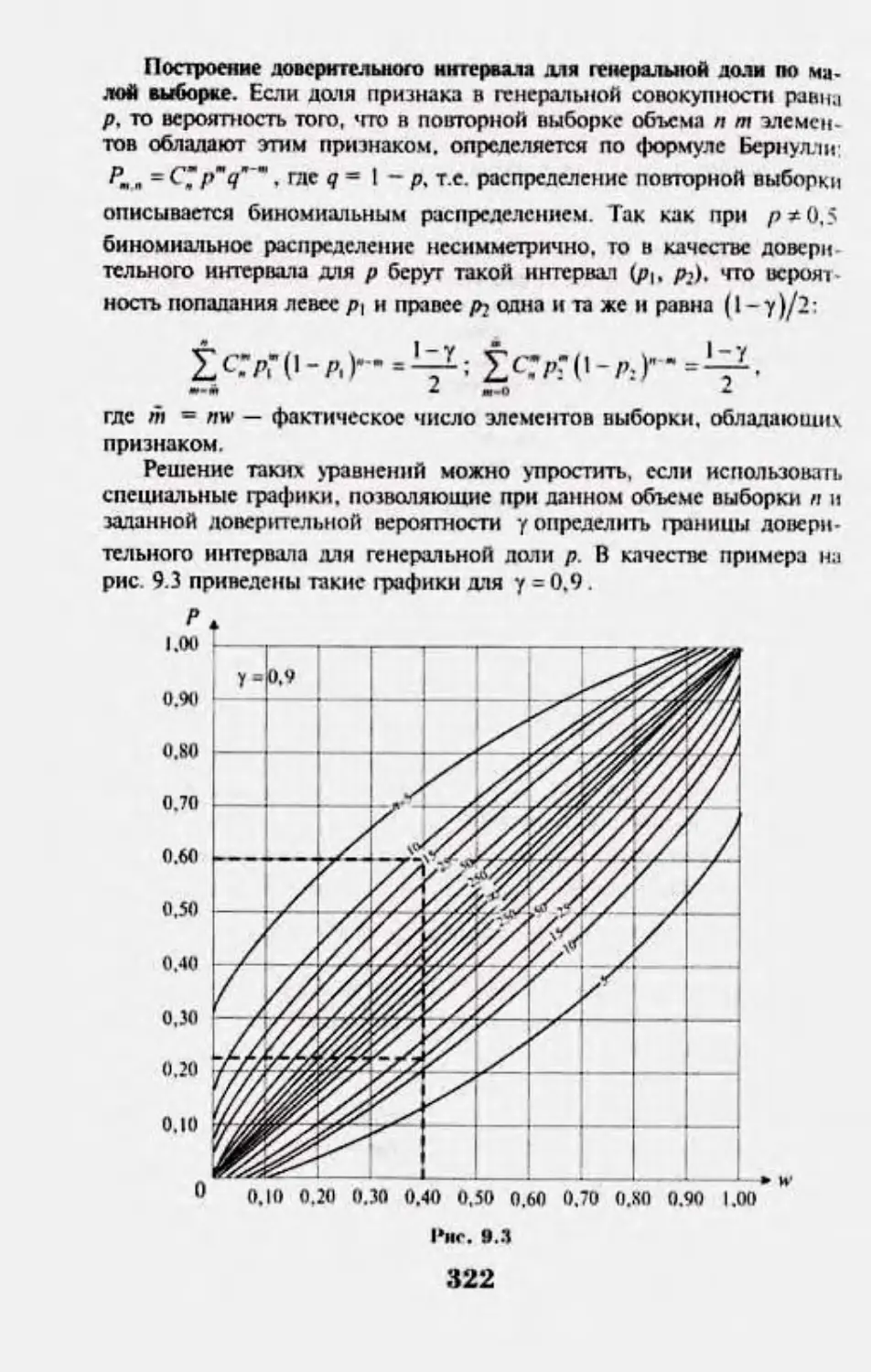
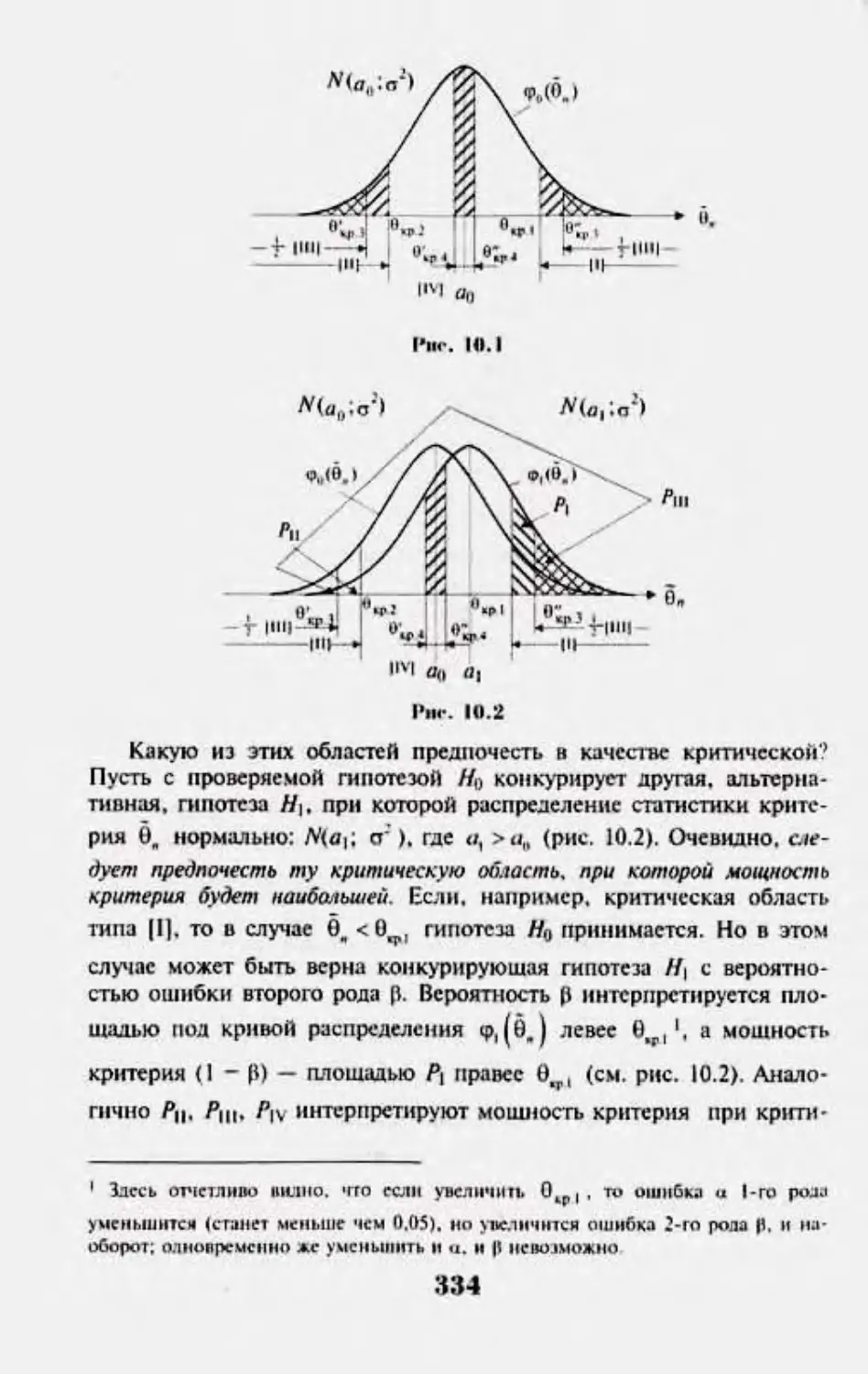
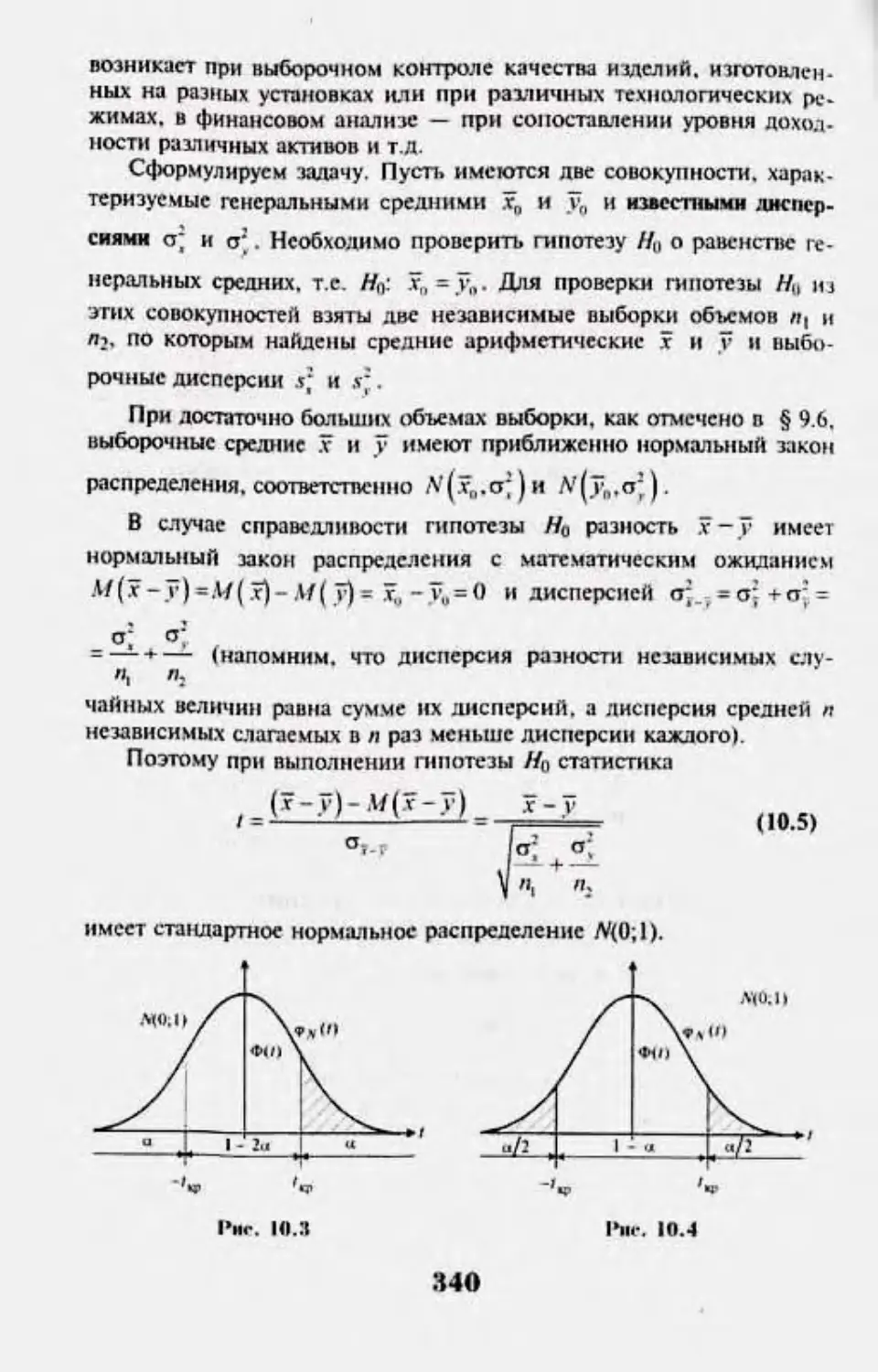
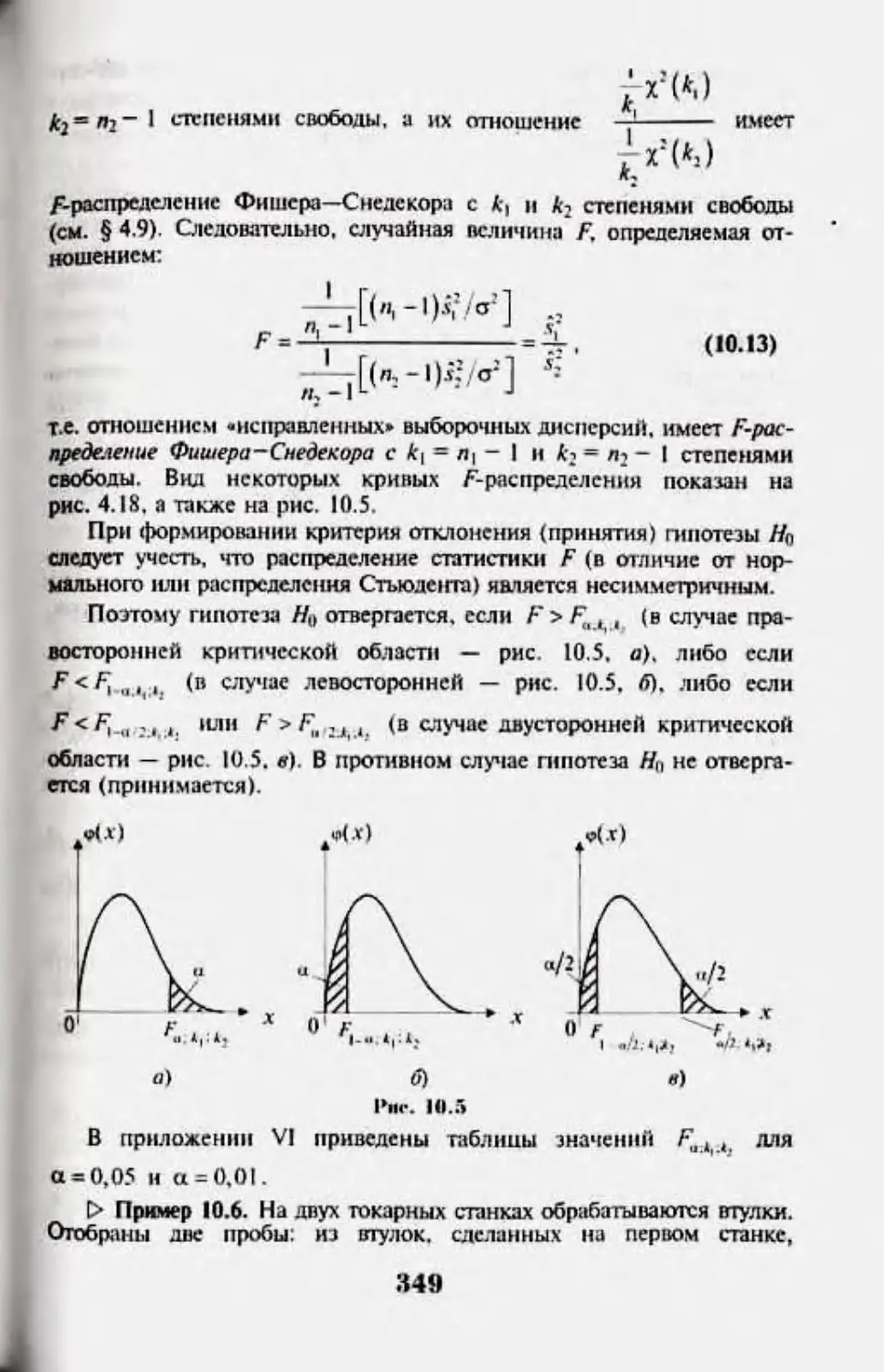
Автор: Кремер Н.Ш.
Теги: теория вероятностей и математическая статистика физико-математические науки теория вероятностей математическая статистика комбинаторный анализ теория графов математика
ISBN: 978-5-238-01270-4
Год: 2007
Текст
Золотой фонд российских учебников
Н.Ш. Кремер
Теория
вероятностей
и
математическая
статистика
Учебник
3-е издание
to и и г и
UNITY
N.Sh. Kremer
PROBABILITY
THEORY
AND
MATHEMATICAL
STATISTICS
Third Edition
Textbook
ю н и т и
UNITY
Moscow • 2007
Н.Ш. Кремер
ТЕОРИЯ
ВЕРОЯТНОСТЕЙ
И
МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА
Третье издание,
переработанное и дополненное
Рекомендовано Министерством образования
Российской Федерации в качестве учебника
для студентов высших учебных заведений,
обучающихся по экономическим специальностям
Ж
ю н и т и
UNITY
Москва • 2007
УДК 519.2(075.8)
ББК 22.!71я73-1+22.172я73-1
К79
Рецензент ьг
кафедра математической статистики и жоиожтрики
Московского еосх-дарственного университета ikohumuku.
статистики и информатики (МЭСИ)
(зап. кафедрой д-р экон. наук. проф. ВС Мхитарян);
д-р фиг-маг. наук. проф. Я.Ф Гапошкшг,
канд техн. наук. доц. ГЛ. Эпштейн
Главный редактор издательства НЛ Эриашвили,
кандидат юридических наук, доктор экономических наук,
лауреат премии Правительства РФ в области науки и техники
Кремер. Наум Шевелевич.
К79 Теория вероятностей и математическая статистика:
учебник для студентов вузов, обучающихся по экономиче-
ским специальностям / Н.Ш. Кремер. — 3-е изд., перераб.
и доп. — М.: ЮНИТИ-ДАНА, 2007. — 551 с. — (Серия
«Золотой (фонд российских учебников»).
ISBN 978-5-238-OI27O-4
Агентство CIP РГБ
Эта книга не таило учебник, но и краткое руководство к решению маач.
Излагаемые основы теории всрояптостей и математической статистики сонро
тюжддктгся большим количеством задач (в том числе экономических). прийо-
димта с решениями и для самостоятельной роботы. При лом упор делается на
основные понятия курса, их теорстико-вероягностныи смысл и применение
Приводятся примеры использования вероятностных и математике-
статистических методов в задачах массового обслуживания и моделях
финансового рынка.
Для студентов и аспирантов экономических спеиналыпхпей и на-
правлений, а также преподавателей вузов, научных сотрудников и эконо-
мистов
ББК 22.171я7Л-Н22.172я73-|
ISBN 978-5-238-01270-4 ОНШ Кремер. 2000. 2003. 2007
&И1ЛАТЕЛКТВО ЮНПТИ-ДАНА. 201)0.2003.2007
Воспроизведение всей книги или любой се части
любыми средствами или п какой-либо форме, в
тохт числе в Интернст-ссти. запрещается без
письменною разрешения издптельства
©Оформление «ЮНИТИ-ДАНА». 2007
Оглавление
Предисловие 10
Введение 12
Раздел 1. Теория вероятностей 15
Г.-ива I. Основные понятия и теоремы теории
вероятностей 16
1,1. Кластч«|мпса1[>1Л событий IB
IX Клкпгггмм* (мфгдкгнмг ucfMwmiocrM 18
1J. С-пши'Пнггкор шфгдслгниг urpcummrni 20
1.4. Геометрические oiiprjr.TriDic Bqioirrnorni 22
IS. Элгметгты komChiuttojmkh 23
1.6. Ннккрглтюикм* iuj'uh .h-iiih- вг|кмтихтгй 27
1.7. Действия над гобыптми 33
1.8. Теорема с.-мпкаиш uejxwmiiMTvn 36
1.9. Условная нг|мит«>т. пХыпы. Тго|1гма умножения
вероттам-тгн. 11с:ши1гнмыг события 37
1.10. Pfiunun? задач 45
1.11. Формула а иной всро>пмш*п1. Формула Байеса 51
1.12. TroprniKo-MH<iacvr'nr»nuu» т|тктишш исниимых iMMumui
м аксйоыаптчепйое поглюгимг теории исрмтюстгй 56
Упражнения 61
Глава 2. Повторные независимые испытания 68
2.1. Форму, ш BejHn.xm 68
2.2. Формула I hwviMiN 71
2.3. Локальная и 1пттра.ий»1Я Цк*(»мулы .Муанрл —Лшхпм-п 72
2.4. ItauHoir .«аджч 78
2-5.1 I<luum»miulwuu< i-хгма 82
Упрожпг1О1л 84
Глава з. (1^1айные вели'тины 87
3.1. Ihnomii' гл^япиной вкпгпшы. Закон |«п<11|м’дглп1ил
aHoqM’nioil r.jyiaiiiioil w-лнчнны 87
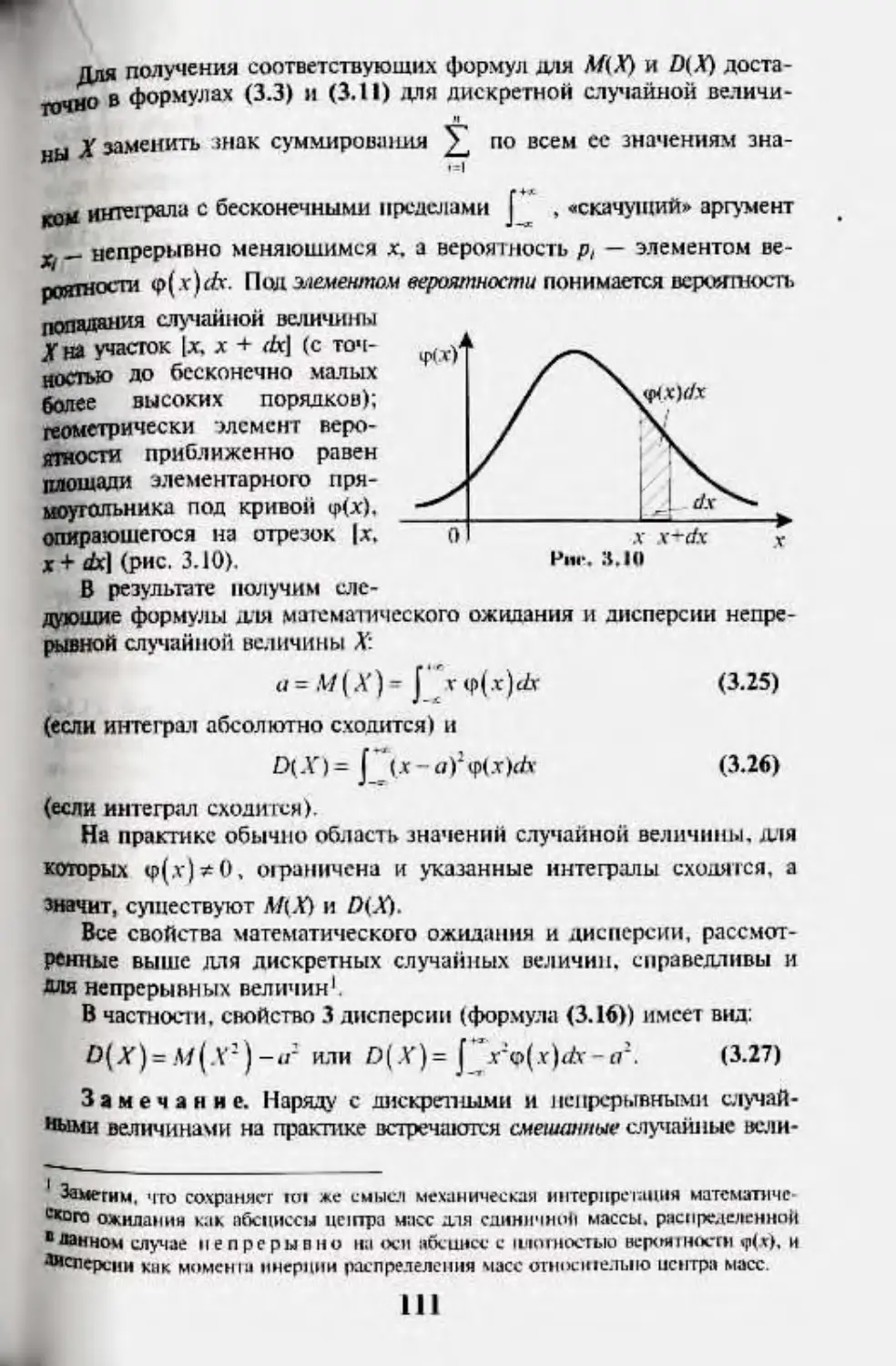
ЗЛ. Млн-мяппи-кне ипершош над сл>яайнымп ar.-nmnm.Mii 91
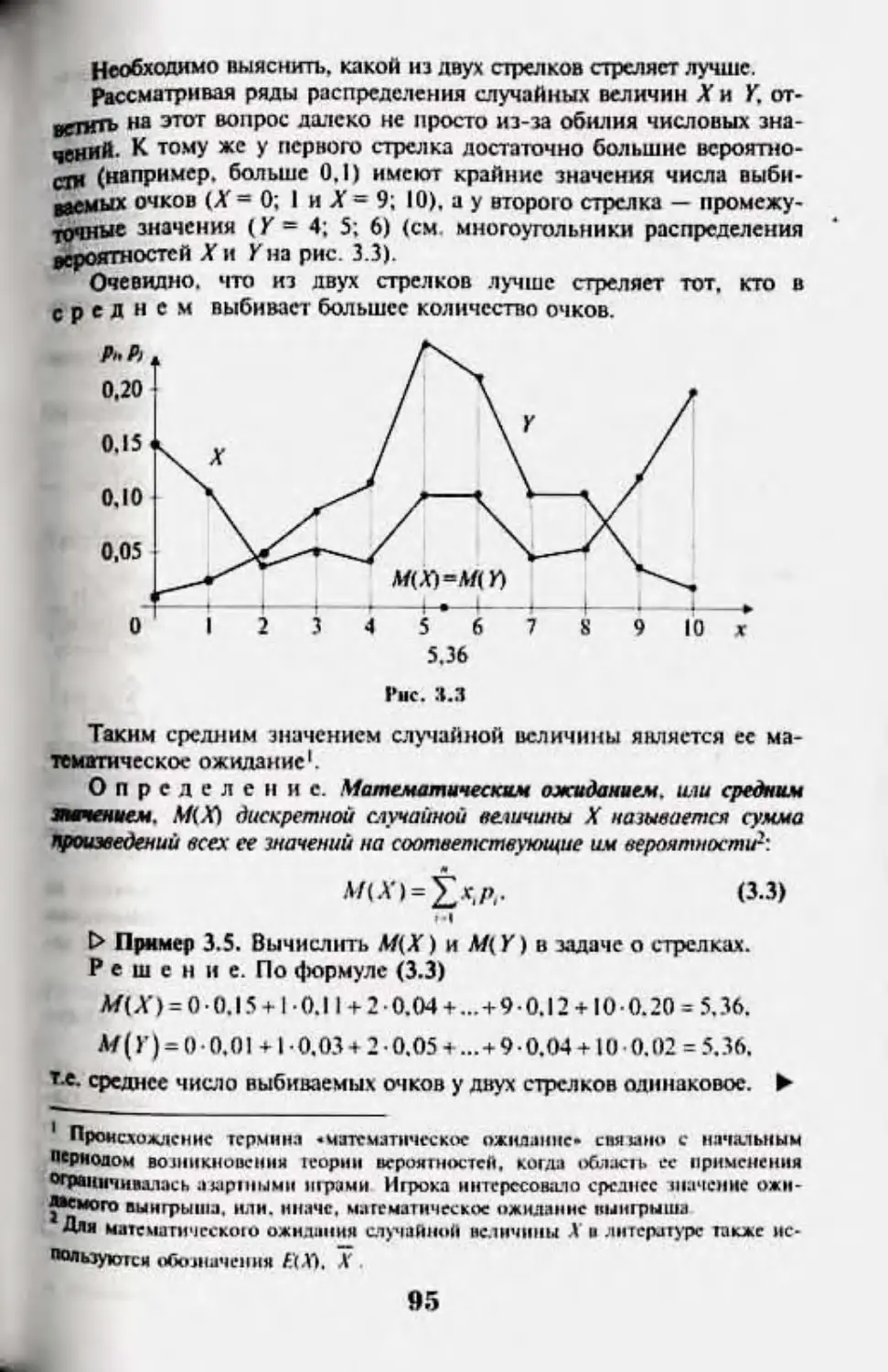
33. .Mim-Mirni'iCT-Ktir ожадмни- днсн}к*пни1 глушАнон nr.-oriiiiiiJ 94
3.4. Дптсроия .иижр-пк.щ глушипой w-urutiiu 98
3.5. Фушнля panq>r;r.'rmm слушАной мличины ЮЗ
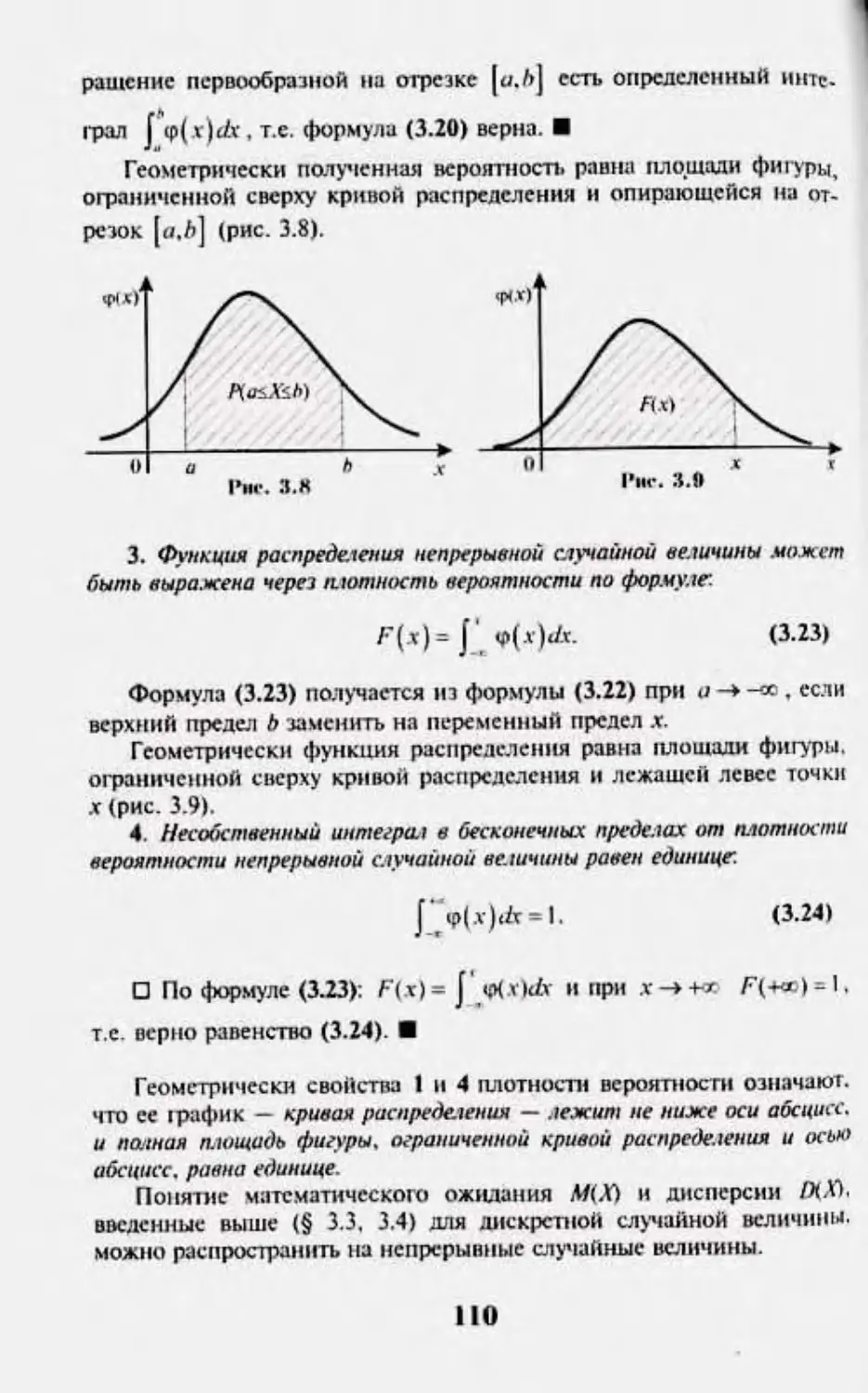
3.6. Нп^м-риплиг слумАныг нгличннм. Иклносп. ш-|х»япн«*П1 106
5
3.7. М«»лл и Mr.uuum. Kiunmuii. Мичипы c-iyuiiiin.ix. iw.iiimiu.
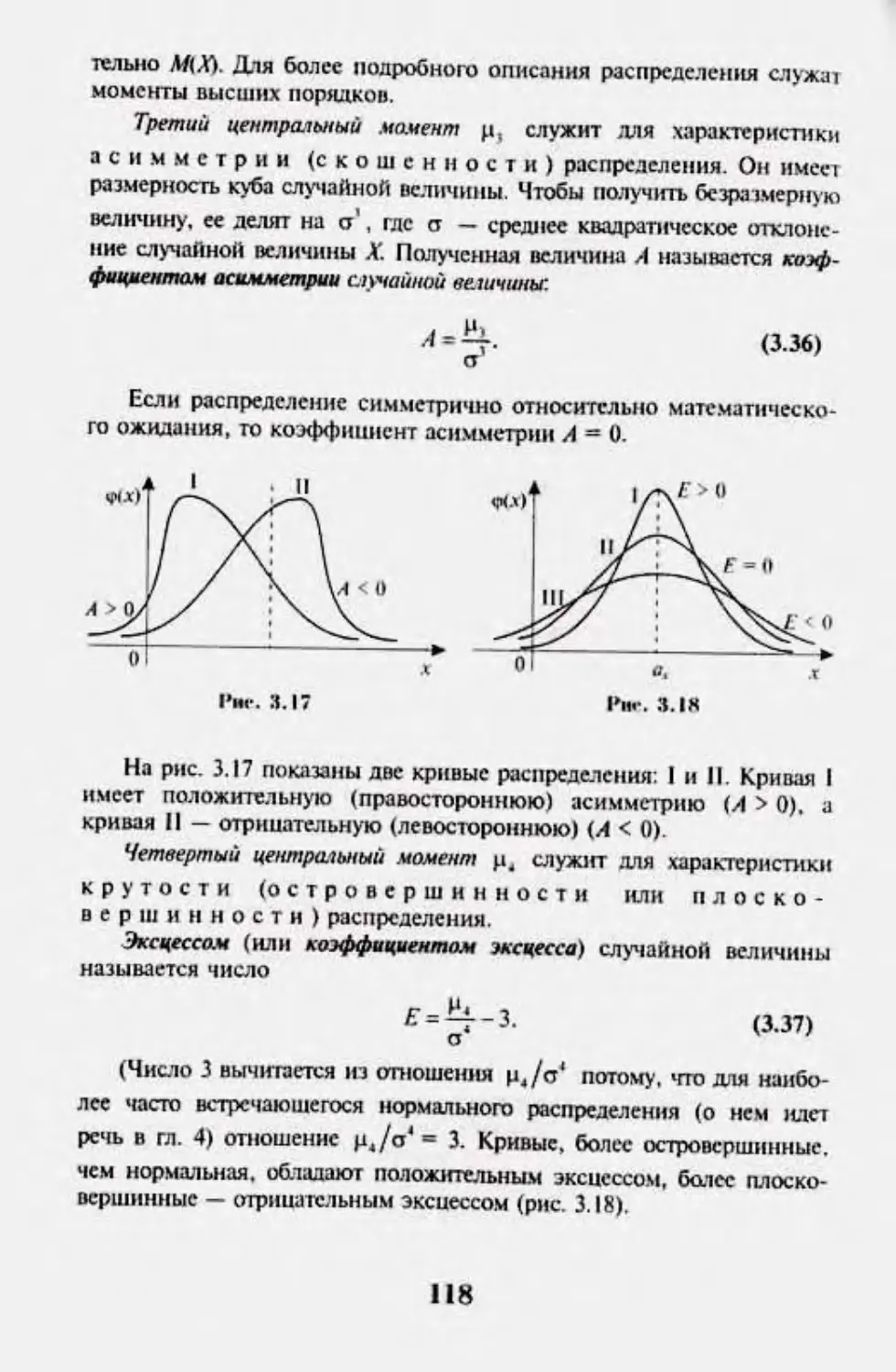
A<HMMiT]HIK и икните 114
3.8. I l|KiiuiH>;vuiuui фупащя I Ю
3.9. Pniinun* задач 121
.Vii|MUt.*iifiiiu< 133
r.uuui 4. Основные ;шконы рнснределешш 141
4.1. biiiKiMiuvujiuul auicuii |*uiq>c.w.ieiiitn I II
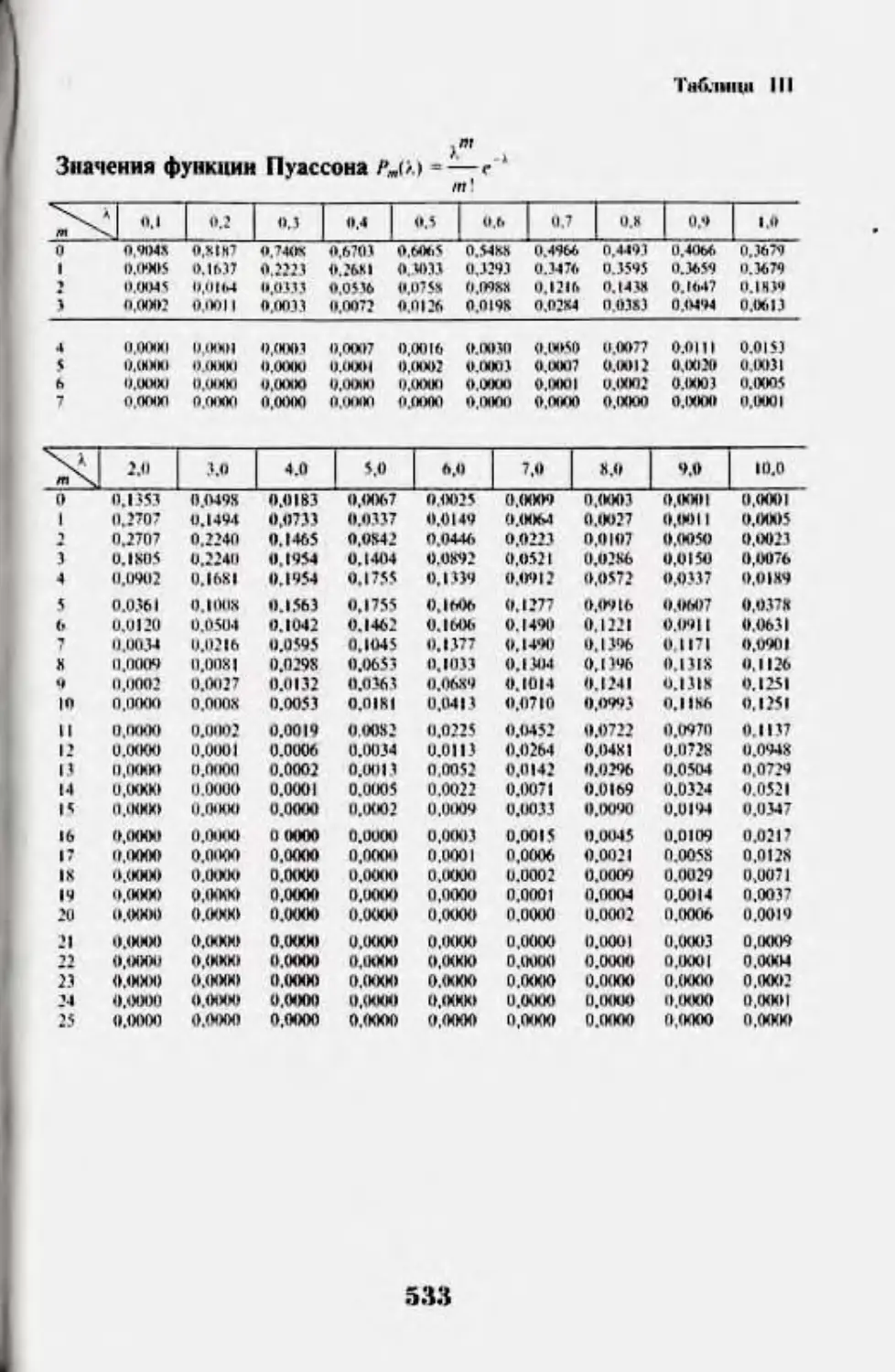
4.2. Зя kt hi |MMiip*,ic.ii*iiiui Пуасгоня 145
4.3. IwMcqarimsoc раптредглняк* к гчх> (ЛЛцснил 1IX
4.4. rinx^>rn>Mcijiw4ecw)c |NM4i|JC.*v*.K4<ir 150
4.5. Равномерный лакни |ми-11|я*д<*.к*11ин 152
4.6. I||'ка.ш1г.1М<ый (wiiirtiniiuuLiiJiijil) зшаи! |»k*ii|m*;b*.ii4IIUI 151
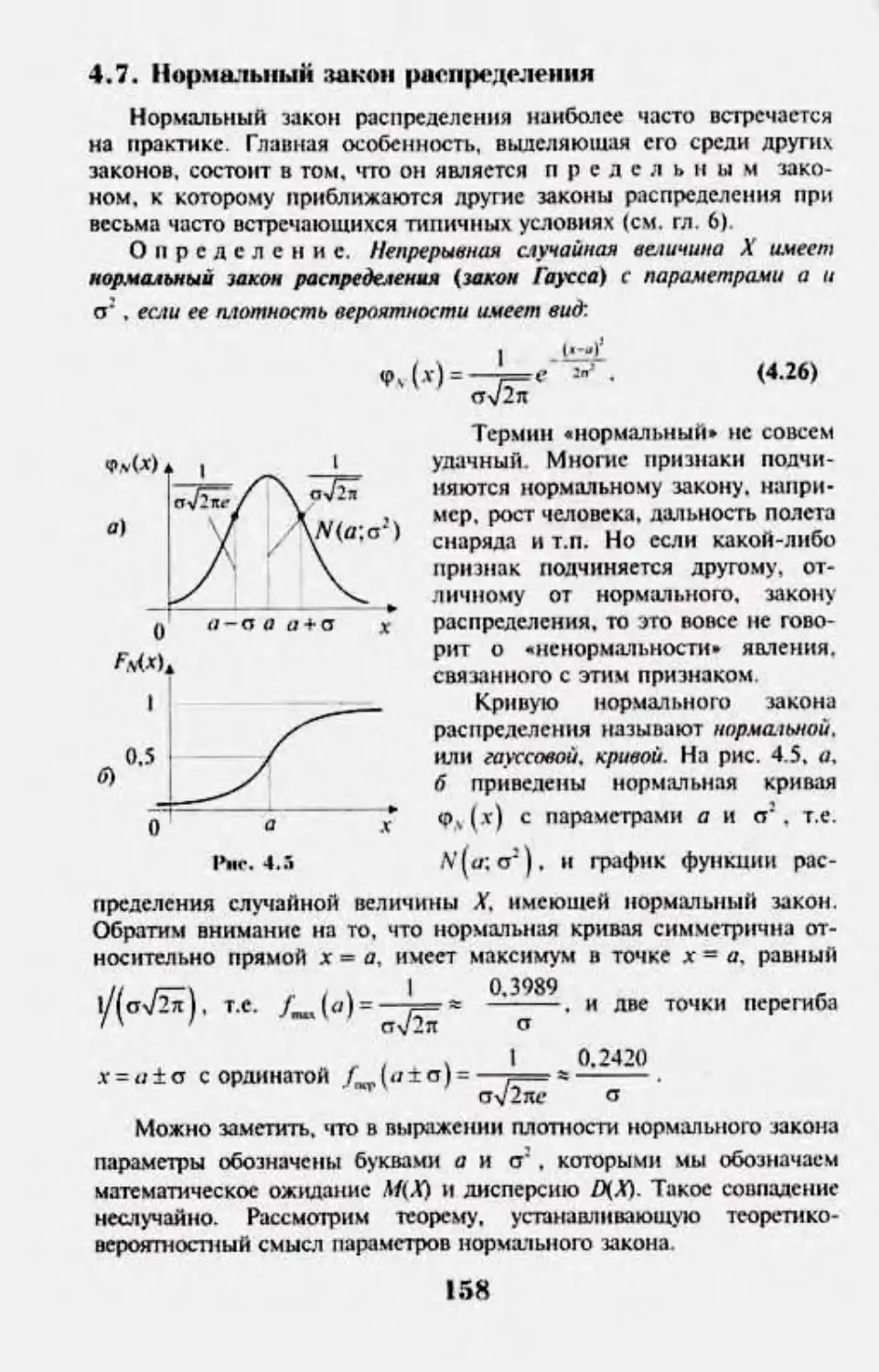
4.7. Нчрмлплплй :uua»i |Nuii|ie.'V*;M4nia 158
4.8. Л<м»р11<|)М11Чггк11-1Ю(1Мдлы1<к* punqe’.tr.wimr 167
•L9. Pmiijir.uvriui»* iv.iwnnjHJx слущГшых im-.iiihiiii. iq««;rmR.wicaiui.\
фуПК1и<11 IIOJIMATIJIMX ПСЛНЧ1Н1 169
>'|||М1ис>и*1шя 172
Глава 5. Многомерные случайные величины 175
5.1. llaiumM* MiHHtiMcptioil случайной величины
it зшаш n* |MMiq*r.v*.N*iuui 175
5.2. <lhiiKtvvi |»i*ii|«'.r.i«iiiiM мн<мич>-р«юй i*.tyuiii№Hi ra*.iiriiiin.i 17!)
53. Il.nmii«m. пгроятинггн .отхмгрний r.r,»Miiii«iii iBMiriitiihi 182
5.4. S'r.HMiin.H* .иконы |MM'iip-.ta-M*iiiiii. Числовые хпракп*(лц*птн
.tKVMqiiioii ••.niai’imai w.uvihhij Prqicrriui IXX
5.5. Лашиимы»* u ih-.uiiuwhmiji* слунитыс w.ihhiihm 192
5.6. Капаргаишл и |«кк|м|нпи1пгг K>q>fM*.iniu!i! 195
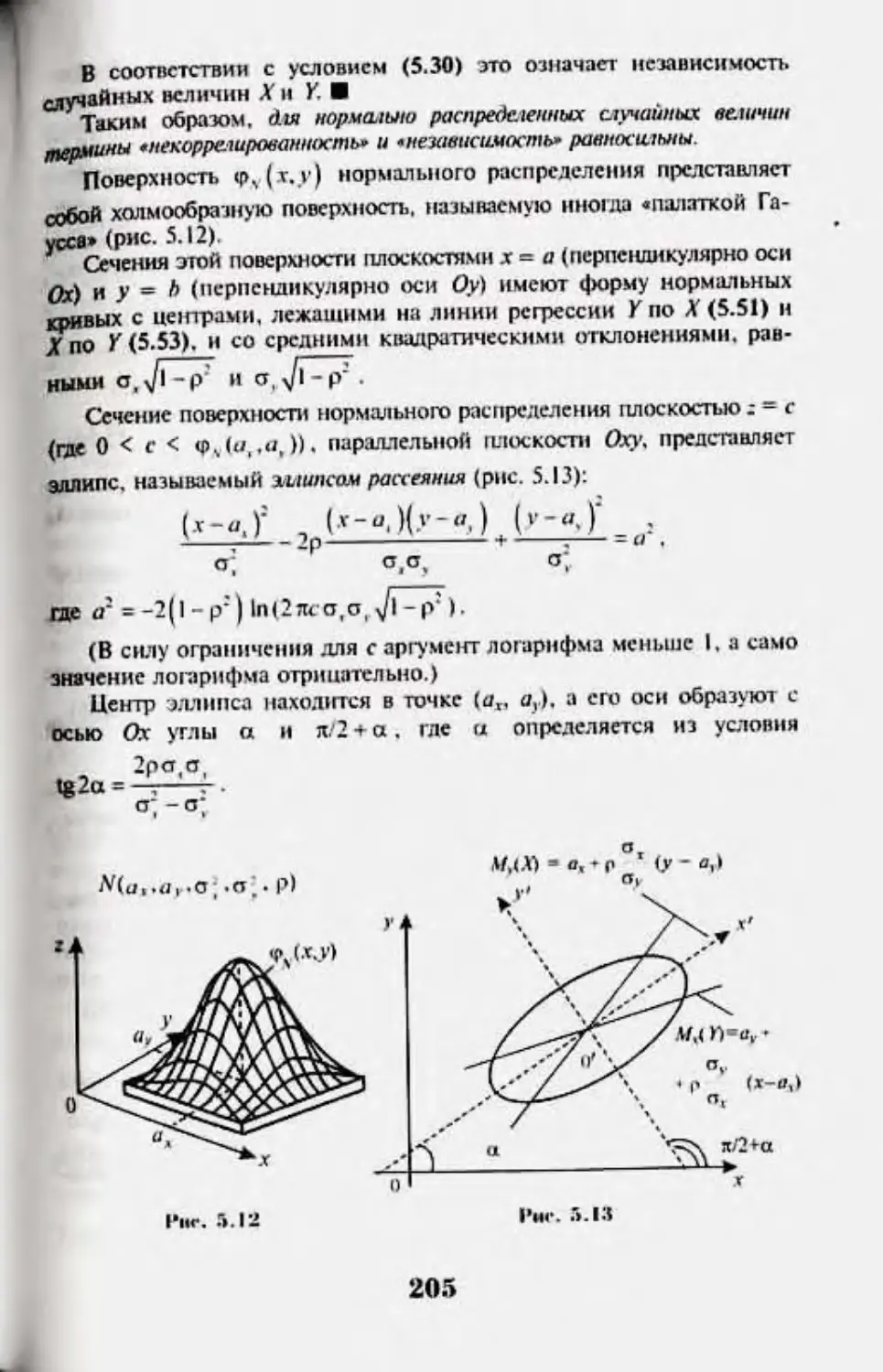
5.7.,'Un'MCpHUfi (o-Mc|)iu.iii} iiopMKiiJiidii :uu:oii |UMiqwar.w*inui 202
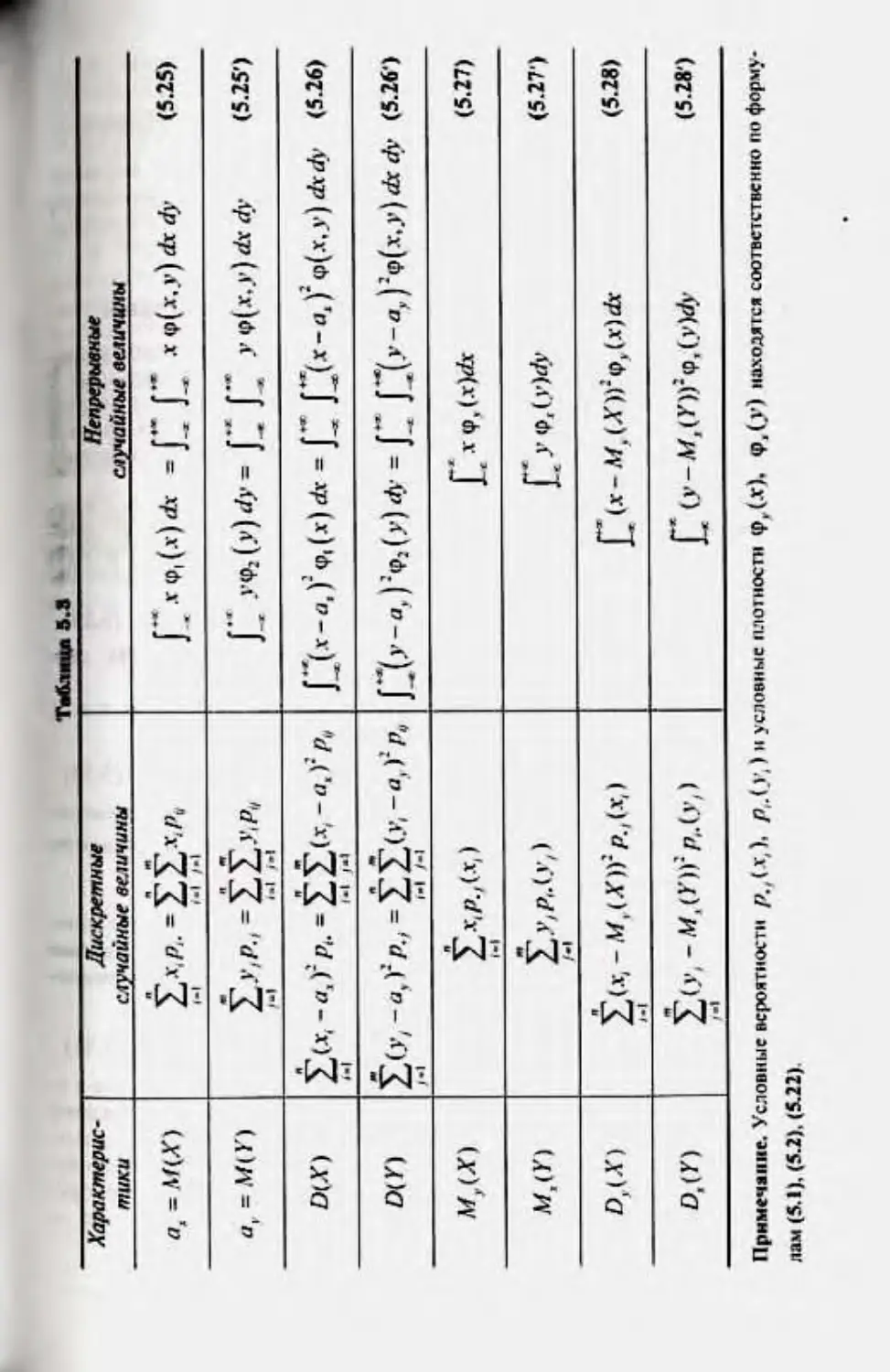
5.8. Фриаша слушйных luviivuni. lioxuuuiuuia .«ikoikhi
|NH-iqit*.u*.vi(iia 207
Уи|М1Ж11П1н>1 213
r.uuM 6. Закон больших чисел и предельные
•1’еоремы 218
6.1.1 l«*|NUv.*»i*nw» Ми|илм«| (.-1ГММП 4<<M.inriui । 218
6.2.111*|«ши41гпм>11сбы| 1H1UI 220
6J. Т«41|и«ма Ч«<1Ы11»гип 223
6.4Л5ч1рсмя Kqmyuji 229
6.5. l{eifT]Mtii.iuui п|и*.-Ц'.шии< тгх^емп 231
.Viiptr/KiM*nii>i 236
6
Глпва 7. Элементы теории случайных п|юцессов
и теории массового обслуживания 238
7.1. Опргж.иимс случайной» нроцсгса и сто Mi|iaK’ni>«irniKJi 238
7.2. Марковские случайные процеегы е дискретными «июлниямн 211
7 J. Основные понятия теории мпегиоол» обслуживания 245
7.4. Потоки еобытнн 2445
75. Уравнения Колмогоронп. Предельные wpoimmrni состояний 250
ТА. Процессы гибели и |иымнож>*ния 251
7.7. СМО с откатами 256
7.8. Понятие о методе гпггнетнческнх испытаний
(методе Моют* Карло) 26)
Упражнения 263
Раздел II. Математическая статистика 266
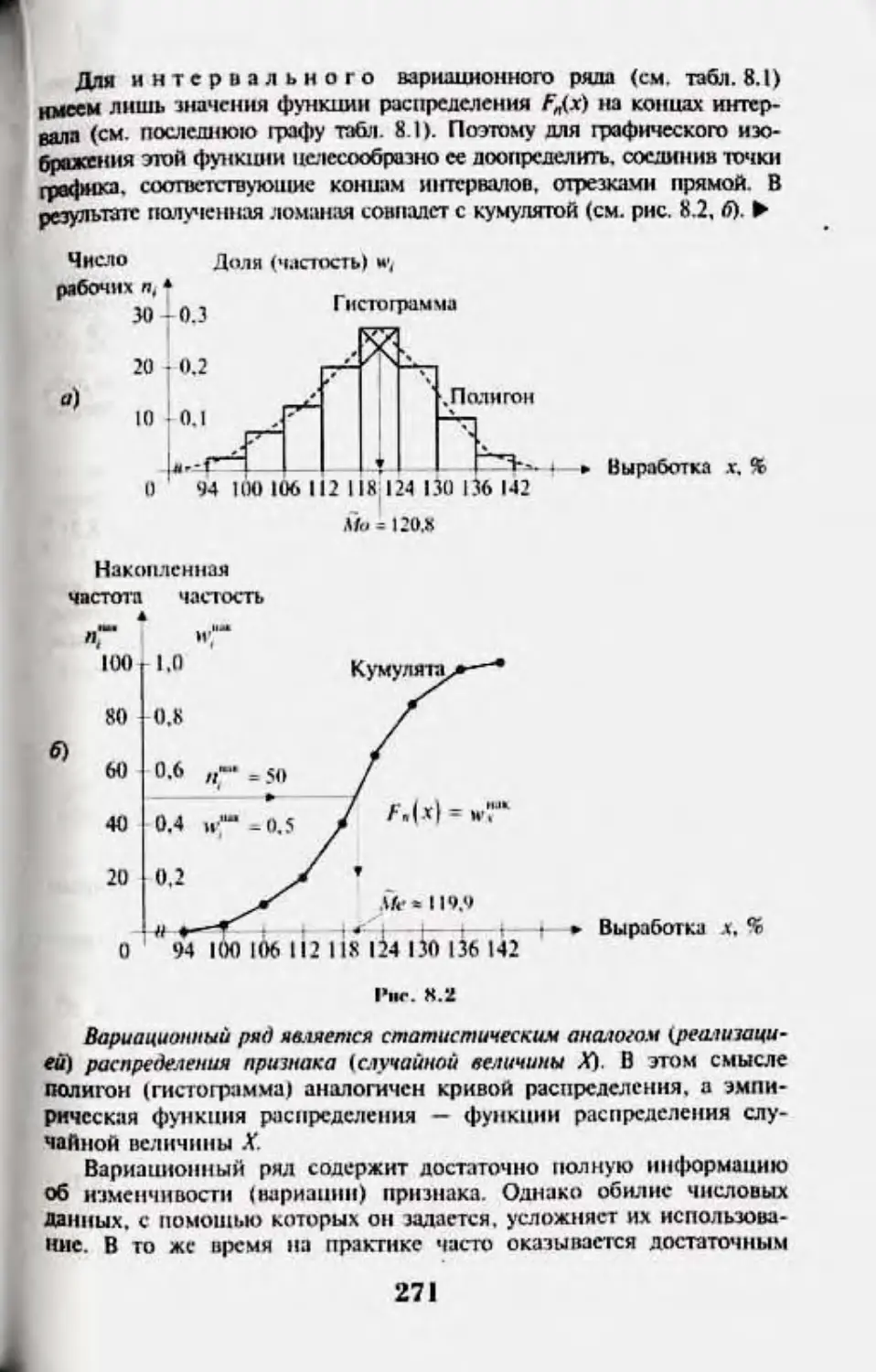
Г.шш 8. Вариационные рщы и их ха|шктеристнки 267
8.1. Вариационные ряды н их rptn|M<4ivKur 1сюбраженне 267
8.2. Средине величины 272
83. Поккип'.п! iui|muuuiii 275
8.4. Упрощенный способ |<1счстп qranrii n|>ni|»Meni4tTwiti н .оинермп 279
85. Нталыи.м* н ц<'1ГГ{м<.1ы<ые чомпгги мрмшмкмпюсп рядя 281
Уприжнпшя 284
Глава 9. Основы математической теории
выборочного метода 286
9.1. Общие nawmui о ныГюр^нюм мстодт 286
93. iltNumie оценки 11лркмсгр1И1 28!)
93. Мстнды 1ШХОЖППШ оценок 293
9.4. Оценки iui|himi*tjmn< п'1и-|1а1ыкй) е1мкма>1имм*п1
по гобгпгнно слумйнон кыбо|ми* 297
93. Опредг.-и*ние ;х|м|»скп11111ых оценок г иомопшо
не|ми«п1<*пш Рло—Крамере Фреше 305
9.6. Понятие 1ппх1нимы1оп» оцпипиння. Дош*р|пглыи1л
псрояпкж’п. it iqjc.K-UJUw ошибки выбо|>ки
9.7. Oiichkii хл|М1Н*п*|як*п1к т«дм.1ьнон сойокмнихтм
1Ю милой пыборке 318
У|фшкн<*1тия 327
Глава 10. П|юверка статистических гипотез 330
10.1. 11рннц)П1 П|>акп1чсско«1 умеренност 330
103. Сптитн'их-кая ппиттш н общим схема се И|м>нсркн 331
103. Проягрка пинпел о |шнен1тнс q«-.unix двух и бмге
сошжуннсхттй 33!)
7
10.4. Проверка пиютга о равенстве долей и|нсииисл в жух
и балет ажжуцнигпа 345
103. Проверка плита о (мшистнс дисперсий даух
U бскГГ СОЯПКМП10Г1ГЙ 348
10.6. Проверка ппв/тга о числовых литаниях парвм1*п>оп 352
10.7. Построение теоретического законе раатдоглення ио
отплным данным. Проверки плита о законе росщх-глення 357
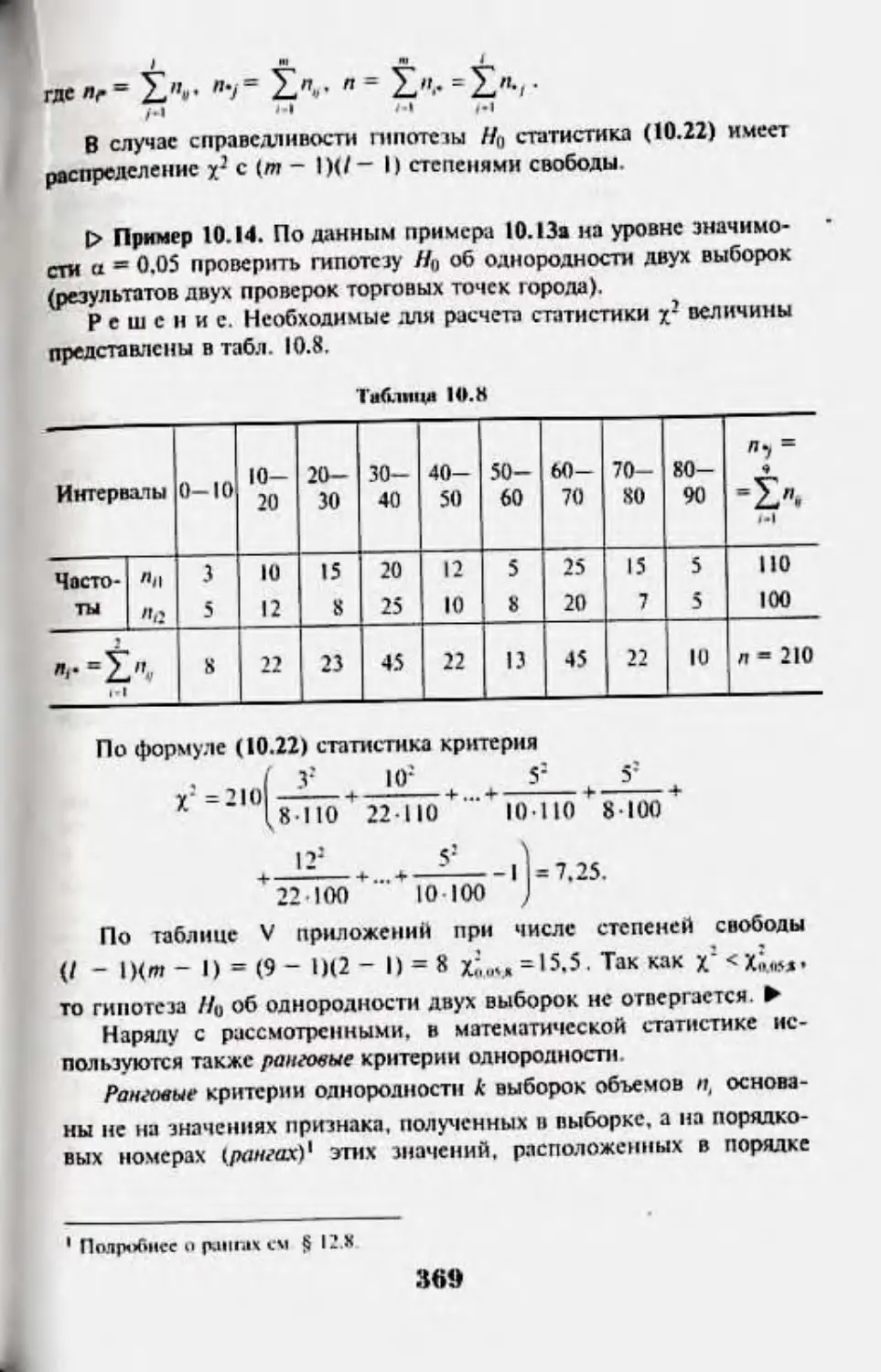
103. Промерю пикта об однородности ныСмцмж 366
103. Понятие о iipoHqwa* гипотез ютолом нослсдоввтглы1ого шшлизв 372
Упражнения 375
Г.мша II. Дисперсионный анализ 379
11.1. Однофакторный дисперсионный анализ 379
1IX Понятие о двухфакгорном дисперсионном анализе 387
У пряж иен ня 393
Глава 12. Корреляционный анализ 395
12.1. Функштоналышя. епгтмгптагкая и хщцгляциошиш
аавнеммотп! 395
12.2. Линейная парная регрессия 398
125. 1u»k|m|j»uuicmt KOfqw.uuuui 4«М1
12.4. Опкшные наипкення кир|1едя1цяяишго анализа.
Двумерная модель 412
125. Проверка значимости и ишгрмалыш <x»r»nai
параметров связи 415
12.6. lu^ipc-uHUKiinior отношение и шцгм* корреляции 410
12.7. Понятие о многомерном кор|1сляцно*!нпм аналпм*
Множп-тнгмный и чаглый гафритлпы корреляции 424
12.8. Рпипжая unjipe.unuui 429
Унражмегаш 436
Глава 13. Регресемоииый шшлнз 439
13.1. Опимише палажеинл рпрнтмоимоп) аналкза.
Пирная ixt^mvcikmiiuix модель 439
13Х 11|пгрвальнал оценки <|птаа(мн регреггии 441
13Л. Проверка лшчнмогти уравнении рнрессмн.
11|гп*]миыыии1 оценка илраметров парной модели 446
13.4. Нелинейная pnptrnui 450
135. Мноиссгтенный [ятргссялнный ышлю 454
13.6. Кооа|ишшкно1ая мяциии и ес кыбороткжя оценка 462
13.7. Оцрггк-лгняг даопяпгдышх тптрвалов
для 1льм|х{япи!пт>н и фикции рстргггми 464
8
13.8. Оценки гапимописш пламенных. 11|хнк1жя ;ошчкм<х*п1
yjxuuteiiH» множттииной ptrjirmni 468
13.9. My.uTHxax'iiiift-nimocn. 472
13.10. Пемигпи* о jipyntx методах мкгимгрниго
rnmrnriccKoin анялва 474
Улрвмаичшм 476
Глава 14. Введение в анализ временных рядов 479
14.1. Общие tuivniiui о временных рядах и додачах их nitaaicin 47!)
142. Сто1инн1а|я<ые в[м*мппп>х' роды
и их xapmcniNK-niKit. Хшхчаццм-.иникишмм фхикилл 481
143. AM&nmmtTKtr пьимшиншипк- (егсиикнвамне) временною
родд (пьс«*Л1чтг нсг.-пяайноЛ компоненты) 484
14.4. HfX’WinU.ir* рОДЫ II ПрОП«КИфОМ1ШГ.
AirroKof»fa*.i)ti(jtn гмтпир-ннй 488
14-5. Aaroftrntrci-ионная модель 494
Угфнжж-ния 495
Глава 15. Линейные peiptHTHOHiiue модели
<|>и>шн<хн!<)го (Минка 497
15.1. Рецихтиониыс модели 497
152. Ри>ючш1Я модмь 49!)
153. Милглм зшик-нмосп! ат кпгатглыкип nojm|xvui 500
15.4. I IqwniuRn-iiiji* it [шикикгныг модели 503
15-5. Модель оценки <|)Н1Ш11гопых лктиион 505
15.6. ('JUCQ. МПОДУ <>Ж111ЛеМ»1(1 ДО\ИД>НМ’ПЛ> И |Я«*КПМ
(Mmi.MiLihiiont пи|т)х*-тя 506
15.7. Многофакти|»1ЫР моделн 507
153. MiHinn|»tiKnipiuui мидель <ац*нк>1 4»iiiiuhiuujx пкпшсж 509
Бнблнотрафнчеекий список 511
Ответы к упражнениям 513
Приложения. Математико-(’гат1ктичес1а!е таб.1ицы 530
Предметный указатель 539
Предисловие
Издательство ЮНИТИ-ДЛНЛ продолжает выпуск учебников и
учебных пособий по математическим дисциплинам для студентов и
абитуриентов экономических вузов.
Мотивацией подготовки данного учебника явилось также то. что в
настоящее время ощущается нехватка доступных для студентов-
экономистов учебников по дисциплине «Теория вероятностей и мате-
матическая статистика» В первую очередь это касается студентов, обу-
чающихся в вузе без отрыва от производства, для многих из которых
учебник служит основным источником учебной информации. Вы-
шедшие из печати в последнее время учебники и пособия по теории
вероятностей и математической статистике ориентированы в основном
на студентов технических вузов и предполагают достаточно высокий
уровень их математической подготовки.
Данный учебник написан в соответствии с требованиями Госу-
дарственного образовательного стандарта и Примерной программой
дисциплины -Математика*, утвержденной Минобразованием РФ.
Основной принцип, которым руководствовался автор при подготов-
ке курса теории вероятностей и математической статистики для
экономистов. — повышение уровня фундаментальной математической
подготовки студе1ггов е усилением се прикладной экономической на-
правленности.
Учебник состоит из двух рахтелов. отражающих основы дисципли-
ны: I «Теория вероятностей* (гл. I «Основные понятия и теоремы тео-
рии вероятностей*; гл. 2 «Повторные независимые испытания»; гл. 3
«Случайные величины»; гл. 4 «Основные законы распределения*; гл. 5
«Многомерные случайные величины»; гл. 6 -Закон больших чисел и
предельные теоремы*) и II «Математическая статистика» (гл. 8 «Ва-
риационные ряды и их характеристики*; гл. 9 «Основы математиче-
ской теории выборочного метода»: гл. 10 «Проверка статистических
гипотез»; гл. II «Дисперсионный анализ*; гл. 12 «Корреляционный ана-
лиз»; нт. 13 «Регрессионный анализ»; гл. 14 «Введение в анализ вре-
менных рядов*). Наряду с этим в учебнике в сжатой форме рассматри-
вается применение вероятностных и математико-статистических мето-
дов в решении ряда прикладных экономических задач: в разделе I —
эго гл. 7 «Элементы теории случайных процессов и теории массового
обслуживания* и в разделе II — гл. 15 «Линейные регрессионные моде-
ли финансового рынка* (гл. 15 (с. 497—510) написана дон Б.Л. Путко).
Известно, что новый учебный материал усваивается студентами
(особенно обучающимися без отрыва от производства) значительно лег-
че. если он сопровождается достаточно большим числом штлюстрирую-
ших его примеров. Поэтому автором сделана попытка соединить в одной
10
книге учебник и краткое руководство к решению задач. При подготовке
задач были использованы различные пособия и методические материа-
лы. Часть задач составлена автором специально для учебника.
Задачи с решениями (в том числе с экономическим содержанием)
рассматриваются на протяжении всего изложения учебного материа-
ла. Более сложные, комплексные, а также дополнительные задачи с
решениями приводятся в ряде глав в специальном параграфе «Реше-
ние задач». Задачи для самостоятельной работы рассматриваются в
конце каждой главы в рубрике «Упражнения* (нумерация задач еди-
ная — начинается в основном тексте главы и продолжается в этой
рубрике). Ответы к этим задачам приводятся в конце книги. Необхо-
димые для решения задач математико-статистические таблицы даются
в приложении. В конце книги приводится развернутый предметный
указатель основных понятий курса.
В третье издание включены новые параграфы: § 3.8 «Произ-
водяшпя функция* в разделе I «Теория вероятностей» и § 10.9 «Поня-
тие о проверке гипотез методом последовательного анализа» в разде-
ле I! «Математическая статистика». Дополнено изложение ряда во-
просов, например, приведены распределения Паскаля, отрицательное
биномиальное и полиномиальное, даны формулы числовых характе-
ристик условных распределений дискретных случайных величин, рас-
смотрены цепи Маркова, немонотонные функции случайных вели-
чин. ранговый критерий Внлкоксонз—Манна—Уитни, сформулиро-
вана теорема Гаусса— Маркова об оценках метода наименьших квад-
ратов. приведен пример многофакторной регрессионной модели
оценки финансовых активов и т.л Добавлены новые задачи с реше-
ниями и для самостоятельной работы. Исправлены замеченные опе-
чатки и неточности
Автор выражает глубокую благодарность проф. ВС. Мхитаряну,
проф. В.Ф. Гапошкину и доп. Г.Л. Эпштейну за рецензирование руко-
писи и сделанные ими замечания.
В книге знаком □ обозначается начало доказательства теоремы,
знаком — ее окончание; знаком > — начало условия задачи,
знаком ► — окончание ее решения.
Введение
Задача любой науки, в том числе экономической, состоит в вы-
явлении и исследовании закономерностей, которым подчиняются
реальные процессы. Найденные закономерности, относящиеся к
экономике, имеют нс только теоретическую ценность, они широко
применяются на практике — в планировании, управлении и прог-
нозировании.
Теория вероятностей — математическая наука, изучающая законо-
мерности случайных явлений. Под случайными явлениями понимаются
явления с неопределенным исходом, происходящие при неоднократном
воспроизведении определенного комплекса условий.
Очевидно, что в природе, технике и экономике нет явлений, в
которых не присутствовали бы элементы случайности. Существуют
два подхода к изучению этих явлений. Один из них — классиче-
ский. или •детерминистский*, состоит в том. что выделяются ос-
новные факторы, определяющие данное явление, а влиянием мно-
жества остальных, второстепенных, факторов, приводящих к слу-
чайным отклонениям его результата, пренебрегают. Таким образом
выявляется основная закономерность, свойственная данному явле-
нию. позволяющая однозначно предсказать результат по заданным
условиям. Этот подход часто используется в естественных (•точ-
ных») науках.
При исследовании многих явлений и прежде всего социально-
экономических такой подход неприемлем. В этих явлениях необ-
ходимо учитывать не только основные факторы, но и множество
второстепенных, приводящих к случайным возмущениям и иска-
жениям результата, т.е. вносящих в него элемент неопределенно-
сти. Поэтому другой подход к изучению явлений состоит в том. что
элемент неопределенности, свойственный случайным явлениям и
обусловленный второстепенными факторами, требует специальных
методов их изучения. Разработкой таких методов, изучением спе-
цифических закономерностей, наблюдаемых в случайных явлениях,
и занимается теория вероятностей.
Математическая статистика — раздел математики, изучающий
математические методы сбора, систематизации, обработки и интер-
претации результатов наблюдений с целью выявления статистических
закономерностей. Математическая статистика опирается на теорию
вероятностей. Если теория вероятностей изучает закономерности
случайных явлений на основе абстрактного описания действитель-
12
пости (теоретической вероятностной модели), то математическая
статистика оперирует непосредственно результатами наблюдений
над случайным явлением, представляющими выборку из некоторой
конечной или гипотетической бесконечной генеральной совокупно-
сти. Используя результаты, полученные теорией вероятностей, ма-
тематическая статистика позволяет нс только оценить значения ис-
комых характеристик, но и выявить степень точности получаемых
при обработке данных выводов.
Если говорип. кратко, теория вероятностей позволяет находить ве-
роятности «сложных* событий через вероятности «простых* событий
(связанных с ними каким-либо образом), а математическая статисти-
ка по наблюденным значениям (выборке) оценивает вероятности
этих событий либо осуществляет проверку предположений (гипотез)
относительно этих вероятностей.
Изучение вероятностных моделей даст возможность понять раз-
личные свойства случайных явлений на абстрактном и обобщенном
уровне, не прибегая к эксперименту. В математической статистике,
наоборот, исследование связано с конкретными данными и идет от
практики (наблюдения) к гипотезе и ее проверке.
При большом числе наблюдений случайные воздействия в значи-
тельной мерс погашаются (нейтрализуются) и получаемый результат
оказывается практически неслучайным, предсказуемым. Это утвер-
ждение (принцип) и является базой для практического использования
вероятностных и математико-статистических методов исследования.
Цель указанных методов состоит в том. чтобы, минуя сложное (а
зачастую и невозможное) исследование отдельного случайного яв-
ления, изучить закономерности массовых случайных явлений, прог-
нозировать их характеристики, влиять на ход этих явлений, контро-
лировать их. ограничивать область действия случайности.
Первые работы, в которых зарождались основные понятия тео-
рии вероятностей, появились в XVI—XVII вв. Они принадлежали
Д. Кардано. Б. Паскалю. П Ферма, X. Гюйгенсу и др. и представ-
ляли попытки создания теории азартных игр с целью дать рекомен-
дации игрокам. Следующий этап развития теории вероятностей свя-
зан с именем Я. Бернулли (XVII - начало XVIII в.), который дока-
зал теорему, теоретически обосновавшую накопленные ранее факты
и названную в дальнейшем «законом больших чисел*.
Дальнейшее развитие теории вероятностей приходится на XVII—
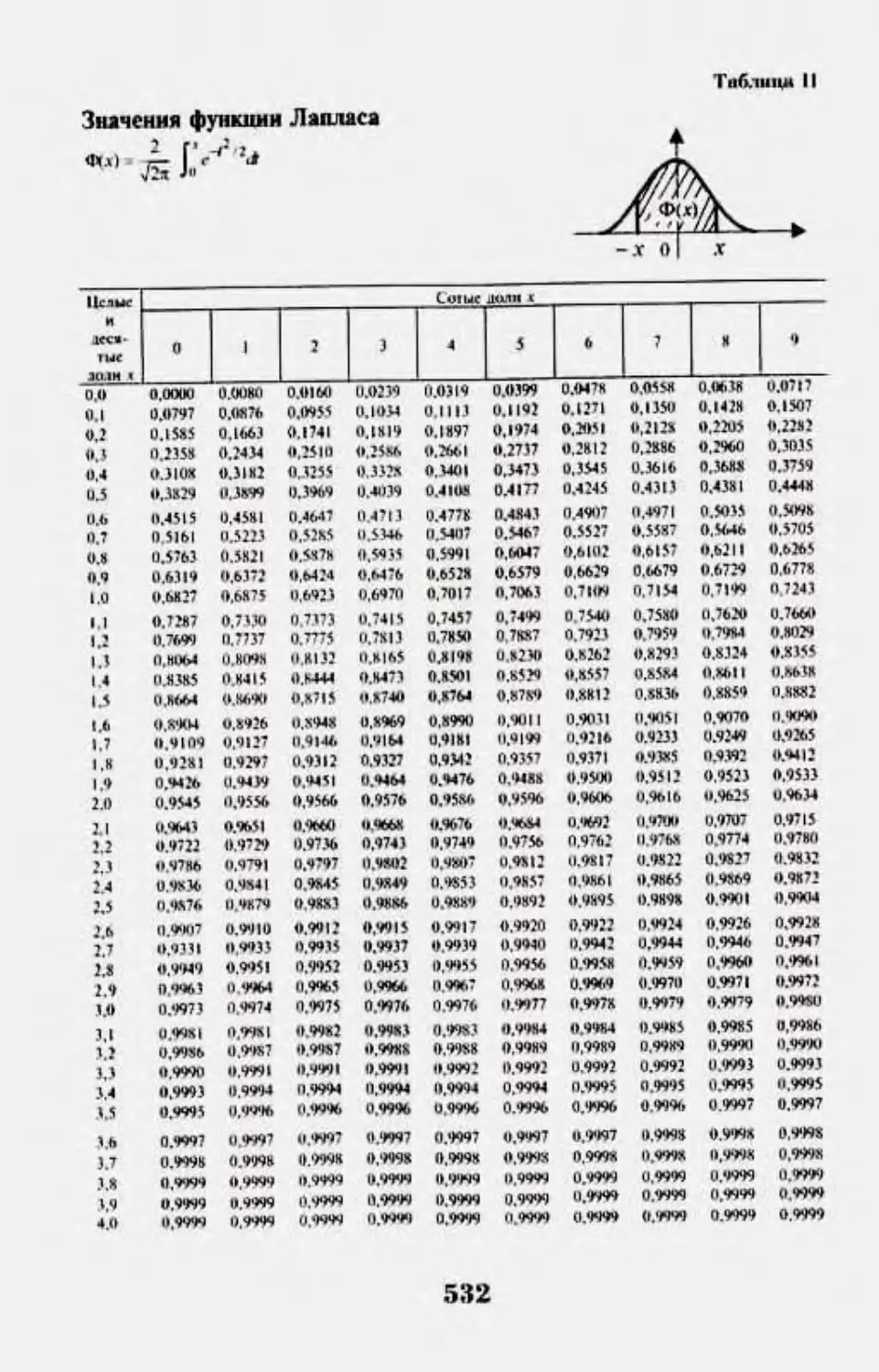
XIX вв. благодаря работам А. Муавра. П. Лапласа. К. Гаусса. С. Пуассо-
на и др. Весьма плодотворный период развития «математики случайно-
го» связан с именами русских математиков ПЛ. Чебышева, А.М. Ляпу-
нова и ДА Маркова (XIX — начало XX в.).
Большой вклад в последующее развитие теории вероятностей и мате-
матической статистики внесли российские математики С.Н. Бернштейн.
В-И. Романовский. А.Н. Колмогоров, А.Я. Хинчин, Ю.В. Линник.
13
Б.В. Гнеденко. Н.В. Смирнов. IO.B. Прохоров и др., а также ученые
англо-американской школы Стыодснг (псевдоним В. Госсета). Р. Фи-
шер, Э. Пирсон. Е. Нейман. А. Вальд и др. Особо следует отметить
неоценимый вклад академика А.Н. Колмогорова в становление тео-
рии вероятностей как математической науки.
Широкому внедрению матемап!ко-статистических методов иссле-
дования способствовало появление во второй половине XX в. элек-
тронных вычислительных машин и. в частности, персональных
компьютеров. Статистические программные пакеты сделали эти ме-
тоды более доступными и наглядными, так как трудоемкую работу
по расчету различных статистик, параметров, характеристик, по-
строению таблиц и графиков в основном стал выполнять компью-
тер, а исследователю осталась главным образом творческая работа:
постановка задачи, выбор методов се решения и интерпретация ре-
зультатов.
Появление мощных и удобных статистических пакетов для персо-
нальных компьютеров позволяет использовать их не только как спе-
циальный инструмент научных исследований, но и как общеупотре-
бительный инструмент плановых, аналитических, маркетинговых от-
делов производственных и торговых корпораций, банков и страховых
компаний, правительственных и медицинских учреждений и даже
представителей мелкого бизнеса. Среди множества используемых для
этих целей пакетов прикладных программ выделим популярные в
России универсальные и специализированные статистические пакеты:
отечественные STADIA. Эвриста, Статистик-консультант. Олимп:
СтатЭксперт и американские STATGRAPHICS. SPSS. SYSTAT.
STATISTICA/w и др.
Раздел
Теория вероятностей
Глава 1. Основные понятия и теоремы теории вероятностей
Глава 2. Глава 3. Глава 4. Глава 5. Глава 6. Повторные независимые испытания Случайные величины Основные законы распределения Многомерные случайные величины Закон больших чисел и предельные теоремы
Глава 7. Элементы теории случайных процессов и теории массового обслуживания
Глава
Основные понятия
и теоремы теории вероятностей
1.1. Классификация событии
Одним из основных понятий теории вероятностей является по-
нятие события.
Случайным событием (возможным событием или просто событи-
ем) называется любой факт, который в результате испытания может
произойти или не произойти.
Под испытанием [опытом, экспериментам) в этом определении
понимается выполнение определенного комплекса условий, в кото-
рых наблюдается то или иное явление, фиксируется тот ши иной
результат Испытание (опыт) может быть осуществлено человеком,
но может проводиться и независимо от человека, выступающего в
этом случае в роли наблюдателя.
Приведем пример ы событий.
I Появление герба (реверса — оборотной стороны) при под-
брасывании монеты.
2. Выигрыш автомобиля по билету денежно-вещевой лотереи.
3. Выход бракованного изделия с конвейера предприятия.
4. Выпадение более 1000 мм осадков в данном географическом
пункте за определенный год.
Событие — это не какое-нибудь происшествие, а лишь возмож-
ный исход, результат испытания (опыта, эксперимента). События
обозначаются прописными (заглавными) буквами латинского алфа-
вита: Л, В. С.
Если при каждом испытании, при котором происходит событие /I.
происходит и событие В. то говорят, что Л влечет за собой событие
В (входит в В. является частным случаем, вариантом В) или В вклю-
чает событие А. и обозначают А <= В. Например, если событие А —
изделие 1-го сорта. В — изделие 2-го сорта, С — изделие стандарт-
ное. то А «= С и В <= С.
Если одновременно А - В и В •=- А. го в этом случае события А и
В называют равносильными и обозначают А = В. Например, события
•нс все изделия данной партии стандартные* и *по крайней мерс од-
но из изделий данной партии нестандартное» янляюгся равносиль-
ными (хотя и имеют различные по форме словесные описания).
События называются несовместными (несовместимыми). если на-
ступление одного из них исключает наступление любого другого. В
противном случае события называются совместными (совместимы-
16
ми). Например, выигрыш по одному билету денежно-вещевой лоте-
реи двух ценных предметов — события несовместные, а выигрыш
тех же предметов по двум билетам — события совместные. Получе-
ние студентом на экзамене по одной дисциплине оценок «отлично»,
«хорошо* и *удовлетвор»пелъно» — события несовместные, а получе-
ние тех же оценок на экзаменах по трем дисциплинам — события
совместные.
Событие называется достоверным (обозначаем буквой Г)), если в
результате испытания оно обязательно должно произойти.
Событие называется невозможным (обозначаем символом 0), если в
результате испытания оно вообще не может произойти. Например, если
в партии все изделия стандартные, го извлечение из нее стандартного
изделия — событие достоверное, а извлечение при тех же условиях бра-
кованного изделия — событие невозможное.
События называются равновозможными, если в результате испы-
тания по условиям симметрии ни одно из этих событий нс является
объективно более возможным. Например, извлечение туза, валета,
короля или дамы из колоды карт либо появление icp6a или решки
при подбрасывании монеты — события равновозможные. Так. если
монета «правильная», выполнена симметрично, то нет никаких ос-
нований считать «появление герба» при подбрасывании монеты со-
бытием объективно более возможным, чем «появление решки».
Равновозможныс события нс могут появляться иначе, чем в ис-
пытаниях. обладающих симметрией возможных исходов; и наше
незнание того, какое из событии объективно более возможно
при отсутствии симметрии исходов, нс может служить основанием,
чтобы считать события равновозможными.
Несколько событий называются единственно возможными, если в
результате испытания обязательно должно произойти хотя бы одно
из них. Например, события, состоящие в том, что в семье из двух
детей: А — «два мальчика». В — «один мальчик, одна девочка*. С —
«две девочки» — являются единственно возможными.
Другой пример. События. состоящие в том. что при 10 выстрелах
число т попаданий в цель: D — т < 2. Е - т < 8, F — т > 5 также яв-
ляются единственно возможными, так как при любом результате
стрельбы обязательно произойдет хотя бы одно из этих событий
(например, при т = 9 — событие Г. при т = I — событие D или Е
н т.д.).
Несколько событий образуют патую группу (полную систему),
если они являются единственно возможными и несовместными ис-
ходами испытания. Эю означает, что в результате испытания обя-
зательно должно произойти одно и только одно из этих событий. Так.
в приведенных двух последних примерах события А. В. С образуют
полную группу, так как они единственно возможные и несовмест-
17
ные, а события /Л Е, F — полную группу не образуют, так как они
только единственно возможные, но совместные1.
Частным случаем событий, образующих полную группу, являют -
ся противоположные события. Два несовместных события, из кото-
рых одно должно обязательно произойти, называются противопо-
ложными. Событие, противоположное событию А, будем обозна-
чать2 .4 . Очевидно. что А - .4, Q - 0. 0 = £2.
Например, «появление герба» и «появление решки* * при подбра-
сывании монеты, «отсутствие бракованных изделий* и «наличие
хотя бы одного бракованного изделия» в парши — события проти-
воположные.
1.2. Классическое оп|м»де.1Рние вероятшм-тн
Для практической деятельности важно уметь сравнивать события
по степени возможности их наступления. Очевидно. события: «выпа-
дение дождя» и «выпадение снега» в первый лень лета в данной мест-
ности. «выигрыш по одному билету» и «вышрыш по каждому из л
приобретенных билетов» денежно-вещевой лотереи — обладают раз-
ной степенью возможности их наступления. Поэтому для сравнения
событий нужна определенная мера.
Численная мера степени объекттпшой возможности наступления
события называется вероятностью события.
Эго определение, качестве н и о отражающее понятие ве-
роятности события, не является математическим Чтобы оно таким
стало, необходимо определить его к о л и ч е с т в с н н о
Пусть исходы некоторого испытания образуют полную группу
событий и равновозможны, т.е. единственно возможны, несовмест-
ны и равновозможны. Такие исходы называются элементарными исхода-
ми. случаями или шансами'. При лом говорят, что испытание сводится к
схеме случаев или «схеме урн» (ибо любую вероятностную задачу для рас-
сматриваемого испытания можно заменить эквивалентной задачей с
урнами и шарами разных цветов).
Случай называется благоприятствующим (благоприятным} собы-
тию л. если появление этого случая влечет за собой появление со-
бытия А.
1 В некоторых курсах теории псроягностсВ и понятие полная группа событий»
нс включается трсбоплние несовместности событий При такой трактовке собы-
тия /). Е. /'также будут обраюоыката полную iруину.
• В литературе события .4 и .4 натыкаю) также ttwuxnu-ihmuHumr.tMMMU, ;> со-
бытие .4 отрицание ч юн ftona шснисм собы тмя -1
1 В теоретико-множественной ipaKiotiKC (см § I 12) такие исходы на житии
ъгсмснтарны м« соДытинми.
IH
Согласно классическому определению веро-
ятность^ события А равна отношению числа случаев, благоприятст-
вующих ему. к общему числу случаев, т.с.
(1.1)
п
где АЛ) ~ вероятность события А;
т — число случаев, благоприятствующих событию Л;
л — обшее число случаев.
t> Пример 1.1. При бросании игральной кости возможны шесть
исходов — выпадение 1, 2, 3, 4. 5. 6 очков. Какова вероятность по-
явления четного числа очков?
Решение. Все л = 6 исходов образуют полную группу собы-
тий и равновозможны, т.с. единственно возможны, несовместны и
равновозможны. Событию А — «появление четного числа очков» бла-
гоприятствуют 3 исхода (случая) — 2, 4 и 6 очков. По формуле (1.1)
АЛ) = 3/6 = 1/2. ►
Классическое определение (точнее, классическая фор-
мула) вероятности (1.1) долгое время, с XVII вплоть до XIX в.,
рассматривалось действительно как определение вероятно-
сти, так как в то время методы теории вероятностей применялись в
основном к азартным играм, которые сводились к схеме случаев,
или в задачах, которые искусственно сводились к этой схеме. В на-
стоящее время формальное определение вероятности не дается (это
понятие считается первичным и не определяется, а при его поясне-
нии используют понятие относительной частоты события (см. § 1.3)).
Поэтому классическое определение (классическую формулу) вероят-
ности (1.1) следует рассматривать не как определение, а как метод
вычисления вероятностей для испытаний, сводящихся к схеме случаев.
Отмстим свойства вероятности события.
I. Вероятность любого события заключена между нулем и едини-
цей. т.е.
0$АЛ)£|. (1.2)
2. Вероятность достоверного события равна единице, т.с.
АО) e I-
3. Вероятность невозможного события равна нулю. т.е.
А0) = 0.
□ Свойства очевидны, так как АЛ) = т/п. а число т благопри-
ятствующих случаев для любого события удовлетворяет неравенству
* Для вероятности события А п литературе нснолыуется также обозначение РПА)
(сокращение слова probability (вероятность)).
I»
О <. т s л , для достоверного события равно п (гл = п) и для невоз-
можного события равно нулю (т = 0).
События, вероятности которых очень малы (близки к нулю) или
очень велики (близки к единице), называются соответственно
практически невозможными или практически достоверными собы-
тиями.
1.3. Статистическое определение вероятности
Выше отмечено, что классическое определение вероятности при-
менимо только для тех событий, которые могут появиться в результате
испытаний, обладающих симметрией возможных исходов, т.е
сводящихся к схеме случаев. Однако существует большой класс собы-
тий. вероятности которых не могут быть вычислены с помощью клас-
сического определения В первую очередь это события, которые не
являются равновозможными исходами испытания. Например, если
монета сплющена, го. очевидно, события «появление герба» и «появ-
ление решки» при подбрасывании монеты нельзя считать равновоз-
можными. и <|юрмула (1.1) для расчета вероятности любого из них
окажется неприменима.
Но есть и другой подход при опенке вероятности событий, ос-
нованный на том, насколько часто будет появляться данное
событие в произведенных испытаниях. В этом случае используется
статистическое определение вероятности.
Статистической вероятностью события /I называется относи-
тельная частота (частость) появления этого события в п произведен-
ных испытаниях, т.е.
Р(Л) = »(Л)=-. (1.3)
п
где Р(Л) — статистическая вероятность события А;
w(A) — относительная частота (частость) события А;
т — число испытаний, в которых появилось событие А;
п — общее число испытаний.
В отличие от * математической» вероятности ?М>. рассматривае-
мой в классическом определении (1.1). статистическая вероятность
/*(Л) является характеристикой опытной, экспериментальной. Если
!\А) есть доля случаев, благоприятствующих событию А. которая
определяется непосредственно, без каких-либо испытаний, то Р( А)
есть доля тех фактически произвело н н ы х и с и ы -
та н и й, в которых событие Л появилось.
Статистическое определение вероятности. как и понятия и ме-
тоды теории вероятностей в целом, применимы не к любым собы-
тиям с неопределенным исходом, которые в житейской практике
20
считаются случайными, а только к тем из них, которые обладают
определенными свойствами1.
|. Рассматриваемые события должны быть исходами только тех
испытаний, которые могут быть воспроизведены неограниченное число
раз при одном и том же комплексе условий. Так. например, бессмыс-
ленно ставить вопрос об определении вероятностей возникновения
войн, появления гениальных произведений искусства и т.п., гак как
речь идет о неповторимых в одинаковых условиях испытаниях, уни-
кальных событиях Или, например, нс имеет смысла говорить о
том. что данный студент сдаст семестровый экзамен по теории ве-
роятностей. поскольку речь здесь идет о единичном испытании,
повторить которое в тех же условиях нет возможности.
И хотя приведенные в примерах события с неопределенным исхо-
дом относятся к категории «может произойти, а может и не произойти»,
такими событиями теория вероятностей не занимается.
2. События должны обладать гак называемой статистической ус-
тойчивостью. или устойчивостью относительных частот. Это означа-
ет. что в различных сериях испытаний относительная частота (час-
тость) события изменяется незначительно (тем меньше, чем больше
число испытаний), колеблясь около постоянного числа. Оказалось,
что этим постоянным числом является вероятность события
(об этом идет речь в теореме Бернулли, приведенной в гл. 6).
Факт приближения относительной частоты, или частости, собы-
тия к его вероятности при увеличении числа испытаний, сводящих-
ся к схеме случаев, подтверждается многочисленными массовыми
экспериментами, проводимыми разными лицами со времен возник-
новения теории вероятностей. Так, например, в опытах Бюффона
(XVIII в.) относительная частота (частость) появления герба при
4040 подбрасываниях монеты оказалась равной 0,5069, в опытах
Пирсона (XIX н.) при 23 000 подбрасываниях — 0,5005, практиче-
ски не отличаясь от вероятности этого события, равной 0.5.
3. Число испытаний, в результате которых появляется событие А,
должно быть достаточно велико, ибо только в этом случае можно
считать вероятность события /\А) приближенно равной се относи-
тельной частоте.
Резюмируя, можно сказать, что теорий вероятностей изучает
лишь такие события, в отношении которых имеет смысл не только
утверждение об их случайности, но и возможна объективная оценка
относительной частоты их появления, Так. утверждение, что при
выполнении определенного комплекса условий 5 вероятность собы-
1 В прикладной литературе нмпсишснис приводимых ниже свойств событий с
неопределенным исходом п исследуемой реальной действительности иногда на-
зываю! условиями действия статистического аисамГня.
21
гия раина р. означает не только случайность события J. но и опреде-
ленную, достаточно близкую к р. (кию появлении события А при боль-
шом числе испытаний-, а значит, выражает определенную объективную
(хотя и своеобразную) связь между комплексом условий S и событием А
(не зависящую от субъективных суждений о наличии этой связи гою
или иного лица). И даже просто существование вероятности р (когда
само значение р неизвестно) сохраняет качественно суть зтого ут-
верждения. выделенную курсивом.
Легко проверить, что свойства вероятности (см. (1.2)). выте-
кающие из классического определения (1.1). сохраняются и при
статистическом определении вероятности (1.3).
1.4. Геометрическое определение вероятности
Одним из недостатков классического определения вероятности
(1.1). ограничивающим его применение, является то. что оно предпо-
лагает конечное ч и с л о возможных исходов испытания.
Оказывается, иногда этот недостаток .можно преодолеть, исполь-
зуя геометр и ч е с к о с он ре дел с и и е вероятности,
т.е. находя вероятность попадания точки в некоторую область (отре-
зок. часть плоскости и т.п ).
Пусть, например, плоская фигура х составляет часть плоской
фигуры G. На фигуру G наудачу бросается точка. Это означает, что
все точки области G -равноправны» в отношении попадания гуда
брошенной случайной точки. Полагая, что вероятность события А —
попадания брошенной точки на фигуру у — пропорциональна пло-
щади этой фигуры и не зависит ни от ее расположения относитель-
но G, ни от формы у. найдем
/’(•») = О-*)
где 5Х и S(t — соответственно плошали областей у и G (рис. 1.1).
Фигуру у называют благоприятствующей (благоприятной) собы-
тию А.
Область, на которую распространяется понятие геометрической
вероятности, может быть одномерной (прямая, отрезок) и трехмерной
(некоторое тело в пространстве). Обозначая меру (длину, площадь,
объем) области через mes. приходим к следующему определению.
Опрел с л е н и с. Геометрической вероятностью события А
называется отношение меры области, благоприятствующей появлению
события А. к мере всей области. т.е
= (1.5)
mes G
22
Риг. I.!
t> Пример 1.2. Два лица — А и В — условились встретиться в
определенном месте, договорившись только о том, что каждый яв-
ляется туда в любой момент времени между 11 и 12 ч и ждет в тече-
ние 30 мин. Если партнер к этому времени еше не пришел или уже
успел покинуть установленное место, встреча не состоится. Найти
вероятность того, что встреча состоится.
Решение. Обозначим моменты прихода в определенное ме-
сто лиц А и В соответственно через х и у. В прямоугольной системе
координат Оху возьмем за начало отсчета II ч. а за единицу изме-
рения — I ч. По условию 0 $ х < I. 0 < у < 1. Этим неравенствам
удовлетворяют координаты любой точки, принадлежащей квадрату
OKLM со стороной, равной 1 (рис. 1.2). Событие С — встреча двух
лиц — произойдет, если разность между х и у не превзойдет 0.5 ч (по
абсолютной величине), те. ly - xl £ 0.5.
Решение последнею неравенства есть полоса х - 0.5 < у х + 0.5,
которая внутри квадрата на рис. 1.2 представляет заштрихованную
область#. По формуле (1.4)
Р(С) = -1-
•5g
так как площадь области # равна площади квадрата G без суммы
площадей двух угловых (незаштрихованных) треугольников ►
-----—г1------= 0.75.
1.5. Элементы комбинаторики
Для успешного решения задач с использованием классического
определения вероятности необходимо знать основные правила и
формулы комбинаторики — раздела математики, изучающего, в ча-
стности, методы решения комбинаторных задач — задач на подсчет
числа различных комбинаций.
Пусть A, (i = I, 2.. л) — элементы конечного множества.
Сформулируем два важных правила, часто применяемых при реше-
нии комбинаторных задач.
23
Правило суммы. Если элемент Л| может быть выбран л( способа-
ми. элемент А2 — другими п2 способами, Л1 — отличными от первых
двух п^ способами и т.д.. Ак — пк способами, отличными от первых
(Л - I). то выбор одного из элементов-. ши Л|, или Л2.... или Л< мо-
жет быть осуществлен П\ + л?+ ...+ пк способами
[> Пример 1.3. В ящике 3(Ю деталей. Известно, что 150 из них —
1-го сорта. 120 — 2-го. а остальные — 3-го сорта. Сколько существует
способов извлечения из ящика одной летали 1-го или 2-го сорта?
Решен и е. Деталь 1-го сорта может быть извлечена л, = 150 спо-
собами, 2-го сорта — п2 = 120 способами По правилу суммы суще-
ствует Л| + п2 = 150 + 120 = 270 способов извлечения одной детали
1-го или 2-го сорта. ►
Правило произведения. Если элемент может быть выбран Л|
способами, после каждого такого выбора элемент А2 может быть вы-
бран п2 способами и т.д., после каждого (Л-1) выбора элемент Ак мо-
жет быть выбран пк способами, то выбор всех элементов Л|. А2, Ак в
указанном порядке может быть осуществлен ntn2...nk способами.
[> Пример 1.4. В группе 30 человек. Необходимо выбрать старос-
ту. его заместителя и профорга. Сколько существует способов это
сделать?
Реше н и е. Старостой может быть выбран любой из 30 уча-
щихся. его заместителем — любой из оставшихся 29. а профоргом —
любой из оставшихся 28 учащихся, т.с Л| = 30, п2 = 29, п\ = 28. По пра-
вилу произведения общее число способов выбора старосты. его замести-
теля и профорга равно ярьл, = 30 • 29 • 28 = 24 360 способов. ►
Пусть дано множество из п различных элементов. Из этого
множества могут быть образованы подмножества из т элементов
(О s m s п). Например, из 5 элементов a. b. с. d. е могут был. ото-
браны комбинации по 2 элемента — uh. cd. eh. ha. се и тл.. по
3 элемента — ahc, cbd, cba. ead и т.л.
Если комбинации из п элементов по т отличаются либо составом
элементов. либо порядком их расположения (либо и тем и другим),
го такие комбинации называют размещениями из п элементов по т
Число размещений из п элементов по т равно
А” = л ( п - 1)(п - 2)...(п - т 4-1), (1.6)
hi coMiioxMic.tdl
или л: = . ”! (1.7)
(л - /л)!
где л! равно произведению п первых чисел натурального ряда. т.с.
я!» 1-2...Л.
24
> Пример 1.5. Расписание одного дня состоит из 5 уроков. Опре-
делить число вариантов расписания при выборе из 11 дисциплин.
Решение. Каждый вариант расписания представляет набор
5 дисциплин из 11. отличающийся от других вариантов как составом
дисциплин, гак и порядком их следования (или и тем и другим), т.е.
является размещением из 11 элементов по 5. Число вариантов распи-
саний. т.е. число размещений из 11 по 5. находим по формуле (1.6)
4 = II I0-9 8 7 = 55 440. ►
5 слмыспюпезсП
Если комбинации из п элементов по т отличаются только со-
ставом элементов, то их называют сочетаниями из л элементов по
т. Число сочетаний из л элементов по т равно
л(л-1)(л-2)..,(л-w-f-l)
1 • 2. .ап
ИЛИ с. = —-------
/л!( п- л»)!
Так как по определению 0! = 1. то = 1. С" = I.
Свойства числа сочетаний:
с; = с;".
с;+ с;" = с;;’.
С>С^С;+... + С; =2".
> Пример 1.6. В шахматном турнире участвуют 16 человек Сколь-
ко партий должно быть сыграно в турнире, если между любыми
двумя участниками должна быть сыграна одна партия?
Решение Каждая партия играется двумя участниками из 16
и отличается от других только составом пар участников, т.е. пред-
ставляет собой сочетание из 16 элементов по 2. Их число находим
по формуле (1.8):
(1.8)
(19)
(1.10)
(1.11)
(1.П)
Если комбинации из п элементов отличаются только порядком
расположения этих элементов, то их называют перестановками из л
элементов. Число перестановок из п элементов равно
Л, = л! (1.12)
> Пример 1.7. Порядок выступления 7 участников конкурса оп-
ределяется жребием. Сколько различных вариантов жеребьевки при
этом возможно?
25
Р е ш с н и с. Каждый вариант жеребьевки отличается только по-
рядком участников конкурса, т.е является переспиювкой из 7 элементов
Их число по формуле (1.12): Р7 = 7! = I • 2 • 3 • 4 • 5 • 6 • 7 = 5040. ►
Если н размещениях (сочетаниях) из п элементов по т некоторые
из элементов (или все) могут оказаться одинаковыми, то такие разме-
щения (сочетания) называют размещениями (сочетаниями} с повторе-
ниями из п элементов по т
Например, из 5 элементов а. Л. с. d. е по 3 размещениями с по-
вторениями будут abe. cba. bed, edb, bbe. ebb, beb. ddd и т а., сочета-
ниями с повторениями будут abe. bed. bbe. ddd и т.д.
Число размещений с повторениями из п элементов по т равно
(1.13)
а число сочетаний с повторениями из п элементов по т равно
где С".„ ! определяется по (формуле (1.8) или (1.9).
£> Пример 1.8. В конкурсе по 5 номинациям участвуют 10 кино-
фильмов. Сколько существует вариантов распределения призов, ес-
ли по каждой номинации установлены: а) различные призы; б) оди-
наковые призы?
Реше н и е. а) Каждый из вариантов распределения призов
представляет собой комбинацию 5 фильмов из К), отличающуюся
от других комбинации как составом фильмов, так и их порядком по
номинациям (или и тем и другим), причем одни и те же фильмы
могут повторяться несколько раз*, т.е. представляет размещение с
повторениями из 10 элементов по 5. Их число по формуле (1.13)
равно
л’м = 10' = 100 000.
б) Если по каждой номинации установлены одинаковые призы,
то порядок следования фильмов в комбинации 5 призеров значения
не имеет, и число вариантов распределения призов представляет
собой число сочетаний с повторениями из 10 элементов по 5, опре-
деляемое по формуле (1.14) с учетом равенства (1.8):
1 Любой фильм МОЖС1 палуииь призы как по одной, гак и по нескольким
(пключая вес пять) номинациям.
26
Если в перестановках из общего числа п элеме1гтов есть к различных
элементов, при этом 1-й элемент повторяется Л| раз. 2-й элеметгг —
п2 раз, А-й элемент — nk раз, причем л, + +...+ лА = п. то такие пе-
рестановки называют перестановками с повторениями из п элементов.
Число перестановок с повторениями из п элементов равно
м*
С ('»Г «•."i I = —7----: (115)
П)! п.! ...nJ.
О Пример 1.9. Сколько существует семизначных чисел, состоя-
щих из цифр 4. 5 и 6. в которых цифра 4 повторяется 3 раза, а циф-
ры 5 и 6 — по 2 раза?
Р с ш е и и е. Каждое семизначное число отличается от другого
порядком следования цифр (причем л, = 3. п2 = 2. я? = 2, а их сум-
ма равна 7), т.е. является перестановкой с повторениями из 7 эле-
ментов. Их число по формуле (1.15):
/»(3: 2;2) =—— = 210. ►
' 3! 2! 2!
1.6. Непосредственное вычисление вероятностей
Для непосредственного вычисления вероятности используется ее
классическое определение (1.1).
> Пример 1.10, Буквы Т. Е. И. Я. Р. О написаны на отдельных
карточках. Ребенок берет карточки в случайном порядке и прикла-
дывает одну к другой: а) 3 карточки; 6) все 6 карточек. Какова ве-
роятность тою. что получится слово: а) «ТОР-; 6) «ТЕОРИЯ»?
Решение, а) Пусть событие А — получение слова «ТОР*.
Различные комбинации трех букв из имеющихся шести представ-
ляют размещения, так как могут отличаться как составом входящих
букв, гак и порядком их следования (или и гем и другим), т.е. об-
щее число случаев п = А,'. из которых благоприятствует событию А
т = 1 случай. По формуле (1.1)
т_ _1_____I__ I
п ~ А", ~ 6-5-4 ’ 120
б) Пусть событие В — получение слова «ТЕОРИЯ». Различные
комбинации шести букв из имеющихся шести представляют собой
перестановки, так как отличаются только порядком следования
букв; т.е. общее число случаев // = /*= 6’, из которых благоприятст-
вует событию В т = I случай. Поэтому
mil I
— — — — — — — - V
п /> 6! 720
27
t> Пример 1.11. Используя условие примера 1.10, на!пи вероят-
ность того, что получится слово «АНАНАС», если на отдельных
карточках написаны три буквы А. две буквы Н и одна буква С.
Решение. Пусть событие В — получение слова «АНАНАС».
Так же, как и в примере 1.10 б, обшее число случаен п- Pti = 6!. но
теперь число случаев т. благоприятствующих событию В, сущест-
вен но больше, так как перестановка трех букв Л, осуществляемая
= 3! способами, и перестановка двух букв Н (Р> = 2! способами)
не меняет собранное из карточек слово «АНАНАС»; по правилу
произведения (см. § 1.5) т = Ру' Р>
Итак,
' п Р„ 6! 60
(Задачу можно решить и иначе, рассматривая комбинации букв
как перестановки с повторениями (см. § 1.5), из которых событию
В благоприятствует I комбинация:
6' I
Р Я =1 : Р„(У, 2; 1=1:—— = —.) ►
3! 2! I! 60
> Пример 1.12. Из 30 студентов 10 имеют спортивные разряды.
Какова вероятность того, что выбранные наудачу 3 студента — раз-
рядники?
Решение. Пусть событие А — 3 выбранных наудачу ciyaci-mi —
разрядники. Общее число случаев выбора 3 студентов из 30 равно
л = С,'„, так как комбинации из 30 студентов по 3 представляют собой
сочетания, ибо отличаются только составом студентов. Точно так же
число случаев, благоприятствующих событию А, равно /»= С’’,. Итак.
- = £k = l^:Z£2^ = ±La0.0.0 ►
и Ci 1-2-3 1-2-3 203
О Пример 1.13. В лифт на l-м этаже девятиэтажного дома вошли
4 человека, каждый из которых можег выйти независимо друг от друга
на любом этаже с 2-то по 9-й. Какова вероятность того, что все пасса-
жиры выйдут: а) на 6-м этаже; б) на одном этаже?
Ре ш е н и е. а) Пусть событие /I — все пассажиры выйдут на 6-м
этаже. Каждый пассажир может выйти со 2-го по 9-й этаж 8 спосо-
бами. По правилу произведения (§ 1.5) общее число способов выхода
четырех пассажиров из лифта равно п = 8 • 8 • 8 • 8 = 84. Число случа-
ев. благоприятствующих событию А. равно т ~ I. Таким образом.
/’(.4) = - = -!- = 0.00024.
п X
28
Р(А) =
6) Пусть событие В — все пассажиры выйдут на одном этаже.
Теперь событию В будут благоприятствовать т = 8 случаев (все пас-
сажиры выйдут или на 2-м этаже, или на 3-м...или на 9-м этаже).
Поэтому
р(0) = - = 4 = 4 = 0-00)95.
' ' п 8‘ 8
(Обшее число способов выхода пассажиров из лифта можно
найти иначе, если учесть, что комбинации номеров этажей, на ко-
торых может выйти из лифта каждый из четырех пассажиров, на-
пример 3456. 4356. 4433. 5666. 5555. 9785 и т.д., представляют собой
размещения с повторениями из 8 элементов (этажей) по 4. Их чис-
ло по формуле (1.13) равно п = jM4=8‘.) ►
О Пример 1.14. По условиям лотереи «Спортлото 6 из 45» уча-
стник лотереи, угадавший 4. 5. 6 видов спорта из отобранных при
случайном розыгрыше 6 видов спорта из 45, получает денежный
приз. Найти вероятность того, что будут угаданы: а) все 6 цифр;
б) 4 цифры.
Реше н и с. а) Пусть событие А — угадывание всех 6 видов
спорта из 45. Обшее число всех случаев, т.е. всех вариантов заполне-
ния карточек спортлото, есть п - . гак как каждый вариант запол-
нения отличается только составом видов спорта. Число случаев. бла-
гоприятствующих событию А. есть т = 1. Поэтому
Р (А) = — =-------------------а 0.00000012.
' 45 44-43-42-41-40
б) Пусть событие В — угадывание 4 видов спорта из 6 выигравших
из 45. Вначале найдем число способов, какими можно выбрать 4 вида
спорта из 6 выигравших, т.е. (’*. Но это еще не все: к каждой комби-
нации 4-х выигравших видов спорта из 6 следует присоединить комби-
нацию 2-х невыитравших видов из 45 - 6 = 39; таких комбинаций
С^.По правилу произведения обшее число случаев, благоприятст-
вующих событию В. равно т = С* -CJ,. Итак.
/>(Д) = ^ = С\С1- =0.00136. ►
П ^44
t> Пример 1.15. В партии КМ) изделий, из которых 4 — брако-
ванные. Партия произвольно разделена на две равные части, кото-
рые отправлены двум потребителям. Какова вероятность того, что
вес бракованные изделия достанутся: а) одному потребителю;
б) обоим потребителям поровну?
29
Рс шс н и с. а) Пусть событие /1 — все бракованные изделия
достанутся одному потребителю. Общее число способов, какими
можно выбрать 50 изделий из 100. равно л = (. Событию А бла-
гоприятствуют случаи, когда из 50 изделии, отправленных одному
потребителю, будет либо 46 стандартных из 96 (и все 4 бракован-
ных) изделий, либо 50 стандартных из 96 (и 0 бракованных); их
число т = - С* + C^Cj. Поэтому
С‘6 .С*-С1’ С’4' I + С*4’ • I 2С’4Л
~ р$41 ~ Ж-.Ч1
2 • 96! • 50! • 50! 2-96!-46!-47-48-49-50 Л11„
46! • 50! 100! 46! • 96! •9798•99 -100
где 100! = 96! • 97 • 98 • 99 • 100. 50! = 46! • 47 • 48 • 49 • 50.
б) Пусть событие В — в каждой партии по 2 бракованных изделия
Теперь событию В будут благоприятствовал, случаи, когда из 50 изде-
лий. отправленных одному потребителю. будут 48 стандартных из 96 и
2 бракованных из 4. их число т - • С;. Поэтому'
= т_ _ С С; = 96! 4! 50! 50! _
и’ С" 48Ь48!-2!-2М00!
= 9б!(2!3-4)(48!-49-50)‘ = 3 4(49.50)' = ()
(48!):2!-2(96! 97.98-99 100) 2-97-98-99 I00
> Пример 1.15а. В магазине было продано 21 из 25 холодильни-
ков трех марок, имеющихся в количествах 5. 7 и 13 штук. Полагая,
что вероятность быть проданным для холодильника каждой марки
одна и та же. найти вероятность того, что остались нераспроданны-
ми холодильники: а) одной марки; б) трех разных марок.
Р с ш с н и е. а) Пусть событие А — остались нераспроданными
холодильники одной марки. Общее число способов, которыми
можно получить 4 (непроданных) холодильника из 25. равно
а? = С.\ . Число способов, которыми можно получить 4 холодильника
первой марки из 5, равно /м, = С4; второй марки из 7 - т. = С* и
третьей марки из 13 — тх = С4,. Событию А ио правилу суммы
(§ 1.5) благоприятствует т = Ш| + пъ + ту = С’4 +С‘ + СД случаев
Поэтому
. = C^C^=5^^ = J51 = O>OW)
п 12 650 12 650
Р(Л) =
30
6) Пусть событие В — остались нераспроданными холодильники
трех разных марок. Событие В может произойти по одному из трех
вариантов. По первому варианту событие В произойдет, если оста-
нутся нераспроданными I, 1, 2 холодильников соответственно 1-й.
2-й и 3-й марок; по второму варианту — 1. 2, I и по третьему вари-
анту останутся нераспроданными 2. I. I холодильников соответст-
венно 1-й. 2-й и 3-й марок Так как до продажи имелось 5 холо-
дильников 1-й марки. 7 — 2-й и 13 холодильников 3-й марки, го по
правилу произведения (§ 1.5) число случаев, благоприятствующих
первому варианту, равно w, = ; второму — /и, = C’lCfc’ii •
третьему варианту — л/, = С^С'С,1,. Общее число случаев, благопри-
ятствующих событию В. равно т = пц + ль + л/j. Теперь
р( в)=™ = с;сс,:,-<-с;с-с,',4с-с;с;, =
w п С'х
5 • 7 • 78 +5-21 • 13 + 10-7-13 5005 А
=-------------------------------=--= 0.396. ►
12 650 12 650
> Пример 1.16. За круглым столом рассаживаются 5 мужчин и
5 женщин. Найти вероятность тою. что: а) никакие два липа одного
пола не сядут рядом; б) супруги сядут рядом, сели эти мужчины и
женщины образуют 5 супружеских пар.
Решение, а) Пусть событие А — никакие два липа одного
пола нс сядут рядом. Общее число способов рассадки 10 лип из
10 местах определяется числом перестановок л = /*|0 = 10!. Если
женщины займут четные места 5! способами, то мужчины будут за-
нимать нечетные места также 5! способами, и наоборот, т.е. число
случаев, благоприятствующих событию А, равно лц = 2< 5!>2. Итак.
' л 10!
2 12^
3 628 800
= 0.00794.
б) Пусть событие В — супруги, образующие пять супружеских
пар, сядут рядом. Теперь число случаев ль, благоприятствующих
событию В, определяется числом 5! всевозможных перестановок
5 супружеских пар. причем в каждой парс возможна перестановка
мужа и жены; по правилу произведения л»у — 5!25. Итак,
v т, 5!2 120-32
л 10! 3 628 800
> Пример 1.16а. В аудитории т = 25 студентов. Найти вероягноегь
того, что хотя бы у двух студентов дни рождения совпадаю!. При ка-
31
ком числе т студентов вероятность того же события не меньше чем
0,95? (Полагаем равновозможность рождений в любой день года.)
Решение. Пусть событие А - дни рождения хотя бы двух студен-
тов из т присутствующих в аудитории совпадают. Найдем вероятность
противоположного события Л — /ши рождения всех студентов различны
Число случаев, благоприятствующих событию Л. есть число
размещений из п - 365 элементов (дней года) по /л, т.е. Лп". Общее
число случаев определяется также числом размещений из л элемен-
тов по т. но размещений с повторениями, т.е. Л* = /Г (см. (1.13))
Согласно классическому определению вероятности
Р( 4) = = "<л-1)-(л-/я-Н)
л" м"
и для п = 365
—11 С)
При т = 25 искомая вероятность, рассчитанная по формуле (*),
составит АЛ) = 0.569.
Вычисляя вероятности АЛ) для различных т, нетрудно ходить-
ся в том. что неравенство АЛ) > 0.95 будет выполняться при т > 47.
т.е. достаточно лишь 47 студентов в аудитории, чтобы с вероятно-
стью. нс меньшей чем 0.95. утверждать, что по крайней мерс у двух
из них дни рождения совпадают. ►
£> Пример 1.17. В купейный вагон (9 купе по 4 места) семи пас-
сажирам продано 7 билетов. Найти вероятности того, что пассажи -
ры попали: а) в два купе; б) в семь купе; в) в три купе.
Решение, а) Пусть событие Л — пассажиры попали в два
купе. Общее число способов выбора 7 любых мест из имеющихся в
вагоне 36 определяется числом сочетаний п = С,в-
Для нахождения чиста mj случаев, благоприятствующих собы-
тию Л, учтем, что 2 купе из 9 можно выбрать С; способами, а
7 мест из имеющихся в двух купе 8 мест — Cg? способами. По пра-
вилу произведения т, = Итак.
/’(Л) = — = S1£l
» Q
36-8
8 347 680
0,0000345.
б) Пусть событие В — пассажиры попали в семь купе. 7 купе из 9
можно выбрать С'.; способами. Семь мест в семи купе можно полу-
32
чип», если в каждом купе выбрать по одному месту из четырех, ‘гто
возможно 47 способами. Общее число случаев, благоприятствующих
событию В. по правилу произведения равно т, =C'J 4 . Итак,
/’(«) =
47
« G,
36 -16 3X4
X 3476X0
0,07066.
в) Пусть событие 1) — пассажиры попали в три купе. 3 купе из 9
можно выбрать CJ способами, а число способов выбора семи мест
из 12 в трех купе определяется сложнее, чем в п. а) и б). Действи-
тельно, возможные варианты выбора 7 мест из 12 в трех купе сле-
дующие: 4 + 2 + 1,3 + 3 + 1, 3 + 2 + 2. а за счет перестановок купе
таких вариантов будет соответственно 6. 3 и 3. Каждый из этих ва-
риантов по правилу произведения может быть получен
CjCjCj. CjCj’Cj. СдС;С; способами соответственно. В результате
общее число случаев, благоприятствующих событию D, равно
да, = G'(6C4‘C;C] +ЗС43С4’с! + ЗС4С4?С;) =
= 84(6-24 + 3 64 + 3-144) = 84-768 = 64 512.
Итак,
Р{П)
<>4 512
8 347 6X0
= 0.00773.
т3
п
1.7. Действия ннд событиями
Введем понятие суммы, произведения и разности событий.
О п р е д е л е н и е. Суммой нескольких событий называется собы-
тие. состоящее в наступлении хотя бы одного из данных событий.
Если /1 и В — совместные события, то их сумма1 А + В обозначает
наступление юти события А, ил» события В. или обоих событий вме-
сте. Если А и В — несовместные события, то их сумма А + В означает
наступление или события А, юти собып<я В.
Определение. Произведением нескольких событий называет-
ся событие, состоящее в совместном наступлении всех этих событий.
Если А, В. С — совместные события, то их произведение1 АВС оз-
начает наступление и события А. и события В, и события С.
О п р е л с л с н и с. Разностью' А — В двух событий А и В назы-
вается событие, которое состоится, если событие А произойдет, а
событие В не произойдет. * *
1 Д.-1Н суммы событий Я и В нс пользуется также обозначение IU В. для npoin-
itcacHHM тех же событии — ЯП В. а хчя их разности А \ В (см § I 12)
? Tl’>pn« ктаянюогй в ШПТШ1М>|«и|. . ITIIIl-SKU
33
> Пример 1.17а. Победитель соревнования насаждается: призом
(событие /I). денежно»» премией (событие Я), медалью (событие О Что
представляют собой события: а) Л + Я, б) ЛВС и) АВ С?
Р с и» е н и с а) Событие А I- В состоит в награждении побели
геля пли при юм. или премией, или и тем и другим
б) Событие АВС состоит в награждении победителя олновре
менно и призом, и премией, и медалью
в) Событие АВ - С состоит в награждении победителя одновре
менно и призом, и премией без выдачи медали ►
Ниже (§ 1.12) рассматривается теоретико-множественная трактов-
ка основных понятий теории вероятностей Здесь же дадим геомет-
рическую интерпретацию основных действий нал событиями с по-
мощью диаграмм Венна.
Пусть, например, внутри прямоугольника (рис. I 3) выбирается
наудачу точка (достоверное событие Q). и событие .-I состоит в по
падании этой точки в меныпий круг (рис. 1.3. а). а событие В — в
больший круг (рис 1.3. о) Тогда сумма событий И + Л означает по-
падание точки во нею ы штрихованную область обоих кругов
(рис 1.3. *п. а произведение АВ в общую часть кругов
(рис. I 3. г). На рис. I 3. й. с заштрихованные области показываю)
события А и В. противоположные событиям А и В. а на рис. 1.3, .>
и з разности событий А — В и В - А
34
> Пример 1.18. Убедиться н справедливости равенств, выра-
жающих законы де Моргана:
а) А + В + ...+ К = А В...К: б) АП...К = J + В +... + К.
Реше н и с. а) Если событие А + В +...+ К состоит в появле-
нии хотя бы одного из данных событий А. В... К. то противопо-
ложное событие .4 •» В +... • К означает непоявление всех данных
событий, т.е. произведение событий IB..К.
б) Если событие АВ...К состоит н совместном наступлении всех
данных событий А. В. .... К. то противоположное событие АВ...К оз-
начает непоявление хотя бы одного из этих событий, т.е. сумму
Х + 8 + ...+ А*. На рис. 1.3. и и к приведенные соотношения между
событиями иллюстрируются на примере двух событий ►
Если событие А представляет собой сумму песо в мест н ы х
событий Л1. Л». .... Ап, т.е. А = At + А; +...+ Лл. то говорят, что собы-
тие А распадается на п частных случаев {вариантов} /1|. А>, .... А„.
Операции сложения и умножения событий обладают следую-
щими свойствам и:
1. А + В = В + а — коммутативность сложения.
2. А + (В + О = (.4 + В} + С — ассоциативность сложения.
3. АВ = ВА — коммутативность умножения.
4. А{ВС) - (АВ)С — ассоциативность умножения.
5. А(В + С) = АВ + .4С; А + ВС = (/1 + + С) — законы ди-
стрибутивности.
Последние дна свойства иллюстрируются на рис. 1.3../ н м.
Из определения операции над событиями вытекают очевидные
равенства:
А + А = 4. .4.4 = .4; J + Q = О. 4Q =. .4; .4 + 0 = А. .40 = 0:
.4+ А = Q. АА = 0; Q *-0 = Q. Q0 = 0.
t> Пример 1.18а. Упростить выражения:
a) D = (.4 + В)( А + В К .4 * В); б) Е = .4 * АВ + ВС + 7с.
Решен и е. а) Используя приведенные выше свойства опера-
ций сложения и умножения событий, получим:
D = (.4 + В X А + В}( .4 + В) = (.4.4 + А В + А В * В В)(.4 + В ).
Так как А А = 0. АВ + АВ = (.4 + .4 )В = ПВ = В. ВВ = В. го
D = (0 ♦ В + Z/X А + В) = В(А 4 В} = АВ 4- ВВ = АВ + 0 = АВ.
б) Используя закон де Моргана (см. пример 1.18) и приведен-
ные выше свойства, получим
Е = {А + АВ)+ ВС * ~АС = .4 + ВС А < .4 +О =
=(я+л)+дс+с)=п+(лс+с)=а ►
35
1.8. Тсо|м>мн сложения вероятностей
Сформулируем теорему (правило) сложения вероятностей.
Теорема. Вероятность суммы конечного числа несовместных собы-
тин ровна сумме вероятностей утих событий:
АЛ + В + ... + Л') =АЛ) + /\В) + ... + АЛ). (1.16)
□ Докажем теорему для схемы случаев. рассматривая сумму двух
событий.
Пусть в результате испытания из общего числа п равновозмож-
ных и несовместных (элементарных) исходов испытания (случаев)
событию А благоприятствует «| случаев, а событию В — пъ случаев
(рис. 1.4).
А т, В - т.
п
Рм.. 1.4
Согласно классическому определению Р( А) = —, /’(В) - .
п п
Так как события .4 и В несовместные. то ни один из случаев,
благоприятствующих одному из этих событий, не благоприятствует
другому (см. рис. I 4). Поэтому событию А + В будет благоприятст-
вовать л/| ч- пь случаев. Следовательно.
= — = /’(//).
п п л
Следствие 1. Сумма вероятностей событий, образующих полную
группу, равна единице:
АЛ) + Р[В} +...+ Pl К) = I (1.17)
□ Если события А, В. К образуют полную группу, то они
единственно возможные и несовместные.
Так как события А. В.... К — единственно возможные, то собы-
тие А + В +...+ Л', состоящее в появлении в результате испытания
хотя бы одного из этих событий, является достоверным1, т.е
А + В + ...+ К = Q и его вероятность равна единице:
АО) = АЛ + Я + ... + Л) = I
1 Полому полную группу событий можно было бы определяй, и иначе, чем и
§ I,! несколько событии образую» пишут группу {систему), если они являются
несовместными исходами испытания и их сумма прсастатияс» собой достонерпое
событие
36
В силу того, что события Я, В, .... А' — несовместные, к ним
применима теорема сложения (1.16>. т.е.
НА + В + ... + К) = А>1) + Н В) + ... + АА) = I.
Следствие 2. Сумма вероятностей противоположных событий
ровна единице-.
НА) + Г(Л)= I. <1.18)
О Утверждение (1.18) следует из того, что противоположные со-
бытия образуют полную группу.
> Пример 1.19. Вероятность выхода изделия из строя при экс-
плуатации сроком до одного гола равна 0.13. а при эксплуатации
сроком др 3 лет — 0.36. Найти вероятность выхода изделия из строя
при эксплуатации сроком от I гола до 3 лет.
Решение. Пусть события J. В. С — выход из строя изделии
при эксплуатации сроком соответственно до I года, от I гада до
3 лет, свыше 3 лет. причем по условию А.4) = 0,13. АО =0.36.
Очевидно, что С = А + В. где А и В — несовместные события. По
теореме сложения АО = НА) + НВ), откуда НВ) = АО ~ НА) =
= 0,36 - 0.13 = 0.23. ►
Замечание. Следует еше раз подчеркнуть. что рассмотрен-
ная теорема сложения применима только для несовместных событий
и попытка се использования в виде (1.16) для совместных событий
приводит к неверным и даже абсурдным результатам. Например,
пусть вероятность события А, — выигрыша по любому билету де-
нежно-вещевой лотереи, т.е. НА,) = 0.05, и приобретено 100 биле-
тов О’ = I, 2. 100). Тогда, применяя теорему сложения, получим,
что вероятность выигрыша хотя бы по одному из 100 билетов, т.с.
АЛ|+Л2+...+4+ -+/1|(ю) = А/1|)+АЛ2)+.,.+АА)+...+А/1|оо) =
= 0.05 + 0,05-...+ 0,05 = 5.
Абсурдность полученного ответа (вероятность любого события не
может быть больше 1) объясняется неприменимостью в данном слу-
чае теоремы сложения, ибо выигрыш по каждому билету, т.е. события
Л|, Л2..являются событиями совместными.
1.9. Условная вероятность события.
Теорема умножения вероятностей.
Независимые события
Как отмечено выше, вероятность НВ) как мера степени объектнв-
ной возможности наступления события В имеет смысл при выполне-
нии определенного комплекса условий. При изменении условий веро-
37
ятность события В может измениться. Так, если к комплексу условий,
при котором изучалась вероятность Pt В), добавить новое условие А. то
полученная вероятность события В. найденная при условии. что событие
.1 произошло, называется условной вероятностью события В и обознача-
ется Р<< В), или А В/A), или Л В | .4).
Строго говоря, «безусловная» вероятность Р(В) также является
условной, гак как она получена при выполнении определенного
комплекса условии.
[> Пример 1.20. В шпике 5 деталей, средн которых 3 стандарт-
ные и 2 бракованные Поочередно из него извлекается по одной
детали (с возвратом и без возврата). Найти условную вероятность
извлечения во второй раз стандартной детали при условии, что в
первый раз извлечена деталь: а) стандартная; б) нестандартная.
Р с in е и и е. Пусть события А и В — извлечение стандартной
детали соответственно в 1-й и 2-й раз Очевидно, что Р(.4) = ^
Если вынутая деталь вновь возвращается в ящик, то вероятность
извлечения стандартной детали во второй раз Р(В} = ^. Если выну-
тая деталь н ящик не возвращается, то вероятность извлечения
стандартной детали во второй раз Р\В) зависит от того, какая деталь
была извлечена в первый раз — стандартая (собьпие А) или бракован-
ная (событие .4). В первом случае В, (В) во втором случае
3
/’(/?) = -, гак как из оставшихся четырех деталей стандартных будет со-
ответственно1 * 3 2 или 3. ►
Найдем формулу для вычисления условной вероятности Р,(В).
□ Пусть из общего числа п ршиювозможных и несовместных (элемен-
тарных) исходов испытания (случаев) событию А благоприятствует т слу-
чаев. событию В — к случаев, а совместному появлению событий А и В. т.е
событию АВ — /случаев (/< т, /< к) (рис 1.5).
1 Следует заметить. что «безусловная» вероятность н >а.'|ечсмия во второй раз
стандартной к-талн Р\Н) (мила втлеченкия дсгаль не возвращается» определя-
ем но формуле полной вероятности (1.31') - см далее § I II
3 2 2 3 3
/'(Я» - Р(А)- /',(/?) ♦ /’(.1)/’((В> = , ♦ _ , т.е га же, что н при возвра-
те и заточенной летали
38
A - т
В - к
АВ - /
И
Рис. 1.5
Тогда, согласно классическому определению вероятности.
рИ=-. Р(М)Л.
п п
После того как событие А произошло, число всех равновозмож-
ных исходов (случаев) сократилось с п до т, а число случаев, благо-
приятствующих событию В. с к до I. Поэтому условная вероятность1
т тп "(••!)
(1.19)
Аналогично
(1.20)
/ч ля)
Умножая правую и левую части равенств (1.19) и (1.20) соответ-
ственно на ЛЯ) и Pi В). получим
Р( АВ} = /»(Л)Л (Л) = Р(В] />Л(Я). (1.21)
Это так называемая теорема (правило) умножения вероятностей:
вероятность произведения двух событий равна произведению вероятно-
сти одного из них на условную вероятность другого, найденную. в пред-
положении. что первое событие произошло.
Теорема (правило) умножения вероятностей2 легко обобщается
на случай произвольного числа событий:
Л/1ЛС...А7.) = АЛ) • РЛ(В) - Рл^С}...Рлвс д<0. <I-22)
Т.е. вероятность произведения нескольких событий равна произведению
вероятности одного из этих событий на условные вероятности других'.
1 Формулу усюпиом верам кости (1.19) мы iio.iv'ih.ih. oiuip.oici. на классическое
определение вероятности И общем случае пл формула служит определением
УсловноЛ вероятности (см § I 12).
2 В случае. если АЛ)₽0 или АЯнО. то соответствующие формулы (1.19) и (1.20)
Для условных вероятностей не имеют смысли, ибо истин можно событие Л или В.
ЗДнако теорема (правило) умножении вероятностей (1.2!) остается верной и при
АЛ)=0. АЯ)=1»
39
при этом условная вероятность каждого последующего события вы-
числяется и предположении, что все предыдущие события произошли.
t> Пример 1.21. Работа электронного устройства прекратилась
вследствие выхода из строя одною из пяти унифицированных бло-
ков. Производится последовательная замена каждого блока новым
до тех пор. пока устройство не начнет работать. Какова вероятность
гою, что придется заменить: а) 2 блока; б) 4 блока?
Ре ш е н и е. а) Обозначим события:
А, — /-й блок исправен, i = I. 2.5;
В — замена двух блоков.
Очевидно, что придется заменить 2 блока, если 1-й блок испра-
вен (4 шанса из 5). а 2-й — неисправен (1 шанс из оставшихся 4).
т.е. В = Я, Я?. Теперь по теореме умножения (1.21)
лл = /’(4Л:)=Р(.ОЛр..)=|1 = 1
б) Пусть событие С — замена 4 блоков. Очевидно, что С =
= 4.4.Я, Яд и по теореме умножения (1.22)
Р(с) = р( 4 А А Л) = Р{ 4) г\ (.4) (я,) 1\,(я,) =
4 3 2 1 I
=---------= -. >
5 4 3 2 5
Г> Пример 1.22. Решип» другим способом задачу, приведенную в
примере 1.11.
Р е ш е н и е. Пусть событие В — получение слова «АНАНАС».
Событие В наступит, если первой окажется карточка с буквой А
(3 шанса из 6), вторая — с буквой Н (2 шанса из оставшихся 5).
третья — с буквой А (2 шанса из оставшихся 4) и т.д. По теореме
умножения (1.22)
3 2 2 1 £ 1 = J_
6 5432 I 60'
Теорема умножения вероятностей принимает наиболее простой
вид. когда события, образующие произведение, назови с и .м ы.
Событие В называется независимым от события А, если его вероят-
ность не меняется от того. произошло событие А или нет. г.с.
/’,(«) = /’(«) (или ЛД/?)=/’(Д().
В противном случае, если f\(B}r Р(В) (или /‘4(/?)*/•’(/?)). со-
бытие В называется зависимым от Я.
Докажем, что если событие В не зависит от А, то и событие А не
зависит от В.
Р(В)
40
□ Так как по условию событие В не зависит от А. то
Л(в) = /’(в>-
Запишем теорему умножения вероятностей (1.21) в двух формах:
Заменяя РДВ) на А Я). получим АЛ)-АЯ) = АЯ)Рд<Л). откуда, .
полагая, что Р{В) *0. получим Р/Х'О = Р[А). т.е. событие А нс
зависит от В.
Таким образом, зависимость и независимость событий всегда вза-
имны. Поэтому можно дать следующее определение независимости
событий.
Два события называются независимыми, если появление одного
из них нс меняет вероятности наступления другого.
О Пример 1.23. Установить, зависимы или нет события А и В по
условию примера 1.20.
Решение. В случае возврата извлеченной детали
Р4(Я) = А,(/?)= Р(Я) = ^. т.е. события А и В независимы. Если
извлеченная из ящика деталь не возвращается, то Р, (В) *
|. т.е. А, (в)* Р(В) и события А и В зависимы. ►
Несколько событий А, В. .... L называются независимыми в сово-
купности (или просто независимыми). если независимы любые лва
из них и независимы любое из данных событий и любые комбина-
ции (произведения) остальных событий. В противном случае собы-
тия А, В..... L называются зависимыми.
Например, три события Л. В. С независимы (независимы в со-
вокупности). если независимы события .4 и В. А и С. 5 и С. А и ВС.
В ЧАС. С и АВ.
Для н е з а в и с и м ы х событий теорема (правило) умножения
вероятностей для двух и нескольких событий примет вид1:
Р( АВ) = Р( А)Р( В). (1.23)
PIABC...KL) = PlA}PiBl...P(L). (1.24)
т.е. вероятность произведения двух или нескольких независимых собы-
тий равна произведению вероятностей этих событий.
1 Формулу (1.23) можно было бы рассматривать и и качестве о пределе-
н и я независимости двух событий Для определения независимости н с -
скольких событий (в совокупности) одной формулы (1.24) было бы уже
недостаточно
41
О Пример 1.24. Вероятность попадания в цель для первого
стрелка равна 0.8, для второго — 0.7, для третьего — 0,9. Каждый из
стрелков делает по одному выстрелу. Какова вероятность того, что в
мишени 3 пробоины?
Решен и е. Обозначим события:
А, — попадание в цель /-го стрелка О’ = 1.2. 3);
В — в мишени три пробоины.
Очевидно, что В- Л|/1у1и причем события Л|. A,. Лу — независи-
мы. По теореме умножения (1.24) для независимых событий
Р(В) = /М|Лу1.0 = Я(/1|)ЛЯ2)Ж/1?) = 0.8-0,7-0.9 = 0.504. ►
Замечание. Говоря о и е з а в и с и м о с т и событий,
отметим следующее
I. В основе независимости событий лежит их физическая независимость.
означающая, что множества случайных факторов. приводящих к тому или
иному исходу испытания, не пересекаются (или почт не пересекаются)
Например, если н цехе имеются две установки, никак не связанные между
собой по условиям производства. то простой каждой установки — события
независимые. Если ли установки связаны единым технологическим цик-
лом, го простой одной из установок завнетп от состояния работы другой.
Вместе с тем если множества случайных факторов пересекаются,
то появляющиеся в результате испытания события не обязательно
зависимые
Пусть, например, рассматриваются события:
А — извлечение наудачу из колоды карты пиковой масти:
В — извлечение наудачу из колоды туза.
Необходимо выяснить, являются ли события .4 и В зависимыми.
На первый взгляд, можно предполагать зависимость событий А и В в
силу пересечения случаев, им благоприятствующих: среди карт пико-
вой масти есть туз, а среди гузов — карга пиковой масти. Убедимся,
однако, в гом. ‘по события А и В независимы
Р( В) = — ~ - (в колоде 4 туза из 36 карт),
36 9
Р((Д) = 1 (в колоде I туз из 9 карт пиковой масти).
Итак. Г, | Я) = Р( В), т.е. события .4 и В независимы1.
1 Независимость события .4 и Я можно показать иначе. убедившись в выполне-
нии равенства (1.23) Так как АЛЯ) = 1/36 (в кололс I пиковый тут из 36 карт).
/ЧЛ) *= 9/36 (п колоде 9 карт пиковой масти из 36). 1/9 (см выше), т.е
f I 9 I )
АЛЛ) * АЛ) А Я) I — — — . слслотатслыто. события 4 и Л независимы. При
к 36 36 9>
добавлении джокера (см. с. 43) имеем АЛ) ~ 9/37. А Я) » 4/37. АЛЛ) = 1/37. тс
/ | 9 4 1
Р( АВ) * Г(.4)Р{ /> )| — - — — | и события Л и В — зависимы.
42
Если же в колоду карг добавлен джокер, то карт станет 37 и соот-
ветствующие вероятности ЛИ) = 4/37, Л<(Я) = 1/9. т.е. ( В) * Р( В)
и события Ии Й зависимы.
2. Попарная независимость нсскапясих событий (т.е. независимость
взятых из них любых двух событий) еще не означает их независимости в
совокупности. Убедимся в этом на следующем примере (примере
С.Н. Бернштейна).
Предположим, что грани правильного тетраэдра (треугольной пи-
рамиды с равными ребрами) окрашены: 1-я — в красный цвет (со-
бытие Л), 2-я — в зеленый (Я). 3-я — в сипни (О и 4-я — во все три
цвета (событие АВС). При подбрасывании тетраэдра вероятность
любой грани, на которую он упадет, в своей окраске иметь одина-
ковый цвет равна 1/2 (так как всего граней 4. а с соответствующей
окраской 2, т.е. два шанса из четырех). Таким образом. ЛЛ) = 1/2.
ЯД)= 1/2. ЛО = 1/2.
Точно так же можно подсчитать, что
PtfiA) = = Рл{ В) = РС<В) = РЛ{С\ = /^О = 1/2
(один шанс из двух), г.е. события /1. В. С попарно независимы Ес-
ли же наступили одновременно два события, например А л В, т.с
АВ, то третье событие С обязательно наступит, т.е Р^С) = I и
аналогично Рас<В) = I, Рщ<А) = I; следовательно, вероятность каж-
дого из событий .4. В или С изменилась, и события А. В и Св сово-
купности зависимы.
При решении ряда задач требуется найти вероятность суммы
двух или нескольких с о в м е с т и ы х событий, г.е вероятность
появления хотя бы одного из этих событий. Напомним,
что в этом случае применять теорему сложения вероятностей в виде
(1.16) нельзя.
Теорема. Вероятность суммы двух совместных событий равна сумме
вероятностей этих событий без вероятности их произведения, т с.
Р(Л + В) = Р(Л) + Р<В) - Р(АВ). (1.25)
□ Представим событие .4 + В, состоящее н наступлении хотя бы
Одного из двух событий А и В. н виде суммы трех несовместных вари-
антов: А + В = АВ 4 АВ + АВ . Тогда по теореме сложения (1.16)
Р( А^В) = /’(АВ) + /»(.4«) + АВ). (1.26)
Учитывая, что А = АВ + АВ, Р(А) = Р( АВ) * Р( АВ), откуда
^(лй) = Р(А) - Р(АВ). и аналогично Р^АВ)-Р(В) Р(АВ), полу-
чим. подставляя найденные выражения в (1.26):
43
/’< .4 + /Л = (/’(.4) - Р< Л/Л | + | Pl В) - Pl .4В)] * P( AB) =
= P(A)>P(B)-P(AB).
В справедливости формулы (1.25) мож-
но наглядно убедиться по рис. 1.6.
В случае грех и более совместных собы-
тий соответствующая формула для вероят-
ности суммы Ал+5+...+Л) весьма громозд-
ка и проще перейти к противоположному
событию L:
L= А + в +... + К - Л В...К (см. пример 1.18).
Тогда на основании (1.18) Р(А + В + ... + А") = 1 - АЛ), или
Р(А + В 4-... + К) = 1 -Р(Л В...К). (1.27)
т.е. вероятность суммы песка!ьких совместных событии А. В. К рав-
на разности между единицей и вероятностью произведения противопо-
ложных событий А. В..... К.
Если при этом события А. В. ... К — н с а а в и с и м ы е. то
Р (А + В + ... + К) = 1 - РС4)Р1В)...Р(К). (1.28)
В частном случае, если вероятности независимых событий рав-
ны. т.е. Р(/1) = Pl В) =...= PIK) = р. то вероятность их суммы
Р(Л+ S+... + А)= I - (I -р)\ (1.29)
(ибо в этом случае Р( А^Р(В)...Р(К) = (I - р)...(! - р) = (1 - [>)”)
> Пример 1.25. На 160 лотерейных билетов приходится 5 выиг-
рышных. Какова вероятность выигрыша хотя бы по одному билету,
если приобретено: а) 2 билета; б) 4 билета?
Р е ш е н и е. Пусть событие А, — выигрыш по /-му билету
(/ = 1.2. 3. 4).
а) По формуле (1.25) вероятность выигрыша хотя бы по одному
из двух билетов
р(4 + 4.)=р(л,)+/’(л)-р(л,4)=
5 5 5 4
= Р( А.) 4 Р( Л ) - Р( А,) Р (А.) = — + -----= 0.098.
' ’ ' • ' " 100 100 100 99
44
6) По формуле <1.27> вероятность выигрыша хотя бы по одному
Из четырех билетов
P(At 4-Л; + J. + Л, )=1-/»(!. Л: Л. Я.) =
95 94 93 92
= 1------------------ 0.188. ►
100 99 98 97
1.10. Решение задач
О Пример 1.26. Вероятность того, что студент сдаст первый эк-
замен. равна 0.9; второй — 0.9; третий — 0.8. Найти вероятность
того, что студентом будут сданы: а) тальке 2-й экзамен; 6) только
один экзамен; в) три экзамена: г) по крайней мере два экзамена;
д) хотя бы один экзамен.
Р е ш с н и е. а) Обозначим события: А, — студент сдаст /-й экза-
мен (/= 1. 2. 3); В — студент сдаст только 2-й экзамен из грех. Оче-
видно, что В = Л, Л, Л,. т.е. совместное осуществление трех событий,
состоящих в том. что студент сдаст 2-й экзамен и не сдаст 1-й и 3-й
экзамены. Учитывая, что события Л|. Ay /К независимы, получим
ЛЯ) = /’(Л, Л. Л,) = Р( Л,) Р[ Л.) Р(~1,) = 0.1 • 0.9.0.2 = 0,018.
б) Пусть событие С — студент сдаст один экзамен из трех. Оче-
видно, событие С произойдет, если студент сдаст только 1-й экза-
мен из трех, или только 2-й, или только 3-й, т е.
Р(<~) = Л’(Л,<.Л, + Л..4.Л. + Л, <..-!,) =
= 0.9 0.1-0.2 4-0.1 0.9 0.2 4-0.1-0,1-0,8 = 0,044.
в) Пусть событие D — студент сдаст все три экзамена, т.с. I) =
я Л|Л1Л.ь Тогда
Р( D} = Р{ Л, Л. Л,) = Р( Л, )Р( Л,) Р{ Л,) = 0.9 • 0.9 • 0.8 = 0.648.
г) Пусть событие Е — студент сдаст по крайней мерс два экза-
мена (иначе: «хотя бы два» экзамена или «нс менее двух» экзаме-
нов). Очевидно, что событие Е означает сдачу любых двух экзаме-
нов из трех либо всех трех экзаменов, т.е.
Е = ДЛ. Л, 4- Д Л?Л, 4- Л.Л.Л, + ДЛ.Л, и
= 0.9 • 0.9 • 0.2 + 0.9 -0.1- 0.8 4- 0.1 • 0.9 • 0.8 4- 0,9 • 0.9 • 0.8 = 0.954.
д) Пусть событие F — студент сдаст хотя бы один экзамен (ина-
че: «не менее одного» экзамена). Очевидно, событие F представляет
сумму событий С (включающего три варианта) и Е (четыре вариан-
45
тп), т.е. F = /1| + Aj + А) = С + £ (семь вариантов). Однако проще
найти вероятность события F. если перейти к противоположному собы-
тию. включающему всего алии варшигг - /•' = Я, * А, - Ях - Я, Я. Як.
т.е. применить формулу (1.27).
Итак,
Р( F) = Р( Я, - Я. + Я,) - I - Р( F) = I - Р(Я. Я. Я,) =
= I - Р< Я,) -А Я. )А Я J = I - 0.1 • 0.1 0,2 = 0,998,
т.е. сдача студентом хотя бы одного экзамена из грех является со-
бытием практически достоверным. ►
[> Пример 1.27. Причиной разрыва электрической пени служит
выход из строя элемента К\ ши одновременный выход из строя двух
элементов — К2 и А?. Элементы могут выйти из строя независимо друг
от друга с вероятностями, равными соответственно 0.1; 0,2; 0,3. Како-
ва вероятность разрыва электрической цепи?
Реше н и е. Обозначим события:
А, — выход из строя элемента K,{i =1.2. 3);
В — разрыв электрической цепи.
Очевидно, по условию событие В произойдет, если произойдет ли-
бо событие А\. либо Aytj. т.е. В= Я| А2А\. Теперь, по формуле (1.25)
= /ЛИ, + Я;Я.О = ЛЯ() + PtAyh) - Р|Я|(Я?Я1)1 =
= АЯ|) + ЛЯ.ОЛЯО - ЛЯ|)ЛЯ2)ЛЯ0 =
= 0.1 + 0.2-0,3 - 0.1 -0.2-0.3 = 0,154
(при использовании теоремы умножения учли независимость собы-
тий Яь Я> и Я1). ►
О Пример 1.28. Производительности трех станков, обрабаты-
вающих одинаковые детали, относятся как 1:3:6. Из нерассортиро-
ванной партии обработанных детален взяты наудачу две. Какова
вероятность того, что: а) одна из них обработана на 3-м станке;
б) обе обработаны на одном станке?
Р е ш е н и е. а) Обозначим события:
Я, — деталь обработана на /-м станке (/ = I, 2. 3);
В — одна из двух взятых деталей обработана на 3-м станке.
По условию
/>( а ) = —!— = о, I. р( а, ) = —-— = 0.3. Р{ Я,) = —-— = 0.6,
’ *' 1 + 346 1 + 3 + 6 1 ” 1 + 3+6
46
Очевидно. что В = ЛИз + + ДИ| + ДИ» (при этом надо учесть. что
либо первая деталь обработана на 3-м станке, либо вторая). По теоремам
сложения и умножения (для независимых событий)
НВ) = ЛИ|)Л40 + НА,Ау) + А4И|) + АЛуЬ) =
= 0.1- 0.6 + 0.3 • 0.6 + 0.6 -0.1+ 0.6 • 0.3 = 0.4Я.
б) Пусть событие С — обе отобранные летали обработаны на
одном станке. Тогда С = Л{Аj + А2А2 + АуАу и
Л О = 0.1 • 0.1 + 0.3 • 0.3 + 0.6 • 0.6 = 0.46 ►
> Пример 1.29. Экзаменационный билет для письменного экза-
мена состоит из 10 вопросов — по 2 вопроса из 20 по каждой из
пяти тем. представленных в билете. По каждой теме студент подго-
товил лишь половину всех вопросов. Какова вероятность того, что сту-
дент сдаст экзамен, если для этого необходимо отвепгп. хотя бы на
один вопрос по каждой из пяти тем в билете?
Реше и н с. Обозначим события:
Л|, А, — студент подготовил 1-й. 2-й вопросы билета по каждой теме:
Bt — студент подготовил хотя бы один вопрос билета из двух по
/-Й теме (/ = I. 2.5);
С — студент слал экзамен.
В силу условия С = ВуВ^ВуВ^В'. Полагая ответы студента по
разным темам независимыми, по теореме умножения вероятностей
(1.24)
Р(С) = Р(Я!)/’(£Г.)Р(Л,)Р(/?,)Р(2?<).
Так как вероятности НВ) (/ = 1. 2.5) равны, го НО = (НВ))'
Вероятность НВ,) можно найти по формуле <1.27) (или (1.25)):
НВ) = = l-PMiJ:)
- - 10 9
= >/<(•<•) = !-- - = 0.763.
Теперь НО = 0.7635 = 0.259. ►
О Пример 1.30. При включении зажигания двигатель начнет ра-
ботать с вероятностью 0.6. Найти вероятность того. что: а) двига-
тель начнет работать при третьем включении зажигания; б) для за-
пуска двигателя придется включать зажигание нс более грех раз.
Ре ш е и и е. а) Обозначим события:
А — двигатель начнет работать при каждом включении зажигания;
В — то же при третьем включении зажигания.
47
Очевидно, что В = Л ЛЛ н /’(а) = Р( А) Р( Л) Р( ЛI = 0.4 • 0.4 • 0.6 -
= 0.096.
б) Пусть событие С — для запуска двигателя придется включать
зажигание не более трех раз. Очевидно, событие С наступит, если
двигатель начнет работать при 1-м включении. или при 2-м. или при
3-м включении. т.с. С = Л + АЛ + А А А. Следовательно.
Р(С) = /Ч А) > Р( Л )/Ч Л) ч /Ч A U4 А) • Р{ Л) =
= 0.6♦ 0.4 0.6 + 0.4• 0,4 0.6 = 0.936 . ►
О Пример 1.31. Среди билетов денежно-вещевой лотереи поло-
вина выигрышных. Сколько лотерейных билетов нужно купить,
чтобы с вероятностью, нс меньшей 0.999. быть уверенным в выиг-
рыше хотя бы по одному билету?
Р е in с н и е. Пусть вероятность события А, — выигрыша по г-му
билету равна р. т.е. АЛ.) = р Тогда вероятность выигрыша хотя бы но
одному из п приобретенных билетов, т.е. вероятность суммы незави-
симых событий Л|. Л),.... А.А„ определится по формуле (1.29):
АЛ, + Л2 + ... + Л„) = I - (I -р)я.
По условию I - (I - р)” > /. где Р = 0.999. откуда
(I - рГ s 1 - ./
Логарифмируя обе части неравенства, имеем
л 1g (I ~ р) S 1g (I - /V
Учитывая, что lg (I - р) — величина отрицательная, получим
По условию р = 0.5. Р- 0,999. По формуле (1.30)
1й0.(Ю1
п>—-------= 9,96. т.е. п > 10 и необходимо купить не мснсс 10 ло-
1й0,5
терейных билетов.
(Задачу можно решить, не прибегая к логарифмированию, путем
подбора целого числа п. при котором выполняется неравенство (J -
— рУ*<1 - Р, т.с. п данном случае | <0.001; так, сше при л = 9
[ - = —— > 0,001 . а гже при п = 10 I — 1 = —-— S 0,001. т.с. п i 10). ►
U/ 512 ’ (2) 1024
48
> Пример 1.3la. Среди клиентов банка 80% являются физиче-
скими линвми и 20% — юридическими. Из практики известно, что
40% всех операций приходится на долгосрочные расчеты, в то же
время из обшего числа операций, связанных с физическими лица-
ми. 30% приходится на долгосрочные расчеты. Какова вероятность
того, что наудачу выбранный клиент является юридическим липом
и осуществляет долгосрочный расчет?
Решение. Обозначим события:
Л — клиент является физическим лицом;
В — клиент осуществляет долгосрочный расчет.
По условию Р[Л) = 0,8; /’(Л) = 0.2; Р(В) — 0,4; РЛ{В) = 0,3. Тре-
буется найти вероятность совместного осуществления событий Л и
В, т.е. Р(ЛВ).
Так как В = АВ + АВ. то
Р(АВ) = Р(В)- Р<АВ) = Р(В)- Р(А)= 0.4-0.80.3 = 0.16. ►
[> Пример 1.32. Два трока поочередно бросают игральную
кость. Выигрывает тот. у которого первым выпадет «6 очков». Како-
ва вероятность выигрыша для игрока, бросающего тральную кость
первым? Вторым?
Р с ш е н и е. Обозначим события:
At — выпадение 6 очков при /-м бросании тральной кости
(/= 1,2....);
В — выигрыш игры троком, бросающим игральную кость первым.
Имеем ЛЛ) = 1/6. Pt Л J = 5/6 при любом /.
Событие В можно представить в виде суммы вариантов:
В = Л, + Л, Л. Л, + Л, Л. Л, Л4 Л, + ... Поэтому
В) = Р(,1,) + /•( Л, А)* Р(.4, А А,< Д) +... =
6 и»/ 6 6
По формуле суммы геометрического ряда с первым ‘«леном
а - 1/6 и знаменателем q = (5/6)J < I
/>(Я) = -^- = —1^ = 1 = 0.545.
1-<7 1-(5/бГ Н
Вероятность Р\ В ) выигрыша игры игроком, бросающим иг-
ральную кость вторым, равна
Л В ) = 1 - Р(В) = I - 6/! I = 5/11 = 0.455.
4»
т.е. существенно меньше, чем игроком, бросающим игральную
кость первым. ►
> Пример 1.33. Вероятность попадания в мишень при каждом вы-
стреле для 1-го стрелка равна 0.7. а для 2-го — 0.8. Оба они делают по
одному выстрелу ио мишени, а затем каждый из стрелков стреляет еще
раз. сети при первом сделанном им выстреле он промахнулся. НаИтп ве-
роятность того, ‘по в мишени ровно 2 пробоины.
Р е ш е н и с. Пусть события:
Л,. В, — попадание в цель соответственно 1-м и 2-м стрелком
при /-м выстреле (/ = I, 2);
С — в мишени ровно 2 пробоины.
Событие С произойдет. если:
• у каждого стрелка по одному попаданию с первого раза;
• у 1-го стрелка — попадание (при одном выстреле), у 2-го
стрелка промах и попадание;
• у 1-го стрелка — промах и попадание, у 2-го стрелка — попа-
дание (при одном выстреле);
• у каждого стрелка — промах и попадание посте двух выстрелов.
Итак.
С= .4,5, *.4,5,5. + Л,5,Л, *45,45..
Исполыуя теоремы сложения для несовместных и умножения
для независимых событий. получим
Р(С) = /’(Л,5, + А. 5,5. + 45,4 + 45.45.) =
= 0.7 0.8 *0.7 0.2 0.8 + 0.3 0.8 0.7 • 0.3 0.2 0.7 0.8 = 0.8736. ►
1> Пример 1.33а. Вероятность гого. что студент сдаст экзамен по
дисциплине А. равна 0.8. Условная вероятность того, что студент
сдаст экзамен по дисциплине 5. равна: 0.5 при условии, что он эк-
замен по дисциплине А сдаст; 0.6 при условии — что нс сдаст.
I) Найти вероятность того, что экзамен хотя бы по одной из
двух дисциплин студент, а) сдаст; б) не сдаст.
2) Являются ли события — сдача экзамена по дисциплинам .4 и
В независимыми?
Р с in с н и с. 1) Пусть события Л и 5 означают, что студент сдаст
экзамены по дисциплинам Л и 5. По условию требуется найти
Pl А + 5) и Р(Л*5). если известно. что /’(Л) = 0.8.
5.(5) = 0.6. 5;(5) = 0.5.
Предварительно найдем*.
Pl AB) = P(A)PtlB) = 0.8 0.6 = 0.48;
Pl АВ) = Р( А) • Pt (В) = 0,2 • 0.5 = 0.10.
где Р( А) = 1 - Р( А) = I - 0.8 = 0,2:
50
p(B)~ Pl АВ + АВ)« 0.48 + 0.10 = О,58.
Теперь по формуле (1.25)
Р( А * В) = /’(.4) + Р{ В} Р(.4В) = 0.8 • 0.58 - 0.48 = 0.9.
Согласно закону дс Моргана А + В = АВ. поэтому
Р( Л+ В)=А>(^В) = 1-Р(ЯВ)= 1-0.48 = 0.52.
2) Так как
РА(В)*Р:,(В). Р,(В)* Р(В). Лг(В)хР(В). Р(АВ)*Р(А)Р(В).
то по любому из этих оснований события Ли В зависимы. ►
1.11- Формула полной вероятности. Формула Байеса
Следствием двух основных теорем теории вероятностей — тео-
ремы сложения и теоремы умножения — яапяются формула полной
вероятности и формула Байеса.
Теорема. Если событие F может произойти только при условии
появления одного из событий (гипотез} /1|. /Ь.Л„. образующих пол-
ную группу, то вероятность события F равна сумме произведений ве-
роятностей каждого из этих событий (гипотез) на соответствующие
условные вероятности события Р
PtF>=^ P(A,)P,(F). (1.31)
fl
□ По условию события (гипотезы) 4(. .4;.../!„ образуют пол-
ную группу, следовательно, они единственно возможные и несовме-
стные (рис. 1.7).
Рис. 1.7
Так как гипотезы А\. А>...А„ — единственно возможные. а со-
бытие F по условию георемы может произойти только вместе с од-
ной из гипотез (см. рис. 1.7), то
F — A\F + AiF + ... + A„F.
В силу того что гипотезы Л|. /Ь..... А„ несовместны, можно
Применить теорему сложения вероятностей:
51
P(F) = A/I|F) + FM3F) + ... + P(A„F) =£P(/f,Fl-
o-i
По теореме умножения P(AIF) = HA,)’ f\(F). откуда и получа-
ется утверждение (1.31).
Формула (1.31) называется формулой полной вероятности. В ча-
стности. для противоположных событий (гипотез) А и А. образую-
щих полную группу, формула (1.31) примет вид:
ЛЛ = F(T)/\(F)+F(.4)P,(F). (1.31’)
Следствием теоремы умножения и формулы полной вероятности
является формула Байеса.
Она применяется, когда событие F. которое может появиться
только с одной из гипотез At, А;.А„, образующих полную группу
событий, произошло и необходимо произвести количествен-
ную переоценку априорных вероятностей этих гипотез
F(/1i). Р(Л2).. Р(/1Я). известных до испытания, те. надо найти
апостериорные (получаемые после проведения испытания) условные
вероятности гипотез Р/ (Л|). Р/(/Ь). F,</1rt).
□ Для получения искомой (|юрмулы запишем теорему умноже-
ния вероятностей событий F \\ А, в двух формах:
PlFAt) = ЛЛ/>(4) = Л/O-F. (Л.
откуда ;(Л . (..л.
или с учетом формулы (1.31) /’(-t)F.(F) = <l33> £/>(л,)г4(г) I-J
Формула (1.33) называется формулой Байеса.
Значение формулы Байеса состоит в том, что при появлении со-
бытия F. т.е. по мере поступления данных, получения новой ин-
формации. мы можем проверять и корректировать выдвинутые до
испытания гипотезы (принятые решения, предполагаемые модели),
основываясь на переходе от их априорных вероятностей к апостери-
орным (рис. 1.8).
Такой подход, называемый байесовским, дает возможность кор-
ректировать управленческие решения в экономике, опенки неиз-
вестных параметров распределения и зучаемых признаков в стати-
стическом анализе и т.п.
52
Исходные
(априорные»
вероятности ninoicj
Поступаю! цис
данные
I Формула
Байеса
Пересмотренные
(апостериорные)
вероятности гапогет
Риг. I.N
Замечание. Если ^ювныс вероятности /’ (F) (/ = 1.2......w)
постоянны, т.е на вероятность события F все гипотезы влияют оди-
наково, то согласно формуле Байеса (1.33) получаем Р, (4) = Р( /1,).
т.е. дополнительная информация о появлении события F нс имеет
никакой ценности, поскольку не меняет наших представлений об
априорных вероятностях гипотез.
[> Пример 1.34. В торговую фирму поступили телевизоры от трех
поставщиков в отношении I : 4 : 5. Практика показала, что телевизо-
ры, поступающие от 1-го. 2-го и 3-го поставщиков, не потребуют ре-
монта в течение гарантийного срока соответственно в 98. 88 и 92%
случаев.
1) Найти вероятность того, что поступивший в торговую фирму
телевизор не потребует ремонта в течение гарантийного срока.
2) Проданный телевизор потребовал ремонта в течение гарантийного
срока. От какого поставщика верояшее всего поступил этот телевизор?
Решение. I) Обозначим события.
Aj — телевизор поступил в торговую фирму от /-го поставщика
(/ = 1,2. 3);
F — телевизор не потребует ремонта в течение гарантийного
срока.
По условию
77777=0Л; '’«(Н=о.9«:
=77777=0-4:
/’<?<’)=7777s=0-S: р‘^=°-п
По формуле полной вероятности (1.31)
Л F) = 0.1 • 0,98 + 0,4 • 0.88 + 0.5 • 0.92 = 0.91.
2) Событие F — телевизор потребует ремонта в течение гаран-
тийного срока; F(f| = I - P(F) = I - 0.91 = 0.09.
53
По условию
/\(Г) = 1-0.98 = 0.02.
(Г) = 1-0.88 = 0.12.
Р, (Г) = 1-0.92 = 0.08.
По формуле Байеса (1.32)
Таким образом, после наступления события F вероятность гипо-
тезы Лу увеличилась с ЖЛу) = 0.4 до максимальной /’ (Л.) = 0.533. а
гипотезы Л3 — уменьшилась от максимальной ЯЛ3) = 0.5 до
Р-(И>) = 0.444; если ранее (до наступления события F) наиболее веро-
ятной была гипотеза Л3. то теперь, в свете новой информации (наступ-
ления события F). наиболее вероятна гипотеза Лу — поступление данно-
го телевизора от 2-го поставщика. ►
[> Пример 1.35. Известно, что в среднем 95% выпускаемой про-
дукции удовлетворяют стандарту. Упрощенная схема контроля призна-
ет пригодной продукцию с вероятностью 0,98, если она стандартна, и
с вероятностью 0.06. сети она нестандартна. Определить вероятность
того, что: I) взятое наудачу изделие пройдет упрошенный контроль;
2) изделие стандартное. если оно: а) прошло упрощенный контроль;
б) дважды прошло упрошенный контроль
Реше н и е. I) Обозначим события:
Л|, Лу — взятое наудачу изделие соответственно стандартное или
нестандартное;
/' — изделие прошло упрощенный контроль.
По условию
ЛЛ|) = 0,95, Л4у) = 0,05. Pjf)=0.98; PJF) = 0,06.
Верояшостъ того, что взятое наудачу изделие пройдет упрошен-
ный контроль, по формуле полной вероятности (1.31):
А О = 0.95 • 0.98 + 0,05 • 0.06 = 0,934.
2, а) Вероятность того, что изделие, прошедшее упрощенный
контроль, стандартное, по формуле Байеса (1.32):
54
2» б) Пусть событие F' — изделие дважды прошло упрошенный
контроль. Тогда по теореме умножения вероятностей
Я (Г) = 0.98-0.98 = 0.9604 и Р, (Г) = 0.06-0,06 = 0.0036.
По формуле Байеса (1.33)
п t 0.95-0.9604
Р. (.4.) =-----------------------= 0.9998.
' ' 17 0.95 0.9604 + 0.05-0.0036
Так как
/>. (Л) = I - (.4,) = 1 - 0.9998 = 0.0002
очень мала, то гипотезу А? о том. что изделие, дважды прошедшее
упрошенный контроль, нестандартное, следует озбросить как прак-
тически невозможное событие. ►
О Пример 1.36. Два стрелка независимо друг от друга стреляют
по мишени, делая каждый по одному выстрелу. Вероятность попа-
дания в мишень для первого стрелка равна 0,8; для второго — 0.4.
После стрельбы в мишени обнаружена одна пробоина. Какова веро-
япюсть того, что она принадлежит: а) 1-му стрелку; б) 2-му стрелку?
Решение. Обозначим события:
At — оба стрелка не попали в мишень;
Аг — оба стрелка попали в мишень;
Ау — 1-й стрелок попал в мишень. 2-й нет;
Л4 — 1-й стрелок нс попал в мишень. 2-й попал;
F — в мишени одна пробоина (одно попадание).
Найдем вероятности гипотез и условные вероятности события F
для этих гипотез:
Р (Л,) = 0.2-0.6 = 0.12. Р$(Р) = 0:
Р ( .4,) = 0.8-0.4 = 0.32. Р(. (F) = 0:
Р(.4, ) = 0.8 0.6 = 0.48. Р4ДР) = 1;
Р(4) = 0.2-0.4 = 0.08, P,JF) = 1.
Теперь по формуле Байеса (1.33)
0.12-0 + 0.32-0 + 0,48-1+ 0.08-1
____________0.08-1____________
0.12 0 + 0.32-0 + 0.48-1 + 0.08-1
= — = 0.857.
7
= 1=0.143,
7
55
т.е. вероятность того, что попал в цель 1-й стрелок при наличии од-
ной пробоины, в 6 раз выше, чем для второго стрелка. ►
> Пример 1.36а. Компания по страхованию автомобилей разде-
ляет водителей на три класса, которые включают 20%, 50% и 30%
водителей соответственно. Вероятности того, что в течение года во-
дитель попадает в аварию, равны 0,01, 0,03 и 0.1 соответственно для
каждого класса. Наугад выбранный водитель два гола подряд из пя-
ти лет срока страховки попадал в аварию. Какова вероятность того,
что он относится: а) к первому классу; б) к третьему классу?
Решение. Обозначим события:
4. Л, А — водитель соответственно первого, второго и
третьего класса;
F — водитель два гола подряд из пяти лет срока страховки по-
падал в аварию.
По условию Р( Л,) = 0.2; Р{ .1,) = 0.5; Д) = 0.3.
Найдем условные вероятности события F (учитываем, что из
пяти лет водитель три года не попадал в аварию, два года — попа-
дал. причем попадал два года подряд, что лает четыре варианта (по
годам I 2. 2—3. 3—4. 4—5)):
(F) = 4 • 0.01’ • 0.99’ = 0.00039;
Р,. (Г) = 4 0.03- -0.97' =0.00329: Р, (F) = 4 0.Г 0.9’ =0.02916.
По формуле Байеса (1.33)
____________У-?0-"0039_____________= 0.007.
0.2 • 0.00039 -*-0.5- 0.00329 + 0.3 • 0.02916
____________0^ 0.02916_____________= 0 835
0.2 0.00039 + 0.5 • 0.00329 + 0.3 • 0.02916
т.е. после наступления события F гипотеза Я, практически невоз-
можна и должна быть отвергнута. ►
1.12. Теоретики-мио/ке^веииая трактовка
основных понятии н аксиоматическое
построение теории вероятностей
Приведем теоретико-множественную трактовку основных поня-
тий теории вероятностей, рассмотренных выше.
Пусть 12 — множество всех возможных исходов некоторого испы-
тания (опыта, эксперимента). Каждый элемент <•> множества 12, т.е
о> е 12, называют элементарным событием, или элементарным исхо-
Л (4)
С (А)
56
а само множество Q — пространством агементарных событий.
Любое событие А рассматривается как некоторое подмножество
(часть) множества П. т.с. A a Q.
Так, в примере 1.1 при бросании игральной кости возможны 6 эле-
ментарных исходов (событий): «| — выпадение I очка. — выпа-
дение 2 очков, .... (Об — выпадение 6 очков, т.е пространство элемен-
тарных событий Q = {«о,, to., a),. G)$, . Событие А. состояшее в
вуттяпении четного числа очков, есть А = {со.. ю4. <о6}.
В задаче о встрече, приведенной в примере 1.2, возможно бес-
конечное несчетное множество элементарных исходов (событий) —
точек (х. у) квадрата OKLM. координаты х и у которых равны мо-
ментам прихода к месту встречи двух лип (см. рис. 1.2), т.е. про-
странство элементарных событий Q — квадрат OKLM. Событие А.
состояшее в том. что встреча двух лиц произойдет, есть заштрихо-
ванная область g на рисунке — часть квадрата, т.е. подмножество
пространства Q: Л с Q.
Само пространство элементарных событий Q представляет собой со-
бытие. происходящее всегда (при любом элементарном исходе со). и назы-
вается достоверным событием. Таким образом. Q выступает в двух качест-
вах: множества всех элементарных исходов и достоверного события.
Ко всему пространству Q элементарных событий добавляется
еще пустое множество 0, рассматриваемое как событие и называе-
мое невозможным событием.
Суммой нескольких событий At. А,, .... Ап называется объедине-
ние множеств Л, U Л. U...U Л„.
Произведением нескольких событий Ль Л?....Л„ называется пе-
ресечение множеств Л| П Л, П...П Л„.
Событием А . противоположным событию Л. называется допол-
нение множества А до О, т.е. П\Л.
На диаграммах Венна (см. § 1.7. рис. 1.3. в. г, д. е) представлены
сумма Л + В. произведение АВ двух событий и события Л . В. про-
тивоположные событиям Л. В.
Несколько событий Л(. Л;...Ап образуют патую группу (патую
систему), если их сумма представляет все пространство элементар-
ных событий, а сами события несовместные, т.е.
£л, = Q и Л(Л =0 (/*>').
Таким образом, под операциями над событиями понимаются опера-
ции над соответствующими множествами. В табл. 1.1 показано соот-
ветствие терминов теории множеств и теории вероятностей.
57
Тиб.пщп I. I
Обозначении Термины
Теории множеств Теории вероятностей
О Множество, пространство Пространство элементарных событий, достоверное событие
о Элемент, точка множест- ва Элементарное событие (эле- ментарный исход)
А, В Подмножество А. В Событие Л. В
А+В =A\JB Объединение (сумма) множеств А и В Сумма событий А и В
ав=аГ\в Пересечение множеств А и В Произведение событий А и В
0 Пустое множество Невозможное событие
А Дополнение множества 1 Противоположное для А со- бытие
АВ~АПВ°£ Множества А и В нс пе- ресекаются События А и В несовместны
А~ В Множества А и В равны События /1 и В равносильны
А с В /1 есть подмножество В Событие /1 влечет за собой событие В
На основе изложенной трактовки событий как множеств перей-
дем к аксиоматическому построению теории вероятностей.
Необходимость формально логического обоснования теории ве-
роятностей, ее аксиоматического построения возникла в связи с
развитием самой теории вероятностей как математической науки и
ее приложений в различных областях.
Такие сформировавшиеся науки, как геометрия, теоретическая
механика, теория множеств, строятся аксиоматически. Фундамен-
том каждой служит ряд аксиом, являющихся обобщением многове-
кового человеческого опыта, а само здание науки строится на осно-
ве строгих логических рассуждений без обращения к наглядным
представлениям.
Аксиоматика теории вероятностей исходит от основных свойств
вероятности событий, к которым применимо классическое или ста-
тистическое определение вероятности. Аксиоматическое определе-
ние вероятности как частные случаи включает в себя и классиче-
ское. и статистическое определения и преодолевает недостатки каж-
дого из них.
.58
Впервые идея аксиоматического построения вероятностей была
высказана российским академиком С.Н. Бернштейном, исходившим
Из качественного сравнения событий по их большей или меньшей ве-
роятности. В начале 1930-х гг. академик А.Н. Колмогоров разработал
иной подход, связывающий теорию вероятностей с современной мет-
рической теорией функций и теорией множеств, который в настоящее
время является общепринятым.
Сформулируем а к с и о м ы теории вероятностей. Каждому со-
бытию А поставим в соответствие некоторое число, называемое веро-
ятностью события А, т е. R.A). Так как любое событие есть множест-
во, то вероятность события есть функция множества.
Вероятность события должна удовлетворять следующим а к -
с и о м а м.
Р.1. Вероятность любого события неотрицательна:
Р(А) > 0.
Р.2. Вероятность достоверного события равна I
ЛЯ) = 1.
Р.З. Вероятность суммы несовместных событий равна сумме веро-
ятностей этих событий, т.е. если А,4} = 0 (/ * j). то
PtAi + А2 + ... + А„) = ЛЛ|) + + ... f ЛЛ).
Для классического определения вероятности свойства, выра-
женные аксиомами Р.2. Р.З. не нужно постулировать, так как эти
свойства были нами доказаны выше.
Из аксиом P.I, Р.2, Р.З можно вывести основные свойства
вероятностей, известные нам из предыдущего изложения:
1. Р(Л) = 1 -РМ).
2. Р(0) = 0.
3. 0 £ PlA) < I.
4. Pt А) < Р( В), если А с. В.
5. Р(А + В) = Р[А) + Р( В) - Pt АВ).
6. Р(А + В) <. Р[А) + Р{В).
В случае произвольного (не обязательно конечного) пространст-
ва элементарных событий Q аксиому Р.З необходимо заменить бо-
лее сильной, расширенной аксиомой сложения Р.З (которую нельзя
вывести из аксиомы Р.З).
Если имеется счетное* множество несовместных событий
А» А]....Ап....(AfAj = 0 при / * Д то
1 Напомним, что множество натыкается счетным. если его элементы можно пе-
ренумеровать натуральными числами
59
Аксиомы теории вероятностей позволяют вычислить вероятно-
сти любых событии (подмножеств пространства Q) через вероятно-
сти элементарных событий (если их конечное или счетное число)
Вопрос о том, откуда берутся вероятности элемоггарных событий,
при аксиоматическом построении теории вероятностей не рассмат-
ривается. На практике они определяются с помощью классического
определения (если испытание сводится к схеме случаев) или статис-
тического определения.
Сформулированные аксиомы не определяют условной вероятно-
сти одного события относительно другого, которая вводится по оп-
ределению.
Определение. Условная вероятность события В относи-
тельно события А есть отношение вероятности произведения этих
событий к вероятности события А, т.е.
(1.34)
ZM)
если Р(А) - 0.
Из этого определения автоматически следует теорема (правило!
умножения вероятностей для любых событий
В последующих главах мы по-прежнему будем ссылаться на тео-
ремы (правила) сложения и умножения вероятаостсй, хотя пра-
вильнее было бы говорить об аксиоме сложения, определении ус-
ловной вероятности.
В более полных курсах теории вероятностей рассматривается
понятие вероятностного пространства, определяемого тройкой ком-
понент (символов} (Q. 5. Р). где (2 — пространство элементарных
событий. S — (т(сигма)-алгебра событий. Р — вероятность. Первую
(Q) и третью (Р} компоненты вероятностного пространства мы уже
рассмотрели в данном параграфе.
Вторая компонента (5) вероятностного пространства — п-алгебра
событий — представляет собой некоторую систему подмножеств
пространства элементарных исходов (событий) Q. Если П конечно
или счетно, то любое подмножество элементарных исходов является
событием, а п-алгебра есть система всех этих подмножеств. Если же
(1 более чем счетно, то оказывается, что не каждое произвольное
подмножество (2 может быть названо событием. Причина этого за-
ключается в существовании так называемых неизмеримых подмно-
жеств. Поэтому в этом случае под событием понимается уже не лю-
бое подмножество пространства £2, а только подмножество из выде-
ленного класса 5, а п-алгебра есть система таких подмножеств. Рас-
смотрение указанных вопросов выходит за рамки данной книги
60
Упражнения
1.37. Слово составлено из карточек, на каждой из которых на-
писана одна буква. Карточки смешивают и вынимают без возврата
по одной. Найти вероятность того. »гго карточки с буквами выни-
маются в порядке следования букв заданного слова: а) «событие»;
б) «статистика».
1.38. Пятитомное собрание сочинений расположено на полке в
случайном порядке. Какова вероятность того, что книги стоят слева
направо в порядке нумерации томов (от 1 до 5)?
1.39. Среди 25 студентов, из которых 15 девушек, разыгрывают-
ся четыре билета, причем каждый может выиграть только один би-
лет. Какова вероятность того, что среди обладателей билета окажут-
ся: а) четыре девушки: б) четыре юноши: в) три юноши и одна де-
вушка?
1.40. Из 20 филиалов Сбербанка 10 расположены за чертой горо-
да. Для обследования случайным образом отобрано 5 филиалов. Ка-
кова вероятность гою. ’гто среди отобранных окажется в черте города:
а) 3 филиала; б) хотя бы один?
1.41. Из яшика, содержащего 5 пар обуви, из которых три пары
мужской, а две нары женской, перекладывают наудачу 2 пары обуви
в другой ящик, содержащий одинаковое количество пар женской и
мужской обуви. Какова вероялюсть того, что во втором ящике по-
сле этого окажется одинаковое количество пар мужской и женской
обуви?
1.42. В магазине имеются 30 телевизоров, причем 20 из них
импорлзых. Найти вероятность того, что среди 5 проданных в тече-
ние дня телевизоров окажется нс менее 3 импортных телевизоров,
предполагая, что вероятности покупки телевизоров разных марок
одинаковы.
1.43. Наудачу взятый телефонный номер состоит из 5 цифр.
Какова вероятность того, что в нем все цифры: а) различные;
б) одинаковые; в) нечетные? Известно, что номер телефона не на-
чинается с цифры ноль.
1.44. Для проведения соревнования 16 волейбольных команд
разбиты по жребию на две подгруппы (по восемь команд в каждой).
Найти вероятность того, что две наиболее сильные команды ока-
жутся: а) в разных подгруппах; б) в одной подгруппе.
1.45. Студент знает 20 из 25 вопросов программы. Зачет счита-
ется сданным, если студент ответит не менее чем на 3 из 4 постав-
ленных в билете вопросов. Взглянув на первый вопрос билета, сту-
дент обнаружил, что он его знает. Какова вероятность того, что сту-
дент: а) сдаст зачет; б) не сдаст зачет?
61
1.46. У сборщика имеются 10 деталей, мало отличающихся лр\|
от друга, из них четыре — первого, по две — второго, третьего и
четвертого видов. Какова вероятность того, что средн шести взятых
одновременно деталей три окажутся первого вила, два — второго и
одна — третьего?
1.47. Найти вероятность того, что из 10 книг, расположенных в
случайном порядке, 3 определенные книги окажутся рядом.
1.48. В старинной игре в кости необходимо было для выигрыша
получитт» при бросании трех игральных костей сумму очков, превос-
ходящую 10. Найти вероятности: а) выпадения II очков; б) выиг-
рыша.
1.49. На фирме работают 8 аудиторов, из которых 3 — высокой
квалификации, и 5 программистов, из которых 2 — высокой квали-
фикации. В командировку надо отправить группу из 3 аудиторов и
2 программистов. Какова вероятность того, что в этой группе ока-
жется по крайней мере I аудитор высокой квалификации и хотя бы
I программист высокой квалификации, если каждый специалист
имеет равные возможности поехать в командировку?
1.50. Два лица условились встретиться в определенном месте
между 18 и 19 ч и договорились, что пришедший первым ждет дру
того в течение 15 мни., после чего уходит. Найти вероятность их
встречи, если приход каждого в течение указанного часа может
произойти в любое время и моменты прихода независимы.
1.51. Какова вероятность того, что наудачу брошенная в круг
точка окажется внутри вписанного в него квадрата?
1.52. При приеме партии изделий подвергается проверке поло-
вина изделий. Условие приемки — наличие брака в выборке менее
2%. Вычислить вероятность того, что партия из 100 изделий, содер-
жащая 5% брака, будет принята.
1.53. По результатам проверки контрольных работ оказалось,
что в первой группе получили положительную опенку 20 студентов
из 30, а во второй — 15 из 25. Найти вероятность того, что наудачу
выбранная работа, имеющая положительную оценку, написана сту-
дентом первой группы.
1.54. Экспедиция издательства отправила газеты в три почтовых
отделения. Вероятность своевременной доставки газет в первое от-
деление равна 0,95, во второе отделение — 0,9 и в третье — 0,8
Найти вероятность следующих событий: а) только одно отделение
получит газеты вовремя; б) хотя бы одно отделение получит газеты
с опозданием.
1.55. Прибор, работающий в течение времени /. состоит из трех
узлов, каждый из которых независимо от других может за это время
выйти из строя. Неисправность хотя бы одного узла выводит при-
бор из строя целиком. Вероятность безотказной работы в течение
«2
времени / первого узла равна 0,9. второго — 0.95. третьего — 0,8.
Найти вероятность того, что в течение времени f прибор выйдет из
строя.
1.56. Студент разыскивает нужную ему формулу в трех справоч-
никах. Вероятность того, что формула содержится в первом, втором и
третьем справочниках, равна соответственно 0.6. 0.7 и 0,8. Найти ве-
роятность того, что эта формула содержится не менее чем в двух
справочниках.
1.57. Произведено три выстрела по пели из орудия. Вероят-
ность попадания при первом выстреле равна 0.75: при втором —
0,8: при третьем — 0.9. Определить вероятность того, что будет:
а) три попадания: б) хотя бы одно попадание.
1.58. Вероятность своевременного выполнения студентом кон-
трольной работы по каждой из трех дисциплин равна соответствен-
но 0.6, 0.5 и 0,8. Найти вероятность своевременного выполнения
контрольной работы студентом: а) по двум дисциплинам: б) хотя бы
по двум дисциплинам.
1.59. Мастер обслуживает 4 станка, работающих независимо
друг от друга. Вероятность того, что первый станок в течение смены
потребует внимания рабочего, равна 0.3, второй — 0,6. третий —
0,4 и четвертый — 0.25. Найти вероятность того, что в течение сме-
ны хотя бы один станок не потребует внимания мастера.
1.60. Контролер ОТК. проверив качество сшитых 20 пальто. ус-
тановил. что 16 из них первого сорта, а остальные — второго. Найти
вероятность того, что среди взятых наудачу из этой партии трех
пальто одно будет второго сорта.
1.61. Среди 20 поступающих в ремонт часов 8 нуждаются в об-
щей чистке механизма. Какова вероятность того, что среди взятых
одновременно наудачу 3 часов по крайней мере двое нуждаются в
общей чистке механизма?
1.62. Среди 15 лампочек 4 стандартные. Одновременно берут
наудачу 2 лампочки. Найти вероятность того, что хотя бы одна из
них нестандартная.
1.63. В коробке смешаны электролампы одинакового размера и
формы: по 100 Вт — 7 штук, по 75 Вт — 13 штук. Вынуты наудачу
3 лампы. Какова вероятность того, что: а) они одинаковой мощно-
сти; б) хотя бы две из них по 100 Вт?
1.64. В коробке 10 красных. 3 синих и 7 желтых карандашей.
Наудачу вынимают 3 карандаша. Какова вероятность того, что они
все: а) разных цветов; б) одного цвета?
1.65. Брак в продукции завода вследствие дефекта А составляет
4%. а вследствие дефекта В — 3.5%. Годная продукция завода со-
ставляет 95%. Найти вероятность того, что: а) среди продукции.
63
нс обладающей дефектом А. встретится дефект В. б) средн забрако.
ванной по признаку Л продукции встретится дефект В.
1.66. Пакеты акций, имеющихся на рынке ценных бумаг, могут
дать доход владельцу с вероятностью 0.5 (для каждого пакета),
Сколько пакетов акций различных фирм нужно приобрести, чтобы
с вероятностью, нс меньшей 0.96875. можно было ожидать доход
хотя бы по одному пакету акций?
1.67. Сколько раз нужно провести испытание, чтобы с вероят-
ностью, не меньшей Р, можно было утверждать, что по крайней
мерс один раз произойдет событие, вероятность которого в каждом
испытании равна р? Дать ответ при р — 0.4 и Р = 0,8704.
1.68. На полке стоят 10 книг, среди которых 3 книги по теории
вероятностей. Наудачу берутся три книги. Какова вероятность, чк»
среди отобранных хотя бы одна книга по теории вероятностей?
1.69. На связке 5 ключей. К замку подходит только один ключ.
Найти вероятность того, что потребуется нс более двух попыток от-
крыть замок, если опробованный ключ в дальнейших испытаниях
нс участвует.
1.70. В магазине продаются 10 телевизоров. 3 из них имеют де-
фекты. Какова вероятность того, что посетитель купит телевизор,
если для выбора телевизора без дефектов понадобится не более трех
попыток?
1.71. Радист трижды вызывает корреспондента. Вероятность то-
го, что будет принят первый вызов, равна 0.2, шорой — 0.3. третий -
0.4. События, состоящие в том. что данный вызов будет услышан, не-
зависимы. Найти вероятность того. *гго корреспондент услышит вызов
радиста.
1.72. Страховая компания разделяет застрахованных по классам
риска: I класс — малый риск, II класс — средний. III класс — боль-
шой риск. Среди этих клиентов 50% — первою класса риска. 30%
второго и 20% — третьего. Вероятность необходимости выплачивать
страховое вознаграждение для первого класса риска равна 0,01. второ-
го — 0.03. третьего — 0,08. Какова вероятность того, что: а) застра-
хованный получит денежное возит рождение за период страхования;
б) получивший денежное возна!ражление застрахованный относится
к группе малого риска?
1.73. В данный район изделия поставляются гремя фирмами в
соотношении 5:8:7. Среди продукции первой фирмы стандартные
изделия составляют 90%. второй — 85%. третьей — 75%. Найти ве-
роятность того, что: а) приобретенное изделие окажется нестан-
дартным; 6) приобретенное изделие оказалось стандартным. Какова
вероятность гою. что оно изготовлено третьей фирмой?
1.74. Два стрелка сделали по одному выстрелу в мишень. Веро-
ятность попадания в мишень для первого стрелка равна 0.6, а для
64
дорого — 0.3- В мишени оказалась одна пробоина. Найти вероят-
ность того, что она принадлежит первому стрелку.
1.75. Вся продукция цеха проверяется двумя контролерами, при-
чем первый контролер проверяет 55% изделий. а второй — остальные.
Вероятность того, что первый контролер пропустит нестандартное
изделие, равна 0.01. второй — 0.02. Взятое наудачу изделие, маркиро-
ванное как стандартное, оказалось нестандартным. Найти вероят-
ность того, что это изделие проверялось вторым контролером.
1.76. Вероятность изготовления изделия с браком на данном
предприятии равна 0.04. Перед выпуском изделие подвергается уп-
рошенной проверке, которая в случае безле<|)сктного изделия про-
пускает его с вероятностью 0.96. а в случае изделия с дефектом — с
вероятностью 0,05. Определить: а) какая часть изготовленных изде-
лий выходит с предприятия; б) какова вероятность того, что изде-
лие, выдержавшее упрошенную проверку, бракованное?
1.77. В одной урне 5 белых и 6 черных шаров, а в другой —
4 белых и 8 черных шаров. Из первой урны случайным образом вы-
нимают 3 шара и опускают во вторую урну. После этого из второй
урны также случайно вынимают 4 шара. Найти вероятность того,
что все шары, вынутые из второй урны, белые.
1.78. Из л экзаменационных билетов студент А подготовил толь-
ко т (т < л). В каком случае вероятность выгатить на экзамене «хо-
роший» для него билет выше: когда он берет наудачу билет первым,
или вторым...или А-м (к < л) по счету среди сдающих экзамен9
1.79. В лифт семиэтажного дома на первом этаже вошли три
человека. Каждый из них с одинаковой вероятностью выхолит на
любом из этажей, начиная со второго. Найти вероятность того, что
все пассажиры выйдут: а) на четвертом этаже; б) на одном и том же
этаже; в) на разных этажах.
1.80. Батарея, состоящая из 3 орудий, ведет огонь по группе,
состоящей из 5 самолетов. Каждое орудие выбирает себе цель слу-
чайно и независимо от других. Найти вероятность того. »гго все ору-
дия будут стрелять: а) по одной и той же цели; б) по разным целям.
1.81. 20 человек случайным порядком рассаживаются за сто-
лом. Найти вероятность того, что два фиксированных лица А и В
окажутся рядом, если: а) стол круглый; 6) стол прямоугольный, а
20 человек рассаживаются случайно вдоль одной из его сторон.
1.82. Имеется коробка с девятью новыми теннисными мячами.
Для игры берут три мяча; после игры их кладут образно. При выборе
мячей игранные от неигранных нс отличаю гея. Какова вероятность
того, что после трех игр в коробке не останется неигранных мячей?
1.83. Завод выпускает определенного типа изделия; каждое из-
делие имеет дефект с верояп гостью 0.7 После изготовления изделие
осматривается последовательно тремя контролерами, каждый из
3 •сроегшчтгП и ияггмап
ш i t Xi in так»
6.5
которых обнаруживает дефект с вероятностями 0.8: 0,85; 0.9 соот-
ветственно. В случае обнаружения дефекта изделие бракуется. Оп-
ределить вероятность того, что изделие: I) будет забраковано;
2) будет забраковано: а) вторым контролером, б) всеми контролерами.
1.84. Из полной кололи карт (52 карты) выбирают шесть карг,
одну из них смотрят; она оказывается тузом, после чего ее смешива-
ют с остальными выбранными каргами. Найти вероятность того, что
при втором извлечении карты из этих шести мы снова получим туз
1.85. В урне два белых и три черных шара. Два игрока поочеред-
но вынимают из урны по шару, нс вкладывая их обратно. Выигрывает
тот. кто раньше получит белый шар. Найти вероятность того, что вы-
играет первый игрок.
1.86. Производятся испытания прибора. При каждом испытании
прибор выходит из строя с вероятностью 0.8. Посте первого выхода
из строя прибор ремонтируется; посте второго признается негодным.
Найти вероятность того, 'по прибор окончательно выйдет из строя к
точности при четвертом испытании.
1.87. Имеется 50 экзаменационных билетов, каждый из которых
содержит два вопроса. Экзаменующийся знает ответ не на все 100 во-
просов. а только на 60. Определить вероятность того, что экзамен бу-
дет сдан, если для этого достаточно ответить на оба вопроса из своей»
билета, или на один вопрос из своего билета и на один (по выбору
преподавателя) вопрос из дополнительного билета.
1.88. Прибор состоит из двух узлов: работа каждого узла безус-
ловно необходима для работы прибора в целом. Надежность (вероят-
ность безотказной работы в течение времени /) первого узла равна O.S.
второго — 0,9. Прибор испытывался в течение времени t. в результат
чего обнаружено, что он вышел из строя (отказал). Найти вероятность
того, что отказал только первый узел, а шорой исправен.
1.89. В группе из 10 студентов, пришедших на экзамен. 3 — подго-
товлены отлично. 4 — хорошо. 2 — посредственно и 1 — плохо. В экза-
менационных билетах имеется 20 вопросов. Отлично подготовленный
студент может ответить на все 20 вопросов, хорошо подготовленный -
на 16, посредственно — на 10. плохо — на 5. Вызванный наугад студент
ответил на три произвольно заданных вопроса. Найти вероятность того,
что студент подготовлен: а) отлично: б) плохо.
1.90. Л. В, С, О — некоторые события. Упростить выражение
Е = (Я*ЯХ.4Ё*С) + С-*-(.4 +ДхО-ьЕ).
1.91. 12 студентов, среди которых Иванов и Петров, занимают оче-
редь в библиотеку Какова вероятность того, что между ними в образо-
вавшейся очереди окажутся ровно 5 человек?
1.92. При игре в бридж между четырьмя игроками раздают 52 кар-
ты по 13 карт каждому. Найти вероятность того. »гто каждый игрок по-
лучит: а) по одному тузу; б) по одной карте каждого достоинства.
66
1.93. Из букв слова -СТАТИСТИКА» путем их случайной переста-
новки формируется новое слово. Найти вероятность того, что: а) вновь
получится слово «СТАТИСТИКА»; б) получится слово, в котором со-
рласные идут подряд
1.94. Чему равна вероятность того, что дни рождения шести наупш
выбранных человек придутся н точности на два месяца?
1.95. Из урны, содержащей три белых и пять черных шаров два че-
ловека вынули поочередно по шару (без возвращения). Какова вероят-
ность того, что первый вынул белый шар. если второй вынул черный шар?
1.96. На сборочной линии завода проводится сборка четырех изде-
лий. Вероятность бездефектной сборки изделия равна 0,8. После выпус-
ка двух изделий линию перенастроили, что повысило вероятность без-
дефектной сборки изделия на 0,05. Найти вероятность того, что ровно
три изделия собраны без дефектов.
1.97. Два стрелка поочередно стреляют по мишени до первого по-
падания. Вероятность попадания для первою стрелка равна 0,2. для вто-
рого — 0,3. Какова вероятность того, что первый сделает больше вы-
стрелов?
1.98. Два руководителя планируют создал» совместное предпри-
ятие, если в течение года каждому из них удается сформировал» свою
долю начального капитала. Вероятности этого равны соответственно 0.4
и 0,7. По истечении года выяснилось, что совместное предприятие не
может быть создано. Какова вероятность того, что каждый участник су-
мел накопить свою долю начального капитала?
1.99. Есть два золотоносных района, поделенных на четыре участка
каждый, причем по прогнозам известно, что вероятность выбрать золо-
тоносный участок равна 3/4 н 1/2 соответственно для первого и второго
районов. Наупш выбран район и куплен один участок, который оказался
золотоносным. Какова вероятность вторичной удачной покупки?
Главн
Повторные независимые
испытания
На практике часто приходится сталкиваться с задачами, кою-
рыс можно представить в виде многократно повторяющихся иены-
таний при данном комплексе условий, в которых представляет
интерес вероятность числа т наступлений некоторого события А в
п испытаниях. Например, необходимо определить вероятность оп-
ределенного числа попаданий в мишень при нескольких выстре-
лах, вероятность некоторого числа бракованных изделий в данной
партии и т.д.
Если вероятность наступления события А в каждом испытании нс
меняется в зависимости от исходов других, то такие испытания назы-
ваются независимыми относительно событии А. Если независимые по-
вторные испытания проводятся при одном и том же комплексе усло-
вий. то вероятность наступления события А в каждом испытании одна
и та же. Описанная последовательность независимых испытаний по-
лучила название схемы Берну.ыи.
2.1. Формула Бернулли
Теорема. Если вероятность р наступления события А в каждом
испытании постоянна, то вероятность Р,„.„ того, что событие А на-
ступит т раз в п независимых испытаниях, равна
(2.1)
где q = I - р.
□ Пусть А{ и Л — соответственно появление и непоявление со-
бытия А в l-м испытании (i - I. 2..л), а В,п - событие, состоя-
щее в том. что в п независимых испытаниях событие А появилось
т раз.
Представим событие Вт через элементарные события А,.
Например, при п = 3. т = 2 событие
Z?. = Я, .4. + /11А,А1 + AfA>At,
т.е. событие А произойдет два раза в трех испытаниях, если оно
произойдет в 1-м и 2-м испытаниях (и не произойдет в 3-м). или в
1-м и 3-м (и не произойдет во 2-м). или произойдет но 2-м и 3-м (и
не произойдет в 1-м).
6R
в обшем виде
В„ - Лл |Л + - +
* .4, А2...А„ „Л.,,.!.../!,,.
(2.2)
те. каждый вариант появления события В„, (каждый член суммы
(2.2)) состоит из т появлений события J и л - т непоявлений. т.е.
из т событий А и из п - т событий А с различными индексами.
Число всех комбинаций (слагаемых суммы (2.2)) равно числу
способов выбора из л испытаний л/, в которых событие А произош-
ло, т.е. числу сочетаний Cf. Вероятность каждой такой комбина-
ции (каждого варианта появления события Я„,) по теореме умноже-
ния для независимых событий равна р"'^'гак как />( А1) = р,
p(,Ai) = q. i = 1.2.л. В связи с тем. что комбинации между со-
бой несовместны, по теореме сложения вероятностей получим
Р.л W-.+ pV = <;’//</
[> Пример 2.1. Вероятность изготовления на автоматическом
станке стандартной детали равна 0.8. Найти вероятности возможно-
го числа появления бракованных деталей среди 5 отобранных.
Решение. Вероятность изготовления бракованной детали
р = 1 - 0,8 = 0.2. Искомые вероятности находим по формуле Бер-
нулли (2.1):
P0J =С? 0.2° -0.84 = 0.32768; />. = CJ • 0.2' • 0.84 = 0.4096;
= С$ • 0.2' • 0.8х = 0.2048; , = С, 0.21 • 0.8* = 0.0512;
Ъ = 0.24-0.8* =0.0064; = С* 0.25 • 0.8° = 0.00032.
Полученные вероятности изобразим графически точками с ко-
ординатами (т. Ртп). Соединяя эти точки, получим многоугольник,
или полигон, распределения вероятностей (рис. 2.1). ►
Рассматривая многоугольник распределения вероятностей (рис. 2.1),
мы видим, что есть такие значения т (в данном случае, одно —
^0= I). обладающие наибольшей вероятностью Ртм.
Число л!ц наступления события А в п независимых испытаниях
называется иаивсроятнейшим, если вероятность осуществления этого
события Р^ п по крайней мере не меньше вероятностей других со-
бытий Ртп при любом т.
69
-ганий, запишем:
Для нахождения
запишем систему нера-
венств:
г,-
(2.3)
Решим первое нера-
венство системы (2.3)
Используя формулы
Бернулли и числа соче-
----1*----------------------------р^'ч'
m„!(п - т0)! (тп + I)!(п - т„ -1)!
Так как (/ц, +1 )’ = /«„!(/>»„ + I), (п - т<,У. = (п - тп — I)!(/» —zw0). то
получим после упрощений неравенство —-—</>—-—р, откуда
п - т„ т„ +1
(mo + I) q > (п - т0) р.
Теперь /л0 (р + q) а пр — q или тп ? пр - q (ибо р + q = I).
Решая второе неравенство системы (2.3), получим аналогично:
т0 i пр + р. Объединяя полученные решения двух неравенств, при-
дем к двойному неравенству:
пр ~ q s /м0 < пр 4 р.
(2.4)
Отметим, что так как разность пр ip - {пр - q) = р + q = 1. ю
всегда существует целое число /и0, удовлетворяющее неравенству
(2.4). При этом если пр + р — целое число, то нам вероятнейших
чисел два: от0 = пр + р и /»' = пр - q.
1> Пример 2.2. По данным примера 2.1 найти наивероятнейшее
число появления бракованных деталей из 5 отобранных и вероят-
ность этого числа.
Реше н и с. По (формуле (2.4) 5 • 0.2 - 0,8 < /Иц < 5 • 0.2 + 0.2
или 0,2 < «о s 1.2. Единственное целое число, удовлетворяющее по-
лученному неравенству, л/о = I, а его вероятность Р| 5= 0.4096 была
получена в примере 2.1. ►
О Пример 2.3. Сколько раз необходимо подбросить игральную
кость, чтобы наивероятнейшее выпадение тройки было равно 10?
70
решение. В данном случае р = -. Согласно неравенству
6
(2.4) »•- - - ^ Ю w • - + - или л-5<60^л + I, откуда 59 < п < 65.
" 6 6 6 6
т.е. необходимо подбросить кость от 59 до 65 раз (включительно). ►
2.2. Формула Пуассона
Предположим, что мы хотим вычислить вероятность Ртп появ-
ления события А при большом числе испытаний п, например,
Рзоо,5оо- По формуле Бернулли (2.1)
D ,.10G КЮ 200 500! гоо 200
= ч - 300,200!' 4
Ясно, что в этом случае непосредственное вычисление по фор-
муле Бернулли технически сложно, тем более если учесть, что сами
р и q — числа дробные. Поэтому возникает естественное желание
иметь более простые приближенные формулы для вычисления Р„ „
при больших п. Такие формулы, называемые асимптотическими,
существуют и определяются теоремой Пуассона, локальной и инте-
гральной теоремами Муавра—Лапласа. Наиболее простой из них
является теорема Пуассона.
Теорема. Если вероятность р наступления события А в каждом
испытании стремится к нулю (р -> 0) при неограниченном увеличении
числа п испытаний (н -> »). причем произведение пр стремится к по-
стоянному числу Х(л/> ->Х). то вероятность Рт_п того, что событие
А появится т раз в п независимых испытаниях, удовлетсоьяет пре-
дельному равенству
Кт/’.,.=/’.(л) = Ц^. (2.5)
•-»* гл!
□ По формуле Бернулли (2.1)
=с: Р-ч"-=-—ц—т-i---------------1>- < । - р) < । - р)
т\
Или, учитывая, что limnp = >.. т.е. при достаточно больших п.
71
Так как lim | I — j = lim | 1 - - j = ...= lim| I-----------------j= I.
lim P - — e ’.
-- "" m!
Строго говоря, условие теоремы Пуассона р > О при л -> х. так
что пр -► а. противоречит исходной предпосылке схемы испытаний
Бернулли, согласно которой вероятность наступления события в
каждом испытании р = const. Однако если вероятность р — посто-
янна и мала, число испытаний п — велико и число а = пр — незна-
чительно (будем полагать, что а = пр < 10). то из предельного равен-
ства (2.5) вытекает приближенная формула Пуассона1.
= (2«)
т\
В табл. III приложений приведены значения функции Пуассона
D> Пример 2.4. На факультете насчитывается 1825 студентов. Ка-
кова вероятность того, что I сентября является днем рождения од-
новременно четырех студентов факультета?
Реше н и с. Вероятность того, что день рождения студента
I сентября, равна р = 1/565. Так как р= 1/365 — мала. п = 1825
велико и А = пр = 1825 (1/365 ) = 5<10. то применяем формулу Пу-
ассона (2.6):
=/’(5)-0.1755(по табл. Ill приложений). ►
2.3. Локальная и интегральная формулы
М у ан ра —Л апласа
Локальная теорема Муавра—Лапласа. Если вероятность р наступ-
ления события А в каждом испытании постоянна и отлична от 0 и I.
то вероятность Р,,,,, того. что событие А произойдет т раз в п неза-
висимых испытаниях при достаточно большом числе п. приближенно
равна*
1 Локалагельспю теоремы приведено и § 6 5. Верой i костный смысл величин пр.
itpq ycKiHuiLiHiuicicH fi § 4 1 (см замечание на с 142-143»
72
где
_ функция Гаусса
к
т - tip
(2.7)
(2.8)
(2.9)
Чем больше л, тем точнее приближенная формула (2.7), назы-
ваемая локальной формулой Муаври—Лапласа. Приближенные значе-
ния вероятности Рт п, даваемые локальной формулой (2.7), на прак-
тике используются как точные при npq порядка двух и более десят-
ков, т.е. при условии npq > 20.
Для упрощения расчетов, связанных с применением формулы
(2.7). составлена таблица значений функции fix) (табл. I. приведен-
ная в приложениях). Пользуясь этой таблицей, необходимо иметь в
виду очевидные свойства функции J{x) (2.8).
I. Функция Дх) является четной, т.е. fl~x) -fix)
2. Функция Дх) — монотонно убывающая при положительных зна-
чениях х. причем при х — х Дх) — 0.
(Практически можно считать, что уже при х > 4 Дх) ® 0.)
О Пример 2.5. В некоторой местности из каждых 100 семей 80
имеют холодильники. Найти вероятность того, что из 400 семей
300 имеют холодильники.
Решение. Вероятность того, что семья имеет холодильник,
равна р = 80/100 = 0.8. Так как п — 100 достаточно велико (условие
npq = 100’0,8(1-0.8) = 64 > 20 выполнено), то применяем локаль-
ную формулу Муавра—Лапласа.
» . 300-400 0.8
Вначале определим по аюрмулс (2.9) г = , = = -2.50.
V400 0.8 0.2
Тогда по формуле (2.7)
Д-2.50) /(2.50) _
НКМ,",г7кЮ-О?8"б:2 = 7М
0.0175
8
*0,0022
(значение /2,50) найдено по табл. I приложений). Весьма малое зна-
чение вероятности Р300.400 не должно вызывать сомнения, так как
•Фоме события «ровно 300 семей из 400 имеют холодильники» воз-
можно еще 400 событий: «0 из 400», «I из 400».. «400 из 400» со
73
своими вероятностями. Все вместе эти события образуют полную
группу, а значит, сумма их вероятностен равна единице. ►
Пусть в условиях примера 2.5 необходимо найти вероятность того,
что от 300 до 360 семей (включительно) имеют холодильники. В этом
случае по теореме сложения вероятность искомого события
/*4оо(ЗОО < т < 360) =Рзоо.4(Ю + ftoi.joo + — + Лчляоо-
В принципе вычислить каждое слагаемое можно по локальной
формуле Муавра—Лапласа, но большое количество слагаемых дела-
ет расчет весьма громоздким. В таких случаях используется сле-
дующая теорема.
Интегральная теорема Муавра—Лапласа. Если вероятность р наступ-
ления события А в каждом испытании постоянна и отлична от 0 и 1. то
вероятность того, что число т наступления события А в п независимых
испытаниях заключено в пределах от а до b {включительно), при доста-
точно большом числе п приближенно равна
Р„(и < т < b) « -!-[Ф( х«) -Ф(х,)]. (2.10)
где Ф(х) = -^= j е' 'dt (2.11)
— функция (или интеграл вероятностей) Лапласа'.
а.п)
\)прч yjnpq
(Доказательство теоремы приведено в § 6.5.)
Формула (2.10) называется интегральной формулой Муавра—
Лапласа. Чем больше п. тем точнее эта формула. При выполнении
условия npq > 20 интегральная формула (2.10). так же как и локаль-
ная. дает, как правило, удовлетворительную для практики погреш-
ность вычисления вероятностей.
Функция Ф(г) табулирована (см. табл. II приложений). Для
применения этой таблицы нужно знать свойства функции
Ф(л).
I. Функция Ф(х) нечетная, т.е. Ф(-х) = -Ф(х).
□ Ф(-х) = -^=| е1 '‘dt. Сделаем замену переменной t =-г.
Тогда dt = —dz. Пределами интегрирования по переменной г будут О
и х. Получим
Ф(-х) = -2£
74
поскольку величина определенного интеграла не зависит от обозна-
чения переменной интегрирования
2. Функция Ф(х) монотонно возрастающая. причем при х -> -к»
ф(х)-> 1 (практически можно считать, что уже при х > 4 Ф(х) - I ).
О Так как производная интеграла по переменному
пределу равна подынтегральной функции при значении
предел3» т.е. Ф'(х) = -у=е ' 2 , и всегда положительна.
верхнему
верхнего
то Ф(х)
монотонно возрастает на всей числовой прямой.
Найдем
lim Ф(х) = lim [ е "‘2 dt = -^= [ V' 2 dt.
Сделаем замену переменной z = //72, тогда Лdz = dt. пределы
интегрирования нс меняются, и
lim Ф(х) = f е ‘ 41dz - ~ • - f е : dz
— ' ' Т2я 4 Л 2 Л
(так как интеграл от четной функции
|>г’Л = 2р ”<*)•
Учитывая, ‘по [ е ‘ dz - Л (интеграг Эйлера—Пуассона). получим
lim Ф( v) =-^=---7п = 1.
•—г vn 2
О Пример 2.6. По данным примера 2.5 вычислить вероятность
того, что от 300 до 360 (включительно) семей из 400 имеют холо-
дильники.
Решение. Применяем интегральную теорему Муавра—
Лапласа {npq = 64 > 20). Вначале определим по формулам (2.12)
300-400 0,8 п 360-400-0,8 е п
х, = .— = = -2.50. х, = . =5.0.
/400-0,8-0.2 ‘ 7400-0,8-0,2
Теперь по формуле (2.10), учитывая свойства Ф(х). получим
Лею (300 <; т < 360) == |[Ф(5.О) -Ф(-2,50)] = |[ф(5.0) + Ф(2.50)] =
*|( 1 + 0.9876) = 0,9938
(ПОтабл. II приложений Ф(2.50) = 0.9876. Ф(5,0)=1). ►
75
Рассмотрим следствие интегральной теоремы Муавра-.
Лапласа.
Следствие. Если вероятность р наступления события Л в каждой
испытании постоянна и отлична от 0 и I, то при достаточно боль-
шой числе п независимых испытании вероятность того, что:
а) число т наступлений события А отличается от произведения пр
не более чем на величину с > 0 (по абсолютной величине), т.е.
(2.13)
6) частость — события А заключена в пределах от а до [3 (вклю-
п
чителыюУ, т.е.
где
- а~р Р~р_-
х//х/ « 7w й
(2.14)
(2.15)
в) частость — события А отличается от его вероятности р не
п
более чем на величину Д>() (/»» абсолютной величине), т.е.
□ а) Неравенство |m-/j/>|<E равносильно двойному неравенству
пр - с £ т <> пр + с. Поэтому по интегральной формуле (2.10)
/’ (|wj - лр| < £) = Ря (пр- к <. т < up + е) =
пр 4^ £ - пр
Фч>ч
-ф
ч
пр - Е - пр
1 ВсрияткостиыГс смысл иелнчины pq/n ycraiciwiKBacTOi и § 4 1
76
б) Неравенство а< — <0 равносильно неравенству а< т < b при
«а и Ь = "Р- Заменяя в формулах (2.10), (2.12) величины а и b
полученными выражениями, получим доказываемые формулы (2.14)
и (2.15).
в) Неравенство |-р | < А равносильно неравенству |ю - лр| < Ан .
п
Заменяя в формуле (2.13) я = Дя. получим доказываемую формулу
(2.16)
[> Пример 2.7. По данным примера 2.5 вычислить вероятность
того, что от 280 до 360 семей из 400 имеют холодильники.
Решение. Вычислить вероятность P4Wt( 280 < т < 360) можно
аналогично примеру 2.6 по основной формуле (2.10) Но проще это
сделать, если заметить, что границы интервала 280 и 360 симмет-
ричны относительно величины tip = 320. Тогда по фор,муле (2.13)
/W280< т < 360 ) = />4011(-40< ж - 320 < 40 ) =
= /Wl'W-320|<40)
40
k 7400-0.8-0,2,
= Ф(5,0)*1. ►
|> Пример 2.8. По статистическим данным в среднем 87% новорож-
денных доживают до 50 лет.
I. Найти вероятность того, что из 1000 новорожденных доля (час-
тость) доживших до 50 лет будет: а) заключена в пределах от 0,9 до
0,95; б) будет отличаться от вероятности этого события не более чем
на 0,04 (по абсолютной величине).
2. При каком числе новорожденных с надежностью 0.95 доля до-
живших до 50 лет будет заключена в границах от 0,86 до 0,88?
Ре ш с н и е. I, а) Вероятность р того, что новорожденный до-
живет до 50 лет. равна 0,87. Гак как п = 1000 велико (условие npq =
“1000 0,87 • 0,13 = 113.1 > 20 выполнено), то используем следствие
интегральной теоремы Муавра—Лапласа. Вначале определим по
формулам (2.15)
0.9-0.87 =2М 0.95 0.87 = ? „
70,87-0.13/1000 ‘ 70.87-0,13/1000
Теперь по формуле (2.14)
..f 0.9 0,95 j « 1[Ф(7,52)-Ф(2,82)] -=
= ~ (1-0.9952) = 0,0024.
77
I, б) По формуле (2.16)
= -0.87
И
<, 0.04 НФ
0,04-У1000
7o.87O.l3
= Ф(3.76) = 0,9998.
^нюо
Так как неравенство | — - 0.87 |< 0,04 равносильно неравенству
п
0.83 £—£0.91, полученный результат означает, что практически
п
достоверно, что от 0,83 до 0.91 числа новорожденных из 1000 дожи-
вут до 50 лет. ►
2. По условию РДО.Зб£ — <0.88) = 0,95. или РД-O.OIS —-
п п
-0,87<0.01) =
Р„
”-0,87
п
£0.01 =0.95.
(*)
По формуле (2.16) при А = 0.01
По табл. II приложений Ф(О = 0.95 при t= 1.96. следовательно.
д7л
—= = /. откуда
Д:
1.96 0.87 0.13
0.01-'
= 4345.
т.е. условие (*) может быть гарантировано при существенном увеличе-
нии числа рассматриваемых новорожденных до п = 4345. ►
2.4. Решение задач
1> Пример 2.9. В среднем 20% пакетов акций на аукционах про-
даются по первоначально заявленной пенс. Найти вероятность того,
что из 9 пакетов акций в результате торгов по первоначально заяв-
ленной цене: I) не будут проданы 5 пакетов; 2) будет продано:
а) менее 2 пакетов; б) не более 2 пакетов; в) хотя бы 2 пакета;
г) нанвероятнейшсс число пакетов.
Рсшенн е. 1) Вероятность того, что пакет акций нс будет
продан по первоначально заявленной цене, р = I - 0,2 = 0,8.
По формуле Бернулли (2.1)
/\ = С.;-0.8s 0.24 = 0,066.
78
2, а) По условию р = 0,2.
/> (т < 2) = Р„„ + />, = С • 0.2“ • 0.8” * С’’ 0,2 • 0.8’ = 0.436.
2. б) РДт< 2) = С... + + А, = С 0.2и -0.8’ + CJ -0.20.8* +
+ С‘ -О.22 0,8’ =0,738.
2, в) Д(до 2» 2) = + ... + />,.
Указанную вероятность можно найти проще, если перейти к
противоположному событию, т.е.
р,(и22) = 1 - Р.(т <2) = I = 1 -0,436 = 0.564 (см. п. 2, а).
2, г) Наивероятнейшее число проданных акций по первоначаль-
но заявленной цене определится из условия (2.4), т.е.
9*0.2 - 0.8</и, < 9-0.2 4 0.2 или 1<до„ <2. т.е. наивероятней-
ших чисел два: до0 = I и тп = 2. Поэтому вероятность
Р^ = /\ 4- Р. 9 = С • 0.2 • 0.8* + С' 0,2: • 0.8' = 0.604. ►
О Пример 2.!0. Завод отправил на базу 10 000 стандартных из-
делий. Среднее число изделий, повреждаемых при транспортировке,
составляет 0,02%. Найти вероятность того, что из 10 000 изделий:
I) будет повреждено: а) 3; б) по крайней мерс 3; 2) не будет повреж-
дено: а) 9997; б) хотя бы 9997.
Решение. 1, а) Вероятность того, что изделие будет повреж-
дено при транспортировке, равна р — 0.0002. Так как р — мала,
я « !0 000 — велико и >. = пр = 10 (ХЮ • 0,0002 = 2^10. следует при-
2‘е“:
менять формулу Пуассона (2.6): А\юооо= •
Эго значение проще найти, используя табл. 1П приложений:
Ру. hi «ио ~ Лз(-) = 0,1804.
I. б) Вероятность /{<„„,( до > 3) может быть вычислена как сумма
большого количества слагаемых:
^onm(w £ 3)= Р).|Ц 00(1 + ^4.10 000 + ••• + Р\<) (100.10 (Ю0.
Но, разумеется, проще се найти, перейдя к противоположному
событию:
^lUOOU ( ^ - -’ ) = I — /’(| ,,и ( ДО < 3) = I - ( цИИИ| + Ру цИИ1, + / j |,„И| ) -
= 1 -(0.1353 - 0,2707 + 0.2707) = 0,3233.
79
Следует отмстить. что для вычисления вероятности /]о 1М)11(ш i 3)
= 10 000) нельзя применить интегральную формулу
Муавра—Лапласа. так как не выполнено условие ее применимости,
ибо tl/Hf =: 2 < 20.
2. а) В данном случае р = I - 0.0002 = 0.9998 и надо найти
^9997joоаь для непосредственного вычисления которой нельзя при-
менить ни формулу Пуассона (р велика), ни локальную формулу
Муавра—Лапласа [npq ~ 2<20). Однако событие «не будет повреж-
дено 9997 из 10 000* равносильно событию «будет повреждено 3 in
10 000*. вероятность которого, равная 0.1804. получена в п. I. а).
2, б) Событие «нс будет повреждено хотя бы 9997 из 10 000-
равносильно событию «будет повреждено не более 3 из 10 000*. для
которого р = 0,0002 и
' 3) — ^(000(1 '* / |<|<а«> + ^I.IIHXHI + ^.1.101ХЮ ~
= 0.1353 + 0.2707 + 0,2707 > 0,1805 = 0.8572. ►
О Пример 2.11. По результатам проверок налоговыми инспек-
циями установлено, что в среднем каждое второе малое предпри-
ятие региона имеет нарушение финансовой дисциплины. Найти
вероятность того, что из 1000 зарегистрированных в регионе малых
предприятий имеют нарушения финансовой дисциплины:
а) 480 предприятий: 6) нам вероятней шее число предприятий: в) нс
менее 480: г) от 480 до 520.
Р с ш с н и е. а) По условию р = 0.5. Так п = 1000 достаточно вели-
ко (условие npq - 10 000 • 0.5(I - 0.5) = 250 > 20 выполнено), то при-
меняем локальную формулу Муавра—Лапласа. Вначале по формуле (2.9)
480-1000 0,5 ,
определим v= . - -1.265. затем по формуле (2.7)’
000 0.5 0.5
/(-1,265) /(1.265) Jl.1792 ^^
4*’"" VlOOOO.50.5 7250 7250
1 При вычислении шзчении .41.265) и Ф( 1.265) испо.п. >усм пшенную интерпо-
ляцию (см габл. I и II приложений):
. . /<1.26М /(1.27) |, .
f(l.265)« , (0.1X04 • 0.I7K1) 0.1792.
. . Ф( 1.26) ♦ Ф( 1.271 |, .
Ф(1,265)« , , (0.7923 • 0.7'759) 0.7‘М1.
80
б) По формуле (2.6) наивероятнейшее число 1000’0.5 -
- 0.5 < < 1000 • 0.5 + 0.5 . т.е. 499.5 < ш„ < 500.5 и целое = 500.
Теперь по формулам (2.9) и (2.7) определим
5и(,-|01,1,-,1'? = 0 и />.........................= 0.0252,
>/1000-0.5 0.5 7250 7250
в) Необходимо найти
/',,,,(„/> 480)= 480 < т < 1000). Применяем интегральную
формулу Муавра—Лапласа (2.10). предварительно найдя по форму-
лам (2.12)
480-1000-0,5 . 1000-1000 0.5 .
v. = . = -1.265. v. = --==^ = 31.6.
' V>000 0.5-0.5 ‘ 7l^O.5O,5
Теперь
(480 ^/н< 1000) = ^[Ф(31,6)-Ф(-1,265)] =
Д[ф(31.6) + Ф(1.265)]=Д(1 +0.7941) = 0.897.
г) Вероятность ^1,„(480< т < 520) можно было найти по той же
интегральной формуле Муавра—Лапласа (2.10). Но проще это сде-
лать. используя следствие (2.13). заметив, что границы интервала
480 и 520 симметричны относительно значения пр = 1000-0.5 = 500:
/?.,.(480 < т S 520 ) = />,„( I т - 5001<20) = Ф | -|= j =
= Ф( 1.265) = 0,794. ►
> Пример 2.12. В страховой компании 10 тыс. клиентов. Стра-
ховой взнос каждого клиента составляет 500 руб. При наступлении
страхового случая, вероятность которого, по имеющимся данным и
оценкам экспертов, можно считать равной р = 0.005, страховая ком-
пания обязана выплатить клиенту страховую сумму размером
50 тыс. руб. На какую прибыль может рассчитывать страховая ком-
пания с надежностью 0.95?
Р е in е н и е. Размер прибыли компании составляет разность
между суммарным взносом всех клиентов и суммарной страховой
суммой, выплаченной л» клиентам при наступлении страхового слу-
чая. т.е.
81
П = 500 • 10 - 5Оло = 50( 100 - л0) тыс. руб.
Для определения л0 применим интегральную формулу Муанра—
Лапласа (требование npq = 10 000 • 0,005 • 0,995 = 49,75 > 20 выпол-
нено).
По условию задачи
(0 s ", S ) = 1[ф(.г,) - Ф( г,)] = 0.95. (2.17)
где т — число клиентов, которым будет выплачена страховая сумма;
- ®~ПР _ [”Р _ 000-0,005 _ 7 Y ~ пр
' Jnpq у q у 0.995 * Jnpq
откуда
ли = пр + г, у]npq = 10 000 0,005 + х: 749.75 = 50 + v, 749.75.
Из соотношения (2.17)
Ф(х.) = 1,9 + Ф(.г,) = 1.9 + Ф( -7,09) ' 1.9 + (-1) = 0.9.
По табл. II приложений Ф(х,) = 0,9 при *2= 1,645.
Теперь лп= 50+ 1.645749,75 = 61.6 и //=50(100 - 61.6) = 1920, т.е
с надежностью 0.95 ожидаемая прибыль составит 1,92 млн руб. ►
2.5. Полиномиальная схема
Как отмечено выше, схема Бернулли представляет последователь-
ность независимых испытаний с двумя исходами. При этом в каждом
испытании событие А может появиться с одной и той же вероятно-
стью р. а событие А — с вероятностью q = 1 - р.
В полиномиальной (мультиномиальной) схеме осуществляется пере-
ход от последовательности независимых испытаний с двумя исходами
Ии А) к последовательности независимых испытаний с к исклю-
чающими друг друга исходами At, А;....Л- При этом в каждом испы-
тании события Ai, Aj, Ак наступают соответственно с вероятностями
Pi, р2..р4. Тогда вероятность Р„ (mlt ль, ..., т*.) того, что в л незави-
симых испытаниях событие Hj произойдет mt раз, А2 - т2, и т.д., со-
бытие Ак - тк раз (Л1| + ль +... + тк = п), определится по формуле:
л!
. т2...пи) = —-— --------- р? р?! ,..р? . (2.18)
л/( ’лк !...л/4 !
82
формула (2.18) получается с учетом того, что событие, состояшее в
появлении в п независимых испытаниях события Л| пц раз. А2 - т2 и
tjl. события Ал — раз (/П| + /л? + ... + тд в л). можно представить
н виде суммы несовместных вариантов, вероятность каждою из кото-
рых по теореме умножения вероятностей для независимых событий
равна рР рГ •••/>? . а число варнатгтов определяется числом переста-
новок с повторениями (1.15) из п элементов
На практике вероятность P„(wPw.......м,) можно получить как
коэффициент при д-р в разложении полинома
(Axi +Р:Х1 + - + АА« Г по степеням х,. х,.. v4.
В частном случае двух исходов при m, ~ т< т2 ~ п ~т> Р\ = Р*
Р2ж q. где q = I - р. формула (2.18) представляет формулу Бернулли
а».
t> Пример 2.12а. Человек, принадлежащий к определенной группе
населения, с вероятностью 0.2 оказывается брюнетом, с вероятностью
0,3 — шатеном, с вероятностью 0.4 — блондином и с вероятностью
0.1 — рыжим. Найти вероятность того, что в составе выбранной нау-
дачу группы из 8 человек: а) равное число брюнетов, шатенов, блон-
динов и рыжих; б) число блондинов втрое больше числа рыжих.
Решение, а) По формуле (2.18) вероятность искомого собы-
тия А равна
8! .
Р(Я) = /Э1(2;2;2;2) =------0,2’ 0.3‘ -0.4- *0.Г =0.0145.
2! 2! 2! 2!
6) Вероятность искомою события В равна сумме вероятностей
двух несовместных событий (вариантов):
Bi — в группе 3 блондина. I — рыжий, а остальные — ни то. ни
другое;
Л — в группе б блондинов и 2 рыжих.
По формуле (2.18). полагая, ‘по р{ = 0.4; = 0.1; /ъ = 1 - (0.4 + 0.1) =
= 0,5, найдем
К*
/>(Д)= Zi(3;l;4) = ——0.4'-0,1 0.5й =0.1120;
3’1! 4!
8! . ,
Р(В:) = />(6;2) = — 0.4” 0,1- =0.0011;
6! 2!
Р{ В) = Р{ В,) + /’(В.) = 0,1120 + 0.0011 = 0.1131. ►
Если вероятности р\. р?. .... Рл наступления событий Л|, А2, .... Ал в
«®Ждом испытании меняются в зависимости от исходов других, то мы
ОДсем схему зависимых испытаний.
83
Последовательность зависимых испытаний, в которых условные
вероятности наступления событий Л(, ... Л в каждом (п + 1-м)
испытании (л = I. 2,...) зависят только от исхода предшествующего
(л-го) испытания, называются цепями Маркова. Цепи Маркова пред-
ставляют один из видов марковского случайного процесса, рассмат-
риваемого (в иной терминологии) в § 7.2.
Упражнения
2.13. Вероятность малому предприятию быть банкротом за вре-
мя ( равна 0.2. Найти вероятность того, «гго из шести малых прел-
приятнй за время t сохранятся: а) два; б) более двух.
2.14. В среднем пятая часть поступающих в продажу автомоби-
лей некомплектны. Найти вероятность того, что среди десяти авто-
мобилей имеют некомплектность: а) три автомобиля; б) менее трех
2.15. Производится залп из шести орудий по некоторому объ-
екту. Вероятность попадания в объект из каждого орудия равна 0.6
Найти вероятность ликвидации объекта, если для этого необходимо
не менее четырех попаданий.
2.16. В среднем по 15% договоров страховая компания выпла-
чивает страховую сумму. Найти вероятность того, что из десяти до-
говоров с наступлением страхового случая будет связано с выплатой
страховой суммы: а) три договора; б) менее двух договоров.
2.17. Предполагается, что 10% открывающихся новых малых
предприятий прекращают свою деятельность в течение года. Какова
вероятность тою. что из шести малых предприятий не более двух в
течение года прекратят свою деятельность?
2.18. В семье десять детей. Считая вероятности рождения маль-
чика и девочки равными между собой, определить вероятность того,
что в данной семье: а) не менее трех мальчиков; б) нс более грех
мальчиков.
2.19. Два равносильных противника играют в шахматы. Что бо-
лее вероятно: а) выиграть 2 партии из 4 или 3 партии из 6; б) нс
менее 2 партий из 6 или не менее 3 партий из 6? (Ничьи в расчет не
принимаются.)
2.20. В банк отправлено 4000 пакетов денежных знаков. Веро-
ятность того, что пакет содержит недостаточное или избыточное
число денежных знаков, равна 0.0001. Найти вероятность того. ч«о
при проверке будет обнаружено: а) три ошибочно укомплектован-
ных пакета; б) не более трех пакетов.
2.21. Строительная фирма, занимающаяся установкой летних
коттеджей, раскладывает рекламные листки по почтовым ящиках*
Прежний опыт работы компании показывает, что примерно в од-
ном случае из двух тысяч следует заказ. Найти вероятность гою. что
84
при размещении 100 тыс. листков число заказов будет: а) равно 48;
б) находиться в границах от 45 ло 55.
2.22. В вузе обучаются 3650 студентов. Вероятность того, что
день рождения студента приходится на определенный день года, рав-
на 1/365. Найти: а) наиболее вероятное число студентов, родившихся
1 мая, и вероятность такого события; б) вероятность того, что по
крайней мерс 3 студента имеют один и тот же день рождения.
2.23. Учебник издан тиражом 10 (ХЮ экземпляров. Вероятность
того, что экземпляр учебника сброшюрован неправильно, равна
0,0001. Найти вероятность того, что: а) тираж содержит 5 бракован-
ных книг; б) но крайней мере 9998 книг сброшюрованы правильно.
2.24. Два баскетболиста делают по 3 броска мячом в корзину.
Вероятности попадания мяча в корзину при каждом броске равны
соответственно 0.6 и 0.7. Найти вероятность того, что: а) у обоих
будет одинаковое количество попаданий; 6) у первого баскетболиста
будет больше попаданий, чем у второго.
2.25. Известно, что в среднем 60% всего числа изготовляемых
заводом телефонных аппаратов является продукцией первого сорта.
Чему равна вероятность того, что в изготовленной партии окажется:
а) 6 аппаратов первого сорта, если партия содержит 10 аппаратов;
б) 120 аппаратов первого сорта, если партия содержит 2(Ю аппаратов?
2.26. Вероятность того, что перфокарта набита оператором не-
верно. равна 0,1. Найти вероятность того, что: а) из 200 перфокарт
правильно набитых будет не меньше 180; б) у того же оператора из
десяти перфокарт будет неверно набитых нс более двух.
2.27. Аудиторную работу по теории вероятностей с первого раза
успешно выполняют 50% студентов. Найти вероятность того, что из
400 студентов работу успешно выполнят: а) 180 студентов, б) не ме-
нее 180 студентов.
2.28. При обследовании уставных фондов банков установлено,
что пятая часть банков имеют уставный фонд свыше 100 млн руб.
Найти вероятность того, что среди 1800 банков имеют уставный фонд
свыше 100 млн руб.: а) нс менее 300; б) от 300 до 400 включительно.
2.29. Сколько нужно взять деталей, чтобы наивероятнейшее
число годных деталей было равно 50. если вероятность того, что
наудачу взятая деталь будет бракованной, равна 0.1?
2.30. Вероятность того, что пассажир опоздает к отправлению
поезда, равна 0,01. Найти наиболее вероятное число опоздавших из
800 пассажиров и вероятность такого числа опоздавших.
2.31. Вероятность того, что деталь стандартна, равна р = 0.9.
Найти: а) с вероятностью 0,9545 границы (симметричные относи-
тельно р), в которых заключена доля стандартных среди проверен-
ных 900 деталей; б) вероятность того, что доля нестандартных дета-
лей средн них заключена в пределах от 0.08 до 0.11.
85
2.32. В результате проверки качества приготовленных для посе-
ва семян гороха установлено, что в среднем 90% всхожи. Сколько
нужно посеять семян, чтобы с вероятностью 0,991 можно было ожи-
дать, что доля взошедших семян отклонится от вероятности изойти
каждому семени не более чем на 0,03 (по абсолютной величине)?
2.33. Вероятность того, что дилер, торгующий ценными бумага-
ми. продаст их, равна 0,7. Сколько должно был, ценных бумаг, «гтобы
можно было утверждать с вероятностью 0.996, что доля проданных
среди них отклонится от 0.7 не более чем на 0,04 (по абсолютной ве-
личине)?
2.34. У страховой компании имеются 10 000 клиентов. Каждый
из них, страхуясь от несчастного случая, вносит 500 руб. Всроя!-
ность несчастного случая 0,0055, а страховая сумма, выплачиваемая
пострадавшему, составляет 50 000 руб. Какова вероятность того,
что: а) страховая компания потерпит убыток; б) на выплату страхо-
вых сумм уйдет более половины всех средств, поступивших от кли-
ентов?
2.35. Первый прибор состоит из 10 узлов, второй из 8 узлов. За
время / каждый из узлов первого прибора выходит из строя, незави-
симо от других, с вероятностью 0,1, второго — с вероятностью 0,2.
Найти вероятность того, что за время i в первом приборе выйдет и л
строя хотя бы один узел, а во втором — по крайней мере два узла.
2.36. Студент рассматриваемого вуза по уровню подготовленно-
сти с верояпюстью 0.3 является •слабым», с вероятностью 0.5 -
•средним», с верояптостью 0.2 — «сильным*. Какова вероятность
того, что из наудачу выбранных 6 студентов вуза: а) число «слабых»,
•средних» и «сильных» окажется одинаковым; б) число «слабых» и
«сильных» окажется одинаковым?
2.37. Два завода производят электролампы. Производительность
первого вдвое выше производительности второго. В среднем 5 ламп
(3 лампы) на каждую сотню в продукции первого (второго) завода
являются бракованными Приобретено 5 ламп, произведенных од-
ним из этих заводов. Из них 2 лампы оказались бракованными. Ка-
кова вероятность того, что купленные лампы произведены первым
заводом? вторым заводом?
Глава 3
Случайные величины
3.1. Понятие случайном величины. Закон распределения
дискретной случайной величины
Одним из важнейших понятий теории вероятностей является
понятие случайной величины.
Под случайной величиной понимается переменная, которая в ре-
зультате испытания в зависимости от случая принимает одно из
возможного множества своих значений (какое именно — заранее нс
известно).
Примеры случайных величин;
I) число родившихся детей в течение суток в г. Москве;
2) количество бракованных изделий в данной партии;
3) число произведенных выстрелов до первого попадания;
4) дальность полета артиллерийского снаряда;
5) расход электроэнергии на предприятии за месяц.
Случайная величина называется дискретной {прерывной}. если
множество ее значений конечное, или бесконечное, но счетное1.
Под непрерывкой случайной величиной будем понимать величину,
бесконечное несчетное множество2 значений которой есть некоторый
интервал (конечный или бесконечный) числовой оси’.
Так, в приведенных выше примерах I)—3) имеем дискретные слу-
чайные величины (в примерах I) и 2) — с конечным множеством зна-
чений; в примере 3) — с бесконечным, но счетным множеством зна-
чений); а в примерах 4) и 5) — непрерывные случайные величины.
Прежде чем перейти к более строгому определению случайной
величины, основанному на теоретико-множественной трактовке ос-
новных понятии, следует отмстить, что возможности использования в
теории вероятностей понятия события, введенного ранее в гл. I. ог-
раничены. Это связано с тем. *гто элементарные исходы (события) в
общем случае имеют нечисловую природу (например. И1гтерес игрока
вызывает не наступление какого-либо случайного исхода в игре, а
связанный с ним размер выигрыша или проигрыша). Яля того чтобы
качественные результаты испытаний отобразить количественно, дос-
таточно каждому элементарному исходу (событию) «;> поставить в со-
ответствие некоторое число, т.е. на множестве элементарных исходов
И задать функцию.
} См. сноску на с 59.
Такое Множество в математике называю! континуума w
Строгое определение непрерывной случайной величины дано ниже.
«7
О п р с д с л с и и е. Случайной величиной X называется функ-
ция. заданная на множестве элементарных исходов (или в простран-
стве элементарных событий)', т.е.
X = /(<>).
где ш — элементарный исход (или элементарное событие, припал-
лежащее пространству Q . т.е. о»е £2 ).
Для дискретной случайной величины множество Н возможных
значений случайной величины, т.е. функции /(«). конечно или
счетно, для непрерывной — бесконечно и несчетно.
Убедимся, например, в том. что случайная величина X — число
дней во взятом наудачу месяце года (невисокосного) есть функция
элементарных исходов (событий) <•>. т.е. X -_/(<«»)- В результате испы-
тания — розыгрыша (выбора наудачу) месяца года — все множество
элементарных исходов (пространство элементарных событий) Q
может быть представлено в виде
Q = |ш|, «2. oj. ..., он),
где с>|, w2, wj.«и — соответственно 1-й, 2-й. 3-й... 12-й месяц
года.
Так как ЛГ(<0|) = 31, Я^ом) = 28. Х(щ) = 31. Х(«<ц) = 30....
А'<«»1>) = 31. то число дней во взятом наудачу месяце года (случай-
ная величина Д') есть функция элементарных исходов (событий) w
Случайные величины будем обозначать прописными буквами
латинского алфавита X, К Z. .... а их значения — соответствующими
строчными буквами х, у.
Наиболее полным, исчерпывающим описанием случайной вели-
чины является ее закон распределения.
О и р е д е л е н и е. Законам распределения случайной величины
называется всякое соотношение, устанавливающее связь между воы
можными значениями случайной величины и соответствующими ин
вероятностями.
Про случайную величину говорят, что она «распределена» по
данному закону распределения или «подчинена» этому закону рас-
пределения.
Для дискретной случайной величины закон распреде-
ления может быть задан в виде таблицы, аналитически (в виде фор
мулы) и графически.
Простейшей формой задания закона распределения дискретно!»
случайной величины X является таблица (матрица), в которой перс-
' В случае бесконечного несчетного множества элементарных событий I) по
определение нуждается н уточнении (связанном с измеримостью функции /(••>»
относительно о-алгебры .У), которое здесь не прютолится. так как ныхо.'ип м
рамки данной книги
«8
числены в порядке возрастания все возможные значения случайной
величины и соответствующие их вероятности, т.е.
*1 ... Xj ••• Хп
Р\ Р1 ... А ... Рп
или/ =
/ = 1. 2..... и).
Такая таблица (матрица) называется рядом распределения дис-
кретной случайной величины.
События А'=Х|, Л = х>...... Х=хп. состоящие в том, что в ре-
зультате испытания случайная величина X примет соответственно
значения Х|. х,. .... х„. являются несовместными и единственно воз-
можными (ибо в таблице перечислены все возможные значения
случайной величины), т.е. образуют полную группу. Следовательно,
сумма их вероятностей равна I. Таким образом, для любой дискретной
случайной ветчины
<3.»
Г*|
(Эта единица как-то распределена между значениями
случайной величины, отсюда и термин ‘распределение».)
Ряд распределения может быть изображен графически, если по
оси абсцисс откладывать значения случайной величины, а по осн
ординат — соответствующие их вероятности. Соединение получен-
ных точек образует ломаную, называемую многоугольником, или по-
лигоном, распределения вероятностей (рис. 3.1).
С* Пример 3.1. В лотерее разыгрываются: автомобиль стоимо-
СТЬю 5000 ден. ед.. 4 телевизора стоимостью 250 ден. ед.. 5 видео-
89
магнитофонов стоимостью 200 лен. ел. Всего продается 1000 билетов
по 7 ден. ел. Составить закон распределения чистого выигрыша, по-
лученного участником лотереи, купившим один билет.
Решение. Возможные значения случайной величины X — чис-
того выигрыша на один билет — равны 0 — 7 = —7 лен. ел. (если билет
нс выиграл). 200 - 7 = 193. 250 - 7 = 243, 5000 - 7 = 4993 ден. ед. (если
на билет выпал выигрыш соответственно видеомагнитофона, теле-
визора или автомобиля). Учитывая, что из 1000 билетов число не-
выигравших составляет 990. а указанных выигрышей соответственно
5. 4 и I. и используя классическое определение вероятности, получим:
АЛ= -7) = 990/1000 = 0,990; f\X = 193) = 5/1000 = 0.005;
Р[Х = 243) = 4/1000 = 0.004; Р(Х = 4993) = 1/1000 = 0.001.
т.е. ряд распределения
X) -7 193 243 4993
Pi 0.990 0.005 0.004 0.001
О Пример 3.2. Вероятности того, что студент сдаст семестровый
экзамен в сессию по лисинилинам А и Б. равны соответственно 0.7
и 0.9. Составить закон распределения числа семестровых экзаменов,
которые сдаст студент.
Решение. Возможные значения случайной величины X —
числа сланных экзаменов — 0. 1, 2.
Пусть А, — событие, состоящее в том. что студент сдаст г-й эк-
замен (/ = 1. 2). Тогда вероятности того, что студент сдаст в сессию
0. I. 2 экзамена, будут соответственно равны (считаем события Л| и
Л; независимыми):
/>( Д' = 0) = /’(Л. А:) = Г(А,) р( Л2) =
= (I - 0.7)(I - 0.9) = 0.3 • 0.1 = 0.03;
Р( .V = I) = Р( Д Л2 + Л,Л.) = Р( Д )Р( А:) + Р( Л.) Р( А:) =
-0.7-0.1 +0.3 0.9 = 0.34.
Р(Х = 2) = Р( А,А.) = Р( А, )Р( А,) = 0.70.9 = 0,63.
Итак, ряд распределения случайной величины
X/ 0 1 2
Pi 0.03 0.34 0.63
90
На рис. 3.2 полученный
ряд распределения пред-
ставлен графически в виде
многоугольника (полигона)
распределения вероятно-
стей. ►
3.2. Математические операции
над случайными величинами
Вначале введем понятие независимости случайных
величин.
Две случайные величины называются независимыми, если закон
распределения одной из них нс меняется от того, какие возможные
значения приняла другая величина. Так. если дискретная случайная
величина X может принимать значения х, (i = I. 2.п). а случайная
величина Y— значения у, (/ = I. 2./л). то независимость дискретных
случайных величин X и К означает независимость событий А’ = х< и У’ = yf
при любых /=1.2..п и /'=1.2...т. В противном случае слу-
чайные величины называются зависимыми.
Например, если имеются билеты двух различи ы х де-
нежных лотерей, то случайные величины X и Г. выражающие со-
ответственно выигрыш по каждому билету (в денежных единицах),
будут независимыми, так как при любом выигрыше по билету од-
ной лотереи (например, при X = х,) закон распределения выигры-
ша по другому билету (У) не изменится. Если же случайные вели-
чины X и Y выражают выигрыш по билетам одной денежной
лотереи, то в этом случае X и Y являются зависимыми, ибо любой
выигрыш по одному билету (X = х<) приводит к изменению вероят-
ностей выигрыша по другому билету (У). т.е. к изменению закона
Распределения Y
В дальнейшем понятие независимости случайных величин будет
Уточнено (см. § 5.5).
Определим математические о пера ц и и над
Дискретными случайными величинами.
Пусть даны две случайные величины:
91
х, *1 Х> ... •V"
А Р\ Р2 ... А»
>/ >’» л ... ут
р\ А р\ ... р\
Произведением кХ случайной величины X на постоянную величину к
называется случайная величина, которая принимает значения кх, с
теми же вероятностями р, (/ = I. 2.п).
/л-й степенью случайной величины X, т.е. Хт. называется случай-
ная величина, которая принимает значения V,* с теми же вероятно
стями =1.2........п).
[> Пример 3.3. Дана случайная величина
X:
X, -2 1 э
Pl 0,5 0.3 0.2
Найти закон распределения случайных величин: a) Y — ЗХ\
6)Z=Z2.
Реше н и е. а) Значения случайной величины К будут 3(-2) = 6;
3-1 = 3; 3 • 2 = 6 с теми же вероятностями 0,5; 0,3: 0.2. т.е.
У, -6 3 6
Pi 0.5 0.3 0.2
6) Значения случайной величины Z будут: (-2)-’ = 4. I2 = I.
2’= 4 с теми же вероятностями 0,5; 0,3; 0.2. Так как значение Z=4
может был. получено возведением в квадрат значений (-2) с вероят-
ностью 0.5 и (+2) с вероятностью 0.2, то по теореме сложения
I\Z = 4) = 0.5 + 0,2 = 0.7. Итак, закон распределения случайной
величины _________________
•/ 1 4
Pl 0,3 0.7
Суммой (разностью или произведением) случайных величин X и >
называется случайная величина, которая принимает все возможные
значения вила х, + yJ (xl-y/ или л; •>',). где i = 1.2./г. /=1.2.т.
с вероятностями Ру того, что случайная величина X примет значе-
ние xt, а X — значение у/
р.,=ф'
92
Если случайные величины X и У независимы, т.е. независимы
любые события Х=х/, У = yt. то по теореме умножения вероятно-
стей для независимых событий
р1^Р(Х^х,)Р(У^у1)^р1р]. (3.2)
Замечание. Приведенные выше определения операций над
дискретными случайными величинами нуждаются в уточнении: ес-
ли среди получаемых значений (.vf.x, ± г , г,г,) встретятся одина-
ковые, то соответствующие их вероятности ( /> или р,,) надо сло-
жить, приписав повторяющемуся значению суммарную вероятность
(см. примеры 3.36 и 3.4).
> Пример 3.4. Даны законы распределения двух независимых
случайных величин:
X, 0 2 4
А 0.5 0.2 0.3
У/ -2 0 2
р\ 0.1 0.6 0.2
Найти закон распределения случайных величин: a) Z=X~ У:
б) U=XY.
Р е ш е н и е. а) Для удобства нахождения всех значений раз-
ности Z = X - К и их вероятностей составим вспомогательную таб-
лицу, в каждой клетке которой поместим в левом углу значения
разности Z = X - К а в правом углу — вероятности этих значений,
полученные в результате перемножения верояпюстей соответст-
вующих значений случайных величин X и У
У) -2 0 2
X) Р/ \ 0.1 0.6 0.3
0 0.5 2 0.05 0 __ 0.30 -2 0.15
2 0.2 4 0.02 2 0.12 ° 0.06
4 0.3 6 0.03 4 0.18 2 0.09
Например, если X = 4 (последняя строка таблицы), а У= -2 (трс-
столбец таблицы), то случайная величина Z-Х- У принимает
Учение Z = 4 - (-2) = 6 с вероятностью P(Z= 6) - АА' = 4) х
»3
x PtY = -2) = 0,3-0,1 = 0,03 (эти числа Z= 6 и Р- 0,03 находятся
в клетке на пересечении последней строки и третьего столбца).
Так как среди 9 значений Z имеются повторяющиеся, то соответ-
ствующие вероятности их складываем по теореме сложения вероятно,
стой (см. замечание на с. 93). Например, значение Z = X - Y - 2 мо-
жет быть получено, когда X =0. Y = -2 (с вероятностью 0.05);
Х=2, Y = 0 (с вероятностью 0.12); Л'=4;Х=2 (с вероятностью
0,09), поэтому
P(Z = 2) = 0.05+0.12+ 0,09 = 0,26 и т.л.
В результате получим распределение
-Л -2 0 2 4 6
Рк 0,15 0.36 0.26 0,20 0.03
Убеждаемся в том. что условие £/>, = I выполнено.
б) Распределение U = XУ находится аналогично п. а).
-8 -4 0 4 8
Л 0.03 0,02 0.80 0.06 0.09
3.3. Математическое ожидание дискретной
случайной величины
Закон (ряд) распределения дискретной случайной величины дает
исчерпывающую информацию о ней. гак как позволяет вычислил,
вероятности любых событий, связанных со случайной величиной
Однако такой закон (ряд) распределения бывает трудно обозримым,
не всегда удобным (и даже необходимым) для анализа. Рассмотрим,
например, задачу.
Задача. Известны законы распределения случайных величин Л'и
Y— числа очков, выбиваемых 1-м и 2-м стрелками.
х, 0 I 2 3 4 5 6 7 8 9 10
Р, 0.15 о. и 0.04 0,05 0.04 0,10 0,10 0,04 0.05 0.12 0.20
У/ 0 1 2 3 4 5 6 7 8 9 10
р' 0.01 0,03 0,05 0.09 0.11 0.24 0,21 0.10 0,10 0.04 0.02
94
Необходимо выяснить, какой из двух стрелков стреляет лучше.
рассматривая ряды распределения случайных величин X и Y. от-
дептть на этот вопрос далеко не просто из-за обилия числовых зна-
чений. К тому же у первого стрелка достаточно большие всроятно-
дн (например, больше 0.1) имеют крайние значения числа выби-
ваемых очков (А' = 0; I и X = 9; 10). а у второю стрелка — промежу-
точные значения (Х= 4; 5; 6) (см многоугольники распределения
вероятностей X и Y на рис. 3.3).
Очевидно, что из двух стрелков лучше стреляет тот. кто в
среднем выбивает большее количество очков.
Таким средним значением случайной величины является ее ма-
тематическое ожидание1.
Определенно. Математическом ожиданием, дш средним
значением. M(Xj дискретной случайной ветчины X называется сумма
произведений всех ее значений на соответствующие им вероятности2:
\ЦХ) = ^.Р,- (3.3)
1-1
Г> Пример 3.5. Вычислить М(Х) и M(Y) в задаче о стрелках.
Р е ш е н и е. По формуле (3.3)
Л/(Л*) = 0-0.15+ 1-0.11+ 2-0.04 + .., + 9-0.12 + 10 0.20 = 5.36.
М (Y) = 0 • 0.01 + I • 0.03 + 2 • 0.05 +... + 9 • 0.04 + 10 0.02 = 5.36.
т.е. среднее число выбиваемых очков у двух стрелков одинаковое. ►
1 Происхождение термина «математическое ожидание» спя мио с начальным
периодом возникновения 1 сори и вероятностей, когда область ее применения
0ГРвимчивхтась аяргными играми Игрока интересовало среднее гначеиие ожн-
ДИмого выигрыша, или. иначе, математическое ожидание выигрыша
Для Математического ожидания случайной величины А в литературе также ис-
пользуюгсм обозначения А(А>. Л'
95
1> Пример 3.6. Вычислить Л/(А) для случайной величины Л — чис-
того выигрыша по данным примера 3.1.
Р е ш е и и е. По формуле (3.3)
Л/(X) = (-7) 0.990 -f 193 • 0.005 * 243 • 0.004 - 4993 • 0.001 = 0.
т.с. средний выигрыш равен нулю. Полученный результат означает,
что вся выручка от продажи билетов лотереи идет на выигрыши. ►
Из приведенного определения следует, что математическое
ожидание заключено между наименьшим и наибольшим значениями
случайной величины.
(Действительно, < Л/(Л'Кл„,д%. что вытекает из очевидною
Я * Я
неравенства У •*„,„/< < £-</’, < ^хт^Р.»ибо. учитывая равенство
м1
к я я
(3.1). У г /> = V, У р. =.л- и аналогично У v о = д- .)
’ • ПМП • I tnm ПьП • I н-4»
Математическое ожидание рассматривают как характеристик}
положения случайной величины, ее центр распределения.
Последний термин связан с м е х а н и ч е с к о й и н -
1 е р п р е г а и и с й математического ожидания. Если предпо-
ложить, что каждая материальная точка с абсциссой х, имеет массу,
равную р( (i =1,2..л), а вся с д и и и ч н а я масса | ^Р, - 1
распределена между этими точками, то математическое ожидание
представляет собой абсциссу центра масс системы материальных
точек. Так, для систем материальных точек, соответствующим рас-
пределениям Л' и Y в примере 3.5, центры масс совпадают: М(Х) =
= М( >) = 5.36 (см. рис. 3.3).
Если дискретная случайная величина X принимает бесконечное. но
счетное множество значений Х|. х?..х„..... то математическим
ожиданием, или средним значением, такой дискретной случайной ве-
личины называется сумма ряди (если он абсолютно сходится):
Л/(А') = £ад. (3.4)
ci
Так как ряд (3.4) может и расходиться, то соответствующая слу-
чайная величина может и нс иметь математического ожидания. На-
пример. случайная величина X с рядом распределения
Xi •> 2? 2’ 2'
р. 1/2 1/2- 1/2' ... 1/2'
96
нс имеет математического ожидания, ибо сумма ряда ^27 2' - ^1
W’ ’ <! М
равна <®. На практике, как правило. множество возможных значений
случайной величины распространяется лишь на ограниченный уча-
сток оси абсцисс, и, значит, математическое ожидание существует.
рассмотрим свойства математического ожидания.
1. Математическое ожидание постоянной величины равно самой
постоянной.
Л/(О = С.
(15)
О Постоянную величину С можно рассматривать как величину, при-
нимающую значение С с вероятностью I. Поэтому Л/(О = С- I = I.
2. Постоянный множитель можно выносить за знак математиче-
ского ожидания, т.е.
M(kX) = кМ(Х). (3.6)
□ Так как случайная величина кХ принимает значения kxl (i =
» 1, 2..л), то М(кХ) - )р, - k£xtpt = кМ(Х).
/•I <»•
3. Математическое ожидание алгебраической суммы конечного
числа случайных величин равно такой же сумме их математических
ожиданий, т.е.’
М(Х± П = М(Х} ± М( И.
(3.7)
□ В соответствии с определением суммы и разности случайных
величин (см. § 3.2) X + Y{X- У) представляют случайную величину,
которая принимает значения х, + yj (х{- yj) (i = I. 2.п\ j = I, 2,
.... m) с вероятностями pv- P ((A* = x,)( Y = >y)|«
Поэтому
w(-v±n=ZL(x. v, }p. =
»-l /-I l-l /•!
Так как в первой двойной сумме х, не зависит от индекса /. по
которому ведется суммирование во второй сумме. и аналогично во
второй двойной сумме у} не зависит от индекса /, то
Mx±r)=Zx.Z₽. *£у, = £л.р, ± =
•-I /-I /-1 1-1 i«l /-1
= Л/(Х)±Л/(Г).И
’ Записываем свойство для двух случайных величин
* Т«рв« »«Р<жпкх1гП и мигшги'ксш rranterma 97
4. Математическое ожидание произведения конечного чист независи-
мых случайных величин равно произведению их математических ожиданий'•
M(XY) = Л/(Л)Л/(П-
□ В соответствии с определением произведения случайных ве-
личин (см. § 3.2), XY представляет собой случайную величину, ко.
торая принимает значения ху} (i = I. 2.п: j = 1, 2...т) с веро.
ятностями р,} = Р |(Х = -V,) (Y- у;)|, причем в силу независимости X
и Y pv= р,р'г Поэтому
cl /•! i«l /•! *«t ;»1
= лаг) л/(> ).
5. Если все значения случайной величины увеличить (уменьшить) на
постоянную С. то на эту же постоянную С увеличится (уменьшится)
математическое ожидание этой случайной величины:
М(Х ± О = М(Х) ± С. (3.8)
□ Учитывая свойства 3 и 1 математического ожидания. получим
М(Х ± О = М(Х) ± М(О = М(Х) ± С.
6. Математическое ожидание отклонения случайной величины от
ее математического ожидания равно нулю:
М\Х- Л/(А)1 = 0. (3.9)
□ Пусть постоянная С есть математическое ожидание2
а = М(Х), т.е. С = а. Тогда, используя свойство 5. получим
М(Х - а) = М(Х) -а = а—а = 0.
[> Пример 3.7. Найти математическое ожидание случайной вели-
чины Z= 8Х- 5 Y+ 7, если известно, что М(Х) = 3, M(Y) = 2.
Решение. Используя свойства I. 2, 3 математического ожи-
дания, найдем
M(Z) = 8Л/(Л) - 5Л/( У) + 7 = 8 • 3 — 5 • 2 + 7 = 21. ►
3.4. Дисперсия дискретной случайной величины
Только математическое ожидание нс может в достаточной сте-
пени характеризован, случайную величину.
1 Записываем свойство для двух случайных величин; случай зависимых случай-
ных величин рассматривается в § 5.6 — см. формулу (5.40)
1 См замечание на с ПН
98
В задаче о стрелках (см. § 3.3) мы убедились в том. *гго Л/(Л) =
вЛ/(У) = 5.36. т.с. среднее количество выбиваемых очков у двух
Щелков одинаковое. Но если у 1-го стрелка, как отмечено выше,
значительные вероятности имеют крайние значения, сильно отли-
чак>щисся от среднего Л/(Л). то у 2-го. наоборот. — значения, близ-
кие к среднему Л /( И (см. рис. 3.3). Очевидно, лучше стреляет тот
стрелок, у которого при равенстве средних значений числа выбитых
очков меньше отклонения (разброс, вариация, рассеяние)
этого числа относительно среднего значения.
В качестве такой характеристики рассматривается диспер-
сия случайной величины. Слово дисперсия означает «рассеяние*.
Определение. Дисперсией D(X) случайной величины X на-
дается математическое ожидание квадрата ее отклонения от ма-
тематического ожидания1:
0(Х) = М[Х- М(Х)]2, (3.10)
или ZX-V) = М(Х - а)2, где а - М(Х).
В качестве характеристики рассеяния нельзя брать математиче-
ское ожидание отклонения случайной величины от се математиче-
ского ожидания М(Х - </). ибо согласно свойству 6 математического
ожидания эта величина равна нулю для любой случайной величины.
Из определения (3.10) следует, что дисперсия D(A) есть величина
пеотрицате. 1мая.
Выбор дисперсии, определяемой по формуле (3.10). в качестве
характеристики рассеяния значений случайной величины X оправ-
дывается также тем. что. как можно показать, математическое ожи-
дание квадрата отклонения случайной величины X от постоянной ве-
лычикы С минимально именно тогда, когда эта постоянная С равна
математическому ожиданию Л/(.¥) = а. т.с.
штЛ/(Л'-С): =Л/(АГ-а)2 =П(Л'). (3.10’)
Если случайная величина X — дискретная с конечным числом
значений, то
ад = £(х,-а): р,. (3.11)
1-1
Если случайная величина X — дискретная с бесконечным, но
счетным множеством значений, то
ад = ^(х,-а)'р,. (3.12)
(-1
1 Для дисперсии случайной величины V и литерлуре используется также обо-
значение vaПЛ). Их), п {см далее определение (3.13)).
99
(если ряд в правой части равенства сходится).
Дисперсия /ХА) имеет размерность квадрата случайной величи-
ны, что не всегда удобно. Поэтому в качестве показателя рассеяния
используют также величину y]D(X\
Определение. Средним квадратическим отклонением
(стандартным отклонением, или стандартом} ст, случайной величи-
ны X называется арифметическое значение корня квадратного из ее
дисперсия
о. =JD(X). (3.13)
t> Пример 3.8. В задаче о стрелках (см. § 3.3) вычислить диспер-
сию и среднее квадратическое отклонение числа выбитых очков для
каждого стрелка.
Решение. В примере 3.5 были вычислены М(Х) = 5.36 и
М( Y} = 5.36. По формулам (3.12) и (3.13)
/ХА) = (0 - 5,36)2,0.15 + (1 - 5.36)2-0,11 + ... +
+ (Ю - 5,36)?*О.2О = 13,61,
ст. = 7^)= 3,69;
/X» = (0 - 5.36)2-0.01 + (1 - 5,36)-’-0.03 + ... +
+ (10 - 5,36)2, D.02 = 4.17.
ст, =7^Х>') = 2.04.
Итак, при равенстве средних значений числа выбиваемых очков
(М(Х) = M(Y)} его дисперсия, т.е. характеристика рассеяния относи-
тельно среднего значения, меньше у второго стрелка (ZXA) < /X >))
и. очевидно, ему для получения более высоких результатов стрельбы
по сравнению с первым стрелком нужно сместить «центр* распре-
деления числа выбиваемых очков, т.е. увеличить М( У). научившись
правильно целиться в мишень. ►
Отметим свойства дисперсии случайной величины.
1. Дисперсия постоянной величины равна нулю:
/ХО = 0. (3.14)
□ ZXO = A/JC- A/(Q|2 = Л/(С- О2 = А/(0) = 0.
2. Постоянный множитель можно выносить за знак дисперсии,
возведя его при этом в квадрат'.
D(kX) = V/XA). (3.15)
100
□ Учитывая свойство 2 математического ожидания, получим
1КкХ) = М\кХ - М(кХ)\2 = М]кХ - кМ(Х)]2 =
= Л2Л/1Х- Ш)|2 = к2О(Х).
3. Дисперсии случайной величины равна разными между матема-
тическим ожиданием квадрата случайной величины и квадратом ее
^тематического ожидания:
ад = М(Х*) - |Л/(Л)|2, (3.16)
или
D(X) = М(Х2} - а2, где а = М(Х\.
□ Пусть М{Х) = а. Тогда D(X) = М(Х - а}2 - MIX2 - 2аХ + о2).
Учитывая, что а — величина постоянная. неслучайная1, найдем
ад = М(Х)2 - 2аМ(Х) + а2 = М(Х2) -2а-а + а2 = Л/( ДГ2) - а2.
Это свойство часто используют при вычислении дисперсии. Вы-
числение по формуле (3.16) дает, например, упрощение расчетов по
сравнению с основной формулой (3.11), если значения х, случайной
величины — целые, а математическое ожидание, а значит, и разно-
сти (X/ - д) — нецелые числа.
> Пример 3.9. По данным примера 3.5 (задачи о стрелках) вы-
числить дисперсии случайных величин А', У, используя свойство 3.
Решение. Вначале найдем
М(X*) = £х‘р, = (Г • 0.15 + Г' • 0.11 +... + 9* • 0,12 * 10’ • 0,20 = 42.34.
М-
Теперь по формуле (3.16)
1ХХ) = М(X2) - а2 = 42,34 - 5,362 = 13.61.
Аналогично D( У) = 4.17. ►
4. Дисперсия алгебраической суммы конечного числа независимых
случайных величин равна сумме их дисперсий2:
D(X 1 И = ад+/ДП. (3.17)
□ По свойству 3:
*XX±Y) = М(Х± П2- 1Ш+ У)]2= М(Х* L 2XY + Y2) - (Л/(Л) + Л/(П12.
1 Из определений как математического ожидания М(Х). так и дисперсии [ЦХ]
0яУЧаЙной величины X (представляющих алгебраические операции нал постоян-
ными величинами значениями л, и их вероятностями р,) следуег. чю сами
2*чА) и D(X) — величины нес.1учайные. постоянные.
вписываем свойство для двух случайных величии: случай зависимых случай-
“Ых величин рассматривается в § 5.6 — см. формулы (5.42). (5.43).
101
Обозначая АЛЛ) = av, Л/( И = «v и учитывая, что для независи.
мых случайных величин Л/(АГУ) = M(X)M(Y), получим
IXА’ ± У) = АЛА'2) ± 2ак/зг + A/( У2) ” 2e/iv - << -
=|А/(А'2) -а; | + |АЛ У2) I = 1ХХ) + IX У).
Обращаем внимание на то. что дисперсия как суммы. птк и раз-
ности независимых случайных величин А' и Y равна с у м м е их дис-
персий. т.е.
LXX + У) = 1\Х - У) = АА) + IX У).
1> Пример 3.10. Найти дисперсию случайной величины Z = ХА -
- 5У+ 7. если известно, что случайные величины А'и У’независимы
и ZXA) = 1.5. IX Y) = I.
Р е ш с н и с. Используя свойства I. 2, 4 дисперсии, найдем
О(7) = 8:О(АГ)+5'О(Г) + 0=64 1,5 + 251 = 121. ►
Если использовать механическую интерпрета-
цию распределения случайной величины, то се дисперсия пред-
ставляет собой момент инерции распределения масс относительно
центра масс (математического ожидания)
Замечание. Обратим внимание на интерпретацию матема-
тического ожидания и дисперсии в ф и и а н с о в о м а н а л и -
з е. Пусть, например, известно распределение доходности X некото-
рого актива (например, акпни), т.е. известны значения доходности
х, и соответствующие их вероятности р, за рассматриваемый проме-
жуток времени. Тогда, очевидно, математическое ожидание АЛА)
выражает среднюю (прогнозную) доходность актива, а дисперсия IX X)
или среднее квадратическое отклонение ov — меру отклонения, ко-
леблемости доходности от ожидаемого среднего значения, т.е. риск
данного актива.
Математическое ожидание, дисперсия, среднее квадратическое
отклонение и другие числа, призванные в сжатой форме выразить
наиболее существенные черты распределения, называются числовыми
характеристиками случайной величины.
Обращаем внимание на то, что сама величина X — случайная, а
ес числовые характеристики являются ветчинами нес л у чай-
ным и. постоянными. Поэтому их часто называют параметрами
распределения случайной величины.
В теории вероятностей числовые характеристики играют боль-
шую роль. Часто удается решать вероятностные задачи. оперируя
лишь числовыми характеристиками случайных величин. Примене-
ние вероятностных методов для решения практических задач в зна-
102
чИТельной мере определяется умением пользоваться числовыми ха-
рактеристиками случайной величины, оставляя в стороне законы
распределения.
3.5* Функция распределения случайной величины
До сих пор в качестве исчерпывающего описания дискретной
случайной величины мы рассматривали закон ее распределения,
др^дставляющий собой ряд распределения или формулу, позво-
ляющие находить вероятности любых значений случайной величи-
ны X. Однако такое описание случайной величины X не является
единственным и. главное, не универсально. Так. оно неприменимо
для непрерывной случайной величины, так как, во-первых, нельзя
перечислить все бесконечное несчетное множество ее значений; во-
вторых, как мы увидим дальше, вероятности каждого отдельно взя-
того значения непрерывной случайной величины равны нулю.
Для описания закона распределения случайной величины X воз-
можен и другой подход: рассматривать не вероятности событий Х= х
для разных х (как это имеет место в ряде распределения), а вероятно-
сти события X < х, где х — текущая переменная. Вероятность Р\Х < х),
очевидно, зависит от х. т.е. является некоторой функцией от х.
О п р с л с л е н и е. Функцией распределения случайной величины
X называется функция Дх). выражающая для каждого х вероятность
того, что случайная величина X примет -значение, меньшее х
Г(х) = Р(Л' <х). (3.18)
Функцию Дх) иногда называют интегральной функцией распреде-
ления или интегральным законом распределения.
Геометрически функция распределения интерпретируется как
вероятность того, что случайная точка .V попадет ленсе аданной
тонких (рис. 3.4).
Х< х
’/////^////////////////////////%;
О X
Риг. 3.4
С* Пример 3.11. Дан ряд распределения случайной величины
X, 1 4 5 7
А 0.4 0.1 0.3 0.2
Найти и изобразить графически се функцию распределения.
103
Решение. Будем задавать различные значения х и находить
для них F(x) = P(X <х).
I. Если xSl. то, очевидно, Г(х) = 0 (в том числе и при х = ।
Г(1)=Р(х<1) = 0).
2. Пусть I <х<4 (например, х = 2); F(x)= Р(Х - I) = 0,4. Оче-
видно, что и Г(4) = Р(Х < 4) = 0,4.
3. Пустъ4<х<5 (например, х = 4,25); F(x) = ₽(.¥<х) = Р(Л'= !)-»•
+Р(Х = 4) = 0.4+ 0.1 =0.5. Очевидно, что и Д5) = 0,5.
4. Пусть 5<х<7. F(x) = [p(A' = l)+P(A' = 4)] + P(A' = 5) =
= 0.5 + 0,3 = 0.8 . Очевидно, что и Д7) = 0,8.
5. Пусть х >7.
Р(х) = [Р(АГ«|)+Р(Х = 4) + Р(АГ = 5)] +Р( А' = 7) =0.8 + 0,2 = 1.
Изобразим функцию Дх) графически (рис. 3.5).
Заметим, что при подходе слева к точкам разрыва функция сохра-
няет свое значение (про такую функцию говорят, что она непрерывна
слева, т.е. lim F(x) = F{a}). Эти точки на графике выделены. ►
a -tu-0
Данный пример позволяет прийти к утверждению, что функция
распределения любой дискретной случайной ветчины есть разрывная
104
ступенчатая функция, скачки которой происходят в точках, соот-
^тствующих возможным значениям случайной величины и равны веро-
ягпностям этих значений. Сумма всех скачков функции Г(х) равна I.
рассмотрим общие свойства функции распределения.
1. Функция распределения случайной величины есть неотрицатель-
на функция, заключенная между нулем и единицей:
0<?(х)<1.
□ Утверждение следует из того, что функция распределения — это
вероятность.
2. Функция распределения случайной величины есть неубывающая
функция на всей числовой оси.
□ Пусть Х| и хо — точки числовой оси. причем х2 > Х|. Пока-
жем, что Л(Х2)> Г(х,). Рассмотрим два несовместных события
Х = (X < X]), В = (х, < X < х,). Тогда А + В = {X < х2).
А + В = (Х< ж,)
________,_____________ ________________„____________ X
4 = (X < Х() v' В = (х, < .V < х,) Л2
Рис. 3.«
Это соотношение между событиями легко усматривается из их
геометрической интерпретации (рис. 3.6). По теореме сложения
Р(А + В)=Р(А}^Р(В)
или
Р (X < х.) = Р (X < X,) + Р (X, < X < X,).
откуда
F(r,)= F(xt)+P(Xl <Х<х2). (3.19)
Тах как вероятность /э(х1 < X < х: )>0. то F(x?)> Г(хД т.е.
Ях) — неубывающая функция.
3. На минус бесконечности функция распределения равна нулю, на
njuoc бесконечности равна единице, т.е.
Г(-ао) = lim F(x) = 0, Л(+оо)= lim F(x) = 1.
О F(-<n) = Р(Х <-«?) = О как вероятность невозможною собы-
тия *<-«.
F(-«») = p(x < 4-х) = | как вероятность достоверного события
<+СО.
105
I
4. Вероятность попадания случайной величины в интервал |хь х2)
(включая Х|) равна приращению ее функции распределения на
интервале. т.е.
Р(х,<Х<х;)=Г(х2)-Г(х1). . (3.20)
□ Формула (3.20) следует непосредственно из формулы (3.19).
Итак, функция распределения любой случайной величины (дис-
кретной или непрерывной) обладает указанными выше свойствами.
Верно и обратное: каждая непрерывная слева функция, удовлетво-
ряющая приведенным свойствам, есть функция распределения не-
которой случайной величины.
О Пример 3.12. Функция распределения случайной величины X
имеет вид:
F(x) =
0
х/2
I
при х < 0.
при 0 < х < 2,
при х>2.
Найта вероятность того, что случайная величина примет значе-
ние: а) в интервале 11:3): б) нс менее чем 1/3.
Р е in е н и е. а) По формуле (3.20)
P(1SX<3)=F(3)-F(1)=I-1 = 1.
Л»
б) Так какА'>х и .¥<л* - противоположные события,
Р(А‘ > л ) = I - Р(Х < v) пли с учетом определения1 (3.18)
х) = I - Г(х). (3.20)
В данном случае по формуле (3.20')
3.6. Непрерывные случайные величины.
Плотность вероятности
Выше дано понятие непрерывной случайной величины, имеющей
бесконечное несчетное множество значений. Приведем теперь более
строгое определение.
1 Если случайная величина X - время жизни человека (другой биосисгемы) или
время безотказной работы устройства, то функцию .У(х) = l-F(X) называют
функцией выживинчя [дожития) или функцией надежности.
106
Определение. Случайная
дичина X называется непрерывной,
ее функция распределения не-
„рерывна в любой точке и диффе-
пею^РУ6^0 вс,°дУ' кроме. быть мо-
лсезп. отдельных точек.
На рис. 3.7 показана функ-
идо распределения непрерывной
случайной величины X. диффе-
ренцируемая во всех точках, кро-
ме трех точек излома.
Теорема. Вероятность любого
отдельно взятого значения непрерывной случайной ветчины равна нулю'.
□ Покажем, что для любого значения Х| случайной величины А*
вероятность P(.V = .v() = 0. Представим /’(А'=х|) в виде
Р(Х = х,) =lim Р( х, < А' < х,).
Применяя свойство (3.20) функции распределения случайной вели-
чины Хи учитывая непрерывность Г(х), получим
P(.V =x,)=lim [F(x.)-F(.r,)] =
lim F(x.)-F(A-,)’F(.r,)-F(.r,) = 0.
До сих пор мы рассматривали испытания, сводившиеся к схеме
случаев, и нулевой вероятностью обладали лишь невозможные собы-
тия. Из приведенной выше теоремы следует, что нулевой вероятно-
стью могут обладать и возможные события, так как событие, состоя-
щее в том. что случайная величина X приняла конкретное значение Х|,
является возможным2. На первый взгляд этот вывод может показаться
парадоксальным. Действительно, если, например, событие а<А'<0
имеет отличную от нуля вероятность, то оказывается, ’гго оно пред-
ставляет собой сумму событий, состоящих в принятии случайной ве-
личиной X любых конкретных значений на отрезке [а. |3] и имеющих
нулевую вероятность. Но никакого противоречия здесь нет, ибо тео-
рема сложения (точнее, аксиома сложения — см. § 1.12) справедлива
только для конечного и счетного бесконечного множества событий, а
Поэтому непрерывную случайную величину можно было определить и иначе:
случайная величина непрерывна, если вероятность любою отдельно взятого се
^чгченим равна нулю.
На практике таких вопросов нс возникает, так как значение любой непрерыв-
ной величины может быть определено лишь с некоторой точностью (абсолютно
точное значение такой величины есть математическая абстракция).
107
множество событий, обозначающих отмеченную сумму, таковым це
является.
Представление о событии, имеющем отличную от нуля вероят-
ность. но складывающемся из событий с нулевой вероятностью, не
более парадоксально, чем представление об отрезке, имеющем оп-
ределенную длину, тогда как ни одна точка отрезка отличной от
нуля длиной нс обладает. Отрезок состоит из таких точек, но сю
длина нс равна сумме их длин.
Далее, рассматривая теорему Бернулли (см. § 6.4). мы убедимся
в том. что при п->х частость события m/л приближается к веро-
ятности этого события. Поэтому из того, что вероятность события
равна нулю, следует только, что при неограниченном повторении
опыта его частость m/л будет приближаться к нулю, т.е. событие
будет появляться сколь угодно редко.
Следствие. Если X — непрерывная случайная величина, то вероят-
ность попадания случайной величины в интересы (Х|. х;) не зависит от
того, является этот интересы открытым или закрытым, т.е.
/’(х, < А' < х.) = Р(х, < .V < х.) = Р(х, < X < х.) = Р(х, S X < .v,).
□ Р(х, < .V <. х.) = Р{ X = х,) + Р(х, < X < х,) + Р( X = X.) =
= 0 + Р(х, < .¥ < х,) + 0 = Р{X] < X < х,)
Аналогично доказываются и другие равенства.
Задание непрерывной случайной величины с помощью функции
распределения не является единственным. Введем понятие
плотности вероятности непрерывной случайной ве-
личины.
Рассмотрим вероятность попадания непрерывной случайной ве-
личины на участок [х. х + Дх]. По формуле (3.20) вероятность
Р(х<Х £ х + Дх) = Г(х +Дг)-Г(х).
т.е. равна приращению функции распределения f\x) на этом участке.
Тогда вероятность, приходящаяся на единицу длины, т.е. средняя
плотность вероятности на участке от х до х + Дх равна
Р(х <, Л’ £ х + Дг) _ Г(х + Дх) - Г(х)
Дг Дх
Переходя к пределу при Дг-»0. получим плотность вероятно-
сти в точке х
.. Р(х< X S х + Дх) .. F(x + Ax)-F(x) . .
lim _1------------- lim _J-----------1_1 = £'( v)
.v-M> дг Дх
108
дредставляющую производную функции распределения Дх) (на-
помним. что для непрерывной случайной величины Дх) — диффе-
ренцируемая функция).
Определение. Плотностью вероятности (плотностью рас-
иредвлення или просто плотностью) ф(х) непрерывной случайной вели-
чины X называется производная ее функции распределения
ф(а) = П'). (3.21)
Про случайную величину X говорят, что она имеет распределе-
ние (распределена) с плотностью ф(х) на определенном участке
оси абсцисс.
Плотность вероятности cp(.v). как и функция распределения
Дх), является одной из форм закона распределения, но в отличие
от функции распределения она существует только для непре-
рывных случайных величин.
Плотность вероятаости иногда называют дифференциальной
функцией или дифференциальным законом распределения.
График плотности вероятности ф( х) называется кривой распре-
деления.
О Пример 3.13. По данным примера 3.12 найти плотность веро-
ятности случайной величины X.
Р е in с н и с. Плотность вероятности ф(х) = F‘(.\:). т.е.
ПРИ Х<0ИХ>2.
р' ' (1/2 при 0<х<2. >
Отметим свойства плотности вероятности непрерывной
случайной величины.
1. Плотность вероятности — неотрицательная функция, т.е.
ф(х)>0.
□ ф(х)2() как производная монотонно неубывающей функции
Ях).
2. Вероятность попадания непрерывной случайной величины в ин-
HtepeaH [п.Л] равна определенному интегралу от ее плотности веро-
ятности в пределах от а до Ь. т.е.
/*(</<.¥ i fr) = J ф(х)</г.
□ Согласно свойству 4 функции распределения
Р(а < Л' 5 b) = F(b) -F(a).
Так как Дх) есть первообразная для плотности вероятности
ЧКх) (ибо Г*(х) = (р(х)), то по формуле Ньютона—Лейбница прн-
(3.22)
109
ращение первообразной на отрезке [а./>] есть определенный инте-
грал j (p(.v)tZv , т.е. формула (3.20) верна.
Геометрически полученная вероятность равна площади фигуры,
ограниченной сверху кривой распределения и опирающейся на от-
резок [«./)] (рис. 3.8).
3. Функция распределения непрерывной случайной величины может
быть выражена через плотность вероятности по формуле'.
F(*)= J’ ф(х)<Л. (3.23)
Формула (3.23) получается из формулы (3.22) при а , если
верхний предел b заменить на переменный предел х
Геометрически функция распределения равна площади фигуры,
ограниченной сверху кривой распределения и лежащей левее точки
х (рис. 3.9).
4. Несобственный интеграл в бесконечных пределах от плотности
вероятности непрерывной случайной величины равен единице.
J' Ф(л){/с = 1. (3.24)
□ По формуле (3.23): F(x)=J <p(.v)c£r и при .v-4-w. Г(+«о) = 1.
т.с. верно равенство (3.24).
Геометрически свойства 1 и 4 плотности вероятности означают,
что ее график — кривая распределения — лежит не ниже оси абсцисс,
и полная площадь фигуры, ограниченной кривой распределения и осью
абсцисс, равна единице.
Понятие математического ожидания Л/(Л) и дисперсии /ХЛ>.
введенные выше (§ 3.3, 3.4) для дискретной случайной величины,
можно распространить на непрерывные случайные величины.
НО
для получения соответствующих формул для М(Х) и D(X} доста-
точно в формулах (3.3) и (3.11) для дискретной случайной величи-
ну X заменить знак суммирования У, по всем ес значениям зна-
t=i
ком интеграла с бесконечными пределами j , «скачущий» аргумент
— непрерывно меняющимся х. а вероятность pt — элементом ве-
роятности (p(.v)tZv. Под элементом вероятности понимается вероятность
попадания случайной величины
X на участок |х. х + r/rj (с точ-
ностью до бесконечно малых
более высоких порядков);
геометрически элемент веро-
ятности приближенно равен
площади элементарного пря-
моугольника под кривой ф(х).
опирающегося на отрезок |х.
х+ dx] (рис. 3.10).
В результате получим сле-
дующие формулы для математического ожидания и дисперсии непре-
рывной слузганной величины X:
а - .V/ ( X) - j v <р(х)dx (3.25)
(если интеграл абсолютно сходится) и
D{ X) = | (х - a}1 <p(.r)dr (3.26)
(если интеграл сходится).
На практике обычно область значении случайной величины, для
которых <p(.v)*O, О1рапичсна и указанные интегралы сходятся, а
значит, существуют М(Х) и D(X).
Все свойства математического ожидания и дисперсии, рассмот-
ренные выше для дискретных случайных величин, справедливы и
Для непрерывных величин1.
В частности, свойство 3 дисперсии (формула (3.16)) имеет вид:
D{X) = М(Х2)-а2 или D(.-V)=j x"q(.v)z/.v - tv". (3.27)
Замечание. Наряду с дискретными и непрерывными случай-
,{Ь1ми величинами на практике встречаются смешанные случайные вели-
Замегнм, что сохраняет ил же смысл механическая интерпретация матсматяче-
ского ожидания как абсциссы центра масс для единичной массы, распределенной
“Данном случае непрерывно на осн абсцисс с цлогностыо вероятности »р(х), и
дисперсии кик момент инерции распределения масс oTmx.it 1елто центра масс.
111
1
чины, для которых функция распределения flx) на некоторых участках
непрерывна, а в отдельных точках имеет разрывы. Примером смешан-
ной случайной величины может служить заработок рабочего, пропор.
циональный его выработке, но не меньший гарантированного размера
оплаты (При х = Л) функция распределения Дх) имеет скачок от нуля
до некоторого значения а при х > Хз непрерывно возрастает.) Ддя
смешанных случайных величин остается справедливой формула (3.20)
вероятности попадания случайной величины на любой шгтервал |хъ х()
1> Пример 3.14. Функция ф(.г) задана в виде:
О при х<1,
(p(.v) = J .4
’' ' — при r > 1 •
X
Найти: а) значение постоянной А. при которой функция будет плот-
ностью вероятности некоторой случайной величины Х\ б) выражение
функции распределения F(.v); в) вычислить вероятность того, что слу-
чайная величина X примет значение на отрезке [2;3]; г) найти мзггемати-
ческое ожидание и дисперсию случайной величины X
Реше и и с. а) Дтя того ‘гтобы ф(х) была плотностью вероят-
ности некоторой случайной величины X она должна быть неотрипа-
тельна, т.е. ф(х) Ъ 0 или — > 0, откуда А >0. и она должна удовле-
творять свойству 4. Поэтому в соответствии с формулой (3.24)
J ф(х)Л = 1.
Следовательно,
J ф(х)^г= J 0<Zv+J -^<Zv = O+liin J-—<& =
откуда А = 3.
б) По формуле (3.23) найдем Fix).
Если х<1. то Л*(х) = J ф(х)</л = J O-cZrsO.
Если х > I. то
Таким образом. F(x) =
О при
. I
1-— при
X
х$1.
х>1.
112
в) По формуле (3.22)
Вероятность Р(2 < < 3) можно было найти непосредственно
как прирашение функции распределения по формуле (3.19):
P(2<*$3) = F(3)-F(2) = (l-l]-(t-l) = ^.
г) По формуле (3.25) вычислим
i-* > Г1 ( 3 \ Cbdx
..x^dx= J 0-Л + J ,r(? j<fc =0+3 Jim { 7 =
л v f 1 Л 3 Г, । ) з
-3 Inn I — = —lim I--T =-.
Л-.Д 2x 1J 2 b~) 2
Дисперсию Z\A) вычислим по формуле (3.27). Вначале найдем
Л/(Л2)= J х'ф(х) <ft = 0+ J .г‘ | I dx = 3
(вычисление интеграла аналогично приведенному выше). Теперь
D(X) = 3-gj:=|.>
Замечание. В ряде случаев, если имеется график функции
распределения Ях), полезно иметь в виду геометрическую интерпре-
тацию математического ожидания Л/(Л) случайной величины X:
Л/(А') = 5,-5|.
ще и 5| — площади фигур, заключенных соответственно между осью
Оу, прямой у = I и кривой у = М на интервале (О;н-<*э) и между кри-
вой у — F{x) и осями Ох и Оу на промежутке (-х;0) (рис. 3.11).
Так. например, для нахождения математического ожидания
случайной величины заданной функцией распределения
ИЗ
F(x). состоящей из участков прямых и дуги окружности (рис. 3.12).
нет необходимости находить ф(л)по формуле (3.21), а затем А/(Л>
по формуле (3.25). Значительно проще найти М(Х), используя его
геометрическую интерпретацию, т.е.
Л/(А') = 5,-5, = 1п/?:-1«Л = 1п(1| _l.l.l = lz2-0.072.
' ' * 4 2 4 l2j 2 2 2 16
Приведенная геометрическая интерпретация позволяет записать
математическое ожидание в виде:
Л/(.Г) = -[ F(x)dx + [ (l-F(x))dv.
3.7. Мода и медиана. Квантили. Моменты
случайных величин. Асимметрия и эксцесс
Кроме математического ожидания и дисперсии, в теории веро-
ятностей применяется еще ряд числовых характеристик, отражаю-
щих тс или иные черты распределения.
Определение. Модой Мо{Х) случайной величины X называ-
ется ее наиболее вероятное значение (для которого вероятность р, или
плотность вероятности ф(х) достигает максимума).
Если вероятность или плотность вероятности достигает макси-
мума не в одной, а в нескольких точках, распределение называется
полимодальным (рис. 3.13).
Мода Мй(Х), при которой вероятность /> или плотность веро-
ятности <р(х) достигает глобального максимума, называется наиверо-
ятнейшим значением случайной величины (на рис. 3.13 это Л/м(,\'),).
Определение. Медианой Ме(Х) непрерывной случайной ве-
личины X называется такое ее значение, для которого
Р(Х < Ме(Х)] = Р(Х> Мс( X)) = 1, (3.28)
114
те. вероятность того, что случайная величина X примет значение,
меньшее медианы Ме{Х) или большее ее, одна и та же и равна
1/2. Геометрически вертикальная прямая х — Ме{Х), проходящая
через точку с абсциссой, ранной Ме(Х), делит площадь фигуры
под кривой распределения на две равные части (рис. 3.14). Оче-
видно, что в точке х = Ме{Х) функция распределения равна 1/2, т.е.
Л) = 1/2 (рис. 3.15).
Отметим важное свойство медианы случайной величины: мате-
матическое ожидание абсолютной величины отклонения случайной вели-
чины X от постоянной величины С минимально тогда, когда эта посто-
янная С равна медиане Me (Л) = /л, т.е.
minA/’(|.¥-C|) = A/(k-d)
с
(свойство аналогично свойству (3.1(H) минимальности среднего квадрата
отклонения случайной величины от ее математического ожидания).
О Пример 3.15. Найти .моду, медиану и математическое ожида-
ние случайной величины X с плотностью вероятности <р(х) = 3х2
при хе[0;1].
Решение. Кривая распределения представлена на рис. 3.16.
Очевидно, что плотность вероятности <р(х) максимальна при
Xе Мо(Х) = I.
Медиану Ме(Х) = b найдем из условия (3.28):
или
| ip(x)<Zv = | 0• dx + £ 3x:dx = х’
откуда
6 = .W<>(,V) = ^1/2^0,79.
115
Математическое ожидание вычислим по формуле (3.25):
Л/(Л')= | хф(х)Л= |' 0 ^+ J' х(З.Г )с& + J” Ocfr=|x
' = 0.75
и
Взаимное расположение точек Л/(А'). Л/е(Л) и Мо(Х) в порядке воз-
растания абсцисс показано на рис. 3.16. ►
Наряду с отмеченными выше числовыми характеристиками для
описания случайной величины используется понятие квантилей и
процентных точек.
О п р с д е л е н и с. Квантилем уровня q (или q-квантилем) на-
зывается такое значение х(/ случайной величины, при котором функция
ее распределения принимает значение, равное q. т.е.
Дд,р = = (3.29)
Некоторые квантили получили особое название. Очевидно, что
введенная выше медиана случайной величины есть квантиль уров-
ня 0,5, т.е. Afe(zY) = х0 $. Квантили Afo.’s и *0.75 получили название
соответственно нижнего и верхнего квартилей*.
С понятием квантиля тесно связано понятие процентной точки
Под 100^%-яой точкой подразумевается квантиль X|-v, т.е. такое зна-
чение случайной величины А', при котором Р(Х >л'.г) = </.
t> Пример 3.16. По данным примера 3.15 найти квантиль хь,з и
30%-ную точку случайной величины X.
Решен» е. По формуле (3.23) функция распределения
F(.v) = J ip(.v)</.v = j 0• cZv + J(|3x:eZv = v’.
Квантиль ход найдем из уравнения (3.29), т.е. г/ । =0.3. откуда
л„, а().67. Найдем 30%-ную точку случайной величины X. или
квантиль Ход, из уравнения .v,’7 =0.7. откуда 5:0.89. ►
Средн числовых характеристик случайной величины особое зна-
чение имеют м о м е н т ы — начальные и центральные.
Опре л е л е и и с. Начальным моментом k-го порядка случай-
ной величины X называется математическое ожидание k-й степени
этой величины:
v, = М(ХА). (3.30)
Определение. Центральным моментом к-го порядка слу-
чайной величины X называется математическое ожидание k-й степени
отклонения случайной величины X от ее математического ожидания:
(3.31)
1 В лкпгратурс встречаются также термины: </сци.ш (пол которыми понимаются
квантили м,|. ...и npuuenmiuu (перценпиии) (квантили ло.щ, Гц.»’...
116
или Ц, - Л/ (х - <?)*. где а - М(Х).
Формулы для вычисления моментов для дискретных случайных
величин (принимающих значения х, с вероятностями р,) и непрерыв-
ных (с плотностью вероятности ф(х)) приведены в табл. 3.1.
Таблиц» 3.1
Момент Случайная величина
Дискретная Непрерывная
Началь- ный Централь- ный (3.32) г-1 Рл =Х(х.-"/а <334) 1-1 v4 = Р’?ф(х)Л (3.33) р, = [‘ (х-а)ф(х)Л (3.35)
Нетрудно заметить, что при к = I первый начальный момент
случайной величины X есть ее математическое ожидание, т.е.
Vj = Af(X) = a, при к = 2 второй центральный момент — диспер-
сия, т.е. р. = D(.V).
Центральные моменты могут быть выражены через началь-
ные моменты V, по формулам:
М,=0.
p?=v,-v;.
р, = V, -3v,v, +2V|.
Ил =v4 ”4vivj + 6v?v:
и Т.Д.
□ Например. щ = М(Х-а)' = М(Х* -ЗоГ: ^а‘Х-и} =
= ЩХ')-ЗаМ(Х: } + М(Х)-и = v, -3v,v. +3v^v, -v’ = v, -3v,v,+
+ 2V|‘ (при выводе учли, что а = М(Х) = v, — неслучайная величи-
на).
Выше отмечено, что математическое ожидание М(Х), или пер-
вый начальный момент, характеризует среднее значение
или положение, центр распределения случайной величи-
ны X на числовой оси; дисперсия ZXA% или второй центральный мо-
мент р., — степень рассеяния распределения X огноси-
117
тельно MIX). Для более подробного описания распределения служа!
моменты высших порядков.
Третий центральный момент р, служит для характеристики
асимметрии (скошенности) распределения. Он имеет
размерность куба случайной величины. Чтобы получить безразмерную
величину, ее деляг на ст', где ст — среднее квадратическое отклоне-
ние случайной величины X. Полученная величина А называется коэф-
фициентом асимметрии случайной величины'.
А-
(3.36)
Если распределение симметрично относительно математическо-
го ожидания, то коэффициент асимметрии /1 = 0.
На рис. 3.17 показаны две кривые распределения: I и II. Кривая I
имеет положительную (правостороннюю) асимметрию (А > 0), а
кривая II — отрицательную (левостороннюю) (Л < 0).
Четвертый центральный момент р4 служит для характеристики
крутости (островершинности или п л о с к о -
в е р ш и н н о с т и ) распределения.
Эксцессом (или коэффициентом эксцесса) случайной величины
называется число
£ = ^--3. (3.37)
ст
(Число 3 вычитается из отношения р4/ст‘ потому, что для наибо-
лее часто встречающегося нормального распределения (о нем идет
речь в гл. 4) отношение р4/о4 = 3. Кривые, более островершинные,
чем нормальная, обладают положительным эксцессом, более плоско-
вершинные — отрицательным эксцессом (рис. 3.18).
118
О Пример 3.17. Найти коэффициент асимметрии и эксцесс слу-
чайной величины» распределенной по так называемому закону Лап-
ласа с плотностью вероят-
ности ф(х) = ^е‘,‘|.
Решение. Так как
распределение случайной
величины X симметрично
относительно оси ординат,
то все нечетные моменты
(как начальные, так и цен-
тральные) равны 0, т.е.
v,=0, v,=0. Щ =0 и в
Рис. 3.19
силу определения (3.36) ко-
эффициент асимметрии А = 0.
Для нахождения эксцесса необходимо вычислить четные началь-
ные моменты1 v. и v4:
V, = J \2q>(x)dr= j = 2 | j”*rV’A-2.
Следовательно,
D(X) = p, = v,-v,:=2-0J = 2 и a, =^D(X) = Vz
x*e‘*dx = 24.
Теперь эксцесс по формуле (3.37)
Е=Ь-3 = ^Т-3 = 3.
° (^)
Эксцесс распределения положителен, что говорит об островер-
шинности кривой распределения ф(х) (рис. 3.19). ►
3.8. Производящая функция
Полезным инструментом при изучении случайной величины яв-
ляется производящая функция.
1 Вычисление получаемых интегралов опускаем и предлагаем его провести чита-
телю самостоятельно.
119
Определение. Функция от параметра f. равная математи-
ческому ожиданию функции е,Л. называется производящей функцией
случайной величины X:
mv(r) = .We*‘. (3.3«)
Производящая функция т,(П содержит в себе сведения о всех
начальных моментах («производит* моменты), т.с. по ней можно
определить функцию распределения, содержащую все сведения о
случайной величине. В этом смысле производящая функция и
функция распределения являются эквивалентными обобщающими
характеристиками случайной величины.
Рассмотрим с в о й с т в а производящей функции.
I. Если тх(1) — производящая функция случайной величины X, то
производящей функцией ветчины сХ будет
(3.39)
2. Производящая функция суммы независимых случайных ветчин
равна произведению производящих функций этих величин:
т. (/) = []»>,(/). (3.40>
Z-* .и
3. Начальные моменты Х--го порядка случайной величины А' равны
значениям k-й производной от функции mx(t) в точке t = 0. т.е.
<’(0) = vt. * = 1, 2,... (3.41)
О Пример 3.17а. Найти производящую функцию, математическое
ожидание и дисперсию случайной величины, распределенной по би-
номинальному закону (см. § 4.1), т.е. дискретной случайной величи-
ны, принимающей значения X = т (т = 0, I......п) с вероятностями
Р„ „ - Р{Х - т) = С"'p”q'"a', где q = I - р.
Реше н и е. Производящая функция такой случайной величины
по фор*<уле (3.38) имеет вид:
т, (Г) = = А/е,т = я =
«-<»
= Хетс'Р"^ ’ = 2ЛТ</х' " =(/х'' +</)"
w-(l м»Л
(последнее равенство напучено на основании формулы бинома Нью-
тона).
Найдем производные функции tnx(t):
m\(t) = np(pe' +g)”‘e/;
т\ (/) = //р[( п -!)/>( ре +чУ :е:‘ + (ре' + q)" 1 ? |.
Найдем начальные моменты vt и v, по формуле (3.41):
120
vt = т\ (0) = пр( р + <;)" 1 - пр, ибо р + q = I:
V. =ш;(()) = п/>|( п-\)p(p + q Г': +(р + </)"'! =
= пр{пр - р + 1) = пр{пр + </).
Следовательно, математическое ожидание М(Х)- v, = «/?.
Для получения формулы дисперсии учтем, что она представляет
второй центральный момент рц (см. § 3.7). т.е.
D( А*) = у. = v, - V'. или D( А') = пр( пр + </)-( пр= npq.
Итак, для биноминального закона
Л/(Л') = пр. D( X) = npq. ►
Производящая функция комплексной случайной величины iX. т.е.
функция g, if) = Me"'. называемая характеристической, широко ис-
пользуется в фундаментальной теории вероятностей.
3.9. Решение задач
О Пример 3.18. По многолетним статистическим данным из-
вестно. что вероятность рождения мальчика равна 0.515. Составить
закон распределения случайной величины X — числа мальчиков в
семье с 4 детьми. Найти математическое ожидание и дисперсию
этой случайной величины.
Решени е Число мальчиков в семье из л = 4 представляет
случайную величину X с множеством значений X = т = 0. I, 2. 3. 4.
вероятности которых определяются по формуле Бернулли:
Р{.V = /и) = CfpV", где q = 1 - р.
В нашем случае п = 4. р = 0,515. q = 1 - р = 0.485.
Вычислим
Р( Д’ = 0) = С? • 0.515” • 0.485‘ = 0.055;
Р( А' = 1) = С] • 0,515' • 0.485 ‘ = 0.235:
Р(Х «2)сС; -0.515: -0.485-’ = 0.375:
Р{ А = 3) = с; • 0.515* 0,485’ = 0.265;
Р( А = 4) = С4 • 0.5154 • 0,485и = 0.070.
(Здесь учтено, что С'У = I. - 4. С; = = 6. (*4‘ - С’ = 4. С\ =1.)
121
Ряд распределения имеет вид
X, 0 1 3 4
Pi 0,055 0.235 0.375 0.265 0,070
Убеждаемся, что ]Г/>, =0.055 + 0.235 + ...+ 0,070 = 1.
/•I
Математическое ожидание М(Х) и дисперсию D(X) можно най-
ти, как обычно, по формулам (3.3) и (3.11). Но в данном случае,
учитывая, что закон распределения случайной величины X би-
номиальный (о нем см. § 4.1). можно воспользоваться прос-
тыми формулами (4.2) и (4.3):
М(Х) = пр = 4-0.515 = 2.06.
IX X} = npq = 4-0.515-0.485 = 0.999. ►
t> Пример 3.19. Радист вызывает корреспондента, причем каж-
дый последующий вызов производится лишь в том случае, если
предыдущий вызов не принят. Вероятность того, что корреспондент
примет вызов, равна 0.4. Составить закон распределения числа вы-
зовов, если: а) число вызовов не более 5; б) число вызовов не огра-
ничено.
Найти математическое ожидание и дисперсию этой случайной
величины.
Реше н и с. а) Случайная величина X — число вызовов кор-
респондента — может принимать значения I. 2. 3. 4, 5. Обозначим
событие At — /-й вызов принят (/ = I, 2, 3, 4. 5). Тогда вероятность
того, что первый вызов принят. Р{Х = I) = ЛЛ|) = 0,4.
Второй вызов состоится лишь при условии, что первый вызов
нс принят, т.е.
/,(Х = 2)=/Э(Й1Л,) = /’(Л,)/’(Л) = (1-0.4).0.4 = 0.24.
Аналогично
р(Х = 3) = />(1,1,^)= Р( 1, )/’(<. )Р(Л ) = 0.6*’ 0.4 =0.144;
/>(х=4) = р(л1л;л1л)=/’(л|)р(й5)р(я,)р(л)=
«-0.61 -0.4 = 0.0864.
Пятый вызов при любом исходе (будет принят, нс принят) — по-
следний. Поэтому
122
P(X=5)=/’(j,.4. Л,/!,) = /’( Л, )f( J, )p(/!1)p(J4 ) = 0.64 =0,1296.
(Вероятность P(X = 5) можно найти и иначе, учитывая, что по-
следний вызов будет или принят, или нет. т.е.
/>( Д' = 5) = />(л, А: А, А, А. + А, А, .< At А,) =
= 0,64 • 0,4 4- 0,64 • 0.6 = 0.64 (0.4 4- 0.6) = 0.64 = 0.1296.)
Ряд распределения случайной величины X имеет вид
X, 1 2 3 4 5
р. 0.4 0.24 0.144 0,0864 0.1296
Проверяем. что £ р, = 0.4 + 0,24 4-... + 0.1296 = I.
>*|
По формуле (3.3) вычислим математическое ожидание:
о = А/(А') = ^зд =
>1
= I • 0,4 + 2 • 0.24 + 3 • 0.144 4 4 • 0.0864 + 5 • 0.1296 = 2,3056.
Так как М(Х) — нецелое число, то находить дисперсию /ХА)
проще не по основной формуле (3.11). а по формуле (3.16). т.е.
ZXA) = М{Х') - а2.
Вычислим
W() = А = ’ • 0.4 4- 2' • 0.24 4- 3- • 0.144 4- 4: • 0.0864 +
ы
4-52-0.1296 = 7.2784.
Теперь D(X) = 7.2784 - 2.30562= 1.9626.
б) Так как число вызовов не ограничено, то ряд распределения
случайной величины X примет вид
2 1 2 3 4 • •• п •••
Р> 0.4 0.24 0.144 0,0864 ... 0.6^' • 0.4 ...
Проверяем, что
£/< =0.4 + 0.244-... + 0.6"*1-0.4 4-... = 0.40 4-0.6 4- ...4-0.6"*' +...) =
123
(использовали формулу суммы сходящегося (|<?|<1) гсометричсско-
а
го ряда: 5 =--- при а = I. q = 0,6).
i-<7
По формуле (3.4) вычислим математическое ожидание
Л/(Х) = £зд=1-0,4 + 2 0.24 + 3 0,144 + ...+л- О.б'1 0.4+ ... =
= 0,4(1 + 2 0.6 + 3 0.6-' + ... + п 0.6' ’ +...).
Для вычисления суммы полученного ряда воспользуемся формулой:
S(x) = l + 2х + 3х*’ +... + ЛГ'”’ +... = (х + № + х’ +... + .v" + ...) =
(т.с. сумма данного ряда является производной сходящегося геомет-
рического ряда при |</| = |х| < !). При х = 0,6
-------г = 6.25. т.е. Л/(Л) = 0.4 • 6,25 = 2.5.
(1-О.бГ
По формуле (3.12) вычислим дисперсию: D(X) - М(Х2} — а2.
Вначале найдем
Л/(А':)=£х;/>( = ,’-0.4 + 2;:0,24 + 3:0.144 + ...-л: 0.6'-*-0.4+ ... =
м
= 0.4(1: + 2: 0.6 + 3:-0.62 +...+ /Г 0.6"-' +...).
Дзя вычисления суммы полученного ряда рассмотрим сумму ряда
Si(x) при |х|<1:
5, (х) = I + 2' х + 3: х; +... + л2х”' +
= (х + 2х' + Зх’ +... + лх" +...) = (x.S’(x)) =
(1-х):+х-2(1-х) _ 1 + х
(1-х)4 "(1-х)’’
При х = 0.6 5, (0.6) = —= 25. т.с. М(Х-’) = 0,4 • 25 = 10.
(1-0.6)
Теперь D(X) = 10 - 2.5- = 3,75. ►
124
Е> Пример 3.20. Среди 10 изготовленных приборов 3 неточных.
Составить закон распределения числа неточных приборов среди
взятых наудачу четырех приборов. Найти .математическое ожидание
и дисперсию этой случайной величины.
Решен» е. Случайная величина X — число неточных прибо-
ров среди четырех отобранных — может принимать значения / = 0.
1.2. 3.
Обшее число способов выбора 4 приборов из 10 определяется
числом сочетаний С\\. Число способов выбора четырех приборов,
среди которых i неточных приборов и 4 - / точных (/ =0, 1,2, 3).
по правилу произведения (см § 1.5) определится произведением
числа способов выбора / неточных приборов из 3 неточных С\ на
число способов выбора 4 - i точных приборов из 7 точных С*", т.е.
С! • С*“. Согласно классическому определению вероятности
/>(ЛГ=/)=Сг5? (/ = 0, 1, 2, 3).
б.
Учитывая, что
c7 = i. с;=з, с;=с;=з. c; = i.
с; = с,'=^^ = 35, С,’=35. с;= —= 21. С) = 7.
’ 1-2-3 1-2 ’
10 9-8-7 ,1Л
с’« =ТГГТ=2,°’
вычислим
/’(х=о)=21 = 1. р(,г = |)= — 6 210 1 2
' ' 210 =±. РИ=3)=Ы 10 ' ’ 210 1 ’ 30’
т.е. ряд распределения будет такой:
*1 0 1 2 3
1/6 1/2 3/10 1/30
Убеждаемся в том, что £/> = 1/6 +1/2 + 3/10 +1/30 = I.
Математическое ожидание М(Х) и дисперсию D<X) вычисляем
по формулам (3.3) и (3.16):
а = Л/(А) =().1 + |.1 + 2— + 3- — =1.2.
6 2 10 30
125
Л/(%:) = 0-' • —+ l: • —+ 22 • — + Зг~ = 2.0
' ' 6 2 10 30
и D( У) = Л/(.)-=2,0-1.2; =0,56. ►
1> Пример 3.21. Ряд распределения дискретной случайной вели-
чины состоит из двух неизвестных значений. Вероятность того, что
случайная величина примет одно из этих значений, равна 0,8. Най-
ти функцию распределения случайной величины, если ее математи-
ческое ожидание равно 3.2, а дисперсия О.!6.
Решение. Ряд распределения имеет вид
*1 *1 &
Л 0.8 0,2
где р, = 0,8. а /л = I - р) = 1 - 0,8 = 0,2.
По условию
а = М(.Г) = 3.2,
/)(.¥) = Л/ (Л'*)- а' = £х’ - сГ = 0,16
<-|
или
0.8 т, + 0.2х, =3.2,
0.8г- +0.2х3 -3.22 =0.16.
Решая полученную систему, находим два решения:
{х,=3. к =3,4.
|х, = 4 ” (х, =2,4.
Аналогично примеру 3.11 записываем выражение функции рас-
пределения:
Г(.г) =
0 при х < 3,
0,8 при 3< 4.
I при х > 4
или F(x) =
0 при
0,2 при
I при
х<2.4,
2,4 <х <3.4.
х>3,4.
[> Пример 3.22. Рабочий обслуживает 4 станка. Вероятность то-
го, 'по в течение часа станок не потребует внимания рабочего, для
первого станка равна 0.9. для второго — 0,8, для третьего — 0.75 и
для четвертого — 0.7. Составить закон распределения случайной
величины X — числа станков, которые нс потребуют внимания ра-
бочего в течение часа.
Решение. Задача может быть решена несколькими способами.
126
Первый способ. Пусть Л4 (Л, ) — событие, состоящее
в том. что А-й станок не потребует (потребует) внимания рабочего в
течение часа. Тогда, очевидно:
Р(Л’= 0) = Р(я, Л, ) = (I-0.9)(|-0,8)(1-0.75)(1-0.7) = 0.0015:
Р( X = I) = Р( Л, Л. А, Л4 + Л, Л; Л, Л 4 + Л, Л,Л, Л, + Л, Л. Л, Л4) =
= 0.9-0.2 0.25 0.3 + 0.1 0.8 0.25 0.34-0.1 -0.2 0.75 0.3 +
+ 0.10.2 0.25 0.7 = 0.0275.
Аналогично находим
Р(Х = 2) = /’(Л.Л.Л^, + Л, Л,Л,Л4 + Л,Л,Л,Л, + Л.Л.Л, Л4 +
+Л, Л. Л, Л4 + Л, Л, Л, Л4) = 0.1685;
Р(Х = 3)= /’(Л,Л.Л,Я4 + Л,Л. Л,Л4 + 4 Л,Л,Л4 + Л,Л.Л,Л4) = 0.4245;
Р[Х = 4) = ЛЛ|Л2ЛгЛ4) = 0.378.
т.е. закон (ряд) распределения случайной величины X имеет biu:
0 1 2 3 4
Р* 0.0015 0.0275 0.1685 0.4245 0.378
Второй способ состоит в том. что заданы законы (ря-
ды) распределения альтернативных случайных величин Xk (к= I. 2. 3.
4), выражающих число станков, нс потрсбующих внимания рабочего
в течение часа (это число для каждого станка равно I. если этот ста-
нок не потребует внимания рабочего, и равно 0, если потребует):
Xt: Х< Ху Х|.
xt 0 1 0 1 х. 0 1 х. 0 1
Рн 0.1 0.9 Р.2 0.2 0,8 Р.У 0.25 0.75 Ра 0.3 0.7
Необходимо найти закон распределения суммы этих случайных
величин, т.с. X = AS + X} + AS + X». Суммируя последовательно (см.
§3.2) АГ| + AS = Z. + AS + AS= Z+ АГ3 = U. AT, + AtS + Xy + X< = U +
+ Ад = X, получим аналопгпю решению примера ЗА:
127
z = х^х2.
-/ 0 1 2
Pt 0.02 0.26 0.72
U= Z+X}:
0 1 2 3
Рт 0.005 0.08 0.375 0.54
и. наконец, распределение X - U + X±, т.е. получили (3.42).
Третий способ. Распределение X можно получить чисто
механически, перемножив биномы (двучлены):
<p4(z) = (0J+0.9z)(0,2 + 0.8r)(0.25+ O,75z)(O.3*O.7r). (3.43)
причем каждый из пяти полученных коэффициентов при ? (к = 0. I.
2, 3. 4) в функции ср, (с) будет выражать соответствующие вероятно-
сти Р(Х = к). Действительно, преобразовав выражение (3.43), получим
Ф4 (г) = 0.0015 + 0.02753 + 0.1685? + 0.4245? + 0.378г4.
где коэффициенты — это вероятности значений случайной величи-
ны Х(3.42). ►
Данный формальный способ основан на том. что искомые веро-
ятности являются коэффициентами при г* производящей функции
случайной величины А' = которой (при _ = е') является
ci
функция фл(-) = */’,’)• Действительно, по свойству (3.40)
«•<
производящая функция суммы независимых случайных величин
равна произведению их производящих функций, в данном случае
биномов (q + />,?) (см. § 3.8).
О Пример 3.23. В 1-й урне содержится 6 белых и 4 черных шара, а
во 2-й — 3 белых и 7 черных шаров. Из 1-й урны берут наудачу два
шара и перекладывают во 2-ю урну, а затем из 2-й урны берут наудачу
один шар и перекладывают в 1-ю урну. Составить законы распределе-
ния числа белых шаров в 1 -й и 2-й урнах.
Решение. Найдем закон распределения случайной величины
X — числа белых шаров в 1-й урне.
Пусть Д(Д) — событие, состоящее в извлечении из первой урны
/-го белого (черного) шара (/ = 1, 2), а В(В} - извлечение из 2-й
урны белого (черного) шара после того, как в нее из 1 -й урны пере-
ложили два извлеченных шара.
В соответствии с условием число X белых шаров в 1-Й урне может
быть равным 4. 5. 6 или 7. Вероятность того, что в 1-й урне останется
4 белых шара, будет равна вероятности совместного осуществления трех
событий: из 1-Й урны извлечены первый шар — белый, второй шар —
128
белый, из 2-й урны извлечен черный шар (после того как в нес перело-
жили два белых шара), т.е.
Р(Л = 4) = />(4и:в)=/’(4)/’Л(л)Ли«)=^|н = ^-
рассуждая аналогично, получим
р(л' = 5) = р(44В+й,4^+445)=
6 4 _8_ 6 £ 5 5 89
10 9 12^10 9 12 10'9’12 “180*
Р( Л' = 6) = Р( л, Л, В + 4 А:В + .4,4в) = _4_ 3 6_ 4 _4_ _£ 6 _4 2_. ’ 10 9 12 10 9 12 10 9 12 "18’ Р(.Г = 7) = Р(4Л.Я) = — — = —. ' ' ' ' ' 10 9 12 30 Итак, закон распределения
А- 4 5 6 7
А 7/36 89/180 5/18 1/30
Убеждаемся в том, что
£ р, = 7/36 + 89/180 + 5/18 +1/30 = I.
Распределение числа Y белых шаров во 2-й урне можно найти
аналогично, но проще это сделать, если учесть, что X + Y = 9 (при
любых значениях xt и уД Поэтому закон распределения случайной
величины Y = 9 - X есть
У/ 2 3 4 5
А 1/30 5/18 89/180 7/36
С> Пример 3.23а. За пятилетие фирма может прекратить свое су-
ществование с вероятностью 1/2. выжить в конкурентной борьбе с
вероятностью 1/3 и разделиться на две фирмы с вероятностью 1/6. В
следующее пятилетие с каждой фирмой может произойти то же самое
с теми же вероятностями. Составить закон распределения числа фирм
к концу второго пятилетия.
Решение. Случайная величина X — число фирм к концу вто-
рого пятилетия — может принимать значения 0. 1,2, 3. 4. Обозначим
5 Teopm •cpornux'tt* м шпештгчесхаа птгхтт
129
события ЛДЯ,) — к концу первого (второго) пятилетия будет / фирм.
г = 0. 1.4 . Известно, что Р( Д,) = 112. Р( Д ) = 1 / 3. Р( Л,) = 1 /6.
В соответствии с условием найдем вероятности:
РЫ = 0) = Р( Д Д + Д в, + Л, в0) = 1 I +1 • 1 +1 - ^ = И;
р(л-=» = р(лд + л:В11Ц.1+1(1.1+1.1]=1:
Р(.Г = 2) = Р(Дв.+Л,в,) = 1-1 + 1[1.1 +
> о о\3 3
6 2 * 2 6, 108’
Р(Х =4)= Р(А:В,) =
1 | 1 1'1 I
б(б’б/ 216’
Более сложные выражения в скобках для вероятностей событий,
происходящих совместно с событием Лэ. связано с тем. что при на-
ступлении события Лэ происходит разделение фирмы на две. из кото-
рых одна (или обе) могут ликвидироваться, выжить либо вновь разде-
литься на две.
Итак, искомый закон распределения
Xj 0 1 2 3 4
А 17/24 1/6 11/108 1/54 1/216
Условие =1 выполнено. ►
1-0
> Пример 3.24. Дана функция распределения случайной вели-
чины
Г(х) =
0
х:/4
I
при л* 5 0,
при 0<х<2,
при х > 2.
Необходимо: а) найти плотность вероятности <р(х); б) постро-
ить графики ф(х) и Дх); в) убедиться в том. что X — непрерывная
случайная величина; г) найти вероятности Р(Х=\), Р(Х<\).
Л1 Х< 2) (две последние вероятности показать на графиках <р(х)
и А(х)); д) вычислить математическое ожидание А/(Л). дисперсию
ZX.V). моду Мо(Х) и медиану Ме(Х}.
Реше н и с. а) Плотность вероятности
130
<p(.v) = F'(v)
10 при х < 0 и при г > 2.
\х/2 при О<х£2.
б) Графики ф(.г) и Дх) изображены на рис. 3.20. а и б.
Рис. 3.20
в) Случайная величина А' — непрерывная, так как функция рас-
пределения Дх) непрерывна, а се производная — плотность вероят-
ности ф(х) — непрерывна во всех точках, кроме одной (х = 2).
г) Вероятность f\X = 1) = 0 как вероятность отдельно взятого
значения непрерывной случайной величины.
Вероятность F\X < 1) можно найти либо по определению функции
распределения (3.18), либо по формуле (3.21) через плотность вероят-
ности ф(х):
l: I
Р(Х < I) = F(I) = — = - (ордината графика ДI) — см. рис. 3.20. 6 —
или
131
lO
0 dx*
4
(площадь под кривой распределения ф(х)на отрезке |0;1| — см.
рис. 3.20, а).
Вероятность Р(1<А*<2) можно найти либо как приращение
функции распределения по формуле (3.20), либо по формуле (3.22)
через плотность вероятности ф(х):
или P(I<A’<2) = J
-t/x
2
f(lSXS2) = F(2)-F(l) = ^-7 = -
(приращение ординаты графика Дх) на отрезке [1:2| — рис. 3.20, (5)
£ 11=2
4’4'4
(площадь под кривой распределения ф(х) на отрезке |1;2| —
рис. 3.20. а).
л) По формуле (3.25) математическое ожидание
0 А =
и = М(Х)
()•<& +
= 0 +
+ 0 =—-2’= —.
6 о 6 3
Если представить распределение случайной величины А' в виде
единичной массы, распределенной по треугольнику (рис. 3.20. «), то
значение М(Х) = 4/3 означает абсциссу центра массы треугольника.
По формуле (3.27) дисперсия IXX) = ЛЛХ-) - а2.
Вначале найдем
Л/(№)
<Zr + 0 = 2.
Теперь D(X) = 2 -
Плотность вероятности ф(х) максимальна при х=2 (см
рис. 3.20, а), следовательно, Мо(Х) = 2.
Медиану MeiX) = b найдем из условия Rb} = —, т.е. — = - , от-
2 4 2
куда b = Ме(Х) = 41 . или через плотность вероятности
I = т.е. 0+ I -<& = — =Т = 7’
J— 1 Jo 2 4 <1 4 2
откуда b = Ме(Х) = V2. ►
132
р> Пример 3.24а. Функция распределения непрерывной случай-
ной величины X, распределенной по закону Коши, имеет вид:
Fix) = А + £arclg — (а > 0).
а
Найти: а) постоянные А и 5; б) плотность вероятности ф(х);
в) вероятность Р(~а< X <а). Убедиться в том, что математиче-
ское ожидание и дисперсия для этой случайной величины не су-
ществуют.
Р е ш с н и е. а) Воспользуемся свойствами функции распределе-
ния F(-<o) = 0. Г(-кю) = 1.
= lim F(x) = lim (J + В arclg — ) = A - B— = 0;
a о
F(-hx) = lim F(x) = lim (J + В arclg —) = A + /?— = I.
*•- * a 2
Из полученной системы уравнений находим .4 = -. В = —. т.е.
2 л
% I I *
F(x) = - + -arclg-.
2 7Т а
б) Плотность вероятности
«Кх) = F'(x) = I 7 + - arclg - | '=-.
12 л а) п(х‘ + а')
в) По формуле (3.20) вероятность
Р(-а < X £ а) = F(a)~ F(-a) = [ — ь— arctg 11-
\ 2 п )
т.е. математическое ожидание не существует, ибо
lim In (№ + а') = V.
Следовательно, нс существует и дисперсия D(X). ►
Упражнения
3.25. Вероятность поражения вирусным заболеванием куста
земляники равна 0.2. Составить закон распределения числа кустов
земляники, зараженных вирусом, из четырех посаженных кустов.
133
3.26. Стрелок ведет стрельбу ио цели с вероятностью попадания
при каждом выстреле 0.2. За каждое попадание он получает 5 очков, а
в случае промаха очков ему не начисляют. Составить закон распреде-
ления числа очков, полученных стрелком за 3 выстрела, и вычислить
математическое ожидание этой случайной величины.
3.27. В рекламных целях торговая фирма вкладывает в каждую
десятую единицу товара денежный приз размером I тыс. руб. Со-
ставить закон распределения случайной величины — размера выиг-
рыша при пяти сделанных покупках. Найти математическое ожида-
ние и дисперсию этой случайной величины.
3.28. Клиенты банка, нс связанные друг с другом, не возвра-
щают кредиты в срок с вероятностью 0,1. Состави л» закон распре-
деления числа возвращенных в срок кредитов из 5 выданных. Найти
математическое ожидание, дисперсию и среднее квадратическое
отклонение этой случайной величины.
3.29. Контрольная работа состоит из трех вопросов. На каждый
вопрос приведено 4 ответа, один из которых правильный. Составить
закон распределения числа правильных ответов при простом угады-
вании. Найти математическое ожидание и дисперсию этой случай-
ной величины.
3.30. В среднем по 10% договоров страховая компания выпла-
чивает страховые суммы в связи с наступлением страхового случая.
Составить закон распределения числа таких договоров среди науда-
чу выбранных четырех. Вычислить математическое ожидание и дис-
персию этой случайной величины.
3.31. В билете зри задачи. Вероятность правильного решения пер-
вой задачи равна 0.9, вгорой — 0.8, третьей — 0.7. Составить закон
распределения числа правильно решенных задач в билете и вычислить
математическое ожидание и дисперсию этой случайной величины.
3.32. Вероятность попадания в цель при одном выстреле равна
0.8 и уменьшается с каждым выстрелом на 0.1. Составит!, закон
распределения числа попаданий в цель, если сделано три выстрела.
Найти математическое ожидание, дисперсию и среднее квадратиче-
ское отклонение этой случайной величины.
3.33. Произведено два выстрела в .мишень. Вероятность попа-
дания в мишень первым стрелком равна 0,8, вторым — 0.7. Соста-
вить закон распределения числа попаданий н мишень. Найти мате-
матическое ожидание, дисперсию и функцию распределения этой
случайной величины и построить се график. (Каждый стрелок дела-
ет по одному выстрелу.)
3.34. Найти закон распределения числа пакетов трех акций, по
которым владельцем будет получен доход, если вероятность получе-
ния дохода по каждому из них равна соответственно 0,5, 0.6, 0,7.
Найти математическое ожидание и дисперсию данной случайной
величины, построить функцию распределения.
134
3.35. Дан ряд распределения случайной величины
X, 2 4
А Р\ Р?
Найти функцию распределения этой случайной величины, если
ее математическое ожидание равно 3.4, а дисперсия равна 0.84.
3.36. Из пяти гвоздик две белые. Составить закон распределе-
ния и найти функцию распределения случайной величины, выра-
жающей число белых гвоздик среди двух одновременно взятых.
3.37. Из 10 телевизоров на выставке 4 оказались фирмы «Со-
ни». Наудачу для осмотра выбрано 3. Составить закон распределе-
ния числа телевизоров фирмы «Сони* среди 3 отобранных.
3.38. Среди 15 собранных агрегатов b нуждаются в дополни-
тельной смазке. Составить закон распределения числа агрегатов,
нуждающихся в дополнительной смазке, среди пяти наудачу ото-
бранных из общего числа.
3.39. В магазине продаются 5 отечественных и 3 импортных теле-
визора. Составить закон распределения случайной величины — числа
импортных из четырех наудачу выбранных телевизоров. Найти функ-
цию распределения этой случайной величины и построить ее график.
3.40. Вероятность того, что в библиотеке необходимая студенту
книга свободна, равна 0,3. Составить закон распределения числа биб-
лиотек. которые посетит студент, если в юроде 4 библиотеки. Найти
математическое ожидание и дисперсию этой случайной величины.
3.41. Экзаменатор задает студенту вопросы, пока тот правильно
отвечает. Как только число правильных ответов достигнет четырех ли-
бо студент ответит неправильно, экзаменатор прекращает задавать во-
просы. Вероятность правильного ответа на одни вопрос раина 2/3 Со-
ставить закон распределения числа заданных студенту вопрос* в
3.42. Торговый агент имеет 5 телефонных номеров потенци-
альных покупателей и звонит им до тех пор, пока не полупи заказ
на покупку товара. Вероятность того, что потенциальный покупа-
тель сделает заказ, равна 0,4. Составить закон распределения чис-
ла телефонных разговоров, которые предстоит провести агенту.
Найти математическое ожидание и дисперсию этой случайной ве-
личины.
3.43. Каждый поступающий в институт должен сдать 3 экзамена.
Вероятность успешной сдачи первого экзамена равна 0.9. второго —
0,8, третьего — 0,7. Следующий экзамен поступающий сдает только в
случае успешной сдачи предыдущего. Составить закон распределения
числа экзаменов, сдававшихся поступающим в институт. Найти мате-
матическое ожидание этой случайной величины.
135
3.44. Охотник, имеющий 4 патрона, стреляет по дичи до перво-
го попадания или до израсходования всех патронов. Вероятность
попадания при первом выстреле равна 0,6. при каждом последую-
щем — уменьшается на 0.1. Необходимо: а) составить закон распре-
деления числа патронов, израсходованных охотником; 6) найти ма-
тематическое ожидание и дисперсию этой случайной величины.
3.45. Из поступивших в ремонт 10 часов 7 нуждаются в общей
чистке механизма. Часы не рассортированы по виду ремонта. Мастер,
желая найти часы, нуждающиеся в чистке, рассматривает их поочеред-
но и. найдя такие часы, прекращает дальнейший просмотр. Составить
закон распределения числа просмотренных часов. Найти математиче-
ское ожидание и дисперсию этой случайной величины.
3.46. Имеются 4 ключа, из которых только один подходит к
замку. Составить закон распределения числа попыток открывания
замка, если испробованный ключ в последующих попытках не уча-
ствует. Найти математическое ожидание, дисперсию и среднее
квадратическое отклонение этой случайной величины.
3.47. Абонент забыл последнюю цифру нужного ему номера те-
лефона, однако помнит, 'гто она нечетная. Составить закон распреде-
ления числа сделанных им наборов номера телефона до попадания на
нужный номер, если последнюю цифру он набирает наудачу. а на-
бранную цифру в дальнейшем нс набирает. Найти математическое
ожидание и функцию распределения этой случайной величины.
3.48. Дана функция распределения случайной величины X
0 при х£ I,
0.3 при 1<л<2.
0.7 при 2<х$3,
I при х > 3.
Найти: а) ряд распределения: б) М(Х) и ЩХ); в) построить мно-
гоугольник распределения и график Дх).
3.49. Даны законы распределения двух независимых случайных
величин
и У.
Г(х) =
X, 0 1 3
р, 0.2 0.5 •>
У. 2 3
Р. 0.4 2
Найти вероятности, с которыми случайные величины принимают
значите 3. а затем составить закон распределения случайной величины
ЗУ - 2Уи проверил» выполнение свойств математических ожиданий и
дисперсий:
Л/(ЗХ- 2У) = ЗМ(Х) - 2Л/()). МЗХ - 2 П = 9ДЛ) + 4ZX П-
136
3.50. На двух автоматических станках производятся одинаковые
изделия. Даны законы распределения числа бракованных изделий,
производимых в течение смены на каждом из них:
а) для первого
X, 0 1 2
р< 0.1 0,6 0.3
б) для второго
0 2
Pi 0.5 0.5
Необходимо: а) составить закон распределения числа производимых
в течение смены бракованных изделии обоими станками; б) проверить
свойство математического ожидания суммы случайных величии.
3.51. Одна из случайных величин задана законом распределе-
ния
X) -1 0 1
Р, 0.1 0.8 0.1
а другая имеет биномиальное распределение с параметрами п = 2, р = 0.6.
Составить закон распределения их суммы и найти математическое
ожидание этой случайной величины.
3.52. Случайные величины X и Y независимы и имеют один и
тот же закон распределения:
Значение 1 2 4
Вероятность 0.2 0.3 0.5
Составить закон распределения случайных величин 2Х и X + Y.
Убедиться в том. что 2Х * X + К но Л/(2Л)= М(Х + У).
3.53. По данным примера 3.52 убедиться в том, что X' * ХУ .
Проверить равенство M(XY) =
3.54. Два стрелка сделали по два выстрела по мишени. Вероят-
ность попадания в мишень для первого стрелка равна 0,6, для вто-
рого — 0.7. Необходимо: а) составить закон распределения общего
числа попаданий; 6) найти математическое ожидание и дисперсию
этой случайной величины.
3.55. Пусть X. Y. 7. — случайные величины: X — выручка фир-
мы, К — ее затраты. 2 = X- Y - прибыль. Найти распределение
прибыли Z. если затраты и выручка независимы и заданы распреде-
лениями:
х, 3 4 5
Р, 1/3 1/3 1/3
У> 1 2
Р) 1/2 1/2
137
3.56. Пусть X — выручка фирмы в долларах. Найти распределе-
ние выручки в рублях Z = X' Y в пересчете по курсу доллара Y, если
выручка Л' нс зависит от курса Y. а распределения X и Y имеют вид
х, 1000 2000
р. 0.7 0.3
У, 25 27
Р/ 0.4 0.6
3.57. Сделано два высокорисковых вклада: 10 тыс. руб. — в
компанию /I и 15 тыс. руб. — в компанию В. Компания А обещает
50% годовых, но может «лопнуть» с вероятностью 0,2. Компания В
обещает 40% годовых, но может «лопнуть» с вероятностью 0,15. Со-
ставить закон распределения случайной величины — обшей суммы
прибыли (убытка), полученной от двух компаний через год. и найти
ее математическое ожидание.
3.58. Дискретная случайная величина X задана рядом распреде-
ления _________________________________________
х< 1 2 3 4 5
Р, 0.2 0.3 0.3 0.1 0.1
Найти условную вероятность события X < 5 при условии, что
Х>2.
3.59. Случайные величины А'ь X? независимы и имеют одина-
ковое распределение
х, 0 1 2 3
Р, 1/4 1/4 1/4 1/4
Найти: а) вероятность события ЛГ| + AS > 2: б) условную вероят-
ность PV| J(Af| + А',) > 2 |.
3.60. Распределение дискретной случайной величины Л' задано
формулой р(Х- к) = Ск2, где к = 1. 2. 3. 4. 5.
Найти: а) константу С; б) вероятность события 2| s 1.
3.61. Распределение дискретной случайной величины АГ опреде-
ляется формулой
ЛХ=А)=С/2Х. к = 0.1.2........
Найти: а) константу С: б) вероятность /’(.¥< 3).
3.62. Случайная величина X, сосредоточенная на интервале
3|. задана функцией распределения F\x) = — х + - • Найти ве-
4 4
роятность попадания случайной величины X в интервал |0; 2]. По-
строить график функции Fix).
138
3.63. Случайная величина X. сосредоточенная на шпервалс |2: 6|. за-
дана функцией распределения Г(х) = ~-(х*’-4х + 4). Найти вероят-
ность того, что случайная величина X примет значения: а) меньше 4;
б) меньше 6; в) не меньше 3; г) не меньше 6.
3.64. Случайная величина X, сосредоточенная на интервале (I: 4).
тяпяна квадратичной функцией распределения Дх) = ах2 + Ьх + с.
имеющей максимум при х = 4. Найти параметры а. Ь. с и вычис-
лить вероятность попадания случайной величины X в интервал
(2; 3J.
3.65. Дана функция
, v |() при х < 0.
Л»“ |Сх<?"* при х £ 0.
При каком значении параметра С эта функция является плотно-
стью распределения некоторой непрерывной случайной величины X'?
Найти математическое ожидание и дисперсию случайной величины X.
3.66. Случайная величина X задана функцией распределения
при х S 0.
при 0< х< I.
при х> I.
Найти: а) плотность вероятности ф(х): б) математическое ожида-
ние М(Ху, в) дисперсию О(Л); г) вероятности Р(Х = 0,5). f\X< 0.5).
ДО,5 s X <. I): д) построить графики ф(х) и Дх) и показать на них
математическое ожидание М(Х) и вероятности, найденные в и. г).
3.67. По данным примера 3.66 найти: а) моду и медиану слу-
чайной величины X: 6) квантиль xfl/1 и 20%-ную точку распределе-
ния X.
3.68. По данным примера 3.66 найти коэффициент асимметрии
и эксцесс случайной величины X.
3.69. Случайная величина .¥ распределена по закону Коши:
Ф(х) = —-——. Найти: а) коэффициент А; б) функцию распределения
I +х*
Дх); в) вероятность Л~1 s X < I). Существуют ли для случайной
величины X математическое ожидание и дисперсия?
3.70. Случайная величина X распределена по закону Лапласа:
ф(х)=Лс' Л|’’. Найти: а) коэффициент А; б) функцию распределения
Лх); в) математическое ожидание М{Х) и дисперсию /ХА). Построить
графики ф(х) и F(x).
3.71. Случайная величина X распределена по закону «прямо-
угольного треугольника» в интервале (0; с) (рис. 3.21). Найти: а) вы-
ражение плотности вероятности <р(х) и функции распределения Нх);
139
б) математическое ожидание Л/(Л). дисперсию D(Xj, центральный
момент мз(Л); в) вероятность Р(с/2 i X s с) и показать ее на данном в
условии графике ф(х) и построенном графике Дх).
3.72. Случайная величина X распределена по закону Симпсона
(равнобедренного треугольника) на отрезке [—3; 3| (рис. 3.22). Най-
ти: а) выражения плотности вероятности ф(х) и функции распреде-
ления Дх); б) числовые характеристики М(Х), D(X). из(Л); в) веро-
ятность Д-3/2 s Х< 3) и показать ее на данном в условии графике
Ф(х) и построенном графике Дх).
Глава 4
Основные законы распределения
В данной главе описаны основные законы распределения дис-
кретных (§ 4.1—4.4) и непрерывных (§ 4.5—4.8) случайных величин,
используемых для построения теоретико-вероятностных моделей ре-
альных социально-экономических явлений. В § 4.9 рассматриваются
распределения случайных величин, используемых в качестве вспо-
могательного технического средства при решении различных задач
статистического анализа.
4.1. Биномиальный закон распределения
Определение. Дискретная случайная величина X имеет би-
номиальный закон распределения с параметрами п и р. если она при-
нимает значения 0, 1.2..т....п с вероятностями
Р(Х - т} = С^p'q'1", (4.1)
где 0 < р < 1.7= I - р.
Как видим, вероятности Р(Х - т) находятся ио формуле Бер-
нулли. полученной выше (гл. 2). Следовательно, биномиальный закон
распределения представляет собой закон распределения числа X = т
наступлений события А в п независимых испытаниях, в каждом из
которых оно может произойти с одной и той же вероятностью р.
Ряд распределения биномиального закона имеет вид:
Х{ 0 1 2 ... т п
Pi «г С'ЯРЧЯ ’ c;p:4z ... e^q" г
Очевидно, что определение биномиального закона корректно,
так как основное свойство ряда распределения £ /? = I выполнено.
1*41
и
ибо £/>, есть не «гто иное, как сумма всех членов разложения би-
нома Ньютона:
ц” + C'„pqn 1 + С1р'чк ' + ... + С7^'</г +...+ р -• р)п = Г = |
(отсюда и название закона — биномиальный).
141
На рис. 2.1 приведен многоугольник (полигон) распределения
случайной величины А', имеющей биномиальный закон распределе-
ния с параметрами п = 5. р = 0.2. а на переднем форзаце учебника -
и при р = 0,3; 0.5; 0.7; 0.8.
Теорема1. Математическое ожидание случайной величины X. рас-
пределенной по биномиальному закону.
М(Х) = пр, (4.2)
а ее дисперсии
Г*Х) = npq. (4.3)
□ Случайную величину X — число т наступлений события А в
п независимых испытаниях — можно представить в виде суммы п
независимых случайных величин Х} + X? + ... + Ад + ... + Х„. каждая из
которых имеет один и тот же закон распределения, т.е.
А* = £ А', . где
X, 0 1
р. Ч Р
Случайная величина Ад выражает число наступлений события А
в k-м (единичном) испытании (А = I. 2..л), т.е. при наступлении
события А .¥д = I с вероятностью р. при ненаступлснии — Xk = 0 с
вероятностью q. Случайную величину А\ называют альтернативной
случайной величиной (или распределенной но закону Бернулли. или
индикатором события Л).
Найдем числовые характеристики альтернативной случайной ве-
личины Ад по с|юрмулам (3.3) и (3.11):
= Л/( V, ) = £.г,д =0 </+ !•/>=/?.
ы
) = £(*, ~и,)-р, =(о-/>)? •*(!-/>) /» =
ы
= Р'Ч + q‘p=pq(p + </)=/*/.
так как р + q = 1.
Таким образом, математическое ожидание альтернативной слу-
чайной величины (4.4) равно вероятности р появления события А в
единичном испытании, а ее дисперсия — произведению вероятности р
появления события .4 на вероятность q его непоявления.
1 Заметим, чго формулы (4.2). (4.3). iipcjicraivwKMiiHc заключение теоремы, были
получены ранее и § 3 К другим способом — с помощью производящей функции
142
Теперь математическое ожидание и дисперсия рассматриваемой
случайной величины X
М(Х) = M(Xi +...+ Xi +...+ Xn) = р +... 4-р * np,
и гж>
D(X) = D(Xi +...+ Xt +...+ Xn) = pq±...+ pq = npq
n put
(при нахождении дисперсии суммы случайных величин учтена их
независимость).
Следствие. Математическое ожидание частости — события в
п
п независимых испытаниях, в каждом из которых оно может насту-
пить с одной и той же вероятностью р. равно р. т.е.
= (4.5)
а ее дисперсия
dW = ^. (4.6)
\ п ) п
_ ,, _ т X т X v
□ Частость события — есть — . т.е. — = —. где X — случайная
п п п п
величина, распределенная по биномиальному закону.
Поэтому
Замечание. Теперь становится понятным смысл аргу-
ментов в функциях Дх) и Ф(.г). содержащихся в локальной и ин-
тегральной теоремах Муавра—Лапласа (см. § 2.3). Так. в функции
„ . т-пр v
fix) аргумент х= . есть отклонение числа X = т появления
события А в п независимых испытаниях, распределенного по бино-
миальному закону, от его среднего значения Л/(Л) = пр. выраженное
в стандартных отклонениях ст, = yfnpq. Аргумент
х = —fi. - &___ в функции Ф(х). рассматриваемой в следствии
интегральной теоремы Муавра—Лапласа, есть отклонение А час-
143
тости т/п события А в п независимых испытаниях от его вероят-
ности р в отдельном испытании, выраженное в стандартных от-
клонениях ст
В гл. 2 установлено, что наивероятнейшес число наступлений
события А в л повторных независимых испытаниях, в каждом из
которых оно может наступить с одной и той же вероятностью р,
удовлетворяет неравенству (2.4). Это означает, что мода случайной
величины. распределенной по биномиальному закону, — число целое —
находится из того же неравенства
пр - q £ Мо( X) < пр + р.
(4.7)
Биномиальный закон распределения широко используется в
теории и практике статистического контроля качества продукции,
при описании функционирования систем массового обслуживания,
при моделировании цен активов, в теории стрельбы и в других об-
ластях. Так, например, полученный в примере 3.18 закон распреде-
ления случайной величины X — числа мальчиков в семье из 4 детей
биномиальный с параметрами п = 4. р = 0,515.
> Пример 4.1. В магазин поступила обувь с двух фабрик в cooi-
ношенни 2:3. Куплено 4 пары обуви. Найти закон распределения
числа купленных пар обуви, изготовленной первой фабрикой. Най-
ти математическое ожидание и среднее квадрап<ческос отклонение
этой случайной величины.
Р е ш е н и с. Вероятность того, что случайно выбранная пара
обуви изготовлена первой фабрикой, равна р - 2/(2 + 3) = 0,4. Слу-
чайная величина X — число пар обуви среди четырех, изготовленных
первой фабрикой, имеет биномиальный закон распределения с пара-
метрами п = 4. р = 0.4. Рял распределения X имеет вид:
л; 0 1 2 3 4
А 0.1296 0,3456 0,3456 0,1536 0,0256
(Значения р, = Р[Х = т), (т = 0. I. 2, 3, 4) вычислены по фор-
муле (4.1): Р(Х = т) = С; 0,4" 0.64 ".)
Найдем математическое ожидание и дисперсию случайной вели-
чины X по формулам (4.2) и (4.3):
М(Х) = пр = 4 • 0.4 = 1.6. /ХА) = npq = 4 • 0.4 • 0,6 = 0.96.
Замечание. Нетрудно заметить, что полученное распреде-
ление двумодальное (имеющее две моды): Мо(Х)\ = I и Мо^Х)^ — 2,
144
так как эти значения имеют наибольшие (и равные между собой)
вероятности. Моду Мо(Х) — число целое — можно найти из нера-
венства (4.7): 4 • 0.4 - 0,6 <ЛЛ>(Х)<40.4 + 0.4 или \$Мо(Х)<2,
т.е. Ш*)| = । и Мо(Х)>~ 2. ►
|> Пример 4.2. По данным примера 4.! найти математическое
ожидание и дисперсию частости (доли) пар обуви, изготовленных
первой фабрикой, среди 4 купленных.
Решение. Имеем п = 4, р = 0.4. По формулам (4.5). (4,6):
Мрфо.4. Dpfl=O±^ = o.O6. ►
\п ) Vп) 4
4.2. Закон распределения Пуассона
Определение. Дискретная случайная величина X имеет
закон распределения Пуассона с параметром а > 0. есп/ она принима-
ет значения 0.1. 2, .... т,... {бесконечное, но счетное множество зна-
чений) с вероятностями
/>(Х = т) = А2£_ = р_(Л). (4.8)
т\
Ряд распределения закона Пуассона имеет вид:
Xi 0 1 •) т • ••
Pi ** ke‘K Ус* 2! • • • XV — ...
Очевидно, что определение закона Пуассона корректно, так как
основное свойство ряда распределения ^р, = 1 выполнено, ибо
сумма ряда
t 2! ml j
(учтено, что в скобках записано разложение в ряд функции е1 при
х = к).
145
На рис. 4.1 показан
многоугольник (ПОЛИГОН)
распределения случайной
величины, распределенной
по закону Пуассона
ДХ= m) = FW(X) с пара-
метрами X = 0,5, X = I.
Х= 2, Х = 3,5.
Теорема. Математиче-
ское ожидание и дисперсия
случайной величины. распре-
деленной по закону Пуассона,
совпадают и равны парамет-
ру X этого закона, т.е.
А/(А)=Х,
ZXA)=X.
(4.9)
(4.10)
□ Найдем математическое ожидание случайной величины X:
7и ZS m! tn(m-l)!
= Хе-1 У'-р~—Г = Хе'х Ь + X + — +... | = ke’'e* = X.
£(m-l)! t 2» J
Дисперсию случайной величины X найдем по формуле (3.16).
т.е. Д(Л) = А/СХ2) - а2. Вначале получим формулу для
/.I «-о т- м.| (т-1)!
= X W + Xe'V = Х: + X.
Теперь D(A’) = (X*+Х)-Х* = Х.
При достаточно больших п (вообще при ?j-> х) и малых значе-
ниях р (р->0) при условии, что произведение пр — постоянная
величина (пр -> X = const), закон распределения Пуассона является
146
хорошим приближением биномиального закона, гак как в этом слу-
чае функция вероятностей Пуассона (4.8) хорошо аппроксимирует
функцию вероятностей (4.1). определяемую по формуле Бернулли
(см. § 2.2). Иначе, при р -> 0 . п —> г . пр -> X = const закон распре-
деления Пуассона является предельным случаем биномиального
закона. Так как при этом вероятность р события А в каждом испы-
тании мала, то закон распределения Пуассона называют часто зако-
ном редких явлений.
Наряду с «предельным» случаем биномиального распределения
закон Пуассона может возникнуть и в ряде других ситуаций. Так. в
гл. 7 показано, что для простейшего потока событий число событий,
попадающих на произвольный отрезок времени, есть случайная вели-
чина, имеющая пуассоновское распределение.
По закону Пуассона распределены, например, число рождения
четверней, число сбоев на автоматической линии, число отказов
сложной системы в «нормальном режиме», число «требований на об-
служивание», поступивших в единицу времени в системах массового
обслуживания, и др.
Отмстим еще, что если случайная величина представляет собой
сумму двух независимых случайных величин, распределенных каж-
дая по закону Пуассона, то она также распределена по закону Пуас-
сона.
t> Пример 4.3. Доказать, что сумма двух независимых случайных
величин, распределенных по закону Пуассона с параметрами X, и X..
также распределена по закону Пуассона с параметром X = X, + X,.
Решение. Пусть случайные величины X = т и Y = п имеют
законы распределения Пуассона соответственно с параметрами Xt и
X,. В силу независимости случайных величин X и К их сумма
Z= Х+ Y принимает значение Z = з с вероятностью
/>(Z = .v)=P(.V = ш) -Р(У-п) =
у Xfe 1 Х.е " _ у А| ~
т' п\ ~L £.,т1п'.~
С-(Х.-t;)у *•»* . е l/,O J у х.
л! 1 '
•
Полагая, что X. + Х, = Х, и учитывая, что У -——— Х.”ЯХ’ =
• £ф-л)’л! 1
= £с"Х; “X" = (X, + X.) '= Х‘. получим P(Z = s) = —у— . т.е. слу-
м< •f*
147
чайная величина Z = X + Y распределена по закону Пуассона с па
раметром X = А,, + X,. ►
4.3. Геометрическое распределение и его обобщения
Определение. Дискретная случайная величина X - т имеет
геометрическое распределение с параметром р, если она принимает
значения 1, 2.т... (бесконечное, но счетное множество значений)
с вероятностями
Р(Х = т) = pq"1 ' , (4.Ц)
где 0 < р < I, q - 1 - р.
Ряд геометрического распределения случайной величины имеет вцд:
Xi 1 2 3 т
А Р PQ ДО2 ... Р<Г 1 ...
Нетрудно видеть, что вероятности р, образуют геометрическую
прогрессию с первым членом р и знаменателем q (отсюда название
«геометрическое распределение»).
Определение геометрического распределения корректно, гак как
сумма ряда
^р, = р + pq + ...+ pef' + ...= р( I + q + L = £ = 1
(так как —— = — есть сумма геометрического ряда У q‘"~' при
*-<? Р Г!
Случайная величина X = т, имеющая геометрическое распределе-
ние, представляет собой число т испытаний, проведенных по схеме
Бернулли, с вероятностью р наступления события в каждом испыта-
нии до первого положительного исхода.
Так, например, число вызовов радистом корреспондента до тех
пор, пока вызов не будет принят, рассматриваемое в примере 3.19. б.
есть случайная величина, имеющая геометрическое распределение с
параметром р = 0,4.
Теорема. Математическое ожидание случайной величины А.
имеющей геометрическое распределение с параметром р.
М(*)=-, (4-,2>
Р
148
а ее дисперсия'
Р'
(4.13)
ще 4 = 1 Р-
[> Пример 4.4. Проводится проверка большой партии деталей до
обнаружения бракованной (без ограничения числа проверенных
деталей). Составить закон распределения числа проверенных дета-
лей. Найти его математическое ожидание и дисперсию, если из-
вестно. что вероятность брака для каждой детали равна 0,1.
решение. Случайная величина X — число проверенных дета-
лей до обнаружения бракованной — имеет геометрическое распределе-
ние (4.11) с параметром р = 0.1. Поэтому ряд распределения имеет вид
Xi 1 2 3 4 ... т • ••
р. 0,1 0,09 0.081 0,0729 0,9я* • 0,1
По формулам (4.12) и (4.13)
М(Л)=-=—= 10. /ХА1=Д- = '^4 = 90. ►
р 0,1 р~ о,Г
Геометрическое распределение при к = I является частным слу-
чаем распределения Паскаля, для которого
Р(Х = т) = Cxj\p'*, т = к, к +1 ....
и числовые характеристики
М(Л') = -. D(A') = M.
Р Р'
Геометрическое распределение характеризует число т испыта-
ний (проведенных по схеме Бернулли с вероятностью р наступления
события в каждом испытании) до первого положительного исхода;
распределение Паскаля — до к-го положительного исхода.
В отличие от закона Паскаля отрицательное биномиальное рас-
пределение характеризует распределение числа т непоявлений события
к-го положительного исхода. Его функция вероятностей
ЛА’ = т) = С1< ,/?</"* w = 0,1,...
и числовые характеристики ) = —; D(X) ~
Р Р'
> Пример 4.4а. Решить задачу 4.4 при условии, что проверка пар-
тил проводится до обнаружения ipex бракованных де талей.
Доказйтельсгво теоремы, связанное с суммированием членов бесконечного
Ряля. Здесь не приводим. Это доказательство аналогично приведенному для ча-
гного случая в решении примера 3.19, б.
149
Ре ш е н и с. Случайная величина X — число проверенных дета-
лей до обнаружения к = 3 бракованных — имеет закон распределения
Паскаля с параметром р = 0,1. т.е. /’(Д' = /л) = С; , -0.1* -0.9"или
X, 3 4 5 т ...
Л 0,001 0,0027 0.00486 о.г’ с*. ,• о. о-’
М(Х) = - = —- = 30, O(.V) = ^- = i^ = 270. ►
р 0.1 рг 0.1=
4.4. Гипергеометрическое распределение
Определение. Дискретная случайная величина X имеет
гипергеометрическое распределение с параметрами п. Л/. N. если она
принимает значения' 0. 1.2. т.min (л. Л/) с вероятностями
Р(Х = т\=С",С>!~”‘
с:
(4.14)
гас М< N, п< Л'; п, М, Л' — натуральные чист.
Гипергеометрическое распределение имеет случайная величина
X = т — число объектов, обладающих заданным свойством, среди п
объектов, случайно извлеченных (без возврата) из совокупности
N объектов. М из которых обладают этим свойством.
Так, распределение случайной величины X — числа неточных
приборов среди взятых наудачу четырех, полученное в примере 3.20,
есть гипергеометрическое распределение с параметрами п = 4,
Л/= 3, jV= 10.
Теорема. Математическое ожидание случайной величины X, имею-
щей гипергеометрическое распределение с параметрами п, М, N, есть
М
М(Х) = п—.
N
(4.15)
а ее дисперсия
<4лб>
Случайную величину X = т, распределенную по биномиальному
закону (4.1). можно интерпретировать как число т объектов, обла-
дающих данным свойством, из общего числа л объектов, случайно
1 Точнее. возможные значения т заключены п границах or max (0. л + М - Л) до
min (л. ЛЛ. при которых существуют Сп , С"'",.
150
извлеченных из некоторой воображаемой бесконечной
совокупности, доля р объектов которой обладает этим свойством.
Поэтому гипергеометрическое распределение можно рассматривать
как модификацию биномиального распределения для случая конеч-
ной совокупности, состоящей из N объектов. М из которых обла-
дают этим свойством.
При N —>*», Л/ оо при условии, что M/N -> р, функция вероят-
ностей (4.14) гипергеометрического распределения стремится к соот-
ветствующей функции (4.1) биномиального закона.
□ Действительно, учитывая равенства (1.8), (1.9), формула
(4.14) примет вид:
Р(Х - т) =-------------------- х
т\
(N-Л/ХЛ’-.W-!)...(#. ЛГ(ЛГ-!).,.(#-л+ 1)
(п-т)\ п'.
После деления делимого и делителя на N" получим
А \ A’aJ ’I Д' .v J
/’(.V = n,) =----:---
т\(п-ту.
(. М
I fi M rt-m + l)
I .V J k A' AM N N J
M
Переходя к пределу при N -> ад. Л/ -> ад, — р, получаем
Л/
формулу (4.1): P(.V = т) = С”/’"</" ". где q = I-.
А
Гипергеометрическое распределение широко используется в
практике статистического приемочного контроля качества промыш-
ленной продукции, в задачах, связанных с организацией выбороч-
ных обследований, и других областях.
[> Пример 4.5. В лотерее «Спортлото 6 из 45* денежные призы по-
лучают участники, угадавшие 3, 4. 5 и 6 видов спорта из отобранных
случайно 6 видов из 45 (размер приза увеличивается с увеличением
числа угаданных видов спорта). Найти закон распределения случайной
величины X — числа угаданных видов спорта среди случайно отобран-
ных шести. Какова вероятность получения денежного приза? Найти
математическое ожидание и дисперсию случайной величины X.
Решени е. Очевидно (см. гл. I, пример 1.14), что число уга-
данных видов спорта в лотерее «6 из 45» есть случайная величина,
имеющая гипсргсометрнческое распределение с параметрами п = 6.
М = 6. А = 45. Ряд ее распределения, рассчитанный по формуле
(4.14), имеет вид:
151
X, 0 1 2 3 4 5 6
Pl 0,40056 0,42413 0,15147 0,02244 0,00137 0,00003 0,00000012
Вероятность получения денежного приза
аЗ$Х<6)=^Р(А' = /) =
i-j
= 0,02244 + 0,00137 + 0,00003 + 0.00000012 = 0,02384*0,024.
По формулам (4.15) и (4.16)
.W(A') = 6 — = 0.8: D(X) = 6 —(I - —111 - — U 0.6145.
45 441 45 Д 45 J
Таким образом, среднее число угаданных видов спорта из 6 все-
го 0.8, а вероятность выигрыша только 0,024. ►
4.5. Равномерный закон распределения
Определение. Непрерывная случайная величина X имеет рав-
номерный (прямоугольный) закон распределения на отрезке |д. Л|, если
ее плотность вероятности ф(х) постоянна на этом отрезке и равна
нулю вне его. т.е.
*(*)“
Ь- а
0
при u<xSh,
при х<а, х>Ь.
(4.17)
Кривая распределения <р(х)и график функции распределения
F(x) случайной величины X приведены на рис. 4.2, а. б.
Теорема. Функция распределения случайной величины X. распреде-
ленной по равномерному закону, есть
152
О прн
(x-a)f(b-a) прн
1 при
х£а.
а <х<Ь,
х >Ь.
ее математическое ожидание
Ш) =
(4.18)
(4.19)
F(x) =
2 ’
а дисперсия
dm = <<м>
□ При х< а функция распределения F(x) = 0.
При а < х <Ь по формуле (3.23)
F(x)= p*L=_2L‘ = £^.
' ' Lb-a b-a* b-a
При x > b очевидно, «по
f(x)= Ги*_Лз£=1.
' ' J- h-a b-a
т.е. формула (4.18) доказана.
Математическое ожидание случайной величины X с учетом его
механической интерпретации как центра масс равно абсциссе сере-
дины отрезка, т.е. М(Х) =
а+Ь
2
Тот же результат получается по формуле (3.25):
Л/(Л') =
Ь' - а' _ а 4- b
2(Ь-а)~~2~'
По формуле (3.26):
D(X)= |‘[х-.М(Х)]2ф(х)Л =
Ян» 6 Y dx _ I ( _ а + b У' “ _
Х” 2 J b-a~ 3[Ь-и)\ 2)
I (Ь-и)' (а-b)' _{Ь-а]‘
= 3(Л-а) 8 8 = 12
Равномерный закон распределения используется при анализе
ошибок округления при проведении числовых расчетов (например,
ошибка округления числа до целого распределена равномерно на
отрезке [-0.5: +0,5|). в ряде задач массового обслуживания, прн
статистическом моделировании наблюдений, подчиненных задан-
153
ному распределению. Так. случайная величина X. распределенная
по равномерному закону на отрезке |0; 1|. называемая «случайным
числом от 0 до 1», служит исходным материалом для получения слу-
чайных величин с любым законом распределения.
О Пример 4.6. Поезда метрополитена идут регулярно с интерва-
лом 2 мин. Пассажир выходит на платформу в случайный момент
времени. Какова вероятность того, что ждать пассажиру придется не
больше полминуты. Найти математическое ожидание и среднее
квадратическое отклонение случайной величины X — времени ожи-
Ф(х)
1*н<*. 4.3
дания поезда.
Р с in е н и е. Случайная вели-
чина X — время ожидания поезда на
временном (в минутах) отрезке |0:2|
имеет равномерный такой распредс-
Поэтому вероятность того, что
пассажиру придется ждать нс более
полмннуты. равна 1/4 от равной
единице плошали прямоугольника
(рис. 4.3), т.е.
По формулам (4.19) и (4.20)
0 + 2 (2-Of 1
g, = JD(X) = ' 0.58 (мин.). ►
4.6. Показательный (экспоненциальный)
закон распределения
Определение. Непрерывная случайная величина X имеет
показательный (экспоненциальный) закон распределения с параметром
X > 0. если ее плотность вероятности имеет вид:
Ф(х) =
Ас " при х£0,
0 при х < 0.
(4.21)
154
Кривая распределения <р(х)и график функции распределения
F(x) случайной величины X приведены на рис. 4.4. а. 6.
Теорема. Функция распределения случайной величины X. распреде-
ленной по показательному (экспоненциальному) закону, есть
° . "Р"г<°' (4.22)
|-е‘м при х £0.
ее математическое ожидание
MW = 7. (4.23)
Л
F(
а дисперсия
-0-' =
Для нахождения дисперсии D{X\ вначале найдем
.V(.¥2)=| x:ip(x)<Zv= lim |ЛгХ*’“,’аЬг =
lim
155
= lim (-A:e'v) + — lim f xX^dx = 0 =-Д-.
1 X*—Jo X X x-
c учетом того, что во втором слагаемом несобственный интеграл
есть М(Х) = 7-. Теперь
D(.r)=.w(x=)-fl==^-±=±
Из доказанной теоремы следует, что для случайной величины,
распределенной по показательному закону, математическое ожидание
равно среднему квадратическому отклонению, т.е.
A/(.Y) = ct, = 1/Х.
Показательный закон распределения играет большую роль в
теории массового обслуживания и теории надежности. Так. напри-
мер. интервал времени Т между двумя соседними событиями в про-
стейшем потоке имеет показательное распределение с параметром
X — интенсивностью потока (см. § 7.3).
Показательный закон распределения (и только он в классе не-
прерывных случайных величин) обладает важным свойством, рас-
сматриваемым ниже.
О Пример 4.7. Доказать, что если промежуток времени Т. рас-
пределенный по показательному закону, уже длился некоторое вре-
мя т. то это никак не влияет на закон распределения оставшейся
части Т\ = Т~х промежутка, т.е. закон распределения 7\ остается
таким же. как и всего промежутка Т.
Ре ш с н и е. Пусть функция распределения промежутка Т опре-
деляется по формуле (4.22), т.е. ДО = 1“ с" . а функция распределе-
ния оставшейся части Т\ = Т - т при условии, что событие Т > т
произошло, есть условная вероятность события Т{ < i относитель-
но события Т> т.т.с. Д(/) = Р7,К(Т\ <{).
Так как условная вероятность любого события В относительно
события А Ра(В) = f\AB)/P(A), то. полагая А- [Т >т), В = (Т, </).
получим
Р| (Т >х)(Т, <01
FAI}-P,.ATI<,} = -^ (4.25)
Произведение событий (Т > т) и 7\ = Т -х< / равносильно со-
бытию т < Т < I + г . вероятность которого
156
/’(т< Г</+ т)= + т)-F(t).
Так как Р(Т > т) = I- Р[Т < г) = I -Г(т), то выражение (4.25)
можно представки, в виде:
НГ-НЖ
40 I-F(t)
Учитывая формулу (4.22). получим
-It
FA') = -^-,-----= l-e-=F(/)>
e
Доказанное в примере 4.7 свойство «отсутствия последействия»
показательного распределения широко используется в марковских
случайных процессах (см. гл. 7)’.
О. Пример 4.8. Установлено, что время ремонта телевизоров есть
случайная величина X распределенная по показательному закону.
Определить вероятность того, что на ремонт телевизора потребуется
не менее 20 дней, если среднее время ремонта телевизоров состав-
ляет 15 дней. Найти плотность вероятности, функцию распределе-
ния и среднее квадратическое отклонение случайной величины X.
Реше н и с. По условию математическое ожидание Л/ (X) = — = 15,
X
откуда параметр /. = 1/15 и по формулам (4.21) и (4.22) плотность
вероятности и функция распределения имеют вил:
ф(х) = ^3': ^(1)=1-/”‘(х>0).
Искомую вероятность Р(Х >20) можно было найти по форму-
ле (3.22). интегрируя плотность вероятности, т.е.
/’(Х2»2О) = Р(2О<Х<+<с) = f —
Jm 15
но проще это сделать, используя функцию распределения:
Р(Х>20) = I - Р{Х< 20) = I - Д20)= 1 -(1 - е7’ )= с77 = 0.264.
Осталось найти среднее квадратическое отклонение о, = М(Х) =
• 15 дней. ►
• В классе дискретных распределений тем же свойстпом обладает только геомет-
рическое распределение
157
4.7. Нормальный закон распределения
Нормальный закон распределения наиболее часто встречается
на практике. Главная особенность, выделяющая его среди других
законов, состоит в том. что он является предельны м зако-
ном. к которому приближаются другие законы распределения при
весьма часто встречающихся типичных условиях (см. гл. 6).
Определение. Непрерывная случайная ветчина X имеет
нормальный чакон распределения (закон Гаусса) с параметрами а и
о:, если ее плотность вероятности имеет вид:
I
<МЛ') = —1г=е зяГ-
(4.26)
Рис. 4.5
Термин «нормальный» нс совсем
удачный. Многие признаки подчи-
няются нормальному закону, напри-
мер. рост человека, дальность полета
снаряда и т.п. Но если какой-либо
признак подчиняется другому, от-
личному от нормального, закону
распределения, то это вовсе не гово-
рит о «ненормальности» явления,
связанного с этим признаком.
Кривую нормального закона
распределения называют нормальной.
или гауссовой, кривой. На рис. 4.5. а.
б приведены нормальная кривая
ФЛ (х) с параметрами а и <Г. т.е.
N'(a: а ), и график функции рас-
пределения случайной величины X. имеющей нормальный закон.
Обратим внимание на то. что нормальная кривая симметрична от-
носительно прямой х = а, имеет максимум в точке х = а. равный
|Д<у>/2я), т.е.
0.3989
------. и две точки перегиба
о
х = а ± а с ординатой (</ ± о) =
1 0.2420
сь/2яс о
Можно заметить, что в выражении плотности нормального закона
параметры обозначены буквами а и <г . которыми мы обозначаем
математическое ожидание М(Х) и дисперсию D(Xi. Такое совпадение
неслучайно. Рассмотрим теорему, устанавливающую теоретико-
вероятностный смысл параметров нормхтьного закона.
158
Теорема. Математическое ожидание случайной величины X. распре-
деленной по нормальному закону, равно параметру а этого закона, т.е.
М(Х) = а, (4.27)
а ее дисперсия — параметру о*. т.е.
2ХА)=а;. (4.23)
□ Математическое ожидание случайной величины X:
Л/(Х) = ГхФ,(х)Л- Г"х ’ е
J-* J— оЛп
„ м х—а
Произведем замену переменной, положив / = —
оЛ
Тогда х = с/ + сЛ/ и dx-ajldi. пределы интегрирования не
меняются и. следовательно,
Л/(.Г) = J —^(а + оЛ/)<?"аЛ^ =
аЛ Г** . а Г* „1 . _ а Г
= —=- I te (// + -= с dt =0 + -f= • Л -и
Jn J-* Л J-* л
(первый интеграл равен нулю как интеграл от нечетной функции по
симметричному относительно начала координат промежутку, а вто-
рой интеграл J e" dt-4^ — интеграл Эйлера—Пуассона).
Дисперсия случайной величины X.
D(X} = [ (х-а)’ q>s (x)dx = f (х-а)'—L=-e **’ dx.
JсгЛя
Сделаем ту же замену переменной х - и + о Л1' как и ПРИ вы‘
числении предыдущего интеграла. Тогда
О(А’) - [ с'2г—\=e" ^-j2dt = z?=- [ re'1’di = --?= [ ide1.
J-» сЛя Л J— Л
Применяя метод интегрирования по частям, получим
О(.Г) = -^ге*г
уП
Г j л О' Г :
+ —j=- I е г//=0 + -у^ уя =о .
-• л J-* уп
159
Выясним, как будет меняться нормальная кривая при измене-
нии параметров а и о: (или а). Если ст= const, и меняется пара-
метр а (Я| < а2 < а3). т.е. центр симметрии распределения, то нор-
мальная кривая будет смещаться вдоль оси абсцисс, не меняя фор-
мы (рис. 4.6).
Рис. 4.6
Если а = const и меняется параметр о" (или а), то меняется ор-
дината максимума кривой /п1ах(я) ~ —!=• При увеличении о орли-
ната максимума кривой уменьшается, но так как площадь под лю-
бой кривой распределения должна оставаться равной единице, то
кривая становится более плоской, растягиваясь вдоль оси абсцисс:
при уменьшении о. напротив, нормальная кривая вытягивается
вверх, одновременно сжимаясь с боков. На рис. 4.7 показаны нор-
мальные кривые с параметрами о, и о,, где а, <о, <аг Та-
ким образом, параметр а (он же математическое ожидание) харак-
теризует положение центра, з параметр а* (он же дис-
персия) — форму нормальной кривой.
Нормальный закон распределения случайной величины X с па-
раметрами а = 0, о2 = 1, т.е. X - /V(0;l), называется стандартны.»
или нормированным. а соответствующая нормальная кривая — стан-
дартной или нормированной.
160
Сложность непосредственного нахождения функции распреде-
ления случайной величины, распределенной по нормальному зако-
ну, по формуле (3.23) и вероятности ее попадания на некоторый
промежуток по формуле (3.22) связана с тем. что интеграл от функ-
ции (4.26) является «нсберушимся» в элементарных функциях. По-
этому их выражают через функцию
Ф(дг) = -у= j е ' 'dt = -j== J с ‘ 2dl (4.29)
— функцию (интеграл вероятностей) Лапласа, для которой составле-
ны таблицы. Напомним, что функция Лапласа уже встречалась нам
при рассмотрении интегральной теоремы Муавра—Лапласа (см.
§ 2.3). Там же были рассмотрены ее свойства. Геометрически функ-
ция Лапласа Ф(.т) представляет собой плошадь под стандартной
нормальной кривой на отрезке (-.г. х] (рис. 4.8)’.
Теорема. Функция распределения случайной ветчины X, распреде-
ленной по нормальному закону, выражается через функцию Лапласа
Ф(х) по формуле:
= Н.ЗО)
1 Наряду с интегралом вероятностей вида (4.29). представляющим функ-
цию Ф(л), в литературе используется его выражения и в bivic других
табулированных функций:
-J— fV' 2dt = 1 Ф(х|. т— f е" 2dt = * * 1 Ф(л), -~r f с ' - Ф( .г </?).
V2x Ju 2 J - 2 2
представляющих собой площади пол стандартной нормальной кривой
соответственно на интервалах [0;л|. (-«>; л]. | г 72. >72).
• Tcopua mpmiikciгй и
161
□ По формуле (3.23) функция распределения:
r г« ।
Mx)s tPx(v)rfv= —i^c 2e’ <**- <4-3l>
J-» J-® сь/2я
Сделаем замену переменной, полагая t--—x = a + ic.
а
dx = cidr, при x -> -х t —> -оо. поэтому
(в силу четности подынтегральной функции и того. что интеграл
Эйлера—Пуассона равен х/л ).
Второй интеграл с учетом формулы (4.29) составляет ~ |
,. ( . I /и I . ( х - а I 1 . ( х - а j _
Итак. Г\ (х =-=•.- +—Ф ------- =_ + _ф ------I
" ' К 2 I, а ) 2 2 I а J
Геометрически функция распределения представляет собой
площадь под нормальной кривой на интервале (—х, х) (см.
рис. 4.9). Как видим, она состоит из двух частей: первой, на интер-
вале (-х, er) v равной 1/2. т.е. половине всей площади под нор-
мальной кривой, и второй, на интервале (а. х), равной
-Ф :--- .
2 I о )
Рассмотрим свойства случайной величины, распределен-
ной по нормальному закону.
1. Вероятность попадания случайной величины Д', распределенной
по нормальному закону, в интервал [хь х2]. равна
Р(х, 5Л-5х.) = 1[ф(/.)-Ф(/,)]. (4.32)
где
х. - а х.-а
----. /, = ----
(4.33)
162
□ Учитывая, что согласно свойству (3.20) вероятность
p(xt < X < х,) есть приращение функции распределения на отрезке
(X|. Xjl. и формулу (4.30), получим
где /| и Ь определяются по формуле (4.33) (рис. 4.10).
2. Вероятность того, что отклонение случайной величины X, распре-
деленной по помольному закону, от математического ожидания а не
превысит величину &> 0 (по абсолютной величине). равна
/э(|Х-а|$Д) = Ф(/), (4.34)
где 1 = —. (4.35)
ст
□ /Л(|Л' - <4 < Д) = Р(а - Д < А' <, и + Л). Учитывая равенства (4.32)
и (4.33). а также свойство нечетности функции Лапласа, получим
На рис. 4.10 и 4.11 приведена геометрическая интерпретация
свойств нормального закона1.
1 Стрелками на рис. 4.10—1.12 отмечены условно
пшх фигур пол нормальной кривой.
и л о in а л и соответствую-*
163
Замечание. Рассмотренная в гл. 2 приближенная инте-
гральная формула Муавра—Лапласа (2.10) следует из свойства (4.32)
нормально распределенной случайной величины при Х| = а, х, - Ь.
а = пр и о, = ^np(j, так как биномиальный закон распределения слу-
чайной величины Х= т с параметрами п и р, для которого получена
эта формула, при и —> х стремится к нормальному закону (см. гл. 6).
Аналогично и следствия (2.13). (2.14) и (2.16) интегральной
формулы Муавра—Лапласа для числа Х = т появления события в
п независимых испытаниях и его частости т/н вытекают из свойств
(4.32) и (4.34) нормального закона.
Вычислим по формуле (4.34) вероятности P(|.V - а| £ Д) при раз-
личных значениях А (используем табл. I! приложений). Получим
при А = ст Р(|А'-4/|<g) = Ф(1) = 0,6827;
при Д = 2п Р(|А'-и|<2ст) = Ф(2) = 0,9545;
при Д = 3о Р(|Л'-</|< Зе) = Ф(3) = 0.9973
(рис. 4.12).
Отсюда вытекает «правило трех сигм».
Если случайном величина X имеет нормальный закон распределен им с
параметрами а и гГ. т.е. Л'(м; а’), то практически достоверно. что
ее значения заключены в интервале (а - За. а + За).
Рис. 4.12
Риг. 4.13
Нарушение «правила трех сигм», т.с. отклонение нормально
распределенной случайной величины X больше, чем на За (по абсо-
лютной величине), является событием практически невозможным,
гак как его вероятность весьма мала:
P(|.V - с/| > За)= I - P(|.V -</| < За) = I - 0.9973 - 0.0027.
164
Заметим, что отклонение Л,, при котором /’(I.V-cJs Д,) =
называется вероятным отклонением. Для нормального закона
д «0.675а, т.е. на интервал (а - 0,675с.«+ 0.675о) приходится
половина всей площади под нормальной кривой.
Найдем коэффициент асимметрии и эксцесс случайной величины
X, распределенной по нормальному закону.
Очевидно, в силу симметрии нормальной кривой относительно
вертикальной прямой х = а. проходящей через центр распределения
а = М(Х). коэффициент асимметрии нормального распределения А = 0.
Эксцесс нормально распределенной случайной величины X най-
дем по формуле (3.37), т.е.
Е = £±-3 =—-3 = 0.
а а*
где учли, что центральный момент 4-го порядка, найденный по
формуле (3.30) с учетом определения (4.26). т.е.
г*' .4 । Л’-1
= | (х-а) —г=е 'п ^т-Зп4
J-r Gyjln
(вычисление интеграла опускаем).
Таким образом, эксцесс нормального распределения равен нулю. и
крутость других распределений определяется по отношению к нор-
мальному (об этом мы уже упоминали в § 3.7).
t> Пример 4.9. Полагая, что рост мужчин определенной возраст-
ной группы есть нормально распределенная случайная величинах X
с параметрами а = 173 и сг = 36:
1) Найти: а) выражение плотности вероятности и функции распре-
деления случайной величины А; 6) доли костюмов 4-го роста (176—
182 см) и 3-го роста (170—176 см), которые нужно предусмотреть в
общем объеме производства для данной возрастной группы;
в) квантиль^,7 и 10%-ную точку случайной величины X.
2) Сформулировать «правило трех сигм» для случайной величи-
ны X.
Решение. I. а) По формулам (4.26) и (4.30) запишем
165
I, б) Доля костюмов 4-го роста (176—182 см) в общем объеме
производства определится по формуле (4.32) как вероятность1
/>(176 < X £ 182) = ) -Ф(г,)] = |[Ф(U0) -Ф(0.50)] =
= -^(0.8664-0.3829) = 0,2418
(рис. 4.13). так как по формулам (4.33)
=12^173.0,50, ^1^12 = 1,50.
6 6
Долю костюмов 3-го роста (170—176 см) можно было определит,
аналогично по формуле (4.32). но проще это сделать по формуле (434).
если учесть. что данный интервал симметричен относительно математи-
ческого ожидания а = М(Х) = 173. т.е. неравенство 170 < X < 176 рав-
носильно неравенству |.V -173| < 3:
Р( 170 < X 5 176) = />(|АГ -173| < 3) = Ф^ |
= Ф( 0.50) = 0.3829
(рис. 4.13).
I. в) Квантиль ай).- (см. § 3.7) случайной величины X найдем из
уравнения (3.29) с учетом формулы (4.30):
. . | | х„, -173
+ =0.7.
откуда
= Ф(/) = 0.4.
По табл II приложений находим t = 0.524 и
ЛЬ.? = 6/ + 173 = 6-0.524 + 173 = 176 (см).
Эго означает, что 70% мужчин данной возрастной группы имеют
рост до 176 см.
10%-ная точка — это квантиль = 181 см (находится анало-
гично). т.е. 10% мужчин имеют рост нс менее 181 см.
2) Практически достоверно, что рост мужчин данной возрастной
группы заключен в границах от а - Зст = 173 - 3 • 6 = 155 до
« + 3ст = 173 >3 -6 = 191 (см), т.е. 155 < А* < 191 (см). ►
В силу особенностей нормального закона распределения, отмечен-
ных в начале параграфа (и в гл. 6), он занимает центральное место в
теории и практике вероятностно-статистических методов. Большое
теоретическое значение нормального закона состоит в том. что с его
помощью получен ряд важных распределений, рассматриваемых ниже.
1 Ъшчсния функции Лапласа Ф(л) определяем по табл II приложений.
166
4.8. Логарифмически-нормальное распределение
Определение. Непрерывная случайная величина X имеет
юарифмически-нормалъное (сокращенно логнормальное распределе-
ние), если ее логарифм подчинен нормальному закону.
Так как при х > 0 неравенства X < х и In X < In х равносильны,
то функция распределения логнормального распределения совпада-
ет с функцией нормального распределения для случайной величины
In X, т.с. в соответствии с формулой (4.31)
I ь (*•**)*
F(x) = Р(.¥ < х) = P(ln А'< Inx) = —7= [ е dt. (4.36)
oV2n
Дифференцируя (4.36) по х. получим выражение плотности ве-
роятности для логнормального распределения
ф(х) = —(4.37)
ау2л х
(рис. 4.14).
Можно доказать, что числовые характеристики случайной величи-
ны X, распределенной по логнормальному закону (437). имеют вше ма-
тематическое ожидание АДА) = не" '. дисперсия D(X\ = а'еп (е° -l).
мода Мо( X) = не” . медиана А/е(Л) = а.
Очевидно, чем меньше
о, тем ближе друг к другу
значения моды, медианы и
математического ожидания,
а кривая распределения —
ближе к симметрии. Если в
нормальном законе пара-
метр а выступает в качестве
среднего значения
случайной величины, то в
логнормальном (4.37) — в
качестве медиан ы.
Логнормальное распре- |*ис- 4.14
деление используется для описания распределения доходов, банков-
ских вкладов, цен активов, месячной заработной платы, посевных
площадей под разные культуры, долговечности изделий в режиме
износа и старения и др.
О Пример 4.10. Проведенное исследование показало, что вклады
населения в данном банке могут быть описаны случайной величи-
ной X, распределенной по логнормальному закону (437) с парамет-
рами а — 530, о; = 0,64.
167
Найти: а) средний размер вклада; 6) долю вкладчиков, размер
вклада которых составляет не менее 1000 ден. ед.; в) моду и медиану
случайной величины X и пояснить их смысл.
Реше н и е. а) Найдем средний размер вклада, т.е.
Л/(X) = аеп'2 = 530?м : = 730 (лен. ед.).
б) Доля вкладчиков, размер вклада которых составляет не менее
1000 ден. ед., есть
Р( X > 1000) = !-/>( X < 1000) = 1 - F( 1000).
При определении Д1000) воспользуемся тем. что функция лог-
нормального распределения случайной величины X совпадает с
функцией нормального распределения случайной величины In X.
т.е. с учетом равенства (4.30) имеем:
F(x)=l+U[j!l£d“£) и
F(1000) = 1 + 1ф[ lnl0^_L"5M ] = 1 + 1ф(0.79) =
= 1 + 1.0.5705 = 0.785.
2 2
Теперь Р(Х>1000) = 1-0.785 = 0.215 (рис. 4.15).
в) Вычислим моду случайной величины Л”:
Л/о( X) = ие п = 530е "w - 280, т.е. наиболее часто встреча-
ющийся банковский вклад равен 280 ден. ед. (точнее, наиболее час-
то встречающийся элементарный интервал с цен гром 280 ден. ед.,
т е. интервал (280 - Л. 280 +Л) ден. ед.).
Если исходить из вероятностного смысла параметра и логнор-
мального распределения, то медиана Ме(Х) — и = 530. т.е. половина
вкладчиков имеют вклады до 530 лен. ед., а другая половина —
сверх 530 лен. ед. ►
ЮН
Наряду с рассмотренными в приложениях теории вероятностей
в экономике применяются распределения Вейбу.ма. Эрланга. Лапла-
са. Парето, логистическое, альфа. бета и др. С ними можно озна-
комиться. например, в 111. |25). [32|.
4.9. Распределение некоторых случайных величин,
представляющих функции нормальных величин
Ниже рассматриваются несколько основных законов, составляю-
щих необходимый аппарат для построения в дальнейшем статистиче-
ских критериев и оценок, применяемых в математ>г1еской статистике.
Х2-распрелеление.
Определение. Распределением (хи-квадрат) с к степе-
нлмв свободы называется распределение суммы квадратов к независи-
мых случайных величин, распределенных по стандартному нормальному
закону, т.е.
<4.38)
Г-1
где Zt (i = I. 2..к) имеет нормальное распределение M0J).
Плотность вероятности х’-распрелсления имеет вид:
О при .V < 0.
где Г(у)= j е'Г '(/f— гамма-функция Эйлера (для целых поло-
жительных значений Г( у) = (у - I)!).
169
Кривые //-распределения для различных значений числа степеней
свободы к приведены на рис. 4.16. Они показывают, *гго х2-распределение
асимметрично, обладает положительной (правосторонней) асиммет-
рией.
При к > 30 распределение случайной величины Z = ^Х" - \Jlk - I
близко к стандартному нормальному закону, т.е. М0;1).
Распределение Стьюдснта1.
Определение. Распределением Стьюдснта (или {-рас-
пределением) называется распределение случайной величины
где Z — случайная величина, распределенная по стандартному нор-
мальному закону, т.е. М0;1);
X' — независимая от Z случайная величина, имеющая //-распре-
деление с к степенями свободы.
Плотность вероятности распределения Стьюденга имеет вид:
гае Г (.у) — гамма-
функция Эйлера в точке у.
На рис. 4.17 показана
кривая распределения
Стьюдснта. Как и стан-
дартная нормальная кри-
вая, кривая /-распреде-
ления симметрична отно-
сительно оси ординат, но
по сравнению с нор-
мальной более пологая
(ее эксцесс Е < 0).
При к -> оо /-распре-
1 С1Ыолс1п — псевдоним английскою статистика В, Госсста
170
деление приближается к нормальному. Практически уже при к > 30
можно считать /-распределение приближенно нормальным.
Математическое ожидание случайной величины, имеющей /-рас-
пределение. в силу симметрии се кривой распределения равно ну-
лю, а се дисперсия (как можно доказать) равна к/(к - 2). т.е.
мо = о. «0=^.
Распределение Фишера—Снедекора.
Определение. Распределением Фишера—Снедехора (или F-pac-
нределением) называется распределение случайной величины
Г = 4. (4.40)
где х ) и х’ (*:) — случайные величины. имеющие х -распределение
соответственно с £| и степенями свободы.
Плотность вероятности F-распределения имеет вид:
ОК Г(у) — гамма-функ-
ция Эйлера в точке у
На рис. 4.18 показа-
ны кривые f-paenpe-
делення при некоторых
значениях числа степе-
ней свободы к\ и к2.
При л -> cn F-pacnpe-
деленис приближается к
нормальному закону.
Рис. 4. IS
171
Упражнения
4.11. Вероятность выигрыша по облигации займа за все время
его действия раина 0.1 Составить закон распределения числа выиг-
равших облигаций среди приобретенных 19. Найти математическое
ожидание, дисперсию, среднее квадратическое отклонение и молу
этой случайной величины.
4.12. По данным примера 4.11 найти математическое ожидание,
дисперсию и среднее квадратическое отклонение доли (частости) выиг-
равших облигаций среди приобретенных
4.13. Составить функцию распределения случайной величины,
имеющей биномиальный закон распределения с параметрами п и р.
4.14. Устройство состоит из 1000 элементов, работающих незави-
симо один от другого. Вероятность отказа любого элемента в течение
времени / равна 0,002. Необходимо: а) составить закон распределения
отказавших за время t элементов; б) найти математическое ожидание и
дисперсию этой случайной величины; в) определил, вероятность того,
что за время / откажет хотя бы один элемент.
4.15. Вероятность поражения цели равна 0.05. Производится стрель-
ба по цели до первого попадания. Необходимо: а) состшипъ закон распре-
деления числа сделанных выстрелов; б) найти математическое ожидание и
дисперсию этой случайной величины; в) определить вероялюсть того, что
для поражения цели потребуется не менее 5 выстрелов.
4.15а . Решить пример 4.15 (п. а. б) при условии, что производится
стрельба по цели до трех попаданий.
4.16. В магазине имеются 20 телевизоров, из них 7 имеют дефек-
ты. Необходимо: а) составил, закон распределения числа телевизоров
с дефектами среди выбранных наудачу пял<; б) найти матсмалтчсское
ожидание и дисперсию этой случайной величины; в) определил, веро-
ятность того, что среди выбранных нет телевизоров с дефектами.
4.17. Цена деления шкалы измерительного прибора равна 0.2
Показания прибора округляют до ближайшего целого числа. Пола-
гая. что при отсчете ошибка округления распределена по равномер-
ному закону, найл<: I) мате.мал1чсское ожидание, дисперсию и сред-
нее квадратическое отклонение этой случайной величины.
2) вероятность того. *по ошибка округления: а) меньше 0,04; б) боль-
ше 0,05.
4.18. Среднее время безотказной работы прибора равно 80 ч
Полагая, что время безотказной работы прибора имеет показатель
ный закон распределения, найти: а) выражение его плолюсти веро-
ятности и функции распределения; б) вероятность того. *гго в тече-
ние 100 ч прибор не выйдет из строя.
4.19. Текущая пена акции может быть смоделирована с помп
щью нормального закона распределения с математическим ожила -
172
нисм 15 лен. ел и средним квадратическим отклонением 0.2 ден.
ед. Необходимо: I) найти вероятность того, что иена акции: а) не
выше 15,3 лен. ед.: б) нс ниже 15.4 лен. ед.; в) от 14,9 до 15.3 лен.
ед.; 2) с помощью правила трех сигм найти границы, в которых бу-
дет находиться текущая пена акции.
4.20. Цена некой ценной бумаги нормально распределена. В те-
чение последнего гола 20% рабочих дней она была ниже 88 ден. ел., а
75% — выше 90 ден. ел. Найти: а) математическое ожидание и сред-
нее квадратическое отклонение цены ценной бумаги; б) вероятность
того, что в лень покупки цена будет заключена в пределах от 83 до
96 ден. ед.; и) с надежностью 0.95 определить максимальное отклонение
цены ценной бумаги от среднего (прогнозного) значения (по абсолют-
ной величине).
4.21. Коробки с конфетами упаковываются автоматически. Их
средняя масса равна 540 г. Известно, что масса коробок с конфета-
ми имеет нормальное распределение, а 5% коробок имеют массу,
меньшую 500 г. Каков процент коробок, масса которых: а) менее
470 г. 6) от 500 до 550 г; в) более 550 г; г) отличается от средней не
более чем на 30 i (по абсолютной величине)?
4.22. Случайная величина X имеет нормальное распределение с
математическим ожиданием а = 25. Вероятность попадания X в ин-
тервал (10; 15) равна 0.09. Чему равна вероятность попадания Л' в
интервал: а) (35; 40); 6) (30; 35)?
4.23. Нормально распределенная случайная величина имеет
следующую функцию распределения: fl.v) = 0.5 + 0,5Ф( х - I). Из
какого интервала (1; 2) или (2; 6) она примет значение с большей
вероятностью?
4.24. Квантиль уровня 0.15 нормально распределенной случай-
ной величины X равен 12. а квантиль уровня 0.6 равен 16. Найти
математическое ожидание и среднее квадратическое отклонение
случайной величины.
4.25. 20%-ная точка нормально распределенной случайной ве-
личины равна 50. а 40%-ная точка равна 35. Найти вероягность то-
го, что случайная величина примет значение в интервале (25; 45).
4.26. Месячный доход семей можно рассматривал, как случайную
величину, распределенную по логнормальному закону. Полагая, «гго ма-
тематическое ожидание згой случайной величины равно 1000 лен. ед., а
среднее квадратическое отклонение 800 ден. ел., найти долю семей,
имеющих доход: а) нс менее 1000 ден. ед.; б) менее 500 ден ед.
4.27. Известно, что нормально распределенная случайная вели-
чина принимает значение: а) меньшее 248 с вероятностью 0,975;
6) большее 279 с вероятностью 0,005. Найти функцию распределе-
ния случайной величины .V
173
4.28. Случайная величина X распределена по нормальному закону
с нулевым математическим ожиданием. Вероятность попадания этой
случайной величины на отрезок от -I до +1 равна 0.5. Найти выраже-
ния плотности вероятности и функции распределения случайной ве-
личины X.
4.29. Имеется случайная величина X. распределенная по нор-
мальному 'закону с математическим ожиданием а и дисперсией а2.
Требуется приближенно заменить нормальный закон распределения
равномерным законом в интервале (а; р): границы а. р подобрать
так. чтобы сохранить неизменными математическое ожидание и
дисперсию случайной величины X.
4.30. Случайная величина X распределена по нормальному за-
кону с математическим ожиданием а = 0. При каком значении
среднего квадратического отклонения о всроялюсть попадания слу-
чайной величины Xв интервал (I; 2) достигает максимума?
4.31. Время ремонта телевизора распределено по показательному
закону с математическим ожиданием, равным 0.5 ч. Клиент сдает в
ремонт два телевизор;), которые одновременно начинают ремонтиро-
вать, и ждет, когда будет отремо1гтирован один из них. После этого с
готовым телевизором он уходит. Найти закон распределения времени:
а) потраченного клиентом; б) которое должен потратить клиент, если
он хочет забрать сразу дна телевизора.
Глава
Многомерные случайные
величины
5.1. Понятие многомерной случайной величины
и закон ее распределения
Очень часто результат испытания характеризуется нс одной случай-
ной величиной, а некоторой ттпелкш случайных величин Х\. Х2, .... Хп,
которую называют также многомерной (п-мерной) случайной величиной
или случайным вектором X = (АГ,. Х2.Х„).
Приведем примеры многомерных случайных величин.
I. Успеваемость выпускника вуза характеризуется системой п слу-
чайных величин А']. AS, ...» Хп — оценками но различным дисцип-
линам. проставленными в приложении к диплому.
2. Погода в данном месте в определенное время суток может быть
охарактеризована системой случайных величин: А'( — температура; AS —
влажность; Ад — давление; Ад — скорость ветра и т.п.
3. Биржевые торги характеризуются системой двух случайных
величин: A'( - валютный курс. Х: — объем продаж.
В теоретико-множественной трактовке любая случайная величины
X, (i = I. 2. .... п) есть функция элементарных событий ш. входящих в
пространство элементарных событий Q (ы g Q). Поэтому и много-
мерная случайная величина есть функция элементарных событий со:
...>.) = /(«).
т.с. каждому элементарному событию ш ставится в соответствие
несколько действительных чисел Х|. х2. .... дп, которые приняли слу-
чайные величины Х\, AS...Хп в результате испытания. В этом слу-
чае вектор х = (Х|. х>, .... х„) называется реализацией случайного век-
тора X = (АГ„ AS..Х„).
Случайные величины Х[. AS..... Хп, входящие в систему, могут
быть как дискретными (см. выше примеры I. 3). так и непрерывными
(пример 2).
> Пример 5.1. Подбрасывают одновременно две тральные кос-
ти; случайная величина X — сумма очков, полученных в результате
испытания; случайная величина Y — их произведение. Показать,
что двумерная случайная величина (AS У) есть функция элементар-
ных исходов (событий) О) .
175
Реше н и с. Множество элементарных исходов (пространство
элементарных событий) состоит из 36 элементарных исходов, т.е.
Q = |w|r oh,.... wM| =
= {1/1. 1/2.. 1/6. 2/1. 2/2...2/6....6/1. 6/2...6/6}.
где элементарный исход, например (д. = 2/3. означает выпадение при
подбрасывании первой игральной кости 2 очков и второй кости —
3 очков. Если результатом испытания является какой-нибудь элемен-
тарный исход (событие) со,. то случайные величины X и У получат
определенные значения; например, при <оч=2/3 Х~5. К = 6. Сово-
купность этих значений (.¥. У) представляет, таким образом, функцию
элементарных исходов (событий) са ►
Геометрически двумерную (Л'. У) и трехмерную (X, У, Z) случайные
величины можно изобразить случайной точкой или случайным векто-
ром плоскости Оху или трехмерного пространства Оху:: при этом слу-
чайные величины Л’. У или Л', У, 7. являются составляющими этих век-
торов. В случае л-мерного пространства (п > 3) также говорят о слу-
чайной точке или случайном векторе этого пространства, хотя геомет-
рическая интерпретация в этом случае теряет свою наглядность.
Наиболее полным, исчерпывающим описанием многомерной
случайной величины является закон ее распределения. При конеч-
ном множестве возможных значений многомерной случайной ве-
личины такой закон может быть задан в форме таблицы (матри-
цы), содержащей всевозможные сочетания значений каждой из
одномерных случайных величин, входящих в систему, и соответст-
вующие им вероятности. Так. если рассматривается двумерная дис-
кретная случайная ветчина (X, У), то ее двумерное распределение
можно представить в виде таблицы {матрицы) распределения
(табл. 5 I). в каждой клетке (/. j) которой располагаются вероятно-
сти произведения событий р,, = Р |(.¥ = л;)( У = >))|.
Та 6. ищи 3.1
X, я Я Ут t /-«
*1 Рч Ph Р\т Pl-
X, Рл Й Pint Рг
...
х„ Рп\ Р* ... Рпт Рл-
t i-t Р-1 Р; Р‘т 1
176
Так как события |(А' = х,)(У = уу)| (/ = I. 2.n\j = 1.2.т),
состоящие в том. »гто случайная величина X примет значение х(, а
случайная величина Y — значение у,. несовместны и единственно
возможны, т.е. образуют полную группу, то сумма их вероятностей
равна единице, т.е.
ЁЁа, = 1-
1-1 /»1
Итоговые столбец или строка таблицы распределения (А. У)
представляют соответственно распределения одномерных состав-
ляющих (X/. д) или (yj, pj).
Действительно, распределение одномерной случайной величины X
можно получить, вычислив вероятность события Х= xt (i = 1,2.п)
как сумму вероятностей несовместных событий:
p.=P(A’ = x,) =
= Р((АГ = х, X)’ = у,) + ... + (А’ = х, X У - у,) + ... + (А' = х4 ХУ = у„)] =
= Л.+- + Я +••••+/>«’£/>»•
Аналогично р, = £рр.
м
Таким образом, чтобы по таблице распределения (табл. 5.1)
найти вероятность того, что одномерная случайная величина при-
мет определенное значение, надо просуммировать вероятности pt)
из соответствующей этому значению строки (столбца) данной
таблицы.
Если зафиксировать значение одного из аргументов, напри-
мер. положить Y = yJt то полученное распределение случайной
величины X называется условным распределением X при условии
К = у, Вероятности р/ (х4) этого распределения будут условными
вероятностями события X = х„ найденными в предположении,
что событие У = уу произошло. Из определения условной вероят-
ности1 (1.34)
{(^ = 4 )(>- = >•,)] л
(5.1)
Аналогично условное распределение случайной ветчины Y при ус-
ловии X = х( задается с помощью условных вероятностей
1 Для услонных вероятностей используются также обозначения Л(х<|уД Я(>у| Х/>.
177
л[(ЛГ~х,)(Г = .р,)] р,
/>(А' = х/) ' Р..'
(5.2)
О Пример 5.2. Закон распределения дискретной двумерной слу-
чайной величины (X. У) задан в табл. 5.2.
Таб.1нци 5.2
у' X/ -1 0 1 2
1 0,10 0.25 0.30 0,15
2 0,10 0.05 0,00 0,05
Найти: а) законы распределения одномерных случайных вели-
чии X и К; б) условные законы распределения случайной величины
X при условии У = 2 и случайной величины Y при условии X = 1;
в) вычислить P(Y< А).
Р е ш е н и с. а) Случайная величина X может принимать зна-
чения:
X = I с вероятностью />| = 0,10 + 0.25 + 0,30 + 0,15 = 0.8;
X = 2 с вероятностью р2 = 0.10 + 0.05 + 0,00 + 0.05 = 0.2.
т.е. ее закон распределения
Xf 1 2
0.8 0.2
Аналогично закон распределения
У) 0 1 2
Р; 0.2 0.3 0.3 0.2
б) Условный закон распределения X при условии, что Y = 2, по-
лучим, если вероятности ptJ, стоящие в последнем столбце табл. 5.2.
разделим на их сумму, т.с. на р( Y = 2) = 0,2. Получим
1 2
Pj<X,) 0,75 0.25
Аналогично для получения условного закона распределения Y
при условии X = I вероятности ру. стоящие в первой строке
табл. 5.2, делим на их сумму, т.е. на р(Х = I) = 0.8. Получим
178
-Ъ -1 0 1 2
АО? 0.125 0.3125 0,375 0.1875
в) Для нахождения вероятностей Л Y < Л) складываем вероятно-
сти событий Р,, из табл. 5.2, для которых yf < х,.
Получим
Р(У< Л) = 0,10 + 0,25 + 0.10 + 0,05 + 0,00 = 0,5. ►
Закон распределения многомерной случайной величины может
быть задан и аналитически. Так. дискретная случайная величина
X = (Xt, X.....V„) имеет полиномиальный (мультиномиальный) закон
распределения, если ее составляющие принимают неотрицательные
значения х, =0.1, 2...п с вероятностями Р(Х}-ту...........
А
Xt = m,). определяемыми по формуле (2.18) (см. гл. 2), где]Гт, =л,
i>i
о<а<ь Ел = |-
5.2. Функция распределения многомерной
случайной величины
Определение. Функцией распределения п-мерной случай-
ной величины (Afj, X,. .... Хп) называется функция F(x,. х,. х„)
выражающая вероятность совместного выполнения п неравенств'
Х\< Х|, Х,< Xi..Х„ < хя, т.е.
F(x,, хг,.... хя) = Р(.У, <xt. X. <х,.Х„ <х„). (S.3)
В двумерном случае3 для случайной величины (X, Y) функция
распределения Дх, у) определится равенством:
Г(х,.у) = Л( Х<х. Г<у). (5.4)
Геометрически функция распределения Дх, у) означает вероят-
ность попадания случайной точки (X. Н в заштрихованную область —
1 Функцию Дх|, г»...хп) называют также совместной функцией распределения
случайных величин Aj, А?..Х„,
1 В основном будем itecrw изложение для двумерной (я = 2) случайной величины;
при этом практически ясе понятии и утверждения, сформулированные для л = 2,
могут быть перенесены и на случай п > 2 Однако рассмотрение двумерной слу-
чайной величины почааляст сделать и итоженне наглядным и менее (ромоадким.
179
M(x, у)
Рис. 5.1
бесконечный квадрант, лежащий
левее и ниже точки М(х, yj
(рис. 5.1). Правая и верхняя гра-
ницы области в квадрант не вклю-
чаются — это означает, что функ-
ция распределения непрерывна
слева по каждому из аргумен-
тов.
В случае дискретной двумерной
случайной величины ее функция
распределения определяется по
формуле:
F(x.y) = • (5.5)
I I
где суммирование вероятностей распространяется на все /. для ко-
торых xt < х, и все J. для которых у7 < у.
Отмстим с в о й с т в а функции распределения двумерной
случайной величины, аналогичные свойствам функции распределе-
ния одномерной случайной величины.
1. Функция распределения Fix. у) есть неотрицательная функция,
заключенная между нулем и единицей, т.е.
0^F(x,.v)Sl. (5.6)
□ Утверждение следует из того, что Fix. у) есть вероятность.
2. Функция распределения Fix, у) есть неубывающих функция по
каждому из аргументов, т.е.
при Х2 > Xi F(X2. у) > /•’(л;. г).
при у2 > л Fix. у>) >F(x.у,). (5.7)
□ Так как при увеличении какого-либо аргумента заштрихован-
ная область на рис. 5.1 увеличивается, то вероятность попадания в
него случайной точки (А' т.е. функция распределения Fix. у).
уменьшиться не может.
3. Если хотя бы один из аргументов обращается в —j., функция
распределения Дх, у) равна нулю. т.е.
F(x, -оо) - F( у) = /'(-х, -ас) = 0,
(5.8)
□ Функция распределения Fix. у) в отмеченных случаях равна
нулю, так как события А' <-». У <—х и их произведение пред-
ставляют невозможные события.
I КО
4. Если один из аргументов обращаете» в +<х>, функция распреде-
ления Я*. >') становится равной функции распределения случайной ве-
личины, соответствующей другому аргументу.
F(x. + *>} = F{(x\
F(+«.y) = F2(y). (5.9)
где F\[x) и Л (у) — функции распределения случайных ветчин X и У, т.е.
Цх} = Р(Х<х). Я(у)=Р(У<у).
□ Произведение события (Х<х) и достоверного события (У < + оо) есть
само событие С¥<х). следовательно, Р(х. + <х>)= Р(Х <х) = F^x).
Аналогично можно показать, что F(+ <х>, у) = Г, (у).
5. Если оба аргумента равны + «о . то функция распределения рав-
на единице:
F(+oo. +со) = 1.
□ Г(+«5,+со)= I следует из того, что совместное осуществление
достоверных событий (X < +оо), (У < +«) есть событие достоверное.
Геометрически функция
распределения есть некоторая
поверхность, обладаю-
щая указанными свойствами.
Для дискретной случайной
двумерной величины (X, У) се
функция распределения пред-
ставляет собой некоторую
ступенчатую поверх-
ность. ступени которой соот-
ветствуют скачкам функции
Ях, у). Риг. 5.2
Зная функцию распределения Я*, у), можно найти вероятность
попадания случайной точки (X. У) в пределы прямоугольника ABCD
(рис. 5.2). т.с. r[(xt S X < .г, )(у, £ У < у,)]. Так как эга вероятность
равна вероятности попадания в бесконечный квадрант с вершиной
Жх?, у2) минус вероятности попадания в квадранты с вершинами
соответственно в точках 4(х,.у.) и С(х,.у,) плюс вероятность по-
падания в квадрант с вершиной в точке D(x}.y\) (ибо эта вероят-
ность вычиталась дважды), то
181
= И v;. Г:) - г(х„7г)-F(x2,y.)+ F(x„у,).
(5.10)
5.3. Плотность вероятности двумерной
случайном величины
Определение. Двумерная случайная величина (X У) называ-
ется непрерывной, если ее функция распределения Дх. у) — непрерыв-
ная функция, дифференцируемая по каждому из аргументов, и сущест-
вует вторая смешанная производная F' (х.у).
Аналогично одномерному случаю вероятность пары отдельно
взятых значений двумерной непрерывной случайной величины рав-
на нулю. т.е. Р(Х= Х|, К=у|) = 0. Это вытекает непосредственно из
формулы (5.10) при х;-*Хр с учетом непрерывности
функции распределения F(x, у).
Для двумерной случайной величины, так же как и для одномер-
ной. вводится понятие плотности вероятности.
Найдем вероятность попадания случайной точки (X У) в прямо-
угольник со сторонами Ат и Ду, т.е.
? = Р[(х< X <х + Ат)(у£ У <у + Ду)].
Полагая в формуле (5.10) Х| = х, хэ = х + Ат, у, = у, у, = у + Ду,
получим, что эта вероятность
i? = [Г(х + Ат. у + Ау)- Г(х, у + Ду)] -
-[Г(х + Ат.у)-Г(х, у)].
Средняя плотность вероятности в данном прямоугольнике равна
отношению вероятности Ф к плошади прямоугольника ДтДу, т.е.
»[(* SX<x + Хх)(у S Г <у+Д>-)]
Ф‘г Дх-Ду ’ ( ’
Будем неограниченно уменьшать стороны прямоугольника, т.е.
Ат->0. Ду —> 0. Тогда, учитывая (5.11), найдем
I Д(х +Ат,у + Ду)-Г(х,у + Ду)
lim Ф<Р= »m — im —----------------------------------— -
л,-.<1 Ду *v-° Ат
.V-'l
- Un,
л*-° Ат
182
Так как функция Г(х. у) непрерывна и дифференцируема по каж-
дому аргументу, то выражение <5.13) примет вид:
lim Ф = lim
л.-о т л. л
г;(х, + Ду) - F'(x%y)
Ду
(5.14)
=[г.'(х’>’)]\ = F.*lv’-4
Определение. Плотностью вероятности (плотностью
распределения или совместной плотностью) непрерывной двумерной
случайной величины (X. У) называется вторая смешанная частная про-
изводная ее функции распределения, т.е.
, . <5:F(x.y) . ,
ф(х,у) = —-1—1 = г;(х.у) . (5.15)
Геометрически плотность ве-
роятности двумерной случайной
величины (А'. И представляет со-
бой поверхность распределения в
пространстве Оху: (рис. 5.3).
Плотность вероятности ф(х.у)
обладает свойства м и. ана-
логичными свойствам плотности
вероятности одномерной случай-
ной величины.
1. Плотность вероятности
двумерной случайной ветчины есть
неотрицательная функция, т.е.
Рис. 5.3
ф(х,у)>0.
□ Свойство вытекает из определения плотности вероятности
как предела отношения (5.13) двух неотрицательных величин, ибо
функция распределения Г(х. у) — неубывающая функция по каж-
дому аргументу.
2. Вероятность попадания непрерывной двумерной ветчины (X,Y) в
область D равна
/>[( А'. Г) е £>] = А ф. (5.16)
Г»
□ Поясним геометрически формулу (5.16).
Подобно тому, как н гл. 4 для одномерной случайной величины
X введено понятие «элемент вероятности», равный ф(х)е&, для дву-
мерной случайной величины (АГ. Y) вводится также понятие «эле-
183
мент вероятности», равный <р(х.у) dx dy. Он представляет (с точно-
стью до бесконечно малых более высоких порядков) вероятность
попадания случайной точки (Л', F) в элементарный прямоугольник
со сторонами dx и dy (рис. 5.4).
У+dy
У
dy
Эта вероятность приближенно
равна объему элементарного паралле-
лепипеда с высотой cp(.v.y). опи-
рающегося на элементарный прямо-
угольник со сторонами dx и dy.
х x+tfx
1*ис. 5.4
Если вероятность попадания од-
номерной случайной величины на
отрезок |о. />| геометрически выра-
жалась площадью фигуры, ограни-
ченной сверху кривой распределения
ф(л) и опирающейся на отрезок
|а, Л|. и аналитически выражалась интегралом J ф(х) dx. го вероят-
ность попадания двумерной случайной веяичшм в область I) на носко-
сти Оху геометрически изображается объемом цилиндрического тела,
ограниченного сверху поверхностью распределения ф(г. г) и опирающе-
гося на область D, а аналитически — двойным интегралом (5.16).
3. Функция распределения непрерывной двумерной случайной вели-
чины может быть выражена через ее мощность вероятности ф(х.у)
по формуле'.
F(x,y)=j | Ф(.т.у) dx dy .
(5.17)
□ Функция распределения Г(х. у) есть вероятность попадания в
бесконечный квадрант D. который можно рассматривать как прямо-
угольник. ограниченный абсциссами —-г. и х и ординатами —г и у
Поэтому в соответствии с формулой (5.16)
Г( х.у) = |[ф(х.у) dx dy = J J ф(х.у) dx dy.
4. Двойной несобственный интеграл в бесконечных пределах от мощ-
ности вероятности двумерной случайной ве тчины равен единице:
J j ф(х.у) dx <Л’ = I .
(5.18)
□ Несобственный интеграл (5.18) есть вероятность попадания
во всю плоскость Оху, т.е. вероятность достоверною события, рав-
184
пая I. Это означает, что полный обьем тела, ограниченного поверхно-
стью распределения и плоскостью Оху, равен I.
Зная плотность вероятности двумерной случайной величины
(X Y), можно найти функции распределения и плотности вероятно-
стей ее одномерных составляющих X и К
Так как в соответствии с равенствами (5.9) Г(х.+со) = Ft (х) и
Г(+<».у)=/г;(у). то, взяв в формулах (5.17) соответственно
ys+ac и х = + т . получим функции распределения одномерных
случайных величин X и У:
/\(х)=( ( ф(х.г)«А-<Л*.
г: г’ (5.19)
Г, (у) =J ] ф(х. y)dxdy.
Дифференцируя функции распределения Г|(х) и F>(y) соответст-
венно по аргументам х и у. получим плотности вероятности одно-
мерных случайных величин X и Y:
Ф, ( V) = J <Р(х. у) dy . Ф; (у) = f ф( V. у) dx. (5.20)
т.е. несобственный интеграл в бесконечных пределах от совместной
плотности ф(х. г) двумерной случайной величины по аргументу х да-
ет плотность вероятности <р.(г). а по аргументу у — плотность
вероятности ф, (х).
Замечание. Если имеется кривая распределения ф(х) од-
номерной случайной величины X. то конкретное значение ее плотно-
сти вероятности в данной точке х определяется геометрически о р -
д и н а т о й кривой ф(х). Если имеется поверхность распределения
<р(х. у) двумерной случайной величины (Л'. У), то конкретное значение
ее совместной плотности в данной точке (х. у) определяется геомет-
рически а п л л и к а т о й поверхности ф(х. у). В этом случае
конкретное значение плотности вероятности ф,(х) одномерной со-
ставляющей Л’ в данной точке х. в соответствии с формулой (5.20).
определится геометрически площадью сечения поверхно-
сти ф(х. г) шкк-костыо Х-х, параллельной координатной плоско-
сти Оу- и отсекающей на оси Ох отрезок х. Аналогично конкретное
значение плотности ф?(у) одномерной составляющей У в данной
точке у есть площадь сечения поверхности ф(х, у) гькккостью У= у.
параллельной координатной плоскости Охе и отсекающей на оси Оу
отрезок у (см. рис. 5.9. на котором значение Ф_.(у) при данном у
представляет площадь сечения, равную s).
185
[> Пример 5.3. Двумерная случайная величина распределена
равномерно в круге радиуса К = I (рис. 5.5). Определить: а) вы-
ражение совместной плотности и функции распределения двумер.
ной случайной величины {X. У); б) плотности вероятности и функ-
ции распределения одномерных составляющих X и У; в) вероятность
того, что расстояние от точки (X, У) до начала координат будет
меньше 1/3.
Ре ш е н и е. а) По условию <р
при х2+/<1.
при х2 + / > I.
Постоянную С можно найти из соотношения (5.18):
f ” !"ч>(•* ‘‘У = J', С А Л- = I
Проше это сделать, исходя из геометрического смысла соотноше-
ния (5.18), означающего, что объем тела, ограниченного поверхно-
стью распределения ф(.х.г) и плоскостью Оху. равен I. В данном
случае, это объем цилиндра с площадью основания я/?2 = д-р = л и
высотой С (рис. 5.6), равный к • С = I, откуда С = \/п. Следовательно,
ф(-г.г) =
1/п
О
при № + у: < I.
при х2 + г2 > I.
Найдем функцию распределения F(x. у) по формуле (5.17):
F(x.y) = f r £ ф(хо’)л 4>‘s-“ J’, tix J dy. (5.21)
Очевидно, что этот интеграл с точностью до множителя 1/л совпадает
с площадью области D — области пересечения круга х2 + у2 < I с беско-
нечным квадрантом ленес и ниже точки М(х, у) (рис. 5.7).
186
1*ис. 5.7
Опустим расчеты интеграла (5.21> для различных х и у, предоставив
их читателю, но отметим очевидное, что при х < -1. -со < у < +оо или
при —»< х <+«, у£ ~1 Лх, у) = 0, так как в этом случае область D —
пустая, а при х> I. у > 1 F (х, у) = I, так как при этом область D пол-
ностью совпадает с кругом х‘ + у: < 1, на котором совместная плот-
ность <р(х, у) отлична от нуля.
б) Найдем функции распределения одномерных составляющих X
и Y. По формуле (5.19) при -1 < х $!
при х < -1,
при -I < х <, I,
при х> I.
Аналогично
’ Можно показать, что для функции 2x/l -х: первообразная сеть х\П-х: +
+ arcsinx.
187
о
*(*)=
- + —(y^l “ У* * arcsin у)
2 я
I
при у < - I.
при -1 < у $ I.
при у >1.
Найдем плотности вероятности одномерных составляющих X и
К По формуле (5.20)
Ф,(х) = [ 4>(.v.y)Jr= f -Jr = -Vl-x: (- I < аг Si).
График плотности <р,(х) показан на рис. 5.8.
Аналогично
Фг(.г) = Г ф(х.уИ=-71-Г (-1<У<1).
л
в) Искомую вероятность
т.е.
вероятность того, что случайная точка (X У) будет находиться в круге
радиуса R} = 1/3 (см. рис. 5.5), можно было найти по формуле (5.16):
но проще это сделать, используя понятие «геометрической вероят-
ности». т.е.
р(х: + Г'< 1) = (яЛ|:)/(лЛ2) = Л):/№= ►
5.4. Условные законы распределения.
Числовые характеристики двумерной
случайной величины. Регрессия
Определена с. Условным законом распределения одной из од-
номерных составляющих двумерной случайной величины (X, У) называется
ее закон распределения, вычисленный при условии, что другая составляю-
щая приняла определенное значение (или попала в какой-то интервал).
Выше (§ 5.1) рассмотрено нахождение условных распределений
для дискретных случайных величин. Там же приведены
формулы (5.1) и (5.2) условных вероятностей:
М*<)=
Р(Г=у,) ’МЛ) Я(х=х,)
188
(5.22)
В случае к е прерывных случайных величин необходимо
определить плотности вероятности условных распределений ip, (л ) и
фД г). С этой целью в приведенных формулах заменим вероятности
событий их «элементами вероятности». т.е. ГЦ А' =л;МГ = у, )| на
ф(х.у) <Zv <А-. Р(Х^ х,) на <р(л ) сЛ\ Р( Y = г ) на <р( v) ch. Р/х,) на
Ф (x)i/x и P,<Vj) на ф, (г) </г. после сокращения на dx и dy получим:
/ \ ,рЬ'-У) л . ф(х.г)
Ф. х =—ту- Ф, >’ =—7-г
Ф:(У) Ф.(*)
Т.е. условная плотность вероятности' одной из одномерных состав-
ляющих двумерной случайной величины равна отношению ее совмест-
ной плотности к плотности вероятности другой составляющей.
Соотношения (5.22), записанные в виде
ф( х. т) = Ф. (v) Ф, (г) = Ф2( г) Ф. (х). (5.23)
называются теоремой (правилам) умножения плотностей распределений.
Используя формулы (5.20), условные плотности вероятностей (5.22)
можно выразшъ через совместную плотность следующим образом:
t k Ф(х.у)
Ф.(х) = —----------------—.
J ф( V. Г) dx
Если, как отмечено выше,
совместная плотность ф(т.г)
двумерной случайной величи-
ны представляет собой геомет-
рически некоторую поверх-
ность распределения, то. на-
пример. условная плотность
фДх) есть кривая распределе-
ния, подобная сечению
этой поверхности плоскостью
Y = у. параллельной коорди-
натной плоскости Ох: и отсе-
кающей на осп Оу отрезок у
(рис. 5 9). и в соответствии с
(5.24) и замечанием на с. 185
получается из нее делением всех ординат на площадь данного сечения
з (т.е. сечение поверхности распределения есть кривая хф.(х). где
< 1 ) (см. рис. 5.9).
Аналогично можно пояснить геометрически и смысл условной
плотности фДу)
1 Дтя условных и'кпиостей верчтиости жиаизукпея также о&лиаченкя <р(л | .у), <»(>• | х).
189
Условные плотности Ф,(х) и <р,(.г) обладают всеми свойствами
«безусловной* плотности. рассмотренной в гл. 3.
Числовые характеристики одномерных составляющих Хи Хи их
условных распределений — математические ожидания Л/(Л'),
и дисперсии D(X), D(Y), условные математические ожидания A/J.V)
и Л/, (У) и условные дисперсии D (X) и DJY) находятся по обыч-
ным формулам математического ожидания и дисперсии, в которых
используются соответствующие вероятности или плотности вероятно-
стей (см. табл. 5.3).
Условное математическое ожидание случайной величины У при
условии X - х, т.е. Л/г( У), есть функция от х, называемая функцией
регрессии или просто регрессией У по Х\ аналогично МУ(Х) называется
функцией регрессии или просто регрессией X по У. Графики этих
функций называются соответственно линиями регрессии (или кривы-
ми регрессии) У по X и X по У ’.
Основные свойства условных математических ожиданий и дис-
персий аналогичны свойствам их «безусловных» аналогов, отмечен-
ных выше (см. § 3.3, 3.4): при этом надо учитывать, что проводи-
мые в них операции понимаются теперь уже не как действия над
числами, а как действия над функциями.
Отметим здесь некоторые дополнительные свойства ус-
ловного математического ожидания.
I. Ест 7. = g(X). где £ — некоторая неслучайная функция от X, то
МАЛЦУ)) = M:(Y).
В частности.
Л/(Л/Л(У)) = М(У)
(правило повторного ожидания).
2. Если Z= g(X), то MAZY) = ZMX(Y).
3. Если случайные ветчины X и У независимы, то
МАУ)-М(У).
□ Докажем в качестве примера (дня непрерывной случайной ве-
личины) правило повторного ожидания М(МАУ)) = М( У). Условное
математическое ожидание МА У) находится по условному распреде-
лению случайной величины У (при условии, что А' = х), задаваемому
условной плотностью вероятности фЛ У). По формуле (5.27’) с уче-
том равенства (5.22) получим
Л/,(У) = [ v<p,(.v)Jv= [ у ------- <Л*.
J. J-» <pt(x)
1 Говорят также: Yun Xи X пи Y.
190
ТМЬмш 5.8
Характерис- тики Дискретные случайные величины Непрерывные случайные величины
а, = М(Х) ts.p.. l-l /•! J х (p, (х) dx = J*,, f ’ * ф(а. г) dx dy (5.25)
а, = М(Г) Ё'-А, = ЁЁаА, l“l tai /а| J Уф;(у)4/г= J, уф(х.у)^Ф* (5.25’)
D(X) £(*. “ а- 'Y Р<- = Z ". Y Р» 4-1 1-1 1-1 j '(x - a,)’ ф, (x) dx = Jf * (x - a, )* ф(х,_v) dx dy (5.26)
D(Y) £(>; - *.*а, = £ - о.)’ pv /•1 i-i х-i )2Фг(>’) = JS ОЛ’"Л‘dy (5.26)
Му(Х) £ хф,(х)Л (5.27)
M,(Y) £t У ^,(y)dy (5.27)
Dy(X) l-t £ (x- Л/,(Х)Г’фДх)е& (5.28)
D,(Y) ^(v, - M,(Y))‘р.Лу,) £ (у-л/,(У)):ф.(ук/у (5.28)
Примечание. Условные вероятности р.,(хД р.Ау,>»« условные плотности ф,(х). Ф,(у) находя гея соответственно по форму-
лам (5.1), (5.2). (5.22).
Теперь
y--v,-~ </v j<p((x)cZr -
<Р,(х) I
УФ(х, y)dxdy- Л/O')
(в соответствии с формулой (5.25')).
5.5. Зависимые и независимые случайные величины
Выше (§ 3.2) введено понятие независимости дискретных слу-
чайных величин X и К основанное на независимости связанных с
ними событий X = х, и У = yj при любых / и /. Теперь можно дать
общее определение независимости случайных величин, основанное
на независимости событий X < х и Y < у, т.е. функций распределе-
ний F|(x) и Л(у).
Определение. Случайные величины X и Y называются неза-
висимыми, если их совместная функция распределения Дх, у) пред-
ставляется в виде произведения функций распределений Д(х) и А(г)
этих случайных величин, т.е.
F{x.y}=Fx(x)Fz(y). <5^)
В противном случае, прн невыполнении равенства (5.29). слу-
чайные величины Л' и Y называются зависимыми.
Дифференцируя дважды равенство (5.29) по аргументам х и у.
получим
ф(х.>’) = ф,(л*)ф:(у). (5.30)
т.е. для независимых непрерывных случайных величин X и Y их совмест-
ная плотность ф(х.у) равна произведению плотностей вероятности
Ф,(х) и ф:(у) этих случайных величин.
Сравнивая формулы (5.30) и (5.23), можно утверждать. что неза-
висимость двух случайных величин X и Y означает, что условные
плотности вероятности каждой из них совпадают с соответствую-
щими ^безусловными» плотностями, т.е.
<М*) = <₽.(•*) и Ф,(.г) = <₽,(>’). (5.31)
До сих пор мы сталкивались с понятием ф у н к ц и о н а л ь-
н о й зависимости между переменными X и Y, когда каждому
значению х одной переменной соответствовало строго определен-
ное значение у другой. Например, зависимость между двумя слу-
чайными величинами — числом вышедших из строя единиц обору-
дования за определенный период времени и их стоимостью -
функциональная.
192
В обшсм случае, при невыполнении условий (5.29)—(5.31).
сталкиваются с зависимостью другого типа, менее жесткой, чем
функциональная.
Определение. Зависимость между двумя случайными ве-
личинами называется вероятностной (стохастической или стати-
слшческой), если каждому значению одной из них соответствует оп-
ределенное (условное) распределение другой.
В случае вероятностной (стохастической) зависимости нельзя,
зная значение одной из них. точно определить значение другой, а
можно указать лишь распределение другой величины. Например, за-
висимости между числом отказов оборудования и затрат на его про-
филактический ремонт, весом и ростом человека, затратами времени
школьника на просмотр телевизионных передач и «пение книг и т.п.
являются вероятностными (стохастическими).
На рис. 5.10 приведены примеры зависимых и независимых слу-
чайных величин X и Y.
На рис. 5.10. а зависимость между X н Y проявляется в том, что с
изменением х меняется как распределение Y, так и условное матема-
тическое ожидание M/Y) (с увеличением х Л/JX) увеличивается). Там
хе показана зависимость Л/Д У) от х. т.е. линия регрессии Y по X.
б)
Toopei кцитпоага « «semiwwt**» стжитпи
193
Гис. 3.10
На рис. 5.10, б зависимость между случайными величинами про-
является в изменении условных дисперсий (с ростом х Dx( У) увели-
чивается). при этом ЛЛ( У) = const, т.е. линия регрессии Y по А' па-
раллельна оси Ох. На рис. 5.10, в случайные величины Y и X неза-
висимы, так как с изменением х распределение случайной величи-
ны Y, а значит, условное математическое ожидание Л/л< У) и услов-
ная дисперсия Д( У) нс меняются.
Риг. 5.11
Таким образом, обобщая, можно
утверждать, ’гго если случайные величи-
ны Y и X независимы. то линии регрес-
сии Y по X и X па Y параллельны коор-
динатным осям Ох и Оу.
О Пример 5.4. По данным приме-
ра 5.3 определить: а) условные плот-
ности случайных величин X и У,
б) зависимы или независимы случай-
ные величины А' и >'; в) условные ма-
тематические ожидания и условные дисперсии.
Р е ш е н и е. а) Найдем условную плотность ф, (г) по формуле
(5.22), учитывая, что ф,(у)*0.
Ф( *-.»•)
<₽,(*) =
при | х| < 71 -г:.
при | .V| > 71 - .г*'.
График ф, (л) при у = 1/2 показан на рис. 5.11.
Аналогично
при |.г|< 71 •
при | v|
194
б) X и Y — зависимые случайные величины, так как
<р(х,у)’еФ|(х)ч>2(.г) или Ф,(х)*Ф,(х). (.г) (см. пример
5.3 и п. а)).
в) Найдем условное математическое ожидание МА У) по формуле
(5-27'). учитывая, что Ф, (у) = —,
2Vl-x:
МА У) = f У Ф, ( .у ) = f - J—г у <Ь -
2VI-.V
Аналогично = | л ф. (л)Л = 0.
Этот результат очевиден в силу того, что крут .г + у: <, I
(рис. 5.5) симметричен относительно координатных осей. Таким
образом, линия регрессии У по X совпадает с осью Ох {МА У) = 0). а
линия регрессии АГ по У — с осью Оу {М>(Xi = 0).
Найдем условную дисперсию DA У) по формуле <5.28'>:
Г [>-«,(Г)]!<Р,<Н<Л = Г' ..1'4 =
J ' 2VI-x’
I .у1
2Vl-xa 3
I - r
3
(Тот же результат можно получить проще — по формуле диспср
сии равномерного закона распределения (4.20):
Аналогично
О.(*)=^уЧ0*Л'*1)-
Таким образом, по мере удаления от начала координат диспер-
сия условных распределений уменьшается от 1/3 до 0. ►
5.6. Ковариация и коэффициент корреляции
Пусть имеется двумерная случайная величина (ХУ), распределе-
ние которой известно, т.е. известна табл. 5.1 или совместная плот-
195
кость вероятности ф(л-.у). Тогда можно найти (см. § 5.4) матема-
тические ожидания Л/(Л) = ov Л/( У) = ау и дисперсии IXX) = о; и
/Л У) = о* одномерных составляющих А' и К Однако математические
ожидания и дисперсии случайных величин X и У недостаточно полно
характеризуют двумерную случайную величину (Х.У). так как не выра-
жают степени зависимости ее состаатяюших АГ и Y Эту роль выполняют
ковариация и коэффициент корреляции.
Определение. Ковариацией (или корреляционным момен-
том) А'и случайных величин X и У называется математическое ожи-
дание произведения отклонений этих величин от своих математиче-
ских ожиданий1, т.е.
А\ = A/[(.V - М(Х)ХУ-М(У))]. (5.32)
или К„ = A/[(.V-аг)(К-а,)].
где = М(Х). ау = М( У).
Из определения следует. что А'9. = Кух. Кроме того.
A'n = A/|( X - а, X А' -«,)] = М(Х - а, У = D( X).
т.е. ковариация случайной величины с самой собой есть ее дисперсия.
Для дискретных случайных величин
Л'п = EEU )U )Рг <533)
!•! /-I
Для непрерывных случайных величин
А'„ = J_. J- (*~И v” а>) r’ v) & 4*. (5.34)
Ковариация двух случайных величин характеризует как сте-
пень зависимости случайных величин, так и их рас-
сеяние вокруг точки (ах,ау). Об этом, в частности, свидетельст-
вуют свойства ковариации случайных величин.
I. Ковариация двух независимых случайных величин равна нулю.
□ Для независимых случайных величин согласно равенству
(5.30) ф(х.у) = Ф,(.г) Ф2(г). Поэтому формула ковариации, напри-
мер. (5.34) для непрерывных случайных величин примет вид:
А'„ = |’"(х-«,)ф1(х)</т J‘ (у-a, |ф:(у)<Л =0.
1 Ковариацию называют еще вторым смешанным центральным моментом случай-
ных величин .V и )‘ Дтя ковариации А и >' используются также обозначения
COV (X Одг
19<)
так как каждый из полученных интегралов есть центральный мо-
мент первого порядка, равный нулю.
2. Ковариация двух случайных величин равна математическому
ожиданию их произведения минус произведение математических ожи-
даний. т.е.
Kry = M(XY) ~ М(Х>- М( Л. (5.35)
или Кку = M(XY) - a^ty.
□ По определению (5.32):
Ку>.= М](Х-av) (Y- ev)| = M(XY-a.Y-а>Х+ а^).
Учитывая, что .математические ожидания М(Л) = а, и М( Л = ау —
неслучайные величины, получим
Кху = М(ХУ) - ахМ( Л - ауМ(Х) + а,ау =
= Л/<*Л - а^у — 0)01 + Oyfly- M(XY) - ОхОу.
3. Ковариация двух случайных величин по абсолютной ветчине не
превосходит произведения их средних квадратических отклонений, т.с.
|Кп|^о,сгг. (5.36)
□ Возьмем очевидное неравенство:
-£И1±^ + £Щ = 2±^г0 (537)
а; а.о, о; о,о,
(учтено. »гго о, и о, — неслучайные величины и дисперсии
D(X) = Л/ (X - и, )•' = о;. D( Y) = М (Y - а, \ = о;).
Неравенство (5.37) равносильно двойному неравенству
“О.о, <ZCH $о,о,. из которого следует доказываемое свойство (536).
197
Ковариация, как уже отмечено, характеризует нс только степень
зависимости двух случайных величин, но и их разброс, рассеяние
Кроме того, она — величина размерная, ее размерность определяет-
ся произведением размерностей случайных величин. Это затрудняет
использование ковариации для оценки степени зависимости для
различных случайных величин. Этих недостатков лишен коэффици-
ент корреляции.
О п р е д с л с н и е. Коэффициентом корреляции' двух случай-
ных величин называется отношение их ковариации к произведению
средних квадратических отклонений этих величин:
Pv=—• (5.38)
о,о.
Из определения следует, что рп = р„ = р. Очевидно также, что
коэффициент корреляции есть безразмерная величина.
Если рассматривать случайные величины X и ¥ как случайные
векторы, их ковариацию — как аналог скалярного произведения
двух векторов, средние квадратические отклонения — как аналоги
длин этих векторов, то коэффициент корреляции представляет ана-
лог косинуса угла между векторами.
Отметим свойства коэффициента корреляции.
I. Коэффициент корреляции принимает значения на отрезке | — I; 1|, т.е.
-irpsl. (5.39)
□ Из неравенства (5.37):
2 ± = 2 ± 2р > 0. откуда -1 < р < I.
о,о»
2. Если случайные величины независимы. то их коэффициент кор-
реляции равен нулю. т.е. р = 0.
□ р = 0, так как в этом случае Кху = 0.
Случайные величины называются некоррелированными, если их
коэффициент корреляции равен нулю. Таким образом, из независи-
мости случайных величин следует их некоррелированность.
Обратное утверждение, вообще говоря, неверно: из некоррелиро-
ванности двух случайных величин еще не следует их независимость
(см. пример 5.6).
3. Если коэффициент корреляции двух случайных величин равен (по
абсолютной величине) единице, то между этими случайными величи-
нами существует линейная функциональная зависимость.
’ Для коэффициент корреляции случайных величин в нперапрс используется
также обозначение eorr (.V. В.
198
D Выше было получено, что
.Г-о, ± Y-at
°. G,
Если р = +1. то 2±2р = 0 и М
= 0.
2 АГ
= 2 ± —- = 2 ± 2р.
стто,,
±
< °. % /
Равенство математического ожидания неотрицательной случай-
ной величины нулю означает, что сама случайная величина тожде-
ственно равна нулю.
Х-а
о,
У-а.
-----= 0 при р = + 1 или
суг
У = д,+—(X-at) при р = ! и К = а,------(Л'-ях)
Ог (Тх
При р = -1. т.с. Хи У связаны линейной функциональной зависи-
мостью.
Замечание. В случае нелинейной функциональной зависи-
мости |р|< I: возможно лаже, что р = 0. Так, например, коэффици-
ент корреляции р между случайными величинами: Л. равномерно
распределенной на интервале [-!:!) (с плотностью вероятности
ф(х) = - и М(.V) = ()). и У = АЛ~ равен нулю, ибо по формуле
(5.35) с учетом равенства (3.25))
К* = М(X • X2) - Л/(X)• Л/(X2) = М (X5) - 0 = j.v • ’ dx = 0.
-I
t> Пример 5.5. По данным примера 5.2 определить ковариацию
и коэффициент корреляции случайных величин X и У.
Решение. В примере 5.2 были получены следующие зако-
ны распределения одномерных случайных величин:
М
V
Найдем математические ожидания и средние квадратические от-
клонения этих случайных величин:
199
а, = Л/(Л') = £л;/>, = 10.8 + 20.2 = 1.2;
i-i
Л/(А'г) = £.r;д = l: 0.8 + 2: 0.2 = 1.6;
f-i
CXX) = M(X2)~a; = 1.6-1.22 = 0.16; a, = ^D(Af) = >/0J6 =0.4;
ay = /И(У)=£т(/>, = (-l)-0,2+0-0.3 +1 0,3т2-0.2 =0,5;
i ।
W:) = £j->, = (-l );-0.2 + O2-O,3 +1:-0,3 + 2:-0.2 = 1.3;
zxn= Л/(Н-<=1,3-0.5;= 1.05; a, = = >Д>5 = 1,025.
Для нахождения математического ожидания M(XY) произведе-
ния случайных величин X и Y можно было составить закон распре-
деления произведения двух дискретных случайных величин (с веро-
ятностями его значений из табл. 5.2)*, а затем по нему найти M{XY).
Но делать это вовсе нс обязательно. Л/(Х)) можно найти непосред-
ственно по табл. 5.2 распределения двумерной случайной величины
(А*. У) по формуле:
Л/(Л'У) = ££ х^,
.-I |-1
к **
где двойная сумма означает суммирование по всем пт клет-
pl
кам таблицы (п — число строк, т — число столбцов):
А/(АГУ) = I -(-1)-0.10 + (-D-O-O.25 + I • 1-0.30 + 1-2-0.15 +
+2 •<-!)• 0,10 + 2-0-0.05 + 2 - 1 - 0 + 2 • 2 • 0.05 = 0.5.
Вычислим ковариацию А'м. по формуле (5.35):
Kty = Л/(АГУ) - ахау = 0.5 - 1.2 • 0.5 = -0.1.
Вычислим коэффициент корреляции р по формуле (5.38):
1 Закон распределения <Л'У) имеет вид:
-2 -1 0 1 2 4
р, 0.1 0.1 0.3 о.з 0.15 0.05
200
т.е. между случайными величинами X и Y существует отрицательная
линейная зависимость; следовательно, при увеличении (уменьше-
нии) одной из случайных величин другая имеет некоторую тенден-
цию уменьшаться (увеличиваться). ►
О Пример 5.6. По данным примера 5.3 определить: а) ковариа-
цию и коэффициент корреляции случайных величин X и У: б) кор-
родированы или некоррелированы эти случайные величины.
Реше н и с. а) Вначале по формулам (5.25), (5.26) найдем ма-
тематические ожидания ах = М(Х} и а,.= М{ У).
и, = | | х<р(х. г) cZv dy = у J х <Zv|dy = 0.
Аналогично av = 0 (то. ’гго ая = ау = 0. очевидно из соображения
симметрии распределения в круге, из которой следует, что центр
его массы лежит в начале координат).
По формуле (5.34) ковариация
К= J J ( х - а,)(у - о,) ф( х.у) dx dy -
= [ f х — — dxdv = — Г vtZvf' vdv-
it J-1 2 -Л7? J
К
Соответственно коэффициент корреляции p =—— =0.
о,а,
б) Так как р = 0. то случайные величины X и У некоррелированы.
В примере 5.4 установлено, что эти случайные величины зависимы:
таким образом, наглядно убеждаемся в том. что из некоррелированно-
сти величин еще не вытекает их независимость. ►
С помощью ковариации можно дополнить и уточнить некото-
рые свойства математического ожидания и дисперсии (рассмотренные
в гл. 3).
I. Математическое ожидание произведения двух случайных вели-
чин равно сумме произведения их математических ожиданий и кова-
риации этих случайных величин:
M(XY) = М(Х) • M(Y) + К» (5.40)
□ Формула (5.40) следует непосредственно из формулы (5.35).
Если А'г, = 0. то
M(XY) = М(Х)М(Г).
(5.41)
201
т.с. математическое ожидание произведения двух некоррелированных слу-
чайных величин равно произведению at математических ожиданий'.
2. Дисперсия суммы двух случайных величин равна сумме их диспер-
сий плюс удвоенная ковариация этих случайных величин:
ДС¥ + П =/ХЛ) + ZXD + 2KV. (5.42)
□ Пусть Z = X + К По свойству математического ожидания
а. = ах + ау Поэтому Z - а: = (X - av) + (Y - л».).
По определению дисперсии
D(X + П = IXZ) =M{Z - «.)•' = М{Х - ах)‘ + 2Л/|(АГ — ot)( Y- ау)| +
+ Л/( У- ау)2 =/**) + 2Л^ + IX Y).
Формула (5.42) может быть обобщена на любое число слагаемых:
S '', | = £о(Л-.) + 2£2Х. (5.43)
X, />| / >>| )>1 /•«
где К1} — ковариации случайных величин X, и Хг
Для некоррелированных (и. разумеется, для независимых) слу-
чайных величин
»| £.V,] = £D(A-.). (5.44)
т.е. дисперсия суммы некоррелированных случайных величин равна сум-
ме их дисперсий.
«5.7. Двумерный (п-мерный) нормальный закон
распределения
Определение. Случайная величина (X. У) называется рас-
пределенной по двумерному нормальному закону, если ее совместная
плотность имеет вид:
где
Л(х..>) =
ф„(х.Л.) =------
2па,(7,71-Р*
(5.45)
г - а,
ст,
_ .г - а, У -
-2р--------------
°. «с
г-а,
о,
1 В § 3.3 свойсгно (5.41) сформулировано для н е з а н и е и м ы х случайных
неднчнн. Теперь выясняегся. что и случае <hyx сомножителей достаточно менее
жесткого требования некоррелированности случайных величин
В случае п{юи шозыю.'о числа сомножителей, как показывает анализ, требование
независимости случайных величин должно быть сохранено.
202
Из определения (5.45). (5.46) следует, что двумерный нормсиъ-
закон распределения определяется пятью параметрами',
a .ov,o\, о\, р т.е. (А’.У) - о;, ст;, р).
Для выяснения теоретике-вероятностного смысла этих парамет-
ров по формулам (5.25)—(5.28). (5.34) найдем математические ожи-
дания случайных величин М{Х} и Л/( У), их дисперсии D{X) и D( У) и
ковариацию А\г Получим после замены фч(х.у)се выражением
(5.45) с учетом равенства (5.46) н вычисления интегралов1:
Л/(Л') =j j х ф s (х. у) dx dy = и,
и аналогично М( У) = а»;
D( А') = j J (х - й, )' ф J.v.у) dx dy = ст;
и аналогично D( У) = ст;;
Кп = J [ (х-а, )(.!’-«, ) Фч (х.у) г/х dy - рст.ст,.
Таким образом, параметры ах и av выражают математические
ожидания случайных величин X и У. параметры ст; и ст; — их дис-
персии. а —— = р — коэффициент корреляции между случайными
ст.ст,
величинами X и Y.
Найдем плотности вероятности одномерных случайных величин
Ли У по формулам (5.20) с учетом равенств (5.45). (5.46):
Ф,(.г)={ Ф.(.т,у)«Л- =---f=e :я’ (5.47)
о,72я
к аналогично
I’-". Г
ф.(у) =---V»* *"• . (5.48)
ст,
Как и следовало ожидать, каждый из законов распределения од-
номерных случайных величин Хн У является нормальным с пара-
метрами соответственно (а,,с;) и (ст,.ст;).
Найдем условные плотности вероятности случайных величин X
и У по формулам (5.22) с учетом равенств (5.45)—(5.48):
ФчСМ’) I "
Ф,<Л> =-----ГТ =------Г , г—е
Ф’(.»’) ojl-p2^
• Вычисление сООтоетсзнумшшх hccoGciпенных inneipajon п § 5.7 опускаем
203
и аналогично Ф,(у) =
Сравнивая полученные выражения условных плотностей ф,(л>
и <р,(у) с плотностями одномерных составляющих (5.47) и (5.48).
убеждаемся в том. что каждый из условных законов распределения
случайных величин X и Г является нормальным с условным матема-
тическим ожиданием и условной дисперсией, определяемыми но
формулам:
М(Х) = а, + р^-(у-а,). (5.49)
G, '
D,(A') = <y;(l-p:), (5.50)
Л/,()') = ^ + р—(х-н,), (5.51)
Gt
П,(Г) = с;|1-рг1. (5.52)
Из формул (5.49). (5.51) следует, что линии регрессии Му(Х} и
Л/,( У) нормально распределенных случайных ветчин представляют со-
бой прямые линии, т.е. нормальные регрессии Y по X и X по Y всегда
линейны.
Из формул (5.50) и (5.52) следует, что условные дисперсии
ОДЛ) и /)Д(У) (а значит, и условные стандартные отклонения о, (А)
и о,(К)) постоянны и нс зависят от значений у или х. Это свойство
называется гомоскедастичностью или равноизменчивостью условных
нормальных распределений и имеет существенное значение в статис-
тическом анализе.
Теорема. Earn две нормально распределенные случайные величины А
и Y некоррелированы, то они независимы.
□ По условию коэффициент корреляции р = 0. Найдем выра-
жение совместной плотности. По формулам (5.45). (5.46) при р = ()
получим:
------------------’°* =Ф,(•<)<?.(у). (5.53)
o,V2n а,72я
где Ф|(х)и ф.(г) — плотности вероятностей одномерных случай-
ных величин X и Y.
204
В соответствии с условием (5.30) это означает независимость
случайных величин X и К
Таким образом, для нормально распределенных случайных величин
термины «некоррелированность» и «независимость» равносильны.
Поверхность ц>у(.т.у) нормального распределения представляет
собой холмообразную поверхность, называемую иногда «палаткой Га-
усса» (рис. 5.12).
Сечения этой поверхности плоскостями х = а (перпендикулярно оси
Ох) н у = b (перпендикулярно оси Оу) имеют форму нормальных
кривых с центрами, лежащими на линии регрессии Y но X (5.51) и
/по Г(5.53). и со средними квадратическими отклонениями, рав-
ными О, 71 “Р: И О, >/| - Р' •
Сечение поверхности нормального распределения плоскостью : = с
(где 0 < с < Ф. (и, ,а,)). параллельной плоскости Оху. представляет
эллипс, называемый эллипсам рассеяния (рис. 5.13):
(х-и,): (х-а,)(у-о.) (>-«.)
-----; 2р + ;—— = О ,
а;------------------------------н.п.-о;
где а' = -2(1 -р*') 1п(2лсстго, Jl - р‘).
(В силу ограничения для с аргумент логарифма меньше I. а само
значение логарифма отрицательно.)
Центр эллипса находится в точке (ах, ау), а его оси образуют с
осью Ох углы а и л/2 + а. где а определяется из условия
ф2а =
2pcr,cr t
о;-о;
205
В случае, если нормально распределенные величины X и Y неза-
висимы, т.е. р = 0. то tg 2u = 0, откуда а = 0 и оси симметрии эл-
липса параллельны осям координат. При этом если ст, = ov =ст. то
эллипс рассеивания превращается в круг, а полученное распределе-
ние с центром в точке («,,</,) называется круговым. Использование
такого распределения облегчает решение многих прикладных задач,
так как случайные величины X и Y осгаются независимыми при лю-
бом повороте координатных осей.
Определение. Случайная величина (A'j, Х^, .... Хп) называ-
ется распределенной по п-мерному нормальному закону, если ее совме-
стная плотность имеет вид:
где а, — математическое ожидание одномерной составляющей А';
(/=1,2....л);
|А’.| — определитель ковариационной матрицы (А',) случайной
величины (А\, X,..Х„):
К
К
(5.55)
•• К
К„'— элементы матрицы, обратной по отношению к ковариа-
ционной матрице (Л').
Из определения (5.54), (5.55) следует, что нормальный закон рас-
пределения л-мерной случайной величины (л-мерного случайного
вектора) Х = (А’|, AS.Хп) характеризуется (л + л (л + 1)/2) параметра-
ми, задаваемыми вектором математических ожиданий а = (д(, а?..... anY и
симметрической ковариационной матрицей (Л'Д где Kv = М\(Х,-
- dJ)(A’/-fl/)| i,j= I, 2.л.
Ковариационная матрица и ее определитель |A'J. называемый
обобщенной дисперсией п-мерной случайной величины, являются анало-
гами дисперсии одномерной случайной величины и характеризуют
степень случайного разброса отдельно по каждой одномерной состав-
ляющей и в целом по п -мерной величине.
206
В качестве характеристики степени рассеивания значении мно-
гомерной случайной величины используется также след ковариаци-
онной матрицы, т.е. сумма се диагональных элементов — дисперсий
одномерных составляющих: tr (А\,) = £ Kt.
I ।
Можно показать, что при л = 2 совместная плотность (5.54)
имеет вил (5.45). (5.46) — совместной плотности двумерного нор-
мального распределения, а свойства л-мерного нормального закона
аналогичны свойствам двумерного.
5.8. Функция случайных величин.
Композиция законов
распре деления
Одной из важных задач в теории ве-
роятностей является определение закона
распределения функции одной или не-
скольких случайных величин. если из-
вестны распределения одного или не-
скольких аргументов. Если дискретная
случайная величина А' имеет закон рас-
пределения j ]. /= I, 2...... л, то
функция Г = /(.¥)— также дискретная случайная величина — имеет
( Л
закон распределения
I Р.
При этом если среди значений / (л;)
встречаются одинаковые, то соответствующие их вероятности надо сло-
жить» приписав / (л;) суммарную вероятность. Так мы поступали ранее
при построении законов распределения функций некоторых дискретных
случайных величин ()’ = kX. Y- X", 7 - Л' + Y. 7. = X -Y.Z - ЛТ) —
см. § 3.2. Обратимся теперь к непрерывным случайным величинам.
Пусть имеется непрерывная случайная величина А'с плотностью ве-
роятности ip(.v). а случайная величина У есть функция от А', т.е.
У - /(X). Требуется найти закон распределения случайной величины У
Пусть функция строго монотонна, непрерывна и диффе-
ренцируема на отрезке |«. />| всех возможных значений случайной вели-
чины Хи /(«) = с. /(/>) = </ (рис. 5.14). Полагаем, что /'(х)>0.
Тогда функция распределения G(v) случайной величины Y = f(X):
207
О при у < с,
g(v)4>’ при с-У-(,‘
тле gfy) — плотность вероятности случайной величины К = /(А).
Если с< y<d.
G(y) = P(Y<y) = P(f(X)<y).
Неравенство /(А' )< г равносильно неравенству X < f ’tv), гле
/~’tv) — функция, обратная функции Дх) на отрезке |д,6]. Поэтому
G(г) = /’[.Г < / \г)] = f J “<p(x)cfr.
По теореме Ь производной интеграла по переменному верхнему
пределу1:
S(.r)=G-(.r)=<|>[/'(.v)] |[/-'(.>’)]' |- (5-56)
(Производную | f ,(r)j‘ берем по абсолютной величине, так как в
случае, если функция Дх) на отрезке |а, />| убывающая, то обратная ей
функция f ‘( г) убывающая и производная [/ ’(>’)] <0. а плотность
вероятности g{y) отрицательной быть не может.)
Если функция г = /(х) на отрезке |а. Л| возможных значений
случайной величины X немонотонна, то обратная функция х = / ’(.г)
неоднозначна, и число ее значений зависит от того, какое значение у
взято (рис. 5.15).
Рис. 5.15
1 Формула (5.56) остается п силе на бесконечном интервале (“*, ♦«j. т.с. при
а с ~ 6 = + ао .
208
в этом случае нетрудно показать (см., например, |7|), что
«(.!) = Ёф[Г,(>’)]|[/',(.1')]'|. (5.56-)
/-1
где А — число значений обратной функции / ‘(г). соответствующих
данному у /''О’). ....4 '(г) — значения обратной функции
jS/‘‘(у). соответствующие данному у.
О Пример 5.6а. Найти плотность вероятности случайной величи-
ны X2, где случайная величина X распределена ио стандартному нор-
мальному закону /V (0; I).
Решение. Функция у = .V не-
монотонна (рис. 5.16).
По формуле (5.56'). учитывая, что
= = получим
ЧУ
g(y) = Ф( - V?) • —7= + Ф( у[у) • —U •
2у]у 2у]у
Для стандартного нормального
I л .
закона ф(х) = -=е * и
>J2n
т.е. представляет плотность вероятности ^-распределения (4.38’) с
к = I степенью свободы, ибо j = Vn. ►
Можно показать, что для нахождения числовых характеристик
случайной величины Y = f(X) не обязательно знать закон ее рас-
пределения. достаточно знать закон распределения аргумента:
а = М(У)=М[/(Х)]= f"/(x)<p(x) A. (5.57>
О(Г) = О[/(Х)]= j" [/(х)-О,]ф(х)Л. (5.58)
или
D(Y)=M<Y:)-a; = (5.58’)
209
t> Пример 5.7. Найти плотность вероятности случайной величи-
ны Y = 1-Х3. где случайная величина X распределена по закону
Коши с плотностью вероятности <р(.г) = ——гг-
к(1+г)
Решение. По условию у = /(.v) = | - .г* 1, откуда
х- f (>’)~ V1 ' Г • Производная (по абсолютной величине)
[/-(>.)] = V=T-
По формуле (5.56) плотность вероятности
1,1 * 3n{l + 7(l-.v)!^(l-.v):
О Пример 5.8. Найти математическое ожидание и дисперсию слу-
чайной величины )'=2-3sin.V, если плотность вероятности слу-
чайной величины А'есть <p(.v) =-^cos.r на отрезке |-л/2. я 2].
Р е ш с н и е. По формуле* (5.57)
а. = Л/(К) = J (2-3sin.t)~cos.v</v = 2.
По формуле- (5.58') дисперсия А)(Г) = .W( Y') - .
М(Г) = J (2-3 sin.v)'-cos.vdr=7 и Д(Г) = 7-2* =3. ►
Из множества задач на составление закона распределения функ-
ции нескольких случайных величин важное для практики значение
имеет задача определения закона распределения с у м м ы двух
случайных величин, т.е. закон распределения случайной величины
Z = X + Y. В случае, если X и Y — независимые случайные величи-
ны. говорят о композиции (свертке) законов распределения.
В гл. 4. в частности, установлено, что сумма двух (и более) аль-
тернативных случайных величин распределена по биномиальному
закону; сумма двух случайных величин, распределенных по закону
Пуассона, также распределена по закону Пуассона.
• Вычисление интегралов предлагаем провести читателю самостоятельно.
1 В данном конкретном случае 1К И проще найти по основной формуле (5.S8)'
г « - » I 9 г» - %
Di К) = J - 3 sin х - 2)" - cosxtZx = - J sin" xcosx (ix - 3.
210
Рассмотрим композицию законов распределения двух непре-
рывных случайных величин. Пусть плотности вероятностей случай-
ных величин X и Y равны соответственно <р, (.v) и <р, (у).
Найдем сначала функцию распределения случайной величины Z:
F(z)= />(Z < z)= Р(Л +)' < z) = jf<p(w) dx dy. (5.5g-)
1).
rufi Dt — множество всех точек плоскости Оху. координаты которых
удовлетворяют неравенству х + у < : (рис. 5.17), ф(х,у) — совместная
плотность двумерной случайной величины (X, К). Так как X и Y — не-
зависимые случайные величины, то А
ф(х,у) = Ф|(г)<рг|у| и формула (5.58') ?
примет вид:
F(z)=| J‘ ‘ Ф,(х)ф.(у)<Л =
’ D. X
= Г ф((х)<Л:Г ф.(у)с/г. —j— —— —♦
J-* 1 • о ’ \ х
Найдем плотность вероятности ф(z): Рмс- 5*17
ф(г)=Г(г)= j фДх)^ j Ф;(у)<А') .
ф(-)= £1Ф1(’г)ф2(2-х)<Л‘. (5.59)
Формулу (5.59) называют формулой композиции двух распределений
или формулой свертки, которая в краткой записи имеет вид:
Ф = Ф! • Ф;.
О Пример 5.9. Найти закон распределения суммы двух случай-
ных величин, распределенных равномерно на отрезке (0; 11.
Р е ш е н и е. Пусть Z = X + У, |де ф, (х) = I при 0 < х £ I и
Ф:(у) = 1 при 0< ,г< !.
По формуле (5.49) плотность вероятности
4>(г)= |'ч>.(г-х)Л-.
Если г < 0, то для 0 <, х < I г - х < 0; если z > 2. то для 0 £ х <> I
z - х >1, следовательно, в этих случаях ф,(с - л)= 0 и <p(z) = 0.
211
Пусть 0<z<2. Подынтегральная функция ф.(г-.г) будет от.
лична от нуля только для значений х. при которых ()< z -х< I или,
что то же самое, при z -1 < х:<>
Если 0 < z < I. то <р( z) = j I • dx = z.
Если I < z < 2 . то ф( 2) = J' J • dx = 2 - z.
Объединяя все случаи, получим:
О
«>(-) =
при z < 0. z > 2.
при 0 < z <, I.
при 1 < z < 2.
(5.60)
Закон распределения (5.60) называется законом распределения
Симпсона или законом равнобедренного треугольника (рис. 5.18).
Вычисление <p(z) можно было провести и иначе: вначале найти
функцию распределения F\z), а затем — ее производную, т.е.
Ф(г) = Г'С). Преимущество такого подхода состоит в возможности
использования геометрической интерпретации функции F{z) как
плошали области D — части квадрата (со стороной, равной 1), ле-
жащей левее и ниже прямой у = z — х (рис. 5.19).
Рис. 3.1»
Действительно (см. рис. 5.19), при 0 <. : $ I So = z2/2 (площадь за-
штрихованного треугольника со стороной г), а при I < z <, 2 St/ = 1 -
- (2 - zr/2 (площадь квадрата без площади незаштрихованного тре-
угольника, сторона которого, как нетрудно показать, равна (2 - г).
Следовательно,
212
О при z < О.
:г/2 npwOSzSl,
Л-’) = ,
1-(2-г)*/2 при lSzS2,
1 при z > 2
и выражение (5.60) для q>(z) получается дифференцированием
Дх). ►
Композиция нормальных законов распределения также имеет нормаль-
ное распределение. Так. если X и Y — независимые нормально распре-
деленные случайные величины, т.е. X - N(<j,.ct^). Y - Л'(а, .о;), то
случайная величина Z = X + Y также нормально распределена:
Z-N(a^at, o;+oj.
Верно н обратное утверждение. Если сумма двух независимых слу-
чайных величин 7. = X + У распределена нормально, то каждая из вели-
чин X. Y сама распределена нормально.
В случае, если нормально распределенные случайные величины X
и Yзависимы (коэффициент корреляции р т 0). то случайная величи-
на Z = X + Y по-прежнему нормально распределена с параметрами
а. = ах + Ор ст; = ст; + ст; + 2рст,о .
Упражнения
5.10. Закон распределения двумерной дискретной случайной
величины (X И задан в табл. 5.4.
T116.1111U1 5.4
у' х, х< 0 1 2 3
-1 0.02 0.03 0.09 0.01
0 0.04 0.20 0.16 0.10
1 0,05 0.10 0.15 0.05
Найти: а) законы распределения одномерных случайных вели-
чин X и У; б) условные законы распределения случайной величины
X при условии У = 2 и случайной величины У при условии X = 1;
в) вероятность Л У > Л).
5.11. Рассматривается двумерная случайная величина (X. У), где
X — поставка сырья. У — поступление требования на него. Извест-
но, что поступление сырья и поступление требования на него могут
произойти в любой день месяца (30 дней) с равной вероятностью.
213
0 при г<0.
, < П =
5е при г > 0;
Определить: а) выражение совместной плотности и функции рас-
пределения двумерной случайной величины (А'. У); б) плотности ве-
роятности и функции распределения одномерных составляющих Л'и
У\ в) зависимы или независимы X и X; г) вероятности того, что по-
ставка сырья произойдет до и после поступления требования.
5.12. Двумерная случайная величина (А'.У) распределена равно-
мерно внутри квадрата Л с центром в начале координат. Стороны
квадрата равны и составляют углы 45° с осями координат. Опре-
делить: а) выражение совместной плотности двумерной случайной
величины (Х.УУ. б) плотности вероятности одномерных составляющих
X и У: в) их условные плотности: г) зависимы или независимы X и У.
5.13. Даны плотности вероятности независимых составляющих
двумерной случайной величины (А', У):
О при у < 0.
2е при у>0.
Найти выражение совместной плотности и функции распреде-
ления двумерной случайной величины.
В примерах 5.14—5.16 определить: а) ковариацию и коэффици-
ент корреляции случайных величин X и У. 6) коррелированы или
некоррелированы эти случайные величины.
5.14. Использовать данные примера 5.10.
5.15. Использовать данные примера 5.11.
5.16. Использовать данные примера 5.12.
5.17. Случайная величина Д'распределена на всей числовой оси
с плотностью вероятности ф(.т) = 0.5е '. Найти плотность вероят-
ности случайной величины У = Д’* и ее математическое ожидание.
5.18. Найти закон распределения суммы двух независимых слу-
чайных величин, каждая из которых распределена по стандартному
нормальному закону, т.с. JV(O:I).
5.19. Двумерная случайная величина определяется следующим
образом. Если при подбрасывании игральной кости выпадает четное
число очков, то А'= I, в противном случае Х= 0; У- I. когда число
очков кратно трем, в противном случае У = 0. Найти: а) законы
распределения двумерной случайной величины (X. И и ее одномер-
ных составляющих; б) условные законы распределения X и У.
5.20. Двумерная случайная величина (А*. У) распределена с по-
стоянной совместной плотностью внутри квадрата ОАВС, где (ОДО).
Л(0;1), В(1;1), С(1:0). Найти выражение совместной плотности и
функции распределения двумерной случайной величины (X. У).
5.21. Поверхность распределения двумерной случайной величи-
ны (X. У) представ.!яет прямой круговой конус, основанием которо-
го служит круг с цегггром в начале координат и с радиусом 1. Вне
214
этого круга совместная плотность двумерной случайной величины
(X У) равна нулю. Найти выражения совместной плотности ф(х, у),
платностей вероятностей одномерных составляющих ф,(х). фХу).
условных плотностей флО0, <М-Т). Выяснить, являются ли случайные
величины X и У: зависимыми, коррелированными.
5.22. Двумерная случайная величина {X. Y) распределена по за-
кону
А
Ф(Х.У) = ;----;---r-j-----г .
I + X* + х* у -* г*
Найти: а) коэффициент А: б) вероятность попадания случайной вели-
чины (X Y) а пределы квадрата, центр которого совпадает с началом ко-
ординат. а стороны параллельны осям координат и имеют длину 2. Уста-
новить, являются ли величины X и У зависимыми; найти ф|(х), ф:(у).
5.23. Совместная плотность двумерной случайной величины (X У)
имеет вид
Ф(х.у) =
С(х' + \т + г*)
О
при OSxS I. о< I.
в остальных случаях.
Найти: а) постоянную С; б) плотности вероятности одномерных
составляющих; в) их условные плотности; г) числовые характерис-
тики ах. ау, /XX. ZX У), р.
5.24. Найти совместную платность двумерной случайной величины
(X У) и вероятность ее попадания в область D — прямоугольник, ограни-
ченный прямыми х = I. х = 2. у = 3. у = 5. если известна се функция рас-
пределения (X И:
/"(х, г) =
-2 ‘ + 2-•
при х>0. г>0.
при х < 0 или у < 0.
5.25. Задана совместная плотность двумерной случайной вели-
20
чины (X У): Ф(х. >) = —---:------—. Найти функцию распре-
л*(16 + х’)(25+г)
деления Дх, у).
5.26. Имеются независимые случайные величины X У. Случай-
ная величина X распределена по нормальному закону с параметрами
ах = 0, о; = 1/2. Случайная величина У распределена равномерно на
интервале (0:1). Найти выражения совместной плотности и функции
распределения двумерной случайной величины (X. У).
5.27. Совместная плотность двумерной случайной величины (X.
У) задана формулой
Ф(х. г) = --е *
1.6л
Найти ах, ау, о;. ст , р.
215
5.28. Независимые случайные величины X. К распределены по
нормальным законам с параметрами «д. = 2. - -3. <т; = I . ст; = ц
Найти вероятности событий:
а) (Х< ах) ( Y < а,.); б) Y< X- 5; в) (|Л| < 1)(|И < 2).
5.29. Задана плотность вероятности <р(х) случайной величины Д',
принимающей только положительные значения. Найти плотность
вероятности случайной величины У. если: а) У= е *; б) У~ In ,V;
в) У=Х\г) Г= 1/А*д) Y = JX
5.30. Случайная величина X равномерно распределена в интер-
вале (-я/2: я/2). Найти плотность вероятности случайной величи-
ны У = sin X.
5.31. Случайная величина распределена по закону Редея с плот-
ностью вероятности
<1И v) =
хе'* 1 при х>0,
О при .V < 0.
Найти закон распределения случайной величины У = е .
5.32. Случайная величина X распределена по закону Коши с плотно-
стью вероятности
ф(х) =------— (-»< х < +»).
Я(1+Х’)
Найти плотность вероятности обратной величины У= \/Х.
5.33. Дискретная случайная величина X имеет ряд распределения
0.2 0.1
0,3 0.4
Найти математическое ожидание и дисперсию случайной вели-
чины У = 2х.
5.34. Имеются две случайные величины X и У. связанные соот-
ношением У= 2 - ЗХ. Числовые характеристики случайной величи-
ны X заданы ах = -I; D(X) = 4. Найти: а) математическое ожидание
и дисперсию случайной величины У; б) ковариацию и коэффициент
корреляции случайных величин X и У
5.35. Случайная величина X задана плотностью вероятности
<p(x) = cosx в интервале (0. я/2); вне этого интервала <р(х) = 0. Най-
ти математическое ожидание случайной величины У- X2.
5.36. Случайная величина X распределена с постоянной плотно-
стью вероятности в интервале (I ;2) и нулевой плотностью вне этого
216
интервала. Найти математическое ожидание и дисперсию случайной
о I
величины У = у.
5.37. Непрерывная случайная величина X распределена в ин-
тервале (0;1) по закону с плотностью вероятности
2х при хе [0:1],
ф(х) =
О при хе [0;1].
Найти математическое ожидание и дисперсию случайной вели-
чины У=АГ2.
5.38. Непрерывная случайная величина распределена по пока-
зательному закону с параметром X = 2. Найти математическое ожи-
дание и дисперсию случайной величины У = е х.
5.39. Случайная величина X распределена по нормальному за-
кону с параметрами а = 0, о2 = 5. Найти математическое ожидание
случайной величины Y- I - ЗХ‘ + 4Х3.
5.40. Имеются две независимые случайные величины X и Y. Ве-
личина X распределена по нормальному закону с параметрами
ах = 1. ст; = 4. Величина Y распределена равномерно в интервале
(0:2). Найти: а) М(Х- П, [XX - У); 6) Л/(АГ2), Л/( Y-).
5.41. Даны плотности вероятности независимых равномерно
распределенных случайных величин X и У: ф|(х) = 0.5 в интервале
(0;2), вне этого интервала ф|(х) = 0; <pj(j) = 0.5 в интервале (0:2),
вне этого интервала ф.Ч.г) = 0. Найти функцию распределения и
плотность вероятности случайной величины Z= А*+ Y.
5.42. Независимые нормально распределенные случайные вели-
I
чины X и Y заданы плотностями вероятности ф|(х) = —7=е • .
V2n
I
Ф2(У) = -7=е • .
х/2л
Найти композицию этих законов, т.с. плотность
вероятности случайной величины 7. = X + У, и числовые характе-
ристики а. и ст'.
Глава 6
Закон больших чисел
и предельные теоремы
Пол законом больших чисел в широком смысле понимается
общий принцип, согласно которому, по формулировке академика
А.Н. Колмогорова, совокупное действие большого числа случайных
факторов приводит (при некоторых весьма общих условиях) к ре-
зультату. почти не зависящему от случая. Другими словами, при
большом числе случайных величин их средний результат перестает
быть случайным и может быть предсказан с большой степенью опре-
деленности.
Под законом больших чисел в узком смысле понимается
ряд математических теорем, в каждой из которых для тех или иных
условий устанавливается факт приближения средних характеристик
большого числа испытаний к некоторым определенным постоян-
ным. Прежде чем перейти к этим теоремам, рассмотрим неравенст-
ва Маркова и Чебышева.
6.1. Неравенство Маркова (лемма Чебышева)
Теорема. Если случайная величина X принимает только неотрица-
тельные значения и имеет математическое ожидание, то для любого
положительного числа А верно неравенство
/э(х>.4)<—k (6.1)
А
□ Доказательство проведем для дискретной случайной величи-
ны X. Расположим ее значения в порядке возрастания, из которых
часть значений Х|. х?.х* будут нс более числа А. а другая часть
х*41..хп будут больше А. т.е.
х, < А. х, < А.х, < Л; х,> Я,х, > А (рис. 6.1).
-----1---------1------1-•--1-------1---------►
х, х2 хд А хЬ| ... х„ х
Рис. 6.1
Запишем выражение для математическою ожидания
*lPl + W2 +••• + +•••+ ад.= Wh
где р\. Р2.Рп — вероятности того, что случайная величина X при-
мет значения соответственно Х|. х?.хп.
218
Отбрасывая первые к неотрицательных слагаемых (напомним. »гго
все х, >0). получим
Xt+ip^i+...+х^ < М(Х). (6.2)
Заменяя н неравенстве (6.2) значения x^i...хп м е н ь ш и м
числом А, получим более сильное неравенство
Л(Ац.| +...+р„) <• Л/(Я) или /\., + .
А
Сумма вероятностей в левой части полученного неравенства пред-
ставляет собой сумму вероятностей событий А=л\.|.... X = хп. т.е.
вероятность события X > А. Поэтому Р (X >А) < -- .
А
Так как события X > А и Л' < А противоположные, то. заменяя
Р(Х>А) выражением 1-Р(А'<.4), придем к другой форме неравен-
ства Маркова:
(6.3)
Неравенство Маркова применимо к любым неотри-
цательным случайным величинам.
О Пример 6.1. Среднее количество вызовов, поступающих на
коммутатор инода в течение часа, равно 300. Оценить вероятность
того, что в течение следующего часа число вызовов на коммутатор:
а) превысит 400; б) будет не более 500.
Решение, а) По условию Л/(.¥) = 300. По формуле (6.1)
Р(Х >400)<^j-. т.е. вероятность того, что число вызовов превы-
сит 400. будет не более 0.75.
б) По формуле (63) Р{ X < 500) > 1 -
300 л .
----= 0.4, т е вероятность то-
500
го, что число вызовом не более 500, будет н с менее 0.4. ►
[> Пример 6.2. Сумма всех вкладов в отделение банка составляет
2 млн руб., а вероятность того, что случайно взятый вклад не превы-
сит 10 тыс. руб., равна 0.6. Что можно сказать о числе вкладчиков?
Р с ш с н и е. Пусть X — размер случайно взятого вклада, ал —
число всех вкладов. Тогда из условия задачи следует, что средний раз-
?()()()
мер вклада М(Х)=------- (тыс. руб.). Согласно неравенству Маркова
и
(6.3): /’(А’< 10) > 1 -или
219
200
Учитывая, что Р( X < 10) = 0.6. получим I-----<0.6. откуда
п
п < 500. т.е. число вкладчиков не более 500. ►
6.2. Неравенство Чебышева
Теорема. Для любой случайной величины, имеющей математиче-
ское ожидание и дисперсию, справедливо неравенство Чебышева:
Р(| Х-а |>е)й-^Ш. <6-4)
где а = М{Х). е >0.
□ Применим неравенство Маркова в форме (6.1) к случайной
величине .Г = (Л'-а)?, взяв * в качестве положительного числа
J = e:. Получим
Так как неравенство (А' - л)2 > £: равносильно неравенству
|.V-u|>r., a Af(.V-a)’ есть дисперсия случайной величины А’, то из
неравенства (6.5) получаем доказываемое неравенство (6.4).
Учитывая, что события |А'-а|>£ и |.V-u|<c противоположны,
неравенство Чебышева можно записать и в другой форме:
Р(| Х-а | (6.6)
ь
Неравенство Чебышева применимо для любых случайных
величин. В форме (6.4) оно устанавливает верхнюю границу,
а в форме (6.6) — н и ж н ю ю границу вероятности рассматри-
ваемого события.
Запишем неравенство Чебышева в форме (6.6) для некоторых
случайных величин:
a) die случайной ветчины X = т, имеющей биномиальный закон
распределении с математическим ожиданием а = М(Х) = пр и диспер-
сией D[X) = npq (см. § 4.1):
Л(|ш-пр|<е)^1--^: (6.7)
б) для частости — события в п независимых испытаниях, в каж-
п
дом из которых оно может произойти с одной и той же вероятно-
т\ . , _>( "И /*/
стью а - М — - />. и имеющей дисперсию D\ — = —:
\ п / \ п ) п
220
4 <6.8)
I n I J nz’
> Пример 6.3. Средний расход волы на животноводческой фер-
ме составляет 1000 л в день, а среднее квадратичное отклонение
згой случайной величины не превышает 200 л. Оценить вероятность
того, что расход воды на ферме в любой выбранный день не пре-
взойдет 2000 л. используя: а) неравенство Маркова; б) неравенство
Чебышева.
Ре ш е н и е. а) Пусть X — расход воды на животноводческой
ферме (л). По условию М(Х) = 1000. Используя неравенство Марко-
ва (6.3). получим Р(Х < 2000) > 1 - = 0*5. т.е. нс менее
чем 0,5.
б) Дисперсия D(A') = o’<200*'. Так как границы интервала
0^X^2000 симметричны относительно математического ожида-
ния М(Х) = 1000. то для оценки вероятности искомого события
можно применить неравенство Чебышева1 (6.6);
Р(X < 2000) = Р(0 < X <. 2000) =
= Я( | Л’-10001 < I000)> I -= 0.96,
т.е. нс менее чем 0.96. В данной задаче оценку вероятности
события, найденную с помощью неравенства Маркова (Р>0.5),
удалось уточнить с помощью неравенства Чебышева (Р £ 0.96). ►
t> Пример 6.4. Вероятность выхода с автомата стандартной дета-
ли равна 0.96. Оценить с помощью неравенства Чебышева вероят-
ность того, что число бракованных среди 2000 деталей находится в
границах от 60 до 100 (включительно). Уточнить вероятность того
же события с помощью интегральной теоремы Муавра—Лапласа.
Объяснить различие полученных результатов.
Решение. По условию вероятность того, что деталь брако-
ванная. равна р = I - 0.96 = 0,04. Число бракованных деталей X = т
имеет биномиальный закон распределения, а его границы 60 и 100
симметричны относительно математического ожидания а = М(Х) =
= пр = 2000 • 0.04 = 80.
Следовательно, оценку вероятности искомого события
* Берем н качестве дисперсии /ХЛ) се максимальное шиченис. рапное 200-. что
позволяет найти опенку вероятности искомою события для любых ятаченнй
0(A) -• 200*
221
P(60<m< 100) = P(-20£m-80 <20) = />( | ш - 801 20)
можно найти по формуле (6.6);
p(|m_80ls20)&1_~J^ = 1_2« =0.808.
4 ' ' 20* 400
т.е. нс менее чем 0.808.
Применяя следствие (2.13) интегральной теоремы Муавра-
Лапласа, получим
Р( |/?»-8()| < 20) =г Ф
20
= Ф(2.28) = 0.979.
т.е. вероятность искомого события приближенно р а в н а 0.979.
Полученный результат Г 0.979 не противоречит оценке, най-
денной с помощью неравенства Чебышева — Р> 0.808. Различие
результатов объясняется тем. что неравенство Чебышева лает лишь
нижнюю границу оценки вероятности искомого события для л ю •
б о й случайной величины, а интегральная теорема Муавра—
Лапласа дает достаточно точное значение самой вероятности Р (тем
точнее, чем больше л), так как она применима лишь для случайной
величины, имеющей определенны й. а именно — биноми-
альный закон распределения. ►
[> Пример 6.5. Оценить вероятность того, что отклонение любой
случайной величины от ее математического ожидания будет не бо-
лее трех средних квадратических отклонений (по абсолютной вели-
чине) — (правим трех сигм).
Решение. По формуле (6.6), учитывая, что D(X) = g' , по-
лучим:
/>( I.Y - J < Зет) 1 - = - = 0,889.
(За)* 9
т.е. не менее чем 0.889. Напомним, что для нормального зако-
на правило трех сигм выполняется с вероятностью Р. равной 0,9973.
т.е. Р = 0.9973. Можно показать, »гго для равномерного закона рас-
пределения Р = I, для показательного — Р = 0.9827 и т.д. Таким
образом, правило трех сигм (с достаточно большой вероятностью
его выполнения) применимо для большинства случайных величин,
встречающихся на практике. ►
О Пример 6.6. По данным примера 2.8 с помощью неравенства
Чебышева оценить вероятность того. что из 1000 новорожденных доля
222
доживших до 50 лет будет отличаться от вероятности этою события не
более чем на 0.04 (ио абсолютной величине).
Решение. Полагая л = 1000, р = 0,87. q — 0,13. по <|юрмуле (6.7)
<0,04 >1-
0,87-0.13
I 000 0,042
= 0.929.
т.е. не менее, чем 0.929. (Напомним, что в примере 2.8, б бы-
ло получено достаточно точное значение вероятности этого события
при использовании следствия из интегральной теоремы Муавра—
Лапласа, ранное 0,9998; различие результатов объясняется так же,
как и в примере 6.4. ►
Замечание. Если математическое ожидание М(Х) > А или
дисперсия случайной величины D(X) > гг, то правые части нера-
венств Маркова и Чебышева в форме соответственно (6.3) и (6.6)
будут отрицательными, а в форме (6.1) и (6.4) будр больше единицы.
Это означает, что применение указанных неравенств в этих случаях
приведет к тривиальному результату: вероятность события больше
отрицательного числа либо меньше числа, превосходящего единицу.
Но такой вывод очевиден и без использования данных неравенств.
Естественно, это обстоятельство снижает значение неравенств Мар-
кова и Чебышева при решении праклпеских задач, однако не ума-
ляет их теоретического значения.
6.3. Теорема Чебышева
Теорема Чебышева. Если дисперсии п независимых случайных вели-
чин Х>. .... А'о ограничены одной и той же постоянной, то при неог-
раниченном увеличении числа п средняя арифметическая случайных
величин сходится по вероятности к средней арифметической их мате-
матических ожиданий д(. Oj..ап, т.е.
.. J X. + У, + ...+У„ а.+д,+...4-Л ,
_*-----2-------2---J-----------М<€ =1 (6.9)
п-»» ( п п I )
или
(6.10)
□ Вначале докажем формулу (6.9), затем выясним смысл фор-
мулировки «сходимость ио вероятности». По условию
А/(У|) - 0|» ЛЯУз) - Д), .... М(Хп) — а,).
223
D(Xt)SC, D(X.)<C...D(X,)^C\
где С — постоянное число.
Получим неравенство Чебышева в форме (6.6) для средней
арифметической случайных величин, т.е. для
ггг,и^...<г,
п
Найдем математическое ожидание М(Х) и оценку дисперсии АЛ):
\ п J
=-Г м (л;) + л/ (.г,)+...+ л/ (х„ ) 1 = .
пL ' J п
= p-[D(X,) + D(X!) + ... + D(.Y.)]s^-(C±£^±C| = ^ = £.
(Здесь использованы свойства математического ожидания и дисперсии и.
в частности. то. что случайные величины Л|. Х>,.... Хп независимы, а следо-
вательно, дисперсия их суммы равна сумме дисперсий.)
Запишем неравенство (6.6) для случайной величины
%=(Xi + X2+...+ Хп} / п\
Х{ + Х2+...+ Хя _ <е 1 > | _ D(X)
л П I ) £"
Так как по доказанному £>(А')< —. то
л
,.£Шг1.Ц«=1__с.
е* с* лс*
и от неравенства (6.11) перейдем к более сильному неравенству:
/>[ W!+--4.<S4+"4|A|_C., (6.12)
I П п } П£‘
В пределе при л-»оо величина -^-г стремится к нулю, и полу-
пс.'
чим доказываемую формулу (6.9).
224
Выясним теперь смысл формулировки •сходимость по вероятно-
сти» и записи ее содержания в виде (6.10). Понятие предела пере-
менной величины X^lim .Y = а или Л' -> а при означает,
что начиная с некоторого момента ее изменения для любого (даже
сколь угодно малою) числа s > 0 будет верно неравенство
|Л-Л<Е- ® круглых скобках выражения (6.9) содержится анало-
гичное выражение1
<£.
где £-Y, /л — случайная величина, а | I /п — постоянное
Однако из неравенства (6.9) вовсе не следует, что оно будет вы-
полняться всегда, начиная с некоторого момента изменения
/л . Так как £.Y, /л — случайная величина, то возмож-
но, что в отдельных случаях неравенство выполняться не
будет. Однако с увеличением числа п вероятность неравенства
4-1 • I
<е стремится к I. т.е. зто неравенство будет выпол-
няться в подавляющем числе случаен. Другими словами, при доста-
точно больших л выполнение рассматриваемого неравенства является
событием практически достоверным, а неравенства противоположного
смысла — практически невозможным.
Таким образом, стремление | £.¥. \/п к j/w следует по-
нимать не как категорическое утверждение, а как утверждение, вер-
ность которого гарантируется с вероятностью, сколь угодно близкой
к 1 при л->«>. Это обстоятельство и отражено в формулировке
теоремы «сходится по вероятности» и в записи (6.10) обозначением
Подчеркнем смысл теоремы Чебышева. При большом чис-
ле п случайных величин Ал.......Хп практически достоверно, что
’ Записываем его кратко с помощью такой суммировании
8 Icopu, •сроив.шгЛ cieinciMu
их средняя X =| £.V, j/л — величина случайная, как угодно
мало отличается от неслучайной величины т.е.
практически перестает быть случайной.
Следствие. Если независимые случайные величины Л|. Ху. А’„
имеют одинаковые математические ожидании, равные а, а их диспер-
сии ограничены одной и той же постоянной, то неравенство (6.12) и
формулы (6.9). (6.10) примут над:
или
-а >1-
пс
(6.13)
(6.14)
(
□ Формулы (6.13)—(6.15) следуют из формул (6.12). (6.9) и
(6.10). так как
м(А-) = ***:♦-+*.) = 1[л/( А-,) + ,tf (Д'.) +... + М(X.)] =
1 / \ па _
= — 4-.,. + и| = — = а.
«V I п
Теорема Чебышева и ее следствие имеют большое практическое
значение. Например, страховой компании необходимо установить
размер страхового взноса, который должен уплачивать страхователь;
при этом страховая компания обязуется выплатить при наступлении
страхового случая определенную страховую сумму. Рассматривая
частоту/убытки страхователя при наступлении страхового случая как
величину случайную и обладая известной статистикой таких случа-
ев, можно определить среднее число/средние убытки при наступле-
нии страховых случаев, которое на основании теоремы Чебышева с
большой степенью уверенности можно считать величиной почти не
случайной. Тогда на основании этих данных и предполагаемой
страховой суммы определяется размер страхового взноса. Без учета
действия закона больших чисел (теоремы Чебышева) возможны су-
щественные убытки страховой компании (при занижении размера
22«
страхового взноса) либо потеря привлекательности страховых услуг
(при завышении размера взноса).
Заметим, что разработкой математических методов и моделей,
применяемых в страховании, .занимается так называемая актуарная
(страховая) математика.
Другой пример. Если надо измерить некоторую величину, истин-
ное значение которой равно аУ проводят п независимых измерений
-уюй величины. Пусть результат каждого измерения — случайная ве-
личина Xj(i= I. 2, .... п). Если при измерениях отсутствуют систе-
матические погрешности (искажающие результат измерения в одну
ц ту же сторону), то естественно предположить, что M(Xt) = а при
любом i. Тогда на основании следствия из теоремы Чебышева сред-
няя арифметическая результатов п измерений £ X, \/п сходится по
k -I >
вероятности к истинному значению а. Этим обосновывается выбор
средней арифметической в качестве меры истинного значения а.
Если вес измерения проводятся с одинаковой точностью, харак-
теризуемой дисперсией 0{Х,) =ст*. то дисперсия их средней
а ее среднее квадратическое отклонение равно сг/Тй. Полученное
отношение, известное под названием «правила корня из п». говорит о
том, что средний ожидаемый разброс средней п измерений в у'н раз
меньше разброса каждого измерения. Таким образом, увеличивая
число измерений, можно как угодно уменьшать влияние случайных
погрешностей (но нс систематических), т.е. увелшшватъ точность оп-
ределения истинного значения а.
Замечание. Если измерительный прибор имеет ючность 8
(например, 8 - половина ширины деления равномерной шкапы при-
бора, по которой производится отсчет), го указанным выше способом
Нельзя рассчитывать получить точность измерения величины а боль-
шую, чем 8. Каждое измерение дает результат с неопределенностью 8 и.
очевидно, их средняя арифметическая будет обладать той же неопреде-
ленностью б. Таким образом, стремиться посредством закона больших
чисел получить значение а с большей степенью точности, чем позволяет
прибор при отдельном измерении, является заблуждением.
Точно так же, как увеличение числа независимых измерений
неизвестной величины в соответствии с формулой (6.15*) приводит
к уменьшению получаемой ошибки, увеличение числа проводимых
227
(не связанных друг с другом) финансовых операций на рынке при
той же доходности приводи! к снижению риска1 Эго связано с гем,
что убытки от одних операций более или менее покрываются при-
былью от других операций. Отсюда следует один из принципов ра-
боты на финансовом рынке, известный как принцип диверсификации
(разнообразия) и вполне согласующийся с народной мудростью: -не
клали все яйца в одну корзину».
О Пример 6.7. Для определения средней продолжительности горе-
ния электроламп в партии из 200 одинаковых ящиков было взято на
выборку по одной лампе из каждого ящика. Оценить вероятность того,
что средняя продолжительность горения отобранных 200 электроламп
отличается от средней продолжительности горения ламп во всей пар-
тии нс более чем па 5 ч (по абсолютной величине), если известно, что
среднее квадратическое отклонение продолжительности горения ламп
в каждом ящике меньше 7 ч.
Ре ш е н и с. Пусть А, — продолжительноегь горения электро-
лампы, взятой из /-го ящика (ч). По условию дисперсия
D(X, )< 7? = 49. Очевидно, что средняя продолжительность горения
отобранных ламп равна (А, + Aj+...+ Аэ»)/200, а средняя продолжитель-
ность горения ламп во всей партии (АЛА|) + А/(А>) +...+Л/(А'?1ю))/2(Ю =
= (О| + + ... + а>(Ю)/200.
Тогда вероятность искомого события по формуле (6.12):
.V, ч .V. •*... *• Л\1Х|
200
ц ♦ а. + ... + u,t)ll
200
<5
200-5'
' 0,9902.
т е. н е мене е чем 0.9902. ►
О Пример 6.8. Сколько надо провести измерений данной вели-
чины. чтобы с верояпзостью не менее 0.95 гарантирован, отклоне-
ние средней арифметической этих измерений от истинного значе-
ния величины нс более чем на I (по абсолютной величине), если
среднее квадратическое отклонение каждого из измерений не пре-
восходит 5?
Реше н и с. Пусть X, — результат /-го измерения (/ = I. 2.п).
а — истинное значение величины, т.е. М{Хд = а при любом /.
Необходимо найти п. при котором
Р
а-,4Л\+...*а;
п
-а <] >0.95.
В соотвегстнии с неравенством (6.12) данное неравенство будет вы-
полняться. если
1 Напомним (см § 3 4), чк> под риском данной финансовой операции мест-
понимается дисперсия или среднее квадратическое отклонение ее доходности
228
1 — ——v — I—2 0.95. откуда —<0.05
ле* п • 1* л
и п % —— = 500, т.с. потребуется не менее 500 измерений. ►
6.4. Теорема Бернулли
Теорема Бернуллн. Частость события в п повторных независимых
испытаниях, в каждом из которых оно может произойти с одной и
той же вероятностью р, при неограниченном увеличении числа п схо-
дится по вероятности к вероятности р этого события в отдельном
испытании:
или
lim Р\
т
-~Р
п
т .Г
-----ТТГ"*/’-
п
(6.16)
(6.17)
= I
□ Заключение теоремы (6.16) непосредственно вытекает из не-
равенства Чебышева для частости события (6.8) при п -> тс .
С м ы с л теоремы Бернулли состоит в том, что при большом
числе п повторных независимых испытаний практически достовер-
но, что частость (или статистическая вероятность) события т/п —
величина с л у ч а Й н а я. как угодно мало отличается от не-
случайной величины р — вероятности события, т.с. практи-
чески перестает быть случайной.
Замечание. Теорема Бернулли является следствием тео-
ремы Чебышева, ибо частость события можно представить как
среднюю арифметическую п независимых альтернативных случай-
ных величин, имеющих один и тот же закон распределения (4.4)
(см. § 4.1). Доказательство теоремы (более громоздкое) возможно
и без ссылки на теорему (неравенство) Чебышева. Исторически
эта теорема была доказана намного раньше более общей теоремы
Чебышева.
Теорема Бернулли дает теоретическое обоснование замены неизвест-
ной вероятности события его частостью, или статистической вероятно-
стью (см. § 1.3). полученной в п повторных независимых испытаниях,
проводимых при одном и том же комплексе условий. Так. например, если
вероятность рождения малышка нам не известна, то в качестве ее значе-
ния мы можем принять частость (статистическую вероятность) этого со-
бытия. которая, как известно по многолетним статистическим данным,
составляет приближенно 0.5) 5.
Теорема Бернулли является звеном, позволяющим связать фор-
мальное аксиоматическое определение вероятности (см. § 1.12) с эм-
пирическим (опытным) законом постоянства относительной частоты
229
(см. § 1.3). Теорема дает возможность обосновать широкое примене-
ние на практике вероятностных методов исследования
Непосредственным обобщением теоремы Бернулли является
теорема Пуассона, когда вероятности события в каждом испытании
различны.
Теорема Пуассона. Частость события в п повторных независимых
испытаниях, в каждом из которых оно может произойти соответст-
венно с вероятностями р\. р2. .... рп. при неограниченном увеличении
числа п сходится по вероятности к средней арифметической вероят-
ностей события в отдельных испытаниях. т.е.
lim /»----——---------— <. с = I
•-** и п J
ИЛИ
(6.18)
п »... п
(6.19)
□ Теорема Пуассона непосредственно вытекает из теоремы Че-
бышева, если в качестве случайных величин Л|, Х2...Х„ рассмат-
ривать альтернативные случайные величины, имеющие законы рас-
пределения вида (4.4) с параметрами р\. р2. .... рп. Так как матема-
тические ожидания случайных величин Х|. Х2...Ха равны соответ-
ственно р\. р2...............................рп, а их дисперсии p.q>.p„qn (см. § 4.1)
ограничены одним числом1, то формула (6.18) непосредственно вы-
текает из формулы (6.9).
Важная роль закона больших чисел в теоретическом обосновании
методов математической статистики и ее приложений обусловила
проведение ряда исследований, направленных на изучение о б щ и \
у с л о в и й применимости этого закона к последовательности слу-
чайных величин. Так. в теореме Маркова доказана справедливость
предельного равенства (6.15) для з а в и с и м ы х случайных вели-
чин X, (i = I. 2./I) при условии
Например, температура воздуха в некоторой местности X, (i = I.
2... 365) каждый день гола — величины случайные, подверженные
существенным колебаниям в течение гола, причем зависимые, ибо на
погоду каждого дня. очевидно, заметно влияет погода предыдущих
дней. Однако среднегодовая температура £.V, /365 почта не меня-
1 Легко показать, что для любого / имеем
Р.Ч. - Р.(* * Р I - Р' ‘ Р. = ~(р. - 0.5) * 0,25 £ 0.25.
230
доя для данной местности в течение многих лет. являясь практически
неслучайной •г «релон редсле иной.
Нахождение общих условий, выполнение которых обязательно
влечет за собой статистическую устойчивость средних, представляет
непреходящую научную ценность исследований в области закона
больших чисел.
Помимо различных форм закона больших чисел в теории вероят-
ностей имеются еще разные формы гак называемого •усиленного зако-
на больших чисел», где показывается не «сходимость по вероятности», а
«сходимость с вероятностью I» различных средних случайных величин
к неслучайным средним. Однако этот усиленный закон представляет
больше интерес в теоретических исследованиях и не столь важен для
его приложений к экономике.
6.5. Центральная предельная теорема
Рассмотренный выше закон больших чисел устанавливает факт
приближения средней большого числа случайных величин к оп-
ределенным постоянным. Но этим не ограничива-
ются закономерности, возникающие в результате суммарного дейст-
вия случайных величин. Оказывается, что при некоторых весьма
общих условиях совокупное действие большого числа случайных
величин приводит к определенно м у. а именно — к
нормальному закону распределения.
Центральная предельная теорема представляет собой группу тео-
рем. посвященных установлению условий, при которых возникает
нормальный закон распределения. Среди этих теорем важнейшее
место принадлежит теореме Ляпунова.
Теорема Ляпунова. Если A'j. АГ». Хп - независимые случайные
величины. у каждой из которых существует математическое ожида-
ние М(Х,) ~ а, дисперсия DlX,) = <г. абсолютный центруемый мо-
мент третьего порядка Л/(|Л*. ц| ) = ш. и
lim ——----— = 0. (6.20)
то закон распределения суммы Y„ = А| + АГ» +.. +Х„ при п —> оо неог-
раниченно приближается к нормальному с математическим ожидани-
И *
ем и дисперсией .
/.I j-i
Теорему принимаем без доказательства.
231
Неограниченное приближение закона распределения суммы
я
= к нормальному закону при п -> г в соответствии со
свойствами нормального закона означает, что
Г.-Ъ".
lim /’
(6.21)
2>.:
где Ф(г) — функция Лапласа (2.11).
Смысл условия (6.20) состоит в том, чтобы в сумме К, = У Л
/. I
не было слагаемых, влияние которых на рассеяние подавляюще
велико по сравнению с влиянием всех остальных, а также нс долж-
но быть большого числа случайных слагаемых, влияние которых
очень мало по сравнению с суммарным влиянием остальных. Таким
образом, удельный вес каждого отдельного слагаемого должен стре-
миться к нулю при увеличении числа слагаемых.
Так. например, потребление электроэнергии для бытовых нужд ы
месяц в каждой квартире многоквартирного дома можно представить
в виде л различных случайных величин. Если потребление электро-
энергии в каждой квартире по своему значению резко не выделяется
среди остальных, то на основании теоремы Ляпунова можно считан»,
что потребление электроэнергии всего дома, т.е. сумма п независи-
мых случайных величин будет случайной величиной, имеющей при-
ближенно нормальный закон распределения. Если, например, н од-
ном из помещений лома разместится вычислительный центр, у кото
рого уровень потребления электроэнергии несравнимо выше, чем в
каждой квартире для бытовых нужд, то вывод о приближенно нор
мальном распределении потребления электроэнергии всего дома бу-
дет неправомерен, гак как нарушено условие (6.20). ибо потребление
электроэнергии вычислительного иеггтра будет играть превалирузо-
щую роль в образовании всей суммы потребления.
Другой пример При устойчивом и отлаженном режиме работы
станков, однородности обрабатываемого материала и т.л. варьирова-
ние качества продукции принимает форму нормального закона рас-
пределения в силу того, что производственная погрешность представ-
ляет собой результат суммарного действия большого числа случайных
величин: погрешности станка, инструмента, рабочего и т.л
Следствие. Если Х\. .¥>.....— независимые случайные величины.
у которых существуют равные математические ожидания Л/(А') = а.
232
сз'\[7г
дисперсии MAJ = о и абсолютные центральные моменты третьего
порядка Л/(|А',-с;| ) = ш, (/= I. 2. //). то закон распределении
суммы Yn - А'| 4- Х> +...+ Х„ при п ->ао неограниченно приближается
к нормальному закону.
О Доказательство сводится к проверке условия (6.20):
lim----!—— =l>m ———— =liin ——— =lim
"wr ..........................
следовательно, имеет место и равенство (6.21).
В частности, если все случайные ветчины X, одинаково распределе-
ны, то закон распределения их суммы неограниченно приближается к
нормальному закону при п -» х.
Проиллюстрируем это утверждение па примере суммирования
независимых случайных величин, имеющих равномерное распреде-
ление на интервале (0. I). Кривая распределения одной такой слу-
чайной величины показана на рис. 6.2. а. На рис. 6.2. б показана
плотность вероятности суммы двух таких случайных величин (см.
пример 5.9). а на рис. 6.2, в — плотность вероятности суммы трех
таких случайных величин (ее график состоит из трех отрезков пара-
бол на интервалах (0. I), (I, 2) и (2. 3) и по виду уже напоминает
нормальную кривую)
Если сложил» шесть таких случайных величин, то получится
случайная величина с плотностью вероятности, практически не от-
личающейся от нормальной.
Теперь у нас имеется возможность доказать локальную и
интегральную теоремы Муавра—Лапласа (см. § 2.3).
Рассмотрим случайную величину Z = т . гдс X = т — чис-
ло появлений события в п независимых испытаниях, в каждом из
которых оно может появиться с одной и той же вероятностью />. т.е.
X = т — случайная величина, имеющая биномиальный закон рас-
пределения. для которого математическое ожидание Л/(Л) = пр и
Дисперсия D(X) - npq.
Случайная величина Z. так же как случайная величина X. вообще
говоря, дискретна, но при большом числе п испытаний сс значения
Расположены на осн абсцисс так тесно, что ее можно рассматривать
как непрерывную с шинностью вероятности <р(г).
233
*-X)
3/4
О
«)
Рис. 6.2
Найдем числовые характеристики случайной величины Z, ис-
пользуя свойства математического ожидания и дисперсии:
и = Af(Z) = (M{X)-np)/Jnptj = (пр-нр) / jnpii = 0,
D(Z) = (D(X)-0)/(Tw) = /i/*y wpg = l.
В силу того, что случайная величина X представляет собой сумму
независимых альтернативных случайных величин (см. §4.1). случай-
ная величина Z представляет также сумму независимых, одинаково
распределенных случайных величин и. следовательно, на основании
центральной предельной теоремы при большом числе п имеет рас-
пределение, близкое к нормальному закону с параметрами а = 0.
<г = I. Используя свойство (4.32) нормального закона, с учетом
равенств (4.33) получим
234
Р(г,^5::Ь1[ф(.-.,)-Ф(.-)]. (6.22)
_ _ . a-wp b-np „ т-пр
Полагая z, ~ , z, = .— , с учетом того, что Z = _L-.
yjnpq ' у]пру Jnpq
получаем, что двойное неравенство в скобках равносильно неравен-
ству a£m£b. В результате из формулы (6.22) получим интеграль-
ную формулу Муавра— Лапласа (2.10):
Р{ и S т S b) = 1 [ф() - Ф ()]. (6.23)
Вероятность Рт п того, что событие А произойдет т раз в п неза-
висимых испытаниях, можно приближенно записать в виде:
Р.. * С(,п - «V w + Лю).
Чем меньше Ьт, тем точнее приближенное равенство. Мини-
мальное (целое) Л/п= I. Поэтому, учитывая формулы (6.23) и
(6.22), можно записать:
С. . « |[Ф(.-;)-Ф(--,)] = Л(=, S 7. < ). (6.24)
Л»
_т-пр _ (да + |)-л/>
EK z, = --------
VW \W
При малых Az имеем
P(z + Az)*<p(z)Az, (6.25)
где ф(г) — плотность стандартной нормально распределенной слу-
чайной величины с параметрами а = 0. «г = I. т.с.
ф(2)= ' с.-4’ . (6.26)
П А (ш + 1 )-///> т-пр 1
Полагая * = z. Лг = г. - г, = -- ' ---=L - —=. из
yjnpq \Jnpq \jnpq
формулы (6.25) с учетом равенства (6.24) полу’шм .юка.»ьную форму-
лу Муавра—Лапласа {1.1Y
С.,.<6.27)
фчч
Замечание. Необходимо соблюдай, известную осторож-
ность. применяя центральную предельную теорему в статистических
Исследованиях. Так. если сумма У Л' при л -> а всегда имеет
235
нормальный закон распределения, то скорость сходимости к
нему существенно зависит от типа распределения ее слагаемых. Так,
например, как отмечено выше, при суммировании равномерно рас-
пределенных случайных величин уже при 6—10 слагаемых можно до-
бтпъся достаточной близости к нормальному закону, в то время как для
достижения той же близости при суммировании х3-распрсделенных
случайных слагаемых понадобится более 100 слагаемых.
Опираясь на центральную предельную теорему, можно утверждать,
«по рассмотренные в гл. 4 случайные величины, имеющие законы
распределения — биномиальный, Пуассона, гипергеометрический. у
(«хи-квадрат»), / (Стьюдента), при «->« распределены асимптоти-
чески нормально.
Упражнения
6.9. Среднее изменение курса акции компании в течение од-
них биржевых торгов составляет 0.3%. Оценить вероятность того,
что на ближайших торгах курс изменится более чем на 3%.
6.10. Отделение банка обслуживает в среднем НЮ клиентов в
день. Оценить вероятность того, что сегодня в отделении банка будет
обслужено: а) не более 200 клиентов; б) более 150 клиентов.
6.11. Электростанция обслуживает сеть на 1600 электроламп,
вероятность включения каждой из которых вечером равна 0,9. Оце-
нить с помощью неравенства Чебышева вероятность того, что число
ламп, включенных в сеть вечером, отличается от своего математиче-
скою ожидания не более чем на 100 (по абсолютной величине»
Найти вероятность того же события, используя следствие из инте-
гральной теоремы Муавра—Лапласа.
6.12. Вероятность того, 'по акции, переданные на депозит, бу-
дут востребованы. равна 0,08. Оценить с помощью неравенства Че-
бышева вероятность того, что среди 1000 клиентов от 70 до
90 востребуют свои акции.
6.13. Среднее значение длины детали 50 см. а дисперсия — 0.1
Используя неравенство Чебышева, оценить вероятность гою, что
случайно взятая деталь окажется по длине нс менее 49,5 и не более
50.5 см. Уточнить вероятность тою же события, если известно. что
длина случайно взятой летали имеет нормальный закон распределе-
ния.
6.14. Оценить вероятность того, что отклонение любой случай-
ной величины от ее математического ожидания будет не более двух
средних квадратических отклонений (по абсолютной величине).
6.15. В течение времени t эксплуатируются 500 приборов. Каж-
дый прибор имеет надежность 0.98 и выходит из строя независимо
от других. Оценить с помощью неравенства Чебышева вероятность
236
тиго, что поля надежных приборов отличается ог 0.98 не более чем
на 0,1 (по абсолютной величине).
6.16. Вероятность сдачи и срок всех экзаменов студентом фа-
культета равна 0.7. С помощью неравенства Чебышева оценить ве-
роятность тою. что доля сдавших в срок все экзамены из
2000 студентов заключена в границах от 0.66 до 0.74.
6.17. Бензоколонка N заправляет легковые и грузовые автомо-
били. Вероятность того, что проезжающий легковой автомобиль
подъедет на заправку, равна 0.3. С помощью неравенства Чебышева
найти границы, в которых с вероятностью, не меньшей 0.79, нахо-
дится доля заправившихся в течение 2 ч легковых автомобилей, ес-
ли за это время всего заправилось 100 автомобилей.
6.18. В среднем 10% работоспособною населения некоторого
региона — безработные Оценить с помощью неравенства Чебышева
вероятность того, что уровень безработицы среди обследованных
10 000 работоспособных жителей города будет в пределах от 9 до
11% (включительно).
6.19. Выход цыплят в инкубаторе составляет в среднем 70%
числа заложенных яиц. Сколько нужно заложить яиц, чтобы с веро-
ятностью. нс меньшей 0.95. ожидать, что отклонение числа вылу-
пившихся цыплят от математического ожидания их не превышало
50 (по абсолютной величине)? Решить задачу с помошью: а) нера-
венства Чебышева: б) интегральной теоремы Муавра—Лапласа.
6.20. Опыт работы страховой компании показывает, что страхо-
вой случай приходится примерно на каждый пятый договор. Оце-
нить с помошью неравенства Чебышева необходимое количество
договоров, которые следует заключить, чтобы с вероятностью
0,9 можно было утверждать, что доля страховых случаев отклонится
от 0,1 не более чем на 0.01 (но абсолютной величине). Уточнить
ответ с помошью следствия из интегральном теоремы Муавра—
Лапласа.
6.21. В целях контроля из партии н 100 ящиков взяли по одной
детали из каждого ящика и измерили их длину. Требуется оценить
вероятность того, что вычисленная по данным выборки средняя
длина детали отличается от средней длины летали во всей партии не
более чем на 0.3 мм, если известно, что среднее квадратическое от-
клонение не превышает 0.8 мм.
6.22. Сколько нужно произвести измерений, чтобы с вероятно-
стью, равной 0.9973. утверждать, что погрешность средней арифме-
тической результатов этих измерений не превысит 0.01. если изме-
рение характеризуется средним квадратическим отклонением, рав-
ным 0,03?
— Элементы теории случайных
Глава / процессов и теории массового
обслуживания
Теория случайных процессов (случайных функций) — это раздел ма-
тематической науки, изучающий закономерности случайных явле-
ний в дина м икс их развития,
7.1. Определенно случайного процесса
и еп» характеристики
Понятие случайного процесса является обобщением понятия
случайной величины, рассмотренной в гл. 3.
Опре д с л спи с. Случайным процессом Х(1) называется про-
цесс, значение которого при новом значении аргумента i является слу-
чайной величиной.
Другими словами, случайный процесс представляет собой функ-
цию. которая в результате испытания может принять тот или инов
конкретный вил, неизвестный заранее. При фиксированном / = /0
представляет собой обычную случайную величину, т.е. с е -
ч е и и е случайного процесса в момент
Примеры случайных процессов:
I) численность населения региона с течением времени;
2) число заявок, поступающих в ремонтную службу фирмы, с
течением времени.
Аналогично тому, как в гл. 3 записана случайная величина в виде
функции элементарного события с». появляющегося в результате ис-
пытания, случайный процесс можно записать в виде функции двух
переменных X(t. со). где <•> С Q, (Е. Т. Х(1. со) G Е и м — элементарное
событие, <2 — пространство элементарных событий. Т — множество
значений аргумента г, Е множество возможных значений слу-
чайной) процесса Х(г. <о).
Реализацией случайного процесса X(t, со) называется неслучайная
функция .\V). в которую превращается случайный процесс X(t) в ре-
зультате испытания (при фиксированном <о), т.с. конкретный вил.
принимаемый случайным процессом X(J), его траектория.
Таким образом, случайный процесс X(i, со) совмещает в себе черты
случайной величины и функции. Если зафиксировать значение аргу-
мента /. случайный процесс превращается в обычную случайную
величину, если зафиксировать со. то в результате каждого испытания
он превращается в обычную неслучайную функцию. В дальнейшем
изложении опустим аргумент <•>. но он будет подразумеваться по
умолчанию.
238
На рис. 7.1 изображено несколько реализаций некоторого слу-
чайного процесса. Пусть сечение этого процесса при данном / явля-
ется непрерывной случайной величиной. Тогда случайный процесс
И/) при данном / определяется плотностью вероятности ф(х. /).
Очевидно. что плот- .
ность ф(х 0 нс является А |
исчерпывающим описани- |—
ем случайного процесса •—/
Д/). ибо она не выражает /
зависимости между ею се- ___
чениями в разные моменты
времени.
Случайный процесс () t-—/ *
X(f) представляет собой |
совокупность всех сече- „ х'
ций при всевозможных 1 иг* '*
значениях /. поэтому для сю описания необходимо рассматривать
многомерную случайную величину (А(Г|), Х(ь)..Au„)). состоящую
из всех сечений этого процесса. В принципе таких сечений беско-
нечно много, но для описания случайного процесса удастся часто
обойтись относительно небольшим количеством сечений.
Говорят, что случайный процесс имеет порядок п. если он пол-
ностью определяется плотностью совместного распределения ф (Х|.
Xi,..., xrt; б. 6.U п произвольных сечений процесса, т.е плотно-
стью л-мерной случайной величины (AVi). A(h).X(tn)>. где Л’<Л> —
сечение случайного процесса Л’(л в момент времени i = I, 2..п.
Как и случайная величина, случайный процесс может быть опи-
сан числовыми характеристиками Если для случайной величины
эти характеристики являются постоянными числами, то для случай-
ного процесса — неслучайными функциями.
Математическим ожиданием случайного процесса Х(1) называется
неслучайная функция которая при любом значении переменной t
равна математическому ожиданию соответствующего сечения слу-
чайного процесса Х(1), т.е. ах(1) = ЛУ|.¥(/)|.
Дисперсией случайного процесса X\i) называется неслучайная функция
при любой значении переменной / равная дисперсии соответствующе-
го сечения случайного процесса Х(1), т.е. Dx(i) =
Средним квадратическим отклонением ax(t) случайного процесса
Х{1) называется арифметическое значение корня квадратного из его
дисперсии, т.е. п, (г) =
Математическое ожидание случайного процесса характеризует
среднюю траекторию всех возможных его реализаций, а его
дисперсия или среднее квадратическое отклонение — р а з б р о с
реализаций относительно средней траектории.
239
Введенных выше характеристик случайного процесса оказывает-
ся недостаточно, так как они определяются только одномерным за-
коном распределения. На рис. 7.2 и 7.3 изображены два случайных
процесса ЛДО и X2(f) с примерно одинаковыми математическими
ожиданиями и дисперсиями.
Если для случайного процесса A'i(r) (см. рис. 7.2) характерно мед-
ленное изменение значений реализаций с изменением /. то для слу-
чайного процесса АпП) (см. рис. 7.3) это изменение происходит зна-
чительно быстрее. Другими словами, для случайного процесса Л|(/1
характерна тесная вероятностная зависимость между двумя его сече-
ниями .V|(/j) и А’|(б), в то время как для случайного процесса A\(/) ла
зависимость между сечениями Л?(/|) и ^>(6) практически отсутствует.
Указанная зависимость между сечениями характеризуется корреляци-
онной функцией.
Определение. Корреляционной функцией случайного процесса
Х{1) называется неслучайная функция
А7/|. l2) = Af|(/(f|) - - аМ)] (7.1)
двух переменных и fj. которая при каждой паре переменных б и /
равна ковариации соответствующих сечений А’(/|) и X(f2) случайного
процесса.
Очевидно. для случайного процесса А'Д/) корреляционная функция
К .(/». /?) убывает по мерс увеличения разности б “ Л значительно мед-
леннее. чем к, (/и /:) лля случайного процесса А%(Г).
Корреляционная функция Kx(t\, г2) характеризует не только сте-
пень тесноты линейной зависимости между двумя сечениями, но и
разброс этих сечений относительно математического ожидания вЛ(г).
Поэтому рассматривается также нормированная корреляционная
функция случайного процесса.
Нормированной корреляционной функцией случайного процесса X(h
240
называется функция
р.м--$М
(7.2)
о Пример 7.1. Случайный процесс определяется формулой
д/) = X cos Mt, где X — случайная величина. Найти основные харак-
теристики этого процесса, если М(Х) = a, D(X) = а2.
решение. На основании свойств математического ожидания
и дисперсии имеем:
ц( ( /) = Л/( .V cos (о /) = cos со/ • М (X) = u cos о/,
£), (t) = l)( X cos w/) = cos’bj/ • D{ X) = <r cos*tot.
Корреляционную функцию найдем по формуле (7.1):
К, (/,,/.) = М [(X cos - a cosw/,)(X cos w/: - и cos о/.)] =
= cos со/, cos со/, • Л / [(Л’ - и){X - а)] = cos (t)/(cos <о/. D (X) =
= a'cos co/(cos co/..
Нормированную корреляционную функцию найдем по формуле (7.2):
. ст* cos со/. cos со/,
Р.('..'2) = 7------г;------TTwL ►
(ст cos СО/, )(СУ cos со/.)
Случайные процессы можно классифицировать в зависимости
от того, плавно или скачкообразно меняются состояния системы, в
которой они протекают, конечно (счетно) или бесконечно множест-
во этих состоянии и т.п. Среди случайных процессов особое место
принадлежит марковскому случайному процессу.
7.2. Марковские случайные процессы
с дискретными состояниями
Случайный процесс, протекающий в некоторой систс.ие S с воз-
можными состояниями 5|. Si, Sj, .... называется марковским, или
случайным процессом без последействия, если для любого момента
времени /о вероятностные характеристики процесса в будущем (при
/ > /0) зависят только от его состояния в данный момент /(> и не за-
висят от того, когда и как система пришла в это состояние; т.е. не
зависят от ее поведения в прошлом (при / < /у).
Пример марковского процесса: система S — счетчик в такси.
Состояние системы в момент / характеризуется числом километров
(десятых долей километров), пройденных автомобилем до данного
момента. Пусть в момент /0 счетчик показывает 5}j. Вероятность то-
го. что в момент / > /0 счетчик покажет то или иное число километ-
ров (точнее, соответствующее число рублей) S|, зависит от 5о, но не
241
зависит от того, в какие моменты времени изменялись показания
счетчика до момента /(>.
Многие процессы можно приближенно считать марковскими. На-
пример, процесс игры в шахматы; система 5 — ipynna шахматных фи-
гур. Состояние системы характеризуется числом фигур противника, со-
хранившихся на доске в момент /<>. Вероятность того. *по в момеш
i > /<) материальный перевес будет на стороне одного из противников,
зависит в первую очередь от того, в каком состоянии находится система
в данный момент а не от того, когда и в какой последовательности
исчезли фигуры с доски до момента
В ряде случаев предысторией рассматриваемых процессов можно
просто пренебречь и применять для их изучения марковские модели
Марковским случайным процессом с дискретными состояниями и
дискретным временем (или цепью Маркова) называется марковский
процесс, в котором его возможные состояния S,.S„ 5,,... можно
заранее перечислить, а переход из состояния в состояние происхо-
дит мгновенно (скачком), но только в определенные моменты вре-
мени /ц. г,. л. называемые шагами процесса.
Обозначил» — вероятность перехода случайного процесса
(системы 5) из состояния i н состояние j. Если эти вероятности не
зависят от номера шага процесса, то такая цепь Маркова называет-
ся однородной.
Пусть число состояний системы конечно и равно т. Тогда ее
можно характеризовать матрицей перехода Р\. которая содержит все
вероятности перехода:
А.
А.
А
Р:
- А.
- А-
Р^
Естественно, по каждой строке
!>.=' /=1.2,
Обозначим р (п) — вероятность того, что в результате п шагов
система перемет из состояния / в состояние j. При этом при / = I
имеем вероятности перехода, образующие матрицу А. т.е.
А»0)=А<-
Необходимо, зная вероятности перехода р<,. найти рДп) — ве-
роятности перехода системы из состояния i в состояние j за п шагов.
С этой целью будем рассматривать промежуточное (между i и j) со-
242
стояние Г, т.е. будем считать, что из первоначального состояния / за к
тагов система перейдет в промежуточное состояние г с вероятностью
рг(Л), после чего за оставшиеся и-к шагов из промежуточного со-
стояния г она перейдет в конечное состояние j с вероятностью
р^п-к}. Тогда по формуле полной вероятности
Ри(м> = ^Лм(*)Р^(н-Л). (7.3)
г-1
формула (7.3) называется равенством Маркова.
Убедимся в том. что. зная все вероятности перехода pu = pjl).
т.е. матрицу Р\ перехода из состояния в состояние за один шаг, мож-
но найти вероятность р„(2). т.е. матрицу А перехода из состояния в
состояние за два шага. А зная матрицу Р^. — найти матрицу Ру пере-
хода из состояния в состояние за три шага, и т.д.
Действительно, полагая п = 2 в формуле (7.3), т.е. к = I (проме-
жуточное между шагами состояние), получим
= = (7.4)
г-1 Г-1
Полученное равенство (7.4) означает, что
Л = = />’.
Полагая п - 3, к = 2. аналогично получим
/> = сл = />/:?=^,
а в общем случае
О Пример 7.!а. Совокупность семей некоторого региона можно
разделить на три группы:
I) семьи, не имеющие автомобиля и не собирающиеся его по-
купать:
2) семьи, не имеющие автомобиля, но намеревающиеся его
приобрести:
3) семьи, имеющие автомобиль.
Проведенное статистическое обследование показало, что матри-
ца перехода за интервал в один год имеет вид
(0.8 0.1
О 0.7
0 0
0.Г
0.3
1 ,
243
(В матрице Р] элемент рц = I означает вероятность того, что
семья, имеющая автомобиль, также будет его иметь, а. например,
элемент руу = 0.3 — вероятность того, что семья, не имевшая авто
мобиля. но решившая его приобрести, осуществит свое намерение в
следующем году, и т.д.).
Найти вероятность того, что: а) семья, не имевшая автомоби-
ля и не собиравшаяся его приобрести, будет находиться в такой
же ситуации через два года; б) семья, нс имевшая автомобиля, но
намеревающаяся его приобрести, будет иметь автомобиль через
два года.
Ре тени е. Найдем матрицу перехода А через два юла:
0.8
0.1
0.7
0
0.1 0.8 0.1
0.3 0 0.7
I 0 0
0.13 0.64 0.15 0,21
0.3 = О 0.49 0.51
I . Д 0 0 I .
0
т.е. искомые в п. а) и б) вероятности равны соответственно р\\ = 0,64.
р>у = 0.51. ►
Далее мы будем рассматривать марковский случайный процесс с
дискретными состояниями и непрерывным временем, в котором, н
отличие от рассмотренной выше цепи Маркова, моменты возмож-
ных переходов системы из состояния не фиксированы заранее, а
случайны.
При анализе случайных процессов с дискретными состояниями
удобно пользоваться геометрической схемой — гак называемым
графом состояний. Обычно состояния системы изображаются пря-
моугольниками (кружками), а возможные переходы из состояния в
состояние — стрелками (ориентированными дугами), соединяющи-
ми состояния.
> Пример 7.2. Построить граф состояний следующего случайно-
го процесса: устройство 5 состоит из двух узлов, каждый из которых
в случайный момент времени может выйти из строя, после чего
мгновенно начинается ремонт узла, продолжающийся заранее неиз-
вестное случайное время.
Реше и и е. Возможные состояния системы: 51, — оба узла ис-
правны; 5| — первый узел ремонтируется, второй исправен; 5; —
второй узел ремонтируется, первый исправен; — оба узла ремон-
тируются. Граф системы приведен на рис. 7.4.
Стрелка, направленная. например, из в 5|. означает переход
системы в момент отказа первого узла, из 5t в — переход в мо-
мент окончания ремонта этого узла.
244
Рис. 7.4
На графе отсутствуют стрелки нз 5v в 5j и из в $2. Это объяс-
няется тем. что выходы узлов из строя предполагаются независи-
мыми друг от друга и. например, вероятностями одновременного
выхода из строя двух узлов (переход из .$) в 50 или одновременного
окончания ремонтов двух узлов (переход из 5j в 5о) можно пренеб-
речь. ►
7.3. Основные понятия
теории массового обслуживания
На практике часто приходится сталкиваться с системами, предна-
значенными для многоразового использования при решении одно-
типных задач. Возникающие при этом процессы получили название
процессов обслуживания, а системы — систем массового обслуживания
(СМО). Примерами таких систем являются телефонные системы, ре-
монтные мастерские, вычислительные комплексы, билетные кассы,
магазины, парикмахерские и т.п.
Каждая СМО состоит из определенного числа обслуживающих еди-
ниц (приборов, устройств. пунктов, станций), которые будем называть
каналами обслуживания. Каналами могут быть линии связи, рабочие точ-
ки, вычислительные машины, продавцы и др. По числу канатов СМО
подразделяют на одноканальные и многоканальные.
Заявки поступают в СМО обычно не регулярно, а случайно, об-
разуя так называемый случайный поток заявок (требований). Обслу-
живание заявок, вообще говоря, также продолжается какое-то слу-
чайное время. Случайный характер потока заявок и времени обслу-
живания приводит к тому, что СМО оказывается загруженной не-
равномерно: в какие-то периоды времени скапливается очень боль-
шое количество заявок (они либо становятся в очередь, либо поки-
дают СМО необслуженными). в другие же периоды СМО работает с
недогрузкой или простаивает.
Предметом теории массового обслуживания является построение
математических моделей, связывающих заданные условия работы
245
СМО (число каналов, их производительность, характер потока зая-
вок и т.п.) с показателями эффективности СМО, описывающими ее
способность справляться с потоками заявок.
В качестве показателей эффективности СМО используются: сред-
нее1 число заявок, обслуживаемых в единицу времени; среднее число
заявок в очереди; среднее время ожидания обслуживания; верояь
ность отказа в обслуживании без ожидания; вероятность того, чю
число заявок в очереди превысит определенное значение, и т.п.
СМО делят на два основных типа (класса): СМО с отказами и
СМО с ожиданием (очередью). В СМО с отказами заявка, поступив-
шая в момент, когда все каналы заняты, получает отказ, покидает
СМО и в дальнейшем процессе обслуживания нс участвует (напри
мер, заявка на телефонный разговор в момент, когда все каналы за-
няты, получает отказ и покидает СМО необслужснной). В СМО с
ожиданием заявка, пришедшая в момент, когда все каналы заняты,
не уходит, а становится в очередь на обслуживание.
СМО с ожиданием подразделяются на разные виды в зависимости
от того, как организована очередь: с ограниченной или неограничен-
ной длиной очереди, с ограниченным временем ожидания и т.п.
Процесс работы СМО представляет собой случайный процесс с дис-
кретными состояниями и непрерывным временем. Математический анализ
работы СМО существенно упрощается, если процесс этой работы -
марковский (см. § 7.2).
Для математического описания марковского случайного процес-
са с дискретными состояниями и непрерывным временем, проте-
кающего в СМО. познакомимся с одним из важных понятий теории
вероятностей — понятием потока событий.
7.4. Потоки событий
Под потоком событий понимается последовательность однород-
ных событий, следующих одно за другим в какие-то случайные мо-
менты времени (например, поток вызовов на телефонной станции,
поток отказов ЭВМ. поток покупателей и т.п.).
Поток характеризуется интенсивностью >. — частотой появления
событий или средним числом событий, поступающих в СМО в еди-
ницу времени.
Поток событий называется регулярным, если события следуют
одно за другим через определенные равные промежутки времени
Например, поток изделий на конвейере сборочного цеха (с посто-
янной скоростью движения) является регулярным.
Поток событий называется стационарным, если его вероятно-
стные характеристики не зависят от времени. В частности, ни-
1 Здесь и в дальнейшем средние величины понимаются как математические
ожидания соответствующих случайных величин.
246
тенсивность стационарного потока есть величина постоянная:
Х(/) = К. Например, поток автомобилей на городском проспекте
не является стационарным в течение суток, но этот поток можно
считать стационарным в определенное время суток, скажем, в
часы пик. В этом случае фактическое число проходящих автомо-
билей в единицу времени (например, в каждую минуту) может
заметно различаться, но среднее их число постоянно и не будет
зависеть от времени.
Поток событий называется потоком без последействия, если для
любых двух непересекаюшнхся участков времени Т| и п число собы-
тий. попадающих на один из них. не зависит от числа событий, по-
падающих на другие. Например, поток пассажиров, входящих в
метро, практически не имеет последействия. А, скажем, поток по-
купателей. отходящих с покупками от прилавка. уже имеет после-
действие (хотя бы потому, что интервал времени между отдельными
покупателями не может быть меньше, чем минимальное время об-
служивания каждого из них).
Поток событий называется ординарным, если вероятность попа-
дания на малый (элементарный) участок времени Л/ двух и более
событий пренебрежимо мала по сравнению с вероятностью попада-
ния одного события. Другими словами, поток событий ординарен,
если события появляются в нем поодиночке, а не группами. На-
пример. поток поездов, подходящих к станции, ординарен, а поток
вагонов не ординарен.
Поток событий называется простейшим (или стационарным пу-
ассоновским). если он одновременно стационарен, ординарен и не име-
ет последействия. Название «простейший» объясняется тем. что
СМО с простейшими потоками имеет наиболее простое математи-
ческое описание. Регулярный поток не является простейшим, так
как обладает последействием: моменты появления событий в таком
потоке жестко зафиксированы.
Простейший поток в качестве предельного возникает в теории
случайных процессов столь же естественно, как в теории вероятно-
стей нормальное распределение получается в качестве предельного
для суммы случайных величин: при наложении (суперпозиции) доста-
точно большого числа п независимых, стационарных и ординарных пото-
ков (сравнимых между собой по интенсивностям (/ = I. 2... п)) по-
лучается поток, близкий к простейшему с интенсивностью Л. равной
сумме интенсивностей входящих потоков, т.е.
/•I
Рассмотрим на оси времени Of (рис. 7.5) простейший поток событий
как неограниченную последовательность случайных точек.
247
____।______________________________• *1__________________________кеш/////./////Я »
0__________________________________t
Рис. 7.5
Пусть случайная величина X выражает число событий (точек),
попадающих на произвольный промежуток времени т. Покажем, что
случайная величина X распределена по закону Пуассона.
□ Разобьем мысленно временной промежуток т на п равных эле-
ментарных отрезков .М ~х/н. Математическое ожидание числа собы-
тии, попадающих на элементарный отрезок Л/, очевидно, равно АЛ/,
где А — интенсивность потока. Согласно свойству ординарности по-
тока можно пренебречь вероятностью попадания на элементарный
отрезок двух и более событий.
Будем считать элементарный отрезок А/ «занятым», если в нем
появилось событие потока, и «-свободным», если не появилось. Веро-
ятность того, что отрезок А/ = т/л окажется «занятым», равна
ХД/^Лт//;; вероятность того, что он окажется «пустым», равна
I -)л/п (чем меньше А/, тем точнее равенства).
Число занятых элементарных отрезков, т.е. число X событий на
всем временном промежутке т. можно рассматривать как случайную
величину, имеющую биномиальный закон распределения, т.е
с параметрами ли р = Кх/п.
(Необходимое для возникновения биномиального закона условие
независимости испытаний, в данном случае — независимость п эле-
ментарных отрезков относительно события «отрезок занят», обеспечи-
вается свойством отсутствия последействия потока.)
При неограниченном увеличении числа элементарных отрезков
л л
.Аг. т.е. при л-»а>, р =-->0 и постоянном значении пронзведе-
п
ния пр = п— = Хт. как отмечено в § 4.2. биномиальное распределение
п
стремится к распределению Пуассона с параметром ат :
P(A'=m)=^-e'u. (7.5)
ж!
248
для которого математическое ожидание случайной величины равно
ее дисперсии: а = о- = /.х.
В частности, вероятность того, что за время х не произойдет ни
одного события (т - 0). равна
Р(Х = 0) = <? ”. (7.6)
[> Пример 7.3. На автоматическую телефонную станцию посту-
пает простейший поток вызовов с интенсивностью X = 1.2 вызова в
минуту. Найти вероятность того, что за две минуты: а) не прилет ни
одного вызова; 6) придет ровно один вызов; в) придет хотя бы один
вызов.
Р е ш с н и е. а) Случайная величина X — число вызовов за две
минуты — распределена по закону Пуассона с параметром
Кт - 1.2-2 = 2.4. Вероятность того, что вызовов нс будет (т = 0).
по формуле (7.5):
/э(ЛГ = О)*е-:4 =0.091.
б) Вероятность одного вызова (т = 1):
/’(.¥ = 1) = 2.4-0.091 =0.218.
в) Вероятность хотя бы одного вы зова:
/’(.¥>1) = 1-/>(Л'=0)= 1-0.091 =0.909. ►
Найдем распределение интервала времени Т между двумя про-
извольными соседними событиями простейшего потока.
В соответствии с (7.6) вероятность того, что на участке времени
длиной г нс появится ни одного из последующих событий. равна
Р(Т>г) = е\ (7.7)
а вероятность противоположного события, т.е. функция распреде-
ления случайной величины Т. есть
и. 0.8)
случайной
F(0 = Р(Т <п = \-е
Плотность вероятности
величины есть производная ее функ-
ции распределения (рис. 7.6). т.е.
ф(П=Г(/)=Лем. (7.9)
Распределение, задаваемое плотно-
стью вероятности (7.9) или функцией
Распределения (7.8), является показа •
пельным (экспоненциальным) (см. §4.6).
Таким образом, интервал времени между двумя соседними произвольны-
249
ми событиями простейшего потока имеет показательное распределение.
для которого математическое ожидание равно среднему квадратиче-
скому отклонению случайной величины:
и обратно по величине интенсивности потока X.
Важнейшее свойство показательного распределения (присущее
только показательному распределению1) состоит в следующем: если
промежуток времени, распределенный по показательному закону, уже
длился некоторое время г, то это никак не влияет на закон распределе-
ния оставшейся части промежутка (Т — т): он будет таким же. как и
закон распределения всего промежутка Т(см. гл. 4. пример 4.7).
Другими словами, для интервала времени Т между двумя лбслс-
доватсльными соседними событиями потока, имеющего показатель-
ное распределение, любые сведения о том, сколько времени протекал
этот интервал, не влияют на закон распределения оставшейся части
Это свойство показательного закона представляет собой, в сущности,
другую формулировку для «отсутствия последействия» — основного
свойства простейшего потока.
Для простейшего потока с интенсивностью X вероятность попа-
дания на элементарный (малый) отрезок времени Л/ хотя бы одною
события потока равна, согласно формуле (7.8).
Pv = Р(Т<.\з) sl-e^^kA/. (7.11)
(Эта приближенная формула, получаемая заменой функции
e ' v лишь двумя первыми членами ее разложения в ряд по степе-
ням А/, тем точнее, чем меньше А/).
7.5. Уравнения Колмогорова.
Предельные вероятности состояний
Рассмотрим математическое описание марковского случайного
процесса с дискретными состояниями и непрерывным временем по
данным примера 7.2. Соответствующий граф состояний процесса
изображен на рис. 7.4. Будем полагать, что все переходы системы из
состояния St в 5, происходят пол воздействием простейших потоков
событий с интенсивностями (/./'= О, I. 2, 3); гак, переход систе-
мы из состояния 5() в 5*1 будет происходить пол воздействием потока
отказов первого узла, а обратный переход из состояния Sj в 3, — пол
воздействием потока «окончаний ремонтов» первого узла и т.п.
Граф состояний системы с проставленными у стрелок интенсивно-
стями будем называть размеченным (см. рис. 7.4). Рассматриваемая сис-
тема 5 имеет четыре возможных состояния: 3^. Зч.
1 В классе непрерывных случайных величин
250
Вероятностью i-го состояния называется вероятность рД/) того,
что в момент t система будет находиться в состоянии S’,. Очевидно,
что для любого момента t сумма вероятностей всех состояний равна
единице:
л
£/>,(») = I. <7.12)
<0
рассмотрим систему в момент / и, задав малый промежуток д/,
найдем вероятность ру(г + ДО того, что система в момент t + Ы бу-
дет находиться в состоянии S®. Это достигается разными способами.
I. Система в момент t с вероятностью />о(О находилась в состоя-
нии ЗЬ, а за время А/ не вышла из него.
Вывести систему из этого состояния (см. граф на рис. 7.4) мож-
но суммарным простейшим потоком с интенсивностью (Xqi + >-02).
Т.е. в соответствии с формулой (7.11), с вероятностью, приближен-
но равной (а<>| + >ч)2)А/. А вероятность того, что система нс выйдет
из состояния Sb, равна 11 - (Aoi + Лад) А/). Вероятность того, чти
система будет находиться в состоянии Sb и не выйдет из него за
время А/, равна по теореме умножения вероятностей:
р0(/)[|-(Х01 + Х«)Д/].
2. Система в момент t с вероятностями р|(0 (или /ъ(0) находилась
в состоянии или Sj и за время А/ перешла в состояние Sb-
Потоком интенсивностью Хш (или Хзо)(см. рис. 7.4) система пе-
рейдет в состояние So с вероятностью, приближенно равной XjoAf
(или ХэоА/). Вероятность того, что система будет находиться в со-
стоянии Sb. по этому способу равна р|(/)ХюД/ (или ^(ОХгоЛО*
Применяя теорему сложения вероятностей, получим:
рп(/ + А/) = Р| (/)Х1(,Д/ + р.(/ JX^.Ar + Д>(/)[| -(Xw + Хо: )А/] .
откуда
р,(>+*)-/>.(') , р.(,)Хи+Р;(,)Хм- (Х„+ка)
Переходя к пределу при дг -> О (приближенные равенства, свя-
занные с применением формулы (7.11), перейдут в точные), полу-
чим в левой части уравнения производную p'0(t) (обозначим ее для
простоты р'о):
Ро ~ ХюР» Хэ»Р; ~ (Xoi + Х02) Ро‘
Получено дифференциальное уравнение первого порядка, т.е.
Уравнение, содержащее как саму неизвестную функцию, так и ее
производную первого порядка.
251
Рассуждая аналогично для других состояний системы 5. можно
получить систему дифференциальных уравнений Колмогорова для веро-
ятностей состояний;
Рь = М + - (Х,„ + Х„; )/>„.
Р: = * М«Ру " )Р:«
Р\ = >»иА + " (Mi + М:)А-
Сформулируем правило составления уравне-
ний Колмогорова. В левой части каждого из них стоит
производная вероятности i-го состояния. В правой части — сумма
произведений вероятностей всех состояний (из которых идут стрелки
в данное состояние) на интенсивности соответствующих потоков
событий минус суммарная интенсивность всех потоков, выводящих
систему из данного состояния, умноженная на вероятность данного (i-го
состояния) — см. рис. 7.4.
В системе (7.13) независимых уравнений на единицу меньше
общею числа уравнений. Поэтому для решения системы необходи-
мо добавить уравнение (7.12).
Особенность решения дифференциальных уравнений вообще
состоит в том. что требуется задавать так называемые начальные
условия, в данном случае — вероятности состояний системы в на-
чальный момент I = 0. Так, например, систему уравнений (7.13)
естественно решать при условии, что в начальный момент оба узла
исправны и система находилась в состоянии 5J). т.е. при начальных
условиях д((0) = I. Р|(0) = /ъ(0) = р3(0) = 0.
Уравнения Колмогорова дают возможность найти все вероятно-
сти состояний как функции времени. Особый интерес представляю!
вероятности системы р,{{} в предельном стационарном режиме, т.е
прн t -> ж. которые называются предельными (финальными) вероят-
ностями состояний.
В теории случайных процессов доказывается, что если число со-
стояний системы конечно и из каждого из них можно (за конечное
число шагов) перейти в любое другое состояние, то предельные веро-
ятности существуют.
Предельная вероятность состояния S, имеет четкий смысл: она
показывает среднее относительное время пребывания системы в этом
состоянии. Например, если предельная вероятность состояния Л’ц.
т.е. А) = 0,5. то это означает, что в среднем половину времени сис-
тема находится в состоянии 5Ь-
Так как предельные вероятности постоянны, то, заменяя в урав-
нениях Колмогорова их производные нулевыми значениями, полу
чим систему линейных алгебраических уравнений, описывающих
252
стационарный режим. Для системы 5 с графом состояний, изобра-
женном на рис. 7.4. такая система уравнений имеет вид:
(^«<1 + )Д> ~ А ^ЧчРг'
(Х|(, + Ап )/?, = ХП|/>„ +
(>-i| + Х„)р, =\,А + A..JA.
Систему (7.14) можно состашпъ непосредственно ио размечен-
ному графу состояний, если руководствоваться правилом, со-
гласно которому слева в уравнениях стоит предельная вероятность
данного состояния р„ умноженная на суммарную интенсивность всех
потоков, ведущих из данного состояния, а справа — сумма произведений
интенсивностей всех потоков, входящих в i-e состояние, на вероятно-
сти тех состояний, из которых эти потоки исходят.
t> Пример 7.4. Найти предельные вероятности для системы S из
Примера 7.2, !раф состояний которой приведен на рис. 7.4. при
Xoi — I. ?ч)2 = 2. /.Ц) - 2, >.ц — 2, Хэл ~ X A’l = 1. Xjt = 3. Xj2 = 2.
Ре ш е н и с. Система алгебраических уравнений, описываю-
щих стационарный режим для данной системы, имеет вид (7.14)
или
-Vo = 2A+3p,.
= + (715)
=2р(|+2р„
(Здесь вместо одного «лишнего» уравнения системы (7.14) запи-
сали нормировочное условие (7.12).)
Решив систему (7.15). получим = 0,40. р\ = 0,20. р, = 0.27.
Рз= 0.13. т.е. в предельном стационарном режиме система 5 в сред-
нем 40% времени будет находиться в состоянии 51, (оба узла ис-
правны). 20% — в состоянии 5| (первый узел ремонтируется, второй
работает». 27% — в состоянии 5'2 (второй узел ремонтируется, пер-
вый работает) и 13% времени — в состоянии (оба узла ремонти-
руются). ►
О Пример 7.5. Найти средний чистый доход от эксплуатации в
стационарном режиме системы Л’ в условиях примеров 7.2 и 7.4, если
известно, что в единицу времени исправная работа первого и второго
узлов приносит доход соответственно в 10 и 6 ден. ед., а их ремонт
требует затрат соответственно в 4 и 2 ден. ед. Оценить экономическую
эффективность имеющейся возможности уменьшения вдвое среднего
253
времени ремонта каждого из двух узлов, если при этом придется вдвое
увеличить затраты на ремонт каждою узла (в единицу времени).
Решение. Из примера 7.4 следует, что в среднем первый
узел исправно работает долю времени, равную plt + /?, = 0.40 +
+ 0,27 = 0.67, а второй узел — р, + р\~ 0.40 + 0.20 = 0.60. В го же вре-
мя первый узел находится в ремонте в среднем долю времени, равную
Pi + ру = 0.20 4-0,13 = 0.33. а второй узел — ру + ру = 0.27 + 0.13 = 0.40.
Поэтому средний чистый доход в единицу времени от эксплуатации
системы, т.е. разность между доходами и затратами, равен
D = 0.67 • 10 + 0.60 6 - 0,33 • 4 - 0.40 2 = К. 1К ден. ед.
Уменьшение вдвое среднего времени ремонта каждого из узлов в
соответствии с формулой (7.10) будет означать увеличение вдвое ин-
тенсивностей потока «окончаний ремонтов» каждого узла, т.е. теперь
Хм» = 4. Хго= 6. Хл = 6. Хд1 = 4и система линейных алгебраических
уравнений (7.14). описывающая стационарный режим системы 5.
вместе с нормировочных* условием (7.12) примет вид1:
*А. = 4 а + 6р;,
6а =Рп+6а.
7 Р: =
/>а +А + А- + /Л = >•
Решив систему, получим р1( = 0.60, pi = 0.15, /ъ = 0.20. /ц = 0.05.
Учитывая, что д> + р> = 0,60 + 0,20 = 0.80. Д) + А = 0.60 + 0,15 = 0.75.
р, + = 0,15 + 0,05 = 0.20, р: + ру = 0.20 + 0.05 = 0,25, а затраты
на ремонт первого и второго узлов составляют теперь соответственно
8 и 4 ден. ед., вычислим средний чистый доход в единицу времени:
Di = 0.80 • 10 + 0.75 6 - 0.20 8 - 0.25 • 4 = 9.9 ден. ед.
Так как Z7t больше D (примерно на 20%). то экономическая це-
лесообразность ускорения ремонтов узлов очевидна. ►
7.6. Процессы гибели и размножения
В теории массового обслуживания широко распространен спе-
циальный класс случайных процессов — гак называемые процессы
гибели и размножения. Название это связано с рядом биологических
задач, где этот процесс служит математической моделью изменения
численности биологических популяций.
Граф состояний процесса гибели и размножения имеет вид, по-
казанный на рис. 7.7.
1 При тайней системы (7.14) одно «лишнее» уравнение исключили
254
Рис. 7.7
Рассмотрим упорядоченное множество состояний системы 5П.
5(, S2... Переходы могут осуществляться из любого состояния
только в состояния с соседними номерами, т.е. из состояния воз-
можны переходы либо в состояние 5i-|. либо в состояние S'*-Л
Предположим, что все потоки событий, переводящие систему
по стрелкам графа, простейшие с соответствующими интенсивно-
стями । или ХЛ.| А.
По графу, представленному на рис. 7.7. составим и решим алгеб-
раические уравнения для предельных вероятностей состояний (их
существование вытекает из возможности перехода из каждого состоя-
ния в каждое другое и конечности числа состояний).
В соответствии с правилом составления таких уравнений (см.
§ 7.5) получим: для состояния 5^
*oiA»=4.A’ <7-16>
ДЛЯ СОСТОЯНИЯ 5| -
Ul2 + Мо)А = МнА) +
которое с учетом равенства (7.16) приводится к виду:
Х|2/7| = Х2|Р2. (7.17)
Аналогично, записывая уравнения для предельных вероятностей
других состояний, можно получить следующую систему уравнений:
\иА> = ^ц»А»
^•иА = А-
.............. <718>
'»».и А-i - А •
к которой добавляется нормировочное условие
Л + А + + <7Л9>
Решая систему (7.18) и (7.19), можно получить
1 При анализе численности популяций считают, что состояние 5* соответствует
численности популяции, равной к. и переход системы и i состояния S* в состоя-
ние 5*.| происходит прн рождении одною члена популяции, а переход в со-
стояние .S, । - при 1н6ели одною члена популяции.
255
-I
> > > A. 1 > '
'*hi '‘ir’io л,пл-1’”л*'г',1Л /
_ - ^Ol - „ - ^»Aei л n - „ /7 7П
Pi - — Po. Pi “ T—:— Pn.......Pn ~ ------—— Ab <7-21)
^10
Легко заметить, что в формулах (7.21) для р\, Р2,.... рп коэффици-
енты при pq — это слагаемые, стоящие после единицы в формуле
(7.20). Числители этих коэффициентов представляют собой прок зу-
дения всех интенсивностей, стоящих у стрелок, ведущих слева направо
от 5^ до данного состояния З* (к = I, 2...л), а знаменатели — произ-
ведения всех интенсивностей, стоящих у стрелок, ведущих справа
налево из состояния 5А до (см. рис. 7.7).
t> Пример 7.6. Процесс гибели и размножения представлен гра-
фом (рис. 7.8). Найти предельные вероятности состояний.
Риг. 7.Я
Решение.
По формуле (7.20) найдем
= 0.706.
по формулам (7.21)
1 2-1
/?1 = _о 706 = 0,176. р> = -----0.706 = 0.118.
4 ’ 3-4
т.е. в установившемся стационарном режиме в среднем 70.6% вре-
мени система будет находиться в состоянии •$>, 17,6% — в состоя-
нии 51 и 11.8% — в состоянии 52. ►
7.7. СМО с отказами
В качестве показателей эффективности СМО с отказами будем
рассматривать:
/1 — абсолютную пропускную способность СМО. т.е. среднее чис-
ло заявок, обслуживаемых в единицу времени;
Q — относительную пропускную способность, т.е. среднюю долю
пришедших заявок, обслуживаемых системой;
Л>гк — вероятность отказа — вероятность того, что заявка по-
кинет СМО необслуженной;
к — среднее число занятых каналов (для многоканальной системы).
256
Одноканальная система с отказами. Рассмотрим задачу.
Имеется один канал, на который поступает поток заявок с ин-
тенсивностью а. Поток обслуживаннй имеет интенсивность и1.
Найти предельные вероятности состояний системы и показатели ее
эффективности.
Система 5 (СМО) имеет два состояния: SJ, — канал свободен. —
канал занят. Размеченный граф состояний представлен на рис. 7.9.
Рнс. 7.9
В предельном стационарном режиме система алгебраических
уравнений для вероятностей состояний (7.14) имеет вид (см. прави-
ло составления таких уравнений на с. 253):
I
т.с. система вырождается в одно уравнение. Учитывая нормировоч-
ное условие рц + р\ = I. найдем из системы (7.22) предельные веро-
ятности состояний
которые выражают среднее относительное время пребывания систе-
мы в состоянии (когда канал свободен) и (когда канал занят),
т.е. определяют соответственно относительную пропускную способ-
ность Q системы и вероятность отказа Рогк:
(7.24)
(7.25)
Абсолютную пропускную способность найдем, умножив относи-
тельную пропускную способность Q на интенсивность потока зая-
вок X:
1 Здесь и и дальнейшем предполагается, что все потоки событий, переводящие
СМО из состояния в состояние, будут простейшими К ним относится и поток
обслуживаннй — поток заявок, обслуживаемых одним непрерывно занятым ка-
налом. Среднее время обслуживания 7^ обратно по величине интенсивности р.
тл. «|/ц.
8 leopui i.ith'-.-tch и «anwnwui ГГШМГПШ 257
(7.26)
Г> Пример 7.7. Известно, что заявки на телефонные переговоры
в телевизионном ателье поступают с интенсивностью равной
90 заявок в час. а средняя продолжительность разговора по теле<|к>.
ну 7,- = 2 мин. Определить показатели эффективности работы СМО
(телефонной связи) при наличии одного телефонного номера.
Решение. Имеем X = 90 (l/ч). 7Л = 2 мин. Интенсивность по-
тока обслуживании нг 1/7,.= 1/2 = 0,5 (1/мин) = 30 (l/ч). По (7.24)
относительная пропускная способность СМО Q = 30/(90 + 30) = 0,25.
т.е. в среднем только 25% поступающих заявок осуществят перего-
воры по телефону. Соответственно вероятность отказа в обслужива-
нии составит = 0.75 (см. (7.25». Абсолютная пропускная спо-
собность СМО по формуле (7.26) А = 90-0,25 = 22,5. т.е. в среднем
в час будут обслужены 22.5 заявки на переговоры. Очевидно, что
при наличии только одного телефонного номера СМО будет плохо
справляться с потоком заявок. ►
Многоканальная система с отказами. Рассмотрим классическую
задачу Эрланга.
Имеется п каналов, на которые поступает поток заявок с интен-
сивностью X. Поток обслужнваний каждого канала имеет интенсив-
ность р. Найти предельные вероятности состояний системы и пока-
затели сс эффективности.
Система 5 (СМО) имеет следующие состояния (нумеруем их по числу
заявок, находящихся в системе): 5ь 5|. 52.5;.5„. где 54 — состоя
ннс системы, когда в ней находится к заявок, т.е. занято к каналов.
Граф состояний СМО соответствует процессу гибели и размно-
жения (рис. 7.10).
Зц
*Р
(А+1)р
5Х
«Р
Риг. 7.10
Поток заявок последовательно переводит систему из любого лево-
го состояния в соседнее правое с одной и той же интенсивностью >.
Интенсивность же потока обслуживания, переводящих систему из лю-
бого правого состояния в соседнее левое, постоянно меняется в зави-
симости от состояния. Действительно, если СМО находится в состоя
нин 52 (два канала заняты), то она может перейти в состояние 5|
(один канал занят), когда закончит обслуживание либо верный, либо
второй канал, т.е суммарная интенсивность их потоков обслуживании
будет 2р. Аналогично суммарный поток обслуживании. переводящий
258
СМО из состояния S, (три канала заняты) в 52. будет имел, интенсив-
ность Зр. т.с. может освободиться любой из трех каналов, и тд.
В формуле (7.20) для схемы гибели и размножения получим для
предельной вероятности состояния
(. X Хг X
А> =
(7.27)
Г_
р 2!р*' А’р1 л!|Г j
X Х>' >•"
где члены разложения — . ----г.... ....... — коэффициенты при в
р 2!р л’ц
выражениях для предельных вероятностей pt. /н........Р/г Величина
Р ~ ~ (7.23)
Р
называется приведенной интенсивностью потока заявок или интен-
сивностью нагрузки канала. Она выражает среднее число заявок,
приходящих за среднее время обслуживания одной заявки. Теперь
Pn =
1+р + —
Р
А!
Р.
л!
(7.29)
Рк =
Р\ = РА). Рз = ~ А)..Ра = 77 Ро....Рп = Ро- (7.30)
2! к\ л!
Формулы (7.29) и (7.30) для предельных вероятностей получили
названия формул Эрланга в ’«есть основателя теории массового об-
служивания.
Вероятность отказа СМО есть предельная вероятность того, что
все п каналов системы будут заняты, т.е.
р = Р"
л!
Относительная пропускная способность — вероятность того, что
заявка будет обслужена:
(7.31)
<2 = 1-/?.,. =1-^ /V
л!
Абсолютная пропускная способность:
(7.32)
Л = Х(? = Х
А. •
(7.33)
Среднее число занятых каналов. т.е. математическое ожидание
числа занятых каналов:
к в£*р»’
где рк — предельные вероятности состояний, определяемые по фор-
мулам (7.29), (7.30).
259
Однако среднее число занятых каналов можно найти нроше. если
учесть. что абсолютная пропускная способность системы А есть цс
что иное, как интенсивность потока обслуженных системой заявок (и
единицу времени). Так как каждый занятый канал обслуживает й
среднем ц заявок (в единицу времени), то среднее число занятых ка-
налов
(7.34)
или. учитывая формулы (7.33). (7.28),
* = Р
л!
(7.35)
t> Пример 7.8. В условиях примера 7.7 определить оптимальное
число телефонных номеров в телевизионном ателье, если условием
оптимальности считать удовлетворение из каждых 100 заявок на
переговоры в среднем не менее 90 заявок.
Р с in с н и с. Интенсивность нагрузки канала по формуле
(7.28) р = 90/30 = 3. т.е. за время среднего (по продолжительности)
телефонного разговора 7,, = 2 мин поступает в среднем 3 заявки на
переговоры.
Будем постепенно увеличивать чисто каналов (телефонных номеров)
л = 2, 3. 4,... и определим по формулам (7.29). (732). (733) для получае-
мой л-каналыюй СМО характеристики обслуживания. Например, при
л = 2 =(1-3 + 372!) ' =0,118 = 0.12: (2= I ~(372’) 0.118 * 0.471;
А = 90 • 0,471 = 42,4. Значение характеристик СМО сведем в табл. 7.1
Тиб.1И1|н 7.1
Характеристика обслуживания Обозна- чение Число каналов <телефонных номеров)
1 2 3 4 5 6
Относительная пропускная спо- собность Q 0.25 0.47 0.65 0.79 0.90 0.95
Абсолютная про- пускная способ- ность А 22.5 42.4 58.8 71.5 80.1 85.3
По условию оптимальности Q >0.9. следовательно, в телевизион-
ном ателье необходимо установить 5 телефонных номеров (в этом
случае Q = 0.90 — см. табл. 7.1). При этом в час будут обслуживаться
в среднем 80 заявок (Л = 80.1). а среднее число занятых телефонных
номеров (каналов) по формуле (7.34) к = 80.1/30 ~ 2,67. ►
260
Пример 7.9. В вычислительный центр коллективного пользо-
вания с тремя ЭВМ поступают заказы от предприятий на вычисли-
тельные работы. Если работают все зри ЭВМ. то вновь поступаю-
щий заказ нс принимается, и предприятие вынуждено обратиться в
другой вычислительный центр. Среднее время работы с одним зака-
зом составляет 3 ч. Интенсивность потока заявок 0.25 l/ч. Найти
предельные вероятности состояний и показатели эффективности
работы вычислительного центра.
решение. По условию п = 3, >. = 0.25 l/ч. 1а, = 3 ч. Интен-
сивность потока обслуживании и = I/7,, = 1/3 = 0,33. Интенсив-
ность нагрузки ЭВМ по формуле (7.28) р = 0.25/0.33 = 0,75. Най-
дем предельные вероятности состояний:
по формуле (7.29): А, = (I + 0.75 + 0.7572! + 0.7573’)'1 = 0.476:
по формуле (7.30): р, = 0.75 • 0.476 = 0.357: р2 = (0.75-/2!) • 0.476 =
= 0,134; ру= (0.7573!) 0.476 = 0.033. т.е. в стационарном режиме
работы вычислительного центра в среднем 47.6% времени нет ни
одной заявки. 35.7% — имеется одна заявка (занята одна ЭВМ).
13,4% — две заявки (две ЭВМ). 3.3% времени — три заявки (заняты
три ЭВМ).
Вероятность отказа (когда заняты все три ЭВМ), таким образом.
Лпк = Рз= о.озз.
Согласно формуле (7.32) относительная пропускная способность
центра Q — I - 0.033 = 0.967, т.е. в среднем из каждых 100 заявок
вычислительный центр обслуживает 96.7 заявок.
По формуле (7.33) абсолютная пропускная способность центра
А = 0.25 • 0.967 = 0.242, т.е. в один час в среднем обслуживается
0,242 заявки.
Согласно формуле (7.34) среднее число занятых ЭВМ к =
= 0,242/0,33 = 0,725, т.е. каждая из трех ЭВМ будет занята обслу-
живанием заявок в среднем лишь на 72.5/3 = 24,2%.
При опенке эффективности работы вычислительного центра не-
обходимо сопоставить доходы от выполнения заявок с потерями от
простоя дорогостоящих ЭВМ (с одной стороны, здесь высокая про-
пускная способность СМО. а с другой — значительный простой
каналов обслуживания) и выбрать компромиссное решение. ►
7.8. Понятие о методе статистических испытаний
(методе Moirre-Kaixio)
Основное допущение, при котором анализировались рассмот-
ренные выше СМО, состоит в том. что все потоки событий, пере-
водящие их из состояния в состояние, были простейшими. При на-
рушении этого требования общих аналитических методов для таких
261
систем нс существует. Имеются лишь отдельные результаты, позво-
ляющие выразить в аналитическом виде характеристики СМО через
параметры задачи.
В случае, когда для анализа работы СМО аналитические методы
неприменимы (или же требуется проверить их точность), использу-
ют универсальный метод статистических испытаний. или. как его
называют, метод Монте-Карло. Название «метод Монте-Карло»
связано с тем. что одним из возможных способов имитации случай-
ных явлений является рулетка, игрой в которую знаменит город
Моттте-Карло.
Для уяснения сути метода Монте-Карло рассмотрим задачу о
вычислении определенного интеграла.
।
Пусть требуется вычислить определенный интеграл J/(.v)<Zv. где
к
Дх) — непрерывная на отрезке |0; 1| элементарная функция, причем
О s/(x) ъ I. Задача носит достаточно общий характер, так как к данно-
му интегралу путем соответствующих линейных подстановок (замен)
»
может быть сведен любой интеграл f(x)dx.
।
Геометрически интеграл J/(.v)Jv представляет собой площадь
о
области 5 пол кривой у = fix) (рис. 7.11).
Будем многократно повторят», опыт, состоящий в бросании нау-
дачу точки в единичный квадрат.
I’ur. 7.11
Используя неметрическое определение
вероятности (§ 1.4). вероятность собьпия А —
попадания брошенной случайной точки
в область S — есть отношение площади
области S к плошали квадрата, т.е.
р(Л) = р- = J/(x)dr.
В соответствии с теоремой Бернулли при достаточно большом
числе опытов п в качестве опенки искомой вероятности р(А) следует
взять частость т/п, которая и будет являться приближенным значе-
нием интеграла по результатам случайных испытаний.
Отличительная особенность применения метода Монте-Карло
состоит в том. что границы, в которых будет заключено истинное
значение неизвестной величины (в данной задаче — вычисляемого
262
интеграла), мы можем указан, нс точно, а лишь с некоторой веро-
ятностью. называемой доверительной (об этом речь пойдет в § 9.6),
Конечно, при реализации метода Монте-Карло не требуется
Проведения реальных опытов по бросанию случайной точки в квад-
рат (или, например, в других задачах — по бросанию монеты, иг-
ральной кости и т.п.). Для этой цели служат специальные компью-
терные программы или датчики случайных чисел (точнее «псевдо-
случайных* чисел, ибо последние не в полной мере удовлетворяют
требованию случайности).
Применение метода Монте-Карло в системах массового обслу-
живания состоит в том. что вместо аналитического описания СМО
проводится «розыгрыш» случайного процесса, проходящего в СМО,
с помощью специально организованной процедуры. В результате
такого «розыгрыша» получается каждый раз новая, отличная от дру-
гих реализация случайного процесса. (Реализации случайного про-
цесса называются статистическими испытаниями — отсюда и вто-
рое название метода.) Это множество реализаций можно использо-
вать как некий искусственно полученный статистический материал,
который обрабатывается обычными методами математической ста-
тистики. После такой обработки могут быть получены приближенно
любые характеристики обслуживания.
При моделировании случайных явлений методом Монте-Карло мы
пользуемся самой случайностью как аппаратом исследования. Для
сложных систем обслуживания с немарковским случайным процес-
сом метод статистических испытаний, как правило, оказывается
проще аналитического, а часто и вовсе единственно возможным.
В данной главе мы ограничились рассмотрением СМО с отказа-
ми. С другими системами массового обслуживания, например СМО
с ожиданием (одноканальными и многоканальными, с ограничен-
ным и неограниченным временем ожидания и др.), можно ознако-
миться. например, в пособии [ 16|.
Упражнения
7.10. Случайный процесс определяется формулой .¥(/) = Xe~*(t > 0),
где X — случайная величина, распределенная по нормальному зако-
ну с параметрами а и о?. Найти математическое ожидание, диспер-
сию, корреляционную и нормированную корреляционную функции
случайного процесса.
7.10а . В моменты времени г,./.,/, производится осмотр ЭВМ.
Возможные состояния ЭВМ: S, — полностью исправна; 5, — имеет
незначительные неисправности: .9, - имеет существенные неис-
правности и может решать ограниченный круг задач; —
полностью вышла из строя. Матрица перехода имеет вил
263
0.3 0.4 0.1 0.2
0 0.2 0.5 0.3
Л =
' О 0 0.4 0.6
,0 0 О J ,
В начальный момент система исправна. Определить вероятности
состояний ЭВМ после трех проверок.
7.11. Постро>пъ граф состояний следующего случайного процесса
система состоит из двух автоматов по продаже газированной воды, каж-
дый из которых в случайный момент времени может был. либо заня-
тым, либо свободным.
7.12. Построить граф состояний системы 5. представляющей
собой электрическую лампочку, которая в случайный момент вре-
мени может быть либо включена, либо выключена, либо выведена
из строя.
7.13. Среднее число заказов на такси, поступающих на диспетчер-
ский пункт в одну минуту, равно 3. Найти вероятность того, что за две
минуты поступит а) 4 вызова; б) хотя бы один: в) ни одного вызова
(Поток заявок простейший.)
7.14. Найти предельные вероятности для систем 5. граф кото-
рых изображен на рис. 7.11 и 7.12.
Риг. 7.11
Рис. 7.12
7.15. Рассматривается круглосуточная работа пункта проведе-
ния профилактического осмотра автомашин с одним каналом (од-
ной группой проведения осмотра). На осмотр и выявление дефектов
каждой машины затрачивается в среднем 0.5 ч. На осмотр поступав
в среднем 36 машин в сутки. Потоки заявок и обслуживании
простейшие. Если машина, прибывшая в пункт осмотра, нс застое!
ни одного канала свободным, она покидает пункт осмотра необслу-
женной. Определить предельные вероятности состояний и характе-
ристики обслуживания профилактического пункта осмотра.
7.16. Решить пример 7.15 для случая п = 4 канала (групп про
ведения осмотра). Найти минимальное число каналов. прн котором
относительная пропускная способность пункт.! осмотра будет не
менее 0.9
264
7.17. Одноканальная СМО с отказами представляет собой одну
телефонную линию, на вход которой поступает простейший поток
вызовов с интенсивностью 0.4 выэовов/мнн. Средняя продолжитель-
ность разговора 3 мин.; время разговора имеет показательное распре-
деление. Найти предельные вероятности состояний и характеристики
обслуживания СМО. Сравнить пропускную способность СМО с но-
минальной. которая была бы. если разговор длился в точности 3 мин.,
а заявки шли одна за другой регулярно, без перерывов.
7.18. Имеется двухканальная простейшая СМО с отказами. На ее
вход поступает поток заявок с интенсивностью 4 заявки/ч. Среднее
время обслуживания одной заявки 0.8 ч. Каждая обслуженная заявка
приносит доход 4 ден. ед. Содержание каждого канала обходится
2 ден. ед./ч. Выяснить, выгодно или невыгодно в экономическом от-
ношении увеличить число каналов до трех.
Раздел
Математическая
статистика
Глава 8.
Глава 9.
Глава К).
Глава II.
Глава 12.
Глава 13.
Глава 14.
Глава 15.
Вариационные ряды и их
характеристики
Основы математической теории
выборочного метода
Проверка статисти’кч’ких гипотез
Дисперсионный анализ
Корреляционный анализ
Регрессионный анализ
Введение в анализ временных рядов
Линейные регрессионные .модели
финансового рынка
Глава
Вариационные ряды
и их характеристики
8.1. Вариационные ряды
и их графическое изображение
Установление статистических закономерностей, присущих мас-
совым случайным явлениям, основано на изучении статистических
данных — сведений о том. какие значения принял в результате на-
блюдений интересующий нас признак (случайная величина X).
О Пример 8.1. Необходимо изучить изменение выработки на одно-
го рабочего механического цеха в отчетном году по сравнению с пре-
дыдущим. Получены следующие данные о распределении 100 рабочих
цеха по выработке в отчетном году (в процентах к предыдущему году):
97.8: 97,0; 101.7; 132.5;142,3; 104.2; 141,0; 122,1.
100 значений
Различные значения признака (случайной величины А) называ-
ются вариантами (обозначаем их через х).
Рассмотрение и осмысление этих данных (особенно при большом
числе наблюдений п) затруднительно, и по ним практически нельзя
предсташпъ характер распределения признака (случайной величины А).
Первый шаг к осмыслению имеющегося статистического мате-
риала — это его упорядочение, расположение вариантов в порядке
возрастания (убывания), т.е. ранжирование вариантов ряда:
хтЛ = 94.0; 94.2;...; 142,3; 141,0 = ,
п -100 значений
В таком виде изучать выработку рабочих тоже не очень удобно
из-за обилия числовых данных. Поэтому разобьем варианты на от-
дельные интервалы, т.е. проведем их группировку.
Число интервалов т следует брать нс очень большим, чтобы по-
сле группировки ряд нс был громоздким, и нс очень малым, чтобы
не потерять особенности распределения признака.
Согласно формуле Стерджеса рекомендуемое число интервалов
т = j + 3,322 1g п, а величина интервала (интервальная разность,
ширина интервала}
V — X
д. шот___mm
1 + 3,322 1g л ’
где хтак - хтт — разность между наибольшим и наименьшим зна-
чениями признака.
267
В примере 8.1 к = (141.0 - 97,0)/(1 + 3.322 IglOO) = 5,76(%).
Примем к = 6,0(%). За начало первого интервала рекомендуется
брать величину ,цич = x,nin - к/2. В данном случае Хц.т| = 97.0 - 6.0/2 =
= 94.0(%).
Сгруппированный ряд представим в виде таблицы (табл. 8.1).
Таблица 8.1
1 Выработка в отчетном году в про- центах к пре- дыдущему X Частота (количест- во рабо- чих) п, Частость (Лыи рабочих) п. и; =— п Накоп- ленная частота п‘ш' Накопленная частость .... н''" = — w
1 94.0-100.0 3 0.03 3 0.03
2 100.0-106.0 7 0.07 10 0,10
3 106,0-112.0 II 0,11 21 0.21
4 112,0-118,0 20 0,20 41 0,41
5 118,0-124,0 28 0,28 69 0.69
6 124,0-130,0 19 0,19 88 0.88
7 130,0-136,0 10 0,10 98 0.98
8 136.0-142.0 > 0.02 100 1.00
У 100 1.00 — —
Числа, показывающие, сколько раз встречаются варианты из данно-
го интервала, называются частотами (обозначаем nj). а отношение их к
общему числу наблюдений — частостями, или относительными часто-
тами, т.е. и* = п/п . Частоты и частости называются весами.
Опре д е л е н и е. Вариационным рядом называется ранжиро-
ванный в порядке возрастания (или убывания) ряд вариантов с соот-
ветствующими им весами (частотами или частостями)1.
Если просмотр первичных, нссгруппированных данных делал
затруднительным представление об изменчивости значений призна-
ка. то полученный теперь вариационный ряд позволяет выявить
закономерности распределения рабочих по интервалам выработки
Мы видим, например, что выработка колеблется от 94,0 до 142.0%
наибольшее число рабочих (28, или 0,28 от общего числа) увеличи-
ли выработку до 118.0—124.0%, уменьшили выработку (в пределах
от 94.0 до 100%) трое рабочих и т.п.
При изучении вариационных рядов наряду с понятием частоты
используется понятие накопленной частоты (обозначаем //"*’). Нако-
пленная частота показывает, сколько наблюдалось вариантов со зна-
• Если вариант л; (г = I. 2. .... п) вариационного ряда рассматривается как слу
чайная величина Л„ получаемая в результате многократного наблюдения интере
сующего нас признака Л. го V, называется порядковой статистикой.
268
ченнем признака, мсныикм х. Отношение накопленной частоты п”“
к общему числу наблюдений и назовем накопленной частостью \г"" .
Накопленные частоты (частости) для каждого интервала находятся
последовательным суммированием частот (частостей) всех предшест-
вующих интервалов, включая данный (см. табл. 8.1). Например, для
х= 124 накопленная частота /Г“ = 3 + 7 + 11 + 20 * 28 = 69. т.е.
69 рабочих имели выработку, меньшую 124%.
Для задания вариационного ряда достаточно указать варианты и
соответствующие им частоты (частости) или накопленные часто™
(частости) (в табл 8.1 приведены и те и другие).
Вариационный ряд называется дискретным, если любые его вари-
анты отличаются на постоянную величину, и — непрерывным (интер-
вальным), если варианты могут отличаться один от другого на сколь
угодно малую величину. Так. вариационный ряд. представленный в
табл. 8.1. — интервальный (проценты выработки условно округлены
до десятых долей). Примером дискретного ряда является распределе-
ние 50 рабочих механического цеха по тарифному разряду (табл. 8.2).
TiiImiiiui 8.2
Тарифный разряд х, 1 2 з 4 5 6 V
Частота (количество рабочих) nt 2 3 6 8 22 9 50
Для графическою изображения вариационных рядов наиболее час-
то используются полигон, гистограмма, кумулятивная кривая
Полигон. как правило, служит для изображения дискретного ва-
риационного ряда и представляет собой ломаную, в которой концы
отрезков прямой имеют координаты (х,. л,), i = 1.2..т.
Гистограмма служит только для изображения интервальных ва-
риационных рядов и представляет собой ступенчатую фигуру из
прямоугольников с основаниями, равными интервалам значений
признака kt = х,(| - х>. i = I. 2.т. и высотами, равными часто-
там (частотаям) п, (в1,) интервалов. Если соединить середины верх-
них оснований прямоугольников отрезками прямой, го можно по-
лучить полигон тою же распределения.
Кумулятивная кривая (кумулята) — кривая накопленных частот
(частостей) Для дискретного ряда кумулята представляет ломаную,
соединяющую точки (х,.л"“) или (х,.»»•““ ). i = 1.2.т. Для интер-
вального вариационного ряда ломаная начинается с точки, абсцисса
которой равна началу первого интервала, а ордината — накоплен-
ной частоте (частости), ранной нулю. Другие точки этой ломаной
соответствуют копнам интервалов.
Весьма важным является понятие эмпирической функции рас-
пределения.
269
Определение. Эмпирической функцией распределения F„(x) на-
зывается относительная частота (частость) того, что признак (случайная
величина X) примет значение, меныиее заданного х. т.е.
ад=и-(.Г<х) = »<. (8.1)
Другими словами, для данного х эмпирическая функция распре-
деления представляет накопленную частость »»•“ -n^fn.
t> Пример 8.2. Построить полигон (гистограмму), кумуляту и
эмпирическую функцию распределения рабочих:
а) по тарифному разряду по данным табл. 8.2;
б) по выработке по данным табл. 8.1.
Решение. На рис 8.1 и 8.2 изображены полигон (гистограмма),
кумулята и эмпирическая функция распределения соответственно
для дискретного (табл. 8.2) и интервального (табл. 8.1) вариацион-
ных рядов. Обращаем внимание на то, что лая дискретного
вариационного ряда эмпирическая функция распределения представ-
ляет собой разрывную ступенчатую функцию по аналогии с функци-
ей распределения для дискрспюй случайной величины (§ 3.5) с той
лишь разницей, что теперь по оси ординат вместо вероятностей
располагаются частости (см. рис 8.1).
Число Доля (частость) w,
270
Для интервального вариационного ряда (см. табл. 8.1)
имеем лишь значения функции распределения Г„(х) на концах интер-
вала (см. последнюю графу табл. 8.1). Поэтому для графического изо-
бражения этой функции целесообразно се доопределить, соединив точки
графика. соответствующие концам интервалов, отрезками прямой. В
результате полученная ломаная совпадет с кумулятой (см. рис. 8.2, <5). ►
Накопленная
частота частость
► Выработка х. %
Вариационный ряд является статистическим аналогом (реализаци-
ей) распределения признака (случайной величины X). В этом смысле
полигон (гистограмма) аналогичен кривой распределения, а эмпи-
рическая функция распределения — функции распределения слу-
чайной величины X.
Вариационный ряд содержит достаточно полную информацию
об изменчивости (вариации) признака. Однако обилие числовых
Данных, с помощью которых он задается, усложняет их использова-
ние. В то же время на практике часто оказывается достаточным
271
знание лишь сводных характеристик вариационных рядов: средних
или характеристик центральной тенденции; характеристик изменчи-
вости (вариации) и др. Расчет статистических характеристик пред-
ставляет собой второй после группировки этап обработки данных
наблюдений.
8.2. Средние величины
Средние величины характеризуют значения признака, BOKpyi
которого концентрируются наблюдения или. как говорят, централь-
ную тенденцию распределения Наиболее распространенной из
средних величин является средняя арифметическая.
О п р с д е л е н и е. Средней арифметической вариационного ряда
называется сумма произведений всех вариантов на соответствующие
частоты, деленная на сумму частот:
Хм
* = —----. (8.2)
п
где х, — варианты дискретного ряда или середины интервалов ин-
тервального вариационного ряда: п, — соответствующие нм частоты:
т — число неповторяюшихся вариантов или число интервалов:
« = •
4-1
Очевидно. что
х = £л;И-, .
1-1
где и = п,/п — частости вариантов или интервалов.
О Пример 8.3. Найти среднюю выработку рабочих по данным
табл. 8.1.
Ре ш с и и е. По формуле (8.2) для интервального вариацион-
ного ряда
_ 97-3 + 103-7+... + l33>10 + l39-2 11П,/вЛ
х =--------------—--------------= Н9,2(%), где числа 9/.
103.. 133. 139 — середины соответствующих интервалов. ►
Для несфуппированного ряда все частоты л, = I (/ = 1.2.л). а
х = -и— (8.3)
л
есть «невзвешенная» средняя арифметическая.
272
Отметим основные свойства средней арифметической, аналогич-
ные свойствам математического ожидания случайной величины.
1. Средняя арифметическая постоянной равна самой постоянной.
2. Если все варианты увеличить (уменьшить) в одно и то же число раз.
то средняя арифметическая увеличится (уменьшится) во столько же раз:
kx = kx или —-------.
п п
3. Если все варианты увеличить (уменьшить) на одно и то же чисю.
то средняя арифметическая увеличится (уменьшится) на то же число:
____ £(х,+с)я, ХхЛ
X + С = X + С ИЛИ —--------= —---+ С.
п п
4. Средняя арифметическая отклонений вариантов от средней
арифметической равна нулю:
х-х =0 или -х) л, =0. (8.4)
1*1
□ При с = х х - с = х - с = х - х = 0.
5. Средняя арифметическая алгебраической суммы нескольких при-
знаков равна такой же сумме средних арифметических этих признаков:.
х + у = х + у.
6. Если ряд состоит из нескольких групп, общая средняя равна
средней арифметической групповых средних, причем весами являются
объемы групп:
Ух, и,
х=-^------. (8.5)
п
где х — общая средняя (средняя арифметическая всего ряда);
х — групповая средняя /-й группы, объем которой равен л,;
/ — число групп.
При решении практических задач могут применяться и иные формы
средней, которые можно получить из средней степенной k-го порядка':
(Ы
1 Болес корректна запись: х4 =---—
п
лястся только для натуральных к > 2
гак как корень А-й степени опреле-
273
X, = V —--------. где x4 > ().
1 n
Легко убедиться в том. что при к = I получаем формулу средней
арифметической. При других значениях к получаем формулы:
к = -1
п
— средней гармонической",
к = 0 (после раскрытия неопределенности при вычислении пре-
дела limx,) х0 = ^х*х"'...х"‘ =п|-|х’ — средней геометрической",
к - 2 х. - \ ------- — средней квадратической и т.д.
V п
Можно показать. что с ростом порядка к степенная средняя воз-
растает. т.е. х ( < х0 < < х, <... (свойство мажорантности средних).
Кроме рассмотренных средних величин, называемых аналитически-
ми, в статистическом анализе применяют структурные, iuih порядковые,
средние. Из них наиболее широко применяются медиана и мода.
О п р е д с л е н и е. Медианой Me вариационного ряда называет-
ся значение признака, приходящееся на середину ранжированного ряда
наблюдений.
Для дискретного вариационного ряда с нечетным числом членов
медиана равна серединному варианту, а для ряда с четным числом
членов — полусумме двух серединных вариантов.
> Пример 8.4. Найти медиану распределения рабочих по тариф-
ному разряду по данным табл. 8.2.
Р е ш е н и е. п = 50 — четное, следовательно. серединных вариазпон
два: Х25 = 5 и хЛ, = 5. Поэтому Me = (хх + л%)/2 = (5 + 5)/2 = 5 (%). ►
Для интервального вариационного ряда находится медианный
интервал, на который приходится середина ряда, а значение медиа-
ны на этом интервале находят с помощью линейною интерполиро-
вания. Не приводя соответствующей формулы. отметим, что медиа-
на может быть приближенно на (щена с помощью кумуляты как зна-
чение признака, для которого п™ -п/2 или и-’,0* = 1/2.
Достоинство медианы как меры центральной тенденции заключа-
ется в том. что на нее не влияет изменение крайних членов варнашг-
274
онного ряда, если любой из них. меньший медианы, остается меньше
ее, а любой, больший медианы, продолжает быть больше се. Медиана
предпочтительнее средней арифметической для ряда, у которого
крайние варианты по сравнению с остальными оказались чрезмерно
большими или малыми.
Определение. Модой Мо вариационного ряда называется
вариант, которому соответствует наибольшая частота.
Например, для вариационного ряда табл. 8.2 мода Мо = 5, так как
этому варианту соответствует наибольшая частота п, = 22. Для интер-
вального ряда находится модальный интервал, имеющий наибольшую
частоту, а значение моды на этом интервале определяют с помошью
линейного интерполирования. Однако проще моду можно найти гра-
фическим путем с помошью гистограммы.
Особенность молы как меры центральной тенденции заключает-
ся в том. что она не изменяется при изменении крайних членов ря-
да, т.е. обладает определенной устойчивостью к вариации признака.
[> Пример 8.5. Найти медиану и моду распределения рабочих по
выработке но данным табл. 8.1.
Ре ш с н и е. На рис. 8.2. б проведем горизош-альную прямую
у = 0.5 (или г = 50). соответствующую накопленной частости
= /-' (д ) = 0.5 (или накопленной частоте =50). до пересече-
ния с графиком эмпирической функции распределения (или куму-
лятой). Абсцисса точки пересечения и будет медианой вариацион-
ного ряда: А/е = 119.9(%).
На гистограмме распределения (см. рис. 8.2. а) находим прямо-
угольник с Наибольшей частотой (частостью). Соединяя отрезками
прямых вершины этого прямоугольника с соответствующими вер-
шинами двух соседних прямоугольников (см. рис. 8.2. а), получим
точку пересечения этих отрезков (диагоналей), абсцисса которой и
будет модой вариационного ряда: A/о =!20,8(%). ►
8.3. Показатели вариации
Средние величины, рассмотренные выше, не отражают измен-
чивости (вариации) значений признака.
Простейшим (и весьма приближенным) показателем вариации
является вариационный размах R, равный разности между наиболь-
шим и наименьшим вариантами ряда:
Наибольший интерес представляют меры вариации (рассеяния)
наблюдений вокруг средних величин, в частности, вокруг средней
арифметической.
275
Средним линейным отклонением вариационного ряда называется
средняя арифметическая абсолютных величин отклонений варнан-
топ от их средней арифметической:
</ = -^-------. . (8.6)
н
я»
(Заметим, что «простая» сумма отклонений £(х,-х)п, не мо-
/•I
жет характеризовать вариацию признака, ибо согласно свойству 4
средней арифметической эта сумма равна нулю для любого вариа-
ционного ряда.)
О и р с д е л е и и с. Дисперсией s' вариационного ряда называется
средняя арифметическая квадратов отклонений вариантов от их
средней арифметической:
___________ (8.7)
п
Формулу для дисперсии вариационного ряда можно записать в виде:
v*=Lu
ы
где ir, = nJ п .
Для несгруппированного ряда (л, = I) по формуле (8.7) имеем:
Е(-Ч-х)*
Г = -^--------
л
Дисперсию ? часто называют эмпирической или выборочной, под-
черкивая. что она (в отличие от дисперсии случайной величины ст )
находится по опытным иди статистическим данным.
Желательно о качестве меры вариации (рассеяния) иметь харак-
теристику. выраженную в тех же единицах, что и значения призна-
ка. Такой характеристикой является среднее квадратическое откло-
нение s — арифметическое значение корня квадратного из дисперсии —
ILUi-^У «<
jpetl—----------- (8.8)
1 л
Рассматривается также безразмерная характеристика — ко-мффи-
циент вариации, равный процентному отношению среднего квадра-
тического отклонения к средней арифметической:
v = ^.|00% (х*0). (8.9)
-V
276
Если коэффициент вариации признака, принимающего только по-
ложительные значения, высок (например, более 100%). то, как правило,
□то свидетельствует о неоднородности значений признака.
Отметим основные свойства дисперсии, аналогичные свойствам
дисперсии случайной величины.
I. Дисперсия постоянной равна нулю.
2. Еаш все варианты увеличить (уменьшить) в одно и то же число
к раз. то дисперсия увеличится (уменьшится) в к2раз'.
£(х,*-Я):„, £(x,-x)’n,
a^-k's\ или —1-----------= к: —-----------.
п п
3. Если все варианты увеличить (уменьшить) на одно и то же чис-
,ю. то дисперсия не изменится'.
Ё[(*,+еНг+с)]Ч £(х,-х)ал,
.Г. . = 5* = ,Г или —---------------= —----------.
И П
4. Дисперсия равна разности между средней арифметической квад-
ратов вариантов и квадратом средней арифметической:
№=х:-х:, (8.10)
где х2=-^------. (8.11)
п
2л "• 2лл* 2л
□ s3 = —---------= ---------2x —----+ X •’ =
n n n n
- xz - 2x • x + x: = x: - x\ ибо 21 п1 - n-
i-l
5. Если ряд состоит из нескольких групп наблюдений, то общая
дисперсия равна сумме средней арифметической групповых дисперсий и
межгрупповой дисперсии:
Г=? + 8:, (8.12)
где л2 — общая дисперсия (дисперсия всего ряда);
средняя арифметическая групповых дисперсий;
ZU~x )Ч
; (8.14)
nt
277
S’=-^----------- (8.15)
n
— межгрупповая дисперсия.
Формула (8.12), известная в статистике как оправило сложения
дисперсий», имеет важное значение в статистическом анализе.
> Пример 8.6. Вычислить дисперсию, среднее квадратическое
отклонение и коэффициент вариации распределения рабочих по
выработке по данным табл. 8.1.
Решение. В примере 8.3 было получено v = 119.2(%). По
определению (8.5) дисперсия
(97-119.2)'-3 <( ЮЗ-119,2)'-7 + ...* (133-119,2)‘'|0+(139-119.2)‘'-2
100
= 87.48.
Среднее квадратическое отклонение л = >/87.48 = 9.35(%): ко-
эффициент вариации по формуле (8.9) х = (9.35/119.2)100= 7,8(%).
Следует отметить. что вычисление дисперсии (особенно в слу-
чае. когда отклонения от средней (х,-х)* выражаются нецелыми
числами), а сами х, — целые, удобнее проводить по формуле (8.10).
Например, в данном примере вначале по формуле (8.11) найдем
7 = 97:-3-,03;.7....-1ЗУ.10 + 139<2 = |д
100
Теперь по формуле (8.10)
Г =?-хг =14 296,12-119.2: =87,48. ►
> Пример 8.7. Имеются следующие данные о средних и диспер-
сиях заработной платы двух групп рабочих (табл. 8.3).
'Гиблина 8.3
Группа рабочих Число рабочих Средняя заработная плата одного рабочего в группе (ден. ед.) Дисперсия за- работной пла- ты
Работающие на одном станке Работающие на двух станках 40 60 2400 3200 180 000 200 000
278
Найти общую дисперсию распределения рабочих по заработной
плат* и его коэффициент вариации.
решение. Найдем общую среднюю по формуле (8.5):
_ 2400-40 * 3200-60
v =-----------------
100
- 2880(лен. ед.).
Найдем среднюю групповых дисперсий по формуле (8.13):
— 180 000 • 40 * 200 000 60 1МЛЛЛ
.г =----------------------= 192 000.
100
Найдем межгрупповую дисперсию по формуле (8.15):
(2400 - 288()/ • 40 * (3200 - 2880 f 60 _ j
100
Используя правило сложения дисперсий (8.12). найдем обшую
дисперсию заработной платы и ее среднее квадратическое отклоне-
ние:
s2 = 192 000 + 153 600 = 345 600; 5 = ^345 600 = 588 (лен. ед.).
По формуле (8.9) коэффициент вариации
588
v = • 100 = 20.4(%). ►
2880
8.4. Упрощенный способ расчета
средней арифметической и дисперсии
Вычисление средней арифметической х и дисперсии
з1 вариационного ряда можно упростить, если использовать не пер-
воначальные варианты х, (/ =1.2.т). а новые варианты
«, = ^. <8.16)
Л
где с и к — специально подобранные постоянные.
Согласно свойствам 2 и 3 средней арифметической и дисперсии
й = = (8.17)
к ) к
откуда
х = йХ+с (8.18)
279
и (8.19)
Учитывая формулу (8.10). а затем равенство (8.17). получим
s; = к:[и: -н:) = А:м: -к:й: = к:и: j -к:и: -(х -с) .
Теперь, заменяя в равенствах (8.18) и (8.19) й и и' их выраже-
ниями (8.2) и (8.11) через варианты uh получим
x=-i^-----к+с. (8.20)
п
-----к2-(х-с)\ (8.21)
п
где w, определяются по формуле (8.16).
Формулы (8.20) и (8.21) дадут заметное упрощение расчетов, ес-
ли в качестве постоянной к взять величину (ширину) интервала по
х, а в качестве с — середину серединного интервала. Если середин-
ных интервалов два (при четном числе интервалов), то в качестве с
рекомендуется взять середину одного из этих интервалов, например,
имеющего большую частоту.
Замечание. Формулы (8.20) и (8.21) для х и s2 носят тех-
нический, вспомогательный характер в позволяют рассчитать харак-
теристики ряда по новым, условным вариантам. Основными же
формулами, вытекающими из определения средней арифметической и
дисперсии вариационного ряда и отражающими их сущность, остают-
ся соответственно формулы (8.3) и (8.7).
О Пример 8.8. Вычислить упрощенным способом среднюю
арифметическую и дисперсию распределения рабочих по выработке
по данным табл. 8.1.
Решение. Возьмем постоянную к. равную величине интер-
вала, т.е. к = 6. и постоянную с, равную середине пятого (одного из
двух серединных) интервала, т.е. с = 121. По (8.16) новые варианты
и,= (х,-121)/6.
Благодаря такому переходу получим вместо вариантов х,= 97.
103. 109. 115, 121. 127. 133 «простые» варианты и, - -4. -3,-2,—1. 0.
I. 2, 3.
Теперь для расчета х и л* по формулам (8.20) и (8.21) необходимо
найти суммы и £u’/j . Их вычисление представим в табл. 8.4.
<-« Г-1
280
Тнблпцп Я.4
/ Интервалы х Середи- на ин- тервал X/ х. -119 г/, = 10 utn, М-i (ui 1 1) п,
1 94,0-100.0 97 -4 3 -12 48 -з 27
2 100.0-106.0 103 -3 7 -21 63 -2 28
3 106.0-112.0 109 —э II -22 44 -1 11
4 112.0-118.0 115 -1 20 -20 20 0 0
5 118.0-124.0 121 0 28 0 0 1 28
6 124.0-130.0 127 1 19 19 19 2 76
7 130.0-136.0 133 2 10 20 40 3 90
8 136.0-142.0 139 3 2 6 18 4 32
V — 100 -30 252 — 292
к х
В итоговой строке табл. 8.4 находим ^u,n, = -30. = 252 .
|>1 Jul
Последний столбец — контрольный. Если таблица составлена
верно, то
£(», -1) и, = ж ~п <где " = Z" )•
<*• <»| г*| 1*1
X
В данном случае У (и, + 1)л, = 292 = 252 + 2(-30)+100. т.е. рас-
<•1
четы проведены верно.
Теперь по формуле (8.20) х = —^-6 + 121 = 119,2(%), по форму-
100
ле (821) .у* = = —-6-119.2-121* =87.48. ►
100 ' '
8.5. Начальные и центральные моменты
вариационного ряда
Средняя арифметическая и дисперсия вариационного ряда яв-
ляются частными случаями более общего понятия — моментов ва-
риационного ряда.
Начальный момент \\ к-го порядка вариационного ряда' опреде-
ляется по формуле:
2».
V, =-^---. (8.22)
н
’ См. сноску ни с. 283.
281
Очевидно, что v, = .v , т.с. средняя арифметическая является на-
чальным моментом первого порядка вариационного ряда.
Центральный момент р4 к-го порядка вариационного ряда опре-
деляется по формуле:
~------------ (8-23)
п
С помощью моментов распределения можно описать нс только
среднюю тенденцию, рассеяние, но и другие особенности вариации
признака.
Очевидно, в силу свойства (8.4), что р, =0, а р, =,г . т.е. цен-
тральный момент первого порядка для любого распределения равен
нулю, а — второго порядка является дисперсией вариационного ряда.
Коэффициентом асимметрии вариационного ряда называется число
Я = Ь = , (8.24)
5 tlS
Если Л = 0. то распределение имеет симметричную форму, т.е
варианты, равноудаленные от .?, имеют одинаковую частоту. При
й>0 (л<0) говорят о положительной (правосторонней) или от-
рицательной (левосторонней) асимметрии.
Эксцессом (или коэффициентом эксцесса) вариационного ряда на-
зывается число
£ = -Ц--3 = —------------3. (8.25)
S ns
Эксцесс является показателем «крутости» вариационного ряда по
сравнению с нормальным распределением. Как отмечено выше (§ 4.7).
эксцесс нормально распределенной случайной величины равен нулю.
Если £>0(Л’<0). то полигон вариационного ряда имеет более
крутую (пологую) вершину по сравнению с нормальной кривой.
О Пример 8.9. Вычислить коэффициент асимметрии и эксцесс
распределения рабочих по выработке поданным табл. 8.1.
Реше н и е. Коэффициент асимметрии и эксцесс вариационного
ряда, приведенного в табл. 8.1. найдем по формулам (8.24) и (8.25):
- (97-119.2)’-3-(103-119,2)’-74-...4 (139-119.2)’ -2
” 100-9,35’ ” ’ ’
282
(97-119.2)*-3+ (103-119.2) -7-• ... + (139-119,2)'-2
E*~ ~ •• “ '
100-9.35
В силу того, что коэффициент асимметрии А отрицателен и
близок нулю, распределение рабочих но выработке обладает незна-
чительной левосторонней асимметрией, а поскольку эксцесс Ё
близок нулю, рассматриваемое распределение по крутости прибли-
жается к нормальной кривой. ►
Средняя арифметическая х . дисперсия и другие характеристи-
ки вариационного ряда являются статистическими аналогами мате-
матического ожидания Л/(Л). дисперсии о и соответствующих ха-
рактеристик случайной величины X.
В табл. 8.5 приведено соответствие терминов (обозначений. фор-
мул) вариационного ряда и случайной величины Подчеркнем, что
вариационный ряд рассматривается в дальнейшем как одна из реали-
заций распределения признака (случайной величины)' А*.
Тиб.ниш Я. 5
Вариационный ряд Случайная величина
Обозначения, формулы Термин Обозначения, формулы Термин
1 2 у 4
— Дискретный ряд — Дискретная случайная ве- личина
— Интервальный рял — Непрерывная случайная ве- личина
X, Вариант X,. X Значение слу- чайной величи- ны
Н’„ И’ Частость А. Р. Р Вероятность
Полигон, лю- то грамма Полигон (мно- гоугольник) распределения вероятностей, кривая распре- деления
1 Если лля характеристик 1мрмапвон110|о ряда nciiojn.iyioioi тс же буквенные
выражения. *по и для случайной величины, то обо шансния этих характеристик
дополняются знаком - (-гильза»).
283
Окончание таи.» Л’5
1 2 3 4
ЕДх) = *\Х < х) Эмпирическая Дх)= Р (X < х) Функция рас-
функция рас- пределения
пределения
Средняя ариф- Математическое
х = 2^х,и; магическая <1 = М(Х)=2^х,рл 1'1 ожидание*
5-'=(х-.?)’ = Дисперсия <Г = Л/[.¥ - ЛЛЛ')]: = Дисперсия*
? 1 II Среднее квад- А <«1 Среднее квадра-
X = у/х2 а - JD(X) = V?
ратичсское гичсскос откло-
отклонение некие
Мо Мода Мо(Х) Мода
Me Медиана Ме(Х) Медиана
Начальный Начальный мо-
момент Л-го y\ = t/p. мент £-го по-
f»l порядка ы рядка’
II м» 1 *1 Центральный Центральный
момент к-го М. = Х1х< W( V)I а момент Л-го по-
«•1 порядка рядка
Коэффициент /1 = р./а’ Коэффициент
асимметрии асимметрии
E = -3 Эксцесс Е = р4/ст‘ -3 Эксцесс
• Формула приведена для дискретной случайной величины.
Упражнения
В примерах 8.10—8.12 дано распределение признака X (случай-
ной величины X). полученной по п наблюдениям. Необходимо':
1) построить полигон (гистограмму), кумуляту и эмпирическую
функцию распределения X; 2) найти: а) среднюю арифметическую
х; б) медиану Me и моду Мо\ в) дисперсию х2. среднее квадратиче-
ское отклонение х и коэффициент вариации й; г) начальные v4 и
• При наличии открытых интервалов значений Л'типа «менее Х|* или «свыше
х< для проведения расчетов их условно заменяют интервалами той же ширины
к. г.с. (Х| - к, д-0 или (хя, ля+Л>
284
центральные р, моменты А-го порядка (к = 1. 2. 3. 4); д) коэффици-
ент асимметрии А и эксцесс Е.
8.10. X — число сделок на фондовой бирже за квартал;
п = 400 (инвесторов).
у 0 1 2 3 4 5 6 7 8 9 10
Л/ 146 97 73 34 23 10 6 3 4 2 2
8.11. X— месячный доход жителя региона (н руб.); п = 1000 (жителей).
х. Менсе 500 500-1000 1000— 1500 1500-2000 2000-2500 Свыше 2500
58 96 239 328 147 132
8.12. X — удой коров на молочной ферме за лактационный пери-
од (в ц); л = 100 (коров).
х. 4-6 6-8 8-10 10— 12 12- 14 14- 16 16- 18 18- 20 20- 22 22- 24 24- 26
1 3 6 II 15 20 14 12 10 6 2
8.13. В таблице приведено распределение 50 рабочих по произ-
водительности труда X (единиц за смену), разделенных на две груп-
пы: 30 и 20 человек.
Прошедшие техническое обучение {группа /) Не прошедшие техническое обу- чение (группа 2)
X, 85 34 96 102 103 63 69 83 89 106
Л/ 2 5 11 8 4 2 6 8 3 1
Вычислить общие и групповые средние и дисперсии и убедиться в
справедливости правила сложения дисперсий.
Глава 9
Основы математической теории
выборочного метода
9.1. Общие сведения о ныбо|ючном методе
В практике статистических наблюдений различают два вила на-
блюдений: сплошное. когда изучаются все объекты (элементы, едини-
цы) совокупности, и несплошное, выборочное. когда изучается часть
объектов. Примером сплошного наблюдения является перепись пасе
ления. охватывающая все население страны. Выборочными наблюде-
ниями являются, например, проводимые социологические исследова-
ния, охватывающие часть населения страны, области, района и т.д.
Вся подлежащая изучению совокупность объектов (наблюдений) называ-
ется генеральной совокупностью. В математической статистике понятие
генеральной совокупности трактуется как совокупность всех мыслимых
наблюдений. которые могли бы быть произведены при данной реальном ком-
плексе условий. и в этом смысле сто нс следует смешивать с реальными
совокупностями, подлежащими статистическому изучению. Так, обсле-
довав даже все предприятия подотрасли по определенным технико-
экономическим показателям, мы можем рассматривать обследованную
совокупность лишь как представителя гипотетически возможной бо-
лее широкой совокупности предприятий, которые могли бы функ-
ционировать в рамках того же реального комплекса условий.
Понятие генеральной совокупности в определенном смысле анало-
гично понятию случайной величины (закону распределения вероятно-
стей, вероятностному пространству), гак как полностью обусловле-
но определенным комплексом условий.
Та часть объектов, которая отобрана для непосредственного изуче-
ния из генеральной совокупности, называется выборочной совокупно-
стью. или выборкой. Числа объектов (наблюдений) в генеральной или
выборочной совокупности называются их объемами. Генеральная со-
вокупность может иметь как конечный, гак и бесконечный объем.
Выборку можно рассматривать как некий эмпирический акало!
генеральной совокупности. Сущность выборочного метода состоит в
том, чтобы по некоторой части генеральной совокупности (ло выбор-
ке) выносить суждение о ее свойствах в целом.
Концепция выборки лежит в основе методологии математической
статистики.
Отмстим преимущества выборочного метода наблюдения по срав-
нению со сплошным:
• позволяет существенно экономить затраты ресурсов (матери-
альных, трудовых, временных);
286
• является единственно возможным в случае бесконечной гене-
ральной совокупности или в случае, когда исследование связа-
но с унн’ггожением наблюдаемых объектов (например, иссле-
дование долговечности электрических лампочек, предельных
режимов работы приборов и т.п );
• позволяет снизить ошибки регистрации, т.е. расхождения ме-
жду истинным и зарегистрированным значениями признака.
Основной недостаток выборочного метода — ошибки исследования,
называемые ошибками репрезентативности (представительства). о ко-
торых речь пойдет ниже.
Однако неизбежные ошибки, возникающие при выборочном ме-
тоде исследования в связи с изучением только части объектов, могут
быть заранее оценены и посредством правильной организации выбор-
ки сведены к практически незначимым величинам. Между тем ис-
пользование сплошного наблюдения даже там. где это принципиально
возможно, нс говоря уже о росте трудоемкости, стоимости и увеличе-
нии необходимого времени, часто приводит к тому, что каждое от-
дельное наблюдение поневоле проводится с меньшей точностью. А это
уже сопряжено с неустранимыми ошибками и в конечном счете может
привести к снижению точност сплошного наблюдения по сравнению
с выборочным.
Чтобы по данным выборки иметь возможность судить о генеральной
совокупности, она должна быть отобрана случайно. Случайность отбо-
ра элементов в выборку достигается соблюдением принципа равной
возможности всем элементам генеральной совокупности быть ото-
бранными в выборку. На практике это достигается тем, «его извлече-
ние элементов в выборку проводится путем жеребьевки (лотереи) или
с помощью случайных чисел, имеющихся в специальных таблицах
или вырабатываемых ЭВМ с помощью датчика случайных чисел.
Выборка называется репрезентативной (представительной), если
она достаточно хорошо воспроизводит генеральную совокупность
Различают следующие в и д ы выборок:
• собственно-случайная выборка, образованная случайным вы-
бором элементов без расчленения на части или группы:
• механическая выборка. в которую элементы из генеральной сово-
купности отбираются через определенный интервал. Например,
если объем выборки должен сосганлять 10% (10%-ная выборка),
то отбирается каждый 10-и ее элемент и т.д.:
• типическая (стратифицированная) выборка, в которую слу-
чайным образом отбираются элементы из типических групп,
на которые по некоторому признаку разбивается генеральная
совокупность;
• серийная (гнездовая) выборка, в которую случайным образом
отбираются не элементы, а целые группы совокупности (се-
рии). а сами серии подвергаются сплошному наблюдению.
287
Используют два способа образования выборки:
• повторный отбор (по схеме возвращенного шара), когда каж-
дый элемент, случайно отобранный и обследованный, воз-
вращается в общую совокупность и может быть повторно
отобран;
• бесповторпый отбор (по схеме невозврашенного шара), когда
отобранный элемент нс возвращается в общую совокупность.
Математическая теория выборочного метода основывается на
анализе собственно-случайной выборки. Рассмотрением этой вы-
борки мы и ограничимся.
Обозначим:
xt — значения признака (случайной величины Л);
N и п — объемы генеральной и выборочной совокупностей;
Nt и п, — число элементов генеральной и выборочной совокупно-
стей со значением признака х(;
М и т — число элементов генеральной и выборочной совокупно-
стей. обладающих данным признаком.
Средние арифметические распределений признака в генераль-
ной и выборочной совокупностях называются соответственно гене-
ральной и выборочной средними, а дисперсии этих распределений —
генеральной и выборочной дисперсиями. Отношение числа элементов
генеральной и выборочной совокупностей, обладающих некоторым
признаком /1. к их объемам, называются соответственно генеральной
и выборочной долями. Все формулы сведем в таблицу (табл. 9.1).
Таблица 9.1
Наименование
характеристики
Средняя
Дисперсия
Доля
Ггнеральная
совокупность
fff
(9.1)
/V
£(-Ч -х0У N,
<Г = (9.3)
Л
(9.5>
Выборка
m
№='•' (9.2)
n
ZU -x)2nt
s2 =(9.4)
n
Замечание. В случае бесконечной генеральной совокупно-
сти (W = о?) под генеральными средней и дисперсией понимается
соответственно математическое ожидание а = и дисперсия п*
288
распределения признака X (генеральной совокупности), а под гене-
ральной долей р — вероятность данного события.
Важнейшей задачей выборочного метода является оценка парамет-
ров (характеристик) генеральной совокупности по данным выборки.
Теоретическую основу применимости выборочного метода со-
ставляет закон больших чисел, согласно которому при неограничен-
ном увеличении объема выборки практически достоверно, что слу-
чайные выборочные характеристики как угодно близко приближа-
ются (сходятся по вероятности) к определенным параметрам гене-
ральной совокупности.
9.2. Понятие оценки параметров
Сформулируем задачу опенки параметров в общем виде. Пусть
распределение признака X — генеральной совокупности — задается
функцией вероятностей ф(л;. 0) = Р(Х - хJCuih дискретной слу-
чайной величины X) или плотностью вероятности ф(.х. 0) (для не-
прерывной случайной величины А), которая содержит неизвестный
параметр 0. Например, это параметр /. в распределении Пуассона
ши параметры а и ст2 для нормального закона распределения и тл.
Для вычисления параметра 0 исследовать все элементы гене-
ральной совокупности не представляется возможным. Поэтому о
параметре 0 пытаются судить по выборке, состоящей из значений
(вариантов) Л|. ... х„. Эти значения можно рассматривать как
частные значения (реализации) п независимых случайных величин
Х\, Х2, .... Хп. каждая из которых имеет тот же закон распределения,
что и сама случайная величина X.
Определение. Оценкой 0„ параметра 0 называют всякую
функцию результатов наблюдений над случайной величиной X (иначе —
статистику), с помощью которой судят о значении параметра 0:
= W',. А\.....VJ.
Поскольку .V|. Ап.Хя — случайные величины, то и оценка 0,
(в отличие от оцениваемого параметра 0 — величины неслучайной,
детерминированной) является случайной величиной, зависящей от
закона распределения случайной величины X и числа п.
Всегда существует множество функций от результатов наблюде-
ний X). X,. .... Х„ (от п «экземпляров» («копий») случайной величи-
ны А), которые можно предложить в качестве оценки параметра 0.
Например, если параметр 0 является математическим ожиданием
случайной величины А', т.е. генеральной средней х„. то в качестве
*0 леувтшхтгЛ л «исыдигкск*! < ijtnnwu
289
его оценки 0. по выборке можно взять: среднюю арифметическую
результатов наблюдении — выборочную среднюю .v, моду Л/о. ме-
диану Me. полусумму наименьшего и наибольшего значений по вы-
борке, т.е. (хппп + хП1М)/2 и т.д. Какими свойствами должна обладай,
опенка 6,. чтобы в каком-го смысле быть «доброкачественной»
оценкой?
Назвать «наилучшей* оценкой такую, которая наиболее близка к
истинному значению оцениваемого параметра, невозможно, так как
выше отмечено, что 0„ — случайная величина, поэтому невозмож-
но предсказать индивидуальное значение оценки в данном частном
случае. Так что о качестве оценки следует судить не по индивидуале
ным ее значениям. и лишь по распределению ее значений в большой се-
ти испытаний, т.е. по выборочному распределению оценки. Если зна-
чения оценки 0и концентрируются около истинного значения па-
раметра 0. т.е. основная часть массы выборочного распределения
оценки сосредоточена в малой окрестности оцениваемого параметра
0. то с большой вероятностью можно считать, что оценка 0, отли-
чается от параметра 0 лишь на малую величину. Поэтому, чтобы
значение 0, было близко к 0. надо, очевидно, потребовать, чтобы
рассеяние случайной величины 0. относительно 0. выражаемое, на-
пример. математическим ожиданием квадрата отклонения опенки
от оцениваемого параметра А/(б„ -0) . было по возможности мень-
шим. Таково основное у с л о в и е, которому должна удов-
летворять «наилучшая* оценка.
Рассмотрим наиболее важные свойства оценок.
О п р е д с л е н и е. Оценка 0, параметра 0 называется не-
смещенной, если ее математическое ожидание равно оцениваемому
параметру, т.е.
А/(б„) = О
В противном случае оценка называется смещенной.
Если это равенство нс выполняется, то оценка (),. полученная по
разным выборкам, будет в среднем либо завышать значение 0 (если
Л/(01т)>0), либо занижать ею (если ,W(0„)<G). Таким образом.
требование несмещенности гарантирует отсутствие систематиче-
ских ошибок при оценивании.
290
Замечание. На первый взгляд, приведенное выше опреде-
ление любой оценки, как всякой функции результатов наблюдений,
было бы более естественным и не таким расплывчатым, если бы в
нем содержалось условие Л/(0П) = 0. К сожалению, этого сделать
нельзя, так как практически важные оценки оказываются смешен-
ными. хотя и слабо.
Если при конечном объеме выборки п Л/(0я)*б, т.е. смещение
оценки Л(0„) = .W(0„)-0*O, но = то такая опенка 0,
называется асимптотически несмещенной.
О п ре л ел с н и е. Оценка 0„ параметра 0 называется со-
стоятельной, если она удовлетворяет закону больших чисел, т.е. схо-
дится по вероятности к оцениваемому параметру:
limP(|e.-0|<s)^. (’-7)
- .г
или G. -> 0.
В случае использования состоятельных оценок оправдывается
увеличение объема выборки, гак как при этом становятся маловеро-
ятными значительные ошибки при оценивании. Поэтому практиче-
ский смысл имеют только состоятельные оценки. Если оценка со-
стоятельна. то практически достоверно, что при достаточно боль-
шом п 6„ = 0 .
Если оценка 0„ параметра 0 является несмещенной, а ее дисперсия
gJ ->0 при п -> х. то оценка ()„ является и состоятельной, ’.-ho не-
посредственно вытекает из неравенства Чебышева:
Р(|ё.-е|<ф|-^.
Так, например, выборочная средняя .? является несмещенной и
состоятельной оценкой генеральной средней л„ (дисперсия а’ -►()
при п -> ас, см. § 9.4), а отдельное выборочное наблюдение
Xk (Л = 1. 2 п) — несмещенной (Л/( Х\ ) = ЛУ(Л’) = ). но не
состоятельной оценкой генеральной средней, гак как ее дисперсия
с: (Xt) = ст’ (X) = ст’ постоянна и не уменьшается с ростом п.
Определение. Несмещенная оценка 0„ параметра 0 назы-
вается эффективной, если она имеет наименьшую дисперсию среди
всех возможных несмещенных оценок параметра 0. вычисленных по
выборкам одного и того же объема п.
291
Так как для несмещенной оценки1 Л-/ (0„ - й) есть ее дисперсия
. то эффективность является решаю щ им свойст-
вом, определяющим качество оценки.
Эффективность оценки 0„ определяют отношением:
•»
е= (9.8)
Ч
где п", и о* — соответственно дисперсии эффективной и данной
оценок. Чем ближе е к I. тем эффективнее оценка. Если е I при
п -> г . то такая оценка называется асимптотически эффективной.
На практике в целях упрощения расчетов используются оценки, не
обладающие высокой эф<|)ективностыо. Так. например, генеральную
среднюю л0 часто оценивают медианой Me выборки, в то время как
эффективной оценкой лп является выборочная средняя л* (§ 9.5).
При нормальном распределении признака в генеральной совокупности
можно показать. что асимптотическая эффективность этой оценки,
т.е. е(Ме) = 2/л = 0,64 при Это означает, что для получения
той же точности и надежности опенки генеральной средней по выбо-
рочной средней нужно использовать лишь 64% обдема выборки, взя-
того при оценке по медиане.
Если при тех же условиях для опенки генеральной средней
л0 использовать статистику 0„ = (.vmil, +.vnii )/2. то (см., например.
24 In п
|23|) се эффективность е(0 I ~ :— с ростом п стремится к нулю, и
п'п
опюсительно приемлемый результат оценивания (по сравнению с эф-
фективной оценкой .v ) возможен при малом объеме выборки.
Другой пример. В практике статистического контроля качества
продукции для оценки генерального среднего квадратическою от-
клонения о широко используют оценку sK = R dn, где
/? = .vnm - .vm,n — вариационный размах. dn — коэффициент, зави-
сящий от объема выборки п. При малых п эффективность оценки .\А-
достаточно высока, но с увеличением п быстро падает. Поэтому
• Дня смешенной оценки, как нетрудно покакпь. Л/ (0„ - 0)? - п; + />’((),> , где
А(0_) — < мщение оценки
292
удовлетворительная оценки ст с помощью может быть достигнута
лишь при п < 10.
В качестве статистических оценок параметров генеральной сово-
купности желательно использовать оценки, удовлетворяющие одно-
временно требованиям несмещенности, состоятельности и эффектив-
ности. Однако достичь этого удается не всегда. Может оказаться,
чю для простоты расчетов целесообразно использовать незначи-
тельно смещенные оценки или оценки, обладающие большей дис-
персией по сравнению с эффективными оценками, и т.п.
9.3. Методы нахождения оценок
Рассмотрим основные методы нахождения оценок.
Согласно методу моментов, предложенному К. Пирсоном, опреде-
ленное количество выборочных моментов (начальных v* или центральных
р4, или тех и других) приравнивается к соответствующим теоретиче-
ским моментам распределения (vt или р4) случайной ветчины X. На-
помним. что выборочные моменты v4 и р4 определяются по форму-
лам (8.22) и (8.23). а соответствующие нм теоретические моменты — по
формулам (3.32)—(3.35):
Mi =Z(.v(-o)*A
м r-t
(для дискретной случайной величины с функцией вероятностей
А =<р(.г,.9)).
v, = J л‘ф(х.0)с/х. И, = f (t-а)* ф(л-.0)с/г
(для непрерывной случайной величины с плотностью вероятностей
Ф(х.0)). где а = М(Х) - см. § 3.7.
t> Пример 9.1. Найти оценку метода моментов для параметра /.
закона Пуассона.
Решение. В данном случае для нахождения единственного
параметра /. достаточно приравнять теоретический v, и эмпириче-
ский v, начальные моменты первого порядка. v, — математическое
ожидание случайной величины X. В § 4.2 установлено, что для слу-
чайной величины, распределенной по закону Пуассона, Л/(А’) = л.
Момент V,. согласно формуле (8.22). равен л. Следовательно, оценка
метода моментов параметра л закона Пуассона есть выборочная сред-
няя х. ►
293
Следует отметить, что сели при использовании данного метола
некоторые моменты равны нулю или не зависят от нужных
параметров, то приходится «пропускать» такие моменты и
переходить к следующим по порядковому номеру. Например, если
оценивается один параметр п‘ нормального икона jV(O; п ),
нужно взять второй момент, а не первый.
Опенки метода моментов обычно состоятельны. однако по эф-
фективности они не являются «наилучшими*, их эффективности
е(0.) часто значительно меньше единицы. Тем не менее метод мо-
ментов часто используется на практике, гак как приводит к сравни-
тельно простым вычислениям.
Основным методом получения опенок параметрон генеральной со-
вокупности по данным выборки является метод максимального (наи-
большего) правдоподобия. предложенный Р. Фишером.
Основу метода составляет функция правдоподобия, выражающая
плотность вероятности (вероятность} совместного появления резуль-
татов выборки Х|. х?....х„:
/-(хр х...v......х,;е) = ф(х|, 0) ф(х.. 0)..,ф(х,, 0)...ф(х„. 0).
ИЛИ L\X), х....х,....х/.О) = |~[ф( г . 0).
i.t
Согласно методу максимального правдоподобия в качестве оценки
неизвестного параметра 0 принимается такое значение . которое
максимизирует функцию Естественность подобного подхода к оп-
ределению статистических опенок вытекает из смысла функции
правдоподобия, которая при каждом фиксированном значении па-
раметра 0 является м с р о й прав л о п о д обмоет и полу-
чения наблюдений х», х2.....хя И опенка 0„ такова, что имеющие-
ся у нас наблюдения Х|. х2..х„ являются наиболее правдоподоб-
ными.
Нахождение опенки ()Л упрощается, если максимизировать не саму
функцию Z., a In L, поскольку максимум обеих функций достигается при
одном и том же значении 0. Поэтому для отыскания оценки параметра 0
(ОДНОГО или нескольких) надо решить уравнение (систему уравнений} прав-
доподобия. получаемое приравниванием производной (частых производ-
ных) нулю по параметру (параметрам) 0:
а затем отобран, то решение, которое обращает функцию In L в
максимум.
294
> Пример 9.2. Найти оценку метода максимального правдоподо-
бия для вероятности р наступления некоторого события А по данному
числу т появления этого события в п независимых испытаниях.
решение. Составим функцию правдоподобия:
/- = (х,. Ь..л,; р) = рр...р(\- /,)(1 - /»)...(! - р).
или
L = />’(1- р)"
Тогда In I. = т In р + (п- т) In (I - р) и согласно уравнению (9.9)
t/in L т п~т . т . ,
------------------. откуда р = — (можно показать, что при р = т/п
dp р 1 - р и
выполняется достаточное условие экстремума функции L).
Таким образом, оценкой метода максимального правдоподобия веро-
ятности р события А будет частость w = — этого события. ►
п
О Пример 9.3. Найти оценки метола максимального правдопо-
добия для параметров а и о2 нормального закона распределения по
данным выборки.
Ре ш е н и е. Плотность вероятности нормально распределен-
ной случайной величины
|
<p4(x;a.cf) = —=е .
ст>/2л
Тогда функция правдоподобия имеет вид:
• I 1
Л(х,..«....г.:а,а:)=р|—--------------------<.
а72я а'(2пр
Логарифмируя, получим:
In /.=-^(1п 0:4-1п(2л))--^7£(л;-и)’.
Для нахождения параметров а и а*’ надо приравнять нулю част-
ные производные по параметрам а и ст2. т.е. решить систему урав-
нений правдоподобия:
? In /.
да
д\п1.
Г <7 2
= ':Zk-«)=0.
±(х. -«У- "
4*1 -С
2»5
откуда оценки максимального правдоподобия равны:
5>, £(.г,-.гУ
О = = .V, Ст" = 1'1 = Л*.
п п
Таким образом, оценками метода максимального правдоподобия
математического ожидания а и дисперсии о* нормально распредаеи-
ной случайной величины являются соответственно выборочная средняя
х и выборочная дисперсия а1. ►
Важность метода максимального правдоподобия связана с его оп-
тимальными свойствами. Так. если для параметра 0 существует эф-
фективная оценка 0^. то оценка максимального правдоподобия единст-
венная и равна 0^. Кроме того, при достаточно общих условиях оцен-
ки максимального правдоподобия являются состоятельными. асимпто-
тически несмещенными, асимптотически эффективными и имеют
асимптотически нормальное распределение.
Основной недостаток метода максимального правдоподобия —
трудность вычисления опенок, связанных с решением уравнений
правдоподобия, чаще всего нелинейных. Существенно также и то,
что для построения оценок максимального правдоподобия и обес-
печения их «хороших» свойств необходимо точное знание типа ана-
лизируемого закона распределения ф(.т.О). что во многих случаях
оказывается практически нереальным.
Метод наименьших квадратов — один из наиболее простых
приемов построения опенок. Суть его заключается и том. что оценка
определяется из условия минимизации суммы квадратов отклонений
выборочных данных от определяемой оценки
О Пример 9.4. Найти опенку метода наименьших квадратов 0„
дня генеральной средней 0 = т„.
Решение. Согласно метолу наименьших квадратов найдем
опенку 0„ из условия минимизации суммы:
и - £(.Т, - 0) -> min .
Используя необходимое условие экстремума, приравняем нулю
производную
“ = -2£( .т, - 9) = 0. откуда £ л; - 0л = 0
- _
и 0„ = —— = г. т.е. оценка метода наименьших квадратов генераль-
п
ной средней х1( есть выборочная средняя х . ►
296
Заметим, что полученная в примере 9.4 опенка метола наи-
меньших квадратов .г для генеральной средней .v(, совпала с оцен-
кой метола максимального правдоподобия для математического
ожидания с; = .тп для нормально распределенной случайной величи-
ны (см. пример 9.3).
И это не случайно, так как функция правдоподобия
Д(х,... 0; ст*) для нормального закона распределения имеет
максимум тогда, когда сумма £(а; -0)’ минимальна.
*|
Метод наименьших квадратов получил самое широкое распро-
странение в практике статистических исследований, так как. во-
первых. не требует знания закона распределения выборочных данных;
во-вторых, достаточно хорошо разработан в плане вычислительной
реализации.
Применение метода наименьших квадратов в задачах корреля-
ционного и регрессионного анализа рассмотрено в гл. 12 н 13.
9.4. Оценка параметров генеральной совокупности
по собственно-случайной выборке
Оценка генеральной доли. Пусть генеральная совокупность содержит
W элементов. из которых Л/обладает некоторым признаком Л. Следует
найти «наилучшую* опенку генеральной доли
/’
А/
.V ’
Рассмотрим в качестве такой возможной опенки параметра р его
статистический аналог — выборочную долю н' =
п
я) Выборка повторная
Выборочную долю можно представить как среднюю арифметиче-
скую п альтернативных случайных величин1 Xh Л'2....Х\, .... Хп. т.е.
и
м? = *-> . где каждая случайная величина Лд (А= I. 2...л) вы-
п
• В учебнике случайные величины, кик прилило, обозначаются прописными
буквами. л их значения строчными. Выборочные среднюю и долю везде обо-
значаем для простоты строчными буквами, соответственно х и н*. При этом
следует понимать. что до проведения наблюдений. когда lapanec неизвестно. ка-
кими они будут, х и »' рассматриваем как случай н ы с величины; после
проведении иап,подгний, когда получены их конкретные значения. — как н е-
сдуча Иные величины.
297
ражаст число появлений признака в Л-м элементе выборки (т.е. при
наличии признака А* = I. при его отсутствии А* = 0) и имеет один и
тог же закон распределения:
(1 1
р, V А/ м N
(9.Ю)
Действительно, вероятность того, что 1-й отобранный в выборку
элемент обладает признаком /I. согласно классическому определе-
нию вероятности равна /ХА) = I) = —, так как из общего числа Л'
N
элементов генеральной совокупности Л/ элементов обладаю! при-
знаком А. Аналогично вероятность того, что 1-й элемент не облада-
.V - М
ет признаком А. равна р(А'| = 0) =----. Так как выборка повтор-
Л’
ная. и каждый отобранный и обследованный элемент вновь воз-
вращается в исходную совокупность, восстанавливая всякий раз ее
первоначальные состав и объем, то вероятности p{Xk = 0) и p(Xk = I)
остаются теми же для любого элемента выборки, и закон распреде-
ления Xk (к = I. 2..п) один и тот же — (9.10).
Случайные величины А'(, АЧ.....А'д...Х„ независимы, так как
независимы любые события А\ = 0. А\ = I (к = 1, 2, .... п) и их ком-
бинации. Например, независимы события А, = I и АГ2= I. так как
М
О = I) = ~. тс- вероятность гою, что 2-й ото-
бранный в выборку элемент обладает признаком А. нс меняется в
зависимости от того, обладал признаком А 1-й элемент или нет. и т.д.
Теорема. Выборочная доля и- = — повторной выборки есть несме-
п
М
щенная и состоятельная оценка генеральной доли р = —. причем ее
N
дисперсия
(9.11)
п
где q = I - р.
□ Докажем вначале н е с мещенность оценки w. Мате-
матическое ожидание и дисперсия частости события в п независи-
мых испытаниях, в каждом из которых оно может наступить с од-
ной и той же вероятностью р. равны соответственно
298
М( н ) = />. Г)( и ) = о* = —
п
где Q = (см- § 4.1).
Так как вероятность того, что .новой отобранный в выборку
элемент обладает признаком Л. есть генеральная доля р. то из пер-
вого равенства вытекает, что частость. или выборочная доля, в1 есть
несмещенная опенка генеральной доли р.
Л nt
Осталось доказать состоятельность оценки и = —
м
которая следует непосредственно из теоремы Бернулли (§ 6.4):
lim Р -- р <г. =1.
п
HJ1H
и*—-—♦ р.
6) Выборка бесповторная
В случае бссиовторной выборки случайные величины Х|.
Х2...Х„ будут зависимыми. Рассмотрим, например, события Х( = I
и Х>- 1 Теперь вероятность />, ДХ. = I) = . так как отобран-
ный элемент (н случае бесповторной выборки) в исходную совокуп-
ность не возвращается, го в ней остасгся всего N — I элементов, из
которых обладающих признаком А М- I. Эта вероятность
— . т.е. события А'| = I и X» = 1 —
Л'
зависимые. Аналогично будут зависимы любые события Хд=1.
Хд = 0 (к = 1.2.. л), а значит, зависимы случайные величины Хь
Х2...ХА.....Xd.
Однако и для бесповторной выборки выборочная доля является
«хорошей» оценкой. Об этом свидетельствует следующая теорема.
Теорема. Выборочная доля и- = — бесповторной выборки есть не-
п
I) не равна /’( A'
М
смещенная и состоятельная оценка генеральной доли р - — . причем
ее дисперсия
(9.12)
где q = I - р.
29»
□ Очевидно, что и для бссповторнон выборки = /?. т.е. и- —
несмещенная оценка для генеральной доли р - M/N. Это связано с
тем, что математическое ожидание суммы любых случайных вели-
чин равно сумме их математических ожиданий (в том числе суммы
зависимых случайных величин, каковой является выборочная доля
и* бес повтор ной выборки).
Найдем дисперсию выборочной доли для бсспоэторной выборки:
J_ Л/1' | _ Л / \ .V - п _ /х/ N - п
п ЛгЛ’ J.V -1 п N -1
где /> = .W/.V. q = 1~ A//.V. г.е. верна формула (9.12) (при выводе форму*
лы для ст'; использовали то. что случайная величина Х= т в случае бес-
по втор ной выборки имеет 1мпергеометрнчсское распределение (см. §4.4).
и ее дисперсия определяйся по (формуле (4.16)).
Для того чтобы лете было понять формулу (9.12). рассмотрим ее
частные случаи и убедимся в справедливости этой формулы.
, /XI ( X “ Л I /X! »
I. При п«.\г ст'*= —--------- = — = <т. т.с. если объем вы-
п Л’ - I J п
борки значительно меньше объема генеральной совокупности, го
выборка практически не отличается от повторной и. естественно,
что дисперсии выборочной доли ст и ст'; приближенно равны.
2. При п = N а? = 0, т.е. если предположить, что объем выборки
равен объему генеральной совокупности, го выборочная доля будет
равна генеральной доле и ее дисперсия будет равна нулю.
[> Пример 9.5. Найти несмещенную и состоятельную оценку до-
ли рабочих цеха с выработкой нс менее 124% по выборке, представ-
ленной в табл. 8.1.
Решение. Несмещенной и состоятельной оценкой генераль-
ной доли Р(Х >124) является выборочная доля
и(.Г£ 124) = (19+ 10 *2)/100 = 0.31. ►
Оценка генеральной средней. Пусть из генеральной совокупности
объема W отобрана случайная выборка Х\. Х>.Х^, .... Хп. где Хк -
случайная величина, выражающая значение признака у А-го элемен-
та выборки (к = I. 2, .... л). Следует найти «наилучшую* оценку для
генеральной средней.
300
Рассмотрим в качестве такой возможной оценки выборочную
среднюю1 х (вспомним, что в примере 9.4 именно г явилась
1-V.
оценкой метода наименьших квадрагов для .vn), т.е. х = —---.
ft
а) Выборка повторная
Закон распределен ня для каждой случайной величины Хк
(к = 1.2...л) имеет вид:
х, *1 Xj ...
А Al Л\ •V •V N. /V
(9.13)
Действительно, вероятность того, что 1-й отобранный в выборку
элемент имеет значение признака Х|. согласно
делению вероятности равна
классическому опре-
так как из общего
числа Л' элементов генеральной совокупности N\ элементов имеют
значение признака Х|. Так как выборка повторная и каждый ото-
бранный и обследованный элемент возвращается в исходную сово-
купность. восстанавливая всякий раз ее первоначальные состав и
объем, то вероятность р(А\ = Х|) = — для любого элемента выбор-
кн, т.е. для к = 1.2.....л. Аналогично можно определить
= xt)
Л;
77
для к =
2...л; 7 = 1.2....л> и убедиться в том.
что закон распределения каждой случайной величины Хк один и тот
же - (9.13).
Случайные величины Х->.......Хк....Хп независимы, так как
независимы любые события Хк = х, (к = I. 2. .... п; i = 1.2.т) и
их комбинации. Например, независимы события А*2 = х) и А'| = Л|.
иб° /\ „ ( V. = х,) = р(X, = х,) = Al.
Л
т.е. вероятность того, что зна-
чение признака у 2-го отобранного в выборку элемента равно Х|. не
меняется в зависимости от того, какое значение признака у 1-го
элемента, и т.д.
Найдем числовые характеристики случайной величины Хк:
1 См. шмечание на с 297.
301
. 2>л
W(^) = £v,P,=^_—=x„. (9.14)
£(*.-* Р<
/W = L(»-.-? )‘ P.= ~-----7-----= °:. (9-15)
A
т.е. математическое ожидание и дисперсия каждой случайной величи-
ны А\ — это соответственно генеральная средняя и генеральная дис-
персия.
Теорема. Выборочная средняя х повторной выборки есть несме-
щенная и состоятельная оценка генеральной средней .7, причем
<Г= — • (9.16)
’ п
□ Докажем вначале н ссмсшенность оценки. Найдем
математическое ожидание выборочной средней г . учитывая формулу
<9.14>:
М(г)=Л/
— ° ,гхп -
-----------= —---------- =-------Ч- = г
п п п "
п
т.е. v — несмещенная оценка для г.
Найдем дисперсию выборочной средней х . учитывая формулу
<9.15) и то. что А’|. Х2.Ад.Х„ — независимые случайные вели-
чины:
O; = D(X) = D Р- = =
----- « ГТ «ГТ « «
п 7
Осталось доказать состоятельность опенки х . кото-
рая следует непосредственно из теоремы Чебышева (6.14):
li.nP(|x-?,|s >:) = !.
ИЛИ
б) Выборка бесповторная
В этом случае случайные величины Х|, А'3.... Х„ будут зависи-
мыми. Рассмотрим, например, события X, = Х| и X, = х,.
N -1
Теперь вероятность ps t ( X. = х,) = , так как отобранный
элемент (в случае бесповторной выборки) в исходную совокупность
302
нс возвращается, го н ней остается всего А'- I элементов, из которых
со значением признака - - I. Эта вероятность />х . (А\ = .х,) не
•V
равна р(Х, = V,) = —. т.с. события А'| = Х| и АЬ = Х| — зависимые.
Аналогично будут зависимыми любые события А* = х, (к = 1. 2. ... п\
/=1.2.....т). а значит, зависимы случайные величины Х|( Л’>......
Хь .... Х„.
Однако и для бесповторной выборки выборочная средняя явля-
ется «хорошей» оценкой. Об этом свидетельствует теорема.
Теорема. Выборочная средняя х бесповторной выборки есть не-
смещенная и состоятельная оценка генеральной средней х„, причем
Теорему принимаем без доказательства. Частные случаи форму-
лы (9.17) аналогичны формуле (9.12) (см. с. 300). т.с. при
п «к .V ст'2 = ст’. при п - N <т': = 0.
t> Пример 9.6. Найти несмещенную и состоятельную оценку
средней выработки рабочих цеха по данным выборки, представлен-
ной в табл. 8.1.
Р е ш е н и е. Несмещенная и состоятельная опенка генераль-
ной средней хи есть выборочная средняя т. найденная в примере
8.3. т.с. х =119.2 (%). ►
Оценка генеральной дисперсии. На первый взгляд, наиболее под-
ходящей оценкой для генеральной дисперсии ст2 является выбо-
рочная дисперсия s2 Следующая теорема свидетельствует о том.
что не является «наилучшей» оценкой.
Теорема. Выборочная дисперсия s' повторной и бесповторной выбо-
рок есть смещенная и состоятельная оценка генеральной дисперсии а
□ Принимая без доказательства состоятельность опенки 5-’. до-
кажем. что она — смещенная оценка В соответствии с формулой
(8.10) х* = х: - v:. На основании свойства 3 средней арифметиче-
ской (§ 8.2) и дисперсии (§ 8.3), если все значения признака умень-
шить на одно и то же число с. то средняя уменьшится на это число,
т.е. х — с = х - с. а дисперсия не изменится:
=< . -(л-г)'=(х-<) -(х-с)’.
Полагая с = хя. получим
л' =(х-л„)* -(х-х,,)’.
303
а) Выборка повторная
Для повторной выборки выборочные значения рассматриваем
как независимые случайные величины Л^. AS...Xk.....Хп. каждая и,
которых имеет один и тот же закон распределения (9.13) с число-
выми характеристиками (9.14) и (9.15), т.е. M(Xk) = х„. D(Xk) = rr.
к:= I, 2..п.
Найдем математическое oxiuiannc оценки s2:
Л/(л:) = Л/
-Л/(?-.?,>)'.
/1
Первый член в правой части
Л/
-
Z(-V
£.w(.r,-x;,)-' £d(a;)
лст*
----= ст
п п
л
Второй член с учетом того, что .? есть несмещенная оценка г„,
т.е. М(х) = х0. и формулы (9.16),
п
п
Л/(.Г-ЛО)- = О(л) = в-: =-
л
Поэтому
ст‘ л -1 .
— =----------ст*.
п п
б) Выборка бесловторная
Как уже рассмотрено выше, для бесповторной выборки А’ь
AS....¥„ — зависимые случайные величины. Можно показать, что
п л-1 Лг , л-I :
.WI.V ) =--------СТ ft----СТ
' 1 п jV-I л
(так как объем генеральной совокупности N, как правило, большой
и Л’ ft .V - I).
Итак, и для повторной выборки, и для бесповторной
Л/(л') = -—-ст’, т.е. s* — смешенная1 опенка о2.
' л
1 Тик хак смешение оценки = Л/(№)- ст’ _ " 'n'-a’s-0 прн
п п
п - > у стремится к пулю. т.е. lim I -0. ю .г п/лл асаиптпгпнчсски несме-
щенния оценка л:
304
Так как ——-<1 и A/(s2)<ct:. то выборочная дисперсия (в
п
среднем, полученная по разным выборкам) занижает генеральную
дисперсию. Поэтому, заменяя о2 на з2, мы допускаем систематиче-
скую погрешность в меньшую сторону. Чтобы ес ликвидировать.
достаточно ввести поправку, умножив з на ------. Тогда с учетом
п -1
(9.4) получим «исправленную* выборочную дисперсию
< = --:---------• (9.18)
п - I п - I
Очевидно, что
-.. .. ,. ( п «п ... ,. п и - I -
Л/ () = А/ -----л- =----- Л/ (Л- ) =-----<Г = ст".
\ л -1 ) п -1 и -1 II
т.е. з: является несмещенной и состоятельной оценкой генеральной
дисперсии ст’.
О Пример 9.7. Найти несмещенную и состоятельную оценку
дисперсии случайной величины X — выработки рабочих цеха по
данным выборки, представленной в табл. 8.1.
Реше н и е. Несмещенной и состоятельной оценкой дисперсии
случайной величины Л* (генеральной дисперсии) ст* является ♦исправ-
ленная» выборочная дисперсия г. В примере 8.6 вычислена выбороч-
ная дисперсия ? = 87,48. На основании формулы (9.18) при п = 100
100
г' = — 87.48 = 88.36. ►
99
Разница между Г и г заметна при небольшом числе наблюде-
ний п. При п > 30 - 40 г а г. т.е. в качестве оценки для ст’ впол-
не можно использовать выборочную дисперсию .Г.
9.5. Определение эффективных опенок с помощью
неравенства Рао— Крамера—Фреше
Выше рассмотрены оценки параметров (характеристик) гене-
ральной совокупности с точки зрения их состоятельности и несме-
щенности. Однако до сих пор нс были затронуты вопросы эф-
фективности этих опенок.
Пусть ф(.г.0)— плотность вероятности признака X (случайной
величины X — генеральной совокупности), если X непрерывна, и
функция вероятностей <р(л;.О) = Р(Л‘ = л;,0), если Д'дискретна.
305
Для широкого класса генеральных совокупностей (при выпол-
нении так называемых условий регулярности функции ф( г,0): диф-
ференцируемости по 0. независимости области определения от 0 и
т.д.. являющихся достаточно общими) имеет место неравенство
Рао—Крамера—Фреше (неравенство информации)'.
(9.19)
' л/(0)‘
где дисперсия опенки 0„ параметра 0;
/(0) — количество информации Фишера о параметре 0. содержа-
щееся в единичном наблюдении и определяемое в дискретном слу-
чае формулой:
/(0)- Л/| (In ф(А*.0))(
Фо (^.0)
ф(.г,.0). (9.20)
Ф(л;.О)
а в непрерывном случае — формулой:
<p(.v, 0) </(). (9.21)
<р(.г. 0)
/ (0) = Л/(( In ф( Л". 0))', J =J
Неравенство информации позволяет найти гот минимум
min />(ёя). который должна иметь дисперсия оценки а- . чтобы
быть эффективной оценкой 6’, т.е. о*, =min
t> Пример 9.8. Найти эффективную оценку генеральной доли /»
повторной выборки.
Ре ш е и и с. Найдем количество информации Фишера lip) по
формуле (9.20). Напомним (см. § 9.4). что в данном случае наблю-
даемая величина X принимает два значения — 0 и I с вероятностя-
ми соответственно: ф (0; р) = д = I - р и ф (I: р) = р. Имеем
т.е.
/(/») =
ф(0;/») +
Фг(°:р)
Ф(0:р)
min
Ф', (Ир)
ф(1:/')
1 £ =_______I
I-/; р р(1-р)’
।= /4|~/>)
п
Ф(1:/>) =
306
Как показано выше, именно такую дисперсию (см. (9.11)) имеет
’ PQ М'-/7) —
выборочная доля и* повторной выборки: ст; = — =-------. Следо-
п и
вателыю, выборочная дат в’ повторной выборки есть эффективная
оценка генеральной доли р. ►
О Пример 9.9. Найти эффективную оценку генеральной средней
хи (математического ожидания а} повторной выборки для нормаль-
но распределенной генеральной совокупности.
Решение. В случае нормального закона распределения
плотность вероятности
Ф, (л. и) =
Тогда
Теперь количество информации Фишера
Минимально возможная оценка дисперсии оценки
min /Я 0 ) = —-— = — .
' пЦа) п
Выше (см. § 9.4) мы установили, что именно такую дисперсию
(см. (9.16)) имеет выборочная средняя х повторной выборки:
ст; = —. Итак, выборочная средняя х повторной выборки для нор-
п
малый) распределенной генеральной совокупности является )ффектив-
ной оценкой генеральной средней а;,. ►
Аналогично примеру 9.9 можно показать, что эффективная
оценка О; генеральной дисперсии ст повторной выборки для нор-
мально распределенной генеральной совокупности должна иметь
минимальную дисперсию min /)(бя) = .
В то же время дисперсия исправленной выборочной дисперсии
л*. являющейся несмещенной оценкой генеральной дисперсии ст:.
307
2п4
как можно показать, есть а‘. =--, т.е. исправленная выборочная
п -1
дисперсия с повторной выборки не является эффективной оценкой
генеральной дисперсии а:.
Выборочные дисперсии — и «исправленная» s' — явтются асимп-
тотически эффективными оценками генеральной дисперсии <г. так
как при л —> л их эффективности, вычисленные по формуле (9.8).
стремятся к единице.
Эффективной же оценкой генеральной дисперсии о: является
статистика
•<=-£(х,-х.)’л,. <9.22)
п . .
но для ее нахождения надо знать генеральную среднюю которая в
большинстве случаев применения выборочною метода неизвестна.
В заключение отметим, что не для всякого закона распределения
может быть использовано неравенство Рао—Крамера—Фреше для
нахождения эффективных оценок параметров, поскольку не всегда
оказываются выполнены условия регулярности функции <p(.v,0). Так.
например, с помощью неравенства информации нельзя получить эф-
фективные оценки для параметров а и b равномерного закона рас-
пределения. так как они непосредственно задают границы области
определения функции <p(.v,G).
9.6. Понятие интервального оценивания.
Доверительная вс|юятность и п|М*д ель пня
ошибка выборки
Выше рассмотрена оценка параметров 0 генеральной совокуп-
ности о д н и м ч и с л о м. т.е. т„ — числом х , р — числом И'.
<г — числом 5‘ или S2. Такие опенки параметров называются то-
чечными.
Однако точечная оценка 0„ является лишь приближенным зна-
чением неизвестного параметра 0 даже в том случае, если она не-
смещенная (в среднем совпадает с 0). состоятельная (стрем1ггся к G
с ростом л) и эффективная (обладает наименьшей степенью случай-
ных отклонений от 0) и для выборки малого объема может сущест-
венно отличаться от 0.
ЗОЯ
Чтобы получить представление о точности и надежности оценки
бп параметра 0. используют интервальную оценку параметра.
Определение. Интервальной оценкой параметра 0 называ-
ется числовой интервал (О<л|).0,/>). который с заданной вероятностью у
накрывает неизвестное значение параметра 0 (рис. 9.!).
0 _________
6J) * б<? *
Риг. 9.1
Обращаем внимание на то, что границы интервала ) и
его величина находятся по выборочным данным и потому являются
случайными величинами в отличие от оцениваемого
параметра (» — величины неслучайной, поэтому правильнее говорить о
том. что интервал «накрывает», а не «содержит» зна-
чение G.
Такой интервал (G'J'.G?’ ) называется доверительным, а вероят-
ность у — доверительной вероятностью, уровнем доверия или на-
дежностью оценки.
Величина доверительного интервала существенно зависит от объ-
ема выборки п (уменьшается с ростом п) и от значения доверитель-
ной вероятности у (увеличивается с приближением у к единице).
Выборочные распределения отдельных оценок 9, (например,
выборочных средней х или доли в) симметричны относительно
параметра 6 (генеральных средней .?0 или доли р), поэтому целесо-
образно рассматривать п принципе доверительный интервал
симметричным относительно параметра 0 . т.е. (0 - А. 0 + А).
В этом случае наибольшее отклонение А несмещенной опенки 0,
от оцениваемого параметра 0, в частности, выборочной средней (или до-
ли) от генеральной средней (или доли), которое возможно с заданной до-
верительной вероятностью у. называется предельной ошибкой выборки1.
1 Значение Д уменьшается (доверительный интервал для параметра U сужается), если
0. — не просто несмещенная. а и эффективная оценка параметра 0 (как. например,
х для г„ (в случае нормальной генеральной совокупности) или и ,гля р)
309
Ошибка Л является ошибкой репрезентативности (представи-
тельства) выборки. Она возникает только вследствие того, что исследу-
ется не вся совокупность, а лишь часть ее (выборка), отобранная случай-
но. Эту ошибку часто называют случайной ошибкой репрезентативно-
сти. Ес нс следует путать с систематической ошибкой репрезентатив-
ности. появляющейся в результате нарушения принципа случайности
при отборе элементов в выборку.
Построение доверительного интервала для генеральной средней и
генеральной доли по большим выборкам. Для построения доверитель-
ных интервалов для параметров генеральных совокупностей могут
быть реализованы два подхода, основанные на знании точного (при
данном объеме выборки п) или асимптотического (при // -»т.) рас*
пределения выборочных характеристик (или некоторых функций от
них). Первый подход реализован далее при построении интерваль*
ных оценок параметров для малых выборок (см. § 9.7). В данном
параграфе рассматривается второй подход, применимый для боль-
ших выборок (порядка сотен наблюдений).
Теорема. Вероятность тога, что отклонение выборочной средней
(или доли) от генеральной средней (или доли) не превзойдет число
Л >0 (по абсолютной величине), равна'.
Р(|х - х„| $ д) = Ф(/) = у. (9.23) Р(|и._ ,,| < д) = ф(,) =
Д
где / = — .
ст
(9.24)
А
где /= —
°)
Ф(/) — функция (интеграл вероятностей) Лапласа.
□ Выше (§ 9.4) показано, что выборочная средняя v и выбо-
рочная доля и* повторной выборки представляют сумму п незави-
симых случайных величин —--------= У
— , где Xk (k = I. 2.......п)
п
имеет один и тот же закон распределения — соответственно <9.13) и
(9.10) с конечными математическим ожиданием и дисперсией. Сле-
довательно. на основании теоремы Ляпунова (см. § 6.5) при п —> ».
распределения х и н> неограниченно приближаются к нормальным
(практически при п > 30—40 распределения х и w можно считать
приближенно нормальными).
Для бесповторной выборки v и и* представляют сумму зависи-
мых случайных величин (см. § 9.4). к которым, вообще говоря, гео-
рема Ляпунова неприменима. Однако можно показать, что и в этом
случае при достаточно больших значениях л н /V - п распределения
х и и- приближенно нормальны.
310
Формулы (9.23) и (9.24) следуют непосредственно из свойства 2
нормального закона (см. § 4.7. формулы (4.34), (4.35)).
Формулы (9.23) и (9.24) получили название формул доверитель-
ной вероятности для средней и доли.
Определение. Среднее квадратическое отклонение выбороч-
ной средней о, и выборочной дат <т4 собственно-случайной выборки
называется средней квадратической (стандартной) ошибкой выборки.
(Для бесповторной выборки обозначаем соответственно ст' и о'.).
Из рассмотренной теоремы вытекают следующие следствия.
Следствие I. При заданной доверительной вероятности у предель-
ная ошибка выборки равна l-кратной величине средней квадратической
ошибки, где Ф( /) = у. т.е.1
Л = го;, (9.25)
Л='о.. (9.26)
Следствие 2. Интервальные оценки (доверительные интервалы) для
генеральной средней и генеральной доли могут быть найдены по формулам:
х - Д < .v0 < Г + А, (9.27)
+ (9.28)
Формулы средних кпшцхгппеских ошибок выборки ст. . ст'-. сти. в,
могут быть легко получены из формул (9.16). (9.17). (9.11), (9.12) соответ-
ствующих дисперсий ст2. ст’,2 . ст;. ст’; . Поместим их в таблицу (табл. 9.2).
Таб.пщн 9.2
Оцени- ваемый параметр Формулы средних квадратических ошибок выборки
повторная выборка бесповторная выборка
Средняя Доля <9и) Грй H’ll-uJ = —-(9’3|> V/1 n Я я It II Л Z Ц «и (9.30) ’4) O.3D
Так как генеральные доля р и дисперсия’ ст2 неизвестны, то в фор-
мулах табл. 9.2 заменяем их состоятельными оценками по выборке —
1 Для бесповпчi[wm выборки в формулах (9.25) и (9.26) вместо ст, и с, берем
cooTiicicnieHiio а' и а'„
311
соответственно и» н s2. ибо при достаточно большом объеме выборки ,t
практически достоверно, что зг «/>. г = а'. При определении средней
квадратической ошибки выборки для дачи, если даже н- неизвестна. н
качестве pq можно взять его максимально возможное значение
(/*?)«» =[р0“/>)].= 0.50.5 = 0.25
(так как pq-p{l- р) = ~(р: -/>) = 0.25- (р- 0.5) . то pq макси-
мально при р = 0.5).
£> Пример 9.10. При обследовании выработки 1000 рабочих цеха
в отчетном голу по сравнению с предыдущим по схеме собственно-
случайной выборки было отобрано 100 рабочих. Получены следую-
щие данные (см. первые две графы табл. 8.1). Необходимо опреде-
лить: а) вероятность того, что средняя выработка рабочих цеха от-
личается от средней выборочной не более чем на 1% (по абсолют-
ной величине); б) границы, в которых с вероятностью 0.9545 за-
ключена средняя выработка рабочих цеха. Рассмотреть случаи по-
вторной и бесповторной выборки.
Решени е. а) Имеем .V = 1000, п = 100. Ранее в примере 8.8
были вычислены х = 119.2(%), s- = 87,48.
Найдем среднюю квадратическую ошибку выборки для средней:
для повторной выборки
По формуле (9.29)
о х /iZd?=o,935(%).
V 100
для бесповторной выборки
По формуле (9.30)
/87.48
av = .----
V ЮО
— | = 0.887(%|
1000 )
Теперь искомую ловерительную вероятность находим по формуле
(9.23):
/’(|x-x(1|sl)= /’(|.г-Г0|<;1) =
= Ф(б^5) = Ф(1-07> = 0,715- =Ф(^) = Ф"-,3) = 0-741-
(Значения Ф(/) находим по табл. II приложений.)
1 Заметим. что в формуле (9.29) «•’ представляет дисперсию кашчсственново призна-
ка X (генеральной соиокутшосги). а в формуле (9.31) величина м - /И I р) - дис-
персию альтернативного при знака А
312
Итак, вероятность того, что выборочная средняя отличается от
генеральной средней нс более чем на 1% (но абсолютной величине),
равна 0,715 — для повторной и 0,741 — для бесповторной выборки.
б) Найдем предельные ошибки повторной и бесповторной вы-
борок по формуле (9.25). в которой / = 2.00 (находим по табл. II
приложений при данной в условии доверительной вероятности у из
соотношения у = Ф(/) = 0,9545).
д = 2.00 0.935 = 1.870(%). | Д'= 2.00 0.887 = 1.774(%).
Теперь искомый доверительный интервал определяем по (9.27):
119,2“ 1Л70< х(| < 119,2 +1.870.
ИЛИ 117.33<х0<121,07(%).
119.2 -1,774 S.vrt <119.2 + 1.774.
ИЛИ 117.43 < v0 <120,97(%).
Таким образом, с надежностью 0,9545 средняя выработка рабочих
цеха заключена в границах от 117,33 до 121.07%, если выборка по-
вторная. и от 117.43 до 120.97%. если выборка бесповторная. ►
|> Пример 9.11. Из партии, содержащей 2000 деталей, для про-
верки по схеме собственно-случайной бесповторной выборки было
отобрано 200 деталей, среди которых оказалось 184 стандартных.
Найти: а) вероятность того, что доля нестандартных деталей во всей
партии отличается от полученной доли в выборке нс более чем на
0,02 (по абсолютной величине): б) границы, в которых с надежно-
стью 0.95 заключена доля нестандартных деталей во всей партии.
Решение. Имеем Д' - 2000. п = 200. т - 200 - 184 = 16 не-
стандартных деталей Выборочная доля нестандартных деталей
w =
т 16
7" 200
= 0.08.
а) По формуле (9.32) найдем среднюю квадратическую ошибку
бесповторной выборки для доли:
/0,08-0,92( . 200 1
200 к 2000 /
= 0.0182.
Теперь искомую доверительную вероятность находим по формуле
(9.24):
/’(|и-/;|<0.02) = ф| 1 =
41 ' V0.0182J
= Ф( 1.10) = 0.729 (по табл. II приложений).
313
т.е. вероятность того, что выборочная доля нестандартных деталей
будет отличаться от генеральной доли нс более чем на 0.02 (по аб-
солютной величине), равна 0,729.
б) Учитывая, что у = Ф(/) = 0.95 и (по таблице) / = 1.96, найдем
предельную ошибку выборки для доли по формуле (9.26)
Д = 1,96 0.0182 = 0,0357. Теперь искомый доверительный интервал
определяем по формуле (9.28): 0.08 - 0,0357 < р <0,08 + 0.0357 . или
0.044 р <. 0.116.
Итак, с надежностью 0.95 доля нестандартных деталей во всей
партии заключена от 0,044 ло 0.116. ►
Объем выборки. Для проведения выборочного наблюдения весь-
ма важно правильно установить объем выборки л. который в значи-
тельной степени определяет необходимые при этом временные, тру-
довые и стоимостные затраты. Дня определения п необходимо задать
надежность (доверительную вероятность) оценки у и точность (пре-
дельную ошибку выборки) Л.
Объем выборки находится из формулы, выражающей предель-
ную ошибку выборки через дисперсию признака. Например, для
повторной выборки при опенке генеральной средней е надежностью
у с учетом формул (9.25) и (9.29) эта формула имеет вил:
СТ' i \ г
Д = /.|— . откуда и = —— . гле ф(г) = у. Аналогично могут быть
V л А’
получены и другие формулы объема выборки, которые сведем в
таблицу (табл. 9.3).
'Гиб.шип D.3
Оцениваемый па- раметр Повторная выборка Бесповторная выборка
Генеральная сред- п = (9.33) п'- <9.34)
няя д- /‘с‘ +NN‘
Генеральная доля п = (9.35) <9.36)
А- /’ pq + л л
Если найден объем повторной выборки л. то объем соответствую-
щей бесповторной выборки п' можно определить по формуле:
. nN
п —-------.
/I + .V
(9.37)
Так как —-— < I . то при одних и тех же точности и надежно-
п + N
сти оценок объем бесповторной выборки а' всегда меньше объема по-
314
вторной выборки п. Этим и объясняется тот факт, что на практике в
основном используется бесповторная выборка.
Как видно из формул (9.33)—(9.36). для определения объема
выборки необходимо знать характеристики генеральной совокупно-
сти о' или р, которые неизвестны и для определения которых
предполагается провести выборочное наблюдение. В качестве этих
характеристик обычно используют выборочные данные л2 или и-
предшествующего исследования в аналогичных условиях, т.е. полага-
ют о: *= (ИЛИ .< ) ИЛИ р * Н’.
Если никаких сведений о значениях ст или р нет. то организуют
специальную пробную выборку небольшого объема, находят оцен-
ку 5: (более точную, чем 5* для малой выборки) или и- и. полагая <г = .г
или р = к*, находят объем «основной» выборки.
При оценке генеральной доли (если о ней ничего неизвестно)
вместо проведения пробной выборки можно в формулах (9.35),
(9.36) в качестве pq = р{\ - р) взять его максимально возможное
значение, равное 0,25, но при этом надо учитывать, что найденное
значение объема выборки будет больше (иногда существенно боль-
ше) минимально необходимого для заданных точности и надежно-
сти оценок.
t> Пример 9.12. По условию примера 9.10 определить объем вы-
борки, при котором с вероятностью 0.9973 отклонение средней вы-
работки рабочих в выборке от средней выработки всех рабочих цеха
не превзойдет 1% (по абсолютной величине).
Решение. В качестве неизвестного значения ст' для определе-
ния объема выборки берем его состоятельную оценку т2 = 87.48. най-
денную ранее в примере 9.10.
Учитывая, что у =Ф(() = 0,9973 и (по табл. II приложений)
г =3,00, найдем объем повторной выборки по формуле (9.33). т.е.
п = З2-87.48/1 = 787.
Объем бесповторной выборки по форхгуле (9.34):
1000-3- -87.48
3:-87.48 +1000-1
= 440.5 = 441.
Объем бесповторной выборки п' мог быть вычислен и по фор-
муле (9.37). так как уже известен объем повторной выборки п. т.е.
, _ 787 1000
787*1000
= 441.
Как видим, при одной и той же точности А = !(%) и надежно-
сти у = 0.9973 опенки объем бесповторной выборки существенно
Меньше, чем повторной. ►
315
1> Пример 9.13. По условию примера 9.11 определить число де-
талей. которые надо отобрать в выборку, чтобы с вероятностью 0.95
доля нестандартных детален в выборке отличалась от генеральной
доли не более чем на 0,04 (по абсолютной величине). Найти то же
число, если о доле нестандартных деталей, даже приблизительно,
ничего неизвестно.
Реше н и с. В качестве неизвестного значения генеральной
доли р возьмем ее состоятельную опенку в» = 0.08. найденную ранее
в примере 9.11.
Учитывая, что у = Ф(/) = 0.95 и (по таблице) t = 1.96. найдем
объем бесповторной выборки по формуле (9.36). т.е.
, 2000-I.962 0,08 0.92
И =----;----------------------г-162.
1.96- • 0.08 0.92+ 2000 0.04-
Объем бесповторной выборки п’ мог быть вычислен и по фор-
муле (9.37). если предварительно был найден объем повторной вы-
борки п по формуле (9.35):
1.96- 0.08 0.92 , 177-2000
п =----------------= 177 и п ------------а 162.
177 + 2000
0.04-
Если о доле р ничего, даже приблизительно, неизвестно, в фор-
муле (9.36) полагаем pq — (pq) = 0.25. Тогда
, 2000 • 1.963 -0.25
П =----;----------------г = 462 ,
1.96- -0.25+ 2000 -0.04-
т.е. полученное возможное значение объема выборки оказалось су-
щественно выше необходимого. ►
Замечание. Если генеральная совокупность бесконечна
(Д'sac) либо объем бесповторной выборки значительно меньше
объема генеральной совокупности (п« .V). расчеты средних квад-
ратических ошибок (для средней и доли) и необходимого объема
бесповторной выборки следует проводить по соответствующим
формулам для повторной выборки.
Построение доверительного интервала .тля генеральной доли по уме-
ренно большим выборкам. Объем выборки может был» не настолько
велик (например, десятки наблюдении), чтобы использовать прибли-
|w( I - и*)
женную формулу (9.31) а„ =.—--------------- вместо точной
V п
Грй л
а. =.— =.-----------. В то же время распределение выборочной
V п У п
доли и* можно по-прежнему считать приближенно нормальным. В
316
згом случае, учитывая формулы (9.24), (9.26). доверительный юггср-
вал для генеральной доли р следует искать из условия
р('~р)
п
(9.38)
Возводя обе части неравенства (9.38) в квадрат, преобразуем его
к равносильному:
(9.39)
п
Областью решения неравенства (9.39) является внутренняя часть
эллипса, проходящего через точки (0:0) и (1:1) и имеющего в этих
точках касательные, параллельные оси абсцисс.
Так как величина w заключена меж-
ду 0 и I. то область D нужно еще огра-
ничить слева и справа прямыми и- = 0 и
w= I (наличие «лишних» областей, вы-
ходящих за полосу 0 < и- < I. объясняет-
ся тем. что при значениях р. близких к
Онли I, допущении о нормальном за-
коне распределения w становится не-
правомерным).
По найденному по выборке значе-
нию w границы доверительного интер- р1|с д о
вала (р}, /ь) для р определяются как точ-
ки пересечения соответствующей вертикальной прямой с эллипсом
(рис. 9.2). Чем больше объем выборки л. тем «доверительный эллипс»
более вытянут. тем уже доверительный интервал.
Границы р\ и Р2 доверительного интервала для р могут был.
найдены из соотношения (9.39) по формуле:
В случае больших выборок, при п >г. величинами t2/n (по
сравнению с I). f2/2n (по сравнению с и-). (г/2л)2 (по сравнению с
Й1 - и')//Л можно пренебречь, и получим:
I и-( I - w)
, а и'+ /. -------- и-Т /о. = + А .
V W
т.е. доказанные ранее формулы (9.28) и (9.26).
О Пример 9.14. По данным примера 9.11 найти границы, в ко-
торых с надежностью 0.95 заключена доля р нестандартных изделий
во всей партии, полшая п = 50. w = 0.08, N = •».
317
Решсни е. По формуле (9.40). учитывая, что г = 1.96. найдем
доверительные Гранины для генеральной доли р:
P,z 1 + 1.96750
1.96’ Л£ /0.08-0.92 ( 1.96 V
-----+ 1.96 J---------+ -----
2-50 V 50 К 2-50J
= 0.110? 0.078 или д =0,032. p, =0.188.
т.е. с надежностью 0.95 доля нестандартных изделий во всей партии
заключена от 0.032 до 0.188. ►
9.7. Оценка характеристик 1'еиеральной
совокупности по малом выборке
На практике часто приходится иметь дело с выборками неболь-
шого объема л < 10 — 20. В этом случае приведенный выше при-
ближенный метол построения интервальной оценки для генераль-
ной средней и генеральной доли неприменим в силу двух обстоя-
тельств:
I) необоснованным становится вывод о нормальном законе
распределения выборочных средней ? и доли и*. так как он основан
на центральной предельной теореме при больших л;
2) необоснованной становится замена неизвестных генеральной
дисперсии ст2 и доли р их точечными оценками соответственно s2
(или 52) и н’. так как в силу закона больших чисел (состоятельности
опенок) эта замена возможна лишь при больших л.
Построение доверительного интервала для генералыюй средней по
малой выборке. Задача построения доверительного интервала для гене-
ральной средней может быть решена, если в генеральной совокупно-
сти рассматриваемый признак имеет нормальное распределение.
Теорема. Если признак {случайная ветчина) X имеет нормальный
закон распределения с параметрами М(Х) = Xq, о; =<г . т.е V(.v„.o:).
то выборочная средняя v при любом п {а не только при н -> л ) име-
. э ».(- о:
ет нормальный закон распределения Л v0.—
I ° л
□ Если в случае больших выборок (при //-+ /?) из любых гене-
t*.
ральных совокупностей нормальность распределения v = —--- обу-
п
словдивалась суммированием большого числа одинаково распределен-
ных случайных величин /п (теорема Ляпунова), то в случае малых
выборок. полученных из нормальной генеральной совокупности, нор-
318
мальность распределения .г вытекает из того. »гго распределение сум-
мы (композиция) любого числа нормально распределенных
случайных величин имеет нормальное распределение (см. § 5.8). Фор-
мулы числовых характеристик для х I д/(7) = D(x) = — I полу-
\ ° п )
чены ранее (см. § 9.4. теорему на с. 302).
Таким образом, если бы была известна генеральная дисперсия о*,
то доверительный интервал можно было бы построить аналогично из-
ложенному выше и при малых л. Заметим, что в этом случае нормиро-
. . . . х-А/(х) х-хп г
ванное отклонение выборочной средней t =-----=-------- Vn имеет
о, о
стандартное нормальное распределение M0J). т.е. нормальное рас-
пределение с математическим ожиданием, равным нулю, и диспер-
сией. равной единице.
Действительно, используя свойства математического ожидания и
дисперсии, получим, что
«(') = )- Af(x„)] = v„ - Т„) = о.
о; = £>(,) = = [O(x)+D(x„)] = A[ — -0 j = I.
Однако на практике почти всегда генеральная дисперсия сг
(как и оцениваемая генеральная средняя .?„) неизвестна. Если за-
менить а: ее «наилучшей* оценкой по выборке, а именно «исправ-
ленной» выборочной дисперсией .<. то большой интерес представ-
ляет распределение выборочной характеристики (статистики)
г = - ,Л<| Jn или, что то же с учетом формулы (9.18). распредсле-
5
х “ /--7
ние статистки / =----->Jn - I .
л
Представим статистику t в виде:
I
(г-хп)/ ?
_________>Jn_
I i л.г’
V z? — 1 (Г
(9.41)
319
Числитель выражения (9-41>. как показано выше, имеет стандартное
нормальное распределение Л<():1). Можно показать (см., например. (3|>.
«по случайная величина ns2/ст имеет ^-распределение с к = п ~ I сте-
пенями свободы. Следовательно (см. § 4.9. определение (4.39)), ста-
тистика / имеет /-распределение Стьюдента с к = п - 1 степенями
свободы. Указанное распределение не зависит от неизвестных пара-
метров распределения случайной величины X. а зависит лишь or
числа к. называемого числом степеней свободы.
Выше (см. § 4.9) отмечено, что /-распределение Стьюдснта на-
поминает нормальное распределение (см. рис. 4.17) и действительно
при к -> «с как угодно близко приближается к нему.
Число степеней свободы к определяется как общее число л наблю-
дений (вариантов) случайной величины X минус число уравнений I, свя-
зывающих эти наблюдения, т.е. к = п - /.
Так. например, дтя распределения статистики /=—-------Jn-I
число степеней свободы к = п - I. ибо одна степень свободы «теря-
ется» при определении выборочной средней г (и наблюдений свя-
заны одним уравнением ^Г.у njn = х).
/•I
Зная /-распределение Стьюдента. можно найти такое критиче-
ское значение /, . что вероятность того, что статистика
t--——>Jn-\ нс превзойдет величину / (по абсолютной велн-
.s
чине), равна у:
Функция 0(/.А) = 2| ф(х.Л) где ф(х.А) — плотность ве-
роятности /-распределения Стьюдснта при числе степеней свободы
к, табулирована. Эта функция аналогична функции Лапласа Ф(/).
но в отличие от нее является функцией двух переменных — / и
к = п - I. При к ->оо функция 6(/Д) неограниченно приближает-
ся к функции Лапласа Ф(/).
Формула доверительной вероятности (9.42) для малой выборки
может быть представлена в равносильном виде:
Г(| х - х0 | S Дм,) = 0(/,я-1) = у, (9.43)
320
где Л..=-^= <»•«)
>Jtt- I
— предельная ошибка малой выборки. Доверительный интервал для
генеральной средней, как и ранее, находится по формуле:
х-Лм, <.^<х+Лм,. (9.45)
О Пример 9.15. Для контроля срока службы электроламп из большой
партии было отобрано 17 электроламп. В результате испытаний оказалось,
что средний срок службы отобранных ламп равен 980 ч, а среднее квадра-
тическое отклонение их срока службы — 18 ч. Необходимо определить:
а) вероятность того, что средний срок службы ламп во всей парши отлича-
ется от среднего срока службы отобранных для испытаний ламп не более
чем на 8 ч (по абсолютной величине); б) границы, в которых с вероятно-
стью 0,95 заключен средний срок службы ламп во всей партии.
Решение. Имеем по условию п = 20, х = 980 (ч) .5=18 ч.
а) Зная предельную ошибку малой выборки Лм,= 8 (ч), найдем
/у из соотношения (9.44):
/ < , = — =— ч/17-l =1.78.
.v 18
Теперь искомая доверительная вероятность по формуле (9.43):
Р(|х-х„|< 8) = 0(1.78; 16) = 0.906. (0(1.78:16) находим по таблице
значений’ ) при числе степеней свободы к = 16).
Итак, вероятность того, что расхождение средних сроков служ-
бы электроламп в выборке и во всей партии нс превысит 8 ч (по
абсолютной величине), равна 0,906.
б) Учитывая, что у = 0(/Л) = О,95 и (по таблице) f0.95;i6~ 2.12. по
формуле (9.44) найдем предельную ошибку малой выборки
2 1218
Дм. = __— = 9.5(ч). Теперь по формуле (945) искомый довернтсль-
V16
ный интервал 980 - 9.5 <.хи <980 + 9.5, или 970,5 S.?o <989.5 (ч), т.е. с
надежностью 0,95 средний срок службы электроламп в партии заключен
от 970.5 до 989.5 ч. ►
'Так как неносредстпснно таблица значений 0(/,Л) в учебнике не приводится,
то вероятность •{ можно найти приближенно, используя табл. IV приложений, в
которой указаны шачення /. ,. полученные из условия 0(/,,) = у. Так. для
к = 16 но >той таблице у = 0.*> при г = 1,75, Болес точно вероятность у. соот-
ветствующую I = 1.78. можно найтн, прибегнув к интерполяции.
1 * Т«цн<, крмтшхге* и »ч:сил!1г»ес>л4 crniunua
321
Построение доверительного интервала для генеральной доли по ма-
лой выборке. Если доля признака в генеральной совокупности равна
р, то вероятность того, *гго в повторной выборке объема п т элемен-
тов обладают этим признаком, определяется по формуле Бернулли:
Р„ „ = Cf, где q - I - р, т.е. распределение повторной выборки
описывается биномиальным распределением. Так как при р*0,5
биномиальное распределение несимметрично, то в качестве доверн
тельного интервала для р берут такой интервал (р(, pj), что вероят-
ность попадания левее р\ и правее /ъ одна и та же и равна (1 - у)/2:
Ё ОГО - А)- = Ц1: ЁС А- (I - А)' - •
~-й ~ и-0 *-
где т = nw — фактическое число элементов выборки, обладающих
признаком.
Решение таких уравнений можно упростить, если использовать
специальные графики, позволяющие прн данном объеме выборки п и
заданной доверительной вероятности у определить границы довери-
тельного интервала для генеральной доли р. В качестве примера на
рис. 9.3 приведены такие графики для у = 0.9.
1»нс. 9.3
322
> Пример 9.16. Опрос случайно отобранных 15 жителей города
показал, что 6 из них будут поддерживать действующего мэра на
предстоящих выборах. Найти границы, в которых с надежностью
0,9 заключена доля граждан города, которые будут поддерживать на
предстоящих выборах действующего мэра.
Р с ш е н и е. Выборочная доля жителей, поддерживающих мэ-
ра. w = т/л = 6/15 = 0.4. По рис 9.3 для у = 0.9 находим при w = 0,4
и для п = 15 по нижнему графику р\ ~ 0,23. а по верхнему — />2 - 0,60.
т.е. доля жителей города, поддерживающих мэра, с надежностью
0.9 заключена в границах от 0.23 до 0,60. Очевидно, что более точ-
ный ответ на вопрос задачи может быть получен при увеличении
объема выборки л. ►
Построение доверительного интервала для генеральной дисперсии.
Пусть распределение признака (случайной величины) X в генеральной
совокупности является нормальным A'( t„;<r). Предположим, что матема-
тическое ожидание A/( X) = .г„ (генеральная средняя) известно. Тогда выбо-
рочная дисперсия повторной выборки Ху..Л;
---------
п
(ее не следует путать с выборочной дисперсией
п
и «исправленной* выборочной дисперсией л‘=------г: если .< ха-
п -1
растеризует вариацию значений признака относительно генеральной
средней х0, то г и л* — относительно выборочной средней .г).
Рассмотрим статистику
Учитывая, что в соответствии с формулами (9.14) и (9.15)
М(Х,) = хи. D(A',) = cr. (/ =1. 2.....л), нетрудно показать, что
M(t) = 0 и <т; = D(t, )= I.
В § 4.9 отмечено, что распределение суммы квадратов п незави-
симых случайных величин , каждая из которых имеет стан-
1-1
дартное нормальное распределение Л1 (0:1). представляет распределе-
ние х: с к = п степенями свободы.
323
т й : ,w-
Таким образом, статистика х = ~г имеет распределение у с
G'
к = п степенями свободы.
Распределение х? не зависит от неизвестных параметров случай-
ной величины Л', а зависит лишь от числа степеней свободы к. Кри-
вые распределения для различного числа степеней свободы показа-
ны на рис. 4.16 (§ 4.9).
Плотность вероятности распределения имеет сложный вид, и
интегрирование ее является весьма трудоемким процессом. Состав-
лены таблицы для вычисления вероятности того, что случайная ве-
личина, имеющая распределение с к степенями свободы, превы-
сит некоторое критическое значение х!» • т.е- Р(х* > Х,м ) = « •
В практике выборочною наблюдения математическое ожидание
л;,, как правило, неизвестно, и приходится иметь дело нс с . а с
Гили л-:. Если X|, AS... Хп — повторная выборка из нормально
распределенной генеральной совокупности, то, как уже отмечено
выше, случайная величина ——
с’
имеет распределе-
ние х’ с к = п - 1 степенями свободы. Поэтому для заданной дове-
рительной вероятности у можно записать:
(9.46)
(графически это площадь пол кривой распределения между х? ”
X;. см. рис. 9.4).
324
Очевидно, ’гго значения х; и Х: определяются неоднозначно
при одном и том же значении заштрихованной плошали1, равной у.
Обычно Xi н X- выбирают таким образом, чтобы вероятности со-
бытий х‘ <Xi и X* >Х- были одинаковы, т.е.
р{х:
_ .. , j ns t
Преобразовав двойное неравенство Xi <—— <Х: в равенстве
о"
* *
(9.46) к равносильному виду -А- < сг < -Ч-, получим формулы дове-
х:> х;
ршпельяой вероятности:
для генеральной дисперсии
и для среднего квадратического отклонения
При использовании таблиц значений у’,л.
венства Р(х‘ > xL ) = а • необходимо
Р(х? < X?) = 1 - X* > X?) • поэтому условие
(9.47)
(9.43)
полученных из ра-
учесть. что
р(х: <х;) = Ц1
•»
равносильно условию Р(х2 > х?) - 1 “ = ~~ • Таким образом,
значения х? и Х: находим по табл. V приложений из равенств:
Р(х2>х,:)=Ц1. <’•“’)
т.е. при к = л — 1
/’(r>xj)=if.
• • *2
Xi ~ Xii.p 2;ч-| ’ X: ~ X(i-fi ?.п ।
(9.50)
1 Прн построении доверительных интервалов для х. и /> мы >ту исолнотначиость
обходили тем. то брали доверительный интервал.’симметричный относительно
несмещенной точечкой опенки Здесь это смысла не имеет, так как в отличие
от выборочных распределений х и *• распределение нс обладает симметрией.
325
t> Пример 9.17. На основании выборочных наблюдений произ-
водительности труда 20 работниц было установлено, что среднее
квадратическое отклонение суточной выработки составляет 15 м
ткани в час. Предполагая, что производительность труда работницы
имеет нормальное распределение, найти границы, в которых с на-
дежностью 0.9 заключены генеральные дисперсия и среднее квадра-
тическое отклонение суточной выработки работниц.
Решение. Имеем у = 0.9; (I -у)/2 = 0.05; (I + у)/2 = 0.95.
При числе степеней свободы к = п - I = 20 - I = 19 в соответ-
ствии с равенствами (9.49) и (9.50) определим х! и X- по табл. V
приложений: х[ = xf.«$w = 10.1 и X: = Хо.оз.н =30.1. Тогда доверитель-
ный интервал для ст’ по формуле (9.47) можно записать в виде:
-^-•15* < а* или 149.5 < а'< 445.6, и для ст по форму-
30,1 10.1
ле (9.48): 7^9.5 <ст< ч/445.6. или 12,2 <с< 21,1 (м/ч).
Итак, с надежностью 0.9 дисперсия суточной выработки ра-
ботниц заключена в границах от 149,5 до 445,6. а ее среднее квад-
ратическое отклонение — от 12.2 до 21,1 метров ткани в час. ►
Замечание. Таблица значений х; ж (прил V) составлена при
числе степеней свободы к от 1 до Зи. При к > 30 можно считать (см
§4.9), что случайная величина ч/зх' \!lk -1 имеет стандартное
нормальное распределение Л'(0;1). Поэтому для определения %; и
Х^ следует записать, что
r(|7V-'/3*~7|<')-<!>(') = Г (9.51)
откуда -I < - Jlk - \ <i и после преобразований
^>/2Л - 1 -/) < х? <^>/2к -1 -*•/)• Таким образом, при расчете довс-
* «0
ригельного интервала при к > 30 надо полагать х[ = ~(х/2А-- 1 - /) .
X: =|(V2Ar-l + /)\rae Ф(/) = У-
£> Пример 9.18. Решить задачу, приведенную в примере 9.17.
при п = 100 работницам.
Решение. При у = Ф(/) = 0.9 по таблице II приложении
t = 1.645, поэтому
326
х- « (72-99-1 -1.645)' =76.8, Х;=| (72-99-1 +1.645) =122.9.
Далее решение, аналогичное примеру 9.17, приводит к доверительным
интервалам для ст: 183,1<ст: <293.0 и для ст: 13,5 < ст< 17,] (м/ч).
Упражнения
9.19. Для исследования доходов населения города, составляю-
щего 20 тыс. человек, по схеме собственно-случайной бесповторной
выборки было отобрано 1000 жителей. Получено следующее распре-
деление жителей по месячному доходу (руб.):
X/ менее 500 500- 1000 1000- 1500 1500— 2000 2000-2500 свыше 2500
Л/ 58 96 239 328 147 132
Необходимо: 1. а) найти вероятность того, что средний месячный
доход жителя города отличается от среднего дохода его в выборке не
более чем на 45 руб. (по абсолютной величине); б) определить грани-
цы, в которых с надежностью 0,99 заключен средний месячный доход
жителей города. 2. Каким должен быть объем выборки, чтобы те же
границы гарантировать с надежностью 0,9973?
9.20. Решить пример 9.!9 при условии, что население города
неизвестно, а известно лишь, что оно очень большое по сравнению
с объемом выборки.
9.21. Поданным примера 9.19 необходимо: I. а) найти вероят-
ность того, ‘по доля малообеспеченных жителей города (с доходом
менее 500 руб.) отличается от доли таких же жителей в выборке не
более чем на 0,01 (по абсолютной величине); б) определить грани-
цы, в которых с надежностью 0.98 заключена доля малообеспечен-
ных жителей города. 2. Каким должен быть объем выборки, чтобы
те же границы для доли малообеспеченных жителей города гаранти-
ровать с надежностью 0.9973? 3. Как изменились бы результаты,
полученные в п. I. а) и 2, если бы о доле малообеспеченных жите-
лей вообще не было ничего известно?
9.22. Решить пример 9.2! при условии, что население города
неизвестно, а известно лишь, что оно очень большое по сравнению
с объемом выборки.
9.23. Из 5000 вкладчиков банка по схеме случайной беспов-
торной выборки было отобрано 300 вкладчиков. Средний размер
вклада в выборке составил 8000 руб., а среднее квадратическое от-
клонение 2500 руб. Какова вероятность того, что средний размер
вклада случайно выбранного вкладчика отличается от его среднего
327
размера в выборке не более чем на 100 руб. (по абсолютной вели-
чине)?
9.24. В результате выборочного наблюдения получены следую-
щие данные о часовой выработке (в ед./ч) 50 рабочих, отобранных
из 1000 рабочих цеха:
Часовая выработка 0.9 1,1 1.3 1.5 1.7 1.9
Число рабочих I 2 10 17 16 4
I) найти (с надежностью 0.95) максимальное отклонение сред-
ней часовой выработки рабочих в выборке от средней во всем цехе
(по абсолютной величине), если выборка: а) повторная; б) беспо-
вторная; 2) найти объем выборки, при котором с надежностью 0.99
можно гарантировать вдвое меньшее максимальное отклонение тех
же характеристик.
9.25. Из партии. содержащей 8000 телевизоров, отобрано 800.
Среди них оказалось 10% не удовлетворяющих стандарту. Найти гра-
ницы, в которых с вероятностью 0,95 заключена доля телевизоров,
удовлетворяющих стандарту. во всей партии для повторной и беспо-
вторной выборок.
9.26. По результатам социологического обследования при опро-
се 1500 респондентов рейтинг президента (т.е. процент опрошен-
ных. одобряющих его деятельность) составил 30%. Найти границы,
в которых с надежностью 0.95 заключен рейтинг президента (при
опросе всех жителей страны). Сколько респондентов надо опросить,
чтобы с надежностью 0.99 гарантировать предельную ошибку со-
циологического обследования не более 1%? Тот же вопрос, если
никаких данных о рейтинге президента нет.
9.27. Каким должен быть объем выборки, отобранной по схеме
случайной бесповторной выборки из партии, содержащей 8000 де-
талей, чтобы с вероятностью 0.994 .можно было утверждать, что до-
ли первосортных деталей в выборке и во всей партии отличаются нс
более чем на 0.05 (по абсолютной величине)? Задачу решить для
случаев: а) о доле первосортных деталей во всей партии ничего не
известно; б) их не более 80%.
9.28. Производятся независимые испытания с одинаковой, но неиз-
вестной вероятностью р появления события А в каждом испытании. Най-
ти доверительный интервал для оценки вероятности р с надежностью
у = 0,95. если в л = 60 испытаниях событие А появилось т = L5 раз.
9.29. Решить пример 9.28 при у =0,9 ; п = 10; т = 2.
9.30. Из большой партии по схеме случайной повторной выбор-
ки было проверено 150 изделий с целью определения процента влаж-
328
НОстн древесины, из которой изготовлены эпз изделия. Получены
следующие результаты:
Процент влажности 11-13 13-15 15-17 17-19 19-21
Число изделий 8 42 51 37 12
Считая, что процент влажности изделия - случайная величина,
распределенная по нормальному закону, найти: а) вероятность того,
что средний процент влажности заключен в границах от 12.5 до
17,5; б) границы, в которых с вероятностью 0.95 будет заключен
средний процент влажности изделий во всей партии.
9.31. По данным 9 измерений некоторой величины найдены
средняя результатов измерений ? = 30 и выборочная дисперсия
36. Найти границы, в которых с надежностью 0.99 заключено
истинное значение измеряемой величины.
9.32. Произведено 12 измерений одним прибором (без система-
тической ошибки) некоторой величины, имеющей нормальное рас-
пределение. причем выборочная дисперсия случайных ошибок из-
мерений оказалась равной 0.36. Найти границы, в которых с надеж-
ностью 0.95 заключено среднее квадратическое отклонение случай-
ных ошибок измерений, характеризующих точность прибора.
9.33. Решить пример 9.32 при п = 100 измерениях.
9.34. Распределение 200 элементов (устройств) по времени без-
отказной работы (в часах) представлено в таблице.
Время без- отказной работы 0-5 5-10 10-15 15-20 20-25 25-30
Число уст- ройств 133 45 15 4 2 1
Предполагая, что время безотказной работы элементов имеет
показательный закон распределения, найти: а) вероятность того, что
время безотказной работы будет заключено в пределах от 3 до 8 ч:
б) границы, в которых с надежностью 0.95 будет заключено среднее
время безотказной работы элементов.
Указание. В качестве оценки параметра л взять величину,
обратную выборочной средней.
Глава
10
Проверка статистических
гипотез
10.1. Принцип практической уверенности
Прежде чем перейти к рассмотрению понятия статистической
гипотезы, сформулируем гак называемый принцип практической уве-
ренности. лежащий в основе применения выводов и рекомендаций с
помощью теории вероятностей и математической статистики.
Если вероятность события А в данном испытании очень маю, то
при однократном выполнении испытания можно быть уверенным в том.
что событие А не произойдет. и в практической деятельности вести
себя так. как будто событие А вообще невозможно.
Этот принцип нс может быть доказан математически; он под-
тверждается всем практическим опытом человеческой деятельности,
и мы постоянно (хотя и бессознательно) им руководствуемся. На-
пример. отправляясь самолетом в другой город, мы не рассчитыва-
ем на возможность погибнуть в авиационной катастрофе, хотя не-
которая (весьма малая) вероятность такого события все же имеется.
Обратим внимание на то. что принцип практической уверенно-
сти о невозможности маловероятных событий сформулирован «при
однократном выполнении испытания». Если же произведе-
но много испытаний, в каждом из которых вероятность события А
даже очень мала, то существенно повышается вероятность того, что
событие А произойдет хотя бы один раз в массе испыта-
ний. Действительно, пусть вероятность АЛ) = а. где а « 1. Тогда
вероятность события В. состоящего в том, что событие А произой-
дет хотя бы один раз в п независимых испытаниях, по формуле
(1.29) равна (при а<< I):
Р(Д) = 1-(1-а)и*1-(1-ла) = па,
т.е. вероятность 1\В) увеличилась по сравнению с /\А) в п раз.
Таким образом, при многократном повторении испытаний мы
уже не можем считать маловероятное событие А практически не-
возможным.
Вопрос о том. насколько мала должна быть вероятность а события
А, ’гтобы его можно было считать практически невозможным, выходит
за рамки математической теории и решается в каждом отдельном слу-
чае с учетом важности последствий, вытекающих из наступления со-
бытия А. В одних случаях считается возможным пренебрегать собы-
тиями. имеющими вероятность меньше 0,05, а в других, когда речь
330
идет, например, о разрушении сооружений, гибели судна и т.п., нельзя
пренебрегать событиями, которые мсмуг появиться с вероятностью,
равной 0,001.
10.2. Статистическая гипотеза и общая схема
ее проверки
С теорией статистическою оценивания параметров тесно связана
проверка статистических гипотез. Она используется всякий раз. когда
необходим обоснованный вывод о преимуществах того или иного спо-
соба инвестиций, измерений, стрельбы, технологического процесса, об
эффективности нового метода обучения, управления, о пользе вносимо-
го удобрения, лекарства, об уровне доходности ценных бумаг, о значи-
мости математической модели и тл.
Определение. Статистической гипотезой называется лю-
бое предположение о виде или параметрах неизвестного закона распре-
деления.
Различают простую и сложную статистические гипотезы. Про-
стая гипотеза, в отличие от сложной, полностью определяет теоре-
тическую функцию распределения случайной величины. Напри-
мер, гипотезы «вероятность появления события в схеме Бернулли
равна 1/2». «закон распределения случайной величины нормаль-
ный с параметрами и = 0. <г = I* являются простыми, а гипотезы
«вероятность появления события в схеме Бернулли заключена ме-
жду 0.3 и 0,6», «закон распределения не является нормальным* —
сложными.
Проверяемую гипотезу обычно называют нулевой (или основной)
и обозначаю! //<». Наряду с нулевой гипотезой Но рассматривают
альтернативную, или конкурирующую, гипотезу Я|, являющуюся ло-
гическим отрицанием //». Нулевая и альтернативная гипотезы пред-
ставляют собой две возможности выбора, осуществляемого в задачах
проверки статистических гипотез.
Суть проверки статистической гипотезы заключается в том. что
используется специально составленная выборочная характеристика
(статистика) ОДх,.....г„). полученная по выборке .... Х„. точное
или приближенное распределение которой известно. Затем по этому
выборочному распределению определяется критическое значение 8,г —
такое, что если гипотеза Яо верна, то вероятность Р(0Я >0мр) = а ма-
ла; так что в соответствии с принципом практической уверенности в
условиях данного исследования событие бп >0м. можно (с некото-
рым риском) считать практически невозможным. Поэтому если в
331
данном конкретном случае обнаруживается значение статистики
0„ > 0ч1, то гипотеза //0 отвергается, в то время как появление значе-
ния 0„ <: О.р считается совместимым с гипотезой Яо. которая тогда
принимается (точнее, не отвергается). Правило, по которому гипотеза
Hq отвергается или принимается, называется статистическим крите-
рием или статистическим тестом.
Таким образом, множество возможных значений статистики кри-
терия (критической статистики) 6, разбивается на два нспсресекаю-
ШИХСЯ подмножества: критическую область (область отклонения гипо-
тезы) W и область допустимых значений (область принятия гипотезы)
В'. Если фактически наблюдаемое значение сгагистики критерия 0п
попадает в критическую область Ж то гипотезу Я» отвергают. При этом
возможны четыре случая (табл. 10.1).
Тнб.шцн 10.1
Гипотеза Ну Принимается Отвергается
Верна Правильное решение Ошибка 1-го рола
Неверна Ошибка 2-го рола Правильное решение
Определение. Вероятность а допустить ошибку l-го ро-
да, т.е. отвергнуть гипотезу Нп. когда она верна, называется уровнем
значимости, или размером, критерия.
Вероятность допустить ошибку 2-го рода, т.е. принять гипотезу
//<)• когда она неверна, обычно обозначают 0.
Определение. Вероятность (1--0) не допустить ошибку 2-го
рода. т.е. отвергнуть гипотезу Hq. когда она неверна, называется
мощностью критерия1.
Пользуясь терминологией статистического контроля качества про-
дукции, можно сказать, что вероятность а представляет «риск по-
ставщика», связанный с забраконкой по результатам выборочного кон-
1 В отличие от простых. при проверке сложных гипотез вероятности ошибок а
и р являются функциями неизвестного параметра; например, <<0) и 0(0)-
функции параметра 0, если нулевая и альтернативная гипотезы предполагают
принадлежность параметра 0 к двум нспересскаюшнмея областям значений В
лом случае вероятность 1-а(0) принят!, гипотезу //„. когда она верна, назы-
вают оперативной характеристикой критерия, а вероятность 1-0(0) отвергнуть
гипотезу //,>. когда она неверна. — функцией мощности критерии
332
троля изделий всей партии, удовлетворяющей стандарту, а вероятность
Р — «риск потребителя», связанный с принятием по анализу выборки
партии, не удовлетворяющей стандарту.
Применяя юридическую терминологию, и — вероятность выне-
сения судом обвинительного приговора, когда на самом деле обви-
няемый невиновен, р — вероятность вынесения судом оправдатель-
ного приговора, когда на самом деле обвиняемый виновен в совер-
шении преступления. В ряде прикладных исследований ошибка
первого рола а означает вероятность того, что предназначавшийся
наблюдателю сигнал не будет им принят, а ошибка второго рода 0 —
вероятность того, что наблюдатель примет ложный сигнал.
Возможностью двойной ошибки (1-го и 2-го рода) проверка ги-
потез отличается от рассматриваемого выше интервального оцени-
вания параметров, в котором имелась лишь одна возможность
ошибки: получение доверительного интервала, который на самом
деле не содержит оцениваемого параметра.
Вероятности ошибок 1-го и 2-го рода (и и 0) однозначно опреде-
ляются выбором критической области. Очевидно, желательно сделать
как угодно малыми а и р. Однако это противоречивые требования:
при фиксированном объеме выборки можно сделать как угодно ма-
лой лишь одну из величин — tx или 0. что сопряжено и неизбежным
увеличением другой. Лишь при увеличении объема выборки возмож-
но одновременн о е уменьшение вероятностей а и р (ем.
пример 10.0).
Какими принципами следует руководствоваться при построении
критической области IV?
Предположим, что используемая для проверки (тестирования)
нулевой гипотезы статистика критерия имеет нормальный
закон распределения а3). В качестве критической области,
отвечающей уровню значимости а = 0.05. можно взять множество
областей — таких, что площадь соответствующих им криволиней-
ных трапеций пол кривой распределения составляет 5/100 от общей
плошали иод кривой распределения. Например (рис. 10.1): |1| —
Область больших положительных отклонений (при >0,?|); |П| —
область больших отрицательных отклонений (при В, <0,р.-)'. |Ш| —
область больших по абсолютной величине отклонений (при
IIV) — область малых по абсолютной величине
отклонений (при 0’р1 <0„ <0*р4) и тщ.
333
ЛЧд,(:ст*>
1'4 а„
Рис. 10.1
М(ап‘><з:) A'Upa*’)
IM a0 at
Рис. 10.2
Какую из этих областей предпочесть в качестве критической?
Пусть с проверяемой гипотезой //() конкурирует другая, альтерна-
тивная, гипотеза Н\, при которой распределение статистики крите-
рия 0„ нормально: Mau о*). где </, >ц, (рис. 10.2). Очевидно, сле-
дует предпочесть ту критическую область, при которой мощность
критерия будет наибольшей. Если, например, критическая область
типа (I]. то в случае 0я <0tpI гипотеза Яо принимается. Но в этом
случае может быть верна конкурирующая гипотеза //, с вероятно-
стью ошибки второго рода р. Вероятность р интерпретируется пло-
щадью под кривой распределения ф,(0.) левее 6,г1 ’. а мощность
критерия (1 - Р) — площадью Р\ правее 0аг, (см. рис. 10.2). Анало-
гично Р||. Рц(, f|v интерпретируют мощность критерия при крити-
1 Здесь отчетливо видно. что если увеличить 0кр|. то ошибка и 1-го рола
уменьшится (станет меньше чем 0.05). но увеличится ошибка 2-го рода р. и на-
оборот; одновременно же уменьшить и а. и |< нсвотможно
334
ческих областях соответственно II. Ill и IV типов (на рис. 10.2 пло-
щади Р\— Р\\- заштрихованы)1. Очевидно, что в данном случае целе-
сообразно выбрать в качестве критической область |1|, т.е. право-
стороннюю критическую область, так как такой выбор гарантирует
максимальную мощность критерия.
Требования к критической области аналитически можно запи-
сать так:
р(б. 6 #’///„) = а,
(ЮЛ)
Р(е<бИ'/Я()=тах,
т.е. критическую область W следует выбирать так, чтобы вероят-
ность попадания в нее статистики критерия 0(1 была минимальной и
равной о. если верна нулевая гипотеза Но. и максимальной в противо-
положном случае.
Другими словами, критическая область должка быть такой,
чтобы при заданном уровне значимости а мощность критерия I — Р
была максимальной. Задача построения такой критической области
W (или. как говорят, построения наиболее мощного критерия) для
простых гипотез решается с помощью следующей теоремы.
Теорема (лемма) Неймона—Пирсона. Среди всех критериев заданного
уровня значимости а, проверяющих простую гипотезу Но против альтер-
нативной гипотезы Н\. критерий отношения правдоподобия является наи-
более мощным.
Поясним смысл этой теоремы, полагая случайную величину X не-
прерывной.
Если верна простая гипотеза Но. то плотность вероятности <р(х) оп-
ределяется однозначно, и функция правдоподобия Ly(x). выражающая
плотность вероятности совмесптого появления результатов выборки (xt.
Xj,.... х„). имеет вид (см. § 9.3):
Л» (-V, <) = <₽„(х, Хр(1 (х.)...ф0 (л„).
Напомним, что функция ........ v„) есть мера правдоподобности
получения выборочных наблюдений Х|, .ъ,.... хя.
Аналогично, если верна простая гипотеза /У|. то функция правдо-
подобия
ЛIV,....х,) = <р, (X, )ф| (х.)... ф, (х„).
В теореме Неймана—Пирсона рассматривается отношение правдопо-
добия L\/U (при * 0); чем правдоподобнее выборка в условиях гипоте-
зы тем больше отношение Li/Ц или его логарифм In (Z-i/io)- А крите-
1 Ан частично перекрывается с А и Ai
335
рий тип олкштенти. по акжмснхю теоремы. н является ндиСхпгг
мощным среди друпа возможных кршернеп
ИсПОЛЫуЯ ДОННЫЙ Кр»ПГрИЙ, МОЖНО НД1ГП1 такую ПОСТОЯННА Ki Г
Нин Ln С = О. *<то
< гкэкккшж» патученной постоянной С (или fl острезетмстся крип*
чсскдя область Н кршгрИЯ и его мощность
t> Пример 10.0. Случайная величина А’ имеет нормальный закон
распределения \(а. ст'». где а - tf(A) не известно, а ст: = ДЛ) и»
мелю. Построить наиболее мощный критерий проверки гипотезы
Но а = против альтернативной //,: я ® в, > о-., Найти и) мощность
критерия, б) минимальный объем выборки, обеспечивающий задан
ные уровень змачимехтзм л и мощность критерия I - 0
Решение Если верни гипотеза /£.. те X - .Ма>; ст;). то
функция прлтыополибня (см § 9.3» имеет вид
4,1 г,.х. I я--------те :<*
ст’(2я) ’
Андлшмчно. если верна гипотеза //t. т е X - М®ь «•>. то
. . . I «-------------
МЧ С.) = —~—-тг
о (2ni
Согласно теореме Неймана Пирсон.» наиболее мощный Крите
рий основан на отношении правдотииобия L|/L> Найдем его лога-
рифм; патучнм
£(х,-<0: £(<.-ц.Г
1П (/.№1 - ---------- - -!-------=
2в’ 2<г
- 7“ (*», Ч) (« < >1 - , Um - Ц. £( 2т, - а, - ц, I =
-<Т । 2 СТ
1 , -.-г - -
= —г(Ц - ц,Х2х - и - а, >п, итю г = ) < п
Дчм построения критерия найдем такую постоянную С (или
In С - cl. что
Полученное выражение для уровня мичимосп! а можно шменип.
ему рлпн4х-н.ты4ым (учитывая монотонность функции In U.jLe) отно
сктсльно т ).
/'(< > с’> и
336
Для определения с’ следует учесть, что если случайная величина
/распределена нормально, т.е. X- N(oq, о2), то ее средняя х также
распределена нормально с параметрами о0 и о2/л (см. § 6.3, 9.3). т.е.
Используя выражение функции распределения нормального за-
кона через функцию Лапласа (4.30), получим
Р(х>с’) = 1-Лх$с') = 1- - + 1ф| =
2 2 I a J
1 •
----------ф
2 2
a.
откуда Ф
с' — а, г—
1-2а или ------~чл=/,_.и и определяющее
о
границ)' критической области И7 значение с' - а,у + f, 2tt .
V»
Следовательно, наиболее мощным критерием проверки гипоте-
зы М»: а = Qq против альтернативной И\. a = 0| > является сле-
дующий: гипотеза Но отвергается, если х > au+ti ia-^\ Яо не от-
a
вергается. если х < aQ + r(.,a -т=.
>Jn
а) Для нахождения мощности критерия определим вначале ве-
роятность р допустить ошибку 2-го рода — принять гипотезу Но,
когда она не верна, а верна альтернативная гипотеза Н\, т.е. X -
* N(a\, о2) или х - Я(в|. ст2/\/л ):
Р = Р v 5 а0 *
о
---Ф
2 2
I.
о
Следовательно, мощность критерия есть
|_р=1+1ф
2 2
о
Рассматривая полученные выражения, еще раз (теперь уже ана-
литически) убеждаемся в том, что уменьшение уровня значимости a
при неизменном объеме выборки л ведет к увеличению вероятности
Р и соответственно к снижению мощности критерия 1 - р. И толь-
337
1
ко при увеличении объема выборки п возможно, уменьшая вероят-
ность а. одновременно уменьшать вероятность [I (увеличивать мош-
ностъ критерия I - |J).
б) При заданных вероятностях ошибок 1-го и 2-го рода а и Ц из
выражения для р нетрудно найти соответствующий объем выборки
по формуле:
В зависимости от вида конкурирующей гипотезы //j выбирают
правостороннюю, левостороннюю или двустороннюю критическую
область. Так. в рассмотренном примере мы убедились, что при кон-
курирующей гипотезе Н\'. а{ > следовало использовать правосто-
роннюю критическую область |1| (см. рис. 10.1. 10.2). Аналогично
можно показать. *гго в случае Н\\ «, < ц, следовало использовать левосто-
роннюю критическую облает». |П|, а при гипотезе //,: о, = щ — двусто-
роннюю критическую область |111|. Гранины критических областей
0,г при заданном уровне значимости и определяются соответствен-
но из соотношений:
для правосторонней критической области
/*(ё.>е.Р)=о. (>0.2)
для левосторонней критической области
/’(9. <0„) = а. (10.3)
для двусторонней критической области
/,(ё.<е.„)=/’(в.>0,.)=^. «юл»
Соответствующий равенствам (10.2) или (10.3) критерий назы-
вается односторонним, а равенству (10.4) — двусторонним.
Следует отметить, что в компьютерных статистических пакетах
обычно не находятся границы критической области 0^. необходимые
для сравнения их с фактически наблюдаемыми значениями выбороч-
ных характеристик 0,Ы|, и принятия решения о справедливости гипоте-
зы Но. А рассч»пывается точное значение уровня значимости (p-valio)
исходя из соотношения Р (0, > 6^., ) = р. Если р очень мало, то ги-
потезу //о отвергают, в противном случае Нц принимают (точнее, не
отвергают; при этом рассчитанное на компьютере значение р может
быть удвоено при выборе двусторонней критической области).
Принцип проверки статистической гипотезы не дает логического
доказательства ее верности или неверности. Принятие гипотезы /Л» в
сравнении с альтернативной Н\ не означает, что мы уверены в абсо-
338
ЛКЛЯОЙ правильности или что высказанное в гипотезе //0 утвер-
ждение является наилучшим, единственно подходящим; просто ги-
потеза М) не противоречил имеющимся у нас выборочным данным,
таким же свойством наряду с //0 могут обладать и другие гипотезы.
Более того, возможно, что при увеличении объема выборки п либо
при испытании Яо против другой альтернативной гипотезы Hi ги-
потеза Но будет отвергнута. Так что принятие гипотезы Но следует
расценивать не как раз и навсегда установленный, абсолютно верный
содержащийся в ней факт, а лишь как достаточно правдоподобное, не
противоречащее опыту утверждение.
В описанной выше схеме проверка гипотез основывается на
предположении об известном законе распределения генеральной со-
вокупности. из которого следует определенное распределение крите-
рия. Критерии проверки таких гипотез называются параметрически-
ми. Если закон распределения генеральной совокупности неизвестен,
то соответствующие критерии получили название непараметрическшд.
Естественно, что непараметрические критерии обладают значительно
меньшей мощностью, чем параметрические. Эго означает, что для со-
хранения той же мощности при использовании непараметрического
критерия по сравнению с параметрическим нужно иметь значительно
больший объем наблюдений.
По своему прикладному содержанию статистические гипотезы
можно подразделить на несколько основных типов:
• о равенстве числовых характеристик генеральных совокуп-
ностей;
• о числовых значениях параметров;
• о законе распределения;
• об однородности выборок (т.е. принадлежности их одной и
той же генеральной совокупности);
• о стохастической независимости элементов выборки.
10.3. Проверка гипотез о равенстве средних
двух и более совокупностей
Сравнение средних двух совокупностей имеет важное практиче-
ское значение. На практике часто встречается случай, когда средний
результат одной серии экспериментов отличается от среднего ре-
зультата другой серии. Прн этом возникает вопрос, можно ли объ-
яснять обнаруженное расхождение средних неизбежными случай-
ными ошибками эксперимента или оно вызвано некоторыми зако-
номерностями* 2. В промышленности задача сравнения средних часто
• В литературе такие критерии называются также свободными от распределения
2 Поэтому проверку гипотез такого типа называют проверкой (оценкой) значимо-
сти (существенности) различия выборочных средних или других характеристик
339
возникает при выборочном контроле качества изделий, изготовлен-
ных на разных установках или при различных технологических ре-
жимах. в финансовом анализе — при сопоставлении уровня доход-
ности различных активов и т.д.
Сформулируем задачу. Пусть имеются две совокупности, харак-
теризуемые генеральными средними х0 и у„ и известными диспер-
сиями <jr и а*. Необходимо проверить гипотезу //у о равенстве ге-
неральных средних, т.с. Но- хп-уп. Для проверки гипотезы Mi из
этих совокупностей взяты две независимые выборки объемов л, и
л,, по которым найдены средние арифметические х и у и выбо-
рочные дисперсии и .V’ .
При достаточно больших объемах выборки, как отмечено в § 9.6.
выборочные средние х и у имеют приближенно нормальный закон
распределения, соответственно Л?(хп.ст;) и N (уп.о;).
В случае справедливости гипотезы Но разность х—у имеет
нормальный закон распределения с математическим ожиданием
Л/(х-у) =А/( х)- Л/( у) = х„-Уи=0 и дисперсией ст;.; = о; + ст; =
= + (напомним, что дисперсия разности независимых слу-
я, л.
чайных величин равна сумме их дисперсий, а дисперсия средней п
независимых слагаемых в л раз меньше дисперсии каждого).
Поэтому при выполнении гипотезы Но статистика
t (х-у}-М(х-у) х-у {]05)
IctJ + о;
V л« п:
имеет стандартное нормальное распределение Л/(0;1).
340
Согласно равенствам (10.2)—(10.4) в случае конкурирующей ги-
потезы Н\: х„>у0 (или Л/,: х(|<у0) выбирают одностороннюю
критическую область и критическое значение статистики находят из
условия (рис. 10.3)
Ф('..) = Ф('..;.) = 1-2а, (10.6)
а при конкурирующей гипотезе //,: x0*J?i> выбирают двусторон-
нюю критическую область и критическое значение статистики нахо-
дят из условия (рис. 10.4)
Ф('„) =Ф(/,..) = 1-а. (10.7)
Если фактически наблюдаемое значение статистики t больше
критического /кр, определенного на уровне значимости а (по абсолют-
ной величине), т.е. |/| > , то гипотеза Hq отвергается. Если |/| <, 1,р,
то делается вывод, что нулевая гипотеза Но не противоречит имею-
щимся наблюдениям.
> Пример 10.1. Для проверки эффективности новой технологии ото-
браны две группы рабочих: в первой группе численностью п, = 50 чел., где
применялась новая технология, выборочная средняя выработка со-
ставила х = 85 (изделий), во второй группе численностью П} = 1Q чел.
выборочная средняя — у = 78 (изделий). Предварительно установ-
лено, что дисперсии выработки в группах равны соответственно
= 100 и о* = 74 . На уровне значимости а = 0,05 выяснить влия-
ние новой технологии на среднюю производительность.
Решение. Проверяемая гипотеза Нп: х0 = у0. т.е. средние вы-
работки рабочих одинаковы по новой и старой -гехнолопадм. В качестве
конкурирующей гипотезы можно взять Н\‘. х0 >у|( или fy : х0*?(>
(в данной задаче более естественна гипотеза Н\, так как ее справед-
ливость означает эффективность применения новой технологии).
По формуле (10.5) фактическое значение статистики критерия
100 74
50 + 70
При конкурирующей гипотезе Я, критическое значение статистики
находится из условия (10.6). т.е. = 1 -2 0.05 = 0.9, откуда по
табл. II приложений = 1,64, а при конкурирующей гипотезе Н? —
из условия (10.7). т.е. ф(гжр) = 1 - 0,05 = 0,95, откуда по таблице
= 41.95 ~ 1.96.
341
Так как фактически наблюдаемое значение / = 4,00 больше кри-
тического значения /кр (при любой из взятых конкурирующих гипо-
тез), то гипотеза //о отвергается, т.е. на 5%-но.м уровне значимости
можно сделать вывод, что новая технология позволяет повысить
среднюю выработку рабочих. ►
Будем теперь предполагать, что распределение признака (слу-
чайной величины) X и Y в каждой совокупности имеет нормальный
закон. В этом случае, если дисперсии о; и о; известны, то провер-
ка гипотезы проводится так же, как описано выше, не только для
больших, но и для малых по объему выборок.
Если же дисперсии ст и о*' неизвестны, но равны, т.е.
а; = о; = о*. го в качестве неизвестной величины ст можно взять
ее оценку — «исправленную» выборочную дисперсию
= —Ц-Ek-•*)*’ ид» •<; =—Ц-Ек-ГГ-
п, -1 ГГ Л; -1 М
Однако «лучшей» оценкой для ст будет дисперсия «смешанной»
совокупности объема Л1 + п2, т.е.
Еи-*):+£(л-Яг _(Я|„^-1).;.; v;+n,s;
л, + л, - 2 ц + л, -2 п, + п2 - 2 ’
а оценкой дисперсии разности независимых выборочных средних
л.г + n,s* f| | '
.V’ - —--------1 — +--
/i,+».-2^ n:)
(обращаем внимание на то. что число степеней свободы к = л( + п2 ~ 2
на 2 меньше общего числа наблюдений Л| + п2, гак как две степени
свободы «теряются» при определении по выборочным данным
средних х и у).
Доказано, »по в случае справедливости гипотезы Но статистка
f = -г-, Л~Г (10.8)
n,s;+n,5;( । । j
у ц + л, - 2 ( п, л.)
имеет /-распределение Стьюдента с к = /ц + п2 - 2 степенями свобо-
ды. Поэтому критическое значение статистки i находится по тем же
формулам (10.6) или (10.7> в зависимости от типа критической об-
342
ласти, о которых вместо функции Лапласа Ф(г) берется функция
G(t.k) распределения Стыодента при числе степеней свободы
д » Я| + лэ-2. т.с. 0(/Л) = 1-2а или 0(/Л)=1-а.
При этом сохраняется то же правило опровержения (принятия)
гипотезы: гипотеза //и отвергается на уровне значимости а, если
р|>/|.1а., (и случае односторонней критической области), либо если
|/|>/|.и< (в случае двусторонней критической области); в противном
случае гипотез;» //0 не отвергается (принимается).
Замечание. Если дисперсии а* и о; неизвестны и не
предполагается, что они равны, то статистика t = (х - у) /я. . также
имеет f-распрсдсление Стыодента. однако соответствующее ему
число степеней свободы определяется приближенно и более слож-
ным образом.
С> Пример 10.2. Произведены две выборки урожая пшеницы: при
своевременной уборке урожая и уборке с некоторым опозданием. В
первом случае при наблюдении 8 участков выборочная средняя уро-
жайность составила 16,2 ц/га. а среднее квадратическое отклонение —
3,2 u/га; во втором случае при наблюдении 9 участков те же характе-
ристики равнялись соответственно 13.9 ц/га и 2,1 u/га. На уровне
значимости а = 0.05 выяснить влияние своевременности уборки уро-
жая на среднее значение урожайности.
Решение. Проверяемая гипотеза Яо: = у„, т.е. средние
значения урожайности при своевременной уборке урожая и с неко-
торым опозданием равны. В качестве альтернативной гипотезы бе-
рем гипотезу Н\\ х0>у„. принятие которой означает существенное
влияние на урожайность сроков уборки.
Фактически наблюдаемое значение статистики критерия по фор-
муле (10.8)
|9-3,2:+8-2.14 I t П
V 8+9-2 (,8 + 9/
Критическое значение статистики ятя односторонней области опреде-
ляется при числе степеней свободы к = Л|+ л2 - 2 = 9 + 8 — 2 = 15 из
условия 0(/.4) = 1 - 2-0.05 = 0.9 , откуда по табл. IV приложений
/о.9;15= 1.75. Так как / = 1.62 < «Ь.9;15= 1.75. то гипотеза Нп принима-
343
ется. Это означает, что имеющиеся выборочные данные на 5%-ном
уровне значимости не позволяют считать, что некоторое запаздыва-
ние в сроках уборки оказывает существенное влияние на величину
урожая. Еще раз подчеркнем, что это не означает безоговорочную
верность гипотезы //0. Вполне возможно, ‘гго только незначитель-
ный объем выборки позволил принять эту гипотезу, а при увеличе-
нии объемов выборки (числа отобранных участков) гипотеза Я(> бу-
дет отвергнута. ►
Сравнение средних нескольких совокупностей. Эта задача рас-
сматривается в гл. II «Дисперсионный анализ».
Исключение грубых ошибок наблюдений. Рассмотренный крите-
рий можно применять для исключения грубых ошибок наблюдений.
Грубые ошибки могут возникнуть из-за ошибок показаний измери-
тельных приборов, ошибок регистрации, случайного сдвига запятой
в десятичной записи числа и т.д.
Пусть, например. ...х„ — совокупность имеющихся
наблюдений, причем х’ резко выделяется. Необходимо решить во-
прос о принадлежности резко выделяющегося значения к осталь-
ным наблюдениям.
Для ряда наблюдений х,, х...х„ рассчитывают среднюю ариф-
метическую v и «исправленное» среднее квадратическое отклоне-
ние з. Прн справедливости гипотезы Нп: х„ = х‘ о принадлежности
• е х-х‘
х к остальным наблюдениям» статистика / = —7— (получаемая как ча-
•V
стный случай из формулы (10.8) при г = х’. /ь- I) имеет /-распре-
деление Стьюдента с к = п - 1 степенями свободы. Конкурирующая
гипотеза //, имеет вид: xj, > х* или < х’ — в зависимости от гою.
является ли резко выделяющееся значение больше или меньше ос-
тальных наблюдений. Гипотеза Нп отвергается, если И>/,р. и при-
нимается. если |/| $ /,р.
> Пример 10.3. Имеются следующие данные об урожайности
пшеницы на 8 опытных участках одинакового размера (ц/га): 26.5:
26,2; 35.9; 30, Г. 32,3; 29.3; 26,1; 25,0. Есть основание предполагать,
что значение урожайности третьего участка х* = 35.9 зарегистрирова-
но неверно. Является ли это значение аномальным (резко выделяю-
щимся) на 5%-ном уровне значимости?
Решение. Исключив значение х* = 35.9. найдем для остав-
шихся наблюдений г =27,93 (ц/га) и з = 2,67 (ц/га). Фактически
344
наблюдаемое значение
35.9-27,93
2.67
= 2.98 больше табличного =
= 6-2«л-| = = следовательно, значение л* =35.9 является
аномальным, и его следует отбросить. ►
10.4. Проверка гипотез о равенстве долей признака
в двух и более совокупностях
Сравнение долей признака в двух совокупностях — достаточно час-
то встречающаяся на практике задача. Например, если выборочная
доля признака в одной совокупности отличается от такой же доли в
другой совокупности, то указывает ли эго на го, что наличие призна-
ка в одной совокупности действительно вероятнее, или полученное
расхождение долей является случайным?
Сформулируем задачу. Имеются две совокупности, генеральные
доли признака в которых равны соответственно pt и р?. Необходимо
проверизъ нулевую гипотезу о равенстве генеральных долей, т.е. Нп:
р\=Р1- Для проверки гипотезы Hq из этих совокупностей взяты две
независимые выборки достаточно большого объема1 л( и л3 Выбо-
ли, т.
рочные доли признака равны соответственно и-, = — и м\ = —-,
А * л.
где /Я| и пъ — соответственно число элементов первой и второй вы-
борок. обладающих данным признаком.
При достаточно больших л( и п2, как отмечено н § 9.5. выбороч-
ные доли w, и и\ имеют приближенно нормальный закон распреде-
ления с математическими ожиданиями р\ и р2 и дисперсиями
н . т.е. соответственно Л д; и
л,---------------------------------------------------л,-П|
‘ J
При справедливости гипотезы Я«: р\ = Pi~ р
разность в; - w, имеет нормальный закон распределения с мате-
матическим ожиданием Л/(и,-и, ) = /?-р = 0 и дисперсией ст; =
Р(1
. Поэтому статистика
1 Здесь ограничиваемся рассмотрением случая больших по объему выборок.
345
(Ю.9)
имеет стандартное нормальное распределение N(0;l).
В качестве неизвестного значения р. входящего в выражение
статистики г, берут ее наилучшую оценку р , равную выборочной
(10.10)
доле признака, если две выборки смешать в одну. т.е.
т. + т,
^+П2
Выбор типа критической области и проверка гипотезы Но осу-
ществляются так же. как и выше, при проверке гипотезы о равенст-
ве средних.
[> Пример 10.4. Контрольную работу по высшей математике по
индивидуальным вариантам выполняли студенты двух групп перво-
го курса. В первой группе было предложено 105 задач, из которых
верно решено 60. во второй группе из 140 предложенных задач вер-
но решено 69. На уровне значимости 0.02 проверить гипотезу об
отсутствии существенных различий в усвоении учебного материала
студентами обеих групп.
Решение. Имеем гипотезу р\ = р,= р. т.с. доли решен-
ных задач студентами первой и второй групп равны. В качестве аль-
тернативной возьмем гипотезу //,: х р,.
При справедливости гипотезы наилучшей оценкой р будет в
соответствии с равенством (10.10) п - - = 0,527. Выбо-
105 + 140 245
рочные доли решенных задач для каждой группы
н*. = — = — = 0.571 и и\ = = 0.493. Статистика критерия
1 л, 105 2 п2 140
по формуле (10.9)
°-57|-°-W =1.21.
Jo.527(1-O.527)(±+i]J
При конкурирующей гипотезе Н\ выбираем критическую дву-
стороннюю область, границы которой определяем из условия
(10.7):Ф(гмг) = I-0.02 = 0.98. откуда по табл. II приложений
гхр = /0 9)i = 2,33. Фактическое значение критерия меньше критиче-
ского. т.е. I < /ЛЧЯ, следовательно, гипотеза принимается, т.е
346
полученные данные нс противоречат гипотезе об одинаковом уров-
не усвоения учебного материала студентами обеих групп. ►
Сравнение долей признака в нескольких совокупностях. Пусть
имеется / совокупностей, генеральные доли которых равны соответ-
ственно Р\. Ръ Pi- Необходимо проверить нулевую гипотезу о ра-
венстве генеральных далей, т.е. М»: р, = р> = ... = рп = р или //<>: д = р
(I — 1.2../). Для проверки гипотезы /7(1 из этих совокупностей
отобраны / независимых выборок достаточно больших объемов
л|, ....П{. Выборочные доли признака равны соответственно
w, =m,/n,. wz~n,'Jn'.. гдс т, — число элементов /-Й
выборки (/= I. 2../). обладающих данным признаком.
Можно показать, что при справедливости гипотезы и при
л->® статистика
У/ = (10.11)
имеет х:-распределение с / — I степенями свободы.
В качестве неизвестного значения р. входящего в выражение
(10.11). берут нанлучшую оценку для р. равную выборочной доле
признака, если все / выборок смешать в одну, т.е.
Р = -^— • <!0.12>
• ’«
Для проверки гипотезы //п обычно берут правостороннюю кри-
тическую область. Гипотеза //0 отвергается, если Х:>Хо.. •• ,дс
~ критическое значение критерия X'- определяемое на уров-
не значимости а при числе степеней свободы I- I.
[> Пример 10.5. По условию примера 10.4 на уровне значимости
а = 0.05 выяснить, можно ли считать, что различия в усвоении
учебного материала студентами четырех групп первого курса суще-
ственны. Дополнительные условия: для третьей группы ту = 63,
Лд= 125. для четвертой группы т4 = 105. п4 = 160.
Реше и и с. Выдвигаем гипотезу Hit: р\= р: = ру - рл,- Р или
Pi — Р (i = I. 2. 3, 4). т.е. доли решенных задач всех групп равны.
Вычислим по формуле (10.12) оценку р :
60.65W + 105 в
105 + 140.125 + 160
347
Выборочные доли решенных задач для каждой группы: и1, =0.571.
и1, = 0.499 (см. пример 10.4), w3 = 63/125 - 0.504, и; = 105/160 = 0,656
Статистика критерия по формуле (10.11)
Х: = о oy-;j| 105(0.571-0.553)' + 140(0.499-0,553)' +
+ 125(0.504-0,553)' +160(0.656-0.553):J = 9.87.
По табл. V приложений Xo.«.j =7,82. Так как x:>xi<.«_>
(9.87 >7.82), то гипотеза Щ отвергается, т.е. различие в усвоении
учебного материала студентами четырех групп значимо или сущест-
венно на уровне а =0,05. ►
10.5. Проверка гипотез о равенстве дисперсии
двух и более совокупностей
Сравнение дисперсий двух совокупностей. Гипотезы о дисперсиях
возникают довольно часто, так как дисперсия характеризует такие
исключительно важные показатели, как точность машин, приборов,
технологических процессов, степень однородности совокупностей,
риск, связанный с отклонением доходности активов от ожидаемого
уровня, и т.д.
Сформулируем задачу. Пусть имеются две нормально распреде-
ленные совокупности, дисперсии которых равны ст* и ст:. Необхо-
димо проверить нулевую гипотезу о равенстве дисперсий, т.е
относительно конкурирующей //,: о; >ст: или ст,: *а;.
Для проверки гипотезы из этих совокупностей взяты две неза-
висимые выборки объемом Л| и гъ. Для оценки дисперсий ст* и ст:
используются «исправленные* выборочные дисперсии л,: и л':.
Следовательно, задача проверки гипотезы сводится к сравнению
дисперсий и 5,:.
При справедливости гипотезы Л/„: ст? = ст: = ст: в качестве
оценки ст* можно взять те же дисперсии s’ и . рассчитанные по
элементам первой и второй выборок.
(л.-l)s*
Напомним (см. § 9.7), что выборочные характеристики -------
ст*
(п.-1)$? .
и —-—:—- имеют распределение х' соответственно с К| = Л| - I и
ст*
348
к2=пт- I степенями свободы, а их отношение —1------ имеет
£г(М
/-распределение Фишера—Снедекора с к} и к2 степенями свободы
(см. § 4.9). Следовательно, случайная величина F. определяемая от-
ношением:
----5=
/Л “ I L J
т.е. отношением «исправленных» выборочных дисперсий, имеет F-pac-
пределение Фишера-Снедекора с к{ = л( - I н к2 = л2 - I степенями
свободы. Вид некоторых кривых F-распределения показан на
рис. 4.18. а также на рнс. 10.5.
При формировании критерия отклонения (принятия) гипотезы
следует учесть, что распределение статистики F (в отличие от нор-
мального или распределения Стыодента) яапяется несимметричным.
Поэтому гипотеза отвергается, если F> Fa l , (в случае пра-
восторонней критической области — рис. 10.5, о), либо если
случае левосторонней — рис. 10.5. /5). либо если
.4. или 2J..4. <в случае двусторонней критической
области — рнс. 10.5. в). В противном случае гипотеза Я(| не отверга-
ется (принимается).
Рис. 10.5
В приложении VI приведены таблицы значений для
а = 0,05 и а = 0.01.
> Пример 10.6. На двух токарных станках обрабатываются втулки.
Отобраны две пробы: из втулок, сделанных на первом станке,
349
Л] = 15 шт., на втором станке — /ь= 18 шт. По данным этих выборок
рассчитаны выборочные дисперсии л'=8,5 (для первого станка) и
.< =6,3 (для второго станка). Полагая, что размеры втулок подчиняют-
ся нормальному закону распределения, на уровне значимости а = 0.05
выяснить, можно ли считать, что станки обладают различной точностью.
Решение. Имеем нулевую гипотезу //„: ст,’ = ст;, т.е. диспер-
сии размера втулок, обрабатываемых на каждом станке, равны.
Возьмем в качестве конкурирующей гипотезу Ht: ст; > ст; (диспер-
сия больше для первого станка). Статистика критерия по формуле
(10.13) (в качестве дисперсии д; , стоящей в числителе, берут боль-
шую из двух дисперсий — это дает возможность, учитывая свойства
F-распредсления, в два раза сократить объем его табличных значений):
1 (15/14)8,5 , з?
£ п. ; (18/17)-6,3
П, ~ 1
По табл. VI приложений критическое значение F-критерия на уров-
не значимости а = 0.05 при числе степеней свободы = Л| - I = Н я
Ь = Л2 - I = 17. т.е. fo,o5;i4:i7 = 2.33. Так как F < Гй„5>|417, то гипотеза
Но не отвергается, т.е. имеющиеся данные нс позволяют считать,
что станки обладают различной точностью.
Замечание. Если в качестве конкурирующей гипотезы в
данной задаче взять гипотезу Ht: ст' * ст;. то. как уже отмечено
выше (см. рис. 10.5. в), следовало взять двустороннюю критическую
область и найти Ft_u :<1 4 и Ft . 4 4 соответственно из условии
< Л-., .-л 4. ) = “ и P(F > Flt ,1(, ) = ^-. При этом гипотеза //.,
отвергается, если полученное значение F < Ft.„ 4 иля
Однако непосредственно по таблицам F-критерия можно найти
лишь правую границу Fa 4 (большую единицы), левую же грани-
цу Ft,a . , к (меньшую единицы) находят из соотношения, доказан-
ного для Г-критерия:
В данном случае при а = 0.05 в задаче следовало найти
^м.кн
3.50
На практике обычно используется таблица значений /'-критерия
(см. табл. VI приложений), в которой приведены значения
и ^г0 позволяег осуществлять проверку гипотезы Но на 5%-
ном и 1%-ном уровнях значимости при использовании односторон-
ней критической области, и на 10%-ном и 2%-ном уровнях значимо-
сти при двусторонней критической области.
Сравнение дисперсий нескольких совокупностей. Пусть имеется /
нормально распределенных совокупностей, дисперсии которых рав-
ны соответственно ст;. ст;'. ст;. и / независимых выборок из каж-
дой совокупности объемов л(, п>.... nt. Необходимо проверить ну-
левую гипотезу о равенстве дисперсий. т.е. //„: ст* = ст; =... = ст; = ст:
или Но: а; = сг (/ = 1. 2./).
Для проверки гипотезы //0 может быть использован критерий
Бартлетта.
Доказано, что при справедливости гипотезы //0 и при условии,
что л, >3 ( / = I. 2./) статистика
£(«,-!) In (г/г)
1 + У----------------!-----
3(/-|)\7T«, -I л,
(в которой
«Л?
г = —-—
и,-I
— исправленная выборочная дисперсия /-Й выборки.
(10.13)
(10.14)
(10.15)
— оценка средней арифметической дисперсий) имеет х‘- распределение
с /- I степенями свободы. Поэтому гипотеза Но отвергается, если
фактически наблюдаемое значение у/ > х\ ( , где х'„. , — крити-
ческое значение критериях2, найденное на уровне значимости а
при числе степеней свободы / - I.
О Пример 10.7. По условию примера 10.5 на уровне значимости
а = 0.05 выяснить, можно ли считать, что станки обладают различ-
ной точностью, если имеются 4 токарных станка и отобраны соот-
ветственно четыре пробы объемов: Я| = 15; л2 = 18; = 25; л4 = 32,
а выборочные дисперсии размеров втулок равны соответственно:
^=8.5; л: =6,3; s;=9,3; л;=5,8.
351
Решение. Имеем нулевую гипотезу На: а' = ст; = ст; = ст; =п
или ст,:=стг(/ = 1, 2, 3. 4).
По формуле (10.14) найдем исправленные выборочные диспер-
сии размеров втулок:
.?* = — • 8,5 = 9,11; .{;=- • 6.3 = 6.67;
*14 - 17
25 , 32
= — -9.3 = 9,69; £ =—5,8 = 5,99.
24 4 31
а по формуле (10.15) — оценку средней арифметической дисперсий
- 15-8,5 + 18 6,3 + 25-9.3 + 32-5,8 659 .
s =------------------------------=----= 7,66.
15 + 18 + 25 + 32-4 86
Статистика критерия по формуле (10.13') равна:
По табл. V приложений х!вм =7,82.
Так как X:<Xo.o>.i (1.87 <7,82), то гипотеза Яо не отвергается,
т.е. имеющиеся данные не позволяют считать, что рассматриваемые
станки обладают различной точностью. ►
10.6. Проверка гипотез о числовых значениях
параметров
Гипотезы о числовых значениях встречаются в различных задачах.
Пусть xt(i =1.2..п) — значения некоторого параметра изделий, про-
изводящихся станком автоматической линии, и пусть а — заданное но-
минальное значение этого параметра. Каждое отдельное значение х, мо-
жет, естественно, как-то отклоняться от заданного номинала. Очевидно,
для того, чтобы проверил, правильность настройки этого станка, надо убе-
диться в том. что среднее значение параметра у производимых на нем из-
делий будет соответствовать номиналу, т.с. проверить гипотезу х„ - и
против альтернативной Яр ^,*а,или Н’2: х,,<и, или Н": хп>и.
При произвольной настройке станка может возникнуть необхо-
димость проверки гипотезы о том. что точность изготовления изде-
лий по данному параметру, задаваемая дисперсий ст:, равна задан-
ной величине ст;. т.с. HQ: о* = сг* или, например, того, что доля
бракованных изделий, производимых станком, равна заданной ве-
личине р0, т.е. Нп: р = и т.д.
352
Аналогичные задачи могут возникнул». например, в финансовом
анализе, когда по данным выборки надо установить, можно ли считать
доходность актива определенного вида или портфеля ценных бумаг. ли-
бо ее риск равным заданному числу; или по результатам выборочной
аудиторской проверки однотипных документов нужно убедиться. можно
ли считать процент допущенных ошибок равным номиналу, и т.п.
В общем случае гипотезы подобною тина имеют вид Hq‘. О = Лн,
где 0 — некоторый параметр исследуемою распределения, а Д„ —
область его конкретных значений, состоящая в частном случае из
одного значения.
При проверке гипотезы указанного типа можно использовать
тот же подход, что и в § 10.2 (см.. например, проверку гипотезы Яо'.
a = fla против альтернативной Н\\ а = Л|>ой при известной диспер-
сии а2 в примере 10.0).
Соответствующие критерии проверки гипотез о числовых значени-
ях параметров нормального закона приведены в табл. 10.2.
ТнСминн 1(1.2
Нулевая гипотеза Предпо- ложения Статистика критерия Альтернативная гипотеза Критерий отклоне- ния гипотезы
с= а0 су2 извест- на 1 -Г 1й С II г: с с. и и и 5= -- ЯЛУ 5 е. г е - г 1' 1- >4-2.1 >'. и
(Г неиз- вестна S/ Ф1-] а - а, > а„ а = а, < а(, “ = Ц * А» 1' 1' > f|-:<. .«-I
°''=^ а неиз- вестно «Г = ст: > ст- ет2 = ст; < ст2 а2 = ст; «ст2 х' >х.» «.1 Х: < Х?-.,л-| либо Х: > Хи Х:
Р “ А» Доста- точно боль- шие п у /,1.7п>| п Р = Ру > А. Р = Ру < Рп Р = Ру * А. J к к >'|м.
'2 Tevpwt «гр»«тжчлп1 u клгштлхи i tnm tnxi
353
Примечание. Критические значения статистик на уровне
значимости а определяют по соответствующим таблицам приложе-
ний исходя из соотношений:
/’(Id <«) = Ф('.-о) = । - a; /’ll /1 < /, ) = 0(ил-.) = I - а.
dr >xL-.)=a-
О Пример 10.8. На основании сделанного прогноза средняя де-
биторская задолженность однотипных предприятий региона должна
составить «о= 120 ден. ел Выборочная проверка 10 предприятий
дала среднюю задолженность х = 135 ден. ед., а среднее квадратиче-
ское отклонение задолженности s — 20 ден. ед. На уровне значимо-
сти 0,05: а) выяснить, можно ли принять данный прогноз; б) найти
мощность критерия, использованного в л. а); в) определить мини
мальное число предприятий, которое следует проверить, чтобы
обеспечить мощность критерия 0.975.
Реше н и с. а) Проверяемая гипотеза х, = ц, =120. В каче-
стве альтернативной возьмем гипотезу х„=«, =135. Так как
генеральная дисперсия о7 неизвестна, то используем /-критерий
Стьюдента. Статистика критерия в соответствии с табл. 10.2 равна
х-ов 135-120 , _ „
f = — ---------. : = 2.25 . Критическое значение статистики
x/Vn-l 20/V10-1
rl-2-O.O5;H>-l = f0.9.9 = 1.83.
Так как |/| (2,25 > 1.83). то гипотеза //0 отвергается, т.е
на 5%-ном уровне значимости сделанный прогноз должен быть от-
вергнут.
б) Так как Д| = 135 > во = 120. то критическая область правосто-
ронняя и критическое значение выборочной средней
_ , 5 5
Л«р “ Д’«» + ^-?и.я-1 /-7 - Ц + /0_»« I— - -
yJn-\ уЛ — |
= 120 +1,83—=2= = 132.2 (ден. ед.),
VlO-l
т.е. критическая область значений для х есть интервал (132,2;+/)
Мощность критерия (см. § 10.2) равна вероятности Р отвергнуть
гипотезу //0. когда верна гипотеза Н\, т.е.
Р = Р(132,2<х<+а>) = 1-1в(сл-|).
где 0 (Г, л - I) — функция, выражающая вероятность попадания
случайной величины, имеющей /-распределение Стьюдента. на от-
354
резок (—Л 0 (аналогична функции Лапласа для нормального распре-
деления (см. § 9.7);
( = -^=22^=_о.42.
.v/Vn-l 20/VlO-l
По табл. IV приложений1 0 (-0,42; 9) =-9 (0.42; 9)«-0.31.
Итак, Р = 0( -0.42; 9) ft | (I + 0.31) ft 0.66.
Л» Л»
в) Воспользуемся решением примера 10.0. 6), в котором форму-
ла (10. Г) объема выборки была получена для случая нормального
закона распределения х. когда известна генеральная дисперсия а2 * *.
Так как у нас а2 нс известна, а известна лишь ее выборочная оценка
, х - ц,
j2, то статистика критерия / =-----.---- имеет /-распределение
S/yJn-\
Стыодента (см. табл. 10.2). и соответствующая скорректированная
формула для п примет вид:
(Zl 1 +,t Ж« 1 ) 5
п =-------------;----.
-Ц.)’
При а = 0.05, |1 = 0,025 (ибо по условию мощность критерия
I - 0 = 0,975). а.) = 120. п, = 135..« = 20 получим:
16. .« ...
п~ g VI» и-1 + '
Так как правая часть равенства сама зависит от неизвестного зна-
чения л, то л находится приближенно подбором. Так. при п = 20.
я = 30. равенство (*) не выполняется (например, при п - 20
20*у««лк»+6..м1-»Г = ~(,.73 +2.09)‘:=24,7), а при п = 25
25 * = "“(1.71 + 2.06)*' =25,3.
Следовательно, необходимо проверить 25 предприятий. ►
Аналогично проверяются и другие гипотезы о числовых значе-
ниях параметров в соответствии с критериями проверки, приведен-
ными в табл. 10.2.
1 Так как непосредственно значения 0(/, л) в данной таблице нет. «внутри» ее п
строке А: » 9 находим близкие к 0,42 шачеиия 0,4(1 и 0,54. соответствующие ве-
роятностям у = 0.3 и •/ = 0.4. т.с. 0(0.40; 9) = 0.3. и 0(0.54; 9) = 0.4. а искомое
значение 0(0.42; 9) « 0.31 накопим интерполированием
355
При проверке статистических гипотез есть и д р у го й под-
х о л. основанный на том. что выше (в § 9.3) для параметров ?„./>. о
были построены доверительные интерна л ы. И если
параметр (или р. или о*) нс попадает в доверительный интервал с
надежностью у = 1-а. т.е. попадает в кр1ггичсскую область, то гипо-
теза //<> отвергается; в противном случае полагают, чго имеющиеся
данные нс противоречат гипотезе Яо.
Достоинством такого подхода, основанного на построении до-
верительного интервала для параметра, является го. что кроме про-
верки гипотезы /7П получается дополнительная информация о воз-
можных истинных значениях параметра. Однако этот подход при-
меним. если в качестве конкурирующих выступают гипотезы типа
v0 *</.//₽ р0. ст’ х ст;. предполагающие выбор двусторонней кри-
тической области.
> Пример 10.9. По данным примера 9.10 на уровне значимости
а ' 0.05 проверить гипотезу о том. что средняя выработка рабочих
всего цеха равна 121%.
Реше н и с. Проверяемая гипотеза /70; v„ = 121(%). Конку-
рирующая гипотеза //,: xj,*l2l. В примере 9.10 с надежностью
7^1-0.05 = 0,95 построен доверительный интервал для
.v0: 117.33 < х„ s 121.07. Так как значение </=121 принадлежит
этому интервалу, то гипотеза Н„ не отвергается, т.е. имеющиеся
данные не противоречат предположению о том. что средняя выра-
ботка рабочих равна 121%. ►
1> Пример 10.10. Поданным примера 9.11 на уровне значимости
о = 0.05 проверить гипотезу о том. что доля нестандартных деталей
во всей партии равна 12%.
Решение. Проверяемая гипотеза Htf. р = 0.12 (или 12%)
Конкурирующая гипотеза р*0.12. В примере 9.11 с надежно-
стью у^1-0,05 = 0.95 построен доверительный интервал для р
0,044 s р < 0.116. Так как значение д, = 0.12 не принадлежит этому
интервалу, то на уровне значимости а = 0,05 гипотеза //и отвергает-
ся. т.е. имеющиеся данные нс позволяют считать, что в партии на-
ходится 12% нестандартных деталей. ►
Г> Пример 10.11. Поданным примера 9.17 на уровне значимости
и = 0,1 проверить гипотезу о том, что среднее квадратическое от-
клонение суточной выработки работниц равно 20 м/ч.
356
Р с ш с н и е. Проверяемая гипотеза 7/0: <Г = 20: = 400. Ковку*
рируюшая гипотеза Ht: сг х 400. В примере 9.17 с надежностью
у = | - 0,1 = 0,0 получен ловер»питна.1й шперцы для er: 157.3 <<г < 468.9.
Так как значение о,; = 400 принадлежит этому интервалу, то на уров-
не значимости а = 0,1 гипотеза //0 не отвергается, т.е. имеющиеся
данные нс противоречат предположению о том. что среднее кшщрати-
ческое отклонение суточной выработки работниц равно 20 м/ч. ►
10.7. Построение теоретического анкона
распределения ио опытным данным.
П|юверка гипотез о законе распределения
Одной из важнейших задач математической статистики является
установление теоретического закона распределения случайной величи-
ны. характеризующей изучаемый признак по опытному (эмпириче-
скому) распределению, представляющему вариационный ряд.
Для решения этой задачи необходимо определить вид и пара-
метры закона распределения.
Предположение о виде закона распределения может быть выдви-
нуто исходя из теоретических предпосылок (например, выполнение
условий центральной предельной теоремы может свидетельствовать
о нормальном законе распределения случайной величины), опыта
аналогичных предшествующих исследований и. наконец, на осно-
вании графического изображения эмпирического распределения.
Параметры распределения, как правило, неизвестны, поэтому их
заменяют наилучшими оценками по выборке, полученными в гл. 9.
Как бы хорошо ни был подобран теоретический закон распреде-
ления. между эмпирическим и теоретическим распределениями не-
избежны расхождения. Естественно, возникает вопрос: объясняются
ли эти расхождения только случайными обстоятельствами, связан-
ными с ограниченным числом наблюдений, или они являются су-
щественными и связаны с тем. »гго теоретический закон распреде-
ления подобран неудачно. Яш ответа на этот вопрос и служат кри-
терии согласия.
Пусть необходимо проверить нулевую гипотезу //0 о том. что ис-
следуемая случайная величина X подчиняется определенному закону
распределения Дэя проверки гипотезы 7/ц выбирают некоторую слу-
чайную величину U. характеризующую степень расхождения теорети-
ческого и эмпирического распределений, закон распределения кото-
рой при достаточно больших п известен и практически нс зависит от
закона распределения случайной величины X.
357
Рнс. 10.0
Зная закон распределения U.
можно найти такое критическое
значение и.„ что если гипотеза Нп
верна, го вероятность гою. что U
приняла значение больше чем и...
т.е. Р((' > w„) = а — мала, где а —
уровень значимости критерия.
Если фактически наблюдаемое и
опыте значение U - и окажется
больше критического: U - и > ип (т.с. попадет в критическую об-
ласть (рис. 10.6)), то в соответствии с принципом практической уве-
ренности это означает, что такие большие значения U практически
невозможны и противоречат гипотезе //«. В этом случае гипотезу /7(1
отвергают. Если же (’ u<wit го расхождение между эмпириче-
ским и теоретическим распределениями несущественно и гипотезу
//0 можно считать правдоподобной или по крайней мерс нс проти-
воречащей опытным данным.
Х2-*фитерий Пирсона. В наиболее часто используемом на практике
критерии f--Пирсона в качестве меры расхождения U берется величина
ранная сумме квадратов отклонений частостей (статистических веро-
ятностей) и; от гипотетических р„ рассчитанных по предполагаемому
распределению. взятых с некоторыми весами с/
= =£f.(“,1 - д,):.
Веса с, вводятся таким образом, чтобы при одних и тех же от-
клонениях (и; -р,)’больший вес имели отклонения, при которых р,
мала, и меньший вес — при которых р, велика. Очевидно, этого
удается достичь, если взять с, обратно пропорциональными вероят-
_ п
н остям р,. Взяв в качестве весов t = — . можно доказать, что при
А
л->« статистика
.-I А
, " ( П - пр, )
или L' = x‘=V------------ (10.16)
м «А
имеет х‘- распределение с k = т - г - 1 степенями свободы, где т —
число интервалов эмпирического распределения (вариационного ряда);
г — число параметров теоретического распределения, вычисленных
по экспериментальным данным.
358
Числа nt = nw< и npi называются соответственно эмпирическими н
теоретическими частотами.
Схема применения критерия х* Для проверки гипотезы //0 сво-
дится к следующему.
I. Определяется мера расхождения эмпирических и теоретиче-
ских частот х по формуле (10.16).
2. Для выбранного уровня значимости а по таблице х;_Рас‘
пределения находят критическое значение х.‘. * при числе степеней
свободы к = т - г - I.
3. Если фактически наблюдаемое значение х больше критическо-
го, т.е. х: > Х.7* • то гипотеза //<» отвсргаегся; если х * Х.м. гипотеза
Hq не противоречит опытным данным.
Замечание. Как уже отмечено, статистика
-(и.-лр,)'
х =2-----------
м пр.
имеет х‘- распределение лишь при и -> зо . поэтому необходимо,
чтобы в каждом интервале было достаточное количество наблюде-
ний. по крайней мерс 5 наблюдений. Если в каком-нибудь интерва-
ле число наблюдений п, < 5. имеет смысл объединить соседние ин-
тервалы1, чтобы в объединенных интервалах л, было не меньше 5.
[> Пример 10.12. Для эмпирического распределения рабочих це-
ха по выработке по данным первых двух граф габл. S.1 подобрать
соответствующее теоретическое распределение и на уровне значи-
мости а = 0.05 проверить гипотезу о согласованности двух распре-
делений с помощью критерия х*
Решение.
По виду гистограм-
мы распределения
рабочих по
ботке (рис.
можно
жить
закон , .
ния признака. Па-
раметры нормаль-
ного закона а и <Г.
являющиеся соот-
ветственно матема-
тическим ожиданн-
Риг. 10.7
выра-
10.7)
прслполо-
нормальный
распределе-
1 Поэтому при нмчнелгкии числа аспеней свободы и качестве величины т бе-
регся соотасгствсино уменьшенное число ингерпалоп
359
ем и дисперсией случайной величины Л', неизвестны, поэтому замени,
см их «наилучшими» оценками по выборке — несмещенными и со-
стоятельнымн оценками соответственно выборочной средней V (|
«исправленной» выборочной дисперсией Г. Так как число наб,по.
дениЙ п = 100 достаточно велико, то вместо «исправленной» г мож-
но взять «обычную* выборочную дисперсию г. В примере 8.8 вычис-
лены v = 119,2(%). .V* = 87,48. j = 9.35(%).
Итак, выдвигаемая гипотеза случайная величина А' — выра-
ботка рабочих цеха — распределена нормально с параметрами и =
= 119.2; а-’ = 87,48, т.е. А - N( 119.2; 87.48).
Для расчета вероятностей р, попадания случайной величины X в
интервал [т|.х1,|] используем функцию Лапласа в соответствии со
свойством нормального распределения:
Например. р,(94 < X < 100)=
100-1)9.2 j ф1 94-119.2 ,
9.35 Г I 9.35 )
= ^[ф(-2.05)-Ф(-2.69)] = 1(-0.9596 + 0.9928) = 0.0166 и соответ-
ствующая первому интервалу теоретическая частота пр\=
= 100-0,0166 * 1.7 и т.д.
Для определения статистики // удобно составить таблицу (табл. 10.3).
Тмб.1111111 10.3
/ Интерна.! к-»..,] Эмпири- ческие час- тоты Вероят- ности Р. Теорети- ческие час- тоты пр, (л, - пр,}- («. ~ пР.)
«А
1 94-100 0.017
5 ho ' ?7,6 5,76 3.758
•> 100-106 7| Ь.059 5.9)
3 106-112 II 0.141 14.1 9,61 р.682
4 112-118 20 3.228 Р2.8 7.84 0.344
5 1 IS—124 2S 3,247 24.7 10.89 3,441
6 124-130 19 1,182 18.2 0.64 3,035
7 130-136 10| , 3,087 8.7]
h- И 1.6 0.16 3,014
8 136-142 2 J 3.029 2.9J
I 100 0,990 99.0 У/=2.27
360
Учитывая, что в рассматриваемом эмпирическом распределении
частоты первого и последнего интервалов (Л| = 3, лх = 2) меньше 5.
при использовании критерия //-Пирсона в соответствии с замеча-
нием на с. 359 целесообразно объединить указанные интервалы с
соседними (см. табл. 10.3).
Итак, фактически наблюдаемое значение статистики х' ~ 2.27,
Так как новое число интервалов (с учетом объединения край-
них) т = 6, а нормальный закон распределения определяется г = 2
параметрами, то число степеней свободы к — т — г — I =
= 6-2-1=3. Соответствующее критическое значение статистики //
по табл. V приложений = 7.82 . Так как '/• < ,, то гипотеза о
выбранном теоретическом нормальном законе N( i 19.2; 87.48) согла-
суется с опытными данными. ►
Замечание. Для графического изображения эмпирического
и выравнивающего его теоретического нормального распределений
необходимо использовать одинаковый для двух распределений мас-
штаб по оси ординат.
Так. если при построении гистограммы эмпирического распрс-
н,
деления по оси ординат откладывать плотность частости —— (где
/7 Дат
Л/ — частота /-го интервала (/ = I, 2.///). Дх — величина интервала.
т — число интервалов, п — число наблюдений, объем выборки), то
выравнивать такую гистограмму будет теоретическая нормальная кри-
вая с плотностью <рч (л) = —L—f'1’ ”' •” , где в качестве параметров
<ь/2я
аист2 используются их состоятельные и несмещенные выборочные
оценки: соответственно средняя v и дисперсия .< (либо г =* л* при
больших л).
Для построения кривой <pv(x) можно использовать таблицу
плотности вероятности стандартного нормального распределения
(табл. I приложений) в соответствии с формулой
, . I . г. . I . х-а х-х
<Рч ') = -/(/). где f/ =-=е и / =-----------s-----.
о У2п а .V
При равенстве величин всех интервалов (как в примере 10.12) часто
бывает удобнее при построении гистограммы эмпирического распре-
деления по оси ординат откладывал» частости »v, = — (см. рис. 10.7)
н
или частоты //,. В этом случае выравнивающей гистограмму кривой
будет растянутая (сжатая) вдоль осн ординат в Дх (или т\х) раз нор-
361
мольная кривая, т.е. кривая ф,(.г) = фч (.r)Av (или кривая
Ф:(х) = Фч (х)лдх).
Точное построение выравнивающей кривой ф,(х) (или ф.(х))
связано с проведением дополнительных расчетов. Их можно избежать,
используя приближенный способ построения (см. рис. 10.7)
В процессе применения //-критерия Пирсона были вычислены веро-
ятности pt и теоретические частоты пр. интервалов распределения.
Учитывая, что в соответствии со свойствами плотности распределения
Фч(х, )Лт, */> (или лцц (л; )Лт * пр,). выравнивающую теоретиче-
скую кривую Ф,(х) (или Ф:(х)) можно построить приближенно по
точкам (х,. р.) (или (х„ лр,)). где в качестве значений х,(/ = 1, 2.л»)
целесообразно взять середины интервалов (см. рис. 10.6). При этом
следует иметь в виду, что .максимум выравнивающей кривой ф,(.г)
(или ф,( х)) будет в точке х = а ~ х и равен
—/’(0) «0.3989— (или —/((j) *0.3989—).
a .v о л
О Пример 10.12а. Имеются следующие статистические данные о
числе вызовов специализированных бригад скорой помощи в час в
некотором населенном пункте в течение 300 ч:
Число вызовов в час х, 0 1 2 3 4 5 6 7 8 V
Частота л. 15 71 75 6Х 39 17 10 4 1 300
Подобрать соответствующее теоретические распределение и на
уровне значимости а = 0.05 поверить гипотезу о согласованности
двух распределений с помощью критерия //.
Р с ш е н и е. Вычислим выборочные среднюю н дисперсию:
_ = g^J).|5 + ... + 8.|
300
л
V K<ni
ГТ ' ' 0--15 + ... + 8* 1
= ---------х =--------------------2,54* * 2.39.
л 300
362
Выдвигаем гипотезу На', случайная величина X — число вызовов
скорой помощи в час — распределена по закону Пуассона с пара-
метром А — 2,54.
В польз)1 этой гипотезы
свидетельствует следующее:
— вызов скорой помощи
для каждого жителя — событие
в целом достаточно редкое;
— полигон частостей (час-
тот) дискретной случайной ве-
личины Д' (рис. 10.8) по своему
виду напоминает полигон пу-
ассоновского распределения
вероятностей при небольших
значениях >. (см. передний
Рис. Ю.х
форзац учебника);
— оценки математического ожидания Л/(А) и дисперсии D(X) —
выборочная средняя и выборочная дисперсия приближенно равны.
т.е. х = л*' (а равенство М(Х) = 1Х.Х). или а = о2. характерно именно
для распределения Пуассона — см. § 4.2).
В качестве неизвестного параметра л. являющегося математиче-
ским ожиданием случайной величины, распределенной по закону Пу-
ассона (см. § 4.2). берем его несмещенную и состоятельную опенку по
выборке — выборочную среднюю, т.е. X = v = 2.54.
Вероятности значений случайной величины А'найдем по формуле (4.8):
р = />(A' = .v =т) =
2.54'е
/»!
Для определения статистики х2 составим таблицу (табл. 10.3а).
Таблица 10.3ц
/ д; = т п> А лА (л, - пр,)2 (и - пр Y ”Р.
1 0 15 0.0789 23.7 75,69 3,194
2 1 71 0.2003 60.1 98.01 1,631
3 2 75 0.2544 76.3 1.69 0.022
4 3 68 0.2154 64.6 11,56 0.179
5 4 39 0.1368 41.0 3.61 0,088
6 5 17 0.0695 20.9 14,44 0.694
7 6 10 0.0294 8.8 1.44 0.164
8 7 4 1 0.0107 3.2 1
5 4,2 0,64 0,152
9 8 1 1 0.0034 ..... L.0 J
300 0,9988 299,6 — X2 = 6.12
363
При расчете х2 объединяем последние два интервала, гак как щ
частоты (лх = 4. лч = 1) меньше 5.
Так как новое число интервалов (с учетом объединения двух
последних) /л = 8. а закон Пуассона определяется г = I парамег*
ром. то число степеней свободы к = т— г- \ = 8 - I - I =6. По
табл. V приложений х?мк.«. = 12,59. Так как х < (6,12 < 12.59).
го гипотеза согласуется с опытными данными. ►
Критерий Колмогорова. На практике кроме критерия X* часто
используется критерий Колмогорова, в котором в качестве меры
расхождения между теоретическим и эмпирическим распределения-
ми рассматривают максимальное значение абсолютной величины
разности между эмпирической функцией распределения Гя(л) и соот-
ветствующей теоретической функцией распределения
D = max|Fj.v)-F(.v)|. (10.17)
называемое статистикой критерия Колмогорова.
Доказано, что какова бы ни была функция распределения Лл)
непрерывной случайной величины X. при неограниченном увеличе-
нии числа наблюдений (л-»оо) вероятность неравенства
Dx/л > л) стремится к пределу
Р(Х)=1- £(-l)V241< (10.18)
4
Задавая уровень значимости и. из соотношения
/’(Ч) = « (Ю.19)
можно найти соответствующее критическое значение X,. В
табл. 10.4 приводятся критические значения а„ критерия Колмого-
рова для некоторых и .
Таблицы 10.4
Уровень зна- чимости а 0.40 0,30 0.20 0.10 0.05 0.025 0.01 0.005 0.001 0,0005
Критиче- ское «каче- ние 0.89 0.97 1.07 1.22 1.36 1.48 1.63 1.73 1.95 2.03
Схема применения критерия Колмогорова следующая.
I. Строятся эмпирическая функция распределения /\(х) и
предполагаемая теоретическая функция распределения F{ v).
364
2. Определяется мера расхождения между теоретическим и эмпири-
ческим распределениями D по формуле (10.17) и вычисляется величина
). = D>/n. (10.20)
3. Если вычисленное значение ). окажется больше критического
X. , определенного на уровне значимости а , то нулевая гипотеза
//о о том, что случайная величина X имеет заданный закон распре-
деления, отвергается. Если то считают, что гипотеза Mi не
противоречит опытным данным.
[> Пример 10.13. Поданным примера 10.12 и табл. 8.1 с помощью
критерия Колмогорова на уровне значимости а = 0.05 проверить ги-
потезу Но о том, что случайная величина .V — выработка рабочих
предприятия - имеет нормальный закон распределения с параметра-
ми а = 119.2: <Г = 87.48. т.е. N( 119,2; 87,48).
Значения эмпирической функции распределения Л'Дх). или на-
копленной частости, вычислены выше в табл. 8.1, а ее график при-
веден на рис. 8.2. б — эти значения и график воспроизводятся соот-
ветственно в табл. 10.5 и на рис 10.9. Для построения теоретиче-
ской функции распределения для нормального закона воспользуем-
ся ее выражением (4.30) через функцию Лапласа:
,v-119.2 ]
9.35 J‘
Г(л) = - + -Ф
I I f 94 -119 2 A I I
Например. Г(94)= - +-ф1 j = - + -Ф( -2.69) = 0.5-
-0.5 0.9928 =0.0036 «0,004 и т.д. Результаты вычислений сведем
в табл. 10.5, а график F(.v) представим на рис. 10.9
ТмГмнцн IO.5
X 94 100 106 112 118 124 130 136 142
F.U) 0.010 0,030 0,100 0,210 0,410 0,690 0,880 0.980 1,000
Нл) 0.004 0,021 0,080 0.221 0,449 0,695 0.878 0.964 0.993
I’m. 10. В
365
х.%
Из рис. 10.9 следует, что
/) = |rjl 18)-F(II8)| = |0.410 - 0.449| = 0.039.
По формуле <10.20) величина Л = Djn = 0,039>/Г00 =0.39 .
Критическое значение критерия Колмогорова по табл. 10.4 рав-
но Х,,„$ = 1.36. Так как а<л.,,0 (0.39< 1.36). то гипотеза Яо согла-
суется с опытными данными. ►
Критерий Колмогорова достаточно часто применяется на прак-
тике благодаря своей простоте. Однако в принципе его применение
возможно лишь тогда, когда теоретическая функция распределения
F(.r) задана полностью. По такой случай на практике встречается
весьма редко. Обычно из теоретических соображений известен лишь
вид функции распределения, а ее параметры определяются по эм-
пирическим данным. При применении критерия /*' это обстоятель-
ство учитывается соответствующим уменьшением числа степеней
свободы. Такого рола поправок в критерии Колмогорова не преду-
смотрено. Поэтому, если при неизвестных значениях параметрон
применить критерий Колмогорова, взяв за значения параметров их
оценки, то получим завышенное значение вероятности Г(Х). а
значит, большее критическое значение . В результате есть риск в
ряде случаев принять нулевую гипотезу о законе распределения
случайной величины как правдоподобную, в то время как на самом
деле она противоречит опытным данным.
10.8. Проверка гипотез об одиородно<пги ныбо|юк
Гипотезы об однородности выборок — это гипотезы о том. что
рассматриваемые выборки извлечены из одной и той же генераль-
ной совокупности.
Пусть имеются две независимые выборки, произведенные из гене-
ральных совокупностей с неизвестными теоретическими функциями
распределения и /<(х). Проверяемая нулевая гипотеза имсез
вил /7,: Л;(л) = Е(л)против конкурирующей //,: ^(х)хЕ(г). Бу-
дем предполагать, что функции FJ(jt) и F,(.v) непрерывны.
Критерий Колмогорова—Смирнова использует ту же самую идею,
что и критерий Колмогорова, но только в критерии Колмогорова
сравнивается эмпирическая функция распределения с теоретиче-
ской, а в критерии Колмогорова—Смирнова сравниваются две эм-
пирические функции распределения.
366
Статистика критерия Колмогорова—Смирнова имеет вид:
-max IF, ( v)-F,. (_v)I, (10.21)
Vw.+w: 1
где F4(.r) и F„ (л) — эмпирические функции распределения, по-
строенные по двум выборкам объемов Л| и п>.
Гипотеза Н(] отвергается, если фактически наблюдаемое значе-
ние статистики X* больше критического Х'р, т.с. X' > Х'р. и прини-
мается в противном случае.
При малых объемах выборок < 20)критические значения Х'р
для заданных уровней значимости критерия можно найти в специаль-
ных таблицах. При оо (а практически при н, >50. п: 2 50)
распределение статистики X’ сходится к распределению Колмогорова
для статистики X . Поэтому гипотеза Яи отвергается на уровне значимо-
сти а , если фактически наблюдаемое значение X’ больше критическо-
го Ха , т.е. X' > Х„ . и принимается в противном случае.
С> Пример 10.13а. В течение месяца выборочно осуществлялась
проверка торговых точек города по продаже овощей Результаты
двух проверок по недовесам покупателям одного вида овощей при-
ведены в табл 10.6.
Тн6.ппш IO.fi
Номер Интервалы Частоты
интернат недовесов. г
п для выборки 1 л для выборки 2
1 0-10 3 5
2 10-20 10 12
3 20-30 15 8
4 30—40 20 25
5 40-50 12 10
6 50-60 5 8
7 60-70 25 20
S 70-80 15 7
9 80-90 5 5
п} = 110 л? = 100
Можно ли считать, что на уровне значимости <1=0.05 по ре-
зультатам двух проверок (случайных выборок) недовесы овощей
описываются одной и той же функцией распределения?
367
Р с in с н и с. Обозначим: л"“* и п'“ — накопленные частоты со-
ответственно выборок 1 и 2; /\ (л; ) = «,"*/л,, Л„ ( v ) =— ши-
чения их эмпирических функций распределения. Результаты вычис-
лений сведем в табл. 10.7.
Гиб. in на 10.7
X, IUB ч /;(ч)
10 3 5 0.027 0,050 0.023
20 13 17 0.118 0,170 0.052
30 28 25 0.254 0,250 0.004
40 48 50 0.436 0,500 0.064
50 60 60 0.545 0,600 0,055
60 65 68 0.591 0,680 0.089
70 90 88 0.818 0,880 0.072
80 105 95 0.955 0,950 0,005
90 110 100 1.000 1,000 0,000
Из последнего столбца видно, ‘по max |Г ( г,)- /\ (,v. )1 = 0.089.
По формуле (10.21) наблюдаемое значение статистики при
Л| = НО. п-> = 100 а* = . ———---0.089 = 0,644. По габл. 10.4 при
VII0 + 100 и
« = 0,05 XOW = I,36.
Так как д' < а(|05 (0.644 < 1.36). то нулевая гипотеза Но не отвер-
нется, следовательно, недовесы покупателям описываются одной и
той же функцией распределения, т.е. они являются устойчивым и
закономерным процессом при продаже овощей в данном городе. ►
Если данные сгруппированы, то для проверки однородности
двух или нескольких выборок можно использовать критерий х2-
Пусть имеется / независимых выборок объемом п( (/ = I. 2..h
и данные выборки сгруппированы в т интервалов (групп), а ?/„ —
число элементов у-Й выборки, попавшей в /-й интервал. Проверяет-
ся гипотеза Н<> о том. что все / выборок извлечены из одной и той
же генеральной совокупности.
В качестве статистики критерия используется величина
, - ‘(/i,,/п>-
x‘ = "L2------------
мы п,.п.
= JyyJ!L_1 ,
(10.22)
36Я
где лг - л7 п
/•I <-• /•! /»1
В случае справедливости гипотезы //0 статистика (10.22) имеет
распределение у2 с (т - I )</ — I) степенями свободы.
О Пример 10.14. Поданным примера 10.13а на уровне значимо-
сти а - 0.05 проверить гипотезу Но об однородности двух выборок
(результатов двух проверок торговых точек города).
Решение. Необходимые для расчета статистики у2 величины
представлены в табл. 10.8.
Таблица 10.8
Интервалы 0-10 IQ- 20 20— 30 30- 40 40- 50 50- 60 60- 70 70- 80 80- 90 = -2>. /!
Часто- ™ н,2 3 5 10 12 15 8 20 25 12 10 5 8 25 20 15 7 5 5 по 100
1’1 8 22 23 45 22 13 45 22 10 л = 210
По формуле (10.22) статистика критерия x.-=2IO|^_+_12L+...+^_+_£_+ V8.I10 22110 ЮНО 8100 12: 52 +——— 1 =7.25. 22-100 10100 J
По таблице V приложений при числе степеней свободы
(/ - l)(m - I) = (9 - 1)(2 - I) = 8 х;111М =15.5. Так как yz <Х<н.5д.
то гипотеза //0 об однородности двух выборок не отвергается. ►
Наряду с рассмотренными, в математической статистике ис-
пользуются также ранговые критерии однородности.
Ранговые критерии однородности к выборок объемов и, основа-
ны не на значениях признака. полученных в выборке, а на порядко-
вых номерах (рангах)' этих значений, расположенных в порядке
1 Полробнсс и рангах см § 12.x
36»
возрастания (убывания) и полученных после упорядочивания объе-
диненной выборки объемом п -^nt.
В критерии Вилкоксона—Манна—Уитни для проверки нулевой
гипотезы однородности двух выборок //,; f-\(x) = F,(x) против аль-
тернативной /У|1 F\(x)*FAx) используется статистика
U = S. - —«.(?/. +1) или U = 5, - — /»,(/». +1), (10.23)
1 2 ' 2 '
где (5,) — сумма рангов наблюдений первой (второй) выборки,
причем обшая сумма рангов
S = 5, + = ~(«| + пг X«i + л; +1 )• (10.24)
Доказано, что если гипотеза Н(1 верна, то при -> х. //. -► -г.
и nt / п. -»л < <х) статистика
6'--’л,л,
г= (10.25)
J-’C^+nJ^n.
I I *
имеет стандартный нормальный закон ЛЧО;1). Поэтому гипотеза
//„ отвергается на уровне значимости а (при п, £ 8. и, £ 8), если
|/1 >/, u. где г,_м определяется по табл. II приложений.
[> Пример 10.14а |30|. Две группы выпускников двух высших
учебных заведений (I и 2) по К) человек в каждой получили оценки
своих административных способностей (в баллах), приведенные в
табл. 10.9.
Тнб.ищн KIJ
26 22 19 21 14 18 29 17 II 34
х.. 16 10 8 13 19 II 7 13 9 21
Можно ли утверждать на уровне значимости и = 0.05, что нс
существуют различия в уровне подготовки выпускников двух вузов?
Решение. I. Составим упорядоченную объединенную вы-
борку объема и = л, + л, =10 + 10 = 20 и определим ранги оценок
выпускников (табл. 10.10).
370
ThImhiui KI. KI
Оценка 7 8 9 10 II II 13 13 14 16
Номер вуза 2 2 2 ? 1 3 2 2 1 2
Ранг 1 2 3 4 5.5 5,5 7.5 7.5 9 10
Опенка 17 18 19 19 21 21 22 26 29 34
Номер вуза 1 1 1 2 2 1 1 1 1 1
Ранг 11 12 13.5 13.5 15.5 15.5 17 18 19 20
2. Находим суммы рангов оценок для первой и второй выборок:
5, = 5.5-9 + 1 1 + 12-13.5±15.5 + 17 * 18 • |9 ► 20 = 140.5;
S, = 1 + 2 + 3 + 4 + 5,5 + 7,5 + 7.5 + 10 + 13,5 + 15.5 = 69,5.
Проверяем выполнение равенства (10.24):
.9 = 10 +10)( 10 +10 +1) = 210. н действительно.
5 = S, +S, = 140,5*69.5 = 210.
3. Находим значения статистик1 U и / по формулам (10.23) и
(10.25):
/; = 140.5--юн = 85.5:
2
85.5- 1 -1010
г = 2 = 2.75.
J ^(10 + 10)10-10
4. По таблице I! приложении при а =0.05 = /„^ = 1.96. Так
как |/| > /, „(2.75 > 1.96).то нулевая гипотеза отвергается, т.е уровни
подготовки выпускников двух вузов существенно отличаются (в пер-
вом вузе он существенно выше, так как 5, >5.). Полученный вывод
интуитивно ясен, так как в объели пенной выборке низкие ранги
(низкие опенки) получили преимущественно выпускники второго
вуза, а высокие рант (высокие опенки) — первою вуза. ►
Тот же принцип, что и в рассмотренном критерии. используется в
других ранговых критериях однородности выборок (критерии Фишера—
мэтса, Крускаю—Уаыиса и др. (см., например. |1]).
1 Если в соответствии с формулой (1(1.23) в качестве шачеиия статистики
Uвзять U 69.5 1 10 11 14.5. то по формуле (10.25) получим г = -2.75.
371
К ранговым относятся также ряд критериев проверки гипотез о
стохастической независимости элементов выборки, таких как: критерий
серий, основанный на медиане выборки; критерий «восходящих» и «нисхо-
дящих» серий; критерий Аббе (см. [I]). Рассмотрение ниженазванных
критериев выходит за рамки данной книги.
В заключение отметим, что при проверке ряда гипотез, напри-
мер. гипотез о законе распределения на заданном уровне значимо-
сти, контролируется лишь ошибка первого рода, но нельзя сделать
вывод о степени риска, связанного с принятием неверной альтерна-
тивной гипотезы, т.е. с возможностью совершения ошибки второго
рола.
10.9. Понятие о проверке гипотез методом
последовательного анализа
Выше (см. § 10.2) было показано, что. используя наиболее мощ-
ный критерий отношения правдоподобия для проверки простой ги-
потезы Н„ против альтернативной //, при заданных уровне значи-
мости и и мощности критерия I -[I. можно найти обеспечивающий
их минимальный объем выборки л (см. формулу (10.1*))- Снизить
это значение п при ф и к с и р о в а н н о м объеме выборки не-
возможно.
Рассматриваемый ниже метод последовательного анализа в прин-
ципе делает возможным при тех же значениях и и 1-0 заметное (п
среднем) уменьшение л, что особенно актуально, если каждое наблю-
дение является дорогостоящим или труднодоступным. Этот метод
принципиально отличается от классического тем, что при его исполь-
зовании заранее не устанавливается объем выборки л. Испытания
проводятся так. что после каждого из них принимается одно из трех
решений:
— нулевую гипотезу /У„ принять (//, отклонить):
— альтернативную гипотезу //t принять (//„ отклонить):
— провести еще одно испытание в случае неопределенности в
принятии гипотезы или /7,.
Следовательно, до проведения испытаний заранее неизвестно, па
каком шаге испытаний N будет принято решение о принятии гипоте-
зы Н„ или Ht, т.е. N — случайная величина с возможными значе-
ниями л.
В качестве критериев принятия гипотезы //„ или //, берутся та-
кие, которые при заданных вероятностях ошибок первого рода и и
второго рода р обеспечивают минимум математического ожидания
372
Наилучшим среди таких критериев является последовательный
критерий отношений правдоподобия (критерий Вальда)
X* £,(Vft.....X,) (Ю.26)
М*.. .....-tj
где ^(ХрХ;....х„) и AjXpX,....х.) — функции правдоподобия при
условии справедливости гипотезы //„ или /У, (см. § 10.2).
Значение критерия 7. определяется после каждого испытания.
Испытания после //-го шага заканчиваются:
принятием проверяемой гипотезы Н„, если
(Ю.27)
I-а
принятием альтернативной гипотезы /•/,. если
>.2—; (10.23)
а
проведением еше одного испытания, если
-L<x<!z£. (10.29)
1 -а а
Процесс проведения испытаний продолжается до тех пор, пока
не будет принята гипотеза Н„ или Л/,.
Проиллюстрируем метод последовательного анализа на примере
контроля качества продукции.
Пусть проверяется нулевая гипотеза /7(| о том, что вероятность
брака в партия изделий не превышает нормативного значения р',
т.е. /7Й: р < р' против альтернативной гипотезы Ht: р > р'.
Заданы граничные значения вероятностей1 /?0 и pt(p„ < р* < р,)
и вероятностей ошибок первого рода а и второго рола р. Все мно-
жество значений р можно разбить на непсресскаюшиеся три облас-
ти (рис. 10.10).
Область Область Область
принятия неопре- принятия
М» делениости
—>------1-----------1---------1----►
О Л /»’ />| । р
Риг. IU.I0
* С целью упрощения схему проиерки сложной гипотезы: //«: Р < Р‘ прогни аль*
тернапгвиой //,: /»?./>’ мы спалим к проверке простой гипотезы
/7и: Д = />!,(//„< д’) прогни альтернативной //,: ’/’*)•
373
Пусть после проверки п изделий число бракованных из них со-
ставляет т с вероятностями р» и р\ и стандартных л - т с вероятно-
стями I - А) и ! “Рь если верны соответственно гипотезы //и и 7/,
Тогда критерий (10.26) примет вид
х=-Ь.=Га'| | . (ю.зо)
Подставляя значение л в формулы (10.27)—(10.29). получим
(после преобразований) соответственно условия принятия гипотезы
//о или Нь или продолжения испытаний:
т <
т Ья,
а„ < т < Ья,
где числа
(10.31)
(10.32)
(10.33)
а =----------!_CL.
Рь I - Ро
in's₽ + „|nb.a
л,=—“--------
taA-tnba
/»» 1 - р.
называются соответственно приемочными и браковочными числами.
Пусть, например, в результате испытаний изделия с номерами I. 4
оказались бракованными, а с номерами 2. 3, 5, 6 — стандартными. Пусть
при заданных лечениях а. 0. />0, /?, линейные функции аргумента
п - ая (10.32) и ЪИ (10.33) имеют вид прямых, показанных на рис. 10.! 1.
374
Как видно из рис. 10.11, полученная ио результатам испытаний
ломаная т(п) выходит из области неопределенности при п = 6, т.е.
достаточно шести испытаний для принятия гипотезы (в данном
случае гипотезы //|).
Упражнения
10.15. По выборкам объемом Л| = 14 и гь= 9 найдены средние
размеры деталей соответственно т= 182 и у = 185 мм. изготов-
ленных на первом и втором автоматах. Установлено, что размер де-
тали, изготовленной каждым автоматом, имеет нормальный закон
распределения. Известны дисперсии ст =5 и о; =7 для первого и
второго автоматов. На уровне значимости 0.05 выявить влияние на
средний размер детали автомата, на котором она изготовлена. Рас-
смотреть два случая: а) конкурирующая гипотеза //,: х„*у0;
б) конкурирующая гипотеза //,: v„ < у1(.
10.16. Расход сырья на единицу продукции составил:
по старой технологии
303 307 308 Всего
п( 1 4 4 9
по новой технологии
303 304 306 308 Всего
•Ь 2 6 4 . 1 13
Полагая, ‘гго расходы сырья по каждой технологии имеют нор-
мальные распределения с одинаковыми дисперсиями, на уровне
значимости 0,05 выяснить, дает ли новая технология экономию в
среднем расходе сырья.
10.17. В рекламе утверждается, что месячный доход по акциям
А превышает доход по акциям В более чем на 0.3% (или на 0.003). В
течение годичного периода средний месячный доход по акциям В
составил 0.5%. а по акциям .4 — 0,65%, а его средние квадратиче-
ские отклонения соответственно 1.9 и 2.0%. Полагая распределения
доходности по каждой акции нормальными, на уровне значимости
0.05 проверить утверждение, содержащееся в рекламе.
10.18. Имеются следующие данные о качестве детского пита-
ния, изготовленного различными фирмами (в баллах): 40. 39. 42. 37.
38. 43. 45, 41. 48. Есть основание полагать. что показатель качества
продукции последней фирмы (48) зарегистрирован неверно. Являет-
ся ли это значение аномальным (резко выделяющимся) на 5%-ном
уровне значимости?
10.19. Вступительный экзамен проводился на двух факультетах
института. На финансово-кредитном факультете из «| = 900 абиту-
375
риентов выдержали экзамен пц = 500 человек; а на учетно-
статистическом факультете из п> = 800 абитуриентов — = 408. На
уровне значимости а = 0.05 проверить гипотезу об отсутствии су-
щественных различий в уровне подготовки абитуриентов двух фа-
культетов. Рассмотреть два случая: а) конкурирующая гипотеза
/7,: />! х /7.; б) конкурирующая гипотеза Н\: рх > р>.
10.20. В результате выборочной проверки качества однотипных
изделий оказалось, что из 300 изделий фирмы Л бракованных 30, из
400 фирмы В — 52. из 250 фирмы С — 21 и из 500 изделий фирмы
D бракованных 74 изделия. На уровне значимости 0.05 выяснить,
можно ли считать, что различия в качестве изделий различных
фирм существенны.
10.21. По данным примера 10.16 выяснить, являются ли суще-
ственными различия между дисперсиями расхода сырья на единицу
продукции при использовании старой и новой технологий: а) на
уровне значимости 0,05 при конкурирующей гипотезе ст; >ст;.; б) на
уровне значимости 0.02 при конкурирующей гипотезе ст; * ст;’..
10.22. Сравниваются четыре способа обработки изделий. Луч-
шим считается тот из способов, при котором дисперсия контроли-
руемого параметра меньше. Первым способом обработано
15 изделий, вторым — 20. третьим — 20. четвертым способом —
14 изделий. Выборочные дисперсии контролируемого параметра при
разных способах обработки соответственно равны 26, 39. 48. 31 еди-
ниц. На уровне значимости 0,05 выяснить, можно ли считать, что
способы обработки деталей обладают существенно различными
дисперсиями. Можно ли признать первый способ «лучшим*? Пред-
полагается. что контролируемый параметр распределен нормально.
10.23. Установлено, что средний вес таблетки лекарства сильного
действия (номинал) должен быть равен 0.5 мг. Выборочная провер-
ка п - 100 таблеток показала, что средний вес таблетки v =0.53 мг.
На основе проведенных исследований можно считать. *гто вес таб-
летки есть нормально распределенная случайная величина со сред-
ним квадратическим отклонением ст, =0.11 мг. На уровне значимо-
сти 0.05: а) выяснил., можно ли считать полученное в выборке от-
клонение от номинала случайным; б) найти мощность критерия,
использованного в п. а).
10.24. Решить пример 10.23 при условии, что п = 20. х - 0.53 мг.
а выборочное среднее квадратическое отклонение лг = 0,11 мг.
10.25. Компания нс осуществляет инвестиционных вложений в
ценные бумаги с дисперсией годовой доходности более чем 0.04.
Выборка из 52 наблюдений по активу А показала, что выборочная
376
дисперсия се доходности равна 0,045. Выяснить, допустимы ли для
данной компании инвестиционные вложения в актив А на уровне
значимости: а) 0.05; б) 0,01.
10.26. Фирма рассылает рекламные каталоги возможным заказ-
чикам. Как показал опыт, вероятность того, что организация, полу-
чившая каталог, закажет рекламируемое изделие, равна 0.08. Фирма ра-
зослала 1000 каталоюв новой, улучшенной (|юрмы и получила 100 зака-
зов. На уровне значимости 0.05 выяснить, можно ли считать, что
новая форма рекламы существенно лучше прежней.
10.27. В соответствии со стандартом содержание активного ве-
щества в продукции должно составлять 10%. Выборочная контроль-
ная проверка 100 проб показала содержание активного вещества
15%. На уровне значимости 0.05 выяснить, должна ли продукция
быть забракована. Рассмотреть два случая: а) конкурирующая гипо-
теза pi * 0.1; б) конкурирующая гипотеза р\ > 0.1.
В примерах 10.28—10.30 на уровне значимости 0.05 проверить
гипотезу о нормальном законе распределения признака (случайной
величины) А'. используя критерии согласия: а) Пирсона;
б) Колмогорова.
10.28. Поданным примера 8.11.
10.29. По данным примера 8.12.
10.30. Поданным примера 9.30.
10.31. По данным примера 9.34 на уровне значимости 0.05 про-
верить гипотезу о показательном законе распределения признака
(случайной величины) X. используя критерий: а) //-Пирсона;
б) Колмогорова
10.32. Имеются две выборки значений (в усл. ед.) объемов 125
и 80 показателя качества однотипной продукции, изготовленной
двумя фирмами:
14 17 20 23 26 29 32 35 38 41
Л, 2 4 10 15 20 27 18 16 8 5
У, 16 20 24 28 32 36 40 44
'h 3 9 12 17 16 13 7 3
Выяснить, можно ли на уровне значимости 0.05 считать, что
рассматриваемый показатель качества продукции двух фирм описы-
вается одной и той же функцией распределения (т.е. выборки из-
влечены из одной генеральной совокупности). Решить задачу, ис-
пользуя критерии: а) Колмогорова—Смирнова; б) однородности
в) Вилкоксона— Манна—Уитни.
377
10.33. Имеются следующие данные о числе сданных экзаменов
в сессию студентами-заочниками:
Число сданных экзаменов х, 0 1 э Ля 3 4 у
Число студстов п. 1 1 I 3 35 60
На уровне значимости а = 0.05 проверить гипотезу о том. »гто слу-
чайная величина X — число сданных студентами экзаменов — распреде-
лена по биномиальному закону, используя критерий: а) х2-Пирсона;
б) Колмогорова.
10.34. Имеются следующие данные о засоренности партии семян
клевера семенами сорняков:
Число семян в одной пробе х, 0 1 2 3 4 5 6 У tee
Число проб п, 405 366 175 40 8 4 ) * 1000
На уровне значимости ч = 0.05 проверить гипотезу о том, ‘по случай-
ная величина X — число семян сорняков — распределена по закону Пу-
ассона, используя критерий: а) х2-Пирсона; б) Колмогорова.
10.35. Фирма-производитель утверждает, что среднее время без-
отказной работы производимых ею электробытовых приборов со-
ставляет по меньшей мерс 800 ч со средним квадратическим откло-
нением о — 120 ч. Для случайно отобранных п = 50 приборов выбо-
рочное среднее время безотказной работы приборов оказалось рав-
ным 750 ч. На уровне значимости а = 0,05: а) выяснить, удовлетво-
ряет ли гарантии вся партия электробытовых приборов: б) найти
мощность критерия, использованного в п. а): в) определить мини-
мальное число приборов, которое следует проверить, чтобы обеспе-
чить мощность критерия, равную 0.98.
10.36. Решип. пример 10.35 при п- 15. если с неизвестно, а
$ = 110 получено по данным выборки.
Глава
11
Дисперсионным анализ
Выше рассмотрена проверка значимости (существенности, дос-
товерности) различия выборочных средних двух совокупностей. На
практике часто возникает необходимость обобщения задачи, т.е.
проверки существенности различия выборочных средних т сово-
купностей (т > 2), Например, требуется оценить влияние различ-
ных плавок на механические свойства металла, свойств сырья на
показатели качества продукции, количества вносимых удобрений на
урожайность и т.п.
Для эффективного решения такой задачи нужен новый подход,
который и реализуется в дисперсионном анализе.
В настоящее время дисперсионный анализ определяется как ста-
тистический метод, предназначенный для оценки «.зияния различных
факторов на результат эксперимента, а также для последующего
планирования аналогичных экспериментов.
Первоначально (1918 г.) дисперсионный анализ был разработан
английским математиком — статистиком Р.А. Фишером для обра-
ботки результатов агрономических опытов по выявлению условий
получения максимального урожая различных сортов сельскохозяй-
ственных культур. Сам термин «дисперсионный анализ» Фишер
употребил позднее.
По числу факторов, влияние которых исследуется, различают
однофакторный и многофакторный дисперсионный анализ.
11.1. Одиофакторный дисперсионный анализ
Однофакторная дисперсионная модель имеет вил:
=Ц + /\ + Е„ , (11.1)
гпс х — значение исследуемой переменной, полученной на /-м уровне
фактора (/ = I. 2,.... т) су-м порядковым номером (/ = 1.2.л);
Ft — эффект, обусловленный влиянием /-го уровня фактора;
е, — случайная компонента, или возмущение, вызванное
влиянием неконтролируемых факторов, т.е. вариацией переменной
внутри отдельного уровня.
Под уровнем фактора понимается некоторая его мера или со-
стояние, например, количество вносимых удобрений, вил плавки
металла или номер партии деталей и т.п.
379
Основные предпосылки дисперсионного анализа:
I. Математическое ожидание возмущения г.г равно нулю для лю-
бых i. т.с.
М(с„) = 0. (11.2)
2. Возмущения Е( взаимно независимы.
3. Дисперсия возмущения е {или переменной ху) постоянна для
любых i, j, т.е.
D(e,)=<r. (П.З)
4. Возмущение ео {или переменная хч) имеет нормальный закон
распределения N {0; ст2).
Влияние уровней фактора может быть как фиксированным, или
систематический (модель I), так и случайным (модель II).
Пусть, например, необходимо выяснить, имеются ли существен-
ные различия между партиями изделий по некоторому показателю
качества. т.с. проверить влияние на качество одного фактора — партии
изделий. Если включить в исследование все партии сырья, то влияние
уровня такого фактора систематическое (модель I). а полученные вы-
воды применимы только к тем отдельным партиям, которые привле-
кались при исследовании; если же включить только отобранную слу-
чайно часть партий, то влияние фактора случайное (модель II). В
многофакторных комплексах возможна смешанная модель 111. в ко-
торой одни факторы имеют случайные уровни, а другие — фиксиро-
ванные.
Рассмотрим эту- задачу подробнее. Пусть имеется т партий из-
делий. Из каждой партии отобрано соответственно п\, п2.....п„ из-
делий (для простоты полагаем, что л, = п2 =...= пт= л). Значения
показателя качества элзх изделий представим в виде матрицы на-
блюдений
% х|2 ... .Т|„ '
= (*„).(/ = I. 2.nr. j = I. 2.п)
Необходимо проверить существенность влияния партий изделии
на их качество.
Если полагай., что элементы строк матрицы наблюдений — это
численные значения (реализации) случайных величин А'|. Х2..Х„„
380
выражающих качество изделий и имеющих нормальный закон рас-
пределении с математическими ожиданиями соответственно
fl|t д2.и одинаковыми дисперсиями о , то данная задача сво-
дится к проверке нулевой гипотезы /70: =а. - ... = ат. осуществ-
ляемой в дисперсионном анализе.
Обозначим усреднение по какому-либо индексу звездочкой (или
точкой) вместо индекса, тогда средний показатель качества изделий /-й
партии, или групповая средняя для /-го уровня фактора, примет вид:
х4,=^—, (11.4)
п
а общая средняя —
m if м.
Zb, IX
х.. = —— - . (11.5)
тп т
Рассмотрим сумму квадратов отклонений наблюдений х„от
общей средней х„:
=££(',. -V -и+
<•1 /•! «-1 ««I /«I
Г- <"б>
1-1 /-1
или Q = Qi + Q> + Qy
Последнее слагаемое
а=2Ё£(*. -\)(\ - г-)=2±(.г.-х_ )22(хЛ -х )=0,
<-1 /-1 М ;«1
так как сумма отклонений значений переменной от ее средней, т.е.
Х(х« ) Равна »УЛЮ-
/-1
Первое слагаемое можно записать в виде:
у = ±±(5;.-я.у=«±(7.-г..)2. (П.7)
/-1
В результате получим следующее тождество:
<?=QI+Q:. (И.8)
381
где (? = £Х(\, ~~ общая, или полная, сумма квадратов от-
1-1 /-1
клонсний;
$ =л^(х„ -г..) — сумма квадратов отклонений групповых
ы
средних от обшей средней, или межгрупповая (факторная) сумма
квадратов отклонений;
\ -V.): — сумма квадратов отклонений наблюдении
<.| f-i
от групповых средних, или внутригрупповая (остаточная) сумма квад-
ратов отклонений.
В разложении (11.8) заключена основная идея дис-
персионного анализа. Если поделить обе части равенства (11.8) на
число наблюдений, го получим рассмотренное выше правило сло-
жения дисперсий (8.12). Применительно к рассматриваемой задаче
равенство (11.8) показывает, что общая вариация показателя каче-
ства. измеренная суммой Q, складывается из двух компонент —
Qf и (А, характеризующих изменчивость этого показателя между
партиями (00 и изменчивость «внутри» партий ((?>). характери-
зующих одинаковую (по условию) для всех партий вариацию пол
воздействием неучтенных факторов.
В дисперсионном анализе анализируются не сами суммы квадра-
тов отклонений, а так называемые средние квадрат ы. яв-
ляющиеся несмещенными опенками соответствующих дисперсий,
которые получаются делением сумм квадратов отклонений на соот-
ветствующее число степеней свободы.
Напомним, что чисто степеней свободы определяется как об-
щее число наблюдений минус число связывающих их уравнений
Поэтому для среднего квадрата л;. являющегося несмещенной
оценкой межгрупповой дисперсии, число степеней свободы
ki = т - I, так как при его расчете используются т групповых
средних, связанных между собой одним уравнением (11.5) А для
среднего квадрата s;. являющегося несмещенной оценкой внут-
ригрупповой дисперсии, число степеней свободы к; = тп - т.
ибо при се расчете используются все тп наблюдений, связанных
между собой т уравнениями (11.4). Таким образом, s'; = Q\/(m - I);
sj = Qz/(mn - т).
Найдем математические ожидания средних квадратов з' и .
подставив в их формулы выражение х,; (11.1) через параметры модели.
382
п
т-1
т-1
wk)=^Tw
L-i
Ц + /\ +£,.- м-г.- с.. )J =
т-1
— М
т -1 77
М £(^.“СМ)' =
+ СГ
(Н.9)
(ибо М 2jj Г,- F. )(ги. - с..) =0 с учетом свойств математическо-
го ожидания, а
=—л/ т Схе> (табл. 1 zb-j Ml f-l w ^^(н + Л + е„-М-^-е,.); = l.l |.| 1 « 1 m . 1 = —Уа; =— Усг-' =— /»cf =o:. (JI.10) m Zi ’ m м m го анализа лредсгавим в виде таблицы Таблица 11.1
« -1 лу дисперсионно l.l).
Компо- ненты диспер- сии Сумма квадратов Число степе- ней свободы Средний квадрат Математическое ожидание среднего квадрата
Меж- груп- повая Внут- ри- груп- повая Общая Q, e=ZZK-J-); /.I /.I . । т — 1 тп - т тп - 1 тп-т т-1 нт' (модель l). па', + о (модель II) а'
383
Для модели 1с фиксирован н ы м и уровнями фактора
F,(i =1.2.т) — величины неслучайные, поэтому
Л/(.г;) = л£( F - F.)’’/(т - I) + сг .
1-1
Гипотеза Но примет вид F = F. (/ = 1,2....т). т.е. влияние всех
уровней фактора одно и то же. В случае справедливости этой гипо-
тезы А/ (а‘) = М (.г;) = ст' .
Для случайной модели II слагаемое F, в выражения
(11.1) — величина случайная. Обозначая ее дисперсию
ст; = М 5^(Л - F.)’ /(ш -1) . получим из (11.9)
М (5') = чст; + ст*,
(ПИ)
и, как и в модели I. Л/(л:) = ст:. В случае справедливости нулевой
гипотезы Но, которая для модели II принимает вид ст; = 0. имеем.
Итак, в случае однофакгорного комплекса как для модели I. гак и мо-
дели II средние квадраты л* и я&гяются несмещенными и, как можно
показал», независимыми оценками одной и пюй же дисперсии ст*.
Следовательно, проверка нулевой гипотезы Но свелась к провер-
ке существенности различия несмещенных выборочных оценок л,
и s; дисперсии ст* . рассмотренной в § 10.5.
Гипотеза Но отвергается, если фактически вычисленное значе-
*
ние статистики F = Ц- больше критического F„ t ( . определенного
Л2
на уровне значимости а при числе степеней свободы = тп - т.
и принимается, если F < Fa.t i^.
Применительно к данной задаче опровержение гипотезы Я(, озна-
чает наличие существенных различий в качестве изделий различных
партий на рассматриваемом уровне значимости.
Замечание. Для вычисления сумм квадратов Q\. Q2, Q час-
то бывает удобно использовать следующие формулы:
—L. (11.12)
n mn
.. t
1.1 f-l fl
384
. . V
. . Z2>.
’ <l,w>
т.е. сами средние, вообще говоря, находить не обязательно.
О Пример 11.1. Имеются четыре партии сырья для текстильной
промышленности. Из каждой партии отобрано по пять образцов и
проведены испытания на определение величины разрывной нагрузки,
результаты испытаний приведены в табл. 11.2.
Таблица 11.2
Помер партии Разрывная нагрузка (кг/см2)
1 200 140 170 145 165
2 190 150 210 150 150
3 230 190 200 190 200
4 150 170 150 170 180
Необходимо выяснить, существенно ли влияние различных партий
сырья на величину разрывной нагрузки. Принять а = 0.05.
Ре ш е н и е. Имеем т = 4. п = 5. Найдем средние значения
разрывной нагрузки для каждой партии по формуле (11.4):
х,. =(200 + 140 + 170 + 145 + 165) / 5 = 164 (кг/см2)
и аналогично
х.# = 170, хч =202 и х^ = 164 (кг/см2).
Среднее значение разрывной нагрузки всех отобранных образ-
цов по формуле (11.5):
х.. = (200 т 140 + ...*!70*180)/20 = 175 (кг/см2)
(или, иначе, через групповые средние.
х..= (164 + 170 + 202 + 164) / 4 = 175 (кг/см2)).
Вычислим суммы квадратов отклонений по формулам (11.6). (11.7):
0 = 5£(.7 - х..)‘ = 5[(164 -175)* + (170 -175)’ + (202 - I75)"' +
♦(164-175)*] = 5-996=4980:
= Z Z (\ )’ = (200 -164 )2 ♦...♦( 165 -164 Г ♦
/•I /•»
+(190 - 170)*' ♦... + ( 150 -170)*’ + ( 230 - 202 )*♦... + ( 200 - 202 )*' ♦
+(>50-164)' +...4 (180-164)’ = 7270;
13 Геирты и мгпипгкчм unninwu
385
<? = ZlU-J-):=(200-l75):+(140-|75):+... + (l70-l75) +
/-I 1*1
+(180—175): = 12 250.
Соответствующее число степеней свободы для этих сумм т - I - з;
/пл — л/= 5’4-4 = 16: /мл — 1 = 5-4-1 = 19.
Результаты расчета сведем в табл. 11.3.
Ткб.|цца 11.3
Компоненты дисперсии Суммы квадратов Число степеней свободы Средние квадраты
Межгрупповая 4 980 3 1660,0
Внутригрупповая 7 270 16 454,4
Общая 12 250 19
Фактически наблюдаемое значение статистики I= Ц- =---------=
л: 454.4
=3,65. По табл. VI приложений критическое значение F-критсрия
Фишера—Снедекора на уровне значимости а = 0.05 при Л| = 3 и
Л'2 = 16 степенях свободы fo.O5:3;i6 = 3,24. Так как F > /Ъ.05:3:1б* то
нулевая гипотеза отвергается, т.с. на уровне значимости а = 0.05 (с
надежностью 0,95) различие между партиями сырья оказывает су-
щественное влияние на величину разрывной нагрузки.
Замечание. С точки зрения техники вычислений сумм 0(.
02, Q проще воспользоваться формулами (11.12)—(11.14), не тре-
бующими вычисления средних. Так, вычислив
У У х, = 200 +140 +... +170 +180 = 3500,
•-I /и
$
= 20°; *,4°: + -+17°:+18°2 =624 75°-
•-I /*1
= (200 + ...+ 165): + (190 + ... + 150)? +
+ (230 +... + 200)* * (150 4 ... + 180): = 3 087 400.
найдем по формулам (11.12), (11.13) и (11.14)
0! = 3 087 400 / 5 - 3500-720 = 4980,
02 = 624 750 - 3 087 400 / 5 = 7270
н
0 = 624 750 - 35OO-/2O = 12 250. ►
386
11.2. Понятие о двухфакторном дисперсионном
анализе
Предположим, что в рассматриваемой в § 11.1 задаче о качестве
различных (т) партий изделия изготавливались на разных (Л стан-
ках и требуется выяснить, имеются ли существенные различия в
качестве изделий по каждому фактору: А — партия изделий, В —
станок. В результате мы приходим к задаче двухфакторного диспер-
сионного анализа.
Все имеющиеся данные представим в виде табл. 11.4, в которой
по строкам — уровни А, фактора А. по столбцам — уровни В, фак-
тора В, а в соответствующих клетках, или ячейках, таблицы нахо-
дятся значения показателя качества изделий хдо (/ = 1,2....т\
1.2..../;* = I, 2..л).
Таб.ищи 11.4
\ в А Si в2 ... В, ... Bl
Ai А) -*•'111 •*211 ...,Хщ -•*2Н *121 *124 *221 *224 ... *1/1. *2/1- ••••*2/4 ... Х|/|,...Л|« *2/1 *2Д
А Ая *1 1 -X.nl 1 Г,н *Д1 */2А *«21 *м24 Хяь Х|/|,,..Л(Л *«!/!•• •ьХ/пЫ.
... X .... -1 ...
Двухфакторная дисперсионная модель и st ее т вид:
*V4 = ц + F, + Gt + + суЪ
(11.15)
где Худ — значение наблюдения в ячейке ij с номером к;
р — общая средняя;
F/ — эффект, обусловленный влиянием /-го уровня фактора Л;
Gj — эффект, обусловленный влиянием /-го уровня фактора В",
lt) — эффект, обусловленный взаимодействием двух факторов,
т.е. отклонение от средней по наблюдениям в ячейке ij от суммы
первых трех слагаемых в модели (11.15);
е,д — возмущение, обусловленное вариацией переменной внут-
ри отдельной ячейки.
Полагаем, что имеет нормальный закон распредстения .V(0;cr). а
вое математические ожидания равны нулю.
3X7
Групповые средние находятся но формулам:
в ячейке —
по строке —
(11.16)
по столбцу —
Общая средняя
т
(П.17)
(11.18)
(П.19)
Таблица дисперсионного анализа имеет вид (табл. 11.5).
Таблица 11.5
Компоненты дисперсии Сумма квадратов Чист степеней свободы Средние квадраты
Межгруп- повая й='"£(?._-X-)’ <•1 т - 1
(фактор Л) т -1
Мсжгруп- J ч
новая /I /- 1
(фактор В)
Взаи.мо- (?,=
действие («-1Х/-1) е>
(АВ) <-l 1-1 ’ ('«-|)(/-|)
Остаточная 1-1 /-1 *.| mln — ml г- а
mln-ml
Общая й-ЁЕЁк.-'-У mln — I
1-1 /-1
388
Можно показал,, что проверка нулевых гипотез Нл, Hr, Нлц об
отсутствии влияния на рассматриваемую переменную факторов Л. В
и их взаимодействия АВ осуществляется сравнением отношений
s' Д;. /•'•’J • -Ч/vi (Для модели I с фиксированными уровнями факто-
ров) или отношений х*/л*. л:/л? • *)/•’< <лля случайной модели II) с
соответствующими табличными значениями F-критерия Фишера—
Снедекора. Для смешанной модели 111 проверка гипотез относительно
факторов с фиксированными уровнями проводится так. как в модели
Л, а факторов со случайными уровнями — как в модели I.
Если л = I. т.с. при одном наблюдении н ячейке, то не все ну-
левые гипотезы могут бып, проверены, так как выпадает компонен-
та Qy из общей суммы квадратов отклонений. а с ней и средний
квадрат л;. ибо в этом случае не может быть речи о взаимодейст-
вии факторов.
t> Пример 11.2. В табл. 11.6 приведены суточные привесы (г) отобран-
ных для исследования 18 пороет в зависимости от метода содержания
поросят (фактор /1) и качества их кормления (фактор В).
'Гнблпцп 11.6
Количество голов в группе (фактор А) Содержание протеина в корме, г (фактор В)
Bt « 80 В: = 100
А, = 30 530. 540. 550 600. 620. 580
,4.= 100 490. 510. 520 550. 540. 560
Лл = 300 430. 420. 450 470, 460. 430
Необходимо на уровне значимости а = 0.05 оценить существен-
ность (достоверность) влияния каждого фактора и их взаимодействия
на суточный привес поросят.
Рсшенн с. Имеем т = 3. /= 2. п = 3. Определим (в г) сред-
ние значения привеса:
в ячейках — по формуле (11.16):
530 *540 + 550 _ Zf|_
д- =---------------= 540 и аналогично д\. =600;
II» !•» ’
х =506,7: х.. =550; х. =433,3; х =453.3;
?i. и.
по строкам - по формуле (11.17):
540 + 600 ...
х. ----------= 570 и аналогично х, = >28.4; х. = 44.>.2;
по столбцам — по формуле (11.18):
540 + 506,7+433,3 _ _ „. ,
х ( =-------------------- 493,3 и аналогично г . = 534.4 .
389
Обшин средний принес — по формуле (11.19):
540 4 600 + 506.7 + 550 + 433.3 + 453.3 _._Л к
х... --------------------------------------- 513.9 (г).
6
Все средние значения привеса (г) поместим в табл. 11.7.
Таблицы 11.7
Количество голов в группе (фактор А) Содержание протеина в корме. г (фактор R)
Я, = 80 52 = 100 5L
4 = 30 хн. =540.0 х.. =600.0 1 • • х,„ = 570.0
4 = 100 х,,. =506.7 х.. =550.0 • • • х:..= 528,4
41 = 300 х„. =433.3 хк. =453.3 Ч. =443.3
X, . х,. =493.3 х. =534.4 • •• x.w =513.9
Из табл. 11.7 следует, что с увеличением количества голов и
группе средний суточный привес поросят в среднем уменьшается, а
при увеличении содержания протеина в корме — в среднем увели-
чивается. Но является ли эта тенденция достоверной или объясня-
ется случайными причинами? Для ответа на этот вопрос по форму-
лам табл. 11.5 вычислим необходимые суммы квадратов отклонении:
(Л = 2 • 3f(57O - 5I3.9)2 * (528.4 - 513,9)-’ + (443.2 - 513.9)2| = 50 011.1;
^2= 3-3 Ц493.3 - 513,9)2 + (534,4 - 513,9)-'| = 7605,6;
21 = 3|(540 - 570 - 493.3 + 513,9)-’ + ... +
+ (453.3 - 443.3 - 534,4 + 513.9)2| = 1211.1;
(?4 = (530 - 540)2 + ... + (550 - 540)-’ + (600 - 600)2 + ... +
+ (580 - 600)- + ... + (470 - 453,3)2 + ... + (430 - 453.3)’= 3000.0:
Q = (530 - 5I3.9)2 + (540 - 5I3.9)2 + ... + (430 - 513.9)-’ = 61 827.8
Средние квадраты находим делением полученных сумм на соответст-
вующее им чисто степеней свободы т - 1 = 2,/- I = I; {nt - 1)(/ - 1) = 2;
mln - ml = 18 - 6 = 12; mln -1 = 18-1 = 17.
Результаты расчета сведем в табл. 11.8.
390
ТаГмшш U.K
Компонента дисперсии Суммы квад- ратов Число степе- ней свободы Средние квадраты
Межгрупповая (фактор А) = 50 011.1 2 .< = 25 005.5
Межгрупповая (фактор В) Q> = 7605,6 1 .< = 7605.6
Взаимодействие (ЛВ) Q; = 1211.1 2 = 605,6
Остаточная (?4 = 3000.0 12 л; = 250.0
Обшая 0= 61 827.8 17
Очевидно, данные факторы имеют фиксированные уровни, т.е.
мы находимся в рамках модели I Поэтому для проверки сущест-
венности влияния факторов А, В и их взаимодействия АВ необхо-
димо найти отношения:
< 25 005.5
х; ’ 250.0
= 100.0; F„
si __ 7605.6
v; 250.0
= 30.4;
„ л; 605.6 „
=-т =-----= 2.42 и сравнить их с табличными значениями (см.
'* .< 250.0
табл. VI приложений) соответственно Л|.о5;2;»2= 3.88; Л1,о5;|;|’ ~ 4.75;
Лл$;2;!2 = 3.88. Так как /•', > F,t(fi:i. и Fn > F„„yi i:. то влияние метода
содержания поросят (фактора Л) и качества их кормления (фактора
В) является существенным В силу того что F,„ < F,t,^.:i:, взаимодей-
ствие указанных факторов незначимо (на 5%-ном уровне). ►
3 а м е ч а и и е. С точки зрения техники вычислений для нахож-
дения сумм квадратов СА- (?:• <?>. ©ь Q целесообразнее использо-
вать формулы:
±[±±v.J'
(7, = -±‘ 1' 1-L _ -1 2Л2------, (11.20)
In mln
zfzzJ2 itixU
у. = 1—L - v-1 '141—L, (i ио
inn nin
.... zz(l>,T
" -• <|1И>
<•1 /-1 Ы n
391
(11.23)
ft* С- Ci- (??- Оь
(11.24)
Так. в рассматриваемом примере 11.2:
= 530 + 540 + - + 460 + 430 = 9250-
i«l /•! 1-1
zizХ-, = 530- + 5402 + ... + 4602 + 4302 = 4 815 300.
I I ?-1 4-1
1 / )
Z ZZ*..
,.| \ *.1
= (530 + 540 + ... + 620 + 58O)2 + ... +
+ (430 + 420 + ... + 460 + 430)2 = 28 820 900.
j = (53°+ 540 + - + 420 + 450)2+-+
+ (600 + 620 + ... + 460 + 430)2 = 42 849 700.
| = (530 + 540 + 550)2 + (600 + 620 + 580)2 + ... +
+ (470 + 460 + 430)-’ = |4 436 900,
и по формулам (11.20)—(11.24):
28 820 900 _ 925(У
1 2-3 3-2-3
42 849ТО0 ?25О^
3-3 3-2-3
0, = 4 815 300 - —436 9-° = 3000 ; 0 = 4 815 300-^^- = 61 827.8 :
3 3-2-3
03= 61 827.8 - 50 011.1 - 7605.6 - 3000 = 1211.1. ►
В заключение отметим, что при решении реальных задач мею-
дом дисперсионного анализа используются статистические про-
граммные пакеты (см., например. |34|).
Отклонение от основных предпосылок дисперсионного анализа -
нормальности распределения исследуемой переменной и равенства
дисперсий в ячейках (если оно не чрезмерное) — не сказывается
существенно на результатах дисперсионного анализа при равном
числе наблюдений в ячейках, но может быть очень чувствительно
392
при неравном их числе Кроме того, при неравном числе наблюде-
ний в ячейках резко возрастает сложность аппарата дисперсионного
анализа. Поэтому рекомендуется планировать схему с равным чис-
лом наблюдений в ячейках, а если встречаются недостающие дан-
ные. то возмещать их средними значениями других наблюдений в
ячейках. При этом, однако, искусственно введенные недостающие
данные не следует учитывать при подсчете числа степеней свободы.
Упражнения
11.3. В течение шести лет использовались пять различных
технологий по выращиванию сельскохозяйственной культуры. Дан-
ные по эксперименту (в u/га) приведены в таблице:
Номер наблюдения (гем)) Технология (фактор .4)
4| <4$
1 1.2 0.6 0.9 1.7 1.0
2 1.1 1.1 0.6 1.4 1.4
3 1.0 0.8 0.8 1.3 1.1
4 1.3 0.7 1.0 1.5 0.9
5 1.1 0.7 1.0 1.2 1.2
6 0.8 0.9 1.1 1.3 1.5
Итого 6.S 4.8 5.4 8.4 7.1
Необходимо на уровне значимости а = 0.05 установить влияние раз-
личных технологий на урожайность культуры.
11.4. На заводе установлено четыре линии по выпуску обли-
цовочной плитки. С каждой линии случайным образом в течение
смены отобрано по 10 плиток и сделаны замеры их толщины (мм).
Отклонения от номинального размера приведены в таблице:
Линия по вы- пуску плиток Номер испытания
1 2 3 4 5 6 7 8 9 10
1 0,6 0.2 0.4 0.5 0.8 0.2 0.1 0.6 0.8 0,8
2 0.2 0.2 0.4 0.3 0.3 0.6 0,8 0.2 0.5 0,5
3 0.8 0.6 0.2 0.4 0.9 1.1 0.8 0,2 0,4 0.8
4 0.7 0.7 0.3 0.3 0.2 0.8 0.6 0.4 0.2 0.6
393
Требуется на уровне значимости а = 0.05 установить зависимость
выпуска качественных плиток отлипни выпуска (фактора А).
11.5. Имеются следующие данные об урожайности четырех
сортов пшеницы на выделенных пяти участках земли (блоках):
Сорт Урожайность по Люкам, ц/га
1 > 3 4 5
1 2.87 2.67 2.16 2.50 2.82
2 2.45 2.85 2.77 2.87 3.25
3 2.32 2.47 2,00 2.40 2.40
4 2.90 2.87 2.25 2.80 2.70
Требуется на уровне значимости а = 0,05 установить влияние
на урожайность сорта пшеницы (фактора А) и участков земли -
блоков (фактора £0
11.6. На четырех предприятиях В\, В2. Ви В4 проверялись три
технологии производства At. А2. Ау однотипных изделий. Данные о
производительности труда в условных единицах приведены в таблице:
'Х А Ах А, Ау
В 1 2 3 1 > 3 1 2 3
Я. 50 54 58 62 60 58 65 71 65
& 54 46 50 64 59 60 59 54 61
By 52 48 50 70 62 60 59 66 64
Ва 60 55 56 58 54 50 71 74 62
Требуется на уровне значимости а = 0.05 установить влияние
на производительность труда технологий (фактора /1) и предприятии
(фактора В).
Глава
12
Корреляционный анализ
Диалектический подход к изучению природы и общества требует
рассмотрения явлений в их взаимосвязи и непрестанном измене-
нии.
Понятия корреляции и регрессии появились в середине XIX в. бла-
годаря работам английских статистиков Ф. Гальтона и К. Пирсона.
Первый термин произошел от латинского ^correlation — соотношение,
взаимосвязь. Второй термин (от лат. • regression — движение назад)
введен Ф. Гальюном, который, изучая зависимость между ростом ро-
дителей и их детей, обнаружил явление •регрессии к среднему» — у
детей, родившихся у очень высоких родителей, рост имел тенденцию
быть ближе к средней величине.
12.1. Функциональная, статистическая
и корреляционная зависимости
В естественных науках часто речь идет о функциональной зави-
симости (связи), когда каждому значению одной переменной соот-
ветствует вполне определенное значение другой. Функциональная за-
висимость может иметь место как между детерминированными (не-
случайными) переменными (например, зависимость скорости паде-
ния в вакууме от времени и т.п.), так и между случайными величи-
нами (например, зависимость стоимости проданных изделий от их
числа и т.п.).
В экономике в большинстве случаев между переменными вели-
чинами существуют зависимости, когда каждому значению одной
переменной соответствует не какое-то определенное, а множе-
ство возможных значений другой переменной. Иначе говоря, каж-
дому значению одной переменной соответствует определенное (услов-
ное) распределение другой переменной. Такая зависимость (связь) по-
лучила название статистической (или стохастической, вероятност-
ной). (О ней уже шла речь в § 5.5.)
Возникновение понятия статистической связи обусловливается
тем, что зависимая переменная подвержена влиянию ряда некон-
тролируемых или неучтенных факторов, а также тем. что измерение
значений переменных неизбежно сопровождается некоторыми слу-
чайными ошибками. Примером статистической связи является за-
висимость урожайности от количества внесенных удобрений, про-
изводительности труда на предприятии от его энерговооруженности
и т.п.
В силу неоднозначности статистической зависимости между К и
АГ для исследователя, в частности, представляет интерес у с р е д -
н е н и а я по х схема зависимости, т.е. закономерность в измене-
395
нии среднего значения — условного математического ожидания1
Л/Х(И (математического ожидания случайной переменной К най-
денного при условии, что переменная X приняла значение х) в зави-
симости от х
Определение. Статистическая зависимость между двум»
переменными, при которой каждому значению одной переменной соот-
ветствует определенное среднее значение, т.е. условное математиче-
ское ожидание другой, называется корреляционной. Иначе. корреляци-
онной зависимостью между двумя переменными величинами называется
функциональная зависимость между значениями одной из них и условным
математическим ожиданием другой.
Корреляционная зависимость может быть представлена в виде:
Л/,(Г) = ф(х) <12.1>
или Л/, (Д') = 4/0). (12.2)
Предполагается, что ф(л) * const и *|/(г)* const . т.е. если при
изменении л или у условные математические ожидания Л/, (Г) и
xV/j.V) не изменяются, то говорят, что корреляционная зависи-
мость между переменными X и Y отсутствует.
Сравнивая различные виды зависимости между X и К можно
сказать, что с изменением значений переменной X при ф у н к -
ц и о н а л ьи ой зависимости однозначно изменяется определен-
ное значение переменной Y. при корреляций н ной — оп-
ределенное среднее значение (условное математическое ожидание) )
а при с т а т и с т и ч е с к о й — определенное (условное) распреде-
ление переменной К (рис. 12.1).
Таким образом, из рассмотренных зависимостей наиболее общей
выступает статистическая зависимость'. Каждая корреляционная
зависимость является статистической, но нс каждая статистическая
зависимость является корреляционной. Функциональная зависи-
мость представляет частный случай корреляционной (об этом речь
еще пойдет ниже, в § 12.3).
’ Для условного математического ожидания в литературе используется также
обозначение ЛЛУ|А’ = .«).
•’ Хотя статистическая зависимость и является наиболее общей из рассмотрен-
ных. она нс отражал любую возможную зависимость между переменными »
условиях неопределенности. Например, можно предполагать, что существует
некоторая зависимость между числом (продолжительностью) военных конфлик
тон и числом изобретений за определенный период времени. Эта зависимость
хотя и сводтпся к зависимости между событиями с неопределенным исходом
(могут произойти или не произойти), но не является статистической, ибо каж-
дому значению одной переменной нельзя поставить в соответствие распределе-
ние другой, так как к таким единичным и неповторяемым и одинаковых услови-
ях событиям, какими являются соответственно военные конфликты и изобрете-
ния, неприменимо само понятие вероятности тем § 1.3).
396
Рис. 12.1
Уравнении (12.1) и (12.2) называются модельными уравнениями
регрессии (или просто уравнениями регрессии} соответственно Y по X
и X по Г1, функции ф(х)к и(г)- модельными функциями регрессии
(или функциями регрессии}, а их графики — модельными линиями рег-
рессии (или линиями регрессии).
Для отыскания молельных уравнений регрессии, вообще говоря,
необходимо знать закон распределения двумерной случайной ветчины
(X, У). На практике исследователь. как правило, располагает лишь вы-
боркой пар значений (х . у,) ограниченного объема. В этом случае речь
может идти об оценке (приближенном выражении) по выборке функции
регрессии. Такой наилучшей (в смысле метола наименьших квадратов)
оценкой является выборочная линия (кривая) регрессии К по X
у. =Ф(Х, Д..Л,....ьг), (12.3)
1дс ут — условная (групповая) средняя переменной У при фиксированном
значении переменной Х= х; Д......Ьр — параметры кривой.
Аналогично определяется выборочная линия [кривая) регрессии X
по Y:
х, =v(y. с„.с,...cj. (12.4)
где х„. — условная [групповая) средняя переменной X при фиксированном
значении переменной Y- у, q......ср — параметры кривой
' Уравнения (12.3). (12.4) называют также выборочными уравнениями
регрессии соответственно Y no X и X по
' Или Кна X и Л на К
1 В дальнейшем для краткости там. где это очевидно по смыслу, мы часто н вы-
борочные уравнения (линии) регрессии будем нлнивагь просто уравнениями
(линиями) регрессии
397
При правильно определенных аппроксимирующих функция*.
ф(л. Ь„. Ь...... Ьг) и ф(г. с„. с,.с.) с увеличением объема выбор-
ки (л -> <г.) они будут сходиться по вероятности соответственно к
функциям регрессии <р(х) и »р(у).
Статистические связи между переменными можно изучать мето-
дами корреляционного и регрессионного анализа. Основной задачей
регрессионного анализа является установление формы и изу-
чение зависимости между переменными. Основной задачей корре -
л яционного анализа — выявление связи между случайными пе-
ременными и оценка ее тесноты.
Вначале (§ 12.2. 12.3) познакомимся с основными понятиями
корреляционного и регрессионного анализа. а затем (§ 12.4-12.7,
13.1-13.8) перейдем к более детальному изучению этих методов.
12.2. Линейная парная регрессия
Данные о статистической зависимости удобно задавать в вше
корреляционной таблицы.
Рассмотрим в качестве примера зависимость между суточной
выработкой продукции Y (т) и величиной основных производствен-
ных фондов X (млн руб.) для совокупности 50 однотипных пред-
приятий (табл. 12.1).
Таллина 12.1
Вели- чина ОПФ. Середи- ны ин- плер- Суточная выработка продукции, т ( Н Всего л, Группо- вая сред няя
млн. руб. (.¥) валов 7-11 П-15 15-19 19-23 23-27 г , т
\ х, 9 13 17 21 25
20-25 22.5 2 1 — — — 3 10.3
25-30 27.5 3 6 4 — — 13 13.3
30-35 32.5 — 3 И 7 — 21 I7.S
35-40 37.5 — 1 2 6 2 11 20.3
40-45 42.5 — — — I 1 2 23,0
Всего п} 5 и 17 14 3 50 —
Групповая сред- няя V . млн руб 25.5 29.3 31.9 35.4 39.2 — —
(В таблице через х, и у, обозначены середины соответствующих
интервалов, а через л, и п, — соответственно их частоты.)
Изобразим полученную зависимость графически точками коор-
динатной (ыоскостн (рис. 12.2). Такое изображение статистической
зависимости называется полем корреляции.
398
Рис. 12.2
Для каждого значения х( (/ = I. 2./). т.е. для каждой строки
корреляционной таблицы вычислим групповые средние
tw
?,= —-----. (12.5)
п,
пае Лу — частоты пар (х„ у,) и л = лт — число интервалов по
переменной К
Вычисленные групповые средние у, помсоим в последнем столбце
корреляционной таблицы и изобразим графически в виде ломаной, назы-
ваемой эмпирической линией регрессии У по X (см. рис. 12.2).
Аналогично для каждого значения у; (/ = 1,2, .... т) по формуле
х, =-^---- (12.6)
вычислим групповые средние х (ем. нижнюю строку корреляцион-
ной таблицы)1, где nt = . I — число интервалов по переменной X.
По виду ломаной .можно предположить наличие л и и с й и о й
корреляционной зависимости У'по X между двумя рассматривасмы-
1 Чтобы не югроможшть чертеж, эмпирическая шния регрессии X по У на
рис 12.2 нс показана
399
мн переменными, которая графически выражается тем точнее, чем
больше объем выборки (число рассматриваемых предприятий) п:
" = ZM- =Zn/ = ZZwv* <127>
i=i /=i /»•
Поэтому уравнение регрессии (12.3) будем искать в виде:
у. =Л0 + ^х. <12-3>
Отвлечемся на время от рассматриваемого примера и найдем
формулы расчета неизвестных параметров уравнения линейной pci-
рессии.
С этой целью применим метод наименьших квадратов, согласно
которому неизвестные параметры м Ь\ выбираются таким обра-
зом. чтобы сумма квадратов отклонений эмпирических групповых
средних у,. вычисленных по формуле (12.5), от значений у, . найден-
ных по уравнению регрессии (12.8). была минимальной:
s=Z(x.. )Ч= Z(h-+^х< -у>)_> min • <12-9*
••I /-1
На основании необходимого условия экстремума функции двух
переменных 5 = 5(/>o. Л|) приравниваем к нулю ее частные произ-
водные. т.е.
^ = 2Z(^+Л^_ЯИ=0-
А. ...
— = 222(А, * l\x, - y).v/i = О,
откуда после преобразований получим систему нормальных уравне-
ний для определения параметров линейной регрессии:
/ j i
^Z"<+ '’•Zл/’'
fl l»l 1*1
/ J I
^Zx<". +/>.Zv''1- =ZY?-"-
f=l t*l <»l
(12.10)
Учитывая (12.5), преобразуем выражения:
Zx-.=z
nt
400
Ы l-l
i w
M /«I
Теперь с учетом (12.7), разделив обе части уравнений (12.10) на
л, получим систему нормальных уравнений в виде:
Л0 + Л,у = у
(12.11)
xy,
где соответствующие средние определяются по формулам:
х = -^---
п
1.УЛ
г = —--
п
(12.12)
лт
п
(12.13)
х;=^---
п
Подставляя значение
=У-Ь,х
(12.14)
(12.14)
из первого уравнения системы (12.11) в уравнение регрессии (12.8),
получим г, = г - Л,х * Л,х. или
Л-.г=Л|(х-х). (12.15)
Коэффициент />| в уравнении регрессии, называемый выбороч-
ным коэффициентом регрессии (или просто коэффициентом регрессии)
Y по X. будем обозначать символом Ьух. Теперь уравнение регрессии
У по Д' запишется так:
.У,-7 = А„(х-х). (12.16)
Коэффициент регрессии Y по X показывает, на сколько единиц в
среднем изменяется переменная Y при увеличении переменной X
на одну единицу.
Решая систему (12.11). найдем
Ьи=А1=^П = ^Д = 4. (12.17)
№ - г Л.‘
401
где — выборочная дисперсия переменной Л (см. формулу (8.10)):
- . Хх-п'
< =Г -Г =-=!------(х)‘; <12.18)
И — выборочный корреляционный момент или выборочная
ковариация1:
/ Я1
ZiW
р = лт-хг= ——----------х г. <12.19)
и
Рассуждая аналогично и полагая уравнение регрессии (12.4) ли-
нейным. можно привести его к виду:
= <12.20)
где = = Л (|2.21)
у*-Г <
— выборочный коэффициент регрессии (или просто коэффициент рег-
рессии) X по Y, показывающий. на сколько единиц «среднем из-
меняется переменная X при увеличении переменной Y на одну единицу;
.Гг=у--у;=—-------(J)’ (12.22)
п
—выборочная дисперсия переменной Y
Так как числители в формулах (12.17) и (12.21) для и ^.сов-
падают. а знаменатели — положительные величины, то коэффициенты
регрессии и Ь^. имеют одинаковые знаки, определяемые знаком р
Из уравнений регрессии (12.16) и (12.20) следует, что коэффициен-
ты Ьух и |/Д„. определяют угловые коэффициенты (тангенсы углов
наклона) к оси Ох соответствующих линий регрессии, пересекаю-
щихся в точке (х. у) (см. рис. 12.4).
О Пример 12.1. По данным табл. 12.1 найти уравнения регрес-
сии Y по X и X по Y и пояснить их смысл.
Р е ш е н и е. Вычислим все необходимые суммы:
1 Для выборочной ковариации переменных X н У исполыустся также оботачс-
ние cov(.V.)’). 5*
402
£x,nt s 22.5- 3 + 27,5- 13 + 32.5-21 + 37,5- 1 1 + 42,5-2 = 1605;
mi
j?x;n, = 22.5--3 + 27.52- 13 + 32.52 - 21 + 37.5-’ - 11 + 42.5-- 2 =
/•t
= 52 612.5;
£y,w, = 9-5 + 13-11 + 17-17 + 21-14 + 25-3 = 846;
/*»
£y;w, = 9--5 + I32-Il + 172- 17 + 2P-14 + 252-3 = 15 226;
Б*
££х,У Д = 22-5 ’9 ’2 + 22-5 •1 - В + - + 42.5 • I • 21 + 42,5 • I • 25 =
м mi
= 27 X95
(обходим все заполненные клетки корреляционной таблицы).
Затем по формулам (12.12)-(12.22) находим выборочные харак-
теристики и параметры уравнений регрессии:
у = 1605/50 = 32.1 (млн руб.); у = 846/50 = 16.92 (т);
s'; =52 612.5/50 - 32,Р= 21.84; .< = 15 226/50 - 16.92-= 18.2336;
М = 27 895/50 - 32.1 • 16.92 = 14,768;
= 14,768/21.84 = 0.6762; Ьх> = 14,768/18,2336 = 0,8099.
Итак, уравнения регрессии
у, - 16,92 = 0.6762 (х - 32.1) или yv= 0.6761v - 4,79.
х, - 32.1 = 0.8099 (у - 16.92) или х,.= 0,8099у + 18.40.
Из первого уравнения регрессии Y по X (его график показан на
рис. 12.1) следует. что при увеличении основных производственных
фондов (ОПФ) X на I млн руб. суточная выработка продукции Y
предприятия увеличивается в среднем на 0,6762 т. Второе уравнение
регрессии X по У показывает, что для увеличения суточной выработки
продукции Y на 1 т необходимо в среднем увеличить ОПФ X на
0.8099 млн руб. (отметим, что свободные члены в уравнениях регрес-
сии не имеют реального смысла). ►
Параметры уравнений регрессии (12.8) могут быть вычислены
упрощенным способом (аналогично тому, как вычислялись числовые
характеристики вариационного ряда в § 8.4). С этой целью от зна-
403
чсний переменных х, и у, переходят к новым значениям и,
л; - с
к
и
у - с' ,
Vj . где к и к’ — величины интервалов, а г и с — середины
к
серединных интервалов соответственно по переменной X или Y. То-
гда в соответствии с формулами (8.20) и (8.21)
£|<л,
х=^--------к+с. (12-23)
п
1^,
у=-^-----к^е, (п.м)
п
I
s;=^-----*!-(х-с). (12.25)
Л
5*=-^-----Г:-(у-с')‘. (12.26)
Покажем, что в этом случае формула для ковариации и (12.19)
примет вид:
Е 1>’Л
р = -^-^----кк'-(х-с)(у-с'). (12.27)
□ Представим правую часть равенства (12.27) в виде:
_ _ ZLw,
и\кк‘ -(х -с)(у -с'), где «у = -^-^- — средняя арифме-
тическая произведений вариантов
.V -с у, -с' х,у.~с,х1 — су + се’
U,V'= ~к ~ ~ кк' ’
Учитывая свойства средней.
и v = —;(.«•- <*’х - су + сс'), откуда
кк
uvkk' - (х - с) (у —<•') = лу - с' х - су + сс’ - (х - с) (у - с') =
= ху - г у = р (по определению (12.13».
404
[> Пример 12.2. По данным табл. 12.1 найти упрошенным спо-
собом уравнения регрессии У по X и X по К и пояснить их смысл.
Реше н и с. Возьмем постоянную к равной величине интер-
вала по переменной X. т.е. к = 5. а постоянную с — равной середи-
не серединного, третьего, интервала, т.е. с = 32.5. Аналогично по
переменной К к' = 4. с'= 17. Итак, и, = (xf- 32,5)/5: 4=<у,~ 17)/4-
Представим корреляционную табл. 12.1 в виде табл. 12.2.
Тнб.1ица 12.2
\ У} 9 13 17 21 25 «I «Л
Xi \ (Я /•1
-2 -1 0 1 2
ui \
22.5 — 1 *• 2д 1: — — — 3 -6 12 10
27,5 -1 3; 6| 4о — — 13 -13 13 12
32,5 0 — 3<, Ни 7b — 21 0 0 0
37.5 1 — 1-1 2п 6. 21 II 11 II 9
42,5 3 Ла — — — Ij !< 2 4 8 6
<МЕ) 5 II 17 14 3 50 -4 44 —
V'/ -10 -11 0 14 6 -1 — — —
20 11 0 14 12 57 — — —
1-1 14 7 0 8 8 — — —• 37
Вычислим необходимые суммы:
=(—2)-3 + (-1) • 13 + 0*21 + 1-11 + 2-2 = -4;
<-|
£//>, = (-2)2-3 + (-I)2-13+ О2-21 + Р-Н +2*-2 = 44;
/-1
= (—2)-5 + (-!)• II + 0-17 + I • 14 + 2-3 = -I;
j-i
X<4S (-2)2’5 + (-l)2-ll + (Р-17 + Р- 14 + 22,3 = 57.
Для упрощения вычислений расчеты указанных сумм целесооб-
разно проводить непосредственно в таблице (см. соответственно два
405
предпоследних столбца и две предпоследние строки со значениями
необходимых сумм в итоговых строке и столбце).
J
Для удобства вычисления суммы вначале рассчиты-
(«I /«I
ваем иц и проставляем эти значения под соответствующими часто-
тами, а затем находим произведения (дл))^, которые суммируем по
строке и столбцу, и записываем полученные числа соответственно в
последнем столбце и последней строке табл. 12.2. Например, на пе-
ресечении первой строки и первого столбца табл. 12.2 получим 2д,
т.е. частота /|ц = 2. w,v, = (-2Х-2) = 4. a (wtr, )//н =4-2 = 8 и т.д.
Итак, суммируя произведения uy,nv в последнем столбце или в
последней строке, получим в правом нижнем углу табл. 12.2
1-1 /-J
Теперь по формулам (12.23)—(12.27) имеем:
-4
г = — 5 + 32.5 = 32,1 (млн руб.);
у = —-4 + 17 = 16.92 (т):
50
44 »
л; =— 5-(32,1-32,5)’ =21,84:
50 ' '
< = ~~4-(16.92 -17)* =18,2336;
р =-^-5-4-(32.1-32.5)(16.92-17) = 14.768.
Далее уравнения регрессии находятся и интерпретируются гак
же. как в примере 12.1. ►
12.3. Коэффициент корреляции
Перейдем к оценке тесноты корреляционной зави-
симости. Рассмотрим наиболее важный для практики и теории слу-
чай линейной зависимости вида (12.16).
На первый взгляд подходящим измерителем тесноты связи Y
от X является коэффициент регрессии bvx, ибо. как уже отмечено,
он показывает, на сколько единиц в среднем изменяется К. когда
X увеличивается на одну единицу. Однако зависит от единиц
измерения переменных. Например, в полученной ранее зависимо-
сти он увеличится в 1000 раз, если величину основных производ-
ственных фондов X выразить не в млн руб., а в тыс. руб.
406
Очевидно, что для «исправления» Ьух как показателя тесноты
связи нужна такая стандартная система единиц измерения, в кото-
рой данные по различным характеристикам оказались бы сравнимы
между собой. Статистика знает такую систему единиц. Эта система
использует в качестве единицы измерения переменной се среднее
квадратическое отклонение $.
Представим уравнение (12.16) в эквивалентном виде:
(12.28)
В этой системе величина
(12.29)
показывает, на сколько величин зу изменится переднем К. когда
X увеличится на одно зх
Величина г является показателем тесноты линейной связи и назы-
вается выборочным коэффициентом корреляции (или просто коэффи-
циентом корреляции).
На рис. 12.3 приведены две корреляционные зависимости пере-
менной Y по X. Очевидно, что в случае а) зависимость между пере-
менными менее тесная и коэффициент корреляции должен быть
меньше, чем в случае (5). так как точки корреляционного поля а) дальше
отстоят от линии регрессии, чем точки поля (5).
Рис. 12.3
Нетрудно видеть, что г совпадает по знаку с (а значит, и с
Ьху). Если г > О (Л„ > 0, 6|у>0). то корреляционная связь между
переменными называется прямой, если г < 0 (Ьух < 0. Ьлу< 0) — обрат-
ной. При прямой (обратной) связи увеличение одной из переменных
407
ведет к увеличению (уменьшению) условной (групповой) средней
другой.
Учитывая равенство (12.17), формулу для г представим в виде:
Отсюда видно, что формула для г симметрична относительно
двух переменных, т.с. переменные X и Y можно менять местами,
Тогда аналогично формуле (12.29) можно записать:
r~bv?L. (12.31)
.V,
Найдя произведение обеих частей равенств (12.29) и (12.31), по-
лучим
= <12:з2>
или r = ±yfb^b^., (12.33)
т.с. коэффициент корреляции г переменных X и Y есть средняя геомет-
рическая коэффициентов регрессии, имеющая их знак.
О Пример 12.3. Вычислить коэффициент корреляции между ве-
личиной основных производственных фондов .¥ и суточной выра-
боткой продукции К (по данным табл. 12.1).
Р е in е н и е. Выше (см. примеры 12.1. 12.2) получили Ьух= 0.6762
и = 0.8099. По формуле (12.33) г = +70.6762-0.8099 = 0.740 (бе-
рем радикал со знаком «+». так как коэффициенты Л,.г и Ьху поло-
жительны). Итак, связь между рассматриваемыми переменными
прямая и достаточно тесная (ибо г близок к I)1. ►
> Пример 12.4. При исследовании корреляционной зависимости
между объемом валовой продукции К (млн руб.) и среднесуточной
численностью работающих X (тыс. чел.) для ряда предприятий от-
расли получено следующее уравнение регрессии X по К: .г,, = 0,2у
- 2,5. Коэффициент корреляции между этими признаками оказался
равным 0,8. а средний объем валовой продукции предприятий со-
ставил 40 млн руб. Найти: а) среднее значение среднесуточной чис-
ленности работающих на предприятиях; 6) уравнение регрессии I
по Х\ в) средний объем валовой продукции на предприятиях со
среднесуточной численностью работающих 4 тыс. чел.
1 См ниже свойство 1 коэффициента корреляции
408
Решение, а) Обе линии регрессии У по X и X по Y пересека-
ются в точке (г). полому х найдем по заданному уравнению регрес-
сии при г = у = 40. т.е. х = 0.2 *40 — 2.5 = 5.5 (тыс. чел.).
б) Учитывая соотношение (12.32). вычислим коэффициент рег-
рессии Л„=
г*
0.8'
0.2
= 3.2. Теперь по формуле (12.16) получим
уравнение регрессии Y по X: ух - 40 = 3,2(х - 5.5) или у, = 3.2х + 22.4.
в) Ух-4 найдем по полученному уравнению регрессии У по X:
Ух-4 = 3.2 • 4 + 22.4 = 35.2 (млн руб.). ►
Отмстим другие модификации формулы л полученные из равен-
ства (12.30) с помощью формул (12.12)—(12.14). (12.8). (12.22):
Для практических расчетов наиболее удобна формула (12.35),
так как по ней г находится непосредственно из данных наблюдений
и на величине г не скажутся округления данных, связанные с расче-
том средних и отклонений от них.
Если данные нс сгруппированы в виде корреляционной таблицы
и представляют п пар чисел (х,. у(). то для вычисления коэффициен-
тов регрессии и корреляции в соответствующих формулах следует
взять Пц - п, = п, - 1. у = /. а У У заменить на £.
1-1 /•! 1-1
t> Пример 12.5. Найти коэффициент корреляции между произ-
водительностью труда Y (тыс. руб.) и энерговооруженностью труда X
(кВт) (в расчете на одного работающего) для 14 предприятий регио-
на по следующим данным (табл. 12.3).
'Гиб.1ици 12.3
Л 2.8 2,2 3.0 3.5 3.2 3.7 4.0 4.8 6.0 5.4 5.2 5.4 6.0 9,0
Л 6.7 6,9 7.2 7.3 8.4 8.8 9.1 9.8 10.6 10.7 II.1 11.8 12.1 12.4
409
Решение. Вычислим необходимые суммы:
£х, = 2.8 +2.2+ ...*6,0+ 9.0 = 64.2;
£х; =2.8: + 2.2* + ... + 6.О2 +9,0: =335.26;
£ у, = 6.7 + 6.9 +... + 12.1 + 12.4 = 132.9;
£у; = 6.72 + 6.92 + ... +12. Г’ + 12.4* = 1313.95:
£ х.у. = 2.8 • 6.7 + 2.2 • 6.9 +... + 6.0 • 12.1 + 9,0 • 12.4 = 650.99.
По формуле (12.35). полагая nt) = п, = п, = I. у = / и заменяя
на получим
|»1 i«l
< < -1 i i
(12.35)
________14-650.99-64.2-132.9________
Jl 4 • 3 35.26 - 64.2: 313.95 - 132.4:
что говорит о тесной связи между переменными’. ►
Отмстим основные свойства коэффициента корреляции (при дос-
таточно большом объеме выборки л), аналогичные свойствам ко-
эффициента корреляции двух случайных величин (§ 5.6).
1. Коэффициент корреляции принимает значения на отрезке !~Г.1|. т.е.
-UrSl. (12.36)
В зависимости от того, насколько | г | приближается к 1. разли-
чают связь слабую, умеренную, заметную, достаточно тесную, тесную
и весьма тесную, т.е. чем ближе | г | к I. тем теснее связь.
2. Если все значения переменных увеличить (уменьшить) на одно и
то же число или в одно и то же число раз. то ветчина коэффициента
корреляции не изменится.
1 См. ниже С1и>йепи> 1 козффнциенга корреляции
410
3. При г = ± I корре. игционная связь
представляет линейную функциональ-
ную зависимость. При зпюм линии рег-
рессии Y по X и X по Y совпадают и все
наблюдаемые значения располагаются
м общей прямой.
□ Найдем lg(p между двумя пря-
мыми регрессии (рис. 12.4) с угловы-
ми коэффицие»гтами А'| = />п и
к2 = —. используя соотвстстную-
щую формулу аналитической гео-
Инс. 12.4
метрии:
k.-kt
1+М, = »„+*„
откуда с учетом соотношений (12.29) и (12.3!)
«Д
lgip =-------;---г.Я (12.37)
г а’ + .г
Из полученной формулы видно, что чем теснее связь и чем
ближе |г| к I. тем меньше угол ф между прямыми регрессии (уже
образуемые ими «ножницы»), а при r= ±1 tgip = <p = O и линии рег-
рессии сливаются (рис. 12.5. а и <5).
4. При г = 0 линейная корреляционная связь отсутствует.
При этом групповые средние переменных совпадают с их общими сред-
ними, а линии регрессии Y по X и X по Y параллельны осям координат.
411
□ Если г = 0. то коэффициент = />vl.= 0, и линии регрессии
(12.16) и (12.20) имеют вид: \\ = г и х,.= х (рис. 12.6).
Риг. 12.»
Равенство г = 0 говорит лишь об
отсутствии линейной корреля-
ционной зависимости (некоррелирован-
ности переменных), но не вообще об
отсутствии корреляционной. а тем
баке статистической зависимости.
Так. например, для зависимо-
стой, представленных на рис. 12.7.
а и б, г = 0 и линии регрессии У
по X параллельны оси абсцисс
Однако по расположению точек
корреляционного ноля отчетливо просматривается взаимосвязь ме-
жду переменными, отличная от линейной корреляционной. Так. в
случае а — это нелинейная корреляционная (почти функциональ-
ная) зависимость; в случае б — статистическая зависимость. прояв-
ляющаяся в данном случае в том. что с изменением х групповые
средние ух не меняются, а меняется лишь рассеяние точек поля от-
носительно линии регрессии.
Выборочный коэффициент корреляции г является оценкой гене-
рального коэффициента корреляции р (о котором речь пойдет дальше),
тем более точной, чем больше объем выборки п. И указанные выше
свойства, строго говоря, справедливы для р. Однако при достаточно
большом п их можно распространить и на г.
12.4. Основные положения корреляционного анализа.
Двумерная модель
Корреляционный анализ (корреляционная модель) — метод, приме-
няемый тогда, когда данные наблюдений или эксперимента можно
412
считать случайными и выбранными из совокупности, распределенной
по многомерному нормальному закону.
Основная задача корреляционного анализа, как отмечено выше.
состоит в выявлении связи между случайными переменными путем
точечной и интервальной оценок различных (парных, множественных,
частных) коэффициентов корреляции. Дополнительная задача корре-
ляционного анализа (являющаяся основной в регрессионном ана-
лизе) заключается в оценке уравнений регрессии одной переменной
по Другой.
Рассмотрим простейшую модель корреляционного анализа —
двумерную. Плотность совместного нормального распределения
двух переменных X и К имеет вил (см. § 5.7):
чч (-v->) =------Ц=т " • < >2.38)
Зпст.ст, V1 ~Р‘
вг, ау — математические ожидания переменных А'и Y.
су;, ст; — дисперсии переменных X н У:
р — коэффициент корреляции между переменными X и
У, определяемый через корреляционный момент (ковариацию) Клу
по формуле (5.38):
Л'„ Л/((А'-«. )() -« )]
р=-----------------------------
ст.ст, °.°,
или с учетом свойства (5.40)
Л/(ЛУ)-и а
Р =--------------
СУ,ст
л *
(12.39)
(12.40)
Величина р характеризует тесноту связи между случайными пе-
ременными X и У. Указанные пять параметров av, ст:, ст • Р дают
исчерпывающие сведения о корреляционной зависимости между
переменными
В § 5.7 показано, что при совместном нормальном законе рас-
пределения случайных величин X и У(12.38) выражения для услов-
ных математических ожиданий, т.е. модельные уравнения регрессии
(12.1) и (12.2). выражаются линейными функциями:
413
M,(Y)-a, + p—-(.r-a,). (12.41)
a,
Л/, (.¥) = «, + P~(У~a, )• (12.42)
CS
Из свойств коэффициента корреляции (§ 5.6) следует, что р ««.
ляется показателем тесноты связи лишь в случае линейной зависимо-
сти (линейной регрессии} между двумя переменными, получаемой. в
частности, в соответствии с равенствами (12.41). (12.42) при их
совместном нормальном распределении.
Из § 5.6 также следует (см. формулы (5.50). (5.52)). что услов-
ные дисперсии равны:
а; (У) = ст; (। - р-'), ст; (х) = ст; (| - р2).
т.е. степень рассеяния значений Y (или X} относительно линии рег-
рессии Y по АГ (или X по У) определяется двумя факторами: дисперси-
ей о* (попеременной Y (X) и коэффициентом корреляции р и не
зависит от значений независимой переменной х(>). По мере прибли-
жения |р| к единице условная дисперсия ст; (У) (ст; (,¥|)->(). и зна-
чения переменных все менее рассеяны относительно соответствующих
линий регрессии, т.е. очевиден смысл коэффнциетгта корреляции как
показателя тесноты линейной корреляционной зависимости.
Генеральная совокупность в определенном смысле аналогична
понятию случайной величины и ее закону распределения (см. § 9.1).
поэтому для вышеназванных параметров используется и другая тер-
минология: ау (или г0) — генеральные средние", ст;, ст; — ге-
неральные дисперсии", Куу и р — генеральные ковариация и коэффици-
ент корреляции.
Для оценки генерального коэффициента корреляции р и мо-
дельных уравнений регрессии по выборке в формулах (12.40)—
(12.42) необходимо заменить параметры я,. ст;, ст;. Кп их со-
стоятельными выборочными оценками — соответственно 7
(12.12), ,v2 (12.18), я] (12.22). |д (12.19). В этом случае получим
знакомые нам формулы для определения выборочного коэффици-
ента корреляции г (12.30) и выборочных уравнений регрессии
(12.16), (12.20). Выше (§ 12.2 и 12.3) те же формулы получены ина-
че — на основе применения метода наименьших квадратов. Совпа-
414
дение результатов объясняется некоторыми ценными свойствами
оценок метода наименьших квадратов.
В § 12.3 мы ввели выборочный коэффициент корреляции г и рас-
смотрели сю свойства, исходя из оценки близости точек корреляци-
онного поля к прямой регрессии без учета предпосылок корреляци-
онного анализа. Однако если эти предпосылки нарушаются (совмест-
ный закон распределения переменных не является нормальным, одна
из исследуемых переменных не является случайной и т.п.), то г не
следует рассматривать как строгую меру взаимосвязи переменных.
12.5. Проверка значимости и нигервалышя оценка
парамет|юв связи
В практических исследованиях о тесноте корреляционной зави-
симости между рассматриваемыми переменными судят фактически не
по величине генерального коэффициента корреляции р (который
обычно неизвестен), а по величине его выборочного аналога г. Так
как г вычисляется по значениям переменных. случайно попавшим в
выборку из генеральной совокупности, то в отличие от параметра р
оценка г — величина случайная.
Пусть вычисленное значение г * 0. Возникает вопрос, объясняется
ли это действительно существующей линейной корреляционной связью
между переменными X н У в генеральной совокупности или является
следствием случайности отбора переменных в выборку (т.е. при другом
отборе возможно, например, г - 0 или изменение знака г).
Обычно в этих случаях проверяется гипотеза //п об отсутствии
линейной корреляционной связи между переменными в генераль-
ной совокупности, т.е. //0: р = 0 против альтернативной
Нр р*0. При справедливости этой гипотезы статистика
г^п - 2
имеет т-распределение Стыодента с к = п - 2 степенями
Поэтому гипотеза //(1 отвергается, т.е. выборочный коэффициент
корреляции г значимо (существенно) отличается от нуля, сели*
гипотезы
(12.43)
свободы.
где /Ьи 4 — табличное значение /-критерия Стыодента. определенное
на уровне значимости и при числе степеней свободы к = п - 2.
’ При использовании одностороннего критерия (п случае альтернативной гипо-
тезы //,: р>0 или //,: р < о } г значим, если р| > г, . ..
415
t> Пример 12.6. Проверить на уровне а = 0,05 значимость ко.
эффиниента корреляции между переменными X и Y по данным
табл. 12.1.
Решение. В примере 12.3 вычислен г — 0.740. Статистика
критерия по формуле (12.43):
VI-0.740:
Для уровня значимости а = 0.05 и числа степеней свободы к = 50 - 2 -
= 48 находим критическое значение статистики /0,95.4$ = 2.01 (см.
табл. IV приложений). Поскольку / > /055.4Х, коэффициент корреля-
ции между суточной выработкой продукции Y и величиной основ-
ных производственных фондов X значимо отличается от нуля. ►
Для значимого коэффициента корреляции г целесообразно най-
ти доверительный интересы (интервальную оценку), который с задан-
ной надежностью у = 1-а содержит (точнее, «накрывает*) неиз-
вестный генеральный коэффициент корреляции р. Для построения
такого интервала необходимо знать выборочное распределение ко-
эффициента корреляции г. которое при рхО несимметрично и
очень медленно (с ростом п) сходится к нормальному распределе-
нию. Поэтому прибегают к специально подобранным функциям or
г. которые сходятся к хорошо изученным распределениям. Чаше
всего для подбора функции применяют преобразование Фишера:
2 = 1|п—. (12.45)
2 I -г
Распределение : уже при небольших п является приближенно
нормальным с математическим ожиданием
.V(2)sl|n12£ + —2— (12.46)
' 2 1-р 2(л-1)
и дисперсией
ст:=——. (12.47)
' л-3
Поэтому вначале строят доверительный интервал для Л/(г):
у/П-1
(12.48)
где /|_ и — нормированное отклонение г, определяемое с помошью
функции Лапласа:
416
ф('„. )=r=l-« (12.49)
При определении границ доверительного интервала для р. т.е.
для перехода от z к р. существует специальная таблица. При ее от-
сутствии переход может быть осуществлен по формуле:
г = lh - = с~ ~с ' , (12.50)
е‘
где th г — гиперболический тангенс z.
jEo?w коэффициент корреляции значим. та коэффициенты регрессии
Ьр и Ьуу также значимо отличаются от нуля, а интервальные оценки
для соответствующих генеральных коэффициентов регрессии и
могут быть получены по формулам, основанным на том. что статисти-
ки (6„-plt)/.\ . (\, имеют /-распределение Стыодента с
(л — 2) степенями свободы:
(12.51)
(12.5Г)
Z-преобраэование Фишера может быть применено при проверке
различных гипотез относительно коэффициента корреляции.
Например, если по данным выборки объема п вычислен коэф-
фициент корреляции г. то для проверки нулевой гипотезы //0 о том.
что генеральный коэффициент корреляции р равен значению р<»,
т.е. Ht). р = рп. используется статистика
; = z(H-z(p„) (12.52)
/ I
Ъ»-3
А для проверки существенности (значимости) различия двух ко-
эффициентов корреляции Г| и а, полученных по выборкам объемов
Л| и п2. т.с. для проверки гипотезы /7|(: pj = pj. применяется стати-
стика
. (12.52')
п+ ’
V ". " 3 “ 3
При достаточных объемах выборки (больших 10) можно считать,
что при выполнении соответствующих нулевых гипотез статистики
14 TcvfM* M-trvimvrrfi • шигчлчпижа! .икепш
417
(12.52) и (12.52') имеют приближенно нормальный закон распреде-
ления. Поэтому (см. § 10.6) гипотеза //() отвергается на уровне зна-
чимости а, если |/|>/, „ (при использовании двустороннего крите-
рия) или р| при использовании одностороннего критерия).
[> Пример 12.7. По данным табл. 12.1 найти с надежностью 0,95
интервальные оценки (доверительные интервалы) параметров связи
между суточной выработкой продукции Y и величиной основных
производственных фондов X.
Реше н и е. Так как коэффициент корреляции X и Y значим
(см. пример 12.5), то построим доверительный интервал для гене-
рального коэффициента корреляции р. применяя ^-преобразование
Фишера. По формуле (12.45)
lin!+°2!!L о.,.™.
2 1-0.740
По формуле (12.49) из условия Ф(/, „ ) = 0.95 по таблице функ-
ции Лапласа находим Го.95s 1.96. По формуле (12.48) построим до-
верительный интервал для
0,9505 - 1.96 , 1 < М (z) s 0.9505 -г 1.96 . 1
750-3 750-3
или 0,6646-' Л/(г)< 1.2364. Находим границы доверительного ин-
тервала для р. используя специальную таблицу или формулу (12.50):
(h 0.6646 < р < ih 1.2364 или 0,581 <р<0,844. В указанных грани-
цах на уровне значимости 0,05 (с надежностью 0,95) заключен гене-
ральный коэффициент корреляции р
Теперь построим доверительные интервалы для генеральных ко-
эффициентов регрессии р„ и р„. Вначале определим средние
квадратические отклонения переменных:
•V. = Jsj = 721.84 = 4.673; л. * = 7*8.2336 = 4.270;
Теперь по формуле (12.51):
4.270 -7> -0.740: 4.
0.6762 -2.01- ------ - < р. <0.6762 + 2.01-
4.673-750-2
270 -^1 -0,740^
4.673-750-2
или 0,4979 < Рп < 0.8545. Аналогично по формуле (12.5Г):
0.5963 ^Р, < 1.0235. ►
418
При содержательной интерпретации параметров р. 0и и 0 сле-
дует считаться в первую очередь с их интервальными (а нс только
точечными) опенками.
|> Пример 12.7а. При исследовании связи между производитель-
ностью труда и уровнем механизации работ на предприятиях одной
отрасли промышленности, расположенных в двух различных рай-
онах страны, вычислены коэффициенты корреляции г( = 0.95 и
г, = 0.88 по выборкам объемов соответственно /»( = 14 и nj = 20.
Выяснить, имеются ли на уровне а = 0.05 существенные различия в
тесноте связи между рассматриваемыми переменными на предпри-
ятиях отрасли в этих районах.
Решение. Проверяемая гипотеза Нп: р| = pj. В качестве альтер-
нативной возьмем гипотезу //<>: р| * рг. т.е. применяем двусторонний
критерий. По формуле (12.51') с учетом соотношения (12.45) статистик:!
2(0.95)-2(0.88) 1.832-1.376 ,
' — —. ~ =----—-------— 1.18.
fj” £ Д,5°
V14-3 ~ 20-3
Так как /< = 1.96. то гипотеза //„ не отвергается, т.е. нет
оснований считать существенным различие показателей связи меж-
ду рассматриваемыми переменными на предприятиях двух районов
страны. ►
12.6. Корреляционное отношение
и индекс корреляции
Введенный выше коэффициент корреляции, как уже отмечено,
является полноценным показателем тесноты связи лишь в случае
линейной зависимости между переменными. Однако часто возника-
ет необходимость в достоверном показателе интенсивности связи
при любой форме зависимости.
Для получения такого показателя вспомним правило сложения
дисперсий (8.12):
(12.53)
где г — общая дисперсия переменной
s’ = —---------. (12.54)
и
х','" — средняя групповых дисперсий л' . или остаточная диспер-
сия —
419
i».
. (12.55)
n
•<=-------------, (12.56)
n
6* — межгрупповая дисперсия
£;= —-------------. (12.57)
г»
Остаточной дисперсией измеряют ту часть колеблемости К. ко-
торая возникает из-за изменчивости неучтенных факторов, нс зави-
сящих от X. Мсжзрупповая дисперсия выражает ту часть вариации
Y, которая обусловлена изменчивостью X. Величина
Ч..= Д (12.58)
получила название эмпирического корреляционного отношения ) по X.
Чем теснее связь, тем большее влияние на вариацию переменной Y
оказывает изменчивость X по сравнению с неучтенными факторами,
тем выше q,. Величина q;,. называемая эмпирическим коэффици-
ентом детерминации, показывает, какая часть обшей вариации У
обусловлена вариацией X. Аналогично вводится эмпирическое корре-
ляционное отношение X по Y:
(*2.59)
Отмстим основные свойства корреляционных отношений' (при
достаточно большом объеме выборки л).
1. Корреляционное отношение есть неотрицательная величина, нс
превосходящая единицу: 0 < q < I.
2. Если q - 0. то корреляционная связь отсутствует.
3. Если q = I. то между переменными существует функциональная
зависимость.
1 '->ти свойства справедливы как для эмпирических корреляционных огношениИ
П. гак и для теоретических R (см ниже»
420
4. л., *«).»• т с в отличие or коэффициента корреляции г (для
которого г, =г1 = г) при вычислении корреляционного отношения
существенно, какую переменную считать независимой, а какую —
зависимой.
Эмпирически корреляционное отношение Г|м является показателем
рассеяния точек корреляционного поля относительно эмпирической линии
регрессии, выражаемой ломаной, соединяющей значения г, Однако в
связи с тем. что закономерное изменение у, нарушается случайны-
ми зигзагами ломаной, возникающими вследствие остаточною дей-
ствия неучтенных факторов, г|„ преувеличивает тесноту связи. По-
этому наряду с ту, рассматривается показатель тесноты связи /?1Л.
характеризующий рассеяние точек корреляционного поля относительно
линии регрессии у, (12.3). Показатель получил название теоретиче-
ского корреляционного отношения ИЛИ индекса корреляции Y по X.
где дисперсии 6; и д' определяются по формулам (12.54)—(12.56).
в которых групповые средние у, заменены условными средними
yt . вычисленными по уравнению регрессии (12.16).
Подобно /?.. вводится и индекс корреляции X по Y:
Достоинством рассмотренных показателей ц и R является го.
что они могут быть вычислены при любой форме связи между пе-
ременными. Хотя »1 и завышает тесноту связи по сравнению с R.
но для его вычисления не нужно знать уравнение регрессии. Кор-
реляционные отношения q и R связаны с коэффициентом корре-
ляции г следующим образом:
0<|r|s/?<n<l. (12.62)
Покажем, что в случае л « и с й н о Й модели (12.3). т.с. зави-
симости г, - у ~ b , (.v - V). индекс корреляции /?,я равен коэффициенту
коррекции г (по абсолютной величине): /?,,-|г| (или Ru =|г|).
□ Полагаем для простоты nt = I (/= I. 2.0.
По формуле (12.60)
421
(гак как из уравнения регрессии г, - у = />„(.\ - v)).
Теперь, учитывая формулы дисперсии, коэффициентов регрес-
сии (12.17) и корреляции (12.30), получим:
Коэффициент детерминации Я2. равный квадрату индекса корре-
ляции (для парной линейной модели — г2), показывает дано общей
вариации зависимой переменной, обусловленной регрессией или изменчи-
востью объясняющей переменной.
Чем ближе R- к единице, тем лучше регрессия аппроксимирует
эмпирические данные, тем теснее наблюдения примыкают к линии
регрессии Если R- = I. то эмпирические точки (л\ у) лежат на ли-
нии регрессии (см. рис. 12.4) и между переменными У и X сущест-
вует линейная функциональная зависимость. Если Я2 = 0. то вариа-
ция зависимой переменной полностью обусловлена воздействием
неучтенных в модели переменных, и линия регрессии параллельна
□си абсцисс (рис. 12.5).
Расхождение между ту и Я2 (или г2) может быть использовано
для проверки л и и е й н о с т и корреляционной зависимости
(см. ниже пример 12.10).
Проверка значимости корреляционного отношения q основана
на том, что статистика
П:
(l-if
(12.63)
(где т — число интервалов по группировочному признаку) имеет
F-распределение Фишера—Снедекора с А| = т - 1 и к> = п - т степе-
нями свободы. Поэтому г| значимо отличается от нуля, если А >
> F,, j , где F,, t — табличное значение F-критерия на уровне зна-
чимости а при числе степеней свободы k[ = т - 1 и = п - т.
Индекс корреляции Л’ двух переменных значим, если значение
статистики
422
R'hi- 2)
f = _L_2 (I2.M)
больше табличного f\,,14,. где A| - I и = n - 2.
> Пример 12.8. По данным табл. 12.1 вычислить корреляцион-
ное отношение г)и и индекс корреляции /?п. и проверить их значи-
мость на уровне а = 0.05.
Решение. Вначале определим п„. Ранее вычислены: общая
средняя F = 16.92, дисперсия < = IX.23 (пример 12.2). групповые сред-
ние у, (табл. 12.1).
Частоты интервалов п, указаны в предпоследней графе той же
таблицы. Для удобства расчеты представим в табл. 12.4.
ТпГмицн 12.4
X) л, у, (у,-Г) п, Л, (У, -у)'ч
22.5 3 10,3 131.5 10.4 127.5
27.5 13 13.3 170.4 13.8 126.5
32.5 21 17.8 16.3 17.2 1.6
37.5 II 20.3 125.7 20.6 149.0
42.5 > * 23.0 73.9 23.9 97.4
X 517.8 — 502.0
Теперь по формуле (12.57) 8; =517,8/50=10.36 и но формуле
(12.58) »1„
Нклб _ , Значение
у 18.23
i](i близко к вели-
чине г = 0.740 (полученной ранее в примере 12.3). Поэтому оправ-
дано сделанное выше на основании графического изображения эм-
пирической линии (ломаной) регрессии предположение о линейной
корреляционной зависимости между переменными.
Для расчета /?,.л по уравнению регрессии ух = 0.6762.x - 4.79 (см.
пример 12.1) находим значения г, . представленные в предпоследней
графе табл. 12.4 Затем аналогично 8'’ =502.0/50 =10.04 и
R = = Jo.55l =0.742. Как и следовало ожидать, ока-
” V 18.23
зался равным г (небольшое расхождение объясняется округлением
промежуточных результатов при вычислении Яух). Поэтому в случае
линейной связи нет смысла вычислять Л,.,, а достаточно ограни-
423
читься вычислением г. Величина коэффициента детерминации
/?’ =0.551 показывает, что вариация зависимой переменной К (су-
точной выработки продукции) на 55,1% объясняется вариацией не-
зависимой переменной X (величиной основных производственных
фондов).
Для проверки значимости . учитывая, что количество интерва-
лов по группировочному признаку т = 5, по формуле (12.63) найдем
F=0.7S4450-5)._,4g2
(1-0.754)(5-1)
Табличное значение /^05.4:45=2,57. Так как F > /шачз» то зна-
чимо отличается от нуля. Аналогично проверяется значимость По
формуле (12.64) /Г= °'(|42о'^2~:)2> = 58-8- Так как F> Гол*,;® = 4.04.
то индекс корреляции значим. ►
12.7. Понятие о многомерном корреляционном анализе.
Множественный и частный коэффициенты
корреляции
Экономические явления чаше всего адекватно описываются
многофакторными моделями. Поэтому возникает необходимость
обобщить рассмотренную выше двумерную корреляционную модель
на случай нескольких переменных.
Пусть имеется совокупность случайных переменных Х\, Х2.
Х(...Xj, .... Хр, имеющих совместное нормальное распределение. В
этом случае матрицу
1 р12 - Pi,'
P:i • •• 1 - р3„ . (12.65)
А рг3 - 1 .
составленную из парных коэффициентов корреляции рц (k j = I. 2.
.... р). определяемых по формуле (9.2), будем называть корреляцион-
ной. Основная задача многомерного корреляционного анализа состоит
в оценке корреляционной матрицы Qp по выборке. Эта задача решается
определением матрицы выборочных коэффициентов корреляции-.
424
(12.66)
где rv (i, j = 1.2.p) определяется по формуле (12.30) или ее мо-
дификациям.
В многомерном корреляционном анализе рассматривают две ти-
повые задачи:
а) определение тесноты связи одной из переменных с совокуп-
ностью остальных (р - I) переменных, включенных в анализ;
6) определение тесноты связи между переменными при фикси-
ровании или исключении влияния остальных переменных, где
7$(р-2).
Эти задачи решаются с помощью множественных и частных ко-
эффициентов корреляции.
Множественный коэффициент корреляции. Теснота линейной
взаимосвязи одной переменной А’, с совокупностью других (р - I)
переменных X,. рассматриваемой в целом, измеряется с помощью
множественного (или совокупного) коэффициента корреляции Pi:,-,
который является обобщением парного коэффициента корреляции
ри. Выборочный множественный, или совокупный, коэффициент кор-
реляции /?4|, г. являющийся оценкой Я ,, ... может быть вычислен
по формуле:
где | q | — определитель матрицы qp‘,
q„ — алгебраическое дополнение элемента г„ той же матри-
цы (равного I).
В частности, в случае трех переменных (р = 3) из формулы
(12.67) следует. *гго
/? ,4 = |^-Ч'Г|* . (12.68)
Множественный коэффициент корреляции заключен в пределах
Os R< I. Он не меньше, чем абсолютная величина любого парного
425
или частного коэффициента корреляции с таким же первичным ин-
дексом.
С помощью множественного коэффициента корреляции (по мерс
приближения /? к I) делается вывод о тесноте взаимосвязи, но не о ее
направлении. Величина R-. называемая выборочным множественным
(или совокупным) коэффициентом детерминации, показывает, какую
долю вариации исследуемой переменной объясняет вариация ос-
тальных переменных.
Можно показать, что множественный коэффициент корреляции
значимо отличается oi нуля, если значение статистики
г_ К'(п-р)
(|-Я-’)(р-1)
(12.69)
где Л. I, «. ~ табличное значение f-критерия на уровне значимости
а при числе степеней свободы = р - I и = и - р.
Частный коэффициент корреляции. Если переменные коррелирую)
друг с другом, то на величине парного коэффициента корреляции
частично сказывается влияние других переменных. В связи с этим
часто возникает необходимость исследовать частную корреляцию меж-
ду переменными при исключении (элиминировании) влияния одной
или нескольких других переменных.
Выборочным частным коэффициентам корреляции между перемен-
ными Xi и Х{ при фиксированных значениях остальных (р - 2) пере-
менных называется выражение
•-.и .г-~Т^- 02ЛО)
фч.. ч.
где qv и qjj — алгебраические дополнения элементов rv и г^ матрицы
qp. В частности, в случае трех переменных (р = 3) из формулы
(12.70) следует, что
Частный коэффициент корреляции rtJ и как и парный коэф-
фициент корреляции г, может принимать значения от —I до I-
Кроме того, Гу 1? вычисленный на основе выборки объема п, име-
ет такое же распределение, что и г, вычисленный по (п -р + 2) на-
блюдениям. Поэтому значимость частного коэффициента корреля-
ции Гу |2 /, оценивают гак же. как и коэффициента корреляции г (см.
§ 12.5), но при этом налагают п' = п -р + 2.
426
D> Пример 12.9. Для исследования зависимости между произво-
дительностью груда (А'|), возрастом (А2) и производственным ста-
жем (Aj) была произведена выборка из 100 рабочих одной и той же
специальности. Вычисленные парные коэффициенты корреляции
оказались значимыми и составили: г)2 = 0.20; гв = 0.41; г2х = 0.82. Вы-
числить множественный коэффициент корреляции /?| у. частные ко-
эффициенты корреляции и оценить их значимость на уровне и = 0.05.
Реше н и с. По формуле (12.68) вычислим множественный
коэффициент корреляции:
R. = ^20"+0,41~-2 0.20-0,41 0.82 = = () ,7
1-0.823
т.е. .между производительностью труда, с одной стороны, и возрас-
том и производственным стажем рабочих — с другой, существует
заметная связь. Множественный коэффициент детерминации
= 0.225 показывает, что вариация производительности труда
рабочих на 22.5% объясняется вариацией их возраста и производст-
венного стажа.
Для оценки значимости по формуле (12.69) вычислим
0.47; (100 3) ~]И
(I-0.47:)-(3-1)
и по таблицам Л распределения найдем /\).05.2.о7 = 3.09. Так как
то Л| ;, значимо отличается от нуля.
По (формуле (12.71) вычислим частные коэффициенты корреля-
ции:
0.20:-0.41 0.82
г,., = -т=-~ --------= - 0.26
- 0.41-)(| -0.82-)
и аналогично 2 ~ 0.44; r2? i = 0.83.
Оценим значимость Патагаем jciohho //' = /»- р + 2 == 100 - 3 + 2 =
*99. Статистика критерия по формуле (12.43):
f = zO26.^2_2>65
VI-0.26*
По таблице /-распределения Стьюдента находим Zo.os.-97» 1.99.
Так как |/|>f(mu7. то частный коэффициент корреляции Г|21 зна-
427
чнм. Тем более будут значимы большие коэффициенты и Ги ।
(в этом можно убедиться таким же образом). ►
Сравнивая частные коэффициенты корреляции с соответст-
вующими парными коэффициентами Су. видим, что за счет «очищения
связи» наибольшему изменению подвергся коэффициент корреляции
между производигельностью труда (А\) и возрастом (АЧ> рабочих (изме-
нилась не только его величина, ио даже и знак: qj = 0.20; г(21 = - 0.26.
причем оба эти коэффициента значимы).
Итак, между производительностью труда (А'|) и возрастом (AS) ра-
бочих существует прямая корреляционная связь (г(2 = 0,20). Если же
устранить (элиминировать) влияние переменной «производствен-
ный стаж» (Ад). го в чистом виде производительность груда (A’t) на-
ходится в обратной по направлению (и опять же слабой по тесноте)
связи с возрастом рабочих (AS) (гцз = -0.26). Это вполне объясни-
мо. если рассматривать возраст только как показатель работоспо-
собности организма на определенном этапе его жизнедеятельности
Подобным образом могут быть интерпретированы и другие частные
коэффициенты корреляции.
Заканчивая краткое изложение корреляционного анализа коли-
чественных признаков, остановимся на двух моментах.
I. Задача научного исследования состоит в отыскании причинных
зависимостей. Только знание истинных причин явлений позволяв
правильно истолковывать наблюдаемые закономерности. Однако
корреляция как формальное статистическое понятие сама по себе нс
вскрывает причинного характера связи. С помощью корреляционно-
го анализа нельзя указать, какую переменную принимать в качестве
причины, а какую — в качестве следствия Например, рассматривая
корреляционную связь между суточной выработкой продукции и
величиной основных производственных фондов (см. пример 12.1),
изменение последней можно считать одной из причин изменения
суточной выработки. Но. с другой стороны, необходимость повы-
шения суточной выработки продукции может повлечь за собой увели-
чение размера основных производственных фондов. Между урожайно-
стью сельскохозяйственных культур и погодными условиями (темпера-
турой, количеством осадков и т.н.) существует корреляционная
связь. Но здесь не возникает сомнений, какая переменная является
следствием, а какая — причиной.
Иногда при наличии корреляционной связи ни одна из перемен-
ных не может рассматриваться причиной другой (например, зависи-
мость между весом и ростом человека). Наконец, возможна ложная
корреляция (нонсенс-корреляция). т.е. чисто формальная связь между
переменными, нс находящая никакого объяснения и основанная
лишь на количественном соотношении между ними (таких приме-
ров в статистической литературе приводится немало). Поэтому при
логических переходах от корреляционной связи между переменными к
428
их причинной взаимообусловленности необходимо глубокое проникнове-
ние в сущность анализируемых явлений.
2. Не существует общеупотребительного критерия проверки опре-
деляющего требования корреляционного анализа — нормальности мно-
гомерного распределения переменных. Учитывая свойства теоретиче-
ской модели, обычно полагают, что отнесение к совместному нор-
мальному закону возможно, если частные одномерные распределе-
ния переменных не противоречат нормальным распределениям
(в этом можно убедиться, например, с помощью критериев согла-
сия); если совокупность точек корреляционного поля частных дву-
мерных распределений имеет вид более или менее вытянутого «об-
лака* с выраженной линейной тенденцией.
Для проверки линейности связи пары признаков можно исполь-
зовать расхождение между квадратами эмпирического корреляци-
онного отношения ц* и коэффициента корреляции r'\ учитывая,
что статистика
(»Г - г
F = ----тг-----гг <12-72)
(m-2)(l-n )
(л — число наблюдений, т — число группировочных интервалов) имеет
^•распределение с А| = т - 2 и к> = п - т степенями свободы.
[> Пример 12.10. По данным табл. 12.1 на уровне значимости
0,05 проверить гипотезу о линейности корреляционной зависимости
между переменными У и X.
Реше н и е. Имеем п - 50. т = 5. В примере 12.3 было получено
г= 0.740. а в примере 12.7 — »| = 0.754. По формуле (12.72)
F _ (0.754 - 0.74(Г И50 - 5) _Q
(5-2K1-0.754J
Так как F< fo.osj;45 = 2.82 (см. табл. VI приложений), то гипо-
теза о линейности корреляционной зависимости между У и А' нс
отвергается. ►
Многомерный корреляционный анализ позволяет с помощью
корреляционной матрицы (12.66) получить оценку модельного
уравнения регрессии — линейного уравнения множественной рег-
рессии. Однако это проще сделать с помощью регрессионного ана-
лиза (см. гл. 13).
12.8. Ранговая корре.тя1Ц1я
До сих нор мы анализировали зависимости между количествен-
ными переменными, измеренными в гак называемых количественных
Шкалах, т.е. в шкалах с непрерывным множеством значений, позво-
ляющих выявить, на сколько (или по сколько раз)
проявление признака у одного объекта больше (меньше), чем у лру-
429
юю (например, производительность труда, себестоимость продук-
ции и т.п.).
Вместе с гем на практике часто встречаются с необходимостью
изучения связи между ординальными (порядковыми) переменными,
измеренными в так называемой порядковой шкале. В этой шкале
можно установить лишь порядок, в котором объекты выстраи-
ваются по степени проявления признака (например, качество жилищ-
ных условий, тестовые баллы, экзаменационные опенки и т.п.). Если,
скажем, по некоторой дисциплине два студента имеют опенки «отлич-
но* и «удовлетворительно*, то можно лишь утверждать, что уровень
подготовки по этой дисциплине первого студента выше (больше),
чем второго, но нельзя сказать, на сколько или во сколько pat
больше.
Оказывается. »гто в таких случаях проблема оценки тесноты свя-
зи разрешима, если упорядочить, или ранжировать, объекты анали-
за по степени выраженности измеряемых признаков. При этом каж-
дому объекту присваивается определенный номер, называемый ран-
гом. Например, объекту с наименьшим проявлением (значением!
признака присваивается ранг I. следующему за ним — ранг 2 и т.д
Объекты можно располагать и в порядке убывания проявления
(значений) признака. Если объекты ранжированы по двум призна-
кам. то имеется возможность оценить тесноту связи между призна-
ками, основываясь на рангах, т.е. тесноту' ранговой корреляции.
Коэффициент ранговой корреляции Спирмена нахо.ъпся по формуле:
р = 1—. (12.73)
п -п
где г, и л, — ранги /-го объекта ио переменным X и К, п — число пар
наблюдений.
Если ранги всех объектов равны (г, = \, / = I. 2.//), то р = I.
т.е. при полной прямой связи р = 1. При полной обратной связи,
когда ранги объектов по двум переменным расположены в обратном
порядке, можно показать, что s()’ =(/?' -л)/3 и по формуле
i-i
(12.72) р = -1. Во всех остальных случаях | р | < I.
При ранжировании иногда сталкиваются со случаями, когда не-
возможно найти существенные различия между объектами по вели-
чине проявления рассматриваемого признака. Объекты, как гово-
рят, оказываются связанными. Связанным объектам приписываю!
одинаковые средние ранги, такие, чтобы сумма всех рангов остава-
лась такой же, как и при отсутствии связанных рангов. Например,
если четыре объекта оказались равнозначными в отношении рас
сматриваемо/о признака и невозможно определить, какие из четы-
430
рех рангов (4. 5. 6. 7) приписать этим объектам. то каждому объекту
приписывается средний ранг, равный (4+ 5 + 6 +7)/ 4 = 5.5.
При наличии связанных рангов ранговый коэффициент корреля-
ции Спирмена вычисляется по формуле:
Р = 1—।. <12.74)
-Г.)
да = г.=нП'.’-'.Н <12-75>
тг, /п, — число грутш неразличимых рангов у переменных Хи Y:
/, — число рангов, входящих в группу неразличимых рангов
переменных Л и Y.
При проверке значимости р исходят из того, что в случае спра-
ведливости нулевой гипотезы об отсутствии корреляционной связи
между переменными при л > 10 статистика
х/1-р;
имеет /-распределение Стьюдента с к: - л - 2 степенями свободы.
Поэтому р значим на уровне а, если фактически наблюдаемое зна-
чение / будет больше критического (по абсолютной величине). т.е.
|г |:>/,, .. где /, 1| И — табличное значение /-критерия Стьюдента.
определенное на уровне значимости п при числе степеней свободы
к = л - 2.
> Пример 12.11. По результатам тестирования 10 студсггтов по
двум дисциплинам /1 и R на основе набранных баллов получены сле-
дующие ранги (табл. 12.5). Вычислить рантовый коэффициент корре-
ляции Спирмена и проверить его значимость на уровне а = 0.05.
Решение. Разности рангов и их квадраты поместим в по-
следних двух строках табл. 12.5.
Tii6.iHiui 12.5
Ранги nochtc- циплшшм Студент, i Всего
1 2 3 4 5 6 7 X 9 10
Л г, 2 4 5 1 7.5 7.5 7.5 7.5 3 10 55
В S. 2.5 6 4 1 2.5 7 X 9.5 5 9.5 55
г,- -0.5 -2 1 0 5 0.5 -0.5 -2 -2 0.5 —
О?" 0.25 4 1 0 25 0,25 0.25 4 4 0,25 39
431
По формуле (12.73) р = I - ~ = 0,763. Однако формула
(12.73) не учитывает наличия связанных рангов.
По дисциплине .4 имеем m, = I — одну группу неразличимых
рангов с /г= 4 рангами; по дисциплине В - т, = 2 — две группы не-
различимых рангов по /д = 2 ранга. Поэтому по формуле (12.75)
Г
Находим „о формуле (12.74)
39
р = 1 - ---------------= о,755.
‘(|0’-10)-(5 + |)
Для проверки значимости р по формуле (12.76)' вычислим
(12.77)
J|0 - 2
t = 0.755-— - = 3.26 и найдем по табл. IV приложений /<»
Vl-O,755:
= 2.31. Так как / > ro.9S;S« то ранговый коэффициент корреляции р
значим на 5%-ном уровне. Связь между опенками двух дисциплин
достаточно тесная. ►
Коэффициент ранговой корреляции Кендалла находится по формуле:
4А
г = I —---------------------------.
л(и-|)
где К — статистика Кендалла2.
Для определения Л’ необходимо ранжировать объекты по одной
переменной в порядке возрастания рангов (I. 2. л) и определить
соответствующие их ранги (rh г2, .... гя) по другой переменной. Ста-
тистика Л’ равна общему числу инверсий (нарушений порядка, когда
большее число стоит слева от меныпего) в ранговой последовательно-
сти (ранжировке) q. г2.гп. При полном совпадении двух ранжиро-
вок имеем Л = 0 и т= I; при полной противоположности можно по-
казал., что К = л(л - 1)/2 и т = - I. Во всех остальных случаях |т| < I
При проверке значимости т исходят из того, что в случае спра-
ведливости нулевой гипотезы об отсутствии корреляционной связи
между переменными (при п > 10) т имеет приближенно нормаль-
ный закон распределения с математическим ожиданием, равным
* В примерил 12.11 и 12.12 использованы приближенно при н = 10 критерии про
верки значимости «хпнегсгвенно р и х, справедливые. вообще юиоря, при л > 10
- Формула тля расчета т при наличии связанных рашов здеез. нс приводится
432
нулю, и средним квадратическим отклонением
12(2» 4 5)
9л(и-1)
По-
этому т значим на уровне а. если значение статистики
т-0
----— Т I-----—
Л, \2(2п *5)
(12.78)
по абсолютной величине больше критического /, „. где Ф(/ь<4) = I - а.
Поясним вычисление рангового коэффициента корреляции
Кендалла на примере.
> Пример 12.12. В результате анкетного обследования для 10 важ-
нейших пилон оборудования, используемого судоводителями во время
вахты, получены следующие ранги по важности оборудования X и по
частоте его использования Y (табл. 12.6). Вычислить ранговый коэф-
фициент Кендалла и оценить его значимость на уровне и = 0.05.
Рсшсни е. В последней строке табл. 12.6 представлены зна-
чения числа инверсий в ранжировках по переменной Y для различ-
ных рангов по переменной X.
менной X. Тогда соответствующий ранг по переменной К г* = 9 и с
учетом последующих рангов (см. табл 12.6) имеем ранжировку по Y
(9. 10. X. 7. 5).
Из пар чисел (перестановок) (9. 10). (9. X). (9. 7). (9. 5) инвер-
сии (нарушения порядка, когда большее число стоит слева от
меньшего) имеются у грех последних пар. т.е. число инверсий рав-
но 3. Аналогично определяются и другие значения числа инверсий
и находится их сумма Л' = 13. Теперь но формуле (12.77)
433
Оценим значимость т. Вычислим по формуле (12.78) значение
статистики / = 0.422 ---------=8.49. по табл. IV приложении
у 2(2-10 + 5)
fa.95 = 1.96. Так как / > fo.95. то ранговый коэффициент корреляции
Кендалла значим на 5%-ном уровне. Связь между рассматриваемы-
ми переменными умеренная. ►
Сравнивая коэффициенты ранговой корреляции р (Спирмена) и
т (Кендалла), можно отметить, что хотя вычисление г более трудо-
емко. коэффициент г обладает некоторыми преимуществами перед
Р при исследовании его статистических свойств (например, возмож-
ностью приближенного построения доверительного интервала для
г) и большим удобством его пересчета при добавлении к п стати-
стически обследованным объектам новых, т.е. при удлинении ана-
лизируемых ранжировок.
Значения коэффициентов р и г тесно связаны между собой.
При умеренно больших значениях п (п > 10) и при условии. >по аб-
солютные величины значений этих коэффициентов не слишком близки
к единице, их связывает простое приближенное соотношение р а 1,5т.
Ранговые коэффициенты корреляции put могут быть использова-
ны и для оценки тесноты связи между' обычными количественными пе-
ременными, измеряемыми в интервальных шкалах. Достоинство р и т
здесь заключается н том. что нахождение этих коэффициентов не требу-
ет нормального распределения переменных, линейной связи между ни-
ми (хотя и предполагает монотонность функции регрессии, отражающей
эту связь). Однако необходимо учитывать, ’гто при переходе от первона-
чальных значений переменных к их рангам происходит определенная по-
теря информации. Чем теснее связь, чем меньше корреляционная зависи-
мость между переменными отличается от линейной, тем ближе коэффи-
циент Спирмена р к коэффициент парной корреляции г.
В практике статистических исследований встречаются случаи,
когда совокупность объектов характеризуется не двумя, а несколь-
кими последовательностями рангов (ранжировками) и необходимо
установить статистическую связь между несколькими переменными.
Такие задачи возникают, например, при анализе экспертных оце-
нок. когда необходимо установить меру их согласованности.
В качестве такого измерителя используют коэффициент конкорда-
ции (согласованности) рангов Кендалла IF. определяемый по формуле1:
!2^О:
И' = —г-Ч---. (12.79)
т'(п -п)
где п — число объектов;
т — число анализируемых порядковых переменных;
1 Формула для расчета IF при наличии свяинных рангов здесь не приводи км
434
D-Ь
П1 (П 4- 1)
(12.80)
— отклонение суммы рангов объекта от средней их суммы для всех
объектов, равной min + I)/2.
Можно доказать, что значения коэффииис1па IF заключены на
отрезке |0. 1|, т.е. О < И' < I. причем IF - I при совпадении всех
ранжировок.
Проверка значимости коэффициента конкордации IF основана
на том, что в случае справедливости нулевой гипотезы об отсутствии
корреляционной связи при п > 7 статистика т(п - I) IF имеет при-
ближенно /“'-распределение с к = п - I степенями свободы. Поэто-
му Назначим на уровне а. если
(12.81)
1> Пример 12.13. Группа из 5 экспертов оценивает качество из-
делий. изготовленных на 7 предприятиях. Их предпочтения пред-
ставлены в табл. 12.7. Вычислить коэффициент конкордации рангов
и оценить его значимость на уровне и = 0.05.
Решение. В итоговой строке табл. 12.7 приведены суммы
рангов изделий по каждому из 7 предприятии, полученных от
5 экспертов. Общая сумма рангов равна 140. Средняя сумма рангов
равна т(п + 1 )/2 = 5(7+1 )/2 = 20 или. иначе, 140/7 = 20.
ТиГмнци 12.7
Эксперт, j Предприятие, i
1 2 3 4 5 6 7
1 1 3 4 2 6 7 5
2 1 2 5 3 6 4 7
3 2 1 7 5 6 4 3
4 1 2 4 6 3 5 7
5 3 1 5 4 2 6 7
5 Сумма рангов 8 9 25 20 23 26 29 140
D -12 -11 5 0 3 6 9 —
D* 144 121 25 0 9 36 81 416
В предпоследней строке табл. 12.7 помещены разности D = - 20,
Г-1
а в последней строке — их квадраты D2.
435
Коэффициент конкордации по формуле (12.79)
И' = 416 _ 0,594. Оценим значимость И/|. Вычислим т (п - I)
5= (7’-7)
Ж = 5 *6’0.594 = 17.83: но табл. V приложений = 12.59. Так
как т (п - 1)И/> х«.«л» то коэффициент конкордации Назначим на
5%-ном уровне. Таким образом, существует достаточно тесная со-
гласованность мнений экспертов. ►
Корреляционный анализ может быть использован и при оценке
взаимосвязи качественных (категоризованных) признаков (переменных),
представленных в так называемой номинальной шкале, в которой воз-
можно лишь различение объектов по возможным состояниям, града-
циям (например, пол. социальное положение, профессия и т.п.). Здесь
в качестве соответствующих показателей могут быть использованы
коэффициенты ассоциации, контингенции (сопряженности), бисериаль-
ной корреляции. Эти вопросы рассмотрены, например, в [2], |25|. |37|.
Упражнения
12.14. Распределение 60 предприятии химической промышлен-
ности но энерговооруженности труда У(кВт*ч) и фондовооружен-
ности X (млн руб.) дано в таблице:
Л У 0-4.5 4.5-9.0 9.0-13.5 13.5-18.0 18.0-22.5 Итого
0-1.4 4 1 — — — 5
1.4-2.8 4 2 — — — 6
2,8-4,2 2 8 1 — — II
4.2—5.6 — 1 20 4 — 25
5.6-7.0 — — 3 3 3 9
7.0-8.4 — — — 1 3 4
Итого 10 12 24 8 6 60
Необходимо: а) найти групповые средние х( и г, и построить
эмпирические линии регрессии: б) оценить тесноту и направление
связи между переменными с помощью коэ<|)фицнснта корреляции;
проверить значимость коэффициента корреляции и построить для
него 95%-ный доверительный интервал; в) вычислить эмпирические
корреляционные отношения и оценил, их значимость на 5%-ном
уровне; г) на уровне значимости 0.05 проверить гипотезу о линейной
1 Используем приближенно при л = 7 критерия проверки шичимекчи И. спра-
ведливый. вообще говоря, при л > 7
436
корреляционной зависимости между переменными У и X; д) найти
уравнения прямых регрессии, построить их графики и найти 95%-ные
доверительные интервалы для коэффициентов регрессии.
12.15. Имеются следующие данные об уровне механизации ра-
бот Х(%) и производительности труда Г (т/ч) для 14 однотипных
предприятий:
X, 32 30 36 40 41 47 56 54 60 55 61 67 69 76
У, 20 24 28 30 31 33 34 37 3S 40 41 43 45 48
Необходимо: а) оценить тесноту и направление связи между пе-
ременными с помощью коэффициента корреляции; проверить зна-
чимость коэффициента корреляции и построить для него 95%-ный
доверительный интервал; б) найти уравнения прямых регрессии.
12.16. При исследовании корреляционной зависимости подан-
ным 20 предприятий между капиталовложениями X (млн руб.) и
выпуском продукции У (млн руб.) получены следующие уравнения
регрессии: у = 1.2.x + 2 и х = 0.7у + 2. Найти: а) коэффициент кор-
реляции между рассматриваемыми признаками и оценить его зна-
чимость на 5%-ном уровне; б) средние значения капиталовложений
и выпуска продукции. Согласуется ли полученный в п. а) результат
с утверждением о том, что генеральный коэффициент корреляции
между А'и К равен 0.95?
12.17. При исследовании корреляционной зависимости между ценой
на нефть X и индексом нефтяных компаний У получены следующие денные:
.7 = 16.2 (лен. ед.), у = 4000 (уел. ед.). = 4. ,s‘=500. р = 40. Необхо-
димо: а) составит!» уравнения регрессии У по X и X по У, б) используя
соответствующее уравнение регрессии, найти среднюю величину индек-
са при цене на нефть 16.5 лен. ед.
12.18. При исследовании корреляционной зависимости между
объемом продукции X (единиц) и ее себестоимости У (тыс. руб.)
получено следующее уравнение регрессии У по X:
г, =-0.0004.x+ 4.22. Составить уравнение регрессии X по У. если
коэффициент корреляции между этими признаками оказался рав-
ным -U.S. а средний объем продукции 7 = 3000 единиц.
12.19. С целью исследования влияния факторов X) — среднеме-
сячного количества профилактических наладок автоматической линии
и А'» — среднемесячного числа обрывов нити на показатель У — сред-
немесячную характеристику качества ткани (в баллах) по данным
37 предприятий легкой промышленности были вычислены парные
коэффициенты корреляции: г =0.105. г, =0.024 и г,, =0.996. Оп-
437
ределнть: а) частные коэффициенты корреляции ги, и г.,и оценить
их значимость на 5%-ном уровне; б) множественный коэффициент
корреляции Rvi2 и оценить его значимость на уровне а = 0.05;
в) множественный коэффициент детерминации. Пояснить смысл по-
лученных коэффициентов.
12.20. При приеме на работу семи кандидатам на вакантные
должности было предложено два теста. Результаты тестирования (в
баллах) приведены в таблице:
Тест Кандидат
1 2 3 4 5 6 7
1 31 82 25 26 53 30 29
2 21 55 8 27 32 42 26
Вычислить ранговые коэффициенты корреляции Спирмена и
Кендалла между результатами тестирования но двум тестам и на
уровне а = 0.05 оценить их значимость.
12.21. На соревнованиях по фигурному катанию девять судей
выставили следующие балльные опенки 10 фигуристам:
Фигурист Судья
1 2 3 4 5 6 7 8 9
1 6.0 5,8 5,7 5,8 6.0 5.9 5.9 5,9 5.8
2 5.4 5,3 5,2 5.3 5.4 5.5 5.6 5,3 5.1
3 5.2 5,0 4,9 5.1 5.2 5.0 4.8 5.3 4.9
4 5,9 5,9 5.8 5.7 5.9 5.8 6.0 5.8 5.7
5 5,0 4,9 4,9 4.9 5.) 5.0 5.0 4,8 4.7
6 5.6 5.5 5.4 5.4 5.5 5.5 5.7 5.6 5.5
7 4.8 4.7 4.6 4,6 4.8 4.9 5.0 4.6 4.5
8 5.4 5.6 5,4 5.5 5,6 5.7 5.4 5.3 5.2
9 5,8 5.7 5,6 5,7 5.8 5.9 5.6 5.7 5.8
10 5.3 5.2 5.1 5.4 5.5 5.4 5.2 5.3 5.2
Вычислит!, коэффициент конкордации рангов и оценить его
значимость на уровне и = 0.05.
Глава 1 3
Регрессионный анализ
В практике экономических исследований очень часто имею-
щиеся данные нельзя считать выборкой из многомерной нормаль-
ной совокупности, например, когда одна из рассматриваемых пере-
менных нс является случайной или когда линия регрессии явно нс
прямая и т.п. В этих случаях пытаются определить кривую (поверх-
ность). которая дает наилучше? (в смысле метода наименьших
квадратов) приближение к исходным данным. Соответствующие
методы приближения получили название регрессионного анализа.
Задачами регрессионного анализа являются установление формы за-
висимости между переменными, оценка функции регрессии, оценка неиз-
вестных значений (прогноз значений) зависимой переменной.
13.1. Основные положения регрессионного анализа.
Парная peqieccионная модель
В регрессионном анализе рассматривается односторонняя зави-
симость случайной зависимой переменной Y от одной (или нескольких)
неслучайной независимой переменной X. называемой часто объясняю-
щей переменной'. Такая зависимость может возникнуть, например, в
случае, когда при каждом фиксированном значении X соответст-
вующие значения Y подвержены случайному разбросу за счет дей-
ствия неконтролируемых факторов. Указанная зависимость Y от X
(иногда ее называют регрессионной) может быть представлена также
в виде модельного уравнения регрессии (12.1). В .силу воздействия
неучтенных случайных факторов и причин отдельные наблюдения у
будут в большей или меньшей мере отклоняться от функции рег-
рессии ф(х). В этом случае уравнение взаимосвязи двух переменных
{парная регрессионная модель) может быть представлено в виде:
Y = <*» (А) + с,
где с — случайная переменная, характеризующая отклонение от
функции регрессии. Эту переменную будем называть возмущающей
или просто возмущением-. Таким образом, в регрессионной модели
зависимая переменная Y сеть некоторая функция фСА1) с точностью до
случайного возмущения с.
1 В литературе У называют также функцией отклика. объясняемой. выходной, ре-
зулыпирующей, зндзкентш переменной, результативны.» признака.», а Л — входной,
предсказывающей. прсзЗик торной. зкзогенной переменной, факторам', регрессором,
фак торным при знаком.
• Переменную »: нааыюают Также остаточной, ИДИ остатком, либо ошибкой.
439
Рассмотрим линейный регрессионный анализ, для которого функция
<р(Л) лине й н а относительно оцениваемых параметров:
ЛМП = Ро+Р|Х (* *3.1)
Предположим, что для оценки параметров линейной функции
регрессии (13.1) взята выборка, содержащая п пар значений пере-
менных (X/, yj, где i = 1,2.п. В этом случае линейная парная рег-
рессионная модель имеет вил:
У, = По + №+ (*3.2)
Отметим основные предпосылки регрессионного анализа.
1. В модели (13.2) возмущение1 с, (или зависимая переменная у,)
есть величина случайная, а объясняющая переменная х, — ветчина
неслучайная2.
2. Математическое ожидание возмущения с, равно нулю:
МЫ = 0. (13.3)
(или математическое ожидание зависимой переменной у, равно ли-
нейной функции регрессии: М(уЦ = По +
3. Дисперсия возмущения г., (или зависимой переменной у() посто-
янна для любого i:
1>Ы = а2 (13.4)
(или Diy,) = п2 — условие гомоскедастичности или равноизменчиво-
сти возмущения (зависимой переменной)).
4. Возмущения е; и £у (или переменные у, и уу) не коррелированы2
Л/(с,с7) = 0 (/*/). (13.5)
5. Возмущение е, (или зависимая переменная у() есть нормально
распределенная случайная величина.
Для получения уравнения регрессии достаточно первых четырех
предпосылок. Требование выполнения пятой предпосылки (т.е. рас-
смотрение «нормальной регрессии*) необходимо для оценки г о ч •
ноет и уравнения регрессии и его параметров.
Оценкой модели (13.2) по выборке является уравнение регрес-
сии ух = Ьц+ Ь\Х (12.8). Параметры этого уравнения Ль и
1 Во всех предпосылках / = 1.2.п.
• При этом предполагается. что среди значений х, (г “ I. 2. и). по крайней
мерс, нс вес одинаковые, так ‘гго имеет смысл формула (12.17) для коэффинн-
сига регрессии.
Требование некоррелированности А.\, = 0 с учетом (5.32) и (13.3) приводи:
к условию (13.5): Kt с - Л/|(с, -0)(е, -0)] - M(?.y.t) = 0. При выполнении
предпосылки 5 это требование равносильно нсшвиснмосгн переменных.
440
Z»i определяются на основе метода наименьших квадратов. Об их
нахождении подробно см. в § 12.2.
Теорема Гаусса—Маркова. Если регрессивная модель удовлетворя-
ет предпосылкам 1—4. то оценки Ь„ (12.14') и Л, (12.17) имеют наи-
меньшую дисперсию в классе всех линейных несмещенных оценок, т.е.
являются эффективными оценками параметров и pt.
Воздействие неучтенных случайных факторов и ошибок наблюде-
ний в модели (13.2) определяется с помощью дисперсии возмущений
(ошибок) или остаточной дисперсии л2. Несмещенной оценкой этой
дисперсии является выборочная остаточная дисперсия
где г, — групповая средняя, найденная по уравнению регрессии;
е, = А’, у — выборочная оценка возмущения или остаток рег-
рессии'.
В знаменателе выражения (13.6) стоит число степеней свободы
л - 2. а не п. так как две степени свободы теряются прн определе-
нии двух параметров прямой Лц и Л,.
13.2. 11|пт|>1мыы1ая оценка функции регрессии
Построим доверительный интервал для функции регрессии, т.е.
для условного математического ожидания Л/Д У), который с задан-
ной надежностью (доверительной вероятностью) у = 1 - а накры-
вает неизвестное значение Л/J Y).
Найдем дисперсию групповой средней ул. представляющей вы-
борочную опенку Мх( У). С этой целью уравнение регрессии (12.15)
представим в виде:
.г. = г+ />,(*-*)• (13.7)
На рис. 13.1 линия регрессии (13.7) изображена графически.
Для произвольного наблюдаемого значения yf выделены его состав-
ляющие: средняя г, приращение />,(х, - .v). образующие расчетное
значение г,. и возмущение et.
Дисперсия групповой средней равна сумме дисперсий двух
независимы х- слагаемых выражения (13.7):
о; = + ст* (.г - .г Г. (13.8)
’ с, называют также невязкой
* Доказательство лото факта здесь нс приводится
441
Рис. 13.1
(Здесь учтено, что (л-.v) — неслучайная величина, при вынесении
которой за знак дисперсии ее необходимо возвести в квадрат.)
Дисперсия выборочной средней у согласно формуле (9.16)
<?.=—. (13.9)
п
Для нахождения дисперсии представим коэффициент рег-
рессии в виде1:
-хКг, -V)
6,=-^--------------. (13.10)
>>i
Тогда
£(х,-?):а;
а- =-Ш-----------=-^-------- (13.11)
£(х, -?)•’] !<*.-*>’
Найдем оценку дисперсии групповых средних (13.8), учитывая
формулы (13.9) и (13.11) и заменяя а2 ее оценкой s2:
(13.12)
1 Раскрыв скобки и разделив числитель и шаменлгсль выражения (13.10) на п.
нетрудно получить уже знакомое выражение (12.17)
442
Исходя из того, что статистика t
имеет /-рас-
пределенис Стьюдента с к = п - 2 степенями свободы, можно (ана-
логично тому, как это сделано в § 9.7) построить доверительный ин-
тервал для условного математического ожидания
У. u.r\. S/W(()')^y, + /Г(М-х,
ах 13)
групповой средней у,.
ipuMiliiu ua
Рис. 13.2
У
У
о
где л, = — стандартная ошибка
Из формул (13.12) и (13.13)
видно, что величина доверительно-
го интервала зависит от значения
объясняющей переменной х при
х = х она минимальна. а по мерс
удаления х от х величина довери-
тельного интервала увеличивается
(рис. 13.2). Таким образом, прогноз
значений (определение неизвестных
значений) зависимой переменной у
по уравнению регрессии оправдан,
если значение объясняющей пере-
менной не выходит за диапазон ее
значений по выборке (причем тем более точный, чем ближе х к г).
Другими словами, экстраполяция кривой регрессии, т.е. ее использо-
вание вне пределов обследованного диапазона значений объясняющей
переменной (лаже если она оправдана для рассматриваемой пере-
менной исходя из смысла решаемой задачи) может привести к
значительным погрешностям.
Построенная доверительная область для Л/. (У) (см. рис. 13.2) оп-
ределяет местоположение модельной линии регрессии (т.е. условного
математического ожидания). но не отдельных возможных значений
зависимой переменной, которые отклоняются от средней. Поэтому
при определении доверительного интервала для индивидуальных значе-
ний г’ зависимой переменной необходимо учитывать еще один ис-
точник вариации — рассеяние вокруг линии регрессии, т.е. в оценку
суммарной дисперсии л' следует включить величину s2. В результате
оценка дисперсии индивидуальных значений у0 при х = хо равна
1 x (X«
— +-------
(13.14)
443
а соответствующий доверительный интервал для прогнозов индиви-
дуальных значений у* будет определяться но формуле:
-Ч - Д, + 'i-...-:*4« (13.15)
> Пример 13.1. Имеются следующие данные (условные) о смен-
ной добыче угля на одного рабочего Y (т) и мощности пласта X (м),
характеризующие процесс добычи угля в 10 шахтах (табл. 13.1).
Таблица 13.1
/ 1 т 3 4 5 6 7 8 9 К)
Xj 8 II 12 9 8 8 9 9 8 12
Л 5 10 10 7 5 6 6 5 6 8
Оценить сменную среднюю добычу угля на одного рабочего для
шахт с мощностью пласта X м. Найти 95%-ные доверительные ин-
тервалы для индивидуального и среднего значений сменной добычи
угля на 1 рабочего для таких же шахт.
Р е ш с и и е. Вначале аналогично тому, как это сделано в при-
мере 12.1. составим уравнение регрессии1. Получим (рекомендуем чи-
10 10 III
тателю получить самостоятельно) ^.т, =94. У .г; =908. У^у, =68.
1-1 <«» |"|
£у; =496. £л;у, =664 и уравнение регрессии у, = -2.75 + 1.016л*.
«-I «-I
т.е. при увеличении мощности пласта X на I м добыча угля на одной’
рабочего Y увеличивается в среднем на 1,016 т (в усл. ед.).
Надо оценить условное математическое ожидание Л/Х.х()). Вы-
борочной оценкой У) является групповая средняя уЛ=8. которую
найдем по уравнению регрессии: y4-s= -2.75 + 1.016*8 = 5,38 (т).
Для построения доверительного интервала для ЛД--и( У) необходимо
знать дисперсию его оценки, т.е. . Составим вспомогательную
таблицу (табл. 13.2) с учетом того, что v = 9.4 (м). а значения у, оп-
ределяются по полученному уравнению регрессии.
1 В расчетах полагаем и,, л, = п, ° \.J ~ i. а У £ шменмем так как ис-
ходные данные нс сгруппированы
444
Tu6.ihiui 13.2
X/ 8 11 12 9 8 8 9 9 8 12 V
(X/" х)2 1.96 2.56 6.76 0.16 1.96 1.96 0.16 0.16 1.96 6.76 24.40
у, = -2,75 + + 1.016л, 5.3S 8.43 9,44 6.39 S.38 5,38 6,39 6,39 5.38 9.44 —
< = - >•» 0.14 2.48 0.31 0,37 0,14 0,39 0.15 1,94 0,39 2.08 8.39
Теперь имеем по форму/ ле (13.12): .< =1,049 ’• л И V. = те (13.6): ? = ± (8-9-4>г~ 10+ 24.4 JO. 189 =0.43: 8 39 J = 1.049. по форму- = 0,189 (т).
По табл. IV приложений /о,95;« = 2.31. Теперь по формуле (13.13)
искомый доверительный интервал:
5.38 - 2.31-0.435 s М^( Л < 5,38 + 2,31-0.435
или 4.38 £ Л £ 6,38 (т).
Итак, средняя сменная добыча угля на одного рабочего для
шахт с мощностью пласта 8 м с надежностью 0,95 находится в пре-
делах от 4,38 до 6,38 т.
Чтобы построить доверительный интервал для индивидуального
значения г* и, найдем дисперсию его оценки по формуле (13.14):
№ -1.049 1+ —+ 8 -9-,4)’ ] = 1.238
10 24.4 )
и s = Ji.238 =1,113 (т).
Далее искомый доверительный интервал подучим но формуле
(13.15):
5.38 — 2,31 • 1,113 < у;., <5,38 + 2.31-1,113
или 2,81 i y^.g S 7,95.
Таким образом, индивидуальная сменная добыча угля на одного
рабочего для шахт с мощностью пласта 8 м с надежностью 0.95 на-
ходится в пределах от 2,81 до 7,95 т. ►
445
13.3. Проверка значимости ураннения регрессии.
Интервальная оценка параметров пирной модели
Проверить значимость уравнения регрессии - значит установить,
соответствует ли математическая модель, выражающая зависимость
между переменными, экспериментальным данным и достаточно ли
включенных в уравнение объясняющих переменных (одной или нескольких)
для описания зависимой переменной.
Проверка значимости уравнения регрессии производится на ос-
нове дисперсионного анализа. В гл. 11 дисперсионный анализ рас-
смотрен как самостоятельный инструмент (метод) статистического
анализа. Здесь же он применяется как вспомогательное средство
для изучения качества регрессионной модели.
Согласно основной идее дисперсионного анализа (см. гл. II)
Х<у, “ У? = - У>*'+’ Л г (,Х 16)
/•I 1*1 1*1
или 2= (13.17)
где Q — общая сумма квадратов отклонений зависимой переменной
от средней, a Qr и Qr — соответственно сумма квадратов, обуслов-
ленная регрессией, и остаточная сумма квадратов, характеризующая
влияние неучтенных факторов.
Убедимся в том. что пропущенное в равенстве (13.17) третье
слагаемое = 2^(у, -уХУ, - у, ) равно нулю. Учитывая уравне-
/-1
ине (13.7) и первое уравнение системы (12.11). имеем:
У., "У =h,(x,-х);
У, ~ У, - У, У, - (У - Л,х) - Ь,х, = (>• - у) - Л,(х. - х).
Теперь
2, =2^(д -.vXv, -,v,) = 2i,£(.v, -х): =0
/•I 1*1
(с учетом соотношения (13.10)).
Схема дисперсионного анализа имеет вил. представленный в
табл. 13.3.
446
ТЫмшщ 13.3
Компоненты дисперсии Сумма квадратов Число степеней свободы Средние квадраты
регрессия i-i т - 1 т - 1
Остаточная v. f-l п — т * = и т
Общая t? Е<у, уг «1 п - 1
Средние квадраты х; и х’ (см. табл. 13.3) представляют собой
несмещенные опенки дисперсий зависимой переменной, обуслов-
ленной соответственно регрессией или объясняющейими) пере-
мснной(ыми) А' и воздействием неучтенных случайных факторов и
ошибок: т — число оцениваемых параметров уравнения регрессии:
л — число наблюдений.
Замечание. При расчете общей суммы квадратов полезно
иметь в виду, что
- №4
е=Уу,г- co in
... и
(формула (13.17') следует из разложения
. (tv."
Р= £(У, - г)2 = £ г; - 2у£ г, + и/ = .
ы (•! <>1 1-1 fl
£у.
учитывая, что г = —— ).
п
При отсутствии линейной зависимости между зависимой и объяс-
няюшсй(ими) переменной(ыми) случайные величины х; = 1(т -!) и
Г = (Z ~имеют х2-распределенис соответственно с т ~ I и п - т
степенями свободы, а их отношение — F-распределсние с теми же
степенями свободы (см. § 4.9). Поэтому уравнение регрессии значимо
на уровне а. если фактически наблюдаемое значение статистики
ед«-|) х- ,м,л
где /•',а , — табличное значение F-критерия Фишера—Снедекора,
определенное на уровне значимости и при А| = /л - 1 и Ь = л - т
степенях свободы.
447
Учитывая смысл величин sj и г. можно сказать, что значение f
показывает, в какой мере регрессия лучше оценивает значение зависи-
мой переменной по сравнению с ее средней.
В случае линейной парной регрессии т - 2 и уравнение регрес-
сии значимо на уровне а. если
(13.18)
Выше (§ 12.6) введен индекс корреляции R (для парной линей-
ной модели — коэффициент корреляции г), выраженный через
дисперсии (см. формулу (12.60)). Тог же коэффициент н терминах
*сумм квадратов» примет вил:
<ш9>
Следует отметить, что значимость уравнения парной линейной
репрессии может быть проверена и другим способом, если оценить
значимость коэффициента регрессии Ь\, что означает проверку нуле-
вой гипотезы о равенстве параметра |1| парной модели (13.2) нулю,
т.е. //„: |J. =0 против альтернативной гипотезы1 /7,: (Л, «0.
Можно показать, что при выполнении предпосылки 5 регресси-
онного анализа (с. 440) статистика f~——— имеет стандартный
нормальный закон распределения МО;!), а если в выражении
(13.11) для оЛ заменить параметр о-’ его оценкой з2. то статистика
f = LA |уи - у/ (13.19')
s угг
имеет /-распределение с к = п - 2 степенями свободы. Поэтому ко-
эффициент регрессии Л| значим на уровне а (гипотеза //(| отверга-
, । h| Ja ~
ется). если р| = —*J2J.V, - О' >/, а доверительный интервал
для |1| имеет вил:
b,Л,' <13.19- >
У г-1 У (-1
1 Здесь и далее используем двусторонние критерии проверки гипотез.
448
Для парной регрессионной модели оценка значимости уравнения
регрессии по F-критсрию равносильна опенке значимости коэффи-
циента регрессии либо коэффициента корреляции г по г-критерию
(см. § 12.5). ибо эти критерии связаны соотношением F = г. А ин-
тервальные оценки для параметра (13.19") — при нормальном
законе распределения зависимой переменной и prr = (12.51)
совпадают.
При построении доверительного интервала для дисперсии возмуще-
, ____ лг 2
ннй о- исходят из того, что статистика —— имеет /‘-распределение с
сг
к - п - 2 степенями свободы. Поэтому интервальная оценка для п2
на уровне значимости а имеет вид (см. формулу (9.47)):
-gL-Scrs . (13.20)
О Пример 13.2. По данным табл. 13.1 оценить на уровне
а = 0,05 значимость уравнения регрессии У по X. Найти интерваль-
ную оценку для параметров р| и сг2.
Решение. 1-й способ. Выше, в примере 13.1. были найдены
10 10
<-|
Вычислим необходимые суммы квадратов по формулам (13.16).
(13.17):
/ ю у
1° IO I 1 AQ-
Q = У (V, - г)" =У у; = 496 - —= 33.6;
77 м Ю 10
Qe = £(у, ->)2 =£< =8.39 (см. табл. 13.2);
«•I <•!
&=<?-{?, =33.6-8,39 = 25,21.
По формуле (13.18*) F = — —12 = 24,04 .
8,39
По таблице F-распределения (табл. VI приложений)
Fo.o5;i;8= 4.20. Так как F> >o.o5;i;8. то уравнение регрессии значимо.
2-й способ. Учитывая, что 6| = 1.016. £(*< - г): - 24.40.
•-I
д2 = 1,049 (см. пример 13.1, табл. 13.2). по формуле (13.19*)
Г= У01-J24.40 =4.90.
71.049
15 Г сори. мрсатпхта1 н ыж.гы«п«че<к*1 гт>т»ггиж*
449
По таблице /-распределения (табл. IV приложений) г0.95;а =
= 2,31. Так как /> /о.95;8» то коэффициент регрессии, а значит, и
уравнение парной линейной регрессии Y по X значимы. Оба спосо-
ба оценки значимости уравнения парной регрессии равносильны,
ибо F= t* (24,40 = 4.902).
Найдем 100 (I - а) = 95%-ный доверительный интервал для па-
раметра Р|. По формуле (13.19")
h nag fl 049
1.016-2.31 ----<В, < 1,016 + 2.31 ----
V 24.40 \ 24.40
или 0.537 < р, < 1,495. т.е. с надежностью 0,95 при изменении мощ-
ности пласта Л” на I м суточная выработка Y будет изменяться на ве-
личину, заключенную в интервале от 0,537 до 1.495 (т).
Найдем 95%-ный интервал для параметра о2.
Учитывая, что а = I - 0,95 = 0.05. найдем по табл. V приложений
Х«:.п-г = Хо,.пм= 17.53« Хьи =Хо.™« = 2’18- По формуле (13.20)
10--,04Ч<о- или 0,599 < о'$4.81 и 0,774$о<2.19.
17,5 2.18
Таким образом, с надежностью 0.95 дисперсия возмущений за-
ключена в пределах от 0.599 до 4.81. а их стандартное отклонение —
от 0,774 до 2,19 (т). ►
13.4. Нелинейная регрессия
Соотношения между социально-экономическими явлениями и
процессами далеко нс всегда можно выразить линейными функ-
циями. так как при этом могут возникать неоправданно большие
ошибки. В таких случаях используют нелинейную (по объясняющей
переменной) регрессию.
Выбор вила уравнения регрессии (8.3) (этот важный этап анализ;!
называется спецификацией или этапам параметризации модели} произ-
водится на основании опыта предыдущих исследований, литературных
источников, других соображений профессионально-теоретического
характера, а также визуального наблюдения расположения точек кор-
реляционного поля. Наиболее часто встречаются следующие вилы
уравнений нелинейной регрессии: полиномиальное \\ = А) + Ь\Х + ... +
+ д^х*. гиперболическое ух = + Ь\/х. степенное yt = b(t • х? •... х'Г .
Например, если исследуемый экономический показатель у при
росте объема производства х состоит из двух частей — постоянной (нс
зависящей от х) и переменной (уменьшающейся с ростом х). то зави-
симость у от х можно представить в виде гиперболы >\ = ди + Ь\/х Ес-
ли же показатель у отражает экономический процесс, который пол
влиянием фактора х происходит с постоянным ускорением или замед-
лением, то применяются полиномы. В ряде случаев для описания эко-
450
комических процессов используются более сложные функции. На-
пример, если процесс вначале ускоренно развивается, а затем, после
достижения некоторою уровня, затухает и приближается к некоторому
пределу, то могут оказаться полезными логистические функции типа
у-Ьа/(\ +
При исследовании степенного уравнения регрессии следует иметь в
виду, что оно нелинейно относительно параметров Л;. однако путем ло-
гарифмирования может быть преобразовано в линейное:
In = In Ьо + />j In Л| + ... + bp In Xp.
Для определения неизвестных параметров до, Ь\......Ьр, как и
ранее, используется метод наименьших квадратов.
> Пример 13,3. По данным табл. 13.4 исследовать зависимость
урожайности зерновых культур У (и/га) от количества осадков X (см),
выпавших в вегетационный период'.
Таблицы 13.4
hfe п/n I
Коли-
чество
осадков
Х/(СМ) 25
Уро-
жай-
ностьу,
(ц/га) 23
27 30 35 36
24 27 27 32
38 39
31 33
2 3 4 5
Решение. Из ка-
чественных соображений
можно предположить,
что увеличение количе-
ства выпавших осадков
приводит к увеличению
урожайности до некото-
рого предела, после чего
урожайность будет сни-
жаться. Учитывая, кроме
того, расположение то-
чек корреляционного
поля (см. рис. 13.3),
можно предположить.
Рис. 13.3
1 То есть в период роста, ратшнм растений.
451
что наиболее подходящим уравнением регрессии будет уравнение
параболы
У, = Ло + bix + Ьхх2.
Его параметры Д). Ь\, находим, применяя метол наименьших
квадратов:
5=Sо*. -):=+ h2x> -yf-*min •
ы <«1
_ 3s ds ds
Приравняв частные производные —. — и —— к нулю, по-
dbu ih:
лучим после преобразований систему нормальных уравнений:
+ Л,£х. +
Г«1 J-I <-1
=1лх«- (13.21)
bl <-| 1-1 г-1
ь*£Х;=11ух-
Ы г-1 4-1 г-1
Для расчета необходимых сумм составим вспомогательную таб-
лицу (табл. 13.5).
Таблица 13.5
/ X/ У/ w X, xf •< У/Х, № Л (>; F
1 25 23 625 15 625 390 625 575 14 375 529 21.7 1,69
2 27 24 729 19 683 531 441 648 17 496 576 24,3 0,11
14 52 24 2704 140 608 7 311 616 1248 64 896 576 24,7 0.46
15 53 25 2809 148 877 7 890 481 1325 70 225 625 23.4 2.44
Е 606 429 25 548 1 115 808 50 158 200 17 371 730 123 12 493 — 45.94
Теперь система (13.21) примет вил:
452
156О + 6066, +
6066o + 25 548Л, +
25 5486й + 1115 8086, +
25 5486, = 429.
1115 8086. = 17 371.
50 158 2006, = 730 123.
Решая эту систему, например, метолом Гаусса, получим 6> = -43,93;
6| = 3,8342; 6г= -0.048361, т.е. уравнение регрессии имеет вид:
ух = -43,93 + 3,8342г - 0.048361лI 2 * *.
Оценим значимость полученной зависимости. С этой целью по
формуле (13.16) найдем суммы (см. итоговую строку табл. 13.5):
=45-94:
»-|
[£.Л
Q = £<У. - У У = £ у; - = 12 493 - ^ = 223,6;
(?№<?”<?« = 223.6 - 45.94 = 177.66.
177.66 (15-3)
По формуле (13.18): F = -------------= 23.2. Табличное зна-
45.94-(3-1)
ченне Fo.o$;2.i’s 3.88. Так как F > F0.05.2j2, то уравнение регрессии
значимо.
Для оценки тесноты связи вычислим индекс корреляции по
формуле (13.19):
I ЕГ I 45.94 /----
R = !-—= l-^—=Jo.795 =0.891.
•’ V (? V 223>6 * В
т.е. полученная зависимость весьма тесная. Коэффициент детерми-
нации /?;, =0,795 показывает, что вариация урожайности зерновых
культур на 79,5% обусловлена регрессией, или изменчивостью коли-
чества выпавших в вегетационный период осадков. ►
В некоторых случаях нелинейность связей является следствием
качественной неоднородности совокупности, к которой применяют
регрессионный анализ. Например, объединение в одной совокупно-
сти предприятий различной специализации или предприятий, су-
щественно различающихся по природным условиям, и т.д. В этих
случаях нелинейность может являться следствием механического
объединения разнородных единиц. Регрессионный анализ таких
совокупностей нс может быть эффективным. Поэтому любая нели-
нейность связей должна критически анализироваться.
453
По расположению точек корреляционного поля далеко не все-
гда можно принять окончательное решение о виде уравнения рег-
рессии. Если теоретические соображения или опыт предыдущих
исследований нс могут подсказать точного решения, то необходимо
сделать расчеты по двум или нескольким уравнениям. Предпочте-
ние отдастся уравнению, для которого меньше величина остаточ-
ной дисперсии. Однако при незначительных расхождениях в оста-
точных дисперсиях следует всегда останавливаться на более
просто м уравнении, интерпретация показателей которого нс
представляется сложной.
Весьма заманчивым представляется увеличение порядка вырав-
нивающей параболической кривой, ибо известно, что всякую
функцию на любом интервале можно как угодно точно приблизить
полиномом у = Д) + Ь[Х + Ь?х2 +...+ Так. можно подобрать та-
кой показатель к. что соответствующий полином пройдет через все
вершины эмпирической линии регрессии. Однако повышение по-
рядка гипотетической параболической кривой может привести к
неоправданному усложнению вида искомой функции регрессии,
когда случайные отклонения осредненных точек неправильно ис-
толковываются как определенные закономерности в поведении
кривой регрессии. Кроме того, за счет увеличения числа парамет-
ров снижается точность кривой регрессии (особенно в случае малой
по объему выборки) и увеличивается объем вычислительных работ.
В связи с этим в практике регрессионною анализа для выравнива-
ния крайне редко используются полиномы выше третьей степени.
13.5. Множественный репммтноннын анализ
Экономические явления, как правило, определяются большим
числом одновременно и совокупно действующих факторов. В связи
с этим часто возникает задача исследования зависимости одной за-
висимой переменной Y от нескольких объясняющих переменных
Л|, Xi..Хп. Эта задача решается с помощью множественного рег-
рессионного анализа.
Обозначим /-е наблюдение переменной у„ а объясняющих пе-
ременных — Хд, Х/2, .... х/?. Тогда модель множественной линейной
регрессии можно представить в виде:
у, = р0 + р,х„ +рЛ, +...+ Ргх„ +г,. (13.22)
где i — 1,2..п. а б( удовлетворяет приведенным выше предпосыл-
кам (13.3)—(13.5).
Включение в регрессионную модель новых объясняющих пере-
менных усложняет получаемые формулы и вычисления. Это приводит
454
к целесообразности использования матричных обозначений. Матрич-
ное описание регрессии облетает как теоретические концепции ана-
лиза, так и необходимые расчетные процедуры.
Введем обозначения: У = (j, у^ ... у„)‘ — матрица-столбец, или
вектор, значений зависимой переменной размера л1;
I X|J Jf), ... Х|Л
I X;i X.J ... х:р
Х =
— матрица значений объясняющих переменных, или матрица тана
размера п х (р + 1) (обращаем внимание на то. что в матрицу Д'до-
полнительно введен столбец, все элементы которого равны I, т.е.
условно полагается, что в модели (13.22) свободный член умно-
жается на фиктивную переменную хЛ, принимающую значение I
для всех /: хЛ1 I (/ = 1, 2.л);
Р = (По ₽| — Пр)‘ — матрица-столбец. или вектор, параметров раз-
мера (р + I);
е = (с| е> ... »:„)' — матрица-столбец, или вектор, возмущений (слу-
чайных ошибок, остатков) размера п.
Тогда в матричной форме модель (13.22) примет вид:
Г= АП + е.
(13.23)
Оценкой этой модели по выборке является уравнение
Г= ХЬ + е.
где b = (Л, Ь\ ... Лр', е = (е, е2... е„)'.
Для оценки вектора неизвестных параметров И применим метод
наименьших квадратов. Так как произведение транспонированной
матрицы <г на саму матрицу е
е'е = (^ t\ ... t'J
= + е; +... + е:„ =
1 Знаком • обозначается операция транспонирования матриц
455
то условие минимизации остаточной суммы квадратов запишется в
виде:
5 = - у,)’ = = с‘е = (Y - XhY( Y-Xb)^ min. (13.24)
«•I »•!
Учитывая, что при транспонировании произведения матриц полу-
чается произведение транспонированных матриц, взятых в обратном
порядке, т.е. (ХЬ)' = Ь'Х', получим после раскрытия скобок:
5 = Г Y - b'XY - Y'Xb + Л’.¥^>.
Произведение Y'Xb есть матрица размера (I * л)[л х (р + |)х
х|(^+ 1)х|| = (|х I), т.е. величина скалярная, следовательно, оно
не меняется при транспонировании: Y'Xb = (УХЬУ - b'X’Y. По-
этому условие минимизации (13.24) примет вид:
5 = ГТ - 2Ь'ХХ + Ь'Х'ХЬ -4 min, (13.24')
На основании необходимого условия экстремума функции не-
скольких переменных ..........Ьр). представляющей (13.24), необхо-
димо приравнять к нулю частные производные по этим переменным
или в матричной форме — вектор частных производных
aS.faS dS ]
ch cf\, cl\ chr J
Для вектора частных производных доказаны следующие формулы1:
с Я
—-(b'c)-c. —(b'Ab) = 2Ab.
cb дЬ
где Лис — вектор-столбцы, а А — симметрическая матрица, в ко-
торой элементы, расположенные симметрично относительно главной
диагонали, равны.
’ Справедливость приведенных формул проиллюстрируем па примере.
Пусть Л> = I ’ |. С = Pl = R 5 j Так как Ь'с - <А1 А2 I ЗА1 * 4А? “
ft'4ft = (ft|ftJ2 ’ I | = 2Л|’+6Л|М »5М. го-^(Л'е) — (ЗА, • 4th) |3| г
13 5ДА-. I ~ ~ t>b r*b \4/
и
' (b'Ab) = (2Af + 66(h. + 56;) = I 4/>l ‘ 6A: 1 = 2 4 A’ | = 2.4Л.
' aft' ’ • (6ft)4ioftJ \з 5|ftJ
456
Поэтому, полагая с - X'Y. а матрицу А = А'Х (она является
симметрической - см. (13.26)), найдем
— = -2A'T' + 2.r;rfr = O,
db
откуда получаем систему нормальных уравнений в матричной фор-
ме для определения вектора Ь:
ХХЬ = ХТ.
(13.25)
Найдем матрицы, входящие в это уравнение’. Матрица XX
представляет матрицу сумм первых степеней, квадратов и попарных
произведений л наблюдений объясняющих переменных:
1
• ••
1
ХТ =
п 2Л» •- Lx* '
2л. 5Х» - Sv*
<SX* Sv* ”• SX* J
(13.26)
Матрица X'Y есть вектор произведений n наблюдений объяс-
няющих и зависимой переменных:
В частном случае из рассматриваемого матричного уравнения
(13.25) с учетом соотношений (13.26) и (13.27) для одной объяс-
няющей переменной (р = I) нетрудно получить уже рассматривае-
мую систему нормальных уравнений (12.10) для нес группирован-
ных данных. Действительно, в этом случае матричное уравнение
(13.25) принимает вил1 2:
1 Здесь под шоком У подразумевается
2 В случае одной объясняющей переменной отпадает необходимость н мннсн
под символом v второго индекса, указывающего номер переменной.
457
" E'-VMJ Z-v.
.Z-ч Zw) I Zm,
откуда непосредственно следует система нормальных уравнений
(12.10) для несгруп пированных данных.
Для решения матричного уравнения (13.25) относительно век-
тора оценок параметров b необходимо ввести еще одну предпосылку
6 для множественного регрессионного анализа: матрица XX явля-
ется неособенной, т.е. ее определитель не равен нулю. Следовательно,
ранг матрицы XX равен ее порядку, т.е. г {XX } = р + I. Из мат-
ричной алгебры известно (см., например. |9|), что г {XX} = г (Л),
значит, r{X} = p + I. т.е. ранг матрицы плана X равен числу ее
столбцов. Это позволяет сформулировать предпосылку 6 множест-
венного регрессионного анализа в следующем виде:
6. Векторы значений объясняющих переменных, или столбцы мат-
рицы плана X, должны быть линейно независимыми, т.е. ранг матрицы
X — максимальный {г{Х) = р + I).
Кроме того, полагают, что число имеющихся наблюдений (зна-
чений) каждой из объясняющих переменных превосходит ранг мат-
рицы X, т.с. п > г{Х) или л>р + 1, ибо в противном случае в
принципе невозможно получение сколько-нибудь надежных стати-
стических выводов.
Решением уравнения (13.25) является вектор
b = (X'Xy'X’Y.
(13.28)
где {XX}'' — матрица, обратная матрице коэффициентов системы
(13.25). а Л")’ — матрица-столбец, или вектор, ее свободных членов
Теорема Гаусса—Маркова, рассмотренная выше для парной рег-
рессионной модели, остается верной и в общем виде для модели
(13.23) множественной регрессии: оценка b-{XX}"' ХУ обладает
наименьшей дисперсией в классе линейных несмещенных оценок, т.е.
является эффектной оценкой параметра |(.
Зная вектор Ь, выборочное уравнение множественной регрессии
представим в виде:
v4 = ^h. (13.29)
где — групповая (условная) средняя переменной Y при заданном век-
торе значений объясняющей переменной Х„ = (1 х,„ х,0 ... лМ().
458
[> Пример 13.4. Имеются следующие данные1 (условные) о смен-
ной добыче угля на одного рабочего У (т). мощности пласта А'| (м) и
уровне механизации работ AS (%), характеризующие процесс добы-
чи угля в 10 шахтах (табл. 13.6).
нейная корреляционная зависимость, найти ее аналитическое вы-
ражение (уравнение регрессии У по ATj и А6).
Решение. Обозначим
5^ fl
Ш U
(напоминаем, что н матрицу плана .¥
8 5'
II 8
12 7
вводится дополнительный
столбец чисел, состоящий из единиц).
Для удобства вычислений составляем вспомогательную таблицу
(табл. 13.7).
Тмблнпз 13.7
/ хн Хц У/ л х2. Л ХЛг УЛ| УЛт *, -о. ->-,г
1 8 5 5 64 25 25 40 40 25 5.13 0.016
2 II 8 10 121 64 100 88 ПО 80 8.79 1.464
3 12 8 10 144 64 100 96 120 80 9,64 1.127
4 9 5 7 81 25 49 45 63 35 5.98 1.038
5 8 7 5 64 49 25 56 40 35 5.86 0,741
6 8 8 6 64 64 36 64 48 48 6.23 0.052
7 9 6 6 81 36 36 54 54 36 6.35 0.121
8 9 4 5 81 16 25 36 45 20 5.61 0.377
9 8 5 6 64 25 36 40 48 30 5.13 0.762
10 12 7 8 144 49 64 84 96 56 9.28 1.631
Z 94 63 68 90X 417 496 603 664 445 — 6,329
• В лом примере исполъиишны данные примера 13.! с добавлением результатов
наблюдений над напой объясняющей переменной .V». при лом старую перемен-
ную X hi примера 13.1 обозначаем теперь Л\
459
Теперь
fl
Л'Х= 8
II
94 63 '
908 603
603 417
5
(см. суммы в итоговой строке табл. 13.7);
I I ...
А')’ = 8 II ...
Л 8 ...
68 1
664
445
Матрицу
Л“'®(А'Х)'определим по формуле
где
Ц — определитель матрицы Л’Х . .4 — матрица, присоединенная к
матрице XX . Получим (рекомендуем читателю убедиться в этом
самостоятельно)
15 027 -1209 -522
.4*= —------1209 201 -108
3738
-522 -108 244
Теперь в соответствии с формулой (13.28), умножая 3iy матрицу на
, получим /» =---
3738
-13 230
3192
1372,
-3.5393
0.8539
. 0.3670
С учетом равенства (13.29) уравнение множественной регрессии
имеет вид: ух = -3,54 + 0.854х| + 0.367x2. Оно показывает, что при
увеличении только мощности пласта А| (при неизменном А'г) ,,а
I м. добыча угля на одного рабочего Y увеличивается в среднем на
0,854 т, а при увеличении только уровня механизации работ X, (при
неизменной А,) — в среднем на 0,367 т.
Добавление в регрессионную модель новой объясняющей пере-
менной AS изменило коэффициент регрессии (У по А\) с 1.016
для парной регрессии (см. пример 13.1) до 0.854 — для множест-
венной регрессии. В этом никакого противоречия нет, так как во
втором случае коэффициент ре|рсссии позволяет оценить прирост
460
зависимой переменной У при изменении на единицу объясняющей
переменной А) в чистом виде, независимо от Х>. В случае парной
регрессии учитывает воздействие на Y нс только переменной
но н косвенно корреляционно связанной с ней переменной Х>. ►
На практике часто бывает необходимо сравнение влияния на
зависимую переменную различных объясняющих переменных, ко-
гда последние выражаются разными единицами измерения. В этом
случае используют стандартизованные коэффициенты регрессии />' и
коэффициенты эластичности Ef(j = 1,2...р):
(13.30)
Е = 6,4- (13.31)
у
Стандартизованный коэффициент регрессии Ь' показывает, на
сколько величин л,. изменится в среднем зависимая переменная Y при
увеличении только j-й объясняющей переменной на х, , а коэффициент
эластичности £, — на сколько процентов (от средней) изменится в
среднем Y при увеличении только Х/ на 1%.
[> Пример 13.5. По данным примера 13.4 сравнить раздельное
влияние на сменную добычу угля двух факторов — мощности пла-
ста и уровня механизации работ.
Реше и и е. Для сравнения влияния каждой из объясняющих
переменных по формуле (13.30) вычислим стандартизованные ко-
эффицненты регрессии:
# = 0,8539 — = 6,728; Ь\ = 0.3670 — = 0.285.
1.83 1,83
а по формуле (13.31) — коэффициенты эластичности:
Е. = 0.8539 — = 1.180; £, =0.3670 —=0.340.
’ 6.8 • 6.8
(Здесь мы опустили расчет необходимых характеристик пере-
менных:
х, =9.4; х. =6.3; у = 6.8; s =1.56; .« =1,42; .« =1.83.)
Таким образом, увеличение мощности пласта и уровня механиза-
ции работ только на одно л\ или на одно л, увеличивает в среднем
сменную добычу угля на одного рабочего соответственно на 0,728л,,
или на 0,285л,, а увеличение этих переменных на 1% (от своих сред-
них значений) приводит в среднем к росту добычи угля соответст-
венно на 1,18% и 0.34%. Итак, по обоим показателям на сменную
461
добычу угля большее влияние оказывает фактор «мощность пласта»
по сравнению с фактором «уровень механизации работ». ►
Преобразуем вектор оценок (13.28) с учетом формулы (13.23):
Л = (.¥\Г) 'Af'(A'0 + c) = (A"A')-,(А"А')р + ‘А"с =
= £0 + (А"А')‘’А"г
или
А = р + (А"Х)‘АГ’е. (13.32)
т.е. оценки параметров (13.28), найденные по выборке, будут со-
держать случайные ошибки.
13.6. Ковариационная матрица
и ее выборочная оценка
Вариации оценок параметров будут в конечном счете опреде-
лять точность уравнения множественной регрессии. Для их измере-
ния в многомерном регрессионном анализе рассматривают так на-
зываемую ковариационную матрицу К, являющуюся матричным ана-
логом дисперсии одной переменной:
^<>0 ^01 ••• Ml;.
к„ кц ... к1г
К — •
М-» — Mr,
где элементы А'(/ — ковариации (или корреляционные моменты) оценок
параметров 0, и 0, (i, j = О, I.р). Ковариация двух переменных
определяется как математическое ожидание произведения отклонений
этих переменных от их математических ожиданий (см. § 5.6). Поэтому
= Л/[(6, - Л/( Л )>(Л - Л/(6,))]. (13.33)
Ковариация характеризует как степень рассеяния значений двух
переменных относительно их математических ожиданий, так и
взаимосвязь этих переменных.
В силу того, что оценки Ьр полученные методом наименьших
квадратов, являются несмещенными оценками параметров 0,. т.е.
M(bf ) = 0,. выражение (13.33) примет вид:
а; = л/1^-р,н/>,-0,)1.
462
Рассматривая ковариационную матрицу К, легко заметить, что
на ее главной диагонали находятся дисперсии оценок параметров
регрессии, ибо
К„ = W,-03*=<^ . (13.34)
В сокращенном виде ковариационная матрица К имеет вил:
(в этом легко убедиться, перемножив векторы (Л - р) и (/> - р)',
Учитывая (13.32), преобразуем это выражение:
К = ,W| [(А'ХУ'ХЪ] |(ХХ) 'Х'с] =
= М1(ХХу' ХЫХ(ХХ)'1 = (ХХ)' Х'ЛЦее’)ХаХ)\
ибо элементы матрицы X — неслучайные величины.
Матрица А/(ее') представляет собой ковариационную матрицу
вектора возмущений с:
Л/(е*) M(zizz) ... AYJejE,,)
Л/(е,е,) Л/(е;) ... Л/(с,с,)
ЛГ(се') =
) Л/(е„е:) ... Л/(е;),
в которой все элементы, не лежащие на главной диагонали, равны
нулю в силу предпосылки 4 о некоррелированности возмущений с,
и г.( между собой (см. (13.5)), а все элементы, лежащие на главной
диагонали, в силу предпосылок 2 и 3 регрессионного анализа (см.
(13.3) и (13.4)) равны одной и той же дисперсии ст:
Л7(е;) = M(z, - 0): = О(е2 ) = <г.
Поэтому матрица Л/(се/) = о’Е, где Е — единичная матрица л-го
порядка. Следовательно, в силу соотношения (13.35) ковариационная
матрица вектора b оценок параметров:
Л'=|(А'%) |А"(ст-£)Н(А'Х)-' хоЧХХНХОИ.ГХГ’.
Х'=о:(Х%)'.
или
(13.36)
463
Итак, с помощью обратной матрицы (.¥Х) определяется не
только сам вектор b оценок параметров (13.28). но и дисперсии и ко-
вариации его компонент.
Входящая в выражение (13.36) дисперсия возмущений неиз-
вестна. Заменив ее выборочной остаточной дисперсией
. £< е.е
Г = —и------- = —. (13.37)
п - (р +1) п - р -1
но формуле (13.36) получаем выборочную оценку ковариационной
матрицы К. (В знаменателе выражения (13.37) стоит п - (р + I), а
не п - 2, как это было выше в формуле (13.6). Эго связано с тем.
что теперь р + ] степеней свободы (а не две) теряются при опреде-
лении неизвестных параметров, число которых вместе со свобод-
ным членом равно р + !.)
13.7. Определение доверительных интервалов
для коэффициентов и функции регрессии
Перейдем теперь к оценке значимости коэффициентов регрес-
сии Ь, и построению доверительного интервала дтя параметров рег-
рессионной модели р, (/= 1.2, .... р).
В силу соотношений (13.34). (13.36) и изложенного выше опен-
ка дисперсии коэффициента регрессии bj определится по формуле:
.<=г|(.Г%)%,
где — несмещенная оценка параметра а2;
'] — диагональный элемент матрицы (Х'Х) '.
Среднее квадратическое отклонение (стандартная ошибка) ко-
эффициента регрессии bj примет вид:
= . (13.38)
Оценка значимости коэффициента регрессии ht означает проверку нуле-
вой пшогезы о равенстве параметр;! р? множественной модели (13.22) ну-
лю, т.е. Я„: р =0 против альтернативной пшогезы Я,: Р? *0.
Эта проверка основана на том, «гго статистика (Л, -р;)Дд име-
ет /-распределение Стыодента с k -п - р - 1 степенями свободы
Поэтому Ь} значимо отличается от нуля на уровне значимости а
464
(гипотеза Яо отвергается), если |/1 = >t},tl „ р ,, где г,
табличное значение / - критерия Стьюдента. определенное на
уровне значимости а при числе степеней свободы к = л - /> -1.
В обшей постановке гипотеза //Оо равенстве параметра 0у за-
данному числу т.е. Но: 0, = 0„ против альтернативной гипоте-
зы //,: 0, *0Н, отвергается, если
Y = (I - и)%-ный доверительный интервал для параметра 0 есть
Л, S Р, . (13.39)
Наряду с интервальным оцениванием коэффициентов регрессии
по формуле (13.39) весьма важным для оценки точности определе-
ния зависимой переменной (прогноза) является построение довери-
тельного интервала для функции регрессии или для условного матема-
тического ожидания зависимой переменной Л/,(Г), найденного в пред-
положении. что объясняющие переменные .¥ь А?...Хр приняли значе-
ния. задаваемые вектором A’„=(l xU1 x:tt... л;.о). Выше такой интер-
вал получен для уравнения парной регрессии (см. (13.13) и (13.12)).
Обобщая соответствующие выражения на случаи множественной
регрессии, можно получить доверительный интервал .гзя Л-/ДГ):
Г «л-г Л. <13-40>
где v, — групповая средняя, определяемая по уравнению регрессии.
(13.41)
— ее стандартная ошибка.
При обобщении формул (13.15) и (13.14) аналогичный довери-
тельный интервал для индивидуальных значений зависимой перемен-
ной у’ примет вид:
,>г -s X s у„ +r<s.. < 13-42>
где
= л>/ь^Л7,(лгх)' .г„ (13.43) 16
16 Тотш Mpcenincirfl ы«ггм«|и'иса> стггш-гмм
Доверительный интервал для дисперсии возмущений а2 в множе-
ственной регрессии с надежностью у = I - а строится аналогично
парной модели ио формуле (13.20) с соответствующим изменением
числа степеней свободы критерия х2:
пх2 л
—-----------<, ст < —---------------
Z* Z*
и 2,»-p-l * l-u 2л»-р I
(13.43')
> Пример 13.6. По данным примера 13.4 оценить сменную до-
бычу угля на одного рабочего для шахт с мощностью пласта 8 м и
уровнем механизации работ 6%; найти 95%-ные доверительные ин-
тервалы для индивидуального и среднего значений сменной добычи
угля на I рабочего для таких же шахт. Проверить значимость коэф-
фициентов регрессии и построить для них 95%-ные доверительные
интервалы. Найти с надежностью 0.95 интервальную оценку для
дисперсии возмущений п2.
Р е ш с н и е. В примере 13.4 уравнение регрессии получено в
виде: уЛ = -3.54 + 0.854.rt + 0.367x2- По условию надо оценить
А/, (У). гле Л' = (I 8 6). Выборочной оценкой Л/, (У) является
групповая средняя, которую найдем по уравнению регрессии: =
= -3.54 + 0.854*8 + 0,367-6 = 5.49 (т). Для построения довери-
тельного интервала для Л'/Ц(У) необходимо жать дисперсию его
оценки — л* . Для ее вычисления обратимся к габл. 13.7 (точнее, к
се двум последним столбцам, при составлении которых учтено, что
групповые средние определяются по полученному уравнению рег-
рессии).
Теперь по (|юрмуле (1337):
.V
6.329
10-2-1
= 0.904
и 5 = ^0.904 =
= 0.951(т).
Определяем стандартную ошибку групповой средней г, по
формуле (13.41). Вначале найдем
15 027
-1209
-522
.V'(XIV) Л-„-<| К 6)J-
.» /Зо
-1209
201
-108
-108
8
244 6
I
3738
(2223 -249 78) 8 =
А
-----(699) = 0.1870.
3738'
Теперь л, = 0.951^6.1870 =0.411 (т).
466
По табл. IV приложений при числе степеней свободы А = 10 -
-2-1=7 находим ? =2.36. По формуле (13.40) доверительный ин-
тервал для Л/, (У) ровен 5.49 - 2.36*0.411 < A/JT) < 5.49 + 2.36*0.411
или 4.52 < Л/, (У )< 6.46 (г).
Итак, с надежностью 0.95 средняя сменная добыча угля на од-
ного рабочего для шахт с мощностью пласта 8 м и уровнем механи-
зации работ 6% находится в пределах от 4.52 до 6.46 т.
Сравнивая новый доверительный интервал для функции регрес-
сии А/, (У). полученный с учетом двух объясняющих переменных,
с аналогичным интервалом с учетом одной объясняющей перемен-
ной (см. пример 13.1), можно шметить уменьшение его величины.
Это связано и тем. что включение в модель новой объясняющей
переменной позволяет несколько повысить точность модели за счет
увеличения взаимосвязи зависимой и объясняющей переменных
(см. ниже).
Найдем доверительный интервал для индивидуального значения
/. при .¥,>(! 8 6):
по формуле (13.43): = 0.951^/1 + 0.1870 = 1.036 (т) и по формуле
(13.42): 5.49 - 2.36 • 1.036 s »•’ < 5.49 + 2.36 • 1.036. т.е. 3.05 S г.; S 7.93 (т)
Итак, с надежностью 0.95 индивидуальное значение сменной
добычи угля в шахтах с мощностью пласта 8 м и уровнем механиза-
ции работ 6% находится в пределах от 3.05 до 7.93 (т).
Проверим значимость коэффициентов регрессии Ь\ и th. В при-
мере 13.4 получены Л| = 0.854 и Ь> - 0.367 Стандартная ошибка х,.
в соответствии с формулой (13.38) равна:
=0.951.—• 201 =0,221. Так как г = =3,81 =2.36. то
* У 3738 0.221
коэффициент______Л, значим. Аналогично вычисляем
.у,. = 0.951’ 244 = 0.243 и /=~^ = 1.51 =2.36. т.е. коэф-
фициент />> незначим на 5%-ном уровне
Доверительный интервал имеет смысл построить только для
значимого коэффициента регрессии Л,-. по (13.39) 0.854 -
- 2.36-0.221 S 0, < 0.854 + 2.36-0.221 или 0.332 < 0, < 1.376.
Итак, с надежностью 0.95 за счет изменения на I м мощности
пласта Х| (при неизменном Ал) сменная добыча угля на одного рабо-
чего Убудет и {меняться в пределах от 0,332 до 1.376 т.
467
Найдем 95%-ныЙ доверительный интервал для параметра л-'
Учитывая, что о = I - 0.95 = 0.05, а/2 - 0.025. I - а/2 = 0.975.
найдем по табл. V приложений при п -р -I = п - 3 степенях сво-
боды Xo.ua.r = *6.0: xi.w75? - Ь69 и по формуле (13.43')
10 0.904 . 10 0.904
---------<, сг <---------
1.69
или 0.565 < с2 < 5.35
16.0
и 0.751 <о: 5 2.31.
Таким образом, с надежностью 0.95 дисперсия возмущений за-
ключена в пределах от 0.565 до 5,35, а их стандартное отклонение —
от 0.751 до 2.31 (т). ►
Формально переменные, имеющие незначимые коэффициенты
регрессии, могут быть исключены из рассмотрения. В экономиче-
ских исследованиях исключению переменных из регрессии должен
предшествовать тщательный качественный анализ. Поэтому может
оказаться целесообразным все же оставить в регрессионной модели
одну или несколько объясняющих переменных, не оказывающих
существенного (значимого) влияния на зависимую переменную.
13.8. Оценка взаимосвязи переменных.
Проверка значимости уравнения
множественной регрессии
Для оценки взаимосвязи между зависимой переменной и совокуп-
ностью объясняющих переменных используется множественный (со-
вокупный) Ko'ulxftuuuenm (индекс) корреляции (см. § 12.6). который
может быть выражен через суммы квадратов отклонений по форму-
ле (13.19):
где <2- Qr и Qf вычисляются во формулам (13.16). (13.17).
Получим более удобную формулу для R. не требующую вычис-
лен ня остатков и остаточной суммы квадратов Q,. = £<.
/►I
□ В соответствии с равенством (13.16)
-?)'=~2?Ё*- + =
|»| |.| 1.1 |«1
= X-v" _ 2у(ну) + луг = УТ - пу2
468
(ибо = у; + у: +... + у* = (у, ... у.)
ы
= Г7).
С учетом условия (13.24’) имеем
£ = XU “ ) ’= ГТ ~ 2Ь'ХГ + Ь'ХХЬ 9 Yy " Ь'ХГ
(ибо в силу равенства (13.25) h'X'Xb -Ь'ХУ).
Наконец.
Уг = С " (?, = >">’ ” ЯУ * - (Уу - h‘x у) = *>'ХГ “ «У*'.
Таким образом.
я = <13,44)
\| Q V И’“"У*
Коэффициент R является обобщением коэффициента корреля-
ции в множественной модели. В зависимости от тесноты связи R
может принимать значения от 0 до I. Величина R2, называемая
множественным коэффициентом детерминации, показывает долю
вариации зависимой переменной, обусловленную регрессией или
изменчивостью объясняющих переменных.
Таким образом, множественный коэффициент детерминации R-
можно рассматривать как меру качества уравнения регрессии, харак-
теристику прогностической силы анализируемой регрессионной модели-.
чем ближе R- к единице, тем лучше регрессия описывает зависи-
мость между объясняющими и зависимой переменными.
Недостатком коэффициента детерминации R2 является то. что
он. вообще говоря, увеличивается при добавлении новых объяс-
няющих переменных, хотя это и не обязательно означает улучше-
ние качества регрессионной модели. В этом смысле предпо’ггитсль-
нее использовать скорректированный (адаптированный, поправлен-
ный) коэффициент детерминации R'. определяемый по формуле
/?•=!- -”"1 (|-/?:). (13.44')
п - р -1' '
Из формулы (13.44’) следует, что чем больше число объясняю-
щих переменных р. тем меньше R' по сравнению с R2. В отличие
от R2 скорректированный коэффициент R1 может уменьшаться
при введении в модель новых объясняющих переменных, не оказы-
вающих существенного влияния на зависимую переменную. Однако
17 Ге>ф«> гп и ипгшигк.
469
даже увеличение скорректированного коэффициента детерминации
/с при введении в модель новой объясняющей переменной не все-
гда означает, что ее коэффициент регрессии значим (это происхо-
дит. как можно показать, только в случае, если соответствующее
значение /-статистики больше единицы (по абсолютной величине),
т.е. | /1>1). Другими словами, увеличение R' еще не означает улуч-
шение качества pei-рессионной модели.
Оценка значимости уравнения множественной регрессии означа-
ет проверку нулевой гипотезы о равенстве нулю р параметров мно-
жественной модели (13.22), т.е. //„; 0, = 0. = ... = 0Г =° против аль-
тернативной гипотезы //,: хотя бы одно 0, *0. j = 1.р.
Критерий значимости любого уравнения регрессии был получен
ранее в § 13.3. Если известен коэффициент детерминации R-, то кри-
терий значимости (13.18) уравнения репрессии может быть записан в
виде:
(I
(13.45)
где А| = р, к2 = п ~ р - 1. ибо в уравнении множественной регрессии
вместе со свободным членом оценивается т = р 1 I параметров.
[> Пример 13.7. По данным примера 13.4 определить множест-
венный коэффициент (индекс) корреляции и проверить на уровне
и = 0,05 значимость полученного уравнения регрессии Y по X| и Х2.
Р с щ с н и е. Вычислим произведения векторов (см. пример 13.4):
Л’А’Т = (-3,54 0.854 0,367)
68
664
<445,
= -3,54 -68 + 0.854 664 + 0,367 • 445 = 489.65
к»
и УТ = £.г,: = 496 (см. итоговую строку табл. 13.7). Из табл. 13.7 на-
<-|
10 и
ходим также £ у, - 68. откуда у = ^у,/п = 68/10 = 6,8 (т).
j .1
Теперь по формуле (13.44) множественный коэффициент (ин-
декс) корреляции
489,65-10-6,8*
496-10-6.8*'
= 70.811 =0.900.
470
Значение R = 0.900. близкое к I. указывает на тесную взаимо-
связь зависимой переменной Y — сменной добычи угля на одного
рабочего и объясняющих переменных — мощности пласта Х\ и
уровня механизации работ Х2. Коэффициент детерминации
R- =0.811 свидетельствует о том. что вариация исследуемой зави-
симой переменной на 81.1% объясняется изменчивостью включен-
ных в модель объясняющих переменных.
Проделав аналогичные расчеты по данным примера 13.1 для
одной объясняющей переменной можно было получить
Л'= 0.866 и IV' = 0.751 (заметим, что в случае одной объясняющей
переменной множественный коэффициент корреляции /?' равен
парному коэффициенту корреляции г). Сравнивая значения R2 и
R,z. можно сказать, что добавление второй объясняющей перемен-
ной Х> незначительно увеличило коэффициент детерминации, оп-
ределяющий качество модели. И это понятно, так как выше, в
примере 13.6, мы убедились в незначимости коэффициента регрес-
сии при переменной
По формуле (13.44') вычислим скорректированный коэффици-
ент детерминации:
9
при р = 1 /?’*=!—(1-0.750 = 0.720;
о
-, 9
при р= 2 R" =l-y(l-0.810 = 0,757.
Видим, что хотя скорректированный коэффициент детермина-
ции и увеличился при добавлении объясняющей переменной Xj, но
это еще не говорит о значимости коэффициента регрессии Ь2 (зна-
чение /-статистики, равное 1,51 (см. § 13.6), хотя и больше едини-
цы. но недостаточно для соответствующего вывода на емлемом
уровне значимости)
Зная Л2 = 0.811. проверим значимость уравнения регрессии.
Фактическое значение критерия по формуле (13.45)
(1-0.8ID-2
больше табличною Л|,О5;2.7 = 4.74, определенного на уровне значи-
мости и = 0.05 при = 2 и к2 = 10 - 2 - 1 = 7 степенях свободы
(см. табл. VI приложений), т.е. уравнение регрессии значимо, сле-
довательно. исследуемая зависимая переменная Y достаточно хоро-
шо описывается включенными в регрессионную модель перемен-
ными Xi и Х2. ►
Следует подчеркнуть, что включенные в регрессионную модель
объясняющие переменные нс должны противоречить теоретическим
471
положениям соответствующей предметной области моделируемого
объекта (например, экономической теории). Меняя состав пере-
менных, получаются новые уравнения регрессии. При этом в поль-
зу добавления в модель (исключения из модели) каждой перемен-
ной могут свидетельствовать: значимость (нсзначимость) ее коэф-
фициента регрессии; возрастание скорректированного коэффици-
ента детерминации /Г; значительное (незначительное) изменение
других коэффициентов регрессии.
Переменная, имеющая веские теоретические основания для
включения, должна быть добавлена в модель (или оставлена в ней),
даже если это противоречит приведенным выше формальным сооб-
ражениям. (Об этом уже упоминалось в § 13.7.)
13.9. Мультнколлннеарность
Под мулътикаляинеарностъю понимается высокая взаимная корре-
.шрованность объясняющих переменных. Мультнколлннеарность мо-
жет проявляться в функциональной (явной) и стохастической
(скрытой) формах.
При функциональной форме мультнколлннеарности по крайней
мере одна из парных связей между объясняющими переменными
является линейной «функциональной зависимостью В этом случае
.матрица А'А' особенная, гак как содержит линейно зависимые век-
торы-столбцы и ее определитель равен нулю, г.е. нарушается пред-
посылка 6 регрессионного анализа Это приводит к невозможности
решения соответствующей системы нормальных уравнений и полу-
чения опенок параметров регрессионной модели
Однако в экономических исследованиях мультнколлннеарность
чаще проявляется в стохастической форме, когда между хотя бы
двумя объясняющими переменными существует тесная корреляци-
онная связь. Матрица А'Х в этом случае является неособенной, но
ее определитель очень мал. В то же время вектор опенок b и его
ковариационная матрица К в соответствии с формулами (13.28) и
(13.36) пропорциональны обратной матрице (А'А'Г1. а значит, их
элементы обратно пропорциональны величине определителя |.Y'V|.
В результате получаются значительные средние квадратические от
клонення (стандартные ошибки) коэффициентов регрессии
Ьц, bi.. bp и оценка их значимости по /-критерию не имеет смыс-
ла, хотя в целом регрессионная модель может оказаться значимой
по Г-крнтерию.
Опенки Ь, становятся очень чувствительными к незначительно-
му изменению результатов наблюдений и объема выборки. Уравне-
ния регрессии в этом случае, как правило, нс имеют реального
472
смысла, так как некоторые из его коэффициентов могут иметь не-
правильные с точки зрения экономической теории знаки н неоп-
равданно большие значения.
Олин из методов выявления мульти коллинеарности заключается
в анализе корреляционной матрицы между объясняющими перемен-
ными Х|, Л;...Хр и выявлении пар переменных, имеющих высокие
коэффициенты корреляции (обычно больше 0.8) Если такие перемен-
ные существуют, го говорят о мультиколлинеарности между ними.
Полезно также находить множественные коэффициенты корре-
ляции между одной из объясняющих переменных и некоторой
группой из них. Наличие высокого множественного коэффициента
корреляции (обычно принимают больше 0.8) свидетельствует о
мультиколлинеарности.
Другой подход состоит в исследовании матрицы XX. Если оп-
ределитель матрицы XX близок к нулю (например, одного поряд-
ка с накапливающимися ошибками вычислений), то это говорит о
наличии мульти колл и неарности.
Для устранения или уменьшения мультнколлннсарностн ис-
пользуется ряд методов. Один из них заключается в том. что из
двух объясняющих переменных, имеющих высокий kox|h|)huiicht
корреляции (больше 0.8). одну переменную исключают из рассмот-
рения. При этом, какую переменную оставить, а какую удалить из
анализа, решают в первую очередь на основании экономических
соображений. Если с экономической точки зрения ни одной из пе-
ременных нельзя отдать предпочтение, то оставляют ту из двух пе-
ременных. которая имеет больший коэффициент корреляции с за-
висимой переменной
Другим из возможных методов устранения или уменьшения
мультиколлинеарности является использование пошаговых проце-
дур отбора наиболее информативных переменных. Например, вна-
чале рассматривается линейная регрессия зависимой переменной Y
от об1>ясняющей переменной, имеющей с ней наиболее высокий
коэффициент корреляции (или индекс корреляции при нелинейной
форме связи). На втором шаге включается в рассмотрение га объ-
ясняющая переменная, которая имеет наиболее высокий частный
коэффициент корреляции с Г и вычисляется множественный ко-
эффициент (индекс) корреляции. На третьем шаге вводится новая
объясняющая переменная, которая имеет наибольший частный ко-
эффициент корреляции с Y, и вновь вычисляется множественный ко-
эффициент корреляции и тл.
Процедура введения новых переменных продолжается до тех пор.
пока добавление следующей объясняющей переменной существенно
нс увеличивает множественный коэффициент корреляции.
473
13.10. Понятие о других методах
многомерного статистического анализа
Многомерный статистический анализ определяется' как раздел
математической статистики, посвященный математическим мето-
дам построения оптимальных планов сбора, систематизации и обра-
ботки многомерных статистических данных, направленных на выявле-
ние характера и структуры взаимосвязей между компонентами иссле-
дуемого признака и предназначенных для получения научных и практи-
ческих выводов.
Многомерные статистические методы среди множества возможных
вероятностно-статистических моделей позволяют обоснованно вы-
брать ту, которая наилучшим образом соответствует исходным стати-
стическим данным, характеризующим реальное поведение исследуе-
мой совокупности объектов, оценить надежность и точность выводов,
сделанных на основании обличенного статистического материала.
С некоторыми разделами многомерного статистического анали-
за, такими, как многомерный корреляционный анализ, множест-
венная регрессия, многомерный дисперсионный анализ (на приме-
ре двухфакторного анализа) мы уже сталкивались в гл. 11 — 13. При-
ведем теперь краткий обзор ряда других методов многомерного ста-
тистического анализа, которые уже нашли отражение в статистиче-
ских пакетах прикладных программ. В первую очередь следует вы-
делить методы, позволяющие выявить общие (скрытые или латент-
ные) факторы, определяющие вариацию первоначальных факторов. К
ним относятся факторный анализ и метод главных компонент.
Факторный анализ. Основной задачей факторного анализа явля-
ется переход от первоначальной системы большого числа взаимосвя-
занных факторов Л’|. AS..Хт к относительно малому числу скрытых
(латентных) факторов Г|. Л. ... />, А < т. Скажем, производитель-
ность труда на предприятиях зависит от множества факторов (обра-
зовательного уровня сотрудников, коэффициента сменности обору-
дования. электровооруженности груда, возраста оборудования, коли-
чества мест в столовых и т.п ), из которых многие факторы связаны
между собой. Используя факторный анализ, можно установить влия-
ние на рост производительности груда лини, нескольких обобщенных
факторов (например, размера предприятия, уровня органнзашш тру-
да. характера продукции), непосредственно нс наблюдавшихся.
Модель факторного анализа записывается в виде:
-а, + ' = ......т' < т' (13.46)
)•»
где aj= М(Х,) — математическое ожидание первоначального фактора А',:
1 См.. Математическая энциклопедия Т. 3. — М : Советская лтнклопедия. 1982.
474
Fj — общие (скрытые или латентные) факторы (/ = 1, 2...к)\
alt — нагрузки первоначальных факторов на общие факторы;
е, — характерные факторы (/ = I, 2./п):
vy — нагрузки первоначальных факторов на характерные факторы.
Первое слагаемое в модели (13.46) — неслучайная составляю-
щая, другие два слагаемых — случайные составляющие.
Особенностью факторного анализа является неоднозначность
определения общих факторов.
Метод главных компонент (компонентный анализ). В отличие от
рассматриваемых в факторном анализе общих факторов, которые
обусловливают большую (но не всю) часть вариации первоначаль-
ных факторов, главные компоненты объясняют всю вариацию и
определяются однозначно. Модель главных компонент имеет вид:
Д’, = Ч + ’ '=1.2, .... т . (13.47)
/-1
Как видим, в модели (13.47) отсутствуют характерные факторы,
так как главные компоненты F; полностью обусловливают всю ва-
риацию первоначальных факторов.
Лия углубления анализа изучаемого явления после выявления
главных компонент рассматривают регрессию на главных компо-
нентах, в которых последние выступают в качестве обобщенных
объясняющих переменных.
Среди других методов многомерного статистического анализа
отмстим методы, позволяющие осуществить классификацию жоно-
мических объектов, г.е. отнесение их к определенным классам. Это
методы дискриминантного и кластерного анализа.
Дискриминязггиый анализ позволяет отнести объект, характеризую-
щийся значениями т признаков, к одной из / совокупностей (классов,
групп), заданных своими распределениями. Предполагается. что / со-
вокупностей заданы выборками (называемыми обучаемыми}, которые
содержат информацию о статистических распределениях совокупно-
стей в m-мерном пространстве признаков.
При отсутствии обучающих выборок могут быть использованы ме-
тоды кластерного анализа, позволяющие разбить исследуемую сово-
купность объектов на группы «схожих» объектов, называемых класте-
рами. таким образом, чтобы объекты одного класса находились на
«близких» расстояниях между собой, а объекты разных классов — на
относительно «отдаленных» расстояниях друг от друга. При этом каж-
дый объект X, (/’ = 1, 2.т) рассматривается как точка в т-мерном
пространстве, и выбор способа вычисления расстояний или близости
между объектами и признаками является узловым моментом исследо-
вания, от которого в основном зависит окончательный вариант раз-
биения объектов на классы.
475
В завершение краткого обзора отметим, что применение мето-
дов многомерного статистического анализа невозможно без исполь-
зования пакетов прикладных программ (см., например. [34|). Под-
робное изложение многомерных статистических методов приведено,
в частности, в учебнике |14|.
УП|М1/КНР111!Я
13.8. Поданным примера 12.14: а) найти уравнение регрессии У
по X; б) оценить среднюю энерговооруженность труда на предприяти-
ях, фондовооруженность которых равна 10 млн руб., и построить для
нес 95%-ныЙ доверительный интервал; в) найти коэффициент детер-
минации Е2 и пояснить его смысл; г) проверить значимость уравнения
регрессии на 5%-ном уровне по F-критерию.
13.9. По данным примера 12.15: а) найти уравнение регрессии
Y по А'; б) найти коэффициент детерминации г2 и пояснить ею
смысл; в) проверить значимость уравнения регрессии на 5%-ном
уровне по F-критерию; г) оценить среднюю производительность
труда на предприятиях с уровнем механизации работ 60% и постро-
ить для нес 95%-ный доверительный интервал; аналогичный дове-
рительный интервал найти дня индивидуальных значений произво-
дительности труда на тех же предприятиях.
13.10. Поданным 30 нефтяных компаний получено следующее
уравнение регрессии между оценкой Y (лен. ед.) и фактической
стоимостью X (дсн- ед.) этих компаний: у, = 0.8750х + 295. Найти:
95%-ные доверительные интервалы для среднего и индивидуально-
го значений оценки предприятий, фактическая стоимость которых
составила 1300 лен. ед., если коэффициент корреляции между пере-
менными равен 0,76. среднее значение переменной X равно 1430 лен
ед., а се среднее квадратическое отклонение равно 270 ден. ед.
13.11. На 10 опытных участках одинакового размера получены
следующие данные об урожайности X (т) и содержании белка Y (%)
для некоторой культуры:
Урожайность, т 9.9 10,2 н.о 11,6 11.8 12.5 12.8 13.5 14,3 14.4
Содержание белка, % Ю.7 10,8 12,1 12,5 12.8 12,8 12,4 11,8 10.8 10.6
Необходимо: а) выровнять зависимость Y от X по параболе вто-
рого порядка и проверить значимость полученного уравнения pci-
рессии; б) оценить тесноту связи между переменными с помощью
индекса корреляции Ryx и коэффициента детерминации /?,’,; в) оп-
ределить, при каком значении урожайности средний процент со-
держания белка будет максимальным; найти этот процент.
476
13.12. Распределение 50 гастрономических магазинов области по
уровню издержек обращения X (%) и головому объему товарооборота
К (млн руб.) представлено в таблице:
у X 0,5 -2,0 2,0-3,5 3,5-5,0 5.0-6.5 6,5-8.0 Итого
4-6 — — — 3 > 5
6-8 — 4 8 8 1 21
8-10 2 5 5 2 — 14
10-12 3 1 5 — — 9
12-14 1 — — — — 1
Итого 6 10 18 13 3 50
Необходимо: а) построить эмпирическую линию регрессии Y по
X; б) выровнять полученную зависимость по прямой и гиперболе и
вычислить остаточную дисперсию для каждого случая; в) оценить
тесноту связи между переменными с помощью эмпирическою кор-
реляционного отношения г|и. коэффициента корреляции г и индек-
са корреляции проверить значимость и и сравнить их по
величине; г) на основании результатов, полученных в п. а), б), в),
определить, какое из двух полученных уравнений регрессии целесо-
образнее использовать для исследования заданной зависимости.
13.13. Имеются следующие данные о выработке литья на одно-
го работающего Л| (т). браке литья X} (%) и себестоимости одной
тонны литья К (руб.) по 25 литейным цехам заводов:
Х|/ х* У) i •Ч/ X2i У/ 1 Х|, X* Л
1 14.6 4.2 239 10 25,3 0.9 198 19 17.0 9.3 282
2 13,5 6.7 254 II 56.0 1.3 170 20 33.1 3.3 196
3 21.5 5.5 262 12 40.2 1.8 173 21 30.1 3.5 186
4 17,4 7.7 251 13 40.6 3.3 197 22 65,2 1.0 176
5 44.8 1.2 158 14 75,8 3.4 172 23 22.6 5.2 238
6 II 1.9 2.2 101 15 27,6 1.1 201 24 33.4 2.3 204
7 20.1 8.4 259 16 88,4 0,1 130 25 19.7 2.7 205
8 28.1 1.4 186 17 16,6 4,1 251
9 22.3 4.2 204 18 33,4 2,3 195
477
Необходимо: а) найти парные, частные и множественный (2 ко-
эффициенты корреляции между переменными и оценить их значи-
мость на уровне а = 0.05; б) найти уравнение множественной регрес-
сии У по и Аэ. оценить значимость этого уравнения и его коэффи-
циентов на уровне а = 0.05; в) сравнить раздельное влияние на зави-
симую переменную каждой из объясняющих переменных, используя
стандартизованные коэффициенты регрессии и коэффициенты эла-
стичности; г) найти 95%-ные доверительные интервалы для коэффи-
циентов регрессии, а также для среднего и индивидуальных значений
себестоимости одной тонны литья в цехах, в которых выработка литья
на одною работающего составляет 40 т. а брак литья — 5%.
13.14. Имеются следующие данные о годовых ставках месячных
доходов по трем акциям за шестимесячный период:
Акция Ji входы по месяцам, %
А 5.4 5.3 4.9 4.9 5.4 6.0
В 6.3 6.2 6.1 5.8 5.7 5,7
С 9.2 9.2 9,! 9,0 8.7 8,6
Есть основания предполагать, что доходы У по акции С зависят
от доходов Aj и Ал по акциям А и В. Необходимо: а) составить
уравнение регрессии У по Aj и Xj; б) найти множественный коэф-
фициент корреляции R и коэффициент детерминации R2 и пояс-
нить их смысл; в) проверить на уровне а = 0.05 значимость полу-
ченного уравнения регрессии; г) оценить средний доход по акции
С, если доходы по акциям А и В составили соответственно 5,5 и
6.0%.
I'.шва
14
Введение в анализ
временных рядов
14.1. Общие сведения о временных рядах
и задачах их анализа
Анализ временных рядов представляет собой самостоятельную,
весьма обширную и одну из наиболее интенсивно развивающихся
областей математической статистики.
Под временным рядом {динамическим рядом, или рядом динами-
ки) в экономике подразумевается последовательность наблюдений
некоторого признака (случайной величины) X в последовательные
равноотстоящие моменты времени. Отдельные наблюдения называ-
ются уровнями ряда, которые будем обозначать х; (/ = 1, 2.л), где
п — число уровней.
В табл. 14 I приведены данные, отражающие пену и спрос на
некоторый товар за восьмилетннй период (усл. ед.), т.е. два времен-
ных ряда — пены товара х, и спроса у, на него.
Тиб. ища 14.1
Год. г 1 2 3 4 5 6 7 8
Цена, х. 492 462 350 317 340 351 368 381
Спрос, у, 213 171 291 309 317 362 351 361
В качестве примера на рис. 14.1 временной ряд у, изображен
графически.
В общем виде при исследовании экономического временного
ряда х, выделяются несколько составляющих:
V, = ", + V, + С, + £, (Г = 1, 2,п).
где и, — тренд, плавно меняющаяся компонента, описывающая чис-
тое влияние долговременных факторов, т.е. длительную («вековую»)
тенденцию изменения признака (например, рост населения, эконо-
мическое развитие, изменение структуры потребления и т.п.);
г, — сезонная компонента, отражающая повторяемость экономи-
ческих процессов в течение не очень длительного периода (года,
иногда месяца, недели и т.л.. например, объем продаж товаров или
перевозок пассажиров в рах1ичные времена года):
<•, — циклическая компонента, отражающая повторяемость эконо-
мических процессов в течение длительных периодов (например,
479
влияние волн экономической активности Кондратьева, демографиче-
ских «ям», циклов солнечной активности и т.п.):
с, — случайная компонента, отражающая влияние не поддаю-
щихся учету и регистрации случайных факторов.
Pur. Ы.1
Следует обратить внимание на то, что в отличие от sf первые
три составляющие (компоненты) v„ ct являются закономерными,
неслучайными.
Важнейшей классической задачей при исследовании экономических
временных рядов является выявление и статистическая оценка основной
тенденции развития изучаемого процесса и отклонений от нес.
Отметим основные этапы анализа временных рядов:
• графическое представление и описание поведения временно-
го ряда;
• выделение и удаление закономерных (неслучайных) состав-
ляющих временного ряда (тренда, сезонных и циклических
составляющих);
• сглаживание и фильтрация (удаление низко- или высокочас-
тотных составляющих временного ряда);
• исследование случайной составляющей временного ряда,
построение и проверка адекватности математической модели
для се описания;
• прогнозирование развития изучаемого процесса на основе
имеющегося временного ряда;
• исследование взаимосвязи между различными временными
рядами.
Средн наиболее распространенных методов анализа временных
рядов выделим корреляционный и спектральный анализ, модели авто-
регрессии и скользящей средней. О некоторых из них речь пойдет ниже.
480
Так же. как ранее вариационный ряд х(, х2 х,, х„ рассмат-
ривался как одна из реализаций случайной величины X. временной
ряд Х|, Х1..х,...хп рассматривается как,одна из реализаций (тра-
екторий) случайного процесса Х(0 (см. § 7.1). Вместе с тем следует иметь
в виду принципиальные отличия временного ряда х, (/ = 1.2.л) от
последовательности наблюдений хь х2....х„. образующих случай-
ную выборку. Во первых, в отличие от элементов выборки члены
временного ряда, как правило, нс являются статистически незави-
симыми. Во-вторых, члены временного ряда не являются одинаково
распределенными.
14.2. Стационарные в|»еменные ряды
и их характеристики.
Лвтокор|м\1яцио11ная функция
Важное значение в анализе временных рядов имеют ста-
ционарные временные ряды, вероятностные свойства кото-
рых не изменяются во времени. Стационарные временные ряды
применяются, в частности, при описании случайных составляющих
анализируемых рядов.
Временной ряд хг (г =1.2..л) называется строго стационарным
(или стационарным в узком смысле), если совместное распределение
вероятностей п наблюдений Х|, х2..х„ такое же, как и л наблюде-
ний Х|+т, х>,.....................x„t. при любых л. i и т. Другими словами, свойства
строго стационарных рядов х, не зависят от момента /. т.с. закон рас-
пределения и сю числовые характеристики нс зависят от /. Следова-
тельно. математическое ожидание ад/) = а. среднее квадратическое
отклонение о,(/)-ст (см. § 7.1) могут быть оценены по наблюдени-
ям х,(/ = I. 2.л) по формулам:
V, = -^—. (14.1)
л
-------• (14.2)
л
Степень тесноты связи между последовательностями наблюде-
ний временного ряда хь х2...хп и Х|+„ х2+т, .... х„,т (сдвинутых от-
носительно друг друга на г единиц, или. как говорят, с лагом х) может
быть определена с помощью коэффициента корреляции
р( . Л/[и-Ц)(л-„,-«)] Л/[(х,-Ц)(х„,-0)] (143)
О, (/)<!, (/ + т) О:
481
ибо М(х, ) = Л/(л;.х ) = о. о, (/) = сг, (/ + т) = ст.
Так как коэффициент р(т) измеряет корреляцию между членами
одного и того же ряда, его называют коэффициентом автокорреля-
ции > а зависимость р(т) — автокорреляционной функцией. В силу ста-
ционарности временного ряда х, (I = 1.2.п) автокорреляционная
функция р(т) зависит только от лага г, причем р(-т) = р(т). т.е.
при изучении р(х) можно ограничиться рассмотрением только по-
ложительных значений г.
Статистической оценкой р(г) является выборочный коэффициент
автокорреляции г„ определяемый по формуле коэффициента корре-
ляции < 12.35’). н которой х, = х„ У(— а п заменяется на п - т:
гх = - - - ->>«» . (14.4)
Функцию г, называют выборочной автокорреляционной функцией.
а ее график — коррелограммой.
При расчете г, следует помнить, что с увеличением т число п - :
пар наблюдений х{, xfit уменьшается, поэтому лаг т должен быть
таким, чтобы число п - г было достаточным для определения г..
Обычно ориентируются на соотношение т < л/4.
Для стационарного временного ряда с увеличением
лага t взаимосвязь членов временного ряда х, и хн., ослабевает и
автокорреляционная функция р(т) должна убывать (по абсолютной
величине). В то же время для ее выборочного (эмпирического)
аналога г,, особенно при небольшом числе пар наблюдений п - г.
свойство монотонного убывания (по абсолютной величине) при
возрастании т может нарушаться.
> Пример 14.1. По данным табл 14.1 для временного ряда у,
найти среднее значение, среднее квадратическое отклонение и ко-
эффициенты автокорреляции (для лагов t » I; 2).
Реше н и с. Среднее значение временного ряда находим по
формуле <14.1):
2_13.,7|+... + 36.
8 ' '
Дисперсию и среднее квадратическое отклонение можно вычис-
лить по формуле (14.2). но в данном случае проще использовать
соотношение
482
s; = у; - у; = 92 478.38 - 296.88: = 4343.61:
л, = >/4343.6] =65.31 (ел).
Найдем коэффициент автокорреляции г, временного ряда (для
лага т = I), т.е. коэффициент корреляции между последовательно-
стями семи пар наблюдений yf и у^| (t — I, 2.7):
л 213 171 291 309 317 362 351
У^ 171 291 309 317 362 351 361
Вычисляем необходимые суммы:
£.»•< = 213 + 171 + ...+ 351 = 2014:
г-1
£ г; = 2132 + I7P + ... + 35Р = 609 506:
£у,.х “ 171 + 291 + ... + 361 = 2162;
i-i
= ПР + 29Р + ... + ЗбР = 694 458;
r-t
£ у, г,.т = 213 • 171 + 171 • 291 + ... + 351 • 361 = 642 583.
Теперь по формуле (14.4) коэффициент автокорреляции
7-642 583-2014-2162 Л
г, = , = 0.725.
77 • 609 506 - 2014* 77 • 694 458 - 2162’
Вычисление коэффициента автокорреляции rj временного ряда
y(t) для лага т = 2, т.е. коэффициента корреляции между последова-
тельностями шести пар наблюдений у, и ул>2 предлагаем провести
читателю самостоятельно. ►
Знание автокорреляционной функции г, может оказать сущест-
венную помощь при подборе модели анализируемого временного
ряда и статистической оценке се параметров.
483
14.3. Ани.1нтическое выравимшише (сглаживание)
B|>eMeiiiiom ряда (выделение
неслучайной компоненты)
Как уже отмечено выше, одной из важнейших задач исследова-
ния экономического временного ряда является выявление основной
тенденции изучаемого процесса, выраженной неслучайной состав-
ляющей ДО (тренда либо тренда с циклической или (и) сезонной
компонентой).
Для решения этой задачи вначале необходимо выбрать в и д
функции Д/). Наиболее часто используются следующие функции:
линейная — Д/) = Ьо + Л|Л
полиномиальная — Л/) = />(| + Ьхг + Ь>г2 +...+ bnin;
экспоненциальная — ,Z(/) = e4’v;
логистическая — / (t) =-------------;
1 + Ле‘‘
Гомпсрца — log, ./ (t) = а - br. где 0< г < I.
Это весьма ответственный этап исследования. При выборе соот-
ветствующей функции /(f) используют содержательный анализ (ко-
торый может установить характер динамики процесса), визуальные
наблюдения (на основе графического изображения временного ря-
да). При выборе полиномиальной функции может быть применен
метод последовательных разностей (состоящий в вычислении раз-
ностей первого порядка Д, = .vr - л;.,, второго порядка
Л/' =ДГ -А,., н т.д.. и порядок разностей, при котором они будут
примерно одинаковыми, принимается за степень полинома).
Из двух функций предпочтение обычно отдается той, при ко-
торой меньше сумма квадратов отклонений фактических данных
от расчетных на основе этих функций. Но этот принцип нельзя
доводить до абсурда: так, для любого ряда из п точек можно по-
добрать полином (п - 1)-й степени, проходящий через все точки,
и соответственно с минимальной — нулевой — суммой квадратов
отклонений, но в этом случае, очевидно, не следует говорить о
выделении основной тенденции, учитывая случайный характер
этих точек. Поэтому при прочих равных условиях предпочтение
следует отдавать более простым функциям. (Подробнее об этом
см. § 13.4.)
Для выявления основной тенденции чаще всего используется
метод наименьших квадратов, рассмотренный в гл. 12. Значения вре-
менного ряда хг или у, рассматриваются как зависимая переменная,
а время t — как объясняющая:
484
yt = ЛО+е,.
(14.5)
где с, — возмущения. удовлетворяющие основным предпосылкам
регрессионного анализа, приведенным в § 13.1. т е. представляющие
независимые и одинаково распределенные случайные величины, рас-
пределение которых предполагаем нормальным.
Напомним, что согласно методу наименьших квадратов пара-
метры прямой г, = />„+Л/ находятся из системы нормальных урав-
нений (12.10). в которой в качестве уберем /. а п,= I:
v «ЛЕ* =Ёл»
а,ё»+а2?:=!>.'•
»•! »•! г«1
а параметры параболы v, -b(l + b,t + h:r — из системы нормальных
уравнении (13.21):
r»l t"l l-l
r*l <•! r»l i«l
i-l i-l r-t r»l
Учитывая, что значения переменной /=1.2....п образуют на-
туральный ряд чисел от I до п. суммы £/. £/2, £/’. £/4 мож-
»»1 г«1 М <•!
но выразить через число членов ряда п по известным в математике
формулам:
uu и(л + 1) -г» , л(и + 1)(2п +1)
2;, = -!-—'; ------' (14.6)
/.I Z 1.1 о
= ,,:<п и): . j-,. = "(" + 1)(2"-И)(Зп! +Зп-|) (м7)
/.I 4 30
[> Пример 14.2. Поданным табл. 14.1 найти уравнение неслу-
чайной составляющей (тренда) для временного ряда yt, полагая
тренд линейным.
485
Реше н >1 е. По формуле (14.6):
Далее £ у, = 213 + 171 + ... + 361 = 2375: £ у; = 213-’ + |7р +
+ ... +361'= 739 827; £.у,/ =213-1 + 171 • 2 + ... + 361 • К = II 766.
Система нормальных уравнений имеет вид:
86п + 366, = 2375.
366„ + 2046, = 11 766.
откуда би = 181.32; Ь\ = 25.679 и уравнение тренда у, = 181.32 +
+ 25.679/ (см. рис. 14.1). т.е. спрос ежегодно увеличивается в сред-
нем на 25.7 ед.
При решении задачи можно было нс выписывать систему нор-
мальных уравнении, а представить уравнение регрессии в виде
. i+„ Ь-
(12.15). т.е. г, - г = 6|(/ - / ). где 7 = -^— =-. у = ——. а кох|>-
п 2 п
фицненг регрессии б| найти по формуле (12.17):
У,' -У.f
Г - Г
где yti = £v//'K y,==^yl/,i'- 7={\+п)/2; Г» (л+1)(2я+1)/б.
Проверим значимость полученного уравнения тренда по F-кри-
терию на 5%-ном уровне значимости. Вычислим с помощью формул
(13.16), (13.17') суммы квадратов:
а) обусловленную регрессией —
(?.=Z<
«!
у,У г = hi tr -
= 25.679
8 )
б) общую —
»л| Г-1
= 739 827 - = 34 748.9;
486
в) остаточную —
(?.. = Q - QK = 34 748.9 - 27 695.3 = 7053.6.
Найдем по формуле (13.18') значение статистики
27 695,3-6 ^ 5(?
£. 7053.6
Так как Л>.о5.1.б = 5,99 (см. табл. VI приложений), то уравне-
ние трепла значимо. ►
При применении метола наименьших квадратов для опенки па-
раметров экспоненциальной. логистической функций или функции
Гомпсрца возникают сложности с решением получаемой системы
нормальных уравнений, поэтому' предварительно, до получения соответ-
ствующей системы, прибегают к некоторым преобразованиям этих
функций (например, логарифмированию и др.).
Другим метолом выравнивания (сглаживания) временного ряда,
т.с. выделения неслучайной составляющей, является метод скользя-
щих средних Он основан на переходе от начальных значений чле-
нов ряда к их средним значениям на интервале времени, длина ко-
торого определена заранее. При этом сам выбранный интервал вре-
мени «скользит» вдоль ряда.
Получаемый таким образом ряд скользящих средних ведет себя
более гладко, чем исходный ряд. из-за усреднения отклонений ряда.
Действительно, если индивидуальный разброс значении члена вре-
менного ряда х, около своего среднего (сглаженного) значения а
характеризуется дисперсией а2, то разброс средней из т членов
временного ряда (х, + х, +...+ х„ )/т около того же значения а бу-
дет характеризоваться существенно меньшей величиной дисперсии,
равной о-’/м. Для усреднения могут быть использованы средняя
арифметическая (простая и с некоторыми весами), медиана и яр.
1> Пример 14.3. Провести сглаживание временного ряда у, по дан-
ным табл. 14.1 методом скользящих средних. используя простую сред-
нюю арифметическую с интернатом сглаживания т = 3 гола.
Реше н и е. Скользящие средние находим по формуле:
Ё-ч
, (14.8)
nt
когда т = (2р - I) — нечетное число; при т = 3 р - I.
Например, при / = 2 по формуле (14.8):
У: = (.V, + »: + ) = “(213 + 171 + 291) = 225 (ед.);
487
при t =3 у, = -(гг + у, + л ) = j( 171 -Г 291 + 309)-257.0 (ел.) и т.л.
В результате получим сглаженный ряд:
f 1 2 3 •1 5 6 7 S
У, — 225.0 257.0 305.7 329.3 343.3 35S.0 —
На рис. 14.1 этот рял изображен графически в пиле пунктирной
линии. ►
14.4. В|Х‘менп1.ге ряды и прогнозирование.
Автокорреляция возмущений
Одна из важнейших задач (этапов) анализа временного (дина-
мического) ряда, как отмечено выше, состоит в прогнози-
ровании на его основе развития изучаемого процесса. При
этом исходят из того, что тенденция развития, установленная в
прошлом, может быть распространена (экстраполирована) на буду-
щий период.
Задача ставится гак: имеется временной (динамический) рял
г, (/ = 1. 2./г) и требуется дать прогноз уровня этого ряда на мо-
мент п + т.
Выше, в § 13,2. 13.6. 13.7, мы рассматривали точечный и интер-
вальный прогнозы значений зависимой переменной т.е. определение
точечных и интервальных оценок Y, полученных для парной и множе-
ственной регрессий для значений объясняющих переменных А’. рас-
положенных вне пределов обследованного диапазона значений А'.
Если рассматривать временной рял как регрессионную модель
изучаемого признака по переменной «время», то к нему могут быть
применены рассмотренные выше методы анализа. Следует, однако,
вспомнить, «по одна из основных предпосылок регрессионного ана-
лиза состоит в том. что возмущения е, (/ = 1.2.п) представляю!
собой независимые случайные величины с математическим ожида-
нием (средним значением), равным нулю. А при работе с времен-
ными рядами такое допущение оказывается во многих случаях не-
верным.
Действительно, если вил функции тренда выбран неудачно, го
вряд ли можно говорить о том. что отклонения от нее (возмущения
с,) являются независимыми. В этом случае наблюдается заметная
концентрация положительных и отри нательных возмущений, и
можно предполагать их взаимосвязь. Если последовательные значе-
ния с, коррелируют между собой, то говорят об автокорреляции
возмущений (остатков, ошибок).
48К
Метод наименьших квадратов, вообще говоря, и в случае авто-
корреляции возмущений дает несмещенные и состоятельные оцен-
ки параметров, однако их интервальные оценки могут содержать
грубые ошибки. В случае выявления автокорреляции возмущений
целесообразно вновь вернуться к проблеме спецификации уравне-
ния регрессии (выбора функции тренда), пересмотреть набор вклю-
ченных в него переменных и т.п.
Наиболее простым и достаточно надежным критерием определе-
ния автокорреляции возмущений является критерий Дарбина—
Уотсона. С помощью этого критерия проверяется гипотеза об отсутст-
вии автокорреляции между соседними остаточными членами ряда и
е,_, (для лага т = I). где е, — выборочная оценка £,.
Статистика критерия имеет вид:
d = ^----------. (М.9)
l-i
Прн достаточно большом п можно ечтггап., что с; ' ' £
г-1
Тогда после несложных преобразований получим, что
"2Ес'1’ >
_£12_____12_____= >
(14.10)
Г»1
Статистика d заключена в границах от 0 до 4; при отсутствии
*
автокорреляции d 2 (так как при этом ,=0); при пашой
положительной автокорреляции </*0
при полной
отрицательной — d » 4 2^е,е,., « I-
Для «/-статистики найдены верхняя </„ и нижняя «/„ критические
границы на уровнях значимости а = 0,01; 0,025 и 0.05.
Если фактически наблюдаемое значение (рис. 14.2):
a) dn< d < 4 - dn, то гипотеза HQ об отсутствии автокорреляции
не отвергается (принимается);
б) d„ d <, du или 4 - dn < d < 4 - d„. то вопрос об отвержении
или принятии гипотезы Нп остается открытым (область неопреде-
ленности критерия);
'8 Тесрч «фипимя и млпигачкш чтети
489
в) 0 < </ <//,„ то принимается альтернативная гипотеза о положи-
тельной автокорреляции;
г) 4 - < d < 4. то принимается альтернативная гипотеза об
отрицательной автокорреляции.
//„ отпер- 1эется ЦЦ..К1ЖИ- тельная антокор- рсляимя) Облое 11. •ICOlipe.JC- лениоетм крнкрни II» принимается icimiic ЛК1ОМ>ррс 1И1Ш11) 1 < >( м.к п. неопрслс 1CMIIOC1II КрШСрии II» отпер- lacrcn (огрнца- телыкя ипгокор- реляции) ।
О d„ d, 2 4 - du 4 - d„ 4
Рис. 14.2
В табл. 14.2 приведен фрагмент таблицы значений статистик d,t и
d„ критерия Дарби на—Уотсона на уровне значимости а = 0.05 .
ТпГыкци 14.2
Число наблюдений п Число объясняющих переменных
Р= । Р = 2 Р 3
d„ /4 dt, d* d„ <4
15 1,08 1.36 0,95 1.54 0.82 1.75
16 1.10 1.37 0.98 1.54 0.86 1.73
17 из 1.38 1,02 1,54 0.90 1.71
18 1.16 1.39 1.05 1.53 0.93 1.69
19 1.18 1.40 1.08 1,53 0.97 1.68
20 1.20 1.41 1.10 1.54 1.00 1.68
25 1.29 1.45 1.21 1.55 1.12 1.66
30 1,35 1.49 1.28 1.57 1.21 1.65
35 1.40 1,52 1.34 1.58 1.28 1.65
40 1.44 1.54 1.39 1,60 1.34 1.66
45 1.48 1.57 1,43 1.62 1.28 1.67
50 1,50 1.59 1.46 1.63 1.42 1,67
Недостатками критерия Дарби на—Уотсона является наличие об-
ласти неопределенности критерия, а также то. что критические зна-
чения //-статистики определены для объемов выборки нс менее 15.
[> Пример 14.4. Выявил, на уровне значимости 0.05 наличие авто-
корреляции возмущений для временного ряда у, по данным табл. 14.1.
Решена е. В примере 14.2 получено уравнение тренда
у, = 181,32 + 25.679/(ед.). В табл. 14.3 приведен расчет сумм, необ-
ходимых для вычисления //-статистики.
490
Тлблшш 14.3
/ >7 = У Г », ?/«7-i
1 213 207.0 6.0 — — 36,0
2 171 232,7 -61.7 6.0 -370.2 3806.9
3 291 258.4 32.6 -61.7 -2011,4 1062.8
4 309 284.0 25.0 32,6 815,0 625.0
5 317 309,7 7.3 25.0 182.5 53,3
6 362 335.4 26.6 7.3 194,2 707.6
7 351 361.1 -10,1 26.6 -268.7 102.0
8 361 386,8 -25.8 -10.1 260.6 665.6
в X г-1 — — — — -1198,0 7059.2
Теперь по формуле (14.10) статистика d > 2(1 г 1198.0/7059.2) = 2.34. По
табл. 14.2 при р = I, л = 15 критические значения dtt = 1.08;
d0 = 1,36. т.е. фактически найденное d = 2,34 находится в пределах
от dn до 4 - dn (1,36 < d < 2,64). Как уже отмечено, при л < 15 кри-
тических значений J-статистики в табл. 14.2 нет, но суля по тен-
денции их изменений с уменьшением л можно предполагать, что
найденное значение останется в интервале (rf„; 4 — dn). т.е. для рас-
сматриваемого временного ряда спроса на уровне значимости 0,05
гипотеза об отсутствии автокорреляции возмущений не отвергается
(принимается). ►
В случае отсутствия значимой автокорреляции возмущений ме-
тодами регрессионного анализа может быть найдена не только то-
чечная, но и интервальная оценка уровней ряда, т.е. осу тес печены
их точечный и интервальный прогнозы.
О Пример 14.5. По данным табл. 14.1 дать точечную и с надеж-
ностью 0.95 интервальную оценки прогноза среднего и индивиду*
ального значений спроса на некоторый товар на момент / = 9 (де-
вятый год).
Реше н и е. Выше, в примере 14.2, получено уравнение рег-
рессии Г; = 181.32 + 25,679/. т.е. ежегодно спрос на товар увеличи-
вался в среднем на 25,7 ед. Надо оценить условное математическое
ожидание У) = г(9). Оценкой у(9) является групповая сред-
няя = 181.32 + 25,679-9 = 412,4 ед.
Найдем по формуле (13.6) оценку ? дисперсии о: (см. габл. 14.3):
X
> I
л-2
7059,2
8-2
= 1176.5
491
Вычислим оценку дисперсии групповой средней по формуле
(13.12>:
з: =1176,5
714.3; л; = /7143 = 26.73 (ед.)
(здесь мы использовали данные, полученные в примере 14.2:
I'
7 = ^-
п
п
£ = 4.5;
» г-1 <-1
= 204 - — = 42 ).
8
По табл. IV приложений /о.9$:б= 2,45. Теперь по формуле (13.13)
интервальная оценка прогноза среднего значения спроса:
412.4 - 2.45-26.73 <7(9)^412.4 + 2.45-26.73
или 346,9<у(9)<477.9 (ед.).
Для нахождения интервальной оценки прогноза инднвидух!ьно-
го значения /(9) вычислим дисперсию его оценки по формуле
(13.14):
1 (9-4.5)
= 1176,5 1 + -+' '
8 42
= 1890.8; .г = 43,48 (ед.),
v .
а затем по формуле (13.15) — саму интервальную оценку для у*(9):
412.4 - 2,45-43.48 <И(9) <; 412.4 + 2.45-43.48
или 305,9 $Г(9)$ 518,9 (ед.).
Итак, с надежностью 0.95 среднее значение спроса на товар на
девятый год будет находиться в пределах от 346.9 до 477.9 (ед.), а его
индивидуальное значение — от 305.9 до 518.9 (ед.). ►
Прогноз развития изучаемого процесса на основе экстраполя-
ции временных рядов может оказаться эффективным, как правило,
в рамках краткосрочного, в крайнем случае, среднесрочного периода
прогнозирования.
Если в рассматриваемой регрессионной модели автокорреляция воз-
мущений существует, то необходимы меры по се устранению (или сни-
жению). С злой целью используются различные методы.
Метод последовательных разностей состоит, в частности, в пере-
ходе от уровней ряда у(, х, к их первым разностям
Ду, = Ун-l ~ Л. Дх, = *;+! ~ х, (/ = 1,2.л) (14.11)
и рассмотрению уравнения регрессии Ду, = /\> + Л|Дхг, в котором
коэффициент />| интерпретируется как средний прирост переменной
492
у, при изменении прироста х, на одну единицу. Метод эффективен,
когда неслучайная составляющая временного ряда представляет
прямую линию.
Другим возможным методом снижения автокорреляции является
включение в модель регрессии времени t в качестве дополнительной
объясняющей переменной:
у, - Z>0 + btXt + b2t. (14.12)
Метат onpajviaH. если он не приводит к мультикоишнеарностн (см.
§ 13.9).
О Пример 14.6. По данным табл. 14.1. отражающей динамику цен х, и
спроса у, некоторого товара за восьмилетий период, выяснить на уровне
значимости 0,05. оказывает ли цена влияние на спрос.
Ре ш е н и е. Если абстрагироваться от тою. что переменные х, и
у, представляют собой временные ряды. то в предположении сущест-
вования линейной регрессии можно получить аналогично примеру
12.1 (или 12.2) уравнение регрессии в виде: у, = 635.2 - 0,8843х,. По
^критерию уравнение регрессии значимо на уровне 0.05. так как
вычисленное значение статистики F= 9.00 > = 5.99.
Однако такой вывод был бы правомерен по крайней мерс при
отсутствии автокорреляции возмущений г., временного ряда зави-
симой переменной у,. Использование критерия Дарби на—Уотсона
показывает наличие существенной автокорреляции остаточного
временного ряда е,= у, —у,. Таким образом, для обоснованного
ответа на вопрос задачи необходимо исключить автокорреляцию
возмущений.
Первый способ. Перейдем в соответствии с равенствами (14.1!)
от уровней ряда у, и х, к их первым разностям Ду, и Дх,. Значения
переменных Дх, и Ду, представим в габл. 14.4.
Тнб.н11ш 14.4
.\х, -30 -112 -33 23 II 17 13
Ду, -42 120 18 8 45 -11 10
Рассчитанное уравнение регрессии: Ду, = 9.94 - 0.7064 Дх,
Проверка уравнения по Г-критерию на уровне 0.05 показывает, что
оно незначимо, гак как /• = 3.96 < /Ь.о$;1Л = 6.61. Итак, нет основа-
ний считать, что иена на данный товар оказывает существенное
(значимое) влияние на спрос.
Второй способ. Включим в модель регрессии время г в качестве
дополнительной объясняющей переменной. Методом наименьших
квадратов (см. § 12.5) получим уравнение (14.12) в виде у, = 380,4
493
- 0.4443 х, + 19.22/. причем коэффициент при переменной /оказал-
ся значимым по /-критерию (/А> = 3.82 > /п.ч$;$ = 2.57). а при пере-
менной Xi — незначимым <//1| = 2.22 < /о.ч5;5 ~ 2,57). Следовательно,
подтверждается вывод о незначимом влиянии цены л, на спрос у, на
данный товар. ►
Одним из распространенных методов устранения автокорреля-
ции является использование авторегрессионной модели.
14.5. Лвто|>егре(*с11О1111ля модель
Для данного временного ряда далеко не всегда удается подоб-
рать адекватную модель, для которой ряд возмущений к, будет удов-
летворять основным предпосылкам регрессионного анализа, в част-
ности. нс будет автокоррелирован.
До сих пор мы рассматривали модели вида < 14.5). в которых в
качестве регрессора выступала переменная / — «время». В настоя-
щее время достаточно широкое распространение получили и другие
регрессионные модели, в которых регрессорами выступают лаговые
переменные, т.с. переменные, влияние которых в регрессионной мо-
дели характеризуется некоторым запаздыванием. Еще одним отли-
чием рассматриваемых в этом параграфе регрессионных молелен
является то. что представленные в них обьясняюшне переменные
являются величинами случайными.
Авторегрессионная модель р-го порядка имеет вид:
х( = Ьц + Ь\ХГ-1+ Ь?хг 2 +...+ bpXt-p + с, (/ = 1.2. .... п), (14.13)
где /\(. />|. ... Ьр— некоторые константы
Она описывает изучаемый процесс в момент / в зависимости от
его значений в предыдущие моменты г I. г 2. ... t - р.
Если исследуемый процесс х, в момент / определяется лишь ст
значениями в предшествующий период / - I. то рассматривают авто-
регрессионную модель 1-го порядка (марковский случайный процесс):
х,= Ли + Л|Х, । + г., (/= I. 2.л). (14.14)
Г> Пример 14.7. В табл 14.5 представлены данные, отражающие
динамику курса акций некоторой компании (лен. ед.).
ТпГмнц» 14.5
1 1 2 $ 4 5 6 7 8 9 10 II
У, 971 1166 1044 907 957 727 752 1019 972 815 823
/ 12 13 14 15 16 17 18 19 20 21 22
У, 1112 1386 1428 1364 1241 1145 1351 1325 1226 1189 1213
494
Используя авторегрессионную модель 1-го порядка, дать точечный и
интервальный прогнозы среднего и индивидуального значений курса
акций в момент / = 23. т.е. на глубину один интервал.
Р с ш е н и е. Попытка подобрать к данному временному ряду
адекватную модель вила (14.5) с линейным или полиномиальным
трендом оказывается бесполезной.
В соответствии с условием применим авторегрессионную модель
вида (14.14). Получим (аналогично примеру 14.2)
X = 284,0 + 0.7503у>_,. (14.15)
Найденное уравнение регрессии значимо на 5%-ном уровне по
f-критерню. гак как фактически наблюдаемое значение статистики
F = 24,32 > Ло.о5.|.|9 = 4,35. Применение критерия Дарбина—Уотсона
свидетельствует о незначимой автокорреляции возмущений е; = у,- у,
(рекомендуем читателю убедиться в этом самостоятельно).
Вычисления, аналогичные примеру 14.5. даюг точечный прогноз
по уравнению (14.15): у, ., = 284,0 + 0.7503 • 1213 = 1194,1 и интер-
вальный на уровне значимости 0.05 для среднего и индивидуального
значений — 1046.6 < г, ,, S 1341.6; 879.1 < у’ < 1509.1.
Итак, с надежностью 0.95 среднее значение курса акций данной
компании на момент / = 23 будет заключено в пределах от 1046,6 до
1341.6 (лен. ед.), а его индивидуальное значение — от 879.1 до
1509,1 (леи. ед.). ►
В данной главе отражены лишь некоторые вопросы (элементы)
анализа временных рядов. С более подробным их изложением мож-
но ознакомиться, например, по |3|. |2б|, а с анализом временных
рядов на компьютере — |34|.
Упражнения
В примерах 14.8—14.10 имеются следующие данные об урожай-
ности озимой пшеницы у, (и/га) за 10 лет:
f 1 2 3 4 5 6 7 8 9 10
16.3 20.2 17.1 7.7 15.3 16.3 19.9 14.4 18.7 20.7
14.8. Найти среднее значение, среднее квадратическое откло-
нение и коэффициенты автокорреляции (для лагов t = I; 2) вре-
менного ряда.
14.9. Найти уравнение тренда временного ряда yh полагая, что
он линейный, и проверить его значимость на уровне 0.05.
14.10. Провести сглаживание временного ряда у, методом скользя-
щих средних. используя простую среднюю арифметическую с интерва-
лом сглаживания: а) т = 3; 6) т - 5.
495
14.11. В таблице представлены данные, отражающие динамику
роста доходов на душу населения у, (ден. ед.) за восьмилетний пе-
риод:
t 1 2 3 4 5 6 7 8
У' 1133 1222 1354 13X9 1342 1377 1491 1684
Полагая тренд линейным: а) найти уравнение тренда и оценить
его значимость на уровне 0.05: б) установить с помошью критерия
Дарбина—Уотсона. является ли остаточный ряд е, автокоррелиро-
ванным на 5%-ном уровне значимости; в) при отсутствии автокор-
реляции возмущений дать точечный и с надежностью 0.95 интер-
вальный прогнозы среднего и индивидуального значений доходов
на девятый год.
Глава
Линейные регрессионные модели
финансового рынка
Каждая ценная бумага — акция, облигация. контракт и другие — в
каждый момент времени обладает стоимостью, которая называется
курсом и устанаштивается рынком (обычно как результат биржевых
котировок). Даже обладая всей полнотой информации о выпустив-
шем бумагу эмитенте, однозначно определить ее курс в заданный
момент времени в будущем, как правило, невозможно. В этом слу-
чае наиболее естественно рассматривать курс ценной бумаги как
значение случайной величины X.
Пусть X, — курс ценной бумаги в момент времени /. а А,., — в
момент времени г + I (обычно единица времени — это промежуток
между котировками). Обратимся к случаю, когда момент времени f
уже наступил, а момент t + 1 cine нет. Рассмотрим величину
X,
Так как Хи । — случайная величина, то и г — тоже случайная ве-
личина. Она называется доходностью ценной бумаги.
Очевидно, что значение именно этой величины определяет при-
влекательность ценной бумаги для инвестора. И одна из главных
задач финансового анализа состоит в возможно более точном пред-
сказании значения величины г.
15.1. Регрессионные модели
Модели, рассматриваемые в финансовом анализе, связывают
случайную величину г с величинами, которые объективно характе-
ризуют финансовый рынок в целом. Такие величины называются
факторами. В зависимое™ от постановки задачи факторы могут
считаться как случайными, гак и детерминированными, т.е. точно
известными величинами.
В самом простом случае выделяется один фактор. Тогда стати-
стическая модель имеет вил:
r = a + 0f + £. (15.1)
Здесь а и Р - постоянные (неизвестные параметры), с— случай-
ная величина, удовлетворяющая условию: Л/А(с) = 0. где Л/, (с) —
условное математическое ожидание случайной величины £ относи-
тельно F. Из этого предположения следует, что и безусловное матема-
тическое ожидание величины е также равно нулю. В самом деле:
Л/(£) = Л/(Л/, (£)) = ().
497
Отсюда также следует, что если фактор Г рассматривается как слу-
чайная величина, то се ковариация с с равна нулю. Действительно,
используя свойства условного математического ожидания, получаем:
cov(F, с)= Л/(Гв)- = Л/(Ге) =
= .W(A/JFe))=.W(F.V/Je)) = O.
Значения коэффициентов а и р нетрудно выразить через чи-
словые характеристики г и F.
cov (г. F) - р cov (F. F) + cov (с. F)
или cov(r.F)=pcov(F,F).
Отсюда
cov (г. F) cov(r.F)
cov(F.F)” D(F)
Перейдя в уравнении модели (15.1) к математическим ожидани-
ям. получим:
Л/(г) = а + pA7(F) +
Но Л/(е) = 0, поэтому
cov (г, F}
и = Л/(г) -|W(F) = Л/(г)-------- Л/(Г).
D(F}
Коэффициент Р называется чувствительностью доходности цен-
ной бумаги к фактору F. Коэффициент а называется сдвигом.
В классическом регрессионном анализе значения факторов F
считаются детерминированными величинами, т.е. модель (15.1)
имеет вид:
rf = а + рл; + е,.
Здесь / = I. .... п — моменты времени — интерпретируются как
номер наблюдения; F\, .... Fn — известные значения факторов; г, —
наблюдаемые выборочные значения случайной величины г; а и р —
неизвестные параметры. Их оценки1 можно построить методом
наименьших квадратов (см. гл. 12):
cov(r.F) "g^-(^)(b]
D(F)
»•! л»1 /
1 Oneнkii параметрон обошичием со знаком
498
Разные модели финансового рынка рассматривают различные
величины в качестве фактора F. Рассмотрим далее основные из этих
моделей.
15.2. Рыночная модель
Олпа из самых распространенных моделей использует в качестве
фактора F доходность рыночного индекса r,w. Рыночным ин-
дексом называется взвешенная сумма курсов акций наиболее значи-
тельных эмитентов финансового рынка. Например, в США наибо-
лее распространены следующие индексы:
DJ {индекс Доу—Джонса) — рассчитывается по 30 наиболее значимым
корпорациям, таким как Microsoft. Coca Cola. General Moton; и тл.;
индекс S&P 500 (Standard and Poor's) — рассчитывается по 500 наи-
более крупным компаниям:
сводный индекс NYSE — для его расчета используются курсы ак-
ций. зарегистрированных на Нью-Йоркской фондовой бирже.
Очевидно, рыночный индекс в определенной степени отражает
состояние экономики в целом. Так что рыночная модель показыва-
ет. насколько доходность ценной бумаги соответствует экономиче-
ской динамике страны (или даже сообщества стран).
Случайная величина с отражает зависимость доходности ценной бу-
маги от обстоятельств. специфических именно для ее эмитента.
Обсудим смысл коэффициента ft в случае рыночной модели.
Доходность рыночного индекса по сути представляет собой ус-
редненную доходность различных ценных бумаг. Если рассматривать
множество всех ценных бумаг, фигурирующих на рынке, то коэффи-
циент ft наудачу выбранной ценной бумаги представляет собой зна-
чение случайной величины (обозначим ее той же буквой ft). Если
ценная бумага включена в индекс, то по самому определению индек-
са имеет место равенство: А/(ft) = 1.
Если конкретное наблюдаемое значение ценной бумаги больше
единицы, значит, се доходность растет в среднем быстрее, чем рынок
в целом. Такне бумаги называются •агрессивными»-. бумаги с коэффи-
циентом ft. меньшим единицы, называются •оборонительными».
[> Пример 15.1. Значения доходности акций Widget Manufacturing
и доходности индекса даны в табл. 15.1.
499
Тпблнци IS-1 | IO|
Год Квартал Доходность WM Доходность индекса
1 I -13.38 2.52
2 16.79 5.45
3 -1.67 0,76
4 -3.46 2.36
2 5 10.22 8,56
6 7.13 8.67
7 6.71 10.80
8 7,84 3.33
3 9 2.15 -5,07
10 7.95 7,10
II -8.05 -11.57
12 7.68 4.65
4 13 4.75 14.59
14 7.55 2.66
15 -2.36 3.81
16 4.98 7,99
Оценить зависимость доходности акций от доходности индекса.
Решение. Метод наименьших квадратов дает следующие ре-
зультаты: р= 0.63. <*х = 0,79. Стандартные ошибки о, = 0.28.
о, =2.03. коэффициент детерминации R- =0,27. Полученные ха-
рактеристики свидетельствуют о том. что доходность акций Widget
Manufacturing существенно зависит от рыночного индекса. Как вид-
но. акции Widget Manufacturing являются ♦оборонительными». ►
На финансовом рынке присутствуют и бумаги с нулевым коэф-
фициентом JJ. В этом случае имеет место соотношение г = г, . отку-
да следует, что ожидаемая доходность ценной бумаги фиксирован-
ная и не зависит от состояния рынка в целом. Такая ситуация ха-
рактерна, например, для облигаций.
15.3. Модели зависимости от касательного порт(|>еля
Другим фактором, часто используемым в линейных регрессион-
ных моделях, является доходность некоторого выделенного портфе-
ля ценных бумаг, который называется касательным. Это понятие
было введено Г. Марковицем в 1952 г. Опишем это понятие.
Пусть на финансовом рынке обращается п ценных бумаг и капи-
тал. равный единице, инвестируется в эти бумаги так. что л; — капи-
тал. инвестируемый в /-ю бумагу. Набор чисел р = Х|.х>, удовле-
творяющий условию л( * л,+...4-ап = I. назовем портфелем ценных
500
бумаг. Разумеется, некоторые числа (xj могут быть нулевыми. (На
самом деле некоторые т, могут быть и отрицательными: соответст-
вующая ситуация называется продажей ценной бумаги без покрытия.
Мы. однако, нс будем углубляться в это понятие.)
Каждому портфелю р соответствует случайная величина гр —
доходность, которая определяется аналогично доходности одной
ценной бумаги. Очевидно, г1, = ^хг). Рассмотрим координатную
i-i
плоскость, на которой по оси ординат откладывается математиче-
ское ожидание доходности (ожидаемая доходность F,). а по оси
абсцисс - стандартное отклонение доходности - ар = ^£>(гг). Ве-
личина называется риском портфеля. Тогда каждому портфелю
может быть поставлена в соответствие точка на такой координатной
плоскости, а все множество допустимых портфелей отображается в
некоторую двумерную фигуру, называемую допустимым множест-
вом (рис. 15.1).
Между множеством всех портфелей и допустимым множеством, ра-
зумеется. нет взаимно-однозначного соответствия. Конечно, два различ-
ных портфеля могут иметь равные значения гг и <зг.
J---------------------------►
О а,
Риг. 15.1
Естественно предположить, что инвестор предпочитает получить
большую доходность с наименьшим риском, т.е. из двух портфелей
с одинаковым значением гг он выберет тот. значение о;, которого
меньше. Это значит, что наиболее предпочтительному портфелю
соответствует точка на куске границы АВ (см. рис. 15.!). Линия АВ
называется эффективным множеством.
501
Проблема выбора точки эффективного множества решается каж-
дым инвестором индивидуально и. казалось бы. зависит от его
склонности к риску (или. наоборот, к избеганию риска). Оказыва-
ется. однако, что эффективному множеству принадлежит точка, ко-
торая является выделенной для всех инвесторов.
Предположим, что кроме приобретения ценных бумаг инвестор
имеет возможность безрискового предоставления и получения зай-
мов. Такое предположение вполне соответствует действительности,
если инвестор имеет возможность покупать государственные обли-
гации и брать кредит. Мы сделаем еше одно предположение (уже
отнюдь нс столь бесспорное), что безрисковое предоставление и
получение займов происходит с одной и той же процентной ставкой
/у, которая называется безрисковой ставкой.
Рассмотрим прямую /, пересекающую ось ординат в точке rf и
касательную к эффективному множеству.
Уравнение прямой / имеет вид г = г, +—(г- - г,).
Рассмотрим портфель р = (х/. хм). где X/ — безрисковые вложения
(положительные в случае приобретения облигаций и отрицательные
при заем? средств) с фиксированной ставкой /у, хм — вложение в порт-
фель, соответствующий точке Л/. Тогда
г. = xfrf + rvFu = (1 - д „ ) rf + хчги = rf+ а„ (- /Jr); ар =
- -
откуда re = r, t—(ru -rf), т.е. точка r ) лежит на прямой I.
° w
Очевидно также, что любая точка полупрямой /, лежащая в первой
четверти, достижима с помощью комбинации (лу. .
Таким образом, при наличии возможности безрискового предос-
тавления и получения займов допустимое множество расширяется, а
эффективным множеством становится прямая /.
502
Портфель, соответствующий точке касания А/ (рис. 15.2). назы-
вается касательным портфелем.
Таким образом, оптимальной для любого инвестора стратегией
оказывается инвестирование части средств в касательный портфель,
а части — в безрисковые облигации. Либо наоборот получение
займа для дополнительного инвестирования в касательный порт-
фель.
Разумеется, на практике точное нахождение касательного порт-
феля невозможно. Но для многих практических целей оказывается
полезной модель, в которой в качестве фактора выбрана доходность
касательного портфеля, а точнее — разница между гм и безрисковой
ставкой г;. Таким образом. Г= г„ - г, и модель имеет вид:
''/= « ♦Р.К ~g) +е^-
гло i — номер пенной бумаги.
15.4. Неравновесные и равновесные модели
Очевидно, что доходности ценных бумаг, обращающихся на
рынке, можно рассматривать в зависимости от времени. При этом
будут зависеть от времени числовые характеристики случайной ве-
личины гг Так же. вообще говоря, будут зависеть от времени и зна-
чения параметров а и 0.
Модель финансового рынка называется равновесной, если число-
вые характеристики входящих в нес случайных величин постоянны
во времени. Экономический смысл подобного предположения оче-
виден: рынок считается «устоявшимся». сбалансированным. В этом
случае можно получить некоторые конкретные результаты, сущест-
венно упрощающие ситуацию.
Будем рассматривай, модель зависимости доходности ценной бу-
маги от доходности касательного портфеля (предполагается, что без-
рисковая ставка получения и предоставления займов для всех участ-
ников рынка одна и га же и равна rjy Если модель равновесная. т.е.
рынок сбалансированный. то касательный портфель удов отворяет сле-
дующему свойству: доля каждой ценной бумаги в нем соответствует ее
относительной рыночной стоимости. Такой портфель называется ры-
ночным и определяется однозначно. Таким образом, рассматривая
равновесные модели, мы будем отождествлять понятия касательного
и рыночного портфеля, доходность которого обозначим г у.
Итак, регрессионная модель для /-Й ценной бумаги имеет вид:
Г + P.v(»w-r, I*s.-
Оказывается. в равновесном случае имеет место следующая теорема.
503
Теорема. Для всех ценных бумаг, обращающихся на рынке, коэффи-
циент а один и тот же и равен безрисковой ставке.
□ Имеем
Рассмотрим портфель р, состоящий из z-й ценной бумаги и ры-
ночного портфеля М в пропорции X/ и 1 - х, соответственно. Ожи-
даемая доходность такого портфеля составит
(15.2)
а стандартное отклонение будет
о,, = ^х/сг + (I - х,<ru + 2х. (I - х, )о,„. (15.3)
Все такие портфели отображаются на кривую, соединяющую
точки / и М (рис. 15.3).
Из равенства (15.2) получаем:
А из равенства (15.3):
_ х,о? - Оу + -2x,alU
dx‘ yfxtf +(l-xJ):<rw +2х,(1-х,)стш
откуда
504
drr (г - ru )yjx;G; +() -x, f a:u ч- 2x, (l - x, )g,w
<4 W - crw + o,„ - 2x,a,w
В точке M x, = 0. отсюда наклон кривом в точке М:
. (,м)
СТМ
Но кривая касается прямой /. поэтому
dr г -С
<15.5)
Ом
Приравняв правые части равенств (15.4) и <15.5), получим
Таким образом, единственным параметром, характеризующим
данную ценную бумагу, является ее чувствительность •бета* к рыноч-
ному портфелю.
15.5. Модель оценки финансовых активов (САРМ)1
Уравнение
G='7+(ru-r/)p„, (15.6)
называется рыночной линией ценной бумаги. Оно определяет зависи-
мость ожидаемой доходности ценной бумаги от ее чувствительности
•бета» (P,w =g1U/a;,).
Рассмотрим портфель
h.....*.}. £•». = ••
Доходность портфеля
$=!>.<;•
1-1
Отсюда имеем, что ожидаемая доходность
1 САРМ — Capital Asset Prising Model
505
r, =2>?;=Ev,★ )2>,0«, = +('„-'>)P,u
t-l Ы t.|
Здесь
Уравнение
(15.7)
называется уравнением модели оценки финансовых активов Для ее
использования необходимо получить опенки параметров касатель-
ного портфеля — ожидаемой доходности и риска, а также ковариа-
ций доходностей ценных бумаг, входяших в /л с доходностью ры-
ночного портфеля.
В качестве аппроксимации рыночного (ненаблюдаемого) порт-
феля обычно выбирается индекс, включающий в себя достаточно
большое число акций (например. S&P 500}.
В реальной ситуации инвестору доступна опенка регрессионного
уравнения
re ~ri =а + Р(',м ~ГЛ <15.8)
Значение параметра в уравнении (15.8) совпадает с таковым в
уравнении (15.7). Поэтому проверка адекватности модели САРМ
сводится к тестированию гипотезы а = 0 в уравнении (15.8).
Если гипотеза и = 0 отвергается, то следует, что рынок пребы-
вает в неравновесной ситуации. Именно в этом случае практическое
значение модели финансовых активов наиболее очевидно.
Так. если доходность ценной бумаги выше той. которая задается
уравнением (15.6). то бумага является переоцененной, в противопо-
ложном случае — недооцененной.
15.6. Связь между ожидаемой доходностью
и риском оптимального портфеля
Пусть для всех участников рынка имеется единая безрисковая
ставка /у получения и предоставления займов. Тогда оптимальным
оказывается портфель, представляющий собой комбинацию касательно-
го и безрискового. Оптимальный портфель имеет вид;
Ани = (*о. Х|, *2.х„).
Здесь х<) — часть (доля) средств, вложенных в безрисковые бума-
ги (казначейские векселя), если jqj > 0. или х0 — заемные средства,
использованные для вложения в касательный портфель, если < 0.
506
Числа X|. х>, .... x„ находятся в том же соотношении. в котором на-
ходятся компоненты касательного портфеля.
Очевидно, что доходности оптимального и касательного порт-
фелей связаны линейным соотношением:
гг = хог, + ,
откуда следует, что коэффициент корреляции p(r,,.rw) = I. т.е.
Таким образом, уравнение САРМ имеет вид:
(г -г )
—----Ч- (15.9)
Оно задает зависимость ожидаемой доходности оптимального
портфеля от его риска.
Рассмотрим геометрический смысл уравнения
(15.9). При сделанных предположениях о безрисковой ставке /у эф-
фективное множество представляет собой прямую / (рис. 15.4).
Из очевидного подобия треугольников следует:
что эквивалентно равенству (15.9).
15.7. Многофакторные модели
Однофакторные модели во многих случаях являются вполне
адекватными, однако чаше всего они оказываются слишком упро-
507
щепными и тогда приходится рассматривай» зависимость доходно-
сти ценной бумаги от нескольких (т) факторов, т.е. линейные рег-
рессионные модели вида:
г, = а + +с, .
<•1
Здесь а. Р4 — параметры, F<4' — факторы, определяющие со-
стояние рынка (/ — номер наблюдения).
Такими факторами могут быть, например, уровень инфляции,
темпы прироста валового внутреннего продукта и др. Если данная
ценная бумага относится к некоторому сектору экономики, то без-
условно следует рассматривать факторы, специфические для данно-
го сектора.
t> Пример 15.2. В табл. 15.2 приведены данные за шесть лет о
темпе роста, уровне инфляции и доходности акций компаний Wid-
get Manufacturing.
Таблица 15.2 14(>|
Год Темп роста ВВП, % (temp) Уровень инфляции. % (inf) Доходность акций. % (Widget)
1-й 5.7 1.1 14.3
2-й 6.4 4.4 19.2
3-й 7.9 4.4 23.4
4-й 7,0 4.6 15.6
5-Й 5.1 6.1 9.2
6-Й 2.9 3.1 13.0
Рассматривается факторная модель вида:
Widget = а temp -+-р,inf .
С помощью метода наименьших квадратов получается уравне-
ние вила:
Widget = 5,77 + 2.17 temp - 0.67inf.
При этом средние квадратические ошибки опенок параметров
р, и р, равны 1.125 и 1.162.
Следует стремиться к возможно меньшему количеству объяс-
няющих переменных (факторов), поскольку кроме усложнения мо-
дели «лишние» факторы приводят к увеличению ошибок оценок.
Так, в рассмотренном примере стандартная ошибка оценки пара-
метра Р: оказалась больше се значения но абсолютной величине.
Это наводит на мысль, что четкой зависимости доходности акций
508
компании Widget от инфляции нет. В этом случае естественно удалить
фактор инфляции и рассматривать зависимости доходности Widget
только от темпа роста ВВП. Соответствующее уравнение регрессии
Widget = а + Р( temp.
оцениваемое с помощью метода наименьших квадратов, имеет вил:
Widget =4 + 2 temp.
При этом ошибка параметра 0, уменьшается и становится рав-
ной 1,002.
Однако в реальных ситуациях порой приходится рассматривать
модели зависимости от десятков и даже сотен факторов.
15.8. Многофакторная модель оценки
финансовых актинов
Один из примеров многофакторной регрессионной модели фи-
нансового рынка является модель вила
(15.10)
где г4 — доходности некоторых выделенных портфелей. Из уравне-
ния (15.10) следует
i-i
что, очевидно, представляет многофакторное обобщение модели
САРМ.
Как и в однофакторной модели, параметры 0, оцениваются с
помощью уравнения
г,-г, + “'•/)• <15.11)
ы
При этом в случае модели САРМ а = 0.
В неравновесном же случае
+ £р.(5 ~rt »
i*i
сеть превышение действительно наблюдаемой средней доходности
актива над «нормальной» доходностью.
Можно получить оценку d , оценивая коэффиниеьгг регрессии а в
уравнении (15.10) по предыстории. Такая опенка называется а-коэф-
фициентом Йенсена.
509
Если d > 0. актив считается успешным (его доходность превыша-
ет нормальную), и тогда его стоит включать в портфель.
Другим показателем, часто используемым для оценки финансово-
го актива, является коэффициент Шарпа
= (15.12)
с/
Коэффициент Шарпа — доля ожидаемой доходности на единицу
риска.
Инвестор, как правило, стремится выбирать активы с большим
коэффициентом Шарпа. Как следует из рис. 15.2, максимальное
значение коэффициента (15.12) достигается на касательном порт-
феле.
Библиографический список
1. Айвазян С.А. Енюков И.С., Меииикин ЛД. Прикладная статистка Основы
моделирования и первичная обработка данных — М.: Финансы и статисти-
ка, 1983.
2. Айвазян С. А., Енюков И.С.. Мешаякин Л Д Прикладная статистика Иссле-
дование зависимостей. — М Финансы и статистика. 1985.
3. Айвазян С.А. Мхитарян В.С. Прикладная статистика и основы эконометри-
ки. - М.: ЮНИТИ, 1998
4. Бочаров ПИ., Печснкин АВ. Теория вероятностей и математическая стати-
стика. — М.; Гарддрика. 1998.
5. Вентцель Е.С Исследование операций Задачи, принципы, методология. —
М : Наука, 1990.
6. Вентцем Е С. Овчаров ЛЛ Задачи и упражнения по теории вероятностей. —
М Высшая школа. 2002.
7. Вентцем Е С, Овчаров Л.А. Теория вероятностей и се инженерные прило-
жения - М : Наука. 1988.
8. Войтенко М.А Руководство к решению задач по теории вероятностей. — М.:
Изд-во ВЗФЭИ. 1988.
9. Высшая математика для экономистов / Пол ред. Н.Ш Кремера — М.: ЮНИ-
ТИ-ДАНА. 2006.
10. Высшая математика для экономических специальностей: Учебник и Практи-
кум / Под ред. Н Ш Кремера. — М.: Высшее образование. 2006.
II. Гмурман В.Е Руководство к решению задач по теории вероятностей и матема-
тической статистике. — М.: Высшая школа, 1979.
12. Гмурчан BE Теория вероятностей и математическая статистика. — М.: Высшая
школа, 1977.
13. Гнеденко Б. В. Курс теории вероятностей — М.: Наука. 1975
14. Дубров А. М.. Мхитарян В С. Трошин Л.И. Многомерные статистические ме-
тоды. — М. Финансы и статистика. 1998.
15. Иванова В М. Калинина В.Н. и др. Математическая статистика — М.: Высшая
школа, 1981.
16. Исследование операций в экономике / Пол ред. Н Ш Кремера. — М.:
ЮНИТИ. Банки и биржи, 1997.
17. Калинина В Н., Панкин В.Н. Математическая статистика — М.: Высшая
школа. 1998.
18. Карасев А. И. Аксютина З.М., Савельева Т.И. Курс высшей математики для эко-
номических вузов. Ч. 2. — М Высшая шкота, 1982.
511
19. Карасев АН.. Кашхман Н.Л.. Кремер //./// Матричная алгебра — М • Изд-во
ВЗФЭИ. 1987.
20. Карасев А.И.. Кремер Н Ш., Савельева Т.Н. Математические методы и модели
п планировании. — М : Экономика. 19X7
21. Калемаев ВЛ. Клшнина В Н Теория вероятностей и математическая стати-
стика - М.: ИНФРА-М. 2004
22. Колмогоров А.И. Основные понятия теории вероятностей. — М.: Наука. 1975.
23. Крамер Г Математические методы статистики: Пер. с англ — М Мир,
1975.
24. Кремер Н Ш Математическая статистика — М.: Экономическое образова-
ние. 1992
25. Кремер Н.Ш., Путко БА., Тришин И.М Математика для экономистов: от
Арифметики до Эконометрики / Под ред Н Ш. Кремера,— М.: Высшее об-
разование. 2007
26. Кремер Н.Ш., Путко БА. Эконометрика. — М.: ЮНИТИ-ДАНА, 2002
27. Математика в экономике: Учеб.-метод. пособие / Пол рея И III Кремер;! —
М Фикстатинформ. 1999
28. Мицкевич И.П.. Свирид Т.П.. Булдык ГМ Сборник задач и упражнений но
высшей математике Теория вероятностей н математическая статистика. -
Минск: Вышэйшяя школа. 1996.
29. Мицкевич Н.П, Свирид ГII. Высшая математика (Теория вероятностей и
математическая статистика). — Минск. Вышэйшая школа. 1993
30. Рунион Р Справочник но нспарамсгричсской статистике. — М Финансы н
статистика. 1982.
31. Смирнов Н. В. Дунин-Барковский И.В. Курс теории вероятностей и математи-
ческой статистики для технических приложений. — М. Наука. 1969.
32. Соколов ГЛ. Чистякова Н.А. Теория вероятностей — М.: Экзамен. 2005.
33. Справочник по прикладной статистике / Под ред Э. Ллойда. У Лидермана:
Пер. с англ — М Финансы и статистика. 1989.
34. Тюрин Ю.Н., Макаров АЛ Статистический анализ данных на компьютерах /
Под ред. В.Э. Фигурнова. — М.: ИНФРА-М. 1998
35. Уотшем ТДж.. Паррамоу К. Количественные методы в финансах: Пер с
англ. — М.; ЮНИТИ; Финансы. 1999.
36. Фадеева Л.И Теория вероятностей и математическая статистика: Курс лек-
ций. — М.: Эксмо, 2006.
37. Ферстер Э.. Ренц Б .Методы корреляционного и регрессионного анализа
Пер. с нем — М.: Финансы и статистика, 1983
38. Хьютсон А Дисперсионный анализ: Пер. с англ — М. Статистика. 1971.
39. Четыркин Е.М., Калихман ИД. Вероятность и статистика. — М.: Финансы и
статистика. 1982
40. Шарп У., Гордон Дж.А.. Бейли Д. Инвестиции: Пер. с англ. — М.: ИНФРА-М.
1997.
41. Экономико-математические методы и прикладные модели / Пол рея В В. Фе-
досеева - М.: ЮНИТИ-ДАНА. 2003
Ответы к упражнениям
Глнва 1
1.37. а) 1//>7=1/71=1/5040=0.000198; 6) Р^Р^/Ры = 2!3!2!2!/10! =
=1/75600 = O.OOOOI32.
!.38. 1/А = 1/5! = 1/120 = 0,00833.
1.39. а) = 0,108; 6) С^/С^ = 0,0166; в) = 0.142.
1.40. а) с;;С-,/с:0 =0,348; 6) I - С^/С^ =0,984.
1.41. ад/с- = ол
1.42. (С?Л f с;с,’о +с*)/с; = 0,809.
1.43. а) 1/(0,9 • 4 ) = 1/27216 = 0,0000367; 6) 9/90000 = 0,0001;
в) 5790000 = 5/144 = 0.0347.
1.44. а)С1С,’4/С,,ь = 8/15=0ЛЗЗ;б)(С’4 + С;С)/СХ =7/15 = 0,467.
1.45. a) (CC>Ct’.,)/Ci = 0,901; 6) 0.099.
1.46. C4’C;Cj /С?о = 0,038.
1.47. ЛЛ1//’ю = 8’31/10! = 0,067.
1.48. а) 0.125; б) 0.5.
1.49. (|-с;7с,')(1-с;/с-)= 0.575.
1.50. 0.4375. 1.62. । - с,; / с,;=0.476.
1.51. 2/л = 0,637. 1.63. a) (C,’ + C,’,)/Ci =0.282;
1.52. С/СХ= 0.0281. 6) (С:с;,+с:сг, )/С,’„ =
1.53. 0.571. = 0,270.
1.54. 1.55. а) 0.032; б) 0.316. 0.316. 1.64. а) аде;/с; =0.184;
1.56. 0.788. б) (адс,ад)/с; =
1.57. а) 0,54; б) 0,995. = 0.137.
1.58. а) 0,46; б) 0.7. 1.65. а) 0.0104; б) 0.625.
1.59. 0,982. 1.66. Нс менее 5 пакетов.
1.60. С]С,;/с;(=0.421. 1.67.
1.61. при р = 0,4, ./= 0.8704,
= 0.344. /г > 4.
513
1.68. I-C’/C,‘o =0,708.
1.69. 0,4.
1.70. 0,992.
1.71. 0,664.
1.72. a) 0,03; б) 0,167.
1.73. a) 0.1725; б) 0,317.
1.74. 0.667.
1.75. 0,621.
1.76. a) 0,9236; 6) 0.0022.
1.77. 0.0073.
1.78. Вероятность одна и та же.
равная т/п.
1.79. a) I/6M.0046;
б) 6/63=1/36 - 0,028;
в) С’/6' =5/54 = 0,093.
1.80. а) 5/5М.04;
б) С; -3!/5’ =0.48.
1.81. а) 2/19*0.105;
б) (2 • 18!+2 • 18 • 18’)/20’=
=0,1.
1.82. 1 • (6/9)(5/8)(4/7)(3/9)х
х(2/8)( 1/7)=5/1764»
*0,0028.
1.83. а) 0,7(1-0.2-0.15-0.1)=
=0,6979;
б) 0.7 0.2-0.85=0,119;
в) 0,7-0.8-0,85-0.9=
=0,4284.
1.84. 1/6+(5/6) • (3/51 )=11/51 *
-0,216.
1.85. 2/5+(3/5)(2/4)(2/3)=О,6.
1.86. 3 • 0,8? • О,2-=О,О768.
1.87. (60/100)(59/99)+(60/100)х
х(40/99)(59/98)»0,504.
1.88. 0.2 • ,9/(1-0,8 • 0.9)=
=9/14=0,643.
1.89. a) *0,579; б) -0,002.
1.90. Л + В + С.
1.91. 1/11.
1.92. а) (4»48!/(12!)4):(52У(13!)4)=
=0,105;
б) (4!)П(13!)4/(52)!*1631(У".
1.93. а) (2!)33!/10!=0.000013;
б) |(6!/3!2!) • (4!/2!2!)-5|:
:|10!/(2!)33!|=0,024.
1.94. С’\((1/6)6-2(1/12f) =
- 0.00137.
1.95. 3/7.
1.96. 0.3944.
1.97. 0,45.
1.98. 1/6; 7/12.
1.99. 8/15.
Глава 2
2.13. а) ^С1р'ц =0.015; б) Р6(т>2) = 1-/>6(т<2)=
= 1-(/’0.6+/,1.б+ А.б) = 0.999.
2.14. а) Pj.vf’C^p'q1 =0.201; 6) />|0(т<3) = Р„.|о+ Л ю =0,678.
2.15. />.(„ г 4) = Ра.ь + 7*5.6 + Рь.ь = 0.544.
2.16. а) iFCt'p'q’ =0.1298; б) Рн)(л1<2)=Л,.|о+/,1.11>=О.544.
2.П. Рь(т s 2)=/*о.б+А.»+Л.б=О.984.
2.18. а) Рю (т г 3) = I - Рю(т < 3) = 1 - (fli.io+T’i.io+A.io) = 0.945;
б) Р„ (т < 3) = Р„„ + />„, + Р. + Рю = 0.172.
514
2.19. a) 2 партии из 4. ибо Д 4 = C;p'q2 =0.375. а РХь = С*р*д' =
= 0.312; б) нс менее 2 партий из 4. ибо Рцт % 2) =
= P:i + />м + =0.688. а Л(/п >3) = I - Л(w <3) = 1 -
+ Р..+ Л.) = 0.656.
2.20. а) А.4(ю= А(0,4) = 0,0072; б) Аоот (т $ 3 ) = Ро.40оо + А .4000 +
+ Л.-мхю + Р}.юо = 0.9992.
2.21. а) Рдл.кккюо = 0,054; б) Рктю(45 < т < 55) =
Аотоот (|гп-лр|<5) =0.522.
2.22. а) т0 = 10; Ло.зь5о= Ло( । 0)=0.1251; Л,650(3</и<3650)=0.9971.
2.23. a) A Kwai = Л(О = 0.0031; б) Лоооо(т£9998) при р =
= 0.9999 равно Лоооо (т < 2) при р = 0,001. т.е. Лоооо (m < 2) =
= А>,|оооо+ Л.юооо + Лмоооо = Л)(О+Л(О+Л( 0 е 0,9197.
2.24. а) </,'</; + (C\p,q; )(<?>.</;) =0.321;
б) (C\ptq; )с/.’ + С;р,:</, (q': + C\p,q;) +А (l -Рг) = °>243.
2.25. з| А.ю= СА4 =0.251; б) Лго.мо = 0.0576.
2.26. а) при р = 0,9 Р>оо(180<т < 200)=0,5; б) при р = 0.1
Ло(ш<2) = /’„=0.930.
2.27. а) Лы>.4от=0.0054; б) Аоо(180< т 400) = 0.977.
2.28. a) Awo(3OO <. т <> 1800) = 0.998; б) Лал(300 S т < 400) = 0.906.
2.29. п = 55.
2.30. ш0=«; А_ХОо=А(«)=0.1396.
2.31. а) 0.88<н <0.92; б) (0.08< и•<;0.11) = 0.8186.
2.32. п = i-pq/:\' =681. где Ф(/) = 0.99|.
2.33. п= грч/&2=т<). где Ф{() = 0.996.
2.34. a) Aoooo(100smsi0000) = 0; Аоооо(50 s т <. 10000)=0.750.
2.35. (I-Л>.ioMI-A-k-A.k) = 0.3235.
2.36. а) Р6(2;2;2)=0,081; б) Р6(0;6;0) + Р6(1;4;1) + Р6(2;2;2) +
+ А(3:0;3) = 0.213.
2.37. 0.839; 0,161.
515
Глава 3
3.25.
3.26.
3.27.
3.28.
329.
3.30.
3.31.
3.32.
3.33.
3.34.
3.35.
3.36.
3.37.
х( О I 2 3 4 ]
(0.4096 0,4096 0.1536 0.0256 0.0016 J’
„ / 0 5 10 15 )
Х 10,512 0.384 0.096 0.008Г М(А)“5лР~3
J ° I 2 3 4 5 '
”1,0.59049 0.32805 0,07290 0.00810 0.00045 0.00001,
М(Х) = пр = 0,5; /ХА) = npq = 0,45.
° I 2 3 4 5 1
(0.00001 0.00045 0.00810 0.07290 032805 0.59049) ’
А/(Л) = пр = 4,5; /ХА) = ад=О,45, где X (тыс. руб.).
Х = Цб4 27/64 9/1
0 12 3 4
0.6561 0,2916 0.0486 0.0036 0.0001
АЯА) = лр = 0,4;
/ХА) = npq = 0.36.
J ° 1 2 3 1
( 0.006 0.092 0,398 0,504 )
V-( ° 1 2 3 '
(0.024 0.188 0.452 0.336/
п(А') = 0.78.
М(Х) = 2.4; /ХА) = 0.46.
A/(A)=2,I; /ХА) = 0,61;
.л Г О I 2 )
Мо.06 0.38 0.J ^='.^А)=0.37;
F(x) = [0 при х < 0; 0,06 при 0 < х < I; 0.44 при 1 < х < 2;
1 при х > 2j.
Jf = (o.006o/o.244 0.2lP(A)=l-8; W7'
F(x) = jo при x < 2; 0,3 при 2 < x < 4; I при x > 4|.
X = (o°3 06 Q l)’ = 1° ПРИ Л ‘ °’ °'3 “РИ 0< x - 1:
0.9 при К xi2; 1 при x>2|.
x- ° 12 И
(o.l 7 оз 03 о.озл
516
3.38.
3.39.
3.40.
3.41.
3.42.
3.43.
3.44.
3.45.
3.46.
3.47.
3.48.
3.49.
3.50.
| О 1 2 3 4 5 1
*0.04196 025175 0,41958 023976 0,04496 0.0020oJ ’
л4° 1 2 Ч
U/14 3/7 3/7 1/14?
F(x) = [0 при х < 0; 1/14 при 0 < х s Г.
1/2 при I < х 5 2; 13/14 при 2 < х £ 3; 1 при х > 3|,
ЧоЗ 0.21 0.К7 0.344з)'ЛЛА^533;В(Л=1-5349-
[ 1 2 3 4 \
' 1/3 2/9 4/27 8/27Л
(12 3 4 5 )
0.4 024 0,144 0.0864 0,1296?
Л/(Л)=2,3056; Р(А)= 1,9626.
^’(о'юо^оУ"^2-62-
а)ДГ = (о.6о!2О.МоУ:6,Л«^'-72:«А)=‘-0*16-
J ; М(Х)= 1,375; ZXAW.401.
.j; Af(A)=2,5; D(A)=1.25; о(АГ)= 1,12.
х4 1 2 3 4'
17/10 7/30 7/120 1/120,
х ( 1 2 3 4 '
" 1025 025 025 0,25,
Z=( 12 3 4 5).
1о.2 02 02 0.2 0,2л '
F(x) = {0 при х < I; 0,2 при I < х < 2; 0,4 при 2 < х s 3:
0.6 при 3<х£4; 0,8 при 4 < х £5; I при х>5}.
Х._ f 2 3'
103 0.4 оз.
; Л/(Л)=3:
Z = ЗА' -2Y =
a) Z=X+ Г=
j; б) Л/(А)=2; D(A)=0.6.
Г-6 -4 -3-1 3 5'
*0.12 0.08 030 020 0,18 0,12
Л/(П=2.6; A/(Z)=-I.O: 7ХА)=1,24; СК П=0,24; D(Z)=12,12.
0,2 3 4 ;б)Ш)-1.2;
0.05 0.30 0.20 0.30 0.15J
Л/(У)=1.0; ,W(Z)=2.2.
: Л/(А)=1.4;
517
SIS
ё = <¥Х7-c = C¥)W -1 = 0 -99-е
•£/1 = (с) J ~(£)d = (£ 5 X > l)d -Ь/L- = J V8=<7 *6/1- = » W£
0 = (9 = X}d = (9 * X * 9)<f (J
•91/91 = (t)/ - (9)j = (9 > X > t}d <a
• I = (9 > X > c)j (9 it/l = (z)d - (fr)j = (fr > X > l}d (* *£9’£
9*0 = (o)/ - (l}d = (l > X > о)</ Z9’£
•9££6‘0 = (£=Ajj +
< (c = *)</+ 0 = X\d + (0 = X)d = <£ 5 x)d (9 *9*0 = О (с I9*£
99^I = fc = xk + fc = X)rf + (lsxV = [l5k-^l)/ (9-99/1=0 O’ 09*£
•(C='X) = ^ {c<(\Y+'y)] = F arj
*9*l = (K)J/(^)J = (»Vc/ (9*8/9 s (гА* *'/)</ (в *6S’£
(9 > Y) = 8 ‘(I < X> = V avj y() = (v)dHw)d = Wd ’«ST
= «'0]=xiS-E
VII * г ~ 01 ~ 9c ~j
к rS 09 £c 9c f
/9/1 C/1 9/1 9/П
I > € Z I J SS €
6’0 = z^<iu + Wdu = (^X/ !97 -
= = (9:^ro «1Г0 ИИГО ^lO’Oj =z W€
•j8*Z = V87 = UXW = vm ‘8*2 = U W = <rW
,(sro ого 6Г0 zi'o WO) _ _ .(S-о го Г0) v _
(91 8 t, г I }-AX-n (91 t \} = tX=z tS£
'9*9 = U+УИ = (/?)/¥ !9‘9 = (¥£)>¥ =
, . . . . v . . /9Г0 ОГО Oc 0 60’0 г 1’0 И)’0>
= (ZW -87 = U)/V =<A'W • o bUUVVVVVCIU EVU I
I 8 9 9 fr € I )
= A +X
'$0 ГО ГОА
.8 t, г J n z ZS(
.(«0'0’^^0 94Г0 9«00)^
3.66. a) <p(x) = jo при x 5 0 и при x > 1; 2x при 0 < x < I j;
б) Af(A) = 0,6667; в) D(X) = 0,0556; r) fl* = 0,5) = 0;
/W<0.5) = 0.25; ao,5 < X< I) = 0,75.
3.67. a) AM A) = I; Me(X} = 0.707; б) ль.д = 0,632; = 0.894.
3.68. a) A = Mj/o’ = -0,566; 6) E = щ/о4 - 3 = -0,6.
3.69. а) Л = 1/п;б) F(x) = (l/n)arctgr+l/2; в) f\-\ < Xs, l)=0,5.
Л/(Л) и D{X) нс существуют, так как выражающие их интегра-
лы расходятся.
3.70. а) Л = л./2; 6) F(x) = {0,5е*>л прих^О; 1 - 0,5е *л при
х > 0); в) М(Х) = 0. ZXA) = 2/л?.
3.71. а) ф(х) = {(2/CMI -х/с) при 0 < х s с; 0 при х > с);
6) М(Х)=с/3-, D(X) = с2/18; р3(/) = с’/135; Лс/2 Д'«г с)=
=1/4.
3.72. а) <р(х) = «1/3)(1-| х|/3) при -3 s х ^3; 0 прн х<-3 или
х > 3); Дх) = {0 при х S -3; (1/18) (х+3)? при -3 < х s 0;
(1/18)(6х -х2+9) при 0<xs3; 1 при х>3); б) М(Х) - 0.
ЩХ) = 1.5; щ(А) = 0; в) А-3/2 s Х< 3) = 7/8.
Глава 4
4.11. Р(Х = m) = CgO.f •0,9”"’. л»=0. 1.2..19; A/(A3 = лр = 1.9;
ZXA3 = npq = 1,71; A/o(A0i = 1» Mo(X)i = 2.
4.12. A/w/„=0.l; ZXm/n)=0.00473.
4.13. f(x) = 10 при x < 0; ^C^pmqn'’n при к < х < к + 1:
т«0
I при X > л}.
4.14. а) Р(Х = л») = 2те 2/т\, т = 0.1.2....; б) М{Х) = >. = 2.
МЛ) = X = 2; в) Р(Х г I) = 1 - Р[Х = 0) = 0.865.
4.15. а) Р(Х= т) = 0,05• 0,95я-1. т = 1.2,...; б) М(Х) = 1/р = 20.
ГХХ) = q/p2 = 380; в) Р( X > 5) = I - Р(Х < 5) = I -
- [Р(X = I) + Р(Х = 2) + Р(Х = 3) + Р(Х = 4)] = 0,8145.
4.15а . а) /’(.Г = гл)=С-.|0,05' 0.95"”‘, w = 0.1,2....;
б) A/(.V) = к/р = 3/0,05 = 60; МА’) = kqlp' = 3 0.95/0.05' = 1140.
4.16. а) Р(Х =т) = СТС^/С^. ш = 0.1.2......5; б) Л/(А) = nM/N =
= 1,75; 1КХ) = лЛ/(1-АУ/Л0(1-л/М/(^-1)=О,898;
в) ЛЛ'=О)=О.О83.
519
4.17. I) ЛЛЛ)=0,1; ЖЛ)=0.00333; о(А') =0.0577;
2.а) Р(0 < X < 0,04) + Р(0.16 < X < 0.20) = 0.4;
б) Р(0,05<.¥ <0.15) = 05
4.18. а) ф(х) = {0 при х < 0; 0.012Se °-п,25л при х £ 0|;
Дх) = {0 при х < 0; I - с~ °*0,Пг при х ;> 0|. б) Р = I -
-Я 100)= 0.286.
4.19. 1.а) Л%£ 15,3) = Л 15.3) = 0.9332; б) Р[Х> 15.4) = 1 -
-Д15.4) = 0,0228; в) Ж 14.9 <, Х<> 15,3) = 0,6246;
2) 14,4 £ Х<. 15,6.
4.20. а) М(Х) *98 (дсп. ед.), п(Х) = 12 (ден. ед.); б) Д83 £ Л <96) =
= 0.461; в) Л = fa = 23,52 (ден. сд.), где Ф(0 = 0,95.
4.21. а) 470) = 0.050; б) Л 500 < Х< 550) = 0,609;
в) НХ> 550) = 0,341; г) Г(|Х-540|< 30) = 0.781.
4.22. о =* 10. Д35 s Х<, 40) = 0.09; б) ДЗО £ Х< 35) * 0,15.
4.23. а) Из интервала (1.2). гак как P(KAf<2) = 0,3414.
а Д2 < Х< 6) = 0.1586.
4.24. а = 15.2: с - 3.1.
4.25. Параметры а * 28.6; а = 255 Л35 < X < 45) * 0.29.
4.26. а) Параметры а * 781; а « 0,703; Р(Х > 1000) = 0,363;
б) Р(Х< 500) = 0.264.
4.27. /\ (х) = 0,5 + 0.5Ф((х -150/ 50).
4.28. фч(х) = 1/(1.48>/2nk' ’'4 W ; Fjx) = 0,5+0.5Ф(х/1.48).
4.29. а = а-(5\!з ; р = а + а7з.
4.30. ст = 7з/2In 2 = 1.47. 4.31. а) <р(х) = |4е '1 при х > 0; 0 при
х < 0); б) <р(х)= {4е:’(1 -е "‘) при ха 0; 0 при х < 0}.
Глава 5
5.10. А-Л-‘ ° ' Ь.[° ' 2 П
1.0.15 0.50 0.35J 1,0.11 0.33 0.40 0.16/
_( 0 ’ 'I у _( 0 I 2 3).
10.225 0.4 0,375) |Д08 0,40 0.32 0.20/
в) P(Y> X) = 0.81.
5.11. а) ф( х. г) = {1/900 при 0 < х < 30. 0 £ у < 30; 0 при х < 0. или
х > 30, или у < 0, или у> 301; Р{х,у)= (0 при х < 0 или при у < 0;
520
(I/900)лу при 0 s х < 30. О < у < 30 (I/30>х при 0 < х s 30. у > 30;
(1/30)у при х>30. О < у < 30; I при х > 30. у > 30); б) Ф|(х) =
=(1/30 при 0 s x s 30; О при х < 0 и х > 30). <₽?(>*) 1/30 при
О < у s 30: при у < 0 и у > 30г, Г|(х) = |0 при х < 0; (1/30)х
при 0 s х < 30; I при х > 30:; Л(у) = (0 при у < 0: (1/30)у при
О <, у < 30; I при у > 30|; в) X и Y независимы:
г) Р[(0$Л'<у)(05У<30)]= 0,5; РГ(у<Л'£30)(0< Г<30)]=0,5.
5.12. а)<р(х, у) = {1/2 при (х. у) 6 Л; 0 при (х. у) «Л |;
б) = jO при |х| >1; 1 + х при -I < х < 0; I - х при
О < х < 11; ф,(х) = |0 при |у| > I; I + у при - I < у < 0; I - у
при 0 < у < I); в) q>, (х) = (0 при |х| > I - |у|; 1/[2(I - |y|)J при
-(I - М) < х < (I - ДО)}, <р.(у) = |0 при |у| > I - |х|:
1/[2(1 - |х||] при (I - |х|) <>•<(! - |х|); г) X и Г зависимы.
5.13. ф(х.у) = [0 при х<0 или у<0; Юс при х > 0. у > 0|;
F {х,у) = (0 при х < 0 или у < 0; (I - е“5‘)( I - е"2г) при
х > 0. у > 0).
5.14. а) Ап.= - 0.012; р = -0.02: б) Хи Скоррелированы.
5.15. А'о.= 0; р = 0; б) Хи Yнекоррелированы.
5.16. А’о.= 0; р = 0: б)Хн С некоррелированы.
5.17. = (0 при у 5 0; /2-Jy при у > 0). Л/( И = 2.
МО;2), т.с.
5.18.
ф(з) = (|/(2>/я)]е :’/4.
5.19.
а) (X У): б) Х)-о= X, \ 0 1 ; х=(° Ч (1/2 1/2) ( 0 1 J/2 1/2/^’
0 1/3 1/6
0 »/з 1/6
о I • Ху».| — 1/2 1/2)
О I '
.2/3 1/3,
; Y =
( 0
[2/3
о
.2/3
1 '
1/3/
I
«Ч
5.20. ф(х,у) = {I при 0 s х s I. О s у s I; 0 — в остальных случаях);
Ях.у) = (0 при х S 0 или у s 0; ху при 0 < х s 1 и 0 < у < 1;
х при 0 < х < I и у > 1; у при х > I и 0 < у < 1; 1 при х > 1 и у > 1).
10 Тюрка кротюоеи и ыопопгксы* тгнепка
521
5.21. ф(х,у) {(3/п)( 1 - Vх? * У* 1 при х-'+уМ; 0 при х2+у2>1); ф|(х,у)
{(3/я) l7l-x2 -х2 ln((l + -7l-x: )/|х|)| прн |.г|<1; О при |х|>1):
Фз(х.у) {(3/п) -У21п((1+7|-/)/Ы)1 при О при
Ы>И; Ф.ЛН = )' Vi-Х2 -X2
|у| < Vl -х2: |х|<1;0 при |y|<Vi-x2 , |х|<1|; ф.(х) =
КП-/*2 + < Ma/1"/ -/ bu(l + 7l-г2 )/],ф при |.г| < Jl-r )Ц<1:
О при |r] < jl-y2 |л| <I): ЛГи У зависимы, так как ф, (х) * ф,(х) .
Ф, (у) * q>2(y) , но не коррелнрованы. так как р = 0.
5.22. а) Л=1/я2; б) Л(-1^51)(-15У$1)]«1/4; Ф|(х)=1/|п(1+хг)|, ф:(х)=
= l/lnd+y2)); X и У независимы, так как ф(х,у) = Ф|(х) ф$(у).
5.23. а) С = 12/11; б) Ф,(х) = 12(.v + х/2+1/21/11. <p,(.v) = 12(у2 +
+ у/2+ 1/2)/1 I; в) ф,(х)= (х2 + х/у+ у2)/ (у2 + у/2+1/2). Ф,(у) = (х2*
+ X/F+ у2)/ (х2 + х/2+1/2); г) о, = а, = 7/11; Р(Х)=Л В=257/3630;
р = -40/257»—0,156. 5.24. ф(х,у) = • In2 2 при х 0, у > 0;
О при х < 0 или у < 0}; /1(1 < X < 2) (3 < У< 5» = 3/128.
5.25. Лху) = |( l/n)arctg(x/4) + 0,5) |( l/a)arclg(y/5) + 0.5).
5.26. Ф(х.у) = )(1/л)е ‘ при 0 < у £ I; 0 при у < 0 или у > I); Дх.у)=
= )О при у < 0; у(0,5 + 0.5 ф(х75 ) при 0 < у s 1; 0.5 + 0.5 ф (х^2 )
при у > I}. 5.27. ах = 2, = -3. а; = а; -1; р = 0.6. 5.28. а) 0,25:
6) 0.5; в) О.25[Ф(3) - Ф< I>| |Ф(2,5) - Ф(0,5)| » 0.0476. 5.29. a) g(y) =
=(1/у) |1и(1/у)| (0<у<1); 6) Ду) = е>' -ф(е‘); в) (1/3^/ Ф^у ). (0< у< «);
г) = (1/(2у77 Ж1/77 > «К** Л) № = 2УФ</) «К У < *)• S-30- №
= {!/[ к-Jl -у21 прн -К у <1; 0 при у <-1 или у > I). 5.31. j?(_v) =
=0,5/Ту (0< у si). 5.32. tfy)el/|n(l+y4 ("»< >< +*)• 5.33. ау = 2.4.
IX У) = 1.99. 5.34. а> а, = 5; [\ У) = 36; б) = 5. р = -I. 5.35. ау =
=(л2 - 8)/4. 5.36. ау = 1п 2; Ж В = 0.5 - 1п22. 5.37. ау = 0.5; IX В =
= 1/12. 5.38. ау = 2Д IX В = 1/18. 5.39. ау = -14. 5.40. М(Х-Г) = 0.
ДЛГ-В = 13/3; б) MtX2) = 5. Л/(У2) = 64/45. 5.41. Е{:) = (0 при 0;
/2/8 при 0< : £ 2; 1 - (4 - z)2/8 при 2 < : < 4; 1 при z > 4|; <р( г) = (О
при г < 0. :/4 при 0< г < 2; I - z/4 при 2 < : < 4; 0 при z > 4).
5.42. ф.у(г) = (1/2х) е 4; аг = 0, о2 = 2.
522
Глава 6
6.9. PsO.I. 6.16. Р > 0.9344.
6.10. а) Р >0.5; б) Р s 2/3. 6.17. 0.2 S и> s 0.4.
6.11. Р >0.9856; Р * 1. 6.18. Р >0.91.
6.12. Р> 0.264. 6.19. а) л <595; 6) л< 121
6.13. Р > 0.6; Р 0.8859. 6.20. л 16000; п =4330.
6.14. Р >0,75. 6.21. Р £0.929.
6.15. Р > 0.996. 6.22. л £3333.
Глава 7
7.10. a^i) = ae b, D^t)= a:e :tAft(/|,b)= . гк(/ь/2) - I.
7.10a . /?|(3) = 0.027; /»;(3) = 0,076: /*,(3) = 0.217: />ДЗ) = 0.680.
7.13. a) P/2)=O.I34; б) P(X > I) = I - Po(2) = 0.9975;
в) Fo(2) = 0,0025.
7.14. p0=8/87. 01=46/87.02=10/87. 05=23/87 (для графа на рис. 7.11);
0о =IO/I7.0| = 4/17,02= 3/17 (для графа на рис. 7.12).
7.15. 0О = Q = 4/7; р\ = Ртк=3/7: А - в/7 (машин в час).
7.16. 0П=О.473. Р|=0,355, 02=0.133. 01=0.033, 04 = Ротк = 0.006;
Q = 0,994. А - 1,491 (машин в час); л=3. 7.17. 0О = Q -
= 0,455. 0| = Ртк= 0.545. А = 0.182 разг./мин.; номинальная
пропускная способность 4|(ОМ = 0.333 разг./мин. почти вдвое
больше. 7.18. При л = 2 0о=О.1О7, 02=0.550. Q = 1 -02=0.450.
4=1,8 заявки/ч. доход D = 7,20 лен. ед./ч; при л = 3 р'„ =
= 0,0677. />;= 0.371, (? = !- pj =0,629, А' = 2.52 заявки/ч.
доход D’ = 10.08 лен. ед./ч; увеличение числа каналов с л = 2
до л = 3 выгодно, так как увеличение дохода (О' - О = 2.88
ден. ед./ч) превосходит увеличение затрат (2 ден. ед./ч).
Глава 8
8.10. 2.а) х = 1,535; б) Л?е = 1; Мо = 0; в) ? = 3,378; л = 1.838;
v = 119.7(%); г) v j = х = 1.535; v 2 = 5.735; v 3 = 30.38;
v4« 201,605; р, = 0; р,= 3.378; р,= 11,2039; р4 =79.494113;
д) А = 1.80; £ = 3.97.
8.11. 2.а) х = 1653 (руб.); б) Ме = 1663 (руб.); Мо = 1665 (руб.).
в) ? = 445591; 5 = 667.5 (руб.); v = 40,4(%);
г) V, = х= 1653; v2 = 317800.
523
8.12. 2д) x =15.6(ц);б) Л?е = 15,4(н); Mo = 14,9 (ц); в) л2= 19Д$ = 4,36(и):
v = 27.9(%); г) V, =л =15.6; v, = 262.36; v, = 4685.76; v4 = 87874,12.
М, =0; ц,= ^ = 19.0; р, = 0.144; щ =898.0048.
8.13. ^=418,42; $>592.05; з; =113.43; < = 400.60; б’»17.82;
? = $> .
Глава 9
9.19. 1.а)/> = Ф (2,19) = 0.9715; б) 1599.9S .v„ < 1706.1 (руб.);
2) л'= 1329.
9.20. 1.а)Р= Ф (2.13) = 0.967; б) 1598.5 S 1707.5 (руб.);
г) л* = 1352.
9.21. 1.а) Р = Ф(1,39) = 0.835; б) 0,00412 < Pi 0.00748;
г) п' = 1605; 3) при \р (1 - р)|тач = 0,25 Рг Ф (0.65) = 0.484;
п' <. 1605.
9.22. 1.а) Р= Ф (1.35) = 0.823; б) 0.0408 i Pi 0.0752;
2) п‘ = 1658; 3) при |/Х I - p)Ux = 0.25
Рг Ф(0.63) = 0,471; п' i 165.
9.23. Р«Ф (0,71) = 0,522.
9.24. 1.а) Л = 0.058 (ед./ч); б) д’ = 0.060(сд./ч); 2) л=347 при по-
вторной выборке и п' = 268 при бесповторной выборке.
9.25. 0,8792 < к < 0.9208 при повторной выборке и 0.8803 i w i 0,9197
при бесповторной выборке.
9.26. От 27.68 до 32.32%; п = 13978; п < 16641 (при отсутствии данных).
9.27. а) п = 756; п' = 691; б) л = 484; л’ = 456.
9.28. 0.16 i р < 0,37. учитывая точную формулу для и нормаль-
ный закон распределения w: 0.14 < р < 0.36. учитывая при-
ближенную формулу для О|Г и нормальный закон н1.
9.29. 0.04 i pi 0.44 (используя рис. 9.3).
9.30. а) Р= 0.718; б) 15,71 i^i 16.37(%).
9.31. 22.9 < х(> s 37,1. учитывая, что /<>.<н,8 = 3.35.
9.32. 0,44 i а < 1,06, учитывая, что Xu.u3s.ii = 21.9; =-V2.
9.33. 0.53 iai 0.70, увпывая, что при аппроксимации х’-расирсцсления
нормальным получаем Хо.«а.« = 127.9; xi.^.w = 72,9.
9.34. а) Р = 0.347; б) 4.40 i xoi 5.60 (ч).
524
Глава 10
10.15. а) Влияние существенно, так как / = 2,82> /Оо5 = 1.96 (дву-
сторонний критерий); б) влияние существенно, так как
г=2.82> f0>q-|.64 (односторонний критерий).
10.16. Новая технология даст значимое уменьшение среднего рас-
хода сырья, так как / = 3.38> гОЛ2о = 1.72 (односторонний
критерий).
10.17. Утверждение в рекламе противоречит имеющимся данным,
так как t = 0,18< Iq^22 = 1.72 (односторонний критерий).
10.18. Значение л>= 48 является аномальным, гак как
t = 2.95 > г(|19 7 = 1.89 (односторонний критерий).
10.19. Существенных различий нет, так как:
а) / = 1.88 < /|195 = 1.96 (двусторонний критерий):
б) 1 = 1.88 < Го.д= 1.64 (односторонний критерий).
10.20. Различия существенны, так как у/ =8.12 > х* ,15, = 7.82 (од-
носторонний критерий).
10.21. Существенных различий нет. так как:
а) F = 1.15 < Л>,О5;Н;12 = 2.85 (односторонний критерий):
б) F — 1,15 < ^0,01:8:12 = 4.50 и F — 1,15 > ^i).99.s.i2 = 0,18, где
^)9чх р =—-— = —— = 0.18 (двусторонний критерий).
f-'^мл 5’67
10.22. Существенных различий нег, так как у/ = 1.54 < х',и, = 7.82
(односторонний критерий). Первый способ существенно
«лучшим* признать нельзя.
10.23. а) Отклонение неслучайно. так как t = 2.73 > /09 = 1.64 (од-
носторонний критерий); б) Р = 0.5 + 0,5Ф(|,09) = 0,862.
10.24. а) Отклонение можно считать случайным, гак как:
а) / = 1.19 < /<|9 |9 = 1,73 (односторонний критерий);
б) Р =0,5-0,50 (0.55; 19) = 0.29.
10.25. Инвестиционные вложения допустимы, так как:
а) х: = 58.5 <xi-i5 M =72,1 (односторонний критерий);
б) х‘ х58.5<х^л,.м = 79.8 (односторонний критерий); таб-
личные значения критерия у/' при к = 51 вычисляем с по-
мощью формулы (9.51).
10.26. Можно считать, так как t = 2.33 > /о ч = 1,64
(односторонний критерий).
10.27. а) Продукция нс должна быть забракована, так как / =
— 1.67 < /09$ = 1.96 (двусторонний критерий); б) продукция
должна быть забракована, так как / = 1.67 > /0 9 = 1.64 (одно-
сторонний критерий)
525
10.28. Гипотеза о нормальном распределении с параметрами
а = 1653, о ’ = 445591 нс отвергается, гак как:
а) х‘ = 2.37 < Холил = 5,99; 6) >. = 0,35 < А0(Н = 1.36.
10.29. Гипотеза о нормальном распределении с параметрами
а = 15,6. сг' = 19,0 не отвергается, гак как:
а) Х; = 1.48 < 4..Мо = 18.3; б) >. = 0,3 <X1lW = 1,36.
10.30. а) Гипотеза о нормальном распределении с параметрами
а = 16,04; <г =4,2384 отвергается, гак как
Х: = 76.4> = "М2; 6) нс отвергается, так как
>. = 0.95 <ЧЮ = 1.36.
10.31. Гипотеза о показательном распределении с параметром
а = 0,2 не отвергается, так как:
а) X" = Ь29< Xo(,<j = 5.99; б) >. = 0,47 < лои5 = 1.36.
10.32. Можно считал., так как: а) >/ = 0,35 < >.() 05 = 1,36;
б) х2 = 12.0 < Xo.os-,7 = 14,1 (если данные xh yt сгруппировать в
одни и те же К интервалов); в) |/1 - 0,98 < = 1.96.
10.33. Гипотеза о биномиальном законе распределения с парамет-
ром р - 0.88 не отвергается, гак как:
а) х2 = 2.71 <Хо.о$;| =3.84; б) л = 0,27 < /.о.в$ = 1,36.
10.34. Гипотеза о законе распределения Пуассона с параметром а = 0.9
не отвергается, так как: а) х* =9.27 <Хо.ом = 9.49;
6) а=0,88 < >^05 =1.36.
10.35. а) Партия не удовлетворяет гарантии, так как / = 2,95 > Го,д=
= 1.64; б) Р = 1 + 1ф(|,30)« ’ + ^ 0,8064 =
=0.903; в) п = (4>.9-л-1 + '(Мл-))2 ’ НО:/5О2 = 70 (найдено
подбором л).
Глава 11
11.3. Влияние типа технологии (фактора А) на урожайность зна-
чимо. так как F = = 9,35 < ;5 = 2,76.
11.4. Влияние линии (фактора А) на качество облицовочных пли-
ток незначимо, так как F = sf 5Z = 1.29 < = 2.87.
526
11,5. Влияние на урожайность: сорта пшеницы (фактора А) значи-
мо (так как F = xf sj = 5.90 > = 3.49): участков земли —
блоков (фактора В} незначимо (так как F - х; /.$; =
= 3,17 <л;О5Л12 = 3.26).
11.6. В рамках модели I (с фиксированными уровнями факторов)
влияние на производительность труда технологий (фактора А)
значимо (так как F = s';/х; = 27.6 > Л\1К. ,4 = 3,40); хозяйства
«|>актора В) — незначимо (так как F = х2/х‘ = 2.03 < /•’.„«, :4 =
= 3.01); взаимодействия факторов А и В — значимо (так как
F = =4.41 = 2.51).
Глаш1 12
12.14. *,=3.15; *,=3.75; *>=6.34. *< = 11.79; *,=15.75;
х* = 19.12 (тыс. руб.); у, = 1.82; у, =3.15; у> =5.02;
у4 = 5,78; у, = 7.0 (кВт *ч); б) г = 0.872; связь тесная и пря-
мая. г значим, так как f = 13.57 > 199553 = 2,00;
0.784 < г < 0.926 (с помощью е-преобразовання Фишера);
в) г|г< = 0.886 (значим, так как F = 41.2 > Л>.05.43' = 2.55);
г|и =0.893 (значим, так как F- 42,5 >/?),о$;5;Я = 2.40):
г) гипотеза о линейной корреляционной зависимости не отвер-
гается. ибо и;, близко к г так. что F= 2.10 < Fo^:v^ =
= 2.78 (или п;, близко к г так. что F = 2,47 < =
=2.55); д) у. = 0.2966* + 1,340; *,. = 2.5609.V - 0.944;
0.2528 < $0,3404; 2.1832 < Р„ <2.9386.
12.15. а) г = 0.969; связь очень тесная и прямая; г значим (так как / =
= 13,59 > А).95;12 = 2.18); 0,901 < г < 0,991 (с помощью .--преоб-
разования Фишера); б) yt=0,5435x + 7.04; х,.= |.7276у~8.94.
12.16. а) г = 0.917 (значим, так как / = 9.75 > /0.95.1s ~ 2.10):
б) х =21.25 (млн руб.); у = 27.5 (млн руб.).
12.17. а) ул=10х + 3838. х> = 0,08у - 303.8;
б) Ух-16.5 ~ 4003 (усл.ед.). Согласуется, так как гипотеза Ни‘.
р = 0,95 (с помощью .--преобразования Фишера) не отверга-
ется. ибо / = 1.08< /0 94=|.96.
12.18. *>.=—1600у + 7832.
12.19. а) г(| 2 = 0.908 (значим, гак как / = 13.0 > rO95 v,=2.02;
527
ry2 i = “0.907 (значим, так как |/| = 12.9 >/0Ч5= 2.02):
6) Я,.и = 0.908 (значим, так как Л= 79,8 > Fo.ofc2.34 = 3.28;
в) Я;12 =0.824.
12.20. р = 0,678 (не значим, гак как / = 2.06 < /995.5 = 2,57;
х = 0,524 (не значим, так как / = 1,65 < ^95 = 1.96.
12.21. И/= 0,922 (значим, так как у2 =74.7 >х».т.ч = 16.9).
Глава 13
13.8. а) ух = 0,2966л + 1,340; б) л.|0 = 4.306 (кВт-ч); 4.075 s
s 4,537 (кВт-ч), учитывая, что /о .45,58=2,00 и
.V, = 0.115(кВт-ч); в) R- = 0,760; г) уравнение регрессии
значимо, так как F-183,7 > fo,o5;i:5S =4.00.
13.9. а) у = 0,5435л + 7.04; б) /?2=0,939; в) уравнение регрессии
значимо, так как F = 184,7 > Л).о5:1:12 ~ 4.75;
г) 38,23 < ЛЛ.Ы|( У) < 41.06 (т/ч). учитывая, что r0.9S;i? =
=2.18; 5, м = 0,647 и 34,88 S < 44.4 (т/ч). учитывая,
что /о.95;|2= 2.18 и л\ = 2.183 (т/ч).
13.10. 1346 < 5 1519 (ден. ед.), учитывая, что го№28 =
=2,О5.а 5, п|м = 42,4 (ден. ед.); 995 S .>•’,1870 (ден. ед.),
учитывая. ЧТО /о.95;28 = н 5Л\ -1М»= 2|3-4 (Дсн- сл
13.11. а) ух = - 50.02 + 10.309л - 0.4237л2; б) Rvx= 0,990;
Я', =0.980: в) у* = 12.7% при х = 12,2 (т).
13.12. 6) уг= 8.465 - 0.5250л. г = 1.633; ух = -0.048+32.6200/л,
г = 1.660; в) и., =0.642 (значим, так как F = 7,92> Го.нм.45 =
=2.59; г= Я>т=~0,619 (значим, так как
|/| = 5.46 >/llQ5 4M = 2.01. (регрессия линейная): Ryx = 0,631
(значим, так как F= 38.4>Г(».о5;|.58=4.04) (регрессия гипербо-
лическая).
13.13. а) г. =-0,851 (значим, гак как kl = 7.77 = 2.07);
г = 0.808 (значим, так как / = 6.58 > = 2,07);
г1: = -0.519 (значим, так как И = 2.91 =2,07);
г, . =-0,857 (значим, так как |/| = 6.89 ,4 =2,06);
528
r;i =-0,815 (значим, так как |/| = 0,815 >/„.*,< =2,06);
/?,1 j = 0.953 (значим, так как F = 109 > ~ 3,44).
б)ул = 210.66 - 1.0238х| + 8.756^2; уравнение регрессии зна-
чимо но F-критерию; коэффициенты 6| и Ь2 значимы по
/-критерию; в) стандартизованные коэффициенты регрессии
= 0,5904. Ь\ =0,5011; коэффициенты эластичности
Е,=-0.185; 4 = 0.150.
13.14. а) уд = 5.62 - О.239х| + О.774х2; б) R = 0.981; в) R- =0,962;
в) уравнение регрессии значимо, так как F = 36,3 >
> = 9.55; г) прн Х|=5.5, х2=6.О ут=8,95(%).
Глава 14
14.8. у, = 16,66 (ц/га); s, = 3.62 (ц/га); г, = 0.035; = -0.339.
14.9. у, = 14,89 + 0.322/. Уравнение тренда незначимо, так как
F=0,56< F0.05:i;8e5,32.
14.10. При/w=3:
/ 1 > 3 4 5 6 7 8 9 10
Л — 17,87 15,00 13,37 13,10 17,17 16,87 17.67 17,93 —
При т=5:
/ 1 2 3 4 5 6 7 8 9 10
Л — — 15.32 15.32 15.26 14.72 16.92 18,00 — —
14.11. у, = 1094.1 + 62.19г, уравнение тренда значимо, так как
F = 32.3 > Foto5iJ;6= 5.99; б) автокорреляция возмушений ря-
да незначимо; в) точечный прогноз у, = 1654 (ден. ед.); с на-
дежностью 0,95 интервальный прогноз: среднего значения
доходов — от 1516 до 1792 (ден. ед.); индивидуального зна-
чения доходов — от 1432 до 1876 (ден. ед.).
Приложения
Математико-статистические таблицы
Значения функции Гаусса до-
Целые
н ле- Сотые доли Л-
сятые
дали Л 0 1 1 | 2 | "1“] 5 | 6 1 ’ 1 S 1 9
0.0 0.39X9 0.39X9 0.39X9 0.3988 0.39S6 0.3984 0,39X2 0.39X0 0.3977 0.3973
0.1 3970 3965 3961 3956 3951 3945 3939 3932 3925 3918
0.2 3910 3902 3894 3885 3876 3867 3857 3847 3836 3825
0.3 3814 3802 3790 3778 3765 3752 3739 3726 3712 3697
0.4 36X3 3668 3653 3637 3621 3605 3589 3572 3555 3538
0.5 3521 3503 3485 3467 3448 3429 3410 3391 3372 3352
0.6 3332 3312 3292 3271 3251 3230 3209 3187 3166 3144
0.7 3123 3101 3079 3056 3034 ЗОН 2989 2966 2943 2920
0.8 2897 2874 2850 2827 2803 2780 2756 2732 2709 2685
0.9 2661 263" 2613 25X9 2565 2541 2516 2492 246Х 2444
1.0 0.2420 0.2396 0.2371 0.2347 0.2323 0.2299 0.2275 0.2251 0.2227 0.2203
1.1 2179 2155 2131 2107 2083 2059 2036 2012 1989 1965
1.2 1942 1919 1895 1872 1849 1826 1804 1781 1758 1736
1.3 1714 1691 1669 1647 1626 1604 1582 1561 1539 1518
1.4 1497 1476 1456 1435 1415 1394 1374 1354 1334 1315
1.5 1295 1276 1257 1238 1219 1200 1182 1163 1145 1127
1.6 1109 1092 1074 1057 1040 1023 1006 0989 0973 0957
1.7 («40 0925 0909 0893 О87Х 0863 0848 0833 0X18 0804
1.8 0790 0775 0761 0748 0734 0721 0707 0694 0681 0669
1.9 0656 0644 0632 0620 0608 0596 0584 0573 0562 0551
2.0 0.0540 0.0529 0.0519 0.0508 0.0498 0.04X8 О.О47К 0.0468 0.0459 0.0449
2.1 0440 0431 0422 0413 0404 0396 0387 0379 0371 0363
2.2 0355 0347 0339 0332 0325 0317 0310 0303 0297 0290
2.3 0283 0277 0270 0264 0258 0252 0246 0241 0235 0229
2.4 0224 0219 0213 0208 0203 0198 0194 0189 0184 01X0
2.5 0175 0171 0167 0163 0158 0154 0151 0147 0143 0139
2.6 0136 0132 0129 0126 0122 0119 0116 0113 оно 0107
530
(htutivauue mafia I
X 1 0 1 I 1 2 1 3 1 4 | 5 I 6 7 | 8 1 9
2.7 0104 0101 0099 0096 0093 0091 18)88 0086 (8)84 0081
2.X 0079 <M>77 0075 0073 (Ю7| 0069 (8)67 0065 (8)63 0061
2.9 0060 0058 0056 0055 (8153 (8151 1Ю50 (MM8 0047 0046
3.0 0.0044 0,0043 0.0042 0.0041 0,0039 0.0038 0,18)37 0.0036 0.0035 0.0034
3.1 0033 0032 0031 0030 0029 0028 (8)27 (8)26 0025 0025
3.2 0024 0023 0022 0022 0021 0020 0020 0019 0018 (8)18
3.3 0017 0017 0016 0016 0015 0015 <8)14 0014 0013 0013
3.4 0012 0012 0012 OOH OOH 0010 0010 0010 <88)9 0(8)9
3.5 0009 0008 0008 0008 0008 0007 0007 ООО? 0007 0006
3.6 0006 0006 0006 0(815 0005 0005 0005 0005 0005 0004
3.7 0004 <MX>4 0004 (8X14 0004 (8)04 0003 0003 <8)03 0003
3.8 0003 0003 0003 0003 0003 (88)2 0002 0002 0(8)2 0(8)2
3.9 0002 IM K> 2 0002 0002 (8Ю2 (88)2 (8)02 0002 0001 ООО!
4.0 4.5 0.0001 0.0001 0.0000160 0.0000015 0,0001 0.0(8) 1 0.0001 0.(8811 0.0001 0.0001 0.0001 0.(88)!
Таблицн II
Значения функции Лапласа
Фл)
_-г -х о| X ►
Целые Сотые дали x
и
КС»- тые (1 1 2 3 4 S 6 7 8 9
□СМИ 1
0.0 0,0000 0.0080 0.0160 U.O239 0.0319 0.0399 U.(M?8 O.O5S8 0.0638 0.0717
0.1 0.079? 0.0876 0.0955 0.1034 0,1113 0.1192 0.12П 0.1350 0.1428 0.1507
0.2 0.1585 0,1663 O.I74I 0.1819 0.1897 0.1974 0,2051 0,21» 0,2205 0.228?
<1.3 0.2358 (1.2434 0,2510 0.25X6 0.2661 0.2737 0.2812 0,2886 0,2960 O.3O3S
0.4 031 ох 0.3182 O.325S 0,332.x 0.3401 0.3473 0,3545 13.3616 0.3688 0.3759
0.5 0,3829 0.3899 0.3969 0.4039 0.4108 0.4177 0.4245 0.4313 0.4381 0.4448
0.0 0.4515 0,4581 0.4647 0.4713 0.4778 (I.4S43 0.4907 0.4971 0.5035 0.5098
о.? 0.5161 и.522.1 0.5285 0.5346 0.5407 0.5467 0,5527 0.5587 0,5646 0.5705
0.8 0.5763 (1.5821 O.S878 0.5935 0.5991 O.MM7 0,6102 0.6157 0.6211 0,6265
0.9 0.6319 0.6372 0,6424 0,6476 0.6528 0.6579 0,6629 0.6679 0.6729 0.6778
1.0 0.6827 0.6875 0,6923 0.6970 0.7017 0.7063 0,7109 0.7154 0.7199 0.724.1
1.1 0.7287 0.7330 0.7373 0.7415 0,7457 0,7499 0.7540 0,7580 0,7620 0.7660
1.2 0.7699 11.7737 0.7775 O.7SI3 0.7850 0.7887 0.7923 0.7959 0.7'184 О.8О2Ч
13 О.НОМ 0.8098 O.K 132 0.8165 U.XI98 0.8230 0.8262 0.8293 0,8324 О.Х355
1.4 0.8.185 0.8415 0.8444 0.8473 0.8501 0.8529 0.8557 O.S5X4 0.Х6П 0.8638
13 0.К6Ы 0.8690 0,8715 0.8740 0,8764 0.878*1 0,8812 0.8836 0.8859 0.8882
1.6 O.S9O4 0.8926 0.8948 0,8969 0.8990 0.9011 0.9031 0.9051 0.9070 0.4090
1.7 0,9109 0.912? 11,9146 0,9164 0,9181 11,9193 n.9216 0.9233 0.9249 0.9265
1.8 0.9281 0.9297 0.9312 0.9327 0.9342 0.9357 0.9371 <1.93X5 П.9.192 0.9412
1.9 0.9426 0.94 39 0,9451 0.9464 0.9476 0.94X8 0.95*30 0.9512 0.9523 0.9533
2.0 0.9545 11.9556 0.9566 0,9576 0.9586 0.9596 0.9606 0.9616 0,9625 0.9634
2.1 0.9643 0.9651 0.9660 0.9668 0.9676 0.9684 0.W2 0.9700 0,9707 0.9715
2.2 0.9722 0.97*7 0.9736 0,9743 0,974'1 11.9756 0.9762 П.976Х 0.9774 0.978(1
2,3 0.9786 0.9791 0.9797 0.9X02 0.980? 0.9X12 0.9817 0.9822 0.9827 0.9832
2.4 0.9836 0.9841 0.9845 0.9849 0.9853 0.9X57 0.9861 0.9865 0.9869 0.9872
23 0.9876 0.9879 0.98X3 0.98X6 0.98X9 0.989» 0.9X95 0.9898 0.9901 0,9904
2.6 II.WJ7 0.9910 0.9912 0,9915 0.9917 0,9920 0,9922 0,9*124 0.9926 0.9928
2.7 0.9331 0.9933 0,9935 0,9937 0.9939 0.9940 0.9942 0,9944 0.9946 0.9947
2.8 0.9949 0.9951 0.9952 0.9953 0.9*155 0,9956 11.9958 0.9959 0.9960 0,9961
2.9 0.9963 0.9964 0,9965 0,9966 0,9967 0,9968 0.9969 0.9970 0.9971 0.9972
.1.0 0.9973 0.9974 0.9975 0.9976 0.9976 0,9977 0.9978 0.9*179 0,9979 0,998(3
3.1 0.9981 (1.9981 0.9982 0,9983 0.9983 0.9984 <1.9984 0.9985 0.9985 0,9*186
1.2 0.9*386 (1.9987 O.99S7 O.998S 0.9988 0,9989 0,9989 0.99X9 0.9990 0,9990
3,3 0.9990 0.9991 0.99*31 0.999) 0.9992 11.99*12 0.9992 O.*3992 0.9993 0.9993
5.4 0.9993 0.9994 0.9991 0,9994 0.9994 0,9994 0.9W5 0.9995 0.9995 0,9995
.3.5 0.9995 0.9996 0.9996 0,9996 0.9996 0.9996 0.9*296 0.9*29(1 0.9997 0,9997
3.6 0.9997 0.9997 0.9997 0.9997 0.9997 0,9997 0.9997 0.9*398 0.9'198 0,9998
3.7 0.9998 0.9998 0.9998 ».WS 0.9998 0.99*18 0.999X 0.9998 0,9998 0,9998
3.8 0.9999 0.9999 0.9999 0.9999 0,9999 0,9999 0.9999 0,99'39 0.99*19 0.9999
1.9 0.9999 0.9999 0.9*799 0,999*1 0.9999 0.9999 0.9999 0.9999 (1.9999 0.9*199
4.0 0.9999 0.9999 0.9999 0.999*1 0.9994 0.9999 0.9*199 0.9999 0.9999 0.9999
532
е 0.3679 •>.3679 <1.1 НУ» 0.0613
о Ш!
е> О © с
х.
Е ЗЯ 23
с о с с
Е ? д 2 г
о о* © с
*< с
V — 7. -! £ с
Е 1 ’© С © = О
- 1 -
п •г* < Й Я S
л — ® а с
© е © с
4?
« X •т
8 е © © е
Q
*Й Й й
Е С ?s:S8 © с = е
X
S г» e-.r-.-j —
S • “£ = 8
X ©©г©’
>.
« х 5х 1х 5 i в г
X с — = с
«V
Я
=
Г) /5 о — *• *•
Oil
о о о с
= si*
е е е е
В§§1
© О © е‘
Hit
ее 88
е © © с
liii
е‘о ее
liii
© = 9 ©
illl
©see
1555
= с о с
ж ж к £
§№
©“ООО
о о — г*, ч© о зе — — •© — — §isss §н = 2* 0.1137 0.0948 0,0729 0.0521 0.0347 0.0217 0.012S 0.0071 0.0037 0.0019 0,0009 0.0004 0.0002 0,0001 0.0000
= © © © © © © © © © ©
© itiO’O Ml 0*0 мооо 1100*0 1(ММ»<) 0.0607 0.0911 0,1171 0.I3IS O.IJIX 0.11X6 ШЦ tliii ii.ii.I 9 О* 9* О 9* О* С* О* О С © С © — ©
ж 0.0003 0.0027 0.0107 0.02X6 O.OS72 ©' ©' © © © © giOiiiiiiilili © 9 © ©* О ©999= = 9 9 =" О
г—“ ^2;i5x 5 5 с © Ь ©©ее© 0140'0 Н0Г0 rofi'o (K.tl'o 06УГО 4441'0 = 8.Ю.1 11 ill
© 8 з 11 i ©©©©© 9 9 9 5 9 9* siti.i ii.i.ti Hitt = О 9 О ©' 0 0 0 9©* 000©©
«41*0 ЮУ 1*0 гшо'о 4££0*0 4900'0 0.1755 0.1462 0,1045 0.0653 0.0363 0.0IRI §§ш iiiii iiiti о о е* о о* с* о* о о о* ©'©©ее'
о т 2 2:5* 7.7. ©' ©‘ ©‘ ©‘ © <n /М 6Г. 00 гч 3 7?.=: 3 — — о с?в о о е о э с? о с liOlitti.iill.ii. 0 0 0 0 9* о о о о о о* О* О О О
с г*. 0.049Я 0.14*1 0.2240 0.224U 0.16X1 хооо’о 4£00'0 180(1'11 9140'0 ИКО'О 81ЮГС1 iiiliiiiitiiil! о о о => о о* о* о о о © е © © о
<< ,0361 ,0120 .0034 ,0009 ,0002 ,0000 ШИШИ islli
а с е © © с э = - = с О О С © = ©009» ©»»©»
** Z / Е © — r< m -г © г- ж у — II 12 13 14 |5 16 17 IX 19 20 21 22 23 24 25
533
Tu6.iinui IV
Значения -критерия Стыодента
Число степе- ней свобо- ды А Вероятность у
0.1 0.2 0.3 0.4 0.5 0.6 0.7 О.Х 0.9 0.95 0.98 0.99
1 0.16 0.32 0.51 0.73 1.00 1.38 1.96 3.08 6.31 12.71 31.82 63.66
2 14 29 44 62 0.82 06 34 1.89 2.92 4.30 6.96 9.92
3 14 28 42 58 76 0.98 25 64 35 3.18 4.54 5.84
4 13 27 41 57 74 94 19 S3 13 2.78 3,75 4.60
5 13 27 41 56 73 92 16 48 01 57 36 03
6 0.13 0.26 0.40 0.55 1.72 1.91 1.13 1.44 1.94 2.45 3.14 3.7|
7 13 26 40 55 71 90 12 41 89 36 00 50
X 13 26 40 55 70 89 11 40 Кб 31 2.90 35
9 13 26 40 54 70 88 10 38 КЗ 26 82 25
10 13 26 40 54 70 88 09 37 XI 23 76 17
II 0.13 0.26 0.40 0.54 0.70 0.88 1.09 1.36 1.80 2.20 2.72 3.11
12 13 26 39 54 69 87 08 36 7Х 18 (►8 05
13 13 26 39 54 69 87 08 35 77 16 65 01
14 13 26 39 54 69 87 08 34 76 14 62 2.98
15 13 26 39 Я 69 S7 07 34 75 13 60 95
16 0.13 0.26 0.39 0.53 0.69 0.86 1.07 1.34 1.75 2.12 2.58 2.92
17 13 26 39 53 69 86 07 33 74 II 57 90
IX 13 26 39 53 69 86 07 33 73 Ю 55 88
19 13 26 39 53 69 86 07 33 73 09 54 86
20 13 26 39 53 69 86 06 32 72 09 53 84
21 0.13 0.26 0.39 0.53 0.69 0.86 1.06 1.32 1.72 2.08 2.52 2.83
22 13 26 39 53 69 86 06 32 72 07 51 82
23 13 26 39 53 6Х 86 06 32 71 07 50 81
24 13 26 39 53 6Х 86 06 32 71 06 49 80
25 13 26 39 53 6S 86 06 32 71 0(1 48 79
26 0.13 0.26 0.39 0,53 0.6Х 0.86 1.06 1.31 1.71 2.06 2.48 2.78
27 13 26 39 53 68 85 06 31 70 05 47 77
28 13 26 39 53 68 85 06 31 70 05 47 76
29 13 26 39 53 68 85 05 31 70 04 46 76
30 13 26 39 53 68 85 05 31 70 04 46 75
40 0.13 0.25 0.39 0.53 0.68 0.85 1.05 1.30 1.6S 2,02 2.42 2.70
60 13 25 39 53 68 85 05 30 67 00 39 66
120 0.13 0.25 0.39 0.53 0.68 0,84 1.04 1.29 1.66 1.98 2.36 2.62
X 13 25 зх 52 67 84 04 28 64 % 33 58
534
Тнб.пщл V
Значения у.;, - критерия Пирсона
Число степе- ней спобо- ли к Верой и «ост 1. а
0.99 0.98 0.95 0,90 0.80 0.70 0.50 0,30 0.20 0.10 0.05 0.02 0.01
1 0,00 0.00 0.00 0.02 0.06 0.15 0.45 1.07 1.64 2.71 3.84 5.41 6.64
2 0.02 0.04 0.10 0.21 0.45 0.71 1.39 2.41 3.22 4.60 5.99 7.82 9.21
3 0.11 0.18 0.35 0.58 им» 1.42 2.37 3,66 4.64 6,25 7.82 9.84 11.3
4 0.30 0.43 0.71 1.06 1.65 2.20 3.36 4.88 5.99 7.78 9.49 Н.7 13.3
5 0.55 0.75 1.14 1.61 2.34 3.00 4.35 6.06 7.29 9.24 II.1 13.4 15.1
6 0.S7 1.13 1.63 2.20 3.07 3.83 5.35 7.23 8.56 10,6 12.6 15.0 16.8
7 1.24 1.56 2.17 2.83 3.82 4.67 6.35 8.38 9.80 12.0 14.1 16.6 18.5
8 1.65 2.03 2.73 3.49 4.59 5.53 7.34 9.52 11.0 13.4 15.5 18.2 20.1
9 2.09 2.53 3.32 4.17 5.38 6.39 8.34 10.7 12.2 14.7 16.9 19.7 21.7
10 2.56 3.06 3.9-1 4.86 6.18 7.27 9.34 11.8 13.4 16,0 18.3 21.2 23.2
II 3.05 3.61 4.58 5.58 6.99 8,15 10.3 12.9 14.6 17.3 19.7 22.6 24.7
12 3.57 4.18 5.23 6.30 7.81 9.03 п.з 14.0 15.8 18.5 21.0 24.1 26.2
13 4.11 4.76 5.89 7.04 8.63 9.93 12.3 15.1 17.0 19.8 22.4 25.5 27.7
14 4.6Zi 5.37 6.57 7.79 9.47 Ю.8 13.3 16.2 18.1 21.1 23.7 26.9 29.1
15 5.23 5.98 7,26 8.55 10.3 11.7 14.3 17.3 19.3 22.3 25.0 28,3 30.6
16 5.81 6.61 7.96 9.31 11,1 12.6 15.3 18.4 20.5 23.5 26.3 29.6 32.0
17 6.41 7.26 8.67 10.1 12.0 13.5 16.3 19.5 21.6 24.8 27.6 31.0 33.4
18 7.02 7.91 9.39 10.9 12.9 14.4 17.3 20.6 22.8 26.0 28.9 32.3 34.8
19 7.63 8.57 10.1 11.6 13.7 15.3 18.3 21.7 23.9 27.2 30.1 33.7 36.2
20 К.26 9.24 10.8 12.4 14.6 16.3 19.3 22.8 25.0 28.4 31.4 35.0 37.6
21 8.90 9.92 И.6 13.2 15.4 17.2 20.3 23.9 26.2 29.6 32.7 36.3 38.9
22 9.54 10.6 12.3 14.0 16,3 18.1 21.3 24,9 27.3 30.8 33.9 37.7 40.3
23 10.2 н.з 13.1 I4.X 17.2 19.0 22.3 26.0 28.4 32.0 35.2 39.0 41.6
24 10,9 12.0 13.8 15.7 18.1 19.9 23.3 27.1 29.6 33.2 36.4 40.3 43.0
25 11.5 12.7 14.6 16.5 18.9 20.9 24.3 28.2 30.7 34.4 37.7 41.7 44.3
26 12.2 13.4 15,4 17.3 19.8 21.8 25.3 29.2 31.8 35.6 38.9 42.9 45.6
27 12.9 14.1 16.1 18.1 20.7 22.7 26.3 30.3 32.9 36,7 40.1 44,1 47,0
28 13,6 14.8 16,9 18.9 21,6 23.6 27.3 31.4 34.0 37.9 41.3 45.4 48.3
29 14.3 15.6 17.7 19.8 22.5 24.6 28.3 32.5 35.1 39.1 42.6 46.7 49.6
50 14.9 16.3 18.5 20.6 23.4 25.5 29.3 33.5 36.2 40.3 43.8 48,0 50,9
535
i'tlft.INlUi VI
Значения л„ 4 ь -критерия Фишера—Сиедекора
и-0.05
1 2 3 4 5 6 7 8 9 10 12 15 20 24 30 40 60 120 СП
। 161 200 216 225 230 234 237 239 240 242 244 246 248 249 250 251 252 253 254
2 18.5 19.0 19.2 19.2 19.3 19.3 19.3 19,4 19.4 19.4 19.4 19.4 19.4 19.4 19.5 19.5 19.5 19.5 19.5
3 10.1 9.55 9.28 9.12 9.01 8.94 8.89 8.85 8.81 8.79 8.74 8,70 8.66 8.64 8.62 8.59 8.57 8.55 8.53
4 7.71 6.94 6.59 6.39 6.26 6.16 6.09 6,04 6.00 5,96 5.91 5,86 5.80 5.77 5.75 5.72 5.69 5.66 5.63
5 6,61 5.79 5.41 5.19 5.05 4.95 4,88 4.82 4.77 4.74 4.68 4.62 4.56 4.53 4.50 4.46 4.43 4.40 4,36
6 5.99 5.14 4.76 4,53 4.39 4.28 4.21 4.15 4.10 4.06 4.00 3.94 3.87 3,84 3.81 3.77 3.74 3,70 3,67
7 5.59 4,74 4.35 4.12 3.97 3.87 3.79 3.73 3.68 3.64 3,57 3.51 3,44 3.41 3.38 3.34 3.30 3.27 3.23
8 5.32 4.46 4.07 3.84 3.69 3.58 3.50 3.44 3.39 3.35 3,28 3.22 3.15 3.12 3.08 3.04 3.01 2.97 2.93
9 5.12 4.26 3.86 3.63 3.48 3.37 3.29 3.23 3.18 3.14 3.07 3.01 2.94 2.90 2.86 2,83 2.79 2.75 2.71
10 4.96 4.10 3.71 3.48 3.33 3.22 3.14 3,07 3.02 2.98 2.91 2.85 2.77 2.74 2.70 2.66 2.62 2.58 2.54
II 4.84 3.98 3,59 3.36 3.20 3,09 3.01 2.95 2.90 2.85 2.79 2.72 2.65 2.61 2.57 2.53 2.49 2.45 2.40
12 4,75 3.89 3,49 3.26 3.11 3.00 2.91 2,85 2.80 2.75 2.69 2.62 2.54 2.51 2.47 2.43 2,38 2.34 2.30
13 4,67 3.81 3.41 3.18 3.03 2.92 2.83 2.77 2.71 2.67 2.60 2.53 2.46 2.42 2.38 2.34 2.30 2.25 2.21
14 4.60 3.74 3.34 3.11 2.96 2,85 2.76 2.70 2.65 2.60 2.53 2.46 2.39 2,35 2.31 2.27 2.22 2.18 2.13
15 4,54 3.68 3.29 3.06 2.90 2.79 2.71 2.64 2.59 2.54 2.48 2.40 2.33 2.29 2.25 2.20 2.16 2.11 2.07
16 4.49 3.63 3.24 3,01 2.85 2.74 2.66 2.59 2.54 2.49 2.42 2,35 2.28 2.24 2.19 2.15 2.11 2.06 2.01
17 4.45 3.59 3.20 2.96 2.81 2.70 2.61 2.55 2.49 2.45 2.38 2.31 2.23 2.19 2.15 2,10 2.06 2.01 1.96
18 4.41 3.55 3,16 2.93 2.77 2,66 2.58 2.51 2.46 2.41 2.34 2.27 2.19 2.15 2.11 2.06 2.02 1.97 1.92
19 4.38 3.52 3,13 2,90 2.74 2.63 2.54 2.48 2.42 2,38 2.31 2.23 2.16 2.11 2.07 2.03 1.98 1.93 I.8S
20 4.35 3.49 3.10 2.87 2.71 2.60 2.51 2.45 2.39 2.35 2.28 2.20 2.12 2.08 2.04 1.99 1.95 1.90 1.84
Продолжение табл. 17
V 1 2 3 4 5 6 7 К 9 10 12 15 20 24 30 40 60 120 л:
21 4.32 3.47 3.07 2.84 2.6Х 2.57 2.49 2.42 2.37 2.32 2.25 2.IX 2.10 2.05 2.01 1.96 1.92 1.87 1.81
22 4.30 3.44 3.05 2.82 2.66 2.55 2.46 2.40 2.34 2,30 2.23 2.15 2.07 2.03 1.98 1.94 1.89 1.84 1.78
23 4.28 3.42 3.03 2.80 2.64 2.53 2.44 2.37 2.32 2.27 2.20 2.13 2.05 2.UI 1.96 1.91 1.86 1.81 1.76
24 4.26 3.40 3.01 2,78 2.62 2.51 2.42 2.36 2.30 2,25 2.18 2.11 2.03 1.98 1.94 1.89 1.84 1.79 1.73
25 4.24 3.39 2.9*) 2.76 2.60 4,49 2.40 2.34 2.28 2.24 2.16 2.09 2.01 1.96 1.92 1,87 1.82 1.77 1.71
26 4.23 3.37 2.98 2.74 2.59 2.47 2.39 2.32 2.27 2.22 2.15 2.07 1.99 1.95 1.90 1.85 1.80 1.75 1.69
27 4.21 3.35 2.96 2.73 2,57 2.46 2.37 2.31 2,25 2.20 2.13 2.06 1.97 1.93 1.88 1.84 1.79 1.73 1.67
28 4.20 3.34 2.95 2.71 2.56 2.45 2.36 2.29 2.24 2.19 2.12 2.04 1.96 1.91 1.87 1.82 1.77 1.71 1.65
29 4.18 3.33 2.93 2.70 2.55 2.43 2.35 2.28 2.22 2.18 2.10 2.03 1.94 1.90 1.85 1.81 1.75 1.70 1.64
30 4.17 3.32 2.92 2.69 2.53 2.42 2.33 2.27 2.21 2.16 2.09 2.01 1.93 1.89 1.84 1.79 1.74 1.68 1.62
40 4.08 3.23 2.84 2.61 2.45 2.34 2.25 2.18 2.12 2.08 2.00 1.92 1.84 1.79 1.74 1.69 1.64 1.58 1.51
60 4.00 3.15 2.76 2.53 2.37 2.25 2.17 2.10 2.04 1,99 1.92 1.84 1.75 1.70 1,65 1.59 1.53 1.47 1.39
120 3.92 3.07 2.68 2.45 2.29 2.17 2.09 2.02 1,96 1.91 1.83 1.75 0.66 1.61 1.55 1.50 1.43 1.35 1.25
X 3.84 3.00 3.60 2.37 2.21 2.10 2.01 1.94 1.83 1.83 1.75 1.67 1.57 1.52 1.46 1.39 1.32 1.22 1.00
а-0.01
1 4052 4999,5 5403 5625 5764 5859 5928 5982 6022 6056 6Ю6 6157 6209 6235 6261 6287 6313 6339 6366
2 98.50 99.00 99,17 99.25 99.30 99.33 99.36 99.37 99.39 99.40 99.42 99.43 99.45 99.46 99.47 99.47 99.48 99.49 99.50
3 34.12 30.82 29.46 28.71 28.24 27.91 27.67 27,49 27.35 27.23 27.05 26.87 26.69 26.60 26.50 26.41 26.32 26.22 26.13
4 21.20 18.00 16.69 15.98 15.52 15.21 14.98 14.80 14.66 14.55 14,37 14.20 14.02 13.93 13.84 13.75 13.65 13.56 13.46
5 16.26 13.27 12,06 11.39 10.97 10.67 10.46 10.29 10.16 10.05 9.89 9.72 9.55 9.47 9.38 9.29 9.20 9.11 9.02
6 13,75 10.92 9.78 9.15 8.75 8,47 8.26 8,10 7.98 7.87 7.72 7.56 7.40 7.31 7.23 7.14 7.06 6.97 6,88
7 12,25 9.55 8.45 7,85 7.46 7.19 6.99 6.84 6.72 6.62 6.47 6.31 6.16 6.07 5.99 5.91 5.82 5.74 5.65
8 11.26 8.65 7.59 7.01 6,63 6.37 6.18 6.03 5.91 5.81 5.67 5.52 5.36 5.28 5.20 5.12 5.03 4.95 4.86
9 10.56 8.02 6.99 6.42 6.06 5.80 5.61 5.47 5.35 5.26 5.11 4.96 4.81 4.73 4.65 4.57 4,48 4.40 4.31
10 10.04 7.56 6.55 5.99 5.64 5.39 5.20 5.06 4.94 4.85 4.71 4.56 4.41 4.33 4.25 4.17 4.08 4.00 3.91
II 9.65 7.21 6.22 5.67 5.32 5.07 4.89 4.74 4.63 4.54 4,40 4.25 4.10 4.02 3.94 3.86 3.78 3.69 3.60
12 9.33 6.93 5.95 5.41 5.06 4.82 4.64 4.50 4.39 4.30 4.16 4,01 3.86 3.78 3.70 3.62 3.54 3.45 3.36
13 9.07 6.70 5.74 5.21 4.86 4.62 4.44 4.30 4.19 4.10 3.96 3.82 3.66 3.59 3.51 3,43 3.34 3.25 3.17
14 8.86 6.51 5.56 5.04 4.69 4,46 4.28 4.14 4.03 3.94 3.80 3,66 ^51 3.43 3.35 3.27 3,18 3.09 3.00
Окончание ma&i. V!
\*| 1 2 3 4 5 6 7 8 9 10 12 15 20 24 30 40 60 120 Ж
15 8.68 6.36 5.42 4.89 4.56 4.32 4.14 4.00 1.89 3.80 3.67 3.52 3.37 3.29 3.21 3.13 3.05 2.96 2,87
16 8.53 6.23 5 .-29 4.77 4.44 4.20 4.03 3.89 3.78 3.69 3.55 3.41 3.26 3.18 3.10 3.02 2.93 2.84 2.75
17 8.40 6. II 5.18 4.67 4..Ч 4.10 3.93 3.79 3,68 3.59 3.46 3.31 3.16 3.08 3.00 2.92 2.83 2.75 2.65
18 8.29 6.01 5.09 4.58 4.25 4.01 3.84 3.71 3.60 3.51 3.37 3.23 3.08 3.00 2.92 2.84 2.75 2.66 2.57
14 8.18 5.93 5.01 4.50 4.17 3.94 3.77 3.63 3.52 3.43 з.зо 3.15 3.00 2.92 2.84 2.76 2.67 2.58 2.49
20 8.10 5.85 4.94 4.43 4.10 З.Х7 3.70 3.56 3.46 3.37 3.2.3 3.09 2.94 2,86 2.78 2.69 2.61 2.52 2.42
21 8.02 5.78 4.87 4.37 4.0-1 3.81 3.64 3.51 3.40 3.3| 3.17 3.03 2.88 2.80 2.72 2.64 2.55 2,46 2.36
22 7.95 5.72 4.82 4.31 3.99 3.76 3.59 3.45 3.35 3.26 3.12 2.98 2.83 2.75 2.67 2.58 2.50 2.40 2.31
23 7.88 5.66 4.76 4.26 3.94 3.71 3.54 3.41 3.30 3.21 3.07 2.93 2.78 2.70 2.62 2.54 2.45 2,35 2.26
24 7.Х2 5.61 4.72 4.22 3.90 3.67 3.50 3.36 3.26 3.17 3.03 2.89 2.74 2.66 2.58 2.49 2.40 2.31 2.21
25 7.77 5.57 4.68 4.18 3.85 3.63 3.46 3.32 3.22 3.13 2.99 2.85 2.70 2.62 2.54 2.45 2.36 2.27 2.17
26 7.72 5.53 4 .(>4 4.14 3.82 3.59 3.42 3.29 3,18 3.0») 2.96 2.81 2.66 2.58 2.50 2.42 2.33 2.23 2.13
27 7.68 5.49 4.60 4.11 3.78 3.56 3.39 3.26 3.15 3.06 2.93 2.78 2.63 2.55 2.47 2.38 2.29 2.20 2.10
28 7.64 5.45 4.57 4.07 3.75 3.53 3.36 3.23 3.12 3.03 2.90 2.75 2.60 2.52 2.44 2.35 2.26 2.17 2,06
29 7.60 5.42 4.54 4.04 3.73 3.50 3.33 3.20 3.09 3.00 2,87 2.73 2.57 2.49 2.41 2.33 2.23 2.14 2,03
30 7.56 5.39 4.51 4.02 3.70 3.47 3.30 3.17 3.07 2.98 2.84 2.70 2.55 2.47 2.39 2.30 2.21 2.11 2.0|
40 7.31 5.18 4.31 3.83 3.51 3.29 3.12 2.99 2.89 2.Х0 2.66 2,52 2.37 2.29 2.20 2.11 2.02 1.92 1.80
ьо 7.08 4,98 4.13 3.65 3.34 3.12 2.95 2.82 2.72 2.63 2.50 2.35 2.20 2.12 2.03 1.94 1.84 1.73 1.60
120 6.85 4.79 3.95 3.48 3.17 2.96 2.79 2.6/1 2.56 2.47 2.34 2.19 2.03 1 95 1.86 1,76 1,66 1.53 1.18
X 6.63 4.61 3.78 3.32 3.02 2.80 2,64 2.51 2.41 2.32 2.18 2.04 1.88 1.79 1.70 1.59 1.47 1.32 I.IM)
ку — число степеней свободы для большой дисперсии. Ь для меньшей дисперсии
11 редметный указатель
Абсолютная пропускная способ-
ность 256-258. 259
Автокорреляционная функция 482
— выборочная 482
Автокорреляция возмущений 488
-- остатков 488
Авторегрессионная модель 494—495
Аксиомы теории вероятностей
59-60
Актуарная математика 227
Альтернативная случайная величи-
на 142
------.дисперсия 142. 312
------. математическое ожида-
ние 142
Асимптотические формулы 71
Байесовский подход 52
Биномиальный закон распределе-
ния 141-145
----, дисперсия 142. 143
------. математическое ожидание
142. 143
Благоприятствующая фигура 22
Благоприятствующий случай 18
Вариант 267
Вариационный размах 275
- ряд 268-272
---дискретный 269
---интервальный 269
---непрерывный 269
Вектор возмущений 455
— значений зависимой перемен-
ной 455
— параметров 455
— случайных ошибок 455
— частных производных 456
Величина интервала 267
Вероятностная зависимость 193.
395
Вероятное отклонение 165
Вероятностное пространство 60
Вероятности состояний 251
----предельные 252
----финальные 252
Вероятность отказа 256. 259
— перехода 242
— произведения двух событий 39
----независимых событий 41
----нескольких событий 39—40
----независимых событий 41
— события 18
— —. непосредственное вычисле-
ние 27-33
----. свойства 19—20
----. теоретике-множестве иная
трактовка 59
----условная 38. 60
— суммы двух совместных событий
43-44
----нескольких совместных событий
44
------несовместных событий 36
Возмущение 380
Временной ряд 479
----. его составляющие 478—479
----. основная задача 480
----. основные этапы анализа 480
----. сезонная компонента 479
----, случайная компонента 479
----стационарный в узком смысле
481
----строго стационарный 479
----. тренд 479
----. циклическая компонента
479-480
Временные ряды стационарные
481
Выборка (выборочная совокуп-
ность) 286
— гнездовая 287
— механическая 287
— представительная 287
— репрезентативная 287
539
— серийная 287
— собственно-случайная 287
— стратифицированная 287
— типическая 287
Выборочная дисперсия 288
---исправленная 305
— доля 288
— средняя 288
Выборочный метол 286—289
---. недостаток 287
---. основная задача 289
---, преимущества 286—287
---. принцип отбора элементов
287
Выравнивание временных рядов
484-488
Гауссова кривая 155
Генеральная дисперсия 288—289
— доля 288
— совокупность 287
— средняя 288—289
Геометрическая вероятность 22—23
Геометрическое определение ве-
роятности 22—23
— распределение 148—149
---, дисперсия 149
---. математическое ожидание
148
Гипергеометрнческос распределе-
ние 150-153
---. дисперсия 150
---. математическое ожидание
150
Гипотеза альтернативная 331
— конкурирующая 331
— нулевая 331
— о равенстве дисперсий двух
совокупностей 348—351
---------нескольких совокупно-
стей 351—352
------долей признака в двух
совокупностях 345—347
--------------нескольких сово-
купностях 347— 348
------средних двух совокупно-
стей 339-344
— основная 331
— статистическая 331
Гипотезы о иконе распределения
339. 357-366
— об однородности выборок 339
366-371
— о стохастической независимо-
сти элементов выборки 330.
372
о числовых значениях парамет-
ров 339, 352-356
Гистограмма 269
Гомоскедастичность 204
Граф состоянии 244
----размеченный 250
Группировка 267
Групповая средняя 388. 45S
Двумерная случайная величина
176-178
------.ее составляющие 176
------. плотность вероятности
182-185
------. плотности вероятное leu
составляющих 185
------, совместная плотность
182-185
------. совместная функция рас-
пределения 179—182
------. свойства 180—182
Двумерный нормальный закон
202-207
------. плотности вероятностей
составляющих 203
------. совместная плотность 202
------, теоретико-вероятностный
смысл параметрон 203
---------. условные дисперсии
204
------, — математические ожида-
ния 204
------, — плотности вероятностей
203—204
------. эллипс рассеяния 205
Децили 120
Диаграммы Венна 34
Диверсификация 228
Динамический ряд 479
Дискриминантный анализ 475
Дисперсионный анализ 379
540
---. влияние отклонений or
предпосылок 392, 393
---двухфакторный 387—393.
405—406
---одно<|закторный 379—386
------. основная идея 382
------. основные предпосылки
380
------со случайными уровнями
факторов 380, 384, 389
------с фиксированными уров-
нями факторов 380. 384,
385
Дисперсия вариационного ряда
276
------, свойства 277—278
------. упрощенный способ рас-
чета 279—281
— выборочная 288
---исправленная 305
— выборочной средней 442
— генеральная 288
— групповых средних 442
— межгрупповая 278
— общая 277
— случайного процесса 239
— случайной величины 98—102
------дискретной (прерывной)
98-100
------. свойства 100-101, 202
------, интерпретация в финан-
совом анализе 102
------. механическая интерпре-
тация 102, III
— функции случайной величины
209-210
Дифференциальная функция рас-
пределения 109
Дифференциальный закон рас-
пределения 109
Доверительная вероятность 263.
309
Доверительный интервал 309
---для генеральной дисперсии
323-326
--------доли для больших вы-
борок 310—313
-------------малых выборок
322-323
-------------умеренно больших
выборок 316—318
------средней для больших вы-
борок 310-313
-------------малых выборок
318-321
------дисперсии возмущений
466
------условного математического
ожидания 441 —443. 465
------индивидуальных значений
зависимой переменкой
443 -444. 465
Доля выборочная 288
— генеральная 288
Дополнение события 18
Доходность ценной бумаги 497
— рыночного индекса 499
Зависимость вероятностная 193,
395
— корреляционная 396
— регрессионная 439
— статистическая 193. 395—397
— стохастическая 193. 395—397
— функциональная 192. 395—397
Зависимые события 41
— случайные величины 91. 192
Задача о встрече 23
— Эрланга 258—260
Закон больших чисел 218
------. теорема Бернулли 229—
230
------. — Пуассона 231—232
------. — Чебышева 223—227
------усиленный 231
— равнобедренного треугольника
212
— распределения Пуассона 145—
148, 248
------. дисперсия 146
------, математическое ожидание
146
---Симпсона 212
---случайной величины 88—89
Законы де Моргана 35
^-преобразование Фишера 416
541
Инверсия 432
Индекс корреляции 421 423
----множественный 468—469
----, проверка значимости 470
Индикатор события 142
Интеграл Лапласа 74—75
Интегральная функция распреде-
ления 103
Интеграл Эйлера—Пуассона 75
Интегральный закон распределения
103
Интенсивность нагрузки канала
246
— потока заявок 257
----событий 246
Интервальная оценка для инди-
видуальных значений зависи-
мой переменной 443—444 . 465
------условного математическою
ожидания 441-443. 465
------уровня временного ряда
491
Интервальная разность 267
Исключение грубых наблюдений
344-345
Испытание 16
Испытания независимые 68
Исход испытания 16
Квантиль случайной величины
116
Квартиль случайной величины
116
Классическое определение веро-
ятности 18—19
Кластер 475
Кластерный анализ 475
Ковариационная матрица 462
Ковариация 196
— выборочная 402. 462
— случайных величин 196
------. свойства 196—197
Количество информации Фишера
306
Комбинаторика 23—27
Комбинаторные задачи 23
Композиция законов распределе-
ния 210-211
Компонеггтнып анализ 475
Континуум 87
Коррелограмма 482
Корреляционная зависимость 397
---линейная 399
---обратная 407
---прямая 407
- таблица 398
функция случайного процесса 2441
---нормированная 241
Корреляционное отношение 419
---теоретическое 421—423
---. проверка значимости
422-423
---эмпирическое 420-421
---. проверка значимости 422
Корреляционный анализ 398.
412-413. 480
---. основная задача 398
---, проверка линейности связи
двух переменных 429
----многомерный 424—426
----. основные задачи 425
Корреляционный момент 196
----выборочный 402, 462
----случайных величин 196
----.свойства 196—197
Корреляция 395
— ложная 428
Коэффициент асимметрии вариа-
ционного ряда 282
---случайной величины 118
— автокорреляции 482
— вариации 276—277
детерминации множественный
426. 469. 470
------скорректированный 469
------эмпирический 420
— конкордаиии (согласованности)
рангов Кендалла 434—435
--------, проверка значимости
435
— корреляции 198.413
---выборочный 406—409
---—. проверка значимости
415-418
---. свойства 410—412
---генеральный 412
542
---случайных величин 198. 413.
414
--------. доверительный интер-
вал 416—417
--------.свойства 198—199
---множественный 425—426
------. проверка значимости
425-426
---частный 426
------. проверка значимости 427
— ранговой корреляции Кендалла
432-433
--------. проверка значимости
432
------Спирмена 430—431
--------. проверка значимости
431
Коэффициеш регрессии генераль-
ный 417
---. доверительный интервал
417. 448. 465
---, проверка значимости 448,
465
---(парная модель) 401—402
---стандартизованный 461
— Шарпа 510
— эксцесса I IS. 2S2
— эластичности 461
Кривая распределения 109
— регрессии 190
Критерии однородности ранговые
369
— свободные от распределения
339
Критерий Аббе 372
— Бартлетта 351
— Вальда 372
— Вилкоксона—Манна—Уитни
370-371
— «ВОСХОДЯЩИХ» И «НИСХОДЯЩИХ*
серий 372
— Дарвина—Уотсона 489—490
— двусторонний 338
— Колмогорова 364—366
— Колмогорова—Смирнова 366—
368
— Крускала—Уоллиса 371
— нспарамегрический 339
— односторонний 338
— отношения правдоподобия
335-336
------последовательный 372
— параметрический 339
- серий, основанный на медиане
372
— статистический 332
— Пирсона х2 (согласия) 358—359
----(однородности) 368—369
— Фишера—Йэтса 371
Критическая область 332—335
----двусторонняя 338
----левосторонняя 338
----односторонняя 338
----правосторонняя 338
----. принцип построения 335,
338
Кумулятивная кривая (кумулята)
269-270
Лаг 481
Лемма Чебышева 218—219
Линия регрессии 190
----нормально распределенных
случайных величин 204
Логнормальное распределение
167-169
------, дисперсия 167
------. математическое ожидание
167
------. медиана 167
------. мода 167
Марковский случайный процесс
241-245
------с дискретными состоя-
ниями и дискретным време-
нем 242—244
-------------непрерывным вре-
менем 244
Математическая статистика 12, 266
Математическое ожидание 95—98
----. геометрическая интерпрета-
ция 113—114
----. интерпретация в финансо-
вом анализе 102
----, механическая интерпретация
96. Ill
543
---непрерывной случайной ве-
личины 111
---, свойства 96. 97—98. 201 —
202
---случайного процесса 239
---случайной величины, рас-
пределенной биномиально
121. 142
---функции случайной величии-
ни 209
---частости события 143
Матрица значений объясняющих
переменных 455
— ковариационная 462—463
— перехода 242
— плана 455
---столбец возмущений 455
---значений зависимой пере-
менной 455
---параметров 455
---случайных ошибок 455
Медиана вариационного ряда
274-275
— непрерывной случайной вели-
чины 114—115
Метод главных компонент 475
— максимального правдоподобия
294-296
------. свойства опенок 296
— Монте-Карло 261—263
— моментов 293—294
---. свойства опенок 294
— наименьших квадратов 296.
297. 400-401. 455-458. 484-
485
— последовательного анализа
372-375
— последовательных разностей
492-493
— скользящих средних 487
— статистических испытаний
261-263
Методы классификации 475
Многомерная случайная величина
175
------дискретная 175
------, закон распределения 176
------непрерывная 175
------. теоретико-множествен-
ная трактовка 175
------. функция распределения
179-182
Многомерный статистический
анализ 474
Многоугольник распределения
вероятностей 69. 89
Множество 56, 58. 87
— счетное 59
Мола вариационного ряда 275
— случайной величины 114
Модели финансового рынка 503.
507-510
Модель главных компонент 475
— линейной множественной рег-
рессии 455
--------.в матричной форме
455
--парной регрессии 440 —441
— оценки финансовых активов
505-506
— скользящей средней 480
Модельная линия регрессии 397
— функция регрессии 397
Модельное уравнение регрессии
397
Момент л-го порядка вариацион-
ного ряда 281—282
-----------начальный 281 — 282
-----------центральный 282
------случайной величины
116-118
-----------начальный 116, 117
-----------центральный 117
Мощность критерия 332
Мультиколлинеарность 472—473
Мультиномиальная схема 82—83
Надежность опенки 309
Наивероятнейшее значение слу-
чайной величины 114
— число 70. 144
Невязка 441
Независимые случайные величи-
ны 91. 192
— события В СОВОКУПНОСТИ 41 —
43
попарно 41—43
544
Некоррелированные случайные
величины 198
Непрерывная случайная величина
87. 107
------. определение 107. 182
------. плотность вероятности
109-110
Неравенство информации 305 —
зоъ
— Маркова 218—219
— Рао-Крамера—Фреше 305-306
--------. условия регулярности
306
— Чебышева 220—221
---для биномиально распреде-
ленной случайной величины.
220
------частости события 220
//-мерный нормальный закон
206-207
------. ковариационная матрица
206
Нонсенс-корреляция 428
Нормальная кривая 155
— регрессия 440
Нормальный закон 158-166
---. вероятность отклонения от
математического ожидания
на величину \ 163—165
---. - попадания в интервал
162-163
---двумерный 202—206
---.дисперсия 159—160
---. коэффициент асимметрии
165
---, математическое ожидание
159. 160
---//-мерный 206—207
---нормированный 160
---. правило трех сигм 164
---стандартный 160
---, функция распределения
161-162
---. эксцесс 165
Область допустимых значений
критерия 332
— отклонения гипотезы 332
— принятия гипотезы 332
Объем выборки 286. 314 315
---бесповторной 314—315
---повторной 314—315
— генеральной совокупности 286
Оперативная характеристика кри-
терия 332
Операции нал множествами 57—
58
---событиями 33—35
Определение вероятности 18
- - геометрическое 23—24
классическое 19
---статистическое 20—22
Опыт 16
Основная тенденция развития
процесса 480
Относительная пропускная спо-
собность 256
Отрицание события 18
Оценка параметра 289
— асимптотически несмещенная
291
---эффективная 292
— значимости различия выбороч-
ных средних 339
— интервальная 309—310
---, свойства 290—293
— несмещенная 290
— смешенная 290
— состоятельная 291
— точечная 308
— эффективная 291—292
Ошибка второго рола 332
— первого рола 332
— представительства 287. 309—310
— регистрации 287
— репрезентативности 287. 309—
310
Пакет прикладных программ 14
Параметризация модели 450
Параметр распределения случай-
ной величины 102. 289
Переменная выходная 439
— зависимая 439
— объясняющая 439
- остаточная 439
— предикторная 439
— предсказывающая 439
— результирующая 439
545
— случайная 439
— экзогенная 439
— эндогенная 439
Переменные категоризованные 436
— качественные 436
— количественные 429
— ординальные 430
— порядковые 430
Перестановки 25
— с повторениями 27
Перцентили 116
Плотность вероятности двумерной
случайной величины 183—185
-----------, нахождение вероят-
ности попадания в
область 183—184
-----------. — дисперсий состав-
ляющих 190. 191
-----------. — математических
ожиданий состав-
ляющих 190. 191
-----------. — функции распре-
деления 184
---, свойства 183—185
---случайной величины 109—
110
---------. вероятность попадания
в интервал 109—110
---------. нахождение функции
распределения 110
---------, свойства 109—110
— распределения 103—106
— случайной величины 207—209
— частости 361
Повторные независимые испыта-
ния 68
Показательный закон 154—157.
249—250
---.дисперсия 155
---, математическое ожидание
155
---. функция распределения 155
Поле корреляции 398
Полигон вариационного ряда 269
— распределения вероятностей 89
Полимодальное распределение 114
Полиномиальная схема 82—83
Полная группа событий 17. 57
------, сумма их вероятностей
36-37
— система событий 17. 57
Портфель ценных бумаг 500. 501
------, его риск 501
------касательный 500. 503
------, допустимое множество 501
------. связь между доходностью
и риском 506—507
------. эффективное множество
501
Порядковая статистика 268
Поток событий 246
---без последействия 247
---ординарный 247
---простейший 247
---регулярный 246
---стационарный 246—247
---стационарный пуассоновский
247
Правило корня из п 227
— произведения 24
— сложения вероятностей 36
---дисперсий 278
— суммы 24
— трех сигм 164
Правило умножения вероятностей
39
---плотностей распределения
189
Практически достоверное событие
20
— невозможное событие 20
Предельная ошибка выборки 309
Предельные вероятности состоянии
252
Принцип диверсификации 228
— практической уверенности 330—
331
Прогнозирование с помощью вре-
менного ряда 488. 491
Прогноз уровня ряда интерваль-
ный 488. 491. 492
------точечный 488. 491
Произведение событий 34. 57. 58
Производящая функция 119—121.
128
---, свойства 120
Пространство элементарных собы-
тий 57
Противоположные события 18. 58
546
----. свойства их вероятностей 37
Процентили 116
Процентная точка распределения
116
Процесс гибели и размножения
254-256
----марковский 241
----с дискретными состояниями
и дискретным временем
242-244
-----------и непрерывным
временем 244
— случайный 241—242
Равенство Маркова 243
Равномерный икон 152—154
----.дисперсия 153
— -. математическое ожидание
153
----. функция распределения 152,
153
Размер критерия 332
Размещения 24
— с повторениями 26
Разноси, событий 33
Ранг 430
Ранги связанные 430—431
Ранговая корреляция 430
Ранжирование 267
Ранжировка 432
Распределение Бернулли 142
— биномиальное 141 — 143
— геометрическое 148—149
- гипср1*ометрическое 150—152
- логарифмически -нормальное
167-168
— нормальное 158—166
двумерное 202—206
круговое 206
«-мерное 206. 207
— отрицательное биномиальное
149
— Паскаля 150—151
— показательное 154-157
— полиномиальное 179
— прямоугольное 152—154
— Пуассона 145—148, 248—249
— равномерное 152—154
— случайной величины 88—89
------, характеристика асиммет-
рии 118
------, — положения 117
------, — рассеяния 117—118
------. — скошенности 118
— /-Стьюдента 170—171
— условное 177—178
— /--Фишера—Снедскора 171
— х* (хи-квадрат) 169—170
— экспоненциальное 154—157
Реализация случайного процесса
238
случайной величины 283
Регрессионная модель доходности
497-498, 505-506, 507-510
Регрессионный анализ 398. 439
---, основная задача 398, 439
- основные предпосылки 440.
458
- — линейный 440
- множественный 454—472
Регрессия 190
— нелинейная 450
— нормальная 440
Регрессор 439
Риск портфеля 501
Рыночная модель доходности 499
Рыночные индексы 499
Рял рас пределен ня 89
Свертка законов распределения
210-211
Сглаживание временных рядов
484
Сдвиг 498
Сезонная компонента 479
с-алгебра событий 60
Симметрия исходов 20
Система массового обслуживания
245-246
---— многоканальная 245
---------с отказами 246. 258—
260
------одноканальная 245
------с отказами 257—258
---с ожиданием (очередью) 246
---. показатели эффективно-
сти 246
547
------. предельные вероятности
состояний 252
— нормальных уравнений 400, 452.
457. 485
------для линейной регрессии 400
------в матричной форме
457
---------квадратичной функции
452. 485
— случайных величин 175
— уравнений правдоподобия 294
Случай 18
— благоприятствующий 18
Случайная величина 87—89
. закон распределения 88—89
дискретная 87—88
. ряд распределения 89
. свойство вероятности ее
значений 89
— —. т-я степень 92
----непрерывная 87
----прерывная 87
----. умножение на число 92
— функция 238
Случайные величины зависимые
91
----, их разность 92—93
----. — произведение 92—93
----. — сумма 92—93
----. математические операции
91-92
----независимые 91
----смешанные 111 — 112
Случайный вектор 175
----. его реализация 175
----. составляющие 176
Случайный процесс 238—239
----без последействия 241—242
----, граф состояний 244
----.его порядок 239
----. дисперсия 239
----, корреляционная функция
240
----.----нормированная 241
---------марковский 241—244
----, математическое ожидание
239
----. реализация 238
---.с непрерывным временем
244
---. — дискретными состояниями
242
---. среднее квадратическое от-
клонение 239
---. траектория 238
Смещение оценки 292
Событие 16, 58
— возможное 16
— достоверное 17. 19. 57
— невозможное 17. 19, 57. 58
— практически достоверное 20
---невозможное 20
— случайное 16
События взаимно-
дополнительные 18
- единственно возможные 17
— зависимые 41
— независимые 41—43
— несовместные 16. 58
— противоположные 18, 58
—. свойства 21—22
—, — операций 35
— ,---. ассоциативность 35
— .---. дистрибутивность 35
— ,---. коммутативность 35
— равновозможные 17
— равносильные 16. 58
— совместные 16
Совместная плотность 182—185
---. вероятность попадания в
область 183
---. геометрическая интерпрета-
ция 183
---. нахождение плотности со-
ставляющей 185
—. — совместной функции рас-
пределения 184
------. — функции распределения
составляющих 185
---, свойства 183—185
Совокупный коэффициент корре-
ляции 425, 468—469
Составляющие случайного вектора
176
— временного ряда 479—480
Сочетания 25
— с повторениями 26
548
Спектральный анализ 480
Спецификация модели 450
Среднее квадратическое отклоне-
ние вариационного ряда 276
------случайной величины 100
------случайного процесса 239
— линейное отклонение вариаци-
онною ряда 276
Средние величины 272—275
---аналитические 274
--- порядковые 274
---. свойство мажорантное™
274
— квадраты 382. 3S4
Средняя арифметическая 272
---. свойства 273 — 274
---. упрошенный способ расчета
'279-281
- выборочная 288
— гармоническая 274
— генеральная 288
— геометрическая 274
— групповая 381. 388. 397. 458
— групповых дисперсий 277
— квадратическая 274
---ошибка выборки 311
------для доли 311
---------средней 311
— общая 381. 388
— степенная //-го порядка 273—274
— условная 397. 458
Стандартная ошибка выборки 311
Стандартное отклонение случай-
ной величины 100
Стандарт случайной величины 100
Статистика 289
— критерия 331
---Колмогорова 364
------Смирнова 367
— порядковая 268
Статистическая вероятность 20
— гипотеза 331
---. принцип проверки 331—332.
— зависимость 192. 396
Статистическая устойчивость час-
тот 21
Статистические пакеты 14. 392
— американские 14
- отечественные 14
— специализированные 14
— универсальные 14
Статистический критерий 332
- тест 332
Статистическое наблюдение 286
— выборочное 286
— сплошное 286
Статистическое определение ве-
роятности 20—22
Страховая математика 227
Сумма квадратов внутригрупповая
382. 384. 391
---межгрупповая 382. 384. 391
- — обусловленная регрессией
446
- - общая 382. 385. 391
---остаточная 382. 446
факторная 382
событий 33. 57. 58
Схема Бернулли 68
— полиномиальная 82—83
— случаев 18
— урн 18
Сходимость по вероятности 225
Теорема Бернулли 229—231
— Гаусса—Маркова 441. 458
— Ляпунова 231—233
— Муавра—Лапласа интегральная
74. 233-235
------. следствия 76—77
------локальная 72—73. 235
— Неймана—Пирсона 335—336
— о вероятности отдельного зна-
чения 107—108
------отклонения выборочной
средней (дачи) от генераль-
ной 310-311
---выборочной дате 298—300
------средней 302—303
------дисперсии 303—304
— Пуассона 230-231
— о равенстве параметра ценных
бумаг безрисковой ставке 504—
505
---связи независимости к не-
коррелированности 204—205
— сложения вероятностей 36—37
------. следствия 36—37
54!)
— умножения вероятностей 39—
40
------, для независимых собы-
тий 41
----плотностей вероятностей IS9
— центральная предельная 231.
235-236
- Чебышева 223-227
Теория вероятностей 12. 13, 15
----. аксиоматическое построе-
ние 58—60
----, теоретико-множественная
трактовка 56—57
— массового обслуживания 245
Траектория случайного процесса
238
Тренд временного ряда 479
Точечная оценка 308
Точечный прогноз 491
Точка множества 58
Точность оценки 314
Тройка компонент вероятностно-
го пространства 60
Уравнения Колмогорова 252
Уравнение регрессии 397
----гиперболическое 450
---- логистическое 451
----нелинейное 450
----полиномиальное 450
----степенное 450
— парной регрессии 44!
------. проверка значимости
446-448
------, упрошенный способ рас-
чета параметров 403—406
— правдоподобия 294
Уровень доверия 309
— значимости критерия 332
Условия регулярности функции
плотности 306
— статистического ансамбля 21
Условная вероятность события 37.
60
------, определение 37. 60
— плотность составляющей 189
-------------. геометрическая
интерпретация 189
— средняя 397. 458
Условное распределение 177.
188-189
Условные дисперсии 190—191.
— математические ожидания
190-192.
Условный закон распределения
188-190
Устойчивость относительных час-
тот 21
Фактор 497
Факторный анализ 474—475
---. модель 474—475
Финальные вероятности состоя-
ний 252
Формула Байеса 52—53
— Бернулли 68
— композиции двух распределений
211
— Муавра—Лапласа интегральная
74-75. 143. 233-235
------. следствия 76—77. 143—144
------локальная 72. 73, 143, 235
— полной вероятности 51—52
— Пуассона 71—72
— свертки двух распределений 211
— Стерджеса 267
Формулы доверительной вероят-
ности для средней и доли
310-311
— Эрланга 259
Функция выживания 106
— Гаусса 73
— Гомперца 484
— дожития 106
— Лапласа 74—75
— линейная 484
— логистическая 484
— мощности критерия 332
— надежности 106
— отклика 439
— полиномиальная 484
— правдоподобия 294
— производящая 119— 12!. 128
— распределения 103
---. вероятность попадания в
интервал 106
---. геометрическая интерпрета-
ция 103
550
----.свойства 104—106
----двумерной случайной вели-
чины 179-182
-----------. вероятность попади*
ния и прямоугольник
181-182
-----------1 геометрическая интср-
иретапия 179-180
----. свойства 180 -182
----л-мерной случайной величины
179
----эмпирическая 271
— случайных величин 207—209
----дисперсии 209—210
------, математическое ожидание
209
---монотонная 207
------немонотонная 208—209
— характеристическая 121
Центральная предельная теорема
231. 235-236
Цепи Маркова 84. 242—244
Цепь Маркова однородная 242
Циклическая компонента 479. 480
Частота интервала 268
- накопленная 268—269
— события 20
----относительная 268
Частость интервала 268
— накопленная 269
— события 20
Числа браковочные 374
— приемочные 374
Числовые характеристики 102
Число степеней свободы 320, 359
Чувствительность доходности 498
Шанс 18
Эксперимент 16
Экспоненциальный закон распре-
деления 154—157, 249—250
------. дисперсия 155
------. математическое ожидание
155
------. функция распределения
155
Экстраполяция кривой регрессии
443
Эксцесс вариационного ряда 282
— случайной величины 118
Элементарное событие 18. 56. 58
Элементарный исход 18. 56—57,
58
Элемент вероятности 111
Эмпирическая линия регрессии 399
— функция распределения 270
Эллипс рассеяния 205
Эффективность оценки 292
Учебник
Кремер Наум ТПсвслспич
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
II МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Авторским редакция
Корректор ГБ. Костром нова
Оригинал-макет Н.В Спасской
Оформление художника А.П. Яковлева
Лицеи шя серии ИД № 03562 от 19 12.2000 i
Санитарно-эшикмип.чогическое включение
№ 77 99 60 953 Д 005315.05.07 or 08.05.2007 г
Подписано I» печать 13.06.2007 <с готовых рх-фаилов). Иц № 1014
Формат 60*90 1/16. Бумага офсетная. Уел печ т. 34.5 Уч -нчл л. 28.5
Тираж 5000 эка Заказ №3932
OCX) .ИЗДАТЕЛЬСТВО ЮНИТИ-ДАНА.
Генеральный директор В.Н Закаидле
123298. Москва. ул Ирины Левченко, I
Тел 8-499-740-60-15. Тел /факс: 8-499-740-60-14
www.unHy-dana.ru E-rnail* unirytf’uniiy-dana ru
Ошечлано и ОАО »ИПК «Ульяновский Дом печати»
432980, г. Ульяновск, ул Гончарова. 14