Автор: Бослаф С.
Теги: теория статистики статистические методы прикладные информационные (компьютерные) технологии методы основанные на применении компьютеров статистика
ISBN: 978-5-94074-969-1
Год: 2015
Текст
СТАТИСТИКА
для всех
Сара Бослаф
Як O'REILLY'
Сара Бослаф
СТАТИСТИКА
ДЛЯ ВСЕХ
STATISTICS
IN A NUTSHELL
Second Edition
Sarah Boslaugh
O'REILLY*
Beijing • Cambridge • Farnham • Koln • Sebastopol • Tokyo
СТАТИСТИКА
ДЛЯ ВСЕХ
Сара Бослаф
щ&
Москва, 2015
УДК 311:004.9
ББК 60.6с515
Б85
Б85 Сара Бослаф
Статистика для всех. / Пер. с англ. П. А. Волкова, И. М. Флямер, М. В. Ли-
берман, А. А. Галицына. - М.: ДМК Дресс, 2015. - 586 с: ил.
ISBN 978-5-94074-969-1
Нужно овладеть статистикой по долгу службы? Хотите получить помощь
при сдаче курса статистики? «Статистика для всех» - ясное и краткое
введение и руководство для всех новичков. Тщательно переработанное и
расширенное, это издание поможет вам глубоко понять статистику, избегая
ошеломляющей сложности многих университетских учебников.
Эта книга - руководство, которое можно приспосабливать к имеющимся
знаниям и нуждам отдельных читателей. Некоторые главы посвящены
темам, которые часто отсутствуют в вводных книгах по статистике. Каждая
глава представляет собой простые для понимания объяснения, дополненные
диаграммами, формулами, задачами с решениями и взятыми из практики
заданиями. Если вы хотите не ломая голову применять распространенные
методы анализа данных и узнать о разнообразных подходах - эта книга для
вас.
УДК 311:004.9
ББК 60.6с515
Original English language edition published by O'Reilly Media, Inc., 1005 Gravcnstcin
Highway North, Scbastopol, CA 95472. Copyright © 2013 Sarah Boslaugh. All rights
reserved. Russian-language edition copyright © 2014 by DMK Press. All rights reserved.
Все права защищены. Любая часть этой книги не может быть воспроизведена
в какой бы то ни было форме и какими бы то ни было средствами без письменного
разрешения владельцев авторских прав.
Материал, изложенный в данной книге, многократно проверен. Но, поскольку
вероятность технических ошибок все равно существует, издательство не может
гарантировать абсолютную точность и правильность приводимых сведений. В связи
с этим издательство пс песет ответственности за возможные ошибки, связанные с
использованием книги.
ISBN 978-1-449-31682-2 (англ.)
ISBN 978-5-94074-969-1 (рус.)
© 2013 Sarah Boslaugh. All rights reserved
© Оформление, перевод па русский язык,
издание, ДМК Пресс, 2015
ОГЛАВЛЕНИЕ
Предисловие 9
Ну хорошо, и что же такое статистика? 9
Основная цель этой книги 12
Статистика в информационную эпоху 13
Структура книги 14
Условные обозначения, используемые в этой книге 18
Благодарности 19
Об авторе 19
Об иллюстрации на обложке 20
Глава 1. Основные понятия, связанные с измерениями 21
Измерение 22
Типы измерений 22
Истинные значения и ошибки 29
Надежность и валидность 31
Смещение измерений 36
Упражнения 40
Глава 2. Теория вероятности 43
О формулах 44
Основные определения 45
Определение вероятности 52
Вычисление вероятности сложных событий 54
Теорема Байеса '. 56
Достаточно разговоров, давайте займемся статистикой! 59
Упражнения 61
Заключительное замечание: связь между статистикой и азартными играми 65
Глава 3. Статистический вывод 67
Распределения вероятностей 68
Независимые и зависимые переменные 76
Генеральные совокупности и выборки 77
Теорема центрального предела 82
Проверка гипотез 87
Доверительные интервалы 91
Значения р 92
Z-статистика 93
Преобразования данных 96
Упражнения 99
¦Л|НННН'! Оглавление
Глава 4. Описательная статистика и графическое
представление данных 107
Генеральные совокупности и выборки 107
Меры центральной тенденции 108
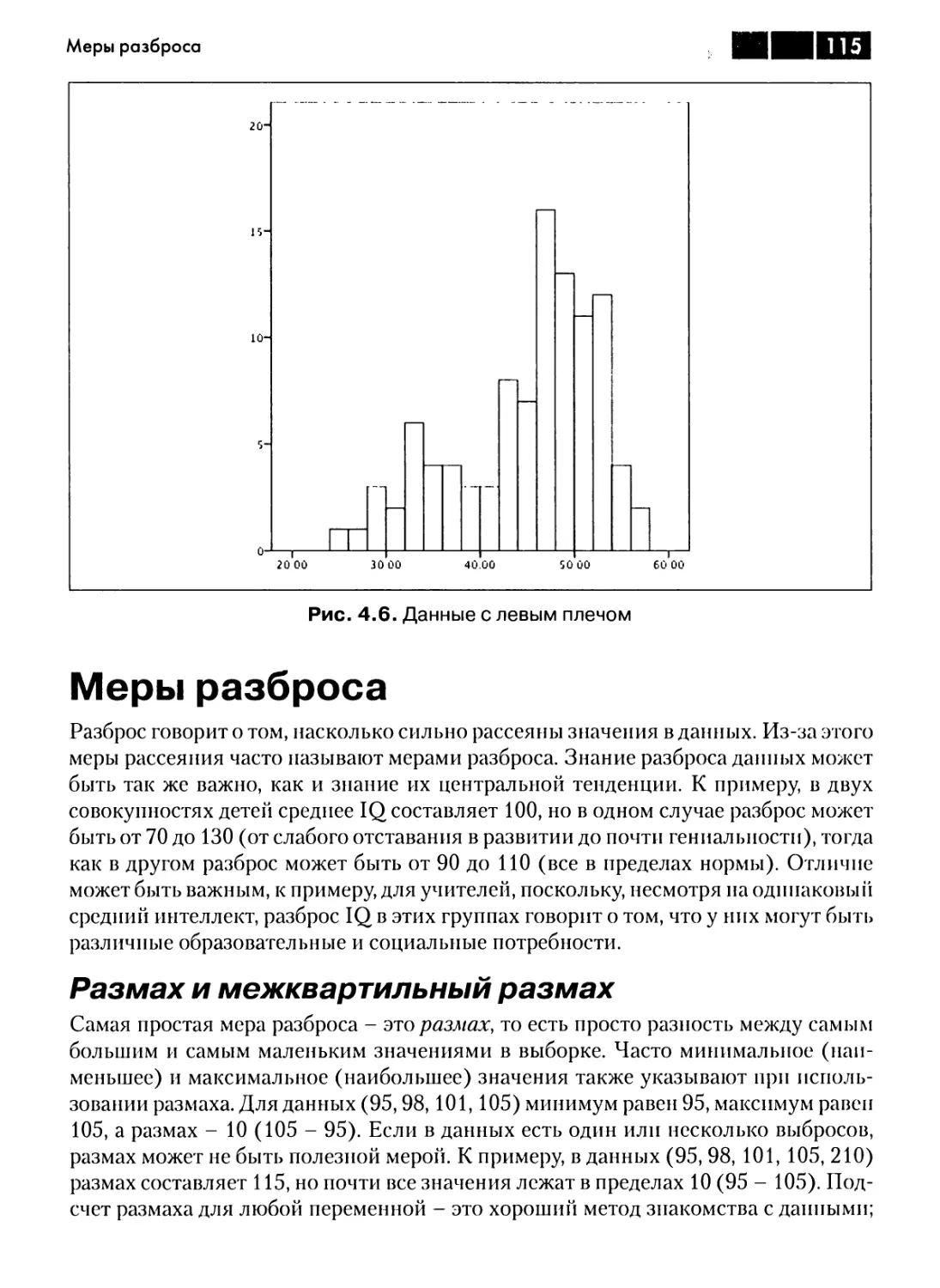
Меры разброса 115
Выбросы 121
Графические методы 122
Столбчатые диаграммы 125
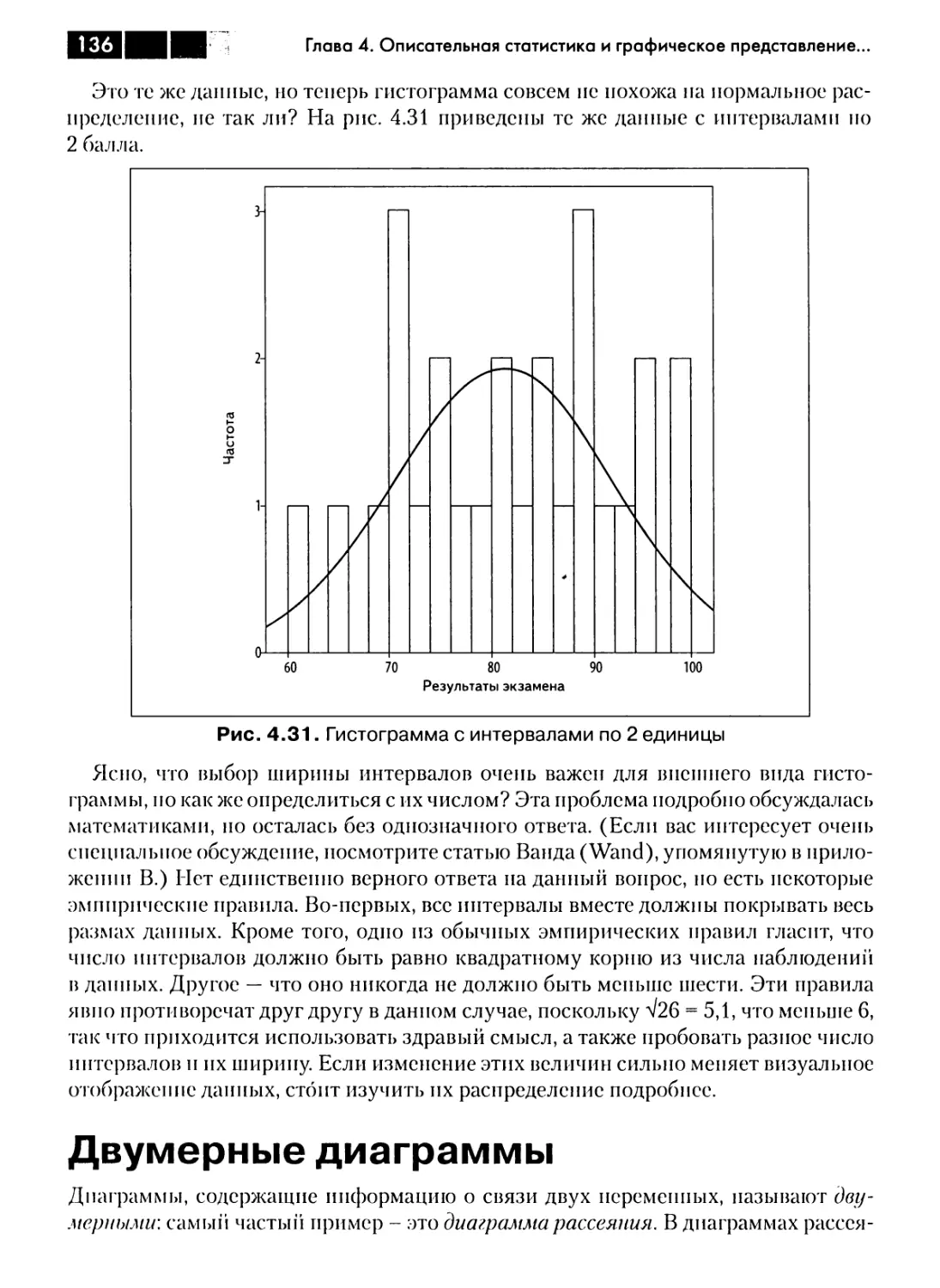
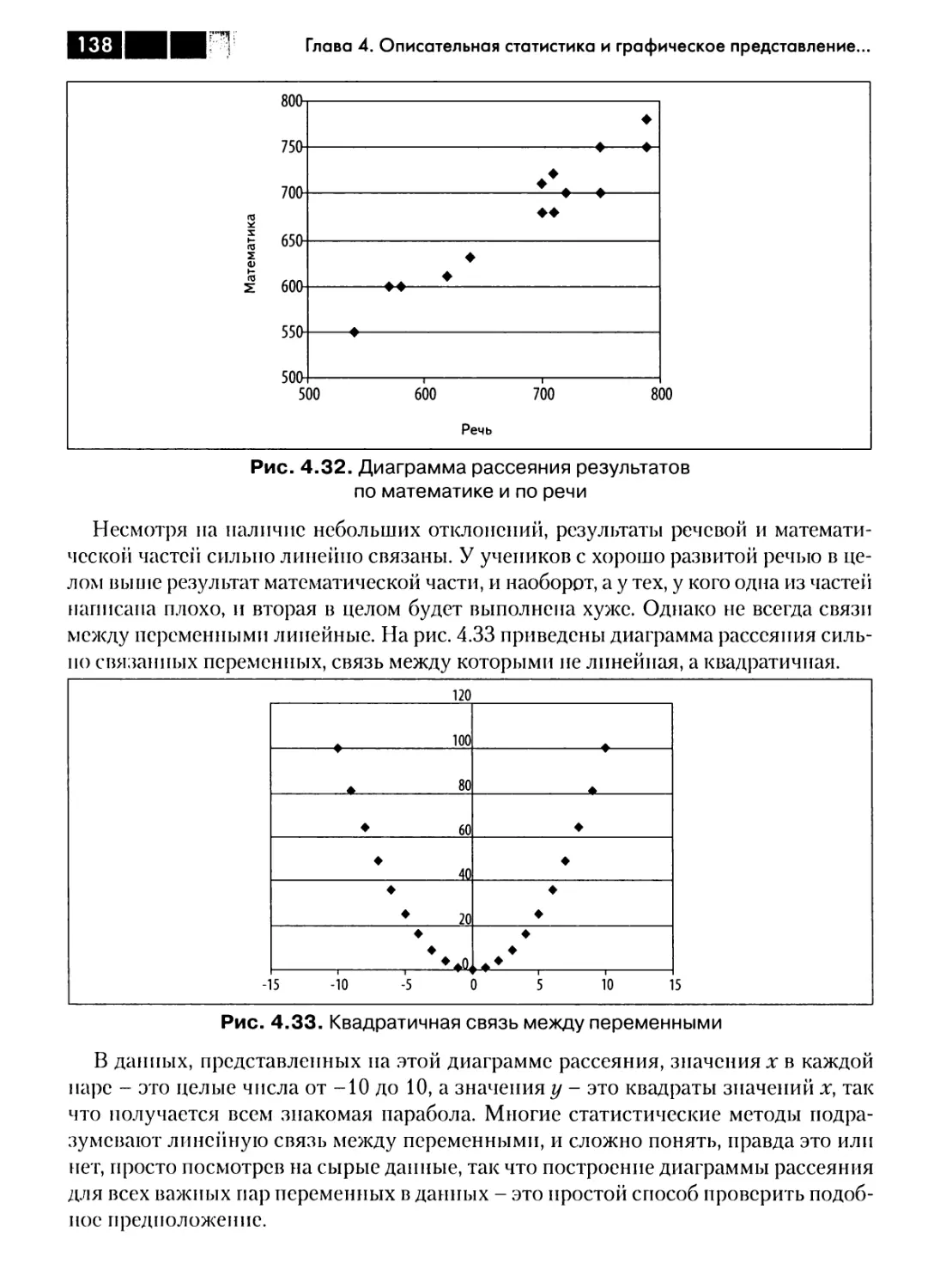
Двумерные диаграммы 136
Упражнения 142
Глава 5. Категориальные данные 146
RxC-таблицы 147
Распределение хи-квадрат 150
Тест хи-квадрат 152
Точный тест Фишера 158
Парный тест МакНемара 160
Пропорции: большие выборки 162
Корреляции для категориальных данных 164
Порядковые переменные 167
Шкала Лайкерта и шкалы семантического дифференциала 171
Упражнения 173
Глава 6. t-критерий 179
f-распределение 179
Одновыборочный f-критерий 182
f-критерий для независимых выборок 184
f-критерий для парных измерений 188
f-критерий для выборокс неравной дисперсией 191
Упражнения 192
Глава 7. Коэффициент корреляции Пирсона 196
Связь 196
Диаграмма рассеяния 198
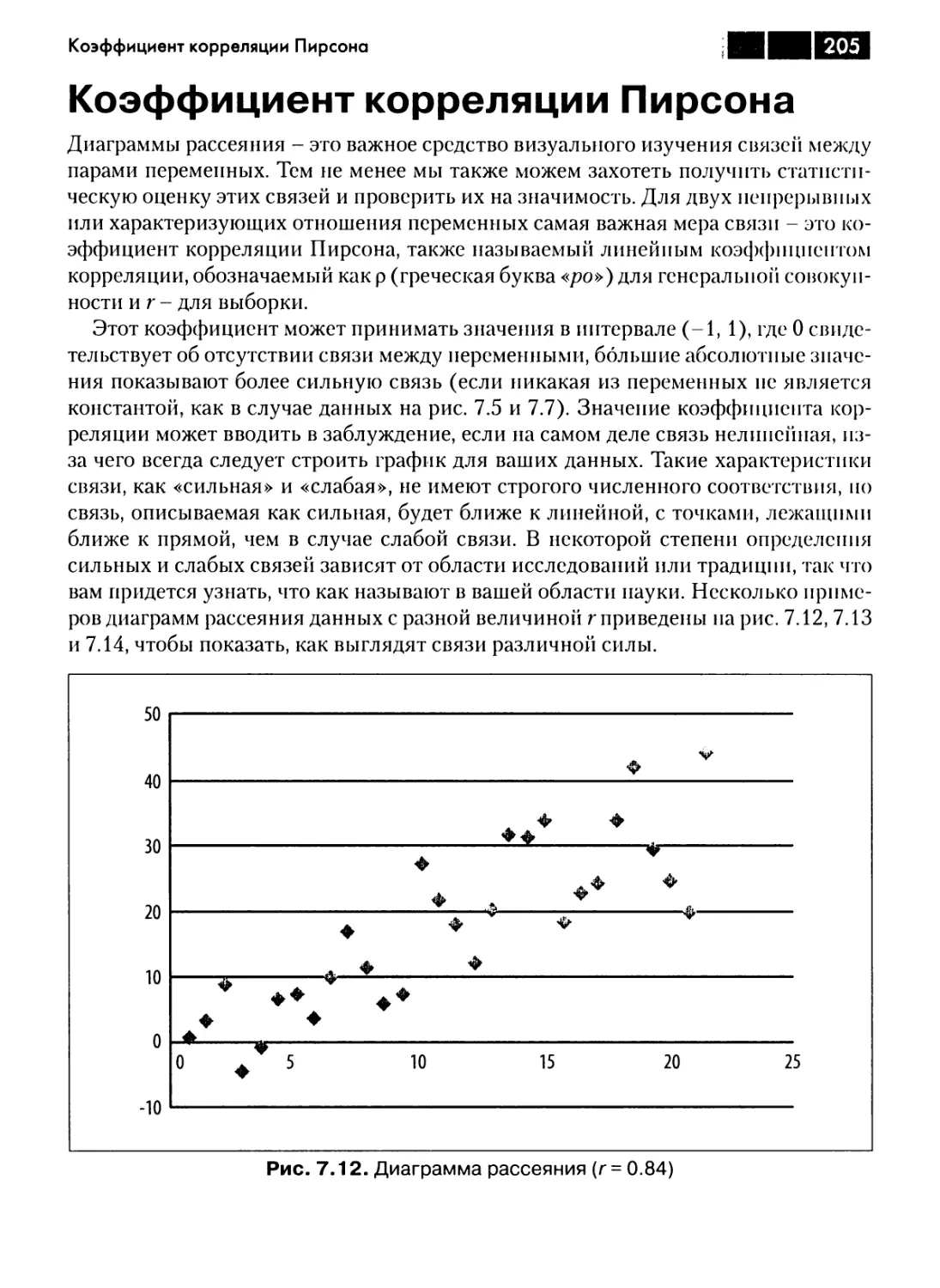
Коэффициент корреляции Пирсона 205
Коэффициент детерминации 210
Упражнения 211
Глава 8. Введение в регрессию и дисперсионный анализ 215
Общая линейная модель 215
Линейная регрессия 217
Дисперсионный анализ (ANOVA) 228
Расчет простой регрессии вручную 235
Упражнения 237
Глава 9. Многофакторный дисперсионный анализ
и ковариационный анализ 245
Многофакторный дисперсионный анализ 245
ANCOVA 254
Упражнен ия 260
Оглавление . HHHHHl^l
Глава 10. Множественная линейная регрессия 265
Модели множественной регрессии 265
Упражнения 291
Глава 11. Логистическая, мультиномиальная и полиномиальная
регрессия 296
Логистическая регрессия 296
Мультиномиальная логистическая регрессия 303
Полиномиальная регрессия 306
Переподгонка 310
Упражнения 312
Глава 12. Факторный, кластерный и дискриминантный анализы... 315
Факторный анализ 315
Кластерный анализ 323
Дискриминантный анализ 327
Упражнения 330
Глава 13. Непараметрическая статистика 332
Независимые выборки 333
Зависимые выборки 341
Упражнения 346
Глава 14. Статистика для бизнеса и контроля качества 349
Индексы 349
Временные ряды 354
Анализ решений 358
Улучшение качества 363
Упражнения 371
Глава 15. Статистика в медицине и эпидемиологии 376
Показатели заболеваемости 376
Отношение рисков 388
Отношение шансов 393
Искажение, послойный анализ и коэффициент Мантеля-Гензеля 396
Анализ мощности 401
Вычисление размера выборки 404
Упражнения 407
Глава 16. Статистика в образовании и психологии 411
Перцентили 412
Стандартизированные баллы 414
Разработка тестов 417
Классическая теория тестов: модель истинных баллов 420
Надежность теста 421
Показатели внутренней непротиворечивости 422
Анализ заданий 426
Современная теория тестирования 430
Упражнения 435
Глава 17. Управление данными 437
Общий подход, а не набор методов 438
¦!¦¦¦
Иерархия 439
Кодификатор 439
Прямоугольный файл данных 442
Электронные таблицы и реляционные базы данных 444
Проверка нового файла данных г 445
Текстовые и числовые данные 449
Пропущенные данные 450
Глава 18. Планирование исследования 453
Словарь основных терминов 454
Наблюдения 457
Квазиэкспериментальные исследования 459
Эксперименты 465
Сбор экспериментальных данных 467
Пример экспериментального дизайна 477
Глава 19. Представление статистических материалов 479
Общие замечания 480
Глава 20. Оценка работ по статистике других авторов 488
Оценка статьи в целом 488
Ошибки в применении статистики 490
Общие проблемы 490
Быстрая проверка 492
Спорные вопросы планирования исследования 495
Описательная статистика 498
Логическая статистика 503
Приложение А. Обзор основных математических понятий 506
Приложение В. Краткий обзор статистических пакетов 530
Приложение С. Ссылки 545
Приложение D. Таблицы вероятностей для распространенных
типов распределений 559
Приложение Е. Интернет-ресурсы 571
Приложение F. Словарь статистических терминов 576
ПРЕДИСЛОВИЕ
Первое издание «Статистики для всех» пользовалось оглушительным успехом,
однако любую книгу можно улучшить, и я благодарна за предоставленную
возможность переработать ее. Мой принцип изложения не изменился: эта книга гораздо
больше предназначена тем, кто хочет размышлять и понимать результаты
статистической обработки данных, чем тем, кто хочет узнать, как пользоваться
конкретным статистическим пакетом программ или углубиться в математические основы
при помощи статистических формул. Эта книга также несколько отличается от
других изданий в этой серии «Руководств для всех» издательства О'Рейлли - она
действительно находится где-то между руководством для тех, кто уже знаком со
статистикой, и учебником для людей, которые только начали осваивать этот
предмет.
Несмотря на продолжающееся проникновение статистики во многие области
нашей жизни, одна вещь осталась неизменной: сказать, что ты работаешь
статистиком, - по-прежнему верный способ испортить приятную беседу на вечеринке.
Почему-то оказывается, что это побуждает людей рассказать мне, как они
ненавидели обязательные занятия по статистике в колледже, или заставляет их
процитировать старую шутку, ставшую популярной благодаря Марку Твену, о том, что
существует три вида лжецов: простые лжецы, отъявленные лжецы и статистики.
Лично я нахожу статистику захватывающей и обожаю работать в этой области.
Я также люблю преподавать статистику, и мне нравится думать, что я заражаю
своим энтузиазмом окружающих. Хотя часто это превращается в напряженную
битву; многие считают, что статистика - это не более чем набор хитростен и
подтасовок для искажения реальности, которые нужны, чтобы одурачить других
людей. Другие занимают противоположную позицию, полагая, что статистика - это
набор волшебных приемов, которые избавят вас от необходимости размышлять
над данными.
Ну хорошо, и что же такое статистика?
Прежде чем погрузиться в технические детали изучения и использования
статистики, вернемся на минуту назад и обсудим, что можно подразумевать под словом
«статистика». Не беспокойтесь, если вы сразу не поймете всю терминологию, она
прояснится в ходе чтения этой книги.
¦ш
Предисловие
Когда люди говорят о статистике, они обычно имеют в виду один или несколько
пунктов из приведенного ниже перечня:
1. Числовые данные, такие как уровень безработицы, число людей,
умирающих ежегодно от пчелиных укусов, или численность жителей г. Нью-Йорк
в 2006 году по сравнению с 1906 годом.
2. Числа, использованные для описания выборок, в противоположность
параметрам (числам, характеризующим генеральную совокупность).
Например, рекламная компания может интересоваться средним возрастом
подписчиков журнала «Спорте Иллюстрейтед» (Sports Illustrated)1. Для
ответа на этот вопрос компания может создать случайную выборку
подписчиков, вычислить среднее значение для этой выборки (статистику) и
использовать его как оценку среднего значения для всей генеральной
совокупности подписчиков (параметра).
3. Определенные методы анализа данных и результаты такого анализа, такие
как ^-статистика или статистика хи-квадрат.
4. Область науки, которая разрабатывает и использует математические
методы для описания данных и формирования суждений о них.
Тот тип статистики, о котором говорится в первом определении, не имеет прямого
отношения к этой книге. Если вы просто хотите найти последние данные о
безработице, здоровье или о любой из множества других тем, по которым правительство или
другие организации регулярно публикуют статистические данные, вам лучше всего
проконсультироваться у библиотекаря или у специалиста в данной области. Если
же вы хотите узнать, как интерпретировать эти данные (понять, например, почему
среднее арифметическое часто бывает плохим показателем средней тенденции, или
сравнить исходные и стандартизованные показатели смертности), то «Статистика
для всех» точно вам поможет.
Понятия, использованные во втором определении, будут обсуждаться в главе 3,
посвященной предсказательным статистикам. Однако эти термины пронизывают
всю книгу. Это отчасти терминологические тонкости (статистики - это числа,
которые описывают выборки, а параметры характеризуют генеральные
совокупности), которые тем не менее подчеркивают ключевой момент применения
статистики. Идея использования информации, полученной при изучении выборки, для
формирования суждений обо всей генеральной совокупности лежит в основе всей
предсказательной статистики, а предсказательная статистика - это основная тема
этой книги (как и большинства других книг, посвященных статистике).
Третье определение также является ключевым для большинства глав этой
книги. Процесс изучения статистики до некоторой степени сводится к освоению
определенных статистических методов, включая такие вопросы, как способы
вычислений и их интерпретации, выбор подходящей статистики в конкретной ситуации и
так далее. На самом деле многие люди, начинающие изучать статистику, держат в
голове в основном это определение. Освоить статистику для них означает узнать,
1 Еженедельный иллюстрированным спортивный журнал, крупнейшее и самое популярное
спортивное iшлапне в США. - Прим. пер.
Ну хорошо, и что же такое статистика?
¦НШ
как выполнять набор статистических процедур. Это не столько неверный подход
к статистике, сколько неполный. Умение применять ряд методов статистической
обработки данных - это необходимая составляющая деятельности статистика, но
это далеко не все, что нужно. Более того, с тех пор как компьютерные программы
сделали применение методов статистического анализа данных существенно проще
для всех вне зависимости от уровня математической подготовки, необходимость
в понимании и интерпретации результатов статистического анализа значительно
превысила необходимость знать, как проводить сами вычисления.
Четвертое определение мне ближе всего, поскольку я избрала статистику своей
профессией. Если вы уже студент или закончили вуз, вам, вероятно, знакомо это
определение, поскольку в наши дни во многих университетах и колледжах или
есть отдельный факультет статистики, или же статистика предлагается как одно
из направлений специализации на математическом факультете. Статистика все
чаще преподается и в средней школе, а в США число учащихся, выбравших
классы с углубленным изучением статистики, быстро растет.
Статистика в университетах - это не только курс для тех, кто решил
специализироваться в этой области. На многих факультетах от студентов требуется
прослушать один или несколько курсов по статистике, помимо тех предметов, на
которых они специализируются. Кроме того, полезно знать, что многие важные
методы современной статистики были разработаны людьми, которые изучили и
использовали статистику во время своей работы в другой области знаний.
Стефан Рауденбуш (Stephen Raudenbush), создатель иерархического линейного
моделирования, изучал основы политического анализа и оценочных исследований
в Гарварде, а Эдвард Тыофт (Edward Tufte), наверное, лучший специалист в мире
по статистической графике, начинал свою карьеру как политолог: он защитил
докторскую диссертацию в Йельском университете по американским движениям в
защиту гражданских прав.
Поскольку статистика все чаще применяется во многих специальностях и на
всех уровнях от управляющих до рядовых рабочих, базовые знания в этой области
необходимо получить многим людям, давно закончившим школу. Они часто
недостаточно обеспечены учебниками, предназначенными для вводных
университетских курсов, а эти пособия слишком специализированы, слишком много
внимания уделяют вычислениям и слишком дороги.
Наконец, статистику нельзя отдать на откуп статистикам, поскольку каждому
из нас следует принимать участие в современной общественной жизни, в
частности понимать многое из того, что вы прочли в газетах и услышали по радио или
телевизору. Рабочие знания по статистике - лучшее противоядие от вводящих в
заблуждение или совершенно ложных числовых данных (исходящих или от
политиков, или рекламных агентов, или от реформаторов социальной сферы),
которые, похоже, составляют постоянно возрастающую часть ежедневно поглощаемой
нами информации. Вот почему классическая книга Дэррила Хаффа (Darryl Huff),
опубликованная в 1954 г., «Как лгать при помощи статистики» ("How to Lie with
Statistics") до сих пор пользуется спросом. Статистику легко использовать
неправильно, стандартные способы искажения статистических данных не меняются на
|[H|f &!' Предисловие
протяжении десятилетий, а лучшая защита против тех, кто хотел бы солгать при
помощи статистики, - стать более образованным, чтобы быть способным выявить
лжецов и немедленно остановить их.
Основная цель этой книги
В продаже существует уже столько книг по статистике, что вы могли бы сильно
удивиться, почему я чувствую необходимость добавить еще одну книгу к этому
множеству. Основная причина заключается в том, что я не нашла ни одной книги
по статистике, которая отвечала бы задачам, поставленным мною в «Статистике
для всех». На самом деле, если позволите на мгновение впасть в поэтическое
настроение, ситуация состоит в том, что, перефразируя состояние старого морехода
Кольриджа, «книги, повсюду книги, но ни одной, по которой можно научиться»2.
Проблемы, которые я постаралась решить в этой книге, таковы:
• нужда в книге, которая была бы посвящена использованию и
пониманию статистики в контексте исследований или прикладной науки, не как
отдельного набора математических методов, а как части процесса
обоснования заключений при помощи цифр;
• необходимость включения таких тем, как теория измерений и управление
данными во введение в статистику;
• необходимость в книге по статистике, которая не была бы посвящена
одной конкретной области знаний. Простейшая статистика в основном
одинакова для всех дисциплин (тест Стыодента работает одинаково для
данных из области медицины, финансов или криминальной юстиции), так
что незачем умножать тексты, представляя одну и ту же информацию
немного в другом ракурсе;
• нужда во введении в статистику, которое было бы компактным, недорогим
и простым для понимания начинающих, избегая снисходительного тона
или излишнего упрощения.
Так кто же предполагаемые читатели «Статистики для всех?» Я вижу три
группы читателей, для которых эта книга будет наиболее полезной:
• учащиеся, которые посещают вводные курсы по статистике в средней
школе, колледжах и университетах;
• взрослые люди, которым нужно освоить статистику для выполнения
текущих задач или для карьерного роста;
• те, кому интересно узнать, что такое статистика, из любопытства.
В этой книге я делаю акцент не на конкретные методы, хотя многим из них вы
научитесь в процессе чтения, а на обосновании заключений при помощи
статистики. Можно сказать, что цель этой книги в меньшей степени заключается в том,
чтобы производить статистические вычисления, и в большей степени, - чтобы
мыслить статистически. Что это значит? Мышление с использованием чисел тре-
2 Имеются в виду строки поэмы английского поэта Сэмюэла Кольриджа «Сказание о старом
мореходе»: «Вода, пода, одна вода/Мы ничего не пьем» (вольный перевод Ы. С. Гумилева). - Прим. пер.
Статистика в информационную эпоху
¦¦¦а
бует определенных навыков. В частности, я делаю упор на осмысление данных и
использование статистики для облегчения этого процесса. Во многих главах
приведены практические задания, которые задуманы как повод пересмотреть
представленный материал и подумать о ключевых понятиях, введенных в данной
главе, они не требуют бездумных вычислений.
Весь материал «Статистики для всех» был переработан, и многие главы
дополнены новыми примерами и упражнениями. В частности, добавлены примеры
работы с пропорциями, а также примеры с использованием реальных наборов данных
из таких источников, как Проект ООН по развитию человечества (United Nations
Human Development Project) и Система слежения за факторами поведенческого
риска (Behavioral Risk Factor Surveillance System). Оба этих набора данных можно
бесплатно скачать из Интернета, так что студенты могут экспериментировать с
ними, а также воспроизвести процедуры, описанные в этой книге. В это издание
также добавлена глава 19. Я сделала это, потому что заметила, что умение доводить
до сведения окружающих статистическую информацию по меньшей мере так же
важно, как и способность выполнять статистические вычисления, в особенности
для тех, кто учится статистике для своей профессиональной деятельности. Также
добавлено несколько новых приложений, в основном для того, чтобы сделать
книгу более самодостаточной и дружественной к читателю. Эти приложения
включают вероятностные таблицы для самых распространенных типов распределений,
перечень информационных ресурсов Интернета, словарь и таблицу
статистических обозначений.
Статистика в информационную эпоху
Стало модным говорить, что мы живем в информационную эпоху, когда люди
получают и распространяют столько сведений, что никто не может быть в курсе
всего. Это клише основано на правдивом наблюдении; общество «тонет» в данных,
и, похожа, эта проблема становится только острее. В этом есть свои плюсы и свои
минусы. К положительным моментам можно отнести то, что широкий доступ к
компьютерным технологиям и электронным средствам хранения и
распространения данных облегчил доступ к информации, так что теперь у исследователей
снизилась потребность в поездках в определенную библиотеку или архив для работы
с печатными источниками.
Тем не менее данные сами по себе ничего не значат. Они должны быть
упорядочены и интерпретированы людьми, чтобы обрести смысл, так что полноценная
жизнь в информационную эпоху подразумевает глубокое понимание данных,
включая способы их сбора, анализа и интерпретации. И поскольку одни и те же
данные могут быть часто интерпретированы разными способами для обоснования
совершенно противоположных заключений, даже людям, которые сами не
работают в области статистики, нужно понимать, как статистика работает и как выявить
безосновательные заявления и аргументы, основанные на неправильном
использовании данных.
ЯШНН1' -i Предисловие
Структура книги
«Статистика для всех» состоит из трех частей: вводная информация (главы 1-4),
где закладывается необходимое основание для понимания последующих глав;
методы предсказательной статистики (главы 5-13); специальные методы, которые
используются в различных областях науки (главы 14-16), и вспомогательные
темы, которые часто являются частью работы статистика, даже если они не
относятся к статистике как таковой (главы 17-20). Вот более детальное содержание
глав.
Глава 1. Основные понятия, связанные с измерениями
Обсуждаются основополагающие вопросы статистики, включая шкалы
измерений, операционализацию, опосредованное измерение, случайные и
систематические ошибки, надежность и валидность, а также типы
смещения измерений.
Глава 2. Теория вероятности
Описаны основные понятия теории вероятности, включая испытания,
события, независимость, взаимное исключение, правила аддитивности и
перемножения, комбинации и перестановки, условную вероятность и
теорему Байеса.
Глава 3. Статистический вывод
Введены некоторые базовые понятия статистического вывода, включая
распределение вероятностей, зависимые и независимые переменные,
генеральные совокупности и выборки, распространенные способы создания
выборок, центральную предельную теорему, проверку гипотез, ошибки
первого и второго типа, доверительные интервалы и значения р, а также
преобразование данных.
Глава 4. Описательные статистики и графическое представление данных
Дана информация о распространенных показателях центральной
тенденции и разброса, включая среднее арифметическое, медиану, моду,
абсолютный размах, межквартильный размах, дисперсию и стандартное
отклонение, а также обсуждаются выбросы. В этой главе рассмотрены наиболее
часто используемые графические способы представления статистической
информации, включая частотные таблицы, столбчатые и круговые
диаграммы, диаграммы Парето, диаграммы типа «стебель с листьями»,
диаграммы размаха и рассеяния, а также линейные графики.
Глава 5. Категориальные данные
Представлен обзор концепций категориальных и интервальных данных,
введено понятие таблицы сопряженности. В этой главе обсуждаются такие
статистические методы, как тест хи-квадрат на независимость, тест
равенства пропорций, критерий согласия, точный тест Фишера, тест МакНемара,
тесты пропорций для больших выборок, а также меры сопряженности для
категориальных и порядковых данных.
Структура книги
¦a
Глава 6. t-критерий
Обсуждается распределение Стыодента, теория и применение теста Стыо-
дента для одной выборки, для двух независимых выборок, для результатов
повторных измерений и в случае неравенства дисперсий.
Глава 7. Коэффициент корреляции Пирсона
При помощи диаграмм, демонстрирующих разную силу связи между двумя
переменными, вводится понятие связи, также обсуждается коэффициент
корреляции Пирсона и коэффициент детерминации.
Глава 8. Введение в регрессию и дисперсионный анализ
Показано отношение линейной регрессии и дисперсионного анализа к
концепции обобщенной линейной модели, и обсуждаются допущения,
которые принимаются при использовании этих видов анализа данных.
Обсуждается и на примерах разбирается применение простой регрессии (для двух
переменных), однофакторного дисперсионного анализа и апостериорного
тестирования гипотез.
Глава 9. Многофакторный дисперсионный анализ и ковариационный анализ
Обсуждаются более сложные схемы дисперсионного анализа, включая
двух- и трехфакторный дисперсионный анализ и ковариационный анализ,
а также поднимается тема взаимодействия переменных.
Глава 10. Множественная линейная регрессия
Регрессионная модель расширяется за счет включения множественных
независимых переменных. Рассмотрены связи между независимыми
переменными, стандартизованные и нестандартизованные коэффициенты,
фиктивные переменные, способы построения моделей, а также отклонения
от допущений, принимаемых при линейной регрессии, включая
нелинейность, автокорреляцию и гетероскедатичность.
Глава 11. Логистическая, мультиномиальная и полиномиальная регрессия
Расширяет применение регрессионного анализа до бинарных данных
(логистическая регрессия), категориальных данных (мультиномиальная
регрессия) и нелинейных моделей (полиномиальная регрессия), также
обсуждается проблема избыточной подгонки модели.
Глава 12. Факторный, кластерный и дискриминантный анализ
Описаны три сложные статистические процедуры: факторный, кластерный
и дискриминантный анализ, обсуждаются группы задач, для решения
которых эти методы могут быть полезны.
Глава 13. Непараметрическая статистика
Обсуждается, когда нужно использовать непараметрическую статистику
вместо параметрической, а также описаны методы для внутри- и
межгрупповых сравнений, включая тесты Вилкоксона, Манна-Уитни, Краскел-
Уоллиса, Фридмана, критерий знаков и медианный критерий.
Глава 14. Статистика для бизнеса и контроля качества
Приведены статистические методы, которые часто используются в бизнесе
Предисловие
и при контроле качества. Описанные аналитические и статистические
процедуры включают в себя индексы, временные серии, критерии принятия
решений минимакс, максимакс и максимин, принятие решений в условиях
риска, деревья решений и контрольные карты.
Глава 15. Статистика в медицине и эпидемиологии
Вводятся понятия и демонстрируются статистические методы, которые
особенно актуальны для медицины и эпидемиологии. В главу вошли такие
темы, как определение и использование отношений, пропорций и долей,
показатели заболеваемости и распространения, исходные и
стандартизованные данные, прямая и непрямая стандартизация, меры риска, искажающие
факторы, коэффициент несогласия (простой и Мантеля-Гензеля), а также
вычисления точности, мощности и объема выборок.
Глава 16. Статистика в образовании и психологии -
Обсуждаются концепции и статистические методы, наиболее часто
используемые в образовании и психологии, такие как перцентили,
стандартизованные баллы, методы создания тестов, классическая теория тестов,
надежность комбинированного теста, меры внутренней согласованности,
включая коэффициент альфа, а также методы анализа заданий. Также
приводится обзор современной теории тестирования.
Глава 17. Управление данными
Обсуждаются практические вопросы управления данными, включая
кодификацию, группировку данных, методы устранения ошибок в файлах,
методы хранения данных в цифровом виде, текстовые и числовые данные
и пропущенные значения.
Глава 18. Планирование исследования
Обсуждаются наблюдения и эксперименты, слагаемые хорошего
планирования исследований, этапы сбора данных, типы валидности и способы
ограничить или предотвратить искажение результатов.
Глава 19. Представление статистических материалов
Рассмотрены основные проблемы представления статистической
информации различной аудитории, затем более детально обсуждается изложение
результатов для специализированных журналов, для общественности и для
коллег по работе.
Глава 20. Оценка работ по статистике других авторов
Содержит руководство по проверке правильности использования
статистики, включая список контрольных вопросов, которые помогут оценить
представление статистических данных, и примеры манипуляций с
корректными статистическими методами для подтверждения спорных
заключений.
В шести приложениях приведены сведения, которые лежат в основе материала,
изложенного в основной части книги, а также указаны источники дополнительной
информации:
Структура книги
Ш
Приложение А. Обзор основных математических понятий
Содержит материалы для самопроверки и обзор основ арифметики и
алгебры для тех, у кого остались лишь ускользающие воспоминания о последнем
курсе по математике. Обсуждаются арифметические правила, экспоненты,
корни и логарифмы, методы решения уравнений и систем уравнений,
дроби, факториалы, перестановки и комбинации.
Приложение В. Краткий обзор статистических пакетов
Представлен обзор некоторых наиболее распространенных компьютерных
программ, используемых для статистических вычислений, приведены
примеры простейшего анализа данных в каждой из программ, обсуждаются
сильные и слабые стороны каждой из них. Рассмотрены такие программы,
как Minitab, SPSS, SAS и R; также обсуждается использование Microsoft
Excel (это не статистический пакет) для статистического анализа.
Приложение С. Ссылки
Аннотированный список литературы к каждой главе включает бумажные
публикации и сайты в Интернете, которые упоминаются в тексте, и прочие
источники, с которых хорошо начать углубленное изучение
соответствующей темы.
Приложение D. Таблицы вероятностей для распространенных типов
распределений
Приведены таблицы для большинства широко используемых
статистических распределений - нормальное, Стьюдента, биномиальное и хи-квадрат.
Даже в эпоху компьютера и Интернета стоит знать, как читать таблицы
распределений, и удобно иметь их под рукой в печатном виде.
Приложение Е. Интернет-ресурсы
Приведен перечень лучших сайтов в Интернете, которые пригодятся тем,
кто учит, использует или преподает статистику. Источники разделены на
общие руководства, словари, вероятностные таблицы, калькуляторы и
учебники.
Приложение F. Словарь статистических терминов
Сюда вошли греческий алфавит (проклятие многих начинающих
статистиков), расшифровка статистических обозначений и краткий словарь для
большинства статистических терминов, использованных в этой книге.
Эта книга - руководство, которое можно приспосабливать к имеющимся
знаниям и нуждам отдельных читателей. Некоторые главы посвящены темам, которые
часто отсутствуют в вводных книгах по статистике, однако я считаю их важными.
Это касается управления данными, изложения статистических результатов и
чтения статистических статей, написанных другими людьми. Эти главы также
послужат полезным справочным материалом для людей, которые внезапно обнаружат,
что их назначили разбираться с данными по проекту, или которым было поручено,
более или менее неожиданно, представить статистические данные о работе их
команды. Ни один из этих сценариев, к сожалению, не слишком редок.
m
Предисловие
Классификация сведений на элементарные и сложные зависит от личных
знаний и задач. Я написала «Статистику для всех» так, чтобы она отвечала задачам
многих категорий читателей. Из-за этого невозможно расположить материал в
идеальной последовательности, так, чтобы это удовлетворяло запросам каждого.
Это соображение приводит нас к важному-заключению: нет никакой
необходимости читать главы в том порядке, в каком они представлены здесь. В статистике
есть много дилемм типа «что было раньше, яйцо или курица?». К примеру, вы не
можете спланировать эксперименты, не зная, какие типы статистической
обработки данных вам доступны, при этом вы не сможете понять, как применяется
статистика, без каких-либо знаний о планировании исследований. Сходным
образом может казаться логичным, что тот, кто занялся управлением данными, уже
имеет опыт статистического анализа, однако я консультировала многих
лаборантов и руководителей проектов, которым было поручено разобраться с объемными
наборами данных до того, как они прослушали хотя бы один курс по статистике.
Так что читайте эти главы в том порядке, который облегчает выполнение стоящих
перед вами задач, и не стесняйтесь пропустить что-то и сосредоточиться па том,
что отвечает вашим конкретным потребностям.
Не весь материал этой книге и актуален для каждого, это наиболее очевидно
для глав 14-16, которые посвящены определенным областям науки (бизнес и
контроль качества, медицина и эпидемиология, образование и психология
соответственно). Однако полезно быть открытым всему новому, если дело касается знания
статистических методов. В данный момент вы можете быть уверенным, что вам
никогда не понадобится проводить нспараметрический тест или логистический
регрессионный анализ, но вы никогда не знаете, что пригодится в будущем. Также
неправильно слишком четко делить методы по областям знаний; поскольку
статистические методы в конечном счете имеют дело с числами, а не с содержанием;
методы, разработанные в одной области знаний, часто пригождаются в другой.
Например, контрольные карты (обсуждаемые в главе 14) были разработаны для
производственных нужд, а теперь широко используются во многих областях от
медицины до образования, тогда как коэффициент несогласия (глава 15),
разработанный в эпидемиологии, теперь применяется ко всем типам данных.
Условные обозначения, используемые
в этой книге
В этой книге принята следующая система обозначений:
Обычный текст
Обозначает названия пунктов меню, опций, кнопок на экране и клавишей
клавиатуры (таких как Alt и Ctrl).
Курсив
Обозначает новые термины, названия файлов и их расширения, путь к
файлам, директории и утилиты Unix.
Об авторе IDS
Нижнее подчеркивание
Ссылки на страницы в Интернете, адреса электронной почты.
Эта пиктограмма обозначает совет, предложение или общее замечание.
\М
^?***\ Эта пиктограмма обозначает предостережение.
Благодарности
На обложке указан только один автор, однако многие люди приложили руку к
созданию этой книги.
Я хотела бы поблагодарить моего агента Нейла Залкинда (Neil Salkind) за
постоянные советы и поддержку; команду О'Рейлли, включая Мэри Трезелер (Магу
Treseler), Сару Шнейдер (Sarah Schneider) и Меган Бланше (Meghan Blanchette),
а также всех статистиков, которые помогали при техническом рецензировании
текста. Я бы также хотела поблагодарить моих далеких от статистики друзей,
которые постоянно требовали от меня объяснять им статистические концепции, что
подтолкнуло меня к написанию этой книги, и моих коллег из центра устойчивой
журналистики в государственном университете Кеннесо (Center for Sustainable
Journalism at Kennesaw State University) за их терпение и снисходительность во
время моего труда над переработкой этой книги. От всей души хочу
поблагодарить мою бывшую коллегу Ранд Росс (Rand Ross) из университета Вашингтона
в Сент-Луисе (Washington University in St. Louis) за то, что она помогала мне не
сойти с ума во время написания первого издания этой книги, и моего мужа Дэна
Пека (Dan Peck) за то, что он был воплощением современного супруга, готового
всегда оказать поддержку.
Об авторе
Сара Бослаф (Sarah Boslaugh) получила докторскую степень по исследованиям
и оцениванию в городском университете Нью-Йорка. В течение 20 лет она
работала как статистический аналитик в различных профессиональных
организациях, включая городской совет Нью-Йорка по образованию (New York City Board of
Education), исследовательское отделение (Institutional Research Office) городского
университета Нью-Йорка, медицинский центр Монтефиоре (Montefiore Medical
Center), отдел социального обеспечения в Вирджинии (Virginia Department of
Social Services), медицинская организация Магеллан (Magellan Health Services),
медицинская школа при университете г. Вашингтон (Washington University School
of Medicine) и организации BJC HealthCare. Она преподавала статистику в разных
шшшшв
Предисловие
аудиториях, а сейчас работает составителем заявок на гранты в государственном
университете Кепнесоу (Kennesaw).
Сара Бослаф уже опубликовала две книги: «Справочник по
программированию в SPSS средней сложности: использование программного кода для
управления данными» ("An Intermediate Guide to SPSS Programming: Using Syntax
for Data Management", SAGE Publications, 2004) и «Вторичные источники
данных в здравоохранении» ("Secondary Data Sources for Public Health", Cambridge
University Press, 2007), а также редактировала «Энциклопедию эпидемиологии»
("Encyclopedia of Epidemiology" for SAGE Publications, 2007).
В 2013 году издательством SAGE опубликована её новая книга, - «Системы
здравоохранения во всем мире: сравнительный справочник» ("Healthcare Systems
Around the World: A Comparative Guide").
Об иллюстрации на обложке
На обложке книги «Статистика для всех» изображен колючий краб-паук (Maja
squinado, Maja brachydactyld). Этот краб обитает в северо-восточной части
Атлантического океана и в Средиземном море. Это самый крупный краб в Европе,
диаметр его карапакса колеблется от 5 до 17 см. Его легко отличить от других крабов
по двум похожим на рога шипам между глаз и шести, или около того, шипикам
расположеным на каждой стороне панциря. Панцирь краба-паука красноватый с
розовыми, коричневыми или желтыми отметинами и вся его поверхность покрыта
мелкими шипами, как следует из названия животного.
Крабы-пауки иногда выползают на берег, но предпочитают глубины от 30 до
180 м. Это одиночные животные, за исключением периода спаривания, когда они
образуют большие скопления. В годы, когда эти крабы особенно многочисленны,
они могут досаждать ловцам омаров, поскольку могут разорять ловушки. Крабы-
пауки сами являются объектом промысла из-за вкусного мяса конечностей.
Самцы крабов-пауков - активные хищники; их, кажущиеся слабыми
конечности, на самом деле довольно мощные и могут открывать раковины небольших
моллюсков, которых крабы поедают. Их конечности имеют два сочленения, так
что крабы-пауки способны достать клешнями до своей спины, чтобы ущипнуть
обидчика, хотя в целом безопаснее его держать за створки панциря. Клешни самок
мельче и менее подвижные, поэтому они более уязвимы для нападения. Для
защиты от врагов, к которым относятся омары, рыбы-губаны и каракатицы, многие
виды крабов-пауков украшают свои колючие панцири водорослями, губками или
грунтом, чтобы лучше замаскироваться на фоне дна.
Изображение на обложке предоставлено естественно-научной библиотекой
Лндекксра (Lydekker's Library of Natural History).
ГЛАВА 1.
Основные понятия,
связанные с измерениями
Для использования статистики при решении определенной задачи необходимо
преобразовать информацию об этой задаче в данные. Это значит, что вы
должны разработать или применить систему присвоения значений, чаще всего
чисел, ключевым для рассматриваемой проблемы объектам или понятиям. Это не
скрытый от понимания непосвященных процесс, а то, что люди делают
ежедневно. Например, когда вы покупаете что-нибудь в магазине, сумма, которую вы
платите, - это измерение: она выражает количество денег, которое вы должны
заплатить, чтобы купить что-то. Аналогичным образом, когда вы утром
становитесь на весы, число, которое вы видите, - это измерение вашего веса. В
зависимости от места вашего проживания это число может быть выражено в фунтах
или килограммах, но принцип присвоения числа физической величине (весу)
сохраняется в любом случае.
Подходящие для анализа данные не обязательно должны быть числовыми.
Например, понятия мужчина и женщина обычно используются в науке и
повседневной жизни для классификации людей, и за этими категориями не стоит никаких
чисел. Аналогично мы часто говорим о цветах объектов, таких как красный и
синий, и к этим категориям также не привязано никаких чисел. (Хотя вы можете
сказать, что этим цветам свойственны разные длины волны света, это знание не
нужно для классификации объектов по цветам.)
Этот тип категориального мышления - привычный ежедневный опыт, и нас
редко раздражает тот факт, что разные категории используются в разных
ситуациях. Например, художник может различать карминовый, малиновый и гранатовый,
тогда как неспециалисту достаточно называть их все красным. Сходным образом
социолог, собирающий информацию о семейном статусе людей, будет различать
никогда не состоявших в браке, разведенных и вдовцов, тогда как для кого-нибудь
человек, относящийся к любой из этих трех категорий, будет просто холостым.
Здесь важно понять, что уровень детализации, используемый при классификации,
должен соответствовать ситуации, исходить из цели классификации и назначения
собранной информации.
шхшшт
Глава 1. Основные понятия, связанные с измерениями
Измерение
Измерение - это процесс систематичного присвоения чисел объектам и их
свойствам для облегчения использования математического аппарата при изучении и
описании объектов и их взаимосвязей. Некоторые типы измерений абсолютно
конкретны: например, измерения веса человека в фунтах или килограммах или
его роста в футах и дюймах или метрах. Обратите внимание, что определенная
система единиц измерения не так важна, как применение определенного набора
правил: мы можем легко преобразовать вес, выраженный в килограммах, в вес,
выраженный в фунтах, например. Хотя любая система единиц измерения может
показаться необоснованной (попробуйте защитить футы и дюймы от нападок того,
кто вырос, используя метрическую систему!), пока система остается постоянной
по отношению к измеряемым признакам, мы можем использовать полученные
результаты для вычислений.
Измерения не ограничены физическими величинами, такими как рост и вес.
Тесты для измерения абстрактных величин, таких как интеллект или
академическая успеваемость, широко используются в образовании и психологии, а
разработкой и улучшением методов исследований этих типов абстрактных конструктов
занимается специальная дисциплина - психометрика. Утверждать, что
определенное измерение точно и осмысленно, более трудно, если его нельзя напрямую
наблюдать. Однако вы можете оценить точность одной шкалы измерений,
сравнивая результаты, которые были получены при помощи другой шкалы, точность
которой известна. Применимость такого подхода при измерении веса не вызывает
сомнений, дело обстоит сложнее, когда вам нужно измерить такой параметр, как
интеллект. В данном случае не только не существует общепризнанных метрик
интеллекта, с которыми можно сравнить новую шкалу, нет даже общего согласия по
поводу того, что подразумевается под интеллектом. Иными словами, трудно
уверенно судить о чьем-нибудь интеллекте, поскольку не существует ясного способа
его измерения и, строго говоря, нет общепринятого определения интеллекта. Эти
вопросы особенно актуальны в социологии и образовании, в которых основная
часть исследований сосредоточена на таких абстрактных понятиях.
Типы измерений
В статистике обычно выделяют четыре типа, или уровня, измерений, эти же
термины могут быть отнесены и к самим данным. Уровни измерений различаются и
по смыслу чисел, используемых в системе измерений, и по типу статистических
процедур, которые корректно применять для обработки данных.
Номинальные данные
Для номинальных данных числа выступают в виде имени или ярлыка и ие имеют
смысла как числа. Например, вы можете создать переменную для пола, которая
принимает значение 1 для мужчин и 0 для женщин. Эти 0 и 1 не имеют смысла как
Типы измерений
шшшш
числа, а выступают в роли «ярлыков», сходным образом вы можете закодировать
эти значения как М и Ж. Однако исследователи часто предпочитают числовую
кодировку значений по нескольким причинам. Во-первых, это упрощает анализ
данных, поскольку некоторые статистические программы не допускают
использования нечисловых значений при определенных типах обработки данных. (Так что
любые нечисловые данные придется перекодировать перед анализом.) Во-вторых,
кодирование данных при помощи чисел позволяет избежать некоторых проблем
при вводе данных, таких как конфликт между прописными и строчными буквами
(для компьютера Мим- разные значения, однако тому, кто вводит данные, они
могут показаться одинаковыми).
Номинальные данные могут иметь больше двух значений. Например, если вы
изучаете связь между опытом игроков в бейсбол и их зарплатой, вы можете
классифицировать игроков по их основной роли, используя традиционную систему:
1 - подающий, 2 - принимающий, 3 - первый полевой игрок и так далее.
Если вы не можете решить, относятся ли ваши данные к номинальному типу,
задайте себе вопрос: отражают ли числа некоторое свойство так, что более
высокое значение означает наличие большего количества этого свойства? Рассмотрим
пример с кодировкой пола, где 0 обозначает женщину, а 1 - мужчину. Есть ли
некоторое свойство пола, которым мужчина обладает в большей степени, чем
женщина?1 Конечно нет, и кодировка будет работать, если обозначать женщин 1, а
мужчин 0. Тот же принцип применим и к бейсбольным игрокам: нет такого качества,
как «бейсбольность», которое свойственно в большей степени полевым игрокам,
по сравнению с подающими. Числа - всего лишь удобный способ обозначения
объектов исследования, и наиболее важно то, что каждому состоянию признака
соответствует свое значение. Другое название номинальных данных - категориаль -
ные} что отражает тот факт, что измерения скорее разделяют объекты на категории
(мужчина или женщина, подающий или полевой игрок), а не измеряют некоторые
присущие им свойства. В пятой главе обсуждаются методы анализа, подходящие
для этого типа данных, и некоторые из разобранных в главе 13 непараметрическнх
методов также подходят для категориальных данных.
Когда данные принимают только два значения, как в случае с женщинами и
мужчинами, их называют бинарными. Этот тип данных настолько распространен,
что для его анализа разработаны специальные методы, включая логистическую
регрессию (обсуждается в главе 11), которая применяется во многих областях
науки. Многие используемые в медицине статистики, такие как отношение шансов
и отношение рисков (обсуждаются в главе 15), были разработаны для описания
взаимосвязи между двумя бинарными переменными, поскольку они очень часто
используются в медицинских исследованиях.
Порядковые данные
Порядковые данные - это данные, которые можно расположить в каком-либо
осмысленном порядке, так что большие значения соответствуют большему про-
Неудачный пример с точки зрения биолога. - Прим. пер.
шшшт
Глава 1. Основные понятия, связанные с измерениями
явлению какого-либо признака, по сравнению с меньшими значениями.
Например, в медицине ожоги часто характеризуются их степенью, которая выражается
через объем поврежденных при ожоге тканей. Первая степень - это покраснение
кожи, слабая боль и повреждение только эпидермиса (наружного слоя кожи).
Вторая степень - это появление волдырей,4 при этом повреждается наружный
слой дермы (слой кожи между эпидермисом и подкожными тканями). Третья
степень ожога затрагивает всю дерму и характеризуется обугливанием кожи и
возможным разрушением нервных окончаний. Эти категории можно
расположить в логической последовательности: ожоги первой степени характеризуются
наименьшим разрушением тканей, ожоги второй степени - более значительным
разрушением, а третьей степени - самым серьезным. Однако не существует
какого-либо метрического аналога линейки или шкалы, чтобы определить, каково
расстояние между этими категориями, или определить, одинаковы ли различие
между ожогами первой и второй степеней и различие между ожогами второй и
третьей степеней.
Многие порядковые шкалы используют ранжирование. Например, кандидаты
на какую-то должность могут быть ранжированы отделом кадров по
привлекательности для найма. Это ранжирование дает понять, какой кандидат наиболее
предпочтителен, какой занимает второе место и так далее, но остается неясным,
сходны ли на самом деле оценки первого и второго кандидатов, или первый
кандидат намного более предпочтителен, чем второй. Можно также ранжировать
страны мира по численности их населения, создав разумный порядок, не говоря
ничего, например, о соотношении различий между 30-й и 31-й странами и различий
между 31-й и 32-й странами. Числа в порядковых данных несут больше смысла,
чем в номинальных, и разработано много статистических методов для полного
использования информации, содержащейся в упорядоченных данных, не
подразумевающих еще каких-нибудь свойств этих шкал. Например, для порядковых
данных имеет смысл рассчитывать медиану (центральное значение), но не среднее
арифметическое, поскольку это подразумевает равное расстояние между баллами
и требует деления, для чего нужны данные, характеризующие соотношения.
Интервальные данные
Интервальные данные характеризуются осмысленным порядком и равными
интервалами между измерениями, отражающими равновеликие изменения
количества любой измеренной величины. Наиболее распространенный пример
интервальных данных - это температура, измеренная по шкале Фаренгейта. Если
вы измеряете температуру по этой шкале, то различие между 10 и 25 градусами
(15 градусов) отражает тот же масштаб изменений температуры, что и различие
между 60 и 75 градусами. Для интервальных данных сложение и вычитание имеют
смысл, поскольку разница в 10 градусов характеризует одинаковую степень
различий в температуре на протяжении всей шкалы. Однако у шкалы Фаренгейта нет
естественного нуля, поскольку 0 на этой шкале обозначает не отсутствие
температуры, а просто относительное положение этого значения на шкале. Умножение и
Типы измерений
шшша
деление не имеют смысла для интервальных данных, поскольку такое
утверждение, как, например, «80 градусов - это в два раза жарче, чем 40 градусов» не имеет
смысла (хотя разумно говорить о том, что 80 градусов - это на 40 градусов жарче,
чем 40 градусов). Интервальные шкалы - это редкость, и придумать еще один
распространенный пример такой шкалы сложно. По этой причине термин
«интервальные данные» иногда используется для описания и интервальных данных, и
данных, характеризующих отношения (обсуждаются в следующем разделе).
Данные, характеризующие отношения
Данные, характеризующие отношения, характеризуются всеми свойствами
интервальных данных (осмысленный порядок, равные интервалы) и естественным
нулем. Многие физические измерения - это данные, характеризующие отношения:
например, рост, вес и возраст - все подходят. Также годится доход: конечно, вы
можете заработать 0 долларов в год или иметь 0 долларов на счету в банке, и это
будет обозначать отсутствие денег. Умножение и деление - осмысленные
арифметические операции для этого типа данных, разумно заключить, что кто-то со $100
имеет вдвое больше денег, чем тот, у кого $50, или что человек в возрасте 30 лет
втрое старше десятилетнего.
Нужно отметить, что хотя многие физические измерения - это данные,
характеризующие отношения, большинство психологических измерений - это
порядковые данные. Это особенно справедливо для исследований ценностей или
предпочтений, которые часто измеряются по шкале Лайкерта (Likert). Например,
человеку можно предъявить утверждение (скажем, «правительство должно
больше вкладывать в образование») и попросить его выбрать ответ из упорядоченного
набора вариантов (например, абсолютно согласен, согласен, нет определенного
мнения, не согласен, абсолютно не согласен). Этим вариантам ответов в
некоторых случаях присваиваются числа (например, 1 - абсолютно согласен, 2 -
согласен и т. д.), и это иногда создает впечатление того, что в этом случае можно
применять методы анализа для интервальных данных или данных, характеризующих
соотношения (например, вычисление среднего арифметического). Правильно ли
это? С точки зрения статистиков - нет, но иногда вам приходится делать то, что
от вас требует начальство, а не то, что вы считаете верным на основании
теоретических знаний.
Непрерывные и дискретные данные
Другое важное различие существует между непрерывными и дискретными
данными. Непрерывные данные могут принимать любое значение вообще или в
определенном диапазоне. Большая часть данных,, которые измеряются в интервальной
шкале или характеризуют отношения, непрерывна: например, вес, рост,
расстояние и доход - это все непрерывные данные.
Во время анализа данных и моделирования исследователи иногда разбивают
непрерывные данные на категории или объединяют в более крупные группы.
Например, вес можно разделить на интервалы по 10 фунтов или возраст, выражен-
Ш1ШШШ
Глава 1. Основные понятия, связанные с измерениями
ный в годах, можно анализировать по возрастным группам: 0-17 лет, 18-65 лет и
старше 65 лет. С точки зрения статистики, между непрерывными и дискретными
данными не существует четкой границы, что нужно учитывать при определении
метода анализа. Также стоит помнить о том, что если вы регистрируете возраст
в годах, вы по-прежнему разбиваете непрерывную переменную на дискретные
категории. На практике применяются различные правила. Например, некоторые
исследователи говорят, что если у переменной есть 10 и более значений (или, в
качестве альтернативы, 16 или более значений), ее можно спокойно анализировать
как непрерывную. Это решение должно быть основано на контексте, созданном
из принятых стандартов в вашей области исследований и типа анализа, который
предполагается применить.
Дискретные переменные принимают только определенные значения, и
между этими значениями существуют четкие границы. Как гласит старая шутка, у
вас может быть два или три, но не 2,37 ребенка, так что переменная «число
детей» - дискретная. На самом деле любая счетная переменная дискретна, считаете
ли вы число книг, купленных за год, или число визитов к врачу во время
беременности. Номинальные данные всегда дискретны, так же как и бинарные или
порядковые.
Операционализация
Люди, которые только начинают заниматься наукой, часто думают, что вся
сложность научного исследования заключается в основном в статистическом анализе,
так что они сосредоточивают свои усилия на изучении математических формул
и методов компьютерного программирования для выполнения статистических
вычислений. Однако один основной аспект исследований имеет очень мало
отношения и к статистике, и к математике, но полностью обусловлен вашим знанием
предмета исследования и внимательным обдумыванием практических проблем
измерений. Этот аспект носит название операционализация, что означает процесс
определения способа описания и измерения признаков.
Операционализация всегда необходима, когда интересующий нас признак не
может быть измерен напрямую. Очевидный пример - это интеллект. Не
существует способа прямого измерения интеллекта, так что вместо этого мы должны
предложить какую-то величину, которую мы можем измерить, такую как баллы
теста на IQ. Сходным образом не существует способа прямого измерения
«готовности к противостоянию катастрофе» для городов, но мы можем операционализи-
ровать этот показатель, составив список задач, которые должны быть выполнены.
Далее мы можем присвоить каждому городу балл «готовности к противостоянию
катастрофе», исходя из того, сколько задач выполнено, в какой мере и
насколько разумно. В качестве третьего примера представим, что вы хотите исследовать
степень физической активности людей. Если у вас нет возможности отслеживать
их активное поведение напрямую, вы можете операционализовать «степени
физической активности» по активности, заявленной в ходе опроса или описанной в
дневнике.
Типы измерений
ттшш
Поскольку многие качества, изучаемые социологами, абстрактны, операцио-
нализация - это распространенная тема обсуждения у представителей этой
специальности. Однако эта проблема также актуальна и для других областей науки.
Например, основные цели здравоохранения - уменьшение смертности и
снижение страданий и тяжести заболеваний. Смертность легко определяется и
измеряется, но этот показатель часто слишком груб, чтобы быть полезным, поскольку, к
счастью, такой исход редок для многих заболеваний. «Тяжесть заболеваний» или
«страдания», - с другой стороны, это показатели, которые важны при многих
исследованиях, однако не существует способов их прямого измерения, так что эти
показатели нужно операционализовать. К примерам операционализации
тяжести заболевания относится определение концентрации вируса в крови у больных
СПИДом. Снижение страданий или улучшение качества жизни может быть опе-
рационализировано как более высокая оценка собственного здоровья, высокие
баллы разработанного показателя качества жизни, улучшившееся настроение,
зафиксированное в результате личной беседы, или уменьшение количества морфия,
необходимого для облегчения боли.
Есть мнение, что даже измерение физических величин, таких как длина,
требует операционализации, поскольку существуют разные способы измерения даже
конкретных свойств, таких как длина. (В одних случаях подходящим
инструментом может быть линейка, в других - микрометр.) Даже если вы согласны с этой
точкой зрения, кажется ясным, что проблема операционализации более
существенна в социологии, где свойства интересующего нас объекта часто нельзя
измерить напрямую.
Опосредованное измерение
Понятие опосредованное измерение обозначает процесс замены одного измерения
другим. Хотя определение опосредованных измерений можно рассматривать как
разновидность операционализации, в этой книге мы рассмотрим их как отдельную
тему. Наиболее частое использование опосредованных измерений - это замена
дешевым и простым измерением другого измерения, которое будет более сложным
или дорогостоящим, если не невозможным для проведения. Другой пример - это
сбор информации об одном человеке путем опроса другого, например вопрос
матери о настроении ее ребенка.
В качестве простого примера опосредованных измерений рассмотрим
некоторые методы, которые полицейские применяют для оценки трезвости людей на
месте. Без портативной медицинской лаборатории полицейские не могут
измерить уровень спирта в крови и напрямую установить, является ли водитель
пьяным, согласно существующим юридическим нормам. Вместо этого полицейский
может использовать удобные для наблюдения признаки нетрезвости, простые
тесты, которые на месте, как принято считать, позволяют оценить концентрацию
спирта в крови, анализ выдыхаемого воздуха или все вышеперечисленное. К
удобным для наблюдения признакам алкогольного опьянения относятся запах
алкоголя, невнятная речь и покраснение кожи. При простых тестах, которые позволяют
ЕШНТ
Глава 1. Основные понятия, связанные с измерениями
на месте быстро оценить степень алкогольного опьянения, испытуемого обычно
просят постоять на одной ноге или следить глазами за движущимся предметом.
При помощи аппарата для получения пробы на алкоголь можно измерить
концентрацию спирта в выдыхаемом воздухе. Ни один из этих оценочных методов
не позволяет напрямую измерить содержание спирта в крови, но они считаются
разумными способами приблизительной оценки, которыми можно быстро и легко
воспользоваться на месте.
Для знакомства с другим распространенным случаем использования
опосредованных измерений рассмотрим разные методы, которые применяются в США
для оценки качества здравоохранения для больниц и отдельных врачей. Трудно
придумать прямой способ измерения качества здравоохранения, за исключением,
возможно, прямого наблюдения за процессом лечения и его оценки согласно
принятым стандартам (хотя тут также можно возразить, ч-го измерения, необходимые
для подобной оценки, все равно будут операционализацией абстрактного понятия
«здравоохранение»). Применение такого метода оценки будет непозволительно
дорогим, при этом придется обучить большую команду оценщиков и полагаться
на согласованность их мнений, и это будет вмешательством в личную жизнь
пациентов. Решение, которое часто используется в качестве альтернативы, - изучать
события, которые считаются показателями хорошей заботы о здоровье: например,
была ли при визите к доктору правильно проведена консультация по избавлению
от табачной зависимости или были ли получены необходимые медикаменты сразу
после госпитализации.
Опосредованные измерения наиболее полезны, если в дополнение к их
относительной простоте проведения они являются хорошими индикаторами той
характеристики, которая нас действительно интересует. Например, если правильное
выполнение описанных выше процедур заботы о здоровье тесто связано с
хорошим состоянием пациента, а плохое выполнение этих процедур или отказ от них
тесно связано с плохим состоянием пациента, то качество выполнения описанных
процедур - это полезное опосредованное измерение качества здравоохранения.
Если такой тесной связи не существует, то применимость опосредованных
измерений менее оправдана. Ни один математический тест не поможет понять,
является ли один параметр хорошим опосредованным измерением для другого, хотя
вычисление статистик, таких как корреляции или тесты хи-квадрат между этими
показателями, поможет прояснить этот вопрос. Кроме того, у опосредованных
измерений есть свои сложности. В примере с оценкой качества заботы о здоровье по
проводимым процедурам предполагается, что без знания отдельных случаев
можно определить, что называется правильным лечением и что доступна информация
о проведенных процедурах. Как и в случае многих вопросов, связанных с
измерениями, выбор хороших опосредованных измерений - субъективное решение,
основанное на знании предмета исследований, традиционных для данной научной
дисциплины подходов и здравом смысле.
Истинные значения и ошибки
Суррогатные конечные точки
Суррогатные конечные точки - это тип опосредованных измерений, используемых в
клинических испытаниях в качестве замены реальных конечных точек. Например,
определенный протокол лечения может быть разработан для предотвращения смерти
(реальная конечная точка), но поскольку смерть при данном состоянии пациентов может быть
редким событием, для более быстрого накопления данных об эффективности лечения
можно использовать суррогатную конечную точку. Обычно это биологический маркер,
связанный с реальной конечной точкой. Например, если лекарство должно
предотвращать смерть от рака простаты, суррогатной конечной точкой может быть уменьшение
размера опухоли или снижение концентрации специфичных антител.
Проблема использования суррогатных конечных точек заключается в том, что хотя
лечение может быть эффективным для улучшения состояния в этих конечных точках, это
не обязательно значит, что оно приведет к успеху при достижении интересующего нас
клинического результата. Например, мета-анализ, проведенный Стефаном Мичильсом
(Stephan Michiels) с коллегами (ссылка приведена в приложении С), показал, что для
местно-распространенных плоскоклеточных карцином головы и шеи коэффициент
корреляции между контролем над расположением (суррогатная конечная точка) и общей
выживаемостью (реальная клиническая конечная точка) колебался от 0,65 до 0,76 (если
результаты были одинаковыми для обеих конечных точек, коэффициент корреляции был
бы равен 1,00).
Суррогатные конечные точки часто неправильно используются, будучи назначенными
постфактум, замещая результат, определенный до начала испытания или в обоих этих
случаях сразу. Поскольку суррогатной конечной точки легче достичь, это может
привести к разработке нового лекарства с доказанной эффективностью, которое может слабо
влиять на реальную конечную точку или даже быть опасным. Более подробное
обсуждение общих вопросов, связанных с суррогатными конечными точками, приведено в статье
Томаса Р. Флеминга (Thomas R. Fleming), ссылка на которую приведена в приложении С.
Истинные значения и ошибки
Мы можем с уверенностью утверждать, что абсолютно точных измерений очень
мало (если они вообще существуют). Это правда не только потому, что измерения
производят и записывают люди, но также потому, что процесс измерений часто
подразумевает присвоение дискретных чисел непрерывным величинам. Одна из
задач теории измерений состоит в осмыслении и количественном выражении
ошибок, содержащихся в определенном наборе измерений, а также в выявлении
источников и последствий этих ошибок.
Классическая теория измерений рассматривает каждое измерение или
наблюдаемое значение как сумму двух составляющих: истинного значения (Т)2 и
ошибки (Е)К Это выражается в следующей формуле:
Х = Т + Е,
где X - наблюдаемое значение измерения, Т- истинное значение, а Е- ошибка.
Например, весы могут показать, что чей-нибудь вес равен 120 фунтам, в то время
2 От англ. true - истинный. - Прим. пер.
'* От англ. error - ошибка. - Прим. пер.
ЕИНН
Глава 1. Основные понятия, связанные с измерениями
как этот человек на самом деле весит 118 фунтов, а ошибка в два фунта
происходит из-за неточности шкалы. Это можно выразить при помощи приведенной выше
формулы как
120=118 + 2,
что представляет собой просто математическое равенство, выражающее связь
между этими тремя величинами. Однако и Г, и Е - это теоретические конструкты. В
реальном мире мы редко точно знаем истинное значение и, следовательно, также
не можем знать точное значение ошибки. Процесс измерений по большей части
заключается в оценке величины и максимизации «истинной» составляющей и
минимизации ошибки. Например, если вы делаете ряд измерений веса одного и того
же человека в течение короткого промежутка времени (так что его истинный вес
можно считать постоянным), используя недавно откалиброванные весы, вы
можете использовать среднее арифметическое всех этих измерений как хорошую оценку
истинного веса этого человека. Затем вы можете трактовать различия между
отдельным измерением и средним значением как ошибку измерений, такую как
небольшую неисправность весов или неточность в считывании и записи результатов.
Случайная и систематическая ошибка
Поскольку мы живем в реальном мире, а не в идеальной вселенной Платона, мы
предполагаем, что в измерениях содержится некоторая ошибка. Однако не все
ошибки имеют одинаковое происхождение, и мы можем научиться жить со
случайными ошибками, но любыми способами должны избегать систематических
ошибок. Случайные ошибки невозможно предсказать: у них нет какой-либо
определенной закономерности, и считается, что они взаимоуничтожаются при
повторных измерениях. Например, считается, что среднее арифметическое ошибок
в серии измерении равно нулю. Так что если кто-нибудь взвесился 10 раз подряд
на одних и тех же весах, вы можете заметить небольшие различия в
зарегистрированных значениях: некоторые будут меньше истинного, а некоторые - больше.
Если истинное значение веса составляет 120 фунтов, возможно, первое
измерение будет равно 119 фунтам (включая ошибку в -1 фунт), второе - 122 фунтам
(с ошибкой в +2 фунта), третье - 118,5 фунта (ошибка в -1,5 фунта) и т. д. Если
весы точные и все ошибки случайны, то их усредненное по многим наблюдениям
значение будет равно 0, а усредненное значение измеренного веса- 120
фунтам. Вы можете постараться уменьшить величину случайной ошибки, используя
более точные приборы, обучив ваш технический персонал правильному их
использованию и так далее, но вы не можете полностью избавиться от случайной
ошибки.
У случайной ошибки есть еще два свойства: она не связана с истинным
значением, а се величина для одного наблюдения не связана с ее величиной для другого
наблюдения. Первое свойство означает, что значение ошибки для любого
измерения не связано с его истинным значением. Например, если вы взвешиваете нескол ь-
ко человек, истинный вес которых различается, вы не будете ожидать, что ошибка
Надежность и валидность
ЕЛ
для каждого наблюдения каким-либо образом связана со значениями истинного
веса этих людей. Это значит, например, что ошибка не должна быть выше при
больших истинных значениях (истинном весе людей). Второе свойство означает,
что ошибочная составляющая каждого измерения независима и не связана с
ошибочной составляющей любого другого измерения. Например, в серии измерений
величина ошибки не должна увеличиваться со временем, так чтобы более поздние
измерения характеризовались бы большей ошибкой. Характеризуя первое
требование, иногда говорят, что коэффициент корреляции между истинным значением
и ошибкой равен 0, а второе требование иногда выражается в утверждении, что
коэффициент корреляции между ошибками равен 0 (корреляция подробнее
обсуждается в главе 7).
В противоположность изложенному выше значения систематической ошибки
имеют заметную структуру, которая формируется не случайно, а часто имеет
причину или причины, которые можно выявить и устранить. Например, весы могут
быть неправильно калиброваны так, что они всегда показывают на 5 фунтов
больше, чем есть на самом деле, так что среднее результатов многократных
взвешиваний человека с истинным весом 120 фунтов будет равно 125 фунтам, а не 120.
Систематические ошибки могут объясняться человеческим фактором, например
техник считывала показания весов под углом, так что она видела стрелку,
указывающую на большие значения, чем на самом деле. Если закономерность
значений систематической ошибки обнаружена, например ее значения
увеличиваются со временем (так что ошибочная составляющая измерений случайна в начале
эксперимента, а затем возрастает), это полезная информация, поскольку можно
вмешаться в ход эксперимента и повторно калибровать шкалу На выявление
источников систематической ошибки и разработку методов для ее обнаружения и
удаления затрачивается много усилий: это подробнее обсуждается в одном из
следующих разделов «Смещение измерений» на стр. 36.
Надежность и валидность
Существует много способов присвоения данным чисел или категорий, и не все из
этих способов одинаково полезны. Для оценки способов измерений (например,
опроса или теста) есть два параметра - надеясностъ и валидность. В идеале нам бы
хотелось, чтобы каждый используемый нами метод был и надежным, и валидным.
В реальности эти качества не абсолютны, а всегда проявляются в некоторой
степени, которая обычно зависит от обстоятельств. Например, опрос, который весьма
надежен для определенных возрастных групп, может быть ненадежен для другой
возрастной группы. Поэтому вместо обсуждения надежности и валидности как
абсолютных величин часто полезнее оценить надежность и валидность способа
измерений для конкретной задачи и допустимость достигнутого уровня надежности
и валидности в определенном контексте. Надежность и валидность также
обсуждаются в главе 18 в контексте планирования исследования и главе 16 в контексте
образовательного и психологического тестирования.
Глава 1. Основные понятия, связанные с измерениями
Надежность
Надежность характеризует согласованность или воспроизводимость
наблюдений. Например, если мы даем одному и тому же человеку один тест дважды,
будут ли результаты сходными? Если мы научили трех людей пользоваться
шкалой качества социальных взаимодействий, затем показали каждому из них одну
и ту лее видеосъемку взаимоотношений в группе людей и попросили оценить
наблюдаемые социальные взаимодействия, будет ли результат одинаков? Если
у нас есть технический работник, который взвесил одну и ту же деталь 10 раз на
одних и тех же весах, будут ли результаты одинаковыми? В каждом случае, если
ответ будет положительным, мы можем сказать, что тест, шкала или работник
надежны.
Многое в теории надежности было разработано исследователями
педагогической психологии, и поэтому показатели надежности часто описываются в терминах
надежности тестов. Однако вопросы надежности не ограничиваются
тестированием в педагогике; те же самые концепции применимы ко многим другим типам
измерений, включая исследования общественного мнения и поведения.
Обсуждение в этой главе будет проведено на базовом уровне. Вычисление
специализированных показателей надежности обсуждается более детально в главе 16
в контексте теории тестирования. Многие показатели надежности основаны на
коэффициенте корреляции (также просто называемом корреляцией), так что
начинающие статистики могут захотеть сосредоточиться на общей логике надежности и
адекватности и отложить обсуждение подробностей их оценки до ознакомления с
коэффициентом корреляции.
Существуют три основных подхода к измерению надежности, каждый из
которых полезен в своей ситуации и имеет свои достоинства и недостатки:
• надежность множественных событий;
• надежность множественных вариантов;
• надежность внутренней непротиворечивости.
Надежность множественных событий, иногда называемая надежностью
повторного тестирования, характеризуется тем, насколько сходные результаты
получаются при повторном использовании теста или шкалы. Из-за этого ее еще
называют показателем временной стабильности, имея в виду стабильность на
протяжении определенного промежутка времени. Например, один и тот же человек
может дважды с интервалом в две недели характеризовать психическое состояние
пациента, основываясь на видеозаписи интервью, а затем сравнить результаты.
Для того чтобы этот тип оценки надежности имел смысл, необходимо, чтобы
измеряемая характеристика оставалась постоянной, поэтому здесь и идет речь о
видеозаписях интервью, а не о двух интервью с пациентом, психологическое состояние
которого может измениться за две недели. Надежность множественных событий
не может быть оценена для непостоянных характеристик, таких как настроение,
или таких характеристик, которые могут измениться в промежуток между
наблюдениями (например, то, как студентка владеет предметом, который она
интенсивно изучает). Распространенный метод оценки надежности множественных собы-
Надежность и валидность
ИЕ1
тий заключается в вычислении коэффициента корреляции между результатами
каждого теста; это называется коэффициентом стабильности.
Надежность множественных вариантов (также называемая надежностью
параллельных форм) характеризует, насколько сходные результаты дают разные
версии тестов или опросников при оценке одной и той же величины.
Распространенный метод оценки надежности множественных вариантов - это расщепление
выборки на две половины, при котором создается набор объектов, который
считается гомогенным, затем половина объектов выполняет вариант Л, а другая
половина - вариант В. Если два (или более) варианта теста предъявляются одним и
тем же людям в одинаковых условиях, то корреляция между результатами для
каждого варианта теста - это показатель надежности множественных вариантов.
Эта корреляция иногда называется коэффициентом эквивалентности.
Надежность множественных вариантов особенно важна для стандартизированных
тестов, которые имеют много версий. Например, разные версии отборочного теста
(SAT, используемого для оценки способностей к тому или иному разделу наук
у абитуриентов американских колледжей и университетов) калиброваны таким
образом, что полученные результаты равнозначны вне зависимости от варианта
теста, который достался данному абитуриенту.
Надежность внутренней непротиворечивости характеризует, насколько
хорошо вопросы, которые составляют инструмент исследования (например, тест
или анкетирование), отражают одно и то же свойство объекта. Иначе говоря,
показатели внутренней непротиворечивости отражают то, насколько согласованно
составляющие одного исследовательского инструмента измеряют одно и то же.
В отличие от надежности множественных событий или вариантов, внутреннюю
непротиворечивость можно оценить, используя один метод или одно наблюдение.
Надежность внутренней непротиворечивости сложнее оценить, чем надежность
множественных событий или вариантов, для этого были разработаны несколько
методов; они подробно обсуждаются в главе 16. Хотя уже здесь можно отметить,
что все эти методы основаны в основном на корреляции между всеми парами
состояний шкалы или вопросов теста. Если такая корреляция высока, то это
интерпретируется как свидетельство того, что все вопросы направлены на исследование
одной и той же величины, и различные статистики, используемые для измерения
надежности внутренней непротиворечивости, будут высокими. Если корреляция
между ответами на разные вопросы будет низкой или непостоянной, статистики
надежности внутренней непротиворечивости будут меньше, и это
интерпретируется как свидетельство того, что вопросы оценивают разные вещи.
Для тестов, составленных из ряда вопросов на одну тему или имеющих сходную
сложность, которые будут учитываться совместно, наиболее полезны два простых
показателя внутренней непротиворечивости: средний коэффициент корреляции
между вопросами и средний коэффициент корреляции по всем вопросам. Для
вычисления среднего коэффициента корреляции между вопросами вы вычисляете
корреляцию между результатами для каждой пары вопросов и усредняете
полученные значения. Для вычисления среднего коэффициента корреляции по всем
вопросам вы суммируете результаты по всем вопросам и затем высчитываете кор-
ЕШ
Глава 1. Основные понятия, связанные с измерениями
реляцию результатов по каждому вопросу с этой суммой. Средняя корреляция по
всем вопросам - это усредненные корреляции суммарного значения с результатом
по каждому вопросу.
Описанная выше устойчивость результатов при расщеплении выборки на две
половины, - это еще один способ оценки внутренней непротиворечивости.
Недостаток этого метода состоит в том, что если вопросы не гомогенны
по-настоящему, разные варианты расщепления будет порождать варианты несопоставимой
сложности, и коэффициент надежности для каждой пары таких вариантов будет
различаться. Метод, который позволяет преодолеть эту сложность, называется
альфой Кронбаха (Cronbach's alpha), или коэффициентом альфа. Он равнозначен
усредненному значению для всех возможных расщеплений выборки на две
половины. Более подробная информация об альфе Кронбаха, включая пример ее
расчета, изложена в главе 16.
Валидность
Валндность характеризует, насколько хорошо тест или балльная шкала измеряют
то, что планировалось измерить. Некоторые исследователи описывают валида-
цшо как процесс сбора свидетельств в пользу выводов, которые предполагается
сделать на основе обсуждаемых измерений. Ученые расходятся во мнениях
относительно классификации типов валидности, и научный консенсус изменяется со
временем, поскольку разные типы валидации объединялись под общим названием
в один год и разделялись в другой. Чтобы не усложнять все, в этой книге мы будем
придерживаться традиционной классификации валидности, включающей четыре
категории: содержательная валидность, конструктивная валидность, совокупная
валндность и предсказательная валидность. Также мы обсудим очевидную
валидность, которая тесно связана с содержательной валидностыо. Эти типы
валидности обсуждаются далее в главе 18 в контексте планирования исследования.
Содержательная валидность характеризует, насколько хорошо измерения
характеризуют ключевое содержание объекта исследований. Этот показатель
особенно важен, если цель состоит в распространении результатов измерений на
более обширную совокупность объектов. Например, кандидатов на должность
программиста могут попросить выполнить проверочное задание, в котором
требуется написать или интерпретировать программу на языках, с которыми
соискатели должны будут работать. Из-за ограничений по времени подобный экзамен
проверяет только часть тех умений и знаний соискателей, которые могут на самом
деле им пригодиться при профессиональном программировании. Однако если
подмножество знаний и умений выбрано удачно, результат подобного экзамена
может быть хорошим показателем способности человека ко всем важным навыкам
программирования, которые понадобятся ему в этой должности. Если это так, то
мы можем сказать, что экзамен содержательно валиден.
Понятие очевидной валидности тесто связано с содержательной валидностыо.
Характеристика с высокой очевидной валидностыо воспринимается
(представителями общественности или тем, кого предполагается оценивать при помощи этой
Надежность и валидность
¦ма
характеристики) как честная оценка изучаемых качеств. Например, если тест по
геометрии за курс средней школы воспринимается родителями выполняющих
его учеников как справедливый тест для проверки знаний по геометрии, этот тест
имеет хорошую очевидную валидность. Очевидная валидность важна для
формирования доверия; если вы утверждаете, что вы оцениваете знания по геометрии,
но родители учеников с вами не согласны, то они могут быть склонны
игнорировать ваши суждения об уровне подготовки их детей по предмету. Кроме того, если
ученики воспринимают тест по геометрии как что-то совершенно иное, они могут
не быть мотивированы к сотрудничеству и старанию, так что их ответы могут не
отражать адекватно их способности.
Совокупная валидность отражает, насколько хорошо выводы, сделанные на
основании измерений, могут использоваться для предсказания другого поведения
или явления, которое измеряется примерно в то же время. Например, если
результаты теста качества работы учащегося сильно связаны с его успеваемостью в
это время или с результатами сходных тестов, этот тест характеризуется высокой
совокупной валидностью. Предсказательная валидность - это сходное понятие,
однако тут рассматривается способность делать предсказания касательно
некоторого события в будущем. Продолжая предыдущий пример, если результаты теста
качества работы сильно связаны со школьной успеваемостью в следующем году
или с должностью, полученной в будущем, этот тест имеет высокую
предсказательную валидность.
Триангуляция
Поскольку каждая система измерений имеет свои недостатки, исследователи
часто используют несколько подходов к измерению одной и той же величины.
Например, в американских университетах часто используется множество источников
информации для оценки способности к обучению школьников старших классов и
вероятности того, что они будут хорошо успевать в университете. К используемым
в этих целях показателям относятся баллы, полученные на стандартизированных
экзаменах, таких как SAT, высокие'школьные оценки, личная мотивация или эссе и
рекомендации учителей. Аналогичным образом решение о приеме на работу в
компанию часто основано на нескольких источниках информации, включая опыт
работы соискателя, его образование, произведенное им впечатление в ходе интервью
и, возможно, образец результатов его работы и один или более тестов на знания и
личностные качества.
Процесс объединения информации из многих источников для получения
истинных или по меньшей мере более точных значений называется триангуляцией,
по смелой аналогии с геометрической операцией установления положения точки
по ее отношению к двум другим точкам с известным положением. Ключевая идея,
лежащая в основе триангуляции, заключается в том, что хотя единичное
измерение некоторого параметра может содержать слишком большую ошибку (или
известного, или неизвестного типа), чтобы быть надежным или валидным само
по себе, объединяя информацию по нескольким типам исследований, по крайней
ЕШ
I 4
Глава 1. Основные понятия, связанные с измерениями
мере некоторые характеристики которых известны, мы можем добиться
приемлемого измерения неизвестной величины. Мы ожидаем, что каждое измерение
имеет свою ошибку, но мы надеемся, что эти ошибки не относятся к одному типу,
так что при помощи нескольких типов измерений мы можем получить разумную
оценку интересующего нас количества или свойства.
Разработка метода триангуляции - непростое дело. Одна исторически
важная попытка этого - матрица со многими параметрами и методами (multitrait,
mukiinethod matrix, MTMM), разработанная Кэмпбеллом и Фиске (Campbell,
Fiske, 1959). Их основная идея состояла в отделении той составляющей измерения,
которая относится к интересующему нас признаку, от той составляющей, которая
характеризует используемый метод измерений. Хотя эта методология меньше
используется в наши дни и ее описание выходит за рамки пособия для начинающих,
упомянутая концепция остается полезной как пример одного из способа
размышлений об ошибке измерений и валидности.
МТММ - это корреляционная матрица для измерений нескольких параметров,
каждый из которых был оценен при помощи нескольких методов. В идеале для
каждого признака должен был быть использован один и тот же набор методов. Мы
ожидаем, что в этой матрице разные измерения одного и того же признака будут
тесно связаны; например, показатели интеллекта, полученные при помощи
нескольких методов, таких как тест, выполненный при помощи карандаша и бумаги,
решение практических задач и структурированное интервью, должны быть тесно
связаны между собой. По той же логике, показатели, характеризующие разные
параметры, которые измеряются одним и тем же способом, не должны быть тесно
связаны; например, показатели интеллекта, поведения и коммуникабельности,
измеренные при помощи бумажной анкеты, не должны существенно коррелировать
между собой.
Смещение измерений
Выявление смещения измерений (measurement bias) важно почти в любой
научной области, но особенно актуально для социологии. К настоящему времени
обнаружено и описано много частных случаев смещения измерений. Мы не будем
перечислять их все, но обсудим несколько наиболее распространенных. Многие
руководства по планированию исследований очень подробно рассматривают
смещение измерений и могут быть использованы как дальнейший источник
информации по этой теме. Ключевая идея заключается в том, что исследователь всегда
должен помнить о возможности смещения измерений, поскольку неспособность
обнаружить смещение и разрешить связанные с ним проблемы может свести на
нет результаты потенциально уникального исследования.
Смещение измерений может произойти на двух основных этапах: во время
отбора объектов для исследования или во время сбора информации об этих
объектах. В любом случае ключевой признак смещения - то, что его источником служит
скорее систематическая, а не случайная ошибка. В результате смещения анали-
Смещение измерений
шшшшш
зируемые данные закономерным образом отличаются от истинного значения, что
может привести к неправильным заключениям, несмотря на применение
корректных статистических методов. В следующих двух подразделах обсуждаются
некоторые из наиболее распространенных типов смещения, объединенные в две
крупные категории: смещение при создании выборки и смещение при сборе и
регистрации информации.
Смещение при создании выборки
Многие исследования производятся на выборках объектов из генеральной
совокупности, будь то больные лейкемией или произведенные на фабрике приборы,
поскольку изучить всю генеральную совокупность было бы недопустимо дорого,
если вообще возможно. Выборка должна хорошо характеризовать генеральную
совокупность (на которую результаты должны распространиться), чтобы
исследователь мог спокойно использовать полученные для выборки результаты для
характеристики всей генеральной совокупности. Если выборка смещена (это
означает, что она нерепрезентативна), выводы, сделанные на основе такой выборки,
могут быть неприменимыми ко всей генеральной совокупности.
Смещение выбора происходит, если некоторые объекты имеют больше шансов
быть включенными в выборку. Этот термин обычно относится к смещению,
которое происходит в процессе составления выборки. Например, телефонные опросы с
использованием номеров из опубликованных справочников по определению
удаляют из числа потенциальных респондентов людей с неопубликованными
номерами или тех, кто сменил телефонный номер после выхода справочника из печати.
Звонки по случайным номерам решат эту проблему, но по-прежнему не позволят
опросить людей, у которых дома нет телефона. Это затрудняет исследование,
поскольку если исключенные из исследования люди систематически выделяются
по исследуемым свойствам (а это очень распространенная ситуация), результаты
исследования будут смещенными. Например, люди, которые живут в домах без
телефона, обычно беднее тех, у кого телефон есть, а люди, у которых есть
только мобильный телефон, обычно моложе тех, у кого есть еще и домашний. Если
уровень доходов или возраст связаны с изучаемой характеристикой, исключение
таких людей из выборки приведет к смещению результатов исследования.
Смещение из-за волонтеров отражает тот факт, что люди, добровольно
вызывающиеся участвовать в исследованиях, обычно не типичны для генеральной
совокупности. По этой причине результаты, полученные на выборках, полностью
составленных из добровольцев, такие как мнения зрителей, позвонивших в студию
телевизионной передачи, не подходят для решения научных задач (если только
генеральная совокупность не представлена людьми, желающими участвовать в
подобных опросах). В этом примере могут проявиться множественные
механизмы неслучайного отбора. Например, чтобы участвовать в опросе, человек должен
смотреть эту телевизионную программу. Это значит, что, скорее всего, этот человек
находится дома; значит, результаты опросов, проводимых в течение рабочего дня,
могут в основном иметь отношение к пенсионерам, домохозяйкам и безработным.
Глава 1. Основные понятия, связанные с измерениями
Для участия в опросе человек должен иметь свободный доступ к телефону и
обладать определенными личностными характеристиками, которые приведут к тому,
что он снимет телефонную трубку и наберет номер с экрана. Проблемы, связанные
с телефонными вопросами, уже обсуждались, и вероятность того, что личностные
характеристики связаны с изучаемыми параметрами, слишком велика, чтобы ее
игнорировать.
Смещение из-за отсутствия ответа - это обратная сторона смещения из-за
волонтеров. Так же как люди, которые добровольно хотят принять участие в
исследовании, отличаются от остальных, люди, которые отказываются участвовать
в исследовании, когда им предлагают это, скорее всего, отличаются от тех, кто в
этом случае принимает приглашение. Вы, возможно, знакомы с людьми, которые
отказываются участвовать в любых телефонных опросах (я сама такая).
Представляют ли такие люди случайную выборку из генеральной совокупности? Вероятно,
нет; например, объединенное исследование состояния здоровья в Канаде и США
выявило не только различия в частоте ответов канадцев и американцев, но
обнаружило смещение из-за отсутствия ответа почти для всех основных показателей
состояния здоровья и доступности здравоохранения (результаты обобщены здесь:
http://bit.lv/TfI6umy
Информационное цензурирование может приводить к смещению результатов
любого повторного обследования (при котором состояние объектов отмечается на
протяжении временного отрезка). Утрата объектов в ходе долгосрочного
исследования - обычная вещь, но настоящие проблемы начинаются, когда объекты выпадают
не случайно, а по причинам, связанным с предметом исследования. Предположим,
мы проводим клиническое исследование двух способов лечения хронического
заболевания. При этом пациенты случайным образом распределяются по группам,
и статус их заболевания отслеживается в течение пяти лет. Благодаря
случайному созданию выборки наши группы полностью равнозначны. Однако со временем
люди из группы с неэффективным способом лечения будут выходить из
исследования, возможно, чтобы получить лечение в другом месте, что будет приводить
к смещению результатов. Если на последнем этапе наша выборка будет состоять
только из тех, кто участвовал в эксперименте до его окончания, и выбывшие из
исследования не будут представлять собой случайную выборку из его изначальных
участников, анализируемая выборка уже не будет такой абсолютно случайной, как
та, с которой мы начали. Напротив, если выбывание из эксперимента связано с
неэффективностью лечения, набор испытуемых на последнем этапе будет смещен
в сторону людей, положительно реагировавших на проводимое лечение.
Информационное смещение
Даже при создании и сохранении идеальной выборки смещение результатов
может произойти из-за методов сбора и записи данных. Этот тип смещения часто
называется информационным, поскольку он влияет на валидность информации,
на которой основано исследование, что, в свою очередь, может сделать
недействительными результаты исследования.
Смещение измерений
ЕЭ
Когда данные собираются при личных или телефонных интервью, между
интервьюером и респондентом возникает социальная связь. Характер этой связи
может по-разному влиять на качество собранных данных. Если смещение вносится
в собранные данные из-за позиции или поведения интервьюера, это называется
смещением результатов из-за интервьюера. Этот тип смещения может быть
создан непреднамеренно, если интервьюер знает цель исследования или статус
респондента. Подобный тип смещения результатов может также иметь место, если
интервьюер выражает свое собственное отношение или мнение, давая понять, что
он отрицательно относится к исследуемому типу поведения, такому как
беспорядочные сексуальные связи или употребление наркотиков, что снижает
вероятность признания респондента в проявлении подобного поведения.
Смещение воспоминаний вызвано тем, что люди, перенесшие тяжелое
заболевание или травму, с большей вероятностью запоминают события, которые они
считают связанными с этим отрицательным жизненным опытом. Например,
женщины, у которых случался выкидыш, скорее всего, провели много времени,
перебирая воспоминания о воздействиях или событиях, которые, с их точки зрения,
могли привести к выкидышу. Женщины, у которых роды протекали нормально,
могли испытывать сходные воздействия, но они не придавали им такого значения
и, следовательно, не вспомнили бы о них при опросе.
Смещением выявления называют тот факт, что определенные характеристики
могут быть с большей вероятностью обнаружены или озвучены у одних людей
по сравнению с другими. Допустим, спортсмены в некоторых видах спорта
подвергаются периодическому тестированию на употребление стимулирующих
физическое развитие препаратов, и результаты этих тестов доносятся до сведения
общественности. Например, пловцы мирового класса периодически проходят тест
на употребление анаболических стероидов, и положительные результаты тестов
официально регистрируются и также часто попадают в новостные сводки.
Спортсмены, которые участвуют в соревнованиях более низкого уровня или в других
видах спорта, могут использовать те же препараты, но поскольку они не проходят
тестов с такой регулярностью или-из-за того, что результаты тестов не доносятся
до сведения широкой общественности, случаи употребления препаратов не
регистрируются. Было бы неправильно предполагать, например, что поскольку случаи
употребления анаболических стероидов чаще регистрируются у пловцов, чем у
бейсболистов, реальная частота употребления стероидов выше в плавании, чем в
бейсболе. Наблюдаемые различия могут быть вызваны более активным
тестированием комитетом по плаванию и большей открытостью этих результатов.
Смещение социальной желательности вызвано стремлением людей представить
себя в выгодном свете. Это часто побуждает, людей давать такие ответы, которые,
по их представлению, понравятся спрашивающему. Учтите, что этот тип смещения
может наблюдаться даже в отсутствие корреспондента, например при заполнении
бумажной анкеты. Этот тип смещения представляет особенно серьезную
проблему в исследованиях, связанных с поведением или позицией, которые осуждаются
в обществе, например преступное поведение, или о которых неудобно говорить,
ЦН№ - Глава 1. Основные понятия, связанные с измерениями
например половая распущенность. Смещение социальной желательности также
может влиять на ответы, если формулировка вопросов указывает на
«правильный», то есть социально желательный ответ.
Упражнения
Здесь размещен обзор тем, затронутых в этой главе.
Задача
Каких возможных типов смещения результатов вам нужно остерегаться при
следующих сценариях, и каково будет вероятное влияние на результаты?
1. По данным университета, средний годовой заработок выпускников
составляет $120 000. Эти данные были получены в ходе опроса
жертвователей в фонд выпускников.
2. Реализация программы, направленной на улучшение учебных
достижений в средней школе, считается успешной, поскольку все 40 учеников,
участвовавших в ней до конца в течение года (из 100, изначально
задействованных в программе), продемонстрировали статистически значимое
улучшение оценок и результатов стандартных тестов на успехи в учебе.
3. Руководитель заботится о здоровье своих подчиненных, поэтому во
время обеденного перерыва он организовал цикл лекций на такие темы, как
здоровое питание, важность физических упражнений и разрушительное
влияние на здоровье курения и алкоголя. Он провел анонимный опрос
сотрудников (при помощи бумажной анкеты) до и после цикла лекций
и обнаружил, что лекции были эффективными, и привели к увеличению
частоты составляющих здорового образа жизни.
Решение
1. Смещение выбора и смещение из-за отсутствия ответов, - оба влияют на
характеристику анализируемой выборки. Заявленная величина среднего
заработка, скорее всего, завышена, поскольку в фонд выпускников
жертвовали, вероятно, самые успешные из них, а люди, которые стеснялись
своего низкого заработка, отвечали с меньшей вероятностью. Можно еще
предположить смещение социальной желательности, которое также
приведет к завышению значений годового заработка, поскольку выпускники,
вероятно, имели тенденцию заявлять о более высоком заработке, чем они
в реальности получали, поскольку желательно иметь высокий уровень
доходов.
2. На свойства анализируемой выборки повлияет информационное
цензурирование. Оценка эффективности программы для учеников средней
школы, вероятно, завышена. Эта программа определенно была полезной для
тех, кто закончил ее, но поскольку более половины участников выбыли по
ходу, мы не можем сказать, будет ли она полезной для среднего ученика.
Может оказаться так, что ученики, участвовавшие в программе до конца,
Упражнения
ШНЕШ
были более умными или мотивированными, чем выбывшие, или же для
выбывших программа не была полезна.
3. Имеет место смещение результатов из-за социальной желательности. Это,
вероятно, приведет к переоценке эффективности цикла лекций.
Поскольку начальник ясно заявил, что он заботится о здоровом образе жизни
подчиненных, они, скорее всего, будут докладывать о более значительном
оздоровлении образа жизни, чем есть на самом деле, чтобы угодить боссу.
Шкала Лайкерта
Шкала Лайкерта - наверное, наиболее часто используемая в социологии шкала
оценок. Этот тип шкалы был впервые описан в 1932 году Ренсисом Лайкертом (Rensis
Likert, 1903-1981), индустриальным психологом, занимавшим должность директора
социологического института при Мичиганском университете с 1946 по 1970 г. Вопросы
с использованием шкалы Лайкерта, как правило, представлены в виде утверждения, и
испытуемым предлагается выбрать свое отношение к нему из упорядоченного
нечетного числа вариантов (наиболее часто пяти, но иногда семи или девяти). Ниже приведен
пример.
В США следует ввести национальную систему страхования здоровья.
1. Абсолютно согласен.
2. Согласен.
3. Нет определенного ответа.
4. Несогласен.
5. Абсолютно не согласен.
Иногда предлагают четное число ответов, так что нейтральный вариант посередине
отсутствует: это называется методом вынужденного выбора, поскольку респондента
вынуждают выбрать, согласен он с данным утверждением или нет. Обычно порядок ответов
меняется один или более раз на протяжении всего опросника так, что иногда 1 значит
«абсолютно согласен», а иногда «абсолютно не согласен», чтобы выявить тех, кто
автоматически выбирает первый или последний ответ, не читая вопроса.
Данные, собранные при помощи шкалы Лайкерта, являются порядковыми, поскольку
хотя варианты ответа упорядочены, нет никакого основания полагать, что различия
между ними равны. Например, у нас нет способа узнать, равно ли различие между
позициями «абсолютно согласен» и «согласен» различию между вариантами «согласен» и «нет
определенного ответа».
Дьюи побеждает Трумэна
Несколько раз выборы президента США сопровождались ошибочными прогнозами
результатов, основанными на смещенных выборках. Всегда забавно видеть, как ошибается
уважаемое издание или организация, однако эти случаи предостерегают нас от
использования результатов, полученных на смещенной выборке, для характеристики
генеральной совокупности.
В 1936 году журнал «Литературное обозрение» (Literary digest), в котором были угаданы
результаты выборов президента США 1916, 1920, 1928 и 1932 годов, предсказал, что
республиканец Элф Лэндон (Alf Landon) одержит полную победу над демократом
Франклином Рузвельтом (Franklin Roosevelt). Однако мы знаем, что Рузвельт выиграл выборы
1936 года с большим отрывом. Проблема журнального прогноза заключалась в том, что
хотя она была основана на большой выборке (более 2,3 млн респондентов из 10 млн
получивших приглашение принять участие в опросе), эта выборка была смещенной, по-
Глава 1. Основные понятия, связанные с измерениями
скольку состояла из тех, кто имел автомобиль или телефон или был подписан на
«Литературное обозрение». В 1936 году доходы этих людей превышали средний уровень, и
они с большей вероятностью были республиканцами. Поскольку для участия в опросе
необходимо было отослать назад почтовую карточку, полученные результаты были
смещены из-за добровольного участия.
В 1948 году каждый серьезный опрос предрекал победу республиканца Томаса Дьюи
над демократом Гарри С. Трумэном. Чикаго Трибюн (Chicago Tribune) даже вышлэ с зэ-
головком нэ первой стрэнице «Дьюи побеждэет Трумэнэ». Хотя технологии опросэ стэли
более совершенными, по срэвнению с 1936 годом, несколько источников смещения ре-
зультэтов опросов были по-прежнему не устрэнены, что привело к неточным прогнозэм.
Однэ проблемэ состоялэ в том, что результэты телефонных опросов были использовэны
без стэтистической попрэвки нэ то, что телефон чэще имели богэтеи, склонные поддер-
жэть Дьюи. Другой фэктор - множество не определившихся со своими предпочтения- I
ми людей в дни перед выборэми, и ни один из опросов не мог определить, зэ кого эти
люди в конечном счете будут голосовэть. Третья проблемэ зэключалась в том, что Дьюи
пользовался большей поддержкой в восточных штатэх, по срэвнению с зэпэдными.
Из-зэ рэзличий в чэсовых поясэх результэты для восточных штэтов стэли известны рэнь-
ше, и в «Трибюн» решили нэпечэтэть прогноз результэтэ, основэнный нэ этих первых
данных. Чего не учли в газете, так это поддержку Труманэ зэпэдными штэтэми, включэя
Кэлифорнию, и это добэвило достэточно голосов для победы нэ выборэх. I
ГЛАВА 2.
Теория вероятности
Статистика основана на теории вероятности. Некоторые считают вероятность
пугающей темой, но нет никакой причины для того, чтобы, затратив достаточно
времени, не разобраться в ней насколько нужно для успешного освоения статистики.
Как и в случае многих других областей науки, «продвинутые» аспекты теории
вероятности могут быть очень сложными и трудными для понимания, но основные
принципы вероятности интуитивно понятны и просты для освоения. Более того,
многие люди уже знакомы с вероятностными утверждениями, начиная с
прогноза погоды, который обещает дождь этим вечером с вероятностью 30%, заканчивая
предупреждением на сигаретных пачках об увеличении вероятности развития рака
легких при курении.
Если, как у большинства взрослых людей, у вас есть один или несколько
страховых полисов, вы уже вовлечены в инициативу, основанную на вероятностном
мышлении. Если вы водите машину или обладаете ею, у вас, скорее всего, есть
полис страхования автомобиля, который на самом деле следовало бы называть
полисом страхования расходов на автомобиль, поскольку он защищает владельца
полиса от чрезмерных расходов, которые потребовались бы при попадании в
аварию. Люди не покупают страховые полисы из-за того, что они собираются во что-
нибудь врезаться; скорее, они признают, что вероятность такого происшествия в
будущем не равна нулю.
Правительство часто требует от автовладельцев иметь полисы из этих же
соображений; это требование - не признание вас плохим водителем, а констатация
того факта, что аварии действительно происходят, и мало кто будет в состоянии из
собственного кармана компенсировать убытки в случае серьезной аварии. В
страховых компаниях работают статистики, которые высчитывают, сколько вы
должны заплатить за полис, учитывая (в числе прочего) вероятность того, что вы
попадете в аварию или на вас подадут иск по любой другой причине, и убыток, который
такой иск принесет компании.
Для понимания основ теории вероятности, изложенных в этой главе, вам не
потребуется больше математических знаний, чем обычно дают в средней школе, а
понимание этих концепций послужит основой для освоения статистических
методов, изложенных в последующих главах. Знакомство с содержанием этой
главы также даст вам возможность понять суть значительной части статистических
шш\
Глава 2. Теория вероятности
методов, с которыми вы имеете шансы когда-либо иметь дело, до тех пор, пока
вы не начнете выполнять «продвинутые» операции или не решите применять
статистику в вашей области исследований. Кроме того, вы научитесь понимать
вероятностные суждения, которые используются в повседневной речи, и оценивать
правильность их использования.
О формулах
Люди, у которых были плохие оценки на уроках математики, часто не любят
формулы, полагая, что это тайная система общения, созданная математиками в
качестве барьера, который позволяет удерживать непосвященных на расстоянии,
оставляя себе все выгодные вакансии. Хотя я никогда не буду утверждать, что
математика и статистика - это простые предметы, представление о формулах как
о барьере для понимания ложно. На самом деле формулы - это сжатый и
недвусмысленный способ передачи важной информации, их можно воспринимать как
набор инструкций, написанных на языке математики. Как говаривал один мой
профессор вычислительной математики: «Посмотри на формулу, затем делай то,
что тебе она скажет».
Преимущество математических формул заключается в том, что они не зависят
от языка, так что о математике могут разговаривать все люди, вне зависимости
от их родного языка или национальности. Не имеет значения, в какой языковой
среде вы выросли, английской, русской или фарси, если вы понимаете язык
математики, вы можете общаться со своими коллегами на математические темы в
некоторой степени независимо от языковых барьеров.
Рассмотрим пример формулы для вычисления среднего арифметического,
называемой в обычном языке усреднением набора чисел, представленной на
рис. 2.1.
1 "
I n_il |
Рис. 2.1. Формула для вычисления среднего значения
Это может выглядеть для вас как греческий (на самом деле это частично так и
есть!), но на самом деле это просто набор указаний по выполнению определенных
вычислений. Давайте рассмотрим ее по частям:
• х - это параметр, для значений которого мы рассчитываем среднее;
• символ х (читается как «х с чертой») обозначает среднее значение х,
которое мы и вычисляем;
• символ х. (читается как «х i-e») обозначает отдельное значение х;
• п обозначает число значений х, используемых для вычисления среднего;
• символ суммы Z обозначает сложение ряда значений, в данном случае всех
значений х. Обозначения сверху и снизу символа суммы означают
сложение всех значений х} от первого (я,) до последнего (х).
Основные определения
iншка
Эта формула «велит» вам вычислить среднее арифметическое, сложив все
значения переменной х} затем разделив их на число наблюдений, которые вы только
что просуммировали. Учтите, что умножение на \/п - это то же самое, что деление
на п.
Представим, что мы хотим вычислить среднее для трех чисел: 1, 3 и 5. Следуя
принятым обозначениям, мы назовем их jct> х2 и хг В этом примере и = 3,
поскольку у нас есть три числа, так что, согласно формуле, мы складываем все числа отх,
до х, и умножаем на 1/3, как показано на рис. 2.2.
*-^2*'-ч<1+3+5>-3
-* !¦!
Рис. 2.2. Вычисление среднего значения для трех чисел
Продолжая изучение статистики, вы познакомитесь с более сложными
формулами, однако алгоритм их использования останется прежним:
1. Поймите, что значит каждый символ и какие математические операции
требуются.
2. Выявите значения, которые заменят каждый символ.
3. Подставьте значения в формулу, выполните указанные операции - и вы
получите нужный результат.
Основные определения
Здесь приведены некоторые ключевые определения, которые нужно знать при
обсуждении теории вероятности.
Испытания
Вероятность связана с результатом испытаний, которые также называются
экспериментами или наблюдениями. Какой бы термин не был использован, главное -
это то, что речь идет про события, исход которых неизвестен. Если бы результат
испытаний был бы в итоге известен, не было бы нужды обсуждать вероятность.
Испытание может быть простым, таким как подбрасывание монетки или
вытягивание карты из колоды, или таким сложным, как наблюдение за тем, останется ли
человек с раком легких в живых через пять лет после постановки диагноза. Мы
будем называть испытанием единичное наблюдение, такое как одно
подбрасывание монетки, а экспериментом - множественные испытания, такие как результат
подбрасывания одной монетки пять раз.
Выборочное пространство
Выборочное пространство, обозначаемое как 5, - это набор всех возможных
элементарных исходов испытания. Если испытание - это однократное
подбрасывание монетки, то выборочное пространство - это S = {орлы, решки} (часто
сокращенно записывается как S = {о,р}), поскольку эти две альтернативы представляют
ЕЁЯНнИв Глава 2. Теория вероятности
все возможные исходы данного испытания. Бросок может завершиться либо
выпадением орла (о), либо выпадением решки (р). Если эксперимент заключался бы
в бросании одной игральной кости с шестью гранями, выборочное пространство
было бы S = {1, 2, 3, 4, 5, 6}, что соответствует шести граням кости, которые могут
выпасть при одном броске. Эти элементарные исходы также называют
элементами выборки. Если эксперимент состоит из множества испытаний, то все
возможные комбинации исходов этих испытаний входят в выборочное пространство.
Например, если испытание состоит в двукратном подбрасывании монетки, то
выборочное пространство таково: S = {(о, о), (о, р), (р} о), (р, р)}, поскольку исходы
могут быть следующими: орлы при обоих бросках, орел в первом броске и решка
во втором, сначала решка, потом орел или решки при обоих бросках.
События
Событие, обычно обозначаемое как Е или любой заглавной буквой, отличной
от S, - это частный случай исхода испытания, оно может состоять из
единственного исхода или набора исходов. Если такой исход или набор исходов имеет
место, мы говорим, что «исход удовлетворяет событию» или «событие произошло».
Например, событие «выпадение орла при одном подбрасывании монетки» может
быть записано как Е = {орел}, а событие «выпадение нечетного числа при
броске одной игральной кости» можно записать как Е = {1, 3, 5}. Элементарное
событие - это исход одного эксперимента или наблюдения, такого как однократное
подбрасывание монетки. Элементарные события могут объединяться в сложные,
как в приведенных ниже примерах объединения и пересечения. События можно
описывать, перечисляя исходы или определяя их логически. Например, если
испытание - это бросок двух игральных костей и нас интересует, как часто сумма
выпадающих чисел бывает меньше шести, мы можем обозначить это как Е = {2,
3, 4, 5} или Е = {сумма меньше шести}.
Обычный способ изображения вероятности событий и комбинаций событий -
это диаграммы Венна, в которых прямоугольник соответствует выборочному
пространству, а круги изображают определенные события. Диаграммы Венна
используются на рис. 2.3-2.6.
Диаграммы Венна
Любой, кто вырос при новой концепции преподавания математики, возможно, помнит
диаграммы Венна из учебника математики в начальной школе. Хотя желание
познакомить учеников начальной школы с теорией множеств может вызывать споры, в этом
точно нет вины английского математика Джона Венна (John Venn, 1834-1923) или его
диаграмм. Диаграммы Венна широко используются в математике и смежных областях
для изображения логических отношений между группами объектов, также они были
адаптированы для использования в других дисциплинах, таких как литература. Венн
провел большую часть своей сознательной жизни, преподавая в Гонвилл-энд-Киз колледже
(Gonville and Caius College) Кембриджского университета, где основной областью его
интересов была логика, и он опубликовал три учебника, включая «Символическую
логику» (1881), в которой диаграммы Венна были введены в обиход. Современные студенты
колледжа имеют перед глазами ежедневное напоминание о достижениях Венна: память
Основные определения
тшшт
о нем была увековечена посредством окна из цветного стекла в столовой, на котором
изображена диаграмма Веннастремя пересекающимися множествами, обозначенными
тремя кругами разного цвета.
Объединение
В результате объединения нескольких элементарных событий создается сложное
событие, которое происходит, если случается хотя бы одно входящее в его состав
элементарное событие. Объединение Е и F записывается как Е U F и означает
«Е и/или F». Обратите внимание, что символ объединения U похож на заглавную
букву U1. Объединение ? и ^соответствует заштрихованной области на диаграмме
Венна в рис. 2.3. Обратите внимание на то, что на этом рисунке изображены два
круга, которые частично перекрываются; это значит, что любая точка
заштрихованной области (любая точка, принадлежащая Е и/или F) удовлетворяет условию
Е U F. Рассматривая это на примере, предположим, что событие - это бросок
игральной кости с шестью гранями и чтоЕ= {1, 3}, F= {1, 2}. Событие Е U
Fпроисходит при выпадении 1, 2 или 3; также можно сказать, что Е U F= {1, 2, 3}.
(
Рис. 2.3. Объединение Ей F(заштрихованная область)
Пересечение
Пересечение двух или более элементарных событий - это сложное событие,
которое происходит, если имеют место все элементарные события. Пересечение Е и F
записывается как Е П Fn обозначает «и Е} и F». Пересечение Е и ^соответствует
заштрихованной области на диаграмме Венна на рис. 2.4; обратите внимание, что
только точки, принадлежащие и Е} и F, удовлетворяют этому условию. Продолжая
наш пример, если событие заключается в бросании игральной кости с шестью
гранями и Е = {1, 3}, F= {1, 2}, то событие Е П F происходит, только если выпадает 1,
поскольку это значение входит в оба набора элементарных событий, так что Е П
F-{1}.
От англ. union - объединение. - Прим. пер.
ЕШНК
Глава 2. Теория вероятности
Рис. 2.4. Пересечение Ей F(заштрихованная область)
Дополнение
Дополнение события - это любое событие из выборочного пространства, кроме
заданного. Дополнение события ? записывают по-разному: как ~?, Ес или Ё и читают
как «не Е» или «дополнение Е». Например, если Е = (числа > 0), то ~Е = (числа < 0).
Продолжая наш пример, если событие заключается в бросании игральной кости с
шестью гранями и Е= {1,3}, то ~Е= {2,4,5,6}. Дополнение FcooTBeTCTByeT
заштрихованной области на диаграмме Венна на рис. 2.5.
~F
Рис. 2.5. Дополнение F(заштрихованная область)
Взаимное исключение
Если события не могут происходить одновременно, они называются взаимно
исключающими. Иначе говоря, если у двух наборов элементарных событий нет об-
Основные определения
шшшшшт
щих событий, то они взаимно исключающие. Например, событие Л = (заработок
больше $100 000) и событие В = (заработок меньше или равен $100 000) -
взаимно исключающие, так же как и события Л = (четные числа) и В = (нечетные числа).
Взаимно исключающие события Е и F изображены на диаграмме Венна на рис. 2.6;
обратите внимание на то, что у них нет общих точек.
Рис. 2.6. Ей F- взаимно исключающие; у них нет общих точек
Независимость
Если два испытания независимы, то исход одного из них не влияет на исход
другого. Иначе говоря, если испытания независимы, то информация об исходе одного
из них не дает никакой информации об исходе другого. Классический пример
независимости - это подбрасывание обычной монетки; если вы подбросили
монетку дважды, результат первого испытания никак не влияет на результат второго
испытания.
Перестановки
В теории вероятности перестановки - это все возможные способы
упорядочивания элементов в наборе. Например, если набор состоит из элементов {а, Ь, с), тогда
перестановки этого набора следующие: (я, Ь, с), (а, с, b), (b, а, с), (Ь, с, я), (с, а, Ь) и
(с, Ь, а). Учтите, что в перестановках важен порядок элементов: (а, Ь} с) - это не та
же перестановка, что (а, с, Ь). Можно рассчитать число перестановок любого
набора уникальных элементов (это значит, что ни один элемент в наборе не
повторяется), используя факториалы, которые обозначаются числом с восклицательным
знаком. Во многих калькуляторах есть кнопках/для вычисления факториалов, но
также их можно вычислить, перемножив все целые числа, равные или меньшие
заданного, вплоть до 1. Вот пример:
3! = 3х2х 1 = 6.
3! читается как «три факториал». Для набора из трех неповторяющихся
элементов существует 3! или шесть перестановок, что согласуется с результатом, который
мы получили выше, выписав все возможные перестановки трех букв. Это логично,
ЕМШ
Глава 2. Теория вероятности
поскольку, если у вас есть три элемента, на первую позицию есть три кандидата
(а} Ь, с в нашем примере), на вторую позицию - два (за исключением того элемента,
который был выбран для первой позиции), на третью позицию - один
(оставшийся после выбора двух предыдущих). Так что у вас есть 3><2х1=6 разных способов
упорядочить эти элементы. Число перестановок растет очень быстро. Например,
5! = 120, а 10! = 3 628 800.
20! имеет настолько большое значение, что не может быть отображено
большинством калькуляторов, если не записать его в экспоненциальном виде:
20! = 2.432902008Е18.
Экспоненциальная запись
Экспоненциальная запись используется для обозначения очень больших или очень
маленьких значений. Использование экспоненциальной записи позволяет не только
сэкономить место (поскольку вам не нужно выписывать множество нулей), но и повышает
точность передачи информации, поскольку число со многими нулями легко прочесть
неправильно. В основе экспоненциальной записи лежит идея о том, что каждое число можно
записать при помощи цифры, большей или равной единице и меньшей 10 (называемой
коэффициентом), умноженной на степень 10 (называемой основанием). Так что число
1234 можно записать в виде 1.234ЕЗ (Е обозначает экспоненту2), что значит 1.234х 103,
то есть 1.234 х 1000. Аналогично 1.234Е-4 обозначает 1.234 х 104 или 1.234x0.0001,
равное 0.0001234. Другой способ трактовки значения Е - это на сколько знаков нужно
переместить десятичную точку влево или вправо. Так что 1.234ЕЗ указывает на
необходимость передвинуть ее на три знака вправо, что даст нам 1234, тогда как при 1.234Е-4
нужно передвинуть ее на четыре знака влево, чтобы получить 0.0001234.
Сочетания
Сочетания схожи с перестановками, за одним исключением - в сочетаниях не
имеет значения порядок элементов. Так что (а, Ь, с) - это то же сочетание, что и (Ь, а, с).
По этой причине для набора элементов (а, Ь, с) существует только одно
сочетание.
Один из способов использования сочетаний и перестановок в статистике - это
расчет числа способов разделения множества элементов на подмножества
заданного размера, что позволяет рассчитать вероятность получения любого заданного
подмножества из множества. В общем случае исходное множество не содержит
повторяющихся элементов, и мы будем использовать это допущение в дальнейшем
обсуждении. Есть несколько способов обозначения сочетаний и перестановок; они
приведены в приложении А вместе с несколькими задачами. В этом разделе мы
будем придерживаться простой системы обозначений, используя Рдля обозначения
перестановок5, а С - для обозначения сочетаний1. Согласно этим обозначениям,
число возможных перестановок двух элементов из трех записывается как ЗР2, а
число сочетаний двух элементов из трех - как ЗС2. Продолжая ранее описанный
От англ. exponent - экспонента. - Прим. пер.
{ От англ. permutation - перестановка. - Прим. пер.
1 От англ. combination - сочетание. - Прим. пер.
Основные определения LJ^B^I
пример, для набора элементов (а, Ь, с) ЗР2 = 6, поскольку есть 6 возможных
перестановок двух элементов из этого набора: (а, Ь)} (а, с), (Ь, с), (Ь, а), (с, а) и (с, Ь).
Для этого набора существуют три сочетания двух элементов: ЗС2 = 3: {а, Ь), (а, с)
и (Ь, с).
Число перестановок для подмножества величины k, происходящего из
множества величины п, вычисляется по формуле, приведенной на рис. 2.7.
(п-к)\
Рис. 2.7. Формула для расчета числа перестановок
Используя эту формулу, можно рассчитать число перестановок двух элементов,
выбираемых из 8 элементов (рис. 2.8).
8! 8!
8/>2 ^56
(8-2)! 6!
Рис. 2.8. Расчет числа перестановок 8Р2
Если вам приходится проводить вычисления вручную, нужно помнить о
правиле сокращения дробей: если выразить числитель и знаменатель в виде
произведения, можно сократить те множители, которые входят в состав и числителя, и
знаменателя. Например:
12/6 = (2 х 2 х 3)/(2 х 3) = 2,
поскольку вы можете сократить и числитель, и знаменатель на (2 * 3).
В случае перестановки 8Р2 не нужно вычислять факториалы перед делением,
поскольку вы можете сократить много множителей. В этом примере:
8! = 8x7x6x5x4x3x2x1
и
6! = 6x5x4x3x2x1,
так что вы можете многое сократить, оставшись с таким выражением:
8Р2 = 8 х 7 = 56.
Если п = k, то число сочетаний будет всегда меньше числа перестановок,
поскольку разный порядок одних и тех же элементов приводит к разным
перестановкам, но не сочетаниям. Это становится ясным при рассмотрении формулы
сочетания, которая представляет собой деление формулы для перестановок на
факториал числа выбранных объектов (рис. 2.9).
п\ пРк
пСк
к\{п-к)\ к\
Рис. 2.9. Формула для расчета числа сочетаний
Глава 2. Теория вероятности
Используя эту формулу, вы можете вычислить число сочетаний двух объектов,
выбранных из 8 объектов, как показано на рис. 2.10.
8С2 =
8!
2!(8-
2)!
8Р2
2! .
56
2
= 28
Рис. 2.10. Расчет числа сочетаний 8С2
Определение вероятности
Существует несколько способов охарактеризовать вероятность, но определение,
используемое в статистике, гласит, что вероятность показывает, как часто
происходит некоторое событие при повторении эксперимента. Например, вероятность
выпадения орла при броске монетки может быть оцененй при наблюдении,
сколько раз выпадет орел в серии бросков. Наверное, если нужно выбрать единственное
самое важное свойство вероятности, то оно таково:
вероятность события всегда находится между Out
Если вероятность события равна 0, это значит, что у него нет шансов случиться,
тогда как вероятность события, равная 1, означает, что оно обязательно
произойдет. В математике принято выражать событие в долях единицы, поэтому мы
говорим, что вероятность события находится между 0 и 1, однако так же правильно
(и более обычно в повседневной речи) рассуждать в терминах процентов, так что
верно будет и то, что вероятность события находится между 0% и 100%. Для
перехода от долей единицы к процентам нужно умножить первые на 100 (процент
означает «на сотню»), так что 0,4 - это 40% (0,4 * 100 = 40), а вероятность 0,85
можно выразить как 85%.
Отрицательная вероятность и вероятность, превосходящая 100%, логически
невозможны и существуют только как фигуры речи. Тот факт, что вероятность
заключена между 0 и 1, имеет математическое обоснование, которое
рассматривается дальше при обсуждении логистической регрессии в главе 11. Этот факт также
служит полезной проверкой ваших вычислений. Если вы получили вероятность
меньше 0 или больше 1, вы определенно где-то ошиблись. Более того, если кто-то
говорит вам, что вы с вероятностью 200% выиграете на бирже, если будете
действовать по его системе, вам, возможно, следует поискать нового консультанта по
инвестициям.
Еще одни полезный факт о вероятности таков:
вероятность выборочного пространства всегда равна 1.
Поскольку выборочное пространство - это все возможные исходы испытания,
общая вероятность для выборочного пространства должна составлять 1. Это
полезный факт, поскольку, хотя мы можем знать вероятность некоторых событий
из выборочного пространства, там могут быть другие, информация о которых у
нас отсутствует. Однако, поскольку мы знаем, что вероятность всего выборочного
пространства равна 1, мы можем вычислить вероятность тех событий, о которых
Определение вероятности LijUIB
у нас нет информации, основываясь на той вероятности, которая остается после
вычитания вероятностей всех известных событий.
Третий полезный факт, который следует из первых двух, таков:
вероятность события и его дополнения всегда равна 1.
Этот факт вытекает из определения дополнения: все выборочное пространство,
кроме события Е, - это дополнение Е. Таким образом, Е и ~Е вместе должны
составлять все выборочное пространство, и общая вероятность Е и ~Е должна быть
равной 1. Это должно быть ясным из рис. 2.5: прямоугольник изображает
выборочное пространство, круг - событие ?, а заштрихованная область внутри
прямоугольника, но вне круга - событие ~?. Вместе Е и ~Е составляют полное
выборочное пространство, и их объединение (Е U F) имеет вероятность 1.
Запись вероятности события
Обычно значения вероятности записывают следующим образом:
Р(Е) = 0,5.
Это должно читаться как «вероятность события Е равна 0,5» или «существует
50%-ная вероятность события Е» (или просто «вероятность Е равна 0,5» или
«существует 50%-ная вероятность ?»). Используя этот формат, можно записать
первый факт о вероятности (о том, что вероятность всегда находится между 0 и 1) как
0<Р(?)<1.
Второй факт о вероятности, который следует из определения выборочного
пространства S как все возможные исходы испытания, можно записать в виде:
P(S) = 1.
Третий факт о вероятности (вероятность события и его дополнения всегда
равна 1) можно записать так:
Р(?) + Р(~?)=1,
что имеет для нас важное следствие:
Р(~Е) = 1-Р(Е).
Это окажется очень полезным при последующих вычислениях. Если мы
знаем вероятность ?, то мы автоматически знаем вероятность ~?, которая составляет
1 - Р(Е). Так что если Р(Е) = 0,4, то Р(~Е) = 1 - 0,4 = 0,6.
Условные вероятности
Часто мы хотим знать вероятность некоторого события, при условии что
произошло другое событие. Это записывается как Р(Е | F) и читается как «вероятность
Е при условии F». Второе событие называется условием, а весь процесс иногда
называется выполнением при условии F. Условная вероятность - важное понятие
в статистике, поскольку мы часто пытаемся установить фактор, который влияет на
результат, например у курильщиков чаще развивается рак легких. Влияние како-
ЮЯ|^И1Нг Глава 2. Теория вероятности
го-либо фактора на исход события можно иначе выразить как то, что вероятность
данного исхода различается в зависимости от наличия или отсутствия данного
фактора. Тот факт, что вероятность рака легких (исход) выше у курильщиков
(фактор), чем у тех, кто не курит, можно выразить при помощи символов
следующим образом:
Р(рак легких | курильщик) > Р(рак легких | некурящий).
Условные вероятности также могут быть использованы для обозначения
независимости. Говорят, что две переменные независимы, если выполняется
следующее равенство:
P(E\F) = P(E).
Это выражение указывает на то, что вероятность Е неизменна, вне зависимости
от наличия переменной F. Продолжая использованный ранее пример, выражение,
которое показывает отсутствие связи между раком легких и курением,
записывается как
Р(рак легких | курильщик) = Р(рак легких).
Вычисление вероятности сложных
событий
Для вычисления вероятности любого из нескольких происходящих событий
(объединения нескольких событий) просуммируйте вероятности отдельных событий.
Вид используемого уравнения будет зависеть от того, являются ли эти события
взаимно исключающими (это значит, что они не могут произойти
одновременно).
Объединение взаимно исключающих событий
Если события взаимно исключающие, как показано на рис. 2.6, то уравнение
простое:
P(EUF) = Р(Е) + P(F).
В качестве практического примера представим колледж, в котором не может
быть двух профильных предметов. Примем вероятность события ? (профильный
предмет - английский язык) равной 0,2 и вероятность события F (профильный
предмет - французский язык) равной 0,1. Эти события взаимно исключающие,
поскольку ученики могут выбрать только один профильный предмет, так что
вероятность события (профильный предмет - либо английский, либо французский
язык) можно вычислить как
P(?Uf) = 0,2 + 0,l=0,3.
Вычисление вероятности сложных событий
¦¦га
Объединение не взаимно исключающих событий
Часто события не взаимно исключающие. Например, в колледже, где можно
выбрать два профильных предмета, события «профильный предмет - английский
язык» и «профильный предмет - французский язык» не взаимно исключающие,
поскольку, вероятно, один человек может выбрать в качестве профильных
предметов и английский, и французский языки. В этой ситуации в уравнение для
вычисления ^(профильный предмет - либо английский, либо французский язык)
нужно ввести поправку на это перекрывание. Согласно рис. 2.4, перекрывание - это
область, принадлежащая и кругу Е, и кругу F (их пересечение, отмеченное
штриховкой). Если вы не учтете, что в колледже, где ученики могут выбрать более
одного профильного предмета, могут найтись люди, специализирующиеся и в области
английского, и в области французского языков, вы рискуете посчитать некоторых
учеников дважды. (Те, кто специализируется и в области английского, и в области
французского языков, будут посчитаны и как те, кто углубленно изучает
английский, и те, кто углубленно изучает французский.)
Для того чтобы учесть возможное перекрывание при подсчете вероятности
одного из двух не взаимно исключающих событий, используйте следующее
уравнение:
Р(Е U F) = Р(Е) + P(F) - Р(Е П F).
Предположим,что Р(профильный предмет - английский язык) = 0,2,
Р(профильный предмет - французский язык) = 0,1 и Р(двойная специализация
на английском и французском) = 0,05. Тогда вероятность специализации студента
на изучении или английского языка, или французского составляет
Р(Е UP) = 0,2 + 0,1 -0,05 = 0,25.
Пересечение независимых событий
Чтобы вычислить вероятность одновременного наступления нескольких
элементарных событий (пересечение нескольких событий), перемножьте их
вероятности. Конкретный вид формулы зависит от того, независимы ли эти события.
Если два события Е и F независимы, то вероятность их совместного
наступления вычисляется просто как
P(EnF) = Р(Е) х P(F).
Предположим, что вы подбрасываете правильную монету (вероятность
выпадения орла равна 0,5, вероятность выпадения решки равна 0,5, результаты каждого
броска независимы). Мы уже указали, что вероятность выпадения орла при любом
броске равна 0,5 и что два испытания независимы, так что вероятность выпадения
орлов при обоих бросках можно вычислить как
Р(Е и F) = 0,5 х 0,5 = 0,25.
шшшш
Глава 2. Теория вероятности
Пересечение не независимых событий
Если два события не независимы, то для вычисления вероятности их совместного
наступления вам нужно знать их условную вероятность. Формула для расчетов
такова:
P(EnF) = P(E)*P(F\E).
Предположим, вы вытаскиваете две карты из обычной колоды в 52 карты, не
возвращая карту в колоду. Половина карт из этой колоды красной масти, а
половина - черной. Эти события (выбор первой и второй карт) не независимы, поскольку
вероятность свойств второй карты зависит от свойств первой. Если вас интересует
вероятность вытащить две карты черной масти, можно рассчитать ее следующим
образом:
Р(Е) = Р(первая карта черной масти) = 26/52 = 0,5;
P(F\ E) = Р{вторая карта черной масти|первая карта черной масти) =
= 25/51=0,49.
Обратите внимание на то, что поскольку вы не возвращаете карту в колоду,
вторую карту вы тянете из колоды в 51 карту, и к этому моменту остается только
25 карт, поскольку вы уже вытащили одну карту черной масти. Используя эти
знания, вы можете рассчитать вероятность вытащить две карты черной масти как
(пересечение Е и F):
Р(Е П F) = 0,50 х 0,49 = 0,245.
Теорема Байеса
Теорема Байеса, также известная как формула Байеса, - это один из наиболее
распространенных способов применения условных вероятностей. Самый типичный
случай применения теоремы Байеса - это расчет вероятности того, что человек с
положительным результатом скринингового теста на определенное заболевание
действительно им болен. В теореме Байеса также используется несколько
введенных ранее базовых понятий теории вероятности, так что внимательное изучение
формулы Байеса, помимо всего прочего, - хороший способ повторить содержание
всей главы. Теорема Байеса для любых двух событий А и В сформулирована на
рис. 2.11.
I р(л I в) -Р{А пв) - Р(в'А)Р{А) I
I Р(В) Р(В\А)Р(А) + Р(В\~А)Р(~А) |
Рис. 2.11. Теорема Байеса
Эту формулу следует использовать, если вы знаете Р(А), Р(В) и Р(В | А), а
хотите знать Р(А | В). Числитель теоремы Байеса учитывает тот факт, что вероятность
пересечения двух событий - это вероятность первого события, умноженная на
вероятность второго события при условии первого. Например, вероятность В при
Теорема Байеса
ШШШШЖ
условии А умножается на вероятность Л, что дает вероятность пересечения А и В}
то есть ситуации, когда Aw В происходят одновременно.
В числителе использован тот же самый факт вместе со знанием о том, что
событие и его дополнение составляют все выборочное пространство и имеют
общую вероятность 1, так что сумма произведения вероятности В при условии А
на вероятность А и произведения вероятности В при условии - А на вероятность
-А даст нам вероятность В.
Представьте себе, что существует скрининговый тест, который выявляет
заболевших с 95%-ной вероятностью и дает отрицательный результат для здоровых с
вероятностью 99%. Клиницисты сказали бы, что этот тест характеризуется 95%-ной
чувствительностью и 99%-ной специфичностью. Предположим, что частота
заболевания в генеральной совокупности составляет 1%. Если мы обозначим
заболевание как D5, отсутствие заболевания как ~Д положительный результат теста как Т,
а отрицательный результат теста как ~Г, вышеупомянутые вероятности можно
записать следующим образом:
Чувствительность = P(T\D) = 0,95;
Специфичность = Р(~Т\ ~D) = 0,99;
Вероятность заболевания в генеральной совокупности = P(D) = 0,01.
Приведенные значения чувствительности и специфичности очень высоки.
Многие часто используемые тесты и процедуры менее точны. Однако все тесты
несовершенны, и возможно, что человек с положительными результатами теста
на самом деле здоров (ложноположительный результат), а человек с
отрицательными результатами теста на самом деле болен (ложноотрицательный результат).
Обычно что вы действительно хотите узнать, так это то, какова вероятность того,
что человек с положительным результатом теста действительно болен?
Используя принятую форму записи условной вероятности, вы хотите узнать P(D \ T). Вы
можете вычислить эту вероятность, используя теорему Байеса, учитывая данные
о чувствительности и специфичности теста и о частоте встречаемости данного
заболевания в генеральной совокупности, как это показано на рис. 2.12.
I Г(р I л -P{D пт) - р(т'D)P(D) I
Р(Т) P(T\D)P(D) + P(T\~D)P(~D)
Рис. 2.12. Теорема Байеса, записанная с использованием
наших обозначений для заболевания и результатов теста
Из этой формулы ясно видно, что вероятность иметь заболевание при
положительном результате теста - это просто вероятность и заболевания, и
положительного результата теста, деленная на вероятность положительного результата теста
(вне зависимости от наличия заболевания).
Используя тот факт, что событие и его дополнение составляют все выборочное
пространство и имеют общую вероятность, равную 1, вы знаете, что частота лож-
ноположительных результатов - это 1 - специфичность:
' От англ. desease - заболевание. - Прим. пер.
ЦвН>. i Глава 2. Теория вероятности
P(T\~D) = 1-0,99 = 0,01.
По этой же причине вы знаете, что вероятность отсутствия данного
заболевания в генеральной совокупности составляет 1 - вероятность наличия
заболевания:
P(~D) = 1 - P(D) = 1 - 0,01 = 0,99.
Используя эти факты и ранее предоставленную информацию, мы можем
вычислить P(D | Т), как показано на рис. 2.13.
WID 2^Ш» 9Ш 0.4897
[(0.95X0.01)] + (0.01)(0.99)] 0.0095 + .00099
Рис. 2.13. Использование теоремы Байеса для вычисления вероятности
наличия заболевания при положительном результате теста
Этот пример демонстрирует важный и не получивший должного внимания (по
крайней мере, у общественности) факт о скрининговых тестах. Даже высокоспе-
цифичный и чувствительный скрининговый тест на редкое заболевание будет
иметь высокую частоту ложноположительных результатов, по сравнению с
частотой истинно положительных результатов. В приведенном примере ожидается,
что около половины людей с положительным результатом теста на самом деле
будут здоровы. Это не обязательно является поводом отказываться от теста, в
особенности если заболевание имеет серьезные последствия, и существует более
точный последующий тест для разделения истинных и ложных положительных
результатов. Однако любое предложение организовать всеобщее обследование
(будь то тест на определенное заболевание или проверка багажа в аэропорту)
обязательно должно учитывать частоту ложноположительных результатов и их
последствия.
Нужно отметить, что частота ложноположительных результатов зависит как от
частоты заболевания в генеральной совокупности, так и от чувствительности и
специфичности скринингового теста. Если частота заболевания составляет 0,005,
а не 0,01, меньше положительных результатов будут истинными, а больше -
ложными, как это видно на примере вычислений, приведенных на рис. 2.14.
п,ъ, ^ (0.95)(0.005) 0.00475
P(D IТ) = = 0.3231
[(0.95)(0.005)] + (0.01)(0.995)] 0.00475 + .00995
Рис. 2.14. Еще один пример использования теоремы Байеса для вычисления
вероятности наличия заболевания при положительном результате теста; обратите
внимание на снижение частоты истинно положительных результатов из-за более
низкой встречаемости заболевания в генеральной совокупности
В этом примере менее одной трети положительных результатов истинные.
Достаточно разговоров, давайте займемся статистикой!
¦¦EI
Преподобный Томас Байес
Теорема Байеса была сформулирована английским министром, преподобным Томасом
Байесом (Thomas Bayes, 1702-1761). Байес изучал логику и теологию в Эдинбургском
университете и зарабатывал на жизнь, занимая должность министра. Однако его
нынешняя слава основана на теории вероятности, которая была разработана им в эссе,
опубликованном посмертно Лондонским королевским обществом. В наши дни
существует отдельная область науки, называемая байесовской статистикой. Она основана на
понимании вероятности как степени уверенности, а не частоты встречаемости. Хотя не
ясно, согласился бы сам Байес с таким определением, поскольку за свою жизнь он
опубликовал сравнительно мало математических работ.
Достаточно разговоров, давайте
займемся статистикой!
Статистика - это что-то, что вы делаете, а не то, про что вы читаете, так что
реальная цель приведенного выше теоретического введения состояла в том, чтобы
снабдить вас знаниями, необходимыми для вычисления вероятности событий и
статистических обоснований. В этой главе также были введены такие понятия, как
независимость, или взаимное исключение, которые понадобятся вам при
использовании более сложных статистических методов.
Цель приведенных ниже задач - помочь вам приобрести некоторый навык
работы с базовыми понятиями теории вероятности. Если для понимания темы вы
предпочитаете выполнить множество задач, то существует много прекрасных
учебников с упором на теорию вероятности; ссылки на некоторые из них
приведены в приложении С.
Если вы впервые беретесь за задачи по теории вероятности, вам может помочь
следующий план работы:
1. Определите, что является испытанием и/или экспериментом.
2. Определите выборочное пространство.
3. Определите событие.
4. Выразите необходимые вероятности и проведите вычисления.
В какой-то момент вы можете почувствовать, что необходимость проходить
каждый из этих этапов отпала, но этот план может пригодиться в начале работы.
В некоторых случаях предлагается альтернативный способ решения, основанный
на другом подходе к задаче.
Монеты, игральные кости и карты
Поскольку во многих примерах, приведенных в этой книге, используются монеты,
игральные кости и карты, этот раздел начинается с их описания.
Игральные кости
Стандартная игральная кость, используемая на Западе, - это куб с шестью
гранями, на которые нанесено разное число точек (от 1 до 6). Допущение, лежащее
E9HIH
Глава 2. Теория вероятности
в основе статистических вычислений, заключается в том, что вероятности
выпадения кости каждой из граней кверху равны, так что каждый бросок кости имеет
шесть равновероятных исходов: 1, 2, 3, 4, 5, 6. Используя специальную
терминологию, набор исходов при броске одной кости имеет дискретное равномерное
распределение, поскольку возможные исходы mojjcho пронумеровать, и каждый из
них имеет одинаковую вероятность. Результаты, полученные при одновременном
броске двух или более костей (или многократного подбрасывания одной и той же
кости), не зависят друг от друга, так что вероятности каждой комбинации чисел
вычисляются путем перемножения вероятностей каждого результата.
Для полной определенности нужно отметить, что «равная вероятность
выпадения каждой грани» выполняется только для костей, используемых в казино, на
которых точки (кружочки, используемые для обозначения числа на каждой
грани) нанесены краской. Вам могут быть больше знакомы кости, на которых точки
сделаны в виде углублений, а не нанесены краской, что приводит к
неравномерному распределению массы и, следовательно, разной вероятности выпадения разных
граней. Однако при теоретических разговорах о вероятности этой разницей
обычно пренебрегают и считают, что выпадение любой грани равновероятно.
Монеты
Стандартная монета, используемая в вероятностных экспериментах, имеет две
стороны, орел и решка. Часто имеют в виду правильную монету, что значит
равную вероятность выпадения орла и решки при каждом броске. Для любой монеты,
правильной или нет, вероятность выпадения орлов и решек считается
постоянной, так что результаты предыдущих бросков не влияют на результаты
последующих. Как и в случае игральной кости, вероятность выпадения орлов и решек на
реальной монете редко в точности составляет 50:50 по ряду физических причин,
включающих дизайн монеты, ее изношенность и стиль бросков, но при
выполнении вероятностных задач эти тонкости следует игнорировать, если только они не
прописаны в условии. Иногда в интересах безопасности эксперименты проводят,
закручивая монетку, а не подбрасывая ее (в результате меньше разящих
объектов летает в переполненном классе). Хотя ожидаемое соотношение 50:50 в этом
случае еще менее правдоподобно, при выполнении вычислений (а не реальном
закручивании монетки и записи результатов) предположите, что это
соотношение работает. Более подробную информацию по этой теме можно получить здесь:
http:/Av\vw.scienccnevvs.org/articles/20040228/fob2.asp.
Игральные карты
Стандартная колода в наши дни состоит из 52 игральных карт четырех мастей:
пики, крести, черви и бубны. Пики и крести - это черные масти, а черви и
бубны - красные. Есть 13 карт каждой масти: туз, нумерованные карты от 2 до 10 и
три фигуры - валет, дама и король. В экспериментах с вытаскиванием карт из
колоды предполагается, что они хорошо перемешаны, то есть вероятность вытащить
любую карту одинакова.
Упражнения
Упражнения
Задача
Если я вытащу одну карту из стандартной колоды в 52 карты, какова
вероятность того, что она будет красной масти?
Решение
1. Испытание - это выбор одной карты из колоды.
2. Выборочное пространство - это все имеющиеся карты, вероятность
вытянуть каждую из них одинакова.
3. Событие - это Е = {красная масть}.
4. Поскольку в колоде есть 52 карты и половина из них (26) красной масти,
вероятность вытащить карту красной масти составляет 26/52 или 0,5.
Ответ - вероятность вытащить карту красной масти из стандартной колоды
составляет 50%.
Задача
Если я один раз брошу игральную кость, какова вероятность, что выпадет число
меньше 5?
Решение
1. Испытание - это один бросок игральной кости с шестью гранями.
2. Выборочное пространство - это числа (1, 2, 3, 4, 5, 6), выпадение которых
равновероятно.
3. Событие - это Е = (одно из 1, 2, 3, 4), которое также можно
рассматривать как объединение четырех элементарных событий, то есть Е = (Е = 1) U
(?=2)U(?=3)U(?=4).
4. Четыре из шести элементарных событий, или возможных исходов,
составляющих выборочное пространство, соответствуют событию ?, так что вероятность
? равна 4/6 или 0,67 (округлено).
Альтернативное решение
К решению этой задачи можноподойти по-другому - вычислить вероятность
каждого элементарного события, которое удовлетворяет событию ?, и сложить их,
поскольку эти события - взаимно исключающие. Тогда вероятность каждого
элементарного события, входящего в ?, равна 1/6; это значит, что в одном случае из
шести выпадет 1, в одном случае из шести выпадет 2 и так далее. В соответствии
с нашим подходом вероятность Е составляет 1/6 + 1/6 + 1/6 + 1/6 или 4/6, что
совпадает с полученным ранее ответом.
Задача
Если я подкину правильную монету дважды, какова вероятность того, что хотя
бы один раз выпадет орел?
Решение
1. Эксперимент заключается в двукратном подбрасывании правильной
(Р = 0,5 и для решки, и для орла) монеты, то есть два независимых
испытания, каждое с вероятностью 0,5.
¦¦Ш
IBhHiv- Глава 2. Теория вероятности
2. Выборочное пространство состоит из следующих исходов: {(о, о), (о, р),
(р, о), (р,р)}, - каждый из которых равновероятен.
3. Интересующее нас событие - это Е = (хотя бы один орел). Три исхода из
выборочного пространства удовлетворяют этому условию: (о, о), (о, р),
(Р. о).
4. Вероятности всех исходов равны, и три из четырех исходов соответствуют
событию Е, так что вероятность Е равна s, или 0,75.
Альтернативное решение
Этот результат можно также получить при помощи математических
вычислений, рассчитав вероятность дополнения этого события и затем вычтя ее из 1,
чтобы получить вероятность самого события. Если событие - это Е = (хотя бы один
орел), его дополнение - это ~Е = (нет орлов, то есть две решки). Вы знаете, что
вероятность выпадения решки при любом подбрасывании правильной монеты равна
0,5, а броски независимы, так что вероятность выпадения двух решек составляет
0,5 х 0,5, или 0,25. Согласно определению дополнения события, 1 - Р(~Е) = Р(Е),
так что 1 - 0,25 = 0,75, или Р(Е). Вероятность выпадения хотя бы одного орла при
двух бросках монеты равна 0,75, что совпадает с полученным ранее ответом.
Задача
Если я вытащу одну карту из стандартной колоды с 52 картами, какова
вероятность того, что это будет фигура (валет, дама или король) черной масти (пики или
трефы)?
Решение
1. Испытание - это выбор одной карты из колоды с 52 картами.
2. Выборочное пространство - это 52 карты, вероятности выбора каждой из
них равны.
3. Событие - это Е = (выбор фигуры черной масти); шесть карт
удовлетворяют этому условию: валет, дама или король пик или треф.
4. Вероятность равна 6/52, или 0,115.
Математическое решение
Р(фигура) = 12/52, или 0,231 Р(черная масть) = 26/52, или 0,5 Р(фигура черной
масти) = Р(фигура) * Р(черная масть) = 0,231 х 0,5 = 0,116.
*у, Обратите внимание, что математическое решение возможно, поскольку веро-
0 % ятность вытащить карту черной масти и вероятность вытащить фигуру незави-
*>Т Л . симы.
Задача
Если я выбираю одну карту из стандартной колоды с 52 картами, какова
вероятность того, что она будет либо черной масти (пики или трефы), либо фигурой
(валет, дама или король)?
Упражнения
¦НЕЭ
Решение
1. Испытание - это выбор одной карты из колоды с 52 картами.
2. Выборочное пространство - это 52 карты, вероятности выбора каждой из
них равны.
3. Событие - это Е = или карта черной масти, или фигура, - это значит, что
любая из 26 карт черной масти или любая из 12 фигур подходит под
условие.
4. Два типа карт, которые удовлетворяют условию, не взаимно исключающие:
некоторые карты черной масти также являются фигурами, и наоборот. Есть
26 карт черной масти: от туза до короля пик (13) и от туза до короля треф
(13). Есть 12 фигур: валет, дама и король, - каждая из которых может быть
четырех мастей. Шесть карт принадлежат обоим категориям: валет, дама,
король пик и валет, дама, король треф, так что 26 + 12 - 6 = 32 карты,
которые удовлетворяют условию, и вероятность равна 32/52, или 0,615.
Математическое решение
Р(черной масти) = 26/52, или 0,500 Р(фигуры) = 12/52, или 0,231 Р(фигуры
черной масти) = 6/52, или 0,115 Р(карты черной масти или фигуры) =
0,500 + 0,231-0,115 = 0,616.
Небольшое различие в ответах (0,615 и 0,616) объясняется ошибкой
округления.
Задача
Если я вытащила одну карту из стандартной колоды с 52 картами и она черной
масти, какова вероятность, что это трефы?
Решение
1. Испытание - это выбор одной карты из колоды с 52 картами.
2. Выборочное пространство - это все карты черной масти, поскольку нас
интересует условная вероятность того, что карта окажется трефами, если ее
масть черная. Таким образом, наше выборочное пространство ограничено
26 картами.
3. Событие - это Е = трефы \ карты черной масти.
4. Вероятность того, что карта окажется трефами, если это карта черной
масти - это 13/26, или 0,5.
••л' ) Обратите внимание, что в этом примере мы вычисляем условную вероятность
\ 0% i (вероятность треф при условии, что вытащили карту черной масти). Неуслов-
М^ Л л ная вероятность выбора трефовой карты, если у нас нет информации о ее цве-
I #|л те> составляет 13/52, или 0,25.
Математическое решение
Р(трефы | черная масть) = Р(трефы и черная масть) /Дчерная масть) = 0,25/0,5
= 0,5.
Учтите, что трефы - это черная масть по определению.
I^lf:'^ Глава 2. Теория вероятности
Задача
Если порядок не имеет значения, сколько есть способов выбрать пять учеников
из 20?
Решение
Это задача на комбинаторику, решение которой через перебор всех возможных
вариантов будет слишком длинным. Вместо этого используем формулу для числа
сочетаний пСк. В этом случае п = 20 и к = 5; ход вычислений приведен на рис. 2.15.
20!
пСк = 15,504
5!(20-5)!
Рис. 2.15. Использование формулы для числа сочетаний для определения числа
способов выбрать пять человек из 20
Задача
В конференции участвуют 80 учеников: 40 мальчиков и 40 девочек. Тридцать
мальчиков и 20 девочек углубленно занимаются математикой. Известно, что
случайно выбранный мальчик углубленно занимается математикой с вероятностью
75%. Однако вы хотите знать, какова вероятность того, что случайно выбранный
углубленно занимающийся математикой ребенок окажется мальчиком. Указание:
используйте теорему Байеса.
Решение
Р(мальчик) = 40/80 = 0,5.
Р(-мальчик) = 40/80 = 0,5.
^(математика | мальчик) = 30/40 = 0,75.
Р(математика | -мальчик) = 20/40 = 0,5.
Ход вычислений приведен на рис. 2.16.
Р{мальчик | математика) =
Р(математика | мальчик) Р(мальчик)
Р(математика\ мальчик) Р(мальчик) + Р(математика | девочка) Р(девочка)
(0.75X0.5)
"[(0.75X0.5)] + [(0.5X0.5)]
0.375
0.625
= 0.600
Рис. 2.16. Применение теоремы Байеса для вычисления вероятности того,
что случайно выбранный углубленно занимающийся математикой ребенок
окажется мальчиком
Вероятность того, что случайно выбранный углубленно занимающийся
математикой ребенок окажется мальчиком, составляет 60%.
Заключительное замечание: связь между статистикой и ...
НМЕЭ
Заключительное замечание:
связь между статистикой и азартными
играми
Статистики любят иллюстрировать теорию вероятности, используя в качестве
примеров монеты, игральные кости и карты, объекты, которые применяются в
азартных играх (или просто играх, как их предпочитают называть в самой игорной
индустрии). Одна причина заключается в том, что эти предметы знакомы
большинству людей. Другая причина состоит в том, что вероятности разных исходов
известны и неизменны и поэтому могут быть использованы для создания простых
примеров применения основных понятий теории вероятности, включая
независимость и взаимное исключение. Преимущество таких примеров заключается еще и
в том, что задачи можно решить с использованием конкретных объектов
(например, вытаскивая карты из колоды) с тем же успехом, что и при помощи
математических уравнений.
Однако тут есть и исторические причины, поскольку многие законы теории
вероятности были сформулированы в связи с азартными играми и умением
использовать игральные кости и карты. На самом деле азартные игры были движущей
силой многих исследований вероятностей разных событий и сочетаний событий,
поскольку способность игрока получить, а не потерять деньги во многом зависит
от его понимания вероятности разных событий, происходящих в данной игре.
Многие историки ставят у истоков современной теории вероятности Шевалье
де Мере (Chevalier de Mere), джентльмена, который был игроком во Франции
XVII века. Он обожал спорить о том, что у него выпадет хотя бы одна шестерка при
четырех бросках одной кости: причина такого желания станет ясной из
следующих абзацев. Однако он также верил, что хорошо спорить о том, что за 24 броска
пары игральных костей у него выпадет хотя бы одна пара шестерок: оказалось,
что это проигрышная идея. К счастью для последующих статистиков, Шевалье
рассказал об этой задаче своему другу - философу Блезу Паскалю (Blaise Pascal),
который обсудил это со своим другом - математиком Пьером Ферма (Pierre de
Fermat). Рассмотрение вопросов такого типа привело к разработке, в числе
прочих вещей, треугольника Паскаля, биномиального распределения и современной
теории вероятности.
Даже в дружеском споре хорошее пари - это то, когда вы, скорее всего,
выиграете более чем в половине случаев. Иначе говоря, вероятность вашего выигрыша в
удачном пари не меньше 0,5. Шевалье первым использовал этот принцип:
вероятность выпадения хотя бы одной шестерки при четырех бросках кости составляет
0,518. Это легко вычислить, рассмотрев вероятность того, что за четыре броска не
выпадет ни одной шестерки, которая составляет (5/6)1. Выпадение хотя бы одной
шестерки - дополнение к выпадению ни одной шестерки, так что Р(хотя бы одна
шестерка из четырех бросков) составляет 1 - (5/6)1 или 1 - 0,482, что равно 0,518.
Это значит, что примерно в 52% случаев Шевалье выигрывал пари.
шш
Глава 2. Теория вероятности
Однако спорить, что при 24 бросках двух костей выпадет хотя бы одна пара
шестерок, - глупо. Существует 36 комбинаций чисел при каждом броске двух костей,
и только одна из них - это две шестерки, таким образом, вероятность невыпадения
двух шестерок при каждом броске составляет 35/36. Поскольку каждый бросок
костей независим, мы можем перемножить вероятности для каждого броска.
Поскольку вероятности не меняются, это значит умножение (35/36) на само себя 24
раза, а это то же самое, что возвести (35/36) в степень 24. Вероятность выпадения
хотя бы одной пары шестерок составляет 1 - Р(невыпадение пары шестерок), или
1 - 0,509, что составляет 0,491. Поскольку эта вероятность меньше 0,5, это
проигрышное пари.
Если вам интересно узнать больше о применении теории вероятностей к
азартным играм, таким как рулетка, кости, двадцать одно, скачки и покер, загляните в
кишу Эдварда Пэкеля «Математика, лежащая в основе азартных игр» (Edward
Packel, «The Mathematics of Games and Gambling»), опубликованную американским
математическим обществом, ссылка на которую приведена в приложении С.
ГЛАВА 3.
Статистический вывод
Статистический вывод - это методология, которая позволяет охарактеризовать
генеральную совокупность или сформировать суждения о ней на основании
информации о выборке, извлеченной из этой генеральной совокупности. Большая
часть практической деятельности в области статистики связана именно со
статистическим выводом. Для облегчения подобных предсказаний разработано
множество сложных методов. Идея предсказательной статистики может показаться
несколько запутанной, так что нам стоит потратить несколько минут, чтобы
подумать о том, что значит использовать статистику для обоснования заключений.
В интернет-словаре Мерриам-Вебстер (Merriam-Webster) есть два
определения термина «вывод (рассуждение)» (inference):
• Переход от одного предположения, утверждения или суждения, считаемого
верным, к другому, истинность которого следует из истинности первого.
• Переход от данных о статистической выборке к обобщениям (в виде
значений параметров генеральной совокупности), как правило, с вычислением
степени уверенности.
Второе значение, которое специфично для статистики, тесно связано с первым.
Логический вывод в общем случае - это способ формирования суждений о
неизвестном, опираясь на уже известное. Статический вывод - это частный случай
логических заключений, при которых формируются суждения о генеральной
совокупности, как было сказано выше.
Люди часто испытывают сложности с разграничением описательной
статистики (descriptive statistics) обсуждаемой в главе 4 и статистического вывода
(inferential statistics), отчасти потому, что некоторые статистические процедуры
используются в обоих типах статистики, хотя могут иметь место незначительные
различия в формулах, а также в интерпретации результатов. К примеру, одна и та
же процедура лежит в основе вычисления среднего арифметического для набора
данных, вне зависимости от того, представляют ли они генеральную совокупность
или выборку: нужно суммировать все значения и разделить полученную сумму на
число значений. Тем не менее есть различия в написании формулы для вычисления
среднего арифметического. Для генеральной совокупности среднее обозначается
греческой буквой и («лш», которую правильно называть параметром, поскольку
это число характеризует генеральную совокупность), тогда как для обозначения
ЕИНН
Глава 3. Статистический вывод
выбочного среднего вы используете латинскую букву х, часто с чертой сверху, х,
(которую правильно называть статистикой, поскольку это число характеризует
выборку). В других случаях между формулами, используемыми для генеральной
совокупности и выборки, существуют более важные различия. Хорошо известный
пример - это формула для дисперсии. Когда вы имеете дело с генеральной
совокупностью, в знаменателе стоит п (число наблюдений), но когда вы работаете с
выборкой, делить нужно на п - 1 (на один меньше, чем число наблюдений). Эти
формулы подробно разобраны в главе 4 (раздел «Меры разброса» на стр. 115), и
если вы новичок в статистике, прочитайте ту главу целиком, прежде чем работать
с этой, поскольку описательная статистика концептуально проще статического
вывода.
Вы можете использовать оба типа статистики в ходе работы над одним
проектом (например, применять описательную статистику для характеристики
выборки и затем - статистический вывод, чтобы решить исходные задачи вашего
исследования), но вы должны четко понимать, какой тип статистики вы используете
в ходе каждого конкретного анализа данных. Для этого полезно задуматься над
целью вашего анализа данных: вы используете его, чтобы просто описать набор
данных, с которым вы проводите вычисления? Или вы хотите распространить
свои результаты на более обширную группу, которую вы не можете изучить
напрямую? В первом случае вам следует применить описательную статистику, а во
втором - статистический вывод. Вот два правила, которые содержат ту же идею,
изложенную другими словами:
• в тех случаях, когда вы изучаете составляющие генеральную совокупность
случаев и не хотите выходить за их рамки, вам следует использовать
описательную статистику;
• в тех случаях, когда изучаемые вами случаи не составляют всей
генеральной совокупности, и вы хотите сделать обобщения, выходящие за рамки
этих случаев, вам следует использовать статистический вывод.
Распределения вероятностей
На практике статистические заключения настолько часто опираются па
допущения о том, как распределены данные, что в статистике принято преобразовывать
данные, чтобы они лучше соответствовали одному из известных типов
распределения. По этой причине наш разговор о предсказательной статистике начинается
с введения понятия теоретического распределения вероятностей и рассмотрения
двух часто используемых распределений.
Теоретическое распределение вероятностей - это выражение, которое
определяет, какие значения будет принимать данный параметр и как часто будет встречаться
каждое из этих значений (или, в случае непрерывного распределения, как часто
будет встречаться данный диапазон значений). Теоретические распределения
вероятностей также часто бывают представлены в графической форме; знаменитая
колоколообразная кривая нормального распределения - один из примеров.
Распределения вероятностей
шшшшт
Теоретические распределения вероятностей полезны для статистического
вывода, поскольку их свойства и характеристики определены. Если реальное
распределение значений имеющегося набора данных близко к теоретическому,
многие вычисления для анализируемых данных могут быть выполнены с
использованием допущений, основанных на свойствах теоретического
распределения. Кроме того, благодаря центральной предельной теореме (которая
разбирается ниже в этой главе) при определенных условиях можно предположить, что
выборочные средние распределены нормально, даже если значения генеральной
совокупности, из которой произошли эти выборки, распределены отлично от
нормального.
Распределения вероятностей часто разделяют на непрерывные, если данные
могут принимать любые значения внутри заданного диапазона, и дискретные,
когда данные принимают только определенные значения. В данной главе в качестве
примера непрерывного распределения рассмотрено нормальное, а в качестве
примера дискретного распределения приведено биномиальное.
Нормальное распределение
Нормальное распределение - наверное, наиболее часто используемый тип
распределения в статистике. Это происходит отчасти потому, что нормальное
распределение адекватно отражает реальное распределение многих непрерывных
переменных, от параметров производственного процесса до результатов проверки
умственных способностей. Вторая причина широкого использования
нормального распределения заключается в том, что при определенных условиях можно
считать, что распределение выборочных статистик, таких как выборочное
среднее арифметическое, будет нормальным, даже если выборки происходят из
генеральной совокупности, для которой нормальное распределение не свойственно.
Данная закономерность обсуждается далее в этой главе в разделе, посвященном
теореме о центральном пределе. Нормальное распределение также называют ко-
локолообразной кривой из-за его характерной формы, или гауссовым
распределением в честь физика и математика Карла Гаусса, который жил в XVIII веке и
использовал нормальное распределении при анализе астрономических данных.
Существует бесконечное множество нормальных распределений, все из которых
в целом имеют одну и ту же форму, но различаются из-за их среднего и (греческая
буква «мю») и стандартного отклонения а (греческая буква «сигма»). Примеры
трех нормальных распределений с разными средними значениями и
стандартными отклонениями представлены на рис. 3.1.
Нормальное распределение со средним арифметическим, равным 0, и
стандартным отклонением, равным 1, известно как стандартное нормальное распределение,
или Z-распределепие. Любое нормальное распределение может быть
преобразовано в стандартное путем преобразования исходных значений в стандартизованные
(этот процесс обсуждается далее в этой главе, а затем в главе 16). Такая процедура
облегчает сравнение генеральных совокупностей с разными средними
значениями и стандартными отклонениями.
Глава 3. Статистический вывод
Для всех нормальных распределений вне зависимости от их среднего значения и
стандартного отклонения характерны некоторые общие свойства. К ним относятся:
• симметричность;
• унимодальность (единственное наиболее частое значение);
• непрерывность значений в диапазоне от минус бесконечности до плюс
бесконечности;
• общая площадь под кривой, равная единице;
• равенство среднего, медианы и моды.
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
Л ix=0,cr =0.45
/\ ц,= 0fo- =2.24
I I ^=-2, а =0.71
\
/ \
J \
5-4-3-2-101234
-
-
Рис. 3.1. Три нормальных распределения
Как было сказано выше, существует бесконечное множество нормальных
распределений, но у них есть общие свойства. Для удобства мы часто описываем
нормальные распределения в терминах единиц стандартного отклонения, а не
характеризуем исходными числами, поскольку это позволяет нам использовать одно и
то же описание для любого нормального распределения.
Поскольку все нормальные распределения имеют одинаковую общую форму,
мы можем сформулировать некоторые суждения о том, как распределены данные
при любом нормальном распределении. Эмпирическое правило гласит, что для
любого нормального распределения:
• около 68% данных находятся в интервале ± одно стандартное отклонение
от среднего;
• около 95% данных находятся в интервале ± два стандартных отклонения
от среднего;
• около 99% данных находятся в интервале ± три стандартных отклонения
от среднего.
Это правило проиллюстрировано на рис. 3.2, где единицами измерения служат
стандартные отклонения.
Распределения вероятностей
Знание этих свойств нормального распределения предоставляет способ решить,
насколько типично конкретное значение данных для генеральной совокупности.
Такие сопоставления облегчаются преобразованием исходных значений данных
(значений в исходных единицах измерения, например вес, измеренный в фунтах
или килограммах) в Z-значения, которые выражают данные в единицах
стандартного отклонения. Преобразование всех значений данных в Z-значения аналогично
преобразованию нормально распределенной генеральной совокупности в
стандартизованное нормальное распределение. По этой причине Z-значения иногда
называют нормализованными значениями, процесс преобразования исходных значений
в Z-значения - нормализацией, а стандартное нормальное распределение - Z-pac-
пределением.
Рис. 3.2. Доля данных, которые попадают в определенные интервалы
нормального распределения
Z-значение - это разница между заданным числом и средним арифметическим,
выраженная в единицах стандартного отклонения. Формула для вычисления
Z-значения для числа из генеральной совокупности с известным средним
арифметическим и стандартным отклонением приведена на рис. 3.3.
Z =
х - /л
а
Рис. 3.3. Формула для вычисления Z-значения
Если переменная х имеет нормальное распределение со средним
арифметическим 100 и стандартным отклонением 5, что можно записать как .г ~JV(100, 5), то
число 105 имеет Z-значение 1 (рис. 3.4).
^ 105-100 , ЛЛ
Z 1.00
Рис. 3.4. Z-значение для числа 105 из генеральной совокупности ~Л/(100, 5)
HHI-:'^ Глава 3. Статистический вывод
Это значит, что число 105 на одно стандартное отклонение больше среднего
арифметического данной генеральной совокупности. Соответственно, число ПО
из этой генеральной совокупности имеет Z-значение 2, а число 85 - Z-значение,
равное -3. Используя ранее сформулированное эмпирическое правило, мы
классифицируем число 105 как превышающее среднее значение, но не выделяющееся
из генеральной совокупности (ожидается, что около 15,9% генеральной
совокупности имеет большие Z-значения). Число 110 - более редкое (большие Z-значе-
ния ожидаются для примерно 2,5% генеральной совокупности), а число 85 меньше
среднего и встречается довольно редко (ожидается, что менее 0,5% значений
генеральной совокупности будут равны ему или меньше).
Одно большое преимущество Z-значений состоит в том, что они облегчают
сравнение значений генеральных совокупностей с разными средними
арифметическими и стандартными отклонениями. Например, рассматривая одну
генеральную совокупность х ~N( 100, 5) и другую у -N(50, 10), мы не можем сразу сказать,
встречается ли число 95 в первой генеральной совокупности реже или чаще
числа 35 во второй генеральной совокупности. Однако такое сравнение можно легко
провести при помощи Z-значсний, как это показано на рис. 3.5 и 3.6.
Рис.
3.5.
Z
95-100
5
-1.00
-значение для числа 95 из генеральной совокупности
35-50
10
-1.50
~Л/(100,5)
Рис. 3.6. Z-значение для числа 35 из генеральной совокупности ~Л/(50, 10)
Переход к Z-зиачениям позволяет перевести обе генеральные совокупности в
одну систему измерений. Теперь мы можем увидеть, что хотя оба значения ниже
среднего в соответствующих генеральных совокупностях, второе значение
выделяется сильнее, поскольку -1,5 дальше отстоит от 0 (среднего значения
стандартного нормального распределения), чем -1,0.
Биномиальное распределение
Мы используем биномиальное распределение в качестве примера дискретного
распределения, то есть распределения величин данных, которые могут принимать
только определенные значения. Представим, что мы подбросили монетку пять
раз: число выпавших орлов может принимать целые значения, такие как 0, 1,2, 3,
5, по не такие значения, как 3,2 или 4,6. Стало быть, величина «число выпадений
орла при пяти подбрасываниях монетки» - дискретная. Биномиальное
распределение может описывать многие типы реальных дихотомических величии данных
(когда возможны только два исхода), начиная от деталей станков, которые могут
быть или бракованными, или пригодными, до студентов, которые могут или сдать,
или провалить экзамен.
Распределения вероятностей :. .ЮН1
События биномиального распределения происходят в результате процесса Бер-
нулли. Одно испытание в процессе Бернулли называется испытанием Бернулли.
Биномиальное распределение описывает число положительных исходов в п
испытаниях процесса Бернулли. «Положительный исход» в данном случае не
обязательно обозначает что-то хорошее, это значит только то, что событие, которое мы
исследуем, произошло. Например, если мы исследуем, сколько деталей станков из
выборки в 10 штук было бракованными, каждая часть будет считаться отдельным
испытанием, а результат испытания будет классифицирован как положительный
исход, если деталь окажется бракованной. Биномиальное распределение
описывает то, с какой вероятностью определенное число деталей из выборки в 10 штук
окажется бракованным, если есть некоторая оценка общей доли бракованных
деталей.
Данные, представленные биномиальным распределением, должны
удовлетворять четырем требованиям:
1. Каждое испытание имеет два взаимоисключающих исхода.
2. Каждое испытание независимо, так что исход одного испытания не влияет
на исход любого другого испытания.
3. Вероятность успешного исхода, обозначенная как р, одинакова для всех
испытаний.
4. Число испытаний определено, оно обозначается как п.
К примерам данных такого типа, которые можно охарактеризовать при помощи
биномиального распределения, относятся число выпавших орлов при
десятикратном подбрасывании монетки, число мужчин в выборке объемом пять из большой
генеральной совокупности, в которой 65% мужчин (эта генеральная совокупность
должна быть достаточно большой, чтобы доля мужчин заметно не изменилась при
изъятии пяти человек), и число бракованных изделий из 20, принадлежащих к
генеральной совокупности, в которой частота брака составляет 1%.
Формула для вычисления вероятности определенного числа успехов при
данном числе испытаний приведена на рис. 3.7.
Рис. 3.7. Формула для биномиального распределения
Формула для сочетания событий приведена на рис. 3.8.
= пСк =
{к к\(п-к)\
Рис. 3.8. Формула для вычисления вероятности сочетания событий
Сочетание, как обсуждалось в главе 2, выражает число способов выбрать к
предметов из п объектов, если порядок не важен. Учтите, что при написании формулы
El
Глава 3. Статистический вывод
биномиального распределения круглые скобки обозначают сочетание, чтобы
сделать формулу легче для восприятия, однако значение этих скобок такое же, как у
обозначения nCk, которое мы использовали в главе 2.
Символ / в этом уравнении обозначает факториал: п! = (п)(п - \){п - 2) ... (1).
Например, 5!=5 x4x3x2*i= 120.
п - это число испытаний. Если мы подбрасываем монетку 10 раз, п = 10.
к - это число успехов. Если мы хотим вычислить вероятность 5 успехов в 10
испытаниях, к = 10.
/; со значениями в диапазоне между 0 и 1 - это вероятность успеха. Если мы
подбрасываем симметричную монету и называем успешным исходом выпадение
орла, то р = 0,5 (это означает, что вероятность выпадения орла при каждом
броске - это 0,5 или 50%).
Биномиальную формулу можно использовать для вычисления вероятности
определенного числа успехов при известной вероятности успеха в каждом испытании
и при заданном числе испытаний. Сокращенный способ записать биномиальную
вероятность - это b(k;ir,p) или Р(к = к;п;р), где к - это число успехов в п
испытаниях, в каждом из которых вероятность успеха равна р. Если бы мы хотели
вычислить вероятность двух успехов в 20 испытаниях ср = 0,4, мы могли бы написать
6(2; 20, 0,4) или Р(к = 2; 20, 0,4).
На рис. 3.9 изображены три графика биномиальных распределений (обратите
внимание па то, что каждая комбинация р\\п даст свое распределение).
0.2
0.18
0.16
0.14
0.12
0.1
0.08
0.06
0.04
0.02
1 1
А
/ \
/ X
1 \
/ \
/ \
- /
У,
) 5 10—
—i—
1
1
15
1
j
^ 20
1 1
___^_^-. n_nc u п_тг|
~~"™——"¦ \) — U.J И II — L\J
р = 0.7 и п = 20~
р = 0.5 и п = 40
i i
25 30 35
Рис. 3.9. Три биномиальных распределения
С увеличением п при постоянном значении р биномиальное распределение все
больше напоминает нормальное распределение. Из практического опыта следует,
что если и пр, и п{\ - р) равны или больше 5, то биномиальное распределение
Распределения вероятностей
может быть хорошо описано нормальным распределением. На рис. 3.9
распределение (р = 0.5, п = 40), согласно этому правилу, может считаться нормальным,
поскольку
пр = 40(0,5) = 20/2(1 -р) = 40(1 - 0,5) = 20.
Тем не менее распределение ср = 0,1 и п = 40 не может быть аппроксимировано
при помощи нормального распределения, поскольку
пр = 40(0,1) = 4.
Сложные вычисления на основе биномиальных распределений обычно
выполняются при помощи компьютерных программ, но мы рассмотрим, как работает
эта формула, на простом примере. Представьте, что мы подбрасываем правильную
монету пять раз; какова вероятность того, что у нас выпадет ровно один орел? Мы
обозначим выпадение орла как «успех» и используем формулу биномиального
распределения для решения этой задачи. В этом примере:
р = 0,5 (по определению правильной монеты орел и решка выпадают с
равной вероятностью);
п = 5 (потому что мы проводим пять испытаний);
к = 1 (поскольку мы вычисляем вероятность ровно одного успеха).
Вероятность ровно одного успеха в пяти испытаниях, при условии что
вероятность успеха в каждом испытании равна 0,5, вычислена на рис. 3.10.
Р(? = 1;5,0.5)= Ю.З'а-О.б)5-1 =0.16
Рис. 3.10. Вычисление Ь(1;5;0,5)
На рис. 3.11 показано, как вычислить сочетание.
!<\ 5! 5x4x3x2x1
\\) 1!(5-1)! 1х (4x3x2x1)
= 5
Рис. 3.11. Вычисление 5С1
А на рис. 3.12 приведено все вычисление целиком.
Рис. 3.12. Подробное вычисление Ь( 1 ;5;0,5)
Мы также можем получить этот результат, используя биномиальную таблицу
на рис. D.8, приложение D.
ЩЛ ^НHi ¦ Глава 3. Статистический вывод
Независимые и зависимые
переменные
Существует много способов классифицировать переменные: один из наиболее
распространенных - разделить их по роли, которую они играют в планировании
исследования или анализе данных. В рамках этого подхода простой способ - это
описывать неременные как зависимые, если они представляют собой результат
исследования, и независимые, если предполагается, что они влияют на значение
зависимой переменной (зависимых переменных). Во многих исследованиях есть
третья категория переменных, контролируемые в исследовании управляющие
переменные (control variables), которые могут влиять на зависимую переменную, но
не представляют особенного интереса.
Учтите, что ярлыки «независимая», «зависимая» и «управляющая»
соответствуют ролям переменных в данном исследовании. Это значит, что данная
переменная (например, вес) может быть независимой в одном исследовании, зависимой
в другом и управляющей в третьем. В дополнение к этому для описания
зависимых и независимых переменных некоторые авторы используют другие названия,
предпочитая зарезервировать специальные названия для определенных типов
исследований. Управляющие переменные вызывают особенные затруднения,
поскольку выделено много их типов в зависимости от их отношения к исследуемым
независимым и зависимым переменным, а также плана исследования.
Управляющие переменные обсуждаются далее в главе 18, однако это обсуждение будет
сфокусировано па независимых и зависимых переменных.
Мы проиллюстрируем идею независимых и зависимых переменных на примере
регрессионного уравнения. Это лишь краткое введение в тему, регрессия подробно
обсуждается в главах 8, 10 и 11.
В стандартной линейной модели, такой как регрессионное уравнение,
основанное на методе наименьших квадратов (МНК), результирующая или зависимая
переменная обычно обозначается буквой У, тогда как независимые переменные
обозначаются как X. Индексы обозначают отдельные переменные: Xv Х2 и так
далее. (МНК - наиболее распространенный тип регрессии; если не указано иначе,
в этой книге «регрессионное уравнение» обозначает «регрессионное уравнение
МНК».)
Это должно стать ясным из принятой формы записи регрессионного уравнения,
показанной на рис. 3.13.
I Y = & + piXl+p2X2 + P3X3 + ...+e I
Рис. 3.13. Регрессионное уравнение
Буква е в этом уравнении обозначает «ошибку» и отражает тот факт, что мы
пе предполагаем, что какое-либо регрессионное уравнение позволит предсказать
значения Ус абсолютной точностью; напротив, мы ожидаем, что всегда будет
наличествовать некая ошибка предсказания. Обратите внимание на то, что перед
Генеральные совокупности и выборки
шлшшж
каждым X в уравнении стоит р, которую называют регрессионным коэффициентом'.
Pt - это регрессионный коэффициент для Xv P2 - это регрессионный коэффициент
для Х2и так далее. Значения этих регрессионных коэффициентов определяются
при помощи математических вычислений, которые позволяют получить лучшее
уравнение из всех возможных для предсказания значений У по значениям
переменных X на основе имеющегося набора данных.
Из-за принятой системы обозначений зависимую переменную также называют
«У-переменной», а независимые - «Х-переменными». К другим терминам,
используемым для обозначения зависимой переменной, относятся результирующая
переменная, переменная-отклик и объясненная переменная. Независимые
переменные также называют регрессоры, предсказывающие или объясняющие переменные.
Некоторые исследователи считают, что термины «независимый» и «зависимый»
следует использовать только в эксперименте (например, при рандомизированном
исследовании эффективности лекарств с контролем). При такой интерпретации
термины «независимый» и «зависимый» подразумевают причинно-следственную
связь, то есть значение зависимой переменной зависит, по крайней мере частично,
от значений независимой переменной, факт, который сложно, если не вовсе
невозможно, установить при наблюдении. (Различие между экспериментом и
наблюдением подробно обсуждается в главе 18.) В этой книге данное правило не
выполняется, поскольку вопросы причинно-следственной связи гораздо более сложны,
по сравнению с разделением исследований на эксперимент к наблюдение; таким
образом, мы будем использовать термин «независимая переменная» для
обозначения переменных, которые отображают результат исследования, и «зависимая
переменная» для переменных, которые, согласно ожиданиям, влияют на результат.
Генеральные совокупности
и выборки
Концепция генеральных совокупностей и выборок, обсуждаемая также в главе 4,
является ключевой для понимания статистического вывода. Определить, что
является генеральной совокупностью, и выбрать подходящий метод получения
выборки может быть довольно сложным (на самом деле многие статистики с
докторскими степенями специализируются на данном типе работы) и требует большего
внимания, чем может быть уделено этому вопросу здесь. Вместо этого мы обсудим
базовые понятия и концепции, а читателю, которому нужна дополнительная
информация по данной тематике, следует обратиться к специализированным
учебным пособиям (некоторые из них перечислены в приложении С) или пройти
углубленный курс теории получения выборок.
Интересующая нас генеральная совокупность (называемая часто просто
«генеральная совокупность») состоит из всех людей или других объектов (например,
атлантических лососей или частей самолетов), которые исследователи хотели бы
изучить, если бы обладали бесконечными ресурсами. Если посмотреть на это с
другой стороны, то генеральная совокупность - это все множество объектов, на
Ш1ШШШ
Глава 3. Статистический вывод
которое исследователи хотели бы распространить свой результат. Это могут быть,
например, все, кто жил в США в 2007 году, или мужчины возрастом 65-75 лет,
у которых диагностирована застойная сердечная недостаточность.
Выборки и переписи
Почти все статистические исследования основываются на выборках из генеральной
совокупности, а не на самой генеральной совокупности. Из этого правила
существуют немногочисленные исключения. Результат периодического сбора данных обо всей
генеральной совокупности называется переписью. Во многих странах
государственные организации проводят перепись населения. Например, в США перепись
населения проводится раз в десять лет и служит разным целям, включая распределение мест
в палате представителей (нижней палате конгресса). Хотя предполагается, что в ходе
переписи собирают информацию о каждом гражданине, на практике это редко
достижимо. Некоторые люди не участвуют в переписи, а иных опрашивают дважды. Поэтому
некоторые статистики считают, что параметры генеральной совокупности будет
аккуратнее оценивать на основании хорошо составленной выборки, а не переписи, или же
что данные переписи должны быть дополнены результатами изучения выборок. Легко
читаемое обсуждение этих вопросов и хороший перечень источников более подробной
информации содержится в статье Иварса Петерсона (Ivars Peterson), ссылка на которую
приведена в приложении С.
Детерминированные выборки
Существует множество способов составления выборки. К сожалению, некоторые
из самых удобных способов основаны на детерминированном отборе объектов,
что делает их уязвимыми для возникновения выборочного смещения. Это значит,
что существует высокая вероятность того, что выборка, составленная при помощи
детерминированного отбора объектов, будет нерепрезентативной, так что
сделанные па основе этой выборки выводы о генеральной совокупности будут
сомнительными. Методы детерминированного отбора объектов популярны, поскольку
с их помощью исследователь может избежать тягостного процесса составления
вероятностной выборки, однако за это удобство приходится платить. Возможность
распространения выводов, сделанных на основании такой выборки, на всю
генеральную совокупность (как правило, основная цель составления выборки) будет
ограниченной, поскольку репрезентативность выборки неочевидна.
Распространенный тип детерминированной выборки - это выборка из
добровольцев. Вот пример: ученый публикует в газете объявление о наборе испытуемых
и включает в исследование всех, кто пожелал принять в нем участие. Это
удобный способ набрать испытуемых, по, к сожалению, те, кто сами вызвались примять
участие в исследовании, не могут представлять никакую генеральную
совокупность. Использование выборки из добровольцев лучше оставить для такой
ситуации, когда составить случайную выборку затруднительно, например для
исследования тех, кто употребляет запрещенные наркотические вещества. Даже учитывая
ограниченную возможность генерализации, на такой выборке из добровольцев
можно получить полезную информацию, особенно на ранних этапах исследова-
Генеральные совокупности и выборки
¦а
ния. Например, можно использовать таких добровольцев для сбора информации
об использовании наркотических веществ в обществе. На основе подобной
информации впоследствии можно составить опросник для работы со случайной
выборкой людей. Тем не менее результаты, полученные для выборки из добровольцев,
будут иметь ограниченную применимость к генеральной совокупности.
Нерепрезентативпые выборки - это еще один распространенный тип
детерминированных выборок. Как и в случае выборок из добровольцев,
нерепрезентативные выборки можно использовать для сбора информации на ранних этапах
исследования, при этом полученные результаты некорректно распространять на
всю генеральную совокупность. Вот пример нерепрезентативной выборки: вы
собираете информацию о покупательских привычках людей определенного
географического района, опрашивая 50 человек, которые делают покупки в торговых
пассажах (моллах). Проблема состоит в том, что эти 50 человек - не случайная
выборка людей из данного района, нет никаких оснований считать, что их ответы
будут отражать покупательские привычки всех жителей этого района. Однако вы
можете использовать результаты этого опроса для составления анкеты, которую
заполнят случайно выбранные жители данного района.
Выборка по группам (квотная, или пропорциональная, выборка) - это метод
составления детерминированных выборок, при котором сборщик данных получает
инструкцию исследовать определенное число или долю объектов из каждой их
группы. Например, в описанном выше случае торгового пассажа исследователь
мог иметь задачу опросить 25 мужчин и 25 женщин или по меньшей мере 20
людей, не принадлежащих к европейской расе. Выборка по группам немного лучше
нерепрезентативной выборки, поскольку в данном случае есть гарантия того, что
будут представлены разные группы объектов. Например, без требований к квотам
выборка людей из торгового пассажа может быть представлена 45 женщинами и
пятью мужчинами, среди которых не будет ни одного неевроиейца. Однако,
поскольку выборка по группам - это детерминированный метод, вы по-прежнему не
узнаете, адекватно ли ее члены представляют генеральную совокупность. В вашей
пропорциональной выборке может быть равное число мужчин и женщин, но будет
ли оно равным для всех людей, которые делают покупки? Выборка по группам
также подвержена одному определенному типу ошибки выборок, риск которой
существует и для нерепрезентативных выборок. Сборщик данных может
опрашивать людей, которые наиболее похожи на него (например, по возрасту) или
которые выглядят наиболее дружелюбными или доступными, что сделает полученные
результаты еще менее применимыми ко всей генеральной совокупности.
Случайные выборки
При получении случайных выборок каждый объект генеральной совокупности
имеет заданную вероятность попадания в выборку. Случайные выборки, хотя
требуют больших усилий при создании, чем детерминированные, предпочтительнее
для использования, поскольку исследователь может обобщать полученные
результаты на всю генеральную совокупность.
ИМ
Глава 3. Статистический вывод
Получение случайной выборки из генеральной совокупности требует наличия
некоторого полного описания ее структуры (списка объектов генеральной
совокупности). В некоторых случаях это полное описание структуры выборки
очевидно. Например, если генеральная совокупность - это ученики какой-то школы, то
описание структуры выборки - это список всех учащихся. В других случаях
такого хорошего описания структуры выборки не существует. Например, телефонная
книга или список номеров может быть использована для опросов, проводящихся
по телефону. Проблема в данном случае заключается в том, что люди, не имеющие
дома телефона, не будут включены в полученную таким способом выборку, хотя
они и могут входить в интересующую нас генеральную совокупность. В ходе
анализа данных можно использовать статистическое взвешивание и другие
процедуры, чтобы сделать полученные на основе выборки результаты более применимыми
ко всей генеральной совокупности.
Основной тип получения случайных выборок - это простое случайное
извлечение (ПСВ). В этом случае все выборки заданного размера имеют одинаковый
шанс быть извлечены. Предположим, вы хотите составить случайную выборку из
50 учеников определенной школы. Вы берете список всех учащихся и случайно
выбираете 50 человек, пользуясь таблицей или генератором случайных чисел.
Поскольку в списке указаны все представители генеральной совокупности и
выбор людей, включаемых в выборку, совершенно случаен, шансы попасть в
выборку одинаковы как для каждого ученика, так и для каждой подгруппы учеников
(в данном примере любая подгруппа размером в 50 испытуемых имеет равную
вероятность быть отобранной для исследования).
В большинстве случаев ПСВ обладают наилучшими статистическими
свойствами из всех способов извлечения выборок, включая наименьшие доверительные
интервалы для оценок параметров, и могут быть проанализированы при помощи
простейших методов. Однако в некоторых случаях использовать ПСВ может быть
невозможно или запредельно дорого. Поэтому для таких ситуаций были
разработаны иные методы создания вероятностных выборок.
Систематическое извлечение выборки сходно с ПСВ. Для систематического
извлечения выборки нужно переписать или перенумеровать все объекты
генеральной совокупности. Вы определяете желаемый размер выборки, а затем
рассчитываете число п, которое определяет алгоритм составления выборки. Вычисление п
происходит путем деления числа объектов в генеральной совокупности на объем
выборки. Предположим, ваша генеральная совокупность состоит из 500
объектов, а вы хотите создать выборку из 25 объектов; в этом случае п = 20, поскольку
500/25 = 20.
Затем вы выбираете случайное начальное значение, которое лежит в диапазоне
от 1 до л, и включаете в выборку объект из генеральной совокупности, который
имеет такой номер, и каждый следующий п-и объект. Предположим, что вы
хотите создать случайную выборку из 100 объектов для генеральной совокупности из
1000 объектов. Шаги по созданию систематической выборки будут следующими:
1. Взять п = 10, поскольку 1000/100 = 10.
Генеральные совокупности и выборки * . ВНнИЕИ
2. Выбрать случайное число в диапазоне от 1 до 10.
3. Выбрать объект с таким номером и каждый следующий десятый объект.
Если случайно выбранное число было равно 7, то выборка будет содержать
объекты под номерами 7, 17, 27 и так далее до 997.
Систематическое извлечение выборок особенно полезно, когда генеральная
совокупность увеличивается со временем, а изначально определенного списка
объектов не существует. Предположим, например, что вы хотите исследовать людей,
которые будут вызваны в суд в наступающем году. В начале исследования вы не
знаете, кто это будет, так что вы оцениваете размер генеральной совокупности,
основываясь на числе людей, вызванных в суд в предыдущем году, определяетесь
с размером выборки и вычисляете п, как это было описано выше. Затем вы
ведете нумерованный список вызываемых в суд людей, выбрав случайное начальное
число, и исследуете человека, попавшего в ваш список под случайным номером, и
каждого п-то после него. Если у вас п = 14, а случайное стартовое число - 10, вы
обследуете десятого человека, 24-го, 38-го и так далее, пока не наберете нужный
размер выборки.
При использовании систематической выборки нужно соблюдать одну
предосторожность: вы должны убедиться в том, что данные не изменяются
периодически так, что это сопряжено с вашим случайным начальным числом и
значением п. Например, если определенные часы или дни работы суда зарезервированы
для рассмотрения дел определенного типа и ваша комбинация начального числа
и параметра п приводит к тому, что люди, рассмотрение дел которых назначено на
этот период, не могут попасть в вашу выборку, она не будет случайной выборкой
из всех людей, которые вызваны в суд.
Существует много типов извлечения сложных случайных выборок - общее
название для методов составления вероятностных выборок с дополнительными
уровнями сложности, по сравнению со ПСВ. В расслоенных
(стратифицированных) выборках интересующая нас генеральная совокупность разделена на
непересекающиеся группы, или слои, на основании общих характеристик. Для людей
такими характеристиками могут служить пол или возраст; для городов это может
быть численность населения или тип управления; для больниц - тип
руководства или число коек. Если сравнение групп или оценка характеристик каждой из
групп - основная задача исследования, расслоенные выборки - это удачный
выбор, поскольку выбор объектов можно организовать так, чтобы каждая
интересующая нас группа была адекватно представлена. Например, ПСВ может не включать
в себя достаточного числа пожилых людей для оценки их характеристик или для
сравнения с людьми среднего возраста. Расслоенная выборка, напротив, может
быть создана таким образом, чтобы чаще выбирать пожилых людей, а затем при
обработке данных можно провести коррекцию на такое смещение частоты.
Гнездовые (серийные, кластерные) выборки извлекаются с использованием уже
имеющихся естественных группировок в генеральной совокупности. Этот подход
часто используется в региональных исследованиях, которые требуют личных
собеседований или отбора биологических проб (например, крови), поскольку носы-
ЕЭ^НН
Глава 3. Статистический вывод
лать исследователей для работы с одним человеком из городка Рукерсвиль (штат
Вирджиния), одним человеком из города Чадрон (штат Небраска), одним - из
Бэрроу (Аляска) и так далее было бы непозволительно дорого. Более экономно
было бы разработать план создания выборки, который бы имел несколько уровней
случайного отбора людей. На уровне страны нужно случайно выбрать несколько
регионов, затем - случайно выбрать штаты в каждом регионе, города - в каждом
штате и так далее вплоть до отдельных домов и людей в этих домах. Гнездовые
выборки дают меньшую точность, поскольку объекты из одной группы (например,
дома в одном городе или города в одном штате) обычно более сходны между собой,
чем объекты, выбранные при ПСВ. Эта потеря точности обычно в достаточной
степени компенсируется большим объемом выборки, которую можно
обследовать, благодаря снижению расходов.
Метод гнездовых выборок может сочетаться с методом выборок,
пропорциональных численности. Например, вы можете захотеть извлечь выборку изо всех
учеников начальной школы. Не существует списка всех учеников начальной
школы в масштабах всей страны (по крайней мере, для США), но вы можете
составить перечень всех начальных школ, а у каждой школы будет список ее учеников.
Так что вы сможете случайно выбрать школы (возможно, в несколько стадий).
Поскольку в разных школах число учеников неодинаково, вам может захотеться
учесть это обстоятельство при составлении выборки, так чтобы число учеников из
маленьких школ не было бы непропорционально большим (поскольку маленьких
школ больше). Затем вы выберете разное число учеников для каждой выбранной
школы, основываясь на общем числе се учащихся. Это значит, что вы выберете
вдвое больше детей из школы с 400 учениками, по сравнению со школой, в
которой учится всего 200 человек. При таком подходе полученная выборка будет
содержать сопоставимое число учащихся из больших и маленьких школ.
Теорема центрального предела
Теорема центрального предела гласит, что распределение значений выборочных
средних близко к нормальному вне зависимости от распределения значений
генеральной совокупности при условии, что выборки достаточно велики. Этот факт
позволяет нам делать статистические заключения, основанные на свойствах
нормального распределения, даже если выборка происходит из популяции,
распределение значений в которой отлично от нормального.
Для выборочного среднего теорему о центральном пределе можно
сформулировать следующим образом:
Пусть X,,... Хп - это случайная выборка из некоторой генеральной
совокупности со средним арифметическим// и дисперсией а2, тогда для достаточно
больших п
а2
X±N(ia,—)>
п
даже если распределение значений в генеральной совокупности отлично от
нормального.
Теорема центрального предела
L ¦¦13
Символ ~ значит, что «распределение близко к», а формулу можно
прочесть как «распределение средних значений X близко к нормальному со
средним арифметическим и и дисперсией о2/п»\
В применимости теоремы о центральном пределе на практике можно убедиться
при помощи компьютерного моделирования, при котором многократно создаются
выборки заданного размера из генеральной совокупности с отличным от
нормального распределения значений. На рис. 3.14 изображено распределение значений
генеральной совокупности из случайно сгенерированных значений, равномерно
распределенных в диапазоне от 0 до 100.
Щ
1Я
щ
5]
0J—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I
0.00 20.00 40.00 60.00 80.00 100.00
Рис. 3.14. Гистограмма для генеральной совокупности с равномерно
распределенными значениями (Л/ = 100) в диапазоне от 0 до 100
Распределение данных, показанное на рис. 3.14, определенно отличается от
нормального. Однако теорема о центральном пределе гласит, что если выборки
достаточного размера получены из генеральной совокупности с отличным от
нормального распределением значений, средние арифметические этих выборок
распределены близко к нормальному. Обратите внимание, что в теореме ничего
не сказано про то, какой размер выборок нужно считать достаточным. Ученые
используют эмпирические правила, такие как распространенное правило, что
выборка должна включать не менее 30 объектов, однако тут нет абсолютных
законов, применимых во всех случаях. Для выборок из генеральной совокупности
с близким к нормальному распределением значений распределение выборочных
средних будет близким к нормальному всего при 10 или 15 объектах в выборке,
тогда как для генеральной совокупности с очень асимметричным распределением
требуется выборка размером 40 объектов и более.
1 Rosner, Bernard. 2000. Fundamentals of Biostatistics, 5th ed.; Brooks/Cole, Pacific Grove, CA, 174.
нмв
Глава 3. Статистический вывод
Выражение «распределение выборочных средних» труднопроизносимо, но его
значение очевидно. Мы уже рассматривали два типа теоретических
распределений (нормальное и биномиальное), хотя ясно, что случайно взятые переменные
тоже имеют какое-то распределение. В данном случае нас интересует
распределение средних значений, рассчитанных для выборок определенного размера,
которые происходят из данной генеральной совокупности. Если мы многократно
будем получать выборки определенного размера, рассчитывать среднее для
каждой из них и графически изображать частоту значений этих средних, результатом
будет распределение выборочных средних. Мы ожидаем, что выборки будут
немного различаться между собой и, таким образом, иметь разные средние значения,
распределенные некоторым образом. Можно предсказать, как именно будут
распределены эти выборочные средние, основываясь па таких факторах, как
распределение значений генеральной совокупности и размер выборки.
Влияние размера выборки на распределение выборочных средних можно
обнаружить, сравнивая рис. 3.15 и 3.16. На рис. 3.15 представлено распределение
выборочных средних для 100 выборок, состоящих из двух объектов каждая, из
генеральной совокупности, распределение значений которой представлено на
рис. 3.14. На рис. 3.16 представлено распределение выборочных средних для 100
выборок объемом 25 объектов, происходящих из того же распределения.
Распределение, показанное на рис. 3.15, по-прежнему похоже па равномерное. Это
показывает, что размер выборки, равный двум, недостаточен для применения теоремы
о центральном пределе для данной генеральной совокупности.
5J
0^
~h
0.00 20.00 40.00 60.00 80.00 100.00
Рис. 3.15. Распределение средних значений для 100 выборок размером п = 2
из генеральной совокупности с равномерно распределенными значениями
Теорема центрального предела
¦¦на
Ha рис. 3.16 показано распределение средних значений для 100 выборок
объемом п = 25, происходящих из генеральной совокупности с равномерно
распределенными значениями (рис. 3.14). Это распределение гораздо ближе к
нормальному, так что размер выборки 25 оказался достаточным для применения теоремы о
центральном пределе для данной генеральной совокупности.
20-
15-
10-
5-
0-
0.00
J
п
п 111111
20.00 40.00
L
И
МП
lllllfil
60.00 80.00
100.00
Рис. 3.16. Распределение средних значений для 100 выборок размером п = 25
из генеральной совокупности с равномерно распределенными значениями
На рис. 3.17-3.19 продемонстрирован тот же принцип для выборок из
генеральной совокупности с ассимметричным распределением значений. На рис. 3.17
показано сильно асимметричное распределение 100 значений генеральной
совокупности.
Рисунки 3.18 и 3.19 показывают, как тип распределения средних значений для
выборок из этой генеральной совокупности изменяется в зависимости от
размера выборок. На рис. 3.18 показано распределение выборочных средних для 100
выборок объемом п = 2, на рис. 3.19 показано аналогичное распределение для 100
выборок объемом п = 25. Так же как и для предыдущего примера с равномерно
распределенными значениями генеральной совокупности, размер выборок п = 2
недостаточен для применения теоремы о центральном пределе, а п = 25 кажется
достаточным.
Глава 3. Статистический вывод
Рис. 3.17. Асимметричное распределение значений генеральной
совокупности (Л/= 100)
Рис. 3.18. Распределение средних значений для 100 выборок размером п = 2
из генеральной совокупности с асимметрично распределенными значениями
Проверка гипотез
¦ШЕЛ
30-
20-
10-
о
Г
L
-4.00 -2.00
0.00
2.00
4.00
Рис. 3.19. Распределение средних значений для 100 выборок размером п = 25
из генеральной совокупности с асимметрично распределенными значениями
Проверка гипотез
Проверка гипотез составляет основу статистического вывода, поскольку
позволяет использовать статистические методы для решения повседневных задач.
Проверка гипотез состоит из нескольких основных этапов:
1. Формулировка рабочей гипотезы, которая может быть проверена
статистическими методами.
2. Формальное описание нулевой и альтернативной гипотез.
3. Выбор подходящего статистического теста, сбор данных, проведение
вычислений.
4. Выработка решения на основании полученных результатов.
Возьмем для примера оценку нового лекарства для снижения кровяного
давления (борьбы с гипертонией). Производитель хочет доказать, что оно при прочих
равных условиях работает лучше, чем все аналогичные средства, так что рабочая
гипотеза может звучать как-нибудь вроде «Гипертоники, получающие новый
препарат X, продемонстрируют более существенное снижение кровяного давления,
по сравнению с гипертониками, которых лечат созданным ранее препаратом У».
Если мы обозначим среднее снижение кровяного давления в группе пациентов,
получающих препарат X, как р,, а в группе с препаратом Y - как р2, то нулевую и
альтернативную гипотезы можно сформулировать следующим образом:
панн
Глава 3. Статистический вывод
Я(): а, < н2
нл- М, > Н2
Я() называется нулевой гипотезой. В данном примере нулевая гипотеза состоит
в том, что лекарство X неэффективнее лекарства У, поскольку снижение
кровяного давления, достигнутое при помощи препарата X, меньше или равно снижению,
наблюдающемуся для препарата У. Нл, иногда обозначаемая как Я,, называется
альтернативной гипотезой. В нашем примере альтернативная гипотеза заключается в
том, что препарат X более эффективен, чем обычное лечение, поскольку пациенты,
получающие препарат X, демонстрируют более выраженное снижение кровяного
давления, чем пациенты, получающие препарат У. Обратите внимание на то, что
нулевая и альтернативная гипотезы должны быть взаимоисключающими (ни один
результат не может удовлетворять обоим условиям) и исчерпывающими (все
возможные результаты должны удовлетворять одному из двух условий).
В данном примере альтернативная гипотеза односторонняя: мы указываем, что
нулевая гипотеза будет отвергнута, если группа, получавшая препарат X,
продемонстрирует более заметное снижение кровяного давления, по сравнению с
группой, получавшей препарат У Мы также можем сформулировать двустороннюю
альтернативную гипотезу, если она будет более уместной для данного
исследования. Например, если бы мы интересовались, различается ли кровяное давление
(не важно, в какую сторону) у пациентов, получавших препарат X и получавших
препарат У, мы бы показали это при помощи двусторонней альтернативной
гипотезы:
Я(): и, = и2
Двусторонние гипотезы более широко распространены в статистике, поскольку,
как правило, вы хотите обнаружить различия любой направленности.
После сбора данных и вычисления статистик можно принять одно из двух
решений:
• отвергнуть нулевую гипотезу;
• не отвергнуть нулевую гипотезу.
Обратите внимание на то, что если мы не можем отвергнуть нулевую гипотезу,
это не значит, что мы доказали ее справедливость. Это значит только то, что наше
исследование не предоставило достаточных доказательств ее справедливости.
Отклонение нулевой гипотезы иногда называется «нахождением
статистически значимого результата», поскольку проводимый статистический анализ данных
должен продемонстрировать не только, например, различия в средних значениях
по группам, а то, что эти различия статистически значимы. Неформальное
значение статистической значимости - это «скорее всего, наблюдающееся не
случайно», а процесс определения того, значимы ли результаты, включает не только
статистические расчеты, но и применение основанных на традициях правил, которые
могут различаться в зависимости от области исследований или других факторов.
Проверка гипотез
ннш
Процесс проверки статистических гипотез включает в себя выбор уровня
значимости, или р-значения (тема, которая подробнее обсуждается позже), которое
определяет, в каком случае результаты, полученные для выборки, будут
достаточно убедительными, чтобы отвергнуть нулевую гипотезу. На практике р-зпаченпе
наиболее часто принимается равным 0,05. Почему именно это значение? Это в
некотором роде произвольно выбранное граничное значение, история которого
отсчитывается с начала XX века, когда статистические критерии
рассчитывались вручную, а значимость результатов определяли путем сравнения статистик
с опубликованными таблицами. Использование р < 0,05 как критерия значимых
результатов критикуется (см. врезку «Противоречия, связанные с проверкой
статистических гипотез»), однако этот критерий сохраняется во многих
исследовательских дисциплинах. Иногда используются другие пороговые р-значения, такие
как р < 0,01 или р < 0,001, однако еще никому не удавалось ввести в практику
использование большего порогового значения, такого какр < 0,1.
Статистический вывод - это мощное средство, которое позволяет
формулировать вероятностные суждения о данных. Однако поскольку эти суждения
вероятностные, а не абсолютно верные, нельзя исключить возможность ошибки.
Статистики определили два типа ошибок, которые можно допустить при формировании
суждений при помощи предсказательной статистики, и установили уровни
ошибок, которые обычно считаются допустимыми. Эти два типа ошибок
представлены в табл. 3.1.
Противоречия, связанные с проверкой
статистических гипотез
Несмотря на повсеместность проверки гипотез в современной статистике и
каноническое пороговое значение статистической достоверности а = 0,05, ничто из
привычного не остается неизменным. Один из основных критиков - это Якоб Коэн (Jacob Cohen),
аргументы которого приведены в том числе и в статье «Земля круглая (р < 0.05)»2.
Существуют существенные критические замечания как по поводу проверки гипотез в
общем, так и по поводу порогового значения 0,05, но ни то, ни другое, похоже, не уйдет в
прошлое в ближайшее время. С одной стороны, нужно установить какой-то стандарт для
определения статистической значимости, чтобы минимизировать возможность
трактовки как значимых различий, которые были получены в результате ошибки выборки или
других случайных факторов. С другой стороны, в значении 0,05 нет ничего сакрального,
хотя иногда его воспринимают именно так. Более того, уровень значимости результатов,
полученных для выборки, подвержен влиянию многих факторов, включая размер
выборки, и переоценка значения р приводит к игнорированию многих причин, по которым в
данном исследовании был или не был выявлен статистически значимый эффект. Для
статистиков очевидно, что если ваша выборка достаточно велика, даже незначительный
эффект будет статистически значимым. Отсюда следует, что статистические методы -
это мощные инструменты, но они не освобождают исследователей от необходимости
использования чувства здравого смысла.
2 The Earth is round (у? < 0.05) // American Psychologist, December 1994, 997-1003.
Глава 3. Статистический вывод
Таблица 3.1. Статистические ошибки первого и второго рода
Решение,
основанное
на анализе
выборки
Не смогли
отвергнуть Н0
Отвергаем Н0
Для генеральной совокупности
верна Н0
Верное решение:
Н0 справедлива, и она
не отвергнута
Ошибка I рода (а)
верна НА
Ошибка II рода (Р)
Верное решение: Н0 ложна,
и она отвергнута
В двух ячейках этой таблицы приведены правильные решения: Я() верна и не
отвергается при исследовании или Н() ложна и отвергается. В двух других ячейках
представлены статистические ошибки I и II рода. Ошибка I рода, также известная
под обозначением а, соответствует ошибке, которую совершают, отвергая нулевую
гипотезу, в то время как она справедлива для генеральной совокупности. Ошибка
II рода, обозначаемая как р, совершается, когда не выполняющаяся для
генеральной совокупности нулевая гипотеза не отвергается в ходе исследования.
Я составила эту таблицу, чтобы сравнить ситуацию во всей генеральной
совокупности (которая, как правило, неизвестна исследователю) с тем суждением о
генеральной совокупности, которое формируется на основании анализа выборки.
Другой способ понять ситуацию - это рассмотреть суд, в котором нулевая
гипотеза состоит в невиновности подсудимого. В ситуации суда есть реальное положение
дел (совершил подсудимый преступление или нет) и есть решение судей,
основанное на предоставленной им информации (виновен подсудимый или нет). Судья
не может знать реальное положение дел в большей степени, чем статистик знает
характеристики генеральной совокупности, так что он может принять правильное
решение, а может совершить ошибку I или II рода. Если судья посчитает
невинного человека виновным, это будет соответствовать ошибке I рода (отвергнуть
нулевую гипотезу о невиновности, когда она справедлива), а если судья объявит
преступника невиновным, он совершит ошибку II рода (не сможет отвергнуть
нулевую гипотезу о невиновности, когда она не справедлива).
Как уже указывалось выше, пороговое значение ошибки I рода принято
считать равным 0,05. Это значит, что мы миримся с 5%-ной вероятностью совершения
ошибки I типа. Иначе говоря, мы понимаем, что, принимая 0,05 за пороговое
значение статистической ошибки I рода, мы имеем 5%-ную вероятность отвергнуть
нулевую гипотезу, когда нам следовало принять ее.
Ошибка II рода пользовалась меньшим вниманием в теории статистики,
поскольку исторически игнорирование реальной закономерности (ошибка II рода)
считалось менее серьезной ошибкой, чем нахождение несуществующей
закономерности (ошибка I рода). Принятые пороговые значения статистической ошибки
II рода равны 0,1 или 0,2. Если р = 0,1, это значит, что у нас есть 10%-ная
вероятность совершить ошибку II рода, то есть 10% вероятности того, что нулевая
гипотеза будет ложной, но мы не сможем отвергнуть ее в своем исследовании.
Величина, обратная вероятности статистической ошибки II рода, называется
мощность и рассчитывается как 1 - р. В последние годы важности достижения
Доверительные интервалы
¦¦El
нужного уровня мощности придается большое значение. Исследователи и гранто-
датели стали заботиться о мощности и, таким образом, об ошибке II рода, отчасти
потому, что они не хотят вкладывать время, деньги и усилия в исследование до
тех пор, пока не будет обеспечена достаточная вероятность обнаружения
существующих закономерностей. Расчет мощности играет важную роль в планировании
исследований, в особенности при определении размера выборки, который
необходим для достижения достаточной мощности; эти вопросы более подробно
обсуждаются в главе 15.
Доверительные интервалы
Когда мы вычисляем одну статистику, такую как среднее, чтобы охарактеризовать
выборку, это называется точечной оценкой, поскольку полученное число
соответствует одной точке на числовой оси. Хотя выборочное среднее - это лучшая
несмещенная оценка среднего значения для генеральной совокупности, мы знаем, что
если взять другую выборку, полученное для нее среднее, скорее всего, будет
другим. Конечно, мы не можем ожидать, что все выборки из одной генеральной
совокупности будут иметь одно и то же среднее значение. Есть смысл задаться
вопросом, насколько точечная оценка варьирует в силу случайных причин, поэтому во
многих областях науки принято приводить и точечные, и интервальные оценки.
В отличие от точечной оценки, которая представлена одним числом,
интервальная оценка - это числовой диапазон.
Один из распространенных типов интервальной оценки - это
доверительный интервал (интервал между двумя значениями, которые представляют собой
верхнюю и нижнюю доверительные границы данной статистики). Формула, при
помощи которой рассчитывается доверительный интервал, зависит от типа
используемой статистики и будет рассмотрена в соответствующих главах. Задача
этого раздела - ввести понятие доверительного интервала. Он рассчитывается
с использованием заранее установленного уровня значимости, часто
называемого а (греческая буква «альфа»), которая наиболее часто принимается за 0,05, как
это обсуждалось ранее. Доверительный уровень рассчитывается как 1 - а или, в
процентном виде, 100(1 - а)%. Таким образом, при а = 0,05 доверительный
уровень составляет 0,95, или 95%, и в научных журналах обычно требуется указывать
95%-ный доверительный интервал в дополнение к точечным оценкам статистик.
Идея доверительных интервалов состоит в том, что если повторить
исследование бесконечное число раз, каждый раз анализируя новую выборку из генеральной
совокупности и используя доверительные интервалы, рассчитанные для каждой
из этих выборок, доверительный интервал будет содержать истинное значение
параметра, которое нужно оценить в данном исследовании, х% раз (где х - это
доверительный уровень). Например, если интересующая нас статистика - это среднее
и мы используем 95%-ный доверительный интервал, после бесконечного числа
извлечений выборки и вычисления выборочного среднего в 95% случаев среднее
значение для генеральной совокупности будет находиться в пределах
доверительного интервала.
Е1Н11Я
Глава 3. Статистический вывод
Доверительный интервал содержит важную информацию об аккуратности
точечной оценки. К примеру, представьте, что у нас есть две выборки студентов, и в
обоих случаях среднее значение IQ (средний коэффициент умственного
развития) составляет 100. Однако в одном случае 95%-ный доверительный интервал
составляет (95, 105), а в другом случае - (80,. 120). Поскольку первый
доверительный интервал намного уже второго, оценка среднего более точна в первом случае.
Кроме того, более широкий доверительный интервал для второй группы
свидетельствует о том, что изменчивость по IQ в этой группе выше (хотя для проверки
этой гипотезы потребуется дополнительный анализ данных).
Значенияр
Очевидно, что при работе с предсказательной статистикой мы в целом пытаемся
оценить значение того, чего не можем измерить напрямую. Например, мы не
можем обследовать каждого гипертоника на планете, но мы можем собрать данные
о выборке людей с повышенным давлением и сделать выводы па основании этой
выборки. Мы знаем, что при таком подходе всегда существует некоторая
вероятность ошибки, включая вероятность того, что значимые результаты будут
получены из-за влияния случайных причин, таких как ошибки извлечения выборки, а не
из-за факторов, представляющих интерес для исследования.
Значение р характеризует вероятность того, что результаты, по крайней мере
настолько же выбивающиеся из общей массы, как которые получены при анализе
выборки, случайны. Слова «по крайней мере настолько же выбивающиеся из
общей массы» включены в определение потому, что многие статистические тесты
основаны на сравнении статистики с некоторым теоретическим распределением, и
часто (как в случае нормального распределения) значения, расположенные ближе
к центру распределения, встречаются чаще значений, расположенных дальше от
центра (выбивающихся из общего ряда). Даже если распределение
асимметрично (как, например, распределение хи-квадрат), сильно отличающие от среднего
значения обычно реже встречаются, так что принцип определения вероятности
результатов, по крайней мере настолько же выбивающихся из общей массы, как
полученные в ходе исследования, остается полезным.
Рассмотрение простого примера может прояснить ситуацию. Представьте, что
мы проводим эксперимент по подбрасыванию «правильной» монеты, то есть
такой монеты, у которой выпадение орла и решки равновероятно при каждом
броске. Формально мы можем записать это в таком виде:
Р(орел) = Р(решка) = 0,5.
Каждый бросок монетки можно назвать испытанием. Поскольку вероятность
выпадения орла при каждом броске равна 0,5, самая надежная оценка числа орлов,
выпавших при 10 испытаниях, - это 5, хотя мы знаем, что в каждом отдельном
случае при 10 бросках может выпасть разное число орлов. Представим, что мы
подбросили монетку 10 раз и 8 раз выпал орел. Мы хотим вычислить значение р
для этого результата, то есть насколько ожидаемо то, что монетка с вероятностью
Z-статистика
¦¦El
выпадения орла при каждом отдельном испытании 0,5 8 раз упадет орлом вверх
в 10 испытаниях.
При помощи таблицы биномиального распределения, компьютерной
программы или формулы бинома Ньютона мы выясним, что вероятность данного
результата (8 орлов при 10 испытаниях) равна 0,0439, означая, что меньше чем в 5%
случаев при 10 подбрасываниях «правильной» монеты выпадут точно 8 орлов.
Вероятность выпадения 9 орлов при 10 испытаниях равна 0,0098, а 10 орлов - 0,001.
Отсюда видно, что чем сильнее результат отличается от ожидаемого (5 орлов при
10 испытаниях), тем менее он вероятен.
Если мы оцениваем вероятность того, что монета «правильная», далекие от
наших ожиданий (5 орлов при 10 испытаниях) результаты дают нам веские
основания считать ее неправильной. При решении задач такого типа мы обычно
вычисляем вероятность не просто полученного результата, но результатов, которые по
меньшей мере настолько же выбиваются из общей массы. В этом случае
вероятность выпадения 8, 9 или 10 орлов при 10 подбрасываниях монетки составляет
0,0439 + 0,0098 + 0,0010, или 0,0547. Это значение р для выпадения по меньшей
мере 8 орлов при 10 подбрасываниях монетки, для которой вероятность выпадения
орла при каждом броске составляет 0,5.
Значения р обычно приводятся в качестве результатов исследований, в которых
задействованы статистические вычисления, отчасти потому, что интуиция - это
плохой индикатор необычности результатов. Например, многие люди могут
думать, что выпадение 8 или более орлов при 10 бросках правильной монеты
необычно. Статистическое определение «необычного» отсутствует, поэтому мы
будем использовать общепринятый стандарт о том, что значение р для наших
результатов должно быть меньше 0,05, для того чтобы мы отвергли нулевую
гипотезу (которая в нашем случае состоит в том, что монета - «правильная»). В данном
примере, что немного удивительно, этот стандарт не выполняется. Значение р для
нашего результата (8 орлов при 10 испытаниях) не позволяет отвергнуть нулевую
гипотезу о том, что монета «правильная», то есть Р(орел) = 0,5, поскольку 0,0547
больше 0,05.
Z-статистика
Z-статистика аналогична Z-значению, которое обсуждалось ранее, за одним
важным исключением: вместо того чтобы оценивать вероятность определенного
значения, теперь мы интересуемся вероятностью определенного среднего значения
для выборки. Z-статистика - это важный пример применения теоремы
центрального предела, которая позволяет вычислить вероятность результата, полученного
для выборки, при помощи нормального распределения, даже если распределение
значений генеральной совокупности, из которой происходит выборка, нам
неизвестно.
Формула для вычисления Z-статистики (рис. 3.20) сходна с формулой для
расчета Z-значения (рис. 3.3).
Глава 3. Статистический вывод
Рис. 3.20. Формула для вычисления Z-статистики
В этой формуле:
х - это среднее значение для нашей выборки;
и - среднее значение для генеральной совокупности;
а - стандартное отклонение для генеральной совокупности;
п - размер выборки.
Существенное различие между формулами для расчета Z-значения и
Z-статистики - это числитель: в случае Z-значения мы делим на а, а в случае Z-значения
мы делим на а/л/п. Обратите внимание на то, что для вычисления Z-статистики
мы должны знать среднее значение и стандартное отклонение для генеральной
совокупности; если мы знаем только среднее, но не стандартное отклонение, мы
вместо этого можем вычислить ^-статистику (обсуждается в главе 6). Вам может
помочь представление о Z-значении как о Z-статистике для выборки из одного
объекта, так что знаменатель будет равен a/Vl, это то же самое, что и а, в
результате мы получим знакомую формулу для вычисления Z-значения.
Знаменатель в формуле для вычисления Z-статистики называется
стандартной ошибкой среднего, иногда сокращаемой как СОСJ или записываемой в виде
а.. Стандартная ошибка среднего - это стандартное отклонение распределения
значений выборочных средних. Поскольку знаменатель делится на Vrc, большие
выборки при прочих равных будут характеризоваться большими значениями
Z-статистики. Это станет ясным, если рассчитать Z-статистику для нескольких
выборок, которые различаются только размером. Предположим, мы создадим три
выборки из генеральной совокупности со средним значением, равным 50, и
стандартным отклонением, равным 10:
выборка 1:х= 52, п = 30;
выборка 2: х = 52, п = 60;
выборка 3: х =52,п= 100.
Расчеты значений Z-статистики для каждой выборки приведены на рис. 3.21,
3.22,3.23.
Z--
52-50
= 10
л/30
= 1.10
Рис. 3.21. Z-статистика для выборки (х = 52, п = 30) из генеральной
совокупности ~Л/(50, 10)
5 В русскоязычном литературе такое сокращение используется крайне редко, а английская аббреииа-
тура SHM (standard error of the mean) широко распространена. - Прим. пер.
Z-статистика
z =
52-50
= 10
л/60
= 1.55
Рис. 3.22. Z-статистика для выборки (х = 52, п = 60) из генеральной
совокупности ~Л/(50, 10)
z =
52-50
= 10
л/Тоо
= 2.00
Рис. 3.23. Z-статистика для выборки (х= 52, п =100) из генеральной
совокупности ~Л/(50, 10)
Эти примеры ясно демонстрируют, что размер выборки существенно влияет на
результаты и что, при прочих равных условиях, большая выборка характеризуется
большим Z-значением. Эта тема гораздо более подробно разбирается в разделе,
посвященном размеру выборки и мощности, в главе 15, а здесь отметим лишь, что
такой результат интуитивно понятен. Z-статистика рассчитывается при делении
числителя на знаменатель, и большие размеры выборки (п) приводят к
уменьшению знаменателя и, следовательно, к увеличению модуля Z-значения (при
условии, что числитель остается постоянным). Мы говорим про модуль, поскольку при
отрицательном числителе Z-значение будет меньшим при больших п (при прочих
равных условиях), хотя все равно более далеким от 0. Например, в данном
примере, если наше выборочное среднее будет равным 48, а не 52, Z-значения будут
равны-1,10,-1,55 и-2,00.
Предположим, мы проверяем двустороннюю гипотезу со значением альфа 0,05.
В этом случае нам также нужны р-значения для каждой выборки, которые
составляют:
выборка 1:р = 0,2713;
выборка 2:р = 0,1211;
выборка 3: р = 0,0455.
Только третья выборка дает значимые результаты, то есть только для этой
выборки значение р меньше заданного уровня а = 0,05, что позволяет нам отвергнуть
нулевую гипотезу. Это подчеркивает важность достаточного объема выборки при
проведении^ исследования.
Вычислить значение р для заданного Z-значения можно несколькими
способами: с использованием статистических программ, онлайн-калькуляторов (http://
graphpad.com/quickcalcs/PValuel.cfm) или вероятностных таблиц.
Вероятностные таблицы для нескольких наиболее распространенных типов распределения,
включая нормальное, приведены в приложении D вместе с инструкциями по их
использованию.
ЕЁЯнНяН Глава 3. Статистический вывод
Преобразования данных
Многие из наиболее распространенных методов статистического анализа
называются параметрическими, это означает, что в их основе лежат определенные
допущения о распределении значений в генеральной совокупности, из которой
происходит выборка. Если данные в выборке свидетельствуют о том, что эти
допущения не выполняются, у исследователя есть в запасе несколько подходов к
анализу данных. Один - использование непараметрических методов, в основе
которых лежит меньше (или вообще никаких) допущений о типе распределения
данных. Непараметрические статистики обсуждаются в главе 13. Другая
возможность - это преобразовать данные некоторым образом так, чтобы выполнялись
допущения, лежащие в основе нужного статистического метода. Существует много
способов преобразования данных, в зависимости от нужного типа распределения
данных и нарушенных допущений. Мы рассмотрим один случай преобразования
набора данных с целью приближения его распределения к нормальному,
однако обсуждаемые нами общие принципы также применимы к другим задачам по
преобразованию данных. Дальнейшую информацию о преобразованиях данных
можно почерпнуть из более полного учебника, например написанного Mosteller и
Tukey (ссылка приведена в приложении С).
Первый шаг в преобразовании данных - это рассмотреть внимательно набор
данных и решить, какое преобразование подходит в данном случае и нужно ли
оно вообще. Для анализа данных с этой целью рекомендуются два подхода. Один
заключается в графическом изображении данных, например в виде гистограммы
с наложенной кривой нормального распределения. Это позволяет визуально
оцепить распределение данных в общих чертах, а также предоставляет возможность
обнаружить выбросы (экстремальные или необычные значения). Понимание
общей формы распределения данных также помогает решить, какой тип
преобразований можно попробовать применить. Второй подход - вычислить одну из статистик,
разработанных для проверки соответствия данных определенному распределению.
Обычно в этих целях используются две статистики - Андерсона-Дарлинга и
Колмогорова-Смирнова. Алгоритмы вычисления этих статистик включены во многие
статистические пакеты, и различные статистические калькуляторы, доступные в
Интернете, также могут вычислять одну из них или обе. К примеру,
статистический калькулятор для проведения теста Колмогорова-Смирнова доступен по этому
адресу: http://juink.de/statistic-calculator/.
Смещенное влево распределение данных (это значит, что низкие значения
более обычны и «хвост» из менее частых высоких значений «тянется» в правой части
гистограммы) может быть приближено к нормальному при помощи извлечения
квадратного корня или логарифмирования. В первом случае вычисляется
квадратный корень каждого значения. Если исходное значение равно 4, преобразованное
значение равно 2, поскольку V4 = 2. При логарифмическом преобразовании
вычисляется натуральный логарифм каждого значения, так что если исходное значение
равно 4, то после преобразования оно равно 1,386, поскольку 1п(4) = 1,386. Каждое
из этих преобразований может быть с легкостью осуществлено при помощи
статистической программы, карманного калькулятора или электронной таблицы.
Преобразования данных
Ha рис. 3.24 представлено смещенное влево распределение данных. На рис. 3.25
показано распределение тех же данных после извлечения из них квадратного
корня, а на рис. 3.26 показаны те же данные после логарифмирования (то есть на
гистограмме представлены натуральные логарифмы данных с рис. 3.24).
Визуальное сравнение этих трех диаграмм позволяет заключить, что
распределение на рис. 3.24 сильно смещено влево и не соответствует наложенной
кривой нормального распределения. Распределение на рис. 3.25 больше похоже на
нормальное, а на рис. 3.26 распределение стало из смещенного влево смещенным
вправо, так что оно тоже отличается от нормального.
Мы также можем провести статистические тесты, чтобы понять, привели ли
преобразования к приемлемому распределению данных. С этой целью мы
рассчитаем одновыборочную статистику Колмогорова-Смирнова (К-С), чтобы оцепить,
насколько хорошо каждый набор данных соответствует идеальному нормальному
распределению. Для расчетов использовали программу SPSS, хотя они могли быть
также проведены при помощи любой другой статистической программы.
Результаты для этих трех наборов данных приведены в табл. 3.2.
Таблица 3.2. Z-статистики Колмогорова-Смирнова и р-значения для трех наборов
данных
Z-статистика
Колмогорова-Смирнова
Р
Исходные
данные
1.46
0.029
Извлечение
квадратного корня
0.66
0.78
Вычисление
натурального логарифма
1.41
0.04
Рис. 3.24. Гистограмма для данных со смещенным влево распределением
(исходные значения)
Глава 3. Статистический вывод
Рис. 3.25. Гистограмма для данных со смещенным влево распределением
после извлечения из них квадратного корня
Рис. 3.26. Гистограмма для данных со смещенным влево распределением
после их логарифмирования
Нулевая гипотеза для одновыборочного К-С теста заключается в том, что
распределение данных соответствует заданному (в нашем случае нормальному).
Альтернативная гипотеза состоит в том, что распределение данных отличается от
заданного. Программа SPSS вычисляет и К-С-статистику (Z-значение К-С), и
Упражнения
; —кп
р-значение для этой статистики, а мы будем придерживаться правила, при котором
нулевая гипотеза отвергается, еслир < 0,05. Согласно результатам из табл. 3.2, мы
отвергаем нулевую гипотезу для исходных и логарифмированных данных, но нам
не удается ее отвергнуть для квадратного корня из данных. Таким образом, если
мы хотим использовать эти данные для методов, предназначенных для работы с
нормально распределенными данными, мы должны использовать преобразование
с извлечением квадратного корня.
Если значения переменной смещены вправо (то есть много высоких значений
с «хвостом» редких низких значений, «протянувшимся» влево), вы можете
«зеркально отразить» данные, а затем извлечь из них квадратный корень или
логарифмировать. Для «зеркального отражения» переменной прибавьте единицу к
максимальному значению в данных и вычтите каждое значение переменной из этого
нового числа. Например, если наибольшее значение равно 35, вычитайте каждое
значение из 36 (то есть 35 + 1), чтобы получить «отраженные» значения. Это
значит, что исходное значение 1 превратится в 35, исходное значение 2 превратится
в 34 и так далее, вплоть до исходного значения 35, отраженное значение которого
равно 1 (36 - 35). Такое «отражение» превращает смещенное вправо
распределение в смещенное влево, а затем можно извлечь квадратный корень из данных или
логарифмировать их и понять, приближают ли эти процедуры распределение
данных к нормальному.
Преобразование данных - не гарантированное решение проблем с
распределением; иногда преобразование только усиливает имеющуюся проблему или
порождает новую! По этой причине преобразованные данные нужно все время проверять
на нормальность, как мы делали перед этим, чтобы убедиться, что преобразование
привело данные к нужному распределению. Учтите также, что преобразование
меняет единицу измерения данных. Например, если вы логарифмировали значения
кровяного давления, единицей измерения стал логарифм единиц, в которых
измеряется кровяное давление. Если вы «зеркально отражаете» значения переменной,
они меняются местами (максимальное значение становится минимальным), так
что интерпретация любой статистики, основанной на этих значениях, тоже
должна быть «зеркально отраженной». По этим причинам действие любого
преобразования данных нужно учитывать при донесении до окружающих и интерпретации
статистических результатов.
Упражнения
Задача
В каждом из приведенных наборов переменных какие, скорее всего, будут
зависимыми, а какие - независимыми при проведении исследования?
1. Пол, потребление алкоголя, стиль вождения.
2. Средний балл в школе, средний балл на первом курсе университета, выбор
профильной дисциплины в университете (до зачисления), этническая
принадлежность, пол.
UIbUHH Глава 3. Статистический вывод
3. Возраст, этническая принадлежность, отношение к курению, вероятность
рака легких.
4. Аккуратность выполнения задания по программированию, тип
полученных инструкций, время тренировки и уровень тревожности.
Решение
Учтите, что на эти вопросы есть более одного правильного ответа. Приведенные
ответы просто представляют собой наиболее распространенные схемы
исследований.
1. Пол - это независимая переменная (ни потребление алкоголя, ни стиль
вождения на него не влияют). Потребление алкоголя - это, скорее всего,
независимая переменная, а стиль вождения - зависимая, так что
исследоваться будет влияние алкоголя и пола на стиль вождения. Хотя можно
разработать экспериментальную схему, в которой роли потребления алкоголя
и стиля вождения поменяются местами, возможно для проверки
предположения о том, что люди склонны уменьшить потребление алкоголя после
серьезной аварии.
2. Средний балл на первом курсе университета - это, скорее всего, зависимая
переменная. По хронологическим соображениям средний балл в школе
будет независимой переменной (поскольку школа идет раньше
университета). Этническая принадлежность и пол - тоже независимые переменные,
поскольку это характеристики человека. По соображениям хронологии
выбор профильной дисциплины в университете - это независимая
переменная, если средний балл первокурсника - переменная зависимая, поскольку
выбор профильной дисциплины осуществляется до поступления, а
средний балл подсчитывается после окончания первого курса.
3. Вероятность рака легких - это, скорее всего, зависимая переменная, а
возраст, этническая принадлежность и стиль курения - независимые.
4. Аккуратность выполнения задания - это, скорее всего, зависимая
переменная, а все остальные - независимые.
Задача
Почему теорема о центральном пределе чрезвычайно важна при использовании
предсказательной статистики?
Решение
Теорема центрального предела гласит, что распределение выборочных средних
приближается к нормальному вне зависимости от типа распределения значений
в генеральной совокупности, из которой происходят эти выборки, если их размер
достаточно велик. Это важно, поскольку при достаточном размере выборки мы
можем использовать нормальное распределение для расчета вероятности
результатов, полученных для выборки, даже если нам неизвестно распределение
значений в генеральной совокупности, из которой происходят выборки.
Упражнения t J^H^I
Задача
Какой тип извлечения выборки описан в каждом из приведенных ниже
сценариев?
1. Цель состоит в сборе информации по дефициту железа в пробах крови у
жителей США. Выборка извлекается из групп испытуемых, которые
выбирают из вложенных друг в друга территорий страны. Регионы выбирают
случайно, внутри них случайно выбирают штаты и так далее до отдельных
домов.
2. Цель состоит в том, чтобы выяснить, как ученики начальной школы
относятся к недавно назначенному директору. Исследователь хочет
проанализировать равное число мальчиков и девочек, так что в школу прислан
интервьюер с указанием опросить по 10 учеников каждого иола из тех, кого он
встретит на игровой площадке по завершении одного учебного дня.
3. Нужно узнать больше о семейной жизни офицеров полиции, работающих
в большом городе, включая то, как влияет на семейную жизнь занятость
супруги(а) офицера вне дома. Есть полный список всех мужчин и женщин,
которые служат офицерами в данном городе, и при помощи компьютера
извлекается случайная выборка из 200 человек, указанных в этом списке.
Эти люди затем опрашиваются по телефону.
4. Директор фабрики озадачен тем, что качество деталей, производимых в
разное время суток, может быть неодинаково (фабрика работает
круглосуточно). План извлечения выборки заключается в отборе 30 деталей 9 раз в
течение рабочего дня, причем время отбора образцов определяется
случайно в пределах каждой из трех частей суток. Для каждой части суток одна
выборка будет взята в первые два часа, одна - в следующие шесть часов, и
еще одна - в последние два часа.
Решение
1. Гнездовая выборка.
2. Выборка по группам (и нерепрезентативная).
3. Простая случайная выборка.
4. Расслоенная выборка.
Задача
У вас есть тест из 10 вопросов, в котором неправильные ответы не штрафуются.
Для каждого вопроса есть пять вариантов ответа, так что метод случайного выбора
дает 20%-ную вероятность правильного ответа на каждый вопрос. При условии
что вы просто угадываете правильный ответ, какова вероятность ровно трех
правильных ответов?
Решение
На этот вопрос можно ответить при помощи биномиального распределения с
п= 10, /г = 3 и р = 0,2, как показано на рис. 3.27.
Глава 3. Статистический вывод
Р(к-
= 3;10,0.20) =
(1&
0.23(1 ¦
-0.2)7
= 0.20
Рис. 3.27. Вычисление Ь(3; 10, 0.2)
Получается, что вероятность получения ровно трех правильных ответов при
заданных условиях составляет 0,2, или 20%.
Согласно рис. D.8 (вероятностная таблица для биномиального распределения
в приложении D), табличное значение вероятности составляет 0,20133, что при
округлении дает 0,20.
Задача
Какова вероятность правильного ответа на три или более вопроса при условиях,
описанных в предыдущей задаче?
Решение
На этот вопрос также можно ответить при помощи биномиального
распределения п = 10, к = 3 ир = 0,2. Проще вычислить вероятность получения правильных
ответов не более чем на два вопроса, а затем вычесть эту вероятность из единицы,
так что мы используем именно этот подход. Мы можем поступить так, поскольку
вероятность всех возможных событий всегда равна 1, а «по меньшей мере три
правильных ответа» и «не более чем два правильных ответа» вместе учитывают все
возможные события. Мы находим необходимые вероятности при помощи бинома
Ньютона:
Р(? = 0) = 0,11
Р(к=\) = 0,27
Р(к = 2) = 0,30
Р(к> 3) = 1 - Р(к< 2) = 1 - (0,11 + 0,27 + 0,30) = 0,32
Таким образом, вероятность получения трех и более правильных ответов при
заданных условиях составляет 0,32, или 32%.
Согласно рис. D.9 (кумулятивная вероятностная таблица для биномиального
распределения в приложении D), табличное значение вероятности для Ь(2; 10,0,5)
составляет 0,67780; 1 - 0,67780 = 0,3222, что при округлении дает 0,32.
Задача
Вычислите Z-зпачения для следующих данных, учитывая, что они происходят
из нормального распределения с и = 100 и а = 2, и при помощи вероятностной
таблицы для стандартного нормального распределения (рис. D.3 в приложении D)
найдите вероятность значений не меньшего, чем каждое из заданных. Указания по
использованию вероятностных таблиц вместе с подробным решением каждой из
этих задач даны в приложении D.
a) 108;
b) 95;
c) 98.
Упражнения
Решение
a) Z = 4; P(Z > 4,00) = 1 - (0,50000 + 0,49997) = 0,00003.
Рис.
b) Z
Рис.
с) Z
„ 108-100 лпп
Z 4.00
2
3.28. Z-значение для числа 108 из генеральной совокупности
= -2,5; P(Z > -2,50) = 0,50000 + 0,49379 = 0,99379.
„ 95-100 пеп
Z 2.50
2
3.29. Z-значение для числа 95 из генеральной совокупности -
= -1,0; P(Z > -1,00) = 0,50000 + 0,34134 = 0,84134.
z.*z"»._lj0o
2
~Л/(100, 2)
~Л/(100, 2)
Рис. 3.30. Z-значение для числа 98 из генеральной совокупности ~Л/(100, 2)
Задача
Каким из приведенных ниже исходных значений свойственно наиболее
экстремальное (то есть сильнее отличающееся от 0 в положительную или
отрицательную сторону) Z-значение?
a) Значение 190 из генеральной совокупности с и = 180 и a = 4;
b) Значение 175 из генеральной совокупности с н = 200 и а = 5.
Решение
Второе значение более экстремальное, поскольку -5,0 дальше отстоит от 0, чем
2,5 (рис. 3.31 и 3.32).
Рис.
3.31
Z-
Z
190-180
4
= 2.50
¦значение для числа 190 из генеральной совокупности
Z =
175-200 _
5
-5.00
~Л/(180,4)
Рис. 3.32. Z-значение для числа 175 из генеральной совокупности ~Л/(200, 5)
Задача
Вычислите Z-статистику для каждой из следующих выборок, которые
происходят из генеральной совокупности со средним значением 40 и стандартным
отклонением 5. Используйте вероятностную таблицу для стандартного нормального
ШН1Н^ Глава 3. Статистический вывод
распределения (рис. D.3 из приложения D) для нахождения вероятности
значения, не превышающего заданное.
a) х = 42, п = 35
b) х = 42, п = 50
c) х = 39, п = 40
d) x = 39,72 = 80
Решение
a) Z = 2,37; P(Z < 2,37) = 0,50000 + 0,49111 = 0,99889.
z =
42-40
= 5
л/35
= 2.37
Рис. 3.33. Z-статистика для выборки (х = 42, п = 35) из генеральной
совокупности ~Л/(40, 5)
Ь)
г-
- 2,83;
P(Z < 2,83) -
¦ 0,50000 + 0,49767 - 0,99767.
Z.«Z40_2.83
750
Рис. 3.34. Z-статистика для выборки (.г = 42, п = 50) из генеральной
совокупности ~Л/(40, 5)
с) Z = -1,26; P(Z < -1,26) = 1 - P(Z > -1,26) = 1 - (0,50000 + 0,39617) =
= 0,10383.
z =
39-40
= 5 "
л/40
-1.26
Рис. 3.35. Z-статистика для выборки (х = 39, п = 40) из генеральной
совокупности ~Л/(40, 5)
(1) Z - -1,79; P(Z < -1,79) = 1 - P(Z > -1,79) = 1 - (0,50000 + 0,46327) =
= 0,03673.
z =
39-40
: 5 "
л/80
-1.79
Рис. 3.36. Z-статистика для выборки (х = 39, п = 80) из генеральной
совокупности ~Л/(40, 5)
Упражнения
Задача
Вы - директор начальной школы. В рамках комплексного обследования одна
из ваших учениц получила в тесте на IQ (интеллект) 80 баллов. Вы знаете, что в
данной возрастной группе значения IQ имеют нормальное распределение с
параметрами ji = 100, а = 15. Какая статистика поможет вам интерпретировать
результат этой ученицы?
Решение
Z-значение поместит результат ученика в контекст распределения значений IQ
других учеников этого возраста. Как показано на рис. 3.37, результат этой ученицы
находится на 1,33 стандартных отклонения ниже среднего значения для ее
возрастной группы. Хотя многие факторы могут влиять на показатель IQ (отсюда и
необходимость в комплексном обследовании), значение IQ ниже среднего позволяет
предположить, что эта ученица будет испытывать больше трудностей в школе, чем
те, кто показал более высокие результаты в тесте на IQ.
^ 80-100
Z = -1.33
15
Рис. 3.37. Z-значение для числа 80 из генеральной совокупности ~Л/( 100, 15)
Используя вероятностную таблицу для стандартного нормального
распределения (рис. D.3 из приложения D), вы можете увидеть, что только для около 9%
учеников (р = 0,09176) ожидаемый IQ не будет превышать указанного.
Р(Ъ < -1,33) = 1 - P(Z > -1,33) = 1 - (0,50000 + 0,40824) = 0,09176.
Задача
Вы - исследователь-медик, изучающий эффект от вегетарианской диеты на
уровень холестерина. Предположим, что значения уровня холестерина в США у
мужчин в возрасте 20-65 распределены нормально со средним значением 210 мг/де-
цилитр и стандартным отклонением 45 мг/децилитр. Вы исследовали выборку из
40 мужчин в данной возрастной группе, которые придерживались вегетарианской
диеты в течение по меньшей мере одного года, и отметили, что средний уровень
холестерина для них составляет 190 мг/децилитр. Какая статистика поможет
поместить вам результат в общий контекст?
Решение
Вы вычисляете Z-статистику, которая позволяет поместить среднее значение
уровня холестерина для вашей вегетарианской выборки в общий контекст мужчин
в США данной возрастной группы. Как показано на рис. 3.38, среднее значение
уровня холестерина у вегетарианцев находится в 2,81 стандартного отклонения
ниже, чем среднее для всей генеральной совокупности мужчин данной возрастной
группы. Это свидетельствует о том, что растительная диета сопряжена с
пониженным уровнем холестерина. Так же как и в примере с IQ, на уровень холестерина
UHl ¦¦¦ Глава 3. Статистический вывод
могут влиять многие факторы, и медицинское исследование этой темы должно
включать больше переменных. Это упрощенный пример для иллюстрации
использования Z-статистики.
190-210
Z = j= 2.81
45
Рис. 3.38. Z-статистика для выборки (х - 190, п = 40) из генеральной
совокупности ~Л/(210, 45)
Используя вероятностную таблицу для стандартного нормального
распределения (рис. D.3 из приложения D), вы увидите, что вероятность получения
результата, который был бы по меньшей мере настолько экстремальным, согласно
двустороннему тесту, составляет 0,00496, так что если ваше значение а = 0,05, этот
результат достаточен для того, чтобы отвергнуть нулевую гипотезу (в данном
случае о том, что растительная диета не влияет на уровень холестерина).
(Z < -2,81) = 1 - P(Z> -2,81) = 1 - (0,50000 + 0,49752) = 0,00248.
P(Z> 2,81) = 0.00248 (поскольку Z-распределение симметрично).
P[(Z< -2,81) OR (Z> 2,81)] = 2 х (0,00248) = 0,00496.
«
ГЛАВА 4.
Описательная статистика
и графическое представление
данных
Большая часть этой книги, как и большинства книг о статистике, посвящена
статистической проверке гипотез, то есть тому, как делать выводы о генеральной
совокупности, используя статистику, рассчитанную по выборке из нее. Однако данная
глава посвящена другому виду статистики: описательной, то есть использованию
методов статистики и графических подходов для представления информации об
изучаемых данных. Практически все, кто связан с обработкой данных,
используют оба вида статистики, и часто вычисление описательных статистик - это
предварительный этап перед итоговой стадией проверки гипотез. Особенно широко
практикуют анализ графического представления данных и расчет простейших
описательных статистик, чтобы лучше почувствовать анализируемые данные.
Всегда полезно узнать свои данные лучше, и почти всегда время, проведенное
за этим занятием, не тратится впустую. Описательная статистика и графическое
представление данных могут быть и окончательным результатом статистического
анализа. К примеру, в бизнесе может потребоваться следить за объемами продаж
в разных местах или для разных продавцов и представлять эти данные с помощью
графиков, без какого-либо применения этой информации для того, чтобы делать
выводы (например, о других местах или годах) с использованием собранных
данных.
Генеральные совокупности и выборки
Одни и те же данные можно рассматривать или как генеральную совокупность,
или как выборку, в зависимости от целей их сбора и анализа. Например,
итоговые оценки за экзамен для всех учеников класса - генеральная совокупность,
если перед нами стоит цель описать распределение оценок в этом классе, но
эти же оценки можно расматривать как выборку, если цель анализа состоит в
том, чтобы на основании этих оценок сделать вывод об оценках других учени-
IEE1
¦
Глава 4. Описательная статистика и графическое представление...
ков (возможно, в других классах или школах). Анализ генеральной
совокупности подразумевает, что ваш набор данных представляет все интересующие вас
объекты, так что вы можете напрямую судить о характеристиках этой группы.
В противоположность этому при анализе выборки вы работаете только с
частью генеральной совокупности, и любые утверждения, которые вы делаете об
этой большей группе на основании выборки, вероятностные, а не абсолютные.
(Обоснование статистики вывода приведено в главе 3.) По практическим
соображениям выборки анализируют чаще, чем генеральные совокупности,
поскольку изучить все члены генеральной совокупности напрямую бывает невозможно
или непозволительно дорого.
Различие между описательной статистикой и статистикой вывода
принципиально, и для проведения различий между ними был разработан набор
условных обозначений и терминов. Хотя эти обозначения несколько различаются в
разных источниках, как правило, числа, которые характеризуют генеральную
совокупность, называют параметрами и обозначают греческими буквами,
такими как и (для среднего) и а (для стандартного отклонения); числа, которые
описывают выборку, называются статистиками и обозначаются латинскими
буквами, такими как х (выборочное среднее) и s (выборочное стандартное
отклонение).
Меры центральной тенденции
Меры центральной тенденции, также известные как меры положения, обычно
одни из первых статистик, которые рассчитывают для непрерывных переменных
из только что полученных данных. Главная цель их расчета состоит в том,
чтобы дать представление о типичном или часто встречающемся значении в данной
переменной. Три самые часто применяемые меры центральной тенденции - это
среднее, медиана и мода.
Среднее
Среднее арифметическое, или просто среднее, - это то же самое, что в быту
называют средним какого-то набора значений. Расчет среднего как меры центральной
тенденции подходит для интервальных или характеризующих отношения данных,
а среднее дихотомической переменной, закодированной как 0 и 1, дает долю
случаев, когда она принимает значение 1. Для непрерывных данных, к примеру
результатов измерения роста или теста на IQ, среднее просто рассчитывают, сложив все
значения и разделив сумму на их число (объем выборки). Среднее генеральной
совокупности1 обозначают греческой буквой и («мю»), тогда как среднее
выборки обычно показывают чертой над обозначением переменной: например, среднее
х обозначается как х и читается как «х с чертой». Некоторые авторы также
используют такую запись и для названий переменных. К примеру, можно обозначить
«средний возраст» как возраст, что читается как «возраст с чертой».
1 В случае генеральной совокупности его также называют математическим ожиданием. - Прим. пер.
Меры центральной тенденции ii iHH^I
Положим, у нас есть генеральная совокупность с пятью элементами и вот
значения переменной х для всех них:
100,115,93,102,97
Мы находим среднее х} сложив все эти значения и разделив на 5 (число
значений):
и = (100 + 115 + 93 + 102 + 97)/5 = 507/5 = 101,4.
Статистики часто используют принятую форму записи суммы, приведенную
в главе 1, которая определяет статистику с помощью описания ее расчета. Расчет
среднего одинаков как в случае выборки, так и в случае генеральной
совокупности; отличие только в символе, обозначающем само среднее. Среднее генеральной
совокупности, записанное в виде суммы, представлено на рис. 4.1.
Рис. 4.1. Формула для расчета среднего
В этой формуле и - это среднее х по генеральной совокупности, п - это число
наблюдений (число значенийх), ах. - это значение х в конкретном наблюдении.
Греческая буква X («сигма») обозначает сумму (сложение), а обозначения под и
над «сигмсЗй» определяют набор значений, к которым должна быть применена эта
операция. В данном случае требуется сложить все значения х от 1 до п. Символ г
обозначает положение в данных, так что хх - это первое значение в данных, х.} - это
второе значение, а хп - последнее. Символ суммы означает, что мы должны
сложить все значения хот первого (х^) до последнего (хц). Таким образом, среднее по
генеральной совокупности рассчитывается с помощью сложения всех значений
исследуемой переменной и последующего деления на общее число значений,
помня, что деление на п - это то же самое, что и умножение на —.
Среднее - это интуитивно понятная мера центральной тенденции, которую
легко осознать большинству людей. Однако среднее в этом качестве следует
использовать не для любых данных, поскольку оно чувствительно к экстремальным
значениям, или выбросам (обсуждается подробнее ниже), и также может вести к
неверным выводам в случае асимметричного распределения данных. Посмотрите
на один пример. Положим, в нашем маленьком примере последнее значение было
297, а не 97. В таком случае среднее будет равно:
п = (100 + 115 + 93 + 102 + 297)/5 = 707/5 = 141,4.
Среднее 141,4 - это нетипичное значение для этих данных. На самом деле
80% данных (четыре значения из пяти) меньше среднего, которое искажено
присутствием одного очень высокого значения.
Эта проблема не просто теоретическая; многие данные тоже распределены
таким образом, что среднее не подходит для них в качестве меры центральной
тенденции. Это часто правда для таких показателей, как данные о доходе на семью в
НИН Глава 4. Описательная статистика и графическое представление...
США. Очень небольшое число крайне богатых семей делает средний доход на
семью гораздо выше типичного, и поэтому вместо среднего дохода часто используют
медианный доход (подробнее про медиану см. ниже).
Среднее также можно рассчитать, используя данные из таблицы частот, то есть
таблицу, показывающую значения данных и то, как часто каждое из них
встречается. Посмотрите на следующий пример в табл. 4.1.
Таблица 4.1. Простая таблица частот
Значение
1
2
3
4
Частота
7
5
12
2
Для того чтобы получить среднее этих чисел, следует использовать колонку
частот как переменную для взвешивания. То есть каждое значение надо умножить
на его частоту. Что касается знаменателя, сложите все частоты, чтобы получить
суммарное п. Среднее затем рассчитывают, как показано на рис. 4.2.
}Л =
я(Х>
с7) + (2х5)-
(7 + 5
(-(3x12)+ (4:
+ 12-
+ 2)
<2)
= 2.35
Рис. 4.2. Расчет среднего по таблице частот
Такой же результат можно получить, если сложить все значения (1 + 1 + 1 + 1
+ ...) и разделить па 26.
Среднее для сгруппированных данных, то есть в которых исходные данные
были разбиты на несколько интервалов в соответствии со значениями, а точные
значения теперь неизвестны, рассчитывается похожим образом. Поскольку мы не
знаем точные значения для каждого наблюдения (мы, к примеру, знаем, что пять
значений попали в интервал между 1 и 20, но не знаем, что это были за
значения), для расчетов мы используем середину интервалов как подстановочное
число вместо точных значений. Таким образом, чтобы посчитать среднее, мы сначала
рассчитываем середину каждого интервала, а затем умножаем его на число
значений в интервале. Для расчета середины интервала сложите его крайние значения
и разделите на 2. К примеру, середина для интервала 1-20 будет:
(1+20)/2=10,5.
Среднее, рассчитанное таким образом, называется групповым средним.
Групповое среднее не так точно, как среднее, посчитанное с помощью изначальных
данных, но часто это единственное, что можно сделать, потому что сырые
данные не доступны. Посмотрите на следующий пример сгруппированных данных в
табл. 4.2.
Меры центральной тенденции
Таблица 4.2. Сгруппированные данные
Промежуток
1-20
21-40
41-60
61-80
81-100
Частота
5
25
37
23
8
Середина
10.5
30.5
50.5
70.5
90.5
Среднее рассчитывают, умножая середину каждого интервала на число
значений в нем (частота) и деля на суммарную частоту, как показано на рис. 4.3.
М:
(10.5 х 5) + (30.5 х 25) + (50.5 х 37) + (70.5 х 23) + (90.5 х 8)
(5 + 25 + 37 + 23 + 8)
= 51.32
Рис. 4.3. Расчет среднего для сгруппированных данных
Один из способов снизить влияние выбросов - это использовать усеченное
среднее, также известно как винсоризованное среднее. Как следует из названия,
усеченное среднее рассчитывают, отсекая, или выбрасывая, определенный процент
крайних значений в распределении, а затем подсчитывают среднее оставшихся
значений. Цель состоит в том, чтобы среднее хорошо представляло большинство
значений, но не подвергалось значительному влиянию крайних значений.
Рассмотрите приведенный ранее пример второй генеральной совокупности с пятью
членами со значениями 100, 115, 93, 102 и 297. Среднее этой совокупности
искажено влиянием одного очень большого значения, так что мы рассчитываем
усеченное среднее, убрав самое большое и самое маленькое значения (эквивалентно
удалению 20% самых больших и самых маленьких значений). Усеченное среднее
рассчитывают так:
(100 + 115 + 102)/3 = 317/3 = 105,7.
Значение 105,7 гораздо ближе к типичным значениям в распределении, чем
141,4 - среднее по всем значениям. Конечно, мы будем редко встречаться с
генеральными совокупностями только с пятью членами, но принцип точно так же
работает и с большими наборами чисел. Обычно удаляют определенный процент
данных с краев распределения. Применение такого подхода следует всегда указывать,
чтобы было понятно, что на самом деле означает приведенное среднее.
Кроме того, среднее можно рассчитывать и для дихотомических переменных,
если закодировать их значения как 0 и 1, и в таком случае среднее будет
эквивалентно проценту случаев, в которых переменная принимает значение 1.
Предположим, у нас есть генеральная совокупность из 10 испытуемых, 6 из которых
мужского пола, а 4 - женского, и мы закодировали мужчин как 1, а женщин как 0.
Расчет среднего даст нам процент мужчин в совокупности:
иптш
Глава 4. Описательная статистика и графическое представление...
и=(1+1+1+1+1+1+0+0+0+ 0)/10 = 6/10 = 0,6, или 60% мужчин.
Медиана
Медиана в данных - это срединное значение, если данные отсортировать по
возрастанию или убыванию. Если есть п значений, то медиана формально
определяется как значение с порядковым номером (п + 1)/2, так что если п = 7}то
срединное значение - это значение с номером (7 + 1)/2, или четвертое значение. Если
значений четное число, то медиана определяется как среднее арифметическое
двух срединных значений. Это формально определяется как среднее значений под
номерами (п/2) и (п/2 + 1). Если значений шесть, то медиана - это среднее
значений под номерами (6/2) и (6/2 + 1), то есть третьего и четвертого. Оба метода
демонстрируются здесь:
• нечетное число значений (5): 1,4,6,6,10; медиана = 6, потому что (5 + 1)/2 = 3,
и 6 - это третье число в упорядоченном списке;
• четное число значений (6): 1, 3, 5, 6, 10, 14; медиана = (5 + 6)/2 = 5,5,
поскольку 6/2 = 3 и 6/2 +1=4, а 5 и 6 - это третье и четвертое значения в
упорядоченном списке.
Медиана лучше среднего в качестве меры центральной тенденции для
симметричных данных или данных с выбросами. Это связано с тем, что медиана основана
на рангах, а не па самих значениях, и по определению половила значений лежит
ниже медианы, а половина - выше, вне зависимости от конкретных чисел. Таким
образом, не имеет значения, есть ли в данных какие-то очень большие или
маленькие значения, потому что они не повлияют на медиану сильнее, чем менее
отклоняющиеся значения. К примеру, медианы всех трех показанных ниже
распределений равны 4:
распределение Л: 1, 1, 3, 4, 5, 6, 7;
распределение Б: 0.01, 3, 3, 4, 5, 5, 5;
распределение В: 1, 1, 2, 4, 5, 100, 2000.
Разумеется, медиана далеко не всегда подходит как мера центральной
тенденции для описания генеральной совокупности или выборки. В чем-то это дело
вкуса; в данном примере медиана, похоже, неплохо отражает данные в
распределениях А и Б, но, видимо, не в распределении В, в котором данные настолько
разбросаны, что использование одного числа для его характеристики вообще может
быть некорректно.
Мода
Третья обычная мера центральной тенденции - это мода, которая несет
информацию о самом часто встречающемся значении. Мода часто полезна при описании
порядковых или категориальных данных. К примеру, представьте, что следующие
числа отражают предпочитаемый источник новостей у студентов, где 1 - газеты,
2 - телевизор, 3 - Интернет:
Меры центральной тенденции
¦¦ИИ
1,1,2,2,2,2,3,3,3,3,3,3,3.
Мы можем видеть, что Интернет - самый популярный источник, поскольку
3 - это модальное (самое частое) значение в этих данных.
Когда моду используют для непрерывных данных, обычно ею называют
определенный промежуток значений (поскольку в случае множества вариантов значении,
обычного для непрерывных данных, не может быть одного числа, встречающегося
заметно чаще других). Если вы собираетесь так делать, стоит задать категории
заранее и использовать стандартные промежутки, если они существуют. К примеру,
возраст взрослых часто собирают с точностью до 5 или 10 лет, и, возможно, если
какие-то данные разделить на промежутки по 10 лет, то модальный возраст будет
40-49 лет.
Сравнение среднего, медианы и моды
В идеально симметричном распределении (таком как нормальное распределение,
обсужденное в главе 3) среднее, медиана и мода в точности совпадают. В
асимметричном распределении все они будут различаться, как показано в данных,
изображенных в виде гистограмм на рис. 4.4, 4.5 и 4.6. Для упрощения расчета моды мы
разбили данные на промежутки по 5 (35-39,99, 40-44,99 и т. д.).
12.И
ю.оЧ
7Н
5-И
2.54
00_| j—|—|—|—j—|—|—|—|—|—|—|—|—|—|—|—|—|—| (
40.00 45.00 50.00 55.00 60.00 65.00
Рис. 4.4. Симметричные данные
пи
¦
Глава 4. Описательная статистика и графическое представление...
Данные на рис. 4.4 приблизительно нормальные и симметричные со средним
50,88 и медианой 51,02; самый частый интервал 50,00-54,99 (37 наблюдений), за
которым следует 45,00-49,99 (34 наблюдения). В этом распределении среднее и
медиана очень близки, а два самых частых промежутка тоже располагаются вокруг
среднего.
юЧ
И
И
И
2-]
о* I ' ' ' I ' ' ' I ' ' ' 1 ' ' ' I ' ' ' I
40.00 50.00 60.00 70.00 80.00 90.00
Рис. 4.5. Данные с правым плечом
У данных на рис. 4.5 есть правое плечо; среднее составляет 58,18, и медиана -
56,91. Среднее больше медианы - это типично для распределений с правым
плечом, поскольку очень большие значения «тянут» среднее наверх, но не оказывают
такого влияния на медиану. Модальный промежуток - это 45,00-49,99 с 16
наблюдениями; тем не менее,в несколько других интервалов попало по 14 наблюдений,
что делает их очень близкими в смысле частоты к модальному промежутку, из-за
чего мода не так полезна в описании этих данных.
У данных на рис. 4.6 есть левое плечо; среднее составляет 44,86, а
медиана - 47,43. Для распределений с левым плечом характерно среднее ниже
медианы, поскольку очень маленькие «значения» тянут среднее вниз, но не
оказывают такого влияния на медиану. Отклонение от симметричности на рис. 4.6
сильнее, чем на рис. 4.5, и это отралсается в большей разнице между средним
и медианой на рис. 4.6, чем на рис. 4.5. Модальный интервал для рис. 4.6 - это
45,00-49,99.
Меры разброса
Рис. 4.6. Данные с левым плечом
Меры разброса
Разброс говорит о том, насколько сильно рассеяны значения в данных. Из-за этого
меры рассеяния часто называют мерами разброса. Знание разброса данных может
быть так же важно, как и знание их центральной тенденции. К примеру, в двух
совокупностях детей среднее IQ составляет 100, но в одном случае разброс может
быть от 70 до 130 (от слабого отставания в развитии до почти гениальности), тогда
как в другом разброс может быть от 90 до 110 (все в пределах нормы). Отличие
может быть важным, к примеру, для учителей, поскольку, несмотря на одинаковый
средний интеллект, разброс IQ в этих группах говорит о том, что у них могут быть
различные образовательные и социальные потребности.
Размах и межквартильный размах
Самая простая мера разброса - это размах, то есть просто разность между самым
большим и самым маленьким значениями в выборке. Часто минимальное
(наименьшее) и максимальное (наибольшее) значения также указывают при
использовании размаха. Для данных (95,98,101,105) минимум равен 95, максимум равен
105, а размах - 10 (105 - 95). Если в данных есть один или несколько выбросов,
размах может не быть полезной мерой. К примеру, в данных (95, 98, 101, 105, 210)
размах составляет 115, но почти все значения лежат в пределах 10 (95 - 105).
Подсчет размаха для любой переменной - это хороший метод знакомства с данными;
I HI Глава 4. Описательная статистика и графическое представление...
необычно большой размах или крайне экстремальные минимальное или
максимальное значения могут быть поводом для дальнейшего исследования. Крайне
высокие или низкие значения или очень большой размах могут возникнуть из-за
таких причин, как ошибка при вводе данных или включение наблюдения из
другой генеральной совокупности, чем та, которую вы исследуете (данные для
взрослого могли случайно попасть в данные, касающиеся детей).
Межквартнльный размах - это альтернативная мера разброса, которая слабее
подвержена влиянию крайних значений, чем размах. Межквартнльный размах -
это диапазон изменчивости 50% данных из середины, который рассчитывают как
разницу между 75% и 25% персентилями. Межквартнльный размах легко
получить с помощью большинства статистических программ, но несложно его
посчитать н вручную с помощью следующих правил (п = число наблюдений, к- это
персснтпль, которую вам надо найти):
1. Отсортируйте все наблюдения по возрастанию.
2. Если пк/\00 - целое (число без десятых или дробной части), то &-ая
персснтпль наблюдений - это среднее наблюдений под номерами nk/\00 и
яА/100+1.
3. Если пк/100 - не целое, /г-ая персентиль совпадает с измерением номер
j + 1, где У — максимальное целое число, меньшее пк/\00.
4. Подсчитайте межквартнльный размах как разность 75% и 25% персенти-
лей.
Рассмотрим следующий набор данных с 13 наблюдениями (1, 2, 3, 5, 7, 8, 11, 12,
15,15,18,18,20):
1. Сначала мы найдем 25% персентиль, то есть к = 25.
2. У нас 13 наблюдений, так что п = 13.
3. (пк)/\00 = (25 Х 13)/100 = 3,25, не целое, поэтому мы используем второй
метод (№ 3 в предыдущем списке).
4. у = 3 (максимальное целое число, меньшее пк/100, то есть меньше 3,25).
5. Таким образом, 25% персентиль - это наблюдение номеру + 1, или
четвертое наблюдение, которое равно 5.
Мы можем проделать те же шаги и для 75% персентили:
1. (/7/0/ЮО = (75*13)/100 = 9,75, не целое.
2. j = 9, максимальное целое, меньшее 9,75.
3. Таким образом, 75% персентиль равна значению номер 9+1, или 10, и
которое равно 15.
4. В итоге межквартнльный размах равен 15 - 5, или 10.
Устойчивость межквартильного размаха к выбросам должна быть очевидна.
У этих данных размах равен 19 (20 - 1), а межквартнльный размах равен 10;
однако если бы последнее значение было равно 200 вместо 20, размах бы составлял
199 (200 - 1), но межквартнльный размах все также был бы равен 10, и это число
лучше бы представляло большинство значений в данных.
Меры разброса
Дисперсия и стандартное отклонение
Самые часто используемые меры разброса для непрерывных переменных - это
дисперсия и стандартное отклонение2. Обе из них описывают то, насколько
отдельные значения в данных отличаются от среднего значения. Дисперсия и
стандартное отклонение рассчитывают слегка по-разному в зависимости от того, что
исследуется, генеральная совокупность или выборка, но в целом дисперсия - это
средний квадрат отклонения от среднего, а стандартное отклонение - это
квадратный корень из дисперсии. Дисперсию генеральной совокупности обозначают как
а2 (произносится как «сигма в квадрате»), а стандартное отклонение - а (греческая
буква «сигма»), тогда как в случае выборки дисперсия и стандартное отклонение
обозначаются как s2 и s соответственно.
Отклонение от среднего для одного значения в данных рассчитывают как
(х. - и), где х - это i-e значение в данных, а и - это среднее всех значений. При
работе с выборкой принцип тот же, только вы должны вычитать среднее но этой
выборке (х) из каждого значения, а не среднее по генеральной совокупности. При
записи в виде суммы формула для расчета суммы отклонений от среднего для
переменной х для генеральной совокупности с п членами показана на рис. 4.7.
п
2и,
/-1
-[Л)
Рис. 4.7. Формула для суммы отклонений от среднего
К сожалению, эта величина не несет особой пользы, потому что она всегда
будет равна нулю, совсем не удивительный результат, если принять во внимание то,
как рассчитывается среднее всех значений в наборе данных. Это легко
продемонстрировать на примере небольшого набора чисел (1, 2, 3, 4, 5). Сначала рассчитаем
среднее:
н = (1 + 2 + 3 + 4 + 5)/5 = 3.
Затем рассчитаем суммы отклонений от среднего, как показано на рис. 4.8.
/-1
= (-2)
-^)
+ (-
= (1-
1) + 0
-3) + (2-
+ 1 + 2 =
-3)-
= 0
КЗ-
-3)-
К4-
-3)-
К5-
-3)
Рис. 4.8. Расчет суммы отклонений от среднего
Чтобы обойти эту проблему, мы работаем с квадратами отклонений, которые
по определению всегда положительны. Чтобы получить средний квадрат
отклонения, или дисперсию, мы возводим каждое отклонение в квадрат, складываем их
все и делим на число наблюдений, как показано на рис. 4.9.
Последнее часто также называют среднеквадратичным отклонением. - Прим. пер.
DQ
Глава 4. Описательная статистика и графическое представление...
"?i
Рис. 4.9. Расчет суммы квадратов отклонений от среднего
Формула дисперсии для выборки отличается, поскольку требует разделить па
п- 1, а не п; причины чисто технические и связаны с числом степеней свободы и
несмещенной оценкой. (Для подробного обсуждения см. статью Вилкинса (Wilkins),
указанную в приложении С.) Формула для дисперсии выборки, обозначаемой как
s2, приведена на рис. 4.10.
п — 1 ^^
Рис. 4.10. Формула дисперсии для выборки
Продолжая наш простейший пример со значениями (1, 2, 3, 4, 5), среднее
равно 3, н мы можем рассчитать дисперсию для этой генеральной совокупности, как
показано на рис. 4.11.
1 п
о"—Ее.
11
-Jl(1-3)i+
¦?[<-2)2+(
4+1+0+1
5
-м)
(2-
-I)2
+ 4
2
3)2 +
+ (0)2
10
" 5
(З-З)2
+(1)2 +
= 2.0
+ (4-
(2)2]
¦З)2
+ (5-
-З)2]
Рис. 4.11. Расчет дисперсии для генеральной совокупности
Если мы примем эти значения за измерения из выборки, а не за члены
генеральной совокупности, дисперсию следует рассчитывать, как показано на
рис. 4.12.
Обратите внимание, что из-за отличия в знаменателе формула дисперсии для
выборки всегда будет давать больший результат, чем формула для генеральной
совокупности, хотя при размере выборки, близком к размеру генеральной
совокупности, отличие будет очень небольшим.
Меры разброса
¦¦по
= ^[(1-3)2+(2-3)2+(3-3)2+(4-3)2+(5-3)2]
= |[(-2)2 + (-1)2+(0)2+(1)2+(2)2]
4
4 + 1 + 0 + 1 + 4 10
4 " 4 "
Рис. 4.12. Расчет дисперсии для выборки
Раз квадраты всегда положительны (если не учитывать мнимые числа), то и
дисперсия всегда будет не меньше 0. (Дисперсия будет равна нулю только в случае,
если все значения переменной одинаковы, а в таком случае переменная является
константой.) Однако при расчете дисперсии мы перешли от наших изначальных
единиц к их квадратам, что может быть неудобно для интерпретации. К примеру,
если мы измеряем массу в фунтах, нам бы было удобно, если бы меры
центральной тенденции и меры разброса тоже выражались в тех же единицах, чтобы не
использовать среднее в фунтах, а дисперсию в фунтах в квадрате. Чтобы
вернуться к изначальным единицам, мы извлекаем квадратный корень из дисперсии; эта
величина называется стандартным отклонением, и она обозначается как а в случае
генеральной совокупности и s для выборки.
Формула для расчета стандартного отклонения для генеральной совокупности
приведена на рис. 4.13.
¦J"!'-1'""'
Рис. 4.13. Формула стандартного отклонения для генеральной совокупности
Обратите внимание, что это просто квадратный корень из формулы для
дисперсии. В предыдущем примере стандартное отклонение можно найти, как показано
на рис. 4.14.
а = л/с? = л/2~=1.41
Рис. 4.14. Связь между стандартным отклонением и дисперсией
Формула для стандартного отклонения для выборки приведена на рис. 4.15.
1ИЯ1
¦
Глава 4. Описательная статистика и графическое представление...
Рис. 4.15. Формула для стандартного отклонения для выборки
Как и для стандартного отклонения для генеральной совокупности, в случае
выборки стандартное отклонение - это квадратный корень из выборочной
дисперсии (рис. 4.16).
s = V7 = V2L5 =1.58
Рис. 4.16. Связь между стандартным отклонением и дисперсией
В целом, в случае двух выборок одного объема с измерениями в одних единицах
(например, две группы по 30 человек, у обеих измеряют массу тела в фунтах), мы
можем утверждать, что у группы с большими дисперсией и стандартным
отклонением больше разброс значений. Однако единица измерения влияет на величину
дисперсии, что может усложнить сравнение разбросов переменных, измеренных
в разных единицах. Очевидный пример: при измерении массы тела в унциях
дисперсия и стандартное отклонение будут больше, чем если измерять ее в фунтах3.
В случае сравнения абсолютно разных единиц, вроде роста в дюймах и массы тела
в фунтах, сравнить разброс еще сложнее. Коэффициент вариации (KB) - мера
относительного разброса, позволяет обойти эту проблему и делает возможным
сравнивать разброс между различными переменными, измеряемыми в разных
единицах. В данном случае KB показан здесь для выборочного разброса, но его можно
точно так же рассчитать и в случае генеральной совокупности, заменив s на a. KB
можно рассчитать, разделив стандартное отклонение на среднее, а затем умножив
на 100, как показано на рис. 4.17.
KB =зх100
х
Рис. 4.17. Формула для коэффициента вариации (KB)
Если вспомнить предыдущий пример, он рассчитывается, как показано на
рис, 4.18.
KB =^х 100 = 52.7
Рис. 4.18. Расчет коэффициента вариации (KB)
KB нельзя рассчитать, если среднее в данных равно 0 (потому что нельзя делить
на пуль), и он особенно удобен, если все значения переменной положительны.
5 I фунт = 16 yiiuiiii. - Прим. пер.
Выбросы
11И1
В случае, если переменная содержит значения обоих знаков, среднее может быть
близким к нулю, что, несмотря на разумный размах в данных, может привести
к обманчивому значению KB: знаменатель будет очень маленьким числом, и это
приведет к очень большому значению KB, хотя стандартное отклонение не
слишком большое.
Польза KB должна стать совсем очевидной, если рассмотреть одни и те же
данные, выраженные в футах и дюймах; к примеру, 60 дюймов - это то же самое, что
и 5 футов. Данные, выраженные в футах, имеют среднее 5,5566, стандартное
отклонение 0,2288; те же данные, выраженные в дюймах, имеют среднее 66,6790 и
стандартное отклонение 2,7453. Тем не менее KB не подвержен влиянию единиц
измерения, и его значение не зависит от них с точностью до ошибки округления:
5,5566/0,2288 = 24,2858 (данные в футах);
66,6790/2,7453 = 24,2884 (данные в дюймах).
Выбросы
Среди статистиков нет полного согласия, как определить выбросы, но практически
все согласны, что важно их выделить и использовать подходящие статистические
методы в случае данных с выбросами. Выброс - это наблюдение в анализируемых
данных, значение которого сильно отличается от других. Его часто описывают как
значение в данных, которое как будто бы происходит из другой генеральной
совокупности или выпадает из интервала типичных значений выборки. Предположим,
вы исследуете учебную успеваемость в выборке или генеральной совокупности,
и почти все испытуемые проучились от 12 до 16 лет (12 лет - окончание средней
школы в Америке, 16 лет - оконченное высшее образование). Однако у одного из
испытуемых значение этой переменной равно 0 (то есть он формально не получил
никакого образования), а у другого - 26 (что предполагает много лет обучения
после получения высшего образования). Вы, наверное, посчитаете эти два случая
выбросами, поскольку их значения сильно отличаются от остальных данных в
выборке или генеральной совокупности. Обнаружение и анализ выбросов - это
важный предварительный этап во многих видах анализа, потому что наличие даже
одного или двух выбросов может кардинальным образом исказить значения
некоторых обычных статистик, таких как среднее.
Кроме того, важно найти выбросы, потому что иногда они могут быть
вызваны ошибками при вводе данных. В предыдущем примере первое, что стоит
проверить, - это правильно ли были записаны значения; может оказаться, что
правильные числа - это 10 и 16, соответственно. Второе, что стоит изучить, - это
принадлежит ли данное наблюдение к исследуемой генеральной совокупности.
Например, не относится ли 0 к продолжительности обучения ребенка, тогда как
данные должны были содержать только информацию о взрослых?
Если такие простые действия не позволяют решить проблему, придется
придумать (по возможности обсудив это с коллегами), что делать с выбросами. Можно
ШМШШ
Глава 4. Описательная статистика и графическое представление...
просто убрать из данных все наблюдения с выбросами до анализа, но
допустимость применения такого метода зависит от области исследований. Иногда
существует статистический метод исправить ситуацию с выбросами, к примеру
усеченное среднее, описанное ранее, хотя такие методы используют не во всех областях.
Другие возможности - это преобразование данных (обсуждается в главе 3) или
применение непараметрических методов (обсуждается в главе 13), на которые
меньше влияют выбросы.
Чтобы по возможности стандартизовать поиск выбросов, были разработаны
различные эмпирические правила. Одно из обычных определений выброса,
использующее межквартильный размах (МКР), состоит в том, что «слабые» выбросы - это те
значения, которые меньше 25% персентили минус 1,5*МКР или больше 75%
пересилит плюс 1,5*МКР. В нормально распределенных данных настолько
отклоняющиеся значения ожидается встретить примерно 1 на 150 наблюдений. «Сильные»
выбросы определяются аналогичным образом, но с заменой 1,5*МКР на 3*МКР;
такие крайние значения ожидаются в нормальных данных примерно 1 на 425 000
наблюдений.
Графические методы
Существует великое множество методов графического представления данных от
самых простых, включенных в программы для работы с электронными таблицами
вроде Microsoft Excel, до очень специализированных и сложных, доступных с
помощью языков программирования вроде R. О правильном и ошибочном
использовании графики в представлении данных написаны целые книги. Лидирующим
(хотя и с противоречивой позицией) экспертом в этой области является Эдвард
Тафти (Edward Tuftc), профессор Йельского университета (магистр в области
статистики и PhD в политических науках). Его наиболее известная работа -
«Графическое изображение числовой информации» (The Visual Display of Quantitative
Information, ссылка дана в приложении С), но все книги Тафти достойны того,
чтобы с ними ознакомиться, всем интересующимся графическим отображением
данных. Абсолютно невозможно рассказать о хоть сколько-нибудь заметной доле
всех методов изображения данных в этом разделе, так что вместо этого мы
обсудим самые обычные подходы, включая и проблемы, связанные с ними.
Легко забыться и приняться за построение навороченных графиков, особенно
из-за того, что программы для работы с электронными таблицами и
статистические пакеты позволяют с легкостью создавать множество видов графиков и
диаграмм. Термин Тафти для графических элементов, не несущих смысловой
нагрузки, - «графический мусор» - точно описывает его отношение к таким
изображениям. Стандарты того, что считают «мусором», а что нет, зависят от
области, по как общее правило стоит использовать простейший вид графика или
диаграммы, который понятным образом представляет ваши данные, при этом
оставаясь в рамках стандартов, принятых в вашей профессии или области
исследований.
Графические методы
шшпп
Таблицы частот
Первый вопрос, который стоит задать самому себе при подборе метода
визуализации данных, - необходимо ли вообще графическое отображение. Это правда, что
часто лучше один раз увидеть, чем сто раз услышать, но в других случаях
таблицы частот оказываются полезнее для представления данных, чем их графическое
изображение. Это особенно важно, когда нас интересует не общее распределение
данных по нескольким категориям, а конкретные полученные значения. Таблицы
частот являются очень эффективным способом представления больших объемов
данных и являются чем-то средним между текстом (абзацами с описаниями
значений данных) и чистой графикой (такой как гистограмма).
Предположим, университет интересуется сбором данных об общем состоянии
здоровья первокурсников. Из-за того, что все больше беспокойства в
Соединенных Штатах вызывает ожирение, одна из вычисляемых величин - это индекс
массы тела (ИМТ), равный отношению массы тела в килограммах к квадрату роста
в метрах. ИМТ - это не идеальный показатель. К примеру, спортсмены часто
показывают как очень низкие результаты (марафонцы, гимнасты), так и слишком
высокие (футболисты, тяжелоатлеты), но его просто подсчитать, и в случае
большинства людей это довольно надежная мера того, насколько у них здоровый вес.
ИМТ - это непрерывная величина, но его часто интерпретируют в терминах
категорий, используя принятые промежутки. Интервалы для ИМТ приведены в
табл. 4.3, согласно данным Центра по предупреждению и контролю заболеваний
(ЦПКЗ, Centers for Disease Control and Prevention, CDC) и Всемирной
организации здравоохранения (ВОЗ), в целом принятым как полезные и верные.
Таблица 4.3. Категории ЦПКЗ и ВОЗ для ИМТ
Интервал ИМТ
< 18.5
18.5-24.9
25.0-29.9
30.0 и выше
Категория
Пониженная масса тела
Нормальная масса тела
Избыточная масса тела
Ожирение
Теперь посмотрите на табл. 4.4, содержащую полностью выдуманные данные о
классификации первокурсников по ИМТ.
Таблица 4.4. Распределение ИМТ среди
первокурсников в 2005 году
Интервал ИМТ
< 18.5
18.5-24.9
25.0-29.9
30.0 и выше
Число
25
500
175
50
Глава 4. Описательная статистика и графическое представление...
Эта простейшая таблица дает нам возможность при беглом просмотре понять,
что большинство первокурсников имеют либо нормальную, либо повышенную
массу тела, и лишь небольшое их число имеют пониженную массу тела или
страдают ожирением. Обратите внимание, что в этой таблице представлены сырые
данные о числе испытуемых в каждой категории, которые иногда называют
абсолютной частотой] эти числа говорят о том, как часто каждое значение встретилось, что
может быть полезно, если, к примеру, вам надо понять, скольких студентов
необходимо проконсультировать о проблемах ожирения. Однако абсолютные частоты
не ставят числа в каждой категории в какой-либо контекст. Мы можем сделать
эту таблицу более полезной, если добавим столбец с относительной частотой,
которая показывает процент от общей суммы, попавший в каждую категорию.
Относительные частоты рассчитывают, разделив число наблюдений в каждой
категории на общее число наблюдений (750) и умножив результат на 100. В табл. 4.5
приведены как абсолютные, так и относительные частоты для этих данных.
Таблица 4.5. Абсолютные и относительные частоты категорий ИМТ
среди первокурсников в 2005 году
Интервал ИМТ
< 18.5
18.5-24.9
25.0-29.9
30.0 и выше
Число
25
500
175
50
Относительная частота
3.3%
66.7%
23.3%
6.7%
Обратите внимание, что относительные частоты должны в сумме давать
приблизительно 100%, хотя может присутствовать небольшая ошибка из-за
округления.
Кроме того, мы можем добавить столбец с накопительной {кумулятивной)
частотой, которая показывает относительную частоту для этой категории и всех
меньших значений, как в табл. 4.6. Накопительная частота для последней
категории должна составлять 100% с точностью до ошибки округления.
Таблица 4.6. Накопительная частота ИМТ в наборе первокурсников 2005 года
Интервал ИМТ
< 18.5
18.5-24.9
25.0-29.9
30.0 и выше
Число
25
500
175
50
Относительная
частота
3.3%
66.7%
23.3%
6.7%
Накопительная
частота
3.3%
70.0%
93.3%
100%
Посмотрев на кумулятивные частоты, можно сразу понять, что, к примеру, у
70% поступивших нормальная или пониженная масса тела. Это особенно полезно
в случае таблиц с большим числом категорий, поскольку позволяет читателю
быстро оценить важные точки в распределении, такие как нижние 10%, медиану (50%
накопительной частоты) или верхние 5%.
Графические методы
Кроме того, можно соорудить таблицу частот для сравнения между группами.
Вас может интересовать, к примеру, сравнение распределений ИМТ среди
юношей и девушек на первом курсе или сравнение поступивших в 2005 году и в 2000
или 1995 годах. В таких ситуациях сырые данные обычно менее полезны (п:з-за
того, что размер курса может различаться), а относительные и накопительные
частоты оказываются пригодными для сравнения. Другая возможность состоит в
подготовке графических изображений, таких как диаграммы, описываемые в
следующем разделе, которые могут сделать подобные сравнения более попятными.
Столбчатые диаграммы
Столбчатые диаграммы особенно удобны для изображения дискретных данных с
небольшим числом категорий, как в случае нашего примера с ИМТ среди
первокурсников. Столбцы в столбчатых диаграммах обычно отделяются друг от друга,
чтобы не возникало ощущения непрерывности; хотя в нашем случае категории
основаны на разбиении непрерывной переменной, они с тем же успехом могут быть
истинными категориями, такими как любимый спорт или область специализации
в учебе. На рис. 4.19 приведена информация об ИМТ среди первокурсников в виде
столбчатой диаграммы. (Если не сказано иное, диаграммы, показанные в этой
главе, были созданы с помощью Microsoft Excel.)
Число студентов
60(Ь
400-
200-
0-
Группы, выделенные по ИМТ,
среди первокурсников 2005 года
'Ш
г-r-i
Пониженная
масса тела
<18.5
н Нормальная
? масса тела
-g 18.5-24.9
2 Повышенная
н масса тела
125.0-29.9
Ожирение
30.0 и выше
Рис. 4.19. Абсолютные частоты категорий ИМТ среди первокурсников
Абсолютные частоты используют тогда, когда надо знать число человек в
определенной категории, тогда как относительные частоты - если необходимо попять
соотношение чисел испытуемых, попавших в разные категории. Относительные
частоты особенно удобны, что мы увидим дальше, при сравнении множества групп,
к примеру чтобы помять, увеличивается или уменьшается год от года доля
студентов с ожирением. В случае простой столбчатой диаграммы решение об
использовании абсолютных или относительных частот не так важно, что можно видеть,
сравнив столбчатую диаграмму с данными об ИМТ у студентов, представленную
ЩЯННнН Глава 4. Описательная статистика и графическое представление...
относительными частотами на рис. 4.20, с теми же данными в виде абсолютных
частот на рис. 4.19. Обратите внимание, что две диаграммы идентичны, за
исключением подписей оси у (вертикальной оси), на которых указаны абсолютные
частоты на рис. 4.19 и проценты на рис. 4.20.
ЙПО/у,
oU/cr
OUytr
ЛП0А-
ZUyCT
Utu-
Группы, выделенные по ИМТ,
среди первокурсников 2005 года
г ¦. 1
1 1
1 1 1
(0<0 (TJ^CT) (TJ<0ct> Ф Zl
i<utn S <и "^ хахл i5
4) К • с; l-<N d) У-СЯ о, из
НИ
ace
<
>рм
ace
8.5
вы
ace
5.0
ЖИ
.0
«2 ?2- О 2CN Og
Рис. 4.20. Относительные частоты категорий ИМТ
среди первокурсников
Использование относительных частот становится очень удобным, если мы
сравниваем распределение студентов по категориями ИМТ в разные годы.
Посмотрите на гипотетическую информацию о частотах в табл. 4.7.
Таблица 4.7. Абсолютные и относительные частоты ИМТ в трех наборах студентов
Интервал ИМТ
Пониженная масса тела
<18.5
Нормальная масса тела
18.5-24.9
Избыточная масса тела
25.0-29.9
Ожирение
30.0 и выше
В сумме
1995
50
400
100
10
560
8.9%
71.4%
17.9%
1.8%
100.0%
2000
45
450
130
40
665
6.8%
67.7%
19.5%
6.0%
100.0%
2005
25
500
175
50
750
3.3%
66.7%
23.3%
6.7%
100.0%
Из-за того, что размеры курса различаются в разные годы, для поиска
зависимостей в распределении студентов по ИМТ удобнее всего использовать
относительные частоты (проценты). В данном случае наблюдалось явное уменьшение
доли студентов с пониженной массой тела, тогда как доля студентов с
повышенной Maccoii тела или ожирением росла. Эту информацию также можно изобразить
с помощью столбчатой диаграммы, такой как па рис. 4.21.
Столбчатые диаграммы
Распределение ИМТ
в трех потоках студентов
80°/сг
60°/сг
40°/а
20°/(г
3|
? 1995
П2000
П2005
5 5*
с 1-М
(В со I
Z от
(TJ <0 СТ)
3 « I
Л О •
О 2 <n
Рис. 4.21. Столбчатая диаграмма распределения ИМТ
среди трех наборов студентов
Это столбчатая диаграмма с группами, которая показывает, что присутствует
слабый, но определенный десятилетний тренд уменьшения доли студентов с
пониженной и нормальной массой тела и роста доли студентов с повышенной массой
тела или ожирением (что в целом отражает изменения среди населения Америки).
Помните, что построение диаграммы не равноценно проведению статистического
теста, так что мы не можем сказать из этого рисунка, что эти изменения
статистически значимы.
Другой вид столбчатых диаграмм, подчеркивающий относительные
распределения значений в каждой группе (в данном случае распределение категорий
ИМТ в трех наборах первокурсников), - это составные столбчатые диаграммы,
что проиллюстрировано на рис. 4.22.
100%-
80%
60°/(Г
40%-
20%
? Ожирение
30.0 и выше
D
Повышенная
масса тела
25.0-29.9
Нормальная
L-l масса тела
18.5-24.9
рп Пониженная
масса тела
<18.5
1995 2000 2005
Рис. 4.22. Составная столбчатая диаграмма распределения ИМТ
в трех наборах студентов
В этом виде диаграмм каждый столбец соответствует одному году сбора данных
и в сумме дает 100%. Относительные пропорции студентов в каждой категории
1ИД1
'"г?
Глава 4. Описательная статистика и графическое представление...
можно легко увидеть, сравнив доли площади столбцов, занятые данной
категорией. Такая организация данных позволяет без труда сравнить много наборов
данных (в данном случае три года) между собой. Сразу же становится ясно, что со
временем уменьшается доля студентов с пониженной и нормальной массой тела и
растет доля студентов с повышенной массой тела или ожирением.
Круговые диаграммы
Всем знакомые круговые диаграммы представляют данные сходным образом с
составными столбчатыми диаграммами: они графически показывают, какую часть
от целого занимают отдельные категории. Круговые диаграммы, как и составные
столбчатые диаграммы, особенно полезны только при небольшом числе
категорий, и если разница между ними достаточно большая. Многие занимают очень
жесткую позицию в отношении к круговым диаграммам, и хотя их все равно еще
часто применяют в некоторых областях, во многих других от них отказываются
как от неинформативных в лучшем случае или даже потенциально вводящих в
заблуждение, - в худшем. Так что я оставляю выбор в зависимости от контекста
и договоренностей за вами; здесь я приведу ту же самую информацию об ИМТ
в виде круговой диаграммы (рис. 4.23) и предоставлю вам самим судить о том,
полезный ли это способ представления данных. Обратите внимание, что это одна
круговая диаграмма, изображающая данные наблюдений одного года, но есть и
другие возможности, включая расположение двух диаграмм рядом (для
сравнения соотношений долей разных групп) и отдельное увеличенное изображение
определенных секторов (чтобы показать их более мелкое разделение на группы).
18°/^
2% 9%
71%
? Пониженная
масса тела
<18.5
rj Нормальная
масса тела
18.5-24.9
? Повышенная
масса тела
25.0-29.9
? Ожирение
30.0 и выше
Рис. 4.23. Круговая диаграмма, показывающая распределение ИМТ
среди первокурсников, поступивших в 2005 году
Флоренс Найтингейл и статистическая графика
Многие люди хотя бы в общих чертах слышали о роли Флоренс Найтингейл (Florence
Nightingale) в создании профессии медсестры и ее героических усилиях в борьбе за
улучшение гигиены и качество ухода в британской армии в ходе Крымской войны. Но мень-
Столбчатые диаграммы
МИРЯ
ше людей знают о ее вкладе в развитие статистической графики, включая эффективное
применение графиков и диаграмм для донесения медицинской информации. Найтин-
гейл также изобрела новый вид графиков, диаграмму в полярных координатах (который
она называла «диаграммой щеголей» (coxcomb chart), а другие - диаграммой розы Най-
тингейл) для изображения и сравнения информации, такой как причины гибели (от ран,
полученных в сражении, болезней и других причин) за каждый месяц среди британских
солдат. Диаграммы Найтингейл привлекли внимание к большой доле смертей солдат от
болезней и позволили ей добиться понимания важности улучшения санитарной
обстановки и гигиены у военного руководства. Многие из диаграмм Найтингейл доступны для
просмотра в Интернете, как и обсуждения ее достижений в этой области. Один из
примеров - это заметка Жюли Рехмейер (Julie Rehmeyer) в Новостях науки (Science News) за
26 ноября 2008 года, «Флоренс Найтингейл: страстный статистик» (http://bit.ly/PvLvSS).
Диаграммы Парето
Графики Парето, или диаграммы Парето, совмещают столбчатые диаграммы и
линейные графики; столбцы показывают частоту или относительную частоту,
тогда как линия показывает накопительную частоту. Большим достоинством
диаграмм Парето является то, что легко видеть, какие факторы наиболее важны
в определенной ситуации и, таким образом, на что следует обращать внимание в
первую очередь. К примеру, графики Парето часто используют в контексте
производства, чтобы понять, какие факторы отвечают за возникновение задержек
или дефектов в процессе изготовления. В диаграмме Парето столбцы
отсортированы в порядке убывания частоты слева направо (так что самая частая причина
расположена левее всего, а самая редкая - правее всего), а линия
накопительной частоты наложена сверху на столбцы (так что вы можете видеть, к примеру,
сколько факторов ответственны за 80% задержек производства). Посмотрите на
гипотетические данные, приведенные в табл. 4.8, которые содержат число
обнаруженных дефектов, связанных с разными участками технологического
процесса на автомобильном заводе.
Таблица 4.8. Обнаружение брака на разных этапах производства
Отдел
Аксессуары
Корпус
Проводка
Двигатель
Коробка передач
Число дефектов
350
500
120
150
80
Хотя очевидно, что отделы, собирающие аксессуары и корпус, ответственны за
наибольшее число выявленных дефектов, сразу не ясно, какую долю общего брака
можно отнести к ним. Рисунок 4.24, который показывает всю ту же информацию
в виде диаграммы Парето (созданной с помощью SPSS), делает это более
понятным.
ЕИМН
Глава 4. Описательная статистика и графическое представление...
Вильфред Парето
Вильфред Парето (Vilfredo Pareto, 1843-1923) был итальянским экономистом, который
открыл то, что сейчас называют принципом Парето, также известным как «мало важного
и много тривиального», или «правило 80:20». Принцип Парето утверждает, что во
многих обстоятельствах 80% активности или результатов происходят из 20% от возможных
причин. К примеру, во многих странах примерно 80% всех богатств принадлежат 20%
населения; аналогичным образом в производстве часто 20% видов ошибок приводят к
80% брака в итоговом продукте; а в здравоохранении 20% от всех пациентов используют
80% от всех медицинских услуг. «Мало важного» в принципе Парето - это 20% от людей,
ошибок и так далее, которые отвечают за основную массу активности, а «много
тривиального» - это 80%, которые в сумме приводят только к 20% активности. Парето лучше
всего известен сегодня как изобретатель диаграмм Парето, которые часто применяют при
контроле качества для обнаружения того, какие процессы приводят к большинству
проблем, таким как жалобы клиентов или бракованные изделия.
Рис. 4.24. Основные причины брака производства
Эта диаграмма говорит нам не только о том, что чаще всего брак
обнаруживается в корпусе и аксессуарах, но и о том, что они ответственны за 75% всего брака.
Мы можем понять это, проведя прямую линию от изгиба в линии накопитель-
нон частоты (который отражает величину накопительной частоты двух наиболее
частых причин брака, корпуса и аксессуаров) до правой оси у. Это упрощенный
пример, и он нарушает правило 80:20 (обсуждается выше во врезке о Вильфредс
Парето), поскольку приведено только небольшое число основных причин
брака. В более реалистичном примере может быть 30 и более возможных причин, и
диаграмма Парето - это простой способ отсортировать их и понять, какие
участки процесса требуют улучшений в первую очередь. Этот простой пример служит
для изображения типичных свойств графика Парето. Столбцы отсортированы от
самого высокого к самому низкому, частоту изображают на левой оси /у, а про-
Столбчатые диаграммы
¦¦ЕЕП
цент - на правой, число случаев из каждой категории указывают внутри каждого
столбца.
Диаграмма «стебель с листьями»
Те виды диаграмм, которые мы обсуждали до сих пор, в первую очередь
подходят для изображения категориальных данных. В случае непрерывных величии
используют другой набор графических методов. Один из простейших способов
графически изобразить непрерывные данные - это график «стебель с листьями»,
который легко сделать вручную и который дает возможность быстро увидеть
распределение данных. Чтобы создать такую диаграмму, разделите ваши данные па
интервалы (используя здравый смысл и ту степень подробности, которая
соответствует вашим задачам) и покажите каждое значение данных с помощью двух
колонок. «Стебель» - это левая колонка, и она содержит одно значение на каждую
строку, а «листья» - это правая колонка, и она содержит по одной цифре па
каждое наблюдение, принадлежащее этой строке. Таким образом, получается график,
который содержит значения данных, но принимает форму, показывающую, какие
данные в каких интервалах встречаются чаще всего. Числа могут быть
произведениями какого-то множителя (например, значения с шагом 10 000 или 0,01), если
это необходимо при каком-то наборе данных.
Приведем простой пример. Предположим, у нас есть набор оценок за экзамен 26
студентов, и мы хотим представить их графически. Вот оценки:
61, 64, 68, 70, 70, 71, 73, 74, 74, 76, 79, 80, 80, 83, 84, 84, 87, 89, 89, 89,
90 92,95,95,98,100.
Логично разделить эти данные на интервалы по 10 единиц, к примеру 60-69,
70-79 и так далее, так что мы делаем «стебель» с цифрами 6, 7, 8, 9 (это десятки,
для тех, кто помнит школьную математику), и «листья» для каждой из них в виде
списка цифр из первого разряда значений, отсортированного слева направо от
меньшего к большему. На рис. 4.25 показан итоговый график.
«Стебель»
6
7
8
9
10
«Листья»
148
00134469
003447999
02558
0
Рис. 4.25. Диаграмма «стебель с листьями» оценок за экзамены
Такая диаграмма показывает не только сами числовые значения и их диапазон
(61-100), но и общую форму их распределения. В данном случае большинство
значений попадает в промежутки, начинающиеся с 70 и с 80, с небольшим числом
значений от 60 до 69 и от 90 до 99, а одно значение равно 100. Форма стороны с
«листьями» на самом деле напоминает повернутую на 90 градусов простейшую
гистограмму (обсуждается ниже) со столбцами шириной по 10.
ВсЯ
Глава 4. Описательная статистика и графическое представление...
Ящики с усами
Ящики с усами, или диаграммы размаха, были разработаны статистиком Джоном
Тыоки (John Tukey) как способ компактного описания и изображения
распределения непрерывных данных. Хотя их можно построить и от руки (как и
большинство других диаграмм, включая столбчатые диаграммы и гистограммы), на практике
их обычно создают с помощью компьютерных программ. Интересно, что точный
метод их построения различается в зависимости от программы, но эти диаграммы
всегда показывают пять важных характеристик данных: медиану, первую и третью
квартили (и, таким образом, межквартильный размах), минимум и максимум.
Центральная тенденция, размах, симметричность и наличие выбросов в данных — все это
можно легко увидеть, взглянув на ящик с усами, и при этом, изображенные рядом
друг с другом, они позволяют легко сравнить несколько разных распределений. На
рис. 4.26 приведен ящик с усами для набора оценок за экзамен, использованного в
предыдущем примере с диаграммой «стебель и листья».
10СМ -т-
щ
щ
М
6СИ
Рис. 4.26. Ящик с усами для данных о результатах экзамена
(построен с помощью SPSS)
Темная линия показывает медиану, в данном случае 81,5. Серый прямоугольник
соответствует межквартильному размаху, так что нижняя его граница - это
первая квартиль (25-ый персентиль), равная 72,5, а верхняя граница - третья
квартиль (75-ый персентиль), равная 87,75. Тыоки называл эти квартили шарнирами,
отсюда одно из английских названий этого вида диаграмм - шарнирный график
(hinge plot). Короткие горизонтальные отрезки с ординатой 61 и 100 показывают
минимальное и максимальное значения, и вместе с отрезками, соединяющими их
с «ящиком» межквартилыюго размаха, они называются усами, отсюда и название
«ящик с усами». Мы сразу можем видеть, что эти данные симметричны, поскольку
медиана расположена приблизительно посередине межквартилыюго размаха, а он
расположен приблизительно в середине всего набора данных.
В этих данных нет выбросов, то есть таких чисел, которые бы были очень далеко
от всех остальных точек. Для демонстрации ящика с усами для данных, содер-
Столбчатые диаграммы
¦МЕШ
жащих выбросы, я заменила значение 100 в этих же данных на 10. На рис. 4.27
приведены ящики с усами двух наборов данных рядом друг с другом. (Ящик для
правильных данных обозначен как «экзамен», а ящик для данных с измененным
значением обозначен как «ошибка».)
100-
80-
60
40
2а
0
т
т
1
#26
Ошибка Экзамен
Рис. 4.27. Ящик с усами с выбросом (построен с помощью SPSS)
Обратите внимание что за исключением одного выброса, два набора данных
выглядят очень похоже; это связано с устойчивостью медианы и межквартильного
размаха к влиянию крайних значений. Отличающееся значение обозначено
звездочкой и подписано своим порядковым номером (26); последняя возможность
есть не во всех статистических пакетах.
Ящики с усами часто используют для сравнения двух или более наборов
данных. На рис. 4.28 приведено сравнение оценок экзаменов за 2007 и 2008 годы,
обозначенных как «Экзамен 2007» и «Экзамен 2008» соответственно.
щ
щ
7W
6(Н 1
5<Н
1 1 1
Экзамен 2007 Экзамен 2008
Рис. 4.28. Ящики с усами для оценок за экзамен в 2007 и 2008 годах
(построены с помощью SPSS)
IFEl
m
Глава 4. Описательная статистика и графическое представление...
Не видя никаких конкретных оценок, я замечаю несколько сходств и различий
между двумя годами:
• самая высокая оценка одинакова в оба года;
• самая нижняя оценка сильно меньше в 2008 году, чем в 2007;
• как размах, так и межквартильный размах (размах 50% данных из
середины) больше в 2008 году;
• медиана в 2008 году немного меньше.
Совпадение самой высокой оценки не удивительно, поскольку можно получить
от 0 до 100 баллов, и каждый год хотя бы один студент набрал максимальное число
баллов. Это пример «эффекта потолка», возникающего в случае, когда величина
не может принимать значений выше какого-то числа, и при этом испытуемые его
достигают. Аналогичная ситуация, если величина не может быть ниже
определенного числа, называется «эффектом пола». В данном случае наименьшим
возможным числом был 0, но все студенты получили больше баллов, поэтому мы не
видим этого эффекта.
Гистограмма
Гистограмма - это еще один часто используемый способ изображения
непрерывных переменных. Она внешне похожа на столбчатую диаграмму, но столбцы
в ней (интервалы, на которые разбиваются значения непрерывного
распределения) располагаются вплотную друг к другу, в отличие от столбцов в столбчатой
диаграмме. Кроме того, обычно у гистограмм больше столбцов, чем у столбчатых
диаграмм. Они не обязаны быть одной ширины, хотя обычно их делают такими.
Ось у (вертикальная) в гистограмме показывает шкалу частот, а не сами значения,
и площадь каждого столбца показывает то, сколько значений попадает в
соответствующий интервал.
На рис. 4.29 показана гистограмма для данных о результатах экзамена, также
построенная с помощью SPSS, с четырьмя столбцами но 10 баллов шириной и с
наложенным нормальным распределением. Обратите внимание, что форма
гистограммы довольно сильно напоминает график «ствол с листьями» для тех же
данных (рис. 4.25), по повернутый на 90 градусов.
Нормальное распределение подробно обсуждается в главе 3; коротко его можно
охарактеризовать как часто используемое теоретическое распределение, которое
имеет знакомую колоколообразную форму, изображенную здесь. Нормальное
распределение нередко накладывают на гистограммы как визуальную точку отсчета,
чтобы мы могли оценить, насколько распределение значений похоже на
нормальное.
Хорошо это или плохо, но выбор числа и размера интервалов для построения
гистограммы может очень сильно повлиять па ее вид. Обычно гистограммы строят
с более чем четырьмя столбцами; на рис. 4.30 приведены те же данные, по
построенные с восемью столбцами шириной но 5 баллов.
Столбчатые диаграммы
Рис. 4.29. Гистограмма с интервалами по 10 единиц
Рис. 4.30. Гистограмма с интервалами по 5 единиц
НИН' Глава 4. Описательная статистика и графическое представление...
Это те же данные, но теперь гистограмма совсем не похожа на нормальное
распределение, не так ли? На рис. 4.31 приведены тс же данные с интервалами по
2 балла.
Рис. 4.31. Гистограмма с интервалами по 2 единицы
Ясно, что выбор ширины интервалов очень важен для внешнего вида
гистограммы, но как же определиться с их числом? Эта проблема подробно обсуждалась
математиками, но осталась без однозначного ответа. (Если вас интересует очень
специальное обсуждение, посмотрите статью Ванда (Wand), упомянутую в
приложении В.) Нет единственно верного ответа на данный вопрос, но есть некоторые
эмпирические правила. Во-первых, все интервалы вместе должны покрывать весь
размах данных. Кроме того, одно из обычных эмпирических правил гласит, что
число интервалов должно быть равно квадратному корню из числа наблюдений
в данных. Другое — что оно никогда не должно быть меньше шести. Эти правила
явно противоречат друг другу в данном случае, поскольку V26 = 5,1, что меньше 6,
так что приходится использовать здравый смысл, а также пробовать разное число
интервалов и их ширину. Если изменение этих величин сильно меняет визуальное
отображение данных, стоит изучить их распределение подробнее.
Двумерные диаграммы
Диаграммы, содержащие информацию о связи двух переменных, называют
двумерными: самый частый пример - это диаграмма рассеяния. В диаграммах рассея-
Двумерные диаграммы
¦¦ЕЗ
ния каждая точка в данных задается парой чисел, часто называемых.г и г/, каждую
точку изображают в координатных осях; этот метод должен быть вам знаком, если
вы когда-то использовали декартовы координаты в школе па уроках
математики. Обычно вертикальную ось называют осью г/, и на ней откладывают значения у
для каждой точки. Горизонтальную ось называют осью х, и на ней откладывают
значения х для каждой точки. Диаграммы рассеяния - это очень важное средство
изучения двумерных связей между переменными, которые подробнее
разбираются в главе 7.
Диаграммы рассеяния
Взгляните на данные, приведенные в табл. 4.9, содержащие результаты
математической и речевой частей Академического оценочного школьного теста на
способности (SAT, Scholastic Aptitude Test) гипотетической группы из 15 учеников.
Таблица 4.9. Результаты теста для 15 учеников
Математика
750
700
720
790
700
750
620
640
700
710
540
570
580
790
710
Речь
750
710
700
780
680
700
610
630
710
680
550
600
600
750
720
Кроме того что все эти результаты достаточно высокие (этот тест калибруют
таким образом, чтобы медианное значение составляло 500, а большинство
результатов сильно выше этого числа), по сырым данным сложно сказать что-то про связь с
результатами выполнения математической и речевой частей теста. Иногда
результаты по математике выше, иногда речевая часть удается лучше, а часто результаты
сходные. Однако построение диаграммы рассеяния двух переменных, такой как
на рис. 4.32, с результатами по математике на оси у (вертикальной) и речевыми на
оси х (горизонтальной) выявляет связь между ними.
IBE1
Глава 4. Описательная статистика и графическое представление...
1атематика
*?.
RfifV,
о\)\г
7^П-
7IYV
650-
<^Л-
СПП-
5
30
¦
600
Речь
¦\
¦¦
700
¦
800
Рис. 4.32. Диаграмма рассеяния результатов
по математике и по речи
Несмотря на наличие небольших отклонений, результаты речевой и
математической частей сильно линейно связаны. У учеников с хорошо развитой речью в
целом выше результат математической части, и наоборот, а у тех, у кого одна из частей
написана плохо, и вторая в целом будет выполнена хуже. Однако не всегда связи
между переменными линейные. На рис. 4.33 приведены диаграмма рассеяния
сильно связанных переменных, связь между которыми не линейная, а квадратичная.
120
100
А 80
¦ 60
¦
40
¦ 20
¦
, ,—±*
+
¦
¦
¦
¦
>**—¦ ¦
Рис. 4.33. Квадратичная связь между переменными
В данных, представленных на этой диаграмме рассеяния, значениях в каждой
паре - это целые числа от -10 до 10, а значения у - это квадраты значений х, так
что получается всем знакомая парабола. Многие статистические методы
подразумевают линейную связь между переменными, и сложно понять, правда это или
нет, просто посмотрев на сырые данные, так что построение диаграммы рассеяния
для всех важных пар переменных в данных - это простой способ проверить
подобное предположение.
Двумерные диаграммы
Hi НИШ
Линейные графики
Линейные графики - это тоже часто используемый способ изображения связей
между двумя переменными, обычно между временем на оси х и какой-то другой
переменной на оси у. Единственное требование для построения линейного
графика, чтобы каждому значению на оси х соответствовало только одно значение па
оси у, так что он не подойдет для таких данных, как результаты теста,
представленные выше. Посмотрите на табл. 4.10 с данными Центра по предупреждению и
контролю заболеваний (ЦПКЗ), показывающими процент взрослых людей с
ожирением в США за каждый год в течение 13 лет.
Таблица 4.10. Встречаемость ожирения среди взрослых в США, 1990-2002
Год
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
2002
Встречаемость ожирения
11.6%
12.6%
12.6%
13.7%
14.4%
15.8%
16.8%
16.6%
18.3%
19.7%
20.1%
21.0%
22.1%
Мы можем видеть из этой таблицы, что встречаемость ожирения равномерно
росла; изредка случалось ее понижение, но чаще всего она увеличивалась па 1-2%
каждый год. Эту же информацию можно представить в виде линейного графика,
как на рис. 4.34, что делает тенденцию к росту с течением времени еще более
заметной.
Хотя этот график является довольно простым методом представления данных,
визуальное воздействие, которое он оказывает, сильно зависит от выбранной
шкалы и интервала оси у (которая в данном случае показывает встречаемость
ожирения). На рис. 4.34 показано разумное отображение данных, но если мы захотим
усилить эффект на зрителя, мы можем раздвинуть шкалу, уменьшив интервал
оси у (вертикальной), как на рис. 4.35.
На рис. 4.35 представлены те же данные, что и на рис. 4.34, но с более узким
интервалом на оси у (10-22% вместо 0-30%), и это визуально увеличивает различия
между годами. Рисунок 4.35 не обязательно показывает неверный способ изображения
данных (хотя многие считают, что всегда стоит включать 0 в случае графика, изоб-
Глава 4. Описательная статистика и графическое представление...
ражающего проценты), но он подчеркивает легкость манипуляции внешним видом
абсолютно правильных данных. Между прочим, выбор вводящего в заблуждение
интервала - это один из верных способов «лгать при помощи статистики» (см. ниже
врезку «Как лгать при помощи статистики», чтобы узнать подробнее об этом).
Рис. 4.34. Ожирение среди взрослых США, 1990-2002
22-
20-
Встречаемость ожирения
12J
10-
У
^/
/^
х~^
1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002
•
Год
Рис. 4.35. Ожирение среди взрослых США, 1990-2002 при использовании
ограниченного интервала для усиления визуального впечатления от тенденции
Двумерные диаграммы
ЯМЕЛ
Этот же прием работает и в обратную сторону - если мы изобразим те же
данные с использованием широкого интервала для вертикальной оси, изменения за
исследуемый отрезок времени покажутся меньше, как на рис. 4.36.
100-
80-
ж
X
X
ф
5- 60-
X
о
л
и
°
Z
* 40-
*¦
ь
и
СО
20-
10-
-
1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002
Год
Рис. 4.36. Ожирение среди взрослых США, 1990-2002, при использовании
широкого диапазона значений по оси ординат для ослабления визуального
впечатления от имеющейся тенденции
На рис. 4.36 показаны те же самые данные об ожирении, что и на рис. 4.34 и
4.35, но с широким интервалом (0-100%) на вертикальной оси для уменьшения
визуального воздействия тенденции. Так какую же шкалу выбрать? Нет
единственно верного ответа на этот вопрос; везде представлена абсолютно одинаковая
информация, и, строго говоря, ни один из вариантов не является ошибочным.
В данном случае, если бы я представляла этот график без каких бы то ни было
других графиков для сравнения, я бы использовала шкалу из рис. 4.34, поскольку
она показывает истинный минимум данных (0%, который является минимально
возможным значением) и создает разумное пространство над максимальным
значением в данных. Вне зависимости от проблем с выбором масштаба для одного
графика, в случае если вы приводите несколько графиков для сравнения (к
примеру, графики, показывающие встречаемость ожирения в нескольких странах за
один и тот же промежуток времени, или графики с различными показателями
здоровья за один и тот же период), они всегда должны иметь одну и ту же шкалу,
чтобы избегать неверной трактовки читателем.
1ЕЯ
Глава 4. Описательная статистика и графическое представление...
Как лгать при помощи статистики
Даррел Хафф (Darrel Huff) был независимым писателем, который одновременно
работал редактором изданий Look («Взгляд»), Better Homes and Gardens («Как улучшить
ваш дом и сад») и Liberty («Свобода»). Однако его лучшей заявкой на известность стала
классическая книга «Как лгать при помощи статистики» (How to Lie with Statistics),
впервые опубликованная в 1954 году. Некоторые считают, что это самая читаемая книга по
статистике в мире. Хафф не был профессиональным статистиком, его представление
темы можно описать разве что как неформальное, а некоторые иллюстрации в этой
книге сейчас бы посчитали оскорбительными, если бы их включили в современную книгу.
Однако данная книга сохранила свою популярность в течение всех этих лет; она все еще
переиздается и была переведена на много языков.
Хафф берет многие из своих примеров «лжи», как он называет обманчивое
представление информации, из СМИ, политических и рекламных текстов. Некоторые из его
самых метких примеров приведены в главе про графическое представление данных, и они
включают такие ошибки, как специально вводящий в заблуждение масштаб и полное
отсутствие подписей по осям. Одна из причин такой популярности этой книги состоит в
том, что многие из методов введения читателя в заблуждение, обнаруженные им в 1954
году, используются и по сей день.
Упражнения
Как и в случае любой другой области статистики, обучение какому-то методу
описательной статистики требует практики. Здесь специально приведены очень
простые данные, потому что если вы сможете правильно применить метод к 10
наблюдениям, вы сможете использовать его и для 1000 наблюдений.
Мой совет состоит в следующем: попробуйте решить задачи несколькими
способами, к примеру вручную, с помощью калькулятора и с помощью любых
доступных вам программ. Даже программы для работы с электронными таблицами,
такие как Microsoft Excel, предоставляют возможность воспользоваться многими
математическими и статистическими функциями. (Хотя польза от применения
этих функций для серьезного статистического анализа находится под вопросом,
они могут быть полезны для первичного анализа; см. ссылки про Excel в
приложении С, чтобы узнать об этом подробнее.) Кроме того, решение проблемы
несколькими способами придаст вам уверенности в том, что вы корректно используете
устройства и программы.
Большинство графиков и диаграмм строят с помощью компьютерных
программ, и хотя у каждого пакета есть преимущества и недостатки, большинство из
них могут создавать большинство диаграмм, если не все, представленные в этой
главе, как и множество других. Лучший способ вникнуть в методы графического
представления данных - это изучить любую доступную вам программу и
практиковаться в изображении данных, с которыми вы работаете. (Если вы в данный
момент не работаете ни с какими данными, в Интернете доступно множество
наборов данных, которые вы можете бесплатно скачать.) Помните, что графическое
представление - это способ общения, и держите в голове то, зачем вы строите тот
пли иной график.
Упражнения ВВП
Задача
Какую из перечисленных мер центральной тенденции следует использовать в
какой ситуации? Придумайте какие-нибудь примеры для каждой из них из вашей
области работы или учебы.
• Среднее.
• Медиана.
• Мода.
Решение
• Медиана подойдет для интервальных или характеризующих отношения
непрерывных симметричных данных без сильных выбросов.
• Медиана подойдет для непрерывных асимметричных данных, ранговых
данных или данных с сильными выбросами.
• Мода чаще всего применяется для категориальных данных или непрерывных
данных, в которых одно из значений встречается сильно чаще остальных.
Задача
Найдите несколько примеров обманчивого применения статистической
графики и объясните, в чем проблема с каждым из них.
Решение
Это не должно быть сложно ни для кого, если вы следите за новостными СМИ,
но если вам не удается это сделать, поищите в Интернете по ключевой фразе
«misleading graphics» (примерный перевод - обманчивые графики).
Задача
Один из следующих наборов данных следует изобразить в виде столбчатой
диаграммы, а другой — в виде гистограммы; определите, какой метод подойдет для
каких данных, и объясните, почему.
1. Данные о росте (в сантиметрах) 10 000 поступивших в университет.
2. Данные о специализациях, выбранных 10 000 поступившими в
университет.
Решение
1. Данные о росте следует изобразить в виде гистограммы, поскольку это
непрерывная переменная, имеющая большое число возможных значений.
2. Данные о специализации лучше изобразить в виде столбчатой диаграммы,
поскольку это категориальная переменная с ограниченным набором
возможных значений (хотя если есть много вариантов специализации, то
более редкие варианты придется объединить для большей ясности).
Задача
Только один из следующих наборов данных подходит для изображения в виде
круговой диаграммы. Определите, какой, и объясните, почему.
1. Заболеваемость гриппом за два последних года, разделенная по месяцам.
НИ' ': Глава 4. Описательная статистика и графическое представление...
2. Число дней больничных, связанных с пятью самыми частыми причинами
госпитализации (пятая категория - это «все остальные», и она включает
все причины отсутствия на работе, кроме первых четырех).
Решение
1. Круговая диаграмма не подходит для данных о заболеваемости гриппом,
поскольку в ней было бы слишком много категорий (24), а многие из них,
вероятно, окажутся очень похожими по размеру (поскольку заболеваемость
гриппом очень мала в летние месяцы), да и на самом деле данные не
отражают части, составляющие единое целое. Лучше в данном случае использовать
столбчатую диаграмму или линейный график, показывающий число случаев
гриппа по каждому месяцу или времени года.
2. Данные о больничных хорошо подходят для круговой диаграммы,
поскольку есть всего пять категорий, и все части в сумме дают 100%. Из данного
описания остается неясным, насколько разные категории (секторы)
отличаются друг от друга по размеру; если они заметно различаются, это еще
один аргумент в пользу использования круговой диаграммы.
Задача
Чему равна медиана следующего набора данных?
832769121
Решение
Данные содержат 9 измерений, что является нечетным числом; таким образом,
медиана - это срединное значение, если отсортировать значения по их величине.
Если рассмотреть этот вопрос с математической точки зрения, раз п = 9 чисел, то
медиана равна числу под номером (п + 1)/2; таким образом, медиана - это число
под номером (9 + 1)/2, то есть пятое число.
Задача
Чему равна медиана следующего набора данных?
7 15 2 6 12 0
Решение
Данные содержат 6 измерений, что является четным числом; таким образом,
медиана - это среднее двух срединных значений, если отсортировать их по
величине, в данном случае 6 и 7. Если рассмотреть этот вопрос с математической
точки зрения, то медиана для набора данных с четным числом измерений равна
среднему чисел под номерами (п)/2 и (п)/2 + 1; в данном случае п = 6, таким
образом, медиана - это среднее чисел под номерами (6)/2 и (6)/2 + 1, то есть третьего
и четвертого чисел.
Задача
Чему равны среднее и медиана следующих (конечно, странных) данных?
1,7,21,3,-17
Упражнения L.'HHH
Решение
Среднее составляет ((1+7 + 21 + 3 + (-17))/5 = 15/5 = 3.
Медиана - это, поскольку число наблюдений нечетное, число под номером
(п + 1)/2, то есть третье. Отсортированные данные выглядят как (-17, 1, 3, 7, 21),
то есть медиана, равная третьему числу, равна 3.
Задача
Чему равны дисперсия и стандартное отклонение следующего набора данных?
Считайте и = 3.
135
Решение
Формула для расчета дисперсии для генеральной совокупности приведена на
рис. 4.37.
Рис. 4,37. Формула для дисперсии для генеральной совокупности
Формула для выборки приведена на рис. 4.38.
Рис. 4.38. Формула для дисперсии для выборки
В данном случае п = 3, х = 3, а сумма квадратов отклонений равна
(-2)2 + О2 + 22 = 8.
Дисперсия для генеральной совокупности равна 8/3, или 2,67, а стандартное
отклонение для генеральной совокупности равно квадратному корню из дисперсии,
то есть 1,63. Для выборки дисперсия составляет 8/2, или 4, а стандартное
отклонение равно квадратному корню из дисперсии, то есть 2.
ГЛАВА 5.
Категориальные данные
Категориальная переменная - это такая переменная, у которой все возможные
значения составляют фиксированный набор категорий, а не чисел, измеряющих
величину па непрерывной шкале. Например, человек может описывать свой пол
как мужской или женский, а деталь может быть или качественной, или
бракованной. Также возможно наличие более двух категорий. К примеру, в Соединенных
Штатах человека можно отнести к республиканцам, демократам или политически
независимым.
Категориальные переменные могут быть таковыми по своей природе (как
принадлежность к определенной партии) без какой-либо числовой шкалы в
основе измерений, так и их можно создать с помощью разбиения непрерывной или
дискретной величины на категории. Давление крови - это мера давления,
оказываемого кровью на стенки сосудов, и она измеряется в миллиметрах ртутного
столба (мм. рт. ст.), но часто её анализируют с использованием категорий, таких
как низкое, нормальное, прсгипертеизия, гипертензия. Дискретные переменные
(то есть такие, которые могут примять определенные значения на промежутке)
также можно сгруппировать в категории. Исследователь может собирать
точную информацию о числе детей в семье (0 детей, 1 ребенок, 2 ребенка, 3 ребенка
и т. д.), но после этого может сгруппировать эти числа в категории для каких-
то целей анализа, к примеру так: 0 детей, 1-2 ребенка, 3 и более детей. Такой
метод группирования часто применяется в случаях, когда вариантов значений
переменной много и некоторые из них обеднены данными. В случае числа
детей в семье, к примеру, в данных вполне может оказаться слишком мало семей
с большим числом детей, и низкие частоты в таких категориях могут негативно
повлиять на мощность исследования или сделать невозможным применение
некоторых статистических методов.
Хотя премудрости группирования непрерывных и дискретных переменных в
категории обсуждаются (некоторые исследователи называют это выбрасыванием
информации, поскольку такой подход приводит к потере информации о разбросе
внутри каждой категории), это обычная практика во многих областях. Разбиение
непрерывных данных проводят по многим причинам, включая как, например, то,
что это принято в данной профессиональной области, так и для решения проблем
с распределением в данных.
RxC-таблицы
ЖММШ
Методы работы с категориальными данными можно применять для анализа
порядковых переменных, то есть таких, в которых значения можно упорядочить
по величине, но расстояние между соседними элементами не обязательно
одинаковое. (Подробнее порядковые переменные обсуждаются в главе 1.) Хорошо
известная шкала Лайкерта (Likert), в которой испытуемые выбирают ответы из
пяти упорядоченных категорий (таких как «Полностью согласен», «Согласен»,
«Затрудняюсь ответить», «Не согласен», «Полностью не согласен»), - это
классический пример порядковой переменной. Существует целый набор аналитических
методов для работы с порядковыми переменными, которые сохраняют
информацию об их порядке. Если есть выбор, лучше использовать специальные методы
для порядковых переменных, чем общие методы для категориальных, поскольку
первые в целом мощнее.
Для категориальных и порядковых данных существуют специальные методы
анализа. В этой главе мы обсудим самые обычные подходы, используемые для
таких переменных, и кроме того, некоторые из этих методов включены и в другие
главы. Отношение вероятностей, отношение рисков и критерий Мантеля-Хен-
зеля (Mantel-Haenszel) описаны в главе 15, кроме того, некоторые
непараметрические методы из главы 13 применимы к порядковым или категориальным
данным.
RxC-таблицы
В случае, когда анализ касается исследования связи между двумя
категориальными переменными, их распределение в данных часто показывают с помощью
RxC-таблиц, которые чаще называют таблицами сопряженности. R в RxC-табли-
це относится к строкам, а С - к колонкам, или столбцам1, и конкретные таблицы
тоже можно описывать по числу строк и столбцов, которые они содержат. Строки
и столбцы всегда называют именно в таком порядке, договоренность, которую
также соблюдают при описании матриц и в записях с индексом. Иногда отдельно
выделяют таблицы 2x2, в которых показывают общее распределение двух
переменных с двумя значениями каждая, и таблицы более высоких размерностей. И хотя
можно считать таблицы 2x2 частным случаем RxC-таблиц, в котором и R, и С
равны 2, эта классификация может быть полезной для обсуждения методов,
разработанных именно под таблицы 2 х2. Выражение R хС читается как «R па С», и то
же применимо к конкретным размерам таблиц, то есть 3x2 читается как «3 на 2».
Положим, нас интересует исследование связи между широкими категориями
возраста и здоровья, а последнее определяется по известной пятибалльной шкале
оценки общего здоровья. Мы решаем, на какие категории разбить возраст, и
собираем данные о выборке испытуемых, классифицируя их по возрасту (используя
выбранные категории) и состоянию здоровья (используя пятибалльную шкалу).
Затем мы смотрим на эту информацию в виде таблицы сопряженности,
организованной как табл. 5.1.
R - от англ. Row, С - от англ. Column. - Прим. персе.
! Глава 5. Категориальные данные
Таблица 5.1. Таблица сопряженности состояния здоровья и возрастных групп
< 18 лет
18-35 лет
40-64 лет
> 65 лет
Великолепное
Очень хорошее
Хорошее
Неплохое
Плохое
Ее можно описать как таблица 4 х5, поскольку она содержит 4 строки и 5
столбцов. Каждая ячейка показывает число людей из выборки с парой
соответствующих исследуемых характеристик: число людей до 18 с великолепным здоровьем,
число людей 18-39 лет с великолепным здоровьем и так далее.
Меры согласия
Описанные в этой книге меры надежности применимы в основном к
непрерывным измерениям. В случае, когда измерения касаются деления на категории,
например классификация деталей на качественные и бракованные, лучше подходят
меры согласия. К примеру, мы хотим сравнить согласованность результатов двух
диагностических тестов на определенное заболевание или проверить, одинаково
ли три наблюдателя расклассифицируют школьников в классе по их поведению
па приемлемое и недопустимое. В обоих случаях некто выбирает одну оценку из
определенного набора категорий, и нам интересно, насколько хорошо результаты
классификации соотносятся друг с другом.
Процент согласия - это самая простая мера согласия; его можно рассчитать,
разделив число случаев совпадения оценок на общее число оценок. К примеру, если из
100 оценок наблюдатели согласны в 80% случаев, то процент согласия составляет
80/100, или 0,8. Большой проблемой простого процента согласия является то, что
высокий процент совпадения может получиться чисто случайно; таким образом,
сложно сравнивать проценты согласия между разными ситуациями, когда
согласованность по случайным причинам может заметно различаться.
Однако этот недостаток можно обойти, используя другую обычную меру
согласия, называемую каппой Кожа, каппа-коэффицепт, или просто каппа.
Изначально эту меру разработали для сравнения результатов двух оценщиков или тестов,
но позднее расширили для использования на большем числе классификаторов.
Использование каппы предпочтительно по сравнению с процентом согласия,
поскольку она включает поправку на случайные совпадения (хотя статистики
спорят о том, насколько эта поправка успешна; подробнее смотрите во врезке ниже).
Каппу легко получить с помощью сортировки результатов в гипотетической сетке
и расчетов, как показано в табл. 5.2. Этот гипотетический пример связан с
согласованностью двух видов тестов па наличие (3+) или отсутствие (3-) определенного
заболевания.
RxC-та блицы
Таблица 5.2. Согласие двух тестов с двумя вариантами результатов
+
Тест 2
Тест 1
+
50
10
60
-
10 60
30 40
40 100
Четыре ячейки с данными часто <
+
-
+
а
с
-
ь
d
Ячейки а и d обозначают согласия (в a - случаи, когда оба теста дали
положительный результат, то есть наличие заболевания, а в d - случаи, когда оба теста
дали отрицательный результат), тогда как Ьис обозначают несогласия.
Формула для каппы выглядит следующим образом:
Р -Р
К = ^ е->
где Р = наблюдаемые согласия, а Ре = наблюдаемые несогласия.
Ро = (я + d)/(a + b + с + d),
то есть число случаев согласия, поделенное на общее число наблюдений. В данном
случае
Ро = 80/100 = 0,80;
Ре = [(а + с)(а + Ь)]/(а + Ь + с: + d)2 + [(b + d)(c + d)]/(a + b + с + d)\
а это число случаев согласия, ожидаемых случайно. Ожидаемое согласие в данном
случае составляет следующее число:
(60*60)/(100*100) + (40*40)/(100*100) = 0,36 + 0,16 = 0,52.
В данном случае каппа рассчитывается таким образом:
1-0.52
Каппа может принимать значения от -1 до +1; значение 0 она примет, если
число наблюдаемых совпадений равно числу ожидаемых случайных, а 1 - если все
наблюдения согласованы. Не существует абсолютных стандартов, по которым
можно судить о том, велико ли данное значение каппы или мало; однако многие
исследователи придерживаются указаний о степени согласования при
определенных значениях каппы, опубликованных Ландисом и Кохом (Landis and Koch) в
1977 году:
идя
Глава 5. Категориальные данные
< 0 Плохое
0-0,20 Слабое
0,21-0,40 Заметное
0,41-0,60 Среднее
0,61-0,81 Сильное
0,81-1,0 Почти идеальное
По этим меркам у нас среднее согласование. Обратите внимание, что процент
согласования составляет 0,80, а каппа - 0,58. Каппа всегда не больше процента
согласования, поскольку она включает поправку па случайные совпадения.
Для альтернативного взгляда на каппу (обращенного к более продвинутым
статистикам) прочитайте следующую врезку.
Неоднозначная каппа
Каппу Коэна часто преподают и широко применяют, но ее использование не лишено
противоречий. Каппу обычно определяют как величину, показывающую согласие сверх
случайного, или, проще говоря, согласие с поправкой на случайность. У нее есть два
применения: как статистика критерия для определения того, согласуются ли два набора
оценок лучше, чем можно было бы ожидать случайно (двумя вариантами ответа: да или
нет), и как мера силы согласования (которая выражается в числе от 0 до 1).
Хотя у большинства исследователей нет проблем с первым применением каппы,
некоторые возражают против второго. Проблема состоит в том, что расчет ожидаемого
случайного согласия основан на том, что оценки независимы, условие, редко
встречающееся на практике. Поскольку каппу часто применяют для оценки согласования между
множеством отдельных оценок одного и того же наблюдения, будь это поведение
ребенка в классе или результаты рентгена у человека с подозрением на туберкулез, мы бы
ожидали чего-то большего, чем случайного совпадения. В таких случаях каппа
переоценивает согласование между тестами, наблюдателями и тому подобное за счет недооце-
нивания наблюдаемого согласования, которое на самом деле случайное.
Критику каппы, включая длинный список относящейся к этому литературы, можно
найти на веб-сайте доктора Джона Уеберсакса (John Uebersax).
Распределение хи-квадрат
При проверке гипотез о категориальных данных нам нужен какой-то способ
оцепить значимость наших результатов. В случае таблиц сопряженности часто
лучшим вариантом статистики является один из тестов хи-квадрат, которые
используют известные свойства распределения хи-квадрат. Распределение
хи-квадрат - это непрерывное распределение, которое широко применяется в
критериях значимости, поскольку многие из их статистик распределены по хи-квадрату
в случае, если нулевая гипотеза верна. Умение соотносить статистику критерия
с известным распределением делает возможным определение вероятности
получить какое-то значение статистики.
Распределение хи-квадрат - это частный случай гамма-распределения, который
определяется только одним параметром, к, числом степеней свободы. В распредс-
Распределение хи-квадрат
лении хи-квадрат есть только положительные значения, поскольку оно основано
на сумме квадратов квантилей, что вы увидите позже, и имеет правую
асимметрию. Его форма изменяется в зависимости от к, особенно сильно при маленьких
значениях параметра, что видно на четырех распределениях хи-квадрат на рис. 5.1.
При приближении к к бесконечности распределение хи-квадрат стремится
(становится очень похожим на) к нормальному распределению.
Функция плотности распределения
вероятности хи-квадрат (1 df)
Функция плотности распределения
вероятности хи-квадрат (2 df)
01—i—i" i i i—г—т—г
0 1 2 3 4 5 6 7 8 9 10
X
Функция плотности распределения
« 1 вероятности хи-квадрат (5 df)
0 1 2 3 4 5 6 7 8 9 10
X
Функция плотности распределения
П1 вероятности хи-квадрат (10 df)
Рис. 5.1. Функция плотности распределения хи-квадрат при различном числе
степеней свободы
На рис. D.11 представлен список критических значений распределения хи-
квадрат, который можно использовать, чтобы определить значимость
результатов критерия. К примеру, критическое значение для уровня значимости 0,05 для
распределения хи-квадрат с одной степенью свободы составляет 3,84. Любой
результат критерия со значением выше данного можно считать значимым для теста
хи-квадрат на независимость таблицы 2 х2 (описывается ниже).
Обратите внимание, что 3,84 = 1,962 и то, что 1,96 - это критическое значение
для Z-распределения (стандартного нормального распределения) для
двухстороннего критерия при уровне значимости 0,05. Это не просто совпадение,
причина этого равенства лежит в математической связи между Z-распределением и
распределением хи-квадрат.
Говоря формально, если X - это независимые переменные, распределенные по
стандартному нормальному закону с и = 0 и а = 1, a случайная величина Q
определяется как
шмж
Глава 5. Категориальные данные
/-1
то Q будет распределена по хи-квадрату с Л-стсиснями свободы.
Два важных момента, о которых стоит помнить, - это что для расчета значения
хи-квадрата необходимо знать число степеней свободы и что критические
значения в целом возрастают с ростом числа степеней свободы. При уровне значимости
0,05 критическое значение для одностороннего теста хи-квадрат с одной степенью
свободы составляет 3,84, по при 10 степенях свободы оно уже равно 18,31.
Тест хи-квадрат
Критерий хи-квадрат - это одни из наиболее распространенных способов
изучения связей между двумя и более категориальными переменными. Проведение
этого теста включает расчет статистики хи-квадрат и ее сравнение с распределением
хи-квадрат, чтобы найти вероятность данного результата критерия. Есть
несколько типов критерия хи-квадрат; если не сказано иное, в данной главе обозначение
«тест хи-квадрат» относится к тесту хи-квадрат Пирсона, одного из наиболее
обычных типов.
Есть три разновидности критериев хи-квадрат. Первый из них называют
критерием независимости хи-квадрат. В случае двух переменных этот критерий
проверяет нулевую гипотезу о независимости переменных друг от друга, то есть об
отсутствии связи между ними. Альтернативная гипотеза состоит в том, что они
зависимы, то есть связаны между собой.
К примеру, мы можем собрать данные о курении и наличии диагноза рака
легких в случайной выборке взрослых. Каждая из этих переменных дихотомическая:
человек или курит, или нет, и у него или диагностирован рак легких, или пет.
Соберем наши данные в таблицу частот, представленную в табл. 5.3.
Таблица 5.3. Курение и рак легких
Курят
Не курят
Диагностирован рак легких
60
10
Не диагностирован рак легких
300
390
При взгляде на эти данные бросается в глаза, что, вероятно, есть связь между
курением и раком легких: у 20% курящих диагностирован рак легких, однако у
некурящих его обнаружили только у 2,5%. Впечатление может быть обманчиво,
поэтому мы проведем тест хи-квадрат на независимость. Вот наши гипотезы:
Н(): курение и рак легких независимы;
Я,: курение и рак легких связаны.
Хотя тесты хи-квадрат обычно рассчитывают с помощью компьютера, особенно
в случае таблиц большего размера, стоит один раз просчитать все шаги вручную
Тест хи-квадрат
1ЯЕ1
в качестве простого примера. Критерий хи-квадрат основан на разнице между
наблюдаемыми и ожидаемыми значениями в каждой из ячеек таблицы 2><2.
Наблюдаемые значения - это просто те, которые мы получили из данных но
выборке (пронаблюдали), тогда как ожидаемые значения - это те, которые мы бы
ожидали увидеть в том случае, если эти переменные независимы. Для расчета
ожидаемых значений воспользуйтесь формулой, приведенной на рис. 5.2.
сумма i-й строки сумма j-го столбца
lJ o6uifm сумма
Рис. 5.2. Расчет ожидаемых значений для ячейки
В этой формуле Е. - это ожидаемое значение для ячейки у, а / \\j обозначают
соответственно строку и столбец ячейки. Эта запись с нижним индексом часто
используется в статистике, так что стоит поговорить о ней сейчас. В табл. 5.4
показано, как такой способ записи используется для обозначения ячеек в таблице 2 *2.
Таблица 5.4. Запись с нижним индексом для таблицы 2 ><2
Ячейка,, Ячейка12 Строка 1 (/' = 1)
Ячейка21 Ячейка21 Строка 2 (/' = 2)
Столбец 10=1) Столбец 2 (J = 2)
В табл. 5.5 добавлены суммы по столбцам и строкам к примеру с курением и
раком легких.
Таблица 5.5. Данные о курении и раке легких с суммами по строкам и столбцам
Курят
Не курят
Сумма
Диагностирован рак легких
60
10
70
Не диагностирован рак легких
300
390
690
Сумма
360
400
760
Частота для ячейки,, составляет 60, для ячейки,., - 300, сумма по первой строке
равна 360, сумма по первой колонке составляет 70 и так далее. Используя запись
с точкой, сумма по строке 1 обозначается как 1., сумма по строке 2 - как 2., сумма
по колонке 1 - .1, и .2 для колонки 2. Логика этой записи состоит в том, что, к
примеру, сумма по первой строке включает значения для обоих колонок, 1 и 2, так
что значение номера колонки замещается точкой. Аналогичным образом сумма по
столбцам включает значения обеих строк, так что обозначения строки
замещаются точкой. В данном примере 1. = 360, 2. = 400, .1 = 70 и .2 = 690.
Значения сумм по колонкам и столбцам называются краевыми значениями,
поскольку их записывают по краям таблицы. Они отражают частоты одной
переменной в исследовании безотносительно ее связи с другой переменной, так что
краевая частота для наличия диагноза рака легких составляет 70, а для курения - 360.
Глава 5. Категориальные данные
Числа в таблице (60, 300, 10 и 390) называют совместными частотами, поскольку
они отражают число испытуемых, имеющих заданные значения обеих
переменных. К примеру, совместная частота для курильщиков с диагнозом рака легких в
данной таблице составляет 60.
Если бы две неременные не были связаны, мы бы ожидали, что частоты в каждой
ячейке были бы равны произведению краевых значений, поделенному на объем
выборки. Другими словами, мы бы ожидали, что совместные частоты определяются
только распределением краевых значений. Это означает, что если курение и рак
легких не связаны, то мы увидим, что число курильщиков с раком легких будет
определяться только числом курильщиков и числом больных раком в выборке. По этой
логике вероятность иметь рак легких должна быть примерно одинаковой у курящих
и некурящих, если курение действительно не влияет па развитие рака легких2.
Используя предыдущую формулу, мы можем рассчитать ожидаемые значения
для каждой ячейки, как показано на рис. 5.3.
360x70 001^
Еи = 33.16
11 760
360x690 п„ПА
Е„ 326.84
'12
760
400x70 пгол
Е21 36.84
21 760
400x690 „плг
Е^ = = 363.16
'22
760
Рис. 5.3. Расчет ожидаемых значений ячеек
Наблюдаемые и ожидаемые значения для данных о раке легких представлены
в табл. 5.6; ожидаемые значения указаны в скобках. Нам нужен какой-то способ
определить, связаны ли различия между ними только со случайностью или они
являются значимыми. Мы можем это сделать с помощью критерия хи-квадрат.
Таблица 5.6. Наблюдаемые и ожидаемые значения в данных о курении и раке легких
Курят
Не курят
Сумма
Диагностирован рак легких
60(33.16)
10(36.84)
70
Не диагностирован рак легких
300 (362.84)
390(363.16)
690
Сумма
360
400
760
Критерий хи-квадрат основан на квадрате разницы между наблюдаемыми и
ожидаемыми значениями в каждой ячейке таблицы и использует формулу,
приведенную на рис. 5.4.
2 Или наоборот, рак легких на курение; пли у них обоих общая причина - как всегда, мы из
статистически значимой связи не можем делать выводы о том, что - причина, а что - следствие. - Прим. перев.
Тест хи-квадрат
*¦-1
(Q(/-V
i-l.y-l ?(/
Рис. 5.4. Формула для расчета значения хи-квадрат
Чтобы понять, что означает статистика хи-квадрат, вам надо выполнить
следующие шаги:
1. Рассчитать наблюдаемые и ожидаемые значения для ячейки 1 г
2. Возвести их разницу в квадрат и разделить на ожидаемое значение.
3. Повторить первые два шага для всех остальных ячеек.
4. Сложить все полученные на шагах 1-3 числа.
Продолжая наш пример, для ячейки,, расчет проходит следующим образом:
(Оц-Еи)2 (60-33.16)2
Еи 33.16
= 21.72.
Повторив это с остальными ячейками, получим следующие значения: 2,2 для
ячейки,2, 19,6 для ячейки.,, и 2,0 для ячейки22. Сумма составляет 45,5, что в
пределах ошибки округления от того, что мы получили, используя статистическую
программу SPSS, 45,474.
Для того чтобы понять, что статистика хи-квадрат означает, вам надо знать
число ее степеней свободы. Форма распределения хи-квадрат зависит от числа его
степеней свободы, и, соответственно, в зависимости от него меняются и
критические значения распределения. В случае простого критерия хи-квадрат число
степеней свободы составляет (г- 1)*(с - 1), то есть (число строк минус 1) умножить
на (число колонок минус 1). Для таблицы 2x2 число степеней свободы составляет
(2 - 1)*(2 - 1) = 1; для таблицы 3x5 их (3 - 1)*(5 - 1) = 8.
Рассчитав значение хи-квадрат и число степеней свободы вручную, мы
можем посмотреть в таблицу значений хи-квадрат, чтобы сравнить наше значение
с соответствующим критическим значением. Судя по рис. D.11 в приложении D,
критическое значение для уровня значимости 0,05 составляет 3,841, тогда наше
число 45,5 сильно его превышает, так что при уровне значимости 0,05 мы должны
отвергнуть нулевую гипотезу о независимости переменных. Если вы незнакомы с
процессом проверки гипотез, вам может быть полезно просмотреть
соответствующий раздел главы 3 до того, как продолжать чтение этой главы. Компьютерные
программы обычно, кроме значения хи-квадрат и числа степеней свободы, выдают
р-значение, и если оно ниже нашего уровня значимости, мы можем отвергнуть
пулевую гипотезу. В данном примере будем использовать уровень значимости 0,05.
Если верить SPSS, р-значение для нашего результата (45,474) меньше 0,0001, что
много меньше 0,05 и говорит о том, что мы должны отвергнуть нулевую гипотезу
об отсутствии связи между курением и раком легких.
Критерий равенства пропорций хи-квадрат рассчитывают ровно так же, как и
критерий независимости, но он проверяет другую гипотезу. Критерий равенства
ЦЦГ;1 Глава 5. Категориальные данные
пропорций используется с данными, взятыми из нескольких независимых
выборок, а нулевая гипотеза состоит в том, что распределение какой-то переменной
одинаково во всех генеральных совокупностях. К примеру, мы можем взять
случайные выборки из разных этнических групп и проверить, одинакова ли частота
рака легких во всех генеральных совокупностях; нулевая гипотеза была бы в том,
что они все одинаковые. Расчеты бы проходили так же, как и в предыдущем
примере: испытуемых надо было бы расклассифицировать по этнической группе и
наличию рака легких, рассчитать ожидаемые значения, статистику хп-квадрат и
число степеней свободы, сравнить статистику с таблицей значений распределения
хи-квадрат с нужным числом степеней свободы или же получить точное
^-значение с помощью статистического пакета.
Критерий согласия хи-квадрат используют для проверки гипотезы о том, что
распределение какой-либо категориальной переменной в генеральной
совокупности совпадает с заданным распределением, тогда как альтернативная гипотеза
гласит, что распределение этой переменной какое-то иное, но не предполагаемое.
Этот критерий рассчитывают, используя ожидаемые значения, основанные на
гипотетическом распределении, и различные категории или группы обозначают
нижним индексом /, от 1 до g (как показано на рис. 5.5).
Рис. 5.5. Формула для расчета критерия согласия хи-квадрат
Обратите внимание на то, что в этой формуле нижние индексы не парные, то
есть, к примеру, ?., а не Е.. Это связано с тем, что для критерия согласия данные
чаще всего организованы в одну строку, поэтому и необходим только один индекс.
Число степеней свободы в критерии согласия хи-квадрат составляет (g - 1).
Положим, мы считаем, что у 10% людей в определенной популяции
пониженное кровяное давление (гипотензия), у 40% нормальное давление, у 30% прегииер-
тензия, а 20% - гипертензики. Мы можем проверить эту гипотезу, набрав выборку
п сравнив наблюдаемые частоты с гипотетическими (ожидаемыми значениями);
мы будем использовать уровень значимости 0,05. В табл. 5.7 приведен пример
возможных данных.
Таблица 5.7. Ожидаемые и наблюдаемые значения распределения кровяного
давления
Ожидаемая
доля
Ожидаемое
число случаев
Наблюдаемое
число случаев
Гипотензия
0.10
10
12
Нормальное
0.40
40
25
Прегипертензия
0.30
30
50
Гипертензия
0.20
20
13
Сумма
1.00
100
100
Тест хи-квадрат
¦МШ
Рассчитанное значение хи-квадрат для этих данных составляет 21,8 с тремя
степенями свободы, и оно значимо. (Критическое значение для уровня
значимости 0,05 составляет 7,815, что можно видеть из таблицы значений хи-квадрат на
рис. D.11 в приложении D.) Поскольку наше расчетное значение больше
критического, мы должны отвергнуть нулевую гипотезу о распределении уровней
кровяного давления в этой популяции.
Критерий хи-квадрат Пирсона подходит для данных, в которых все
наблюдения независимы (то есть, к примеру, каждого испытуемого измеряют только
1 раз), а категории взаимно исключающие и перекрывают все возможные
значения (то есть в каждом случае можно однозначно отнести испытуемого к ровно
одной ячейке). Кроме того, предполагается, что ни в одной из ячеек ожидаемое
значение не меньше 1, и не более чем у 20% ячеек ожидаемое значение меньше 5.
Причина возникновения двух последних требований связана с тем, что
критерий хи-квадрат асимптотический, и его некорректно применять к разреженным
данным (то есть таким, в которых у одной или нескольких ячеек маленькая
ожидаемая частота).
Поправка Йейтса па непрерывность - это процедура, разработанная
британским статистиком Франком Йейтсом (Frank Yates) для критерия независимости
хи-квадрат при работе с таблицами 2><2. Распределение хи-квадрат непрерывное,
однако данные, используемые в критерии хи-квадрат, дискретные, и поправка
Йейтса была придумана как раз для того, чтобы исправить это несоответствие.
Поправку Йейтса очень легко применить. Вам просто надо вычесть 0,5 из
абсолютного значения разницы наблюдаемых и ожидаемых значений до возведения в
квадрат; это слегка понижает значение статистики хи-квадрат. Формула
хи-квадрат с поправкой Йейтса на непрерывность приведена на рис. 5.6.
I , ''-^-С(1О,7-?,71-0.5)2 I
^= ^ Е
Рис. 5.6. Формула хи-квадрата с поправкой Йейтса на непрерывность
Идея поправки Йейтса состоит в том, что уменьшение значения хи-квадрат
приводит к уменьшению вероятности ошибки первого рода (ошибочного
отвержения нулевой гипотезы). Однако использование поправки Йейтса одобряется
далеко не всеми; некоторые исследователи считают, что она может приводить к
слишком сильной коррекции с понижением мощности и повышению вероятности
ошибки второго рода (ошибочного неотвержения нулевой гипотезы). Некоторые
статистики отвергают поправку Йейтса в принципе, хотя другие находят ее
полезной в случае разреженных данных, особенно если хотя бы в одной ячейке
ожидаемая величина меньше 5. Менее противоречивый метод работы с такими данными
в случаях, когда предположения о распределении, упомянутые выше (не более
20% ячеек с ожидаемым значением меньше 5 и без ячеек с ожидаемым значением
меньше 1), не выполняются, - это использование точного теста Фишера, который
обсуждается ниже, вместо критерия хи-квадрат.
вшн
Глава 5. Категориальные данные
Тест хи-квадрат часто рассчитывают и для таблиц большего размера, чем 2><2,
хотя для в таких ситуациях обычно используют компьютерные программы,
поскольку с ростом числа ячеек расчеты быстро становятся очень громоздкими. Нет
никакого теоретического ограничения на число строк и столбцов, которые можно
включить, но два фактора создают практические ограничения: возможность
сделать адекватные выводы (попробуйте это сделать с таблицей 30x30!) и
необходимость избегать пустых ячеек, что было сказано ранее. Иногда данные собирают в
виде большого числа категорий, но потом их объединяют в меньшее число групп,
чтобы избежать пустых ячеек. К примеру, информацию о семейном положении
можно собирать в виде большого числа категорий (женат/замужем, холост/не
замужем, в разводе, проживание с партнером, вдовец/вдова и т. п.), но для
некоторых видов анализов исследователь может решить сократить число категорий
(к примеру, до женат/замужем и холост/не замужем) из-за недостаточного числа
испытуемых в более мелких категориях.
Точный тест Фишера
Точный тест Фишера (или просто тест Фишера) - это непараметрический
критерий, аналогичный тесту хи-квадрат, но его можно применять с небольшим
количеством данных или в случае разреженного распределения данных, которые не
подходят под требования хи-квадрата. Тест Фишера основан на
гипергеометрическом распределении и рассчитывает точную вероятность наблюдения такого
распределения, как в данных, или более экстремального, отсюда и слово «точный»
в названии. Это не асимптотический тест, так что он не ограничен правилами о
разреженности, которые относятся к тесту хи-квадрат. Обычно для расчета теста
Фишера используют компьютерные программы, особенно для таблиц большего
размера, чем 2 х2, из-за занудности расчетов. Ниже следует простой пример с
таблицей 2x2.
Положим, нас интересует связь между употреблением некоего уличного
наркотика п внезапной остановкой сердца у молодых людей. Поскольку наркотик
незаконный и новый для нашего района, и, кроме того, остановки сердца очень редко
встречаются у молодых людей, мы не смогли собрать достаточно данных, чтобы
провести тест хи-квадрат. В табл. 5.8 приведены данные для анализа.
Таблица 5.8. Точный тест Фишера: расчет связи между употреблением
нового уличного наркотика и внезапной остановкой сердца у молодых людей
Употребляли наркотик
Не употребляли наркотика
Сумма
Остановка сердца
7
5
12
Нет остановки сердца
2
6
8
Сумма
9
11
20
Маши гипотезы:
Точный тест Фишера
ВВНЕШ
Н(): риск внезапной остановки сердца у употреблявших и не употреблявших
наркотика одинаковый.
Ht: риск внезапной остановки сердца у употреблявших новый наркотик выше.
Точный тест Фишера рассчитывает вероятность получить результат не менее
экстремальный, чем тот, который был найден в исследовании. Более
экстремальный результат в данном случае - это такой, в котором отличие в частоте внезапной
остановки сердца у употреблявших и не употреблявших наркотик еще больше,
чем в наших данных (при том же объеме выборки). Пример более экстремального
результата приведен в табл. 5.9.
Таблица 5.9. Более экстремальное распределение данных для примера
с употреблением наркотика и внезапной остановкой сердца
Употребляли наркотик
Не употребляли наркотика
Сумма
Остановка сердца
8
4
12
Нет остановки сердца
1
7
8
Сумма
9
11
20
Формула точной вероятности для таблицы 2 ><2 приведена на рис. 5.7.
гх\г2\сх\с2\
Р n\a\b\c\d\
Рис. 5.7. Формула точного теста Фишера
В данной формуле «!» означает факториал (4! = 4 * 3 * 2 х 1), а ячейки и
краевые значения обозначены в соответствии с табл. 5.10.
Таблица 5.10. Табличная запись
а Ь г}
с d г2
c^ с2 п
В нашем случае a = 8, Ъ = \,с = 4,d= 7, г, =9, г2 = И, с, = 12, с2 = 8 \\п = 20.
Почему эта таблица более экстремальна, чем наши данные? Потому что если бы между
употреблением наркотика и внезапной остановкой сердца не было бы связи, мы
бы ожидали увидеть такое распределение, как на табл. 5.11.
Таблица 5.11. Ожидаемые данные при условии независимости
Употребляли наркотик
Не употребляли наркотика
Сумма
Остановка сердца
5.4
6.6
12
Нет остановки сердца
3.6
4.4
8
Сумма
9
11
20
ЕШНН
Глава 5. Категориальные данные
В наших наблюдаемых данных связь между употреблением наркотика и
внезапной остановкой сердца сильнее (больше смертей, чем ожидаемое значение для
употреблявших наркотик), так что любая таблица, в которой связь еще сильнее,
чем наблюдаемая в данных, более экстремальна и, таким образом, менее вероятна
в случае, если употребление наркотика и остановка сердца независимы.
Чтобы найти /^-значение для точного теста Фишера вручную, нам бы пришлось
найти вероятности всех более экстремальных таблиц и сложить их. К счастью,
алгоритмы расчета теста Фишера включены практически во все статистические
пакеты, и существует множество онлайн-калькуляторов, которые могут сделать
этот расчет за вас. Используя калькулятор, доступный на странице,
поддерживаемой Джоном С. Пеццуло (John С. Pezzullo), профессором фармакологии и биоста-
тпстики в отставке, мы находим одностороннее/^-значение точного теста Фишера
для данных из табл. 5.7, и оно составляет 0,157. Мы используем односторонний
критерий, поскольку паша гипотеза односторонняя; пас интересует, не повышает
ли новый наркотик риск внезапной остановки сердца. Используя уровень
значимости 0,05, мы не можем считать этот результат значимым, так что мы не
отвергаем нулевую гипотезу о том, что новый наркотик не связан с увеличением риска
внезапной остановки сердца.
Парный тест МакНемара
Критерий МакНемара (McNemar) - это вид теста хи-квадрат, который применяют
13 тех случаях, когда данные получены из связанных выборок, или в случае парных
данных. Например, мы можем использовать тест МакНемара для анализа
результатов опроса общественного мнения до и после просмотра испытуемыми
политической рекламы. В данном примере от каждого человека мы получим два ответа,
один до и второй после просмотра. Мы не можем использовать эти два ответа на
один и тот же вопрос как независимые, так что не можем применять критерий
хи-квадрат Пирсона; вместо этого мы предполагаем, что два ответа, полученные
от одного и того же испытуемого, будут более сильно связаны, чем два ответа,
полученные от случайных людей. Тест МакНемара также подойдет для анализа
ответов пар муж-жена или братьев и сестер на один и тот же вопрос. В случае
братьев и сестер или мужей-жен, хотя данные и получены от разных людей, каждый
человек в паре настолько сильно связан с другим, что мы ожидаем, что они будут
более похожими, чем случайные люди из генеральной совокупности. Критерий
МакНемара также можно применять для анализа данных, собранных па группах
испытуемых, настолько похожих по ключевым свойствам, что их больше нельзя
считать независимыми. К примеру, в медицинских исследованиях иногда изучают
встречаемость некоторого заболевания в зависимости от возраста, пола, расовой
принадлежности или национальности и подобных характеристик и применяют
такие тесты, как критерий МакНемара, поскольку испытуемые настолько сильно
похожи, что их считают скорее связанными выборками, чем независимыми.
Положим, мы хотим определить эффективность политической рекламы для
влияния на мнение людей о смертной казни. Один из подходов сделать это со-
Парный тест МакНемара
НПШ1
стоит в сборе мнения людей о том, поддерживают они высшую меру или нет, до
и после просмотра 30-секундного ролика, пропагандирующего отмену смертной
казни. Посмотрите на гипотетические данные в табл. 5.12.
Таблица 5.12. Критерий МакНемара для мнения по поводу смертной казни
до и после просмотра политической рекламы
До просмотра
ролика
За смертную казнь
Против смертной казни
Сумма
После просмотра ролика
За смертную
казнь
15
10
25
Против
смертной казни
25
20
45
Сумма
40
30
70
Больше людей были против смертной казни после просмотра ролика, чем до
того, но достоверно ли отличие? Мы можем это проверить с помощью критерия
хи-квадрат МакНемара, который рассчитывается по формуле па рис. 5.8.
.» (Ь-сУ
Ь + с
Рис. 5.8. Формула для теста хи-квадрат МакНемара
Эта формула использует метод указания ячеек с помощью буквенных
обозначений по такой схеме, как в табл. 5.13
Таблица 5.13. Способ буквенного обозначения ячеек в таблице 2x2
а Ь
с d
Обратите внимание, что формула основана исключительно на распределении
дискордантных пар (Ь и с), в данном случае тех, в которых человек изменил свое
мнение после просмотра ролика. Статистика МакНемара распределена по хи-
квадрату с одной степенью свободы. Расчеты приведены на рис. 5.9.
I (25-Ю)'_ 225 ~ I
Л 25 + 10 35 I
Рис. 5.9. Расчет критерия хи-квадрат МакНемара
Как вы можете увидеть из таблицы значений хи-квадрат (рис. D.11 в
приложении D), при уровне значимости 0,05 критическое значение распределения хи-
квадрат составляет 3,84, так что наш результат свидетельствует о необходимости
отвергнуть нулевую гипотезу о том, что просмотр ролика никак не влияет на
мнение людей о смертной казни. Кроме того, с помощью компьютерного анализа я
определила, что точная вероятность получить такую (6,43) или более экстремальную
шмшшш
Глава 5. Категориальные данные
статистику хи-квадрат составляет 0,017, если бы мнение людей не менялось после
просмотра ролика, что подчеркивает значимость результатов этого исследования
и необходимость отвергнуть нулевую гипотезу.
Пропорции: большие выборки
Пропорция - это доля, в которой все случаи из числителя также входят и в
знаменатель. К примеру, мы можем говорить о пропорции (доле) студенток в каком-то
университете. В числителе будет стоять число студенток, а в знаменателе - число
всех студентов университета, как мужского, так и женского пола. Или же мы можем
говорить о доле студентов какого-то университета, специализирующихся на химии.
В числителе будет число студентов-химиков, а в знаменателе - число всех
студентов университета (вне зависимости от специализации). Пропорции более подробно
обсуждаются в главе 15. Данные, которые можно описать в терминах пропорций, -
это особый случай категориальных данных, в которых есть две категории: студенты
мужского и женского пола в первом примере, химики и не химики во втором.
Многие статистики, обсуждаемые в этой главе, такие как точный тест Фишера
и критерии хи-квадрат, можно использовать для проверки гипотез о
пропорциях. Однако в случае достаточного объема выборки можно применять некоторые
дополнительные виды критериев, которые используют нормальное приближение
биномиального распределения; это возможно из-за того, что, как говорилось в
главе 3, биномиальное распределение начинает очень напоминать нормальное с
ростом п (объема выборки). Какого объема выборки достаточно? Эмпирическое
правило гласит, что как пр, так и п{\ - р) должны быть не меньше 5.
Поставьте себя на место менеджера на фабрике, который утверждает, что 95%
шурупов определенного вида, выпускаемых на фабрике, имеют диаметр между
0,50 и 0,52 сантиметра. Один из клиентов жалуется, что в недавней поставке было
слишком много неразмерных шурупов, так что вы решили взять выборку из 100
шурупов и измерить их, чтобы посмотреть, сколько из них соответствует
стандарту. Вы проведете одновыборочный Z-критерий, чтобы проверить вашу
предполагаемую гипотезу о том, что 95% шурупов соответствуют указанным стандартам, со
следующими гипотезами:
Н():я>0,95;
Н,: Ж 0,95,
где я - это доля шурупов, соответствующих стандартам, в генеральной
совокупности (диаметр между 0,50 и 0,52 см). Обратите внимание, что это односторонний
критерий; вы будете рады, если хотя бы 95% шурупов соответствуют стандарту,
и счастливы, если даже больше, чем 95%. (Лучше всего было бы, если бы 100%
соответствовали стандартам, но не бывает идеально точного производственного
процесса.) В вашей выборке 91 шуруп соответствовал указанным размерам.
Достаточен ли этот результат для того, чтобы при уровне значимости 0,05 отвергнуть
пулевую гипотезу о том, что хотя бы 95% шурупов этого типа, произведенных на
вашей фабрике, соответствуют стандартам?
Пропорции: большие выборки <ИнИ
Формула для расчета одновыборочного Z-теста пропорций приведена па рис. 5.10.
Z--
Р-л0
1л0(1-л0)
V п
Рис. 5.10. Формула для одновыборочной Z-статистики для пропорций
В этой формуле п{) - это предполагаемая пропорция в генеральной
совокупности, р - это пропорция в выборке и п - это объем выборки.
Подстановка чисел в эту формулу дает Z-значение, равное -1,835, как показано
на рис. 5.11.
г_ 0.91-0.95 _ -0.0400 __
т (0.95) (0.05) " 0.0218
100
Vs
Рис. 5.11. Расчет одновыборочной Z-статистики для пропорций
Критическое значение для одновыборочного Z-критерия при нашей гипотезе и
уровне значимости составляет -1,645. Наша статистика -1,835 более
экстремальна, чем это значение, так что мы отвергаем нулевую гипотезу и заключаем, что
меньше 95% шурупов этого вида, произведенных на нашей фабрике,
соответствуют указанным стандартам.
Кроме того, мы можем проверять отличия между пропорциями в генеральных
совокупностях в случае большого объема выборок. Предположим, нас
интересует доля курящих старшеклассников, и мы хотим сравнить этот показатель у двух
стран. Нашей нулевой гипотезой будет то, что пропорции в двух странах
одинаковы, так что мы проведем двухсторонний тест со следующими гипотезами:
Н(): я, = я2;
Считая, что предположения об объеме выборок выполнены (пр >5,п(1 - р) > 5
для обеих выборок), мы можем применить формулу с рис. 5.12 для расчета
Z-статистики для разницы между пропорциями для двух генеральных совокупностей.
Z =
V2
Р\-
2ЕЖ
Рг
7Ш
1
Рис. 5.12. Формула для расчета Z-статистики равенства пропорций
В этой формуле р, - это пропорция в выборке 1,р2 - это пропорция в выборке 2,
п{ - это объем выборки 1, п2 - это объем выборки 2 и р - это объединенная
пропорция, рассчитанная как сумма успехов в обеих выборках (в данном случае число
курильщиков), разделенная на сумму объемов выборок.
|НЩр ' Глава 5. Категориальные данные
Предположим, мы взяли выборки по 500 старшеклассников в каждой из стран; в
стране 1 выборка включала 90 курильщиков; в стране 2 обнаружилось 70 курящих
испытуемых. Достаточно ли нам этих данных, чтобы отвергнуть нулевую
гипотезу о равенстве пропорций курящих старшеклассников в /щух странах? Мы можем
проверить это с помощью двухвыборочного Z-теста, как показано на рис. 5.13.
0.18-0.14
Z
/0.16(1-0.16) 0.16(1-0.16)
V 500 + 500
0.04
.023
= 1.74
Рис. 5.13. Расчет Z-статистики для разницы двух пропорций
Обратите внимание: наша объединенная пропорция составляет
(90 + 70)/(500 + 500) = 160/1000 = 0,16.
Это Z-зиачеиие менее экстремально, чем 1,96 (значение, необходимое для того,
чтобы отвергнуть нулевую гипотезу при уровне значимости 0,05; вы можете
проверить это с помощью таблицы нормального распределения (рис. D.3 в
приложении D)), так что мы не можем отвергнуть нулевую гипотезу о равенстве долей
курильщиков среди старшеклассников в двух странах.
Корреляции для категориальных
данных
Самая обычная мера связи двух переменных, коэффициент корреляции Пирсона
(обсуждается в главе 7), требует того, чтобы переменные были хотя бы
интервальными. Тем не менее были разработаны меры связи для категориальных и
порядковых данных, и они имеют смысл, сходный с коэффициентом корреляции Пирсона.
Эти меры часто рассчитывают с помощью статистических программ или онлайп-
калькуляторов, хотя можно это сделать и вручную.
Как и в случае коэффициента корреляции Пирсона, корреляции, обсуждаемые в
этом разделе, - это исключительно меры связи, и ни в кое случае нельзя делать
выводы о причинно-следственных взаимодействиях только на основании
коэффициента корреляции. Есть огромное множество подобных мер, некоторые из которых
известны под несколькими названиями; здесь описаны некоторые из самых часто
используемых статистик. Хороший подход в случае, если вы используете
статистический пакет, - это посмотреть, какие из мер он поддерживает, а затем изучить,
что из них подходит для ваших данных, поскольку существует очень большое
разнообразие видов корреляций.
Бинарные переменные
Фи - это мера степени связи между двумя бинарными переменными (двумя
категориальными переменными, каждая из которых принимает только два значения).
Фи рассчитывают для таблиц 2 *2; VКрамера (Cramer's V) аналогична фи для таб-
Корреляции для категориальных данных
ВНЕШ
лиц большего размера. Используя метод указания ячеек как в табл. 5.10, формула
для расчета фи приведена на рис. 5.14.
ad-be
^l(a + b)(c + d)(a + c)(b + d)
Рис. 5.14. Формула для фи-статистики
Мы можем рассчитать фи для данных по курению/раку легких из табл. 5.3, как
показано на рис. 5.15.
I (60X390)- (300X10) I
ф= , = 0.24
| л/360 + 400 + 70 + 690
Рис. 5.15. Расчет фи-статистики
Кроме того, фи можно рассчитать, разделив статистику хи-квадрат на п и взяв
квадратный корень из полученного значения, как показано на рис. 5.16.
ф=.
гт
J-
V п
Рис. 5.16. Альтернативная формула для фи-статистики
Обратите внимание, что первый метод расчета может дать как положительный,
так и отрицательный результат, тогда как второй - только положительный,
поскольку статистика хи-квадрат всегда положительна1. Значение фи, полученное с
помощью статистики хи-квадрат по второму методу, можно считать за абсолютное
значение результата расчета по первой формуле. Это хорошо видно при анализе
данных из табл. 5.14.
Таблица 5.14. Пример для фи
10 20
20 10
Рассчитав фи по первой формуле, мы получили -0,33, а по второй - 0,33. Вы
можете проверить это с помощью компьютерного пакета или онлайн-калькулято-
ра, или же проведя расчеты вручную. Разумеется, если бы мы поменяли порядок
следования колонок, мы бы получили положительный результат с помощью
обоих методов. Если у колонок нет естественного порядка (к примеру, если они
представляют из себя неупорядоченные категории вроде цвета), нас может не заботить
направление связи, а только ее сила. В других случаях ситуация может быть иной,
к примеру если колонки представляют из себя наличие или отсутствие болезни.
В последнем случае надо быть внимательными к расположению данных в
таблице, чтобы избежать неверной интерпретации результатов.
'* Кроме того, если не учитывать мнимых чисел, квадратный корень всегда неотрицателен. - Прим.
перев.
пя
Глава 5. Категориальные данные
Интерпретация фи не так однозначна, как интерпретация коэффициента
корреляции Пирсона, поскольку максимальное и минимальное значения фи зависят
от краевого распределения данных. Если обе переменные разделены ровно 50 на
50 (половина с одним значением, половина - с другим), фи может принимать
значения (-1, +1) при расчете по первому методу и (0, 1) - по второму. Если у
переменных распределение иное, то фи может принимать меньший набор значений.
Это подробнее обсуждается в статье Дэвенпорта и Эль-Саихурри (Davenport and,
El-Sanhurry), упомянутой в приложении С. Помня об этом ограничении, в
остальном интерпретация фи сходна с таковой для коэффициента корреляции Пирсона,
так что значение -0,33 говорит о средней отрицательной связи (следует помнить,
что нет точного определения «средней силы связи», и такой результат может
считаться сильным в одной области и довольно слабым - в другой).
V Крамера - это обобщение фи для таблиц, больших, чем 2x2. Формула для
V Крамера сходна с таковой для второго метода расчета фи, что показано на
рис. 5.17:
у n(min г-1, с-1)
Рис. 5.17. Формула для расчета V Крамера
где в знаменателе стоит п, умноженное на меньшее число из (г- 1) и (с - 1), то есть
минимум из двух чисел: число строк минус 1 и число столбцов минус 1. Для
таблицы 4 хЗ это число будет 2, то есть 3-1. Для таблицы 2 х2 формула для V Крамера
совпадает с формулой для второго метода расчета фи.
Предположим, значение хи-квадрат для таблицы 3x4 с п = 200 составляет 16,70.
V Крамера для этих данных приведена па рис. 5.18.
I ушШ..03о |
V 200(2)
Рис. 5.18. Расчет V Крамера
Точечно-бисериальный коэффициент корреляции
Точсчно-бисериальный коэффициент корреляции - это мера связи между
дихотомической и непрерывной переменными. Математически он эквивалентен
коэффициенту корреляции Пирсона (подробно обсуждается в главе 7), но из-за
дихотомичпости одной из переменных можно применять другую формулу для
расчета.
Предположим, что нас интересует сила связи между полом (дихотомическая
переменная) и ростом (непрерывная переменная) у взрослых.
Точечно-бисериальный коэффициент симметричен, как и коэффициент корреляции Пирсона, но для
простоты обозначения мы запишем пол как X и рост как У, причем закодируем У
так: 0 - мужчины, 1 - женщины. Мы берем выборку мужчин и женщин и рассчи-
Порядковые переменные
тываем точечно-бисериальный коэффициент корреляции с помощью формулы,
приведенной на рис. 5.19.
грь-
Xx-Xjp(l-p)
Рис. 5.19. Формула для точечно-бисериального коэффициента корреляции
В этой формуле X, - это средний рост женщин, Х() - средний рост мужчин,
р - доля женщин, sx. - стандартное отклонение X.
Предположим, в нашей выборке средний рост мужчин составляет 69,0 дюйма1,
64,0 дюйма5 - средний рост женщин, стандартное отклонение роста составляет 3,0
дюйма", и в выборке 55% женщин. Мы рассчитываем корреляцию между полом и
ростом у взрослых, как показано на рис. 5.20.
грЬ-
.*L
--?.
(64-
-69)^0.55(0.45)
3
-0.829
Рис. 5.20. Точечно-бисериальная корреляция между полом и ростом
Корреляция на уровне -0,829 - это показатель сильной связи, что говорит о том,
что рост и пол каким-то образом тесно взаимосвязаны в популяции США.
Корреляция отрицательная, поскольку мы закодировали женщин (которые в среднем
ниже) как 1, а мужчин - как 0; если бы мы закодировали эту переменную
наоборот, корреляция бы составляла 0,829. Обратите внимание, что средние и
стандартное отклонение, использованные в этом подсчете, близки к реальным данным по
США, так что сильная связь между полом и ростом существует не только в этом
упражнении, но и в жизни.
Порядковые переменные
Самая обычная статистика для корреляции порядковых данных (то есть тех, в
которых данные упорядочены в смысле «меньше-больше», но нет равного расстояния
между значениями) - это ранговая корреляция Спирмена (Spearman's rank-order
coefficient), также называемая ро Спирмена или г Спирмена, иногда обозначаемая /;.
Ро Спирмена основана на рангах данных по величине (первый, второй, третий и так
далее), а не на самих значениях. Ранжирование класса - это пример порядковых
данных; ученику с наибольшим средним баллом присваивают номер один, со
вторым по величине средним баллом - номер два и так далее, но при этом вы не
знаете, такая же ли разница между первым и вторым учениками, как между вторым и
третьим. Даже если данные на самом деле измеряются на непрерывной шкале, как
средний балл в школе, часто при поступлении в колледжи используются именно
ранги из-за сложностей в сравнении оценок в разных классах и школах.
1 Примерно 175 см. - Прим. перев
J Примерно 162 см. - Прим. перев.
() 7.62 см. - Прим. перев.
Глава 5. Категориальные данные
Для расчета ро Спирмсна прорапжируйте все значения каждой переменной по
отдельности, поставив в соответствие равным значениям усредненный ранг. Затем
посчитайте разницу в рангах для каждой пары значений и рассчитайте ро Спирме-
на с помощью формулы, приведенной на рис. 5.21.
Рис. 5.21. Формула для ро Спирмена
Положим, пас интересует связь между временем, проведенным за учебой в
неделю, и результатом итогового экзамена. Мы собираем данные об обеих
переменных, как показано в табл. 5.15 (данные упрощены для иллюстрации, чтобы
минимизировать ручные расчеты).
Таблица 5.15. Число часов, потраченных на учебу каждую неделю, и результат
экзамена
Студент
1
2
3
4
5
6
7
8
9
10
Время учебы
(часы)
10
12
8
15
4
11
6
7
9
5
Ранг
7
9
5
10
1
8
3
4
6
2
Результат
экзамена
93
98
99
100
92
90
80
82
84
75
Ранг
7
8
9
1
6
5
2
3
4
1
d.
i
0
1
-4
0
-5
3
1
1
2
1
d2
t
0
1
16
0
25
9
1
1
4
1
Похоже, что большие затраты времени на учебу связаны с более высокой
оценкой, однако связь не идеальная (студент № 3 получил высокую оценку, хотя
потратил среднее количество времени на учебу, а студент № 5 получил хорошую оценку,
хотя занимался относительно немного). Мы рассчитаем ро Спирмена, чтобы
получить более точную оценку этой связи. Обратите внимание на то, что мы возводим
разницу в рангах в квадрат, так что не имеет значения, вычитаете вы ранг времени
обучения из ранга оценки (как сделали мы) или же наоборот. Сумма d? составляет
58, ау;о Спирмена для этих данных показана на рис. 5.22.
г =1- = 1-0.35 =0.65
10(99)
Рис. 5.22. Расчет ро Спирмена
Порядковые переменные
ВЯН1Ш
Это подтверждает то, что мы предполагали, посмотрев на данные: есть
достаточно сильная, но не идеальная связь между затратами времени на занятия и
результатом экзамена.
Гамма Гудмана и Краснела (Goodman and Kruskal's gamma), часто называемая
просто гамма, - это мера связи между порядковыми переменными, которая
основана на числе коикордаитных и дискордантпых пар в двух переменных. Иногда ее
называют мерой монотонности, поскольку она говорит о том, как часто
переменные принимают значения в том порядке, который ожидается. Если я вам скажу,
что две переменные положительно связаны друг с другом и что второе число в
переменной 1 больше, чем первое, то вы будете ожидать, что второе число в
переменной 2 тоже выше первого. Тогда это будет конкордантная пара. Если же второе
число в переменной 2 будет меньше, чем первое, это будет дискордантная пара.
Для ручного расчета гаммы мы сначала должны получить распределение частот
для двух переменных, сохраняя в них естественный порядок.
Представьте себе гипотетические данные об ИМТ (индекс массы тела, мера
отношения массы к росту) и кровяном давлении. В целом высокий ИМТ связан с
высоким давлением, но это не так для каждого отдельного человека. У некоторых
полных людей нормальное давление, а у некоторых людей с правильным весом
давление повышено. Есть ли сильная связь между массой тела и кровяным
давлением в данных в табл. 5.16?
Таблица 5.16. Пример данных для расчета гаммы
ИМТ
Нормальный
Повышенный
Нормальный
25
10
Кровяное давление
Прегипертензия
15
10
Гипертензия
5
25
Формулы для расчета гаммы используют обозначение ячеек как в табл. 5.17.
Таблица 5.17. Обозначения ячеек для расчета гаммы
a b с
d e f
Сначала нам надо найти число коикордаитных (Р) и дискордантпых пар (Q)
следующим образом:
Р = а (е +7) + bf= 25(10 + 25) + 15(25) = 875 + 375 = 1250,
Q = с (d + ё) + bd = 5(10 + 10) + 15(10) = 100 + 150 = 250.
Затем гамму рассчитывают так, как показано на рис. 5.23.
I P~Q 1250-250 п?п I
у = = =0.67
' P + Q 1250 + 250
Рис. 5.23. Расчет гаммы Гудмана и Краскела
ЦЩ' Глава 5. Категориальные данные
Смысл гаммы ясен: если есть сильная связь между двумя переменными, доля
конкордантных нар должна быть выше; таким образом, чем больше гамма, тем
более слабой связи она соответствует. Гамма симметрична, поскольку ист разницы,
какая из переменных рассматривается как зависимая, а какая - как независимая;
значение гаммы будет одинаковым в любом случае. Гамма не делает поправку на
равные ранги в данных.
Морис Ксидалл (Maurice Kendall) разработал три немного отличающихся вида
порядковой корреляции как альтернативы гамме. Статистические компьютерные
программы иногда используют более сложные формулы для расчета этих статистик,
так что стоит проверять, какой именно метод расчета используется, по руководству
к программам. Все варианты статистики тау Кендалла, как и гамма, симметричны.
Тау-а Кендалла основана на разнице числа конкордантных и дискордантных
пар, разделенной на меру, основанную па общем числе пар (п = объем выборки),
как показано на рис. 5.24.
Рис. 5.24. Формула для тау-а Кендалла
Тау-b Кендалла - это похожая мера связи, основанная на конкордантных и
дискордантных парах, с учетом поправки на число равных рангов. Если назвать
переменные X и У, тау-fe рассчитывается как Р - Q, поделенное на геометрическое
среднее числа пар X с уникальным рангом (Х{)) и числа пар Ус уникальным рангом
(У()). Тау-6 может достигать 1,0 и -1,0 только в случае квадратных таблиц (таблиц
с одинаковым числом строк и столбцов). Формула для тау-й Кендалла приведена
па рис. 5.25.
ч
л[(Р~1
P-Q
¦Q+x0)(P<
н(2н
^о)
Рис. 5.25. Формула для тау-Ь Кендалла
В этой формуле Х{) - это число пар X с уникальным рангом, У() - это число пар У
с уникальным рангом.
Тау-с Кендалла используют для неквадратных таблиц и рассчитывают, как
показано на рис. 5.26.
rc=(P-Q)
2m
n2(m -1)
Рис. 5.26. Формула для тау-с Кендалла
В этой формуле m - это число строк или столбцов, в зависимости от того, какое
из них меньше, а п - это объем выборки.
Шкала Лайкерта и шкалы семантического дифференциала BB^I
d Сомерса (Somers's d) - это асимметричный вариант гаммы, так что расчет
статистики меняется в зависимости от того, какую из переменных мы считаем
независимой, а какую - зависимой. Кроме того, d Сомерса отличается от гаммы в том,
что она включает поправку на число пар с равным рангом в независимой
переменной. Если гипотеза заключается в том, что X предсказывает значение Y, d Сомерса
будет поправлено на число равных рангов вХ. Если, наоборот, У предсказывает
X, то поправка будет касаться равных рангов в Y. Как и в тау-6, равные ранги в d
Сомерса удаляются из знаменателя. Используя обозначения Х() = число
уникальных рангов в X, a Y{) = число уникальных рангов в Y, d Сомерса рассчитывают, как
показано на рис. 5.27.
б/(предсказаиие Y по X) =
^(предсказание X по У) =
P-Q
P-Q
P + Q+Y{]
Рис. 5.27. Формулы для d Сомерса
Симметричное значение для d Сомерса можно получить, взяв среднее от двух
асимметричных значений, полученных по этим формулам.
Шкала Лайкерта и шкалы
семантического дифференциала
Исследователи разработали несколько типов шкал для измерения свойств, у
которых нет естественной единицы измерения, таких как мнения, отношения и
впечатления. Самая известная из таких шкал - это шкала Лайкерта, предложенная Ренсисом
Лайкеротом (Rensis Likert) в 1932 году и широко используемая по сей день в самых
различных областях от образования до здравоохранения и менеджмента. В
типичном вопросе, построенном по шкале Лаймерта, испытуемому дают утверждение и
предлагают выбрать из упорядоченного списка возможных ответов. К примеру:
Мои занятия в Высшей школе Линкольна (Lincoln East High School)
подготовили меня к занятиям в университете.
1. Полностью согласен.
2. Согласен.
3. Затрудняюсь ответить.
4. Не согласен.
5. Полностью не согласен.
Это классическая порядковая шкала; мы можем быть достаточно уверены, что
«Полностью согласен» показывает более сильное согласие, чем «Согласен», а
«Согласен» - более сильное, чем «Затрудняюсь ответить», однако мы не знаем,
одинаково ли отличие между «Согласен» и «Полностью согласен» с отличием между
«Затрудняюсь ответить» и «Согласен», и одинаковы ли они для разных испытуемых.
|fj?J[Щ|НН :'* Глава 5. Категориальные данные
Методы работы с категориальными и порядковыми данными, описанные в этой
главе, подходят для анализа данных, собранных с помощью шкалы Лайкерта, как и
некоторые непараметрические методы, описанные в главе 13. Тот факт, что ответы
в шкале Лайкерта часто обозначают номерами, иногда приводит к использованию
исследователями методов, разработанных для интервальных данных. К примеру,
вы можете найти опубликованные статьи, где указаны среднее и дисперсия для
данных, собранных с помощью шкалы Лайкерта. Исследователь, выбирающий
такой путь (использования данных, собранных с помощью шкалы Лайкерта, как
интервальных), должен понимать всю противоречивость этого подхода и что многие
издатели не примут подобного анализа, а задача по доказательству возможности
отхода от порядковых и категориальных методов в случае анализа таких данных
целиком и полностью лежит на самом исследователе.
В шкале Лайкерта часто используют пять уровней реакции испытуемого,
поскольку, как считается, три уровня не дают достаточного числа вариантов ответа,
тогда как семь предоставляют слишком большой выбор. Кроме того, есть данные,
что люди не любят выбирать крайние значения из многих вариантов. Однако
некоторые исследователи вообще предпочитают четное число вариантов ответа,
обычно четыре или шесть, чтобы убрать среднюю категорию, которую
испытуемые могут выбирать по умолчанию.
Шкала семантического дифференциала похожа на шкалу Лайкерта, за тем
исключением, что отдельные варианты ответа не имеют названия, а обозначены
только крайние значения. Предыдущий вопрос из шкалы Лайкерта можно
переформулировать в стиле семантического дифференциала следующим образом:
Пожалуйста, оцените вашу академическую подготовку в Высшей школе Линкольна
в отношении требований университетского обучения:
Великолепная подготовка 12 3 4 5 Недостаточная подготовка
Из-за отсутствия необходимости давать названия отдельным точкам в
шкалах семантического дифференциала часто используют больше вариантов ответа.
Пользуется популярностью десятибалльная шкала, поскольку людям знакома
десятибалльная система оценки (отсюда и популярная в английском языке фраза
«a perfect 10», обозначающая высшую оценку чего-либо; дословно переводится
как «идеальная десятка»). Как и в случае шкалы Лайкерта, шкалы
семантического дифференциала по своей природе порядковые, хотя в случае большого числа
предложенных вариантов некоторые исследователи считают, что можно
анализировать их как интервальные.
Ренсис Лайкерт (1903-1981)
Ренсис Лайкерт (произносится с ударением на первый слог) был американским
социологом, специализировавшимся на исследовании организации и теории управления.
Лайкерт получил степень бакалавра (ВА) социологии в Мичиганском университете в
1926 году, а степень кандидата психологических наук (PhD) в Колумбийском
университете в 1932 году; он разработал шкалу Лайкерта как часть своей диссертации. Лайкерт был
основателем Института социологии Мичиганского университета и был его директором с
Упражнения
1946 до 1970 года; последние годы своей жизни он консультировал корпорации и писал
книги по теории управления. Главный вывод его работы делает его очень популярным
среди мотивированных студентов и работников по всему миру: Лайкерт разработал
основы управления на основе участия и методов организации, ориентированных на
человека, на базе своих исследований, показавших, что существует обратная связь между
принуждающим стилем управления и эффективностью работы сотрудников.
Упражнения
Вот несколько вопросов на повторение тем, обсужденных в этой главе.
Задача
Каковы измерения таблиц 5.18 и 5.19? Сколько будет степеней свободы в
критерии независимости хи-квадрат для таких данных?
Таблица 5.18. RxC-таблица (а)
Таблица 5.19. RxC-таблица (б)
Решение
Размерности таблиц равны 3x4 (таблица а) и 4x3 (таблица б). Помните, что
таблицы описывают как R*C, то есть (число строк)х(число столбцов). Число
степеней свободы для первой таблицы равно (3 - 1)(4 - 1) = 6 и (4 - 1)(3 - 1) = 6
для второй, поскольку число степеней свободы для хи-квадрата рассчитывают как
(г-1)(с-1).
Задача
Рассчитайте процент согласия и каппу по данным из следующей таблицы.
Таблица 5.20. Согласие двух оценщиков
Оценщик 1 +
-
Оценщик 2
+
70
30
100
-
15
25
40
85
55
140
Глава 5. Категориальные данные
Решение
Процент согласия = 95/140 = 0,68.
Каппа = 0,30.
Рп = (70 + 25)/140 = 0,68.
Р. = (85*100)/(140*140) + (40*55)/(140*140) = 0,54.
0.68-0.54
1-0.54
Рис. 5.28. Расчет каппы
Задача
Какова нулевая гипотеза критерия независимости хи-квадрат?
Решение
Переменные независимы, что одновременно означает, что совместные частоты
можно точно предсказать с помощью краевых частот.
Задача
Какова нулевая гипотеза критерия равенства пропорций хи-квадрат?
Решение
Нулевая гипотеза состоит в том, что две или более выборки, взятые из разных
генеральных совокупностей, имеют одинаковое распределение изучаемых
переменных.
Задача
Какая статистическая мера подойдет для оценки связи между двумя
независимыми переменными, приведенными в табл. 5.21? Каково значение этой
статистики, какие выводы можно из него сделать?
Таблица 5.21. Две независимые переменные
D+ D-
Е+ 25 10
Е- 2 5
Решение
Поскольку это таблица 2^2 и в двух ячейках ожидаемые значения меньше 5
(ячейки с и г/), следует использовать точный тест Фишера. Значение, полученное
с помощью компьютерной программы, составляет 0,077, что не дает оснований для
того, чтобы отвергнуть нулевую гипотезу об отсутствии связи между Е и D.
Задача
Каковы ожидаемые значения для табл. 5.22? Чему равна статистика
хи-квадрат? Каковы ваши выводы по поводу связи между вхождением в группу риска и
заболеванием, судя по этим данным?
Упражнения
ииипд
Таблица 5.22. Расчет ожидаемых значений
D+ D-
Е+ 25 30
Е- 15 5
Решение
Ожидаемые значения приведены в табл. 5.23.
Таблица 5.23. Ожидаемые значения: решение
D+ D-
Е+ 29.3 25.7
Е- 10.7 9.3
Хи-квадрат (1) = 5,144, р = 0,023. Этого достаточно, чтобы отвергнуть нулевую
гипотезу о независимости вхождения в группу риска от заболевания. Мы можем
сделать тот же вывод, основываясь на таблице хи-квадрат (рис. D.11 в
приложении D): 5,144 больше критического значения на уровне значимости 0,025 (5,024)
для одностороннего критерия хи-квадрат с одной степенью свободы, что говорит
о том, что мы должны отвергнуть нулевую гипотезу, если мы используем уровень
значимости 0,05.
Задача
В табл. 5.24 представлены политические предпочтения семейных пар.
Рассчитайте соответствующую статистику, чтобы проверить, независимы ли
политические предпочтения мужей и жен от их супруги или супруга.
Таблица 5.24. Политические предпочтения мужей и жен
Муж
Республиканец
Демократ
Жена
Республиканец
20
20
Демократ
30
20
Решение
Из-за того, что данные взяты из связанных пар, в данном случае подходит тест
МакНемара. Расчеты приведены на рис. 5.29. Значение хи-квадрата МакНемара
равно 2,00, что ниже критического значения для критерия хи-квадрат с одной
степенью свободы при уровне значимости 0,05, так что у нас нет оснований отвергнуть
нулевую гипотезу о независимости политических предпочтений мужей и жен друг
от друга.
2 (30-20)2 100 ^ЛЛ
tf =- 2.00
Л 30 + 20 50
Рис. 5.29. Расчет критерия МакНемара
ШЯНИН Глава 5. Категориальные данные
Задача
Какую из тау-статпстик Ксидалла следует применить при анализе данных в
табл. 5.25?
Таблица 5.25. Уровень образования и удовлетворенность работой
Образование
Неполное среднее
Среднее
Неполное высшее
Высшее
Удовлетворенность работой
Не удовлетворен
45
15
30
10
Нейтральное
отношение
20
15
10
15
Удовлетворен
10
20
25
30
Решение
Следует использовать тау-с Ксидалла, поскольку таблица не квадратная (в ней
4 строки и 3 колонки).
Задача
В чем проблема при анализе данных, полученных с помощью шкалы Лайксрта
и подобных шкал отношения как интервальных данных?
Решение
Нет естественной метрики для таких искусственных конструктов, как
отношение или мнение. Мы можем разрабатывать порядковые шкалы (то есть
ответы можно ранжировать по степени согласия, например) для их измерения, но нет
никакой возможности определить, равномерно ли распределены точки на такой
шкале. Таким образом, данные, собранные с помощью таких шкал, как шкала
Лайксрта, и подобных, следует анализировать как порядковые или категориальные, а
не интервальные или характеризующие отношения.
Задача
В какой ситуации вы бы использовали V-статистнку Крамера?
Решение
V Крамера - это более общий вариант фи-статистики, который характеризует
силу связи между двумя категориальными переменными с более чем двумя
уровнями. Для бинарных переменных V Крамера эквивалентна фи.
Задача
Вы узнали результаты государствепого опроса, которые гласят, что 30%
студентов университетов не удовлетворены своей внешностью. Вы хотите узнать,
сохраняется ли пропорция в вашем местном университете (20 000 студентов), так
что вы берете случайную выборку объемом в 150 студентов и узнаете, что 30 не
удовлетворены своей внешностью. Проведите соответствующий тест, чтобы
узнать, значимо ли отличается пропорция в вашем университете от результатов
государственного опроса.
Упражнения
Решение
Вопрос требует использовать одновыборочиую Z-статистику с двухсторонним
критерием (поскольку вас интересует наличие отличий в результатах опроса в
нашем университете от результатов по всей стране в любую сторону). Статистика
теста приведена на рис. 5.30.
Z-
0.30 - 0.20
/0.30(1-0.30)
V 150
0.10
~ 0.037
= 2.70
Рис. 5.30. Расчет одновыборочной Z-статистики для пропорций
Используя стандартный уровень значимости 0,05 и двухсторонний критерий,
мы видим, что критическое Z-зиаченис составляет 1,96 (вы можете его найти па
рис. D.3 в приложении D). Наше Z-зпачеиие больше критического, так что мы
отвергаем нулевую гипотезу о равенстве пропорций студентов, не удовлетворенных
своей внешностью, в вашем университете и по всей стране.
Парадокс Симпсона
Парадокс Симпсона описывает те ситуации, когда направление связи обращается при
объединении данных из нескольких групп. Он хорошо известен среди фанатов бейсбола.
К примеру, даже если у игрока А средний счет (batting average, доля успешных ударов)
выше, чем у игрока Б в каждом из двух годов, тем не менее в среднем за оба года у
игрока А счет может быть ниже. Посмотрите на табл. 5.26.
У игрока Б был выше счет в каждом из годов, однако если их объединить, то его счет
окажется ниже. Этот феномен возникает из-за разного числа ударов каждого игрока в
каждом из годов.
Таблица 5.26. Парадокс Симпсона в бейсболе
Игрок
А
В
2000
Удары
10
85
At-bats
50
400
Среднее
0,2
0,213
2001
Удары
200
50
At-bats
600
145
Среднее
0,333
0,345
Объединенные
Удары
210
135
At-bats
650
545
Среднее
0,323
0,248
Парадокс Симпсона был причиной споров о половой дискриминации при поступлении
в университет несколько лет назад. Иск, поданный против Калифорнийского
университета, был отклонен, поскольку было показано, что та дискриминация, которая имелась
на первый взгляд (меньший процент женщин, чем мужчин, поступил в университет),
может быть объяснена тем, что поступление определяется на уровне факультета, и
большинство женщин поступали на те факультеты, куда процент принятых абитуриентов был
в целом ниже, тогда как большинство мужчин, наоборот, поступали на те факультеты, где
процент принятых абитуриентов был выше. На самом деле на большинство факультетов
приняли мужчин даже немного меньше, чем женщин, но эта ситуация оказалась
обращенной при объединении данных со всех факультетов.
Также парадокс Симпсона проявляется при оценке лекарств, когда лекарство Л
проявляет себя лучше, чем лекарство Б, в обеих выборках, но оказывается менее
эффективным, если выборки объединить. Некоторые статистики полагают, что в таких
обстоятельствах это вообще не следует называть парадоксом, потому что это тогда означает, что
между двумя переменными есть какая-то причинная связь.
Глава 5. Категориальные данные
Таблица 5.27. Обзор
Название критерия
Процент согласия
Каппа Коэна
Тест независимости
хи-квадрат
Критерий хи-квадрат
равенства пропорций
Критерий согласия
хи-квадрат
Точный тест Фишера
Критерий МакНемара
Z-критерий пропорции
для больших выборок
Z-критерий равенства
пропорций для двух
больших выборок
Фи
V Крамера
Точечно-бисериальная
корреляция
Ро Спирмена
Гамма Гудмана
и Краскела
Тау-а Кендалла
Тау-Ь Кендалла
Тау-с Кендалла
всех тестов, упомянутых в этой главе
Тип данных
Одна категориальная
переменная, две оценки
Одна категориальная
переменная, две оценки
Две или более категориальные
переменные
Одна категориальная
переменная, выборки из двух или более
генеральных совокупностей
Одна категориальная
переменная, предполагаемое
распределение для нее
Две категориальные
переменные; данные могут быть
разреженными
Одна дихотомическая
переменная, измеренная на парах
Дихотомическая переменная,
одна большая выборка
(лр>5, л(1 -р)>5)
Дихотомическая переменная,
две большие выборки
(пр>5,л(1 -р)>5)
Две бинарные переменные
Две категориальные
переменные
Одна дихотомическая и одна
непрерывная переменная
Две ранжированные
переменные
Две порядковые переменные
Две порядковые переменные
Две порядковые переменные
Две порядковые переменные
Что проверяется
Насколько хорошо оценки
совпадают?
Насколько хорошо оценки
совпадают после поправки на случайность?
Независимы ли переменные?
Распределена ли переменная
одинаково во всех популяциях, из
которых взяты выборки?
Распределена ли переменная по
предполагаемому закону в
генеральной совокупности, из которой
взята выборка?
Независимы ли все переменные?
Равны ли пропорции в парах?
Отличается ли пропорция в
генеральной совокупности от
заданной?
Одинаковы ли пропорции
переменной в генеральных совокупностях,
из которых взяты выборки?
Насколько сильно связаны
переменные?
Насколько сильно связаны
переменные?
Насколько сильносвязаны
переменные?
Насколькосильносвязаны
переменные?
Насколько сильно связаны
переменные (на основании конкордантных и
дискордантных пар)?
Насколькосильносвязаны
переменные (на основании конкордантных и
дискордантных пар)?
Насколькосильносвязаны
переменные (на основании конкордантных и
дискордантных пар)?
Насколькосильносвязаны
переменные (на основании конкордантных и
дискордантных пар; можно
использовать для неквадратных таблиц)?
ГЛАВА 6.
f-критерий
^-распределение было впервые описано химиком, работавшим над контролем
качества в пивоварне Гинесс (Guiness) в Ирландии, Уилльямом Сили Госсетом
(William Sealy Gosset). Госсет представил ^-распределение в статье под
псевдонимом Стыодент (Student); именно поэтому ^-распределение также часто
называют распределением Стыодента, а ^-критерий — критерием Стыодента. Есть
три основных типа ^-критериев, все они имеют отношение к проверке разницы
в средних значениях и включают сравнение статистики теста с
^-распределением для определения справедливости полученной величины статистики в случае
верности нулевой гипотезы. Однофакториый дисперсионный анализ (ANOVA)
с двумя факторами математически эквивалентен ^-критерию, но ^-критерий
настолько часто применяется, что заслуживает отдельной главы. Кроме того,
понимание логики ?-критерия должно помочь в понимании более сложной логики
дисперсионного анализа.
{-распределение
Если вы незнакомы со статистикой вывода, то, прежде чем читать дальше, вам
может быть полезно сначала ознакомиться с главой 3. Статистические выводы
о реальных данных основываются в том числе и на знании распределения
вероятности. В главе 3 мы обсуждали нормальное и биномиальное распределения; в
данной главе мы познакомимся с ^-распределением. Как и нормальное
распределение, ^-распределение непрерывное и симметричное. В отличие от нормального
распределения, форма ^-распределения зависит от числа степеней свободы
выборки, то есть числа параметров, которые могут изменяться. В случае
^-распределения основной эффект на число степеней свободы оказывает размер выборки,
и у тестов для более крупных выборок в целом больше степеней свободы, чем в
случае небольших выборок. Расчет числа степеней свободы для различных
типов ^-критериев будет обсуждаться в разделах, посвященных соответствующим
типам критериев.
Как отмечалось выше, Госсет разработал ^-распределение для практических
задач. Будучи работником отдела контроля качества в пивоварне Гинесс, он
пытался разрешить проблему использования выборки ограниченного размера. Главное
Глава 6. f-критерий
наблюдение Госсета касалось влияния объема выборки на вероятность того, что
среднее по генеральной совокупности лежит не дальше определенных границ от
среднего выборки. Существует две основные причины использования
^-распределения при проверке различий в средних: работа с совокупностью, которая, как
мы считаем, распределена нормально, и неизвестное стандартное отклонение
генеральной совокупности, когда нам приходится использовать стандартное
отклонение выборки как замену отклонению генеральной совокупности. Если мы
работаем с выборкой слишком маленького объема, чтобы применить центральную
предельную теорему, и мы не уверены в нормальности распределения генеральной
совокупности, из которой мы взяли выборку, то нам придется применять
непараметрические тесты (обсуждаются в главе 13).
0.4
Функция плотности ^-распределения
(1 степень свободы)
0.4
0.3
Функция плотности t- распределения
(10 степеней свободы)
S 0.2
0.
s..
о:
О
О.
2 о.
т—I—I—I—I—I—I—I—г
-5-4-3-2-1012345
X
Функция плотности /-распределения
4 (20 степеней свободы)
0
l*i—г—т—i—i—i—г
-5-4-3-2-1012345
X
Функция плотности /-распределения
q, (30 степеней свободы)
Т-5! 1 1 1 1 1 Г
5-4-3-2-1012345
X
Рис.6.1. Четыре f-распределения
Как показано на рис. 6.1, ^-распределение напоминает нормальное
распределение, причем главное отличие состоит в более «тяжелых» хвостах, что говорит о
том, что крайние значения в ^-распределении встречаются чаще, чем в
нормальном. С ростом объема выборки (и, соответственно, числа степеней свободы)
^-распределение становится все более похожим па нормальное.
Госсет обнаружил, что в случае выборки из нормально распределенной
совокупности и использования стандартного отклонения выборки для оценки дисперсии
совокупности распределение средних выборок из этой совокупности по
переменной х можно описать формулой, представленной на рис. 6.2.
f-распределение
шшмш
х- и
t = —-
S
Рис. 6.2. Формула г-распределения
В этой формуле х - это среднее выборки, и - это среднее генеральной
совокупности, 5 - это стандартное отклонение выборки, а п - это объем выборки.
Эта формула очень напоминает формулу Z-значения, приведенную в главе 3;
единственное отличие заключается в том, что при вычислении ^-статистики
используется стандартное отклонение выборки, тогда как при вычислении
Z-значения - отклонение генеральной совокупности.
В приложение D входит таблица (рис. D.7) с верхними критическими
значениями ^-распределения для различных степеней свободы; мы говорим о «верхних
критических значениях», поскольку ^-распределение симметрично, поэтому нет
никакого смысла выписывать также и нижние значения (они будут равны
значениям в данной таблице со знаком «минус»). Из-за того, что в таблицу включены
только положительные значения, для нахождения критического значения в
двухстороннем ^-критерии мы берем колонку со значением а, равным половине
искомого. Для двухстороннего критерия с а = 0,05 мы должны использовать столбец
для а = 0,025. Неудивительно, что с ростом объема выборки критические значения
^-распределения стремятся к таковым для стандартного нормального
распределения. Например, мы знаем (из рис. D.7 в приложении D, как и из обсуждения в
главе 3), что в стандартном нормальном распределении для двухстороннего теста
с а = 0,05 верхнее критическое значение равно 1,96. Для двухстороннего теста с
использованием t-распределения с а = 0,05 верхнее критическое значение зависит
от числа степеней свободы (df). Для df = 1 оно составляет 12,706; для df= 100
верхнее критическое значение равно 2,228; для df =30 - 2,042; для df = 50 - 2,009; для
df= 100 - 1,984; для бесконечного числа степеней свободы верхнее критическое
значение составит 1,96.
Уилльям Сили Госсет
Уилльяма Сили Госсета часто рассматривают как первого промышленного статистика
современности. Хотя его работа была мотивирована прагматическими интересами его
работодателя (Артур Гиннесс, Сын и Ко - Arthur Guiness, Son & Со - изготовители пива),
его прикладные результаты послужили основой для возникновения набора важнейших
статистических тестов, основанных на распределении, которое он описал. После
систематического применения близких методов, таких как корреляция, для решения рабочих
задач он выделил фундаментальное ограничение выборок малого объема и методик,
которые подразумевают большое число наблюдений и/или экспериментов для
определения статистической значимости. Более поздние методы, такие как дисперсионный
анализ, разработанный Р. А. Фишером (R. A. Fischer), в значительной степени полагаются на
выведенное Госсетом f-распределение. Жизнь и работа Госсета служат великолепным
примером взаимодействия между прикладными и теоретическими исследованиями.
HJUf Глава 6. f-критерий
Одновыборочный f-критерий
Одно из возможных применений ^-критерия состоит в сравнении средних выборки
и совокупности с известным средним. Например, вас интересует влияние свинца
на умственное развитие детей. Вы знаете, что в среднем пятилетние дети в США
получают 100 баллов в определенном тесте на умственное развитие. У вас есть
выборка из 15 пятилетних детей, контактировавших со свинцом, и вы хотите узнать,
не повлияло ли это на их умственные способности, измеряемые при помощи
упомянутого теста. Вы также знаете, что в целом результаты теста в генеральной
совокупности распределены по нормальному закону. Ваша нулевая гипотеза состоит
в том, что пет разницы между выбранной группой и генеральной совокупностью в
целом, и вы проводите двухсторонний ?-тест с уровнем значимости 0,05.
Формула для одновыборочного ^-критерия показана на рис. 6.3.
Рис. 6.3, Формула одновыборочного г-критерия
В этой формуле х обозначает выборочное среднее, р() - это среднее для
сравнения (средний уровень умственного развития для всех 5-летних детей в США),
s - это стандартное отклонение вашей выборки, и п - это ее объем.
Формулы для расчета среднего и стандартного отклонений выборки показаны
на рис. 6.4 и 6.5.
Рис. 6.4. Расчет выборочного среднего
Рис. 6.5. Расчет выборочного стандартного отклонения
В этой формуле х - это отдельное значение х, х - это выборочное среднее, s -
это выборочное стандартное отклонение, а п - это объем выборки.
Также существует расчетная формула для стандартного отклонения выборки,
математически идентичная формуле с рис. 6.4, но более простая для ручного
расчета; она приведена па рис. 6.6.
Одновыборочный f-критерий
Рис. 6.6. Расчетная формула для выборочного стандартного отклонения
Если вам хочется попрактиковаться в использовании этих формул, то в конце
главы приведен полностью разобранный пример. Для его решения предположите,
что выборочное среднее равно 90, стандартное отклонение равно 10, а объем
выборки - 15, и используйте эти данные для расчета ^-статистики, как показано па
рис. 6.7.
90-100 00^
' = -fo- = -3-87
л/15
Рис. 6.7. Расчет одновыборочного f-критерия
Число степеней свободы для одновыборочного ^-критерия равно п - 1; в данном
примере df = 15 - 1 = 14. Из таблицы верхних критических значений
^-распределения (рис. D.7 в приложении D) мы видим, что для двухстороннего ^-критерия
с 14 степенями свободы и уровнем значимости 0,05 оно равно 2,145. Поскольку
абсолютное значение ^-статистики в наших данных превосходит верхнее
критическое значение (|-3,87| > 2,145), мы отвергаем нулевую гипотезу о том, что в
среднем контактировавшие со свинцом дети выполняют тест на умственное развитие
столь же успешно, как и все дети их возраста в популяции. Из-за того, что разность
среднего и ^-статистики отрицательна, мы также можем утверждать, что в среднем
их умственные способности ниже, чем в генеральной совокупности всех детей их
возраста.
Доверительный интервал для одновыборочного
t-критерия
Кроме статистики критерия и величины достоверности, нам часто нужно
рассчитать и доверительный интервал. Доверительный интервал (ДИ1) - это диапазон
значений вокруг среднего: если мы будем брать бесконечное число выборок того
же размера из той же генеральной совокупности, х% раз истинное среднее
генеральной совокупности будет попадать в доверительный интервал, рассчитанный
из выборок. Если мы рассчитаем 95%-ный доверительный интервал (самый часто
применимый), то х = 95, так что мы можем утверждать, что 95% всех
доверительных интервалов, рассчитанных из бесконечного числа выборок этой генеральной
Или CI, от англ. confidence interval. - Прим. пер.
1ШНИ
Глава 6. f-критерий
совокупности, будут включать в себя ее истинное среднее. Говоря более общо,
доверительный интервал говорит нам об аккуратности точечной оценки, такой как
выборочное среднее. Широкий доверительный интервал указывает на то, что если
бы мы взяли другую выборку, то могли бы получить отличающееся выборочное
среднее, тогда как если он узкий, то, взяв другую выборку, мы, скорее всего,
получили бы достаточно близкое значение выборочного среднего.
Формула для расчета двухстороннего доверительного интервала для среднего в
случае одновыборочного /-критерия приведена на рис. 6.8.
С/,-а =Х±
( \
ш
Рис. 6.8. Формула доверительного интервала для одновыборочного f-критерия
В нашем примере, а = 0,05, х = 90, df = п - 1 = 14,5= 10, /()()Г)М = 2,145 (из
таблицы па рис. D.7 в приложении D), и п = 15.
Подстановка этих значений в формулу дает нам ответ, приведенный на
рис. 6.9.
С/095 = 90 ± (2.145) -7= = 90 ± 5.54 = (84.46,95.54)
Рис. 6.9. Расчет доверительного интервала для одновыборочного f-критерия
95%-ный доверительный интервал для нашей оценки истинного среднего
составляет (84,46,95,54). Заметим, что эти числа иногда называют нижней и верхней
границами доверительного интервала; в этом примере нижняя граница составляет
84,46, а верхняя - 95,54.
При расчете одностороннего доверительного интервала замените ± либо на +,
либо на -, в зависимости от необходимости. Для расчета доверительного
интервала с другой вероятностью попадания среднего в него используйте
соответствующее критическое значение из таблицы /.-значений. Например, для одностороннего
90%-го доверительного интервала с 20 степенями свободы верхнее критическое
значение /-распределения составляет 1,325.
f-критерий для независимых выборок
/-критерий для независимых выборок, также называемый двухвыборочным
^-критерием, сравнивает средние двух выборок. Задача этого теста состоит в проверке,
равны ли средние генеральных совокупностей, из которых были взяты выборки.
Предполагается, что члены двух выборок не связаны (никто не измерен дважды,
нет братьев п сестер и т. п.) и выбраны из своих совокупностей независимо.
Кроме того, мы предполагаем, что генеральные совокупности имеют приблизительно
нормальное распределение, если только объемы выборок недостаточно велики,
чтобы применить центральную предельную теорему, и дисперсии двух совокупное-
f-критерий для независимых выборок
ННЕЕЭ
тей приблизительно равны. Этот критерий часто применяют во многих областях,
и обычно для его расчета используют компьютерные программы, которые также
включают критерий равенства дисперсий совокупностей (например, тест Левене,
тест Брауна-Форсайта (Brown-Forsythe test) или тест Бартлетта (Bartlett's test))
и методы для исправления ситуации, если это предположение оказывается
неверным.
Формула для расчета ^-критерия для независимых выборок приведена на рис. 6.10.
| . (*1-*2)-(Ц-^2)
lik+i)
(ni-l)sf + (n2-l)s22
пх+п2-2
Рис. 6.10. Формула для расчета f-критерия для независимых выборок
В этой формуле х их,- это средние двух выборок,
jij и и2 - это средние двух генеральных совокупностей,
s21 - это объединенная дисперсия,
п{ ип2- это объемы двух выборок, а
52, и s22 - это дисперсии двух выборок.
Заметим, что часто нулевая гипотеза ^-критерия для независимых выборок
состоит в том, что разница между истинными средними равна 0, тогда выражение
(jj1 - u2) можно опустить.
Число степеней свободы для двухвыборочного ^-критерия составляет
(п] + п2 - 2), то есть на 2 меньше, чем общее число элементов двух выборок.
Это сложная формула, но стоит сделать шаг назад и посмотреть на ее общую
форму до того, как застрять в деталях. Формула для двухвыборочного ^-критерия
для независимых выборок сходна с таковой для одновыборочного ^-критерия в
том, что числитель - это разница между средними, а знаменатель - мера разброса,
включающая как разброс внутри выборок, так и их объем. Статистика парного
теста тоже будет следовать этой общей форме, хотя и будет отличаться в некоторых
тонкостях.
Давайте рассмотрим пример. Стар как мир вопрос о том, кто находится в
лучшей форме - мужчины-футболисты или мужчины-танцоры в балете; поэтому
спортивный физиолог организует исследование для ответа на него совместно с
местной группой исследователей из госпиталя. Две группы - это независимые
совокупности, поскольку пи один из футболистов не танцует в балете. Два списка
танцоров и футболистов ведутся их соответствующими профессиональными
ассоциациями, из них следует, что и футболистов, и танцоров можно найти по всей
где
2
^IBH Глава 6. f-критерий
стране; испытуемые выбираются случайным образом из каждой группы.
Поскольку и танцоры, и футболисты - очень занятые люди, удается договориться только
с 10 членами каждой группы. Всех участников исследуют с помощью набора
заданий на физическую подготовку, включая ходьбу, бег и прыжки, а также измеряют
соответствующие физиологические показатели, такие как постоянство частоты
сердечных сокращений, скорость распространения пульсовой волны и т. п. Эти
измерения вместе образуют единый показатель физической формы,
принимающий значения от 0 до 100. Опыт использования подобного метода оценки с этим
способом подсчета результатов показывает, что эти показатели распределены в
генеральной совокупности приблизительно нормально.
Всех участников исследуют в одном и том же учреждении в одно время дня, а их
результаты оценивают и объединяют одни и те же врачи. Результаты обеих групп
приведены в табл. 6.1.
Таблица 6.1. Результаты оценки физического
состояния футболистов и танцоров балета
Танцоры балета
89.2
78.2
89.3
88.3
87.3
90.1
95.2
94.3
78.3
89.3
Футболисты
79.3
78.3
85.3
79.3
88.9
91.2
87.2
89.2
93.3
79.9
Мы будем использовать значение а = 0,05 в этом исследовании. Вы можете
рассчитать ^-статистику целиком вручную, используя формулы для подсчета
стандартного отклонения, приведенные в данной главе ранее (и помня, что
дисперсия - это квадрат стандартного отклонения). Для ускорения этого процесса мы
рассчитали необходимые величины за вас, назвав танцоров балета группой 1, а
футболистов - группой 2:
хх = 87,95
х2 = 85,19
5,2в 32,38
s22 = 31,18
Если бы мы использовали компьютерную программу, мы могли бы проверить
предположение о равенстве дисперсий с помощью теста Лсвеие (или
альтернативного - это обсуждается подробнее дальше в этой главе, в разделе, посвященном
/"-критерию для выборок с неравной дисперсией), проверяющего нулевую гипоте-
f-критерий для независимых выборок I ИИ^И
зу о том, что дисперсии двух совокупностей равны. (Если мы не можем отвергнуть
эту нулевую гипотезу, то можно применять ^-критерий.)
Объединенная дисперсия выборок рассчитывается, как показано на рис. 6.11.
2_(10-1)32.38 + (10-1)31Л8_
Sp 10 + 10-2
Рис. 6.11. Расчет объединенной дисперсии
Число степеней свободы elf = п{ + п., - 2 = 18. Наша нулевая гипотеза состоит в
том, что в среднем спортивная форма в двух группах одинакова, то есть \i{ - [х.} = 0.
Для проверки этой нулевой гипотезы мы рассчитываем ^-статистику, как показано
на рис. 6.12.
Рис. 6.12. Расчет f-статистики
На рис. D.7 в приложении D мы видим, что верхнее критическое значение для
двухстороннего ^-критерия с уровнем значимости 0,05 и 18 степенями свободы
составляет 2,101. Абсолютное значение нашей ^-статистики ниже него (то есть
ближе к нулю), так что мы не можем отвергнуть нулевую гипотезу и заключаем,
что это исследование не дало никаких доказательств различной физической
подготовки у футболистов и танцоров балета.
Доверительный интервал для t-критерия
для независимых выборок
Для расчета двухстороннего доверительного интервала для этого типа ^-критерия
мы используем формулу, приведенную на рис. 6.13.
а~-ьМьЩЩ
где
2
2 _(nl-l)s*+(n2-l)s2
пх+п2-2
Рис. 6.13. Формула доверительного интервала для f-критерия
для независимых выборок
Есть несколько моментов, касающихся этой формулы, которые стоит отметить:
• это доверительный интервал для разницы между средними двух
совокупностей;
|[^|Щц| Глава 6. f-критерий
• для значения ?«,,//- мы берем верхнее критическое ^-значение для df и
половины заданного значения альфа из таблицы ^-распределения, такой как на
рис. D.7 в приложении D;
• если бы это был односторонний доверительный интервал, мы бы
использовали верхнее критическое /"-значение для а, а не для у> и поставили бы знак
«плюс» или «минус», а не ±, в зависимости от направления интервала;
• формула включает ранее рассчитанный делитель из формулы ^-критерия
для независимых выборок.
Для наших данных мы используем а = 0,05 и рассчитываем 95%-ный
двухсторонний доверительный интервал; результат показан на рис. 6.14.
I С/,_а = 2.76 ± (2.10)(2.73) = (-2.97,8.49) I
Рис. 6.14. Расчет 95%-го двухстороннего доверительного интервала
для f-критерия для независимых выборок
Заметьте, что этот интервал включает 0, который является нашим нулевым
значением (значением, с которым мы сравнивали выборочные средние, согласно
нашей нулевой гипотезе); такой результат ожидаем для этих данных, поскольку
мы не увидели статистически значимые различия и не отвергли нулевую гипотезу
ранее.
f-критерий для парных измерений
Для проведения /-критерия для повторных измерений, также известного как
/-критерий для зависимых выборок, или парный ^-критерий, элементы двух выборок
должны быть не независимы, а связаны каким-то образом. Иногда данные в
выборках - это измерения, сделанные дважды на одних и тех же людях, например
кровяное давление до и после приема лекарства. Иногда данные собирают для
людей, родственных каким-то образом, например мужей и жен или чьих-то
потомков. Иногда данные получают из выборок разных людей, но слишком сходных по
другим характеристикам, так что их уже нельзя рассматривать как независимые
выборки. Измерения рассматриваются как парные, то есть выборки должны быть
одного размера.
Формула для расчета ^-статистики для парного ^-критерия основана на
разностях, рассчитанных для каждой пары элементов выборок. Статистика теста
приведена на рис. 6.15.
^-(ц-д2)
—
л/л
Рис. 6.15. Формула для парного f-критерия
f-критерий для парных измерений
ill]
В этой формуле d = средняя разница, \х{ и р2 - это средние двух совокупностей,
s(j - это стандартное отклонение разниц, а п - число пар.
Нулевая гипотеза для парного ^-критерия обычно состоит в том, что средняя
разница (d) равна 0, тогда как альтернативная гипотеза говорит, что она отлична
от 0. Как и с двухвыборочным ^-критерием, часто величина (и, - р2)
предполагается равной 0, и в таком случае ее можно опустить.
Под разницей понимается просто отличие в значениях парных измерений,
например кровяное давление до лечения минус кровяное давление после лечения.
Мы рассчитываем эту разницу для каждой пары, а затем вычисляем их среднее
и стандартное отклонение для расчета ^-статистики. Заметим, что п в контексте
парного ^-критерия относится к числу пар, а не числу измерений. Число степеней
свободы df = п- 1.
Вы можете разобраться в этом лучше, если посмотрите на пример.
Предположим, мы хотим проверить эффективность программы диеты с физическими
упражнениями в снижении общего уровня холестерина у мужчин среднего возраста.
Мы решили использовать парный ^-критерий, поскольку мы будем измерять
уровень холестерина дважды для каждого подопытного, до начала программы и еще
раз после ее окончания. Этот метод иногда называют «использование объектов
как их собственные контроля», поскольку, измеряя каждого человека дважды, мы
надеемся убрать или минимизировать влияние всех индивидуальных
особенностей, не относящихся к тому, что нас интересует, то есть тому, как уровень
холестерина испытуемого изменяется в зависимости от диеты и программы упражнений.
Мы считаем, что изменения уровня холестерина в ответ на условия эксперимента
в генеральной совокупности распределены приблизительно нормально, и у пас
всего лишь 10 испытуемых, так что парный ^-критерий - это подходящий метод.
Экспериментальные данные приведены в табл. 6.2.
Таблица 6.2. Уровень холестерина до и после диеты и упражнений
до
220
240
225
180
210
190
195
200
210
240
После
200
210
210
170
220
180
190
190
220
210
Разница (d) (После - До)
^20
-30
-15
-10
10
-10
-5
-10
10
-30
Очевидно, что у большинства испытуемых уровень холестерина понизился
после окончания программы, но была ли разница статистически значимой? Для
¦шнм
Глава 6. f-критерий
выяснения этого мы рассчитаем парную ^-статистику, используя следующие
значения, полученные из данных:
^ —11;
5,= 13,9.
Мы проведем двухсторонний парный ?-тест с уровнем значимости 0,05. Наша
нулевая гипотеза состоит в том, что средние совокупностей равны, то есть их
разница равна 0; ^-статистика для этих данных приведена на рис. 6.16.
I -11-0 ~~ I
г = -Тз^- = -2-50
л/io
Рис. 6.16. Расчет парного f-критерия
Поскольку у нас всего 10 пар, то степеней свободы 9 (df = п - 1). Используя
таблицу верхних критических значений для ^-распределения (рис. D.7 в
приложении D), мы нашли, что критическое значение для двухстороннего ^-критерия
с 9 степенями свободы и а = 0,05 составляет 2,262. Абсолютное значение нашей
^-статистики превосходит это число, поэтому мы отвергаем нулевую гипотезу и
заключаем, что упражнения и диета оказали значимый эффект на общий уровень
холестерина. Поскольку средняя разница и ^-статистика отрицательные, мы также
можем утверждать, что оздоровительная программа привела к снижению
холестерина у се участников.
Вы можете задаться вопросом, что это за две генеральные совокупности, о
которых мы говорим в данном примере. Измерения до программы рассматриваются
как взятые из генеральной совокупности мужчин среднего возраста, а измерения
после - из генеральной совокупности мужчин среднего возраста, прошедших
оздоровительную программу. Разумеется, вторая генеральная совокупность
существует только в теории, поскольку это новая программа, то есть что мы на самом
деле делаем, так это предполагаем, что произойдет с обидим уровнем холестерина
в первой генеральной совокупности, если вся она пройдет через исследуемую
программу.
Доверительный интервал для t-критерия
для парных измерений
Для расчета доверительного интервала в случае парного ^-критерия используйте
формулу, показанную на рис. 6.17.
С7,.а -d±
( )
ы
ш
Рис. 6.17. Формула для доверительного интервала для парного f-критерия
f-критерий для выборок с неравной дисперсией
Расчеты для данных из нашего примера приведены на рис. 6.18.
Рис. 6.18. Расчет двухстороннего 95%-го доверительного интервала
для парного f-критерия
Обратите внимание, что этот доверительный интервал не включает 0; этого
следовало ожидать, поскольку мы увидели значимый результат, применив
/-критерий, то есть отвергли нулевую гипотезу о том, что средняя разница равна 0.
f-критерий для выборок с неравной
дисперсией
Одно из допущений, лежащих в основе ^-критерия для независимых выборок,
состоит в приблизительном равенстве дисперсий генеральных совокупностей, из
которых взяты выборки; это также называют предположением об однородности
дисперсии, или, проще, предположением об однородности. Если это условие не
выполняется и дисперсии генеральных совокупностей в реальности различаются,
возрастает риск ошибок как первого, так и второго рода. Это связано с
объединением дисперсий выборок при проведении ?-теста для независимых выборок, и
результаты этого теста сильно искажаются, если выборки взяты из совокупностей
с отличающейся дисперсией. Задача проверки гипотезы о двух независимых
выборках с различающейся дисперсией известна под названием проблемы Берен-
са-Фишера (Behrens-Fisher), и было предложено несколько ее решений.
Если вы используете статистическую программу для проведения ?-тсста для
независимых выборок, то, скорее всего, она включает алгоритм проведения
одного или нескольких тестов на однородность дисперсии. Примеры такого рода
тестов включают тест Левене, тест Брауна-Форсайта и тест Бартлетта. Тест Ле-
вене основан на среднем, а критерий Брауна-Форсайта - это расширение теста
Левене, использующее усеченное среднее либо медиану. Тест Бартлетта наиболее
чувствителен к отклонениям от нормальности (это не то же самое, что равенство
дисперсий), так что его следует применять, только если вы уверены в примерно
нормальном распределении совокупностей, из которых взяты выборки. Важно
тут, однако, использовать любой из этих тестов, если это вам доступно, чтобы
проверить условие однородности. Технические детали различных тестов со ссылками
на профессиональную литературу про них доступны в Руководстве по
инженерной статистике национального института стандартов и технологий (Engineering
Statistics Handbook of the National Institute for Standards and Testing), документ
свободно доступен в Интернете (http://itl.nist.gov/div898/handbook/index.htmy
Если предположение об однородности не выполнено, вы можете использовать
один из непараметрических аналогов ^-критерия для независимых выборок
(обсуждается в главе 13) или применить ^-критерий для выборок с неравной диспер-
|ВНЯ: Глава 6. f-критерий
смей, также известный как ?-тест Велча (Welch's Mest). Выбор одного из этих
вариантов особенно важен, когда вы работаете с небольшими выборками, или когда
вы хотите быть очень аккуратными с выводами, ^-критерий Велча использует
немного отличающуюся формулу для расчета ^-статистики и сложную формулу для
расчета числа степеней свободы.
Для расчета ^-статистики тест Велча использует формулу, приведенную на
рис. 6.19.
t = -
J,-3c2
\S1A
Рис. 6.19. Формула для f-критерия Велча
В этой формуле х, и х2 - это выборочные средние, s* и s.22 - это выборочные
дисперсии, а я, и п2 - объемы выборок.
Обратите внимание, что формула для критерия Велча не включает
объединенную дисперсию. Серьезное усилие требуется при подсчете числа степеней
свободы для теста Велча, что видно на рис. 6.20.
Hf
(2 2 \
S\ S2
КП\ П2>
2
S\ , ^2
п\{п-Х) n\{n2-\)
Рис. 6.20. Формула для расчета числа степеней свободы для критерия Велча
Рассчитав ^-статистику и число степеней свободы, вы продолжаете анализ так
же, как и с любой другой ^-статистикой, сравнивая ваш результат с таблицей
критических значений /-распределения (такой как на рис. D.7 в приложении D) и
принимая решение в соответствии с ней.
Упражнения
Хотя вы могли бы использовать статистический пакет, такой как Minitab, SPSS,
STATA пли SAS, для расчета ^-критерия и его уровня значимости, поработав с
некоторыми примерами вручную, можно лучше понять внутреннее устройство
этого критерия. Далее, если вам понадобится изучить ситуации, связанные с
работой пли учебой, включающие небольшие выборки, вы можете начать
тренироваться в работе с ними, используя ^-критерий. Если вы понимаете детали расчета
/-критерия вручную, тогда использование статистического пакета станет для вас
значительно проще. Кроме того, многие статистические пакеты выдают довольно
запутанные результаты, если вы не знаете, на что в них смотреть; так что самостоя-
Упражнения ВВП
тельная проработка некоторых примеров может поспособствовать обнаружению
нужной информации в море чисел.
Задача
Менеджер на фабрике обеспокоена высоким числом несчастных случаев на
предприятии, которым она управляет, поэтому она организует программу
безопасности, включающую образование рабочих, улучшение освещения на фабрике
и назначение премий бригадам, улучшившим свои показатели по этой проблеме.
Среднее число инцидентов в неделю до программы было равно 5, а распределение
было приблизительно нормальным. Она хочет знать, изменилось ли оно после
начала программы. Она берет выборку из 15 недель после программы и использует
служебные записи для определения числа происшествий, случившихся в течение
каждой из этих недель. Данные представлены в табл. 6.3. Какой тест следует
применить, чтобы определить, изменилось ли среднее число происшествий в неделю
после начала программы? Какова статистика критерия и что она говорит об
эффективности программы?
Таблица 6.3. Число происшествий за неделю
Номер недели
Число
происшествий
1
5
2
6
3
6
4
4
5
5
6
3
7
2
8
7
9
5
10
4
11
1
12
0
13
3
14
2
15
5
Решение
Она должна использовать одновыборочный ^-критерий, сравнивая среднее
число происшествий в неделю, рассчитанное для 15 недель после программы, со
средним по совокупности недель до программы. Она должна использовать
двухсторонний критерий, поскольку существует вероятность, что частота инцидентов
увеличилась после начала программы, и ей точно стоит узнать об этом. Таким
образом, она проведет двухсторонний одновыборочный ^-критерий с нулевой
гипотезой о том, что пет достоверной разницы между средними выборки и генеральной
совокупности, и она будет использовать стандартный уровень значимости 0,05.
Вот информация, необходимая для расчета статистики:
н() = 5 (дано)
п = 15 (дано)
х = 3,87
s = 2,00
Сначала мы рассчитываем выборочное среднее и стандартное отклонение, как
показано на рис. 6.21 и 6.22.
^ 58
x = J=i ?? = 3.87
п 15
Рис. 6.21. Расчет выборочного среднего
Глава 6. f-критерий
Рис. 6.22. Расчет выборочного стандартного отклонения
Затем мы подставляем эти числа в формулу для статистики одновыборочного
/-критерия, как показано на рис. 6.23.
S
3.87-5.00
" 2.00 "
л/15
-1.13
0.52 "
-2.17
Рис. 6.23. Расчет одновыборочного f-критерия
У нас 14 степеней свободы (df = п - 1). В соответствии с рис. D.7 в
приложении D верхнее критическое значение для двухстороннего теста с 14 степенями
свободы и при уровне значимости, равном 0,05, составляет 2,145. Абсолютное
значение нашей /-статистики превосходит критическое значение, поэтому мы
отвергаем нулевую гипотезу об отсутствии различий между частотой происшествий
за педелю до и после начала программы безопасности. Поскольку разница между
выборочным средним и средним генеральной совокупности отрицательная, как и
/-статистика, мы, кроме того, можем заключить, что программа снизила частоту
инцидентов.
Задача
Каков 95%-ный доверительный интервал для нашей оценки среднего
генеральной совокупности при таких результатах?
Решение
Мы рассчитываем 95%-ный двухсторонний доверительный интервал, как
показано на рис. 6.24.
у
CIl.a=x±
-41
i)-~> Ш)
= (2.76,4.98)
Рис. 6.24. Расчет 95%-го доверительного интервала
для одновыборочного f-критерия
Обратите внимание, что верхнее критическое значение 4,97 очень близко к
среднему по совокупности. Этого можно было ожидать, поскольку наша
выборочная /-статистика еле-еле превосходит критическое значение при значимости 0,05;
Упражнения
то есть мы с трудом достигли стандартной величины, для того чтобы отвергнуть
нулевую гипотезу о равенстве разницы между выборочным средним и средним
генеральной совокупности нулю.
Задача
Каков 90%-ный доверительный интервал для нашей оценки среднего по
совокупности при таких результатах по выборке?
Решение
Для расчета 90%-го доверительного интервала все, что нам нужно изменить в
формуле, использованной в предыдущем задании, - это верхнее критическое
значение. Используя рис. D.7 в приложении D, мы видим, что для двухстороннего
доверительного интервала критическое значение для уровня значимости 0,10 при
df = 14 составляет 1,761. Подставив это в формулу, получим результат,
показанный на рис. 6.25.
Ch.a=x±\
= 3.87 ±(1.761)1
/2.00^
1л/15у
= (2.96,4.78)
Рис. 6.25. Расчет 90%-го доверительного интервала
для одновыборочного f-критерия
Обратите внимание, что 90%-ный доверительный интервал уже, чем 95%-иый
для того же набора данных. Этого следует ожидать из-за меньших критических
^-значений, используемых для 90%-го интервала. Другими словами, 90%-ный
доверительный интервал включает меньше суммарной вероятности, чем 95%-ный, так
что неудивительно, что он уже него.
Таблица 6.4. Различные f-критерии и их применение
t-критерий
Одновыборочный
f-критерий
Двухвыборочный
f-критерий
Парный
f-критерий
f-критерий для
выборок с
различающейся дисперсией
Тип данных
Одна выборка, непрерывные данные,
приблизительная нормальность
Две независимые выборки,
непрерывные данные, приблизительная
нормальность, приблизительно
равная дисперсия
Две связанные выборки, равный
размер выборок, непрерывные
данные, приблизительная нормальность
разниц
Две независимые выборки,
непрерывные данные, приблизительная
нормальность
На какой вопрос дает ответ
Относится ли выборка к
совокупности с заданным средним?
Относятся ли выборки к
совокупностям с равными средними?
Относятся ли выборки к
совокупностям с равными средними?
Относятся ли выборки к
совокупностям с равными средними?
ГЛАВА 7.
Коэффициент корреляции
Пирсона
Коэффициент корреляции Пирсона - это мера линейной связи между двумя
интервальными или характеризующими отношения переменными. Хотя существуют
другие типы корреляции (некоторые из них обсуждаются в главе 5, включая
коэффициент ранговой корреляции Спирмена), коэффициент корреляции Пирсона
наиболее обычен, а слово «Пирсона» часто опускают, и мы просто говорим про
«корреляцию» или «коэффициент корреляции». Если не сказано иное, в данной
книге «корреляция» относится к коэффициенту корреляции Пирсона.
Корреляции часто рассчитывают в разведочной фазе исследовательского проекта, чтобы
увидеть, как связаны друг с другом различные непрерывные переменные, также
часто для исследования этих связей строят диаграммы рассеяния (обсуждаются
в главе 4). Тем не менее некоторые корреляции являются интересными сами по
себе, их можно проверять на достоверность, и их логично использовать как
отдельные величины. Понимание коэффициента корреляции Пирсона - это основа для
понимания линейной регрессии, так что стоит потратить время на изучение этой
статистики и как следует понять, что она вам говорит о связи между двумя
переменными. Самое главное в корреляции - то, что это мера наблюдаемой связи, сама
по себе она никак не может выявить причину. Многие переменные в реальном
мире сильно коррелируют друг с другом, но эти связи могут объясняться случаем,
влиянием других переменных или другими неизвестными причинами. Даже если
между величинами есть причинно-следственная связь, она может работать в
другую сторону, чем мы предполагаем. Поэтому даже самая сильная корреляция сама
по себе не может свидетельствовать о причинно-следственной связи; она может
быть подтверждена только с помощью постановки эксперимента (обсуждается в
главе 18). В этой главе мы обсуждаем общее значение связи в контексте
статистики и затем подробно разбираем коэффициент корреляции Пирсона.
Связь
Повседневная жизнь полна переменными, которые кажутся ассоциированными
пли связанными друг с другом, и обнаружение этих связей и есть основная задача
Связь
ШШЕШ
науки. Однако ничего сложного или загадочного в понимании взаимосвязей
между величинами нет; люди все время думают в терминах связей и часто ассоциируют
с ними причинно-следственные взаимодействия. Родители, которые наставляют
детей питаться больше овощами и меньше - нездоровой пищей, вероятно,
делают это, поскольку думают, что есть связь между рационом и здоровьем, а атлеты,
которые тратят много часов на тренировки, скорее всего, делают это, потому что
считают, что интенсивные тренировки приведут их к успеху. Иногда такие
здравые мысли поддерживаются экспериментальными данными, иногда - нет, но
людям, похоже, свойственно замечать, что некоторые события вроде бы происходят
одновременно, и верить, что одно из них вызывает другое. Как ученые (пли просто
люди, понимающие в статистике) мы должны привыкнуть задаваться вопросами,
является ли кажущаяся связь реальной, и если да, то есть ли в ней причинно-
следственные взаимоотношения.
Вот несколько примеров выводов, основанных на наблюдениях, но, очевидно,
неверных:
• Есть сильная связь между продажами морожелого и числом утонувших,
так что причина этого в том, что люди идут купаться слишком рано после
того, как съели мороженое, у них сводит мышцы, и они тонут.
• Есть сильная связь между результатом теста на словарный запас и
размером обуви, что можно объяснить тем, что у высоких людей мозг больше, и
поэтому они могут запомнить больше слов.
• Число аистов в регионе сильно связано с уровнем рождаемости, так что,
очевидно, аисты и правда приносят детей.
• Мэр города заметил сильную корреляцию между победами местной
спортивной команды в соревнованиях и парадами1 и решил проводить больше
парадов, чтобы улучшить результаты местных команд.
Вот настоящие объяснения:
• И потребление мороженого, и плавание более обычны в теплое время года,
так что очевидная связь объясняется влиянием третьего фактора,
температуры (или времени года).
• Исследование проводили на школьниках, а их возраст не учитывали.
Вероятно, старшие дети окажутся выше (с большим размером обуви) и будут
иметь более обширный словарный запас, чем младшие дети; таким образом,
наблюдаемая связь обусловлена третьей переменной, возрастом.
• Аисты чаще встречаются в сельской местности, а рождаемость также
обычно выше вне городов, так что связь объясняется влиянием другого фактора,
типа местности.
• Это обращенная причинно-следственная связь - парады проводят после
побед в чемпионатах, так что успешный сезон для команд - это причина
парадов, а не проведение парадов улучшает их результаты.
В оригинале - ticker-tape parades, то есть парады, сопровождающиеся посыпанием конфетти и
нарезанной бумагой с близлежащих зданий. - Прим. пер.
шмв
Глава 7. Коэффициент корреляции Пирсона
Стоит заметить, что дажеесли логичная причинасвязи двух переменных
отсутствует, связь между ними можно обнаружить просто по случайности. Это особенно
важно для исследований очень больших выборок, когда даже слабая корреляция
может оказаться статистически значимой, но при этом не иметь никакого
практического значения. Также стоит отметить, что даже в случаях сильных связей
между переменными, таких как курение и рак легких, она может проявляться очень
по-разному на уровне отдельных случаев. Некоторые люди курят на протяжении
многих лет и никогда не заболевают, в то время как некоторые несчастные
получают рак легких, даже если не курили никогда в своей жизни.
Диаграмма рассеяния
Диаграмма рассеяния - это полезное средство для изучения взаимоотношений
между переменными, и обычно создание таких диаграмм для непрерывных
переменных проводится па разведочной стадии работы с данными. Диаграмма
рассеяния - это диаграмма для двух непрерывных переменных. Если идея эксперимента
подразумевает, что одна из переменных является независимой, а вторая зависит
от нее, то первую откладывают по оси х (горизонтальной), а вторую - по оси у
(вертикальной); если такие взаимоотношения неизвестны, то не имеет значения,
какая переменная отложена на какой оси. Каждому члену выборки соответствует
одна точка на графике, описываемая набором координат (х, у); если вы когда-либо
использовали картезианские координаты2 в школе, то вы уже знакомы с этим
процессом. Диаграммы рассеяния дают вам возможность почувствовать общие
свойства связи между переменными, включая такие, как направление (положительное
или отрицательное), силу (сильная или слабая) и форму (линейная, квадратичная
и т. п.). Кроме того, диаграммы рассеяния - это хороший способ получить общее
впечатление о разбросе данных и увидеть, есть ли какие-то выбросы, случаи,
которые на первый взгляд не похожи на остальные.
Важно исследовать двумерные связи (связи между двумя переменными),
поскольку многие часто используемые методы предполагают, что они линейные,
предположение, совсем не обязательно соблюдаемое для произвольной пары
переменных из каких-то данных. Линейность в данном контексте означает
«расположение на прямой линии», в то время как любые другие взаимосвязи
считаются нелинейными, хотя мы можем охарактеризовать другие типы связи и более
конкретно, например как квадратичную или экспоненциальную. Разумеется, мы
не ожидаем, что в реальности данные идеально подходят под какую-то
математическую модель; под линейной связью мы подразумеваем ситуацию, когда данные
кажутся расположенными поблизости от прямой линии.
Кроме того, мы можем создать матрицу диаграмм рассеяния, в которой
представлено множество таких диаграмм, так что мы можем легко увидеть связи
между парами переменных. На рис. 7.1 показана такая матрица диаграмм рассеяния,
созданная Ллойдом Курье (Lloyd Currie) из Национального института стандартов
п технологии (National Institute of Standards and Technology) для изучения свя-
2 Картезианские координаты также часто называют декартовыми. - Прим. пер.
Диаграмма рассеяния
¦¦1Ш
зей между четырьмя загрязнителями: калием, свинцом, железом и оксидом серы.
Диаграммы рассеяния для каждой пары переменных расположены на
пересечении соответствующих столбцов и строк, так, в ячейке (1, 2) (первая строка, второй
столбец) показана связь между калием и свинцом, а в ячейке (1,3)- между калием
и железом и так далее.
Данные о загрязнении
О ЗаО 700 О ЛХС 6СО0
Калий
г
г
2
2V2~2"-v
м<гг*"2~г
2
2 ш/
2 „2.-2- I
Свинец
г
^Г'Г2
*%?&*•*
г г ,
*,22
'i2 г J
Г, 7 2
Железо
ьН*"2"'2
А-,
Оксид
серы
юн
О 25I-J SCO О 100 200
Рис. 7.1. Матрица диаграмм рассеяния для четырех загрязнителей
Взаимосвязи между непрерывными
переменными
В линейной алгебре мы часто описываем связи между двумя переменными с
помощью уравнения вида:
у = ох + Ь.
В этой формуле у - это зависимая переменная, х - независимая переменная,
a - коэффициент наклона, b - константа.
Заметим, что иногда вместо а в данном уравнении используют т - это другой
способ записи, никак не меняющий смысла уравнения. Как я, так и b могут быть
положительными, отрицательными или равняться нулю. Для нахождения
значения у для заданного значения х вам надо просто умножить х на а} а затем
прибавить Ь. Такие уравнения, как это, описывают идеальную связь (зная значения „г,
а и Ь, мы можем найти точное значение г/), тогда как уравнения, описывающие
реальные данные, обычно включают также величину ошибки, показывая наше
понимание того, что уравнение дает нам предсказанное значение у, которое может не
совпадать с истинным. Тем не менее стоит посмотреть на графики, точно заданные
уравнениями, чтобы почувствовать, как при построении выглядят идеальные
связи; это должно помочь замечать схожие тенденции в реальных данных.
На рис. 7.2 показана взаимосвязь между двумя переменными, х и г/, которые
связаны идеальной положительной связью: х = у. В этом уравнении b = О, а = 1, и
ИВ11
Глава 7. Коэффициент корреляции Пирсона
в каждом случае значения х и у совпадают. Это уравнение выражает
положительную связь, поскольку с ростом значения х так же растет и у; в графике с
положительной связью точки идут из нижнего левого угла в верхний правый.
15
10
5
-15 -10 -5 ^*
.¦* -5
И -10
-15
а
.¦-
¦¦¦•¦
0 5 10 15
Рис. 7.2. График модели у = х
На рис. 7.3 изображена отрицательная зависимость между х и у: эти точки
описываются уравнением у = -х.В этом уравнении а = -1, b = 0. Заметьте, что при
отрицательной зависимости при росте значения х значение у уменьшается, а точки
на графике идут из верхнего левого угла в нижний правый.
15
- - iff
¦ . 10
¦*¦¦;
-15 -10 -5
-5
-10
-15
°*Ф 5 10 15
••-.,
V
Рис. 7.3. График модели у = -х
На рис. 7.4 показана положительная зависимость между х и у, определенная
моделью у = Зх + 2. Заметьте, что эта связь все так же идеальна (в том смысле что,
зная модель и значение д:, мы можем рассчитать точное значение у) и выглядит как
прямая линия. Однако, в отличие от двух предыдущих графиков, линия больше
не проходит через начало координат (0, 0), потому что значение b (константы)
равно 2, а не 0.
Диаграмма рассеяния
¦¦ЕЯ
25
20
15
10
5
-15 -10 -5 J
ф -10
t* -15
¦ -20
-25
^
ф
5Ф
*¦
0 5 10 15
Рис. 7.4. График модели у = Зх + 2
В трех предыдущих случаях уравнение прямой указывало на сильную связь
между переменными. Однако это не всегда так; прямая может показывать
отсутствие связи между переменными. Даже если одна из переменных постоянна (то есть
ее значение не меняется), в то время как значение другой переменной непостоянно,
то такое взаимоотношение все равно можно выразить в виде уравнения (и
графика) прямой для несвязанных переменных. Например, уравнение х = -3, которому
соответствует график на рис. 7.5; вне зависимости от значения у значение х всегда
одно и то же, таким образом, между х и у нет никакой связи. Коэффициент
наклона этого уравнения не определен, поскольку в уравнении, использованном для его
расчета, нулевой знаменатель.
6
Ф 4
¦
#1
Ь 2
-6 -4 -2 0
* "2
¦
-6
2 4 6
Рис. 7.5. График модели х = -3
Уравнение для расчета коэффициента наклона приведено на рис. 7.6:
Глава 7. Коэффициент корреляции Пирсона
Рис. 7.6. Уравнение для расчета коэффициента наклона прямой
где л", и х, - это два произвольных значения х из данных, а у{ и у2 -
соответствующие значения у.
Если х{ и х2 совпадают, у этой дроби знаменатель равен нулю, так что уравнение
и коэффициент наклона не определены.
Уравнение у = -3 также описывает отсутствие связи между хиу,в данном
случае из-за того, что коэффициент наклона равен нулю. В этом уравнении у всегда
равен -3 вне зависимости от того, чему равен х. График для этого уравнения -
горизонтальная линия, как показано на рис. 7.7.
6
4
2
-6 -4 -2 0
-2
ф ф ф 4^ -^>
-4
-6
2 4 6
*^г* *ж ^^ ^^ ^г
Рис. 7.7. График модели у = -3
Для реальных данных мы не ожидаем, что уравнение будет идеально описывать
связь между переменными, а график будет идеальной прямой, даже если имеется
довольно сильная линейная зависимость. Посмотрите на график на рис. 7.8, где
изображены почти те же данные, что и на рис. 7.9; отличие состоит в том, что к
данным мы прибавили некоторую случайную ошибку, так что идеальная прямая
больше не наблюдается. Взаимосвязьхиу все равно линейная и положительная,
по мы больше не можем точно предсказать значение у по значению х с помощью
уравнения. Другими словами, знание значения х помогает нам предсказать
значение у (в противоположность предсказанию без знания х), но мы понимаем, что
паше предсказанное значение у может на сколько-то отличаться от истинного
значения изданных.
Диаграмма рассеяния
30
25
20
15
10
-15 -10 -5^ф* 5
•* .,.
¦ ф -15
-20
Ф
¦ г
* ¦
Ф ф.
0 5 10 15
Рис. 7.8. График для сильной положительной связи
-15
Ф
-10
Ф
30
25
20
15
10
5
"5 ¦ -5
-10
¦ ¦-Is
-20
W
•ffti
1 4^
Ф
4"
Ф ^ Ф
4*
¦ ¦
5 10 15
20
Рис. 7.9. График для более слабой положительной связи
Две переменные могут быть связаны сильно, но не линейно. В качестве
знакомого примера можно привести уравнение у = х2} которое описывает идеальную
связь, поскольку при известном значении х мы знаем абсолютно точно, чему
равен у. Тем не менее эта зависимость квадратичная, а не линейная, что можно
видеть на рис. 7.10. Возможность заметить сильные нелинейные связи - это одна из
важнейших причин для построения графиков по вашим данным.
На рис. 7.11 показан другой обычный тип нелинейной зависимости,
логарифмическая, определенная уравнением у = 1п(дг), где In означает «натуральный
логарифм от».
Глава 7. Коэффициент корреляции Пирсона
120
4 100
* 80
Ф
60
Ф
Ф 40
¦ 20
V
Ф
¦
Ф
Ф
Ф
-15 -10 -5 ° 5 10 15
Рис. 7.10. График идеальной квадратичной зависимости
Рис. 7.11. График идеальной логарифмической зависимости
Если вы заметили нелинейную зависимость в своих данных, то может
оказаться, что ее можно преобразовать в зависимость, близкую к линейной; это подробнее
обсуждается в главе 3. Узнавать такие нелинейные зависимости и помнить разные
способы их «исправления» - важное умение для всех, кто работает с данными.
В случае данных, показанных на рис. 7.10, если мы преобразуем г/, взяв
квадратный корень от него, и затем построим зависимость Vt/ отх, мы увидим, что
зависимость стала линейной. Аналогично, в случае данных, приведенных на рис. 7.11,
мы можем преобразовать у в е-1 и построить диаграмму его зависимости от х} тогда
мы увидим линейную зависимость между переменными.
Коэффициент корреляции Пирсона
Коэффициент корреляции Пирсона
Диаграммы рассеяния - это важное средство визуального изучения связей между
парами переменных. Тем не менее мы также можем захотеть получить
статистическую оценку этих связей и проверить их на значимость. Для двух непрерывных
или характеризующих отношения переменных самая важная мера связи - это
коэффициент корреляции Пирсона, также называемый линейным коэффициентом
корреляции, обозначаемый как р (греческая буква «ро») для генеральной
совокупности и г - для выборки.
Этот коэффициент может принимать значения в интервале (-1, 1), где 0
свидетельствует об отсутствии связи между переменными, большие абсолютные
значения показывают более сильную связь (если никакая из переменных не является
константой, как в случае данных на рис. 7.5 и 7.7). Значение коэффициента
корреляции может вводить в заблуждение, если на самом деле связь нелинейная, из-
за чего всегда следует строить график для ваших данных. Такие характеристики
связи, как «сильная» и «слабая», не имеют строгого численного соответствия, но
связь, описываемая как сильная, будет ближе к линейной, с точками, лежащими
ближе к прямой, чем в случае слабой связи. В некоторой степени определения
сильных и слабых связей зависят от области исследований или традиции, так что
вам придется узнать, что как называют в вашей области науки. Несколько
примеров диаграмм рассеяния данных с разной величиной г приведены на рис. 7.12, 7.13
и 7.14, чтобы показать, как выглядят связи различной силы.
50
40
30
20
10
0
-10
¦ -
фф
ф
¦ ¦¦ ¦
л ¦ *
* фф *ф
ф ¦
0 ^ 5 10 15 20
25
Рис. 7.12. Диаграмма рассеяния (г = 0.84)
Глава 7. Коэффициент корреляции Пирсона
25
20
15
10
5
0
(
Ф
Ф
Ф Ф
ф Ф Ф
Ф Ф
ф ^ Ф ф
Ф *
ФФ ¦ +
) 5 10 15 20 25 30
35
Рис. 7.13. Диаграмма рассеяния (г = 0.55)
25
20
15
10
5
п
Ф
ф Ф
ф
4Ь ? 4b>
ф
ф
ф
ф *^
ФФ ¦ ф ¦ А ффф^ ¦
^ф ж ф^ ^ ^ф
0 5 10 15 20 25 30
35
Рис. 7.14. Диаграмма рассеяния (г = 0.09)
Хотя коэффициенты корреляции часто рассчитывают с помощью
компьютерных программ, их так же легко рассчитать вручную. Формула для коэффициента
корреляции Пирсона представлена на рис. 7.15.
Рис. 7.15. Формула коэффициента корреляции Пирсона
Коэффициент корреляции Пирсона ^^^И^^ИЕ+Я
В этой формуле SSx - это сумма квадратов отклонений х, SSt - это сумма
квадратов отклонений у и SS - это сумма квадратов отклонений х и у.
Все этапы этих расчетов просты, но процесс может быть утомительным,
особенно для данных большого объема. Для расчета суммы квадратов х необходимо
проделать следующее:
1. Из каждого значения х вычесть среднее по всем значениям х. Это называют
отклонениями.
2. Возвести каждое отклонение в квадрат.
3. Сложить все квадраты отклонений (отсюда название «сумма квадратов
отклонений»).
На рис. 7.16 это показано в виде формулы.
ssx-2(*,-*)2
/-1
Рис. 7.16. Формула суммы квадратов отклонений
В этой формуле xi - это отдельное значение х,х- это среднее по всем
значениям х и п - это объем выборки.
Из этой формулы хорошо понятно, как вычислять SSx, но ее использование
может потребовать большого количества времени. Сумму квадратов отклонений
можно получать также с помощью расчетной математически тождественной
формулы, показанной на рис. 7.17, ручной расчет с помощью которой может оказаться
менее утомительным.
SS
X
п
i-i
/ »
2*
\м
п
\2
)_
Рис. 7.17. Расчетная формула для суммы квадратов х
Первая часть формулы указывает на то, что нужно возвести каждое значение х
в квадрат, а затем сложить их. Вторая часть указывает на необходимость возвести
сумму всех значений х в квадрат, а затем разделить эту сумму на объем выборки.
Затем, чтобы получить SSx, нужно вычесть вторую величину из первой.
Для расчета суммы квадратов отклонений у повторите ту же процедуру, но со
значениями у и средним по значениям у.
Процесс расчета ковариации сходен, но вместо возведения отклонений для
каждого значения х или у в квадрат вам надо перемножить соответствующие значения
отклонений для х и у друг на друга. Этот процесс представлен в виде формулы на
рис. 7.18.
I ^ I
/-1
Рис. 7.18. Расчет суммы квадратов отклонений хиу
ИНН' ' Глава 7. Коэффициент корреляции Пирсона
Также существует расчетная формула для суммы квадратов отклонений х и г/,
которая приведена на рис. 7.19.
Рис. 7.19. Расчетная формула для суммы квадратов отклонений х и у
Принцип использования этих формул может стать понятнее после изучения
примера. Предположим, мы получили выборку 10 американских
старшеклассников и анализируем результаты выполнения ими разделов Академического
оценочного теста (Scholastic Aptitude Test), направленных на проверку вербальных и
математических умений, которые приведены в табл. 7.1. (В каждом разделе этого
теста можно получить от 200 до 800 баллов.) Для облегчения восприятия данных
мы выстроили их в порядке увеличения баллов, полученных за вербальные
умения, но это никак не связано с расчетами.
Таблица 7.1. Баллы за разделы Академического оценочного теста,
направленные на проверку вербальных и математических умений
Ученик
1
2
3
4
5
6
7
8
9
10
Речь
490
500
530
550
580
590
600
600
650
700
Математика
560
500
510
600
600
620
550
630
650
750
Вот информация, которая вам понадобится для использования расчетных
формул (или чтобы проверить себя, если вы подсчитали эти величины
самостоятельно):
я-10.
= 5790
п
^х,2 =3 390 500
Коэффициент детерминации
( >' \
1"
К"1 )
п
= 5790
3 612 500
^ (*,>>,.)= 3 494 000
Затем мы подставляем эти числа в расчетные формулы, как показано на
рис. 7.20.
5 7902
SSX = 3 390 500 38 090
10
5 9702
SSV = 3 612 500 = 48 410
' 10
^=3494 000-(579°)(5970)~37 370
ху 10
37 370
г = , = 0.87
V(38 090)(48 410)
Рис. 7.20. Расчет г для вербальных и математических результатов
Академического оценочного теста
Корреляция между речью и математикой в этом тесте составляет 0,87 - сильная
положительная связь, говорящая о том, что ученики, которые получают высокие
результаты в одной части, так же чаще хорошо выполняют вторую. Заметьте, что
корреляция симметрична, так что мы не должны постулировать, что одна
переменная влияет на другую, а только то, что мы увидели связь между ними.
Проверка статистической значимости
коэффициента корреляции Пирсона
Мы также хотим определить, значима ли данная корреляция. Нулевая гипотеза
для корреляционного анализа обычно следующая: переменные не связаны, то есть
г=0, и именно эту гипотезу мы проверяем в этом примере; альтернативная
гипотеза состоит в том, что гф 0. Мы будем использовать уровень значимости 0,05
и рассчитаем статистику для проверки значимости отличия наших результатов
от 0, как это показано на рис. 7.21. Эта статистика имеет ^-распределение с (п - 2)
степенями свободы; степени свободы - это статистический термин, характеризую-
НИ*'-4- Глава 7. Коэффициент корреляции Пирсона
щий число величии, которые могут меняться в определенной ситуации. Это также
число, которое нам надо знать, чтобы использовать правильное ^-распределение
для оценки наших результатов.
Рис. 7.21. Формула для проверки статистической значимости коэффициента
корреляции Пирсона
В рис. 7.21 г - это коэффициент корреляции Пирсона для выборки, п - это ее
объем. Для наших данных расчет приведен на рис. 7.22.
0.87V10-2 2.46 с м
t = , 5.02
Vl-0.872 0.49
Рис. 7.22. Расчет теста на значимость корреляции между баллами
за математическую и вербальную части Академического оценочного теста
В соответствии с таблицей ^-распределения (рис. D.7 в приложении D)
критическое значение для двустороннего ^-критерия с 8 степенями свободы при а = 0,05
равно 2,306. Поскольку наше расчетное значение, равное 5,02, превосходит
критическое, мы отвергаем нулевую гипотезу о том, что результаты в математической и
вербальных частях не связаны. Мы также рассчитали точное р-значение для этих
данных с помощью онлайн-калькулятора и получили двустороннее р-значение,
равное 0,0011, что также показывает, что наши результаты очень маловероятны,
если на самом деле эти переменные не связаны в генеральной совокупности, из
которой мы брали выборку.
Коэффициент детерминации
Коэффициент корреляции показывает силу и направление линейной связи
между двумя переменными. Вам также может понадобиться узнать, какую долю
дисперсии одной переменной можно связать с другой переменной. Для
нахождения этой величины вы можете рассчитать коэффициент детерминации,
который равен просто г2. В нашем примере с тестом г1 = 0,872 = 0,76. Это означает,
что 76% дисперсии в результатах вербальной части можно связать с результатом
для математической части, и наоборот. Мы еще поговорим о коэффициенте
детерминации в главах, посвященных регрессии, потому что очень часто одной из
задач при построении регрессионной модели является поиск набора
независимых переменных, которые могут объяснять большую долю дисперсии зависимой
переменной.
Упражнения
Упражнения
Задача
Какие из приведенных диаграмм рассеяния (рис. 7.23,7.24 и 7.25) указывают на
то, что две переменные линейно связаны? Установите для них направление связи
и оцените ее силу, то есть коэффициент корреляции Пирсона для
соответствующих данных. Учтите, что никто не ожидает от вас определения точного значения
коэффициента корреляции на глаз, однако полезно уметь его правдоподобно
предсказывать.
-10
35
30
25
20
15
10
* 5
*
0
Ф
tfh
¦ ¦
10
Ф
15 20
Ф
Ф
25
35
Рис. 7.23. Диаграмма рассеяния (а)
1.0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.1
0.1
0
(
Ф
)
Ф Ф
л.
ф ¦ ф 4
+
* <k
¦ 4
Ф
J»L Ф #
¦ А Ф
Ф
10 10 15 20 25 30
35
¦нш
Рис. 7.24. Диаграмма рассеяния (Ь)
ИИ
Глава 7. Коэффициент корреляции Пирсона
90
¦ 80
70
Ф 60
¦ 5°
40
^ ¦ 30
20
4i+ » 1
¦
*
lir
¦¦
^tiii
-15 -10 -5 0 5 10 15
Рис. 7.25. Диаграмма рассеяния (с)
Решение
a) Сильная положительная связь (г = 0,84).
b) Слабая связь (г = 0,11).
c) Нелинейная квадратичная связь. Заметьте, что г = -0,28 для этих данных -
это достаточно большой коэффициент корреляции, так что без диаграммы
рассеяния мы могли легко не заметить нелинейную природу связи между
этими двумя переменными.
Задача
Найдите коэффициенты детерминации для каждого набора данных из
предыдущей задачи, если это имеет смысл, и проанализируйте их.
Решение
a) r* = 0,842 = 0,71;
71% дисперсии одной переменной может быть объяснен дисперсией другой
переменной.
b) ;^ = 0,112 = 0,01;
1% дисперсии одной переменной может быть объяснен дисперсией другой
переменной. Этот результат указывает на то, насколько слабой на самом
деле является корреляция величиной в 0,11.
c) г и 1* не применимы для переменных, связь между которыми нелинейна.
Задача
Некоторые исследования выявляли слабую положительную корреляцию
между ростом и умственными способностями (последние измеряются величиной
IQ), то есть более высокие люди в среднем немного умнее. Используя формулы,
Упражнения
ИСТ
представленные в этой главе, рассчитайте коэффициент корреляции Пирсона для
данных, представленных в табл. 7.2, где указан рост (в дюймах) и результаты
теста IQ для 10 взрослых женщин. Затем проверьте корреляцию на статистическую
значимость (проведите двусторонний тест с уровнем значимости 0,05),
рассчитайте коэффициент детерминации и проанализируйте результаты. Для удобства мы
обозначим рост как х и IQ - как у.
Таблица 7.2. Рост и IQ
Студент
1
2
3
4
5
6
7
8
9
10
Рост (дюймы)
60
62
63
65
65
67
68
70
70
71
IQ
103
100
98
95
110
108
104
110
97
100
Решение
Расчеты приведены на рис. 7.26 и 7.27.
и = 10.
2^, =661
/ = 1
П
JV =43817
/=1
5>,=1025
/=1
п
ЛИ
? (ад )= 67 777
/=1
Глава 7. Коэффициент корреляции Пирсона
6612
SS =43 817 124.9
10
10252
SSV = 105 327 264.5
у 10
гп ,„„„„ (661)(1025) ^лг
SSXV = 67 777 - - 24.5
ху 10
24.5
г= , =0.135
V(124.9)(264.5)
Рис. 7.26. Расчет корреляции между ростом и Ю
Коэффициент детерминации = г2 = 0,018.
0.135V10-2 0.382
t , 0.385
Vl-0.1352 0.991
Рис. 7.27. Расчет f-статистики для корреляции между ростом и IQ
В этих данных мы наблюдаем слабую (г = 0,0135, i2 = 0,018) положительную
связь между ростом и IQ; тем не менее эта связь не значима (t = 0,385, р > 0,05),
так как мы не отвергаем нашу нулевую гипотезу об отсутствии связи между
переменными.
Если вы заинтересовались данным вопросом, посмотрите статью Кейса и
Пирсона (Case and, Pearson), ссылка на которую дана в приложении С; хотя в первую
очередь эта статья касается связи между ростом и заработком, в ней также
обобщены исследования роста и интеллекта.
ГЛАВА 8.
Введение в регрессию
и дисперсионный анализ
Регрессия и дисперсионный анализ (ANOVA)1 - два метода, использующие
общую линейную модель (GLM)2. Если идея линейной функции вам не до конца
ясна, просмотрите обсуждение коэффициента корреляции Пирсона в главе 7.
В главах с 8 по 11 мы опишем статистические методы, в том числе достаточно
сложные, основанные на простейшем принципе линейной связи между двумя или
более переменными. Эта глава представляет самые простые линейные модели,
простые регрессии и однофакторный дисперсионный анализ; в главах с 9 по 11
я опишу более сложные методы из семейства общих линейных моделей.
Методы обработки данных, описанные в этих главах, почти всегда реализуются с
использованием компьютерных программ; к счастью, большинство из этих методов
достаточно обычны, так что они присутствуют в любом статистическом пакете.
Кроме того, обычно несложно разобраться, как использовать определенный
пакет, если вы понимаете теоретические аспекты, лежащие в основе модели. По этой
причине мы сконцентрируемся на объяснении того, как эти модели работают, но
оставим советы достаточно общими, так чтобы их можно было применить к
большинству программ.
Общая линейная модель
В основе всех методов из семейства общих линейных моделей лежит
предположение о том, что зависимая переменная является функцией одной или более
независимых переменных. Мы часто рассуждаем в терминах предсказания или
объяснения зависимой переменной, используя набор независимых переменных, но
давайте сделаем шаг назад, чтобы разобраться, что же значит, что одна переменная
является функцией другой (или их набора, но, чтобы упростить задачу, для
начала мы остановимся на простейшем случае одной зависимой и одной независимой
переменной). Вы, возможно, помните функции типа у =f(x) с уроков алгебры; это
1 От англ. ANalysis Of Variance. - Прим. пер.
1 От англ. General Linear Model, не следует путать с обобщенной линейной моделью - Generalized
Linear model. - Прим. пер.
Ш . Глава 8. Введение в регрессию и дисперсионный анализ
уравнение говорит о том что, зная значение х, мы можем вычислить значение у,
следуя процедуре, определенной в функции/(х). Вот несколько примеров
функций:
• // = х означает, что значение у всегда такое же, как и значение х, так что
(х,у) = (1, 1), (2, 2), (3,3). Запись вида (х, г/) = (1, 1), (2, 2) и так далее - это
просто короткий способ сказать: «Если х= 1, то у = 1; если х = 2, то у = 2»
и так далее;
• у = ах означает, что значение у является произведением значения х и
константы а. Если а = 3, то (х, у) = (1, 3), (2, 6), (3, 9) и так далее; значение у
всегда в три раза больше значения х. Если а = 0,5, то (х, у) = (1, 0,5), (2, 1),
(3, 1,5) и так далее. В этом типе модели а часто называют коэффициентом
наклона уравнения;
• у = ах + /; означает, что значение у всегда является суммой произведения х
па константу а и константы Ь. Заметьте, что сначала х умножается на а, а
затем к произведению прибавляется Ь. Если а = 1 и b = 5, то (х, у) = (1, 6),
(2, 7), (3, 8) и так далее. В этом типе модели b часто называют константой
уравнения, потому что его значение не меняется; каково бы ни было
значение х, значение b всегда одно и то же;
• у = х2 означает, что значение у равно квадрату значения х, то есть значению
х, умноженному само на себя. Таким образом, (х, у) = (1, 1), (2, 4), (3, 9) и
так далее.
В этой главе мы рассмотрим случай уравнений только с двумя переменными;
этот тип уравнений всегда может быть описан как у = ах + b (помните, что b - это
константа, а не переменная).
Запись линейных уравнений
Существует несколько способов записать линейное уравнение, но основные его части
остаются неизменными. Для описания простого линейного уравнения с одним
предиктором и константой достаточно записать его как у = ах + Ь. В этом уравнении у - это
зависимая переменная, а - это коэффициент наклона и b - константа3. Константа
определяет величину, которой соответствует точка пересечения прямой с осью у; то есть
соответствует значению у при х = 0. Коэффициент наклона определяет связь между х и у:
насколько изменяется у при изменении х на одну единицу? Вы можете помнить описание
этого коэффициента из учебника алгебры как «подъем на пробег»; в данном случае
подъем относится к изменению величины у, а пробег - изменению х. Если вы чувствуете, что
нужно вспомнить алгебру линейных уравнений, прочитайте обзор «Взаимосвязи
между непрерывными переменными» на стр. 199 в главе 7 и попробуйте решить несколько
практических задач из приложения А на эту тему.
Другой способ записи чаще используется в статистике при описании линейных
уравнений, особенно для уравнений с множеством независимых переменных. В этой записи
простое линейное уравнение записывается в виде у = р0 + Р1х1 + е, где ро - это константа,
р1 - коэффициент наклона, а е - остаток или ошибка, которая включается из-за того,
:\
В английском языке для /; существует термин intercept, аналога которому нет в русском, означающий
«пересечение»: эта константа определяет место пересечения прямой с осью ординат; аналогично a
по-английски называют slope, то есть «склон», потому что именно наклон прямой определяется этим
коэффициентом. - Прим. пер.
Линейная регрессия
ШШШ1
что при работе с настоящими данными (в противоположность манипуляциям с
алгебраическими выражениями) мы не ожидаем абсолютно точного предсказания значения у по
уравнению. Остаток или ошибка представляет из себя разницу между наблюдаемым и
вычисленным из уравнения значениями у.
В статистике термин «коэффициент» в отношении р, используется чаще, чем
«коэффициент наклона», поскольку мы нередко работаем с уравнениями со многими
независимыми переменными (множественная линейная регрессия), когда ни одна из независимых
переменных не определяет целиком наклона прямой. Значение коэффициента во
множественном линейном уравнении определяет предсказываемое изменение в значении у
при изменении значения х на одну единицу при условии, что все остальные независимые
переменные постоянны. Таким образом, в уравнении у = ро + Вуху + В^2 + В^ъ + е есть три
независимые переменные (х,, х2 и х3), а коэффициент В, определяет предсказываемое
изменение у при изменении х, на одну единицу при постоянных х2 и х3.
Линейная регрессия
Предположим, что модель у = ах + Ъ описывает связь между двумя переменными,
х и у. В алгебре эта зависимость может быть идеальной, то есть значение у
абсолютно точно предсказывается значением х. Приведенные ранее примеры
соответствуют как раз такому типу моделей. Если мы скажем, например, что у = 2х + 7,
мы знаем, что при значении х = 0, то у будет равен 7. В этом случае коэффициент
корреляции всегда будет 1,00, показывая идеальную связь, мы всегда можем
безошибочно предсказать значение у по значению х.
Как бы то ни было, в статистике мы часто пытаемся подобрать уравнение для
реального набора данных. В этом случае мы не ожидаем получить идеальную связь
между х и у. То есть мы не предполагаем, что мы всегда сможем предсказать
значение у по значению х без ошибки. Жизнь гораздо более разнообразна, чем закрытая
система математики, и даже самые сильные наблюдаемые в реальном мире связи
крайне редко идеальны с математической точки зрения.
Рассмотрим взаимосвязь между ростом и массой тела у взрослых людей.
Интуитивно понятно, что эти две переменные должны быть сильно положительно
связаны; в целом более высокие люди весят больше, чем более низкие. И тем не менее
эта связь не идеальна; мы все можем вспомнить низких, но довольно полных
людей и высоких, но очень легких. Аналогично мы ожидаем увидеть положительную
связь между числом лет получения образования и заработком среди людей
трудоспособного возраста; в целом более образованные люди зарабатывают больше.
Однако эта связь тоже не идеальна; один из богатейших людей в мире, Билл Гейтс,
не закончил колледж, и многие университетские города полны людей с учеными
степенями на низкооплачиваемой работе. При работе с реальными данными мы не
ожидаем получить идеальные связи, но пытаемся найти полезные. Например, мы
не можем получить уравнение для точного предсказания человеческого роста на
основе веса (даже с помощью гораздо более сложного выражения, включающего
множество других переменных). Вместо этого мы хотим создать уравнение,
которое было бы полезно для наших целей и улучшало бы наши предсказательные
способности, в том смысле что, зная рост человека, мы могли бы, используя урав-
ЕГСМН I
Глава 8. Введение в регрессию и дисперсионный анализ
пение, сделать лучшее предсказание массы его тела, чем мы сделали бы, не зная
его роста.
Мы могли бы изучать взаимосвязь между ростом и массой тела с помощью
диаграмм рассеяния и коэффициента корреляции, но линейная регрессия позволяет
нам сделать шаг вперед. Регрессионный анализ можно представить как
проведение прямой линии (регрессионной прямой), изображающей взаимосвязь между
двумя переменными; эту линию часто накладывают на диаграмму рассеяния для
дальнейшего уточнения связи. Посмотрите на диаграмму рассеяния на рис. 8.1.
Рис. 8.1. Диаграмма рассеяния роста в метрах и массы тела
в килограммах для 436 взрослых американцев
Это диаграмма рассеяния роста (в метрах) и массы тела (в килограммах) для
436 взрослых американцев; данные получены с помощью случайного выбора из
данных системы наблюдения за поведенческими факторами риска 2010 года\
медицинского исследования, проводимого в Америке ежегодно. (Вы можете
подробнее узнать о ней и скачать данные для собственного анализа с этого сайта: http://
vvww.cdc.gov/brfss/technical_infodata/surveydata/2010.htm.) Как и ожидалось,
связь положительная и в целом линейная (данные более или менее
концентрируются вдоль линии), но далека от идеала: большинство точек не лежит на
регрессионной прямой (линии, наложенной на диаграмму), и некоторые достаточно
далеки от нее. Это типичный результат, который можно получить для реальных
данных; связи не идеальные, но если ваша модель хорошая, они могут оказаться
достаточно сильными, чтобы быть полезными.
1 Behavioral Risk Factor Surveillance System (BRFSS) - американская программа Центра па
контролем п профилактикой заболеваний по мониторингу за поведенческими рисками, проводимому по
телефону. Самая большая подобная программа в мире. - Прим. пер.
Линейная регрессия
—1ПП
В данном случае коэффициент корреляции (г) и коэффициент детерминации
(г1) между ростом и массой тела равны соответственно 0,47 и 0,22. Это значит, что
около 22% дисперсии массы тела может быть связано с ростом, совсем не
идеальное предсказание или объяснение, но значительно более хорошее, чем 0.
Уравнение регрессии для этих данных таково:
у = 91*-74.
Коэффициент наклона равен 91, константа - 74. Для нахождения
предсказываемого значения массы тела человека подставьте вместо х его рост в метрах, и
останется только произвести вычисления. Это уравнение предсказывает, что человек
с ростом 1,8 метра будет иметь массу тела 89,8 кг, потому что:
у = 91(1,8) -74 = 89,8.
Разумеется, если бы мы по-настоящему хотели предсказывать массу тела, мы
бы разработали более сложную модель, включающую такие факторы, как пол и
возраст, но этот пример служит хорошей иллюстрацией основных принципов
простой регрессии. Вы могли заметить, что хотя корреляция не требует указывать,
какая переменная является независимой, а какая от нее зависит, вам приходится
делать такой выбор при работе с регрессией. Я назначила массу тела зависимой
переменной, а рост - независимой, что осмысленно, потому что рост у взрослого
человека постоянен и может рассматриваться как причинный фактор для массы
тела. (При прочих равных, включая телосложение, высокие люди в целом весят
больше, чем низкие.) Не думаю, что я могла бы как-то защитить позицию о
первичности массы тела по отношению к росту.
Можно посчитать линию регрессии вручную (я делала это в аспирантуре, а до
тех пор, пока компьютеры не получили широкого распространения, все делали
это таким образом), но гораздо чаще для этих расчетов используют
статистические программы. Регрессия - это очень часто встречающаяся процедура, и
практически любой статистический пакет, который вы можете использовать, вероятно,
будет включать в себя возможности по расчету регрессии. Для тех же, кто захочет
расчитать параметры регрессии вручную, в конце данной главы приведен
решенный пример.
Даже если вы не планируете проводить регрессию вручную, стоит ближе
познакомиться с логикой этого процесса. Когда статистический пакет выдает линию
регрессии для набора данных, он подбирает уравнение, соответствующее линии,
максимально близкой ко всем точкам одновременно. Это часто описывают как
минимизацию квадратов отклонений, где квадраты отклонений - это суммы
квадратов отклонений между каждой точкой данных и линией регрессииГ). Это легко
проиллюстрировать на примере простой регрессии, потому что тут участвуют только
два измерения (независимая и зависимая переменные); тот же принцип применим
и к более сложным моделям (с большим число переменных), но в этом случае его
сложнее проиллюстрировать из-за большего числа измерений.
По-русски обычно это называют «методом наименьших квадратов» - Прим. пер.
ЕуЭИнмН Глава 8. Введение в регрессию и дисперсионный анализ
Посмотрите на рис. 8.2. Это диаграмма рассеяния для небольшого набора
данных с наложенной линией регрессии. Обратите внимание, что хотя регрессионная
прямая лежит достаточно близко ко всем точкам, ни одна из них не лежит на
самой линии; это не необычно, особенно для небольших наборов данных, потому что
задача заключается в построении линии, максимально близкой ко всем точкам,
даже если она не содержит ни одну из них. На рис. 8.2 вы можете провести
вертикальные линии от каждой точки к линии регрессии; длина каждой такой линии
соответствует ошибке предсказания, или отклонению, для каждой точки. Если вы
возведете в квадрат длину каждой линии и сложите полученные числа, это будет
суммой квадратов отклонений для этого набора данных. Линия регрессии
строится таким образом, чтобы минимизировать все эти квадраты отклонений, так что
она лежит настолько близко ко всем точкам, насколько это возможно для прямой
липни. Разницу между каждой точкой и линией регрессии также называют
остатком, потому что она представляет изменчивость в данных, не объясняемую
уравнением прямой. «Минимизацию квадратов отклонений» также можно называть
«минимизацией ошибок предсказания» или «минимизацией остатков».
7.00-
6.00-
5.00-
>-4.00-
3.00-
2.00-
1.00-
1.00 2.00 3.00 4.00 5.00 6.00
X
Рис. 8.2. Ошибки предсказания в небольшом наборе данных
Допущения
Как в случае большинства статистических процедур, в ходе линейной регрессии
приходится делать некоторые предположения об анализируемых данных; если
они нарушаются, то результат анализа может быть неверным. Важнейшие условия
для проведения простой линейной регрессии включают:
Линейная регрессия
IEED
Подходящий тип данных
Результирующая переменная должна быть непрерывной, представленной
интервальными или характеризующими отношения данными и
неограниченной (или хотя бы варьирующей в широких пределах); независимая
переменная должна быть непрерывной или дихотомической. Категориальные
независимые переменные с более чем двумя значениями можно
перекодировать в набор дихотомических фиктивных переменных; это обсуждается
в главе 10.
Независимость
Каждое значение зависимой переменной независимо от других значений.
Это допущение нарушается, если есть некоторая зависимость от времени,
например, или если некоторые из зависимых переменных - это измерения
объектов, объединенных в группы (такие как члены одной семьи или
ученики одного класса), так что это повлияет на значение зависимой
переменной. Выполнение этого допущения можно проверить, зная сами данные и
то, как они были получены.
Линейность
Отношения между независимой и зависимой переменными напоминают
прямую линию. Это предположение проверяется с помощью изображения
данных на графике; если его форма существенно отличается от прямой, вам
может понадобиться преобразовать одну или обе переменные либо выбрать
другой метод.
Распределение
Непрерывные переменные приблизительно нормально распределены и не
имеют выбросов. Распределение непрерывных переменных можно
проверить «на глаз» с помощью построения гистограммы и с помощью
статистических тестов на нормальность, таких как тест Колмогорова-Смирнова.
Выброс определяют как значение, находящееся далеко от остальных
значений той же переменной в наборе данных; иногда его описывают как
значение, которое не похоже на другие. Определение выбросов отчасти
субъективно, оно обсуждается дальше в главе 17 и может быть многоступенчатым
процессом. (Необычное значение данных может как появиться, например,
в результате ошибки, так и быть, по всей видимости, верным.)
Гомоскедастичность
Ошибки предсказания постоянны на всем промежутке данных. Это
означает, что, например, ошибки не становятся меньше, если у уменьшается,
а с увеличением у не растут. Это предположение проверяется с помощью
построения графика связи между стандартизованными остатками и
стандартизованными предсказанными значениями; данные должны
напоминать облако без каких-либо указаний на то, что ошибки предсказания не
постоянны на всем промежутке. Рисунок 8.3 показывает гомоскедастичные
данные, а рис. 8.4 — гетероскедастичные.
ЦН№Ч' Глава 8. Введение в регрессию и дисперсионный анализ
Независимость и нормальность ошибок
Ошибка предсказания для каждой точки не должна зависеть от ошибки
предсказания других точек, и остатки должны быть нормально
распределены. Предположение о независимости проверяется тестом Дарбина-Уот-
сона (обсуждается ниже), а предположение о нормальности - с помощью
построения графика остатков (ошибок).
з
% 2 • • # • •
Б • ••
° 1 • •
ф 1 • • • •
I • . •
| о •••••••
со
2 • • •
ГО a w
1 • • •
8- ,# ¦ - *
-3-2-10 1 2 3
Стандартизованные предсказанные значения
Рис. 8.3. Гомоскедастичность
атки
о
о
ные
ван
тизо
а.
i
Ста
3
2
1
0
-1
-2
-3
• •
• ¦ • •
•
•
-3 -2 -1
•
• •
•
•
•
•
• .
•
•
0
•
•
•
•
# •
•
•
#
•
1
•
•
•
•
•
•
•
• •
2 3
Стандартизованные предсказанные значения
Рис. 8.4. Гетерокедастичность
Предположим, нас интересует уровень рождаемости среди подростков
(отношение числа родов молодых женщин 15-19 лет к их общему числу) и то, какие
Линейная регрессия
¦МЕШ
факторы на уровне страны влияют на него. Наше первое предположение состоит
в том, что подростковая рождаемость может быть связана с равноправием полов,
и мы предполагаем, что она ниже в тех странах, где у женщин больше прав. Мы
проведем регрессионный анализ для проверки этой гипотезы, используя данные,
скачанные с сайта проекта ООН по развитию человечества (http://hdr.undp.org/
en/statistics/data/). Мы будем использовать индекс неравенства полов (ИНП)
как независимую переменную; этот индекс складывается из пяти переменных,
характеризующих репродуктивное здоровье женщин, число прав и
возможностей, а также их участие в работе, и принимает значения от 0 до 100 (в наших
данных от 6,5 до 79,1), где меньшие значения соответствуют большему равенству.
Заметьте, что это так называемые популяционные, или обобщенные, данные;
значение каждой переменной относится к стране в целом, а не к отдельным людям.
Нет ничего плохого в использовании таких данных, но стоит быть аккуратным,
чтобы делать выводы на том же уровне обобщения, на каком собраны
исследуемые данные; в нашем случае результаты будут относиться к уровню страны, а не
отдельных людей.
Начнем с проверки наших предположений. Таблица частот свидетельствует,
что переменные непрерывны и их значения колеблются в достаточно широком
диапазоне, а также что у нас есть 135 измерений со значениями обеих переменных,
что более чем достаточно для простого регрессионного анализа. Кроме того, наши
данные независимы, потому что данные для каждой страны собирали отдельно.
Наше третье предположение, линейность, можно проверить с помощью
диаграммы рассеяния. Как видно по рис. 8.5, тут мы сталкиваемся с проблемой:
зависимость, скорее, не линейна.
1-
ф
с;
СУ>
У
m -р
ч- 0)
ъ *
X ч-
3" 1
I 1Л
* I
юсти,
енщи
(D л
«да
000
а*
)СТКОВОЙ
родов н
X. о
ьпод
(числ
i
>
2S0.O-
200.0"
150.0-
100.0-
so.o-
.о-
о
о
о
сР
ф О
о°
оо •
о о <Р°
V°§°o°
° о ф о °0 0
$0 О О
о ° _ ft оо
о о oqO <Po о о
о о о V о 'Ь Q
1 1 1 1
.000 .200 .400 600
Индекс неравенства полов
о
600
Рис. 8.5. Диаграмма рассеяния подростковой рождаемости
и индекса неравенства полов
Ш1ШШ
Глава 8. Введение в регрессию и дисперсионный анализ
Мы проделываем логарифмическое преобразование (обсуждается в главе 3)
уровня подростковой рождаемости и видим, что теперь переменные уже связаны
гораздо более линейно. Диаграмма рассеяния преобразованных данных
изображена на рис. 8.6.
6.00-
5.00-
^-ч 40°"
'Б4
н
и
О
2t 3.00-
&
*JZ 2.00-
1.00-
.00-
°о
о *<Ф°Оо?0
фо о о
о ° Л fc оо
о о oqO фо w о
° ^ о
о о of ° ^ о
с8о° n ° °
ЪЬсРо0 ° о°оо
о°оо °*
о о о0 о
о° * о о
о °
о
о
1 1 1 1
.000 .200 .400 .600
Индекс неравенства полов
о
1
.800
Рис. 8.6. Диаграмма рассеяния для натурального логарифма подростковой
рождаемости и индекса неравенства полов
Мы проверим нормальность наших переменных с помощью теста
Колмогорова-Смирнова (К-С). Тест К-С сравнивает распределение переменной с эталонным
распределением. (Эталоном в данном случае служит нормальное распределение.)
Нулевая гипотеза теста К-С заключается в том, что переменная была получена из
эталонного распределения, так что в данном примере если мы не сможем
отвергнуть нулевую гипотезу, то сможем принять предположение о том, что генеральная
совокупность нашей переменной распределена нормально. Обе гистограммы (не
показаны) выглядят достаточно нормальными, а тест К-С не показал достоверных
отличий (К-С = 1,139, р = 0,149 для натурального логарифма уровня подростковой
рождаемости; К-С= 1,223,/? = 0,101 для индекса неравенства полов).
Мы проверим последние два допущения после проведения регрессии. Мы
полагаем, что неравенство полов влияет на подростковую рождаемость, и мы
преобразовали уровень подростковой рождаемости, взяв его натуральный логарифм (LN),
так что наша регрессионная модель выглядит так:
LN(подростковая рождаемость) = (3() + р^ИНП) + е.
Это другой стиль записи, чем мы использовали ранее в этой главе, но он чаще
применяется при обсуждении регрессий, так что самое время переключиться на
него. Наша зависимая переменная У в данном случае - это LN(подростковая рож-
Линейная регрессия
¦винтя
даемость); константой, ранее обозначавшейся как Ь, теперь является р(); а
коэффициент наклона, выше обозначенный я, теперь записан как Рг Эта запись будет
особенно удобна при обсуждении регрессии с несколькими независимыми
переменными, потому что их тогда можно обозначать Рр р2 и так далее; эти члены
называют коэффициентами.
Разные статистические пакеты выдают результаты в разном виде, но в них
достаточно много общего, чтобы можно было понимать результат простой
регрессии, полученный в любом из них, если вы знаете, как понять результат хотя бы в
каком-то виде. Мы будем показывать самую важную информацию о результатах
анализа просто в виде таблиц, чтобы избежать предпочтения одной системы перед
остальными.
В первую очередь мы хотим оценить общее качество нашей модели. Оно обычно
выражается в терминах F-статистики и вероятности и оценивает, лучше ли вся
модель, чем ее отсутствие. Другими словами, значения ^-статистики и вероятности
позволяют сравнить нашу модель с моделью, в которой все коэффициенты
равны 0 (нулевая модель). Нас также интересует, какую долю дисперсии зависимой
переменной может объяснить наша модель; возможна ситуация, особенно с
большими наборами данных, когда модель с достоверными коэффициентами
объясняет лишь малую долю всей дисперсии.
F-статистика для этой модели составляет 190,964 с 1 и 185 степенями свободы и
р-значением меньше 0,001; таким образом, мы заключаем, что лучше такая модель,
чем никакой. /?-значение, или корреляция, составляет 0,714, а коэффициент
детерминации, или R2, составляет 0,509; это значит, что индекс неравенства полов может
объяснить больше 50% дисперсии подростковой рождаемости в странах из нашего
набора данных. Заметим, что, несмотря на то что в данном случае мы работаем
только с двумя переменными, корреляции и регрессии обычно обозначаются заглавной
буквой /?, и мы следовали этой договоренности. Статистика Дарбина-Уотсона для
этих данных составляет 2,076, подтверждая независимость остатков в наших
данных (это хорошо). Статистика Дарбина-Уотсона лежит в интервале от 0 до 4, а ее
значение 2 показывает абсолютную независимость; наше значение очень близко к 2,
так что мы можем считать условие о независимости ошибок выполненным.
Коэффициенты регрессии для этой модели приведены в табл. 8.1.
Таблица 8.1. Таблица коэффициентов для регрессионного анализа предсказания
индекса неравенства полов и натурального логарифма подростковой рождаемости
Константа
ИНП
Нестандартизованные
коэффициенты
В
1.798
4.446
Станд. ошибка
0.112
0.244
Стандартизованные коэффициенты
Бета
0.845
t
16.118
18.221
Значимость
< 0.001
< 0.001
Столбец, обозначенный как В в «Нестандартизованных коэффициентах»,
показывает наши коэффициенты для уравнения регрессии. В данном случае уравнение
принимает следующий вид:
ЕЕЭ
Глава 8. Введение в регрессию и дисперсионный анализ
LN(подростковая рождаемость) = 1,798 + 4,446(ИНП) + е.
Это говорит нам о том, что на каждую единицу ИНП натуральный логарифм
подростковой рождаемости увеличивается примерно на 4,4 единицы; эта связь
положительна, что подтверждает нашу догадку о том, что более сильное
неравенство приводит к более высокой подростковой рождаемости. Столбец «Станд.
ошибка» показывает стандартные ошибки для оценок коэффициентов. Столбец
«Бета» в «Стандартизованных коэффициентах» содержит, как подсказывает
название, стандартизованные коэффициенты регрессии; это может быть полезно в
регрессионном анализе со множеством независимых переменных, измеряемых в
различных масштабах. Столбец t показывает ^-статистику для каждого
коэффициента и рассчитывается как отношение В к соответствующей стандартной ошибке.
Например, для ИНП:
^ = 4,446/0,244 = 18,221.
Последняя колонка показывает значимость ^-статистики. Мы обычно не
беспокоимся о значимости константы (все, что отсюда следует, - это значимо ли она
отличается от нуля, что обычно не интересует исследователя), но нам интересна
значимость коэффициентов при независимых переменных. В нашем случае ИНП
входит в модель для предсказания подростковой рождаемости с высокой
значимостью (р< 0,001).
Может быть полезным подумать о том, что же мы проверяем с помощью этого
анализа. Наша главная цель - понять, влияет ли неравенство полов на уровень
подростковой рождаемости; если ^-статистика для неравенства полов в таблице
коэффициентов не значима, это означает, что мы можем убрать эту величину из
нашего уравнения. Другими словами, незначимый результат для неравенства
полов означал бы, что коэффициент для него значимо не отличается от нуля, то есть
можно убрать его из нашей модели без вреда для способности уравнения
предсказывать или объяснять зависимую переменную.
Последним шагом должна быть проверка наших предположений, чтобы быть
уверенными в адекватности полученных результатов. Мы можем проверить
гомоскедастичиость (предположение 5) с помощью построения графика
остатков против стандартизованных предсказанных значений; результат показан на
рис. 8.7.
Это классическое облако данных, не дающее никаких оснований предполагать
непостоянство ошибки предсказания, так что условие гомоскедастичности
выполнено. Наконец, мы проверим нормальность распределения наших остатков, создав
их гистограмму (не показана) и рассчитав статистику Колмогорова-Смирнова;
ее значение составляет 1,355 (р = 0,51), так что наши данные проходят тест на
нормальность.
Не все статистические анализы дают значимые результаты. В табл. 8.2 мы
показываем результат регрессионного анализа, пытающегося использовать число
женщин в стране (в тысячах) для предсказания индекса неравенства иолов для
страны.
Линейная регрессия
ШШШк
статки
о
ованные
ГО
г
ь
о_
(0
Z
«О
н
и
2.00000-
1.00000-
ооооо-
1.00000-
2.00000-
з.ооооо-
4.00000-
о
о
0 °0 о Д \°о о,
ооо» о о° ° «b ° о _# о
° ° %° * ° оо >
о° о о «>
° о8„ °„
о <в °° о о 0 о°о о
u о
о о
о
о
о
о
о
1 1 1 1
2.00000 1.00000 .00000 1.00000
Стандартизованные предсказанные значения
о
1
2.00000
Рис. 8.7. Диаграмма рассеяния стандартизованных остатков
и стандартизованных предсказанных значений
Таблица 8.2. Таблица коэффициентов регрессии для предсказания индекса
неравенства полов по числу женщин (в тысячах)
Константа
Число женщин
(тысячи)
Нестандартизованные
коэффициенты
В
0.282
0.000
Станд. ошибка
0.074
0.000
Стандартизованные
коэффициенты
Бета
0.306
t
3.806
1.285
Значимость
0.002
0.217
По ^-значению (1,285) и значимости (0,217) ясно, что число женщин в стране
достоверно не предсказывает равенство полов; другим свидетельством в пользу
этого результата служит нулевая величина нестандартизованного коэффициента
для этой переменной. Диаграмма рассеяния двух переменных (рис. 8.8)
показывает, что связь между ними случайна, и, логически рассуждая, нет причин для того,
чтобы в странах с большим числом женщин (что соответствует просто странам с
большим населением) был больший или меньший уровень неравенства иолов, чем
в странах с малым числом женщин, так что мы не будем обсуждать этот анализ
дальше.
Глава 8. Введение в регрессию и дисперсионный анализ
.600-
.400-
X
з:
.200-
.000"
О
о о
О °
о о
° о
о° °
о
о
о
о
о
о
1 1 1 1 1 1
.000 200.000 400.000 600.000 800.000 1000.000
Женское население (тысячи)
Рис. 8.8. Диаграмма рассеяния женского населения (в тысячах)
и индекса неравенства полов
Дисперсионный анализ (ANOVA)
Дисперсионный анализ (ANOVA) - это статистическая процедура, используемая
для сравнения средних значений определенной переменной в двух и более
независимых группах. Ее так называют, потому что расчет включает разделение
дисперсии, соотнесение наблюдаемой в данных дисперсии с различными причинами или
факторами, включая групповую принадлежность. Тем не менее из-за того, что эту
процедуру применяют для сравнения средних между группами, многие студенты
думают, что настоящее название должно быть A-MEAN-A0. И все же ANOVA - это
полезный метод, особенно при анализе данных продуманных экспериментов
(таких как изучение разницы между контролем и экспериментальными группами в
клинических испытаниях).
Основная статистика для ANOVA - это F-отношение, которое может быть
использовано для определения статистической значимости различий между
группами. Например, нас может интересовать проверка эффективности трех лекарств,
которые должны понижать кровяное давление; мы можем сформировать четыре
группы гипертоников и дать каждой из них одно из лекарств (и одна из групп
будет служить контролем, то есть они либо не будут получать никаких лекарств,
либо их будут лечить стандартными методами). Через некоторое время мы мо-
Мсап по-анг.пшекп означает «среднее значение». - Прим. пер.
Дисперсионный анализ (ANOVA)
¦¦ЕШ
жем измерить кровяное давление пациентов, участвующих в исследовании,
чтобы увидеть, повлияли ли на него достоверно какие-то из лекарств, а также есть
ли достоверная разница между действием разных лекарств. ANOVA рассчитает
F-отношение для сравнения групповых средних, статистическую значимость
которого мы проверим, используя заранее заданный стандарт, такой какр < 0,01 или
р < 0,05.
Простейший вариант ANOVA включает одну группирующую (независимую)
переменную и одну предсказываемую; по этой причине он называется одно-
факторный дисперсионный анализ. Глава 9 описывает более сложные варианты
ANOVA, включая двух- и трехфакторный дисперсионный анализ
(многофакторный дисперсионный анализ) и анализ данных с учетом непрерывной ковариаты
(ANCOVA7).
Однофакторный дисперсионный анализ
Простейший вариант дисперсионного анализа - это однофакторный дисперсионный
анализ, в котором при формировании групп для сравнения используется только одна
переменная. Данную переменную часто называют «фактором», и этот термин еще
более обычен при использовании более сложных вариантов ANOVA. Предположим,
нас интересует эффективность нового лекарства, которое должно снижать сахар в
крови у больных диабетом второго типа; мы можем проверить ее с помощью
дисперсионного анализа, сравнив новое лекарство с другим уже используемым препаратом.
Фактором в данном исследовании служит используемое лекарство, и у него есть два
уровня: новый и старый препараты. Фактор в однофакторном дисперсионном
анализе может иметь и более двух уровней: в предыдущем примере о сравнении трех
препаратов для снижения давления и контроля у одного фактора было четыре уровня.
Однофакторный дисперсионный анализ с двумя уровнями аналогичен
^-критерию. Наша нулевая гипотеза в таком анализе обычно гласит о равенстве средних
двух групп, тогда как альтернативная говорит о том, что средние различны
(двусторонний тест) или различаются в определенном направлении (односторонний
тест). Даже если есть значимое отличие в средних между двумя группами, мы
не можем ожидать, что значения в двух группах не будут перекрываться; на
самом деле отсутствие такого перекрытия очень необычно. Также мы ожидаем, что
внутри каждой группы будет наблюдаться изменчивость, и однофакторный
дисперсионный анализ принимает в расчет изменчивость внутри групп (например,
изменчивость в уровне сахара среди пациентов, принимающих новое лекарство)
и изменчивость между группами (разницу между пациентами, принимающими
исследуемый и стандартный препараты).
Дисперсионный анализ также подразумевает соблюдение некоторых условий
для его правильного применения. Поскольку линейная регрессия и ANOVA - это
на самом деле два способа исследовать данные, используя общую линейную
модель, неудивительно, что некоторые из предположений дисперсионного анализа
совпадают с предположениями для регрессии.
От англ. ANalysis of COVAriance. - Прим. пер.
шшмшш
Глава 8. Введение в регрессию и дисперсионный анализ
Типы данных
Зависимая переменная должна быть непрерывной, представленной
интервальными или характеризующими отношения данными и неограниченной
(или хотя бы изменяющейся в широком интервале); факторы
(группирующие переменные) должны быть дихотомическими или категориальными.
Независимость
Каждое значение зависимой переменной не должно зависеть от других ее
значений. Это условие может нарушаться в ситуациях, когда, например,
имеется какая-либо временная зависимость или некоторые из значений
были измерены у объектов, объединенных в группы (такие как члены
одной семьи или дети, учащиеся в одном классе) так, что это повлияло на
зависимую переменную. Это предположение можно проверить только с
помощью ваших знаний о данных и способе, которым они были получены.
Распределение
Непрерывная переменная распределена приблизительно нормально в
каждой группе. Распределение можно проверить с помощью гистограммы («на
глаз») и с помощью статистических тестов на нормальность, таких как
критерий Колмогорова-Смирнова.
Однородность дисперсии
Дисперсии всех групп должны быть приблизительно одинаковыми. Это
проверяется с помощью теста Левина (Levene test); нулевая гипотеза
состоит в том, что дисперсия однородна, то есть если результат теста Левина
статистически не значим (обычно применяют критерий а < 0,05), то
дисперсии достаточно сходны.
Дисперсионный анализ считают робастным методом, что означает, что он
может хорошо работать даже в ситуациях, когда некоторые условия нарушаются;
например, если размеры групп одинаковы, получаемая ^-статистика достаточно
надежна даже в случае, когда распределение непрерывной переменной отлично
от нормального. Аналогичным образом при одинаковых размерах групп F-статис-
тика устойчива к нарушениям предположения об однородности дисперсии. Если
вы хотите почитать еще о спорах по поводу этих вопросов, в приложении С
упомянута соответствующая статья Гласса (Glass). Тем не менее нарушения условия
независимости могут сильно исказить результаты, так что перед использованием
ANOVA следует быть уверенным, что это условие соблюдено.
Предположим, мы сравниваем два метода тренировок по подъему большого
веса, и наши измерения показывают увеличение поднятого веса после трех
месяцев тренировок одним или другим методом. Наша нулевая гипотеза состоит в том,
что средние в обеих группах после тренировок равны; другими словами, в среднем
никакой из методов не лучше другого. В начале эксперимента мы случайным
образом выбираем, каким способом каждый из испытуемых будет тренироваться, и
измеряем средний вес, который они могут поднять; средние были приблизительно
равны. Диаграмма размаха на рис. 8.9 показывает улучшение «грузоподъемности»
после трех месяцев; хорошо видно, что испытуемые, тренировавшиеся по первому
Дисперсионный анализ (ANOVA)
EED
методу, в целом оказались успешнее, поскольку первая группа имеет большую
медиану, представленную в виде черной линии в середине «ящика», и весь интервал
расположен выше. Тем не менее видно, что в обеих группах есть изменчивость, и
имеется значительное перекрытие выборок. Не все члены первой группы
улучшили свой результат больше, чем все члены второй группы, только в среднем первая
группа показала более хороший результат.
50.00-
4000-
о
Q) 3000-
0Q
20.00"
10.00-
1
1.00
Группа
i
2.00
Рис. 8.9- Увеличение поднятого веса после трех месяцев тренировок
одним из двух методов
На самом деле в группе 1 среднее улучшение составляет 34,21 фунта, а в
группе 2 - 26,42 фунта. Значима ли эта разница статистически? Для ответа на этот
вопрос мы проведем однофакторный дисперсионный анализ. Сначала рассчитаем
простейшую статистику по этим данным, как показано в табл. 8.3.
Таблица 8.3. Описательная статистика по данным о подъеме веса
(два метода тренировок)
Группа
1
2
В целом
N
15
15
30
Среднее
34.21
26.42
30.32
Станд. откл.
7.38
6.16
7.76
Нижняя граница
95%-го
доверительного интервала
30.13
23.01
27.41
Верхняя граница
95%-го
доверительного интервала
38.31
29.83
33.22
Заметим, что размеры групп одинаковы, в группах приблизительно одинаковы
дисперсии, и 95%-ные доверительные интервалы для средних двух групп не
перекрываются (хотя они почти соприкасаются). Также мы рассчитали статистику
ВЕЯ
Глава 8. Введение в регрессию и дисперсионный анализ
Левина, чтобы проверить однородность дисперсии наших групп; наш результат
(0,626, /; = 0,435) не дает оснований отвергнуть нулевую гипотезу об
однородности, так что мы можем применять дисперсионный анализ.
Статистические результаты дисперсионного анализа обычно представляют в
виде таблицы, похожей на табл. 8.4.
Таблица 8.4. Результаты однофакторного дисперсионного анализа данных
о подъеме веса (два метода тренировки)
Между группами
Внутри групп
В целом
Сумма
квадратов
455.86
1294.52
1750.38
df
1
28
29
Средний
квадрат
455.86
46.23
F
9.86
Значимость
0.004
Руководствуясь стандартом а < 0,05, эти результаты можно считать
значимыми, так что мы можем отвергнуть нулевую гипотезу о том, что средние двух групп
равны; на самом деле метод 1 привел к достоверно более хорошим результатам,
чем метод 2. Это простая таблица дисперсионного анализа, потому что у нас был
только один фактор с двумя уровнями, но стоит потратить немного времени и
посмотреть на ее части, потому что это поможет понять более сложные таблицы.
В таблице есть три строки: одна содержит данные для межгрупповой
дисперсии, одна - для внутригрупповой, и одна - для общей. Суммируя внутри- и
межгрупиовые суммы квадратов и степени свободы (df), мы получаем значения
для всей выборки. Дисперсия между группами -это дисперсия, связанная с
групповой принадлежностью, то есть с той, которая определяется методом тренировок.
Внутригрупповая дисперсия - это дисперсия значений в каждой группе; как мы
видели на диаграмме размаха на рис. 8.9, значительная дисперсия была как
внутри каждой из групп, так и между группами. Число степеней свободы отражает то,
сколько параметров могут изменяться при вычислении каждой части статистики;
общее число степеней свободы равно п - 1 (на один меньше, чем число
испытуемых), число степеней свободы между группами равно k - 1 (на один меньше числа
групп), внутригрупповое число степеней свободы равно п - k. Сумма квадратов
(SS8) - это сумма возведенных в квадрат отклонений между группами, внутри
групп и в целом, тогда как средний квадрат (MS9) - это сумма квадратов,
разделенная на число степеней свободы, как в этом примере:
55(между) = 455,86/1 = 455,86;
55(внутри) = 1294,52/28 = 46,23.
F-статистпка - это отношение меж- и внутригрупповой сумм квадратов, как в
этом примере:
F= 455,86/46,23 = 9,86.
8 От англ. Sum of Squares. - Прим. пер.
[) От англ. Mean Square. — Прим. пер.
Дисперсионный анализ (ANOVA)
¦МЕШ
Наш статистический пакет автоматически рассчитал значимость ^-статистики,
но мы также могли сравнить значения с табличными (по аналогии с нормальным
распределением и другим таблицами, включенными в приложение D).
Поскольку F-таблицы имеют две степени свободы (для числителя и знаменателя), они
довольно громоздки, так что мы не стали включать их в эту книгу; тем не менее
вы можете найти F-таблицу тут: http://www.itl.nist.gov/div898/handbook/eda/
section3/eda3673.htm.
Апостериорные тесты
Если у вас есть только две группы, то значимые различия по ^-критерию говорят о
том, что их средние различаются. Однако если у вас более двух групп, ваш
дисперсионный анализ мог показать значимый результат ^-критерия (называемого
универсальным критерием), что означает, что средние групп различаются, но при этом
вы все равно не сможете сказать, к каким парам групп это относится. Для ответа на
этот вопрос можно провести апостериорный тест; как и говорится в названии, этот
тест применяют после того, как вы получили значимый результат универсального
/^-критерия. Есть целый набор апостериорных тестов, и некоторые из них чаще
применяются в одних областях, а другие - в других. Один из хороших вариантов - это
тест Шеффа (Scheffe test), который проверяет различия между всеми парами групп
на статистическую значимость и учитывает факт проведения множества тестов на
одних и тех же данных (использование теста Шеффа контролирует частоту
экспериментальных ошибок и не увеличивает вероятности ошибки первого рода).
Предположим, что мы сравниваем три метода тренировок по подъему веса, а не
два. Описательная статистика для этих данных представлена в табл. 8.5.
Таблица 8.5. Описательная статистика для данных по подъему веса
(три метода тренировки)
Группа
1
2
3
В целом
N
15
15
15
45
Среднее
34.21
26.42
30.04
30.32
Станд. откл.
7.38
6.16
9.22
7.76
Нижняя граница
95%-го
доверительного интервала
30.13
23.01
24.94
27.41
Верхняя граница
95%-го
доверительного интервала
38.31
29.83
35.15
33.22
Размеры всех трех групп равны, что является оптимальным для проведения
дисперсионного анализа. Судя по групповым средним, группа 3 имеет более низкие
результаты, чем группа 1, но более высокие, чем группа 2.95%-ный доверительный
интервал для группы 3 перекрывается с интервалами двух других групп, так что
будет интересно посмотреть, что нам скажут апостериорные тесты для этих трех
методов тренировки.
Тест Левина дает значение 1,447 (р = 0,247), так что требование
однородности дисперсии выполнено. Результаты дисперсионного анализа представлены в
табл. 8.6.
Глава 8. Введение в регрессию и дисперсионный анализ
Таблица 8.6. Результаты дисперсионного анализа данных по подъему веса
(три метода тренировки)
Между группами
Внутри групп
В целом
Сумма
квадратов
456.04
2483.76
2940.36
df
2
42
44
Средний
квадрат
228.30
59.14
F
3.86
Значимость
0.029
F-статистика значима, то есть средние трех групп различаются. Однако мы
хотим узнать больше - достоверно ли выше результаты группы 1, чем групп 2 и 3,
например? А результаты группы 3 значимо лучше, чем у группы 2? Для ответа на
этот вопрос мы проводим апостериорный тест Шеффа, что дает нам результаты,
приведенные в табл. 8.7 и 8.8.
Таблица 8.7. Результаты апостериорного теста Шеффа для данных
о подъеме веса (три метода тренировки)
Группа 1
1
1
2
2
3
3
Группа J
2
3
1
3
1
2
Средняя
разница
(I-J)
7.80
4.17
-7.80
-3.62
-4.17
3.62
Станд.
ошибка
2.81
2.81
2.81
2.81
2.81
2.81
Значимость
0.029
0.341
0.029
0.442
0.341
0.442
Нижняя граница
95%-го
доверительного интервала
0.67
-2.95
-14.92
-10.75
-11.30
-3.50
Верхняя граница
95%-го
доверительного интервала
14.92
11.30
-0.67
3.50
2.95
10.75
Таблица 8.8. Гомогенные группы из апостериорного теста Шеффа
(три метода тренировки)
Группа
2
3
1
Значимость
N
15
15
15
Группы для а = 0.05
1
26.42
30.04
0.442
2
30.04
34.22
0.341
Таблицы 8.7 и 8.8 показывают один и тот же результат, но информация
организована по-разному. Посмотрев на таблицы, мы можем увидеть, что среднее
группы 1 отличается от среднего группы 2, но не от среднего группы 3, которое, в свою
очередь, не отличается от среднего группы 2.
Таблица 8.7 представляет все возможные попарные сравнения между группами;
половина таблицы избыточна, поскольку представлены как сравнение группы 1
с группой 2, так и группы 2 с группой 1. Например, первая строка представляет
Расчет простой регрессии вручную
МЕШ
сравнение группы 1 с группой 2 (приняты обозначения «группа I» и «группа J»).
Разница в средних между этим группами составляет 7,80, и разница достоверна
(р = 0,029). 95%-ный доверительный интервал для этой разницы средних
составляет (0,067, 14,92); заметим, что он не включает нуль. Вторая строка табл. 8.7
представляет из себя сравнение групп 1 и 3; средняя разница составляет 4,17, и
она не достоверна (р = 0,341). Заметим для сравнения, что доверительный
интервал включает нуль (-2,95, 11,30). В третьей строке сравниваются группы 2 и 1;
результат ровно тот же, что и в первой строке, с точностью до знака (поскольку
в третьей строке среднее группы 1 вычитается из среднего группы 2, тогда как
в первой строке среднее группы 2 вычиталось из среднего группы 1). В строке 4
показано сравнение средних групп 2 и 3; разница в средних составляет -3,62, и она
не достоверна (р = 0,442). Строки 5 и 6 совпадают со строками 2 и 4.
Столбцы табл. 8.8 соответствуют гомогенным наборам групп; в гомогенном
наборе средние включенных групп не отличаются достоверно друг от друга. В
данном случае группы 2 и 3 формируют гомогенную группу (столбец 1); группы 1 и 3
также гомогенны (столбец 2).
Расчет простой регрессии вручную
Коэффициенты регрессии можно рассчитать вручную, используя суммы
квадратов, дисперсии X и Y и несколько других величин, которые можно вычислить
без помощи компьютера. Проблема с ручным расчетом регрессии не в том, что он
включает какие-то особенно сложные этапы, а в том, что с набором данных
любого размера работа становится очень утомительной и способствующей ошибкам.
Тем не менее пройти через модифицированную версию этого процесса может быть
полезным для понимания смысла коэффициентов регрессии, и именно для этого
приведен следующий раздел.
Мы заметили ранее, что при работе с реальными данными мы не ожидаем
получить идеальное предсказание по уравнению регрессии. На самом деле мы
предполагаем, что будут некоторые различия между наблюдаемыми и
предсказываемыми по модели значениями. Мы также обсуждали квадраты отклонений, которые
являются квадратами разностей каждого наблюдаемого и предсказанного по
уравнению значений. Сумма квадратов отклонений - это сумма квадратов ошибок, и
она рассчитывается, как показано на рис. 8.10.
п
Рис. 8.10. Сумма квадратов ошибок
В этой формуле у. - это наблюдаемое значение, а у. - это предсказанное
значение (в соответствии с уравнением регрессии) для него. Поскольку значение^
определяется по уравнению регрессии (or. + Ь)} сумма квадратов ошибок также
может быть записана, как показано на рис. 8.11.
Глава 8. Введение в регрессию и дисперсионный анализ
п
SSE = ^(yi-(axi+b))2
1-1
Рис. 8.11. Другой способ записи суммы квадратов ошибок
Цель регрессии состоит в минимизации суммы квадратов, что будет означать,
что предсказанные значения лежат максимально близко, насколько это возможно,
к наблюдаемым. Формулы, необходимые для расчета простейшего
регрессионного уравнения, приведены на рис. 8.12-8.15. Учтите, что 5vv - это дисперсия х, а
S - это ковариация х и у.
Рис. 8.12. Расчет дисперсии х
Рис. 8.13. Расчетковариациихиу
Рис. 8.14. Расчет коэффициента наклона простого уравнения регрессии
Рис. 8.15. Расчет константы простого уравнения регрессии
Предположим, что вам дали значения из рис. 8.16, рассчитанные на основе
данных о связи IQ {у) с ростом в метрах (х); вы можете использовать эту информацию
для расчета линии регрессии для этих данных. Вы также могли бы рассчитать эти
величины вручную, но этот процесс крайне трудоемок даже для небольших
наборов данных - настолько трудоемок, что на самом деле вы легко забудете, для чего
вы вообще все это считаете.
Упражнения
2*-
1у-
2*1-
2/-
Х*У
л-21
33.25
2 486
= 53.01
= 299 676
= 3 973.04
Рис. 8.16. Данные, необходимые для расчета простого уравнения регрессии
Используя уравнения и данные из рис. 8.16, мы рассчитываем уравнение
регрессии следующим образом:
1х/п = 33,25/21 = 1,58;
1у/п = 2486/21 = 118,38;
5п. = 53,01 - (33,25)2/21 = 0,36;
Sxl = 3973,04 - (33,25)(2486)/21 = 36,87;
я = 36,87/0,36 =102,42;
Ъ = 118,38 - [(102,42)(1,58)] = -43,44.
Уравнение регрессии представляет из себя следующее:
у =102,42*-43,44 + е
или
IQ = 102,42(рост) - 43,44 + е.
Для человека ростом 2 метра уравнение предсказывает IQ = 161,40
(гениальность!), поскольку:
102,42(2)-43,44 =161,40.
Нет необходимости подчеркивать, что это искусственный пример, который
иллюстрирует метод регрессии; у нас нет цели запятнать умственные способности
кого-то, вне зависимости от роста.
Упражнения
Регрессия
Первая группа вопросов использует данные программы развития ООН для
изучения величин, связанных с подростковой рождаемостью (частотой родов женщин
15-19 лет в данной стране, выраженной как число родов на 1000 женщин этой
IF1'
Глава 8. Введение в регрессию и дисперсионный анализ
возрастной группы). Вы решили посмотреть на уровень образования в стране,
включая такой показатель, как «средняя длительность обучения взрослых»,
предполагая, что в тех странах, где среднее число лет, потраченных на образование,
выше, подростковая рождаемость должна быть ниже.
Задача
На рис. 8.17 представлена диаграмма рассеяния двух переменных (с
использованием натурального логарифма подростковой рождаемости, как обсуждалось
ранее в этой главе). Что она говорит об их взаимоотношении, и поддерживает ли
она проведение простого регрессионного анализа с использованием этих двух
переменных?
6.00-
рождаемости
о о о
о о о
1 1 1
Логарифм
о
1.00-
.оо-1
°" Я Й ° о °
0 ° со* о *Ъ*° л
°°°>*о°°?^ое о
0 о о о "° <?о о
О О© О О
00 cPL ° 8 о
° о <**> о о о <9 о
о ° в ° ?Р °
° ° ъ oV°°85 ° о°
О О (р О
о ° ° ° 9)
0°
о о
о
1 1 1 1 1 1
.00 2.50 5.00 7.50 10.00 12.50
Среднее число лет обучения у взрослых (годы)
Рис. 8.17. Диаграмма рассеяния натурального логарифма подростковой
рождаемости и средней длительности обучения взрослых
Решение
Диаграмма рассеяния показывает достаточно сильную отрицательную
взаимосвязь. (Более высокий уровень образования связан с более низким уровнем
подростковой рождаемости.) Обе переменные выглядят непрерывными и имеют
значительный размах, что позволяет проводить регрессионный анализ.
Задача
Регрессионный анализ выдал результаты, показанные в табл. 8.9; заполните
пропущенное значение для R в квадрате и проинтерпретируйте информацию в
табл. 8.9.
Упражнения
Таблица 8.9. Информация о модели
Я
0.663
Я2
Статистика Дарбина-Уотсона
2.199
Решение
К2 равно 0,440 (найдено возведением 0,663 в квадрат). Это коэффициент
детерминации для модели, и он означает, что 44,0% всей дисперсии натурального
логарифма уровня подростковой рождаемости можно объяснить влиянием средней
длительности обучения взрослых. Статистический тест Дарбина-Уотсона
проверяет предположение о независимости ошибок, а значение 2 показывает
абсолютную независимость; поскольку мы получили значение, очень близкое к 2 (2,199),
мы можем заключить, что это предположение выполняется.
Задача
Ниже приведена таблица коэффициентов из того же самого регрессионного
анализа. Заполните пропущенные значения ^-статистики, напишите уравнение
регрессии и проанализируйте информацию из этой таблицы.
Таблица 8.10. Таблица коэффициентов регрессии, предсказывающей натуральный
логарифм подростковой рождаемости по среднему значению длительности
обучения взрослых в стране
Нестандартизованные
коэффициенты
Стандартизованные
коэффициенты
В
Станд. ошибка
Бета
Константа
Средняя продолжительность
обучения взрослых
5.248
-0.217
0.146
0.019
-0.663
Значимость
< 0.001
< 0.001
Решение
^-статистика для константы составляет 35,945 и -11,421 для среднего времени
обучения взрослых; она рассчитывается как отношение В соответствующей
величины к его стандартной ошибке. Для константы:
5,248/0,146 = 35,945.
Уравнение регрессии для этого анализа выглядит следующим образом:
тхт/ чг-о/олгл.-г* среднее число лет
LN(подростковая рождаемость) = 5,248 - 0,217 * обучения взрослых.
Это уравнение говорит о том, что предсказываемый логарифм подростковой
рождаемости уменьшается на 0,217 единицы при уменьшении времени обучения
взрослых в стране на 1 год. ^-статистики и их тесты значимости говорят нам, что
оба коэффициента регрессии достоверно отличаются от нуля. Коэффициент Бета
(-0,663) для средней продолжительности учебы взрослых - это
стандартизованный коэффициент регрессии для этой переменной (-0,217); он не особенно
полезен для простого уравнения регрессии, но может быть использован в моделях со
множеством независимых переменных, измеряемых в разных единицах, для
сравнения их значимости.
кяя
Глава 8. Введение в регрессию и дисперсионный анализ
Этот анализ поддерживает представление о наличии достоверной
отрицательной связи между уровнем образования в стране и частотой подростковых родов:
в среднем уровень подростковой рождаемости ниже в тех странах, где взрослые
учились дольше.
Дисперсионный анализ
Эти вопросы используют данные Системы наблюдения за поведенческими
факторами риска за 2010 год (BRFSS, ежегодный обзор информации, связанной со
здоровьем, для США). Хотя вы можете скачать данные с BRFSS, анализ в этом
разделе основан на случайной выборке из данных 2010 года, так что не стоит
ожидать ровно таких же результатов, если вы проведете анализ самостоятельно.
Вас интересует, есть ли взаимосвязь между астмой и массой тела. Вы будете
применять дисперсионный анализ для проверки того, есть ли достоверная разница в
массе тела между теми людьми, которым никогда не ставили диагноз астмы, и теми,
которым когда-либо его ставили. Ваша групповая переменная, диагностирование
астмы - дихотомическая, а зависимая переменная, масса тела - непрерывная. Поскольку
результаты исследования интересуют американских чиновников, вы будете измерять
массу в фунтах, а не килограммах. (В данных имеются обе единицы измерения.)
Задача
На рис. 8.18 изображена диаграмма размаха для диагноза астмы и массы тела в
фунтах. Какую информацию о данных вы можете получить из этой диаграммы?
Если вы незнакомы с диаграммами размаха, вы можете просмотреть
соответствующий раздел в главе 3.
350-
% зоо-
фунт
со
Сообщенная масса
боб
50-
17>
182846383
013 219 273
° О
С
94
i i I
1 2 7
Когда-либо ставили диагноз астмы
Рис. 8.18. Диаграмма размаха для диагноза астмы и массы тела в фунтах
Упражнения
¦¦ЕШ
Решение
Вы должны очень заволноваться, увидев эту диаграмму, которая является
хорошим примером того, почему очень важно смотреть на данные. Во-первых, там есть
три группы данных по диагнозу астмы, а не две; быстро просмотрев книгу кодов
(также доступна здесь: http://www.cdc.gov/brfss). мы видим, что 7 - это
пропущенные значения, так что мы должны исключить эти случаи из нашего анализа.
В обеих валидных группах (с и без диагноза астмы) есть выбросы; это те случаи,
которые изображены в виде кружочков, а номер рядом с ними показывает номер
строки с таким значением. Это поднимает вопрос о том, нормально ли
распределена масса тела, так что, перед тем как продолжить, мы это проверим. В итоге
медианные массы тела для двух групп почти совпадают, что говорит о том, что
эта переменная может оказаться не самой многообещающей, если нас интересует
поиск факторов, сильно связанных с астмой. Тем не менее мы продолжим наш
анализ, поскольку обнаружение отсутствия значимости также дает полезную
информацию.
Задача
Мы создали гистограмму для массы тела и рассчитали статистику
Колмогорова-Смирнова для этой переменной; гистограмма представлена на рис. 8.19, а
статистика Колмогорова-Смирнова оказалась равно 1,898 (р = 0,001). В итоге что
они говорят нам про распределение массы тела в данных?
60-
50-
40-
{5
о
о 30-
аг
20-
ю-
pi
IM
К
К
Ш\
И
л
л
/А
—*-*^ п 1 1 III
0 1 1 1
50 100 150
1-1
41
N
h\
и\
П_\
Ш
П ч1
1111 11 ИУД гтц
200 250 300 350
Сообщенная масса тела в фунтах
Рис. 8.19. Гистограмма массы тела в фунтах
ШЕЯ
ящ
Глава 8. Введение в регрессию и дисперсионный анализ
Решение
Гистограмма имеет положительную асимметрию (более высокие значения
встречаются чаще, чем ожидается из нормального распределения); это ясно при
сравнении распределения реальных данных (столбцы гистограммы) с
наложенной нормальной кривой (показывающей идеальное нормальное распределение).
Статистика Колмогорова-Смирнова достоверна, то есть нам придется отвергнуть
нулевую гипотезу о том, что эта переменная распределена нормально.
Задача
Мы взяли натуральный логарифм от массы тела и проверили нормальность
еще раз; в этом случае гистограмма (не показана) выглядела приблизительно
нормальной, а статистика Колмогорова-Смирнова была равна 0,961 (р = 0,314),
подтверждая достаточную нормальность. Кроме того, мы рассчитали статистику
Колмогорова-Смирнова для каждой группы отдельно; ни одна из них не была
достоверной, так что мы уверены, что распределения внутри групп также
нормальные. Диаграммы размаха для преобразованных данных показаны на рис. 8.20; что
они говорят нам о данных?
6.00-
5.S0-
1п(масса тела)
4.50-
182в50
383 179
1 1
да нет
Когда-либо ставили диагноз астмы
Рис. 8.20. Диаграмма размаха для преобразованных
величин масс тела
Решение
В группе, получавшей диагноз астмы, все еще сохраняется группа выбросов, но,
поскольку данные достаточно нормальные, мы продолжим наш анализ. Группа с
диагностированной астмой имеет немного более высокую медиану, чем «здоро-
Упражнения
¦¦ЕШ
вая» группа, но обе группы значительно перекрываются. Мы продолжим
проводить дисперсионный анализ с этими данными.
Задача
Статистика Левина для этого анализа составляет <0,001 (р = 0,983). Зачем мы
рассчитываем статистику Левина, и что нам говорит этот результат?
Решение
Статистика Левина проверяет, верно ли предположение об однородности
дисперсии. Нулевая гипотеза состоит в том, что дисперсии разных групп
однородны; в данном случае мы не получили достоверного значения для этой
статистики, так что мы можем считать предположение об однородности
дисперсии верным.
Задача
В табл. 8.11 даны некоторые описательные статистики для преобразованной
массы тела в наших данных. Что вы можете заметить в этой таблице, и какие
последствия от этого будут для анализа?
Таблица 8.11. Описательная статистика для преобразованной массы тела
для людей, получавших и не получавших диагноза астмы в течение жизни
Группа
Был поставлен
диагноз астмы
Не был поставлен
диагноз астмы
В целом
N
44
390
434
Среднее
5.19
5.13
5.16
Стан д. откл.
0.24
0.24
0.24
Нижняя граница
95%-го
доверительного
интервала
5.12
5.10
5.11
Верхняя граница
95%-го
доверительного
интервала
5.27
5.15
5.16
Решение
Самое первое, на что стоит обратить внимание, - это то, что размеры групп
сильно отличаются, что говорит о том, что наши данные не оптимальны для
проведения дисперсионного анализа (ANOVA лучше всего работает в случае
сбалансированных выборок). Второе - это то, что средние выборок достаточно
сходны, а 95%-ные доверительные интервалы сильно перекрываются, намекая на не
слишком сильную взаимосвязь между постановкой диагноза астмы и массой
тела. Все равно стоит закончить анализ; отрицательный результат тоже может
оказаться полезным.
Задача
Результаты дисперсионного анализа приведены в табл. 8.12; что они говорят
о связи между наличием диагноза астмы и массой тела? Используйте обычную
a = 0,05 для проверки на достоверность.
Глава 8. Введение в регрессию и дисперсионный анализ
Таблица 8.12. Результаты однофакторного дисперсионного анализа о связи
диагноза астмы и массы тела
Между группами
Внутри групп
В целом
Сумма
квадратов
456.04
2483.76
2940.36
df
2
42
44
Средний
квадрат
228.30
59.14
F
3.86
Значимость
0.029
Решение
Этот анализ нашел достоверную связь (F= 3,86,р = 0,029) между наличием
диагноза астмы и массой тела. В соответствии с табл. 8.11 люди, которые когда-либо
получали диагноз астмы, в среднем имеют более высокую массу тела, чем те, у кого
астму никогда не находили.
«А*
Поскольку мы преобразовали массу тела в ее натуральный логарифм, наши
средние (табл. 8.11) показывают натуральные логарифмы массы тела.
Чтобы получить эти величины в более осмысленном виде, нам необходимо
преобразовать их обратно в изначальные единицы (фунты). Мы можем сделать
это с помощью взятия экспоненты от средних из табл. 8.11:
е519= 179,5;
е513= 169,0.
Мы можем добавить эту информацию во второе предложение наших
результатов, так что оно выглядит следующим образом: «Люди, которым когда-либо
ставили диагноз астмы, имеют в среднем более высокую массу тела
(среднее = 179,6 фунта), чем те, которым никогда не ставили такого диагноза
(среднее = 169,0 фунта)». Преобразование обратно в изначальные величины также
указывает на опасность, связанную с работой с преобразованными данными: разница,
которая может выглядеть очень маленькой (5,19 и 5,13), может оказаться гораздо
более внушительной в изначальных величинах (179,5 и 169,0).
Поскольку данные системы наблюдения за поведенческими факторами
риска собираются в один момент времени, невозможно ответить на вопрос о
причинно-следственной связи в отношении массы тела и ожирения.
Возможно, астма приводит к увеличению массы тела (например, уменьшая
возможности для тренировок), или же увеличенная масса тела может
приводить к астме (к примеру, из-за увеличения нагрузки на легкие). Также
возможно, что есть какие-то еще дополнительные факторы, которые могут
объяснить наблюдаемые взаимоотношения, например увеличенная масса
тела и астма могут быть ассоциированы с нищетой.
ГЛАВА 9.
Многофакторный
дисперсионный анализ
и ковариационный анализ
В главе 8 кратко обсуждались простая регрессия и дисперсионный анализ
(ANOVA). В данной главе представлены более сложные варианты
дисперсионного анализа: многофакторный дисперсионный анализ (дисперсионный анализ с
несколькими группирующими переменными, или факторами) и ковариационный
анализ (модель дисперсионного анализа, включающая непрерывную переменную,
или ковариату). В главе 10 обсуждаются подобные расширения для модели
простой регрессии.
В большинстве исследований используются как минимум две группирующие
переменные. Принципы таких моделей основаны на однофакторном дисперсионном
анализе, но более сложная модель порождает дополнительные трудности:
например, измерение взаимодействий между факторами. Такие типы анализа почти
всегда выполняются в компьютерных статистических пакетах. К счастью, все пакеты
имеют много общего, поэтому, обучившись понимать результаты выдачи одного
пакета, легко понять и результаты, полученные в другой программе. Мы представляем
данные анализа в общем виде, насколько это возможно, чтобы читатель мог понять
их вне зависимости от того, какой программой он пользуется сам.
Многофакторный дисперсионный
анализ
Влияние единственного фактора относительно редко интересует современного
исследователя. Напротив, гораздо чаще нам интересно влияние нескольких
факторов и, возможно, их взаимодействие. Многофакторные планы (дисперсионные
анализы, включающие несколько факторов) дают возможность оценить
совместный эффект, оказываемый несколькими факторами на зависимую переменную.
Нас может интересовать как главный эффект - эффект каждого фактора самого
по себе, так и эффект взаимодействия - эффект сочетаний факторов. Как и одно-
факторный дисперсионный анализ, многофакторный анализ лучше всего подхо-
ЕШНН!
Глава 9. Многофакторный дисперсионный анализ...
дит для спланированных экспериментов и одинаковых размеров ячеек плана, то
есть приблизительно одинакового числа объектов в каждой подгруппе или
ячейке, сформированной всевозможными сочетаниями факторов. Главные допущения
для многофакторного дисперсионного анализа те же, что и для однофакторного
(см. главу 8). Особенно важны независимость наблюдений и однородность
дисперсии. В основном статистические пакеты предоставляют статистические тесты
на однородность дисперсии: например, тест Левина. Независимость наблюдений
достигается на этапе планирования эксперимента.
Самые обычные многофакторные планы: а * b (двухфакторный) и а * b * с
(трехфакторный). Возможны и более сложные планы, но результаты их
обработки становится очень сложно интерпретировать. Более высокие уровни сложности
проще аппроксимировать моделью линейной регрессии. Как и в случае
однофакторного дисперсионного анализа, каждый фактор является категориальной
переменной как минимум с двумя уровнями, а зависимая переменная - непрерывной
переменной, измеренной в абсолютной или интервальной шкале.
Взаимодействие
При исследовании более одного фактора приходится решать вопрос
взаимодействия факторов. По определению, взаимодействие - это зависимость эффекта
одной переменной от уровня другой переменной. Другими словами, эффект одной
переменной зависит от величины другой переменной. Это проще понять,
рассматривая графики предельных случаев взаимодействия и его отсутствия. Подобные
графики редко получаются для реальных данных, но полезны в качестве
иллюстрации.
Рассмотрим некоторые гипотетические данные по отношениям силы сжатия
руки (данные эксперимента, измеренные в фунтах на квадратный дюйм) и двух
факторов: пола и употребления алкоголя. Если между факторами нет
взаимодействия, то график с данными может выглядеть похоже на рис. 9.1.
Этот график демонстрирует отсутствие взаимодействия между потреблением
алкоголя и полом: сила сжатия (ось у) уменьшается с ростом потребления
алкоголя (ось х) как для женщин, так и для мужчин. Скорость уменьшения одинакова
для обоих полов, поэтому линии параллельны, и мужчины имеют силу сжатия
сильнее при любом уровне потребления алкоголя.
Рисунок 9.2 отражает данные с взаимодействием, потребление алкоголя влияет
на силу сжатия по-разному для мужчин и для женщин. По сути, эффект
противоположный: потребление алкоголя увеличивает силу сжатия для женщин и
уменьшает для мужчин.
Линии не обязательно должны пересекаться при наличии взаимодействия: на
рис. 9.3 показано взаимодействие, характеризуемое не параллельными, но
расходящимися линиями; эффект алкоголя на силу сжатия больше для женщин, чем
для мужчин.
И на рис. 9.2, и на рис. 9.3 наблюдается зависимость эффекта алкоголя на силу
сжатия от уровня или величины третьей переменной - пола; соотношения между
Многофакторный дисперсионный анализ
ШШША
алкоголем и силой сжатия различны для мужчин и женщин. Конечно, нельзя
сказать, является ли взаимодействие значимым, просто глядя на график; для этого
требуется статистический тест.
20.00"
18.00-
16.00-
Среднее силы сжатия
о о о
о о о
1 1 1
&.00-
6.00-
\
\
\
\
1 1 1
нет/низкое среднее высокое
Потребление алкоголя
Пол
мужчины
женщины
Рис. 9.1. Данные без взаимодействия
20.00-
18.00-
Z
»-
X 16.00-
»силы
Ф 14.00-
Cpeflh
12.00-
ю.оо-
\
\
\
\
\
\
\
\
1 1 1
нет/низкое среднее высокое
Потребление алкоголя
Пол
мужчины
женщины
Рис.9.2. Данные с взаимодействием
КЕЕ1
Глава 9. Многофакторный дисперсионный анализ...
20.00-
18.00-
р. 16.00-
X
н
(0
U 14.00-
5
^
X
55 1200-
дне
О. 10.00-
U
8.00-
6.00-
\.
^\^
^"\
1 1 1
нет/низкое среднее высокое
Потребление алкоголя
Пол
мужчины
женщины
Рис. 9.3. Данные с взаимодействием
Двухфакторный дисперсионный анализ
Показатели работоспособности часто различаются внутри популяций, и
уменьшение силы сжатия, например, может коррелировать с некоторыми
клиническими характеристиками. Ваша исследовательская группа интересуется изучением
того, как два фактора - пол и потребление алкоголя - соотносятся с силой сжатия
и как эти факторы взаимодействуют. Перед вами три начальных вопроса
исследования:
1. Влияет ли пол на силу сжатия?
2. Влияет ли потребление алкоголя на силу сжатия?
3. Влияет ли совместное действие пола и потребления алкоголя на силу
сжатия?
Будем рассматривать потребление алкоголя как дихотомическую переменную,
противопоставляя друг другу тех, кто употреблял алкоголь как минимум неделю,
тем, кто не употреблял.
Наши гипотезы могут быть формально записаны следующим образом:
Главный эффект пола
Н(): ист разницы в силе сжатия между мужчинами и женщинами.
Н,: есть разница в силе сжатия между мужчинами и женщинами.
Главный эффект алкоголя
Н(): нет разницы в силе сжатия между пьющими и трезвенниками.
Н,: есть разница в силе сжатия между пьющими и трезвенниками.
Многофакторный дисперсионный анализ
ШШЕ22
Взаимодействие пола и алкоголя
Н(): влияние потребления алкоголя на силу сжатия одинаковое для мужчин
и женщин.
Ht: влияние потребления алкоголя на силу сжатия разное для мужчин и
женщин.
В табл. 9.1 представлены выборочные данные для первых 12 случаев,
полученных в лаборатории по силе сжатия (всего п = 50). Силу сжатия измерили шести
женщинам и шести мужчинам, в каждой тендерной группе было по три пьющих и
три непьющих (определяемые по тому, выпивал ли человек как минимум неделю
или же никогда не пил).
Таблица 9.1. Соотношения между силой сжатия (зависимая переменная)
и полом и потреблением алкоголя (независимые переменные)
Пол
Женщина
Женщина
Женщина
Женщина
Женщина
Женщина
Мужчина
Мужчина
Мужчина
Мужчина
Мужчина
Мужчина
Алкоголь
Да
Да
Да
Нет
Нет
Нет
Да
Да
Да
Нет
Нет
Нет
Сила сжатия
(фунт на квадратный дюйм)
19
20
21
30
25
28
31
30
35
32
35
32
Два главных эффекта тестируются по разности средних по выборке,
основанных на нулевых гипотезах:
ц - и =0;
•МУЖЧИНЫ ~Ж(Ч11ЦПНЫ '
Ц - LL =0.
•алкоголь ~Гк'л алкоголя
Обратите внимание, что нулевые гипотезы для главных эффектов
сформулированы в терминах оценок различий; утверждается, что две величины
одинаковы - это то же самое, что их разность равна 0. Гипотезы взаимодействия
обычно выражаются в терминах разностей. В данном примере утверждение о том, что
между женщинами и мужчинами нет разницы в том, как влияет алкоголь на силу
сжатия, может быть выражено как:
"мужчины/алкоголь "мужчины/беи алкоголя "женщины/алкоголь "жпицпны/Гнм алкоголя"
Данное исследование было очень близко к сбалансированному: в нем
принимали участие 24 женщины и 26 мужчин, 24 пьющих и 26 трезвенников. Коэффи-
шшшш
Глава 9. Многофакторный дисперсионный анализ...
циент детерминации К1 для модели был 0,566, что означало объяснение двумя
факторами и их взаимодействием 56,6% дисперсии силы сжатия, наблюдаемой в
этой выборке данных. Тест Левина (F= 0,410,p = 0,746) показал, что допущение об
однородности удовлетворено. Выборочные средние следующие:
• Главный эффект пола: женщины (25,25), мужчины (31,65).
• Главных эффект алкоголя: алкоголь (26,71), без алкоголя (30,31).
Средние по полу и потреблению алкоголя представлены на рис. 9.4.
32.5-
зо.о-
Сила сжатия
2 5.0-
22.'г
\
1
нет
~~ —
\
ч
ч
i
да
Алкоголь
Пол
ркенщины
— 'мужчины
• женщины
мужчины
Рис. 9.4. График средних для эффектов пола и потребления алкоголя
на силу сжатия
Кажется, в данном случае присутствуют оба главных эффекта и эффект
взаимодействия: в нашей выборке у мужчин большая сила сжатия, чем у женщин; у
выпивающих меньшая сила сжатия, чем у трезвенников; и эффект потребления алкоголя
на силу сжатия больше для мужчин, чем для женщин. Чтобы понять, значимы ли
различия статистически, требуется двухфакторный дисперсионный анализ.
Некоторые статистические пакеты выдают множество таблиц, из которых
только отдельные особенно полезны. В данном случае нас интересует тест на
статистическую значимость главных эффектов и эффект взаимодействия в модели.
Ключевые данные из дисперсионного анализа представлены в табл. 9.2.
Таблица 9.2. Дисперсионный анализ различий силы сжатия (зависимая
переменная) для пола и потребления алкоголя (независимые переменные)
Величина
Скорректированная модель
Свободный член
Сумма
квадратов
733.085
40 426.436
df
3
1
Средний
квадрат
244.362
40 426.436
F
20.033
3299.504
Значимость
< 0.001
< 0.001
Многофакторный дисперсионный анализ
¦¦ЕШ
Величина
Пол
Алкоголь
Пол'алкоголь
Ошибка
Сумма
Скорректированная сумма
Сумма
квадратов
504.806
148.325
80.769
561.095
42 135.000
1294.180
df
1
1
1
46
50
49
Средний
квадрат
504.806
148.325
80.769
12.198
F
41.385
12.160
6.622
Значимость
< 0.001
0.001
0.013
Используя уровень значимости а = 0,05 и рассматривая строки пол (главный
эффект), алкоголь (главный эффект), пол*алкоголь (эффект взаимодействия),
получаем, что все три эффекта значимы, как мы и предполагали из графиков
средних. Обзор результатов приведен ниже.
В данном плане оба главных эффекта и взаимодействие значимы:
Главный эффект пола: F(l,46) = 41,385, р < 0,001.
Направление эффекта показывает, что в целом женщины имеют более
низкую силу сжатия, чем мужчины.
Главный эффект алкоголя: F(l,46) = 12,160, р = 0,001.
Направление эффекта показывает, что в целом те, кто потребляет алкоголь,
имеют более низкую силу сжатия, чем те, кто не выпивает.
Взаимодействие пол * алкоголь: F( 1,46) = 6,622, р = 0,013.
Взаимодействие показывает, что и пол и алкоголь действуют совместно,
причем потребление алкоголя ассоциировано с большим снижением силы
сжатия у женщин сравнительно с мужчинами.
Обратите внимание, что стоит остерегаться утверждений, содержащих
причинно-следственные связи («потребление алкоголя ухудшает силу сжатия»), так как
данное исследование - всего лишь наблюдение: мы спрашиваем у людей,
выпивают ли они, и измеряем их силу сжатия, но не назначаем им алкоголь и не
фиксируем после изменения в силе сжатия. Связь между потреблением алкоголя и
силой сжатия может объясняться множеством факторов. Например, возможно,
что спортсмены воздерживаются от употребления алкоголя, согласно правилам
тренировки, и также имеют увеличенную силу сжатия из-за своих тренировок.
Трехфакторный дисперсионный анализ
Двухфакторная модель может быть легко расширена до трех факторов. Вы
показали значимость главных эффектов пола и потребления алкоголя на силу сжатия,
но теперь ваша группа обнаружила другие факторы, которые могут влиять на силу
сжатия. В литературе часто обсуждается влияние возраста на силу сжатия, причем
отмечается снижение силы сжатия после 40 лет. Вы решаете добавить еще одну
категорию возраста (до 40 лет или за 40), для того чтобы определить, влияет ли
возраст и так ли сильно, как другие факторы. Таблица 9.3 демонстрирует первые
12 случаев в данном исследовании.
ЕЁЭШИнН Глава 9. Многофакторный дисперсионный анализ...
Таблица 9.3. Отношения между силой сжатия (зависимая переменная) и полом,
потреблением алкоголя и возрастом (независимые переменные)
Пол
Женщина
Женщина
Женщина
Женщина
Женщина
Женщина
Мужчина
Мужчина
Мужчина
Мужчина
Мужчина
Мужчина
Алкоголь
Да
Да
Да
Нет
Нет
Нет
Да
Да
Да
Нет
Нет
Нет
Сила сжатия
(фунт на квадратный дюйм)
19
20
21
30
25
28
31
30
35
32
35
32
Возраст
Моложе 40
Старше 40
Моложе 40
Старше 40
Моложе 40
Старше 40
Моложе 40
Старше 40
Моложе 40
Старше 40
Моложе 40
Старше 40
Тестируемая гипотеза становится более сложной с тремя факторами, потому что
потенциально имеются семь гипотез: главные эффекты пола, алкоголя и
возраста; двухфакторные взаимодействия пол*алкоголь, пол*возраст, алкоголь*возраст;
трсхфакторное взаимодействие пол*алкоголь*возраст. Выше была приведена
формализация двухфакторного взаимодействия. Для трехмерного
взаимодействия тестируемая нулевая гипотеза может быть определена как «различие во
влиянии потребления алкоголя на силу сжатия между мужчинами и женщинами
одинаково в двух возрастных категориях».
Чтобы получить график средних с тремя факторами, как ни странно, требуется
построить две зависимости: для объектов моложе 40 и для объектов старше 40.
График средних изображен на рис. 9.5.
Из графика средних можно предположить, что возраст будет являться важным
фактором для прояснения интересующих отношений, так как он, оказывается,
взаимодействует и с полом, и с потреблением алкоголя. Ключевые результаты
представлены в табл. 9.4. Мы будем использовать а = 0,05 для измерения
значимости эффектов в этой модели.
Таблица 9.4. Дисперсионный анализ различий в силе сжатия для пола,
потребления алкоголя и возраста
Величина
Скорректированная модель
Свободный член
Пол
Алкоголь
Сумма
квадратов
864.583
35 902.885
548.630
128.214
df
7
1
1
1
Средний
квадрат
23.512
35 902.885
548.630
128.214
F
2.075
3510.081
53.637
12.535
Значимость
<0.001
<0.001
<0.001
0.001
Многофакторный дисперсионный анализ
Величина
Возраст
Пол*алкоголь
Пол'возраст
Алкоголь*возраст
Пол*алкоголь*возраст
Ошибка
Сумма
Скорректированная сумма
Сумма
квадратов
0.003
33.446
75.758
0.226
49.491
429.597
42 135.000
1294.180
df
42
50
49
Средний
квадрат
0.003
33.446
75.758
0.226
49.491
10.229
F
0.000
2.370
7.407
0.022
4.839
Значимость
0.986
0.078
0.009
0.883
0.033
3 5.0-
3 2.5-
зо.о-
27.5-
X 25.0-
U 22.5-
{
X
§_ 35.0-
U
32.5-
зо.о-
2 7.5-
25.0-
22.5"
нет да
Алкоголь
старше 40 моложе 40
Возраст
IIs
Рис. 9.5. График средних для трехфакторного дисперсионного анализа
Два из трех главных эффектов в модели значимы:
Главный эффект пола: F(l,42) = 53,637,р < 0,001.
Направление эффекта показывает, что в целом у женщин сила сжатия
меньше, чем у мужчин.
Главный эффект алкоголя: F(l,42) = 12,535, р = 0,001.
Направление эффекта показывает, что в целом у выпивающих сила сжатия
меньше, чем у трезвенников.
Главный эффект возраста: F(l,42) = 0,000, р = 0,986 (незначимый).
ИЕЯ
Глава 9. Многофакторный дисперсионный анализ...
Одно из двухфакторных взаимодействий важно:
Взаимодействие пол х алкоголь: F(l,42) = 2,370,р = 0,078 (незначимый).
Взаимодействие пол * возраст: F(l,42) = 7,407, р = 0,009.
Различие в силе сжатия для пьющих и непьющих у мужчин заметно
зависит от возрастной группы, в то время как у женщин зависимость несильно
меняется. Сила сжатия для мужчин возраста 40 и старше почти не зависит
от того, принимают ли они алкоголь; для мужчин младше 40 употребление
алкоголя связано со снижением в силе сжатия. Снижение силы сжатия при
употреблении алкоголя больше для женщин в возрасте от 40 и старше, по
сравнению с более молодыми женщинами, но это различие между
возрастными категориями не так велико, как у мужчин.
Взаимодействие алкоголь * возраст: F(\,42) = 0,022,р = 0,883 (незначимо).
Трехфакторное взаимодействие значимо:
Взаимодействие пол х алкоголь х возраст: F(l,42) = 4,893, р = 0,033.
Эти результаты интересны тем, что хотя главный эффект возраста не значим,
одно включающее возраст двухфакторное взаимодействие значимо (пол*возраст),
так же как и трехмерное пол*алкоголь*возраст. Еще интересно, что
взаимодействие иол*алкоголь не значимо в трехфакторной модели, но было значимо в двух-
факторной. Это демонстрирует идею, применимую и к регрессии: при
добавлении или удалении элементов модели значимость других переменных будет тоже
меняться. При представлении результатов сложной модели всегда необходимо
уточнять, какая именно модель была протестирована, так как предикторы часто
взаимодействуют друг с другом; возможно, что при другом варианте анализа
возраст будет значимым предиктором силы сжатия.
Хотя возраст и не имеет значимого главного эффекта в данной модели,
требуется оставить его в анализе, потому что обычно включается любая переменная,
значимая во взаимодействии, так же как и в главном эффекте. Результаты данного
анализа одновременно достаточно интересные и интригующие, чтобы обосновать
необходимость дальнейших исследований. Еще одна возможность, которая может
оказаться полезной, - переключиться на уравнение регрессии и включить возраст
как непрерывный предиктор (использовать возраст в годах как предиктор, вместо
того чтобы разбивать его на категории моложе/старше 40). Другая возможность -
то, что двух категорий возраста недостаточно, и, возможно, 40 - не лучшая линия
разделения; это можно также исследовать в будущем.
ANCOVA
Ковариационный анализ (ANCOVA)1 - это разновидность многофакторного
дисперсионного анализа, которая позволяет включать в модель непрерывную ковариату.
Наиболее часто эту модель используют для контроля возможного эффекта ковариа-
ты. Например, возможно, вас интересуют заработки выпускников колледжей в за-
От ингл. ANalysis of COvanance and VAriation. — Прим. пер.
ANCOVA JIHIEEEI
висимости от их области знаний (естественные науки, гуманитарные науки, бизнес
и т. п.). Можно рассмотреть модель дисперсионного анализа (ANOVA) с зависимой
величиной - заработной платой, - и категориальным фактором - областью знаний.
Однако если ваши данные включают не только недавних выпускников, но и людей,
работающих в данной сфере разное время, вы обнаружите, что это может влиять на
заработную плату, так как в целом заработок увеличивается с возрастом и/или с
количеством лет работы в данной области. Время работы или возраст можно
контролировать добавлением одной из этих переменных в качестве непрерывной ковариа-
ты в план дисперсионного анализа, таким образом получив план ковариационного
анализа. При ковариационном анализе можно пользоваться несколькими ковариа-
тами. Хотя добавление потенциально вмешивающихся факторов как ковариат для
контроля - не самое лучшее решение, это правильнее, чем просто их игнорировать.
Вот один из способов рассуждать о таком использовании ковариационного анализа:
контролируя эффект непрерывной ковариаты (или ковариат), вы проверяете
отношения между фактором и непрерывным результатом, считая значение ковариаты
одинаковым во всех случаях. На примере области исследований и зарплаты,
используя возраст как непрерывную ковариату, вы проверяете, в каком отношении были бы
два фактора, если все объекты исследования были бы одинакового возраста.
Другой типичный пример использования ковариационного анализа -
уменьшение остаточной или ошибочной дисперсии в плане. Мы уже знаем, что одной
из целей статистического моделирования является объяснение дисперсии в
выборке данных; что модели, объясняющие больше дисперсии и имеющие меньшую
остаточную дисперсию, в основном предпочтительнее, чем те, которые объясняют
меньше. Если получается снизить остаточную дисперсию включением одной или
более непрерывных ковариат в план, то обнаружить отношения между
интересующими факторами и зависимой величиной может быть проще.
Для ковариационного анализа используются те же допущения, что и для
ANOVA, за исключением двух дополнительных:
Подходящие данные
Результирующая переменная и ковариаты должны быть непрерывными,
измеренными в интервальной или характеризующей отношения шкале,
иметь неограниченные или хотя бы колеблющиеся в широком диапазоне
значения; факторы (группирующие переменные) должны быть
дихотомическими или категориальными. Это допущение проверяется проверкой
данных с помощью частотных таблиц, гистограмм и так далее.
Независимость
Каждое значение результирующей переменной должно быть независимым
от других значений. Например, это условие может нарушаться, если
присутствовала некоторая временная зависимость наблюдений, или
измерения проводили у объектов, объединенных в большие группы (члены одной
семьи или одноклассники) таким образом, что они влияли на зависимую
переменную. Это допущение контролируется знанием данных и тем, как
они были собраны.
ИЕСТ
Глава 9. Многофакторный дисперсионный анализ...
Распределение
Результирующая переменная должна иметь приблизительно нормальное
распределение внутри каждой группы. Распределение результирующей
переменной может быть проверено с помощью гистограммы (пристальным
изучением, просмотром данных) или с помощью статистического теста на
нормальность, такого как тест Колмогорова-Смирнова.
Однородность дисперсии
Дисперсия внутри каждой группы должна быть приблизительно
одинаковой. Это проверяется такой процедурой, как статистика Левина; нулевая
гипотеза такая, что дисперсия однородна, так что если результаты
статистики Левина не значимы (обычно критерий а < 0,05), то это означает, что
дисперсии достаточно однородны для дальнейшей обработки.
Независимость ковариат и эффектов факторов
Дисперсия, объясненная ковариатой, должна быть специфичной и не
перекрываться с дисперсиями, объясненными факторами. Это чаще всего
является проблемой исследований, в которых не используется случайный
выбор; если две группы различаются по ковариате и это объясняет
некоторую дисперсию результирующей переменной, то невозможно отделить
дисперсию, объясненную фактором, от объясненной ковариатами. Если
случайный выбор невозможен, лучшим подходом будет определить,
меняются ли значимо уровни ковариаты среди остальных групп; если это так,
не используйте ковариату. Играет роль также здравый смысл: можно ли
представить такой разумный случай, чтобы объясненная данной
ковариатой дисперсия объясняла определенную долю дисперсии результирующей
величины? Если нельзя, то не используйте ковариату.
Однородность регрессионных наклонов
Отношения между ковариатой и зависимой величиной должны быть
одинаковыми для всех групп. Это можно проверить с помощью создания и
нанесения на график регрессионных линий для ковариаты и зависимой
величины отдельно для каждой группы и с помощью вычисления эффектов
взаимодействия и их тестирования на значимость. Регрессионные линии
должны быть аппроксимированы параллельными прямыми; их наклоны
должны быть приблизительно одинаковыми. Эффект взаимодействия не
должен быть значимым.
Продолжая рассматривать пример с силой сжатия, исследовательская группа
озаботилась тем, что в модели не учтена важная переменная: тренировались ли
исследуемые. Интуитивно понятно, что работа может улучшить силу сжатия,
поэтому они решили добавить еще одну переменную в модель: минуты в неделю,
потраченные испытуемым на физическую активность. Это - непрерывная
величина с широким диапазоном, так что она может быть добавлена как непрерывная
ковариата к полу и потреблению алкоголя (независимые переменные) и силе
сжатия (зависимая переменная).
ANCOVA
шшшл
Первое допущение, которое требуется проверить: объясняет ли новая ковариата
специфичную дисперсию (допущение 5). Мы можем представить разумный
случай, когда время, проведенное за упражнениями, может объяснить специфичную
дисперсию для силы сжатия. И мы можем вычислить средние ковариат в группах:
если эти средние не различаются значимо, мы продолжим анализ. В целях
демонстрации мы вернемся к двухфакторной модели с факторами пола и потребления
алкоголя, добавив в качестве ковариаты интенсивность упражнений, измеренных
как продолжительность упражнений в минутах в неделю.
Мы используем однофакторный дисперсионный анализ (аналогично
использованию ?-теста) для средних величин длительности упражнений в минутах для
каждого пола и потребления алкоголя; главные результаты представлены в табл. 9.5.
Как можно видеть, хотя средние длительности занятий в неделю различаются
между мужчинами и женщинами, они не значимы на уровне а = 0,05 при
сравнении потребляющих и не потребляющих алкоголь.
Таблица 9.5. Результаты однофакторных дисперсионных анализов длительности
упражнений в неделю по факторам пола и потребления алкоголя
Переменная
Пол
Потребление алкоголя
Подгруппа
Мужчины
Женщины
Да
Нет
Среднее
100.74
87.64
106.01
83.78
F
1.069
3.209
Значимость
0.306
0.080
Также нам необходимо проверить однородность регрессионных наклонов
(допущение 6). Как и в случае оценки нормальности, мы протестируем это допущение и
графически, и статистически. Для графического теста построим диафаммы рассеяния с
регрессионными линиями для соотношения между силой сжатия (результат) и
упражнениями (ковариата) для мужчин и женщин, а также для употребляющих алкоголь и
трезвенников. Для каждой пары групп наклоны должны быть приблизительно
одинаковыми. Диафаммы рассеяния и рефессионные линии для пола представлены на
рис. 9.6, а для употребления алкоголя - на рис. 9.7.
На обоих графиках нет ничего подозрительного; углы наклонов оказались
приблизительно одинаковыми; это хорошие новости для допущения однородности
наклонов. Проведем также статистический тест этого допущения с помощью
составления модели, включающей эффект взаимодействия ковариаты и фактора.
(Составим отдельные модели для каждого фактора.) Если этот эффект окажется
незначимым, мы допустим однородность наклонов для этих данных. Результаты
анализа представлены в табл. 9.6 и 9.7.
Стоит заметить, что единственная причина использования этих моделей -
проверка значимости эффекта взаимодействия; мы не проверяем теорию, так что нам
не важно, подходит ли модель, значимы ли другие эффекты и тому подобное. Как
можно видеть в табл. 9.6 и 9.7, ни один из эффектов взаимодействия не значим;
для взаимодействия пол*упражненияр-значение равно 0,702, для взаимодействия
алкоголь*упражненияр-значение составляет 0,939. Эти результаты говорят о том,
Ш1ШШ
Глава 9. Многофакторный дисперсионный анализ...
что, используя уровень значимости = 0,05, допущение об однородности углов
наклона верно в данном анализе (для данной выборки), так что можно продолжить
ковариационный анализ.
35-
30-
25-
20-
Сжатие
зо-
25-
20-
15-
О
О
О
1
.00
о
о
о
о о
о о о
о__
1
50.00
<ю о о
о о
-Сх______0 О
о
0 00
о
о о
оо а> о о
о
(D Q___ О
О О D
О
О ОО
о
1 1
100.00 150.00
Упражнения
200.00
Z
1
Жен
л
2С
Z
Рис. 9.6. Отношения между длительностью упражнений в неделю в минутах
и силой сжатия для мужчин и женщин
35-
30-
25-
20-
Сжатие
зо-
25-
20-
15-
О
О
о
!
.00
о
о
о о
о о
о
о
о
о
1
50.00
о о о
о
о
о о о о
о
оо о
о
О CD
о
о о
о о о
(DO О
ии О
о о
о о о
о
1 1 1
100.00 150.00 200.00
5
нет
Упражнения
Рис. 9.7. Отношения между длительностью упражнений в неделю в минутах
для потребляющих и не потребляющих алкоголь
ANCOVA
ШШШ1
Таблица 9.6. Тестирование допущения об однородности наклонов для пола
и упражнений
Величина
Скорректированная модель
Свободный член
Пол
Упражнения
Пол*упражнения
Ошибка
Сумма
Скорректированная сумма
Сумма
квадратов
560.053
7807.479
69.358
40.686
2.363
734.127
42 135.000
1294.180
df
3
1
1
1
1
46
50
49
Средний
квадрат
186.684
7807.479
69.358
40.686
2.363
15.959
F
11.698
489.212
4.346
2.549
0.148
Значимость
<0.001
<0.001
0.043
0.117
0.702
Таблица 9.7. Тестирование допущения об однородности для алкоголя
и упражнений
Величина
Скорректированная модель
Свободный член
Алкоголь
Упражнения
Алкоголь 'упражнения
Ошибка
Сумма
Скорректированная сумма
Сумма
квадратов
161.863
6619.891
29.800
0.019
0.146
1132.317
42 135.000
1294.180
df
3
1
1
1
1
46
50
49
Средний
квадрат
53.954
6619.891
29.800
0.019
0.146
24.616
F
2.192
268.931
1.211
0.001
0.006
Значимость
0.012
<0.001
0.277
0.978
0.939
Тест Левина для ковариационного анализа силы сжатия, включающего
фактор потребления алкоголя, пол и ковариату упражнений, имеет значение 0,292
(р = 0,381); этот результат не значимый, так что допущение о равных
дисперсиях принимается. R1 для этой модели равно 0,576, то есть эти факторы объясняют
57,6% всей дисперсии силы сжатия в данных. Это небольшое улучшение К2 = 0,566
для двухфакторного дисперсионного анализа (факторы = пол, алкоголь),
обсужденного ранее в этой главе. Результаты ANCOVA представлены в табл. 9.8.
Таблица 9.8. Ковариационный анализ силы сжатия с факторами пол и потребление
алкоголя и ковариатой длительность упражнений в минутах в неделю
Величина
Скорректированная модель
Свободный член
Упражнения
Сумма
квадратов
745.596
7289.554
12.511
df
4
1
1
Средний
квадрат
186.399
7289.554
12.511
F
15.290
597.957
1.026
Значимость
<0.001
<0.001
0.316
кяд
Глава 9. Многофакторный дисперсионный анализ...
Величина
Пол
Алкоголь
Пол*алкоголь
Ошибка
Сумма
Скорректированная сумма
Сумма
квадратов
517.299
117.498
78.573
548.584
42 135.000
1294.180
df
1
1
1
45
50
49
Средний
квадрат
517.299
117.498
78.573
12.191
F
42.434
9.638
6.445
Значимость
<0.001
0.003
0.015
Оба фактора и их взаимодействия значимы, а ковариата - нет:
• для пола F(l,45) = 42,434,р = <0,001;
• для алкоголя f(l,45) = 9,638,р = 0,003;
• для пол*алкоголь F(l,45) = 6.445,р = 0,015;
• для упражнений F(l,45) = 1,026,р = 0,316 (не значимо).
Так как мы не улучшили качество модели добавлением ковариаты, можно
проверить, есть ли лучший способ измерить упражнения. Возможно, важен тип
занятий: у тех, кто занимается тяжелой атлетикой, сила сжатия наверняка будет
улучшена, по сравнению с теми, кто бегает большие дистанции, например. Возможно,
упражнения лучше регистрировать в виде дихотомической или категориальной
переменной; может быть, различие между теми, кто занимается и вообще не
занимается, важнее, чем время, уделяемое упражнениям (в этом случае упражнения
будут скорее фактором, чем ковариатой). Это демонстрирует, почему любой
исследовательский проект обычно представляет собой непрекращающуюся работу:
вы начинаете с какой-то идеи, проверяете её, улучшаете идею и тестируете снова.
Намыливаете, смываете и повторяете, как говорится в мире рекламы - не
ожидайте получить наилучшую модель с первого раза.
Упражнения
Задача
Вы планируете провести двухфакторный дисперсионный анализ; как часть
процесса вы проводите тест Левина, который даетр-значение = 0,045. Что это
означает для вашего анализа?
Решение
Тест Левина является тестом на однородность при дисперсионном анализе:
проверкой того, что в каждой группе приблизительно одинаковые дисперсии.
Нулевая гипотеза состоит в том, что дисперсии равные, так что если тест Левина
не значим, допущение о равенстве дисперсий принимается, ANOVA можно
продолжить. В данном случае, используя стандартный уровень значимость a = 0,05,
тест Левина значим, то есть допущение об однородности нужно отвергнуть,
ANOVA продолжать нельзя без изменения входных данных или иного решения
проблемы.
Упражнения III
Задача
Вы работаете с двухфакторным дисперсионным анализом; один из ваших
факторов имеет два, другой - три уровня. В ходе анализа данных вы строите график
средних, изображенный на рис. 9.8. Интерпретируйте график и его значение для
статистического анализа.
Оценка пределов средних зависимой переменной
102.00-
X
X
и
g 100.00-
I
с
2
I
6
о »$0°"
96.00-
А
/ \
1 \
1 \
'
i i i
1.00 2.00 3.00
фактор 2
1.00
2.00
фактор 1
Рис. 9.8. График средних для дисперсионного анализа
Решение
Взаимодействие между факторами возможно. В целом уровни 1 и 3 фактора 1
ассоциированы с низкими результатами, а уровень 2 фактора 1-е высокими. Тем
не менее этот эффект больше для случаев с уровнем 1 фактора 2, так что,
возможно, эффект фактора 1 частично зависит от уровня фактора 2.
Задача
В табл. 9.9 представлены результаты двухфакторного дисперсионного анализа,
график средних которого был рассмотрен в предыдущей задаче. Какие выводы о
взаимодействии факторов и результирующей величине можно сделать при
одновременном рассмотрении таблицы и графика средних? Используйте уровень
значимости а = 0,05.
Глава 9. Многофакторный дисперсионный анализ...
Таблица 9.9. Дисперсионный анализ с двумя факторами
Величина
Скорректированная модель
Свободный член
Фактор 1
Фактор 2
Фактор 1 *фактор 2
Ошибка
Сумма
Скорректированная сумма
Сумма
квадратов
145.392
198 801.665
103.782
17.849
23.762
4060.418
303 007.475
4205.810
от*
5
1
2
1
2
24
30
29
Средний
квадрат
29.078
298 801.665
51.891
17.849
11.881
169.184
F
0.172
1766.133
0.307
0.105
0.070
Значимость
0.971
0.000
0.739
0.748
0.932
Решение
Ни факторы, ни их взаимодействия не соотносятся значимо с зависимой
переменной. Результаты следующие:
Фактор 1: F(2,24) = 0,307, р = 0,739 (незначимый);
Фактор 2: F(l,24) = 0,105,р = 0,748 (незначимый);
Фактор 1*Фактор 2: F(2,24) = 0,070, р = 0,932 (незначимый).
Это иллюстрирует тот факт, что не каждый анализ дает значимый результат и
что не следует увлекаться рассмотрением графиков средних. В данном случае, судя
по графику средних, можно предположить наличие взаимодействия в данных, но
дисперсионный анализ дает понять, что и главные эффекты каждого фактора, и их
взаимодействия незначимо отличаются от 0. Для исследовательской команды это
означает, что пора начинать всё с чистого листа. К2 данной модели 0,035, то есть
модель объясняет менее 4% дисперсии зависимой переменной.
Задача
Вы планируете ковариационный анализ с одной непрерывной ковариатой и с
одним фактором с тремя уровнями. На стадии проверки допущений
ковариационного анализа вы строите графики (рис. 9.9). Что отражают эти графики, какое
допущение проверяют, и что можно заключить, глядя на них?
Решение
Это диаграммы рассеяния с проведенными регрессионными линиями для
результирующей переменной (ось у) и ковариаты (ось х); каждый уровень фактора
представлен на отдельном графике. Такой тип графиков используют для проверки
допущения однородности наклонов. Это свидетельствует в пользу схожести
отношений между ковариатой и результирующей величиной для всех уровней фактора.
Если это так, то наклоны регрессионной линии для ковариаты и результирующей
величины должны быть приблизительно одинаковыми для всех уровней фактора.
Упражнения
ш
В данном случае наклон для уровня 2 более крутой, чем для уровней 1 и 3, но без
статистического тестестирования трудно говорить о значимости различий.
О
2
СО
Ковариата
Рис. 9.9. Графики, проверяющие допущение ковариационного анализа
Задача
Для продолжения проверки допущения ковариационного анализа, описанного
в предыдущей задаче, вы осуществили анализ, который дал результаты,
приведенные в табл. 9.10. Используйте уровень значимости а = 0,05.
Таблица 9.10. Результаты теста допущения ковариационного анализа
Величина
Скорректированная модель
Свободный член
Фактор
Ковариата
Фактор'ковариата
Ошибка
Сумма
Скорректированная сумма
Сумма
квадратов
742.689
19 233.663
93.367
487.758
129.749
3463.121
303 007.475
4205.810
df
5
1
2
1
2
24
30
29
Средний
квадрат
148.538
19 233.663
46.683
487.758
64.875
144.297
F
1.029
133.292
0.324
3.380
0.450
Значимость
0.453
0.000
0.727
0.078
0.643
УТЯЖ
Глава 9. Многофакторный дисперсионный анализ...
Решение
Это статистический тест на однородность наклонов; если наклоны однородны,
эффект взаимодействия фактор*ковариата должен быть незначимым. В данных
результатах эффект взаимодействия незначим (F= 0,450, р = 0,643), так что
различие наклонов незначимое, ковариационный анализ можно продолжать.
Задача
Продолжая решение проблемы предсказания силы сжатия, которая
обсуждается на протяжении всей главы, исследовательская команда решила, что тренировка
силы может быть лучшим предиктором силы сжатия, чем упражнения в целом.
К двухфакториой модели с дихотомическими факторами пол
(мужчина/женщина) и потребление алкоголя (да/нет) они добавили непрерывную ковариату:
минуты в неделю, потраченные на тренировку силы. После проверки допущений
ковариационного анализа они протестировали модель и получили результаты,
приведенные в табл. 9.11. К2 для этого ковариационного анализа 0,628.
Интерпретируйте результаты табл. 9.11 и сравните с результатами в табл. 9.8.
Таблица 9.11. Ковариационный анализ силы сжатия с факторами пол
и потребление алкоголя и ковариатой длительность упражнений в минутах в неделю
Величина
Скорректированная модель
Свободный член
Тренировка силы
Пол
Алкоголь
Пол*алкоголь
Ошибка
Сумма
Скорректированная сумма
Сумма
квадратов
813.327
6622.003
80.242
388.763
63.086
34.597
480.853
42 135.000
1294.180
df
4
45
50
49
Средний
квадрат
203.332
6622.003
80.242
388.763
63.086
34.597
10.686
F
19.029
619.711
7.509
36.382
5.904
3.238
Значимость
<0.001
<0.001
0.009
<0.001
0.019
0.079
Решение
Данная модель объясняет больше дисперсии (62,8%), чем модель, включающая
упражнения в качестве ковариаты (57,6%). В данной модели оба фактора и кова-
рпата значимо соотносятся с результатом, силой сжатия; взаимодействия
факторов не значимы. Основные результаты следующие:
для полаД1, 45) = 36,382,/? = 0,001;
для алкоголя F(l, 45) = 5,094, р = 0,019;
для пол*алкоголь F(l, 45) = 3,238, р = 0,079 (незначимый);
для тренировок силы F(l, 45) = 7,509,р = 0,009.
тл
ГЛАВА 10.
Множественная
линейная регрессия
В главе 8 была представлена простая линейная регрессия, в которой одна
независимая переменная использовалась для предсказания, или объяснения, значений
зависимой переменной. Эта модель полезна для ознакомления с принципами
линейной регрессии, но в реальности простая регрессия используется редко. Гораздо
шире распространена множественная линейная регрессия, в которой две или более
независимых переменных связаны с одной зависимой переменной.
Множественная регрессия является обычным исследовательским методом, который
используется во многих областях, включая естественные и социальные науки, медицину и
образование. Одна из привлекательных сторон множественной регрессии -
гибкость; переменные предикторов могут быть непрерывными, категориальными или
дихотомическими, при этом в одном уравнении возможно использование любой
комбинации типов. При использовании категориальной переменной она должна
быть переведена в набор дихотомических фиктивных переменных. Этот метод
тоже будет освещен в данной главе. При увеличении сложности множественных
независимых переменных требуется выполнение дополнительных допущений, и
они также обсуждаются в данной главе. И наконец, методы построения моделей
с множественными предикторами полезны для получения наилучшей модели в
конкретном случае; эти методы тоже обсуждаются в данной главе.
Модели множественной регрессии
Исследование моделей простой линейной регрессии, коэффициента двумерной
регрессии и его квадрата (коэффициента детерминации) используются для
введения в общие понятия регрессионного анализа; в реальности на работу с
уравнениями регрессии с двумя переменными тратят время только в некоторых областях
исследований. Рассмотрим модели предсказания изменений климата, такие как
глобальные климатические модели1 и даже более сложные атмосферно-океаии-
ческие модели общей циркуляции (МОЦ)2. Эти модели были разработаны за
1 General Circulation Models (GCMs). - Прим. пер.
1 Atmosphere-Ocean General Circulation Models (AOGCM). - Прим. пер.
ЕШНН
Глава 10. Множественная линейная регрессия
последние 30 лет для увеличения точности предсказания погодных
закономерностей. В этих моделях учитываются и оцениваются возможные соотношения
между сотнями и тысячами самых разных переменных. Например, в середине 70-
х модели были сосредоточены на переменных состояния атмосферы, тогда как в
ближайшем будущем будут доступны модели, основанные на данных об
атмосфере вместе с информацией о поверхности земли, океаническом и морском льде,
наличии сульфатных и несульфатных аэрозолей, геохимическом цикле углерода,
динамике растительности и химии атмосферы. При объединении этих
дополнительных источников изменчивости в крупномасштабную статистическую модель
стало возможным предсказание качественно разных типов погодной активности в
разных пространственных и временных масштабах.
В данной главе мы будем работать с множественной регрессией в гораздо
меньшем масштабе. В реальности это вполне естественно. На самом деле полезная
регрессионная модель может быть построена с использованием относительно малого
числа переменных-предикторов (скажем, от 2 до 10), несмотря на то что при
построении моделей люди, возможно, рассматривают гораздо больше предикторов
перед выбором тех, которые останутся в конечной модели. Существует много
способов построения регрессионной модели и много целей; нет одного наилучшего
способа построения, но возможен лучший способ построения данной модели для
данной цели. В этой главе будет предложен общий совет, поэтому вам придется
самостоятельно разбираться с тем, что принято и ожидается в вашей
профессиональной сфере. Вот простой пример: регрессионная модель может быть построена
по принципу парсимонии (включение относительно малого числа переменных,
каждая из которых объясняет большую долю дисперсии) или по принципу
объяснения максимального количества дисперсии (скорее всего, в этом случае модель
будет включать больше переменных, из которых каждая будет объяснять
некоторую дополнительную небольшую долю дисперсии). Ни один из подходов не
является лучшим при любых обстоятельствах, так что лучше всего заранее знать, что
ожидается в вашей области исследования или работы.
В разных областях знаний различается степень того, насколько теоретическая
обоснованность и трактовка моделей управляет работой статистиков. В научном
сообществе теоретическое объяснение ценится высоко, и построение модели по
одной частной выборке не одобряется. Однако в деловом мире построение
моделей автоматизированными методами (например, методы с включением или
исключением переменных, обсуждаемые дальше в этой главе) может быть
полностью приемлемым. При обсуждении я больше склоняюсь к теоретическому
подходу, так как провела большую часть карьеры в научном мире. Тем не менее
существуют особые ситуации, в которых может потребоваться и более
практический подход. Повторюсь, суть состоит в осознании традиций и ожиданий
статистического анализа в конкретно вашей сфере деятельности, а также того, что и
почему вы делаете.
При регрессионном моделировании важны два основных принципа. Во-первых,
каждая включенная в модель переменная должна иметь свой собственный вес, то
есть она должна объяснять уникальную дисперсию результирующей переменной.
Модели множественной регрессии
¦неш
Очень часто применяется такое правило, что каждая переменная должна объяснять
статистически значимое количество дисперсии. На самом деле регрессионную
модель нельзя сделать хуже (уменьшить объясненную дисперсию) добавлением
новой переменной, но даже модели, построенные по принципу максимизации
объясненной дисперсии в целом, имеют некоторые правила определения, достаточно
ли данная переменная улучшает модель и может ли она быть сохранена в модели.
Во-вторых, при работе с множественными предикторами нужно ожидать, что
некоторые из них обычно коррелируют как с зависимой переменной, так и друг с
другом; из этого следует, что добавление или удаление предиктора, скорее всего,
поменяет коэффициенты при всех переменных в модели. Это очень важно при
интерпретации результатов: не достаточно утверждать, что переменная Л -
незначимый предиктор результирующей ?, придется сказать, что переменная А -
незначимый предиктор Е в модели, включающей переменные В, С и D.
Формально модели множественной линейной регрессии имеют вид:
где У- зависимая переменная, Р() - константа, Xv Xv ... Хп - независимые
переменные, р0, р ,... р - коэффициенты, а е - остаточный член или ошибка модели. То же
самое было описано в главе 8, тем не менее, основные моменты стоит рассмотреть
сейчас. Зависимая переменная (У) и независимые переменные (XvXr ... Хп) -
данные наблюдений, а константа (р()) и коэффициенты (Р(), Рг ... р/;) - значения,
вычисляемые алгоритмом линейной регрессии так, чтобы минимизировать остаток
или ошибку (е) в модели. Для данного случая (i) предсказание величины У.
вычисляется с помощью умножения данных наблюдаемых величин (Xv X2 и т. д.) на
соответствующие коэффициенты (р,, Р2и т. д.) и добавлением р(). Разность между
наблюдаемой величиной У. и предсказанной величиной Y. - ошибка предсказания,
или остаток е. для данного случая. Коэффициенты определяются так, чтобы сумма
квадратов остатков была минимальна. (Остатки должны быть возведены в
квадрат, потому что некоторые из них положительны, некоторые - отрицательны и в
сумме дают 0, если их не возводить в квадрат.)
Допущения простой регрессии (обсужденные в главе 8) также имеют место
и для множественной регрессии. Кроме того, при использовании более одного
предиктора приходится волноваться о мультиколлинеарности. Это означает,
что ни один из предикторов не должен сильно коррелировать с каким-либо
другим. В частности, ни одна из предикторных переменных не должна быть
линейной комбинацией других; иными словами, нельзя включать в качестве
предикторов переменные Д В и Л+Б в одну модель. Можете смеяться, но это очень
легко - составить новую переменную и забыть убрать её компоненты из
списка предикторов. Сильно скоррелированные предикторные переменные обычно
объясняют одинаковую дисперсию результирующей переменной, что скрывает
от нас отношения отдельных переменных с результирующей. К тому же
модели, содержащие сильно скоррелированные предикторы, обычно нестабильны, то
есть добавление или удаление одной переменной из модели может кардинально
поменять коэффициенты и значимость остальных предикторов. (Мы ожидаем
КЯ1
Глава 10. Множественная линейная регрессия
не значительное, а малое изменение при добавлении или удалении переменной.)
К счастью, большинство статистических пакетов имеют встроенные функции
проверки мультиколлинеарности в моделях регрессии, и её наличие можно
оценить после построения модели.
Мы будем строить модель регрессии для предсказания подростковой
рождаемости (числа родов для девушек в возрасте от 15 до 19 лет на 1000 человек) по
набору других демографических переменных. Мы будем использовать данные
программы развития ООН *. Вы можете скачать эти данные здесь: http://hdr.undp.
org/en/statistics/data/ - и попробовать провести анализ самостоятельно в любой
используемой вами статистической системе или даже попробовать построить еще
лучшую модель. Сейчас мы будем работать лишь с некоторыми переменными,
чтобы демонстрация оставалась простой, но в вашем собственном анализе нет
причин ограничиваться только ими. Другое важное замечание: эти данные - по-
пуляционные, измеренные в масштабах страны; то есть любые замеченные нами
соотношения могут трактоваться лишь в масштабах страны (а не
распространяться на отдельных людей, например).
Первым делом посмотрим на наши возможные переменные. Как обсуждалось в
главе 8, уровень подростковой рождаемости не имеет нормального распределения,
но его натуральный логарифм распределен нормально, поэтому мы можем
использовать преобразованную переменную как результирующую. На рис. 10.1 показана
гистограмма распределения натурального логарифма уровня рождаемости; она
действительно выглядит нормальной, и статистика Колмогорова-Смирнова
(измеряет вероятность того, что переменная происходит из нормального
распределения, обсуждалась в главе 8) для этой переменной 1,139 (р = 0,149), следовательно,
это распределение не слишком отличается от нормального.
Мы считаем, что хорошие предсказания может дать ожидаемая
продолжительность жизни при рождении, которую можно рассматривать как индикатор общего
уровня здоровья в стране. Однако ожидаемая продолжительность жизни точно не
имеет нормального распределения, как видно из гистограммы на рис. 10.2. Судя
по всему, есть две группы стран: одна группа с явно низкой ожидаемой
продолжительностью и почти равномерным распределением приблизительно от 45 до 65,
другая группа с высокой ожидаемой продолжительностью и приблизительно
нормальным распределением с центральным значением около 75. Поверим, что между
странами с низкой и высокой ожидаемой продолжительностью (а не с высокой и
очень высокой ожидаемой продолжительностью) есть важное различие, поэтому
разобьем случаи на две группы, чтобы это отразить. Примерно в одной трети
случаев продолжительность составляет 66 лет или меньше, и это как раз приходится
на тот промежуток, в котором, кажется, и заключается основное различие между
меньшей группой стран с низкой продолжительностью жизни и большей группой
стран с высокой продолжительностью, поэтому мы будем использовать значение
66,0 лет для разбиения ожидаемой продолжительности жизни на категории
низкой или высокой.
United Nations Development Project. - Прим. пер.
Модели множественной регрессии
25-
20-
ота
Част
ю-
5-
о-
[tfl
WL
/шг
/п
fiffl
14
г Ш HI И
п
\\ 1
Ш
Ш
\ш
\\Ш
К
JI_J_l_J_j_L_l
.00 1.00 2.00 3.00 4.00 5.00 6.00
1од(рождаемость)
Рис. 10.1. Гистограмма для натурального логарифмического преобразования
величины уровня подростковой рождаемости
Среднее = 67.99
Станд. откл. = 10.346
N = 194
40.0 50.0 60.0 70.0 80.0
Ожидаемая продолжительность жизни (лет)
Рис. 10.2. Гистограмма для ожидаемой продолжительности жизни при рождении
Глава 10. Множественная линейная регрессия
Другая переменная, которая может помочь построению модели, - валовый
национальный доход (ВНД4) на душу населения, выраженный в международных
долларах с учетом паритета покупательной способности (ППСГ)). Этот показатель
позволит нам сравнить относительный достаток или бедность разных стран. В
целом у стран с большим ВНД меньше подростковая рождаемость, следовательно,
это должен быть хороший предиктор для нашей модели. Преимущество
использования ВНД, выраженного в ППС, в том, что он отражает возможность покупки
эквивалентных товаров в разных странах, таким образом, включает в себя
информацию о разных уровнях цен и позволяет избежать проблемы изменений
межнационального валютного курса. Позже мог бы возникнуть вопрос, выражался ли
доход в других странах в той же валюте, что и в данной, - в американских
долларах, например. Гистограмма ВНД на душу населения представлена на рис. 10.3; ее
центр тяжести сильно смещен влево. Мы вычисляем натуральный логарифм от
ВНД, показанный на рис. 10.4. Он выглядит гораздо ближе к нормальному
распределению, и статистика Колмогорова-Смирнова подтверждает нормальность
(К-С = 0,737, р = 0,649), поэтому в модели будем использовать логарифмически
преобразованный ВНД.
1од(ВНД)
Рис. 10.3. Гистограмма ВНД (ППС 2005 в международных долларах)
на душу населения
1 GNI, gross national income. - Прим. пер.
"' РРР, purchasing power parity. - Прим. пер.
Модели множественной регрессии
Рис. 10.4. Гистограмма натурального логарифма ВНД
(ППС 2005 года в международных долларах) на душу населения
Нам может оказаться полезной и другая переменная - ожидаемое время
школьного обучения. Логично предположить, что страны, которые хотят и имеют
возможность вкладывать средства в образование своих детей, могут также иметь более
низкий уровень подростковой рождаемости. Эта переменная отражает математическое
ожидание того, сколько лет школьного обучения окончит ребенок, основанное на
текущих данных о возрасте учащихся. На рис. 10.5 показано распределение числа
ожидаемых лет обучения; обрыв справа объясняется ограничением статистики
возрастом 18 лет. Как ни странно, статистика Колмогорова-Смирнова свидетельствует
о допустимом нормальном характере распределения (К-С = 0,975, р = 0,298),
поэтому мы можем включить эту переменную в нашу модель без изменений.
Наконец, мы учтем процент урбанизации, то есть процент населения данной
страны, проживающий на территории городов. Эта переменная достаточно
нормально распределена, как показывают гистограмма (рис. 10.6) и тест
Колмогорова-Смирнова (К-С = 0,893, р = 0,403).
Следующее, что нам требуется проверить, - это линейность. Зависимость
между каждой непрерывной независимой переменной и результирующей должна
напоминать прямую. Все точечные графики (не приведены) показывают линейную
зависимость, поэтому мы можем считать допущение верным.
1ТЯ1
Глава 10. Множественная линейная регрессия
ш\
ш\\
J\}\\\\\
ПИП
1 cupK 1 1 1 1 1 1 1 1
1
Nn
N
L
ш
\Ш
11111111^-
.0 5.0 10.0 15.0 20.0
Ожидаемое число лет школьного обучения для детей
(годы)
Рис. 10.5. Гистограмма для ожидаемых лет школьного обучения
20-
15-
Частота
1
5"
Jmffl
rffl
Ш
пш
и
м\\\\\\
1 1 1
0 20.0 40 0
тН
ИКп
Шп
К
Nn
ш
1 1 1 1
60.0 fiO.O 100 0 120.0
Население, процент урбанизации
Рис. 10.6. Гистограмма для процента населения, проживающего
на территории городов
Модели множественной регрессии
¦НЕШ
Хотя регрессионный анализ даст в том числе статистику мультиколлинеарнос-
ти, мы хотим рассмотреть взаимоотношения между переменными предикторов
еще и с помощью матрицы корреляций. Это покажет нам, близка ли какая-то пара
предикторов друг с другом. Матрица корреляций (её верхний треугольник) для
трех непрерывных предикторов отображена в табл. 10.1.
Таблица 10.1. Корреляционная матрица для натурального логарифма ВНД,
процента урбанизации и ожидаемых лет школьного обучения
Юд(ВНД)
Проц. урбаниз.
Ожид. обуч.
Юд(ВНД)
1.000
Проц.урбаниз.
0.723
1.000
Ожид. обуч.
0.805
0.644
1.000
Неудивительно, что все три предиктора близки. Запомним этот результат до
построения модели. Еще можно рассмотреть взаимоотношения между дихотомической
переменной и остальными тремя, проводя одномерные дисперсионные анализы для
различий средних трех непрерывных переменных для двух групп. Неудивительно,
что все три теста сильно значимы, как показано в табл. 10.2. Страны с высокой
ожидаемой продолжительностью жизни более урбанизированы, имеют больший ВНД и
большее математическое ожидание школьных лет обучения.
Таблица 10.2. Средние и результаты одномерного дисперсионного анализа
в странах с высокой и низкой ожидаемой продолжительностью жизни
для натурального логарифма ВНД, процента урбанизации и ожидаемых лет
школьного обучения
Переменная
Проц. урбаниз.
1од(ВНД)
Ожид. обуч.
Ожид.
продолжит.
< 66 лет
> 66 лет
< 66 лет
> 66 лет
< 66 лет
> 66 лет
Среднее
35.5
63.8
7.3
9.2
8.6
13.3
Станд.
откл.
15.8
21.0
0.9
1.0
2.5
2.0
F
89.158
188.163
206.874
Значимость
< 0.001
< 0.001
< 0.001
Согласно теории, все рассматриваемые переменные имеют отношение к
подростковой рождаемости, поэтому мы начнем с модели, включающей все эти
переменные в качестве предикторов. Эта модель значительно лучше нулевой модели
(F(4, 182) = 53,500, р < 0,001) и имеет R = 0,735 и К2 = 0,540, то есть она объясняет
54% дисперсии уровня подростковой рождаемости. Основная статистика
регрессионного анализа представлена в табл. 10.3.
^¦|H№ i Глава 10. Множественная линейная регрессия
Таблица 10.3. Таблица коэффициентов для модели 1
Константа
Юд(ВНД)
Проц.урбаниз.
Ожид. обуч.
Ожид. продолж. жизни
Нестандартизованные
коэффициенты
В
7.706
-0.360
0.002
-0.073
-0.234
Станд. ошибка
0.377
0.072
0.003
0.029
0.159
Стандартизованные
коэффициенты
Бета
-0.487
0.059
-0.233
-0.114
t
20.949
-4.993
0.794
-2.513
-1.474
Значимость
< 0.001
< 0.001
0.428
0.013
0.142
Как и для простой регрессии, каждая строка в этой таблице представляет
информацию об одном из предикторов в модели. Отличие от простой регрессии
заключается в том, что влияние каждого предиктора измерено в контексте полной
модели. Так как мы знаем, что предикторы близки друг к другу, то предполагаем,
что они перекрываются по объясняемой дисперсии результирующей переменной.
В регрессионной модели, когда все предикторы включаются одновременно (как мы
поступили здесь), каждому предиктору засчитывается только его уникальная
объясняемая дисперсия. Это может объяснить, почему переменные, которые должны,
кажется, быть хорошими предикторами подростковой рождаемости (процент
урбанизации и ожидаемая продолжительность жизни), не значимы в этой модели.
Основные результаты отдельных предикторов следующие:
Ь&ВНД): (3 = -0,360, t = -4,993, р < 0,001.
ВНД на душу населения - значимый предиктор уровня подростковой
рождаемости в модели, также включающей процент урбанизации, ожидаемое
время школьного обучения и дихотомическую ожидаемую
продолжительность жизни. Коэффициент отрицательный, то есть страны с более высоким
ВНД имеют в среднем более низкие уровни подростковой рождаемости.
Процент урбанизации: р = -0,002, t = 0,794, р = 0,428.
Доля людей, проживающих на городской территории, - незначимый
предиктор уровня подростковой рождаемости в модели, также включающей
логарифм ВНД, ожидаемые годы школьного обучения и дихотомическую
ожидаемую продолжительность жизни.
Ожидаемые годы школьного обучения: р = -0,073, t = -2,153, р = 0,013.
Ожидаемые годы школьного обучения - значимый предиктор уровня
подростковой рождаемости в модели, также включающей процент
урбанизации, логарифм ВНД и дихотомическую ожидаемую продолжительность
жизни. Коэффициент отрицательный, то есть страны с большим
ожиданием времени школьного обучения имеют в среднем более низкие уровни
подростковой рождаемости.
Модели множественной регрессии
ШШМШШ
Дихотомически разделенная ожидаемая продолжительность жизни:
Р = -0,234,; = -1,474, р = 0,142.
Ожидаемая продолжительность жизни при рождении (разбитая на <66 лет
и >66 лет) - незначимый предиктор уровня подростковой рождаемости в
модели, включающей также процент урбанизации, ожидаемые годы
школьного обучения и логарифм ВНД.
Так как в этой модели у нас несколько предикторов, стоит взглянуть на
стандартизированные коэффициенты (бета) в этой таблице. Абсолютные значения
этих коэффициентов говорят о том, какие из тестируемых предикторов объясняют
большую долю дисперсии в модели (это нельзя определить напрямую из
коэффициентов, так как они измерены в разных шкалах). Согласно этому показателю,
log(Bb^) объясняет большую долю дисперсии (бета = -0,487), после него следуют
ожидаемые годы школьного обучения (бета = -0,233), дихотомическая переменная
продолжительности жизни (-0,114) и процент урбанизации (р = 0,059). Как и
следовало ожидать, два значимых предиктора имеют наибольшие коэффициенты /?.
Теперь мы повторно построим модель только со значимыми предикторами, но
сначала стоит заметить кое-что еще. При многофакторном дисперсионном
анализе (глава 9) взаимодействия между переменными тестировались автоматически.
В случае регрессии это не так: если вы желаете проанализировать взаимодействие,
нужно указать это в модели заранее. Этот вопрос решается после того, как стало
ясно, какие предикторы будут включены в модель.
Мы проверяем вторую модель, включающую только log(BIH^) и
ожидаемые годы школьного обучения. Эта модель значительно лучше нулевой
(F(2, 184) = 105,21, р < 0,001), R = 0,685, R1 = 0,470, следовательно, удаление двух
переменных из модели привело к уменьшению объясняемой дисперсии всего
на 7%. Как мы и ожидали, это подтверждает предположение, что близкие
предикторы объясняли большей частью одну и ту же дисперсию уровня подростковой
рождаемости. Основная статистика этого регрессионного анализа представлена в
табл. 10.4.
Таблица 10.4. Таблица коэффициентов для модели 2
Константа
Юд(ВНД)
Ожид. обуч.
Нестандартизованные
коэффициенты
В
7.837
-0.366
-0.085
Станд. ошибка
0.345
0.063
0.027
Стандартизованные
коэффициенты
Бета
-0.495
-0.271
t
22.730
-5.827
-3.190
Значимость
< 0.001
< 0.001
0.002
Оба предиктора значимы, и абсолютные значения этих коэффициентов и
^-статистики увеличились (в частности, для ожидаемых лет школьного обучения). Это
еще больше подтверждает предположение, что они перекрывались с двумя
переменными, которыми мы пренебрегли в модели. Основные результаты для
отдельных предикторов следующие:
ЕШНН
Глава 10. Множественная линейная регрессия
log(BHJI): р = -0,366, t = -5,827, р < 0,001.
ВНД на душу населения - значимый предиктор уровня подростковой
рождаемости в модели, включающей ожидаемую продолжительность
школьного обучения. Коэффициент отрицательный, то есть страны с большим
ВНД имеют в среднем более низкие уровни подростковой рождаемости.
Ожидаемые годы школьного обучения: (3 = -0,085, t = -3,190,р = 0,002.
Ожидаемые годы школьного обучения - значимый предиктор
подростковой рождаемости в модели, включающей ВНД на душу населения.
Коэффициент отрицательный, то есть страны с более длительным обучением
имеют большие уровни подростковой рождаемости.
Следующее, что мы хотим сделать, - это протестировать взаимодействие
между ВНД на душу населения и ожидаемой продолжительностью школьного
обучения. Для этого мы добавим в модель взаимодействие ^(ВНД)*ожид. обуч. и
посмотрим, является ли оно значимым. Эта модель объясняет больше дисперсии
(К2 = 0,546) и дает интересные результаты об отношении наших предикторов, как
показано в табл. 10.5.
Таблица 10.5. Таблица коэффициентов для модели 3
Константа
Юд(ВНД)
Ожид. обуч.
1од(ВНД)*ожид. обуч.
Нестандартизованные
коэффициенты
В
5.039
-0.019
0.159
-0.029
Станд. ошибка
1.280
0.165
0.111
0.013
Стандартизованные
коэффициенты
Бета
0.026
0.507
-1.193
t
3.936
-0.118
1.436
-2.267
Значимость
< 0.000
0.906
0.153
0.025
Добавление взаимодействия поменяло все. ВНД на душу населения и
ожидаемые годы школьного обучения - уже не значимые предикторы в модели,
включающей взаимодействие; изменилась направленность влияния ожидаемых лет
обучения. Взаимодействие - единственный значимый предиктор в модели, но мы
все же оставим все три элемента в модели, так как взаимодействие имеет значение
только в контексте главных эффектов. Из значимости взаимодействия следует, что
эффект одной переменной меняется в зависимости от уровня другой переменной.
В данном случае эффект ВНД на подростковую рождаемость изменяется в
зависимости от ВНД на душу населения. Объяснять взаимодействие при
использовании непрерывных переменных особенно сложно, но картина может проясниться,
если посмотреть на график их взаимодействий.
Рисунок 10.7 представляет собой график средних для логарифма уровня
подростковой рождаемости (ось у) на низком, среднем и высоком уровнях
ожидаемой продолжительности школьного обучения (прерывистые линии) и
логарифма ВНД (ось х). Низкий уровень определен как нижняя треть
значений для данной переменной, средний уровень - как центральная треть,
высокий уровень - как верхняя треть.
Модели множественной регрессии
шашшк
5.00-
? 4.50-
I
cl
Ф
а.
о
? 4.00-
еде
Q.
с
0)
¦о 3.50-
ненн
0)
и
о
w 1.00-
2.50-
Оцененные пределы средних 1од(рожд.)
ч.
^v
Nu
сэ—¦ ГЧччч^
N.
'\. \,^^
\ ^ >в
^
\
\
\
\
\
1 Г 1
1.00 2.00 3.00
вндз
Показаны только оцениваемые средние
графЗ
1.00
— 2.00
— 3.00
Рис. 10.7. Средние натурального логарифма уровня подростковой
рождаемости для низкого, среднего и высокого уровней логарифма ВНД
и ожидаемых лет обучения
По рис. 10.7 ясно: хотя высокий ВНД и высокая продолжительность обучения
в школе оба ассоциированы с низкими уровнями подростковой рождаемости,
степень уменьшения в действительности зависит от их взаимодействия. Заметьте,
что для самых высоких уровней школьного обучения нет стран в нижней трети по
ВНД, так как эта линия имеет только две точки.
Для стран с низким уровнем ожидаемой продолжительности школьного
обучения уменьшение уровня подростковой рождаемости почти линейное по
трем уровням ВНД. Для стран со средним уровнем обучения разница между
высоким и средним ВНД выражена лучше. Уменьшение подростковой
рождаемости для стран с высоким уровнем обучения гораздо больше при переходе со
среднего на высокий ВНД, чем уменьшение для стран с одновременно
маленьким или средним уровнем обучения.
Рисунок 10.8 показывает другой способ рассмотрения этого взаимодействия.
На нем мы имеем точечные графики ожидаемых лет школьного обучения и
натуральный логарифм подростковой рождаемости на низком, среднем и высоком
уровнях ВНД. Наклон регрессионной прямой (показатель взаимодействия
между натуральным логарифмом подростковой рождаемости и годами ожидаемого
обучения) заметно больше для более высоких уровнях натурального логарифма
ВНД, что снова указывает на взаимодействие между двумя предикторами. Ин-
EH1IIH
Глава 10. Множественная линейная регрессия
терссен тот факт, что хотя по всему диапазону данных отношения между
натуральным логарифмом подростковой рождаемости и ожидаемой
продолжительностью школьного обучения явно сильные (К2 = 0,44), внутри любой из трех
категорий ВНД эти взаимоотношения много слабее (0,188 - для стран нижнего
уровня ВНД, 0,052 - для стран среднего уровня, 0,168 - для стран высокого
уровня). Это указывает на сильные взаимодействия между нашими предиктор-
ными переменными.
Рис. 10.8. Отношения между натуральным логарифмом подростковой
рождаемости и ожидаемыми годами обучения для стран с низким, средним
и высоким уровнем ВНД
Очевидно, мы не исчерпали возможности анализа взаимоотношений между
ВНД, ожидаемыми годами обучения и подростковой рождаемостью. Также
очевидно, что мы не объясним уровень подростковой рождаемости только лишь
двумя переменными, но, по крайней мере, в целях демонстрации мы имеем рабочую
модель. Статистика Дарбина-Уотсона (Durbin-Watson) для этой модели равна
0,195, что очень близко к нулевому значению 2, поэтому можно принять
допущение о независимости ошибок. Статистика Колмогорова-Смирнова для
стандартизованных остатков в этой модели: 0,663 (р = 0,772), и гистограмма на рис. 10.9
выглядит близкой к нормальной, поэтому можно принять допущение о
нормальности распределения остатков.
Модели множественной регрессии
¦¦ЕШ
5 1
Ч Г
Ш
1
irllll
s 1 Г
Q 1-т-рТ 1
Ml
п
п\
ki
Ш
к
111 HrrN--
3.00000 2.00000 1.00000 .00000 1.00000 2.00000 3.00000
Стандартизованный остаток
Рис. 10.9. Гистограмма стандартизованных остатков для модели 3
Будем оценивать допущение об однородности дисперсии с помощью
построения диаграммы зависимости стандартизованных остатков от стандартизованных
предсказанных величин, как показано на рис. 10.10.
Этот график приближенно является облаком точек без каких-либо признаков
неоднородности, поэтому примем допущение об однородности дисперсии.
Еще следует рассмотреть мультиколлинеарность предикторных переменных.
Осуществим это с помощью подсчета допустимости (tolerance) и фактора
инфляции дисперсии (ФИД) (Variance Inflation Factor) для предикторов в нашей
модели; эта опция поддерживается многими алгоритмами регрессии. Стоит заметить,
что ФИД - лишь обратная величина допустимости (ФИД = 1/допустимость),
поэтому интерпретация любой из этих двух статистик должна давать одинаковый
результат. Существует множество эмпирических правил интерпретации
допустимости и ФИД. Одно из популярных правил - допустимость не должна быть
меньше 0,1 или ФИД больше 10. Если использовать этот стандарт, то в наших данных
есть проблема, как показано в табл. 10.6.
Таблица 10.6. Анализ мультиколлинеарности для модели 3
Предиктор
Юд(ВНД)
Ожид. обуч.
1од(ВНД)*ожид. обуч.
Допустимость
0.50
0.20
0.01
ФИД
20.04
50.35
11.73
ШШШМШШ-
Глава 10. Множественная линейная регрессия
з.ооооо-
2.00000-
V
ато!
анный ост
1 1
ш
О
го
»-
S" 1.00000-
X
(0
ь
о
2.00000-
з.ооооо-
о о
о °оо о
• °°0° с?о° °
° ° б^° о о
9о° о °o°00ft °о^о0А°о0
о ° о © о те
о осР° rfP * 00 ° °/|о
оо^о * о@о>°ооо* ° °
«о V «оо <Р о оо 0
0 ° °* о оо°
° о о о 0°
° о -,
о
о о° о
о
о о
1 1 1 1 1 1
3.00000 2.00000 1.00000 .00000 1.00000 2.00000
Стандартизованное предсказанное значение
Рис. 10.10. Гистограмма стандартизованных остатков для модели 3
Однако другие ученые считают, что принятые значение ФИД и устойчивости не
указывают на некорректную регрессионную модель; возьмите в качестве примера
статью ОЪрайена (O'Brien), процитированную в приложении С. Мы знаем, что
наши предикторные переменные сильно коррелируют. Следовательно, если бы
мы продолжили анализ, то рассматривали бы больше переменных для включения
в модель, возможно, выбросили бы одну или обе эти переменные или
скомбинировали их (может быть, вместе с некоторыми другими). Продолжим интерпретацию
текущей модели, чтобы закончить пример.
Уравнение регрессии для наших данных:
log(poжд.) = 5,039 - 0,019(log(BHA)) + 0,159(Ожид. обуч.) =
= 0,029(к^(ВНД)*ожид. обуч.) + е.
Хотя коэффициенты при log(BI^) и Ожид. обуч. незначимо отличаются от О
в этом анализе, мы оставим их в уравнении, так как член взаимодействия сам по
себе имеет значение только в контексте уравнения, которое включает переменные,
участвующие во взаимодействии. Заметьте также, что было бы неверно
интерпретировать коэффициенты при log(Bbm) и Ожид. обуч. без отсылки к их
взаимодействию: напротив, каждый коэффициент должен быть интерпретирован в
контексте полного уравнения.
Мы можем использовать это уравнение для предсказания значения уровня
подростковой рождаемости для страны, если даны величины ВНД надушу
населения и ожидаемая продолжительность школьного обучения. Заметьте, что обе
переменные - и рождаемость, и ВНД - являются логарифмически преобразо-
Модели множественной регрессии
ванными, поэтому если эти переменные даны нам в исходном виде, мы должны
взять логарифм, перед тем как включать их в уравнение. Наши результаты,
полученные из уравнения, будут выражены в единицах логарифма уровня
рождаемости. Так как это вряд ли будет осмысленным показателем для большинства людей,
мы можем перевести результат в уровень подростковой рождаемости, понять его
будет гораздо проще. Стоит отметить, желательно, чтобы входные данные для
предсказания лежали в пределах значений, включенных в исходную выборку;
другая возможность - применить модель вне диапазона использованных
значений, но мы этого не хотим, так как нельзя утверждать верность регрессионного
уравнения вне диапазона значений, использованных для его построения.
Предположим, мы хотим посчитать предсказанный уровень подростковой
рождаемости для страны с ВНД на душу населения 12 000 (ППС в международных
долларах, как определено ранее) и с ожидаемым обучением в школе в течение
12 лет. В первую очередь нам необходимо перевести исходную статистику в
натуральный логарифм:
1п( 12000)- 9,393.
После этого можно подставить значения в уравнение и посчитать:
log(Oжид. рожд.) = 5,039 - 0,019(9.393) + 0,159(12) - 0,029(9,393*12) =
= 3,500.
Стоит заметить, что мы удалили член ошибки (е), так как сейчас мы
считаем предсказанный ^(рожд.): известно, что между предсказанной величиной и
действительной, измеренной для страны с такими значениями переменных X,
может быть ошибка предсказания. Теперь пересчитаем предсказанное значение
log(poжд.) потенцированием:
е3-™-33,12.
Этот результат говорит о том, что, согласно нашей регрессионной модели,
страна с ожидаемым школьным обучением 12 лет и ВНД 12 000 ППС в
международных долларах имеет предсказанную подростковую рождаемость 33,12 на 1000.
Фиктивные переменные
Множественная линейная регрессия может использовать либо непрерывные, либо
дихотомические предикторные переменные. Но иногда требуется работать с
переменными, имеющими более чем две категории. В этом случае нужно преобразовать
категориальную переменную в некоторый набор дихотомических, или фиктивных,
переменных. Предположим, что колледж желает провести некоторое исследование
начальных годовых заработков своих выпускников 2010 года. Данные
представлены так, чтобы отражать средний балл" студента и область обучения
(гуманитарные, общественные или естественные науки). Средний балл записан в два разряда
с определенным максимальным уровнем 4,0 (идеально, или твердое «отлично»)
GPA - grade point average. - Прим. пер.
вгя
Глава 10. Множественная линейная регрессия
и минимальным уровнем 0,0 (провал по всем предметам), хотя реальные данные
заключены между 2,5 и 4,0. Данные приведены по выпускникам, поэтому можно
ожидать более высоких оценок, чем средняя оценка по всему колледжу Заработная
плата выражена в тысячах долларов и колеблется от 19,6 до 58,6.
Желательно включить область обучения в нашу модель предсказания
начальной заработной платы, но сперва нужно преобразовать эту переменную в
фиктивные (дихотомические) переменные. Нельзя включить её в модель просто так:
статистический пакет будет интерпретировать номера, использованные для значений
этой переменной, как численные значения (например, 2 больше 1), тогда как в
действительности они - просто маркеры категорий. Существует насколько
способов преобразования в фиктивные переменные. Сейчас будет продемонстрирован
один из наиболее популярных методов.
Мы имеем категориальную переменную с четырьмя категориями, то есть нам
нужно создать три фиктивные переменные для преобразования информации,
содержащейся в этой переменной. Вообще говоря, если переменная имеет k
категорий, то для её замены требуется k - 1 фиктивных переменных. Нам
необходимо выбрать одну категорию для того, чтобы использовать её в качестве опорной;
остальные категории будут с ней сравниваться.
Для данного анализа выберем гуманитарные науки как опорную категорию,
потому что для неё показана самая низкая заработная среди четырех групп, как
следует из табл. 10.7. Выбор группы с наименьшей заработной платой даст
положительные коэффициенты для остальных категорий, что может оказаться проще
для объяснения широкой публике (например, родителям абитуриентов).
Таблица 10.7. Средние годовые заработные платы для выпускников
колледжа четырех основных направлений обучения
Направление
Гуманитарные науки
Естественные науки
Социальные науки
Образование
Средний заработок
(тысячи долларов)
22.7
56.3
28.9
28.0
Стандартное
отклонение заработка
11.4
9.3
10.1
8.1
Схема преобразования фиктивных переменных показана в табл. 10.8.
Таблица 10.8. Представление фиктивных переменных
для направлений обучения
Направление
Гуманитарные науки
Естественные науки
Социальные науки
Образование
*i
0
1
0
0
*2
0
0
1
0
*з
0
0
0
1
Модели множественной регрессии
ШНЕШ
Мы создали три новые фиктивные переменные X, Х2 и Xv и придаем им
значение 0 или 1 в зависимости от направления обучения. Для нашей опорной
категории гуманитарных наук все три фиктивные переменные имеют значение 0.
Для каждого из остальных трех направлений одна из фиктивных переменных
имеет значение 1, причем для других она имеет значение 0. Такая комбинация трех
фиктивных переменных однозначно определяет каждое направление обучения: в
случае значений Х = 0, Х2 = 1 и X., = 0 мы знаем, что направление обучения -
социальные науки.
Уравнение регрессии, предсказывающее заработную плату по направлению
обучения, следующее:
В этом уравнении Р() будет средним заработком для обучающихся
гуманитарным дисциплинам. Например, р, будет отражать различие между выпускниками,
специализирующимися в естественных науках, и выпускниками гуманитарного
направления. Регрессионные коэффициенты для этих данных представлены в
табл. 10.9.
Таблица 10.9. Результаты регрессии для уравнения, включающего фиктивные
переменные
Константа
*,
*2
*э
Нестандартизованные
коэффициенты
В
22.682
33.611
6.247
5.288
Станд. ошибка
3.102
4.386
4.386
4.386
Стандартизованные
коэффициенты
Бета
0.905
0.168
0.142
t
7.313
7.662
1.434
1.206
Значимость
<0.000
<0.000
0.163
0.236
Уравнение для этих данных следующее:
Сред, заработок = 22,682 + 33,611(ХХ) + 6,247(Х2) + 5,288(X:J) + е.
Для подсчета среднего заработка для любого из четырех направлений обучения
мы просто подставим значения переменных X в это уравнение и решим его.
Например, кто-то имеет область образования, закодированную следующим образом:
X, = О, Х2 = 0 и Х{ = 1. Подставляя эти значения в уравнение, получим:
Предок, средн. зараб.(образование) = 22,682 + 33,611(0) + 6,247(0) +
+ 5,288(1) = 27,97.
Это средний заработок для выпускников в этой области образования, и он
совпадает с соответствующим числом в табл. 10.7 (в пределах ошибки округления).
Если выполнить такое же упражнение для остальных трех направлений, вы
обнаружите, что подсчитанные с помощью регрессионного уравнения значения для
ЕН«В
Глава 10. Множественная линейная регрессия
этих направлений также совпадут со значениями, представленными в табл. 10.7.
^-критерии для каждого коэффициента проверяют отличие от 0. Так как
переменные - фиктивные и в качестве опорной группы использовалось направление
гуманитарных наук, ^-статистика говорит о том, является ли стартовый заработок для
студентов данного направления значимо отличающимся от заработка студентов
направления гуманитарных наук. Из табл. 10.9 можно увидеть, что есть значимое
различие между начальным заработком для точных и гуманитарных наук, так как
X, значимо отличается от 0 (t = 7,662, р < 0,001), при этом два других сравнения не
значимы. Из этого следует важное замечание о фиктивном преобразовании: если
вы знаете, какие сопоставления вам нужно провести, не сомневайтесь и
определите фиктивные переменные так, чтобы осуществить эти сравнения.
Методы построения регрессионных моделей
Только что мы рассмотрели довольно простые регрессионные модели, но часто
при построении моделей приходится начинать с 10, 20 или даже большего числа
независимых переменных, рассматриваемых как кандидаты на включение в
модель. Но даже для меньшего числа предикторов вам, возможно, захочется
применить формальный процесс построения моделей. Многие статистические пакеты
включают несколько альтернативных алгоритмов построения моделей, некоторые
системы позволяют комбинировать разные методы или алгоритмы внутри одной
модели.
Существуют две категории методов построения моделей: пошаговые методы,
которые сами выбирают предикторы для включения и исключения, и методы
выбора наилучшего подмножества7, для которых задаются рассматриваемые
предикторы для включения на каждом шаге. Термин подмножество8 относится
к группе предикторов, которые вводятся в модель одной группой или
рассматриваются для включения как группа. При построении моделей в этой главе мы
использовали все предикторы как одно подмножество, но, как мы увидим, есть и
другие возможности. Термин «пошаговый» относится к методу выбора предик-
торной переменной для включения внутри подмножества. Пошаговые методы в
целом автоматизированы и сами выбирают, какую переменную внутри
подмножества добавлять или оставлять в модели, используя указанный пользователем
критерий.
Автоматизированные методы построения моделей приняты не во всех
направлениях исследований, в основном потому, что они основаны на данных вашей
выборки больше, чем на теоретических соображениях. Это вызывает очевидные
трудности, так как мы часто строим модели с целью поставить нашу выборку в
общий контекст. Другой недостаток автоматизированных методов - в том, что
они, по сути, эквивалентны выполнению множества тестов значимости на одних
и тех же данных без какой-либо поправки на инфляцию вероятности ошибки
' Blocking method - дословно «метод разбиения на блоки», в русскоязычной литературе принят
термин «метод выбора наилучшего подмножества» - Прим. пер.
<s «Block» - блок - Прим. пер.
Модели множественной регрессии
¦¦ЕШ
в эксперименте, что увеличивает вероятность ошибки I рода. Тем не менее
автоматизированные модели считаются приемлемыми в некоторых
направлениях исследований и работы, и если они приемлемы в вашей конкретной области,
почему бы их не использовать. Единственное, о чем следует всегда помнить: три
разных пошаговых метода могут дать три разные регрессионные модели, так что
придется обосновать выбор метода.
Отчасти основой автоматизированных методов для построения моделей
является мера, называемая частной корреляцией9, - корреляция между двумя
переменными с удалением эффекта одной или более других переменных. В
автоматизированных алгоритмах регрессии частная корреляция используется для определения
однозначной дисперсии, объясненной предикторной переменной, чтобы выбрать
предиктор, который сильнее связан с результирующей переменной при
измерении в присутствии остальных предикторов. Даже в модели, для которой вы сами
определяете включаемые предикторы и их порядок, тестирование частичной
корреляции может быть полезным для измерения значимости отдельных
предикторов в присутствии остальных.
Всего существует три основных пошаговых метода построения моделей:
Метод с исключением (backward removal)
Все предикторы из подмножества добавляются в модель одновременно и
далее удаляются один за другим, пока удаление переменных не начинает
значимо снижать качество модели. Этот алгоритм рассматривает
переменные для удаления по уникальной дисперсии, объясненной ими в полной
модели. Переменная, объясняющая меньшую дисперсию (с наименьшей
частной корреляцией), рассматривается как первый кандидат на удаление,
и после удаления этой переменной следующим кандидатом на удаление
становится переменная, объясняющая наименьшую дисперсию, и так
далее. Пользователь определяет критерий удаления переменной и показатель
качества модели.
Метод с включением (forward entry)
В модель добавляется одна переменная за раз, начиная с той, у которой
самая большая абсолютная корреляция с зависимой переменной. Для второго
и последующих предикторов переменная выбирается так, чтобы она
имела наибольшую частную корреляцию с предиктором, который объясняет
большую часть уникальной дисперсии зависимой переменной. На каждую
переменную может действовать указанный пользователем критерий
включения в модель. В основном он основан на улучшении качества модели или
индивидуальной значимости предиктора.
Метод с включением и исключением (пошаговый, stepwise)
Пошаговый метод является комбинацией методов включения и
исключения. Предикторы вводятся в регрессионную модель по одному в
зависимости от того, насколько они улучшают модель. Каждый раз, когда
добавляется новый предиктор, уже включенные в модель предикторы
9 Partial correlation иногда переводится как частичная корреляция. - Прим. пер.
кгя
Глава 10. Множественная линейная регрессия
оцениваются и могут быть удалены, если они уже незначимо улучшают
качество модели.
Методы выбора наилучшего подмножества не автоматизированы, но с их
помощью вы можете вводить или тестировать переменные группами. В данной главе
мы вводили все переменные одной группой, но бывают случаи, когда вы можете
захотеть вводить переменные отдельными подмножествами. Один из примеров:
вы хотите узнать, как подмножество переменных улучшит качество модели после
того, как другое подмножество уже включено в модель. Например, вам
понадобилось подготовить общественное мероприятие с целью побудить людей
упражняться и улучшать здоровье. Вы знаете, что многие демографические факторы (пол,
национальность или этническая группа, доход и т. д.) также связаны с
упражнениями и здоровьем, и вы хотите отделить дисперсию упражнений и здоровья,
связанную с проведенным мероприятием, от дисперсии, объясняемой
демографическими факторами. Для этого, скорее всего, вы сначала введете
демографические переменные в уравнение одной группой, а затем переменные, связанные с
мероприятием, второй группой. Таким образом, результирующая дисперсия,
объясненная вашими исследованиями, будет дополнительной к объясненной
демографическими переменными. Такой тип модели особенно полезен в исследованиях,
основанных на наблюдениях, когда вы не можете использовать случайное
разбиение на группы для контроля влияния переменных (демографических, например),
которые могут соотноситься с результатом.
Метод выбора наилучшего подмножества может быть также совмещен с
автоматизированным методом благодаря использованию одного
автоматизированного метода в одном блоке и другого (или никакого) - в другом блоке. Продолжим
предыдущий пример: возможно, у вас имеются измерения некоторого числа
демографических показателей, из которых вы не можете с уверенностью выбрать
объясняющий наибольшую дисперсию в вашей модели. Если в вашей области
исследований допускается использование автоматизированных процессов
построения модели, вы можете ввести все демографические переменные одной группой и
позволить алгоритму решить, какие из них наиболее полезны для объяснения
дисперсии результирующей переменной. После этого вы можете ввести переменные
из вашего собственного исследования в качестве второй группы, чтобы узнать, как
много дисперсии они объясняют сверх описанной демографическими
переменными. Для второй группы не нужно использовать какой-либо автоматизированный
метод построения моделей, можно просто ввести все ваши переменные
одновременно.
Давайте рассмотрим простой пример, для того чтобы проанализировать эффект
использования различных пошаговых методов. Представьте, что вы - педагог,
заинтересованный в поиске зависимости между IQ и традиционными
показателями общих способностей (вычислительный и речевой навыки, навыки чтения
и мыслительной способности), а также нетрадиционными показателями
(музыкальные способности и физическое состояние). Часть данных выборки показана
в табл. 10.10.
Модели множественной регрессии
Таблица 10.10. Данные, показывающие зависимость между традиционными
и нетрадиционными показателями общих способностей и Ю
IQ
85.0
90.0
95.0
100.0
100.0
100.0
105.0
105.0
110.0
110.0
115.0
120.0
Вычисление
3.0
3.0
4.0
4.0
5.0
5.0
6.0
6.0
7.0
7.0
8.0
9.0
Чтение
5.0
6.0
6.0
7.0
7.0
8.0
8.0
8.0
9.0
9.0
10.0
10.0
Речь
7.0
7.0
7.0
8.0
8.0
8.0
8.0
8.0
8.0
8.0
9.0
9.0
Физическое
состояние
10.0
10.0
9.0
9.0
8.0
7.0
6.0
5.0
4.0
3.0
3.0
1.0
Музыкальность
6.0
6.0
7.0
7.0
8.0
9.0
8.0
7.0
6.0
6.0
5.0
4.0
Мышление
10.0
10.0
8.0
5.0
6.0
5.0
4.0
5.0
6.0
9.0
10.0
9.0
Вы решаете исследовать отношения между переменными при помощи
вычисления всех попарных корреляций и их статистической значимости, как показано в
табл. 10.11 (только верхний треугольник). Неудивительно, что большинство
традиционных измерений (вычисление, чтение и речь) сильно положительно
коррелируют с IQ (** = р < 0,01). Также неудивительно, что многие из этих мер высоко
коррелируют друг с другом. Значит, любая регрессионная модель, включающая
несколько из них, будет, скорее всего, иметь высокий уровень коллинеарности.
Однако оценка мыслительной способности несильно связана с большинством
остальных переменных (кроме музыкальных навыков), и физическое состояние
имеет строго отрицательную корреляцию с IQ и несколькими другими мерами
способностей. Кроме того, удивительно отсутствие связи между IQ и
музыкальными способностями.
Таблица 10.11. Попарные связи между традиционными и нетрадиционными
показателями общих способностей и IQ
IQ
Вычисление
Чтение
Речь
Физическое
состояние
Музыкальность
Мышление
IQ
1.000
Вычисление
0.978**
1.000
Чтение
0.976**
0.963**
1.000
Речь
0.914**
0.887**
0.912**
1.000
Физическое
состояние
-0.955**
-0.986**
-0.954**
-0.836**
1.000
Музыкальность
-0.427
-0.481
-0.381
-0.337
0.503
1.000
Мышление
-0.073
0.026
-0.055
-0.103
-0.062
-0.738**
1.000
ЕГЕ11
Глава 10. Множественная линейная регрессия
Если вас больше интересует не проверка конкретной теоретической модели,
а исследование отношений переменных внутри этого набора данных, то вы,
вероятно, решите использовать автоматизированный метод для построения вашей
модели. Вы решаете построить две модели, используя два метода (методы с
включением и метод с исключением), и далее сравнить эти две модели. Для метода с
включением вы устанавливаете критерий добавления р < 0,05 (коэффициент для
любого предиктора должен удовлетворить этому стандарту, для того чтобы быть
включенным в модель); для метода с исключением вы устанавливаете критерий
удаления F> 0,100 (переменная будет удалена, если уровень изменения
вероятности F-статистики не ниже 0,100).
Метод с включением
В методе с включением первым в модель вводится предиктор с наиболее
сильной парной корреляцией с IQ (г = 0,978) - вычислительные навыки. В этой
модели К2 = 0,956, и такая модель в целом значимая, с F(l, 10) = 217,36,;; = 0,000. Ни
один другой предиктор не дает значимого улучшения качества модели, так что
это и есть наша окончательная модель, её коэффициенты показаны в табл. 10.12.
Такой результат одновременно и удивляет (так как другие исследователи
обнаруживали близкие отношения IQ и других переменных, например мыслительной
способности), и не удивляет (так как большинство наших предикторов настолько
сильно коррелируют, что мы могли бы ожидать большого перекрытия между
любыми объясняемыми дисперсиями IQ).
Таблица 10.12. Окончательная регрессионная модель, построенная
с использованием автоматизированного метода с включением
Константа
Вычисление
Нестандартизованные
коэффициенты
В
74.318
5.122
Станд. ошибка
2.043
0.347
Стандартизованные
коэффициенты
Бета
0.978
f
36.374
14.743
Значимость
0.000
0.000
Таблица 10.13 отражает информацию о переменных, исключенных из финальной
модели. Можно заметить, рассматривая ^-статистики и значимость колонок, что
некоторые из них очень близки к порогу включения, особенно «Чтение» (t = 2,239,
р = 0,052). Легко представить, что, если бы вы составили выборку из других
наблюдений, «Чтение» могло бы быть включено в модель, а «Счет» - исключено.
Регрессионная модель, полученная при помощи метода с включением:
IQ = 74,318 + 5,122(Счет) + е.
Одно огромное преимущество использования метода с включением состоит в
быстром нахождении минимальной модели, объясняющей наибольшее количество
дисперсии в вашей выборке данных. Это особенно полезно, если у вас имеется
большое число предикторов, но никаких определенных теоретических соображений по
поводу того, как они соотносятся друг с другом и с результатом, и вы хотите только
Модели множественной регрессии
ШШЕШ
получить наилучшую модель для ваших данных. Этот подход похож на «добычу
данных»10 тем, что вы просто хотите узнать, какая информация содержится в ваших
данных, и не намереваетесь рассматривать их как выборку из генеральной
совокупности или распространить результат на другие данные. Проблема этого подхода в
том, что модель, построенная автоматизированным методом, может сильно
зависеть от специфичного набора данных, использованных для построения модели. Это
действительно является проблемой, если вы собирается распространить результат
из вашей выборки на генеральную совокупность. Если множество ваших
предикторов сильно коррелируют друг с другом и с результирующей переменной (как в
нашем примере), небольшие различия в их корреляциях могут приводить к высокой
нестабильности модели. Если вы составите другую выборку, то модель, полученная
теми же автоматизированными методами, может выглядеть немного иначе, чем
модель, полученная из вашей первоначальной выборки.
Таблица 10.13. Переменные, исключенные из окончательной модели регрессии,
построенной с помощью автоматизированного метода с включением
Модель
Чтение
Речь
Физическое состояние
Музыкальность
Мышление
Бета
.467
.219
.288
.057
-.098
t
2.239
1.648
.716
.737
-1.594
Значимость
0.052
0.134
0.492
0.480
0.146
Частичная
корреляция
0.598
0.482
0.232
0.239
-0.469
Допустимость
0.072
0.213
0.029
0.768
0.999
Метод с исключением
Метод с исключением начинается с включения в модель всех заданных предик-
торных переменных, которые после удаляются одна за другой, начиная с той
переменной, которая вносит наименьший вклад в дисперсию. Модель перестраивается
заново при каждом удалении, поэтому вклад каждой переменной пересчитывается
для каждой новой модели.
В табл. 10.14 представлены пять моделей, полученных по пути к окончательной
модели. После каждой итерации одна независимая переменная удаляется,
начиная с «Речи», и далее «Физическое состояние», «Музыкальность» и «Мышление».
В табл. 10.15 показаны коэффициенты для моделей в каждой итерации, а также
соответствующие значения t и их значимость.
Напомним, что предыдущий метод с включением дал нам только одну
независимую переменную, «Счет», включенную в модель. Интересно, что, используя
метод с исключением, мы пришли к окончательной модели, включающей два
предиктора, «Счет» и «Чтение». Также поучительно наблюдать за тем, как
коэффициенты меняются с удалением переменных из модели, - это подчеркивает, что обыч-
10 Data mining - интеллектуальный, или глубинный, анализ данных - собирательное название
методов обнаружения в данных ранее неизвестных закономерностей и извлечение из этого
практической пользы. - Прим. пер.
I л7"1Г
Глава 10. Множественная линейная регрессия
но добавление или удаление переменной из модели изменяет коэффициенты для
большинства или всех остальных переменных.
Таблица 10.14. Пошаговое моделирование линейной регрессии с исключением
Модель
1
2
3
4
5
Введенные переменные
Мышление, Вычисление,
Музыкальность, Речь,
Чтение, Физическое состояние
Удаленные
переменные
Речь
Физическое
состояние
Музыкальность
Мышление
Метод
Включение
Исключение (критерий: вероятность
удаляемого F > 0.100)
Исключение (критерий: вероятность
удаляемого F>0.100)
Исключение (критерий: вероятность
удаляемого F > 0.100)
Исключение (критерий: вероятность
удаляемого F>0.100)
Таблица 10.15. Стандартизованные коэффициенты для каждой итерации
моделирования
Модель
1
2
3
Константа
Вычисление
Чтение
Речь
Физическое
состояние
Музыкальность
Мышление
Константа
Вычисление
Чтение
Физическое
состояние
Музыкальность
Мышление
Константа
Вычисление
Чтение
Нестандартизованные
коэффициенты
В
64.480
3.827
3.070
.048
1.011
-1.222
-.742
64.514
3.851
3.088
1.026
-1.224
-.743
80.511
2.449
2.863
Станд. ошибка
20.702
2.369
1.749
2.628
1.423
0.864
0.445
18.819
1.822
1.301
1.040
0.777
0.402
9.530
1.137
1.279
Стандартизованные
коэффициенты
Бета
0.731
0.487
0.003
0.305
-0.167
-0.169
0.735
0.490
0.310
-0.167
-0.169
0.467
0.454
t
3.115
1.616
1.755
0.018
0.710
-1.414
-1.668
3.428
2.114
2.373
0.986
-1.575
-1.848
8.448
2.153
2.239
Значимость
0.026
0.167
0.140
0.986
0.509
0.216
0.156
0.014
0.079
0.055
0.362
0.166
0.114
0.000
0.068
0.060
Упражнения
ШШШЙ
Модель
4
5
Музыкальность
Мышление
Константа
Вычисление
Чтение
Мышление
Константа
Вычисление
Чтение
Нестандартизованные
коэффициенты
-1.179
-0.785
68.274
3.149
2.476
-0.294
64.655
2.765
2.945
0.775
0.399
5.524
1.122
1.352
0.253
4.649
1.093
1.316
Стандартизованные
коэффициенты
-0.161
-0.179
0.601
0.393
-0.067
0.528
0.467
-1.522
-1.968
12.360
2.806
1.831
-1.161
13.908
2.529
2.239
0.172
0.090
0.000
0.023
0.105
0.279
0.000
0.030
0.050
Окончательная модель регрессии, полученная с помощью метода с
исключением (модель № 5 в табл. 10.14), следующая:
IQ = 64,655 + 2,765(Вычисление) + 2,945(Чтение) + е.
Эта модель объясняет 97,2% дисперсии IQ, что немного больше, чем модель
метода с включением (95,6%). Хотя обе модели объясняют почти одинаковое
количество дисперсии, интересно отметить отличие коэффициентов. Модель,
полученная методом включения, имеет большую константу и больший коэффициент для
навыка вычислений. Эти различия, скорее всего, объясняются тем, что некоторое
количество дисперсии, объясненной навыком «Счет» в первой модели,
объясняется навыком «Чтение» во второй и что включение второго предиктора
естественно уменьшает константу, так как каждый результат IQ теперь объясняется двумя
оценками умственных способностей, а не одной.
Упражнения
Множественная линейная регрессия может быть использована для изучения
разных типов исследовательских задач, как показано в нижеследующих
примерах.
Пример 1
Как специалист по кадрам вы заинтересованы в мотивационных факторах,
связанных с продуктивностью (результирующая переменная) ИТ-групп (групп,
занимающихся разработкой информационных технологий), основанной на метрике
KLOC (kilolines of code) - тысячи строк кода, написанного за неделю. Считается,
что на продуктивность влияют четыре мотивационных фактора: они могут быть
основаны либо на внутренней, либо на внешней мотивации и быть либо
самооценочными, либо оцениваемыми со стороны. Для измерения этих факторов
разработаны четыре шкалы, которые используются как предикторные переменные в
модели (в скобках оригинальные названия):
КЕЯ1
Глава 10. Множественная линейная регрессия
• самооценка внутренней мотивации (IS - intrinsic self-report);
• внешняя оценка внутренней мотивации (Ю - intrinsic observed);
• самооценка внешней мотивации (ES - extrinsic self-report);
• внешняя оценка внешней мотивации (ЕО - extrinsic observed).
KLOC выражен в тысячах строк кода; четыре предиктора измерены в
шкале от 0 до 100. Описательная статистика для этих переменных представлена в
табл. 10.16.
Таблица 10.16. Описательная статистика для четырех типов мотивационных
факторов и KLOC
Переменная
Продуктивность (KLOC)
Самооценка внутренней мотивации (IS)
Наблюдение внутренней мотивации (Ю)
Самооценка внешней мотивации (ES)
Наблюдение внешней мотивации (ЕО)
п
50
50
50
50
50
Среднее
3.5
41.3
54.7
27.1
40.7
Станд. ошибка
2.3
14.8
19.4
16.5
25.5
Верхний треугольник корреляционной матрицы для этих переменных показан
в табл. 10.17; корреляции cp-value 0,05 или менее обозначены звездочкой (*).
Таблица 10.17. Корреляционная матрица для четырех типов мотивационных
факторов и KLOC
KLOC
Внут. самооц. (IS)
Внут. наблюд. (Ю)
Внеш. самооц. (ES)
Внут. наблюд. (ЕО)
KLOC
1.00
Внут.
самооц. (IS)
0.25
1.00
Внут.
наблюд. (10)
0.12
-3.70*
1.00
Внеш.
самооц. (ES)
0.43*
-1.70
0.18
1.00
Внут.
наблюд. (ЕО)
0.67*
0.35*
-0.18
0.61*
1.00
Задача
Что вы заметили в корреляционной матрице такого, что могло бы помочь в
определении регрессионной модели для этих данных?
Решение
Во-первых, два из четырех предикторов имеют значимую парную корреляцию с
результирующей переменной: самооценка внешней мотивации (г = 0,43,р = 0,002)
и внешняя оценка внешней мотивации (/-= 0,67, р < 0,001); отдельные/7-value не
были включены в табл. 10.17, но взяты из компьютерной выдачи. Во-вторых,
некоторые из наших предикторов имеют значительную корреляцию друг с другом,
и это нужно держать в голове при построении нашей модели. Пары близких
предикторов: самооценка внешней мотивации и внешняя оценка внутренней
мотивации (/'= -0,37,;; = 0,008), самооценка внутренней и внешняя оценка внешней
Упражнения
¦¦ESI
мотивации (г = 0,35, р = 0,013), самооценка внешней и внешняя оценка внешней
мотивации (г= 0,612, р < 0,001).
Вы решаете включить все четыре предиктора в вашу регрессионную модель;
эта модель объясняет 51,5% дисперсии KLOC и дает коэффициенты и значимость
тестов, как показано в табл. 10.18. Общий тест качества модели дает результат
F(4, 45) = 11,927, р< 0,001.
Таблица 10.18. Таблица коэффициентов для регрессионного анализа
предсказания KLOC из четырех типов психологических факторов
Константа
В нут. самооц. (IS)
Внут. наблюд. (Ю)
Внеш. самооц. (ES)
Внут. наблюд. (ЕО)
Нестандартизованные
коэффициенты
В
-0.989
0.022
0.023
0.003
0.062
Станд. ошибка
1.253
0.023
0.009
0.023
0.015
Стандартизованные
коэффициенты
Бета
0.129
0.280
0.019
0.660
t
-0.790
0.970
2.370
0.124
4.044
Значимость
0.434
0.337
0.017
0.902
< 0.001
Задача
Интерпретируйте информацию табл. 10.18, запишите уравнение регрессии и
предположите, какой может быть следующий шаг, чтобы попытаться понять
отношения между этими переменными.
Решение
Уравнение регрессии для этих данных следующее:
KLOC = -0,989 + 0,022(Внут. самооц.) + 0,023(Внут. наблюд.) +
+ 0,003(Внеш. самооц.) + 0,062(Внеш. наблюд.) + е.
Эта модель значительно лучше нулевой модели, но только два из четырех пре-
дикторных переменных значимо отличаются от 0: 10 (t= 2,370, р = .017) и ЕО
(t = 4,044, р < 0,001). В зависимости от цели вашего анализа вы можете
остановиться здесь или продолжить исследование данных. Вы знаете из корреляционной
таблицы, что в этой выборке данных самооценка внутренней мотивации значимо
коррелирует с внешней оценкой и внутренней мотивацией, и внешней. Это
может объяснять недостаток значимости самооценки внутренней мотивации в этой
модели, поэтому вы можете запустить модель только с самооценкой внутренней
мотивации в качестве предиктора и посмотреть, сколько дисперсии объяснено
только ею. Вы также можете добавить больше переменных в модель, например
пол; возможно, мотивация мужчин и женщин устроена по-разному.
Пример 2
Вы - консультант по менеджменту в отделе розничных продаж, проводящий
исследование движений на рабочем месте и затрат времени для определения того,
шмшш
Глава 10. Множественная линейная регрессия
какой из двух предикторов (размер штрих-кода или точность продавца) имеет
наибольший эффект на производительность кассы, измеренной в товарах в секунду.
На вопрос трудно ответить, так как единицы измерения в каждом случае
различны: размер штрих-кода измеряется в квадратных сантиметрах, в то время как
точность кассира измеряется как доля успешных с первого раза сканирований товара.
Ваш клиент хочет увеличить производительность, так как покупатели жаловались
на длинные очереди в магазине. Однако большие сканеры дороже маленьких, а
тренировочные курсы для работников требуют затрат и при этом не обязательно
повышают точность. Менеджер хочет узнать, тратить ли больше денег на
тренировки (пли наем лучших работников) или покупку больших сканеров, поэтому вы
решаете провести исследование, чтобы увидеть, какая переменная имеет больший
вклад в производительность: размер сканера или точность кассира.
Производительность и точность - непрерывные переменные; хотя размер
штрих-кода теоретически является непрерывной переменной, в этой выборке
данных он имеет только три значения (2см2, 4 см2 и 6 см2), поэтому вы решаете
работать с ним как с категориальной переменной. В исследовании участвуют
сканеры только трех размеров; описание непрерывных переменных представлено в
табл. 10.19.
Таблица 10.19. Информация для производительности кассы и точности кассира
Переменная
Пропускная способность
Точность
N
30
30
Среднее
0.76
81.31
Стан д. откл.
0.36
4.38
Минимум
0.20
73.62
Максимум
1.50
91.13
Задача
Ваше первое задание - составить схему фиктивных переменных для размера
сканера. Используйте наименьший размер сканера как опорную категорию и
переведите значения в такое количество переменных Х} сколько нужно для
однозначного представления размера сканера.
Решение
Наиболее очевидная схема представлена в табл. 10.20. Стоит заметить, что
переменные сохраняют порядок значений переменной. Значение 2 см2 должно быть
перекодировано со значениями 0 для переменных Х] и Xv в то время как коды для
4 см2 и 6 см2 можно поменять местами, при этом кодирование по-прежнему
удовлетворяет условию обозначения 2 см2 как опорной.
Таблица 10.20. Схема фиктивных переменных
Размер
2 см2
4 см2
6 см2
*,
0
1
0
*2
0
0
1
Упражнения ^^Н^^1Е?ЁЯ
Предположим, вы проверили все необходимые допущения и проводите
регрессионный анализ, используя схему фиктивных переменных, представленную
выше. Эта модель значительно лучше модели (F(3, 26) = 21,805, р < 0,001) и
объясняет 68,3% дисперсии производительности. Коэффициенты для этого анализа
представлены в табл. 10.19.
Задача
Запишите уравнение регрессии, основанное на информации из табл. 10.21, и
дайте рекомендации менеджеру, основанные на данных вашего анализа.
Таблица 10.21. Данные по производительности и точности кассира
Константа
Точность
*.
*г
Нестандартизованные
коэффициенты
В
0.737
-0.003
0.071
0.685
Станд. ошибка
0.917
0.011
0.094
0.015
Стандартизованные
коэффициенты
Бета
-0.034
0.094
0.909
t
0.803
-0.246
0.756
6.491
Значимость
0.429
0.808
0.456
<0.001
Решение
Уравнение регрессии:
Производительность = 0,737 - 0,003(Точность) + 0,071(Х,) + 0,685(Х2) + е.
Регрессионный анализ (п = 30) проверил эффекты точности кассира (доля
успешных с первого раза сканирований) и размера сканера (в см2) и
производительность (число просканированных продуктов в секунду). Практический контекст
этого исследования - условия розничной продажи, приводящие к увеличению
производительности. В исследование вошли сканеры трех размеров (2 см2, 4 см2,
6 см2). И производительность, и точность были приблизительно нормально
распределены; производительность имела диапазон от 0,20 до 1,50, среднее 0,76 и
стандартное отклонение 0,36; точность имела диапазон от 73,62 до 91,13 со
средним 81,31 и стандартным отклонением 4,38.
Регрессионная модель объяснила 68,3% дисперсии производительности.
Точность кассира не была связана с производительностью (t = -0,246, р = 0,808), но
размер сканера - был. Большой сканер (6 см2) имел значимое преимущество
перед наименьшим (2 см2) (t = 6,491, р = 0,000). Сканер среднего размера (4 см2) не
давал определенного преимущества перед самым маленьким (t = 0,756,/? = 0,456).
Я рекомендую покупать большие сканеры, размером в 6 см2, так как этот размер
является наиболее сильно соотносящейся с увеличением производительности
переменной.
шту
ГЛАВА 11.
Логистическая,
мультиномиальная
и полиномиальная регрессия
Множественная линейная регрессия - это мощный и гибкий метод, способный
справиться со многими различными типами данных. Однако существует много
других видов регрессии, более подходящих для определенных видов данных или
для описания определенных связей между переменными. Мы обсудим некоторые
из этих видов регрессии в данной главе. Логистическая регрессия подходит для
таких ситуаций, когда зависимая переменная дихотомическая, а не непрерывная,
мультиномиальная - работает в случае категориальных зависимых переменных
(с более чем двумя категориями), а полиномиальная - больше подходит для
случаев, когда связь между независимой и зависимой переменными описывается с
помощью уравнения, включающего многочлен (например, с х2 или х]). Если вам
незнакомо понятие «отношение вероятностей», вам было бы полезно сначала
прочесть посвященный ему раздел главы 15, поскольку отношение вероятностей
играет ключевую роль в интерпретации результатов логистической регрессии.
Логистическая регрессия
Множественную линейную регрессию можно использовать для поиска связей
между одной непрерывной зависимой переменной и набором независимых
переменных, которые могут быть непрерывными, дихотомическими или
категориальными; в случае категориальных независимых переменных их необходимо
перекодировать в набор дихотомических фиктивных переменных.
Логистическая регрессия во многом напоминает множественную линейную
регрессию, по ее применяют в том случае, если зависимая переменная
дихотомическая (то есть может принимать только два значения). Ее значение может быть
как дихотомическим по своей природе (человек либо закончил школу, либо нет),
так п может представлять разбиение непрерывной или категориальной
переменной на две группы (кровяное давление измеряется па непрерывной шкале, но для
целей анализа испытуемых можно разбить на две группы: с повышенным давлс-
Логистическая регрессия ; ]|И^|1Е&Э!
нием и с нормальным). Зависимую переменную в логистической регрессии
традиционно кодируют как 0-1, где 0 обозначает отсутствие какой-то характеристики,
а 1 - ее наличие. Зависимая переменная в логистической регрессии - это логнт,
что есть преобразованная вероятность данного значения исследуемой
характеристики; можно легко преобразовать логиты в вероятности и наоборот, что мы
увидим позже.
Вы можете задаться вопросом, почему нельзя просто использовать
множественную линейную регрессию с категориальной зависимой переменной. На то есть
две причины:
1. Для категориальных переменных не выполняется условие гомоскедастич-
ности (равенства дисперсий).
2. Множественная линейная регрессия может выдавать значения за
пределами допустимого интервала 0-1 (наличие или отсутствие).
Логит также называют логарифмом вероятностей по причинам, очевидным из
его определения. Если р - это вероятность того, что объект исследования будет
обладать данным свойством, то логит для этого объекта определяется, как
показано на рис. 11.1.
логит (р) = log- = \og(p)-\og(l-p)
Р
Рис. 11.1. Определение логита (логит-функции)
Для преобразования вероятностей в логиты используют натуральный
логарифм (с основанием ё).
Не считая использования логита как зависимой переменной, уравнение для
логистической регрессии с п независимыми переменными записывается очень
сходно с уравнением для линейной регрессии, что можно видеть на рис. 11.2.
логит(/?) = P0+faX]+P2X2...+ PnXn+e
Рис. 11.2. Уравнение логистической регрессии
Как и в случае линейной регрессии, существуют показатели качества модели
для всего уравнения (сравнивающие ее с нулевой моделью, в которой все
коэффициенты нулевые) и тесты для каждого отдельного коэффициента (проверяющие
для каждого из них нулевую гипотезу о том, что коэффициент незначимо
отличается от нуля). Смысл коэффициентов, однако, иной; вместо их интерпретации в
ключе линейных изменений зависимой переменной мы говорим в терминах
отношения вероятностей (обсуждается в данной главе и в главе 15; обратите внимание,
что отношение вероятностей часто используется в медицинской и
эпидемиологической статистике).
Как и в случае линейной регрессии, логистическая регрессия требует
выполнения нескольких условий, касающихся используемых данных:
EHS11
Глава 11. Логистическая, мультиномиальная и полиномиальная...
Независимость
Как и во множественной линейной регрессии, каждый испытуемый не
должен зависеть от других испытуемых, так что нельзя использовать
несколько измерений, проведенных на одном человеке, членах семьи и так далее
(если родство может изменить значения пары испытуемых но сравнению
со случайно выбранными людьми).
Линейность
Между хотя бы одной из непрерывных независимых переменных и логи-
том зависимой переменной наблюдается линейная зависимость. Это
проверяется с помощью создания модели с логитом как зависимой переменной и
независимыми переменными в виде всех непрерывных независимых
переменных, их натуральных логарифмов и их взаимодействий друг с другом.
Если взаимодействие окажется незначимым, мы можем считать, что
линейность соблюдена.
Отсутствие мультиколлинеарности
Как и в случае множественной линейной регрессии, ни одна из
независимых переменных не должна быть линейной функцией других независимых
переменных, и они не должны быть слишком сильно связаны друг с другом.
Первый запрет в этом определении абсолютен (обычно нарушается только
по рассеянности исследователя, например если он включает в уравнение
в качестве независимых переменных величины a, b и а + /?); вторая часть
открыта для обсуждения, и ее выполнение оценивается с помощью
критериев мультиколлинеарности, используемых при проведении
регрессионного анализа. Как обсуждается в главе 10, специалисты не имеют единого
мнения по поводу того, насколько неабсолютная мультиколлинеарность
опасна для регрессионной модели.
Нет полного разделения
Значение одной переменной нельзя точно предсказать по значению(ям)
другой переменной или их набора. Эта проблема чаще всего возникает в
случае, если у вас есть несколько дихотомических или категориальных
переменных в модели; данное условие можно проверить с помощью
составления таблиц сопряженности по этим переменным и проверки, что в них нет
пустых ячеек.
Положим, вас интересуют факторы, влияющие на степень обеспеченности
населения Соединенных Штатов медицинским страхованием. Вы берете случайную
выборку 500 испытуемых из данных Системы наблюдения за поведенческими
факторами риска (BRFSS) 2010 года, ежегодное исследование взрослых в США
(подробнее про эту систему - см. главу 8). Наличие страховки - это
дихотомическая переменная; после исследования нескольких потенциальных факторов вы
решаете использовать пол (дихотомическая переменная) и возраст (непрерывная
переменная) как независимые переменные. В этом наборе данных у 87,4%
респондентов есть страховка, их средний возраст составляет 56,4 лет (стандартное
отклонение 17,1 лет), а 61,7% из них - женщины.
Логистическая регрессия
1ЕД
Посмотрев на условия применимости логистической регрессии, мы можем
сказать, что первое из них выполняется, поскольку известно, что данные этого опроса
собирают опытные исследователи в соответствии с национальным планом. Для
оценки линейности между логитом и возрастом мы создадим регрессионную
модель, включающую возраст, натуральный логарифм возраста и взаимодействие
между ними. Результаты приведены в табл. 11.1.
Таблица 11.1. Проверка линейности между возрастом и логитом
Возраст
(.п(Возраст)
Возраст*1п(Возраст)
Константа
В
1.305
-9.353
-0.218
15.862
Станд. ошибка
1.136
7.884
0.198
13.055
Вальд
1.321
1.407
1.209
1.476
df
1
1
1
1
Знач.
0.250
0.235
0.271
0.224
Ехр(В)
3.690
0.000
0.804
7.74Е6
Единственное, что нас сейчас интересует в этой таблице, - это значимость
взаимодействий. Это проверяется с помощью статистики Вальда (Wald),
разновидности хи-квадрата. Как можно видеть из колонки значимостей, в нашей модели
взаимодействие незначимо, таким образом, мы можем считать условие
линейности выполненным.
Мы оценим мультиколлинеарность с помощью проведения линейной
регрессии с проверкой на мультиколлинеарность. Мы получили значение
толерантности, равное 0,999, а ФИД (фактор инфляции дисперсии) оказался равен 1,001 для
обеих переменных, что означает, что мультиколлинеарность в данном случае не
представляет проблемы. Как обсуждалось в главе 10, стандартное эмпирическое
правило состоит в том, что толерантность не должна превышать 10, а ФИД не
должен быть меньше 0,10. Отсутствие мультиколлинеарности неудивительно,
потому что эти данные получены из случайной выборки на уровне государства по
большому диапазону возрастов (от 18 и старше в данном случае), соответственно,
нет оснований предполагать наличие связи между возрастом и полом.
Для проверки наличия полного разделения мы создаем таблицу сопряженности
между нашей дихотомической переменной (полом) и зависимой переменной
(наличием медицинской страховки). Эти частоты приведены в табл. 11.2.
Таблица 11.2. Проверка на полноту разделения
Страховка
Отсутствует
Имеется
Пол
Женщины
32
234
Мужчины
20
167
У нас нет пустых ячеек; на самом деле у нас нет даже почти пустых ячеек.
Последний случай может представлять проблему, хотя это и не полное разделение,
IFBCTI
Я
Глава 11. Логистическая, мультиномиальная и полиномиальная...
поскольку такая ситуация может привести к очень большим стандартным
ошибкам оценок и, соответственно, широким доверительным интервалам. Чтобы
увидеть, как может выглядеть полное разделение, посмотрите на гипотетические
данные, представленные в табл. 11.3.
Таблица 11.3. Гипотетические данные с полным разделением
Страховка
Отсутствует
Имеется
Пол
Женщины
62
234
Мужчины
0
167
В данном примере все те, у кого нет страховки, женского пола. Таким образом,
если мы знаем, что у кого-то нет страховки, мы сразу же знаем, что это женщина;
вот что подразумевается под полным разделением. На практике полное
разделение чаще встречается с категориальными независимыми переменными
(предположите, что мы также включили в модель такие переменные, как работа, семейное
положение и образованность), если некоторые из них неравномерно распределены
по отдельным категориям. Модель логистической регрессии не сработает в случае,
если имеется полное разделение, так что лучше всего попробовать перекодировать
переменную. Если у семейного положения есть шесть категорий (женат/замужем,
вдовец/вдова, в разводе, холост/не замужем, проживание с партнером того же
пола, проживание с партнером противоположного пола), возможно, вам удастся
так их объединить, чтобы получилось 2-3 категории, в каждую из которых
попадает достаточно испытуемых, чтобы избежать проблемы разделения.
Разумеется, вы должны уметь защитить свой выбор объединяемых категорий. К примеру,
если в вашем случае важно только то, женат/замужем испытуемый(ая) или нет,
вы вольны перекодировать данную переменную для отражения этого факта. Даже
если у вас в данных нет полного разделения, правильно избегать переменных с
очень малым числом испытуемых в определенных категориях, поскольку, как
говорилось ранее, в таких ситуациях доверительные интервалы оценок будут
чрезвычайно широкими.
Проверив выполнение всех условий, мы продолжаем наш анализ. В
логистической регрессии качество модели в целом определяется несколькими способами. Во-
первых, существует критерий для коэффициентов модели, проверяющий, лучше
ли наша модель в целом, чем нулевая модель без коэффициентов (omnibus test);
модель проходит этот тест со статистикой хи-квадрат (2 степени свободы), равной
16,686 (р < 0,001). Кроме того, мы рассчитываем три других показателя
качества модели: -2 логарифма правдоподобия, R2 Кокса и Снелла (the Cox&Snell R2)
п R2 Нагелкерке (the Nagelkerke R2). Показатель -2 логарифма правдоподобия в
чем-то аналогичен сумме квадратов остатков в линейной регрессии. Сложно
интерпретировать его значение само по себе, но он полезен при сравнении двух и
более вложенных моделей (моделей, в которых большая из них включает все
независимые переменные из меньшей), поскольку чем меньше значение -2 логариф-
Логистическая регрессия
¦¦ЕЛ
мов правдоподобия, тем лучше модель. Мы не можем рассчитать R Пирсона или
R2 для логистической регрессии, по существуют две статистики вместо этой
величины: R2 Кокса и Снелла и R2 Нагелкерке. Обе основаны на сравнении логарифма
правдоподобия нашей модели и нулевой модели; поскольку максимум R2 Кокса
и Снелла никогда не достигает теоретического максимального значения, равного
1,0, R2 Нагелкерке использует поправку, приводящую к тому, что оно всегда
больше первого. Обе из них интерпретируют так же, как и коэффициент детерминации
в линейной регрессии, то есть они описывают долю дисперсии зависимой
переменной, объясняемую моделью. Из-за поправки R2 Нагелкерке в целом принимает
более высокие значения, чем R2 Кокса и Снелла для одной и той же модели. В
нашем случае -2 логарифма правдоподобия равны 301,230, R2 Кокса и Снелла равно
0,038, a R2 Нагелкерке равно 0,073. Коэффициенты для этой модели представлены
в табл. 11.4.
Таблица 11.4. Коэффициенты для логистической регрессии, предсказывающей
наличие медицинской страховки по полу и возрасту
95% ДИ для Ехр(В)
Мужской пол
Возраст
Константа
В
0.030
0.035
0.118
Стан д.
ошибка
0.310
0.009
0.475
Вальд
0.010
16.006
0.062
df
1
1
1
Знач.
0.922
< 0.001
0.804
Ехр(В)
1.031
1.036
1.125
Нижняя
граница
0.561
1.018
Верхняя
граница
1.893
1.054
Мы перекодировали пол в новую переменную, Мужской пол, со значениями 0
для женщин и 1 для мужчин; это проще интерпретировать, поскольку нам не надо
запоминать, как какая категория была закодирована. Как и с линейной
регрессией, критерии для константы нам обычно не интересны. Независимые переменные
оцениваются с помощью хи-квадрата Вальда (the Wald chi-square); значения до-
стоверностей интерпретируют так же, как р-значения в любых других
статистиках. В данном случае мы видим, что возраст достоверно предсказывает наличие
страховки (хи-квадрат Вальда (1 df) равен 16,006, р < 0,001), тогда как мужской
пол - нет (хи-квадрат Вальда (1 df) p = 0,922). Вспомнив, что мы закодировали
страховку так, что 0 - это ее отсутствие, а 1 - наличие, легко видеть, что,
поскольку, коэффициент для возраста положительный, с увеличением возраста
вероятность наличия страховки у человека тоже растет.
Столбец Ехр(В) дает нам отношение вероятностей для каждой независимой и
зависимой переменной с поправкой на все остальные переменные в модели;
последние две колонки показывают 95%-ный доверительный интервал для
отношения вероятностей с поправкой. Если вы незнакомы с отношениями вероятностей,
вам лучше прочитать раздел главы 15 о них, прежде чем двигаться дальше,
потому что тут приведено лишь очень краткое объяснение. Как видно из названия,
отношение вероятностей - это частное вероятностей двух возможных событий.
КБЯ
Глава 11. Логистическая, мультиномиальная и полиномиальная...
В данном случае это отношение вероятности иметь страховку, если испытуемый
мужского пола, к таковому, если это женщина. Нейтральное значение для
отношения вероятностей равно 1; значения выше 1 говорят о повышенной вероятности, а
ниже 1-о пониженной. Отношение вероятностей для мужчин выше 1 (1,031), это
значит, что в этом наборе данных у мужчин больше вероятность иметь страховку,
чем у женщин. Однако этот результат статистически не значим, что следует из
/^-значения для статистики Вальда (0,922) и того факта, что 95%-ный
доверительный интервал для отношения вероятностей (0,561, 1,893) включает нейтральное
значение 1. Таким образом, мы можем утверждать, что в модели,
предсказывающей наличие страховки по полу и возрасту, пол не имеет значимой
предсказательной силы.
Посмотрев на вторую строку таблицы, мы видим, что возраст имеет значимую
предсказательную силу для наличия страховки в модели, включающей пол.
Исправленное отношение вероятностей равно 1,036, а 95%-ный доверительный интервал
равен (1,018, 1,014); обратите внимание, что доверительный интервал не включает
единицу Отношение вероятностей для возраста и мужского пола выглядит очень
небольшим (совсем немного больше 1), но помните, что это отношение на самом
деле характеризует разницу в вероятностях при увеличении возраста на 1 год;
например, вероятность иметь страховку для человека возраста 35 лет в сравнении с
34 годами (и с поправкой на пол). Для установления ожидаемого изменения на
более протяженном промежутке времени вам необходимо возвести отношение
вероятностей в степень, равную числу лет в промежутке. К примеру, предсказываемое
отношение вероятностей иметь страховку при десятилетней разнице равняется:
1,036'°= 1,424.
Часто при сообщении о своих результатах полезно приводить гипотетические
примеры такого рода совместно с самими результатами, чтобы аудитория легче
понимала важность непрерывных переменных. Уравнение логистической модели
в данном случае получилось следующее:
Логит(р) = 0,118 + 0,030(мужской пол) + 0,035(возраст) + е.
Как отмечалось ранее, несмотря на значимое отличие нашей модели от нулевой
при предсказании наличия страховки, она не объясняет заметной доли
дисперсии в данных (определено с помощью подсчета псевдо-R2). Это неудивительно,
потому что, вероятно, важную роль в данном случае играет множество других
переменных, кроме возраста и пола; если бы мы продолжали анализ, мы бы точно
проверили важность наличия работы и заработка, к примеру. Также мы бы могли
попробовать разбить возраст на моложе/старше 65 лет, поскольку мы знаем, что
почти все люди старше 65 имеют медицинскую страховку по Федеральной
программе страхования Medicare1. Мы также могли бы попробовать построить модель
только для людей моложе 65, поскольку не ожидаем увидеть заметного
разнообразия в наличии страхования у людей 65 лет и старше.
Это на.танпе одной ил программ страхопаппя в США. - Прим. пер.
Мультиномиальная логистическая регрессия ВНИ
Преобразование логитов в вероятности
Люди, незнакомые со статистикой, вряд ли будут понимать, что такое логит, так
что, как правило, лучше представлять результаты в единицах, которые они поймут.
Для логистической регрессии очевидным выбором будут вероятности. К счастью,
логистическое уравнение для любого набора независимых переменных можно
преобразовать, используя вероятности, по следующей формуле:
р уравнение логистической регрессии
Предсказанная вероятность = : '
г * /a i „уравнениелогистическом регресемпч
Продолжив наш пример с данными BRFSS, мы можем найти вероятность того,
что у человека есть страховка, подставив его или ее значения в наше уравнение, а
затем преобразовав его по формуле, представленной выше. К примеру, для
мужчины (х] = 1) в возрасте 40 лет (х, = 40), предсказанный логит равен:
Предсказанный лошт(р) = 0,118 + 0,030(1) + 0,035(40) = 1,548.
Затем мы подставляем это значение в формулу для предсказанной
вероятности:
Предсказанная вероятность = е{,гт / (1+ eirriH) = 0,825, или 82,5%.
Мультиномиальная логистическая
регрессия
Если у вас есть данные, по всем параметрам подходящие под логистическую
регрессию, но только с зависимой категориальной переменной (более чем с двумя
категориями), то использование мультиномиальной логистической регрессии
может оказаться тем, что нужно. Возвращаясь к данным BRFSS, нас
интересует, какие переменные могут предсказать состояние здоровья. К счастью, данные
этого опроса включают переменную, характеризующую состояние здоровья по
шкале, часто применяемой в медицине и здравоохранении. Нередко
характеризуемая как «самооценка общего здоровья», эта переменная включает ответы
людей о том, какая из пяти категорий лучше всего описывает их состояние здоровья
в целом:
1. Великолепное.
2. Очень хорошее.
3. Хорошее.
4. Неплохое.
5. Плохое.
Ответы на этот вопрос в нашей выборке представлены в табл. 11.5.
Глава 11. Логистическая, мультиномиальная и полиномиальная...
Таблица 11.5. Самооценка общего здоровья
Великолепное
Очень хорошее
Хорошее
Неплохое
Плохой
Частота
64
149
136
65
21
Процент
14.7
34.3
31.3
14.9
4.8
Суммарный процент
14.7
49.0
95.2
80.2
100.0
Мы будем использовать возраст (непрерывная переменная) и пол
(дихотомическая) в уравнении мультиномиальной логистической регрессии для
предсказания самооценки состояния здоровья. Поскольку у нас довольно мало
испытуемых попало в одну из категорий в зависимой переменной, мы
составим таблицу сопряженности с полом, чтобы проверить, не будет ли какая-то
из ячеек пустой или почти пустой; если так, это окажется проблемой по той
же причине (полное или почти полное разделение), которая обсуждалась при
разборе логистической регрессии. Результаты показаны в табл. 11.6.
Таблица 11.6. Таблица сопряженности общего состояния здоровья и пола
Состояние здоровья
Великолепное
Очень хорошее
Хорошее
Неплохое
Плохой
Женщины
36
92
80
45
15
Мужчины
28
57
56
20
6
Тут есть как хорошие новости, так и плохие: несмотря на то что пустых ячеек
не оказалось, в одной из них всего лишь 6 испытуемых (мужчин с плохим
здоровьем), что может привести к довольно широким доверительным интервалам. Мы
решаем объединить две нижние категории и продолжить наш анализ. Нам
необходимо выбрать одну из категорий как категорию сравнения для анализа;
компьютерный алгоритм затем сравнит каждую из остальных категорий с этой, чтобы
понять, есть ли достоверные различия с какой-то из них. Мы выбираем категорию
«Великолепное».
Качество модели в мультиномиальной логистической регрессии можно
оценить теми же методами, что и в биномиальной логистической регрессии. -2
логарифма правдоподобия для данной модели равны 660,234 (это может быть
полезно знать для сравнения с более сложными моделями), и наша модель
достоверно лучше нулевой модели без независимых переменных (х2 (6 df) = 19,194,
р = 0,004). Статистики псевдо-Я2 говорят нам, что мы объясняем только неболь-
Мультиномиальная логистическая регрессия
¦ШЕЕЭ
шую долю дисперсии (К2 Кокса и Снелла = 0,043, К1 Нагелкерке = 0,046), но это
и неудивительно: следует ожидать, что, кроме возраста и пола, еще очень многие
вещи будут влиять на общее здоровье человека. Кроме того, мы рассчитали
критерии отношения правдоподобий, которые говорят нам об изменении качества
модели при удалении одной из независимых переменных. Если качество модели
значимо понижается (что проверяется с помощью статистики хи-квадрат), это
говорит о большом вкладе удаленной переменной в предсказание значения
зависимой переменной. Данные этого теста приведены в табл. 11.7.
Таблица 11.7. Критерий отношения правдоподобий для мультиномиальной
регрессии, предсказывающей общее состояние здоровья по возрасту и полу
Константа
Возраст
Мужской пол
-2 логарифма правдоподобия
сокращенной модели
660.234
675.719
660.609
Хи-квадрат
0.000
15.485
3.375
df
0
3
3
Знач.
0.001
0.337
В каждом случае «сокращенная модель» обозначает модель без анализируемой
переменной. Из этой таблицы мы можем видеть, что возраст - это значимая
переменная, определяющая общее состояние здоровья, тогда как пол таковой не
является. Константа в данном случае не изучается, поскольку ее удаление не меняет
число степеней свободы модели. Как мы сказали ранее, более низкое значение
-2 логарифмов правдоподобия соответствует лучшей модели, так что мы не
удивлены заметному росту этой величины при удалении возраста из модели (675,719
против 660,234) и при этом крайне незначительному изменению (660,608 против
660,234) при удалении фактора «пол».
Оценки параметров для нашей полной модели приведены в табл. 11.8. Обратите
внимание, что это на самом деле данные по трем моделям одновременно,
поскольку коэффициенты оцениваются для каждого из наших сравнений («очень
хорошее» против «великолепного», «хорошее» против «великолепного» и «неплохое/
плохое» против «великолепного»).
Таблица 11.8. Оценки параметров модели мультиномиальной регрессии,
предсказывающей общее состояние здоровья по возрасту и полу
95%ДИдляЕхр(В)
Общ.
категория
здоровья
Очень
хорошее
Константа
Возраст
Мужской
пол = 1
В
0.681
0.001
0.227
Станд.
ошибка
0.519
0.009
0.003
Вальд
1.723
0.004
0.562
df
1
1
1
Знач.
0.189
0.949
0.454
Ехр(Б)
1.001
1.255
Нижняя
граница
0.984
0.693
Верхняя
граница
1.018
2.274
ивя
Глава 11. Логистическая, мультиномиальная и полиномиальная...
95%ДИдляЕхр(В)
Общ.
категория
здоровья
Хорошее
Неплохое/
плохое
Константа
Возраст
Мужской
пол = 1
Константа
Возраст
Мужской
пол = 1
В
-0.142
0.015
0.095
-1.766
0.030
0.559
Станд.
ошибка
0.542
0.009
0.307
0.638
0.010
0.348
Вальд
0.068
2.836
0.096
7.740
8.701
2.581
df
1
1
1
1
1
1
Знач.
0.794
0.092
0.057
0.005
0.003
0.108
Ехр(Б)
1.015
1.100
1.030
1.748
Нижняя
граница
0.998
0.602
1.010
0.884
Верхняя
граница
1.033
2.009
1.051
3.457
Наши опасения при виде низких значений псевдо-i?2 в данной модели
оправдались: только одна независимая переменная значима для одного из сравнений, а
именно «возраст» для сравнения «Неплохого/плохого» против «Великолепного»
здоровья. Поскольку коэффициент положителен (0,030), а Ехр(Л), или отношение
вероятностей, выше единицы, мы можем утверждать, что больший возраст связан
с более высокой вероятностью иметь «Неплохое/плохое» здоровье, чем
«Великолепное». Обратите внимание, что 95%-ный доверительный интервал для
«возраста» в этом сравнении (1,010, 1,051) не включает нулевого значения 1,0, результат,
который можно ожидать из значимой статистики хи-квадрат Вальда для данной
независимой переменной в этом сравнении.
Полиномиальная регрессия
До сих пор вы много узнали о подборе моделей, где связь между зависимой
переменной и одной или несколькими независимыми линейная, то есть значение
зависимой переменной можно предсказать с помощью взвешенной линейной
суммы независимых переменных плюс константа. На плоскости такие отношения
выглядят как прямые линии с ненулевым наклоном. Однако многие явления
описываются нелинейными законами, и вам нужно уметь моделировать и такие связи.
Любая связь, не являющаяся строго линейной, по определению нелинейна, так
что обсуждение нелинейного моделирования должно быть очень широким. В этом
разделе вы узнаете о двух из наиболее часто используемых моделях регрессии,
основанных на квадратичных и кубических многочленах2.
В квадратичной модели есть как линейный, так и квадратичный член для
независимых переменных, тогда как кубическая включает линейный,
квадратичный н кубический члены; принцип состоит в том, что вы включаете как все
более низкие степени, так и наивысшую. У каждой кривой есть набор экстремумов,
2 Также на английский манер их называют «полиномами» (англ. polinomials), отсюда и название
метода полиномиальной регрессии. - Прим. пер.
Полиномиальная регрессия
число которых на один меньше наивысшего показателя степени1, таким образом,
у квадратичной модели будет один максимум1, а у кубической - один максимум
и один минимум. На рис. 11.3 приведена квадратичная зависимость (у = х2), а на
рис. 11.4 - кубическая (у = г*).
40.00-
30.00-
^20.00-
10.00-
.00-
•
•
•
i
-5.0
•
•
1
-2.5
•
1
.0
X
•
•
•
1
2.5
•
•
•
1
5.0
Рис. 11.3. Квадратичная зависимость (у = х2)
300.00-
200.00-
100.00-
Ъ .00-
-100.00-
-200.00-
-300.00-
•
•
•
1
-5.0
• •
1
-2.5
•
.0
X
•
• •
2.5
•
•
•
5.0
Рис. 11.4. Кубическая зависимость (у = х3)
Точнее говоря, число экстремумов не превышает эту величину; простейший пример несоответствия -
у =-¦ хК У кривой, соответствующей этому уравнению, нет ни одного экстремума. - Прим. пер.
1 Или минимум. - Прим. пер.
ЕЫЗ^ИнИ Глава 11. Логистическая; мультиномиальная и полиномиальная...
Давайте посмотрим на пример из спортивной психологии. Закона Иеркеса-Дод-
сона, впервые сформулированный в 1908 году, постулирует квадратичную
зависимость между возбуждением (независимая переменная) и спортивным результатом
(зависимая переменная). Для многих спортсменов достижение оптимума
физиологического возбуждения, соответствующего максимуму зависимой переменной,
ведет к достижению их цели - выступить максимально хорошо. Если спортсмены
недостаточно возбуждены, они выступят плохо; и наоборот, если они
перевозбуждены, они также покажут плохие результаты.
Однако если связь между возбуждением и качеством выступления на самом
деле кубическая, рост возбуждения будет в итоге приводить к улучшению
выступления, что противоречит предсказанию квадратной модели. Полиномиальную
регрессию можно использовать для проверки качества квадратичной и
кубической моделей, и это позволит принять лучшую зависимость из них в качестве более
правильной модели, описывающей связь возбуждения с качеством выступления
спортсменов.
Уотерс, Мартин и Шретер5 придумали эксперимент для проверки квадратичной
зависимости между кофеином (веществом, вызывающим возбуждение) и
умственными способностями с помощью набора тестов. В ходе эксперимента требовалось
через равный промежуток времени вводить по одной дозе кофеина (6 * 100 мг);
это должно было дать практические эффекты и привести к улучшению
результатов с каждой попыткой вне зависимости от возбуждения. Любая остаточная
дисперсия, объясняемая квадратичным членом, - это свидетельство связи между
возбуждением и качеством работы.
Вы могли бы задаться вопросом, почему участников исследования просто не
приглашали прийти несколько раз для прохождения теста со случайным выбором
дозы кофеина при каждой попытке. Причины были этического характера;
исследователи хотели заметить любые нежелательные реакции на кофеин при низких
дозах, что было бы невозможно при первой попытке со случайной постановкой
эксперимента, поскольку некоторые испытуемые сразу получили бы самую
высокую дозу; кроме того, исследователи хотели минимизировать необходимое число
визитов испытуемых. Для улучшения качества контроля в эксперименте авторы
решили использовать повторяющиеся измерения, среди которых один раз
испытуемые получали плацебо, а другой - дозы кофеина (одинарный слепой метод).
Если экспериментатор замечал нежелательную реакцию, эксперимент
прекращался. Порядок использования плацебо и кофеина выбирали случайно.
Согласно плану, в эксперименте были как зависимые сравнения, так и
независимые, первые должны были показать зависимость от дозы, а вторые -
подтвердить, что наблюдаемые явления не объясняются случайностью (или привычкой).
Здесь приведен только анализ повторных, зависимых измерений. Анализ
проводят последовательно, используя сначала количество кофеина, затем его квадрат
и куб. В табл. 11.9 приведены данные для выборки испытуемых, которые можно
получить в таком эксперименте.
"' Walters, P. A., Martin, F, & Schrcter, Z. (1997). «Caffeine and cortical arousal: The nonlinear Yerkes-
Dodson Law.» Human psychopharmacology: clinical and experimental, 12, 249-258.
Полиномиальная регрессия ^^И^^нЕЁ
Таблица 11.9. Связь между количеством кофеина и когнитивными функциями
Омг
10.0
8.0
15.0
14.0
15.0
10.0
8.0
15.0
14.0
15.0
100 мг
15.0
10.0
16.0
17.0
16.0
15.0
10.0
16.0
17.0
16.0
200 мг
17.0
14.0
18.0
21.0
18.0
17.0
14.0
18.0
21.0
18.0
300 мг
18.0
16.0
24.0
22.0
20.0
18.0
16.0
24.0
22.0
20.0
400 мг
15.0
12.0
20.0
21.0
18.0
15.0
12.0
20.0
21.0
18.0
500 мг
13.0
10.0
17.0
17.0
16.0
13.0
10.0
17.0
17.0
16.0
600 мг
11.0
9.0
15.0
13.0
12.0
11.0
9.0
15.0
13.0
12.0
Для линейной модели у = (3() + $sxx + е} где у - это результат тестов, ах -
количество кофеина, не было практически никакой связи между переменными: R2 = 0,001,
и F-статистика также показала, что коэффициент при количестве кофеина
незначимо отличался от О (F(1, 68) = 0,097, р = 0,757).
Для квадратичной плюс линейной модели, у = р{) + (^.г, + fi.pc2 + е, обнаружилась
достоверная связь между количеством кофеина и результатами тестов. Для этой
модели R2 = 0,462, F(2, 67) = 28,81 ир < 0.001. Таблица коэффициентов этой
модели, табл. 11.10, говорит о том, что как линейный, так и квадратичный член вносят
значимый вклад в качество модели, причем сильная линейная связь сопутствует
отрицательному квадратичному члену. Относительный вклад обоих членов в
суммарную модель, что видно из абсолютных значений стандартизованных
коэффициентов, вполне сравним (В .. .. = 2,314 против 6 .. = -2,448).
Таблица 11.10. Квадратичная модель для предсказания результатов тестов
по потребленному кофеину
Кофеин
Кофеин2
(Константа)
Нестандартизованные
коэффициенты
в
0.044
-7.429Е-5
12.014
Станд. ошибка
0.006
0.000
0.784
Стандартизованные
коэффициенты
Бета
2.314
-2.448
t
7.166
-7.580
15.324
Значимость
<0.001
<0.001
<0.001
Модель с кубическим, квадратичным и линейным членом, у = (3() + Ргг| + р^т,2 +
Ртг1 :* + е, не объяснила достоверно больше дисперсии в качестве выполнения
тестов, а коэффициент при кубическом члене не отличается достоверно от нуля,
подтверждая, что модель с линейным и квадратичным членами лучше всего подходит
для объяснения связи между потреблением кофеина и спортивными успехами".
() По-видимому, авторы экстраполируют выводы об эффекте кофеина па умственные способности
также и на результаты в спорте. - Прим. перев.
ЕЮ Hi
Глава 11. Логистическая, мультиномиальная и полиномиальная...
Переподгонка
Одна из самых поразительных возможностей современных статистических
пакетов состоит в том, что вы можете автоматически выбрать и провести любое
число сложных статистических тестов по нажатию одной кнопки. Применение этих
возможностей при построении моделей может быть полезным, если вы просто
смотрите на данные с разных сторон, или ваша первоначальная гипотеза
оказалась неверной, и вы пытаетесь разобраться, что же на самом деле происходит в
данных. Тем не менее многие статистики хмурятся при построении моделей
исключительно на основании ваших данных и сравнивают это с «выуживанием»
закономерностей наугад, а если используется нелинейная регрессия, называют это
произвольной подгонкой под кривые. Мы обсуждали опасности, которые таит
механистичное построение моделей, в главе 10, но все предостережения здесь еще
более актуальны, поскольку вы не просто добавляете и убираете переменные, но
еще и трансформируете их. Тем не менее такой метод построения моделей
допустим в некоторых областях, так что, если так и обстоят дела в вашей области, нет
причин не использовать все возможности, которые предоставляют современные
статистические пакеты. Некоторые из них позволяют произвести расчет
множества линейных и нелинейных моделей связи между двумя переменными, а дальше
просто выбирать ту, которая лучше всего объясняет ваши данные.
Если вы решите попробовать применить такой метод построения моделей, вам
стоит знать, какие при этом существуют опасности. Мы проиллюстрируем это
простым примером. Вообразите, что вы врач, которого интересует связь между
курением и кровяным давлением, и результаты вашего небольшого эксперимента
приведены в табл. 11.11. Вы знаете, что между этими переменными существует
связь, но как эксперту в суде вам надо установить наиболее сильную связь
между ними. Часть данных, касающихся диастолического давления и числа сигарет в
день, приведена в табл. 11.11.
Таблица 11.11. Взаимосвязь между диастолическим
кровяным давлением и числом выкуриваемых сигарет за день
Диастолическое кровяное давление
80.0
75.0
90.0
80.0
75.0
95.0
90.0
100.0
110.0
140.0
Сигарет в день
0.0
0.0
1.0
0.0
0.0
10.0
20.0
25.0
30.0
35.0
Переподгонка
¦¦ЕЛ
Сводка результатов построения нескольких моделей (с диастолическим
давлением как независимой переменной, а числом сигарет в день как независимой)
представлена в табл. 11.12. Как вы можете видеть из нее, кроме линейной,
возможно еще много видов связи между двумя переменными. Еще более
удивительно, что модель, включающая линейный и кубический члены, объясняет 97%
дисперсии диастолического давления. Никто до того не отмечал кубическую связь
между этими переменными, так что вы думаете, что нашли очень убедительный
аргумент.
Таблица 11.12. Связь между диастолическим кровяным давлением и числом
выкуренных за день сигарет
Зависимость
Линейная
Квадратичная
Кубическая
Составная
Рост
Экспоненциальная
Информация о модели
Я2
0.781
0.869
0.970
0.813
0.813
0.813
F
28.518
23.118
64.155
34.853
34.853
34.853
df1
1
2
3
1
1
1
df2
8
7
6
8
8
8
Знач.
0.001
0.001
0.000
0.000
0.000
0.000
Оценки параметров
Константа
78.423
80.984
79.069
79.007
4.370
79.007
ь1
1.246
-0.386
3.975
1.013
0.012
.0120
ь2
0.053
-0.299
ь3
0.007
Имеют ли R2, рассчитанные при таком подходе, какое-то реальное значение?
И да, и нет; один из рисков при таком «выуживании результатов» - это переиод-
гонка (или переобучение - overfitting). Это означает, что ваша модель слишком
хорошо аппроксимирует данные и объясняет не только достоверные зависимости,
но и случайные отклонения. Поскольку задачей статистического анализа
являются обобщение результатов и перенос их на другие выборки из той же генеральной
совокупности, переподгонка мешает достижению этой цели. Вы можете получить
модель, которая замечательно описывает ваши данные, но она совсем не
обязательно подойдет для каких-то других данных, так что она не привносит новых
полезных знаний в вашу область.
Лучшая защита от переподгонки - построение моделей на основании теории.
Если вы решите строить свою модель с помощью механистичных подходов,
следует проверять ее на многих выборках, чтобы быть уверенным, что вы моделируете
важные взаимосвязи в данных, а не случайный шум. Если доступно только
ограниченное число выборок, например в случае, когда получение данных
сопровождается уничтожением образца, можно применять методы создания повторных
выборок (resampling), или создания искусственных выборок на основе имеющихся
данных, таких как бутстреп (bootstrapping) или «складной нож» (jackknife); они
обсуждаются в книге Ефрона (Efron), упомянутой в приложении С.
ИНН ^ Глава 11. Логистическая, мультиномиальная и полиномиальная...
Упражнения
Задача
Вы сравниваете две вложенных модели логистической регрессии (модели, где в
большей есть все независимые переменные, включенные в меньшую). У модели Л
-2 логарифма правдоподобия равны 200,465; у модели Б - 210,395. Какая из
моделей лучше описывает данные?
Решение
Модель А лучше подходит под данные; при сравнении двух вложенных моделей
лучше та, у которой -2 логарифма правдоподобия меньше.
Задача
Вы планируете проведение логистической регрессии с одной дихотомической
и одной категориальной независимой переменными. Следующая таблица
показывает таблицу сопряженности значений у и двух независимых переменных
(лг, и х2). Вас ничего не напрягает при ее просмотре? Если да, как бы вы исправили
проблему?
Y=0
Y=^
x2=^
Х2 = 2
Х2=1
х? = 2
25
27
34
41
32
17
6
36
20
32
23
5
Решение
Хотя пустых ячеек тут нет, но есть две с очень небольшим числом наблюдений
(6 и 5), что может привести к большим доверительным интервалам. Если
возможно (и теоретически это можно обосновать, в соответствии со смыслом
переменной л:,), лучшим решением было бы объединить вторую и третью категории этой
переменной.
Задача
Вы провели логистическую регрессию для предсказания вероятности
исключения старшеклассников на основании их GPA и пола как независимых переменных.
Вот ваше уравнение регрессии:
Логит{р) = 4,983 + 1,876(Мужской пол) - 2,014(GPA) + е.
Исключение {у) закодировано как 1 = исключен, 0 = не исключен.
GPA - это непрерывная переменная со значениями от 0,00 до 4,00.
Мужской пол (переменная, кодирующая пол учеников) закодирован
как 0 = женский пол, 1 = мужской пол.
Какова предсказанная вероятность быть исключенной у девушки с GPA = 3,0?
Упражнения
Решение
Для расчета вероятности подставьте значения для женского пола и GPA в
уравнение логистической регрессии и затем пересчитайте результат по следующей
формуле, чтобы получить вероятность быть исключенным:
, уравнение логистической регресси
Предсказанная вероятность = ¦
* * (А _|_ р уравнение логистической регресепч
Предсказанный логит равен:
Логит(р) = 4,983 + 1,876(0) - 2,014(3.0) = -1,059.
Предсказанная вероятность быть исключенным равна:
Предсказанная вероятность = е 1()59/(1 + е и)5У) = 0,258 = 25,8%.
Задача
Продолжая вопрос предсказания вероятности исключения из старшей школы,
вы решили включить в анализ еще одну переменную: то, окончила ли мать
ученика старшую школу (0 = не окончила, 1 = окончила). После проведения
необходимых проверок данных вы строите модель и получаете коэффициенты и
результаты проверок значимости, показанные в табл. 11.13. Эта модель достоверно лучше,
чем нулевая модель для предсказания исключения из старшей школы (хи-квад-
рат (3) = 28,694, р < 0,001); значение К2 Кокса и Снелла составляет 0,385, а К2 На-
гелкерке - 0,533.
Таблица 11.13. Коэффициенты уравнения логистической регрессии,
предсказывающей вероятность исключения из старшей школы по полу,
GPA и образованию матери
Мужской пол
GPA
Мать закончила
старшую школу
Константа
В
2.107
-1.599
-2.430
5.021
95% ДИ для Ехр
Станд.
ошибка
0.770
0.756
1.104
2.420
Вальд
7.495
4.466
4.847
4.305
df
1
1
1
1
[В)
Знач.
0.006
0.035
0.028
0.038
Ехр(В)
8.224
0.202
0.088
151.526
Нижняя
граница
1.819
0.046
0.010
Верхняя
граница
37.170
0.890
0.766
Проанализируйте информацию в этой таблице, включая то, какие из
независимых переменных значимы для этой модели, в каком направлении влияют и что
означают столбцы Ехр(В) и 95%-ный доверительный интервал.
Решение
Все независимые переменные в этой модели достоверно связаны с
вероятностью того, что школьника исключат из старшей школы. У юношей больше шансов
ви
Глава 11. Логистическая, мультиномиальная и полиномиальная...
быть исключенными (В = 2,107; хи-квадрат Вальда (1) = 7,495, р = 0,006). Более
высокий GPA предсказывает уменьшение вероятности исключения (В = -1,599;
хи-квадрат Вальда (1) = 4,466, р = 0,035), как и окончание матерью старшей школы
(В = -2,430; хи-квадрат Вальда (1) = 4,867, р = 0,028).
Столбец Ехр(В) содержит исправленные отношения вероятностей для каждой
независимой переменной. Как и ожидалось, у мужского пола отношение больше 1
(8,224), то есть у юношей более чем в 8 раз выше шанс быть исключенными, чем у
девушек, после поправки на GPA и образование матерей; 95%-ный доверительный
интервал для мужского пола составляет (1,819, 37,170). Отношение вероятностей
для GPA и окончания матерью старшей школы меньше 1, что указывает на то, что
высокий GPA и лучшее образование матери понижают шансы быть исключенным.
Отношение вероятностей и доверительные интервалы составляют 0,202 и (0,046,
0,890) для GPA и 0,88 и (0,010, 0,766) при наличии матери, окончившей старшую
школу. Обратите внимание, что ни один из интервалов не включает нейтрального
значения 1; этого можно ожидать из того факта, что все независимые переменные
достоверно предсказывают значение зависимой.
ГЛАВА 12.
Факторный, кластерный
и дискриминантный анализы
Сейчас используется больше статистических методов, чем можно описать в одной
книге. На самом деле существует больше методов статистического анализа, чем
кто бы то ни было смог бы освоить за свою жизнь. Тем не менее часто полезно
быть знакомым с методом, даже не умея его применять. Вам может, к примеру,
понадобиться прочитать статью с описанием приема, которым вы не владеете, пли
вы можете решить, что вам необходимо освоить метод или нанять консультанта,
владеющего им, после того как вы прочитали, как кто-то другой использовал этот
метод в своих исследованиях. Эта глава рассказывает о применении нескольких
продвинутых статистических методов на конкретных примерах; при этом
обучения самим методам не будет, поскольку цель главы - в том, чтобы помочь
читателю понять, когда один из этих методов можно применить в определенном
исследовании. Приёмы, описанные в данной главе, включают факторный, кластерный
и дискриминантный анализ.
Факторный анализ
В факторном анализе (ФА) используются стандартные переменные для
сокращения набора данных с помощью анализа главных компонент (АГК) (Principal
Component Analysis) - наиболее широко применяемого метода сокращения
размерности. Он основан на прямоугольном разложении исходной матрицы для
создания выходной матрицы, состоящей из набора ортогональных компонент (или
факторов), которые учитывают наибольшую долю разброса переменных
начальной матрицы. Этот процесс обычно выдает меньшее число выходных компонент.
В терминах линейной алгебры АГК работает с матрицей ковариаций для создания
набора собственных векторов и собственных значений. Компоненты выходной
матрицы - это линейные комбинации входных переменных; компоненты
создаются так, чтобы первая из них учитывала наибольший разброс данных, а каждая
последующая - максимально возможную величину остаточного разброса при
условии некоррелированного направления в пространстве. Более общий
вариант АГК- канонический корреляционный анализ Хотеллинга (ККА) (Hotelling's
ия
Ы1.
Глава 12. Факторный, кластерный и дискриминантный анализы
canonical correlation analysis (CCA)), который, подразумевая многомерное
нормальное распределение, может быть использован для проверки независимости
двух наборов переменных.
В первую очередь АГК применяется для достижения трёх основных целей:
1. Для создания ортогональных переменных при проверке гипотез с
использованием методов, основанных на общей линейной модели.
2. Для сжатия большого числа переменных до числа, с которым легче
работать.
3. Для нахождения скрытых переменных в больших массивах данных,
которые представлены высоко скоррелированными входными переменными.
Хотя первые две задачи обычно решаются с помощью АГК, к третьей чаще
приступают с использованием факторного анализа (ФА), который также основан на
прямоугольном разложении, но может включать более сложные приемы, в
частности такой, как максимизирующее дисперсию вращение (varimax). О некоторых
из подобных приемов вы узнаете из этой главы. Заметьте, что в ФА выбранные
главные компоненты называются общими факторами, а корреляции с исходными
переменными называются нагрузками факторов.
Посмотрим на пример из области психометрики. Исторически ФА
использовался для проверки различных теорий умственной деятельности и интеллекта,
включая гипотезу о едином общем факторе, лежащем в основе интеллекта и
соперничающей с ней гипотезы о множестве таких ортогональных факторов. В свою
очередь, общие выводы, полученные в ходе обширных исследований интеллекта
и сознания в популяции, позволили надежно выделять индивидуальные различия
с помощью набора тестов. На процесс понимания индивидуальных отличий и их
компенсации сильно повлияли идеи Карла Фридриха Гаусса, первооткрывателя
распределения Гаусса, или нормального распределения, развитые более поздними
работами Бесселя, который открыл уравнение своего имени для внесения
поправок в наблюдения, сделанные разными астрономами.
Ранние попытки изучить интеллект с помощью количественных переменных
начались с исследований таких ученых, как Джеймс Каттел (James Cattell), которые
пробовали измерять интеллект наборами ментальных тестов, таких как скорость ре-
акци и, скорость движения и сила хватки. Более поздние работы показали, что
результаты выполнения этих тестов не были скоррелированы с реальной академической
успеваемостью. Как бы то ни было, работа Чарльза Спирмена (Charles Spearman) об
общем факторе интеллекта, g, извлеченном из результатов группы психологических
тестов, привела к широкому распространению в психометрике методов, схожих с ФА
и АГК. Более поздние работы Луиса Леона Тёрстоуна (Louis Leon Thurstone) и
других дали основание предполагать наличие как минимум двух независимых факторов
сознания, лежащих в основе интеллекта: вербальный (речевой) фактор - L и фактор
счёта (arithmetic) - Q Даже сейчас такую характеристику интеллекта можно
увидеть в стандартных тестах, таких как Академический оценочный тест на способности
(SAT, Scholastic Aptitude Test), который проходят многие американские студенты,
планирующие поступать в университет, и экзамен для поступающих в вуз или ас-
Факторный анализ
¦¦EQ
пирантуру - Вузовский оценочный тест (GRE, Graduate Record Examination). Оба
теста включают три основные части: речь, письмо и математика, - в общих чертах
соответствующие лингвистическому фактору (речь и письмо) и фактору счёта,
предложенному Тёрстоуном.
Рассмотрим типичный психометрический пример, в котором в качестве входной
матрицы использованы результаты ряда интеллектуальных и ментальных тестов,
а выходная матрица будет иметь меньшую размерность. Здесь термин «матрица»
относится только к численной информации, организованной в структуру,
соответствующую каждой части информации. Анализ может опираться на определенную
гипотезу. Например, специальная психологическая теория может предсказать два
фактора (скажем, L и Q) - это означает, что будут выбраны только два фактора,
значимых для максимальной величины дисперсии. С другой стороны, если
исследование носит разведывательный характер, допустимо, чтобы набор данных
частично определял число выбранных факторов, следуя некому стандартному критерию
или правилу. Обычно наиболее используемым критерием для сохранения фактора
является критерий Гутмана-Кайзера (Guttman-Kaiser), который отбирает только
собственные значения, превосходящие единицу (в случае применения ФА). Следуя
указанному правилу, факторы отбираются, если дисперсия, за которую они
отвечают, превышает среднюю для переменной, если дисперсия равномерно распределена
по всему набору входных данных. Другие критерии сохранения факторов
включают процедуру частичной корреляции Велицера (Velicer partial correlation procedure),
тест Бартлета (Barthlett's test) и модель сломанной трости (broken-stick model),
в то время как для более наглядного представления используется так называемая
«диаграмма каменистой осыпи» собственных значений (scree plot) для определения
того, какой из факторов следует сохранить. С помощью такой диаграммы вы
графически представляете собственные значения и выбираете те из них, которые, подобно
каменистой осыпи, скапливаются у подножия.
Предположим, у вас есть набор данных с результатами стандартного набора
тестов; данные для первых пяти участников показаны в табл. 12.1. Психологу нужно
определить, лежит ли фактор общей способности к пониманию в основе процесса,
включающего все компоненты интеллекта, или здесь присутствуют чёткие
факторы, в значительной степени отвечающие за отдельные переменные. Например,
существенно ли фактор L связан со способностями читать и говорить, а
независимый фактор Q - со способностями к счёту и геометрии.
Таблица 12.1. Результаты психометрических тестов
Чтение
8
5
2
8
10
Музыка
9
6
3
9
7
Счет
6
5
2
10
1
Речь
8
5
6
9
10
Спорт
5
6
8
8
5
Письмо
9
5
6
10
10
Геометрия
10
5
4
6
2
ЕЮ Hi Hi
Глава 12. Факторный, кластерный и дискриминантный анализы
Первый этап обработки данных - создание матрицы парных корреляций среди
всех переменных. Таблица 12.2 показывает верхний треугольник такой матрицы.
Это удобный метод определить, какие переменные существенно связаны между
собой, а какие - нет. Первая строка для каждой пары отображает коэффициент
корреляции Пирсона - г, вторая строка/? - уровень значимости.
Таблица 12.2. Корреляции между переменными психометрического теста
Чтение
Музыка
Счет
Речь
Спорт
Письмо
Геометрия
г
Р
г
р
г
р
г
р
г
р
г
р
г
р
Чтение
1.000
Музыка
0.535
0.111
1.000
Счет
-0.253
0.481
0.249
0.488
1.000
Речь
0.860
0.001
0.262
0.464
-0.501
0.140
1.000
Спорт
-0.469
0.172
-0.263
0.463
0.206
0.568
-0.236
0.511
1.000
Письмо
0.762
0.010
0.380
0.278
-0.307
0.389
0.895
0.001
0.054
0.881
1.000
Геометрия
-0.386
0.270
0.069
0.850
0.758
0.011
-0.569
0.086
0.266
0.458
-0.291
0.415
1.000
Корреляции в таблице являются подкреплением идеи независимости факторов
QnL.
Для L:
• Процесс речи и результаты чтения высоко скоррелированы (г= 0,860,
р = 0,001).
• Результаты по чтению и письму высоко скоррелированы (г =0,765,
р< 0,010).
• Результаты по речи и письму высоко скоррелированы (г = 0,895, р< 0,001).
Для Q:
• Результаты по геометрии и счёту высоко скоррелированы (г =0,758,
р<0,011).
Ни одна из прочих переменных (к примеру, способности к спорту или музыке)
не имеет существенной корреляции с другими переменными, поэтому можно
ожидать, что два интерпретируемых фактора и будут результатом ФА.
Первый шаг после вычисления АГК - выяснение того, какая величина
дисперсии учитывается факторной структурой. Это делается путём изучения общностей
(communalities), как показано в табл. 12.3 в столбце с названием «Выборка». Из
него видно, что некоторые переменные, такие как музыка, имеют сравнительно
Факторный анализ
¦¦ЕЮ
низкий показатель общности (0,779), в то время как другие переменные, такие
как письмо, имеют очень высокую общность (0,967). Переменные с высокой
общностью имеют высокую величину дисперсии, объясняемую выбранными
факторами, в то время как у переменных с низкой общностью остаётся много иеобъяс-
ненной дисперсии.
Таблица 12.3. Общности
Чтение
Музыка
Счет
Речь
Спорт
Письмо
Геометрия
Начальные значения
1.000
1.000
1.000
1.000
1.000
1.000
1.000
Выборка
0.929
0.779
0.868
0.955
0.943
0.967
0.814
Таблицы 12.4-12.6 показывают, соответственно, начальные собственные
значения, суммы квадратов нагрузок и суммы квадратов нагрузок после вращения,
полученных из ФА. Эти таблицы являются чрезвычайно важной и значимой
частью результатов для интерпретации. Из табл. 12.4 можно видеть, что первые
три фактора составляют 89,37% дисперсии, что сразу даёт возможность ощутить
мощность такого инструмента, как АГК, поскольку он позволил сразу свести семь
переменных к трём факторам, принимая во внимание все вариации в массиве
данных! Таблица 12.5 даёт значения трёх извлечённых факторов перед вращением,
а табл. 12.6 показывает те же факторы после того, как было применено вращение
(varimax) с использованием максимизации дисперсии и нормализации Кайзера
(Kaizer normalization). Вращение (varimax) поворачивает оси факторов с
сохранением ортогональности, при этом максимизируя сумму дисперсий нагрузок.
Заметьте, что это не влияет на общую величину дисперсии, подсчитанную по трём
факторам, но относительная пропорция дисперсии между факторами меняется.
Таблица 12.4. Начальные собственные значения
1
2
3
4
5
6
7
Начальные собственные значения
Суммарно
3.488
1.651
1.117
0.425
0.234
0.067
0.018
% дисперсии
49.829
23.591
15.958
6.069
3.343
0.952
0.258
Совокупный %
49.829
73.420
89.378
95.446
98.789
99.742
100.000
Э^^||Н : Глава 12. Факторный, кластерный и дискриминантный анализы
Таблица 12.5. Суммы квадратов нагрузок после выборки
Суммарно
3.488
1.651
1.117
% дисперсии
49.829
23.591
15.958
Совокупный %
49.829
73.420
89.378
Таблица 12.6. Суммы квадратов нагрузок после вращения
Суммарно
2.846
2.066
1.345
% дисперсии
40.653
29.517
19.208
Совокупный %
40.653
70.170
89.378
Людям, знакомым с ФА, порою кажется, что в вращении есть какое-то
жульничество, особенно потому, что оно используется в качестве вспомогательного
средства для интерпретации факторных нагрузок и для обнаружения скрытой
структуры. Тем не менее это вполне легитимная техника обработки данных, которая
служит весьма полезной цели, помогая исследователю вылавливать переменные,
наиболее сильно связанные с каждым фактором.
Преимущества вращения можно увидеть, сравнивая табл. 12.7 и 12.8, которые
представляют матрицы компонент для анализа до и после вращения. Для
компоненты 1, которая соответствует скрытому фактору I, можно увидеть, что вращение
имеет эффект увеличения нагрузок, соответствующих наиболее скоррелирован-
ным переменным, таким образом, что способности в письме, чтении и речи имеют
самые высокие нагрузки на этот фактор. После вращения компонента 2, которая
соответствует фактору Q, имеет более высокие нагрузки для счёта и геометрии,
в то время как нагрузки для некоррелированных переменных, таких как
музыка, теперь сравнительно снизились. У компоненты 3 высокая нагрузка только для
спорта, поэтому, хотя она представляет вполне явный фактор, она не отражает
никакой скрытой структуры и не будет учтена в анализе. Таким образом, вращение
помогло нам выяснить, какие результаты тестов (чтение, музыка и т. д.) наиболее
тесно связаны с нашими двумя компонентами.
Таблица 12.7. Матрица компонент до вращения
Чтение
Музыка
Счет
Речь
Спорт
1
0.902
0.386
-0.582
0.955
-0.403
Компонента
2
0.328
0.775
0.727
0.009
-0.059
3
-0.085
-0.174
0.028
0.209
0.882
Факторный анализ
¦¦ESI
Письмо
Геометрия
1
0.819
-0.664
Компонента
2
0.235
0.597
3
0.491
0.130
Таблица 12.8. Матрица компонент после вращения
Чтение
Музыка
Счет
Речь
Спорт
Письмо
Геометрия
1
0.859
0.593
-0.158
0.869
-0.046
0.955
-0.246
Компонента
2
-0.144
0.490
0.917
-0.438
0.176
-0.164
0.846
3
-0.412
-0.433
0.050
-0.088
0.954
0.169
0.195
Графическое исследование данных также помогает выяснить связи между
переменными. Возвращаясь к вопросу о выборе собственных значений, рис. 12.1
графически представляет упомянутую выше «диаграмму каменистой осыпи» как
результат анализа, где каждый кружок соответствует одному из собственных
значений в табл. 12.4. Более высокие значения соответствуют большей дисперсии,
откуда с очевидностью следует, что после третьего собственного значения остальные
собственные значения ничего существенного к общей картине не добавляют. Если
вы изобразите собственные значения как камни, скатывающиеся вниз по склону,
станет ясно, что существует некий изгиб к горизонтали на третьем и четвёртом
собственных значениях (правда, в интерпретации «диаграмм каменистой осыпи»
присутствует субъективный элемент), в то время как собственные значения от
четвёртого до седьмого просто «осыпаются» в кучу у подножия. Поэтому остаются
только две или три компоненты, которые имеет смысл рассматривать при анализе,
и это соответствует результатам использования критерия Гутмана-Кайзера;
компонента 3 имеет значение, едва превышающее 1,000.
Рисунок 12.2 демонстрирует эффект от вращения данных в пространстве трёх
измерений. По нему можно понять, что переменные, связанные с фактором L
(письмо, речь и чтение), тесно сгруппированы в трёхмерном пространстве, так же
как и переменные, связанные с фактором Q (счёт и геометрия). Отметим, что две
другие переменные (спорт и музыка) примерно равноудалены от центров двух
компонентных групп (кластеров). Довольно часто влияние вращения легче
отследить в трёхмерном пространстве, нежели по таблицам нагрузок.
Глава 12. Факторный, кластерный и дискриминантный анализы
4.000-
з.ооо-
значение
Собственное
о о
о о
о о
.000"
О
1.00
О
2.00
О
0
О
1 1 1
3.00 4.00 S.00
Номер собственного значения
о
i
6.00
о
!
7.00
Рис. 12.1. Диаграмма каменистой осыпи
гм
Компонента
1.0-
0.5-
0.0-
-0.5-
-1.0
-
Диаграмма компонент
Счет О Музыка О
Геометрия О
ЧтениеО
ПисьмоО
Спорт О Речь О
^~^Г по ~~Г~ ЩШ \, о.о ^
и °5 7 0 U ° ***Ъ
Рис. 12.2. Пространственная диаграмма компонент
Кластерный анализ
ННЕЕЕ]
Таблица 12.9 описывает выходную матрицу после процедуры ФА. Она
показывает результаты для трёх компонент первых пяти участников тестирования, если
это тесты GRE (вузовский оценочный тест) или SAT (академический оценочный
тест) - это те самые результаты, которые можно сообщать участникам
тестирования. Заметим, что точность результатов зависит от вашей компьютерной
программы.
Таблица 12.9. Результаты по трём компонентам для каждого участника
Участник
1
2
3
4
5
Компонента 1
0.518
-1.170
-1.396
1.094
0.706
Компонента 2
(О)
1.132
-0.128
-1.207
1.198
-1.049
Компонента 3
(Спорт)
-0.095
0.084
1.619
1.128
0.014
Так же как и все другие техники обработки данных, о которых вы узнали из этой
книги, АГК и ФА имеют ряд базовых предварительных условий, которые должны
выполняться, если требуется получить обоснованные и/или надёжные
результаты. Для АГК и ФА наиболее часто используются большие базы данных, потому
что, как правило, чем больше набор данных, тем надёжнее результаты. В случае
психометрики удается добиться постоянной надёжности, если тестирование
проводится на сотнях тысяч испытуемых из разных лингвистических и национальных
групп. Другое основное условие - число объектов превосходит число переменных
во входной матрице. Как правило, тесты на статистическую значимость не
используют АГК, поэтому пиковые и другие потенциально возможные источники
отклонений не представляют столь существенной проблемы, как, скажем, при работе с
ANOVA. АГК также предполагает линейную корреляцию - это означает, что ни
одна из переменных не может быть ни нулём, ни абсолютно скорреллированной
с другой.
Кластерный анализ
Кластерный анализ (КА) представляет собой набор технических приёмов,
который позволяет сгруппировать объекты на основе их значений для одной и
более переменных. Некоторые методы кластерного анализа размещают объекты по
группам путём разделения, в то время как другие методы создают иерархические
деревья, которые показывают систематические связи между группами и их
прототипами. Связанный с КА метод - дискримипантный анализ (ДА) (Discriminant
Function Analysis, DFA) - может быть использован для уточнения правил
распределения объектов по группам, основываясь на понимании параметрической
структуры групп. ДА лучше работает для прогнозирования групповой
принадлежности, чем кластерный анализ без ДА. Зачастую эти два метода применяют-
ШЁШШШШ
Глава 12. Факторный, кластерный и дискриминантный анализы
ся совместно. Кластерный анализ полезен тогда, когда число групп изначально
неизвестно. Если же это число установлено, то ДА может быть использован для
прогнозирования принадлежности к группе для каждого объекта по
отдельности.
КА весьма полезен при двух сценариях. В первом случае вам может быть
известно, сколько групп вы ожидаете найти в каждом наборе данных, и вы передаёте это
число алгоритму, который и определяет размещение объектов по группам (метод
к-средних, или k-means). В другом случае число групп, которое существует в
действительности, неизвестно, и тогда вы хотите при помощи этого метода определить
его.
Кластерный анализ является в высокой степени эмпирическим инструментом;
его успех в значительной степени зависит от качества поставляемых данных. КА
работает путём выбора входного вектора Ус п объектами и р переменными,
располагая каждый из п объектов в одну из k групп. Каждая изр переменных измеряет
одно направление изучаемого объекта. Если продолжить рассмотрение примера
из психометрики, каждая переменная там может представлять результат по
определённому типу тестируемых способностей (чтение, письмо и т. д.). Алгоритм
создаёт на вероятностной основе k кластеров, устанавливая центроиды (или центры
тяжести кластеров) и направляя каждый объект к ближайшему центроиду.
Объекты перемещаются между кластерами для минимизации внутрикластерных
различий и максимизации межкластерных различий. Процесс продолжается до полного
схождения в соответствии с заранее определённым критерием. Следует отметить,
что поскольку в начальном назначении центроидов присутствует некоторая
случайность, не всегда можно получить одинаковый ответ.
Целью расчётов в кластерном анализе является подтверждение того, что все
члены групп \...к похожи на другие члены их групп и отличаются от членов
других групп. Сходство или несходство определяется специфическими
расстояниями. К ним относят следующие:
Эвклидово расстояние
Это геометрическое расстояние между двумя точками в многомерном
пространстве.
Манхэттэновское расстояние
Поквартальное расстояние по типу Манхэттэна, где улицы
перпендикулярны друг другу1.
Расстояние Махаланобиса
Расстояния между точками внутри кластера увеличиваются, а между
кластерами уменьшаются.
Рассмотрим ещё раз пример из психометрики. Показав, что способности
испытуемых определяют три фактора, психолог теперь заинтересован в выяснении,
имеется ли некоторое основание для классификации учащихся по разным группам обу-
1 Млн расстояние между двумя точками определяется как сумма разностей их координат. - Прим.
пер.
Кластерный анализ
¦¦ЕЭ
чения на основе этой скрытой структуры, потому что выявленные факторы для I,
Q и Спорт ортогональны друг к другу. Вопрос в специализации: если у испытуемых
определены способности к спорту, лингвистике или вычислениям, они могут быть
направлены, соответственно, в классы, специализирующиеся в этих дисциплинах.
(Возраст, в котором такая специализация должна происходить, - это другой
вопрос). Главная проблема при подобном подходе заключается в том, что некоторые
испытуемые могут иметь способности более чем в одной дисциплине и
идеализированное представление, даваемое вращающейся матрицей нагрузок, показанное
на рис. 12.2, может не отражать всех возможных случаев.
Для выяснения того, соответствуют ли три явные группы в этом наборе данных
конкретным членам, подходящим лингвистическому, вычислительному и
спортивному направлениям, психолог выбирает кластерный анализ. Поскольку мы
полагаем, что есть три группы, это количество k = 3 и передаётся в работу алгоритму
с запросом идентифицировать эти три группы и направить каждого учащегося в
соответствующий класс обучения.
Начальные центры тяжести кластеров показаны в табл. 12.10, и после
нескольких итераций алгоритм приходит к решению с окончательным определением
принадлежности первых пяти объектов к определённому кластеру, а также положения
центров кластеров и попарных расстояний между ними (табл. 12.11-12.13;
верхний треугольник только для табл. 12.13). Начальные центры кластеров связаны
с корреляциями и соответствующими главными компонентами из предыдущего
анализа. Кластер 1 прочно связан с чтением, речью и письмом; кластер 2 - со
счётом и геометрией; кластер 3 - со спортом. Несмотря на то что в процессе итерации
наблюдаются определённые изменения, подобное разделение довольно
устойчиво. Окончательное расположение групп является обычной функцией расстояния
от каждого центроида. Попарные расстояния между центроидами также в
значительной степени устойчивы. Таким образом, оказывается, что расстояния между
группами успешно увеличены, и нет проблем в их разделении. Увеличение числа
объектов при анализе несомненно улучшит надёжность результата.
Таблица 12.10. Начальные центры кластеров
Чтение
Музыка
Счет
Речь
Спорт
Письмо
Геометрия
1
10.00
9.00
3.00
10.00
6.00
10.00
3.00
Компонента
2
3.00
9.00
10.00
2.00
6.00
4.00
9.00
3
2.00
3.00
2.00
6.00
8.00
6.00
4.00
Глава 12. Факторный, кластерный и дискриминантный анализы
Таблица 12.11. Решение по кластерам: членство в кластерах
Номер объекта
1
2
3
4
5
Кластер
1
3
3
1
1
Расстояние
6.565
2.915
2.915
7.078
4.468
Таблица 12.12. Решение по кластерам: окончательное
расположение центров кластеров
Чтение
Музыка
Счет
Речь
Спорт
Письмо
Геометрия
1
8.57
8.86
4.00
9.00
5.14
9.00
3.86
Компонента
2
3.00
9.00
10.00
2.00
6.00
4.00
9.00
3
3.50
4.50
3.50
5.50
7.00
5.50
4.50
Таблица 12.13. Решение по кластерам: окончательные попарные
расстояния между кластерами
Кластер
1
2
1
2
12.971
3
8.562
9.925
Таблица 12.14 показывает результаты определения значимости каждой
переменной для разграничения групп (англ. discriminability), полученные с помощью
дисперсионного анализа (ANOVA - см. главу 8). Эти результаты не
интерпретируются как итоги точного тестирования статистической значимости в смысле
проверки гипотезы, но они весьма полезны при обнаружении переменных, которые
помогают различить кластеры между собой. Результаты письма, речи и чтения
оказались значимыми (что и ожидалось), но результаты комплектования второго
и третьего кластеров (соответственно, счёт и геометрия и спорт) оказались
незначимыми. Первый результат имеет смысл хотя бы потому, что высокие значения
по письму, речи и чтению действительно помогают различить первую и вторую
группы, но отсутствие различимости у третьего кластера оказалось сюрпризом
(хотя и это неудивительно, если вспомнить результаты АГК, где третий фактор
Спорт имел собственное значение, едва превышавшее 1, и учитывал всего лишь
15% дисперсии).
Дискриминантный анализ
¦МЕЗ
Таблица 12.14. Результаты дисперсионного анализа по способности
к различению
Чтение
Музыка
Счет
Речь
Спорт
Письмо
Геометрия
Кластер
Ср. квадр.
28.893
15.321
17.000
26.950
2.771
17.550
11.571
)
df
2
2
2
2
2
2
2
Ошибка
Ср. квадр.
1.745
1.622
9.214
0.643
4.122
1.786
8.194
df
7
7
7
7
7
7
7
F
16.558
9.443
1.845
41.922
0.672
9.828
1.412
Значимость
0.002
0.010
0.227
0.000
0.541
0.009
0.305
Дискриминантный анализ
Дискриминантный анализ (ДА) (Discriminant Function Analysis, DFA)
используется для формулировки правил, которые позволяют классифицировать объекты
по двум или более группам, основываясь на линейной комбинации переменных;
при этом сами группы известны перед началом анализа, а целью последнего
является нахождение переменных, наиболее эффективных в прогнозировании
принадлежности новых объектов к этим группам. Однажды мне пришлось
участвовать в исследовании, целью которого был прогноз расового и этнического состава
групп студентов университета, которые не смогли заполнить определённую часть
анкеты (информацию, необходимую для отсылки федеральному правительству).
В том случае мы знали, какие категории используются федеральными органами
для расовой и этнической идентификации, и нам было нужно использовать
другую информацию в заполненных частях анкет для распределения студентов по
соответствующим группам.
Цель ДА - определение функции или функций, которые максимизируют
различия между группами, тем самым достигая наибольшей возможной точности при
распределении объектов по группам. Как правило, эти функции представляют из
себя линейные комбинации входных переменных и называются линейные дискры-
минантные функции (linear discriminant functions, LDFs). Кластерный анализ и
классификационный анализ в некотором роде пытаются решить одну проблему
разными средствами: оба ищут максимум различных функций (например,
максимизируя расстояния или точность распределения).
Опять вернёмся к примеру из психометрики. При известном расположении
групп, полученном после кластерного анализа, ДА можно использовать для
определения ряда дискриминантных функций, обеспечивающих максимальное
разделение между группами. После этого можно проверить нулевую гипотезу
равенства групповых средних для каждой переменной. В случае двух групп это можно
i^lHi Глава 12. Факторный, кластерный и дискриминантный анализы
сделать с помощью ?-теста; при большем числе групп для этого нужен F-тест.
Результаты из в табл. 12.15 указывают на то, что есть существенные различия: для
чтения F(2, 7) = 16,558, р = 0,002; для музыки F(2, 7) = 9,443, р = 0,010; для речи
F(2, 7) = 41,922, р = 0,001; для письма F(2, 7) = 9,828, р = 0,009. Таким образом,
основываясь на значимости переменных для разграничения групп, можно
оставить только тесты по чтению, музыке, речи и письму, сохраняя большие
расстояния между группами.
Таблица 12.15. Проверка равенства групповых средних
Чтение
Музыка
Счет
Речь
Спорт
Письмо
Геометрия
Лямбда Уилкса
0.174
0.270
0.655
0.077
0.839
0.263
0.713
F
16.558
9.443
1.845
41.922
0.672
9.828
1.412
«*i
2
2
2
2
2
2
2
df2
7
7
7
7
7
7
7
Значимость
0.002
0.010
0.227
< 0.001
0.541
0.009
0.305
Таблица 12.16 характеризует две канонические дискриминантные функции,
необходимые для распределения объектов по группам. Интересно, что первая
функция учитывает 96% дисперсии, в то время как вторая - только 4%.
Таблица 12.16. Канонические дискриминантные функции
Функция
1
2
Собственное
значение
79.224
3.287
% дисперсии
96.0
4.0
Совокупный %
96.0
100.0
Каноническая
корреляция
0.994
0.876
Таблица 12.17 показывает расчётные значения лямбды Уилкса, которая
используется для оценки значимости дискриминантных функций в многомерном
пространстве. В строке, обозначенной «от 1 до 2», приведены показатели значимости для обеих
функций, а в строке, обозначенной «2», - только для второй функции. К сожалению,
в этом виде анализа даже две функции совместно не в состоянии существенно
дифференцировать группы. Вероятно, это отражает тот факт, что функция 1 забирает на
себя слишком высокую часть дисперсии, а набор данных сравнительно мал, поэтому
в данном случае анализу недостаёт мощности.
Таблица 12.17. Значения лямбды Уилкса
Тест функции
от 1 до 2
2
Лямбда Уилкса
0.003
0.233
Хи-квадрат
23.362
5.822
df
14
6
Значимость
0.055
0.443
Дискриминантный анализ
¦¦ЕШ
В табл. 12.18 даны стандартные коэффициенты канонических дискриминант-
ных функций. Они являются аналогами стандартных коэффициентов регрессии и
показывают связь между каждым измерением способностей и функциями,
выведенными при проведении анализа.
Таблица 12.18. Стандартные коэффициенты
канонических дискриминантных функций
Чтение
Музыка
Счет
Речь
Спорт
Письмо
Геометрия
Функция
1
-0.706
1.838
-0.364
3.686
-0.150
-1.884
1.916
2
-0.141
-0.368
-0.707
1.409
1.309
-2.030
0.945
В табл. 12.19 представлена структурная матрица; значения в таблице являются
каноническими коэффициентами корреляции случайных величин и могут
толковаться как факторные нагрузки, то есть они показывают вклад каждой переменной
в каждую случайную величину. Из этой таблицы можно видеть нагрузки чтения и
музыки на функцию 1 и нагрузки письма, речи, счёта, геометрии и спорта на
функцию 2. Эти значения слегка отличаются от тех, которые можно было бы ожидать
от, скажем, АГК или кластерного анализа, но не следует забывать, что алгоритмы,
используемые в каждом виде анализа, имеют свои цели, поэтому неудивительно,
что результаты не совпадают.
Таблица 12.19. Структурная матрица
Чтение
Музыка
Счет
Речь
Спорт
Письмо
Геометрия
Функция
1
0.243
0.188
0.115
0.379
-0.046
-0.055
-0.043
2
-0.140
0.034
-0.708
0.433
-0.331
-0.225
0.121
И наконец, табл. 12.20 демонстрирует связь между двумя дискриминантными
функциями и центроидами групп.
ЛВНЩЦд ; Глава 12. Факторный, кластерный и дискриминантный анализы
Таблица 12.20. Функции к центроидам групп
Номер кластера для объекта
1
2
3
Функция
4.804
-14.483
-9.573
-0.169
-3.465
2.324
Упражнения
Найдите несколько профессиональных статей в вашей области, в которых
используются методы, приведенные в этой главе, и посмотрите, как используется каждый
метод и как объясняются результаты. Для начала ниже даны несколько
примеров:
• Крэйг А. Дэпкен и Даррсп Грант. Калькуляция цен сервисных услуг в
Главной бейсбольной лиге: анализ главных компонент. (Craig A., and Darren
Grant. 2011. "Product pricing in Major League Baseball: A principal components
analysis." Economic Inquiiy 49 (April): 474-488.)
Дэикеп и Грант используют анализ главных компонент для исследования
факторов, влияющих на стоимость концессий, билетов и парковки в
Главной бейсбольной лиге США.
• Ханна С. Уильямсон, Томас Н. Бредбери, Томас Е. Трэйл и Бенджамен Р.
Карни. Факторный анализ шкалы оценок семейных отношений в штате
Айова. (Williamson, Hannah С, Thomas N. Bradbury, Thomas E. Trail, and
Benjamin R. Karney. 2011. "Factor analysis of the Iowa Family Interaction
rating scales " Journal of Family Psychology 25(6): 993-999.)
Уильямсон и коллеги используют анализ главных компонент для
выявления факторной структуры способа описания различных типов
вербального и невербального поведения супругов в общении; новизна их подхода
заключается в применении метода, использовавшегося для белых супругов
среднего класса, к примерам расово разных пар с низким уровнем дохода.
• Майкл Н. Тума, Рейнольд Декер и Сорен В. Шольц. Обзор проблем и
скрытых препятствий при применении кластерного анализа в
сегментации рынков. (Tuma, Michael N., Reinhold Decker, and Soren W. Scholz. 2011.
"A survey of the challenges and pitfalls of cluster analysis application in market
segmentation." International Journal of Market Research 53(3): 391-414.)
Тума, Декер и Шольц рассматривают некоторые методы кластерного
анализа, использовавшегося при сегментации рынков за последние 50 лет, и
предлагают лучшие практические решения этой проблемы.
• Барабара К. Кайе и Томас Джонсон. Блог что надо: Кластерный анализ
причин оценки разных типов блогов как заслуживающих доверия. (Кауе,
Barbara К., and Thomas J. Johnson. 2011. "Hot diggity blog: A cluster analysis
Упражнения
ШМЕЕО
examining motivations and other factors for why people judge different types of
blogs as credible." Mass Communication and Society 14(2): 236-263.)
Кайе и Джонсон используют кластерный анализ для выявления групп
людей, которые оценивают различные типы блогов (общеинформативные,
медиа/журналистика, военные и относящиеся к войне, корпоративные и
персональные) в качестве источников информации, заслуживающих
полного доверия.
• Ричард Гонсалес. Распознавание пола детей но костям черепа с помощью
дискриминантиого анализа. (Gonzalez, Richard. 2012. "Determination of sex
from juvenile crania by means of discriminant function analysis." Journal of
Forensic Sciences 57(1): 24-34.)
ГЛАВА 13.
Непараметрическая статистика
Основа статистического анализа - оценка параметров распределения, то есть
оценка свойств генеральной совокупности по информации, полученной из
выборки, взятой из этой совокупности. Многие из самых обычных статистических
методов полагаются на то, что исследуемое распределение принадлежит к
какому-то известному типу, например оно нормальное, чтобы выводы, сделанные по
результатам теста, были осмысленными; эти методы называются
параметрическими1. Но что же делать, если вы знаете или подозреваете, что генеральная
совокупность отнюдь не подходит под требования определенного статистического
теста? В таких ситуациях используют другой набор статистических методов,
называемых испараметрическими. Они не зависят от распределения, то есть делают
мало или не делают вовсе никаких предположений о свойствах распределения
данных; некоторые говорят, что они зависят от распределения меньше, поскольку
отдельные непараметрические тесты все-таки требуют выполнения
определенных требований к распределению генеральной совокупности, но в целом они
менее строгие, чем в случае параметрических тестов.
Ыепарамстрические статистики часто применяют при исследовании данных,
если их получали скорее как ранги, а не как чистые значения, или же при
тестировании значения заменяются на ранги из-за опасений по поводу распределения
сырых данных. Ранговые данные, по определению, являются порядковыми, что
обсуждается в главе 1, и их нельзя анализировать методами, предназначенными
для интервальных или характеризующих отношения данных. Знакомым
примером может служить ранжирование класса по баллам2: учеников в школе можно
ранжировать по баллам, и хотя мы можем быть уверены в порядке их следования
в списке (студент № 1 всегда имеет более высокий балл, чем студент № 2), мы не
можем быть уверены в промежутке между рангами (эти студенты могут иметь как
и почти идентичный балл, так и сильно различающийся).
Если ваше исследование предполагает использование определенной
параметрической статистики, но данные не подходят под ее требования, то часто можно
1 Потому что они используют оценки параметров наперед .'заданного распределения. - Прим. пер.
2 В Америке п других западных странах нахождение в вершине списка класса - очень важное
достижение при, например, поступлении в университет, поэтому всем знакомо ранжирование учеников
но баллам. - Прим. пер.
Независимые выборки
l HHIEE9
применить непараметрический аналог. Существует множество
непараметрических статистик, кроме нескольких, описанных в этой главе, и учебник Вилльяма
Коновера (William Conover) «Практическая непараметрическая статистика»
(Practical Nonparametric Statistics), упомянутый в приложении С, включает
схему, помогающую выбрать непараметрический тест для вашей комбинации данных
и статистической задачи.
Кроме того, вы можете найти такую схему и в Интернете; ссылка на ее вариант
от министерства здравоохранения (Department of Health) Великобритании
приведена в приложении С.
В этой главе представлены медианный критерий, U-критсрий Маина-Уит-
ни (Mann-Whitney U test), ранговый парный критерий Вилкоксоиа (Wilcoxon
matched pairs signed rank test), тест Краскелла-Уоллиса (Kraskal-Wallis test) и тест
Фридмана (Friedman test). Несколько непараметрических тестов приведены в
главе 5, включая тест хи-квадрат (chi-square test), точный тест Фишера (Fisher's exact
test), тест МакНемара (McNemar's test), фи (phi), V Крамера (Cramer's V),
корреляция Спирмена (Spearman's correlation), гамма Гудмана и Краскела (Goodman
and Kruskal's gamma), тау Кендалла (Kendall's tau) и d Сомерса (Somers's d).
Медиана и межквартильный размах, которые часто используют при отличном от
нормального распределении, обсуждаются в главе 4.
Непараметрические методы более робастные, чем их параметрические аналоги,
то есть на них слабее влияют отклонения от предположений модели или необычные
значения в выборке (такие как выбросы), но обычно менее мощные, чем
параметрические критерии. Из-за этого в том случае, если ваши данные подходят под
параметрический критерий, используйте его; если же это не так, то используйте
непараметрический метод (или преобразуйте данные, как описано в главе 3).
Независимые выборки
В этом разделе описаны некоторые часто использующиеся непараметрические
критерии для сравнения независимых выборок, в общем основанные на ранговой
сумме и ранговом среднем.
Тест ранговой суммы Вилкоксона
Для описания порядковых данных используют две основные статистики:
ранговая сумма и ранговое среднее. Рассмотрим следующий пример их
использования. Отборочный комитет Олимпийских игр должен выбрать лучшую команду
по тэквондо из двух штатов (Калифорния и Невада), чтобы она представляла
Соединенные Штаты. Поскольку, кроме индивидуальных зачетов, будут и
групповые, к которым члены команд готовились вместе, команды нельзя
перемешивать, чтобы получить составную команду из самых лучших спортсменов; вместо
этого необходимо выбрать одну или другую команду как целое. Каждый член
команд получил общий балл за свое выступление, основанный на числе кирпичей,
который он сумел разбить за пять минут тестирования. Результаты приведены
в табл. 13.1.
¦cKEJ ^^Ш ВНЦ [:.; Глава 13. Непараметрическая статистика
Таблица 13.1. Результаты членов команд по тэквондо из двух штатов
Калифорния
4
5
6
6
7
8
9
9
9
9
Невада
2
3
3
4
4
5
10
10
11
11
Более высокий балл указывает на более хорошие навыки (разбил больше
кирпичей). Попытка проанализировать результаты на глаз дается трудно; баллы членов
команды Калифорнии более сходны и сгруппированы в более узком диапазоне,
тогда как результаты невадцев более разбросаны и включают как очень высокие, так
и очень низкие баллы. Поскольку четыре спортсмена с самыми высокими
баллами - выходцы из Невады, у вас может появиться соблазн выбора этой команды, но
медиана для нее составляет всего лишь 4,5, тогда как у Калифорнии она равна 7,5.
Нет никаких оснований предполагать, что данные происходят из
нормального распределения, а объем выборки в 10 человек не дает возможности применить
центральную предельную теорему. Также мы не можем считать, что данные равно
интервальные; хотя два кирпича - это однозначно больше, чем один, мы не можем
быть уверены, что у сумевших разбить два кирпича навыки по тэквондо в два раза
лучше. (На самом деле подобная интерпретация наверняка была бы
неправильной.) Нам гораздо удобнее думать, что разбить два кирпича - лучше, чем один, без
уточнения, насколько лучше.
Самым подходящим способом описания таких данных являются ранги, а
отнюдь не значения. Мы припишем ранг каждому испытуемому и просуммируем
все ранги для каждой из команд. Для подсчета рангов обе команды объединяют,
каждый член каждой команды нумеруется по возрастанию (более высокий ранг
означает большее число разбитых кирпичей). Таблица 13.2 показывает, как
проходит этот процесс.
Таблица 13.2. Ранжирование членов команд
Калифорния
4
Невада
2
3
3
4
4
Ранг
1
2
3
4
5
6
Независимые выборки
ВЕЯ
Калифорния
5
6
6
7
8
9
9
9
9
Невада
5
10
10
11
11
Ранг
7
8
9
10
11
12
13
14
15
16
17
18
19
20
А что с равными значениями? Везде, где мы их увидели, следует вместо
обычного ранга подсчитать средний ранг как сумму рангов этих значений, деленную на
число равных значений; например, равные второе и третье значения оба получат
ранг 2,5. Таблица 13.3 показывает новые ранги с учетом равных значений.
Таблица 13.3. Ранги для оценок выступления борцов тэквондо
с учетом равных значений
Калифорния
4
5
6
6
7
8
9
9
9
9
Невада
2
3
3
4
4
5
10
10
11
11
Ранг
1
2.5
2.5
5
5
5
7.5
7.5
9.5
9.5
11
12
14.5
14.5
14.5
14.5
17.5
17.5
19.5
19.5
^|B|L :'' Глава 13. Непараметрическая статистика
Затем для каждой группы вычисляют сумму рангов, складывая
соответствующие ранги, как показано на рис. 13.1.
^к(КалифоР?шя)= 5+ 7 5+ 9.5+ 95+ U + 12 + U5+ 145+ U5 + U5 = U2.5
2Л (Невада) =1 + 2.5 + 2.5 + 5 + 5 + 7.5 + 17.5 + 17.5 + 19.5 + 19.5=97.5
Рис. 13.1. Расчет суммы рангов
Если группы приблизительно равны, мы бы ожидали, что суммы рангов будут
приблизительно одинаковы. Это сравнение честно только в том случае, когда у
нас равны объемы выборок, как в данном примере. Кроме того, мы можем
подсчитать средние рангов - более хорошая статистика для групп разных размеров,
как показано на рис. 13.2.
- 112.5
R (Калифорния) = ——— = 11.25
97.5
R (Невада) = = 9.75
10
Рис. 13.2. Расчет средних рангов
Сравнение средних рангов дает нам ответ, что команда Калифорнии
выступила лучше, чем команда из Невады. Таким образом, используя ранговые
методы, отборочный комитет должен выбрать команду из Калифорнии, поскольку
их средний ранг выше. Что же делать, если мы хотим проверить, достоверно ли
отличие между командами? Мы можем использовать Z-критерий для
определения, является ли различие между двумя группами достоверным на стандартном
уровне значимости 0,05. По нулевой гипотезе у этих двух групп средние ранги
равны, так что мы можем рассчитать ожидаемую сумму рангов, как показано на
рис. 13.3:
Щ/ -
**1 (Я,
+ п2
±1) =
10(10 + 10
2
±R
= 105
Рис. 13.3. Расчет ожидаемой суммы рангов
где пЛ и п2 - это объемы первой и второй выборок соответственно.
Обратите внимание, что ожидаемая сумма рангов никак не зависит от
значений элементов выборок, только от их числа; если у вас есть две группы по 10
образцов в каждой, то ожидаемая сумма рангов всегда будет 105. В последнем
примере вы можете видеть, что у одной группы (Калифорния) сумма рангов
выше ожидаемой, а у другой (Невада) - ниже. Z-критерий можно вычислить на
основании среднего и стандартного отклонения W, как показано на рис. 13.4.
Независимые выборки
Рис. 13.4. Формула для расчета рангового Z-критерия
В этой формуле W - это меньшая из двух сумм рангов, нц/ - это ожидаемая
сумма рангов, которую мы рассчитали ранее, a gw - это стандартная ошибка3,
рассчитываемая по формуле на рис. 13.5.
ow=.
\п\П2(пх + п2 +1)
У 12
|10(10)(10 + 10 + 1)
V 12
Рис. 13.5. Расчет оценки стандартного отклонения для рангов
В этой формуле пх и п2 - это объемы выборок в первой и второй группах
соответственно, а 12 - это константа. Обратите внимание, что стандартное отклонение
рангов зависит только от объемов выборок, но не от значений их элементов.
Статистика Z-критерия для этих данных рассчитывается, как показано на рис. 13.6.
13.23
Рис. 13.6. Расчет Z-критерия для рангов
Используя стандартную таблицу значений нормального распределения
(рис. D.3 в приложении D), мы видим, что у такого результата р-значение выше,
чем 0,05; таким образом, мы не можем отвергнуть нулевую гипотезу.
В данном случае мы использовали нормальное приближение для критерия
суммы рангов Вилкоксона, поскольку и п] > 10 и п2 > 10. Для меньших объемов
выборок следует рассчитывать суммы рангов для каждой группы, как мы это и делали, а
затем сравнивать значения сумм с таблицей вероятностей различных значений Т.
Такая таблица доступна здесь: http://bit.ly/TfXwoR.
U-критерий Манна-Уитни, который выдаст ту же Z-статистику для заданного
набора данных, тоже используется для такого типа данных. Оба критерия можно
использовать вместо двухвыборочного ^-критерия, если нет уверенности в
нормальности данных.
Критерий знаков
Критерий знаков - это непараметрический аналог одновыборочного ^-критерия,
и он используется для проверки, равняется ли медиана выборки заданному
значению. Часто тест знаков использует ранги и биномиальное распределение для
проверки гипотез о дихотомических данных, то есть данных только с двумя
возможными значениями. Значения данных делятся на две группы: выше (+) или
,} В принципе, стандартная ошибка и стандартное отклонение, как это названо ранее и позднее, - это
не одно и то же. - Прим. пер.
ЕШНШ
Глава 13. Непараметрическая статистика
ниже (-), чем предполагаемая медиана; число элементов со значением выше этой
медианы - это п+, а со значением ниже - п-. По нулевой гипотезе выборка взята
из распределения с заданной медианой; в таком случае эта классификация задает
биномиальное распределение с я = 0,5; каждое значение рассматривается как
попытка, и результат - это + или -, а каждый из вариантов имеет вероятность 0,5.
Обратите внимание, что я (греческая бука «пи») - это обозначение вероятности в
генеральной совокупности, ар - вероятности в выборке. Тест знаков использует
биномиальное распределение для нахождения вероятности наблюдаемого
результата в том случае, если нулевая гипотеза верна.
Поставьте себя на место медика-исследователя, изучающего новое
метаболическое заболевание, временно называемое диабет типа X. Похоже, что диабет
тина X проявляется позже (то есть возраст появления первого симптома у больного
выше), чем у диабета второго типа; медианный возраст проявления у последнего
составляет 35,5 лет. Ваша нулевая гипотеза состоит в том, что я < 0,50, то есть не
более чем у 50% людей с диабетом типа X болезнь проявляется в возрасте 35,5 лет
пли позднее; альтернативная гипотеза состоит в том, что я > 0,50, то есть более чем
у 50% больных диабетом типа X болезнь проявляется после 35,5 лет. В
исследуемой выборке 40 пациентов с диабетом типа X, у 36 болезнь проявилась в возрасте
после 35,5 лет: п+ = 36. Вы используете нормальное приближение биномиального
распределения с поправкой на непрерывность, чтобы узнать, насколько вероятен
такой результат при уровне значимости 0,05 и верна ли нулевая гипотеза. Расчеты
приведены на рис. 13.7.
I z_(X±0.5)-n/7_(36-0.5)-[(40)(0.5)]_15.5_^0 I
| V/i/7(l-/7) У40(0.5)(0.5) л/10 |
Рис. 13.7. Вычисление статистики теста знаков
Здесь X - это число наблюдаемых величин выше медианы (и+), 0,5 - это
поправка на непрерывность (отрицательная в данном случае, поскольку наша
гипотеза говорит, что я > 0,5), пр - это медиана биномиального распределения
(ожидаемое значение X, если верна нулевая гипотеза), -yjnp(l - р) - это стандартное
отклонение биномиального распределения, а п - объем выборки.
Используя стандартную таблицу нормального распределения (рис. D.3 в
приложении D), вы видите, что вероятность такого результата составляет 0,00002, что
гораздо меньше, чем уровень значимости 0,05, так что вы отвергаете нулевую
гипотезу о том, что возраст проявления диабета типа X равен или ниже такового для
диабета второго типа.
Медианный критерий
Дальнейшие исследования метаболизма в вашей лаборатории дают основания
полагать, что диабет типа X может быть поделен на два подтипа - тип Х] и тип Хг и
поднимают вопрос о том, не ассоциированы ли эти подтипы с возрастом
проявления. Вы решили исследовать выборку из других 40 человек, 20 из которых предва-
Независимые выборки
¦¦ЕШ
рительно получили диагноз подтипа Xv а другие 20 - Х.г Вы решаете использовать
медианный критерий, разделяющий испытуемых из обеих выборок на две
группы - выше или ниже медианы для объединенной выборки (с испытуемыми из
обеих групп). В данном случае медиана объединенной выборки составляет 36,4 года;
вы решаете использовать уровень значимости 0,05 и провести двухсторонний тест,
поскольку вам будет интересна разница в возрасте в обе стороны.
В группе с подтипом Хх у 12 испытуемых возраст выше медианного, а у 8 -
ниже. Из группы с подтипом Х2 у 9 испытуемых возраст был выше медианного,
а у 11 - ниже. Нулевая гипотеза состоит в том, что п у двух групп равны. Если у
какого-то испытуемого возраст равен медианному, данные о нем не используются
в анализе. В табл. 13.4 приведены все частоты.
Таблица 13.4. Частоты встречаемости возрастов у больных диабетом
типаХ, итипаХ2
ТипХ,
ТипХ2
В сумме
Выше медианы
12
9
21
Ниже медианы
8
11
19
В сумме
20
20
40
Для проверки значимости различий в этих данных можно использовать тест
хи-квадрат на независимость (обсуждается в главе 5). Можно применить
формулу для быстрого вычисления х\ в которой ячейки описываются как в табл. 13.5,
а затем найти вероятность получившегося хи-квадрата при нулевой гипотезе о
независимости (испытуемые из каждой совокупности с равной вероятностью имеют
возраст ниже медианного).
Таблица 13.5. Значения ячеек для теста хи-квадрат на независимость
Тип
*,
*г
Сумма по
столбцам
Выше медианы
а
с
а + с
Ниже медианы
b
d
b + d
Сумма по строкам
а + Ь
c + d
п
Так выглядит расчет хи-квадрата на основе этих данных:
2_ n(ad-bc)2 40[(12xll)-(8x9)]2 _Qt)Q1
Х (а + Ь)(с + d)(a + c)(b + d) (12 + 8)(9 +11)(12 + 9)(8 + 11)
Используя таблицу для распределения хи-квадрат (рис. D.11 в приложении D),
находим, что при одной степени свободы наш результат (x2Q: = 0,902) можно
получить с вероятностью больше 0,10. Таким образом, мы не можем отвергнуть
нулевую гипотезу и заключаем, что наше исследование не дало оснований полагать
разницу в возрасте проявления для диабета типа Хх и типа Х2.
ешзнм
Глава 13. Непараметрическая статистика
Н-критерий Краскела-Уоллиса
Н-критсрин Краскела-Уоллиса - это непараметрический аналог однофакторного
дисперсионного анализа. Также можно его считать расширением критерия суммы
рангов Вилкоксона для более чем двух групп. Этот критерий проверяет
гипотезу о равенстве медианы нескольких групп и не требует одинакового объема всех
выборок. Предположим, вы хотите сравнить успешность работы трех команд
продавцов, одной - из шести человек, а двух - из пяти. Наша задача состоит в выборе
лучшей команды на основании ее недавних успехов. Их продажи за последний
квартал (в тысячах долларов) приведены в табл. 13.6.
Таблица 13.6. Квартальные продажи в тысячах долларов
Команда А
10
10
12
13
14
15
Команда Б
8
8
9
9
14
Команда В
6
8
10
14
15
Нашим первым шагом будут ранжирование индивидуальных суммарных
продаж без учета принадлежности к группе и присвоение ранга в случаях равных
значений, как показано в табл. 13.7.
Таблица 13.7. Ранжированные квартальные продажи
Команда А
10
10
12
13
14
15
Команда Б
8
8
9
9
14
Команда В
6
8
10
14
15
Ранг
1
3
3
3
5.5
5.5
8
8
8
10
11
13
13
13
15.5
15.5
Зависимые выборки :^Н^|
Мы используем Н-критерий Краскела-Уоллиса с уровнем значимости 0,05,
чтобы проверить, есть ли достоверные различия между работой этих трех групп.
Формула для этого критерия приведена на рис. 13.8.
12 vi 7]2
н i^-V^-3(;v + i)
Рис. 13.8. Формула для Н-критерия Краскела-Уоллиса
В этой формуле N - это суммарный объем выборки (во всех трех выборках
вместе),
я. - это объем /-й выборки,
Г - это сумма рангов i-й выборки, а
12 и 3 - это константы.
Как рассчитать Т. для выборок, показано на рис. 13.9.
2=8 + 8 + 10 + 11 + 13 + 15.5=65.5
2=3 + 3 + 5.5 + 5.5 + 13 = 30
2=1 + 3 + 8 + 13 + 15.5=40.5
Рис. 13.9. Расчет суммы рангов
Подставим эти значения в формулу для Н-критерия Краскела-Уоллиса, как
показано на рис. 13.10.
и- п
16(16+1)
65.52 302 40.52
+ +
-3(16 + 1) = 2.96
Рис. 13.10. Расчет Н-критерия Краскела-Уоллиса
Для проверки значимости полученного значения хи-квадрат мы сравниваем его
со значением хи-квадрата с двумя степенями свободы (на один меньше числа групп)
из приложения D. Наше значение ниже табличного (5,991) для уровня значимости
0,05 и df= 2, так что мы не можем отвергнуть нулевую гипотезу о равенстве медианы
всех трех групп.
Зависимые выборки
В этом разделе мы рассмотрим несколько часто используемых непараметрических
тестов для зависимых выборок.
Парный критерий Вилкоксона
Парный критерий Вилкоксона (Wilcoxon Signed Rank Test) можно использовать
как непараметрический аналог парного ^-критерия. Он подходит для тех ситуа-
ЕШВМ
Глава 13. Непараметрическая статистика
ций, когда данные представлены как парные измерения, то есть, к примеру, до и
после воздействия для одного и того же испытуемого или измерения братьев и
сестер или мужей и жен. Нулевой гипотезой для этого теста обычно является то,
что средняя разница между членами пары равна 0. Парный критерий Вилкоксона
не предполагает нормальности, но для него необходимо хотя бы симметричное
распределение, так что нельзя применять его в случае очень асимметричных
распределений.
Положим, нас интересует влияние упражнений на умственную деятельность и
настроение. У нас есть выборка из 40 малоподвижных взрослых, которые
добровольно участвуют в программе упражнений и проходят через набор
физиологических тестов до начала программы и после ее завершения. В данном конкретном
исследовании нас интересует 100-балльная шкала настроения, в котором 0
соответствует апатии, а 100 - сильному эмоциональному переживанию. Мы
анализируем настроение членов выборки до начала программы и после нее. Мы проведем
двухсторонний тест с нулевой гипотезой об отсутствии разницы между
настроением до и после упражнений с уровнем значимости 0,05.
В табл. 13.8 мы приводим выдержку из данных этого исследования для
иллюстрации процесса расчета этого критерия. (Процесс довольно механистичен и
включает процедуру ранжирования, обсужденную ранее.) Для каждой пары значений
мы рассчитываем разницу и ее абсолютное значение. Мы ранжируем абсолютные
значения разницы, а затем уже снова приписываем им знак. Если для какого-то
испытуемого разница равна 0, то он исключается из исследования, а если есть
одинаковые значения разностей, то им будет соответствовать средний ранг (то есть
если у испытуемых с рангами 3, 4 и 5 значения разностей равны, то мы припишем
им всем ранг 4).
Таблица 13.8. Упражнения и настроение
Испытуемый
1
2
3
4
5
40
До
упражнений
60
65
52
74
65
70
После
упражнений
68
70
50
85
60
77
Разница
(после - до)
8
5
-2
11
-5
7
Модуль
разницы
8
5
2
11
5
7
Ранг модуля
разницы
5
3
1
6
3
4
Ранг со
знаком
5
3
-1
6
-3
4
В пяти случаях разница равнялась 0, так что после удаления этих
испытуемых п = 35, что является достаточно большой выборкой (эмпирическое правило:
п > 25), чтобы использовать приближение парного теста Вилкоксона для больших
выборок для получения Z-значения, вероятность которого мы можем определить,
используя стандартную таблицу нормальных значений. Сумма положительных
рангов равняется 380.
Зависимые выборки ;Ц
После удаления пар равных значений у нас есть 35 пар, так что мы
рассчитываем нормальное приближение парного критерия Вилкоксона, используя формулу
с рис. 13.11.
z = -
4
|л(л + 1)(2л + 1)
V 24
Рис. 13.11. Парный критерий Вилкоксона для больших выборок
В данной формуле Т - это сумма положительных рангов, п - это число пар,
а 4 и 24 - константы.
Обратите внимание на сходство с Z-статистикой:
п(п + 1)
это ожидаемая сумма рангов, а
л(л + 1)(2л + 1)
J-- — - это стандартная ошибка, так что эта формула сравнивает
V 24 значения, которые мы получили из нашей выборки, с
ожидаемым (аналогичным математическому ожиданию
генеральной совокупности) и делит разницу на меру разброса.
Использование наших значений дает результат, показанный на рис. 13.12.
z = -
4
|л(л +1X2/1 + 1)
V 24
,оп 35(35 + 1)
380- —
4 106
(35(35+ 1X70 + 1)
i 24
Рис. 13.12. Расчет парного критерия Вилкоксона для больших выборок
с подставленными значениями
Используя стандартную таблицу значений нормального распределения
(рис. D.3 в приложении D), мы находим вероятность получить такое значение,
как 0,28914, и оно значительно выше нашего уровня значимости в 0,05, так что
мы не можем отвергнуть нулевую гипотезу.
Если бы у нас был меньший набор данных (п < 25), то мы бы использовали
вариант парного критерия Вилкоксона для малых выборок. Для него вам надо так
же, как и в случае критерия для больших выборок, присвоить каждой паре
значений ранг со знаком, а затем рассчитать сумму как положительных рангов (F),
так и отрицательных (Г ). Затем вам надо будет сравнить эти значения с таблицей
критических значений для парного критерия Вилкоксона. (Такая таблица есть в
статье Вилкоксона [1957], процитированной в приложении С, а ее версии
доступны в книгах по статистике и в Интернете: http://facultyweb.berry.edu/vbissonnette/
ЕШНН
Глава 13. Непараметрическая статистика
tables/wilcox_t.pdf.) В случае двухстороннего теста вы отвергаете нулевую
гипотезу в том случае, если Т или Т ниже критического значения, приведенного в
таблице для вашего объема выборки.
Тест Фридмана
Тест Фридмана - это расширение парного теста Вилкоксона для нескольких
связанных выборок; также можно его воспринимать как непараметрический
аналог дисперсионного анализа для зависимых выборок. Положим, нас попросили
оцепить уровень физической подготовки команды борцов тэквондо. Заставляет
задуматься следующая вещь: поскольку на соревнованиях спортсменам может
потребоваться выступить много раз за несколько часов, необходимо исследовать,
способны ли они сохранять высокий уровень своего выступления на протяжении
длительного времени. Мы проводим тренировочное соревнование и оцениваем
качество выступления каждого спортсмена по десятибалльной шкале (10 - это
великолепное выступление, а 0 - провальное) после одного часа соревнований, двух
часов и трех часов. Мы считаем, что такая шкала порядковая (9 - это выше, чем 8),
по не равиоинтервальиая или абсолютная. (Мы не знаем, одинаково ли отличие
между 8 и 9 и между 7 и 8 и в два ли раза лучше выступление с оценкой 8, чем с
оценкой 4.) Таким образом, мы будем проводить тест Фридмана для исследования
изменений в уровне мастерства спортсменов за три периода времени. Наша
нулевая гипотеза состоит в том, что они выступают одинаково хорошо в течение всех
трех часов, и мы проводим двухсторонний тест с уровнем значимости 0,05.
Данные этого исследования приведены в табл. 13.9.
Таблица 13.9. Выступление спортсменов на спарринге в ходе трех часовых
периодов
Спортсмен
1
2
3
4
5
6
7
8
1 час
9
9
6
8
8
9
9
7
2 часа
8
7
8
7
7
8
8
5
Зчаса
7
8
7
6
6
7
7
6
Первым действием должно быть ранжирование выступлений каждого атлета;
например, для спортсмена 1: самый низкий балл он получил после третьего часа,
средний - после второго, а самый высокий после первого. Эти ранги приведены
в табл. 13.10. Кроме того, обратите внимание на последнюю строку, содержащую
суммы рангов для каждого временного промежутка.
Зависимые выборки
Таблица 13.10. Ранжирование выступлений каждого спортсмена после трех
периодов по часу
Спортсмен
1
2
3
4
5
6
7
8
Сумма рангов
1 час
3
3
1
3
3
3
3
3
22
2 часа
2
1
3
2
2
2
2
1
15
Зчаса
1
2
2
1
1
1
1
2
11
Формула для расчета критерия Фридмана приведена на рис. 13.13.
bt(t + l)
Рис. 13.13. Формула критерия Фридмана
В этой формуле Ъ - объем выборки, t - это число измерений каждого
испытуемого, s. - это сумма рангов для каждого периода, а 12 и 3 - константы.
В нашем примере b = 8, t = 3, а значения для s. - это 22, 25 и 11. Подставив эти
значения в формулу, получаем результат, показанный на рис. 13.14.
Г =
12(222+152+112)
8(3)(3 + 1)
-3(8)(3 + 1) = 7.75
Рис. 13.14. Расчет критерия Фридмана
Эта статистика имеет распределение хи-квадрат с двумя степенями свободы
(df= ?-1=2). Используя рис. D.11 из приложения D, видим, что критическое
значение для такого распределения с уровнем значимости 0,05 составляет 5,991;
наша статистика превосходит это число, так что мы отвергаем нулевую гипотезу об
отсутствии отличий между выступлениями в разные промежутки времени. Судя
по исходным данным, качество выступлений со временем падает у большинства
спортсменов, это значит, что им следует уделить больше времени тренировкам.
Использование теста Фридмана не ограничивается измерениями,
разделенными временем, его также можно применять для оценки влияния лекарств или
в любой другой экспериментальной ситуации, где необходим непараметрический
подход.
ЕШНН
Глава 13. Непараметрическая статистика
Упражнения
Вот несколько упражнений, чтобы вспомнить темы, обсужденные в этой главе.
Задача
Положим, вы хотите провести тест Фридмана, но обнаруживаете, что в данных
есть совпадающие значения. К примеру, некоторые спортсмены из примера про
выступление команды по тэквондо в трех промежутках времени получили
повторяющиеся баллы. В таком случае у вас появилась необходимость использовать
средние ранги для этих испытуемых. В табл. 13.11 приведены результаты 8
спортсменов по шкале, обозначающей успешность выступления; измерения были
сделаны после одного, двух и трех часов тренировочного соревнования. Проведите тест
Фридмана для этих данных, используя нулевую гипотезу о постоянстве качества
выступления спортсменов в течение этих трех часов с уровнем значимости 0,05, и
решите, принять пулевую гипотезу или отвергнуть. Для равных значений задайте
средний ранг; то есть для баллов (6, 6, 5) ранги будут (2,5, 2,5, 1).
Таблица 13.11. Успешность выступления спортсменов на спарринге в трех
промежутках времени (с равными значениями)
Спортсмен
1
2
3
4
5
6
7
8
1 час
8
6
6
8
9
9
8
8
2 часа
8
6
8
7
9
8
7
7
Зчаса
6
7
7
6
7
7
6
7
Решение
В табл. 13.12 приведены рассчитанные ранги и суммы рангов.
Таблица 13.12. Ранги успешности выступления на спарринге в трех часовых
промежутках времени (с равными значениями)
Спортсмен
1
2
3
4
5
6
1 час
2.5
1.5
1
3
2.5
3
2 часа
2.5
1.5
3
2
2.5
2
Зчаса
1
3
2
1
1
1
Упражнения
¦¦ЕЕЗ
Спортсмен
7
8
Сумма рангов
1 час
3
3
19.5
2 часа
2
1.5
17
Зчаса
1
1.5
11.5
Расчет критерия Фридмана показан па рис. 13.15.
8(3)(3 + 1)
Рис. 13.15. Расчет критерия Фридмана с равными значениями
Есть две степени свободы {elf = t - 1). Из таблицы значений распределения
хи-квадрат (рис. D.11 в приложении D) мы видим, что критическое значение для
уровня значимости 0,05 при df=2 составляет 5,991; наша статистика меньше этой
величины, так что мы не можем отвергнуть нулевую гипотезу.
Задача
Маркетолог интересуется сбором информации о демографии фанатов
различных футбольных команд. Поскольку часто разрабатывают специальные
маркетинговые кампании для разных возрастных групп, важным является определение
медианного возраста болельщика определенной команды. Вы отвечаете за
статистику в этом проекте, и вы набираете случайную выборку членов клуба фанатов
одной из двух команд (Л и Б); вы собираете по телефону данные об этих людях,
включая их возраст. Вы определили, что общий медианный возраст (в обеих
группах вместе) равен 27,5 года, и разделяете болельщиков на старшую и младшую
половины, проведя границу по медиане. Ваши данные приведены в табл. 13.13.
Если вы проводите исследование с нулевой гипотезой об отсутствии различий в
медианном возрасте между двумя группами с уровнем значимости 0,01, каково
будет ваше решение?
Таблица 13.13. Сравнение возрастов болельщиков двух футбольных команд
Команда
А
Б
Сумма по столбцам
Выше медианы
30
60
90
Ниже медианы
70
40
110
Сумма по строкам
100
100
200
Решение
Вы решили использовать медианный тест, поэтому рассчитали значение хи-
квадрата для данных, проверяя нулевую гипотезу о независимости (поскольку
равенство медиан возрастов болельщиков обеих команд означает, что возраст не
связан с тем, за какую команду человек болеет). Вы используете быструю расчетную
KfEll
Глава 13. Непараметрическая статистика
формулу для вычисления х2, использованную в разделе этой главы про медианный
тест, и сравниваете ваши результаты с критическим значением распределения хи-
квадрат.
Расчеты приведены на рис. 13.16.
, n(ad-bc)2 200[(30 х 40) - (70 х 60)]2
* " (а + Ь)(с + d)(a + c)(b + d) " (100)(100)(90)(110)
Рис. 13.16. Расчет хи-квадрата для медианного критерия
Из таблицы значений хи-квадратов (рис. D.11 в приложении D) вы видите, что
значение для df= 1 и уровня значимости 0,01 составляет 9,210. Ваша статистика
теста больше, чем это число, так что вы отвергаете нулевую гипотезу о равенстве
медиан возрастов болельщиков двух команд. Результат: х2 = 18,18, р < 0,01.
Посмотрев на таблицу с данными, вы видите, что фанаты команды А в целом, видимо,
моложе, чем болельщики команды Б, поскольку только 30% фанатов команды А
старше медианного возраста, в отличие от 60% более старших болельщиков
команды Б.
ГЛАВА 14.
Статистика для бизнеса
и контроля качества
Многие статистические методы, используемые в бизнесе и контроле качества,
основаны на базовых приемах, включая тест хи-квадрат (обсуждаемый в главе 5),
тест Стыодента (глава 6), регрессию и дисперсионный анализ (главы с 8 по 11).
Однако для достижения специфических целей бизнеса и контроля качества
разработаны другие методы, которые станут предметом обсуждения в этой главе.
Индексы
Индексы часто используются в бизнесе, чтобы измерить изменения во времени
количества или цены определенного товара или набора товаров и услуг. Один
широко известный пример - это индекс потребительских цен (ИПЦ), который равен
средней цене определенного количества товаров и услуг, которое считается
типичным для американской семьи. В США этот индекс вычисляется ежемесячно
статистическим управлением министерства труда; этот показатель используется
для оценки уровня инфляции и расчета прибавок к заработной плате и пенсии.
Хотя ИПЦ много критикуется, он оказался весьма эффективным в качестве
обобщенного показателя средней стоимости жизни и позволяет сравнивать этот
показатель в разные эпохи и в разных регионах. ИПЦ или сходный индекс также
вычисляется в Канаде, Китае, Израиле, Новой Зеландии, Австралии и многих
европейских странах.
Вычисление индексов может быть очень простым (если индекс отражает
изменение цены или количества товара) или очень сложным (когда индекс отражает
взвешенное среднее для ряда товаров и услуг, как это происходит в случае ИПЦ).
Простой числовой индекс выражает изменение во времени цены или количества
одного товара, такого как число телевизоров, проданных за одну унцию золота.
Для вычисления простых индексов нужно выбрать базисный период, который
используется для сравнения. Индекс будет характеризовать изменения цены или
количества по отношению к этому базисному периоду. При вычислении простого
индекса необходимы три этапа:
1. Узнать цену или количество товара в интересующий нас отрезок времени.
|Щ Глава 14. Статистика для бизнеса и контроля качества
2. Выбрать базовый период и узнать цену или количество для того года.
3. Вычислить значение индекса для каждого периода времени, используя
формулу, приведенную на рис. 14.1.
/, = — х 100
Y
Рис. 14.1. Формула для вычисления простого индекса
Здесь 1( = индекс в момент времени t,
Y( = цена или количество в момент времени t, a
У() = цена или количество в базисный период.
Предположим, мы хотим провести мониторинг состояния автомобильной
промышленности в США за последние 20 лет. В рамках этого исследования мы можем
создать индекс, который отражает число собираемых за год автомобилей, по
сравнению с первым годом. Если у нас есть данные за 1986-2005 годы, то 1986 год
будет базисным, а число автомобилей, произведенных в этом году, будет обозначено
как Y{). Рассмотрите табл. 14.1, в которой приведены малые вымышленные числа
для иллюстрации вычисления простого индекса.
Таблица 14.1. Данные для вычисления простого индекса
Год
1985
2005
Число выпущенных автомобилей
5 000
4 000
Вычисление индекса для этих данных показано на рис.
*2005
-i2*xioo.
5000
= 80
14.2.
Рис. 14.2. Вычисление простого индекса
Индекс, равный 100, свидетельствует о том же количестве или цене, как в
базовый период. Индекс, превышающий 100, говорит о снижении количества или
цены, а индекс больше 100 означает увеличение количества или цены, по
сравнению с базовым периодом. Одно из существенных преимуществ индексов состоит
в том, что они позволяют сравнивать характеристики, выраженные в разных
величинах и с разным размахом величин. Например, используя индексы, мы можем
легко сравнить относительное снижение или увеличение продукции автомобилей,
мотоциклов и велосипедов за определенный период времени.
Составной индекс совмещает информацию о цепе или количестве нескольких
типов товаров или услуг. Например, мы можем подсчитать количество пива,
продаваемого в Шотландии тремя крупнейшими пивоваренными компаниями, как сумму
количества пива, проданного каждым изготовителем. Если мы будем производить
эти подсчеты в течение нескольких лет и выберем один год в качестве базового
Индексы ЫН1^И^шЯ
периода, мы может вычислить значение индекса для каждого года, так же, как мы
делали для простого индекса в предыдущем примере. Этот тип индекса называется
простой составной индекс, поскольку он вычисляется путем объединения
информации из разных источников без использования какого-либо способа взвешивания.
Если при вычислении индекса мы используем некоторый тип взвешивания,
такой индекс называется взвешенным сложным. Индексы цен часто взвешены,
например в соответствии с количеством проданных товаров. Есть несколько
способов проведения взвешивания, поскольку количество купленных товаров может
меняться в зависимости от выбранного периода времени, и выбор весов может
существенно повлиять на вычисленное значение индекса. Однако как только
правила взвешивания определены, вычисления становятся очень простыми. Для
каждого периода времени рассчитывается общая цена, и индексы для каждого периода
времени вычисляются аналогично простым индексам.
При вычислении индекса Ласпейреса (Laspeyres) значения параметров в
течение базового периода используются в качестве весов, так что инфляция или
дефляция измеряется для заданной корзины товаров или услуг. ИПЦ - это пример
индекса Ласпейреса; величины, используемые для определения весов, основаны
на исследованиях покупок более чем 30 000 семей с 1982 по 1984 год. Этапы
вычисления Ласпейреса таковы:
1. Собрать информацию о ценах (Р , Р ,..., Pk) для каждого периода времени
для каждого наименования товара (с 1 по k), которые будут включены в
индекс.
2. Собрать информацию об объемах покупок (Qu , Q2i, ..., Qk( ) для базового
периода для каждого наименования товаров, которые входят в индекс.
3. Выбрать базовый период (t{)).
4. Вычислить взвешенные суммы для каждого временного периода при
помощи формулы, приведенной на рис. 14.3.
у
Рис. 14.3. Формула для вычисления взвешенной суммы для определенного
периода времени
5. Вычисление индекса Ласпейреса, 1(У посредством деления взвешенной
суммы для каждого периода времени на взвешенное среднее для базового
периода и умножения на 100, как показано на рис. 14.4.
/,-Нг х10°
'-1
Рис. 14.4. Формула для вычисления индекса Ласпейреса
МИ' Глава 14. Статистика для бизнеса и контроля качества
В табл. 14.2 приведен простой пример вычисления индекса Ласпейреса для
потребительской корзины, содержащей всего два типа товаров.
Таблица 14.2. Пример вычисления индекса Ласпейреса
Продукт
Хлеб
Молоко
Базовое количество
(2000 год)
10
20
Цена в 2000 году
1.00
2.00
Цена в 2005 году
1.50
4.00
Взвешенное среднее для 2000 года составляет:
(10 х 1,00)+ (20x2,00) = 50,00.
Для 2005 года взвешенное среднее равно:
(10 х 1,50)+ (20x4,00) = 95,00.
Индекс Ласпейреса для этой потребительской корзины в 2005 году при
использовании 2000 года в качестве базового периода вычисляется так, как показано на
рис. 14.5.
Рис. 14.5. Вычисление индекса Ласпейреса
При вычислении индекса цеп Пааше (Paasche) используются взвешенные
суммы с учетом количества товаров, приобретенных в каждый период времени.
Преимущество такого подхода заключается в возможности учесть изменения в
покупательских предпочтениях. Например, если цена товара возрастает, то люди
начинают реже его покупать и переключаются на менее дорогие аналоги.
Например, если цена говядины растет быстрее, чем цена курятины, то люди будут чаще
покупать курицу, а не говядину. Это изменение в предпочтениях покупателей не
может быть отражено в индексе Ласпейреса, но учитывается индексом Пааше.
Действия мри вычислении индекса Пааше сходны с таковыми при вычислении
индекса Ласпейреса. Основное различие заключается в том, что нужно собрать
информацию об объеме покупок в каждый период времени, и эта информация
используется при вычислении взвешенных средних. Для вычисления индекса
Пааше необходимо:
1. Собрать информацию о ценах (Ри, Р2(,..., Pkt) для каждого периода времени
и каждого наименования (от 1 до k), которые входят в состав индекса.
2. Собрать информацию об объемах покупок для каждого временного отрезка
(Q1(, Q2l,..., Qkl) для каждого наименования, входящего в индекс.
3. Выбрать базисный период (t{)).
4. Вычислить взвешенные суммы для каждого отрезка времени, используя
формулу, приведенную на рис. 14.6.
Индексы
Рис. 14.6. Формула для вычисления взвешенных сумм для одного периода
времени при помощи индекса Пааше
5. Вычислить индекс Пааше - 1(, путем деления взвешенной суммы для
каждого временного отрезка на взвешенную сумму для базового периода и
умножения на 100, как показано на рис. 14.7.
Рис. 14.7. Формула для вычисления индекса Пааше
Для вычисления индекса Пааше мы используем данные, приведенные в
табл. 14.3.
Таблица 14.3. Вычисление индекса Пааше
Продукт
Хлеб
Молоко
Количество
в 2000 году
10
20
Цена
в 2000 году
1.00
2.00
Количество
в 2005 году
15
15
Цена
в 2005 году
1.50
4.00
Взвешенная сумма для 2000 года составляет:
(10 х 1,00)+ (20x2,00) = 50,00.
В 2005 году взвешенная сумма равна
(15 х 1,50)+ 15x4,00) = 82,50.
Индекс Пааше для этой корзины товаров в 2005 году с использованием 2000
года в качестве базового периода вычисляется так, как это показано на рис. 14.8.
82 5
Д™ -х 100 = 165.0
'2005
50.0
Рис. 14.8. Вычисление индекса Пааше
Обратите внимание на то, что хотя цены в обоих примерах были одинаковыми,
разные методы взвешивания привели к значительным различиям в двух
значениях индекса (190 и 165). Преимущество индекса Пааше заключается в
возможности сравнивать цены для корзины товаров с учетом объемов их продаж в каждый
из временных периодов. Недостаток состоит в том, что нам нужно собирать эту
ЕШВШ
Глава 14. Статистика для бизнеса и контроля качества
информацию (количество приобретенных товаров) для каждого отрезка
времени, что может быть недопустимо дорого. Другой недостаток индекса Пааше -
поскольку н цены, и востребованность товаров меняются с течением времени,
трудно сравнивать индекс Пааше для любых двух временных периодов, если один из
них не является базовым.
Критика в адрес индекса потребительских цен (ИПЦ) в США
ИПЦ - это основной показатель динамики цен в США, который рассчитывается в
некотором виде статистическим управлением министерства труда с 1919 года. Он
используется во многих целях, включая характеристику инфляции и расчет социального
пособия, пенсии и пособия по безработице. Неудивительно, что индекс, используемый для
многих целей, подвергается разносторонней критике. К принципиальным возражениям,
которые приводят к растущему игнорированию ИПЦ, относят следующие.
Изменение качества и искажение показателей из-за недавно появившихся
товаров
ИПЦ не учитывает улучшение качества некоторых товаров, таких как электронные
устройства. DVD-плеер, который стоит $150 в 2005 году, может быть существенно более
качественным и, значит, более ценным для потребителя, чем тот, который стоил $100
в 2000 году, однако это повышение качества не отражено в ИПЦ. Аналогично,
поскольку используется фиксированная потребительская корзина, новые новые товары
своевременно не включаются в ее состав в ее состав. В результате снижение цены на
начальной стадии (обычное для новых электронных устройств) не регистрируется этим
индексом.
Смещение результатов в результате замены продукта
Использование фиксированной потребительской корзины (весй корректируются один
раз в 10 лет) не позволяет зарегистрировать изменение покупательских предпочтений
вследствие колебаний цен. Например, если цена мяса растет быстрее, чем цена другой
белковой пищи, такой как птица или яйца, покупатели могут в основном перейти на эти
продукты, однако такой сдвиг не отразится на значениях ИПЦ.
Смещение в результате использования крупных магазинов
Поскольку информация о ценах собирается при анализе продаж в обычных
универмагах, новые способы продаж, такие как гипермаркеты или интернет-магазины, не
достаточно учтены при вычислении ИПЦ.
Временнь1е ряды
Временные ряды часто используются в бизнес-статистике для отображения
изменения величин во времени. Строго говоря, временной ряд - это
последовательность измерений некоторой величины, сделанных в разные моменты времени.
Приведенный выше пример с числом автомобилей, произведенных в каждый год
с 1986 по 2005, подходит под это определение, так же как и измерения, которые
позже обсуждаются в этой главе в разделе, посвященном контрольным картам.
Временные ряды могут быть использованы в целях описания или формулировки
статистических выводов; последнее включает прогнозирование или предсказание
величин для предстоящих периодов времени. Однако читатель должен помнить,
Временные ряды
ПНЕШ
что анализ временных рядов - это сложная тема со многими
специализированными приемами и что в этом разделе у нас есть возможность ввести лишь некоторые
термины, проиллюстрировав их несколькими простыми примерами. Всем, кто
планирует работать в этой области, следует ознакомиться с учебником по данной
теме, такими как книга Роберта С. Шамвэя «Временные ряды и их использование
с примерами на языке R» (Robert S. Shumway "Time Series and Its Applications:
With R Examples", изд-во Springer). Учтите, что некоторые авторы, например
Табачник (Tabachnick) и Фидель (Fidell), считают, что правильное использование
анализа временных рядов возможно, если у вас есть как минимум 50 точек.
Одно из свойств временных рядов заключается в том, что данные во
временной последовательности не независимы друг от друга, как это ожидается в
стандартной обобщенной линейной модели, для них характерна автокорреляция. Это
значит, что значение величины в данный момент времени связано со значениями,
которые идут перед и после нее, а возможно, и с более удаленными значениями
этого временного ряда.
Считается, что данные временных рядов - стационарные, этозначит, что их
свойства, такие как среднее, дисперсия и автокорреляционная структура, постоянны на
всем протяжении временного ряда. Для достижения стационарности данные перед
обработкой иногда подвергаются дифференцированию) это значит, что значение для
данного момента времени вычитается из значения для какого-то предшествующего
момента времени. Период времени между двумя соседними наблюдениями
называется лаг. Методы, необходимые для определения нужного типа
дифференцирования и его автоматизированного проведения, входят в состав статистических
пакетов, предназначенных для анализа временных рядов. Для стабилизации дисперсии
перед началом анализа могут быть проведены другие преобразования данных, такие
как извлечение квадратного корня или логарифмирование.
Для описания составляющих временного ряда часто используются аддитивные
модели, такие как
Yi = Tt + Ci + Si + R,.
В этой модели к составляющим тренда Y( относятся:
Т( - долговременный тренд, общий тренд за все время исследований;
С( - циклический эффект, колебания вокруг долговременного тренда из-за
состояния бизнеса или экономики, такие как периоды общей рецессии или
экспансии экономики;
S( - сезонный эффект, колебания из-за времени года (например, различия
между зимними и летними месяцами);
R( - остаточный, или ошибочный эффект, который остается после того, как
учтены долговременный, циклический и сезонный эффекты; может отражать как
случайные события, так и редкие, такие как ураганы или эпидемии.
Значительная часть анализа временных рядов посвящена объяснению
изменчивости этих составляющих во времени. Идея похожа на разбиение дисперсии на
составляющие в моделях дисперсионного анализа, однако в основе лежат иные
математические приемы.
ЕШНН
Глава 14. Статистика для бизнеса и контроля качества
Точные значения регистрируемых на протяжении отрезка времени
переменных, также известные как нескорректированные («сырые») временные ряды,
почти всегда характеризуются значительной изменчивостью. Она может скрыть
основные тренды, которые используются для объяснения закономерностей и
точного прогнозирования. Для борьбы с этой проблемой разработаны разные методы
сглаживания. Они могут быть разделены на две основные группы: методы
скользящего среднего, при которых для ряда последовательных точек вычисляется
определенный тип среднего, и это среднее вычитается из исходных значений, и экспо-
ненцирование, при котором для взвешивания исходных значений используются
показательные ряды.
Для вычисления простого скользящего среднего (ПСС) нужно взять невзве-
шенное среднее определенного числа точек (п) перед нужным моментом времени.
Число п часто называют окном из-за представления о том, что для вычисления
скользящего среднего используется окно, включающее п точек (окно шириной п).
По мере продвижения по временному ряду окно перемещается таким образом, что
в него попадают разные точки ряда, и среднее для определенного момента
времени рассчитывается для попавших в окно точек. Например, при вычислении ПСС
по пяти точкам среднее будет вычисляться по данному значению и предыдущим
четырем.
ПСС для каждой новой точки включает одно новое значение и исключает одно
старое, снижая тем самым флуктуации. От этого свойства и происходит название
«скользящее среднее» - поскольку самое старое значение «ускользает», будучи
«вытесненным» новым. Сходные приемы применяются при определении рейтинга
профессиональных игроков в теннис, хотя в этом случае вычисляют скорее общую
сумму баллов, а не среднее. Баллы каждого игрока в данную неделю - это сумма
его баллов, набранных за предыдущие 52 недели, а каждую неделю эта сумма пере-
считывается, поскольку результаты самой давней недели удаляются, а результаты
последней недели добавляются.
Чем больше ширина окна, используемого для ПСС, тем сильнее сглаживаются
колебания, поскольку каждая новая точка имеет относительно мало влияния, по
сравнению со всеми использующими при усреднении точками. В какой-то момент
данные могут стать настолько сглаженными, что важная информация об
имеющихся закономерностях будет утеряна. Кроме того, чем шире окно, тем больше
данных придется выкинуть (поскольку понадобится больше точек для
вычисления каждого среднего значения). Это видно на примере, приведенном на рис. 14.9
и в табл. 14.4.
Как и ожидалось, наибольшие колебания наблюдаются для исходных данных,
меньше колебаний - для усреднения с окном шириной в два наблюдения, и очень
мало - с окном шириной в четыре наблюдения.
Когда используется окно шириной в два наблюдения, то нужно выбросить всего
одно наблюдение (поскольку перед ним нет никакого наблюдения, необходимого
для вычисления среднего). При использовании окна шириной в четыре
наблюдения нужно выкинуть первые три точки, поскольку ни у одной из них нет трех
предшествующих наблюдений, чтобы посчитать среднее. Это не такая большая
Временные ряды
проблема, если у нас есть много наблюдений, но для набора данных из всего 10
наблюдений это приводит к заметной потере информации.
>1
О
(Г
7_
г
2 О"
X
с с:
л J
* 4
i 1
1 J
2 i
5 z
г
0-
*^^^ \ / A" •-
—i 1 1 1—
r >--
V ""A /a
1 1 1
.исходные
данные
n=2
¦n=4
5 6 7
Время
10
Рис. 14.9. Исходные данные и скользящие средние сл = 2ип = 4
Таблица 14.4. Простое скользящее среднее для окон разной ширины
Время
Исходные
данные
л = 2
п = 4
1
5
2
6
5.5
3
3
4.5
4
7
5
5.25
5
4
5.5
5
6
6
5
5
7
8
7
6.25
8
5
6.5
5.75
9
2
3.5
5.25
10
6
4
5.25
Центрированное скользящее среднее (ЦСС) сходно с ПСС, однако
используемое для усреднения окно включает и предыдущие, и последующие наблюдения.
Например, для ЦСС с шириной в три наблюдения среднее для второго
наблюдения составит 4,67, или (5 + 6 + 3)/3. Учтите, что последующие наблюдения - это
результаты измерений, а не предсказанные значения; они последующие только в
том смысле, что получены позже, чем центральное значение при вычислении
данного ЦСС. Пример приведен в табл. 14.5.
Таблица 14.5. Центральное скользящее среднее (л = 3) для приведенных выше
данных
Время
Исходные данные
л = 3
1
5
2
6
4.67
3
3
5.33
4
7
4.67
5
4
5.67
6
6
6.00
7
8
6.33
8
5
5.00
9
2
Взвешенное скользящее среднее (ВСС) учитывает значения, попадающие в окно
заданной ширины, однако более близкие к рассматриваемому наблюдению
значения получают больший вес. По умолчанию используются веса из
арифметической, а не экспоненциальной последовательности. Обычно рассматриваемому
значению присваивают вес п} где п - это ширина окна. Каждое следующее
наблюдение, используемое при подсчете ВСС, имеет все меньший вес по мере удаления
ЕЭ
Глава 14. Статистика для бизнеса и контроля качества
от анализируемого значения. Используя эту систему для вычисления ВСС для
пяти дней, анализируемому дню будет присвоен вес 5, предыдущему дню - 4 и так
далее до пятого дня с весом в 1. Эта взвешенная сумма делится на сумму весовых
множителей, которая будет равна [п (п - 1)]/2. ВСС уместна в любой ситуации,
когда предполагается, что идущие подряд значения будут наиболее тесно связаны,
и эта связь убывает с увеличением расстояния между точками.
Экспоненциальное скользящее среднее (ЭСС) также придает больше веса
близко расположенным наблюдениям, однако веса, присваиваемые отстоящим дальше
наблюдениям, убывают не в арифметической, а в экспоненциальной
последовательности. Для вычисления ЭСС определяется константа экспоненциального
сглаживания а, находящаяся в интервале от 0 до 1. Эта константа связана с
шириной окна, п, согласно формуле, приведенной на рис. 14.10.
I 2 I
а =
п + 1
Рис. 14.10. Формула для вычисления константы для экспоненциального
скользящего среднего
В данном случае а = 0,2 соответствует /2 = 9, поскольку 2/10 = 0,2. Затем а
используется согласно формуле на рис. 14.11, в которую включаются новые члены,
пока они не станут такими маленькими, что ими можно пренебречь.
ЭСС =
Рх
+ (1-
- сс)р2 +
1+(1-
(1-
-«)
<*)2р3+(1-
+ (1-а)2 +
а)3/?4 + ...
..
Рис. 14.11. Формула для вычисления экспоненциального скользящего среднего
В приведенной выше формуле р{ - это измерение в тот момент времени, для
которого вычисляется ЭСС, р2 - предыдущее измерение, p.s - предпредыдущее
измерение и так далее. Знаменатель стремится к 1/а по мере увеличения
числа включенных в вычисление наблюдений, и 86% веса присваивается первым п
наблюдениям. В данном случае п - это не ширина окна при вычислении ЭСС, как
это было при вычислении ПСС и ВСС; последняя точка определяется значением а
и представлением исследователя о величине значения, которым можно
пренебречь.
Анализ решений
Мы принимаем решения ежедневно, однако как мы приходим к принятию
наилучшего решения, особенно в ситуациях, когда многое (например, большая сумма
денег) поставлено на кон? Анализ решений - это набор специальных приемов,
методологий и теорий, которые используются для систематизации процесса принятия
решений с целью повышения его качества. В рамках теории принятия решений
существует много направлений, и каждое может быть полезным в определенной
ситуации. Этот раздел посвящен нескольким наиболее распространенным мето-
Анализ решений
ЕШ
дам анализа решений, которые помогут получить представление о его
составляющих, а также помогут разобраться в реальных случаях принятия решений.
Процесс анализа решений будет описан на примере финансовых убытков и прибылей,
однако также может быть использован для других показателей (например, личной
удовлетворенности или улучшения качества жизни), если их можно измерить.
При анализе решений процесс принятия решения обычно выполняется в виде
последовательности этапов, что не так уж и отличается от действий,
предпринимаемых для проверки гипотез. Анализ решений также весьма похож - за
исключением выбора и применения математической модели (шаги 5 и 6) - на обычный
процесс принятия решений, в который мы вовлечены ежедневно. Помимо
возможности принятия лучшего решения, выполнение описанных ниже шагов (а
также их обоснование) должно облегчить объяснение причин принятия какого-либо
решения человеку, который не принимал в этом участия. Вот основные этапы:
1. Охарактеризуйте ситуацию, включая внешние обстоятельства (любые
процессы реального мира, которые могут повлиять на результат). Внешние
обстоятельства должны быть изложены как взаимно исключающие и
исчерпывающие события, например высокий/средний/низкий спрос или
аномальное/нормальное количество осадков.
2. Перечислите возможные варианты, то есть альтернативные решения,
которые могут быть приняты, они называются действия.
3. Укажите возможные исходы или последствия.
4. Выявите выгоды и затраты, связанные со всеми возможными сочетаниями
решений и исходов.
5. Выберите подходящую математическую модель.
6. Примените модель, используя информацию из пунктов 2-4.
7. Примите решение, основываясь на лучшем ожидаемом, согласно
предсказаниям модели, исходе.
Выбор методологии анализа решений зависит частично от количества
информации о ситуации. Есть три типа контекстов, в которых можно использовать
теорию принятия решений:
• принятие решений в условиях определенности;
• принятие решений в условиях неопределенности;
• принятие решений в условиях риска.
Принятие решений в условиях определенности предполагает, что внешн ие
обстоятельства в будущем известны, так что для принятия решения необходимо лишь
указать возможные варианты и их выгоды, чтобы сделать выбор, который
неминуемо приведет к оптимальному решению. Эту ситуацию мы не будем обсуждать
далее, поскольку она не требует математического моделирования, и тут ие может
быть никаких сомнений о том, что является лучшим выбором.
Принятие решений в условиях неопределенности - это более
распространенная ситуация; мы не знаем вероятность разных внешних обстоятельств и
должны принять решение, основываясь только на анализе выгод и затрат,
сопряженных с разными действиями при разных внешних обстоятельствах. Например,
ШМНн
Глава 14. Статистика для бизнеса и контроля качества
если мы решаем, в каком городе открыть ресторан, успех этого действия
зависит частично от экономического климата в том городе, где мы откроем
ресторан, однако мы можем не располагать оценками экономического климата в
разных городах в будущем. Аналогично, если мы решаем, какой сорт растений
посадить, наш урожай будет частично зависеть от количества осадков за
вегетационный период, однако у нас может быть недостаточно знаний, чтобы
предсказать, сколько выпадет осадков.
Принимая решения в условиях риска, мы знаем вероятности каждого исхода
(или имеем разумные оценки этих вероятностей) и можем сочетать эти знания с
информацией об ожидаемых выгодах для выбора оптимального решения.
Минимакс, максимакс и максимин
Информацию, необходимую для принятия решения в условиях
неопределенности, можно обобщить в виде таблицы результатов, где строки соответствуют
действиям, которые можно предпринять, а столбцы - внешним обстоятельствам.
Предположим, что мы раздумываем, куда стоит вложить деньги, в организацию
большого мероприятия на открытом воздухе, в устройство меньшего мероприятия
в помещении, или вообще не организовывать ничего. Допустим, что дело
происходит в климатической зоне, где в это время года обычны ураганы с ливнем, и мы не
можем с должной степенью уверенности сказать, какова вероятность такого
урагана в день мероприятия. Организация мероприятия будет стоить $50 000. Таблица
результатов может выглядеть как табл. 14.6.
Таблица 14.6. Таблица результатов для вклада денег в организацию события
Действия
Мероприятие на открытом воздухе
Мероприятие в помещении
Не вкладывать деньги
в организацию мероприятия
Дождь
-$50 000
$200 000
$0
Погода
Нет дождя
$500 000
$200 000
$0
На мероприятие на открытом воздухе придет больше людей, чем в помещение,
так что если в тот вечер не будет дождя, то мы получим больше денег (прибыль
$500 000). Если будет идти дождь, то мероприятие отменится, и мы потеряем
деньги, ничего не получив взамен (убыток $50 000). С другой стороны, мероприятие
в помещении принесет одинаковую прибыль ($200 000) вне зависимости от того,
будет ли идти дождь: меньше, чем мероприятие на открытом воздухе в хорошую
погоду, но больше, чем оно же под дождем. Наконец, мы можем решить, что
вкладывать деньги в театрализованное мероприятие слишком рискованно, и найти им
другое применение.
Мы можем создать таблицу потерь вследствие неиспользования благоприятных
возможностей (упущенных выгод), в которой будут указано, сколько мы
упустили возможность заработать, выбрав тот или иной образ действий. Для нашей гипо-
Анализ решений
тетической схемы «вложений в организацию мероприятия в дождливой стране»
эта таблица будет выглядеть как табл. 14.7.
Таблица 14.7. Таблица упущенных выгод для вклада денег в организацию события
Действия
Мероприятие на открытом воздухе
Мероприятие в помещении
Не вкладывать деньги
в организацию мероприятия
Дождь
$250 000
$0
$200 000
Погода
Нет дождя
$0
$300 000
$500 000
Обратите внимание, что в этой таблице нет отрицательных значений. Лучшим
действием при данных погодных условиях будет то, при котором упущенная
выгода будет равна $0, тогда как для остальных действий указана сумма, которая
упущена из-за неоптимальной стратегии действий при данных погодных
условиях.
Для принятия решений в условиях неопределенности разработаны три
алгоритма - минилшкс, максимакс и максимин. Алгоритм мшшмакс позволяет выбрать
действие так, чтобы минимизировать упущенную выгоду. Для принятия решения
по этому алгоритму нужно проанализировать таблицу упущенных выгод, чтобы
найти максимальную упущенную выгоду для каждого действия и выбрать
действие, для которого это значение минимально. В этом примере:
наибольшая упущенная выгода (на открытом воздухе) = $250 000;
наибольшая упущенная выгода (в помещении) = $300 000;
наибольшая упущенная выгода (не вкладывать деньги) = $500 000.
Согласно алгоритму минимакс, мы решим вложить деньги в организацию
мероприятия на открытом воздухе, поскольку в этом случае упущенная выгода будет
минимальной из трех рассмотренных вариантов действий.
Стратегия максимин подразумевает выбор действия с наибольшей
минимальной прибылью. Эту стратегию называют выбором пессимистов, поскольку в
данном случае отдают предпочтение варианту с наибольшей минимальной прибылью
или наименьшими потерями - лучший выбор при неблагоприятных условиях.
В этом примере:
наибольшая упущенная выгода (на открытом воздухе) = -$50 000;
наибольшая упущенная выгода (в помещении) = $200 000;
наибольшая упущенная выгода (не вкладывать деньги) = $0.
Используя стратегию максимин, мы проведем мероприятие в помещении,
поскольку самое плохое, что может произойти в этом случае, - мы заработаем
$200 000 вне зависимости от погодных условий.
Стратегия максимакс предполагает выбор действия, которое характеризуется
наиболее высокой максимальной выгодой. По этой причине максимакс может
ЕВШШШ
Глава 14. Статистика для бизнеса и контроля качества
быть назван алгоритмом для оптимистов, поскольку в данном случае выбор
делается в пользу оптимального действия при наиболее благоприятном состоянии
внешних факторов. В нашем примере:
наибольшая упущенная выгода (на открытом воздухе) = $500 000;
наибольшая упущенная выгода (в помещении) = $200 000;
наибольшая упущенная выгода (не вкладывать деньги) = $0.
Согласно алгоритму максимакс, мы выберем мероприятие на свежем воздухе,
поскольку в данном случае мы получим наибольшую максимальную выгоду.
Принятие решений в условиях риска
Если вероятности разных внешних обстоятельств известны или могут быть
достаточно аккуратно оценены, мы находимся в ситуации принятия решений в
условиях риска. Допустим, что в предыдущем примере мы знали вероятность дождя
в тот вечер, на который было назначено мероприятие. Если вероятность дождя
составляет 0,6, то вероятность отсутствия дождя - 0,4, поскольку это взаимно
исключающие события. Мы добавим эту информацию в табл. 14.8.
Таблица 14.8. Таблица результатов разных действий при данных вероятностях
разной погоды
Действия
Вероятность
Мероприятие на открытом воздухе
Мероприятие в помещении
Не вкладывать деньги в
организацию мероприятия
Погода
Дождь
0.6
-$50 000
$200 000
$0
Нет дождя
0.4
$500 000
$200 000
$0
Ожидаемый
результат
$170 000
$200 000
$0
Ожидаемый результат вычисляется путем умножения результата при каждом
сочетании действий и погодных условий на вероятность данной погоды.
Например, для проведения мероприятия на открытом воздухе
Е{резулыпат) = (0,6)(-50 000) + (0,4)(500 000) = -30 000 + 200 000 = 170 000.
Мы выбираем вариант с наилучшим ожидаемым результатом. В данном случае мы
бы организовали мероприятие в помещении. Для применения этого метода нужно
иметь разумные оценки вероятности разных внешних условий. Если бы
вероятности в приведенном выше примере поменялись местами, то наилучший ожидаемый
результат был бы достигнут при проведении мероприятия на открытом воздухе.
Деревья решений
Если вероятность разных результатов при данных действиях известна, то можно
построить дерево решений, которое иллюстрирует возможные действия и их
результаты при разных внешних условиях и может быть использовано для поиима-
Улучшение качества LJhH^I
ния результатов при разных комбинациях действий и внешних условий. Дерево
решений, содержащее ту же информацию, что приведена в табл. 14.8, показано на
рис. 14.12.
Действия Внешние условия Результат
Мероприятие у Дождь (0.6) $50,000
на открытом /
воздухе \ Нет дождя (0.4) $500,000
, Дождь (0.6) $200,000
Мероприятие
в помещении
".Нетдождя (0.4) $200,000
Нет вложений
<;
у Дождь (0.6) $0
^ Нет дождя (0.4) $0
Рис. 14.12. Дерево решений для примера с выбором места проведения
мероприятия
Улучшение качества
Концепция улучшения качества (УК) родилась в 1920-х годах, когда Вальтер Ше-
варт (Walter Shewhart) начал разработку статистического подхода к
исследованию изменчивости в промышленности. Интерес к УК резко возрос в 1950-х годах
после публикации работы В. Эдвардса Деминга (W. Edwards Deming), который
разработал статистический метод, основываясь на результатах Шеварта. По
иронии судьбы, метод Деминга был сначала не признан на его родине (США), но с
энтузиазмом воспринят в Японии, где технологии УК были использованы на
производстве с таким успехом, что японские компании смогли поспорить за
превосходство, а некоторых случаях и одержать верх над американской
промышленностью. В ответ на это американские компании стали использовать технологии УК в
1980-х годах; «Моторола» и «Дженерал Электрик» - одни из наиболее известных
пионеров применения этих методов.
Существует много подходов к УК, включая распространенную программу,
известную под названием «Шесть сигм» (6а), которая является частью общего
подхода, называемого комплексное управление качеством. Этот раздел книги
сфокусирован на основах УК, общих для многих таких программ, и не содержит жаргона
и акронимов, специфичных для любой конкретной программы. Он также
посвящен статистической методологии, используемой при УК, хотя читатель должен
помнить о том, что большинство программ УК имеет много аспектов и включают
психологические и организационные подходы наряду с методами измерения и
статистического анализа.
Хотя идея УК зародилась в производственном секторе, сейчас ее применяют в
других областях, включая здравоохранение и образование. «Качество», наверное,
ЕШ
Глава 14. Статистика для бизнеса и контроля качества
стало модным словом в наш век, так что рассмотрение основных аспектов
измерения и улучшения качества может оказаться полезным для людей, которые
работают в самых разных областях. Всюду, где качество может быть определено и
измерено, концепция УК может предложить полезные инструменты.
Первый шаг при измерении чего-либо - определить эту характеристику.
Качество в контексте УК обычно определяется с позиции покупателя;
высококачественный продукт удовлетворяет потребительским нуждам и предпочтениям. В
производстве это может означать детали механизмов с определенными промерами и
сроком службы. В здравоохранении это может означать визит к доктору, который
удовлетворит жалобы пациента и не будет подразумевать долгого ожидания или
других вызывающих отвращение моментов. Запросы и предпочтения
потребителя нужно перевести в характеристики продукта, которые можно измерить. Если
взять пример со здравоохранением, «отсутствие чрезмерного времени ожидания»
можно оиерационализировать как «время ожидания составляет не более 10
минут». Это позволит оценить, удовлетворяет ли стандартам каждый визит.
Аналогичным образом можно задать конкретные промеры для деталей механизмов и
оценивать, выдерживаются ли промеры данных деталей в рамках диапазона,
определенного заказчиком.
Язык УК характерен для промышленности, в нем часто упоминаются
продукты, которые создаются в результате процессов, являющихся частью системы.
Например, компания может изготавливать болты (продукт) при помощи серии
процессов (таких как разрезание, штамповка и полировка), и это является частью
системы, которая преобразует сырье (такое как металл) в продукт (болты).
Характеристики любого процесса - это переменные. Например, не любой
изготовленный болт будет обладать заданными параметрами. УК во многом имеет дело
с определением допустимых пределов изменчивости, регистрируя изменчивость
в ходе процесса, выявляя причины и находя решения, если продукт выходит за
пределы допустимой изменчивости.
Схемы прогона и контрольные карты
Контрольные карты, разработанные Вальтером Шевартом в 1920-х годах, - это
основной графический прием, позволяющий отслеживать вариации. Схема прогона -
это улучшение базовой версии контрольной карты, которая представляет собой
график временного ряда, на котором отображена некоторая характеристика продукта
по осп у и время или порядковый номер продукта по оси х. Часто изображенные
на графике точки являются статистиками, такими как среднее, вычисленными для
небольших выборок продукта, а не отдельными значениями.
Отображая на графике выборочные средние, мы можем вспомнить теорему о
центральном пределе и подразумевать нормальное распределение значений на графике
вне зависимости от типа распределения отдельных значений в генеральной
совокупности. Это важно при использовании правил для определения, вышел ли процесс
из-под статистического контроля. Если на графике приведены исходные значения,
то эти правила можно использовать только при нормальном распределении данных,
Улучшение качества
¦¦ЕШ
однако отображение сырых значений может быть полезным для визуального анализа
имеющихся вариаций во времени.
Мы ожидаем обнаружить изменчивость продукта, созданного при любом
процессе, однако мы не предполагаем, что распределение данных изменится, как по
положению (среднее или медиана), так и по разбросу данных (стандартное
отклонение или размах). Если распределение характеристик процесса не меняется во
времени, мы говорим, что процесс находится под статистическим контролем пли
просто под контролем. Если распределение характеристик меняется с течением
времени, мы говорим, что процесс вышел из-под статистического контроля или
просто вышел из-под контроля. Мониторинг источников вариации и борьба с ними
с целью удержания процесса под контролем или обретения этого контроля
называется статистическое управление технологическим процессом.
В любом процессе существуют два основных источника общей изменчивости:
общие причины и специальные, или определимые, причины. Общие причины
изменчивости связаны с организацией всего процесса и влияют на все его результаты.
В производстве к общим причинам можно отнести освещение на заводе, качество
сырья и квалификацию рабочих. Если общими причинами объясняется слишком
большая доля изменчивости, организация процесса должна претерпеть
изменения. Возможно, освещение можно улучшить, рабочих - больше обучать, задания
разбить на более мелкие этапы, чтобы повысить аккуратность выполнения или
найти более подходящий источник сырья. Этот тип корректировки процесса в
целом относится к сфере ответственности руководства и не вовлечен в тот тип
анализа данных, который обсуждается в этом разделе.
Для наших задач процесс, у которого есть только общие причины вариации,
считается находящимся под контролем. Напротив, мы сосредоточимся на
специальных причинах вариации - действиях или событиях, которые не являются составной
частью организации производственного процесса. Специальные причины обычно
действуют ограниченное время и влияют лишь на малую часть процесса. Рабочий
может утомиться и не быть способным выполнять работу аккуратно, или могут
сбиться настройки станка, который начнет производить детали с параметрами,
выходящими за пределы допустимых значений. Контрольные карты
используются для выявления момента выхода процесса из-под статистического контроля и
могут помочь в обнаружении специальных причин вариации.
На контрольные карты обычно помещают осевую линию, проходящую через
среднее или медианное значение исследуемой характеристики. Осевая линия
служит точкой отсчета для оценки отдельных значений, например для оценки того,
насколько сильно отличаются отдельные значения от центрального. Положение
этой осевой линии обычно определяется заранее аналитиком и представляет
собой скорее ожидаемое значение, характеризующее процесс, который находится
под контролем (протекает правильно, обеспечивает выработку приемлемой
продукции), а не среднее по всем данным. Также на контрольных картах принято
соединять соседние точки отрезками, что позволяет легче видеть закономерности в
последовательности измерений. Оба этих момента продемонстрированы на
гипотетической схеме прогона (рис. 14.13).
шмн
Глава 14. Статистика для бизнеса и контроля качества
6.0
~ 4.5-
?3.0-
CD
00-
JVJ\nAf^\hf-
4 v ^ V V
1 5 9 13 17 21 25 29
Порядковый номер изделия
Ч~
i
33
hr
V
37
Рис. 14.13. Контрольная карта веса 40 болтов, выраженного в унциях
(отдельные значения), с осевой линией, проведенной через значение 3
Эта контрольная карта отображает вес 40 последовательно изготовленных в ходе
воображаемого производственного процесса болтов. По оси у отложен вес каждого
болта в унциях, ось х соответствует порядковому номеру изделия, а осевая линия
проведена через среднее значение 3. Таким образом, мы можем заметить, что первые
три болта были немного легче среднего, четвертый - тяжелее и т. д. Мы также можем
видеть, что изменчивость случайна, и вес болтов колеблется вокруг среднего, а самый
долгий период (последовательные значения, изменяющиеся в одном направлении)
состоит из четырех значений (с 29 по 32).
В представленных на рис. 14.3 данных не прослеживается никакой
закономерности (неудивительно, ведь они были созданы при помощи генератора случайных
чисел!) - это один из признаков того, что процесс находится под контролем.
Контрольные карты на рис. 14.14-14.19 демонстрируют некоторые закономерности,
которые можно выявить при помощи схем прогона, и это может говорить о необ-
ходимости дальнейших исследований.
6.0-
f з.о-
ш
0.(Ь
1 1 1
1 3 5
¦ i i i
7 9 11 13
Порядковый номер изделия
i
15
i
17
19
Рис. 14.14. Контрольная карта с восходящим трендом
Обратите внимание, что на этой стадии, поскольку мы рассматриваем отдельные
значения, мы ищем общие закономерности, а не проводим статистические тесты.
Вскоре мы обсудим более строгие правила для определения закономерностей в
данных, которые не могут быть объяснены случайной изменчивостью, а должны
быть исследованы как доказательство выхода процесса из-под контроля.
Улучшение качества
5-
I 4-
& 2-
1-
vA\AV^V^w\
1 4 7 10 13 16 19 22 25 28
Порядковый номер изделия
6.0-
X
I3*
* 1 5-
0.0-
Рис. 14.15. Контрольная карта с нисходящим трендом
_^--v
V /* *^*V .Х*^ ^^^V "р*5-
N^/ ху ЧчИ'
1 4 7 10 13 16 19 22 25 28
Порядковый номер изделия
Рис. 14.16. Контрольная карта с цикличной изменчивостью
7.5-
I 5.0-
а-
X
•Ь 2.5
и
СО
0.0-
-Av^Vv^VvY\A
1 4 7 10 13 16 19 22 25 28
Порядковый номер изделия
Рис. 14.17. Контрольная карта с увеличением вариации
10-
'х 5-
X
3"
X
>ч
о
со
-5-
i i
1 4
i
7
10 13 16 19 22
Порядковый номер изделия
i
25
28
Рис. 14.18. Контрольная карта с выбросом (единичное экстремальное значение)
Глава 14. Статистика для бизнеса и контроля качества
6.0
? «¦
? 3.0-
и
а»
Л 1.5-
0.0-
vV^vA^
i i i i i i i i i i
1 4 7 10 13 16 19 22 25 28
Порядковый номер изделия
Рис. 14.19. Контрольная карта с изменением уровня
(сдвиг среднего значения вверх)
Если контрольные карты основаны на средних значениях, то благодаря теореме
о центральном пределе мы можем использовать нормальное распределение для
выявления значений или закономерностей, которые будут чрезвычайно
нехарактерны для процесса, находящегося под статистическим контролем. Для
выявления процесса, вышедшего из-под контроля, разработан ряд правил, основанных
на распределении значений, ожидаемом, если бы они происходили из выборок с
нормальным распределением со средним и дисперсией, наблюдающимися в
процессе, когда он находится под контролем.
Использование стандартного отклонения для определения допустимых границ
изменчивости продукта послужило источником названия программы «Шесть
сигм», поскольку сигма (а) используется для обозначения стандартного
отклонения. Идея, которая лежит в основе программы «Шесть сигм», заключается в
достаточном снижении вариации, так чтобы продукт, параметры которого
укладываются в диапазон ±3а, все еще удовлетворял покупателя.
Как обсуждалось в третьей главе, при нормальном распределении данных
вероятность попадания данных в определенный диапазон значений известна. Доля
данных из нормального распределения, которая попадает в различные диапазоны,
заданные числом стандартных отклонений по отношению к среднему, показана на
рис. 14.20.
Рис. 14.20. Вероятность попадания данных в определенные диапазоны
нормального распределения
Улучшение качества
Era
Как было описано в третьей главе, из этого рисунка ясно, что при нормальном
распределении в пределах одного стандартного отклонения от среднего
находится 68,2% значений. Вероятность того, что наблюдение попадет в интервал между
одним и двумя стандартными отклонениями больше или меньше среднего,
составляет около 27,2%, вероятность попадания в интервал между двумя и тремя
стандартными отклонениями больше или меньше среднего и равна примерно 4,2%,
а вероятность нахождения за пределами трех стандартных отклонений больше
или меньше среднего - около 0,2%. Иначе говоря, в повторных выборках из
генеральной совокупности с нормальным распределением значений мы ожидаем, что
около 68% выборочных средних будет находится в пределах одного стандартного
отклонения от среднего, около 95% - в пределах двух стандартных отклонений и
около 99% - в пределах трех стандартных отклонений.
Контрольная карта с добавлением контрольных пределов интерпретирует эту
информацию так, что распределение точек отложено на оси г/, а по оси х идет время
или порядок отбора образцов. Разные диапазоны обычно снабжены подписями,
как показано на рис. 14.21.
На этой контрольной карте:
1. Зона Л, или зона трех сигм, - это диапазон между двумя и тремя о от осевой
линии.
2. Зона 5, или зона двух сигм, - это диапазон между одной и двумя о от осевой
линии.
3. Зона С, или зона одной сигмы, - это значения в пределах одной а от осевой
линии.
+3а
+2а
+1сг
Осевая линия
-1а
-2а
-За
В
С
С
в
Порядковый номер наблюдения
Рис. 14.21. Контрольная карта с диапазонами, выраженными в сигмах
Эти зоны используются совместно с правилами анализа закономерностей для
определения, находится ли процесс под контролем.
Поскольку для определения, находится ли процесс под контролем, важны и
среднее значение, и изменчивость выборок, контрольные карты обычно изготав-
кяд
Глава 14. Статистика для бизнеса и контроля качества
ливаются парами - на одной отображаются средние значения для выборок, а на
другой - изменчивость. Для анализа среднего значения непрерывных данных
используется корта х (называемая так, потому что х, которое произносится как «х с
чертой», используется в статистике для обозначения среднего). Изменчивость
иллюстрируется либо s-картой, отражающей стандартное отклонение выборок1,
либо r-картой, на которой показан размах2 значений.
Перечисленные ниже правила анализа закономерностей применяются для
интерпретации данных с карт средних значений, однако эти правила можно
использовать и для анализа других типов контрольных карт. Этот перечень -
сочетание нескольких наборов правил, включая правила Вестерн Электрик (Western
Electric), разработанные для одноименной компании (теперь вошедшей в состав
«Амсрикан телефон энд телеграф» - AT&T) и опубликованные впервые в 1956
году, и правила Нельсона, разработанные Ллойдом С. Нельсоном (Lloyd S. Nelson)
и впервые опубликованные в 1984 году.
Признаки, при проявлении которых процесс считается вышедшим из-под
контроля согласно правилу анализа закономерностей, следующие:
1. Любое значение попадает вне зоны А (дальше от осевой линии).
2. 9 последовательных значений попадают в зону С или кнаружи от неё по
одну сторону от осевой линии.
3. 6 последовательных значений уклоняются в одном направлении, то есть
параметр постоянно увеличивается или уменьшается.
4. 14 последовательных значений «скачут» попеременно то вверх, то вниз.
5. 2 из 3 последовательных значений попадают в зону Л или кнаружи от нее с
одной и той же стороны от осевой линии.
6. 4 из 5 последовательных значений попадают в зону В или кнаружи от нее
по одну сторону от осевой линии.
7. 15 значений подряд попадают в зону С.
8. 11 последовательных значений попадают в зону В или кнаружи от нее.
Если данные бинарные, а не непрерывные (например, если объекты просто
классифицируются как бракованные или приемлемые), вместо контрольных
карт для средних значений можно строить р-карты или пр-карты, основанные
на биномиальном распределении. Учтите, что биномиальные данные в сфере
контроля качества называются данными по относительному распределению.
Если вас интересует число дефектов, а не число бракованных деталей (когда у
детали может быть несколько дефектов), вместо контрольных карт для средних
значений создаются с-карты и и-карты. Поскольку все они обычно создаются
при помощи компьютерных программ, мы не будем здесь подробно обсуждать
эти карты. Самое главное, что правила их интерпретации сходы с правилами для
контрольных карт со средними значениями. Приведенный ниже набор правил
поможет разобраться, какой тип контрольной карты нужно использовать для
разных типов данных:
1 От англ. standard deviation - стандартное отклонение. - Прим. пер.
2 От англ. range - размах. - Прим. пер.
Упражнения '^H^l
1) выборочные средние для непрерывных данных (картах);
2) число бракованных деталей в выборках равного размера (яр-карта);
3) доля бракованных деталей в выборках разного размера (р-карта);
4) среднее число дефектов на деталь для выборок равного размера (с-карта);
5) среднее число дефектов на деталь для выборок разного размера (м-карта).
В. Эдварде Деминг и Япония
Япония не всегда была промышленным центром, каким мы знаем ее сейчас. В первую
половину XX века в Японии производились в основном недорогие товары, а
промышленная инфраструктура страны сильно пострадала во время Второй мировой войны. Однако
после войны победившие союзники отрядили группу инженеров, чтобы помочь Японии
возродить ее экономику.
Одной из составляющих мероприятий по возрождению было обучение японских
производителей статистическим методам контроля качества. В 1950 году при содействии
японского союза ученых и инженеров В. ЭдвардсаДеминга (1990-1993), статистика,
который учился вместе с Вальтером Шевартом, пригласили прочесть курс лекций о
контроле качества. Во время своего визита Деминг также встретился с руководством многих
ведущих японских компаний.
Деминг произвел такое впечатление на глав японских промышленных компаний, что
они учредили две ежегодные награды за успехи в области улучшения качества его имени:
приз Деминга для отдельных лиц (присуждается людям, которые внесли важный вклад в
исследования, разработку методологии, распространение идей в области комплексного
управления качеством) и приз за применение идей Деминга для компаний
(присуждается за выдающееся улучшение результата при помощи применения идей комплексного
управления качеством). Дальнейшую информацию об этих наградах можно найти на
сайте института Деминга (http://demina.org).
Упражнения
Вот краткое повторение тем, затронутых в этой главе.
Задача
Рассчитайте простой индекс для 2000 года, используя каждый из приведенных
в табл. 14.9 годов в качестве базового. Что вы узнали из этих результатов о
влиянии выбора базового периода?
Таблица 14.9. Данные для вычисления индекса
с использованием различных базовых периодов
Год
1970
1980
1990
2000
Цена
1000
1500
2000
1500
Глава 14. Статистика для бизнеса и контроля качества
Решение
12{т = 150, если принять за базовый 1970 год, 100 - если сравнивать с 1980 годом,
и 75, если базовый год - 1990. Это показывает важность выбора базового периода
при вычислении индекса. Отсюда ясно также, почему важно не позволить
политическим или иным посторонним соображениям повлиять на этот выбор.
Индекс для 1970 года как базового вычисляется следующим образом:
12Ш) = (1500/1 000) х 100 = 150;
для 1980 года как базового:
/2()()() = (1500/1 500) х 100=100;
для 1990 года как базового:
12Ш) = (1500/2 000) х 100 = 75.
Задача
Вычислите индексы Ласпейреса и Пааше для 2000 года, используя данные из
табл. 14.10 и выбрав 1990 год в качестве базового. Почему эти индексы
различаются?
Таблица 14.10. Данные для сравнения индексов Ласпейреса и Пааше
Продукт
Говядина
Курица
Количество
в 1990 году
100 фунтов
100 фунтов
Цена
в 1990 году
$3 /фунт
$3 /фунт
Количество
в 2000 году
50 фунтов
150 фунтов
Цена
в 2000 году
$5 /фунт
$3.5/фунт
Решение
Индекс Ласпейреса равен 141,67, индекс Пааше составляет 87,5. Наблюдаемая
разница обусловливается разными правилами присвоения весов: при расчете
индекса Ласпейреса используются веса базового года, а для индекса Пааше - веса
индексного года. В данном случае в 1990 и 2000 годах общее количество мяса было
равным, однако в 2000 году покупали меньше говядины и больше курицы, по
сравнению с 1990. Оценка инфляции на основании индекса Ласпейреса не отражает
этого изменения в поведении потребителей.
Ход вычисления индекса Ласпейреса показан на рис. 14.22, а индекс Пааше
вычисляется так, как показано на рис. 14.23.
(100
(100
Рис.
(50:
(100
х5.00)-
хЗ.ОО)-
ьЦООх
НЮ0>
: 3.50)
: 3.00)
х100 =
= 141.67
14.22. Вычисление индекса Ласпейреса
к 5.00)4
хЗ.ОО)-
•(150 х
f(100>
3.50)
с 3.00)
х100 =
= 129.17
Рис. 14.23. Вычисление индекса Пааше
Упражнения ,1Н^1
Задача
Вычислите простое (ПСС) и центрированное (ЦСС) скользящее среднее для
п = 3 и п = 5 для шестого наблюдения из табл. 14.11.
Таблица 14.11. Данные для вычисления ПСС и ЦСС
Время
Исходные данные
1
3
2
5
3
2
4
7
5
6
6
4
7
8
8
7
9
9
Решение
ПСС(п = 3) = (7 + 6 + 4)/3 = 5,7.
ПСС(и = 5) = (5+ 2 + 7 + 6 + 4)/5 = 4,8.
ЦСС(и = 3) = (6 + 4 + 8)/3 = 6,0.
ЦСС(А2 = 5) = (7+ 6 + 4 + 8 + 7)/5 = 6,4.
Обратите внимание на то, что поскольку в этих данных есть восходящий тренд,
оценки ЦСС выше, особенно при более широком окне.
Задача
Допустим, вы думаете, где открыть канцелярский магазин, в большом или
маленьком городе. В большом городе потенциальный заработок будет выше, однако
выше будут и убытки (из-за больших организационных расходов). Успех
магазина будет во многом зависеть от экономической ситуации в момент его открытия.
Если торговля в городе расширяется, у вас есть хороший шанс заработать, но если
дела ухудшаются, вы можете с трудом вернуть затраченные деньги.
В табл. 14.12 приведены исходы дела в двух возможных ситуациях. Примите
решения, пользуясь критериями минимакс, максимакс и максимин.
Таблица 14.12. Данные для сравнения разных мест открытия канцелярского
магазина
Размещение
Крупный город
Маленький город
Экономическая ситуация
Хорошая
$200 000
$100 000
Плохая
$10 000
$20 000
Решение
Для применения алгоритма минимакс нужно составить таблицу упущенных
выгод вроде табл. 14.13.
Таблица 14.13. Таблица упущенных выгод при возможных сценариях открытия
канцелярского магазина
Размещение
Крупный город
Маленький город
Экономическая ситуация
Хорошая
$0
$100 000
Плохая
$10 000
$0
Глава 14. Статистика для бизнеса и контроля качества
Решение по алгоритму минимакс - это действия, минимизирующие
упущенную выгоду; в данном случае мы решим разместить свой магазин в большом
городе.
Решение по алгоритму максимакс - это действия, при которых максимальный
доход будет наибольшим, в данном случае мы опять решим разместить свой
магазин в большом городе.
Решение по алгоритму максимин - это действия, характеризующиеся самым
большим минимальным доходом, так что в данном случае мы решим разместить
свой магазин в маленьком городе.
Задача
Какие правила расположения точек закономерностей нарушены, судя по
контрольной карте на рис. 14.24?
Рис. 14.24. Контрольная карта с нарушениями закономерностей
Имейте в виду, что в данном случае среднее равно 3, а стандартное отклонение -
0,5, так что осевая линия проходит через значение 3, диапазон трех сигм находится
между 1,5 и 4,5, двух сигм - между 4,0 и 2,0, и одной сигмы - между 3,5 и 2,5.
Решение
Все нарушения обозначены на рис. 14.25 и перечислены ниже.
5-
4^
3-
2-
V
i 1\ Т Л
1 1
1 5
i
9
С1>2
V _А • /V / \_ з л ; 1
i i i i i i
13 17 21 25 29 33
Порядковый номер наблюдения
i
37
4
(**>гЧ/
i i
41 45
UCL =4.5
4
3.5
Х=3
2.5
2
LCL=1.5
Рис. 14.25. Контрольная карта с обозначенными нарушениями закономерностей
ния ШНЕШ
Девять точек подряд находятся по одну сторону от осевой линии
(правило 2).
Одна точка находится вне диапазона трех сигм, то есть кнаружи от зоны Л
(правило 1).
Шесть точек подряд «идут» в одном направлении (правило 3).
Четыре из пяти последовательных точек находятся вне диапазона одной
сигмы (зона В или дальше от осевой линии) по одну сторону от осевой
линии (правило 6).
гая*'
ГЛАВА 15.
Статистика в медицине
и эпидемиологии
Многие статистические показатели, используемые в медицине и
эпидемиологии, включая тест Стыодепта (обсуждается в главе 6), коэффициент корреляции
(глава 7) и разные типы регрессии и дисперсионного анализа (главы с 8 по 11),
применяются также в других областях пауки. Однако некоторые статистические
показатели (такие как вероятность успешного исхода) были специально
разработаны для нужд медицины и эпидемиологии, а другие (например, определение
мощности и объема выборки), хотя и используются в других областях, так часто
применяются в медицине и эпидемиологии, что рассматриваются именно в этой
главе.
Показатели заболеваемости
Прежде чем перейти к специализированным показателям заболеваемости, стоит
обсудить значения нескольких терминов, с которыми часто возникает путаница
при использовании в повседневной речи. Мы всегда можем выразить частоту
заболеваемости в числе случаев. Например, в прошлом году в городе Л
зарегистрировано 256 случаев туберкулеза, а в городе В - 471. Исходные числа полезны людям,
которые распределяют средства в настоящее время и планируют их распределение
в будущем, поскольку им нужно знать, сколько случаев туберкулеза (и других
заболеваний) ожидается в следующем году, чтобы соответственно распределить
ресурсы. Однако для исследовательских задач и для планирования на национальном
и международном уровне заболеваемость полезнее выражать в относительных,
а не абсолютных величинах, поскольку нам часто хочется посмотреть на
тенденции во времени или в разных регионах с разной численностью населения.
Например, приведенные выше гипотетические исходные значения позволяют
предположить, что ситуация в городе В хуже, чем в городе Л, но если численность жителей
города В в пять раз превышает численность жителей города Л, то это утверждение
выполняется с точностью до наоборот. Аналогичным образом число заболеваний
может расти из-за роста численности населения, так что для проведения
сравнений нам нередко нужно перевести число случаев в другие показатели.
Показатели заболеваемости
шшшмшт
Отношения, доли и частоты
Три связанных показателя - это отношения, доли и частоты. Отношение (ratio)
выражает величину одной переменной по сравнению с величиной другой
переменной, эти числа не должны обладать какими-то определенными свойствами
или относиться к одному объекту. Отношения могут быть выражены в виде Л:В
или Л на Б и обычно приводятся к стандартным единицам, чтобы облегчить
сравнение, таким как \\В или А на 10 000. Нас может интересовать отношение числа
мужчин со СПИДом к числу женщин со СПИДом в США. Согласно данным
центров по контролю и профилактике заболеваний, в 2005 году в США жило 769 635
мужчин и 186 383 женщины со СПИДом. Таким образом, отношение больных
мужчин к больным женщинам составляет 769 635:186 383, что также можно
записать как 4,13:1. Вторая формулировка яснее демонстрирует, что в США в 2005
году число мужчин со СПИДом более чем вчетверо превосходило число женщин
со СПИДом.
В эпидемиологии и здравоохранении обычно используют два типа отношений -
это отношения рисков и отношения благоприятных исходов, которые обсуждаются
позже в этой главе. Для вычисления отношений сравниваемые характеристики не
обязательно должны быть выражены в одинаковых единицах измерения; широко
использующийся показатель для сравнения доступности медицинской помощи в
разных странах - это отношение числа больничных коек к численности
населения. Этот показатель часто выражается в числе коек на 10 000 человек.
Согласно данным Всемирной организации здравоохранения, в 2005 году в Англии было
39 коек на 10 000 человек, в Судане - 7, а в Перу - 11, из чего можно сделать вывод,
что стационарное лечение более доступно в Англии, чем в двух других странах.
Такой тип отношений часто называется частотой (rate), хотя он не соответствует
строгому определению частоты (обсуждается ниже), поскольку в знаменатель не
входят единицы измерения времени.
Доля (proportion) - это частный случай отношения, в котором все объекты,
входящие в числитель, также входят и в знаменатель. Возвращаясь к предыдущему
примеру, если мы захотели узнать долю мужчин среди всех больных СПИДом в
США, мы бы разделили число мужчин на общее число случаев заболевания
(число больных мужчин плюс число больных женщин), как это показано на рис. 15.1.
769 635 + 186 383
Рис. 15-1. Вычисление доли
Доли часто выражаются в процентах, что означает буквально на сотню {cent па
латыни - это 100). Для перевода в проценты доли нужно умножить на 100:
0,805 х 100 = 80,5%.
Долю мужчин от всех жителей США со СПИДом можно также выразить как
80,5 процента, или 80,5%.
Глава 15. Статистика в медицине и эпидемиологии
Частота (rate), строго говоря, - это доля, в знаменатель которой входят
характеристики времени. Например, мы нередко измеряем частоту сердцебиения в
ударах в минуту и частоту заболеваний или увечий в числе случаев за неделю,
месяц или год. Показатели заболеваемости или смертности часто приводят в виде
частоты, умноженной на 1000 или 100 000 на единицу времени, поскольку легче
сравнивать такие числа, как 3,57 и 12,9 за год на 100 000 человек, чем 0,0000357 и
0,0000129 в год на одного человека.
Преобразование частот в стандартные единицы измерения облегчает сравнения
популяций разного размера. Например, поданным центров по контролю и
профилактике заболеваний, смертность в США в 2004 году составила 816,5 на 100 000
человек в сравнении с 1076,4 на 100 000 человек в 1940 году и 954,7 на 100 000
человек в 1960 году. В 2004 году умерло больше человек, чем в оба других года
(2 397 615 человек в 2004 году, 1 417 269 человек в 1940 году и 1 711 982
человека в 1960 году), но поскольку численность населения США также увеличивается,
ежегодная смертность в расчете на 100 000 человек уменьшается.
Это продемонстрировано на простом примере с использованием
вымышленных данных (табл. 15.1).
Таблица 15.1. Показатели численности населения и смертности
в течение нескольких лет
Год
1940
1950
1960
1970
Число смертей
75
95
110
125
Численность
населения
50 000
60 000
75 000
90 000
Число смертей
на 100 000 человек
150.0
158.3
146.7
138.9
Можно видеть, что хотя число смертей ежегодно увеличивается, численность
населения растет еще быстрее, поэтому смертность в расчете на 100 000 человек
уменьшается в каждый из годов, по которым у нас есть данные. Для вычисления
смертности (частоты смертей) на 100 000 человек используйте формулу,
приведенную на рис. 15.2.
число смертей
х 100 000
численность населения
Рис. 15.2. Вычисление смертности на 100 000 человек
Таким образом, используя данные из табл. 15.1, смертность на 100 000 человек
в 1940 году рассчитывается так, как показано на рис. 15.3.
75
50,000
х 100 000
Рис. 15.3. Вычисление смертности на 100 000 человек в 1940 году
Показатели заболеваемости
шшшп
Один вопрос, возникающий при вычислении частоты для долгого периода
времени, такого как год, заключается в выборе числа, которое будет стоять в
знаменателе, поскольку численность населения в течение этого периода нельзя считать
постоянной. Одно из распространенных решений - использовать численность
населения в середине этого периода (например, года).
Существует несколько других проблем, связанных с выражением
заболеваемости. Одна - приводить ли данные о числе заболевших людей или о числе
заболеваний. Например, если бы вы изучали гигиену ротовой полости, вы могли бы
интересоваться разрушениями зубов, однако у одного человека может быть
больше одной дырки. Вас будет интересовать число людей, у которых есть хотя бы одна
дырка в зубах, или общее число дырок?
Сходный вопрос возникает при изучении переходных состояний. Допустим,
если вы изучаете бездомных, интересуетесь ли вы, сколько людей были
бездомными хотя бы один раз за определенный период времени, или будете ли вы
считать каждый случай бездомности, понимая, что каждый человек мог лишиться
дома в данный период времени более одного раза. Это проблемы выбора единицы
анализа, то есть вы должны решить, что вы изучаете (человека, у которого может
быть одна или несколько дырок в зубах, или число отдельных зубов, в каждом из
которых может образоваться дырка), и собирать данные, помня о своем решении.
Единицы анализа обсуждаются подробнее в главе 3.
Распространенность заболевания
и заболеваемость
Когда мы говорим о числе случаев заболевания в эпидемиологии и медицине, мы
сразу должны решить, считаем ли мы все существующие случаи болезни или
только новые случаи. Обычному человеку это может показаться несущественными
тонкостями, но для людей, работающих в медицине и эпидемиологии, это
различие существенно, поскольку нам часто бывает нужно отделить вновь возникшие
случаи заболевания от уже существующих. Например, в этом случае мы можем
определить эффективность мер по ликвидации антисанитарии для
предотвращения новых случаев заболевания. Мы отделяем вновь возникшие случаи
заболевания от уже существующих, измеряя два показателя частоты заболеваний:
распространенность заболевания и заболеваемость.
Распространенность заболевания характеризует число случаев заболевания,
которые отмечены в данной популяции в определенный момент времени.
Распространенность заболевания характеризует подверженность популяции
заболеванию, не делая различий между новыми и уже существующими случаями;
диабетик, выявленный в день проведения исследования, фиксируется так же, как
диабетик, живущий с этим диагнозом 20 лет. Распространенность заболевания
особенно полезна для тех, кто занимается распределением ресурсов, поскольку
им нужно знать размер проблемы наряду с прогнозом на будущее.
Распространенность заболевания становится все более важным показателем, поскольку
внимание эпидемиологов в индустриальную эпоху переместилось с инфекционных
ЕШНШ
Глава 15. Статистика в медицине и эпидемиологии
заболеваний на хронические. Это происходит потому, что хронические
заболевания и состояния часто неизлечимы, но и не приводят к быстрому смертельному
исходу, так что человек может жить с таким заболеванием или состоянием годы,
если ему оказывают правильную медицинскую помощь.
Распространенность заболевания определяется как доля людей в популяции с
определенным заболеванием в данный момент времени и вычисляется, как
показано на рис. 15.4.
число случаев заболевания
Р :
численность населения
Рис. 15.4. Определение распространенности заболевания
Если в результате исследования выяснили, что из 150 000 жителей одного
города 671 - диабетики, то распространенность диабета в том городе на момент
исследования составит 671 человек на 150 000, или 447,3 на 100 000. Принятые
единицы, такие как число людей на 100 000, обычно используются при
изложении результатов для простоты сравнения. Поскольку распространенность
заболевания свидетельствует о состоянии популяции в определенный момент времени,
ее иногда называют точечной распространенностью. Учтите, что «точка» может
быть календарной единицей времени, такой как день, или периодом в жизненном
цикле или другой последовательности событий, такой как начало менопаузы или
первый день после операции. Распространенность иногда называют частотой
распространения, особенно когда речь идет о длительных периодах времени, таких
как год, хотя, строго говоря, это неправильно, поскольку в знаменателе не стоят
единицы измерения времени.
Заболеваемость вычислить сложнее, поскольку для этого нужно определить
три се составляющие. Заболеваемость характеризует число новых случаев
заболевания или состояния, развившихся в группе риска за определенный интервал
времени. Группой риска считаются люди, у которых данное состояние может
возникнуть. Например, мужчины не могут забеременеть, так что они не входят в «группу
риска» по беременности. Аналогичным образом, если человек уже заразился ВИЧ
(вирусом, который вызывается СПИД), то он не может заразиться им еще раз
(и не может выздороветь, насколько нам известно), так что в популяцию,
подверженную риску заражения ВИЧ, входят только ВИЧ-отрицательные люди. И
распространенность заболеваний, и заболеваемость используются не только для
характеристики заболеваний и состояний, но и образа жизни; например, мы можем
говорить о распространении курильщиков в Мексике или о начавших курить в
2005 году учениках определенной школы.
Существует два типа заболеваемости: кумулятивная заболеваемость и
плотность заболеваемости. Кумулятивная заболеваемость (КЗ) вычисляется как доля
заболевших людей за определенный отрезок времени (рис. 15.5).
Показатели заболеваемости
¦МЕЛ
число случаев заболевания
КЗ = за определенный период
численность населения
Рис. 15.5. Формула для вычисления кумулятивной заболеваемости
КЗ используется для оценки вероятности того, что у находящегося в группе
риска человека за данный отрезок времени разовьется определенное заболевание
или состояние, так что важно определить протяженность этого отрезка времени.
КЗ для возникновения рака груди у женщин за один год после начала приема
оральных контрацептивов и за 10 лет различается.
Формула для вычисления КЗ подразумевает, что всю группу риска можно
обследовать на протяжении всего заданного периода; это значит, что по умолчанию
заболеваемость - это доля. Если состав группы риска меняется на протяжении
заданного периода, то вместо этого нужно вычислять плотность заболеваемости
(incidence density), также известную как частоту заболеваемости. Этот
показатель используется, если люди включаются в исследование после его начала или
выбывают до его завершения. Для вычисления плотности заболеваемости
необходимо выразить знаменатель в единицах человеко-времени, что показывает, как
долго наблюдали каждого человека. Время наблюдения каждого человека часто
называют его временным вкладом в исследование.
Подсчет единиц человеко-времени показан на примере данных из табл. 15.2.
В ней представлены вымышленные данные по частоте послеоперационного
инфицирования в двух больницах. Поскольку в этих больницах находится разное
число пациентов, а пациенты пребывают там разное время, нам нужно вычислить
плотность заболеваемости, используя единицы человеко-времени в качестве
знаменателя. Мы будем анализировать частоту осложнений в перерасчете на 100 па-
циенто-дней. Каждый пациенто-день можно рассматривать как возможность для
инфицирования, так что использование этой величины в качестве знаменателя
позволяет учесть разницу в возможности для заражения.
Таблица 15.2. Данные о послеоперационном инфицировании в двух больницах
Больница
1
1
1
Всего для первой больницы
2
2
2
2
Всего для второй больницы
Порядковый
номер пациента
1
2
3
1
2
3
4
Число дней
в больнице
30
25
15
70
45
30
50
75
200
Была ли
инфекция?
Нет
Да
Нет
1
Да
Нет
Нет
Да
2
ИНН • Я Глава 15. Статистика в медицине и эпидемиологии
Частота инфекций в перерасчете на 100 пациенто-дией вычисляется так, как
показано на рис. 15.6.
число инфекций
х100
число пациенто-дней
в исследовании
Рис. 15.6. Вычисление частоты инфекций в перерасчете на 100 пациенто-дней
Так, для этого примера вычисление частоты заболеваний для первой больницы
приведено па рис. 15.7, а для второй - на рис. 15.8.
1
70
х10() =
= 1.43
па
100
Рис. 15.7. Вычисление частоты инфекций в перерасчете на 100 пациенто-дней
для первой больницы
2 х 100 = 1.00 на 100
200
Рис. 15.8. Вычисление частоты инфекций в перерасчете на 100 пациенто-дней
для второй больницы
Хотя во второй больнице отмечено больше случаев послеоперационных
инфекций, они произошли за пропорционально большее число человеко-дней, так
что частота послеоперационных инфекций ниже во второй больнице, чем в
первой.
Связь между распространенностью определенного заболевания и
заболеваемостью им сильно зависит от его длительности. Если это кратковременное
заболевание (такое как обычный насморк), то для него распространенность будет
ниже заболеваемости. Напротив, если данное заболевание длится долго
(типично для многих хронических болезней типа диабета), то распространенность
превысит заболеваемость. Изменения распространенности заболевания с течением
времени связаны с изменениями или заболеваемости, или длительности
заболевания. Например, частота заболевания смертельным недугом может снизиться,
но его распространенность может увеличиться из-за появления новых методов
лечения, которые позволяют людям с таким заболеванием дольше жить
(увеличение средней длительности такого заболевания). Аналогично заболеваемость
может увеличиться, но распространенность этого заболевания при этом может
снизиться из-за появления новых методов лечения, которые позволяют быстрее
победить недуг.
Распространенность заболевания можно математически выразить как
произведение заболеваемости и продолжительности болезни, как показано на рис. 15.9.
Показатели заболеваемости
¦ШЕШ
P=/xD
Рис. 15.9. Связь между распространенностью заболевания (Р),
заболеваемостью (/) и продолжительностью болезни (D)
Если две эти характеристики известны, можно вычислить третью. Например,
если заболеваемость составляет 75 человек на 100 000, а средняя годовая
распространенность заболевания - 45 человек на 100 000, то среднюю
продолжительность заболевания можно вычислить, как показано на рис. 15.10.
I - Р 45/100 000 45 ~~~~^ I
D= — = — = — =0.6 года
I 75/100 000/гоЭ 75/год
Рис. 15.10. Вычисление средней продолжительности недуга при известных
заболеваемости и распространенности заболевания
При этом подразумевается постоянство условий на всем протяжении
исследований и отсутствие значительных изменений заболеваемости или
продолжительности болезни. Эту формулу также можно использовать для оценки изменений
распространенности заболевания при других значениях заболеваемости или
продолжительности болезни. Например, если заболеваемость определенным недугом
будет оставаться на уровне 125 человек на 100 000, но продолжительность этой
болезни снизится с 0,6 лет до 0,1, то ее распространенность упадет с 75 до 12,5
случаев на 100 000 человек за год. Аналогично если продолжительность болезни
увеличивается, то ее распространенность возрастает. Если заболеваемость будет
равна 200 случаям на 100 000 человек в год, но продолжительность болезни
увеличится с 0,5 года до 2 лет, распространенность увеличится с 100 до 400 случаев
на 100 000 человек за год.
Общие, категоризированные
и стандартизованные частоты
По умолчанию термин частота обычно означает общую частоту. Общая
частота - это частота для всей исследуемой генеральной совокупности, без
взвешивания или поправок.
Распространенный пример - это общая смертность. По данным центра
контроля заболеваний, общая смертность от рака в США в 2003 году составляла
195,5 человек на 100 000. В общих частотах нет ничего плохого, но иногда нам
необходима более подробная информация, или нужно внести поправки в частоты,
чтобы сравнивать их более осмысленно. К примеру, общая смертность от рака в
США в 2003 году была неодинаковой в разных этнических и возрастных
группах, для людей разного пола и для разного типа рака. Изучение этих различий
может представлять интерес для исследователей, и в этом случае им захочется
посмотреть на категоризированные частоты, в которых и числитель, и
знаменатель характеризуют определенную часть популяции или один тип заболевания.
ШМШЯШм
Глава 15. Статистика в медицине и эпидемиологии
В 2003 году в США смертность от рака у мужчин составила 201,4/100 000, а для
женщин - 182,0/100 000. В тот же год общая смертность от рака легких составила
76,9/100 000, а от меланомы - 2,7/100 000.
Для американцев европейского происхождения общая смертность от рака
составила 203,8/100 000; для афроамериканцев - 164,3/100 000, результат, который
может показаться парадоксальным, если не сообразить, что возросшая ожидаемая
продолжительность жизни часто связана с ростом смертности от рака.
Умирающий в младенчестве, скорее всего, умирает не от рака, но человек, разменявший
восьмой десяток, имеет гораздо большую вероятность связанной с раком смерти.
Это справедливо и для смертности вообще. Как правило, вероятность смерти в
следующем году гораздо выше у 90-летнего человека по сравнению с 12-летним.
По этой причине при сравнении смертности у разных популяций или в разные
периоды времени обычно делают поправку на возраст, а также могут делать
стандартизацию по категориям, таким как этническая принадлежность или пол.
Важность поправки на возраст можно увидеть при сравнении общей
смертности от рака и смертности от рака с поправкой на возраст в США в 2003 году
(табл. 15.3).
Таблица 15.3. Общая смертность от рака и смертность от рака с поправкой
на возраст (на 100 000 человек) в США в 2003 году
Всего
Европейцы
Афроамериканцы
Азиаты/жители тихоокеанских
Индейцы/исконные жители
Испанцы
островов
Аляски
Общая
смертность
191.5
203.8
164.3
79.4
69.3
60.3
Смертность
с поправкой на возраст
190.1
188.3
234.5
114.3
121.0
127.4
Отсюда становится ясно, что хотя общая смертность от рака максимальна у
американцев европейского происхождения, это отчасти объясняется их более высокой
ожидаемой продолжительностью жизни. Большая ожидаемая продолжительность
жизни означает существование большого числа американцев преклонного
возраста, когда смертность от рака увеличивается. После введения поправки на возраст
смертность от рака оказывается самой высокой у афроамериканцев.
Существуют два типа стандартизации - прямая и непрямая. Оба используются
для сравнения уровня заболеваемости и смертности в разных популяциях после
избавления от влияния других характеристик популяции - таких как возрастная
или половая структура. При прямой стандартизации одна из популяций
используется в качестве эталона для сравнения, и характеристики популяций с
поправками, которые нужно сравнивать, вычисляются с использованием весов, полученных
для «эталонной популяции». Рассмотрим гипотетический пример
распространенности артрита среди людей с разным статусом занятости (табл. 15.4).
Показатели заболеваемости
Таблица 15.4. Распространенность артрита у людей с разным статусом занятости
Статус занятости
Работающий
Безработный
Численность
населения
10 000
5 000
Число человек
с артритом
387
892
Частота больных на
1000 человек
38.7
178.4
Судя по этим данным, частота (на самом деле доля) артрита более чем вдвое
выше у безработных, чем у работающих людей. Может ли это объясняться тем,
что людей с тяжелым артритом «выкидывали» с рынка труда? Помогает ли работа
обуздать артрит? Обе идеи имеют право на существование, однако более логичное
объяснение заключается в том, что люди старше 65 лет с большей вероятностью и
не работают, и страдают артритом. Для проверки влияния возраста на различия в
распространении артрита у людей с разным статусом занятости нужно вычислить
частоты артрита с поправкой на возраст, используя «эталонную» популяцию. Во-
первых, нужно оценить распространенность заболевания у работающих и
неработающих людей разных возрастных групп, как это сделано в табл. 15.5.
Таблица 15.5. Распространенность заболевания у работающих и неработающих
людей разных возрастных групп
Возрастная
группа
18-44
45-64
65+
Всего
Работающие
ленность
5 000
4 500
500
10 000
Число
людей,
страдающих
артритом
127
260
105
387
Доля людей
страдающих
артритом,
на 1000
человек
25.4
57.7
210.0
38.7
Неработающие
ленность
1000
1 500
2 500
5 000
Число
людей,
страдающих
артритом
32
100
760
892
Доля людей
страдающих
артритом,
на 1000
человек
32.0
66.7
304.0
178.4
Глядя на заболеваемость артритом в отдельных возрастных группах
работающих и неработающих людей, мы видим, что в каждой возрастной группе частота
артрита немного выше среди неработающих людей, чем среди работающих (при
анализе данных по всем возрастным категориям вместе наблюдалась
противоположная закономерность). Также можно видеть, что, как мы и подозревали, среди
людей старше 65 лет, среди которых артрит наиболее широко распространен,
гораздо больше неработающих (50%), чем работающих (5%).
Учтите, что в этой таблице для простоты расчетов мы использовали очень
широкие возрастные границы (соответствующие молодым и пожилым работающим
взрослым, а также пенсионерам). Чаще используют более узкие категории,
например с интервалом в 10 лет.
Можно использовать частоты для отдельных возрастных групп для
вычисления ожидаемого числа людей с артритом для работающих и неработающих людей,
- 1 :
Глава 15. Статистика в медицине и эпидемиологии
анализируя возрастную структуру «эталонной» популяции. Обычно в качестве
«эталонной» популяции для подобных вычислений используют данные из
авторитетного источника, такого как данные американского бюро переписи населения
о населении США в 2000 году. Ожидаемое число людей с артритом приведено в
табл. 15.6.
Таблица 15.6. Ожидаемое число людей с артритом в разных возрастных категориях
и с разным статусом занятости
Возрастная
группа
18-44
45-64
65+
Всего
Эталонная
популяция
Численность
100 000
70 000
30 000
200 000
Работающие
Частота
(на 1000
человек)
25.4
57.7
210.0
Ожидаемое
число
больных
2540
4039
6300
12 879
Неработающие
Частота
(на 1000
человек)
32.0
66.7
304.0
Ожидаемое
число
больных
3200
4669
9120
16 989
Ожидаемое число больных было подсчитано для каждой возрастной группы
работающих и неработающих людей при помощи умножения соответствующих
частот заболевания на число людей в данной возрастной категории в «эталонной»
популяции. Это можно рассматривать как один из типов взвешивания, и это то
же самое, что оценить ожидаемое число больных в популяции при условии, что ее
возрастная структура будет такой же, как в «эталонной» популяции. Например,
для работающих людей в возрасте 18-44 лет ожидаемое число больных
вычисляется, как показано на рис. 15.11.
Е = частота х
число
человек'
25 А
1000
х 100 000 = 2 540
Рис. 15.11. Ожидаемое число больных среди работающих людей
в возрасте 18-44 лет
Для неработающих людей старше 65 лет ожидаемое число больных
вычисляется, как показано на рис. 15.12.
304
Е -частота х^- — ж 30 000 =9 120
Рис. 15.12. Ожидаемое число больных среди неработающих людей старше 65 лет
Общее число ожидаемых больных для работающих и неработающих людей
рассчитывается путем сложения результатов для каждой возрастной группы.
Можно видеть, что если бы у двух групп людей возрастная структура была
одинаковой, то среди работающих ожидалось бы меньше больных артритом (12 879),
Показатели заболеваемости
ШМЕИЭ
чем среди неработающих (16 989). Мы можем развить это наблюдение,
вычислив частоту артрита для каждой группы, разделив ожидаемое число больных на
общую численность группы и затем умножив на 1000 (чтобы получить частоту в
расчете на 1000 человек). Для работающих людей это вычисляется, как показано
на рис. 15.13.
х 1000 = 64.4 на 1000
200 000
Рис. 15.13. Частота встречаемости артрита среди работающих людей
с поправкой на возраст
Для неработающих людей частота артрита с поправкой на возраст составит
84,9 человека на 1000. Сравнение этих величин свидетельствует, что частота
артрита выше у неработающих людей по сравнению с работающими, по эта
разница намного меньше, чем та, что указана в табл. 15.5. Учтите, что частоты с
поправкой на возраст, вычисленные при помощи прямой стандартизации, не
являются реальными частотами для любой группы людей; они дают представление
об ожидаемых частотах в одной или нескольких группах, если бы их возрастная
структура совпадала с возрастной структурой «эталонной» группы.
Непрямая стандартизация подразумевает противоположный подход. В этом
случае категоризованные частоты для некоторой «эталонной» популяции
применяются к категориям двух и более групп. Применив непрямую
стандартизацию к нашему примеру с артритом, мы можем рассчитать ожидаемое число
больных, если возрастной состав больных в обеих группах будет одинаковым и
сохранится реальная возрастная структура. Частоты (вымышленные)
приведены в табл. 15.7.
Таблица 15.7. Непрямой метод стандартизации
Возрастная
группа
18-44
45-64
65+
Всего
Частота
заболевания в «эталонной»
популяции
(на 1000 человек)
30
60
200
Работающие
Численность
5000
4500
500
10 000
Ожидаемое
число больных
150
270
100
520
Неработающие
Численность
1000
1500
2500
5000
Ожидаемое
число больных
30
90
500
620
Можно использовать эти значения для вычисления стандартизованного
показателя заболеваемости (СПЗ), разделив число зарегистрированных заболеваний
(из табл. 15.5) на ожидаемое число заболеваний (из табл. 15.7). Расчет этого
показателя для работающих людей показан на рис. 15.14.
Глава 15. Статистика в медицине и эпидемиологии
СПЗ =
наблюдаемое число
заболеваний
ожидаемое число
заболеваний
387
520
= 0.744, шш74.4%
Рис. 15.14. Стандартизованный показатель заболеваемости
для работающих людей
Для неработающих людей стандартизованный показатель заболеваемости равен
0,695, или 69,5%. Если этот показатель равен единице, то у нас наблюдаемое число
заболеваний равно ожидаемому. В нашем примере стандартизованный показатель
заболеваемости и для работающих людей, и для неработающих меньше единицы,
это значит, что зарегистрировано меньше заболеваний, чем ожидалось.
Стандартизованный показатель заболеваемости превосходит единицу, если регистрируют
больше заболеваний, чем ожидали.
Если мы имеем дело со смертями, а не с заболеванием артритом, то можно
использовать тот же прием для вычисления стандартизованного показателя
смертности, часто используемого для сравнения смертности в разных группах людей;
разница состоит в том, что мы подсчитываем случаи смерти, а не заболевания.
Отношение рисков
Во многих медицинских и эпидемиологических исследованиях анализируют связь
между двумя дихотомическими переменными. Распространенный пример, - это
подверженность какому-либо фактору риска (такому как контакт с асбестом или
курение табака) и развитие какого-либо заболевания или состояния (асбестоза
или рака легких). Фактор может быть наследственным, таким как пол или
этническая принадлежность, и не обязательно негативным; например, регулярная
физическая активность положительно действует на здоровье.
Связь между двумя дихотомическими переменными часто представляют в виде
таблицы сопряженности, также называемой таблицей 2><2, или два на два, из-за ее
размерности (две строки и два столбца). Таблицы сопряженности также
обсуждаются в пятой главе, и здесь применимы те же принципы. Однако в
эпидемиологических исследованиях существует стандартный способ построения таблиц
сопряженности, продемонстрированный в табл. 15.8.
Таблица 15.8. Таблица 2x2
Воздействие
Всего
Есть
Нет
Заболевание
Есть
а
с
а + с
Нет
b
d
b + d
Всего
a + b
c + d
a+b+c+d
Расположение (строки - Воздействия, столбцы - Заболевания) и порядок
(сначала - Есть (наличие), потом - Нет (отсутствие)) групп приняты для многих эпи-
Отношение рисков
демиологических исследовании, так что разумно следовать этим правилам, если
у вас нет причины поступить по-иному. Объекты исследования распределяются
по группам согласно их подверженности воздействию и наличию заболевания, и
ячейки, обозначенные буквами я, Ь, с, d, содержат частоты для каждого сочетания
воздействия и болезни. Например, в ячейке а указана частота подверженных
воздействию больных, а в ячейке d - частота не подверженных воздействию
здоровых.
Частоты в ячейках а> Ь, с, d иногда называют комбинированными (joint
frequencies), поскольку люди в этих ячейках разделены с учетом наличия и воздействия,
и заболевания. По краям таблицы приведены суммы по строкам и столбцам,
часто называемые краевыми частотами (marginal frequencies). Например, а + b - это
число подверженных воздействию людей вне зависимости от их здоровья. Общее
число исследованных людей выражается как а + b + с + d.
Отношение рисков (ОР), также называемое относительным риском, - это
оценка вероятности развития заболевания у людей, подверженных воздействию, по
сравнению с не подверженными воздействию. Это отношение доли подверженных
воздействию больных к доле не подверженных воздействию больных. Отношение
рисков вычисляется, как показано на рис. 15.15.
Qp _a/(a + b)
с 1{с + d)
Рис. 15.15. Формула для расчета отношения рисков
Отношение рисков можно также трактовать как отношение частоты
заболеваний в подверженной воздействию группе (Зи) к частоте заболеваний в не
подверженной воздействию (3()) группе (рис. 15.16).
заболеваемость в подверженной
воздействию группе Зи
' заболеваемость в не подверженной 3
воздействию группе °
Рис. 15.16. Выражение отношения рисков через частоту заболеваний
Для исследований, в которых знаменатель выражен в единицах
человеко-времени, проводятся аналогичные вычисления, только вместо частоты заболеваний
используется плотность заболеваний (ПЗ), как показано на рис. 15.17.
Рис. 15.17. Выражение отношения рисков через плотность заболеваний
Давайте рассмотрим данные вымышленного исследования, организованного с
целью проверить, есть ли связь между потреблением пищи с высоким
содержанием жира (воздействие) и диабетом II типа (заболевание). Данные представлены в
табл. 15.9.
Глава 15. Статистика в медицине и эпидемиологии
Таблица 15.9. Связь между потреблением пищи с высоким содержанием
жира и диабетом II типа
Есть воздействие
Нет воздействия
Всего
Есть заболевание
350
200
550
Нет заболевания
1200
1900
3100
Всего
1550
2100
3650
Риск диабета II типа при употреблении пищи с высоким содержанием жира
вычисляется, как показано на рис. 15.18.
350
а + Ь 1550
= 0.226
Рис. 15.18. Риск для подвергающейся воздействию группы
Это число больных людей, подвергающихся воздействию (те, кто ел жирную
пищу и болел диабетом II тина), деленное на общее число подвергавшихся
воздействию людей (всех, кто ел жирную пищу, вне зависимости от их здоровья).
Риск заболеть диабетом II типа, не будучи подверженным воздействию (не
потребляя жирную пищу), - показан на рис. 15.19.
200
c + d 2100
= 0.095
Рис. 15.19. Риск для не подвергающейся воздействию группы
Относительный риск заболевания диабетом у тех, кто ел жирную пищу, по
сравнению с теми, кто ее не ел - это отношение этих двух типов риска (отсюда и
термин - отношение рисков), как показано на рис. 15.20.
ОР =
ОР?+
ОР?.
а/(а +
с/(с +
Ъ)
d)
0.226
" 0.095
= 2.38
Рис. 15.20. Отношение рисков для подвергавшихся воздействию людей
по сравнению с неподвергавшимися
Относительный риск больше единицы значит, что воздействие увеличивает
риск заболевания. Если между воздействием и заболеванием пет связи, то
относительный риск равен единице, а если воздействие благотворно (ассоциировано с
уменьшением риска заболевания), то относительный риск будет меньше единицы.
В данном случае мы бы сказали, что у людей, употребляющих пищу с высоким
содержанием жира, риск заболеть диабетом II типа в 2,38 раза выше, чем у тех, чей
рацион содержит нормальное или пониженное количество жиров.
Отношение рисков |Н^^1Е01
Как и многие другие статистические параметры, значения отношения рисков
приводят с доверительными интервалами (ДИ). При вычислении этих
доверительных интервалов нужно учитывать, что распределение отношения рисков
смещено вправо, поскольку его значения снизу ограничены нулем, а сверху не
ограничены. Чтобы избавиться от этой асимметрии, нужно взять натуральный
логарифм (In) отношения рисков, что приблизит их распределение к нормальному.
При вычислении доверительных интервалов для отношения рисков необходимо
взять натуральный логарифм отношения рисков, вычислить для него
доверительный интервал, а затем взять натуральный антилогарифм значений
доверительного интервала, чтобы вернуться к исходным единицам измерения. Учтите, что
статистики иногда записывают ех как ехр(х).
Существует несколько способов вычисления доверительного интервала для
отношения рисков, самое простое - это использовать компьютерную программу. Тем
не менее эти вычисления можно провести и вручную, в общем случае при помощи
формулы с рис. 15.21.
ДИ = (OP) exp[±z^Var(ln(OP))]
Рис. 15.21. Общая формула для вычисления доверительного интервала (ДИ)
для отношения рисков (ОР)
В этой формуле г - это значение стандартного нормального распределения,
соответствующее нужному уровню доверительного интервала; чаще всего это
значение составляет 1,96, что соответствует двустороннему 95%-му доверительному
интервалу. Если отношение рисков оценивается при помощи отношения шансов
(обсуждается ниже) по данным исследования случай-контроль, то
доверительный интервал можно вычислять, используя значения из таблицы 2x2.
ДИ = (flrf/bc)exp[±zV(l/a + 1/b + 1/с + 1/d)]
Рис. 15.22. Формула для вычисления доверительного интервала для отношения
рисков, оцененного через отношение шансов
При использовании значений из табл. 15.9 для 95%-го доверительного
интервала эта формула применяется, как показано на рис. 15.23.
дИ = 350(1900)ехр(±1.96л/1/350 + 1/1200 + 1/200 + 1/1900)
200(1200) v
= (2.77)ехр(±0.19)
= (2.30,335)
Рис. 15.23. Вычисление доверительного интервала с использованием
формулы для отношения шансов
[321 Hi
Глава 15. Статистика в медицине и эпидемиологии
Поскольку полученный доверительный интервал не включает единицу, мы
заключили, что связь между диабетом II типа и потреблением нищи с высоким
содержанием жира значима.
Для интерпретации относительного риска важен период времени, в течение
которого собирали данные. Риск развития многих хронических заболеваний
возрастает но мере увеличения продолжительности воздействия, например следует
ожидать, что риск рациона с высоким содержанием жиров для развития диабета
II типа будет выше в исследовании длительностью 10 лет, чем при сборе данных в
течение одного года. Это особенно актуально при изучении смертности,
поскольку в достаточно длительном исследовании вероятность смерти всех объектов
составляет 100%!
Атрибутивный риск; атрибутивная доля риска
и число людей, которых нужно лечить
Поскольку у нс подвергающихся воздействию людей тоже есть определенный
риск заболеть, в эпидемиологии также используется понятие атрибутивного
риска (АР) (attributable risk). Это абсолютный эффект воздействия на возникновение
заболевания, то есть риск заболевания в подверженной воздействию группе, но
сравнению с ненодверженной. Атрибутивный риск полезен в качестве
показателя пользы или вреда некоторого воздействия для охраны здоровья, поскольку из
подверженной воздействию группы удаляют те случаи заболеваний, которые, как
предполагают, случились бы даже без воздействия. АР также можно использовать
для оценки эффекта от предотвращения определенного воздействия, вычисляя
число заболеваний, которые удалось бы избежать, избавившись от данного
воздействия. Атрибутивный риск вычисляется путем вычитания частоты
заболеваний в не подверженной воздействию группе (3()) из частоты заболеваний для
подверженной воздействию группы (Зи). В нашем примере с жирной пищей и
диабетом II типа это будет выглядеть, как показано на рис. 15.24.
АР -Зв-30 = 0.226-0.095 =0.131
Рис. 15.24. Вычисление атрибутивного риска (АР)
Таким образом, употребление большого количества жиров увеличивает
заболеваемость диабетом второго типа на 131 случай из 1000 людей. Если между
воздействием и заболеванием не существует связи, то в подверженной воздействию
группе не будет дополнительных случаев заболеваний и атрибутивный риск будет
равен нулю.
Доля атрибутивного риска (АР%, также называемая этиологической долей) -
это /юля случаев в подвергающейся воздействию группе, которую можно
объяснить наличием этого воздействия и можно предотвратить, устранив
воздействие. Для нашего примера этот показатель можно вычислить, как показано на
рис. 15.25.
Отношение шансов
ИИ—ЕГД
АР Зи-3() 0.226-0.095
АР% = — х 100 = ——- х 100 х 100 = 58.0%
3^ Зв 0.226
Рис. 15.25. Вычисление доли атрибутивного риска (АР%)
Мы интерпретировали бы это, сказав, что воздействие было виной 58%
заболеваний в подверженной ему группе.
Долю атрибутивного риска можно также вычислить через отношение рисков,
как показано на рис. 15.26.
I ОР-1 2.38-1 I
АР% = х 100 х 100 = 58.0%
| ОР 238 |
Рис. 15.26. Вычисление доли атрибутивного риска через отношение рисков
Число нуждающихся в лечении больных - это число пациентов, которых нужно
подвергнуть специальному лечению (в противоположность стандартному
лечению или плацебо) или оградить от воздействия, чтобы уменьшить число больных
людей в группе на одного. Этот показатель полезен для оценки ожидаемой выгоды
от нового лечения в будущем, он обратно пропорционален атрибутивному риску.
В нашем примере атрибутивный риск составил 0,131, поэтому число
нуждающихся в лечении больных равно 1/0,131 = 7,6. Этот показатель обычно округляют до
целых чисел (пожалуйста, никаких частей больных!), так что в нашем случае
можно сказать, что восьми людям нужно воздержаться от избыточного употребления
жиров, для того чтобы в дайной группе стало одним диабетиком меньше.
Отношение шансов
Представление об отношении шансов было разработано в исследованиях случай-
контроль, методологии, которая применяется в эпидемиологии для упрощения
исследования редких или медленно развивающихся заболеваний, так что
обычные перспективные исследования было бы трудно осуществить. В исследованиях
случай-контроль людей выбирают на основании наличия заболевания - случаи
больны, а коитроли здоровы. Эти две группы затем сравнивают по
подверженности воздействию. В подобных исследованиях нельзя вычислять отношение рисков,
поскольку оно чувствительно к числу контролей (здоровых людей), а это число в
исследованиях случай-контроль определяют, исходя из плана, а не частоты
заболевания в популяции. Как будет показано далее, отношение шансов имеет
преимущество, поскольку, в отличие от отношения рисков, оно нечувствительно к числу
контролей (здоровых людей).
Отношение шансов (ОШ) (odds ratio) (вероятность успешного исхода) - это
отношение вероятности воздействия в опытной группе к вероятности воздействия
в контрольной группе. Это математически эквивалентно отношению вероятности
заболевания в подверженной воздействию группе к вероятности не подверженной
воздействию группе, так что вы можете встретить другое определение этого тер-
Глава 15. Статистика в медицине и эпидемиологии
мина. В таблице 2><2 вероятность воздействия при наличии заболевания равна а/с,
а вероятность воздействия в отсутствие заболевания - b/d. Отношение шансов
вычисляется по формуле, приведенной на рис. 15.27.
вероятность воздействия
при наличии заболевания
вероятность воздействия
при отсутствии заболевания
ОШ =
ale
ad
~Ъ~с
Рис. 15.27. Формула для вычисления отношения шансов (ОШ)
Предположим, у нас есть исследование случай-контроль влияния курения на
возникновение рака легких. В табл. 15.10 приведены вымышленные данные.
Таблица 15.10. Связь между курением и
Есть воздействие
Нет воздействия
Всего
Есть заболевание
50
25
75
раком легких
Нет заболевания
2000
1900
3900
Всего
2050
1925
3975
о
гношенме шансов может быть вычислено,
ОШ
50/25
~ 2000/1900
как показано на
= 1.90
рис.
15
28.
Рис. 15.28. Вычисление отношения шансов
Обратите внимание, что отношение рисков для этих данных примерно такое же
(рис, 15.29).
50/2050
ОР 1.88
25/1925
Рис. 15.29. Вычисление отношения рисков
Если заболевание или состояние редки (практическое правило заключается в
том, что частота заболевания должна быть меньше 10% во всех группах), то
отношение шансов - это хороший способ оценки отношения рисков. Причина
требований «редкости заболевания» заключается в том, что как только заболевание
становится более частым, отношение шансов начинает сильнее отличаться от
отношения рисков. Это показано на примере данных вымышленного исследования
случай-контроль курения и рака легких (табл. 15.11).
Таблица 15.11. Курение и рак легких
Есть воздействие
Нет воздействия
Всего
Есть заболевание
50
20
70
Нет заболевания
50
100
125
Всего
100
120
195
Отношение шансов
Ha этот раз заболевание широко распространено и среди подверженных
воздействию объектов, и среди неподверженных; рак легких есть у 50% курильщиков и
у 16,5% некурящих. Отношение шансов для этих данных вычислено на рис. 15.30, а
отношение рисков - на рис. 15.31.
Рис.
ОШ
15.30.
50(100) 5000
" 20(50) " 1000 "
• 5.0
Вычисление отношения шансов
_ 50/100 „ Л
ОР = = 3.0
20/120
Рис. 15.31. Вычисление отношения рисков
Разница между 5,0 и 3,0 существенна и связана с тем, что «правило 10%»
нарушено; для таких данных отношение шансов - плохая оценка отношения рисков.
Отношение рисков, в отличие от отношения шансов, также чувствительно к
числу контролей. Предположим, что поскольку контроли легче найти, чем
случаи, мы увеличили число контролей в десять раз (маловероятно, поскольку
уменьшение эффективности исследования наблюдается при соотношении контролей и
случаев 4:1, но полезно в демонстрационных целях). Тогда мы получим данные,
представленные в табл. 15.12.
Таблица 15.12. Курение и рак легких при десятикратном увеличении числа
контролей
Есть воздействие
Нет воздействия
Всего
Есть заболевание
50
20
70
Нет заболевания
500
1000
1500
Всего
550
1020
1570
Отношение шансов не отличается от того, что было вычислено для данных из
табл. 15.11, как показано на рис. 15.32, но отношение рисков отличается (рис. 15.33).
ОШ =
50(1000) 5000
20(500) " 1000
= 5.0
Рис. 15.32. Отношение шансов не меняется при увеличении числа контролей
20/1020
Рис. 15.33. Отношение рисков меняется при увеличении числа контролей
Доверительный интервал для отношения шансов можно вычислить при
помощи метода, описанного в предыдущем разделе «Отношение рисков» (стр. 388).
EZMH
Глава 15. Статистика в медицине и эпидемиологии
Шансы
Отношение шансов - важный показатель в медицинских и статистических
исследованиях, однако он основывается на понятии, незнакомом или непонятном на интуитивном
уровне большинству людей: это шансы. Шансы некоторого события - это просто другой
способ выражения его правдоподобности, сходный с вероятностью; разница
заключается в том, что вероятность вычисляется при помощи деления числа событий на общее
число испытаний, а шансы вычисляются как отношение числа событий к числу не-со-
бытий. Если рассматривать пример из эпидемиологии, то шансы курильщика заболеть
раком легких вычисляются путем деления числа курильщиков с раком легких на число
курильщиков без рака легких (а/b из нашей таблицы сопряженности). Вероятность рака
легких у курильщиков вычисляется посредством деления числа курильщиков с раком
легких на общее число курильщиков {а/(а + Ь)).
Поскольку и шансы, и вероятность используют одни и те же величины, вы можете
преобразовать один показатель в другой при помощи следующих формул:
Шансы = вероятность/^ - вероятность),
Вероятность = шансы (1 + шансы).
Предположим, что Р{А) = 0.5,или50%.ТогдашансыЛсоставят0.5/1 -0.5 = 1.0.Этодолж-
но иметь смысл на интуитивном уровне: вероятность 50% значит равные шансы
наступления и ненаступления события, то же самое означают и шансы, равные 1.0. Рассмотрев
обратную ситуацию, если шансы составляют 1, то вероятность равна 1/(1+1) = 0.5.
Отношение шансов - это просто частное двух шансов, например шансов рака легких
у курильщиков и шанса рака легких у некурящих (математически тождественное
отношению шансов курения у больных раком легких и здоровых). Отношение шансов можно
вычислить, подставив вероятности в приведенную на рис. 15.34 формулу (где шансы,
и шансы2 - это шансы исхода при двух условиях, а р1 и р2 - это вероятности исхода при
двух условиях).
ОШ _шшш\ __ P\d-P\)
шапсы2 р2(\-р2)
Рис. 15.34. Вычисление отношения шансов
с использованием вероятностей
Искажение, послойный анализ
и коэффициент Мантеля-Гензеля
Искажение - это ситуация, в которой наблюдаемая статистическая связь
объясняется, хотя бы отчасти, неизученными различиями исследованных групп.
Искажение иногда называют проблемой «третьей переменной»; связь между двумя
переменными, например воздействием и заболеванием, маскируется или искажается
третье]! переменной, связанной с первыми двумя. Искажение может быть внесено
более чем одной переменной, но для простоты мы расскажем о методах работы с
одним искажающим фактором.
При работе в области эпидемиологии нужно знать о возможности искажения
данных, особенно при наблюдениях, когда принадлежность объекта к группе не
определяется исследователем. Например, при исследованиях эффектов от куре-
Искажение, послойный анализ и коэффициент Мантеля-Гензеля
¦Н1ЕШ1
ния нужно учитывать, что курение - это добровольное дело (люди сами решают,
курить им или нет), а курильщики могут отличаться от некурящих людей но
многим признакам (таким как употребление алкоголя, рацион питания или уровень
образования).
По возможности лучше избавляться от искажающих факторов при планировании
исследования. Рандомизация - это метод выбора объектов в экспериментальных
исследованиях, поскольку теоретически она позволяет избавиться от всех возможных
искажающих факторов одновременно. Это происходит потому, что, как правило,
случайное распределение объектов по группам должно привести к примерно
одинаковому распределению любых возможных искажающих факторов в каждой группе,
включая те факторы, о существовании которых исследователь не подозревает.
Два других метода, которые можно использовать при наблюдениях для
минимизации действия известных или предполагаемых искажающих факторов, - это
ограничение и сопоставление. Недостаток обоих методов - это обретение контроля
только над теми искажающими факторами, которые были включены в
исследование. При использовании ограничения исследователь анализирует только часть
генеральной совокупности, выбранную по значениям потенциального искажающего
фактора. Например, в медицинских исследованиях часто используют только
мужчин или только женщин, чтобы избежать влияния пола на связь между
воздействием или заболеванием. Недостаток этого подхода - ограничение применимости
результатов исследования; если для определенной группы мужчин будет
выявлена связь между употреблением алкоголя и психопатологией, немедленное
распространение этой закономерности на женщин будет неоправданным, поскольку они
не участвовали в исследовании.
Сопоставление - это другой прием для обретения некоторого контроля над
известными искажающими факторами. В этом случае анализируются все уровни
искажающего фактора, но объекты распределяются по группам таким образом,
чтобы искажающие факторы были равномерно рассредоточены по этим группам.
Сопоставление часто используется в исследованиях случай-контроль, в которых
контроли подбирают так, чтобы они соответствовали вошедшим в выборку
случаям. Существуют разные методы сопоставления, но все они основаны на сходном
распределении значений искажающих факторов по группам.
Существуют два способа проведения сопоставления. При прямом
сопоставлении объекты сравниваются по одному. При частотном сопоставлении
распределение объектов по группам организуют так, что в каждой группе присутствует
равное количество искажений. Если искажающие факторы - это иол и возрастная
группа, то при прямом сопоставлении женщинам возраста 60-70 лет в
экспериментальной группе будут соответствовать женщины этого же возраста в
контрольной группе. При частотном сопоставлении руководитель проекта позаботится о
том, чтобы в опытную и контрольную группы было включено равное число
женщин и людей из разных возрастных категорий. Частотное сопоставление иногда
называют сопоставлением по группам, поскольку вы можете думать о группах,
определенных разными комбинациями признаков (например, мужчины в возрасте
20-29 лет, мужчины в возрасте 30-39 лет и так далее). Частотное сопоставление
ЕЕ!
Глава 15. Статистика в медицине и эпидемиологии
особенно популярно в исследованиях случай-контроль, поскольку часто сначала
выбирают случаи, а потом подыскивают соответствующие им контроли.
Поскольку вы знаете, как распределены параметры случаев, то можете подобрать контроли
со сходным распределением признаков.
Если от влияния искажающих факторов нельзя избавиться при планировании
исследования, этим можно заняться во время анализа данных. Для этого
существует множество статистических методов, включая многомерный анализ, который
может быть довольно сложным. Однако в эпидемиологии от искажений
избавляются более простыми методами, особенно в исследованиях с одним воздействием
и одним заболеванием. Ниже описан один из наиболее распространенных методов
для оценки и контроля искажения: вычисление и сравнение простого
коэффициента несогласия и коэффициента несогласия Мантеля-Гензеля.
При определении переменной как искажающего фактора не предполагают
причинной связи; на самом деле считается, что многие наиболее обычные
искажающие факторы лишь связаны с другими параметрами. Переменная считается
искажающим фактором при выполнении трех условий:
1. Она должна быть связана с воздействием.
2. Она должна быть связана с заболеванием независимо от ее связи с
воздействием.
3. Она не должна находиться посередине логической цепочки, связывающей
воздействие и заболевание.
Четвертое, скорее практическое, чем теоретическое, требование заключается в
том, что значения искажающего фактора должны быть неравномерно
распределены между исследуемыми группами. Например, если мы знаем, что возраст может
быть искажающим фактором для смертности, но в определенном исследовании
возрастная структура всех исследуемых групп сходна, то в данном случае
возраст - это не искажающий фактор.
Давайте в качестве примера рассмотрим исследование благотворного эффекта
добровольной физической активности в свободное время (воздействие) на
возникновение сердечных приступов (инфаркт миокарда или ИМ, заболевание); мы
полагаем, что эта связь может искажаться возрастом. Все три требования выполнены:
1. Возраст связан с физической активностью (в среднем молодые люди
занимаются спортом больше, чем пожилые).
2. Возраст - это фактор риска для ИМ вне зависимости от физической
активности (в среднем вероятность ИМ выше у пожилых людей).
3. Возраст не находится посредине логической цепочки, связывающей
физическую активность и ИМ (нет такого механизма, при помощи которого
физическая активность влияла бы па возраст человека, а возраст - на
вероятность ИМ).
Один из способов обретения контроля над искажающим фактором - это
использование послойного анализа, при котором исследуемые группы разделяют на
слои или подгруппы согласно значениям искажающего фактора. Стратификация
по возрастным группам - это обычный случай. Как обсуждалось в предшествую-
Искажение, послойный анализ и коэффициент Мантеля-Гензеля
¦¦ЕШ
щем разделе, посвященном стандартизованным частотам, население разных стран
характеризуется разной возрастной структурой; в некоторых странах больше
молодых людей, а в других - больше пожилых. Возраст связан со смертностью и
распространенностью многих болезней. По этим причинам при сравнении
смертности и заболеваемости между разными странами обычно проводят разделение
по возрастным категориям, а затем стандартизацию, так чтобы распределение
возрастов в сравниваемых группах было сопоставимым.
Вот пример, демонстрирующий необходимость оценки искажающего фактора.
В 2007 году смертность в США составляла 8,26 смерти на 1000, а в Эквадоре - 4,21
смерти на 1000. Следует ли это интерпретировать как свидетельство в пользу
более здорового образа жизни эквадорцев по сравнению с американцами? Это
интересная гипотеза, однако она не подтверждается при исследовании более
подробных таблиц продолжительности жизни, которые показывают, что смертность
эквадорцев выше смертности американцев в каждой отдельно взятой возрастной
категории. Например, для возрастной группы 45-49 лет вероятность смерти у
американцев составляет 0,00341, а у эквадорцев - 0,00513.
Разница в смертности наблюдается из-за различий в возрастной структуре этих
двух популяций. В Эквадоре, как и в большинстве развивающихся стран, высока
доля молодых людей. В США, как и в большинстве промышленно развитых стран,
больше пожилых людей, у которых вероятность смерти выше. Это различие было
бы упущено при анализе только общих показателей смертности, но становится
ясным, когда послойный анализ позволяет избавиться от влияния искажающего
фактора (возраста) на результат (смертность).
Не существует четкого теста на искажение, но есть способы исследовать
действие потенциальных искажающих факторов на интересующую нас связь и на
основании этого решить, существуют ли искажающие факторы. Стандартные действия
при определении искажающих факторов следующие:
1. Вычислить показатель связи без учета искажающего фактора.
2. Разделить исследуемую группу на основе искажающего фактора, то есть
разделить ее на подгруппы по значениям искажающей переменной.
3. Вычислить показатель связи с поправкой.
4. Сравнить исходный показатель связи со скорректированным показателем;
разница более чем в 10% обычно считается свидетельством в пользу
искажения.
Подходящий показатель связи зависит от плана исследования; мы рассмотрим
послойный анализ с использованием исходных значений отношения шансов и
значений с поправкой Мантеля-Гензеля (Mantel-Haenszel). Учтите, что
использование этой поправки требует соблюдения двух условий: общий объем выборки
должен быть большим, а показатель связи между воздействием и результатом
должен варьировать от 0,5 до 2,5.
Оценка Мантеля-Гензеля отношения шансов при послойном анализе
позволяет объединять информацию из нескольких таблиц сопряженности с
использованием формулы, приведенной на рис. 15.35.
Глава 15. Статистика в медицине и эпидемиологии
Рис. 15.35. Формула для вычисления отношения шансов
с поправкой Мантеля-Гензеля
В этой формуле:
к - это число таблиц сопряженности,
г - это одна из таблиц («слоев», на которые разделена выборка),
п - число объектов в слое,
ar br с. и d. - это значения ячеек в этой таблице сопряженности.
Предположим, нас интересует связь между курением и заболеваниями печени.
Известно, что курильщики в среднем чаще употребляют алкоголь, а употребление
алкоголя - это независимый от курения фактор риска для болезней печени, который
не находится в логической цепочке посередине между курением и заболеваниями
печени. Таким образом, употребление алкоголя - это потенциальный искажающий
эффект, наличие которого мы проверяем, разделив выборку по употреблению
алкоголя (как дихотомической переменной: употребляющие алкоголь люди и
непьющие) и сравнив исходное и скорректированное значения отношения шансов.
Исходные данные представлены в табл. 15.13.
Таблица 15.13. Курение и заболевания печени до разделения выборки на группы
Есть воздействие
Нет воздействия
Всего
Есть заболевание
50
30
80
Нет заболевания
100
120
220
Всего
150
150
300
Отношение шансов для этих данных вычислено на рис.
OUT
ad
= ~b~c"
50(120)
= 30(100)
= 2.00
15.36.
Рис. 15.36. Вычисление отношения шансов для исходных данных
Высокое положительное значение отношения шансов свидетельствует о
положительной связи курения с заболеваниями печени: у курильщиков вероятность
таких заболеваний вдвое выше по сравнению с некурящими людьми. Чтобы
узнать, является ли потребление алкоголя искажающим фактором, мы построили
отдельные таблицы сопряженности для людей, употребляющих и не
употребляющих алкоголь (табл. 15.14 и 15.15).
Искажение, послойный анализ и коэффициент Мантеля-Гензеля НШНЕЕ
Таблица 15.14, Курение и заболевания печени у не употребляющих алкоголя людей
Есть воздействие
Нет воздействия
Всего
Есть заболевание
40
30
70
Нет заболевания
35
45
80
Всего
75
75
150
Таблица 15.15. Курение и заболевания печени для употребляющих алкоголь людей
Есть воздействие
Нет воздействия
Всего
Есть заболевание
60
50
110
Нет заболевания
15
25
40
Всего
75
75
150
Для этих данных мы можем вычислить отношение шансов с поправкой
Мантеля-Гензеля, как это показано на рис. 15.37.
(40x45)7150 (60x25)7150
(30 х 35)7150 + (50x15)7150
Рис. 15.37. Вычисление отношения шансов с поправкой Мантеля-Гензеля
Поскольку разница между исходным и скорректированным значениями
отношения шансов превышает 10% от исходного значения 2,0, мы заключаем, что
употребление алкоголя - это искажающий фактор для связи между курением и
заболеваниями печени, который нужно учитывать в подобных исследованиях.
Анализ мощности
В этом разделе речь пойдет о теоретических аспектах мощности и размера
выборки, и будут представлены несколько простых примеров. Вычисления
необходимого размера выборки и мощности часто просты, но они также имеют свою
специфику; разные планы исследований требуют использования разных формул, и
их незачем перечислять, поскольку все они приведены в справочниках. Для тех,
кто работает в области медицины и эпидемиологии, мы особенно рекомендуем
главу, посвященную вычислениям объема выборки, из «Руководства по
эпидемиологии» (Handbook of Epidemiology, Springer). Во многих компьютерных
программах, таких как SAS и Minitab, есть встроенные процедуры для проведения анализа
мощности и вычисления нужного размера выборки, калькуляторы этих величин
также есть в Сети; хорошую коллекцию ссылок на онлайн-калькуляторы можно
найти здесь: http://statpages.org.
ОПТ,,. =
/-1
уаА
Ml"
i-l Ui
EESHhH Глава 15. Статистика в медицине и эпидемиологии
При статистическом выводе всегда есть вероятность принять неверное
решение, поскольку статистический вывод о генеральной совокупности опирается на
вычисления, сделанные на основе выборки. Как обсуждалось в третьей главе, при
статистическом выводе возможны два обычных типа ошибок:
1). статистическая ошибка первого рода (а), когда вы ошибочно отвергаете
нулевую гипотезу;
2). статистическая ошибка второго рода (Р), когда вы не можете отвергнуть
нулевую гипотезу, в то время как она неверна.
Иными словами при ошибке I рода вы находите закономерность, где ее нет, а
при ошибке II рода - пропускаете существующую закономерность.
Мощность - это вероятность отвергнуть нулевую гипотезу, когда она неверна
(1 - Р). Нам бы всем хотелось, чтобы мощность была все время высокой,
однако практические соображения, в особенности финансовые затраты и доступность
объектов, вынуждают нас идти на компромисс. Принято, чтобы мощность
составляла хотя бы 80%, то есть вероятность обнаружить в вашей выборке
существующую в генеральной совокупности закономерность составляло бы 80%. Это значит,
что в 20% случаев вы не найдете закономерность там, где вы должны были это
сделать. Также часто используется стандартное значение мощности, равное 90%.
На мощность влияют четыре основных фактора:
1. Уровень а, то есть Р (ошибки I рода): более высокая а увеличивает
мощность.
2. Различия в результате между группами (мощность выше при больших
различиях).
3. Изменчивость (при маленькой изменчивости мощность выше).
4. Размер выборки (мощность выше при большей выборке).
Изменение любого из этих параметров при постоянных значениях остальных
переменных приведет к изменению мощности в указанную сторону. Уровень а
обычно выбирают равным 0,05 или менее (например, 0,01); увеличение а дает
более высокую мощность. Увеличение межгрупповой разницы в результатах также
увеличивает мощность. Эту разницу можно повысить, оптимизировав
воздействие, так чтобы оно имело более выраженный эффект, или выбрав такие группы
объектов, для которых ожидаемые различия в результатах были бы выше.
Уменьшение изменчивости также повышает мощность. Уменьшить изменчивость иногда
можно путем оптимизации измерений или выбора исследуемых объектов
(например, уменьшив диапазон возраста или дохода). Однако наша способность
контролировать эти параметры обычно незначительна.
Таким образом, нам остается только размер выборки - единственный фактор,
который находится под контролем исследователя при планировании проекта.
При прочих равных условиях больше объектов = больше мощности. Однако
обследование большего числа объектов обычно требует больших средств и усилий со
стороны исследовательской группы. Цель анализа мощности - найти разумный
компромисс, при котором была бы достигнута приемлемая мощность, а вы бы не
обанкротились и не набрали бы больше данных, чем нужно.
Анализ мощности НИН ЕЕ
Понятие мощности наряду с ошибками I и II рода можно прояснить, рассмотрев
рис. 15.38.
Рис. 15.38. Диаграмма мощности для двух генеральных совокупностей
с нормальным распределением значений
На рис. 15.38 проиллюстрировано вычисление мощности, при котором нулевая
гипотеза заключается в том, что среднее значение для генеральной совокупности
равно 100, а альтернативная гипотеза - в том, что оно равно 115. Считается, что
распределение значений обеих генеральных совокупностей близко к нормальному.
На этом рисунке левая кривая распределения (светло-серая) соответствует нулевой
гипотезе. Правая кривая (темно-серая) соответствует альтернативной гипотезе.
Вычисления мощности всегда проводят для конкретной альтернативной
гипотезы. В этом случае альтернативная гипотеза заключается не просто в том, что
среднее значение превышает 100, а в том, что оно равно 115. Обратите внимание
на то, что при проверке гипотез речь идет о средних значениях для генеральной
совокупности, хотя при этом используются средние значения, вычисленные для
выборок. Для простоты изложения в этом примере обе генеральные совокупности
характеризуются одинаковым стандартным отклонением, равным 15.
В данном случае тестируется односторонняя гипотеза, поэтому определено
единственное граничное или критическое значение, обозначенное пунктиром.
Если выборочное среднее превышает это значение, то нулевая гипотеза должна
быть отвергнута. Если выборочное среднее меньше критического значения, то
нулевую гипотезу не отвергают. Критическое значение 112,5 было выбрано на
основании генеральной совокупности, соответствующей нулевой гипотезе, у которой
среднее равно 100, а стандартное отклонение - 15; это критическое значение для
а = 0,05, поскольку 95% значений этой генеральной совокупности находится слева
от 112,5, а 5% - справа.
Площадь под кривой распределения значений, соответствующей нулевой
гипотезе, справа от критического значения представляет вероятность ошибки I рода
или вероятность отвергнуть нулевую гипотезу, когда она справедлива. В нашем
примере эта вероятность равна 0,05.
Площадь под кривой распределения значений, соответствующей
альтернативной гипотезе, слева от критического значения - это вероятность ошибки II рода,
если верна альтернативная гипотеза (среднее значение генеральной совокупности
равно 115). Это вероятность того, что если настоящее среднее равно 115,
выборочное среднее будет меньше критического значения 112,5.
Ц_Л_ЦНт Глава 15. Статистика в медицине и эпидемиологии
Площадь этой кривой справа от критического значения - это мощность теста
для данной нулевой гипотезы. Она соответствует вероятности того, что если верна
альтернативная гипотеза (среднее для генеральной совокупности равно 115), то
выборочное среднее будет больше критического значения 112,5, и мы решим, что
среднее в генеральной совокупности больше 100.
Давайте на нашем примере рассмотрим, как каждый из указанных выше
четырех факторов может увеличить мощность, считая, что факторы могут меняться
только по одному.
1. Если увеличить а до 0,1, то критическое значение было бы меньше
(сместилось влево), и мощность бы увеличилась, тогда как вероятность ошибки
II рода уменьшилась бы (площадь под кривой левее критического
значения стала бы меньше).
2. Если бы увеличилась величина эффекта, например среднее значение для
«альтернативной» генеральной совокупности было бы 120, а не 115, то
распределение этой генеральной совокупности сместилось бы вверх. В
результате снизилась бы вероятность ошибки II рода и увеличилась мощность.
3. Если уменьшилось бы стандартное отклонение, то распределения этих
двух генеральных совокупностей были бы более узкими (сильнее
сгруппированными вокруг среднего), таким образом, они бы меньше пересекались.
Это бы привело к снижению вероятности ошибки II рода и увеличению
мощности.
4. Если бы объем выборки увеличился, то эффект был бы сходен с
уменьшением стандартного отклонения, что привело бы к снижению вероятности
ошибки II рода и увеличению мощности.
Один из хороших способов познакомиться с влиянием разных факторов на
мощность - это поэкспериментировать с графическим калькулятором мощности;
в качестве примера такого калькулятора можно привести «Приложение для
вычисления мощности» (Statistical Power Applet, http://wise.cgu.edu/power_applet/
powcr.asp), созданное Клермонтским университетом (Clarcmont Graduate
University).
Вычисление размера выборки
Как было упомянуто выше, каждый тип вычислений мощности или
необходимого размера выборки требует использования подходящей формулы. Однако если
понять принципы планирования научных исследований и анализа мощности, то
найти нужную формулу будет несложно. Здесь приведены два простых примера
вычисления объема выборки, поскольку они хорошо иллюстрируют принципы
этого процесса и могут быть выполнены при помощи ручного калькулятора.
Доверительный интервал для процентов
Одна из распространенных задач - это определение размера выборки,
необходимой для вычисления процентов с приемлемой точностью. Например, вы можете
Вычисление размера выборки НнНИЕЕ
вычислять степень согласия между разными сотрудниками, которые
анализируют медицинские карты, в процентах с точностью до 5%. Или же вы проводите
анализ доли взрослых людей в популяции, которые сделали прививку от гриппа,
и хотите оценить долю иммунизированных людей с точностью до 10%. В этом
случае анализ мощности не проводится, поскольку нет гипотезы, которую
нужно проверять, однако размеры выборки вычисляются, потому что нужно
определить минимальный размер выборки, необходимый для получения заданного
уровня точности.
Формула, используемая для вычисления двустороннего доверительного
интервала, приведена на рис. 15.39.
Рис. 15.39. Формула для вычисления объема выборки для двустороннего
доверительного интервала заданного уровня точности для процентного
соотношения
В этой формуле:
п - это необходимый объем выборки,
я (греческая буква «пи») - предполагаемое процентное соотношение в
генеральной совокупности,
Z - значение стандартного нормального распределения, соответствующее
половине уровня а,
со (греческая буква «омега») - половина ширины нужного доверительного
интервала (если мы используем доверительный интервал в 10%, то половина его
ширины - это 5%).
Мы хотим вычислить двусторонний доверительный интервал для а = 0,05, так
что Z= 1,96. Мы считаем, что я = 0,8, и нам нужен доверительный интервал в 10%
(0,10), так что со = 0,05. Подстановка этих значений в уравнение даст результат,
приведенный на рис. 15.40.
Рис. 15.40. Вычисление объема выборки для двустороннего доверительного
интервала заданного уровня точности для процентного соотношения
Мы округляем эту оценку до 246, поскольку обычно долей объектов не
существует! Так что нам нужно исследовать 246 объектов, при условии что наша оценка
значения я верна, чтобы получить 95%-ный доверительный интервал шириной в
0,10 (0,05 меньше оценочного значения и 0,05 больше него).
EEI Hi HI
Глава 15. Статистика в медицине и эпидемиологии
Мощность для теста на различие
между двумя выборочными средними
(тест Стьюдента для независимых выборок)
В качестве простого примера вычисления мощности давайте рассмотрим расчет
числа объектов в группе, которое нужно, чтобы провести двусторонний тест
Стьюдента для независимых групп с приемлемой мощностью. Формула представлена
на рис. 15.41, 5 - это величина эффекта, расчет которой приведен на рис. 15.42.
п = -, L—
Рис. 15.41. Формула для расчета числа объектов в тесте Стьюдента
для независимых выборок
О
Рис. 15.42. Вычисление величины эффекта в тесте Стьюдента
для независимых выборок
В данном случае значение а определяется при помощи любого подходящего
для рассматриваемых данных метода, который используется для вычисления
стандартного отклонения в тесте Стьюдента (подробное объяснение см. в
главе 6). Для применения этой формулы нам нужны Z-значения и для а, и для р. Мы
по-прежнему будем использовать 95%-ный доверительный интервал для
двустороннего теста, так что Z-зпачение для (1 - а/2) будет равно 1,96. Мы вычислим
объем выборки, нужный для достижения 80%-ной мощности, так что Z-зпачение
для 1 - р будет равно 0,84. Учтите, что если бы мы проводили односторонний
тест, Za было бы равно 1,645, а если бы вычисляли 90%-ную мощность, то Z,
было бы равно 1,28.
Как было указано ранее, величина эффекта - это различие между двумя
генеральными совокупностями, деленное на подходящий показатель дисперсии. Если
и, =25, ц2 = 20, а а = 10, то размер эффекта составит 0,5. Мы можем подставить
полученные значения в формулу для вычисления объема выборки, как это
показано па рис. 15.43.
I 2(1.96 + 0.84)2 ~~ I
п= = = 62.72
| 0^ |
Рис. 15.43. Расчет необходимого числа объектов в тесте Стьюдента
для независимых выборок
Мы округлили полученный результат до целого числа, так что нам нужно по
меньшей мерс 63 объекта в каждой группе, чтобы с вероятностью 80% найти
значимое различие между двумя группами при величине эффекта, равной 0,5.
Упражнения
шшшм
Как лгать при помощи процентов?
Вы не можете проработать в области статистики достаточно долго без того, чтобы
кто-то не показал свою образованность, процитировав в какой-нибудь форме афоризм,
приписываемый английскому политику Бенджамину Дизраэли (Benjamin Disraeli) и
популяризированный в США Марком Твеном, о том, что существует три вида лжецов: лжецы,
отъявленные лжецы и статистики. Существует даже популярная книга Даррелла Хуфа
(Darrell Huff) «Как лгать при помощи статистики» («How to Lie with Statistics» (Norton)),
которую иногда называют самой востребованной книгой по статистике в мире. Одна из
целей книги Хуфа, так же как и этой, - не научить вас лгать при помощи статистики, а
помочь уличить других людей во лжи.
Один из наиболее простых способов солгать (или ввести кого-либо в заблуждение,
если вы предпочитаете такую формулировку) при помощи статистики - это привести
проценты без указания исходных данных, технология, полюбившаяся политикам, но не
только им. Например, если вы услышите, что частота заболеваний холерой в США
увеличилась на 100%, вы можете считать это поводом для беспокойства, пока не узнаете,
что речь идет об увеличении с одного случая до двух. Аналогичным образом 50%-ное
увеличение риска возникновения рака от какого-либо редкого воздействия
(влияющего, скажем, лишь на 15 человек во всей стране) не так значимо для здоровья нации,
как 5%-ное увеличение риска для обычного воздействия (которое может повлиять на
миллионы людей).
Проценты также могут вводить в заблуждение, поскольку люди часто забывают о том,
что увеличение и уменьшение процентов несимметрично. Если число выпускников
определенного колледжа в один год увеличится на 10%, а в следующий год
уменьшится на 10%, число выпускников не будет равно исходному. Предположим, изначально у
нас было 100 000 выпускников. Увеличение их числа на 10% даст нам 110 000 человек.
Уменьшение этого числа на 10% даст нам 99 000 (110 000 * 0,9) человек, это меньше
исходного значения.
Упражнения
Вот ряд вопросов, которые помогут вам освежить в памяти темы, затронутые в
этой главе.
Задача
Классический пример использования таблиц сопряженности в
эпидемиологии - это исследование вспышки пищевых отравлений. Если много людей
отравилось после посещения ресторана, департамент здравоохранения организует
исследование с целью выявить пищу, которая послужила причиной отравления.
Это осложняется тем, что заболевшие люди, возможно, ели несколько блюд, а
некоторые люди, которые ели то же самое, остались здоровыми. Один из подходов
к этой проблеме - это опросить потребителей о том, что они ели и были ли у них
симптомы отравления. Затем данные представляют в виде серии таблиц
сопряженности, таких как табл. 15.16 и 15.17, в которых в роли воздействия выступает
определенный тип пищи, а в роли болезни - пищевое отравление. Вычислите
отношение рисков для двух указанных блюд и обоснуйте свое решение о том, какое
из этих блюд, скорее всего, послужило причиной отравления.
Глава 15. Статистика в медицине и эпидемиологии
Таблица 15.16. Таблица сопряженности для употребления
ростбифа и пищевого отравления
Есть воздействие
Нет воздействия
Есть заболевание
15
20
Нет заболевания
85
80
Таблица 15.17. Таблица сопряженности для употребления
салата из цыпленка и пищевого отравления
Есть воздействие
Нет воздействия
Есть заболевание
80
20
Нет заболевания
20
80
Решение
Отношение рисков для ростбифа вычислено на рис. 15.44.
ОР =
а/(а + Ь) 15/100
c/(c + d)~ 20/100
= 0.75
Рис. 15.44. Вычисление отношения рисков для употребления ростбифа
и пищевого отравления
Отношение
рисков для салата из цыпленка вычислено па рис. 15.45.
ОР
а/(а + Ь)
с /(с + d)
80/100
~ 20/100
= 4.0
Рис. 15.45. Вычисление отношения рисков для употребления салата
из цыпленка и пищевого отравления
Если рассматривать только эти два блюда, то, похоже, виновником отравления
был салат из цыпленка, поскольку люди, которые его ели, в четыре раза чаще
испытывали симптомы пищевого отравления, чем те, кто не притрагивался к салату.
Ростбиф оказывал слабый благотворный эффект, возможно, поскольку те, кто ел
ростбиф, с меньшей вероятностью ели еще и салат из цыпленка. Шансы
отравления у тех, кто ел ротбиф, были на три четверти ниже, чем у тех, кто не ел его.
Задача
Вычислите отношение шансов и доверительный интервал для данных
исследования случай-контроль о связи использования оральных контрацептивов и рака
легких (табл. 15.18).
Таблица 15.18. Таблица сопряженности для употребления
оральных контрацептивов и рака легких
Есть воздействие
Нет воздействия
Есть заболевание
30
20
Нет заболевания
70
80
Упражнения
Решение
Отношение шансов вычисляется, как показано на рис. 15.46.
ad 30(80)
ОШ = —^—^ — 1.71
be 20(70)
Рис. 15.46. Вычисление отношения шансов для использования
оральных контрацептивов и рака легких
Чтобы проверить, отличается ли это отношение шансов от единицы, вычислим
95%-ный доверительный интервал, как показано на рис. 15.47.
ad
ДИ =— ехр|
be
I
7 1 1 1 Г
±2Л — + — + - + -
\а Ъ с Ъ
= 1.71ехр ±1.96J—+ — + — + —
\ V30 70 20 80 j
(0.89,3.28)
Рис. 15.47. Вычисление 95%-го доверительного интервала для отношения
шансов для использования оральных контрацептивов и рака легких
Доверительный интервал (0,89, 3,28) включает единицу, так что это
исследование не демонстрирует значимой связи между употреблением оральных
контрацептивов и раком легких.
Задача
Вычислите и интерпретируйте значения атрибутивного риска, доли
атрибутивного риска и числа нуждающихся в лечении больных, используя следующую
информацию:
• заболеваемость у подверженных воздействию людей = 0,05;
• заболеваемость у не подверженных воздействию людей = 0,02.
Решение
Необходимые вычисления представлены на рис. 15.48.
Ар =1е-10 =0.05-0.03 = 0.02
АР% =^—х 100 =0.40
0.05
Число 1
нуждающихся = = 50
в лечении больных 0.02
Рис. 15.48. Вычисление атрибутивного риска, доли атрибутивного риска
и числа нуждающихся в лечении больных
¦НЯНИ ^ Глава 15. Статистика в медицине и эпидемиологии
Увеличение заболеваемости при появлении воздействия составляет 0,02, или 20
человек на 1000. С воздействием связано 40% заболеваний, и нужно будет
устранить воздействие на 50 человек, чтобы стало одним случаем заболевания меньше.
Задача
Вычислите размер выборки, достаточный для оценки процентного
соотношения с 95%-иым доверительным интервалом шириной в 10%, если предполагаемое
значение равно 0,7.
Решение
Используйте формулу для нахождения размера выборки для процентных
соотношений и подставьте в нее нужные числа:
Z,_u/2= 1,96; со = 0,10; я = 0,70.
Вычисления (рис. 15.49) показали, что выборка должен состоять из 81
объекта.
п = ' 1-а/2>> [я(1 - ж)] = [ — 1 [0.70(0.30)] = 80.7
О)
V0.10
Рис. 15.49. Вычисление объема выборки, нужной для оценки процентного
соотношения
Задача
Вычислите размер выборки, необходимый для теста на различие средних, при
помощи одностороннего теста Стыодента для независимых выборок с мощностью
90% и величиной эффекта 0,4.
Решение
Подставьте в нужную формулу указанные числа:
Z =1,645; Z =1,28; 5 = 0,4
Вычисления (рис. 15.50) показали, что в каждую группу должно войти 107
объектов.
п ¦•
_Az*
+ Z,
б2
-1
2(1.645 + 1.28)2
0.16
= 106.9
Рис. 15.50. Вычисление объема выборки, нужной для теста Стьюдента
с независимыми выборками
ГЛАВА 16.
Статистика в образовании
и психологии
Многие статистические методы, используемые в образовании и психологии,
обычны в других областях исследований, к ним относится тест Стыодента (разобран в
главе 6), различные регрессионные модели и дисперсионный анализ
(обсуждаются в главах 8-11) и тест хи-квадрат (предмет главы 5). Обсуждение теории
измерений, приведенное в первой главе, также полезно, поскольку в большинстве
исследований в области образования и психологии задействованы конструкты,
которые не могут быть измерены напрямую и не имеют очевидных единиц
измерения. Примерами таких конструктов служат предрасположенность к техническим
специальностям, самоэффективность1 и устойчивость к переменам. В этой главе
акцент сделан на статистические методы, используемые в психометрике, которая
имеет дело с созданием, оценкой валидности и применением тестов и измерений
человеческого интеллекта, знаний, умений и психологических характеристик,
таких как личные качества.
Первый вопрос, который у вас может возникнуть в связи с использованием
статистики в образовании и психологии, - зачем это вообще нужно. В конце
концов, разве каждый из нас - не уникальная личность, и разве смысл образования
и психологии не заключается в том, чтобы принимать каждого человека во всем
богатстве его индивидуальности вместо сведения его к набору чисел или
сравнения с остальными людьми?
Это ценное соображение, которое учитывает то, что уже знают все, кто работает
с людьми: исследование людей во многих отношениях значительно сложнее, чем
работа в точных науках или на производстве, поскольку люди бесконечно
разнообразнее химических молекул или орехов2. Изменчивость и индивидуальность
людей особенно затрудняет связанные с ними исследования. Верно также, что
хотя некоторые исследования в области образования и психологии проводятся
для формулировки общих суждений о группах людей, значительная часть этих
исследований направлена на понимание и помощь отдельным индивидуумам,
каждый из которых характеризуется своими социальными особенностями, семей-
1 Вера и эффективность собственных действий. - Прим. пер.
~ Автор явно недооценивает сложность других живых систем. - Прим. пер.
ЕОИНШ
Глава 16. Статистика в образовании и психологии
ными историями и другими контекстуальными сложностями, что сильно
затрудняет сравнение одного человека с другим.
Однако стандартные статистические процедуры могут быть полезны даже при
весьма специфических обстоятельствах, таких как разработка подходящего
образовательного плана для одного студента или психотерапевтического режима для
одного пациента. Принимать подобные решения сложно, но это было бы еще
сложнее без использования стандартных образовательных или психологических
тестов, позволяющих получить числовые значения, которые можно сравнивать с
соответствующими значениями для других людей. Никто не предлагает в подобных
ситуациях руководствоваться лишь формальными стандартизованными тестами
и анкетами; в образовании и психологии большую роль также играют интервью
и наблюдения. Однако к преимуществам использования формальных процедур
тестирования и стандартизованных тестов относятся следующие соображения:
1. Объективные сравнения облегчаются при использовании нормативной
группы. Например, испытывает ли данный восстанавливающийся после
травмы пациент больше побочных эффектов, чем это обычно наблюдается
у людей, восстанавливающихся после подобной травмы? Сравнимы ли
навыки чтения данного ученика с навыками других учеников его возраста и
года обучения?
2. Стандартизированное тестирование позволяет быстро получить
результаты; не нужно ждать конца учебного года, чтобы выяснить, какие ученики
испытывают проблемы из-за плохого владения языком, и незачем
устраивать продолжительные интервью или обследования, чтобы понять, что
пациент страдает от серьезных проблем с памятью.
3. Стандартизированные тесты предъявляются в определенных условиях и
могут считаться объективными, так что единственный параметр, который
оценивается, - это способности ученика или пациента, а не его внешность,
коммуникабельность (если она не имеет отношения к исследуемому
параметру) или прочие не относящиеся к делу факторы.
4. Многие стандартизированные тесты не требуют высокой квалификации
для их проведения (в отличие, например, от клинических интервью) и
могут быть предъявлены нескольким людям одновременно, что делает тесты
особенно полезными в скрининговых исследованиях.
Перцентили
Во многих странах школьников оценивают при помощи тестов, результаты
которых выражаются в перцентилях', один школьник может характеризоваться 70-м
перцентилем по чтению и 85-м перцентилем по математике, тогда как другой
школьник имеет 80-й перцеитиль по чтению и 95-й - по математике.
Перцентили - это вид соотнесенной с нормой оценки, называемой так, поскольку
индивидуальный балл помещен в контекст нормальной группы, то есть людей, сходных с
тем, кто выполняет тест. Для школьников это обычно другие дети, которые учатся
в этом классе в данной стране. Соотнесенная с нормой оценка используется при
Перцентили
ПНЕШ
любом тестировании, в котором относительный результат человека (по
сравнению с определенной группой) важнее абсолютного.
Перцентили для результата отдельного человека - это доля людей в
нормальной группе, которые имели более низкий результат, так что перцентиль 90
означает, что 90% нормальной группы показали худший результат. Здесь на примере
мы кратко объясним, как найти перцентили для результатов экзамена, который
сдавали 100 студентов. (На экзаменах национального масштаба нормальная
группа будет намного больше, а изменчивость результатов будет выше, но этот пример
иллюстрирует саму идею.)
Первый шаг - это перевод исходных результатов в перцентили для создания
частотной таблицы, в которую входит столбец с суммарным процентом, как показано
в табл. 16.1. Для нахождения перцентиля для отдельного результата используйте
суммарный процент для ближайшего предыдущего результата (расположенного
в таблице на строку выше). В данном примере человек, получивший 96 баллов на
экзамене, характеризуется 75-м перцентилем (это значит, что 75% студентов
получили баллы ниже 96), а человек с 85 баллами характеризуется 25-м перцентилем.
Сотого перцентиля нет, поскольку, рассуждая логически, 100% человек,
выполнявших тест, не могли получить баллы ниже тех, что вошли в таблицу. Однако
нулевой перцентиль присутствует; он соответствует человеку, набравшему 53 балла,
поскольку никто не получил более низкого балла.
Таблица 16.1. Баллы, полученные 100 студентами за экзамен
Балл
53
55
58
61
65
67
70
71
78
80
82
84
85
86
88
90
91
Частота
1
2
1
2
3
1
2
3
2
4
2
2
5
4
3
5
7
Процент
1.0%
2.0%
1.0%
2.0%
3.0%
1.0%
2.0%
3.0%
2.0%
4.0%
2.0%
2.0%
5.0%
4.0%
3.0%
5.0%
7.0%
Суммарный процент
Го%
3.0%
4.0%
6.0%
9.0%
10.0%
12.0%
15.0%
17.0%
21.0%
23.0%
25.0%
30.0%
34.0%
37.0%
42.0%
49.0%
ЕШНГ
Глава 16. Статистика в образовании и психологии
Балл
92
93
94
95
96
97
98
99
100
Частота
8
7
5
6
4
3
7
6
5
Процент
8.0%
7.0%
5.0%
6.0%
4.0%
3.0%
7.0%
6.0%
5.0%
Суммарный процент
57.0%
64.0%
69.0%
75.0%
79.0%
82.0%
89.0%
95.0%
100.0%
При использовании стандартизированных тестов на национальном уровне
нормальная группа, используемая для определения перцентилей, гораздо больше, и,
как правило, вычислять перцентили для отдельных студентов не требуется.
Вместо этого разработчик теста обычно предоставляет шкалу для перевода исходных
баллов в перцентили.
Стандартизированные баллы
Стандартизированные баллы, также называемые нормализованными баллами, или
Z-значением, выражают исходные баллы в числе стандартных отклонений выше
пли ниже среднего. Это преобразует исходные баллы так, что их можно оценить,
соотнося со стандартным нормальным распределением, которое подробно
обсуждается в третьей главе. Стандартизированные баллы часто используются в
образовании и психологии, поскольку они помещают результаты в общий контекст, и,
таким образом, их можно считать разновидностью соотнесенной с нормой оценки.
Для часто используемых шкал, таких как шкала Вичслера для оценки
интеллекта взрослых людей (Wechsler Adult Intelligence Scale, WAIS), средине значения и
стандартные отклонения известны и могут быть использованы при вычислениях;
для этой шкалы среднее равно 100, а стандартное отклонение - 15. Для
преобразования исходных баллов в стандартизированные используйте формулу,
приведенную на рис. 16.1.
П z = ^± I
| О |
Рис. 16.1. Формула для вычисления Z-значения
В этой формуле:
X - это исходное значение,
и - это среднее значение для генеральной совокупности, а
а - это стандартное отклонение для генеральной совокупности.
Преобразование в Z-зпачемия позволяет разместить все результаты на общей
шкале, у которой в случае стандартного нормального распределения среднее
Стандартизированные баллы
¦НЕЮ
равно 0, а дисперсия - 1. Кроме того, распределение Z-значений имеет
известные свойства нормального распределения. (Например, около 66% значений будут
находиться в пределах одного стандартного отклонения от среднего.) Мы можем
преобразовать исходное значение шкалы WAIS, равное 115, в Z-зиачение, как
показано на рис. 16.2.
I ^ 115-100 _ I
Z = 1.00
| 15 I
Рис. 16.2. Вычисление Z-значения
Используя таблицу для стандартного нормального распределения (Z-pacnpe-
деления), приведенную на рис. D.3 из приложения D, мы видим, что Z-значение 1
свидетельствует о том, что 84,1% участников получили такие же или меньшие
баллы, как данный испытуемый. Для примера давайте представим, что мы также
проводим тест на математические способности, который характеризуется средним
значением 50 и стандартным отклонением 5. Если какой-то человек получил 105
баллов по тесту WAIS (рис. 16.3) и 60 - по тесту на математические способности
(рис. 16.4), мы можем легко сравнить эти результаты, используя Z-значения.
I ^ 105-100 „00 I
Z 0.33
| 15 I
Рис. 16.3. Вычисление Z-значения (тест WAIS)
I ^ 60-50 _ I
Z = 2.00
| 5 |
Рис. 16.4. Вычисление Z-значения (тест на математические способности)
Эти Z-значения свидетельствуют, что интеллект тестируемого немного выше
среднего, а его математические способности заметно превышают средние.
Некоторым кажется, что стандартизированные баллы сбивают с толку, в
частности потому, что человек может иметь нулевое или отрицательное значение (а в
стандартном нормальном распределении половина значений меньше среднего и
поэтому отрицательные). Поэтому Z-значения иногда конвертируют в Т-зпачения
с использованием более интуитивно понятной шкалы, со средним значением 50 и
стандартным отклонением 10. Преобразование Z-значений в Т-значения можно
выполнить при помощи следующей формулы:
T=Z(10) + 50.
Если у человека Z-значение равно 2,0 (что означает, что его или ее результат на
два стандартных отклонения выше среднего), его можно преобразовать в Т-значе-
ние следующим образом:
Г=(2,0х 10)+ 50 = 70.
Аналогичным образом Z-значение -2,0 соответствует Т-значению 30.
Поскольку вряд ли чей-нибудь результат будет на пять или более стандартных от-
ист
Глава 16. Статистика в образовании и психологии
клонений меньше среднего, Т-значсния почти всегда положительны, что делает
их более простыми для понимания многих людей. Например, результаты
клинических шкал второй версии минесотского многофазного исследования личности
(Minnesota Multiphase Personality Inventory-II, MMPI-II), часто используемые
для выявления и оценки тяжести психиатрических состояний, выражаются
в Т-зиачсниях.
Стсшайп* - это еще один метод перевода исходных значений в значения
стандартного нормального распределения. Станайны делят значения на 9 категорий
(1-9), каждая из которых соответствует половине стандартного отклонения
стандартного нормального распределения. Среднее шкалы станайнов равно 5, и в эту
среднюю категорию попадают значения, которые соответствуют Z-зиачениям
от -0,25 до 0,25 (четверть стандартного отклонения выше и ниже среднего).
Основное преимущество станайнов перед Z- или Т-значениями заключается в том,
что представление результатов в виде принадлежности к категории, а не точных
значений помогает противостоять человеческой привычке придавать значение
небольшим различиям в полученных результатах.
Поскольку для нормального распределения более характерны расположенные
вокруг среднего, а не сильно уклоняющиеся значения, станайны, близкие к
центральному значению 5, более обычны, чем значения, близкие к 1 или 9. Обратите
внимание также на то, что распределение станайнов симметрично, так же как и
распределение значений стандартного нормального распределения, так что ста-
найн 1 так же часто встречается, как и станайн 9, станайн 2 так же распространен,
как и станайн 8, и так далее. Иллюстрация этих двух принципов представлена
в табл. 16.2, в которой указаны значения станайнов, соответствующие значения
стандартных Z-значений и доля значений, приходящихся на каждую категорию
дсвятибаллыюй шкалы.
Таблица 16.2. Станайны
Станайн
1
2
3
4
5
6
7
8
9
Диапазон
Z-значений
Z<-1.75
-1.75<Z<=-1.25
-1.25 <Z<=-0.75
-0.75 <Z<=-0.25
-0.25 <Z<= 0.25
0.25 <Z<= 0.75
0.75 <Z<= 1.25
1.25 <Z<= 1.75
Z> 1.75
Доля подобных
значений в выборке
4%
7%
12%
17%
20%
17%
12%
7%
4%
Этот термин означает оценку по девятибаллыюй шкале и происходит от сокращения английских
слон standard nine (стандартная девятка) - stanine. Общепринятый перевод термина па русский
я;*ык отсутствует. - Прим. пер.
Разработка тестов
ШШПЕк
Станайпы можно вычислить, зная Z-зпачения, по следующей формуле:
Станайн = (2 х Z) + 5.
Значения стаиайнов округляют до ближайшего целого числа; половинные
значения округляют в меньшую сторону. Предположим, у нас есть Z-значение -1,60.
Его преобразуют в станайн 2, как показано ниже:
Станайн = (2 х -1,60) + 5 = 1,8.
Ближайшее целое число - это 2, и это соответствует значению станайна,
приведенному в табл. 16.2 для Z-значения -1,60.
Z-значение 1,60 соответствует станайну 8, поскольку:
Станайн = 2(1,60)+ 5 = 8,2.
Ближайшее целое число 8, и это значение станайна соответствует
приведенному в табл. 16.2 для Z-значения 1,60.
Разработка тестов
Многие тесты в психологии и образовании используются для так называемого объ-
ект-центрированного измерения, задача которого - разместить индивидуумов в
континууме, руководствуясь определенными характеристиками, такими как
способность к изучению языков или ревность. Создание и валидация теста - это огромный
объем работы. (Когда я училась в магистратуре, студентам запрещали писать
диссертацию, для которой нужно было создавать и апробировать новый тест, поскольку
боялись, что в таком случае они никогда не защитятся.) Бремя по убеждению всех
коллег в осмысленности результатов теста полностью лежит на его создателе. Таким
образом, первый шаг для любого человека, который начинает работать в новой для
него области, - проверить, не подходят ли ему уже существующие и
апробированные тесты. Однако, особенно если вы работаете в новой области или с группой,
которой до этого пренебрегали, для ваших задач может не существовать подходящего
теста. В этом случае единственный выход - создать и опробовать новый тест.
Тесты могут быть соотнесенными с нормой и соотнесенными с критерием.
Соотнесенные с нормой тесты мы уже обсудили; их цель - поместить индивидуума
в контекст определенной группы. Напротив, цель соотнесенного с критерием
теста - сравнить индивидуума с некоторым абсолютным стандартом, скажем, чтобы
понять, приобрел ли он минимальную заранее заданную компетентность по
учебному предмету. В соотнесенных с критерием тестах каждый выполнивший тест
может получить высший балл, или же все могут получить низший балл, поскольку
испытуемых оценивают путем сравнения с некоторым заранее заданным
стандартом, а не друг с другом. Хотя результаты соотнесенных с критерием тестов могут
быть непрерывной переменной (например, число в диапазоне от 1 до 100), часто
также определяют пороговое знамение (одно число), так что каждый, кто получил
пороговое или более высокое число баллов, считается прошедшим испытание, а
получившие меньше баллов - нет.
ЕПМН 1
Глава 16. Статистика в образовании и психологии
Большинство тестов состоит из множества отдельных пунктов (обычно
письменных вопросов), которые комбинируют (часто просто суммируя), чтобы
получить общий балл за тест. Например, тест на владение языком может состоять из
100 вопросов, за правильный ответ на каждый из которых начисляется 1 балл, а
за неправильный - 0. Общий балл за тест для каждого человека можно
вычислить, просуммировав баллы за правильные ответы. Во многих статистических
процедурах, используемых для анализа тестов, приходится иметь дело со связью
между отдельными вопросами и связью между отдельными вопросами и общим
баллом.
Хотя общие баллы за тесты широко используются, они могут сбивать с
толку при оценке способностей или достижений. Одна трудность заключается в том,
что обычно все вопросы имеют одинаковый вес по отношению к общему баллу,
хотя не все они могут быть одинаково сложными. Различие между человеком,
который проваливает некоторые простые вопросы, но правильно отвечает на более
сложные, и человеком, верно отвечающим на простые вопросы и пасующим перед
сложными, теряется, если общий балл получают простым суммированием баллов
за разнородные вопросы.
Среднее значение и дисперсия для дихотомических вопросов (на которые
можно ответить верно или неверно) вычисляются с использованием значения
сложности вопроса, обозначаемого как р. Сложность вопроса - это доля испытуемых,
правильно ответивших на него. Если группа, используемая для оценки сложности
вопроса, состоит из Л^человек,/? вычисляется для одного вопроса (/'), как показано
на рис. 16.5.
число людей, правильно ответивших
на вопрос j
Рис. 16.5. Формула для вычисления сложности вопроса
Если ответы на дихотомические вопросы оцениваются как 0 или 1 (0 -
неверный ответ, 1 - верный), то среднее - это то же самое, что и доля людей, правильно
ответивших на вопрос (рис. 16.6).
п
j "'-"''"IT I
Рис. 16.6. Формула для вычисления сложности дихотомических вопросов
В этой формуле X - это отдельные вопросы, a N- число испытуемых.
Дисперсию для отдельного дихотомического вопроса можно вычислить, как
показано на рис. 16.7.
1 j-PjtX-Pj) |
Рис. 16.7. Формула для дисперсии дихотомического вопроса
Разработка тестов
¦¦ЕЮ
Коэффициент корреляции между двумя дихотомическими вопросами,
называемый также фи-коэффициентом, обсуждается в главе 5.
Вычисление дисперсии общего балла требует знания и дисперсии для каждого
вопроса и их ковариации. Если условие нулевой или отрицательной корреляции
между всеми парами переменных не выполняется, то дисперсия общего балла
всегда будет больше, чем сумма дисперсий для отдельных вопросов. Хотя дисперсия
общего балла обычно вычисляется при помощи компьютерных программ, полезно
знать ее формулу, поскольку она характеризует связь между соответствующими
величинами. Ковариацию для пары характеристику и к (не важно,
дихотомических или непрерывных) можно вычислить, как показано на рис. 16.8.
°jk = Pjkaj°k
Рис. 16.8. Формула для вычисления ковариации пары вопросов
В этой формуле:
<з к - ковариация двух вопросов,
рк - корреляция двух вопросов, а
о и ак - дисперсии этих вопросов.
Часто нас интересует дисперсия общего балла, такого как балл Уза тест,
состоящий из множества вопросов. Поскольку для каждой пары вопросов существуют
две идентичные ковариации (ковариация j с к и ковариация к с Д ковариацию
общего балла У можно вычислить, как показано на рис. 16.9.
i<j
Рис. 16.9. Формула для вычисления ковариации общего балла
Условие г <j в приведенной выше формуле обеспечивает учет лишь
неповторяющихся ковариации. Затем для получения нужного числа ковариации мы
умножаем каждую уникальную ковариацию на два.
Число ковариации растет быстрее числа добавляемых в тест вопросов.
Например, если мы добавим пять вопросов в тест, в котором уже есть столько вопросов,
то число дисперсий увеличится с 5 до 10, а число ковариации - с 20 до 90.
Число ковариации для п вопросов рассчитывается как п(п - 1); так что для теста с
пятью вопросами 5 есть 5(4) = 20 ковариации. Тест с 10 вопросами
характеризуется 10(9) = 90 ковариациями. Число уникальных ковариации равно [п(п - 1)]/2,
так что пяти вопросам соответствуют 10 уникальных ковариации, а 10
вопросам - 45.
В большинстве случаев суммирование баллов за отдельные вопросы для
получения общего балла увеличивает дисперсию последнего, поскольку дисперсия
общего балла увеличивается за счет дисперсий отдельных вопросов, а также их
ковариации со всеми вопросами теста. Относительные масштабы роста
дисперсии выше, если вопросы добавляют в короткий тест, а не длинный, и дисперсия
максимальна, если ответы на разные вопросы высоко скоррелированы, поскольку
E^Sl^^lnB Глава 16. Статистика в образовании и психологии
это приводит к большим ковариациям между ними. При прочих равных условиях
более высокая дисперсия возникает при средней сложности вопросов (р = 0,5),
сильно скоррелированных между собой.
Классическая теория тестов:
модель истинных баллов
В идеальном мире все тесты были бы абсолютно надежными. Это значит, что если
одинаковых людей несколько раз протестировать при одинаковых условиях на
предмет какой-либо устойчивой характеристики, то они каждый раз получили
бы одинаковые баллы, а систематическая ошибка (се определение дано позже)
при определении баллов отсутствовала бы. В таком случае мы могли бы с
уверенностью утверждать, что наблюдаемые баллы идентичны истинным баллам и что
наблюдаемые баллы адекватно отражают реальные показатели человека, вне
зависимости от того, какую характеристику оценивает данный тест. Однако в реальном
мире наблюдаемые баллы зависят от многих факторов, и повторяющиеся тесты,
выполненные одним и тем же человеком, часто дают разные результаты. По этой
причине мы должны осознавать различие между истинными и наблюдаемыми
баллами. Мы делаем это, вводя понятие ошибки измерения, которая соответствует
разнице между наблюдаемым и истинным результатами.
Ошибка измерения может быть случайной или систематической. Случайная
ошибка измерений - это результат случайных обстоятельств, таких как
температура в комнате, различия в процедуре проведения теста или колебания настроения
или внимательности испытуемого. Мы не ожидаем, что случайная ошибка будет
смещать результаты теста в том или ином направлении. Случайная ошибка делает
измерения менее точными, но не изменяет результатов определенным образом,
поскольку ожидается, что она увеличивает значения в одном случае и уменьшает в
другом, таким образом, самоуничтожаясь при достаточно большом числе
испытаний. Из-за существования большого числа потенциальных источников случайной
ошибки мы не можем надеяться на полное избавление от нес, но нам требуется
уменьшить ее, насколько это возможно, чтобы повысить точность наших
измерений. С другой стороны, систематическая ошибка измерений смещает результаты в
определенном направлении, но не имеет ничего общего с исследуемым
конструктом. В качестве примера можно привести ошибку измерений во время экзамена по
математике, вызванную плохим знанием языка, в результате чего экзаменуемый
не смог правильно прочесть указания по выполнению заданий. Систематическая
ошибка - это источник искажения результата, и от нее при тестировании нужно
по возможности избавляться.
Психолог Чарльз Спирмен (Charles Spearman) сформулировал классические
понятия истинных и наблюдаемых значений в начале XX века. Спирмен
описал наблюдаемое значение X (результат, который реально получает испытуемый
при тестировании), которое состоит из истинной составляющей (7) и случайной
ошибки (Е):
Надежность теста
НЕЕП
Х = Г + Е
Подразумевается, что при бесконечно большом числе испытаний случайный
компонент самоуничтожается, так что среднее или ожидаемое значение
наблюдаемых результатов становится равным истинному результату. Для испытуемого^ это
можно записать в таком виде:
Г. = ?(Х) = мЛ.
где Т - истинное значение для испытуемого j, E(X) - ожидаемое значение для
этого испытуемого, наблюдаемое при бесконечно большом числе испытаний, а
\ix - среднее наблюдаемое значение для этого испытуемого при тех же условиях.
Таким образом, ошибка - это разница между наблюдаемым и истинным
значениями для испытуемого:
Е=Х-Т.
j j j
Ожидаемое значение ошибки для одного испытуемого при бесконечно
большом числе тестирований равно 0. Поскольку в этом определении «ошибка»
означает только случайную ошибку, считается, что истинное значение и ошибка имеют
следующие свойства:
• для генеральной совокупности испытуемых среднее значение ошибки
равно 0;
• для генеральной совокупности испытуемых корреляция между истинным
значением и ошибкой равна 0;
• корреляция между ошибками для двух случайно выбранных испытуемых,
выполняющих два варианта одного и того же теста или проходящих
независимо одно и то же тестирование, равна 0.
Надежность теста
Когда мы предъявляем тест определенному человеку, мы беспокоимся и о том,
насколько полученный результат отражает истинный результат этого человека.
Используя принятую у теоретиков терминологию, нас интересует индекс надежности,
который рассчитывается как отношение стандартного отклонения для истинных
значений к стандартному отклонению наблюдаемых значений (рис. 16.10).
Рхт
"¦"
от
<*х
Рис. 16.10. Формула для вычисления индекса надежности
В этой формуле ау. - это стандартное отклонение для истинных значений в
генеральной совокупности экзаменуемых, а ох - это стандартное отклонение для
полученных ими баллов.
Надежность теста иногда описывают как долю общей изменчивости
результатов теста, которую можно объяснить истинной изменчивостью
(противопоставленной ошибке).
ВЕЯ
Глава 16. Статистика в образовании и психологии
На практике истинные баллы неизвестны, так что индекс надежности нужно
оценивать при помощи наблюдаемых баллов. Один способ сделать это - провести
два параллельных теста для одной и той же группы экзаменуемых и использовать
корреляцию между результатами по двум вариантам теста, называемую
коэффициентом надежности, как оценку индекса надежности. Параллельные тесты должны
удовлетворять двум условиям: одинаковая сложность и одинаковая изменчивость.
Коэффициент надежности - это оценка отношения дисперсии истинных
значений к наблюдаемой дисперсии значений, его можно интерпретировать просто
как коэффициент детерминации (;^) обобщенной линейной модели. Если тест
характеризуется коэффициентом надежности 0,88, мы можем интерпретировать это
как то, что 88% дисперсии наблюдаемых значений объясняются изменчивостью
истинных значений, а оставшиеся 0,12 или 12% должны быть отнесены на счет
случайной ошибки. Для вычисления корреляции между истинными и
наблюдаемыми результатами этого теста нужно извлечь квадратный корень из
коэффициента надежности, так что для данного теста корреляцию между истинными и
наблюдаемыми баллами можно оценить как -0,88 или 0,938.
Коэффициент надежности можно оценить несколькими способами. Если мы
оцениваем коэффициент надежности, предъявляя один и тот же тест тем же
экзаменуемым дважды, это называется методом повторного тестирования, а
корреляция между значениями теста в этом случае называется коэффициентом
устойчивости. Мы также можем оценить коэффициент надежности, предложив
два эквивалентных варианта теста тем же самым испытуемым в той же ситуации;
это метод альтернативной формы, а коэффициент корреляции между
результатами называется коэффициент эквивалентности теста {коэффициент надежности
альтернативных форм). Если используются и разные варианты теста, и разные
условия, то корреляцию между результатами в этом случае называют
коэффициентом устойчивости и эквивалентности. Поскольку этот коэффициент имеет два
источника ошибок, варианты теста и условия тестирования, в целом для данной
группы испытуемых его значения должны быть ниже и коэффициента
устойчивости, и коэффициента эквивалентности.
Показатели внутренней
непротиворечивости
Другой подход к оценке надежности - это использование показателей внутренней
непротиворечивости, которые можно вычислить после однократного применения
теста одной группе испытуемых. Показатели непротиворечивости используются
для оценки надежности, поскольку в составные тесты входит несколько вопросов,
выбранных из множества возможных вопросов. Оценка внутренней
непротиворечивости - это предсказание, насколько сходными будут результаты одного
человека, если он ответит на другие вопросы из того же множества.
Рассмотрим задачу по разработке теста для проверки знаний ученика по курсу
алгебры за среднюю школу. Первый шаг при разработке такого теста - это решить,
Показатели внутренней непротиворечивости
какие темы включить в него. Затем будет составлен перечень вопросов, которые
позволят оценить знания ученика по этим темам. Часть этих вопросов будет
использована в окончательном варианте теста. Цель такого экзамена - не просто
понять, насколько хорошо ученик справляется с вошедшими в тест заданиями, по и
как он в целом освоил всю программу по алгебре за курс средней школы. Если
вошедшие в тест вопросы представляют адекватную выборку из содержания курса,
то результат тестирования будет надежным показателем овладения материалом
учениками. Однородность вопросов - это также ценная характеристика такого
рода теста, поскольку это показатель того, что все вопросы проверяют одинаковое
содержание и не имеют технических недостатков, таких как неудачная
формулировка или неверный учет результатов, вследствие чего успех выполнения данного
задания будет не связан с успехами в алгебре.
«Натаскивание» на тесты
В некоторых ситуациях ученикам нужно выполнять ряд тестов (так называемых
итоговых, или ключевых, тестов), которые используются для определения, можно ли им
перейти на следующую ступень обучения в школе (например, перейти из пятого класса в
шестой) или закончить этап обучения (например, среднюю школу). Поскольку ясно, что
администрация и учителя заботятся, чтобы их ученики хорошо справились с тестами,
некоторые школы выделяют часть учебного времени специально для подготовки к
экзаменам. (Помимо беспокойства за качество образования учеников, учителей и
администрацию также могут оценивать по результатам выполнения этих тестов их учениками.)
Если задача заключается в том, чтобы добиться более высоких успехов при выполнении
теста, а не улучшить свои знания и умения по предмету, то это часто называется
«натаскиванием» на тест. Например, ученики могут посвящать свое время выполнению заданий
именно в том формате, который будет использован в предстоящем тесте, или свести
свое обучение к известному кругу задач или информации, которые войдут в тест, вместо
изучения разнообразных тем и применения умений многими способами.
Что же не так с «натаскиванием» на тест? Проблема заключается в том, что
проверяющие учебные достижения тесты основаны на допущении, что входящие в них вопросы
представляют случайную выборку из всех возможных вопросов по предмету и что
успешность выполнения предъявленных заданий данного теста - хороший показатель общего
овладения материалом. Если это допущение выполняется, то результаты ученика для
другой выборки вопросов будут сходными. Это допущение не выполняется, если
ученики и учителя знают заранее, какие вопросы войдут в тест, и готовятся только к ним; в
этом случае по результатам теста невозможно судить об овладении всем материалом
по теме.
Предположим, что мы проверяем знания учеников по математике. Одна из тем - это
доказательства в геометрии; студенты должны уметь формулировать двурядные
доказательства данной теоремы. Если ученикам преподавали общий метод формулировки
доказательств, то их знания в равной степени применимы ко всем заданиям на
доказательства в данном тесте, так что их результаты выполнения теста должны быть хорошим
показателем их общих успехов в данном разделе математики. Однако если их учитель
заметил, что из года в год на экзаменах спрашивают только несколько типов
доказательств, он может просто добиваться, чтобы ученики запомнили, как формулировать
данные типы доказательств. Это пример «натаскивания» на тест. В данном случае
способность учеников формулировать те доказательства, которые они запомнили, не
обязательно связана со способностью формулировать другие типы доказательств. Таким
образом, невозможно по результатам данного теста судить об их общей способности
формулировать доказательства.
^|в| Глава 16. Статистика в образовании и психологии
Методы расщепления совокупности надвое
Для измерения внутренней непротиворечивости методами растепления
совокупности надвое (split-half methods) нужно разделить тест на две части, или
варианта, обычно две половины равной длины, которые считаются сходными. Каждый
испытуемый выполняет тест целиком. Разделение теста проводят несколькими
способами, включая попеременное распределение (четные номера вопросов идут
в один вариант, нечетные - в другой), учет соответствия содержимого или
случайное распределение. Какой бы метод не использовали, если исходный тест состоит
из 100 вопросов, в каждую из двух половин войдут 50 вопросов. Коэффициент
корреляции между результатами выполнения двух частей называется
коэффициентом эквивалентности. Этот коэффициент недооценивает надежность
исходного теста, поскольку длинные тесты обычно надежнее коротких. Для оценки
надежности исходного теста по коэффициенту эквивалентности его двух половин
можно использовать прогностическую формулу Спирмана-Брауна (Spearman-
Brown prophecy formula), приведенную на рис. 16.11.
1 + Рав
Рис. 16.11. Прогностическая формула Спирмана-Брауна
(для коэффициента эквивалетности)
В этой формуле:
рху - это оценка надежности исходного теста, а
рЛН - это наблюдаемая корреляция, то есть коэффициент эквивалентности,
между этими двумя половинами тестов.
Для корректного применения этой формулы две половины теста должны в
точности соответствовать друг другу. Если коэффициент эквивалентности двух
половин теста равен 0,5, надежность теста рассчитывается, как показано на
рис. 16.12.
Л 2(0'5) П*7
дуу, = =0.67
Нхх 1 + 0.5
Рис. 16.12. Вычисление коэффициента эквивалентности
Второй метод оценки надежности исходного теста при помощи его разделения
надвое - это вычисление разницы между результатами выполнения каждой из
двух половин для каждого испытуемого. Дисперсия полученных различий - это
оценка дисперсии ошибок для надежности, так что 1 минус отношение дисперсии
ошибок к общей дисперсии также можно использовать как показатель
изменчивости. На рис. 16.3 приведена формула для применения этого второго метода.
Рис. 16.13. Еще одна формула для вычисления коэффициента эквивалентности
Показатели внутренней непротиворечивости |Н^1
Здесь о2п - это дисперсия разницы результатов, a o2v - это дисперсия
наблюдаемых значений.
Оценки надежности этими методами совпадут, если дисперсия для двух
половин теста будет одинаковой. Чем сильнее различаются дисперсии для двух
половин, тем сильнее будет оценка по формуле Спермана-Брауиа превышать
оценку, сделанную при помощи метода разницы значений. Оценка надежности
любым из методов будет зависеть от способа распределения заданий по
половинам теста, поскольку при разном распределении заданий корреляции между
половинами теста и набор значений разницы дисперсий будут разными.
Коэффициент альфа
Есть несколько методов оценки надежности с использованием ковариации
между ответами на отдельные вопросы, которые позволяют обойти проблему
множественных вариантов разделения теста надвое; ниже представлены три таких
метода. Альфу Кронбаха (Cronbach's alpha) можно использовать для вопросов с
двумя или более вариантами ответа, тогда как две формулы Кюдера-Ричардсона
(Kuder-Richardson) подходят только для вопросов с двумя вариантами ответа.
Показатель внутренней непротиворечивости, рассчитанный при помощи любого
из этих методов, обычно называется коэффициент альфа, он эквивалентен
усредненному значению коэффициентов согласия при разделении теста надвое всеми
возможными способами. Строго говоря, коэффициент альфа - это оценка не
коэффициента надежности, а его нижней границы (иногда называемой
коэффициентом точности). Однако часто при интерпретации результатов на эту тонкость не
обращают внимания, и коэффициент альфа обычно приводят без обсуждения.
Учтите, что вычисление коэффициента альфа для сколь-нибудь длинного теста
утомительно, и поэтому обычно производится при помощи компьютерных
программ. Тем не менее все равно полезно знать формулу и применить ее для простых
вычислений, чтобы понимать, какие факторы влияют на коэффициент альфа.
Альфа Кронбаха - наиболее обычный метод вычисления коэффициента
альфа и так часто называется коэффициент альфа в компьютерных программах,
созданных для анализа надежности. Этот коэффициент рассчитывается по формуле,
приведенной на рис. 16.14.
Рис. 16.14. Формула для вычисления альфы Кронбаха
Здесь k - это число вопросов, о2. - дисперсия для z-ro вопроса, 62х - общая
дисперсия для всего теста.
Предположим, что у нас есть тест из пяти вопросов с общей дисперсией 100 и
дисперсиями для отдельных вопросов 10; 5; 6,5; 7,5 и 13. Вычисление альфы Кронбаха
для этих данных показано на рис. 16.15.
Глава 16. Статистика в образовании и психологии
а=—|1- —1=0.725
5-Ц 100 /
Рис. 16.15. Вычисление альфы Кронбаха
Для вычисления коэффициента альфа существует несколько формул Кюде-
ра-Ричардсона; две из них, которые разумно использовать для дихотомических
вопросов, приведены ниже. Обратите внимание на то, что формула KR-21 - это
упрощенный вариант формулы KR-20; она подразумевает, что все задания имеют
одинаковую сложность. KR-20 и KR-21 дают идентичные результаты при
одинаковой сложности заданий; если это не так, то KR-21 дает более низкие результаты
по сравнению с KR-20. Формула KR-20 приведена на рис, 16.16.
Рис. 16.16. Формула Кюдера-Ричардсона, вариант KR-20
Здесь к - это число вопросов,;;. - сложность данного задания, d2Y - общая
дисперсия для всего теста.
Обратите внимание на то, что формула KR-20 идентична формуле для
вычисления альфы Кронбаха, за исключением того, что дисперсия для отдельного задания
выражена по-другому, чтобы учесть тот факт, что KR-20 используется для
дихотомических вопросов.
Формулу KR-20 можно упростить, допустив, что все вопросы имеют
одинаковую сложность, так что не нужно вычислять дисперсии для отдельных вопросов,
а затем суммировать их. Такое упрощение позволяет получить формулу KR-21
(рис. 16.17).
Рис. 16.17. Формула Кюдера-Ричардсона, вариант KR-21
Здесь к - это число вопросов, Д - сложность данного задания (часто
оценивается как X), 62х - общая дисперсия для всего теста (часто оценивается как s2v).
Анализ заданий
При подготовке тестов часто создают большой пул заданий, проверяют их на
испытуемых, сходных с теми, для кого этот тест предназначен, и формируют
окончательный набор заданий, которые вносят наибольший вклад в валидность и
надежность теста. Анализ заданий - это набор процедур, используемых для проведения
тестов и описания ответов испытуемых на рассматриваемые вопросы, включая
распределение ответов на каждый вопрос и связь между ответами на каждый
вопрос и другими критериями.
Анализ заданий
mmzsi
Прежде всего при анализе заданий рассчитываются среднее и дисперсия для
каждого задания. Для дихотомических заданий среднее - это также доля
испытуемых, правильно ответивших на вопрос, она называется сложностью задания,
илир, как говорилось выше. Общий результат за тест для одного испытуемого -
это сумма сложностей всех заданий, что равно сумме вопросов, па которые был
дан правильный ответ. Среднее значение сложности задания - это сумма
сложностей всех заданий, деленная на число заданий, как показано на рис. 16.18.
I ~к I
| ^fc |
Рис. 16.18. Формула для вычисления средней сложности заданий
В этой формуле рх - сложность i-ro задания, a k - общее число заданий.
Поскольку сложность задания - это пропорция, дисперсия для отдельного
задания вычисляется как
Часто выбирают задания с наибольшей дисперсией, чтобы увеличить
эффективность теста для разграничения людей с разными способностями. Дисперсия
максимальна, когдар = 0,5, в чем вы можете удостовериться, вычислив дисперсию
для некоторых других значений р:
Если р = 0,50, а) = 0,5(0,5) = 0,2500.
Еслир = 0,49, а] = 0,49(0,51) = 0,2499.
Если р = 0,48, о' = 0,48(0,52) = 0,2496.
Если р = 0,40, а] = 0,40(0,60) = 0,2400.
Учтите, что дисперсия дляр = 0,49 ир = 0,51 одинакова, так же как и дисперсия
для р = 0,48 ир = 0,52, и так далее.
Во многих обычных форматах тестирования, особенно с множественным
выбором, испытуемые могут улучшать свои результаты, пытаясь угадать ответ, если не
знают его. Это значит, что значение р для вопроса будет выше, чем доля
экзаменуемых, которые действительно знают проверяемый вопросом материал. Иначе
говоря, наблюдаемые значения постоянно будут выше реальных, поскольку
наблюдаемые значения завышаются при успешном угадывании. Поэтому, когда формат
задания позволяет угадывать (например, в случае вопросов со многими
вариантами ответа, когда неправильные ответы не штрафуются), при расчете
наблюдаемой сложности задания необходим дополнительный шаг для максимизации
дисперсии. Это достигают путем прибавления к сложности задания величины 0,5/ш,
где т - это число вариантов ответа на данный вопрос. Эта формула подразумевает,
что все варианты ответа имеют равную вероятность быть выбранными, если
экзаменуемый не знает правильного ответа. Наблюдаемая сложность задания р(), при
которой предполагается, что истинная сложность равна 0,5 (половина экзаменуе-
¦ШИ Глава 16. Статистика в образовании и психологии
мых знает правильный ответ без угадывания), для разных значений т будет такой,
как указано в табл. 16.3.
Таблица 16.3. Сложность заданий с поправкой на угадывание
Число вариантов ответа
2
3
4
Ро
0.5 + 0.5/2 = 0.75
0.5 + 0.5/3 = 0.67
0.5 + 0.5/4 = 0.625
Дифференцирующий потенциал задания описывает, насколько хорошо оно
разделяет экзаменуемых с большим и малым количеством тестируемой
характеристики, будь то знания географии, музыкальные способности или депрессия. Обычно
составитель теста выбирает положительно дифференцирующие задания, этозначит,
что на них с высокой вероятностью ответят правильно или положительно люди с
большим количеством определенной характеристики, а люди с малым
количеством данной характеристики ответят неправильно или отрицательно. Например,
если вы проверяете математические способности, на положительно
дифференцирующие вопросы с большей вероятностью ответят ученики с высокими
математическими способностями, в противоположность ученикам с низкими
математическими способностями, которые, скорее всего, ответят неверно. Противоположное
свойство - это отрицательная дифференциация] продолжая наш пример,
отрицательно дифференцирующее задание будет с большей вероятностью выполнено
верно учеником с низкими знаниями, по сравнению с много знающим учеником.
Отрицательная дифференциация обычно является основанием для исключения
вопроса из теста, если только оно не используется для выявления людей, которые
лукавят при ответе (например, в исследовании психического здоровья).
В этом разделе описаны четыре индекса дискриминирующего потенциала
задания, затем обсуждается индекс дискриминирующего потенциала, который можно
связать либо с общими баллами за тест, либо с внешним критерием. Если все
вопросы имеют умеренную сложность (что характерно для многих тестов), все пять
индексов дадут сходные результаты.
Индекс дискриминации применяется только к дихотомическим вопросам; он
позволяет сравнить долю правильно ответивших экзаменуемых в двух группах.
Эти две группы часто формируются, используя баллы за весь тест; например, 50%
лучших экзаменуемых часто сравнивают с 50% худших экзаменуемых или 30%
лучших сравнивают с 30% худших. Для вычисления индекса дискриминации (D)
применяется следующая формула:
D=P„-P,>
гдс/;;/ - это доля лучших испытуемых, которые справились с заданием, а/?, - доля
худших испытуемых, которые справились с заданием.
Если 80% лучших экзаменуемых правильно выполнили задание, и этого же
добилось только 30% худших экзаменуемых, то индекс дискриминации будет равен
Анализ заданий
ШШЕШ
D = 0,8 - 0,3 = 0,5.
D варьирует в диапазоне (-1, +1). D = 1,0 значит, что каждый из лучших
экзаменуемых выполнил задание верно, и с ним не справился никто из слабой группы,
так что это задание имеет очень высокий дискриминирующий потенциал; D = 0,0
означает, что задание выполнили равные доли испытуемых из сильной и слабой
групп, так что это задание вообще не имеет дискриминационного потенциала. На
индекс дискриминации влияет алгоритм формирования групп; например, если
сильная группа составлена из 20% экзаменуемых, показавших лучшие результаты,
а слабая - из 20% экзаменуемых с худшими результатами, мы ожидаем получить
более высокий индекс дискриминации.
Для индекса дискриминации не существует тестов на значимость и
абсолютных правил для определения приемлемого значения. Эмпирическое правило,
предложенное Эбелем (Ebel, 1965; полная ссылка приведена в приложении С),
гласит, что D> 0,4 - это приемлемое значение (задание можно использовать),
D < 0,2 - неприемлемое значение (от задания можно отказаться), а
промежуточные значения свидетельствуют о том, что задание нужно доработать так, чтобы
D превысил 0,4.
Точечный коэффициент бисериальиой корреляции, обсуждаемый в главе 5, - это
мера связи между дихотомической и непрерывной переменными; его можно
использовать для измерения корреляции между отдельным дихотомическим
заданием (за которое можно получить либо 0, либо 1 балл) и общим баллом за тест
(подразумевая, что в тесте содержится достаточно заданий, чтобы считать общий
балл непрерывной переменной).
Коэффициент бисериальной корреляции можно вычислять для дихотомических
заданий, если подразумевается, что качество выполнения задания обусловлено
скрытой переменной с нормальным распределением. Формула для вычисления
коэффициента бисериальной корреляции приведена на рис. 16.19.
/ \
Рьь -
Я-Иг
1 °х )
1 \
\А
\у)
Рис. 16.19. Формула для вычисления коэффициента бисериальной корреляции
Здесь и+ - усредненный общий балл за тест для экзаменуемых, которые
правильно ответили на данный вопрос,
jix - это усредненный общий балл за тест для всех экзаменуемых,
ах - стандартное отклонение для общего балла за тест для всех экзаменуемых,
р - сложность задания,
У - Y-координата (высота кривой) для стандартного нормального
распределения сложности заданий (взятая, например, с рис. D.3 в приложении D).
Предположим, что для данного вопроса н+ = 80, их = 78, av = 5 и р = 0,5. Расчет
коэффициента бисериальной корреляции для него показан на рис. 16.20.
ЕЕЗНВ
Глава 16. Статистика в образовании и психологии
/80-78V0.5000\ __
phi=\ =0.5014
У,т { 5 A0.3989J
Рис. 16.20. Расчет коэффициента бисериальной корреляции
Бисериальпая корреляция всегда выше, чем точечная бисериальная
корреляция, вычисленная для тех же данных, и эти различия особенно заметны, если
/; < 0,25 пли/; > 0,75. Коэффициент бисериальной корреляции более
предпочтителен в качестве показателя сложности задания, когда подразумевается, что в основе
дихотомических результатов выполнения задания лежит нормальное
распределение, и задача состоит в выборе очень легких или очень сложных вопросов, или тест
будет использован для экзаменуемых с очень разными способностями.
Разобранный в главе 5 коэффициент фи отражает связь между двумя
дихотомическими переменными. Если переменные исходно не были дихотомическими, а
были получены посредством преобразования непрерывной переменной с
нормальным распределением значений (например, результат в виде сдал/не сдал,
полученный при использовании порогового значения для непрерывной переменной), для
них более предпочтителен коэффициент тетрахорической корреляции, поскольку
диапазон фи ограничен при разной сложности заданий. Тетрахорические
корреляции также используются при факторном анализе и моделировании
структурных уравнений. Коэффициент тетрахорической корреляции редко рассчитывают
вручную, но его вычисление предусмотрено в некоторых стандартных
компьютерных программах для статистической обработки данных, включая SAS и R.
Современная теория тестирования
Хотя классическая теория тестирования до сих пор применяется в разных
областях, современная теория тестирования (СТТ) (item response theory)"1 - это
важный альтернативный подход. Каждый работающий в области психометрики
должен быть знаком с СТТ, которая используется сейчас все шире, от медицины до
криминологии. СТТ в дальнейшем, возможно, будет использоваться еще более
активно, поскольку возможности ее применения предусмотрены в наиболее
распространенных статистических программах. СТТ - это сложная тема, которую здесь
можно лишь кратко описать; те, кто хочет познакомиться с ней подробнее,
должны прочесть учебник (например, Hambleton, Swaminathan, Rogers, 1991). Список
компьютерных программ для применения СТТ приведен на http://winstcps.com/
rasch.htm.
СТТ избавлена от некоторых недостатков классической теории тестирования,
главный из которых заключается в том, что методы классической теории не
позволяют отделить характеристики экзаменуемого от характеристик теста. В рамках
классической теории способности экзаменуемого выражаются в терминах
конкретного теста, а сложность данного теста определяется при помощи отдельной
Общепринятый перевод этого термина на русский язык отсутствует. Иногда встречается название
«теория текстовых заданий». - Прим. пер.
Современная теория тестирования
пННЕЕЛ
группы испытуемых. Это происходит потому, что в классической теории
сложность задания определяется как доля экзаменуемых, выполнивших это задание
верно; для одной группы испытуемых данное задание может быть
классифицировано как сложное, поскольку лишь несколько человек выполнили его верно, а для
другой группы оно будет интерпретировано как легкое, потому что с ним
справится большинство. Аналогичным образом по результатам одного теста экзаменуемая
может считаться хорошо освоившей материал, поскольку она получила высокие
баллы, а другой тест, явно основанный на том же материале, покажет, что она
плохо овладела материалом, поскольку получила низкий балл.
Из того, что оценки сложности задания и способностей экзаменуемого в
классической теории тестирования переплетены, вытекает сложность адекватной оценки
способностей экзаменуемых, которые выполнили разные тесты, или
ранжирования заданий тестов, выполненных разными группами испытуемых, по сложности.
В классической теории тестирования проводились попытки устранения этих
проблем разными способами, такими как включение набора общих заданий в разные
варианты теста, однако основная проблема остается.
• Результаты выполнения определенного задания экзаменуемым можно
объяснить теми его способностями, на проверку которых направлен тест, и
способности считаются латентной, ненаблюдаемой переменной.
• Связь между результатами выполнения определенного задания группой
испытуемых и их способностями можно выразить при помощи
характеризующей задание кривой (ХЗК) (item characteristic curve).
Способности обычно обозначают греческой буквой «тета» (0), а сложность
задания выражают числом от 0 до 1. ХЗК изображают в виде сглаженной линии на
графике, где по вертикальной оси отражают вероятность правильного ответа на
вопрос, а по горизонтальной - способности экзаменуемого по такой in кале, где 6
имеет среднее значение 0 и стандартное отклонение 1. ХЗК - это возрастающая
функция, так что для более способных экзаменуемых (с высоким значением 0)
предсказанное значение вероятности правильного ответа на вопрос будет всегда
выше. Это показано на теоретической ХЗК (рис. 16.21).
Модели СТТ обладают следующими достоинствами, по сравнению с
классической теорией тестирования:
1. Модели СТТ фальсифицируемы] соответствие этих моделей данным можно
оценить и определить, насколько конкретная модель подходит для
определенных данных.
2. Оценка способностей экзаменуемого не зависит от теста; она проводится
на основании общего показателя, что позволяет сравнивать испытуемых,
выполнявших разные тесты.
3. Оценка сложности задания не зависит от экзаменуемого; она проводится
на основании общего показателя, что позволяет сравнивать задания,
выполнявшиеся разными группами.
4. В рамках СТТ для результатов каждого испытуемого вычисляются
стандартные ошибки, а не предполагается (как в классической теории тестиро-
ЕВДЯ^^нНВ; Глава 16. Статистика в образовании и психологии
ваиия), что стандартные ошибки одинаковы для результатов всех
испытуемых.
5. В рамках СТТ при оценке способностей экзаменуемого учитывается сложность
заданий, так что два человека, справившихся с одинаковым числом заданий,
могут иметь разные оценки способностей, если один выполнил более сложные
задания, чем другой.
Одно из следствий, вытекающее из пунктов 2 и 3, состоит в том, что в СТТ
оценки способностей испытуемого и сложностей задания инвариантны. Это значит, что,
если не брать в расчет ошибку измерения, любые два экзаменуемых со сходными
способностями имеют равную вероятность правильно ответить на данный вопрос, а
вероятность правильного ответа экзаменуемого на два задания сравнимой сложности
одинакова.
I 100-1 ^^~— I I
§ 0.5W /
°'251 /
0.001-1 Г*! I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I
-3-2-10123
Лежащая в основе латентная переменная (0)
Рис. 16.21. Теоретическая кривая, характеризующая задание
Обратите внимание на то, что хотя в этом обсуждении мы предполагаем, что
задание можно выполнить или верно, или неверно (отсюда и такие формулировки,
как «вероятность правильного выполнения задания»), СТТ можно применять в
случаях, где нет верного или неверного ответа. Например, в психологической
анкете, направленной на выявление установок, сложность задания можно выразить
как «вероятность согласия с утверждением», а 0 - это степень или выраженность
измеряемого качества (такого как положительное отношение к гражданской
активности).
Несколько широко используемых в СТТ моделей различаются по
характеристикам заданий, которые они учитывают. Для всех моделей СТТ свойственны
следующие допущения.
Одномерность
Задания в тесте оценивают только одно качество; на практике это
объясняется требованием того, чтобы результаты выполнения теста можно было
объяснить одним основным фактором.
Современная теория тестирования
Локальная независимость
Если способности экзаменуемого остаются неизменными, то зависимость
между его ответами на разные вопросы отсутствует; то есть результаты
выполнения разных заданий не зависят друг от друга.
Простейшая модель СТТ включает только одну характеристику заданий -
сложность задания, обозначаемую Ь.. Это логистическая модель с одним
параметром, называемая также моделью Раша, поскольку она была создана датским
математиком Георгом Рашем (Georg Rasch). X3K для этой модели вычисляется при
помощи следующей формулы:
Р№ =
о-ь,
1 + е1
где Р.(9) - вероятность правильного ответа на вопрос г для экзаменуемого со
способностями 6, a 6. - сложность задания L
Сложность задания определяется как точка на шкале способностей (ось .г), для
которой вероятность правильного выполнения задания равна 0,5. Более
сложные задания может выполнить половина экзаменуемых, если их общий уровень
достаточно высок, а для простых заданий достаточно более низких способностей
экзаменуемых в целом, чтобы половина из них справилась с заданием. В модели
Раша ХЗК для вопросов разной сложности имеют одинаковую форму и
различаются только положением. Это видно на рис. 16.22, на котором показаны ХЗК для
нескольких заданий разной сложности, но с одинаковым дифференцирующим
потенциалом.
Рис. 16.22. Кривые, характеризующие задания разной сложности,
но с одинаковым дифференцирующим потенциалом:
задание А - самое сложное, задание В - самое простое
Помня о том, что 6 - это мера способностей экзаменуемого, можно видеть, что
для правильного выполнения задания А с 50%-ной вероятностью нужно больше
способностей, по сравнению с другими заданиями, кривые для которых
расположены левее. Также ясно, что для представленных на графике заданий наименьшее
количество 0 нужно для 50%-ной вероятности правильного ответа на вопрос В. Так
что можно сказать, что вопрос В - самый простой, а вопрос А - самый сложный. Вы
ЕШМН
Глава 16. Статистика в образовании и психологии
можете лучше понять это, если проведете на графике горизонтальную линию у = 0,5,
а затем из точки пересечения этой линии с каждой кривой опустите перпендикуляр
на ось х. Точка пересечения такого перпендикуляра с осью х - это значение G,
необходимое для того, чтобы правильно ответить на вопрос с 50%-ной вероятностью, и
это количество явно больше для задания Л, по сравнению с заданием В.
Модель СТТ с двумя параметрами включает дифференцирующий потенциал
задания, а.. Этот параметр обусловливает разный наклон кривых,
характеризующих задания. Вопросы, для которых характерны более крутые кривые,
эффективнее для дифференциации экзаменуемых со сходными знаниями, чем вопросы, для
которых характерны более пологие кривые, поскольку в первом случае
вероятность успешного ответа на вопрос быстрее меняется, по сравнению с изменением
способностей испытуемого.
Сложность задания пропорциональна углу наклона кривой в точке, где Ь. = 0,5, то
есть когда ожидается, что половина экзаменуемых выполнит задание верно.
Обычно а. колеблется в диапазоне (0,2), поскольку от отрицательно дифференцирующих
заданий (на которые с большей вероятностью ответит более слабый экзаменуемый)
обычно отказываются и поскольку на практике дифференцирующий потенциал
задания редко превышает 2. В логистическую модель с двумя параметрами
обычно входит коэффициент масштабирования Д который добавляют, чтобы добиться
максимально возможного соответствия логистической функции кумулятивному
нормальному распределению.
ХЗК для логистической модели с двумя параметрами вычисляется при помощи
следующей формулы:
Кривые для двух заданий, различающихся и по сложности, и по
дифференцирующему потенциалу, показаны на рис. 16.23.
I ^Т
°-31
О.ОН—I I I I I I I I I I I
-3-2-10123
6
Рис. 16.23. Кривые, характеризующие задания, которые различаются
и по сложности, и по дифференцирующему потенциалу
Трсхфакторная логистическая модель включает дополнительный параметр, с,
который специалисты называют параметр уровня псевдослучайности. Это нижняя
Упражнения
шшмшшт
асимптота для ХЗК, которая показывает вероятность случайно выполнить задание
правильно экзаменуемыми с низкими способностями. Этот параметр часто
называют параметром угадывания, поскольку для слабых экзаменуемых единственный
способ ответить правильно на сложный вопрос - это угадать ответ. Однако часто с.
меньше, чем ожидается при случайном угадывании, поскольку составители тестов
умеют придумывать неправильные ответы, которые покажутся верными слабым
ученикам. ХЗК для логистической модели с тремя параметрами вычисляется при
помощи следующей формулы:
/>(0) = с,+(1-с,) е DaAe_bi)-
Модель с тремя параметрами изображена на рис. 16.24; в нее включен
достаточно высокий параметр угадывания, на что указывает тот факт, что кривая
пересекает ось у в районе значения 0,2. Это значит, что человек с очень низким 6 примерно
с 20%-ной вероятностью выполнит задание верно.
1.СХН
0.7SJ /
% 0.5W /
0.2Я ^^^
0.0Н—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—i—I—I—I—I—I—I—I
-3-2-10123
е
Рис. 16.24. Кривая, характеризующая задание с достаточно высоким значением
параметра угадывания
Упражнения
Здесь представлен ряд вопросов для повторения тем, рассмотренных в этой
главе.
Задача
Для данных, представленных в табл. 16.1:
1. Каков перцентиль для 80 баллов?
2. Какой балл имеет 75-й перцентиль?
Решение
Перцентиль можно найти, посмотрев на кумулятивную вероятность для
следующего по величине балла (выше интересующего вас). Для нахождения балла,
соответствующего заданному перцентилю, выполните обратное действие.
^¦¦Вш Глава 16. Статистика в образовании и психологии
1. Балл 80 соответствует 17-му перцентилю.
2. Балл 96 соответствует 96-му перцентилю.
Задача
Представьте себе, что вы работаете с опубликованным тестом со средним баллом
100 и дисперсией 400. Преобразуйте следующие баллы, полученные отдельными
людьми, в Z-значения, Т-значения и станайны.
1. 70.
2. 105.
Решение
1. Для 70: Z=-l,5, T= 35, астанайн = 2.
2. Для 105: Z= 0,25, Т= 52,5, астанайн = 5.
Необходимые вычисления для значения 70 приведены на рис. 16.25 и ниже.
20
Рис. 16.25. Вычисление Z-значения
Г = -1,5(10) + 50 = 35.
Опанайн = 2(-1,5) + 5 = 2,0.
Необходимые вычисления для значения 105 приведены на рис. 16.26 и ниже.
„ 105-100 п^
Z 0.25
20
Рис. 16.26. Вычисление Z-значения
Г = 0,25(10) + 50 = 52,5.
Станайн = 0,25(2) + 5 = 5,5; округляется вниз до 5.
ГЛАВА 17.
Управление данными
Вы могли бы задаться вопросом, что делает глава об управлении данными в книге
по статистике. Вот объяснение: использование статистики обычно подразумевает
анализ данных, а надежность статистических результатов во многом зависит от
надежности проанализированных данных, так что если вы будете использовать
статистику, вам нужно знать что-то об управлении данными вне зависимости от
того, будете ли вы заниматься этим сами или поручите кому-то другому.
Довольно странно, что об управлении данными редко говорят па занятиях по
статистике, так же как и во многих офисах и лабораториях; некоторые профессора
и руководители проектов, похоже, верят, что данные волшебным образом
преобразуются в подходящий вид без вмешательства человека. Однако люди, которые
ежедневно работают с данными, имеют совсем другое мнение на этот счет. Многие
описывают соотношение между управлением данными и их анализом при помощи
правила 80/20, которое означает, что в среднем 80% времени, затраченного на
работу с данными, уходит на их подготовку к анализу, и лишь 20% времени посвящено
самому анализу данных. С моей точки зрения, управление данными
обеспечивается как общим знанием проблемы, так и умением выполнить ряд специфических
задач. Оба этих аспекта можно преподать и выучить, и, хотя некоторые люди
действительно способны получить эти знания неформальным способом (методом проб
и ошибок, так сказать), это не может быть хорошим обоснованием для того, чтобы
пустить все на самотек. Напротив, более разумно - отнестись к управлению
данными как к умению, которое, как и все прочие умения, можно приобрести, и нет
никаких оснований пренебрегать коллективной мудростью, накопленной до вас.
Качество анализа частично зависит от качества данных, факт, блестяще
сформулированный программистами: «мусор на входе - мусор на выходе» (garbage in,
garbage out, GIGO). Эта же концепция применима и к статистике; самый лучший
статистик не может получить надежные результаты из данных, которые
представляют собой кашу. Процесс сбора данных хаотичен по своей природе, и данные
редко попадают к вам в идеальном виде готовыми к анализу. Это значит, что когда-то
между сбором и анализом данных кто-то должен проделать грязную работу с
самим файлом данных - проверку, реорганизацию и прочие действия по подготовке
данных к анализу. Как правило, этот процесс не покрыт завесой тайны, однако он
требует систематичного подхода, руководимого знанием свойств данных и спо-
EQU^HhI Глава 17. Управление данными
собов их дальнейшего использования, наряду с заинтересованным отношением,
сопряженным со здравым смыслом.
У аббревиатуры GIGO есть и другая расшифровка: «мусор на входе -
убеждения на выходе». Эта фраза отражает огорчительную склонность некоторых людей
верить в то, что все, что выдает компьютер, верно, что можно расширить до столь
же огорчительного убеждения о том, что любые результаты, полученные при
помощи статистических методов, должны быть истинными. К сожалению, в обоих
случаях мы не можем избавиться от необходимости рассуждать; и компьютеры, и
статистические методы могут давать бессмысленные результаты, если они
основаны на неправильных данных. Простейшим примером является следующее: тот
факт, что вы можете вычислить среднее и дисперсию для любого набора чисел
(даже если они представляют собой номинальные или порядковые данные,
например), не значит, что эти числа имеют смысл, не говоря уже о том, представляют ли
они надежную общую характеристику данных. Использовать корректные данные
и выбрать правильный метод их обработки - это задача аналитика, поскольку
статистическая программа просто выполняет заданные вами операции и не может
оценить ни качество данных, ни адекватность применяемой процедуры.
Если ваш интерес ограничен изучением статистических процедур, вы можете
захотеть пропустить эту главу. Аналогичным образом, если у вас нет
практического опыта работы с данными, эта глава может показаться полностью абстрактной,
и вам может захотеться лишь бегло ознакомиться с пей или отложить ее
прочтение до того момента, когда вам придется реально иметь дело с данными. С другой
стороны, при любых обстоятельствах вам может все равно показаться полезным
понимать па базовом уровне, что происходит при управлении данными, и знать,
что может произойти, если это не сделано правильно. Кроме того, всегда хорошо
знать больше, чем это требуется при данных обстоятельствах, особенно
учитывая, что смена специальности свойственна для современной жизни. Вы никогда не
сможете предугадать, когда представление об управлении данными даст вам
преимущество мри поступлении на должность, а чтение этой главы должно помочь
вам уверенно говорить на эту тему, возвышая вас над конкурентами. Кроме того,
если управление данных войдет в круг ваших будущих обязанностей, сведения из
этой главы помогут вам на базовом уровне понять, почему управление данными
важно и как оно осуществляется.
Общий подход, а не набор методов
Поскольку для сбора, хранения и анализа данных используется множество
методов и компьютерных программ, в одной главе невозможно дать инструкции по
управлению данными, которые работали бы в любых обстоятельствах. Поэтому
в данной главе мы сосредоточимся на общих подходах к управлению данными,
включая рассмотрение общих для многих ситуаций вопросов наряду с общим
описанием процесса приведения исходных данных к пригодному для анализа виду.
Если бы мне нужно было дать один-единственный совет по управлению
данными, он бы прозвучал так: ни на что не надейтесь. Не надейтесь, что файл с дай-
Кодификатор
ШШШ1
ными, который был вам предоставлен, - это именно тот файл, который вы
должны анализировать. Не надейтесь, что все переменные были перенесены из одной
программы в другую без потерь. (На одну только эту тему могут быть написаны
целые тома, и каждая версия программы, похоже, несет новый набор проблем.)
Не надейтесь, что качество ввода данных контролировалось или что кто-нибудь
еще проверял данные на наличие логически невозможных значений. Не надейтесь
на то, что человек, который поручил вам этот проект, знает, что значения важной
переменной отсутствуют в 50% случаев или что другая переменная не была
закодирована так, как было указано в инструкции. Сбор данных и их ввод в
компьютер производится людьми, которые то и дело совершают ошибки. Большая часть
процесса управления данными заключается в обнаружении этих ошибок и или
их исправлении, или изобретении способа обойти их, чтобы данные можно было
нормально обработать.
Иерархия
Не увлекаясь слишком сильно армейскими аналогиями, можно отметить, что для
эффективного управления данными в ходе крупного проекта необходимо
определить структуру, или иерархию, людей, которые отвечают за разные части
процесса. Столь же важно, чтобы каждый участник проекта знал, кто уполномочен
принимать определенные решения, так что, когда проблема появляется, ее можно
разрешить быстро и разумно. Это может звучать как размышления, основанные
на здравом смысле, однако на самом деле данные условия не всегда выполняются
на практике. Если вводящий данные в компьютер сотрудник обнаружил, что в
поступающих к нему данных многие переменные имеют пропущенные значения, он
должен точно знать, кому доложить об этой проблеме, чтобы исправить ситуацию,
пока проект еще находится на стадии сбора данных. Если аналитик во время
предварительного исследования файла данных обнаружил неправдоподобные
значения, он должен знать, кто уполномочен принять решение о том, что следует делать
с такими данными, так что они могут быть исправлены или перекодированы до
начала основного анализа. Если такие вопросы сложно решать, сотрудники,
скорее всего, будут самостоятельно принимать решения или отказываться что-либо
делать, оставляя вас с данными неясного качества.
Кодификатор
Кодификатор (codebook - лабораторный журнал) - это классический инструмент,
который применяется в любом проекте, сопряженном со сбором и анализом
данных. Кодификатор - это просто способ сбора и организации важной информации
о проекте. Иногда кодификатор - это физический объект, такой как блокнот на
спирали или скоросшиватель с тремя кольцами, а иногда это электронный файл
(или набор файлов), который хранится на компьютере. В некоторых проектах
используется комбинация этих способов, когда большая часть информации хра-
ЕЕЕ1
Глава 17. Управление данными
иится в электронном виде, однако что-то или все распечатывается и хранится в
скоросшивателе. В сущности, не важно, какой метод вы выберете, главное, чтобы
основная информация о проекте и наборе данных была надежно записана и
сохранена для дальнейшего использования.
Кодификатор должен содержать информацию как минимум по следующим
темам:
• информация о проекте и методы сбора данных;
• методы ввода данных в компьютер;
• решения, принятые относительно данных;
• процедуры кодировки.
Информация о проекте включает его цели, график, финансирование и
сведения о команде (исходный состав и все изменения, обязанности каждого человека).
К информации о методах сбора данных относятся сведения о времени и способах
их сбора, о том, был ли использован какой-либо контроль, и о том, кто на самом
деле собирал данные. Если была использована какая-либо форма вроде анкеты, ее
копию нужно включить в кодификатор вместе с инструкциями, которыми
руководствовались сборщики данных. Решения, принятые относительно данных, - это
такие вопросы, как определение выбросов (значений, которые находятся слишком
далеко от всех остальных значений) или других необычных данных, подробная
информация о любых объектах, которые были исключены из анализа, и о
причинах этого, а также указание процедур замещения пропущенных данных или других
манипуляций с такими данными. Информация о процедурах кодировки содержит
расшифровку значений переменных, способы и причины их перекодировки, а
также коды и их обозначения.
Информация о вводе данных особенно валена, когда данные собирают в одном
виде, например как распечатанные на бумаге анкеты, а анализируют в другом,
таком как электронный файл. Однако даже если используется компьютерная
система телефонного опроса или другой метод сбора данных в электронном виде,
кодификатор должен содержать информацию о процессе получения отдельных файлов
и их преобразованиях. Часто, но не всегда преобразование электронных файлов
проходит успешно, но при каждом преобразовании файла есть вероятность его
повреждения. При обнаружении повреждения файла может понадобиться
проследить историю его преобразований, чтобы выяснить, что произошло, и
придумать, как исправить это. Сведения об обучении людей, которые вводят данные, и
о любых использованных методах контроля качества (например, повторный ввод
части данных) также должны быть зафиксированы.
По моему опыту, компании, данные которых представляют собой
протоколы ежедневных деловых операций, лучше документируют процесс, чем ученые
и другие люди, работающие над малыми проектами, когда данные собираются
отдельно для каждого проекта. Этому есть несколько причин. Во-первых, если
сбор и сохранение данных продолжаются, относительно легко установить набор
стандартов и следовать им. Во-вторых, в крупных компаниях, которые
постоянно имеют дело с данными, работают люди, занимающиеся только управлением
Кодификатор
НШЕП1
данными, и эти люди проходят специальное обучение, соответствующее их
задачам. В академических учреждениях дело, как правило, обстоит противоположным
образом; в лаборатории может выполняться много проектов, в каждом из которых
задействованы разные наборы данных, каждый со своими особенностями. Дело
часто осложняется тем, что обязанность сбора и упорядочивания данных может
лежать на студентах с минимальным опытом и квалификацией или на людях с
учеными степенями, которые являются экспертами в своем деле, однако
незнакомы с базовыми аспектами управления данными (и, возможно, не интересуются
ими).
Главная причина, по которой вам нужен кодификатор или его аналог, - это
необходимость хранения информации о каждом проекте и его данных, так чтобы
те, кто присоединялся к проекту или анализировал данные по истечении
значительного времени после окончания их сбора, знали, что это за данные и как их
интерпретировать. Существование надежного кодификатора также полезно для тех,
кто участвовал в проекте с самого начала, поскольку ничья память не абсолютна,
и легко забыть о том, какое решение было примято шесть месяцев или два года
назад. Легкодоступная информация из кодификатора также значительно
сэкономит время, когда наступит черед описания результатов или когда вам потребуется
объяснить суть проекта новому аналитику.
Данные редко анализируются точно в том виде, в котором они были собраны.
Перед началом анализа кому-то нужно изучить файл данных и решить, что делать
с такими проблемами, как наличие неправдоподобных и пропущенных значений.
Все эти решения должны быть записаны наряду с местом нахождения каждой
версии файла. Заархивированную версию исходного файла следует сохранить
где-нибудь, так чтобы ее нельзя было изменить и чтобы можно было позже
перекодировать данные по-другому или заменить поврежденную более позднюю
версию файла. Также неплохо сохранять все версии файла после каждого серьезного
редактирования для того случая, если вы решите, что действия на этапах 1, 2, 3 и
5 были верными, а на этапе 4 - нет. Возможность вернуться к версии 3 убережет
вас от необходимости возвращаться к исходной черновой версии. Также нужно
записать число переменных и объектов в каждой версии файла и структуру файла.
При каждом преобразовании файла нужно убедиться, что в новой версии осталось
верное число переменных и объектов, а знание структуры файла пригодится, если
нужно будет использовать не названия, а порядок переменных (например, если
последняя переменная не уцелела в ходе преобразований файла). Если
используется какой-либо метод работы с пропущенными данными, нужно указать его
подробные характеристики и характер преобразования файла.
Записи об использованных в проекте процедурах кодировки, возможно,
займут больше всего места в кодификаторе. В данном случае нужно зафиксировать
информацию об исходных названиях переменных, подписях, добавленных к
переменным и их значениям, обозначениях, пропущенных при применении этих
данных. Здесь также нужно привести список новых переменных и описание способа
их получения (например, преобразование существующих переменных или
перекодировка непрерывной переменной в категориальную).
Глава 17. Управление данными
Прямоугольный файл данных
Существует много способов хранить данные в электронном виде, но наиболее
распространенный формат - это прямоугольный файл данных. Этот формат должен
быть знаком каждому, кто использовал электронные таблицы типа Microsoft Excel.
Хотя статистические пакеты, такие как SAS или SPSS, могут читать данные,
хранящиеся в разных форматах, прямоугольные файлы данных используются часто,
поскольку это облегчает обмен данными между разными программами.
Самая важная характеристика прямоугольного файла данных - это то, как он
организован. В предназначенных для статистического анализа данных принято,
чтобы строки соответствовали объектам, а столбцы - признакам. Определение
объекта частично зависит от типа планируемого анализа и затрагивает
концепцию, которая известна как единица анализа (обсуждается подробнее в
одноименной врезке на стр. 444). Поскольку иногда данные об одном объекте записываются
на нескольких строках или данные о нескольких объектах могут содержаться в
одной строке, некоторые предпочитают говорить, что одна строка соответствует
одной записи, а не одному объекту.
На рис. 17.1 показана небольшая часть данных национального исследования
общественного мнения (General Social Survey) 1993 года, проводимого
Национальным центром изучения общественного мнения (National Opinion Research Center)
при университете г. Чикаго практически ежегодно, начиная с 1972 года. В каждой
строчке содержатся данные об одном человеке, обозначенном при помощи
переменной id (первый столбец). В каждом столбце даны значения
соответствующей характеристики. Например, второй столбец содержит значения переменной
wrkstat, в которой закодирован ответ человека на вопрос о форме занятости, а в
третьем столбце указаны значения переменной maiital, соответствующие ответу
респондента на вопрос о его семейном статусе.
1 lid
2
h
5
6
7
8
9
10:
11
12!
13:
14
15
16
17
18:
19!
20:
21
22
23
24
И < >
Uks
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
>i\GSS93/
25
0
0
25
22
24
22
0
0
0
31
24
0
0
о
22
32
24
98
9
43
45
78
83
55!
75!
31!
54
29
23:
61!
63!
33!
36!
39!
55
55:
2
5:
0:
2
2
2
3
2
34
36
44
80
zodiac
5
8
2
99
10
3:
10:
11!
7!
з:
4
ю:
99
3
3!
11!
3:
1:
9!
4
educ
2
6
11
99
7[
12
7
9:
4
12
2
8
99
1
12
8
12:
10
7!
2
degree:
11
16
16
15
17
11
12
12
18
18
18
15
12
4
10'
14
8
15
16
16
Рис. 17.1. Прямоугольный файл данных в программе Excel
Прямоугольный файл данных
Ш11ЕШ
На рис. 17.2 приведен тот же фрагмент файла данных в SPSS. Основное
различие заключается в том, что файле Excel названия переменных (id, wrkstat)
записаны в первой строке, тогда как в файле SPSS названия переменных связаны с
данными, но не образуют отдельную строку. Это различие в формате приводит к
тому, что при преобразовании данных из Excel в SPSS вам будет казаться, что одна
строка пропала, но на самом деле это связано с тем, что строка с названиями
переменных используется в Excel, но не в SPSS. Перенос данных из одного формата в
другой часто сопряжен с такими странностями, так что полезно знать что-то о том,
как каждая система или программа поступит с разными типами данных.
1
2
3
4
5
6
7
8
э
10
11
12
13
14
15
16
17
18
19
20
21
22
id
I
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1Б
17
18
19
20
21
22
wrkstat | marital | aqewed [
1
1
1
2
5
5
1
5
1
2
l
1
1
5
4
1
7
1
1
1
3
2
31 20 j
5 o:
3 25:
5
5
l
1
1
3
5
5
5
1
4
5
5
5
I
1
1
1
1
0;
0
25
22
24;
22^
o!
0
0
31
24
0:
0
0
22
»
24
24
23!
sibs (
3:
2
4
1
2
2
з;
i
i
1
0
0
3
4
0
96
9
'
2
5
0
childs j
1 j
6!
0
o;
0
2
21
2
2]
0:
0
0
1:
4
3;
1
4
0
1
2
2
3:
age |
43 j
44:
43
45
78
83:
55
75:
311
54
29!
23:
61
63
33;
36
39:
55
55;
34
36
44
birthtno j zodiac |
В 6
2 11
99 99;
10; 7
3: 12
10 7
11 9
7 4
3| 12
2
10 8
99; 99
3; 1
3; 12
11 8
3 12
1 10
9 7
4: 2
6 3
Bl 5
educ
11
16
16
15
17
12
18
18
18
15
12
4
10
14
8
15
16
16
14
18
degree
Рис. 17.2. Прямоугольный файл данных в программе SPSS
Хотя данные в электронных таблицах могут быть организованы по-другому,
например признакам могут соответствовать строки, а объектам - столбцы, эти
подходы обычно не используются, если данные предназначены для импорта в
статистическую программу. Кроме того, хотя электронные таблицы позволяют хранить
другие типы информации, помимо данных и названий переменных (такие как
заголовки и формулы), эту информацию нужно удалить перед импортом данных в
статистическую программу.
При определении структуры хранения данных в электронном виде вы должны
руководствоваться основным критерием - облегчением их планируемой обработки.
В частности, помните, что какую бы программу вы бы не собирались использовать
для анализа данных (Minitab, SPSS, SAS или R), у нее есть свои специфические
требования к формату данных, и от вас требуется предоставить данные в таком
формате, который используется выбранной программой. К счастью, многие программы
для статистического анализа данных имеют встроенные процедуры, которые
позволяют преобразовать данные из одного формата в другой, однако это не избавляет
ответственного за управление данными и/или их анализ от необходимости
определить, какой формат данных требуется для конкретной процедуры, и преобразовать
данные в этот формат перед началом анализа.
Ш1ШШ
Глава 17. Управление данными
Единица анализа
Единица анализа в исследовательском проекте - это основная единица, которая
представляет интерес при данном виде анализа данных. Например, при исследовании
школьной успеваемости единицей анализа может быть ученик, класс, школа, район или
город. В медицинских исследованиях единицей анализа может быть визит к врачу,
пациент, врач, отделение больницы или вся больница. Мы говорим о единице анализа,
поскольку одни и те же данные можно обработать с использованием разных единиц
анализа. Например, при одной обработке данных нас может интересовать успеваемость
отдельных учеников, при другой - уровень образования, достигнутый разными школами, а
при третьей - различия в уровне обученности школьников в ряде городов.
Данные, специфичные для одной единицы анализа, часто называют принадлежащими
к определенному уровню. В примере с данными о школах характеристики отдельных
учеников (возраст, пол и т. д.) будут называться данными индивидуального уровня, а
характеристики школ (такие как тип финансирования) называются данными школьного уровня.
Хотя в некоторых областях науки по-прежнему допускается смешивать данные разных
уровней при статистическом анализе, это может привести к сбивающим с толку
результатам. Напротив, все чаще ожидают, что при объединении данных разных уровней в одном
статистическом анализе будут использоваться специализированные приемы, такие как
многоуровневое моделирование.
Электронные таблицы
и реляционные базы данных
Даже если данные, собранные в ходе проекта, будут в конечном итоге
проанализированы при помощи специализированной статистической программы, обычно их
собирают и/или вводят в компьютер в другой программе, такой как Excel,
Microsoft Access или FileMaker. Вводить данные может быть проще в этих программах,
чем в любом статистическом пакете, и у многих людей они уже стоят па
компьютере (в особенности Excel), снижая число лицензий на специализированные
статистические программы, которые нужно покупать. Excel - это электронная таблица,
a Access и FileMaker - это реляционные базы данных (базы данных с поддержкой
соединения отдельных записей). Все три программы могут открывать
электронные файлы, созданные в других программах, и сохранять файлы в разных
форматах, что делает их полезными при переносе данных из одной программы в другую.
Кроме того, все три можно использовать для просмотра данных и вычисления
и росте й ш и х статиста к.
Электронные таблицы полностью подходят для ввода простых наборов данных
в малых проектах. Преимущество электронных таблиц - это их простота; вы
можете создать новый файл данных, просто открыв новую электронную таблицу и
вводя данные в окно, и весь набор данных будет содержаться в одном документе.
Новичкам несложно пользоваться электронными таблицами, их формат
побуждает вводить данные в виде прямоугольной таблицы, облегчая обмен данными
между разными программами.
Реляционные базы данных могут быть более предпочтительными для более
крупных пли сложных проектов. Реляционная база данных состоит из ряда от-
Проверка нового файла данных
wiiggg
дельных таблиц, каждая из которых выглядит похоже па отдельную страницу
электронной таблицы. В хорошо разработанной базе данных каждая таблица
содержит определенный тип данных, а таблицы связаны при помощи ключевых
переменных. Это значит, что внутри базы данные для одного объекта (например, для
одного человека) могут содержаться во многих отдельных специализированных
таблицах. База данных для учеников может содержать одну таблицу для их
домашних адресов, другую - для дат их рождения, еще одну - для дат поступления и
так далее. Если данные нужно перенести в другую программу для анализа, запись
прямоугольного файла данных, содержащего всю нужную информацию в одной
таблице, можно осуществить в программе для работы с реляционными базами
данных. Главное преимущество реляционной базы данных - это эффективность;
данные никогда не бывает нужно вводить более одного раза, а для одних и тех же
данных могут быть сделаны разные записи. Для примера со школой это означает,
что по одному адресу могут проживать несколько братьев и сестер, однако в
электронной таблице информацию об адресе нужно вводить отдельно для каждого
ребенка, увеличивая вероятность опечаток или неправильного написания.
Проверка нового файла данных
Предположим, что вам только что прислали новый файл данных для анализа. Вы
прочитали сопроводительную информацию о проекте и знаете, какой тип анализа
необходимо провести, однако, прежде чем начать, вам нужно убедиться, что файл
находится в порядке. В большинстве случаев перед началом анализа вам
понадобится ответить на приведенные ниже вопросы (как минимум). Чтобы ответить
на них, вы должны открыть файл данных и, в некоторых случаях, провести
некоторые простые процедуры, такие как создание частотных таблиц (обсуждаются в
главе 4). В некоторых статистических программах есть специальные процедуры,
которые помогают проверить новый файл данных, однако основные
необходимые процедуры можно провести в любом статистическом пакете. Тем не менее вы
можете также захотеть справиться в одном из специализированных руководств о
конкретных методах проверки данных и устранения в них ошибок, реализованных
в определенных статистических пакетах; некоторые из таких книг упомянуты в
приложении С.
Вот некоторые из основных вопросов, на которые нужно ответить при начале
работы с новым файлом:
1. Сколько в нем наблюдений?
2. Сколько в нем переменных?
3. Есть ли повторяющиеся наблюдения (допущенные непреднамеренно)?
4. Верно ли преобразованы значения переменных, названия и подписи?
5. В разумных ли пределах варьируют данные?
6. Сколько данных отсутствует и есть ли в этом какая-либо закономерность?
Вы должны знать, сколько наблюдений должно быть в полученном вами файле
данных. Если это не согласуется с реальным числом наблюдений в файле, воз-
шмп
Глава 17. Управление данными
можно, вам прислали не тот файл (что не так редко случается) или файл был
поврежден в ходе преобразований (тоже не редкость). Если число наблюдений в
вашем файле не соответствует вашим ожиданиям, вам нужно вновь обратиться к
источнику данных и получить правильный неповрежденный файл, перед тем как
продолжать его анализ.
Если число наблюдений верно, нужно также убедиться в правильности числа
переменных в файле. Причиной неправильного числа переменных может быть не
только не тот файл данных, но и те же самые повреждения файла при переносе
из одной программы в другую. В особенности нужно иметь в виду то, что
некоторые программы накладывают ограничения на число переменных, если это так, вам
нужно найти другой способ преобразования полного файла. Если это невозможно,
отберите часть переменных, которые вы будете использовать при анализе (при
условии, что вы не собираетесь анализировать все переменные исходного файла), и
просто преобразуйте этот меньший файл. Третий вариант - преобразовать файл
по частям, а потом объединить их.
Если у вас есть файл с правильным числом строк и столбцов, вы хотите узнать,
пет ли в нем непредумышленно повторенных записей. Для этого нужно связаться
с кем-нибудь, кто был вовлечен в сбор данных по проекту, чтобы узнать, что
представляют собой повторяющиеся наблюдения и есть ли в файле данных ключевая
переменная, содержащая уникальные идентификаторы (если вам незнаком этот
термин, см. размещенную ни лее врезку «Уникальные идентификаторы»). Определение
повторяющегося наблюдения зависит от единицы анализа. Например, если
единица анализа - это визит в больницу, нормально, если одни человек имеет несколько
записей в файле (поскольку он мог посетить больницу несколько раз). С другой
стороны, в случае файла, где указаны смертные случаи, вы будете ожидать, что одному
человеку соответствовует одна запись. Для обнаружения повторяющихся записей
существуют разные методы в зависимости от используемого программного
обеспечения и специфики набора данных. Иногда для этого нужно просто убедиться в том,
что ни один уникальный идентификатор (например, идентификационный номер)
не встречается чаще одного раза, тогда как в других случаях вам может
понадобиться искать повторяющиеся записи, которые имеют одинаковые значения нескольких
пли всех переменных.
Уникальные идентификаторы
Идея уникальных идентификаторов чрезвычайно важна для управления данными и
знакома тем, кто работает с базами данных, но может быть новой для тех, кто никогда не
создавал базы данных или не был иным образом задействован в управлении данными.
Идентификатор - это код, обычно числовой, который обозначает наблюдения в наборе
данных. Уникальный идентификатор - это код, который имеет уникальные значения для
каждого наблюдения. Простейший способ присвоить уникальные идентификаторы
каждому случаю - это использовать идентификационные номера (такие как
регистрационный номер пациента в системе здравоохранения). Даже если уникальные обозначения
уже имелись, простые последовательные идентификационные номера обычно
предпочтительнее, поскольку это позволяет бороться с нарушением конфиденциальности.
Проверка нового файла данных
Ш1ЕЕЯ
В большинстве наборов данных нужен как минимум один уникальный идентификатор
для каждой потенциальной единицы анализа. Например, если данные о медицинской
клинике можно анализировать или на уровне пациентов, или на уровне отдельных
визитов, то нужно, чтобы один идентификатор был уникальным для каждого пациента, но
общим для всех записей о данном пациенте, а другой идентификатор должен обозначать
все записи, относящиеся к одному визиту (диаграммы, анализы крови и т. д.).
Уникальный идентификатор полезен для того, чтобы подтвердить отсутствие повторяющихся
записей, выявить общие записи для одной единицы исследования (например, все
посещения больницы одним человеком) и предотвратить перемешивание записей для разных
людей. В большом файле могут фигурировать, например, несколько Петров Ивановых1,
и вы бы не хотели, чтобы записи о них смешались. Аналогичным образом данный Петр
Иванов мог приходить в больницу пять раз за год; просматривая его историю болезни,
вы хотите легко выявить все относящиеся к нему записи.
Проверка того, что все значения, названия переменных и подписи верны, - это
следующий этап обследования файла. Сохранение правильных значений наиболее
важно, поскольку названия и подписи можно создать заново, однако сами данные
должны быть правильными, а в процессе преобразования файла может случиться
много неожиданностей. К вещам, за которыми нужно следить, относятся
правильный тип переменных (иногда числовые переменные неожиданно преобразуются
в текстовые, или наоборот; см. следующий раздел о числовых и текстовых
переменных), длина значений текстовых переменных (которые часто обрезаются или
заполняются незначащими символами во время преобразований) и правильность
значений, особенно дат. Во многих статистических пакетах можно вывести на экран
информацию о тине, длине и подписях каждой переменной, и эту возможность
нужно использовать, чтобы убедиться в том, что все преобразовано, как ожидалось.
Названия переменных во время преобразования файла могут неожиданно
меняться, поскольку у разных программ есть разные требования к допустимым
названиям переменных. Например, в Excel название переменной может начинаться
с числа, а в SAS и SPSS2 - нет. В некоторых программах длина названий столбцов
может достигать 64 знаков, а некоторые - обрезают названия до 8 знаков, это
ограничение может привести к повторяющимся названиям переменных или замене
на формальные названия, такие как varP. Хотя данные обычно можно
анализировать вне зависимости от того, как названы отдельные переменные, странные п
бессмысленные названия доставляют дополнительные неудобства пользователю
и могут снизить эффективность анализа. Если данные предполагается открывать
в нескольких программах, нужно спланировать это заранее. В частности, нужно
предусмотреть ограничения, накладываемые на названия переменных каждой из
программ, которые предполагается использовать, и создать совместимые со всеми
этими программами названия переменных.
Подписи переменных и их значений очень удобны при работе с файлом данных,
однако они часто вызывают проблемы при переносе файлов из одной программы
1 В оригинале Bill Smith. - Прим. пер.
2 И в R. - Прим. пер.
* От англ. variable - переменная. - Прим. пер.
ШШШШ1
Глава 17. Управление данными
пли платформы в другую. Подписи переменных - это сопряженные с переменной
текстовые предложения, которые являются одним из способов обойти
ограничения длины названий. Например, переменной wrkstat из примера с национальным
опросом общественного мнения можно присвоить подпись «Форма занятости в
предыдущие шесть месяцев», которая гораздо лучше отражает содержание этой
переменной. Подписи значений сходны с подписями переменных, однако они
относятся к значениям каждой переменной. Продолжая рассматривать наш пример,
мы можем присвоить подпись «Полная занятость» значению 1 переменной wrkstat,
«Частичная занятость» значению 2 и так далее. Как бы не были удобны подписи
переменных и значений, они часто неправильно переносятся из одной программы
в другую, поскольку в каждой программе такая информация хранится по-разному.
Одно из решений может быть следующим: если вы знаете, что данные будут
анализироваться в нескольких программах и/или платформах, используйте простые
названия переменных, такие как v\ и v2, и простые числовые коды для значений
(О, 1,2 и т. д.), а затем напишите команды (короткую компьютерную программу),
которые можно запустить в каждой программе или платформе, присваивающие
подписи переменным и их значениям.
Следующий этап - проанализировать сами значения набора данных и понять,
правдоподобны ли они. Некоторые простые статистические процедуры (такие как
вычисление среднего и дисперсии числовых переменных) помогают убедиться,
что значения не изменились при преобразованиях (при условии, что вы знаете
значения среднего и дисперсии данных до их преобразования). Даты нужно
проверять особенно аккуратно, поскольку они являются особенно частым источником
проблем из-за того, что в разных программах даты представлены в разных
форматах. Обычно даты хранятся в виде числа единиц измерения времени (дней или
секунд), прошедшего после определенной точки отсчета. К сожалению, кажется,
каждая программа использует свою точку отсчета, и некоторые программы также
измеряют время в разных единицах, вследствие чего даты часто переводятся из
одной программы в другую неверно. Если вы не можете правильно преобразовать
даты, сохраните их как текстовую переменную, которую потом можно
использовать для повторного создания дат в новой программе.
Даже если вы убедились, что данные преобразованы верно, с ними все равно
могут возникнуть проблемы. Одна вещь, которую нужно проверять, - это
наличие неправдоподобных или лежащих вне диапазона значений. Это можно легко
сделать, посмотрев на частоты значений (или на минимум и максимум, если у
переменной много значений), чтобы убедиться, что они осмысленны и согласуются с
тем, как была закодирована переменная. (Частотные таблицы обсуждаются в
главе 4.) Если файл данных маленький, также возможно просто отсортировать
значения каждой переменной и посмотреть па наименьшие и наибольшие значения.
Третий вариант, если вы используете Excel, - использовать фильтр данных, чтобы
выявить все возможные значения определенной переменной. Обычные проблемы,
которые приходится выявлять, - это лежащие вне диапазона значения (человек
в возрасте 150 лет), недопустимые значения (3 для переменной, которая может
принимать только значения 0 и 1) и несовместимые значения (новорожденный
Текстовые и числовые данные
ИМ ВЕД
младенец, который записан как выпускник). Если вы обнаружили необычные
значения или очевидные ошибки после того, как убедились, что файл преобразован
правильно, кому-то нужно решить, как поступить в этом случае, поскольку как
только вы начнете статистический анализ, программа будет использовать все
предоставленные данные как верные.
Последний шаг перед началом анализа - это оценить количество пропущенных
данных и их закономерности. Ваша первая задача - это выявить
распространенность пропущенных данных, это можно сделать при помощи анализа частот
значений. Вторая задача - изучение закономерностей пропуска данных во многих
переменных. Например, есть ли такие переменные, значения которых
отсутствуют чаще всего? Есть ли строки, в которых много пропущенных данных, тогда как
остальные полностью или в основном заполнены? Есть ли в файле информация о
причинах пропуска данных (например, отказался ли человек отвечать па вопрос
или его просто не спрашивали), и если да, то как закодирована эта информация?
Наконец, нужно решить, как поступить с пропущенными данными - тема, которая
обсуждается позже в этой главе.
Текстовые и числовые данные
В большинстве программ хранения данных и их статистической обработки есть
существенное различие между текстовыми и числовыми переменными, хотя они
могут называться по-разному. Значения текстовых переменных, которые
называются также строковыми или буквенно-числовыми, могут включать буквы, числа,
пробелы и символы, такие как #. (Допустимые специальные символы различаются
в разных программах.) Текстовые переменные хранятся в виде
последовательности закодированных значений; наиболее часто используются такие системы
кодировки, как EBCDIC (extended binary coded decimal interchange code, расширенный
двоично-десятичный код обмена информацией) и ASCII (american standard code
for information interchange, американский стандартный код обмена
информацией). Поскольку текстовые переменные хранятся в виде последовательностей
кодов, каждый с определенной позицией внутри переменной, положение символов
можно определять при помощи специальных процедур. Например, многие языки
программирования позволяют выделить первые три символа текстовой
переменной и сохранить их в виде повой текстовой переменной.
Числовые переменные хранятся скорее в виде значений, а не символов,
используемых для записи этих значений. Их, в отличие от текстовых переменных, можно
использовать в математических и статистических операциях, таких как сложение
и вычитание. В некоторых системах для числовых переменных также
допустимы определенные символы, такие как десятичный разделитель в виде точки или
запятой и знак доллара. Есть одна вещь, о которой нужно помнить, - значения
текстовых переменных, закодированные при помощи ведущих нулей (0003), при
преобразовании в числовые переменные потеряют эти нули (3).
Способ хранения значений числовых переменных и их точность различаются в
зависимости от платформы и программы. Вы должны помнить, что при преобра-
Пропущенные данные
ШИШ!
работать проще всего, поскольку полные наблюдения можно рассматривать как
случайную выборку из всего набора данных. К сожалению, полностью случайные
пропуски редко встречаются на практике. Случайные пропуски не зависят от
значений отсутствующих данных, но связаны со значениями других задействованных
в анализе переменных. Неспособность ответить на вопрос о семейном доходе
может быть связана с уровнем образования. Неслучайные пропуски - это, к
сожалению, наиболее частый случай, который с наибольшей вероятностью внесет
систематическую ошибку в статистический анализ. Пропуски этих данных связаны с их
собственными значениями. Например, слишком полные люди могут отказаться
отвечать на вопрос об их весе, а люди с непрестижной работой с меньшей
вероятностью расскажут о своей должности.
Это обсуждение может показаться несколько теоретическим; как вы можете
узнать, к какому типу нужно отнести пропущенные данные, если вы, по
определению, не знаете, какие значения были пропущены. Ответ состоит в том, что вы
должны принять решение, основываясь на знании генеральной совокупности и
своем опыте в данной области исследований. Поскольку большая часть методов
статистического анализа подразумевает, что у вас есть полные лишенные
систематических ошибок данные, если значительная часть данных пропущена, вам
(или тому, кто уполномочен принимать такие решения) нужно придумать, как
поступить с ними. Применение некоторых из предлагаемых ниже способов может
потребовать советов консультанта по статистике или использования программ,
специально разработанных для работы с пропущенными данными, так что
бюджет вашей организации наряду с доступностью таких экспертов и программ также
сыграет роль при принятии решения. Здесь перечислены некоторые возможные
пути решения проблемы. Наиболее предпочтителен первый, хотя такое решение
не всегда можно исполнить (и даже если попытки предпринимаются, они могут
быть неудачными). Третий вариант находится на втором месте по
предпочтительности в большинстве случаев. Варианты с пятого по седьмой редко бывают
оправданы со статистической точки зрения, однако иногда применяются на практике.
1. Приложить дополнительные усилия для восполнения пропущенных
данных, выяснив причину их отсутствия.
2. Применить другой способ анализа данных, такой как многоуровневая
модель, вместо классической модели повторных измерений.
3. Восстановить пропущенные значения при помощи методов наибольшего
правдоподобия вроде тех, что доступны в модуле MVA программы SPSS,
или использовать методы множественного замещения пропущенных
значений, реализованные в таких программах, как SAS PROC Ml, для
исследования распределения пропущенных значений1. В ходе восстановления
пропущенных данных они замещаются на значения, основанные на
существующих данных, в результате чего мы получаем полный набор данных.
Множество современных методов работы с пропущенными данными реализовано в программе R.
Подробные инструкции по их применению приведены, например, в книге Роберта Кабакова «R в
действии» (издательство «ДМК Пресс», 2014). - Прим. пер.
ЗНАНИИ Глава 17. Управление данными
4. Создать дополнительную переменную (0, 1) для обозначения
пропущенных данных наряду с замещением пропущенных данных.
5. Удалить строки или столбцы с большим количеством пропущенных
данных. (Это допустимо, только если проблема заключается в небольшом
числе строк и/или столбцов, которые не очень важны для вашего анализа, и
это может послужить источником систематической ошибки, если данные
пропущены не полностью случайно.)
6. Использовать замещение при условии, замещая пропущенные значения на
имеющиеся (не рекомендуется, поскольку может привести к занижению
дисперсии).
7. Использовать простое замещение, заменив пропущенные значения,
например, средним значением (не рекомендуется, поскольку почти всегда
приводит к сильной недооценке дисперсии).
\ШШШ
ГЛАВА 18.
Планирование исследования
Часто одна из обязанностей статистика - это планирование исследовании.
Чтобы хорошо справиться с этой задачей, нужно знать основные типы организации
исследований, представлять себе их сильные и слабые стороны и быть в
состоянии применить это знание для разработки планов исследований, которые
позволяют ответить на разные вопросы. Вы также должны знать традиции в той
области науки, на которой вы специализируетесь, а именно какой тип
исследований обычно используется для анализа определенного типа данных или для
ответа на конкретный вопрос. Планирование исследований - это слишком
обширная тема, чтобы ее можно было обсудить в одной главе, так что здесь мы
только затронем основные проблемы планирования исследований и рассмотрим
самые распространенные типы этих планов. Обычно планирование
исследований представляет собой компромисс между тем, что ученый хотел бы получить в
идеале, и тем, чего можно достичь. При выборе и разработке плана исследования
следует руководствоваться наиболее важными задачами, а также традициями в
данной области науки. Нам бы всем хотелось выполнить исследование, которое
бы находилось под полным контролем (это значит, что экспериментатор мог бы
манипулировать всеми важными для исследования факторами пли как-то иначе
контролировать их) и при этом проходило бы в полностью естественных
условиях (то есть все измеряемые явления были бы точно такими, как в реальном
мире). Однако контроль и естественность часто противоречат друг другу, и одни
из признаков компетентного исследователя - это умение решить, насколько
можно пожертвовать одним ради другого. Один из факторов, влияющий на то,
какое решение будет принято, - это цель исследования. Это выявление
факторов, лежащих в основе какого-то явления, как часто бывает в фундаментальной
науке, или оптимизация выхода либо результата определенного процесса с
минимизацией затрат и усилий, что характерно для исследований в бизнесе и
технологии? Практические и этические соображения также часто играют роль -
некоторые планы исследований просто невозможно реализовать, поскольку они
недопустимо дороги или считаются неэтичными, а исследователь должен быть в
курсе этических норм выполнения экспериментов, бытующих в обществе и
науке.
ESlli^m ! Глава 1 8. Планирование исследования
Словарь основных терминов
Планы исследований могут быть разделены на три типа: экспериментальный,
квазиэкспериментальный и наблюдение. В экспериментальных исследованиях
объекты распределяются по группам или категориям случайным образом. Классический
пример эксперимента - это рандомизированное исследование с контролем,
проводимое в медицине, в котором пациенты случайно разделяются на
экспериментальную и контрольную группы, подвергаемые определенному лечению, и
результат регистрируется для обеих групп. Эксперимент с контролем считается самым
«сильным» типом исследования, с точки зрения достоверности выводов на основе
результатов (на самом деле некоторые считают результаты экспериментов с
контролем эталоном доказательства), однако провести такое исследование не всегда
возможно или практично. Исследования следующего уровня качества -
квазиэкспериментальные, в которых есть некоторая группа для контроля или сравнения,
по объекты попадают в опытную и контрольную группы неслучайно. При
наблюдениях исследователь не разделяет объекты на группы, а отмечает связь разных
факторов и результатов в том виде, в котором они существуют в реальном мире.
Хотя эксперименты предпочтительнее, поскольку они снижают систематическую
ошибку (тема, обсуждаемая в главе 1), преимущество квазиэкспериментов и
наблюдений заключается в минимизации влияния экспериментатора на
естественный ход событий. Это особенно важно при исследовании людей, поскольку их
поведение во многом зависит от ситуации, и поведение испытуемого в лаборатории,
когда он знает, что за ним наблюдают, может сильно отличаться от его поведения
в повседневной жизни. Опять же, решения о нужном типе исследования зависят
от приоритетов исследователя и его возможностей с практической и этической
позиций.
Фактор - это независимая переменная в научном исследовании, то есть
считается, что эта переменная как-то влияет на значение зависимой (результирующей)
переменной. Часто план эксперимента подразумевает наличие нескольких
факторов. Если вы изучаете детское ожирение, в свое исследование вы можете включить
ожирение у родителей, бедность, рацион, уровень физической активности, пол и
возраст. Некоторые ученые называют любой план исследования, который
включает более одного фактора, факторным планом] другие относят это название только
к таким планам, в которых реализованы все возможные сочетания значений
факторов, называемым также полными факторными (перекрестными) планами. Вас
может интересовать влияние каждого фактора по отдельности (главный эффект)
и их совместное влияние (эффект взаимодействия). Вы можете считать, что
рацион влияет на развитие детского ожирения (главный эффект), но влияние рациона
зависит от пола ребенка (эффект взаимодействия).
Исследования также можно классифицировать по соотношению между
временем событий и временем сбора информации о них. В перспективных
исследованиях данные собирают, начиная с момента старта исследования. Группа,
объединенная общей временной характеристикой, будь то время включения в исследование
пли год рождения, называется когортой, так что в перспективном исследовании
Словарь основных терминов
Ш1ВЯ
когорт собирают информацию о группах люден (или других объектов) на
протяжении времени. В противоположность этому в ретроспективных исследованиях
собирают информацию о событиях, которые произошли за некоторое время до
начала исследования. Что касается типов данных, то исследователи часто делят
их на первичные и вторичные. Первичные данные собирают и анализируют в
рамках конкретного исследовательского проекта, тогда как вторичные данные
собирают с одной целью, а впоследствии анализируют с другой целью. У каждого типа
данных есть свои достоинства и недостатки, некоторые исследователи работают
только с одним типом данных, а некоторые - с обоими. Основное достоинство
первичных данных - их специфичность; поскольку их собирают в рамках того же
проекта, в котором и анализируют, такие данные отвечают конкретным задачам
данного проекта. Кроме того, те, кто анализирует первичные данные, скорее всего,
хорошо знают, когда и как они были собраны. С другой стороны, поскольку сбор
данных дорог, объем данных, собранных одним ученым или исследовательской
группой, ограничен. Самое главное достоинство вторичных данных - их
количество. Поскольку вторичные данные часто собирают государственные учреждения
или крупные научные организации, такие как Национальный центр исследования
общественного мнения (базирующийся в Чикаго), они часто имеют
национальный или международный масштаб и могут собираться в течение многих лет,
достигая такой широты покрытия, о которой отдельные исследователи могут только
мечтать. К недостаткам вторичных данных относится то, что вам приходится
использовать их в том виде, в каком они представлены, что они могут не
соответствовать в точности целям вашего исследования, и что могут быть ограничения в
характере использования данных. (Например, требования конфиденциальности
могут заключаться в недоступности данных для отдельных людей.)
Последняя деталь - единицы анализа. Единица анализа (обсуждается
подробнее в главе 17) - основной предмет исследования. В социологии единица анализа -
обычно отдельный человек, однако ей также может быть группа людей, входящая
в состав более крупной совокупности, такой как школа, завод или страна.
Исследования, единицей которых является не один организм, а популяция, называются
популяционными. Хотя популяционные исследования могут быть полезными для
определения потенциальных направлений исследований (связь между рационом
с высоким содержанием жиров и сердечными заболеваниями) и они относительно
дешевы, поскольку в основном используют вторичные данные, к выводам,
полученным в ходе этих исследований, нужно относиться с осторожностью, так как для
них свойственно заблуждение генерализации. Заблуждение генерализации
возникает, когда считается, что связи, проявляющиеся на одном уровне (скажем,
национальном), также сохраняются на другом уровне (индивидуальном). На самом деле
сила и/или направление связей, выявленных для одной единицы анализа, может
значительно измениться при изучении другой единицы анализа. В классической
работе В. С. Робинсона (W. S. Robinson), ссылка на которую приведена в
приложении С, содержатся примеры заблуждений генерализации в серии исследований
связи между расовой принадлежностью и грамотностью в США при группировке
данных по географическим регионам разного уровня.
ЕЕМН
Глава 1 8. Планирование исследования
Система обозначений Кука и Кампбелла
Томас Д. Кук (Thomas D. Cook) и Дональд Т. Кампбелл (Donald T. Campbell)
разработали способ обозначений разных планов исследований, который использовали и
видоизменяли многие ученые. Основные элементы такого условного обозначения - это О для
наблюдения1 (сбора данных), Хдля воздействия, Я для рандомизации2, пунктирная
линия для обозначения групп, созданных без рандомизации, и подстрочные индексы для
обозначения последовательности наблюдений и воздействий. Рандомизированный план
исследований со снятием показателей до и после воздействия с экспериментальной и
контрольной группами, согласно Куку и Кампбеллу, будет обозначен так, как показано на
рис. 18.1.
R 01 X О
R 0, 02
Рис. 18.1. Рандомизированный план исследования
со снятием показателей до и после воздействия
Эта схема означает, что объекты были случайно распределены в экспериментальную и
контрольную группы, обе группы были сначала обследованы, потом на
экспериментальную, но не на контрольную группу, оказали воздействие, затем обе группы были вновь
обследованы. Этот план эксперимента обычен для медицинских исследований, где
экспериментальное воздействие - это лекарство или другой тип лечения; контрольная
группа не получает этого лечения, а подвергается стандартному лечению или вообще
лишается его. В последнем случае такая контрольная группа иногда называется группой
плацебо.
Квазиэкспериментальный план со снятием показателей до и после воздействия
обозначается, как показано на рис. 18.2.
I ._°:__х__°г I
| "о" """У |
Рис. 18.2. Квазаэкспериментальный план исследования
со снятием показателей до и после воздействия
Квазиэкспериментальный план отличается тем, что распределение объектов по
группам не случайно. Часто при этом плане исследования используют уже существующие
группы, такие как класс или школа; группа, на которую не оказывали воздействия,
называется группой для сравнения.
Простота и гибкость обозначений Кука и Кампбелла объяснюет их неослабевающую
популярность. Эти ученые также многое сделали для привлечения внимания к
использованию неудачных планов экспериментов в образовательных и социальных
исследованиях и для выявления проблем, возникающих при попытках формулировки выводов на
основе данных, полученных в ходе таких экспериментов. Их список факторов, ставящих
под угрозу достоверность и надежность результатов, замечательно служит ученым как
напоминание о множестве аспектов, которые могут поставить под вопрос выводы даже
хорошо спланированных исследований. Классический учебник Кука и Кампбелла по
планированию исследований обновлен Вильямом Шадишем (William Shadish) и упомянут в
приложении С.
От англ. observation - наблюдение. - Прим. пер.
От англ. randomization - рандомизация. - Прим. пер.
Наблюдения
Наблюдения
Наблюдения обычно проводят, если нет возможности провести эксперимент или
если сбор информации об объектах в естественной среде обитания важнее наличия
контроля, который возможен только в эксперименте. В качестве примера первой
причины рассмотрим исследование влияния курения на здоровье человека. Такое
исследование можно провести только в виде наблюдения, поскольку велеть
некоторым людям курить неэтично, ведь известно, что это вредит здоровью. Вместо
этого мы наблюдаем за людьми, которые решили курить, и сравниваем показатели
состояния их здоровья с некурящими. В качестве иллюстрации второй причины
рассмотрим исследование асоциального поведения учеников начальной
школы. Поскольку такое поведение может быть вызвано определенными аспектами
школьной жизни, исследователи могут решить обследовать учеников в обычных
классах, а не привозить их в лабораторию.
Один хорошо известный тип наблюдений - это план с контролем и
случаями, часто используемый в медицине, чтобы исследовать болезни, которые редко
встречаются или медленно проявляются. В данном случае применять
перспективное исследование когорт непрактично, поскольку вам понадобится наблюдать за
очень большой когортой, чтобы иметь шанс наблюдать необходимое число
испытуемых с таким заболеванием, а исследование должно продолжаться 20 или 30 лет
(или дольше), пока у членов когорты начнет проявляться это заболевание. План
с контрольными случаями позволяет избежать подобных затруднений, поскольку
исследование начинается с группы больных людей {случаи), затем составляется
еще одна группа людей (контроль), которые не имеют данного заболевания, но по
всем остальным параметрам сходны с представителями первой группы. Подобные
исследования обычно нацелены на обнаружение факторов (рацион, контакт с
химическими веществами на производстве, курение, употребление прописанных
лекарств), которые позволяют различить случаи и контроля, в надежде обнаружить
ключевой(ые) фактор(ы), объясняющий(е), почему у случаев есть заболевание, а
у коитролей - нет. Некоторые отнесли бы план с контролем и случаями к
квазиэкспериментам, поскольку он включает контрольную группу, однако термин
«квазиэксперимент» чаще используется для описания перспективных экспериментов,
в которых группы формируют и наблюдают за ними в течение времени.
Мощность плана с контролем и случаями во многом зависит от степени
сходства между случаями и контролями; в идеале, контроли должны быть во всем
идентичны случаям, за исключением отсутствия заболевания. На практике наиболее
часто соответствия достигают всего лишь по нескольким переменным, которые
считаются важными, с точки зрения риска возникновения заболевания, такие
как возраст, пол, наличие сопутствующих заболеваний и стиль курения.
Недавно был разработан метод улучшения соответствий - баллы
предрасположенности, который, используя разные факторы, позволяет оценить вероятность данного
испытуемого быть случаем или контролем. Этот метод впервые предложили
использовать Дональд Рабин (Donald Rubin) и Пол Розенбаум (Paul Rosenbaum), в
приложении С процитирована статья, в которой они описывают данный метод.
ШШ1Ш1
ЕШНН
Глава 1 8. Планирование исследования
Перекрестный план подразумевает однократное наблюдение; наиболее
распространенный пример - это сбор данных при помощи анкеты или интервью.
Собранные при этом данные представляют собой «моментальный снимок»
состояния людей в данный момент. Хотя перекрестные исследования могут быть
чрезвычайно полезными для отслеживания трендов в популяциях и для сбора
разнообразной информации для большого числа людей, они менее полезны для
установления причинно-следственной связи из-за отсутствия временной
последовательности данных. Например, в ходе перекрестного анкетирования можно
выяснить, сколько часов в день человек смотрит телевизор и каковы его рост и
вес. Используя эту информацию, исследователь может вычислить индекс массы
тела (индикатор ожирения) для всех обследованных людей и исследовать связь
между проведенным у телевизора временем и тучностью. Однако исследователь
не может утверждать, что просмотр телепрограмм вызывает ожирение,
поскольку все данные были собраны для одного момента времени. Иначе говоря, даже
если данные покажут, что тучные люди в среднем дольше смотрят телевизор, чем
худые, это не поможет вам узнать, толстеют ли люди от просмотра телепередач
или они сначала становятся толстыми, а потом начинают проводить больше
времени у телевизора, поскольку более активное времяпрепровождение становится
затруднительным.
Исследование когорт в некоторых случаях также можно отнести к
наблюдению. Хороший пример - это знаменитое фрамингамское исследование сердечной
деятельности, при котором в 1948 году начали наблюдать когорту из более чем
5000 мужчин, живших во Фрамингаме (Framingham, Массачусетс, США), чтобы
выявить факторы, связанные с кардиоваскулярными заболеваниями (болезнями
сердца). Мужчины, участвовавшие в исследовании, изначально были в возрасте от
30 до 62 лет и не имели симптомов кардиоваскулярных заболеваний. Каждые два
года они посещали исследователей, чтобы те могли собрать данные об их здоровье
на основе лабораторных анализов, тестов на физическое развитие и истории
заболеваний. Это исследование продолжается по сей день, включив две последующие
когорты, в том числе супругов, детей и внуков первоначальных участников. Это
исследование внесло важный вклад в установление основных факторов,
увеличивающих риск сердечных заболеваний (высокое кровяное давление, курение,
диабет, высокий уровень холестерина и отсутствие физической активности), наряду с
выявлением связи между заболеваниями сердца и такими факторами, как возраст,
триглицериды в крови и психосоциальные аспекты.
Основная критика в адрес наблюдений - это трудность, если не невозможность
разделить влияние разных переменных. Например, некоторые наблюдения
показали, что умеренное потребление вина сопряжено с лучшим состоянием здоровья,
по сравнению с полным отказом от алкоголя, однако невозможно установить,
объясняется ли этот эффект употреблением вина или другими
характеристиками любителей вина. Например, те, кто пьет вино, могут в целом иметь более
здоровый рацион, по сравнению с непьющими, или, возможно, эти люди могут пить
вино, потому что их здоровье крепче. (К примеру, алкоголь противопоказан при
лечении от определенных заболеваний.) Чтобы попытаться исключить подобные
Квазиэкспериментальные исследования
\ ШВШШШШ
альтернативные объяснения, исследователи часто собирают данные о разных
факторах, которые не имеют первоочередной важности для данной темы, и включают
эти дополнительные факторы в статистическую модель. Такие переменные,
которые не являются ни результирующими, ни основными независимыми,
называются контролирующими, поскольку они включены в уравнение для контроля их
действия на результат. Такие переменные, как возраст, пол, социоэкономическпй
статус, расовая/этническая принадлежность, часто включаются в медицинские
и социологические исследования, хотя они не являются ключевыми, поскольку
ученых интересует влияние основных независимых переменных на
результирующую, после того как будет учтено влияние этих контрольных переменных. Однако
подобные поправки, сделанные постфактум, всегда несовершенны, поскольку вы
никогда не можете знать обо всех переменных, которые способны повлиять на
результат, и существуют практические ограничения количества данных, которые вы
способны собрать и включить в любой анализ.
Хотя наблюдения с позиции статистической мощности в целом считаются
более слабыми, у них есть одна важная особенность: результирующие переменные
(такие как человеческое поведение) молено наблюдать в естественных условиях,
увеличивая их экологическую достоверность, или степень, в которой
наблюдаемые параметры не созданы искусственно в узких рамках эксперимента. Более
того, некоторые наблюдения подразумевают участие исследователя в изучаемом
процессе. Если это участие скрыто от испытуемых, в связи с подобной
хитростью могут возникнуть этические соображения, так что нужно позаботиться о
том, чтобы экспериментальные процедуры не принесли непреднамеренного
вреда испытуемым.
Квазиэкспериментальные
исследования
Квазиэкспериментальные исследования сходны с экспериментальными
использованием контрольной группы или группы для сравнения, но отличаются тем, что
участники распределяются по группам не случайно. Квазиэкспериментальные
исследования часто используются в полевых исследованиях (когда данные собирают
в естественных условиях, а не в лаборатории или другой очевидно искусственной
обстановке) и особенно популярны в образовательных и социологических
исследованиях, где экспериментальный план часто будет неосуществимым. Например,
если вы хотите исследовать эффективность нового способа обучения математике,
вы можете обучать один класс по-старому, а другой - по-новому; в конце
учебного года вы сравните достижения учеников в обоих классах. Это не эксперимент,
поскольку ученики не распределялись случайно в экспериментальную группу
(новый метод) и контрольную (старый метод), но в школьных реалиях
настоящий эксперимент был бы невозможен. Вместо этого выбирают сходную группу
учеников для сопоставления с учениками из экспериментальной группы (которых
ЕНЗНИ
Глава 1 8. Планирование исследования
будут обучать по-новому) - компромиссное решение, которое лучше, чем полное
отсутствие группы для сравнения.
Польза от квазиэкспсрименталыюго метода будет яснее, если мы сравним его с
некоторыми более слабыми методами, применение которых часто нерационально.
Терминология и условные обозначения, используемые в этом разделе,
разработаны Томасом Д. Куком и Дональдом Т. Кампбеллом (см. врезку «Система
обозначений Кука и Кампбелла» на стр. 456 и ссылку на работу Шадиша в приложении С)
и широко распространились среди ученых. Три особенно слабых, но до сих пор
широко распространенных плана - это исследование одной группы только после
оказания воздействия, исследование неравноценных групп только после оказания
воздействия и исследование одной группы до и после воздействия. Как отмечают
Кук и Кампбелл, результаты исследований, проведенных по таким схемам, могут
объясняться таким множеством факторов, помимо тех, что интересовали ученых,
что из них сложно сделать какой-либо вывод.
При исследовании одной группы только после оказания воздействия на одну
группу оказывают экспериментальное воздействие, а затем собирают данные об
этой группе, как это показано на рис. 18.3.
X О
Рис. 18.3. План исследования одной группы только после оказания воздействия
Этот план так же прост, как он выглядит; вы оказываете на группу воздействие,
а затем однократно обследуете ее членов. Это может быть полезным, если у вас
есть полученная из других источников информация о состоянии
экспериментальной группы до оказания воздействия. Такой подход можно использовать на
начальных этапах исследования для сбора описательной информации, которую
затем можно использовать для разработки более аккуратного плана основного
исследования. Однако вне контекста подобное исследование значит немногим
больше, чем «мы что-то сделали, а затем что-то измерили». Если честно, что значат
полученные данные? Очень сложно, если не невозможно обосновать заключения
о причинно-следственных связях, сделанные но результатам подобного
исследования, поскольку на все результаты могло влиять множество факторов, помимо
экспериментального воздействия. Без точного знания состояния группы до
экспериментального воздействия сложно сказать что-то о том, как изменились ее
члены, а без контрольной группы невозможно утверждать, что изменения произошли
из-за воздействия. Другие возможные объяснения наблюдаемых изменений - это
случайность, влияние внешних событий, созревание (естественные процессы
роста; эта причина особенно актуальна при исследованиях детей и подростков) и
влияние внимания исследователя.
Исследование неравноценных групп только после оказания воздействия имеет
одно достоинство, по сравнению с описанным выше планом: сравнение с группой,
которая не испытывала экспериментального воздействия, но была обследована
одновременно с экспериментальной группой, как показано на рис. 18.4.
Квазиэкспериментальные исследования
¦МШ1
X
0
0
Рис. 18.4. План исследования неравноценных групп только после оказания
воздействия
Этот план исследования может быть полезен для получения предварительных
описательных данных, если из других источников известно изначальное
состояние обеих групп, а использование группы для сравнения (в идеале настолько
сходной с экспериментальной, насколько это возможно, такой как параллельный
класс в той же школе) дает некоторую информацию, которая помогает поместить
наблюдения в контекст. Данные о контрольной группе помогают отбросить
некоторые альтернативные объяснения, такие как созревание (подразумевается, что
обе группы имели одинаковый возраст и сопоставимые значения измеряемых
параметров). Однако различия между экспериментальной и контрольной группами
могут быть вызваны их изначальным несходством, а не вмешательством, а отказ
от случайного распределения наряду с отсутствием информации об исходном
состоянии групп не позволяет отбросить это объяснение для любых межгрупповых
различий.
Исследование одной группы до и после воздействия обозначается так, как
показано на рис. 18.5.
о, х о2
Рис. 18.5. План исследования одной группы до и после воздействия
Хотя сбор информации об экспериментальной группе до экспериментального
воздействия определенно полезен, в данном случае на основе данных,
полученных в ходе данного исследования, по-прежнему невозможно прийти к причинно-
следственным заключениям. Это происходит из-за существования множества
альтернативных объяснений наблюдаемых результатов. Помимо очевидных вещей,
таких как созревание и влияние внешних факторов, при подобном плане
исследования нужно всегда помнить о возврате в среднее состояние, в особенности если
экспериментальная группа была выбрана из-за высоких или низких показателей
некоторой величины, связанной с предметом исследования. Предположим,
некоторую группу детей, которая характеризовалась плохими навыками чтения
(тестирование до воздействия), дополнительно тренировали в чтении (воздействие).
Они могли показать заметно лучшие результаты при тестировании после
воздействия, чем до него, однако описание данных различий как результата воздействия не
может быть доказано результатами исследований, поскольку все измерения
содержат случайную ошибку. (Это подробно обсуждается в главе 16.) Например,
каждый ученик из нашего воображаемого исследования характеризуется истинными
навыками чтения, однако каждое конкретное измерение этих навыков (результат
шмшт
Глава 1 8. Планирование исследования
теста на чтение) содержит некоторую ошибку измерения, которая может
завысить или занизить реальные навыки этого ученика. Таким образом, ученик,
который показал плохие навыки чтения на одном испытании, может показать лучшие
навыки на следующем просто из-за случайной ошибки измерения, тогда как его
реальные навыки чтения остались неизменными. Если фокусная группа выбрана
из-за их выдающихся результатов (например, дети, которые плохо справились с
тестом на чтение), вероятность возврата к норме, которая выражается в более
высоких баллах во втором тестировании, повышается.
Кук п Кампбелл приводят много квазиэкспериментальных планов, которые
более предпочтительны, чем три описанных выше (см. ссылку на книгу Shadish,
Cook, Campbell в приложении С, для получения дальнейшей информации по
этой теме); все они представляют попытки улучшить контроль в тех ситуациях,
где невозможно случайным образом разделить объекты на группы. Один простой
пример - это план с обследованием до и после воздействия и контрольной группой,
проиллюстрированный на рис. 18.6.
о,
о,
X
ог
%
Рис. 18.6. План с обследованием до и после воздействия и контрольной группой
При таком плане выбирают сходную с экспериментальной контрольную
группу, однако объекты не распределяются по группам случайно; вместо этого чаще
всего используются уже существующие группы. Измерения проводят для обеих
групп, потом на экспериментальную группу оказывают воздействие, затем
измерения вновь проводят для обеих групп. Основной недостаток этого эксперимента
заключается в том, что без случайного распределения объектов эти группы могут
оказаться несравнимыми в полной мере; рассмотрение результатов первого
обследования обеих групп помогает преодолеть это затруднение, но не полностью. Еще
одна проблема такого плана - сам факт любого вмешательства может повлиять на
результат (поэтому на контрольную группу иногда оказывают другое воздействие,
которое, как считается, не повлияет на результат), также эти две группы могут
иметь разные свойства, выходящие за рамки эксперимента. У разных классов
могут быть разные учителя; разные города могут характеризоваться разной
экономической ситуацией и так далее.
Прерванные временные ряды, проиллюстрированные па рис. 18.7 и 18.18, - это
квазиэксперимент, который может включать, а может и не включать контрольную
грУгтУ-
""о;"о;"о7о""о7"о6"о""оГо7
Рис. 18.7. Прерванные временные ряды с контрольной группой
Квазиэкспериментальные исследования
МЕЕЯ
00000 Х0000
1 2 3 4 v5 w6 7 w8 9
Рис. 18.8. Прерванный временной ряд (без контрольной группы)
Число наблюдений может варьировать в зависимости от исследования, однако
основная идея состоит в том, что в течение некоторого времени проводят ряд
измерений, затем оказывают воздействие, и ряд измерений продолжается. Этот план
часто используют для оценки судебной или социальной политики, которая влияет
на большие группы людей, такой как закон, обязывающий водителей
пристегиваться, или повышение платы домовладельцев за вывоз мусора. Несколько измерений
проводят до воздействия, чтобы установить линию отсчета, и после воздействия,
чтобы определить новый уровень. Многократные измерения нужны, чтобы учесть
естественные колебания изучаемой величины. Например, даже без всякого
изменения законодательства число дорожно-транспортных происшествий варьирует
от месяца к месяцу. В идеале значения линии отсчета должны колебаться вокруг
какой-то величины, и измерения после воздействия должны колебаться вокруг
нового значения, изменившегося в ожидаемую сторону. Добавление контрольной
группы в этот план увеличивает уверенность исследователя при формулировке
заключений, поскольку это позволяет учитывать внешние воздействия, которые
могут повлиять на результат. (Массовая природоохранная акция может заставить
людей перерабатывать и компостировать отходы вне зависимости от увеличения
платы за вывоз мусора.)
Предположим, правительство штата озабочено высокой смертностью при
ДТП и решает снизить предельно допустимую скорость на шоссе, ожидается,
что это решение приведет к снижению смертности. Поскольку снижение
максимально допустимой скорости повлияет на всех водителей этого штата, у нас
нет возможности взять контрольную группу; в качестве такой группы можно
использовать соседний штат со сходной демографической ситуацией и
смертностью на дорогах. Данные, полученные в ходе данного исследования,
представлены на рис. 18.9.
Черная линия отражает число смертей в ДТП в опытном штате, серая линия - в
контрольном; вертикальная пунктирная линия обозначает время вмешательства
(введения ограничения скорости). Можно увидеть, что в двух штатах смертность в
ДТП в течение пяти месяцев до вмешательства была сравнимой; затем смертность
снизилась в опытном штате и стабилизировалась на новом, более низком уровне,
как и ожидалось в случае, если закон будет эффективным для снижения
смертности в ДТП. Такого эффекта не было обнаружено в контрольном штате (на самом
деле она, скорее, немного увеличилась). Это укрепляет уверенность в том, что
принятый закон, а не другой фактор привел к наблюдаемому снижению смертности в
ДТП. Конечно, также следует провести статистический анализ, чтобы убедиться в
значимости этих изменений, однако график показывает, что вмешательство
действительно имело нужный эффект.
Глава 1 8. Планирование исследования
— — Опыт
¦ Контроль
1 2 3 4 5 6 7 8 9 10
Месяц
Рис. 18.9. Влияние ограничения максимально допустимой скорости
на смертность в результате ДТП
Действительно ли «Спорте Иллюстрайтед» приносит несчастье?
Вы могли слышать о несчастье, приносимом «Спорте Иллюстрайтед»3, - мнение о том,
что спортсмены, попадающие на обложку этого журнала, подвержены какому-либо
проклятию, что приводит впоследствии к плохим результатам в спорте или другим
несчастьям. Те, кто верит в это, могут привести множество примеров в поддержку своей теории.
Бен Хоган (Ben Hogan) - один из величайших игроков в гольф своего времени - появился
на обложке «Спорте Иллюстратед» 10 января 1949 года только для того, чтобы через
несколько недель получить не совместимые с карьерой травмы в автокатастрофе.
Белорусский гимнаст Иван Иванков на обложке сентябрьского номера журнала в 2000 году
был назван лучшим спортсменом мира, а вскоре после этого не допущен до
соревнования за медали Олимпийских летних игр 2000 года.
Каждый знает, что отдельные случаи - это не доказательство, так что три
корреспондента «Спорте Иллюстрайтед» проследили судьбы спортсменов более чем с 2000 обложек
журнала. Вот их заключение: более чем треть (37.2%) людей с обложки пострадали от
несчастных случаев вскоре после публикации, при этом несчастным случаем называли
все - от снижения личных или командных результатов до увечья или смерти. Конечно, для
того чтобы проверить этот результат на статистическую значимость, нам нужно гораздо
больше информации, включая частоту несчастных случаев для каждого спортсмена на
протяжении его карьеры; поскольку сбор таких данных был бы чрезвычайно трудоемким,
если не невозможным, эта задача, возможно, останется нерешенной.
Однако у нас есть гораздо более простое объяснение: возврат в среднее состояние.
Спортсмены, которых выбирали для обложки «Спорте Иллюстрайтед», обычно
показывали наивысшие результаты в их виде спорта на тот момент, а поскольку результаты любого
человека меняются, легко понять, что их результаты не всегда будут оставаться на том
высоком уровне. Суеверные люди могут с легкостью трактовать это снижение
результатов как злой рок, а не естественную изменчивость. Более подробная информация на эту
тему представлена в статье Александра Вольфа (Alexander Wolff) с соавторами,
процитированной в приложении С.
Sports Illustrated - еженедельный иллюстрированный спортивный журнал, крупнейшее и самое
популярное спортивное издание США. - Прим. пер.
0) v
О. *
fflO
Q.O
2 <q
/\ ' » ¦¦¦¦¦¦
¦¦-¦¦* в v •- ,
у
; "^s—
Эксперименты
Эксперименты
Экспериментальные исследования дают самое строгое доказательство причинно-
следственной связи, поскольку в хорошо спланированном эксперименте влияние
многих источников изменчивости контролируется или уничтожается, что позволяет
нам с большей уверенностью считать, что наблюдаемые эффекты объясняются
экспериментальным воздействием, а не иными причинами. Есть три элемента любого
эксперимента, а их план может варьировать от очень простого до очень сложного:
• Единицы эксперимента - исследуемые объекты. При экспериментах с
людьми единицами принято называть участников, при условии что они активно
вовлечены в процесс эксперимента.
• Комбинации условий эксперимента - воздействия, оказываемые на каждую
единицу эксперимента.
• Отклики - данные, собранные после экспериментальных воздействии, на
основе которых будет оценен эффект от воздействия.
Кроме условий, изучение которых является частью эксперимента, может
считаться, что другие переменные могут повлиять на отклик. Некоторые из них - это
характеристики объектов; в случае людей они могут включать такие параметры,
как пол и возраст. Эти характеристики могут интересовать исследователей
(можно предположить, что условия больше действуют на мужчин, чем на женщин),
или это могут быть помехи или управляющие переменные, которые маскируют
связь между воздействием и откликом. Вам хочется нейтрализовать воздействие
этих переменных на отклик, и обычно это делается при помощи примерно равного
присутствия ключевых помех и управляющих переменных в экспериментальной
и контрольной группе. Как правило, случайное распределение объектов делает
распределение признаков в каждой группе, таких как пол и возраст, примерно
одинаковым; если этого недостаточно, то можно использовать приведение в
соответствие или объединение в блоки, как это описано ниже.
В некоторых экспериментальных планах проводится сравнение между
базисным значением для каждого объекта до воздействия и его измерением после
воздействия. В этом случае говорят о зависимых выборках (within-subjects design),
такой план дает высокую степень контроля, поскольку участники служат
контролем самим себе. Пример теста Стыодента для приведенных в соответствие нар
объектов, описанный в главе 6, - это пример плана с зависимыми выборками. При
плане с независимыми выборками (between-subjects design) сравниваются разные
объекты, и часто эти объекты приводятся в соответствие но одной или более
характеристикам, чтобы обеспечить наиболее четкое сравнение объектов из
контрольной и экспериментальной групп.
Характеристики хорошего экспериментального
плана
Задача эксперимента - определить эффект от экспериментального воздействия;
он часто выражается в виде различий между значениями переменной-отклика
И—ВИД
ШЕЯ\
Глава 1 8. Планирование исследования
для экспериментальной и контрольной групп. Важно корректно распределить
объекты между этими группами; ведь способ распределения объектов - это
основное различие между экспериментом и наблюдением. Основная задача
любого экспериментального плана - минимизировать систематические ошибки при
сборе данных или (еще лучше) избавиться от них. По многим причинам -
включая этические и экономические соображения - количество собранных данных
должно быть минимально достаточным для ответа на определенный вопрос,
стоящий перед исследователем. Использование эффективных способов
создания выборки и вычисления мощности (тема, подробно обсуждаемая в главе 16)
позволяет убедиться, что в эксперимент вовлечено минимально возможное
число объектов и что результат может быть достигнут с минимальными затратами
средств и усилий.
Эффективный исследовательский план значительно облегчает последующий
анализ данных. Например, если вы организуете эксперимент так, чтобы не
пропускать значения, вам не нужно будет думать о кодировании пропущенных данных
и о каких-либо ограничениях в интерпретации результатов, которые могут
впоследствии возникнуть (это предмет главы 17), включая систематические ошибки,
которые могут сопутствовать неслучайно пропущенным данным.
Теория статистики гибка в том смысле, что многие сложные планы
экспериментов можно проанализировать, однако на практике большинство статистик
(а следовательно, экспериментальных планов) основано на требованиях
обобщенной линейной модели. Это упрощает анализ, поскольку многие методы, такие
как корреляция и регрессия, основаны на этой модели. Однако, чтобы корректно
использовать обобщенную линейную модель, эксперимент должен быть
спланирован с учетом нескольких важных факторов, включая сбалансированность и
ортогональность.
Сбалансированность означает, что разным комбинациям условий подвергнуто
одинаковое число объектов в рамках каждого экспериментального блока.
Сбалансированные планы характеризуются большей мощностью, чем несбалансированные
планы с тем же числом объектов, несбалансированный план также может отражать
сбой в процессе распределения объектов по группам. Случайное распределение но
группам, слепые методы и выявление систематических ошибок - механизмы,
которые используются, чтобы убедиться, что сбалансированность сохраняется; все это
обсуждается ниже в этой главе.
Ортогональность означает, что эффекты от разных воздействий можно
независимо оценить, и они не взаимодействуют. К примеру, если у вас есть два типа
экспериментальных воздействий и вы строите экспериментальную модель,
которая объясняет их действие на объекты, то можно убрать любое из воздействий из
модели и получить тот же ответ для оставшегося воздействия.
Ни одна из этих вещей не так сложна, как кажется на первый взгляд, и если
вы будете следовать некоторым широко известным правилам и шаблонам мно-
гофакториого плана, вам не придется беспокоиться о более редких
исключениях.
Сбор экспериментальных данных |В^^1Е^Э
Сбор экспериментальных данных
Итак, вы хотите начать эксперимент, но как это сделать? В этом разделе приведена
общая схема исследовательского процесса, примерно в той последовательности, в
которой нужно выполнять эти действия, однако в своем плане вы должны
учитывать, как эксперименты вроде того, который вы собираетесь провести,
организуются в вашей области исследований. Иными словами, стойте на плечах гигантов;
если вы проводите научные эксперименты, посмотрите некоторые статьи из
научных журналов вашего профиля и убедитесь в том, что организация экспериментов
и анализ данных, которые вы проводите, согласуются с теми, что обычно проводят
в вашей области науки. Процесс рецензирования, хотя и не безупречный,
удостоверяет, что методология, использованная в статье, одобрена по меньшей мере
двумя экспертами. Если у вас есть консультант или руководитель, вы можете
также посоветоваться с ним - нет смысла изобретать колесо. В производстве или
промышленности найти образец может быть труднее, однако технические
отчеты данной компании и проводимый ранее анализ должны послужить в качестве
примера - даже если они не проходили рецензирования, - который вы можете
использовать в качестве руководства.
Нужно сказать, что вы будете удивлены, насколько вариации и городская
мифология влияют на план эксперимента, так что давайте перечислим все этапы по
порядку:
1. Выделите объекты, которые вы хотите измерить.
2. Определите воздействия, которые вы хотите оказать, контрольные
переменные; которые вы будет использовать.
3. Назначьте уровни воздействий.
4. Определите результирующие переменные, которые вы будете измерять у
объектов.
5. Сформулируйте верифицируемую гипотезу, которая предсказывает эффект
от воздействия на результирующие переменные.
6. Проведите эксперимент.
7. Проанализируйте результаты.
План (шаги 1-5) может казаться простым, когда он бегло упомянут, однако
давайте рассмотрим подробнее каждый этап, чтобы понять, что на самом деле
происходит.
Определение задействованных в эксперименте
объектов
Вспомните, что статистики вычисляются для выборок и являются оценкой для
параметров генеральной совокупности, из которой происходят выборки. Чтобы
быть уверенным, что эти оценки аккуратны, большинство статистических
процедур предполагает, что объекты были выбраны из генеральной совокупности
случайным образом. (Планы с сопоставлением наблюдений и зависимыми
выборками - очевидное исключение из этого правила.) Систематическая ошибка может
ЕНЯ
Глава 1 8. Планирование исследования
легко вкрасться в план на этой начальной стадии, и вдобавок обстоятельства могут
сложиться так, что этой ошибки непросто избежать.
Например, многие психологические исследования используют в качестве
подопытных студентов-психологов. Это делается для выполнения двух задач.
Во-первых, во время курсовой работы студенты знакомятся с разными планами
экспериментов и из первых рук получают знания о постановке эксперимента; во-вторых,
такие участники доступны для исследования. В некотором смысле гомогенность
студентов как объектов является чем-то вроде контроля, поскольку в этом случае
участники имеют сходный возраст, распределение по полам, географическое
происхождение, культурные традиции и так далее. Однако они не представляют собой
случайную выборку из генеральной совокупности, и это может ограничивать
применимость выводов из ваших данных. Научные статьи, основанные на выборке
студентов, могут больше сказать нам о поведении студентов, чем о генеральной
совокупности в целом; значимость этого уточнения зависит от типа проведенного
исследования. Эта проблема не ограничивается психологией; несмотря на
ожидаемый случайный отбор объектов, на практике исследователи многих
специальностей выбирают свои объекты неслучайным образом. Например, медицинские
исследования часто проводятся на пациентах определенной больницы или
клиники, тогда как результаты распространяются на всю генеральную совокупность;
оправданием этому служит независимость биологических закономерностей от
места проведения исследования, так что результаты, полученные на одном наборе
пациентов, должны распространяться и на другой сходный набор пациентов.
Важно знать, какие ожидания и традиции относительно составления выборки и
корректности генерализации результатов существуют в вашей области исследований,
поскольку ни одно из правил не затрагивает всех областей науки.
Что означает случайный отбор в этом контексте? Представьте себе лотерею,
в которой каждый горожанин вытаскивает билетик. Все билетики помещены в
большую коробку и перемешаны вращением во многих направлениях. Затем
помощника просят выбрать один билетик, запустив в коробку руку и выбрав
первый билетик, к которому он прикоснулся. В этом случае у всех билетиков равный
шанс быть выбранным. Если вам нужно 100 человек для контрольной группы и
100 - для экспериментальной, вы можете выбрать их при помощи этой
процедуры, когда первые 100 билетиков будут соответствовать контрольной группе, а
следующие 100 - экспериментальной. Конечно, вы можете чередовать билетики, так
чтобы первый соответствовал контрольной группе, второй - экспериментальной
и так далее. Если выбор по-настоящему случаен, эти два подхода будут
равнозначными. Для абсолютно случайного выбора важно, чтобы выбор каждого отдельного
участника не зависел от выбора любого другого.
Разные способы составления выборок подробно описаны в главе 3. Основная
вещь, которую нужно помнить, - в реальном мире получение случайной выборки
из генеральной совокупности часто невозможно или нерационально, и
практические соображения заставляют вас составлять выборку на основе меньшей
генеральной совокупности, чем та, на которую вы хотите распространить выводы
(к которой, как вы считаете, применимы ваши результаты). Это не проблема, если
Сбор экспериментальных данных
шшшшлш
вам ясно, когда и где выборка была получена. Представьте себе, что вы
микробиолог, который хочет изучить бактерии, живущие в больницах. Если вы используете
фильтр с порами диаметром 1 мкм (микрометр), все более мелкие бактерии не
попадут в исследуемую генеральную совокупность. Это ограничение при сборе
материала внесет систематическую ошибку в исследование; однако, до тех пор,
пока вы будете отдавать себе отчет в том, что генеральная совокупность, о которой
вы делаете выводы, - это бактерии крупнее 1 мкм, и ничего, кроме этого, ваши
результаты будут корректными. В реальности мы часто хотим распространить свои
результаты на большую генеральную совокупность, чем та, из которой происходит
выборка, и наши возможности в этой области зависят от ряда факторов.
В медицинских или биологических исследованиях распространение
результатов за пределы генеральной совокупности, из которой происходит выборка,
обычно, поскольку считается, что основные биологические процессы одинаковы
у всех людей. Поэтому предполагается, что результаты медицинского
исследования, проведенного в одной больнице, имеют отношение к пациентам всего мира.
(Конечно, это касается не любого медицинского исследования.) Также нужно
помнить о том, что исчерпывающее описание ограничений вашей выборки
позволяет получить корректные результаты, которые пополнят общий объем знаний.
Поскольку многие подобные исследования проводятся в определенной области
науки, их результаты могут быть распространены на генеральную совокупность.
Например, проведение тестов на время реакции на английские слова может быть
использовано для формулировки заключений о восприятии и познавательной
деятельности англоговорящих людей. Последующие эксперименты, нацеленные на
расширение применимости результатов, могут быть такими же, но использовать
немецкие слова и говорящих по-немецки людей, французские слова и говорящих
по-французски людей и так далее. Действительно, так и получают более общие
результаты в науке.
Определение воздействий и контроля
Воздействия - это манипуляции или вмешательства, которые вы желаете
провести для достижения экспериментального эффекта. Предположим, что
фармацевтическая компания потратила миллионы долларов на разработку нового лекарства
от глупости и после многих лет лабораторных испытаний его действие требуется
проверить на практике. Компания организует клиническое испытание, в котором
1000 участников отбираются случайно по фамилиям, указанным в
национальной телефонной базе, составив по-настоящему случайную выборку из
генеральной совокупности по таким значимым параметрам, как возраст, пол и так далее.
К счастью, все выбранные участники согласились участвовать в эксперименте
(каждый хочет стать умнее, верно?), так что компании не пришлось беспокоиться
о том, что кто-то отказался или выбыл из эксперимента (оба этих события могут
внести систематическую ошибку в результаты). Все участники были исследованы
в один и тот же день при одинаковых условиях (расположение, температура,
освещение, стул, стол и так далее). В 9 утра участники прошли тест на интеллект при
швишмшд
Глава 1 8. Планирование исследования
помощи компьютера; в полдень они приняли дозу лекарства от глупости, запив
его водой; и в три часа дня они выполнили тот же самый тест на интеллект. Их
результат в среднем улучшился на 15%! Персонал компании пришел в экстаз, они
послали результаты эксперимента на лондонскую фондовую биржу, что привело к
росту акций этой компании. Но что же было не так с этим экспериментом?
Во-первых, поскольку каждый проходил тест точно в том же месте и при тех
же условиях, результат нельзя автоматически распространить на другие места и
условия. Если бы участники выполняли тест при другой температуре, результаты
могли бы различаться. Кроме того, некоторые составляющие экспериментальной
обстановки могли оказать воздействие на результат - скажем,
использовавшиеся стул или стол или содержание кислорода в помещении, - и эти осложняющие
факторы сложно исключить.
Во-вторых, тот факт, что начальное и экспериментальное испытания всегда
проводили в одинаковом порядке, используя дважды один и тот же тест, почти
точно внес вклад в повышение интеллекта на 15%. Есть основания предположить,
что первое выполнение теста оказало обучающий эффект, учитывая, что вопросы
во второй раз были в точности те же самые (или даже если они были заданы в той
же форме).
В-третьих, нет никакого способа проверить, не сыграла ли роль какая-либо
посторонняя переменная, поскольку данный эксперимент был проведен без
контроля; например, питье воды в полдень (в этой ситуации) могло оказать какой-то
физиологический эффект на уровень интеллекта во второй половине дня.
Наконец, участники могли испытать эффект плацебо, при котором они
ожидали, что их интеллектуальные способности после приема лекарства улучшатся. Это
широко известное явление в психологии, его проверка требует создания
дополнительной контрольной группы, которая будет исследована при таких же
обстоятельствах, но с «пустышкой» вместо настоящего лекарства.
К экспериментальному плану можно сделать множество критических
замечаний, но, к счастью, есть четко описанные способы улучшения эксперимента при
помощи контроля. Например, если половина случайно отобранных объектов
будет случайно определена в контрольную группу, а другая половина - в
экспериментальную, тогда контрольной группе можно дать «пустышку», а
экспериментальной - лекарство от глупости. В этом случае обучающий эффект от двойного
прохождения теста, а также эффект от самого участия в эксперименте можно
оценить на контрольной группе, а любые различия в результатах двух групп могут
быть проверены статистически.
Конечно, настоящие клинические испытания лекарств устроены иначе, эти
испытания проводятся поэтапно с четкими задачами на каждом этапе, начиная с
выявления эффекта от широкого диапазона доз, проверки токсичности и так далее с
постоянным наличием контрольной группы, пока не будет найдена оптимальная
и безопасная доза, которая дает нужный медицинский эффект. Участников почти
никогда не выбирают случайно из генеральной совокупности, но вместо этого их
проверяют на соответствие набору определенных требований (возраст, здоровье и
так далее). Однако после создания выборки объекты, как правило, случайно рас-
Сбор экспериментальных данных
ШШШЙ
пределяются между экспериментальной и контрольной группами - это важный
аспект экспериментального плана, который позволяет избежать систематической
ошибки, уравняв опытную и контрольные группы, насколько это возможно.
Определение уровней воздействий
На практике вас может не интересовать именно выделение факторов, влияющих
на результат эксперимента, - вы можете хотеть просто исключить все
возникающие систематические ошибки. Этого часто можно достичь при помощи
сбалансированного плана, при котором равное число участников подвергаются разным
комбинациям воздействий. К примеру, если вы интересуетесь, повышает ли
лекарство от глупости интеллект у всех людей, в вашу выборку должно войти равное
число мужчин и женщин, тест нужно предъявлять разное число раз и так далее.
Однако если вам нужно определить, влияет ли пол или частота приема лекарства
на эффект от него, эти переменные нужно в явном виде включить в число
факторов и указать их уровни в плане. Для категориальных переменных, таких как
пол, задать уровни или категории (мужской и женский) легко. Однако для
непрерывных переменных (таких как время суток) легче приурочить уровни к целым
часам (в данном случае 24 уровня) или просто выделить утро, день и вечер (три
уровня). Выделение уровней и экспериментальных эффектов зависит от цели
исследования. Уравновешивание баланса и рандомизация также могут быть
использованы для избавления от систематической ошибки. Разумеется, воспроизведение
результатов на расширенной выборке или в других пространственно-временных
рамках важно для оценки возможности генерализации результата.
После определения уровней воздействий исследователи обычно говорят
о воздействиях и их уровнях как о формализованном факторном плане вида
А^я,) х А2(п2) х ... Ах(пх), где Л, ... Ау - это воздействия, а п{ ... nv - это уровни
каждого воздействия. Например, если вы хотите обозначить эффект от пола и времени
суток на действие лекарства на интеллект и у вас есть контрольная и
экспериментальная группы, то у вас будет три воздействия со следующими уровнями:
ПОЛ: мужской/женский
ВРЕМЯ СУТОК: утро/день/вечер
ПРЕПАРАТ: лекарство/плацебо
Таким образом, план можно записать как ПОЛ(2) * ВРЕМЯ СУТОК(З) х
ПРЕПАРАТ^), что можно прочесть как план 2 на 3 на 2. Анализ главных эффектов для
каждого воздействия и взаимодействия между ними обсуждается в главах,
посвященных анализу данных.
Воздействия или характеристики?
В естественных и гуманитарных науках существует одно важное различие в
определении воздействия. Слово «воздействие» (treatment) относится к активному
использованию какого-либо действия, интенсивность которого может меняться, например доза
лекарства от глупости. Однако в социологии воздействием часто называют
фиксированную величину, такую как пол. Стбит такую характеристику называть воздействием, ведь
zsnmm
Глава 1 8. Планирование исследования
она не меняется? Как называть планы, использующие подобные характеристики, -
экспериментальными, квазиэкспериментальными или просто наблюдениями? Ключевой
момент здесь - продемонстрировать причинную связь между воздействиями и
откликами, поскольку использование воздействия постоянной силы оставляет открытым
вопрос о том, какие именно характеристики экспериментальных единиц на самом деле
отвечают за разницу между уровнями воздействия. Поэтому некоторые исследователи
предпочитают называть независимые переменные, такие как пол, характеристиками, а
не воздействиями, а некоторые используют название «независимые переменные» для
всех переменных, которые, как считается, влияют на результаты. В конечном счете
подобные соображения накладывают ограничения на заключения, которые можно сделать
из результатов эксперимента. В технологии цель эксперимента может быть более
конкретной, например установить величину эффекта, определить оптимальные комбинации
и пропорции разных воздействий и их уровней, которые позволят максимизировать
переменную-отклик.
Определение результирующих переменных
Иногда результирующая переменная очевидна, но в других случаях бывает
нужно измерить более одной переменной, в зависимости от точности, с которой
переменная операционализирует некоторое абстрактное понятие. Интеллект - это
хороший пример; это абстрактное понятие может показаться простым для
неспециалиста, однако не существует способа измерить интеллект напрямую. Вместо
этого в качестве результирующих переменных измеряется много показателей
интеллекта в разных сферах (числовой, аналитический и т. д.), которые можно
объединить в одно число (коэффициент умственного развития, IQ), выявив скрытую
структуру в связанных результирующих переменных. Существуют сложные
методики (описанные в главе 12), которые помогают организовать и сократить число
результирующих переменных в меньший, более осмысленный (с позиции
интерпретации) набор признаков.
Лучшим подходом при работе со сложным неоднозначным понятием, таким как
интеллект, могут быть использование набора приемов для получения
результирующих переменных и последующее определение качества их согласования друг с
другом. Конечно, способы определения согласованности результирующих
переменных играют важную роль при оценке адекватности экспериментальных
планов.
Существуют три тина результирующих переменных: основные, отклики и
промежуточные. В предыдущем разделе мы видели, как основной показатель
интеллекта был использован для определения прямого экспериментального
воздействия на переменную-отклик (ум). Промежуточная переменная используется для
об'ьяснения связи мелсду воздействием и результирующей переменной, когда
эта связь непрямая, но контролируемая. Если вы хотите определить причинно-
следственные связи как часть объяснительной модели, вам точно нужно знать
обо всех вовлеченных в процесс переменных.
В некоторых исследовательских планах различие между воздействиями и
промежуточными переменными может быть неважным. Например, если вы химик и
Сбор экспериментальных данных НН^^ВЕ^Э
интересуетесь химическими свойствами воды, вы более охотно будете работать на
уровне частиц атома (протоны, нейтроны, электроны), чем на субатомном уровне.
В психологии, напротив, промежуточным переменным часто уделяется гораздо
больше внимания, особенно если цель исследования - определить, как протекает
некий психологический процесс.
В очень сложных системах непредвиденные вмешательства (или
ненаблюдаемые промежуточные переменные) могут повлиять на результат, особенно если
такие переменные сильно скоррелированы с воздействием или влияют на
проведение эксперимента, изменяя наблюдаемое поведение. Таким образом, может быть
трудно понять, обусловлено ли наблюдаемое изменение результатов именно
оказываемым воздействием. Другая общая закономерность - тем больше промежуток
времени между оказываемым воздействием и наблюдаемым ответом, чем больше
вероятность того, что некоторые промежуточные факторы повлияют на результат
и, возможно, приведут к сомнительным заключениям. Например, сезонные
факторы, такие как температура, влажность и так далее, оказывают очень сильный
эффект на характеристики сельскохозяйственной продукции, и этот эффект
может быть более выраженным, чем воздействие (новый тип удобрений), которое
является предметом исследования.
Проверка гипотез в сравнении с добычей
информации из данных
Учитывая, что уровень достоверности р < 0.05 значит, что 1 из 20 экспериментов
приведет к статистической ошибке первого рода, на исследователе лежит ответственность
так организовать эксперимент, чтобы он согласовался с явлениями, соответствующими
модели или теории, или пытался объяснить их. Однако у некоторых исследователей есть
привычка собирать большой объем данных для многих результирующих переменных и
пытаться связать их с определенными воздействиями на выборку. Этот подход,
применяемый в широком масштабе, называется добыча информации изданных (data mining).
Эта форма вторичного анализа данных чрезвычайно полезна для исследования больших
наборов данных, часто собранных посредством наблюдений или полученных из разных
источников. В простейшем виде цель добычи информации из данных состоит в
определении корреляций между многими переменными, что может впоследствии послужить
основанием для разработки плана эксперимента. В качестве альтернативы в условиях
промышленности добыча информации из данных может использоваться для создания
алгоритмов принятия решений на производстве, основываясь на обнаруженных связях.
Например, анализ банковской базы данных может выявить, что клиенты с доходом более
$100 000 и живущие по одному адресу более трех лет никогда не отказываются
выплачивать внутренний заем. Таким образом, банк может решить выдавать заем только тем
клиентам, которые соответствуют этим требованиям и пока не имеют займа. Однако в
данном случае не устанавливают никаких общих причинных связей; правила принятия
решений по своей природе сугубо утилитарны.
Добыча информации из данных чаще критикуется при традиционном
экспериментальном подходе; считается недопустимым отказываться от процесса формулировки
гипотез и их проверки, а проведение многих статистических тестов в надежде на то, что
что-то будет статистически значимым, называется выуживанием результатов. Причина
этого заключается в том, что значения р корректны для одного теста, а не для множества
сходных тестов, проведенных для одних и тех же данных. При множественных тестах в
шшмт
Глава 1 8. Планирование исследования
пределах одного эксперимента частота статистических ошибок первого рода почти
точно выше, чем для одного теста (за исключением полностью независимых тестов). Для
корректировки значений р при множественных тестах разработано несколько
статистических процедур, включая поправки Гринхауса-Гейсера (Greenhouse-Geisser) и Бонфер-
рони (Bonferroni).
Слепой метод
Вы, возможно, слышали об эффекте плацебо, когда члены контрольной группы
проявляли некоторые свойства, характерные для экспериментальной группы.
Этот эффект обусловлен многими аспектами, включая эффект ожидания
(поскольку при испытаниях лекарств, например, действующее вещество и его
известные эффекты и риски известны пациентам), наряду с систематической ошибкой,
вызванной поведением экспериментаторов, дающих лекарство или собирающих
результаты. К примеру, если экспериментатор знает, что испытуемый получает
настоящее лекарство, он может относиться к пациенту более внимательно, чем если
он выдает «пустышку». Соответственно, на собирающего данные
экспериментатора также может подействовать коллективное знание об опытной и контрольной
группах.
Использование одинарного, двойного или тройного слепых методов помогает
эффективно контролировать подобные источники ошибок.
Одинарный слепой метод
Участник эксперимента не знает, в какой группе он находится - опытной
или экспериментальной.
Двойной слепой метод
Ни участник эксперимента, ни сотрудник, выдающий ему лекарство, не
знают, в какой группе находится участник эксперимента.
Тройной слепой метод
Ни участник эксперимента, ни сотрудник, выдающий ему лекарство, ни
сотрудник, собирающий данные, не знают, в какой группе находится
участник эксперимента.
В маленьких лабораториях один и тот же человек может и выдавать лекарство,
и собирать данные; так что тройной слепой метод часто так же просто применять,
как и двойной. Хотя применение слепого метода весьма необходимо, это не
всегда можно сделать на одном или нескольких уровнях. Например, многие взрослые
люди знакомы с физиологическим эффектом от выпивки, так что использование
плацебо для имитации эффекта от алкоголя, не влияющего при этом на время
реакции, при исследовании влияния алкоголя на время реакции будет
затруднительным. (А если плацебо повлияет на время реакции, то его нельзя будет
использовать в качестве эффективного контроля.) В других случаях бывает
возможно создать эффективное плацебо, так что участники эксперимента не будут
знать, в какую группу они попали. Основной принцип таков - в экспериментах
нужно использовать слепой метод везде, где это возможно; это составляющая об-
Сбор экспериментальных данных
¦И1ВЯД
щих усилий по отделению эффекта от нахождения в экспериментальной группе
от эффекта по воздействию и удалению внешних факторов, которые запутывают
картину.
Ретроспективная поправка
В предыдущем разделе мы упомянули систематическую ошибку, которая может
произойти в результате информированности сборщика информации о статусе
испытуемого. Еще один потенциальный источник ошибки возникает при наличии
нескольких сборщиков информации или разных инструментов для ее получения,
что приводит к плохо сравнимым суждениям о результатах контрольной и
опытной групп. Хорошая тренировка сборщиков информации может уменьшить
значимость этого источника ошибки, для ее уменьшения можно использовать другие
способы. Например, результаты нескольких сборщиков информации можно
усреднить для достижения консенсусного значения. Другая возможность -
исследование всего массива результатов, полученных одним сборщиком, и попытка
ретроспективной поправки обнаруженной систематической ошибки.
Объединение в блоки и латинский квадрат
Цель объединения в блоки - это постановка экспериментов таким образом, чтобы
сравнимые (и желательно идентичные) ответы были получены при одном и том
же воздействии. Идея заключается в том, чтобы использовать как можно больше
априорной информации об экспериментальных единицах для объединения их в
экспериментальные блоки так, чтобы все объекты данного блока одинаково
реагировали на воздействие. Наверное, наиболее знаменитый пример объединения в
блоки - это использование в психологических исследованиях однояйцевых
близнецов для изучения эффекта наследственности и воспитания, поскольку
однояйцевые близнецы имеют идентичный генотип. Если близнецы, например,
разлучаются при рождении или посещают разные школы, воздействие внешних факторов
можно определить, держа генетику «под контролем». Преимущество объединения
в блоки однояйцевых близнецов заключается в том, что изменчивость из-за
одного фактора (генетического) можно четко контролировать; недостаток -
ограниченность числа нужных объектов, а число разделенных однояйцевых
близнецов - еще меньше.
Приведение объектов в соответствие друг другу позволяет ограничить влияние
внешних факторов на план эксперимента. Разницу в результатах между объектами
можно контролировать, ставя в пару объекты, похожие по максимально
возможному числу могущих запутать результаты (или коррелирующих с воздействием)
факторов. В психологических исследованиях это обычно означает приведение в
соответствие по таким факторам, как возраст, пол, интеллект, однако в
экспериментах на восприятие иногда учитываются такие специфические факторы, как
острота зрения или цветовая слепота.
Бывает невозможно привести участников в соответствие по всем возможным
внешним источникам воздействия, однако во многих областях исследования су-
Глава 1 8. Планирование исследования
шествуют хорошо известные критерии, эффективность приведения в соответствие
по которым показана ранее. Преимущество парных планов заключается в том, что
на уровне отдельных объектов вы можете более определенно показать, что
экспериментальный эффект действительно существует, чем надеясь, что рандомизация
сгладит все различия. Дальнейшее улучшение - использование
рандомизированного блочного плана, который позволяет исследователю оказывать воздействие на
парные объекты случайным образом, сохраняя контроль при помощи приведения
объектов в соответствие, одновременно сохраняя низкую систематическую
ошибку посредством рандомизации.
Практическое правило при планировании исследования - по возможности
объединять объекты в блоки, а если это невозможно, то применять
рандомизацию.
Вспомните, что план с попарным соответствием объектов по возможности
контролирует внешние факторы при помощи приведения в соответствие объектов из
экспериментальной и контрольной групп по важным переменным. Дальнейший
контроль можно обрести, сделав объекты своими собственными контролями? как
в плане для зависимых групп (как в примерах, которые обсуждаются в разделе из
главы 6, посвященном тесту Стыодента для зависимых выборок), хотя это не
всегда возможно или разумно сделать. Планы для зависимых выборок часто
используются в психологии; однако поскольку многие эксперименты подразумевают
некоторое изменение поведения или восприятия, можно задуматься об осложняющем
дело эффекте обучения. Если все объекты испытали контрольное воздействие, а
затем - экспериментальное (или наоборот), то, конечно, на результаты может
влиять эффект обучения (или систематической ошибки созревания).
Однако рандомизация вновь предлагает противоядие в виде латинского
квадрата, который представляет собой несмещенный способ рандомизизации
распределения участников по воздействиям. Для любого экспериментального плана с
//-условиями, в которые помещают каждого участника (Г,, T2,..., Г), испытания для
каждого участника группируют и рандомизируют при помощи латинского
квадрата для обеспечения разной последовательности воздействий для каждого
участника. Например, если время реакции на пять объектов измеряют в испытаниях
Г,, Т2, Tv TA и Tv так что у = 5, и у нас есть пять участников, то рандомизированный
латинский квадрат позволит создать план, показанный в приведенной ниже
таблице, который определит порядок предъявления стимулов.
Л 75 72 7з Тл
73 72 Тл Тъ Л
74 7з 75 7"1 72
7s Тл 71 72 7з
*v
72 71 7з Тл Тъ
Пример экспериментального дизайна
1ИЯ
Таким образом, использование латинского квадрата позволяет быть уверенным,
что любая изменчивость между объектами одинаково влияет на все воздействия.
Учтите, что в латинском квадрате 5><5 существует 161 279 других случайных
конфигураций, которые сохраняют ту характерную особенность, что никакой столбец
или ряд не содержит одного номера более одного раза. Если ваш
экспериментальный план требует хотя бы однократного предъявления воздействий в их
изначальном порядке (Гр Tv Tv Тл и Г5), можно использовать усеченную форму квадрата -
поскольку порядок воздействий сохраняется в первом ряду и столбце? - однако
для этого варианта возможно лишь 55 перестановок. Латинский квадрат для
небольшого числа условий легко можно создать вручную, однако вы можете найти
таблицу латинских квадратов в Интернете наряду с простыми алгоритмами их
создания.
Пример экспериментального дизайна
В этом разделе кратко разобран реальный пример эксперимента и обсуждаются
решения, принятые по поводу плана. Проведено сравнение возможного хода
эксперимента при использовании двух обычных планов, и на примерах показаны
сильные и/или слабые стороны каждой стратегии.
Франсис X. Мартин и Дэвид А. Т. Сиддл (Frances H. Martin, David A. T. Siddle,
2003; полная ссылка приведена в приложении С) решили выявить главные
эффекты от алкоголя и транквилизаторов, наряду с их взаимодействием, на время
реакции, способность реакции Р300 и время между предъявлением стимула и реакции
Р300. Последние два параметра оцениваются при помощи связанных с событием
потенциалов в мозге через 300 мс после предъявления стимула. Все три
характеристики связаны с разными механизмами обработки информации в мозге.
Необходимость исследования вытекает из более ранних работ, которые
независимо показали существование эффекта от алкоголя и транквилизаторов, но не от их
взаимодействия. Кроме того, в исследованиях роли алкоголя на результирующие
переменные обычно использовали большие дозы, а работы, связанные с
транквилизаторами, анализировали сильные препараты, тогда как для этого исследования
выбрали слабый транквилизатор - темазепам. Итак, сформулировали три вопроса:
1. Оказывает ли алкоголь значимый главный эффект на любую из
результирующих переменных?
2. Оказывает ли темазепам значимый главный эффект на любую из
результирующих переменных?
3. Есть ли взаимодействие между алкоголем и темазепамом?
В эксперименте участники выступают в роли контроля для самих себя.
Факторный план был следующим: 2 (алкоголь, контроль) * 2 (транквилизатор,
контроль); так что каждый участник эксперимента подвергался четырем испытаниям
при следующих условиях:
• отсутствие алкоголя и темазепама;
• только алкоголь;
вдд
Глава 1 8. Планирование исследования
• только темазепам;
• и алкоголь, и темазепам.
Результаты эксперимента свидетельствовали о значимом главном эффекте
темазепама на способность реакции Р300 (то есть этот эффект был выражен и
при употреблении алкоголя, и без него) и значимом главном эффекте алкоголя
на время реакции и задержку реакции Р300. Однако между этими факторами не
было значимого взаимодействия. Поскольку главные эффекты алкоголя и
темазепама различаются и не взаимодействуют, исследование подтвердило
независимое действие алкоголя и темазепама на разные процессы обработки информации
в мозге.
Если бы вы планировали этот эксперимент, что бы вы сделали? Выбрали бы
план с приведенными в соответствие парами объектов вместо сравнения
объектов самих с собой? Это бы уменьшило число испытаний для каждого участника,
однако в данном случае сравнение объектов с самими собой позволило обойтись
малым числом участников (N = 24), а для демонстрации эффекта при
сравнении разных объектов понадобилась бы большая выборка. Без сомнения, вы бы
отбирали участников случайно, возможно, используя фамилии из телефонного
справочника и номера страниц и столбцов, полученные при помощи генератора
случайных чисел. Надежность данных не вызывает сомнений, поскольку
используемые результирующие переменные широко применяются при описании
процессов обработки информации в мозге. Вы бы также позаботились о слепом методе
при выдаче алкоголя или темазепама, чтобы убедиться, что контроль для
каждого из воздействий воспринимается участниками так же, как и само воздействие.
Увеличите ли вы число факторов? Возможно, взаимодействие между алкоголем и
тсмазепамом проявляется лишь при высоких дозах, так что, может быть, план 3x3
будет более подходящим. Тут возникает уже не только научный, но и этический
вопрос: вы хотите минимизировать дозу транквилизатора, полученную каждым
испытуемым, и при отсутствии бесспорного теоретического обоснования (или
клинических фактов или наблюдений) для ожиданий противоположного эффекта
выбор плана 2x2 будет разумным.
ГЛАВА 19.
Представление статистических
материалов
Для подготовки успешного письменного или устного сообщения необходимо
излагать результаты, учитывая специфику аудитории. Если вам придётся иметь
дело со статистикой по работе или при выполнении курсовой, есть вероятность,
что ваша ответственность не закончится вместе с расчётами - скорее всего, вам
придётся довести эти результаты и выводы, сделанные на их основе, до сведения
кого-нибудь другого. Этим кем-то может оказаться ваш шеф, коллеги, аудитория
профессиональных статистиков, журналисты, соученики и так далее -
возможности столь же разнообразны, сколь разнообразны контексты, в которых
статистика используется сегодня.
Ключом к успешному общению является выбор соответствующей подачи
материала для аудитории или формы письменного изложения или презентации.
Иногда предполагаемый выбор вполне очевиден. Если вы пишете статью в
профессиональный журнал, возможный формат (включая всё, от разделов до ссылок
и литературы), скорее всего, уже полностью предопределён, и вам остаётся
заглянуть в уже опубликованные статьи в этом же журнале для дальнейшего
руководства. Обращение к более широкой аудитории - такой как газета или популярный
журнал - требует другого набора приёмов, потому что вам придётся представлять
ключевые моменты так, чтобы не смутить читателя техническим жаргоном (или,
что ещё хуже, не вынудить его бросить чтение и двигаться дальше). Написание
статьи или составление презентации по заказу организаций выдвигает иные
требования, потому что вам часто придётся реагировать немедленно на реплики
людей с весьма разным уровнем понимания статистики.
Основное внимание в этой главе бу/^ет уделено письменной форме изложения,
но значительная часть этих советов может применяться и к устному общению,
включая таковое на профессиональных конференциях. Имеется множество
добротных ресурсов, обсуждающих, к примеру, такие вопросы, как организация
хорошей слайдовой презентации, и некоторые из них перечислены в приложении С.
PERI
Глава 19. Представление статистических материалов
Общие замечания
За исключением случаев, когда научная статья пишется для профессионалов,
статистика, скорее всего, сама по себе будет играть вспомогательную роль, зато тема
вашей презентации или статьи должна сразу привлечь внимание. Поэтому
существует опробованная общая практика заявлять вначале наглядные результаты,
а затем показывать показатели статистики, которые подкрепляют ваши выводы.
«Участники, выполнявшие упражнения и соблюдавшие диету, похудели в среднем
на 20 фунтов в течение шестимесячного курса занятий, в то время как те
участники, которые просто соблюдали диету, потеряли в среднем 15 фунтов; разница
оказалась статистически значимой (?=2,75, р = 0,0071)» - такая формулировка
относительной эффективности двух планов снижения веса более эффективна,
нежели «Мы обнаружили, что ^-статистика равна 2,75, что указывает на
существенную разницу по группам». Некоторые называют такую подачу «Конец в
начале - КВН» (Bottom Line Up Front, BLUF).
Определите, какой уровень точности вас устраивает, и округляйте значения
соответственно. Если программа даёт точность до восьмого знака после запятой, это
не значит, что вы должны показывать их все, а если вы так делаете, то это может
восприниматься негативно. В частности, в таблицах данных чрезвычайно
утомительно читать цифры с кучей десятичных знаков, равно как и трудно сравнивать
эти данные, поэтому, как правило, лучше сводить, скажем, число 10,77953201 к 10,8
или 10,78. Если вы имеете дело с очень большими или очень малыми числами, то
принятые научные сокращения типа 2,38* 10 * вместо 0,0000238 и способы
выражения «х на у» делают значения более ясными для восприятия, при этом последнее
обычно используется в демографической статистике, к примеру такое-то
количество больничных коек на 1000 населения или убийств на 100 000 населения.
Помните, что ваша аудитория не всегда так же, как вы, знакома с
использованным типом анализа, посему ей требуется приложить больше усилий для того,
чтобы уяснить смысл результатов. Не бойтесь повторяться в разных местах и формах
изложения, например один раз в тексте, а другой - в таблице или диаграмме. Этот
принцип особенно важен, когда вы имеете дело с неспециализированной
аудиторией, имеющей туманное представление о статистике (или которая просто
пропускает абзацы с цифровыми данными), но зато может легко понять
представляемую концепцию через грамотно сделанную графику.
Всегда разумно указывать источник данных, которые вы подвергаете анализу,
особенно если эти данные не ваши. Формулировка «Данные квартального отчёта
по занятости и оплате, опубликованные вчера Управлением трудовой статистики,
показывают...» указывает читателям, что вы использовали стандартный источник,
что помогает им интерпретировать результаты, зная, что каждый набор данных
имеет свои ограничения и особенности. Это правило особенно относится к
информации, собранной источником, заинтересованным в результатах анализа, поэтому
если ваша работа о пользе употребления мандаринов для здоровья основана на
сведениях, собранных Ассоциацией производителей мандаринов, указать эту
информацию в самом начале - просто ваш долг перед читателями.
Общие замечания
¦¦ЕЯ
Часто важно включить какую-то информацию о выборке и методах сбора
данных. В профессиональной статье вам придётся обсуждать эти вопросы детально,
но даже в статье, предназначенной для неспециалистов, вам, скорее всего,
захочется поделиться информацией о размере выборки, методе отбора объектов и способе
сбора данных. Если ваша статистика была посчитана на удобной выборке, равной
20, и если данные целиком основаны на персональном опросе этих людей (то есть
данные получены непосредственно от самих людей, а не какими-то косвенными
способами), об этом нужно четко заявить, для того чтобы читатель мог
использовать эту информацию при оценке значимости ваших результатов.
Ссылаясь на пропорции, необходимо включать и основу отсчёта, то есть
информацию о том, что опасные преступления в городе Л участились вдвое, можно
толковать как увеличение от 1 до 2 случаев, а можно - как от 500 до 1000. Оба
примера представляют удвоение, но выводы, по сути, совершенно разные.
Возможности неверного толкования и непонимания при указании только процентов
без базовых показателей даже шире, чем при рассмотрении объектов разных
размеров. Если сообщается, что в городе Б уровень преступности повысился на 25%,
а в городе В - только на 15%, вам необходимо дать читателям информацию, что в
городе Б проживает 300 человек и в нём зафиксировано 4 опасных преступления
за прошлый год, а в городе В 3 миллиона жителей и там отмечено 50 000 таких
преступлений за тот же период.
Если приводятся данные опроса, полезно включать подлинный текст
некоторых или всех вопросов, особенно если перечень короткий. Но даже тогда, когда
невозможно дословное изложение всех вопросов, следует, по крайней мере, дать
ясное представление об общем положении дел. Например, желательно, чтобы в
опрос, касающийся потребления лекарств, включался ряд уточняющих разделов
типа применение лекарств в течение всей жизни, в последние годы, в последние
30 дней или применение время от времени, и каждая такая область должна
содержать в качестве результата разный процент людей, являющихся потребителями
лекарств.
Написание профессиональной статьи
В определённом смысле технически написать такую статью легче всего, поскольку
формат и аудитория абсолютно ясны. Специалисты быстро овладевают стилем
научно-технических изданий, наиболее известных в своей области, поэтому эти
замечания больше ориентированы на студентов и молодых исследователей,
работающих над своими первыми статьями. По умолчанию подразумевается, что при
написании следует использовать все доступные ресурсы, включая помощь ваших
профессоров и кураторов, руководящие указания издания, в котором вы
намереваетесь публиковать вашу работу, указания этого издания для рецензентов
(иногда такие материалы доступны на сайтах журналов) и статьи, опубликованные
ранее в этом журнале. Часто университеты и исследовательские организации имеют
журнальные клубы с целью помочь своим студентам и персоналу держать руку на
пульсе текущих исследований, и, без сомнения, вы должны воспользоваться таки-
шимшш:
Глава 19. Представление статистических материалов
ми возможностями, если они имеются в наличии (презентации в журнальных
клубах будут обсуждаться в главе 20). Ориентация среди основных научных изданий
в области вашей работы, равно как и в исследованиях, которые они публикуют,
является весьма полезным залогом продолжения научной карьеры начинающего
учёного.
Безусловной отправной точкой написания статьи является то, что вам есть
что сказать - нечто важное, что может заинтересовать других в вашей области
исследований. Для того чтобы иметь это «нечто», необходимо быть в курсе всех
проблем и дискуссий в этом направлении, обладать знаниями, почерпнутыми из
литературы, и взаимодействовать с вашими наставниками и кураторами.
Подобные знания помогут также выбрать целевой журнал для публикации. В
большинстве научно-технических дисциплин имеется чёткая иерархия журналов, и нужно
выбрать один, который публикует статьи, соответствующие теме именно вашей
работы. К тому же следует подумать о качестве и относительном рейтинге
избранного издания, потому что вы изначально заинтересованы в широкой аудитории
и воздействии вашей работы на то, что происходит в этой области исследований.
Следует оценить влиятельность этого журнала, средний индекс цитирования в
данном журнале за предыдущие два года - чем выше такой индекс, тем выше
показатель влияния. Выбор журнала может потребовать некоторой негласной
информации, которую могут дать более опытные коллеги и которая, собственно, есть
процесс проб и ошибок. Не будет выглядеть необычной и отсылка статьи в журнал
более широкого профиля, при этом держа в уме возможную переадресацию в
другие журналы, если более престижные издания не примут вашу работу.
Написание статьи
Очевидно, что написание статьи в определённый журнал означает следование
формату этого журнала. К счастью, несмотря на то что существует масса
научных журналов, имеется также много общего в используемых стилях, ибо стиль
есть средство достижения общей цели, заключающейся в содействии доведения
результатов ваших изысканий до аудитории специалистов.
У многих журналов имеется строгий формат написания статей, который
определяет основные части статьи, их порядок и формат для ссылок (сносок,
заключительных комментариев и библиографии). Многие из тех, кто занимается наукой,
используют программное обеспечение (такое, к примеру, как менеджер ссылок
EndNote и его аналоги) для организации поиска ссылок, комментариев и
литературы, поскольку это облегчает изменение формата цитирования, если статья была
отвергнута одним журналом и требуется подать её в другой, использующий иной
формат. Кроме того, обычно журналы также дают правила стиля самого текста
статьи. Например, когда число следует писать словом (один), а когда цифрами (1),
когда использовать активный или пассивный залог. Большинство пишущих
придерживается одного из общепринятых стилей, которые диктуют подобные
правила. Общепринятые стили, в частности, включают правила, установленные АРА
(American Psychological Association, Американская ассоциация психологов),
Chicago/Turabian (метод выборки цитирования Чикаго/книга Кэти Турабьян по
Общие замечания
¦¦ЕШ
стилю научных статей), АР (Associated Press, издательство Ассошиэйтед Пресс)
и ICJME (International Committee of Medical Journal Editors, Международный
комитет издателей медицинских журналов). Задача в том, чтобы найти описание
стиля журнала, в который вы подаёте статью, и следовать ему.
Профессиональные научные статьи обычно включают следующие разделы
(хотя и под разными наименованиями):
Реферат или краткое изложение (Abstract)
Это краткое резюме ваших исследований и выводов, обычно ограниченное
размером (например, 250 слов), который устанавливает журнал. Вероятнее
всего, этот раздел вашей статьи будет прочитан в первую очередь, поэтому
важно, чтобы он был лаконичен и захватывал внимание читателя. Этот
раздел нужен вам для того, чтобы убедить аудиторию, что вы преподносите ей
нечто важное и предлагаете ваши основные результаты.
Введение/Обзор литературы (Background/literature review)
Этот раздел анализирует текущее состояние знаний в области
исследования и устанавливает уровень вашего собственного вклада. Конечно, можно
повеситься, пытаясь прочесть всё когда-либо написанное по вашей теме, и
никогда не написать своей статьи. Во избежание того и другого примите
помощь ваших консультантов, наставников и/или коллег, которые помогут
вам найти нечто среднее.
Методы (Methods)
Эта часть статьи объясняет, что вы делали в своём исследовании, включая
такие детали, как исследуемая выборка и применённый инструментарий.
Часто читатель вскользь просматривает этот раздел, чтобы определиться,
представляет ли изложенное в статье какой-то интерес для него, посему
убедитесь, что этот раздел отвечает всем важным вопросам, касающимся
того, как именно вы проводили это исследование.
Результаты (Results)
Этот раздел представляет, что конкретно вы нашли после проведения
исследования, включая результаты всех проведённых статистических тестов.
После реферата это, скорее всего, наиболее важная часть статьи в смысле
доведения до читателей значимости вашей работы. Читатель в основном
хочет знать, что, собственно, вы нашли нового в предлагаемом
исследовании.
Обсуждение (Discussion)
Здесь вы объясняете полученные результаты в контексте других
исследований, обсуждаете границы применения (возможно, ваша выборка
представляет только один географический регион или ограничена только теми
людьми, для которых английский является родным) и предлагаете
дальнейшие пути развития темы.
Как правило, каждый раздел (и возможные подразделы внутри него) узнаётся
по заголовкам. Этот стандартный элемент стиля помогает в передаче информации,
ЕШНН
Глава 19. Представление статистических материалов
имея в виду, что типичный читатель не вычитывает профессиональные
публикации с начала до конца. Вместо этого более распространена практика
просматривать множество статей (или даже просто вступлений к ним), выбирая некоторые
разделы, которые кажутся более значимыми для более или менее внимательного
рассмотрения (возможно, методы и результаты), и, в конце концов, отбирая
несколько разделов для полного прочтения.
Таблицы и графики (см. главу 4) играют ключевую роль во многих научных
работах. Поскольку читатели чаще просматривают введение, методы и
результаты, чтобы уяснить, заинтересует их статья или нет, они могут обратить внимание
и на таблицы и графики, дабы увидеть стоит ли тратить своё драгоценное время
на данный материал. По этой причине если вы собираетесь использовать
таблицы и графики, делать это нужно убедительно. Все таблицы и графики должны
рассказывать некую историю и должны иметь самодостаточные подписи (то есть
читатель не должен рыскать по всему тексту, выискивая, что означает та или иная
таблица или график).
Процесс рецензирования
У каждого журнала свой алгоритм работы с авторами, и если вам повезёт, этот
процесс может быть объяснён на сайте журнала. В основном процесс рецензирования
проходит примерно так:
1. Вы посылаете статью (сегодня это делается с помощью электронной почты).
2. Редактор и/или несколько добровольцев-рецензентов (обычно таких же
профессионалов в данной области) читают статью и отвечают с одной из
ниже приведенных формулировок решения:
• принимается (с некоторыми поправками или без таковых);
• требуется переработать и подать заново;
• отказать.
3. Ваша реакция: праздновать принятие, делать соответствующие поправки и
подавать заново или подавать в другой журнал.
В большинстве журналов очень редко принимают статью в первоначальном
виде, то есть без правки. Некоторые статьи, принятые к публикации, требуют
незначительной переработки, но даже если статья принимается без замечаний, стоит
ожидать обоюдных бесед, в наши дни главным образом по электронной почте,
касающихся требований редакции.
Отзыв редакции типа «переработать и подать заново» - дело обычное и не
может служить основанием для разочарования, так как это означает, что статья
понравилась рецензентам и они просто хотят поработать с вами, для того чтобы
сделать статью более приемлемой для публикации в данном журнале.
Большинство рецензентов искренне хочет помочь вам улучшить качество статьи, поэтому
нужно весьма серьёзно относиться к их предложениям. Обычно после
доработки статьи вы вновь отсылаете её вместе с сопроводительным письмом, в котором
указываете, как именно вы отреагировали на каждое предложение рецензентов.
Общие замечания
ННЕШ!
Если же у вас есть причина не следовать какому-либо совету редакции, будьте
любезны пояснить это в вашем ответе. Совсем не обязательно следовать всему тому,
что говорят рецензенты, но оставлять без ответа их замечания означает для них,
что или вы невнимательно читали их комментарии, или просто проигнорировали
их - ни то, ни другое не является правильным, если вы хотите, чтобы ваша статья
появилась в журнале.
Иногда статья никогда не попадает под рецензию - много журналов
практикуют систему, в которой редактор собственной персоной определяет, находится
ли статья в рамках его журнала, и примерно оценивает её качество, решая,
стоит ли посылать её на рецензию или нет. Если он всё же решит послать статью на
рецензирование, то, скорее всего, рецензенты порекомендуют отвергнуть её. Но
даже если это произойдёт, вы можете послать её в другой журнал (если только не
решите, основываясь на выводах рецензентов, просто отказаться от публикации).
Но даже если статья посылается в другой журнал, следует учесть комментарии
рецензентов: возможно, вы захотите отреагировать на некоторые из них для
усиления статьи перед отсылкой в другой журнал. С другой стороны, вы можете не
захотеть слишком угождать одной небольшой группе рецензентов ради отсылки
материала другой кучке рецензентов. Нет никакой гарантии, что эта вторая кучка
согласится с мнением первой, и вам не придётся переделывать некоторые
произведенные изменения вторично для другого журнала.
Процесс рецензирования может разочаровать, особенно если вы сталкиваетесь
с ним впервые. Нельзя отрицать, что некоторые рецензенты трудны в общении
и/или несправедливы, а иногда в этот процесс вмешивается политика, но если на
карту поставлена научная карьера, вам придётся научиться работать по этим
правилам. Мой категорический совет - не принимать близко к сердцу этот процесс,
а вместо этого научиться работать с ним и использовать мудрость ваших старших
коллег, чтобы найти свой путь его прохождения.
Исторически рецензирование анонимно. Тем не менее некоторые журналы,
такие как Публичная научная библиотека (Public Library of Science, PloS),
поощряют открытость этого процесса (в этом случае автор статьи знает имена
рецензентов). В научной среде происходили и продолжаются дискуссии об альтернативах
рецензированию или его реформе, чтобы сделать его более согласованным и менее
спорным, но для большинства журналов подобные изменения где-то в будущем,
если предвидятся вообще.
Написание статьи для широкой аудитории
Статья для более широкой аудитории, для газеты или журнала общего профиля
выдвигает другой набор требований. Вы не станете себя обманывать тем, что в
этом случае большинство читателей знает или интересуется статистикой. Скорее
всего, их интересует предмет статьи (здоровье, экология, образование и так
далее). Это означает, что вам следует высветить в первую очередь результаты и их
практическое применение, нежели детали использованной методологии, а также
то, что нужно ясно объяснить ключевые концепции статистики на повседневном
языке.
ЕШНИГ
Глава 19. Представление статистических материалов
Так же как в случае с профессиональными научными журналами, популярные
издания имеют свои руководящие указания и целевую аудиторию, и, перед тем
как начать писать статью, вы должны знать и то, и другое. Существует ряд поводов
для негодования редакторов, получающих совершенно негодные для публикации
статьи, и это целое искусство - найти подходящую манеру изложения для
соответствующего рынка изданий, но это уже ваша проблема, а не забота редактора, и
подача статьи, не вписывающейся в рамки публикаций, просто означает, что вы не
удосужились прочесть ваш труд перед отсылкой по желаемому адресу.
Те, кто затрагивают технические проблемы в статьях для широкой аудитории,
часто описывают свой труд над статьёй как работу рассказчика. Вы же не хотите
вывалить на читателей массу информации и цифр, нет, вам хочется построить
изложение материала как рассказ, охватывающий контекст и передающий важность
того, что вы хотели сказать. Нужно быть избирательным. Нельзя включить весь
поток данных стостраничного исследования работы правительства в один
газетный материал, поэтому ограничьтесь одним или несколькими основными
положениями и организуйте их в некое повествование.
Популярные научные статьи часто полагаются на наглядность образов,
сопровождающую абстрактные понятия (или на реальные картинки и словесные
описания), и такие работы должны использовать повседневный язык с заменой
технических терминов, чтобы среднестатистический читатель легко понял, о чём
идёт речь. Также нужно объяснить читателю важность вашей темы, например,
возможно, новое исследование выявило какой-то существенный риск для
здоровья или обнаружило, что не существует никаких свидетельств того, что некое
социальное явление вообще имеет место. Общим правилом является то, что чем
более неожиданный или противоречивый результат, тем больше времени нужно
уделять его объяснению и тем многочисленнее должны быть свидетельства в его
поддержку.
Написание статьи по заказу организаций
Сообщение или презентация по заказу - штука довольно хитроумная, так как вам
придётся обращаться к весьма смешанной аудиторией в смысле технического и
статистического понимания предмета, а ставки в то же время будут высокими, ну,
например, от результатов, которые вы представите, будет зависеть политика
компании. В таких случаях полезно подумать над созданием как основных положений
для руководства заказчика (ОПР), так и над представлением детального
доклада. В письменной форме ОПР должны быть краткими, содержащими суммарные
результаты более длинного и детального сообщения, должны быть написаны не
техническим языком и включать ключевые моменты более длинного сообщения.
Как следует из определения, ОПР такого рода предназначены для менеджеров
высшего уровня, у которых нет ни времени, ни технической подготовки для анализа
всего материала, но есть необходимость понять информацию, заложенную в этот
материал. Часто такого рода сообщения предлагают не только информацию, но
также и рекомендации или набор предложений лицу, принимающему решения.
Общие замечания
ШШШШМ
При написании ОПР легко понять, как реализуется концепция их создания:
вначале пишут полный доклад, включающий все необходимые детали, а затем
составляют более краткое суммарное сообщение, написанное простым и понятным
языком. Тут вам нужно уметь подкреплять любое своё утверждение данными и
результатами анализа, взятыми из основного доклада. Общие положения
предназначены не для представления новых точек зрения или не подкреплённых общих
рассуждений, но для обощения результатов, заявленных в основном сообщении.
Каким образом концепцию ОПР можно применить к презентациям? Если вас
позвали что-то рассказывать смешанной технической и общей аудитории, вам
следует подумать о двух презентациях: презентации для руководящего состава,
которую можно понять без специальных знаний или с их минимумом, и
презентации со всеми деталями и расчётами, которые захотят получить специалисты.
Фокус в том, что обе презентации нужно делать одновременно. Тогда слайды
должны отображать версию для руководства, возможно, с минимальным количеством
подробностей в виде отступлений и сносок. Но можно подготовить и раздаточный
материал к вашей презентации со всеми подробностями, которые могут
заинтересовать специалистов. Поскольку вы, будучи экспертом в статистике, знаете все
технические детали вашего проекта, подготовка такой двухуровневой
презентации не потребует много дополнительных временных затрат.
Обращаясь к смешанной аудитории, вы также должны быть готовы объяснять
технические нюансы по каждому ключевому моменту (почему выбран такой
именно статистический тест или как можно интерпретировать результат?) таким
образом, чтобы как слушатели-неспециалисты, так и коллеги-статистики смогли
понять суть. Ничто так быстро не разрушает доверия к вам, как неспособность
объяснить важные моменты презентации, и аудитория быстро станет
нетерпеливой, если вы не сможете общаться с ней на её языке.
ГЛАВА 20.
Оценка работ по статистике
других авторов
В этой главе рассказано, как читать и оценивать работы по статистике,
представляемые авторами, включая материалы, содержащиеся в опубликованных статьях
и корпоративных презентациях. Глава начинается с общих рассуждений об
оценке научных статей и затем фокусируется на том, какими методами следует
проводить разбор статей и презентаций и какими общими уловками их авторы
пытаются скрыть слабые места представляемых материалов. В определённом смысле
эта глава имеет самую широкую применимость из всех, представленных в этой
книге, так как даже если вы сами никогда не планировали и не применяли
статистического анализа, вы получаете хорошую возможность понимать статистические
результаты, представляемые другими, как на работе или в учебном заведении, так
и в повседневной жизни просто как гражданин, владеющий информацией.
Оценка статьи в целом
Довольно часто вас просят оценить не только материалы по статистике в статье,
но всю статью в целом. Поначалу это может отпугнуть, особенно если вы
сталкиваетесь с этим впервые, но если этим заниматься систематически, всё становится
легче. Если вы рецензируете статью для какого-то конкретного журнала, должен
существовать набор требований или какая-то иная форма для руководства в
процессе оценки. Если таковых нет, просмотрите другие издания в этой сфере, чтобы
найти такие требования или руководства, которые могут оказаться полезными для
вас, при условии что они существуют. Например, такие материалы есть у
журнала «Профилактика хронических заболеваний» (Preventing Chronic Disease),
выпускаемого Центрами регулирования и профилактики заболеваний (Centers for
Disease Control and Prevention). В этой главе представлены общие рекомендации
по оценке статей в виде вопросов, которыми вы задаётесь при прочтении каждой
части статьи в процессе рецензирования любой научной работы.
Краткое изложение (Реферат) или Введение
Является ли тема исследования интересной и значимой? Достаточно ли
детализированы основные положения (включая результаты статистического
Оценка статьи в целом
¦¦ЕШ
анализа), чтобы быть уверенным, что статья базируется на собственном
существенном исследовании автора? Подтверждаются ли утверждения,
заявленные во введении, результатами, изложенными в самой статье? (На
удивление часто не поддерживаются!)
Обзор литературы
Оправдывает ли приведенная литература тему исследования, убеждая вас,
что проведенная работа действительно важна и необходима?
Действительно ли даны ссылки на существующие и современные источники? Неплохо
при оценке просмотреть старые статьи на эту же тему, особенно если они
считаются классическими в этой области; при этом отсутствие материалов
нескольких последних лет наводит на мысль, что рассматриваемая статья
некоторое время пролежала в столе (то есть была написана, но не
опубликована). Недостаточное использование текущих материалов может
свидетельствовать о том, что тема исследования уже не является важной для
этой области или что указанная литература вытащена из старой работы и
не обновлена.
Построение исследования
Какая схема применена - наблюдение, псевдоэкспериментальная,
экспериментальная? Какие специальные методы использованы - ANOVA, линейная
регрессия, факторный анализ и т. п.? Соответствует ли план исследования
приведенным данным и заявленной теме? Можно ли было построить
исследование более удачным способом? Ясно ли представлены гипотезы?
Данные
Понятно ли, каким образом была получена выборка и зачем? Достаточно ли
ясно описаны процессы сбора данных, их обработки и анализа? Не видите
ли вы подозрительных моментов, таких, например, как разный размер
выборок при использовании разных видов анализа, которые адекватно не
освещаются в статье? Соответствуют ли взятые данные теме исследования?
Результаты и выводы
Достаточно ли ясно описаны результаты и насколько они соответствуют
заявленным допущениям? Действительно ли результаты соответствуют
сделанным выводам? Обоснована ли информация в таблицах и графиках (и не
только для статистических тестов) настолько, что они создают хорошее
впечатление о работе и результатах? Есть ли в тексте возможные неясности и
прорехи, которые следовало бы обсудить, но этого не было сделано? Имеют
ли результаты практическую и статистическую ценность? Достаточно ли
чётко очерчены рамки применимости данного исследования?
Есть вероятность оказаться слишком критичным - мы ведь живём в реальном
мире, в конце концов, и не хотим, чтобы лучшее было врагом хорошего, не говоря
уже об идеальном. При оценке исследования важно также понимать, какие
стандарты существуют в выбранной специальной области, и ваши более умудрённые
опытом коллеги прекрасно помогут вам в этом.
ЩIBI: ¦¦! Глава 20. Оценка работ по статистике других авторов
Ошибки в применении статистики
В широком понимании неправильное применение статистики можно разделить на
две явные категории: основанное на незнании и преднамеренное. Неверное
применение статистики в результате незнания возникает тогда, когда автор пытается
использовать для подкрепления доводов описательный или логический подход к статистике,
но техника, тесты и/или методология этому не соответствуют. Преднамеренное
манипулирование статистикой появляется тогда, когда пытаются скрыть, затуманить или
неверно истолковать полученные результаты. Интуитивно можно предположить, что
незнание в большинстве случаев проявляется при работе с такими сложными
процедурами, как многомерный анализ (и это, безусловно, так), но оказывается, что даже
базовые описательные статистические процедуры тоже применяются неправильно.
Намеренное искажение также является подводным камнем в описательной
статистике, начиная с вводящих в заблуждение осей графиков до игнорирования внутренних
допущений тестов с целью подогнать результаты под значимые.
В этой главе некоторые примеры взяты из современной дискуссии вокруг
изменения климата и глобального потепления, потому что настроение людей по этому
поводу резко меняется во многих странах в последние годы. Но цель состоит не в
том, чтобы убедить в правильности того или иного мнения, касающегося климата,
а просто дать реальные примеры некоторых трудностей проведения
статистических исследований, их толкования и передачи результатов другим людям.
Общие проблемы
Если вам дали набор безупречных статистических результатов, которые должны
доказать или подтвердить некие доводы, теорию или предложение, начните с
нижеприведенного вопросника, чтобы начать задавать нелицеприятные вопросы:
Репрезентативность выборки
Если исследователь пытается делать статистические выводы о
совокупности, используя некую выборку, то каким образом она была получена?
Действительно ли эта выборка случайна? Были ли сомнительные
моменты в процессе выбора объектов? Результаты любого статистического теста
будут обоснованными, если выборка на самом деле хорошо представляет
совокупность, к которой автор пытается применить логику. В отдельных
случаях выборки могут искусственно создаваться так, чтобы доказать
какое-то ложное утверждение. С другой стороны, возможно искажение из-за
добровольцев, если кто-то соглашается участвовать в выборке, а кто-то нет.
Для того чтобы статистические выводы о совокупности заслуживали
доверия, выборка должна быть реально репрезентативной с исключением всех
возможных двусмысленностей.
Искажения при опросе
Если данные собираются путём опроса или интервью, как были составлены
вопросы и как собирались ответы? Принимайте во внимание не только воз-
Общие проблемы J^B^I
можность «силового» опроса (то есть опроса, истинная цель которого - не
получение информации, а влияние на мнение опрашиваемых), но также и
необъективность распространенного желания нравиться (то есть тенденцию
опрашиваемых давать ответы, которые, по их мнению, опрашивающий
желает услышать и/или которые создают лучшее впечатление о них самих).
Сознательные искажения
Представляет ли автор свои доводы и утверждения в объективной и
нейтральной манере или налицо намерение обосновать результат любой
ценой?
Отсев данных и отказы
Каким образом отсеянные данные принимаются во внимание при анализе?
Если участники опроса выбирались случайно, но некоторые из них
отказывались от участия, как они учитывались в анализе? Как автор работал с
этим «истончением» данных?
Размер выборки
Достаточно ли велики размеры принятой выборки для исключения нулевой
гипотезы? Настолько ли велики размеры выборки, чтобы отвергнуть
практически любую нулевую гипотезу? Выбран ли размер выборки на основе
расчётов мощностей?
Эффективность результатов
Если результат статистически значимый, указана ли величина эффекта?
Если нет, то как устанавливается степень важности результата? Имеет ли
результат смысл в контексте исследуемого явления?
Параметрические тесты
Используются ли в анализе параметрические тесты, в то время как
целесообразнее было бы использовать непараметрические?
Выбор тестов
Правильно ли подобран статистический тест для шкалы измерения
переменных? Для измерения комбинации различных зависимых и
независимых номинативных, порядковых, интервальных и характеризующих
отношения переменных используются разные статистические техники.
Связи и случайность
Является ли единственным свидетельством причинно-следственного
взаимодействия только мера связи между переменными, например
корреляция? Если так, то некорректно заявлять о причинности связи, даже если
переменная названа зависимой от независимой переменной.
Обучение и тестовая выборка
Применяется ли при разработке модели тот же набор данных, который
используется и при тестировании? Если так, то существуют ли какие-то
основания предполагать, что эта модель не будет работать так же хорошо с
другим набором данных? Эта проблема типична для задач распознавания
образов.
ЩЩ/l i ! Глава 20. Оценка работ по статистике других авторов
Операционализация
Действительно ли переменная, взятая для измерения некого отдельно
взятого явления, измеряет его? Если нет, то разумна ли в этом случае
операционализация этого явления? Это общая проблема в психологии, когда
скрытые переменные, такие как развитость интеллекта, измеряются
косвенно путём проведения разных когнитивных тестов.
Допущения
Подтвердились ли допущения, лежащие в основе достоверности теста?
Каким образом исследователь убеждается, что его предположения
верны? Например, если тест предполагает, что совокупность распределена
нормально, а на самом деле является бимодальной, результаты теста не
будут иметь смысла.
Тестирование нулевой гипотезы
Чтобы определить, взяты ли две группы из одной и той же совокупности
или из разных совокупностей, общепринято проверять нулевую гипотезу,
что группы взяты из одной совокупности. Такая практика исходит из основ
научной методологии, в которой теории подкрепляются многочисленными
надёжными тестами отвергнутых нулевых гипотез скорее, чем
использование более прямолинейного (что очевидно) подхода, заключающегося в
проверке непосредственно самой гипотезы. Опасайтесь попыток в любой
части исследования доказать теорию одним-единственным
экспериментом.
Применение слепого метода
Были ли в исследовании использованы слепой, двойной или тройной
слепой методы? Например, не могли ли участники или исследователи
вставить некие сомнительные данные, заранее зная об условиях проведения и
проверки эксперимента?
Проверка
Медицина: соответствует ли эффект лечения, демонстрируемый в
предварительной или окончательной моделях лечения, проверкам с введением
плацебо в ту же парадигму эксперимента для контроля эффекта плацебо?
Спланированный эксперимент является наилучшим (некоторые могут
сказать - единственным) способом получения надёжных логических выводов из
имеющихся данных.
Быстрая проверка
Структура исследований, использующих статистику, на удивление однообразна.
Если вы рецензируете какую-то работу, попытайтесь определить
последовательность событий в процессе проведения исследования. Начинали ли исследователи
свою работу с одной гипотезы, а затем поменяли точку зрения после получения
результатов? Применялось ли множество тестов с последующими поправками post
hoc (то есть по результатам), чтобы убедиться, что их материалы могут дать значи-
Быстрая проверка
ШШ1Ш
мый, подтверждённый проверками результат? Не распределяются ли результаты
одного исследования на несколько статей с целью продлить и усилить значимость
вклада авторов? Прощупывание статьи серьёзными вопросами подобно работе
детектива, опрашивающего субъекта о перемещениях в определённый день и час:
несовпадения и смена легенд легко выводят на чистую воду!
Исследования, использующие статистику, желательно проводить в
соответствии с нижеприведенными общими правилами:
• Предполагая, что началу исследования предшествует период наблюдений и
изучения, задачи работы должны быть заявлены в первую очередь.
Исследователи должны иметь сформулированные гипотезы (а также
соответствующие нулевые гипотезы) задолго до начала сбора данных. В противном случае
проверка гипотез окажется несостоятельной, а само исследование приобретёт
оттенок «выуживания результатов». Известно, чтор = 0,05 представляет
вероятность 1 к 20 совершения ошибки первого рода, и поскольку ежегодно в
научных журналах публикуются тысячи работ с подобными утверждениями,
множество противоречащих этому «фактов» могут без колебаний вызывать
вопросы. Это тот самый случай, когда независимая повторяемость и
надёжность чрезвычайно важны для целостности научного подхода.
• Необходимо отчётливо представлять связь между рассматриваемой
совокупностью и сделанной выборкой. Статистические выводы о всей
совокупности людей на основе выборки из высокообразованных, здоровых,
принадлежащих к среднему классу студентов колледжей со всей очевидностью
неприемлемы.
• Гипотезы должны быть связаны с влиянием конкретных независимых
переменных (предиктор) на зависимые переменные (итог). Таким образом,
очень важно знать как можно больше о зависимых переменных, особенно
любую причину их изменений. Это наиболее важно, когда подразумевается
или известно, что зависимые переменные должны быть высокоскоррелиро-
ванными (т. е. присутствует мультиколлинеарность). Зависимые
переменные должны быть измеряемы и полностью операционализировать
принятые концепции.
• В сложных проектах, где учитываются как основные воздействия, так и
взаимодействия, желательно рассматривать все возможные сочетания этих
действий.
• Процессы случайных выборок и работа с выпавшими данными и отказами
должны формализовываться на ранних стадиях, чтобы предотвратить рост
искажений. Помните, что подлинно репрезентативная выборка должна
быть действительно случайной. Если получить абсолютно
рандомизированную выборку не удается, вполне возможно идентифицировать
отдельные группы и произвести выборку в пропорции к частоте этих групп в
общей совокупности. Если же случайная выборка не используется (а это
часто именно так), то это ограничение должно быть обосновано, и на него
следует обратить внимание.
ЕШМН
Глава 20. Оценка работ по статистике других авторов
• Для проверки должен отбираться самый простой тест из возможных, то
есть такой простой тест, который тем не менее позволяет исследовать
рассматриваемые выводы. Безусловно, техники многомерного анализа
невероятно важны, но если нужно провести простое сравнение, они могут быть
просто не уместны.
• Тесты следует выбирать, основываясь на известных или ожидаемых
характеристиках данных.
• В идеале в работе должен быть освещен каждый полученный результат,
даже если исследование не подтвердило его статистическую значимость.
Отказ от этого ведёт к систематическим ошибкам в публикациях
(publication bias), в которых обнародуются только значимые результаты, рисуя
ошибочную картину существующего уровня знаний. Не бойтесь писать
об отклонениях, несущественных результатах проверки или о неудачных
попытках тестирования нулевых гипотез - не всякий эксперимент должен
заканчиваться существенным научным результатом!
Ошибка публикаций и график-воронка
Легко впасть в наивное заблуждение, что научные публикации в самом деле
отображают правильную картину нашего коллективного знания в любой научной области. Если
провести серьёзный анализ литературы и найти четыре статьи, доказывающие
эффективность какого-либо лекарства, и ни одной статьи, опровергающей эту эффективность,
это как будто свидетельствует о том, что данный препарат действительно работает, не
так ли? К сожалению, это не всегда соответствует действительности. Причиной
является систематическая ошибка в литературе, вызванная публикацией материалов в угоду
характеру и направленности тематики исследований, иначе называемой «проблемой
сброса в стол» (file drawer problem), то есть тенденции публиковать только статистически
значимые результаты, а статьи без таковых оставлять неопубликованными (складывать
в столе). Существуют и другие подвохи, влияющие на общую картину, получаемую из
опубликованных исследований. Например, литература на английском может быть более
доступна, чем не менее, а иногда и более, достойные внимания статьи на других языках,
что, скорее всего, исключает их частое цитирование в других публикациях. (Индекс
цитирования иногда используется для оценки важности статей или их влияния.)
Одним из путей выявления ошибки публикаций является создание так называемого
графика-воронки, в котором каждая точка представляет опубликованную работу и
горизонтальная ось - это логарифм отношения частот (log odds ratio) статьи, а
вертикальная - стандартная ошибка. Если ошибки публикаций нет, то следует ожидать картину,
похожую на перевёрнутую воронку, как показано на рис. 20.1.
Отметим, что в работах с большей стандартной ошибкой (то есть с меньшей точностью
исследования) выявляется большая вариативность результатов (шире область
значений логарифма отношения частот), в то время как для более аккуратных исследований
кластеры этого логарифма ближе к единственному значению. Заметим также, что этот
график в основном симметричен, тем самым показывая, что публиковались работы с
положительными, отрицательными и несущественными результатами. График-воронка, в
общей форме представленный на рис. 20.1, показывает, что ошибка публикации не столь
важна в данной конкретной области исследований.
График-воронка на рис. 20.2, напротив, указывает на наличие ошибки публикаций -
почти половина воронки пуста, так как мало работ с нейтральным или негативным
результатом. Этот график сам по себе не доказывает наличия ошибки публикаций
(некоторые другие возможности содержатся в документе Кохрановского «Сотрудничества»,
процитированного в приложении С), но он вполне предполагает её возможность.
Спорные вопросы планирования исследования
¦¦ЕШ
ф
ф
ф
ф
-10 12 3
Логарифм отношения частот
Рис. 20.1. График-воронка, предполагающий небольшую ошибку публикаций
или её отсутствие
0.0
I °-5
(0
X
н
о.
d 1.5
Стан
2.0
•
¦>
Ф
Ф ф
ф
Ф
ф Ф
• •
-10 12
Логарифм отношения частот
3
Рис. 20.2. График-воронка, предполагающий наличие ошибки публикаций
Спорные вопросы планирования
исследования
Если в итоге мы хотим получить какие-нибудь осмысленные выводы, то обычно
планирование исследования по интересующей нас тематике требует соблюдения
определённых инструкций, представленных в главе 18. Тем не менее значительная
часть исследователей полностью игнорирует эти руководящие указания, особенно
в случаях, когда работа предназначена для статей, основанных на сенсационных
заголовках для привлечения внимания читателя или обозревателя. Но даже если
о.о
0.5
1.5
2.0
ф Ф
Ш1ШШ
Глава 20. Оценка работ по статистике других авторов
нужные процедуры соблюдены и получены достоверные результаты, смысл этих
результатов можно исказить, если сообщение в новостях преподаст публике то,
что относится к одному отдельно взятому исследованию, как фундаментальный
сдвиг в знаниях.
Дисперсия
Знание дисперсии существенно для всех систем. Дисперсия может происходить из
реально признанных источников (действительные изменения в структуре
населения), равно как и вследствие ошибок измерения. Изменчивость может быть
цикличной, так что исследования, выполненные в отдельный момент времени, могут
не всегда выявлять локальные минимумы системы. В климатических системах,
к примеру, изменения температуры главным образом происходят благодаря
промышленной революции и соответствующему увеличению выпуска парниковых
газов, поэтому как можно отличить дисперсию вследствие нормальных
циклических явлений от тех, которые могут быть отнесены непосредственно к деятельности
человека? И это одна из критических проблем, с которыми сталкивается наука
об окружающем пространстве, ибо наша атмосфера реально потеплела со
времени последнего ледникового периода безо всякого вмешательства людей ещё до
промышленной революции. Идея заключается в том, что вопросы изменчивости
необходимо обсуждать в научных статьях, помещая результаты в контекст
ожидаемой естественной изменчивости.
Генеральная совокупность
При определении генеральной совокупности важен контекст для уточнения
границ применения логических выводов из отдельно взятой работы. Если все члены
совокупности каким-то образом измерены и отсутствуют отсев данных и отказы,
статистика вообще не нужна, потому что можно вычислить необходимые
параметры без ухищрений. Однако такая ситуация в исследованиях встречается редко.
Частью проблемы определения совокупности является некое фундаментальное
непонимание природы исследуемой совокупности. Представьте, что некий опрос
проводился в штате Юта, а результаты экстраполированы на население штата
Калифорния, или опрос проводился в Италии, но применён к Дании. Это может
показаться нормальным, так как в первом случае оба штата не только находятся в
одной стране, но и географически расположены сравнительно близко, а во втором
оба объекта находятся в Западной Европе. И всё-таки в каждом случае имеется
много различий: размеры и разнообразие экономик, этнический и расовый состав
населения и т. д., поэтому бремя создания работы, в которой такие обобщения
оправданы, ложится на исследователя.
Создание выборки
Существуют два ключевых аспекта создания выборки: размер и рандомизация.
Достоверная репрезентативная выборка должна быть достаточно большой и
основанной на принципе случайности, то есть рандомизированной, чтобы обеспе-
Спорные вопросы планирования исследования
ШШША
чить точную оценку (статистическую) всех параметров совокупности. Получение
достаточной большой выборки, которая адекватно характеризует генеральную
совокупность, - трудная задача, вычисления статистической мощности
(обсуждается в главе 15) определенно предоставляют возможности для этого - в терминах
статистических тестов, - однако более хитроумные схемы сбора данных являются
попыткой обнаружить все источники изменчивости в генеральной совокупности,
которые могут вызвать смещение результатов, и отобрать объекты с учетом этого
факта. Планирование рандомизированной выборки - это лучший способ избежать
многочисленных типов ошибок при отборе, но это не всегда удаётся осуществить.
Статья всегда должна описывать, как создавалась выборка, и обсуждать
последствия применения нерандомизированной выборки.
Проверка
В одной из недавних статей было показано, что назначение антидепрессантов
многим участникам клинического эксперимента оказалось не более
эффективным, чем использование плацебо. То есть ожидание эффекта от лечения в итоге
вылилось в одинаковое снятие депрессивной симптоматики как при применении
плацебо, так и при использовании таблеток с активным ингредиентом. Эффект
плацебо у людей развит чрезвычайно сильно, и большинство исследований
обязано обеспечивать какую-то ясную проверку, когда они стремятся
продемонстрировать воздействие лечения. В медицине и фармацевтике такие методы уже хорошо
работают. Когда создание контрольных групп невозможно (например, при
моделировании климата), статья должна по возможности предоставить определённого
рода контекст для приведенных результатов (исторические данные, результаты
других исследований).
Сила совпадений
Если статистическая значимость выражается какр = 0,01 илир = 0,05, это
означает, что существует вероятность 1 к 100 или 1 к 20, соответственно, совершения
ошибки первого рода. Тогда если р = 0,05, повторение эксперимента приведёт к
ситуации, когда 19 из 20 событий окажутся значимыми, а 1 событие из 20 -
незначимым. Вот почему независимые повторности и воспроизводимость
эксперимента столь важны. К тому же мир полон совпадений, а эксперименты несут в
себе ошибки измерений. Взаимодействие совпадений и ошибок измерений могут
привести к совершенно дурацким и неожиданно «значимым» открытиям,
которые на самом деле невозможно связать с реальными закономерностями при всём
желании. Представим на минуту, что вокруг солнца вращается двадцать планет
Земля, и вы выбираете для исследования глобального потепления одну из них.
Вы обнаруживаете корреляцию между повышением промышленной активности
и температурой за последние 200 лет. Поскольку вам известно, что существует
вероятность 1 к 20 совершения ошибки первого рода, вы, скорее всего, проверите
несколько других планет или проведёте эксперимент на всех из них и с половиной,
выступающей в качестве контроля для остальных.
ЕНЯ1
Глава 20. Оценка работ по статистике других авторов
Вы понимаете, что трудность тут заключается в понимании причин
глобального потепления. У вас нет никаких других 19 планет, на которых можно было бы
поэкспериментировать или проверить вашу модель, но в то же время вы знаете, что
вероятность совершения ошибки I рода весьма велика. Такая же проблема
возникает при определении эпицентров заболеваний: например, имеется наблюдение,
что некоторые виды заболеваний часто встречаются в некоторых географических
регионах, при этом жители этих регионов в качестве причины подозревают
влияние окружающей среды. Однако такой тип аргументации чувствителен к фокусам
типа хитрой стрельбы по мишени, когда вы сначала стреляете, а потом подносите
цель к месту, куда попала пуля; идея состоит в том, что географический регион
распространения болезни определён после того, как эпицентр заболевания уже
замечен. Кроме того, чисто случайно в некоторых городах, регионах и т. д. могут
часто встречаться определенные заболевания по тем же причинам, как при
подбрасывании монеты время от времени могут подряд выпадать орёл или решка.
Суть в том, что всегда следует быть начеку с исследованиями, которые
пытаются основываться на случайности, особенно если результаты работы противоречат
тому, что известно из других, более правильно спланированных исследований.
Описательная статистика
Правильная интерпретация статистических тестов сложна и уязвима для
ошибок. В то же время применение описательной статистики, в свою очередь, имеет
шокирующую потенциальную способность генерировать ошибочное понимание
и аргументацию. Некоторые из таких ошибок вызваны преднамеренными
попытками ввести в заблуждение и увести в сторону. Другие - просто результат плохого
выбора. В этом разделе вы узнаете о некоторых общих проблемах, связанных с
описательной статистикой, особенно с выбором меры центральной тенденции и
графической информации.
Показатели центральной тенденции
Вопрос выбора соответствующей меры центральной тенденции возникает всегда,
когда распределение данных отличается от нормального, и чем экстремальнее
отклонение (особенно вследствие наличия выбросов в данных), тем более важным
становится выбор. В правоассиметричных совокупностях (то есть в генеральных
совокупностях с относительно малым числом высоких значений) среднее
арифметическое будет выше медианы, и если значения выбросов существенно выше
значений остальной генеральной совокупности, среднее арифметическое в качестве
показателя центральной тенденции может вводить в заблуждение. В этом кроется
причина того, почему информация о размерах дохода или стоимости
недвижимости обычно представляется медианами, а не средними значениями - наличие
нескольких очень богатых людей или нескольких очень дорогих зданий внутри
совокупности может исказить среднее, не оказывая суидественного влияния на
медиану.
Описательная статистика
ШШШМ
Меры центральной тенденции могут также вводить в заблуждение, если выборка
и/или генеральная совокупность изменяются от одного измерения к другому.
Средняя стоимость домовладений является классическим примером - их цены
основываются исключительно на продажах в течение какого-то периода времени, скажем,
одного года. Вычисленное среднее должно несомненно меняться от года к году, если
только все проданные за год дома не будут перепроданы снова и никаких других
продаж домов не будет. Можно с уверенностью сказать, что такое событие
маловероятно. И всё-таки заинтересованные домовладельцы часто накидывают 10% к
прежней средней цене, намекая таким образом на то, что реальная цена их домов
увеличилась в той же пропорции. Там, где совокупность изменяется сама по себе,
скажем при строительстве и продаже множества новых домов за год, медиана
несомненно увеличится. И тем не менее существующие строения могут продаваться
по той же самой цене, если не меньшей, чем год назад. Более достоверным способом
определения средней цены построек было бы произвести выборку из совокупности
так, чтобы каждый дом имел равный шанс на оценку и входил в выборку. Более
того, поскольку отношение существующих домов к вновь построенным известно,
эту выборку можно впоследствии стратифицировать так, чтобы можно было
указать средние цены домов обоих типов и/или затем их сгруппировать.
Во избежание чрезмерного влияния крайних событий для удаления их из анализа
иногда применяется простое правило. Скажем, события, отличающиеся на два
стандартных отклонения - выше и ниже среднего, - можно опустить перед
статистическими вычислениями, также можно удалить определенную долю данных, например
верхние и нижние 10%, и такая практика называется обрезкой данных (trimming).
Исключение крайних значений из анализа тоже помогает минимизировать влияние
ошибок измерения: например, в экспериментах на время реакции участникам
нередко становится ужасно скучно, и они теряют стимул. Если у компьютерной
программы время отклика равно 2 секундам, а стимул теряется, то стандартное время
реакции порядка 20-80 миллисекунд увеличивается до 2000 миллисекунд, что на
два порядка выше обычной величины. И если от таких наблюдений не избавляться,
то среднее может быть изрядно преувеличено.
Ключевым моментом в этом примере является то, что хотя тут и присутствуют
законные основания для удаления выделяющихся значений, любая правка
выборки авторами после её формирования должна быть доведена до читателя и строго
обоснована. Правильной практикой при рецензировании статей является
отслеживание размеров выборки на протяжении всей статьи: если приведенная
выборка отличается от первоначальной, то дано ли этому резонное объяснение? Если
исследователь удалил какие-то данные, дал ли он ясные объяснения и
обоснования? Был ли произведен анализ чувствительности модели, то есть были ли данные
проанализированы дважды, один раз со всеми значениями и второй - с
исключёнными выбросами, для изучения влияния удаления экстремальных величин?
Стандартная ошибка и доверительные интервалы
В статьях необходимо приводить стандартную ошибку данных, особенно если речь
идет о сравнении среднего для двух групп. Стандартная ошибка - это оценка стан-
Глава 20. Оценка работ по статистике других авторов
дартного отклонения распределения выборки (такого как распределение
выборочного среднего) и, следовательно, оценка изменчивости приведенной статистики.
На практике стандартная ошибка определяется как отношение стандартного
отклонения к корню квадратному из п; следовательно, при всех прочих равных
обстоятельствах стандартная ошибка уменьшается по мере увеличения
размера выборки, а параметры оценки становятся более надёжными. Как правило, в
большинстве областей исследования даётся доверительный интервал для каждой
оценки (например, для среднего), равно как и стандартная ошибка среднего.
Доверительный интервал даёт меру точности оценки, и в статье не просто должны быть
представлены доверительные интервалы, но и обсуждён их смысл. Если
доверительный интервал широкий, это должно быть раскрыто не только с точки зрения
точности рассматриваемого исследования, но и в рамках обобщения результатов.
Графическое представление данных
Графика является доступным способом представления численной информации.
В то же время во многих случаях графики используются не совсем по правилам,
например отсутствуют обозначения осей, смысл которых нельзя правильно
понять, или имеют место манипуляции, предпринимаемые для сокрытия или
улучшения реальных связей между переменными. В научной работе численные
данные должны быть приведены наряду с их графическим представлением, в то время
как в популярных медиа показывают лишь графику, что умножает возможности
для манипуляций.
Старая поговорка «Картинка заменяет тысячу слов» безусловно верна, но
тысяча слов может кардинально изменяться в зависимости от выбора шкалы.
Рисунок 20.3 показывает вымышленный ряд температур, которые повышаются в
пределах от 70 до 77 градусов по Фаренгейту за столетний период. Повышение
температуры почти идеально скоррелировано со временем (г = 0,94); этот факт
может быть либо подчеркнут, либо затушёван в графической презентации.
Рисунок 20.3, конечно же, показывает значительно быстрое линейное повышение.
70 Ф-
69
1940 1950 1960 1970 1980 1990 2000 2010 2020 2030 2040
Рис. 20.3. Повышение температуры за сто лет
Описательная статистика
Однако растягивание горизонтальной оси за счёт сжатия вертикальной
неожиданно создаёт видимый эффект куда более медленного подъёма температуры, как
показано на рис. 20.4.
Рис. 20.4. Повышение температуры за сто лет при растянутой горизонтальной оси
Заметим, что если температурную шкалу настроить на 0 градусов от начала
отсчёта вместо 68, то связь ещё больше сгладится, и визуально обе переменные
станут некоррелированными, как показано на рис. 20.5.
Рис. 20.5. Повышение температуры за сто лет при увеличенном диапазоне
по вертикальной оси
Конечно, если поступить наоборот и растянуть вертикальную ось, то подъём
температуры покажется ещё более существенным (рис. 20.6).
Такие дезориентирующие графики, как на рис. 20.5 и 20.6, редко встречаются в
научных публикациях, но следует быть всегда начеку при попытках ввести
читателя в заблуждение путём странного выбора диапазонов, осей и других фокусов.
К сожалению, подобные трюки часто встречаются в популярной прессе, поэтому
illH: Глава 20. Оценка работ по статистике других авторов
необходимо быть особенно внимательным, работая с графической информацией
из публикаций, предназначенных для широкой читательской аудитории.
Рис. 20.6. Повышение температуры за сто лет при растянутой вертикальной оси
Экстраполяция и тенденции
Общепринятым инструментом в маркетинге является экстраполяция известных
связей между двумя переменными для прогнозирования тенденции вне
измеренного диапазона. Например, если индекс S&P500 (фондовый индекс)
увеличивался на 10 пунктов каждые 10 недель, биржевые игроки могут чувствовать
известную уверенность при совершении сделок, прогнозируя такое же увеличение на
10 пунктов в течение следующей недели. Здесь применение простой линейной
экстраполяции даёт максимально вероятную оценку, но из-за того, что биржа
подвержена множеству случайных изменений, индекс не всегда будет подниматься в
соответствии с предыдущими результатами. Если система нелинейна, линейная
экстраполяция неприменима.
Полезным может оказаться и поиск тенденций, и это тоже обычная практика
во многих областях деятельности. Но когда изучаемая система не является
детерминированной и подвержена случайным или беспорядочным ошибкам, польза от
такого прогноза ограничена, и возможны ужасно нелепые в смысле точности и
несоответствия реальности результаты. Любые прогнозы, предлагаемые в статье,
должны быть тщательно проверены и оправданы, равно как и любые
экстраполяции на области, находящиеся вне рассматриваемого диапазона измеренных
данных.
Логическая статистика
ЕЗ
Логическая статистика
До сих пор вы познакомились с ключевыми проблемами структуры исследований
и описательной статистики, которые часто присутствуют в сообщениях о
проведенных исследованиях. Иногда обман скрывается за неверной презентацией
анализа, а опускание ключевой статистики должно ещё более укрепить ваши
подозрения. В статистике вывода нужно также быть готовым к неправильному или не
соответствующему применению некоторых тестов. Наиболее важной проблемой
является повторяющееся игнорирование многомерных тестов корректности
допущений, в то время как результаты таких тестов чрезвычайно чувствительны к
нарушению допущений. В исследовательской статье следует чётко объяснять, каким
образом соответствующие допущения тестировались и какие меры были
предприняты, если таковые имели место, перед проведением анализа данных.
Статистические тесты допущений
Ниже приведены несколько типичных нарушений распространённых
статистических тестов и механизм тестирования, если допущения были нарушены. Если
статья не рассматривает, как тестируются допущения, у вас должны появиться
сомнения в правильности результатов.
f-тесты
?-тесты для двух выборок предполагают, что эти выборки не связаны между
собой, в противном случае нужно использовать парный t-тест (более подробно
?-тесты обсуждаются в главе 6). «Несвязанные» в данном контексте означают
независимые, то есть выборки можно проверять на линейную независимость,
используя коэффициент корреляции. В то же время проблему может представлять
автокорреляция, если данные собирались в течение некоторого
продолжительного периода времени.
?-тесты подвержены влиянию экстремальных значений, поэтому следует
обращать внимание на то, были ли данные проверены на наличие таких значений, и
если какие-то были найдены, то что с ними делали. Следует отметить, что
удаление выбросов значений на основе надёжных статистических показателей резко
отличается от пренебрежения нежелательными данными, а удаление последних
просто усиливает впечатление неприемлемости результатов.
?-тесты предполагают, что дисперсии двух групп одинаковы (потому что
дисперсии объединены как часть теста), поэтому в статье должны быть ссылки на
использование одного из тестов на однородность дисперсии, какие методы
корректировки были предприняты при необходимости или вместо стандартного
?-теста, был ли задействован тест, не опирающийся на однородность переменных
(например, t-тест Уэлша или непараметрический тест).
Другим допущением при ^-тестировании является нормальность
распределения обеих переменных, при условии что размеры выборок достаточно велики,
чтобы было можно применить центральную предельную теорему. Повторюсь, долж-
КБЯ
Глава 20. Оценка работ по статистике других авторов
ны быть приведены объяснения, каким образом тестировались допущения и, если
нужно, какие меры коррекции применялись.
ANOVA
В ANOVA (см. главы 8 и 9) имеется большое количество допущений, которые
необходимо подтвердить, и всегда нужно прямо указывать, подтверждается
определённое допущение или нет (что лучше, чем призрачные надежды на то, что оно
как-то подтверждается, или игнорирование этого вопроса). ANOVA предполагает
независимость и нормальность распределений, но наиболее важным допущением,
с точки зрения практической перспективы, является равенство дисперсий.
Применение ANOVA будет наиболее надёжным, если исследование
сбалансировано (когда размеры выборок примерно равны); результатом асимметричных
распределений и неодинаковых изменений может быть недостоверность F-Tecra.
Статья, использующая ANOVA, должна объяснять, как тестировались все
допущения и какие меры применялись для коррекции и упорядочивания, если они имели
место.
Линейная регрессия
Линейная регрессия (см. главы 8 и 10) подразумевает независимость ошибок
независимых и зависимых переменных. Это допущение может не выполняться,
если присутствует, предположим, сезонный эффект (скажем, уровень продаж
мороженого в жаркие месяцы будет выше). Желательно, чтобы в статье описывалось,
каким образом тестировалось это допущение (в общем случае это проверяют с
помощью анализа регрессионных остатков) и что было проделано, если было
обнаружено отсутствие независимости ошибок (к примеру, был использован анализ
временных рядов вместо линейной регрессии).
Презентация в журнальном клубе
У многих исследовательских организаций и академических кафедр есть так
называемые журнальные клубы, которые представляют группу людей, регулярно встречающихся
для обсуждения опубликованных работ в своей области науки. Там могут предлагаться
пицца или другие кулинарные изыски для повышения посещаемости. Часто эти встречи
концентрируются на одной или двух статьях, каждую из которых сначала представляют, а
затем она подвергается разбору членами клуба. Как же лучше всего подготовиться, если
подошла ваша очередь представлять свою работу? Без сомнения, вы будете
придерживаться всех принятых правил клуба, и всё-таки ниже даны некоторые советы, которые
могут оказаться полезными:
1. Отберите работу, которую стоит представить коллегам. Помните, что вы отберёте час
или больше времени у своих коллег, а они не менее заняты, чем вы. Начинайте читать
отдельные части других статей в вашей области, а затем выберите одну с
интересной гипотезой, или с хорошей структурой исследования, или с адекватным подбором
данных для получения твёрдого заключения.
2. Прочтите свою статью хотя бы три раза: первый раз, чтобы осмыслить аргументы,
второй раз критически, и третий раз, чтобы выбрать основные моменты, которые вы
хотите подчеркнуть во время презентации. Избегайте соблазна просто пробежаться
по тексту в'порядке изложения материалов. До представления вы должны знать свой
Логическая статистика
¦¦ЕШ
материал настолько хорошо, чтобы спокойно говорить о важных моментах статьи, а
не просто выдавать информацию, напечатанную на страницах.
3. Впишите статью в определённый контекст. Кто ещё работает над этой темой, как
теория в данной статье соотносится с другими статьями в вашей области и т. д.? И ещё
кто спонсирует это исследование и имеются ли какие-нибудь явные конфликты
интересов?
4. Коротко опишите основную терминологию или методы статистики, которые могут
оказаться неизвестными для слушателей, включая, если требуется, разбор того, как
они применяются в статье.
5. Определите временные границы презентации, имея в виду время, отведенное для
доклада, и допустимое время для вопросов и обсуждения. Многие находят полезным
прикинуть время для разных частей сообщения (что-то типа примерного
хронометража), чтобы убедиться, что у вас будет достаточно времени для изложения наиболее
важных моментов исследования.
6. И никак нельзя считать нечестной игрой, если вы попросите коллег, которым вы
доверяете и которые будут на презентации, задать несколько вопросов, оговоренных
заранее, на случай, если начало обсуждения затянется. Это также неплохой путь
направить дискуссию в русло, по которому вы хотели бы проводить обсуждение.
ПРИЛОЖЕНИЕ А.
Обзор основных
математических понятий
Вам не нужно быть асом в математике, чтобы понять статистику, а современные
карманные калькуляторы и компьютерные программы могут выполнить
большую часть монотонной работы за вас. Однако для статистических
умозаключений необходимо хорошо понимать принципы работы с числами, включая
основные арифметические и алгебраические правила. Хотя каждый может научиться
бездумно выполнять вычисления, если вы не понимаете смысла получаемых при
этом чисел, ваши усилия могут быть бесполезными или контрпродуктивными.
Кроме того, всегда интереснее знать, что ты делаешь, и если вы.действительно
понимаете значение полученных чисел и можете объяснить это окружающим, то вы
обнаружите, что имеете большое преимущество перед другими кандидатами, не
важно, в школе или на работе.
Если от математики, которую вы учили в школе, остались только туманные
воспоминания, не волнуйтесь; таких людей много! Даже если вы хорошо успевали по
алгебре в средней школе, краткий обзор основных концепций облегчит ваш путь в
статистику, а проработка нескольких простых упражнений поможет прояснить ум,
перед тем как вы займетесь более сложными вычислениями. Выполнение простых
вычислений - это также хороший способ познакомиться с новым калькулятором
или новой компьютерной программой. Начните с работы над вычислениями, для
которых вы знаете правильный ответ, и вы будете более уверенно использовать
этот метод для решения новых задач.
Мой учитель арифметики говорил нам, что ученики при выполнении
домашних заданий чаще всего делают ошибки в алгебраических вычислениях. Он прав,
причем чаще всего мы ошибаемся, применяя правила, изученные еще в младших
классах средней школы! Тот же принцип работает в статистике; в той математике,
которая вам нужна, нет ничего сложного, по крайней мере на начальном уровне, но
вам нужно очень хорошо владеть материалом, и его нужно освежить в памяти. Вот
поэтому в этом приложении представлен дружественный обзор некоторых
основных математических понятий, который, я надеюсь, уменьшит ваше беспокойство и
освежит воспоминания тех, кто не помнит точно, когда ему приходилось
перемножать экспоненты или рисовать график в декартовых координатах.
Обзор основных математических понятий
¦¦ЕЗ
Если вы хотите проверить, как много вы помните, можете прямо перейти к
задачам в конце этой главы; если вы хорошо справитесь со всеми темами, можете
спокойно пропустить это приложение. С другой стороны, если вы плохо
выполнили эти задания, у вас может появиться желание дополнить материалы из этого
приложения обзором по алгебре, предназначенным для первокурсников. Если вы
поймете, что статистика нравится вам настолько, что вы хотите
специализироваться на ней, со временем вам придется прослушать несколько семестров курса
вычислительной математики или статистических вычислений, но тот уровень
математики находится далеко за пределами приемов, представленных в этой книге.
Арифметические правила
Часто бывает полезно думать о числах как о точках на числовой прямой, на
которой маленькие числа находятся слева, а большие - справа. Вы можете помнить
числовую ось с начальной школы (рис. А.1).
I I I I I I I I I I I I I I I
-6-5-4-3-2-10123456
Рис. А.1. Числовая ось
Идея числовой оси полезна для статистики, поскольку мы часто говорим о
значении в распределении как о «расположенном правее», тогда как на самом деле
мы имеем в виду «более высокое значение». При проверке гипотез вы часто
встретите утверждение, что значение «по меньшей мере, такое же экстремальное» или
«по меньшей мере, так же сильно удалено от среднего», что также отсылает вас к
числовой прямой. Распределения, такие как нормальное распределение,
симметричны, и у них есть единственное наиболее часто встречающееся центральное
значение; по мере удаления от центрального значения (влево или вправо) значения
становятся менее вероятными.
Числа могут иметь положительный или отрицательный знак; если не стоит
никакого знака, подразумевается, что он положительный. Абсолютное значение а
записывается как \а\ и означает расстояние, на которое а отстоит от нуля на
числовой прямой, не важно, в положительную или в отрицательную сторону. Это значит,
что если а = -5 и Ь = 5, их абсолютные значения равны: \с\ = \Ь\ = 5. Иначе говоря,
абсолютное значение числа равно его значению после удаления знака минус, если
он есть. Согласно этому правилу, |-5| больше |4|, хотя и 4 больше (находится правее)
-5, поскольку 5 (абсолютное значение |-5|) больше 4 (абсолютного значения |4|).
При суммировании чисел с одинаковыми знаками сложите их абсолютные
значения, сохраняя знак:
3 + 5 = 8, -3 + -5 = -8.
Складывая два числа с разными знаками, вычтите их абсолютные значения и
оставьте знак большего по модулю числа:
-3 + 5 = 2, 3 + -5--2.
(jjjjj Ц| Щ |v | Приложение А
Для сложения более двух чисел с разными знаками сгруппируйте их по знакам,
сложите абсолютные значения внутри каждой группы, а затем вычтите
отрицательные значения из положительных:
-3 + 5 + -2 + 4 = (5 + 4) - (3 + 2) = 4.
Можно видеть, что прибавление отрицательного значения аналогично
вычитанию отрицательного. Это можно формально выразить в виде следующего
правила:
а - b = а + -Ь.
Так что:
2-5 = 2 + (-5) = -3.
Для умножения чисел с одинаковыми знаками перемножьте их абсолютные
значения. Если все значения положительные, результат будет положительным.
Если все значения отрицательные, подсчитайте число минусов. Если число
минусов четное, результат будет положительным; если нечетное - отрицательным:
4(2) = 8, -4(-2) = 8, -4(-2)(-3) =-24.
Для умножения чисел с разными знаками перемножьте их абсолютные
значения, а затем подсчитайте число минусов; если оно четное, результат
положительный; если нечетное - то отрицательный:
-4(2)(-3) = 24, -4(2)(3) = -24.
При делении чисел с одинаковыми знаками поделите их абсолютные значения,
результат должен быть положительным. При делении чисел с разными знаками
поделите абсолютные значения и сделайте результат отрицательным:
10/5 = 2, -10/-5 = 2, 10/-5 = -.2
Порядок арифметических действий
Обычно мы решаем арифметические выражения слева направо, а арифметические
действия выполняем в следующем порядке1:
1). то, что в скобках;
2). возведение в степень и корни;
3). умножение и деление;
4). сложение и вычитание.
В оригинале указано, что «Многие школьники выучили эту последовательность благодаря
мнемоническому правилу»: «Пожалуйста, простите мою дорогую тетушку Сапли», первые буквы английского
варианта этой фразы «Please excuse my dear aunt Sally» соответствуют первым буквам английских
названий соответствующих арифметических действий: parentheses - скобки, exponents - возведение в
степень, multiply - умножать, divide - делить, add - складывать, subtract - вычитать. Нетрудно
придумать русскоязычный аналог этой фразы, однако, насколько мне известно, в русскоязычном сообществе
этот мнемонический прием не используется. - Прим. пер.
Обзор основных математических понятий ?.¦:. jiHIH
Если несколько скобок вложены друг в друга, вы проводите вычисления по
порядку, двигаясь изнутри наружу. В табл. А.1 показано несколько примеров.
Таблица А. 1. Примеры порядка арифметических действий
Выражение
2+5x10
(2 + 5)х10
10 х22
(10х2)2 + 5
10-4/(2 + 2)
[5 + 3(4 + 6)]/(3 + 2)
Правило
Сначала умножение, потом сложение
Сначала - выражение в скобках
Возведение в степень делают раньше умножения
Сначала действие в скобках, потом возведение в
степень, затем сложение
Сначала действия в скобках, потом деление, затем
вычитание
Начинаем со внутренних скобок, сначала умножаем,
затем складываем
Результат
52
70
40
405
9
7
Свойства действительных чисел
Действительные числа - это тип чисел, известных нам из повседневной жизни и
наиболее часто используемых в математике и статистике. У них может быть
дробная часть, и поэтому к ним относятся рациональные числа, такие как 4 и 7/5, и
иррациональные числа, такие как я (3,1415...) и квадратный корень из двух (1,4142...),
но не мнимые или комплексные числа (которые при возведении в квадрат дают
отрицательное число). Если не указано иное, во всем этом обзоре имеются в виду
действительные числа. К свойствам действительных чисел относятся следующие:
• ассоциативность при сложении и умножении:
(я + Ь) + с = а + (Ь + с), так что (1 + 2) + 3 = 1 + (2 + 3) = 6,
a(b*c) = (a*b) с, так что 2 х (3 х 4) = (2 х 3) х 4 = 24;
• коммутативность при сложении и умножении:
а + b = b + а, так что 5 + 4 = 4 + 5 = 9,
а х Ь = b x а, так что 2x3 = 3x2 = 6;
• дистрибутивность при умножении:
a(b + c) = ab + ас, так что 5(2 + 3) = 5(2) + 5(3) = 10 + 15 = 5(5) = 25;
• аддитивная идентичность нуля: прибавление нуля к любому числу дает
само это число:
а + 0 = я, так что 5 + 0 = 5;
• мультипликативная идентичность нуля: при умножении любого числа на
нуль получается нуль:
а х 0 = 0, так что 5(0) = 0;
• мультипликативная идентичность единицы: умножение любого числа на
единицу дает само это число:
я(1) = а, так что 5(1) = 5;
HlH:'; Приложение А
• инверсивное свойство сложения: сумма любого числа и обратного ему равна
нулю:
а + -а = 0 и -а + а = 0, так что 5 + -5 = 0 и -5 + 5 = 0;
• правило двойного минуса: два минуса взаимоуничтожаются:
-(-а) = а, так что -(-5) = 5;
• инверсивное свойство умножения:
а х (1/я) = 1, если а Ф 0 (поскольку результат деления на 0 не определен),
так что 5 х (1/5) = 1.
Показатели степени и корни
Показатель степени указывает, сколько раз нужно умножить основание само на
себя:
• а" = а * а * а ... п раз, так что 2А = 2 х 2 х 2 х 2 = 16,
где а - это основание, а п - показатель степени;
• а2 обычно называют «а в квадрате», а сР - «а в кубе»; также можно
произносить их как «а во второй степени» или «а во второй» и так далее, и такая
система используется для степеней выше 3 {а1 читается как «а в седьмой
степени»);
• умножение степенных выражений с одинаковым основанием: сложите
показатели степени, сохранив исходное основание:
ат х а" = ат +", так что З2 х 3:* = З2 +' = З5 = 243;
• правила возведения степенных выражений в степень:
(ат)п = ат\ так что (22)' = 2fi = 64,
(аЬ)" = а"Ь", так что (5 х 4)2 = 52 х 42 = 400 = 25 х 16,
(а/Ь)" = а"/Ь", так что (3/4)2 = 32/42 = 9/16, если п ф 0;
• нулевой показатель степени: любое отличное от нуля число, возведенное в
степень 0, равно 1:
а{) = 1, так что 245° = 1 и -8° = 1 (значение 0° не определено);
• отрицательный показатель степени - это то же самое, что деление на
основание, возведенное в указанную степень (по модулю):
аЛ = \/а и а'1 = 1/я2, так что 2 ' = 1/2 и 2 2 = 1/22 = 1/4,
(а/Ь)-п = {Ь/аУ, так что (5/3)2 = (3/5)2 = 9/25;
• при делении степенных выражений с одинаковым основанием
рассчитывайте разность степенных показателей:
ат/ап = а'" " (если а Ф 0), так что 3г,/32 = З5 -2 = 3' = 27.
Извлечение корня из числа - действие, противоположное возведению в
степень: корень гг-ой степени из х - это число а, такое что а" = х. Это может быть
легче понять, если рассмотреть квадратный корень, то есть корень второй степени
из числа. Квадратный корень из 9 - это 3, поскольку З2 = 9. Формально 3 - это
главный квадратный корень из 9 (-3 - это тоже квадратный корень из 9), но этим
Обзор основных математических понятий ;^НИ
различием часто пренебрегают на практике. Аналогично корень третьей степени
из 125 - это 5, поскольку 5:* = 125. Корень третьей степени также называют
кубическим корнем; для степеней выше третьей приняты названия корень четвертой
степени, корень пятой степени и так далее.
Свойства корней
На рис. А.2-А.4 показаны несколько важных правил работы с корнями.
<\[ab = Vtf Vfc, если ua,ub>0
Рис. А.2. Правило перемножения корней
Рис. А.З. Правило деления корней
^ =U[a~\ =a\ еслииа, ub>0
Рис. А.4. Правило возведения корней в степень
Вы можете самостоятельно применить эти правила, используя калькулятор,
как показано на рис. А.5.
л/4х16 = л/4 л/16 =2x4 = 8
(27 _ р=3=0.75
V64 Уб4 4
V81 = (Vs")2 = 8> = 4
Рис. А.5. Применение правил работы с корнями
Логарифм (часто обозначаемый как log) - это степень, в которую нужно
возвести данное основание, чтобы получить требуемое число. Для основания
10 - log1()100 = 2, поскольку 102 = 100. Хотя основанием может служить любое
число, в статистике часто имеют дело со степенными функциями с основанием е.
Их также называют натуральными логарифмами и записывают как In x, что значит
log^x. Основание е - это иррациональное число 2,718, которое полезно для
описания многих процессов в естественных («натуральных») науках, отсюда и название
«натуральный логарифм». В научных калькуляторах обычно есть кнопка LN для
вычисления натуральных логарифмов, а во многих компьютерных программах
для этой цели есть встроенная функция. Однако вам следует быть осторожными;
иногда функция для вычисления натурального логарифма сокращенно называет-
Ц|Щ j Приложение А
ся LOG, а не LN, так что вам нужно выяснить правильное обозначение для того
калькулятора или компьютерной программы, которую вы используете.
Равенство \пх = 1,5 эквивалентно записи в1Г> = х. В этом случае х = 4,48
(округлено), поскольку е1-5 = 4,48, и мы можем сказать, что натуральный логарифм 4,48
равен 1,5. Следующие принципы выполняются для логарифмов по любому
основанию (в этих примерах основание обозначено буквой Ь)\
• \ogh 1 = 0, поскольку Ь{) = 1 (потому что любое число в нулевой степени =1);
• log/; b = 1, поскольку б1 = Ъ (потому что любое число в первой степени равно
само себе);
• log/; bx = х (поскольку по определению логарифм Ьх - это х, если основание
равно Ь)\
• buv, где х > 0 (поскольку log/; х - это степень, в которую нужно возвести Ь,
чтобы получить х).
Также в статистике используются следующие свойства логарифмов:
• log/; MN = log/; M + log/; N (логарифм произведения - это сумма логарифмов
множителей);
• log/; M/N = log/; M - log/; N (логарифм частного - это разность логарифмов);
• log,,M" = plog/;M.
Эти правила можно проверить самостоятельно при помощи карманного
калькулятора, например для натуральных логарифмов:
1п(2 х 4) = 1п2 + 1п4 = 0,693 + 1,386 = 2,079;
1п(2/5) = 1п2 - 1п5 = 0,693 - 1,609 = -0,916;
1п2' = 3 1п2 = 3(0,693) = 2,079.
Учтите, что логарифмы для чисел между 0 и 1 отрицательны, а логарифмы для
чисел меньше нуля не определены. (Если вы попытаетесь вычислить In -1 на
вашем калькуляторе, появится сообщение об ошибке.)
Решение уравнений
При решении уравнений вам помогут следующие их свойства:
• Если а = Ь} то а + с = b + с (прибавление константы к обеим частям
уравнения не меняет его);
• Если а = Ь, то а- с = b - с (при вычитании константы из обеих частей
равенства оно не меняется.;
• Если а = Ь, то ас = be (умножение обеих частей равенства на константу не
меняет его);
• Если с Ф 0, то а/с = b/с (деление обеих частей равенства на ненулевую
константу не меняет его).
Это свойства пригождаются при решении линейных уравнений, так же как и
описанные выше свойства действительных чисел. Например, чтобы решить
уравнение
Обзор основных математических понятий LJhIII
5(х - 4) = 40,
раскройте скобки в левой части:
5х-20 = 40.
Затем выделите х, прибавив 20 к обеим частям:
5х = 60.
Затем поделите обе части на 5:
х=12.
Для проверки решения нужно подставить 12 в исходное уравнение:
5(12 - 4) = 5(8) = 40, что является верным.
Для более сложных задач нужно группировать подобные члены следующим
образом:
2(Зх+1) = 5(х + 2)
6х + 2 = 5х + 10 Раскрываем скобки с обеих сторон.
х + 2 = 10 Вычитаем 5х из обеих сторон.
х = 8 Вычитаем 2 из обеих сторон.
2(24 + 1) = 5(8 + 2) = 50 Проверка: подставляем 8 вместо х в исходное уравнение.
Логарифмы полезны для решения уравнений, в которые входят возведенные в
степень значения; вы можете прологарифмировать обе стороны, а затем
использовать свойства логарифмов для нахождения неизвестного. Например, используя
основание 10:
5х = 3
log 5х = log 3 Логарифмируем обе стороны.
х log 5 = log 3 Используем правило для логарифмов степенных
выражений.
х = log 3 /log 5 = 0.683 Делим обе части на log 5.
5°683 = 3 Проверка: подставляем 0.683 вместо х в исходное
уравнение.
Системы уравнений
Система уравнений, также называемая системой совместных уравнений, - это набор
алгебраических уравнений с общими переменными. Решение системы уравнений
означает нахождение общего решения, значений переменных, которые будут верны
для всех уравнений в системе. Если существует общее решение (это справедливо
для всех представленных здесь случаев), система называется непротиворечивой',
если нет, система называется противоречивой. Системы уравнений можно решать
графически (прочертив соответствующие уравнениям линии; решение - это точка
пересечения) или алгебраически. Ниже мы продемонстрируем второй метод.
Решение некоторой системы уравнений - это хороший способ освежить свои
знания по алгебре и развить умение рассуждать логически. Простой подход к
решению системы уравнений, который сработает для представленных здесь приме-
шпшш
Приложение А
ров, - это упростить каждое уравнение, насколько это возможно, а затем решить
систему, используя или метод подстановки, или метод сложения и вычитания. Мы
проиллюстрируем вышесказанное при помощи систем двух уравнений с двумя
неизвестными, хотя эти же принципы можно использовать для решения более
сложных систем, например трех уравнений с тремя неизвестными. Однако этот уровень
сложности приближается к такому, когда удобнее решать сложные задачи,
используя матрицы - тема, которая выходит за пределы нашего базового обзора.
Вот пример использования метода подстановки для решения системы двух
уравнений с двумя неизвестными (х и у):
2х + у = 6, Зх-2у = 16.
Найдите у в первом уравнении:
у = 6 - 2х.
Подставьте найденное значение вместо у во второе уравнение:
За:- 2(6 - 2х) = 16.
Найдите х во втором уравнении:
Зд: - 12 + Ах = 16, 1х = 28, х = 4.
Подставьте это значение в первое уравнение, чтобы найти у:
у-6-(2х4)--2.
Так что решение таково: (4, -2). То есть х = 4, у = -2. Проверьте, подставив эти
значения в уравнения:
2(4) + (-2) = 6, 3(4) - (2 х -2) = 16.
При использовании метода сложения (или вычитания) для решения той же
системы уравнений нужно складывать или вычитать подобные члены из двух
уравнений, чтобы избавиться от одной переменной и затем найти вторую. Часто
необходим дополнительный шаг, который заключается в умножении одного или
обоих уравнений на константу, чтобы одна из переменных (х или у) уничтожилась
при сложении двух уравнений или вычитании одного уравнения из другого. В
нашем случае мы умножаем первое уравнение на 2:
2[2х + у = 6] превращается в Ах + 2у = 12.
Затем мы подставляем это уравнение (которое идентично исходному,
поскольку мы всего лишь умножили обе его части на константу) в систему и прибавляем
ко второму уравнению. На рис. А.6 показаны дальнейшие преобразования
приведенной выше системы уравнений.
Ах
+
Ъх
= 1х
+ 2у-
-2у-
+ 0у
= 12
= 16
= 28-
так что
х '-
28
~Т
= 4
Рис. А.6. Решение системы уравнений при помощи метода сложения
Обзор основных математических понятий
Затем полученное значение можно использовать для нахождения у в другом
уравнении:
2(4) + у = 6, так что у = -2, 3(4) -2у= 16, так что у = -2.
Таким образом, мы получаем тот же ответ, что и при использовании метода
подстановки: (4, -2).
Графическое решение уравнений
Точки в многомерном пространстве обычно описывают при помощи декартовых
координат, называемых также прямоугольными координатами, которые
представляют собой просто значения каждого измерения в системе, описывающей
положение конкретной точки. Мы проиллюстрируем эту систему на примере двух
измерений, поскольку их легче изобразить на бумаге, однако та же идея может быть
применена для большего числа измерений.
Положение точек в двумерном пространстве определяется при помощи
плоскости с двумя осями, х (горизонтальной) и у (вертикальной), как показано на
рис. А.7. Каждая точка на этой плоскости описывается двумя числами, „г-коорди-
натой и г/-координатой, которые всегда указываются в этом порядке. Например, у
точки (2,3)х-координата равна 2, а г/-координата равна 3; точка (-1,5, -2,5) имеет
х-координату -1,5 и г/-координату -2,5.
А ОСЬ у
10+
5+
I I I I I I I I I I I I I
-10 -5
-5+
-10+
I I I I | I I I I | I I I >
\ 5 10
" Х(0,0)
начало координат
Рис. А.7. Декартова система координат
Линейные уравнения можно записать в виде у = тх + Ъ, где т называется
угловой коэффициент, а Ь - свободный член (отрезок, отсекаемый на оси у от начала
Ill
Приложение А
координат); этот способ обозначения называется уравнением прямой с угловым
коэффициентом. Прямые могут характеризоваться при помощи других
обозначений, у = ах + Ь, в данном случае а - это угловой коэффициент, a b - свободный
член. Любой способ обозначений дает уравнение прямой с угловым
коэффициентом. Для графического изображения линейного уравнения (в которое не входят
квадратные члены или члены высшей степени) в декартовых координатах найдите
две или более пар координат, которые удовлетворяют уравнению, и соедините их
прямой линией. Вот простой пример:
у = 2х+ 4.
Ниже представлены возможные решения. (Учтите, у этого уравнения
существует бесконечное множество решений.)
х = О, у = 4; х = 1, у = 6; х = -2, у = 0.
Графически эти решения можно представить, как это сделано на рис. А.8.
к ОСЬ у
i i i I i i i i I i I/ i
-10 -5 Й,0)
-10+
I I I I | I I I I | I I I >
5 10
Рис, А.8. Линия, соответствующая уравнению у = 2х + 4
Вот интерпретация составляющих уравнения:
Угловой коэффициент
Насколько увеличится у при увеличении х на одну единицу.
Свободный член
Значение у при х = 0, то есть значение, где линия пересекает ось у.
Даже не рисуя графика, вы можете интерпретировать уравнение и предсказать
новые значения у, зная х. Посмотрите на это уравнение:
у = -Зх + 6.
Обзор основных математических понятий
,Н1
Мы знаем, что эта линия пройдет из верхнего левого угла в нижний правый,
поскольку угловой коэффициент отрицательный (в противоположность тому, что
показано на рис. А.8, где угловой коэффициент был положительным). Мы также
знаем, что по мере увеличения х у уменьшается, и наоборот. Свободный член (6)
указывает на то, что линия пересечет ось у в значении 6. Мы можем вычислить
координаты некоторых точек, через которые проходит линия, как показано ниже
(рис. А.9) (проще первым делом определить точки, в которых линия пересекает
оси). В табл. А.2 приведены некоторые возможные значения.
Таблица А.2. Некоторые значения, через
которые проходит линия у = -Зх + 6
X
2
0
1
У
0
6
3
А ОСЬ у
I I I | I I I I | I I I I
-10
-5 (-2,0)
-10+
I I I | I I I >
10
Рис. А.9. Линия, соответствующая уравнению у = -Зх + 6
Другой способ записи уравнения прямой - это использование так
называемого уравнения пучка прямых с центром в точке. Этот формат использует тот факт,
что, зная угол наклона прямой и одну точку на ней, мы можем отобразить линию
и вычислить координаты любой ее точки. Аналогичным образом если нам
известны две точки, лежащие на прямой, мы можем вычислить угол ее наклона. Иначе
говоря, прямую линию можно однозначно определить двумя точками или одной
IhH|':'J Приложение А
точкой и углом наклона. Уравнение пучка прямых с центром в точке записывается
следующим образом:
у-ух = т(х-хх),
где т - это угловой коэффициент, а (х, у) и (xv z/,) - две точки на прямой.
Угловой коэффициент можно найти, зная две точки на прямой, при помощи формулы,
приведенной на рис. А. 10.
т = ^А
Рис. А. 10. Формула для нахождения углового коэффициента линии
Вы можете запомнить это как «угловой коэффициент = возвышение над
горизонталью», где возвышение - это изменение в значениях г/-координат (изменение
по вертикальной оси), а горизонталь - это изменение в значениях х-координат
(изменение по горизонтальной оси) для двух точек. Если у нас есть точки (0, 6) и
(2,0), угловой коэффициент для проходящей через них прямой можно вычислить,
как показано на рис. А.11.
т
6-
=
0-
-0
=
-2
6
-2
= 3
Рис. А. 11. Нахождение углового коэффициента для прямой
Это соответствует угловому коэффициенту из предыдущего примера. Если бы
наша линия проходила через точки (6, 6) и (4, 2), ее угловой коэффициент можно
было вычислить, как показано на рис. А. 12.
6-2 4
т = = — = 2
6-4 2
Рис. А. 12. Нахождение углового коэффициента для другой прямой
Продолжая работу с этим примером, если мы знаем, что линия с угловым
коэффициентом 2 проходит через точку (6, 6), мы можем найти ^/-координату для 4,
используя уравнение пучка прямых с центром в точке:
у - ух = т{х - *,), 6 - ух = 2(6 - 4), -у] = 4 - 6 = -2у{ = 2.
Линейные неравенства
Уравнение связывает два выражения знаком равенства; например, у = тх + Ъ - это
уравнение прямой. Часто мы хотим связать два выражения знаками неравенства,
которые означают, что две части не равны. Некоторые часто используемые в
неравенствах символы приведены в табл. А.З.
Обзор основных математических понятий
Таблица А.З. Часто используемые в неравенствах символы
Символ, аббревиатура
Ф, <>, NE2
<,LT3
>,GT4
<, <=, LE5
>, >=, GE6
~
Значение
He равно
Меньше, чем
Больше, чем
Меньше или равно
Больше или равно
Примерно равно
Примеры
a*b,a<>b,aNE5
а < b, a LT 5
а > Ь, a GT 5
a<b,a<=bt al_E5
а>Ь,а>=Ь, aGE5
а~Ь, а~5
Аббревиатуры, в особенности такие как GE и LE, часто используются для
обозначения неравенства при написании компьютерного кода.
Мы можем оценить неравенства с точки зрения логики или правдивости.
Например, если а = 5иЬ = 6, тоа<6иа<Ь верны, тогда как а > 5 и а > b ложны. Для
линейных неравенств действуют следующие правила:
1. Если одинаковое число прибавить к обеим частям неравенства, то оно не
изменится.
Если а<Ь,тоа+х<Ь+х\\а-х<Ь-х.
6 < 10, так что (6 + 4) < (10 + 4) и (6 - 1) < (10 - 1).
2. Если умножить или разделить обе части неравенства на одно и то же
положительное число, то неравенство не изменится.
Если а > Ь, то ах > Ьх и а/х > Ь/х.
5 > 3, так что (5 х 2) > (3 х 2) и (5/2) > (3/2).
3. Если умножить или разделить обе части неравенства на одно и то же
отрицательное число, то неравенство изменится на противоположное.
Если а<Ь,то а(-х) > Ь(-х).
2 < 4, так что 2(-3) > 4(-3) и 2/-3 > 4/-3, то есть -6 > -12
и -2/3 > -4/3.
Линейное неравенство можно решить тем же способом, что и линейное
уравнение. Например:
4(3* + 2) < 20
12д: + 8<20
12х<12
х< 1
2 от англ. not equal. - Прим. пер.
'* от англ. less than. - Прим. пер.
А от англ. greater than. - Прим. пер.
5 от англ. less than or equal. - Прим. пер.
() от англ. greater than or equal. - Прим. пер.
III Приложение А
Дроби
Дробь - это просто способ выразить результат деления одного числа на другое.
Верхнее число называется числитель, а нижнее - знаменатель (рис. А. 13).
числитель
дробь =;
знаменатель
Рис. А. 13. Числитель и знаменатель дроби
На рис. А. 14 представлены некоторые основные свойства дробей. (Во всех
случаях не подразумевается деление на 0.)
1.
2.
3.
4.
5.
а
b
а
Т =
а
а
а
~Ъ =
а
~~Ь
с в том и только в том
^ если
а
1
ас
~Ьс~
-а
= Т =
act =
а
~-Ь
--be
случае,
Рис. А. 14. Свойства дробей
Учтите, что свойство 4 вытекает из свойства 3: любое число, деленное на само
себя, дает 1, так что умножение на — как в данном случае, означает просто
умножение на 1 и не меняет значения дроби. Это свойство также позволяет упрощать
дроби, сокращая общие делители, как показано на рис. А. 15.
8
24
Ах
8x1
~8хЗ
'у2
1
~3
ЛГ1
2хуъ
Рис. А. 15. Упрощение дробей
Вспомните из нашего обсуждения степенных показателей, что у_1 = \/у.
Для вычитания или сложения дробей нужно привести их к общему
знаменателю. Вы можете помнить из начальной школы упражнение «найти наименьший
общий знаменатель», но для наших целей пойдет любой общий знаменатель. Если
у дробей есть общий знаменатель, то нужно просто сложить или вычесть
числители, оставив знаменатель прежним, как показано на рис. А. 16.
Обзор основных математических понятий . g]j
а Ъ а + Ь
—+ - =
С С С
Рис. А. 16. Сложение дробей с общим знаменателем
Если у дробей нет общего знаменателя, вам нужно привести их к общему
знаменателю при помощи умножения или деления, затем провести сложение или
вычитание и упростить результат, сократив общие делители, например так, как
показано на рис. А. 17.
5
—+
6
2
4
10
= +
12
6
12
16
= =
12
4
3
или
А
1-
3
Рис. А. 17. Сложение дробей с приведением их к общему знаменателю
I3- называется смешанным числом, поскольку оно состоит из целой и дробной
частей. -J называется неправильной дробью, поскольку ее числитель превосходит
знаменатель. Чтобы преобразовать неправильную дробь в смешанное число,
извлеките из дроби столько целых чисел, сколько это возможно, так что в результате
получится целое число плюс представленный в виде дроби остаток, как показано
на рис. А.18.
4
— =
3
3
= —+
3
1
3
,1
= 1-
3
Рис. А.18. Преобразование неправильной дроби в смешанное число
Для умножения дробей перемножьте числители и знаменатели по отдельности,
а затем упростите результат, как показано на рис. А. 19.
а
с
9
5
Ъ
х — =
d
10
х —
27
ab
cd
90
~ 135
2
"з
Рис. А. 19. Перемножение дробей
При делении дробей умножайте на обратную дробь. Это допустимо, поскольку
деление нах - это то же самое, что умножение на \/х (то есть деление - это то же
самое, что умножение на величину, обратную делителю). Это показано на рис. А.20.
а
Ъ
3
4
с
1_ —
d
1
7-
2
а
d
= — х —
Ъ
3
с
2
= — х — =
4
1
ad
=
be
6
= — =
4
А
1-
2
Рис. А.20. Деление дробей
ЮЯ1
Приложение А
Дроби также можно выражать в десятичных дробях или процентах. Процент -
это всего лишь дробь со знаменателем 100 (cent = 100 на латыни). При помощи
калькуляторов легко преобразовать любую дробь в десятичную, а затем - в
проценты, умножив ее на 100; на некоторых калькуляторах даже есть специальная
кнопка для автоматического представления частного в виде процентов. Так что:
1/4 = 0,25 = 25%, 6/4 = 1,5 = 150%.
Чтобы вычислить процент от числа, умножьте это число на соответствующую
проценту десятичную дробь. Например, 40% от 30 = 0,4(30) =12. Для вычисления
прибавки к какому-либо исходному числу умножайте на 1,0 плюс прибавка;
например, результат увеличения на 20% можно вычислить посредством умножения
на 1,2, поскольку умножение на 1,0 даст вам исходное значение, а умножение на
0,2 дает 20%-ную прибавку. Поэтому увеличение на 100%, что соответствует
удвоению, означает умножение на 2,0 (1,0 для исходного значения, 1,0 для
прибавки). Для вычисления результата уменьшения исходного числа умножайте на 1 -
уменьшение; например, чтобы найти результат уменьшения 100 на 10%, умножьте
100 на 0,9, то есть 100(.9) = 90.
Факториалы, перестановки
и сочетания
Факториал числа - это само это число, умноженное на все целые числа меньше
него вплоть до 1. Факториал п записывается как п! и означает п(п - 1)( п - 2) ... (1),
так что:
5! = 5(4)(3)(2)(1) = 120
и
10! = 10(9)(8)(7)(6)(5)(4)(3)(2)(1) = 3 628 800.
У многих калькуляторов есть кнопка для вычисления факториалов, обычно
обозначенная как / или х/, наряду с кнопками для вычисления перестановок и
сочетаний пРг и пСг. Если у вашего калькулятора есть эти кнопки,
экспериментируйте с ними, прорабатывая этот раздел. Содержащие факториалы дроби часто
можно упростить, сократив их на общие делители, важное свойство, поскольку
факториалы быстро становятся очень большими числами, как мы видели на
примере 10!. Польза от сокращения на общие делители должна быть понятна из
примера, приведенного на рис. А.21.
10! 10x9x8x7x6x5x4x3x2x1 л/л Л _
— = 10x9=90
8! 8x7x6x5x4x3x2x1
Рис. А.21. Сокращение на общие делители в задаче с факториалами
Факториалы полезны в таких задачах, где нужно разместить конечное число
объектов в определенном порядке. Например, сколько существует способов
расположить пять книг на полке? У вас есть пять вариантов для первой книги, четы-
Обзор основных математических понятий
¦¦ЕШ
ре - для второй (поскольку первая книга уже стоит, и ее нельзя выбрать еще раз),
три - для третьей, два - для четвертой и один для пятой. Так что ответом будет
5! = 120.
Если вас интересует число способов расположить подмножество объектов из
конечного набора различающихся объектов, для получения ответа можно
использовать перестановки. На самом деле нахождение числа способов, которыми можно
расположить пять из пяти объектов, как в предыдущем абзаце, - это задача на
перестановки, в которой подмножество соответствует всему множеству. Однако
чаще задачи на перестановку имеют дело с чем-то вроде числа способов выбрать
три книги из пяти. Существует несколько принятых обозначений перестановок,
так что взгляните на рис. А.22, где показано число способов упорядочивания
/объектов, выбранных из п объектов.
P(n,r) = nPr =-^—
| (п-г)! I
Рис. А.22. Формула для перестановок
Число способов упорядочивания трех объектов, выбранных из пяти, показано
на рис. А.23.
5РЗ =— 60
| (5-3)! |
Рис. А.23. Определение числа перестановок
Учтите, что 0! принято считать равным 1, а не 0, чтобы избежать проблем при
делении на 0.
В перестановках порядок объектов имеет значение. Если бы мы составляли,
например, набор из трех букв, выбранных из первых пяти букв английского
алфавита, то (я, Ьу с) будет иной перестановкой, чем (я, с, Ь). Если порядок неважен, мы
имеем дело с сочетаниями, а не перестановками. Сочетания - это число разных
наборов из г объектов, которые можно получить из п объектов, если наборы из
одинаковых объектов, построенных в разном порядке, считаются одинаковыми.
При выборе трех букв из первых пяти букв алфавита (а} Ь, с) это такое же
сочетание, как и (а, с, Ь). Как и в случае с перестановками, для сочетаний не существует
единственного принятого обозначения, а все способы таких обозначений для
сочетания г объектов, выбранных из п объектов, представлены на рис. А.24.
С(п,г) = пСг = \ =— -
\г) г\(п-г)\
Рис. А.24. Разные способы обозначения сочетаний
Подсчет числа способов выбора трех объектов из пяти, если порядок неважен,
показан на рис. А.25.
ШЁШШШ
Приложение А
5СЗ =
5!
3!(5-
3)!
= 10
Рис. А.25. Определение числа сочетаний
Упражнения
Ниже приведен обзор понятий, обсуждаемых в этом приложении.
Арифметические правила и действительные числа
Вы лучше оцените ваш уровень освоения математики, если выполните первые
семь разделов без использования калькулятора, - то есть если вы задействуете
свои знания алгебры для решения их вручную. В случае ответов с буквенными
переменными (такими как х или у) просто выразите их в простейшей форме.
1. 3 + (-8) =
2. 6/-3 =
3. (-8г/)(-6г) =
4. 2 + 5/10 =
5. (2 + 5)/10 =
6. 6 + 32-5 =
7. (3 + 2)2 =
8. [12(5)-2(3)]/(Зх2) =
9. -(3-5х) =
10. 6(4 + 2.г) - х(5) =
И. 3(4Д) =
12. 5.г(4-2) =
13. (5х + 6)(3) =
Возведение в степень, корни и логарифмы
1. 2" =
2. (1/4)* =
3. (-х)1 =
4. (.г')2 =
5. 22(2') =
6. х5{х2) =
7. (4х2)2 =
8. 2 ' =
9. х2/х' =
10. (2/3)2 =
11. (7г/2)' =
12. (5/9) ' =
13. хУх2 =
14. (27/8)"+ =
15. (4/9)+ =
Обзор
основных математических понятий
¦¦НЕЭ
16. V7=
17. \/27У =
18. ^4x16 =
19. 1* =
20. J—-
Натуральные логарифмы
1. е°-
2. In 1 =
3. logI0100 -
4. Iog10(5x2)-
5. Ine3-
Решение уравнений с нахождением х
1. Зд: + 7 = 20
2. (1/3)х = 6
3. 3(х + 2) = 2(х + \)
4. 4х = 3(.г-2) + 7
Системы линейных уравнений
1. Зх-2г/ = 6 и х+2г/= 14
2. х + Зг/ = -1 и 2х + г/ = 3
Линейные уравнения и декартовы координаты
1. Заполните приведенную ниже таблицу с использованием линии,
соответствующей уравнению у = Зх + 2.
Таблица А.4. Нахождение декартовых координат
X
0
1
-1
У
0
2. Чему равны угловой коэффициент и свободный член в уравнении
у = -х + 5?
3. Если в уравнении у = 6 - 2х х увеличится на 2, что произойдет с у?
4. Найдите угловой коэффициент прямой, проходящей через данные точки
(5,3) и (2,-1).
ЦЦр Приложение А
5. Найдите ^/-координату для прямой при х = -3, если известно, что угловой
коэффициент этой прямой равен -1 и она проходит через точку (2, 4).
Линейные неравенства
1. Если a < b, как соотносятся За и 36?
2. Если а < Ь, как соотносятся -2а и -2Ь?
3. Выразите х из следующего неравенства: 5(2х -1) > 8.
4. Выразите х из следующего неравенства: Зх(2) GE 4.
Простые и десятичные дроби и проценты
1.
2.
Зх2у
1
5ху
~6
>V
у5
8 3 _
10 15 ~
8/
2у
5
—х
4
Зх
V
7'
7_
5 '
3
7_
3~
2
<— =
X
14 _
10 "
2 _
Зх"
7' 5 ' 10
8. iUA =
3 Зх
Замечание: для ответа на следующие четыре вопроса можно использовать калькулятор.
9. Чему равны 20% от 75?
10. Выразите 7/21 в виде десятичной дроби.
11. Если мы продали 500 единиц товара в прошлом году, а в этом году продажи
увеличились на 10%, сколько единиц товара мы продали за этот год?
12. Если мы продали 500 единиц товара в прошлом году, а в этом году продажи
упали на 20%, сколько единиц товара мы продали за этот год?
Факториалы, перестановки и сочетания
Замечание: для выполнения заданий из этого раздела можно использовать калькулятор.
Обзор основных математических понятий
ЕЯ
1. 7! =
2. 6Р4 =
3. 8СЗ =
х!
4. =
U-1)!
5. Сколько существует способов расположить на поле команду из девяти
игроков, если у нас всего есть 15 игроков (порядок важен)?
6. Сколько всего существует разных сочетаний (порядок неважен) пяти
предметов, выбранных из десяти разных предметов?
Ответы
Арифметические правила и действительные числа
1. 3 + (-8) = -5
2. 6/-3 = -2
3. (-8y)(-6z) = 48yz
4. 2 + 5/10 = 2,5, или 2 1/2
5. (2 + 5)/10 = 7/10,или0,7
6. 6 + 32-5=10
7. (3 + 2)2 = 25
8. [12(5)-2(3)]/(3x2) = 9
9. -(3 - 5х) = -3 + 5*
10. 6(4 + 2х) - х(5) = 24 + 12 х - 5х = 24 + 7х
11. 3(4/х) = 12/х,или12х'
12. 5х(4-2) = 10х
13. (5х + 6)(3) = 15х+18
Возведение в степень, корни и логарифмы
1. 2°-1
2. (1/4)2= 1/16, или 0,0625
3. (-х)4 = х<
4. (я3)2-*"
5. 22 (2:)) - 25 - 32
6. х5 (х 2) = г1
7. (4*2)2 = 82 = 64
8. 2-'- 1/2, или 0,5
9. х1/х% = х 2, или 1/х2
10. (2/3)2 = 4/9, или 0,444...
11. (7г/2)' = 7г/2
12. (5/9) ' = 9/5, или 1-3-, или 1,8
13. хУх2 = х7
14. (27/8) w = 2/3
ESI Hi HP
Приложение А
15. (4/9)|/2 = 2/3
16. 47 = xl
17. фл/=Ъу
18. 8
Натуральные логарифмы
1. e°=l
2. In 1 = О
3. log,,, 100 = 2
4. Iog10(5x2)-1
5. In., - 3
Решение уравнений с нахождением х
1. Эх + 7 = 20: х = 13/3, или 4 1/3
2. (1/3)*-6: а-=18
3. 3(х + 2) = 2(л-+1): х=-4
4. 4х = 3(.г--2) + 7: дт — 1
Системы линейных уравнений
1. Зх - 2у = 6 и х + 2г/ = 14: решение = (5, 4,5)
2. .г + Зг/ = -1 и 2х + у = 3: решение = (2, -1)
Линейные уравнения и декартовы координаты
1.
X
0
-2/3
1
-1
У
2
0
5
-1
2. Угловой коэффициент = -1, свободный член = 5
3. у уменьшается на 4
4. 4/3
5. у -9
Обзор основных математических понятий
Линейные неравенства
1. 3a<3b
2. -2a>-2b
3. 10х> 13, илих> 13/10
4. х GE 4/6, или х GE Уз
Простые и десятичные дроби и проценты
1. _3*V-
2.
-=3х2>>
1
5ху V _ 5xz2
б/ ~ by1
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
8 3 _ 24 6
10 15 ~ 30 30 ~
2j> 3
5 7 _ 35 11
4 3 ~ 12 ~ 12
3x 2 _ 6
7Xjc~7
7 14 _ 7 10
5 ' 10 ~ 5 14 ~
x 2 x 3x x2
з~"з7~з~ Т~Т
15
0,333
550
400
Факториалы, перестановки и сочетания
1. 7! = 5040
2. 6Р4 = 360
3. 8СЗ=56
4. х
5. 15Р9 - 1,816,214,400
6. 10С5 = 252
ПРИЛОЖЕНИЕ В.
Краткий обзор
статистических пакетов
В некоторый момент вашей карьеры в статистике вам, возможно, понадобится
использовать статистические программы; теоретические познания и карманный
калькулятор помогают только до определенной степени. К счастью, мы живем в
эпоху, когда для упрощения статистических вычислений легко можно
воспользоваться разными типами программ. Многие статистики работают с одним или
более стандартными статистическими пакетами, такими как SAS или SPSS.
Статистический пакет - это обычно собрание статистических процедур с общим
интерфейсом, разработанное для упрощения работы по выполнению
статистического анализа и сопряженных задач, таких как управление данными. Главное, что
нужно помнить о статистических пакетах, - то, что, как и любые другие
компьютерные программы, - это всего лишь средство для достижения цели. У каждой
программы есть свои достоинства и недостатки, и, по крайней мере на начальном
уровне, вы, скорее всего, будете использовать ту программу, которая уже
установлена на вашем компьютере или там, где вы учитесь. Если впоследствии вам
понадобится освоить новый статистический пакет (скажем, для другой должности),
это не должно стать существенным затруднением. Если вы хорошо понимаете
теоретические основы статистики и обладаете хотя бы минимальными
способностями для работы на компьютере, вы сможете сообразить, как использовать почти
любой статистический пакет.
Однако начало работы с новым статистическим пакетом может показаться
трудным делом, особенно если ваш босс или инструктор уже считает вас
экспертом в этом вопросе! Опубликованные руководства или файлы помощи в
Интернете могут быть, а могут и не быть полезными в самом начале; удивительно большое
число таких руководств подразумевает, что вы уже знакомы с той программой, о
которой идет речь, хотя именно знакомства вам и недостает. Так что цель этого
приложения - предоставить краткий обзор нескольких наиболее
распространенных статистических пакетов с особым вниманием к вещам, которые могут быть
важными для нового пользователя или которые не всегда ясно прописаны в
документации.
Еще одна задача, которую я пытаюсь выполнить в этом приложении, - это
продемонстрировать вам сильные и слабые стороны каждой программы и показать,
Краткий обзор статистических пакетов
¦МЕШ
в каких ситуациях разумно использовать каждую из них. Конечно, я могу
основываться только на личном опыте, и мои идеи - определенно не последнее слово
в данной теме. Существует множество обзоров разных программ, и если вы
когда-нибудь окажетесь в ситуации выбора программы, выполняющей определенные
задачи, которую нужно приобрести для вашего отдела, вам, возможно, захочется
начать поиск в Интернете, в литературных источниках по вашей специальности
или и там, и там, используя ключевую фразу вроде «сравнение статистических
пакетов».
Minitab
Minitab - это статистический пакет, разработанный в государственном
университете Пенсильвании в 1980-е годы и теперь продаваемый находящейся в частной
собственности компанией Minitab, Inc. Эта программа часто используется в качестве
обучающей в курсах статистики для начинающих, а также широко используется
в бизнесе и контроле качества. Хотя Minitab - это коммерческий продукт, с сайта
компании можно скачать пробную версию, которая работает в течение 30 дней.
Minitab предпочитают использовать в некоторых курсах статистики для
начинающих, поскольку она легка в применении; согласно сайту компании, это наиболее
широко используемая при обучении в колледжах и университетах программа во
всем мире. В стандартную комплектацию входит обширная система файлов
помощи и демонстрационных материалов, которая сделала программу популярной среди
новичков. Однако те свойства программы, которые помогают новичкам быстро ее
освоить, такие как опора на меню и предоставление лишь ограниченного выбора
методов анализа, могут сделать ее не подходящей для более сложных случаев.
Minitab может импортировать и экспортировать файлы в нескольких
форматах, включая свой собственный формат рабочей таблицы (с расширением *.mtw)
и проекта (*.mpj), а также формат Excel (*.xls) и текстовые файлы (*.txt). Данные
хранятся в прямоугольном виде, как показано на рис. В.1. Строки пронумерованы,
а столбцы обозначаются как CI, C2 и так далее. Названия переменных можно
добавлять в затененную строку между названием столбца и самими данными. И
данные, и названия столбцов можно вводить прямо в рабочей таблице Minitab.
Рис. В.1. Рабочая таблица Minitab
Ill'
Приложение В
Команды в Minitab обычно запускаются при помощи меню; они записываются
в рабочем окне вместе с результатами, которые могут быть выражены в виде
текста; фрагмент рабочего окна с бинарным логистическим регрессионным анализом
показан на рис. В.2. Каждый графический результат записывается в отдельном
окне (что может привести к значительному разрастанию числа открытых окон во
время анализа!). Все результаты вместе с набором данным, использованным при
анализе, можно сохранить в виде проекта Minitab, а наборы данных и диаграммы
можно сохранить в виде отдельных файлов разных форматов.
НТВ > Blogistic 'CHD' = CHD CAT AGE CHL SHK ECG;
T
Results for: evans
Binary Logistic Regression: CHD versus CAT. AGE. CHL. SMK. ECG
Link Function: Logit
Response Information
Variable Value Count
CHD 1 71 (Event)
0 538
Total 609
Logistic Regression Table
Predictor
Constant
CAT
AGE
CHL
SHK
Coef
-6.76472
0.776079
0.0325374
0.0093670
0.828039
SE Coef
1.13218
0.333091
0.0151541
0.0032332
0.304211
Z
-5.97
2.33
2.15
2.90
2.72
P
0.000
0.020
0.032
0.004
0.006
Odds
Ratio
2.17
1.03
1.01
2.29
954
Lower
1.13
1.00
1.00
1.26
CI
Upper
4.17
1.06
1.02
4.15
0.416540 0.292459 1.42 0.154 1.52 0.85 2.69
Log-Likelihood = -201.337
Test that all slopes are zero: G = 35.884, DF * 5, P-Value = 0.000
Goodness-of-Fit Tests
Method Chi-Square DF P
Pearson 588.700 586 0.461
Deviance 397.129 586 1.000
Hosmer-Lemeshow 16.062 8 0.041
Table of Observed and Expected Frequencies:
(See Hosmer-Lemeshow Test for the Pearson Chi-Square Statistic)
Obs 0 2 5 9 6 8 8 4 6 23 71
Exp 1.8 2.8 3.7 4.4 5.2 6.3 7.3 8.8 11.5 19.2
0
Obs 60 59 56 52 55 53 53 57 55 38 538
Exp 58.2 58.2 57.3 56.6 55.8 54.7 53.7 52.2 49.5 41.8
Total 60 61 61 61 61 61 61 61 61 61 609
Measures of Association:
(Between the Response Variable and Predicted Probabilities)
Pairs Number Percent Summary Measures
Concordant 25869 67.7 Somers' D 0.36
Discordant 11933 31.2 Goodman-Kruskal Gamma 0.37
Ties 396 1.0 Kendall's Tau-a 0.08
Total 38198 100.0
Рис. В.2. Рабочее окно Minitab
Краткий обзор статистических пакетов
¦¦1БЕ1
В Minitab можно вычислять разные описательные статистики, создавать разные
диаграммы, проводить вычисления мощности и размера выборки, генерировать
случайные числа и осуществлять некоторые более сложные статистические процедуры,
такие как линейную и логистическую регрессию; однако доступные опции часто до
удивления ограничены, по сравнению с такими статистическими пакетами, как SAS
или SPSS. Так что если вы раздумываете о приобретении Minitab, имеет смысл
выполнить некоторые из предполагаемых видов анализа при помощи пробной версии,
чтобы понять, представляют ли эти ограничения проблему для ваших задач.
Наиболее выгодно Minitab смотрится в области контроля качества и связанных с
ним задач в бизнесе; согласно сайту компании, это мировой лидер в этом сегменте.
Часто Minitab - это статистический пакет, который осваивают вместе с правилом
шести сигм и аналогичными аспектами контроля качества. Специфические задачи
бизнеса и контроля качества можно легко решить в Minitab, включая анализ
экспериментальных планов, схемы прогона, контрольные карты (для создания
контрольных карт в главе 14 использовался Minitab), методы временных рядов, диаграммы
причинно-следственных связей, диаграммы Парето (распределение брака по
причинам) и анализ мощностей.
В продаже имеется множество руководств по Minitab наряду с учебниками по
статистике, в которых используются примеры из Minitab; поиск в
интернет-магазине Amazon или в вашем любимом магазине технической книги должен открыть
перед вами множество возможностей. Поиск в Интернете также позволит
обнаружить множество руководств и других справочных сайтов по Minitab.
SPSS
SPSS - это статистический пакет общего назначения, который был впервые
выпущен в 1968 году. Он широко используется социологами (название исходно
означало статистический пакет для социологии - Statistical Package for the Social
Sciences), а также широко применяется в других областях, включая медицину, бизнес
и образование. Этот пакет за время своего существования сменил несколько
названий. Версия под названием SPSS-X вышла в 1980-х годах (название
соответствует основному списку рассылки, посвященному SPSS); с 2009 по 2010 год SPSS
называлась PASW; а с тех пор как SPSS была приобретена IBM в 2010 году, новые
версии программы стали называться IBM SPSS (например, IBM SPSS Statistics
19.0, выпущенная в августе 2010 года). Для простоты мы будем использовать
называние SPSS для всех версий этой программы.
Возможности SPSS находятся между возможностями Minitab и SAS; эта
программа более сложна и имеет больше аналитических инструментов, чем Minitab, но
ее возможности более ограничены, по сравнению с SAS. С другой стороны, многие
новички считают, что легче освоить SPSS, чем SAS, и многие считают, что SPSS
лидирует в области форматирования и документирования данных. В особенности
после приобретения IBM при разработке SPSS стали уделять особое внимание
приложениям для предсказательного анализа, и это могло особенно понравиться
людям, работающим в этой области.
Приложение В
В SPSS возможны экспорт и импорт данных во многих форматах и в
непрямоугольном виде; однако набор данных всегда преобразуется в прямоугольный файл
данных SPSS, известный как системный файл (с расширением *.sav).
Метаданные (информация о самих данных), такие как форматы переменных,
пропущенные значения, подписи столбцов и значений, хранятся вместе с набором данных.
Возможны два способа отображения данных: окно данных (data view) (рис. В.З)
и окно переменных (variable view) (рис. В.4), то есть просмотр метаданных. Ввод
информации может осуществляться напрямую в любом из окон, то есть данные
можно ввести в окно данных, а названия переменных, подписи и тому подобное
можно ввести в окно переменных.
Si
>i3
Irntii _
USEEQUIP
2
2
1
2
2
2
2
1
2
1
2
2
2
2
SMOKE100 !
1
2
1
1
1
2
2
2
2
2
1
2
1
1
Visible ?
VETEF
2 28
2 28
7 18
2 28
2 18
2 18
2 \i
2 28
2 28
2 18
2 18
2 18
2 55
2 1?
Рис. В.З. Окно данных в SPSS
во
Si
I
rntiH
-J
1
2
3
i
S
i
7
8
9
10
11
12
Nairn
ASTHMA2
ASTHNOW
QLACTLM2
USEEQUIP
МОШОН
U5ENOW3
ACE
l>lr>PANC2
MRACE
VETERAN2
MARITAL
сшиж»
„,.,-.
Type
Numeric
Numeric
Mimic
Nun-eric
Numeric
Numeric
Numeric
Numeric
String
Numeric
Numeric
Width Decimals Label
G EVER TOLD HA...
С STILL HAVE AS. .
id ACTIVITY UM1...
;0 HEALTH PROBL.
0 SMOKED AT LE.
0
0
С
с
D
0
USE ОГ SMOKE.
REPORTED ACE
HISPANIC-LA "П..
MULTIPLE RACE
Ncnc
(1, Vtll..
Nonf:
None
Ncnc
None
None
None
ARE YOU A VET. , None
MARITAL STATUS None
NUMBER ОГ CM,
None
None'
None
None
Mom
None
None
MOM
None
None
None
Columns
5
9
10
10
10
5
10
s
10
9
10
-,
Align
S Right
Щ Right
Ш Right
Щ Right
Ш Right
Ж Right
Ж Right
Ш Left
S Right
Ж Right
Ж Right
-— гм-w.
it.
§.
4
0'
0
4'
&
4
0'
cf
0'
Nominal
Nominal
Nominal
Nommal
No И in al
Scale
NomJrol
Nominal
Nominal
Nominal
Role
\ Input
\ Input
\ Input
\ Input
N Input
\ Input
\ Input
\ Input
N Input
\ Input
\ Input
\ Input
4
Рис. В.4. Окно переменных в SPSS
SPSS можно полностью управлять при помощи кода, который вводят или
прямо в окно команд, или пишут в любом текстовом редакторе, а затем вставляют в
окно команд (рис. В.5). Файлы программного кода SPSS имеют разрешение *.sps.
Краткий обзор статистических пакетов
Синтаксис SPSS относительно легок для написания и понимания, что должно
быть видно по фрагменту кода, приведенного на рис. В.5. Вы, вероятно, можете
догадаться, что делает этот код, даже никогда не использовав SPSS. Вот подсказка:
строки, которые начинаются со знака *, - это комментарии, адресованные
программисту, а не выполняемые программой команды. Данная программа
перекодирует непрерывную переменную exercise в дихотомическую переменную exe?c_cat}
добавляет подписи к новой переменной и ее значениям и создает сводную и
частотную таблицы для этих двух переменных.
щ class demo week 3.sps - SPSS Syntax Editor
File Edit View Data Transform Analyze Graphs Utilities Run Add-ons Window Help
? %» I? M > %
*2) Recording.
* If not using predetermined categories, look at the distribution of your data first (but dont print huge frequency tables!),
freq exercise/histogram norrnal/stats = mean median.
* NB: no missing values in this data set (missing < 0).
recode exercise (0 thru 5= 1) (5.01 thru hi = 2) into exerc_cat.
val labels exerc_cat 1 "0-5 hrs/wk" 2 "> 5 hrs/wk".
var label exerc_cat "exercise categories".
* check the receding,
crosst exercise by exerc_cat.
freq exerc_cat.
* Recodmg through the menus: Transform/Recode into different variables.
RECODE exercise
(0 thru 4.8=1) (4.801 thru Highest=2) INTO exc_cat2 .
VARIABLE LABELS exc_cat2 'categorized exercise'.
EXECUTE
crosst exercise by exc_cat2.
freq exc_cat2.
Рис. В.5. Окно команд в SPSS
Некоторые люди предпочитают использовать интерфейс меню, и почти любой
статистический анализ или способ управления данными в SPSS может быть
выполнен таким образом. Я предпочитаю рассматривать меню как альтернативный
способ создания кода, который можно сохранить в файле так, чтобы брать лучшее
от каждого способа. Я могу использовать меню для создания кода незнакомой мне
команды, а затем сохранить этот код, задокументировав проведенный анализ, а
при последующей обработке данных я могу повторно использовать этот код или
изменить его. Второй фрагмент кода на рис. В.5 был создан при помощи меню;
верный признак этого - команды, написанные прописными буквами (RECODE,
VARIABLE LABELS и так далее). Для создания кода при помощи меню
выберите необходимые пункты в командном интерфейсе меню, а затем нажмите Paste,
а не ОК на заключительном этапе, как показано на рис. В.6. В результате этого
команды будут сохранены в отдельном файле или добавлены к существующему
файлу с командами, если он уже открыт. С другой стороны, если вы просто хотите
выполнить анализ и не заботитесь о сохранении командного кода, нажмите вместо
этого ОК, и анализ будет немедленно проведен. Статистические результаты будут
идентичными в любом случае.
т
Приложение В
Невозможно на отведенном месте перечислить все доступные типы анализа;
обзор возможностей SPSS представлен на ее сайте (http://www.spss.com). Это
дорогая программа, но в образовательных целях ее можно приобрести дешевле, а
университеты часто покупают лицензию, так что они могут предоставить
сотрудникам и студентам бесплатный или заметно более дешевый доступ к SPSS.
! $ Employee Code [id] \
i ty Previous Experience (is
Minority Classification |i
| <$r Current salary (thousarj
\ & Beginning salary (thouj
?
Ш
Layer 1 of
?
Row(s):
; j?jj Educational Level \ye<
Colurnn(s):
Ф Months since Hire [job
I 0K
[ Paste ]
I Reset ]
j Cancel J
( Help j
I i Display clustered bar charts
I | Suppress tables
I Statistics... I | Cells.
Format..
Рис. В.6. Использование меню для создания
командного кода в SPSS
SAS
SAS - это статистический пакет программ, разработанный в государственном
университете Северной Каролины в 1960-е годы, а с 1976 года он стал
коммерческим продуктом, который распространяет институт SAS. SAS - это следующий
уровень сложности, по сравнению с SPSS. SAS иногда сложнее использовать, но
она предоставляет гораздо больше возможностей с точки зрения доступных
типов анализа и гибкости определения параметров и выполнения процедур.
Основной недостаток SAS для начинающих - это система, основанная на программном
коде, а широта выбора параметров даже для простого анализа может показаться
избыточной на первый взгляд. SAS также менее дружественна в том, что касается
управления данными и метаданными; например, она сохраняет формат данных в
отдельных файлах (а не связывает информацию о формате с файлом данных, как
SPSS), и при каждом открытии файла данных нужно указывать в программном
коде расположение файла формата. Однако язык SAS стал стандартным во
многих профессиях, а помощь при изучении и использовании SAS легче получить, по
сравнению с SPSS, и с сайта программы, и от службы помощи, и из многих книг и
веб-сайтов.
Краткий обзор статистических пакетов
-¦¦ЕЗ
SAS во многом схожа с SPSS. Это всеобъемлющий статистический пакет,
который способен выполнить столько типов анализа, что здесь не хватит места,
чтобы перечислить их, и может читать и записывать данные в разных форматах. SAS
слишком дорога для одного человека, но ее можно приобрести для школы или
работы. Основное различие между SAS и SPSS заключается в том, что SAS в
основном ориентирована на программный код. Многие статистики и так
предпочитают работать с программным кодом, отчасти потому, что они (как и я!) настолько
старые, что научились пользоваться компьютером до появления графического
интерфейса, а отчасти из-за того, что (как это упоминалось в разделе, посвященном
SPSS) программный код можно распространять и использовать повторно. Кроме
того, создание программного кода помогает обдумывать анализ данных, чего
может не произойти, если щелкать по пунктам меню. Однако для тех, кто только
начинает работать со статистикой, отсутствие меню может казаться в большей
степени препятствием, чем достоинством. Ситуацию можно улучшить, используя
проверенный временем метод - можно изменять написанный кем-то код так,
чтобы он удовлетворял вашим задачам, и в Интернете размещено столько
аннотированных фрагментов кода SAS, что вы можете научиться писать программы на
языке SAS, просто используя этот метод.
У SAS есть три основных окна: окно кода (syntax window), в котором вы
можете набирать свой код или вставлять его из другой текстовой программы; окно
протокола (log window), в котором записываются все действия за текущую
сессию, включая предупреждения и другие сообщения от программы, и окно вывода
(output window), куда по умолчанию выводятся результаты статистических
процедур (они могут быть направлены в другие места, например в HTML, *.rtf или
*.ods). При использовании SAS вы открываете файл данных SAS или
импортируете данные в другом формате (таком как Excel или текстовый файл), вводите
команды в окно кода и проверяете результаты в окне вывода. Вид окон кода и
протокола представлен на рис. В.7.
В окне кода продемонстрированы три основные особенности
программирования в SAS. Во-первых, расположение файлов данных SAS указывается при
помощи команды libname, а сами файлы данных имеют состоящее из двух частей
название: библиотека.название_файла_дапных. В данном случае мы назначили
библиотеку у (это название произвольно, и многие используют однобуквенные
названия, поскольку их проще набирать) существующей в данной директории:
C:\Documents and Settings\sboslaugh\Desktop\CHQE Projects\ BH Dip Analysis\
и затем обратились к файлу y.sbdip0601f который хранится в данной директории.
Программы SAS состоят в основном из двух блоков:
1). DATA, который открывает, преобразует и сохраняет файлы данных;
2). PROC, который производит статистический анализ файлов.
В окне протокола повторяются все введенные команды и содержатся
программные сообщения, например о том, что наша команда libname была успешно
выполнена.
Приложение В
3177
3178
3179 title "Health insurance coverage by gender: Missouri BRFSS data 2007";
3180 proc freq data = brfss.mo; tables hlthplan * sex;
3181 where hlthplan = 1 or hlthplan = 2;
3182 run;
NOTE: Ther« were 5252 observations read from the data set BRFSS.MO.
WHERE hlthplan in (1. 2);
MOTE: PROCEDURE FREQ used (Total process tine):
real time 0.04 seconds
cpu time 0.03 seconds
" ANALYSIS STARTS HERE;
1ЛВГШ11Г. brfss ! C:\r-oojwc; nr.5 arid Sett гида\ 5*Ь5632\ r-esktop\ 2007 bi:fss\';
-data brfss.mo; set brfss.brfss2007;
4h~i:e state = ?'); run;
title "Health игзпгзпсе coverage by gender: Missouri BP.FSS data 2СЮ7";
Sproc ?re<j data - brfss.mo; tables hlthplan * sex;
where hlthplan = 1 or hlthplan = i>;
nin;
A
|
Рис. В.7. Окна кода и протокола в SAS
На рис. В.8 показан фрагмент окна вывода SAS.
The l Ш Ц (Procedure
Stat 1 • ut: ¦ г or feb le < 11 Ml KDOB 1 »y PCJHOD
Statist К Qf Value
СЫ-Square Б 3.43 70
L i be 1 I hood Ra t i о Ch i -Squar « 1 4.2716
Rente 1-Нес..—<ч им-Square i o.4t;:«/
Phi Coefficient 0. MK4
Eurtt iiuj«M«:y fm.-ffit M?nt 0.П5Б
I'rwcr's V 0.1164
UftRNINft: AT', ut th#> rail:; bavr к*.pt:»;t.ftd CtHifits
lh.it» '., Cln-IIijiMK' nay twt Ы* я v,H id
» ISher 4 1 R«Cl ?«•!
Tfthb- Probability (P) Г..0В1Е-0Е,
IV <- P 0.8013
Banple Btxa ¦ ?5ft
IV Ofa
0.7414
0.6400
0.4<H>9
lest
...
Рис. В.8. Окно вывода в SAS
В SAS есть два других окна, между которыми можно переключаться, используя
ярлыки в их нижних углах. Окно результатов (results window) (рис. В.9)
показывает общий перечень результатов, полученных во время сессии; выбор любой
папки позволяет вывести на экран следующий уровень детализации. Окно
обзора (explorer window) (рис. В.10 и В.11) дает доступ к разным библиотекам SAS.
(Любая созданная пользователем библиотека, такая как у в нашем случае, должна
быть задана при помощи команды libname во время текущей сессии SAS.) Выбор
папок позволяет получить более высокий уровень детализации.
Краткий обзор статистических пакетов III lEEU
Учтите, что можно открыть набор данных SAS в виде электронной таблицы (как
на рис. В. 12), которая в SAS называется форматом просмотра таблицы (viewtable).
Это можно сделать, выбрав файл в окне обзора, и таким образом данные можно
вводить или редактировать напрямую. Однако обычно в SAS эти действия
выполняются при помощи программного кода.
ТОРБОХ
Щ Table 2 of РЕЯ ЮС» * ТОРБОХ
¦ '[0 Table 3 of PERIOD * ТОРБОХ
+ J$ Table 4 of PERIOD • ТОРБОХ
* Ш Means: The SAS System
* .if? r-ot1 '• T^e 5A~' System
Рис. В.9. Окно результатов
Active Libraries
m
Brfss
m
Mylib
1 |fl|
Sasuser
1 в
Work
ш
Maps
Ш 1
Sashelp
1
Transprt
1
Рис. В. 10. Окно обзора в SAS
Behdip4 Sbdip0607
Рис. В.11. Содержание библиотеки данных (три файла SAS) в окне обзора SAS
ист
Приложение В
1
2
3
4
5
6
7
3
9
10
willhlp!
3.00
5.00
5.00
4.00
5.00
5.00
3.00
4.00
4.00
3.00
RSPRE0!
3.00
4.00
5.00
4.00
5.00
5.00
3.00
4.00
4.00
3.00
chlp :
3.00
5.00
5.00
4.00
5.00
5.00
5.00
5.00
3.00
5.00
COORD
3.00
5.00
5.00
4.00
5.00
5.00
5.00
5.00
3.00
3.00
DISRSPCTl
3.00
5.00
5.00
4.00
5.00
5.00
5.00
5.00
4.00
5.00
MEDS |
4.00
5.00
5.00
5.00
4.00
5.00
3.00
5.00
5.00
4.00
MDATT |
4.00
5.00
5.00
4.00
5.00
5.00
4.00
4.00
5.00
5.00
Рис. В12. Набор данных SAS в формате просмотра таблицы
В изучении SAS вам поможет множество книг наряду с качественными
интернет-ресурсами, и это сообщество программистов на языке SAS - серьезный довод
в пользу использования этого языка.
R
R - это язык программирования, который также выполняет функции
статистического пакета, поскольку многие статистические процедуры (компьютерные коды,
позволяющие выполнить определенное задание) уже написаны. R отличается от
других обсуждавшихся в этом приложении пакетов - запатентованных
продуктов, лицензии на использование которых нужно покупать, поскольку R можно
бесплатно скачать из Интернета. R - это чрезвычайно мощный язык, а новые
процедуры постоянно создаются и размещаются в Интернете статистиками и
программистами со всего мира.
Свободный доступ - это серьезное преимущество, так что вы можете
удивляться, почему все вокруг до сих пор не используют R для статистической обработки
данных. Ответ заключается в том, что R сложнее использовать, чем другие пакеты,
обсуждавшиеся в этом приложении, особенно впервые и для того, кто не обладает
значительными способностями или опытом в программировании. Использование
R также требует от программиста больше думать о том, что он делает, по
сравнению с SPSS или SAS. Хотя это определенно полезно с образовательной точки
зрения, люди, желающие всего лишь вычислить несколько простых статистик,
возможно, сочтут время, которое нужно потратить для преодоления первоначальных
затруднений, чрезмерным.
С другой стороны, если вы начали изучать R в то же время, что и статистику,
овладение этой программой может быть не труднее, чем знакомство с какой-либо
другой. Существует несколько вариантов графического интерфейса, и по мере
того как R становится все более распространенным, могут быть разработаны даже
более дружественные для пользователя приложения. Сейчас происходит что-то
вроде естественного эксперимента, поскольку язык R все чаще используется для
обучения основам статистики, так что, возможно, через 10 лет мы будем способны
ответить на этот вопрос. Если вы планируете заняться статистикой всерьез, вам
Краткий обзор статистических пакетов
1ВД1
нужно лучше познакомиться с R, поскольку это наиболее мощный и гибкий язык
из доступных на сегодняшний день, который может стать языком для общения
между статистиками всего мира в ближайшем будущем.
Для использования R его нужно сначала установить на ваш компьютер. Самый
легкий способ сделать это - пойти на веб-страницу CRAN (http://cran.r-project.
org, Comprehensive R Archive Network - всеобъемлющий архив R) и следовать
инструкциям. На следующем этапе, если вы не чрезвычайно тверды духом (или
не уже ас программирования), необходимо найти хороший учебный текст по R;
существует множество книг, а многие источники размещены в Интернете, включая
те, которые есть здесь: http://www.r-project.org1.
R - это командно-ориентированный язык; вы вводите команды в командную
строку, а R-интерпретатор реагирует в интерактивном режиме, или выполняя
команду, или выводя сообщение об ошибке. Эти команды довольно компактны, если
сравнивать их с используемыми в SPSS и SAS, и могут показаться таинственными
непосвященным; однако, после того как вы научитесь использовать R, вы начнете
ценить эту эффективность. Лучший способ освоиться с R, даже в большей
степени, чем с другими обсуждаемыми в этом приложении языками, - это выполнить
на компьютере несколько простейших заданий, используя пособия. Логику языка
R легче понять в ходе его практического применения, а не чтения чьих-нибудь
разъяснений.
Еще одна вещь, которую вам нужно знать про R, - то, что это
объектно-ориентированный язык (как и, например, Java, C++ и Smalltalk); это значит, что все, что
вы создаете при помощи R, - это объекты, с которыми можно работать далее при
помощи команд. Каждый объект относится к определенному классу, это означает,
что он обладает определенными характеристиками и внутренней организацией,
которые позволяют выполнять с ним некоторые действия.
Microsoft Excel
Строго говоря, Microsoft Excel - это вовсе не статистический пакет, хотя он иногда
используется в качестве такового. Excel - это приложение для работы с
электронными таблицами, созданное корпорацией Microsoft, которое часто используется
для работы с данными из-за его повсеместного распространения (он, например,
устанавливается на многие новые компьютеры, продаваемые в США), простоты
использования и того факта, что несколько основных статистических пакетов
имеют готовые процедуры для импорта и экспорта данных в формате Excel. В Excel
также можно создавать графики и диаграммы и проводить некоторые типы
статистического анализа, хотя вы должны знать, что статистические процедуры Excel
имеют ряд хорошо известных изъянов (http://www.daheiser.info/excel/frontpage.
html), так что разумность его использования для чего-нибудь, помимо базовых
диаграмм и вычислений, сомнительна. С другой стороны, Excel может полностью
1 На русском языке в издательстве «ДМК Пресс» недавно вышли две книги: Шипунов А. Б. и др.
«Наглядная статистика. Используем R!» и Кабаков P. «R в действии». - Прим. пер.
ЕШ1 III
Приложение В
отвечать вашим нуждам, или он может быть программой, которую стоит выбрать
для учебного курса. Просто помните, что Excel - это приложение для работы с
электронными таблицами, а не статистический пакет, и действуйте
соответствующим образом.
Excel хранит данные в отдельных электронных таблицах, которые называются
рабочими листами (worksheet); несколько рабочих листов объединяются ърабочие
книги (workbook). Отдельные значения данных хранятся в ячейках, образуемых
пересечением строки и столбца. Например, ячейка Л1 - это пересечение столбца Л
и строки 1. И отдельные рабочие листы, и рабочие книги имеют расширение *.xls
(или *.xlsx в новых версиях). Электронная таблица выглядит как прямоугольный
набор данных, но предоставляет намного больше возможностей, включая
встроенные функции для вычислений с использованием части данных, например
отдельных строк или столбцов. В Excel также есть много вариантов формата хранения
данных, вывода их на экран и печати; отдельные ячейка, столбец или строка могут
быть отформатированы как текстовые или числовые данные, им может быть
присвоен разный формат дат и так далее.
На рис. В. 13 вы можете видеть рабочий лист (лист 1, как показывает
закладка внизу) из рабочей книги, состоящей из трех листов; вы можете переключаться
между этими листами при помощи закладок внизу (обозначенных в этом
примере как Sheet 1, Sheet2 и Sheet3). Строки идут по горизонтали, как в стандартном
прямоугольном наборе данных, так что у нас есть строка 1, строка 2 и так далее.
Столбцы идут по вертикали, так что у нас есть столбец Л, столбец В и так далее.
Отдельные ячейки обозначены сочетанием столбца и строки, так что верхняя
левая ячейка - это Л1, следующая ячейка справа - В1, а соседняя ячейка снизу - Л2.
Обозначения Л1, Л2 и т. д. называются адресами ячеек.
А В С D Е 1
1
2
3
4
5
6
7
8
9 ;
10
11
12
13
14
•1С
< < > M\sheetl/Sheet2/Sheet3/ \<\
Рис. В. 13. Рабочий лист Microsoft Excel
Краткий обзор статистических пакетов
Данные можно напрямую вводить в рабочий лист, который в случае Excel
применяет форматы по умолчанию, исходя из типа введенных данных. Эти
форматы можно изменять, используя команды меню Формат/Формат ячеек (Format/
Format Cells); на рис. В. 14 показаны некоторые форматы дат. Если вы используете
Excel для сбора данных, которые потом будут перенесены для анализа в другую
программу, вы должны знать, что форматирование часто теряется или
искажается в процессе переноса данных. Поэтому, особенно если вы работаете с датами и
временем (которые из-за их сложности и разного способа хранения в разных
программах часто искажаются при переносе из одной программы в другую),
некоторые исследователи предпочитают импортировать все данные Excel в текстовом
формате, а затем назначать нужный формат уже после импорта в ту программу, где
данные будут анализироваться.
Number J Alignment
Category:
Patterns i Protection
General
Number
Currency
Accounting
Time
Percentage
Fraction
Scientific
Text
Special
Custom
Font j Border
Sample
! 3/12/2007
lype:
:Wednesday, March 14, 2001
3/14
3/14/01
03/14/01
14-Mar
14-Mar-01
Locale (location):
English (United States)
d
Date formats display date and time serial numbers as date values. Except for
items that have an asterisk (*), applied formats do not switch date orders
with the operating system.
Рис. В. 14. Некоторые примеры форматов, доступных в Excel
Названия переменных можно размещать в первой строке, и во многих
статистических пакетах есть возможность распознавать эти имена при импорте данных.
Однако, поскольку содержащая названия переменных строка считается строкой
данных в Excel, но не в таких программах, как SPSS, SAS и R, импортированный
файл будет содержать на одну строку меньше, чем исходный файл Excel. Это
может вызвать беспокойство, поскольку кажется, что одна строка потеряна, но на
самом деле это несоответствие вызывается всего лишь различием в способе
хранения данных.
Еще одна ловушка для непосвященных при переносе данных из одной
программы в другую - это разные правила для имен переменных. Ваш дух может быть
сломлен, если вы потратите много времени на ввод осмысленных названий
переменных в электронную таблицу только для того, чтобы они приобрели вид Varl,
щмк
Приложение В
Var2 и так далее после импорта файла в статистический пакет. Если вы хотите
импортировать названия переменных, следуйте правилам конечной программы, так
что если вы собираетесь импортировать данные в SPSS, соблюдайте требования
SPSS к обозначению переменных, когда вы вводите их названия в электронную
таблицу Excel. Другое решение - это использовать простые названия (такие как
vl, v2 и т. д.) в Excel, а затем написать код в конечной программе для добавления
осмысленных названий переменных после их импорта.
В Excel можно создавать множество диаграмм и графиков. При этом вы
вставляете их в рабочий лист, а затем их можно сохранить как отдельный объект или
вставить в другие программы, такие как Microsoft Word.
В Excel можно с легкостью производить основные арифметические операции, и
его возможности электронной таблицы особенно полезны, если нужно выполнять
вычисления для многих строк или столбцов чисел. В Excel также реализован набор
встроенных функций, который позволяет производить основные статистические
процедуры с любым набором строк, а арифметические операции вы можете
производить, задав уравнение, которое должно быть решено. В любом случае функцию
или формулу вводят в ячейку, в которой отобразится результат вычислений.
ПРИЛОЖЕНИЕ С.
Ссылки
Предисловие и общие источники
• Abelson, Robert P. 1995. "Statistics as Principled Argument." Hillsdale, NJ:
Lawrence Erlbaum.
Абельсон, преподававший в Иельском университете на протяжении 42 лет,
прекрасно обсуждает, как разобраться в статистике и с ее помощью попять
все остальное.
• Frey, Bruce. 2006. "Statistics Hacks: Tips and Tools for Measuring the World
and Beating the Odds." Sebastopol, CA: O'Reilly.
Это собрание коротких увлекательных эссе, в которых статистические
концепции объясняются на примерах из повседневной жизни от проверки на
случайность результатов «случайного» перемешивания данных при
помощи вашего iPod'a до использования правила Бенфорда для обнаружения
фальсифицированных данных.
• Huff, Darryl. 1954. "How to Lie with Statistics." Repr., New York: W.W. Norton,
1993.
Книга Хаффа, вышедшая впервые в 1954 году, остается классическим
описанием того, как при помощи даже простейших статистических приемов
можно ввести людей в заблуждение, смутить их или даже напрямую
солгать. Читатели, которые способны мириться с устаревшими примерами
и (особенно) стереотипными иллюстрациями, сочтут эту тонкую книжку
прекрасным источником знаний и веселья.
• Levitt, Steven D., Stephen J. Dubner. 2005. "Freakonomics: A Rogue Economist
Explores the Hidden Side of Everything. New York: HarperCollins.
В этом бестселлере, по отзывам «Нью-Йорк Тайме», экономист из
Чикагского университета использует теорию экономики и статистический
анализ для исследования вопросов от наличия обмана в борьбе сумо до того,
приведет ли легализация абортов к снижению уровня преступности. Хотя
это популярная книга, в некоторых университетах она рекомендуется для
обязательного прочтения.
ист
Приложение С
• Salsburg, David. 2001. "The Lady Tasting Tea: How Statistics Revolutionized
Science in the Twentieth Century." New York: W.H. Freeman.
Эта популярная история посвящена применению статистики и теории
вероятности для решения научных проблем в XX веке, ключевую роль играют
судьбы и достижения пионеров статистики, таких как Рональд Фишер
(Ronald Fisher), Карл Пирсон (Karl Pearson) и Джерси Нейман (Jerzy Neyman).
• Tucker, Martha A., and Nancy D. Anderson. 2004. "Guide to Information
Sources in Mathematics and Statistics." Westport, CT: Libraries Unlimited.
Это путеводитель по источникам информации о математике и статистике;
целевая аудитория - это библиотекари, но исследователям эта книга также
будет полезной. Сюда вошли поисковые средства, журналы, справочники,
биографические и исторические материалы и книги по применению
математики в других областях науки.
Глава 1
• Carmines, Edward G., and Richard A. Zeller. 1979. "Reliability and Validity
Assessment." Thousand Oaks, CA: Sage.
Один из первых выпусков в серии «маленьких зеленых книг» издательства
Сейдж, в котором описаны классические методы для оценки надежности и
значимости и приведено краткое обсуждение методов факторного анализа.
• Fleming, Thomas R. 2005. "Surrogate endpoints and FDA's accelerated
approval process." Health Affairs 24 (January/February): 67-78.
Флеминг обсуждает применение суррогатных конечных точек в
клинических испытаниях, направленных на получение ясных доказательств
преимущества определенных препаратов и других способов лечения, а также
описывает несколько ситуаций, при которых лечение, которое было
эффективным для суррогатных конечных точек, может быть бесполезным в
случае реальных конечных точек.
• Hand, D.J. 2004. "Measurement Theory and Practice: The World Through
Quantification." London: Arnold.
Хэнд приводит прекрасное обсуждение теории и практики измерений,
включая главы, посвященные частным проблемам в областях психологии,
медицины, физики, экономики и социологии.
• Michiels, Stefan, Aurelie Le Maitre, Marc Buyse, Tomasz Byrzykowski, Emilie
Maillard, Jan Bogaerts, et al. 2009. "Surrogate endpoints for overall survival
in locally advanced head and neck cancer: Meta-analyses of individual patient
data." The Lancet Oncology 10 (April): 341-350.
Статья, основанная на 104 клинических случаях, посвящена исследованию
применимости двух суррогатных конечных точек для оценки успешности
лечения плоскоклеточного рака головы и шеи. Вывод состоит в том, что
выживание без рецидивов в течение определенного времени лучше корре-
УИМЕ9
лирует с общим выживанием (истинная конечная точка), чем контроль над
положением патологии.
• Uebersax, John. "Kappa coefficients." http://www.john-iiebersax.com/stat/
kappa.htm.
Приведено подробное обсуждение достоинств и недостатков
коэффициента каппа в рамках общего обсуждения статистик согласия.
Глава 2
• Hacking, Ian. 2001. "An Introduction to Probability and Inductive Logic."
Cambridge: Cambridge University Press.
Эта книга была написана как вводный текст для студентов-философов, но
будет оценена всеми, кто хотел бы получить представление об основных
идеях статистики посредством слов, а не формул.
• Mendenhall, William, et al. 2008. "Introduction to Probability and Statistics."
13th ed. Pacific Grove, CA: Duxbury Press.
Это популярный учебник по теории вероятности и статистике для
студентов, не изучавших вычислительную математику.
• Packel, Edward W. 2006. "The Mathematics of Games and Gambling."
Washington, D.C.: Mathematical Association of America.
В книге прослежены связи между азартными играми (включая нарды,
рулетку и покер) и математикой и статистикой в стиле, который
рассчитывает на знания математики всего лишь в рамках средней школы. Приведено
множество иллюстраций и упражнений.
• Ross, Sheldon. 2005. "A First Course in Probability." 7th ed. Prentice Hall.
Введение в основы теории вероятности, проиллюстрированное многими
примерами, для студентов, которые изучили основы вычислительной
математики.
Глава 3
• Cohen, J. 1994. "The earth is round (p < .05)." American Psychologist 49: 997-
1003.
Это классическая статья одного из наиболее ярких критиков консервации
значения альфа = 0,05 как абсолютного показателя статистической
значимости или отсутствия таковой.
• Dorofeev, Sergey, and Peter Grant. 2006. "Statistics for Real-Life Sample
Surveys: Non-Simple-Random Samples and Weighted Data." Cambridge:
Cambridge University Press.
Это хорошо написанное руководство по созданию выборок и анализу
данных опросов, где простой случайный выбор объектов невозможен (это
часто имеет место).
шмн
Приложение С
• Mosteller, Frederick, and John W. Tukey. 1977. "Data Analysis and Regression:
A Second Course in Statistics." Reading, MA: Addison Wesley.
Это классический учебник по статистике вывода, в который входит глава
по преобразованию данных.
• National Institute of Standards and Technology. Engineering Statistics
Handbook: Gallery of Distributions, http://www.itl.nist.gov/div898/handbook/
cda/section3/eda366.htm.
Прекрасная демонстрация 19 распространенных статистических
распределений, включает многочисленные иллюстрации, формулы и обычные их
способы применения.
• Peterson, Ivars. 1997. "Sampling and the census: Improving the decennial
count." Science News (October 11).
В этой, ясно написанной, статье обсуждаются проблемы, связанные с
усилиями по сбору данных во время переписи населения в США, и
противоречия, связанные с выборочными исследованиями в процессе переписи.
• Rice Virtual Lab in Statistics. "Simulations/Demonstrations." http://onlines-
tatbook.com/stat_sim/index.html.
На этом сайте размещено много ссылок на модели, написанные на языке
Java, которые иллюстрируют статистические концепции, включая теорему
о центральном пределе, доверительные интервалы и преобразование
данных.
Глава 4
• Cleveland, William S. 1993. "Visualizing Data." Summit, NJ: Hobart Press.
В этой книге обсуждается эффективное графическое представление
данных со многими примерами; также разобраны визуальные и
психологические принципы, которые лежат в основе эффективного графического
представления информации.
• Erceg-Hurn, David M., and Vikki M. Mirosevich. 2008. "Modern statistical
methods: An easy way to maximize the accuracy and power of your research."
American Psychologist 63: 591-601.
Обсуждаются устойчивые статистические методы, включая усеченные
средние, и приводятся аргументы в пользу их более широкого применения.
• Robbins, Naomi. 2004. "Creating More Effective Graphs." Hoboken, NJ: Wiley.
Простое в использовании руководство, в котором приведены примеры
хороших и плохих способов графического представления одной и той же
информации, эта книга помогает использовать графические методы для более
эффективного представления статистической информации.
• Tufte, Edward R. 2001. "The Visual Display of Quantitative Information." 2nd
ed. Cheshire, CT: Graphics Press.
Ссылки
¦¦ЕШ
Эта книга послужила вехой, навсегда изменившей характер
использования графики для представления статистической информации. Почитатели
иногда спорного подхода этого автора захотят ознакомиться и с другими
его работами, включая Beautiful Evidence (2006).
• Wand, M. P. 1996. "Data-based choice of histogram bin width." The American
Statistician 51(1): 59-73.
Эта публикация не предназначена для слабых духом или неподготовленных
математически людей, зато в ней содержится исчерпывающее
профессиональное исследование разных правил для определения нужного числа
интервалов в гистограммах.
• Wilkins, Jesse L. M. 2000. "Why divide by N-l?" Illinois Mathematics Teacher
(Fall): 13-18. http://scholar.vt.edu/access/content/user/wilkins/Public/
IMT.pdf.
Это ясный и подробный ответ на вопрос, который неизменно возникает на
уроках статистики и который оказалось на удивление сложно разъяснить:
почему при вычислении выборочной дисперсии мы делим на (п - 1), а не на
п?
Глава 5
• Agresti, Alan. 2002. "Categorical Data Analysis." 2nd ed. Hoboken, NJ: Wiley.
Это стандартный учебник для продвинутых курсов по анализу
категориальных данных. Он может быть сложным для новичков, но ясно написан
и охватывает все темы от таблиц сопряженности до линейных моделей.
• Davenport, Ernest С, and Nader A. El-Sanhurry. 1991. "Phi/phimax: Review
and synthesis." Educational and Psychological Measurement 51(4): 821-828.
Это обсуждение диапазона ф в связи с разными распределениями данных и
поиском возможного решения.
Глава 6
• Fisher, R. А. 1925. "Applications of'student's' distribution." Metron 5: 90-104.
В статье обсуждаются различия между способами использования
характеристик распределения Стыодента.
• Gosset, William Sealy. 1908. "The probable error of a mean." Biometrika 6(1):
1-25.
Это оригинальная статья, в которой обсуждаются характеристики
распределения Стьюдента.
• Senn, S., and W. Richardson. 1994. "The first t-test." Statistics in Medicine
13(8): 785-803.
Эта статья посвящена первому применению теста Стыодента в
клинических испытаниях.
И5Я1
Приложение С
Глава 7
• Case, Anne, and Christina Paxson. 2008. "Stature and status: Height, ability,
and labor market outcomes." Journal of Political Economy 116(3), 499-532.
В этой статье обсуждается положительная связь между ростом и доходом, и
утверждается, что наблюдаемая связь объясняется положительной связью
между ростом и когнитивными способностями.
• Holland, Paul W. 1986. "Statistics and causal inference." Journal of the
American Statistical Association 81(396): 945-960.
Описаны сложные взаимосвязи между необходимостью выяснения
причинно-следственной связи и статистическими методами, доступными для
анализа определенных типов данных.
• Spearman, С. 1904. "The proof and measurement of association between two
things." American Journal of Psychology 15: 72-101.
Это, возможно, наиболее влиятельная статья на тему измерения силы
взаимосвязей за всю историю психологии.
• Stanton, Jeffrey M. 2001. "Galton, Pearson, and the peas. A brief history of
linear regression for statistics instructors." Journal of Statistics Education 9(3).
Чрезвычайно легко читаемое введение в историю развития идей, лежащих
в основе корреляции и регрессии.
Глава 8
• Cohen, J., Cohen P., S. G. West, and L. S. Aiken. 2003. "Applied Multiple
Regression/Correlation Analysis for the Behavioral Sciences." 2nd ed. Hillsdale, NJ:
Lawrence Erlbaum Associates.
Прекрасный учебник для освоения основ простой и множественной регрессии.
• Dunteman, George H., and Moon-Ho R. Но. 2006. "An Introduction to
Generalized Linear Models." Thousand Oaks, CA: SAGE Publications.
Одна из «маленьких зеленых книжек» издательства Сейдж. Это тонкое
(72 страницы) издание предоставляет прекрасный обзор обобщенных
линейных моделей для тех, кто без труда разбирается в математических уравнениях.
• Galton, Francis. 1886. "Regression towards mediocrity in hereditary
stature." Journal of the Anthropological Institute 15: 246-263. http://galton.org/
essays/1880-1889/galton-1886-jaigi-regression-stature.pdf.
Это оригинальная статья о возврате в среднее состояние.
• Glass, G. V., Peckham,R D. and Sanders J. R.. 1972. "Consequences of failure to
meet assumptions underlying the analysis of variance and covariance." Review
of Educational Research 42: 237-288.
Подробный разбор допущений, лежащих в основе дисперсионного и
ковариационного анализов, и последствий нарушения этих допущений для
анализа данных.
ШЕН1
Глава 9
• Fisher, R. A. 1931. "Studies in crop variation. I. An examination of the yield of
dressed grain from Broadbalk." Journal of Agricultural Science 11: 107-135.
Описание оригинальных экспериментов и формулировок, лежащих в
основе дисперсионного анализа.
• Miler, G. A., and Chaplin J. P.. 2001. "Misunderstanding analysis of covariance."
Journal of Abnormal Psychology 110(1): 40-48.
Ясное обсуждение корректного использования дисперсионного анализа
данных и того, что можно, а чего нельзя делать при помощи этого метода.
Глава 10
• Achen, Christopher H. 1982. Interpreting and Using Regression. Thousand
Oaks, CA: Sage Publications.
«Маленькая зеленая книжка» издательства Сейдж, в которой дано
прекрасное введение в корректную (и осторожную) интерпретацию моделей
множественной линейной регрессии.
• Jacard, James, Robert Turrisi, and Wan С. К.. 1990. Interaction Effects in
Multiple Regression. Thousand Oaks, CA: Sage Publications.
Еще одна «маленькая зеленая книжка» издательства Сейдж, в которой
ясно обобщены теоретические и практические аспекты эффектов
взаимодействия в регрессионных моделях.
• O'Brien, R. М. 2007. "A caution regarding rules of thumb for variance inflation
factors." Quality & Quantity 41: 673-690.
Автор доказывает, что применение принятых практических правил
усиливает проблемы, вызванные мультиколлинеарностью, а стандартные
подходы к устранению мультиколлинеарности могут вызвать больше проблем,
чем они решают.
Глава 11
• Bates, Douglas M., and Donald G. Watts. 1988. Nonlinear Regression Analysis
and Its Applications. New York: Wiley.
Это очень полезный учебник по основам аппроксимации кривых и
нелинейному моделированию.
• Efron, Bradley. 1982. The Jackknife, the Bootstrap, and Other Resampling
Plans. Philadephia: Society for Industrial and Applied Mathematics.
Классический учебник по повторному составлению выборок.
• Hosmer, David W., and Stanley Lemeshow. 2000. Applied Logistic Regression,
2nd ed. New York: Wiley.
Изложение практического подхода к логистической регрессии и ее
приложениям для продвинутых студентов и специалистов.
EEElHiH
Приложение С
Глава 12
• Gould, Stephen Jay. 1996. "The Mismeasure of Man." W. W. Norton &
Company.
Эта прекрасная книга описывает историю тестов на интеллект и
(неправильного применения различных методов многомерного анализа для
понимания различий между людьми.
• Hartigan, J. A. 1975. "Clustering Algorithms." New York: Wiley.
Эта книга - современная классика, полностью охватывающая
фундаментальные понятия кластерного анализа, включая метрики расстояния,
достаточно подробно, чтобы сделать возможным применение всех описанных
алгоритмов.
Глава 13
• Conover, W. J. 1999. "Practical Nonparametric Statistics." Hoboken, NJ:
Wiley.
Эта книга достойна своего названия1; это прекрасный справочник для
людей, которым нужно узнать, как проводить корректные непараметрические
тесты в конкретной ситуации, и которым не нужно долгое теоретическое
обсуждение каждой статистики. В книге приведена полезная схема,
которая позволяет найти непараметрический аналог любого параметрического
теста.
• HealthKnowledge. "Parametric and non-parametric tests for comparing two or
more groups." http://www.healthknowledge.org.uk/public-health-textbook/
research-methods/lb-statistical-methods/parametric-nonparametric-tests.
Это набор полезных схем, которые помогут вам подобрать подходящую
непараметрическую статистику для разных аналитических ситуаций. Эти
схемы были созданы в рамках популярного онлайн-курса по
здравоохранению, разработанного английским департаментом здравоохранения.
• Mann, H. В., and Whitney D. R.. 1947. "On a test of whether one of two random
variables is stochastically larger than the other." Annals of Mathematical
Statistics 18: 50-60.
В этой статье описано расширенное применение теста Манна-Уитни для
выборок разного размера.
• Wilcoxon, F. 1945. "Individual comparisons by ranking methods." Biometrics
Bulletin 1:80-83.
Это оригинальная статья, в которой описан тест Манна-Уитни для
выборок одинакового размера.
• Wilcoxon, F. 1957. Some Rapid Approximate Statistical Procedures. Stamford,
CT: American Cyanamid. Revised with R. A. Wilcox, 1964.
«Практическая нсиараметрпческая статистика». - Прим. пер.
шшшш
Это оригинальные и переработанные статьи, которые описывают текст
Вилкоксона, включая таблицу пороговых значений.
Глава 14
• Clemen, Roger T 2001. "Making Hard Decisions: An Introduction to Decision
Analysis." Pacific Grove, CA: Duxbury Press.
В этом учебнике, посвященном разным подходам к анализу решений,
сделан акцент на логические и философские вопросы, которые сопутствуют
принятию решений.
• The Economist Newspaper. 1997. "Numbers Guide: The Essentials of Business
Numeracy." Hoboken, NJ: Wiley.
Этот полезный карманный справочник описывает операции с числами,
которые используются в бизнесе, включая индексы, задачи, связанные с
вложениями и ипотекой, прогнозы, проверку гипотез, теорию принятия
решений и линейное программирование.
• Gordon, Robert J. 1999. "The Boskin Commission Report and its aftermath."
Paper presented at the Conference on the Measurement of Inflation, Cardiff,
Wales, http://faculty-web.at.northwestern.edu/economics/gordon/346.pdf.
Здесь обобщены критические соображения по поводу индекса
потребительских цен, включая те индексы, которые были обнародованы в отчете
комиссии Боскина (Boskin) в 1995 году, в котором обосновывалось
завышение уровня инфляции индекса потребительских цен.
• Shumway, Robert, and David S. Stoffer. 2006. "Time Series Analysis and Its
Applications: With R Examples." New York: Springer.
В эту популярную книгу по анализу временных серий вошел программный
код на R (свободный язык программирования).
• Tague, Nancy. 2005. "The Quality Toolbox." 2nd ed. Milwaukee, WI: American
Society for Quality.
В этом справочнике приведены обзор и краткая история контроля качества
с алфавитным перечнем методов, используемых в данной области, включая
стандарные статистические и графические процедуры, такие как диаграммы
размаха и проверка гипотез, и более специализированные инструменты,
такие как контрольные карты и диаграммы причинно-следственных связей.
Глава 15
• Cohen, Jacob. 2002. "A power primer." Psychological Bulletin 112 01ИУ)-
Это увлекательное введение в концепцию мощности предварено
исследованием Коэна с соавторами, посвященным игнорированию оценки
мощности в опубликованных работах.
• Ahrens, Wolfgang, and Iris Pigeot, Eds. 2004. "Handbook of Epidemiology"
New York: Springer.
шшмт
Приложение С
Этот справочник по эпидемиологии состоит из глав по отдельным темам,
написанным экспертами в каждой области. Глава, посвященная
вычислению размера выборки и анализу мощности, содержит формулы и примеры
наиболее распространенных планов исследований, используемых в
медицине и эпидемиологии.
• Hennekens, Charles H., and Julie E. Buring. 1987. "Epidemiology in Medicine."
Boston: Little, Brown.
Это легко читающееся введение в эпидемиологию, начиная с базовых
понятий до планирования исследований и типов анализа.
• Pagano, Marcello, and Kimberlee Gauvreau. 2000. "Principles of Biostatistics."
2nd ed. Pacific Grove, CA: Duxbury Press.
Это введение в биостатистику подходит для базового университетского
курса; оно проще и менее детально, чем предыдущий учебник.
• Rosner, Bernard. "Fundamentals of Biostatistics." 6th ed. Pacific Grove, CA:
Duxbury Press, 2005.
Прекрасное введение в биостатистику для аспирантов или для тех, кто
хочет глубже вникнуть в теоретические нюансы, чем это позволяет сделать
указанный выше учебник.
• Rothman, Kenneth J., et al. 2008. "Modern Epidemiology." 3rd ed. Philadelphia:
Lippincott, Wilkins, and Williams.
Это очень подробное обсуждение эпидемиологии, включая несколько глав,
написанных приглашенными авторами, для студентов, которые желают
полностью овладеть предметом.
Глава 16
• Crocker, Linda, and James Algina. 2006. "Introduction to Classical and Modern
Test Theory." Independence, KY: Wadsworth.
Это обновленная версия стандартного учебника, непревзойденного в части
описаний моделей, основанных на классической теории тестирования.
• Ebel, R. L. 1965. "Measuring Educational Achievement." Englewood Cliffs, NJ:
Prentice Hall.
Этот текст послужил источником правил для интерпретации индекса
дискриминации, которые процитированы в главе 16.
• Embretson, Susan, and Steven Reise. 2000. "Item Response Theory for
Psychologists." Mahwah, NJ: Erlbaum.
Это базовый учебник, который использует интуитивный подход к
современной теории тестирования с использованием многих схем и аналогий с
классической теорией тестирования.
• Hambleton, Ronald К., et al. 1991. "Fundamentals of Item Response Theory."
Thousand Oaks, CA: Sage Publications.
Здесь представлено чрезвычайно ясное введение в современную теорию
тестирования, где объяснено, как она преодолевает некоторые ограничения
классической теории тестирования.
• Tanner, David E. 2001. "Assessing Academic Achievement." Boston: Allyn and
Bacon.
Этот ясный текст, написанный для учителей и администраторов,
затрагивает основные проблемы академического тестирования и оценивания;
обсуждаются актуальные вопросы (достоверная оценка, итоговое
тестирование, адаптированное для компьютера тестирование) наряду с обычными
темами, такими как классическая теория тестирования и сравнение оценок,
соотнесенных с нормой и критерием.
Глава 17
• Boslaugh, Sarah. 2004. "An Intermediate Guide to SPSS Programming: Using
Syntax for Data Management." Thousand Oaks, CA: Sage.
Книга посвящена основным аспектам управления данными и
предназначена для людей, которые будут управлять данными и анализировать их,
используя SPSS. В книгу входит программный код для выполнения многих
задач.
• Cody, Ron. 1999. "Cody's Data Cleaning Techniques Using SAS Software."
Cary, NC: SAS Institute.
Описаны приемы проверки и очистки данных при помощи SAS, включая
многие примеры стандартных процедур и программный код SAS для их
выполнения.
• Hernandez, M.J. 2003. "Database Design for Mere Mortals: A Hands-On Guide
to Relational Database Design." 2nd ed. Upper Saddle River, NJ: Addison
Wesley.
Это хороший справочник по теории и практике организации баз данных.
Изложение касается принципов, применимых к любой базе данных, а не
указаний по использованию определенного программного продукта.
• Levesque, Raynald. Raynald's SPSS Pages.
http://www.spsstools.net/.
Два сайта, поддерживаемые опытным SPSS-программистом; оба содержат
советы, полезные приемы и примеры кода.
• Little, Roderick J. A., and Donald B. Rubin. 2002. "Statistical Analysis with
Missing Data." 2nd ed. Hoboken, NJ: Wiley.
Эта книга о пропущенных данных - стандартный справочник по предмету.
Однако он не для слабых духом и подразумевает наличие значительных
математических способностей у читателя.
ИЯ1
Приложение С
Глава 18
• Christensen, Larry В. 2006. "Experimental Methodology." 10th ed. Boston: Al-
lyn & Bacon.
Это очень легко читаемое и полное введение в планирование исследований
и экспериментов, особенно в образовании и психологии.
• Fisher, R. А. 1990. "Statistical Methods, Experimental Design, and Scientific
Inference: A Re-issue of Statistical Methods for Research Workers, the Design
of Experiments, and Statistical Methods and Scientific Inference." Oxford:
Oxford University Press.
Если вы хотите ознакомиться с оригинальным обоснованием многих
экспериментальных планов и проблем, изложенных в этой главе - это лучший
источник.
• The Framingham Heart Study, http://www.framinghamheartstudy.org/.
Это официальный сайт одного из наиболее масштабных, продолжительных
и знаменитых перспективных групповых исследований за всю историю
медицины.
• Martin, E, and Siddle D.. 2003. "The interactive effects of alcohol and Temaze-
pam of P300 and reaction time." Brain and Cognition, 53(1): 58-65.
Эта статья была использована в качестве примера плана исследования в
главе 18.
• Robinson, W. S. 1950. "Ecological correlations and the behavior of individuals."
American Sociological Review 15(3): 351-357. Reprinted in the International
Journal of Epidemiology (2009).
http://ije.oxfordjournals.org/content/early/2009/01/28/ije.dyn357.full.
pdf+html.
Это классическая публикация на тему заблуждений в популяционных
исследованиях, проиллюстрированных данными о корреляции между
грамотностью и расовой принадлежностью и национальностью.
• Rosenbaum, Paul R., and Donald В. Rubin. 1983. "The central role of the
propensity score in observational studies for causal effects." Biometrika 70: 41-55.
В этой статье описана концепция степени предрасположенности, которая в
настоящее время широко используется в медицинских исследованиях
случай-контроль.
• Shadish, William R., Thomas D. Cook, and Donald T. Campbell. 2001.
"Experimental and Quasi-Experimental Designs for Generalized Causal Inference."
Florence, KY: Wadsworth Publishing.
Это обновленная версия классического текста о планировании
исследований; не самая лучшая книга для начинающих, но необходимая для
каждого, кто хочет по-настоящему овладеть этой темой.
• Wolff, Alexander, Albert Chen, and Tim Smith. 2002. "That Old Black Magic."
Sports Illustrated 96 (January): 50-62.
В статье оценена обоснованность разговоров о «несчастье, приносимом
Спорте Иллюстрэйтед», явлении, часто упоминаемом в качестве
классического примера возврата к среднему.
Глава 19
• Alley, Michael. 2003. "The Craft of Scientific Presentations." New York: Springer.
Целая книга, посвященная рассмотрению разных стилей представления
результатов научных исследований (например, сравнению информирующего
и мотивирующего стилей). В книге содержится множество примеров
наряду с общими принципами, позволяющими сделать презентацию успешной
или неуспешной.
• LaMontaigne, Mario. "Planning a scientific presentation."
http://www.biomech.uottawa.ca/english/teaching/apa6905/lectures/
presentation-style.pdf.
Это компьютерная презентация о том, как делать хорошие компьютерные
презентации, с забавными примерами некоторых неудачных подходов.
• "Slides from NISS/ASA Technical Writing Workshop for Young Researchers ...
and Some Other Stuff." (August 2007).
http://wwwpublic.iastate.edu/~vardeman/RTGWritingStuff.html.
Это собрание слайдов и других ресурсов, посвященных написанию научных
статей для профессиональных журналов, выполненное в рамках рабочего
совещания, финансированного Американским статистическим обществом
и Национальной независимой статистической службой; основная целевая
аудитория - это студенты и молодые исследователи, которые пишут
первую научную статью, однако там есть много советов, которые будут
полезны и более опытным ученым.
• Ternes, Reuben. 2011. "Writing with statistics." Purdue Online Writing Lab.
http://owl.english.purdue.edu/owl/resource/672/1/.
Это основное руководство по представлению статистических данных для
студентов. В лаборатории интернет-публикаций (OWL, Online Writing
Lab) создана и другая полезная информация для людей, пишущих научные
тексты, включая руководства по написанию резюме и основным системам
ссылок и написанию статей по медицине, медсестринскому делу и
техническим специальностям.
• The OPEN Notebook.
http://www.theopennotebook.com.
Сайт, посвященный научной журналистике, нацелен на широкую
аудиторию и представляет сочетание практических советов и взгляда изнутри на
^HhH':J Приложение С
написание широко известных статей и книг (таких как «Вечная жизнь
Генриетты Лаке»).
United Nations Economic Commission for Europe. 2009. Making Data
Meaningful.
http://www.unece.org/fileadmin/DAM/stats/documents/writing/MDM_
Partl_English.pdf;
http://www.unece.org/fileadmin/DAM/stats/documents/writing/MDM_
Part2_English.pdf:
http://www.unece.org/fileadmin/DAM/stats/documents/writing/MDM_
Part3_English.pdf:
Этот текст в трех частях написан для менеджеров, специалистов по
связям с общественностью и прочих далеких от науки людей. В первой части
рассказано, как превратить статистическую информацию в рассказ,
который завладеет вниманием слушателей и передаст важную информацию,
во второй части обсуждается, как представлять статистические результаты
(и вербально, и графически), а третья часть посвящена взаимодействию со
СМИ.
Глава 20
• Good, Phillip I., and James W. Hardin. 2006. "Common Errors in Statistics (and
How to Avoid Them)." Hoboken, NJ: Wiley.
Этот справочник позволяет избежать распространенных ошибок в
статистической методологии и аргументации.
• Alderson, Phil, and Sally Green, eds. 2009. The Cochrane Collaboration
Learning Material for Reviewers.
http://www.cochrane-net.org/openlearning/.
Здесь представлено ясное обсуждение систематической ошибки при
отборе статей для публикации, написанное для поддержания усилий группы
Кохрейна (Cochrane Collaboration), международной организации, цель
которой - стимулирование обоснованных решений в здравоохранении.
• Книга Дэррила Хуфа «Как лгать при помощи статистики» (Darryl Huffs
«How to Lie with Statistics»), которая упоминалась в качестве общего
источника в начале этого приложения, также чрезвычайно актуальна для
этой главы.
ИДЯ
Дда
ПРИЛОЖЕНИЕ D.
Таблицы вероятностей
для распространенных
типов распределений
Таблицы вероятностей для разных распределений размещены во многих
учебниках и Интернете; в этом разделе для вашего удобства таблицы приведены вместе
с решенными примерами из основной части. Одно предостережение: существует
более одного способа представить значения вероятности для любого
распределения, так что часто имеет смысл потратить несколько минут, чтобы сообразить, как
устроена данная таблица, перед ее использованием.
Таблицы вероятностей - это, возможно, пережиток того времени, когда
статистические калькуляторы и компьютерные программы еще не были
легкодоступными, но эти таблицы полезны даже в нашу эпоху электроники. Для правильного
использования таблицы вероятностей вам нужно задуматься об интересующем
вас распределении и о том, как оно соотносится с вашей научной задачей. Так что
несколько минут работы с таблицей вероятностей не пройдут даром, даже если вы
рассчитываете произвести большую часть или все необходимые статистические
расчеты при помощи компьютерных программ.
Вошедшие в эту главу таблицы, за исключением биномиального
распределения, взяты из электронного справочника по статистическим методам (NIST/
SEMATECH e-Handbook of Statistical Methods), размещенного в Интернете
(http://itl.nist.gov/div898/handbook/index.htm) американским
Национальным институтом стандартов и технологий (National Institute of Standards and
Technology). Таблицы для биномиального распределения, также находящиеся в
открытом доступе, были созданы Вильямом Найтом (William Knight), бывшим
профессором информатики и математики университета Ныо Брунсвика (New
Brunswick), и размещены на его сайте (http://www.math.unb.ca/~knight/utility/).
Учтите, что в случае непрерывных распределений, таких как нормальное, мы
всегда рассуждаем в терминах площади под кривой (что соответствует
вероятности всех результатов, составляющих эту площадь), а не вероятности одного
значения распределения. Это значит, что мы можем вычислить P(Z > 2,00) или
P(Z< -1,80), но не P(Z = 2,00) или P(Z = -1,80). Этому есть техническое объяс-
|Ц : Приложение D
пение; в дискретном распределении у точки (такой как 2,00) нет площади и,
следовательно, нет вероятности. Это ограничение относится только к непрерывным
распределениям, и для дискретных распределений можно найти вероятность
отдельных значений.
Стандартное нормальное
распределение
На рис. D.3 указана площадь под кривой нормального распределения,
соответствующая вероятности того, что 0 < х < |я|, то есть вероятности того, что значение х
лежит в диапазоне между 0 и абсолютным значением некоторого а. Предположим,
что а = 0,5. Площадь 0 < х < 0,5 выделена цветом на рис. D.I.
Рис. D.1. Площадь 0 < х < 0,5 для стандартного нормального распределения
Из таблицы вероятностей для нормального распределения, представленной на
рис. D.3, видно, что площадь этой области, соответствующая вероятности
значения в диапазоне (0, 0,5), равна 0,19146. (Помните, что общая площадь под кривой
нормального распределения равна 1,0.) Мы находим это значение, двигаясь вниз
по столбцу х до строки 0,5, а затем - до пересечения со столбцом 0,00. Значение в
ячейке на пересечении этих столбца и строки - это вероятность значения в
диапазоне от 0 и абсолютного значения а (в данном случае между 0 и 0,5). Это значение
0,19146- и площадь под кривой нормального распределения между значениями
0 и 0,5, и вероятность для значения в диапазоне между 0 и 0,5 для стандартного
нормального распределения.
Поскольку стандартное нормальное распределение асимметрично, в этой
таблице приведены только положительные значения, но площадь для отрицательных
значений а можно легко вычислить. Например, Р(0 < х < 0,5) = Р(0 > х > -0,5) =
Р(-0,5 < х < 0). Площадь (-0,5 <х< 0) залита цветом на рис. D.2, и вероятность
равна 0,19146.
Таблицы вероятностей для распространенных
-4-3-2-101234
Рис. D.2. Площадь -0,5 < х < 0 для стандартного нормального распределения
X
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
4
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
00
00000
03983
07926
11791
15542
19146
22575
25804
28814
31594
34134
36433
38493
40320
41924
43319
44520
45543
46407
47128
47725
48214
48610
48928
49180
49379
49534
49653
49744
49813
49865
49903
49931
49952
49966
49977
49984
49989
.49993
49995
49997
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Площадь под кривой нормального распределения от 0 до X
01
00399
04380
08317
12172
15910
19497
22907
26115
29103
31859
34375
36650
38686
40490
42073
43448
44630
45637
46485
47193
47778
48257
48645
48956
49202
49396
49547
49664
49752
49819
49869
49906
49934
49953
49968
49978
.49985
.49990
.49993
.49995
.49997
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
02
00798
04776
08706
12552
16276
19847
23237
26424
29389
32121
3 4614
3 6864
38877
40658
42220
43574
44738
45728
46562
47257
47831
48300
48679
48983
49224
49413
49560
49674
49760
49825
49874
49910
49936
49955
49969
49978
.49985
.49990
.49993
.49996
.49997
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
03
01197
05172
09095
12930
16640
20194
23565
26730
29673
32381
34849
37076
39065
40824
42364
43699
44845
45818
46638
47320
47882
48341
48713
49010
49245
49430
49573
49683
49767
49831
49878
49913
49938
49957
49970
49979
49986
49990
.49994
.49996
.49997
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
04
01595
05567
09483
13307
17003
20540
23891
27035
29955
32639
35083
37286
39251
40988
42507
43822
44950
45907
46712
47381
47932
48382
48745
49036
49266
49446
49585
49693
49774
49836
49882
49916
49940
49958
49971
49980
49986
49991
49994
49996
.49997
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
05
01994
05962
09871
13683
17364
20884
24215
27337
30234
32894
35314
37493
39435
41149
42647
43943
45053
45994
46784
47441
47982
48422
48778
49061
49286
49461
49598
49702
49781
49841
49886
49918
49942
49960
49972
49981
49987
49991
49994
49996
49997
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
06
02392
06356
10257
14058
17724
21226
24537
27637
30511
33147
35543
37698
39617
41308
42785
44062
45154
46080
46856
47500
48030
48461
48809
49086
49305
49477
49609
49711
49788
49846
49889
49921
49944
49961
49973
49981
49987
49992
49994
49996
49998
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
07
02790
06749
10642
14431
18082
21566
24857
27935
30785
33398
35769
37900
39796
41466
42922
44179
45254
46164
46926
47558
48077
48500
48840
49111
49324
49492
49621
49720
49795
49851
49893
49924
49946
49962
49974
49982
49988
49992
49995
49996
49998
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
08
03188
07142
11026
14803
18439
21904
25175
28230
31057
33646
35993
38100
39973
41621
43056
44295
45352
46246
46995
47615
48124
48537
48870
49134
49343
49506
49632
49728
49801
49856
49896
49926
49948
49964
49975
49983
49988
49992
49995
49997
49998
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
09
03586
07535
11409
15173
18793
22240
25490
28524
31327
33891
36214
38298
40147
41774
43189
44408
45449
46327
47062
47670
48169
48574
48899
49158
49361
49520
49643
49736
49807
49861
49900
49929
49950
49965
49976
49983
49989
49992
49995
49997
49998
Рис. D.3. Таблица вероятностей для стандартного нормального распределения
||| |ЕП
ЕШНН
Приложение D
Один из способов ориентироваться в незнакомой таблице вероятностей - это
найти несколько известных значений. Например, Z-значение для 1,96 должно быть
вам знакомо в связи с 95%-ми двусторонними доверительными интервалами. Если
вы найдете ячейку на пересечении 1,9 (строка) и .06 (столбец), вы увидите значение
0,47500. Это Р(0 < х < 1,96), и если вы удвоите его, добавив вероятность для Р(-1,96
< х < 0), вы получите 0,95, или 95%. Иначе говоря, 0,025 площади под кривой
стандартного нормального распределения лежит выше значения 1,96 и 0,025 - ниже
значения -1,96, так что всего 5% значений стандартного нормального распределения
находятся за пределами диапазона (-1,96, 1,96). Вот почему при использовании
значения альфа, равного 0,05, для основанного на нормальном распределении
статистического теста результат, который соответствует стандартным значениям, выходящим
за пределы диапазона (-1,96,1,96), считается значимым; настолько выбивающееся
из общей массы значение будет встречаться менее чем в 5% случаев, если
справедлива нулевая гипотеза.
Проработка нескольких примеров может сделать эту таблицу более понятной.
Часто для вычисления вероятности некоторого результата требуется сложить
вероятности с обеих сторон от нуля. Например, в главе 3 (рис. 3.4) мы выяснили, что
Z-значение для числа 105, происходящего из генеральной совокупности с
распределением х ~ N(100,5), равно 1,00. Найти вероятность значения, большего или равного
105, из генеральной совокупности с распределением х ~ N(100,5) - это то же самое,
что найти вероятность Z-значения не меньше, чем 1,00, для стандартного нормального
распределения. Простейший способ вычислить P(Z> 1,0) - это найти площадь под
кривой для значений меньше Z= 1,00, а затем вычесть эту площадь из 1,0 (общей
площади под кривой нормального распределения). Площадь под кривой левее Z= 1,00
включает площадь от минус бесконечности до нуля и от нуля до 1,00. Мы знаем, что
первая равна 0,5 (поскольку половина площади под кривой стандартного
нормального распределения находится левее нуля, а другая половина - правее), и, используя
таблицу, мы узнаем, что вторая площадь равна 0,34134. Таким образом, если мы
обозначим значение какХ:
Р(Х< 105) = P(Z< =1,00) = 0,50000 + 0,34134 = 0,84134,
Р(Х> 105) = P(Z> 1,00) = 1 - 0,84134, или 0,15866.
Если вернуться к исходной задаче, этот результат свидетельствует о том, что
вероятность того, что значение превысит 105, составляет около 15,9%, если
распределение значений в генеральной совокупности описывается как -N(100, 5). Иначе
говоря, значение 105 в такой генеральной совокупности находится примерно в
верхних 16% значений. На рис. D.4 эта площадь выделена цветом.
В главе 3 (рис. 3.5) мы также узнали, что значение 95 из генеральной
совокупности с распределением N-(100, 5) преобразуется в Z-значение -1,00.
Предположим, мы хотим узнать, какая доля значений лежит ниже этого уровня. Чтобы
сделать это, мы используем два факта:
• по определению стандартного нормального распределения площадь ниже 0
(между минус бесконечностью и нулем) равна 0,5;
Таблицы вероятностей для распространенных.,
площадь между -1,00 и 0 равна 0,34134 (так же как и площадь между 0
и 1,00).
i ~Х^ 1 1 1
-4 -3 -2 -1 0
i ^Т i
12 3 4
Рис. D.4. Площадь под кривой стандартного нормального распределения
для P(Z> 1,00)
Таким образом, площадь под кривой левее -1,00 равна 0,5 - 0,34134 или 0,15866.
Обратите внимание на то, что эта площадь под кривой равна площади правее
Z= 1,00, ожидаемый результат, учитывая симметричность стандартного
нормального распределения. Эта площадь показана цветом на рис. D.5.
1 Т —1 1
-4 -3 -2
10 12 3 4
Рис. D.5. Площадь под кривой стандартного нормального распределения
для P(Z< 1,00)
При работе с таблицей вероятностей можно легко запутаться, какую площадь
вы вычисляете, так что может быть полезно схематически изобразить, что вам
нужно сложить или вычесть, чтобы получить ответ.
В главе 3 (рис. 3.6) мы вычислили, что значение 35 из генеральной
совокупности с распределением ~JV(50, 10) преобразуется в Z-значение -1,50. Для
вычисления вероятности значения из этой генеральной совокупности, превышающего 35,
мы заметили, что в ответ войдет площадь между -1,5 и 0, а также площадь правее
нуля (между нулем и плюс бесконечностью).
P(Z> -1,5) = 0,43319 + 0,50000 = 0,93319.
Так что вероятность значения выше 35 в этой генеральной совокупности равна
93,3%. Это соответствует выделенной цветом площади на рис. D.6.
шмн :
Приложение D
i Т^—i Н 1 1 1 -:==т 1
-4-3-2-101234
Рис. D.6. Площадь под кривой стандартного нормального распределения
для P(Z< -1.5)
При нахождении вероятности при помощи таблицы для стандартного
нормального распределения не важно, представляет ли Z-значение одно число или
выборочное среднее. В главе 3 (рис. 3.21) мы вычислили Z-статистику для выборочного
среднего, равного 52, из выборки с 30 значениями, происходящей из генеральной
совокупности со средним 50 и стандартным отклонением 10. Это выборочное
среднее соответствует Z-значению 1,10. Вероятность Z-значения не меньше этого
мы вычисляем следующим образом:
P(Z> 1,10) = 1 - P(Z< 1,10) = 1 - (0,5000 + 0,36433) = 0,13567.
Если вместо этого мы хотим вычислить вероятность значения не меньше
данного, это нужно делать следующим образом:
P(Z< 1,10) = (0,5000 + 0,36433) = 0,86433.
Как и раньше, 0,5 соответствует вероятности значения от минус бесконечности
до нуля, а 0,36433 характеризует вероятность значения от 0 до 1,10.
Вот вероятности для других примеров Z-распределения из главы 3.
Рис. 3.22: Z= 1,55
P(Z> 1,55) = 1 - P(Z< 1,55) = 1 - (0,50000 + 0,43943) = 0,06057
P(Z< 1.55) = (0.50000 + 0.43943) = 0,93943
Рис. 3.23: Z= 2,00
P(Z> 2,00) = 1 - P(Z< 2,00) = 1 - (0,50000 + 0,47725) = 0,02275
P(Z< 2,00) = (0,50000 + 0,47725) = 0,97725
Распределение Стьюдента
Поскольку распределение ^-статистики зависит от числа степеней свободы,
таблицы для распределения Стьюдента обычно сокращены и содержат только
определенные критические значения (иначе эти таблицы были бы необъятными).
В таблице, представленной на рис. D.7, число степеней свободы указано в столбце,
обозначенном буквой v. Это односторонние критерии, и поскольку распределение
Стьюдента симметрично, для вычисления двусторонней вероятности нужно
выбрать столбец для значения, вдвое меньшего, чем то, что вас интересует.
Таблицы вероятностей для распространенных...
ЕЯЯ
Верхние критические значения для распределения
Стьюдента с v степенями свободы
Вероятность превышения критического значения
Рис. D.7. Избранные критические значения для распределения Стьюдента
Приложение D
Предположим, вам нужно найти критическое значение для двустороннего теста
Стыодента с 20 степенями свободы и а = 0,05. Вы выбираете столбец для 0,025
(поскольку 0,05/2 = 0,025), доходите до пересечения со строкой v = 20 и находите
критическое значение, равное 2,086. Это означает, что ^-критерий для вашего
эксперимента должен быть больше, чем 2,086, или меньше, чем -2,086, чтобы
нулевую гипотезу можно было отвергнуть.
Если вы проводите односторонний тест с v = 20 и а = 0,05, нужно
воспользоваться столбцом, обозначенным 0,05, дойти до пересечения со строкой v = 20, как и в
предыдущем случае, тогда мы узнаем, что критическое значение составляет 1,725.
Хотя эта таблица для распределения Стыодента не дает вам точных
вероятностей для любого ^-значения, вы можете использовать ее для проверки гипотез.
Например, в главе 6, рис. 6.7, мы вычислили ^-статистику, равную -3,87, для
одностороннего теста Стыодента с 14 степенями свободы. Для двухстороннего теста
со значением а = 0,05 критическое значение составляет 2,145 (пересечение строки
для 14 степеней свободы и столбца с вероятностью 0,25 на рис. D.7). Вычисленное
нами значение сильнее отличается от нуля, чем критическое, так что мы отвергаем
эту нулевую гипотезу.
В главе 6, рис. 6.12, мы вычислили ^-статистику, равную 1,01, для двухвыбороч-
ного теста для двух независимых групп с 18 степенями свободы и а = 0,05. Глядя на
рис. D.7, мы понимаем, что критическое значение в данном случае равно 2,101.
Вычисленная нами ^-статистика меньше по модулю (ближе к нулю), чем критическое
значение, так что в данном случае мы не можем отвергнуть нулевую гипотезу.
Биномиальное распределение
Поскольку биномиальные распределения различны для каждой комбинации п up,
таблицы биномиального распределения могут быть довольно большими. К счастью,
биномиальное распределение можно аппроксимировать нормальным, если и пр, и
п{\ - р) больше или равны 5, так что особой надобности в таблицах для больших
значений п нет. Здесь мы приводим часть таблиц вероятностей и кумулятивных
вероятностей для биномиального распределения, созданных профессором
Университета Ныо-Брунсвика Вильямом Найтом, полные версии таблиц доступны на его
сайте (http://www.math.unb.ca/~knight/utility/). На рис. D.8 представлены
вероятности для п = 3-10, а на рис. D.9 - кумулятивные вероятности для п = 3-10.
Для вычисления вероятности биномиального распределения вам нужно знать
п (число испытаний), к (число успехов) и р (вероятность успеха в любом
испытании). Сначала найдите таблицу для нужного п, а затем в пересечении строки
для к и столбца для р прочтите искомую вероятность (на рис. D.8) или
кумулятивную вероятность (на рис. D.9) для указанного результата. Например, в главе 3
(рис. 3.10) мы вычислили, что 6(1;5, 0,5), вероятность ровно одного успеха в пяти
испытаниях ср = 0,5, равна 0,16. Чтобы убедиться в правильности этого
вычисления с помощью табл. D.8, мы найдем таблицу для п = 5, а затем - пересечение
строки для к = 1 и столбца для р = 0,5. Вероятность будет равна 0,15625, что после
округления даст нам такой же результат, какой был ранее вычислен. Если мы хотим
Таблицы вероятностей для распространенных...
узнать вероятность не более чем одного успеха в пяти испытаниях - вероятность О
или 1 успехов, то мы используем таблицу кумулятивных вероятностей (рис. D.9).
Выполнив ту же последовательность действий, мы обнаружим, что вероятность О
или 1 успехов в пяти испытаниях ср = 0,5 равна 0,18750. Мы могли бы получить
то же значение, сложив вероятности нуля и одного успехов на рис. D.8:
0,03125 + 0,156250 = 0,18750.
0 | o.ti'i 0.412 o.m o.nA o.m о, on* o.uh о.тя o.aoi
j j 0.2*1 ».Ш o.Mi P.4U o..i>s o.i&» q.ui •.Ml •.Ml
2 | 0.02? 0,044 0.11» 0.211 0.173 0.433 0.441 0.114 0.242
1 j 0.001 0.00» 0.027 0.044 0.125 0.21* 0.243 0.Ы2 0.72»
\ P- .1
.2
4
0 I 0.4361 0.4314 0.2401 0.1294 0.O623 0.0234 0.0011 0.0014 Э.СЭ01
> | 0.2*14 0.40*1 0.4114 0.1434 0.2300 0.1314 0.073» 0.023* 0.03)1
2 j 0.0186 0.1316 0.2646 0.143b 0.2730 I.MM 0.244» 0.1324 00464
i | 0.0016 I.NM t.*2M D*MM i.MM I.14M в.41441 c.tc'ie. i.Mll
4 | 0.0031 0.O014 0.0011 0.0234 0.0423 0.1244 0.2401 0.4C»* 0.4341
К S P-.l
.3
0 I ¦.MM! 0.32769 0.16907 0.077)6 0.0
i j 1.1ЛМ 0.40460 D..1h0i1 О
2 | 0.072*0 0.20410 0.20*70 0
1 j 0.O0M10 0.03120 1.1)121 0
4 j 0.UO04S 0.006*0 0. U2.11S I
3 I 0.00001 0.00012 0.O0241 0
125 0.01024 0.00241 1.1*1)1 С.ОО0О1
01024 0.01123 0.07774 0.14107 0.22741 0.3*04»
1 | 0
4 | О
1 | I,
>.33144 0.26214 0.11745 О
t.MMl fl.Hiii u.ia2*i о
>.0)142 0.24374 0.12114 0
>.01438 0.0»l»2 0.18522 О
1.11Ш O.Qi-iU •.•MM О
OC0O1 0.00131 3.01021 0
0O300 0.00006 0.00073 0
04466 0.01562 B.OC410 О
IMO i.iUTi о.олкйл о
11104 0.224)1 0.1)124 0
27648 0.31250 C.2764V О
11A24 O.Jllifl 6..11104 0
02114 0.0*173 0.11442 0
00410 1,11*1] 0.О4666 0
OOCTJ 0.03006 D.O&300
01022 1.МШ O.OiV.'lOS
03*34 0.01334 C.OG132
16522 0.CB192 0.01458
0. I.'НИ.'
0.17201
0. 12400
0.02 246
•.•MM
0.00317
O.Ol
0.204i<2 0.0A21* 0
0.3*703 0.24704 0
0.27523 1.)1T« 0
Cl. 1МЙ il. J Jhh'i и
0..12RK) fi.0412* О
0.004)0 0.02300 0
0. 00036 0.0015,7 0
0.000ft) H.OUJ2 2 0
02,'•»•> t.MTti o.ciut(i4 l.lOM) o.
12044 0.0344* 0.01720 0.30337 3
24127 0.16*06 0.07741 0.02500 0
24010 0.21.144 0..41** 0.04/24
j<m* 0.21Л** 0.210.10 o.22(i*-# a
07741 -3.14404 0,26127 0.21743 3
01720 •«•94*1 0.13064 0.24706 0
00164 1.11711 0.02)44 1.1MM 0
0 3014 С
00*30 С
.02*6)
0.02 «"'Mi
I 0.12400
) 0.17 201
0.42017 0
0.2S264 0
0.1*880 0
о.01107 a
0.0043* 0
0.00041 0
0.001)02 U
0.00000 0
O.OOOOO 0
16777
31354
2*163
l*6fi:l
04311
0091»
Mill
COCCI
NW
С.0Э743
c.:»T65
0.29648
0.2S412
0.13614
0.04668
0.00132
С.ОСЭ07
0
0
0
0
0
0
0
31410
03958
20902
2)flh4
21224
12396
0412-»
00714
0ОС66
3
0
0
ft
3
a
I
3
a
031*1
D3125
1393»
>tl>|
27)44
21B75
1043 в
0)133
00191
0
0
•
0
1
0
и
1
0
OO044 0
00796 0
04129 О
12 1Й6 0
23224 0
2786» 0
20102 0
01*31 0
01680 0
03O07
03122
01000
0*6ьй
11414
25412
2464Й
1*743
05765
С.0С300 0
D.OCOQB 0
С.ОС115 0
[. .и..-l.h О
0.04311 0
•.SUM о
0.211*0 0
C.33S34 0
B.56T77 0
ЗОСЗО
ooc so
0QC02
14ЙА0
34261
I3JM1
J
.7
Ш
11422 0.0*01* U.OlC'fi* 0-0014* 0.0002* 0.00002 •.•MM 0.
301** C. 13349 0.0*0-47 3.0173» 0.001*4 0.СЭ041 0.00302 0.
10199 0.266*3 0.16124 0.BTO21 0.02123 0.0O1B6 О.ОС029 0.
1)614 0.266ЙЛ |,|1Щ 0.1ЙЮК 0.07412 1.4ШМ •.MI7I 0.
06406 0.17133 0.23012 3.2440» 0.11722 0.07391 0.01432 0.
01652 0.O73S1 0.16722 0.2*609 0.25092 0.11133 0.06606 0.
60274 0.02 100 0.0)412 0-16*06 0.2*0*2 0.266Я1 0.17616 0,
0002» I.0MM 0.33121 0.07031 0.14124 0.2641J 0.1ЙИ* 0,
00OO2 0.00041 0.00354 0.01)39 С.О6047 0.15345 0.101*» 0.
.60000 0.00002 0.0002*. 0.0.111* О.ОЮОв O-iHOl* 0.11*22 0,
I I I
• I I
I I I
I I I
.00744 0.
.00091 0.
4MM o.
.00030 0.
1721»
1*7*2
1A/42
.2
о I :
i t «
2 | 1
:.03)13 o,
| 0.01116 0
i Л.О0141 0
! •.•MM 0,
j I.MMI 0.
! o.ooooo о
i o.ooooo o.
I o.ooooo o.
10737 0.
26844 0.
10144 a.
30113 0.
08B0№ 0.
OOCi* 3
OOC07 0
.00000 0
30330 3
2**11
20012
10212
•MM
•MM
СЭ243
MOM
•MM
OC609
040)1
1 MM
3U»»
250*2
2 0.1 Sri
0.3009» 5,03313 (
0.00977 0.00157 (
0.6*144 0.01062 t
0.1171» 0.0424T (
O.2O308 0.1
0.00*30 o.:
0.03676 0-t
0. 10242 -.':
O.luftJl Л
0.24Ш 0.2
0.22347 0.30199 0.1937
00167 0.004?) fi.0*011 0.12106 Й.21..-4* 0.1Й742
0C31C 0.300»* 0.03603 0.33123 0.13737 0.l4l*t
.14*
о.2*йоч о.зоапк
0.10*0* l.MMI
0.1171» 0.214*9 <
0.0*395 0.12093 I
I.NMI 6.0СЭО0
l.MMI o.ooooo
). f..'i о !.-i 0.00000
).03O7» 0.00301
m 0.00914
.03642 0.00141
tUN l.ltlil
).23131 C.03MC
Рис. D.8. Вероятности для биномиального распределения для л = 3-10
Приложение D
О | 0.81 0.64 0.41 0.16 ft. 2*. ЯЛ* O.OT 0.04 0.01
i j a.4i e.»« o.n ft.и а.чч а.«4 a.is о.м о.и
3 | 1.30 8.00 1.03 1.03 I.M 1.С0 1.30 1.00 J.03
7>»л
.1
.8
0 I 0.729 0.312 0.343 0.216 О.125 0.344 0.027 0.008 0.001
1 I 0.972 С.89* 0.784 0.04В 0.500 0.352 0.214 0.104 5.028
2 | О. И» 0.992 О.973 0.936 0.*Т5 О. 1*4 С.«57 0.488 0.2)1
х j i.aoa i.cao коса i.ooo i.ono i.aoa i.cao l.ftM 1.000
В \ Г*.I .2 ..1 .4 . 1 .6 .7 .Я . 1
0 0.6362 0.4094 0.2431 0.1394 0.042» 0.0354 0.OC91 0.0014 0.0631
1 \ 0.94T7 0.1193 0.691? 0.47S3 0.И21 0.1792 0.013? 0.0373 O.OCS?
2 : J,»») 0.9728 0.9183 O.B27I 0.8873 0.J2*» Q.M8J 0,1838 0.0323
J I 0.9199 0.9984 0.991? 0.9744 0.9J73 0.8704 0,7599 0.5904 O.J439
4 j 1.0000 1.0030 1.0000 1.0030 1.0030 5.0000 1.0C30 l.MN 1.0030
.»
0 I о.4ча4'» с.лгзка влево? o.o7?7s a.ami 0.01024 0.002*:» o.oco.u o.eaoaj
1 I 0.9L81* G.7372S O.S2822 0..1.1*16 a.lSVSG 0.06J0* 0.01078 O.OC672 ft.COO**
2 e.HUI 0.14Jft8 0.81692 0,*BJ3* а.Юйвв О.ЛП44 ft.lAiaft 6.01712 0.0389*
J I 9.99954 0,9912» 3.94932 0.91398 3.I12J0 0.4«364 9.471TJ 0.34272 3.61144
4 j 0.M999 C.9994I 0.99T37 0.*»»T* 9.94173 0.9222* 3.83193 0.«?332 0.19*32
3 ; 1,30300 I.O30S9 1.30306 1.03063 1.90030 S.0C9C3 1.096-30 1,00303 I .MM*
1 у .;
0 l 0.
1 I 0,
2 I 0.
л I o,
4 Л
1 1
a
0.418.10 0
j »•«*»> 0
2
)
5
Ъ
8.97432 0
9.99727 0
0.99982 0
0.99999 0
1.03030 0
1,МВ0» l
2D17 2
41612
83197
»«6«*
MM!
99943
93999
0
0
1
С
с
с
г.
1
0821%
13*41
44767
1739»
9Т229
994-21
4997?
а
а
3
3
0
э
1
П*.">'1 O.OCJfil O.CKilfi* 0.OO022
1***1 о.вблз
41990 0.23636
T2621 0.39309
90374 0.77244
9*114 0.93153
99834 0.99219
oocoo 1.08MI
1.61*84 0.3011»
'.99424 0.92819
3.28979 0.13604
.58010 0.75293
3.8*137 0.1.7058
V91233 0.9174,5
1. cocao 1.oocoo
o.oaoai
0.&ЗОЛ1
0.03443
е.оззэ*
ft, (MM
С 42329
0.79029
fi
a
3
э
3
0
3
5114» C.26214 O.Uttf 0.0«*<S« 0.03562 0.0C410 «.MM) 0.00006 0.00000
88174 0.61116 0.42018 0.2112*. 0.10118 0.04016 ft.01094 0.00160 O.C<3O0*
9**1* ft.MJU 0.74*11 0.1*4.12 O.Mttl 0.17923 0.010*7 0.01616 t\ .tulil
Mill 0.181ft* 0.921V1 0.82080 0.61,621 0.411168 ft.2Vi«1 0.01888 0.01181
91114 0.1H140 0.9*10* 6.191ft» .1.89062 й.ШИ 0.11181 0.***** ft.114»*
30309 C.**9»t 0.99937 0.19193 9.9143* 0.9333* 9.81311 0.73'** 3,46834
90908 1.03030 1.30509 1.03089 1.909-30 1.03OC3 1.9303.0 1.09309 1.09030
OOfi'JO
aaeat
90318
80273
a | o.*to*i a.i*Ti? &.en** a.ai«*e< e.oeni ft.MOM a.aoaa? о.оавеа а.лолао
1 | 8.8ШО 0.30333 0.33333 3.10418 0.33*1* 0.93*33 0.90139 0.0308» 3.90300
2 j 9,96191 3,19672 0.33277 9.32319 0.24433 3,64982 3.31134 6.09222 9.80692
J j 0.99498 0.94372 0.80593 0.59439 0.1*128 0.1U67 0.53797 0,01041 Э.ВОС43
4 j 0.99957 0.98959 0.9*20} 3.82*33 0.4-3672 0.43392 0.19*10 0.05428 0.00502
5 j 0,9999» 0.9987? 0.9BS7] 3.95019 0.*3347 0.684Ы 0.*4823 0.20109 3.03809
« i I,MOM 0.99992 0.99*71 Э.9М4* 0.964*4 0.8SO62 0.(4*70 0.49*6» O.i*6»0
i j i.fiaono i.aoooa o.ii'»ii a.w» o.iisgi a.ift.uo 0.942.11 d.»:i32i a.s«ii.i
I | I4MM I.49MM I.MM4) I .MOM 1.0X041 1.MOO0 i.oi.noa i.oaofto i.ooooo
0.O4O3S 9.9263» 0.031*3 9.69024 9.90902 6.09039 9.80690
0,19*03 0.07054 0.01932 0.C3J9O t.MMJ 0.00003 3.00000
0.46783 Э.211Т9 0.0B9B* 0.02333 0.00*29 O.O0O3] 0.00000
0.2-5391 0.C9933 0.02329 0.0030T 0 . 0OCO6
43.MM0 0.МИ1 0.098*1 0,0193» 0.00089
O.J4S09 ft.1»7J1 0.2701* ft.0B«,«4 O.MOJl
O.^lOl»! B.TMtl l,|3?il 0,2(1180 0.01,29?
0.19111 О.Ч^ЛЗО 0.'7Я0*Г 0.1214А 0.80*0(1 0.М31ТЧ O.JiSi*
0.4*948 a.**«i4 б.+4«г.1 e.«i««> a.81**1 o.Mttl a.*m»
1.03053 1.90690 1.00303 1.636 30 1.90903 t.09099 1.30690
1.482Ы '.
M)MJ <
).10ft*1 t
I .I.-Ч.ПО 0.111*9 0.99171 0
1.0MM 0
I .0-3090 1
L.С9080 2
.4
Л
3484» 0.10731 0
13*1* O.J»5»3 0
921*1 ».tntd a
9«i7o |,t?»U a
19817 t).W7tl 0
»4**1 0.98.1 (S.I ¦
•9999 0.99*1» 3
30Э09 0.99*92 1
ОС 000 t.tMM 0
OOOOO l.OMM 0
MM* l.coooo l
02825
14931
S*21R
64461
Hill
11241
• 1942
MM]
99V86
0O03C
О.ОСЬОЗ 0..СО09* 0.0СЧ3.1В 0.O00C1 0.00000 0
0.0**36 0.CIC'»4 0.001*8 0.O0OU 3.000O0 0
0.1K»21 0.C«,469 O.0i229 C.0fti19 a..000i(ft 0
D.18?28 П.1118ft 0.01*76 0.OJCJ49 O.ftOftM 0
o.s.ma 0.31*91 |,1Ш4 0,0*7.15 a,.oo6.i? о
с..«.1176 a.6i.iai o.t*6*ft ft.нал a.a.ui* о
0,94*3* 9,12*13 0,61732 С.J30.19 3.138»? 0
0.91771 0.9*332 0.»3271 6.41721 9.31326 0
C.99VJZ 0.9892* 0,953*4 0.83069 O.C2439 0
0,99993 0.99932 0.99393 C.97S?5 0.8921.3 0
1.0ГЗСЭ l.COOOO 2.00300 l.O'OOOO l.MMO I
ОЙ141
012*3
0731»
26 293
Рис. D.9. Кумулятивные вероятности для биномиального распределения
для п = 3-10
Предположим, мы хотим ответить на другой вопрос: какова вероятность хотя
бы одного успеха в пяти испытаниях с р = 0,5? Самый простой способ найти
ответ - вычислить вероятность нуля успехов, а затем вычесть ее из 1. Поскольку
Таблицы вероятностей для распространенных...
¦¦ЕШ
й(0;5,0,5) = 0,03125 (вероятность нуля успехов), вероятность более чем нуля
успехов, то есть одного и более успеха, равна 1 - 0,03125, или 0,96875.
Распределение хи-квадрат
Распределение хи-квадрат несимметрично, как видно по рис. D.10, и поэтому
верхние и нижние критические значения различаются. На практике верхние
критические значения используются гораздо чаще, и поэтому в это приложение включены
только они. Форма кривой распределения хи-квадрат варьирует в зависимости от
числа степеней свободы, и у каждого распределения есть отдельный набор
критических значений. Из-за ограничений в объеме мы приводим таблицу вероятностей
для первых 40 степеней свободы; таблица для первых 100 степеней свободы наряду
с таблицей для нижних критических значений доступна в Интернете в
электронном справочнике по статистическим методам (NIST/SEMATECH e-Handbook of
Statistical Methods, http://itl.nist.gov/div898/handbook/eda/section3/eda3674.htmy
П 7
U.3
0.25 -
Z 0.2-
*THO<
о 0.15-
0).
m
§ 0.1-
I
H
O
= 0.05-
a = 0.025
I
0 5
\^a = 0.025
10
X
i
15 20
Рис. D.10. Распределение хи-квадрат, двусторонний тест (а = 0.05)
Для использования таблицы вероятностей для распределения хи-квадрат
(рис. D.11) найдите строку, соответствующую числу степеней свободы
(обозначенную v), а затем дойдите до пересечения со столбцом с вероятностью для
интересующего вас верхнего критического значения (в случае одностороннего теста).
Для теста хи-квадрат с одной степенью свободы и а = 0,05 критическое значение
равно 3,841. Это то значение, которое вычисленная в тесте статистика должна
превосходить, чтобы можно было отвергнуть нулевую гипотезу. Иначе говоря, если
нулевая гипотеза справедлива, есть только 5% вероятности, что в эксперименте
с одной степенью свободы статистика хи-квадрат будет больше или равна 3,841.
Для теста хи-квадрат с пятью степенями свободы и a = 0,01 критическое значение
равно 15,086.
EZ3IIII
Приложение D
Рассмотрим пример из табл. 5.7 (глава 5). В эксперименте значение хи-квадрат
было равно 21,8 при трех степенях свободы. Из таблицы вероятностей на рис. D. 11
видно, что критическое значение для а = 0,5 и трех степеней свободы равно 7,815.
Наше значение превосходит табличное, следовательно, мы отвергнем нулевую
гипотезу.
Верхние критические значения для распределения
хи-квадрат
V
I
2
3
4
5
6
7
а
9
10
11
1.2
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
3 3
34
3 5
36
37
38
39
40
с v степенями свободы
Вероятность превы
0.10
2.706
4.605
6.251
7.779
9.2 36
10.645
12.017
13.362
14.684
15.987
17.275
18.549
19.812
21.064
22.307
23.542
24.769
25.989
27.204
28.412
29.615
30.813
32.007
33.196
34.382
35.56 3
36.741
37.916
39.087
40.256
41.422
42.585
43.745
44.903
46.059
47.212
48.363
49.513
50.660
51.805
0.05
3.841
5.991
7.815
9.480
11.070
12.592
14.067
15.507
16.919
18.307
19.675
21.026
22.362
23.685
24.996
26.296
27.587
28.869
30.144
31.410
32.671
33.924
35.172
36.415
37.652
38.885
40.113
41.3 37
42.557
43.773
44.985
46.194
47.400
48.602
49.802
50.998
52.192
5 3.384
54.572
55 .758
шения крит
0.025
5.024
7.378
9.348
11.143
12.83 3
14.449
16.013
17.535
19.023
20.483
21.920
2 3.337
24.736
26.119
27.488
28.845
30.191
31.52 6
32.852
34.170
35.479
36.781
38.076
39.364
40.646
41.923
43.195
4 4.461
45.722
46.979
48.232
49.480
50.72 5
51.96 6
53.203
54.437
5 5.668
56.896
58.120
59.342
шеского значения
0.01
6.635
9.210
11.345
13.277
15.086
16.812
18.475
20.090
21.66 6
23.209
24.725
26.217
27.688
29.141
30.578
32.000
3 3.4 09
34.805
36.191
37.566
38.932
40.289
41.6 38
42.980
44.314
45.642
46.963
48.278
49.588
50.892
52.191
53.486
54.776
56.061
57.342
58.619
59.893
61.162
62.428
63.691
0.001
10.828
13.816
16.266
18.467
20.515
22.458
24.322
26.125
27.877
29.588
31.264
32.910
34.528
36.123
37.697
39.252
4 0.790
42.312
43.820
45.315
46.797
48.268
49.728
51.179
52.620
54.052
55.476
56.892
58.301
59.703
61.098
62.487
63.870
65.247
66.619
67.985
69.347
70.70 3
72.055
7 3.402
Рис. D.11. Верхние критические значения для распределения хи-квадрат
ПРИЛОЖЕНИЕ Е.
Интернет-ресурсы
В Интернете размещено множество статистических ресурсов, и никакой
опубликованный список в принципе не может быть полным, кроме того, его составители
и не стремятся к этому; иногда переизбыток информации - это так же плохо, как
и недостаток. Как справедливо для Интернета в целом, не каждый сетевой ресурс
точен или надежен, так что пользователь должен решить, подходит ли ему данный
источник. Перечисленные здесь сайты поддерживаются надежными
организациями, включая федеральное правительство, факультеты статистики в университетах,
профессиональных статистиков и компании, которые создают широко
используемые статистические продукты.
Общие источники
Вычислительный статистический онлайн-ресурс (The Statistics Online
Computational Resource).
http://socr.ucla.edu/SOCR.html
Многие ресурсы, включая интерактивные инструменты и материалы курсов,
на статистическом сайте Калифорнийского университета в Лос-Анджелесе.
Виртуальная статистическая лаборатория Раиса (Rice Virtual Lab in
Statistics).
http://onlinestatbook.com/rvls.html
Коллекция ресурсов, включая онлайн-учебники, симуляции и
демонстрации, примеры исследований и инструменты статистического анализа.
Сайты для статистических вычислений.
http://statpages.org/index.html
Ссылки на многие инструменты, включая деревья решений, бесплатные
статистические программы, онлайн-калькуляторы и графические
программы, поддерживаемые Джоном Пеззулло (John С. Pezzullo), заслуженным
профессором биостатистики и фармакологии.
Демонстрационный проект Вольфрама (Wolfram Demonstrations Project):
статистика.
Н^^1 ИНН Г:- * 1'
______ Ь { Приложение Е
http://demonstrations.wolframxom/topic.html?topic=Statistics&limit=20
Коллекция интерактивных инструментов, имеющих отношение к
статистическим разделам демонстрационного проекта Вольфрама, все написаны
открытым кодом и могут быть запущены на любом стандартном
компьютере под Windows, Macintosh или Linux.
StatLib: данные, программы и новости от статистического сообщества.
http://lib.stat.cmu.edu/index.php
Сайт, предназначенный для распространения статистических программ,
наборов данных и информации, поддерживаемый Университетом Карнеги
Меллона (Carnegie Mellon).
CAUSEweb.
http://wvvw.causeweb.org/resources/links.php
Обширная коллекция ссылок, полезных для обучения статистике,
созданная Юха Пурайненом (Juha Puranen) из университета Хельсинки и
размещенная на сайте консорциума по улучшению университетского
статистического образования (Consortium for the Advancement of Undergraduate
Statistics Education, CAUSE). Коллекция разделена на материалы к
курсам, наборы данных, демонстрации, статистические программы и тексты;
многие ссылки будет полезными практикующим статистикам наряду с
преподавателями.
Спросите доктора Математику (Ask Dr. Math).
http://mathforum.org/dr.math/
Архивы ответов на вопросы по математике и по статистике, по которым
можно осуществлять поиск. Уровень сложности вопросов варьирует от
начальной школы до колледжа.
Обзор математических понятий, подготовленный на факультете
математики и статистики университета Макмастера.
http://www.math.mcmaster.ca/lovric/rm/MathReviewManual.pdf
Приведен обзор математических понятий от основ алгебры до
вычислительной математики наряду с советами о том, как учить и понимать
статистику. По каждой теме есть решенные задачи и проверочная работа.
Виртуальная интернет-лаборатория: статистика.
http://www.stat.ufl.edu/vlib/statistics.html
Коллекция ссылок, составленная на факультете статистики университета
Флориды; сюда вошли такие разделы, как источники данных,
образовательные организации, распространители программного обеспечения,
рассылки и новостные группы.
Совет колледжей: домашняя страница стандартного курса статистики.
http://apcentral.collegeboard.eom/apc/public/courses/teachers_corner/2151 .html
Интернет-ресурсы 1^Н^^1ЕШ
Коллекция ссылок на материалы, которые имеют отношение к
стандартному курсу статистики в американских средних школах (АР Statistics course),
разработанному советом колледжей (организация, которая разработала и
проводит тестирование). Сюда входит информация о самом тесте (включая
тесты на практическое применение знаний), учебные материалы и
короткие статьи на статистические темы, входящие в курс.
Словари
• Статистический словарь StatSoft.
http://www.statsoft.com/textbook/statistics-glossarv/
Подробный словарь, поддерживаемый производителем программы Statistics.
• EXCITE! Словарь эпидемиологических терминов.
http://www.cdc.gov/excite/nbrary/glossary.htm
Словарь эпидемиологических терминов, поддерживаемый американскими
центрами по контролю и профилактике заболеваний; определения взяты из
третьего издания «Основ эпидемиологии в здравоохранении», курса для
самообразования, разработанного специалистами вышеупомянутых центров.
• Карманный статистический словарь.
http://www.mhhe.com/biisiness/opsci/bstat/keyterm.mhtml
Словарь терминов, используемых в бизнес-статистике, составленный Хардео
Сахаи (Hardeo Sahai) и Анвером Хуршидом (Anwer Khurshid) и
размещенный на сайте отделения высшего образования издательства McGraw-Hill.
• Словарь Шести сигм.
http://www.micquality.com/six_sigma_glossary/index.htm
Словарь терминов, используемых при контроле качества в рамках
программы Шесть сигм, размещенный на сайте MiC Quality, компании, которая
организует курсы по обучению технологии Шесть сигм и разрабатывает
учебные материалы.
• Словарь многоуровенного анализа.
http://www.paho.org/English/DD/AIS/be_v24n3-multilevel.htm
Словарь терминов, используемых в многоуровенном анализе, написанный
Анной В. Диез Ру (Ana V. Diez Roux), профессором университета
Колумбии, и размещенный на сайте пан-американской организации
здравоохранения.
Таблицы вероятностей
• Таблицы вероятностей для разных распределений.
http://itl.nist.gov/div898/handbook/eda/section3/eda367.htm
ШЁШшт
Приложение Е
Общедоступные таблицы для стандартного нормального распределения,
распределения Стьюдента, F-распределения и хи-квадрат-распределения
от национального института стандартов и технологий.
• Вильям Найт (William Knight): общедоступные статистические таблицы.
http://www.math.unb.ca/~knight/utility/
Общедоступные таблицы доверительных интервалов для медианы, U-тес-
та, критерия знаков, биномиальных коэффициентов, квадратных корней,
вероятностей для биномиального распределения, стандартного
нормального распределения (включая сокращенную таблицу для обучения),
распределений Стьюдента, хи-квадрат, F от профессора Вильяма Найта из
университета Ныо Брунсвика.
Онлайн-калькуляторы
• QuickCalcs: онлайн-калькуляторы для ученых.
http://graphpad.com/quickcalcs/index.cfm
На сайте, поддерживаемом разработчиком программного обеспечения для
ученых GraphPad, представлены разнообразные статистические онлайн-
калькуляторы.
• Приложения для проекта Cybergnostics.
http://www.stat.tamu.edu/~west/applets/
Коллекция статистических калькуляторов и графических демонстраций
статистических понятий, созданных Р. Вебстером Вестом (R. Webster West),
профессором статистики техасского университета; эта коллекция особенно
полезна для обучения, поскольку она позволяет студентам заниматься
моделированием и изменять параметры разных распределений, наблюдая за
изменением формы кривых этих распределений.
• Программы для вычисления мощности и размера выборки.
http://www.epibiostat.ucsf.edu/biostat/sampsize.html
Ссылки на многочисленные калькуляторы для мощности и размера
выборки и связанные с ними информация и программы на сайте, созданном
Стивом Шибоски (Steve Shiboski), профессором отделения эпидемиологии и
биостатистики калифорнийского университета в Сан-Франциско.
• Приложения на языке Java для вычисления мощности и размера выборки.
http://homepage.stat.uiowa.edu/~rlenth/Power/
Графический интерфейс для ответа на многие обычные вопросы о
мощности и размере выборки, созданный Расселом В. Лентом (Russell V. Lenth),
профессором статистики и делопроизводства университета Айовы;
программу можно запустить на сайте или установить на компьютер
пользователя.
Интернет-ресурсы
ВИД
Онлайн-учебники
• Электронный учебник по курсу общей статистики.
http://wiki.stat.ucla.edu/socr/index.php/EBook
Онлайн-учебник для стандартного курса статистики с вычислительного
статистического калифорнийского университета в Лос-Анджелесе.
• Статистика с самого начала.
http://www.bmj.com/about-bmj /resources-readers /publications/statistics-
square-one
Девятое издание этого учебника по статистике особенно полезно
медицинскому персоналу.
• База знаний о методах исследований.
http://www.socialresearchmethods.net/kb/
Онлайн-учебник, созданный Вильямом М. К. Трочимом (William M. К. Тго-
chim), профессором анализа стратегий и менеджмента Корнелльского
университета; в него входят разделы, которые обычно преподаются в курсе но
исследовательским методам в социологии, включая планирование
исследований, создание выборки, аналитические приемы и изложение результатов.
• Электронный учебник по статистике от StatSoft.
http://www.statsoft.com/textbook/
Этот учебник от компании-производителя Statistica включает информацию
о многих сложных методах, в том числе CHAID1, методы поиска
информации в данных (data mining) и моделирование структурных уравнений.
Автоматическая детекция взаимодействий - разновидность деревьев решений. - Прим. пер.
ПРИЛОЖЕНИЕ F.
Словарь статистических
терминов
Одна из сложностей любой профессии - необходимость выучить специфическую
терминологию. В этом приложении приведен краткий справочник по основным
терминам и обозначениям, использованным в этой книге; статистическая
терминология рассмотрена гораздо подробнее в таких справочниках, как
«Кембриджский статистический словарь» (The Cambridge Dictionary of Statistics, Cambridge
University Press, 2010) и «Краткая статистическая энциклопедия» (Concise
Encyclopedia of Statistics, Springer, 2008).
Таблица F.1. Греческий алфавит
Прописная
буква
А
В
Г
Л
Е
Z
н
0
I
к
Л
м
Строчная
буква
а
Р
Y
6
?
?
п
э
I
к
Л
М
Греческое
название
Альфа
Бета
Гамма
Дельта
Ипсилон
Зета
Эта
Тета
Йота
Каппа
Лямбда
Мю
Прописная
буква
N
=¦
О
П
Р
I
т
Y
Ф
X
Ф
Q
Строчная
буква
V
*
о
тт
р
о
т
и
ф
X
ф
ш
Греческое
название
Ню
Кси
Омикрон
Пи
Ро
Сигма
Тау
Упсилон
Фи
Хи
Пси
Омега
Словарь статистических терминов
Таблица F.2. Статистические обозначения
Символ
S
Е
и
п
Р(А)
Р(А\В)
Р(~А)
е
In
1одх
X
X
М
s
о
S2
*\
о2
п
N
г
ГРь
rs
У
\' ТБ' ТС
Ф
Р
Q
Значение
Выборочное пространство (теория вероятности)
Событие (теория вероятности)
Объединение наборов
Пересечение наборов
Вероятность события А
Вероятность события А при условии В
Вероятность события, дополнительного к А (вероятность не-А)
Константа Эйлера, иррациональное число 2.718 ...
Натуральный логарифм (логарифм по основанию е)
Логарифм по основанию х
/-й член выборки х
Выборочное среднее
Среднее значение для генеральной совокупности
Выборочное стандартное отклонение
Стандартное отклонение для генеральной совокупности
Выборочная дисперсия
Дисперсия для объединенной выборки
Дисперсия для генеральной совокупности
Размер выборки
Размер генеральной совокупности
Выборочная корреляция
Точечная бисериальная корреляция
Корреляционный коэффициент Спирмена
Гамма Гудмана и Крускала
Тау-Д тау-8 и тау-С Кендалла
Фи (мера связи между двумя бинарными переменными)
Согласованные пары (мера связи для порядковых переменных)
Несогласованные пары (мера связи для порядковых переменных)
ls:J
Приложение F
Символ
p
X2
О
E
RxC
Ho
HA,H1
a
CO.
I
nPk
паЩ
n!
t
df
Z
ss
MS
',
Qit
Pit
Tt
Ct
St
Rt
RR
OR
ORMH
D+,D-
Значение
Корреляция для всей генеральной совокупности
Хи-квадрат
Наблюдаемое значение (хи-квадрат)
Ожидаемое значение (хи-квадрат)
Таблица с R строками и С столбцами
Нулевая гипотеза
Альтернативная гипотеза
Альфа, вероятность статистической ошибки первого рода
Бета, вероятность статистической ошибки второго рода
Сумма
Перестановки
Сочетания
п факториал, то есть п * {п - 1) * (п - 2) х ... 1
f-критерий Стьюдента
Степени свободы
Стандартное нормальное значение/распределение
Сумма квадратов
Среднее квадратичное
Индекс для времени t (статистика в бизнесе)
Количество продукта / в период времени t (статистика в бизнесе)
Цена продукта / в период времени t (статистика в бизнесе)
Долговременный тренд (временное ряды)
Периодическое воздействие (временнь'ю ряды)
Сезонные изменения (временнь'ю ряды)
Остаточный, или ошибочный, тренд (временные ряды)
Отношение рисков (относительный риск)
Отношение шансов
Отношение шансов Мантеля-Гензеля
Заболевание, нет заболевания (эпидемиология)
Словарь статистических терминов
Символ
Е+, Е-
5
Т
Е
X
А.
а
KRon, KR,.
Значение
Воздействие, отсутствие воздействия (эпидемиология)
Дельта, величина эффекта (вычисления размера выборки и мощности)
Истинное значение, истинная составляющая (теория измерений)
Ошибочная составляющая (теория измерений)
Наблюдаемое значение (теория измерений)
Оценка надежности (прогностическая формула Спирмана-Брауна,
теория измерений)
Коэффициент альфа (теория измерений)
Алгоритмы Кудера-Ричардсона 20 и 21 (теория измерений)
Абсолютное значение
Значение числа без учета его знака; абсолютные значения -4 и 4 равны 4.
Используя обозначения: |-4| = |4| = 4.
Альфа (а)
Вероятность статистической ошибки I рода в экспериментах, то есть
вероятность отвергнуть нулевую гипотезу, когда она справедлива.
Априорная гипотеза
Гипотеза, сформулированная до проведения тестов.
Бета (Р)
Вероятность статистической ошибки II рода в экспериментах, то есть
вероятность принять нулевую гипотезу, когда она ложна. 1 - р = мощность.
Бинарные переменные
Переменные, которые могут принимать только два значения; также
называются дихотомическими.
Валидность (validity)
Насколько точно показатель измеряет то, что он должен измерять.
Взаимодействующая переменная (interaction variable)
Переменная, при разных значениях которой изменяется характер связи
между двумя другими переменными.
Внутренняя непротиворечивость
В теории тестирования - степень, в которой вопросы теста измеряют одну
и ту же характеристику.
Данные, характеризующие отношения (ratio data)
Данные, которые можно упорядочить, имеющие равный интервал между
соседними значениями и естественный нуль.
Двойной слепой метод
См. Слепой метод.
ЕШНН
Приложение F
Диапазон
Разница между самым большим и самым маленьким значениями.
Дискретные данные
Данные, которые могут принимать только определенные значения.
Дисперсия
Показатель изменчивости ряда чисел, вычисляемый как
среднеквадратичное отклонение от среднего.
Дихотомические переменные
См. Бинарные переменные.
Доля
Отношение, в котором все случаи, попавшие в числитель, также
включены и в знаменатель, например пропорция женщин, заболевших раком в
США (числитель - это все люди, мужчины и женщины, заболевшие раком
в США).
Единовременное обследование
Исследование, при котором данные собирают в один момент времени.
Заболеваемость (incidence)
В медицине и эпидемиологии число новых случаев заболеваний или
состояний в рассматриваемой популяции за определенный период.
Зависимые переменные
Переменные, которые считаются находящимися под влиянием других,
независимых переменных, включенных в план исследования.
Индексы
В статистике для экономики и бизнеса - числа, используемые для
измерения изменений во времени количества и/или цены товара или
набора товаров; широко известный пример - это индекс потребительских
цен.
Интервальные данные
Данные, которые могут быть упорядочены и для которых предполагаются
равные интервалы между последовательными значениями.
Информационное смещение (information bias)
Систематическая ошибка из-за способа сбора и регистрации данных.
Истинное значение
В теории измерений - значение, измеренное без ошибки.
Категориальные данные
Данные, которые не имеют числового значения и в которых числа служат
лишь условными обозначениями (как в случае пола или цвета).
Когорта
Группа людей, объединенная некоторым временным фактором (например,
рожденных в 1950 году или поступивших в колледж в 2000 году).
Словарь статистических терминов
¦НЕЛ
Максимакс
Метод принятия решений в условиях недостатка информации, при
котором стоит цель увеличения максимально возможной прибыли.
Максимин
Метод принятия решений в условиях недостатка информации, при
котором стоит цель увеличения минимально возможной прибыли.
Медиана
Центральное значение в наборе чисел, упорядоченных по возрастанию.
Межквартильный размах
Диапазон, в который попадают центральные 50% значений переменной.
Мешающая переменная (confounding variable)
Переменная, связанная и с независимой, и с зависимой переменной и не
стоящая между ними в цепочке причинно-следственных связей.
Минимакс
Метод принятия решений в условиях недостатка информации, при котором
стоит цель уменьшения упущенных возможностей.
Мода
Самое частое значение переменной.
Мощность
Вероятность отвергнуть ложную нулевую гипотезу. Мощность = 1 - /?, то
есть 1 - Р(статистическая ошибка II типа).
Наблюдаемое значение
В теории измерений - зарегистрированное значение какого-либо
показателя, включая ошибку измерения.
Надежность
Показатель непротиворечивости или воспроизводимости измерений с
течением времени.
Надежность конструкта
Степень, в которой измерение или серия измерений адекватно
характеризует конструкт (например, интеллект).
Надежность критерия
Степень, в которой измерение коррелирует с чем-нибудь еще, например
насколько сильно баллы теста на IQ коррелируют со школьной
успеваемостью.
Надежность характеристики
Степень, в которой инструмент (такой как тест) адекватно отражает
исследуемую характеристику.
Независимые переменные
Переменные, которые, как считается, оказывают влияние на другие,
зависимые переменные, включенные в план эксперимента.
Ш^аХШШШЯШЛ' Приложение F
Непараметрическая статистика
Статистика, не основанная на предположениях о распределении гене-
ралыюй(ых) совокупности(ей), из которых происходят данные, или
основанная на менее точных предположениях, по сравнению с
параметрическими данными.
Непрерывные данные
Данные, которые могут принимать любые значения или любые значения в
определенном диапазоне.
Одинарный слепой метод
См. Слепой метод.
Операционализация
В исследованиях - процесс определения концепции и разработки способа
ее измерения.
Опосредованное измерение (proxy measurement)
Замена одного измерения другим.
Отношение
Способ выражения связи между величиной двух значений; эти значения
не обязательно измеряются в одних и тех же единицах (например, число
больничных коек на 1000 человек).
Ошибка
В теории измерений - ошибочная составляющая наблюдаемого значения.
Параметрическая статистика
Статистика, основанная на знании распределения генеральной(ых)
совокупности(тей), из которой(ых) происходят данные.
Перспективное исследование
Исследование, в котором наблюдение за объектами (и сбор данных)
планируют проводить в течение долгого времени в будущем.
Плацебо
В плане эксперимента - воздействие, которое, как считается, не оказывает
никакого эффекта.
Порядковые данные
Данные, которые можно упорядочить, то есть расположить по величине, но
для которых интервалы между последовательными значениями не
обязательно будут равными.
Пост-хоктест
Тест, который проводится после какого-то другого теста; например, пост-
хок тесты проводят после дисперсионного анализа, чтобы узнать, какие
пары групп различаются.
Распространенность заболеваний
В медицине и эпидемиологии - число случаев заболеваний в
определенный момент времени; учитываются и новые, и уже существующие случаи.
Словарь статистических терминов I j ^ЦЩЩЩ
Ретроспективное исследование
Исследование событий, которые уже произошли.
Систематическая ошибка
Ошибка по какой-то неслучайной причине; систематическая ошибка
приводит к завышению или занижению наблюдаемых значений и, таким
образом, вызывает смещение результатов.
Слепой метод
При планировании эксперимента - лишение вовлеченных в исследование
людей информации о важных аспектах исследования, например о том, какие
участники подвержены экспериментальному воздействию, а какие -
получают плацебо. В одинарном слепом эксперименте информация утаивается от
испытуемых. В двойном слепом эксперименте информация держится в тайне
и от испытуемых, и от исследователей, проводящих эксперимент. При
тройном слепом эксперименте информация не разглашается среди испытуемых, а
также проводящих исследование и анализирующих данные ученых.
Случайная ошибка
Ошибка, которая возникает по случайности. Случайные ошибки делают
измерения менее точными, но не вызывают смещения результатов.
Смещение (bias)
Систематическая ошибка, которая может привести к некорректной
интерпретации результатов
Смещение в случае неответов (nonresponse bias)
Систематическая ошибка, возникающая из-за того, что некоторые
участники отказываются участвовать в исследовании или предоставлять
некоторую информацию.
Смещение из-за воспоминаний (recall bias)
Смещение в результатах из-за того, что жизненные обстоятельства
заставляют некоторых людей лучше запоминать определенные события.
Смещение из-за выявления (detection bias)
Систематическая ошибка из-за более простого обнаружения некоторых
качеств у одних людей по сравнению с другими.
Смещение из-за добровольцев
Частный случай смещения выбора, который происходит из-за сбора
данных из составленной добровольцами выборки.
Смещение социальной желательности
Смещение из-за стремления людей представить себя в наиболее выгодном
свете.
Смещение отбора (selection bias)
Смещение результатов из-за способа создания выборки.
Создание детерминированной выборки
Создание выборки, когда вероятность выбора любого объекта или комби-
Приложение F
нации объектов неизвестна; примерами служат нерепрезентативные и
пропорциональные выборки.
Составление вероятностных выборок
Методы составления выборок, при которых вероятность выбора каждого
объекта генеральной совокупности известна; в качестве примера можно
привести простые случайные и расслоенные выборки.
Специфичность
В медицине и эпидемиологии - вероятность того, что результат теста на
заболевание будет отрицательным у здорового человека.
Среднее
Арифметическое среднее для набора чисел.
Стандартное отклонение
Квадратный корень из дисперсии; для набора чисел - это квадратный
корень из среднего для квадратных отклонений от среднего.
Стандартная ошибка
Стандартное отклонение для распределения выборочных средних.
Статистическая значимость
Результат, который, скорее всего, получен не случайно.
Статистическая ошибка Ipoda
Отказ от нулевой гипотезы, когда она справедлива.
Статистическая ошибка IIрода
Принятие ложной нулевой гипотезы.
Степени свободы
Число переменных, которые могут изменяться в уравнении или при
расчете статистики.
Тройной слепой метод
См. Слепой метод.
Уникальный идентификатор
Код или переменная, которая используется для обозначения всех записей,
относящихся к одной единице анализа (например, идентификатор
пациента для обозначения всех оказанных ему медицинских услуг).
Управляющие переменные
Переменные, которые включены в исследование не потому, что они сами
по себе представляют интерес, а потому, что предполагают их влияние
на ключевые переменные, и исследователь хочет учитывать их
воздействие.
Факторный план эксперимента
Эксперимент, в котором задействованы две или более категориальных
переменных и их взаимодействия. В полном факторном плане в исследование
входят все возможные комбинации переменных.
Словарь статистических терминов
¦¦БЭ
Частота
Отношение, в которое входят единицы времени, например несчастные
случаи на производстве за год.
Чувствительность
В медицине и эпидемиологии - вероятность того, что больной человек
будет иметь положительные результаты теста на заболевание.
Шкала Лайкерта
Один из вариантов упорядоченной оценочной шкалы, разработанной
психологом Ренсисом Лайкертом (Rensis Likert); в шкале Лайкерта
содержатся утверждения, а люди должны выразить степень согласия или несогласия
с ними, используя упорядоченную шкалу.
Кинги издательства «ДМК Пресс» можно заказать в торгово-издательском
холдинге «Планета Альянс» наложенным платежом, выслав открытку или письмо по
почтовому адресу: 115487, г. Москва, 2-й Нагатинский пр-д, д. 6А.
При оформлении заказа следует указать адрес (полностью), по которому
должны быть высланы книги; фамилию, имя и отчество получателя. Желательно также
указать свой телефон и электронный адрес.
Эти книги вы можете заказать и в интернет-магазине: www.alians-kniga.ru.
Оптовые закупки: тел. (499) 782-38-89
Электронный адрес: books@alians-kniga.ru.
Сара Бослаф
Статистика для всех
Главный редактор Мовчан Д. А.
dmkpress@gmail.com
Перевод с английского Волкова П. А, Флямер Я. М.,
Либерман М. В., Голицына А. А.
Корректор Синяева Г. И.
Верстка Паранская Н. В.
Дизайн обложки Мовчан А. Г.
Формат 60х901/1(Г Гарнитура «Петербург».
Печать офсетная. Усл. печ. л. 42,63.
Тираж 200 экз.
Веб-сайт издательства: \?\у\?.дмк.рф
Статистика для всех
Нужно овладеть статистикой по долгу службы? Хотите получить помощь при сдаче
курса статистики? «Статистика для всех» — ясное и краткое введение и руководство
для всех новичков. Тщательно переработанное и расширенное, это издание поможет
вам глубоко понять статистику, избегая ошеломляющей сложности многих
университетских учебников.
Каждая глава представляет собой простые для понимания объяснения, дополненные
диаграммами, формулами, задачами с решениями и взятыми из практики заданиями.
Если вы хотите, не ломая голову, применять распространенные методы анатиза данных
и узнать о разнообразных подходах — это книга для вас.
• Узнайте об основных понятиях теорий измерений и вероятностей,
управления данных и планирования исследований.
• Познакомьтесь с основными методами статистической обработки
данных, включая корреляционный анализ, тесты Стьюдента, хи-квадрат
и Фишера, а также методы анализа непараметрических данных.
• Овладейте более сложными методами, основанными на обобщенных
линейных моделях, такими как дисперсионный и ковариационный
анализ, множественная линейная регрессия и логистическая регрессия.
• Используйте и интерпретируйте статистические данные в бизнесе,
контроле качества, медицине и здравоохранении, образовании и
психологии.
• Доводите свои результаты до общего сведения и критически
анализируйте статистические данные, полученные другими авторами.
Сара Бослаф (Sarah Boslaugh) — доктор наук, магистр здравоохранения. Составитель заявок на
гранты в университете Кенессо (KennesawState University). Работала как статистик и программист
более 20 лет. Автор книг «Руководство по программированию в SPSS среднего уровня сложности»
("An intermediate guide to SPSS programming", издательство Сейдж, Sage), «Источники вторичных
данных в здравоохранении» ("Secondary data sources for public health ", издательство Кембриджского
университета), «Статистика для всех» С Statistics in a nutshell", первое издание, издательство О"'Рей-
лли, O'Reilly) и редактор книги «Энциклопедия эпидемиологии» ("The encyclopedia of epidemiology",
издательство Сейдж:, Sage).
ISBN 978-5-94074-969-1
Интернет-магазин:
www. d nikpress. com
Книга - почтой: O'REILLY*
orders^ aJians-knka.ru IIIII