Математическое и цифровое моделирование для инженеров и исследователей - Смит Дж. М.

Автор: Смит Дж. М.
Теги: автоматика системы автоматического управления и регулирования интеллектуальная техника технология управления оборудование систем управления техническая кибернетика кибернетика материалы инженерия машиностроение математическое моделирование переводная литература
Год: 1980
Похожие
Элементы математического моделирования в программных средах Matlab 5 и Scilab
Структурное моделирование объектов и систем с распределенными параметрами.
Справочник инженера по АСУТП: Проектирование и разработка
Справочник инженера по АСУТП: проектирование разработка.
Текст
                    МАТЕМАТИЧЕСКОЕ
И ЦИФРОВОЕ
МОДЕЛИРОВАНИЕ
ДЛЯ___________
ИНЖЕНЕРОВ
и иссле-
дователей
MATHEMATICAL MODELING
AND DIGITAL SIMULATION
FOR ENGINEERS AND SCIENTISTS
JON M. SMITH
JMSA Systems Research and Analysis
St. Louis, Missouri
A Wiley-Interscience Publication
JOHN WILEY & SONS
NEW YORK LONDON SYDNEY TORONTO
ДЖОН М. СМИТ
МАТЕМАТИЧЕСКОЕ
И ЦИФРОВОЕ
МОДЕЛИРОВАНИЕ
ДЛЯ
ИНЖЕНЕРОВ
И ИССЛЕДОВАТЕЛЕЙ
Перевод с английского Н. П. ИЛЬИНОЙ
МОСКВА « МАШИНОСТРОЕНИЕ *
1980
ББК 32.81
См50
УДК 681.5.01
Научный редактор д-р техн, наук О. А. Чембровский
Смит, Джон М.
См50 Математическое и цифровое моделирование для инжене-
ров и исследователей/Пер. с англ. Н. П. Ильиной; Под ред
О. А. Чембровского. — М.: Машиностроение, 1980.— 271 с.
В пер.: 1 р. 50 к.
Книга посвящена комплексному моделированию процессов протекающих в
различных системах, с помощью цифровых вычислительных машин. Рассмотре-
ны численные методы моделирования непрерывных процессов, высокоточного диф-
ференцирования, интегрирования, разработки оптимальных фильтров. Дан ана-
лиз численного моделирования, который приводит к дискретной динамической
системе.
Книга предназначена для инженеров и научных работников, занимающихся
моделированием процессов.
30501-58
См-------------58-80.	1502010000
038(01)-80
ББК 32.81
6Ф0.1
© A Wiley-Interscience Publication John Wiley & Sons New York—London—Syd-
ney—Toronto
(6) Перевод на русский язык, «Машиностроение», 1980 г*
СОДЕРЖАНИЕ
Предисловие............................................................ в
Часть I. Введение в математическое моделирование
Введение...............................................................10
Глава 1. Математическое	моделирование	непрерывных	процессов	...	13
Глава 2. Математическое	моделирование	дискретных	процессов	...	74
Часть II. Численные методы моделирования линейных систем на циф-
ровых вычислительных машинах
Глава 3. Введение в моделирование линейных систем.....................110
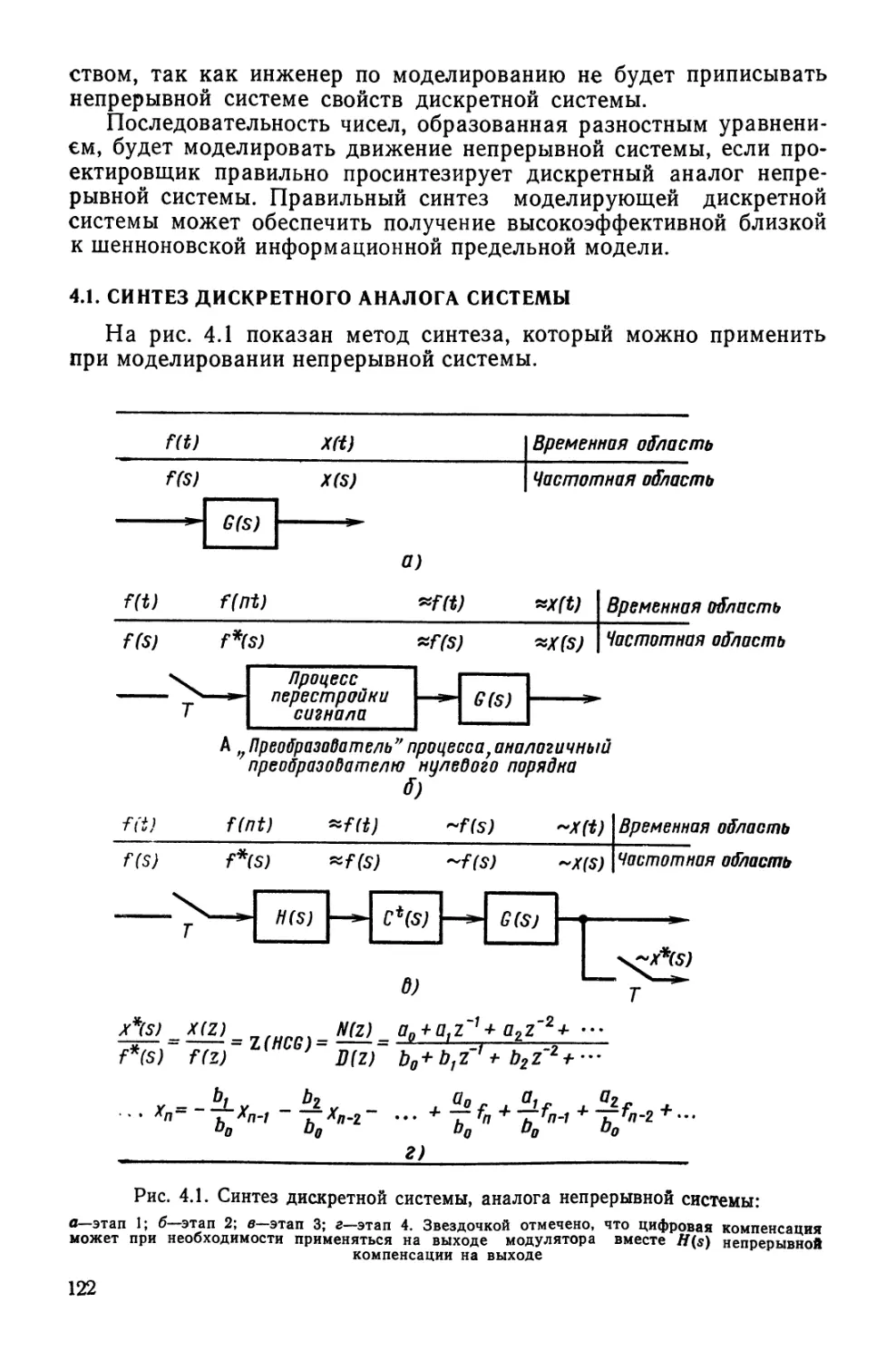
Глава 4. Дискретно-аналоювое моделирование............................121
Глава 5. Сущность методов подбора корней..............................154
Часть III. Численные методы моделирования нелинейных систем на
цифровых вычислительных машинах
Глава 6. Моделирование нелинейных систем..............................170
Глава 7. Современные методы численного интегрирования	. . .	.	181
Глава 8. Классические методы численного интегрирования	.... 207
Часть IV. Методы ускоренных вычислений
Глава 9. Гнездовые скобочные выражения и экономизация Чебышева 232
Приложения
А.	Методы подстановки для исследования передаточных функций с
помощью моделей...................................................249
Б. Таблица z-преобразований Жюри..................................253
В.	Т-интегрирование нулевого порядка и его связь с теоремой о сред-
нем значении......................................................260
Предметный указатель............................................  268
Моим родителям
Мариусу Элвину Смиту
Долорес Элизабет Смит
ПРЕДИСЛОВИЕ
Эта книга о скоростных методах численного моделирования. Не-
когда разработанные численные методы в основном не изменились
в течение длительного времени. Спрашивается, для чего же нуж-
на еще одна книга на столь старую тему?
Ответом является само содержание книги. Шеннон показал,
что существует предельное количество информации о непрерывном
процессе с конечным числом элементов, которая обеспечивает до-
статочные знания о его протекании.
Так, при цифровом моделировании непрерывных систем рас-
сматривается применение таких численных методов, которые обес-
печивают высокоточную надежную информацию о моделируемой
системе. В связи с этим в книге обсуждаются численные методы,
обеспечивающие точное моделирование непрерывных систем или
процессов при наименьшем числе выбранных параметров и наи-
меньшем объеме вычислений.
Следует отметить, что немногие из численных методов являют-
ся и точными и экономичными. За исключением классических чис-
ленных методов, включенных для полноты изложения, методы, из-
ложенные в данной книге, относятся к периоду после 1959 года.
При этом большинство из них, относящихся в особенности к моде-
лированию нелинейных систем, было разработано в середине или
начале 70-ых годов.
К современным численным методам относятся эффективные
скоростные алгоритмы, обеспечивающие при реализации:
—	уменьшение стоимости моделирования при одновременной
многопараметрической обработке информации;
—	высокоточное моделирование и управление в реальном мас-
штабе времени:
—	потенциальную устойчивость в процессе моделирования;
—	высокую точность промежуточных операций;
—	устойчивую связь параметров моделируемой системы и мо-
дели;
—	использование стандартных числовых интеграторов, хорошо
«настраиваемых» на решение системы уравнений;
—	применение новых численных методов, которые не могут быть
заменены эквивалентными классическими методами;
6
_____идеальное использование цифровых ВМ с ограниченной ем-
костью, таких, как 16-битовые микропьюторы, и более современ-
ных 8-битовых микропроцессоров.
В данной книге предлагается методика математического мо-
делирования непрерывных и дискретных систем. Тема этой книги
была навеяна большим количеством семинаров и лекций, проведен-
ных в США, которые подвели меня, если не к необходимости, то,
во всяком случае, полезности углубленного обзора понятий ма-
тематического моделирования непрерывных и дискретных систем.
Читателю полезно выяснить основные положения математичес-
кого моделирования и его языка, затем проследить детали матема-
тического моделирования в других книгах.
Опытный инженер найдет в книге общепринятый математичес-
кий язык для установления связи между изучаемыми физически-
ми процессами и уравнениями, решаемыми с помощью цифровых
ВМ.
Без «физического чутья» моделируемого процесса и понимания
процедуры его математизации в математической модели на цифро-
вой ВМ трудно осуществить эффективное проектирование модели.
Эта книга прежде всего написана для инженеров и исследова-
телей, участвующих в математическом моделировании динамиче-
ских процессов на цифровых ВМ.
Описываемые здесь численные методы основаны на использо-
вании технологии дискретных систем, оперирующих с выбороч-
ными данными. При этом процессы рассматриваются как во вре-
менной, так и частотной областях, что придает рассмотрению боль-
шую наглядность.
Некоторые классические методы излагаются здесь исключи-
тельно с целью демонстрации определенной преемственности сов-
ременных и классических методов, а также в тех случаях, когда с
их помощью полезно решать определенные современные задачи.
В представленных материалах обсуждаются:
1.	Последовательность решения и математический аппарат мо-
дели.
2.	Применение предлагаемых методик на больших ВМ, мини-
компьютерах и микрокомпьютерах.
3.	Достоинства и недостатки каждого метода.
4.	Применяемые выражения, обычно табулируемые для облег-
чения технологии построения моделей при решении разнообразных
задач.
Особое внимание уделено практической стороне использования
предлагаемых методов, необходимых инженерам, исследователям
и программистам, занимающимся цифровым моделированием.
При изложении классических методов, используемых в цифро-
вом моделировании, опущены выводы аналитических зависимостей,
которые можно найти в других источниках, и лишь некоторые из
них в интересах полноты изложения приводятся подробно.
Материалы этой книги базируются на том допущении, что циф-
ровое моделирование приводит к дискретной динамической систе-
7
ме. Это оправдано по той причине, что фильтрация, настройка, ста-
билизация, управление, анализ и синтез осуществляются в такой
модели точно так же, как и в дискретной системе.
Эта точка зрения расширяет арсенал численных методов ма-
тематического моделирования, так как включает не только тради-
ционные методы вычислительной математики, но и методы, разви-
тые в теорию автоматического регулирования импульсных, дис-
кретных систем, широко освещенных в многочисленной, хотя и
разбросанной литературе. Предлагаемая точка зрения приводит к
получению новых методов моделирования, которые не могут быть
заменены классическими приемами.
Различные элементы матобеспечения разрабатывались в то или
иное время различными группами и к тому же в различных местах
применительно к различным задачам. Ввиду этого проектировщик,
использующий моделирование, не должен надеяться на возмож-
ность механического смешения различных разработок без соответ-
ствующего синтеза модели при соответствующей подгонке имею-
щихся идей матобеспечения, применявшегося в связи с другими
задачами.
В практике проектирования сложных систем обычно предусмат-
риваются соответствующие регулирующие устройства, применяе-
мые для подбора параметров коэффициента усиления при точной
настройке спроектированной системы. В этой книге предлагается
серия примеров математических моделей, позволяющих осущест-
влять их доводку с помощью регулировки и подстройки.
Книга имеет ярко выраженную практическую, а не теоретиче-
скую направленность. Но несмотря на это я стремился к кратко-
му и достаточно строгому освещению математических вопросов,
оставаясь в то же время в рамках практических целей машинного
проектирования.
Одна из основных задач, которую я перед собой при этом ста-
вил, заключалась в том, чтобы заинтересовать читателя матема-
тическим моделированием с использованием дискретных систем.
При рассмотрении этой особенности показано, что существует еще
множество проблем при разработке методов моделирования, кото-
рые требуют дискретизации данных. В связи с этим книга широко
иллюстрирована большим числом простых примеров, привлекаемых
для демонстрации особенностей излагаемых методов, с детальным
рассмотрением их использования для моделирования на ВМ.
В процессе рассмотрения технических методов обсуждаются их
недостатки. В принципе не существует какого-либо универсального
метода решения любой задачи. Поэтому одной из основных задач
является нахождение и выбор частного метода сообразно с пред-
варительной оценкой его преимуществ и недостатков.
Книга содержит девять глав, некоторые из которых содержат
много разделов. При написании книги по главам ставилась зада-
ча уйти от обобщений при создании математических моделей, что
является скорее искусством, чем наукой.
В части I читатель знакомится с идеями математического мо-
8
делирования, с его методиками и формами представления моделей,
которые проходят через всю книгу. В части II показаны методики
моделирования линейных систем. В части III представлены спосо-
бы моделирования нелинейных систем. В части IV обсуждается
метод наискорейшей функциональной оценки, который хорошо из-
вестен опытным исследователям, однако, как показывает мой опыт,
совершенно не известен начинающим. Эта часть включена для пол-
ноты изложения и, не неся в себе оригинальных положений, содер-
жит полезную информацию.
В части I содержится введение в математическое моделирова-
ние, которое содержит две главы, раскрывающие математические
особенности описания непрерывных и дискретных процессов. Они
близки темам, продолжающимся в части II.
В части II, излагающей «Численные методы моделирования ли-
нейных систем на цифровых вычислительных машинах», содер-
жится три главы, описывающие методы решения систем уравне-
ний, моделирующих непрерывные линейные системы. Применение
каждого метода рассматривается в реальном и произвольном мас-
штабах времени. Здесь представлены специальные методы для
миникомпьютеров и микрокомпьютеров, а также таблицы наиболее
часто встречающихся разностных уравнений для моделирования
дискретных процессов.
В части III, посвященной «Численным методам моделирования
нелинейных систем на цифровых ВМ», содержится три главы, со-
держащих примеры систем, требующих численного интегрирова-
ния систем нелинейных уравнений, и методы составления разност-
ных уравнений для моделирования нелинейных систем.
• В части IV, содержащей «Высокоскоростные способы модели-
рования», включена единственная глава, в которой рассмотрено
применение гнездовых скобочных форм, полиномы Чебышева и
рациональные разложения в полиномы, позволяющие осуществлять
оперативное и точное решение сложных математических выраже-
ний.
Материалы книги базируются на 26-летнем опыте лекторской
деятельности по изложению современных численных методов, ос-
нованных на использовании метода дискретных выборок данных.
Я, несомненно, в долгу перед моими коллегами, сотрудничающи-
ми в кампании Боинг, Макдоннелл Астронавтике Компэни-Хаустон
Оперэйшэнз, отделение Спэйс энд Мисайлэс кампании Локхид,
Эм-Ай-Ти, университете во Флориде, лабораториях Белла и лабо-
раториях Чарлза С. Дрэйпера.
Выражаю мою благодарность моим друзьям доктору Ричарду
Хэммингу и доктору Джеральду Розенбауму за помощь в редакти-
ровании рукописи, а также за корректуру Джеку Ван Вую и ма-
шинистке Флоренс Пижо.
Сан Луи, Миссури
Ноябрь, 1976
Джон М. Смит
9
Часть I
ВВЕДЕНИЕ
В МАТЕМАТИЧЕСКОЕ
МОДЕЛИРОВАНИЕ
ВВЕДЕНИЕ
Обобщенная структурная схема процесса построения модели
показана на рис. 1.1, а более подробная структура процесса при-
ведена на рис. 1.2. Исходной позицией процесса проектирования
модели является сама моделируемая система, а результатом ее —
модель. Несмотря на то, что процесс содержит четыре этапа ма-
шинного проектирования, такое подразделение является условным,
так как каждый этап тесно связан с предыдущим и последующим.
Первым шагом при проектировании является выбор наиболее
подходящей тематической модели. Этот этап должен обеспечить
получение наиболее удачной математической модели.
В данной книге системы проектируются, как правило, с исполь-
зованием структурных схем, построением систем уравнений и дру-
10
Спидометр
Вращаю-
щаяся
магнит-
ная головка
Физическая
система
80
Угловая
скорость
колеса
<У(5>		
	И	8(s)
	Ts + 1	
		
		
		
Oman 1 Подготовка ма- тематической модели системы		
п=п+1
If	1-es7		k	
	s		Ts+1	
ENTER
п=0
(on=f(nt)
PRINT
п,6
=п
6(2)
т
ооо=хх.хх
01 птах=ХХХХ
02Т=хх.хх
03t=xx.xx
/74 k=xx.xx
05 п~О
06 U)n=f(nT)
07 ci-expt-T/t)
08 Т1=к(1-С1)ып
09 Т2-С19
10 6=Т1 + Т2
11 TITLE; N,TH ETA
12 PRINT; n,6
13 П>ПтохjGO ТО
14п=П + 1
15 GO ТО 06
16 EXIT
16
			
Счетчик циклов	Матема- тическая модель системы	Моделиру- ющая ма- темати- ческая модель	Ошибка
n	6	6	€
0	0	0	0
1	0,776	0,600	-0,176
2	0,950	0,840	-0,110
3	0,990	0,936	-0,054
			
Расшифровка результатов
| EXIT |
Этап 2	Этап 3	Этап 4
Подготовка матема-	Подготовка	Испытание,
тической модели	программы	проверка
для моделирования	ВМ для модели	и отладка модели
Рис. 1.2. Пример подробной структуры процесса проектирования модели
гимн математическими приемами, обеспечивающими получение
алгоритма.
Вторым этапом процесса проектирования является подготовка
математической модели для моделирования. Задача решается при-
ведением к структурной схеме дискретного процесса и приведе-
нием системы уравнений к дискретной форме. Этот этап завер-
шается, следовательно, двумя результатами: математическим опи-
санием и структурной схемой всей дискретной системы. Структур-
ная схема полученной дискретной системы должна быть идентич-
на структурной схеме непрерывной системы по потоку информации.
Операторы должны будут иметь ясное представление о харак-
тере моделируемой системы. Это облегчается тем, что при постро-
ении дискретной схемы мы не утрачиваем аналогии с непрерывным
процессом.
Все методы, представленные в этой книге, связаны с синтезом
дискретных систем, аналогичных моделируемым непрерывным, ди-
скретным или комбинированным системам.
Третьим этапом является написание программы для осущест-
вления математического моделирования. Это решающий этап, со-
держащий строгое соблюдение временных соотношений в синтези-
руемой математической модели. В частности, при моделировании
одной из одногерцевых систем в истинном масштабе времени, для
которой выборочный период составляет 1/20 с, а запаздывания в
обратной связи достигают одного интервала выборки, могут воз-
никнуть фазовые смещения в 16 периодов.
По опыту автора наибольшее число проблем возникает при пе-
реходе от задач 2-го этапа к задачам 3-го этапа.
Необходимо подчеркнуть, что задача, стоящая перед 2-м эта-
пом, содержит в качестве важного элемента выработку требова-
ний к условиям моделирования. Они обычно определяются на ос-
новании анализа условий, вытекающих из 1-го этапа, на основа-
нии которого закладывается математическая модель системы.
И опять же, на основании опыта автора, только установлением
тождественности можно подготовить условия, при которых она
соблюдается и проверяется с помощью контрольных схем. Этот
этап особенно существен для решения задач 4-го этапа, проверки
и отладки модели.
Только после того, как проектировщик модели определит сово-
купность критериев, получаемых в процессе испытания и обеспе-
чивающих проверку требований тождественности для отладки мо-
дели, можно с уверенностью переходить к операционной фазе.
Здесь следует указать, что не во всех случаях необходимо при
моделировании стремиться к условиям высокой точности и высокой
надежности, вследствие этого возможно создание более выгодных
в этих случаях упрощенных моделей, обладающих повышенным
быстродействием. Это приводит к интересному направлению соз-
дания -параллельно действующей с основной моделью упрощенной
шунтирующей системы, которая обеспечивает на языке програм-
мы вычислительной машины контроль полученного результата.
12
Уверенность в добротности разработанной модели зависит от уве-
ренности в выбранном матобеспечении, зависящем от вводимых
численных методов, от языка модели или от численных методов,
применяемых в программе ВМ. По этой причине в данной книге
подвергаются детальному обсуждению преимущества и недостатки
различных численных методов в явном и неявном виде при введе-
нии соответствующего языка моделирования. По этой причине тща-
тельно подобраны примеры, чтобы получить уверенность в эффек-
тивности применения каждого метода применительно к определен-
ным условиям. Это не исключает ошибки от неправильного при-
менения того или иного метода.
Для того чтобы избежать этого (и в это автор верит), специ-
алисту необходимо развивать интуитивное чутье, оправдывающее
применение данного метода.
Эта книга, содержащая 2, 3 и 4-й этапы, посвящена главным
образом принципам модельного проектирования, подготовке ма-
тематической модели к моделированию, к программированию мо-
дели на ВМ, проверке и отладке модели. Так как подготовка мате-
матической модели строго зависит от исходной модели, и так как
система математической модели обычно тождественна исходной
системе, часть I посвящена обзору методов математического моде-
лирования и анализу физических систем. Характеристики непре-
рывных и дискретных систем изучаются с точки зрения установле-
ния требований к модельному проектированию во временной и
частотной областях при помощи анализа как обеих систем, так и
их моделей.
Глава 1 МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
НЕПРЕРЫВНЫХ ПРОЦЕССОВ
Необходимость в моделировании систем часто возникает по
следующим причинам:
1.	При необходимости осуществления экономического поиска
рациональной системы, сложный характер которой не может быть
выявлен в лабораторных условиях или на масштабной модели.
2.	При необходимости проверки справедливости системы моде-
лирующих уравнений, применяемых в системах управления.
3.	При необходимости оценки реакции системы на комплекс ре-
гулирующих воздействий, при выявлении оптимальных управлений,
при выборе альтернативных решений динамики системы.
Математическое моделирование осуществляют на базе матема-
тического описания непрерывного процесса, который подвергается
исследованию построением математической модели, позволяющей
получить те же результаты, что и при моделировании на лабора-
13
Правильно спроектированная математическая модель отражает
(в определенных рамках) характеристики анализируемого анали-
тического процесса.
Границы эффективного моделирования полностью определяются
допущениями, принятыми при проектировании модели. Неучет осо-
бенностей допущений может привести к ошибочным заключениям
по результатам моделирования.
При проектировании моделей необходимо иметь полный и хо-
рошо определенный перечень допущений, на которых строится
модель, а затем, определив их влияние на результат моделирова-
ния, выявить те из них, которые являются доминирующими. Одним
из способов является принятие допущений об отсутствии в системе
люфтов, зон нечувствительности, чрезмерных перегрузок*, приво-
дящих к необходимости введения ограничений эффективной обла-
сти применения модели по параметрам входной информации, за
которыми существенны искажения результатов моделирования.
Существует определенное количество методов получения сис-
тем уравнений для описания непрерывных физических процессов.
В области механики законы Ньютона и соотношения действующих
на свободные тела сил приводят к системе дифференциальных
уравнений второго порядка, описывающих динамику системы.
Уравнения Лагранжа и его энергетические построения приводят
к системам совместных уравнений, описывающих динамику меха-
нических систем. Если ньютоновские и лагранжевы уравнения
представляются в одинаковых системах координат, то мы прихо-
дим к одним и тем же уравнениям. При выводе моделирующих
уравнений сравнительно редко используется классический метод
Гамильтона, где для получения системы дифференциальных урав-
нений первого порядка в обобщенных координатах и обобщенных
моментах применяются известные гамильтоновские энергетические
соотношения и уравнения Гамильтона, описывающие динамику ме-
ханических систем. Очевидно, причиной, по которой гамильтонов-
ская формулировка механики широко не используется при созда-
нии моделей механических систем, является необходимость исполь-
зования труднопонимаемого обобщенного момента, и на этом фоне
термины ньютоновской формулировки динамики механических си-
стем более предпочтительны.
Метод Шредингера обеспечивает математическое описание диф-
ференциальных уравнений, описывающих явления и динамику в
квантовой механике. Таким образом, закон Ньютона, уравнения
Лагранжа, уравнения Гамильтона и метод Шредингера являются
основными методами получения математических описаний механи-
ческих систем.
Несмотря на то, что физические законы описываются соответ-
ствующими уравнениями, являющимися математическими моделя-
ми динамики этих процессов, утверждение, что все математические
модели могут быть получены непосредственно из физических зако-
* Некоторые нелинейности систем рассмотрены в этой главе ниже.
14
нов, неверно. Многие системы сегодня моделируют с помошг-с про-
ведения лабораторных экспериментов. Однако не всегда в процессе
моделирования можно идентифицировать полученные результаты
модели и натуры в частотной или временной области. Современ-
ные системы так сложны (содержат множество соединений, внут-
ренние нелинейности, ненаблюдаемые состояния), что метод отож-
дествления их параметров при лабораторном моделировании для
получения эмпирических зависимостей представляет проблему.
В связи с этим эта книга начинается с той посылки, что диф-
ференциальные уравнения, описывающие динамику непрерывного
процесса, — известны. В этой главе раскрываются свойства и ха-
рактеристики уравнений, их преобразования в различных областях,
их свойства в каждой области, граф-ическое и схематическое пред-
ставление систем для большей наглядности и проникновения в ди-
намику систем, которые они моделируют.
Рассматриваются линейные и нелинейные дифференциальные
уравнения, их структурные схемы, стационарные и нестационарные
линейные системы. Для исследования характеристик непрерывного
процесса с точки зрения описания системы и функций возмущаю-
щего воздействия используется аппарат преобразований Фурье и
Лапласа. Описываются спектральные характеристики и рассматри-
ваются устойчивость, параметры установившихся процессов ли-
нейных стационарных систем. Представлены также линейные и не-
линейные векторно-матричные уравнения (вектора состояния) и их
структурные схемы, представляющие непрерывный процесс.
Ввиду сжатости пунктов в части I основное внимание уделяет-
ся восстановлению основных понятий, определений и форм запи-
си. Внимание уделялось в основном пунктам, представляющим ин-
терес для специалистов, занимающихся проектированием моделей.
Тем не менее, начинающий найдет в главе весьма полезные ма-
тематические разработки и положения для проектирования и от-
работки моделей, а также для понимания динамики систем.
1.1.	ЛИНЕЙНЫЕ СИСТЕМЫ
Моделирование линейных систем применяется главным образом
по четырем причинам, а именно:
1.	Технологические системы и их модели часто бывают линей-
ными, по крайней мере, в определенных границах.
2.	Точные решения линейных систем уравнений могут быть лег-
ко найдены.
3.	Существуют специальные высокоточные методы моделиро-
вания линейных систем.
\С помощью линейных систем можно оценить искажения в не-
линейных системах.
Аналитические методы решения нелинейных систем существуют
скорее как исключение, чем как правило. Даже при возможности
ОпХп°ЖАеНИЯ точных Рвений необходимы приближенные методы.
пРеДеленные методы аппроксимации часто принадлежат к мето-
15
дам оценки конкретного варианта и требуют детального рассмот-
рения, чтобы избежать обобщений.
В первой части этой главы обратим внимание на линейные си-
стемы, так как их математические модели имеют большие возмож-
ности для аналитического описания, чем математические модели
нелинейных систем.
На протяжении всей книги главным вопросом будет определе-
ние реакции системы на заданную функцию возмущающего воз-
действия.
Допустим, возмущающая функция Изменяющаяся во вре-
мени, вызовет реакцию ri(t) и вторая возмущающая функция /г(0
вызовет реакцию r2(t).
Тогда можно записать
ЛЮ-УЛО;
Для линейной системы
ZiW+AW-nW+rH/).	(1.1)
Уравнение (1.1) описывает принцип суперпозиции: суперпози-
ция индивидуальных возмущающих воздействий приводит к реак-
ции, которая является суперпозицией индивидуальных реакций.
Характерным свойством линейной системы является допусти-
мость принципа суперпозиции.
Следствием принципа суперпозиции является:
1.	Отсутствие какого-либо возмущающего воздействия, влияю-
щего на другие возмущающие воздействия.
2.	Отсутствие пересекающихся реакций, вызванных различны-
ми возмущающими воздействиями.
3.	Сочетание возмущающих воздействий может быть выявлено
по сочетанию реакций определением зависимости каждого возму-
щающего воздействия от реакции и последующего объединения
или наложения реакций для определения суммарной реакции си-
стемы на суммарное возмущающее воздействие.
Другим выводом, который следует из принципа суперпозиции,
является то, что если на линейную систему действует п одинако-
вых возмущающих воздействий, то реакция от такого воздействия
определится как п одинаковых реакций, каждая из которых явля-
ется реакцией системы на одно возмущающее воздействие, т. е.
«/(/) —«г (/).	(1.2)
Из (1.2) видно, что линейные системы сохраняют масштабный
фактор возмущающего воздействия при переходе от входа к вы-
ходу системы. Это свойство линейных систем называют принципом
однородности.
Если соотношения (1.1) и (1.2) справедливы для линейных си-
стем, то это не означает, что выполнение одного или другого усло-
вия достаточно для определения свойств линейной системы.
16
Рис. 1.1. Простая нелинейная система, удовлетворяющая принципу суперпозиции
и обладающая неоднородностью
Система линейна тогда и только тогда, когда удовлетворяются
как (1.1), так и (1.2).
Хорошо известный пример нелинейной системы, когда выдержи-
вается принцип суперпозиции, но не выдерживается свойство одно-
родности, показан на рис. 1.1.
Кроме того, линейная стационарная система характеризуется ее
реакцией на периодическое возмущающее воздействие.
Если периодическое возмущающее воздействие обладает часто-
той F, то стационарная линейная система ответит на него периоди-
ческой реакцией с частотой F.
Короче говоря, реакция стационарной линейной системы обла-
дает теми же спектральными компонентами, что и возмущающие
воздействия.
Полагают, что линейная система должна быть стационарна,
если
(1.3)
где Т — произвольное время запаздывания.
1.2. МОДЕЛИРОВАНИЕ ЛИНЕЙНОЙ СИСТЕМЫ
Линейные системы — это такие системы, динамика которых
моделируется линейными уравнениями.
Это могут быть линейные алгебраические уравнения, линейные
дифференциальные уравнения, линейные разностные уравнения
или их комбинации.
Рассмотрим дифференциальное уравнение
=	0-4)
гДе t — независимая переменная; f(t)—функция возмущающего
воздействия иг — реакция.
Коэффициенты а0, ai и а2 — система параметров. Коэффициен-
ты могут изменяться или не изменяться от времени, они, как пра-
вило, полностью определяются количеством и типом элементов в
системе.
Уравнение (1.4) —простое дифференциальное уравнение второ-
о порядка. Кроме того, уравнение (1.4) является линейным урав-
нием по следующим причинам:
17
I) ни переменная г, ни какие-либо ее производные нз содержат
степени больше первой;
2) ни один из его членов не содержит произведений двух или
большего числа одних и тех же зависимых переменных или про-
изведений зависимой переменной на какую-либо производную.
Допуская принцип суперпозиции, мы приходим к следующему:
ач	+а0Г! = /1 ;
a2-^r+al^- + a0r2:=f2-
dt2 at
Складывая эти уравнения, убеждаемся, что принцип суперпози-
ции выполняется:
#2	(Г1 + Гэ) + а\	(Г1 + г2) ~Г а0 (Г1 + Г2) = (/1 + А)-
at2	at
В дальнейшем мы увидим, что принцип суперпозиции справед-
лив для любых стационарных и нестационарных процессов.
Любое обыкновенное дифференциальное уравнение n-го поряд-
ка можно записать как
an W (г) + ап_х (/)	(г) + ... + а. (/) г (/) = f (/),	(1.5}
dtn	dtn~x
где коэффициенты и возмущающее воздействие даны как функции
независимой переменной t. Говорят, что это уравнение однород-
ное, если возмущающее воздействие равно нулю, и неоднородное,
если возмущающее воздействие отлично от нуля.
Можно записать (1.5) в форме
= Л	(1.JS).
если обозначим
L=an{t)	ап_х (/) -±— +... + а0 (t),	(1.7).
dtn	dtn~l
где L является оператором, зависимой переменной г.
Используя (1.6), можно сформулировать следующие основные-
свойства линейных дифференциальных уравнений.
1.	Умножение зависимой переменной г на постоянный множи-
тель равносильно умножению оператора на ту же самую кон-
станту:
ЦКг)=КЦг).	(1-8)
Если L(r) =0 (случай однородного уравнения), то
£(Л>)=0.	(1.9).
Из этого следует, что r(t), являющееся решением однородного
уравнения L(r) =0, служит также решением случая Kr(t).
2.	Замена г на ri + r2, где и г2 линейно независимы, приводит
к сумме двух линейных операторов, один от и, другой от г2.
18
В связи с этим понятно, что
(г14~г2) = L(г1)4“(гг)	(1- Ю)
и
^(г1±г2) = 0 только при А(г1) = £(г2) = 0.	(1. И)
Соотношения (1.10) и (1.11) утверждают, что если г{ и г2 яв-
ляются решениями однородного уравнения L(r)=0, то тогда и
Гг[-г2 является также его решением.
Из свойств 1 и 2 видно также, что если ri(/), r2(t),..., rn(t) —
линейные независимые решения однородного линейного дифферен:
циального уравнения, то L(r)=0, также и для их линейных ком-
бинаций С{Г1 + с2г2-{-СзГ3+ ... + спгп, когда с — независимые кон-
станты
3.	Решение г^=С\Г\ + с2г2+ ... -\-спгп с п независимыми констан-
тами является общим решением однородного дифференциального
уравнения при условии, что п частных решений гь г2, ...,гп линей-
но независимы. И, наоборот, решения должны быть линейно не-
зависимы, если ни одно из них не может быть выражено через
линейные комбинации других.
Общее решение однородного уравнения часто называют допол-
нительной функцией.
4.	Если гч — частное решение неоднородного уравнения при
L(r4) =/(/), то сумма этого частного решения и дополнительной
функции является полным решением неоднородного линейного диф-
ференциального уравнения.
Вообще, любое решение (1.4) может быть записано как комби-
нация дополнительной функции и частного решения (иногда назы-
ваемого частным интегралом):
г(/) = Гд(/) + гч(/).	(1.12)
Можно заметить, что если r(t) —решение (1.4) и гч — частное
решение (1.4), то
£(г —гч)-—£(г)~£(гч)=/(/) —/(/)=0.
Отсюда г—гч = гд является решением однородного уравнения, ко-
торое из-за свойств произвольной постоянной с может быть выра-
жено
Г —r4 = c1rl + c2r2 + ...+c„rn.
Перенеся частное решение этого уравнения вправо, получим же-
лаемое решение.
5.	Для нахождения численных значений п констант требуется
знание п значений решения уравнения и его производной. Неизвест-
ные коэффициенты определяют решением системы уравнений при
подстановке численных значений реакций и их производных.
Заметим, что их значения можно брать в известные, не обяза-
тельно одинаковые моменты времени.
19
1.3. РЕШЕНИЕ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ
Важным направлением численных методов решения дифферен-
циальных уравнений, рассматриваемых в данной книге, являются
решения стационарных и нестационарных линейных дифференци-
альных уравнений.
Эти методы не’включают преобразующие функции и операто-
ры. Хотя решения не записываются в векторно-матричной форме,
методы решения пригодны для решения дифференциальных урав-
нений в матричном представлении.
Кроме того, несмотря на то, что преобразования Лапласа при
решении линейных дифференциальных уравнений проще и во мно-
гих случаях более традиционны, чем классические методы, сущест-
вуют определенные ограничения в применении метода трансформа-
ции функций. Методом преобразования Лапласа нельзя, например,
решать линейные дифференциальные уравнения с переменными
коэффициентами. В этом случае классические методы решения
могут позволить решить многие неустойчивые уравнения, имеющие
практическое значение.
Освежим наши знания классических методов решения диффе-
ренциальных уравнений.
Для ряда реальных систем методы преобразования Лапласа
в случае их применимости становятся громоздкими, особенно, ког-
да условия задачи зависят от времени (или значений независимой
переменной).
Эта особенность справедлива также для линейных дифференци-
альных уравнений с постоянными коэффициентами.
Классические методы требуют знания этих условий.
Начнем изучение классических методов с простого процесса,
описываемого уравнением первого порядка. Общее линейное диф-
ференциальное уравнение первого порядка имеет следующий вид:
^-+а(/)г=/(/).	(1.13)
at
Это уравнение решается, если заметить, что оба члена левой
части выражения (1.13) при некоторых условиях являются резуль-
татом взятия производной от произведения (гы), полученного ум-
ножением г на неизвестную функцию и, зависящую от t.
Таким образом,
А_(гй)=й^_ + г^-.	(1.14)
Сравнивая (1.13) и (1.14), видим, что умножением левой и
правой частей (1.13) на неизвестную функцию «(/) получим
и_ЁИ + иа(/)г=«/(/).	(1.15)
20
Чтобы левая часть уравнения (1.15) точно соответствовала про*
взводной от произведения (ги), необходимо следующее условие:
dt v
Интегрируя, находим
1пи= J a(t)dt.
Таким образом,
(1.16)
Так как коэффициент а является заданной функцией времени, и
может быть найдено из уравнения (1.16).
Подставляя и в уравнение (1.4), сможем записать
-£-(re^)dz)=/(Z)e^<)rf/.
Тогда
/(/)еИ0Л<//+с].	(1.17)
Заметим, что выражение в скобках — это тип свертки. Позже
мы еще раз столкнемся с интегралом свертки в разделе преобра-
зования Лапласа. Решение, представленное (1.17), является необ-
ходимым решением уравнения (1.13). Зафиксируем форму записи
(1.17). Она появится снова в более общем виде при решении ли-
нейных матричных дифференциальных уравнений. Это связано с
тем, что простые линейные дифференциальные уравнения в век-
торно-матричной записи имеют первый порядок. Решение общих
линейных дифференциальных уравнений первого порядка имеет
особое значение; в уравнениях с порядком, отличным от единицы,
подобные решения отсутствуют.
Из-за отсутствия общих решений линейных дифференциальных
уравнений высоких порядков оставшаяся часть этой главы посвя-
щается рассмотрению конструктивных методов решения таких ста-
ционарных линейных дифференциальных уравнений.
Возвратимся снова к классическим методам решения дифферен-
циальных уравнений, так как они более освоены и традиционны,
чем методы трансформации.
Ниже приведены классические методы решения задач для не-
прерывных систем.
Рассмотрим линейные процессы
x-\-kx = f(t).
21
Из уравнения (1.17) известно, что
t /	t	\
—рМт / t	(Мт	\
л=е 0 I J/(t)e& dx-\-C I.
Пример 1. Если k — постоянная величина и f(t) = O,
х=Се~к‘.
Если /=0, х=х0,
Х — Хй0~Ы.
Пример 2. Если k — положительная константа и f(t)=A (кон-
станта),
'	л	‘
х=Се-‘'4-Де-*'^е*Мт=Се-»'+	(е»’) =
о	о
л	л
=Сегы 4- (ew — 1)—С е~« + у (1 - е~«).
Если / = 0, х=х0,
.Xq=C.
И, наконец, получаем
х=х0е-«+4(1-е-«).
Заметим, что
lim(x) = — при &>0.
f —►оо	k
Это можно видеть из самого дифференциального уравнения
x-\-kx — A.
При установившемся движении х=0, что приводит к
x = A]k.
Пример 3. Если k — постоянно, f (/) = t и Хо=О, получим
г	е~м г
х == е~и 1 т e*’ dx\ х=—-— \ kx e^dt.
о	о
Интегрируя по частям, получим
л~ь* г 1	1 /	1 W г |<	/ е*т \1<1
х=---- \ dx qm---\k e^dx I =-- (t e*T) — I ——) =
л Lj k J J*L l0 \ k /kJ
0	0
22
При больших t
xx — (t——V если ^>0.
Таким образом, если стационарные процессы описываются урав-
нением первого порядка, то после того, как экспонента достигает
исчезающе малого значения, решение уравнения движения системы
определяется через угловой коэффициент, сдвинутый на время,
численно равное угловому коэффициенту \/k.
Пример 4. Если	где k0 — константа и /(/)=0, то
—f»oxdt
х=Се °	; х=Се_‘,(,/2. Заметим, что если t—О, х=х0. Таким
образом, х=х0е-‘»/’/2.
Пример 5. Если k(t)=kot и f(t)=Aot, где k0 и Ао — постоянны,
a ko — положительно, то
t
х = Л’0е_*|>/,/2-{-е_*<>/’/2 j* Дот eft°'t’/2 dt;
6
.-ЛоР/2 1
х=Х0е~к<>1,/2 -|-------\ Дот е*»т,/2 k0 rft;
*0
х=ДГ0е-‘«/,/2+^-(1 -e-*»'1/2).
Заметим, что
lim(x)=^- при &0>0.
t->60	kft
Пример 6. Если k (/) = «> tg(w/) и /(/)=0,
t
—Jo> tg(<ot)d T
x=Ce 0	;
у -Q £lncos(tt>f )"
x=C cos (<»/).
Если / = 0, x=x0,
x=Xq cos (w/).
Этот интересный результат показывает, что решение колеба-
тельного характера не обязательно связано с системами, описыва-
емыми линейными уравнениями второго порядка.
Некоторые нестационарные дифференциальные уравнения пер-
вого порядка могут быть преобразованы таким образом, что их ре-
шением может стать любая желательная функция при f(/)=0:
здесь k(t)—линейный функциональный преобразователь.
23.
Например, если необходимо преобразовать функцию вида
x=Xot~at,
vjifi а — константа, имеем
k=a.
Для преобразования такой функции, как распределение Гаусса
x=Xoe~at* при а>0, мы получим преобразующую функцию в
виде
k(t)=2at.
Другие .виды линейных функциональных преобразователей
представлены в табл. 1.1.
Таблица 1.1
Линейные функциональные преобразователи некоторых
наиболее часто встречающихся функций при
x+k(t)x=Q
*(0	*оета'	Хое+а“	Хо ^atn	Xq sin (<oZ)	cos (<oZ)	*(/±n	Xot^ai
А(0	±а	±2at	±nattl~A	—w Ctg (u>t)	<0 tg (<o/)	y-nt-i	(±a-t~V)
Наконец, можно преобразовать входную функцию f(t) в неко-
торую функцию g(t), используя линейный функциональный преоб-
разователь
g <<>
Например, если g(/) = sin («>/) при f(t)= sin(W), получим
k } = Sin И)-cos И) =! _ ctg ((в/).
sin («/)
Другим примером может быть случай, когда g(t)=U(t)* при
f(t) =sin (®0.
Тогда при линейный функциональный преобразователь
примет вид
jinG-O-MO =sin((u/)>
k «(О
Конечно, существуют практические трудности в преобразова-
нии функций такого рода, особенно, когда искомый результат име-
ет колебательный вид, так как в этом случае линейный функци-
ональный преобразователь имеет в знаменателе g(t)—функцию,
приобретающую нулевое значение.
* U(t)—единичная функция;
(°приг<°;
I 1 при t > 0.
24
1 4. КЛАССИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ СТАЦИОНАРНЫХ
ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ВЫСОКИХ
ПОРЯДКОВ
Так как не существует общих аналитических решений линей-
ных дифференциальных уравнений (стационарны они или нет) вы-
ше первого порядка, мы не в состоянии распространить общий ме-
тод предыдущего раздела на уравнения более высокого порядка.
В этой части мы стремимся максимально использовать опера-
ционные методы (иные, чем метод линейных функциональных пре-
образований) при решении линейных дифференциальных уравне-
ний.
Допустим, D означает операцию дифференцирования по неза-
висимой переменной.
Тогда
ОД —.
= dt
Из этого следует, что
О"(г)=-^-(г).	(1.18)
dt*
Оператор D обладает следующими свойствами:
(Dmf-Dn)r(t)==Dmr(t)-]-Dnr(t);	(1-19)
[(Dm + £>") + Dl] г (t)=[Dm + (О" + О')] г (/);	(1. 20)
(Dm • Dn) г (t)=Dm+nr (t)=D*+mr(t)=.(D* • Dm) г (/);	(1.21)
Dm (Dn  Dl) r(t)=(Dm- Dn) Dl г (/);	(1.22)
L>z(Z>+Dn)r (/) = (£>'+"* +£>*+") r(0-	(1.23)
Дифференциальное уравнение первого порядка
^_ + ar=/W	(1.24)
at
может быть представлено с помощью оператора в виде
(Dа) г=f {t).	(1.25)
Таким образом,
rW=(“DT^)/(Z)-	(h26)
Из уравнения (1.17) следует:
г(/)=е-^{| fix) е^)ЛЛ+с}.
Для случая, когда a(/)=const, имеем
r(/)=e-fl< (У/(т)еаМт-|-С).	(1.27)
Таким образом,
(-577)f (/)	е-а' {$f (т) е<” d*+с)-	(1 •28)
25
l/{D + a) —это символическая запись трансформации f(t), при-
водящей к образованию суммы дополнительных и частных реше-
ний.
Теперь рассмотрим стационарное дифференциальное линейное
уравнение второго порядка
Й2	0- 29>
С помощью оператора D получим
(a2D*+a,D+а0) г = f (/),	(1. 30)
что можно представить с помощью элементарных сомножителей
как
	(D-s^D	-s2)r=/(/),	(1.31)
где		(af — 4a2a0)1/2 2a2	(1.32)
	— ai 2a2	(я2 — 4д2а0)1/2 2a2	(1.33)
Заметим, что S! и s2 могут быть комплексными. Дополнитель-
ное решение получается из следующих выражений:
=c^lt (h34)
\ D—Si J
и
=C2e*«/.	(1.35)
\ D~ s2 /	/(f)-0
Таким образом, дополнительное решение уравнения (1.30) за-
писывается в форме
гд=пд+г2д=С1е^+С2е^<.	(1.36)
Частное решение неоднородного уравнения (1.31) записывает-
ся как
ИЛИ
-Ml- (1-37)
l D—Si L\ D—s2 ) JJ
На основании (1.27) можно записать
---- ----1 f W — e-s*' f № e"‘T dx-	(1.38)
D — S% /	J
Заметим, что С в (1.28) связано дополнительным решением и
равно нулю.
26
Соединяя (1.37) и (1.38), получим
гч=f (?t) ei,Xi dxx — ei,z е<«*-м-ч e~s«x>f (?) d?t d?2.
-k(l-39)
Полное решение является суммой дополнительного и частного
решений уравнения (1.29).
В связи с этим имеем
r=C1ei*'+C2es«<+es-<	Je-r«x« f (?)dxxdx2. (1.40)
Этот метод может быть обобщен для решения стационарных
линейных дифференциальных уравнений п-го порядка.
Рассмотрим систему, описываемую стационарным линейным
дифференциальным уравнением
Jnr	нп~1
а„ _|_ ап_х	г +... + аог=/ (/).	(1.41)
dtn	dtn—1
В операционной записи (1.41) принимает вид
(ап Dn+ап_х D"-' +... +а0) г=f (/).	(1.42)
Тогда:
1.	Напишем характеристическое уравнение, заменяя оператор
D на s, и полученный операторный полином приравняем к нулю.
2.	Определим п корней этого полинома n-го порядка.
3.	Если п корней не равны, то дополнительное решение (1.41)
принимает вид
гд=С, е*-' + С2	. + Ся еЧ	(1.43)
4.	Частное решение уравнения (1.41) может быть найдено ме-
тодом последовательного интегрирования.
Оно примет вид
гч=е^	J е<*‘-5*)т... j e“V/(T)dT< (1.44)
5.	Общее решение (1.41) является суммой дополнительного и
частного решений.
6.	При наличии кратных корней характеристического уравне-
ния решение представляется в виде, показанном в разд. 1.6.
7.	Если в частном решении встречаются какие-либо экспоненци-
альные выражения, повторяющие аналогичные выражения допол-
нительного решения, общее решение может быть видоизменено
способом, аналогичным тому, который применяется при наличии
кратных корней.
Приведем некоторые примеры применения операционных мето-
дов решения стационарных линейных дифференциальных урав-
Символическое выражение dri, dx2, dx$ .. dxn.
27
Пример 1. Рассмотрим стационарный процесс, описываемый
следующим линейным дифференциальным уравнением:
x-\-kx=f(t).
Представляя его в операторной форме, получим
(D-H)x=/(/).
Заменяя D на $ и полагая f(/)=0, получим характеристическое
уравнение
s J-£=0.
Это уравнение имеет один корень
$1 = — k.
Таким образом, дополнительным решением дифференциального
уравнения является
хл—Сх е~и.
Как и раньше, если t=0, х=х0, то
x,=xoe~w.
Частное решение задается выражением
t
х,=е*,/Je-**’если /(/)=0, хд=0.
Если f (t) =A и А постоянно, то
t
x„=e~kl J A ^dx=y (1 - e-«).
о
Если f(t)=Aot, где Ло — константа,
t
x4=Hoe-w tefttt/t; хч=-^— (t—i-j.
о	'
Пример 2. Рассмотрим стационарное линейное уравнение
^-4-А—=/(/).
dfl 1 dt J
В операторной записи имеем
(D2 + W)x = /(/)
или
[(D+0)(D+^)]x=/(f).
Как и раньше, характеристическое уравнение получается све-
дением /(/) к нулю и D к s.
Тогда
(а+0)($4-£)=0.
28
Так как Sj=O и s2=—k,
t	t
х=хд++C2e,*<-j-e**' Jj e5*’ f(x)dx2,
о	о
если /(/)=0, x=Ci+C2e_w. А если /(/)=A (константа), то
x=C1+C2e-«+^-(l-e-«).
Если /(/)=А0/ (Ao —константа), то
x=C1+C!e-“+4(e--l) + Az.
«2	k
Пример 3. Уравнению
соответствует характеристическое уравнение
s3+3s2+4s+2=0,
корнями которого являются
«!=-1; s2= —1-(-/; s3= — \-j,
где J—V— 1. Дополнительное решение имеет вид
х=Ci	+ С2 е* + С3 е*»‘=Ct е~‘+е"' (С2 е><-фС3
=Cj е_( -|-e~z [(С2 -|- С3) cos (f)-}-/(С2—С3) sin (/)],
так как
е^ = cos (/)+J sin (/).
1.5.	МЕТОД НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ
Для получения частных решений в разд. 1.4 применялся метод
последовательных решений. Другим, более простым методом явля-
ется метод неопределенных коэффициентов. Преимуществом яв-
ляется то, что он включает лишь операции дифференцирования и
не требует интегрирования. Ограничением является то, что он не-
применим ко всем типам функций, но полезен для функций, пред-
ставленных в табл. 1.2. Для рассматриваемых нами целей он не
несет строгих ограничений, как это имеет место в некоторых слу-
чаях, рассмотренных вначале, при использовании других методов.
Дифференциальные уравнения, которые описывают линейные си-
стемы, имеют решения, которые для большинства рассматривае-
мых процессов могут быть составлены при использовании этих
простых функций.
Метод неопределенных коэффициентов прост в применении и
приводит к простым решениям.
Для линейных дифференциальных уравнений с постоянными
‘Коэффициентами потенциальные функции составляются из суммы
29
или произведения функций табл. 1.2, при этом частный интеграл
или частное решение является суммой или произведением соответ-
ствующих выражений, представленных в правой колонке таблицы.
Таблица 1.2
Потенциальные функции частных решений
Образование потенциальной функции	Образование частного решения
Постоянная, k	Постоянная, А
Степень независимой переменной, tn (п— целое число) Экспоненциальная функция, е1* Косинусоидальная функция, cos (yt) Синусоидальная функция, sin (yt)	п Ряд S Amtm 0 Экспоненциальная функция Ai cos (yt) -Ь Л2 sin (yt) Ai cos (yt) -Ь Л2 sin (yt)
При подстановке потенциальных функций и соответствующих
им частных решений необходимо приравнять соответствующие ко-
эффициенты в правой и левой частях получаемых равенств.
При использовании этой простой методики необходимо осущест-
влять дополнительные преобразования только в двух случаях:
если характеристическое уравнение обладает нулевыми кор-
нями;	‘
если потенциальная функция содержит элементарные функции,
аналогичные содержащимся в дополнительных решениях.
Если характеристическое уравнение содержит нулевой корень,
то возможно преобразование частного интеграла, приводящего к
интегралу, решение которого дано в табл. 1.2.
Это преобразование может быть распространено на случай, ког-
да характеристическое уравнение обладает кратными нулевыми
корнями.
Во втором случае при наличии кратных корней характеристиче-
ского уравнения может быть применен метод неопределенных ко-
эффициентов.
1.6.	РЕШЕНИЕ СОВМЕСТНОЙ СИСТЕМЫ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ
УРАВНЕНИЙ ОПЕРАЦИОННЫМИ МЕТОДАМИ
Решение системы линейных дифференциальных уравнений с по-
стоянными коэффициентами, содержащих одну независимую пере-
менную и несколько зависимых, — общеизвестно.
Операционный метод, который обсуждается в этой работе, стан-
дартен и полезен в решении совместных уравнений.
Самым коротким решением системы совместных дифференци-
альных уравнений с одной независимой переменной является
уменьшение данной системы уравнений до одного уравнения.
30
Это уравнение затем может быть решено операционным мето-
дом, обсуждающимся в разд. 1.4.
Рассмотрим систему двух стационарных линейных дифферен-
циальных уравнений
hi U>) х+gl (D) у = Л (/); й2 (D) х+g2 (D) у = /2 (/).
Следующими действиями они могут быть представлены как
g2 (D) [Й1 (D) х + gl (D) у]=g2 (D) fx (t)
и
gi (Р1 [А2 (£>) х + g2 (D) у]=gx (£>) f2 (t)
и после вычитания (для исключения у) преобразованы к виду
[g2(D)й, (D)-gl (D)й2(О)] х =g2(D) Л (/) -gl (i) f2[t).
Если оба уравнения умножить соответственно на hx(D) и h2(D),
найдем
[Й! (D) g2 (£>) - й2 (D) gl (£>)] у=й2 (£>) Л (/) - Й! (D) /2 (/).
Эти уравнения могут быть решены операционными методами.
1.7.	ОБЛАСТЬ ПРИМЕНЕНИЯ ЧАСТОТНЫХ МЕТОДОВ
ПРИ МОДЕЛИРОВАНИИ НЕПРЕРЫВНЫХ ПРОЦЕССОВ
Прежде чем рассмотреть особенности метода моделирования,
необходимо познакомиться с основными особенностями областей
применения частотных и временных зависимостей, в которых мож-
но успешно применять эти методы.
Ввиду этого рассмотрению условий моделирования и проекти-
рования моделей в настоящей части книги предпошлем область
применения частотного метода.
Разложение периодических функций в ряд Фурье
Любая периодическая функция f(0) может быть разложена в
ряд Фурье, если имеет период 2Т и удовлетворяет следующим ус-
ловиям Дирихле:
1.	Обладает конечным количеством перегибов в течение од-
ного периода.
2.	Имеет ограниченное число максимумов и минимумов в тече-
ние одного периода.
+г
3.	Интеграл	|/(0)|rf0 —ограничен.
—г
Рядом Фурье является
00
+ 2 1ап СО8(П0) + ЙЯ sin (п0)],	(1.45)
л-1
31
где ап—~ V/(6) сое (га 9) dO при п—0, 1,2,...;	(1.46)
Л J
—тс
тс
Ьп=~ /(9) sin (ra9)d9 при га=1, 2,...	('1.47)
— ТС
Большинство функций, рассмотренных в этой книге, зависит от
времени (если не в явной, то, по крайней мере, в неявной форме).
Уравнения (1.45), (1.46), (1.47) преобразуются к виду, учиты-
вающему, что периодическая функция с периодом Т может быть
выражена через параметр времени, если учесть, что 0 меняется в
течение всего периода в соответствии с соотношением
0=2л(//Т)=<	(1.48)
где а=2л/Т.
Подставляя (1.48) в (1.45), (1.46) и (1.47), получим
/(z)=-y-+^[®ncos(raa>/) + />„sin (га<о/)];
Г/2
2 г-
гап=— \ f (/)cos(n&t)dt при ra=0, 1, 2,...;
-Г/2
Г/2
=	/ (/) sin (nut)dt при ra=0, 1, 2,...
-Г/2
(1-49)
(1.50)
(1.51)
Функции /(/) можно придать и другой известный в теории уп-
равляющих систем вид:

COS (га<о/— ф’п);
п-1
(1-52)
^я=(4+^)1/2;
\ ап /
(1.53)
(1.54)
Из уравнения (1.52) видно, что периодическая функция (удов-
летворяющая условию Дирихле) f(t) может быть представлена
как среднеарифметическая величина (за весь период Т) * * при ну-
+«
* Это можно видеть из (1.46), где ап = 2/2л J f (0) cos n6d6 при n=0 (1.46)
—ТС
принимает вид а0=2(1/2я f /(O)rf0) = 2 (среднеарифметическое значение / в
—ТС
интервале 2я); таким образом, aQ/2 равно среднеарифметическому значению / (0).
3
левой частоте синусоидальных компонент, являющихся целыми
кратными основной частоты (2л/Т).
Амплитуда и относительная фаза этих компонентов даны в
(1.53) и (1.54). Зависимость сп от и® называется амплитудным
спектром функций времени f(/).
Значение этой функции при ® = 0 является, как указывалось,
среднеарифметическим. Зависимость фазы Тп от и® называется
фазовым спектром f(t).
Комбинация амплитудного и фазовых спектров используется
для определения устойчивости динамических процессов.
Графики сп и Тп от п® являются дискретными и изображаются
прерывистыми функциями.
Эти функции наносят на график в виде линий, соединяющих
значения ординаты и абсциссы (см. рис. 1.3). Иногда они наносят-
ся как линии спектра. Это связано с тем, что с увеличением Т
уменьшается ®, и плотность линий возрастает.
При неограниченном увеличении Т дискретный спектр стано-
вится непрерывным и ряд Фурье превращается в интеграл Фурье.
Далее будет более подробно рассмотрен этот вопрос.
В зависимости от того, какими свойствами симметрии облада-
ет функция, ряд Фурье принимает тот или иной вид.
Возможны следующие характерные случаи:
1.	Когда периодическая функция четная и удовлетворяет ус-
ловию
/(/)=/(_/).	(1.55)
2.	Когда периодическая функция нечетная и удовлетворяет
условию
(1.56)
Разложенные в ряд нечетные функции содержат только синусы.
3.	Периодическая функция с периодом Т содержит только чет-
ные гармоники, удовлетворяющие условиям
/(7 ± 7?2)=/(/).	(1.57)
4.	Периодическая функция с периодом Т содержит только не-
четные гармоники,	если она удовлетворяет условию	i
/(/±Г/2)=-/(/).	(1.58)
5.	Любая	функция,	обладающая симметрией,	может быть пред-
ставлена четной и нечетной функцией
/(О + /(О 
2^2'
При анализе такой периодической функции важно определить
наличие упрощающих свойств по симметрии. Если они существу-
Ют, то известны упрощения рядов Фурье, позволяющие при опре-
делении коэффициентов Фурье осуществлять интегрирование на
половине периода. Указанные случаи представлены в табл. 1.3.
2	493	о.
Упрощения в рядах Фурье при различных условиях симметрии
Таблица 1.3
Условия симметрии	Упрощения	ап	bn
/(0=/(-0 /(0= - /(-0	Содержатся только косинусы Содержатся только синусы Для четных функции Для нечетных функций Для четных функций Для нечетных функций	Т/2 4 с Г	/2лп \ "I — \ [7(0 cos 0 0 Т/2 4 ( Г	/2ли \ "| ~ \ [/(Ocos[— jtjdt 0 L 0 0 Т/2 4 г Г к /2лп \ 1 — ц/ cos \ J dt 0	0 Т/2 4 Г Г	/2лл \ I у- Ц/ (0 sin [— ] fl dt о L Т/2 4 i Г	/2лп \ I —	[/(0 sin [ —1 t\dt Р L 0 0 Т/2 4 f Г	/2лп \ 1 Tj [/(Osin[— 0
Пример 1. Хорошо известным
и часто используемым примером,
который обладает большой на-	 -
глядностью (как иллюстрация
для начинающих, ознакомление с	•
областью частотного анализа)	t____
при определении параметров раз-
ложения в ряд Фурье, является * *" 4
периодическая прямоугольная рис j 2
функция (прямоугольная волна), ис'
представленная на рис. 1.2.
Эта разрывная функция * описывается
уравнений:
' 11 I_____L
X X зт т
4	2	4
Периодическая прямоуголь-
ная функция
следующей системой
/(0=
(1.59)
Заметим, что f(t) —функция четная. Следовательно, ряд Фурье
будет состоять только из косинусоидальных функций. Так как
(о7’=2л, коэффициенты при косинусах можно выразить как
Т/2
а„=-у-	/0 cos di;	(1.60)
о
ап — —sin (дю/)|Г/ 4;	(1.61)
п<оГ	1о
Дя=2/0[—(”"/2) 1 при п=1, 2,...	(1.62)
L ПЛ J
И
а0=-у- при п=0.	(1.63)
То, что коэффициенты при синусах равны нулю, видно из сле-
дующего:
772	Т/4
2 г	2 с
bn=— \ fa sin (n<&f)dt = — \	=
—Т/2	—Т/4
—	—2/0 Г	/>п(лТ \	/—пыТ \"| п
=-----— COS (n^t)	=----COS --------- — COS -----11 = 0.
<*n	-T/4	<*n L \ 4 /	\	4 J]
Используя (1.63) и (1.64), запишем
/	=	f cos(<o/)—— cos (3<о/) —|———• COS(5u)/) —
2 я L	I 3	5
—J-cos(7«rf)4-...	(1.64)
* Непрерывная везде, кроме точек разрыва.
2*
35
2fa
Зо 5cj 7cj 9cj
2f0
77%
t .
110)
Амплитудный спектр f(t)
представлен на рис. 1.3, а графи-
ки частных решений (1.64)—на
рис. 1.4. Фазовый спектр изменя-
ется от 0 до л для всех значений
1г, начиная от 0 при п<в = 0.
Рис. 1.3. Амплитудный спектр перио-
дической прямоугольной функции,
представленной на рис. 1.2
Пример 2. Рассмотрим разложение в ряд Фурье периодической
треугольной функции, представленной на рис. 1.5. Данная функция
обладает следующими условиями симметрии:
/(0=-/(-') и	_/(/).
(1.65)
Первое условие означает, что коэффициенты при косинусах
должны быть равны нулю. Второе условие предполагает, что ко-
эффициенты при четных гармониках должны быть равны нулю.
В силу этого разложение функции в ряд Фурье содержит только
коэффициенты Ьп и при этом только те, которые являются нечет-
ными (т. е. &2n+i). При определении коэффициентов Фурье и на-
личии двух указанных условий симметрии интегрирование осущест-
вляется в интервале одной четвертой части периода. Выражение
т
этой функции при С< <7	— имеет вид
ZW=(4^o-	(1-66)
Тогда получим
Г/4
Ьп=~т\	(1.67)
О
(L68)
fUTl2 \ 2 /
На основании предыдущего напишем
f(t)= fsinto/—sin + sin 5u>Z — sin 7а>/-|-..Л (1. 69)
Фазовый спектр в этом случае изменяется от 0 до л для всех
значений пш, начиная от Чго=О. Амплитудный спектр периодиче-
ской треугольной функции представлен на рис. 1.6.
Свойства частотной характеристики можно выявить из рассмот-
рения следующих примеров.
1. В случае параллельного смещения оси абсцисс имеем
36
Рис. 1.5. Периодическая треуголь-
ная функция
Рис. 1.4. Частные случаи выражения (1.64),
иллюстрирующие особенности преобразова-
ния Гиббса (отклонения от прямоугольной
функции) рядом Фурье, аппроксимирую-
щим прямоугольную разрывную функцию
(где К — константа) и в разложении меняется только «коэффици-
ент усреднения» а0. Раскроем также влияние условий задачи на
особенности симметрии. Это особенно наглядно, когда ось абсцисс
смещена на величину среднеарифметического значения заданной
функции /(/). При этих условиях свойства симметрии не изменя-
ются.
В примере 1 в ряде Фурье существуют только нечетные гармо-
ники. Данная периодическая прямоугольная функция наглядно
обнаруживает свои свойства симметрии при исследовании f(t) —
2. Параллельный перенос оси ординат (который означает сме-
щение во времени) не меняет численные значения гармоник пери-
одической функции и влияет только на значения синусов и коси-
нусов в разложении в ряд Фурье. Величины рп2=ап2+Ьп2 не из-
меняются для периодических функций от времени. Это является
основной причиной, по которой в спектральном анализе частотный
метод занимает ведущее положе-
ние при машинном проектиро-
вании.
На основании этого читатель
может убедиться в действенности
частотного метода и для непре-
рывных процессов.
3. На примере 1 показывает-
ся, что амплитуда гармонических
составляющих периодической
прямоугольной функции, облада-
ющая конечным числом разры-
вов, уменьшается пропорциональ-
но 1/п.
На примере 2 показано, что
8f0
fr)z
3cj
tif
у,
Рис. 1.6. Амплитудный спектр перио-
дической треугольной функции
37
амплитуда гармонических составляющих периодической непрерыв-
ной треугольной функции, обладающая разрывами производных,
уменьшается пропорционально 1/п2.
Следовательно, этим доказано, что коэффициенты (а) разло-
жения в ряд Фурье периодических функций, имеющих один или
большее число разрывов, уменьшаются пропорционально 1/п (с
ростом п) и коэффициенты (6) разложения в ряд Фурье периоди-
ческих непрерывных функций, но имеющих разрывы первых про-
изводных в одной или большем количестве точек, уменьшаются
пропорционально 1/п2 (с ростом п).
4. С помощью ряда Фурье в интервале — Т/2</<7/2 могут
быть аппроксимированы и непериодические функции f(t).
Если ряды определены с внешней стороны интервала, то необ-
ходимо убедиться, что f(t) аппроксимируется периодом Т внутри
интервала.
Экспоненциальная форма рядов Фурье
Ряды Фурье в тригонометрической форме, содержащей синусы
и косинусы, исторически появились раньше. Однако они могут
быть представлены и в экспоненциальной форме. Эта форма легче
в обращении и обеспечивает переход к интегралу Фурье и пре-
образованиям Фурье.
Мы приведем, однако, тригонометрическую форму записи ряда
Фурье, чтобы сделать нагляднее этот переход:
со
=-у +^^(ancosn«)/ + ^nsin(*M') ПРИ <«=2я/7'; (1.70)
П=1
Т/2
9	<
ал=— \ f	при n = 0, 1, 2,...;	(1.71)
—Г/2
Т/2
9	(*
Ьп—— \ /(/) sin при n=0, 1, 2,....	(1.72)
—Т/2
Согласно формуле Эйлера
sin (n«rf)=— (е^ - е-^');	(1. 73)
cos(n«M!)=2_(e^<“z + e-^m/).	(1.74)
Подставляя (1.73) и (1.74) в (1.70), находим
/1-1
38
/ co=«о + 2 (а«e/w+а-«еУпт<).	(1 •7б)
п-1
где	a„=-i-(a„-/6„) при п>0;	(1.77)
«-„=у (ая+/дя) при п<0;	(1.78)
а0=-у- при п=О-	(1-79)
Второй член в (1.76) может быть записан в ином виде, если
осуществлять замену п на —п, и соответственно пределы сумми-
рования
2 О-я &na,t = 2 але/лш<-	(1.80)
л=1	п— 1
В результате выражение (1.76) может быть упрощено объеди-
нением в простую сумму
/(/)= 2 а„е><	(1.81)
п—1
Эта запись является экспоненциальной формой рядов Фурье.
Комплексные коэффициенты могут быть получены подстановкой
выражений (1.71) и (1.72) для ап и Ьп в (1.77):
Г/2
ап=-±- J	для всех целых чисел п. (1.82)
-Г/2
В выражении (1.81) п принимает отрицательное значение. Это
приводит к возникновению отрицательных частот*, которые не
имеют физического смысла для реальных физических систем. Они
возникают от математических преобразований синусоидальных и
косинусоидальных функций в пары экспоненциальных функций.
Затруднения, связанные с использованием экспоненциальных
рядов Фурье в связи с наличием комплексных функций и «отри-
цательных частот», часто отмечаются как их недостаток. Эти не-
достатки могут быть устранены, если учесть, что значения коэф-
фициентов рядов Фурье должны быть действительными, если f(t)
действительная функция t. Разработка экспоненциальной формы
рядов Фурье обязана тому, что она непосредственно ведет к ин-
тегралу Фурье и преобразованию Фурье, что важно для распрост-
ранения положений частотного метода на непериодические функ-
ции, и к развитию преобразований Лапласа.
* Читатели, занимающиеся проектированием электротехнических систем, дол-
жны представить положительные и отрицательные частоты как пару вращающих-
ся в противофазе электродинамических систем в комплексной плоскости, суммар-
ное движение которых изображается на действительной оси.
39
Интегралы Фурье и преобразование Фурье
Амплитудный спектр рассмотренных периодических функций —
дискретен (является линейным спектром). Как уже отмечалось,
увеличение Т уменьшает основную частоту 2л/Т и уплотняет ам-
плитудный и фазовый спектры. В пределе дискретный спектр
стремится к плавной кривой, называемой непрерывным амплитуд-
ным спектром. Кроме того, при Т—>оо f(t) перестает быть пери-
одической функцией. Дальнейшей задачей является осуществле-
ние построения непрерывного амплитудного спектра непериодиче-
ских функций с помощью разложения в ряды Фурье, содержащие
периодические функции. Непериодические функции представляют
интерес, так как отражают фактическую картину протекания раз-
личных процессов.
Таблица 1.4
Трансформации в формулах Фурье
Ряд Фурье	Наименование	Интеграл Фурье
По)	Гармоническая компонента	<0
(0	Основная частота	Доз
т	Период	£2л/Д(о
Если f(t) —непериодическая функция, следует изменить запись
полученных выражений, так как при стремлении частоты 2л/Т к
нулю Т становится бесконечным, а п абсурдным. Это связано с тем,
что хотя основная частота о в непрерывном спектре может при-
нимать любое значение, это обстоятельство не может быть рас-
пространено на п. По этим причинам формулы Фурье требуют
некоторой корректировки в соответствии с трансформациями
табл. 1.4.
Тогда (1.81) и (1.82) примут вид
/(/)= yj aa>e-'w при%>=0, + Д<о, + 2Д«>;	(1.83)
— оо
Т/2
\	(1-84)
-Г/2
Подставляя (1.84) в (1.74), находим
~	Г/2
/(/) = -А_|~^	/(/)e->/rfi'le>zto.
-оо -т/2
(1.85)
40
Теперь пусть Т—>оо; тогда получим
/(0=-L lira
2л г->оо
Т/2
-Т/2
dt \ До) _
—/ (t)&~iwt dtjefa/ d<s>.
(1.86)
Выражение (1.86) является изображением функции f(t) с по-
мощью интеграла Фурье.
Определим преобразование Фурье, полагая
g(o»)= J
(1-87)
Ввиду этого из (1.86) следует, что
И
/(/)=-L. g(m)ei*dt
(1.88)
g(<») = j f(t^->a,dt.
(1.89)
Уравнения (1.88) и (1.89) называют парным преобразованием
Фурье, gfa) называют преобразованием Фурье функции /(/), а
[ (/) — обращением преобразования Фурье.
Иногда используется следующая форма записи:
g(«)=F{/(/)};	(1.90)
/(O^-HgWh	(1.91)
Пример 3. Рассмотрим амплитудный спектр единичного прямо-
угольного импульса с амплитудой f0 и продолжительностью Т, как
показано на рис. 1.7:
/о, 0</<Т;
О, 0>/>Т.
Тогда
г
С /о е~у“' dt =-^- (1 - е->9;
4
gU\=2h- sin (!£.\е-Я»>г/2).
6' '	( 2 /
(1.92)
(1.93)
(1.94)
sin (<07*72)
<>772
(1.95)
41


Рис. 1.7. Прямоугольный
импульс
ir?wi
Рис. 1.8. Амплитудный спектр прямоугольного
импульса
График амплитудного спектра прямоугольного импульса представ-
лен на рис. 1.8.
Пример 4. Рассмотрим функцию
/(/) = /-Л
Разложение функции f(t) в ряд Фурье в интервале 0</<1
имеет следующий вид:
6„=0;
ао—~
о
3 _1о“ 3
«я=4 \(z-^cos
о
nrfcos(nrtO । t . ,
ал = 2 U—-—-ч--------sin (плЛ1 —
LI л2л2 1 пл	}
- cos (пл/)--sin (пл/)+ sin (nn/)jp ;
Г/cos (пл)— 1 \	/ 2 cos пл \"|
[\ п2л2 )	\ п2л2 /] ’
— 2(1 +cos пл)
-------- ~~~ •
п------п2л2

Таким образом,
—-M-^-cos(2n/)+-^- cos(4л/)+ JL(6«0+...l.
О Л/ 4	10	<*0	j
Пример 5. Ряд Фурье функции ех на интервале 0<х<2 облада-
ет особенностью, т. е. содержит синусы и косинусы, где выпукло
подчеркивается «нечетность».
42
В этом случае
2
а0= f exrfx=e2— 1;
2
z.	g2_ 1
an= \ ex cos(nnx)rfx = ——-;
о
2
bn= ex sin (nnx)dx =	П •
о
Таким образом,
ex=(e2— 1) p + - у cos (лх)	cos (2лх)4~...
z i \	/ 2 \	1
•.. — I-----1 sin (ax) —I------1 sin(2jtx)— ...k
\ I2 + 1 /	k \ 22 + 1 )	v	J
Очевидно, для больших п
в то время как
Для больших п нечетные составляющие разложения функции
е® доминируют во всем интервале 0<х<2.
Данная книга посвящена прикладным проблемам исследования
воздействия периодической функции, которая может быть разло-
жена на ряд синусоидальных компонент ряда Фурье, на линейную
систему и реакции этой системы, представленной также в виде
суммы синусоидальных компонент, каждая из которых является
реакцией на соответствующую компоненту воздействующей функ-
ции.
Таким образом, результат получается наложением совокупности
индивидуальных воздействий, преобразуемых к реакции с помо-
щью периодических функций. Выходная реакция системы обладает
при этом синусоидальными волнами той же частоты, что и у воз-
действующей входной функции, и отличается только величиной фа-
зы и амплитуды, а система может быть охарактеризована переда-
точной функцией, от которой зависят соответствующие изменения
амплитуды и фазы. Эта передаточная функция характеризуется
однозначным соответствием между выходом и входом системы. Она
является функцией только входных частот. Необходимо обратить
внимание на то, что последнее утверждение основывается на осо-
бенностях связи характеристик системы, времени и частоты.
Это обстоятельство проясняется после того, как мы проследим
связь между «синусоидальной волной на входе» и «синусоидальной
43
волной на выходе» во времени» которая показывает, что амплитуд-
ное и фазовое изменения зависят только от частоты синусоидаль-
ной входной волны. В этом смысле мы переносим задачу из вре-
менной области в частотную.
Использование теории рядов Фурье позволяет исследовать
спектр устойчивых реакций системы на периодические воздействия,
не включая области непериодических возмущений и переходных
процессов.
Вместе с тем применение преобразований Фурье позволяет
переносить рассмотрение непериодических функций из временной
в частотную область. Реакция системы на данное воздействие мо-
жет быть определена с помощью обратного преобразования Фурье,
произведения преобразований Фурье, функции воздействия и пере-
даточной функции. При динамическом анализе систем приме-
нение преобразований Фурье имеет два ограничения, что приводит
к необходимости использования более гибкого преобразования
Лапласа.
Первым ограничением является то, что обратное преобразова-
ние Фурье включает несобственные интегралы, которые часто вы-
зывают трудности в интегрировании.
Второй, более значительной трудностью является то, что интег-
ралы не сходятся для большого числа наиболее употребимых в ин-
женерной практике передаточных функций, включающих ступен-
чатую функцию, sin, |sin | и tn (при п— 1, 2, 3,...).
Например, преобразование Фурье единичной ступенчатой функ-
ции
/(/)=( °’ /<0:	(1.96)
• U, />0
принимает вид интеграла
g (<o)= (	di=-^~ ” = .eos(^)-;sin(<oQ ,
J	— >	—>
о	о
который не может быть вычислен, так как синус и косинус колеб-
лятся внутри предельных значений и не определены при бесконеч-
ном аргументе.
Найти решение в этом случае можно таким преобразованием
f(/), чтобы интеграл Фурье сходился при введении «фактора схо-
димости», которым является е~а/, приводящий к преобразованию
Лапласа. В этом случае
	/,(O = e-V(/)=f°’eZ	^о; >0.	(1.98)
Тогда			
со
g (<о) = е~в/ е-л0' dt =
о
е~(«+»*
—(а + /“)
(1.99)
44
1.8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Альтернативой для изменения преобразуемой функции являет-
ся изменение преобразующего ядра. Оно заключается в том, что
преобразуемая функция умножается на е о/, которое дополняет
преобразующее ядро интегрирования е>т/. Преобразование прини.-.
*1ает вид
g (.>) = f [e-°z f (/)] dt\	g (<o)=j f (Z) e~<a+»z dl',
6	~	’	(1.100)'
F(s)= j /(/) e~stdf.
о
Обратное преобразование принимает вид
1
2л
1
2л/
e-’VM
Таким образом,
\ g((o)e<e+^z dw>
2л «)
— оо
g’W d (/ю) =
-/oo
1
2л/
a 4- Joo
\ S (ш) f d (a + /id)
a—j’oo
a+joo
= —-—	F(s)^stds.
2nj J
a—j’oo
(1.101)
Уравнения (1.100) и (1.101) называют преобразующей парой
Лапласа. Если интеграл (1Л00) сходится, то функция f(t) может
быть преобразована с помощью оператора Лапласа. Большинство
встречающихся в прикладных задачах функций может быть преоб-
разовано с помощью оператора Лапласа. Примеры функций типа
V и е/Л (п=1, 2, 3,...), которые не могут быть преобразованы с
помощью оператора Лапласа, в дальнейшем из рассмотрения ис-
ключаются. Это объясняется тем, что функции, которые не могут
быть представлены экспоненциальными структурами, оператором
Лапласа не преобразуются. Смысл этого утверждения очевиден.
По поводу функции f(Z) следует сказать следующее: 1) неза-
висимая переменная t не обязательно должна выражать время;
2) для обеспечения однозначности преобразования Лапласа функ-
ция /(/) должна быть однозначной; 3) она может иметь конечное
число конечных разрывов; 4) если функция имеет разрыв при /=0,
нижний предел интеграла должен приближаться к нулю с поло-
жительной стороны. Наконец, обратное преобразование Лапласа
(1.101) может быть вычислено с помощью теории вычетов, что уп-
рощает эту операцию.
Преобразования Лапласа с применением элементарных функ-
ций и операций над ними позволяют сводить довольно сложные
45
для решения дифференциальные уравнения к решению алгебраи-
ческих уравнений в изображениях.
Преобразования Лапласа позволяют:
1)	осуществлять преобразование периодических функций с ко-
нечными разрывами (или разрывами производных) в простые ал-
гебраические функции;
2)	преобразовывать операции интегрирования и дифференциро-
вания во времени в операции умножения и деления в частотной
области;
3)	осуществлять преобразования интегродифференциальных
уравнений в алгебраические;
4)	в случае решения дифференциальных уравнений осущест-
влять определение произвольных постоянных;
5)	в удобной форме исследовать устойчивость линейных систем
по их реакции на импульсное возбуждение.
Существует достаточно обширный перечень литературы по до-
вольно сложным методам анализа линейных систем с применением
преобразований Лапласа. Основным фундаментом этой литерату-
ры служит сравнительно небольшой перечень теорем, которые мы
приведем без доказательств, имеющихся во многих источниках.
Теорема 1. Преобразование Лапласа для суммы двух функций
равно сумме преобразований каждой из них:
А(Л + /2) = А(/1)-1-А(/2).	(1.102)
Теорема 2. Преобразование Лапласа произведения функции на
постоянную величину равно произведению этой постоянной на пре-
образование Лапласа этой функции:
L(cf)=cL(f).	(1.103)
Эти две теоремы выражают линейную природу преобразований
Лапласа.
Теорема 3. Теорема смещения. Если оператор Лапласа Lf (t) =
= F(s), то
r)] = e-^F(s).	(1. 104)
Добавим, что функция смещения имеет значение также для
дискретных устройств, где смещение во времени естественно.
При игнорировании этой важной оговорки возникают ошибки,
и особенно при применении теоремы смещения к разностным урав-
нениям.
Теорема 4. Оператор Лапласа периодической функции f(t) ра-
вен 1/(1 — e~rs), умноженной на оператор Лапласа f(t) по перво-
му периоду:
(1.105)
Теорема 5. Теорема дифференцирования. Если функция f(t) и
46
ее производные могут быть преобразованы с помощью оператора
Лапласа и если L[f(O]=F(s), то
/ (0-+-).	(1-106)
Теорема 6. Теорема интегрирования. Если Lf(f)=F(s), то
zh(1Л07)
Lo J
Теорема 7. Если L[f(t)] = F(s) и первая производная может быть
преобразована с помощью оператора Лапласа, то
/(0-(-)=lini /(Z)=limsF(s).	(1. 108)
/->0+	5->оо
Теорема 8. Если L[f(/)]=F(s) и первая производная может
быть преобразована с помощью оператора Лапласа, то
lim /(/)=HmsF (s).	(L109)
/-►00	5->0
" /
=Fl(s)F2(s). (1.110)
Теорема 9. Теорема свертки. Если А [/\ (/)] = 7^($) и 1[/2(/)1=
=F2(s), то
£ J	=L
Теорема свертки особенно важна, так как она позволяет по-
лучить реакцию системы на функцию воздействия. Интеграл сверт-
ки позволяет получать частное решение для многих дифференци-
альных уравнений, которые могут быть преобразованы с помощью
оператора Лапласа и у которых функция воздействия может быть
также преобразована с помощью оператора Лапласа.
Теорема 10. Если L(f) =F(s), то
£{e^/(/)} = F(s-a).	(1.111)
Теорема 11. Теорема изменения масштаба. Если Lf(t)=F(s), то
Lf(ai)=±F(±:
Л \ л t
(1.Н2)
Теорема 12. Если Lf(t) =F(s), то
L{t-f{t)}^-\y-^-F{s).	(1.113)
Теорема 13. Если Lf(t)=F(s) и существует lim	то
L {J^-} = j>(s)<Zs.	(1-114)
Для получения выражений (1.100) и (1.101), помимо методов,
указанных выше, существует поистине огромное количество преоб-
разований различных функций с помощью оператора Лапласа.
47
Чтобы избежать сложных операций при решении дифференци-
альных уравнений, созданы таблицы функций и их преобразований
с помощью оператора Лапласа. Книга Е. С. Леви «Преобразова-
ния Лапласа» (Мак Гроу-Хилл, Нью-Йорк, 1969) содержит таб-
лицы 1200 преобразований Лапласа в сжатой форме. Таблицы та-
кого рода в основном были опубликованы в Макдоннелл-Дуглас
(автор таблиц Леви создал их, работая в кампании Дуглас Аирк-
рафт в Санта Монике, Калифорния).
С помощью преобразований Лапласа могут быть решены диф-
ференциальные уравнения преобразованием результирующего опе-
ратора. Оператор Лапласа является в этом случае изображением
решения дифференциального уравнения. Если функцию можно
разложить в ряд, то изображение функции будет также изобра-
жением ряда.
Таким образом, если может быть осуществлено разложение в
степенной ряд некоторой функции, то может быть найдено и ее
изображение Лапласа, также представленное соответствующим
рядом.
Если
00
то
Несомненно, изображения Лапласа для рядов tn должны при
этих условиях сходиться.
Пример 1. Если	—единичная ступенчатая функция,
то
оо	£
LU(t)= f	=
о	о
i. ( *~st \\L u	1
= lim ----- =lim ----------1==—.
£-*<» \ S /|o 4-coo \ S / S
На этом простом примере видно, что результат может быть
получен только тогда, когда
Re(s)>0 или а>0,
где s= (о+/а)) — комплексное число.
Пример 2. Если f (0 =t, то
—St	о—st х\Г	1
—-------—I =— при s>0.
S	«2 J|o	$2
48
Интегрируя по частям, найдем
{/р st р	1
----------1 =— ПрИ $>о.
S $2 Ло $2
Пример 3. Если /(/)=еа<, то
«	00	оо
Leat —	\	ekdk.>
с	7 о"
где k~(s — a)t и Leat = {——Vo — 1) = —-—.
\s — а /	s— а
Пример 4. Если f(t) = sin(co/), то
00
L { sin (со/)} = e~s/ sin со/rf/
6
—е st [s sin (to/) + to’cos (to/)]  to
$2 -|— o)2	$2	o)2
Пример 5. Если f(t) =cos (art), to
cos (<«/)=——— sin (orf);
to dt
тогда
L cos (co/) == — L — sin (co/) = (—($) (---) ;
V	to dt V 7	\ to P 7 \ $2 + ш2 / ’
L COS (co/) =------.
V 7	$2 + to2
Пример 6. Если f(t) =sh(/), to
L {sh (co/)} = L p-e-^+^dt;
о	о
£{sh (<>/)}=-^- L {em<} + -b L (е-и/};
Z{sh(<o/)}= — [—i---------=	.
2 (s — to S -|“ to J s2 — <o2
Пример 7. Рассуждая так же, как и в примере 5, мы можем за
писать
L {ch (ш/)}=(—W ——) (s) = —— .
Пример 8. Если f(t) —te-*, и так как
£(/)=l/S2(
получим
£{/е-ш/}—______________________-___=______________.
(s + <о)2	«2 4- 2<I>S 4- й>2
Пример 9. Если /(/)=е-//т sin (<*>/), то
£{sin (<о/)}=-------sin (ю/)}
$2 -|- (о2
4$
И
Це-Ч* sin (<в/)}=--------.
v	s2 4- (2/TJ) s + («2 + 1/-C2)
Пример 10. Если f(/)=sin (at), то изображение решения диф-
ференциального уравнения, которое имеет f(t) в качестве своего
решения, может быть получено следующим образом:
cos (<»/); /"(/) = —<о2 sin (arf) = — <о2/ (/).
Тогда
L {sin (ш/)}=L {f" (t)+ю2/ (/)=0}=s2L{f(t)} +
-H2M/(/)}-WW'(O)=o
и
(s2 + <o2)Z{/(/)}=s/(0)+/'(0);
(О* j	\S*	0)2 J
Теперь f(0) =0 и /'(0)=«>-
Пример 11. Если f (/) = / sin (о/), то
Lf(t) =---—W -2-— .
J V ’ dS \S2 A-($2 -I- <o2)2
Обратное преобразование Лапласа
Обратное преобразование Лапласа записывается в комплекс-
ной интегральной форме как
а+/оо
estf(s)ds.
<3— JOO
Для определенных преобразований Лапласа прямое использо-
вание этого интеграла для получения оригинала является наибо-
лее быстрым методом достижения цели. Другими, наиболее рас-
пространенными методами нахождения оригинала обратным пре-
образованием Лапласа являются следующие.
1.	Поисковые таблицы (наипростейший и наискорейший ме-
тоды).
2.	Применение разложений в виде правильной дроби G(s) =
= N(s)/D(s) *, которая может быть представлена как сумма эле-
ментарных дробей типа
A	As А-В	As2 A- Bs А-С
(as 4- b) ' (asi A- bs A-c) ’ (as3 4- bs% A-cs Ard) ’
общий знаменатель которых соответствует знаменателю G(s).
* D(s) имеет больший порядок, чем ^(s).
50
3.	Метод разложения G(s) в ряд по степеням s, который об-
ратным преобразованием можно привести к степенному ряду по
степеням t.
4.	Метод решения дифференциального уравнения обратным пре-
образованием его изображения с помощью оператора Лапласа
G(s).
Пример 12
£—1 /5 4~ ^1 _ S — ш2 )  Z,-1 / I I _	$ I_______^2	1 
I S3 S2 + “д J	I $2	53	®2 + “д S2 + “д J
= /_|_J^._COs((O/t/)_|_^2. Sin
2
Пример 13
£—1 /____5____1	£—1 / (s — 2)4-2 1 
(s2—4s4-20j t (s—2)2+16 J
— £-1 / s~2	1-1 1 £-1 I 4	1 —
1(5-2)4-16/	2	|(S_2)24-16j
— e2z cos (4/) + — e2/ sin (4/)=e2/ fcos(4('J—L sjn
2	*4	' 7 1 2
Пример 14
e~Ts
(5 4- 1/т)4
= А-1[е-^{£/(/)Я,
где
Тогда
/(/)=£-! (-----i--1
J l(s 4- l/n)‘J
6
г (	\"i	e—(*—ПЛ (f т\з
L~^~Ts L J —----1 = ---------U(t — T).
L I	6 JJ	6
Функция может быть записана так же, как
, е_г. .	(-L(/_r)>e-<'-r>« (>?•;
6 0 /<л
Пример 15
Z”1 [--i---1 = ^-1 (------1——+ — +— ) =
(«2(5 4- I)2/	l(S4-l)2	5 4- 1	52 ' 5 /
=/е-<4-2е-/4-/-2.
Пример 16
—1 ( 35 4~ 7 ) д । 1 35 4~ 7 1 д । 1 S'"А , В 1
( s2—2s — 3)	1(5 — 3) (s 4-1) J Is—3 54- 1J’
Это получено разложением на элементарные дроби
35 4-7	_ Л , Д
(s—3)(5 4- 1) — 5— 3	5 4-1
51
или
ЗН-7=Д($+1)+В(«-3)=(Д+В)«+И-ЗВ).
Так как
Л + #=3, Д-35=7.
Решая систему, найдем
Д=-4 и 5 = -1.
Это даст:
£-1----3s + 7-= £ f ( ——'l — ( ——U = 4c° — e •
(s-3)(s + l)	|\s —3/ \s + 1/1
Решение дифференциальных уравнений
Дифференциальное уравнение
хх-\-х = f(t)
с начальным условием
х(0)=0
может быть решено с помощью изображений Лапласа
£(1x4-*)=£/(');
т£(х) + £(х) = £/(/);
х [sx(s) — x(0)]4--*(s)=f(s);
(TS + 1) x’(s) = /(«) + tx (0);
Второй член в правой части этого уравнения является допол-
нительным решением. Первый член — частное решение дифферен-
циального уравнения. Частное решение дано в общей форме, по-
этому можно рассмотреть ряд условий.
1.	Если f (/) =0, то /♦'(s) =0 и
£-1	=о.
(TS + 1)
2.	Если f (t)=U (I), то F(s)=l/s и
£-1	£-1 (--1----1=1 - е-'/\
Its+1J (s (ts + 1)J
3.	Если /(/)=е~а/, то /г($)=а/($4-а) и
£—i f______5Д________] = ( 1 1 (е~at — е—1'"1)
I (s + 1/т)(s + а) /	\1 — ха)
52
Условия устойчивости
Устойчивость линейной системы оценивается по характеру ее
реакции на импульсйое воздействие.
В этом случае изображение решения через передаточную функ-
цию связывается с изображением импульсного воздействия в виде
дельта-функции при t=0. Тогда
После преобразований получим
Z8(0)= 1,
что следует из следующих операций:
at
Ll (0) ~ L — {U (/)}=sLU (/) = s (— 'I = 1.
dt	\ s )
Изображением реакции системы на импульсное воздействие"
будет
что приводит к
x(t)=L~1x(s)== l-e-</'t= 1 • е5п0люс<*.
В связи с этим можно сделать следующие замечания:
1. Устойчивость процесса определяется местоположением полю-
са на плоскости s. Когда Re («полюс) <0, этот процесс устойчив, так
как показательная функция имеет отрицательное значение степени,
что приводит к уменьшению начального отклонения во времени;
говорят, что система обладает асимптотической устойчивостью.
При положительной степени показательной функции начальное-
возмущение неограниченно возрастает во времени; говорят, что сис-
тема неустойчива. Наконец, если возмущение сохраняет во време-
ни постоянное значение, система не обладает асимтотической ус-
тойчивостью.
2. Изображение реакции системы тождественно передаточной
функции системы (как мы увидим в разд. 1.9). Применение преоб-
разования Лапласа при решении стационарных линейных диффе-
ренциальных уравнений более высокого порядка в своей основе не-
сет те же соображения, что и для процесса, описываемого уравне-
нием первого порядка.
Выводы по характеру устойчивости системы, описываемой урав-
нением более высокого порядка (содержащей полиномы «), тожде-
* «полюс — значение полюса ( — — 1 (нримеч. ред.).
53*
ственны по своей идее с примером системы, описываемой уравне-
нием первого порядка. Для того чтобы линейная система, описы-
ваемая дифференциальным уравнением п-го порядка, была устойчи-
ва, все п полюсов должны быть либо меньше нуля, либо равны нулю.
1.9.	СТРУКТУРНЫЕ СХЕМЫ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
Структурные схемы появились в качестве наглядных образов
проектируемых комплексных систем.
Связь между параметрами проектируемых систем и их динами-
кой может быть потеряна, если они представляются только сис-
темой математических уравнений. Альтернативой структурных схем
является наглядное представление причинных отношений между
входом и выходом каждого элемента системы. Причинные соотно-
шения между входом и выходом каждого элемента системы назы-
ваются элементарными передаточными функциями. Каждый блок
структурной схемы имеет свою передаточную функцию. Однопара-
метрические системы имеют один вход и один выход. Как правило,
блоки структурных схем являются многопараметрическими и име-
ют более одного входа и выхода, связанных между собой векторно-
матричными уравнениями. Простейшая структурная схема может
связать вход с выходом системы, как это показано на рис. 1.9.
Главной характеристикой структурной схемы является сигналь-
ный поток на входе и выходе в виде однонаправленного процесса
с преобразованием его внутри блока подобно тому, как оператор
передаточной функции действует на входной сигнал для преобразо-
вания его в выходной.
Так (как показано на рис. 1.10) оператор суммирования скрыт
внутри блока и на блоке это действие изображается символом сум-
мирования.
Символ разветвления потока сигнала на его пути представлен
на рис. 1.11.
Эта система символов представляет:
а)	элементы системы, содержащие передаточные функции;
б)	суммирование потоков сигналов;
в)	разветвление потока сигнала, который может быть использо-
ван для получения развитой системы блоков, содержащих алгебру
управляющих передаточных функций, построения эквивалентных
систем, упрощения передаточных функций системы и достижения
большей наглядности проектирования и взаимодействия среди мно-
гих элементов комплексной системы.
Использование структурных схем при математическом модели-
ровании систем с замкнутым циклом создает особую обозримость
и доходчивость.
Л
f( )
* Обозначает	у= ffx)
Рис. 1.9. Простейшая структурная схема—блок—символ
54
-----Л.—э- обозначает
(±)Т(±)	z=±x±t)
АЛ
, обозначает
' разветвление’
Рис. 1.10. Общепринятое обоз-
начение суммирования
Рис. 1.11. Обозначение развет-
вления тракта сигнала
В связи с актуальностью темы инженеры достигли высокого
уровня мастерства в применении структурных схем для решения
алгебраических уравнений замкнутых систем.
Большинство из используемых структурных схем преобразова-
ний сигналов представлено в табл. 1.5.
Пример 1. Структурная схема содержит преобразование
У/х= 1/(«+1)-
Заметим, что
w/(s) + z/(s)=x(s).	••• y(s)=x(s) —xsy(s).
В связи с этим структурная схема уравнения будет выглядеть
как
Можно также осуществить преобразование nsy(s)+y(s)=x(s)z
Тогда
Эти структурные схемы идентичны передаточной функции, так
как сигнал изменяется.
rs+1
Физически каждая структурная схема обладает отличительной
особенностью.
55
Г и поЬые структурный схемы и ^::ьйВалентнЬ1е соотношения, применяемые
В структурном анализе
Таблица 1.5
ЛреыГразоОания	Типовая структура			Эквивалентная схема				Уравнения
Перемена (ГлокоВ				—				b=aY,Yz
Взаимный оймен сумматоров	a +z-\Q - Ьх-ч	d -Хь +Хс			a +^da+cL.^ d ——ЧегЧг)—±-*- +р? +-|ь				d=a-b+c
Перестроение сумматоров	_а	,+ф	d_^ Ь	С			i С5				d=a-b-c
Смещение (Глока за сумматор	и ? гур	& - -1 f				I/Y			d=aY-с
Смещение сумматора за (Глок				<Г тт С5				c=(a-b)Y
Смещение (Глока за точку ответвления	— о			b	<^Г С5 т о —1 > о-				b ~aY
Смещение точки отВетВления за (Глок	а	. , пл ь			Д' Г71	Ь-				a II C3 II II C3
	а					j//y			^.ь]	
Смещение сумматора за точку ответвления			С	ь ч *4- । лЧ				c=a- b
Смещение точки ответвления за сумматор	О —и > 1 о Iх			со +м + J Ч- ° s> *3				c = a-b а = с + ь
b
Объединение каскадных блокад	а	г-,	г-, ь —НКННК1—*			а			У,У2		ь		1 b=aYtYz
Удаление блока из прямой петли	^-4^			•ЧИН*			1 уг	1—1 +^-\Ч *ЕНф—*			d=a(Yi~Yz)
Вдедение блока д прямую петлю	а	—HZihjKjp—		а	Т Lit	r*EhEHSh* *——-*					d=aY1-a
Устранение прямой петли	а	гЧЗЧ©— 	Ч5Н		а			У,~Уг		d		d^aiYj-Yz)
Устранение блока из контура обратной сдязи	Чф—Eh		d		1 Уг						d=^~ 1 + Y,YZ
Вдедение брона б контур обратной бдязи	а + (		Jv I		d								->Е}Г		1 + У,
		1 1									
Устранение контура обратной сдязи	ЧЭ—Eh (HJ*—		d	а				У, 1 + У,Уг			£		
			d r	а				У,		d ,		“-°,.У,
	а	Ч гЛ	*		а			1		d		d=a-^- /+ Yz
		Т__Й*-					/ + y2				
Вдедение контура обратной сдязи	g->И—			У			/-г,			d	d = aYj
	—d *			г			у, 1		d		d = aYt
о
Рис. 1.12. Пружинная демпфируемая система со
спаренной массой:
Ki—постоянная первой пружины; Кг—постоянная второй
пружины; гп\—масса первого груза; т?— масса второго
груза; (/—отклонение т\ от положения равновесия; х—
отклонение т2 от положения равновесия
Первая структурная схема может рас-
сматриваться как позиционная система с
коэффициентом обратной связи, представ-
ляющим диссипативный элемент.
Вторая структурная схема может быть
рассмотрена как позиционная система, со-
держащая однократный интеграл позицион-
ного рассогласования, т. е. интеграл разно-
сти между значением сигнала х и значени-
ем у.
Пример 2. Получим передаточную функцию системы
Два элемента контура могут быть объединены следующим об-
разом:
7
S('ES^7)
У
Тогда передаточная функция для процессов в замкнутом конту-
ре получится как
или
Передаточная функция при этом имеет вид
х (s)	т$2 4- $ 4-1
58
Пример 3. Рассмотрим движение свободной спаренной пружин-
ной системы, представленной на рис. 1.12, используя ее передаточ-
ную функцию и не прибегая к уравнению Лагранжа.
Позиция 1. Если т2 перемещается в направлении +х и если
нет других одновременных перемещений, с помощью равновесия
сил, действующих на т2, можно составить следующую структурную
схему:
Позиция 2. Если mi перемещается в направлении +у и если нет
других одновременных перемещений, равновесие сил, действую-
щих на тх, дает возможность представить структурную схему в
следующем виде:
Позиция 3. Объединяя позиции 1 и 2, найдем
На этом примере показывается «физическая причинность» быст-
рого построения структурной схемы относительно сложного про-
цесса с недостаточными начальными данными о характере измене-
ния сил и движения. Эти структурные схемы могут быть быстро и
без затруднений сведены к алгебраическим структурам и, если
есть необходимость, уравнениям движения, которые могут быть по-
лучены после простых алгебраических преобразований в виде пе-
59
редаточной функции и последующего применения к ней обратного
преобразования Лапласа.
Вероятно, самым важным моментом в применении структурных
схем является то, что специалист должен обладать «хорошим чуть-
ем» задачи при ее разработке указанным способом.
Применять структурную схему для вычислений можно только
после того, как аналитически или на вычислительной машине будет
получена исходная информация, которую необходимо заложить в
математическую модель. В основе построения схем должны лежать
физические процессы в системе, а не математические свойства урав-
нений. «Физический» подход отличается тем, что не зависит от то-
го, применяется ли для математического описания закон Ньютона
или уравнение Лагранжа, в которых аналитические нюансы доста-
точно удалены от физических свойств системы.
Те, кто имеет дело с исследованиями вращательных движений,
должны познакомиться с пока еще не очень широко известной ра-
ботой Le Compte, который разработал простой подход (он назвал
его двухвекторной гиромеханикой) * для анализа вращательного
движения. Она основана на физическом проникновении в суть ги-
родвижения через структурную схему движения, угловую скорость,
вращательный момент и координату единичных векторов, так как
система реагирует на скручивающие воздействия. Обычно простые
математические модели вращательного движения могут быть раз-
работаны на основании гиромеханики, которая принесла большое
количество интересных изобретений, среди которых такие, как ак-
тивные демпферы нутаций, целевые управляющие системы тел вра-
щения, трансляционные управляющие системы тел вращения, прос-
тые датчики колебаний.
1.10.	ИЗОБРАЖЕНИЕ СИСТЕМЫ В ФОРМЕ ВЕКТОРА СОСТОЯНИЯ
Линейные динамические системы n-го порядка описываются ли-
нейными дифференциальными уравнениями n-го порядка, которые
могут быть преобразованы в систему п линейных дифференциаль-
ных уравнений первого порядка:
xl W = аПх1 + #12*2 + • • • + а1пХп + ^11^1 + ^12^2 + • • • +
х2^) = ^21Х1~\~а22Х2-[~ •••~\~а2пХп~\~	^22и2~\~ ••• + ^2mUm)	( 1 • 1 16)
хп (^) = ^п!х1 “4“ &п2х2 + • • • “И ^ппХп “4“	“4“ ^п2^2 Н” • ‘ • “4" ^птпУ'т'
п функций в этой системе дифференциальных уравнений являются
функциями, определяющими состояние системы. Они могут быть
переписаны в матричной форме
(1.И7)
* «Simply Mechanized Attitude Control for Spinning Vehicles». G. W. Le
Compte and J. G. Bland. Journal of Spacecraft and Rockets. Nov.—Dec, 1964.
60
Обозначая входной вектор как
Можно видеть, что здесь обнаруживается аналогия между полу-
ченным результатом и однопараметрическим случаем, когда еди-
ничный выход выражается через единичный вход с помощью пере-
даточной функции. Развивая эту аналогию, изменим обозначения
дифференциальных уравнений /г-го порядка через обозначения од-
нопараметрического случая, используя для этого символику п-мер-
ных векторов состояния, которые приведут к системе алгебраичес-
ких уравнений связи между входом и выходом системы
У1 = cl1 “Г ^12х2 + • • • 4~ С1пХп 4" ^114" d 12^2 4" • • • +
У2 = C2lx 1 4" с22х2 4* •' • 4" с2пхп 4" ^21^1 4" ^22и2 4~ • • • 4" d2mUm>	( 1 • 120)
Ук = CklXl 4* ck2x2 4" ♦ • • 4" cknxn 4" dkxux 4- dk2U2 +... + dkmUm.
Как (1.119), так и (1.121) могут быть записаны в более простой
векторной форме, где векторы выделяются жирным шрифтом:
X = AX4BU;	(1. 122)
Y = CX + DU.	(1. 123)
Обычно нет прямого соответствия между векторами состояния
системы векторных уравнений и функциями на входе и выходе.
Если матрица D равна нулю, система уравнений может быть упро-
щена:
X = AX + BU;	(1. 124)
Y = CX.	(1.125)
Эта система уравнений может иметь векторно-матричный вид
или может быть представлена в форме записи одной переменной
61
состояния системы. А — обычно называют матрицей системы, В —
матрицей входа, С — матрицей выхода. Этот тип математического
описания имеет общий характер и прост по форме. Теоретическое
значение такой формы записи подчеркивает общность преобразо-
ваний в линейных системах. Многие теоремы n-размерного вектор-
ного пространства посвящены отождествлению значительного
количества свойств динамических процессов. Например, идея п-раз-
мерного векторного пространства может быть использована в сис-
темах управления, в частности, при проектировании оптимальных
систем управления путем сведения к максимуму векторно-скаляр-
ного произведения, представляющего выходной вектор регулируе-
мой системы при заданном векторе входного управляющего сигна-
ла. Современные методы фильтрации также основаны на миними-
зации скалярного произведения, представляющего выходной вектор
фильтра при заданном векторе шума на входе. В некоторых сис-
темах оптимального управления с фильтрами стараются объеди-
нить оба метода.
Несмотря на то, что методы решения линейных дифференциаль-
ных уравнений хорошо изучены, использование векторно-матрич-
ной записи имеет большое практическое значение. Она не может
быть непосредственно использована для решения линейного диффе-
ренциального уравнения n-го порядка. Однако векторно-матричный
метод дает решение системы п линейных уравнений первого поряд-
ка, которое вместе с тем идентично решению дифференциального
уравнения системы n-го порядка.
Хотя векторно-матричные выражения для линейных систем не
устранены из области математического моделирования, их прони-
кновение в эту область не получило большого размаха, так как бо-
лее полное представление о характеристиках и свойствах систем
создали аналитические выражения, которые приводятся к подроб-
ным структурным схемам. Именно это является решающим факто-
ром при синтезе эффективных комплексных систем.
Уравнения состояния (1.124) и (1.125) стационарных линейных
систем можно решать либо методами преобразования, либо приме-
нением интеграла свертки.
Применив преобразование Лапласа к (1.124), найдем
sX(s)-X(O+)=AX(s)+BU(s).	(1. 126)
Таким образом,
X(s)=(sI-AHX(O+)+(sl-AHBU(s).	(1. 127)
Как видно из рис. 1.13, это выражение может быть сведено к
структурной схеме. Применяя либо метод приведения к структур-
ной схеме, либо решая уравнение состояния системы при помощи
(1.124), можно записать
t
Х(/)=Ф(/)Х(0+)+ Ca>(/-T)BU(T)rfT, (1. 128)
62
Исходные усло-
вия системы
Рис. 1.13. Векторно-матричная структурная схема линейных стационарных про-
цессов
где переходная матрица определяется следующим соотношением:
Ф=£_,($1 —А)-1.	(1.129)
Решением уравнения состояния (1.124) с использованием интег-
рала свертки будет
Х = ехр[А(/-/0)]Х(/0) +jexp[A(/--t)]BU(t)4/T,	(1.130)
где экспонента матрицы определяется как
ехр[А(/)]=1+А/+^-+...	(1.131)
Первый из этих двух методов более пригоден при анализе устой-
чивости систем, в то время как использование обратных матриц,
включающих обратное преобразование Лапласа матрицы переда-
точной функции, представляет собой реакцию, на импульсное воз-
действие системы и не может быть осуществлено с помощью вы-
числительной машины.
Последний из методов более применим при использовании чис-
ленных методов, когда матрицы преобразования раскладываются
в бесконечные матричные ряды. Для различных физических систем
эти ряды обычно сходятся. Интегралы свертки при исследованиях
применяются более охотно, несмотря на то, что вычисление переход-
ных матриц с конечным числом элементов усложняется необходи-
мостью вычисления матриц п2 порядка бесконечного ряда, где п—
количество векторов состояния в задаче, что в лучшем случае тру-
доемко.
При рассмотрении линейных стационарных систем уравнения
записываются либо с помощью фазовых переменных, либо в форме
Жордано. Изображение передаточной функции через фазовую пе-
ременную имеет вид
y(s)	B(CfeSft~1 + C»-lSft~2+ ... +C2S + C1)	,, .ops
и (s)	s" + ansn~l + an—\sn~2 4- ... 4- a2s + ax
63
и
Это может быть представлено структурной схемой на рис. 1.14.
Структурная схема той же системы, записанная в нормальной
форме Жордана, представлена на рис. 1.15. Запись в нормальной
форме Жордана можно получить из (1.132)
У _	B(cas*-1 + cft-is*~2+ ... +c2s + ci) Z1
путем преобразования знаменателя (1.132), где Xi — полюс пере-
даточной функции.
Производя разложение в ряд элементарных дробей,
J/ d\ ।	с?2	।	।	। dn
и s—Xi s—Хг s—Хз	s—Х„
Таким образом,
_L=dl-^)_ + d.2^+d3^
и	" /“ч	"
получим
(1. 136)
где
и (s) и ($) и (s)
—£L_=_J— ПрИ /— 1, 2,..., п.
u(s)	S—
zn(s)
п u(s) ’
(1.137)
(1. 138)
64
Рис. 1.15. Структурная схема сис-
темы n-го порядка в нормальной
форме Жордана
Тогда
y=dxzx-\-d2z2 + ... -\-dnzn.
(1. 139)
Во временной области имеем
—и, при /=1, 2,..., /г;	(1.140)
y = ^idizi.	(1-141)
И в векторно-матричной форме
Z=XZ+r«;	(1.142)
#=CZ,	(1. 143)
где
(1. 144)
В матричной терминологии лямбды, фигурирующие в нормаль-
ной записи Жордана, являются корнями характеристического урав-
нения матрицы А, которые (опять же) являются полюсами переда-
точной функции. Так как соответственное значение матрицы X ин-
вариантно к любым линейным преобразованиям, существуют ли-
нейные методы преобразования для численной оценки лямбды в
выражении Жордана.
Системы матричных уравнений при использовании в моделях
систем должны быть соподчинены с преобразованными матрицами
состояний.
Решение линейных нестационарных систем [А, В и С в (1.124)
и (1.125) нестационарны] в векторно-матричной форме задается
как
t
Х=Ф(/,/0)Х(/0)+(Ф(Лт)В(т)и(т)</т;	(1. 145)
*0
Y=C(/)X(/),	(1.146)
3	493
65
где переходная матрица принимает вид
Ф(/, /0)=ехр
(1.147)
Выражение (1.145) является решением (1.124), если А, В и U
нестационарны, что можно доказать подстановкой.
И, наконец, решение линейных векторно-матричных дифферен-
циальных уравнений возможно методом их подбора.
Обсуждаемые в этой книге методы фокусируются на рассмот-
рении матрицы перехода от одного решения к другому. Переход-
ные матрицы обладают достаточно удобным свойством, по которо-
му переход, осуществляемый через и этапов с помощью одной мат-
рицы, равен произведению п матриц на интервалах промежуточ-
ных переходов:
Ф(/2, /0)=Ф(/2, /ОФ^, /0).	(1.148)
Это свойство справедливо как для стационарных, так и для не-
стационарных линейных систем. Другим важным свойством пере-
ходных матриц является свойство «предыдущей позиции» и обра-
щение с помощью переходной матрицы в «обратную позицию»:
ф-Ц^^-Ф^).	(1.149)
Во всех представленных случаях применялась переходная мат-
рица для решения дифференциальных уравнений.
Далее мы познакомимся еще с одним методом интегрирования
дифференциальных уравнений вектора состояния.
1.11.	НЕЛИНЕЙНЫЕ СИСТЕМЫ
Нелинейными системами являются все системы, не являющи-
еся линейными.
Моделирование — это способ, обычно применяемый при исследо-
вании динамики нелинейных систем, если нет общего метода их
решения и анализа. В этой книге нелинейные системы рассматри-
ваются для полноты изложения, а моделирование их непрерывных
процессов обсуждается крайне сжато.
В моделировании встречаются два простых нелинейных процес-
са с жесткой нелинейностью и гладкой (гибкой) нелинейностью.
Процессы с гибкой нелинейностью описываются дифференциальны-
ми уравнениями. Системы с жесткой нелинейностью характеризу-
ются возможностью описания (по крайней мере ее части) разными
уравнениями при разных условиях. Классическим примером гибкой
нелинейности системы являются колеблющийся маятник с больши-
ми углами отклонения и осциллятор Ван-дер-Поля.
Нелинейные уравнения четвертого порядка встречаются при
описании вращательного движения среди нелинейных уравнений,
связанных с процессами модуляции и демодуляции в высокочастот-
ных передатчиках и приемниках, при проектировании нелинейных
фильтров в современных системах управления, а также в уравнени-
66
ях движения спутников.
Примеры гибких нелиней-
ных элементов даны на рис.
1.16, а примеры нелинейных
элементов, включающих реле,
зоны нечувствительности и опе-
раторы абсолютного значения,
представлены на рис. 1.17.
Структурные схемы как для
гладких, так и для жестких не-
линейных процессов обладают
наглядностью, особенно при
нахождении аппроксимирую-
щих уравнений при решении
нелинейных процессов в задан-
ном интервале.
Примером упрощения, кото-
рое можно произвести с нели-
нейными системами, является
реле с нелинейной мертвой 30- Рис. 1.16. Примеры элементов с глад-
кой, показанное на рис. 1.17.	кой нелинейной связью
Такие реле характерны для
открытых и закрытых управляющих систем. Если отклонения при
х=0 малы по сравнению с зоной нечувствительности, динамика
процесса не зависит от у. С другой стороны, если отклонения х ле-
жат далеко за пределами зоны нечувствительности, вправо, дина-
мика системы должна находиться под воздействием +у. Если рас-
смотреть отклонения х, находящиеся на равном расстоянии справа
или слева от зоны нечувствительности при достаточно высокой
частоте по сравнению с частотой реакции системы, ступенчатая не-
линейность может быть заменена наклонной прямой (аппроксима-
цией), угловой коэффициент наклона которой равняется уровню
выхода, разделенному на половину размера зоны нечувствитель-
ности.
Подобные аппроксимации могут быть осуществлены и для дру-
гих систем с нелинейными жесткими связями, а «качественный»
линейный анализ позволяет предвидеть характеристики таких не-
линейных систем.
Системы с гибкими нелинейными связями всегда могут быть
выражены системой дифференциальных уравнений первого поряд-
ка в виде
X (Z)=f (X, U,/),	(1.150)
где X—n-мерный вектор выхода; U—л-мерный вектор входа; t —
независимая переменная.
Если t содержится в неявном виде, то (1.150) сводится к виду
X(/)=f(X, U).	(1.151)
67
3*
Структурная схема {1ёзвани^
Уравнение
Рис. 1.17. Примеры элементов с жесткой нелинейной связью
При U(0=0 система будет автономной, и ее уравнение прини-
мает вид
Х(/)=/(Х(/)).	(1.152)
Хотя нелинейные дифференциальные уравнения не имеют общих
методов своего решения в законченной форме, нелинейные вектор-
но-матричные уравнения решаются численно на вычислительных
машинах численным интегрированием.
Структурные схемы для нелинейных систем с гладкими связями
строятся на базе фазовой переменной следующим образом:
1)	по структуре нелинейного дифференциального уравнения
системы;
2)	в соответствии с порядком решения уравнения относительно
высших производных;
3)	применением блоков кратного интегрирования для определен
ния выходного сигнала системы;
4)	введением в контур обратной связи нелинейного оператора.
После построения структурной схемы системы можно осущест-
вить с ее помощью решение либо линейных, либо нелинейных урав-
нений, производя поиск решения в виде рядов по следующим эта-
пам.
Этап 1. Подготовка структурной схемы фазовой переменной для
непрерывного процесса.
68
Рис. 1.18. Структурная схема в фор-
ме фазовой переменной y+ky2—f
Рис. 1.19. Структурная схема фазо-
вой переменной y+kty=f(t)
Этап 2. Создание сходящихся
для решения дифференциального
сигнала и последовательным его преобразованием с помощью пере-
даточной функции в последующий вид входного сигнала или на-
чальных условий.
Пример 1.
Этап 1. Нелинейное дифференциальное уравнение
y-ky*=f(t),
аппроксимирующих многочленов
уравнения упрощением входного
для которого примем
у(0)=0, y(Q)=Y,
может быть представлено структурной схемой фазовой переменной,
показанной на рис. 1.18.
Этап 2. На основании структурной схемы имеем
у0=У-,
t/i = r+J(-Ar2)rf/=r-)fer2/=r(l-kYt);
О
y2=Y Г1-Ш-|-Л2Г2^2 —y-YI;
Пример 2.
Этап 1. Нестационарное линейное дифференциальное уравнение
у -\-kty
для которого примем
£(0)=0, jf(O)=K, /(/)=0,
представлено структурной схемой фазовой переменной, как показа
но на рис. 1.19.
Этап 2. Из структурной схемы видно, что
Уо=Г;
kYV
2

2
09
kY&.&Yfi „/. kt , gift
У^ = У l + (
2"«1
= Ye~ktt/2.
Пример 3.
Этап 1. Уравнение
(l-^2)i/-2^ + «(«+!)«/=/(/),
где £(0)=0, y(Q)=Y, y^)=Y, f(t)=Q,
может быть представлено структурной схемой фазовой переменной,
как показано на рис. 1.20.
Заметим, что
о
/
1 —Z2
можно схематизировать как
Этап 2. Исследуя структурную схему рис. 1.21, можно записать
у= y-^n(n+V)Ydt2+... +
+ f Ydt— fjj Yn(n+\)dt* + ^Ytdt2-\-...
Таким образом,
У=ГГ1 - „(«+!)-£-+.. .1+Кр-(«- 1)(я + 2)4+...
L	J L	и»
Сравнивая примеры 1 и 2, можно сделать следующие заклю-
чения.
1. Системы с гладкой нелинейностью приводят к более слож-
ным выражениям для многочленов, чем у линейных. В этом смысле
нелинейные системы более сложны, чем линейные того же порядка.
2. В отличие от нелинейных уравнений решения в виде аппрок-
симирующих рядов в линейных системах могут быть получены не-
посредственно из структурной схемы, исключая необходимость при-
менения промежуточных многочисленных полиномов.
Первое выражение ряда для нелинейной системы — это началь-
ное условие, являющееся входным сигналом структур ой схемы.
Рис. 1.20. Структурная схема решения уравнения (1—t2)y—2ty+n(n+l)y=f(t)
через фазовую переменную
Вторым выражением ряда является начальное условие, которое
пришло к выходу структурной схемы после первого прохождения
по цепи обратной связи, подвергаясь воздействию соответствующих
математических операторов.
Подобным же образом получают п-е выражение в бесконечном
ряде прохождением начальных условий по контуру п—1 до того,
как оно прибавлено к решению.
Такое упрощение применяется также и при решении линейных
систем независимо от того, являются ли они стационарными или
нет.
В случае линейного дифференциального уравнения входной сиг-
нал проходит по прямой части контура, преобразовываясь в вы-
ходной. Второе выражение проходит от одной замкнутой цепи к
другой через оператор умножения на п(п+1), и затем через два
оператора интегрирования.
Выражения более высокого порядка получают таким же спосо-
бом — последовательным прохождением по замкнутым контурам.
Рис. 1.21. Упрощенная структурная схема решения уравнения (1—-2ty+
+n(n+l)y=f(t) через фазовую переменную
71
1.	Y проходит непосредственно к выходу.
2.	Y проходит по внешнему контуру.
3.	Y проходит по внутреннему контуру через операцию умноже-
ния на 2t, затем проходит к выходу через два оператора интегри-
рования.
Необходимо отметить, что для составления сходящихся рядов
достаточно сравнительно небольшой практики.
Этот способ эстетически более притягателен, чем педантичный
классический метод получения решений ординарных линейных
дифференциальных уравнений с помощью рядов. Он был разрабо-
тан автором для моделирования контрольных случаев и для иссле-
дования условий, при которых реакция системы приобретает моно-
тонно возрастающий ряд, т. е. условия, при которых коэффициенты
в решении дифференциальных уравнений с помощью ряда не содер-
жат знакопеременных коэффициентов. Оказывается, что с точки
зрения ряда одним из необходимых условий устойчивости является
то, что он должен быть знакопеременным. Конечно, это условие не
является достаточным для определения устойчивости, системы.
Только что описанный метод математически эквивалентен мето-
ду Пикарда для решения ординарных дифференциальных уравне-
ний, независимо от того, линейны они или нелинейны, стационарны
или нестационарны, автономны или неавтономны.
Если вы помните, по методу Пикарда производится не только
решение ординарных дифференциальных уравнений с помощью ря-
дов, но он является основой для теорем, которые гарантируют
существование решения дифференциального уравнения, являюще-
гося единственным, и что бесконечные ряды сходятся на всех ин-
тервалах, где существует решение дифференциального уравнения.
Другим методом решения нелинейных дифференциальных урав-
нений первого порядка, которые можно встретить в виде включений
в системы, являются решения в форме Г(х, у) =С. Тогда решением
нелинейного дифференциального уравнения первого порядка будет
-^-= /(х, у)=	,	(1. 153)
dx	Q(x,y)
так что
Pdx = Qdy.	(1. 154)
Тогда
+	(1.155)
если
-^-=Р(х, у) и -?f-=Q(x,y)	(1.156)
дх	ду
и, кроме того,
— = -^-;	(1.157)
72
это следует из того, что между этими двумя условиями имеет ме-
сто
&F _ &>Р
дудх дхду
Тогда полагают, что (1.153) становится точным решением, а реше-
ние F(x, у)— С может быть получено из (1.156). Так, например, из
первого уравнения (1.156) получим
F{x, y)=J Р(х, y)dx4-R(y),
где R(y) — произвольная функция от у.
Используя второе уравнение (1.156), имеем
^^=Q(-v, у) Р(х,y)dx.
Таким образом,
(1.158)
(1. 159)
(1.160)
(1.161)
Если (1.153) не обладает точным решением, функция h(x, у) из
условия
d(hP)d(hQ)
ду дх
(1. 162)
может применяться как интегрирующий множитель.
Другим методом, который не содержит в себе прямого решения
нелинейного дифференциального уравнения, является метод преоб-
разования.
Этот метод позволяет с помощью специальной преобразующей
функции зависимой переменной трансформировать нелинейное
уравнение в линейное. Примером может служить уравнение Бер-
нулли
ох
(1. 163)
которое преобразуется в линейное дифференциальное уравнение
.^£.=(1 — n)/(x)«+g(x)(l-n)	(1.164)
при помощи преобразующего соотношения г=у'~п. Интегрируя
один раз, мы решаем уравнение Бернулли.
Уравнение Риккати в обобщенной форме
^-\-а(х)у-\-Ь(х)у2=с{у)	(1.165)
может быть преобразовано в линейное дифференциальное уравне-
ние второго порядка использованием преобразующего соотношения
dz ( \ \
dx \b(x) г) *
(1. 166)
73
И наоборот, однородное линейное дифференциальное уравнение
второго порядка
а'(х)-^—b' (х)	+ с' (х) z — 0	(1.167)
может быть преобразовано в уравнение Риккати подстановкой
dz)dx=d(x)yz. Мы будем встречаться с уравнением Риккати мно-
го раз, общим решением которого будет выражение
A(x) + kB(x)_	л 168)
у C(x) + kD(x)
где k — константа.
Глава 2 МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ДИСКРЕТНЫХ ПРОЦЕССОВ
При цифровом моделировании мы имеем дело с непрерывными
функциями [принадлежащими действительным значениям *(/)]>
дискретными функциями [соответствующими кратным целым зна-
чениям аргумента х(пТ)=хп] и эквивалентными соотношениями
между ними. Это объясняется тем, что на практике представляют
интерес непрерывные системы, движение которых описывается не-
прерывными функциями, дискретные системы, чье движение опи-
сывается дискретными функциями, принимающими последователь-
ные числовые значения, и системы, представляющие сочетание двух
предыдущих, динамика которых описывается эквивалентными соот-
ношениями. Кроме того, представляют интерес рекуррентные соот-
ношения, которые применяются при описании как дискретных, так
.и непрерывных процессов. Рекуррентные соотношения позволяют
упрощать вычисление последовательности чисел (или последова-
тельности значений функций), где значение каждого нового числа
(или функции) вычисляется на базе текущего и предыдущего зна-
чения чисел (или функции).
Разностные уравнения, рекуррентные соотношения
и их определения
Прежде всего определим разностное уравнение и рекуррентное
соотношение. Разностное уравнение — это средство описания дина-
мики систем. Оно имеет решение, описываемое дискретными функ-
циями, областью решения которых являются действительные числа.
Рекуррентные формулы позволяют определить, например, 100-е
число на основании 99-го и предыдущих чисел. Обычно в литерату-
ре применяют запись, по которой трудно выявить отличие решения
разностного уравнения от рекуррентной формулы.
74
Например, уравнение
X(t)=Xoe-<f+T)
является решением непрерывного процесса, описываемого уравне-
нием первого порядка (Х+Х=0), содержащего «смещение во вре-
мени» при начальном условии Xq. Для дискретной функции решение
во времени, представляемое в форме (пТ+уТ), имеет вид
Ха=Хое-^т.
Эта функция приводится к рекуррентной на основании выражений
Хп-е-гЛ’л_1 = 0; Х(О)=е-тгХо.
В рекуррентной форме мы имеем зависимость n-го члена {Хп} от
ранее вычисленного числа {Хп-i}. Следовательно, полученное урав-
нение является рекуррентным уравнением. Таким образом, рекур-
рентное уравнение, связывающее друг с другом во времени после-
довательности чисел в соответствии с выражением Хп — Х(пТ+уТ),
является,также разностным уравнением.
Если у = 0, то числовая последовательность может быть отнесе-
на как к ее n-му значению, так и к n-му интервалу времени пТ.
Если уУ=0 и индекс п означает порядковый номер вычислений,
осуществленных с помощью рекуррентного соотношения, то после-
довательность чисел {Хп} означает состояние системы к моменту
времени t= (п+у)Т.
Ряд дифференциальных уравнений, содержащих фазовый сдвиг,
рассмотрен в следующих главах; здесь же нам необходимо отме-
тить это обстоятельство, чтобы подчеркнуть различие между рекур-
рентными и разностными уравнениями.
В данной книге рекуррентные формулы записаны с одинаковы-
ми знаками и не включают ошибок вычисления, выходящих за рам-
ки ошибок округления чисел. Рекуррентные формулы получаются
при осуществлении численного дифференцирования, когда последо-
вательность Хп аппроксимируется X(t) |пГ. Остановимся подробнее
на проблеме аппроксимации.
Рекуррентная формула
Х^е-тХ^
может быть приведена к виду
(/)—Хо e~z при t = nT
или
Х’2(/)=Лг0е_<'+‘*) при t = nT, sj== const,
или
X’3(Z)=(X'o+e2)е~' ПРИ i = nT, s2=const,
или, наконец,
^4(^ = (X'04-®2)e_(/+‘,) при i--=nT, Sj и е2—const.
75
Предполагаем, что ei и 82 — неизвестные ошибки, возникающие
от неточного представления зависимости от времени цли Хо- Это
могут быть ошибки, возникающие вследствие отбрасывания членов
ряда, ошибки операторов при управлении вычислительными опера-
циями, ошибки при небрежности введения данных и длительном
хранении в памяти, ошибки программирования.
Другим источником ошибки моделирования (и цифрового регу-
лирования) является процесс вычисления системы с обратным
контуром, когда вычисляется прямой контур до вычисления обрат-
ного. Это приводит к запаздыванию при расчете замкнутых конту-
ров. Это временное запаздывание не может быть вычислено учетом
движения сигнала по непрерывному замкнутому контуру.
Таким образом, источники ошибок для рекуррентных и непре-
рывных форм моделируемых или контролируемых систем анало-
гичны.
Трудности в понимании разностного уравнения в форме
возникают тогда, когда последовательность Хп сравнивается с
X (/) | пт и они не согласуются на некоторую величину, результат
чего может быть истолкован следующим образом:
Классическая точки зрения
1. Хп обладает отклонением из-за
ошибки в Хп-i (какие бы причи-
ны ее не вызвали)
' 1. Хп обладает ошибкой из-за ошибки в
Xn-i (то же, что и в классическом
толковании)
Современная точка 2. Хп обладает временным смещением от-
зрения	носительно X (/)|л7-
3. Хп обладает ошибкой как из-за оши-
бок в Хп_ъ так и из-за ошибок во
времени.
Ясно, что, если задано уравнение
хп=^хп_г
и вычисленное значение не совпадает с контрольным значением,
то ошибка может объясняться как ошибкой согласования во вре-
мени, так и ошибкой оценочной функции или сочетанием обоих.
Далее мы увидим, что ошибка оценочной функции (зависящая
от отбрасывания членов ряда и округления) может быть объясне-
на и как ошибка согласования.
Для уменьшения ошибки при отбрасывании членов обычно при-
нимают более мелкие шаги, так как ошибка меняется как степень
величины шага и при е'—АТ’3 означает, что для шага (АТ/2)
( дг \3_«(дг)3
Д 2 ) ~ 8
76
Проще уменьшить ошибки за счет согласования, изменяя время
выхода на печатное устройство.
Первый способ является достаточно дорогим способом умень-
шения ошибки, так как необходим больший объем вычислений для
решения данной задачи. Он обладает тем преимуществом, что все
переменные состояния могут выводиться на печать при одном и
том же значении времени *.
Преимуществом второго способа является то, что вычисления
проводятся более экономично (из-за большего размера шага), но
зато все параметры состояния сравниваются с параметрами не-
прерывной системы при несколько ином времени. В последнем слу-
чае имеется тот очевидный факт, что время не инвариантно при
преобразовании дифференциального уравнения в моделируемое
разностное уравнение.
Это приводит нас к двум видам времени — реальному времени
и времени решения задачи, идея которого будет более подробно
рассмотрена далее в книге.
Уравнения в приращениях и рекуррентные формулы
Типичные примеры уравнений, описывающие дискретные систе-
мы, приведены ниже.
Уравнения в конечных разностях
—+ «/=0;
Ду + Д7 y = °-
Уравнения в приращениях
.Уп+Л^Т-\)уп = 0.
Рекуррентные формулы \^п ^Т^Уп i + //r
\Уп~ АУп— 1 f П'
Нелинейные разностные уравнения уп = А G/n-i)2+fn.
Термин «уравнения в приращениях» часто используется для
описания всех этих уравнений и является результатом того, что он,
возможно, возник из понятия уравнения в конечных разностях.
Простые линейные разностные уравнения могут быть получены
преобразованием линейных дифференциальных уравнений с по-
мощью формул численного интегрирования и написания их в форме
уравнений в приращениях. Нелинейные разностные уравнения мо-
гут быть получены подобным же способом, в результате преобразо-
вания нелинейных дифференциальных уравнений с помощью фор-
мул численного интегрирования и написания их в форме нелиней-
ных дифференциальных уравнений в приращениях.
самом деле, не все они печатаются при одном и том же времени, как
мы уже это видели и встретим далее.
77
Например, если дифференциальное уравнение имеет вид
х —х=0, где хо=О,
и мы используем прямоугольную формулу интерполирования *
ХЛ = Х/|_1
то получим
хл^хЛ_1 + Гхя,
откуда
/ 1 \
хп= ----------------------------Хл_1.
Л I । гр I П I
В том случае, если
х — №=0 при хо=О;
лп = x„_iУхд; Тхп— хп-^-хп_1 = 0,
найдем
-----—’|/1-47’х._1.
2Т 2Т
Заметим, что, так как мы рассматриваем эти уравнения как ре-
куррентные, знак приближения записывается вместо знака ра-
венства.
Задача для студентов
Квадратное уравнение 7хп2—xn+xn-i=0	имеет решение
± /1-47'х„_1.
Почему второе выражение выбрано отрицательным?
2.1. РАЗНОСТНЫЕ УРАВНЕНИЯ
Разностные уравнения возникают, когда динамика дискретных
процессов выражается в форме уравнений в конечных разностях,
таких, как
bmy=f(yn, Ьуп, &уп,...,Ьт-1уя, п).
Так как
=Уп ~ Уя-ъ ^У = tyn ~ ^Уп-i=Уп~ 2Уп-1+У п-2,
вместо разностного уравнения m-го порядка получим
Уп = ё(Уп, Уп-1, Уп-2, Уп-^-->Уп-т>
* Численное интегрирование только аппроксимирует аналитическое интегри-
рование, поэтому в формуле численного интегрирования употребляется знак
«приблизительное равенство».
78
Если f (и поэтому g) и т начальных условий
Уо> Уь Уъ->Ут-1
известны, то определяют единственное решение разностного урав-
нения.
Рассмотрим, например, линейное разностное уравнение второго
порядка
уп — 6уп_1 + 8уп-2=п при go=3, 01 = 2.
Предположим, что коэффициенты в уравнении постоянны и функ-
ция определена только при t=nT, когда n=0, 1, 2,... Это уравнение
мы называем уравнением второго порядка, так как оно содержит
разность значения зависимого переменного в двух соседних интер-
валах. Это уравнение мы можем назвать линейным, так как оно не
содержит степени больше первой или произведений зависимой пе-
ременной.
Классические методы решения линейных разностных уравнений
подобны методам решения линейных дифференциальных уравне»
ний. Решение состоит из двух частей — дополнительного и частно-
го. Общее решение является суммой обоих решений.
Дополнительное решение — это общее решение однородного
уравнения при равенстве нулю силовой функции:
Ул-б0я_1 + 80я_2=О.
Это уравнение решается способом, аналогичным тому, который
применяется при решении дифференциальных уравнений, а именно,
методом подбора решения, допустим в виде ап.
Тогда, если
уп—Сап,
где а и С — константы, мы найдем при подстановке в разностное
уравнение, что
(а2 —6а-|-8) = 0.
Это — характеристическое уравнение, которое имеет корни
at = 2; я2=4.
Полная запись дополнительного решения имеет вид
0Я =	“J” ^2^2 = Ct2n -|- С24п.
Используя начальные условия, найдем, что, если п=0, то
3=С[ -|-С2
и при п= 1
2=2Ci-|-4C2.
Решая эту систему совместных уравнений, найдем С] = 5 и С2=2.
Таким образом,
0Я=5(2)«-2(4Г.
79
Чаше встречаются линейные разностные уравнения в виде
ао (Уп~\~а1(. пТ) уя_х -|-... 4- am (пТ) ya_m—f (пТ).
Мы можем его переписать в форме
а^Уп+z~lyn 4- a2z~2yn 4-... 4- amz~myn= f(nT),
где z°=l и z~m является оператором смещения (т. е. г~туп=Уп-т)-
Тогда
(«о«° 4- axz~l 4-... 4- amz~m) уп= f (пТ);
L(z)yn=fn.
Если fn=0, для всех п удобно искать решение в виде
у=Сгп.
Подставляя его в разностное уравнение, получим характеристи-
ческое уравнение
(аог« 4- ах г"~14-... + атгп~т)=0.
Если а, постоянны, — этот многочлен имеет т корней. Если кор-
ни действительные и имеют различное значение, уравнение прини-
мает вид
i/„=C1r?+C2r2n + - + Cm<-".
Если а,- — действительные числа, а некоторые корни комплекс-
ные, то решение принимает вид
Уп ^Г1(а14-/р1)п4-Г2|а2'— Z₽2)" + --- (декартовы координаты);
yn—Qn{Cx cosn04-C2 sin «0)4-.•• (полярные координаты).
Если корни действительные и равные, то решение примет вид
Уп=(Ci 4- с2« 4- •  • 4- С*/?-1) г".
Если /п¥=0, то возникает задача нахождения частного решения
разностного уравнения. Найденное частное решение складывается
с дополнительным, образуя общее или полное решение разностного
уравнения:
общее Уп — частное уп+дополнительное уп-
2.2. ЧАСТНОЕ РЕШЕНИЕ
Частное решение неоднородного уравнения может быть получено
методом, аналогичным методу получения частного решения неод-
нородного дифференциального уравнения. В частности, в некото-
рых случаях, подобных рассмотренному в разд. 1.5, может быть ис-
пользован метод неопределенных коэффициентов.
Как было указано раньше, метод неопределенных коэффициен-
тов применяется для нахождения частных решений, когда силовая
функция F(k) может быть выражена через часто встречающиеся
соотношения. В этом случае мы предугадываем вид частного ре-
шения, которое должно быть связано с видом силовой функции.
Метод неопределенных коэффициентов прост в применении и
80
приводит к простым результатам. Для линейных дифференциаль-
ных уравнений с постоянными коэффициентами, чья возмущающая
или возбуждающая функция составлена из суммы или произведе-
ния возмущающих функций, сведенных в табл. 2.1, где частные ре-
шения являются суммой или произведением функций, представлен-
ных в правой колонке. Если это решение подставляется в разност-
ное уравнение, то коэффициенты в правой и левой частях прирав-
ниваются для определения коэффициентов частного решения. Этот
метод содержит несложные преобразования. Если возмущающая
функция содержит член, имеющийся и в дополнительном решении,
то его учитывают при формировании общего решения, а при ее
представлении в виде степенного ряда должна быть проведена
оценка частного решения в виде степенного ряда такого порядка
относительно k, который позволит получить достаточно точное ре*
шение.
Таблица 2.1
Применение метода неопределенных коэффициентов в частных решениях
линейных разностных уравнений
Виды возмущающих функций	Виды частных решений
k	k
а	Aa
Многочлен Р (k) порядка m	Aokm 4- A]km 1 4- ... 4- Am
sin (ak)	A cos (ak) 4- В sin (ak)
cos{ak)	A cos (ak) 4- В sin (ak)
акР (k)	ak (AQkm 4- A^-1 4- ... 4- Am)
ак sin (bk)	ак [Л cos (bk) 4- В sin (££)]
ak cos (bk)	ак [Л ccs (bk) 4- В sin (£&)]
Пример.
Решим уравнение
Хп^ТХп^ = п\
Однородное уравнение имеет вид
хл+тхл_1=о.
Дополнительное решение получим в следующем порядке.
Этап 1. Допустим, что решение существует в виде Хд(п)=ап.
Подставляя его в однородное уравнение, имеем
а«(1+Га-1)=0.
Таким образом,
а=-Т
и	Хя(п)=С( — Т)п.
81
Этап 2. В соответствии с табл. 2.1 допустим, что Хч(п) =АгП2+
+Д1П+Д0, в то время как возмущающая функция имеет вид и2.
При подстановке Хч (п) получим
Д2/124~ А]П“I-До4~ ТАг (л — 1 )24* Т'А\ (п — 1)И-ТAq^^h2
или
Д2/124” А±п 4- Др -|- 71 АгП2 — 2Т АгП 4“ 71 Аг “I- Т А\П — Т А1 4~ Т Др — zz2;
(1 + т) А2п2 4- (А! - 2ГД2 + ТА i) п + (До+ТА2 - ТA , + Т До) = zz2
Так как левая часть равна правой, если Хч — решение разност-
ного уравнения, для любых значений п, приравнивая коэффициен-
ты при равных его степенях, получим систему для нахождения
трех неопределенных значений Ai, Аг, Аз-
(14-7’)Д2=1;	(2.1)
Д1-27'Д2+ТД1 = 0;	(2.2)
Др 4~ ТДр 4* ТД2 — ТА 1 = 0.
Из уравнения (2.1)
А — 2ТА2 2Т
1 1+7	(1 +Т)2 *
Из уравнения (2.2)
Г 1	_ 2Т 1
4 = Г(Л2-Л!) = [1 + 7 ~ (1 + n2J .
' 0	1 + 7	14-г
Г 27 1
Г 1—-------
А _ I 1 + 7 J Т(\ — Т)
°	(1 + 7)2	(1 + Г)3 *
Таким образом,
х п2 I 2Г" I п1-?-)
4	1 + 7 1 (1 + 7)2 1 (1 +Т)3
2Сп-2Сд(/г)4-^ч(/г) = С1(-Г)«4
п2 . 2Тп . 7 (1 — Г)
1 + 7	(1 + TyJ' (1 + Г)3
Изображение дискретной системы
с помощью переменной состояния
Как и дифференциальные уравнения, разностные уравнения мо-
гут быть записаны в виде вектора состояния. Это обнаруживается
при переходе от разностного уравнения n-го порядка к п разност-
ным уравнениям первого порядка. Решение каждого отдельного
дифференциального уравнения представляет собой вектор. Сово-
82
купность п векторов называется вектором состояния. Так как век-
тор начальных условий и вектор возмущающих функций сказыва-
ются на векторах решений разностных уравнений первого порядка,
мы говорим, что состояние на входе претерпевает изменения. Пере-
ход от состояния к состоянию осуществляется с помощью матрицы
перехода.
Общая система векторно-матричных уравнений имеет вид
Y(/i4-l)=B(n)Y(n) + X(n),
где {X (л)} — известная последовательность векторов.
Если заданы начальные условия ¥0, то общее решение примет
вид
п
Y(«)=P„oYo + 2P„/X/_1,
/-1
где	1ВЛ—2 ••• By
и
РЛЛ=«.
Если	8^ = 8^=... =В;=В,
то общее решение примет вид
Y(n)=B'iY(0)4-2B'I_yx;-i-	(2.3)
Пример. Рассмотрим однопараметрическое дифференциальное
уравнение первого порядка т -\-y = e~kt при т и k — положи-
тельных постоянных, 1/(0) = 1. Это уравнение может быть аппрок-
симировано разностным уравнением
т (у„ — уп_х) + Д7уп_х = ЬТ е~*лАГ при ДТ — положительной констан-
те;
I ДУ	ДУ  Ъп ДТ
Уп-Уп-x-V — Уп-1=—е кпкТ',
X	X
уп — (\ ——\уп-1 = ^~- е-*л4Г (стандартная форма).
\ X ]	X
Используя уравнение (2.3), запишем решение в следующем
виде:
п
9.=(1 - f у й+у (1 - ^у-' m е--
\ X / А» \ X /	\ X /
Таким образом,
ДУ \	. гду
У1= 1---— Уо+—
\ X /	X
ДУ \ / ДУ \
дт \2
т /
83
Так же как и при решении дифференциальных уравнений, кон-
станты в решении разностных уравнений определяются на основа-
нии известных условий. Нет необходимости за известные прини-
мать начальные условия задачи, это могут быть любые условия,
где последовательность значений решения {Хп} известна.
Другим способом решения линейных разностных уравнений с
постоянными коэффициентами является метод /-преобразований.
Сделаем краткий обзор Z-преобра юваний и их основных
свойств.
2.3. / ПРЕОБРАЗОВАНИЕ
/-преобразование возникло из необходимости определения вы-
борки дискретных значений сигнала в форме последовательности
чисел, которую используют инженеры связи и управления для ис-
следования управления выборкой данных и в телеметрических сис-
темах.
Инженеры столкнулись с задачей определения «пульсаций» дан-
ных в выбранной последовательности в частотной области.
Проблема математического анализа в частотной области заклю-
чается в том, чтобы с помощью преобразования Фурье или Лапла-
са получить возможность решать разностные уравнения. Здесь цель
сводится к необходимости решения задач инженерами, занимаю-
щимися управлением, применить преобразование Лапласа и Фурье
для получения последовательности выборок или последовательно-
сти чисел.
Математически принято, если
£/(/)=F(s),
то можно записать
Для решения этой проблемы был в конце концов применен спо-
соб, использующий хорошо известную дельта-функцию, которая:
а) может быть преобразована с помощью операторов Фурье и Лап-
ласа; б) образует последовательность непрерывных хорошо из-
вестных функций, которые образуются модулированием системы
дельта-функциями; в) приводит к преобразующей паре, которая
допускает алгебраические действия в разностных уравнениях, по-
добно тому как преобразования Лапласа приводят к алгебраичес-
ким действиям при решении дифференциальных уравнений.
Кроме того, что более важно, характеристики этой последова-
тельности смодулированных импульсов в частотной области почти
соответствуют характеристикам выборочных данных, так что они
используются в телеметрии и в определенном типе систем связи.
Подход к преобразованиям Лапласа и Фурье в области дискрет-
ных значений функций изображен в табл. 2.2.
Для целых чисел, кратных выбранному периоду Т, существуют
соответствующие значения /(/), которые образуют последователь-
84
ность {/(пТ)}. Хотя эта дискретная функция сама по себе не может
быть преобразована ни с помощью оператора Лапласа, ни операто-
ра Фурье, однако с помощью дельта-функции (которая сама по*
себе непрерывна, везде хорошо определена и может быть преобра-
зована и с помощью оператора Лапласа и Фурье) модулированием
ее значениями функции f(t) может быть определена в выбранный
момент, как показано в колонке.
Таблица 2.2
Последовательность величин, представленная как ряд
промодулированных дельта-функций и ее преобразований
с помощью оператора Лапласа
1	2	3	4	5
	/(0	6(/-т)	/(0 8 0-т)	£{/(/)8(/-т))
0	/(0)	8(0)	/(0)8(0)	/(0)
т	/(/)	8(Z-T)		/ (D esT
2Т	/(27)	8(Z—27)	f(2T)b(t—2T)	/ (27) e~2sr
ЗТ	/(37)	8 (t — 37)	/(37) 8 (/ — 37)	/ (37) e~3sr
пТ	(/(«D)	b(t — пТ) 2 8(t-пТ) 0	f(nT) b’(j — пТ) f (0*=5 / (nt)h(t<—nT) 	0		 Ряд промодулированных имлульсов	/ (пТ) e~nsT 4/(0*) = = 2 / (n7) e~nsT 	0	 	
Каждая строка в колонке 4 является непрерывной функцией,
везде хорошо определенной, чье основание (на интервале под дель-
та-функцией) равно f(nT). Ряд смодулированных импульсов, обра-
зованный суммированием по колонке 4, является непрерывной
функцией, хорошо определенной на всем интервале, которая может
быть преобразована с помощью операторов Лапласа и Фурье. В ко-
лонке 5 показано преобразование с помощью оператора Лапласа
последовательности смодулированных импульсов.
Из табл. 2.2 видно, что последовательность смодулированных
импульсов, преобразованных с помощью оператора Лапласа и ее
обратное преобразование может быть осуществлено с помощью со-
отношения
L (F* (/)) = 2 / («Л e~"sr £ F* (s);
О
00
О
85<
Предположим, z = eJ/; эта пара преобразования Лапласа пере-
водит в форму Z-преобразования, которое записывается как
О
/* (О А 2 / (пТ) 8 (/ - пТ) A Z-1 (F (Z)).
О
В данной книге с целью обзора мы приводим /-преобразование
для некоторых важных функций и операций.
Рассмотрим функцию	Z-преобразование функции f(t)
получается следующим образом:
Z (/) A Z 2 (*Л 8 (* - nT)=(QT) z-°+(T) z-1 + (2Г) Z-2 Н-... +
О
+ (ra7’)z-" + ...-r(z-i + 2z-2 + 3z-3+...+«z-'’+-)=-^^-.
Рассмотрим функцию /(/)=eeZ. Z-преобразование функции
f (t) развивается следующим образом:
Z (eat) = 1 + е.аТ z~' + е2аГ Z-2 + е3аГ z~3 +... =--= г .
v ’ г	т	~	г 1 — earz-i z—er
Z-преобразование единичной ступени U(t) можно получить, исполь-
зуя Z-преобразование экспоненциальной функции, приравнивая а
к нулю.
Z(£7(/)) = limZ(ea')=lim(-г—..
k V а-+0	a-+o\z—Q~at ) Z — 1
/-преобразование функций синуса и косинуса можно получить в
виде
Применяя
Z (еа')|а-Уш.
теорему Эйлера
е^“'= cos'(<o/)+J sin (°Ю>
найдем
т / • t iw	г sin ("О
Z(sin (юл)=----------------1— --------
” гч — 2г cos (<•>?) 4-1
и
Z (COS K))= 2[z-cosK)L_
z2 — 2z COS (co/) + 1
Наиболее часто встречающиеся в книге пары Z-преобразований
собраны в табл. 2.3 (см. Приложение Б для Z-преобразований).
86
Z-преобразования некоторых функций
Таблица 2.3
оо
F(s)	f(O	Z (F (s))—Z (f (t))=F (z)
1	u(t)	z
S		z — 1
1	t	Tz
S2		(Z- 1)2
J		ft	Пг (z+ 1)
$3	2	2{z — 1)3
1	*3	T3z (z^ + 4z + 1)
$4	3-2	6(z-l)<
1		(nyfe+O-V)]’
S	(n—1)1	L z— 1 J
1		z
	-at	^r-oT
$4-0	e	z— e
1		Tz^~aT
(s 4-0)2	t<Tat	(г_е-аГ)2
1	& -at	zT%i~aT	гТ2е~2аГ
(s 4- 0)3	2 e	2(г-е-аГ)2 + (z-e“ar)3
a		z(l-e~ar)
s(s 4-0)	i — e	(z— 1) (z— e~aT)
a	af_(l_e-a<)	Tz _	(1 —e~ar)z
+ a)	a	(z — 1)2 a (z — 1) (z — e-ar)
a	If	2	2	2 _,Д	T2z	(aT—2) Tz	z	z
$3 ($ g)		—— ft— — t 4- т — “6 2 \	a	aft aft	/	(z— I)3 + 2a (z— 1)2 + a2 (z— 1) “ a2 (z_e-a7')
Продолжение табл. £.3
F(s)	/ (0	Z(F (s»=Z(f(t))-F(z)
(О0	Sin Wg/ COS *>p/		z sinr(a)0T)
S2 -|- (Oq s		г2 — 2г cos (“оГ) + 1 z [г — cos («орТ)]
S2 4- g)q		z2 — 2z cos (««оГ) + 1 z sh (apT)
o>0	sh (ш0О	z2 — 2z ch («oqT) + 1 z[z—ch(a>0T)]
S2-- “o		
s	ch («oqO	— 2z ch (&qT) 4- 1
s2 — “0		z	z
b— a	e—а/_е-г>/	z — eTaT	z-e~bT
(s + a)(s + b) (b — a)(s + c) (s + a) (s 4- b) 	ab			(c — a)z	(b—c) z
	(c — a) e~at + (b—c) e~bl	z — e-dr + z — Q~bT z	bz	az
	1 + —e-a/- —e-w	z— 1	(a—b) (z—e aT) (a—b)(z—e aT)
s (s + a) (s + b) ab (s + c)	a—b	a — b	cz	b(c —a) z	a(b — c) z
	c b (c — a) e~at	a(b — c) t~bt	z—i	(a— b)(z—e~aT)	(a—b)(z—e~br)
s (s + a) (s + b) 	1		(a—b)	+	(a— b) e~at	e~bt	a~ct		£_	 +	£	+
		(b—a) (c—a){z—e aT) (a—b) (c—b) (z—e~bT) +	£	
(s +a) (s + b) (s + c) 	<°p		(b—a) (c—a)	(a—b) (c—b) + (a—c) (b—c)	(a—c) (b—c) (z—e—cT) 	ze~aT sin (црГ)	
(s + a)2 + o>2 s + a		
	e~at sin (<o0Z)	z%— 2ze~ar cos (w0T) 4- e—2aT z^ — ze~aT cos (<*)рГ)
(s 4- a)2 4- Wq	e—at cos (<o00	
		^2— 2ze~aT cos (&T) 4- e~2aT
Теоремы преобразований
Теорема смещения. Если функция f(t) имеет Z-преобразование
Zf (t) = F(z), и если kT — действительное положительное число, а
k — целое положительное число, то
Z [/ (/ — ЛГ)]=z~kF (z); Z [/ (/ - fcT)]=z*F (z).
Теорема конечного значения. Если функция f(t) может быть
преобразована с помощью Z-преобразования, Zf(t)=F(z), то
lim f =	/(n7')=lim zF (z).
Теорема начального значения. Если функция f(t) может быть
подвергнута Z-преобразованию Zf(t)=F(z) и если функция F(z)
не содержит полюсов вне единичной окружности или на ее грани-
це, то
=	f («T) = lim I -—X—F(z
2.4. ОБРАТНОЕ Z-ПРЕОБРАЗОВАНИЕ
Обратное Z-преобразование обладает рядом особенностей и
свойств. Как уже указывалось, Z-преобразование имеет следующий
вид:
Z f (/)=Z /* (/) = Z	f № 8 (/ - пТ)=F (z).
Обратим внимание на то, что функция /(/), строго говоря, не
равна функции /*(£), однако при Z-преобразовании функция при-
нимается равной функции
Данное соотношение несправедливо при обратном /-преобразо-
вании, что видно из следующего неравенства:
Z-iF(z)/2/(n7)8(/-"7)-
Например, при
ZU(f)
Z — 1
cos(o>/),	если	шГ=0,	2л,	4л,...;
1 sin (ш/), если	<оГ=0,	л,	2л,	Зл,...;
ch(o>/),	если	<о=0;
e-aZ	если	а=0.
Это означает, что при одном и том же Z-преобразовании данной
акции f(t) существует множество функций g(t), чьи дискретные
89
значения приобретают значения f(nT), тождественные g(t)- Это
свойство можно наблюдать на рис. 2.1.
При обратном /-преобразовании часто применяется два метода:
— метод разложения в степенной ряд;
— метод разложения на элементарные дроби.
Представленный в этой книге материал использует только ме-
тод разложения в степенной ряд. Существует еще и третий метод,
прямой метод, который включает интегрирование по контуру в
плоскости Z. Этот метод мало пригоден для инженеров и обсуж-
даться не будет. Он упомянут здесь только для полноты изложения.
Метод разложения в степенные ряды
при обратном /-преобразовании *
По этому методу многочлен из z разлагается в степенной ряд
из z~x делением. Коэффициенты каждого члена степенного ряда со-
ответствуют значению функции /(0 при n-м выбранном моменте
Z-1F (z)=Z-1 (---—пJ = Z-1 /-----1---=
v ’ \z—e~aT) [l — z-ie-*7)
= Z~l (1 + z~x е~аГ + z“2 е~2аГ z~3 е~3аГ+ ...);
Z-1 (	=18(0) + е-аГ 8 (t - T) + е-2вГ 8 (/ - 2T)+
+ е-3вГ8(/ - 3T) + ...
Заметим, что если
у (*) _J g
x(z) z—е~аТ
то соответствующее рекуррентное уравнение имеет вид
^+l + e“f Уп + *п+1-
Если х=0 для всех значений п и t/o=l, то результатом решения
будет последовательность из уп‘-
j g—аТ g—2аТ g—ЗдГ
Мы видим, что эти значения связаны с коэффициентами при
разложении в степенной ряд передаточной функции F(z) области Z.
В табл. 2.4 объединены следующие основные моменты оператор-
ного метода Z-преобразования.
1.	Написание последовательности чисел в форме, которая позво-
лит произвести преобразование с помощью оператора Лапласа ли-
бо Фурье.
2.	Преобразование функции f(t) в функцию F(z).
3.	Преобразование функции F(s) в функцию F(z).
4.	Определение вида разностного уравнения на основании вида
функции F(z), что можно использовать при вычислении последова-
тельности {f(nT)}.
* Одностороннее Z-преобразование.
90
Рис. 2.1. Множество функций
может проходить через одну и
ту же систему точек
Отсюда становится ясным, что можно осуществить следующие
переходы:
—	от разностного уравнения к функции F(z);
—	от функции F (z) к функции f* (t);
—	от функции F(z) к функции f (t);
—	от функции F(z) к функции F(s);
—	от функции F(s) к функции F(z) и т. д.
Все это нужно помнить при реализации метода Z-преобразова-
ния, которое позволяет осуществлять переход от дифференциаль-
ного уравнения к моделируемому уравнению в следующей последо-
вательности:
дифференциальное
уравнение и возмуща- yp(s\ yf(t] >F(z) > разностное
ющая функция извест- ' '	' I \ >	\ > уравнение
ного вида
Переход от разностного уравнения к дифференциальному урав-
нению осуществляется в обратной последовательности:
разностное ^p(s)^f(t)*^f(f)^p(s)^. дифференциальное
уравнение	' '	7	'' ’ v ’ уравнение
Осуществляя операцию по реализации этой последовательности,
можно ее прервать или начать с некоторого момента. Полная по-
следовательность осуществляется только при переходе от диффе-
ренциального уравнения к разностному уравнению и наоборот.
2.5.	РЕШЕНИЕ ЛИНЕЙНЫХ РАЗНОСТНЫХ УРАВНЕНИЙ С
ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ МЕТОДОМ
Z-ПРЕОБРАЗОВАНИЯ
Вооружившись теперь методом Z-преобразования, мы сможем
решать линейные разностные уравнения с постоянными коэффици-
ентами (1), осуществляя Z-преобразование правой и левой частей
разностного уравнения (2) применением алгебры Z-преобразования
Краткая запись операторного метода Z-преобразования функций
временной области их дифференциальных и разностных уравнений
Таблица 2.4
Преобразования	Определения	L {/* (/)} = S f е nsT =	(*) 0 Z-1 {F* (5)} = / (0) Ь (/- 0) + / (7) Ь (/- 7) + / (27) Ь (/- 27) + ... Допустим	z esr
Начиная с первой строки таблицы сверху вниз, раположена после- довательность преобразо- ваний	Тогда	00	__ F (г) А / (пТ) z n~Z {/*(/)};	Эти уравнения называют парным 0	Z-преобразованием. Они являются ' логическим продолжением преобра- f* (0 4 2 Л(«г)8 <<-лГ) = Z-1 (*)} • 30вания Лапласа 0 г-	7 Преобразования Лапласа и дифференциальные уравнения Y=f(t)\ Уо = О L (Y(t)) = sy(s) и, если /(/) = Z7(/), тогда £./(<)= — и Г(«)= 1/«2.	Г(/) = < S
Z-преобразования функ- ций временной области и функции s-области	Z (0 4 Z 2 («0 8 (* — пГ) = z (S“2) = (ОГ)г-О + (Т)г-1 + (2Г) г2 + ... + (пТ) г~пТ = 0 = 0 4- Тд-14- 2Гг-2 4- ... 4- (лГ)= Т (г-1 4- 2г-2 4- Зг-З-ь... 4-лг~л4-...); ,	Tz FW~ («-IF’
2-преобразования и раз- ностные уравнения	Преобразования функций f'(z) в разностное уравнение для вычисления последовательности f(nT) р	У (г)	TZ	Tz-i X (z)	(z— 1)2	1—2z-l 4-£-2’ то	(I _ 2z-i + z-2) У (г) == 7>-1 x (г); у (s) — 2e~sT у (s) + e""25,7 у (s) = T^TsTx (s)l у (0 - 2y (t - T) 4- У (t- 27) = 7x (/ - 7); у (nT) = 2y ((zz -1)7)- у ((n - 2) 7) 4- Tx ((n - 1) 7).
для получения решения уравнения дискретной системы, подвергаю-
щейся воздействию произвольной возмущающей функции (частное
решение), и решения ее однородного уравнения в зависимости от
начальных условий (дополнительное решение).
Рассмотрим разностное уравнение
хп=Ах„_1 + /„ при х(О) = Хо,
которое в результате Z-преобразования примет вид
x(z) = Az-1x(z) + /(z).
Решение x(z) примет вид уравнения
z ““ A z ““ А
которое при обратном преобразовании приводит к дискретной
функции *
Первый член уравнения является решением однородного урав-
нения или дополнительным решением, а остальные члены ряда яв-
ляются частным решением. Между прочим, мы видим, что коэффи-
циент Ап переносит начальные условия xQ на величину х(пТ), ко-
торая может быть получена непосредственно из разностного урав-
нения в соответствии со следующим:
/л=0 для всех /г,
тогда
хп=Axn—v
Так как
•^71—1 == Ахп^2^
то
= А2Хд_2.
Подобным образом
хп—Апх$.
Все это приводит к векторно-матричной записи [см. уравнение
(2.3)] как к средству распространения дискретных состояний в на-
правлении п равных временных интервалов через п повторяющих-
ся переходов.
В табл. 2.3 представлены Z-преобразования, которые полезны
при решении разностных уравнений, обеспечивая связь функций во
гттАииаЕ<?и	(z)/(z—4)] имеет замкнутую форму, изображение частного ре-
шения ооычно находится по таблице Z-преобразований.
93
временной области, «-области и z-области. Кроме того, как будет
показано, они полезны для упрощения получения разностных урав-
нений при моделировании.
2.6.	ПРЕДСТАВЛЕНИЕ РАЗНОСТНЫХ УРАВНЕНИЙ В ВИДЕ КОНЕЧНЫХ
И БЕСКОНЕЧНЫХ РЯДОВ
Одним из полезных свойств разностного уравнение является их
возможность написания в виде конечных и бесконечных рядов.
В общем случае мы имеем дело с представлением разностного
уравнения в виде беконечных рядов, т. е. с выражениями вида
хп ~ a‘xn—i 4“ bjQn—j-
Частный случай представления разностного уравнения может
иметь вид
хп = CjQn-j-
С его помощью вычисляется дискретная функция хп, представ-
ляющая реакцию системы на дискретное возмущающее воздей-
ствие.
В качестве примера получения и решения разностного уравне-
ния рассмотрим исходное дифференциальное уравнение
xx-\-x=Q(t) при х(0)=0,
которое приводится к разностному уравнению вида
х„=е-^	+ (1 - е-г/’) Q„_p	(2.4)
Передаточная функция для этого дискретного процесса записы-
вается в виде
х(г)__1 — &~Tiz
Q (г) z— &~r,z'
Используя разложение в степенной ряд, получим *
х (2) = (1 - e-r/’) (z-1 + е-г/’ г-2+е-2/’ г~3 +...) Q (z),
которое при обращении и отбрасывании членов выше третьего по-
рядка примет вид**
хп=(1 -	(Q„-i + е-гл Q„-2 + е-2ГЛ Qn-з).
Это выражение характеризует конечную память выражения
(2.4). Она полезна при моделировании систем, описываемых раз-
ностными уравнениями, у которых Т приблизительно равно т. Кро-
ме того, оно полезно при вычислении с помощью вычислительных
машин или при ручном счете результатов воздействия шума на
дискретные системы, описываемые разностными уравнениями.
*	Отражает бесконечную память системы на Q воздействия.
*	* Конечная память Q воздействия (три члена в этом примере).
94
Наконец, на основании сказанного выше можно показать, что
если x(z) записана в функции Q(z), то бесконечный ряд становит-
ся дискретной формой интеграла свертки
t
x(t)=^ h(t — т) Q (т) dx.
G
Рассмотрим дисперсию шума на выходе как результат его про-
хождения через систему, описываемую разностным уравнением, в
виде конечного ряда, вычисление которого не представляет особого
труда.
Такое разностное уравнение имеет вид
хп = 2	!•
При возведении в квадрат оно будет выглядеть следующим об-
разом.
хп — 2
Стационарная возмущающая функция * в виде белого и несме-
щенного случайного или квазислучайного шума приводится к дис-
персии выходного сигнала через дисперсию в виде
	~ V а’
.. e2 = /j а‘'
aQ
Заметим, что дисперсия передаточной функции, выраженной
бесконечным рядом, больше суммы квадратов коэффициентов в
системе с конечной памятью.
Возвращаясь к нашему примеру системы первого порядка, на-
помним, что конечная память разностного уравнения видна из вы-
ражения
x„^(l-e-^)(Q/,_1+e-^Q„_2+e-2^QZ!_3+...);
при возведении его в квадрат получим
4 = (1 - е-г/х)2 (Qn-i + е_2Г/х Q„_2 + e-^/t Q„_3 +...).
Если допустить отсутствие смещения (EQ = 0), стационарность
(EQn=EQ«_i = EQ«_2=...), взаимную независимость (E(Qn_]X
XQn-2)=0) случайными (или квазислучайными), Q< можно прий-
ти к передаточной функции дисперсии вида
(1 - е-г/х)2 (1 + е-2Г/х + е-</’+...).
_________°<?
* Признаки: стационарности -> Е = Е ;
отсутствия смещения -► Е (Хп) = 0;
белого шума Е (^пхт)т^п = 0.
95
Заметим, что это дискретное выражение представляет теорему
Парсеваля
a2 = p2(Z) ФЛ>
О
где h(t) является импульсной переходной функцией системы, а Ф
спектральной плотностью входного сигнала.
В определенных случаях передаточная функция дисперсии мо-
жет быть записана несколько иным образом. В этом случае
О* _(1_е-^)2
02	(1-е-2^)	Ц-е-г/;'
Пои нестационарном шуме отношение дисперсий может быть
представлено в виде
ах2_(1-е-^)2
а2 ,_е-2ГЛ ’
которое приводит л рекуррентному соотношению дисперсий разно-
стного уравнения
,2 =	(1 - е-г/^2 02	.
п	лп—1 1 к	7 чп— 1
2.7.	МАТЕМАТИЧЕСКИЕ СВОЙСТВА ДИСКРЕТНЫХ ВЫБОРОК
И ИХ ПРЕОБРАЗОВАНИЙ
При синтезе дискретных систем, которые аппроксимируют не-
прерывные системы, необходимо, чтобы читатель был способен осу-
ществлять замену непрерывного процесса дискретным. Такую за-
мену можно осуществить с помощью специальных быстродействую-
щих устройств для получения дискретных значений сигнала в
строго определенные интервалы времени, его преобразования в со-
ответствии со структурой преобразующих операторов и преобразо*
вания результирующего сигнала в аналоговую форму.
Таким образом, для завершения синтеза разностных уравнений
при переходе от аналогового процесса к дискретному вводятся
устройства получения дискретных значений сигналов для их даль-
нейшего преобразования с помощью передаточной функции к сиг-
налу на выходе.
Если эти устройства для получения дискретных значений сигна-
ла на выходе разрывают аналоговую схему изменения сигнала во
времени, то они могут использоваться для процесса перестройки.
Более подробно об этом сказано в гл. 4.
Очень важно понять свойства процесса выделения дискретных
значений сигнала и их связь с перестройкой сигнала. При подобной
замене непрерывного процесса дискретным вводится два источника
ошибок. Первый — это то, что искажается частотный спектр непре-
рывной функции, которая стала дискретной. Второй — это то, что
96
Устройство
дискретизации
fft)
f*nT
сигнала
Временная
область
Частотная
область
W Z7f 0 2tf ЧтГ
I Г	ГТ
Рис. 2.2. Влияние дискретизации сигнала на спектр функции f(t)
происходит спектральное искажение из-за смещения фазы (появля-
ется время запаздывания).
Спектральное искажение, связанное с процессом выделения дис-
кретных значений сигнала, можно определить, изучая спектраль-
ные характеристики промодулированного ряда импульсов:
/*(/)=/(/гГ)8(/-«Г).
Допуская, что преобразование функции f(t) с помощью опера-
тора Фурье f(ja) известно, преобразование функции f*(t) с по-
мощью оператора Фурье может быть представлено как
оо
f* =-у	F U (ш+
— оо
где ®s является частотой выборок дискретных значений сигнала.
Сравнение спектров исходной непрерывной системы и спектров
ряда смодулированных импульсов представлено на рис. 2.2. Перед
тем как продолжить наши рассуждения, необходимо остановиться
на некоторых обстоятельствах. Заметим, что если функция f* (]'<&)
обладает синусоидальной волной частотой 1 Гц, а выборка реали-
зуется с частотой 10 выборок в секунду, то спектр содержит смо-
дулированный ряд импульсов при частотах 1, 11, 21, 31, 41, 51
вплоть до 1001 Гц и далее.
Эти высокочастотные компоненты спектра промодулированного
ряда импульсов вносятся для преобразования высокочастотных
компонентов ряда Фурье. При этом моделирующая функция опре-
деляет каждый элемент спектральной линии. Если непрерывная
функция обладает синусоидальной волной частотой 11 Гц, она ста-
новится дискретной при частоте выборки 10 Гц, при этом ее ряд
обладает и более высокочастотными компонентами, такими, как
4	493
97
Рис. 2.3. Смещение спектра частотной свертки при выборке дискретных значений
сигнала на самых низких частотах
21, 31, 41, 51 Гц, но помимо этого мы можем обнаружить частоту
1 Гц.
Это является результатом того, что как синусоидальная волна
в 11 Гц модулирует частоту 10 Гц, точно также сигнал с частотой
в 1 Гц модулируется с частотой в 10 Гц. Этот тип спектрального
смещения называют частотной сверткой (с частотами 11, 21, 31, 41
и вплоть до 1 Гц, при осуществлении выделения дискретных значе-
ний в 10 Гц), что и наблюдается, если выделяются дискретные зна-
чения сигнала со скоростями ниже половины наибольшей частоты
компонентов спектра данной функции. Это спектральное смещение
и перекрытие областей спектров можно наблюдать на рис. 2.3.
Таким образом, выделение дискретных значений сигнала может
привести к двум видам смещения спектра:
—	наложению спектра или частотной свертки;
—	введению высокочастотных компонентов из-за модуляции
дельта-функции.
2.8.	ПРОЦЕССЫ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
Преобразование сигналов — это термин, который применяется в
теории дискретных систем и относится к преобразованию сигнала
из дискретных значений в непрерывные.
Из рис. 2.2 видно, что спектр непрерывной функции с ограни-
ченной полосой может быть восстановлен, если выделенные дис-
кретные значения пропускаются через идеальный фильтр, имеющий
однозначную передаточную функцию с частотой пропускания в ди-
апазоне от <»s/2 до нуля.
Практическая реализация преобразователей сигналов приводит
нас к процессам, которые отличаются от идеальных, но в то же
время достаточны по своим параметрам для решения большинства
инженерных задач.
98
fft)
f
0
Зкстраполятор
нулевого
порядна
~f(t)
i
t
0)
Импульс-реакция
T
S)
aft)
• Зависимость
экстраполятора
Составляющие
импульс-реакциа


Рис. 2.4. Зкстраполятор нулевого порядка:
а—исходной является непрерывная функция во времени; применение ступенчатой аппрокси-
мации в аналого-цифровом моделировании позволяет упростить задачу синтеза дискретных
аналогов непрерывных систем; б—импульс-реакция; в—структурная схема и результат про-
хождения через нее сигнала. Им пульс-реакция =й/=~/=й(О—и(1—Г); L(~/)=l/s-e-5^/s—
= (1—e~sT) Is - ~/(5)
В этой книге мы касаемся больше математической модели пере-
стройки, чем ее физически реализуемой структуры. При преобра-
зовании мы имеем дело с двумя видами характеристик: с отдель-
ными точечными данными возмущающей функции на входе и со сту-
печатыми значениями результирующих функций.
Простейшим типом преобразователя является зкстраполятор
нулевого порядка, который с помощью многочлена нулевого поряд-
ка перестраивает последовательность дискретных значений решет-
чатой функции на входе в последовательность ступенчатых функ-
ций на выходе.
В этой книге нулевой порядок зкстраполятора применяется в
двух случаях:
—	когда он используется в качестве процесса при синтезе дис-
. кретных систем, аппроксимируя непрерывные системы;
—	при моделировании с помощью аналого-цифрового комплек-
са, где зкстраполятор применяется в качестве преобразователя ин-
формации из цифровой формы в аналоговую.
На рис. 2.4 представлен процесс преобразования с помощью
экстраполятора нулевого порядка во временной области, а на рис.
4*	99
Рис. 2.5. Характеристики экстраполятора нулевого порядка в частотной области.
Преимущества: простота применения и понимания; очевидны недостатки в срав-
нении с экстраполятором первого порядка, видимые при рассмотрении n-го ин-
тервала (см. рис. 2.7 и 2.9). К недостаткам относятся: полупериодное запазды-
вание модели, некоторое затухание в полосе частот, несущих информацию, сла-
бое затухание сигнала за информационной полосой
2.5 представлены графики амплитудной и фазовой характеристик
этого преобразования.
Частотные характеристики экстраполятора нулевого порядка
определяются приравниванием s=j<a в передаточной функции
....	1—е_/тГ	2	. /<оГ\
f (jw)=-----------=— еsin I----------),
/о)	<0	\ 2 /
из которой можно получить амплитудное и фазовое смещение *
f (/<1)1 z 
J ’ шТ/2	2 '
Заметим, что экстраполятор нулевого порядка вносит значи-
тельное фазовое запаздывание в проходящие через него высокочас-
тотные компоненты любого сигнала. Это ключ к пониманию его
особенности, о которой упоминается на протяжении всей книги.
Последнее легко объяснить, используя координату времени, если
рассмотреть сложный периодический сигнал, преобразуемый экст-
раполятором нулевого порядка.
Представим, что мы исследуем этот экстраполятор с помощью
ряда Фурье. Тогда экстраполятор нулевого порядка вносит вре-
мя запаздывания с половиной периода в каждой из функций сину-
са и косинуса ряда. Очевидно, мы обнаружим значительное влияние
на результат, если период дискретного сигнала соизмерим с перио-
дом высокочастотной составляющей сигнала.
Существует экстраполятор первого порядка, который осуществ-
ляет экстраполяцию с помощью последовательности линейных
функций, образующих зубчатообразное приближение к непрерыв-
ной функции. Это видно на рис. 2.6. Экстраполятор первого поряд-
ка преобразует последовательность многочленов первого порядка
Ньютона—Грегори в непрерывный сигнал.
—символ фазового угла; фазовый угол равен — <оГ/2.
100
a)
Рис. 2.6. Экстраполятор первого порядка. Формула экстраполяции:
~ f(t)= fn + [(/л — /л-О/У] У — пТ) на интервале пТ < (n -I- 1) Г;
-/(«) = [(1 + Гл)/Т][(1 - e-rs)/s]2
Частотные характеристики экстраполятора первого порядка мо-
гут быть представлены как
f (»=Т (1 + (^П)1/2 ( sin	) £ tg-i шГ - о>Т,
что показано на рис. 2.7. Доминатные члены в фазовых выраже-
ниях указывают на то, что процессы преобразования вносят за-
паздывания в Т/2 при экстраполяторе первого порядка исходя из
шенноновского предела (cos/2). Экстраполятор л-го порядка должен
помочь построению кривой через п точек, вводя эффективное за-
паздывание сигнала* приблизительно на Т/2 по сравнению с за-
мененным им непрерывным сигналом.
Экстраполятор треугольного типа (рис. 2.8, 2.9) не содержит
этих запаздываний. С точки зрения физического смысла этот эк-
страполятор нереализуем из-за того, что его передаточная функция
I
I
ws 2ш3 Зы5
2
Рис. 2.7. Частотные характеристики экстраполятора первого порядка. Преимуще-
ство: нет затухания в информационной полосе частот (малый коэффициент уси-
ления). Недостаток: запаздывание равно почти полному периоду выборки, ко-
торый в 2 раза больше фазового смещения экстраполятора нулевого порядка
Только в информационной полосе.

101
fl)
Аппроксимация трапецией на каждом
шаге (трапеция может быть получена
суммированием б соответствии с
треугольной экстраполяцией)
а)
Рис. 2.8. Треугольная экстраполяция. Формула интерполяции:
~f(0=fn + [(fn+r—fn)fT](t—пТ) на интервале пТ < t < (п 4- 1) Г; ~ / (s) =
= ег*$2 [(1 —е“5Г)/$]2
должна располагать нереализуемой аппаратурно величиной функ-
ции, опережающей на период (т. е. значением /п+ь до того как оно
вычислено).
Нашей задачей является показать применение экстраполяторов
в математических моделях, с помощью которых мы можем решить
разностные уравнения, применяемые при моделировании непрерыв-
ных систем. В математике экстраполяция методом треугольников
приводит к уравнениям'В неявном виде, которые всегда могут быть
решены как линейные уравнения с постоянными коэффициентами,
так и в виде нелинейных уравнений. Поэтому мы можем утвер-
ждать, что экстраполяция методом треугольников является необхо-
димым процессом моделирования. Преобразование сигнала — важ-
ный процесс при синтезе дискретных систем, который необходим
большому количеству современных методов, обеспечивающих ап-
проксимацию непрерывных систем. Если осуществить сравнение
информационных потоков при моделировании одной и той же не-
Рис. 2 9. Частотные характеристики треугольного экстраполятора. Преимущества:
нет фазового смещения или запаздывания сигнала, хорошее затухание с внеш-
ней стороны информационной полосы. Недостаток: затухание в самой информа-
ционной полосе

102
прерывной системы от цифровой машины и от аналоговой, возник-
нут определенные трудности.
Например, непрерывный процесс G(s) обладает следующей
структурной схемой:
----------- o(s)
----------- B(s) -
где О — выходной сигнал системы, а I — входной сигнал.
Каждому дифференциальному уравнению, которое связывает
значения сигналов на выходе и входе, может быть поставлено в со-
ответствие разностное уравнение, которое с помощью функции
H(z) связывает О и/.
Функция H(z) может быть получена из следующей последова-
тельности:
1.	Получение разностного уравнения на основании перехода в
дифференциальных уравнениях к конечным разностям *.
2.	С помощью Z-преобразования разностного уравнения.
3.	Получение передаточной функции H(z) для разностного
уравнения.
В этом случае мы можем сделать наглядной дискретную систе-
му, которая аппроксимирует непрерывную систему с помощью
структурной схемы
Hz)-------- 0(z)
----H(Z) ---------
После всех алгебраических преобразований бывает трудно свя-
зать функции H(z) и G(s) и, следовательно, G(s)—с физической
сущностью моделируемой системы. Надо обладать определенной
интуицией к физической системе, чтобы легко связать математичес-
кую модель и результат расчетов на вычислительной машине с фи-
зической системой, представленной G(s). Для многих случаев бы-
вает совершенно невозможно связать функции H(z) с G(s) в фи-
зической системе.
Тем, кто проектирует непрерывную систему на цифровой вычис-
лительной машине, известны неприятности, начинающиеся при
проектировании системы второго порядка, которая даже при пра-
вильном моделировании все-таки будет вызывать необходимость
найти моделирующее разностное уравнение, обладающее четырьмя
дополнительными полюсами и двумя новыми нулями: результатом
является просто подстановка достаточно точного числового интег-
ратора третьего порядка в дифференциальное уравнение, которое
описывает непрерывную систему второго порядка.
метолм^°ЖНО использовать также методы численного интегрирования или иные
Д перехода от дифференциальных уравнений к разностным.
10&
Рассмотрим систему на простом примере:
х-\-х=f при хо=О,
которая имеет один действительный корень при —1. Передаточная
функция этой системы имеет вид
х 1
G(s)= -(s) =----
г S+1
Если использовать общепринятую формулу численного интегри-
рования *
хп=хл_! + у (Зх„_1 — х„_2)
для интегрирования дифференциального уравнения, то можно пря-
мой подстановкой найти, что
^п~^п—1 +	[3 (./л—1 -^/1—1) (/п—2 '^/1—2)]
ИЛИ
“Ь ( ~2-О ------2~ Х/1~2 = ~2	-/л-2)’
Производя Z-преобразование этого разностного уравнения, най-
дем, что
['г2+(т“1)г_т]л(2)=Т(3г-1)/(2)’
передаточная функция которого имеет следующий вид:
x(z) =	(Т/2) (Зг-1)	= н , .
f(z) £2+ (3772—1)2— Т/2	1 h
Таким образом, приходим к заключению, что
f(S)
X(S)
можно промоделировать на цифровой вычислительной машине при
помощи соотношения
f(z)
(ТЦ) (3-1-1}
1ЧЗТ/2-1)т-Т/2
x(z)
* Особенно при моделировании в реальном масштабе времени.
104
В связи с изложенным возникают следующие вопросы: «Как
сделать систему, обладающую двумя полюсами и одним нулем,
похожей на систему с одним полюсом?» и «Целесообразно ли про-
ектирование непрерывной системы с помощью математической мо-
дели дискретной системы?»
Выходом из этой дилеммы является прежде всего то, что автор
должен верить в возможность синтеза дискретного аналога непре-
рывного процесса. Затем необходимо связать функцию H(z) с G(s).
Эти процессы первоначально были получены авторами Жюри, Ту,
Фаулером независимо (примерно в одно и то же время) и впослед-
ствии обнаружены многочисленными инженерами, «рабочей зада-
чей» которых был синтез гибридных информационных систем (а не
гибридного моделирования на вычислительной машине), которые
могут быть описаны разностными уравнениями. Разностные урав-
нения программировались на цифровой вычислительной машине,
так что вычислительная машина оперировала с дискретным анало-
гом непрерывного процесса. Краеугольным камнем являлся про-
цесс преобразования сигнала.
Рассмотрим следующий пример.
Дискретным аналогом непрерывной системы будет
f(s)
1 X(s)
+ 1
Дискретизация
сигнала на Сходе
Перестройка
сигнала на Сходе
f(s)
f(t)
f(z) Частотная область (40)
f*(nT) Временная область (ВО)
f(z)
T
1 - e’sr
f(s); 40
BO
s
Управление	f(s)	f(z)
кепрерыдной f(t)	:
системой c	_	>	z__E_
помощью непре- T	S
рыбной функции	L
f(s)
f(t) Г......; •
l's+ /
X(s); 40
X(t) i BO
Выдорка на —
Выходе. Этот T
элемент позволяет
нам представить раз~
постное уравнение,
ныйТхпП Оискрет-
Пыходом ° диснРетным
f(z)
i-e~ST
s
/
T1S+ 1
ffzPz( s /($+//( z~e
xn~e'r/vxn.t + n-e'T/^-z
~Xtt)
T
105
Теперь можно утверждать следующее:
Передаточная функция дискретной системы
имеет один полюс, как и функция G(s).
Полюс дискретной системы является полюсом плоскости s, ото-
браженным в плоскости z, что видно из соотношения
гДе5/;
с Т
7	—а°полюс'
полюс V ’
откуда следует, что
^ПОЛЮС l/'t» е , ^ПОЛЮС е / .
Коэффициент разностного уравнения является переходной мат-
рицей для этой однопараметрической задачи»
Используется не метод численного интегрирования, а оператор-
ный метод. Этот способ является более предпочтительным, так как
сохраняет связь с физикой системы при цифровом моделировании
лучше, чем чисто алгебраический способ.
Этот метод обсуждается дальше, в гл. 4.
2.9.	УСТОЙЧИВОСТЬ ДИСКРЕТНЫХ СИСТЕМ
Устойчивость линейных дискретных систем с постоянными коэф-
фициентами может быть изучена как в плоскости s, так и в плос-
кости z.
В плоскости s критерием устойчивости может быть то, что по-
люсы системы находятся в ее левой половине. В дискретных сис-
темах предполагают, что система является устойчивой, если полюс
расположен на плоскости z в области меньшей или равной единице.
Этот критерий плоскости z вытекает из того факта, что левая по-
S-плоскость устойчивости Z-ллоскость устойчивости
Lms	tm z
•	Полюса функции G(s)
в левой полуплос -
кости указывают,
Полюса функции H(z) находя-
щиеся внутри единичной ок-
ружности указывают на то,
что функция H(z) устойчива
—Rez
Res
•	Полюса функции
G(s) в правой полу-
плоскости указывают
на то,что функция
G(s) неустойчива
а)
Полюса функции H(z) на-
ходящиеся с внешней
стороны единичной окруж-
ности показывают на то/
что функция H(z)
неустойчива
Рис. 2.10. Условия устойчивости дискретной системы:
а_уСЛ0ВИя устойчивости на плоскости $; б—условия устойчивости на плоскости z
106
Рис. 2.11. Устойчивая дискретная система. Типичные характеристики при:
а—полюса на действительной оси и б—комплексно сопряженные полюса
ловина плоскости s отображается внутренней частью единичной
окружности на плоскости г. Все это представлено на рис. 2.10 и
следует из соотношения
z=es/.
Расположение полюса в плоскости s определяет характер про-
текания процесса во временной области, так же как и местонахож-
дение полюса в плоскости z, что показано на графике рис. 2.11.
Действительные полюсы, находящиеся на левой действительной по-
луоси, не обеспечивают решения эквивалентной заменяемой непре-
рывной системы (за исключением тех случаев, когда непрерывные
системы заменяются дискретными, имеющими больший интервал,
чем дискретность выборки). Дискретные системы, полюсы которых
находятся на действительной оси в левой полуплоскости z, обычно
не применяются при моделировании непрерывных систем.
2.10.	УРАВНЕНИЯ СОСТОЯНИЯ ДИСКРЕТНЫХ СИСТЕМ
Выше мы видели, что линейные стационарные системы могут
описываться векторно-матричными уравнениями
X — AX + BU;
Y = CX,
где X — вектор состояния; Y — вектор на выходе; U — вектор на
входе; А, В, С — постоянные матрицы.
Решением данной системы уравнения может быть
t
X = е>1('-'о) X (/0) 4- J ел<^) BU (т) dx.
^0
Дискретные векторно-матричные уравнения могут быть получе-
раюо3 НдПРеРывных векторно-матричных уравнений следующим об-
1 = пТ при тг = О, 1, 2,...
107
Преобразование
нулевого
порядка,
£
5
~^/7
Рис. 2.12. Образование вектора состояния при дискретной аппроксимации систе-
мы X=AX+BU
Систему дифференциальных уравнений первого порядка будем
решать с помощью разностного уравнения первого порядка. При
этом значения экстраполированных параметров движения системы
определяются по их текущим значениям. Это можно видеть из сле-
дующего:
Х„=ел(лГ-/о’Х(/0)+ f
/о
(Д+1)Г
Х„+1 = ел<«7'+г-<»)Х(/0)+ | ел<«г+г-^Ви(т)</т.
^0
Сравнивая эти уравнения, видим, что
(«+1)Г
X„+1 = e^X„+ J* e^+^)BU(T)rft
Yn+i — СХя+1.
При постоянных коэффициентах системы
Ф=елг.
В и С вычисляются только один раз. Если интеграл решается чис-
ленно (что является обычным способом в комплексных задачах),
то подынтегральное выражение должно быть вычислено на каждом
шаге. Альтернативой является применение разностного уравнения
в векторно-матричной записи. Если синтезируется дискретная ап-
проксимация этой системы уравнения, то можно использовать ме-
тодику получения разностного уравнения, изложенную в разд. 2.7.
Теперь рассмотрим непрерывный процесс, показанный на рис.
2.12. Он может быть упрощен до вида, показанного на рис. 2.13.
Из этой модели очевидно, что X — это реакция системы на ступен-
чатые воздействия Un на входе. За ступенькой величина Un посто-
янная, так же как А, В, С.
Таким образом, интеграл может быть упрощен до следующего
вида:
fOrfr Вил,
108
Рис. 2.13. Упрощенная структура системы, представленной на рис. 2.12
который легко получается. Тогда моделирующее разностное урав-
нение принимает вид
Хл+1 = ФХ„+Тил, где Ф=елг
(т	\
и	Т=	В; Уя+1 = СХл+1.
\о	J
Подобные проработки могут быть сделаны и для нестационар-
ной линейной системы. Но так как коэффициенты меняются со вре-
менем, возможны только незначительные упрощения, и уравнения
преобретают менее простую структуру для понимания и примене-
ния. Мы упомянули о них ради полноты изложения.
Часть II
ЧИСЛЕННЫЕ МЕТОДЫ
МОДЕЛИРОВАНИЯ ЛИНЕЙНЫХ СИСТЕМ
НА ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИНАХ
Глава 3. ВВЕДЕНИЕ В МОДЕЛИРОВАНИЕ
ЛИНЕЙНЫХ СИСТЕМ
Анализ линейных систем с постоянными коэффициентами имеет
большое значение из-за того, что он часто встречается при проек-
тировании непрерывных процессов. При нахождении параметров
проектируемых систем для определения типа передаточной функ-
ции обычно исследуются выходные Динамические характеристики
линейных систем при заданном входе.
В этой главе рассматривается синтез рекуррентных формул,
которые могут применяться при вычислении параметров динами-
ческого процесса с выборочными дискретными значениями его пе-
редаточной функции.
Вводятся ключевые понятия и приводятся разностные динами-
ческие уравнения, полученные на базе динамических дифференци-
альных уравнений, т. е. основное внимание уделяется нахождению
разностных уравнений, чьи характеристики корней, полюсов, нулей
и фазы подобны таким же характеристикам в дифференциальных
уравнениях непрерывной системы. Затем показываются примеры
использования разностных уравнений для моделирования непре-
рывного процесса, описываемого дифференциальным уравнением.
В гл. 4 и 5 этот способ моделирования доведен до практических
приложений.
3.1. РЕШЕНИЕ РАЗНОСТНЫХ УРАВНЕНИЙ МЕТОДАМИ ПОДСТАНОВКИ
ПРИ ЧИСЛЕННОМ ИНТЕГРИРОВАНИИ
В гл. 7 и 8 мы найдем примеры многих классических формул
интегрирования, включая формулу интегрирования Эйлера, интег-
рирования методом прямоугольников, методом трапеций, Т-интег-
рирование и ряд формул численного интегрирования дифференци-
альных уравнений методом прогноза и коррекции.
Существует способ использования дифференциального уравне-
ния для численной оценки приращений, который позволяет пред-
сказывать решение дифференциального уравнения вблизи от на-
чального состояния.
110
Другим способом численного интегрирования является образо-
вание разностных уравнений.
Рассмотрим дифференциальное уравнение первого порядка с
постоянными коэффициентами
xx-\-x=Q,	(3. 1)
где x=x(t); Q = Q(t), а т — постоянная.
Дальше рассмотрим формулу интегрирования Эйлера
xn = xn-l~k^'xn-l-	(3-2)
Применяя дифференциальное уравнение и формулу интегриро-
вания, можно получить решение в виде скорости
*л-1 = + (<2л-1--*л-1)>	(3.3)
которое можно подставить в формулу численного интегрирования
^л=^л-1 + ^-(<?л-1-^л-1).	(3.4)
и
При очевидных преобразованиях получается разностное урав-
нение или рекуррентная формула решения дифференциального
уравнения в явном виде
(3.5)
\ Т /
Рекуррентная формула дает возможность вычислить, например,
значение результирующей функции на 100-м шаге на основании
данных, образованных на 99-м шаге. Индексация функций в рекур-
рентной формуле позволяет вычислить их значения при решении
дифференциального уравнения методом итерации. Она также ука-
зывает время, при котором функция приобретает значение х(/) в
момент t = nT, если решение началось при пТ = 0.
При t=/=nT индексация позволяет определить примерные значе-
ния функций в их последовательности, полученной в результате
решения разностного уравнения.
Применение рекуррентных формул- в решении дифференциаль-
ных уравнений имеет два преимущества. Они уменьшают объем
вычислений при моделировании разностных уравнений, упрощают
процесс линеаризации и интегрирования в неявном виде.
В этих формулах скорость переменной состояния является
функцией состояния. Существует формула интегрирования с по-
мощью метода трапеций, которая имеет вид
1	1).	(3. 6)
При интегрировании с помощью метода трапеции п+1 значение
например, вычисляется на основании знания п+1 значения ско-
рости х. Следовательно, для оценки х в этом дифференциальном
уравнении требуется значение xn+i, Оно находится в уравнении в
неявном виде, так как в решении является функцией, зависящей
111
от самой себя. Если формулы интегрирования в неявном виде при-
меняются для получения разностных уравнений, то эти уравнения
'могут быть решены алгебраически. Например, рассмотрим неявное
интегрирование по Эйлеру (интегрирование методом прямоуголь-
ников), которое принимает вид
xn=xn-i+T*n-	(3.7)
Из дифференциального уравнения видно, что
xn~~{Qn xn)i	(3-8)
т
откуда при подстановке в формулу прямоугольного интегрирова-
ния получим
хп=Хп-\ И- ~ (Q/i	(3.9)
т
Заметим, что это уравнение обладает неявной формой, так как
хп является функцией самой себя. Однако это уравнение может
быть преобразовано к следующему виду:
~~хп = хп—1~}~~' Qn'i (1 Н	хп~хп—1 + ““ ^п'
и	и \ и )	и
•	хп=( — -----1 хп-1 + (Qn.	(3.10)
•	• " \ 1 + т/и) п 1 v и + г/н / п	k 7
Попробуем сравнить выражение Эйлера для неявной формы с
выражением в явной форме с точки зрения числовой устойчивости,
числовой ошибки и способа получения решения дифференциально-
го уравнения.
Устойчивость этих разностных уравнений первого порядка пол-
ностью определяется величиной первого коэффициента в разност-
ном уравнении. Так, если выражение
—1— 1 + 1-
1 + Г/т	т
Интегрирование в неявном виде	Интегрирование в явном виде
превышает ±1, то разностное уравнение становится неустойчивым.
Например, если а=2 в разностном уравнении уп^ауп-\ при на-
чальном значении функции, равном единице, получим результат,
представленный в табл. 3.1.
Таблица 3.1
Неустойчивые характеристики разностного уравнения
Уп = ауп-1(а=2)
п	1	2	3	4	5 . . . .
Уп	1	2	4	8	16 ... .
112
Однако заметим, если а = 0,9, разностное уравнение устойчиво,
что видно из табл. 3.2.
Таблица 3.2
Устойчивые характеристики разностного уравнения
</п=аг/п_1(а=0,9)
п	1	2	3	4	5 . . . .
Уп	1	0,9	0,81	0,729	0,6561 ....
Этот пример делает более наглядным анализ, например, раз-
ностного уравнения первого порядка, полученного с помощью не-
явного интегрирования методом Эйлера.
В данном случае нашей целью является определение условий,
при которых размер шага интегрирования и постоянной времени
системы обеспечивают устойчивость разностного уравнения и не
приводят его к числовой неустойчивости.
Поэтому мы сначала определим условия, при которых величи-
на а меньше или равна единице, т. е.
Решая неравенство для Т/т, видим, что устойчивая область для
разностных уравнений, полученных с помощью интегрирования
Эйлера в явном виде, есть
0< — <2.
15
Изучая разностное уравнение, полученное для интегрирования
методом прямоугольников (интегрирование Эйлера в неявной фор-
ме) , видим, что условия, при которых
I 1
I 1 + Г/и
есть 0< —.
и
Разностное уравнение, полученное с помощью Эйлера методом
прямоугольников, более устойчиво, чем полученное в явном виде.
Это является характерным примером более общего результата, к
которому приводят линейные дифференциальные уравнения с по-
стоянными коэффициентами. Они интегрируются с помощью раз-
ностных уравнений в неявном виде и обеспечивают более устойчи-
вые решения, чем уравнения, которые получены с помощью формул
интегрирования в явном виде. Поэтому еще раз подчеркиваем это
преимущество интегрирования в неявном виде для получения ус-
тойчивых разностных уравнений моделирования непрерывных про-
113
Теперь обратимся к точности этих моделирующих разностных
уравнений. В табл. 3.3 представлена последовательность значений
решения разностного уравнения, полученного в результате интегри-
рования в явной и неявной форме на единичном шаге. Наибольшая
точность получается в формуле при интегрировании в неявном
виде. В целях обеспечения устойчивости разностных уравнений,
полученных при помощи формул Эйлера, эти разностные уравне-
ния исследовались при соотношении шага интегрирования к посто-
янной времени 3/2.
Таблица 3.3
Сравнение разностных уравнений, полученных
интегрированием в явной и неявной форме (Г/т=1,5)
Нормализо- ванное время	Точность	Интегрирование в неявном виде		Интегрирование в явном виде	
	х(пГ)	х (пТ)	ошибка	х (пТ)	ошибка
Т/т=О	0	0	0	0	0
Т/т=1,5	0,776	0,600	—0,176	1,500	+0,724
77т=3,0	0,950	0,840	—0,110	0,750	—0,200
Т/т=4,5	0,990	0,936	-0,054	1,125	+0,135
Как видно, при этих условиях разностное уравнение, полученное
при интегрировании в неявной форме, обладает большей точностью,
чем разностное уравнение, полученное с помощью интегрирования
в явной форме. Это подчеркивает еще одно свойство разностных
уравнений, полученных с помощью интегрирования в неявном виде
для моделирования линейных систем с постоянными коэффициен-
тами. Их преимуществом является большая точность.
Наконец, изучим устойчивость полных разностных уравнений.
Поступим следующим образом. Рассмотрим неоднородное урав-
нение (так как в однородном уравнении все конечные условия сос-
тояния устойчивости приближаются к нулю, сравнение сделать не-
возможно) .
Для непрерывных и дискретных уравнений результирующий
шаг описывается выражениями, которые имеют вид
У=Q (1 -	уп=(1 - —)	1+V Qn-i’
\ Т /	т
Точное	Явное
(1 + г/т)	+ (Т7777)Qn'
Неявное
При УСТОЙЧИВОМ СОСТОЯНИИ Z->OO Хп=Хп-Ь
Таким образом, окончательное значение можно записать как
limy(/) = Q;	=	yn=Qn.
/-►00
Точное	Неявное	Явное
114
Отсюда как неявное, 'Так и явное разностные уравнения дости-
гают одного и того же окончательного значения, равного оконча-
тельному значению ступенчатой функции входного сигнала.
Однако рекуррентная формула, полученная с помощью интегри-
рования в неявном виде, является и более устойчивой и более точ-
ной, чем формула, выведенная с помощью интегрирования в явном
виде.
Эти рекуррентные формулы особенно полезны в оценке реакции
системы на произвольную функцию возмущающего воздействия. В
случае, если шаг интегрирования мал в сравнении со значением
наибольшего периода колебаний функции возмущающего воздейст-
вия, рекуррентные формулы можно использовать для вычисления
реакции системы на произвольную функцию возмущающего воз-
действия для оценки ее эффективности.
Затруднение связано с формулой интегрирования в неявном ви-
де при вычислении реакции системы на произвольную функцию
возмущающего воздействия в связи с допущением, что она рас-
сматривается в момент п.
Если функция возмущающего воздействия имеет вид
f=f(y, С.
оценка функции fn соответствует
fn=f(y* пТ),
в которой уп еще не определено.
Мы располагаем только значениями yn-i. В этом случае для
оценки у мы должны применить формулу экстраполяции, учитыва-
ющую ее последние значения, или можно полагать yn-i как ап-
проксимацию уп. Это можно сделать, если компоненты функции
возмущающего воздействия (с точки зрения анализа Фурье) обла-
дают более низкой частотой, чем собственная частота системы, за-
данная дифференциальным уравнением.
Вычислим некоторые значения функции возмущающего воздей-
ствия для системы, допускающей yn^yn-i. Образуем несколько
первых членов функции /. Используя таблицу, оценим скорость из-
менения функции f. В этом случае можно просто использовать
формулу экстраполяции для проведения первой оценки уп на осно-
вании уп_{ и уп-2- Автор находит, что не часто возникает необходи-
мость применения метода экстраполяции при практической оценке
решений применительно к дифференциальным уравнениям.
Эта техника получения разностных уравнений для моделирова-
ния динамики непрерывных процессов чрезвычайно полезна при
моделировании динамических нелинейных процессов. Одной из
проблем, однако, является то, что большинство разностных урав-
нений в неявной форме не может быть решением нелинейных диф-
ференциальных уравнений, т. е. уравнение в неявном виде является
нелинейным уравнением и обычно может быть решено только с по-
мощью итерационного метода. Однако разностные уравнения явно-
115
го вида легко получаются и подставляются в выражение, которое
может быть оценено значительно легче, чем при осуществлении
численного интегрирования нелинейного уравнения.
3.2. УСТОЙЧИВОСТЬ РАЗНОСТНЫХ УРАВНЕНИЙ
Рекуррентные формулы для моделирования непрерывных дина-
мических процессов предполагают, что разностные уравнения име-
ют тот же порядок, что и дифференциальные уравнения, которые
должны быть промоделированы. Корни разностного уравнения
определяются с учетом соответствующих корней дифференциаль-
ного уравнения и учитывают «коэффициент корректировки» так же>
как и при подборе окончательного выражения разностного уравне-
ния, соответствующего исходному дифференциальному уравнению.
Для примера рассмотрим непрерывный процесс первого поряд-
ка с постоянными коэффициентами
xx-\-x=Q.
Допустим, что это уравнение имеет решение
х = е5/.	(3. 11)
При подстановке получим показательное уравнение
(т$+1)е*' = 0,	(3. 12)
которое имеет характеристический корень
(3. 13)
т
В этом случае решение однородного дифференциального урав-
нения принимает вид
х = с^~Ч\	(3.14)
Решение неоднородного уравнения можно получить с помощью
интеграла свертки, который может быть получен на базе решения
однородного уравнения, образующего свертку с функцией возму-
щающего воздействия:
t
x = ^Q{k)^V'dk.	(3.15)
Тогда полное решение дифференциального уравнения примет
вид
j* Q(#)efe/X dk-\-c1
il
(3. 16)
Подобные способы могут применяться для дифференциальных
уравнений первого порядка, с помощью которых осуществляется
либо анализ во временной области, либо для решения используют-
ся преобразования Лапласа, либо Z-преобразования.
116
Представим, что мы собираемся моделировать непрерывный
процесс с помощью разностного уравнения, корни и конечное зна^
чение решений которого соответствуют таким же корням и конеч-
ному значению решения непрерывного процесса.
Допустим, что разностное уравнение имеет следующий вид:
ахп_ 1 -J- bQn,	(3. 17)
а решение разностного однородного уравнения имеет вид
хп = с^~пТ1\	(3. 18}
При подстановке получим показательное уравнение, соответст-
вующее разностному уравнению
г1е-«^(1-ае^)=0.	(3. 19)
Чтобы корни разностного уравнения соответствовали корням
дифференциального уравнения, требуется
а = е-т/\	(3.20)
Это определяет коэффициент в разностном уравнении, который
выполняет роль полюса соответствия между разностным и диффе-
ренциальным уравнениями:
x„=e-W„_i.	(3.21)
Этот метод должен гарантировать соответствие разностного-
уравнения динамики дифференциальному уравнению динамики,
так как их корни эквивалентны и образуют эквивалентные решения
при разложении обоих в экспоненциальный ряд. При помощи этого’
определяем конечное выражение разностного уравнения и подбира-
ем с его помощью конечное значение решения дифференциально-
го уравнения. Изложенный здесь метод более простой для тех не-
однородных разностных уравнений, которые имеют вид
+	(3.22)
где устойчивость состояния разностного уравнения с подобранным
корнем достигается в том случае, если
Qn = Qn-1’ Хп~ Хп—!•
Тогда
хп = _е—т/т^п-	(3.23)
При включении коэффициента корректировки в виде
6=1-е~^	(3.24)
разностное уравнение принимает точно такое же окончательное
значение, как и в исходном дифференциальном уравнении. Таким
образом, моделирующее разностное уравнение примет вид
хп =	+ (1 - е^Л) Qn.	(3. 25)
Заметим, что решение этого однородного разностного уравнения
соответствует точному решению однородного дифференциального
117
уравнения. Оно образует последовательность решений, которые
являются точными для реакции на ступенчатое воздействие Q(Z) =
и образует решения, которые являются хорошей аппрокси-
мацией дифференциального уравнения реакции на произвольное
возмущающее воздействие.
Заметим, что это разностное уравнение не может стать неустой-
чивым независимо от размера шага интегрирования, так как выра-
жение всегда меньше единицы независимо от того, как будет
велико Т при т>0.
Из табличных значений явствует, что между решением дина-
мического разностного уравнения и решением непрерывного диф-
ференциального уравнения возникает значительная ошибка. Одна-
ко из уравнения (3.25) становится ясным, что решения разностных
уравнений являются запаздывающими по сравнению с непрерывны-
ми решениями. С точки зрения динамики они идентичны дифферен-
циальному уравнению за исключением эффекта фазового смеще-
ния. Конечно, можно уменьшить размер шага для сведения двух
кривых ближе, но этот способ и не точный и не эффективный при
уменьшении этого рода ошибок. Им можно компенсировать эту
фазовую ошибку определением с помощью интерполяции времени
получения последовательности реакций в разностном уравнении по
сравнению с дифференциальным уравнением и затем учесть это
время смещения в таблице последовательности решений разност-
ного уравнения.
Допустим, нам известно, что в четвертой графе таблицы вели-
чин реакций расположено, истинно непрерывное решение в диапа-
зоне между t = 3T и 4 Г. Используя обратную интерполяцию, можно
определить, при каком времени дискретное решение приближается
к непрерывному решению, и затем выбрать соответствующий про-
межуток времени, за который рассчитываются интервалы пТ.
Необходимо обратить внимание на то, что при решении, полу-
ченном при помощи разностного уравнения, а также при помощи
формул численного интегрирования, исследователь сталкивается с
проблемой времени, которое отличает характер процесса во вре-
мени исходной системы от характера процесса во временной после-
довательности пТ. Эта проблема заключена в дисркетной аппрок-
симации непрерывного по времени процесса, отличного от последо-
вательности значений пТ. Отсюда индекс в рекуррентных форму-
лах в большей мере относится к числу итераций, чем к промежут-
ку времени пТ.
Исследователь должен уметь связывать последовательность по-
лучаемых результатов с реальным временем, сравнивая эти ре-
зультаты с контрольным примером процесса, протекающего в ис-
тинном непрерывном времени. По собственному опыту автора мно-
гие инженеры и программисты, обратив внимание на проблему вре-
мени, стараются сравнить результаты, полученные при непрерыв-
ных и дискретных операциях вычисления, осуществленных во вре-
мени пТ, вместо того, чтобы понять, что численное интегрирование
является аппроксимирующим процессом.
118
Синтез моделирующих разностных уравнений методом динами-
ческих аналогий также содержит проблемы времени.
Дискретные системы обладают, например, различием в потоке
информации цепи обратной связи, в зависимости от того, содержит
ли она численные интеграторы или разностные уравнения. Таким
образом, исследователь при выборе квантования последовательно-
сти значений в непрерывном и дискретном процессах должен это
учитывать.
Проблема возникает также при выборе слишком большого шага
интегрирования, в том случае, когда остро встает вопрос экономич-
ности вычислений во времени, так как с увеличением шага интег-
рирования рабочая нагрузка ЦВМ существенно уменьшается.
Некоторые из часто встречающихся линейных процессов и их
моделирующие разностные уравнения, в которых применяются ме-
тоды динамической аналогии, представлены в табл. 3.4.
Таблица 3.4
Разностные уравнения для наиболее часто встречающихся линейных
систем с постоянными коэффициентами *
0(5)
/(О
Разностные уравнения,
применяемые при моделировании
_/____i_
f ~ з
I	1
f = S2
У _	1
X	XS Ч- 1
У XS
х xs Ч- 1
9
У _	wn
х + 2^wns + w2n
dt
I = ^f(t)dt2
In — I n-A + T f n
T2
^n—l In~2 4" ~2~ (f * fn—l)
—Т/т	—T/t
Уп=ъ	+	—e )xn
Уп=ъ ThУп-i + e r/~ (xn —
Уп = АУп-i ~ Byn-2+( 1 — A + B) xn
-
A =2e~CwnT cos{w„T(l—C2)*/2}
B=e~KwnT
при 0 < £ < 1
* См. дополнительную фильтрацию, разд. 5.7 содержит моделирование вы-
соких порядков, имеющих нули и полюсы с использованием простых переда-
точных функций.
В гл. 4 и 5 мы встретимся с большим количеством подобных
уравнений.
Выбор параметров решения разностных уравнений, применяе-
мых при моделировании, необходимо увязывать с числом итераций
в интервале времени пТ. Для этого осуществляют сравнение дис-
119
кретного решения с контрольным примером непрерывного решения,
что приводит к выявлению временных параметров с помощью ана-
лиза, подобного рассмотренному ранее.
Разностные уравнения, полученные непосредственно на основа-
нии динамической аналогии, обладают важными общими свойст-
вами.
При рассмотрении устойчивости эти разностные уравнения ока-
зываются устойчивыми, если устойчивы исходные дифференциаль-
ные уравнения. Это обусловлено тем, что корни разностного урав-
нения подбираются на основании корней дифференциального урав-
нения, и, следовательно, если непрерывный процесс устойчив, то
дискретный процесс также устойчив. Это справедливо при величине
корней дискретной системы, равной или меньшей единицы, неза-
висимо от того, каким способом они формируются. Например, в
случае уравнения первого порядка, которое мы здесь рассмотрим,
корни дискретной системы могут быть представлены как
е-^Л,
которые всегда меньше или равны 1 при Т>0 и т>0. Единственное
условие, которое накладывается на применение разностного урав-
нения, состоит в том, что скорость получения дискретных значений
функции возмущающего воздействия должна быть равна удвоенно-
му наибольшему значению ее частоты.
Более детально это изложено в гл. 1, где обсуждаются скорости
моделирования. Кроме того, конечные значения дискретного раз-
ностного уравнения всегда подбираются, исходя из этих значений
непрерывного разностного уравнения, независимо от периода дис-
кретизации и без необходимости знания окончательного значения
корректирующего коэффициента. Это объясняется тем, что конеч-
ные значения текущей и предыдущей реакций системы при устой-
чивых процессах имеют одно и то же значение. При подстановке
окончательного значения в разностное уравнение можно вычислить
функции возмущающего воздействия на входе, которые находятся
подбором таких же самых окончательных значений в моделируе-
мых динамических непрерывных процессах.
В этих моделирующих разностных уравнениях есть ограничение.
Непрерывная система второго порядка может обладать тремя со-
вершенно различными динамическими характеристиками: когда
два корня системы действительны и равны; когда они действитель-
ны и неравны; когда оба корня комплексны. В устойчивых динами-
ческих непрерывных системах второго порядка с комплексными
корнями колебания демпфируются, реакция системы с действитель-
ными корнями не носит колебательного характера, имеет в резуль-
тате демпфирования апериодический характер движения. В каж-
дом случае необходим самостоятельный тип разностных уравнений.
Поэтому для определения характера разностного уравнения нужно
знать, какое место занимают корни на комплексной плоскости. Это
особенно важно, если коэффициенты дифференциального уравне-
ния меняются во времени так же, как и в случае линейной системы
120
с переменными коэффициентами. Если коэффициенты меняются со
временем, то для решения могут быть использованы разностные
уравнения при их кусочно-линейной аппроксимации уравнениями
с постоянными коэффициентами подбором результатов, близких к
решению, полученному методом численного интегрирования диф-
ференциального уравнения с переменными коэффициентами. Одна-
ко, если корни, меняющиеся со временем, пересекают действитель-
ную ось, то необходимо осуществлять переключение с одного раз-
ностного уравнения на другое, а именно, одно разностное’уравне-
ние моделирует динамический процесс при неравных действитель-
ных корнях, другое разностное уравнение моделирует динамику,
если корни действительные и равные; и существует еще одно раз-
ностное уравнение в случае комплексных корней. Выбор соответст-
вующего ряда разностных уравнений достаточно прост, но заметим,
что разностные уравнения неявного вида, которые получены в
разд. 3.3, не нуждаются в их изменении и поэтому могут быть более
пригодны с точки зрения быстроты моделирования непрерывных
процессов с переменными коэффициентами.
Глава 4. ДИСКРЕТНО-АНАЛОГОВОЕ
МОДЕЛИРОВАНИЕ
В этой главе рассматривается дискретно-аналоговый метод мо-
делирования линейных стационарных систем. Этот метод может
быть с таким же успехом применен и к нестационарным линейным
и нелинейным системам. Метод позволяет синтезировать дискрет-
ные системы, являющиеся аналогом непрерывных систем. Поэтому
в главе получаются разностные уравнения, которые описывают та-
кую дискретную систему, которую используют для программирова-
ния на цифровой вычислительной машине. Последовательность
решений разностного уравнения безусловно относится к выбранной
дискретной системе, а не к непрерывной. Поскольку дискретная
система является аналогом непрерывной системы, можно опреде-
лить последовательность решений разностных уравнений, позволя-
ющих характеризовать движения непрерывной системы.
По этому методу дискретная система синтезируется таким об-
разом, чтобы переработка сигнала в ней являлась аналогом пере-
работки сигнала в непрерывной системе. Такое разностное уравне-
ние дискретной системы решается на цифровой вычислительной
машине, моделируя такую переработку. Таким образом, этот метод
является одним из видов аналогового моделирования.
Очевидно, что преимуществом этого метода, как и любого ана-
логового метода, является то, что проектировщики и моделисты
находятся ближе к непрерывной системе, хотя они знают, что циф-
ровая вычислительная машина вычисляет движение дискретной,
а не непрерывной системы. Это является значительным обстоятель-
121
ством, так как инженер по моделированию не будет приписывать
непрерывной системе свойств дискретной системы.
Последовательность чисел, образованная разностным уравнени-
ем, будет моделировать движение непрерывной системы, если про-
ектировщик правильно просинтезирует дискретный аналог непре-
рывной системы. Правильный синтез моделирующей дискретной
системы может обеспечить получение высокоэффективной близкой
к шенноновской информационной предельной модели.
4.1.	СИНТЕЗ ДИСКРЕТНОГО АНАЛОГА СИСТЕМЫ
На рис. 4.1 показан метод синтеза, который можно применить
при моделировании непрерывной системы.
f(t)	x(t)	Временная область
f(S)	x(s)	Частотная область
G(s) ------
а)
fit)	f(nt)	«fit)	«x(t)	Временная область
f(S)	f*(S)	«f(S)	«x(s)	Частотная область
A Преобразователь”процесса,аналогичный
преобразователю нулевого порядна
t)
f(t) f(nt) ~f(i)	~f(s)	~X(t) Временная область
f(s) f*(s)~f(s)	~f(s)	~X(S) \ частотная область
x*(s) . xrzj	00 + 0,2''+ a2z'2 + •••
f*(S) f(Z) ' D(Z) bo+bjZ'1 + b2z~2
bo
' • *n= ”	“ T“ *n-z ~
°O	Oq
г)
Рис. 4.1. Синтез дискретной системы, аналога непрерывной системы:
а—этап 1; б—этап 2; в—этап 3; г—этап 4. Звездочкой отмечено, что цифровая компенсация
может при необходимости применяться на выходе модулятора вместе H(s) непрерывной
компенсации на выходе
122
Этап 1. Составление структурной схемы непрерывной системы.
Этап 2. Включение квантизаторов вектора состояния на трактах
интересующего входного сигнала. Если необходимо осуществить
такой дискретный процесс, модулятор производит только пульса-
цию. Ясно, что это еще не является дискретным аналогом непре-
рывного процесса. Для того чтобы создать аналог непрерывного
процесса в непрерывной системе, вводится процесс перестройки
сигнала [Н($)] после каждого модулятора.
Этап 3. Корректировка искажения процесса перестройки сигна-
ла осуществляется компенсатором [С(«)].
Этап 4. Получение уравнения, описывающего эту дискретную
систему.
Этап 5. Составление программы вычислений разностных урав-
нений на цифровой вычислительной машине и интерпретация ре-
зультата моделирования для исследования непрерывной системы.
Заметим, что при таком способе моделирования линейные дина-
мические процессы не искажаются. Только непрерывный поток сиг-
нала преобразуется к дискретному потоку введением модулятора
и процесса перестройки на выходе сигнала. Для того чтобы синте-
зировать дискретную систему, аналогичную непрерывной системе,
нужно просто разорвать непрерывный информационный поток на
дискретный информационный поток. Чем чаще производится
выборка дискретной системы, тем ближе дискретная система ап-
проксимирует непрерывную систему. Кроме того, в этом случае все
корни остаются в характерных местах на плоскостях «их. При
этом методе непрерывный процесс остается таким же. Только про-
текание сигнала отличается от протекания сигнала непрерывной
системы.
Интересны информационные аспекты выборки дискретного зна-
чения сигнала и процессов перестройки (нет необходимости рас-
сматривать числовую неустойчивость на этой стадии).
Обычно компенсация перестройки сигнала — процесс линейный.
Могут быть применены два типа компенсации: линейная непрерыв-
ная компенсация и линейная дискретная (цифровая) компенсация
сигнала. Как уже указывалось в гл. 2, фазовое смещение и затуха-
ние связано с процессом дискретизации сигнала непрерывного вида.
Этот нежелательный эффект можно уменьшить с помощью компен-
сирующего фильтра. Например, если для перестройки сигнала при-
меняется преобразователь первого порядка, то запаздывание по
сравнению с заменяемым непрерывным сигналом равно половине
периода дискретного сигнала. Для того чтобы устранить эффект
запаздывания, полученный при использовании преобразователя ну-
левого порядка, применяется полупериодный компенсационный
ввод.
На рис. 4.2 показан дискретный аналог, применяемый в системе
второго порядка. Заметим, что блок-схема дискретного аналога
тождественна блок-схеме гибридной модели этой же системы вто-
рого порядка (аналоговая вычислительная машина + цифровая вы-
числительная машина).
123
•	Уравнение движения системы
у = 2$ыпу + ы2у = ы„х/ при х(О)=О=х(О)
ф Передаточная функция системы
y(s)=— г
х s2+ 2£ыПз + о)„
ф Структурная схема системы
е Сист:::а упрощается Введением однопериодного
компенсационного Обода
y(S)
Т УШ
ф Передаточная функция дискретной системы, полученная
в результате следующих преобразований:
ум=7	1 (____“L_____)=<i-a+b)z2
X(Z) ' s '	\ з2+2£шп + ы%' Az2+Bz+C
О Здесь А=2е'*ШпТсоз{ыпТ(1- $2)’/г^; B=e'2ib>nT
•	При моделировании используется разностное уравнение
следующего вида:
Уп = АУп-Г вУп+ (1-А + В)Хп
Рис. 4.2. Дискретный аналог непрерывной системы второго порядка
Функция возмущающего воздействия должна следовать из циф-
ровой вычислительной машины через преобразователь Ц/А и пере-
страиваться в аналоговый сигнал, который должен быть использо-
ван для управления непрерывным процессом второго порядка в
аналоговой вычислительной машине. Выход аналоговой вычисли-
тельной машины должен быть выведен через конвертер А/Ц для
преобразования данных в цифровую форму при определении выхо-
да непрерывной системы.
На рис. 4.3 представлен типичный дискретный аналог непрерыв-
ной системы второго порядка. В этом примере модулятор и преоб-
разователь нулевого порядка на входе сигнала и модулятор на вы-
ходе сигнала приблизительно эквивалентны переходу Ц/А, а пере-
ход А/Ц связан с гибридным моделированием. Переписывая пере-
даточную функцию от модулятора к модулятору, мы получим пере-
даточную функцию дискретного процесса, которая является анало-
гом непрерывного процесса второго порядка, моделируемого на
аналоговой вычислительной машине. Обращение этой передаточной
функции в дискретную функцию является процедурой получения
разностного уравнения, которое можно использовать в цифровой
124
Рис. 4.3. Дискретно-аналоговый метод моделирования линейных непрерывных
систем на вычислительных машинах
вычислительной машине для моделирования процесса второго по-
рядка *.
Дискретно-аналоговая структурная схема на рис. 4.1 показыва-
ет, что различие между дискретной и непрерывной системами со-
держится в процессе выборки и перестройки. При моделировании
существенны условия точности, так как метод связан исключитель-
но с точностью моделирования и перестройки сигнала. Все это име-
ет значение, так как, глядя слева на процесс перестройки, мы фо-
кусируем внимание на точности, тогда как, глядя справа, мы фо-
кусируем внимание на устойчивости процесса. В дискретно-анало-
говом методе различают условия устойчивости и условия точности.
4.2.	ДИСКРЕТНО-АНАЛОГОВОЕ ОБОБЩЕНИЕ
На рис. 4.4 представлено обобщение дискретно-аналогового ме-
тода. Процесс в нижней ветке потока сигнала —это дискретизиро-
ванная часть непрерывного сигнала, изображенного в верхней вет-
ке потока сигнала. На выходах модуляторов мы имеем дискретные
значения сигнала непрерывного процесса на выходе системы, его
дискретную аппроксимацию.
На всем протяжении книги, когда рассматриваются ошибки,
мы полагаем, что ошибка равна разнице между выбранными значе-
ниями непрерывного процесса и выбранными значениями его же
Дискретной аппроксимации на выходе. Дискретная аппроксимация
состоит из преобразования H(s), компенсации C(s) и непрерывно-
го процесса y=f(x, t, у). Компенсация C(s) нейтрализует искаже-
ние, вводимое преобразованием H(s) в сигнал x(t). Глядя на про-
цесс компенсации слева, мы имеем дело с точностью, с которой
функция возмущающего воздействия x(s) восстанавливается из
* В гл. 5 можно найти разностное уравнение (за исключением коэффициента
2 в числителе), которое может быть получено также отображением полюсов
плоскости s iB полюсы плоскости z, таким образом, чтобы получить передаточ-
ную функцию области г, чьи полюсы и конечные значения подобраны из тех же
параметров, что и у непрерывной системы.
125
Рис. 4.4. Непрерывная система и ее дискретный аналог
последовательности выбранных значений. Эти обстоятельства
включают:
—	выборку дискретных значений при достаточно высокой час-
тоте, чтобы восстановить функцию возмущающего воздействия
Я(5);
—	понимание влияния модулятора спектра функции x(s);
—	понимание причин искажения как фазового, так и амплитуд-
ного спектра функции x(s), вводимого электрической цепью преоб-
разователя
—	определение компенсации, которая может свести к миниму-
му искажение спектра х как от Н ($), так и от модулятора.
Точность и информационное содержание функции возмущающе-
го воздействия х(з) являются условиями между первым модуля-
тором и компенсирующей сетью; между компенсирующей сетью на
выходе и последним модулятором основным условием является ус-
тойчивость моделируемого процесса.
Заметим, что y(s) = G(s)-x(s). Таким образом, применяя тео-
рему свертки, найдем, что y(s) является реакцией функции G(s)
на функцию возмущающего воздействия x(s). Так как х(з) на про-
тяжении периода моделирования известна, то y(s) может быть вы-
числена за тот же период времени умножением характеристики
G(s) на известную функцию возмущающего воздействия х(з). По-
скольку последовательность функций x(s) аппроксимируется про-
извольной функцией х(з), то предполагают, что решение'y(s) явля-
ется реакцией G(s) на произвольную функцию возмущающего воз-
действия х(з).
Заметим только, что реакция системы при начальных условиях
(решения этой однородной системы) как для дискретной аппрок-
126
Y(0)
Рис. 4.5. Обобщение дискретно-аналогового метода
симации, так и для непрерывного процесса тождественна, т. е. ре-
акция на начальные условия при дискретно-аналоговом методе рав-
нозначна той реакции непрерывной системы, у которой начальные,
условия не проходят через модель, преобразователь и компенсиру-
ющую сеть.
В связи с этим не следует обращать внимания на то, что теоре-
ма Грина (где в линейных системах с начальными условиями мож-
но обращаться как с возмущающими функциями и наоборот) при
дискретно-аналоговом методе точно не выдерживается.
На рис. 4.5 показано векторно-матричное обобщение дискретно-
аналогового метода для линейного и гладкого нелинейного процес-
са. И еще раз, нижняя ветвь движения сигнала является дискрет-
ной аппроксимацией непрерывного процесса, описываемого верхней
траекторией сигнального потока. В таком случае структурная схе-
ма обобщается для включения как линейного, так и нелинейного
процесса.
Как уже обсуждалось, точно такие же принципы допускаются
для строго линейной стационарной системы. То есть принципы,
связывающие первый модулятор и компенсирующую сеть на выхо-
де, основываются на перестройке функции возмущающего воздей-
ствия с достаточной точностью, для того чтобы аппроксимировать
возмущающие воздействия как во временной, так и в частотной об-‘
ластях. А принципы, связывающие компенсационную сеть на вы-
ходе и последний модулятор, основываются на решении системы
Уравнений при известной функции возмущающего воздействия и
Начальных условиях.
В дискретном аналоге время решения задачи отличается от вре-
мени в истинном масштабе при непрерывном процессе. Время обоз-
начается параметрами т и t в дифференциальном уравнении и в их
выбранных модельных значениях. Компенсирующая сеть обеспечи-
127
Рис. 4.6. Обобщение дискретно-аналогового метода и метода численного интег-
рирования системы дифференциальных уравнений
вает компенсацию запаздываний, возникающих в модели в процес-
се восстановления. Нет необходимости в том, чтобы время в дис-
кретно-аналоговом процессе было таким же, как в истинном не-
прерывном процессе, так как могут появиться систематические
запаздывания, связанные с вычислением векторного интеграла в
дискретном аналоге, т. е. прямая цепь должна быть рассчитана до
того, как обратная цепь замкнута. В дискретном аналоге нелиней-
ных уравнений, с помощью которых осуществляется интегрирова-
ние на вычислительных машинах, в том числе сопоставление с ана-
литическим решением, возникает добавочное запаздывание, кото-
рое изменяет время решения задачи в дискретной системе по срав-
нению с реальным временем в непрерывной системе. Кроме того,
при крупномасштабном моделировании часто практикуются различ-
ные пакеты программного обеспечения, расположенные в различ-
ных группах и в различных местах. В таких случаях возникают
трудности управления временем информационного потока; при про-
граммном обеспечении возникают необъявленные запаздывания,
которые позже могут быть учтены моделирующим инженером пос-
ле отладки программ. Это можно видеть из рис. 4.6, где дискретный
интегратор (цифровой интегратор) представлен с помодцью процес-
сов восстановления и компенсации, который включает времен-
ную задержку при замыкании обратной цепи (е-5Г вдоль цепи).
Важным свойством разностных уравнений, применяемых в дис-
кретно-аналоговом методе, является присущая им стабильность не-
зависимо от размера шага, конечно, в том случае, если моделиру-
ется стабильный процесс. И в более общем случае разностные урав-
нения обладают устойчивыми характеристиками, как и дифферен-
циальные уравнения непрерывной системы.
Как показано на рис. 4.5, если период выборки велик по срав-
нению с постоянной времени процесса, то процесс легко достигает
устойчивого состояния. Однако это неверно для численно интегрп-
128
руемой системы, показанной на рис. 4.6. Если ординарные диффе-
ренциальные уравнения решаются не аналитически, а численным
интегрированием, то может возникнуть числовая неустойчивость.
Короче говоря, если дифференциальное уравнение может быть
решено при наличии возмущающей функции (частное решение) и
для начальных условий (решение однородного уравнения), то раз-
ностное уравнение, которым описывается это решение, будет обла-
дать устойчивостью характеристик.
В этой книге рассматриваются процессы перестройки с помо-
щью преобразователей нулевого, первого, второго и треугольного
вида, а не процессы непрерывной компенсации, которая обычно яв-
ляется опережающей, запаздывающей, опережающе-запаздываю-
щей или переносной опережающей компенсацией. Существуют дру-
гие типы процессов перестройки, которые здесь не рассматривают-
ся, но имеют большое значение для развития моделирования,— это,
например, самонастраивающиеся процессы Портера — Стонемана
«кардинального преобразования», которые перестраивают функции
в точно ограниченной полосе. Существуют также и нелинейные
компенсирующие фильтры. Эти процессы здесь также не рассмат-
риваются, так как существуют фундаментальные работы, в кото-
рых положено только начало исследованиям по применению дан-
ных методов, еще далеко не доведенных до конца.
4.3.	ДИСКРЕТНО-АНАЛОГОВЫЙ МЕТОД И ГИБРИДНОЕ
МОДЕЛИРОВАНИЕ
В разд. 4.2 упоминалось, что дискретно-аналоговый метод подо-
бен гибридному машинному методу моделирования непрерывной
системы. Это положение нуждается в дальнейшем развитии по раз-
личным причинам.
На рис. 4.7 показана структурная схема гибридного моделиро-
вания линейного стационарного процесса G(s), где дискретные
значения функции возмущающего воздействия (вычисленные на
цифровой вычислительной машине) перестраиваются на аналого-
вой цифровой машине методом выборки дискретных значений и
преобразования, а затем реализуются в непрерывном процессе
G(s) (путем реализации на аналоговой вычислительной машине),
выход которого претерпевает дискретизацию и затем возвращается
по обратной цепи к цифровой вычислительной машине. Теперь дол-
жно быть очевидно, что дискретно-аналоговый метод является ана-
логом и при гибридном моделировании функции G(s).
В этом смысле, иногда дискретно-аналоговый метод называют
гибридно-аналоговым. С помощью разностных уравнений обычно
моделируют G(s) на цифровой вычислительной машине, при этом
могут быть получены такие же результаты, как и на аналоговой
вычислительной машине при исключении влияния напряжения ее
квантователя (функция квантователя — сделать дискретными уров-
ни напряжения аналога, что можно достичь с помощью цепи пре-
образователя). Во-первых, заметим, что разностные уравнения, по-
5	493	129
Аналоговая вычислительная машина
Рис. 4.7. Моделирование G(s) с помощью гибридной ВМ. Ключевые данные о
дискретно-аналоговом методе базируются на основании его аналогии с гибрид-
ными системами:
1.	Если G(s) является устойчивым, то отношение у (г) к х(г) будет устойчивым независимо
от шага Т. 2. Если y(s) имеет частотные составляющие вплоть до соп Гц, то нижняя часто-
та квантования должна быть порядка 7соп. Так как во многих случаях 7’т1п«1/7шп. Боль-
шинство моделируемых процессов плохо реализуется при Т=1/2®п (нижний предел Шенно-
на) по различным причинам (либо у не ограничен полосой частот, либо значительна ошиб-
ка квантования и т. д.). В силу этого практическое значение приобретает T—\i7G)n. 3. Ес-
ли высокочастотные составляющие y(s) выходят за значение 1/2Т, то считается, что оин бу-
дут стремиться к еще более низким частотам в процессе моделирования на цифровой ВМ.
В случае, если Т переменно, следует применить перед последним модулятором специализи-
рованный фильтр. Однако подобный метод автору применять не приходилось
лученные для процесса дискретно-аналогового моделирования,
будут более точными, чем заменяемый гибридный процесс, в кото-
рый включается влияние квантователя. Во-вторых, пределы точно-
сти решения разностного уравнения определяются по точности вы-
числения коэффициентов разностного уравнения, по точности
самого решения разностного уравнения на цифровой ВМ, которые
значительно выше, чем при решении на эквивалентной аналоговой
ВМ. Это происходит от того, что точность вычислений на аналого-
вой ВМ обеспечивается потенциометрами и обычно ограничивается
одной долей от 103 или 104, в то время как получение коэффициен-
тов на цифровой ВМ реализуется с точностью одной доли от 2",
где п — число бит информации в арифметическом регистре цифро-
вой ВМ.
Из этого следует, что нет необходимости привязывать механизм
аналоговой ВМ к быстродействующим аналоговым процессам, если
разностные уравнения могут быть записаны и вычислены на цифро-
вой ВМ с большей точностью, чем это может быть достигнуто на
гибридной ВМ.
В-третьих, при гибридном вычислении применяется процесс пре-
образования нулевого порядка. Это требует введения модулятора
с задержкой на полпериода во все компоненты функции возмущаю-
щего воздействия. Этот эффект компенсируется обычно в цифровой
ВМ при помощи цифрового фильтра. При дискретно-аналоговом
методе компенсация может быть включена там, где удобно, на пути
сигнального потока между преобразователем перестройки и непре-
рывным процессом G(s), либо с помощью цифрового фильтра, ли-
130
Рис. 4.8. Цифровая компенсация
бо с помощью эквивалентной цифровой компенсации, как указано
на рис. 4.8.
Так Как передаточная функция коммутативна в z линейных ста-
ционарных процессах, то тождественные результаты можно полу-
чить установкой цифрового фильтра на выбранном выводе G(s).
Тогда можно прийти к заключению, что условия, которые голжны
подтверждать наличие быстродействующих линейных стационар-
ных процессов в аналоговой части гибридного моделирования, дол-
жны быть связаны с аппаратурными средствами или другим анало-
говым процессом, а не с процессом аналогового вычисления.
Как упоминалось в предыдущей части, если процесс устойчив,
то разностное уравнение также будет устойчивым, что видно из
этой аналогии. При гибридном моделировании устойчивость непре-
рывного процесса в аналоговой ВМ не зависит от выбранного пери-
ода, с которым в сеть перестройки вводится функция возмущающе-
го воздействия. По данной причине дискретно-аналоговым разност-
ным уравнениям присуща устойчивость. Из этого можно сделать
вывод, что если разностные уравнения имеют устойчивые решения
и полюсы разностного уравнения, находящиеся в плоскости z, бу-
дут отображать полюсы плоскости непрерывной системы, если ото-
бражения производятся в плоскости s, то перестройка функции воз-
мущающего воздействия никаким образом не повлияет на динами-
ческие характеристики модулируемого непрерывного процесса.
Также очевидно, что процесс цифровой компенсации, представ-
ленный на рис. 4.8, может быть обобщен в векторно-матричной за-
писи, как показано на рис. 4.9. Вообще компенсация, применяемая
в дискретно-аналоговом методе, может быть либо дискретной, либо
непрерывной.
Передаточная функция £>(z) дискретного фильтра может быть
передаточной функцией с модулятором, с процессом перестройки,
и тогда фильтр непрерывной компенсации следует за модулятором
и дискретная передаточная функция может быть связана с эквива-
лентным непрерывным фильтром. Причина сохранения непрерыв-
ного потока сигнала в дискретизированном аналоговом процессе
связана с сохранением опережений и задержек в дискретной систе-
ме, которая моделирует непрерывную компенсацию. По этой при-
чине непрерывная компенсация широко применяется в данной ра-
боте.
Рис. 4.9. Векторно-матричная цифровая компенсация
5*
131
Наконец, как в дискретно-аналоговом методе, так и при чисто
гибридном моделировании важно рассмотрение задачи идентифи-
кации отождествления и частотного огибания.
Предположим, что идеальный осциллятор связан с гибридной
ВМ. Если короткий импульс входит от цифровой ВМ в эту систему
через преобразователь Ц/А, система будет колебаться:
z/=sin (<оя/-|-Ф).
Если частота квантования преобразователя А/Ц устанавливает-
ся при (Ds=100(Dn, ее легко будет определить из дискретных значе-
ний, так как функция стала синусоидальной волной с частотой соЛ.
Если (os = (Dn (или около этого), то цифровая ВМ будет обеспе-
чивать постоянный вывод из преобразователя А/Ц. Очевидно, где-
то между (ds = lOOcon и (ds = (On ЦВМ потеряет способность отслежи-
вать простую синусоидальную волну. Наибольшая частота, с кото-
рой ЦВМ способна различать дискретизированные значения, — это
Так, если мы моделируем на АВМ систему, которая обладает
составляющими в частотной области большими, чем (os/2, то они
окажутся в ЦВМ такими же низкочастотными колебаниями. Этот
эффект называют обратной частотной сверткой. Дело в том, что
при применении преобразования А/Ц нужно либо быть уверенным
в том, что отсутствуют высокочастотные составляющие сигнала,
который дискретизируется, либо включить фильтры непосредствен-
но перед преобразователем А/Ц. Это так же, как было в дискрет-
но-аналоговом методе. Если моделируемый непрерывный процесс
обладает высокочастотными составляющими, описывающее их раз-
нсотное уравнение для вычисления движения обеспечит функцио-
нирование модели и правильно вычислит высокочастотное движе-
ние; но системы, которые функционируют, используя выходные зна-
чения разностных уравнений, будут переводить функцию возмуща-
ющего воздействия к более низкой частоте, чем движение самой
системы. Если разностные уравнения имеют резонанс при низких
частотах, то результаты моделирования при большой дискретности
могут ввести в заблуждение и вызваь неверные заключения. Этого
явления не происходит, если применяемый метод используется точ-
но. При затруднении точного определения cds можно установить
o)s5>g)h, где сон — наибольшая частота реакции системы.
4.4.	ПРОБЛЕМА ЕДИНСТВЕННОСТИ
Рассмотрим следующий процесс:
*1 *
*4	($ + ^) (S + Ь)
Цифровая аппроксимация этой непрерывной системьигредстав-
лена на рис. 4.10.
Для простоты обсуждения будем применять не компенсацию,
а перестройку в искаженном процессе из-за дискретизации. Запи-
сывая передаточную функцию области г от модулятора к модуля-
тору при //($)=(1—е“5')/$» можно получить уравнение
132
Рис. 4.10. Дискретный аналог дифференциатора с ограниченной полосой
р-лг р-дГ
~х1я=(е-г+е-Ы) - е-«^>гх1я_2+	----X
Х^-х^).
Мы видим, что процесс дифференцирования происходит при раз-
ности в интервале между х^п и лг4д_1 в последнем члене уравнения
в процессе экспоненциального сглаживания Х\п_х и х1д_2. Диф-
ференциатор с ограниченной полосой может моделировать разност-
ное уравнение. Для моделирования с использованием дифференци-
атора с ограниченной полосой можно применять разностное урав-
нение.
Другая дискретная система, которая могла бы применяться при
моделировании, может быть представлена рис. 4.11.
Для описания дискретного процесса между двумя первыми и
двумя последними модуляторами используются два разностных
уравнения. Эти уравнения при совместном решении образуют по-
следовательность аппроксимирующих решений — выбранных зна-
чений непрерывного процесса.
Разностные уравнения могут быть представлены следующим
образом:
/п _сГ\ /	\
~хз__|1 — е J / s J___ г — 1
х4 \ s	z~e~al*
_hr , (1 —
•.~Х1/г“е Х1п-1+	! Хзд-Г
В этом случае члены первого разностного уравнения образуют
дифференциальную функцию с первой операцией сглаживания;
Рис. 4.11. Второй пример дискретного аналога дифференциатора с ограниченной
полосой:
== Нъ = (1 —е sT)ls—эксполятор нулевого порядка
133
5)
Рис. 4.12. Параллельное (а) и последовательное (б) решение разностных урав-
нений в процессе моделирования
второе разностное уравнение образует вторую операцию сглажи-
вания. Низкопропускной фильтр первого разностного уравнения
является высокопропускным фильтром дифференциатора с ограни-
ченной полосой.
Заметим, что преобразование нулевого порядка обычно приме-
няется для получения дифференциатора. Ясно, что производная
ступеньки равна только нулю, и таким образом, можно ожидать,
что передаточная функция высокопроходного фильтра будет равна
нулю.
Однако производная, применяемая в низкопропускном фильтре
l/(s + a), прослеживается при дифференцировании использованием
простой конечной разности в х4.
Полагают, что при дифференцировании разностного уравнения
разностное уравнение с х3, являющегося функцией х4, может быть
решено параллельно с разностным уравнением для Xi, являющего-
ся функцией х3. Так, из первого разностного уравнения получается
х3, а во втором разностном уравнении содержится Хзп_х- По этой
причине 1 находится в прямой цепи потока сигнала на рис. 4.12.
Однако, если впервые вычисляется х3 на основании х4 и затем
этот результат используется для дискретной аппроксимации узко-
полосного фильтра, тогда выход первого разностного уравнения
может быть прямо использован при вычислении выхода второго
разностного уравнения, устраняя таким образом г-1 в прямой цепи.
2г1 — это физический оператор, и он зависит от способа вычис-
ления, при котором применяются разностные уравнения. Это не
является частью дискретно-аналогового метода. Этот факт часто
упускается при обсуждении дисркетных аппроксимаций непрерыв-
ных систем.
Картина потока сигнала или структурная схема дискретного
процесса^ который моделирует непрерывный процесс, может вклю-
чать не только математику процесса, но также и обработку данных
в процессе вычисления.
По мнению автора, это является одной из наиболее часто встре-
чающихся ошибок при дифференцировании разностного уравнения.
Третья аппроксимация этой непрерывной системы изображена
134
Рис. 4.13. Еще один дискретный аналог дифференциатора с ограниченной полосой
пропускания:
Я1 =[(1 + sT)/s] [(1- esr)/s]2 и Я2 = Нз=(1-е4Г)/«
на рис. 4.13. И опять сначала разностные уравнения будут решать-
ся параллельно, а затем последовательно.
Разностное уравнение от модулятора к модулятору для диффе-
ренциатора имеет вид
• ~ х, - &-aTXr> I (1 -е~аГ) -
. .~Л2П—е	x2n_j-|-	хзп-1
(1 _ e-W)
~ X! „=е	x2„_r
В этом случае процесс перестройки был применен до дифферен-
циатора, так что пилообразная функция становится дифференциру-
емой. Здесь применялся преобразователь нулевого порядка, ввиду
этого приращение каждой ступеньки было равно нулю и передаточ-
ная функция должна была быть равна нулю.
Таким образом, процесс перестройки должен включать рассмот-
рение возмущающего воздействия.
При последовательном осуществлении этого процесса вновь по-
лученные результаты х3 вычисляются с помощью первого разност-
ного уравнения, но не применяются сразу же во втором разностном
уравнении; подобным же образом выход второго разностного урав-
нения не применяется сразу же в третьем разностном уравнении.
Конечно, нет причин, по которым проектировщик не смог бы ис-
пользовать эти разностные уравнения по своему усмотрению, хотя
третье разностное уравнение для решения нуждается в знании х2
при п—1, а не при л, и второе разностное уравнение требует зна-
чения х3 при п—1, а не при л. Необходимо ввести z~x в обратную
связь этого процесса.
При большом шаге эти два выбранных периода задержки мо-
гут обладать разрушительными влияниями на всю динамику любой
системы, включая данный пример с дифференциатором с ограни-
ченной полосой пропускания.
135
Моделируемая
система
Уравнения	; х2л=е’%.,*(*-е’%;
Уравнение 1 Уравнение 2	Уравнение 3
ппгм^п^тс С помощью уравнения 1 находят х,, которое сразу же подстад-
Последовательность ляется q уравнение 2, которое определяет х2 , а вслед за змия
решения	применяется в уравнении 3.	Ztt
б)
Рис. 4.14. Нежелательный (а) и предпочтительный (б) способы моделирования
тракта сигнала
На рис. 4.14 приведена последовательность данного моделиро-
вания, где первое разностное уравнение используется для питания
второго и второе — для питания третьего.
Из этих примеров следует: первое, — не существует уникальной
системы разностных уравнений для моделирования любого непре-
рывного процесса; второе, — возникает вопрос, какая же из систем
уравнений является лучшей для моделирования непрерывной сис-
темы; третье, — при параллельном решении системы уравнений ре-
шение может осуществляться в любом порядке, но при последова-
тельном решении должен точно соблюдаться намеченный порядок
в соответствии с первыми, вторыми и третьими операциями.
Определенные трансляторы на ФОРТРАНе могут перевести
разностные уравнения в программу ВМ. Это может помочь в пре-
одолении запаздываний при дискретно-аналоговом методе.
Что касается вопроса точности, целесообразно помнить следу-
ющее правило: устранение наибольшего количества аппроксимаций
в дискретно-аналоговом методе может быть достигнуто введением
наименьшего количества процессов дискретизации и перестройки.
Во многих случаях при использовании изображений на диспле-
ях и мониторах отпадает необходимость в промежуточных векторах
состояния, обращения к дискретизации и перестройки во всех- век-
торах состояния.
4.5. РЕШЕНИЕ УПРОЩЕННОГО РАЗНОСТНОГО УРАВНЕНИЯ
Решение разностных уравнений в дискретно-аналоговом методе
для линейных стационарных систем включает осуществление z-npe-
образования произведения управляющей, компенсирующей и пере-
даточных функций непрерывного процесса.
136
Часто возникают трудности, если G(s), C(s) и H(s) хотя бы
отчасти комплексны.
Например, при использовании дискретных преобразователей ре-
шение передаточной функции примет формы, указанные далее:
-^(z)=Z/7(s)C(s)G(s).
При использовании преобразователя нулевого порядка
=	; -2_(z) = £ZzJz(— У (4.1)
S	I	Z \ S )
Преобразователь первого порядка дает
О = (г -1\2z ГCO(l + Ts) I
I ' ' \ z / L Ts^ J
при	piy.	(4.2)
Треугольный преобразователь дает
О,. (г— Yft ~ t CG \ и, .	(1—e~ir)2esr
т(2)=1—J-Z(—) при //(S)=3-----------.	(4.3)
Во всех этих случаях, даже если в данных преобразователях
применяется простейшая компенсация, решение упрощается незна-
чительно.
При C=es< (4.1) становится равным
т=<г-1)г(т)-
При C=ert (4.2) становится равным
О = (г — 1)2 z Г (l + rs)G I
I z L Tst J’
При С=1 (4.3) становится равным
О _ (г— 1)2 z / а \
I z \Ts1 )'
Передаточные функции в круглых скобках достаточно сложны
даже в этих простых выражениях и часто нуждаются в анализе,
отличающемся от простого поиска табличного значения z-преобра-
зования для определения передаточных функций z-области.
Все это нужно иметь в виду для того, чтобы искать возмож-
ность свести данный процесс решения к простой необходимости по-
иска табличного значения z-преобразования.
Это можно проделать следующим образом.
Каждую G(s) в круглых скобках можно свести к структурной
схеме, как показано на рис. 4.15. Выбирая выход каждой G(s) и
перестраивая выбранные значения, мы образуем дискретный ана-
лог этих процессов (рис. 4.16). В этих выражениях z-преобразова-
ние между первыми двумя модуляторами является случаем таб-
137
Рис. 4.15. Структурная схема сложной части преобразования
личного поиска преобразования G(s), и дискретная передаточная
функция, образованная между вторыми двумя модуляторами,— та-
кой простой случай табличного поиска ^-преобразования.
При дискретно-аналоговом методе с применением преобразова-
теля перестройки нулевого порядка упрощенной формулой решения
разностного уравнения будет
-y- — TZG(s).	(4.4)
Аналогично, при дискретно-аналоговом методе, где применен
преобразователь перестройки первого порядка, упрощенное реше-
ние может быть представлено формулой
I 2z	k
Z6WZ(^)(^)

Рис. 4.16. Дискретная аппроксимация линии связи
138
при треугольной перестройке
T“t(^)Z0W
Еще одна полезная компенсация, которую мы обсуждали, при-
водит к выражению *
/	z	v ’
Во всех этих случаях сложность z-преобразования объединен-
ных вместе компенсации и непрерывной системы была уменьшена
и сведена к табличному поиску z-преобразования G(s) и умноже-
нию на передаточную функцию цифрового фильтра, в которой
включены два уровня аппроксимации общего метода. По этой при-
чине результирующие разностные уравнения обладают двойным
уровнем аппроксимации.
Мы рассмотрим, при какой степени эти разностные уравнения
аппроксимируют непрерывную систему.
Рассмотрим процесс первого порядка
X _ 1
/ ts 4-1
который при аппроксимации с помощью упрощенного преобразова-
теля нулевого порядка дискретного метода аппроксимации дает
передаточную функцию
Г Z ('----)= (Г/'В)_^/ =
\ rs + 1 / z — е /
которая приводит к разностному уравнению
х^е-^х^ + Ш
\ и /
Дискретно-аналоговая передаточная функция будет иметь вид
х ______________________!\ —е~~г/т\
f \г_е-т1г)
и разностное уравнение
хп=е^Хп-! + (1 ~ е~ГЛ) Д.
Очевидно, числитель передаточной функции упрощенного раз-
ностного уравнения является разложением первого порядка пере-
даточной функции. Таким образом, конечное значение упрощенного
разностного уравнения не будет равно конечному значению непре-
рывного процесса.
При t/x меньше 1, эта аппроксимация все же приемлема. Все
указывает на то, что к этому разностному уравнению можно приме-
* X— регулируемый параметр усиления и у — параметр регулировки по фа-
зе. Оба параметра могут быть приспособлены аналитически или эмпирически для
согласования моделируемого разностного уравнения с дифференциальным урав-
нением, которым описывается моделируемая система.
139
йить константу й эмпирически приспособить его для получения
правильного конечного значения или откорректировать аналитиче-
ски определения конечных значений дискретных и непрерывных
систем, и подобрать константу для того, чтобы эти конечные значе-
ния соответствовали. После того, как все это проделано, убежда-
емся, что (4.4) удобно записать в виде
О т _ ZO(s) ?«-'")];	5)
I ZGis)/^ ’
где п — порядок знаменателя ZG(s) и т — порядок числителя
ZG(s).
Так, для нашего примера
Z[G(s)] =---izffc ПРИ ^=1, w = l
г|0(5)]=т_1^;
передаточной функцией моделирующего разностного уравнения бу-
дет
х (1 — е~г/т) z
f ~ z-e^
Подобным же образом производится моделирование колеба-
тельного звена
-° =Z--------2Jo---=Z(e-^ sin «>0/)=-----------------------------
(s 4-a)2-J-<oq	'	g2—2ze aT cos {<^T) 4- e
Теперь
ZO(s)U
_____e aT sin (<oq T)___
1 — 2e—aT cos (w0 T) + e~2аГ
и n=2, в то время как m=l. Так, передаточная функция моделиру-
ющего разностного уравнения примет вид
[ 1 — еГаТ cos (ц>р Г) 4- е—2аГ] z2
z^ — 2z &~аТ cos («о Т) 4- е—2аГ
что приведет к разностному уравнению модели
<р„=2е-вГ cos (<о0 Т)	— е-2вГ <р„_2 + (1 — е“аГ cos (®0 D + е“2вГ) /„.
Просто, не так ли?
Некоторые выражения в знаменателе ZG(s) вида (z—1) не по-
зволяют
[Z О «_,]-*
стать определенным. В этих случаях мы прибегаем к помощи ори-
гинала решения упрощенного разностного уравнения или разделя-
ем ZG(s) =H(z) на две части:
-^=/Z(z)=F(z)S(z).
140
Тогда процесс обратится в последовательность двух разный
уравнений
Например, \/s(s + a) обладает ^-преобразованием
z (1 — е~аГ)
(г-1)(г-е-аГ)'
Это может выглядеть как

к
1=е£
z-e~aT
Применяя метод решения упрощенного разностного уравнения
(4.5) к первой части, найдем
-£ТГ= (1---~-ar-=>/"=(е-ЛГ)<1 - е“аг)
г—е~аТ
Тогда вторая часть обращается при помощи метода решения
упрощенного разностного уравнения (4.4) к виду:
у Tz ______	I
-f-=—г => ^=^-1+Г'Л-
Так, соединяя систему уравнений
/п=е-вгг-я_1_|_(1 _е-ат)Хя. уп== ^я1_|_ т1п,
можно моделировать систему l/[s(s+a)].
Другой способ виден из записи, в которой применяются два
разностных уравнения для моделирования этого процесса:
Возвращаясь к другим упрощающим методам получения пере-
даточных функций разностного уравнения, найдем, что упрощаю-
щий преобразователь перестройки первого порядка образует пере-
даточную функцию для нашего процесса первого порядка
X	(Зг—1)Г/2ч
/	(г-е-^) ’
из которого получается разностное уравнение
(3/„- /„_!).
При треугольном преобразователе передаточная функция при-
нимает интересную форму:
X ________(z2 + г) T/2v___
f z2 — (1 + e-r/t) z 4- e-r/T ’
которая обращается в разностное уравнение
х„ = (’ - е-гл) Хп^ - е-г/хХя_2_|_^
Передаточная функция является квадратичной и обладает дву-
мя полюсами при 1 е_//т. Динамический эффект полюса при 1 ком-
пепсируется нулем при —1.
Наконец, передаточная функция при упрощенном дискретно-
аналоговом методе с компенсацией коэффициента усиления, пере-
менного по фазе, имеет вид
х г X (Т/т) [у* + (1 - у)]
/	(г-е~г/т)
которая обращается в разностное уравнение
=e-r/’x„_j +X (Г/т) [у/„ + (1 - у) /„-J.
Заметим, что при у=1 п Х=(1 — е-7'/'')/(Г/т) это разностное
уравнение становится искомым разностным уравнением. Более под-
робно об этом будет сказано ниже.
Очевидно, что все эти полюсы находятся справа. Некоторые вы-
ражения содержат дополнительные нули, что может привести к до-
полнительным корням при использовании систем с обратной
связью.
В итоге методы решения упрощенных разностных уравнений
приводят к дискретным аппроксимациям, конечные значения кото-
рых могут отличаться от тех же конечных значений аппроксимиру-
емой непрерывной системы. Исключением из этого правила явля-
ется процесс компенсации нулевого порядка, что прослеживается
в (4.5). Этот упрощенный метод приводит к разностному уравне-
нию, которое можно применять во многих случаях. Полюсы дис-
кретной системы подбираются по полюсам непрерывной системы.
Хотя окончательное их значение при малых периодах точно не
совпадает со значениями корней этих систем, аппроксимация не-
прерывной системы первого порядка все же близка к ним.
Кроме того, если конечное значение непрерывной системы мо-
жет быть определено, то можно применить дополнительную посто-
янную в числителе передаточной функции, для того чтобы подо-
брать конечное значение дискретной системы, соответствующей
значению непрерывной системы.
Наконец, и что самое важное, решение упрощенного разностно-
го уравнения приводит к табличному методу поиска простого z-npe-
142
образования для определения разностных уравнений для всех пе-
редаточных функций.
Ряд разностных уравнений, полученных применительно к этому
методу, представлен в табл. 4.1.
4.6. МЕТОД ФАУЛЕРА *	_	;
При изучении сложных линейных систем с нелинейными элемен-
тами, такими, как мертвые зоны или ограничители, необходимо от-
делить линейные элементы системы.
Например, как показано на рис. 4.17, в простой системе с огра-
ничением скорости первого порядка мы видим, что необходимо за-
писать эту систему, как процесс с обратной связью вместо единич-
ной передаточной функции 1/($+1). Моделирование этой системы
требует большей тщательности для получения соответствующих
моделирующих разностных уравнений.
М. Е. Фаулер изучил эту систему достаточно детально. Его ра-
бота широко известна проектировщикам управляющих систем и ин-
женерам по моделированию, как способ преодоления опорных мо-
ментов в применении линейных методов для изучения нелинейных
процессов. Фаулеровская методика приводится здесь из-за харак-
терных особенностей, полезных для широкого класса задач моде-
лирования непрерывной системы.
Применяя метод Фаулера в течение восьми лет, автор пришел к
заключению, что он позволяет осуществлять высокоточное цифро-
вое моделирование линейных и некоторых нелинейных процессов.
Фаулеровское объяснение пути, по которому он пришел к дан-
ному методу, базируется на комплексе результатов, которые он по-
лучил за годы работы в четырех областях: линейных непрерывных
систем, линейных дискретных систем, нелинейных непрерывных
Рис. 4.17. Простая нелинейная непрерывная система
* «А New Numerical Method for Simulation», Simulation, vol. 6, No. 2,
pp. 90-92, Fabruary 1966; vol. 6, pp. v and vi, June 1966; vol. 8, pp. 308—310,
June 1967.
143
Таблица 4.1
Разностны? уравнения для цифрового моделирования

Рекуррентная формула (нижний индекс л относится к числу
переходов в уравнении)
1
s + a
1
($ 4- д)2
<*>0
«S2 +
S
(1-е~дГ)г
(1 —e~gr)2g2
(г-е-*г)2
(2— 2 COS (OgT) Z2
^2 — 2z COS wo т + 1
z (1 — cos <о0Г)—1 (z —cos mqT)
Уп = (e aT) yn-i + (1 — e aT) xn
Уп={^ аТ)Уп-\—(с 2вГ) У п-2 + U —1е аТ)2ха
Уп = (2 cos a>oТ) у— уп-.2 + (2—2 cos ш0Т) хп
Уп = (2 cos шоО Уп-1 — У п-2 +
«2+ “о
<*>0
(s + a)2 + <0q
z% — 2z cos <o0 T + 1
(1 — 2e aT cos top Г + e 2дГ) z^
Z2 __ z2eTaT cos (OqT + e~2aT
COS <*>о
1 — COS <jOq Т
Уп=2(е аГ cos ЩТ) Уп-l —2аГ) У п-2 +
4- (1 — 2е—аГ cos a>o Т 4- е“2аГ) хЛ
-H-=G(s)
X
--T(z)
X
(s 4-a)
(s 4- a)2 4- °o
(1 — e grcos(oqT)—1 [гг2—(e аТсоз^Т)г]
z% — z2e~aT cos a>0 T 4- e~2gr
Tz
z — 1
1
«2
(s-t-c) (b—a)
(s + a) (s + b)
T?Z
(г-1)2
(c — д)(1 —e'“T)z (6—c)(l— e bT)z
_________________________fc-T*
______ab
(s + a) (s + b)
Tz __________bTz_______
z — 1 + (a — b) (z — e-er)
_______aTz________
(a—b) (z—e~bT)
Продолжение табл. 4.1
Рекуррентная формула (нижний индекс л относится к числу
переходов в уравнении)
Уп = 2 (е аТ cos (О0 Т) yn-i — (е 2аГ) уп_2 +
е аТ cos (oq Т \
--------------- *л-1
1—е ai coswqT /
Уп — Уп—1 + Тхп
Уп = 2</л—1 — У п-2 + Т^Хп
Уп — On + Рп
On = е~аТОп-1 + (с — а) (1 — е~аГ) хп
Рп = е~ЬТРп-1 + (Ь - с) (1 - e-w) х„
Уп— Оп + Рп+ $п
On = On-1 + Тхп
Рп = е-аГ Рп-1 + ( У . ) хп
\ а — О )
Q	( ЛТ \ у-
— е дл-1+	] хп
\ а — /
систем и нелинейных дискретных систем. Никому в Соединенных
Штатах не удалось иметь такой опыт в данной области. Когда он
сжал весь этот накопленный опыт и поместил сущность результа-
тов в одну статью или одну лекцию, бывало трудно для не имею-
щих практики следовать за развитием его мысли. По мнению авто-
ра, именно это приводило к некоторой критике работы Фаулера.
Прошло много времени с тех пор, когда метод был впервые сфор-
мулирован, и он выдержал испытание временем.
Вероятно, эта глава и тщательно подобранный пример проил-
люстрируют неоспоримым образом полезность метода Фаулера.
Фаулер сделал интересное заключение, что если кто-либо синте-
зирует дискретную систему, все линейные элементы которой обла-
дают «характерными» корнями, и если 1/з заменяется на Tz/z—1
(во всех случаях), то цепь этих линейных элементов может быть
замкнута и систему можно рассматривать как замкнутую, при этом
она:
—	обладает рядом полюсов справа;
—	может быть подобрана для получения требуемого конечного
значения выходного параметра;
—	может быть скорректирована для того, чтобы получить тре-
буемую фазу;
—	может быть отрегулирована таким образом, чтобы полюсы
замкнутой цепи имели необходимые значения.
На основании этих позиций Фаулер создал метод, который те-
перь носит его имя.
Кроме того, рассмотрим простую нелинейную систему, представ-
ленную на рис. 4.17.
Эта система действует как линейная система до тех пор, пока
величина х2 не станет достаточно большой, чтобы достичь предела
х3. При |х2| за зоной, допускаемой ограничителем линейности, х3
ограничено до величины а или —а, в зависимости от того, является
ли х2 положительной или отрицательной.
Если система действует в линейной области, она обладает пере-
даточной функцией
•Ч 1
Xi , TS + 1
которая имеет единственный полюс при
		1_
®1ЮЛЮС______ •
и
Можно подвести некоторый итог по методу Фаулера* *.
Для синтеза дискретного аналога непрерывной системы исполь-
зуют ее структурную схему в следующей последовательности:
Этап 1. Подставляем Tzl(z—1) для каждого Ifs.
Этап 2. Подставляем
И —	для каждого O(s).
	Z \ S J
* Это является авторской интерпретацией работы Фаулера.
146
Рис. 4.18. Дискретная система для моделирования системы, представленной на
рис. 4.17
Этап 3. Добавляем операцию k в прямую цепь, значение кото-
рой может быть установлено по местоположению полюсов замкну-
той цепи.
Этап 4. Добавляем передаточную функцию на входе для полу-
чения реакции замкнутой линейной системы, подобной исходной
системе.
Применяя метод Фаулера к задачам-примерам, можно соста-
вить структурную схему дискретной системы, представленную на
рис. 4.18.
В этом примере мы не используем этап 2. Если х3 имеет предел
и эта система является линейной дискретной системой, то она име-
ет передаточную функцию
kTzI(z) =H^J^
z— 1 +kT '
которая обладает полюсом при гПОлюс=1—kT.
Для приведения в соответствие полюса дискретной системы с
полюсом непрерывной системы нам необходимо, чтобы
^НОЛЮС == е^ПОЛЮС т или чтобы 1 — &Г = е“7Л
11ГМ**
Так, если мы установим
l-e"7^
k
Т
можно гарантировать, что дискретная система с обратной связью
будет вести себя подобно непрерывной системе с обратной связью
Рис. 4.19. Дискретный аналог непрерывной нелинейной системы
147
Рис. 4.20. Дискретный аналог нелинейной системы, представленной на рис. 4.19,
при выходе х3 за предел мнимой оси
при х3, выходящем за предел. Мы можем теперь начертить блок-
схему моделируемой дискретной системы, как показано на рис. 4.19.
Эта система обладает передаточной функцией замкнутой цепи
=I (г) (1~е ГЛ)г-.
Если х3 выходит за предел, то было бы желательно, чтобы дис-
кретная система, представленная на рис. 4.19, вела себя подобно
дискретной системе, показанной на рис. 4.20, где C(s) компенси-
руется при искажении, вводимом H(s).
Для этого примера будем применять преобразователь нулевого
порядка (1 — e~sT)/s и компенсацию esT/2 для компенсации запаз-
дывания вполовину периода, вводимого преобразователем.
Таким образом, целесообразной передаточной функцией для
дискретной системы, которую мы пытаемся получить для модели-
рования нелинейного процесса, является
/ х4 \ =2/1 ~(&st/2\ ( 1 \ = (1 — е~г/2т) г + (е~г/2т — е~г/т)
\ *1 )d \ s /	+1 /	г—e~T/‘t
Чтобы найти /(z), мы приравниваем эту передаточную функцию
к действительной передаточной функции дискретной моделирую-
щей системы:
Xj  / Х4 \
*1	\ *1 /р’
(1-е-Г/2г)г + (е-Г/2г_е-Г/Т)
,(1- e-r'2t) Z + (е"^- е~^)
1 ’	(i_e-^)z	•
Окончательной формой дискретного моделирования нелинейного
процесса может быть структура, показанная на рис. 4.21.
Следует сделать следующие замечания:
— эта методика достаточно сложна для того, чтобы в системах
более высокого порядка обойтись без специальной аналитической
помощи. Фаулер предвидел эту необходимость и разработал про-
грамму ВМ для осуществления метода. Программа, являющаяся
148
Рис. 4.21. Окончательная форма дискретной системы, предназначенной для моде-
лирования нелинейной системы, представленной на рис. 4.17. Здесь а=1 —
— е~г/2х; b = е~г/2х — е“г/х; с = 1 — е-г/х; k == (1 — е-г/х)/Т
коммерчески пригодной, содержится в ВМ с наименованием CSAP
или «Control Systems Analysis Program»*;
— I(z) может быть приравнена к единице и коэффициент уси-
ления k может быть определен эмпирически методом проб и оши-
бок. Это устраняет необходимость CSAP и обеспечивает полу-
чение результатов, которые являются достаточно точными для мно-
гих случаев прикладного моделирования;
— автор удержался от обсуждения поведения корней нелиней-
ного процесса в плоскости s. Здесь обсуждается создание в линей-
ной дискретной системе с замкнутым циклом режима, подобного
режиму линейно-дискретной системы с желаемой передаточной
функцией. Это происходит из представления о том, что если нели-
нейная система линеаризуется, то она ведет себя аналогично сис-
теме, показанной на рис. 4.20;
— этот интересный результат дает возможность утверждать»
что, так как информационный поток дискретной системы аналоги-
чен информационному потоку непрерывной системы, то дискретная
нелинейная система будет вести себя так же, как непрерывная не-
линейная система. И это несомненно так.
На рис. 4.22 показано моделирование системы, представленной
на рис. 4.23, по методу Фаулера. Целью является получение пере-
даточных функций с полюсами и нулями передаточных функций
замкнутых циклов с желаемой аппроксимацией.
Метод, примененный Фаулером для синтеза моделирующих сис-
тем, позволил впервые получить полюсы для функций, полученных
^-преобразованием.
Рис. 4.22. Модель системы, изображенной на рис. 4.23. Представлена благодаря
любезности фирмы Интэрнэйшнл Бизнэс Машинз Корпорэйшн
♦ Программа анализа управляющих систем (примеч. ред.).
149>
Рис. 4.23. Нелинейная непрерывная система, примененная Вейснером для срав-
нения численных методов цифрового моделирования. Представлена благодаря
любезности фирмы Интэрнэйшнл Бизнэс Машинз Корпорэйшн
Для первой передаточной функции
5
s + 2
полюс в записи через ^-преобразование есть г —е~2Г; при 7 = 0,5
имеем z— 0,3679.
Передаточная функция, полученная ^-преобразованием, которая
применяется при интегрировании 1/$, имеет вид:
Tz
Z — 1
Заметим, что для вычисления внутренних передаточных функ-
ций нет необходимости использовать аппроксимации на входе.
Только те передаточные функции, которые обладают дискретизиро-
ванными входами, подходят к этим условиям.
Выражения в числителе для внутренних передаточных функций
определяются относительно просто согласно следующему правилу:
коэффициент усиления установившегося состояния передаточной
функции области z приравнивается к такому же коэффициенту пе-
редаточной функции области s.
Для многих линейных систем установившееся состояние может
быть вычислено приравниванием $ = 0 и г=1 в функции #(z). Для
передаточной функции области s коэффициент усиления является
отношением постоянного члена числителя к постоянному члену зна-
менателя. В случае установившегося состояния коэффициент уси-
ления передаточной функции области z является суммой коэффи-
циентов числителя, деленных на сумму коэффициентов знамена-
теля.
Для передаточной функции
5
s 4- 2
коэффициент усиления передаточной функции равен 2,5.
Как было указано ранее, полюс соответствующей г при Г=0,5
есть z — 0,3679.
Таким образом, 0,6325 — это сумма коэффициентов знаменате-
ля. Тогда сумма коэффициентов числителя должна быть
-0,6325X2,5=1,581.
150
В случае, если числитель либо знаменатель не имеют постоян-
ного значения, нужно разделить s на соответствующий коэффици-
ент. Например, передаточная функция
_______________________________
s2 4- 2s
может быть подобрана делением знаменателя на з, чтобы получить
две умножаемые функции
/_1\ / 5 \
\ з / \ з 4- 2 /
Передаточная функция, соответствующая ^-преобразованию,
может быть записана в форме
/ А \ / В \
1 / \z — o~2r) ’
Используя соотношения \ls-+Tzl(z—1) и s->(z—1)/Tz, можно по-
казать, что передаточная функция остаточного члена коэффициен-
та усиления установившегося состояния может быть найдена по
правилу, представленному ранее.
Коэффициенты числителя, необходимые для получения правиль-
ного установившегося значения, затем соединяются в один, который
применяется как коэффициент при наибольшем значении степени
(наибольшая степень знаменателя). Передаточные функции, пред-
ставленные на рис. 4.22, были получены Фаулером, применявшим
методику, которая была только что изложена.
На рис. 4.24 показано местоположение корня части замкнутой
цепи системы, представленной на рис. 4.22, как функции Кь для
случая Ка = 1. Здесь Кь — коэффициент усиления прямой цепи, вве-
денный в прямую цепь системы (см. рис. 4.22). Он используется
как способ графического изображения местоположения корня сис-
темы, если с ней работают как с линейной системой.
Можно видеть, что местоположение корня корректируется так-
же в непрерывной системе за исключением значений Кь (рис. 4.25).
Если Ка = 0,903, корректировка корней верна при KL=l. Корректи-
ровка при Kl<1 неточна, но достаточна. Этот ввод и корректиров-
ка Ка в данном случае являются необходимыми для получения
правильного промежуточного ответа при моделировании замкнуто-
го контура.
В некоторых случаях может быть необходимо включить транс-
портную задержку в контур. В системах высшего порядка при
^-преобразованиях могут образоваться значительные опережения, и
местоположения корня выйдут за пределы мнимой оси. Это может
быть скорректировано добавлением одного или нескольких членов
в числителе.
Влияние добавочных (запаздывающих) членов в числителе пе-
редаточных функций состоит в повороте местоположения корня по
направлению к мнимой оси.
151
m(s;
Lmtsj
Рис. 4.24. Положение корня непре-
рывной нелинейной системы при ее
линеаризации и Хз, выходящем за
предел мнимой оси. Представлен бла-
годаря любезности Интэрнэйшнл Биз-
нес Машинз Корпорэйшн
KL= 1,0
KcOtW2
8^0,384
2,5
2,0
1,5
1,0
0,5
Re-----------х-”> ।------------U
-2,5 -7,0 -1,5 -1,0 -0,5
Рис. 4.25. Положение корня при мо-
делировании по методу Фаулера.
График представлен благодаря лю-
безности Интэрнэйшнл Бизнэс Ма-
шинз Корпорэйшн
И теперь единственно, что остается вычислить, — это аппрокси-
мацию на входе. Это можно осуществить так же, как и раньше.
Желаемой передаточной функцией при 7=0,5 является
z / 5Я0 е~°>255 \  0,12985*2 4- 0,51604* + 0,06657
\ $2 4- 2s + 5 /	*2 4- 0,65542* 4- 0,36788
Передаточная функция найдена:
0,1825*2 4- 0,7245* 4- 0,093
*2
Этим подтверждается, что данная передаточная функция на
входе, умноженная на передаточную функцию замкнутого контура
x5/xi рис. 4.22, даст желаемую передаточную функцию.
Результаты данного моделирования, где использован ступенча-
тый вход, представлены на рис. 4.26.
Разностными уравнениями, которые использовались для полу-
чения результатов, являлись
хг = 0,1825%! + 0,7245%! (- 1) + 0,093%! (- 2);
x2=xi—х5( —1);
х3=0,3675х3 (-1)4-1 ,428х2;
х4=х3, если х3^Спредельному значению; х4 = предельному значению
со знаком хз, если Хз>предельного значения;
*5=xs(— 1) +0,5х4.
132
?ис. 4.26. Реакция на ступенчатое
воздействие, ограниченная при t—
= —0,25. График представлен благо-
даря любезности Интэрнэйшнл Биз-
нес Машинз Корпорэйшн
Рис. 4.27. Моделирование с использованием метода подстановки Тастина. Пред-
ставлено благодаря любезности Интэрнейшнл Бизнес Машинз Корпорэйшн
Рис. 4.28. Реакция модели на ступенчатый вход при использовании метода Тас-
тина. Представлено благодаря любезности Интэрнэйшнл Бизнэс Машинз Корпо-
рэйшн
153
Следует заметить, что х2 вычисляется с помощью последнего
значения х&. Это самое последнее имеющееся значение х5, так как
текущее значение в этой системе уравнений вычисляется пос-
ледним.
Для сравнения этого метода с другими, часто применяемыми,
Фаулер разработал метод подобия в моделировании при помощи
метода Тастина* (рис. 4.27). Результаты моделирования для вели-
чины ступеньки, равной 2, по методу Тастина представлены на
рис. 4.28. Этот пример включен здесь только из-за того, что он ил-
люстрирует важность положения о том, что даже прекрасный метод
Тастина может привести к затруднению, если используется непра-
вильно.
Вероятно, самой значительной причиной применения дискретно-
аналогового метода, или метода Фаулера, является то, что сам ме-
тод заставляет исследователя осмыслить его систему. Подстановоч-
ные методы Тастина, Труксаля и других авторов этого сделать не
могут. Их методики пригодны для получения системы уравнений.
Однако по ним трудно сказать, насколько подобна или не подобна
полученная дискретная система той, которую они собираются мо-
делировать.
Глава 5. СУЩНОСТЬ МЕТОДОВ
ПОДБОРА КОРНЕИ
В гл. 4 мы обсуждали метод Фаулера для моделирования ли-
нейных систем с включением нелинейных элементов, передаточная
функция замкнутого контура которых корректируется передаточ-
ной функцией разностного уравнения, полученного с использовани-
ем дискретно-аналогового метода.
По ходу изложения при обсуждении особенностей моделирова-
ния в гл. 4 мы уже говорили о необходимости нахождения корней
непрерывного дифференциального уравнения по корням модули-
рующего разностного уравнения, что составляет сущность модели-
рования непрерывных процессов. Эта тема рассматривается в дан-
ном специальном разделе из-за того, что некоторые детали подбо-
ра корней достаточно запутаны и нуждаются в специальном объ-
яснении. Кроме того, понятие подбора корней в разностном урав-
нении по таким же корням дифференциального уравнения пони-
мается лучше при применении преобразований Лапласа, где урав-
нения движения характеризуются передаточными функциями.
На прошедших семинарах по современному состоянию числен-
ных методов после опубликования работы Фаулера ** автор часто
слышал критику в том же духе, что и критика метода Фаулера по
* См. прил. А.
♦♦ «А New Numerical Method for Simulation», Simulation, vol. 6, No. 2, pp. 90—
02, February 1966; vol. 6 pp. v and vi, June 1966; vol. 8, pp. 308—310, June 1967,
154
поводу методов подбора корней. Так как его работу можно рас-
сматривать как специальный случай изложенных здесь методов, то
основная критика была направлена по поводу перенесения методов
синтеза и анализа линейных непрерывных систем на нелинейные
системы. Кроме того, метод Фаулера в некоторой степени трудно
применять инженерам, начинающим работать в области модельно-
го проектирования, из-за того, что требуется глубокое знание
свойств как непрерывных, так и дискретных систем.
Работа Фаулера может быть охарактеризована как метод под-
бора корней системы разностных уравнений с помощью корней
системы дифференциальных уравнений. В этом случае подбор сис-
темы корней разностного уравнения с помощью системы корней
дифференциального уравнения является специальным случаем ме-
тода Фаулера.
Методы подбора корней для дискретизированных непрерывных
систем были изучены большим числом аналитиков, работающих в
области управляющих систем; среди них Ту, Жюри, Корн, Фран-
клин, Калман.
В действительности, в рекуррентных формулах состояния, по-
лученных многими новаторами того времени, их корни подбира-
лись в соответствии с корнями дифференциальных уравнений, опи-
сывающих непрерывный процесс. Все это указывает на причины
того, что разностные уравнения с подобранными корнями являют-
ся предметом меньшей критики, чем метод Фаулера.
Идея применения разностных уравнений с соответственно по-
добранными корнями приходила в голову не только известным
ученым фундаменталистам, но и инженерам-исследователям во
всем мире, занятым моделированием. Дэн Розамонд из Мак-До-
нелл Дуглас Корпорэйшн, Билл Эдвард из Локхида, Дэйв Лэнг и
Рональд Баулез из НАСА, Стейман от Боинга вместе с Эллиот
Пуйроном, Брайном Шонмакером и другими авторами и членами
служебного персонала проектировщиков, осуществляющих модели-
рование со сменным экипажем программы Аполлон, были среди ин-
женеров, применявших метод подбора соответствующих корней
или ему эквивалентного метода для моделирования непрерывных
систем. Они обратились к этим методам, так как для решения
задач в науках, связанных информатикой (т. е. связь, управление,
проектирование ВМ), стало использоваться моделирование класси-
ческими численными методами, которые часто приводили к значи-
тельной числовой неустойчивости и требовали стабилизации цифро-
вого моделирования при малом шаге. Это в лучшем случае приво-
дит к удорожанию моделирования, а *в худшем случае к неточно-
сти моделирования (из-за округленной ошибки). Многие классиче-
ские методы неприменимы для моделирования в реальном масшта-
бе времени, как это требуется для человека, находящегося в конту-
ре тренажера, из-за того, что:
— время, требуемое для выполнения одного прохождения через
программу моделирования на ВМ, больше, чем наибольший раз-
мер шага, необходимый для сохранения устойчивости;
155
•— при численных методах моделирования динамики движения
в ряде случаев не могут сохраниться как устойчивость, так и точ-
ность.
По-видимому, естественно приступить к решению задачи о чис-
ловой неустойчивости регулированием корней моделирующей сис-
темы методами подбора их соответствующих значений.
Классические численные методы сфокусированы в основном на
числовой точности, а современные методы, на основании работы
Норберта Винера 1943 г., обращены как к числовой точности, так
и к числовой устойчивости. При этом одновременное соблюдение
устойчивости (в частотной области) и точности (во временной об-
ласти) при проектировании более выгодно, чем проектирование с
каждой точки зрения в отдельности.
5.1.	МЕТОДЫ ПОДБОРА СООТВЕТСТВУЮЩЕГО КОРНЯ
Под числовой неустойчивостью в моделировании обычно пони-
мается несвязанная сложная числовая ошибка, вытекающая либо
при ограничении, либо при округлении, либо от комбинаций обеих
мер. Одним из подходов к решению вопроса об ошибке ограниче-
ния является уменьшение размера шага в задаче моделирования
до такой величины, чтобы разностные уравнения моделирования
или процесс численного моделирования стал устойчивым. Затем
проводятся испытания для определения минимального шага, при
котором ошибка округления приводит к значительной ошибке в мо-
делировании. В основном это не является проблемой при исполь-
зовании больших вычислительных машин. Однако для миником-
пьютеров и микрокомпьютеров * ошибка округления наименьших
значащих цифр может, например, иногда приводить к ошибкам в
значащих цифрах разности больших чисел. Обычно находят алго-
ритмы моделирующих систем для устранения неустойчивости, воз-
никающей из-за ошибок (от отбрасывания членов и округления).
Методы подбора соответствующего корня совершенно непохо-
жи ни на применяемые дискретно-аналоговый метод, ни на метод
подстановки **.
Эти методы особенно полезны при моделировании линейных
стационарных систем, являются ли они непрерывными или дискрет-
ными и основаны ли они на той концепции, что любой метод мо-
делирования в конце концов сводится к разностному уравнению
или системе разностных уравнений, которые могут быть решены
на цифровой ВМ.
Система разностных уравнений будет иметь ряд характеристи-
ческих корней, конечных значений выходных параметров и неко
торого фазового соотношения непрерывной системы, которую пы-
таются промоделировать. Кроме того, в любой системе дискретных
моделирующих уравнений: 1) разностные уравнения будут в пре-
деле при стремлении шага к нулю приближаться к дифференци-
* На 16 бит и 8 бит соответственно.
♦* См. прил. А.
156
альным уравнениям; 2) полюсы, нули и конечное значение диск-
ретной системы будут приближены к полюсам, нулям и конечному
значению непрерывной системы. Интуитивно, видимо, можно ожи-
дать, что если синтезируется система разностных уравнений, полю-
сы, нули и конечное значение которой подобраны в соответствии с
непрерывной системой на выходе, мы можем получить систему
моделирующих разностных уравнений для моделирования непре-
рывной системы.
Без сомненния, это именно так. Целью подбора соответствую-
щих корней при моделировании является образование разностных
уравнений, динамические характеристики которых подобны дина-
мическим характеристикам непрерывной системы, которая моде-
лируется. Так как динамические характеристики непрерывной сис-
темы полностью характеризуются ее корнями и конечным значе-
нием, то, по-видимому, можно осуществить подбор корней и конеч-
ного значения моделирующего разностного уравнения в соответст-,
вии с теми же величинами системы, которая моделируется.
Метод подбора соответствующего корня подобен дискретно-
аналоговому методу: оба фокусируются на динамических характе-
ристиках процесса, который моделируется, и ни один из них не
включает численного интегрирования.
Метод подбора корня не похож на дискретно-аналоговый ме-
тод, так как первый является аналитическим методом для синтези-
рования разностного уравнения, чтобы моделировать непрерывный
процесс, в противоположность методу синтеза дискретной системы,
сходной с непрерывной системой.
5.2.	ПОДБОР ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК
ПЕРЕДАТОЧНОЙ ФУНКЦИИ РАЗНОСТНОГО УРАВНЕНИЯ
В СООТВЕТСТВИИ С ПЕРЕДАТОЧНОЙ ФУНКЦИЕЙ
ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
Цель подбора динамических характеристик — синтез разност-
ного уравнения, чтобы:
—	иметь такое же число полюсов и нулей, как в дифференци-
альном уравнении, описывающем непрерывный процесс;
—	иметь полюсы и нули, подобранные в соответствии с полю-
сами и нулями в дифференциальном уравнении;
—	иметь конечное значение, подобранное в соответствии с ко-
нечным значением дифференциального уравнения;
—	регулировать фазы для лучшего подбора реакции дискрет-
ной системы в соответствии с реакцией непрерывной системы.
Эта цель может быть достигнута для передаточных функций
следующим девятиступенчатым алгоритмом.
1.	Определение передаточной функции, необходимой для моде-
лирования при помощи преобразования Лапласа.
2.	Вычисление полюсов и нулей передаточной функции, пред-
ставленной в этапе 1.
157
3.	Отображение полюсов и нулей s-плоскости в z-плоскости, ис-
пользуя соотношения
О' ----р $ПОЛК><Л- Z -р!®НУЛ1Л
^полюс v	’ ^нуль v
4.	Образование полинома передаточной функции в z-преобра-
зовании с полюсами и нулями, определенными в этапе 3.
5.	Определение конечного значения непрерывной системы на
реакцию единичной ступени.
6.	Определение конечного значения дискретной системы на ре-
акцию единичной ступени.
7.	Подбор конечного значения дискретной системы в соответст-
вии с конечным значением непрерывной системы введением посто-
янной в передаточную функцию, образованную на этапе 4.
8.	Добавление корней к передаточной функции дискретной сис-
темы до тех пор, пока порядок знаменателя дискретной системы
не будет соответствовать порядку числителя дискретной системы.
9.	Обратное z-преобразование z-передаточной функции, полу-
ченной на этапе 8, для образования моделирующего разностного
уравнения.
Для развития разностных уравнений, использующих этот алго-
ритм, система должна удовлетворять следующим условиям:
—	быть линейной;
—	обладать преобразованием Лапласа;-
— быть асимптотически устойчивой и удовлетворять теореме ко-
нечного значения: кроме того, конечное значение не должно рав-
няться нулю.
Разностное уравнение, образованное данным способом, не
только устойчиво, но и точно, т. е. решение однородного разност-
ного уравнения точно подбирается в соответствии с однородным
решением дифференциального уравнения.
Разностное уравнение позволит с достаточной точностью вы-
числить последовательность дискретных значений решения одно-
родного непрерывного процесса и позволит точно вычислять после-
довательность решения непрерывной системы при ступенчатых
функциях возмущающего воздействия. Из этого следует, что по-
скольку последовательность значений дискретизируется при часто-
те, по крайней мере в два раза превосходящей (номинально от 5
до 7 раз) наибольшую частоту функции возмущающего воздейст-
вия, для моделирования реакции непрерывной системы на произ-
вольную функцию возмущающего воздействия можно применить
разностное уравнение.
Пример. Получить разностное уравнение для моделирования
простой системы xx+x=f.
Этап 1.
хх-\^х= f при х(0)=0;
Z.(tx+x=/)=(ts+
X __ 1
f w 4- Г
158
Этап. 2
$ полюс
Этап 3
Z	— р 5полюс^ — р—Г/т
полюс * * * * v * * * *	v .
Этап 4
1	_ Р
z — е~т,х q
Этап 5
$"для теоремы о конечном значении Преобразрвание Лапласа единичной£ступени (U)
„ ......................... „ - ............... ~
lim s ——	— | =1.
$->o I \us 4- 1/ \ s J)
LT—передаточная функция системы
Этап 6
Z—1
---для теоремы о конечном значении
z
Z-преобразование (ZF) единичного шага
1
1
г-е^
г->11 z \ z—е—*'* )\z — 1/J	1—е т!х
ЕТ—пъуъда'гъч.кая. функция моделирования
Этап 7
х ~k р — k
f q
h
Подбор конечного значения =>-----гт;=1-
1 —Q—'
*=1-е-гл.
С учетом этого
1-е-г^
k
г_й~Т!^
Этап 8
х (1 — е г/х)
/ - 2-е~г^
Этап 9
х — г-1 е~т/х х—(. 1 — е-7'/’) /.
Произведем обратное Z-преобразование (для проверки):
хя—е~т/х хя-1=(1 - е-г/') /я.
159
5.3. ЗАМЕЧАНИЯ О МЕТОДЕ ПОДБОРА СООТВЕТСТВУЮЩЕГО КОРНЯ
Некоторыми узкими местами в методе подбора соответствую-
щего корня являются следующие положения.
1. Теорема о конечном значении должна привести к результа-
ту, не равному нулю, иначе величина подобранной постоянной, со-
ответствующей конечному значению, не может быть определена.
Это может произойти у большого числа систем как реакция на про-
изводную входного сигнала или при ступенчатом входе, когда их
значение разно нулю. В этих случаях существуют две альтерна-
тивы:
а)	вычислить реакцию при устойчивом состоянии на единичный
пилообразный импульс;
б)	переписать передаточную функцию системы так, чтобы диф-
ференцирующее устройство проявлялось как дополнение к фильт-
ру с ограниченной пропускной способностью.
Дополнительное фильтрование изложено в этой главе дальше.
2.	Корнями непрерывной системы второго порядка могут быть:
а) действительные и равные (предельно демпфируемая реак-
ция);
б)	действительные и не равные (демпфируемая реакция);
в)	комплексные и сопряженные (колебательная реакция).
Для каждого из этих случаев требуется свое уравнение.
Дело в том, что каждое разностное уравнение действительно
только для определенной области в плоскости — s или z. Эта ситу-
ация, очевидно, характерна не только для систем второго порядка,
но для систем более высокого порядка.
3.	Разностным уравнениям, полученным этим способом, прису-
ща устойчивость, если система, которую они моделируют, являет-
ся устойчивой. РАЗМЕР ШАГА НЕ ИГРАЕТ НИКАКОЙ РОЛИ!
Проверим это на нашем примере, заметив, что
^полюс=е-г/’ <1 при Т'/т > 0.
Важно то, что разностное уравнение
=е-г/т хл_! + (1 - е-г/т) /„ при т > 0
не может стать неустойчивым. Моделирование при помощи данно-
го уравнения устраняет проблему числовой неустойчивости!
Это справедливо для всех разностных уравнений, полученных
только что описанным способом. Так как моделирующие разност-
ные уравнения не могут стать неустойчивыми, возникает вопрос,
как установить скорость квантования?
Ответ определяется теоремой Шеннона.
5.4.	ТЕОРЕМА ШЕННОНА И ЕЕ ЗНАЧЕНИЕ ДЛЯ МОДЕЛИРОВАНИЯ
Теорема Шеннона. Если функция f(t) не содержит частот вы-
ше, чем © герц, то она вполне определяется присущими ей орди-
натами системы точек, находящихся по крайней мере на расстоя-
160
t
Рис. 5.1. Выявление частотных харак-
теристик f(/), представляющих инте-
рес. Особенность этого процесса упо-
минается, например, в книге, содер-
жащей гармонический анализ,
Р.. В. Хэмминга «Численный анализ
для инженеров и исследователей»,
Мак Гроу-Хилл, 1972
с2
пункция.
Ханна f
L L 1 i 11 &
т т т т т т
100
—-------30%
Наибольшая частота,
представляющая
ч интерес, ~4,2Т
L_J___I____
12 3 4 5 6 ы
%
Г Т Т Т Т Т
8,4/Т < ^модуляции < 42/7"
Номинальная а)^дуляции -30/Т
нии 1/(о секунд друг от друга *. В современных терминах мы могли
бы сказать, что если /(/) ограничена поясом при (oL, минимальная
скорость, при которой мы можем промодулировать /(f), это 2<оь.
Так как большинство функций, встречающихся при моделирова-
нии, не ограничены определенной полосой, то минимальная часто-
та, с которой мы проводим модуляцию /(/), должна быть от 5 до
10 раз выше наибольшей частоты, необходимой для описания f(t).
На точный вопрос, что же означает «наибольшая частота», пред-
ставляющая интерес, четкого ответа не существует. Автор приме-
нил следующий метод для определения «HFI» **.
1.	Выбирается участок известной реакции системы, которая мо-
делируется; на участке существуют быстрые изменения состояния
системы.
2.	Вырезается «окно» участка исследуемой функции при помо«
щи функции Ханна.
3.	Вычисляются коэффициенты (частотных составляющих) для
12-членного ряда Фурье выбранного участка.
4.	Корректируются коэффициенты для выбранного участка.
5.	Возводятся в квадрат коэффициенты (вычисление показате-
ля степени составляющих спектра).
* «Communications in the Presence of Noise», Claude E. Shannon, Proceedings
of the IRE, January 1949.
**HFI — наибольшая частота, представляющая интерес (примеч. ред.).
6	493	161
6.	Осуществляется построение графика совокупной части об-
щей энергии, представленной компонентами энергетического спект-
ра.
7.	Выявляется наибольшая частота, представляющая интерес, —
частота, при которой совокупная часть энергетической кривой пе-
ресекает 90% энергетической линии.
Этот процесс отчетливо виден на рис. 5.1.
5.5.	МОДЕЛИРУЮЩАЯ СИСТЕМА ВТОРОГО ПОРЯДКА
Другой, более сложный пример подбора корня сделает метод
более ясным и проиллюстрирует некоторые тонкости, которые
только что обсуждались.
Пример. Система
f $2 + 2£о)л$ -|- а)2
является математической моделью непрерывного процесса второго
порядка с демпфированием £ и собственной частотой <оп. Урав-
нения движения кораблей, автомобилей, самолетов, датчиков, оп-
ределенные экономические явления могут характеризоваться этой
простой системой или по крайней мере обладать ее элементами в
математической модели, которая является такой же системой вто-
рого порядка.
При £=1 эта система обладает двумя реальными корнями
При £ = 0 эта система станет чисто колебательной с парой ком-
плексных сопряженных корней
$ = + ]Л —± /<»л.
При £>1 корни действительны и неравны, система предельно
задемпфирована.
Наконец, при £<1 корни комплексно-сопряженные и имеют
вид
51=	+	1	52 =	— V \ “С2-
Следуя правилу подбора соответствующего корня (при этом,
однако, мы будем двигаться последовательно к характерной форме
передаточной функции разностного уравнения), попытаемся опре-
делить передаточную функцию вида
х (г)________kz^_____
f (z) (z — ztl)(z— гп.с) ’
где	ги = е5иолюсг=^-^пт^^пг
z __ е "опряж. _ ^лт	V1—)в
162
После подстановки и небольших алгебраических преобразова-
ний найдем
х ___________________kz^__________
f z^~z{c2e ^пТ ccs у 1 —С2)1+е 2С<°л7
Допустим,	А = 2 е“Са>лГ cos (юпТ \ 1 — £2), В = е~2:°‘«г.
Применяя теорему о конечном значении и приравнивая конеч-
ное значение дискретной передаточной функции к передаточной
функции непрерывной системы, найдем
Таким образом, передаточная функция моделирующего разно-
стного уравнения примет вид
х __(1 — Л + В) *2
f z^ — Az + В ’
и моделирующее уравнение может быть представлено как
z2x — Azx-[- Вх = {\ —	z<2f-
Для того чтобы получить разностное уравнение в более удоб-
ном виде связи текущих и последующих величин, разделим пра-
вую и левую части на г2:
х-Az~'x + Bz~2x = (l - А + В)
найдем
хп — Ахп_х + Вхп-ъ=(1 “ + #) f п*
Таким образом, моделирующим разностным уравнением явля-
ется
Хп = Ахп-\ ~ ^Хп-2 + (1 ~ А + В) f п.
Для данного случая заметим, что система резонирует при
(О7? = (Оп I7 1— С2.
Если нам ничего не известно о функции возмущающего воздей-
ствия, нужно ее выбирать по крайней мере так, чтобы можно бы-
ло возбудить резонансную частоту системы, которая становится
моделирующей. В этом случае можно установить
7<ол |/1 - С2 < выборки.
Пример переходного процесса этой системы показан на рис. 5.2.
Заметим, что данное уравнение не только точно, но и устойчиво для
больших интервалов.
6*
163
Рис. 5 2. Реакция системы (an2l(s2 + 2£(ons-1-
+ (ог.2) на единичное ступенчатое воздейст-
вие при £=0,3; (Dn = 13 рад/с; (о3=10 вы-
борок в секунду и	— С2) = 5,07
На самом деле, легко можно показать, что
I^полюсов! 1 С0Л 1
для данной системы второго порядка.
5.6.	ПРИМЕНЕНИЕ МЕТОДА ПОДБОРА КОРНЕЙ ПРИ
МОДЕЛИРОВАНИИ ДИСКРЕТНЫХ СИСТЕМ
Нет ничего необычного в том, что встречаются задачи модели-
рования с помощью цифровой системы, когда частота выборки
цифровой модели отличается от частоты выборки в моделируемом
процессе.
Автор встретился с этой ситуацией в программе «Аполлон», где
возникла необходимость промоделировать (при 10 выборках в се-
кунду) цифровой автопилот (ЦАП), который действовал при выб-
ранном интервале выборки в 40 миллисекунд (25 выборок в секун-
ду), ЦАП имел фильтр вида
Д-=2,62 f 2,~0’98 ] = D (z),
[	\ г— 0,64) v
который был выполнен с использованием разностного уравнения
=0,64?„_1 + 2,62 (/„ - 0,981 /л_1).
Целью являлось установление устойчивых характеристик £>(z).
Мы установили местоположение полюсов и нулей в «-плоскости
и скорректировали полюс и нуль в z-плоскости для того, чтобы от-
считывать разницу в периоде выборки. Мы поняли, что полюс и
нуль фильтра ЦАП в «-плоскости имеется при
-^-1п (z\,ojnoc) = si,ojlloc = 3n,	In (ZHy^b) $нуль °н-
В случае, если Т=4Х10~2 с (действительный интервал выбор-
ки ЦАП),
оп = 251п (0,64) =25X —0,4463= —11,16; <тн=251п (0,98) =
=25Х —0,0202= —0.505.
Полюсом и нулем в z-плоскости при 7=0,1 с были
гнуль=е-0’0505 =0,9508; гполюс=е->>>16=0,3277.
164
Таким образом, новая передаточная функция фильтра ЦАП
может принять вид
.	.1г — 0,9508 \
D, (z) = k I-------- ,
\ z—0,3277 /
где k определяется подбором ступенчатой реакции фильтра реаль-
ного ЦАП при помощи моделирующего фильтра.
Фильтр реального ЦАП обладает ступенчатой реакцией в виде:
выходной	(z) = 2,62 ( ——/—-—'j
’	U— 0,64)/\z — 1/
конечное значение которого
(2,62) (0,02)
(0,36)
Моделирующий фильтр обладает конечным значением
, 0,0492	с.,
k-------= FV..
0,6723 s
Так как нам необходимо, чтобы FVS=FV, определим k следу-
ющим образом:
k = (0,6723) (2,62) (0,02) = j 98g9
(0,0492) (0,36)
Окончательно
z 1 / \	1 пооп ( ** — 0,9508 \
О. (z)= 1,9889 ---------- .
м	\ г— 0,3277 /
И наконец, моделирующее разностное уравнение принимает
вид
?л=0,3277?„_l + 1,9823 (/п - 0,9508/„_1).
Это уравнение дает вполне удовлетворительные результаты.
Распространение метода подбора корней на другие дискретные
системы будет дано далее.
Подобные вопросы обсуждались в разд. 5.3 и использовались
при моделировании дискретной системы.
5.7.	ДОПОЛНИТЕЛЬНАЯ ФИЛЬТРАЦИЯ И ЕЕ ПРИМЕНЕНИЕ
В ЦИФРОВОМ МОДЕЛИРОВАНИИ
Часто применяемым методом фильтрации в области управления
и связи является дополнительная фильтрация, которая приводит
к многим полезным и удивительным результатам.
Например, применяя дополнительные низкочастотные фильт-
ры, можно получать решения с высокой точностью. Кроме того,
частотный спектр функции возмущающего воздействия можно
разложить на части и оперировать с ними, а затем вновь соеди-
нить его в случае уверенности, что это свойство в частотной облас-
ти так же закономерно, как и во временный области. Наконец, кон-
165
цепция дополнительной фильтрации вытесняет при проектировании
фильтров догадки и тайны и делается более доходчивой.
Рассмотрим фильтр G(s), структурная схема которого пред-
ставлена на рис. 5.3. Если G(s) —простой низкочастотный фильтр
вида
O(s) = —1—,
XS + 1
ТО МЫ понимаем, ЧТО ВЫХОДОМ фильтра является Хнизной частоты, ИЛИ,
что то же, низкочастотные составляющие х($). Теперь рассмотрим
дополнительный фильтр
Этот простой широкополосный фильтр, который пропускает все
частоты, отбрасываемые низкочастотным фильтром 1/(ts+ 1), и от-
брасывает частоты, пропускаемые низкочастотным фильтром.
Из этого следует, что, если суммировать выходы этих двух
фильтров, мы можем снова получить x(s) (рис. 5.4).
Чтобы понять это, заметим, что
_Е£_ + _^ = 1.
TS + 1 TS + 1

G(S)
*(рилы< .
Рис. 5.3. Структурная схема G(s)
Низкая частота х
Х(са)
x(oj)
Предполагаемая
зависимость
со
Высокая частота х
Предполагаемая
'^зависимость
1 Xjt
Рис. 5.4. Структурная схема двух дополнительных фильтров
Мы видим, что, если фильтр представлен в виде G(s), его до-
полнением является просто 1 — G(s).
Из этого следует, что, так как
од=1-о,
166
Рис. 5.5. Дополнительный фильтр, эквивалентный фильтру G
можно получить выход фильтра, используя его дополнение, как по-
казано на рис. 5.5. Так, если фильтр имеет вид
rs -ь 1 ’
не входя в обычные проблемы дифференцирующего устройства,
так как его нелегко выполнить (будь то аналоговая или цифровая
фильтрация), можно применить дополнение G(s), показанное на
рис. 5.6.
Фильтры с определенной полосой пропускания, фильтры, огра-
ничивающие по уровню, и дифференциаторы могут быть представ-
лены, как показано на рис. 5.7.
Концепция дополнительного фильтрования вводится по следу-
ющим причинам.
1.	Дополнительная фильтрация вносится без изменения в циф-
ровой фильтр.
2.	Это позволяет моделировать передаточные функции, обла-
дающие нулями, используя только передаточные функции с полю-
сами. Так, простые системы первого и второго порядка с низкой
пропускной способностью, рассмотренные в разд. 5.3 и 5.5,— это
все, что необходимо для моделирования даже самых сложных пе-
редаточных функций.
3.	Это дает проектировщику, применяющему моделирование,
необходимое понимание для проектирования специальных частот-
ных фильтров.
4.	Это обеспечивает проектировщику емкость в выборе различ-
ных фильтров при моделировании.
Пример. Промоделируем (s + a)/(s-b6), используя только раз-
ностные уравнения для низкопропускного фильтра.
Этап 1
s -|- & s । л
I s b s -|- b s b
Рис. 5.6. Высокочастотный фильтр и его формирование на базе низкочастотного
фильтра
167
Предполагаемая
зависимость
Фильтр с ограни-
ченной полосой
пропускания
ФОПП
Фильтр
низкочастотный
х
1	\
rz Фильтр
низкочастотный
1
rzs+1
полоса
пропускания
Фильтр, ограни-
чивающий по уровню
Высокая частота
Рис. 5.7. Фильтры с определенной полосой пропускания, фильтры с ограничени-
ем по уровню и дифференциатор, включающий в себя низкочастотные фильтры
х = {х—[s/(ts+ 1)]х} (1/т). Следовательно, х = [sf (xs +1) ]х
1
с
1
Рис. 5.8. Моделирование
(s-ha)/(s + 6) при помощи низкочас-
тотных фильтров. Для пояснения от-
метим следующие преобразования
разностных уравнений:
(fl)« = е“&г (<?!)„-! + О - e-ftr)
(<Р2)л = In, (<Рз)п = е ЬТ (<р3)л-1 +
+ (д/^).(1 е In, (tn) = (?i)n 4~
+ (?2)л 4- (?з)п
168
Этап 2
$  $	111___ $	$ I 1	— I 1
<$ “h* b s -f- b	s -|- b s H- b s “I- b
Этап 3
s + a —b  j  a _ <t
s + b s + b s + b I ’
который может стать моделируемым при помощи
<р _— (1 — еГьт) z , 1 . а/б(1— еГьт) г
I (г-е~ьт)	(г-е-67-)	•
Структурную схему этой системы можно узнать из рис. 5.8.
Системой уравнения этого моделирования является
п	л—1
*2л = ^Я’
?3 --=е-6г<р3	+(а//>)'(1-е-6г)/„;
°л	п—1
'Р=?1 + ?г+?з-
Часть III
ЧИСЛЕННЫЕ МЕТОДЫ
МОДЕЛИРОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
НА ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИНАХ
Глава 6. МОДЕЛИРОВАНИЕ
НЕЛИНЕЙНЫХ СИСТЕМ
В этой главе представлены методы составления разностных
уравнений для моделирования нелинейных систем, которые могут
быть описаны нелинейными дифференциальными уравнениями. Не-
которые результаты были получены при решении определенных за-
дач, и здесь представлен ряд из них, опубликованных в последнее
время.
Эта глава относится к цифровому моделированию непрерывных
систем, описываемых нелинейными дифференциальными уравне-
ниями вида
' х = Р (х, /).
Ряд исследователей решали эту проблему на базе современных
численных методов. Фаулер исследовал эту проблему с точки зре-
ния подбора корней. Среди наиболее интересных его работ было
эмпирическое исследование моделирования нелинейных систем,
описываемых уравнениями
x — kx2=f(t), х(О)==х0, постоянная, и /(/) = 0.
Эта система может быть представлена структурной схемой,' как
показано на рис. 6.1.
Вследствие этого протекающие в ней процессы можно рассмат-
ривать как линейные, имеющие кусочно-постоянные коэффициен-
ты на протяжении шага цифрового моделирования.
Фаулер на основании этого метода разработал систему разност-
ных уравнений и показал, что реакция этой простой системы на
начальное условие (или, в соответствии с уравнением равновесия,
на ступенчатое воздействие на входе) была ниже по сравнению с
истинной реакцией непрерывной системы. Однако он нашел, что
время реакции системы и модели сравнивается, когда коэффици-
ент усиления обратной связи системы увеличивается на множи-
тель 2 (рис. 6.2).
Задачей, несомненно, является выяснить, когда состояние рав-
новесия системы приближается к неустановившемуся значению.
170
Рис. 6.1. Структурная схема модели Рис. 6.2. Структурная схема системы
системы х~kx2=f(t)	х—(2kx)x=f(t)
|/ при f = const, £<0
Это очевидно из следующего: в устойчивом состоянии х = 0 и, сле-
довательно,
установившегося состояния2=21/ —~~~ При y = COnst, k О
' k
для моделируемой системы, поскольку
•^установившегося состояния ==
для системы, которая заложена в кусочно-линейное разностное
уравнение, задается скорректированное время реакции моделируе-
мой системы. Очевидным решением было добавление коэффициен-
та усиления в прямую часть контура к входу f. Распространение
этого метода на другие более сложные нелинейные дифференциаль-
ные уравнения содержит ряд трудностей. На этой стадии Фаулер
сделал интересные исследования и показал, что 2kx является
якобианом этой нелинейной системы:
x = kx2-\-
-^- = 2kx=J —Якобиан.
дх
Другие авторы получили аналогичные результаты при приме-
нении различных методов. Все они сводятся к тому, что якобиан
является не только средством изучения местной устойчивости не-
линейных процессов, но и ключевым параметром к быстрому мо-
делированию.
Однако встретились трудности получения метода преобразова-
ния нелинейного дифференциального уравнения в кусочно-линей-
ное дифференциальное уравнение, в котором:
1)	постоянный коэффициент был таким же, как якобиан нели-
нейного дифференциального уравнения;
2)	конечное значение подобрано по конечному значению нели-
нейного дифференциального уравнения.
В начале 1970-х годов был сделан ряд попыток, которые в ос-
новном не увенчались успехом. Частные методики были разработа-
ны для частных систем, к общим методам приблизиться не уда-
171
Усовершенствованные методе!
моделирования нелинейных
Методы быстрых
решений разност-
ных уравнении
систем
Методы быстрого
численного интег-
рирования
стрые решения
усочно-линейных
разностных уравнений тных уравнений
Быстрые решения УсоВершенство-
нелинейных ризное- Ванный числовой
интегратор
Улучшенные оценю
подынтегральных
выражений
Рис. 6.3. Пути усовершенствования моделирования нелинейных систем
лось. На этой стадии автор принял несколько отличный метод, ко-
торый оказался необычайно простым и легко применимым, и изло
жил его впервые. Этот подход приводит к улучшению эффектив-
ности численно интегрируемых нелинейных дифференциальных
уравнений путем улучшения оценки подынтегрального выражения
(рис. 6.3).
Интересно, что это приводит к методу, разработанному для ку-
сочно-линейных дифференциальных уравнений, удовлетворяющих
одному или двум свойствам, упомянутым ранее. Как оказалось,
разностные уравнения были идентичны тем уравнениям, которые
исследовал Рональд Баулез, применявший совершенно отличную
методику: методику экспертных консультаций *. Оба метода рас-
сматриваются в этой главе.
6.1. УСОВЕРШЕНСТВОВАНИЕ ОЦЕНОК ПОДЫНТЕГРАЛЬНОГО
ВЫРАЖЕНИЯ
Разработка улучшенного метода численного интегрирования
нелинейных дифференциальных уравнений из опыта автора и его
убеждения должна базироваться на том, что численное интегриро-
вание легче применить в цифровом моделировании непрерывных
процессов, чем в методах моделирования разностных уравнений.
Кроме того, такой подход легче осмыслить, он более полезен для
инженеров, занимающихся моделированием, с ограниченным опы-
том. По этой причине этот метод будет рассмотрен первым.
Метод в ретроспективе обманчиво прост, но, чтобы к нему прий-
ти, потребовалось три года. Целью является преобразование нели-
нейного дифференциального уравнения в кусочно-линейное диффе-
ренциальное уравнение с постоянным коэффициентом, являющим-
ся якобианом нелинейной системы и конечное значение которого
* Или экспертных оценок (прямей, ред.).
172
соответствует конечному значению нелинейной системы. Таким
образом, коэффициент этого линейного дифференциального уравне-
ния вычислен на основании якобиана и сохраняется постоянным
на шаге интегрирования.
Кусочно-линейное дифференциальное уравнение решается с ис-
пользованием алгоритма в три этапа:
Этап 1. Дифференцирование нелинейного дифференциального
уравнения (приводящее к определению коэффициента, которым яв-
ляется якобиан нелинейного процесса).
Этап 2. Подстановка исходного дифференциального уравнения
в результирующее выражение этапа 1 (это гарантирует, что конеч-
ное значение кусочно-линейного дифференциального уравнения
будет подобрано в соответствии с конечным значением нелинейного
дифференциального уравнения).
Этап 3. Численное интегрирование дифференциального уравне-
ния, полученного на этапе 2, определение якобиана, зафиксирован-
ного на шаге интегрирования.
Пример одного процесса
	X = kx2 f (/).	(6.1)
Этап 1	x=(2kx)x-\- f (/).	
Этап 2	x—(2kx){kx2-\-	f (/);	(6.2)
		(6.3)
Этап 3
Двойное численное интегрирование
i-J(^2+/O + /W.
Выбираем J и фиксируем на всем интервале интегрирования.
Двойное интегрирование (6.3) протекает значительно быстрее,
чем единичное интегрирование (6.1), так как размер шага интег-
рирования в случае (6.3) может быть сделан большим, чем удво-
енный шаг (двойное интегрирование) при (6.1).
Этот метод можно сделать более общим следующим образом:
X = f(X, /);	(6.4)
такая система может быть проинтегрирована численно применени-
ем кусочно-линейного дифференциального уравнения, представлен-
ного ниже.
Этап 1
X = JX + -(^ ° 	(6.5)
dt	v '
Этап 2
x=jf(x,/)+^H!_o.	(б,6)
dt
173
Рис. 6.4. Структурная схема числен-
ного интегрирования нелинейного
дифференциального уравнения (6.4)
Этап 3
Численно интегрируя
X = Jf(X, t) + .f) ?(X’ ° ,
dt
выбираем J и фиксируем на всем интервале интегрирования.
Разница между классическими методами и методом подборки
соответствующего якобиана может быть наглядно видна при срав-
нении их структурных схем. Классический подход представлен на
рис. 6.4.
На рис. 6.5 показан кусочно-линейный метод, при котором под-
бирается якобиан, фиксируемый на каждом шаге интегрирования.
Другим путем для усовершенствования численного интегриро-
вания кусочно-линейного дифференциального уравнения может
быть метод, показанный на рис. 6.6. Этот метод иллюстрирует чис-
ленное интегрирование (6.3).
Из двух кусочно-линейных методов автор предпочитает метод,
показанный на рис. 6.6, так как он явно гарантирует, что условие
равновесия (конечное значение) будет удовлетворено. Более опре-
деленно, если достигается равновесие:
-^у- = 0 при Х = 0;
тогда из (6.3)
X = Jf (Х,/)+—=>O=f(X, /),
dt
в то время как из (6.2)
X = JX + — =>0 = JX,
1 dt
Рис. 6.6. Структурная схема числен-
ного интегрирования кусочно-линей-
ного дифференциального уравнения
(6.6)
Рис. 6.5. Структурная схема числен-
ного интегрирования кусочно-линей-
ного дифференциального уравнения
(6.5)
174
которое не гарантирует, что f(X, /)=0. И на самом деле это оче-
видно из рис. 6.5. Если числовая ошибка будет входить в послед-
ний интеграл, то она никогда не будет сведена на нет процессом в
замкнутом контуре вокруг X. Короче говоря, последнее интегриро-
вание — это интегрирование открытого контура, которое будет
отклоняться от любого конечного значения в зависимости от сум-
мы числовой ошибки, полученной последним интегрированием. Это
не тот процесс, который показан на рис. 6.6.
Математический ход решения дифференциального уравнения
представлен на рис. 6.7.
Теперь нам нужно было бы поинтересоваться, почему (6.2),
'6.3) и математическая схема решения (6.7) указывают на явное
вычисление J? Почему применяется дифференциальное уравнение
x = J (kx> + /(/)) + /(/)	(6.7)
вместо упрощенного алгебраического вида (6.5)? В этом случае
алгебраическое упрощенное уравнение должно иметь вид
x = 2^x3 + 2^/(J +	(6.8)
Ответ содержится в данной главе и подчеркивает, что данным
методом управляют два различных эффекта:
1. Получение и применение якобиана.
2. Применение и получение конечного значения.
При изучении рис. 6.7 мы видим, что якобиан известен в урав-
нении. Так как равновесие доказано (/=0 и х = 0) , ясно, что
х=^/Гпри / — constant, &<0,
как и должно быть.
Существует другая причина для написания этого уравнения в
виде (6.3). Для многих задач это — форма скоростной численной
сценки уравнения. Дифференциальным уравнениям, переписанным
в форме (6.3), необходимо наименьшее количество арифметических
операций и объем памяти для оценки производной.
Например, если мы выполняем (6.8) на миникомпьютере или
настольном микрокалькуляторе с ограниченной памятью, нам нуж-
на (в худшем случае) следующая программа вычисления:
x = 2x&X&XxXxxxSTOCLR2xxx fxk-[-/RCL-f-*,
8 умножений, 2 сложения, 2 памяти =12 арифметическим операци-
ям, в то время как (6.2) может программироваться (в худшем слу-
чае) как
x = AxxSTO х х-|-/RCLx2x f-\~,
4 умножения, 2 сложения, 3 памяти = 8 арифметическим операциям.
Несмотря на то, что разница между 12 и 8 операциями может
показаться не такой большой для данного примера, она дает
* Предполагается машинный язык.
175
Вычисление
параметров
задачи
Вычисление _
приращений
Двойное инте-
грирование
X ПО X,
(например, инте-
грирование
только по
Эйлеру)
Оператор
печати
Корректировка
времени
аппроксимации
Счетчик
циклов
Рис. 6.7. Иллюстрация математической последовательности численного интегри-
рования уравнения (6.5). Следует обратить внимание, что х, обеспечиваемое при
первом цикле численного интегрирования (е), позволяет осуществлять вывод на
печать и закрыть обратный цикл, вычисляя х с помощью х и t
в сумме на 50% больше операций, чем это необходимо. На самом
деле, если принимать во внимание, что примерно 5 мкс необходи-
мо для выполнения операции сложения и 9 мкс для операции ум-
ножения на типовой ВМ CDC типа 6400, то разница времени вы-
числения арифметической операции может составить до 78% лиш-
него времени.
Если эффективность не выше номинальной, то (6.8), безуслов-
но, также удовлетворительно, как и (6.2).
176
Сделаем замечание несмотря на то, что метод был вполне
разработан для моделирования сложного вращательного движе-
ния нелинейных фильтров, нелинейных систем экономики и динами-
ческих процессов в инерциальных системах универсального подве-
са, он совершенно не оценен с точки зрения ограничений числен-
ного метода, и не был применен ни с одним численным интегралом,
кроме Т-интегратора *.
Все это изложено здесь, чтобы облегчить понимание, которое
может быть полезно читателям, внимательно следящим за особен-
ностями применения нелинейного моделирования.
В данной книге изложено состояние дела на время публикации.
«.2. РЕШЕНИЕ УРАВНЕНИЯ Х = Jf+df/dt
В ЗАМКНУТОМ ЦИКЛЕ
Чтобы получить кусочно-линейное уравнение для моделирова-
ния полностью нелинейного процесса, описываемого
X = f(X, /),
необходимо решить кусочно-линейное дифференциальное уравне-
ние
X = JX + —
dt
в замкнутом цикле. Решая это уравнение, можно предположить,
что f известно. В этом случае можно предположить, что преобра-
зователь перестраивает f в последовательность ступенчатых зна-
чений, и будем искать ответ системы на ступенчатую функцию воз-
мущающего воздействия.
X = JX при J=constant.
Метод, который мы использовали для аналитического вывода
разностного уравнения системы, представлен на рис. 6.8.
Сначала мы найдем однородное уравнение
X —JX = 0
для получения матрицы переходного состояния ф. Предположим,
что его решением будет
Х = еА/.
При подстановке мы найдем
(A —J)=O,.:A=J.
Решением однородного уравнения становится
X^eJZC.
♦ См. гл. 7.
177
Рис. 6.8. Структурная схема цифрового моделирования при х —f(x, t)
При t=0
Х^Х0 = С и J = J0.
Таким образом,
Х=е^Х0;
Ф = z; Фо = ет°
Частным решением неоднородного уравнения становится
Х = ~0Х0+\ф(/-т)^-Ц
\ dt h
о
д f
где----постоянная по шагу интегрирования.
dt
Вычисляя интеграл, мы получим выражение:
X-e’o'Xo + Jo'1 (/-е-М)/1В ,
\ dt Jo
которое еще раз интегрируется для получения окончательной фор
мы разностного уравнения
Х-Х^ f Х( )Л,
о
откуда
X —X0-|-J6’1(e'i>z —/)Xo+Jo'2(eJ»z-t	.
\ dt Jo
Из этого следует, что
I Х„— X„_t+(еJ"-Ir - /) Х„_,+J„_2, (еJ«-- Т Jn_, - /) [tt)
1 dt In- 1
или по причинам, которые будут обсуждаться позже,
X^X^+J^! (eJ«-i7 - /)	+	(eJ«-tr-7'Jn_! -/)/<- .
\ Of ~r--l
так как	X„_! =
!7.s
Пример. Для простой однопараметрической задачи
x=kx2-\-f(t) при /(/) = 0;
при J7-i = l/2£x„-i.
Тогда моделирующим разностным уравнением будет
xn=x„_!+ 1/2^хл_! (e2ft-r»-ir — 1) (kx2n-i),
которое упрощается до
хп—1 /1 I 2kx„ <Т\
хп = -^-{^+е «-1).
Этот пример иллюстрирует ограниченность метода кусочно-ли-
нейного разностного уравнения.
Вычисление шагов гарантируется тем, что каждое приращение
шага берется в соответствии с характеристиками местной устойчи-
вости нелинейного дифференциального уравнения, но конечное зна-
чение вычисляется способом разомкнутого цикла суммированием
приращений шагов.
Применение этих разностных уравнений не слишком полезно
при моделировании без использования метода корректировки
ошибки.
Интересно, что в некоторых ситуациях методы корректировки
ошибки применены как стандартные. Они являются численным ин-
тегрированием уравнений вращательного движения.
Уравнения движения вращающегося тела применяются при про-
ектировании практически всех транспортирующих систем—от ав-
томобилей до подводных лодок, самолетов и переносятся на кос-
мические корабли.
Для этих случаев распространенные методики моделирования
вращательного движения содержат:
уравнение Эйлера,
уравнения четвертого порядка,
уравнения направляющих косинусов.
Эти методики зависят от методики расчета оценки прямоуголь-
ной координатной системы, содержащей прямоугольные состав-
ляющие вращения (за исключением неортогональных уравнений
Эйлера).
Если система критерию ортогональности не удовлетворяет, то
производится незначительная коррекция координатной системы в
сторону ортогональности. В таком процессе преобразования поло-
жения прямоугольной координатной системы допускаемые ошибки
в вычислении устойчивого состояния никогда не достигают значи-
тельных величин.
«.3. АЛГОРИТМ ЛОКАЛЬНОЙ ЛИНЕАРИЗАЦИИ БАУЛЕЗА
Рональд Баулез из НАСА получил уравнение, идентичное урав-
нению (6.9) для моделирования нелинейных систем с помощью
кусочно-линейных разностных уравнений. Он с большим успехом
179
применял метод, названный ЛЛ (локальная линеаризация) алго-
ритмом, в моделировании вращательного движения самолета с
высокими характеристиками.
Баулез опубликовал свою работу в 1973 * г.
Этот документ демонстрирует значительный прорыв в быстро-
действующее моделирование вращательного движения. Он приме-
нил анализ возмущения для получения разностного уравнения.
Метод реализуется следующим образом. Зададимся
X=cf(X,f);
f может быть разложена в многопараметрический ряд Тейлора . f
=	+	8Х+(!Щ 8/ + ...,
\С'А/п	\	/ П
где	ВХ = (Х —Х„) и 8/=(t — nT).
Таким образом,
x=i(X„ ex+Q« + ....
Заметим, что
— (8Х) = Х;
dt
мы можем также написать
(8 X) = J„ 8 X + f„ +	(/ - пТ\
что является дифференциальным уравнением первого порядка.
Если Jn, fn и (df/d/)n выдерживаются постоянными на всем
промежутке Т, то оно становится кусочно-линейным дифференци-
альным уравнением с постоянными коэффициентами. Решение
примет вид
8 X = (V (еГ V_ /) f„ + (J71)2 (eV_ / _ т J„)	.
1	\ ot )п)
Тогда можно записать
Хл+1 = Хл-|- о X.
Его сравнение с уравнением (6.9) доказывает, что результаты
идентичны, хотя предполагаемые процессы до некоторой степени
различны. Без сомнения, рассмотренное ранее ограничение сохра-
няется для ЛЛ алгоритма.
И, наконец, как итог, подчеркнем, что методы разностных урав-
нений при моделировании, включающем большое количество век-
торов состояния, вызывают значительные трудности, если якобиан
меняется при каждом переходе от одного шага к другому.
* Развитие и применение алгоритма локальной линеаризации для интегриро-
вания уравнений скоростей четвертой степени в задачах моделирования полета в
реальном времени. Баркер, Баулез и Вильямс, НАСА TN-D-734/, дек :97б
180
Это особенно заметно, когда якобиан является слабообуслов-
ленной матрицей. Несомненно, все эти факторы влияют на решение
о том, использовать ли кусочно-линейные разностные уравнения
для моделирования нелинейных систем, либо численно интегриро-
вать уравнения движения.
Глава 7. СОВРЕМЕННЫЕ МЕТОДЫ
ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
В классических разработках по численному интегрированию»
средневзвешенные оценки интегрируемой функции на интервале ин-
тегрирования обычно основаны на методах аппроксимации поли-
номами.
Если решать сложную систему уравнений (возникающую, на-
пример, при цифровом моделировании в реальном времени, цифро-
вых компьютерных управляемых системах и други?; дискретных ин-
формационных системах), при аппроксимации появляются фазо-
вое смещение и амплитудное искажение.
Влияние ошибок на каждую систему уравнений различно, а
при их объединении часто возникает неточность и неустойчивость.
В настоящее время разработаны цифровые интеграторы, снаб-
женные цифровыми фильтрами с регулируемым «коэффициентом
усиления по фазе». Средневзвешенные оценки интегрируемых
функций производятся фильтрами с изменяющимися фазовыми и
амплитудными характеристиками, проходящими через численные'
интеграторы, для выработки параметров регулирования ошибки.
Эти параметры могут быть выбраны с целью компенсации сме-
щения по фазе и искажения амплитуды независимо от источника.
Найдено, что введение перестройки интегрируемой функции при
фильтрации искажения приводит к простым формулам численно-
го интегрирования, которые можно «настроить» на систему интег-
рируемых уравнений. В частности, числовая точность и устойчи-
вость регулируются настройкой фазы и амплитуды передаточной
функции интегратора. «Настройка» и во временной области и в час-
тотной не имеет эквивалента в классическом численном интегриро-
вании.
Цифровые интеграторы приводятся к определенным формулам
классического интегрирования смещением фазы интегрируемой
функции. Это приводит к интересному выводу о том, что многие
классические цифровые интеграторы по существу различаются
только величиной фазового смещения интегрируемой функции.
7.1.	ВЫБОРКА ДАННЫХ ПРИ ЧИСЛЕННОМ ИНТЕГРИРОВАНИИ
В этой главе формулы численного интегрирования получены
путем:
18Ь
О)
f)
0)
Непрерывная
система
Дискретная
аппроксимация.
Перестройка
сигнала перед
компенсацией
Дискретная
аппроксимация.
сигнала после
компенсации
x^t)
пере„-
стройна
НепрерыО- x2(t)
процесс
Непрерыв-
ная компен
сация
~X;(t) ^xz(t)
HenpetXJTl ~х2(пТ\
ный Н>-------------
процесс | Т
-Х^ПТ)
Перестройка ^(У^^'диснретЦ^
шэнппгг ппппр. >\наЯ КОМПгН-
сация
Процесс
пере-
стройки
Непрерыв-
ный
процесс
*x2(t)
^x2(nT)
~Т
-Xj(t)
т
~Xf(t)
Рис 7.1. Дискретные методы аппроксимации непрерывных систем
1)	синтезирования дискретной аппроксимации для непрерывно-
го интегрирования;
2)	написания разностного уравнения, описывающего дискрет-
ную систему.
Разностное уравнение является формулой численного интегри-
рования.
Методы синтеза дискретных систем, которые аппроксимируют
непрерывные системы, представлены на рис. 7.1.
На рис. 7.1, а показан непрерывный процесс, который аппрок-
симируется дискретным процессом. На рис. 7.1, б показана диск-
ретная аппроксимация непрерывного процесса, где перестраиваю-
щийся (непрерывный) сигнал компенсируется для ликвидации ис-
кажения. На рис. 7.1, в компенсация перестройки применена к
дискретному сигналу до его перестройки. Особенно полезны методы
аппроксимации непрерывных систем с помощью дискретных, пред-
ставленных на рис. 7.1. Они в значительной мере отделяют инфор-
мационные соотношения от соотношений устойчивости исходя из
выбранного процесса перестройки и фильтрации компенсации.
Процесс перестройки может быть выбран исходя из рассмотре-
ния временной области и информационного содержания (такого
как скорость выбора дискретных данных, ошибки квантования,
свертывания спектра и алгоритма интерполяции), тогда как про-
цесс компенсации перестройки выбирают исходя из частотной об-
ласти и устойчивости (по таким показателям, как фазовое смеще-
ние, амплитудный спектр, место полюса и нуля, местоположение
корня).
Метод аппроксимации, который основан на рассмотрении как
временной, так и частотной области, приводит к лучшей аппрокси-
мации, чем методы, которые основаны на рассмотрении только вре-
менной или только частотной области.
1	Для разработки компенсационных интеграторов желательно
применять преобразователи нулевого, первого, второго порядка и
182
треугольного типа. Амплитудный спектр этих процессов перестрой-
ки изложен в гл. 2.
Беглый взгляд на частотные характеристики этих преобразова-
телей показывает, что они относятся к более высокому порядку
процесса перестройки и обладают большим отклонением при бо-
лее высоких частотах.
Понятно, что перестройка интегрируемой функции привносит*
полупериодное запаздывание по времени в перестроенный сигнал.
Это запаздывание возрастает по мере роста порядка процесса пе-
рестройки.
7.2.	КРАТКИЙ ОБЗОР ДИСКРЕТНЫХ АППРОКСИМАЦИЙ
НЕПРЕРЫВНЫХ ФУНКЦИЙ
На рис. 7.2 показана простая дискретная аппроксимация для
непрерывного интегрирования. Рис. 7.2, а содержит структурную
схему непрерывного интегрирования. Дискретная аппроксимация
этого процесса представлена на рис. 7.2, б.
В этом случае преобразователь нулевого порядка применяется
для перестройки подынтегрального выражения. Процесс перестрой-
ки с помощью преобразователя нулевого порядка эквивалентен
преобразованию интегрируемой функции с помощью подбора по-
линома кривой (аппроксимация Ньютона — Грегори), полученной
по дискретным значениям интегрируемой функции.
Соотношение передаточной функции через z-преобразование X
и X имеет вид *
X (г) z \ s / \ s ) ’
(7.1)
а)
б)
с$>х=^~хти т х(о>=о
x=f„x(Tidr xW^O
Jo
Рис. 7.2. Преобразование нулевого порядка при интегрировании
* Численное интегрирование позволяет вычислять лишь приближенное зна-
чение интеграла, что подчеркивается знаком «приблизительное равенство».
1S3
‘.•реодразсданио перья го порядка
г
Рис. /.3. Преобразование первого порядка при интегрировании
Разностным уравнением, которое описывает эту дискретную
аппроксимацию непрерывного интегрирования, является
ХП=ХЯ^ТХП^.	(7.2)
Это формула Эйлера, которая описывает процесс выборки данных
при непрерывном интегрировании интегрируемой функцией, пере-
строенной с помощью преобразователя нулевого порядка.
На рис. 7.3 показан дискретный эквивалент непрерывного ин-
тегрирования при преобразовании процесса перестройки первого
порядка (аппроксимация полиномом первого порядка Ньютона—
Грегори), применяемый для перестройки интегрируемой функции.
Разностное уравнение, описывающее этот процесс, может быть
получено следующим образом:
Произведя обратное преобразование, найдем разностное урав-
нение
*п = *n-i + (Г/2) (3X„_t - АГ„_2).	(7.4)
Здесь мы найдем, что процесс перестройки через преобразование
первого порядка приводит к формуле интегрирования Адамса вто-
рого порядка и снова к хорошо известному результату.
И наконец, численное интегрирование, основанное на перестрой-
ке с преобразованием второго порядка, которые видно на рис. 7.4,
приводит к явному интегратору Адамса—Бэшфорта
Хп	+ Г/12 (23ХП^ - 16ХЛ_2 + 5ХЛ_3).	(7. 5)
Так как процессы перестройки более высоких порядков относят-
ся к аппроксимирующим, но различающимся полиномам Ньюто-
на—Грегори более высокого порядка, следует ожидать, что будут
найдены иные классические интеграторы, соответствующие процес-
су перестройки такого рода.
С точки зрения системы, осуществляющей выборку данных, эти
интеграторы различаются характером процесса перестройки ин-
тегрируемой функции. Точность перестройки интегрируемой функ-
ции связана с точностью и устойчивостью интегратора. Это снова
184
Преобразование второго nojvrffafc
^K(Z)
Т '
Рис. 7.4. Интегрирование с преобразованием второго порядка
заостряет наше внимание на процессе перестройки интегрируемой
функции, характеристики и свойства которой — предмет особых
исследований в области управления выборкой данных и систем ин-
формации. В этом плане интересны методы управления устойчиво-
стью системы управления выборкой данных. Они будут применять-
ся здесь для преодоления цифровой неустойчивости. Кроме того,
несомненно, эти методы выборки данных будут применены в уп-
равлении искажением сигнала перестройки — главным источником
цифровой ошибки и неустойчивости численного интегрирования.
7.3.	НАСТРОЙКА ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
Источники ошибки в численном интегрировании многочисленны.
Вместо выявления компенсации для каждого источника ошибки
при составлении разностных уравнений, используемых при числен-
ном интегрировании, включают переменную компенсирующую
фильтрацию по фазе — амплитуде, которая может быть определе-
на аналитически в соответствии с критерием системы или эмпири-
чески методом проб и ошибок.
Оба метода будут обсуждаться.
Три непрерывных фильтра со смещением по фазе применяются
при поиске интеграторов настроечного типа (Г-интеграторы) (см.
табл. 7.1). Эти фильтры «опережения» ограничивают разложение
в ряд оператора е+5Г.
Интегратор преобразования нулевого порядка с непрерывной
компенсацией коэффициента усиления по фазе и единичным нулем
виден на рис. 7.5. Передаточной функцией отношения X и X явля-
ется
,7.6)
^Квантование Перестройка Компенсация Интегрирование Квантование
Рис. 7.5. Структура интегратора нулевого порядка: Т — период интегрирования;
Л параметр компенсации коэффициента усиления; у — параметр компенсации
по фазе
185
Непрерывная компенсация
Таблица 7.1
Тип
ко дпенсации
Передаточная
функция
Получение
Нуль первого
Порядка
Полюс первого
порядка
1 4- yTs
1
1 —yTs
Q+1T _ ! + Y Ts +	— +	_ 1 + yTs
P + lTs 1
'	e~1TS
1 — yTs 4-
y^TW
2
1
1 — yTs
Полюс/нуль
первого порядка
2 + yTs
2—yTs
e + VTs ____________
e-I7’s/2
yTs y?T2s2
1 + 2 +	8	+ '"	2 +
yTs y^TW-	2—yTs
Отсюда находим формулу численного интегрирования
Хп	+ ХГ {уХп + (1 - Y) Хп-г}.
(7.7)
(7.8)
(7. 9)
(7. 10)
При помощи непрерывной компенсации с фильтром «опереже-
ние — запаздывание» с единичным полюсом и единичным полю-
сом—нулем мы найдем следующие формулы численного интегриро-
вания соответственно:
хп =- (1 - eVi) Хп^ - е^Хп_2 + XT’ [{1 + Y (1 - е~^)> Хп^ -
_(ei/7 4-Y(i_eVT)|AV2];	(7.11)
хп (1 - е^) Хп^ - е™Хп_2 +
д-XT [{1 + Y (1 - е-2'T)}	- {е’Л+Y (1 - е^)} Хл_2].	(7.12)
Мы видим, что преобразование нулевого порядка с помощью
компенсации с единственным нулем приводит к формуле интегри-
рования, коэффициенты в которой — простые выражения.
186
Треугольное
преобразование Компенсация
Рис. 7.6. Цифровая аппроксимация непрерывной компенсации
Подобным же образом при преобразованиях более высокого по-
рядка коэффициенты полученной формулы интегрирования при
компенсации с единичным нулем просты по форме. Эти формулы
сведены в табл. 7.2.
Настроечные интеграторы также были разработаны при помощи
дискретной компенсации. Простой тип дискретной компенсации
фильтром был разработан получением дискретного эквивалента
непрерывной компенсации, применяемой в процессе перестройки
с помощью преобразования треугольного типа (рис. 7.6).
Передаточная функция этого дискретного процесса
п/ ч X . [z— 1 \2 7 / 1 -J- yTs \
D(z}^— = kz\----- Z ——— =
X \ z )	\ Ts )
z (—^_+	1 ;
Z ) l(z— 1)2	(Z— 1)2 I
D(z)^ = l{yz + (\-y)}.	(7.13)
Таблица 7.2
Формула интегрирования с непрерывной компенсацией
Процесс
экстраполяции
Разностное уравнение
Экстраполятор
нулевого порядка
Экстраполятор
первого порядка
Экстраполятор
второго порядка
Экстраполятор
треугольного типа
Хп =	+ \Т {уХп + (1 - у) Хп-1]
Хп = Х„_! + -у- (у (Y + 2) хп -
- (2Y2 + 2Y - 3) Xn-i + (Y2 - 1) Х„_2}
Хп = Хп -1 +	{(2y3 + 9y2 + 12Y) Хп -
— (6y3 + 21Y2 4- 12Y - 23)	+
+ (6y3 + 15y2 - 16) Xn-2 -(2Y3 + 3Y2 -5) X
XT
Xn=Xn-i+— (y2^4 + (1 + 2y-2Y2)X„_1 +
+ (1-2Y + y2)X„-2}
187
Дискретно скомпенсированные цифровые интеграторы, полу-
ченные обращением передаточной функции следующим путем
X ( .	ч ~ /Я ($)\
Л.	\ 5 /
где D(z)—передаточная функция дискретной компенсации и
H(s) — передаточная функция преобразования перестройки.
- у)}-—;
3	\	/
откуда
— у)}!-————),
X Г 1 k Г"1 Z JI (Z- 1)2 J
2L ~ \T + —
X [	z —1 J’
(7.14)
(7. 15)
(7. 16)
которое обращается в разностное уравнение
^л-^л_1 + ХГ{у^л + (1-у)^л_1}.	(7.17)
Интересно, что это такое же выражение, что и при непрерывной
компенсации с единичным нулем в перестройке с преобразованием
нулевого порядка.
В табл. 7.3 представлены формы численного интегрирования
для преобразований более высокого порядка, где использована эта
простая амплитудно-фазовая дискретная компенсация.
Таблица 7.3
Формула интегрирования с дискретной компенсацией
Процесс экстраполяции	Разностное уравнение
Зкстраполятор нулевого порядка	Xп ~ Хп_1 4- \Т {уХп 4- (1 —у) Xn—i}
Зкстраполятор первого порядка	Хп=Хп^ + -у-{ЗуХ,г + (3-4у) ±„-1 + + (Y-l)X„-2}
Зкстраполятор второго порядка	Хп — Xи—1 + ]2	п + (23 + 39у)	1 + 4- (21у — 16)AFn_2 + 5(l —у) Хп — 3}
Зкстраполятор треугольного типа	хп ~ Хп-! -4- —— {ухп 4-	4- (1 — у) Хп-2}
188
7.4.	ОБЪЕДИНЕНИЕ КЛАССИЧЕСКИХ РАЗРАБОТОК
ПО ЧАСТОТНОЙ ОБЛАСТИ
Представленные в предыдущем разделе формулы численного
интегрирования обладают интересным свойством, приводящим к
определенным, хорошо известным классическим интеграторам при
определенных значениях фазы и коэффициента усиления.
Например, при Х=1 и у-действительному числу, кратному по-
ловине, формула численного интегрирования нулевого порядка
^л-^л_1 + >Т{у^„ + (1-у)Хп-1}	(7-18)
принимает форму, показанную в табл. 7.4.
Таблица 7.4
Приведение скомпенсированных интеграторов к определенным
классическим интеграторам при определенных значениях
Уравнение инхегрирования
Наименование
I
Хп ХЛ_1 + 7’(2Х„_1-А-П)
Хп = Xи—1 + Т (Xn—i)
Хп^ Х„_1 + у (Х„ + *»-1)
Xa^Xn_l+T(Xn)
т
п = Xn—i + — (ЗХЛ — Хп_ i)
= Xw__1 + T(2A/l-Xn_1)
2
О
4-1
Метод Эйлера
Метод трапеций
Метод прямоугольни-
ков
Метод неявного инте-
грирования второго по-
рядка Адамса
— 1
1
Отсюда могут быть найдены многие классические численные ин-
теграторы и формулы интегрирования более высокого порядка для
чисел, кратных у= 1/3, 1/4, 1/5, ..., 1/п, где п —целое число. Количе-
ство подобных выражений намного больше, чем мы указали. Важ-
но, что восемь формул интегрирования табл. 7.2 и 7.3 приводят к
большому числу классических формул. Таким образом, многие ши-
роко известные классические формулы численного интегрирования,
каждая из которых получена самостоятельно, на самом деле пред-
ставляют тот же самый интегратор, отличаясь только величиной
фазового смещения интегрируемой функции.
Заметим, что эти интеграторы являются членами бесконечного
ряда интеграторов, связанных по фазе, основой которых является
189
также единая формула интегрирования. В основном все эти ин-
теграторы отличаются от классических общностью фазовых связей
интегрируемой функции. Кроме того, несмотря на то, что это менее
важно, интеграторы с фазовыми связями характеризуются нали-
чием коэффициентов, которые являются функциями, а не числами.
Симметричность выражения формул интегрирования первого
порядка вблизи у = + 1/2 (см. табл. 7.4) возникает из-за того, что
процесс перестройки интегрируемой функции с помощью преобра-
зователя нулевого порядка привносит полупериодное запаздывание,
которое компенсируется полупериодным опережением при
Y = +1/2.
Заметим единообразие весовых функций обоих выражений в
формуле интегрирования. Ясно, что если нет иного фазового сме-
щения, нежели вводимое процессом перестройки, можно осуще-
ствлять трапециевидное интегрирование, не обладающее фазовым
смещением в интеграле.
Важно понять, что компенсирующие цифровые интеграторы об-
ладают параметром фазового смещения. Из этого следует особен-
ность применения явных или неявных интеграторов. Эта гибкость
рассмотренного интегратора является существенным отличием от
применяемых компенсирующих цифровых интеграторов и других
методов интегрирования.
Более подробно Г-интегратор
x„=x„-i + 7'X[yx„+(1 — Y)3c„-i]
может быть применен с использованием только последнего значе-
ния х, но скомпенсированного при помощи опережения периода вы-
борки у. Так что применяя
Y' = Y+b
получим
x„=x„_i + 7'X[(y+ 1)+-1 + Y-^ra-2]
или
x„ = xn_1 + n[Y,x„_1 + (! -Y')^n-2]-
Все, кто обычно применяет явные числовые интеграторы в мо-
делировании, сочтут полезным упоминание, что формулы Т-интег-
рирования могут быть записаны через выражения последних зна-
чений интегрируемой функции простым изменением индексов в
каждом из членов интегрируемой функции соответственно от п до
п—1; от п—1 до п—2; от п—2 до п—3 и т. д.
Чтобы получить обоснованную характеристику с помощью ин-
тегратора, необходимо ввести опережение периода выборки (для
компенсации введенного запаздывания):
1)	изменением формулы интегрирования, как показывалось ра-
нее;
2)	численно, добавлением единицы к значению у.
190
7.5.	ПРИМЕНЕНИЕ УПРАВЛЯЕМОГО ИНТЕГРИРОВАНИЯ
В этой главе будет обращено особое внимание на применение
интегратора нулевого порядка для упрощения задач. Последний
упростит аналитические решения и заставит объединить принципы
применения компенсирующих интеграторов при моделировании,
управлении и в других системах информации. С точки зрения ус-
тойчивости, обладая первым порядком, интегратор можно так на-
строить, чтобы не ввести в динамический процесс полюсов больше,
чем может дать истинное непрерывное интегрирование. Это не яв-
ляется исключением и для многих интеграторов более высокого по-
рядка, включая интеграторы Рунге—Кутта.
Подстановка интеграторов более высокого порядка (явных или
неявных) в дифференциальное уравнение приводит к разностному
уравнению с большим числом полюсов, чем в дифференциальном
уравнении, из которого оно получено. При больших размерах шага
интегрирования эти дополнительные Полюсы часто влияют на ус-
тойчивость интегрируемых уравнений движения больше, чем любой
другой источник ошибки.
С точки зрения точности, теорема о среднем гарантирует, что
при использовании интегратора нулевого порядка можно точно ин-
тегрировать в заданном интервале при соответствующем выборе
средних значений Д-. ^-интегрирование нулевого порядка облада-
ет параметром транспортного опережения у, который может быть
подобран по точности при заданном интервале времени выбора
дискретных данных интегрируемой функции. Для линейных систем
с постоянными коэффициентами у подбирают постоянной. В систе-
мах же с коэффициентами, изменяющимися во времени, или у ли-
нейных систем у подбирают переменными эмпирически или ис-
пользованием алгоритмов изменения фаз (что аналогично алгорит-
мам переменного шага).
Интегрирование с переменной фазой проводится при фиксиро-
ванном размере шага интегрирования, а фаза подбирается для по-
лучения желаемой точности интегрирования — в этом суть новой
разработки в приложении к численному интегрированию для точ-
ного реального времени *.
Там, где необходимо регулировать фазовое смещение и влияние
дополнительных полюсов, полученных при интегрировании с ма-
лым размером шага и высоким порядком разложения интегрируе-
мой функции, подобранные интеграторы низкого порядка позволят
нам скомпенсировать эти эффекты непосредственно при помощи
компенсирующей фильтрации.
7.6.	АНАЛИТИЧЕСКИЙ ВЫБОР ОТНОШЕНИЯ ФАЗЫ
К КОЭФФИЦИЕНТУ УСИЛЕНИЯ
Можно использовать много аналитических критериев для выбо-
ра единственных X и у. Например, можно выбрать X и у таким об-
разом, чтобы получить соответствие между корнями моделирующе-
* См. прил. В.
191
Рис. 7.7. Линейная непрерывная сис-
тема первого порядка с постоянными
коэффициентами
го разностного уравнения и корнями моделируемой системы. Кроме
того, у и X могут быть выбраны так, чтобы свести к минимуму
среднеквадратичное отклонение между реакцией непрерывной сис-
темы и реакцией аппроксимирующей системы при известной пере-
даточной функции. Во многих случаях эти и другие критерии поз-
воляют приводить к удовлетворительной дискретной системе, ап-
проксимирующей непрерывные системы либо при моделировании
с применением цифровых управляющих машин или для отбора
цифровой информации.
Интересно, что различные методы выбора X и у при решении
сложных комплексных задач редко приводят к одинаковым X и у
Этот недостаток (т. е. уникальность синтезированных дискретных
систем, которыми аппроксимируются непрерывные системы) явля-
ется хорошо известным свойством дискретного системного синтеза.
Например, фазу и коэффициент усиления выбирают подбором со-
ответствующего корня следующим образом.
Рассмотрим линейную непрерывную систему первого порядка с
постоянными коэффициентами, показанную на рис. 7.7. Уравнени-
ями движения, которые описывают этот процесс, являются
X=F — kX\ Х(0) = 0,	(7.19)
где F — возмущающая функция системы.
Дискретная система, которую можно использовать для аппрок-
симации этой непрерывной системы, показана на рис 7.8.
В обратном контуре e~sT является показателем неявной функ-
ции дискретных систем, где прямой цикл вычисляется раньше, чем
можно просчитать и замкнуть обратный контур. Эта система пред-
ставлена для г-области на рис. 7.9.
Передаточной функцией дискретного процесса является
=	{у^ Ч- (1 — Y)}	(7 20)
F (z) z^ +(UTy— l)z +НТ(1 — у) ’	'
Рис. 7.8. Линейная дискретная система первого порядка с постоянными коэффи-
циентами — аналог линейной непрерывной системы первого порядка с постоян-
ными коэффициентами
192
Рис. 7.9. Дискретная аппрок-
симация при записи в форме
^-преобразования
Характеристическими полюсами дискретной системы второго
порядка являются
=	1{ЖуЧМШ(1-?Г.	(7.21)
Одним полюсом непрерывного процесса является
(7.22)
Мы можем подобрать полюсы дискретной системы второго по-
рядка с замкнутым циклом при помощи полюса непрерывной сис-
темы первого порядка с замкнутым циклом. Для этого, приравни-
вая у=1, устраним один из корней дискретной системы второго
порядка. Затем выберем X так, чтобы подобрать полюс оставшейся
дискретной системы в соответствии с полюсом непрерывной сис-
темы.
При v=l передаточной функцией дискретной системы станет
=-----—------ (7.23)
F (z)	z+(k\T— ])	v
с полюсом при
4,олюс=1-^.	(7.24)
Для того чтобы подобрать полюс непрерывной системы в соот-
ветствии с тем же полюсом дискретной системы, X выбирается из
условия
ZMm^s^T^-kT= 1 -k\T.	(7. 25)
Решая (7.25) относительно X, найдем
1 — е~кт
(7-26)
Подставляя у и А в передаточную функцию и перемножая, полу-
чим выражение
X (z) _ z(\ — erkT)
F(z)	(z — e~kT)
которое обращается в разностное уравнение
^„ = e-^X„_1 + (l-e-^)F„.
(7.27)
(7. 28)
Из всего этого видно, что выбор X и у путем подбора соответствую-
щего корня приводит к интегрированию, которое является точным
при однозначном решении непрерывной системы и при ступенча-
7	493	193
гой реакции. Оно является хорошей аппроксимацией при реак-
ции вычисляемой системы на произвольные функции возмущающе-
го воздействия и неспособно стать неустойчивым независимо от то-
го, какой размер шага интегрирования выбран (так как величина
полюса передаточной функции разностного уравнения есть e~fer, ко-
торое всегда меньше, чем 1, если k>0).
7.7.	ЭМПИРИЧЕСКИЙ ВЫБОР ОТНОШЕНИЯ ФАЗЫ
К КОЭФФИЦИЕНТУ УСИЛЕНИЯ
Так как интегратор с переменным отношением фазы к коэффи-
циенту усиления приводит ко многим, хорошо известным цифровым
интеграторам с фиксированным интервалом, то эмпирический вы-
бор опережения и коэффициента усиления не представляет ничего
иного, чем метод проб и ошибок при выборе интегратора, который
используется при данной системе уравнений.
Методика эмпирического подбора X и у состоит в следующем.
1.	Приравниваем у = Х=1.
2.	Образуем контрольный случай при	WB— часто-
та выборки дискретной части сигнала и Wi — частота информации,
представляющей интерес.
3.	Приравниваем U7B=10U^i и выбираем у, для того чтобы са-
мым лучшим образом подобрать контрольный случай.
4.	Выбираем X, чтобы лучше подобрать соответствующий конт-
рольный случай.
5.	Повторяем этапы 3 и 4.
При использовании интегратора нулевого порядка, приравни-
вая Xi=yi = 1, преобразуем интеграторы переменного отношения
опережения к коэффициенту усиления в прямоугольные интегра-
торы. Прямоугольное интегрирование обладает тем свойством, что
нет необходимости вводить дополнительные корни в дискретную
систему.
Таким образом, непрерывная система n-го порядка преобразу-
ется в дискретную систему я-го порядка; дальнейшая подборка ко-
эффициента усиления может означать выбор корней дискретной
системы в соответствии с корнями непрерывной системы.
И, наконец, эмпирический «настроечный» интегратор может
быть упрощен во многих случаях по следующему правилу:
1)	у влияет на промежуточную неустойчивую характеристику, а
не на установившийся режим;
2)	%=/=1 может влиять на устойчивое состояние; при изменяю-
щемся X устойчивое состояние нужно проверять.
При полете летательных аппаратов модель системы является
примером моделирований, где различные номинальные условия
полета требуют различных значений величин опережения и коэф-
фициента усиления (в зависимости, например, от того, убраны или
выпущены закрылки, убрано или выпущено шасси, велико или ма-
ло число Маха). Для каждого условия у и X подбираются повторе-
нием четырехэтапной «настроечной» методики. Эти коэффициенты
194
усиления и фазы хранятся и исполь-
зуются при моделировании, когда
осуществляются соответствующие
условия (например, если рукоятка
закрылка поставлена в нижнее поло-
Рис. 7.11. Импульсная переходная
функция аппроксимированной систе-
мы второго порядка при Т=0,001 с
Рис. 7.10. Линейная непрерывная сис-
тема второго порядка с постоянными
коэффициентами
жение, рукоятка шасси перемещена в верхнее положение, Мах>0,5
и т. д.).
Пример эмпирического выбора фазы и коэффициента усиления
линейной непрерывной системы второго порядка с постоянными ко-
эффициентами представлен на рис. 7.10.
Уравнением, описывающим движение этой системы, является
X=F-KwnX-VDlnX-,	(7.29)
С=0,3, Аг(0)=Л'(0)==0;	(7.30)
wn=l Гц.	(7.31)
В этом примере первое приближение получается первичным
определением реакции от единичного воздействия при частоте вы-
борки дискретных значений в 1000 раз большей, чем естественная
частота системы.
На рис. 7.11 показан пример единичного коэффициента усиле-
ния при у = +3 и у= —3. Очевидно, что при данной небольшой
частоте влияние небольшого фазового смещения незначительно.
На рис. 7.12,а, б и в показано влияние у (при Х=1) на часто-
ты выборки 100 Гц.
На рис. 7.13, а, бив показано влияние изменения у при частоте
выборки 10 Гц.
Заметим, что во всех случаях каждый выбранный период опе-
режения (у= 1, Х=1) приводит к промежуточным функциям, кото-
рые очень хорошо согласуются с первичными, даже без подбора
коэффициента усиления.
Легко показать (рис. 7.Г2), что приравниванием у=1 устраня-
ются два корня в некоторых дискретных системах четвертого по-
рядка. Обычно этим пользуются при моделировании линейных сис-
тем с постоянными коэффициентами, когда, принимая y=il, умень-
шают число корней в линейной системе. Подобранный коэффици-
ент усиления может быть использован для нахождения местополо-
жения корня дискретной системы в соответствии с местоположени-
7*
195
Рис. 7.12. Импульсная переходная
функция аппроксимированной систе-
мы второго порядка при Т=0,'01 с
Рис. 7.13. Импульсная переходная
функция аппроксимированной систе-
мы второго порядка при Т=0,1 с
ем корня непрерывной системы. Это положение несправедливо при
нелинейных уравнениях.
Пример эмпирического выбора X и у нелинейной системы пока-
зан на рис. 7.14. Эта задача была использована Бейзнером для
исследования метода Фаулера, интеграторов Гурка и метода Адам-
са для моделирования в реальном масштабе времени как простой
пример составных систем с замкнутым контуром, содержащих ли-
нейные элементы, жесткие нелинейности и интеграторы. В этой
задаче представлено простое сравнение любых заданных методов
или комбинации методов в простой форме и поэтому динамические
свойства системы могут быть предопределены либо на машине,
либо вручную аналитически. Процесс в этой системе может быть
рассмотрен как линейный второго порядка с внедренным нелиней-
ным ограничителем скорости. Это справедливо при достаточно низ-
кой скорости, т. е. когда |Х3|^1 и процесс приобретает стацио-
нарный линейный вид, передаточной функцией которого является
.	(7.32)
2^5	4- 2s 4- К
Рис. 7.14. Пример решения задачи с нелинейностью
196
Рис. 7.15. Дискретный вариант системы, представленной на рис. 7.16
При ступенчатых входах, где величина М достаточно низка
(т. е. |М| < 272), данная система достигнет своего устойчивого
состояния при равенстве функции на выходе ее значению на вхо-
де. Частоты и демпфирование подбираются по характеру выходной
функции системы второго порядка. При этом
Wn=VK, ^=\iVk,
что следует из ограниченности скорости при величине Х3, достига-
ющей единицы.
Устойчивый режим процесса первого порядка, соответствующий
Л7(($ + 2), отвечает k[2. Он достигает 68% своего устойчивого ре-
жима за 1/2 с. В течение этого времени влияние обратной связи
возрастает медленно и не сможет обеспечить скорость Х3 выходя-
щей за предел единицы, если величина Лг4 больше, чем 2/К. Для
этой системы при К=5
1^ = 2,236 рад/с--=0,356 Гц; £-0,447
и при единичных шагах порядка 2,5 будет реализовываться ско-
рость Х3, большая, чем единица.
Характерная дискретная система, которая обычно моделирует
рассматриваемую, имеет вид, представленный на рис. 7.15. В это?!
дискретной системе процесс A7(s-|-2) аппроксимируется выборкой
и перестройкой нулевого порядка при помощи опережения в пол-
периода для компенсации запаздывания, вводимого процессом пе-
рестройки нулевого порядка. Разностным уравнением, которое опи-
сывает этот процесс, является
Л',, = ^Х.,_, + А ((1 _ e-Г) + (е-г - е-W) Х,^}.
В этом примере Т-интегратор нулевого порядка, для нахождения
решения Х2 желательно применить уравнение
Программа моделирования показана на рис. 7.16.
Заметим, что для текущей оценки берется текущее значение
^5 и последнее значение Хь Как упоминалось раньше, это происхо-
дит из-за того, что обработка цифровых данных прямого контура
должна быть осуществлена до того, как обратная связь будет
замкнута. Введение физического запаздывания в данные связано
не с моделирующими разностными уравнениями, а с динамически-
ми характеристиками информационного потока в цифровой ВМ.
Это запаздывание также показано в обратном контуре (рис. 7.17).
197
^n~X5n X1n-i
4=e‘%-; +


Г2- V -'
X2n=*3r.
V
= 1
“в
логика
предельногь
насыщения
2П~
xin=xin-i+aT\lxzn+(1~t)X2n-i
^4
Х2П.:
Хзп-Г хзп
Рис. 7.16. Программа ВМ
для моделирования нелиней-
ной контрольной задачи
В рассматриваемом примере применялся выборочный период в
0,5 с; отношение выборочной частоты к собственной
2=5.613.
Wn 0,356 Гц
что близко к шенноновскому пределу, при котором возможна пере-
стройка непрерывной функции в дискретную.
Характеристика дискретной
системы при ступенчатом входе
2,5 показана на рис. 7.17 для раз-
> личных значений у. Контрольный
случай был получен сведением
шага интегрирования к 0,0001.
Размер шага интегрирования яв-
ляется небольшой гарантией того,
что при изменении у от +3 до
—3 фазовое смещение в решении
не достигнет ±0,3 м-рад и вели-
чина интервала распечатки не бу-
дет меняться на величину, боль-
шую чем 5-10-4.
Из рис. 7.17 видно, что допус-
тимая приемлемая
ледовательности
большом размере
щью контрольного
исходит при 1 и у~ 1.
7*0$'
2,5
2,0
1,5
1,0
Исходный,
вариант
7-1
7*0,9
Рис. 7.17. Результаты моделирования
Реакция на
единичный
импульс____
о *	2	3	4	5 б
Время (секунды)
подгонка пос-
решений при
шага с помо-
решения про-
* ч. в. с. — число выборок в секунду.
19
7.8.	ИНТЕГРИРОВАНИЕ С ПЕРЕМЕННОЙ ФАЗОЙ
Интегрирование с переменной фазой сходно с интегрированием
при переменном размере шага, критерием которого является дос-
таточная точность, при двухэтапном интегрировании с размером
шага, равным 1/2, или при интегрировании в один этап. В этом слу-
чае фаза имеет незначительное опережение. При необходимости
производится дополнительное опережение фазы и еще раз применя-
ется критерий точности.
Таким образом, при недостаточной точности, достигнутой при
первом этапе интегрирования с опережением по фазе, осуществля-
ют последующие этапы до тех пор, пока критерий не удовлетво-
рен.
Критерий точности удовлетворяется при у, который согласуется
с допускаемым первоначальным шагом и обеспечивает интегриро-
вание следующих этапов. При подборе фазы вычисление произво-
дится со «стороны контура» за тысячную долю секунды по сравне-
нию с интегрированием, которое обычно протекает за время этапа
в 0,1 с. Это позволяет регулировать точность численного интегри-
рования в реальном масштабе времени. В отличие от интегрирова-
ния при переменном шаге интегрирование с переменной фазой про-
текает при одинаковом шаге, выбираемом с точки зрения требова-
ния задачи по точности.
Обсуждаемый здесь алгоритм переменной фазы — это простей-
ший вариант первоначального ознакомления с рассматриваемым
методом. Очевидно, существует большое количество алгоритмов, в
которых будет допускаться Т-интегрирование, для того чтобы прий-
ти к адаптивным видам. Те из них, с которыми автор часто стал-
кивался, являются вариантами этого основополагающего понятия.
С практической точки зрения параметры фазы и коэффициента
усиления могут применяться для компенсации систематических
ошибок вычисления (а не округления случайной) независимо от
источника. При разработке крупномасштабного цифрового или
гибридного моделирования или при разработке цифровых управля-
ющих систем их элементы часто разрабатываются различными
группами в различное время, а иногда и в различных местах. Ког-
да эти части объединяются вместе и собираются в целую систему,
обнаруживается нестыковка в виде небольших фазовых смещений
во многих элементах. Это приводит к дополнительной задаче ус-
тойчивости системы. В этих ситуациях формулы интегрирования
переменного соотношения фазы и коэффициента усиления использу-
ются для интегрирования уравнений движения с параметрами фа-
зы и амплитуды (X и у), подобранными эмпирически либо на осно-
вании хорошо подобранного контрольного примера, либо по оценке
суммарного фазового и амплитудного смещения, возникшего в
процессе моделирования.
199
7.9.	СВОЙСТВА ИНТЕГРАТОРОВ
Сравнивая табл. 7.2 и 7.3, мы видим, что дискретно скомпенси-
рованные интеграторы проще непрерывно скомпенсированных. Эта
особенность приводит сама по себе к сравнительно простому пред-
ставлению о свойствах дискретно скомпенсированных интеграторов;
далее они будут изучаться более детально. Непрерывно скомпен-
сированные интеграторы представлены только ради полноты изло-
жения.
Предопределение числовой ошибки в любых, даже самых прос-
тых случаях управляющих систем чаще всего весьма затрудни-
тельно. Как для цифрового моделирования, так и для цифрового
управления большее практическое значение представляет способ
определения ошибки системы с помощью системы уравнений.
Полезной мерой характеристики передачи ошибки числового
интегратора (его сглаживающей способности при цифровом управ-
лении или воспроизведении в реальном масштабе времени) являет-
ся его реакция на шум, который характеризуется дисперсией «скач-
ка» от шага к шагу процесса численного интегрирования. Как для
дискретных, так и для непрерывно скомпенсированных чисновых
интеграторов «скачок» от шага к шагу задается как
ЬХП = (ХП-ХП^=\Т[УХЛ^-^ХП-Л	(7.33)
Дисперсия ДХП задается средним значением ДХП2 как
al.v = Е (ЬХ2)=№Е (Y2^2„+2у (1 - Y) XпХ+ (1 — Y)2 XLj,
(7.34)
где Е — оператор математического ожидания.
При нулевой коррелированности стационарных случайных (или
псевдослучайных) значений последовательности X имеют
(7.35)
и
Е(Х2п) = Е(Х2п^)=4.	(7.36)
Таким образом, характеристика «белого шума» представляется
как
32х=Х2Л(2У2-2У+1)4.	(7.37)
Значение у, которое сводит к минимуму дисперсию этого интег-
ратора, равно 1/2, и минимум передаточной функции дисперсии для
интегратора — это
2
= —.	(7.38)
2
Подобные результаты могут быть получены и для других ин-
теграторов. Уравнения распространения дисперсии, как для неп-
200
рерывно, так и для дискретно скомпенсированных интеграторов
представлены в табл. 7.5.
Таблица 7.5
Уравнения ошибки интегратора		
Процесс экстраполяции	Непрерывная компенсация	Дискретная компенсация
Экстраполятор	адХ = Х272Х	W х
нулевого порядка	X (2у2—2у + 1) а2х	
		Х(2у2-2у+ 1) <2х
	9	Х2Т2	<>	Х2Г2
Экстраполятор	а!х = —(6У4+12уЗ_	аАХ = —д—Х
первого порядка	4	4
	_ 6у2- 12у + 10) а2х	X (26у2 — 26у + 10) а2 А
Экстраполятор второго порядка	Х2Г2 «дх= -^-(80уб+450у5+	о	Х272 адх = 144 (2516у2 —
	4- 723у4 + 457у3 —	— 2516у+810) э2х
	-1189у2—522у—248)	
Экстраполятор	=— (бу4— 12у3+	’lx = X-7^(2Y2-2Y + 2)a2
треугольного типа	4	
	+ 6у2 + 2) а2х	
В табл. 7.6 представлены значения у, которые приводят к ми-
нимуму дисперсии для этих интеграторов наряду с минимумом их
передаточных функций. График нормализованных передаточных
функций дисперсий в зависимости от функции параметра фазового*
смещения у для дискретно скомпенсированных интеграторов пока-
зан на рис. 7.18.
Таблица 7.5
Характеристики интеграторов при минимальной дисперсии
Процесс э1&траполяиии	Ts при минимальной дисперсии		Пере сточная функция при минимальной дисперсии	
	Дискретная компенсация	Непрерывная компенсация	Дискретная компенсация	Непрерывная компенсация'
Экстраполятор нуле- вого порядка	у= 1/2	у = 1/2	Х2Г2/2	Х272/2
Экстраполятор первого порядка	у= 1/2	у = 0,5714	7X272/8	Х272
Экстраполятор второго порядка	у = 1/2	у = 0,250	10X272/8	4X272
Экстраполятор тре- угольного типа	У = 1/2	у = 0 и 1	3X272/8	Х272/2
2011
Рис. 7.18. Передаточная функция нор-
мализованной дисперсии параметра
фазового смещения у для дискретно
скомпенсированных интеграторов
Минимальные дисперсии
дискретно скомпенсированных
интеграторов сведены во вто-
рую колонку табл. 7.7. Каждый
из интеграторов содержит ал-
горитм интегрирования в неяв-
ной форме, который может
быть применен как корректи-
рующее устройство в алгорит-
ме прогнозирования. Прогнози-
рующее устройство находится
принятием в этих алгоритмах
величины у = 0. Прогнозирую-
щие пары представлены в
табл. 7.7.
Подобные результаты могут
быть получены и из непрерыв-
но скомпенсированных интег-
раторов. Наконец, интеграторы
настройки обладают следую-
щими общими свойствами.
Таблица 7.7
Дискретно скомпенсированные интеграторы минимальной дисперсии
Процесс экстраполяции	Формула коррекции Су минимума дисперсии)	Формула прогноза Су=О)
Зкстраполятор нулевого порядка	кт Хп = X п—1+ g X	Хп ~ Xn-i 4- lTXn—i
Зкстраполятор первого порядка	X (х„ + Х„_!) кт Xn=Xn_l + —	X -X 4-^- лп—Хп-\+
	(ЗХ„ + 2Хп^+Хп-2)	
Зкстраполятор второго порядка	Л„ = ХЛ_1 + ^-	Хп = X +
	(6Хл+13Лл-1- - 12Хл_2 +5Лл_3)	(23ХЛ_1-)6ХЛ*.2 + 5ХЛ_3)
	или Хп=Хп_1+—(12Хп+	
	+25*п_1-25Хл-1+12Хл_з)	
Зкстраполятор треугольного типа	X — X + Лп — лп-1~г 4 (Хп 4“ ^п—1 4- *п-2)	= X п—1 4" XT , . +	~ (^л-1 + Хп-2)
202
1.	В непрерывно скомпенсированных интеграторах у при мини-
мальной дисперсии стремится к нулю от максимального значения,
равного 1/2 по мере роста порядка процесса преобразования.
2.	Для дискретно скомпенсированных интеграторов минималь-
ная дисперсия имеет место при у, равной 1/2, и не зависит от про-
цесса перестройки.
3.	Распространение дисперсии чувствительно к увеличению фа-
зового смещения по мере увеличения порядка процесса перестрой-
ки.
4.	Минимум дисперсии растет по мере увеличения порядка про-
цесса перестройки.
7.10.	СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ
Изучение распространения дисперсии дает возможность про-
никнуть в механизм достижения требуемой точности и чувствитель-
ности ошибки от значения амплитуды, однако информация по фа-
зе не может быть получена интегральными операциями над пара-
метрами случайного процесса.
В этом смысле плодотворен анализ в частотной области, кото-
рый дает представление как о фазовых, так и об амплитудных ха-
рактеристиках исследуемых интеграторов. Спектральные характе-
ристики этих интеграторов дают возможность изучать особенности
их практического применения.
Одним из простых методов определения частотной характерис-
тики этих интеграторов является, во-первых, образование переда-
точной функции в z-области на базе разностного уравнения, во-вто-
рых, переход из z-плоскости в плоскость W, при этом используется
преобразование
(7 39)
и последующее преобразование из ^-области в частотную область
через промежуточные алгебраические и тригонометрические соот-
ношения
(7.40)
и
& = tg(^V	(7.41)
Этот метод приводит к амплитудной и фазовой информации в
ограниченном интервале (ю^сов/2), где а>в — частота выборки.
Следуя этому методу амплитуды, спектр и фазовое смещение свя-
зывают с интегратором преобразования нулевого порядка.
Передаточной функцией интегратора при преобразовании нуле-
вого порядка является
203
Подставляя	1 +VF z =	, 1 —IF	(7.43)
найдем	JL	1+(2у~1)^	(7.44)
	\ТХ ( '	21F	
Подставляя		(7.45)
найдем	X ,	(2 у — 1) tg (лш/<ов) — } ,	(7. 46)
	\ТХ v	tg (лю/юв)	’	
на основании	которого запишем	
	, х .2 {(y—4")2tg(3t“/“»)}—1	(7.47)
	ЦГХ J “	{2 tg(JIto/a>B)}2	
и	*	
	?=tg-1 {(y — 1/2) 2 tg (лш/шв)} — 90°.	(7.48)
Очевидно,	что спектральная характеристика этого	интегратора
значительно отличается от непрерывного интегрирования, где		
	/ у \о (у) = 1До2 и ?=90°.	(7.49)
Заметим, что хорошая аппроксимация при непрерывном интег-
рировании достигается при у =1/2, Х=1. Тогда
(у \2	1
—р) = Ит {4 tg2 (лсо/<ов)}-1	;	(7. 50)
кТХ )	а)->о
lim(<p)=-90e.	(7.51)
О) -*0
Кроме того, заметим, что амплитудный спектр симметричен от-
носительно у= 1/2 (7.47), а фазовый спектр несимметричен (7.48).
Кроме того, (Л(gj))2 зависит как от у, так и от X, в то время как
фаза зависит только от у. Эта разница между фазовой и амплитуд-
ной частотными характеристиками предполагает эмпирический ме-
тод выбора у и X при Г-интегрировании, применяемом в сложных
нелинейных системах с замкнутым контуром.
1. Сначала выбирается у для оценки фазовых ошибок.
2. Затем выбирается X для сведения к минимуму амплитудных
ошибок.
Уравнение (7.48) показывает, что при у ='1/2 этот интегратор
(примененный в неявной форме) будет обладать только искажени-
ем амплитудного спектра, и параметр коэффициента усиления X
204
может быть выбран для того, чтобы свести к минимуму это иска-
жение.
Таким образом, если амплитудный спектр моделируемого про-
цесса известен, дисперсия между амплитудным спектром непрерыв-
ного процесса и его дискретной аппроксимацией может быть све-
дена к минимуму выбором X. Параметры к и у могут быть выбра-
ны и эмпирически и аналитически, как обсуждалось в разд. 7.3.
И, наконец, так как в целом верно, что если к «устанавливает мас-
штаб» выхода интегратора, то это может повлиять на установивше-
еся решение системы уравнений, если установившийся интегратор
на входе не равен нулю. В этих случаях к всегда должна прирав-
ниваться к 1.
Спектральный анализ интеграторов более высокого порядка мо-
жет быть осуществлен аналогичным образом *. Итак, мы нашли,
что:
1.	Все эти интеграторы аппроксимируют непрерывное интегри-
рование при со->0 и Х=1.
2.	Для дискретно скомпенсированных интеграторов фазовое
смещение зависит только от у, тогда как [4 (со)]2 зависит и от X и
от у.
3.	Фазовые ошибки являются основным источником неточности
при интегрировании, если размер шага интегрирования велик по
сравнению с естественным периодом системы интегрируемых урав-
нений.
4.	Амплитудные ошибки являются основным источником неточ-
ности при интегрировании, если шаг интегрирования мал по срав-
нению с естественным периодом системы интегрируемых уравне-
ний.
7.11. УСТОЙЧИВОСТЬ ХАРАКТЕРИСТИК
Существуют две точки зрения, которые нужно рассмотреть при
изучении устойчивости числового интегратора: это собственная ус-
тойчивость интегратора и влияние интеграторов на устойчивость
регулируемого или моделируемого процесса.
Собственная устойчивость интегратора, с точки зрения управ-
ления и моделирования, характеризуется устойчивостью как интег-
ратора, так и дифференциатора. Корень настроечного интегратора
нулевого порядка равен +1, поэтому он нейтрально устойчив. Ве-
личина z-полюса дифференциатора представляется выражением
|2п0ЛюС| = |^|,	(7.52)
которое меньше или равно 1 для всех у^ 1/2.
Мы пришли к выводу, что интегратор первого порядка устойчив
при всех у^ 1/2. Кроме того, нашли, что, так как у увеличивается,
* Marc L. Sabin, «Bode Magnitude and Phase-Angle Characteristics of the
Tunable Integrators», vol. 6, Part. 1, Proceedings of the Sixts Annual Pittsburgh
Modeling and Simulation Conference, April 24—25, 1975.
205
превосходя 1/2, то точное интегрирование получается вплоть до
критического значения у, за которым точность интегратора умень-
шается.
Заметим, что трапециевидное интегрирование (у= 1/2) нейтраль-
но-устойчиво как для интегратора, так и для дифференциатора.
Нашли, что два корня треугольного и дискретно скомпенсиро-
ванного интегратора первого порядка равны 0 и +1; подобно ин-
тегратору нулевого порядка это устойчивые интеграторы. Величи-
ны полюсов этих интеграторов при использовании их в качестве
дифференциаторов равны
1ДолЮс|= ±^-{1-4y(1-Y))i/2	(7.53)
zy zy
и
|ZnMl0C| = -fc^-±-fc^-{(3-4Y)2-12Y(l-Y)}1/2| (7.54)
оу	оу	I
соответственно.
Они-оба меньше или равны 1 для всех значений у^1/2.
Нашли, что такие же результаты справедливы для дискретно
скомпенсированного интегратора второго порядка. Из этого мож-
но сделать заключение, что скомпенсированный интегратор может
быть устойчив для всех значений у, однако только при у, больших
1/2, можно гарантировать, что интегратор обладает внутренней ус-
тойчивостью в процессе вычисления.
Обычный метод изучения влияния интегратора на числовую ус-
тойчивость системы интегрируемых уравнений — это подстановка
формульного выражения интегратора (в явном или неявном виде)
в интегрируемые дифференциальные уравнения таким образом, что-
бы образовать разностные уравнения. Параметрами этого разност-
ного уравнения интегратора являются коэффициенты, получаемые
с помощью исходного дифференциального уравнения, и величина
шага интегрирования. Устойчивость разностных уравнений изуча-
ется на подготовленных диаграммах устойчивости, показывающих
комбинации коэффициентов дифференциального уравнения и раз-
меров шага интегрирования, при которых интегрирование будет
обладать числовой устойчивостью.
Представленные в табл. 7.2 и 7.3 Г-интеграторы не нуждают-
ся в анализе подобного типа. Эти интеграторы обладают парамет-
рами с регулируемой устойчивостью, которые можно выбрать та-
ким образом, чтобы сделать процесс интегрирования не только ус-
тойчивым, но и высокоточным.
Достаточно сказать, что если коэффициент в формуле интегри-
рования содержит в себе фазовое смещение, параметры коэффи-
циента усиления и размер шага интегрирования, то можно осуще-
ствить устойчивое и точное интегрирование системы уравнений.
206
Глава 8. КЛАССИЧЕСКИЕ МЕТОДЫ
ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
В этой главе рассматриваются классические численные методы
интегрирования. Метод численного интегрирования, представлен-
ный в гл. 7, относительно новый и практически мало применявший-
ся (приблизительно было проделано 100 моделирований за время
написания книги). Даже этот ограниченный опыт, однако, указы-
вает на то, что он является гибким и значительным методом интег-
рирования.
Была проделана работа по сравнению Г-интегрирования (кото-
рое обладает гибкостью при проектировании) с классическими ме-
тодами, которые не всегда удобны для решения задач.
Классические методы включены для полноты содержания, так
как некоторые из них особенно полезны при решении разностных
уравнений и при цифровом моделировании.
Выводы уравнений для ряда методов здесь опущены, так как
могут быть найдены в таких прекрасных книгах, как, например,
«Численные методы для исследователей и инженеров»
Хэмминга.
Как упоминается в гл. 7, существует большое количество чис-
ленных методов. Здесь же представлены те из них, которые могут
быть пригодны в моделировании. Критерии, по которым обычно
производят выбор алгоритма, как правило, включают точность,
скорость, устойчивость и простоту.
При проектировании могут быть введены как полезные числен-
ные интеграторы r^-го порядка, так и интеграторы, имеющие за-
паздывание с периодом, равным п/2, которое нежелательно с ^очки
зрения устойчивости.
Указанные выше обстоятельства необходимо иметь в виду осо-
бенно, если речь идет о моделировании сложных (больших поряд-
ков) систем в истинном масштабе времени, когда в контур включен
человек.
Такого типа моделирование часто характеризуется периодом
времени (размером шага интегрирования) от 0,05 с до 0,1 с.
Например, формула моделирования четвертого порядка, кото-
рая включает оценку скорости на основании последних четырех пе-
риодов выборки может в замкнутых контурах с обратной связью
вызывать запаздывание 0,1—0,2 с.
Моделирование системы с замкнутым контуром с собственной
частотой в 1 Гц и такой большой задержкой может привести к фа-
зовому смещению от 16 до 32°. С такими данными ни ручное, ни
моделируемое автоматическое управление не только нежелательно,
но и недопустимо.
Большинство управляющих систем оперирует с фазовым смеще-
нием не более 3°.
207
С другой стороны, при исследовании траектории классические
интеграторы дают погрешность порядка
где п — порядок формулы интегрирования.
При небольшом Т анализ ошибки в классическом интегрирова-
нии указывает на то, что для повышения точности желательны ин-
теграторы более высокого порядка.
При рассмотрении особенностей использования классических
численных интеграторов целесообразно иметь в виду следующее:
1.	Какие методы более пригодны для получения квадратур (оп-
ределенное интегрирование) и какие более пригодны при неопре-
деленном интегрировании дифференциальных уравнений.
2.	Какие методы применимы при моделировании в истинном
масштабе времени.
3.	Какие методы применимы при моделировании в произволь-
ном масштабе времени.
4.	Какова устойчивость данного цифрового интегратора (т. е
собственная устойчивость применительно к моделированию систе-
мы).
5.	Какова точность каждого метода по минимизации и рас-
пространению дисперсии.
6.	Какая временная задержка (среднеинтегральная задержка)
может ожидаться при применении конкретного интегратора.
Этот параметр при умножении на наивысшую частоту, пред-
ставляющую интерес, является оценкой фазового смещения, связан-
ного с интегратором, и таким образом является оценкой степени
влияния формулы интегрирования на замкнутые обратные связи в
системе моделирования с замкнутым контуром. Правилом—указа-
телем является сведение фазового смещения при моделировании в
замкнутом контуре к градусу или около того. Это дает значения
для оценки размера шага интегрирования, которые необходимы
для моделирования непрерывного процесса.
Мы будем в основном рассматривать два типа интегрирова-
ния — определенные и неопределенные интегралы.
Определенный интеграл задается как
ь
у(й)=у(<2)+[ f(x)dx,	(8.1)
а
в то время как неопределенный интеграл задается как
t/(x)^y(a)+f/(O^.	(8.2)
а
Определенным интегралом вычисляется одно число, которое яв-
ляется площадью под кривой, ограниченной функцией, а неопреде-
ленный интеграл — это осуществление операции, обратной взятию
производной от интегрируемой функции, вследствие чего образу-
208
ется первообразная функция, а интеграл может принимать мно-
жество числовых значений в зависимости от произвольной посто-
янной.
В этой книге данное различие является маловажным, так как
предсказывающая — корректирующая концепция численного ин-
тегрирования дифференциальных уравнений может быть рассмот-
рена как последовательность перемежающегося определенного и
неопределенного интегрирования. В зависимости от того, какой
способ для схематизации выберет читатель для численного интег-
рирования в его деталях, имеет смысл изучать оба понятия.
Таким образом, мы будем изучать определенные интегралы с
точки зрения квадратур (вычисления площади под кривой) и не-
определенные интегралы с точки зрения интегрирования дифферен-
циальных уравнений.
Сначала рассмотрим определенные интегралы.
8.1.	ОПРЕДЕЛЕННОЕ ИНТЕГРИРОВАНИЕ
Вычисление площади под произвольной кривой обычно осуще-
ствляется с помощью замены ее функции (известной, но трудно ин-
тегрируемой аналитически) аппроксимирующей совокупностью бо-
лее простых легко интегрируемых функций.
Интегрирование в этом случае сводится к поиску, например, сте-
пени аппроксимирующего многочлена произвольной функции, а
затем интеграла от него.
В классической математике такая аппроксимация встречается
наиболее часто. При соответствующем выборе коэффициентов по-
линома степени п он обеспечивает получение достаточного аппрок-
симирующего выражения исходной функции.
Аналитические подстановки или другие методы аппроксимации
при решении определенных и неопределенных интегралов настоль-
ко привлекательны, что почти все специалисты по численным ме-
тодам находят новые пути для решения многих классических и не-
которых новых задач.
Несмотря на то, что велик соблазн осветить здесь методы ин-
тегрирования некоторых сложных функций, сосредоточим наше вни-
мание все-таки на классических разработках, которые просты и не-
сложны в применении.	*
Читателю должно быть известно огромное количество хороших
математических методов численного интегрирования, разработан-
ных в последние 20 лет в связи с внедрением цифровых ВМ и при-
менением численных методов в решении сложных технологических
задач.
Конструкции, системы связи, системы управления, проектирова-
ние летательного аппарата, проектирование химических предпри-
ятий — это только некоторые области, где моделирование систем с
помощью различных матриц и функций численного интегрирова-
ния, которые, как правило, нейтрально устойчивы (при большом
Шаге интегрирования), привело к новым понятиям интегрирования.
8	493	эпа
Специалисты по строительной механике разработали специаль-
ные формулы численного интегрирования для интегрирования
своих «дифференциальных уравнений прочности». Специалисты-
аналитики по управлению разработали формулы описания процес-
сов в частотной области. И специалистами по моделированию бы-
ли разработаны специальные формулы одноэтапного интегрирова-
ния в истинном масштабе времени.
Несмотря на то, что подобного рода задачи могут встретиться,
все-таки основное внимание нами будет уделено классическим ме-
тодам, которые являются общими и широко распространенными
для большинства функций, легко поддающихся аналитической об-
работке.
Кроме того, следует отметить, что по этим классическим мето-
дам имеется обширная литература.
Интегрирование методом трапеций
Если мы аппроксимируем функцию f(x) на ограниченном ин-
тервале	линией, соединяющей точки на границах интер-
вала, то можно написать уравнение для аппроксимирующей функ-
ции по интервалу как
У W = f («) + (^~/(а)] (х ~ аУ
у (х) =	+	.	(8 3)
Ь — л
Интегрируя (8.3), найдем
ь
\ y[x)dx = ^f{b} + f{a^(b-a).	(8.4)
а
Уравнение (8.4) вычисляет площадь под прямой линией интер-
поляции между конечными точками. Это называют интегрировани-
ем методом трапеций, так как на каждом шаге площадь замкнута
трапецией, образованной прямыми линиями, соединяющими точки
ординат, двумя ординатами и отрезком ее абсциссы. Если интер-
вал велик, то интегрирование методом трапеций может привести к
большой числовой ошибке интегрирования. Уменьшение этой ошиб-
ки возможно при применении правила трапеций на меньших интер-
валах независимой переменной.
Если вычисление осуществляется для равно отстающих друг от
друга интервалов Дх, интегрирование методом трапеций принимает
вид
ъ
/ (х) dx = Дх	+ <(а + Дх) + f (а + 2Дх) +... +	. (8.5)
а
Метод трапеций при интегрировании не является самым прос-
тым (более просто интегрирование по Эйлеру, по видоизмененным
210
методам Эйлера, прямоугольное интегрирование), и его формула
не дает наименьшую ошибку при минимальном объеме вычисле-
ния, однако он прост в применении, полезен в поверочных расче-
тах и легко запоминается.
При поиске рациональных формул интегрирования мы осущест-
вляем абстрактные рассуждения и ищем наилучший способ нахож-
дения средних значений функции, ее производной на интервале и,
наконец, интеграла, по которому оценивается ошибка округления
и отбрасывания, подбирается смещение фазы и амплитуды, т. е.
осуществляется поиск наиболее добротных формул численного ин-
тегрирования в данной задаче.
В конце концов аналитическое интегрирование сравнивается с
приближенным численным интегрированием, с помощью которого
оцениваются различия между методами интегрирования для конк-
ретной задачи. Ясно, что здесь содержатся трудности как при тех-
ническом анализе самих интегральных кривых, так и при вычисле-
нии площади под кривой дискретной функции. Интегрирование ме-
тодом трапеций может быть чрезвычайно полезно и достаточно
точно вследствие возможности выбора необходимого количества
интервалов.
8.2.	ОШИБКА В ИНТЕГРИРОВАНИИ МЕТОДОМ ТРАПЕЦИЙ
Мы не предполагаем осуществить здесь вывод формул интег-
рирования или формул ошибок, а собираемся предложить таблицу
наиболее употребимых из них и свести их к виду, который приго-
ден при моделировании. Рационально, однако, начать изучение
ошибки с простой формулы интегрирования, для того чтобы затем
понять ошибку более сложных формул. Следуя Хеммингу, мы ис-
следуем ошибку отбрасывания в алгоритме интегрирования с помо-
щью метода трапеций использованием разложения подынтеграль-
ной функции в ряд Тейлора. Сравнивая оба результата, можно оп-
ределить ошибку, связанную с процессом аналитической подстанов-
ки в численное интегрирование.
Запишем интегрируемую функцию в виде разложения в ряд Тей-
лора
/W=/(a)-|-(x_a)/'(а)+/"(«)+...	(8.6)
и подставим его в обе части формулы интегрирования методом тра-
пеций; тогда левая часть даст
+	+	/"(«) + -.	(8.7)
в то время, как правая часть примет вид
’ 2	а) f (а) +”	/,,(а)+->- + /(£)^ + е» (8. 8)
где Дх=(&—а).
8*
211
После сокращения одинаковых выражений в обеих частях урав-
нения получим формулу ошибки при отбрасывании членов:
g + (b-a£ г (а)+ _ =	(д);	(8 9)
4	о!
(8.Ю)
\ о! 4 /	О
Если допустить, что наибольшую величину в формуле ошибки
имеет первый член разложения ряда *, можно записать
(8.11)
12	V 7
или более полно
е	при а 0	(8- 12)
Если рассматриваемая функция и используемый интервал ин-
тегрирования приводят к большим значениям членов более высоко-
го порядка, то эта формула ошибки безусловно непригодна.
Тем не менее многие практические технические задачи поз-
воляют использовать выражение (8.42) при оценке ошибки интег-
рирования с использованием метода трапеций.
Не так важна формула характерной ошибки при интегрирова-
нии методом трапеций, как важен сам метод ее получения. В этом
частном примере мы применили разложение в ряд Тейлора для
интегрируемой функции для того, чтобы получить величину ошиб-
ки, связанную с отбрасыванием членов ряда. Как альтернативу,
можно применить разложение функции в ряд Фурье для определе-
ния влияния отбрасывания членов ряда на точность в частотной
области.
Другим аппроксимирующим полиномом может быть полином
Чебышева f(x), который дает иной вид формулы ошибки интегри-
рования.
Толкование результатов каждой из упомянутых формул ошибки
различно, величина же ошибки постоянна; ошибка характеризуется
только формулой интегрирования, а не аппроксимирующим поли-
номом, используемым для оценки формулы ошибки.
На рис. 8.1 показано, что при вогнутых функциях значение
интеграла от интегрирования с помощью метода трапеций будет
несколько больше, чем точное значение, в то время как при вы-
пуклых функциях это значение будет несколько ниже. При интег-
рировании волнообразных функций интервалы должны устанавли-
ваться таким образом, чтобы ошибки аппроксимирующего ядра на
одном интервале были скомпенсированы ошибками на другом ин-
* Это нехарактерное допущение для оценки эффективности скоростных
формул интегрирования, в частности, такого, как Т-интегрирование, так как целью
является сделать интервал наибольшим.
212
Рис. 8.1. Иллюстрация ошибки огра-
ничения при интегрировании методом
трапеций. Источник: Дж. М. Смит
«Научное исследование на микро-
калькуляторе», Вили, 1975. С разре-
шения издателя
тервале. Формула ошибки при интегрировании методом трапеций
может быть преобразована к виду
е ~ _/»-<> A*2. f" (9) при а < 0 < Ь.	(8. 13)
Для оценки ошибки с помощью (8.12) и (8.13) необходимо вы-
явить значения минимальной и максимальной ошибки, а по ним
среднюю ошибку интегрирования на интервале.
Иногда рассматривают значение наихудшей ошибки. Существу-
ет еще целый ряд альтернатив. В таком случае, что же является
критерием оценки ошибки?
На этот вопрос нет простого ответа. С точки зрения приклад-
ных наук ошибка, определяемая (8.9), имеет большее значение, чем
те, на которых наиболее часто акцентируется внимание в книгах
по численному методу. Процесс вывода формулы ошибки является
более фундаментальным вопросом, чем вопрос возможности вычис-
ления инженером или ученым собственной формулы ошибки при
рассмотрении своей конкретной задачи.
Студент или начинающий специалист относится осторожно к
формулам ошибки, часто стремясь вывести собственную формулу
для конкретной задачи. Оценка ошибки при числовой аппроксима-
ции и при аналитических вычислениях не всегда может быть прос-
то выражена, особенно при наличии неопределенных выражений.
Анализ ошибки является сам по себе искусством.
8.3.	ИНТЕГРИРОВАНИЕ МЕТОДОМ СРЕДНЕЙ ТОЧКИ
При интегрировании методом средней точки используют сред-
нее значение производной по интервалу интегрируемой функции,
исходя из того, чтобы площадь под кривой была равна площади
под аппроксимирующей функцией.
В этом смысле формула интегрирования методом средней точки
Хэмминга особенно проста и является удобным введением в общий
213
метод получения аппроксимирующих многочленов при аналити-
ческой подстановке. Рассмотрим формулу интегрирования вида
J / (х) dx=Wi/	-j- w2/'	•	(8- 14)
а
Коэффициенты весовой функции Хэмминга могут быть легко по-
лучены с помощью условия, из которого формула должна обеспе-
чить при f(x) = 1. Тогда
b — a = Wi.	(8. 15)
В случае f (х) —х имеем
---2---) + ®2-	(8-16)
Можно определить оба коэффициента Хэмминга, решая эти
уравнения совместно:
_ / />2—Д2 \ __ (1>—Я)(Д +6) _ / />2 — д2 \ _ / £2—^2 \ _0
\	9	/	9	\	9	)	\	9	/	’
\	2	/	2	\	2	/	\	2	/	(8. 17)
w1 = b~ а.
Поэтому найдем формулу интегрирования методом средней
точки в виде
ь
\f(x)dx=(b-a)fP-±±\.	(8.18)
Полученное рассмотренным способом интегрирование методом
срединной точки приводит к интегрированию методом прямоуголь-
ников. То есть, площадь, образованная выбранным прямоугольни-
ком при среднем значении ординаты на интервале, тождественно
равна площади под кривой на этом же интервале. Сначала, воз-
можно, и кажется парадоксальным, что интегрирование методом
прямоугольников практически эквивалентно интегрированию мето-
дом трапеций, т. е. формулы, основанные на одном значении f, мо-
гут быть по точности равносильны двухточечным формулам интег-
рирования методом трапеций.
На самом деле интегрирование методом прямоугольников мо-
жет быть выполнено с желаемой точностью, если выбранная точ-
ка интервала удовлетворяет теореме о среднем.
Таким образом, мы еще раз убеждаемся, что интегрирование
методом прямоугольников может быть выполнено с такой же точ-
ностью, что и аналитическое интегрирование функции, ограничен-
ной на интервале, если они обладают равными площадями. Этот
факт отражен в формуле (8.18).
И, снова, для того чтобы найти выражение ошибки отбрасыва-
ния, можно использовать ряд Тейлора
/(х)=/(а) + -(£=^- /'(а)+-И /"(«) + ...,	(8. 19)
214
где на основании подстановки в формулу (8.18) найдем выражение
е + (b-a^ f, (д)+ . = 1Ца)з f, (а)(	20)
о	о
которое упрощается и принимает вид
.	(8.21)
При
s > (*-д)3Г(0)
20
Сравнивая (8.21) и (8.12), мы видим, что интегрирование с по-
мощью средней точки методом прямоугольников является более
точным, чем интегрирование методом трапеций.
Обобщая формулу интегрирования методом средней точки, най-
дем
J f(x)dx=bx [/ (а+-у-)+ /(*4~)+
где формула ошибки представляется как
е ~ (*~2Д4)Лх2 /" (9) при а < 0 < Ь.	(8.22)
Заметим, кроме того, что обобщенное интегрирование методом
трапеций можно видоизменять включая конечные наружные точки
интервала [а, &]. Видоизмененный метод трапеций представляется
формулой
\/(х)^=Дх[^- + /(а + Дх)+/(а + 2Дх) + ... + ад +
+	+	+	(8.23)
где ошибка, связанная с видоизмененным интегрированием мето-
дом трапеций, может быть представлена как
е=	при (а-|-Дх)<6<(/>+Дх).	(8.24)
Еще одно популярное определение интегрирования
Правило Симпсона, вероятно, наиболее часто применяемая
формула, которая имеет вид
2Дх
/(х)^=-^-(/0+4Л + Л).	(8.25)
о
21S
Связанная с ней формула ошибки имеет вид	*
е==—/'"'(9) при 0<С9<С2Дх.
Прекрасным свойством правила Симпсона является то, что с
его помощью интегрируются кубические уравнения, даже если вы-
бираются только три точки интегрируемой функции, и, кроме того,
оно обладает незначительными ошибками при Дх меньше 1/2.
Правило Симпсона может быть также обобщено (на четное чис-
ло интервалов) в соответствии с формулой
>	Дх
J /(х)^ = -^(/о+4/1 + 2/2+4/з+2/4+... + /2я),	(8.26)
х0
и его формула ошибки имеет вид
е —	5 /""(0) при 0 <(х0 + 2/гДх).	(8.27)
В2Д-У2
k 2!
+	(8.28)
Вероятно, наипростейшей формулой обобщенного интегрирова-
ния является формула Эйлера—Маклорена
j7(x)rfx=Ax(-^- + /1 + /2+/3+... + -^L]-
Х0
Ее формулой ошибки будет
£2^ = { 9пД(ХХ2)!+'~') К<хИ(Л)2'+21} ПРИ <9<1;	(8-29)
здесь B2k — число Бернулли.
Правило трех восьмых для определенного интегрирования пред-
ставляется формулой
р(х)^х = -^(/0 + ЗЛ + 3/2 + /3).	(8.30)
х0
Связанная с ним формула ошибки имеет вид
s =—/""(0) при хо<0<;х3.	(8.31)
80
Для квадратур применяются два типа формул, если большин-
ство значений интегрируемой функции в выбранных точках извест-
но. Это формулы определенного интеграла Боде и формулы Нью-
тона—Котеса. Правила Боде для квадратур представлены в табл.
8.1, а формулы Ньютона—Котеса сведены в табл. 8.2.
Формулы высокого порядка, такие, как формулы Ньютона —
Котеса и формулы Боде, могут обладать некоторыми весьма не-
желательными свойствами при больших п. Для некоторых анали-
216
тических и дискретных функций последовательность интегралов ин-
терполирующих полиномов не сходится.
Таблица 8.1
Формулы Бодэ для вычисления определенных интегралов
Формула интегрирования	Формула погрешности
С	2Дх \ / (х) dx = — (7/о + 32/i + 12/2 + 32/з + 7/4) х0 Хо г	5Дх \ f{x)dx =—(19/0 + 75/! +50/г + 50/з + J	zoo Хо	8Ax7/vl (в) “	945 275Дх7 /V1 (9) 12 096
+ 75Л+19/5)
хЛ С	Дх \ / (х) dx = — (41/о + 216/! + 27/2 + 272/3 + Хо	_ 9Ax9/vnl (6) 1400
+ 27/4 +216/5+ 41/6)
X» \ / (х) dx -	(751/0 + 3577/1 + 1323/2 + J	1 / zoU Хо	_ 8183Дх9/У1П (9) “	518 400
+ 2989/з + 2989/4 + 1323/5 + 3577/6 + 751/7)
хо \ / (X) dx -	(989/о + 5888/1 - 928/2 + J	14 1/5 Хо	2368Дх11/ х (9) “	467 775
+10496/з-4540/4+10 496/5—928/6+5888/7+989/8)
Кроме того, коэффициенты этих формул интегрирования вели-
ки и содержат переменные знаки, при которых возрастает погреш-
ность округления.
Формулы Ньютона—Котеса чаще применяются при больших
значениях п в основном по этим причинам. При малых значениях
они могут быть упрощены до хорошо известных формул, таких, как,
например, обсуждавшихся ранее формул метода трапеций и фор-
мулы правила Симпсона. Несмотря на то, что правило Боде обхо-
дит недостатки, связанные с переменными знаками, в сравнении с
формулами Ньютона — Котеса, при нем тоже есть проблемы схо-
димости для определенных, редко встречающихся функций.
Интегрирование методом трапеций приводит к приемлемой точ-
ности и погрешности округления, обладает приемлемым объемом
вычислений интеграла любой функции. Оно рекомендуется для
решения научно-технических задач, где необходимы небольшие
абсолютные погрешности.
217
Таблица 8.2
Формулы определенного интегрирования Ньютона — Котеса при
интегрировании функций, значения которых на концах либо не
определены, либо неизвестны, либо представляют особые точки
Формула интегрирования
Формула погрешности
*8
С	ЗДх
/ (*) dx = — (/i + /2)
х.
х<
f	4Дх
\ f(x)dx = — (2/i-/2 + 2/з)
J	о
х0
с	5Дх
J f(x)dx = — (ИЛ + /2 + /з+П/4)
Х0
ХЛ
С	бДх
/ (х) dx = — (11/! + 14/2 + 26/з- 14/4 + 11/5)
х.
\ / (х)	=	(611/1-453/2 + 562/3 +562/4-
J	1440
-453/5+611/б)
\ / (х) dx =	(460/1 - 954/2 + 2196/3 - 2459/4 +
J	945
+ 2196/5- 954/6 + 460/7)
Дх3
/" (•>
14Дх5 45	/IV	(9)
95Дх5		
144	/У	(6)
41Дх7	-VI	
140	гх	(в)1
5257AxL /У|(|)
3956 Дх^ -Уш
14175 f
8.4.	ОСНОВНЫЕ ПОЛОЖЕНИЯ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Численное интегрирование неопределенных интегралов осуще-
ствляется методами, применяемыми для решения дифференциаль-
ных уравнений.
Например, если нам задано уравнение
(8.32)
мы решаем его с помощью неопределенного интеграла
«/ = ^о + J /(Л y>dt-	(8-33)
Из уравнения (8.33) очевидно, что решение зависит от самого
дифференциального уравнения. Поэтому основная задача неопре-
218
деленного интегрирования — выразить неопределенные интегралы
в неявной форме.
Заметим, что неопределенные интегралы в явном виде
У=Уо^	(8.34)
являются особым случаем решения дифференциального уравнения
вида
-^-=/(4	(8.35)
Численное интегрирование уравнения такого типа можно вы-
полнить аналитически, и его мы здесь не рассматриваем.
Наипростейшим алгоритмом численного интегрирования неоп-
ределенного интеграла является формула Эйлера
Уп+1=Уп + ^ (77) •	(8-36)
\ ах /п
Здесь мы видим, что вычисление (yn+i) осуществляется на ос-
новании ранее вычисленного значения (уп) и его производной
(dy!dx)n, которая определяется обычно непосредственно из диф-
ференциального уравнения, решаемого относительно у. Так как
вычисление нового значения у основано на вычислении старого
значения у' и старого значения у, оно относится к категории про-
цессов с разомкнутым циклом, и новое значение у основано на
экстраполяции предварительно известных данных с определенной
погрешностью.
Процесс определения новых значений у представляет собой
простой переход от одной области их значения к другой в соответ-
ствии с процедурой решения дифференциального уравнения. В це-
лом метод состоит в том, чтобы, начиная с некоторых начальных
условий (которыми ЯВЛЯЮТСЯ Xq, #о), вычислять наклон, используя
дифференциальное уравнение, заданное в виде
г/о=/(ха, у0).
Затем осуществляем переход на интервал h в направлении
прямой, имеющей наклон, равный производной во второй точке,
которую затем считаем новой начальной точкой. Процесс повторя-
ем вновь. Если принимаются достаточно малые интервалы, то
можно надеяться, что последовательность значений решения,
представляемая этой методикой, будет находиться близко к реше-
нию дифференциального уравнения. В целом здесь есть все эле-
менты решения дифференциального уравнения с помощью неоп-
ределенного численного интегрирования.
Для каждого шага в процессе численного интегрирования дол-
жна быть просчитана таблица значений х, у, у' и &у. Кроме того,
задача должна решаться не только в соответствии с особенностя-
ми дифференциального уравнения, но и в соответствии с его на-
219
чальными условиями. В этом случае возможно выбрать подходя-
щий интервал интегрирования и формулу интегрирования, которая
точна для данного интервала.
8.5.	НЕОПРЕДЕЛЕННОЕ ИНТЕГРИРОВАНИЕ МОДИФИЦИРОВАННЫМ
МЕТОДОМ ЭЙЛЕРА
Альтернативой к ликвидации вводимого при вычислении запаз-
дывания является выбор среднего значения функции на интерва-
ле, а не ее значения на его границах.
Например, можно начать решение с начальных условий t/=0,
х = 0. При интегрировании с помощью формулы интегрирования
Эйлера
Уп-Уп~1 = Му'п-1
необходимы условия выбора интервала Дх.
Самым простым способом является экспериментальное опреде-
ление Дх, при котором интегрирование дифференциального урав-
нения будет точным (зависит от специалиста по аналитике).
Рассмотрим решения этого дифференциального уравнения при
х = 0,05; 0,1; 0,2 и 0,3. Результаты сведены в табл. 8.3.
Таблица 8.3
Решение уравнения dy!dx=e~у—х2
X	Точное решение у	Решение методом Эйлера			
		Дх=-0,05	|	Дх-0,10	Дх=0,2	Дх-0,3
0,0	0,0				
0,1	0,09498	0,09694	0,09900	—	—
0,2	0,17977	0,18261	0,18557	0,19200	—
0,3	0,25389	0,25672 .	0,25964	—	0,27300
0,4	0,31667	0,31872	0,32077	0,32506	—
0,5	0,36731	0,36786	0,36833	—	—
0,6	0,40488	0,40329	0,40152	0,39756	0,39333
0,7	0,42839	0,42407	0,41942	—	—
0,8	0,43686	0,42923	0,42119	0,40395	—
0,9	0,42929	0,41782	0,40582	—	0,35277
1,0	0,40477	0,38895	0,37264	0,33749	—
Сравнение решений, полученных численным интегрированием,
с точным решением показывает, что точность решения зависит от
размера шага интегрирования. В основном это верно для всех чис-
ленных интегралов, даже если размер шага интегрирования явля-
220
ется частью «ответного времени» * дифференциального уравнения.
Недостатком метода Эйлера являются вводимые систематиче-
ские погрешности смещения фазы и запаздывание (экстраполяции)
на каждом шаге. Метод может быть модифицирован (модифициро-
ванное интегрирование Эйлера) и приводит к лучшим результа-
там, т. е. к большей точности, по существу при том же методе и
том же объеме работы, или к той же самой точности, но при мень-
шем объеме работы.
Это аналогично получению формулы метода трапеций для
средней точки, полученной в разд. 8.3.
Задачей является преобразование интеграла
^"+1 у' (x)dx,	(8.37)
хп—1
при использовании формулы средней точки (см. разд. 8.3).
Мы хотим предсказать следующее значение у на основании нас-
тоящих и прошлых значений независимой переменной.
Предсказанное срединное значение приводит к
Рп+1 = ^л-1 + 2(Дх)^п.	(8.38)
Используя предсказанное значение, можно вычислить наклон
прямой в предсказанной точке решением дифференциального урав-
нения
Pn+i = f(xn+x, рп+г)	(8.39)
и затем применить правило трапеций для получения корректиров-
ки вычисленной точки:
Уп+1=Уп-}"^ (Pn+i + Уп)-	(8.40)
Коррекцией называется уточнение значения уп+\. Мы применя-
ем при этом срединный наклон в интервале.
Короче говоря, этот метод состоит из трех этапов.
Этап 1. Пишем среднее значение функции для поиска предпо-
лагаемого значения уп+\> задаваемое формулой
/’л+1==Уя-1 + 2(Дх)^.	(8.41)
Этап 2. Вычисляем производную при предсказанном значении,
которая определяется с использованием дифференциального урав-
нения, описываемого системой
Pn+i = f (хя+1, ра+1).	(8. 42)
* Приблизительное время, необходимое для перехода из одного состояния
равновесия к другому, строго применимо только к дифференциальным уравне-
ниям, независимой переменной которых является время; однако это понятие
применяется более широко.
221
Этап 3. Вычисляем значения t/n-n> применяя интегрирование ме-
тодом трапеций:
Уп+1 = Уп + -^-(Уп-[-Уп+1)-	(8.43)
Этот процесс предсказания и коррекции приводит к наименова-
нию этого этапа интегрирования, как численное интегрирование
прогноза—коррекции.
Ряд алгоритмов прогноза и коррекции представлен в конце
этой главы; они могут применяться при нахождении неопределен-
ных интегралов дифференциальных уравнений.
£.6. НАЧАЛЬНЫЕ ЗНАЧЕНИЯ
В нашем предварительном анализе мы допустили, что облада-
ем величинами зависимых и независимых переменных при началь-
ной или исходной точке. Однако алгоритму необходимы не только
начальные значения, но и более ранние значения. Предшествую-
щие значения могут быть получены двумя способами. Они могут
быть вычислены на ВМ или вычислены вручную аналитически.
Здесь представлены оба метода.
Ручной метод вычисления основан на применении разложения
функции в ряд Тейлора
у(х+Дх)=у(х) + Дх/(х) + ~-	+	(8.44)
Производные для разложения в ряд Тейлора могут быть найде-
ны из дифференциального уравнения повторным дифференцирова-
нием. Количество членов зависит от размера шага и желаемой точ-
ности. Все это может быть легко получено путем эмпирических
непрерывных оценок вплоть до получения желаемой точности.
Метод машинного счета основан на повторном применении
формулы корректировки. Если нам задана начальная точка (Хо,
Уо), мы можем оценить предыдущую точку (х_ь «/_]) методом неиз-
мененного интегрирования Эйлера, оперируя в обратном направле-
нии следующим образом:
x~i = x0 — х;
У-1=Уо~ &ху'о (первая оценка ^_j).	(8.45)
Мы можем использовать оценку предварительного значения у
в соответствии с дифференциальным уравнением для получения
производной и предшествующего значения у.
Формула корректировки с помощью метода трапеций может
быть затем повторена для того, чтобы итерационно скорректиро-
вать предварительную оценку, если не будет достигнута желаемая
точность при вычислении.
Системой уравнений для процесса коррекции является
z/Li = /(x-i, 1/_1)(первая оценка y'-iY
222
У-\=Уо~ -y-(^o+^li) (вторая оценка y-J; (8.46)
у!1=/(х_1, f/_i) (вторая оценка y'_i);
Если после нескольких итераций предшествующее значение у
не стабилизировалось, размер шага интегрирования может быть
уменьшен вдвое; просчитывается предварительное значение Уп-цъ
и процесс повторяют для вычисления уп-\-
Альтернативой является применение значения Уп-уъ для оцен-
ки значения уп+1/2 и повторение процесса, чтобы получить опере-
жение в половину шага вплоть до уп+\-
Эти значения затем применяют в качестве начальных значений
в алгоритме интегрирования прогноза и коррекции.
8.7. ОЦЕНКИ ОШИБКИ И ИЗМЕНЕННЫЙ ПРОЦЕСС ПРОГНОЗА
И КОРРЕКЦИИ
Только что обсуждавшаяся формула прогноза является форму-
лой интегрирования с использованием средней точки и имеет со-
ответствующую формулу ошибки
еп=~-*/,п(9).	(8.47)
О
Формуле коррекции, представленной в разд. 8.2, соответствует
формула ошибки
гк=-^У1П(е)-	(8.48)
Так как формула ошибки содержит противоположный знак,
разница между прогнозируемым и скорректированным значениями
имеет вид
У и У К	(«/точи ~~ ®|1) (l/точн ®к).	(8. 49)
Таким образом, при любом заданном шаге разница между про-
гнозируемым и скорректированным значениями выражается как
--^-Дх3^).	(8.50)
Кроме того, мы видим из (8.49), что приблизительно на четыре
пятых разница содержит составляющую предсказания и на одну
пятую — составляющую коррекции. Для продолжения процесса ин-
тегрирования нужно продолжить процедуру прогноза и коррекции.
Если мы прогнозируем с помощью уравнения
Рп+1 — Уп-1 И- 2Дх£/п,	(о. 51)
то можем сразу же изменить значение этого прогноза, применяя
предшествующее значение разности прогноза и коррекции и фор-
мулу
__4
тп+^Рп+1—{рп-сп).	(8.52)
О
223
Тогда мы применим дифференциальное уравнение для вычис-
ления измененной производной
rn«+i = /(x„+i, /ип+1),	(8.53)
которая затем корректируется путем
сп+1=^Уп + -~(пг'„+1-\-уп)	(8.54)
и приводит к окончательному значению
У п+1 — cn+i Н—(Pn+i ~ cn+i)-	(8.55)
Методика прогнозирования, коррекции, а также последующего
нового изменения является чем-то вроде стремления к пределу, к
которому мы стремимся в решении дифференциальных уравнений,
рассчитываемых вручную.
Более прогрессивные методы также громоздки.
8.8. ЕЩЕ ОДНО ПРИМЕНЕНИЕ ФОРМУЛ ЧИСЛЕННОГО
ИНТЕГРИРОВАНИЯ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Существует большое число наиболее употребимых алгоритмов
прогнозирования и коррекции, пригодных для решения ординарных
дифференциальных уравнений.
Этими самыми популярными формулами использования накло-
на в точке являются прогнозирующие выражения Эйлера и сред-
него значения. Они задаются в виде
Уп+1 = Уп + (Дх)у'а при е~Дх2;
i/„+i = t/„_iH-2(Ax)t/n при s — Дх3
и обычно применяются в соединении с формулой коррекции мето-
да трапеций
Уп+1 = Уп+ -^~(Уп+1+ У'п) ПРИ £~Д^3-
Другим, часто применяемым, чрезвычайно полезным является
метод Адамса. Формулы четвертого порядка прогноза и коррекции
Адамса даются в виде
У п+1 = Уп+№>Уп - 59f/n-i + 37Уя-2 - 9У«-з) пРи е ~ Дх5;
yn+i==yn+-^(9y„+1+l9y„-5z/n_1 + y;_2) при е —Дх5.
Числовая устойчивость этих методов и ошибки округления свя-
заны с переменой знаков коэффициентов, что может привести к
известным трудностям.
224
Методы Рунге — Кутта
Методы Рунге—Кутта основываются на разложении неявной
функции в ряд Тейлора с сохранением членов более высоких по-
рядков в результате сочетания численных оценок производных
функции на определенных интервалах независимой переменной.
Так как методы Рунге—Кутта являются еще одним вариантом при-
менения метода разложения в ряд Тейлора, они ограничены и не
могут быть применены для функций, которые не могут быть разло-
жены в ряд Тейлора, или если интегрируемая функция имеет раз-
рыв, то решение осуществляется вплоть до разрыва и затем снова
продолжается, начиная от разрыва.
Метод Рунге—Кутта второго порядка (метод Хана) может
быть представлен как
У«+1 =У« +^-“(^1 + ^2) при е~Дх3,	(8.56)
где	А’1 = Дх/(х„, уп); k2 = Дх/(хл + Дх,
В методах Рунге—Кутта применяется интегрирование Эйлера
на каждом шаге. Так, чтобы вычислить (8.56), необходимо снача-
ла вычислить kx и k2. Для вычисления k2 необходимо вычислить
предыдущее значение y(.y+k\). Очевидно, что это равноценно ме-
тоду Эйлера. Таким образом методика содержит первоначальное
применение метода Эйлера для вычисления первой оценки г/п+ь
которая затем применяется вместе с хп+Ах для вычисления зна-
чения производной при х(п+Ах), чтобы получить k2. Затем, при-
меняя kx и k2, образуют (8.56).
Другой формой уравнения Рунге—Кутта второго порядка яв-
ляется
Уп+1=Уп + к2 при е~Дх3;
kx = Lxf(xn, уа); ^ = Дх/(х„+ -у-,	(8-57)
В этом выражении kx применено для того, чтобы при сдвиге на
половину шага от хп к хп + Дх/2 определить уп + &1/2, откуда, учи-
тывая хп + Ах/2 в соответствии с (8.57), вычисляется k2. И снова
должно быть применено интегрирование по Эйлеру, чтобы осущест-
вить первую половину шага и первый полный шаг путем оценок
среднего значения скорости по интервалу.
' Еще один метод Рунге—Кутта может быть представлен в двух
видах. Одним из них является
при е~д*4;
kx = дх/ (х„, 1/„); k2 = Дх/ (х„+~, Уп 4-	;
Л3== Дх/(хя-|-Дх, yn-\-2k2 — kJ.
225
Это является самым распространенным и удобным видом ин-
тегрирования методом Рунге—Кутта третьего порядка.
Другим видом этого метода Рунге—Кутта является система
третьего порядка
!/п+1 = «/я + -^-+тЛз ПрИ е~Дх4;
^=Дх/(х„, упу,
Л2=Лх/(хп+-^-,	+	;
'	О	О /
, А /. /	, 2Дх . 2^ \
Л3 = Дх/ х„+—.
\	О	О /
Двумя наиболее употребимыми выражениями для численного
интегрирования методом Рунге—Кутта четвертого порядка явля-
ются
ул+1={/л+-у+-у+'т+‘у при е~д*5;
Л1 = Дх/(х„, уа\,
^2=дх//х„+-у-, у„+-у);
Л3=Дх/(х„+-^-, ул + -у);
#4= Дх/(х„-1-Дх, f/n + A-з)
И
!/л+1=!/л + -^-+-^-+^-+-^- при е~Дх5;
О	О	о	о
^ = Дх/(х„, у„);
^2=Дх/(х„+-у-,
£3=Дх/(х„+-Ц^-, {/„+*2- -y);
Л4=Дх/(хл-|-Дх,	—^ + ^1)-
Точность этого интегратора четвертого порядка зависит от фор-
мулы остатка, которая выражает погрешность пропорционально
Дх5. Хемминг указывал на справедливую критику этого метода,
связанную с неучетом всей предыдущей информации. Однако, сле-
дует отметить, что и эти методы интегрирования легко использо-
вать в общих случаях.
Все методы разложения в ряд Тейлора основаны на его огра-
ничении, которое может быть хорошо определено при следующих
преобразованиях:
226
2	О
^{/(/+Л}=[1+Г5 + ^-+^-+...)/(5),
\	ZI	<51	]
чьи амплитудные характеристики в частотной области ограничены
таким образом, чтобы ограничить многочлен s.
Методы Рунге—Кутта, как и любой метод вычисления в конеч-
ных разностях, который основан на ограничении членов разложе-
ния в ряды Тейлора, имеют ограничения в частотной области по
характеристикам передаточной функции ограниченного ряда Тей-
лора.
Спектральные характеристики интегралов Рунге—Кутта опре-
деляются количеством членов, оставленных в разложении ряда
Тейлорй.
Кроме того, если встречаются разрывы в переменной состоя-
ния, алгоритмы Рунге—Кутта, которые основаны на уменьшении
вдвое интервала интегрирования до тех пор, пока сравнение полно-
го шага с половиной шага не приведет в этих условиях к выбору
размера шага интегрирования, неэкономичны. Вдобавок методы
Рунге—Кутта не обладают формулами остаточного члена *, из ко-
торых получаются выражения для оценки погрешности, и они не
дают возможности оценить на каждом шаге ее величину как в ал-
горитмах прогноза, так и в алгоритмах коррекции. Это является
самьцл слабым местом метода Рунге—Кутта, которое может при-
вести к слабо регулируемым погрешностям алгоритмов. Все же,
даже с этими ограничениями, легкость программирования и при-
менения интегрирования методом Рунге—Кутта на больших ВМ
делает эту формулу привлекательной. Он обладает рядом удобных
свойств по учету начальных условий и позволяет оперировать ими
автономно.
При моделировании или применении численного интегрирова-
ния в отборе данных на микрокомпьютерах автор рекомендует
изучение других методов, в частности метода интегрирования с на-
стройкой (гл. 7) и алгоритмы предсказания и коррекции этой
главы.
Во всех методах, представленных в этой части, рассматривает-
ся дифференциальное уравнение первого порядка, записываемое в
виде y'=f(x, у), так как даже в более общем случае дифференци-
альные уравнения n-го порядка могут быть сведены к п дифферен-
циальным уравнениям первого порядка. Следовательно, эти мето-
ды применимы к системам уравнений или к уравнениям высоких
порядков.
* За исключением примененных недавно интеграторов типа Фельберга Рун-
ге — Кутта.
227
Специальные методы интегрирования
Можно получить ряд методов решения дифференциальных
уравнений высшего порядка, содержащих специальные алгоритмы
предсказания и коррекции. Несмотря на то, что они не могут быть
признаны самыми целесообразными для численного решения диф-
ференциальных уравнений, тем не менее эти методы упрощают вы-
числения.
Например, алгоритмы прогнозирования и коррекции Мильна
для дифференциальных уравнений первого порядка имеют вид
п. [у„+1=:4'л-з+^(2//п-Ул_1 + 2у„_2)
111	6
К	при е ~ Дх5;
У п+1 = У п-1 +	(У П-1 + 4У’п + У’п + 1^
<5
рй+1=//в-5+^ (11//;- Щп^ + 26уп_2- 14у„_3+ 11у„_4)
?	при е~Дх7.
У п+1=Уп-з+(7y'n+l-\-32y'n-i-12yn_i-\-32y'n_2+7 уп_3)
Формулы прогнозирования и коррекции Мильна для дифферен-
циальных уравнений второго и третьего порядка записываются
следующим образом:
У п+1 = У п-2+3(Уп~ У п-1) + &х2 (у’п - у’п_г)
при е ~ Дх5;
П
К
J-J1 Ул+1— Уп-2 I ”\Уп Уп-1)^^л \Уп Уп-1>
кЦ /.„ = у. +	(</„, + ».)-	(S„, - й
('«+=у.-г+3(». -	к -
У.^ = У.+^(ЯМ-+ при —
Для систем дифференциальных уравнений вида
= у, z); z'=g(x, у, z)
по Рунге—Кутту можно записать
Уп+1-Уп+^-+-Т	3
Z Z при £ — Дх3,
2л+1 = zn Н—
^ = Ах/(х„, у„, г„);
/! = Дх^(х„, уп, znY,
А>2 = Дх/(х„ + Дх, +	^n + Zj);
Z2 = Axg(x„-|-Ax,	+	^-j-Zj).
228
Способ Рунге—Кутта для систем уравнений четвертого поряд-
ка принимает вид
„	_ I ^1 + 2#2 + 2&3 + ^4 ф
Уп + 1—^Уп\	Q’
_____	। Л ~н 2/2 + 2/з + Z4 '
zn+l zn~T	Q	’
^ = Дх/(хл, у„, zny,
li = bxg(xn, уп, zny
^2 = Дх/(х„ + -у , y+Y’ *n + l"):
l2=^xg(xn^^~, Уп-\~> г«+4г);
Л3=Дх/^Х„ + -у-, У„ + -у,
/3 = Дх/(х„+-у-, г/«+-у’ *« + §) ;
*4=Дх/(хл + Дх, */„ + &,, г„+/з);
/4=Дх/(хл + Дх, ул + ^з, г„ + /3).
Для дифференциального уравнения второго порядка
/' = /(х, у, у')
по методу прогноза и коррекции Мильна имеем
Уп+1=Уп-з Н з (2ул_2 yn_i + 2уп}
при е —Дх5;
У'п+1 = Уп^+^-(у’п_1+^Уп+Уп+^
по методу Рунге—Кутта получим
У п+1 = Уп~\~ ^хУп Н	(^1 “Г ^2 + ^з)
.	при е — Дх5;
У п+1= У п Н—(^1 + ^2 + 2^3 + ^4)
^ = Дх/(х„, уп, упУ,
*2 = Дх/(хлН—упД——yn+-_L, 0«+у-):
t	/ I	..I ^Хуп I ^Xkl , I kl \
£3=Дх/(хл+ —, уп-\----— + —, Уп+-^У’
^4=Дх/^Хл-|-Дх, уп ^хуп -]	^-2-, уп -1-
Для дифференциального уравнения второго порядка вида
У"=/(х, у)
229
метод Мильна дает
У п+1=Уп+У п-2 - У п-3 +	(%;++5у’п_2)
д	при е~Дл6;
У п+1=%Уп ~ У п-2 + — (y'n+l + 10уп+/п_1)
метод Рунге—Кутта
t а Г ' । /	4- 2^2
Уп+1 = Уп +	УПТ (	£	) ’
L v /J при е— Дх4;
1/;+,=й+т+^-+т
^ = Дх/(хя, «/„);
-	.	. [	। Дх . Дх , . Дх <\
Л2 = Дх/(х„+— уп + — уп-\——k^ ;
А3=Дх/(хл + Дх, yn-\-^xy'n-\--^- k^.
Выражения Рунге—Кутта для дифференциального уравнения
второго порядка, содержащие значение скоростей, интегрируются
методом Эйлера. Для небольших машин с ограниченной памятью
эти альтернативные формы численной оценки интегралов особенно
полезны, потому что они обходятся без интегрирования двух диф-
ференциальных уравнений первого порядка, что было бы необхо-
димо при решении уравнения второго порядка.
Некоторые заключения общего характера по методам
прогноза и коррекции
Проведена большая работа по разработке методов прогноза и
коррекции. Эти способы изучали и развивали Хэмминг, Мильна,
Адамс, Бэшфорт и другие авторы. Авторский опыт в методах прог-
ноза и коррекции приводит к следующим рекомендациям.
1.	При использовании одношаговых алгоритмов в случае моде-
лирования в естественном масштабе времени на малогабаритных
машинах необходимо исследовать погрешности округления, особен-
но при наличии разности малых чисел. В то время как модифика-
торы в основном уменьшают погрешность численного интегрирова-
ния иногда путем введения коэффициента 10, они могут увеличить
погрешность округления в микрокомпьютерных устройствах.
На своем опыте автор убеждался, что модификатор уменьшает
точность интегрирования на большом интервале.
2.	Если встречается числовая неустойчивость при моделирова-
нии в истинном масштабе с применением алгоритмов прогноза и
коррекции с модификаторами, устойчивость процесса интегрирова-
ния может быть улучшена их устранением.
3.	При моделировании в истинном масштабе времени (где фик-
сируется размер шага интегрирования и модификаторы не могут
230
применяться для его изменения), объединяя порядок уровней точ-
ности, можно повысить точность вычисления в целом.
4.	Так же, как и любой метод численного интегрирования, ос-
нованный на интегрировании интерполированных или экстраполи-
рованных многочленов, эти методы чувствительны к разрывам в ин-
тегрируемых функциях. При больших ошибках и при любом задан-
ном шаге интегрирования модификатор может быть указателем
разрыва. В этом случае алгоритм интегрирования сам может быть
модифицирован таким образом, чтобы не изменить размера шага
интегрирования до тех пор, пока большая ошибка модификатора
соблюдается при выбранных п периодах.
Другим способом является изменение размера шага интегриро-
вания в том случае; если модификатор обнаруживает изменение
точности процесса интегрирования.
5.	Обсуждаемым здесь методам прогноза и коррекции необхо-
димы начальные значения. В настоящее время методы Рунге—Кут-
та широко применяются для вычисления каждого шага процесса
интегрирования, но часто забывается, что для этих методов необ-
ходимы четыре итерации для каждого следующего шага, в то вре-
мя как в методах прогноза и коррекции необходимы две итерации.
При этом в обоих методах достигается одинаковая степень точно-
сти.
Часть IV
МЕТОДЫ
УСКОРЕННЫХ
ВЫЧИСЛЕНИЙ
Глава 9. ГНЕЗДОВЫЕ СКОБОЧНЫЕ ВЫРАЖЕНИЯ
И ЭКОНОМИЗАЦИЯ ЧЕБЫШЕВА
В этой главе представлены определенные элементарные методы
совершенствования эффективности расчетных функций. Эти мето-
ды просты, легко применяются и запоминаются. Они имеют широ-
кое применение и полезны проектировщикам, начинающим модели-
ровать. Эти методы хорошо известны большинству специалистов по
системам матобеспечения. Те инженеры, кому неизвестны эти ме-
тоды, познакомятся с оценкой скоростной функции.
9.1. ГНЕЗДОВОЕ ВЫРАЖЕНИЕ
Многие функции, представляющие интерес для специалистов,
могут быть записаны степенными рядами, которые можно полу-
чить, применяя разложения Тейлора, Маклорена, полиномы Чебы-
шева и т. д. Кроме того, ряд эмпирических данных может быть по-
добран с помощью степенного ряда. Таким образом, всегда необ-
ходимо иметь дело с полиномом
/(х)=а0 + а1х+а2х* 1 2 + а3х3 4+...+а„хя-[-...	(9.1)
Вычисление этого ряда содержит следующие операции опреде-
ления п членов частной суммы f (х):
(1) Вычисление х и хранение в X
(2) Хранение х в У
(3) Умножение
(4) Умножение
(п+2) Умножение
(п+3) Вызов ап
(п+4) Умножение
(п+5) Вызов предыдущего члена суммы f(x)
(п+6) Хранение предыдущего члена суммы f(x)
232
Таблица 9Л
Известные разложения в ряд при гнездовой
скобочной форме записи
Re х
/ У / 2w / Зу \ \ \
1П(Х)=Ы l-dr !- Q Р-"Г	прий = (х-1), \х—11 < 1
I	1 о \	^'/11
arcsin (х) х
при | х | < 1
233
• Продолжение табл. 9.1
л 1 [	1 /	3 \\
arctg(x)^T--ll-—Д1-—2Ипри|х|>1
Таблица 9.2
Аппроксимация полиномами некоторых часто встречающихся функций
<1) 1g (х) = / (ai + /2 \а3 + /2 (а5 + /2 (а7 + j J + е (х).
Здесь t = (х— 1) (х 4- 1)“!
« | е (х)| < 10-7, где 10-1/2 < х < 13+1/2
при
ах = 0,868591718; а3 = 0,289335524; а5 = 0,177522071; а7 = 0,094376476;
а9 = 0,191337717.
(2)	1g (х) = t (ах 4- а3/2) 4- е (х),
где t = (х— 1)(х4- О-1; а\ =0,86304 и а3 = 0,36415.
Тогда | в (х)| < 10“4, где 10~^* 2 3 4 5 < х < 10+1/2.
(3) In (1 4- х) = х (ai 4- х (а2 4- х (а3 4- х(сц 4- л5х))^ 4- е (х).
Здесь ai = 0,99949556; а2 = 0,49190896; а3 = 0,28947478; а4 =—0,13606275;
а5 = 0,03215845.
Тогда | £ (х)| < 10—5, где 0 < х < 1.
(4) In (1 4- х) = х I ах 4- х I а2 4- х а3 4- х
4-е (х).
Здесь ai= 0,9999964239; а2 = —0,4998741238; а3 = 0,33117990258; а4 =
= 0,2407338084; а5 = 0,167654071; аб = —0,0953293897; а7 = 0,0360884937;
а8 = 0,0064535442 и | £ (х)| < 3-10—8, где 0 < х < 1.
(5)	е х= 1 4-x(ai 4-л2х)4-е(х),
где ах — —0,9664 и а2 = 0,3536.
Тогда | £ (х)1 < 3- Ю-з, 0 < х < In 2.
234
Продолжение табл. 9.2
(6)	е х = 1 + х (ai + х (аг + х (а3 4- а4х)) j,
где а! = 0,9998684; а2 = 0,4982926; а3 = —0,1595332; а4 = 0,0293641.
Тогда | е (х)| < 5-10—5, где 0 < х < In2.
(7)	sin (х) = х (1 4- х2 (02 4- а**2)) + ** М,
где а2 = —0,16605 и 04 = 0,00761.
Тогда | е (х)| < 2-10-4, где 0 < х < л/2.
(8)	sin (х) = х 1 4- х2 ^02 4- *2	4- *2 (^6 + *2 (Л8 + Лю*2))]^ + *<(*>>
где 02 = -0,166666664;	04 = 0,0083333315; 0б = —0,0011984090; j * 08 =
= 0,0000027526; 01о = —0,0000000239.
Тогда | е (х)| < 2-10—9, где 0 < х < л/2.
(9)	cos (х) = 1 4- х2 (02 4- 04х2) 4- е (х),
где 02 = —0,49670; 04 = 0,03705.
Тогда | е (х)| < 9-10~4, где 0 < х < л/2.
(10)	cos (х) = 1 4- х2 ^а2 4- х2 ^04 4- х2 (06 4- х2 (08 4- 0юх2)) j j 4- e (х),
где 02 = -0,4999999963; 04 = 0,0416666418; 06 = —0,001388839; 08 =
= 0,0000247609; 0ю =—0,000000605.
Тогда | е (х)| < 2-10-9, где 0 < х < л/2.
(11)	tg (х) = х (1 4- х2 (а2 4- 04х2)) 4- хе (х),
где 02 = 0,31755; 04= 0,20330.
Тогда | е (х)| < Ю—з, где 0 < х < л/4.
(12)	tg (х) = х ^1 4- х2 ^02 4- х2 (а4 4- х2 ^0б 4- х2 (08 4- х2 (а10 4- 012х2)),
где 02 = 0,3333314036; 04 = 0,1333923995; 0б = 0,0533740603; 08 = 0,0245650893;
а10 == 0,0029jI>5_50; 0i2 = 0,0095168091.
Тогда | е (х)| < 2-10~3, где 0 < х < л/4.
(13)	ctg(x)= ^-(1+х2(а2+а4х2))+-^-,
где а2 =- —0.332867; а5 = -0,024369.
Тогда | е (х)| < 3-10-5, где 0 < х < л/4.
(14)	ctg (х) = — (1 + х2 (а2 + х2 (а4 + х2 (а6 + х2 (а8 + а10х2))]) ] +
где Я2 = —0,3333333412; а4=—0,0222220287; а6 = 0,0021177168; а8 =
= —0,0002078504; а10 = —0,0000262619.
Тогда j е (х)| < 4- 10—ю, где 0 < х < л/4.
235
Продолжение табл. 9.2
(15)	arsin(x) =-^- — (1 — х)1'2^а0 + х (fli + х (а2 + «з*))) +е (*)>
где а0 = 1,5707288; ах = —0,2121144; а2 = 0,0742610; а3 = —0,0187293.
Тогда | е (х)| < 5-10~5, где 0 < х < 1.
(16)	arctg (х) = х [а^ Н- *2 («з + *2 (^5 + х2 (а7 н- а9х2)) j j Н- £ (х),
где ai = 0,9998660; а3 = —0,3302995; а5 = 0,1801410; а7 =—0,0851330; а9 =
= 0,0208351.
Тогда | е (х)| < 10—5, где —1 < х < 1.
Общее число рассматриваемых операций приблизительно равно
— —12.
2
Запишем полином (9.1) с помощью гнездовой процедуры
4“ Х (а1 + Х (а2 4" х (а3 4“ * • • 4“ Х (ап-2 4" х (ап-1 4- апХУ) •••)))•
Число операций уменьшается, потому что образуется естествен-
ная для ВМ последовательность действия, которая не требует из-
быточных умножений. Типичной последовательностью операций
вычисления частной суммы f (х) в гнездовом виде является:
(1)	Вычисление х и хранение в X
(2)	Вызов ап
(3)	Умножение
(4)	Вновь вызов ап-х
(5)	Сложение
(6)	Вызов X
(7)	Умножение
Общее число рассматриваемых операций приблизительно 7п.
Сравнивая эти два метода, мы видим, что число операций, не-
обходимых для вычисления ряда в стандартной записи, возрастает
пропорционально квадрату числа членов ряда, в то время как чис-
ло необходимых операций при вычислении ряда в гнездовой записи
пропорционально числу членов в ряде. Гнездовые формы обраба-
тываются быстрее, чем стандартные формы. Заметим также, что
если ряд вычисляется с помощью гнездовых записей, уменьшается
необходимость в использовании памяти ВМ при промежуточных
вычислениях. Наиболее употребимые ряды приведены в табл. 9.1.
Эти формулы удовлетворяют условию сходимости.
Другим методом вычислений этих функций является подбор по-
линомов кривой с широким диапазоном изменения аргумента. Эти
полиномы позволяют точно вычислять логарифмические, экспо-
236
ненциальные и трансцендентные функции. Табл. 9.2 составлена из
таких полиномов для наиболее известных функций.
Функции могут быть записаны в выражениях, которые легко
вычисляются следующими методами.
Метод 1
а)	найдем или составим таблицу значений интересующей нас
функции с интересующей точностью;
б)	подготовим интерполирующий полином, который проходит
через интересующие нас выбранные в таблице точки и охватыва-
ет интересующий диапазон аргумента;
в)	установим максимальную погрешность аппроксимирующего
полинома в интересующем интервале;
г)	если точность удовлетворительна, запишем полином в гнез-
довой скобочной форме и используем его для приближенной оцен-
ки функции.
Если таблица отсутствует или нет времени для ее составления,
используют метод 2.
Метод 2
а)	подготовим аппроксимирующий многочлен функции в инте-
ресующем интервале;
б)	применим схему экономизации Чебышева (см. разд. 9.2) для
уменьшения порядка полинома;
в)	проверим полином на точность по интересующему интервалу
аргумента;
г)	если полином не достаточно точен, включаем большее коли-
чество членов в первоначальный аппроксимирующий полином до
экономизации Чебышева и применяем метод Чебышева для того,
чтобы снова проверить полином;
д)	если полином достаточно точен, запишем в гнездовой скобоч-
ной форме и используем для вычисления функции.
Вопрос о точности оценочной функции достаточно сложен.
Инженеры часто ограничиваются точностью функции, равной
10-3. Другие исследователи утверждают, что достаточно ограни-
читься процентом погрешности оценочной функции, равной 10-3.
В чем же разница? Для того чтобы оценить е~х при х = 3, по перво-
му критерию необходимо 12 членов разложения ряда Тейлора
е~х в окрестностях нуля. Второму критерию необходимо только
восемь членов ряда. Почему? Ответ простой, потому что первый
критерий ошибки является абсолютным:
абсолютная ошибка = истинная — приближенная.
Второй же критерий является относительным критерием ошибки:
истинная—приближенная абсолютная ошибка
относительная ошибка =-----------------------------
истинная
истинная
Так как абсолютная ошибка меньше истинной, то знаменатель
должен быть больше, чем числитель, и таким образом критерий
относительной ошибки удовлетворяется при меньшем количестве
членов ряда, чем критерий абсолютной ошибки.
237
Другим обстоятельством является то, что большинство инже-
неров привыкло оперировать процентами (или относительной ошиб-
кой). Хотя при высокоточном моделировании в современных тео-
ретических разработках необходима высокая абсолютная точность,
в обычном техническом моделировании удовлетворяются несколь-
кими процентами относительной точности и, следовательно, неболь-
шим количеством членов ограниченного бесконечного ряда иссле-
дуемой функции.
9.2. ПОЛИНОМЫ ЧЕБЫШЕВА
В этой главе рассматриваются решения с помощью полиномов,
которые могут применяться для аналитических решений, а не
только при самом моделировании, при скоростном моделировании
разложения функций, представляемых медленно сходящимися ря-
дами. Существует возможность модификации рядов к виду, обеспе-
чивающему более быструю сходимость с помощью методики эко-
номизации Чебышева или с помощью рациональных методов при-
ближения полиномом. Аппроксимация полиномом функции, разла-
гаемой в ряд, обладает тем преимуществом, что может быть запи-
сана в гнездовом скобочном виде и эффективно (быстро) с высо-
кой точностью вычислена. Таким образом, вопрос заключается в
необходимости улучшения сходимости аппроксимирующего ряда
заданной функции.
Полиномы Чебышева могут применяться в уникальном процес-
се, обычно называемом экономизацией, для преобразования разло-
жения функции в быстросходящийся полином. С помощью теоре-
мы аппроксимации Чебышева можно преобразовать таблицы бес-
конечных рядов в быстросходимые ряды (погрешность которых из-
вестна). Эти полиномы затем должны быть записаны в гнездовом
виде для вычисления с помощью скоростной функции. Из полино-
мов Чебышева можно составить таблицы отображения большого
количества математических функций опережения (существующих
в значительном количестве), что необходимо при вычислении ско-
ростной функции. Из-за легкости преобразования процесс эконо-
мизации доступен различным специалистам, ввиду чего мы и ос-
танавливаемся на этих удивительных свойствах полиномов Чебы-
шева и их применении в рядах для обеспечения наилучшей сходи-
мости.
Полиномы Чебышева обладают пятью важными математиче-
скими свойствами.
1.	Они являются ортогональными полиномами с соответствую-
щей весовой функцией, определенной либо на непрерывном интер-
вале, либо на ряде дискретных интервалов.
2.	Они равно пульсирующие функции, т. е. изменяются между
равным максимальным и минимальным значениями.
3.	Нули полиномов Чебышева чередуются один за другим.
4.	Все полиномы Чебышева удовлетворяются трехчленным ре-
куррентным соотношением.
238
5.	Они легко вычисляются и обращаются в форму степенного
ряда на основании исходной формы.
Все эти свойства образуют аппроксимирующую функцию мини-
макс (т. е. в процессе приближения минимизируется максималь-
ная ошибка). Аппроксимация Чебышева отличается от метода при-
ближения с помощью наименьших квадратов, где минимизируется
сумма квадратов ошибок. При приближении методом наименьших
квадратов максимальная ошибка может принимать достаточно
большое значение. В аппроксимации Чебышева средняя ошибка
часто может принимать большое значение, а минимизируется мак-
симальная ошибка.
Определение полиномов Чебышева
Полиномы Чебышева определяются просто соотношениями
Т. (х) = 1;	(9.2)
Тп (х) = cos (п0);	(9.3)
cos0 = x.	(9.4)
Из (9.3) очевидно, что полиномы Чебышева ортогональны (в
чем можно убедиться подбором соответствующего весового коэф-
фициента), так как косинус является ортогональной функцией и
cos (п0) является полиномом в степени п величины 0.
Отмечая тригонометрическое тождество
cos(п1)0 + cos(^—1)9 = 2 cos 0 cos n0,	(9. 5)
можем сразу же написать, что
Тп+1-\-Тп_1=2хТп.	(9.6)
Гя+1=2х7'я-7’я_1.	(9.7)
Применяя это рекуррентное соотношение к полиномам Чебы-
шева, можно легко получить последующие полиномы следующим
образом. Так как То=1 и Тг=х, с помощью (9.7) найдем
T2=2xTi—Т0=2х2—1.
И тогда, начиная с Т\=х и Тг=2х2—1 и снова применяя рекуррент-
ную формулу (9.7), найдем
Т2 - 2xT2—T,i=4%з—Зх.
Продолжая подобным образом, можно образовать таблицу по-
линомов Чебышева:
Го=1.
7\ = х,
Г2 = 2х2—1,
7'3=4х3 —Зх,
Г4=8х<- 8х2+ 1,
239
Т5=16х5-20х3 + 5х,
Г6 = 32x6 - 48X4 + 18x2 - 1,
Г7=64x7 - 112x5 + 56x3 - 7x,
T8 = 128x8 - 256x6 +1 бОх4 - 32x2 +1.
Заметим, что, кроме того, можно образовать таблицу степеней
х в выражениях полиномов Чебышева, проводя решение относи-
тельно степеней х из этой таблицы:
1=?;,
х=7'1,
х2=(7'0 + Г2)/2,
хЗ=(ЗЛ + 7’3)/4,
х4=(ЗГ0+4Л + 7'4)/8,
хб-(ЮЛ + 57’з + Л)/16,
х6=(1ОТо+157’2+6Т4+Л)/32,
х7=(35Л + 21Т3 + 7Т5 + Г7)/64,
х«=(357; + 567; + 28Л + 87"6 + Т3)/128.
Важное свойство полиномов Чебышева состоит в том, что во
всех полиномах степени п имеется коэффициент опережения 1 и что
полиномы Чебышева (при делений на 2П-1) обладают наименьшим
экстремальным значением в интервале
' — 1<№С +1.
Не существует других полиномов степени п, чьи коэффициенты
опережения равны 1 и которые обладают меньшим экстремальным
значением, чем
в интервале
— 1 <х <-|-1.
Это является важным положением, так как утверждает, что если
аппроксимировать функцию на интервале | х |	1 при помощи по-
линомов Чебышева, ограниченных п членами, максимальной ошиб-
кой приближения будет
i/2"-1.
Разложим функцию f(x) в ряд с помощью полиномов Чебышева:
п
f№=VanTn(x).	(9.8)
я=0
Метод аппроксимации f(x) с помощью полиномов Чебышева
(первоначально отнесенный к Ланкрозу) является простым в упот-
240
реблении и обладает улучшенной сходимостью любого ограничен-
ного разложения функции f(x) в ряд. Рассмотрим применение это-
го разложения, содержащего:
1)	написание ограниченного ряда аппроксимирующих полино-
мов f (х) в гнездовой форме;
2)	представление этого разложения полиномом с выражениями
полиномов Чебышева;
3)	ограничение нового ряда одним или более двух членов;
4)	представление полиномов Чебышева с помощью выражений;
содержащих х;
5)	представление этого полинома в гнездовой скобочной форме
для удобства вычислений.
Например, если представить выражения функции в виде
т
/(х) = ^апхп	(9.9)
и переписать (9.9) в гнездовой скобочной форме
f (*) = «о + X (Ц1 + х (а2 +... + х (ат_х+атх)...)),
то этот ряд можно привести к ряду полиномов Чебышева, начиная
от внутренних скобок, в виде
am-i + amx=am_J\+am7\.	(9.10)
Можно умножить п—е скобочное гнездо
Л + ~\~апТ'п	(9.11)
на х и добавить к нему следующий коэффициент степенного ряда
am_n_ii, чтобы получить (л+1)-е гнездо.
Тогда, применяя соотношения
хГ0=Т1; х7'я=(7’я+1 + Г„_1)/2,	(9. 12)
приводим степенной ряд в л-х скобках, осуществляя преобразова-
ние в (n+1) степенной ряд полиномов Чебышева следующим об-
разом:
а'г~12Гп— Ъ-- + (-£^)^+(«о±-^)л+
+ (am_„_1+-^-)T0.	(9.13)
Процесс получения коэффициентов на любой стадии разложе-
ния полинома Чебышева f(x) может быть наглядно изображен с
помощью рис. 9.1. Здесь коэффициенты заданной стадии образуют
коэффициенты следующей стадии в соответствии с этой схемой.
В этом методе коэффициент, связанный с /л-м членом началь-
ного ряда
атхт,
9	493
241
Рис. 9.1. Процесс получения коэффициентов в разложении f(t) на полином Че-
бышева. Источник: Дж. М. Смит «Научное исследование на микрокалькуляторе»,
Вили, 1975. С разрешения издателя
преобразуется к соответствующему члену в разложении с помо-
щью полинома Чебышева
Таким образом, если ограничить разложение полинома Чебы-
шева f(x), начиная с /n-го члена, ошибка должна быть порядка
«m/z"1-1, а не ат, что могло бы быть в первом приближении поли-
нома (табл. 9.3). В этом смысле, говорят, что разложение Чебы-
шева сходится быстрее, чем первоначальное разложение. Другими
словами, если начальная аппроксимация функции была выполне-
на с точностью до некоторой величины, то аппроксимация полино-
мом Чебышева будет иметь почти такую же точность (при такой
же ошибке) с меньшим количеством членов. Это и называется
процессом экономизации.
Методика следования из (9.10) в (9.13) указывает основной
способ получения аппроксимаций полинома Чебышева f(x) для п
членов. Таблицы степеней х в членах полиномов Чебышева, пред-
ставленные ранее и повторяемые здесь для удобства, пригодны
для непосредственной подстановки степеней х при их эквивалент-
ности полиному Чебышева:
1=7'о>
x=7'i,
х2=(Т0 + 72)/2,
хз=(37\4-Т3)/4.
х4=(ЗГ+4Т2 + Т4)/8,
х5=(ЮЛ+57'з + 75)/16.
В этом способе степенной ряд вида
f (х)=а0 4- atx -|- а2х2 +. • • + атхт
может быть превращен в разложение полиномов Чебышева
Л(х)=&0+ь, Л + ь2 Т2+... Ьт Тт.
242
Таблица 9.3
N
Разложение fN(x)= апхп с помощью полинома Чебышева
л=0
Разложение в степенной
ряд по х
Разложение с помощью полинома Чебышева
/о — а0
/1 = ЛО 4- Я1Х
/2 = До +	4- Л2х2
/з = ао 4-	4-
4- а2х% 4- л3*3
/4 — ао 4- а\х 4- #2*2 4-
4- 0з*3 4- я4х4
/5 = до 4- cl\x 4- л2х2 4-
4- я3*3 4- л4х4 + а5х5
аоЛ)
ао^о 4- а$л
Для того чтобы этот процесс был точным, ряд должен быть за-
писан в такой форме, где вычисляется /(х) при х на интервале
—Isgjxsg; 4-1. Записанное разложение в терминах полиномов Че-
бышева может быть заменено на полиномы через х на основании
представленной ранее таблицы, переписываемой здесь для удобст-
ва в виде
т0=1,
Л=Х,
Т2=2х2— 1,
7’з=4х3 —Зх,
Tt=8x*—8х2+ 1,
Т5= 16л5 — 20х3 + 5х,
а затем упрощено с помощью алгебраических преобразований и
записано в гнездовом виде для быстрого счета.
Предположение Хэмминга легко проследить на примере
г/= 1п(1+х)^х-х2/2+х3/3,	(9.14)
9*
243
чтобы наглядно представить метод экономизации. Прямой подста-
новкой вместо степенной х это разложение можно записать в виде
степенного ряда с помощью членов, содержащих полиномы Чебы-
шева, следующим образом:
^Г,_(Л±^) + (?й_±2к);
У==-Г0/4+(1+“)Л—(9.15)
Отбрасывая последний член в степенном ряде (9.14), получаем
погрешность (е), составляющую 0,25, а у (при х=1) в степенном
ряде (9.15) при отбрасывании последних двух членов
£= 1/12— 1/4= —0,1666....
Это понятно, так как значение величины полиномов Чебышева
меньше или равно единице для всех х на интервале O^x^l.
Таким образом, можно написать
=	+	(9. 16)
обеспечивающую большую точность, чем обеспечена в (9.14). Это
и есть процесс экономизации. Используя определения полиномов
Чебышева, можно переписать (9.16) в виде
, у = 1п(1+х)^-А+-^||---------2^+_L=x(], 25-0,5%).
Сравнение численных результатов экономизированного полинома
второго порядка и неэкономизированного полинома второго по-
рядка представлено в табл. 9.4. Экономизированное квадратное
уравнение обладает меньшей средней ошибкой —0,0646, чем не-
Зкономизированное квадратное уравнение 0,0795, и, кроме того,
наименьшей максимальной ошибкой 0,1 при х = 0,5 на интервале
1.
Таблица 9.4
Сравнение экономизированных и неэкономизированных
квадратных уравнений
х	Точное г/ = 1п (14-х)	Экономизированное у=х (1,25-0,5х)		Неэкономизирова иное z/ = лг—0,5_ха	
		У 1	ошибка	У 1	ошибка
0,1	0,09531018	0,1200	—0,0246	0,0950	0,0003
0,3	0,26236426	0,3300	—0,0676	0,2550	0,0074
0,6	0,47000363	0,5700	—0,0999	0,4200	0,0500
0,9	0,64185389	0,7200	—0,0781	0,4950	0,1469
1,0	0,69314718	0,7500	—0,0569	0,5000	0,1931
244
Осуществив методы функциональной оценки, мы поняли, что
записью полиномов в скобочно-гнездовом виде достигается точ-
ность пятого и шестого порядка с таким же количеством операций,
какое требуется при оценке полинома третьего порядка без скобоч-
ной записи. Далее можно обнаружить, что при экономизации Че-
бышева можно обеспечить точность полиному высокого порядка
за счет точности полиномов низкого порядка, значительно умень-
шая тем самым количество числовых операций. Кроме того, мож-
но заметить, что, применяя критерий относительной ошибки, мож-
но уменьшить число требуемых членов полинома. Так, относитель-
ная точность полинома пятого порядка, полученная с помощью
полиномов Чебышева, может быть эквивалентна неэкономизиро-
ванному разложению полинома седьмого или восьмого порядка.
Тогда, если полином Чебышева записать в гнездовой скобочной
форме, он обеспечивает такую точность операциям, которая обыч-
на в разложении полиномов свыше восьмого или девятого порядка.
Таким образом, оценочная аппроксимация полиномом Чебышева в
гнездовом скобочном виде уменьшает рабочую нагрузку в терми-
нах относительной ошибки по сравнению с полиномом аппроксима-
ции f(x) девятого порядка до ее величины, соответствующей приб-
лиженному полиному f(x) второго или третьего порядка. Это при-
водит к уменьшению объема числовых операций на порядок. В це-
лом способ оценки математических функций предусматривает сле-
дующее.
1.	Написать функцию с помощью полинома усеченного вида в
терминах относительной ошибки.
2.	Переписать выражение таким образом, чтобы интервал, в ко-
тором находится оцениваемая функция /(%), был равен —
+1.
3.	Экономизировать ряд, применяя полином Чебышева.
4.	Переписать аппроксимацию Чебышева в гнездовом скобоч-
ном виде.
5.	Все это применить для численной оценки.
Численная оценка полиномов Чебышева
Полезно знать, что представленная здесь рекуррентная форму-
ла для получения полинома Чебышева
тп (X)=2хТ	(х) - Т п_2 (х)
может быть применена к численной оценке полиномов Чебышева.
Начальное значение рекуррентной формулы может быть вычислено
при То= 1, Тч=х.
Таким образом, разложение функции в полином Чебышева, од-
нажды записанное, нет необходимости переписывать в степенной
ряд от х, а сразу же можно проводить численную оценку. Напри-
мер, уравнение
у = 1п(1+х)--^-+-^Г1--^ + 2к (9.17)
245
является аппроксимацией Чебышева In (1+х), что было получено
ранее. Используя рекуррентную формулу с учетом того, что То=1.
Т,1—х, можно численно оценить уравнение (9.17) первой оценкой
численного значения для пяти полиномов Чебышева, например при
х=0,3:
Го=1,
Л=0,3,
Т2 = (2) (0,3) Тх - То=2 • 0,3 • 0,3 - 1 = - 0,82,
73=(2) (0,3) Т2 - Тх = - 2 • 0,3 • 0,82( - 0,3) = 0,792.
Все это мы можем подставить в разложение степенного ряда
для численной оценки ряда
у=1п(1,3)^- 1/4 + (15/12)0,3- 1/4(—0,82)+ 1/12(—0,792)=0,2640;
у=1п(1,3)=0,26236426.
Эта процедура позволяет удобно оценивать полиномы Чебыше-
ва высоких порядков (вплоть до 20-го). Несмотря на то, что воз-
можно написание разложения функций в полином Чебышева в гнез-
довой скобочной форме, оно громоздко, и начинающий может спот-
кнуться, если он забыл, с какими скобками принято обращаться в
процессе числовой оценки. Другим вариантом является первое вы-
числение численных значений полиномов Чебышева и затем под-
становка их в уравнение разложения полинома, хотя это и не при-
водит непосредственно к оценке полиномов высшего порядка.
Пример. Экономизируем разложение ряда Маклорена: ех=1 +
+х+х2/2+х3/6+х4/24+х5/120+х«/720+ ...
Так как
1=Г0
х=Ть
х2=1/2(Т0 + Т2),
хЗ=1/4(ЗЛ + 7’з),
1/8(ЗТ0 + 47'2 + Л),
х5=1/16(10Т1 + 57’з+7'5),
х6 = 1 /32 (1ОТ0 + 15Т2+6Г4 + Т6),
мы можем переписать е* как
ех=То + Тх + 1/4 (То + Т2) +1 /24 (3 Тх + Т3) + V192 (ЗГ0 + 4Г2 X Т4) +
+1/1920(107'1 + 57'3+...)+1/23О4О(1ОТо+157'2+...) + ...;
ех = 1,2661 То + 1,13027’1+0,2715Т2 + 0,044373 +...;
ех = 1,2661 + 1,1 ЗОЗх+0,2715 (2х2 - ’1) + 0,0444 (4х3 - Зх) +...;
ех^ 0,9946+ 0,9974х+0,5430х2+0,1771л3+...
246
Таблица 9.5
Сравнение полинома Маклорена с экономизированным
полиномом Чебышева
X	ех	Маклорен	Чебышёв	Ошибка по Маклорену	Ошибка по Чебышеву
1,0	2,7183	2,6667	2,7120	0,0516	0,0063
0,8	2,2255	2,2053	2,2307	0,0202	—0,0052
0 6	1,8221	1,8160	1,8267	0,0061	—0,0046
0,4	1,4918	1,4907	1,4917	0,0011	0,0001
0,2	1,2214	1,2213	1,2172	0,0001	0,0042 
0,0	1,0000	1,0000	0,9946	0,0000	0,0054
Заметим, что члены, включающие То. Т\, Т2 и Тз, были получе-
ны при подстановках полиномов из шести членов в ряд Маклоре-
на. Таким образом, мы выявили вклад шестого члена на фоне пер-
вого и последующих членов — эффект, за счет которого получена
экономизация. Сравнение результатов расчета с использованием
экономизированного полинома Чебышева и полинома Маклорена,
содержащих четыре члена каждый, представлено в табл. 9.5. За-
метим, что ошибка при использовании метода Чебышева макси-
мальна при х=0, а ошибка при применении метода Маклорена при
этом минимальна. Это происходит от того, что приближение
Маклорена вначале имеет характер касания по сравнению с ми-
нимаксным характером приближения Чебышева на интервале
(0,1). Это иллюстрируется графиком рис. 9.2.
Пример. Осуществим аппроксимацию sinx полиномом Чебы-
шева, используя метод экономизации. В этом же простом примере
применим аппроксимацию sin х полиномом Маклорена, основыва-
ясь опять же на том, что она отцентрована в интервале —1^х^
+1. Имеем
Тогда
sin X = Л - 4- <ЗГ1 + Гз) + 4т (1071 + 5Гз +
/Л	JLi/j&V
169
sin —
192
г.—— ГзН—— т5.
1	128	1 1920	5
Более высокие степени х ряда Маклорена могли бы внести даль-
нейший вклад в уточнение коэффициентов Тц, Т3 и Т$. Однако это
доля небольшая, особенно для первых членов Тх. Член х5, в част-
ности, изменяет коэффициент 7ц менее, чем на 1%, а член х7 из-
меняет Л менее, чем на 0,01 %'.
247
Рис. 9.2. Ошибка экономизации Че-
бышева при разложении в ряд Мак-
лорена функции ех. Источник:
Дж. М. Смит «Научное исследование
на микрокалькуляторе», Вили, 197’5.
С разрешения издателя
Рис. 9.3. Сравнение ошибок аппрок-
симации при разложении в ряд Мак-
лорена и при экономизированном по-
линоме Чебышева функции sinx. См.
Дж. М. Смит «Научное исследование
на микрокалькуляторе», Вили, 1975.
С разрешения издателя
Экономизируя аппроксимацию Чебышева (опуская член 7$),
найдем
169 ~	5 ~
---- 1 1----------1 Q.
192	1	128	15
Подставляя
Л—х;
7"з = 4х3 —Зх.
найдем
sin х 0,9974л — 0,1562л3 = л (0,9974 — 0,1562л2).
Ошибки аппроксимации функции sin х методом Маклорена и
экономизированной аппроксимации Чебышева сравнены на графи-
ке рис. 9.3.
9.3. ССЫЛКИ
При изучении следует иметь в виду работу Ричарда Хэмминга
«Численные методы для инженеров и исследователей», Мак Гроу-
Хилл, 1973, гл. 28, 29 и 30. В связи с решением примеров, приве-
денных в этой главе, целесообразно ознакомиться с работой Курти-
са Ф. Джеральда «Прикладной численный анализ», Эддисон—
Весли, 1970.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ А
МЕТОДЫ ПОДСТАНОВКИ ДЛЯ ИССЛЕДОВАНИЯ ПЕРЕДАТОЧНЫХ
ФУНКЦИЙ С ПОМОЩЬЮ МОДЕЛЕЙ
Метод подстановки при использовании передаточных функций
с помощью моделей заключается в предварительном получении
разностного уравнения с помощью следующего метода:
1. Выявления f(z), определяющей s-1 в передаточной функции
моделируемой системы;
2. Получения разностного уравнения с помощью обращения пе-
редаточных функций г-области.
Хорошо известный метод подстановки Тастина приводит к дос-
таточно устойчивым, хотя и недостаточно точным, разностным
уравнениям для моделирования непрерывного процесса. Тастин по-
лучил функцию /(z) в своем методе следующим образом:
что следует из ограничения разложения в ряд ln(z) Лорана.
Таким образом,
т /Z+ 1\
2	—V
Пример. Используя метод Тастина, выведем разностное уравне-
ние, моделирующее систему первого порядка:
Следуя методу, получим
У 1
х xs + 1
у 1/д
772 (г 4-1)
и + 1/S
ц(г-1) + Г/2 (г 4-1)
249
/ Т/2и \
I------- (1 4-г-1)
Г/2т (г + 1)	=	Т/2т(1 + г-1)	__\14-Г/2т/
(1 +T/2t) z 4- (772т-1) (14- 772т) - (1 - 772т) г~1	1 _ /1—772т \
\14-772t/
Таким образом,
Переходя к разностному уравнению, найдем
Теперь давайте рассмотрим свойства разностного уравнения. Сна-
чала заметим, что
_/1-Г/2тх
полюс |j + 772iJ
И ЧТО
1 ini |г110Люс|	1 •
Г->оо
Таким образом, разностное уравнение устойчиво независимо от то-
го, насколько велико значение Т. Это весьма существенное качест-
во метода Тастина, которое распространяется на разностные урав-
нения высоких порядков.
Далее заметим, что передаточный коэффициент
1 — 772т
1 4- 772т
является ограниченным разложением ряда е~г/х. Это легко увидеть
из
с-т/х_ 7 е-г/2т ~1 — Т/2т
еГ/2т 1+7/2'С’
Это означает, что разностное уравнение обеспечивает на каждом
шаге лишь удовлетворительную аппроксимацию непрерывного дви-
жения при Т/2х<^ 1.
Автор для метода Тастина обычно пользуется величиной Т =
=т/15. Говоря иными словами, частота квантования должна быть
не менее чем в 15 раз выше основной частоты моделируемой сис-
темы. Многие из тех, кто применял метод Тастина, пользовались
более низкими частотами квантования. Опыт автора указывает на
то, что разностные уравнения, оставаясь устойчивыми, обеспечивают
переход на шаге с абсолютной ошибкой порядка 10~3—10-4 при
o)s=15(on, где (Оз — частота квантования, а (оп — собственная час-
тота моделируемой системы. Эти значения меняются от системы к
системе и их не следует понимать буквально. Они даны здесь для
ориентировки и являются иллюстрацией эвристического выбора
рационального значения, как подхода автора при использовании
небольшого шага в методе Тастина.
250
Внимательный читатель заметит, что передаточная функция при
s-1 в методе Тастина не что иное, как передаточная функция ин-
тегрирования методом трапеций
что является численным интегратором неявного вида. То что ме-
тод Тастина основан на применении алгоритма интегрирования в
неявном виде, предрешает успешность его применения в качестве
метода подстановки.
Поскольку метод Тастина прост в применении к интегрирова-
нию в неявном виде и аналогичен методам трапеций дифференци-
альных уравнений движения, его можно использовать для решения
определенных нелинейных дифференциальных уравнений.
Очевидно, достаточно просто перенести метод постановки на
другие численные методы. Это доступно каждому и для этого не-
обходимо осуществить ^-преобразование интегратора, получить
его передаточную функцию. Затем эту функцию можно подставить
в выражение s-1 моделируемой системы.
Пример.
х л = х п_ 1 -р Тхп.
^-преобразование приводит к
(1 — z-1) х = Тх.
. х __ Tz
’ * X Z — 1’
которое обычно при моделировании
у s-i
X и + $—1
приводит к
У = Tz =____________________Г/Т_______=_______Г/Т_____
X 1 ' т(г—l) + r 1 — Z-1 4-(Г/т)г-1	1 —(1 — Г/т) z~i ’
обращающееся в разностное уравнение
Уп = (1 - W У п-1 + О) хп.
Для подстановки можно применить Т-интегратор. Его передаточ-
ной функцией является
ХГ[уг + (1 —у)]	_s__n
г- 1 J
где X, и у можно применить для настройки интегратора при реше-
нии уравнения движения моделируемой системы, обсуждавшейся
в гл. 7.
Существует достаточно обширная литература по методу под-
становки. Некоторые из наиболее часто используемых алгоритмов
при подстановке представлены в табл. А.1.
251
Таблица A.l
Наиболее часто употребляемые интеграторы в прикладном методе подстановки
l/Sk	Метол	Оператор	Метод i	Оператор
1/s	Тастин Мэдвед — Труксаль	Т Z+ 1 2 z — 1 Т z+ 1 2 z— 1	Точное z-преобразование z-форма	Тг Z — 1 Т г + 1 2 z— 1
1/S2	Тастин Мэдвед — Труксаль	П	+ 2z + 1 4	(Z- 1)2 Т2 z2 + 4г + 1 6	(z— 1)2	Точное z-преобразование z-форма	Г2г (г - 1)2 7*2 гч -|- Юг + 1 12 (г —1)3
1/S3	Тастин Мэдвед — Труксаль	ТЗ гЗ + Зг-2 + Зг + 1 8	(z—1)3 ТЗ гз± 11г2+ 11г + 1 24	(г— 1)3	Точное z-преобразование z-форма	ГЗг (г + 1) 2 (г— 1)3 ТЗ г(г+ 1) 2 (г-I)3
1/S4	Тастин Мэдвед — Труксаль	Ti Zi + 4гЗ Н- 6г2 + 4г + 1 16	(г —1)4 7*4 г4 + 26г3 + 66г2 + 26г + 1 120	(г— 1)4	Точное z-преобразование z-форма	Т4 z (z2 + 4г + 1) 6	(г-1)4 T4 Z (z2 + 4г + 1) 6	(г— 1)4
„	1	f XrtY-z+U—у)])л
Примечание. Подбор интегратора в общем случае осуществляется с помощью выражения	:----?
ПРИЛОЖЕНИЕ Б
ТАБЛИЦА z-ПРЕОБРАЗОВАНИИ ЖЮРИ*
Таблица 1
z-преобразовательные пары
। Номера по пор. 1	Дискретная временная функция / (л): п > 0	^-преобразование F (z)-C\f (n)]s Izl > R=2 / (n) г~Л n=*Q
1	2	3
1	и (л) = 1* ^при п > 0	z
		z — 1
2	--ЛП	z
	е	z —e~*
3		z
	п	1)2
4	П2	г(г+1) (*- 1)3
5	п3	Z (z2 + 4z + 1)1
		(г-1)4
6		z(z*+ 11г2-|- 11г + 1)
		(Z- 1)5
7	д5	z (z4 + 26z3 + 66z2 + 26z + 1)
		(z-l)6
8	пк	
9	и (п — k)	z~k+1
		z — 1
10		F(eezr)
11	Л(2) = п (п — 1)	2—-— (.2- 1)3
12	п™ = п(п — 1)(л— 2)	3!	Z
		(Z- 1)4
13	п(*)= 71 (л — 1) (л —2)... (Л— k+ 1) i		*1	Z bx. (z— l)*+l
* Жюри Е. И. Теория и применение метода z-преобразований. Вили, Нью-
Йорк, 1964.
253
Продолжение табл. I
1	2	3
14	n(ft)/ (n), nk = n (n 4- 1) (n 4- 2)...	у	\ k fe	& f \ *1
	... (п + Л-1)	( — 0 z
15	( — l)ft n (n—1) (n —2)...	Jz zF<^ (z),	(z) =	s- F (z)
	... (n — k 4- 1) /л_Л+1 —	dsr
16		F^{z)
17	(- l)ft (n - 1) (n - 2)... (n - k) fn_k	F^ {z)
18	nf(n)	— zF^(z)
19	n^f (n)	z2F^ (z) + zMl\z)
20	n3f (n)	— nSF^ (z) — 3z2F<2> (z) — zF^> (z)
21	cn	tcfz
	n\	
22	(1ПС)"	C^z
	n\	
23		{az + c)k
	\n)	’ W (£ —n) !nl	zk
24	(n + k\si ~	zk+l
	( k /	{z—c)k+l
	cn	
25		(n = 1, 3, 5, 7....) n\	sh —I \ 2 J
	cn	, f c \
26	— (n=0, 2, 4, 6,...) nl	'"(v)
	sin (an)	z sin a
27		z^ — 2z cos a 4- 1
28	cos(an)	z (z— cos a)
		z2 — 2г cos a 4- 1 z2 sin ф 4- г sin (a — ф)
29	sin (an 4- ф)	
		z2 — 2z cos a 4- 1
30	ch(an)	z (z— ch a)
		z2— 2z ch a 4- 1
	sh (an)	z sh a
31		z2— 2z ch a 4- 1
	1	t z
32	— , n > 0	In	
	n	z— 1
* Следует отметить, что fn означает, то же, что и f(n)-
254
Продолжение табл. I
2
3
1—с~а”
п
sin ап
п
cos ап
------, п > О
п
(и 4-1) (и 4-2)... (и 4-^-1)
(£-1)!
, г~е
а 4- In----т“ , а > О
z — 1
. sin а
а + tg“x------, а > О
z — cos а
In—т=========~
•/ г2 — 2г cos а 4- 1
1
1——	,^=2,3,...
г /
е1^
z— 1

41
42
43
44
45
( 1)(л-Р)/2
при п > р и п — /2-четном; = О
при п < р или п— р-ъъчыпмл.
fnlk}ЬП1Ь' п= mk(~m = 0>	2> ")
= 0,	/14 mk
ап / d \п
апТп (х) = ап cos (п cos-1 х)
Ln (х) _ "VI /п\ ( — х/
nl ~ £t\r) rl
г-0
нп (X) _	(-l)n-ftxn-2*
n! ' kl(n— 2*)!2Л
апР™ (х) = ап (1 - x^)mft	(х)’
m равно целому числу.
Z
у z^— 2xaz 4- а2
z (z — ах)
z% — 2xaz 4- а2
—£— е-г/(г-1>
Z — 1
е—z/z—1/2х8
(2/п) 1
2mm\ Х
(z2— 2xaz + a2)m+1'2
255
1
46
47
48
49
50
51
52
53
54
55
Продолжение табл. I
2
3
п (х)	( d \т Ln(x)
—.«равно целому
числу.
п 4 L Z(z) а (л) J
де F (г) и G (z) — рациональные поли-
номы z одинакового порядка
________________1___________
т (т 4- 1) (т 4- 2)... (т 4- п)
sin (ап)
nl
cos (ап)
п!
п
2 fkgn—k
Л=0

In
O(z)
ecOs°/*sin
sin a
z
eCOSI/zcos/'-^
F(z)G(z)
k fkgn—k
2 & f kg n—k
Л=.О
an 4- ( —a)n
2a2
an—$n
a —p
(n 4- k)(k)
(n — k)^
.«(«_*)
ml e
1	n;
— sin — n
n	2
cos a (2n— 1)
----7--------, n>Q
2n-i
— Pw{z)G(z),
dz
Л(2) (л) О (z)
1
г2 — a2
z
(г— a) (z— p)
t. s z
k г (г-1)й+1
1 z 4- 2 г cos a 4- 1
----y=- In---------t=------------
4 у z z — 2 у z cos a + 1
Продолжение табл. I
1

з
61
62
63
64
65
66
67
68
69
70
71
у п	1
(У ~1)2+ 1 -У ~(1-У)2
Y-1V 1-Y U-Y (1—Y)2/
ап cos лп
е~ап cos ап
е~~ап sh (ап 4- ф)
(Y_a)2 + [}2
(а2 + р2)"/2 sin (пе+ф) ...J.
+ ?[(а _ Y)2 + р2]1/2 и-‘е а
(г—у) (г — I)2
г (г 4- Др)
(г —у) (г- 1)2
Z
z + а
z(z— е“а cos а)
z2 — 2z е“а cos а -b е2а
г? sh ф + г е~а sh (а — ф)
г** — 2z е“а ch а + е~2а
(г-у)[(г-а)24-?2]
пул 1 Зуп 1 Гп(и—1)
(Y-l)3~ (y-1)4 + Т 1(1-у)2 “
4п	6	1
“ (1-Y)3 + (1-Y)4 J
k
v₽0
/00
n
fn+2 /0=0
n + 1 ’ fl = о
________1 + Др______j_
(1-Y) [(l-«)2 + ?2]
(Y + ao)Yn _ .
(y-1)[(y-«)2+P2]
,	[а2 + p2]”/2 [(Др + g)2 4- p2]V2
+ ₽ [(« - l)2 + ₽2] 1/2 [(а_у)2-|-р2]1/2
X sin (nO + Ф 4- X), ф = Ф1 + Фг,
z
(г_у)2(г~1)з
z(z — l)ft
(г—ea)ft+1
P~^F(p)dp+
J	л-Ч) п
z
г]'Л(р) dp
z
________г (г 4-Др)_____
(Z_1)(Z_Y) [(2. _ а)2 + [J2]
257
Продолжение табл. I
1
2
3
72 (л + 1) еая — 2п е’ (л+1> + е“(л+2) (п-1)
73
cosan
1)л-----, п > О
п
74
(п + k) !
----;---/л+ь fn=* 0 при 0 < п < k
пI
4- Л
76
77
78
79
80
81
82
п Я
— пап cos — п
„ 1 + COS ЛП
пап -------------
„ Л 1 + COS ЯП
a" sin — п-----------
4	2
„ / 1 4~ COS ЯП	я \
а (	2	~ cos —nj
Рп (X)
п !
--------/п>0, РТ* — 0 при п<т
(п + т)\	п
1
-—;—— , а > 0, Re ? > 0
(п 4- а) р
83
84
85
86
/ 1 + cos ЯП	я \
а ------------------4-cos — п)
сп
—, n= 1, 2, 3, 4,...
п
сп
— , и = 2, 4, 6, 8,...
п
/Z— 1 \2
\z — еа)
1д________£________
г2 4- 2г cos а 4- 1
dk
(-V)kz2k-^rU4z)]
P~(1+h)fr<P>aP
z
2д2г2
(г 4- а2)2
___2д2г2
(г2—а2)2
д2г>2
г* +
2а2г2
г4 — д4
е^’/о (/Г=ТГ2г-1)
Ф(г~ 1, а, р), где Ф(1, ₽, а) =
= С (?, а) равно обобщенной функции
Римана
2г4
г4 — д4
In г — In (г— с)
In г — -у- 1п(г2— с2)
сг(г4- с)
(г-с)З
258
Продолжение табл. I
1	2х	3
87	пЧп	cz + 4c z + g2) (*— c)4
88	пксп	dP(z/c)	. t, о
89	л	и/2 \ ~“ST" 2j а + 1 х 1=0	_____Z2 __
		z4 4- 2д2г2 + M
	X ал“2—4z (а4 — Ь*У	
90	iff (п)9 k > 0 и целое число	~zd^F1 {z)’ Fi (г)=c lnk~lf (л)1
91	(я _ 1) (я_ 2) (л—3)... (и—Л-Н)	>	1
	(Л— 1) t	(г—a)ft
92	k(k — l)(fe—2)... (fe—n + 1)	(1+0*
	nt	
93	nan cos bn	[(z/a)3 + z]a\ cos b — 2 (zjaft [(zffl- 2 (г/a) cos b + 1]2
94	nan sin bn	(г/д)3 sin b — (z/a) sin b
		[(z/ayi— 2 (z/a) cos b 4- 1]2
95		nan	z(a—2z)	/	a \	2 In 1 —	— — z «2	\	z /	a
	(n + 1) (n + 2)	
96	(-O'1	2 ]/ z/a tg~i Уа[г —
	(n 4- 1) (2n + 1)	z t /	a \ — — In 1 4- — I a \	z /
97	an sin an	z cos a	a sin a
	n + 1	1g 1	4- a	z — a cos a
		z sin a	z2 — 2az cos a 4- a2 4-	In	 2a	z2
98	an cos (n/2) sin a (n + 1)	z	z2 4- 2az sin a 4- a2 — In —		 4a z2 — 2azsina4-a2
	n+ 1	
99	1	ch (z”1/2)
	(2n)l	
259
Продолжение табл. I
3
100
101
102
п !
/ _1_\
~ 2 1(-а)я
V П /
/ J_
I “ 2
\ л/2
Вп (*) — полиномы Бернулли
„ л
a ccs п
103
W п (х) Д полиномы Чебышева второ-
го рода
105 Qn (х) = sin (п cos-i х)
/z/ (z— а)
_____z
у/ & —
elz
г(е^-1)
2Г2
z^—lxz ч- 1
z sin л/m 1 + z~m
z- — 2г cos л/m 4-1 1 — z~m
z
z^ — 2xz 4- 1
ПРИЛОЖЕНИЕ В
Т-ИНТЕГРИРОВАНИЕ НУЛЕВОГО ПОРЯДКА И ЕГО СВЯЗЬ
С ТЕОРЕМОЙ О СРЕДНЕМ ЗНАЧЕНИИ *
Т-интегратор нулевого порядка является простым числовым ин-
тегратором прямоугольного типа, который можно подобрать для
решаемой задачи. Этот интегратор синтезирован таким образом,
что его частотные характеристики могут варьироваться. Таким об-
разом, Т-интегратор может быть подобран для точного и эффек-
тивного интегрирования во многих разнообразных случаях. Все
Т-интеграторы обладают устойчивостью, точностью и параметрами
регулирования шума, которые можно изменять.
При подборке Т-интегратора для интегрирования линейной сис-
темы с постоянными коэффициентами его параметры могут быть
выбраны для осуществления точного численного интегрирования,
при этом они инвариантны во времени. Т-интегрирование нулевого
порядка, применяемое для численного интегрирования нелинейных
систем или линейных систем с переменными во времени коэффи-
циентами, часто более точно, чем при использовании численных
интеграторов высоких порядков. Возникает вопрос: «Почему же
Т-интегрирование так точно?» В этом дополнении как раз лредстав-
*Смит Дж. М. Т-интегрирование нулевого порядка и его отношение к тео-
реме о среднем значении. Т. 6, Ч. I. Доклады 6-й ежегодной конференции по мо-
делированию в Питсбурге, апрель 24—25, 1975.
260
лен ответ на вопрос. Это происходит из-за того, что интегрирова-
ние нулевого порядка можно осуществить, применяя теорему о
среднем значении интегрального исчисления. Теорема о среднем
значении (в простейшем изложении) доказывает, что существует
интегратор прямоугольного типа, точно интегрирующий произволь-
ную непрерывную функцию в ограниченном интервале. Таким об-
разом, окончательно Т-интегрирование нулевого порядка — это
концепция численного интегрирования с использованием теоремы о
среднем значении.
Теорема о среднем значении в интегральном исчислении
Допустим f' непрерывна на ограниченном интервале [а, Ь].
Тогда существует такое число 0, для которого при a^.Q^b
ь
^f'dt=(b-a)f'^).	(В. 1)
а
В дальнейшем мы будем ссылаться на (В.1) или на формуль-
ное выражение теоремы о среднем значении. Левая сторона урав-
нения является интегралом, с помощью которого нам хотелось
идеально провести счет, а правая сторона демонстрирует возмож-
ность счета с помощью численного интегрирования методом пря-
моугольников.
Из теоремы о среднем значении следует, что интегрирование
методом прямоугольников позволяет точно интегрировать произ-
вольную подынтегральную функцию на интервале [а, &], если чис-
ло 0 определено. Одним из лучших подтверждений того, что автор
нашел применение теоремы о среднем значении для оценки интер-
валов, — это обратиться, например, к Куранту *. Теорема о сред-
нем значении проиллюстрирована графиком на рис. В.1 для слу-
чая, когда f — простая линейная функция. В этом случае 0, удов-
летворяющая -уравнению о среднем значении, является средним
значением на интервале.
Предлагаются четыре варианта представления теоремы о сред- •
нем значении для оценки интегралов.
Допустим, f' непрерывна в ограниченном интервале [а, 6]. Тог-
да существуют числа X и у, так что
Вариант 1.
(п+1)Т
f f'(t)dt=Tf'(nT-\-yT).
nt
Вариант 2.
(п + 1)Г
nt
* Courant R. Differential and Integral Calculus. Wiley Interscience, Vol. 1, 2nd
Ed., 1937, 1959 reprint, pp. 126—128.
261
Рис. В.1. К теореме о среднем
значении:
ь
(b-a)f’(V)=\f’(x)dx
а
Рис. В.2. Варианты теоремы о
среднем значении
Вариант 3.
(п+\)Т
j* fr(t)dt = TT' fr (пТ -|-$ Г) —явная форма.
nt
Вариант 4.
(n+V)T
J f'(t)dt = T\fr 1)^ + уЛ — неявная форма.
nt
Три из этих вариантов представления проиллюстрированы на рис.
В.2. Первый служит для того, чтобы сместить подынтегральную
функцию во времени на величину уТ. Это смещение интегрируемой
функции во времени относительно пТ позволяет эффективно выби-
рать средние значения. Второй вариант позволяет изменить мас-
штаб текущего значения интегрируемой функции (при помощи па-
раметра X) таким образом, чтобы прямоугольная область, образо-
ванная «Х/(пТ)» и базой «Г», удовлетворяла уравнению о среднем
значении. С помощью третьего и четвертого вариантов осуществ-
ляют и масштабирование и смещение во времени интегрируемой
функции. В этом случае требуется найти комбинации к и у, удов-
летворяющие теореме о среднем значении. Отличие между форма-
ми 3 и 4 состоит в том, что время смещения в варианте 3 отнесено
к текущему его значению, а время смещения в варианте 4 — к пос-
ледующему его значению.
Вывод формулы Т-интегрирования
Получение формулы численного интегрирования основано на
теореме о среднем значении, включающей синтез прямоугольного
интегратора. При этом осуществляется следующее:
262
Рис. В.З. Схема Т-интегрирования
1) синтезируется структурная схема представления теоремы
о среднем значении;
2) выводится формула интегрирования применением методик
Z-преобразования.
Окончательное решение задачи осуществляется с помощью
операций, представленных на рис. В.З, и четырех форм представ-
ления теоремы о среднем значении. Указанная на рис. В.З струк-
турная схема является процедурой разработки передаточной функ-
ции Т-интегратора, полученного /-преобразованием, и содержит
следующее:
1)	преобразование процесса перестройки нулевого порядка;
2)	масштабирование и фазовое смещение или процесс «фаза—
фильтрация»;
3)	сам процесс непрерывного интегрирования.
Обращая передаточную функцию Т-интегратора нулевого по-
рядка, мы найдем формулу численного интегрирования в неявном
виде:
хя=х„_1 + ХТ[ух„ + (1-у)х„_1].	(В. 2)
Эта формула интегрирования является дискретной аппроксима-
цией теоремы о среднем значении, где X и у находятся таким обра-
зом, чтобы удовлетворялось уравнение среднего значения. Во-пер-
вых, заметим, что это формула неявного интегрирования, где хп —
функция хп, а для многих систем хп является функцией хп. Неоп-
ределенное интегрирование не позволяет точно оценить хп, но хп
можно оценить либо с помощью экстраполяции, либо другим при-
ближенным методом. Для того чтобы приспособить этот интегра-
тор к интегрированию в явном виде (хп — функция хп^\ и других
последующих значений скорости), нужно переписать
x(2')	~е~*Г (?.с™г)( 1 \ —+ O
х(г) \ s '	\ s / I z— 1	)’
а (В.2) — в виде
хп = х„_1 + Г Т [(у + 1)	+ ух„-2].
где Г — постоянная масштаба при текущей функции, отличающей-
ся от % функцией, смещенной на интервал. Таким образом, компен-
сируется смещение подынтегрального выражения при замене хп на
Хп-^\- Эта особенность находит отражение в прямой цепи структур-
ной схемы, что связано с отличием в представлении четвертой фор-
мы теоремы о среднем от третьей формы.
263
Выбор значений параметров X и у
Любому способу выбора к или Г и у на первом этапе предшест-
вует применение метода Рунге—Кутта или другого классического
интегратора высокого порядка для интегрирования дифференци-
альных уравнений, а затем вычисляют у, принимая Х=1, или вы-
числяют %, принимая у=1. Этот хорошо известный процесс подго-
товки интегратора определением X, у или обоих сразу (при взаим-
ной увязке между у и к) можно осуществить через определенные
интервалы времени моделирования (скажем, на каждом 100-м
шаге). В конечном счете систему управления Т-интегратора наст-
раивают так, чтобы он стал достаточно точным интегратором вы-
сокого порядка на определенном интервале моделирования во вре-
мени. Если подставить в нелинейное дифференциальное уравнение
x = F(x, t) интеграторы нулевого порядка, то можно получить сис-
тему разностных уравнений, где ks и у$ — ее параметры.
Осуществим процесс программирования разностных уравнений
на цифровой ВМ. Для этого получим сначала один или несколько
контрольных случаев решения систем дифференциальных уравне-
ний с применением численных методов интегрирования и использо-
ванием интеграторов Рунге—Кутта четвертого порядка. Теперь фа-
зы и коэффициенты масштабирования могут быть выбраны эмпи-
рически:
1.	Выбором параметров разностного уравнения, обеспечиваю-
щего интегрирование с шагом, соответствующим частоте, превы-
шающей в 7—10 раз частоту динамического процесса.
2.	Установлением к=1/
3.	Эмпирическим подбором у до тех пор, пока результат вычис-
лений с помощью разностного уравнения не будет обеспечивать хо-
рошее совпадение * с результатом вычислений численным методом
интегрирования дифференциальных уравнений.
4.	Выбором к, обеспечивающего при выбранном у устойчивое
решение уравнений **.
Эмпирический способ быстр и точен при моделировании линей-
ных процессов с постоянными коэффициентами, в которых подоб-
ранные параметры остаются инвариантными во времени. В нели-
нейных процессах они обычно меняются во времени, однако часто
система параметров может быть определена «в среднем», например,
если с инженерной точки зрения такой прием интегрирования хо-
рошо согласуется в наиболее существенной области переменных
состояния динамической системы. Указанный прием может быть
использован, если условия моделирования или управления, а так-
же элементы системы меняются несущественно от прогонки к про-
гонке (например, цифровой фильтр, встроенный в систему управле-
* При любом количестве критериев.
** Необходимо обеспечить условие, при котором ks не будет выполнять функ-
цию «коэффициента усиления системы». Проверка с помощью контрольного вари-
анта как раз нужна автору, чтобы исключить такую возможность. Обычно Х=1.
264
ния ВМ, или условия процесса моделирования этого числового
сЬильтра в модели системы управления).
Однако в процессе инженерного проектирования модели с ме-
няющимися от прогонки к прогонке параметрами в случае приме-
нения этого приема, подходящего для линейных систем, необходи-
мо предусматривать время от времени прогонки контрольного ва-
рианта с уменьшенным шагом, для того чтобы понять и оценить,
существует ли динамика изменения параметров системы. Парамет-
ры настройки модели могут быть оценены аналитически. Эти пара-
метры, например могут быть выбраны (для линейных систем)
подбором (определением) корней характеристических уравнений *
дискретной модели с помощью уравнений непрерывной системы.
В системах, имеющих более одного интегратора, обнаруживает-
ся бесконечное число комбинаций % и у для каждого из интеграто-
ров, обеспечивающего решение системы решаемых уравнений. Оп-
ределенные интеграторы более предпочтительны при промежуточ-
ных решениях, чем другие, а связанные с этими интеграторами фа-
зовые характеристики и коэффициенты усиления будут доминиро-
вать при решении динамических систем.
Настроечные операции интеграторов в моделях или системах уп-
равления выполняются эмпирически достаточно быстро подстрой-
кой сначала низкочастотных внешних цепей, а затем внутренних
или высокочастотных цепей. Это итеративный процесс, который, по
опыту автора, работающего с системами 10—20 порядка, занима-
ет не более 1 —1,5 ч при настройке модели вручную в четырех-
пяти контрольных точках. Эмпирическая подстройка интеграторов,
спроектированных моделей систем или систем управления весьма
эффективна. Большинство систем управления обладает адаптив-
ными свойствами, обеспечивающими самонастройку своих харак-
теристик в каждой отдельно взятой системе, нуждающейся в под-
стройке. Подстройку моделируемой системы осуществляет элемент,
функционирующий параллельно с Т-интегратором в широком диа-
пазоне условий, однако, как правило, настроенный на конкретные
условия применения. Для настройки модели необходимы опреде-
ленные значения критериев. Исходными посылками при их выборе
являются либо определенные инженерные соображения, либо ана-
литические оценки, а определение их значений на модели возмож-
но применением «отладочных потенциометров», обычно использу-
емых при аналоговом моделировании. В частности, в программе
«Аполлон» настроечные операции Т-интеграторов осуществлялись
в цифровых компьютерах через преобразователи А/Ц с помощью
потенциометров аналоговых компьютеров.
Во многих случаях отладка модели осуществляется для ее ис-
пользования в широком диапазоне условий. Обычно отладка бази-
руется на контрольных вариантах задач, реализуемых при самом
* Дискретная система уравнений получается с помощью Z-преобразования
Т-интегратора для 1/s в ее передагочной функции, полученной с помощью преоб-
разований Лапласа в линейных системах с последующим переходом из Z-области
к разностным уравнениям.
265
малом шаге интегрирования с % или Г = 1 и у=0. Одновременно с
подстановкой модели для работы в контрольном варианте осуще-
ствляется подготовка аналогичной модели для работы в скорост-
ном режиме (например, в истинном масштабе времени для процес-
сов в системах управления или в тренажерах с участием человека
в контуре) с шагом интегрирования до 1/7(ог* и подгонкой настра-
иваемых параметров до требуемых значений. Регулируемые пара-
метры могут зависеть от основной динамической переменной, яв-
ляясь монотонной функцией от нее. Так, например, у может зави-
сеть от числа Маха следующим образом: у = а0 + ^1М + а2М2, и для
регулировки в этом случае необходимо определить три коэффици-
ента степенного ряда, обеспечивающих «нормальное» функциони-
рование регулятора с изменением М.
Подобные методы применяются, например, в авиационных тре-
нажерах, где к тому же настраиваемые параметры имеют несколь-
ко выражений, которые включаются в зависимости от того, выпу-
щено или убрано шасси, выпущены или убраны закрылки.
Целью многих моделирующих устройств является нахождение
и согласование рациональных динамических характеристик моде-
лируемых процессов. В этом случае настройка с помощью интегра-
тора для решения системы уравнений ранее осуществлялась после-
довательной подстановкой выражения одного интегратора в дру-
гой вплоть до получения «динамического соответствия», обеспечи-
вающего получение хорошо согласованных числовых интеграторов.
При регулировании параметров Г-интеграторов по временному сме-
щению и коэффициентам.усиления для лучшего удовлетворения
теоремы о среднем используются их выражения в неявном виде.
Управление точностью интегрирования при фиксированном шаге
Одним из подходов к управлению точностью интегрирования
при фиксированном шаге является изменение у до тех пор, пока
Т-интегрирование при выбранном шаге не будет достаточно близко
к результату Т-интегрирования с удвоенным шагом на одинаковом
интервале. В этом случае интуитивная догадка о возможности ис-
пользования Т-интегратора нулевого порядка перерастает в уве-
ренность, что интерполяция ступенчатой функцией может быть под-
держана с точки зрения удобства отладки. Эта экстраполяция не-
прерывной функции позволяет, таким образом, достичь цели в слу-
чае правильной центровки ступенчатой функции. Если ступенча-
тая функция отцентрирована «в среднем» относительно непрерыв-
ной интегрируемой функции, то и в этом случае дополнительное
уменьшение шага или измельчение шага квантования вдвое сущест-
венно не изменит точности процесса интегрирования. Таким обра-
зом, этот прием оценки правильности выбора параметров ступен-
чатой функции, аппроксимирующей непрерывную функцию, при
интегрировании является оправданным, так как только в случае
* со, — наибольшая частота моделируемой системы в герцах.
266
неудачной центровки изменение шага вдвое может значительно
повлиять на точность. Поэтому важно, чтобы определение
необходимости изменения у в каждом из п шагов было бы оцене-
но при таком уменьшении шага в два раза (в уравнении с фикси-
рованным у). Проблема заключается в определении уверенности
возможности такой ступенчатой аппроксимации по сравнению с ап-
проксимацией непрерывной функции, которая может быть получе-
на уже при первых вычислениях. Пробный расчет необходим и для
определения характера изменения величины ошибки при измене-
нии величины шага, приводит ли это к увеличению или уменьшению
ошибки. Если точность увеличивается, то изменение у в ходе ее
определения было в правильном направлении. Если точность
уменьшается, у изменилось неправильно, и необходимо осущест-
вить удвоение количества шагов, что может изменить результат
оценки. Как только локальное значение найдено, можно продол-
жить моделирование, в том числе увеличивая шаг во времени. За-
тем у подбирают вновь. Несомненно, подобные проверки проводят-
ся и в высокоскоростном поверочном моделировании и при этом
стремятся к фиксированным значениям величины шага.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
А Абсолютная ошибка, см. ошибка
абсолютная
Автономная система 68
Аналитическая подстановка 209
Аналитический выбор отношения
фазы к коэффициенту усиления
191
Аналог 121
— гибридный 129
Аналогово-дискретный преобразо-
ватель 122, 132
Аппроксимирующие многочлены
69, 234, 238
Асимптотическая устойчивость 53
Б Белый шум 200
Бернулли число 216
Бесконечная память 94
Боде интегрирование 217
В Вектор шума 62
Векторно-скалярное произведение
62
Векторное пространство 62
Весовая функция, коэффициенты
Хемминга 214
Винер Норберт 156
Возмущающая функция 16
-------периодическая 33, 43
------- псевдослучайная 95
-------реакция на воздействие 16
-------случайная 95
Временная область 44
Временное смещение в разностном
уравнении 76
Время
— запаздывания 76
— печати 77
— решения задачи 77
Выходная матрица 62
Выходной вектор 61
Г Гармоники четные, нечетные 33
Гармонические составляющие 37
Гибридная аналогия 129
Гибридное моделирование 129
Гиромеханика 60
Гнездовая скобочная форма 233
Д Дельта-функция 53
Демпфер нутации 60
Дискретно-аналоговое моделиро-
вание 121
Дискретные системы
----аппроксимация 183
----компенсация, формулы интег-
рирования 189
----моделирование 164
----процесс 74
----спектр 33
----уравнение состояния 107
----устойчивость 106
----функции 74
Дифференциальные уравнения
----кусочно-линейные 172
----линейные 20
----линейные 170
----постоянные коэффициенты 20
----решение 52
Дифференцирующее устройство 167
Дополнительная функция 19
Дополнительное решение 26
3 Запаздывание 100
Запись матричная
----вектор 61, 68
----нелинейных уравнений 67
268
---передаточная функция 63
--вход 61
--выход 61
И Импульсное воздействие 53
Интеграл
—	неопределенный 208
—	определенный 208
—	свертки 21, 63
— Фурье 39
Интегратор
— Гирка 196
—	нулевого порядка 201
—	первого порядка 201
— Рунге—Кутта 191
— явный Адамса—Бешфорта 184
Интегрирование
— моделированное Эйлера 220
— методом трапеций 111, 211
—неопределенное 218
—	определенное 209
—	ошибка 211
—	по контуру 90
—	с переменной фазой 199
—	явное 111
—	неявное 112
Интерполяция 210
К Калман, метод 155
«Кардинальное преобразование»
129
Квадратура 209
Классические методы решения ли-
нейных дифференциальных урав-
нений 20
Корни характеристического урав-
нения, матрицы 65
Коэффициенты
— неопределенные 29
— Фурье 33
Краткое описание операторного
метода 90
— таблица Жюри 253
Кратные корни 27
Курант Р 261
Л Линейно-независимые решения 19
Линейные дифференциальные урав-
нения 21
---------высоких порядков 21
---------классические методы реше-
ния 20, 25
кусочно-линейные 170, 179
-------матричной записи 21
-------нестанционарные 20
-------станционарные 20, 25
Линейный спектр 4'0
Локальная линеаризация (ЛЛ)
179, 180
алгоритм Баул я 179, 180
М Масштаб времени
-------реальный 199
Математическое моделирование
10, 62
-------высокоточное
-------гибридное 129, 199
-------дискретного аналога 121
-------дискретных систем 164
-------линейных систем ПО
-------нелинейных систем 170
-------непрерывных систем 66
-------условия 31
-------цифровое 165
Матрица экспоненциальная 63
Матричный бесконечный ряд 63
Метод
— Адамса 196, 224
— Гамильтона 14
— Пикарда 72
— подстановки 249
— разложения в ряд 51
— Рунге — Кутта 225
— Тастина 153, 249, 251
— Фаулера 170, 136, 143
— Шредингера 14
Н Настройка 185
Начальные значения 222
Неортогональные уравнение Эйле-
ра 179
Непрерывная компенсация 186
-----формула интегрирования 187
Непрерывная функция 183
-----ограниченная полосой 98
Непрерывные процессы 13
Непрерывный спектр 33
Нечетные
— гармоники 33
— периодические функции 32
269
О Обратный контур 76, 128
Обратное преобразование
---Лапласа 50
---Фурье 44
Однородные уравнения 18
Операторный метод 30
---смещения 80
---запись 28
Общее решение 19
Оптимальные управляющие систе-
мы 62
Основная частота 40
Отрицательные частоты 39
Ошибка
— абсолютная 237
—	временная 76
—	интегратора 201
—	интегрирования 211
—	регулирование 181
—	относительная 237
—	оценки 223
П Память бесконечная 94
Параллельное смещение 36
Первообразная функция 209
Передаточная функция 44
--- дисперсии 96
Переходная матрица 63
Подбор
— динамических характеристик
154,	155, 156, 160, 162
—	корней 154
Погрешность округления 217
Полиномы
— Ньютона—Грегори 183
— Чебышева 243
Правило Симпсона 216
Преобразование Лапласа 45
---обратное 50
---периодических функций 46, 49
---суммы 46
---таблица 48
Преобразовательная пара Фурье 41
Приближенный метод 15
Принцип однородности 16
Причинные соотношения между
входом и выходом 54
Прогноз, коррекция 223
Производные, разрывы, преобра-
зования Лапласа 45, 47
Простой переход 219
Р Разложение на элементарные дро-
би 50
решение 52
Разностные уравнения
----движения 74
---- линейные 79
----нелинейные 77
----с постоянными коэффициен-
тами 91
----спутников 67
Реакция системы 16
Рекуррентные формулы 74
Реле 68
Ряд Тейлора 211
Ряд Фурье
----практическое применение 42
----разложение периодической
функции 31
----экспоненциальная форма 38
С Самолет с высокими летными ха-
рактеристиками 180
Скомпенсированное интегрирова-
ние 189
Спаренная пружинная система 59
Спектр функции
----дискретный 33
----искаженный 204, 97
Среднеарифметическое значение
функции 33
Стационарная возмущающая
функция 95
Суперпозиция
— принцип 16
Т Таблица г-преобразования Жюри
253
Телеметрия 84
Теорема
—	дифференцирования 46
—	изменение масштаба 47
—	конечного значения 89
—	свертки 47
— Парсеваля 96
Теория вычетов 45
Т-интегратор
—	— нулевого порядка 260
Трансляционные управляющие сис-
темы 60
270
У Управление точностью 266
Упрощенное разностное уравнение
136
Уравнение Бернулли 73
Уравнение Рикатти
----решение 74
Уравнения
— векторно-матричные Лагранжа
— движения 60
— дифференциальные, кусочно-ли-
нейные 172
— интегродифференциальные 46
— прочности 21'0
— состояния дискретной системы
ПО
разностные 74, 77, 94, 116, 144
Уравнения Эйлера 179
----интегрирование 112
----неортогональные 179
---- неопределенное интегрирова-
ние 220
Ф Фактор сходимости 45
Физическая причинность 59
Фильтр нелинейный 66
Фильтр определенной полосы про-
пускания 168
Фильтрация, дополнительная 165
Формула дискретной компенсации
188
Формула Эйлера 38
Формула непрерывной компенса-
ции 187
Функции равнопульсирующие 238
Функция Хана 161
X Характеристика белого шума 200
Характеристика дисперсии интег-
рирования 201
Характеристики устойчивости сис-
тем 106, 205
Характеристическое уравнение 27
Хемминг, весовые коэффициенты
214
Ц Цифровое моделирование 165, 170
Цифровой автопилот 164
Ч Частотное решение 19
Частотная свертка 98
Частотная обратная свертка 132
Частотная область 44, 189
Частота выборки 203
Частотные методы для непрерыв-
ных процессов 31
Члены ограниченной памяти 94
Ш Шеннон
— теорема 160
— информационная предельная
модель 122
— информационный предел 101
Э Эквивалентные соотнощения 74
Экономизация ряда Маклорена
246
Экономизация Чебышева 232
Эмпирический подбор соотношения
фаза — коэффициент усиления
194
Я Ядро преобразования 45
Якобиан 171
ИБ № 2691
Джон М. Смит
МАТЕМАТИЧЕСКОЕ
И ЦИФРОВОЕ МОДЕЛИРОВАНИЕ
ДЛЯ ИНЖЕНЕРОВ
И ИССЛЕДОВАТЕЛЕЙ
Редактор А. С. Коровкин
Художественный редактор С.С. Водчиц
Технический редактор Н. Н. Скотникова
Корректоры И. М. Борейша и А. П. Озерова
Переплет художника С. Н. Орлова
Сдано в набор 07.05.80
Подписано в печать 18.07.80.
Формат 60X90V16 Бумага типографская № 1.
Усл. печ. л. 17,0.	Уч.-изд. л. 17,05.
Тираж 10 000 экз. Заказ 493. Цена 1 р. 50 к.
Издательство «Машиностроение:», 107076,
Москва, Б-76, Стромынский пер., д. 4.
Московская типография № 8 Союзполиграфпрома
при Государственном комитете СССР
по делам издательств полиграфии
и книжной торговли.
Хохловский пер., 7.