Сборник задач по элементарной алгебре - Ляпин С.Е., Баранова И.В., Борчугова З.Г.

Автор: Ляпин С.Е. Баранова И.В. Борчугова З.Г.
Теги: математика алгебра задачи по алгебре
Год: 1973
Похожие
Конкретная математика. Основание информатики
Библиотечка Квант 22. Задачи по математике. Алгебра и анализ
Комбинаторный анализ. Задачи и упражнения
Введение в математическую статистику
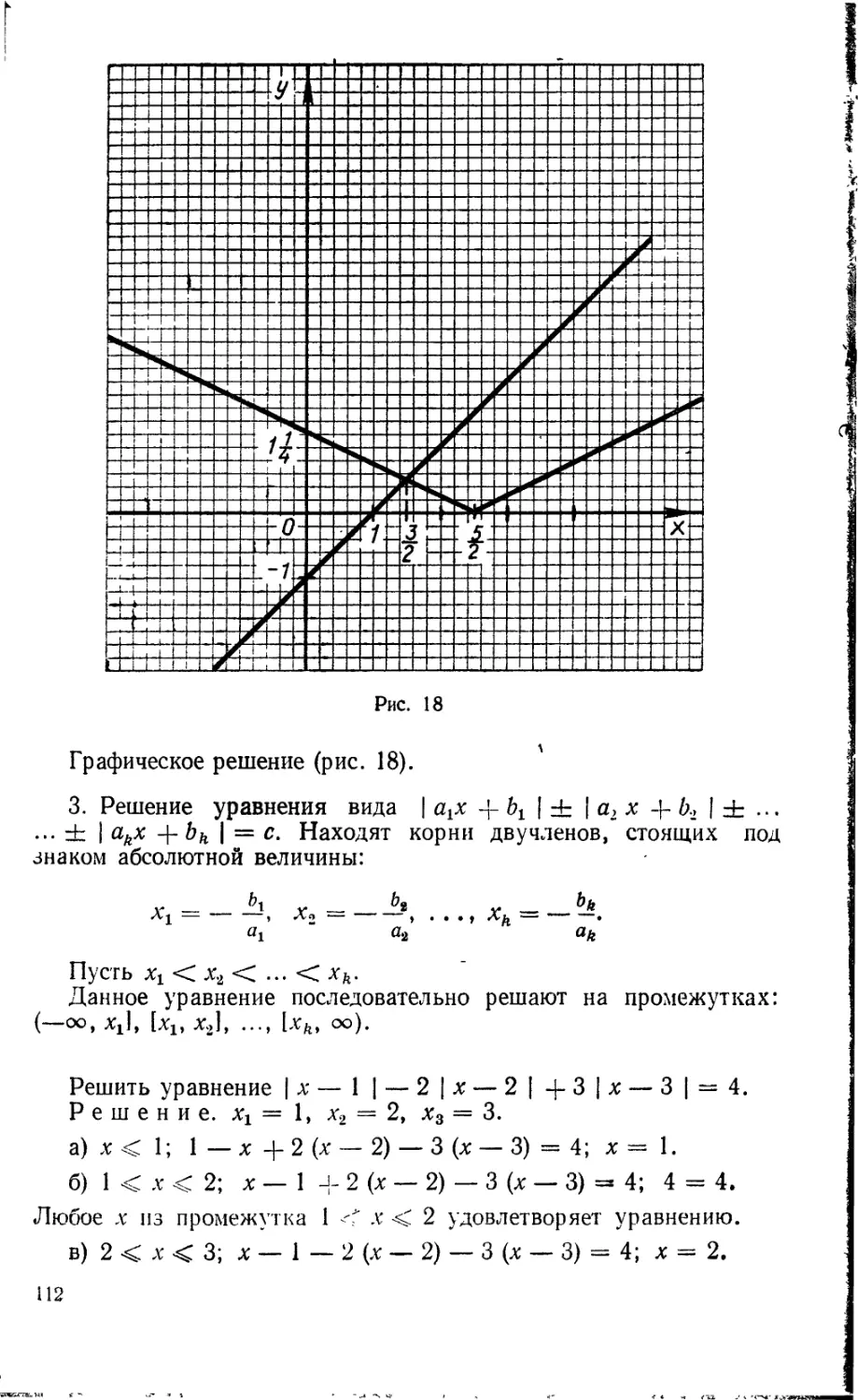
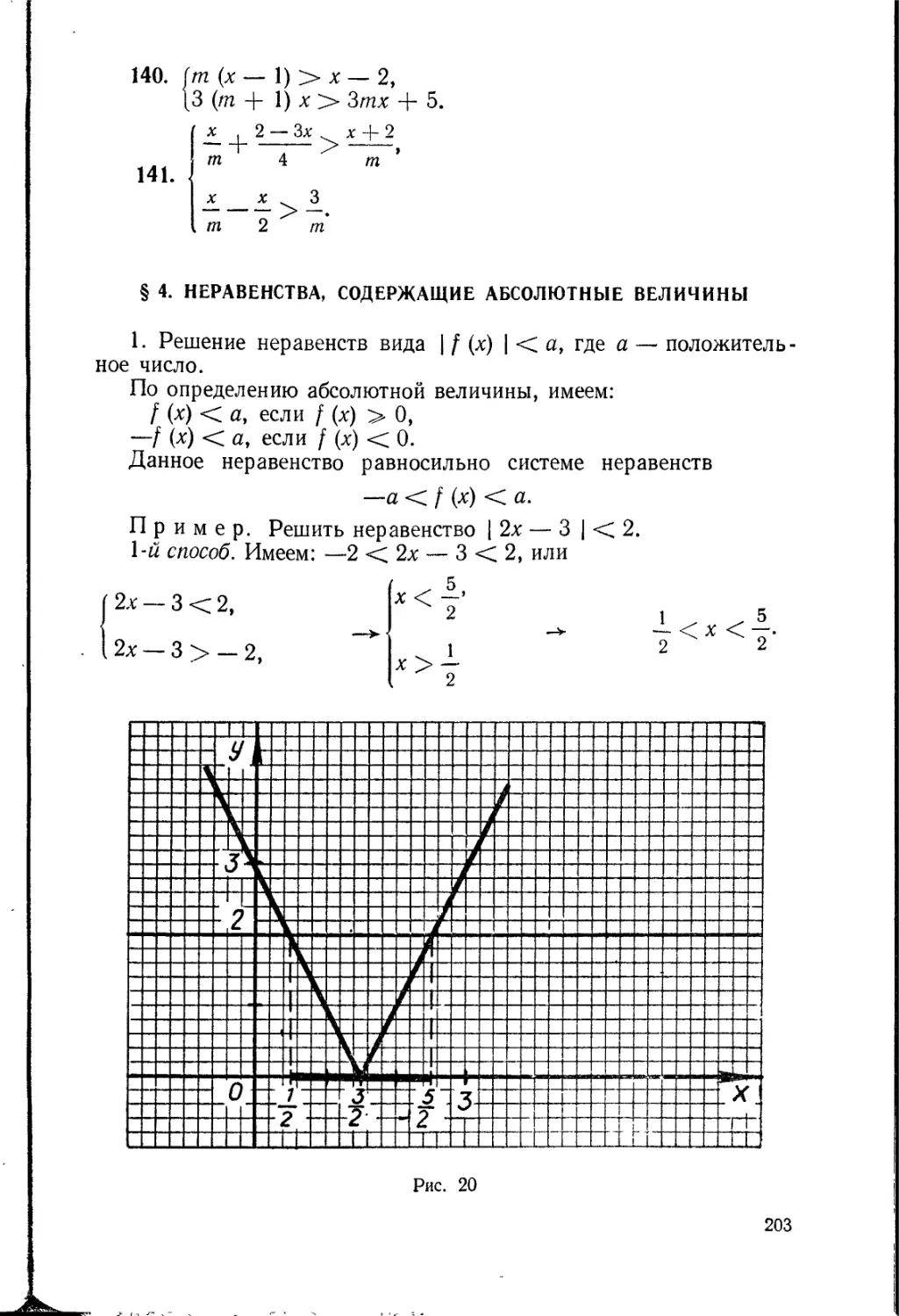
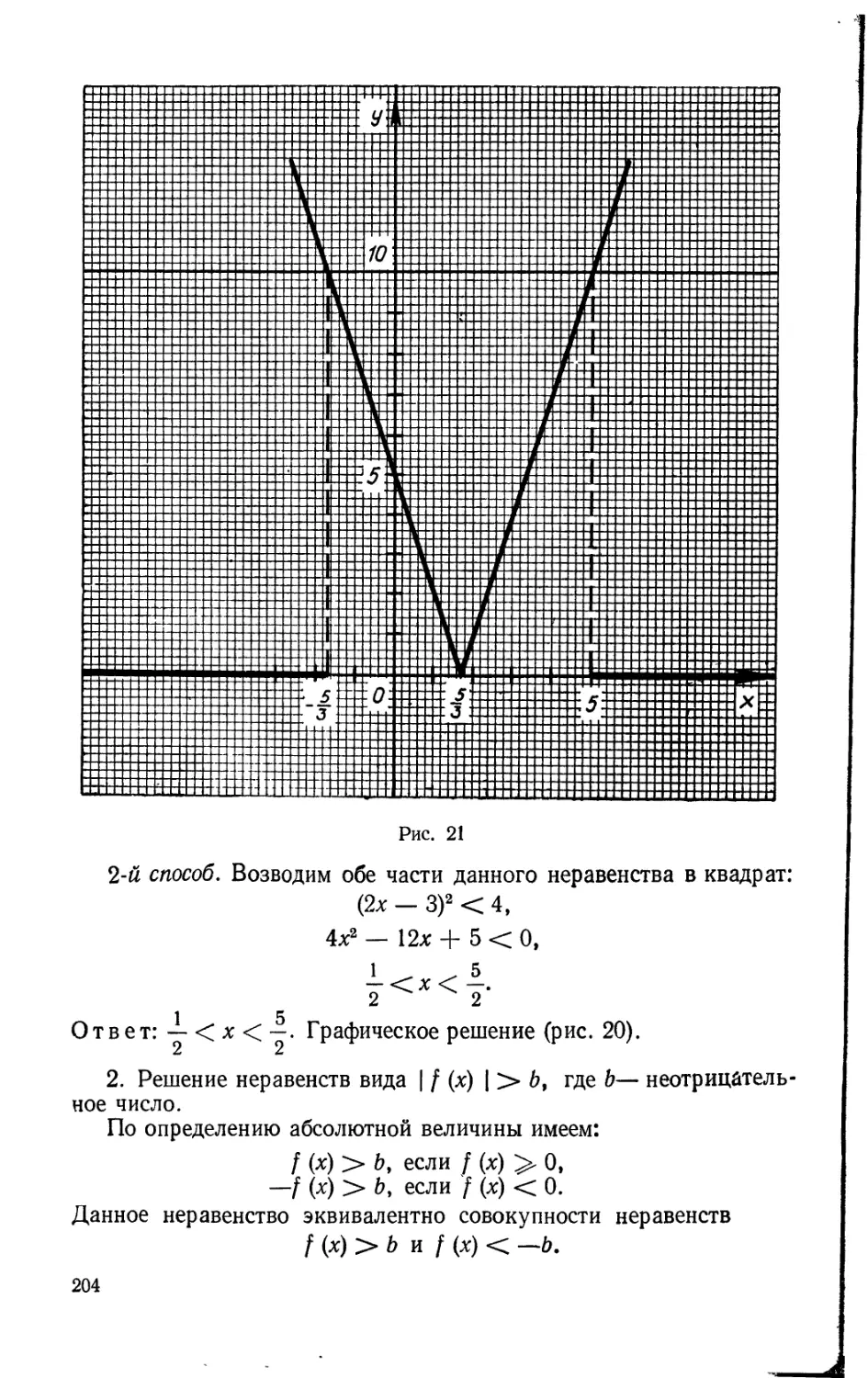
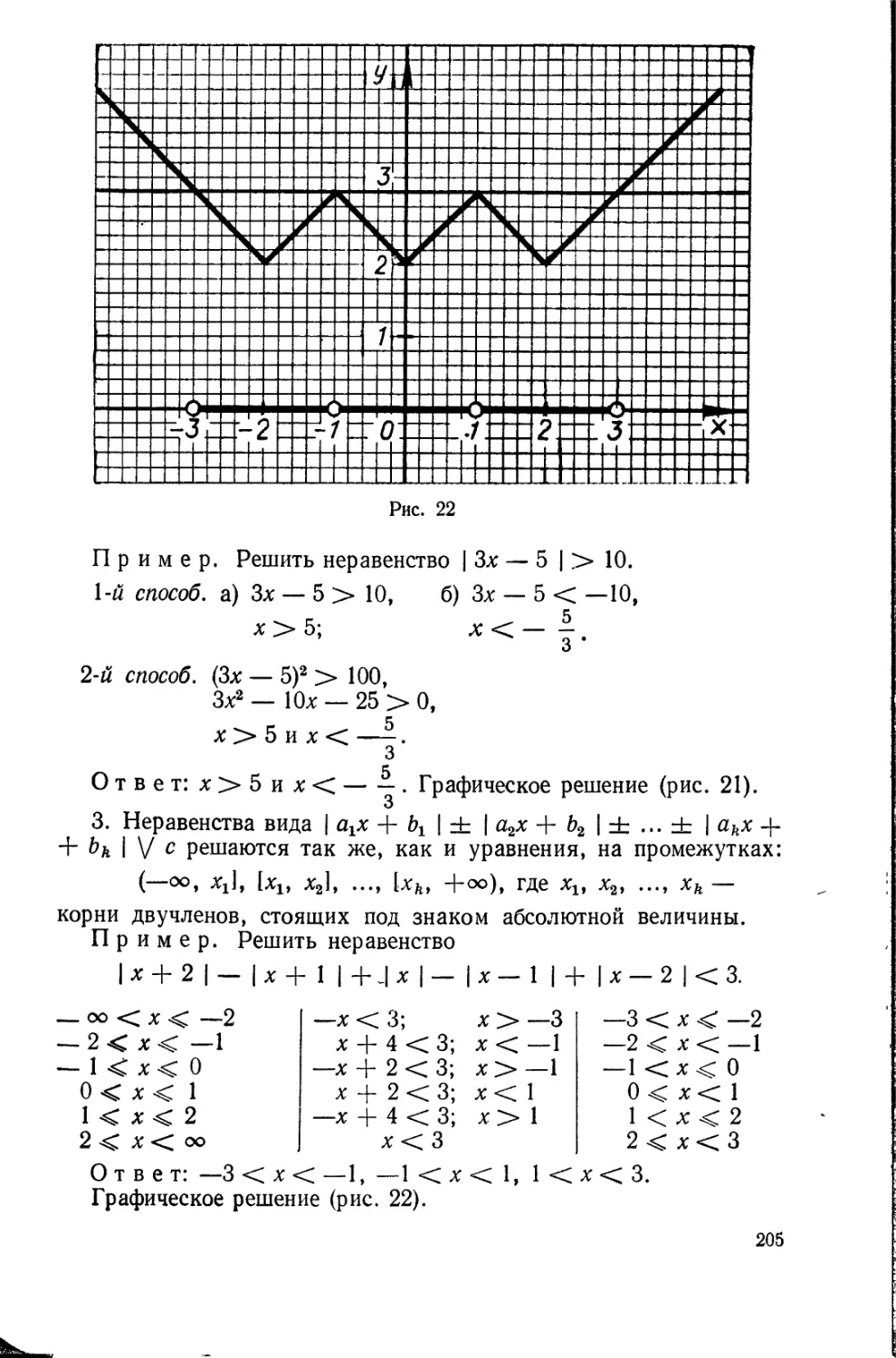
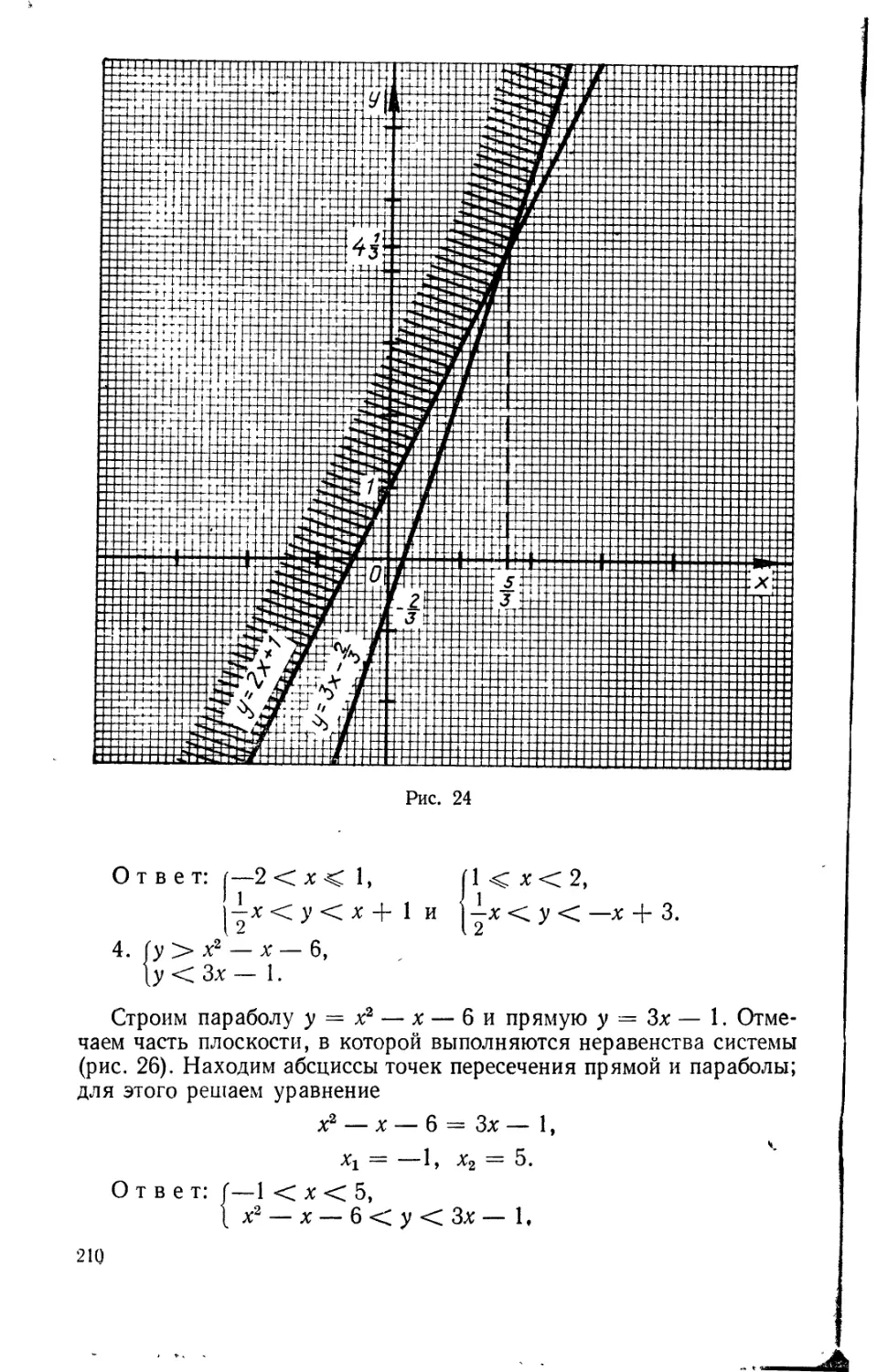
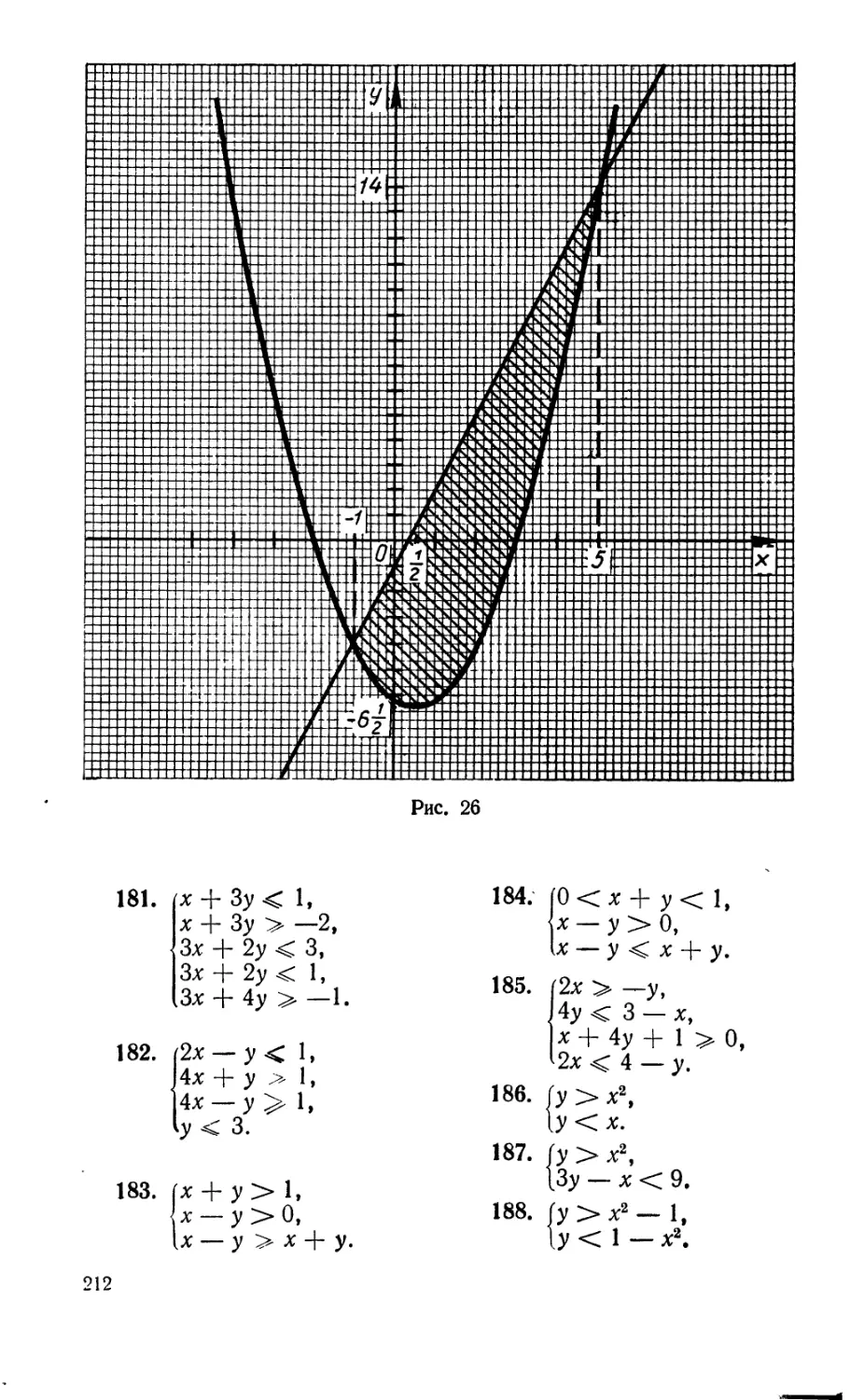
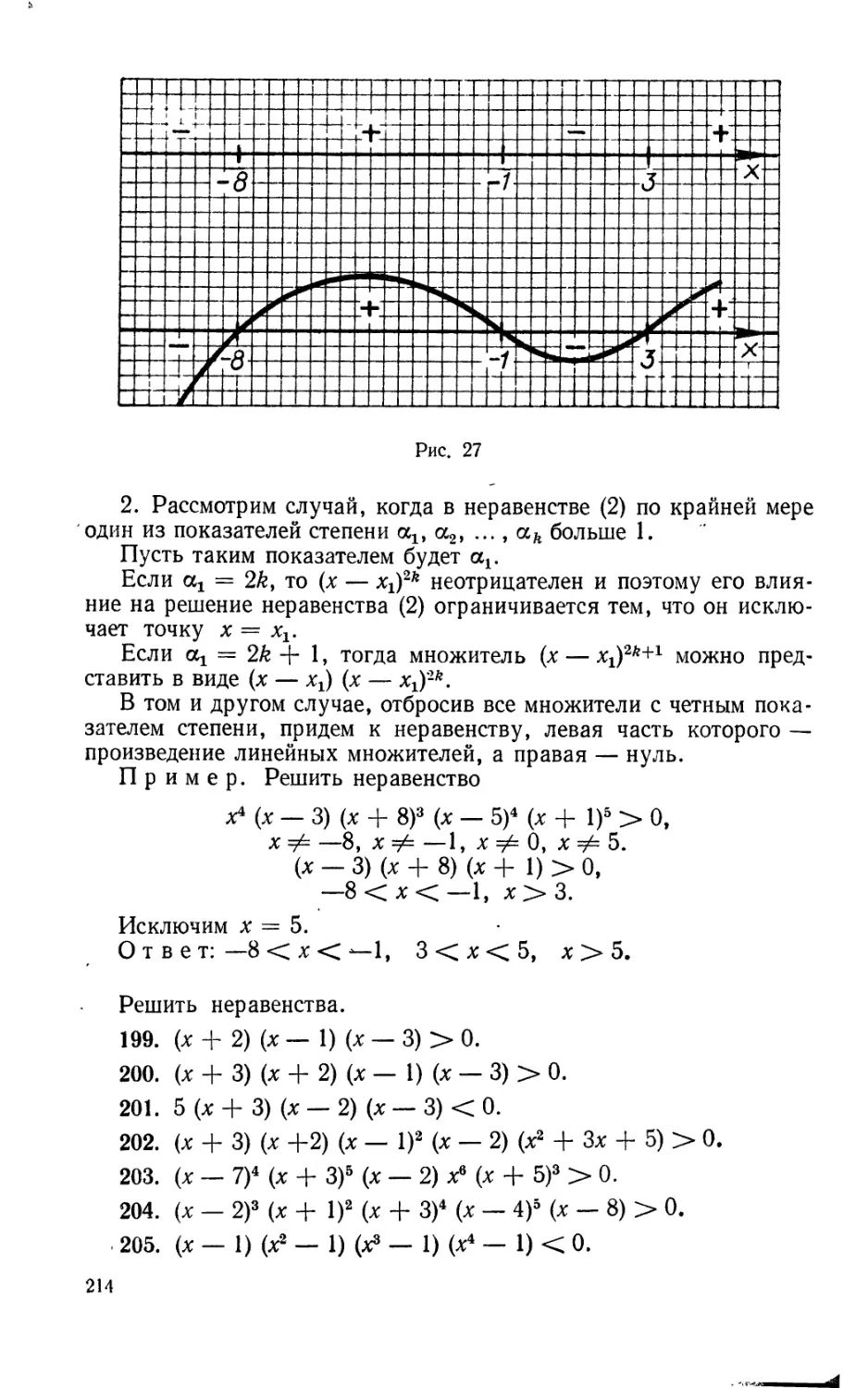
Текст
                    
С. Е. ЛЯПИН,
И. В. БАРАНОВА,
3. Г. БОРЧУГОВА
Сборник
задач
по элементарной
алгебре
Допущено Министерством просвещения СССР
в качестве учебного пособия для студентов
физико-математических факультетов
педагогических институтов
Издание второе, переработанное, дополненное
МОСКВА «ПРОСВЕЩЕНИЕ» 1973
512
Л97
Второе издание задачника (1-е в 1960 г.) основательно перера-
ботано и дополнено в связи с новыми требованиями к школьной
математике. Сборник задач охватывает многие вопросы школьного кур-
са алгебры, в некоторых разделах выходит за его пределы. Данный
сборник может служить пособием для проведения практикума по
элементарной математике в педагогических институтах по спе-
циальности № 2104 «Математика».
Ляпин С. Е. и др.
Л 97 Сборник задач по элементарной алгебре. Учеб, пособие
для студентов физ.-мат. фак. пед. ин-тов. Изд. 2-е перераб., доп.
М., «Просвещение», 1973,
351 с.
Перед загл. авт.: С. Е. Ляпин, И. В. Баранова, 3. Г. Борчугова.
„	0662 — 677
Л-------------
М103 (03) —73
32 — 73
512
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ ....................................................... 5
Глава I. Целые числа .............................................. 6
§ 1.	Метод математической индукции .............................. —
§ 2.	Действия над целыми числами ............................... 13
§ 3.	Делимость суммы, разности, произведения. Наибольший общий
делитель. Наименьшее общее кратное.............................. 24
§ 4.	Простые числа ............................................. 27
§ 5.	Применение теории делимости к решению неопределенных уравне-
ний в целых числах ............................................. 29
§ 6.	Делимость чисел Гаусса .................................... 33
§ 7.	Систематические числа ..................................... 38
Глава II. Рациональные числа. Иррациональные числа ....	41
§ 1.	Сравнение положительных рациональных чисел ................. —
§ 2.	Сокращение дробей ......................................... 42
§ 3.	Операции над рациональными числами (дробями) .............. 43
§ 4.	Конечные и бесконечные периодические систематические дроби. 45
§ 5.	Иррациональные числа ..................................... .48
Глава III. Комплексные числа. Алгебраические и трансцендентные
числа ............................................................ 50
§ 1.	Комплексные числа	.................................... —
§ 2.	Алгебраические и трансцендентные числа .................... 55
§ 3.	Числовые кольца и поля .................................... 58
Глава IV. Тождественные	преобразования ........................... 59
§ 1.	Действия с многочленами .................................... —
§ 2.	Разложение на множители и теорема Безу .................... 60
§ 3.	Наибольший общий делитель и наименьшее общее кратное ...	65
§ 4.	Дроби ..................................................... 66
§ 5.	Радикалы .................................................. 69
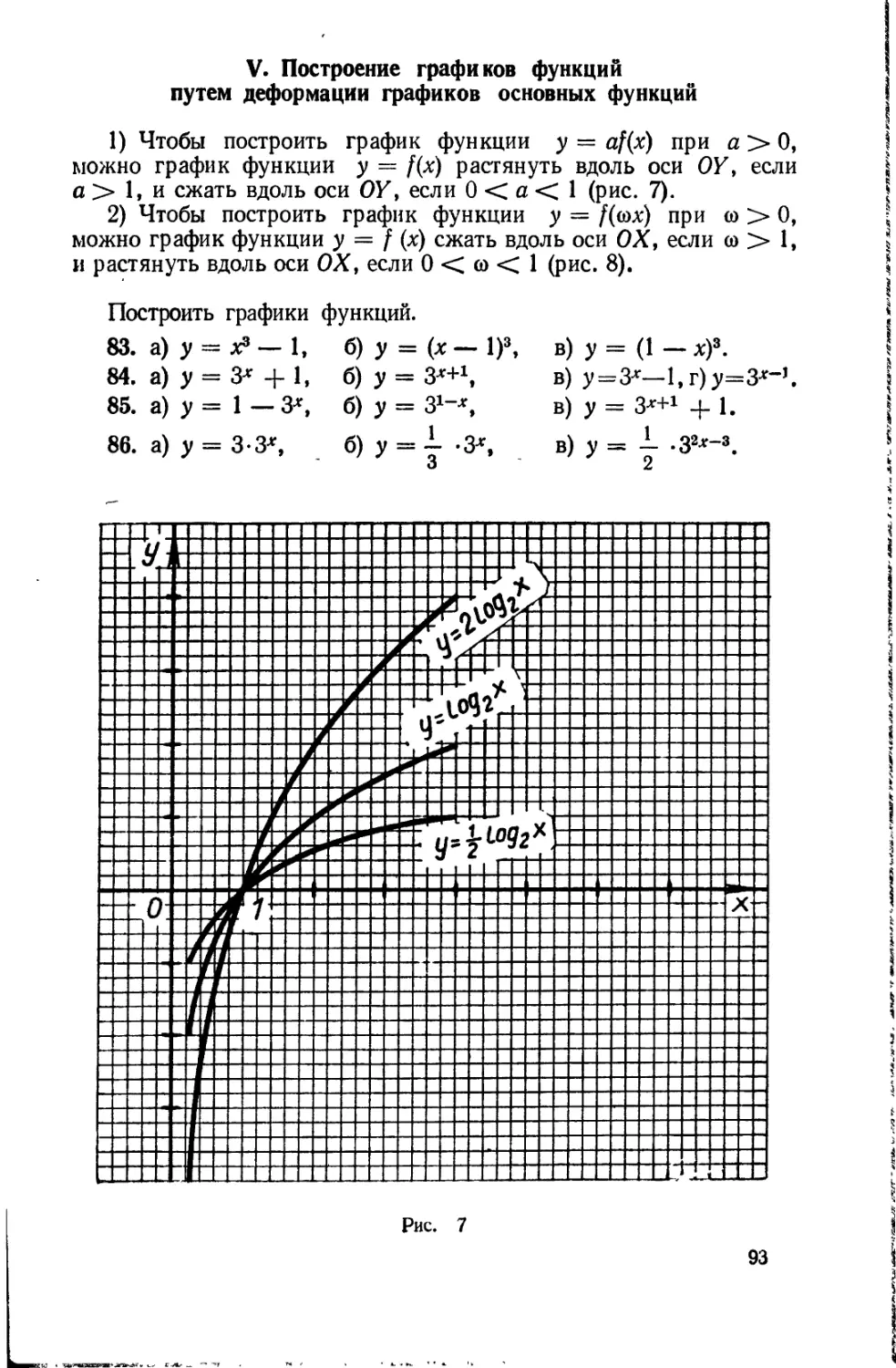
Глава V. Функции ...............................................   79
§ 1.	Область определения функции ................................ —
§ 2.	Область изменения функции .................................-82
§ 3.	Четные и нечетные функции ................................. 84
§ 4.	Возрастание и убывание функции........................  .	85
§ 5.	Способы построения графиков функций ....................... 87
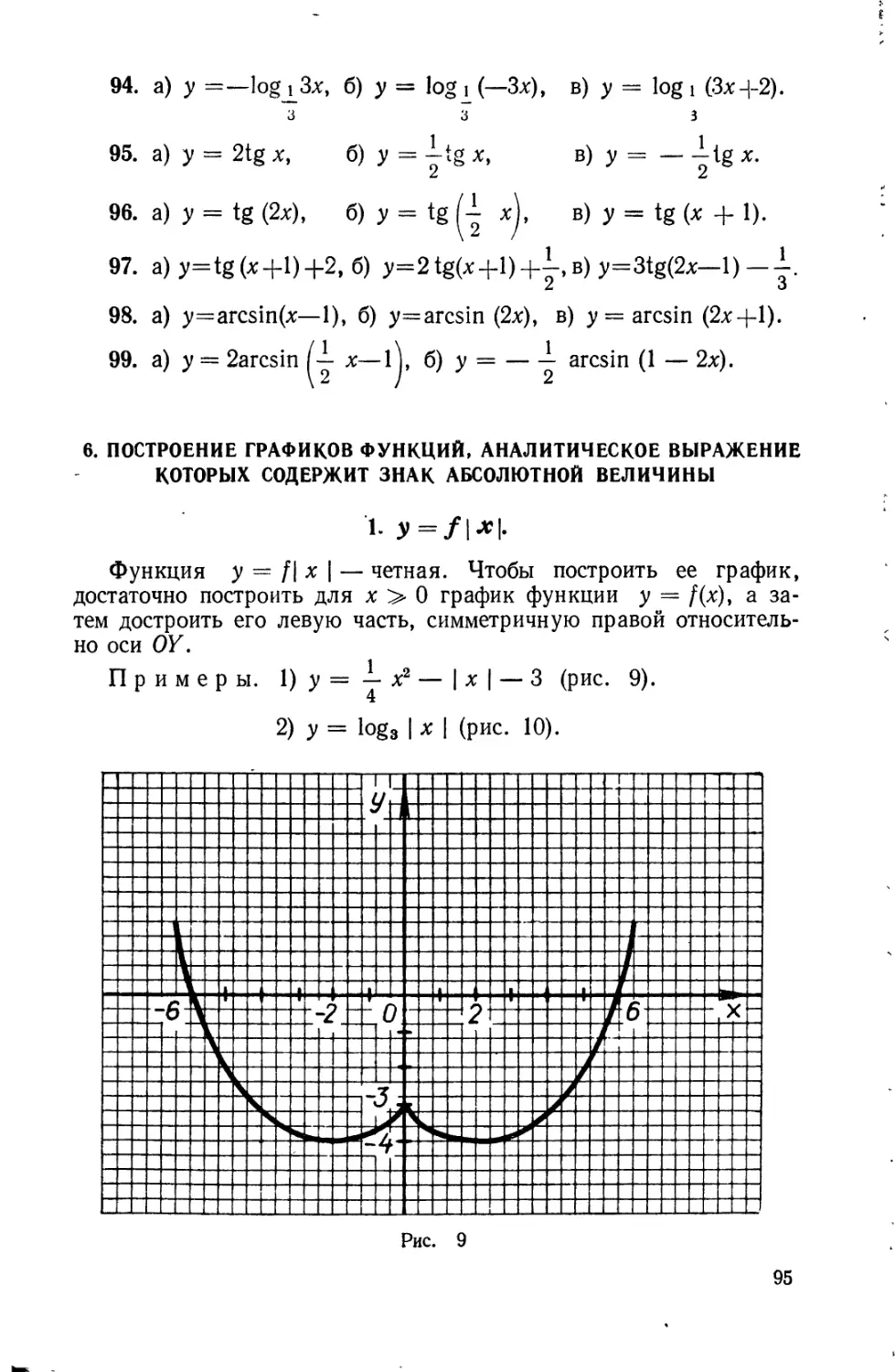
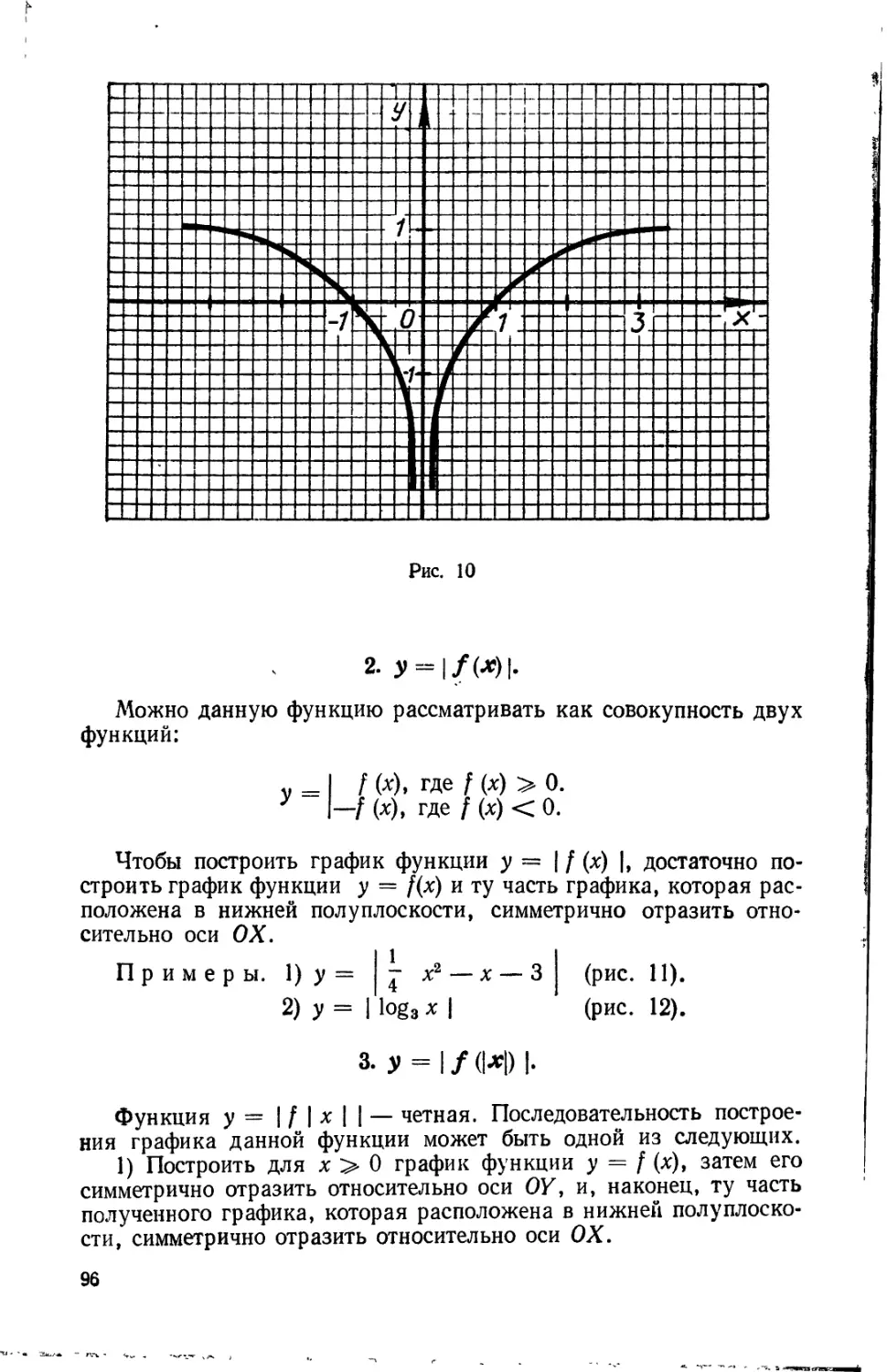
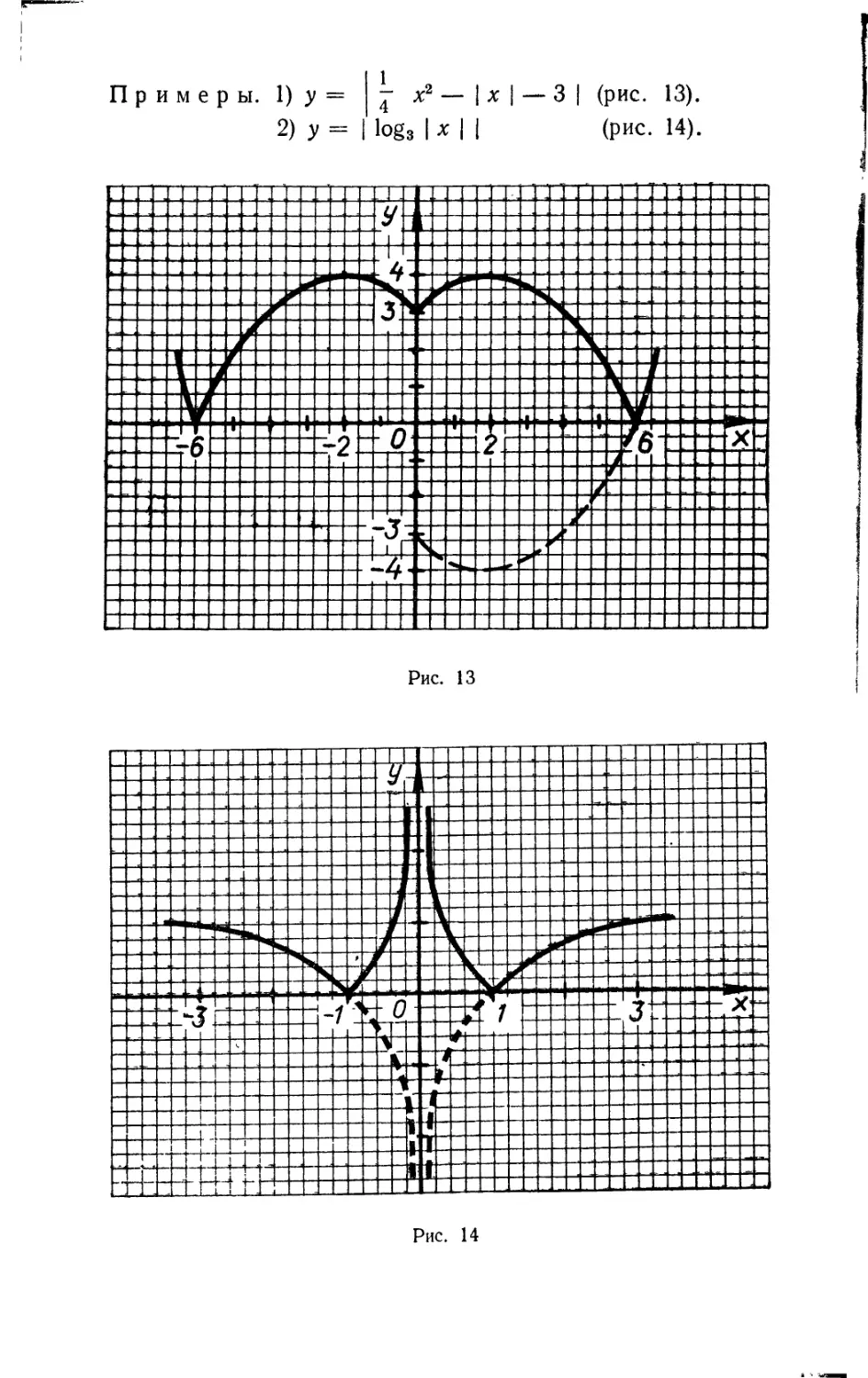
§ 6.	Построение графиков функций, аналитическое выражение которых
содержит знак абсолютной величины.............................. 95'
3
Глава VI. Рациональные алгебраические уравнения .................... 102
§ 1.	Равносильность уравнений ..................................... —
§ 2.	Решение уравнений с параметрами .........................•.	108
§ 3.	Уравнения, содержащие знак абсолютной величины ............. 109
§ 4.	Квадратные уравнения ....................................... 114
§ 5.	Трехчленные уравнения, приводящиеся к квадратным уравнениям. 118
§ 6.	Возвратные уравнения ....................................... 119
§ 7.	Частные методы решения алгебраических уравнений ............ 122
§ 8.	Дробно-рациональные уравнения .............................. 124
Глава VII. Системы рациональных алгебраических уравнений ...	128
§ 1.	Основные методы решения систем уравнений ..................... —
§ 2.	Системы линейных уравнений .................................. 131
§ 3.	Исследование систем линейных уравнений ..................... 134
§ 4.	Системы нелинейных алгебраических уравнений ................. 138
Глава VIII. Иррациональные уравнения и их системы .......	146
Глава IX. Решение задач с помощью составления уравнений и систем
уравнений .......................................................... 157
Глава X. Логарифмы. Показательные и логарифмические уравнения и
их системы	...................................... 173
$ 1.	Логарифмы ..................................................... —
§ 2.	Показательные и логарифмические	уравнения ................... 176
§ 3.	Системы показательных	и	логарифмических	уравнений .......... 185
Глава XI. Неравенства ......................................... . . .	189
§ 1.	Доказательство неравенств ......................................—
§ 2.	Равносильность неравенств .................................. 197
§ 3.	Линейные неравенства с одним неизвестным и их системы ....	199
§ 4.	Неравенства, содержащие знак абсолютной величины ........... 203
§ 5.	Квадратные неравенства ..................................... 206
§ 6.	Системы неравенств первой и второй степени с двумя неизвестными. 208
§ 7.	Алгебраические неравенства высших степеней с одним^неизвестным. 213
§ 8.	Дробно-рациональные неравенства с одним неизвестным ....	215
§ 9.	Иррациональные неравенства ................................  218
§ 10.	Неравенства, содержащие показательную и логарифмическую
функции ......................................................... 221
Глава XII. Прогрессии и	ряды .................................... 226
§ 1.	Прогрессии .................................................... —
§ 2.	Ряды ....................................................... 233
Глава XIII. Комбинаторика.	Бином Ньютона ...................... 238
§ 1.	Комбинаторные задачи	....................................... 241
§ 2.	Комбинаторные тождества и уравнения ........................ 245
§ 3.	Бином Ньютона .............................................. 247
Ответы и указания .................................................. 252
ПРЕДИСЛОВИЕ
В данное издание «Сборника задач по элементарной алгебре»
по сравнению с первым его изданием внесены существенные изме-
нения, вызванные, в частности, новым учебным планом и програм-
мами для математических факультетов пединститутов. Так, в связи
с исключением из учебного плана курса элементарной математики
в ряде случаев задачам предшествуют краткие теоретические све-
дения. Более полно представлен вопрос о числовых множествах:
включен материал о вещественных и комплексных числах, об алге-
браических и трансцендентных числах. Раздел о делимости чисел
расширен и дополнен вопросами о решении неопределенных урав-
нений в целых числах, о числах Гаусса. Более подробно рассмотре-
ны вопросы о функциях, об уравнениях и неравенствах, о ком-
бинаторике. Значительно обновлена вся система задач: исключен
ряд однотипных задач, внесено большое количество новых задач;
для многих задач пересмотрены указания к решению, чтобы сде-
лать их менее подсказывающими.
Главы I и II, за исключением параграфа о числах Гаусса и ряда
задач на неопределенные уравнения, написаны И. В. Барановой.
Параграф «Числа Гаусса» и некоторые задачи на неопределенные
уравнения составлены |Н. Н. Матвеевой]. Глава III написана
К. П. Козловым. Остальной материал задачника, в первом изда-
нии составленный С. Е. Ляпиным, подвергнут существенной пере-
работке, при этом главы IV и X доработаны Л. И. Ляпиной, главы
V, VI, VII, VIII, IX и XI переработаны 3. Г. Борчуговой, глава
XIII составлена Л. И. Кабеховой. Общая редакция издания при-
надлежит И. В. Барановой.
Авторы выражают искреннюю признательность рецензентам и
особенно сотрудникам кафедры алгебры и теории чисел Свердлов-
ского государственного педагогического института за предложения,
несомненно способствовавшие улучшению задачника.
Авторы
29.9.1971
Ленинград
ГЛАВА I
ЦЕЛЫЕ ЧИСЛА
§ 1.	МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Метод математической индукции — дедуктивный метод дока-
зательства, основанный на аксиоме, называемой аксиомой индукции
(или принципом индукции). Существует несколько утверждений,
принимаемых за аксиому индукции (см., например, статью И. В. Про-
скурякова в ЭЭМ1, том I).
В данной книге в качестве аксиомы индукции используется сле-
дующее утверждение:
Если некоторое предложение S справедливо для неотрицатель-
ного целого числа а и из предположения о его справедливости для
неотрицательного целого числа k> а следует справедливость его
для непосредственно следующего за k числа k + 1, то предложение S
справедливо для любого целого неотрицательного числа п > а.
За число а, как правило, принимают наименьшее неотрицатель-
ное целое число, обладающее свойством S.
Доказательство с использованием аксиомы индукции состоит
из трех этапов: проверки справедливости доказываемого утвержде-
ния для некоторого целого неотрицательного числа (наименьшего
из множества, указанного в условии); допущения справедливости
доказываемого утверждения для некоторого целого неотрицатель-
ного числа k\ доказательства справедливости этого утверждения
для числа k + 1 при использовании допущения. Ссылка на акси-
ому индукции позволяет считать доказанным утверждение для лю-
бого целого неотрицательного числа, не меньшего» числа, исполь-
зованного на первом этапе доказательства.
Метод математической индукции может быть использован и
для доказательства утверждений, заданных на множестве целых
чисел, если добавить доказательство справедливости утверждения
и для числа k — 1.
1 Энциклопедия элементарной математики, кн. I. Арифметика. И. В. Про-
скуряков, гл. III. М.—Л., Гос. изд-во технико-теоретической лит-ры, 1951.
6
Применение метода математической индукции к
доказательству свойств чисел натурального ряда
Доказать:
1.	Сумма п первых чисел натурального ряда равна
2.	Чему равна сумма первых п нечетных натуральных чисел?
3.	Сумма квадратов п первых натуральных чисел равна
п(п + 1) (2п + 1)
6
4.	I2 + З2 + ... + (2п— I)2 = п(2п~-Р (2п + , где п — любое
натуральное число.
5.	а) — 1 + 3 — 5 + ... + (—1)" (2п — 1) = (—1)" п;
б) 1 — 22 + З2 — 42 + ... + (—I)"-1/!2 = (— 1)"-1Я^-+-?-),
где п — любое натуральное число.
6.	Сумма кубов п первых чисел натурального ряда равна
п2(п +1)2
4
7.	Для любого натурального числа п справедливо равенство
1-2 + 2-3 + ... + п (п. + 1) = -п(п + ^(п + 2) •
8.	1 -4 + 2-7 + ... + п (Зп + 1) = п (п + I)2, где п — лю*
бое натуральное число.
9.	Для любого натурального п
1 • 2 • 3 +2 • 3 • 4 + ... + п (п + 1) (п + 2) = ”	+ 2)<п + 3\
4
10.	Для любых натуральных пир имеет место равенство
1-2 ... р + 2-3 ... р (р + 1) + - + п (п + 1) ... (п + р - 1) =
_ П (П + 1) (п + 2) • • • (п + Р)
Р + *	*
11.	При натуральном п справедливо равенство
2-12+ 3-22 + ... + п (п — I)2 + (п + 1)п2=
п (п + 1) (« + 2)(3п + 1)
=	1-3.4
7
12.	При 1 и натуральном п справедливы тождества:
а) 1 4- х + х2 + ... + хп =
х”41 — 1 .
X — 1
| П 2 I | п х—(n + 1) хл+1 + ПХП+2
О) X + 2х2 + ... + ПХП = ------------ - - ------1-----
(1-х)2
13.	1 4- 2 + 22 + ••• + 2я-1 = 2" — 1, где п — любое на-
туральное число.
14.	1 • 1! 4- 2-2! 4- ••• 4- «•«! = (» 4~ 1)! — 1, где п — любое
натуральное число.
15.	k\ 4- k-kl 4- (k + 1) (k 4- 1)! 4- ... + n-n! = (» + 1)1,
где n и k — натуральные числа, n > k.
16.	(n 4- 1) (« 4- 2) ... (ft + n) = 2”. 1-3 ... (2n — 1), где n —
любое натуральное число.
17.	При любом натуральном п справедливо тождество
А + JL .и + 2» + 1 =	1
4	36 1 л2(л 4-1)2 (n 4- I)2
18.	fi — IWi _ 1)... h--------!— 1 =
\	4/\	9/ [	(n4-l)2J 2л 4-2
ральное число.
19.	Если п — натуральное число, то
1_± + ±_... + _!----------_1_
2	3	2з — 1 2п л +1 и + 2
где n — нату-
2п
20.	При натуральном п
_2— _|_ __L_ 4-... _]---!-------= _
1-33.5	(2л — 1) (2л 4- 1) 2л 4-1
21.	При натуральном п
1	, I ,	1	4.	4.	»	=	«
1 • 4	4 • 7	7 • 10 "И (Зл — 2) (Зл 4-1)	Зл4-1’
22.	При натуральном п
4	- _L_ 4- _L_ +	|	»	_ п .
1	.5	5-9	9-13	(4л —3) (4л4-1) 4л 4-1 '
23.	При натуральном п справедливо тождество
1	,	22	_______л^_______ _ л (л 4- 1)
1 • 3 ' 3 • 5 "Г "Г (2л—1) (2л 4-1)	2(2л 4-1)'
8
24.	При натуральном п
—--------------Ь-------------------F ••• 4~--------------------------
1 • 2 • 3	2 • 3 • 4	п (п + 1) (л + 2)
£П
2
2 (л + 1) (п + 2) J
25.	При натуральном п
---!-------1-------н ... Н----------------------=
1-3-5	3-5-7	(2л •—1) (2л 4-I) (2л + 3)
__ П (п + 1)
2 (2л + 1) (2л + 3)'
26.	При любом натуральном п
1 , 1 , ,______________________________1_____________=
1 - 2 • 3 • 4 "Г 2 • 3 - 4 • 5 "t” " ”л (л + 1) (« + 2) (л + 3) (л + 4)
_ £ Г £____________I___________
з[б (п + ])(п + 2)(л + 3).‘
27.	При любых натуральных а и п
1 _|___________!______|_... ,_______!___________ п
а (а 4-1)	(а+1)(а + 2)	(а + л — 1) (а + л) а (а 4-л)’
OR а4“1_|_а+3.а-|-7 .	. а-\-2п — 1
28- — + —+— + -+------------------2п---=
ta__1W2”___1)
i----------- 4- п, где а и п — любые натуральные числа.
29.	+ ... +	= 1----(п — натуральное число).
зо.	+ + (-п«.+ =
1!	2!	1V 7	п\
t 1 \и — О ••• (* — л)
= (— 1 )п •  --— --------— при действительном х и натуральном п
п!
1	9	4	2n	1	2W+1
31.-------—------1	--1---... -I----- = —------1---г
1+х	1 -j~ №	1 -j~ X4	1-|_х2П х — 1	1 _х
при натуральном п и п = 0; | х | #= 1.
х . х2 х4	, х2”’1	1	х—-х*п
1—ха 1—х*	1—X8	1 —х2 1—*	1—X3
при натуральном п и n = 0; | х |	1.
9
Применение метода математической индукции
к решению вопросов делимости чисел
33.	Доказать, что сумма кубов трех последовательных натураль-
ных чисел делится на 9.
34.	Доказать, что при любом целом п:
а)	п3 +	5п	делится	на	6;
б)	п3 +	Пи	»	»	6;
в)	п4,+	6га3 +	11п2	+	6п	»	»	24;
г)	и® —	Зп5 +	6п4 —	7п3 + 5п2 — 2п »	»	24.
35.	Доказать, что при любом целом неотрицательном п:
а)	у» — 1	делится на 9;
б)	4я + 15п — 1	»	»	9;
В) з2«+2 _ 8П _ 9	»	»	64;
г)	32Я+1 + 40м _ 67	»	»	64;
д)	2я+2-Зя + 5п — 4	»	»	25;
е)	62я + 3«+2 + 3я	»	»	11.
36.	Доказать, что при любом целом неотрицательном п справед-
ливы утверждения (знак «•» означает «делимость нацело»):
4) 7Я+2 + 82я+4 : 57;
Чб) 11«+2 + 122я+1: 133;
' - в) 25я+3 + 5Я-3.«+2: 17;
\) " г) 2я+5-34я + 53я+4 : 37;
1, д) З3я+2 + 5-23я+4: 19;
\| е) з2л+2.52Л _ 3зл+2.22Л : 1053.
37.	Доказать, что при целом четном т, при натуральном четном
(или равном 0) п справедливы утверждения:
а)	пг3 + 20m • 48;
б)	20я + 16я — 3я — 1 : 323.
38.	Доказать: а) число 7 + Т2 + 73 + 74 + ... + 7я делится
на 100 при любом натуральном п, кратном 4;
б)	чтобы число 9я — 1 делилось на 10*, достаточно условия:
п = 10*-1, где k — натуральное число, большее единицы.
39.	Доказать, что при любом целом а число а? — а делится
на 42.
10
------------------------------- _______________________—ft |
40.	Доказать, что при любом целом~а и простом”/? число аР — а
делится на р) если числа аир взаимно простые, то а₽-1 — 1 делит-
ся на р (малая теорема Ферма).
41.	Доказать: число о4л+1 — а делится на 30 при любом целом
а и целом неотрицательном п.
42.	При любом целом а и целом неотрицательном п числа а
и о4л+1 оканчиваются одной и той же цифрой.
Применение метода математической индукции
' к решению разных задач
43.	Доказать, что сумма членов каждой горизонтальной строки
данной таблицы равна квадрату количества чисел в ней:
1
2,	3, 4,
3,	4, 5, 6, 7
4,	5, 6, 7, 8, 9, 10
44.	Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21,..., первые два члена ко-
торого 0 и 1, а каждый следующий получается от сложения двух
предыдущих, называется рядом Фибоначчи или рядом Ламе. Обо-
значив через а0, alt а2, ... соответственно первый, второй и т. д.
члены этого ряда, доказать справедливость следующих равенств:
а)	an+i — ао + ai + ^2 4“ ••• + Яп-1 + 1;
б)	Oq + а2 + ... + а2п — («1 + «з + ••• + о2п-1) — Огп-i — 1;
а) = ^П—1 * ^л+1 — 1,
г) &п+р—1 ~ ^п—1'^p—l 4~ ^п'^рг
Д) <W1 = ak + 4+Ь
45.	Доказать, что число, состоящее из 3" единиц, делится на Зл.
46.	Дано: ух =4> Уп = 4 + Д°казать: уп_х < уп <^.
47.	Дано: an+1 = а^ап — a0-«n-i; «о = 2, ах = 3. Доказать:
ап = 2Л + 1.
48.	Дана последовательность натуральных чисел ип, для ко-
торой «х = 1, uh = ил_х + k. Доказать: un + un+! = (и + I)2.
11
49.	а) Имеются два числа а и Ь. Составим последовательность
пар чисел a, b\ alt bL-, а2, Ь2;...; ап, Ьп\ ... по следующему закону:
а + b	+ Ь.
«1 = ——; а, = ——...
1	2	2	2
Доказать:
ап = а 4- — [b — aWl — —V, bn = а 4- — (Ь — а) (14---—\
3 \	) \	4я/	3	\	2 • 4 я /
б) Числа последовательности а1( а2, ..., ап определяются еле*
дующими условиями: aQ = а, а± = Ь, ап+! =
Доказать: ап- =	+ (— 1)я-1
50.	а) Последовательность задана рекуррентной формулой:
ап — an-i cos х 4- cos (п — 1) х, п > 2.
Найти общий член, если at = 1.
' б) Последовательность задана рекуррентной формулой:
ап — 2ап-1 cos х — ап-.2, п~> 3.
Найти общий член, если аг = 1, а2 = 2 cos х.
51.	Доказать: каковы бы ни были произвольные натуральные
числа tn, п, k, существует натуральное число N такое, что
(]/щ 4- п — ]/7n)ft= YN + пк — УТ/.
52.	Доказать тождество
(1 4- х) (1 4- х2) ... (14-х2"	= 1 4- х 4- х2 4- ... + х2 Л
53.	Доказать:
(1 — х) (1 — х2) ... (1 — х«) 4- х (1 — х2) ... (1 — хя) +
4-х2 (1 — х3) ... (1 — Xя) + ... 4- х* (1 — х*+х) ... (1 —хя)4-..: +
4-	Xя-1 (1 — хя) 4- хя = 1.
54.	Доказать тождество
1 + 1 + 2х±1
^1^2
। (^1 + 0 (а2 + 1) ।	। (Д1+ *) (^2+ О fa + 1) =
аха2 ••• ctn+i
(fli + 1) ... (an+i + 0
. ala2 аП+1
где at 0, i = 1, 2, 3, ... ,п, л+ 1.
12
55.	Дано: а + 6 = tn, аВ = а\ Л, = т--
т— 1
Л« = т — -------------, Л4 = т —
6	а *
т —----
т—1
т
а
т
т—1
А+1 = т —- (m #= 1; а =# Р; & > 1).
Л*
тт	л (“Л+1 — ₽"+1) — (а" — Р")
Доказать, что Л_ = *-----—!—-—-——
*	п (ал — Рл) — (ал~1 — рл-1)
56.	Доказать, что при натуральных значениях k и п число
kn+2 + (k + 1)2л+х делится на число k2 + k + 1.
57.	Доказать, что если п — нечетное число, то
1 + гс-1 1 (п-1)(п-3)	, (n-l)(n-3)...2 в п
+ п — 2 + (п —2)(п —4) "Г (я — 2)(п — 4)... 1
58.	Зная, что число (р — 1)!	1 делится на р тогда и только
тогда, когда р — простое число (теорема Вильсона), доказать,
что п! [р — (п + 1)1! + (—1)” (0 < п < р — 1) делится на р
тогда и только тогда, когда р — число простое.
. 7
7*
59.	Доказать, что если число Ак=7г составлено из k
семерок, то Лп — Ар делится на 34 300 при п и р, не меньших 2.
60.	Даны п монет одинакового достоинства, среди которых име-
ется одна фальшивая, отличающаяся весом. Доказать, что если
п < 3*, то достаточно k взвешиваний на чашечных весах, чтобы об-
наружить фальшивую монету.
§ 2. ДЕЙСТВИЯ НАД ЦЕЛЫМИ ЧИСЛАМИ
Зависимость между компонентами
и результатом арифметических действий
61.	Доказать: если одно из слагаемых а суммы умножить на
натуральное число k, то сумма увеличится на число, равное данно-
му слагаемому, умноженному на k — 1, т. е. на a (k — I); если одно
из слагаемых а суммы разделить на натуральное число k, то сумма
уменьшится на число, равное данному слагаемому, деленному на k
и умноженному на k — I, т. е. на (a: k) (k — 1); если уменьшаемое
увеличить в k раз, то разность увеличится на число, равное умень-
шаемому, умноженному на k— 1; если вычитаемое увеличить в k
раз, то разность уменьшится на число, равное вычитаемому, умно-
женному на k — 1.
13
62.	Установить, как изменится разность, если уменьшаемое
уменьшить в k раз; если вычитаемое уменьшить в k раз; если умень-
шаемое и вычитаемое увеличить (или уменьшить) в одно и то же
число раз.
63.	Установить, как изменится произведение двух множителей,
если один из них увеличить в несколько раз, а другой уменьшить
во столько же раз; если один из них увеличить в k раз, другой
уменьшить в п раз; если один из них уменьшить (или увеличить)
на несколько единиц.
64.	Установить, как изменится частное, если делимое увеличить
в несколько раз; если делитель уменьшить (или увеличить) в несколь-
ко раз; если делимое увеличить в несколько раз, а делитель умень-
шить во столько же раз.
65.	Установить, как изменится остаток (при делении с остатком),
если делимое и делитель увеличить (или уменьшить) в одно и то же
число раз.
66.	Доказать, что если делимое (при делении с остатком) есть
сумма нескольких чисел, то остаток от деления этой суммы на не-
которое число не изменится, если уменьшить или увеличить одно
или несколько слагаемых на число, кратное делителю.
67.	Доказать, что если делимое (при делении с остатком) есть
произведение нескольких чисел, то остаток от деления этого про-
изведения на некоторое число не изменится, если уменьшить или
увеличить один из множителей на число, кратное делителю.
68.	Доказать, что при делении большего числа на меньшее де-
лимое всегда больше двойного остатка.
69.	а) Какое число можно прибавить к делимому (при делении
с остатком), чтобы частное не изменилось?
б)	Какие числа можно прибавить одновременно к делимому и
делителю (при делении с остатком), чтобы частное не изменилось?
70.	При каком условии деление числа А (с остатком) на два
последовательных числа а и а + 1 дает в частном одно и то же
число?
Некоторые приемы умножения
Доказать (№ 71—81):
71.	Чтобы двузначное число умножить на 9, достаточно из дан-
ного числа вычесть число десятков, увеличенное на единицу, и к
результату приписать дополнение числа единиц до 10.
72.	Чтобы двузначное число умножить на 99, достаточно умень-
шить это число на единицу и к результату приписать дополнение
данного числа до 100 (двумя цифрами).
73.	Чтобы двузначное число, сумма цифр которого меньше 10,
умножить на 11, достаточно между цифрами десятков и единиц вста-
вить сумму десятков и единиц.
14
74.	Чтобы двузначное число, сумма десятков и единиц которо-
го не меньше 10, умножить на 11, достаточно между цифрой десят-
ков, увеличенной на единицу, и цифрой единиц вставить избыток
суммы десятков и единиц над 10.
75.	а) Чтобы перемножить два двузначных числа, последняя
цифра которых 1, а сумма цифр десятков меньше 10, достаточно
перемножить цифры десятков и к этому произведению приписать
сумму цифр десятков и единицу; б) чтобы перемножить два дву-
значных числа, последняя цифра которых 1, а сумма цифр десятков
не меньше 10, достаточно к произведению цифр десятков, увели-
ченному на 1, приписать избыток суммы цифр десятков над 10 и
единицу.
76.	Чтобы найти произведение двух двузначных чисел, у ко-
торых цифры десятков разнятся на 1, а сумма цифр единиц равна 10,
достаточно взять большее из чисел, возвести в квадрат цифру
десятков, вычесть единицу и к результату приписать дополнение
до 100 квадрата цифры единиц.
77.	Чтобы вычислить произведение двух двузначных чисел,
у которых: а) одинаковы цифры единиц или десятков, а сумма цифр
десятков или единиц равна 10; б) цифры одного числа одинаковы,
а сумма цифр другого числа равна 10, достаточно произведение
цифр десятков сложить с повторяющейся цифрой и к результату
приписать двумя цифрами произведение цифр единиц.
78.	Чтобы умножить нечетное число на 15, достаточно к этому
числу прибавить частное от деления этого числа, уменьшенного на 1,
на 2 и к результату приписать цифру 5.
79.	Чтобы четное число умножить на 15, достаточно к этому
числу прибавить частное от деления его на 2 и к результату припи-
сать 0.
80.	Чтобы умножить число на 25, достаточно найти частное от
деления этого числа на 4 и к результату приписать 00; 25; 50 или 75
в зависимости от того, равен ли остаток соответственно 0, 1,2, 3.
81.	Чтобы двузначное число умножить на 101, достаточно при-
писать справа к данному числу само это число.
Признаки делимости
82.	Дано трехзначное число, цифры которого суть последова-
тельные натуральные числа. Если составить новое число, цифры
которого взяты в обратном порядке, то разность между большим
М меньшим из этих чисел делится на 198. Доказать.
V 83. Доказать, что разность между трехзначным числом и чис-
лом, составленным из этих же цифр, но взятых в обратном порядке,
делится на 9.
•J 84. Доказать, что всякое трехзначное число, написанное оди-
наковыми цифрами, делится на 37.
15
85.	Доказать, что если имеются два трехзначных числа, каждое
из которых не делится на 37, но их сумма делится на 37, то шести-
значное число, составленное из этих двух чисел, делится на 37.
86.	Доказать, что если трехзначное число делится на 37, то
имеются и другие трехзначные числа, составленные из тех же цифр,
которые делятся на 37.
87.	Доказать, что если число делится на 6, то сумма цифры еди-
ниц с учетверенной цифрой каждого из остальных разрядов числа
делится на 6 и обратно.
88.	Доказать, что если число делится на 8, то сумма цифры еди-
ниц с удвоенной цифрой десятков и с учетверенной цифрой сотен
делится на 8 и обратно.
89.	Пусть a, b, с, d обозначают соответственно единицы, десят-
ки, сотни и тысячи некоторого числа. Доказать, что это число де-
лится на 4, если а + 2Ь делится на 4, и обратно; оно делится на 8,
если а + 2Ь + 4с делится на 8, и обратно; оно делится на 16, если
а + 2Ь + 4с + делится на 16 и b — число четное, и обратно.
90.	Доказать, что число, имеющее четное число цифр, первая '
и последняя из которых — единицы, а остальные — нули, делится
на 11.
91.	Доказать, что число, состоящее из четного числа одинако-
вых цифр, делится на 11.
92.	Сумма цифр трехзначного числа равна 7. Доказать, что
число будет делиться на 7, если цифра единиц будет равна цифре
десятков.
93.	Пользуясь общим признаком делимости, установить при-
знаки делимости на числа: 11, 101, 33.
94.	Доказать следующий признак делимости на 13: на 13 де-
лятся только такие числа, у которых сумма числа всех десятков с
учетверенной цифрой единиц делится на 13. Показать, что, приме-
няя этот признак достаточное число раз, всегда можно задачу све-
сти к делимости на 13 двузначного числа.
95.	Доказать, что необходимым и достаточным условием дели-
мости данного числа N на 17 является следующее: если сумма уд-
военной цифры единиц и утроенного числа десятков N делится на 17,
то и число N делится на 17.
96.	Наугад выбрано 1973-значное число, делящееся на 9. Сум-
му его цифр обозначим через а, сумму цифр числа а обозначим Ь,
сумму цифр числа b обозначим с. Чему равно с?
Деление с остатком. Делимость чисел
97.	Написать равенства, выражающие деление целого числа а
на натуральное число b с остатком при следующих значениях а
и Ь: а = —5, b ~ 2; а = —117, b — 31.
98.	Доказать, что любое натуральное число можно представить
в виде 2п или 2п + 1, где п — натуральное число или нуль.
16
99.	Доказать, что любое натуральное число можно предста-
вить в виде Зп, Зп + 1 или Зп + 2, где п — натуральное число
или нуль.
100.	Доказать, что если каждое из двух натуральных чисел при
делении на 3 дает в остатке 1, то их произведение при делении на 3
тоже дает в остатке 1.
101.	Доказать, что если одно из двух натуральных чисел при
делении на 3 дает в остатке 1, а другое — остаток 2, то их произве-
дение при делении на 3 дает в остатке 2.
102.	Доказать, что произведение двух последовательных на-
туральных чисел при делении на 3 дает в остатке нуль или 2.
103.	Если два целых числа при делении на одно и то же нату-
ральное число дают равные остатки, то разность данных чисел де-
лится на это натуральное число. Доказать.
104.	Если разность двух целых чисел делится на натуральное
число, то эти целые числа дают равные остатки при делении на дан-
ное натуральное число. Доказать.
105.	Если целые числа alt аг, , апи blt Ь2, ..., bn дают соответ-
ственно равные остатки при делении на натуральное число k, то
числа aj + «2 + ... + ап и dj + Ь2 + ... + Ьп, а±а2 ... ап и ЬгЬ2 ...
... Ьп дают также равные остатки при делении на k. Доказать.
106.	Если целые числа аи b при делении на натуральное число с
дают равные остатки, то одинаковые натуральные степени их при
делении на с тоже дают равные остатки.
Примечание. Целые числа, дающие равные остатки при делении на
некоторое натуральное число т > 1, называются равноостаточными или срав-
нимыми друг с другом по модулю т.
107.	Доказать, что если п — натуральное число, то
п(п + 1)(л + 2) —число натуральное.
108.	Доказать, что произведение двух последовательных четных
чисел делится на 8.
109.	Доказать, что произведение четырех последовательных на-
туральных чисел делится на 24.
ПО. Доказать, что произведение пяти последовательных нату-
ральных чисел делится на 120.
111.	Доказать, что разность между кубом натурального числа
и самим числом делится на 6.
112.	Доказать, что разность между кубом нечетного числа и
самим числом делится на 24.
113.	Доказать, что квадрат всякого нечетного числа, уменьшен-
ный на единицу, делится на 8.
114.	Доказать, что разность квадратов двух последовательных
нечетных чисел делится на 8.
115.	Доказать, что разность квадратов двух нечетных чисел
делится на 8.
17
116.	Доказать, что произведение квадрата натурального числа
на натуральное число, предшествующее этому квадрату, делится
на 12.
117.	Доказать, что сумма кубов трех последовательных нату-
ральных чисел делится на 3.
118.	Доказать, что сумма двух последовательных натуральных
степеней числа 2 делится на 6.
119.	Доказать, что сумма трех последовательных натуральных
степеней числа 2 делится на 14.
120.	Доказать, что сумма двух последовательных степеней лю-
бого натурального числа а делится на произведение этого числа
и числа, за ним следующего.
121.	Доказать, что' разность между квадратом числа, не деля-
щегося на 3, и единицей делится на 3.
122.	Доказать, что ах2 — а22 + а32 — ... + a22n-i — а\п де-
лится на 24, если ай — нечетные числа, не кратные 3 (k = 1,
2.......2л).
123.	Доказать, что, какими бы ни были натуральные числа а
и Ь, где а > Ь, одно из чисел: а, Ь, а + Ь, а — Ь — делится на 3.
124.	Доказать, что, какими бы ни были натуральные числа
а и Ь, где а > Ь, одно из чисел: а, Ь, а + Ь, а — Ь, 2а + Ь, 2а —
— b — делится на 5.
125.	Доказать, что если а и b — натуральные числа, то число
ab (а2 + 62) (а2 — й2) делится на 5.
126.	Доказать, что сумма 1919 +6969 делится на 44.
127.	Доказать, что следующие выражения делятся на 1969:
а) 1647 — 489 — 1023; б) 2вл+178 + 2«+178 — 2вя — 2« при не-
четном п; в) 36п+178 — Зя+178 — 36П Зл ПрИ четном Пф
128.	Доказать:
а)	всякое число, не делящееся на 2 и на 3, может быть пред-
ставлено в виде 6л + 1 или би + 5, где п — натуральное число
или нуль;
б)	произведение двух чисел вида 6л 4- 1 или 6п + 5 есть число
вида 6р + 1;
в)	произведение чисел вида 6 л + 1 и 6м 4- 5 есть число вида
6р + 5.
129.	Доказать, что квадрат целого числа или делится на 4,
или при делении на 4 дает в остатке 1.
130.	Доказать, что число, являющееся квадратом натураль-
ного числа, или делится на 3, или при делении на 3 дает в
остатке 1.
131.	Доказать, что если число не делится на 5, то его квадрат,
увеличенный или уменьшенный на 1, делится на 5.
132.	Доказать, что если число не делится на 7, то его куб, уве-
личенный или уменьшенный на единицу, делится на 7.	i
133.	Показать, что сумма квадратов двух целых чисел только
тогда делится на 7, когда каждое из этих чисел делится на 7.
18
134.	Доказать, что куб любого натурального числа либо делит-
ся на 9, либо, будучи увеличенным или уменьшенным на единицу,
делится на 9.
135.	Доказать, что произведение трех последовательных на-
туральных чисел, среднее из которых — квадрат, делится на 60.
136.	Доказать, что произведение трех последовательных на-
туральных чисел, среднее из которых — куб, делится на 504.
137.	Показать, что при всяком целом нечетном значении а
выражение а4 + 7 (7 + 2а2) делится на 64.
138.	Доказать, что при любом натуральном п выражение
п (п2 + 5) делится на 6.
139.	Доказать, что при любом натуральном п выражение
п (2п + 1) (7п + 1) делится на 6.
140.	Доказать, что при любом натуральном а выражение а3 +
+ Па делится на 6.
141.	Доказать, что если (и, 6) = 1, то выражение п2 — 1 де-
лится на 24.
142.	Доказать, что при натуральном п выражение 2п* — п4 —
—"п2 делится на 36.
;	143. Доказать, что при всяком целом а выражение (а2 4~ За +
+ I)2 — 1 делится на 24.
144.	Доказать, что при всяком нечетном х выражение х3 -f- Зх2 —
— х — 3 делится на 48.
\) 145. Доказать, что при всяком целом значении п выражение
п4 + 6п3 + 11п2 + 6п делится на 24.
146.	Доказать, что при всяком целом значении п выражение
п (п4 — 125п2 + 4) кратно 120.
147.	Доказать, что при всяком целом значении п выражение
п (п2 — 1) (п2 — 5п + 26) делится на 120.
148.	Доказать, что многочлен п5 — 5п3 + 4п при всяком целом
значении п представляет собой число, делящееся на 120.
149.	Доказать, что при любом натуральном п выражение 6п5 +
+ 15п4 + Юп3 — п кратно 30.
150.	Доказать, что при всяком нечетном п выражение п8 — п* —
— п4 + п2 делится на 1152.
151.	Доказать, что при нечетном п выражение п12 — п8 — п4 +
+ 1 делится на 512.
152.	Доказать, что ab (а4 — Ь4) делится на 30, где а и b — лю-
бые натуральные числа.
153.	Доказать, что выражение а2Ь2 (а4 — Ь4) (а4 — 1) при лю-
бых натуральных а и b делится на 900.
154.	Доказать, что выражение ап+4 — ап делится на 30, где а
и п — любые натуральные числа.
155.	Доказать, что выражение п2 (га4 — 1) делится на 60 при
любом натуральном п.	'
156.	Доказать, что разность между пятой и первой степенями
любого натурального нечетного числа, не меньшего 3, делится на
240.
19
157.	Установить, может ли выражение а (а2 — 1) (а2 — 4) при
любом натуральном а делиться на 720.
158.	Доказать, что выражение п (п2 — 49) (п2 + 49) делится на
30 при всяком натуральном значении п.
159.	Доказать, что при натуральных значениях хну выражение
(х2у3 — 4х2у) (х4 + х2 — 2) делится на 216.
160.	Выбрать для у такое натуральное значение, чтобы выраже-
ние (у2+ 1) х3 + (у3 — 1) х делилось на 6 при любом натуральном х.
161.	Доказать, что при целом неотрицательном п выражение
32я+2-4 _|_ 32/1 — 36 делится на 64.
162.	Доказать, что при всяком целом значении а выражение
а7 — 5а5 + 4а3 кратно 360. При каких целых значениях а это вы-
ражение кратно 1080?
163.	Натуральное число п выбрано так, что сумма 1 + 22 +
+ З2 + ... + п2 не делится на 5. Найти остаток от деления на 5
суммы: 1 + 2 + 3 + ... + п.
164.	Доказать, что при нечетном п число Iя + 2я + ... + (а —
— 1)я делится на 1 + 2 + 3 + ... 4- (а — 1) + а.
165.	Найти наименьшее число, делящееся на 7, которое при де-
лении на 2, 3, 4, 5, 6 дает в остатке 1.
• 166. Найти наименьшее целое число, дающее при делении на
2, 3, 4, 5, 6 соответственно остатки 1, 2, 3, 4, 5.
167.	Доказать, что при делении ряда чисел jV, 2N, 3N, ...,
(D — 1) N на D получится D — 1 различных остатков, если
(N, D) = 1.
168.	Используя задачи 40 и 106, найти остатки от деления:
а)	142Б6 на 17;
б)	6592 на 11;
в)	7100 + II100 на 13;
г)' 131в — 225-515 на 3 и на 37;
д)	(116 + 1717)21 на 8;
е)	З333 + 1 на 5;
ж) 4343 _ 1717 на ю.
169.	Используя задачи 40 и 106, решить задачу 36.
Разные задачи, связанные с делимостью
и делением с остатком
170.	Даны две последовательности: ah = 32k+1 + 33*+1 + 4,
bk = 32*+! — 3*+4 -|- 4. Доказать, что при любом натуральном k
одно из чисел последовательностей ак или bk делится на 5.
171.	Найти все шестизначные числа а1а2а3а4а5а6, удовлетворяю-
щие условию: а^аза^щ = (а^йз +
20
172.	Найти все шестизначные числа a1a2a3a4a5a(;, являющиеся
точными квадратами и удовлетворяющие условию:	— аха2а3—
= 100.
173.	Найти четырехзначное число, равное квадрату числа,
выраженного двумя последними цифрами данного четырехзначного
числа.
174.	Доказать, что для всякого натурального п, взаимно про-
стого с 10, найдется число вида 101 ... 01, кратное п.
175.	Найти все трехзначные числа, при делении каждого из
которых на 11 получается частное, равное сумме квадратов значе-
ний отдельных цифр данного числа.
176.	Найти трехзначное число, являющееся квадратом нату-
рального числа k, и такое, что произведение его цифр равно k — 1.
177.	Двузначное число в сумме с числом, записанным теми же
цифрами, но в обратном порядке, дает квадрат натурального числа.
Найти все такие числа.
178.	Доказать, что сумма произведения четырех последователь-
ных натуральных чисел и единицы есть квадрат натурального числа.
179.	Доказать, что сумма квадратов двух нечетных чисел не
может быть квадратом целого числа.
180.	Доказать, что сумма квадратов пяти последовательных
целых чисел-не может быть квадратом целого числа.
181.	Доказать, что числа вида Зп — 1, 5п + 2, 5п — 2, 7п +
+ 3, 7п — 1 и 7п — 2, где п — целое число, не могут быть, квадра-
тами целых чисел.
182.	Показать, что числа вида 12п + 5, где п — целое число,
не могут быть квадратами целых чисел.
183.	Если 2т — 1 = а-b, где т, а, b — натуральные числа,
причем b — больше единицы, то числа а + 1 и b — 1 делятся на
одну и ту же наивысшую степень двух.
184.	Какое число надо прибавить к выражению (п2 — 1)р (п —
— l)'4-1, чтобы оно делилось на п?
185.	Доказать, что число 2n3ft + 4nft + 10 ни при каких нату-
ральных п и k не может быть произведением последовательных на-
туральных чисел.
186.	Доказать, что число А не может быть четвертой степенью
натурального числа, если А — 5 делится без остатка на 9.
187.	При каких целых значениях k выражение k (k2 — 1) (k2 —
— 4) кратно 480?
188.	Доказать, что сумма четных степеней трех последователь-
ных четных чисел не может равняться четной степени какого-
либо целого числа.
189.	Доказать, что сумма одинаковых четных степеней девяти
последовательных целых чисел не может равняться никакой сте-
пени целого числа (показатель степени больше единицы).
190.	В натуральном ряду чисел от 1 до 2310 включительно есть
числа, делящиеся порознь на 2, 3, 5, 6, 7, 10, 11, 14, 15
21
и т. д., вообще — на делитель числа 2310. Сколько чисел, порознь
делящихся на каждый делитель числа 2310? Найти общее реше-
ние задачи.	'___
191.	Найти наименьшее натуральное число вида п — аа ... а
с четным количеством цифр, кратное 131.
Разные задачи на действия с целыми числами
192.	Доказать, что всякие два числа, оканчивающиеся на 1
или 5, 6, 25, 76, 376, 625, 90 625, дают в произведении число,
оканчивающееся теми же цифрами.
193.	Доказать, что если в квадрате натурального числа число
десятков нечетное, то цифр единиц в нем может быть только 6.
194.	Доказать, что сумма 1+2 + 3+ ... + п (п — натураль-
ное число) не может оканчиваться цифрами 2, 4, 7, 9.
195.	В некотором натуральном числе произвольно переставили
цифры. Доказать, что сумма исходного и полученного чисел не
может быть равна числу 99 ... 9.
1973
196.	До какого числа надо довести обыкновенную таблицу умно-
жения, чтобы сумма всех заключенных в ней чисел была равна
36 100?
197.	При умножении четырехзначного числа, состоящего из
разных цифр, на 9 получилось в произведении число, которое от-
личалось от множимого только тем, что между цифрами тысяч и
сотен оказался нуль. Найти множимое.
198.	Вычислить:
Д — 1059 • /1025)* 5 ( 1048576\« /6560\3 /15624,8 . /9801\*
~	’ \1024/ ' \ 1048575/ ' \6561 J ' \15625/ ’ \9800/ ’
199.	Сколько цифр имеет число:
1 I юч J0^104-1) । 104(104-1>(104-g). I- +р
1-2	1-2-3
104 -f-1 членов
200. Найти четыре последовательных натуральных числа, про-
изведение которых есть 1680.
201. Найти три целых последовательных числа такие, чтобы
сумма всех возможных отношений между ними была числом целым.
202. Найти числа, оканчивающиеся на цифру а (а = 2, 3, 4,
5, 6, 7, 8, 9) и обладающие тем свойством, что если последнюю
цифру переставить в начало числа, то число увеличится во столько
раз, сколько единиц в переставляемом числе.
22
203.	Разложить на множители: 218 + З18.
204.	Доказать, что:
а)	числа 49, 4489, 444 889 и т. д., полученные путем вписывания
в середину предыдущего числа 48, — квадраты натуральных чи-
сел;
б)	числа 16, 1156, 111 556 и т. д., полученные путем вписывания
в середину предыдущего числа 15, — квадраты натуральных чи-
сел;
в)	числа 1331, 1 030 301, 1 003 003 001 и т. д., полученные при
последовательном увеличении количества нулей между цифрами
1, 3, 3, 1, — кубы натуральных чисел.
205.	В следующих числах найти неизвестные цифры при ука-
занных условиях:
а)	число 1234ху делится на 8 и на 9;
б)	число 4х87у6 делится на 56;
в)	число хур 138 делится на 7, число 138хур при делении на 13
дает в остатке 6, число xly3p8 при делении на 11 дает в остатке 5;
\ г) число x52ypk делится на 11, и сумма его цифр делится на 11.
206.	Ряд последовательных нечетных чисел: 1, 3, 5, 7, ...,
2k + 1 разделяют на группы: 1; 3 и 5; 7, 9 и 11; 13, 15, 17 и 19
и т. д., содержащие 1, 2, 3, ..., п членов данного ряда. Доказать,
что суммы членов этих групп есть кубы чисел 1, 2, 3, ..., п соответ-
ственно.
207.	Доказать, что всякое число, делящееся на 2я, есть сумма
2я-1 последовательных нечетных чисел.
208.	Доказать, что всякая натуральная степень числа п есть
сумма п последовательных нечетных чисел.
209.	Все натуральные числа выписаны подряд, начиная от еди-
ницы.- Определить, какая цифра стоит на 32 454-м месте.
210.	Какая цифра занимает n-е место в ряду, составленном из
натуральных чисел:
1234567891'011121314 ... 99100101102 ... ?
211.	Найти целое трехзначное число, всякая целая степень ко-
торого имеет такие же цифры сотен, десятков и единиц, как и само
это число.
212.	Найти четырехзначное число, зная, что оно является квад-
ратом натурального числа и что цифры его распадаются на две пары;
состоящие из одинаковых цифр.
213.	Найти двузначное число, обладающее тем свойством, что
если сложить его с суммой кубов его цифр, то получится число, на-
писанное теми же цифрами, но в обратном порядке.
214.	Найти такие числа К, что если N делится на К, то и любое
число, полученное из числа N перестановкой порядка цифр, де-
лится на К.
23
§ 3. ДЕЛИМОСТЬ СУММЫ, РАЗНОСТИ, ПРОИЗВЕДЕНИЯ.
' НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ.
НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
В § 3 приняты следующие условные обозначения:
(а, Ь) — наибольший общий делитель чисел а и Ь\
[а, й] — наименьшее общее кратное чисел а и Ь.
215.	Доказать, что если ab 4~ cd делится на а — с, то ad 4- be
делится на а — с.
216.	Найти необходимое и достаточное условие того, чтобы
сумма чисел an b делилась бы на с, если а и & на с не делятся.
217.	Сумма и произведение двух чисел делятся на некоторое
третье число. Что можно сказать о делимости каждого из данных
двух чисел на это третье число, если оно простое, если оно состав-
ное?
218.	Даны два взаимно простых числа т и а. Известно, что раз-
ности da — be и а — b делятся на т. Доказать, что разность с — d
делится на т.
219.	Если N — натуральное число и N = р*' р%2 ... р*п,
где pt — различные простые числа, аг — натуральные числа или
нуль, то количество делителей числа W определится формулой
т (N) = (ах + 1) (а2 4- 1) ... (ап 4- 1). Доказать.
220.	Найти все делители числа 572, используя каноническое
представление этого числа. Сколько делителей имеет число 572 а?Ьс,
если: 1) а, Ь, с — различные простые числа, большие 20; 2) а = 31,
b = 32, с = 33?
221.	Доказать: если сумма всех делителей некоторого числа
вдвое больше этого числа, то сумма чисел, обратных этим делите-
лям, равна 2.
222.	Доказать: а) не существует целых чисел a, b, с, k, удовлет-
воряющих равенствам:
abek — а — 11 ... 1;
1970
abek — b =
11 ... 1;
1971
abek — с —
abek — k =
11 ... 1;
1972
11 ... 1;
1973
б) не существует целых чисел a, b, с, k таких, что выражение
ях3 4- Ьх2 4- сх 4- k равно 1 при х = 19 и равно 2 при х = 62.
24
223.	Доказать: если разность ар — Ьр делится на р, то она раз-
делится и на р2, где а и b — целые числа, р — простое число.
224.	Если р и q — последовательные нечетные числа, то рр +
+ qi кратно р + q. Доказать.
225.	Найти (а, с) и (Ь, с), если а = 1775 + 30 621 • 1733 —
— 1735;
b = 1735 + 30 621 • 1773 — 1775;
с = 1734 + 30 6212 + 1774.
226.	Каким может быть наибольший общий делитель двух чи-
сел по сравнению с их разностью?
- 227. Доказать, что два последовательных нечетных числа —
числа взаимно простые.
228.	Доказать, что общий наибольший делитель двух после-
довательных четных чисел равен 2.
' 229. Доказать, что если даны три последовательных натураль-
ных числа, то произведение двух последовательных натуральных
чисел и третье натуральное число либо взаимно простые, либо име-
ют наибольшим общим делителем число 2.
230.	Доказать, что числа п, п + 1 и 2п + 1 — попарно взаим-
но простые.
„ 231. Доказать, что	2n + lj = 1.
232.	Доказать, что если числа а и b взаимно простые, то каждое
из этих чисел взаимно простое с суммой и разностью данных чисел.
233.	Доказать, что если (a, b) = 1, то (а + Ь, а— b) = 1 или
(а + Ь, а — Ь) = 2.
234.	Доказать, что если (a, b) = 1, то произведение этих чи-
сел и их сумма, произведение этих чисел и их разность — числа
взаимно простые.
.	235. Доказать, что если (a, b) = 1 и р — простое число, то
(а ± b, abp) = 1 или (а ± b, abp) = р.
236.	Доказать, что если числа а и b взаимно простые, то их
сумма и неполный квадрат разности тоже числа взаимно простые
или имеют общий наибольший делитель, равный 3.
237.	Доказать, что если числа а и b взаимно простые и одно из
них четное, а другое нечетное, (числа разной четности), то
[(а + Ь)п, (а — b)n} = 1.
238.	Доказать, что если числа а и b взаимно простые, то наиболь-
ший общий делитель чисел ас и b равен наибольшему общему дели-
телю чисел b и с.
239.	Доказать, что если (а, &) — d,ro (а + be, а b (с — 1)] =
= d.
240.	Доказать, что если числа а и b взаимно простые, то суммы
На + 2Ь и 18а + 5£> имеют своим общим наибольшим делителем
19 или 1.
25
241.	Доказать, что общий наибольший делитель чисел а и Ь
совпадает с общим наибольшим делителем чисел 5а + 36 и
13а + 86.
242.	Найти необходимое и достаточное условие того, чтобы число
т было наименьшим общим кратным чисел а и 6.
243.	Установить, чему может быть равно наименьшее общее
кратное трех последовательных натуральных чисел.
244.	Установить, будет ли наименьшее общее кратное двух чи-
сел делиться на наибольший общий делитель этих чисел.
245.	Доказать, что наибольший общий делитель суммы двух
чисел и их наименьшего общего кратного совпадает с наибольшим
общим делителем этих чисел.
246.	Доказать, что для любых п натуральных чисел наиболь-
ший общий делитель наименьшего общего кратного п — 1 из них
и n-го числа равен наименьшему общему кратному наибольших
общих делителей каждого из п — 1 чисел и n-го числа.
247.	Установить, как может быть изменено правило нахожде-
ния наибольшего общего делителя двух чисел путем последователь-
ного деления (алгоритм Евклида), если удвоенный остаток больше
меньшего числа.
248.	Установить сравнительную величину остатков rfe+2 и rk
(k — 1, 2, 3, ...) в системе равенств при последовательном делении
большего из двух чисел на меньшее, меньшего числа на первый оста-
ток и т. д. (алгоритм Евклида).
249.	Доказать, что если числа тип взаимно простые, ат — 1
делится на d и ап — 1 делится на d, то а' — 1 делится на d, где t —
произвольное натуральное число.
Разные задачи, связанные с понятием наибольшего общего делителя
и наименьшего общего кратного
* 250. Найти наибольший общий делитель всех значений, которые
принимает выражение 7"+2 + 82л+1 при п целом и неотрицатель-
ном.
251.	Доказать, что при всяком четном значении п выражение
п2 (п2 — 4) (п2 — 16) делится на 23 040.
252.	Доказать, что 1 + 4rq есть квадрат числа, если г равно
разности между произведением двух чисел и их общим наиболь-
шим делителем, a q равно отношению наименьшего общего кратного
к наибольшему общему делителю тех же двух чисел.
253.	Показать, что: 1) произведение двух натуральных чисел,
разность между которыми равна 3, не может быть квадратом на-
турального числа, кроме случая, когда меньшее число есть 1;
2) произведение двух последовательных натуральных чисел не
может быть квадратом натурального числа.
254.	Дано, что ни а, ни 6 не делится на нечетное простое число р
и что разность квадратов этих чисел делится на натуральную сте-
26
пень р. Доказать, что либо сумма, либо разность чисел а и b делится
на эту степень р.
255.	Найти числа а и & по следующим условиям:
1)	(а, Ь) = 13;	[а, Ь] = 1989;
2)	а + b = 667,	= 120;
(аб)
3)	[а, М = 8100,	]/"а + Vb = 48.
256.	Доказать, что наименьшее общее кратное чисел 1, 2, ...
..., 2п равно наименьшему общему кратному чисел п + 1, п + 2, ...
..., 2п.
257.	Доказать, что число (а — b) ]^ab делится на 24, если ab
есть квадрат числа и если а и b — натуральные числа одинаковой
четности.
258.	Найти целые числа п, делящиеся на все целые числа, не
большие п.
§ 4. ПРОСТЫЕ ЧИСЛА
4 259. Доказать, что если а и b — неравные нечетные простые
числа, то (а + Ь, а — Ь) = 2.
4 260. Какие числа, заключенные между числами 2320 и 2350;
40 322 и 40 330; 3 628 802 и 3 628 810, простые, а какие составные?
4 261. Доказать, что число ]Л22 499 ... 9100 ... 09 + 3 при k >2
k '
имеет простыми делителями только числа 2, 3, 5.
' 262. Найти все простые числа р такие, что р + 10 и р+14 тоже
являются простыми числами.
" 263. Найти такие значения для а, при которых все три числа:
а, а + 4, а + 14 будут простыми.
264. Известно, что р и 8р2 + 1—простые числа. Найти р.
) * 265. Дано, что р — целое положительное число и что каждое
из чисел р, 8р2 + 1 — простые числа; доказатьчто 8р2 — р + 2
тоже простое число.
- 266. Найти числа, представляющие собой кубы натуральных
чисел и имеющие вид 13р + 1, где р — простое число.
- 267. Доказать, что если р и 2р + 1 — числа простые и р не
меньше 5, то 4р + 1 — число составное.
268.	Доказать, что если а — простое число вида 4k + 1, то а2
может быть представлено в виде 24n + 1.
' 269. Доказать, что а4 + 4 есть составное число при любом на-
туральном а, большем единицы.
270.	Доказать, что при натуральном k числа вида 24ft+2 + 1 —
составные.
27
271.	Установить, простыми или составными будут числа вида
х4* + 24р+2, если х — целое число.
г 272. Доказать, что квадрат любого простого числа, кроме 2 и 3,
при делении на 12 дает в остатке 1.
' 273. Доказать, что если а есть простое число, отличное от 2 и 3,
то а2 — 1 делится на 24.
* 274. Доказать, что разность четвертых степеней двух простых
чисел, больших 5, делится на 240.
" 275. Доказать:
а)	любое простое число при делении на 30 может дать в остатке
только простое число или 1;
б)	квадрат любого простого числа, большего 5, при делении на
30 может дать в остатке только 19 или 1.
* 276. Три простых числа а, b и с, большие 3, образуют арифмети-
ческую прогрессию. Доказать, что разность этой прогрессии де-
лится на 6.
- 277. Доказать, что если число N составное, то и число 2N — 1
тоже составное.
278. Доказать, что если число N имеет нечетный делитель
6 > 1, то число 2N + 1 составное.
, 279. Справедливо ли утверждение: если 2N + 1 — число со-
ставное, то N имеет нечетный делитель; если N не имеет нечетных
делителей, то 2N + 1 — число простое?
- 280. Справедливы ли утверждения: если 2N — 1 — составное
число, то N — составное число; если N — простое число, то 2N — 1
тоже простое число?
" 281. Доказать, что если произведение 1-2-3 ... п не делится на
п + 1 (п > 3), то п + 1 — простое число.
' 282. Простым или составным будет число 2-3-5-7 ... р + 1,
где р — простое число?
283. Доказать, что выражение (1 + — + —+ ... Ч-------—) X
\	2	3	р— 1/
X (р — 1)! делится на р, где р — простое число, большее 2.
ч-	284. Доказать, что если аР — 1 кратно простому числу р, то
оно кратно и р2.
285.	Доказать, что всякое простое число, большее 3, выражает-
ся формулой 6n± 1, где п — натуральное число. Верно ли обрат-
ное утверждение?
286.	Доказать, что всякое простое число, большее 2, выража-
ется формулой 4n ± 1, где п — натуральное число. Верно ли об-
ратное утверждение?
287.	Доказать, что сумма двух простых чисел делится на 12,
если их разность равна 2 и меньшее больше 3.
« 288. Все простые числа, не превосходящие данного простого
числа р, разбиты на две группы а, Ь, с, ..., k и а, р, ..., у так, что
число х, определяемое разностью x = abc...k — а р ... у, за-
ключается между 1 и р2. Доказать, что х — простое число.
28
§ 5. ПРИМЕНЕНИЕ ТЕОРИИ ДЕЛИМОСТИ
К РЕШЕНИЮ НЕОПРЕДЕЛЕННЫХ УРАВНЕНИЙ В ЦЕЛЫХ ЧИСЛАХ
Неопределенные уравнения — уравнения, содержащие более
одного неизвестного. Под одним решением неопределенного уравне-
ния понимается совокупность значений неизвестных, которая обра-
щает данное уравнение в верное равенство.
В данном параграфе будут рассмотрены задачи, связанные с на-
хождением только целых решений неопределенного уравнения,
или, как говорят, «с решением неопределенных уравнений в целых
числах». При этом будут рассмотрены как уравнения первой сте-
пени с двумя неизвестными, так и уравнения степени выше первой
и с количеством неизвестных два и более. Для решения уравнений
второго типа, имеющихся в этом параграфе, оказывается достаточ-
ным использовать известные факты о делимости целых чисел.
Например, для решения в целых числах уравнения х5 — х3 =
= уар, где у и р — простые числа, достаточно преобразовать его
к виду
х3 (х2 — 1) = уар
и провести следующие рассуждения: если имеются целые решения
этого уравнения, то у3р • х3, так как (х3, х2 — 1) = I (доказать!),
но (у3, р) = 1, р/х3; следовательно, у3 делится на х3, что возможно,
если х = у, т. е. х — простое число. Тогда х2 — 1 =р, (х—1)х
х(х + 1) — р, что возможно, если х— 1 = 1, х + 1 = р, т. е.
х = 2, у = 2, р = 3.
Для решения в целых числах уравнения вида ax + by = с,
где а, Ь, с — целые числа, отличные от нуля, приведем ряд теоре-
тических положений, которые позволят установить правило ре-
шения. Эти положения основаны также на уже известных фактах
теории делимости.
Теорема 1. Если (a, b) = d, то существуют такие целые
числа.х и у, что имеет место равенство ах + by = d.
(Это равенство называется линейной комбинацией
или линейным представлением наибольшего обще-
го делителя двух чисел через сами эти числа.)
Доказательство теоремы основано на использовании равенств
алгоритма Евклида для нахождения наибольшего общего делителя
двух-чисел (наибольший общий делитель данных чисел выражается
через неполные частные и остатки, начиная с последнего равенства
в алгоритме Евклида).
Пример. Найти линейное представление наибольшего обще-
го делителя чисел 1232 и 1672.
Решение. 1) Составим равенства алгоритма Евклида:
1672 = 1232-1 + 440,
1232 = 440-2 + 352,
440 = 352 -1 + 88,
352 = 88-4, т. е. (1672, 352) = 88.
2) Выразим 88 последовательно через неполные частные и остат-
ки, используя полученные выше равенства, начиная с конца:
88 = 440 — 352-1 = (1672 — 1232) — (1232 — 1672-2 +
+ 1232-2) = 1672-3— 1232-4, т. е. 88 = 1672-3 + 1232-(—4).
Теорема 2. Если в уравнении ах + by = 1 (a, b) = 1,
то уравнение имеет по крайней мере одно целое решение.
Справедливость этой теоремы следует из теоремы 1. Таким обра-
зом, чтобы найти одно целое решение уравнения ах + by = 1,
если (a, b) = 1, достаточно представить число 1 в виде линейной
комбинации чисел а и Ь.
Пример. Найти целое решение уравнения 15х + 37у = 1.
Решение. 1) 37 = 15-2 + 7,
15 = 7-2 + 1.
2) 1 = 15 — 7-2 = 15 — (37 — 15-2) • 2 ± 15 х
X 5+ 37. (_2),
т. е. х0 = 5, у0 = —2 — решение данного уравнения. u
Теорема 3. Если в уравнении ах + by = с (a, b) = d > 1
и с не делится на d, то уравнение целых решений не имеет.
Для доказательства теоремы достаточно предположить про-
тивное.
Пример. Найти целое решение уравнения 16х — 34у = 7.
Решение. (16,34) = 2, 7 не делится на 2, уравнение целых
решений не имеет.
Теорема 4. Если в уравнении ах + by = с (a, b) = d> 1
и с • d, то оно равносильно уравнению ахх + Ьгу — с1( в котором
(ai, К) = 1.
При доказательстве теоремы следует показать, что произвольное
целое решение первого уравнения является также решением вто-
рого уравнения и обратно.
Теорема 5. Если в уравнении ах + by = с (a, b) = 1,
то все целые решения этого уравнения заключены в формулах'.
х = хос + bt,
' У = У<£ — at,
где х0, у0 — целое решение уравнения ах + by = I, t — любое
целое число.
При доказательстве теоремы следует показать, во-первых,
что приведенные формулы действительно дают решения данного
уравнения и, во-вторых, что произвольное целое решение этого
уравнения заключено в приведенных формулах.
Приведенные теоремы позволяют установить следующее прави-
ло решения в целых числах уравнения ах + by — с, где (a, b) = 1:
1)	находится целое решение уравнения ах + by = 1 путем
представления 1 как линейной комбинации чисел а и b (существу-
30
ют и другие способы отыскания целых решений этого уравнения,
например при использовании цепных дробей);
2)	составляется общая формула целых решений данного урав-
нения: х = xQc + bt, у = уос — at, где х0, у0 — целое решение
уравнения ах + by = 1, t — любое целое число.
Придавая t определенные целые значения, можно получить
частные решения данного уравнения: наименьшие по абсолютной
величине, наименьшие положительные (если можно) и т. д.
Пример. Найти целые решения уравнения 407х — 2816у =
= 33.
Решение. 1) Упрощаем данное уравнение, приводя его к
виду 37х — 256у = 3.
2)	Решаем уравнение 37х — 256у = 1.
256 = 37-6 + 34,
37 = 34-1 + 3,
34 = 3-11 + 1.
1 = 34 - 3-11 = 256 - 37-6— 11 (37 - 256 + 37-6) =
= 256-12 — 37-83 = 37-(—83) — 256-(—12), т. е.
х0 = —83, у0 = —12.
3)	Общий вид всех целых решений данного уравнения:
х = — 83- 3 — 256/ = —249 — 256/,
у = -12-3 — 37/ = —36 — 37/.
Положив / = —1, получим хх = 7, ух = 1 и общие формулы
решений примут вид: х = 7 — 256/, у = 1 — 37/.
289.	Дать полные доказательства всех теорем, приведенных в
начале параграфа. Доказать: если хХ( ух — целое решение уравне-
ния ах + by = с, где (a, b) = 1, то все целые решения этого урав-
нения заключены в формулах:
х = хх + bt,
У = Ух — at,
где / — любое целое число.
290.	Представить в виде линейных комбинаций наибольшие
общие делители следующих пар чисел: 15 и 73; 4862 и 720; 192 и 168;
2438 и 321; 15 843 и 435; 8264 и 242.
291.	Решить уравнения в целых числах, используя возможность
представления наибольшего общего делителя двух чисел в виде
их линейной комбинации:
а)	27х — 40у =	1;	г)	13х — 15у	= 7;	ж)	42х + 34у = 5;
б)	54х + 37у =	1;	д)	81х + 52у	= 5;	з)	253х — 449у=3;
в)	107х + 84у =	1;	е)	24х — 56у	= 72;	и)	73х + 85у = 7.
292.	Найти год рождения тех людей, которым в годовщину пя-
тидесятилетия Советской власти исполнилось столько лет, какова
сумма цифр года их рождения.
31
293.	Доказать, что можно найти такое число х, умножив на ко-
торое данное число р, взаимно простое с 10, получйм произведение,
оканчивающееся заданными цифрами abc ... k (всего п цифр).
294.	На какое наименьшее число надо умножить 7, чтобы про-
изведение оканчивалось на 123?
295.	Найти все четырехзначные простые числа, начинающиеся
и оканчивающиеся цифрой 1.
Задачи № 296—304 относятся к решению в целых числах раз-
личных неопределенных уравнений.
296.	Найти все целые решения уравнения:
а)	ху = х + у;
б)	р (х + у) = ху, где р — простое число;
в)	ху + Зх — 5у = —3.
297.	Найти натуральные значения корней уравнений:
а) х2 — 4ху + 5у2 = 169;
в) х8 — y5z = х6, где у и z — простые числа.
298.	Решить уравнения в целых числах:
а)	2у + 1 = х3, где у — простое число;
б)	3* — у3 = 1;
в)	2* + 1 = ЗЛ
299.	Найти целые корни уравнения:
а)	1 + х + х2 + х3 = рУ, где р — простое число;
б)	х2 + х = у4 + у3 + у2 + у;
в)	х2 + Зу2 = 4z2 + 12;
. а	b . с	1
г)	— — —|—, где а, Ъ, с — целые числа.
х	у z
300.	Доказать, что уравнение 2Х2 — 5у2 = 7 не имеет целых
решений.
301.	Доказать, что следующие уравнения не имеют целых ре-
шений:
а)	х2 — 7у2 = 0;	г)	2х2 — I = 5у;
б)	Зх2 — 4у2 = 13;	д)	Зх2 + 2 = у2;
в)	Зх2 + I = 5у;	е)	15х2 — 7у2 = 9.
302.	Доказать, что следующие уравнения не имеют целых ре-
шений:
а)	х3 + 6х + 6 = 0;
б)	х2 + Зх + 5 = 121у;
в)	х5 4- Зх4у — 5х3у2 — 15х2у3 + 4ху4 + 12у5 = 33;
г)	х10 + ах7 + b = 0, где а и b — нечетные числа.
303.	Дано уравнение (х + а) (х + b) = 1, где а и b — целые
неравные числа. Доказать, что уравнение не имеет целых решений.
32
304.	Дапо уравнение с целыми коэффициентами:
xk + CjX*-1 + ... + aft-iX 4- ah = 0.
Левая часть его при х — 0 и х == 1 дает нечетные числа. Доказать,
что уравнение не имеет целых решений.
Задачи № 305—310 приводят к необходимости решить неопре-
деленное уравнение в целых числах.
305.	Найти все натуральные х, для которых выражение 22х + 5
является квадратом натурального числа.
306.	Найти четырехзначные числа, которые, будучи приписаны
справа к числу 400, дают полный квадрат.
307.	Найти наименьшее натуральное число N, обладающее сле-
дующими свойствами:
а)	его запись в десятичной системе счисления оканчивается циф-
рой 6;
б)	если переставить цифру 6 из конца числа в его начало, то
полученное число будет в 4 раза больше данного.
308.	Найти четырехзначные числа, каждое из которых делится
на 11 и сумма цифр каждого равна 11.
309.	Доказать, что каждое целое неотрицательное число п
можно представить, и притом единственным образом, в виде
п (х 4~ У)2 4~ 3* 4~ У
2	’
где х и у — целые неотрицательные числа.
310.	а) Числа 12, 14, 37, 65 являются одним из решений уравне-
ния ху — xz 4- yt = 182. Определить, значением какой буквы бу-
дет каждое из данных чисел.
б) Доказать, что не существует натуральных чисел х и у, отно-
шение произведений каждого из которых на следующее за ним чис-
ло было бы кратно натуральной степени 4.
в) Число начинается 1. Если эту цифру переставить с первого
места на последнее, то число увеличится втрое. Найти это число.
Сколько существует чисел, удовлетворяющих условию задачи?
§ 6.	ДЕЛИМОСТЬ ЧИСЕЛ ГАУССА
Задачи данного параграфа требуют простейших сведений о ком-
плексных числах. Поэтому они могут быть рассмотрены и после
главы «Комплексные числа».
. Основным разделом темы «Целые числа» является теория дели-
мости, которая дает возможность ставить и решать различные за-
дачи. Результаты арифметики целых чисел можно переносить, в
некоторых случаях, на совокупности, отличные от множества це-
лых чисел. В частности, теория делимости целых чисел может быть
перенесена на множество так называемых чисел Гаусса.
2 Заказ 1089
33
Комплексные числа с целыми компонентами обычно называют
числами Гаусса, по имени математика, впервые исследовавшего
свойства этих чисел.
Очевидно, сумма, разность и произведение двух чисел Гаусса
будут числом Гаусса, и целые рациональные числа составят подмно-
жество чисел Гаусса. Частное же двух чисел из этого множества не
обязательно будет иметь целые компоненты, т. е. может не быть
числом Гаусса.
В этом параграфе будут сформулированы определения делимо-
сти чисел Гаусса и их нормы. В качестве задач будет предложено
провести доказательства некоторых свойств и теорем, которые по-
могут глубже овладеть вопросами теории делимости чисел Гаусса
и применить их к решению алгебраических уравнений.
Введем следующие обозначения. Числа Гаусса будем
обозначать прописными (заглавными) латинскими буквами, их
компоненты — строчными латинскими буквами.
Например, А = а + Ы, В = х + yi, где а, Ь, х, у — целые
рациональные числа.
Определение делимости. Число Гаусса А делится на
число Гаусса В тогда и только тогда, когда найдется число Гаусса
С такое, что А = В С.
Пример. 3 4- 5i = (1 + 0-(4 + 0; следовательно, 3 4- 5/
делится на каждый из сомножителей, но это же число не делится на
2 4- i (проверить). Применяя определение делимости, доказать сле-
дующие свойства делимости чисел Гаусса.
311.	Каждое число Гаусса А делится на себя и на единицы,
т. е. на числа 1, —1, I, —I.
312.	Если А делится на В, В делится на С, то А разделится на С.
313.	Если А = а 4- Ы, В = х 4- yi и А делится на В, то число,
сопряженное с Л, т. е. Л = а — Ы, разделится на число, сопряжен-
ное с делителем, т. е. на В = х — yi.
314.	Нуль делится на любое не равное нулю число Гаусса. Ни
одно число Гаусса не делится на нуль.
315.	Если Л делится на В и С — любое отличное от нуля чис-
ло Гаусса, то А-С разделится. на В-С.
316.	Если Л делится на В и k — натуральное число, то Л* раз-
делится на В*.
317.	Если Лъ'..., Ак делится на В, то, каковы бы ни были числа
Гаусса С1( .... Ск, сумма ЛрС^ 4~ ••• 4~ Ак-Ск разделится на В.
318.	Если Л = а 4- bi и р = (а, Ь), то Л будет делиться на р.
319.	Если А = а + bi и а, b — целые рациональные числа,
одновременно либо четные, либо нечетные, то Л делится на 1 4- *>
—1 4- i, 1 — i, —1 —~ i.
320.	Если А = а + bi и а и b — взаимно простые нечетные
числа, то Л делится на 1 4- i, —1 4- i, 1 — i, —1 — i и не делится
на квадраты этих чисел.
34
321.	Если А делится на В, то каждое из четырех чисел А, —А,
—Ai, Ai разделится на каждое из следующих четырех чисел В,
—В, —Bi, Bi.
Для получения дальнейших свойств делимости чисел Гаусса
оказалось полезным поставить в соответствие каждому числу
Гаусса целое неотрицательное число, называемое его нормой.
Определение нормы числа Гаусса. Нормой числа Гаус-
са А = а + bi называется сумма квадратов его компонент, т. е.
число а2 Ь2. Обозначение нормы:
N (А) — а2 + Ь2.
Доказать следующие свойства нормы чисел Гаусса.
322.	Норма каждого числа Гаусса А равна произведению этого
числа на сопряженное с ним.
323.	Норма нуля есть нуль. Норма всякого отличного от нуля
числа Гаусса есть число натуральное.
324.	Только четыре единицы, т. е. числа 1, —1, i, —i, имеют
норму, равную единице.
Г 325. Норма целого рационального числа а равна его квадрату,
т. е. N (а) = а2.
326.	Норма произведения А-В равна произведению норм сомно-
жителей, т. е. N (А-В) = N (A)-N (В).
327.	Если А делится на В, то и норма А делится на норму В.
328.	Если норма А не делится на норму В, то и число А не де-
лится на число В.
Замечание. Обратное утверждение не всегда справедливо. Например,
3 + i не делится на 2 + i (проверить), но норма первого числа, равная 10, де-
лится на норму второго числа, равную 5.
329.	Норма любого числа А, не равного нулю, делится на это
число.
330.	Если число А делится на число В, то и норма А разделится
на число В.
331.	Если число А делится на норму В, то число А разделится
на число В.
332.	Для того чтобы натуральное число Р было нормой числа
Гаусса А, необходимо и достаточно, чтобы его можно было предста-
вить в виде суммы квадратов двух целых рациональных чисел.
Замечание. Очевидно, не всякое натуральное число обладает этим
свойством. Например, целые числа 3, 7, 11, 19 и многие другие нельзя пред-
ставить в-виде суммы квадратов двух целых рациональных чисел.
333.	Существует лишь конечное количество чисел Гаусса, нор-
ма которых не превосходит фиксированного натурального числа Р.
Выяснить геометрический смысл этого свойства.
334.	Каждое не равное нулю число Гаусса имеет лишь конеч-
ное количество делителей.
2*	36
335.	Каждое натуральное число Р, отличное от единицы и являю-
щееся нормой числа Гаусса, делится на числа Гаусса, отличные от
единиц и чисел Р, —Р, Pi, —Pi.
336.	Если А — число Гаусса, норма которого — число четное,
т. е. N (Л) = 2k, то компоненты этого числа имеют одинаковую чет-
ность. Если норма А — число нечетное, то компоненты числа А
имеют разную четность.
337.	Если А — любое число Гаусса, то Л5 — Л делится на сле-
дующие восемь чисел: 2 4* i, —2 + i, 2 — i, —2 — /, 1 + 2i, —1 +
+ 2i, 1 — 2t, —1 — 2i.
338.	Если A = a + bi, a = 10c + cx, b — Юр 4- ръ то, для
того чтобы Л делилось на числа 2 + i, —2 + i, 2 — i, —2 — i,
1 + 2i, —1 + 2i, 1 — 2i, —1 — 2i, 3 + i, —3 + i, 3 — i, —3 — i,
1 + 3t, —1 + 3i, 1 — 3i, —1 — 3t, достаточно, чтобы число Гаус-
са сх + pti делилось на эти числа.
339.	Если А = а + bi, а — Юс + с1( b — Юр •+ р1( то, для
того чтобы число Л делилось на 4 + i, —4 + i, 4 — i, —4 — i,
1 + 4i, —1 + 4i, 1 — 4i, —1 — 41, достаточно, чтобы число Гаус-
са 2Ci 4- Зс + (2pi + 3p)t делилось на эти числа.
340.	Если А = а + bi, а = 102с + Юс + с, b = Ю2р + Юр 4-
4- р, то Л делится на 6 4- i, —6 4- i, 6 — i, —6 — i, 1 + 6i, —1 4-
-j- 6i, 1 — 6t, —I — 6t.
341.	Пусть A — a + bi и В — x + yi, причем x, у — взаимно
простые целые числа. Разделим Л на В, применяя правило деления
комплексных чисел, получим:
А__ ах 4-by . —ay + by
В ~ х2 + у2 + Xs + у2 1'
Тогда если первая компонента частного — целое рациональное
число, то и вторая компонента будет целым, и наоборот. Доказать.
342.	Используя указанные в предыдущих задачах свойства,
найти делители следующих чисел Гаусса:
А = 777 4- Uli, В = 153 4- 374/.
343.	Если Ф (х) = Хк 4- Схх»-1 4- ... + Ck — полином, коэф-
фициенты которого — числа Гаусса и Л его корень, то свободный
член Ск делится на Л.
344.	Если Ф (X) — Хк 4- С^Х*-1 4- ••• 4- Ck — полином, коэф-
фициенты которого — числа Гаусса и Л его корень, то Ф (1) де-
лится на 1 — Л, Ф (—1) делится на 1 4- Л, Ф (i) делится на i — А,
Ф (—0 делится на i 4- Л.
345.	Если хотя бы одно из чисел 1 4- i, —1 4- i> 1 — i, —1 — i
является корнем полинома Ф (х) = хк 4- Сгхк~г 4- ... 4- Ск, у ко-
торого коэффициенты — числа Гаусса, то компоненты его свобод-
ного члена Cfe = Сх 4~ C2i, т. е. числа Clt С.,, должны иметь оди-
наковую четность.
36
346.	Найти числа Гаусса, которые являются корнями следую-
щих уравнений:	/
а)	х4 — х3 — х — 1 =0;
б)	х4 — 2Х3 + 4х2 + 2х — 5 = 0;
в)	х4 — 2Х3 + 4х2 — 2х + 3 = 0;
г)	х4 + бх3 + 6х2 — 8 = 0;
д)	х4 + 2Х3 + 8х2 + 2х + 7 = 0;
е)	х4 + 8Х3 — 12х2 + 104х — 20 = 0;
ж)	х4 + 4х3 + 2х2 + 2х + 4 = 0;
з)	х3 + Зх — 21 = 0;
и)	х3 — 6tx + 4 (1 — i) = 0;
к)	х3 + 3tx2 — 3 (1 + 2i)x + 10 — 57 = 0.
347.	Найти числа Гаусса, каждое из которых является корнем
полинома, и разложить эти полиномы на произведение множите-
лей первой степени:
а)	Ф (х) = х4 + 2Х3 + 2х2 + 10х + 25;
б)	Фг (х) = х3 — 3 (2 + 1)х* + 18 (2 + t)x — 1087.
348.	Если Ф (х) =	+ ... + Cft — полином, у
которого коэффициенты числа Гаусса и Со=#0, тогда, если умно-
жить все члены этого полинома на С9к~г и положить у = Сах,
можно получить новый полином, у которого все коэффициенты бу-
дут числами Гаусса, старший коэффициент, т. е. коэффициент при
ук, будет равен единице, а корни этих полиномов будут связаны за-
висимостью ух = CqXx. Доказать.
349.	Найти числа Гаусса, которые являются корнями следую-
щих уравнений:
а)	8Х3 — 12х2 — 2х + 3 = 0;
б)	8Х4 + 4х3 — 2х2 + х — 1 = 0;
в)	2 (—1 + Ох3 + 3(1 + i)x — 21 = 0;
г)	2Х3 — 37х +1 — i = 0.
350. Если Ф (х) = х* + Qx*-1 + ... + Ck — полином, коэф-
фициенты которого — числа Гаусса, и если этот полином при зна-
чении х = 0 и х=1 принимает значения, которые являются числа-
ми Гаусса с нечетной нормой, то ни одно число Гаусса не может быть
корнем такого полинома; в частности, полином не будет иметь и
целых рациональных корней. Доказать.
351. Показать, что числа Гаусса не являются корнями следую-
щих уравнений:
а)	х4 + 2Х3 + 5х2 + 4х — 5 = 0;
б)	х4 — 2х3 — 9х2 + 6х + 9 = 0.
§ 7.	СИСТЕМАТИЧЕСКИЕ ЧИСЛА
352.	Что называется основанием системы счисления? Какое
число может быть принято за основание системы счисления?
353.	Написать первые пятнадцать чисел натурального ряда в
системах счисления с основанием g, равным 5, 7, 12.
354.	Написать в троичной, пятеричной, семеричной и тринад-
цатеричной системах счисления число, содержащее 27 единиц в
десятичной системе счисления.
355.	Записать 38,0 по основаниям g = 2, 3, 4, 5, 6, 7, 8, 9,
11, 12.
356.	Сколько единиц (в десятичной системе счисления) содер-
жит наибольшее однозначное число в троичной системе счисления;
наибольшее двузначное число в двоичной системе счисления; наи-
большее пятизначное число в пятеричной системе счисления?
357.	Могут ли в семеричной или пятеричной системе счисления
быть числа, записанные в виде 567, 1238, 1029?
358.	Составить таблицу сложения однозначных чисел для си-
стем счисления с основанием, равным 7, 12, 15.
359.	Составить таблицы умножения однозначных чисел для си-
стем счисления с основанием, равным 3, 6, 7, 12.
360.	Найти а, Ь, с, если abc& = cbas.
361.	Выполнить указанные действия:
а)	23 3346 -1- 33 020в + 444в + 12 341в;
б)	43 (10) (11) 512 + 3 (10) 612 + 4 (11) 2512;
в)	10 010 0113 — 2 210 0223;
г)	1 (11) (10) (Ю)12 — 9 (11) 712;
д)	343 224, • 1257;	з) 322 2215 :’4,;
е)	34 1125-34445;	и) 471 2228 : 278;
ж)	34 71812-2612;	к) 51 (10) 3406ц :548и.
362.	В каких системах счисления возможны равенства:
а) *12 + 13 = 30; б) 2-3 = 12; 4 в) 30 : 2 = 14;
2 + 4 =10;	6-6 = 51;	30 : 2 = 12;
17 + 38 = 54;	12-12=144; 1520:12 =123;
89 + 69 = 103;	12-7 =80;	55:13 = 4?
363. Установить, по какой системе счисления выполнены дей-
ствия, а)	и найти неизвестные цифры: ч,??2	_?????? Х ?2	'	? 1?5		|??5 1??7
	, ??0? -*”??? 1 ? ? ? ? 1	3?? ??0 _??? ??5 0	1
38
364.	Число 4561 записано в десятичной системе счисления.
Как оно запишется в пятеричной системе счисления? Число
38446 записано в десятичной системе счисления. Как оно запишется
в семеричной системе счисления? Число 34 567 записано в восьме-
ричной системе счисления. Как оно запишется в десятичной систе-
ме счисления? Число 276 записано в двенадцатеричной системе
счисления. Как оно запишется в десятичной системе счисления?
Число 386 записано в тринадцатеричной системе счисления. Какой
оно будет иметь вид в восьмеричной системе счисления? Число
(11) (10) (10) записано в двенадцатеричной системе счисления. Как
оно запишется в десятичной системе счисления?
365.	В десятичной системе счисления число записано в виде 16.
В какой системе счисления оно запишется в виде 31? В десятичной
системе счисления число записывается как 33. В какой системе
счисления оно запишется в виде 53? Число имеет 63 единицы в де-
сятичной системе счисления. В какой системе счисления оно запи-
шется в виде 77?
366.	Число 1241 записано в пятеричной системе счисления.
В какой системе счисления оно запишется как 304? Число 41 за-
писано в восьмеричной системе счисления. В какой системе счис-
ления оно запишется как 201?
367.	В какой системе счисления число 57 896, написанное по
десятичной системе счисления, изобразится в виде 3 323 041?
368.	Найти в десятичной системе счисления трехзначное число,
которое, будучи написано в системе счисления с основанием 9,
дает число, написанное теми же цифрами, как и искомое, но в обрат-
ном порядке.
369.	Доказать, что в системе счисления, основание которой
есть а, удвоенное число, предшествующее основанию, и квадрат
числа, предшествующего основанию, записываются одними и теми
же цифрами, но взятыми в обратном порядке.
370.	Число, записанное десятью девятками, делится на 9091;
число, записанное двенадцатью девятками, делится на 9901. Дели-
тели — простые числа вида 104 — 103 + 102 — 10 + 1 и 104 —
— 102 + 1 соответственно. Верно ли, что в системе счисления с
основанием 9 число, записанное десятью восьмерками, делится на
94 — 93 + 92 — 9 + 1; число, записанное двенадцатью восьмерка-
ми, делится на 94 — 92 + 1 и что эти делители — простые числа?
371.	Установить, как выразится сумма квадратов п первых на-
туральных чисел в системе счисления с основанием п, большим 6.
372.	Установить, как выразится сумма п первых натуральных
чисел в системе счисления с основанием и.
373.	Показать, что любое натуральное число может быть пред-
ставлено в виде суммы различных степеней числа 2.
374.	Доказать, что число 144 будет квадратом натурального
числа в системе счисления с любым основанием, большим 4.
375.	Доказать, что число 1331 будет кубом натурального числа
в системе счисления с любым основанием, большим 3.
39
376.	В какой системе счисления число 16 324 есть квадрат чис-
ла 125?
377.	Пусть число А по десятичной системе счисления изобража-
ется 2/п цифрами, каждая из которых есть 4; число В — т + 1 —
цифрами, каждая из которых 2; число С — т — цифрами, каждая
из которых 8. Доказать, что число А + В + С 4- 7 есть квадрат
натурального числа.
378.	Пусть А, В, С — три целых числа, записанных в деся-
тичной системе счисления:
А — при помощи 2т цифр, каждая из которых 1;
В — при помощи т + 1 цифр, каждая из которых 1;
С — при помощи т цифр, каждая из которых есть 6. Доказать,
что А + В + С + 8 есть квадрат натурального числа.
379.	Число кратно 136, если оно в двоичной системе имеет
вид 100 ... 0100 ... 01010 ... 0, где k = 33, п = 89, р = 13.
k	п	р
Доказать это утверждение.
380.	Найти все натуральные числа х, произведение цифр ко-
торых в десятичной системе равно х2 — 10х — 22.
381.	Доказать, что в любой системе счисления числа 10 101,
101010 101, 1010 101010 101, 10 101010 101010 101 и т. д.—
составные.
382.	Найти все системы счисления, в которых признаком дели-
мости любого числа на данное число d является делимость суммы
его цифр на число d.
383.	Установить, в каких системах счисления сохраняется из-
вестный признак делимости чисел на 3 и на 9.
384.	Установить, в каких системах счисления известный приз-
нак делимости на 3 справедлив для чисел 4, 5, 6.
385.	Найти наименьшее основание системы счисления, в кото-
рой справедливы следующие признаки делимости:
а)	если сумма цифр некоторого числа делится на 5, то и само
число разделится на 5;
б)	если число, образованное двумя последними цифрами про-
извольного числа, делится на 7, то и само число разделится на 7.
386.	Найти признаки делимости на числа 3, 4, 7 в системах
счисления с основаниями 13 и 5.
387.	Установить признак делимости на 13 в пятеричной и две-
надцатеричной системах счисления.
388.	Дана последовательность целых чисел, каждое из которых
изображается в системе счисления с основанием р всеми значащими
цифрами, но не содержит цифру дважды. Указать среди этих чисел
такйе два, отношение которых равно наибольшему целому числу
(Р>2).

ГЛАВА II
РАЦИОНАЛЬНЫЕ ЧИСЛА. ИРРАЦИОНАЛЬНЫЕ ЧИСЛА
§ 1. СРАВНЕНИЕ ПОЛОЖИТЕЛЬНЫХ РАЦИОНАЛЬНЫХ ЧИСЕЛ
1.	Доказать, что от вычитания из числителя и знаменателя пра-
вильной дроби одного и того же натурального числа, меньшего
числителя, дробь уменьшается, а от вычитания из числителя и зна-
менателя неправильной дроби одного и того же натурального чис-
ла, меньшего знаменателя, дробь увеличивается. Установить, как
изменится при этом разность между числителем и знаменателем
в данной и полученной дробях.
2.	Что произойдет с правильной дробью, если к ее числителю
прибавить (отнять) натуральное число п? Если к знаменателю ее
прибавить (отнять) натуральное число п? Если к числителю и зна-
менателю ее прибавить (отнять) натуральное число п? Аналогич-
ные вопросы в случае неправильной дроби.
3.	Как изменится величина дроби, если числитель ее увеличить
на его величины, знаменатель увеличить на его величины?
4.	Доказать: если — < —, то — < S-i£2 <
4* ^з
если	- то a + gl <g + ai+ga	fli+ga
bi b b 4- bi b 4" bi 4" b3	bi 4* b2
где а, Ь, аг, Ьъ а2, Ь2 — натуральные числа.
5.	Найти натуральное число п, чтобы дробь -”~4 была квад-
«4-17
п I 4
ратом несократимой дроби; чтобы дробь была квадратом
несократимой дроби.
2	5
6.	Найти натуральные а и Ь, чтобы дроби ---- и — были
а -|- b	ab
равны.
7.	Найти натуральные числа а и Ь, если число, обратное их раз-
ности, в три раза больше числа, обратного их произведению.
8.	Доказать, что не существует правильной дроби, равной дроби,
числитель которой есть разность между знаменателем и числителем
этой дроби, а знаменатель — сумма числителя и знаменателя ее.
3.42.5З пП~2	J
9.	Доказать, что дроби —(ПуП— и 2»----------j Равны-
1	3	5	999
10.	Доказать, что произведение — • — • — .. меньше 0,01.
11.
жения
Доказать, что при любом натуральном п следующие выра-
10" 4-2 1О'! 4- 8 10й 4-5
есть целые числа: —-—; ------11—.
3	9	5
41
12. Показать, что ни
п — 6 п — 5
выражения —— и ——
при каких натуральных значениях п
не могут быть одновременно равны
целым числам.
аг_kt
13. Доказать, что -------- не может быть целым числом, если
ab
а и b — неравные, отличные от нуля целые числа.
14. Показать, что ни при каком целом значении х дроби
№ —Зх + 4. х24-5х —9. х24-Зх-|-15	, павны пе-
	. 	. 	 Нс МО1 уТ СЫ1Ь DdoHbl Це-
49----------------------------169-121
лым числам.
15. Найти такие правильные дроби, каждая из которых: 1) от
уменьшения ее числителя и знаменателя на 1 обращается в
2) от увеличения ее числителя и знаменателя на 1 обращается в Д
16. Найти дробь, числитель которой есть а, знаменатель —
двузначное число ab, если эта дробь равна —.
6а
17.	Доказать, что не существует натурального числа п такого,
чтобы дробь — была равна —.
ab	п
18.	Найти дробь, числитель которой есть произведение двух
однозначных целых чисел, а знаменатель,— двузначное число, со-
ставленное из тех же цифр, взятых в том же порядке, как и множи-
тели в числителе, если она равна дроби с числителем 1.
19.	Дана правильная дробь, числитель и знаменатель которой —
двузначные числа, причем цифра единиц числителя одинако-
ва с цифрой десятков знаменателя. Найти все дроби, которые
при зачеркивании этой одинаковой цифры сохраняют свою ве-
личину.
20.	Найти несократимую дробь если а и b — однозначные
ь
натуральные числа и число, обратное &, есть
21.	Во множестве трехзначных чисел найти такое, отношение
которого к сумме его цифр имеет наименьшее значение.
§ 2. СОКРАЩЕНИЕ ДРОБЕЙ
22.	Доказать, что если правильная дробь несократима, то дробь,
дополняющая данную до единицы, тоже несократима.
23.	Доказать, что если данная дробь несократима, то дроби
с числителем, равным сумме и разности числителя и знаменателя
данной дроби, и знаменателем, равным произведению числителя
на знаменатель данной дроби, тоже несократимы.
42
24. Дробь сократима.
a~b
Сократима или несократима
дробь —?
ь
25.	Сократимой или несократимой будет дробь, полученная
после исключения целого числа из сократимой дроби? из несокра-
тимой дроби?
23.	Сократимой или несократимой будет дробь	Дробь
------, где а — натуральное число?
2а -j- 1
27.	При каких целых значениях п дробь  ”	1— несократима?
28.	Дробь — несократима. Доказать:
ь
1 \	а2 + ab + Ь2
1)	дробь ----!----5------несократима;
а + ь
Cl I Ь
2)	дробь ——— несократима или сократима только на 3;
а2—a&+Z>2
/у2 _1_ А2 /тЗ _±. АЗ	АН _1_ АЛ
3)	дроби —£— , ----------и вообще --------, где п — натураль-
ab	ab	ab
ное число, несократимы.
29.	Доказать, что дробь
натуральных а.
30.	Доказать, что дробь
а3 + 2а
—зд2 । несокРатима ни ПРИ каких
2п2—1
2п + 1
где п — натуральное число,
несократима.
5д2 । 1
31.	Доказать, что если дробь —-2— , где п — натуральное
число, равна целому числу, то дроби — и — несократимы.
2	3
32.	Доказать, что если дробь у несократима, то дробь ——а
где п — натуральное число, или несократима, или сократима
только на делителя числа п + 2.
33.	Доказать, что если и j- — правильные равные
дроби, то первая из них сократима на 9.
§ 3. ОПЕРАЦИИ НАД РАЦИОНАЛЬНЫМИ ЧИСЛАМИ (ДРОБЯМИ)
34.	Найти условия, при которых:
а)	сумма двух несократимых дробей равна целому числу;
б)	разность двух несократимых дробей равна целому числу;
в)	произведение двух несократимых дробей равно целому числу;
г)	частное двух несократимых дробей равно целому числу.
43
г
I
35.	Доказать, что если знаменатели двух несократимых дробей —
взаимно простые числа, то их сумма и разность — дроби несокра-
тимые.
36.	Дробь — несократима. Выяснить, сократима или несократима
ь
сумма дробей с числителем 1 и знаменателем а и а-\-Ь соответственно.
37.	Найти условие, при котором разность двух дробей, имею-
щих одинаковые числители, выразится дробью с тем же числи-
телем.
38.	Найти условие, при котором сумма двух несократимых
дробей равна их произведению; разность двух несократимых дро-
бей равна их произведению.
39.	Доказать, что не существует двух несократимых дробей,
сумма и произведение которых были бы целыми числами.
40.	Доказать, что если ——правильная дробь, то — = —-— +
b	b k +1
4-	а~п -, где k — частное, ап — остаток от деления числа b
b(k +1)
на число а.
41.	Пользуясь предыдущей задачей, доказать, что всякую пра-
вильную дробь можно представить в виде суммы нескольких дро-
бей с числителем 1.
42.	Доказать, что сумма данной дроби и обращенной всегда
больше 2 (дробь не равна 1).
43.	Доказать: если abck = 1, где a, b, с, k — положительные
числа, то а2 + Ь2 + <? + k2 + ab + ас + ak + bk + be + ck > 10.
44.	Зная, что x, у, p — различные рациональные числа, свя-
занные с данными рациональными числами a, b, с, k (а=£ 0, Л =# 0)
следующими соотношениями: ах3 + bx2 + сх + k = 0, ay3 4- by2 +
+ су + k = 0, ар3 + bp2 + ср + k = 0, найти сумму дробей
1 + 1 + -•
X У Р
45.	Доказать, что при целом а и натуральном п выражение
/ а™ ,_____1_\ _ / а2п ,	1 • \
1 о« + 1/ \ал-|-1 ' а" — 1/
есть целое число. Указать область допустимых значений для а.
гг	л” (х — 1)(х+1)	2(0,5—х)
46.	Доказать, что сумма дробей	—1	„ и	—-—у
равна сумме их кубов. Указать область допустимых значений для х.
47.	Доказать, что если дано п дробей с положительными числи-
телями и знаменателями, то дробь, числитель которой есть сумма
числителей данных дробей, а знаменатель — сумма знаменателей
данных дробей, заключена между наибольшей и наименьшей из
данных дробей.
48.	Доказать, что сумма 1 + —+ —+••• +— при достаточ-
2	3	п
но большом п будет больше всякого наперед заданного числа А.
I
44
§ 4. КОНЕЧНЫЕ И БЕСКОНЕЧНЫЕ ПЕРИОДИЧЕСКИЕ
СИСТЕМАТИЧЕСКИЕ ДРОБИ
В данном параграфе имеется в виду известным следующее:
1)	Дробь, числитель которой есть целое систематическое число,
знаменатель — натуральная степень основания системы счисле-
ния, называется систематической дробью.
anGn + an-iG"-1 + ... + ajG + а,, _ a^-i-ap
Gm	Gm ’
где G — основание системы счисления (натуральное число, боль-
шее единицы), ап, an-lt ... , ага0— однозначные числа этой систе-
мы счисления, п и т — любые натуральные числа этой же системы
счисления.
2)	Если а — правильная дробь, то она может быть представле-
на в виде а — О, Ь2 Ь2 ... bmQ\
если а — неправильная дробь, то она может быть представлена
в виде а =	... сх, Ь2Ь2 ... Ь,„в, где сь.с1( bu b2, ..., bm—
однозначные натуральные числа системы счисления с основа-
нием G.
3)	Действия с систематическими дробями, представленными
как в форме, указанной в п. 1, так и в форме, указанной в п. 2,
выполняются по правилам, аналогичным соответствующим прави-
лам в десятичной системе счисления.
4)	При записи обыкновенных дробей в форме, аналогичной
указанной в п. 2, имеют место случаи, обобщающие факты, из-
вестные для десятичной системы счисления:
а)	если знаменатель несократимой дроби — взаимно прост с
ь
основанием системы счисления G, то дробь может быть представле-
на в виде «чистой периодической систематической дроби».
Пример.^ =0, (1)в, где (5, 6) = 1;
б)	если каноническое разложение знаменателя несократимой
дроби— содержит простые множители, отличные от простых множи-
ь
телей основания системы счисления, то дробь — обращается в «сме-
ь
шанную периодическую систематическую дробь».
Пример.-1- = 0,0(2)4, 124 = 2-3, 4 = 2-2;
12j
в)	если каноническое разложение знаменателя несократимой
а
дроби — содержит только те простые множители, которые входят
ь
в каноническое разложение основания системы счисления, то дробь
— обращается (может быть представлена) в «конечную систематиче-
ь
скую дробь».
45
П р и м е р. - = 0,243в, 40 = 23-3, 6 = 2-3, (15, 40)e = 1;
406
г)	правила обращения «периодических систематических дробей»
в обыкновенные аналогичны соответствующим правилам, установ-
ленным для десятичной системы счисления.
Примеры. 0, (23)в = — = — , так как 23в = 5-3; 556 =
55в	11в
1,3 (2497)ls=l +
32497 — 3	4
(11)	(11)(11) (11) 012	"	13И*
Справедливость обобщений, указанных в пи. 2—4, может быть
доказана читателем самостоятельно или найдена в соответствующей
литературе, например в книге «Арифметика»1
49.	Ответить на следующие вопросы:
1)	Существует ли рациональное число, обращающееся в беско-
нечную непериодическую десятичную дробь?
2)	Какие обыкновенные дроби обратятся в конечные система-
тические, какие — в чистые и какие — в смешанные периодиче-
ские в системе с основанием 12?
3)	Конечной или бесконечной десятичной дробью будет сумма
двух конечных десятичных дробей? произведение? разность?
4)	Всегда ли частное от деления двух конечных десятичных дро-
бей выразится конечной десятичной дробью? Если не всегда, то
при каком условии частное выразится конечной десятичной дробью?
5)	Сумма и разность двух чистых периодических дробей — перио-
дическая ли дробь?
6)	Произведение двух периодических дробей — всегда ли есть
периодическая дробь?
7)	Частное от деления двух периодических дробей — всегда ли
есть периодическая дробь?
50.	Доказать,- что сумма трех чисел, обратных трем последова-
тельным натуральным числам, обращается в смешанную периоди-
ческую десятичную дробь.
11	2
51.	Доказать, что сумма дробей —; —— и - —-обращается в
смешанную десятичную периодическую дробь при любом натураль-
ном п.
52.	Доказать, что дроби —;	---------- обращаются
2п2 + 1 п2 4- п + 1
в чистые периодические десятичные дроби при любом натураль-
ном п.
1 М. К. Гребенча и С. Е. Ляпин. Арифметика. М., Учпедгиз,
1952.
46
53.	Доказать: для умножения чистой периодической систе-
матической дроби на 10* достаточно перенести в ней запятую на k
знаков вправо, а для умножения ее на -Ц — перенести запятую
10й
на k знаков влево, где k — натуральное число.
54.	Если дробь — несократима и обращается в смешанную пе-
ь
риодическую десятичную дробь, то число цифр до периода в этой
смешанной дроби будет равно наибольшему показателю степеней
чисел 2 и 5, с которым эти числа входят в каноническое разложение
знаменателя дроби Ь.
55.	Доказать, что сумма чистой и смешанной периодических дро-
бей не может быть равна целому числу.
56.	Доказать, что сумма двух чистых периодических дробей,
имеющих разные длины периодов, не может быть равна целому
числу.
57.	Доказать, что произведение двух чистых периодических
дробей, каждая из которых меньше единицы, есть также чистая
периодическая дробь.
58.	Доказать: если сумма двух правильных чистых периодиче-
ских систематических дробей меньше единицы, то для вычисления
ее достаточно найти чистую периодическую дробь, длина периода
которой равна наименьшему общему кратному длин периодов дро-
бей слагаемых.
59.	Доказать: для вычисления разности двух чистых периоди-
ческих систематических дробей достаточно найти дробь, длина пе-
риода которой равна наименьшему общему кратному длин перио-
дов компонентов.
60.	Дана несократимая дробь, знаменатель которой не делится
на 3, и эта дробь обращается в чистую периодическую десятичную
дробь. Доказать, что период данной дроби есть число, делящееся
на 9.
61.	Дана несократимая дробь, знаменатель • которой — число,
взаимно простое с 5, и эта дробь обращается в смешанную периоди-
ческую десятичную дробь. Доказать, что последние цифры перио-
да и числа, стоящего до периода, или одинаковы, или отличаются
друг от друга на 5.
62.	Дана несократимая дробь, знаменатель которой — число
нечетное, и эта дробь обращается в смешанную периодическую де-
сятичную дробь. Доказать, что последние цифры числа, образован-
ного цифрами, стоящими до периода, и числа, образованного циф-
рами периода, — числа одинаковой четности.
63.	Доказать, что всякое нечетное число, не оканчивающееся
на 5, есть делитель числа, записанного в десятичной системе счис-
ления с помощью одних единиц.
64.	Доказать, что всякое целое число А есть делитель числа,
выраженного цифрой 9, повторенной конечное число раз, сопровож-
денной несколькими нулями (десятичная система счисления).
47
Обобщить задачу на случай любого целого систематического
числа.
65.	Доказать, что если дробь - при обращении в десятичную пе-
риодическую дает в периоде четное число цифр, причем цифры вто-
рой половины периода дополняют цифры первой половины перио-
да до 9, то число п есть делитель числа вида 10p + 1, где р — чис-
ло цифр в периоде дроби.
66.	Обыкновенная дробь, знаменатель которой — простое чис-
ло (десятичная система счисления) представлена в виде периодиче-
ской дроби, период которой содержит четное число 2п цифр. Дока-
зать, что сумма n-й и (k + м)-й цифр этой дроби равна 9 при любом
значении k.
67.	Доказать, что бесконечная десятичная дробь
0,1234567891011...,
полученная вписыванием после 0 всех натуральных чисел, не будет
периодической десятичной дробью.
§ 5. ИРРАЦИОНАЛЬНЫЕ ЧИСЛА
68.	Доказать иррациональность следующих чисел: ]/ 5; fr' 7;
у 12345,67: log., 5.
69.	Дано выражение:
N = 1 +------Ц----
Доказать, что N = К 2.
70.	Доказать, что сумма, разность, произведение, частное
(делитель не равен нулю) двух рациональных чисел есть число ра-
циональное.
71.	Доказать справедливость следующего утверждения:
а)	сумма, разность, произведение, частное двух иррациональ-
ных чисел может быть рациональным числом;
б)	сумма, разность, произведение, частное двух чисел, одно
из которых рациональное (не равное нулю), другое— иррациональ-
ное, не могут выражаться рациональным числом.
72.	Зная, что среднее арифметическое k первых цифр числа л
стремится к числу 4,5, доказать, что при этом число 10 — л обла-
дает этим же свойством.
73.	Доказать, что если а — рациональное (иррациональное)
число в десятичной системе счисления, то оно останется принадле-
жащим тому же множеству, если будет записано по другому осно-
ванию.
74.	Представить следующие иррациональные числа в виде си-
стематических дробей с пятью десятичными знаками: ]/* 5 — в
двоичной системе счисления, 2 — в троичной системе счисления,
48
15.	Доказать, что если корень натуральной степени из целого
положительного числа не есть целое число, то он не может быть и
рациональным числом.
76.	Доказать, что логарифмы целых положительных чисел, не
равных целой степени основания, есть числа иррациональные.
77.	Доказать, что арифметический корень натуральной сте-
пени из бесконечной непериодической систематической дроби не
может быть равен конечной систематической дроби.
78.	Доказать, что при извлечении квадратного корня из двух
рациональных положительных чисел, не являющихся точными
квадратами, не могут получиться одинаковые последовательности
десятичных знаков.
79.	Дано: а и Р — вещественные числа. Доказать:
а)	если | а | < р, то —Р < а < Р;
б)	если. —Р < а < р, то | а | < Р;
в)	| а + Р | < |а | + I Р I >
г)	| а — Р | > | а | — |Р|.
80.	Доказать методом математической индукции, что для лю-
бых вещественных чисел о^, а2, ...» справедливы соотношения:
а)	( ах -|- а2 + ••• I ’С I ai I I а2 I + ••• + I 1>
б)	| ах-а2 ... aft | = | ах | • | а2 | ... | aft |.
Г Л A В A III	'
КОМПЛЕКСНЫЕ ЧИСЛА. АЛГЕБРАИЧЕСКИЕ
И ТРАНСЦЕНДЕНТНЫЕ ЧИСЛА
§ 1.	КОМПЛЕКСНЫЕ ЧИСЛА
Введем следующие обозначения: Re (z), Im (z), arg г, | z|. Они
означают соответственно вещественную часть, мнимую часть, аргу-
мент, модуль комплексного числа z, а z — число, сопряженное г.
1.	Построить точки, изображающие комплексные числа:
а) 2; б) —5; в) V~2\ г) (—^, 0); д) —1 -f-i; е) 2 — 5ц ж) (-1,
1 \	.	л . л	л	л\
- ; з) coS O -|-t sin 0; и) cost -J- i sin -; к) 2 (cos, 4-1 sinr ;
л) 3 (cos л + i sin л).
2.	Найти алгебраическую форму комплексных чисел, которые
изображаются точками:
Лг (0, 4)1 А (-1. 2); А3 (-1, 1); Л4 (1, 0).
о	
3.	Представить в алгебраической форме следующие числа:
а) (-1, 2); б) (0, 3);	в) (-4,	0);	г)(-1,	?);	1
д) 2 V 2 (cos — + i sin	—'j; " е)	2]/ 2 (cos — л	i sin — д');	1
\	4	4/	\	4	4/
ч о ( л . . . л\	\ о /	2л	. . . 2л\
ж) 3 cos —р i sin — I;	з) 8	cos-]- t sin —	.
\	6	6/	\	3	3/
4.	Дано: arg z = —35°. Найти: а) формулу, по которой можно »
получить все аргументы г;
б)	наименьший положительный аргумент z;
в)	будет ли угол, равный 500°, аргументом z?
5.	Дано: arg z — ф. Чему равен arg z?
6.	Доказать, что для любых комплексных чисел справедливы
соотношения
] 2^1 1 — I I С I Z1 22 I I Z1 I + I Z2 I •
Выяснить, при каких условиях имеет место равенство.
7. Доказать тождество	'
I Z1 + *2 Г + I Z1 — г2 12 = 2 (| zx |2 + | z2 |2), где zx, z2 —
комплексные числа.
Каков геометрический смысл
этого тождества?
60
8.	Найти геометрическое место точек, изображающих комплекс-
ные числа:
а) | z | = а\ б) arg z = Л
О
9.	Найти комплексные числа z такие, что
| z | > | 3 - 4i | .
10.	Найти геометрическое место точек, изображающих комплекс-
ные числа г, удовлетворяющие неравенствам:
а)	|	z | < 3; б) | z j >3; в) |	z — 3i | <	5;
г)	|	z —	3 + i | < 3; д) | z — 2 — i | > 2;
е)	|	z	2i | <Z 3; ж) 2 <Z I z	| < 3;
з)	1	< |	z — 2 4- 4i | < 5.
11. Где расположены точки, изображающие комплексные чис-
ла, удовлетворяющие условиям:
а) | z — 5t | = 8; б) | z — 1 — i | < 4; в) | z — а | 4- I 2 —
- Ъ | = 5; г) lz- 1 |2 4-|z + 1 [2 = 4; д) | г | = | г - 1- ;
О
е) Re (z) > с; ж) Im (z) < с; з) 0 < Re (iz) < 1; и) | z | < Im (г) +
+ Re (г); к) log, | z —3 | >log, | z | ; л) log , ,|г~1.1,+ ^>
-з	г	Т 31г -11
м) 1 < | z Д-t |<2, — < argz< у-;н)2< |г |< 3, у <argz<y л.
12. Среди комплексных чисел, удовлетворяющих условию
| z — 5t | < 3, найти число, имеющее наименьший положительный
аргумент.
13. Представить в тригонометрической форме комплексные
числа:
а) 2; б) —5; в) i; г) —3i; д) 1 — i ]/3; е) 1 — i; ж) —3 (cos у—
— i sin — 'j;	з)	cos (-------------—'l	4-	i sin —	;	и) sin —	—	i cos	"	;
7 /	\	2 /	2	9	9
к) —2(cos — 4-t’sin —); л) 1 4-cos— л 4-isin—л; м) 1 —cosa 4-
\	8	8 /	5	5
4- i sin a, где	0 < a < л; н)	cos q>	— i sin q>;	0)	—cos	<p	4-	i sin q>;
n) —cos ф — i sin ф; p) 1 4- c°s a 4- i sin a.
14.	Доказать справедливость основных законов сложения и
умножения для комплексных чисел.
15.	Построить геометрическое изображение компонент и ре-
зультатов действий:
а) (2 4- 50 4- (1 — 30, б) (—3 4- 40 — (2 4- О-
51
16.	Комплексные числа г, и г2 изображаются точками, находя-
щимися в I и III координатных углах. Найти то тки, изображаю-
щие числа:
а) 21 4-г2; б) ?х 4-z2; в) \ г) zx 4-2.; д) zx — z2;
е) 2t — г2; ж) zx — г2; 3)	— z2.
17.	Выполнить действия:
а)	(а — а0 4- (За 4- 2Ы) — [(а — Ы) — (—5а — 10W)];
б)	(5 — 20 — (8i — 3).— [(2 — 40 — (3 4- 240 — 7].
18.	Найти необходимое и достаточное условие того, чтобы сум-
ма двух комплексных чисел а 4- Ы и с 4- di была бы: а) числом
вещественным, б) числом чисто мнимым.
19.	Найти необходимое и достаточное условие того, чтобы ком-
плексное число а 4- Ы было: а) равно своему сопряженному, б)
равно противоположному своего сопряженного числа.
20.	Найти все комплексные числа, каждое из которых сопря-
жено с самим собой.
21.	Выполнить действия:
_____	6
а)	(]ЛЗ - 0 (]Г2 - i ]/3); в) — ;
б)	( — 34- 8») • 20	r) -/~3-Н /Г.
22.	Найти х и у, считая их вещественными:
а)	(4 — 0 х (2 -|- 50 у = 8 4- 9t;
б)	(3 4- 0 х — (1 — 20 у = 7.
23.	Найти х и у из системы:
a)	fix — 2у = —0
|(1 4- 0 х — 2iy = 3-]- 0
б)	((1 — 0х—(I 4-0у = —1+ь
Ц—2 4- 20 х — 2у = —4.
24.	Решить уравнение:
а) | z | — 2z = — 1 — 80 б) 2 | 2 | —3z = 1 — 121.
25.	Найти точку, изображающую следующие числа:
a) z.2, + 0 б) ^1 — 2; в) -‘ — 2 —i; r) zf г 4-3 4- 5i, где
г2	z2
?! -- 2) 2 / cos — i sin 1 , z2 — 2]/~Z I cos	» sin ~ j*
52
26.	Доказать, что модуль произведения двух комплексных чи-
сел равен произведению модулей этих чисел, а аргумент — сумме
их аргументов.
27.	Доказать формулу Муавра (cos <р +1 sin ф)и = cos n<p -J-
4- i sin n<p для любого целого n.
28.	Найти модуль частного от деления любого неравного нулю
числа на сопряженное ему.
29.	Доказать, что если два комплексных числа с ненулевой
мнимой частью таковы, что их произведение и сумма — веществен-
ные числа, то они сопряжены. Верно ли это утверждение, если мни-
мая часть комплексного числа равна О?
30.	Найти все комплексные числа, каждое из которых сопряже-
но: а) со своим квадратом, б) со своим кубом.
31.	.Вычислить: a) in, б) in i "+1 -f-1"+2 -|- in+3, где n — це-
лое число.
32.	Найти наименьшее натуральное значение п, при котором
(1 — ij" окажется положительным числом.
33.	Определить и из условия (1	1)“ = (1 — 0"» если п —
целое число.
34.	Вычислить: а) (1 — i)*, где k — целое число; б)
где п > 2 — целое число.
35.	Доказать, что всякая целая положительная степень
комплексного числа есть число комплексное.
36.	Вычислить:
37.	Вычислить z" + — > если г + — = 1, где п —целое число.
7П	7
оотт	2 /	7	. . 7 \	3 /	5 л
38.	Даны числа = — cos — л + i sin — л ,	= — cos — 4-
+ i sin — 1 Найти Zi , zl,
9J
39.	Составить формулы, выражающие cos nx и sin nx через
cos x и sin x.
Выразить через cos x и sin x: a) cos 2.v; 6) sin 2x; в) cos 3x;
r) sin 4x.
40.	Выразить tg nx через tg x, где n — целое положительное.
53
41.	Вычислить:
(1 — t/ З)12 —(1 + t/ з)8
(-1+Оы
42.	Найти аргумент комплексного числа zr = z2 — z, если
z = cos ф + i sin <p.
43.	Доказать следующие равенства:
a)	= 1 - tg2cc + c" tg4“ - - +л>где A= (-
n—i
при n — четном, A — (— 1) 2 C"7* tgn-1a при n — нечетном;
6)	=c"tg a -c"tg3a + c«tg5a+-+A>где
л—2	n—1
Л = (— 1) 2 Cn~? при n — четном, A = (— 1) 2 tgna
при n — нечетном.
44.	Найти сумму:
a)	sin х + sin 2x 4- ... 4- sin nx;
6)	cos x + cos 2x + ... + cos nx.
45.	Вычислить сумму S = 1 4- z 4- z2 4-... +zn~l, где z =
2л	2л	/
= cos — 4- i sin —•
n ‘ n
46.	Доказать, что все значения 1 являются степенями одного
из них.
47.	Доказать, что совокупность всех значений У 1 замкнута
относительно действий умножения и деления.
48.	Доказать, что все значения z, где z — комплексное число,
можно получить, умножая какое-нибудь одно значение этого корня
на все значения у 1.
49.	Показать, что число
2k л . . . 2k л
е — cos-------И * sin —
п	п
(где k > 1, п 2 — целые числа) является первообразным корнем
степени — из единицы, где d — наибольший общий делитель чисел k
d
и п.
50.	Найти все значения корней и построить их геометрическое
изображение:
а)^2ГГ; б) ^8; в) ^^27; г) ^Т; д) ^2^2?; е)
6 Г 1 — t ~
ж) ; з) ]/	|/"з + i .
54
51.	Найти корни уравнения Xе = У 3 + i и показать, что им
соответствуют вершины правильного многоугольника.
52.	Вычислить:
_____625
(-3 + 4Z)2
5 + 6/ДЫ
6 — 51/
|0/ (3	3 + 4) — t(4 /3 — 3)
53.	Решить уравнение
x*+x54-x44-x34-xa-]-x + l = 0.
§ 2.	АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ ЧИСЛА
В этом параграфе под словом поле будем всюду понимать
числовое поле. Число г называется алгебраическим отно-
сительно поля £2, если оно является корнем некоторого полинома
ненулевой степени над данным полем.
Число, не являющееся алгебраическим относительно поля
£2, называется трансцендентным относительно £2.
В частности, если £2 есть поле рациональных чисел, то слова
«относительно поля £2» обычно опускают и говорят просто об алге-
браическом или трансцендентном числе. Мы будем поступать также.
Пусть £2 — некоторое поле и а — некоторое число. Под [£2,
а] будем понимать поле, порожденное множеством, состоящим из
£2 и а.
54.	Доказать, что всякое число, являющееся корнем полинома
с целыми коэффициентами, является алгебраическим и обратно.
55.	Доказать, что всякое комплексное число является алгебра-
ическим относительно поля вещественных чисел.
56.	Доказать, что алгебраическим будет всякое число, получаю-
щееся из рациональных чисел при помощи действий сложения,
вычитания, умножения, деления и извлечения корня.
57.	Зная, что число ар есть трансцендентное число, если а и
Р — алгебраические числа, р — иррациональное число, а#=1,
а 0 (теорема Гельфонда — Шнейдера), доказать, что все деся-
тичные логарифмы рациональных чисел, не являющиеся сами ра-
циональными числами, являются трансцендентными числами.
58.	Доказать, что все числа вида 1g k являются трансцендент-
ными, где k — целое число, большее 1 и отличное от натуральной
степени числа 10.
59.	Доказать, что cos 20° — число алгебраическое.
60.	Доказать, что sin 10° — число алгебраическое.
55
61.	Доказать, что если t—трансцендентное число относитель-
но поля й, то всякое число вида , где f (х), g (х) — полиномы
&(0
над Й, тоже трансцендентно относительно й.
62.	Определить степень числа г = --К? относительно поля
рациональных чисел и найти числа, сопряженные ему относитель-
но этого поля.
63.	Определить степень числа
2 /Т
относительно:
а)	поля рациональных чисел,
б)	поля [R, У2], где R — поле рациональных чисел,
в)	поля вещественных чисел,
г)	поля комплексных чисел.
64.	Для числа
1 з\
2 ~ Т 1 ~/
найти числа, сопряженные с z относительно поля рациональных
чисел.
65.	Найти необходимое и достаточное условие, когда число z
будет алгебраическим относительно поля Q первой степени.
66.	Найти степень мнимого числа z и все числа, с ним сопряжен-
ные относительно поля вещественных чисел.
67.	Найти степень числа z и все числа, с ним сопряженные
относительно поля рациональных чисел:
а) г = /3 + V2;	6)z = ^-i^;
68.	Найти степень числа z и все числа, с ним сопряженные
относительно поля вещественных чисел:
a)	+
69.	Какой вид имеют элементы простого алгебраического расши-
рения:
а) [7?, КЗ], б) [/?, f/2], в) Ц?, К2,оК5], г) [/?, Л, д) [/?,
^3 ], е) [/?, V~2 + J/'З], ж) ]£, У~2 +	1, где R — поле ра-
циональных чисел.
56
70.	Пусть /? — поле рациональных чисел, I = х—.	Пока-
зать, что л С [/?, /], и записать его в виде —, где f (х) и g (х) —
&\ч
полиномы над R.
71.	Какой вид имеют элементы простого алгебраического расши-
рения [D, Л, где D — поле вещественных чисел.
72.	Пусть а = / 3 — одно из значений кубического корня.
Образует ли а) множество элементов вида a + ba, где а, b — ра-
циональные числа, простое алгебраическое расширение поля R
рациональных чисел; б) множество элементов вида а + Ьа2, где
а, b — рациональные числа, простое алгебраическое расширение
поля R рациональных чисел?
73.	Показать, что множество чисел вида а + Ьа, где а, b —
рациональные числа и а — один из корней полинома р (х) = х2 —
— х + 3, образует простое алгебраическое расширение поля ра-
циональных чисел.
74.	Пусть R — поле рациональных чисел, a Q = V 5 1.
Доказать, что й есть простое алгебраическое расширение поля R,
и найти какЬй-нибудь примитивный элемент.
75.	Пусть R — поле рациональных чисел, Q2 = fK 2, У3, Л-
Доказать, что й2 есть простое алгебраическое расширение R, и
найти какой-нибудь примитивный элемент.
76.	Освободиться от иррациональности в знаменателе следую-
щих выражений:
а) 2^~5 + 1	. б) 13#Т-1)	^25 + уг5~-2
,/'25 + у/Т+2’	^25 —	+ I ’
.	/7+1	. „ч 23	. .	4
г)  	> Д) — з > е) —	—>
/7+/7—1	1+/2+2/4	1 + /2 — УЗ
Ж)—4?=—7=‘> 3) ~	5—“=; и)	—+-1 ir-------->
1—У2 + /2 у 2— 1 + У2 У3 + у9+р27 + 3
2 + /2 + /3 + У‘б ‘
77.	Освободиться от иррациональности в знаменателе:
а)	—где а — корень уравнения х4 — х3 4 2х + 1 = 0;
б)	а2 + 2а —1, где а _ кореш, уравнения х3 + х2 + Зх + 4 = 0;
а® + 2а + 1
в)	—2а+ 4—, где а — корень уравнения х4 + 4х3 + 2х + 2 = 0;
а3 + 4а2 + 2
г)	——, где а — корень уравнения х3 — Зх + 1 = 0;
а + 1
57
д)
1
а+ 2’
где а — корень уравнения лл — 2v — 2 = 0;
е) ----——, где а — корень уравнения х3 + 3%+ 1 =0,
а2 + 2а — 1
§ 3. ЧИСЛОВЫЕ КОЛЬЦА И ПОЛЯ
Определить, является ли кольцом, полем:
78.	Множество натуральных чисел.
79.	Множество, состоящее из 0 и натуральных чисел.
80.	Множество целых чисел.
81.	Множество положительных рациональных чисел.
82.	Множество нечетных чисел.
83.	Множество четных положительных чисел.
84.	Множество целых чисел, кратных k, где k — число нату-
ральное.
85.	Множество чисел 0; ±2; ±4; ±6; ...;	... .
86.	Множество чисел 0; ±3; ±6’; ...; ±3п; ... .
87.	Множество 0; I2; 22; ...; п2; ... .
88.	Множество 1; ±3; ±32; ...; ±3"; ... .
89.	Множество рациональных чисел.
а
90.	Множество рациональных дробей вида где k — целое
положительное число, а и b — рациональные числа, причем b 0.
ах-\-Ь
91.	Множество дробей вида где a, b, с, d — рацио-
нальные числа, end одновременно не равны 0.
92.	Множество дробей вида
ах2к + Ьхк + с
aiXim +	+ Ci ’
где а, b, с, аг, Ьг, сг — рациональные числа и alt bt, сг — одновре-
менно не равны 0.
93.	Множество действительных чисел.
94.	Множество чисел вида р q 2, где р и q — любые целые
числа.
95.	Множество чисел вида а У 2 + b У 3, где а и b — любые
целые числа или равные нулю.
96.	Множество чисел вида а У2 Ц- ЬУЗ -|-с У&, где а, Ь,
с — любые целые числа.
97.	Множество чисел вида аУ~- где a, b, с, d — любые
c + dV2
целые числа, end одновременно не равны нулю.
98.	Множество комплексных чисел.
99.	Множество чисел вида ai, где а — любое вещественное
число.
58
ГЛАВА IV
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
Равенство, верное при всех допустимых значениях входящих
в него букв, называется тождеством.
Примерами тождеств могут служить следующие равенства:
1) л? — 2ху 4-у2 = (х — у)2; 2) *2~у' = ~ у> Iх + У), ПрИ
#= 0; 3) 1g х2 -}- 1g (х — I)2 = 1g (х2 (х — 1)21 при х =4= 0 и х =# 1;
4) х —у = х2 4- ху 4- у2 при х =# у; 5) ху = Ух — У у при
х О, У О’» 6) 1g х 4- 1g у = 1g (ху) при х > 0, у > 0.
Множество допустимых значений букв, входящих в правую
часть тождества, может совпадать со множеством допустимых
значений букв, входящих в левую часть этого тождества (см. при-
меры тождеств 1, 2, 3), а может и не совпадать с ним (см. примеры
тождеств 4, 5, 6). В первом случае тождества иногда называют а б-
солютными тождествами, а во втором — неабсолют-
ными тождествами.
Замена одного выражения другим, тождественно ему равным,
называется тождественным преобразованием.
Если два выражения абсолютно тождественны, то замена одно-
го из них другим не изменяет множества допустимых значений букв,
входящих в заменяемое выражение.
Если же два выражения неабсолютно тождественны, то замена
одного из них другим изменит (сузит или расширит) множество
допустимых значений букв, входящих в заменяемое выражение.
Нет нужды отказываться от осуществления таких преобразований
там, где они могут оказаться полезными. Однако необходимо да-
вать себе отчет в особенностях этих преобразований, хотя их также
принято называть тождественными.
Во всех задачах настоящей главы рассматриваются алгебра-
ические выражения в области действительных чисел. При решении
задач следует обращать внимание на множество, в котором рас-
сматриваемые выражения имеют смысл.
§ 1.	ДЕЙСТВИЯ С МНОГОЧЛЕНАМИ
1.	В многочлене f (и) = н3 4-2м2 — Зи 4-5, сделав замену
и -- х 4- 2у — г, вычислить коэффициент при х2.
2.	Доказать тождество
(а2 4- &2) • (с2 4- d2) = (ас — bd)2 4- (be — ad)2.
3.	Доказать тождество
(а2 4 Ь2 4- с2) (т2 4- п2 4- р2) = (ат (- Ьп 4- ср)2 +
4- (сп — Ьр)2 4- (ар — ст)2 4- (ап — Ьт)2.
59
4.	Если а, b, с, d — положительные действительные числа
+ ft4 + о4 +	= 4abcd, то а — b = с = d.
5.	Если х + у + г = 0, то х3 + у3 23 = Зхуг.
6.	Если a -f- b + с = 0, то
(а2 Ь2 + с2)2 = 2 (а4 + ft4 4- с4).
7.	Если (х2 + у2 + г2) (а2 4- ft2 4- а2) = (ах 4- fty 4- cz)2, то
X	У	Z	1
— = — = —, где а, &, с, х, у, z — действительные числа.
а	b	с
8.	Если (а + Ь 4- с)2 = 3 (Ьс 4- са 4- aft), то а ~ b — с (а, Ь,
с — действительные числа). ’
9.	Если s = а 4- b 4- с, то
(as 4- be) (bs 4- са) (cs 4- ab) — (b + c)2 (c 4- a)2 (a 4- ft)2.
10.	Если s = a 4-—» to s2 (s2 — 4) 4- 2 = a4 •
a	a*
11.	Доказать, что xy (Зх 4-2) (5y 4-2) есть разность квадра-
тов двух целых многочленов с целыми коэффициентами.
12.	Многочлен 2х2 — 21ху — 11у2 — х 4- 34у — 3 разложить на
множители первой степени с целыми коэффициентами относитель-
но х и у.
13.	Если х2 4- z2 = а2; у2 4- z2 = ft2, то ft2x4 — a2y4 4- (a2 —
— ft2) z4 = a2ft2 (a2 — ft2).
14.	Разложить на множители первой степени с целыми коэф-
фициентами многочлен х2 — 5ху 4- 4у2 4-х 4- 2у — 2.
15.	Не перемножая двучлены, представить в каноническом виде
произведение (х 4- 2) (х 4- 3) (х — 5).
16.	При каком условии трехчлен ах2 + Ьх 4-е в поле действи-
тельных чисел является квадратом двучлена первой степени?
17.	Найти условия, при которых многочлен
ах3 4- ftx2 4- ех 4- d
является кубом двучлена первой степени.
18.	Найти коэффициенты А, В, С, D, при которых многочлен
f (х) = х4 4- ^х3 4- Вх2 — 8х 4- 4
будет полным квадратом многочлена <р (х) = х2 4- Сх 4- D.
19.	Известно, что сумма коэффициентов одного многочлена
равна т, другого п. Найти сумму коэффициентов многочлена,
являющегося произведением двух данных многочленов.
§ 2.	РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ И ТЕОРЕМА БЕЗУ
Разложить на множители над полем действительных чисел.
20.	х4 — х2 (а2 4-1)4- а2.	22. х4 4- 5х2 4- 9.
21.	х3 4- (а — 1) х 4- а.	23. а5 — 4а3 4- 8а2 — 32.
60
24.	х2у + ху2 + х2г 4- xz2 4- у2г -|- yz2 4- 2xyz.
25.	х2у 4- ху2 4- Л 4- xz2 4- y2z 4- yz2 4- 3xyz.
26.	х5 4-х3 4-х.
27.	х4 — х3 -|- 2х2 4-х — 3.
28.	х4 4- х3 4- Зх2 4- 2х 4- 2.
29.	х8 — х4 4- бх3 — бх2 4- 9х — 9.
30.	х’ — х® — х5 4-х4 — х3 4-х2 4-х — 1.
31.	х4 4-4у4.
32.	Разложить на множители над полем рациональных чисел
х3 4- х 4-1.
33.	х4 4-х2 4- 1.	35. X4 4-х2 4-3.	37. х* 4-Зх2 4-3.
34.	х4 4-1.	36. х4 —х2 4-2.	38. хв 4-27.
39.	Разложить на множители над полем рациональных чисел
1х12.
Решить задачи, используя теорему Безу.
4О.	Если многочлены f (х) и ср (х) не делятся на многочлен
ф (х), то может ли сумма этих многочленов делиться на ф (х)? Если
может, то при каком условии?
41.	При каком условии сумма двух многочленов делится на
х— 1, если каждый многочлен не делится на х— 1?
42.	При каком условии сумма двух многочленов делится на х2 4-1»
если каждый многочлен не делится на х2 4- 1?
43.	Если каждый из многочленов f (х) и <р (х) не делится на мно-
гочлен ф (х), то может ли произведение этих многочленов делиться
на ф (х)?
44.	При каком условии произведение двух многочленов делится
на х2 — 1, если каждый многочлен не делится на х2 — 1?
45.	Найти два таких многочлена, чтобы каждый из них не де-
лился на х2 — Зх 4- 2, а произведение их делилось бы на х2 — Зх 4-
4- 2.
46.	Не производя деления, установить, делится ли1 выражение
(х3 — 8)5 4- (х2 — 4)3 на двучлен (х — 2).
47.	Не производя деления, установить, делится ли выражение
(х4 — Юх2 4- 16) 4- (х4 — Их2 4- 24) на х2 — 8.
48.	Найти условие делимости (х 4-1)"1 4- (х — 1)т на х, где
т — натуральное число.
49.	Доказать, что (ах 4- by)3 4- (Рх 4- ау)3 делится без остатка
на (а 4- Ь) (х 4- у).
50.	Доказать, что (х2 — ху 4- у2)5 4- (х2 4- ху 4- У2)8 делится
без остатка на 2х2 4- 2у2.
1 В данной задаче и последующих имеется в виду деление нацело.
61
51.	Определить, делится ли выражение (х2 х — I)21 4-
-|- (х2 — х 4- 1)2я на х2 — х.
52.	Делится ли многочлен (х 4-1)2я— х2я— 2х—1 на 2х34-
4-Зх2 4-х?
53.	Показать, что произведение (хт—1) (х"1-1 — 1) (Xя1-2 — 1)
делится на произведение (х — 1) (х2 — 1) (х3 — 1) при т > 2.
54.	При каком значении % выражение (х8 4-1) (х 4- 1) 4-
4- к (х4 — Зх2 4-1) разделится на х2 4- 1.
55.	При каком значении а и b многочлен а(х* 4-у* — х®у2) 4-
4- Ь (х — у)2 х2у2 4- х* разделится на (х 4- у) (2х — у)?
56.	Определить, делится ли многочлен х4"-2 — х4"-4 4- х4"-6 —
— ... 4-х2 — 1 на х4 — 1 (п — натуральное число).
57.	При каком п (п — натуральное число) многочлен 1 4- х2 4-
4-х4 4- ... 4-х2'1-2 разделится на многочлен 1 4-х 4-х2 4-... 4-
4- xn—1?
58.	Определить, делится ли многочлен 1 4-я4 4-*8 + ••• 4-я4"
на многочлен 1 4-х2 4-х4 -|- ... -{-х?п.
59.	Найти условие делимости многочлена хт +хт~1 -J-...4-
4- х 4- 1 на хл 4- хп~1 4-... 4-я 4-Д (тип — целые положитель-
ные числа).
60.	Определить, делится ли многочлен 1 а4 -|- а8 4-... 4-
4-авл-4 на многочлен 1 4-а2 4-а4 4-... 4-а4я-2.
61.	Определить, делится ли многочлен (х 4- 1)4я 4-х2" 4-4я 4- 1
на х2 4- 1 (и — натуральное число).
62.	Делится ли многочлен х4" -f-x4*4-1 4-х4с+2 4-x4<z+3, где
а, Ь, с, d — натуральные числа, на многочлен х3 4-х® -{-х 4- 1?
63.	Найти первые семь членов произведения (1 -|- х 4- & 4-
4-х3 4-... 4- хя-1) (1 — х 4- х2 — х3 4-... ± хя-1), где п — на-
туральное число.
64.	Найти первые семь членов разложения (1 4-х 4-х2 4-х3 4-
4-... 4-х”-1)2.
65.	Доказать, что 32я+2 — 2я+1 делится на 7 (п — натуральное
число или 0).
66.	Доказать, что 34я+4 — 43я+3 делится на 17 (п — натуральное
число или 0).
67.	Доказать, что 33я+2 4- 5-23г+1 делится на 19 (п — натураль-
ное число или 0).
68.	Доказать, что 32я+2 4- 2вя+1 делится на 11 (п — натураль-
ное число или 0).
69.	Доказать, что 52я+1 4- 2"+4 4- 2я+1 делится на 23 (п — на-
туральное число или 0).
70.	Доказать, что 32(я+1)  52я — 3’<+2.28я делится на 117 (п —
натуральное число).	,
71.	Доказать, что 11я+2 4-122я+1 делится на 133 (п — нату-
ральное число или 0).
72.	При каком условии 72я+4 — 24я+2 делится на 65 (п — нату-
ральное число)?
62
73.	Доказать, что при натуральном числе п, большем 1, выра-
жение 72л — 42л — 297 делится на 264.
74.	Доказать, что 5*72(л+1) -j-23n при натуральном числе п
делится на 41.
75.	Доказать, что 4"+1п — (я 4- 1) 4Л 4- 1 делится на 9 (я —
натуральное число).
76.	Доказать, что 240 4- 23® 4- 235-32 4-27-Зп 4-23-311 4-22 х
X З13 делится на 1892.
77.	Доказать, что 32л+1 4- 40я — 67 делится на 64 (я —
натуральное число).
78.	Доказать, чю при любом натуральном п выражение 62л4-
4-Зя+2 4- Зл делится на 11.
79.	Доказать, что при любом натуральном п выражение 10" 4-
4- 18я — 1 делится на 27.
80.	Доказать, что при любом целом п > 0 выражение 72л —
— 48я — 1 делится на 482.
Разложить на множители над полем действительных чисел.
81.	(х2 4- х)2 + 4 (х2 4- х) — 12.
82.	(х2 4- х)2 — 14 (х2 4- х) 4- 24.
83.	а2х2 4- а (36 4-а) х 4*26 (а 4- 6).
84.	Зх (у 4- z) 4- у (2х 4- 3z) 4- z2 4- 2 (х2 4- у2).
85.	(х2 4-х 4-1) (х2 4-х 4-2) — 12.
86.	(X2 4- 4х + 8)2 4- Зх (х2 4- 4х 4- 8) 4- 2Х2.
87.	(х2 4- х 4- 4)2 4- 8х (х2 4-х 4-4) 4- 15х2.
V 88. 2 (х2 4- бх 4-1)2 + 5 (х2 -)- бх 4-1) (х2 4-1) 4- 2 (х2 4-1)2.
У89. (х 4-1) (х 4- 2) (х 4- 3) (х 4- 4) — 24.
У90. (х 4-1) (х -|- 3) (х 4- 5) (х 4- 7) 4-15.
✓ 91. 4 (х 4- 5) (х 4- 6) (х 4- 10) (х 4-12) — Зх2.
92. Доказать, что (х — 1) (х — 3) (х — 4) (х — 6) -]- 10 поло-
жительно при всех значениях х.
93. Доказать, что (х -J- а) (х 4- 2а) (х 4- За) (х 4- 4а) -|- а4 есть
квадрат трехчлена.
94.	При каком значении h выражение х (х 4- а) (х -|- 6) (х 4-
4- а 4- 6) 4- 6 будет точным квадратом?
95.	х3 — 19х — 30.	99. х3 -|- Эх2 + 23х 4- 15.
96.	х3 — 7х — 6.	100. х3 — х2 — 21х 4- 45.
97.	х3 4-Эх2 4-Их —21.	’• 101. 27Х3 —27Х2 4- 18х —4.
98.	х3 4- бх2 4-Зх — 9.	102. х4 — х3 4-2Х2 4-х — 3.
103.	2Х4 4- 7х® — 2Х2 — 13х 4- 6.
104.	2Х4 — Xs — Эх2 4- 13х — 5.
105.	х4 — 2х® — Зх2 4- 4х 4- 4.
106.	х4 — 2х® — Их2 4- 12х 4- 36.
107.	х4 + 2х® — 16х2 — 2х 4-15.
108.	14х — 4 4- 27Х4 — Эх2.
109.	9хг 4- 4Х3 — 1 — 12Х4.
ПО. а5 — 6а4 4- 16а3 — 32а2 4- 48а — 32.
111.	а® 4-2а5 4-9а4 4- 16а3 4- 24а2 4-32а 4-16.
63
112.	x3 -j-	+ xyz 4- y2z — y3.'
113.	a2" — ain — 2a7" — a10".
114.	x3 4- 2y3 — 3xy2.
115.	x1 4- 6xJy -|- 8x2y2 — 6xy3 — 9y4.
116.	(y 4-z) (z 4-x) (x 4-y) 4-xyz.
117.	(x2 — y2) (x 4- y) 4- z (x 4- y)2 — z2 (x — y) — z3.
118.	xyz (x3 4- У3 + 23) — y3z3 —	— л?у3.
119.	б3^ (b — c) 4- c3a3 (c — a) 4- a363 (a — b).
120.	c2 (a 4- b) 4- b2 (c 4- d) 4- be (a 4- d) 4- ad (b 4- c).
121.	2 (a2b2 4-a2c2 4- 62c2) — (a4 4-64 -f-c4).	3
122.	x (y2 4- yz 4- z2) 4- у (z2 4- zx 4- x2) 4- z (x2 4- xy 4- y2).
123.	x54-x4y 4-2y5— x2y3—xy4—2x3y2. Доказать, что данный
многочлен будет неотрицателен при всех положительных значени-
ях х и у.
124.	(х2 — ху 4- у2)3 4- (х2 4- ХУ + У2)3.
125.	х3 4- Зху 4- У3 — 1-
126.	х3у2 4- y3z2 4- z3x2 — х2у3 — y2z3 — z2x3.
127.	х3 4- ху (х 4- у) 4- у3 4- yz (у 4- г) 4- z3 4- zx (х 4- г).
128.	x3y2z 4- y3z2x 4- &х‘У — xy2z3 — yz2x3 — zx2y3.
129.	x8y3z2 4- y5z3x2 4- z^y2 — x2y3z8 — у Ух8 — z2x3y5.
130.	Доказать, что многочлен (х 4- I)4 — х4 — 2х — 1 делится
на х (х 4- 1) (2х 4- 1)> и найти частное.
131.	Доказать, что многочлен (х — 2)4 4- (х — I)2 — 1 делится
на (х — 1) (х — 2), и найти частное.
132.	Разложить на множители (х 4- у)5 — х8 — у8.
133.	Разложить на множители (х -|- у)’ — х1 — у7.
134.	Доказать, что х8 4- У5 — л4у — ху4 > 0 при всех положи-
тельных значениях х и у.	i
135.	(a — 6)s 4- (Ь — с)3 4- (с — а)3.	’
136.	(а 4-й 4-е)3 — (а3 4- & 4-е3).	1
137.	а (Ь 4- с)2 4* 6 (с 4- а)2 4- с (а 4-	Ь)2	—	Aabc.
138.	а (Ь 4- с — а)2 ~г b (с 4- а — Ь)2	-|- с (а	4-	b — с)2 4-	,
4- (Ь 4-е — а) (с 4- а — Ь) (а 4- 6 — с).
139.	(Ь с — а) (с 4- а — Ь) (а 4- b — с) 4- а (а — Ь 4- е) (а 4-	।
4-6 — с) 4- b (а 4-6 — с) (6 4-е — а) 4- с (Ь 4- с — а) (а — b 4-е).
140.	х (у2 — z2) у (z2 — х2) 4- z (х2 — у2).
141.	(6 — с) (Ь 4- с)2 4- (с — а) (с -|- а)2 4- (а — Ь) (а 4- 6)2.
142.	(а 4- b 4- с) (Ьс 4- са -|- ab) — abc.
143.	(а 4-6 4-е)3 — (6 4-е — а)3 — (с 4- а — 6)3 — (а 4- 6—с)3.
144.	а (6 — с)3 4- 6 (е — а)3 ~(с (а — Ь)3.	4
145.	х (у 4- z) (у2 — z2) 4- у (z 4- х) (z2 — х2) 4- z (х 4- у) (х2 —
— У2)-
146.	(6	—	с) (6 4- с)3 4- (е —	а) (с -|- а)3	4- (а — 6) (а 4- 6)3.
147.	(а	4-6 4-с)4 — (а 4-6)4	— (6 4-с)4 - (с 4-а)4 + а4 4-
4-64 4-с4.
148.	а2	(6	4- е — 2а) 4- 62 (с	4- а. — 26)	-|- с2 (а 4-6 — 2с) 4-
4- 2 (с2 —	а2)	(с — 6) 4-2 (а2 —	62) (а — с)	-|- 2 (62 — с2) (6 — а).
149.	8 (а + 6 4- с)3 — (6 4- с)3 — (с 4- а)3 — (а 4- 6)3.
64
150.	(у — z)5 — (z — х)5 + (х — у)5.
151.	(а +	b +	с)5	—	(а5 + 65 + с5).
152.	(а +	b 4-	с)5	—	(Ь + с — а)5 — (с	+ а — Ь)'а	—	(а	4-
4* b с)°.
153.	а4 (Ь — с)	4-	fe4	(с — а) +с*(а —	Ь).
154.	а2 (а	4- Ь)	(а	с) (Ь — с) 4- Ь2 (Ь	+ с)	+ а)	(с	—	а) +
4- с2 (с 4- а) (с 4- Ь) (а — Ь).
155.	(Ь — с) (Ь+ с)4 4- (с — а) (с 4- а)4 4- (а — Ь) (а 4- fe)4.
156.	а2 (Ь — с)	(с 4-	а	— b ) (а	+ Ь — с) 4- Ь2 (с — а) (а	4- b —
— с) (6 4- с — а)	4- с2	(а	— Ь) (Ь	4- с — а) (с 4- а — Ь).
157.	а (Ь — с)5 4- b (с — а)5 4- с (а — fe)s.
158.	а3 (Ь — с)	(с —	d)	(d — b)	— Ь3 (с — d) (d — а) (а —
— с) 4- с3 (d — а)	(а —	Ь)	(Ь — d)	— d3 (а — Ь) (Ь — с) (с —	а).
159.	(b +c — a — d)i(b — c)(a — d) 4- (с 4- а — b — d)4X
X (с — а) (Ь — d) 4- (а 4- b — с — d)4 (а — Ь) (с — d).
160.	&W (b — с) (с — d) (d — b) — cW (с — d)(d—a)X
Х(а — с) 4- d2a2b2 (d — а) (а — b)(b — d) — a2b2c2 (a — b)(b — c)x
X(c — a).
161.	X8 4- y3 4- 2® — 3xyz.
§ 3.	НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ
И НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
Найти НОД разложением на множители или последовательным
делением многочленов.
162.	Зх2	— 4х 4- 1	и	4Х4 — бх3 4-х2.
163.	Эх4	4- бх2 4-' 1	и	Зх3	4- 2х2 4-1.
164.	2Х4 — Зх3 — 8х2 4- 12х и бх3 — 15х2 -|- бх.
165.	2Х3	4-х2 4-4х	2 и	2х® 4-х2	бх	3.
166.	Зх5	— х4 — Зх	4-	1 и	Зх4 -|- х3 4- х2	4- х — 2.
167.	2х® — 5х4 4- Эх3 — 7Х2 4-4х и 4х« — 12х* 4- 19Х4 — ISx3 4-
_|_ 4х2.
168.	1) ая 4-2a2 — а — 2, а3 — За2— а 4-3 и 2а3 — а2 — 2а 4.
+1;
2)	Зх3 — 7х2у 4- 5ху2 — у3, х2у 4- Зху2 — Зх3 — у3 и Зх3 4-
4- 5х2у -|- ху2 — у3.
169.	Найти НОД d (х) для следующих многочленов Д (х) и
f2 (х) и представить его в виде d (х) —	(х) А (х) 4- Д (х) В (х),
где Л (х) и В (х) — некоторые многочлены:
1)	/1 W = 4Х4 — 2х® — 16Х2 4- бх 4- 9,
Д (х) = 2Х3 — х2 — бх -|- 4;
2)	Д (х) = х4 — х3 — 4х2 4- 4х 4- 1,
Д (х) = х2 — х — 1.
Найти НОК.
170.	х3 4- Зх2 — х — 3 и х3 4- Зх2 4- х + 3.
171.	4Х3 — 8х2 4-Зх —б и 12Х3 4-4х2 4-9х 4-3.
3 Заказ 1089	65
172.	х4 — 2х® + 2х — 1 и х4 — 2х® + 2х2 — 2.г 4- 1.
173.	2х2 — х — 6, Зх2 — 7х 4- 2 и бх2 4- 7х — 3.
174.	хз _ 27, х2 — 15х + 36 и Xs — Зх2 — 2х + 6.
175.	2х2 — 23х 4- 11, 2Х3 — 5х2 — 196х 4-99 и 2х3 — Зх2 —
— 200х — 99.
§ 4. ДРОБИ
Сократить дроби.	
176.	а2 — За 4~ 2	р7 2аг — аЬ — № а2 _ 5а + 6 ‘	2а2 — 5аЬ 4- 362’
178.	+	_ 2	179 дП+ХЬП-Х_аП-ХЬП+Х а6 4“ 8	*	’ am+xbm~x — агп~хЬ,п+х'
180.	хп+г _ 2хп + хи-2	Зхл+1 — Юх" 4- Зх"-1 ’
	х”+2 — xn+l 4- хл~4 — хл~2'	' Зхл+1 — 8хл — Зх'8’1 '
182.	5х2— х — 4	'	183 З*2	+ 9 х3 — 1	х5 + 5х3 + 6
184.	х4 — х3 — х + 1	185	~Ь g2 + 2а6 + 2ас 4~ 26с х4 — 2х3 — х2 — 2х 4- 1	а2 — Ь2 — с2 — 26с
186.	а2 — ЗаЬ 4- ас 4- 262 — 26с	а4 — 16
	а2 — b2-}-2bc— с2	а4 — 4а34~8а2 — 16а 4- 16
188.	х4 4-х2у2 4-У4 189> х84-х44-1 .	190> х84-х44-х24- (х — У) (*3 — У3)	х2 4- х 4- 1	х3 4- х2 4- х 4- 1 ’
191.	х3 — 1	192	— ^с3 + с3а — х4 4- х2 4~ 1	а2& — об2 4" №с — Ьс4 4" с2а — са2
193.	(X 4- У)7 — х7 — у7	J94.	X3 4- у3 4- Z3 — Зхуг (х 4- у)5 — х5 — у5 *	’ (х — у)2 4- (У — г)2 4- (г — х)2
195.	(а — 6) (а 4~ 6 4~ с) (а 4~ 6 — с)
	2а2&2 4- 2а2с2 4- 262с2 — а1 — Ь4 — с4 ’
196.	(а 4- 6 4- с)4 — (а 4- b)4 — (b+ с)4 — (с 4- а)4 4~ Д4 4- Ь4+с4 12аЬс (а 4- b 4* с)
197.	d(a — b)(b — c)+b(a — d)(c — d) с (а — 6) (с — d) 4- а (6 — с) (с — d)
198.	(х2 — у2)3 4~ (У2 —‘ z2)3 + С?2 — *2)3 (х —У)34-(у —г)34-(2 —х)3
199.	ат-п тп~1 _р т-1п _|_ ап-т тп^а171^ 4- 2 4-/wr1a,I”/n
Произвести действия.'	
	.	1	,	\	3	
	Х24-Зх4-2	(х-Н)(х4-2)(х + 3)’
66
201.	(+ aW—-----------лА — (+ лА (—---------а
\а + х / \а — х ] \а + х J \а — х t
^+-^~
202.	а Ь + с. . Г1 4-
1	1	[	2bc ]’
а Ь-\-с
203.		----4----------------4-----------------------------.
а (а 4-6) (а 4-6) (а 4-6 4-с)	(а 4- ft 4- С) (а 4- 6 4- с 4- d)
204.	—!------1---------!------1-------5--------1-
а (а 4-1)	(а4-1)(а4-2)	(а4-2)(а4-3)
--------------+---------!----.
(а + 3)(а + 4)	(а4-4)(а4-5)
205.	-L-4--1- +-^~ + — 4--^-+- 16
1—	X 14- х 1 4-х2	1 4-Х4	1 +Х8	1 + х1в
206 а + 3  fl2 —	2a3 — а (1 — 5a) — 1
’ 2a—1	4a2 — 4а 4- 1	8а3—12а2-|-6а — 1 ’
207.		1--- : —----------------.
208.	Доказать тождество
1	2. 4- 1+2 + (Д+!)(>+!) | (а+!)(& + !) (с4-1)
a ab	abc	abed
(а 4- l)(d+l)(c + l)(d4-l)
abed
209.	Доказать тождество
а2(с —Ь) ,	Ь2(а — с) (	^(Ь — а)
Ьс	ас	ab
а(с — Ь) ,	ь (а — с)	с (Ь — а)
Ьс	‘ ас Н	ab
= а 4- b 4- с.
210.	Доказать тождество
а2 (х — Ь) (х — с) . Ь2 (х — с) (х — а) . с2 (х — а) (х — Ь)_ 2
(а — Ь) (а — с) (Ь — с)(Ь — а) (с — а)(с — Ь) Х '
211.	Доказать тождество
--------е----------+------------ь.--------+------------1---------
(х — а) (а — Ь) (а — с) (х — Ь) (Ь — а) (Ь — с) (х — с) (с — а) (с — Ь)
________________________	х
(х — Ь) (х — а) (х — с)
3*
67
Произвести действия.
212.
М . У\
у2 ха \ у х)
213 ( а*+аЬ . а*ь + аЬ* м*\ . /д4 —д —3д3 + 3д2 ,
\ 'а2 + Ь2	а* — b* )	\ а3Ь — Ь*
• Д4 + fl2 — 2д3 \
a2b2 + д/?3 + 64 J
2|^ х	. х2 + * — 1 1 [ х2 — х —-1____2х3
X2 — 1	X3 — X2 + X — I X3 + X2 + X + 1 X4 — 1 •
215в	(х-11у + 1)2 + (2х + У-3)2 _ 2х-[-у — 3 .
2х2 —21ху—Пу2 —х + 34у —3 х—Пу + Г
21g /	1 — х х3 + х — 2	\ . /	1 +х ___1—х+ХА
\х2 + х3 —х4	х6 — х3—2х2 — х/ \х3 + х44-х6 х5 /
2	2
-с-г-1УгЧЧ-+(“ + 6+с>а-
— Н— J ~F — “F —
b с J Ьс ас ab
218 х5 + 2х*+х(1-/5') + 1_____________1
4(х4 + х3 + х2 + х+ 1)	2(х2+1)4-л-(1+/5)’
219.	а .	(g + &Hg + с) _i_	.	<6 + с) (6 + Д) । с	.	(с	+ а) (с + Ь)
(д — Ъ) (а — с)	(Ь — с) (Ь — д)	(с	— а)(с — Ь) *
220.	а2 •	(а +	+ с)	.	bz	. (Ь + с) (Ь + а)	,	с2 ,	(с + л)(с+6)
(а — Ь) (а — с)	(Ь — с) (Ь — а)	{с	— а) (с —Ь)
221.	Доказать, что если сумма двух дробей равна 1, то квадрат
первой дроби, сложенной со второй, равен квадрату второй дроби,
сложенной с первой дробью.
ау—Ьх сх—аг	Ьг—су х у г
222.	Доказать, что если ---— —~— =--------> то
’	с о а а Ь с
ялп г а b	с? Ч- fe3 а тт
223.	Если — — —, то----------- —. Доказать.
b с ь2 + с3 с
лпл г?	a — b b — с с—а
224.	Если х —--------; у —-; z =---, то
а + Ь Ь-[- с с -|- а
(1 4- х) (1 + у) (1 4- z) = (1 — х) (1 — у) (1 — z). Доказать.
68
225.	Если	= ... = Ч то
Ъг ьа b3 bk
(м = Pb?+ mb% + lb$ + ...+sb% ’
где р, tn, t, ...» s — натуральные числа. Доказать.
§ 5. РАДИКАЛЫ
Число х называется значением корня n-й степени из числа А
или просто корнем n-й степени из А, если хп = А. В этом случае
употребляется обозначение при помощи знака радикала
п/~л
х = у А.
Действие нахождения корней называется извлечением
корня. Необходимо иметь в виду, что действие извлечения корня,
вообще говоря, неоднозначно, т. е. возможен случай, когда xt Ф
х2, но HXj= у^А, и х2 = у^ Л (т. е. х? = х? = Л).
Если Л есть действительное неотрицательное число, то всегда
существует, и притом единственное, значение корня у7" Л, само явля-
ющееся действительным неотрицательным числом. Это значение
корня называется арифметическим.
Нередко употребление знака Л ограничивают лишь арифме-
тическим значением корня. В частности, так будет сделано в настоя-
щем параграфе. Во всех задачах в выражении вида У А А будет
предполагаться действительным неотрицательным, а само УА
арифметическим значением корня из Л (тем самым выражение / Л
всюду будет иметь вполне определенный однозначный смысл).
В связи со сказанным следует всегда иметь в виду, что при про.
извольном действительном Л мы должны считать УЛ* = | Л |
(так как при отрицательном Л арифметическим значением корня
]/Т2 является число —Л = | Л |).
Все тождественные преобразования в задачах этого параграфа
осуществляются на базе обычных правил и свойств арифметических
действий и общеизвестных свойств действия извлечения корня,
непосредственно получаемых из исходного определения.
Пример. Найти значение выражения
л	— 4	1 f т . -| f п
А = —---------,' если х = I/ —h I/ —.
и имеют арифметические значения, если ~ > О,
— > 0, т. е. ти > 0.
tn
69
1) Преобразуем данное выражение, если т >* 0, п > О,
х2 = * 4- " + 2,
п т
Тогда
2п | т — и |
2п | tn — п |
tn + п — | т — п |
т — п । = т — п,
| т — п | = п — т,
л 2п (т — п)
если т > п,
если т <,п.
_______.	• = т — п.
т + п — т + п
Если т < п, А ------2Mn-m)----=
т + п — п + tn	tn
2) Преобразуем данное выражение, если т < 0, п < 0. Для
этого случая надо учесть, что
Vтп	= Vtn2+Vti2 = |/n| + |n|= — т — п,
поэтому
А = 2п | от — п |
(— т — п) — | т — п |
Тогда:
если т > п, А =---------------__ »(» —
—от—п—т+п	т ’
если т < п, А ==--g«(n —»»)-_ т _
— от — п —n-f-m
Вычислить1.
226. (4]/37j)v
227. (V745624T76)!.
1 Индекс внизу показывает, с какой точностью отыскивается данное выра-
жение.
228. (3 /О,О7)о>о1.
231.
3 /532
/й.
0,01
229. (/43|)г 230.
8	' 9
232. (/863)0>01.	233. (/4 + Г5')0>01.
234. (У 4 + V 2,5 )0)01.	235. (У5 + 2 V 3 )0,01.
Упростить выражения:
236	|	। /1331
/Т /17	/19 уТТ ’
237.	2 У//5^+3 У40 /12 — 2yi5/2L
238.	/176 —2/275 —/891 +/1584.
239.	//25 — 1 /245 — /180 + /80.
240.	У9 + /Т7- У9 — /17.
241.	У /23 —/Г• У /23 + /"7 + 6/ 5 /2“+ 7 X
X У 5/Г—7.
242.	30 У ± + З^у f+5 /144.
Освободиться от иррациональности в знаменателе.
243.	_ 2У_____244. -^-2У°- _.
/ 2 + / 3 + / 5	/5 + / 6 + / 7
245.		У-------246. 7 -  . J ,—.
3 + г2—/3	/з + ^9 + /27 + 3
247.	-т=--—---т=--(и вычислить с точностью до 0,01).
/ 10 +у 15 +/14 +/21
248.	-----7=~Ч------т=.
2 + / 2 + /3 + / 6
15
249.	--7=----;=-----7=---7=-----т=- (и вычислить с точностью
/Ю + /20 + /40 —/5 —/80 4
до 0,01).
250.
/ / а + У 5
/У ~а — /У
„С1 Ууа^уь 252 Гггз+^2
V У а + У b V 2 V 3 - У 2
71
253.		---- (и вычислить-с точностью до 0,01).
2-/з
254.	„	-—г-тг (и вычислить с точностью до 0,01).
2/ 2 +37з
255.	у—	—3	- (и вычислить с точностью до 0,001).
/2+)'5+|/2-у 5
256.	у 	———	— (и вычислить с точностью до 0,001).
/11 + I И- /11- у s’
257.
259.	260. ----!----.
/3+/ 2	(3-/1)5
А~К А..-в, где А > 0, В > 0, А2 > В.
2
Упростить выражения, применяя формулу преобразования слож-
ного квадратного радикала, доказанную в задаче 201.
262.	75— 12/21’.	263. V 4/2+ 2/6.
264. 4/ 7 + /48. 265. 4/ 6 + /20	266. 4/ 17+ 12/ 2?
267. ]/ 28 — 16/11	268. У 17 _ 4 /’э 4 4/5?
269.	У^/5 — Уз — V 29 — 12/К
270.	- -	1 __--------- 1---.
/7 — /24 + 1	/7 + У 24 — 1
271.	2 /з+Т/б-/ 13 + /48.
272.	I _г+/7 =. , _г+У V
273.	Z2x + 2/x2 —у2.	274. V+ 2 /№— 1.
72
275.	У Ь — ЧУаЬ — a*.
276.	(a -f- x2)2 + (a — x1)2 , где x = 4 (a — 1).
277.	Представить в виде разности двух радикалов
х =
Найти значение х при г = 2, а = 1.
278.	Доказать тождество:
1/2 (2а + f/a2 —t>2) У а — /а2^2 = J/(a + 6)3 — У(а — Ь)э,
если а > О, b > 0, а > Ь.
279.	При каком условии радикал Ут + Уа -]~УЬ 4- У~с
можно представить в виде суммы трех радикалов Ух +Уу +Уг~,
где х, у, z — положительные рациональные числа?
280.	Упростить У 8 + J/8 4- 1/20 4- ]/40.
281.	Упростить У12)/24 + ]/39 + 1/Ю4.
282.	Число 12 разложить на два множителя, один из которых
есть У5 +’|/3'+К2?
283.	Разложить 2 (х 4- у) на два множигеля, один из которых
есть
]/(%+ 1)2+(У+ О2 + l/(x-l)2-i-(y-l)2.
284.	Если - =	то УТа 4- УВЬ + УСс 4	=
а b с d
— "j/* (ct + b -J- c -j~ d) (^4 4~ В + C + Z?). Доказать.
Разложить на множители.
285.	yG? 4- Уху3 — Ух?у — У у4.
286.	(х — 1) Ух — (у — 1)Уу.
287.	(х 4- Ух -i 1) (х 4- I)2 4- (1 — У(х + I)3) (х 4- 1) 4-
288.	(1 4- х)2 — 2х — (1 — х)2.
73
289.	Упростить
1 f х3 —Зх + (х2—1). -?f X3 — Зх — (х2 — 1)У
У ----------------+ у ---------------,
где | х | >2.
290.	Извлечь квадратный корень из многочлена
(х2+4)-4(х+ -4 +12-
\ х/ . \ х /
Упростить выражения.
291 '/](3/ад)5 • (/ад4]3
5
а11
n2-J- П f q t 11 Л 1 /-г—
292.	/xm(m’+1)- /x2mt
(	г~	1- 1 -1
293. зУ^у2” — pz • х 3 у 3 : 2х2у2.
I	/ху	J
295.
x8n~18yz4
(X + у)2я
6
296.
Л 3/ а2-2а& + &2 , 3f а2 + 2а& + *2 \ (	°2
I]/-------------+ У-------^гь-----)
299. }/ 2 + /5 .
300 1/11 +3/Г + 2]/Г2+ )/5	301.	4 + 2у 3 -
ЗС0- V --------------2-----------•	г 10 + 6 КЗ-
302.	Доказать, что /20+ 14/2+ /20—14 |/2 =4.
74
303.	Доказать, что 1^51/2 + 7— уЛ5/2 -7=2.
304.	Показать, что если а, Ь, с — рациональные числа и
а + b у/ 2 + с У 4 — 0, то а — b = с = 0.
310. Доказать тождество
если а > 2.
Упростить выражения. Указать ту область определения этих
выражений в множестве действительных чисел, в которой они сами
имеют действительные значения.
75
-2
— J^x2 8x -h 16.
5 I
2	”9	1	r_______ ,_________
3I4	* — *__________(x _	2 . %2 /—	1 T &
(x + l)(x2 + l) \	1 + X2)	’	14-x2
Найти значение выражений.
322.	||Ц1 + /Н)5-’г(1 — ]/а)5] - (а/5 — I)2} : 2а2 при
а = 5 — ]/5.
76
/5-3
2
2
2
(1 —X2)	2 + 1	:
2
£
при x — 2a2 (1 + а)"1, если
£ £
(m + x)2 +(m —x)2
324.
(1-
> 2
2
a
325.
при X =
2mn
2	2
(tn + x) — (tn — x)
326.
прих = -^-
r 6(1+ /n2)
327.
У a + bx — У a — bx
1 _L __
(x -j- d) (x — d) -J- (x d)
при x = a ———, tn > 0, n > 0.
m3 — n3
£
(x-a)3
i
328.
_ L _ L
(x2 + a8) 2 + (x2—a2) 2
—2
J
329.
при x = a
2	2
_(x2 + a2)	— (x2 — a2)
9	9	9^	9
(a + x) (x + 6)	+(a-x)	(x-b)
1 Я-8
_(a-}-x) 2 (x + 6)
при x = Vab, a> b>0.
26 /х2 — I
330. - — ~ - - при
x — ]Лг2 — 1
331. i пр„
x =
x =
2	2	2
— (a — x) (x — b)
, гдеа>0,д>0.
, где a>0, b>0.
2	2
332. (1 — ax) (1 + ox)-1 (1 + bx) (1 — bx)
при x — a
1 jr> где 0 < a < b < 2a.
77
ззз. —4——	при х = У£.
1 + )/ 1 + 2х 1 — pl — 2х	4
334.	Уgjx	при х = 12* +	где а и
Уа + х — Ух + Ь	4	4z2	2
£
Ь — действительные числа и z > | а — b |2.
L _L
335.	(1 + х-x)-24- (1 — л"1)"2 при х '= (1 — а-1)2 (1 + а-1) 2,
если а > 1.
336.	[x-z + a Зх 3) 2 +\а-24-а Зх 3) 2
/ 2_	£\£
при х = \Ь3 —а3 )2.
337.	(х-1 + а-1) (х + а)п — Ь-1^1
п / п п \—1
при х = аЬп+'\а+{— bn+l) .
338.	ху-Ух—при х _ ± L + г, у = 11Ь + 1\
ху + Ух2 — 1У>2 — 1	2 ' а'	2 \	ь '
339.	Числа х, у удовлетворяют равенствам:
(х + ]/х2 + а2)(у + /у2 4-й2) = с2, г = х/у24- й2 + у/х2 4- а2.
Найти г в зависимости от а, Ь, с.
ГЛАВА V
ФУНКЦИИ
Переменная величина у называется функцией переменной вели-
чины х, если каждому значению х соответствует некоторое оп-
ределенное значение у.
§ I. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ
Множество всех тех значений, которые принимает аргумент х
функции у — f (х), называется областью определения
этой функции.
Если область определения функции не указана, то функция рас-
сматривается для всех действительных значений аргумента, кото-
рым соответствуют действительные значения функции. Областью
определения функции, заданной явной аналитической формулой
(без дополнительных условий), считают множество всех тех значе-
ний аргумента, для которых все указанные в формуле операции вы-
полнимы. Такая область определения называется естествен-
ной (или областью существования).
Приведем примеры аналитических формул, в которые вхо-
дят операции, ограничивающие область существования функции.
1) У =	2) у = ^Ptf), Р(х)>0-, 3) у =
= logeP(x), Р(х) > 0;	4)y = tgP(x), P(x)^(2k +l)i;
5) у = ctg Р (х), Р (х) =# nk; 6) у = arc sin Р(х), —1<Р(х)< 1;
7) у = arc cos Р(х), —1 < Р(х) < 1.
Пусть требуется найти область определения функции
______Ух2 —4
— log2 (х2 + 2х — 3) •
Чтобы найти область определения данной функции, следует решить
систему неравенств:
х2 — 4 > 0,
х2 + 2х — 3 > 0,
log2 (х2 4- 2х — 3) =£ 0.
Ответ: х <—1—J/5, —1—]/5<х<—3, х > 2.
Найти область определения функций.
1.	(Устно.)
а)	У =	У =Vх2 — 5х + 6, у =]/б—х— х2, у =]/х24-х+1,
79
У = ]/ —5 4-2х —х2,	у —У — (х — а)2, у =У — х-г	1 -,
у 2 + х
=	(х-1)(х + 2)
У х(х + 5)Кх2 + 6х + 8 ’
б)	У = 5/х + 2/-х, у = 1g (х — 2), у = 1g Igx, у = log2 (х2 —
— 4х — 5),
у = log, (Зхг-40 2),,- >8	, У -18 —г
о
в)	у == tg (х — 1), у = ctg (х 4- -2-\ у = tg(sinх), у = -	1	,
\	4 J	1 + sin 2х
у = logj cos х, у = log2 (1 — tg х);
"2
г)	у = arc cos (х — 1), у = arc sin Зх, у — arc sin У~х, у =
— аге sin (sin х), у = etg arc cos х.
2.	у = 2/х—1 —
У 4— х
3.	у =	4- г + ]/х2 —6х + 9.
х + 2
4.	у =	+ 2/Г^х 4-Ух2— 1.
5.	у = /16 —х2 —3 /х2 —4.
О. V =------------г — — - -2ZT-.
х2 4- 1	У 4 — Зх — ха
9. у = /х2 —7х 4-12 —	.
Ух - 4
10. у = У (2 —х)(3,5 —х)(х —8).
-3)(10-х)
(х— 1) X2
80
13.
14.
15.
16.
Л(х8 + х+1)(х-3)
х2 + 4х + 3
Г (ха+ 1)(х —2)
х2 — 4x4-3
г 217-7 б+1Л
х2 — 5х + 6
Гх —2 , , Г 1 —
х2.
17.
1
V1 —/х4-2
18.
1
19.
У 4 —/15 4* 2х —х2’
1
20.
21.
22.
23.
24.
25.
26.
У /х-|-8—/5x4-20 4-2’
y = log3_x(x2 — 1).
у	9 + 1g (х 4-1).
У = 1g (3- /Г+1).
у = 31g (х- 2)
ух — 4
у = |/1g (х2 — 5х 4-7).
у = Ух2 — 5х-}-44- 1g(х4- 2).
y = lg-T^4^-2^^3.
27.
y=lg**-fa + 8.
z & х2 — Эх 4- 20
,	/x2-7x+12 4-lg(x-l)
у =-------------------
29. у = |/1о6/—
30.
/х2 —3x4-4
х 1g (х — 5)
31 у- 1* + 8
3L У “1-1^ (i-х)’
а-
81
32. у = lg[x(x—1)(х+2)].
34.	у = 1gx(x~2) (* + 3)
s (2x 4- 1) (x - 4)
35.	у =---------- 1
log2 И 6 + X — X2
36.	у =--------!---------.
log8 (x2 — 2x — 8) — 4
37.	у = tg/4 —x2.
38.	у = |/\sinx 4- cosx)3— 1.
39.	у = 1 4- ]/lg cos x.
40.	у = /lofesinx
у X2— 3x 4-2’
41.	y = arcsin(x—1)4-—L==-.
V 5x — 1
42.	у =----.
arc sin (x — 3)
4„	_ arc cos (x — 2) 4- V9 — x2
У~ log8(5 —2x)
44 v = arc sin (x — 2)
’ y yiog3(x2-l) --Г
§ 2. ОБЛАСТЬ ИЗМЕНЕНИЯ ФУНКЦИИ
Множество всех тех значений, которые принимает сама функ-
ция у = f (х), называется областью изменения этой
функции.
Можно найти область изменения функции, исследуя аналити-
ческое выражение функции или разрешая данное уравнение функ-
ции относительно х.
Примеры. Найти область изменения функции:
1-й способ. Область определения данной функции х =И= —1. Для
нахождения области изменения удобно данную функцию записать
в таком виде:
82
з
Дробь ----- принимает в области определения функции все-
х +1
возможные значения, кроме нуля. Следовательно, областью изме-
нения данной функции является множество всех действительных
чисел, кроме у = 2.
2-й способ. Разрешают данное уравнение функции относитель-
но х. Получают: х =	. Откуда следует, что у может быть
2 —у
любым действительным числом, кроме 2.
2) у — 2 cos2 -| + tg х ctg х.
Область определения данной функции х =/= -у k, где k = О,
±1, ±2, .... На этой области данная функция и функция г —
= 2 cos2 + 1 имеют одну и ту же область изменения.
Найти область изменения z.
О < cos2 — < 1.
2
l<2cos2 - +К 3.
2
Исключить из области изменения z те значения, которые z при-
нимает при х = k:
k = 0, х = 0, z = 3,
k= 1,х = — , z = 2,
2	’
k = 2, х = л, z = 1.
При других значениях k значения z совпадают с одним из полу-
ченных трех значений, которые эта функция принимает только при
Л 1_
х — k.
2
Итак, областью изменения функции y = 2cos2-|- 4-tgxctgx
являются действительные числа, удовлетворяющие неравенствам
Найти область изменения функции.
45.	а) у = х2 — 4х 4- 7,	б) у = 8х — х- — 10.
46.	а) у =----—-----,	б) у —------------.
15 + 2х—х8	2х —х2 —5
83
47.	а) у -	б) у =
' 7 х — 3’	’ у х —3
48.	а)у = -£-а,	6)y=-^f-.
1 + №	х* + 1
50. a) y=Vx2 + V(x— 1)2,б) у = /х2—2x4-14-Vx24-2x4-1.
51. а) у = log (х — 2) + 5,
52. а) у = 4 sin х 4- 3 cos х,
54. а) у = lg (1—2cosx),
log,—
б) у = 5 х.
б) у = 12 sin х — 5 cos х.
б) у —----------.
3— sin 2х
б) у = logj fl — ^-sinxY
55. а) у = (sinх 4- cosх)2 — -—cos4x — cos
2sin 2х
а , / л .	\ , tg х (1 + cos 2х)
б) у х= ctgxctg — + х + -?
\ 2	/ 2cosx
56. а) у = 3arccos f х —
б) у = у arc sin (х + 1).
§ 3. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
Функция у = /(х) называется четной, если при всех значе-
ниях х из области определения этой функции /(—х) = — /(х)
Функция у = /(х) называется нечетной, если при всех
значениях х из области определения этой функции f(—х) = — /(х).
Область определения четной и нечетной функции симметрична
относительно начала координат.
Установить четность или нечетность следующих функций.
57. а)	у = х* — 2х2 4-2,	\ . 1 Г) У = х 4- -, X
б)	у = 2х3 4- 3,	д)у=..+1'
в)	у = X3 — X,	е) у = 5 — х
58. а)	у = х 4- sinx,	в) у = cos (х — а),
б)	у = sin2x 4- cos х,	Г) У =tg(x —а).
84
59.	а) у = J/1 — х2, в) у = ]/1 + х + х2 —	1 — х 4- х2,
б)	У —	(2х — 5)2 + У(2х + 5)2 , г) у = j/x4 4-х3 4- 4 —
— j/x4 —х3 4- 4 .
60.	а)	у _
61.	а)	у = 1g х3,	г)	у =	1g 1(1	— х2) (1 4- х2)],
б)	У = lg(x2— 1),	fl)y =	lgj-^,
В)	У = lg(x 4-	/1 + х2),	е)	у =	1g	.
2 — х
62.	у — х2 4-1: а) на отрезке [—2,31; б) на отрезке [—4, 41.
63.	Доказать, что сумма, разность, произведение и частное
четных функций есть также четная функция.
64.	Доказать, что сумма и разность нечетных функций есть
функция нечетная, а произведение и частное нечетных функций —
функция четная.
65.	Доказать, что сумма двух функций различной четности не
является четной, а также нечетной функцией.
§ 4. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ
Функция /(х) называется возрастающей (убываю-
щ е й) на данном промежутке, если при произвольных двух различ-
ных значениях аргумента, из данного промежутка, большему зна-
чению аргумента соответствует большее (меньшее) значение функ-
ции.
Примеры. Найти участки возрастания и убывания функций.
1) у = х2 4- Зх — 108.
Решение. Пусть х2 > хх. Найдем разность у2 — ух и устано-
вим, при каких значениях х она положительна, при каких — отри-
цательна.
у2 — У1 = (х2 4- Зх2 — 108) — (xi 4~ 3xi — 108) = (х2 х2)[(х2 4~
4~ xi) + 31 •
х2 — Xj > 0, так как х2 > хх. Следовательно, знак разности
зависит от знака выражения х2 -|- Хх 4- 3.
з
х2 + xi + 3 > 0 при х2 >	,
Х2 Х1 3	0 ПрИ X}
3
2
85
3	3
Итак, если х >-------, то у возрастает; если -------, то у убывает.
2) У = -г.
X2
Решение. Пусть х2 > хх и хх =/= 0. Найдем разность у2 — ух
и установим ее знак.
а	а	[ 1	1 \ У 2	"“2	Г	I —2	2~ / *2	Х1	\Х2	Х1 /		2	2 а (л*1	х2)	
		*1 х22	
__ a — х2) (хх + х2)
”” х2 х2
Л । Лсу
Х1 — х2 < 0; Х1 Х2 > 0.
Знак разности у2 — уг зависит
от знака выражения a (Xj 4- х2).
Возможны случаи:
1)	а >	0,	х2	>	xi >	0;
2)	а >	0,	хх	<	х2 <_	0;
3)	а <	0,	х2	>•	хх >	0;
4)	a <	0,	хх	<	х2 <	0;
у убывает, если х С (0, со).
у возрастает, если х £ (—оо, 0).
у возрастает, если х £ (0, оо).
у убывает, если х£ (—оо, 0).
Найти участки возрастания и убывания функций.
66.	а) у = ах2,	б) у = х2 — Зх + 2,	в) у=—2х24-4х—3.
67.	\ а. а) у = -’ X	б) У = х+ X	ч	2х -f“ 3 в) У - J •
68.	а) у = х3 —	4, б) у = х3 + х,	в) у = х3 -|- 2х -f-1.
69.	а) у = х2л+1	, где п — натуральное	число;
	б) у = х2л,	где п — натуральное число.	
70.	а) у = Кх ,	б) у = -Ух + 2,	в) У = V хг 4- 4,
	х	V— г) у = / X ,	4<— д) У = V X3.	
71.	а) у = 2х,	<)Х 1 9- Г б) у - 3-х, в) у - ах, г) у -	2	
72. а) у = (1)’Л б) у = З**2-0 3+1.
73. а) у = 1g х, б) у = 1g -Ц в) у—1g (5 4- х), г) у = 1g (3—х).
86
§ 5. СПОСОБЫ ПОСТРОЕНИЯ ГРАФИКОВ ФУНКЦИЙ
Графиком функции у = f (х) называется множество всех
точек плоскости, координаты которых (х, [ (х)).
I. Построение графика функции «по точкам»
Этот способ вытекает из определения графика функции. Он
является длинным и недостаточно надежным способом построения
графика функции. Применяется в школьном курсе математики при
первоначальном знакомстве с простейшими функциями.
II. Построение графика функции на основании результатов
исследования функции
(без использования понятия производной)
Примеры. 1) Построить график функции у = ]/х2 — L
Для построения графика функции исследуем ее, придерживаясь
общей схемы исследования.
1.	Нахождение области определения.
х2 — 1 > 0. х С (—оо, —1] (J [1, со).
2.	Определение четности или нечетности.
f (- х) = /(-х)2-Г =	= f (х).
Функция у = Ух2 — 1 — четная. Дальнейшее исследование
будем вести для х С [1, со).
3.	Выделение промежутков монотонности.
хх > х2 > 1.
М-Г+l'^i
2	2
= -z Х|~Х2	>0.
К х i — i + V 4 “1
При возрастании значений х от 1 до оо значения у возрастают.
4.	Нахождение корней функции и промежутков знакопостоян-
ства.
Если х С [1, оо), то Ух2 —1=0 при х = 1. -
Ух2 — 1 > 0 при всех х с (1, оо).
5.	Область изменения функции.
Если х = 1, то у = 0. Если х -> оо, то у -> оо. Следовательно,
у € [0, оо).
6.	Исследование на выпуклость и вогнутость.
f (1+ID > Z(l) + H/2j
' \	2 J 2
График функции — выпуклая кривая.
87
				1 _				
	и Т									
								
					о.						
				с						
					—			
				— /•	—		-	
					—			
					-			
				.0:	"	h			
-		_-2		ч			1		2				 _ X
					—			
							L- _J		
Рис. 1
На основании результатов исследования строим график функ-
ции (рис. 1).
2) Построить график функции у = ~*~4.
х — 1
Для исследования удобно данную функцию записать в таком
виде:
У=3 + —Ц.
1.	Область определения: (—оо, 1) (J (1, оо).
2.	Не является ни четной, ни нечетной.
3.	Возьмем два произвольных значения х± и х2 (х2 > хх) из
области определения функции и установим знак разности:
/3-4-	? (____( 3 [	\	~	*з)
\ х2 — 1 /	\ х, —1/	(х2 —1)(х1 —1)
хх — х2 < 0, (х2 — 1) (хх — 1) > О и при х2 > хх > 1, и при
1 > х2 > хх. Разность отрицательна, следовательно, функция
убывает во всей области определения.
4.	Зх = 0	при х = — —,
х — 1	3*
>0	при х > 1 и х < - - ,
х— 1	3
< 0	при - ± < х < 1,
х — 1	3
88
5.	Исследуем поведение функции вблизи точки разрыва и при
х ->- оо и х -> —оо.
Если значения х, возрастая, стремятся к 1, то значения данной
функции неограниченно убывают (у->—оо). Если значения х,
убывая, стремятся к 1, то значения данной функции неограниченно
возрастают (у -> оо).
Если х->-—оо, то значения данной функции стремятся к 3,
оставаясь меньше 3.
Если х-> оо, то значения данной функции стремятся к 3, оста-
ваясь больше 3.
6.	С возрастанием х от —оо до 1 значения функции убывают от
3 до —оо; с возрастанием х от 1 до оо значения функции убывают от
оо до 3.
На основании полученных результатов исследования строим
график функции (рис. 2).
89
-1ТТО7МИ» -S’* “ЯЬ JflWTW?
Построить графики функций.
74.
\	1	X 4- 1 ч
а) у = б) у =--------------------, в) у =
х + 2	х
ч 3 — 2%
•, г) У = ~---------------•
1 — х
75.	а) у = 3-^, б) у = 2-±^, в) у = 2-=^.
76.	а) у = Ух2 — Зх + 2 , б) у = ]ЛГ=х2',
в) У = У 4х — х2 + 5 .
77.	а) у = Ух2-! , б) у = Ух- 1 Ух + 1,
в) У=Кх+1— У1 — X.
79.	а) у = ——!-----------, б) у =-------------!------,
х2 + 2х — 8	' ' 4х —х2 4-5
в) у —---------5-----.
х2 — 2х + 3
80.	а) у = —— , б) у = ——,	в) у = log3 -,
10g2 X	log ! X	X
2
г) у = log 1
А X
81.	а) у = logjlog2x, б) у = log^log2х, в) у = logjog^x.
2	2
82.	а) у = log2 , б) у = log| х, в) у = log3_x (х2 — 1).
III. Построение графиков функций
путем сдвига графиков основных функций
или сдвига осей координат
Пусть у = /(х) — одна из основных функций и ее график по-
строен.
1) Чтобы построить график функции у = f (х) 4- с, можно или
график функции у = /(х) сдвинуть вдоль оси OY на с единиц в
сторону, совпадающую со знаком с, или перенести параллельно ось
ОХ в сторону, противоположную знаку с (рис. 3).
2) Чтобы построить график функции у = f(x -|- с), можно или
график функции у — f(x) сдвинуть вдоль оси ОХ на с единиц в сто-
рону, противоположную знаку с, или перенести параллельно ось
OY в сторону, совпадающую со знаком с (рис. 4).
90
Рис. 3
91
IV. Построение графиков функций путем симметричного отображения
относительно осей координат графика основной функции
1) Чтобы построить график функции у — —f(x), можно по-
строить изображение, симметричное графику функции у = f(x)
относительно оси ОХ (рис. 5).
2) Чтобы построить график функции у = /(—х), можно по-
строить изображение, симметричное графику функции у = f(x)
относительно оси OY (рис. 6).
92
V. Построение графиков функций
путем деформации графиков основных функций
1) Чтобы построить график функции у = af(x) при а > О,
можно график функции у = f(x) растянуть вдоль оси OY, если
а > 1, и сжать вдоль оси OY, если 0 < а < 1 (рис. 7).
2) Чтобы построить график функции у = /(сох) при о > О,
можно график функции у = f (х) сжать вдоль оси ОХ, если со > 1,
и растянуть вдоль оси ОХ, если 0 < о < 1 (рис. 8).
Построить графики функций.
83. а) у = х3 — 1,	б) у = (х — I)3, в) у = (1 — х)3.
84. а) у = 3*4-1,	б)у = 3*+1, в) у=3*—1,г)у=3*~’.
93
87.	а) у = -Ц-, б) у = -Ц - 2, в) у = -Ц- + 2.
X — 1	X — 1	X — 1
88.	а) у = Ух — 1, б) у = Ух — 1, в) у — Ух — 1 4-2.
89.	а) у = ЗУх— 1, б) у =- /х 4-1, в) у =	—2.
3	2
90.	а)	у = У2х 4- 1,	б) у = У2х 4- 1,	в)	у	= у/1 х — 1.
91.	а)	у—2—Ух—1,	б) у=2—У2х—1,	в)	у	= 1—1х-}-1.
92.	a)	y=logLx 4-1,	б) у = log±(x4-l),	в)	y=log±(x4-l)4-3.
93.	а)	у = logj_ (Зх),	б) у = logj_ И Л	в)	у = log , (1 — х).
3	У \ 3 )
94
94.	а) у =—logj_3x, б) у = log^(—Зх), в) у = log i (Зх-|-2).
3	3	3
95.	а) у = 2tg х,	б) у = ytg х,	в) у —-----|tg х.
96.	а) у = tg (2х),	б) у = tg (1	в) у = tg (х 4-1).
97.	a)y=tg(x+l)+2,6) y=2tg(x+l)+i B)y=3tg(2x-1)-1
2	□
98.	a) y=arcsin(x—1), б) y=arcsin (2х), в) у = arcsin (2x4-1).
99.	а) у = 2arcsin fy х—б) у = — arcsin (1 — 2х).
6. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ, АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ
КОТОРЫХ СОДЕРЖИТ ЗНАК АБСОЛЮТНОЙ ВЕЛИЧИНЫ
1.	у=/|Х|.
Функция у — х | — четная. Чтобы построить ее график,
достаточно построить для х > 0 график функции у = Дх), а за-
тем достроить его левую часть, симметричную правой относитель-
но оси OY.
Примеры. 1) у = х2 — | х | — 3 (рис. 9).
2)	у = log3 I х | (рис. 10).
95
Рис. 10
2.	3» = |/(Х)|.
Можно данную функцию рассматривать как совокупность двух
функций:
I f (х), где f (х) > 0.
I—f (X), где f (х) < 0.
Чтобы построить график функции у = | f (х) |, достаточно по-
строить график функции у — f(x) и ту часть графика, которая рас-
положена в нижней полуплоскости, симметрично отразить отно-
сительно оси ОХ.
Примеры. 1) у = j - х2 — х — 3 (рис. 11).
2)	у = I log3 х |	(рис. 12).
з.	у = 1/(И)Ь
Функция у = | f | х | | — четная. Последовательность построе-
ния графика данной функции может быть одной из следующих.
1)	Построить для х > 0 график функции у = f (х), затем его
симметрично отразить относительно оси OY, и, наконец, ту часть
полученного графика, которая расположена в нижней полуплоско-
сти, симметрично отразить относительно оси ОХ.
96
2)	Построить для х > 0 график функции у = f (х), затем ту
часть полученного графика, которая расположена в нижней полу-
плоскости, симметрично отразить относительно оси ОХ и, наконец,
полученный график симметрично отразить относительно оси OY.
4 Заказ 1089
Примеры. 1) у = | х2 — |х| — 3 | (рис. 13).
2)	у = I log3 I -V I I	(рис. 14).
Рис. 14
4.	Кусочно-линейная функция
Графиком кусочно-линейной функции является ломаная линия.
Для построения графика находят уравнения звеньев ломаной.
Пример, у = ] х — 1 | — | х — 2 | + | х — 3 | — | х —
4 I + I х — 5 | .
Точки излома 1, 2, 3, 4, 5 (корни функций, стоящих под знаком
модуля).
Находим уравнение звеньев ломаной.
х 1, У ~~ 1 х “Н х 7— 2 -(- 3 — х —х — 4 — х	5 —
— —х	3.
1	х 2, у = х 1 —|- х — 2 -j— 3 — х —х 4 — х -|- 5
= х -|- 1.
2	< х < 3, у — х — 1 + х + 2 + 3 — х + х — 4 — х + 5 »
= —х -|- 5.
3	< х < 4, у = х — 1— х + 2 — 3 -1-х 4-х - 4 — х + 5 =
— х — 1.
4	х 5, у х 1 х —2	3 —х х —4 — х —|— 5
= —х 7.
5	< х, у = х — 1 — х 4- 2 — 3 + х — х + 4 -|-х — 5 = х — 3.
Зная уравнения звеньев ломаной на каждом промежутке, строим
график данной функции (рис. 15).
4*
99
Построить графики функций.
100.	а) у = | х | — 2, б) у = 1 — | х | , в) у = I х 4- 2 |,
1
г) у = — -1 х | + 2, д) у = | 1 — | х | |.
101.	а) у = л- -j- | х 4- 3 | , б) у = х 4- | 2х 4- 3 в) у = 2х—
- |х +1 | 4-2.
102.	а) у = хг —	5	| х |, б) у = 4	| х	| — х2	—	3,	в)	у	=	|	4х —
—	х2 —	3 |, г) у = |	4	| х | — х2 — 3	|.
103.	а) у = (х-	1)	(2- | х |), б)	у	=	(1	4-	| х	|)	(2- |	х|),
в)	у =	| х2 — 5х 4- 6 |	— х.
104.	а) у = (5- | х |) (1 4-х), б) у=(5-|х|)(|х|4-
4-1), в) у = (5 — х) i х 4-1 | .
105.	а) у — | х |3 — 1, б) у = | х3 | — 1, в) у = | х3 — 1 | ,
Г) У = I (X 4- З)3 — 2 | , Д) у = i (X — 2)3 4-1 |.
106.	а) у = -п»	б) у = Lil, в)у = -^£,
|х|	X	|х|
г) у — —L—,	д) у = —L—.
’ ?	|х-2|	>	|х| — 2
107.	а) у = 3_£±_2 , б) у = ^±2 , в)у = |3|£Н2
’	Х-1 ’	' 7	|Х| — 1	I |х|-1
108.	а) у — ---1---, б) у =------------1-------,
х2 — 2|х| — 8	'	[х2 —2х —8|
в) у =--------1---.
|х2 —2|х| —8|
109.	а) у = Kkl > б) у — | х| , в) у — К|х| — 2,
г) у = }/|х| — 2, д) у = 2 — /1 — |х| .
ПО. а)
в)
у = Ух? — з I X I + 2 ,
у = Л Г 2 I х | — 1 г)
Г 1x14-1
б) у у
1 / 2 I X | — 1
Г |х| + 1 '
У =
111.	а) у = 2 1И,	6)y = ^Kl, в)у = 2-21*1,
г) у = |2|ж,-,-1|.
112.	а) у = 4W“’ , б) у == 4|V-11 , в) у =	‘ ,
Г)У = Ы •
100
1
ИЗ
б) у =
.	„1*1-2
в) у = 2
114	а) У = !ogjx|, 2	б) у =	1 log2x|, 2	в) У = 1 log±|х||. 2
115	а) У = 1О&-J-7 ,	б) у =	10g2 -	, в) у = | log2 1 .
	|х|		X	1 W
116.	а) у = log 1 -Ц,	У =	Io? . —	. В) у = log ! 7 | ,
	7^1		-2Х	1 4 и 1
117.	. 1		1	V	1 Rl V 	 - -
		VJf У —		о/ у —	•_
	logj |х|		| 1о?4 X 1 ’	1 log4 |х||
118.	. 1 V 	 		V —	 1	—	r\ V —
	<*/ У	,	и) у —		, Щ У	। ,
	1<И ! I X |		1 log । X I	1 log_| И 1
	*5		~з	3
119.	а) у = | sin 2х |,	б) у =	sin 2| х	|, в) у — 2 — cos|x
	г) у = 1 cos| X11.			
120. а)
1 — X2
у = ] arc sin х |, б) у = arccos|x|, в) у — arcsin
у = | 4х — 1 | — | 2х — 3 | + | х — 2 | , б) у — | х —
121.	а)
— 1 | — | х 4-21 — 1 2х — 31+13 — х |.
122.	а) у — | 5 — х | + | 5х + 4 | — | х — 1 | + | х + 21,
б) у = | 1 — х|+|х-3|-|х+2| — | 5 — 2х | .
123.	а) у = | х2 + 2х | + j х2 — 5х + 6 | , б) у = | ^-х2 —
+ |2х! + 1х_1|.
I 4	4 I
124.	а) у = | 2 — | 1 — | х | 11, б) у = | | | | х | — 2 | —
— 1 | — 2 |, в) у = | log2 | | х | — 1 ||.
+
ГЛАВА VI
РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
§ I. РАВНОСИЛЬНОСТЬ УРАВНЕНИЙ
I. Пусть функции f(xt у, ... , z) и <р(х, у, ... , z) определены на
некотором множестве А. Поставим задачу: найти множество X,
на котором эти функции принимают равные значения, другими сло-
вами, найти все значения х, у, ... , z, для которых выполняется ра-
венство
/ (X, У...г) = ф (х, у.....г).	(1)
При такой постановке задачи равенство (1) называется урав-
нением с неизвестными х, у, ... , г.
Множество А называется множеством (областью) допусти-
мых значений неизвестных для данного уравнения.
Множество X называется множеством решений данного
уравнения.
Для уравнения с одним неизвестным f (х) = ф (х) всякое его
решение х — а называется корнем уравнения.
Решить уравнение — значит найти множество всех его решений.
Множества решений данного уравнения зависит от числового
множества, над которым оно рассматривается. Например, урав-
нение х2 = 2 в поле рациональных чисел не имеет корней, в поле
действительных чисел имеет два корня х = ± ]/2.
Процесс решения уравнения состоит в последовательной заме-
не данного уравнения другим, более простым уравнением. Воз-
никает вопрос о законности такой замены. Всегда ли получается
уравнение с тем же множеством решений?
Ответ на этот вопрос дает теория равносильности уравнений.
Пусть даны два уравнения с одними и теми же неизвестными и
рассматриваемые на некотором множестве At
fl (х, у, ... , z) = ф! (х, у, ... , г),	(1)
/2 (х, у, ... , z) = ф., (х, у.г).	(2)
Обозначим множество решений jравнения (1) через Mf а уравне-
ния (2) — через N.
Если М cz X, то уравнение (2) называется с л е»д ст в и е м
уравнения (1).
Если М то уравнения (1) и (2) называются равносиль-
н ы м и.
Понятие равносильности обладает свойством транзитив-
ности.
Два уравнения могут быть равносильными относительно одного
числового множества и не быть равносильными относительно дру-
гого числового множества. Например, уравнения 2х — 6 = 0 и
х3 — Зх2 — 2х -|-6 = 0 равносильны на множестве рациональных
чисел и не равносильны на множестве действительных чисел.
102
Равносильны ли уравнения:
1.	2х + 1 = 3 и 2х = 2 на множестве действительных чисел?
2.	= 9,5 и х (х— 1) = 2 на множестве натуральных
чисел? на множестве действительных чисел?
3.	2х — 6 = 0 и х2 — 5х J- 6 = 0 на множестве действитель-
ных чисел?
4.	х (х — 1) — 2 (х — 1) ~ 0 и (х — 1) (х — 2) — 0 на мно-
жестве действительных чисел?
5.	Зх + 1 = 7 и (Зх + 1) (х — 1) = 7 (х — 1) на множестве
действительных чисел?
6.	х — 1 = 0 и (х — 1) (х2 — 3) = 0 на множестве действитель-
ных чисел? на множестве натуральных чисел?
7.	ха + 1 = 0 и х4 4~ 1 = 0 на множестве рациональных чисел?
на множестве действительных чисел?
8.	х2 = 4 и х4 = 16 на множестве действительных чисел? на
множестве целых чисел?
II. При замене одного уравнения другим, более простым часто
приходится выполнять тождественные преобразо-
ван и я. Всегда ли при выполнении тождественных преобразова-
ний полечим уравнение, равносильное данному (см. главу IV)?
Пусть дано уравнение
„ К (х, у, ... , Z) = cpt (х, у, ... , Z)	(1)
с множеством допустимых значений неизвестных Мг. После выпол-
нения тождественных преобразований в одной или в обеих его ча-
стях получили уравнение
/г (х, у, ... , г) = <р2 (х, у.z)	(2)
с множеством допустимых значений неизвестных Л12. Если при
этом:
1)	Л4г = Л42, то уравнения (1) и (2) равносильны.
2)	cz Л42, то уравнение (2) может иметь посторонние для
уравнения (1) решения, принадлежащие множеству М2—Мг\
если таких решений не окажется, то уравнения (1) и (2) равно-
сильны.
3)	М± М2, то в множество решений уравнения (2) могут
не войти решения уравнения (1), принадлежащие множеству
— М2. Если потери решений не произойдет, то уравнения (1) и (2)
равносильны.
4)	М19 с одной стороны, обогащается новыми значениями,
а с другой стороны, теряет некоторые из них, то уравнение (2) мо-
жет быть неравносильно уравнению (1) как в силу потери ре-
шений, так и приобретения решений, посторонних для уравне-
ния (1).
103
Примеры нарушения равносильности уравнений, вызван-
ного тождественными преобразованиями.
I)	]	•- 3, (1) ML = {х | х > 2}.
]z2x2 — х —6 = 3,	(2) М, = {х | х > 2 и х < —1,5},
Xi = 3, х2 = —2,5, Xi С Mi, х2 С ML.
Тождественное преобразование расширило множество Мх.
Уравнение (2) не равносильно уравнению (1). Уравнение (2) имеет
еще корень х = —2,5, принадлежащий множеству М., —	—
= {х|х<—1,5}.
2)	1g (х - 5)2 = 2, (1) Afj = (х | х ? (-оо, 5) U (5, оо)}.
21g (х — 5) = 2, (2) М2 = {х | х С (5, оо)}. х — 15.
Тождественное преобразование сузило множество Л4Х. Уравне-
ние (2) не равносильно уравнению (1). Уравнение (1) имеет еще ко-
рень х = —5, принадлежащий множеству М2 — М2 = {х | х £
С(—оо, 5)}.
3)	1g [х (х + 9)1 + 1g = 0, (1) Mi = (х | х < -9 и х> 0}.
1g х + 1g (х +9) + 1g (х h 9) — lg x -= 0, (2) M> = (х | х >
>0}.
21g (х 4- 9) = 0, (3) Мя - {х | х > —9 }.	х = —8.
При переходе от уравнения (1) к уравнению (2) тождественное
преобразование сузило множество М19 при переходе от уравнения (2)
к уравнению (3) — расширило множество Л12. Уравнения (2) и (3)
не равносильны уравнению (1) и не равносильны между собой.
Тождественные преобразования привели к потере корня х = —10,
принадлежащего множеству Мг — Л12 = {х | х < —9}, и прио-
бретению постороннего корня для уравнения (1) х — —8, принад-
лежащего множеству М3 — М> = {х | —9 < х < 0}.
Вывод. При решении уравнений необходимо следить за из-
менением множества допустимых значений неизвестного. В случае
расширения его следует проверять, не является ли найденное
решение посторонним для данного уравнения. В случае сужения
необходимо убедиться, не являются ли выпавшие значения неиз-
вестных решениями данного уравнения. Задача нахождения по-
терянных решений не всегда легко выполнима, поэтому желательно
избегать тождественных преобразований, ведущих к сужению мно-
жества допустимых значений неизвестных уравнения.
Равносильны ли уравнения в поле действительных чисел?
9. л3 -1 —---- = х	и х3 = х.
Л* X
10. 3x^1 + —---------— =9 — х И Зх+1 =9 — х.
х — 2 х — 2
104
11. ~—J- = 2
х — 1
12. Г = 3
х — 1
14.	х2 — — =- О
X
15.	Ig	х-	=	О
16.	1g	х’	=	О
17.	1g	л4	=	О
18.	Ig — = О
<11 (X)
и л- 1 = 2.
и л' -г 1 — 3.
и х - 1 = 2.
и х- — 2х — О.
и 21g х — О.
л 51g х = О.
и 2 1g | х | = О.
и lj/(x) — lg<p(x) =0.
19.	х2 — х — 1 = 1 и Ig (х2 — х — 1) = 1g 1.
20.	xr	+ Зх + 2	=	х	-и	1	и 1g (х2 4- Зх + 2) =	Ig (х	4-	1).
21.	х2	4- 2х + 2	=	1	и	Ig	(х2 4- 2х 4- 2) = Ig 1.
22.	Ig	х 4- ig (х	— 3)	=	1	и	IgJ (x — 3) xl = Ig 10.
23.	Ig	(л- -Ь ИЗ)	4-	Ig	(x	-}/3) = 0и Ig l(x 4- ИЗ)	(x	-/3)1 =
= 0.
24.	31g (—x) = Ig x2 и —x3 = x2.
III.	При решении уравнений выполняют преобразования, осно-
ванные на теоремах:
Теорема 1. Уравнения
Дх, у, ... ,z) = ф(х, у, ... , z)	(1)
и
f (х,у, ..., 2) + <о(х, у, ... , г) = <р(х, у, ... , г) + со(х, у, ... , z) (2)
равносильны, если функция ю(х, у, ... , z) определена на множестве
всех допустимых значений неизвестных уравнения (1).
Замечание. Если <о(х, у, ..., z) определена не при всех допустимых
значениях неизвестных уравнения (1) и теряет смысл при каких-либо системах
значений неизвестных, являющихся решением уравнения (1), то при переходе
ог уравнения (1) к уравнению (2) произойдет потеря решений.
Пример ы: 1) Дано уравнение 2х 10, которое имеет только
один корень х = 5.
а)	Прибавим к обеим его частям функцию со (х) = ——,
х —5
теряющую смысл при х = 5. Получим уравнение 2х 4- —— =
х — 5
== 10 + —Ц; , не равносильное данному, гак как х 5 не явтя
егся его корнем.
105
б)	Прибавим к обеим частям данного уравнения функцию со (х) =
= ——, теряющую смысл при х = 2. Получим уравнение 2х +
х — 2
-|- —5— = 10 -|- —, равносильное данному, так как оно
х — 2	х — 2
имеет тоже только один корень х = 5.
2) Дано уравнение х (х — 1) = 0; множеством допустимых зна-
чений неизвестного является множество всех действительных чисел.
Уравнение имеет два корня: xt = 0 и х2 = 1.
Прибавим к обеим частям данного уравнения функцию со (%) =
= 1g х, область определения которой х > 0. Получим уравнение
х (х — 1) + 1g х = 1g х, не равносильное данному, так как х = 0
не является его корнем.
Теорема 2. Уравнения f(x, у, = ср(х, у, ... , z) (1) и
Дх, у, ... , z)-co(x, у, ... , z) = ср(х, у, ... , z)-G)(x, у, ... , z) (2) равно-
сильны, если функция со (х, у, ..., z) определена и отлична от нуля на
множестве всех допустимых значений неизвестных уравнения (1).
Замечание. Если условия теоремы, касающиеся функции а>(х, у, ..., г),
не выполняются, то уравнение (2) может быть не равносильно уравнению (1).
Может произойти потеря решений, если со(х, у, ... , г) теряет смысл при каких-
либо системах значений неизвестных, являющихся решением уравнения (1).
Уравнение (2) может иметь посторонние решения для уравнения (1), если
со(х, у, ..., z) при некоторых допустимых системах значений неизвестных равна
нулю, но эта система значений неизвестных не является решением уравнения (1).
Примеры. Дано уравнение х2 = 2 — х, множеством допу-
стимых значений х является множество всех действительных чисел.
Уравнение имеет два корня: xL = 1 и х2 = —2.
а) Умножим обе части данного уравнения на со (х) = ——
1 —Л'2
теряющую смысл при х=1 и х =—1. Получим уравнение
х2- —— = (2 — х) • ——, не равносильное данному, так как оно
1— х2	1—х2
имеет только один корень х = —2. Умножение обеих частей данного
1 .
уравнения на ---привело к потере корня х = 1.
1—	х2
б)	Умножим обе части данного уравнения на со (х) = —
*4-1
теряющую смысл при х = —1. Получим уравнение х2- —— =
х 4- 1
= (2 — х)- ---- , равносильное данному, так как оно имеет два
корня: xt = 1 и х2 = —2.
в)	Умножим обе части данного уравнения на со (х) = х — 3,
обращающую в нуль при х = 3. Получим уравнение х2 (х — 3)
= (2 — х) (х — 3), не равносильное данному, так как оно имеет
три корня: X} = 1, ха = —2, х3 — 3. Умножение обеих частей дан-
ного уравнения на х — 3 привело к появлению постороннего корня
х = 3.
106
Равносильны ли уравнения на множестве действительных чисел?
25. х — 1 = 2х — 6 и х — 1 -j- J х2 + 4 — 2х — 6 4- Ух2 +4.
26. 5х — 2 = 2х 4 и 5х — 2 4- 1g (х2 4- 3) = 2х 4- 4 + 1g (х2 +
+ 3).
27.	х + 5 = 15 — хи х 4- 5 +	= 15 — х -[-Ух.
28.	х — 2 = 4 — х и х — 2 4- — = 4 — х 4- —.
х - 3	л - 3
29.	х2 — 5х 4- 6 = 0 и х2— 5х 4- 6 4- —-— = ——.
х —2 X —2
30.	2х — 3 = 9 — х и2х — 3 4- | r 1 — х = 9 — х 4-]/1 — х.
31.	Зх — 2 = 6 — х и Зх — 2 4- 1g (1 — х2) = 6 — х 4“ 1g (1—
— х2).
32.	х — 3 = 0 и (х — 3) • (х2 4- 1) = 0.
33.	х2 — 5х 4- 6 = 0 и (х2 — 5х 4- 6) • —— = 0.
х — 2
34.	х — 2 = 0 и (х — 2) (х 4- 3) = 0.
35.	х2 — 2х — 3 = 0 и (х2 — 2х — 3)-2v = 0.
36.	/(х) = 0 и Дх)-ач^> = 0.
37.	— = — и (х — 1) (х — 1) = (х — 2) (х — 3).
х — 2 х — 1
38.	1+1 = 5^ и (z+ 1) (z —3) = (z — 5)(z — 1).
г — 1 г — 3
39.	5 _ 1212е = -1- и 5(х —4) —(5 —х) = — 1.
X—4	4—х
х — 4
40.	----------1---—— =----5---- и 2x4-(х—4)(Х—2)=х-|-2.
(х4-2)(х-2) х(х + 2)	х(х-2)	v	’
41.	^ = /‘Г* с и (х—1)(х2—5х 4-6) = (х —2)(х2—1),
х — 2 х2 — 5х + 6
42>	+	и 3(х2 —2х) , 2(х2 4-1) = 5х3.
х2 + 1	3 Зх- + 3
43.	х — 2 = 7 — 2х и (х — 2)2 = (7 — 2х)2.
44.	Зх — 1 = 4х — 2 и (Зх — I)4 = (4х — 2)‘,
45.	/ (х) = (р (х) и {[ (х)]2 = [<р (х)12,
46.	f (х) = <р (х) и I/ (х)1А = [<р (х)]*,
47.	2*'rjI/7W = Ф (х) и / (х) = ф2*+* (х),
48.	х2 — 1 = 0 и Ух2 —1=0.
49.	Шф/фМ = 0 И УГуГ¥У) = 0.
107
50.	При каком условии уравнения
/,(У)	/,(*) J-M*> н 21121	М»)
<Pi(*)	’h(') т <(2(*)	'l.(')	<|2(Л)
равносильны?
51.	Будут ли равносильны уравнения на множестве действитель-
ных чисел
х1 — 5х + 6 _ ,г — 2	и х2 — 5х 4- 6   (г2— 5х -L (И 4~ (х — °) ?
х — 1 Зх — 7	х — 1	(х — 1) 4* (Зх — 7)
52.	Будут ли равносильны уравнения на множестве действитель-
ных чисел
1 М*) _	1	М*)	и	ГМ*) — Гф,!.')'  ГМ*>	- Гф2Ь) >
Г 41 (*)	I	<М*)	I МЛ) -г I	41U)	|	/»(Л)	Г J <Р2(Х)
53.	Верно ли утверждение, что уравнения
IM*)	=	1'М*)	и	I /i(*> - 1	<Р1(*) _	1 Цх)	Гф2(*)~
1 <Pi(*)	I <М*Г	I /и*) — I	<р2(*)	1	Мл)	— I ч2(л)
равносильны на множестве действительных чисел?
54.	Будут ли равносильны уравнения на множеаве действитель-
ных чисел
Г*2 — Зх ____	г*2 н- х
V х2 — 2х -г 3	] х2 -- Зх 3
]' х2 — Зх  Г*~ — 3* 4~Г*24~*?
) х2 — 2х 4- 3~ I X2—2x4 3 — I х2 4- Зх -г 3 ’
§ 2. РЕШЕНИЕ УРАВНЕНИЙ С ПАРАМЕТРАМИ
Решить уравнение, содержащее параметры, — это значит для
каждой допустимой системы значений параметров найти множество
всех решений данного уравнения.
Примеры. Решить уравнение на множестве действительных
чисел.
1) ах 4-
, Зх -ь	1
3	2
Решение. 6 (а — 1) х = 3 — 6Z? -|- 4аЬ.
n f .	3- 27; (3—20
Если а 1, то х -----------~ .
6 0—1)
Если а = 1, то уравнение примет вид 0-х— 3 — 2ft, и если
о	з
Ь — —, то х — любое действительное число; если b Ф —, то урав-
2	2
пение не имеет решений.
108
Ответ: при а 1 х = -—
6 (п — 1)
при а = 1 и b = — х — любое действительное число;
при а = 1 и b — уравнение не имеет решений.
2)	(3 4- 2а — а2) ] х = а — 3. М = {х | х > 0}.
а)	Если 3 -г 2а — а2 4= 0, т. е. а 4= 3 и а 4= — 1, то
]ЛХ = —g~3	=________3	1 	1 у Q.
3 4- 2а — а-	(а — 3) (а -j- 1) а + 1 ’ а 4- 1	*
а < — 1; х = —-— при а < — 1.
(а-1)2 Н
б)	Если а — 3, то уравнение примет вид
0-]Т= 3 — 3,
х — любое неотрицательное число.
в)	Если а — —1, то уравнение примет вид
0-Тх= —1—3,
уравнение решений не имеет.
Ответ: при а< —1 х =----------1---:
(а -h I)2
при а — 3 х > 0;
при а > —1 и а =4= 3 уравнение не имеет решений.
Решить уравнения на множестве действительных чисел.
55.	(2а — 1) х = За 4- (а + 2) х.
56.	а2х 4- 2 = а (х 4- 2).
57.	т (тх — 1) = 3 (тх — 1).
58.	a (ab 4- 1) х 4- Ь2 = а2 4- (о3 4- Ь) х.
59.	26х 4~ &х == х (а 4~ ^) 4~ 4” сх,
60.	а (1 — ах) = 4Ь — 2ах.
61.	(ab 4- 2) х 4- а — 2& 4- (Ь 4- 2а) х.
62.	(а2Ь2 4- 36) х 4- а2 = Ь2 + (9а2 4- 462) х.
§ 3.	УРАВНЕНИЯ, СОДЕРЖАЩИЕ ЗНАК АБСОЛЮТНОЙ
ВЕЛИЧИНЫ
1) Решение уравнений вида f (| х |) = а.
По определению абсолютной величины, данное уравнение распа-
дается на совокупность двух смешанных систем:
[f W = а. и Я (—х) = а,
109
Так как функция /(|х|) четная, то ее корни будут существовать
парами противоположных чисел, т. е. если а — корень уравнения,
то и —а также будет корнем данного уравнения. Следовательно,
достаточно решить лишь одну из этих двух систем.
Пример. Решить уравнение х2 — х — 6 аналитически и
графически.
Решение. (х2 — | х | = 6,
(х > О,
х — 3.
Ответ: хх = — 3, х2 = 3.
Графическое решение (рис. 16).
2) Решение уравнения вида | f (х) | = <р (х).
Решение такого уравнения распадается на совокупность двух
смешанных систем:
(/ (х) = <р (х),	(/ (х) = —ф (х),
[Ф (х) > О [ф (х) > 0.
НО
Рис. 17
Примеры. 1. | 2х — 51 = х — 1.
Решение.
а)	! 2х — 5 = х — 1,
Ь— 1 >0,
х = 4.
б)	(2х — 5 = 1 — х,
[х—1 > 0,
х = 2.
Ответ: хх = 2, х.3 = 4. Графическое решение (рис. 17).
2. I—— —| = х—1.
| 2	4 I
а)	б)	1* 1 1 II 1 *
	2	4	2	4
	X — 1 > 0.	X — 1 >0.
	' 1	3
	X —	X = —,
	2	2
	X > 1,	х> 1,
		3
система решений не имеет.		х = —. 2
		Ответ:
111
Графическое решение (рис. 18).
3. Решение уравнения вида | atx -ф bt | ± | а, х Ь., | ± ...
... ± I akx -р bh | = с. Находят корни двучленов, стоящих под
знаком абсолютной величины:
Г -	у _	у _ bk
«1	а2
Пусть Хх < ха < ... < xh.
Данное уравнение последовательно решают на промежутках:
(—оо, xj, [хп х2], .... [xfe, оо).
Решить уравнение | х — 1 | — 2 | х — 2 | 4- 3 | х — 3 | = 4
Решение. xr = 1, х2 = 2, х3 = 3.
а)	х < 1; 1 — х 4- 2 (х — 2) — 3 (х — 3) = 4; х — 1.
б)	1 < х < 2; х — 1 + 2 (х — 2) — 3 (х — 3) =» 4; 4 = 4.
Любое х из промежутка 1 'Г х < 2 удовлетворяет уравнению.
в)	2 < х < 3; х — 1 — 2 (х — 2) — 3 (х — 3) = 4; х = 2.
112
г)	х > 3; X — 1 — 2 (х — 2) + 3 (х — 3) = 4; х = 5.
Ответ:1<х<2их=5.
Графическое решение (рис. 19).
Решить уравнения аналитически и графически.
63.	1 4- | х | = 0,5.
64.	1 — | х | = 0,5.
65.	-|х| — - = 11.
3 1 1	2	2
66.	0,3 I х I — 1 = 3 — 0,5 I х |.
67.	2 | х | — 4,5 = 5 — | | х |.
68.	| х — 2 | = 3.
69.	| х | = х + 2.
70.	| х | = 2х + 1.
71.	|—х 4-2 | = 2х 4-1.
ИЗ
72.	| Зх — 4 | = —x + 4.
73.	Zi±*-x= L3x~51.
5	2
74.	|x — 1 | 4- |x — 2 | = 1.
75.	| x — 2 | 4- | x — 3 | + | 2x — 8 | = 9.
76.	|	4x — 1 | — | 2x —	3 | 4- | x — 2 | = 0.
77.	|	x — 1 | 4- | x + 2	| — | x — 3 | =» 4.
78.	|	x — 1 | — | x 4- 2	| — | 2x — 5 | 4. | 3 — x| = —3.
79.	|	| | | x | - 2 | - 1	| - 2 | = 2.
80.	| 2 — | 1 — |x | | | = 1.
§ 4. КВАДРАТНЫЕ УРАВНЕНИЯ
81.	При каком значении k корни уравнения (k — 1)х® — 2 (k 4-
4-1 )х k 4-4 = 0 будут равны между собой?
82.	Доказать, что корни уравнения х2 — 2ах 4- а2 — Ь2 — с2 =
= 0 действительные, если а, b и с — действительные числа.
83.	При каком значении а уравнение (а 4- 3)х2 4- (2а 4- 3)х 4-
4- а 4- 5 = 0 имеет действительные корни?
84.	Доказать, что если р, k, п — рациональные числа, то корни
уравнения (р 4- k 4- п)х2 — 2 (р 4- k)x 4- (р 4- k — /г) = 0 ра-
циональны.
85.	Доказать, что корни уравнения х2 4- рх 4- q = 0 всегда
рациональны, если р = п 4-~, где р, п, q—рациональные числа
и п #= 0.
^‘2
86.	Доказать, что уравнение -—|-—— = 1, где а и b — дей-
х х — 1
ствительные числа и одновременно неравные нулю, имеет действи-
тельные корни.
87.	Доказать, что корни уравнения х2 — (k 4- «)х 4- (kn —
— р2) — 0 действительные (k, п и р—действительные числа).
Найти условие, при котором корни этого уравнения будут равны
между собой.
88.	Доказать, что корни уравнения а (х — &) (х — с) 4- b (х —
— а) • (х — с) 4- с (х — а) (х — Ь) = 0 всегда действительные.
89.	Доказать, что уравнение (а2 4- Ь2 4-с2)х2 4-2(а4-д-|-
4- с) х 4- 3 = 0 не может иметь действительных корней, если а,
Ь, с не равны между собой.
90.	Доказать, что корни уравнения (а2 4- Ь2 4- с2) х2 — 2 (аах 4-
4- ЬЬХ 4- ссх) х -|- а/ Ь2 4- с2 = 0 мнимые, за исключением слу-
чая, когда а : ах = b : Ьх = 'с : сх.
91.	При каком значении а уравнение (а 4~ 5) х2 4- (2а — 3) х 4-
4- а — 10 = 0 имеет действительные корни одного и того же знака?
114
92.	Дано уравнение: 9х2 — (2 — а) х — (6 4- а) — 0. Опреде-
лить, при каком значении а:
1)	уравнение имеет равные корни:
2)	уравнение имеет корни, равные по величине и противополож-
ные по знаку.
93.	При каком значении k уравнение х2 — 7х 4- k = 0 имеет
один корень а = —2.
94.	В уравнении 2х2 — Их 4- т — 0 найти т, если 2а — 0 =
s 2, где а и 0 — корни уравнения.
95.	Найти условие, при котором разность корней уравнения
х2 4- рх -|- q = 0 равна т.	-	(
96.	Даны два уравнения х2 -|- ах 4- 1 = 0 и х2 4- х 4- а — 0.
При каком значении а уравнения будут иметь общий корень?
97.	При каком значении а один из корней уравнения х2 —^х 4-
4- а’ = 0 будет квадратом другого?
98.	Найти условие, при котором разность квадратов корней
с2
уравнения ах2 + bx -f-c = 0 равна —
а2*
99.	Найти соотношение между коэффициентами уравнения ах2 4-
Ьх 4- с = 0, если один корень вдвое больше другого.
100.	При каком значении k один корень уравнения (k2 — 5k 4-
4- 3) х2 4- (3k — 1) х 4- 2 = 0 вдвое меньше другого.
101.	При каком значении к корни уравнения 2х2 4- (2Х — 1) х 4-
4- X — 1 =0 удовлетворяют соотношению За — 40 = 11 (а и 0 —
корни уравнения)?
102.	При каком значении X корни уравнения (2Х — 1) х2 4*
4- (5Х 4- 1) х 4- (ЗХ 4- 1) = 0 относятся как 3 : 2?
103.	Пусть Pi-p2 — 2 (</! 4* <?’)• Доказать, что по крайней мере
одно из уравнений х2 ргх 4-	= 0 или х2 4- р2х 4- qt = 0
имеет действительные корни.
104.	Уравнения х2 4- рх 4- q = 0 и рх 4* 72 = 0 имеют общий
корень. Найти зависимость между р и q.
105.	Доказать, что если уравнения ах2 4- Ьх 4- с = 0 и Ах2 4-
4- Вх 4- С = 0 имеют общий корень, то
(Ас — Са)2 = (АЬ — Ва) (Вс — СЬ).
106. Если один из корней уравнения х2 4- Рх 4- Я в 0 равен
обратному значению корня уравнения х2 4- тх 4- п. = 0, то (рп —
— т) (qm — р) — (qn — I)2. Доказать.
107.	Доказать, что корни уравнения ах2 fta 4-с = 0 обратны
корням уравнения сх2 4- Ьх 4- а — 0.
108.	Доказать, что если 0 и а — корни уравнения х? 4- Ьх 4-
4- Ь2 4- а = 0, то а2 4- а0 4- 02 4- а = 0.
109.	Какому условию удовлетворяют коэффициенты уравнения
Л । 9
х2 4- рх 4- q = 0, если а = где а и 0 — корни уравнения?
П5
ПО. Дано уравнение ах2 -\-bx 4-с = 0, корни которого a
и р. Составить новое квадратное уравнение, корни которого были
,	Г).	В
бы — и —
Р a ‘
111.	Составить квадратное уравнение, корни которого были
бы равны сумме и произведению корней уравнения ах2 4- Ьх 4- с =
= 0.
112.	а и р — корни уравнения х2 — 5х 4- 3 = 0. Не решая урав-
нения, составить квадратное уравнение, корни которого были бы
a 2Р и Р J- 2a.
113.	Дано уравнение ах2 Ьх 4-с = 0, корни которого a
и Р; составить новое квадратное уравнение, корни которого были бы
,1 а 1	1
a + — и р + —
а	р
114.	В уравнении Зх2 -\-ах — 2 = 0 определить а так, чтобы
корни уравнения аир были бы связаны зависимостью а2 4- р2 =
= !?•
9
115.	Не решая уравнения ах2Ьхс = 0, доказать, что
а® + а2р 4~ ар2 4- р® есть число рациональное, если коэффициен-
ты а, Ь и с — рациональные числа (а и р — корни уравнения).
116.	Если а и Р — корни квадратного уравнения с рациональ-
ными коэффициентами х2 4- рх 4- Q = 0, то выражение а4 4~ а®Р 4~
4- а2р2 4- ар« 4- Р4 рациональное. Доказать.
117.	Дано уравнение Зх2 — 18х 4- 5 = 0. Не решая уравнения,
вычислить ар2 — Ра2, где а и Р — корни уравнения.
118.	а и р — корни уравнения х2 — 5х 4- 3 = 0. Не решая урав-
нения, составить квадратное уравнение с корнями а4 и р4.
119.	Не решая уравнения lx2 4- 4х 4- 5 = 0, вычислить выра-
жение 4a® — бар2 4- 4Р3 — 6a2p, где а и Р — корни уравнения.
120.	Дано уравнение х2 4- рх 4-<7 = 0, корни которого
и	1.1
Не решая уравнения, вычислить выражение — 4-"^.
121.	Дано уравнение х2 + рх -\-q = 0, корни которого
Не решая уравнения, вычислить выражение
—— 4-—.
(2a 4- З)2	(23 + З)2
a
и
a
и
122.	Дано уравнение х2 + рх -\-q = 0, корни которого а и р.
Не решая уравнения, вычислить выражение

123.	Не решая уравнения х2 4- рх 4- q = 0, вычислить следую-
щее выражение: а’Р4 4- Р7а4, где аир — корни уравнения.
124.	Дано уравнение х2 4- рх -f- q = 0. Найти коэффициенты
р и q и корни этого уравнения а и р, если a 4-1 и р 4- 1 удовлетво-
ряют уравнению х2 — р2х pq = Q.
116
Найти корни уравнения с точностью до 0,001 с недостатком
125. № — 2 (1 4-]2) л- + 2 ]л2 = 0.
126.	х2 |/Т— (2	/З) х 4- 2 = 0.
127.	(2х 4- 2) (х ~ 1) = 5х 4- 6.
128.	х (2х 4- 3) 4- (12х + 6) = 0.
129.	8х (х 4- 2) 4- 3 (х 4- 1) 4- 1 = 0.
Решить уравнения на множестве действительных чисел.
130. х2 — 2 (а 4-1) х 4- 4а = 0.
131.	а + 2Ь = — ~ 4Z)V.
а —
132.	х (х 4-3) -L- а (а — 3) = 2 (ах — I).
133.	х2 -|- (а 4- с) х — 2а (а — с).
134	Л' <х , а — Ь__________2х
а- 2аЬ 4- Ь- Л а + b a -j- b
135.	(а — Ь) х2 — (а2 ab /У) х 4- ab (2а 4- Ь) = 0.
136.	а (а 4- 2) х2 4- 2х — а- 4- 1 = 0.
137.	/;х2 — а — (а — Ь) х.
138.	а (а -ь 1) х2 4- х — а (а — 1) = 0.
139.	(т- т - - 2) х2 4- (2m2 4- т 4- 3) х = 1 — т\
140.	(2х2 — Зх — 2) /г2 4- (1 — х2) m2 = тп (1 4- х;).
Решить уравнения аналитически и графически.
141.	х2 4-2,5 |х |— 1,5 = 0.	142. х2 4- 6 | х | 4- 8 = 0.
143.	х2 — 6 | х | 4- 8 = 0.	144. | х — 3 | = (х — З)2.
145.	(х 4- I)2 = | х + 3 | .	146. | 2х — 3 | = (2х — З)2.
147.	| х2 — 4 | = х2 — 4.
148.	| —х2 4- 1 | = —х2 4- 1.
149.	|	х2 — Зх	4-	2	|	=	Зх	- х2 —	2.
150.	|	2х — х2	—	1	|	=	2х	— х- —	1.
151.	|	5х — х2	—	6	|	—	х2	— 5х	6.
152.	|	х2 — 5х	4-	6	|	—	5х	— х2 —	6.
153.	lx2—1 | = — |х | 4- 1.
154.	11 х2 — 2х + - I + I—Зх + 4! -
I 2	2 I I 2	I 4
117
§ 5.	ТРЕХЧЛЕННЫЕ УРАВНЕНИЯ.
ПРИВОДЯЩИЕСЯ К КВАДРАТНЫМ УРАВНЕНИЯМ
Трехчленное уравнение вида
Ах2" + Вх" + С = О,
где п > 2 — натуральное число, при помощи подстановки хп = у
сводится к квадратному уравнению
Ду2 + By -4- С — 0.
Частным видом трехчленного уравнения является биквадратное
уравнение Ах* + Вх2 + С = 0.
При м е р. Решить уравнение х6 — 17х3 + 16 = 0.
Введем новое неизвестное у = х3. Получим уравнение у2 —
— 17у + 16 = 0, решениями которого являются ух = 16, у2 = 1.
Подставим в равенство у = х3 значения уг и у2. Получим два
двучленных уравнения х3 = 1 и х3 = 16. Решения этих уравнений
хх = 1, Чз= ~Х±2УЗ  *4= 2>^, х5(в = У2(-1±1УЗ) бу-
дут решениями данного уравнения.
155.	Не решая уравнения, определить, действительные или
мнимые имеет оно корни.
а)	5х* — 8х2 + 3 = 0;
б)	х* — 5х2 + 9 = 0.
156.	При каком значении % уравнение имеет два равных корня?
а) х4 + (31 + 1) х2 +1 = 0,
б) х4 + (31 — 1) х2 + 21 + - = 0.
157.	Составить биквадратное уравнение, имеющее в числе своих
корней /3 и |/2.
158.	Составить биквадратное уравнение с рациональными коэф-
фициентами, зная, что один из корней равен ]/2 + ]/5.
159.	Найти q в уравнении х4 — Зх2 + q = 0, зная, что хх +
+ х2 = 2 (хг и х2 — корни уравнения).
Решить уравнения на множестве комплексных чисел.
160.	х4 — 13х2 + 36 = 0.
161.	х4 + 26х2 — 360 = 0.
162.	2х4 + Зх2 + 3 = 0.
163.	2х8 + х4 — 15 = 0.
164.	36х8 — 13х4 +1 = 0.
118
165.	(2х — I)» + 3 (2х — I)3 — 10 = 0.
166.	(х — 2)« — 19 (х — 2)3 = 216.
। 167. Найти действительные корни уравнения (1 + х)8 4- (1 4“
-4. х2)1 = 2Х4.
168.	Решить уравнения на множестве действительных чисел
графическим способом:	,
а)	х4 4- Зх2 = 0;
б)	х4 -|- 4Х2 — 5 = 0;
в)	х4 — 4х2 4- 3 = 0;
г)	х4 4- Зх2 4- 2 = 0.
109.	Определить, при каком значении т корни уравнения
х4 — (3 п — 5) х2 + (т 4- I)2 = 0 составляют арифметическую про-
ip ссаю.
170.	Определить, при каком значении X корни уравнения х4 —
— (ЗХ 4- 1) х2 4- 2Х 4- 1 =0 составляют арифметическую прогрес-
сию.
§ 6.	ВОЗВРАТНЫЕ УРАВНЕНИЯ
Общий вид возвратных (симметричных) уравнений ахп 4-
4- Ьх'1'1 4- схп-"1 4- ... 4- сх2 4- Ьх 4- а = 0, где а =/= 0.
Возвратное уравнение не может иметь число 0 своим корнем.
Если возвратное уравнение имеет своим корнем число а, то оно
. 1
имеет корень, равный —
а '
При решении возвратного уравнения часто применяется подста-
новка у = х 4—
х '
Пример ы. Решить уравнения на множестве комплексных
чисел.
1.	бх4 — 13Х3 4- 12х2 — 13х 4- 6 = 0.
Дано возвратное уравнение четной степени. Разделим обе части
уравнения на х2. Получим уравнение
бх2 — 13х -'г 12 — 13-1 4- 6-— = 0.
X	X2
Сгруппируем попарно члены, равноотстоящие от начала и от
конца.
6 (х2 + —'l — 13 (х 4- Д 4- 12 = 0.
\	X2/	\ X )
Введем новое неизвестное у = х 4-—, тогда х2 4~— = у2 — 2.
X	X2
Получим уравнение 6 (у2 — 2) — 13у 4- 12 — 0, решениями ко-
торого будут У1 = О, у2 =
V
119
_ 1
Подставив полученные значения у в равенство х -\- — = у,
2	з
найдем решения данного уравнения х1>2 = ±«, х3 = —, х4 =—•
3	—
2.	х’ _|_ 2х* — 5Х5 — 13.г‘— 13-t3 — 5х2 + 2х + 1 = 0.
Дано возвратное уравнение нечетной степени. Такое уравнение
всегда имеет корень %! = —1, следовательно, его левая часть де-
лится на х 1.
(х + 1) (х* 4-х5 — 6х4 — Ух3 — бх2 4- х 1) — 0.
Таким образом, решение возвратного уравнения нечетной сте-
пени свелось к решению возвратного уравнения четной степени.
х6 4- х& — 6х4 — 7Х3 — 6v: х 4- 1 = 0.
Делим обе части уравнения па г’:
(> + 4) + (х'2 + - ) - 6 (х + - 7 = 0,
\ X3 /	\ X- /	\ X I
У = X 4- -, X2 4- 4 = у2 — 2, Xs 4- 4 = у1 — Зу,
X	Xw	х3
у3	уЗ _ 9у — 9 = 0.
У1 —	1, у, — 3, у3 =	3.
х 4- — = — 1, х 4- —  3 х 4- — = — 3.
X	XX
Откуда	_	_	_
— 1 4- i | '3	3'15	.	— 3 4 ) '5
Xi,i —	7)	’ Xi-:> — ~ о ’	~	9	•
ЗОх4 — Их3 — 228Х2 4- 17х + 30 = 0.
3.
Дано уравнение, в котором коэффициенты членов, равноот-
стоящих от начала и конца, при четных степенях равны, а при не-
четных степенях противоположны (возвратное уравнение II рода).
Разделим обе части уравнения на х2 и сгруппируем попарно
члены, равноудаленные от начала и от конца.
ПА /..О	,	1 \
--1 — 228 -0,
X /
L, = yS 2,
ЗОу-— 17у — 168 - 0,
У, = 2|, у2 = -2,1,
1	21	1	8
X-----=-----, X---.
х	10	х	3
Откуда Xi = — |, х.2 = х3 = 3, х4 = — |
2	и	и
120
4.	х4 — Зх3 -l 9№ — 27х 4- 81 = 0.
Если положить х — Зи, то получим возвратное*уравнение от-
носительно и. Можно данное уравнение решить и так, Разделим
обе части уравнения на 9х2:
— — - + 1 —— + — = 0,
9	3	3-х	9-х2
1(у2-18)-1у+1=0,
У	«д
у2 — Зу — 9 = 0,
,9	3 — 315	,9	34-3 ]Л5
X + — =--------, X 4- — — — у'----------.
1 х	2	*	1 х	2
Откуда л-1)2 = | (1 а ]л5 ± i Г 10-2/5) ,
= 7 0 — ।	' V Ю 4- 2 /б) .
Решить уравнения на множестве комплексных чисел.
171. л4 + бх3 4- 2х2 — 5х 4- 1 = 0.
172.	бх4 — 13г1 + 12л-2 — 13х 4- 6 = 0.
173.	х4 — 10х3 4- 26х2 — Юх + 1 = 0.
174.	2л4 + Зх3 — 4х2 — Зх 4- 2 = 0.
175.	ЗОх4 — 17Х3 — 228х2 4- 17х 4- 30 = 0.
176.	15х4 — 16х3 — ЗОх2 4- 16х 4- 15 = 0.
177.	Зх4 4- 7х* + 7х 4- 3 = 0.
178.	2х‘ — Эх3 + 9х 4- 2 = 0.
179.	12г’ — 56х4 4- 107л-3 — 107х2 + 56х —12 = 0.
180.	15л-’ 4- 34л4 4- 15л2’ — 15х2 — 34х — 15 = 0.
181.	хв 4- Зх5 + бх4 4- 7х3 4- бх2 4- Зх -(- 1 = 0.
182.	12г5 + 18х4 — 45.x3 — 45х2 4- 18x4- 12 = 0.
183.	бх3 — х2 — 20х 4- 12 = 0.
184.	х4 4- 1 = 2 (1 4- х)4.
185.	(1 4-х2)2 4-2ах (1 — х2).
121
186.	В возвратном уравнении х4 4- рх? 4~ Зх2 4- Рх + 1 = О
определить р так, чтобы произведение двух корней равнялось 2.
187.	Дано возвратное уравнение х4 4- рх3 4- дхг + рх 4- 1 — 0.
Доказать, что если оф = 2, то р и q связаны зависимостью 4р2 —
— 18<? 4-45 = 0 (а и р — корни уравнения).
188.	Составить возвратное уравнение четвертой степени, в
числе корней которого были бы 5, 3, у
189.	Доказать, что если в уравнении ах4 4- Ьх3 4- сх2 4- dx 4-
4- е = 0 коэффициенты удовлетворяют соотношению а : е =
= b2: d2, то уравнение решается, как возвратное, подстановкой у =
, ь
— х —|— —
X ‘
Решить уравнения на множестве комплексных чисел.
190.	х4 4- 2х3 — 11х2 4- 4х 4- 4 = 0.
191.	х4 — 2Х3 — 23Х2 4- 8х 4- 16 == 0.
192.	2л-4 — 21х3 + 74х2 — 105х 4- 50 = 0.
193.	2х4 — 15Х3 4- 40х2 — 45х 4-18 = 0.
,194. 27.x® ф 27Х5 — 117Х4 + 195х2 — 75х — 125 = 0.
195.	5х4 — 14Х3 — 79х2 4- 84х + 180 = 0.
§ 7.	ЧАСТНЫЕ МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
1.	Метод разложения левой части уравнения = 0
на множители
Этот метод решения основан на теореме:
Если функции (х), /2 (х), .... fn (х) определены на некотором
множестве М, то на этом множестве уравнение
равносильно совокупности уравнений
fi (х) = 0
А (х) = о
fn (х) =0
Решить уравнения на множестве комплексных чисел разложе-
нием на множители.
196.	х3 — Зх — 2 = 0.
197.	х3 — 19х — 30 = 0.
198.	2х3 — х2 — 1 = 0.
199.	х3 4- х — 2 = 0.
122
200.	х3 4- 4х2 4 бх 4 4 = 0.
201.	бх4 — 13х3 — 27х2 4 40х — 12 = 0.
202.	9х2 4-4Х3 = 1 + 12x4.
203.	х4 4 х? 4 х2 4- х 4 1 = 0.
204.	х5 + х3 + х = 0.
205.	х3 — бх4 4 Эх3 — бх2 4 8х = 0.
206.	Зх7 4- х? + Зх4 4 х3 4- 15с 4-5 = 0.
207.	8х7 — бх6 — 4х4 4- Зх3 4- 8х — 6 = 0.
208.	х? 4- 2х* 4- 4Х4 — Збх3 4- 32х* — 72х 4 48 = 0.
209.	(х3 + х2 4- 1)! 4 (х3 — х2 4 I)2 = 2Х4.
210.	(х — I)3 4 (2х 43)3 = 27х® 48.
211.	х5 — (х 4 2)8 = —2.
212.	(х — 1) (х — 2) (х — 3) = 24.
213.	х* 4 (1 — а2)х 4а = 0.
214.	х (х2 — 2) = а (х2 4 2ах 4 2).
215.	х4 4 2а3х = а4.
216.	х3 4 рх2 4 (р — 1 4—— 'j х 4 1=0.
\ р — 1 /
217.	(а —- х)3 4 (Ь — х)3 = (а 4 b — 2х)3.
218.	х3 (с — Ь1) 4 Ь1 (х — с1} 4 с3 (Ь — х2) 4 bcx (bcx — 1) =
= 0.
219.	ах4 4- Ьх3 4 сх4 4 dx 4 е =* 0, если а4^«&4^ =
= d 4 е.
220.	Найти действительные корни уравнения (14x4х3)2 =
=	(1 4 х2 4 х4) при | а | > 2.
« — 1
2. Метод введения нового неизвестного
Иногда при решении уравнений высокой степени с целью упро-
щения полезно ввести новое неизвестное.
Пример, (х2 4x4- 1) (х2 4 х 4 2) — 12 = 0.
Введем новое неизвестное у = х2 4 х 4 1 • Данное уравнение при-
мет вид
у (у 4 1) - 12 = 0.
Корни полученного уравнения 54 = —4, у.2 = 3. Подставляя
вместо у найденные значения, получим два квадратных уравнения:
х2 4 х 4 1 = —4 и х2 4 х 4 1 — 3.
Решения этих уравнений Xi)2 = ~ 1	*.?» х9 =—2, х4 = 1
будут решениями данного уравнения.
123
Решить уравнения на множестве комплексных чисел методом
введения нового неизвестного.
221.	(х2 + 5х)2 — 2 (х2 4- 5л) — 24 = 0.
222.	(х2 + 2х)2 — 11 (х2 4- 2л) = 15.
223.	(х2 — 2х — I)2 — Зх2 — бх — 13 = 0.
224.	(х2 + х + I)2 — Зх2 — Зх - 1 = 0.
225.	(2х2 — х + 5)2 + 3 (2хг — х — 1) — Г) = 0.
226.	(х2 — 5х 4- 7)2 — (х — 2) (х — 3) = 1.
227.	(х — 1) х (х 4- 1) (х 4- 2) = 24.
228.	(х 4- 4)	(х	t	5) tx 4- 7)	(х	4-	8) =	4.
229.	(х 4- 1)	(х	4-	2) (х 4- 3)	(х	4-	4) =	120.
230.	(х — 2)	(х	4	1) (х 4- i)	(х	4-	7) =	19.
231.	(х2 4- х	4-	1)	(2х2 4- 2х	—	3)	= —3 (1 — х — х2).
232.	(2х2 4- Зх — 2) (5 — бх — 4х2) = —о (2х- 4- Зх 4- 2).
§ 8. ДРОБНО-РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Применяя теоремы равносильности уравнений, можно заменить
дробно-рациональное уравнение целым алгебраическим уравнением.
Надо помнить, что мы производим преобразования, которые могут
привести к появлению посторонних корней. Отбор посторонних
корней можно производить или путем сопоставления с множеством
допустимых значений неизвестного, или путем проверки корней.
Примеры. Решить уравнения на множестве действитель-
ных чисел.
I)	--—- = 3 — х — х2.
1 -р X -р X"
Так как 1 4- х 4- х2 не обращается в нуль ни при каком действи-
тельном значении х, то данное уравнение равносильно уравнению
3 = (3 — х — х2) (1 4- х 4- х2).
Введем новое неизвестное у = 1 4- х 4- х2. Получим уравнение
3 = (4 — у) у, решениями которого будут yt = 1, у., = 3.
Подставляя значения у, получим два квадратных уравнения:
х24-х = 0 и х24-х — 2 = 0,
решения которых хА = 0, х2 = — 1, х3 = —2, х4 = 1 будут реше-
ниями данного уравнения.
2) — =	-----3. /И : х * 4.
х — 4 х — 4
Умножая обе части уравнения на х — 4, получим: 9 — х — 5 —-
— Зх 4- 12, OIкуда х = 4.
124
Сопоставляя полученный корень с множеством допустимых зна-
чений неизвестного М, приходим к выводу, что данное уравнение
корней не имеет.
X "Т“ 1	9.1	. .	,	.
3) -------=-----------------. М: х ф 1, х Ф- —4.
2(х—1)	2(х + 4)	х—1
(х + 1) (х 4- 4) = 9 (х - 1) 4.2 (х 4- 4),
х2 — 6х 4-5 = 0,
хг = 5, х2 = 1.
х., £ М, следовательно, является посторонним для данного
уравнения. Уравнение имеет один корень х = 5.
х2 ,	х4-1	1	1	„
4) —------1-----— = -------------• Мх =£ -4-2.
х3—4	2 (х — 2)	2 —х х4-2
2х2 + (х 4- 1) (х 4- 2) = —2 1(х 4- 2) 4- (х — 2)1,
Зх2 4- 7х 4- 2 = О,
хх = —2, х2 = —-i- . хг£ М.
Уравнение имеет один корень х = —
3
Решить уравнения на множестве действительных чисел.
233. 234.	2	5	2	3	 х—14 х — 13 х— 9 х—11 12x4-1 _ 9х —5	108х — Зб.у- — 9 6х — 2	Зх + 1	4(9х2— 1)
235.	12x4- 1	4	.	3	_ q
	2х2 — 7х + 5 2х — 5 х — 1
236.	х2 + 2х + 2 . х2 + 8х 4* 20 _ х2 4-4х + 6 , х2-1- 6x4' 12 .	4*	.	.... — .	. . .|.
	х4-1	х4-4	х + 2	х + 3
237.	5(6 —х) _ 10 (5 — х) _ Ц . 6 —х
	х —2 ~ 3(х —4)	3 х —4*
238.		4			 4--Л_=0.
	2х3 4-Зх3 — 8х — 12	Xs — 4	2х24-7х + 6	.2x4-3
	1	21	3,1
239.	—-	1		 -г— + — -	.
	2х 4- 3	2х3 4- Зх- — 2х — 3	х3 — 1	2х3 + 5х -)- 3
94А	1	1	,	1	х~*	_ о
	г-	-	V.
	2x4-3 х3 —16	2х34-11х4-12	2х34-3х3—32х — 48
	10	,	3	7	ох —9,4
241.	Н-	—	4~
	6х3 —х— 12 3x 4- 4	6х3 — х — 12	2х —3
242.	4х2 4- 29х 4- 45 — (х 4-1) (2х 4- 15) (х - 1) (х 4- 5)
	[2 (х — I)]2 — 2 (х 4-1) (х — 2)	(х - 1) (х - 2) '
125
243.	3	_	1	3 х2 -г х — 2 х (х — I)2 ‘ х (х — 3)
244.	—•	!	+	!	1	= о. х24-7х	х24-7х-)-6 х2 + 7х + 18 х2 + 7x4-12
245.	х	।	Зх 4~ 1	х 4~ 34	q 2х2 +12х 4- Ю 1 4х2 + 16х — 20	х3 + 5х2 — х — 5
246.	/х 4-— Г4-х = 42——. \	X /	X
247.	Х2+ - + 6|х+ -'l =23. X3	\	X /
248.	^ + 18= ю/х__4\ 3 х3	\3 х/
249.	2 (1 4- -) + 3 (^±??= 14. \ х /	\ х 1
250.	10	~ 	= 6 — X — X2. 1 + X + X*
251.	ха 4- X 4- 1 _ 7_ . Х4-1 х2 — X + 1	9 х — Г
252.	2	3	_ £ х24-2х —2 х2 — 2x4-3 — 2'
253.	24	12	, , 	 =	4 X2 — х. х2 — 2х х2 — х
254.	Зх2 — 4а 	 Зх	х ах — а — Зх + 3 а — 3 х — 1
255.	/ а	,	\ / х	\	/ х	,	\ / а	\	1 п 	Их	а —	Н	х = 10. \х + а	]\х — a	)	\х + а	/ \х — а	}
256.	а _ Ь 1 — bx 1 — ах
257.	т	п 	т — п х — т х — п х — р
258.	а-\- Ь а — b	а	Ь —|— -		 г		—- * х — а х — Ь х — а х — b
259.	ab — х Ь — сх b — ах Ьс — х
260.	а 4- с	а -г с _ 1 х — а	х 4- с 2
261.	Ь2, 4- 2а	b _ х	х ах -4 2а + Ьх 4~ 2Ь х 4“ 2 а 4" Ь х + 2
232.	ах2 4~ &х 4- с _ ах 4- Ь тх2 4- пх 4- р тх + п
126
263.	X	.	X	.	1	Cl -J- 3 — ab	ах —За х — 3	ах — За — bx + ЗЬ
264.	х	х	।	1	_ 	а + 3	 а2 ab ах -f- За х + 3 ах + За + Ьх + ЗЬ
265.	X го 1 II р
266.		!	।	!	।	L	।	L_ ~ о. x~ra + b x — a + b x-j-a — b 1 х — а — b
267.	а- + ах + х2   а2 а1 — ах + х2	х2
268.	5	_	3 Зх — k kx — 4 *
269.	1 • 1 4- 1 =	1 х	a	b af/if /
270.	1	,	1	_ 1 _1 х + й ' х — Ь Ь	а
271.	& — а2~ь* - &2 (* + 2> ‘ 2х — х2	х — 2
272.	.	1	а — b . аb X -J	== —	1- — х	а + 6 а — b
273.	10	8	9	_ q х2 — 4ах	х2 — 4ах 4- За2	х2 — 4ах + 4а2
Решить уравнения аналитически и графически.
274. а)	31 х | + 2 |х|-1	= 3,
275. а)	2 — 3 | х [ 1 +|х|	= 1,
276. а)	31x1-2 |х|-1	= 2,
1 Зх -|“ 2 1 | х — 1 1	= 3,	в)	|31х|4-2 1 1*1-1	= 3.
| 2 — Зх |	1,	в)	2 —3|х| I	= 1.
1 1 4-х 1			1+1*1 1	
| Зх —2	^2,	в)	I 3| х | —2	2.
| X — 1			1 1*1-1	
ГЛАВА VII
СИСТЕМЫ РАЦИОНАЛЬНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
§ I. ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ
Системой К уравнений с неизвестными х, у,	, z называ-
ется множество, содержащее k уравнений.
(А (х, у, ... , z) = ча (х, у, ... , z)
А (х, у, ..., г) = <р, (х, у...z)	qj
7л (х, у, ... , г) = q>ft (х, у, ..., z),
где правые и левые части всех уравнений являются функциями,
которые рассматриваются совместно в общей части их областей
определения.
Решением системы (1) называется система чисел х — а,
у = Ь, ... , z = с, удовлетворяющая каждому ее уравнению.
Решение записывается или в виде последовательности чисел
(а, Ь, ... , с), или в виде
х — а у = b системы г	или таблицей Z — с	X	У		г
	а	b		с
Система уравнений, имеющая по крайней мере одно решение,
называется совместной. Совместная система называется опре-
деленной, если она имеет конечное число решений, и неопре-
деленной, если множество ее решений бесконечно.
Система, не имеющая ни одного решения, называется несов-
местной или противоречивой.
Две системы с одними и теми же неизвестными, рассматриваемые
на некотором множестве А, называются равносильными относи-
тельно множества А, если всякое решение любой из этих систем
является решением и другой из них.
Две равносильные системы уравнений могут состоять из одина-
кового и различного количества уравнений. В частности, система
уравнений может быть равносильна одному уравнению.
Процесс решения системы состоит в последовательной замене
данной системы равносильной ей системой более простого вида.
Основные методы получения систем уравнений, равносильных
заданной (метод подстановки и метод алгебраического сложения),
основаны на теоремах:
Теорема 1. Если из одного уравнения данной системы (1)
выразить одно неизвестное через остальные, а затем подставить
это выражение во все другие уравнения системы, то полученная си-
с тема будет равносильна данной.
128
Теорема 2. Если к одному из'уравнений системы (1), умно-
женному на множитель f (х, у, ..., г), имеющий смысл и не обращаю-
щийся в нуль при всех допустимых системах значений неизвестных,
прибавить некоторые другие ее уравнения, умноженные на любые
множители <р (х, у, ..., г), определенные при всех допустимых си-
стемах значений неизвестных, а остальные уравнения оставить без
изменения, то получим систему, равносильную данной.
Пример ы. Решить системы уравнений.
1. х 4- 2у + 5г — —9,
х — у + Зг = 2,
,х2 4- у2 4- г2 = 14.
Из первых двух уравнений выразим х и у через г, для этого ре-
шим систему двух линейных уравнений.
(х 4- 2у 4- 5г = —9,
|_х — у 4- 3z == 2.
_	54-Иг	11+2г
Откуда х =--------—, у =-------------— .
Подставляем значения х и у в третье уравнение. Получаем урав-
нение второй степени 67г2 4- 77г 4- 10 — 0, корни которого гх =
2. |'2х — у — ху — 14,
|х 4- 2у 4- ху = — 7.
Данная система равносильна системе
|3х L у — 7,
(л- 4- Ъ т V =" —7>
в которой первое уравнение получено алгебраическим сложением
уравнений данной системы.
/Методом подстановки находим решения системы
X	3	__2 	2
У	— 2	14
При решении систем уравнений часто применяют метод введе-
нии новых неизвестных.
5 Заказ 1089
129
Пример. Решить систему уравнений
/15	7
------=9,
х у
1 + 1 = 35.
I* у
Положив — = а, —= Ь, получим систему линейных уравнений
X У
относительно а и Ь:
f 15а —76 = 9,
|4а + 9Ь = 35.
Решение такой системы легко найти.
Используя специфические особенности системы уравнений,
применяют различные частные и искусственные приемы.
Примеры.
1. х2 + у2 = 5,
I ху = 2.
При решении этой системы используем свойства корней квадратно-
го уравнения.
1-й способ. 2-й способ.
(X +У)2 = 9,
ху = 2.
х -|-у = ± 3,
ху = 2.
(х2 + у2 = 5,
( х2у2 = 4.
z2 — 5z + 4 = О,
Zi = 1, z2 = 4.
2. (х2 4- у2 = 2,5ху,
|х — у = 0,25ху.
Первое уравнение системы является однородным уравнением.
(х — О
_ 0 — решение системы.
Найдем другие решения, считая, что х =# О, у =# 0. Введем новое
неизвестное у = tx.
Получим уравнение х2 4- /2х2 = 2,5х2/, или t2 — 2,5/ +1 = 0.
Откуда 4 = 2, /2 = 2.
130
Подставляя во второе уравнение у — 2х и х = 2у, получим урав-
нения 0,5х1 2 3 * 5 4- х — 0 и у (0,5у — 1) — 0.
Откуда находим решения данной системы
fxi = —2,	(х2 = 4,
1Ух = —4.	[у2 = 2.
3.
(х + у) (х + г) = а,
(х + у) (у + г) = Ь,
(х + г) (у + г) = с.
Перемножим уравнения системы.
(х + У) (х + z) (у 4- z) = ± У abc. Разделим полученное урав-
нение на каждое уравнение системы:
х -{- у = ~ ^abc t
с
. X + Z =	,
ь
у + Z = *	
а
Такую систему легко решить методом алгебраического сложения.
Ответ:
§ 2. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Решить системы уравнений.
1. (Зх — 4у 4- 5z = 18,
12х 4- 4у — 3z = 26,
lx — бу 4- 8z = 0.
3. (10х —9z = 19,
{ 8х — у = 10,
I у — 12z = 10.
5. (х 4" 2у 4~ z 4~ Т = 0,
< 2х 4- у — z — 1 =0,
(Зх — у 4- 2z — 2 = 0.
2. (2z 4- 5 = Зх,
(х 4- бу 4- 4z = 10,
l8y — 5х 4- 2 = 0.
4. (х 4- у 4- z = 6,
12х 4- У — z = 1,
(Зх — у 4- z = 4.
/х 4- у = 4,
2у 4- z = 11,
Зг 4- 2и = 29,
,4« 4- Зх = 31.
5*
131
С - Ф О ‘° Го О	р р Р
25.
26.
' 2x + Зу + 4г -|” 5и —- —~2,
Зх + у + 2г 4- 4и = 1,
4х J- бу + Зг 4- lu = i,
, 5х 4- 2у 4- г 4- 4u =4.
Xj 4- Хо ““ ЗХд -- 1 ,
2х^ 4- х2 ~~ 2х3 == 1,
*1 4- Х2 +	~ 3,
Xj 4~ 2х2 Зх3 — 1.
СЛ to
28.	(х2	+ Х3 + *4 + Хэ		4~ х6 =	з,
	Х1	+ хз	4- х4 4" хз	4* хв ~	5,
	Х1	4“ Х2	+ х4 4"	4- хз —	4,
	Х1	4“ Х‘2	+ Х3 4“ Х5	+ хз =	7,
	Xi		-+- х3 4~ xi	+ л4 ~	И,
	*1	4- х2 -р хз 4~ xi		4- х5 =	10.
29.	Х'1	х2	4- хз 4~ xi	4“ Л<5 + Х6 —	
	Х1	+ Х3	-’г xi 4- х3	4- хз —	2,
	Х1	-р X.,	4- х4 4- Ъ>	4- Ч	3,
	Х1	4-х;	4- хз 4- Ъ	“Г Х6 =	4,
	Х1	+ Х2	+ хз 4_ xi	~Г	“	5,
	Х1	+ х2	4- х3 -4 х4	4~ х5 =	6.
30.	X!	J- X?	+ л4 4~ •••	4~ хп	= 1,
	Х1	4- х3	4" Х 4 + • ”	4~ хп	: 2,
	Х1	х2	4~ х4 4” ***	4~ хп —	 з,
	Л'1	4-х2	+ хз 4“ •••	+	= п
31.	х4 -р 2х2 4“ Зл'з -’р 4х4 -р ... -|- /1хл 1Ъ\\	х’2 4- 2х3 4 Зх4 4- ... 4- (п — 1) хп (// — 1) х4 4~ ^х2 4“ хз 4_ 2х4 + ... 4- (п —	« а„ = а2, 2) хг1 =
	2xr -J- 3х2 -) 4х3 -j- ... 4- хп	ип» у
32.	(х, — х, — х3 — ... — х„	= 2а,	
33.	! ю	1	1	1* 2^ 4*	2? 1+1	1	1	+ .1?	,Г-	£ 1+'*| II •+”'| 1 1 1 ;	।	। +:4| 1 ~Ь	ьЗ to ~	9 *	I О’ цг ”	1 + 1	“ 11 II	н II II Г*Г“	
133
34» Xj 4* x.j а^,
Xg 4* x3 — ®2,
	1 + ХП	Яд—1> хп + Х1 =	•	
35. 1+J = У+1 = *4-у	36. 1 20~	21	17	1		(x : у : 2 : и = 1 : 2 : 3 : 4, |9x 4“ 7у 4- 3z 4“ 2a == 200.
37. 1	(х : у : z : и = 0,1 (6) : 0, (3) : 0, у И-	==	(5): 0, (6),
38.	£ — L — L — «	39. а Ь с d ’	& 1 * II II n | M II Я. | Я
	,x4-y4-z4-a = s.	ax 4- fJy 4- yz 4- 6a = s.
40.	х 4~ У 4" z = nx = ту, ,rx = pz.	
§ 3. ИССЛЕДОВАНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Исследовать систему уравнений — это значит решить вопрос
о ее совместности или несовместности, и если она совместна, то
найти все ее решения.
Примеры. Исследовать систему уравнений.
1.	(ах 4- у = 2,
|х + у = 2а.
Решение.	-
Определитель данной системы Д = а — 1. Если а =# 1, то си-
стема определенная.
При а = 1 имеем (х 4- у = 2,
1х 4- у = 2.
Система неопределенная.
2.	((а 4” 5) х 4“ (2а 4~ у (За 4* 2) == О,
[(За 4-10) х 4- (5а 4- 6) у — (2а 4- 4) = 0.
Решение. Д = (а 4- 5) (5а 4- 6) — (2а 4- 3) (За 4-10) =
= -а (а - 2).
Если Д = —а (а — 2) #= 0, то система определенная. Если
Д = —а (а — 2) = 0, т. е. а = 0 или а — 2, то система может
быть неопределенной или несовместной.
При а = 0 имеем: (5х 4- Зу — 2 = 0,
(10х 4- бу — 4 = 0.
Система неопределенная.
При а = 2 имеем: (7х 4- 7у — 8 = 0,
(16х 4- 16у	8 = 0.
Система несовместная.
134
3.	(ax — у — b,
[bx. 4- у = a.
Решение. A = a A-b.
1)	Если A = a 4- b ф 0, т. e. a	—b, то система определенная.
2)	Если a = —b, то имеем: (ax — у — —a,
[—ax 4- у = a —
система неопределенная; в частности, при a = 0 и i = Оее реше-
нием служит пара чисел: х — любое число, у = 0.
Исследовать системы уравнений.
41.	(ах 4-у = 2,	42. (Зх +аУ — 5a2,
(х 4- у = 2а.	|3х — ay = a2.
43.	(x 4- ay — 1 = 0,
[ax — 3ay — (2a 4- 3) = 0.
44.	((a 4- 5) x 4- (2a 4-,3) у — (3a 4- 2) = 0,
((3a 4- 10) x 4- (5a 4- 6) у — (2a 4- 4) = 0.
45.	((a — 1) x 4- 2ay 4-2 = 0,
[2ax 4- (a — 1) у — (a — 1) = 0.
46.	((2a — 3) x — ay — 3a 4-2 = 0,
I—5x + (2a 4- 3) у 4-5 = 0.
47.	((a — 1) x 4- (a 4- 1) у — 2 (a2 — 1) = 0,
[(a2 — 1) x 4- (a2 4- 1) у — 2 (a3 — 1) = 0.
48.	(a (a — 1) x 4- a (a 4-1) у = a3 4- 2,
[(a2 — 1) x 4- (a3 4-1) у = a4 — 1.
50.
ax — у = b,
bx -f- У — о.
Ax — 5y -|- mz = 3,
lx — lly -J- nz = 3,
ix 4- у + pz = 3.
bx + ay = c, '
ex + oz = b,
cy bx = a.
49. fay — bx — О,
- x = b — a.
4- by = a +bb,
bx 4- ay — ah 4- b.
51. (ax
52.
54.
53. |'ax 4- у 4-2 = 4,
jx 4~ by 4- z == 3,
lx 4- 2by 4- z = 4.
55.	Может ли быть система уравнений
(ах 4- by = al,
[bx 4- су = bl
неопределенной или несовместной?
Исследовать системы уравнений.
56.	((а2 4- д2) х 4- (а2 —	Ь2) у	=	а8,
[(а 4- Ь)	х	4-	(а — Ь)	у	=	а.
57.	|(а	5)	х	4-	(а — Ь)	у	=	а2	4-	ft2,
((а — 5)	х	4-	(а 4- Ь)	у	=	а2	—	Ь2,
135
58.	Определить параметры тар так, чтобы система
j(3m — Зр 4- Ь) х (8т — Зр — а) у = 1,
|(2т — Зр Ь) х 4- (4m — р) у = 2
была неопределенной.
Исследовать, совместны ли уравнения.
59. (2х — Зу = 1,
{% — 2у = 3,
(Зх — 2у = 1.
61.
Зх — 2у = 5,
бх — 4у = 10,
9х — бу = 12.
60. |5х —Зу = —1,
4х 4-Зу = 10,
(2х — Зу = —4.
62. 12х — 4у = 3,
] х — 2у = 5,
(Зх — бу = 7.
63.	Определить а таким образом, чтобы уравнения
(ах 4- у = 1,
X 4- у = 2,
(х — у = а
были совместны.
64.	Найти такие значения параметра а, чтобы уравнения
Зх — 4у = а (а1 4- 12),
5х — бу = 2а (а 4- 3),
7х — 8у = 12 (4 — а)
были совместны.
65.	Определить а таким образом, чтобы уравнения
у — 2х = О,
• (2а 4- 5) х 4- (За 4- 1) у 4-3 = 0,
(а 4- 5) х 4- (2а 4- 3) у — 18 = 0
были совместны.
66.	Найти необходимое и достаточное условие того, чтобы урав-
нения
(atx 4- 6Ly = Ci,
!a.,x 4- b2y — c.,,
ЬзХ 4- bsy = cs
были совместны.
67.	Найти значения параметров а и Ь, при которых были бы
совместны уравнения
2х — у = ab,
х 4- Зу = а2 4~
х 4- у = 52— — а2 — Ь2,
7
х — у = 2аЬ — 26—
Л	7’
136
68.	Совместны ли уравнения
(х + ay = b 4- с,
I х Ьу = с + а,
(х + су = a -j- Ь,
где а, Ь, с — действительные числа, связанные соотношением
я2 + Ь2 4- с2 — 1?
Исследовать систему уравнений.
69.	|(b2 4-f2) х + &Ьу ~ ас,
labx 4- (с2 4- я2) у -= Ьс,
'сах 4- Ьсу -- а1 4- Ь',
где я, Ь, с — действительные числа и я2 4- b2 4-са — 1.
/0. Iх4 4- Х2 ~Н хз 4-х4 — О,
। х4 4- Зх, + 6х3 4- Юх4 = О,
1х4 4- х2 4” 4д3 4“ Юх4 — 0.
71. I х4 4" х3 4- х4 = О,
। Х| 4" х., 4- х4 == О,
12л4 4“ х% 4- х3 4" 2х4	1.
72.
73.
х4 — х> 4“ Зх3 — х4 — 1,
х4 — Зх, 4- х3 4— х4 •== О,
х4 — 2х, 4- 2х3 = 0.
Х| — 2х, 4- Зх3 4х4 4- 2х3 — О,
2Х| 4~ ЗХ2 4х3 4” х± — 2х=, О,
Зл'| 2х2 4- 4х3 4- х4 — Зх^ — О,
4х4 4- Зх2 — х3 — 2х4 — 4х5 = 0.
74. При каком значении параметра я система уравнений
I 2х4 х, 4- х3 4- х4 — 1,
х4 4- 2х, — х3 4- 4х4 = 2,
1х4 4- 7х2 — 4х3 4- 11х4 = а
имеет решения?
Исследовать систему уравнений.
75. |ях 4- У 4- 2 = 4,
\ х 4“ by 4“2 === 3,
1х 4- 2Ьу 4-2 = 4.
76. (ах +У 4-2 = Ь
х 4-ЯУ-4-2 = а;
U 4- У 4- «2 = а ’
77.
'их 4“ у 4*2 4-	1 •
х 4- ау 4- 2 4- — а,
х 4- у 4- az 4- I = а2,
х 4- у 4- г 4- ai = я3.
137
§ 4. СИСТЕМЫ НЕЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Решить системы уравнений.
9 = 0,1.
х + у
6
* + у
83. Г(5х — 1) (Зу + 2) = (2х + 1) (9у — 2),
[(Зх + 2) (2у - 9) = -(х + 2) (у + 9).
84.	[1 + 1+J_ = 9,	85’	ЗХУ _ g	86.	
	xyz	х + у	х + у
	1+1+1=11,	=3,	Уг
	X у л о		У + г
	± + ± + ± = 13,	-^— = 4.	ZX —- = q.
	X	Z	V	Ь4-г	\z + x
	1 + 1 + 1 = 15.		
	у	Z	V		
87. xyz = a (yz — zx — ху) = b (zx — ху — yz) = с (ху —
— yz — гх).
138
88,
'х~ _ 5
Г~8’
89.
Зх — 4 у + 5г = 248.
х : у = 5 : 3,
у : г = 6 : 7,
г : и = 21 : 4,
У + г = _9__
, хг—и2 68
х = 2_
Z 11 ’
90. Г(2х + у) : (Зх + г) : (у + г) = 1 : 2 : 3,
|21х + 31у + 42г = 15.
91.
х (у 4* г) : у (г + х) : г (х + у} = р : q : г,
—I—I— = р 4~ q +г'
X у Z
92. (	ху = 12, х — 2у — 2 = 0.	93. Гх2 + 4у2 — Зх — 2 = (2х 4* Зу = 5.	
94. J	2х2 — Зу = 23, 3/ _ 8х = 59.	95. (5х2 + 14у = 19, (7у2 4- Юх = 17.	
96.	х2 + Зу2 — хг = 6, 2х — у + Зг = 11, х + 2у — 2г = 1.	97.	х2 4~ У2 = 25, ху = 12.
98. J	х4 + у4 = 97, ху = 6.	99. (х 4- ху 4- У = 11, |х — ху 4- у = 1.	
100.	(ху + х + у = И, |х2у + У2Х = 30.	101.	‘t Ч| II ьэ II со
102.	(5ху + Зх2 = 57, [15ху — х2 = 81.	103. |	х2 4- ху 4- х = 10, У 4- ху 4- у = 20.
104.	(Хг _ / = 16, (х + у = 8.	105.	оГ II 1 -«1 х
			4—4 = 16. X2	у2
106.	((х + 2у)2 — (у — 2х)2 [(х + 2у) + (У — 2х) =	= 168, = 12.	
107.	(х2 = 13х + 4у, [у2 = 4х + 13у.	108.	fx2 (х 4- у) = 80, |х2 (2х — Зу) = 80.
109.	(х — у = 2, (х3 — у3 = 8.	ПО. 1	х 4- у = 5, х3 + у3 = 65.
111.	(х2 4* у2 — а,		fx , у _ 10
	- + - = ь. и2 у2	112. ।	У х	3’ [х2 _ у2 = 8.
113.	х + У | х— у 5_	114. ।	(х4-У . х —у _ 10
	х — у х + у 2* + у2 = 20.		। х — у х + у	3 1 1х2 + у2 = 5.
139
115. f(x + # 4 (x J- у)2 — 117= О,
(x — у — 25.
116. (Зх2 — 8ху + 4у2 = О,	117. (х2 4- 2у2 = 17,
(х2 + у2 + 3 (х — у) = 0.	’ (бх2 — ху — 12у2 — О.
118.' (х2 4- ху 4* у2 = 19 (х — У)2»
(х2 — ху + У2 = 7 (х — у).
119. (Зх2 - 8ху 4- 4у2 = О,	120. (х2 + ху = 12,
(х2 + у2 4- 13 (х — у) = 0.	(ху — у2 = 2.
121. (х2 — 4у2 = 9,	122. [х2 4- Зху — 54,
(ху 4- 2у2 = 3.	(ху 4- 4у2 — 115.
123,	124. /(.х2+ у2) - = 6,
(2л- -г 2ху 4* у = 26.	у
(х1— у2) 2 = 1.
.	X
125. (х2 4- Зху = 7,
(ху 4- Зу2 = 14.
127. (х3 —Зху2 = 1,
(Зх2у — у3 = 1.
129.	X3	у3	__]5
	У х	“ 2*
	L — L: у	X	” 2*
131.	4	Ъ £zVy = 39L 4	2
	IV-	* 1
133. [х2 4- ху 4- у2 = 13,
|х 4- у = 4.
135. (х2 4- У2 = Ю,
(х 4~ ху 4- У = 7.
137. I-4-- =18,
У х
(х4- у = 12.
139. (х 4- у 4- ху = —1,
(X2 4- у2 — (X 4- у) =
126. (х2 — 2ху 4- Зу2 = 9,
(х2 — 4ху 4- 5у2 = 5.
128. (ху (х 4- у) ~ 30,
(х3 4- у3 = 35.
130. (2х2 - Зху = 9 (х — 2у),
(л2 — Зу2 = 6 (х — 2у).
132. (х2 4у2= |ху,
72:7.	|х-у=1ху.
134. (4 (х 4- У) --= Зху,
]х -Г у -Г X2 4- у2 = 26.
136. (х2 — ху 4- у2 = 19,
(х4 4- х2у2 -- у4 = 931.
138. I- -u f. = 3,
I У  х
(х -г у = 2.
140. (х2 4* ху 4- у2 = 49,
(х4 4~ х2у2 т у4 = 931.
141. (Zv’y2 — у3х2 = 36,
(2х2у — у2х = 6.
140
142.
J- у~ = 9,
У х
/хг V*
143.	-4-— =12,
У х
144.	/ху + ху3 = 6,
|х + ху2 + ху* = 9.
146.
£±Г +	5,
1 — ху 1 1 + ху
145.	/(х + у)3 (х — у)2 = а,
1(х + у)2 (х-у)3 = Ь.
147. ) г3 — у3 = 26,
|х4 — у4 = 20 (х у).
- + - =
х у 4 ’
+	= 4.
, 1 -г ху 1 — ху
148.
/х2у 4- у2х — 20
1 ! 1 ~ А
17 т 7“ 4*
149.	/(х — у)2 — (х — у) = 6,
|2 (х2 4- у2) = 5ху.
150.	(| 3--)' 4- (3 4-	? = 38,25,
\	х4- У/ \ ' х — у)
1ху == 3.
151.	/ху (х + у) = 30,	152. ((х2 4- у2) (х3 + у3) = 280,
[х3 4- у3 ~ 35.	|х 4- у = 4.
153. /х®у 4- ху = а,	154. /х 4~ У = 4,
/х2 — у2 — Ь.	/х4 4~ у4 — 82.
155. /х + у = 19,	156. /(х2 + у2) ху = 78,
/(х — 8)4 4- (у — б)4 = 272.	(х4 + у4 = 97.
157. /х2 — ху 4- У2 = 7,
/х4 + х2у2 4- У4 = 133.
159. /х4 4- х4у4 4- У4 = 33,
|х — ху 4- у = 1.
161. /(х2 + 1) (у2 4- 1).= Ю,
[(х 4- у) (ху — 1) = 3.
158. /х3 4- х3у3 4- у3 = 17,
|х 4- ху + у = 5.
160. /5 (х4 4- у4) = 41 (х2 4- У2),
|х2 4- ху 4- у2 = 13.
162. |х3 — у5 = 3093,
/х — у = 3.
163.	/(х2 — х 4- 1) (у2 — У 4* 1) = 3,
1(х 4- 1) (у 4- 1) = 6.
164.	[х2 4- 4ху — 2у2 = 5 (х 4- У)»
/5х2 — ху — у2 = 7 (х 4- У)-
165.	/х3 4- х2у 4- ху2 4- у3 = а2 (х — у),
[х3 — х2у 4- ху2 — у3 — Ь'1 (х 4_ У)-
141
166.	1 -f- x . 1 —у  4 1 + у ‘ 1 —x — 13’ !+x	1+y =9 1— у 1-x 13’
167.	«-±2=’xy, x — у 2 xy + 1  3x xy — 1	2y
168.
169.
fx2 — у2 — 7,
|xy (x2 + у'1) = 300.
x®y + xy3 = (x + #,
x4y + xy4 = -| (x + y)3.
'	о
170.
'A +4 + у = 8 + 4у I
. у2 у X
12y2
x2
4y2 = x + xy.
171. fx4 + x2y2 + y4 = 481,
[x2 -j- xy + y2 = 37.
172. (x (x + 1) (3x + 5y) = 144,
|x2 + 4x + 5y — 24.
173. fx8 + ye = 65,
+ y* = 17.
174. Г(1 + x2) y2 + 2 (x - y) (1 + xy) = a,
[xy — у = b.
175.
’ (x — У)2 + 1 _ a2
(x + y)2+l “&+?
x2 = (a — b)2 + 1
У2 + 1 (a + b)2 + Г
176. J(x + y) (xy + 1) = 4,5xy,
((x2 + y2) (x2y2 + 1) = 6,25x2y2.
177	+	>21
 Xs + у	13’
x + у = 2.
178. (yz = 24,
{zx = 10,
Ixy = 15.
142
179.	С II II II £
180.	(х + у = аху, у + z = byz, [z + х = сху.
181.	|-4--4-- = 1» х у г ах = by = cz.
182.	у + 2х + z = а (у + х) (г + х), z + 2у + х = b (z + у) (х + у), х 4- у + 2z = с (у + z) (х + г).
183.	4-4-4- II II II <4
184.	.	ху х4-у =	— , 1+х/ Х + 2=1+^
185.	[(х2 + у2) (х2 + г2) = а, (х2 + у2) (у2 + z2) = Ь, (х2 + z2) (у2 + г2) — с.
186.	yz __ 10 х 3 ’
	zx _ 15
	7" 2’
	со | ю II
187.	х (х + у + z) = а2, У (х + у + z) = Ь2, .Z (х + у + z) = с2.
188. (	ху + хг = 229, yz 4- ух — 255, zx + zy = 196.
189.
f(x +	У)	(х	+	У	+	г) = 72,
(х +	г)	(х	+	у	+	z) = 96,
(у +	z)	(х	+	у	+	г) = 120.
143
190. Гх2 — (у — z)2 = а,
у2 — (z — х)2 = Ь,
\z2 — (х — у)2 = с.
191.	(х (х	+ у +	z)	+ yz	=	238,
(у (х	+ у +	z)	+ zx	--	187,
|z (х	4- у +	z)	+ ху	=	154.
192.
-^-=а.
У 4-z
^=Ь,
2 —X
-
х + У
193.	[х + у + z = 13,
X2 4- у2 4- z2 = 91,
1у2 = xz.
194.	|х2 4- 4ху 4- бу2 = 33,
<х2 + 4xz 4- 12г2 — 9,
1у2 4- 3yz 4- 2z2 == 0.
195.	|х 4- У 4- z = а,
|х2 4- у2 4- г2 = а2,
1ху 4- bz — 0.
196.	lx + y + z= 1,
х2 + у2 4- z2 = 1,
lx3 4~ У3 + z3 = 1.
197.	(х 4- у + z = 0,
lx2 4- у2 4- z2 = х3 4- у3
I xyz = 2.
198.	I x 4" 2y 4" z — 19,
x2 + 4y2 4- z2 = 133,
Ixz = 4y2.
199.	ixy 4- yz 4- zx = 11,
jx2 4- y 2 4- z2 — 14,
I xyz = 6.
•200. {x2 4- yz у 4- z,
ly2 4- xz == x 4- z,
\z2 4- xy = x + y.
201.	fx 4- у = 5z,
x2 4- y- = 13z,
lx3 4- y3 — 35z.
202.	12 (x + y) =- xy,
]xy 4- yz 4- xz = 108,
I xyz — 180.
144
203.	rx2y + yz — а, х2 + yz = Ь, [х2уг 4- z = с.		
204.	IX (у — z)	+	у	(у +	z)	=	а, у (z — х)	+	z	(г -г	х)	=--	Ь, [z (х — у)	4-	X	(X +	у)	=	С.		
205.	(у 4- г)2 — х2 = а2, (г + х)2 — у2 = Ь1, (х 4- у)2 — z2 = с1.		
206.	|(а-1)*У _ а । 1	207.	v2 * <»2	9*2
	х + у		л ~|— у — Z 	 С
	(а-2)хг _	, 2		2ху	z у\+ г'2— х2   « 2yz	х ’
	х H-z		
	(а-З) уг	3		22 -Н X2 — У2 __ Ь
	1 У4-г		2xz	у
Решить графическим способом системы уравнений.
208.	fxy = 2, jx 4- у = 3.		209.	(у = X2 — X — 1, {ху = 2.
210.	(у = х2 — 2х — 3, |у = х — 1.		211.	Гу = х2 — 2х — 5, [ху = —6.
212.	fx2 4- У2 = 5, |х 4- у = з.		213.	+ у2 = 13, = х2 —7.
214. 216.	((х - 2)2 + (у - I)2 = [х — у = 2. fx2 — 2х 4* У2 — 4у = 1у = х2— 1.	: 1, о,	215.	|х2 — Зх -у у2 — 4)' =0, (X = у.
217.	|х2 4- у2 = 25, {ху = 12.		218.	(X2 — у2 = 3, (х — у - 1.
ГЛАВА VIII
ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И ИХ СИСТЕМЫ
Уравнение f (х, у, ... , z) = О называется иррациональным,
если f (х, у, ... , z) есть алгебраическая иррациональная функция
от неизвестных.
Способы решения:
1.	Замена иррационального уравнения смешанной рациональ-
ной системой.
з---------------
Пример. Решить уравнение у х + 1 = у х — Зна множе-
стве действительных чисел.
Решение. Пусть Ух + 1 = у, Ух — 3 = z.
Составим смешанную систему
(У = 2,
ул = х 4- 1,
' z2 = х — 3,
z > 0.
Решение системы сводится к решению уравнения z3 — z2 — 4 =
= 0, откуда z = 2, х = 7.
Ответ: х = 7.
2.	Возведение обеих частей уравнения в одну и ту же степень.
При решении иррациональных уравнений этим способом надо
иметь в виду следующие теоремы равносильности уравнений:
2h-H __
Теорема 1. Уравнение УR (х) = Р (х) равносильно в поле
действительных чисел уравнению R (х) = Р2А+1 (х).
Теорема 2. Уравнение УR(x) = Р (х) равносильно в поле
действительных чисел смешанной системе (R (х) = Р2А (х),
]Р (х) > 0.
Необходимо помнить, что при решении уравнений этим способом
множество допустимых значений неизвестных может расшириться.
Это иногда приводит к появлению посторонних решений, которые не
будут принадлежать множеству допустимых значений неизвестных.
Кроме того, если при возведении обеих частей уравнения в чет-
ную степень не накладывать условия Р (х) > 0 (теорема 2), то
могут появиться посторонние решения, принадлежащие множест-
ву допустимых значений неизвестного данного уравнения. В этом
случае необходимо делать испытание корней, принадлежащих мно-
жеству /Допустимых значений неизвестных подстановкой их в дан-
ное уравнение.
Пример. Решить уравнение на множестве действительных
чисел.
УхТ8 — /5х 4- 20 4- 2 = 0,
146
Решение I. М = {х \х	—4}.
/х 4- 8 4- 2 —У5х + 20. Обе части уравнения неотрицательны.
х И- 8 4~ 4 Ух + 8 4- 4 = 5х 4~ 20.
Ух 4- 8 = х + 2. Накладываем дополнительное условие х ~>
> —2:
х2 4- Зх — 4 = 0.
xi = 1> х2 = —4 не удовлетворяет дополнительному условию.
Ответ: х = 1.
Решение II. М = {х ] х >—4}.
Ух + 8 4- 2 = У5х 4- 20.
Ух 4- 8 = х 4- 2.
х2 4- Зх — 4 = 0,
хх = — 4, х2 = 1.
Оба корня принадлежат М. Проверяем, являются ли хх = —4
и х2 = 1 корнями данного уравнения.
У—4 + 8 4- 2 =# У 5-(—4) 4- 20,
У1 4- 8 4- 2 = У5-1 4- 20/
Ответ: х = 1.
3.	Исключение радикалов в иррациональном уравнении домно-
жением на сопряженный множитель. _________
Пример. ]/Зх24-5х4-8—/Зх2 4- 5х 4- 1 = 1.	(1)
Решение. Умножим обе части уравнения на
/Зх2 4- 5х 4- 8 4- /Зх2 + 5х 4- 1.
Получим: /Зх2 4- 5х 4- 8 4- /Зх2 4- 5х 4- 1 = 7.	(2)
Сложив уравнения (1) и (2), придем к квадратному уравнению
Зх24- 5х — 8 = 0, корни которого хх= —| и х2= 1 будут корня-
ми данного уравнения.
Искусственные приемы
Примеры.
1. Vх 4- 3 — 4 /Г=Л 4-Кх 4- 8 — 6 /х— 1 = 1.
Решение.	(х—1)—4]/х—14-4 4~	(х—1)—6/х—14-9=1.
V (/3/Т- 2)2 4- V (/7^1 - З)2 = 1.
|/х— 1 — 2 | 4- |/х- 1 -3 | = 1.
147
1)	Vx — 1 < 2 -> 1 < X < 5.
2 — О — 1 + 3 * — JOO = 1.
0—1 = 2.
х = 5. *
2)	2 < ] О1 < 3->5 < x < 10.
O — 1—2+3 — | x — 1 = 1.
1	= 1.
5	< x < 10.
3)	0—1 > 3-> x > 10.
О _ 1 _ 2 + О — 1 — 3 = 1.
О— i = з
x = 10.
Ответ: 5 < x < 10.
2. у' (a + x)2 + 4 y(a — x)2 = 5 yra2 — x2.
Решение. Еслиа=/=0, то x — а не является корнем уравнения,
з
Разделим обе части уравнения на у (а — х)2.
Получим:
а -I- х	а ‘ х
а) 1/	= 1. б) I/ — ^'= 4.
у а — х	у а — х
х = 0.	х = — а.
65
Если а — 0, то уравнение имеет один корень х — 0.
Ответ: если а 0, то х, = 0, х2 = — а;
если а = 0, то х = 0.
Решить уравнения на множестве действительных чисел.
з г— в,—
1. » х + j х — 2 = 0.
3. х5—ЗЗх2 |'7 + 32 = 0.
5. 2 х + 5 — 63 р/' А.
2. 5у‘ х + 2 = 3 х.
4. лл — Зх 0+2 = 0.
з _	3	0
6.	2х у х — Зх 1^/ А = 20.
148
7.	№ + 11 + W + Н = 42.
8.	x2 — ]	= 21.
Xs 4- (a2 — X-) ) a2 — x-
9. ......  7.	----= a2.
X 4- I <i~ — x2
10.	] "(x — 2)2 + K(x -r i)2 = ] '(x + 2)-’, x > 0.
II.	] rx2 — 4x + 4 - I — Ox - 9 - I' X2 - 2.V r Г
) -b I x^i 2 /'TZT
12.	—=-------~= = T I /	•
УЗ — x — У x — 4	3 | x — 4
13.	]T+x+j/T^x = 1.
14.	У 23 + 1 2x 4- I 5д-2 — 21x — 68 = 5.
15.	x — a 4- Г а2 г x | x2 — a2 — b2.
16.	I 1 + x J x~— 24 = a' — 1.
18.	x2 -r 5x 4- 4 = 5 Vx2 + 5x + 28.
19.	(x + 5) (x — 2) 4- 3 ]лх(х-г 3) = 0.
20.	x2 4- 4x — 8	|/8x	+	20 = 0.
21.	л2 — 3x — 6	ГЗх	4-	18	0.
22.	x2 — Зх — 2	)л2х	+	6 =	0.
23.	x10 — Xs — 2	4-2 =	0.
24.	/Лх2+ Вх-r С + |/Лх2-г Вх + Сх = р.
25.	х2 — Зх — 5 | 9х2 + х — 2 = 2,75 — —х.
9
26.	Ух + 5-4 | ТТЛ + Кх + 2-2| х+“1 = 1.
27.	1'4х + 2 + J 4х — 2 = 4.
28.	|^4 — х + | 5 + х = 3.
29.	] 25 — х + | +Г+х = 2.
30.	Y1 + х + х2 + | 1 — х 4- х2 — 4.
149
31.	/х2 + х 4~Т = /х2 —х + 1 + 1.
32.	х /Г+ Ух — 2 = 4 (Ух — 1).
33.	х2 + 2 (х + 1) У7+ Зх = 8.
34.	х3 + 4х (х — I)1-6 + Зх2 — 8х + 4 = 0.
35.	Xе — х3 — 2х2 — 1 = 2 (х — х3 + 1) Ух.
36.	(х + 2)2 4- 2 (х + 2) Ух — 3 Ух — 2х = 46.
37.	2 (х + Ух2 — 1) = (х — 1 + Ух 4- I)2.
38.	х (х — 2 Ух^~1) = 2 Ух^~1 — Зх.
39.	(х — 1) [1 — х (1 4- 2 Ух)\ = х3 — (х - Ь)2.
40.	2х 4- 1 4- х Ух2+ 2 4- (х 4- 1) /х2 + 2х + 3 = 0.
41.	а3 4- 2 (х — а) = За Зу (х — а)2.
42.	Vа — У а 4- х = х.
43.	х = а 4- Ка 4- Ух.
44.	(1 4- /Г+х) УТГх 4- (1 4-Т/Т^х) пУГ^~х = 2 (1 4-
4-	у41 — х2) VУ1 — х2.
45.	Ух+ ]/х —/П^х= 1.
46.	Кб 4- х 4- 4 Ух 4- 1 = 2 4- Ух 4- 1.
47.	Vх 4- 2 4- 2 УТ+~1 + Кх + 2 — 2 Ух~+1 = 2.
48.	]/ х — УхУ^~2 4- Vх 4- Ух —2 = 2.
49.	/4х —3 4- /бГ+1 = У 15х 4- 4.
50.	]/FT9 4- У^~—9 = УТ4- 5.
51.	У(х - 1) (х - 2) 4- У(х - 3) (х - 4) = У2.
52.	У2х2 4- Зх 4- 5 4- /2х2 —3x4- 5 = Зх.
53.	УУ+~5 4- /Г+3 = /2х+"7.
54.	Vх (1 + Ух) — И х (1 + х) = УТ+~х — К1 + Ух.
55.	Уа+Ух + Уа2 — Х =	а+/а2-х а-У^-х
56.	(1 - Vyx + 1) И/х + 1 « Ух.
150
57.	(1 + х) V1 + х — (1 — х) У1 — х = х.
58.	2 (х - 1) = (Ух- 1) (/2=ТГ + 1).
59.	±х = (/Г+7- 1) (/1^7+ 1).
60.	х + Ух + /7+2 + /х2 + 2х = 3.
61.	у<х + 45 — у^х — 16 = 1.
62.	^54 + /7+ /б4 — /7 = /18.
63.	/(8 — х)2 + (27 + х)2 = 3/(8 —х) (27 + х) + 7.
64.	Ьх У а + х + ab У а У х = а /х3.
65.	/ (а + х)2 — /а2 — х2 + /(а — х)2 = Ь.
66.	/а + х — уа + /х + /а — х — У а — /х — 0.
67.	У 1 + /7= 2— 1 — /7
69.	Vх + У х2 — х3 + V1 — х + у/"х (I — х)2 = 1»
70.	/(а + х)2 + 4 у/г(а—х)2= 5 /а2 — х2.
71.	ула + х + \/ а — х — '/а2 — х2.
72.	V х? + /х*а2 + Vа2 + /а4х2 = Ь.
73.	У(1 + х)2—(/1 +х —1) /1 + /1 +х =1.
74.	а + х + { а — х = 2/а2 — х2.
75.	/(х+ I)2 + /(х- I)2 = 4/х^Т.
76.	/(х + а)8 + 2 /х3 = 3 /х2 (х + а).
77.	(1 + у'х) v х2 + (1 + у^а) уга2 = 2у^ах (1 + frax).
78.	|/(Зх-5)3 - /(5-Зх)-3 = - 5?.
79.	(У х—1 + /х+ I)2 + 5 [/(х~ I)2 — /(х + I)2 J +
+ 6 [/7^1 — /х+ I]2 = 0.
80.	(/7+7 + /Т3^)3 (|/х+7 — / х —а )= 2Ь.
151
81.
X
lf12 + * = 211 J*
12.	3 1 л-
П г--:-- П г----;- П
82.	>' а~^х । V а + х _ -\/ х.
а	х b
83.	л ^х — а — (х +• а)-1 у^(х 4- о)-1 = а '^х — а.
84.	а*х'г~* 4- yran~kxk — 2 y'bx, где п > 2k > О, b > а > 0.
Д_	Х2 _|_ (1 _|_ т а2(«-т>) ^а2 = 2 р ах (1 +
+ / (ах)"-"' ).
86. хп -f- j/ апхп~ -г + 1/Г(2">х" — Ь.
i_	i_
87. [(х + аУ 4- (х - a)«f + Цх 4- аУ - (х - а)"] ’ =
i_
= [(х + аУ + Ь"? + {(х 4- ау- Ь"? .
। п ~
а+\ х
а
89 /3-х 4-/х-2 =	1
/3 —х — Ух^2 5 — 2х’
Of) У5=Л- + 4/Д _ 2 М~х
/5 — х — ) 'х — 2	3 |/ х — i
94. 	-.... 4-	6 	= -Ц.
J'3x4-10 J (х±2) (Зх-Н 10)	) х + 2
95. р « + х —	|/ 2а 4- х.
96 -v ~~ l_£zz £
J х — 2и. -р I' х т
152
97.	1/‘~A* 4-1=0.
i -j- ax p 1 — bx
98.	.V	1 x	1	1	£Z1L	j---------* л' ~ 1	,	I.
I' X	— 1	— I	x — 1	x — ) X- —	1
9g	*	0 x	- 1	)3 >	x - 1	_	x2 - 2л- }	x	-4 x — 1 =
x— (|	x -г 1)	л —(|	x	— 1)
100.	+	+
x — I x- — a* + a
lot. y±±H±_LL + 1 ~ > 7	2
| 1 — | x 4- I X Kl + I X Г- 1 X
102.	1 -у2 + л'^6 + Гх-—x —4 _
j x~ -J- x -j- 6 — | x“ — x — 4
103.	~\/_l I/Lx4 =2.
V b-j-x'V a — x
104 1 1 -r >'' + t 1 — x- _ p_
 trt. m - m ------- .
|/ 1 4- x2 - | 1 — x2 4
106	. I x I' x — V X — Vx = 4 ]/ “jy-
107	1 a + * _	Уа — х
| a 4- Г° Г x У a — У a — x
Ю8. J-ZEL+1ZEL г	=
| X2 -j- 1 — ) X1 — 1	I X2 T 1 T I ~ 1
109. | \vi y |/'ГТТ = -^.
110.	a — x	,	a + x	— У a •	i
	a	a — x	\f a + У а ф x		
111.	1 +*— r 2X-T-X2	= „зГ2 4-X	— ГГ	'1
	1 -f- x -p 2x + x2	2 — X	— Ух	
112.	-i [ Ю 12 4-	/ о 12 = 1/ 12		 1/ x1		X2.	
	У	X2	V	X2		4
153
Решить графически уравнения.
ИЗ. /х = х.
114.	/х = х — 2.
115.	Vx = 2х — 6.
116.	= _Lx+ 1L.
У 2	8	4
117.	/7= 2х2 — 1.
118.	/х+“1 = х— 1.
119.	/Зх —5 = х2 — 7.
120.	/4^х + /5 + х = 3.
121.	/25 —х + VW+~x = 2.
122.	/х = - + 1-.
х 4
123.	/х+1 = -.
X
124.	/Г+2 = /8 = А
Решить системы уравнений на множестве действительных чисел.
125.
7___4	_ 5_
уг'х^т	/7+6" ~3.’
—= 21
х — 7 fy + 6	6
х: у: г = 1:27:64,
i_ i_	1
х3 + у3	г3 = 24.
127. |/х + /у = 3,
|ху = 4.
128. (3/Г4- Vy = 3,
|ху = 8.
154
{з ,- з л—
у х — у у = 2,
ху — 27.
130. (х = 6 /х~+~у,
(у = 2 ]/х 4- у.
131. ((х2 + ху + у2) Ух2 + у2 = 185,
Цх2 — ху 4~ у2) Р^х2 4* у2 = 65.
132.
ух3 + V У3 = 35,
*Ух~+ v4F= 5-
1зз. (х + у — 10*
134. (х + у — Ух 4- Уу — 2 ]/~ху = 2,
1/х 4- У У = 8.
135.
х 4-у = 12.
12
---,
X—У
136.
ху = 15.
137.
-1 [ Зу —2х . д / 4у = 2 у~2 ,
у у У Зу —
3(х2 4-1) = (у 4-1)(у — х 4-1).
138. (х 4- у 4- Уху = 14,
]х2 4- у2 4- ху = 84.
}/х3у 4- Уху3 = 78.
3?-------ь--------------
140.	7х — 11у = Ух 4- у = Ух 4- 9у.
141.	(х2 4- У Уху = 420,
(у2 4- х Уху = 280.
155
142.	[xVx_ + у]/У= 341,
U Г у + у Ух = 330.
143.	1У £±Z_-|3- *EL _
J Г х — у У х 4- у 2
[л2 —у2 = 32.
144.	[У 6х + 5 — |/4х — Зу =
(6х + Зу = 4.
145.
х3 + xyz = У xyz,
у3 + xyz = У xyz,
Z? + xyz = У xyz.
146.	(Ух + у у + Уг = 4,
IX + у + Z = 6,
х2 + у2 + Z2 = 18.
147.
Ух -г У у = Z,
2х 4- 2у + а — 0,
г4 -г az2 4- b — 0.
ГЛАВА IX
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СОСТАВЛЕНИЯ УРАВНЕНИЙ
И СИСТЕМ УРАВНЕНИЙ
1.	Шестизначное число начинается слева цифрой 1. Если эту
цифру перенести с первого места слева на последнее место справа,
то вновь полученное число будет втрое больше первоначального.
Найти первоначальное число.
2
2.	Отношение двух положительных чисел составляет —. Если
увеличить меньшее из них на 1000, а большее на 2000, то отношение
их будет Найти оба числа.
3.	Двузначное число, деленное на сумму своих цифр, дает в
частном 4 и в остатке 3; если цифры этого числа переставить, то
получится число на 5 больше ушестеренной суммы его цифр. Найти
число.
4.	Сумма цифр двузначного числа равна 7. Если к каждой циф-
ре прибавить по 2, то получится число, на 3 меньшее удвоенного
первоначального числа. Найти это число.
5.	Сумма цифр двузначного числа равна 9. Если цифры этого
5
числа переставить, то получится число, составляющее — перво-
6
начального. Найти это число.
6.	Двузначное число больше учетверенной суммы его цифр на
3; если к этому числу прибавить 18, то получится число на 18
меньше числа, написанного теми же цифрами, но в обратном поряд-
ке. Найти это число.
2
7.	Число десятков двузначного числа составляет у числа еди-
ниц, а число, написанное теми же цифрами, но в обратном порядке,
больше первоначального числа на 18. Найти число.
8.	Сумма двух двузначных чисел равна 68. Если написать
большее из них и приписать к нему справа меньшее, то получится
число на 2178 больше того числа, которое получится, если при-
писать меньшее число к большему слева. Найти числа.
9.	— суммы двух чисел без их разности составляют 16; полураз-
ность этих чисел, умноженная на 8, равна их полусумме. Найти
числа.
10.	Частное от деления целого числа D на целое число Е равно 4,
а остаток равен 30. Если сложить делимое, делитель, частное и оста-
ток, то полученная сумма будет равна 574. Найти делимое и дели-
тель.
11.	Дробь обратится в единицу, если к числителю прибавить 2;
если же к знаменателю прибавить 3, то дробь обратится в —. Най-
ти эту дробь.
157
12.	Если к числителю дроби прибавить 3, а к знаменателю 1,
то вновь полученная дробь будет равна у; если из числителя вы-
честь 5, а из знаменателя 3, то вновь полученная дробь будет рав-
на -j. Найти дробь.
13.	Трехзначное число уменьшается на 99, если написать его
цифры в обратном порядке. Сумма цифр числа — 14, причем сред-
няя цифра равна сумме остальных цифр. Найти число.
14.	Сумма цифр трехзначного числа равна 12; сумма цифр его
сотен и десятков кратна 9. Если от искомого числа отнять 99, то
получится число, записанное теми же цифрами, но в обратном по-
рядке. Найти число.
15.	Сумма цифр трехзначного числа равна 12. Число единиц
1 .
этого числа равно —числа, выраженного цифрами сотен и десятков
4
(написанных в том же порядке); цифра сотен равна — числа, выра-
23
женного цифрами десятков и единиц, написанных в том же порядке.
Найти число.
16.	Найти три числа, удовлетворяющих следующим условиям:
первое из них, деленное на второе, дает в частном 4 и в остатке 12;
второе, деленное на третье, дает в частном 5 и в остатке 5; наконец,
первое, деленное на третье, дает в частном 21 и в остатке 12.
17.	Число 100 разделено на три части таким образом, что про-
3	2
изведение первой части на —, частное от деления второй части на —
з
и произведение третьей части на — находятся в отношении 3:9:4.
5
Найти величину каждой части.
18.	Знаменатели трех дробей соответственно равны 3, 6 и 15.
у
Найти эти дроби, если сумма всех дробей равна 1—. Если числи-
тель первой дроби увеличить на 1 и сложить полученную таким обра-
зом дробь со второй дробью, то получится 1—, разность второй и
з
третьей дроби равна —.
19.	Разделить 96 на 3 части так, чтобы от деления первой части
на вторую получилось в частном 2 и в остатке 7, а от деления вто-
рой части на третью в частном получилось бы 1, а в остатке 3.
20.	Найти четырехзначное число по следующим данным: оно
остается таким же, если записать его цифры в обратном порядке,
сумма его цифр равна 24, а число, образуемое двумя его цифрами,
стоящими справа, больше числа, образуемого двумя его цифрами,
стоящими слева, на 36.
21.	Если переставить в трехзначном числе цифры сотен и де-
сятков, то число уменьшится на 90; если переставить цифры десят-

158
ков и единиц, то число уменьшится на 18; если же переставить циф-
ры сотен и единиц, то число уменьшится на 297. Найти число.
22.	Число 23 разделено на 4 части; если прибавить к первой
части 1, вычесть из второй части 2, умножить третью часть на 2 и
разделить четвертую часть на 3, то получатся равные результаты.
Найти эти части.
23.	Сумма четырех чисел равна 64. Первое число относится ко
второму как 5 : 6, второе к третьему как 2 : 3, а третье к четвертому
как 3 : 4. Найти числа.
24.	Сумма цифр четырехзначного числа равна 15; число, изо-
браженное двумя крайними цифрами этого числа, взятого в поряд-
ке их написания, равно — числа, изображенного двумя средними
цифрами; число, изображенное двумя первыми цифрами этого чис-
8	.
ла, равно — числа, изображенного последними двумя цифрами;
сумма цифр сотен и тысяч равна цифре десятков. Найти число.
25.	Определить четыре числа по следующим условиям: сумма —
2	5	3
первого и — второго равна 8; разность между — второго и — третьего
равна 6; сумма — третьего и — четвертого равна 9; разность меж-
6	7
4	1
ду — четвертого и — первого равна 26.
5	4
26.	Первое число при делении на второе дает в частном 2 и в
остатке 3. Второе число при делении на третье дает в частном 1
и в остатке 8. Третье число при делении на четвертое дает в частном 2
и в остатке 1. Сумма всех четырех чисел равна 76. Найти эти четы-
ре числа.
27.	Четырехзначное число, сложенное с числом, изображенным
последними тремя его цифрами, дает в сумме 2818. Разность между
числом сотен и числом тысяч этого четырехзначного числа равна 8.
Сумма числа сотен и числа единиц равна 18. Разность между чис-
лом единиц и удвоенным числом тысяч равна 7. Найти число.
28.	Одна из цифр двузначного числа на единицу больше другой,
а сумма квадратов этого числа и числа, полученного от перестанов-
ки его цифр, равна 1553. Найти число.
29.	Найти двузначное число, зная, что оно в сумме с числом,
составленным из тех же цифр, но взятых в обратном порядке, дает
121 и что произведение его цифр равно 28.
30.	Числитель дроби на 3 меньше знаменателя. Если к числи-
телю прибавить 5, а из знаменателя вычесть 4, то полученная дробь
будет в 4 раза больше первоначальной. Найти дробь.
31.	В первый раз знаменатель дроби увеличили на 3, а во вто-
рой раз уменьшили на 5. Сумма полученных таким образом дробей
159
9
оказалась равной у. Найти знаменатель этой дроби, зная, что чис-
литель ее равен 2.
32.	Найти дробь по следующим условиям: числитель на 2 мень-
ше знаменателя; если к числителю и знаменателю прибавить по 5
и полученную таким образом дробь умножить на обратную искомой
4
дроби, то получится
33.	Найти двузначное число, зная, что число единиц искомого
числа на 2 больше числа его десятков и что произведение числа на
сумму его цифр равно 144.
34.	Некоторое число есть произведение трех последовательных
положительных целых чисел. Сумма частных, полученных от деле-
ния этого числа на каждое из трех составляющих его множителей,
равна 74. Найти число.
35.	Цифра десятков двузначного числа вдвое больше цифры
его единиц. Если переставить цифры числа, то произведение вновь
полученного числа на первоначальное будет равно 2268. Найти
число.
36.	Найти четырехзначное число, являющееся точным квадра-
том, у которого цифра тысяч одинакова с цифрой десятков, а цифра
сотен на 1 больше цифры единиц.
37.	Два двузначных числа образованы из одних и тех же цифр,
ио взятых в различном порядке. Произведение этих чисел равно
3154; меньшее число больше утроенной суммы своих цифр на 5.
Найти числа.
38.	Если числитель некоторой дроби увеличить на 13, а знаме-
натель на столько же уменьшить, то получится обратная дробь.
Если же числитель и знаменатель увеличить на 13, то произведение
первоначальной дроби на полученную дробь будет равно Найти
дробь.
39.	Если сумму двух чисел сложить с суммой их квадратов,
то получится 86, а если к разности квадратов этих же чисел приба-
вить разность самих чисел, то получится 26. Найти числа.
40.	Найти два числа, зная, что их разность, разность их квадра-
тов и разность их кубов находятся соответственно в отношении
1:3:7.
41.	Если двузначное число разделить на произведение его цифр,
то результат будет равен 6. Если же цифры переставить и вновь по-
лученное число разделить на сумму его цифр, то частное будет рав-
но 7. Найти число.
42.	Сумма двух чисел равна 3, а сумма чисел, обратных данным,
27 тт v '
равна —. Наити числа.
43.	Сумма двух чисел, умноженная на сумму квадратов этих
чисел, равна 369, а разность их, умноженная на разность их квадра-
тов, равна 9. Найти числа.
160
44.	Сумма цифр трехзначного числа равна 11, а сумма квадра-
тов тех же цифр 45. Если от искомого' числа отнять 198, то получит-
ся число, написанное в обратном порядке. Найти это число.
45.	Найти три числа, зная, что сумма их равна 36; большее
число на 6 меньше суммы двух других чисел, а отношение большего
числа к сумме квадратов среднего и меньшего чисел равно 1 : 15.
46.	Найти трехзначное число по следующим условиям: частное
от деления искомого числа на сумму его цифр равно 48; частное от
деления произведения цифр этого числа на их сумму равно 10—, циф-
з
ра десятков есть среднее арифметическое остальных цифр.
47. Сумма трех чисел равна 13, а сумма квадратов тех же чисел
равна 61. Сумма удвоенного первого числа и утроенного второго
равна 18. Найти эти числа.
48. Найти трехзначное число по следующим условиям: сумма
его цифр равна 9, сумма квадратов его цифр равна 29; если же пере-
ставить цифры искомого числа в обратном порядке, то новое число
будет на 99 меньше искомого.
49. Сумма трех чисел равна 42. Первое число равно разности
между квадратом второго числа и третьим числом. Определить эти
числа, зная, что первое число при делении на 4 дает в частном второе
число и в остатке — третьего числа.
5
50.	Найти три числа по следующим условиям: разность кубов
первого и второго чисел равна 98; сумма удвоенного второго и утро-
енного третьего равна 12; сумма утроенного третьего и удвоенно-
го первого равна 16.
51.	Найти три числа по следующим условиям: сумма утроен-
ного первого числа и куба второго равна 155; сумма удвоенного
квадрата первого числа и утроенного куба третьего равна 203;
1	2
куб третьего и у куба второго дают в сумме 42—
52.	Найти четырехзначное число по следующим условиям:
произведение крайних цифр равно 40; произведение средних цифр
равно 28; цифра тысяч на столько меньше цифры единиц, на сколько
цифра сотен меньше цифры десятков; если к искомому числу при-
бавить 3267, то получится число обращенное.
53.	Сумма цифр трехзначного числа равна 12. Сумма цифр его
сотен и десятков кратна 9. Если от искомого числа отнять 99, то
получится число, записанное теми же цифрами, но в обратном по-
рядке. Найти число.
54.	Число лет некоторого человека в 1962 году равнялось сумме
цифр его года рождения. Сколько лет ему было в этом году?
55.	При делении шестизначного числа, состоящего из одинако-
вых цифр, на четырехзначное, также состоящего из одинаковых
Цифр, в частном получается 233 и некоторый остаток. Если отбро-
сить в делимом и делителе по одной цифре, то частное не изменится,
а остаток уменьшится на 1000. Найти делимое и делитель.
6 Закач 1089
161
56.	Какие цифры на третьем и на пятом месте необходимо под-
ставить вместо нуля в числе 3 000 003, чтобы вновь полученное
число делилось на 13.
57.	Найти число по следующим условиям: если к нему приба-
вить число а, полученную сумму умножить на b и к произведению
прибавить т, то получится п.
58.	По дороге в одном и том же направлении едут два велосипе-
диста. Первый велосипедист проезжает в час 11 км, второй —
14 км. Первый проехал пункт А в 11 ч утра, второй проехал пункт В,
расположенный далее по направлению движения, в 2 ч дня. Зная,
что расстояние между пунктами А и В равно 21 км, определить, на
каком расстоянии от пункта А второй велосипедист догонит первого.
59.	Турист отправляется в поход из А в В и обратно, проходя
весь путь за 3 ч 41 мин. Дорога из А в В идет сначала в гору, по-
том по ровному месту, потом под гору. На каком протяжении до-
рога тянется по ровному месту, если скорость ходьбы туриста в
гору 4 км/ч, по ровному месту — 5 км/ч и под гору — 6 км)ч, а
расстояние АВ равно 9 км?
60.	Турист, идущий из деревни на железнодорожную станцию,
пройдя за первый час 3 км, рассчитал, что он опоздает на поезд на
40 мин, если будет двигаться с той же скоростью, поэтому остальной
путь он проходил со скоростью 4 км/ч и прибыл на станцию за 45 мин
до отхода поезда. Найти расстояние от деревни до станции.
61.	Из города А в 12 ч вышел поезд. В 14 ч того же дня вышел
другой поезд и нагнал первый поезд в 20 ч того же дня. Определить
средние скорости обоих поездов, зная, что сумма их средних скоро-
стей равна 70 км/ч.
62.	Из двух городов, расстояние между которыми равно 63 км,
вышли одновременно два пешехода и встретились через 9 ч. Опре-
делить среднюю скорость обоих пешеходов, зная, что если бы первый
шел в 1— раза скорее, а второй — в 2 раза скорее, то они встрети-
лись бы через 5 ч 15 мин.
63.	Два велосипедиста выехали одновременно и едут в одном
и том же направлении по кругу, имеющему в окружности 900 м.
Велосипедист, едущий быстрее, через каждые 18 мин настигает дру-
гого. Если они поедут одновременно из одного и того же пункта
навстречу друг другу, то они будут встречаться через каждые 2 мин.
Найти скорость каждого велосипедиста.
64.	Турист ехал 5 ч на пассажирском поезде, затем 4 ч на скором
поезде и всего проехал 440 км. Если бы он ехал 2 ч в поезде, кото-
рый проходит в час на 10 км больше пассажирского, и 5 ч в поезде,
который проходит в час на 8 км больше скорого поезда, то он про-
ехал бы то же расстояние. Найти скорость каждого поезда.
65.	Поезд прошел некоторое расстояние с постоянной скоростью.
Если бы он проходил в час на 6 км больше, то потратил бы на про-
162
хождение этого расстояния на 4 ч меньше, а если бы он проходил
в час на 6 км меньше, то потратил бы на прохождение этого расстоя-
ния на 6 ч больше. Найти это расстояние.
66.	За 3 ч пароход прошел 48 км по течению реки и 16 км про-
тив течения. В другой раз тот же пароход за 5 ч прошел 72 км по
течению реки и 32 км против течения. Определить скорость тече-
ния реки и скорость парохода в стоячей воде.
67.	Первый поезд проезжает расстояние между станциями А
и В на 10 мин скорее, чем второй. Сумма времени, в течение которо-
го тот и другой поезд проходят расстояние от А до В, равна 50 мин.
Определить скорости поездов и расстояние от А до В, зная, что сум-
ма скоростей обоих поездов равна 2,5 км/мин.
68.	Два автомобиля выезжают одновременно навстречу друг
другу из Л в Ви из В в Л. После встречи одному из них прихо-
g
дится быть в пути 2 ч, а другому----ч. Найти скорость автомо-
8
билей, если АВ равно 210 км.
69.	Из Л в В и из В в Л одновременно вышли два пешехода.
Когда первый прошел половину пути, второму осталось пройти
24 км, а когда второй прошел половину пути, первому осталось
пройти 15 км. Сколько километров останется пройти второму пеше-
ходу, когда первый закончит переход?
70.	Из А в В выезжают одновременно автомашина «Победа»
и велосипедист, а из В в Л в то же время — автомашина «Москвич».
Автомашины встречаются через 2,4 ч, а велосипедист и «Москвич»
встречаются на расстоянии 48 км от А. Найти скорость автомашин
и велосипедиста, если велосипедист затрачивает на путь в 30 км
на 2,5 ч больше, чем «Победа», и его скорость в 4 раза меньше, чем
у «Москвича».
71.	Два пешехода вышли одновременно навстречу друг другу
и встретились через 3 ч. Во сколько времени пройдет все расстояние
каждый из них, если первый пришел в то место, из которого вышел
второй, 2-i- часами позже, чем второй пришел в то место, откуда
(Вышел первый?
М 72. Пешеход прошел с определенной скоростью 8 км-, затем,
увеличив скорость на 1 км/ч, прошел еще 5 км. Если бы все прой-
денное им расстояние он прошел с той же скоростью, с какой шел
последние 5 км, то он был бы в пути на 24 мин меньше. Определить
первоначальную скорость пешехода.
73.	Из двух пунктов Л и В, отстоящих один от другого на 480 км,
навстречу один другому идут два поезда. Если бы поезд из Л вышел
на 2 ч раньше другого, то встреча их произошла бы на середине
пути. Если же они выйдут одновременно, то по прошествии 6 ч
расстояние между ними будет равно первоначального. Во сколько
времени каждый поезд проходит все расстояние от Л до В?
6*
163
74.	Два грузовых автомобиля едут навстречу один другому.
Расстояние между ними 180 км. Первый проезжает в час на 6 км
больше второго, а второй проезжает в час число километров, вдвое
большее числа часов, которое проходит до их встречи. Сколько ки-
лометров в час проезжает каждый автомобиль?
75.	Два автомобиля, легковой и грузовой, выезжают из одного
города в другой. Легковой автомобиль проезжает на 15 км/ч боль-
ше, чем грузовой, и успевает приехать часом раньше. Расстояние
между городами 180 км. Сколько километров в час проезжает каж-
дый автомобиль?
76.	Пассажир проехал на поезде 30 км и, пробыв на станции
20 мин, вернулся с обратным поездом, делающим в час на 3 км
4
более. Общая продолжительность поездки была равна 2— ч. Оп-
ределить скорости поездов.
77.	Велосипедист, выезжающий из пункта А, должен приехать
в пункт В через 3 ч. Одновременно с ним из пункта С выезжает дру-
гой велосипедист, и, чтобы успеть приехать в В вместе с первым
велосипедистом, он должен проезжать каждый километр на одну
минуту скорее, чем первый. Расстояние от С до В на 6 км больше
расстояния от А до В. Определить эти расстояния.
78.	Расстояние между городами А и В равно 100 км. Из города
А в город В отправляются одновременно два автомобиля. Первый
делает в час на 10 км больше второго и прибывает в В на 50 мин
раньше второго. Определить скорость каждого автомобиля.
79.	Из Л в В одновременно выезжают два автомобиля и направ-
ляются по двум различным дорогам; длина одной из них — 77 км
а другой — 97— км. Автомобиль, идущий более длинной дорогой,
делает на 5 км/ч больше и прибывает в В на 4 мин раньше другого.
Определить скорости автомобилей.
80.	Турист предполагал пройти 26 км с некоторой скоростью.
Но с этой скоростью он шел всего 1 ч, а затем стал проходить на
1 км/ч меньше. В результате он пробыл в пути на 1— ч больше,
чем предполагал. С какой скоростью турист предполагал пройти
путь?
81.	Два пешехода идут навстречу друг другу из двух деревень
Л и В. Вышли они одновременно. При встрече оказалось, что пер-
вый прошел на 2 км больше, чем второй. Продолжая движение,
первый приходит в В через 40 мин, а второй — в Л через 1у ч
после встречи. Как велико расстояние между Л и В?
82.	Два тела движутся по сторонам прямого угла по направле-
нию к вершине со скоростями 3 и 4 см/сек. В некоторый момент
времени первое тело отстояло от вершины угла на 21 см, а второе —
на 28 см. Через сколько времени расстояние между телами будет
равно 5 см?
164
83.	Два тела А и В двигаются по двум прямым линиям, пере-
секающимся под прямым углом. Скорость тела А равна 4 м/сек,
а скорость тела В — 3 м/сек. В данный момент тело А отстоит от
точки пересечения на 300 м и движется по направлению к ней, а
тело В отстоит от точки пересечения на 250 м и движется от нее.
Через сколько времени расстояние между телами будет равно
1825 м?
84.	Центры двух окружностей движутся по двум пересекающим-
ся под прямым углом путям по направлению к точке пересечения.
Центр первой окружности, радиус которой равен 46 см, удален
от вершины угла на 2248 см и движется со скоростью 7 см/сек.
Центр второй окружности, радиус которой равен 14 см, удален от
вершины угла на 1628 см и движется со скоростью 5 см/сек. Через
сколько времени окружности будут внешне касаться?
85.	Два автомобиля выехали одновременно из одного пункта
и едут в одном и том же направлении. Скорость первого автомоби-
ля 50 км/ч, а второго — 40 км/ч. Спустя полчаса из того же пункта
и в том же направлении выехал третий автомобиль, который обо-
гнал первый автомобиль на 1— ч позже, чем второй. Определить
скорость третьего.автомобиля.
86.	Расстояние между городами Ли В равно 195 км. Одновремен-
но из обоих городов навстречу друг другу выходят два поезда и
идут до встречи 3 ч; после встречи поезд из А тратит на прохожде-
13
ние расстояния от места встречи до В на — ч больше, чем тратит
поезд, идущий из В, на прохождение расстояния от места встречи
до А. Определить скорость каждого поезда.
87.	Автомобиль проехал расстояние между городами А и В.
Если бы скорость автомобиля была бы на 5 км/ч меньше, то автомо-
биль потратил бы на 0,7 ч больше. Определить расстояние между
городами А и В и скорость автомобиля, если известно, что это рас-
стояние на 15 км больше утроенной скорости автомобиля.
88.	Гребец проезжает расстояние в 16 км по течению реки на 6 ч
скорее, чем против течения; при этом скорость лодки в стоячей
воде на 2 км/ч больше скорости течения. Определить скорость
лодки в стоячей воде и скорость течения.
89.	С морской пристани одновременно отходят два парохода
по двум взаимно перпендикулярным направлениям. Спустя — ч
после отплытия пароходов кратчайшее расстояние между ними бы-
ло 15 км, а спустя еще 15 мин оказалось, что один из пароходов был
от пристани на 4-^- км дальше другого. Определить скорость каждо-
го парохода.
90.	Из двух городов выезжают навстречу друг другу два ту-
риста. Проехав число дней, равное разности между числами кило-
165
метров, проезжаемых ими в 1 день, они встретились после того,
как первый проехал 216 км. Расстояние между городами 3S6 км.
Сколько километров проезжает в день каждый?
91.	Три парохода совершают рейсы между пристанями А и В.
Первый пароход проходит в час на 3 км больше, чем второй, и весь
рейс совершает на 2 ч скорее второго. Второй проходит в час на
3 км больше, чем третий, и весь рейс совершает на 3 ч скорее треть-
его. Определить скорость третьего парохода и расстояние между
пристанями А и В.
92.	Из города А вышел пешеход, проходящий а км/ч. Через
t ч вслед за ним из того же города выехал велосипедист, проезжаю-
щий с км/ч. Через сколько времени велосипедист догонит пешехода?
93.	По дороге в одном и том же направлении едут два велоси-
педиста. Первый проезжает в час км, второй — v2 км. Первый про-
ехал пункт А на t ч ранее, чем второй пункт В, расположенный
далее по направлению движения, чем пункт А. Расстояние между
пунктами А и В равно d км. Определить, на каком расстоянии от
пункта В один велосипедист догонит другого.
94.	Расстояние между двумя городами S км. Товарный поезд,
скорость которого на а км больше скорости пассажирского поезда,
проходит это расстояние на t ч скорее пассажирского. Во сколько
часов товарный поезд проходит расстояние между городами?
95.	Поезд был задержан на станции на t мин. Чтобы наверстать
потерянное время, он увеличил свою скорость на а км/ч и на следую-
щем перегоне в b км опоздание ликвидировал. Какова была ско-
рость поезда до его задержки на станции?
9
96. Расстояние между пунктами А и В равно S км. Причем —
3
этого расстояния — асфальтированное шоссе. Автомобиль на ас-
фальтированном шоссе имеет скорость, на v км/ч большую скорости,
с которой он проходит остальную часть пути — грунтовую дорогу.
Определить скорость автомобиля на асфальтированном шоссе и
на грунтовой дороге, если все расстояние АВ автомобиль проходит
за t ч.
97. Из города А в город В выехал мотоциклист, а из В в Л на-
встречу ему выехал велосипедист. При встрече оказалось, что вело-
сипедист проехал а км, а мотоциклист — на d км больше. Продол-
жая путь после встречи с прежними скоростями, велосипедист
приехал в А через t ч после того, как мотоциклист приехал в В.
Определить скорости велосипедиста и мотоциклиста, если мотоцик-
лист проезжает на b км/ч больше велосипедиста.
98.	Два велосипедиста выезжают одновременно навстречу друг
другу из пунктов А и В, расстояние между которыми d км, и через
час встречаются. Не останавливаясь, они продолжают путь с преж-
ней скоростью, и первый прибывает в пункт В на t ч скорее, чем
второй в пункт А. Найти скорость каждого велосипедиста.
99.	Пешеход отправился из города А в город В. Расстояние
между этими городами d км. В то же время из В в А выехал велоси-
166
педист. Встреча произошла через t ч после их отправления из Л и
В. После встречи велосипедист приехал в город А на а ч раньше,
чем пешеход пришел в город В. Найти скорость пешехода.
100.	Два грузовика одновременно выезжают с одного и того же
склада в пункт, отстоящий от него на а км. Один едет со скоростью,
большей на т км/ч, чем другой, и приходит к месту назначения на
п ч раньше. С какой скоростью едет каждый грузовик?
101.	Два лыжника проходят расстояние а км-, первый из них,
скорость которого на b км/ч меньше, чем скорость другого, прохо-
дит это расстояние на b ч больше. Найти скорость каждого лыжника.
102.	Турист рассчитывал пройти а км за определенное время;
пройдя b км, он отдохнул 15 мин и, чтобы прийти вовремя, увели-
чил скорость на с км/ч. Определить первоначальную скорость дви-
жения туриста.
103.	Два самолета вылетают одновременно из пункта А в пункт
В, расстояние между которыми S км. Скорость первого самолета
на т км/ч меньше скорости второго, поэтому первый самолет при-
летает в В на п ч позже второго. Найти скорость первого самолета
и время, затрачиваемое им на перелет из А в В.
104.	Пароход за а ч прошел b км по течению. В другой раз паро-
ход за с ч прошел d км против течения реки. Определить скорость
течения реки и скорость парохода в стоячей воде.
105.	Моторная лодка прошла а км по течению реки и b км про-
тив течения за т ч; в другой раз в тот же промежуток времени лод-
ка прошла с км по течению реки и d км против течения. Найти ско-
рость моторной лодки в стоячей воде и скорость течения реки.
106.	Лодка проезжает расстояние между пристанями А и В
за а ч, идя по течению реки. В стоячей воде лодка проходит Ь км/ч.
Определить, во сколько времени лодка совершит обратный путь,
если известно, что скорость течения реки в час, выраженная в кило-
п
метрах, составляет — числа часов, за которое лодка совершает
т
обратный путь.
107.	Моторная лодка прошла по течению реки расстояние
S км от пункта А до пункта В и повернула обратно в пункт А. Не
доходя до А р км, лодка остановилась. На весь путь от Л до В и
обратно до остановки лодка потратила t ч. Определить собственную
скорость лодки (скорость лодки в стоячей воде), если скорость те-
чения реки а км/ч.
108.	Двое рабочих вместе могут выполнить некоторую работу
в 10 дней. После 7 дней совместной работы один из них отказался,
и другой окончил работу, проработав еще 9 дней. Во сколько дней
каждый рабочий отдельно может выполнить всю работу?
109.	Двое рабочих, работая вместе, окончили работу в 2 дня.
Определить, во сколько времени окончит эту же работу каждый из
них, работая отдельно, зная, что если бы первый проработал два
167
5
дня, а второй — один день, то они вместе сделали бы — всей ра-
боты.	°
ПО. Некоторое число рабочих выполнили работу в несколько
дней. Если число рабочих увеличится на 3, то работа будет сделана
на 2 дня скорее, а если число рабочих увеличится на 12, то на 5
дней скорее. Определить число рабочих и время, необходимое для
выполнения этой работы.
111.	Двое рабочих взялись выполнить некоторую работу за
30 дней. В начале седьмого дня один из них заболел, а другой про-
должал работу, которую окончил в 40 дней. Во сколько дней может
каждый из них выполнить эту работу, работая один?
112.	В двух бочках находится жидкость. Если перелить из пер-
з
вой во вторую 12 л, то во второй бочке окажется — жидкости, остав-
шейся в первой; если же из второй перелить в первую бочку 20 л,
то в первой станет вчетверо больше жидкости, чем во второй. Сколь-
ко литров жидкости имеется в каждой бочке?
113.	Две трубы, действуя одновременно, наполняют бассейн
в 1 ч 12 мин. Определить, во сколько времени могла бы наполнить
бассейн каждая труба в отдельности, зная, что если бы вторая труба
была отливной (сточной), то при одновременном открытии обеих
труб бассейн наполнился бы за 6 ч.
114.	Некоторую работу взялись выполнить трое рабочих.
Первый и второй, работая вместе, могут выполнить эту работу за
3,6 ч, первый и третий — за 4 ч, а второй и третий — за 5у ч. Во
сколько времени каждый рабочий, работая отдельно, выполнит
данную работу?
115.	Трое рабочих выполняют некоторую работу в 2 дня. Опре-
делить, во сколько времени выполнит эту работу каждый из рабо-
чих, работая один, зная, что первый и второй, работая вместе,
выполнят ту же работу в 4 дня, а второй и третий — в 3 дня.
116.	Для наполнения бассейна были одновременно открыты
1 1	3
3 трубы. Спустя 1— ч, когда — бассейна было уже наполнено, засо-
рилась первая труба, и бассейн продолжали наполнять остальные
две трубы; через 3 ч после засорения первой трубы оказалось, что
19
водой наполнено — бассейна; тогда закрыли третью трубу, и вто-
24	1
рая труба наполнила бассейн за 2— ч. Во сколько времени каждая
труба в отдельности может наполнить бассейн?
117.	Бассейн наполняется тремя трубами в течение 1 ч. Если
открыть первую и вторую трубы, то бассейн наполнится за
1 ч 20 мин\ если же открыть вторую и третью трубы, то бассейн напол-
нится за 1-j ч. Во сколько времени наполнит бассейн каждая труба
отдельно?
168
118.	Два сосуда одинакового веса содержат разные количества
воды. Вес сосуда А с водой составляет — веса сосуда В с водой.
5
Если перелить содержимое сосуда В в сосуд А, то вес сосуда А с
водой будет в 8 раз больше, чем вес пустого сосуда В. Зная, чго вес
воды в сосуде В на 50 г больше веса воды в сосуде А, найти вес
каждого сосуда (пустого) и вес воды в каждом сосуде.
119.	Чан наполняется двумя кранами А и В. Наполнение чана
только через кран А длится на 22 мин дольше, чем только через
кран В. Если же открыть оба крана, то чан наполнится в 1 ч. Во
сколько времени может каждый кран в отдельности наполнить чан?
120.	Один рабочий выполняет некоторую работу на 12 дней
з
скорее другого. Совместно ту же работу они выполнили за 14— дня.
5
Во сколько дней может выполнить работу каждый из них в отдель-
ности?
121.	Два каменщика, из которых второй начинает работу на
1-| дня позже первого, могут выстроить стену за 7 дней. Если бы
эта работа была поручена каждому отдельно, то первому потребо-
валось бы на 3 дня больше, чем второму. Во сколько дней каждый
из них отдельно выстроит стену?
122.	В бассейн проведены три трубы. Первые две, действуя сов-
местно, наполняют бассейн в то же время, в какое наполняет бас-
сейн одна третья труба. При этом вторая труба, действуя одна,
наполняет бассейн на 5 ч скорее первой трубы и на 4 ч медленнее
третьей. Во сколько времени наполняет бассейн каждая труба от-
дельно?
123.	Колхозник при косьбе конной косилкой увеличил часовую
производительность на 0,1 гаи участок в 5 га скосил на 1 ч 40 мин
скорее. Определить часовую производительность косилки.
124.	Трое рабочих могут совместно выполнить некоторую ра-
боту за 2у ч. Первый рабочий может выполнить ту же работу вдвое
скорее третьего и на 1 ч скорее второго. Во сколько часов каждый
из них, работая самостоятельно, может выполнить эту работу?
125.	Бассейн наполняют 3 трубы. Первая и вторая трубы,
работая одновременно, могут наполнить этот бассейн за 10,8 ч,
вторая и третья — за 7— ч. За сколько часов каждая из труб, дей-
ствуя отдельно, может наполнить бассейн, если известно, что пер-
вая труба наполняет его на 13у ч скорее третьей?
126.	А и В вместе выполняют некоторую работу за с ч, Л и С
вместе — за b ч, а В и С вместе — за а ч. Во сколько времени все
они вместе выполнят данную работу?
127.	Один рабочий ежедневно изготовляет а деталей, а другой —
Ь деталей. Через сколько дней количества изготовленных ими де-
169
талей будут между собой равны, если первый к данному дню уже
изготовил с деталей, а второй d деталей?
128.	Двое рабочих, работая вместе, выполняют некоторую ра-
боту в b дней. Если каждый из них выполнял бы эту работу один,
то первый из них окончил бы всю работу на а дней позже второго.
Определить, во сколько дней каждый из них может выполнить всю
работу, работая один.
129.	Двое рабочих должны выполнить некоторую работу в оп-
ределенный срок. Первый работал на а дней меньше срока и зара-
ботал b руб., а второй — на а дней больше срока и заработал с руб.
Если бы первый работал столько дней, сколько второй, а второй
столько дней, сколько первый, то они получили бы поровну. В
какой срок каждый рабочий выполнит эту работу?
130.	На обработку одной детали рабочий А затрачивает на
п мин меньше рабочего В. Сколько деталей обработает каждый из
них за t ч, если А обрабатывает за это время на т деталей больше,
чем В?
131.	При помощи двух труб надо выкачать 100 гл воды. Две тру-
бы неодинакового сечения выкачивают в 1 ч а гл воды. Первая тру-
ба выкачала 50 гл воды, а затем всю оставшуюся воду выкачала вто-
рая труба. Вся работа была выполнена за п ч. Сколько гектолитров
воды можно выкачать каждой трубой отдельно в 1 ч?
132.	На железнодорожном полотне две бригады рабочих укла-
дывали шпалы. Первая бригада работала на t дней больше второй
и за время работы уложила шпалы на S км пути. Вторая бригада
укладывала шпал в день на т км пути больше первой и за время
своей работы уложила на п км пути меньше, чем первая. Сколько
километров пути прокладывает каждая бригада за 1 день?
133.	Сплавлено два слитка золота 84-й и 64-й пробы и получено
50 г золота 76-й пробы. Сколько весил каждый из сплавленных
слитков?
134. Сплавлено 4 дг золота одной пробы и 6 дг золота другой
пробы и получено золото 62-й пробы. Какой пробы было золото
первого и второго слитка, если при сплаве их поровну получается
золото 61-й пробы?
135.	Сплавлено 30 г серебра некоторой пробы с медью, получился
сплав 63-й пробы. Определить, какой пробы было серебрю и сколько
взяли меди, зная, что если бы для сплава взяли серебра 20 г, а не
30 г, то получился бы сплав 56-й пробы.
136.	Сплавлено золото двух проб, причем золота 1-й пробы бы-
ло взято в два раза меньше, чем золота 2-й пробы, и получился сплав
68-й пробы. Определить пробу золота обоих сортов, зная, что если
бы в сплав вошло золота 1-й пробы в 3— раза больше, чем золота
п
2-й пробы, то проба сплава равнялась бы 62—.
170
/ 137. Руда из одного рудника содержит 72% железа, руда из
второго рудника — 58% железа. Смешано некоторое количество
первой руды с некоторым количеством второй руды, получили ру-
ду, содержащую 62% железа. Если бы для смеси взяли каждой ру-
ды на 15 кг больше, чем взяли в первом случае, то получили бы ру-
ду, содержащую 63,25% железа. Сколько было взято руды каждого
сорта для составления смеси?
/ 138. Имеется сталь двух сортов с содержанием никеля в 5% и
40%. Сколько нужно взять каждого из этих сортов стали, чтобы
получить 140 т стали с содержанием никеля в 30%?
с/139. При смешении трех сортов суперфосфата, высшего сорта
(20% усвояемого фосфор а), первого сорта (18% усвояемого фосфора)
и второго сорта (16% усвояемого фосфора), было получено 1000 кг
с 18,8% усвояемого фосфора. Сколько было взято суперфосфата
каждого сорта, если суперфосфата первого сорта было на 300 кг
больше, чем суперфосфата второго сорта?
140.	Сплавлено серебро трех различных проб: 56, 60 и 72-й.
Получилось 16 г серебра 65-й пробы. Сколько вошло в сплав сереб-
ра каждой пробы, если известно, что, изъяв из сплава серебро 56-й
пробы, получили бы сплав 68-й пробы?
141.	Имеется спирт трех сортов. Если смешать два ведра спирта
первого сорта, 3 ведра второго и 5 ведер третьего сорта, то получит-
ся смесь 83°. Если смешать 5 ведер спирта первого сорта, 1 ведро
второго и 4 ведра третьего, то получится смесь 79°. Если же сме-
шать 2 ведра спирта первого сорта, 5 ведер второго и 3 ведра треть-
его сорта, то получится смесь 81°. Определить крепость спирта
каждого сорта.
142.	Смешаны спирты различной крепости и получено 10 ве-
дер спирта в 79°. Сколько взято того и другого спирта, если первый
спирт имеет крепость 85°, а число градусов, выражающее крепость
второго, на 66 больше числа ведер второго спирта?
143.	Вычислить вес сплава золота 920-й пробы, зная, что если
прибавить к сплаву 300 г 880-й пробы и из вновь полученного спла-
ва взять 200 г, .заменив их 200 г 833-й пробы, то получится сплав
893-й пробы.
(/144. Из бутыли, наполненной доверху кислотой, отлили 6 л,
затем долили ее водой и вновь отлили 5 л смеси. Определить вмести-
мость бутыли, если известно, что вода после второго отливания со-
ставляла 20% всей смеси.
145.	Из сосуда, содержащего 60 бутылок кислоты, отлито не-
сколько бутылок и долито такое же количество воды. Затем взято
столько же бутылок, сколько в первый раз, и еще 20 бутылок, пос-
ле чего сосуд вновь долит водой. Кислоты в полученной после это-
го смеси оказалось на 10 бутылок меньше, чем воды. Сколько бу-
тылок было отлито в первый раз?
146.	Сплавлено серебро двух сортов, причем получилось а г
сплава &-й пробы. Первый сорт был с-й пробы. Сколько было взято
171
граммов того и другого сорта, если проба второго сорта серебра на
d больше числа граммов того же сорта?
147.	Смешаны спирты различной крепости и получена смесь
крепостью в а°. Спирт первого сорта имеет крепость &°, и взято его
с ведер. Определить крепость спирта второго сорта, если число ве-
дер его на d меньше числа, выражающего его крепость в градусах.
148.	В цистерне было а л чистого спирта. Из нее отлили некото-
рое количество спирта и долили столько же воды. Потом отлили
такое же количество смеси, после чего в цистерне осталось b л
спирта. Сколько литров спирта отлито в первый раз?
149.	Из сосуда емкостью а л, наполненного спиртом, два раза
брали по одинаковому количеству содержимого и каждый раз до-
полняли водой, после чего в сосуде осталось b л чистого спирта.
По скольку литров отливали каждый раз из сосуда?
150.	Сколько килограммов товара одного сорта ценою а руб.
за килограмм надо смешать с т килограммами другого сорта ценою
b руб. за килограмм для получения смеси ценою р руб. за килограмм?
ГЛАВА X
ЛОГАРИФМЫ. ПОКАЗАТЕЛЬНЫЕ
И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
И ИХ СИСТЕМЫ
§ I. ЛОГАРИФМЫ
Определение. Логарифмом числа N при основании а>0
и а =/= 1 называется показатель степени, при возвышении в которую
числа а получается число N.
а'°еак = л/.
В поле действительных чисел нуль и отрицательные числа не
имеют логарифмов.
При решении задач будем использовать определение логарифма,
свойства логарифмов чисел и формулу перехода от одной системы
логарифмов к другой. Формула перехода
iogi # = i0goy. -Ц_
logaf>
дает возможность найти логарифмы чисел при основании Ь, если
известны логарифмы чисел при основании а,
Число —— называется модулем перехода от лога-
loga6
рифмов чисел по основанию а к логарифмам чисел по основанию Ь.
При N = а формула имеет вид
log,а = —, или log, а  loga b = 1.
logao
1.	Доказать, что .логарифмы последовательных членов геоме-
трической прогрессии образуют арифметическую прогрессию с раз-
ностью, равной логарифму знаменателя данной геометрической про-
грессии.
2.	Чему должно равняться основание логарифма числа а, если
число а равняется своему логарифму?
3.	Логарифм какого числа равен основанию системы логариф-
мов, т. е. loga х — а?
Найти х.
4	%==3i + iog36 .	5. х = 24 + 1ое23 .	6. х = 103,g3 .
7. х = 271 “log’ 2 .	8. х = а1 + loga 6.
9. х= j/102 + rlg16 .	10. х = a1 - 1ОКо ь .
173
11. X=a2,°Sa6.-
12. х = аг,oga 6 с
13. x = a3-ios“b.	14. x = 5log/^4 + 21og=3 .
1	logs (j-logs _9 \
15. x = 4410g2 3 + 21og,<4 .	16. % = 9	' V 3 /.
17.	Зная, что 1g 2-lg 5 = 0,2104, вычислить 1g 2 и 1g 5 с тремя
десятичными знаками.
18.	Зная, что 1g 2 = а, найти логарифмы следующих чисел:
125; /1Д5; 0,025; ^0,0125.
19.	Зная, что loge 2 = а, найти log3 6.
3.--
20.	Зная, что 1g 64 = а, найти 1g у 25.
21.	Дано: loge 2 = а. Найти log6 9.
22.	Дано: log3e 8 = а. Найти log3e 9.
23.	Дано: 1g 122,5 = а и 1g 7 = b. Найти 1g 5.
24.	Дано: 1g 3 = а и 1g 2 = b. Найти log5 6.
25.	Дано: log54 = a и log53 = Ь. Найти log2512.
26.	Дано: log4 125 = а. Найти 1g 64.
27.	Дано: log14 2 = а. Найти log49 16.
28.	Дано: log12 27 = а. Найти loge 16.
29.	Найти 810g45-10g5\
30.	Вычислить без помощи таблиц логарифмов
100,5-lg(0,375-/Ю» — Iog2j/J- 0,0625.
10g6 logftfl
31.	Доказать, что а	= log6a.
32.	Доказать, что logafe ап=~-.
33.	Доказать, что log п ар =—'
34.	Доказать, что отношение -ogaP- не зависит от осно-
logafe
ван и я логарифмов.
35.	Доказать, что loga-~  - = 1 -|- loga5.
36.	Доказать, что log6n ап = logz> а logfe п .
1 + п
37.	Доказать, что log пап +1 = + 1 log* а.
ba	1 + nlog^a
174
38.	Доказать, что log „4.1 abn = —ogft а + п
°	1 + n
39.	Дано: y Ю1 — z = 10 1 ~4
1
Доказать, что x = 101 - №.
40.	Если a2 + b2 = 7ab, to 1g = — 0g a ig ьу Доказать.
3	2
41.	Доказать, что при любых положительных значениях а
и N имеет место равенство
—!— I -------!----1-----!----1---1----= 10 log ..а.
loga N loga2 N loga3 Л/ loga4 TV	N
42.	Вычислить loga a an x (при x У= 1), зная loga x; loga x;...
,..;loganx.
43.	Если а и b суть длины катетов, с — длина гипотенузы, то
log,+, а + log,_, а = 21ogc+, a log,_, а. Доказать.
44.	Доказать, что если а, &, с — члены геометрической прогрес-
сии с положительными членами, то
logfl N — logfr N = logfl N
log TV — logr TV logc TV*
45.	Доказать тождество
loga N log, + log, N log, N + log,(V log^ =
logabc N
46.	Если х(у + г~х) = y(? + x —У) = г(х + У — ?)
Igx	Igy	lg2
TO Xyyx = zxXz = уггУ.
Вычислить при помощи таблиц логарифмов.
47.	^0^^0,4914.
48.	-j3/" 6,2 * уЛ0,1267
V 0,9981
49.	Л/"(0,83)2 К 0,06352
*	(l.l)2^ (0,04135)2
з.-------
50.	0,4782 • (2,011 )2 У (4.003)2
 I	---------—•
(1,306)2 / (10,11)«
175
3	_______ ______________ о /	J>
51.	5,613 . ’/(0,06371)-V (0.2165)! .	52. 1/ 0,637 + у 0,7315.
_ г	- 3 Г-------- '
11,03- У 0,09153 у (0,3014 V
55. yZ (4,552)2 jZ (0.2)2 /о,6672
10,11 I” (0,4512)2
§ 2. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
Если f (х) — элементарная трансцендентная функция, то урав-
нение вида f (х) = 0 называется элементарным транс-
цендентным уравнением.
В элементарной алгебре рассматриваются частные виды таких
уравнений и специальные приемы их решения.
Простейшее показательное уравйение имеет вид:
ах — Ь, где а > 0, а 1, b > 0.
Уравнение имеет единственное решение. При а < 0 уравнение не
имеет решений.
Простейшее логарифмическое уравнение имеет вид:
loga х = Ь, где а > 0, а Ф 1, b — любое действительное число.
Тогда уравнение имеет единственное решение х = аь.
Уравнения вида ам = <p (х), loga f (х) = ср (х), где f (х) и
ср (х) — алгебраические или трансцендентные функции, решаются,
как правило, графически.
Например, — ср (х) строят графики двух функций: у —
= а/(х) и у = <р (х); если графики имеют общие точки, то абсциссы
точек пересечения являются решениями уравнения; если графики
не пересекаются, то уравнение не имеет решения.
Пример. log9 х + log*, 3=1.
Решение. Область допустимых значений неизвестного: х>
> 0. В данном уравнении основания логарифмов различные. Про-
изведем преобразования, приводящие к одному основанию, напри-
мер основанию 9. Из свойств логарифмов известно, что если осно-
вание логарифма и логарифмируемое число возвести в степень п
(п — целое число), то величина логарифма не изменится, т. е.
logx, 3 = logx<9.
Тогда log9 х + logxl 9=1.
176
Учитывая, что log/ 9 = —-—, имеем:
log»*4
log» х + —— = 1.
41og9x
4 log| x — 4 log9 x + 1 = 0.
О т в e t: x = 3.
log,, X = y.
Можно за основание логарифмов взять другое число, например
3; тогда
log9 х = у 1°ёз х,
так как если извлечь корень n-й степени (п — целое число) из осно-
вания логарифма, оставив без изменения логарифмируемое число,
то логарифм увеличится в п раз. Имеем:
1°§х- 3 = 	. Тогда заданное уравнение примет вид:
— log3 х Н--------- 1,
2	2log3x
(logs X — I)2 = 0, log3 X = 1, X = 3
Значение неизвестного х = 3 принадлежит области определения
данного уравнения. Проверка показывает, что х = 3 есть корень
данного уравнения.
Пример. 21g х — 1g (х — 1) = 1g а.
Решение. Область допустимых значений х и параметра а
определяется неравенствами х>1; а>0. Потенцируя, имеем:
а-f- V а2 — 4а	а — К а2 — 4а
корни этого уравнения хх = —1; х2  -----------------------------
Чтобы корни были действительными числами, должно выпол-
няться неравенство а2 — 4а > 0, или а > 4 (а = 0 не удовлетво-
ряет условию задачи).
При а > 4 оба значения неизвестного удовлетворяют области
определения уравнения:
. _а — \г а2 — 4а . а 2	/а2 — 4а _
2
0;
(а — 2) + > а2 — 4а
х2 > 1; хг > 1;
при а > 4 имеем два различных корня: хг, х2,
при а = 4 имеем корень х = 2.
177
Решить показательные уравнения.
56. ^128 = 44
57. б3"* = 216.
-------------
58. 23х = у 512.
- (4)-' - П-
6°. 5^2 = 625i
62. /П* . /IV ?Z
\3/	\8j	64*
63. 61*1 = 36.
64.	7|-|х| = 49.
65-	3'(Г“<- .
66.	2х-5х = 0,1 (10х-1)5.
67.	|Т/~1;/т== 2
\ 4 / . г 3.	16 *
68.	xx’-5x + 6 = l.
69.	(5л2+*-2)<3-*> = 1.
70.	2х2-6х-2,5 = 16]/£
71.	(0,11)х’-5 = 0,001331.
х + 5	х+ 17
72.	32х-7 = 0,25- 128х-3.
х + 1 __
73.	3х у 8х = 36.
.74. 23 + Ч 24 = З/Т.
75.	51 +1085 cosx = 2,5.
76.	атх + п . ърх + q = а(гп-г>х — п . +1)х~q
178
78.	(a4 — 2а2Ь2 + Ь4)х~1 =	» a>b>0.
79.	2х — 2X~2 = 3.
80.	3х — 3х-2 = 8.
81.	2-Зх+3 — 5-Зх~2 = 1443.
82.	5х"1 + 2х — 5х + 2х+2 = 0.
83.	10х + 10х-1 = 0,П.
84.	10х —5х-1-2Х~2 = 950.
3 — х
86.	3х-2-НО, (3)]’“* — [0,(1)] 2 =99.
87.	5х-4 —5х-5 —2-5х-6 = 2-3х-4,
88.	2ГГ+ 2 — 2 У~+1 = 12 4- 2УГ~
89.	]/зх“54 — 7Кзх“58 = 162.
90.	(0,1)-(*2"5* + 8)= 100.
91.	5 (7*> = 7<5*\
92.	23* (2х — 1)~ 1 — 22х(2х + 1)“ 1 — (2* — 1)~ ’ + (2* + 1)" * -
= а + 2, где а > 0.
93.	уЙ + 2х у/*2 — бх = 9, где х > 0.
94.	52х — Iх — 52х-35 + 7Х-35 = 0.
95.	3 • 4Х + -• 9* + 2 = 6-4* + 1—- • 9х + 1.
3	2
gg 4Х____ $Х — 0,5 _ qX 4- 0,5 _ 22х ~ 1
97.	52-54-5® ... 52х = 0,04-28.
98.	а1 • а3 • а5... а2х-1 = п, где а > 1.
99.	1 4- а + а2 4- а* + ... 4- ах-1 4- ах = (1 4- а) (1 4- а2)Х
х (1 4- а4) (1 + а8).
100.	И2*-1— 132*-1 4- 112х_2 4- 132х-2 = 0.
101.	2х 4- 2х + 1 4- 2х+2 4- 2х + 3 = 3х 4- 3х + 1 4- Зх+ 24- Зх + 3.
102.	72х — 6-7х 4-5 = 0.
103.	4х — 9-2х 4- 8 = 0.
104.	52х-1 + 5х+‘ = 250.
179
105.	8х+ ‘ — 82х~' = 30.
106.	22 + х — 22-х = 15.
107.	2-73х —5-49®х + 3 = 0.
(§Г+(£Г= '«
109.	9х + 6х = 4х.
ПО. 22х + 2Х-3Х = 32х.
111.	gr _ 6х = 4х+0+
112.	3-4Х + 2-9х = 5-6х.
113.	9-52х~4 + 4-58-2х= 325.
114.	2х — 3 • 20,5(х~3) = 26.
115.	4х-2 — 17 • 2х-4 +1=0.
116.	9х + 4х = 2,5-6*.
117.	4Гх~2 + 16 = 10 • 2ГхГГ.
118.	4Х+У*^ — 5 . 2*+’/^2-1 = 6.
119.	22х+’+ 32x+I = 5 • 6х.
120.	42х+1 + 22х+6 = 4 • 8х+’.
121	27х I 3^"^"х 1 3I—х 1 27—х 	368
“Г"	729 ' ’
122.	27х + Зх+4 = 702.
123.	8х + 18х —2-27х = 0.
124.	2х — 2- (0,5)2х — (0,5)х —1=0.
125.	23х — Л — б(2х —= 1.
90-V	1	2^—* /
126.	53х + 9-5х + 27-(5~3х + 5~х) = 64.
127.	24х — 23x+1 — 22х + 2Х+1 + 1 = 0.
128.	Xх + 139х-х — 108х~2х = 32.
129.	—2 • 10<х+	= ю'—х3—х
130.	16х + 625х — 3- 100х — 2-4х (4х — 25х) + 2-40х = 0.
131.	^9—^'6 =^4.
132.	]/а2 — Ь2, = 3 ab . ’
133.	(И2— /з)Х + (/2 + /з)Х = 4.
180
134. ( V4 —/1б)* + (У4 + ]Л15 )* = (2 /2 )X.			
135.		1 | <м |оо 		" |со |О1	= 3. 2/
Решить графически уравнения.			
136.	2х - 4.	137. 3~х = 3.	138. 2Х~* = 1.
139.	23х = 8.	140. 2х = х.	141. 2х = х + 2.
142.	3х = — х2. 3	143. 2V = х2.	144. 2х = х2 — 2х.
145.	2~х = УУ	146. 2х = ]/4 —х2.	147. 2х = У5-х2.
148.	2х = —. X	-4-	150. 2Х‘ = 2.
151.	З*2 = 10.	152. 2Х‘ = - х+ -. 3	3	153. 2*2 = х2 + 12.
154.	2*2—* _ 1	155. 2хг~х = х + 1.	156. 2Х~* + -L- = 0.
Решить логарифмические уравнения.
157.	lg(x + l) = 2 1g 4-lg2
158.	1g (0,5 + х) = 1g 0,5 — 1g x.
159.	Ig2x	_ 2 lg(4x—15)
160.	loga(35-x3) = a loga (5 — x)
161.	1g (x2 4- 75) - 1g (X - 4) = 2.
162.	1g Ух1 — 55х + 90 = 0,5 [1g (х — 36) + 1g 21.
163.	1g 1^+7-<g2_ = - 1.
lg 8 — lg (х — 5)
164.	1g (x3 + 8) — 0,5 1g (x2 + 4x + 4) = 1g (58 + x).
165.	lg(/^H+l) = 3.
1g yAx — 40
166.	1g ]/5x —4 + 1g Vx~+1 = 2 + 1g 0,18.
167.	2 lg]/x2 — 36 + 11g (x3 + 3x2 + 3x + 1) — 1g (x + 6) =
= 21g 5 + 1g 2.
168.	1g J/TTx + 31g VT^x = 1g У1 —x2 + 2.
181
169 'gWgH-Sx-ex2) = 3
lg(2x—1)
170.	Ig (1 + ax) — Ig a = Ig Ig b — c.
171.	x (1 — Ig5) = Ig (2х + x — 1).
172.	Ig (x2 — x — 6) — x = Ig (x + 2) — 3.
173.	Ig (2* 4- x — 4) = x (1 — Ig 5).
174.	Ig (6-5x — 25-20*) = x + Ig 25.
175.	log4 (x + 3) — log4 (x — I) = 2 — lg4 8.
176.	Ig (10x)-lg (0,lx) = Ig Xs — 3.
177.	Ig V75 + 5/57=2 = |.
178.	log4 {21og3 [1 + log2 (1+3 log2x)]} =1
179.	Ig | 2x — 3 | — Ig 1 3x — 2 | = 1.
180.	log2 (x + I)2 + log2 | x + 11 = 6.
181.		--------- 2.
Jg| 4x- 15|
183.	log2 (9х-1 + 7) = 2 + log2(3*-‘ + 1).
184.	2loge(—2x) = log381.
185.	410g*T-1 = 0,5.
186 4loge*(x“"3)+Iog25 = 5Q
187.	Ig 2 + Ig (4X~2 + 9) = 1 + Ig (2х-2 + 1).
188.	1 (9log25X+* — 910g2‘x) — logfr 2 /2 = 9log^‘
189.	5'g* _ 3's*-1 = 3lgx+I — 5lgx-1.
190.	3logax+’ + 3x10g«3 = 2. a > 0, а ф 1.
191 / JL\log3|fx+1-----2
= ]Z2(x- 1).
/	1 \	/ x___	\
192. 2 Ig2 + 1 +-) lg3 — lg(y 3 + 27 = 0.
1	4
193 ।____________________z____— з
5-41g(x+l) l+lg(x + l)
194. 0,llg4x — lg2x + 0,9 = 0.
182
195.	2,og=3 • x’~,og‘(7’5*) = 1.
196.	x4<'g*+7> = 10lg*+1.
197.	xlg'x+Igx’+3 _______________?______________
1 1 *
V1+x—1 Ух+1+l
198.	(0,4)lg2;v+1 = (6,25)2-lgxl.
199.	log, 5/5 - | = log3 /5.
200.	x'~lgx = 0,01.
201.	0,1 xlgx-2 = 102.
202.	x'+lgx = 100.
203.	Vx'eYx = 10.
lg*+7
204.	x 4 = 10lg*+‘.
205.	(0,l)_[lg(x+2)+2—lg20] = 2 (x 6).
206.	x¥~ = V"xx.
207.	X21g’x“’’51g* = /Jo.
208.	log3 log3 log3 x = 0.
209.	loga log3 logft x = 0.
210.	log4 log2 logs x=
211.	logs log8 log2 x = logs 2—1.
212.	logs x + log/rx + log, x = 6.
213.	21ogx 3 4- log3v 3 4- 31og9x 3 = 0.
214.	log3 (l°g22 x — 31og2 x 4- 5) = 2.
215.	log, 2-log, 2 = log, 2.
16	64
216.	log5x + log3 x = 1.
217.	log, /1 4- x + 3 log^ (1 — x) = log^ (1 — x2)2 4- 2.
1	T	Тб
218.	log2 I 2x — 5 |4- log2 I x 4- 20 | = -Д-
183
219.	Vlog* 5 У5 + log/r 5 У5 • log/r x = —Уб.
220.	Iogx У2х  log2x = — 1.
221.	]/31og2(—x) = log2 Ух2.
Решить уравнения и исследовать относительно параметров.
Параметр — действительное число.
222.	1g х — 1g (х — 2) = tn.
223.	2 lg х — lg (х — 1) = lg a.
224.	loga x + logv a — b.
225.	lg (ax) + lg x = lg (x — 1).
227.	loga x log* x = loga b.
228.	loga2 x + log? a = 1.
229.	loga x log* c-(l + logc a) = log* x logc x loga c.
230.	1 + log, = (lg lg n — 1) log, 10.
231.	logx+1 a + loga, a = 0.
232.	2 log,, a + loga, a + 3 loga2* a = 0.
233.	3 loga2* x + — log * x = 2.
2 Vf
2
234.	log m x + log „ a — -r=.
&am	уmn
Решить уравнения, если a > 0, a =# 1, & > 0, b^l.
235.	log^s J/х + loga/? x3 = logaa j x .
236.	Кloga У ax + logx ax + у loga j/ logx j/-^- = a.
237.
log2X   2 loga x
10^2	10g_l_ a
b
= log3 X • logax.
238. 1 + log* (2 log a — x) logv b ==
Решить графически уравнения.
239. lg x = x — 1.
241. lg x = x2 — 2.
2____
'leg* x ‘
240. lg x = x + 1.
242. lg x = Ух — I.
184
243. Ig (x + 1) = x— 1.
245. lgx = yx.
247. Ig (1 — x) = 2*.
244. Ig x — x2.
246. Ig x = 2~x.
248. Ig (x2 — 2x) = у x — 8.
§ 3. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ И ЛОГАРИФМИЧЕСКИХ
УРАВНЕНИЙ
Пример. Решить систему уравнений, исследовать относи-
тельно параметра а
1g (*—!) + 1g (У — 1) = 1g а, ху = 3.
Решение. Область определения неизвестного: х > 1; у > 1.
Значениями параметра а могут быть только положительные числа
а > 0.
Решая систему, получим (х + у = 4 — а,
( ху = 3,
х и у будут корнями квадратного уравнения.
z2 — (4 — a)z + 3 = 0,
откуда
____ 4 — а — У а2 — 8а + 4	4 — а + У а2 — 8а + 4
21 —	2	>	г2 —	g———-.
Корни будут действительные числа, если а2 — 8а + 4 > 0;
откуда а > 4 + 2 УЗ, а < 4 — 2 УЗ. Учитывая, что а > 0,
имеем:
0 < а < 4 — 2 УЗ, а > 4 + 2 УЗ.
Если а > 4 + 2 УЗ, то
. _ 4— а — У а2—8а+ .4	. _	2 — а — /а2 — 8а + 4	„
X 1—	2	1 —	2	<'U’
т. е. х< 1. Следовательно, при а> 4 + 2УЗ система не имеет
решений.	_
Если а = 4 + 2 УУ то х =	~ ~ 2	= — УЗ,
система не имеет решений.
При а = 4 - 2 УЗ х = 4-4 + 2/3 в
система имеет одно решение.
п л	.	<-> 1 г o’	1	4 — а — У а2 — 8а Ч- 4	,
При 0	< а < 4	— 2 у 3	х — 1	=----------------------1	=
2 - а — У а2 — 8а 4- 4 _ _____20	. п
2	— 2 — а + У а2 — 8а + 4	и’
х > 1, у > 1, система имеет два решения.
185
и логарифмических уравнений.
Решить системы показательных
249. [	у*2—7*4-12	= J, х + У = 6.		
250.	[5х- 8у = 512 000, х + У = 7.	251.	(/7 = 2,
252.	2х (х + у) = 10, Ух + у = 5.	253.	{/х + у =2, 1(х + у) • 3х = 279 936.
254.	(2х • Зу = 24, (2у • 3х = 54.	255.	(3х • 5у = 75, (ЗУ • 5х = 45.
256.	[х2у-1 = 5, [ху+2 - 3.	257.	/у = 9, 1/324 = 2х2.
258.	/3 • /15 = 0,25, [/5 : /о^ = 1.	259.	ху = 256. .2 /8Г2 = Зх.
260.	82х+* = 32 • 24у~1, [5 • 5*-у = V252у+>-	261.	/F = 32 /§у , /3х = 3 /9*-*'.
262. I	[ху = ух, (Х3_= у2.	263. 1	л /х + у = 2 /3, {(х + у)-2У~х = 3.
264. ।	[Зх _ 22у = 77, 1/3* — 2у = 7.	265. 1	[642х + 642у = 12, । 64х+у = 4 /2.
266. j	[Э-б* + 7-2х+у = 457, [6-5х — 14- 2х+у = —890.	267. (	х2у = 16 + 6-хУ, х2у 5 = у-хУ + 5у2.
268.	(1 + У)х = юо, (у<_2у2+ 1Г*= 1	(У + I)2		
269.	(у + 1)х = 10000, (у2 _ 1)2х-2 = 0L- 02Х , Г	(У + 1)х ’	270.	[ЫТ - 5°. ,(9999х-у-‘)х2+6у2-60 =1.
271.	1 ,5/“ х3 = /у8, 4	!5/“ у = ИХ2, 7 = V* + /7 .	272.	Ч: 'с II II II И
1R6
273.
8
xz = у3 ,
2
lg (* + у) — 1g 5	_ j
lg x + lg у — lg 6
_________— Igx__________
lg(*4-6) — (igy + lg 6)
274. (5x + 2y = 100,
|lg x — lg у = lg 1,6.
275. (lgx-lgy=l,
(x + y2 - 200.
276.
1.
277. fig (x2 + y2) — 1 = lg 13,
(lg (x + y) — lg (x — y) = 3 lg 2.
278. Hg (x — y) — 21g 2 = 1 — lg (x + y),
(lg x — lg 3 = lg 7 — lg y.
280. (log., м 4- log.z v — 2,
[u2 + v = 12.
282. (3* • 2y = 576,
(l°g/2- (У — *) = 4-
284. (lg2 x + lg2 у = 7,
(lg x — lg у = 2.
279. ( log4 x — log., у = 0,
(x2 — 5y2 + 4 = 0.
281. (logxy (x —y) = 1,
(logxy (x + y) = 0.
283. (xy = 40,
= 4.
285. (xy = a2,
|lg2 x + lg2 у = -| lg2a2, где
286. (5 (logy x + logx y) = 26,
(xy = 64.
287' |l°gO (! + y) = 2 — ,0§a У>
log* x + logfc у = 4.
288. (з1с«з*__2log'y = 77,
|3iog,/r_ 21°g“>' = 7.
289.
lg pxn ym = tnn. + 1,
lg (x'g^) _ lm_\2
,lg(ylgy) \»/
290, ^^^yyy = 10,
(2x + 2y = 5.
291.
103-is(^-y) = 250,
| V~y -
187
292. I	у э = x,	293. (ху = yx,	
	у3 = X2.	\px = q>-
294. (	ху = у*,	295. (р log* а + q logv а = 0,	
1	хР = у’.	lx? — 4yP = 0.
296. (	a*by = ab,	297. ((ох)'«а = (£>у)х®*, ху = 1.	
298. <	~lg*+ ylgy — Ig (4 — /х) (25/^7 — 125-5^ = 0.	= o,
299.	log^ + log02 у = |,	30°- logj.X + logfty = |.	© <ra ",	II 'C 1* II	л cT o* oq aa ч: н
301. ( 303. 1	Xx+y _ yi2 _ o,	302. <xx+y = yx~y, yx+y — x3.	|x2y = 1. 7- 3x+1 — 2*3y+*_-*+1 = 9, 2-3-v+1 Зу+г-х = 27, Ig (x + у + z) — 3 Ig x = Ig yz + 0,3010.	
304. 305. 306. 307. 1 308. 1	Ig (x + 3y + 2z) = Ig x + -i- _!2__2^=20> 2г-2У	44 23 • 22у-г — 5 • 2х-2 = 52. 2*ТУ — у^а — 0( y*+y = гР, Юз-^-у) = 250. log2 X + log4 у + log4 z = 2, logs У + logs z + log9 X = 2, llog4 z + logie X + logie у = 2. Ig (1 — x) — Ig (1 — y) = Iga, xy = 2. (logy x + log* у = j , lx 4* У = a + a2.	Ig 2,
309.	flga x + lg2 у = | lgaa2, Ixy = a2.	
ГЛАВА XI
НЕРАВЕНСТВА
§ 1. ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВ
Доказать неравенство — это значит показать, что одно алгебра-
ическое выражение больше или меньше другого при всех значениях
входящих букв или при указанных условиях.
Существует несколько способов доказательства неравенств.
Рассмотрим некоторые наиболее часто применяемые способы.
1-й способ. Составляют разность между левой и правой частями
доказываемого неравенства и определяют ее знак.
Примеры.
1. Доказать, что 1 + 2л4 > 2х® 4- х2.
Доказательство.
1 + 2х* — х2 — 2х® = (х4 — 2х* 4- х2) + (х4 — 2х2 + 1) =
= (х»—х)2 + (х2 — I)2 > 0.
Если х Ф 1, то разность положительна; если х — 1, то разность
равна нулю. А это и значит, что 1 4- 2Х4 > х2 + 2х®.
2. Доказать, что при положительных а, Ь, с
ab (а + b) + Ьс (Ь + с) + ас (а + с) > babe.
Доказательство.
ab (а + b) + Ьс (Ь + с) + ас (а + с) — 6аЬс = а2Ь 4- ab2 4-
4- Ь2с 4- te2 4- а2с + ас2 — 2аЬс — 2аЬс — 2abc = Ь (а — с)2 4-
4- а (Ь — с)2 + с (Ь — а)2 > 0,
следовательно, ab (а + Ь) + Ьс (Ь + с) + ас (а + с) > (заЬс.
2-й способ. Преобразуют одно или несколько очевидных нера-
венств к виду доказываемого неравенства.
Примеры. 1. Доказать, что а2 4- 63 > а2Ь 4- ab2
при а 4- Ь > 0.
Доказательство. Возьмем очевидное неравенство а2 4-
+ Ь2 > 2аЬ. Вычтем из обеих частей неравенства по ab, получим
а2 4- 62 — ей) > ab. Умножим обе части полученного неравенства
на а 4- Ь > 0, получим (а2 4- Ь2 — ab) (а 4- b) > ab (а + Ь), или
а3 4- Ь3 > а2Ь 4- ab2.
2. Доказать, что если а, Ь, с — натуральные числа, то
ab 4- Ьс 4- ас < ЗаЬс.
Доказательство. Возьмем очевидные неравенства:
ab < abc, be < abc, ас < abc\ сложив их почленно, получим доказы-
ваемое неравенство ab 4- Ьс 4- ас < ЗаЬс.
3-й способ. Предположив, что данное неравенство справедливо,
преобразуют его к очевидному неравенству.
Замечание. При доказательстве неравенства этим способом необходи-
мо наблюдать, чтобы из каждого следующего неравенства можно было получить
предыдущее. Соблюдение этого требования гарантирует правильность заключе-
ния о том, что если получено -очевидное неравенство, то справедливо и исходное,
в противном случае это заключение не будет верным.
189
4
Примеры. 1. Доказать, что при т> 0 т -]-------> 3.
т2
Доказательство. Предположим, что данное неравен-
ство справедливо, тогда справедливо неравенство т3 — Зт2 4- 4 О
Представив левую часть полученного неравенства в виде про-
изведения, получим неравенство (т. 4- 1) (т — _2)2 0, которое
очевидно.
Из каждого полученного при преобразованиях неравенства мож-
но получить предыдущее. Значит, данное неравенство верно.
2. Доказать, что если а, Ь, с и d — положительные числа, то
]/(a + c)-(b + d) > Vab + У cd.
Доказательство. Предположим, что данное неравен-
ство справедливо. Тогда после возведения обеих частей его в квад-
рат получим неравенство
(а + с) • (Ь 4- </) ab 4- 2 У abed 4- cd.
Вычитая из обеих частей по ab 4~ cd, получим неравенство cb 4-
4- ad > 2 ]/ abed, которое легко приводится к очевидному неравен-
ству (У сЬ — У ad)2 0.
Принцип обратимости сохранен, т. е. из каждого последующего
неравенства можно получить предыдущее, следовательно, данное
неравенство верно.
4-й способ. Применяют Для доказательства неравенств некото-
рые замечательные неравенства и свойства средних величин.
Примеры. 1. Доказать, что если
Xi, х2, ..., хп, у1( у2, •••» Уп
положительные числа, то
Ух^У1 + УхгУг + ••• + УхпУп <
< У Xi 4- х2 4- ... 4- хп-Уу! 4- Уг 4- ... 4- Уп-
Доказательство. В неравенстве Буняковского—Коши
(я А 4аЛ+ ••• + апЬп)2 < (ах2 4- Яг2 4- ... 4- On2) (V + b2 4-
4- ... 4- Ьп2) положим а2 — хх, я2г ~ х2. ап2 = хп, Ь2 = ух,
Ь22 = у2, ..., Ьп2 = уп. Получим неравенство
УХ1У1 + Ух^У2 4- ••• 4- УхпУп)2 < (А 4- х2 4-	4- хп) (ух 4-
4" Уг + ••• + Уп)-
Извлечем квадратный корень из правой и левой частей.
У-Wi + /хУ2 4-  4- Ухпуп <
< У Xi + х2 4- ••• 4- хп • ГУх 4" у2 4~ ... 4- Уп.
Получили доказываемое неравенство.
2. Доказать, что если a.2i ..., ап — положительные числа, то
(ах + а2 + ... + ап) + — + - + -Ц > л2.
\а1 а2	ап)
190
Доказательство. Применим для доказательства дан-
ного неравенства свойство среднего арифметического и среднего
геометрического для чисел а19 а2) ..., ап и для чисел—, —,
#1	^2
+ а2 + - + ап > nyal-ai...a~
1 , 1 , , 1 1 1 1
—1------F ••• Ч— > п 1 /
а2	ап	V	а2 аП
'Ь
(1)
(2)
Перемножив неравенства (1) и (2), получим доказываемое неравен-
ство.
5-й способ. Применяют для доказательства неравенств метод
математической индукции.
Пример. Доказать, что при любом натуральном п справедли-
во неравенство —-----1—!--I- ... Ч----— > 1.
п + 1 п + 2	Зп +1
Доказательство.
1)	Проверим справедливость неравенства для п = 1:
l + i + l^i.
2	3	4	12
При п = 1 неравенство справедливо.
2)	Предположим, что неравенство справедливо при некотором
п = k > 1, т. е.
-1-+ _1_ +... + —1—> 1. (1)
/г + 1 k + 2 1 3k +1	'
3)	Докажем справедливость неравенства при п = k + 1, т. е.
— + — + ...+ -J—> 1:	(2)
/г + 2 Хг + 3	З/г + 4
Преобразуем левую часть неравенства (2):
А: + 2	* + 3	"	3/г + 4 — G + 1	k-\-2 + + Зй + 1) +
Ч-(—^—+—^—+ —-------------Ч-
\3fc + 2 3k + 3 3k + 4 k + 1)
i , i ,	।	1
k + 1 ’r k + 2 -T" " 3k + 1
больше 1 по предположению (1). Следовательно, для доказательст-
ва неравенства (2) достаточно доказать неравенство
__L_ + _L_ + _1---------1_>о.
3/г + 2 3k+ 3 3k+ 4 k+l
Предположим, что неравенство (3) справедливо, тогда
1 1 > 1_______________1
3k + 2 + 3k + 4 k + 1 3k + 3 ’
6/г Ч 6	2 q g
9fea + 18/г + 8	3 (fe + 1) ’
(3)
191
Получили очевидное неравенство. Принцип обратимости сохра-
нен, следовательно, неравенство (3) доказано.
Если к числу, большему 1, прибавить неотрицательное число,
то сумма и подавно будет больше 1. Значит, неравенство (2) справед-
ливо.
На основании аксиомы математической индукции можно утвер-
ждать, что данное неравенство справедливо при всяком натураль-
ном п.
Доказать неравенства (в задачах, в которых не дано дополни-
тельных указаний, под буквами следует понимать любые дей-
ствительные числа).
1.	а1 + ab + Ь2 > 0.
2.	а2 — ab + b2 < ab.
3.	а2 + Ь2 + с2 ab + ас + be.
4.	а2 + b2 + с2 + 3 > 2 (а + b + с).
5.	<1.
1 “I- cP
6.	2а2 + Ь2 + с2 > 2а (Ь + с).
7.	а2 + с2 > 2Ь2, если а : b = b : с.
g /а + Ь + ctb + ас + Ьс
’ \ з У з ’
9.	—	< — + — , если а > 0 и b > 0.
а b Ь2 а2
10.	ab + ас + be > abc, если а, Ь, с — положительные числа,
меньшие 1.
11.
а + Ь
1 -j- a -j- b
——|——, если а
1 +□ 1+ь
0 и &>0.
12.	(1 + аг) (1 + а2) ... (1 + ап) 2я, если аг > 0 (1 < i <
< п) и а&ъ ... ап — 1.
13.	(1 — х) (1 — у) (1 — z) > 8xyz, если х, у, г — положитель-
ные числа и х + У + z = 1.
14.	а* + Ь* + с4 > abc (а + b + с), если а, Ь, с — положитель-
ные числа.
15.	а4 + Ь* а?Ь + аб3.
16.	а4 + 2а36 + 2а& + t»4 > 6аг&2, если а и b одного знака.
17.	abc (Ь + с — а) (а + с — b) (а + b — 1с), если а, Ь, с —
числа положительные и сумма любых двух чисел больше третьего
числа.
18.	(ах + Яг + а3)2 < 3 (а/ + а^ + а82).
19.	(ах + а2 + ... + ав)2 < п (а^ + а/ + ... + ап2).
20.	х2 + у2 + г2 > —, если х + у + z = 1.
з
192
21.	4а4 — 4а3 + 5а3 — 4а + 1 > 0.
22.	х5 + У5 — х*У — ху4 > 0, если х, у — положительные числа.
23.	х8 — х5 + х2 — х + 1 > 0.
24.	(а + b 4- с)3 — (а3 + Ь3 + с3) > (а + Ь) (Ь 4- с) (с + а),
если а, Ь, с — положительные числа.
25.	(а + b)2 < (1 + с) а2 + (1 + —) Ь2, где а, Ь, с — любые
С
действительные числа, с — положительное число.
26.
ат — Ьт
ат + Ьт
сг —	. п
-----г при m > я и а > р > 0.
ап + Ьп Е
27.	l+a.+^+...+a..>{L±, а> L
а + а3 + а8 4-... + а3”-1 п
29.	— 4- — > 2, если и а2 — положительные числа.
«2	«1
Для доказательства неравенств № 30—35 использовать нера-
венство № 29.
30.	З’®67+3",’67>2.
31.	ad + be	bc + ad 4, еслиположительные числа.
bd	ас
34.	Xj 4- х2 4-... + хп ----1 И ... 4—	2/1.
%1 х2	Хц
35.	lg а + logfl 10 > 2, если а > 1.
36.	Доказать методом математической индукции, что среднее
арифметическое положительных чисел не меньше среднего геомет-
рического этих чисел:
gl ~Ь ^2 +
П
где alt a2i ... , ап — положительные числа.
Для доказательства неравенств № 37—53 использовать свойство
среднего арифметического и среднего геометрического положитель-
ных чисел.
37.	(а + Ь) (Ь + с) (с + а) > 8abc; если а, Ь, с — положитель-
ные числа.
7 Заказ 1089
193
38.	(1 + a) (1 + b) (1 + c) > 8, если a, b, c — положительные
числа и abc = 1.
39.	]Л(а + a)(b 4- 0)< i (a 4- b) -f- у (a 4- 0), если a, 0, a, b —
положительные числа.
40.	У ab	, если a> 0 и b > 0.
a+b _ _ _
4\. a + b + с > У ab + У be + У ас, где a, b, c — положи-
тельные числа.
42.	(a + 1) (b + 1) (a 4- c) (b + c) l&abc, если a > 0, ft > 0, c > 0.
43.	(a + 1) (b + 1) (a + c)3 (b 4- с)3	256a2b2c3, если a, b, c —
положительные числа.
44.	Va& + Уа&з 4- ... + У an^an <	4- «2 + ... +
4- an), где a,- — положительные числа.
45.	]/4a 4- 1 4- У4b 4- 1 4- У 4c 4- 1 <. 5, если a 4- b 4- c =
= 1 и a, b, c — положительные числа.
46.	(У a 4- УЬ)* > 64ab (a 4- b)2, если а и b— положительные
числа.
47.	a3 4- &3 + с3 > ЗаЬс, если a, b, c — положительные числа.
48.	па^ ... an < a? 4- a2n 4- ... + an", где n — натуральное
число и a, >0 (1 < i < n).
49.	— 4- — + — 4- — > n> если ax, a2,..., an — положительные
a2 a3	al
числа.
50.	n+i/~abn < —-, где а и b — положительные числа, п —
«4-1
натуральное число.
51.	1
\ 2 /
и(п-И)
52.	1.22-33-44...n'I<(^i^) 2 .
53.	aa+b+c • ba+i,+e • ca+b+e > -(a4~ b 4- c).
з
Доказать неравенства.
54.	a 4	----> 3, если a > b > 0.
(a — b) b
55.	11 4- IWj 4-	> 9, если x>0, y>0 и x4-y=l.
\	x)\ y)
56.	- 4- 7 + - < °8 +3b* ПРИ abc> °*
abc	a3b3c3
57.	—5	1-J-4 ... 4- — > —, где n — натуральное число и n> 1.
п +1 n + 2	2п	2
194
58.	—!	J------<------!----1---1-----h ... 4--!---<
n + 1 n + P +1 (n + D2 (n + 2)2	(n+p)2
<--------, где пир — натуральные числа и п > 1, р > 1.
п п + р
59.	а2 + Ь2 + с2 + d2 -г ab + ас + ad + be + bd + cd > 10,
если a, b, c, d — положительные числа, произведение которых рав-
но 1.
60.	3 (1 + а2 4- а4) > (1 + а + а2)2.
61.	ab + ]/(1 — а2) (1 — Ь2) < 1, если | а | < 1, | b | < 1.
62.	а4 + &4	, если а + b = 1.
8
63.	Доказать, что если сумма k положительных переменных
чисел есть постоянное число х + у + z + t + ... + v = А, то
произведение этих чисел будет наибольшим при их равенстве
Л
x=y=z=t= ... = V = — .
k
64.	Доказать, что если сумма k положительных переменных чи-
сел х + у + z+ ... + v есть число постоянное, равное Л, то про-
изведение хт уп zp ... vr, где т, и, р, ..., г — натуральные числа,
будет наибольшим, когда — =— = — — ... = — .
т п р	г
65.	Доказать, что если произведение k положительных перемен-
ных чисел есть число постоянное, то сумма этих чисел будет наимень-
шей при их равенстве.
66.	Доказать, что если произведение k положительных перемен-
ных чисел xmynzP...tr — Л есть число постоянное, то сумма
х + у + ... + t будет наименьшей при условии — = — = ... = —.
т п	г
67.	Доказать, что если четыре положительных числа пропор-
циональны, то сумма наибольшего и наименьшего больше суммы
остальных двух чисел.
68.	Из всех прямоугольников с данным периметром найти
тот, который имеет наибольшую площадь.
69.	Из всех параллелепипедов с данной суммой длин трех вза-
имно перпендикулярных ребер найти тот, объем которого наиболь
ший.
70.	Найти наибольшее значение ху при условии 5х + 7у = 20.
71.	Наити наименьшее положительное значение дроби -—.
X
72.	Найти наибольшее значение произведения (х + З)2 (2 — х)3.
73.	Найти при х > 0, а > 0, & > 0 наименьшее значение дроби
(а + х) (6 + X)
х
7*
195
74.	Найти наибольшее значение функции у =
X2
х2+1 ’
32х2
75.	Найти наибольшее значение дроби -----.
х44-16
76.	Доказать методом математической индукции неравенство
Буняковского — Коши.
где а;, bt > 0.
п	\2 п п
z=i	j	i=i i=i
Для доказательства следующих неравенств № (77—80) исполь-
зовать неравенство Буняковского — Коши.
77.	(а-\-Ь) (— + — I > 4, если а, b — положительные числа.
\ а Ъ ]
78.	(а 4- b 4-с) (— 4- -- 4- -Ц > 9, если а, Ь, с — положительные
\а ь с ]
числа.
79.	(хх 4- х2 4- - 4- *п) (— + — 4- •••+ -) > п2> если хх, х2, ...
\ Х1 Х2	ХП/
хп — положительные числа.
80.	Если а2 4- 62 4~ с2 = 1 и х2 4- У2 + z2 = 1 и х, у, г Ф а, Ь, с,
то —1 < ах 4- by 4-.cz < 1.
Доказать неравенства методом математической индукции.
81.	Доказать, что при натуральном п, большем 4, справедливо
неравенство 2" > п2.
82.	Доказать, что 2я > 2п 4- 1 при натуральном п > 3.
83.	Доказать, что 2я > п3 при натуральном п 10.
84.	Доказать, что 22	> п\ при натуральном п > 2.
85.	Доказать справедливость неравенства [2--- )я > п, где
\ п /
п — натуральное число, большее единицы.
86.	Доказать —— 4—— 4- ••• 4- — > —, где п — натуральное
число, большее 1.
87.	Доказать, что при любом натуральном п, большем 1, имеет
1,1,1,	,1^1
место неравенство — 4- — 4- — 4- — 4- —t < 1.
88. Доказать, что при любом натуральном п, большем 1, имеет
1,1,	,	1	1/~
место неравенство 4- у- 4- ••• 4- -у = > V »•
89. Доказать, что для любых целых положительных чисел ах,
02, .... ап имеет место неравенство
— 4- — 4- - 4- — > «•
Од
196
90. Доказать, что
14--<(14--У <14--4--^
для любого целого положительного k < п.
91. Доказать, что для любого натурального п, большего 1,
имеет место неравенство
4я (2л)!
П + 1	(л!)2
92. Доказать, что для любого натурального п, не меньшего 6,
имеет место неравенство
/ п\Л
п_\"
3 / '
93.	Доказать, что при х > —1 и натуральном п справедливо
утверждение: (1 + х)" У 1 + пх (неравенство Бернулли — Коши).
94.	Доказать, что 2я-1 (а" + Ь") > (а + Ь)п, где а + b > 0,
а ф b и п — натуральное число, большее 1.
95.	Доказать, что при любом х> 0 и при любом натуральном п
справедливо неравенство
X" хп-г xn-i 4.... + J_4-J_+l>rt+i.
Xя'4 Xя*2 Xя
96.	Доказать, что если хг + х2 + ... + хп = А, причем ни одно
из чисел хх, х2, ...» хп не равно нулю и неотрицательно, то
Х1 х2	х„ А
97.	2! 4! 6! ... (2п)! > [(п + 1)!]я.
4я (2пУ
98.	——	гДе «— натуральное число, большее 1.
99.	п! > Уп".
100.	У ——
I =1
п
п.
• хп
§ 2. РАВНОСИЛЬНОСТЬ НЕРАВЕНСТВ
Пусть функции f (х, у....z) и ф (х, у, ..., г) определены на не-
котором множестве А. Поставим задачу: найти множество X,
на котором значения одной из функций больше (меньше) значений
другой из них, другими словами, найти все значения х, у.......z,
для которых выполняется неравенство
f (х, у... z) > ф (х, у, ..., z)
или
f (х, у, .... Z) < ф (х, у..Z).	(1)
197
При такой постановке задачи каждое из неравенств (1) называ-
ется функциональным (алгебраическим) неравенством с
неизвестными х, у, ..., z.
Множество А называется множеством (областью) до-
пустимых значений неизвестных для данного неравенства.
Множество X называется множеством решений дан-
ного неравенства.
Решить неравенство — значит найти множество всех систем
значений х, у, ... ,z, для которых данное неравенство выполняется.
Два неравенства называются равносильными, если мно-
жества всех решений их совпадают, т. е. если всякое решение каж-
дого из них является решением другого.
Обычно в процессе решения неравенства, как и при решении
уравнения, заданное неравенство заменяют равносильным ему не-
равенством, более простым.
Такая замена чаще всего основывается на теоремах.
Теорема 1. Неравенства
f (х, у, ... , Z) V ф (х, у.г)	(1)
и
f (х, у,... ,г) + (0 (х, у,... ,z) v <р(х,у,... ,z) + со(х, у,... ,z) (2)
равносильны, если функция со (х, у, ..., z) определена на множестве
допустимых значений неизвестных неравенства (1).
Замечание. Знак V означает один из символов >, <.
Теорема 2. Неравенства
f (х, у, ..., z) V ф (х, у, ..., z)	(1)
и
f (х, у, ... , z) со (х, у, ... , z) V Ф (*, У, ••• , z) • ю (*,	••• > ?) (2)
равносильны, если значения функции со (х, у, ..., z) положительны
при всех допустимых системах значений неизвестных неравенства (1).
Теорема 3. Неравенства
f (х, у, ..., z) V Ф (х, у, ..., г)	(1)
и
f (х, у, ... , z) со (х, у, ..., г) Л ф (х, у, ... , z) со (х, у, ..., z) (2)
равносильны, если значения функции со (х, у, ..., z) отрицательны
при всех допустимых системах значений неизвестных неравенства (1).
Замечание. Знак Л означает, что неравенство (2) противоположного
смысла по отношению к неравенству (1).
При решении неравенств, так же как и при решении уравнений,
можно потерять и приобрести решения.
Если при решении уравнений не всегда легко было найти по-
терянные решения, то при решении неравенств не всегда легко най-
ти как потерянные, так и приобретенные решения. Обнаружить
обычной проверкой потерянные решения неравенства довольно за-
труднительно. При решении неравенств целесообразно выполнять
равносильные преобразования.
198
Равносильны ли неравенства на множестве действительных чисел?
101.	х2 < —1 и — (5х4 + 3) > 0.	102. х > 0 и х2 > 0.
103.	х — 3 > 2 и х — 3 + -J— >2 4- _.
х — 7	' х — 7
104.	5х < 0 и 5х + - < 1.
X X
105.	х > 1 и х + — > 1	.
4 — х	4 — х
106.	Зх + 1 > 1 и (Зх + 1) + (х — 4) > х — 4.
107.	х — 3	>	2	и	(х — 3) (х	+	I)2 > 2 (х + I)2.
108.	х — 3	>	2	и	(х — 3) (х	—	1) > 2 (х — 1).
109.	—х2 — 5х 6 < 0 и х2 + 5х — 6 < 0.
ПО. х — 1	>	0	и	(6х2 + Зх	+	5) (1 — х) < 0.
111. —2 (х	—	х2	— 3) (4х —	1) > 0 и 4х — 1 > 0.
113.
114
115.
116.
117.
118.
119.
и ^2(<-3)>0.
х — 3
и 1 > 2 (х — 3).
и (х — 2) (5 — х) > 0.
112. — >2
х — 3
1
х — 3
х —2^
5 — х
 * ~2 > 0 и (х —2)(5 —х) >0.
х2 (5 — х)	v м '
—— > —-— и (х + 5)2 < (х +
(х + 5)2 (х + 1)2 v
X	X
х2 — Зх + 1 X2 + Зх Н-
г \ л 5 — х 4
5 — х > 4 и --> —
х2 “I- Зх 4- 2
2
120.
х2 —Зх 4-1.
1 х2 < 49.
4
2
О
и
1	/ 7
— х < 7 и
2
§ 3. ЛИНЕЙНЫЕ НЕРАВЕНСТВА С ОДНИМ НЕИЗВЕСТНЫМ
И ИХ СИСТЕМЫ
1. Линейные неравенства
Линейное неравенство с одним неизвестным в общем виде можно
записать так:
а±х + Ьг V а2х + b2,	(1)
где alf b19 а2, Ь2 — действительные числа.
199
Неравенство (1) можно заменить равносильным ему неравенст-
вом ах V Ь.
Пусть знак V обозначает >, тогда будем иметь неравенство
ах > Ь, решениями которого будут
b	л	b	г\
х > — , если а > 0;	х < —, если а < 0;
а	а
у х £ D, если а — 0 и Ь < 0.
Нет решений, если а = 0, 6 > 0.
Пример. Решить неравенство
(а2 + а + 1) х — За > (2 + а) х + 5а.
Решение.
(а2 + а + 1) х — (2 + а) х > 5а + За,
(а2 — 1) х > 8а.
Если |а| > 1, то х> -’.
а2 — 1
Если |а| < 1, то х < —.
а2 — 1
Если а = 1, то неравенство примет вид 0 • х > 8 и не будет
иметь решений.
Если а = —1, то неравенство примет вид 0 • х >> —8 и будет
выполняться при любых значениях х.
Решить неравенства.
121.	5х— а> ах — 4.
122.	х — 2~> т — пх.
123.	— — тх — 1 > —[х (т + 1) + т].
3
124.	Зах + b > ах + 26.
125.	ах + 62 > Ьх + а2.
126.	а2х + ab> Загх + Ьс.
127.	- + — > —— —.
а а2 а а2
128.	- — 5 > - + а — 4.
а	а
< па ах + b ах — b	л 1 л
130. —— >----------- при а > 0, b > 0.
а — b а-\-Ь
131. Решить неравенства графически:
а) 2х — 1 > 3; б) х + 1 > 2х — 1; в) 2х — 2 > 4 — х.
200
СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ
После замены каждого неравенства системы простейшим нера-
венством, ему эквивалентным, получим одну из следующих систем:
1)(х>тп, 2)(х<.т, 3)(х>т, 4)(х<т,
jx > п; |х < п; |х <С и; (х > п.
Если т > п, то системы имеют решения:
1) х > т; 2) х < п; 3) нет решений; 4) п < х < т.
Пример.
Решение.
1) а > —3,
Решить систему неравенств ((а + 3) х < 5а 4- 6,
1х > 3.
'	. 5а + 6
х < ——,
а 4- 3
Чтобы найти решение системы при а > —3, надо сравнить числа
5а + 6 Q
—-— И 3.
а 4-3
^±^V3.
а 4- 3
5а 4- 6 V За + 9.
2а V 3.
а\/ —
2
3	5а 4~ 6	п
Следовательно, если а > —, то —— > 3, и тогда решением
2	а + 3
системы будут:
о v 5a 4- 6,
О Л	————— *
a + 3
5a + 6 . о
—— < 3 и система
а 4" 3
6
л -------,
а 4~ 3
х> 3.
если — 3
3
—, то
2
5а +
не имеет решений.
2) а < — 3,
Сравним числа и 3 при а < — 3,	у 3.
r	а4-3	а-ЬЗ
5а 4~ 6 Д Зи 4~ 9> cl А
Так как а < —3, то знак Д соответствует знаку <; следова-
тельно,
5а + 6>3,
a 4“ 5
и, значит, решением системы при а < —3 будут:
5a 4* 6
Х>-----—.
а 4- 3
20!
3) a = —3. Данная система примет вид
|0 • х -< —9,
I х> 3.
Система решений не имеет.
о	5а + 6
т вет: если а < —3, то х > —!—;
а + 3
3 о 5а 4-6
если а > — , то 3 < х < —!;
2	«4-3
з
если —3 < а < —, то решений нет.
Решить системы неравенств.
132. (5 (х 4- 1) + 6 (х + 2) > 9х + 3,
\7х — 3 (2х + 3) > 2 (х — 8).
133.
' х 7 Зх 5
4	8^4	2’
х + 1 < 2	1 — 2х
. 4	3
134.
2х —4>х+ 16,
X I 1	. Q	Л 1
-----h 3 < х — 6—,
2	4
к
-Х<% + 19,4.
3
5 - X _ g . 2х — 1
4	З-’
> 0,3 (х+ 12),
6 — 5х . Зх — 1	7
-----4---->7 — х.
(52
136. Решить системы неравенств графически:
135. ,
а)	1х — 4 > О,
(3 — х < 0;
б)	) 2х — 3 < 0,
U — 4х > 0;
в)
—х + 1 > 0,
3
.2 — х > 0.
Решить системы неравенств.
137. ,(а + 3)х
1х < 3.
< 5а + 6,
138.	(а (х — 2) > х — 3,
|9 (а + 1) х > 9ах + 8.
139.	I т (х — 2) > х — 3,
Ц2т 4- 3) (х — 1) > (m — 1) (х 4- 2).
202
140.	(т (х — 1) > х — 2,
[3 (т + 1) х > Зтх + 5.
141.
— _|_ — Зх > х + 2
т 4 т ’
х ____х > 3
, т	2 т
§ 4. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ АБСОЛЮТНЫЕ ВЕЛИЧИНЫ
1. Решение неравенств вида | f (х) | < а, где а — положитель-
ное число.
По определению абсолютной величины, имеем:
/ (х) < а, если f (х) > 0,
—f (х) < а, если f (х) < 0.
Данное неравенство равносильно системе неравенств
—а < f (х) < а.
Пример. Решить неравенство | 2х — 3 | < 2.
1-й способ. Имеем: —2 < 2х — 3 < 2, или
203
Рис. 21
2-й способ. Возводим обе части данного неравенства в квадрат:
(2х — З)2 < 4,
4х2 — 12х + 5 < О,
1	5
Ответ: — < х < —. Графическое решение (рис. 20).
2. Решение неравенств вида | f (х) | > Ь, где b— неотрицатель-
ное число.
По определению абсолютной величины имеем:
f (х) > Ь, если / (х) > 0,
—f (х) > Ь, если f (х) < 0.
Данное неравенство эквивалентно совокупности неравенств
/ (х) > b и f (х) < —Ь.
204
Пример. Решить неравенство | Зх — 5 | > 10.
1-й способ, а) Зх — 5 > 10, б) Зх — 5 < —10,
х > 5;	х < — —
3 •
2-й способ. (Зх — 5)2 > 100,
Зх2 _ 10х _ 25 > 0,
х > 5 и х <.---.
з
Ответ: х> 5 и х<. —	. Графическое решение (рис. 21).
3. Неравенства вида | агх + bY | ± | а2х 4- Ь2 | ± ... ± | акх 4-
+ bh | V с решаются так же, как и уравнения, на промежутках:
(—оо, xj,	х2]....1хй, +оо), где xlt х2, ..., хк —
корни двучленов, стоящих под знаком абсолютной величины.
Пример. Решить неравенство
|x + 2|-|x+l|+Jx|-|x-l|+|x-2|<3.
-- ОО < X < —2
— 2 < х < —1
— 1 < х < О
О < х < 1
1	< х< 2
2	< х < оо
—х < 3;
х + 4 < 3;
—х + 2 < 3;
х 4~ 2	3;
—х 4	3:
х > —3
х < —1
х > —1
X < 1
X > 1
—3 < х < —2
—2 < х < —1
—1 <х< О
0< х< 1
1 < х < 2
2< х<3
х < 3
Ответ: —3 < х < —1, —1 < х < 1, 1 < х <; 3.
Графическое решение (рис. 22).
205
Решить неравенства аналитически и графически.
142.	а)	| 2х — 5	| < 7; б) |	3 — х | <	4.
143.	а)	| Зх — 5	| > 10; б) |	5 — х |
144.	а)	| х — 2 |	< 2х — 10;	б) | 2х —	1 | > х — 1.
145.	а)	| х 4- 2 |	> | х | ; б)	| х | > |1	— х	|.
146.	а) | 2х	+ 3 |	> |	4х —	3 |; б) | х — 1 | < | 2х — 1 |.
147.	|	2х —	3	| —	| Зх	+ 7	|	> 0.
148.	|	2х 4-	7	| —	| Зх	+ 5	|	> 0.
149.	|	2х 4-	5	| —	| Зх	— 7	|	< 0.
150.	| х —	1	| 4-	I 2х — 6 | < 3.
151.	|х —	1	| 4-	|х — 3 | > 2.
152.	| х —	1	|4-	| х 4- 2 | — | х — 3|>4.
153.	|х4-2|4-|х4-1|4-|х — 4|>9.
154.	| х —	1	| —	| х — 2 | 4- | х — 3 | — | х — 4 |4- |х —
— 5 | < 3.
155.	| х 4- 2 | — | х 4- 1 1+ I х | — | х — 1 |4- | х — 2 | >
>2,5.
§ 5. КВАДРАТНЫЕ НЕРАВЕНСТВА
Неравенство второй степени с одним неизвестным в общем виде
можно записать так:
fljX2 4- М 4- q V «2*2 + Ь2х + с2.	(0
где а2, blt b2, си с2 — действительные числа, и а2 одновремен-
но не равны нулю.
Неравенство (1) можно заменить равносильным ему неравенством
ах2 4- Ьх 4- с V 0.
При решении неравенств второй степени используют результа-
ты исследования квадратного трехчлена у = ах2 + Ьх + с.
-----ах2 4- Ьх 4- с > 0------
а > 0	а < 0
D >	0	X < И X > х2	А < х < х2
D =	0	Любое х ф хА = х2	Нет решений
D<	0	х — любое число	Нет решений
f а < 0	а > 0
---- ах2 4- Ьх 4- с < 0 -----
206
Примеры. Решить неравенства.
1. 56х2 + ах — а2 < 0.
Решение. D = 225а2 > 0. х,= — —, х, = —.
7	8
Если а>0, то — — < х < —.
7	8
Если а <. 0, то < х < — -у.
Если а = 0, то неравенство не имеет решений.
2. п2 (х2 + 1) + 6 > а2 + 2 (п2х + 3).
Решение. п2х2 — 2п2х + п2 — а2 > 0.
D = п2а2 >0. xr — х2 — где п о
п	п
т?	п ~ п —а	п + а
Если ап > 0, то х <-- и х > ——.
п	п
Если ап < 0, то х< —— и х >-----.
п	п
Если а = 0, п Ф 0, то х — любое число, не равное 1.
Если п = 0, нет решений.
Решить неравенства аналитически и графически.
156.	а)	х2 — Ьх + 6	>	0;	г)	14 — Ьх — х2 < 0;
б)	х2 — 10% + 25	> 0;	д)	х + 2 — 6х2 > 0;
в)	х2 + 4х + 5	<	0;	е)	— х2 + Зх + 6 < 0.
з
157.	а)	6 < х2 — 5х	+	12	< 8; б)	—8 < х2 + 8х + 8	<	—4.
158.	а)	х2 < —Зх;	в)	2х2 — 1 > х;
б)	х2 > 2х — 5;	г)	х2 — 4 < 4 — 2х.
159.	а)	|	х2 — х — 6	| >	4;	г)	х2 — | х | > 6;
б)	|	х2 — х — 3	| <	9;	Д)	I —4Х2 — 6х — 5	| < 9;
в)	|	2Х2 — 9х +	15 |	>	20;	е)	| х2 — 5х | < 6.
160.	а)	|	х2 — х — 6	| >	3 +	х;
б)	lx2 — 6х + 8 | < 5х — х2;
в)	| 5х —	х2 — 6	| > х2	—	5х	+	6;
г)	| х2 —	Зх + 2	| > Зх — х2	—	2;
д)	| х2 +	6х + 5	| > х2	—	8х	4-	16.
161.	а)	| х2 —	1 | < |	х + 2	| ;
б)	| 2х — 5 | > 2 | х2 — 1 | ;
в)	| х2 — Зх + 2 | > | х2 + Зх + 2 |.
Решить неравенства.
162.	х2 — бтх + 25m2 > 0.
164. х2 + 7ах > ах — а2.
166.	(а — 2) х2 — х — 1 > 0.
163. 56х2 + ах > а2.
165. 26а2 -j- х2 > Юах.
207
167.	При каких действительных значениях а неравенство ах2 —
— 7х + 4а < 0 выполняется при всех действительных значениях х?
168.	Найти все действительные значения т, при которых нера-
венство тх2 — 4х -h 3m + 1 > О удовлетворяется при всех поло-
жительных значениях х.
169.	При каких действительных значениях а неравенство (а —
— 4) х2 + 10х + a < 4 выполняется при любых значениях х?
170.	При каких действительных т множество решений неравен-
ства х2 + тх + т2 + 6т <_ 0 содержит интервал 1 < х <z 2?
§ 6. СИСТЕМЫ НЕРАВЕНСТВ ПЕРВОЙ И ВТОРОЙ СТЕПЕНИ
С ДВУМЯ НЕИЗВЕСТНЫМИ
Неравенство / (х, у) V 0 (1), где f (х, у) — функция первой или
второй степени, имеет бесконечное множество решений. Неравен-
ству (1) удовлетворяют координаты всех точек плоскости, лежащих
выше или ниже графика функции f (х, у).
Множеством решений системы неравенств первой и второй сте-
пени является пересечение множеств решений неравенств, вхо-
дящих в систему. Решение системы записывается системами вида
(а<х<Ь,	илир<у<Л,
Vi (х) < у < f.2 (х)	(х) < х < <р2 (х).
Часто при решении таких систем неравенств комбинируют гра-
фический и алгебраический методы.
Примеры. Решить системы неравенств.
1. (у > х + 2,
|у < 2х — 3.
Решение. По свойству транзитивности неравенств данная
система равносильна системе
(х -f- 2 2х — 3,	(5 х оо,
(х + 2 < у < 2х — 3	1 х + 2 < у < 2х — 3.
Графическое решение (рис. 23).
2. (2х — у + 1 < О,
[9х — Зу — 2 < 0.
Решение, (у >2х-(-1,
|у > Зх —
9	-5
Неравенство Зх---->2x4-1 выполняется при х > ^.
3	5
Неравенство Зх —	< 2х + 1 выполняется при х < —.
Ответ: ^-5	|х < -|,
1	3	2 и »
у > Зх----q 1у > 2х + 1»
Графическое решение (рис. 24).
208
Рис. 23
3.
У<
У <
У>
х -|~ 1,
—х -|- 3,
1
Строим прямые у — х + 1, у = —х + 3, у = и отмечаем
полуплоскости, в которых выполняются неравенства системы
(рис. 25). Искомая область представляет из себя внутренние точки
треугольника Xp42^3- Найдем абсциссы точек А19 А2, Л3; для это-
го решим уравнения:
х + 1 =
х + I = _х + 3,
—х = —х + 3.
2
х-^ == —2, х2 == х3 2.
209
Ответ: [—2 < х < 1, f 1 < х < 2,
11	. 1	< 1	I о
1—X < у < X + 1 И I — X < у < —х + 3.
I 2	I 2
4.	(у > х2 — х — 6,
[у < Зх — 1.
Строим параболу у = х2 — х — би прямую у = Зх — 1. Отме-
чаем часть плоскости, в которой выполняются неравенства системы
(рис. 26). Находим абсциссы точек пересечения прямой и параболы;
для этого решаем уравнение
х2 — х — 6 = Зх — 1,
хх = —1, х2 = 5.
Ответ: Г—1 < х <. 5,
( х2 — х — 6 < у < Зх — 1,
21Q
Решить системы неравенств и дать геометрическое истолкование.
171.	(у<х — 1,
(у > 2х — 3.
172.	(у>х— 1,
|у > —х + 2.
173.	(2у — Зх > 4,
\2х — у > 8.
174.	(х — у> 1,
[у — х > 1.
175.	(у _ х — 2 > О,
[у — 2х -|~ 3	0.
176.	(Зх + 5у>7,
[4х + 5у < 9.
177.
178.
179.
180.
(у < х + 1,
У < — X + 9,
у > х— 1.
□
х + у > 4,
х — у < 4,
Зх + 8 > 4 — у.
/у < х + 3,
у + х< 3,
у < х + 1,
у < 1 — х,
у > —1 — х,
у > X — 1.
211
Рис. 26
181.
х + Зу < 1,
х + Зу > —2,
Зх + 2у < 3,
Зх -|- 2у < 1,
Зх + 4у > —1.
184.
185.
182.
(2х — у < 1,
4х + У > 1,
4х — у > 1,
1у < 3.
183. (х + у > 1,
<х — у > О,
U —у > х + у.
О < х + у < 1,
х — у > О,
(X — у < X + у.
'2х > —у,
4у < 3 — х,
х + 4у + 1 > О,
\2х < 4 — у.
186. Гу >х2,
Ь<х.
187.
188.
у > X2,
Зу — х < 9.
У > х2 — 1,
у < 1 — х2.
212
189. [у > x2 — 5x + 6,
(у < 4-
190.
191.	Гх>у2,
(x < 2. .
192.	fx < y2,
I—x < y2,
1у <4.
193.	(y > x1,
(y < 4 — x2.
194.	(x + у + 1 < 0,
lx2 + У2 < 25.
195.
196.
197.
198.
0 < x2 + y2 < 1,
x + у > 0,
X + у > X2 + у2.
X2 + y2> 1,
x + у > 0,
lx + у < X2 + у2.
х2 + у2> 1,
У>0,
_ X2 -|- у2
У
§ 7. АЛГЕБРАИЧЕСКИЕ НЕРАВЕНСТВА ВЫСШИХ
СТЕПЕНЕЙ С ОДНИМ НЕИЗВЕСТНЫМ
Решение неравенства вида Р (х) V 0 (1), где Р (х) = а^х" 4-
+ Я1 х”-1 + ... + ап_г х + ап — многочлен над полем действитель-
ных чисел, рекомендуется проводить методом интервалов.
Известно, что Р (х) = а (х — Xj)"» ... (х — xft)“* • (х2 4- ргх +
4-	... (х2 4- ртх 4- Ят/т, где хг, х2, .... хк — действительные
корни Р (х); множители второй степени не имеют действительных
корней.
Так как множители второй степени положительны при любых зна-
чениях х, то неравенство (1) равносильно неравенству
а (х — xj"- ... (х — xft)“* V 0.	(2)
1. Рассмотрим случай, когда ах = а2 — ... = ак = 1,
а (х — X]) ... (х — хк) V 0.	(3)
Предположим, что действительные корни многочлена Р (х)
расположены в порядке возрастания: хх < х2 < ... < хк.
В каждом из интервалов (—оо, хх), (хх, х2) ... (хк, оо) Р (х)
сохраняет постоянный знак, а проходя через нуль, меняет свой знак
на противоположный. Поэтому для решения неравенства (3) до-
статочно определить знак данной функции для какого-нибудь од-
ного интервала, например (—оо, xj.
Это можно сделать или путем вычисления значения левой части
неравенства (3) в какой-либо точке интервала (—оо, xj, или путем
подсчета числа отрицательных сомножителей.
При решении неравенства методом интервалов удобно приме-
нять графическую иллюстрацию (рис. 27).
213
2. Рассмотрим случай, когда в неравенстве (2) по крайней мере
один из показателей степени а1г а2, ..., ah больше 1.
Пусть таким показателем будет аг.
Если ах = 2k, то (х — хх)2* неотрицателен и поэтому его влия-
ние на решение неравенства (2) ограничивается тем, что он исклю-
чает точку х = х1.
Если а1 — 2k + 1, тогда множитель (х— Xj)2^1 можно пред-
ставить в виде (х — хх) (х — xx)2ft.
В том и другом случае, отбросив все множители с четным пока-
зателем степени, придем к неравенству, левая часть которого —
произведение линейных множителей, а правая — нуль.
Пр и м е р. Решить неравенство
х4 (х — 3) (х + 8)3 (х — 5)4 (х + I)5 > О,
х =/= —8, х =# —1, х =# 0, х =/= 5.
(х — 3) (х + 8) (х + 1) > О,
—8 < х <—1, х>3.
Исключим х = 5.
О т в е т: — 8 < х < —1, 3<х<;5, х > 5.
Решить неравенства.
199.	(х + 2) (х — 1) (х — 3) > 0.
200.	(х + 3) (х + 2) (х — 1) (х — 3) > 0.
201.	5 (х + 3) (х — 2) (х — 3) < 0.
202.	(х +	3) (х +2) (х — I)2 (х — 2) (х2 + Зх +	5) > 0.
203.	(х —	7)4 (х +	З)5 (х	—	2) Xе (х + 5)3 > 0.
204.	(х —	2)3 (х +	I)2 (х	+	З)4 (х — 4)5 (х — 8)	>	0.
205.	(х —	1) (х2 —	1) (х3	—	1) (х4 — 1) < 0.
214
206.	(х + 2) (х — I)2 (х — 2) (х2 + Зх + 5) < 0.
207.	(х3 — 2х2 — 5х + 6) (х2 — х + 1) > 0.
208.	х3 + 5х2 + Зх — 9 > 0.
209.	х4 — бх3 4- 11х2 — бх < 0.
210.	х4 — Зх3 + Зх2 — Зх + 2 < 0.
211.	(х — 1) (х2 + 1) (х3 — 1) (х4 4- 1) < 0.
212.	(х8 — 1) (х4 — 1) < 0.
213.	(х3 — 1) (х — 1) > 0.
214.	х4 — 13х2 4- 36 > 0.
215.	х4 — 29х2 + 100 > 0.
216.	20 — 25х« — 121Х2 < 0.
217.	27 — 37х2 — 16Х4 < 0.
218.	Зх2 (х — 4)2 < 32 — 5 (х — 2)2.
•
§ 8. ДРОБНО-РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
С ОДНИМ НЕИЗВЕСТНЫМ
При решении дробно-рациональных неравенств с одним неиз-
вестным часто пользуются теоремой.
Теорема. Неравенство V 0 на множестве допустимых
Q(x)
значений неизвестного х равносильно неравенству Р (х) Q (х) V 0.
Решение дробно-рациональных неравенств можно свести к
решению совокупности систем неравенств. Например, неравенство
Р(х) п
.... > 0 сводится к решению совокупности систем i
(Р (х) > О, IP (х) < 0,
(Q (х) > 0 и (Q (х) < 0.
При решении дробно-рациональных неравенств вида
Р, (х) . . Р2(х)	Л
V надо помнить, что если неизвестен знак общего
<?i(x)	Q2(x)
знаменателя дробей, то не имеем права на него умножать обе части
данного неравенства.
Примеры. Решить неравенства.
1. Ъх-Ъ < 0
х — 4
Решение. 1-й способ. М: х #= 4.
Данное неравенство равносильно на множестве М неравенству
(2х — 3) (х — 4) < 0, решение которого 1,5 < х < 4.
2-й способ. Дробь принимает отрицательные значения, если чле-
ны дроби имеют разные знаки. Решение данного неравенства сво-
дится к совокупности двух систем;
215
Г2х — 3 > 0, и (2х — 3 < О, — система не имеет решений.
— 4 < О — 4 > О
1,5 < х < 4.
Ответ: 1,5 •< х < 4.
9 2х — 5 \ 1
х+~3
Решение. Л4: % #= —3.
Перенесем 1 в левую часть неравенства, получим неравенство,
равносильное данному:
2х 5 1 \	% 8 гл	s- о
------1 > 0  > 0 х < —3 и х > 8.
х+з---х+З
Ответ: х < —3 и х > 8.
Решить неравенства.
219. а) — >2;
х — 3
б) ^—^<2;
х —2
в)
X	1
Зх — 1 < "з *

220. ^±.1 + 1 >
х—2	2 х—2
221. —	1 " °
х — 1
1
222
223.
224.
225.
226
227.
2 3
+ 3 х + 2
Зх — 5 Зх — 8
х— 1 х — 1 *
(х— 1) (х — 2)	1
(х-3)(х-4)
- х~3— >0.
х2 + 4х + 3
ух2-4х + 3 р
х2 — 7х + 10
х2 - 1
Зх — 7 — 8х2
228.
229.
х2 — 2х + 3
ха(х—1) —(х—1)
230.
(х-1)(х2-х + 1)
231.
X3 — 1
х2 — 2х + 1
Зх — 5 - х2
216
232.
4х2 — 5х — 1
2х2 — 5х + 3
233 (х+1)(х + 2)(х + 3)	0
’ (2х — 1)(х + 4) (3 — х)
234.  ^ + 2х-5 >0.
х®— х2 — 4х + 4
235.
х3 + 4х2 4- X — 6 Q
х3 + 2х2 — 5х — 6
236.	+> о.
х4 — Зх3 + Зх2 — Зх + 2
Решить неравенства аналитически и графически.			
237. а) —	3|х|	1;	б)	I 2-3|х|| j
1 +|Х 238. а)	<2;		б)	1 1 + 1*1 1 31*1-г>2.
1 X — 1 239. а) ^±2 >з;		б)	|х| —1 4М±2|<3.
х — Решить нер 240. 1 х— 1 241.	1—- 1 х— 1 242.	I		 1 * + 243.	*		 1 х + 2 244.	1?^ | X2 — 1 245.	1^^	-1 авенства. > 1. 1 10 2 Jx—1 |<2. с + 2 I j	L	1*1 — 1 1
] х2 + Зх + 2 | 246. I ** —3*~1 I < з. 1 X2 + X + 1 1 247. При каком действительном значении k неравенство			
выполняется при любом д		х2 — fex + 1 I g X2 + X + 1 1 .ействительном значении х?	
217
I
Решить неравенства.
248.	> 5.	249.	> qx—b^
ах — 1	а — ха
250.		— >
2	х + а	2
251.	___—
k	X — k	k
252	~х ~ * — х
m 4- 1	2 (m — 1) m 4- 1 *
253.	+ !----2а>а2.
X — 1
254.	+ \
2х — х2 х — 2
, 255. Найдите действительные значения т, при которых пера*
венство
________х2 — 8х 4- 20____ q
тх- 4~ 2 (т 4- 1) х 4~ 9m 4* 4
выполняется для любых действительных значений х.
§ 9. ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
Решение иррациональных неравенств с одним неизвестным на
множестве действительных чисел основано на теореме.
Теорема. Неравенства f (х) V ф (х) и fn (х) V фп (х) рав-
носильны на множестве А, если на этом множестве / (х) > 0 и
Ф (х) > 0.
Откуда следует, что решение иррациональных неравенств сво-
дится к решению равносильной ему рациональной системы нера-
венств.
Необходимо иметь в виду, что при возвышении обеих частей
неравенства в одну и ту же степень можно приобрести решения за
счет расширения множества допустимых значений неизвестного.
Поэтому необходимо полученное решение согласовать с множест-
вом допустимых значений неизвестного данного неравенства.
Кроме того, необходимо рассмотреть случай, когда одна из ча-
стей неравенства может принимать отрицательные значения, иначе
можно потерять решения.
Примеры. Решить неравенства на множестве действитель-
ных чисел.
1	— 2* — х2 < |
Решение. Левая часть неравенства может быть как неотри-
цательной, так и отрицательной.
218
24 — 2х — х2 > О,
х > О,
24 — 2х — х2 ।
№
24 — 2х — х2 > О,
х < О,
— 6 < х < 4,
х>0	->3<х<4,
х < — 4 и х > 3;
(— 6 < х < 4,
( х < О
->— 6 < х < О.
У 24 — 2х — х2
х
Ответ: —6 <	С х <	: о и з < х <	4.
2. х>]/2х4~	24.		
Решение.	2х -	Ь 24 > 0,	f х > —12,
	х	>0,	-> I х > 0 -► х > 6,
	. х2:	> 2х 4- 24	1 х< —4 и х>6.
Ответ: х > 6.
Решение. 3|^6 + х — х2 > 4х — 2.
Найдем множество М допустимых значений неизвестного;
х £ [—2, 31.
Правая часть неравенства может быть как неотрицательной,
так и отрицательной.
а)	4х — 2 > О,
1
х > —,
2
9 (6 + х — х2) > (4х — 2)2	—1 •
полученное решение принадлежит М;
~ [4х — 2 < 0,	[ х < —,
б)	I г--------- 2
13^6 4-Х — х2> 4х — 2
Ответ: —2 < х < 2.
2,
2
£
2
Решить неравенства на множестве действительных чисел.
256. /х>—1.
257.	/2х —5> 7.
258.	I/ —-<3.
259.	> 1.
V 2 — х
260.	Vx+ 1 >]/х— 1.
219
огг
•<? + РЛ < x — q/t + X — VД -982
О < Ч ‘О < о И1гээ 'q + V < х — г<? Д + х — 8р Д *S83
•» < gx — xvz Л + ~ г”4 W
’0<zy —гр4 + у3 ’883
,*Л	£4 — *—IД	*4 + *—14
z	г	г	383
21 X гу —14
S£> I I 182
’Z£ —хдД < 61 — У£Д — si — xz Л ’6Z3
; g — хд— <e — хд — g —хд -gzs
Iх ~ 9 4 >9~у4 —3 + *4 'LLZ
.’9 — уг 4 + I +х4 < 9 + х 4 '9LZ
4 > 1 +х~гх4 —3+xs + gX4 ’SZ3
'£ < 8Х — Х9 Д + гх —6Д 4Z3
*8 < 8 + хД — I ДхгД -8ZZ
ч > I + хД + I + хгД -ZLZ
’Z + гХ < I + зХД (г — X) 4Z3
’I — z* < I + гхД (х Д J) *o£S
— 3 < 9 — хд + гхзд ‘692
‘ХЪ<% + гх — х + 9 Д £ ’89g
'XZ + £ > (х — g) (£ — х) 4 Y93
•3 —x<Qi — xg —гхД *992
’х — 8 > 01 — xg — гхД -^2
‘х ~ £ > 6 + xg /| -g92
•х <g + хД '292
•у + д4 >Х— !Д 392
287. У a — х + Уb — х>Уа-У Ь — 2х.
2§с __1 I______!_2>____-___
Ух —а Ух + а Ух2 — а2
§ 10. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПОКАЗАТЕЛЬНУЮ
И ЛОГАРИФМИЧЕСКУЮ ФУНКЦИИ
При решении показательных и логарифмических неравенств
применяются свойства показательной и логарифмической функций.
На основании свойства монотонности этих функций можем утверж-
дать, что
1) если а > 1, то равносильны неравенства хх > х2 и > а*»;
хх > х2 > 0 и log0 хх > loga х2;
2) если 0 < а < 1, то равносильны неравенства хх > х2 и
ах> < ах‘; хх > х2 > 0 и logo хх < logo х2.
Решение многих неравенств, содержащих показательную и ло-
гарифмическую функции путем введения новой неизвестной, сво-
дится к решению алгебраических неравенств.
Примеры. Решить неравенства.
1- logo,5 logs
Решение. Так как основание логарифма меньше 1, то лога-
рифм отрицателен, если он берется от числа, большего 1, т. е.
Так как основание логарифма больше 1, то логарифм больше 1,
если он берется от числа, большего основания, т. е.
х2 — 2х
х — 3
Решения полученного неравенства 3 < х < 4 и х > 6 будут
решениями данного неравенства.
2.	1g (х2 - 3) > 1g (х + 3).
Решение.
Данное неравенство равносильно системе неравенств
1 х2 — 3 > х + 3,	( х < —2 и х > 3,
| х + 3 > 0	—*" 1 х	—3,
—► —3 < х < —2 и х > 3.
3. (log3 х)3 4 — (log 1	— 20 log2 х + 148 < 0.
\	2 4/
Перейдем к основанию логарифма 2.
(log2 х)4 — 25 (log2 х)2 + 144 < 0.
221
25z2 + 144 < 0.

<v
О
со
со
О
сч
сч
О
сч
CD
05
сч
00
сч
Од
сч
00
Од
сч
о
а»
сч
Сч
с
со
Ci
сч
303. 3х-
сч
304.	21*1 < 1024.
305.	З1 ж+21 + З1 1 > 28.
306.	1g2 к — 2 1g х —8<0.
307.	llg2x>- — — Igx.
12 s 3	4
308.	logo,5(3x — 1) < logo,5 (3 — x).
309.	1g (x3 - 3) > 1g (x + 3).
310.	logo.i (x2 + 1) < logo.i (2x —5).
31L logi ji~3<!ogi (8—*)•
Г	Г
312.	1g (x2 — 2x — 2) < 0.
313.	log5 (x2—11x4-43) >2.
314.	log2 (x2 — 5x 4* 6) > 3.
315.	lg(-—-
\x — 1
316.	1g (x — 1) 4- 1g (x — 2) < 1g (x 4- 2 ).
317.	log7 x — log, (2x — 5) < log7 2 — log, (x — 3).
318.	log2 (]/x + 3 — x — 1) 4- log2 1 < 0.
319.	log, log2 > 0.
L 1
2
320.	Iglgj=l>-1.
2 — x
321.	log2 log3^-J < log log ^±-J.
x + 1	1. L x — 1
2	3
322.	18'«-3|8« + 3 > 1.
1g X — 1
д2з lg2x4-21gx —6	।
Igx
324. IgU2 —	+ 8) j
1g (X - 8)
325. 1f log2^f < 1.
У 1 —x
4OR ^1Og0.SX“81 +2 / I
ozo.-------	-	\ 1.
logo,5 X — 1
223
327.	log] log5 (/x2 + 1 + x) < log3 log] (V x2 + 1 — x).
3	5
328.	log2log3ii-l < log] log] ^1.
Г г
329 0 5Iogs i°go’2 ~~ °*8) < 1
330. 1,25’-(,og2 x)8 < 0,642 + '°g/2 *.
]og2jt —2	2 (1 4-log2 x)
331. 0,8	<0,64
. Зя—1
332.	°g? 2x+3 > 1.
333.	log2(2A‘ — 1) logi(2x+i- 2) > - 2.
334.	| log2 x | > 5.
335.	log3 | 2x — 7 | < 1.
336.	\x\x‘~x~2<l.
337.	| 4 — log2 x | > 2.
338.	2 > | log2 | x | |.
339.	|log_i_ (1 — x)|>2.
2
340.	|log3(x-4) |< 1.
341.	| log± (x - 2) | > 1.
з
342.	Ig | 3x — 14 | < 1.
343.	| log2 (x2 + x —4) | < 1.
345.	1о&+з 16 > 2.
346.	log2x_ з x ;> 1.
347.	log3j(._2 x <Z 1.
348.	log/-^<0.
X — о
349.	I„gjll±.5<-1.
x 6 — 5x
5
350.	log i x > logx 3 — —
3 2
351.	logv_2 (x2 — 8x + 15) > 0.
352.	logx_3 (x2 — 4x + 3) < 0.
224
353.	logx2 (2 + x) < 1.
354.	(x — 2X2-e*+8> 1.
355.	(x2 — 8x+ 15)x-e < 1.
356.	loga x 4- 6 > 16 logv a.
357.	1оя0х>61(^ a — 1.
358.	10go X 4- loga (x + 1) < loga (2x + 6)-
359.	21ogx a2 —31oga2X> 1.
360.	log2a x — logo x < 0.
361.	(loga x 4- 1) (loga x — 2) (loga x — 5) < 0.
362.	1 + log°* > 1.
1 4 logax
8 Заказ 1089
ГЛАВА XII
ПРОГРЕССИИ. РЯДЫ
§ 1. ПРОГРЕССИИ
Общий вид арифметической прогрессии: alt + d,
ar + 2d, d — разность прогрессии.
Общий вид геометрической прогрессии: ult uYq, urq2....
q — знаменатель прогрессии.
Формулы для нахождения n-го члена и суммы п первых членов
арифметической и геометрической прогрессий:
ап = «х 4- d (п — 1), ип = Щ""1,
q _ (01 + ал)п	о . «И?" —1)
п .
2	q — 1
Сумма бесконечно убывающей геометрической прогрессии
$ = где |<?| < 1.
1 — я
1.	Доказать, что если второй член арифметической прогрессии
есть среднее пропорциональное между первым и четвертым члена-
ми, то шестой член будет средним пропорциональным между чет-
вертым и девятым членами.
2.	Число членов арифметической прогрессии равно 10. Сумма
членов, стоящих на четных местах, равна 15, а на нечетных местах
равна 12,5. Найти все члены прогрессии.
3.	Первый член арифметической прогрессии равен 2, второй и
третий соответственно равны квадратам двух последовательных
натуральных чисел. Найти прогрессию.
4.	Могут ли длины сторон прямоугольного треугольника обра-
зовать арифметическую прогрессию?
5.	Найти сумму: 1002 — 992 + 982 — ... + 22 — 1.
6.	Если все члены арифметической прогрессии умножить на
одно и то же число, будет ли новая числовая последовательность
представлять собой арифметическую прогрессию?
7.	В арифметической прогрессии даны ее члены ат+п = Д;
ат-п = В. Найти ат а ап.
8.	Числа а2, Ьг, с2 образуют арифметическую прогрессию. До-
1 1 1 , .
казать, что числа	также образуют арифметическую
прогрессию.
9.	Показать, что для всякой арифметической прогрессии
Ох, а2, а3, .... ап имеют место равенства
ах — 2а2 + а3 = 0;
ai — За3 — а4 = 0;
Ох — 4а2 -г 6as — 4а4 + аь = 0,
226
и вообще при всяком п > 2 имеем:
С„а2 4* Сп(13	... i Сп ап 4- <zn+i ~ 0.
10.	Доказать, что если alt а2, ..., ап образуют арифметическую
прогрессию, то ——|----------1------1- ... 4-Ji.
^1^2	^2^3	^3^4	aian
11.	Решить уравнение 1 4- 7 4~ 13 4- ••• 4~ * = 280.
12.	Решить уравнение (х 4- 1) 4- (х 4- 4) 4- ••• 4- (х 4- 28) =
= 155.
13.	Найти арифметическую прогрессию, если сумма ее п членов
равна 2/г2 — Зп.
14.	Найти десятый член арифметической прогрессии, если сум-
ма ее п членов равна Зп2 — 2п.
15.	Найти арифметическую прогрессию, у которой сумма лю-
бого числа членов, начиная с первого, в четыре раза больше квад-
рата числа членов.
16.	Найти сумму первых тридцати нечетных чисел, которые при
делении на 5 дают в остатке 1.
17.	Найти арифметическую прогрессию, в которой пятый член
равен 18, а сумма п членов равна — суммы 2п членов.
4
18.	Доказать, что если п — число целое положительное, то
(п 4- I)4 — п4 есть сумма 2п 4- 1 последовательных целых чисел.
19.	Дано: 23 = 3 4- 5;
24 = 7 4~ 9;
З2 = 1 + 3 4- 5;
З4 = 25 + 27 + 29;
54 = 121 4- 123 4- 125 4- 127 4- 129,
и вообще всякая степень некоторого числа может быть представле-
на как сумма некоторых чисел, отличающихся на 2; количество
слагаемых зависит от основания степени. Вывести общий закон.
20.	Сумма членов некоторых арифметических прогрессий, чле-
ны которых суть целые числа, равняется четвертой степени числа
членов. Найти, к-акая зависимость должна существовать между
числом членов, первым членом и разностью прогрессии.
21.	Сумма членов некоторых арифметических прогрессий, чле-
ны которых — целые положительные числа, равняется кубу числа
членов:
1 4- 7 = 8 = 23;
1 4- 9 4- 17 = 27 = З3;
1 + 11 + 21 4- 31 = 64 = 43;
4 4- 12 + 20 + 28 = 64 = 43;
13 4- 15 4- 17 + 19 = 64 = 43.
Указать, какая зависимость должна существовать между числом
членов, первым членом и разностью прогрессии.
22.	Какое натуральное число может быть представлено как
сумма последовательных чисел, начиная с 1?
8*	227

23.	Найти натуральное число, равное сумме всех ему предше-
ствующих натуральных чисел.
24.	Пусть Sj — сумма первых членов,
S2 — сумма п2 первых членов,
Х3 — сумма п3 первых членов
некоторой арифметической прогрессии. Доказать, что
(п2 - п3) + -Ь (и3 - nJ + (пх - п2) = 0.
П2	П3
25.	Найти сумму всех несократимых дробей со знаменателем 3,
заключающихся между положительными числами т и п(т <_ п).
26.	Доказать, что если в арифметической прогрессии сумма п
первых членов равна г?р и сумма k первых членов равна k2p, то
сумма р первых членов равна р3.
27.	Доказать, что если в арифметической прогрессии Sm = Sn,
ТО Sm-f-n = 0.
28.	В арифметической прогрессии — = ™. Доказать, что
п2
ат 2т—I
ап ~ 2п — 1
29.	Доказать, что в геометрической прогрессии произведение чле-
нов, равноотстоящих от концов, равно произведению крайних членов.
30.	Показать, что 1+ 2-4- 22 4- ••• 4- 25п-1, где п —натураль-
ное число, кратно 31.
31.	Доказать, что 1 4- 3 4- З3 4- ... 4- З6"-1 кратно 364 (п —
натуральное число).
32.	Доказать, что произведение п членов геометрической про-
п(п—1)
грессии равно urnq 2 .
33.	Доказать, что во всякой геометрической прогрессии сумма
членов четвертого, пятого и шестого есть среднее геометрическое
между суммой первого, второго и третьего и суммой седьмого, вось-
мого и девятого членов.
34.	Могут ли числа 10, 11 и 12 быть членами одной и той же гео-
метрической прогрессии?
35.	Доказать, что если в геометрической прогрессии каждый
член вычесть из следующего за ним члена, то последовательные раз-
ности составят также геометрическую прогрессию.
36.	Найти условие, при котором произведение двух произволь-
ных членов геометрической прогрессии будет некоторым членом
этой же прогрессии.
37.	Найти условие, при котором числа а, b и с представляют
k-й, п-й и р-й члены одной и той же геометрической прогрессии.
38.	Доказать, что если Л, В и С — n-й, р-йи^-йчленыоднойи
той же геометрической прогрессии, то Др-ь • Bk~n > Сп~р = 1.
39.	Доказать, что в геометрической прогрессии любые четыре
члена um, unt uh, щ, для которых tn + п = k + /> связаны соот-
ношением um-un = uk-ut.
228

40.	Могут ли длины сторон прямоугольного треугольника обра-
зовать геометрическую прогрессию?
41.	Что можно сказать о числах a, b, с, d, если они, взятые в
любом порядке, образуют всегда геометрическую прогрессию?
42.	Доказать, что если а, &, с, d составляют геометрическую
прогрессию, то (а2 + Ь2 + с2) (Ь2 + с2 + d2) = (ab + be + cd)2.
43.	Доказать, что если числа a, by с, d составляют геометриче-
скую прогрессию, то (а — с)2 + (Ь — с)2 + (Ь — d)2 = (а — d)2.
44.	Доказать, что если три числа х, у и z составляют геометри-
ческую прогрессию, то (х + у + z) (х — у + ?) = %2 + у2 + z2.
45.	Если А и В есть (р + £)-й, (р — k)-h члены геометрической
прогрессии с положительными членами, то р-й член ее равен АВ,
а k-й член равен А у f — I. Доказать.
46.	В геометрической прогрессии дано:
ат+п - А и ащ-п. = В. Найти ат и ап.
47.	Знаменатель геометрической прогрессии равен
Показать, что каждый член, начиная со второго, равен разности
двух соседних с ним членов.
48.	Даны две прогрессии:
арифметическая alt a2t а3, ..., ап, ... и
геометрическая их, и2, и3, ...» ип , ...,
причем все члены этих прогрессий положительны и обе прогрессии
возрастающие. Кроме того, = и^, а2 = и2. Доказать, что все
члены арифметической прогрессии, начиная с третьего, меньше со-
ответствующих членов геометрической прогрессии, т. е. что
ап < и-п ПРИ всех « > 2.
49.	Доказать, что сумма квадратов нечетного числа членов гео-
метрической прогрессии делится на сумму первых степеней этих
членов.
50.	Доказать, что в геометрической прогрессии, имеющей 2п
членов, отношение суммы п членов, стоящих на четных местах, к
сумме п членов, стоящих на нечетных местах, равно знаменателю
прогрессии.
51.	Сумма 2п членов геометрической прогрессии, у которой пер-
вый член а и знаменатель q, равна сумме п членов геометрической
прогрессии, у которой первый член b и знаменатель q2. Доказать,
что b = а + aq.
52.	Найти сумму: S = (а + b) + (а2 + ab + &2) + ... + (ап +
+ ап~хЬ + ... + &").
53.	Если ап есть п-й член, a Sn — сумма п членов геометрической
прогрессии alt aYq, axq\ ..., то avSn = anS'n, где S’n =	+
+ ... + a1q~Xn~1'>. Доказать.
54.	Пусть Sn = Ui + u2 + ... + un, Пп = щи2 ... un и S'n =
= — + — + ... + Ц— • Доказать, что Д2П-(5'П) = (Sn)n.
«1	"19	«19"’1
229
55.	Доказать, что сумма п членов геометрической прогрессии,
в которой р-й член равен (— 1)ра1р, при всех значениях р равна
[(—1)« а4" — II.
а4 -И 1
56.	Если SH; S2n; S3n суммы п, 2п и Зм первых членов одной и
той же геометрической прогрессии, то
Sn ^2п) = (^зп 5П)2. Доказать.
57.	Найти сумму 2 Si = Sx + S2 + S3 + ... + Sn, если Si
есть сумма i членов данной геометрической прогрессии.
58.	Пусть S®; ...; S(n} суммы п членов геометрических
прогрессий, знаменатели которых последовательно равны числам
1, 2, 3, ..., п и первый член каждой прогрессии равен 1. Доказать,
что 5(„° 4- S’„2) + 2Sn’ + ... + (n -	= 1 + 2« + 3« 4-
-f- ... 4- nn.
59.	Найти сумму n членов геометрической прогрессии, первый
член которой равен а, а последний Ь.
60.	Сумма первых трех членов геометрической прогрессии рав-
на 31, а сумма первого и третьего членов равна 26. Найти прогрес-
сию.
61.	Произведение первых трех членов геометрической прогрес-
сии равно 64, а сумма кубов этих членов равна 584. Найти прогрес-
сию.
62.	Возможна ли такая геометрическая прогрессия, у которой
сумма первого и четвертого членов была бы втрое больше суммы
второго и третьего членов?
63. Сумма первых трех членов геометрической прогрессии рав-
на 13; частное от деления суммы первых двух членов на сумму вто-
рого и третьего членов равна —. Найти прогрессию.
3
64.	В геометрической прогрессии и2 + uQ = 34; и3 + щ = 68;
Sn = 63. Найти ulf q и п.
65.	В геометрической прогрессии 1, %, х2, ..., х2п> произведение
членов с нечетными номерами равно 64, а произведение членов с
четными номерами равно 32. Найти пи х.
66.	Найти три числа, образующие геометрическую прогрессию,
зная, что их сумма равна 26 и сумма их квадратов 364.
67.	Найти геометрическую прогрессию, если сумма первых че-
тырех членов равна 15, а сумма квадратов тех же членов равна 85.
68.	Сумма четырех членов геометрической прогрессии равна 30,
а сумма их квадратов 340. Найти данные числа.
69.	Найти четыре числа, образующих геометрическую прогрес-
сию, если известно, что сумма их равна т, а разность между суммой
квадратов крайних и средних членов равна п2.
70.	Найти сумму: (х +	—	+ (х2	4- — ?+	... + (хп	+ — Г.
\	*)	\	\ х,г)
230
71.	Решить систему уравнений
хг__х2 __а
х2	Х3	Хл'
= 8X4+	х2	Х3	“Г ^4 = ^5.
72.	Решить систему уравнений
^1   Х2   Х3  	_ хп-1.
Л'2	-V3	х4	хп
xY — 8х4;	+ х2 4~ хз “г ••• ~Ь хп 15.
73.	Решить систему уравнений:
Х1 __ х2 _____ Х3 ___	_ ХП.
xi + 1 х2 + 3 х3 4- 5	хп + 2/г — 1
✓Vi + Х2 + Х3 4~ ••• + хп
74.	Решить систему уравнений
Х1 ___ Х2 ______ Х3 _	_ ХП
4- 1 х2 + 1 Х3 + 1	Хп + 1
		,	, 1 , 1 ,	,1 Ю
+ х2 + ••• + хп~\---1---Ь — Н— — V*
xi х2	хп 3
75.	Могут ли числа 2; ]Лб; 4,5 быть членами геометрической
или арифметической прогрессии?
76.	Возможны ли три таких числа а2, а3, чтобы они были од-
новременно первыми, вторыми и третьими членами арифметической
и геометрической прогрессий?
77.	Найти условия, при которых квадраты трех последователь-
ных членов арифметической прогрессии составляют геометрическую
прогрессию.
78.	Доказать, что если ху, у2 и z2 составляют последовательные
члены арифметической прогрессии, то числа у, z, 2у — х составля-
ют последовательно члены геометрической прогрессии.
79.	Вместимость колокола воздушного насоса равна а а
вместимость цилиндра поршня равна Ь Найти упругость возду-
ха под колоколом воздушного насоса после 6 качаний поршня,
если до качания она равнялась 1 атм.
80.	В арифметической прогрессии 11 членов. Первый член ра-
вен 24. Первый, пятый и одиннадцатый члены составляют геометри-
ческую прогрессию. Написать члены арифметической прогрессии.
81.	В арифметической прогрессии, содержащей 9 членов, пер-
вый член равен 1, а сумма всех членов равна 369. Геометрическая
прогрессия также имеет 9 членов, причем первый и последний чле-
ны ее совпадают с соответствующими членами данной арифмети-
ческой прогрессии. Найти седьмой член геометрической прогрес-
сии.
82.	Три числа составляют геометрическую прогрессию. Если вто-
рой член увеличить на 8, то данная геометрическая прогрессия
231
обратится в арифметическую, но если затем третий член будет
увеличен на 64, то она опять обратится в геометрическую прогрес-
сию. Определить эти числа.
83.	Три числа, сумма которых 114, можно рассматривать как
три последовательных члена геометрической прогрессии или как
первый, четвертый и двадцать пятый члены арифметической про-
грессии. Найти эти числа.
84.	Между числом 3 и неизвестным числом вставлено еще одно
число так, что все три числа образуют арифметическую прогрессию.
Если средний член этой прогрессии уменьшить на 6, то получится
геометрическая прогрессия. Найти неизвестное число.
85.	Найти четыре числа, из которых первые три составляют гео-
метрическую прогрессию, а последние три числа — арифметиче-
скую прогрессию; сумма крайних чисел равна 14, а сумма средних
чисел равна 12.
86.	Если к четырем числам, составляющим геометрическую про-
грессию, прибавить соответственно 4; 21; 29 и 1, то получим четыре
числа, составляющих арифметическую прогрессию. Найти числа.
87.	Если от четырех чисел, составляющих арифметическую про-
грессию, отнять соответственно 6; 18; 22 и 2, то получится четыре
числа, составляющих геометрическую прогрессию. Найти эти
числа.
88.	Найти предел суммы членов бесконечно убывающей геомет-
рической прогрессии ]/2 + —	+ ... .
89.	Найти предел суммы членов бесконечно убывающей гео-
метрической прогрессии (]/5 — 2) — (7 — 4 )/5) + ... .
90.	Найти знаменатель бесконечно убывающей геометрической
прогрессии, зная, что предел суммы членов вдвое больше суммы
первых п членов.
91.	Найти предел суммы членов бесконечного ряда:
92.	При каком значении а предел суммы членов бесконечно убы-
вающей геометрической прогрессии 2а + а]^2 а + ... равен 8?
93.	Найти
S = (а2 — Ь2) + (а + b) +	+ •••, где а — b > 1.
а — b
94.	Сумма членов бесконечно убывающей геометрической про-
грессии равна 9, а сумма квадратов ее членов равна 40,5. Найти
прогрессию.
95.	Первый член бесконечно убывающей геометрической про-
грессии равен 1. Каждый из остальных членов в 2— раза мень-
6
ше суммы двух смежных с ним. Найти предел суммы членов про-
грессии.
232
96.	Найти бесконечно убывающую геометрическую прогрессию,
зная, что первый ее член равен 1, а каждый член в 3 раза больше
суммы всех следующих за ним членов.
97.	Сумма первых четырех членов бесконечно убывающей гео-
метрической прогрессии равна 15. Сумма первого и четвертого чле-
нов в 1,5 раза больше суммы второго и третьего. Найти предел
суммы п членов прогрессии.
98.	Найти предел выражения
99.	Сколько надо взять членов в бесконечно убывающей гео-
метрической прогрессии 8; 7; ..., чтобы их сумма отличалась от
предела суммы меньше, чем на 0,01?
100.	При каком значении х прогрессия
a-j-x . а — х . (а— х\3
------1------------ -j- ...
а — х а-\-х \а + х/
есть бесконечно убывающая. Найти предел суммы членов про-
грессии.
101.	Сторона квадрата равна а. Середины сторон этого квадрата
соединили отрезками. Получился новый квадрат. С этим квадратом
поступили так же, как и с данным, и т. д. Найти предел суммы
периметров и предел суммы площадей этих квадратов.
102.	Сторона равностороннего треугольника равна а. На высо-
те его построен новый равносторонний треугольник. На высоте но-
вого равностороннего треугольника построен еще равносторонний
треугольник и т. д. Найти сумму периметров и сумму площадей всех
этих треугольников.
103.	В равносторонний треугольник со стороной а вписан круг.
В этот круг вписан новый равносторонний треугольник. В этот
треугольник опять вписан круг и т. д. Найти сумму длин окружно-
стей и сумму площадей всех этих кругов.
104.	В шар радиуса г вписан куб. В этот куб вписан новый шар.
В шар опять вписан куб и т. д. Найти сумму площадей поверхно-
стей и сумму объемов всех этих кубов и сумму площадей поверхно-
стей и сумму объемов всех шаров.
§ 2. РЯДЫ
Выражение вида и± + и2
..., unt ... — данные числа,
дом или просто рядом,
членами ряда. Член
ряда.
Sn =	+ ^2 + ••• 4" ип
мой ряда.
+ и3 +’... + ип + ..., где и19 и2, ...
называется бесконечным р я-
Числа и19 и2, ..., ип, ... называются
ип называется общим членом
называется частичной с у м-
233
При п = 1, 2, 3, ... получаем Slt S2, S3, ... поел едова-
тельпость частичных сумм данного ряда. Если lim Sn = S,	г
то ряд называется сходящимся, число S — его суммой.	,*
Если Sn при п оо предела не имеет или он равен оо, то ряд назы-
вается расходящимся и сумма такого ряда не существует.
105.	Вывести формулу для суммы квадратов п натуральных
чисел: I2 + 22 + З2 + ... + /г2.
106.	Вывести формулу для суммы кубов п натуральных чисел:
I3 + 23 + З3 + ... + п3.
107.	Показать, что при любом нечетном натуральном числе п
п3 — п
выражение —является целым числом.
108.	Найти сумму п членов ряда Sn = 1-22 + 2-32 + 3-42 +
+ --• + (п — 1) п2.
109.	Найти сумму п членов ряда Sn = I2 + З2 + 52 + Т2 + ...
... + (2п— I)2.
ПО. Найти сумму п членов ряда Sn = 2-12 + 3-22 + 4-32 + ...
... п (п — I)2 4- (п 4- 1) п2.
111.	Найти сумму п членов ряда Sn = (п 4- 1) « 4- 2п (п —
— 1) 4- 3 (п — 1) (п — 2) 4- 4 (п — 2) (п — 3) + ... + п • 2-1.
112.	Найти n-й член ряда треугольных чисел: 1; 3; 6; 10; 15;
21; ... .
113.	Найти сумму п членов ряда Sn = 1 + 3 + 6+ 10 +
П (п + 1)
4- 15 4- ... 4--4^-
114.	Найти сумму п членов ряда Sn = 1 4- 4 + 10 + 20 4- ...
, п (п+1) (п + 2)
1-2-3
115.	Найти сумму п членов ряда Sn = 1 + 3 + 5 + 7 + ...
... + (2п — 1).
116.	Найти сумму п членов ряда Sn = 1-2 + 2-5 + 3-8 + ...
... + п (Зп — 1).
117.	Найти сумму п членов ряда Sn = 1 + 7 + 19 + 37 + ...
... + (Зп2 — Зп + 1).
118.	Доказать, что п + 3 (п — 1) + 5 (п — 2) + ... + [2 (п —
— 2) — 1] • 3 + [2 (п — 1) — 11-2 + 2п — 1 = I2 + 22 + ... + п2.
119.	Найти сумму п членов ряда Sn = 1 + 15 + 65 + 175 +
+ ... + (4п3 — 6п2 + 4п — 1).
120.	Найти сумму п членов натурального ряда чисел, восполь-
зовавшись разностным методом.
234

т
121.	Найти сумму п треугольных чисел разностным методом:
sn = 1 + 3 + 6 ч- 10 + 15 + ... + п(п±У>-- .
122.	Найти сумму п членов ряда разностным методом:
Sn= 1 + 4 + 10 + 25 + ... +	1)(” + 2).
п	1-23
123.	Найти сумму п членов ряда Sn= 1 + 54- 15 + 35 + ...
, n(n + l)(»4-2) (п +3)
"~Г	1 • 2 • 3-4
124.	Найти сумму п членов ряда Sn = 1 + 2-3 + 2-4-5 +
+ 2-4-6-7 + ... + 2-4-6 ... (2п — 2) (2n — 1).
125.	Найти сумму п членов ряда Sn = 1-2 + 1-3-4 + 1-Зх
Х5-6 + 1-3-5-7-8 + ... + 1-3-5 ... (2n — 1) - 2п.
126.	Найти сумму п членов ряда Sn — 1-2-3 ... k + 2-3-4 ...
... (k + 1) + 3-4-5 ... (k + 2) + ... + n (n + 1) ... (n + k — 1).
127.	Найти сумму n членов ряда
S — ____!___L ____I---1--L J------1____
n 1 • 2	2- 3	3 • 4	n («4-1)’
128.	Найти сумму n членов ряда
S =—+ — + —+ I 1
n 1 • 3 "r 3- 5	5- 7	” -r (2n —l)(2n4-l) *
129.	Найти сумму n членов ряда
S =	1	_i_	1 i 1	+	.	1
n 2 •	5 ' 5 •	8	8 • 11 '	'	(3n — l)(3n 4-2)	'
130.	Найти сумму n членов ряда
S 1	।1	।	1	।	।	1
n 4 • 11 ' 11 • 18 ~ 18  25 *Г ' '	(7n — 3) (7n 4-4) '
131.	Найти сумму n членов ряда
5 _	1___।_____!_____|_ j_________1______
n 1 - 2 • 3	2 • 3 • 4	n (n 4-1) (n 4- 2) *
132.	Найти сумму n членов ряда
S = —!------1-----J------1------!------4 — 4--------------------
n 3-7-11	7-11-15	11.-15-19	(4n—1) (4«+3) (4«4-7)’
133.	Найти сумму n членов ряда
5 1  1 ' 1
n 1-2-3.4	2-3-4-5	3-4•5 • 6
+ - 4-----------------------•
n (n + 1) (n + 2) (n 4- 3)
235
134.	Найти сумму п членов ряда
<j _________1______1______!______i_
n 1-2-3-4-52-3-4-5-6
+ ... -j----------!------------.
n(n + l)(n + 2)(n + 3)(«-44)
135.	Найти предел суммы п членов ряда
s = —5------1-----!---1---------------и....
2 • 7 • 12	7-12-17	12-17-22
136.	Найти предел суммы п членов ряда
S = - + - + - + - + ... 4---------1- ... .
3	8	15	24	п2 — 1
137.	Найти предел суммы п членов ряда
2	2.3	2-3-4
138.	Найти предел суммы п членов ряда
S=-A_ + . 5	...7	_
(1 • 2)2	(2 • З)2	<3 • 4)2
139.	Найти сумму п членов ряда
п I  3Т3 • 5 1 5 - 7 1	' (2га — 1) (2п 4-1) *
140.	Найти предел выражения
—А.....4-— 2—+	_ 4-... 4----!--------,
n24-P	n24- 22 zi2 4-32	n24-(n — I)2
когда п-> оо (и — натуральное число).
141.	Найти сумму п членов ряда
е 1	,	2	,	4	.	8	.	,2"	о
$п — " , 1 А" а । . А" ’7' '. A- g  А- ••• А—п-’ х >2.
х 4- 1 х2 4- 1 х4 + 1 х8 4-1 х2 +1
142.	Вывести формулу для суммы ряда, полученного от пере-
множения членов арифметической прогрессии на соответствующие
члены натурального ряда чисел: 4-а, а 4- d, а 4- 2d, .... а 4- (п —
— 1) d и 4-1, 2, 3, .... п, т. е. для Sn = а 4- 2 (а 4- d) 4- 3 (а 4-
4- 2d) 4- ... 4- п[а+ (п — 1) d].
143.	Вывести формулу для суммы п членов ряда, члены кото-
рого получаются от перемножения соответствующих членов двух
арифметических прогрессий: 4-а; а 4- р\ а 4- 2р\...; а 4- (п — 1) р
и 4-Ь; b 4- q; b + 2q; ...; b 4- (п — 1) q, т. е. для Sn = ab+(a +
+ р) (b + q) + (а + 2р) (Ь 4- 2q) 4- ... 4- la 4- (n —• 1) pl X
XlH (n-1) q).
236
144.	Найти сумму: Sn = а 4~ аа + ааа + аааа + ••• + аа ... а,
п
где а — определенная цифра.
145.	Найти сумму: 86 = 3 + 33 + 333 + 3333 + 33 333 +
+ 333 333.
146.	Найти сумму п членов ряда Sn = 1 4- 2а 4* За2 4- ...
... + па"-1, где а 0 и а =4= 1.
147.	Найти сумму п членов ряда
Sn = 1 + За + 6а2 + 10а3 + ••• + | (« + 1) а""1.
148.	Найти сумму: S5 = 1 + 3-2 + 6-4 + 10-8 + 15-16.
149.	Найти сумму п членов ряда
Sn = 1	2а3 + За® 4- 4а9 + ... 4* па3"-3, где а =# 1.
150.	Найти сумму: 8 = 1 4- 2а + За2 4* 4а3 4- ... 4-
4-(п 4- 1) а" + ..., где | а | < 1.
151.	Найти сумму:
8 = —4- -4-- 4-... 4- - 4- ...
2	22	23	2"
152.	Найти сумму: 8 = 1 4- За 4- 5а2 4- 7а3 4- 9а4 4- ...
где | а | < 1.
153.	Найти сумму:
8=1 4- За 4- 6а24-10а34- ... +	4- •••. где | а | < 1.
154.	Найти сумму: 8 = 1 4* 4а 4~ 9а2 4- ••• 4~ (я + 1)2а" 4*
4- ...» где 1 а | < 1.
155.	Найти сумму:
8 = аг 4- (а 4- ab) г2 4- (а 4- ab 4- ab2) ,г3 4- ••• . где 0 < г < 0
и 0 < b < 1.
156.	Найти формулы для п-го члена и для суммы п членов ря-
да, у которого разности 2-го порядка равны 0.
157.	Найти, воспользовавшись разностями, сумму п натураль-
ных чисел: 8П= 14-24-34- ... 4- п.
158.	Найти формулы для n-го члена и для суммы п членов ряда,
разности 2-го порядка которого постоянны.
159.	Воспользовавшись формулой для разностей, найти:
8n = I2 4- 22 4- З2 4- ... 4- п2.
237
ГЛАВА XIII
КОМБИНАТОРИКА. БИНОМ НЬЮТОНА
Теория соединений, или комбинаторика, изучает некоторые опе-
рации над конечными множествами. Эти операции приводят к по-
нятиям перестановок, размещений и сочетаний. Комбинаторика
решает также и задачи, связанные с этими операциями. Основны-
ми задачами являются следующие:
1)	определение вида соединений,
2)	подсчет числа соединений.
1.	Перестановки
Всевозможные упорядоченные множества, составленные из дан-
ных п элементов, называются перестановками.
Число возможных перестановок из п элементов обозначается сим-
волом Рп и определяется по формуле Рп = nl
Пример. Сколькими способами можно раскрасить диаграм-
му из четырех столбцов четырехцветной шариковой ручкой так,
чтобы каждый столбец был окрашен в определенный цвет?
Решение. Р4 = 1-2-3-4 = 4! = 24.
2.	Размещения
Размещениями из п элементов по т называются всевозможные
упорядоченные подмножества, содержащие т элементов
из данных п.
Число возможных размещений из п элементов по т обозначается
символом А™ и находится по формуле
=п(п-1)(п-2)...(п-/п+1) = -5Ц
“	(п—т)\
где п и m — натуральные числа и 0 < т < п.
Пр и м е р. Сколько словарей надо издать, чтобы можно было
непосредственно выполнять переводы с любого из пяти языков:
русского, немецкого, английского, французского, итальянского —
на любой другой из этих пяти языков?
Решение. Так как нужны словари для двустороннего перево-
да, то вместе с русско-английским словарем должен быть издан и
англо-русский словарь и т. д. Поэтому число всех словарей равно
числу всех упорядоченных пар из пяти элементов, т. е. А$ = 20.
3.	Сочетания. Свойства сочетаний
Сочетаниями из п элементов по т называются всевозможные
подмножества, содержащие т элементов из данных п.
238
Число возможных сочетаний из п элементов по т обозначается
символом С™ и определяется по формуле
п(п— 1) ... (п — т+ 1)
— —————-	,
т\
или
pin =	_
п т\ (п — т)1 9
или С =	,
гт г т-п
где 0 < т < п, а т и п — натуральные числа.
Пример. 12 человек играют в городки. Сколькими способа-
ми они могут разбиться на команды по 4 человека в каждой?
Решение. Число способов выбрать четырех человек из 12
равно числу сочетаний из 12 по 4, т. е^ С = —р = 495.
Свойства сочетаний:
1)	С % = С„~т. Это соотношение позволяет ускорить вычис-
ление числа сочетании из п элементов по т при т > - .
2)	С-1 + С = C++
з)	скп = c^z} + Cj + С4 +... + cfci.
Следствие.
СП—k f>n—k I —k-— 1 I —k—2 I . z^O
n = Crt_1 4" ^r/—2	+	3 ф ••• + bft—1.
4)	C + C + C^+... + C2 = 2".
Эти свойства упрощают вычисления.
Примеры.
1.	Со = С350 = 501' 4|-"'~ = 19 60°-
2.	С}£ + С\% =	= Со = 2°°-;у- = 19 900.
3/оП ।	—1
. С9 4" С9 = Сю.
4.	С° + С| + cl + ... + С = С?2 = С= -772-з1^9- = 495«
Соединения с повторениями
Наряду с соединениями, в которые каждый из п различных эле-
ментов некоторого множества входит один раз, можно рассматри-
вать соединения с повторениями, допускающие появление одного
и того же элемента более одного раза.
Пусть дано п групп элементов. Каждая группа содержит не-
сколько одинаковых элементов. Такое деление на группы бывает,
например, в ящике для наборного шрифта, где в одну группу вхо-
дят одни и те же элементы, в разные группы — разные элементы'.
239
1.	Перестановки с повторениями
Перестановки из п элементов, в каждую из которых входит а
элементов а, р элементов Ь, у элементов с и т. д. % элементов I, где
а + р + у + ... + % = п, называются перестановками
из п элементов с повторениями.
Число всевозможных перестановок с повторениями обознача-
ется символом Pa.p.v.к, и оно может быть найдено по формуле
р •	= (<* + Р + т + - + М! = п
а, ₽.v,... ,Л а! (3! у! ... %!	al pi у! ... X! ’
Примеры.
1.	Имеется 5 кружков: 3 белых и 2 черных. Сколько различных
узоров можно составить из этих кружков, располагая их в ряд?
5!
Решение. Р» ,= — = 10.
’2	3! 2!
2.	Сколько анаграмм можно составить из слова «математика»?
Решение. Р?,з,21 i.i =-----—--= 151 200.
’	'	213121ПШ!
2.	Размещения с повторениями
Размещения из п элементов, в каждое из которых входит т
элементов, причем один и тот же элемент может повторяться в каж-
дом размещении любое число раз, но не более т, называются разме-
щениями из п элементов по т с повторениями.
Число всевозможных размещений с повторениями из п
элементов по т элементов в каждом обозначается символом А™ и вы-
числяется по формуле А™ = пт.
Пример. В стену здания вмонтированы 8 гнезд для флажков.
В каждое гнездо вставляется либо голубой, либо красный флажок.
Сколько различных случаев распределения флажков на здании?
Решение. А% = 28 = 256.
3.	Сочетания с повторениями
Сочетания из п элементов, в каждое из которых входит т эле-
ментов, причем один и тот же элемент может повторяться в каждом
сочетании любое число раз, но не более т, называются сочетаниями
из п элементов по т с повторениями и обозначаются С”.
Число С™ всевозможных сочетаний с повторениями вычисляют
по формуле
рШ ____ f'tn _______
— C/n+rt—1 —
n(n + 1) (ft+ 2) - (n + m — \)
1 • 2 -3 ... tn
Пример. В почтовом отделении продаются открытки 10 сор
тов. Сколькими способами можно купить 12 открыток?
240
Решение. Порядок покупки открыток несуществен. Поэ-
тому всякий набор купленных открыток представляет собой соче-
тание с повторениями из 10 по 12. Таким образом, число способов
произвести покупку 12 открыток равно С}^ — С^.
§ I. КОМБИНАТОРНЫЕ ЗАДАЧИ
При решении комбинаторных задач необходимо вначале опре-
делить вид соединения. При этом можно руководствоваться пра-
вилами для установления вида соединений, вытекающими из при-
знаков, определяющих понятие того или иного из этих видов. Та-
ких правил несколько. Приведем одно из них.
Пример. Научное общество состоит из 25 человек. Надо
выбрать президента общества, вице-президента, ученого секретаря
и казначея. Сколькими способами могут быть сделаны эти выборы,
если каждый член общества может занимать лишь один пост?
Решение. Так как производятся выборы на различные долж-
ности, то порядок элементов имеет значение. Следовательно, имеем
либо перестановки, либо размещения. В соединения из 25 эле-
ментов входят 4 элемента, т. е. не все элементы, значит, каждый на-
бор представляет собой размещение из 25 элементов по 4. Таким обра-
зом, выборы могут быть сделаны
Л25 = 25-24• 23-22 = 303 600 способами.
Во многих комбинаторных задачах полезно использовать сле-
дующие два правила:
Правило суммы. Если объект А может быть выбран т
способами, а объект В — п способами, то выбор «либо А, либо В»
может быть осуществлен т + п способами.
Правило произведения. Если объект А может быть
выбран т способами и после каждого из таких выборов объект В,
в свою очередь, может быть выбран п способами, то выбор «А и В»
в указанном порядке может быть осуществлен m-п способами.
241
Пример. Из трех инженеров и девяти экономистов должна
быть составлена комиссия в составе 7 человек. Сколькими способами
может быть составлена комиссия, если в нее должен входить хотя
бы один инженер?
Решение. В комиссии может быть: а) 1 инженер и 6 экономис-
тов, б) 2 инженера и 5 экономистов, в) 3 инженера и 4 экономиста.
а)	Выбор одного инженера из трех возможен Сз = 3 способа-
ми, а шести экономистов из девяти — Сэ. По правилу произведе-
ния число способов выбора одного инженера и шести экономистов
равно Сз-Сд.
б)	Выбор двух инженеров из трех возможен способами, а
выбор пяти экономистов из девяти — Сэ. По правилу произведе-
ния, число способов выбора двух инженеров и пяти экономистов
равно Сз-Сэ-
в)	Выбор трех инженеров из трех возможен Сз способами, а
выбор четырех экономистов из девяти — Сд. По правилу произве-
дения число способов выбора трех инженеров и четырех экономи-
стов равно Сз-Сд.
Таким образом, общее число способов выбора комиссии, в сос-
тав которой входил бы хотя бы один инженер, по правилу суммы
равно:
c'-q + q.c| + q.q.
Решить задачи.
1.	Какие два математических термина, состоящих из одинако-
вых букв, но разно расположенных, зашифрованы в слове «фарим-
гол»? Сколько слов из этих букв пришлось бы составить, чтобы най-
ти зашифрованные термины?
2.	Сколькими способами можно выбрать из 15 человек партию
людей для работы? В партию может входить любое число людей:
1, 2, 3, ... , 14, 15.
3.	Сколько размещений из т элементов по п будет начинаться
с первого элемента?
4.	Сколько размещений из т элементов по п будет начинаться
любым элементом за исключением первого?
5.	Сколько можно составить четырехзначных чисел из 5 разных
цифр: 0, 1, 2, 3, 4?
6.	Сколько четных четырехзначных чисел можно изобразить
цифрами 2, 3, 5 и 7?
7.	Сколько четных пятизначных чисел можно изобразить циф-
рами 2, 3, 4, 5, 9?
8.	Сколько пятизначных чисел, кратных 5, можно изобразить
цифрами 0, 1, 2, 3, 5?
9.	Составлены размещения из 10 элементов по 7 элементов.
Сколько из этих размещений будут содержать: а) первый элемент,
б) второй и четвертый элементы?
242
10.	Составлены) размещения из 10 элементов по 7 элементов.
Сколько из этих размещений не будут содержать: а) первого эле-
мента, б) третьего и пятого элементов?
11.	Составлены размещения из иг элементов по п. Сколько из
этих размещений будут содержать k данных элементов, если k < п?
12.	Составлены размещения из т элементов по «.Сколько из
этих размещений не будут содержать k элементов, если k < «?
13.	Сколько всех делителей у числа 210?
14.	Сколько всех делителей у числа 30 030?
15.	Определить число всех диагоналей 5-, 8-, 12- и 15-угольника.
16.	Из двух спортивных обществ, насчитывающих по 100 фех-
товальщиков каждое, надо выделить по одному фехтовальщику для
участия в состязании. Сколькими способами можно это сделать?
17.	У одного человека есть 7 книг по математике, а у другого —
9 книг. Сколькими способами они могут обменять друг с другом по
две книги?
18.	Из состава конференции, на которой присутствуют 52 чело-
века, надо избрать делегацию, состоящую из 5 человек. Сколькими
способами можно это сделать?
19.	В местком избрано 9 человек. Из них надо выбрать предсе-
дателя, секретаря и культорга. Сколькими способами это можно
сделать?
20.	Сколькими способами можно расставить 20 книг в книжном
шкафу с 5 полками, если каждая полка может вместить все 20 книг?
21.	Сколько существует треугольников, длины сторон которых
принимают одно из следующих значений: 4 см, 5 см, 6 см, 7 см?
22.	30 человек голосуют по 5 предложениям. Сколькими спосо-
бами могут распределиться голоса, если каждый голосует только
за одно предложение и учитывается лишь число голосов, поданных
за каждое предложение?
23.	Для премий на математической олимпиаде выделено 3 экзем-
пляра одной книги, два экземпляра другой и. один экземпляр
третьей книги. Сколькими способами могут быть вручены премии,
если в олимпиаде участвовало 20 человек и никому не дают двух
книг сразу? Та же задача, если никому не дают двух экземпляров
одной и той же книги, но могут быть вручены две или три различные
книги.
24.	В библиотеке имеются учебники по физике трех различных
авторов, учебники по химии двух различных- авторов и учебники
по математике пяти различных авторов. Каково наибольшее число
студентов, которые взяли не меньше чем по одной книге каждого
из трех видов при условии, что ни один студент не взял все книги,
одинаковые с другим студентом?
25.	Лифт, в котором находятся 9 пассажиров, может останавли-
ваться на 10 этажах. Пассажиры выходят группами по два, три и
четыре человека. Сколькими способами это может произойти?
26.	12 ученикам выданы два варианта контрольной работы.
Сколькими способами их можно посадить в два ряда, чтобы рядом не
243
было одинаковых вариантов, а у сидящих друг за другом был один
и тот же вариант?
27.	Сколькими способами можно переставить буквы слова «ло-
гарифм» так, чтобы 2, 4 и 6-е места были заняты согласными бук-
вами?
28.	Из лаборатории, в которой работают 20 человек, 5 сотрудни-
ков должны уехать в командировку. Сколько может быть различ-
ных составов этой группы, если начальник лаборатории, его заме-
ститель и главный инженер одновременно уезжать не должны?
29.	Из 10 спортсменов, из которых 2 гребца, 3 пловца, а осталь-
ные бегуны, нужно выделить команду из 6 человек для предстоя-
щих соревнований. Сколько может быть случаев создания команды,
в которую бы вошли не менее одного спортсмена от каждого вида
спорта?
30.	На полке находится т 4- п различных книг, из которых
т — в черных переплетах, ап — в красных. Книги переставля-
ются всевозможными способами. Сколько существует различных
положений книг, при которых книги в черных переплетах занима-
ют т первых мест? Сколько таких положений, при которых книги
в черных переплетах стоят рядом?
31.	Из 15 рабочих, в число которых входят 5 плотников и 4
штукатура, требуется создать бригаду в 8 человек. Сколькими спо-
собами можно укомплектовать бригаду так, чтобы в нее вошли не
менее трех плотников и не менее двух штукатуров?
32.	Во скольких точках пересекаются 10 прямых линий, если
между ними нет параллельных прямых и через каждую точку пере-
сечения проходит не более двух прямых?
33.	Во скольких точках пересекаются 8 прямых линий, если
две из них параллельны между собой и через каждую точку пере-
сечения проходит не более двух прямых?
34.	Во скольких точках пересекаются 15 прямых линий, если
четыре из них параллельны между собой и через каждую точку пе-
ресечения проходит не более двух прямых?
35.	Вычислить сумму пяти средних элементов девятой строки
треугольника Паскаля (биномиальные коэффициенты для п = 1,
2, ... записаны в виде последовательности строк).
36.	Вычислить сумму четырех средних членов десятой строки
треугольника Паскаля.
37.	Вычислить сумму четырех крайних членов одиннадцатой
строки треугольника Паскаля.
38.	Сколькими способами можно разместить 10 пассажиров в
трех вагонах?
39.	Буквы азбуки Морзе состоят из символов (точек и тире).
Сколько букв можно изобразить, если потребовать, чтобы каждая
буква содержала не более пяти символов?
40.	Сколько различных четырехзначных чисел, делящихся на
4, можно составить из цифр 1, 2, 3, 4, 5, если каждая цифра может
в записи числа встречаться несколько раз?
244
§ 2.	КОМБИНАТОРНЫЕ ТОЖДЕСТВА И УРАВНЕНИЯ
Комбинаторные тождества могут быть доказаны:
а)	путем тождественных преобразований с использованием
основных формул;
б)	методом математической индукции;
в)	с помощью теоретико-множественных соображений.
Примеры.
Доказать тождества.
1. .	— = 2х(2х + 1).
2х— 1^2х-п
Решение. Преобразуем правую часть равенства, используя
формулы числа размещений и перестановок.
Р2Х+1	_	(2x4-1)!	_ (2х +1)! _ 9 п
л	-2х{2х+ ”
2. Р + 22 + З2 + ... + п2 = С2+1 + 2 (С2 + CLi + - + Cl). (1)
Решение. Вычислив сумму С2+2 + С2п+1, находим
Г2 , Г2 _(л + 2)(л+1).(л+1)л_, П2
Ьп+2 "Г Ьга+1 = ----------1------ = (П + 1) .
Итак, (п + I)2 = С2+2 + C2+i.	(2)
а) Допустим, что равенство (1) верно при п = k, т. е.
I2 + 22 + З2 + - -И2 = C2k+l +2 (Cl + Cl-i + ... + Cl).
Докажем, что при этом равенство (1) верно и при п = k + 1. Для
этого сложим его с тождеством (2). Тогда получим:
I2 + 22 + з2 +... + *2+ (*+ 1)2=c1+2+2(^+1+cUcL1+... + С$.
Таким образом, равенство (1) остается верным при переходе от
п = k к п = k + 1. Но оно верно при п = 2, что проверяется не-
посредственным вычислением. В силу принципа математической
индукции равенство (1) справедливо при любом натуральном п > 2.
Зх>П	1 I zVl—1	।	1	.	. f^n— 1
•	1 -f- С/л—2 “Г ^т— 3 “г ••• "Г ^п— 1-
Решение. Число сочетаний из т элементов по п разделим
на группы так, чтобы в первую группу вошли сочетания, начинаю-
щиеся первыми элементами, во вторую — вторыми, в третью —
третьими и т. д. до тех пор, пока не будут исчерпаны все сочетания.
Элементы в сочетаниях записаны в порядке возрастания их индек-
сов. Определим, на сколько групп по указанным признакам разби-
лись сочетания из т элементов по п. Каждая группа не может со-
держать начальных элементов предыдущих групп. Поэтому число
элементов, из которых составляется каждая последующая группа,
уменьшается, а число элементов, входящих в сочетание, остается
постоянным, равным п. Следовательно, индекс начального элемента
245
последней группы будет таким, что разность между числом всех
элементов и этим номером будет равна числу элементов, входящих
в сочетание, уменьшенному на единицу, т. е. если х — порядковый
номер последней группы, то т — х ~ п — 1, или х = т — п + 1.
Доказать тождества.
дб д5
41.	=(п-4)2.
Ап
43. Л*=-^-.
?n-k
45. Л* • Pn_ft = п\
47. Л?о • Р10-п = Ю • Р9.
49. А„ = nAknZ\.
42	‘	__ ^2
44. Ап~х = Рп.
дк— 1 р t
46. Aj----ILf = 1.
Г п-1
48. Ahn = ALi + kAk~\.
50. С'"+' + Сп~1 + 2С? = О1.
ОЬ -f; Gn—1 -f- ••• -f-	10 = Cn-jil -CjS'd-
52.	Доказать, что если C„t = С'т и k #= I, то I + k — m.
53.	Найти x, если Cx = Cx.
54.	Cjl} = 36. Найти Pn.
55.	Найти n и г, если Arn = 272 и C„ = 136.
56.	Доказать, что C% : <X = 1 • 3 • 5 - <4n — 0 .
[1 • 3 • 5... (2n — l)j2
57.	Найти пит, если Cffl : С+1 : C^i1 = 5:5:3.
58.	Найти n и г, если C^-1 : Crn : C^1 = 2:3:4.
59.	На сколько увеличится число сочетаний из 7 элементов по
2, если ввести 8-й элемент, оставив сочетания парными?
60.	Показать, что непосредственное определение числа парных
сочетаний приводится к суммированию разностной прогрессии.
61.	На сколько увеличится число сочетаний из 7 элементов по
3, если ввести 8-й элемент, оставив сочетания тройными?
62.	Пользуясь общей формулой члена парных сочетаний, вы-
вести формулу суммы квадратов т членов натурального ряда чисел.
63.	Пользуясь общей формулой числа тройных сочетаний, вы-
вести формулу суммы кубов т членов натурального ряда чисел.
64.	Показать, что непосредственное определение числа трой-
ных сочетаний сводится к суммированию ряда парных произведе-
ний.
246
Решить уравнения.
— А'1	р ,	р
65.	—------- = 89.	66.	= 720.	67. —V13.... = 720.
А*	рз	А^РХ.Ь
68.	Ахп = хАхп~\ 69. -3^ — - 240.
Лл-4-4
§ 3.	БИНОМ НЬЮТОНА
Формула (х + а)" = хп + СпХп-1а-|- qxn-2a2 4- ...
... + С"-1ха"-1 4- ап называется биномом Ньютона.
Любой член бинома определяется по формуле
П+1 = Ск x*~W.
Коэффициенты С°, С„, С2п, .... С”-1, Ch называются биномиаль-
ными. Они обладают следующими основными свойствами:
1.	Коэффициенты членов, равноудаленных от начала и от кон-
ца разложения бинома, равны между собой.
, В самом деле, коэффициентом (kA- 1)-го члена разложения явля-
ется С„, а коэффициентом (k + 1)-го члена разложения от конца
или (п — k + 1)-го члена от начала есть С%~к , но Ск = Ch~h.
2.	Сумма всех биномиальных коэффициентов равна 2".
Действительно, при х = а = 1 имеем:
(1 + 1)« = 1 + С\ + С„2 + ... 4- СГ1 + Сп\
откуда 2" = С» + Сп + Сп + ... +	+ q .
3.	Сумма биномиальных коэффициентов, стоящих на четных ме-
-стах, равна сумме биномиальных коэффициентов, стоящих на не-
четных местах.
В самом деле, при х = 1, а = — 1 имеем:
(1 - 1)" = 1 - q + q - q + ... +
откуда i + q + q + ... = q + q + q + ... .
4.	Коэффициент (k + 1)-го члена разложения бинома равен про-
изведению коэффициента fe-ro члена на показатель степени х
в этом члене, деленному на k.
Действительно, С» = С • n ~	1, где С„-1 есть коэффици-
k
ент &-го члена, — коэффициент (k + 1)-го члена разложения
бинома, а (п — k + 1) — показатель степени х в этом члене, ч
247
Пример. В разложении бинома (]/х 4- первые три
коэффициента образуют арифметическую прогрессию. Найти все
рациональные члены разложения.
Решение. Первые три члена разложения имеют вид:
(Ух У; п(Уху-х
п (п — 1)
2
(У~хУ~2
1
2
1
22 (У~хУ
Их коэффициенты 1;
грессию, поэтому 1 4-
—— образуют арифметическую про-
8
— 2- —. Решая получен-
8	2
ное уравнение относительно п, получим: п = 1 и п = 8. При п = 1
разложение не имеет рациональных членов.
При п = 8 (k + 1)-й член разложения имеет вид:
8—k k
П+1 = сЖГ)'-<^ = сГ±^-г
где k = 0, 1, 2, 3, 4, 5, 6, 7, 8.
, Требуется найти рациональные члены. Для того чтобы член был
л	8 — k k
рациональным, необходимо и достаточно, чтобы-------=
2	4
' 16—3k А	.
=----- было целым, что возможно при fe, делящемся на 4,
4
т. е. при k = 0, 4, 8. Следовательно, рациональные члены разло-
жения есть:
7\ = х4; Т, = — х; Т9 = — х~2.
5	8	9	256
70.	Вычислить 1,0005зв с точностью до 0,001.
71.	Вычислить (1 — УЗ)4 с точностью до 0,001.
72.	Разложить по формуле бинома Ньютона (1 + 2t)7.
73.	Разложить по формуле бинома Ньютона (а 4- ЫУ 4- (а —
— ыу.
74.	Доказать, что в разложении (1 4- i)4ft+2 сумма членов, стоя-
щих на нечетных местах, равна 0.
75.	Доказать, что если А означает сумму членов, стоящих на
нечетных местах, а В — сумму членов, стоящих на четных местах
в разложении (х 4- а)"> то А2 — В2 = (х2 — а2)”.
76.	Найти пятый член разложения бинома (2х]/х — Ух)2.
77.	Найти средний член разложения бинома 12х 4-	.
78.	Найти наибольший коэффициент в разложении бинома
[(1 4-x)(i- 1)Г.
\х /J
248
79.	Найти значение показателя т в разложении бинома
(1 + а)т, если коэффициент пятого члена равен коэффициенту
девятого члена.
80.	Определить А~, если пятый член разложения
не зависит от х.
81.	Найти пятый член разложения бинома | -Д- Vх । .если
\У х а ]
отношение коэффициента третьего члена к коэффициенту второго
11
члена равно
82.	В разложении бинома (У1 + х — V1 — х)и коэффициент
третьего члена разложения равен 28. Найти средний член разло-
жения.
83.	Найти наименьшее значение показателя т в разложении
(1 + х)т, если отношение коэффициентов двух каких-либо соседних
членов разложения равно 7 : 15.
84.	В разложении бинома (х + сумма коэффициентов
на 240 меньше суммы коэффициентов разложения бинома (а + Ь)2п.
Найти третий член первого разложения.
85.	Найти член, содержащий х4 в разложении бинома
(]/х + Vx)9.
/	1 \1в
86.	В разложении бинома у х + зт= найти член, содержащий
\	ух/
уЗ
I П	1 \1000
87.	В разложении бинома %5 + — найти член, не завися-
щий от х.
88.	В разложении бинома (j/"a + /а-1)15 найти член, не зави-
сящий от а.
89.	Найти члены, не содержащие х, в разложении бинома
а + х) (1 +-ЦГ.
L \	*/J
/	—	1 \я
90.	В разложении бинома [а v а_ +	_ опреде-
\	6	. yAz28 /
лить член разложения, не содержащий а, если сумма биномиальных
коэффициентов трех первых членов разложения равна 79.
91.	Определить х, если четвертый член разложения бинома
/ 1g /Г 1	\7
110	+ .----| равен 3 500 000.
92.	В разложении бинома (а	определить член,
\ г 3 дз/
содержащий а в третьей степени, если сумма биномиальных коэф-
249
фициентов, стоящих на нечетных местах в разложении бинома,
равна 2048.
/ 1 V~b \п
93.	В разложении бинома	определить
член разложения, содержащий 66, если отношение биномиальных
коэффициентов четвертого и второго членов равно 187.
94.	В разложении бинома (х х —	определить член
\ /
разложения, не содержащий %, если сумма биномиальных коэффи-
циентов второго члена от начала и третьего от конца разложения
равна 78.
95.	Отношение коэффициента третьего члена к коэффициенту
_1 з__________________________________	2
пятого члена разложения бинома (х 2 — ]/ х)п равно Найти тот
__ 5
член бинома, который содержит х 2.
96.	Найти, при каких значениях х в разложении бинома (]/2х +
.	1 \т	1 nr-
+	сумма третьего и пятого членов равна 135, если сумма
биномиальных коэффициентов трех последних членов равна 22.
97.	Найти х, у и z, если известно, что второй, третий и четвертый
члены разложения (х + у)г равны 240, 720, 1080.
98.	Коэффициенты пятого, шестого и седьмого членов разложе-
ния бинома (I + х)« составляют арифметическую прогрессию.
Найти п.
99.	При каком значении п коэффициенты второго, третьего и
четвертого членов разложения бинома (х + у)" составляют арифме-
тическую прогрессию?
100.	Найти члены, не содержащие иррациональности, в разло-
жении бинома (}/ 3 +	2)5.
101.	Найти члены, не содержащие иррациональности, в разло-
жении бинома (уЛ3 + у 2)24.
102.	Найти все рациональные члены разложения (/х — угх)21.
1 _i
103.	Найти все рациональные члены разложения (х3 — у 3)19.
104.	Сколько рациональных членов содержится в разложении
(]/ 2 + уЗ)100?
105.	Найти номера трех последовательных членов разложения
(а + Ь)23, коэффициенты которых образуют арифметическую про-
грессию. '
106.	Доказать, что разность между коэффициентами при хк+1
и хк в разложении (1 + х)п+1 равна разности между коэффициен-
тами хк+1 и хк~1 в разложении (1 + х)п.
107.	Доказать, что в разложении (а + Ь)п (а > 0 и b > 0),
где п — целое положительное число, не может быть трех одина-
250
новых последовательных членов. При каких условиях разложение
имеет два одинаковых последовательных члена?
108.	Найти наибольший член разложения (1 + 1/2)50.
109.	Найти наибольший член разложения (]/2 + ]/3)101.
НО. Доказать, что 62" + 3"+2 4~ 3я делится на 11, где п —
натуральное число.
111. Доказать, что 32я+3— 24м + 37 делится на 64, где п —
натуральное число.
112. Используя разность 32я+1— 5п, составить выражение,
кратное 64.
Доказать тождества.
113.
114.
115.
116.
117.
Сп - 2С„ + ЗС3 -... + (- \у-ЫСпп = 0.
С„ + 2С2 + ЗС3 + ... + пСпп = п- 2я-1.
С°п + 2С'п + ЗС2п 4-... 4- (п 4- 1) С„ = (п 4- 2) • 2я’1.
/-.О	1 .'-Л ।	1	, /	1 \п ^п	I
-f- — Gn
2. о
r 0 .	I Cn
cn 2«+l — 1
'n — 2я-1, если n — четное,
г + Cn + ... + Cn = 2я-1, если n — нечетное.
C»^2C" L 4.	4	”C;	"<” + '>
" z~':	;4+"'Tc"'' “2 “
C° 4- 2d 4- 22C2n 4-... 4- 2"C = 3я.
„	22C'	23C2	2Я+’СЯ
2c:+v+~+- + 7T? =
- +_____-----ь----!—
1(«— 1)!	31 (n —3)1	51 (n —5)!
1	1 r2 , 1 r3 . (— I)"-1
- C„ -- c„ 4-	- ... 4-
118.
120.
121.
122.
123.
3Я+1 _ 1
1
H------!— = —
(n—1)! nl
,n ___	n
n —	; ?•
и
ОТВЕТЫ И УКАЗАНИЯ
ГЛАВА I
§ 1
1. При n = 1 утверждение справедливо, так как 1=1. Допустим, что
утверждение справедливо для п = k, и докажем его справедливость для
Ife j | \
п = &+ 1;	= Sft + (k+ 1), но Sk=------------ по предположению, значит,
о k(k+\) .	(k + \)(k + 2)
5*+i=------2---+	+ 0 =--------2---------’
2. Непосредственным вычислением устанавливаем: 1 + 3 = 22, 1 + 3 +
+ 5 = З2 и т. д. Выскажем предположение: сумма первых п нечетных чисел рав-
на квадрату числа их. При п = 1 предположение верно, так как 1=1; допустим,.
что оно верно и для п — k, докажем справедливость его для п— k + 1:
S^+i = Sk + (2k + 1), noSk — k2 по предположению, значит, Sk+1—(k +1)2.
5. a) Sft+l = Sft + (—l)ft+i (2k + 1).
15. При k = 1 получим предыдущую задачу. Поэтому достаточно, сослав-
шись на эту задачу, провести доказательство индукцией по п. Обратить внимание
на интересный факт, доказанный в этой задаче: рассматриваемая сумма не зави-
сит от значения k. Например, 1! + 1 • 1! + 2 • 2! + ... + п • и! = 1000! +
+ 1000 • 1000! + ... + п • п!, так как 1000! = 1! + 1 • 1! + 2 • 2! + ... +
+ 999 • 999! (при п 1000).
.«о о	1	1	(	1	1	1 \
19’ ft+1 _ Sk + 2k + 1 “ 2k + 2 “	+ 2 + k 4- 3 + " + 2k) +
! / 1 1 \
+ 2k + 1 + V: 4-1 ~ 2k + 2/ '
2ft+1
31. Sft+1 = Sk 4- ft+1 .
1 -f A
34.	а) При n = 0 утверждение справедливо; S^+1= Sk + 3k (k + 1) + 6;
Sk-i = sk — %k (fe —1) —6.
в) Доказать, что разности, составленные из данного выражения при
п=&+1,п=6и при п — k, п = k — 1, делятся на 24.
35.	а) Применить метод индукции дважды или преобразовать S^+1 к виду
S*+i = Sk • 7 - 9 (2k - 1).
36.	д) Преобразовать данное выражение к виду 27л • 9 + 10 • 8Л. Тогда
S*4-i= 8Sft+ 171 ' 27*’
37.	а) Доказать справедливость утверждения при т — 0, m = 2k + 2 и
т = 2k — 2.
38.	а) Учесть, что 7 + 72 + 73 + 74 = 28 00.
б) Доказать, что каждое из чисел 98, 96, 94, 92 при делении на 5 дает в ос-
татке 1, и представить 910*— 1 в виде произведения двух множителей: 92* 106-1—
__1 и 98.106-1 _|_ 96.юб—1 94.Ю&—1 92.106-1 1.
252
40.	Доказательство провести индукцией по а. При а — 0 утверждение спра-
ведливо; S^+1 — Sk + р • А, где А — целое число (обосновать, используя раз-
ложение по формуле бинома Ньютона), = Sk + р • В, где В — целое число.
Второе утверждение задачи — следствие первого.
41.	Учесть, что число вида 4n + 1 не обязательно простое и 30 = 5 * 6.
42.	Задача сводится к доказательству того, что число а4'г+1— а делится на 10
(см. предыдущую задачу).
43.	Общий вид строк таблицы: n, п + 1,	2, ... , Зп —2. Всего 2п — 1
чисел. S^+1 = Sk — k -|- (3k — 1) +36 4“ (3k “hl).
44.	а) Имеем: ak+1 « ak + ak^ = a0 + ax + ... + ak_2 + 1 + ak^ = ad+
+ aY + ... + ak^ + 1.
б)	Имеем: aQ + a2 + ... + a2k + a2k+2 — (ax + a3 + ... +
+ a2fc-l + a2fe+l) — a0 + a2 + • • • + a2k — (fll + a3 + - + a2k-l) + a2k+2~ a2k+l =
— a2k-l 14” ^2& = (a2k-1 + a2k) 1 — a2fe+l 1»
в)	Допустим, что утверждение справедливо для п = 2k, докажем справедли-
вость его для п =» 2k + 2.
a2fe4-2 = (й2&+14" fl2ft)2=a2fe-hl ~^~a2k~i~ ^a2k+l • a2k = a2k+l~i~ a2^-l,a2Jfe+l+2fl2^+lX
X — 1 — a2k+l * К^2Й+1 + a2k) +(а2Й-1+а!2Д’)]“1 = a2&+l (a2k~2 + a2fc+l)“ 1 =
: ^2Й+1 *
Аналогично доказывается и для нечетного п.
г,	д) Справедливость утверждений может быть доказана методом математиче-
ской индукции аналогично уже проведенным доказательствам. Свойство д) мож-
но доказать, пользуясь свойством г). Для этого достаточно положить п = k + 1,
р = k + 1.
45.	Допустим, что утверждение справедливо для п = k, т. е. для числа
А = 11 ... 1, и докажем его справедливость для числа В= 11 ... 1.
3^	3^+1"
Имеем: В =11... 1 00... 0 4- 11 ... 100... 0 4-11... 1 = А • 10зй-24- А- 103*4-А,
“ ^3^	3й “
но А по допущению делится на 3й; следовательно, В = Д(10зА'2+ 10зй4*1)
делится на Зй+1, так как множитель в скобках имеет сумму цифр, кратную 3,
следовательно, делится на 3.
46.	Доказать справедливость двух неравенств: ул_х < и у„ < “ .
47.	аА+1 = Зак — 2aft_1= 3 (2й4- 1) — 2(2й-14-1)=3-2й4-3—2й— 2= 2й+14-1.
2	/	1 \	2	/	1 \
а, + ь„ “+1 (‘- °>1Г»)+ “ + 7 “>('+	)
49.	а) а^+1 —	=
2	!	1	1 \
- -----------------i-------------------- "> + 7 (к- »> (-	
Аналогично доказывается и для
52.	Прип = й4-1 имеем: (1 4- х) (1 4-х2) (1 4- х1)... (1	х2*) = (14-х 4-х24-
4-... 4- х2*-1) (1 4- х2*)=1 4- х 4- х2 4- х4 4-... 4- х2Й+2*-1 = 14-х4-х24-.-4-х2*+~1
м с о , («1 + 1) («2+1)-(^4-1) («*+14-1)
54.	o£+i =	-j-	-------------------------------- =
^^2 akak+lak+2
__ (fll ~h 1) (^2 ~Ь 1)	+1 )	| (Q1 + 1) (^2 ~h 1)	(^4-1 4~ 1) __
aYa2 ...	aia2 ••• ak+i ak+2
253
(g, +1) (02 + n - (gftlt + l) v {. ,	1	_
E=	X I 1 Г | —
ax6J2 ... cik+x	\ ak+2 /
_ («1 + 1) (a2 + 1) - (afe+i + О <ak+* 4- 1)
aia2 ak+lak^2
55.	Для доказательства справедливости утверждения при п — 2 надо пре-
а2 4- р2 4- сф — а — Р
образовать выражение для Л2 к виду А2 = ----------------, умножив
а + р— 1
числитель и знаменатель на а — р.
Чтобы доказать справедливость утверждения для п = k + 1 при условии,
что оно справедливо для п = k, надо использовать равенство Ak+1 — (а + ₽)—
ар
56.	Докажем для переменного п. При п = 1 имеем: kn+2 + (k + 1)2я+1=»
= k* + (k + I)3 = 2fe3 + 3k + 1 + 3k2 = 2k (k2 + k + 1) + k2 + k + 1,
т. e. делится на k2 + k + 1.
Допустим, что делимость имеет место при п = р, и докажем, что она имеет
место и для п = р + 1.
Имеем:

fe(p+l)4-2 + (fe + l)2P+3 kP+2 » fe + (fe + 1)2P+1 (fe + I)2
_ kP+2 - fe + (fe + 1)2P+1 (fe2 + 2fe + 1) fep+2- fe +fe2(fe+l)2W+2fe(fe+l)2p+1
(fe+l)2^+l k [kP+2+(k +1)2W] + (fe + l)2p+1 (fe2 + fe + 1) __
/г2+&+1~	fc2+/e + l	~
k2 + k +1
Но по допущению это число целое.
57.	Проверить справедливость утверждения для п — 1; допустить его спра-
ведливость для п — 2k — 1 и доказать справедливость утверждения для п =
«= 2k + 1, выразив 32й+1 через S2fc_r
58.	Составить сумму данных выражений при и=&ип=£+1и доказать,
что второе слагаемое делится на р.
59.	Из условия задачи следует, что Ап и Ар должны давать одинаковые
остатки при делении на 34 300. Докажем это, найдя, например, остаток от деле-
ния А 2 на 34 300, а затем обобщим с помощью метода математической индукции.
1)	Найдем остаток от деления Л2 = 7? = 823 543 на 34 300.
А2 = V = 823 543 = 34 300 • 24 + 343.
2)	Допустим, что такой же остаток при делении на 34 300 дают все Ak при
k п, и докажем справедливость утверждения для k = п + 1, т. е. допустим,
что Л = 34 300яп + 343.
3)	д ____ ^Ап т е Л 7^4	-|-343 —, y4(8575a/i -j-85)-J-3 „ у4В
X 73= 74В • 343 = (100fe + 1) 343 = 34 300& + 343, так как при возведении
числа 7 в степень, кратную 4, получается число, оканчивающееся цифрами 01
(доказать).
60. Используем метод математической индукции. Предположим, что число
пр_1 удовлетворяет условию 3^~2<	З^"1 и что для обнаружения фальшивой
монеты достаточно р — 1 взвешиваний. Возьмем пр монет и разделим их на три
группы так, чтобы в двух равных группах было по З^-1 (или меньше) монет, а
число монет в третьей группе было бы не больше З^1. Положив на чашки весов
две группы из равного количества монет, определим, в какой из трех групп со-
держится фальшивая монета (одно взвешивание). Согласно допущению для вы-
деления фальшивой монеты из этой группы достаточно (р — 1) взвешиваний, т. е.
всего р взвешиваний. Предположение, очевидно, справедливо при /г — кт. е.
при п = 2 и при п = 3.
254
§ 2.
62.	Пусть D = а — buDt- (a:k) —• b " p — b, где a — kp\ kp = pk =»
= p (k — 1) -f- p. Тогда D = a — b — pk — b p (k — 1) + p — b =
= p (k — 1) -r Dr или £>x D — p (k — 1) = D — (a : k) (k — 1).
63.	Пусть P = a ♦ b и Pi — (a : k) (b  k), где а делится на k и k — нату-
ральное число, тогда Рг = [(а : k) • k\ > b (ассоциативность умножения), но
(а : k) • k = а, следовательно, Р± = а • b ~ Р.
64.	Пусть а : b = k, откуда а = bk\ если с — некоторое натуральное чис-
ло, то ас => bkc, или ас — b (kc), но (ас) : b — kc (см. определение), или (ас) : b —
— (а : Ь) • с.
65.	Пусть а = bk + г, где г > 0, но меньше Ь. Пусть с — некоторое нату-
ральное число, тогда ас = (bk)c + rc~ (bc)k + г, но г меньше Ь; значит, гс
меньше Ьс и гс — остаток от деления ас на Ьс. Значит, остаток увеличился в с раз.
66.	Пусть а = bk + г, где г — натуральное число, меньшее Ь, и пусть также
а = х± + х2 + ... + хп. Обозначим через аА сумму: аг = х± + х2 + ... + хп+
+ cb, где с — натуральное число. Тогда аг = (хх + х2 + ... + хп) + cb —
= а + cb — (bk + г) + cb = (k + с) b + г.
69.	а) Пусть a — bk 4- г, где 0 < г < Ь, и а + х = bk + гх; откуда х =
« bk + гх — bk — r—rY — г, т. е. х -г г < Ь, или х < b — г;
б) см. пункт а).
70.	См. решение задачи 69;	k (а + 1) A < (а + 1) (k + 1).
71.	А — 10а ~г Ь — данное	двузначное	число. А-9 = (10а + Ь)	•	(10 —	1)	=
= 100а	+ ЮЬ — 10а — b = 10 [(10а + b) — (а + 1)] + (10 — Ь).
72.	А — 10а ~г b — данное	двузначное	число. А • 99 — (10а	+	Ь)	•	(100—
—1) =	1000а	+ ЮОЬ — 10а	— b = 100 (10а + b — 1) + [100 — (10а + Ь)].
73.	А —	10а + b — данное двузначное число, а + b < 10. А • 11 =
= (10а + Ь) (10 + 1) = 100а + 10Ь + 10а + b = 100а + 10 (а + Ь) + Ь.
76.	А =	10а + Ь, В =	10 (а + 1) + (10 — Ь) — данные двузначные числа.
А •	В = (10а	+ Ь) [10 (а +	1) 4- (10 — Ь)] = 100а2 4- Ю0а 4- Ю0а — ЮаЬ +
4- ЮаЬ + 10Ь + ЮЬ — Ь2 = (100а2 + 200а 4- 100 — 100) 4- (100 — 100- Ь2 4“
4- 20Ь) = 100 [(а 4- I)2 — 1] + ЮО — (10 — Ь)2.
77.	Положить А = 10а + Ь, В — 10а + (10 — Ь) и найти А • В.
(д________1 \
А 4-----2/’ Ю + 5, где А —данное нечетное'число.
79.	См. решение задачи 78.
80.	Натуральное число может иметь один из видов: 4k, 4k + 1, 4k 4- 2,
4k 4" 3. Пусть A = 4k 4" 3, тогда A • 25 = (4k 4" 3) • 25 = 100/s 4~ 75, где k —
частное от деления числа А на 4. Аналогично доказывается и для первых трех
случаев.
82.	Обозначить данное трехзначное число через ЮОп + 10 (п + 1) +
(п 4" 2) и вычислить указанную в условии задачи разность.
83.	Обозначить данное трехзначное число через А • 100 4" В • 10 4- С,
причем А > С. Составить разность согласно условию задачи, учесть, что С < А,
и подсчитать сумму цифр полученного числа.
85.	Пусть А и В — данные числа (трехзначные), причем А + В делится
на 37, но ни А, ни В не делятся на 37. Шестизначное число, составленное из дан-
ных трехзначных чисел, имеет вид 103А + В = 999А + (А + В), или 103В 4~
4- А = 999В + (А *+ В). В обоих случаях полученное шестизначное число де-
лится на 37.
86.	Пусть трехзначное число 100А + 10В + С делится на 37, т. е. 100А +
+ 10В + С == 37k, где k — целое число. Составим другое трехзначное число
из тех же цифр, например 100В 4- ЮС 4~ А, но 10В = 37k — 100А — С; значит,
100В + ЮС + А = 370/? — Ю00А — ЮС 4- ЮС + А = 3706 — 999А делится
на 37. Установить, какие еще перестановки цифр данного числа дают число, де-
лящееся на 37.
87.	Число 10 и его степени при делении на 6 дают в остатке 4, так как Юл в
« IQj^O = 9 ... 9 + 1 = 3 • (3 ... 3) 4“ 1 + 3 — 3 = 3 • (33 ... 3 — 1) +
а	а	а	а
255
4-4=3«3 ... 32 + 4. Установить остаток, который даст при делении на 6
л—1
число N = ап\0п + ая_110'г-1 + ... + а0.
90.	Доказательство проведем методом математической индукции. Пусть
в данном числе п нулей, где п — число четное.
а)	При п = 2 утверждение справедливо, так как 1001 делится на 11.
б)	Допустим, что утверждение справедливо при п = 2k, и докажем, что оно
будет справедливо при этом и для п = 2k + 2; N => 10 ... 01 = 10 ... 01 +
' ST"
+ 990 ... 0= 10 ... 01 + 99 * 10 ... 0, но 10 ... 01 делится на И по допуще-
"Ik+l """‘ЯГ'
нию и 99 делится на 11.
91.	См. задачу 90.
92.	Пусть цифра десятков данного трехзначного числа есть х, цифра еди-
ниц — у, тогда цифра сотен будет 7 — х — у, причем 7 — х — у > 0, или
х + У < 7... (1). Рассматриваемое число имеет вид 100 [7 — (х + у)] + 10х +
+ у = 700 — 90х— 99у ... (2). Если х =* у, то это число приводится к виду
700 — 189х, т. е. к числу, кратному 7, так как 700 и 189 делятся на 7. Обратно,
если 700— 90х — 99у кратно 7, то х = у (доказать!).
93.	Число N = ап10л + аЛ_Л0'г“1 + ... + яг10 + а0 делится на 11, если
число Q = (а0 + а2 + ... + a2k + ...) — (а± + а3 + ... + a2fc+i + •••) Делится
на 11, и обратно.
Число N делится на 101, если число Q = (ад, + а5а4 + ...) — («3«2+
+ «7£б_+ •••) делится на 101, и обратно. Число JV делится’на 33, если Q = ага0 +
+ «за2 + ••• делится на 33, и обратно.
94.	Пусть а — число десятков данного числа А, b — цифра единиц. Обозна-
чив сумму а + 4Ь через Ар составить разность 10А! —А и установить справед-
ливость утверждения. Рассмотрев разность А — Ар установить, какое из этих
чисел больше.
95.	Пусть N = 1 Оу + х; тогда (2х + Зу) + 17у = 20у + 2х = 2(10у + х)=
2W, т. е. число N делится на 17, если делится на 17 число 2х + Зу, и обратно.
96.	О т в е т: с = 9.
Учесть, что а 9 • 1973 = 17 757 — пятизначное число, тогда b С 9 • 5 8=3
>=45 — двузначное число, делящееся на 9.
98.	Любое натуральное число при делении на 2 дает в остатке 0 или 1.
100.	А = 3k + 1, В = Зп + 1, А • В =» Зр + 1, где р = 3kn + k + n.
101.	См. задачу 100.
102.	А = п (п+1). Рассмотреть возможные виды числа п : п = 3k, п=*
= 3k + 1, п = 3k + 2.
103.	Пусть а и b — данные целые числа, т — натуральное число. Учесть,
что тогда а = mq1 + г, b = mq2 + г, где 0 < r < m, qv q2 — целые числа.
104.	Учесть, что по условию задачи а = qm + b, где q — целое число.
105.	Учесть, что из условия данной задачи и задачи 103 следует делимость
на k каждой из разностей: аг — Ьг, а2 — Ь2, ..., ап — Ьп, Составить сумму этих
разностей. Учесть также, что из условия задачи следует:
«1 = bl + kqt
^2 =
ап~ + Мп»
где qlt q2, ..., qn — целые числа. Составить произведение этих выражений.
107.	Доказать делимость числителячдроби на 2 и на 3.
109.	Показать, что имеет место делимость на 3 и на 8.
115.	А = 2 (п — k) ♦ 2 (n + k + 1). Из чисел п — k и n + k + 1 одно
четное (доказать!).
116.	Разложить полученный многочлен на множители.
122.	а) См. задачи 115, 118.
256
123.	Если а или b делится на 3, то справедливость утверждения очевидна.
Если а и b не делятся на 3, но при делении на 3 дают одинаковые остатки, то
а — b делится на 3; если а и b при делении на 3 дают разные остатки, то а + b
делится на 3, так как разными остатками при делении на 3 могут быть только
числа 1 и 2, которые в сумме дают 3.
124.	См. задачу 123.
125.	Рассмотреть различные случаи: а или b (или оба) кратно 5; а и b не кра-
тны 5, но при делении на 5 дают одинаковые остатки; а и b не кратны 5, но при
делении на 5 дают остатки, сумма которых кратна 5; а и b не кратны 5 и при де-
лении на 5 дают разные остатки, сумма которых не кратна 5. Можно использо-
вать также задачу 40.
126.	Следует доказать делимость выражения на 4 и на 11, для чего преобра-
зовать данное выражение к виду 1919 + 6969 = (20 — I)19 + (68 + I)69 (делится
на 4), а также к виду 1919 + 6969 = (22 — З)39 + (66 + З)69 = 1U + З69—
— З19 = 11/г + З19 • (З50 — 1) = 11/г + З19 (24310 — 1), но 24310 — 1 делится
на 11, по задаче 40.
127.	Обратить внимание на то, что 1969 = 11 • 179, преобразовать данное
выражение (а) к виду (210 — 1) (21?8 — 1) и использовать задачу 40. Остальные
задачи решаются аналогично.
128.	а) Число, не делящееся ни на 2, ни на 3, не делится и на 6, т. е. может
быть представлено в виде 6n + 1 или 6п + 5, так как остальные числа, не крат-
ные 6 (6п + 2, 6п + 3, 6п + 4), делятся или на 2, или на 3.
б, в) Вычислить указанные произведения и установить их вид.
129.	Целое число может быть четным, т. е. иметь вид 2п, или нечетным, т. е.
иметь вид 2n + 1; рассмотреть квадраты таких чисел.
130.	Целое число может иметь вид Зп, Зп + 1 или Зп + 2; установить вид
квадратов этих чисел.
131.	Целые числа, не делящиеся на 5, имеют вид 5п + 1, 5п + 2, 5п + 3,
5п + 4 или 5п ± 1; 5п ± 2; установить вид квадратов этих чисел. Можно ис-
пользовать задачу 40.
132.	См. решение задачи 131.
133.	Натуральное число, не делящееся на 7, может иметь вид 76 + 1,
7k + 2, 7k + 3, 7k + 4, 7k + 5, 7k + 6 или 7p ± 1, 7p ± 2, 7p ± 3. Найти
квадраты этих чисел и показать, что ни одна из комбинаций этих чисел, как
сумм двух слагаемых, не дает числа, делящегося на 7.
134.	См. решение задачи 130.
135.	По условию задачи имеем: (п2 — l)n2 (n2 + 1). Доказать делимость
этого выражения на 4, 3 и 5.
136.	По условию задачи имеем: А =» (п3 — l)n3 (n3 + 1) и 504 — 23 • З2 • 7.
' 137. Преобразовать данное выражение, учтя, что число а нечетное, т. е.
имеет вид 2k + 1.
138.	Установить делимость данного выражения на 2 и 3.
139.	См. задачу 138.
140.	Преобразуем выражение, данное в задаче: а3 + 11а = а3 — а + 12а =
= (а — 1)а (а + 1) + 12а.
141.	Если (п, 6) = 1, то (п, 2) = 1 и (п, 3) = 1, и, значит, п — 1 и n + 1 —
последовательные четные числа, произведение которых делится на 8 (почему?).
Известно, что произведение трех последовательных натуральных чисел делится
на 3, т. е. (п — l)n(n + 1) делится на 3, но п делиться на 3 не может, так как
согласно условию задачи (п, 3) == 1; значит, одно из чисел (п — 1) или (n + 1)
делится на 3.
142.	Разложить данный многочлен на множители и рассмотреть делимость
произведения на 4 и на 9.
143.	Разложить данный многочлен на множители.
144.	Разложить данный многочлен на множители и учесть, что х имеет вид
2n + 1.
145.	Разложить данный многочлен на множители.
146.	Выделить слагаемые, кратные 120, оставшееся выражение разложить
на множители.
147.	Преобразовать данный многочлен в сумму двух слагаемых.
9 Заказ 1089
257
148.	Разложить данный многочлен на множители.
149.	Разложить данное выражение на множители; установить делимость
произведения на 2, на 3, на 5.
150.	Разложить данный многочлен на множители, разложить число 1152
на множители и доказать делимость произведения на каждый из этих множителей.
151.	Разложить данный многочлен на множители и доказать его делимость
на 29.
152.	Разложить данный многочлен на множители. См. задачи 125, 40.
154.	Учесть, что ал+4 — ап = ап (а4 — 1).
155.	См. решение задачи 154, имея в виду, что А = п2(п4—1) = (п — 1)«Х
Х(и+ l)n(n2 + 1). Провести доказательство, не ссылаясь на задачу 154.
156.	По условию задачи имеем: А = (2п + I)5 — (2п + 1) = (2и + 1) X
X [(2n + I)4 — 1] = 2п (2п + 1) (2n + 2)[(2n + I)2 + 1]. См. задачу 40.
157.	Преобразуем выражение, данное в условиях: А = а (а2 — 1) X
X (а2 — 4) = (а — 2) (а — 1)а (а + 1) (а + 2). Данное выражение делится на
720 при любом значении а, кроме а = 3.
158.	Пусть А = п (п2 — 49) (п2 + 49).
А делится на 2, так как либо п, либо п2 + 49 — числа четные;
А делится на 3, так как если п кратно 3, то справедливость утверждения
очевидна, если же п не кратно 3, то п может иметь вид 3^+1 или 3k — 1, тогда
п2 — 49 = 3(3fc2 ± 2k) — 48 делится на 3.
Рассуждая аналогично, можно показать, что А делится на 5. См. задачу 40.
159.	Преобразуем данное выражение: (х2у3 — 4х2у) (х4 + х2 — 2) =
= х2 (х2 — 1) (х2 + 2)у (у2 — 4). Число у (у2 — 4) кратно 3 (проверить); число
х2 (х2 — 1) (х2 + 2) кратно 8, так как при х четном х2 кратно 4, а х2 + 2 кратно
2; при х нечетном х2 — 1 кратно 8 (проверить); число х2 (х2 — 1) (х2 + 2) кратно
9 (проверить). Следовательно, А кратно 3 • 8 • 9 = 216.
160.	Преобразовать данное выражение к виду у2 (х3 — х) + х (у + 1)у2 +
+ х (х — 1) (х 4- 1), показать делимость первого и третьего слагаемых на 6,
установить делимость второго слагаемого на 2 и найти выражение для у, чтобы
х (у + 1)у2 делилось на 3, положив х = 1.
Ответ: у должен быть числом вида 3k или вида 3k — 1.
161.	Представить рассматриваемое выражение в виде 4 (32Л+2 + 8м — 9) и
рассмотреть случаи: п — число четное; п — число нечетное.
162.	Преобразовать данное выражение к виду: а2 (а — 2) (а— 1) X
X (л + 1) (л + 2); показать, что (а — 2) (а — \)а (а +1) (а + 2) делится
на 120; показать также, что это выражение делится на 9, т. е. что рассматривае-
мое выражение делится на наименьшее общее кратное чисел 120 и 9. Установить
что если а делится на 3, то а3 делится на 27, т. е. данное выражение делится на
наименьшее общее кратное чисел 120 и 27, т. е. делится на 1080. Показать, что
если а не кратно 3, то а может быть представлено в следующем виде: а = 9k ± 1;
а = 9k ± 2; а = 9k ± 4, и непосредственной проверкой установить, что если
число а вида 9k ± 1 и 9k ± 2, то данное выражение кратно 1080, в остальных
случаях оно не кратно 1080.
163.	S =1 + 22+ ... + п2— —	"•(см. задачу 3), причем S—це-
6
лое число. Если число п вида 5/г, 5^+4 или 5&+2, то множители и, n + 1 или
2п + 1 кратны 5, а следовательно, и числовая величина S будет кратна 5, так как
S — число целое, а знаменатель этого выражения не делится на 5. Значит, число
п может быть одного из видов: 5k + 1 или 5k + 3. Поэтому сумма 1 + 2 + ... +
. п (п 4-1)
+ п =-------—— приводится к одному из двух выражении:
(5k + 1) (5k + 2) k (5k + 3)
«1=	2	=	2	' 5+1
ИЛИ
S2 = ,.g + W<). = 5» (St+7), + 6 Но ч>сла ( (a +!) _ , (5i +
258
четные, следовательно, сумма 1 + 2 + 3 + ... + п при делении на 5 дает в
остатке 1.
164.	Пусть 1" + 2я + ... + (k — 1)п + kn = Ak. Тогда 2Ak = [Iя + 2п +
+ ... + (k — 1)я 4- kn] + \kn + (k — 1)я + ... 4~ 2я 4~ Iя] = (Iя + kn) 4-
4- [2й 4“ (6 — 1)я]4“ ... 4" [(6я 4“ 1)] ... (1). Но при нечетном п каждая из ско-
бок делится на сумму х 4" (k —х + 1) = & 4~ 1; следовательно, 2Ak делится
на k 4“ 1, а 2Аа делится на а 4- 1. Но 2Аа = 2[1Я 4- 2п + ... 4~ (л — 1)я] 4-
4- 2ап= 24a_x4- 2ап ... (2). По доказанному выше 2Аа_1 кратно а, следователь-
но, 2Аа тоже кратно а. Значит, число 2Аа кратно числам а и а + 1, но (а, а 4~
4“ 1) = 1; следовательно, 2Аа делится на а (а 4- 1), т. е. 2Аа = а (а 4- 1) • В...
(3), или 1« + 2» + ... + (а - !)»+ ап = В • —= В (1 + 2 + ... + а),
т. е. 1л 4" 2я + ... 4” (а — 1)я 4" ап делится на 1 4~ 2 4" ••• 4~ а при нечетном п.
165.	Наименьшее число, делящееся на 2, 3, 4, 5, 6, есть 60, следовательно,
искомое число имеет вид 60& + 1 и одновременно кратно 7. Искомое число 301.
166.	Прибавив к искомому числу 1, получим число, делящееся и на 2, и на 3,
и на 4, и на 5, и на 6. Найти наименьшее из таких натуральных чисел. Искомое
число 59.
167.	Пусть mN = QD 4- i\ и m±N = QrD 4- г2. Если i\ = г2» T0 (Qi — Q)X
%D= (тг — m)N; так как (D, N) = 1, то — m делится на D, что невозможно,
если т и тх есть различные числа ряда 1, 2, 3, ... D — 1, значит, ф г2.
168.	а) 1416 при делении на 17 дает в остатке 1 (задача 40); (1416)16 при деле-
нии на 17 тоже дает в остатке 1 (задача 106). Ответ: 1.
б)	Учесть, что 6592 = 6590 • 36. Использовать задачи 40 и 105. О т в е т: 3.
в)	Учесть, что 796 и 1196 при делении на 13 дают в остатке по 1. О т в е т: 12.
г) 0; д) 5; е) 4; ж) 0.
170.	Установить, делится или не делится на 5 разность и произведение со-
ответствующих членов этих поеледователь ностей.
171.	Обозначив а1а2а3= 4, а4а5а6 = В, получим следующее условие: 1034 4-
+б=(А+в)2, или (103—1)А=(4+б)(А+б—1), или А = —---.
Рассмотрев возможные случаи делимости (4 4~ В)(4 4" В— 1) на 27 и 37, полу-
чим числа: 998 001, 494 209.
172.	204 304, 301 401, 525 625, 544 644. См. предыдущую задачу.
173.	Введя обозначение: abed — искомое число, получить равенство
100(10^4“ Ь) = (10с 4~ <0 (Юс 4“ d — 1). Обратить внимание на то, что правая
часть равенства — произведение двух последовательных двузначных чисел,
делящееся на 100; найти эти числа и установить, какая из пар чисел удовлетво-
ряет условиям задачи. Ответ: 5776.
174.	Рассмотреть п чисел вида 101, 10 101,... , 1 010 101 ... 01 и допустить,
что ни одно из них не делится на п, взаимно простое с 10. Доказать, что тогда
среди этих чисел найдутся два, разность которых должна делиться на п, опре-
делить вид этой разности и установить противоречие с допущенным.
175.	Ответ: 550 и 803. Представив искомое трехзначное число в виде
100а + 106 4- с, будем иметь: а 4~ 6 + с С 27; а — 6 4~ с = 0 или а — b + с =
= 11 (по признаку делимости чисел на 11, см. задачу 93); 100а 4" 106 -j- с =
= 11 (а2 4“ 62 4“ с2) по условию. Преобразовав последнее равенство при условии
с
а — 6 4" с = 0, получим уравнение а2 4~ (с — 5) а 4“ с2 — — = 0, решив кото-
рое относительно а и имея в виду, что с может быть только выражено цифрами
0, 2, 4, 6 (доказать), получим число 550. Аналогичные рассуждения при условии
а — 6 4“ с = И приводят к числу 803.
176.	По условию задачи 100 < k2 < 1000, следовательно, 10 < k < 31.
Пусть k2 = ЮОх 4~ 10у 4~ z, xyz = k — 1, причем z =# 0, так как в этом случае
все произведение было бы равно нулю, и z нечетное, так как в противном случае
k четное и k — 1 нечетное, чего не мржет быть при четном z. Кроме этого, z может
быть равным только 1, 5 и 9 (на эти числа оканчиваются квадраты нечетных чи-
сел), Из таблицы квадратов выбираем трехзначные числа, оканчивающиеся на
9*
259
1, 5 и 9, произведение цифр которых не больше 31. Это числа 121, 225, 361 и 441.
Условию задачи удовлетворяет одно число 361.
177.	Пусть двузначное число есть 10а + Ь, тогда по условию зада-
чи 10а + Ь+ \0Ь + а= 11 (а + b) — k2. Следовательно, k2 делится на 11,
а значит, и k делится на 11, т. е. k2 делится на 121. Определить возможные значе-
ния для а и Ь, если а + b — 11. Искомые числа есть 29, 38, 47, 56, 65, 74, 83, 92.
178.	Разложить выражение, вид которого определяется условием задачи,
на множители: п (п + 1) (п + 2) (п + 3) + 1 — (п2 + За) (п2 + Зп + 2) + 1 =
= (п2 + Зп)2 + 2 (п2 + Зп) + 1 = (п2 + Зп + I)2.
179.	Пусть 2п + 1 и 2k + 1 — два нечетных числа. Сумма их квадратов —
число четное. Установить, что если эта сумма является квадратом целого числа,
то она должна быть кратна 4, и показать, что в данном случае это невозможно.
180.	Рассмотреть числа вида п —2, п — 1, п, п + 1, п + 2. Найти сумму
их квадратов, преобразовать ее в произведение и показать, что множитель про-
изведения, отличный от 5, не может быть кратен 5.
181.	Пусть А — некоторое целое число, тогда А = В • k + р, где р — не-
отрицательное число, меньшее В; А2 = В2 • k2 + 2Bkp + р2, т. е. А2 и р3 при
делении на В дают одинаковые остатки, так как А2 — р2 делится на В (почему+
а) Если В = 3, то р может принимать значения 0,1 и 2, ар2 соответственно
значения 0, 1 и 4, но 4 =-3 • 1 + 1; значит, р2 может быть равно 0 или 1 (р < 3),
откуда А2 = Зп или А2 = Зп + 1, но не Зп — 1.
б)	Если В = 5, то р может принимать значения 0, 1, 2, 3 и 4, а р2 — значе-
ния 0, 1, 4, 9 и 16 или А2 = 5п, 42 = 5п + 1, 42 = 5п + 4, но не 5п + 2 или
5п — 2.
Аналогично доказываются остальные утверждения.
182.	Число вида 12п + 5 можно представить как 3k — 1, так как 12п + 5 =
«= 12п + 6 — 1 = 3 (4п + 2) — 1, но в таком виде нельзя представить квадрат
натурального числа (см. предыдущую задачу).
183.	2т — 1 — число нечетное, следовательно, числа а и b тоже нечетные,
а + 1 и b — 1 четные. Пусть высшие степени 2, на которые делятся а + 1
и b — 1, будут соответственно 2х и 2у, тогда а + 1 == 2х • u; b — 1 = 2у • v,
где и и v — числа нечетные. Откуда а= 2х • и — 1, b = 2у • v + 1, ab —
= (2х • и — 1) • (2у • t>+ 1), или ab = 2x+yuv + 2хи — 2yv — 1 = 2т— 1, или
2x+yuv + 2хи — 2yv = 2m.
Если х < у, то 2x(2yuv — 2у~х* v + и) = 2т, но это равенство невозможно,
так как число 2yuv — 2y~xv + и нечетное ввиду нечетности пив то же время
число это больше единицы, так как 2yuv > 2y~xv.
Аналогично если х > у, то невозможно равенство 2у (2xuv + 2х~уи— v)=
= 2т, так как v нечетное и не равно единице. Следовательно, х = у.
184.	Имеем:, (п2 — 1)^ • (п — 1)^+1 = (п + (п — 1)2^41. Если из (п + 1)^
вычесть единицу, то получим величину, кратную п, т. е. (п + 1)^ — 1 = ап.
Откуда (п + 1)^ = ап + 1. Также (п — 1)2^+1 + \ — Ьп и (п — l)2P+i =	— 1.
Имеем: (ап + 1) (Ьп — 1) = abn2 + Ьп — ап — 1. Следовательно, если к дан-
ному выражению прибавить единицу, то оно будет кратно п.
185.	Обозначив nk = р, преобразовать данное выражение к виду
(Зр3 + Зр + 9) - (р - 1)р (р + 1) + 1.
Учесть, что произведение трех и более последовательных натуральных чисел
делится на 3 (см. задачи 102 и 107).
186.	По условию задачи имеем: А — 5 = 9х, А = 9х + 5. Допустим, что
Д =	Где у — целое число, и у — 9k ± р, где k — целое число, а р может
принимать одно из значений: 0, 1,2, 3, 4. Тогда А = у4 = (9k ± р)4 — 9п + р4.
Следовательно, А дает при делении на 9 такой же остаток, что и р4. Но р4 может
иметь одно из значений: 0, 1, 24, З4, 44 и при делении на 9 может давать в остат-
ке соответственно 0, 1,7, 0, 4; значит, и А при делении на 9 дает такие же остат-
ки, что противоречит условию.
187.	Преобразуем данное выражение: k (k2 — 1) (k2 — 4)=(/?— 2) (k — 1)х
yk (k + 1) (k + 2); оно делится на 120, причем 120 = 15 • 8 и 480=15 • 32.
Если k — четное число, т. е. k = 2т, то k (k2 — 1) (k2 — 4) = 8 (m — l)mX
Х(пг+ 1) • (2m + 1) • (2m— 1). Чтобы это число делилось на 32, достаточно,
чтобы т было кратно 4.
260
Если т — нечетное число, то рассматриваемое выражение делится на 32.
Следовательно, т должно быть вида т — 4t или т = 2t + 1; откуда k = 84,
k = 4^+2, где t — любое целое число.
Если k — нечетное число, т. е. k »= 2т + 1, то k (k2 — 1) (/г2 — 4) =
= 4m (т + 1) (2т + 1) (2т — 1) (2т + 3).
Для того чтобы это выражение было кратно 32, необходимо и достаточно, чтобы
т (т + 1) было кратно 8, что возможно лишь при т = St или т + 1 = 8^;
откуда k = 2т + 1 = 16^+1 или /г = 16^ — 1. О т в е т: k *= St, k =4t + 2,
fe=16f+l, k = 16/ — 1.
188.	Учесть, что если число при делении на 3 дает в остатке 1, то любая его
натуральная степень при делении на 3 тоже дает в остатке 1; если же число при
делении на 3 дает в остатке 2 => 3 — 1, то любая четная степень его дает при де-
лении на 3 в остатке 1, а нечетная —2. Значит, из четных степеней трех последо-
вательных чисел одна делится на 3, а две другие дают при делении на 3 в остат-
ке 1. Следовательно, сумма этих степеней при делении на 3 дает в остатке 2, но
такого остатка не может дать при делении на 3 никакая четная степень целого
числа, так как целое число может иметь вид N = 3k, N — 3k + 1, N = 3k + 2 =
= 3kr — 1.
189.	Из предыдущей задачи имеем, что сумма четных степеней трех последо-
вательных целых чисел при делении на 3 дает в остатке 2; значит, сумма четных
степеней девяти последовательных чисел при делении на 3 дает в остатке 6, т. е.
делится на 3. Доказать, что эта сумма не делится на З2 = 9, чем и будет доказано
утверждение задачи. Рассмотреть сумму 0 + I2* + 22k + 32Л + 42ft + 52fe +
+ 62ft + 72Л + 82^, показать, что она дает такой же остаток при делении на 9,
как и сумма 2 (1Л + 4k + 7*), и учесть, что число k может иметь один из видов:
=== Зп, k = Зп + 1, k = Зп + 2.
190.	Пусть N = nD. Первое число, делящееся на D, есть D, второе — 2D,
третье — 3D и т. д., последнее число есть nD, или N. Следовательно, от 1 до N
делятся на D следующие числа: D, 2D, 3D, ... , nD=> N, т. е. всего чисел, удовлет-
воряющих условию, будет п.
191.	Ответ: п= 11 ... 1, где цифра 1 повторяется 130 раз. Число п мож-
102* — 1
10—1 ’
но представить в виде а*
Задача сводится к отысканию наименьшего на-
турального значения k, при котором 102Й — 1 делится на 131. Задача 40 позво-
ляет утверждать, что число, составленное из 130 одинаковых цифр, делится на
131 (пояснить). Остается доказать, что число, составленное из меньшего количе-
ства одинаковых цифр, не делится на 131 (обратить внимание на то, что 2k долж-
но быть делителем 130).
192'	N, ° 10006 + 376 }	= (1°3а + 376) (103й + 376) “ 1О’а6+
+ 376 • 1(А + 376 • 1036 + 3762 = 103 (108а6 + 376а + 3766 + 141) + 376.
Аналогично доказывается и в остальных случаях.
193.	(10а 4- Ь)2 «=» 10 (10а2 + 2а6) + Ь2; 10а2 + 2аЬ — четное число; сле-
довательно, Ь2 должно содержать нечетное число десятков, что возможно только,
если Ь2 == 16 или Ь2 = 36.
п (п | 1)
194.	Известно, что 1 + 2 + 3 + ... + п	. Установить, какими
цифрами оканчиваются произведения и полу произведения двух последователь-
ных однозначных чисел.
Ответ: 3, 6, 0, 5, 1, 8.
195.	Допустив противное, доказать, что четное число должно быть равно
9 • 1973, что невозможно.
196.	Пусть искомое число есть х. Тогда сумма всех чисел, входящих в табли-
цу» будет (1 + 2 + 3 + ... + х) • (1 + 2 + 3 + ... + х) == 36 100, откуда
1 + 2 4-... + №> 190, —190 и № 19.
197.	Представить 9 в виде 10—1 и рассмотреть вид произведения, которое
может получиться при условии задачи.
261
198.	1025s = 510 • 41s;
1024s = 2S0;
1 048 5768 = 2180;
1 048 5758 = 38 • 5“ • ll8 • 31s • 418;
65603 = 21S • 53 • 413;
65613 = 324;
15 6248 = 224 • 316 • 78 • 318;
15 6258 = 548;
98014 = 318 • ll8;
98004 = 212 • 58 • 78;
A = 219«.
199.	Данный ряд чисел представляет собой разложение бинома Ньютона,
если положить х = 1; а = 1; п = 104, т. е. (1 + I)1’4 = 21’4 = 210 °00. Харак-
теристика логарифма этого числа ЗОЮ, следовательно, число 210 000 имеет ЗОН
цифр.
200.	Учесть, что х (х 4- 1) (х + 2) (х + 3) < (х + 2)4, х (х + 1) (х + 2) X
Х(х + 3) > (х + I)4. Искомые числа: 5, 6, 7, 8.
201. Пусть три целых последовательных числа будут х — 1, х, х+ 1. По
х	XX + 1 х______1
условию задачи -; + —— +-----+-----Н-
X — I х+ 1 X X
тановить, при каком условии —-— целое число,
X2 — 1
х—1	х+1	6х2
---- 1 --- —. --- ус.
х+1	х-1	X2— 1
учтя, что (х2, Xs—1)= 1, т. е.
х2 — 1 = 1, или х2 — 1 = 2, или х2 — 1 = 3, или х2 — 1 = 6. Искомые числа:
—3, —2, —1 или 1, 2, 3.
202.	Пусть искомое число х, а его последняя цифра а, тогда число без послед-
. Х~ а
ней цифры выразится .
Новое число, которое получится после перенесения
в числе х последней цифры на
х — а
первое место, будет а • 10я1 Н-.
х — а
По условию имеем: —---------1- а • 10я1 = а • х, или а • 10w+1—а = х(10а—1).
Отсюда видно, что для получения искомого числа х нужно делить число, выражен-
ное цифрой а с неопределенным количеством нулей, на число 10а — 1 до тех пор,
пока в остатке не получится а. Давая а различные значения, получим искомое
число.
203.	1) 218 + З18 = (2е + З6) (212 — 2е • 3е + З12) = 13 • 61 • (212 — 2е X
ХЗ6 + З12), так как 26 + 3е = (22)3 + (З2)3 = (22 + З2) (24 — 22 • З2 + З4) =
= 13 • 61.
2)	212 — 2е • З6 + З12 = (З6 — 26)2	+ 6е = (З3 —	23)2	•	(З3 +	23)2 +
+ 6е = (3 — 2)2 (3 + 2)2 (З2 + 3 • 2 + 22)2 .	(З2	— 3  2 +	22)2	+	6е =	А.
Обозначим 2-3=6, тогда 3 + 2= 5= k — 1; З2 + 3 • 2+ 22 — 19 = 25—6 =
= (6 — 1)2 — 6; З2 — 3 • 2 + 22 = 7= k+	1;	66 =/г2;	64	=	3662.	Тогда
А = (62 + 1) (2k2 + 1) (562 + 1) = 37 • 73 • 181	(обосновать!).
204.	а) Общий вид чисел 4 • 10я- (10«-J+ 10я~2+ ... + 1) + 8 • 10 (10я-2+
/ 10я — 1 \	/10я-1— 1\
+ 10я'3 + ... + 1) +9 = 4 • 10я • I---------------J+ 8 - 10 -I----------) +9=»
. 4 . ю2Я + 4 • 10я + 1	/ 2 • 10я + 1 \2	,
= ----------------------- = I---------------I , так как 2 • 10я + 1 всегда делится
/ 2 • 10я + 1 V
на 3 без остатка, то I----------I — целое число.
205.	а) Если число 1234xi/ делится на 8, то 4ху делится на 8, т. е. 400 + 10х +
+ У = 8р ... (1).
Чтобы 1234 ху делилось на 9, достаточно, чтобы сумма 1 + 2 + 3 + 4+
+ х + у делилась на 9, т. е. 10 + х + у = 9g... (2).
262
Наибольшее значение х + у равно 18, следовательно, 28. Из уравне-
ния (2) 9^ > 10, т. е. q > 1, следовательно, q может иметь только два значения:
2 и 3. Вычтя из равенства (1) равенство (2), получим 390 + 9х = 8р — 9д, или
р = 49+х + ^ +
х + д — 2
8
Чтобы р было числом целым, необходимо, чтобы х + q — 2 делилось на 8.
Если q = 2, то х = 0 или х = 8; если q = 3, то х = 7.
Из уравнения (2) имеем: у — 9q — х — 10, следовательно, у = 0 или у — 8;
значит, искомые числа есть: 123 480 или 123 408.
б)	По признаку делимости числа на 8 имеем: 7у6 делится на 8
или 706 + 10у = 86; следовательно, сумма остатков от деления 706 на 8 и 1 Оу
должна делиться на 8, т. е. сумма 2у + 2 должна делиться на 8, или 2у + 2 =
= 8fep но у С 9; следовательно, у = 7 или у = 3. Если у — 3, то 408 736 +
+ 104 • х делится на 7 или 6 + 4х = 7/г2, но х 9, откуда х = 2 или х = 9.
Если у = 7, то, рассуждая аналогично, находим х = 6. Получаем следующие
числа: 428 736, 498 736, 468 776.
в)	313 138, 495 138.
206.	По условию задачи имеем следующее разбиение ряда нечетных чисел
на группы: 1 + (3 + 5) + (7 + 9 + 11) + (13 + 15 + 17 + 19) + ... . п-я
группа имеет перед собой 1+2 + 3 + ... + (п—1) нечетных чисел, т. е. ~~—~
п (п — 1)
й наминается с >г %---И нечетного числа. Всякое fc-e нечетное число есть 2k—1;
„ Л Г п (п— о
следовательно, первое число рассматриваемой группы есть 2 ---------
—1 = п (п — 1) + 1. Приняв это число за 1-й член арифметической прогрессии
с разностью 2 и числом членов п, найдем ее сумму: S — п (п — 1) + 1 +
+ „(„-!)+ 3 + ... + »(«- 1>+ 2»- 1 = "(r.-l) + l+M.-l> + 2»-lx
X п = л3.
2
2
207.	Пусть N = 2п • k. Возьмем прогрессию: 2х+1, 2х + 3, ... ,
2х + 1 + 2 (2я"1 — 1), разность которой 2, а число членов 2я-1. Сумма всех
членов данной прогрессии есть: S = (2х + 1 + 2я-1— 1) • 2я-1. Положив (2х+
+ 1 + 2я-1 — 1) • 2я"1 = 2я • /г, найдем, что первый член данной прогрессии
есть 2k — 2Я"1+ 1, а последний 2k + 2я"1— 1 и N = (2k — 2я-1+ 1) + (2k —
- 2я-1 + 3) + ... + (2k + 2я-1 — 1).
208.	Пусть W . Возьмем прогрессию: 2х + 1; 2х + 3; ... ; 2х + 1 +
+ 2 (п — 1), разность которой 2, число членов п. Сумма всех членов этой про-
грессии будет S = (2х + п) • п. Полагая (2х + п) • п = па, найдем, что первый
и последний члены прогрессии будут: n<x"-l—-n+ 1 и + п — 1 и что па =
=	_ п + 1) + (Па~1 — п + 3) + ... + (na~l + п — 1).
209.	Однозначных чисел всего 9, двузначных 99 — 9 = 90, трехзначных
999 — 99 = 900 и вообще п-значных 9 • 10я"1. Однозначные числа в выписанном
ряду займут 9 мест, двузначные 90 • 2 = 180 мест, трехзначные 900 • 3 = 2700
мест, четырехзначные 9000 • 4 = 36 000; следовательно, искомая цифра будет
принадлежать четырехзначному числу.
Цифры, принадлежащие не более чем трехзначному числу, будут иметь но-
мера от 1 до 9 + 180 + 2700 = 2889.
Для того чтобы узнать, сколько четырехзначных чисел уложится в проме-
жутке от 2889-го места до 32 454-го места, надо разность 32 454— 2889 = 29 565
разделить на 4, получим 29 565 = 4 • 7391 + 1; таким образом, искомая цифра
будет принадлежать числу 8391 и стоять на первом месте слева, т. е. искомая
цифра 8.
263
210.	1) Однозначных чисел 9, двузначных 90 и вообще m-значных (10w— 1) —
—	—1)= 9 • 10m<l. Чтобы узнать число мест, занятых числами от 1 до
m-значных включительно, надо вычислить сумму:
S = 9. 1 + 9 • 2 • 10 +-9 • 3 • 102 + ... + 9m • 10w-1
(так как m-значных чисел 9 • 10т-1 и каждое из них занимает т мест).
2)	Искомое число S имеет вид (m — 1) 88 ... 89, так как при умножении
т-1
9 на k получится 8 и k — 1 в уме. Действительно, при fe = 2; 9 • k « 18 утверж-
дение справедливо. Допустим, что 9 • k = (k — 1) • 8. Тогда 9 (k + 1) =
= (Ю — 1) . (k -г 1) = 10fc + 10 — k — 1 + (k — 1) = 106 4- 8 = £8.
Следовательно, 9 • 1 + 9*2* 10+9*3* 102 + ... + 9m • IO"1'1 ==
= (m — 1) 88 ... 89.	(1)
m— 1
3)	Если n имеет форму (1), то искомая цифра будет 9, так как последнее из
m-значных чисел оканчивается 9.
4)	Если п не имеет форму (1), то надо взять ближайшее меньшее число вида
(1) и вычесть из п. Например, п = 75 830, ближайшее число вида (1) будет
38 889; 75 830 — 38 889 = 36 941. Эта разность покажет, сколько занято мест
(т + 1)-значными числами до искомой цифры включительно.
5)	Полученную разность разделим на (m + 1). Если деление произойдет
без остатка, то искомая цифра на единицу меньше последней цифры частного.
Если же при делении получается остаток а, то к частному надо прибавить 10ш и
взять в полученном числе а-ю цифру слева, так как (Ь + 1)-е число из (m + 1)-
значных есть 10ш + Ь.
211.	Вычтя из N2 число N, получим согласно условию число, оканчивающее-
ся тремя нулями; следовательно, N2 — N кратно 1000. Таким образом, искомое
число заключается среди таких трехзпачных чисел N, которые удовлетворяют
условию: N2 — N делится на 1000. N2 — N = N (N — 1), но (N, N — 1) = 1;
следовательно, необходимо, чтобы одно из чисел N и А — 1 делилось на 125,
а другое на 8, так как 1000 = 125 • 8.
Допустив, что N делится на 125, установить, какое из трехзначных чисел,
кратных 125, будучи уменьшенным на 1, делится на 8. Затем, допустив, что N
целится на 8, найти его, учитывая, что А — 1 должно делиться на 125. Искомые
значения АЛ 625 и 376.
212.	По условию задачи имеем: = 1000х + ЮОу + Юх + у, или N2 =*
•“ Ю00х + ЮОу + 10у + х, или N3 == Ю00х + ЮОх + 1 Оу + у.
Откуда = 1010х + 101у = 101 (10х + у), т. е. делится на 101; следо-
вательно, если N± удовлетворяет условию задачи, то Юх + У — 101, что невоз-
можно, так как Юх + у < 99. Имеем также N2~ Ю01х + ПОу, N2 делится
на 11, следовательно, N2— II2 • z2, т. е.
1000 о 9999
----< z2<------
121	121
и 3 < z < 9.
Испытывая для z все возможные значения, получаем, что только при z = 8 усло-
вие задачи удовлетворяется, т. е. N2~ II2 • 82 = 882 = 7744. Аналогично для
N3 получаем число 7744.
213.	По условию задачи имеем: 10х + у + х3 + у3 — 10у + х, или х3 +
+ у3 == 9 (у — х). Сумма кубов должна быть однозначна или двузначна; следо-
вательно, ни одна из цифр числа не может быть больше 4. Она не может быть и рав-
на 4, так как в этом случае сумма кубов цифр была бы больше 60, а число, на-
писанное в обратном порядке, было бы меньше 50.
Нельзя взять и цифры 3, так как тогда сумма кубов должна делиться на 9
(см. равенство в начале решения), но этого не будет, если одна цифра будет 3,
а другая отлична от 3. Единственное решение — число 12 : 12 + I3 + 23 = 21.
264
214.	Пусть k есть n-значное число. Тогда среди п + 2-значных чисел, деся-
тичная запись которых имеет вид \^ага2 ... ап, найдется по крайней мере одно,
которое делится на k. Пусть это число есть 10/^ Ь2 ... Ьп. Тогда по условию зада-
чи оба числа brb2 ... &л10 и btb2 ... Ьп01 делятся на k, их разность равна 9 и
также делится на k. Но у 9 делителями могут быть только 1, 3 и 9, следователь-
но, искомыми числами являются 1, 3 и 9.
§ 3
215.	(ab + cd) — (ad+ be) — b (а — с) — d (а — с).
216.	Использовать соотношения при делении с остатком.
217.	а) Пусть а+ b делится на т и ab делится на т, причем т— число
простое. Если ab делится на т, то хотя бы одно из чисел а или b должно делить-
ся на т. Но а + Ь делится на т; следовательно, если одно из чисел делится на пг,
то и другое число делится на т.
б)	Простые множители числа т (все) должны быть делителями числа а либо
числа Ь, и сумма остатков от деления этих чисел на т должна быть равна т или 0.
218.	Если а— b делится на /и, то ас— Ьс тоже делится на т. Составить
разность ас— Ьс— (ad— be),
219.	Использовать метод математической индукции, имея в виду количество
различных простых делителей в каноническом разложении числа N.
220.	Число 572 имеет 12 делителей, число 572а3Ьс имеет 192 делителя.
W N
221.	Учесть, что если pi, р2, . . . , р — делители числа N, то—-, — ,. ..
р‘ "
..., — тоже делители числа N (доказать!), т. е. эти совокупности чисел совпа-
Pk
дают.
222.	а) Если допустить противное, то a (bek— 1) = 11 ... 1, т. е. а — не-
четное число; нечетные также b, с, k, что противоречит условию (показать).
223.	Пользуясь задачей 40, доказать: (аР — ЬР)— (а— Ь) делится на р,
т. е. а — b делится на р и а = pk + b.
224.	Пусть р > д, тогда р— 1 = q + 1. Рассмотреть выражения рР — 1
и их сумму.
226.	Наибольший общий делитель двух данных чисел должен быть делите-
лем их разности.
227.	Допустим, что данные числа есть 2n + 1 и 2п + 3 и что их общий наи-
больший делитель есть d. Учесть, что тогда разность (2п + 3) — (2п + 1) должна
делиться на d,
229.	Учесть, что из данных чисел два числа могут быть четными, а одно не-
четным или два нечетных и одно четное.
231.	По предыдущей задаче (n, 2п + 1) = 1 и (п + 1, 2п + 1) = 1. Из чи-
сел п и п + 1 одно обязательно четное, пусть четным числом будет п. Допустим,
что 2п + 1^ = d, тогда (п, 4п + 2) = 2d, значит, п делится на 2d; 4п + 2 то-
же делится на 2d, следовательно, 2 должно делиться на 2d, что возможно при
d = 1, т. е. 2п + 1 j = 1. Откуда	, 2п + 1^ = 1.
232.	Допустим, что (а, а ± b) = d > 1, тогда а должно делиться на d и
а ± Ь должны делиться на d, а следовательно, и b делится на d, тогда (а, Ь) то-
же делится на d, что противоречит условию, так как (a, b) = 1. Аналогично до-
казывается, что (b, а ± b) — 1.
235.	Допустим, что (а ± b, abp) = d, тогда а ± b делится на d, abp делится
на d, но (ab, а ± b) = 1 (см. задачу 234), следовательно, р делится на d, а так
как р — простое число, то d = 1 или d = р, т. е. (a ± b, abp) = 1 или р.
236.	Преобразуем выражение а2 + Ь2 — ab: а2 + Ь2 — ab= а2 Ь2 +
+ ЗаЬ — ЗаЬ — ab = а2 + b2 + 2аЬ — ЗаЬ = (а + Ь)2 — ЗаЬ. Пусть (а + Ь,
265
(a +	b)9 — 3ab) «• d,	тогда (a + b)9 — ЗаЬ делится на d,	откуда	ЗаЬ делится
на d.	Итак,	(a +	b) и	ЗаЬ делятся на d, но по предыдущей задаче (а + 6, ЗаЬ) =
= 1	или (а	+ 6,	ЗаЬ)	= 3; следовательно, d = 1 или d =	3, т. е.	(а + 6, а2 +
+ Ь2	— ab)	= 1,	или	(а + 6, а2 + Ь2 — ab) = 3.
238. Применить метод доказательства от противного, допустив, что (ас, Ь) =*
*= d> (с, Ь).
239.	Применить метод доказательства от противного, допустив, что
(а + be, а + b(c — 1)) = d1 > d.
240.	Пусть (11а + 2b, 18а + 5b) = d, т. е. На + 2Ь делится на d и 18а +
+ 5Ь делится на d, откуда 55а + 106 делится на d и 36а + 106 делится на d,
разность этих выражений тоже делится на d, т. е. 19а делится на d. Аналогично
рассуждая, находим, что и 196 делится на d, но (а, 6) = 1; следовательно, 19
делится на d, откуда следует, что d — 1 или d = 19.
241.	См. решение задачи 240.
242.	Приняв /и = [а, 6], вычислить наибольший общий делитель частных
[а, 6]	[а, 6]	г м а ' b i	,
----- и 	, используя равенство [а, 6] =	 (необходимое условие),
а 6-------------------------------------------(а, 6)
Доказать достаточность этого условия.
243.	а) Если данные числа попарно взаимно простые, т. е. (п, п + 2) — 1,
(п, п + 1) = 1, (п + 1, п + 2) — 1, то [n, п + 1, п + 2] = п (п + 1) (п + 2).
б)	Если данные числа попарно не взаимно простые, т. е. (п, п + 2) = 2
(см. задачу 228), тогда (п (п + 1), п + 2) = 2 (см. задачу 229) и [n, п + 1] ==
=n (п + 1), откуда
[п, д+1, п + 2] = [л(л+1), п + 2] =
и (и + 1) (и + 2) п(п + 1) (и+ 2)
(п (п + 1), п+2)	2
245.	Пусть (а, 6) = d, (а + 6, [а, 6]) = d', тогда а + 6 делится на d', —
d
ab
тоже делится на d', т. е. а + 6= d'k, = d'k', (k, k') = 1. С другой стороны»
d
ab
а = ud, b — dv\ следовательно, a + b = d (и + v), — = udv, или d (u +
d
+ o)= d'k, udv —d'k'. Откуда d'k делится на d и d'k' делится на d, но (k, k')—
= 1; следовательно, d' делится на d. Аналогично доказывается, что d делится
на d'.
246.	Использовать метод математической индукции.
247.	Пусть а = bq + г, 6 — г < г, т. е. 6 < 2г, тогда а = 6 (q + 1) —
— (6 — г) и вместо г можно рассматривать (6 — г).
Пример. (6552, 448) = ?
/ способ
6552 = 15 • 448 — 168;
448 = 3 • 168 — 56;
168 = 3 • 56;
(6552, 448) = 56.
II способ
6552 = 448 • 14 + 280;
448 = 280 • 1 + 168;
280 = 1 • 168+ 112;
168 = 1 • 112 + 56;
112 = 2 • 56;
(6552, 448) = 56.
248.	а = bq + гх, а > 6; 0 < г\ < 6;
6 = Mi + г2, 0 < r2 < rf,
>1 = r2q2 + r3, 0 С r3 < r2,
rk~rk+i ‘	+ гЛ+2» 0 <	< Г£+ь
2
Если гЛ+2 < гЛ+1, то rk > rk+2/ qk+1 + rk+2 и rk > 2rk+2, т. e. rk+2< rk.
266
g
249.	Рассмотреть последовательное деление т на п (tn > п) и доказать,
что ari — 1 делится на dt где г, — последовательны^ остатки при делении т на
п, а следовательно, а — 1 делится на dt но
а*— 1 = (а— 1) (а^ + ... + 1).
250.	Представим данное выражение в виде 7Л+2 + 82л+1 + 1п • 8 — 1п • 8 =
= (7Л+2 + 7Л • 8) + (82Л+1 — 7Л- 8) = 7Л (72 + 8) + 8 [(82)Л — 7Л] = 57 • 1п +
+ 8 (64л — 7Л). Число 64ft — 7ft кратно разности 64 — 7 = 57, а потому и
все рассматриваемое выражение кратно 57. При п = 0 это выражение равно 57,
следовательно, искомый наибольший общий делитель есть 57.
251.	Пусть п — четное число вида 2m, тогда п2 (п2 — 4) (п2 — 16) =
= 64 (т — 2) (т — 1) т (т + 1) (т + 2) т. Показать, что
(т—2) (m—1) m(m-H) (m+2)m делится на 120; (т—2) (m—1)т и m(m+l) (m+2)
делятся на 6.
252.	Пусть рассматриваемые два числа есть а и b\ d — их обилий наиболь-
ab	ab
ший делитель, тогда т = [а, 5] = — ; 1 + 4rq = 1 + 4 (ab — d) • — =
d	tr
ab	/ab\%
*= 1 - 4 • -~+ 4 I —- | = 1 — 4m + 4m2 = (2m — I)2,
d	\ d /
253.	1) Пусть имеем квадраты натуральных чисел m2 и (т + п)2, откуда
(т + л)2 — т2 = 2тп + л2. Установить, при каких значениях m и п эта раз-
ность получит наименьшее значение.
2)	По второму условию данной задачи имеем, что (m, т+ 1) « 1, поэтому
произведение т (т + 1) может быть квадратом натурального числа, если каж-
дый из сомножителей есть квадрат натурального числа. Использовать вывод
пункта 1.
254.	Показать, что одно из чисел а + b или а — b не кратно р, предположив
обратное. Учесть также, что а2 — Ь2 = (а — Ь) (а + Ь) делится на рп.
255.	1) а= 117, 5= 22;
2)	а = 552, 5=» 115;	. ; > < . \ .
а =1 435, b = 232.
3)	Пусть d — наибольший общий делитель искомых чисел, х и у — частные
от деления этих чисел на d. По условию задачи имеем: dxy = 8100 (1), dx +
+ У dy = 48 (2). Покажем, что dx и dy — квадраты натуральных чисел:
dx = 482 + dy + 2 • 48 • /dy.
dx — натуральное число, следовательно, dy — квадрат натурального числа,
аналогично dx — квадрат натурального числа. Но из равенства (1) ясно, что
dxy
dxy тоже квадрат натурального числа, следовательно, и числа х = — , у =
= — — квадраты натуральных чисел. Полагая х — а2, у = b2, d= z2, на-
dx	____ ________
ходим из равенств (1) и (2) a2b2z2 = 8100, У z2a2 + Уz2b2 = 48.
abz = 90,1
г (а + Ь) = 48,/
15 _ ab
откуда —— = —• . Дробь т. : несократима, так как если х и у, а и Ь—числа
а + b 8	а + b
взаимно простые, то (ab, а + b) = 1, откуда а = 5, b = 3, или а — 3, b = 5,
z=6.
Искомые числа: 900 и 324, так как dx = z2a2 = 36 • 25 = 900, dy = z2b2 —
= 36 • 9 = 324, или наоборот.
267
256.	Пусть [1, 2, 3.2n]« М, [п + 1, п Ч- 2, ...» 2n) = М'. Так как М
кратно числам п + 1,	, 2п, то Л1 делится на NV. С другой стороны, в ряду чи-
сел п + 1, п + 2, ... , 2п всегда можно найти хоть одно число, кратное любому
из чисел 1, 2, ... , п (1).
Действительно, пусть а — одно из чисел последовательности (1); ха — об-
щий вид чисел, кратных а, где х — натуральное число.
п	п	п
Решая неравенства п <ха < 2п, получим — < х < 2 — , (2);"так как — >1,
а	а - а
то для х всегда можно найти хоть одно натуральное число. Таким образом, при
надлежащем выборе х число ха равно одному из чисел п + 1, п + 2, ...» 2п (3).
Следовательно, М', кратное любому числу ряда (3), кратно ха и потому
кратно а, где а— любое число ряда (1); будучи уже кратно всем числам ряда (1)
М' кратно Л4, их наименьшему кратному; следовательно, М' делится на М.
Значит, М = М'.
а	b
257.	Пусть (a, b) =» d, тогда « х, = у и (х, у) « 1. Получим!
а	а
“ ХУ‘ ПУСТЬ х= •" Р"П ’	где Р1>
Pt....рп, 41, Чг, > 9m— различные простые числа, 04,а2....а„, f2.....
натуральные числа.
Тогда ху =« р*1 • р®2... Рпп •	• <$* ••• Утт » так как (*» У) h то в
ряду простых чисел pv р2, ...» рп, qv q2, ...» qm нет одинаковых, а потому имеем
каноническое разложение ху.
ab
Но по условию ab есть квадрат натурального числа, причем ху == ~ ;
следовательно, ху — квадрат натурального числа, что возможно, ч если каждый
показатель ар а2, ...,ал, рх, р2, ...»	— число четное, так как каждое из чисел
х и у — квадрат натурального числа.
Полагая х « т2, у 3=3 п2, где пг и п — целые числа, имеем: а dx = dm2,
b *= dy == dn2, откуда (a — b) Уab^ (dm2 — dn2) . yd2m2n2 = d2 (m2 —
— n2)mn. Если а и b — оба нечетные, то т и n, как их делители, тоже нечетные,
т. е. т = 2k + 1, п = 21 + 1; следовательно, т2 — п2 = (2k + I)2 — (21 + 1)2=
=а 4 [& (k + 1) — I (I + 1)], k (k + 1) и I (I + 1) — числа четные; следователь-
но, т2 — п2 делится на 8, а потому (а — Ь) У~аЬ делится на 8.
Аналогичный вывод получается, если а и b четные. Если одно из чисел тип
кратно 3, то и тп кратно 3, т. е. (а — Ь) • УаЬ делится на 3.
Если m и п не кратны 3, то т2 — 1 и п2 — 1 кратны 3; следовательно, число
(т2 — 1) — (п2 — 1) = т2 — п2 тоже кратно 3, а следовательно, и число
(а — Ь)У ab кратно 3, но (8,3) =» 1; значит, (а — Ь)Уab делится на 24.
258.	Допустим, что п делится на все числа т, не большие У п, Составим
общее наименьшее кратное М всех таких чисел т. В него, очевидно, будут вхо-
дить все простые числа, меньшие Уп, причем каждое простое число р в такой
степени_£, что рк^У~п, но рй+1>]Лп. Допустим, что число простых чисел, мень-
ших Уп, равно /; эти простые числа обозначим через pv р2,	, рр Наименьшее
общее кратное всех чисел, меньших Уп, представляет собой произведение
pf1 • Р22... Pit , где k19 k2, ..., ki определяются неравенствами р^< Уп <
< p^z+1 < p2ki , 1“ 1, 2, I. Перемножая эти неравенства, получим М
< (Уп)1 < М2. Но так как согласно допущению п должно делиться на М, то
М < п; следовательно, (У п)1 < п2, откуда I < 4; так как рр р2, ..., pi — все
простые числа, меньшие Уп, то р4 = 7 > Уп (четвертое простое число есть 7)
и п < 49. Непосредственной проверкой устанавливаем, что требуемым свойством d
обладают только числа 24, 12, 8, 6, 4, 2.	d
268
§ 4
259.	Если простые числа не равны между собой, то они и взаимно простые
(см. решение задачи 233).
260.	После применения признаков делимости на 2, 3, 5, 7 останется иссле-
довать числа 2323, 2329, 2333, 2339, 2341, 2347. Первые два из этих чисел делятся
соответственно на 23 и 17. Далее достаточно проверить делимость числа 2333
на 19, 29, 31, 37, 41, 43, 47 и сравнить полученные остатки с остальными из ис-
следуемых чисел. Среди остальных промежутков все числа составные, так как
8! = 40 320 и 3 628 800 = 90-8! (см. доказательство теоремы о наличии в на-
туральном ряду сколь угодно длинных отрезков, не содержащих простых чисел).
261.	Преобразовать подкоренное выражение к виду (15 -10^ — З)2.
262.	Простое число может иметь следующий вид: р = 3, р = 3fe + 1, р =
= 3k + 2. Если р = 3, то р + 10 = 13 и р + 14 = 17 удовлетворяют условию
задачи. Если р = 3/г + 1, то р + 10= 3&+11, р + 14 = 3k + 15 — числа
составные. Если р = 3k + 2 то р + 10 = 3k + 12 — число составное, следо-
вательно, р = 3.
263.	а = 3 (см. решение задачи 262).
264.	р = 3 (см. решение задачи 262).
265.	См. решение задачи 262.
266.	По условию задачи имеем: х3 = 13р + 1, или х3 — 1 = 13р, но
х3 — 1 = (х — 1) (х2 + х + 1); следовательно, (х — 1) (х2 + х + 1) = 1 Зр, от-
куда либо х — 1 = 13, либо х2 + х + 1 = 13. Значит, хг = 14, х2 = —4,
х3 = 3. Искомые числа 143 = 2744 = 13-211 + 1, (—4)3 = —64 = 13 X
X (—5) + 1; З3 = 27 = 13 • 2 + 1.
„ г-г	(2р + 2) (2р + 1) 2р 2р(2р+1)(р + 1)
267.	Показать, что выражение ---------------= ------------------- —
1-2-3	3
число целое. По условию задачи р и 2р + 1 — числа простые, следовательно,
р + 1 делится на 3, а потому 4р + 1 = Зр + (р + 1) — число составное.
268.	По условию задачи а2 = 16fe2 + 3k + 1 = 4fe (46 + 2) + 1. Рас-
смотреть делимость произведения 4/г (4fe + 2) на 8 и на 3, имея в виду, что по
условию задачи 4k + 1 — число простое, большее 3.
269.	Прибавить и вычесть 4а2.
270.	Полагая х = 2	2 , разложить х4 + 1 на множители.
Пример. 258 + 1 = 288 230 376 151 711 745 — число составное.
271.	Учесть, что х4* + 24^+2 = (x2k + 22^+1)2 — 22^+2 • х2Л.
272.	Любое натуральное число можно представить в виде 6n + 1, 6п + 2,
6п + 3, 6п + 5, 6п. Установить, какие из этих чисел могут быть простыми, най-
ти их квадраты и остатки от деления этих квадратов на 12.
273.	а2 — 1 = (а — 1) (а + 1). Учесть, что а — простое число, отличное
от 3, и доказать делимость этого выражения на 8 и на 3.
274.	Использовать задачи 40 и 122, имея в виду, что 240 = 5-48.
275.	а) Установить, какой вид могут иметь простые числа, если рассматри-
вать делимость их на 30; найти квадраты этих чисел и проверить, какие остатки
они дают при делении на 30.
б) Учесть, что если а = bq + г, где 0 г < д, то (а, Ь) = (Ь, г).
276.	По задаче 272, простые числа имеют вид 6n + 1 или 6п + 5, следова-
тельно, из трех простых чисел два имеют одинаковый вид. Но данные числа свя-
заны и следующей зависимостью; а = а, b = а + х, с = а + 2х. Разность этих
чисел, равная х или 2х, с одной стороны, кратна 6, с другой стороны —х (два из
чисел имеют одинаковый вид, следовательно, их разность есть 0)., следовательно,
разность прогрессии х кратна 6.
277.	Пусть N делится на d, тогда 2N — 1 делится на 2d — 1, т^ е. число
2^ — 1 составное.
Пример. N = 15, 215 — 1 = 32 767 делится на 25 — 1 = 31; 32767
делится на 23 — 1 = 7, так как 15 делится на 5 и на 3.
269
("U ("Ye	"
278.	2W + 1 = 2 '6 / + 1; 2^ ' +1 делится на 2б + 1.
Пример. 26 + 1 = 65, а 65 делится на 22 + 1» так как 6 имеет нечетный
делитель 3.
279.	Утверждения не справедливы, что подтверждает следующий пример:
232 + 1 = 4 294 967 297 = 641 • 6 700 417 — число составное, но 32 не имеет
нечетного делителя.
280.	Утверждения не справедливы, что подтверждает следующий пример:
211 — 1 = 2047 — 23 • 89 — число составное, но 11 — число простое.
281.	Если бы п + 1 было числом составным, то оно должно было бы иметь
простых делителей среди чисел 2, 3,..., п, т. е. произведение 1 • 2 ... п должно
было бы делиться на п + 1, что противоречит условию.
282.	Число 2 • 3 • 5 • 7 ... • р + 1 может быть простым, но тогда большим
р, а может быть и составным, но тогда имеющим простые делители, большие р.
Примеры. 2 • 3 • 5 • 7 • 11 + 1 = 23 11 — число простое; 2 • 3 • 5 X
Х7 • 11 • 13 + 1 = 30 031 = 59 • 509 — число составное.
283.	Преобразовать первый множитель, сгруппировав слагаемые, одинаково
расположенные от концов суммы.
284.	Учесть задачу 40 и то, что если а — 1 • р, то и ak — 1 • р, где k — на-
туральное число.
288.	Допустим, что х — составное число, и пусть рх, р2, ..., рп — все про-
стые множители, на которые оно разлагается; тогда х = р^1 • р®2... р“л ия > 2.
Среди простых чисел рр р2, ..., рп есть по крайней мере одно число, меньшее р,
так как если бы каждое из них было не меньше р, то произведение двух из них
было бы не меньше р2 и мы имели бы, что х р2, что противоречит условию.
Пусть это простое число (меньшее р) есть qt причем оно должно быть сомно-
жителем одного из произведений а • 0... у или а • Ь* с... k, так как ряд а, Ь, с,...,
6, а, 0, ..., у представляет все простые числа, не превосходящие р. Но тогда х
делится на q, одно из произведений тоже делится на q; следовательно, и второе
произведение должно делиться на q, что невозможно, так как q — простое число,
встречающееся только в одном из этих произведений. Следовательно, х — про-
стое число.
291.	а) /х == 3 + 40/,
(у = 2 + 27/;
б)	/х = —13 + 37/,
(у = 19 — 54/;
в)	(х — 11 + 84/,
|у = —14 _ Ю7/;
г)	(х = 4 + 15/,
1у = 3 + 13/;
292.	1951. Задача сводится
Их + 2у = 57.
§ 5
Д) /х = —7 + 52/,
1у= 11 + 81/;
е)	(х = 3 + 7/,
1У = 3/;
ж)	уравнение целых решений не имеет;
з)	(х = 71 + 449/,
|у = 40 + 253/.
к решению неопределенного уравнения
293.	Пусть (р, 10) = 1 и дано число abc ... /г, состоящее из п цифр, тогда
уравнение рх — 10пу = 1 имеет целые положительные решения. Умножив обе
части уравнения на число abc...k, получим искомое число х {abc ... k), где х —
корень уравнения рх — 10лу = 1.
294.	См. задачу 293.
295.	Выделим из ряда чисел 1001, 1011, 1021, ..., 1991 все числа, делящиеся
на простое число р. Пусть х — число десятков, которое, сложенное с числом 1001,
1001 + Юх
обращает его в число, делящееся на простое число р, т. е. пусть------=у,
Р
где у — целое число. Получаем неопределенное уравнение ру— Юх = 1001,
1001
причем 100 > х > 0; у >-----, р + 2, р 5, так как ни одно из чисел рассмат-
Р
270
риваемого ряда не делится ни на 2, ни на 5; р не может быть больше 43, так как
]/1991 == 44,6... Следовательно, для р возможны только такие значения: 3, 7,
11, 13, 17, 19, 23, 29, 31, 37, 41, 43, и для решения задачи будем иметь двенадцать
уравнений вида
ру — 10х = 1001.
Решая эти уравнения, находим значения для х, умножив их на 10 и сложив с
числом 1001, получим составные числа, а выделив эти числа из данного ряда,
получим простые числа.
296.	а) хг =0; ух = 0; х2 =2; у2 = 2. Представить данное уравнение в
виде (у — 1) (х— 1) = 1 и, допустив, что оно имеет целые решения, рассмотреть
все возможные случаи, когда произведение двух целых чисел может быть равно 1.
б)	Шесть решений, из которых три, например, такие: xi = 2р, yi = 2р;
х2 — 0, у2 = 0; хз == р + 1, Уз — р + р2. Представить данное уравнение в виде
(х — р) (у — р) = р2 и провести рассуждения, аналогичные приведенным в
предыдущей задаче.
в)	Двенадцать решений.
Представить данное уравнение в виде (у + 3) (5— х) = 18 и рассмотреть
все возможные случаи, допустив, что уравнение имеет целые решения.
297.	а) Преобразовать уравнение к виду (х— 2у)2 + у2 = 132 и рассмотреть
его, имея в виду, что 169 = 132 + О2; 169 = 52 + 122.
• ’ б) Девять решений, в том числе такие пары чисел, как 210 и 15, 112 и 16.
Преобразовать уравнение к виду (х — 14) (у — 14) = 196.
в) 2, у - 2, г - 7. Преобразовать данное уравнение к виду х5 (х3 — 1)=
= y5z, установить, что х должен быть простым числом, равным у.
298.	а) х = 3, у = 13. Преобразовать уравнение к виду (х — 1) (х2 + х +
+ 1) = 2у.
б)	х= 2, у=з2. Преобразовать уравнение к виду (у + 1)(у2— у+ 1)=3Х.
в)	х= 3, у=з2; х = 1, у = 1. Установить, есть ли еще целые решения у
этого уравнения, если есть — найти их.
299.	а) х=0, у = 0; х = 1, у == 2. Преобразовать уравнение к виду
(1 + х) (1 + х2) = рУ.
б)	Решениями уравнения будут следующие пары чисел: 0 и 0; 0 и —1; —1 и
—1; — 1 и 0; 5 и 2; —6 и 2, где первое число пары — значение х, второе число
пары — значение у.
Преобразовать данное уравнение так, чтобы в обеих частях его можно было
бы выделить полные квадраты, установив те значения у, при которых равенство
не может иметь места, испытать оставшиеся значения.
в)	х = 6k (k + 1); у =2^+1; z=3fe(^+l); у = ± 2, х = ± 2z, где
г — любое целое. Преобразовать уравнение так, чтобы его части представляли
собой произведение.
г)	х : у : z ==> auk : п (bk + cri) : k (bk + cn), n и k — целые числа.
300.	Допустив, что уравнение имеет целые решения, получим, что у должен
быть нечетным числом, т. е. иметь вид у = 2т + 1, откуда х2 — 10m2 — 10m =
= 6, т. е. х — четное число или х = 2п; тогда 2п2 — 5m (т + 1) = 3, что не-
возможно, так как оба компонента разности — четные числа.
301.	а) Допустив, что уравнение имеет целые решения, установить количе-
ство простых множителей 7 в каноническом разложении чисел х2 и у2.
б)	Приведя уравнение к виду 3 (х2 — 1) — 4у2 = 10, рассмотреть делимость
его членов на 4.
в,	г) Установить, какими цифрами могут оканчиваться числа в левых ча-
стях равенства, если предположить, что уравнения имеют целые решения.
д)	Учесть, что если уравнение имеет целые решения, то у не делится на 3,
т. е. имеет вид у = 3k ± 1.
е)	Установить, что если предположить, что уравнение имеет целые решения,
то у2 должно быть кратно 3, и использовать полученный вывод.
302. а) Допустив существование целых решений, рассмотреть случаи: х = 0,
х > 0, х < 0.
б) Разложить левую часть равенства на множители и учесть, что 33 = 11 *3.
271
г) Обратить внимание на то, что выражение х7 (х3 + а) — четное число прй
любом целом х.
303.	Учесть, что произведение двух целых чисел может быть равно 1 только
в определенных случаях (рассмотреть каждый из них).
304.	Допустив, что уравнение имеет целое решение х0, представить левую
часть уравнения в виде произведения х — х0 на соответствующий многочлен и
использовать условия задачи.
305.	Множества чисел, определяющиеся формулами х= 22fe2 — 14fe + 2 и
х = 22k2 — 30& + 10, где k — натуральное число или нуль. Обозначив 22х +
+ 5 = а2, преобразовать полученное выражение к виду а2 — 16 = 11 (2х — 1);
установить, что тогда а — нечетное число, имеющее вид а = (2k — 1) • 11 ± 4,
где k — натуральное число или нуль; выразить х через k.
306.	1001 и 8004. Приняв искомое четырехзначное число за у, обозначив
точный квадрат через х2, будем иметь: х2 — 4 • 106 = у. Найти целые решения
этого уравнения, удовлетворяющие условию задачи.
307.	153 846. Задача сводится к решению неопределенного уравнения вида
4 (10х + 6) = 6 • 10У-1 + х, где х — число всех десятков в искомом числе. Пос-
ле упрощений решение уравнения сводится к отысканию таких натуральных
значений у, при которых Ю^-1 — 4 делится на 13.
308.	2090, 3080, 4070, 5060, 6050, 7040, 8030, 9020. Обозначив искомое число
через 1000х+ ЮОу + 10fe + р, учтя признак делимости на 11 и условие зада-
чи, получить уравнение 2 (х + k) = 11 (n + 1), где п — некоторое целое число,
которое и решить, учтя условие задачи.
309.	Обозначив х + у = kt получим иное выражение для п, а именно: п а
k (k + 1) , Л
«== —-—- + х, где 0 < х С Ь.
Показать: 1) при k = 0, 1, 2 и т. д. получим группы чисел 0; 1, 2; 3, 4, 5;
6, 7, 8, 9;... , образующие отрезок расширенного натурального ряда сколь угодно
большой длины;
2) число п попадет в одну и только одну из групп этого отрезка.
310. а) х = 37, у= 12, z = 14, t= 65. Представить данное уравнение в
виде х (у — z) + yt = 2 • 7 • 13 и доказать, что х 14, х =# 65; затем предста-
вить его в виде у (х + /) — xz = 2 • 7 • 13 и доказать, что у =# 14, у #= 65. Ис-
следовать оставшиеся возможности, вновь получая неопределенные уравнения.
б) Задача сводится к доказательству того, что уравнение х(х+1)=4лу (у + 1),
где п — натуральное число, не имеет натуральных решений. Допустив
противное, доказать, что тогда х имеет вид bnk или bnk — 1 и исследовать квад-
ратное уравнение, полученное при замене х через одно из указанных выражений.
в) 142 857, '142 857 142 857 и т. д. Задача сводится к решению в натураль-
ных числах уравнения 3 (10х + n) = 10n + 1, где п — число, изображенное
всеми цифрами искомого числа, кроме 1; х — количество цифр числа п. *
§ 6
311.	Для того чтобы доказать, что одно из заданных чисел делится на дру-
гое, достаточно найти частное так, чтобы оно было числом Гаусса. Действитель-
но, в настоящей задаче соответственные числа Гаусса легко найти: А= А * 1,
А = 1 • А, А = —1 • (—Л), А = i • (—/Л), А = — Z (/Л).
312.	По условию Л делится на В, В делится на С. По определению делимости
это значит, что найдутся числа Гаусса X и У такие, что А = ВХ и В = CY.
Подставляя произведение, полученное для В, во второе равенство, получим:
Л =» С • (УХ), где УХ есть число Гаусса. Следовательно, по определению Л
делится на С.
313.	По условию Л делится на В, это значит, что найдется число Гаусса
Xi + yxZ такое, что а + bi = (х + у i) • (хх + yxi). Теперь нетрудно проверить,
применяя правило равенства комплексных чисел, что будет справедливо и
а — bi = (х — yi) • (хх — y^i).
314.	Использовать решение предыдущих задач, в частности задачи 311.
315.	Использовать решение задачи 312.
316.	Использовать решение задачи 312.
272
317.	Использовать решение задачи 312.
318.	По условию а = р • а± и b = р • тогда А р • (а± + Ьр).
319.	Разделить А на указанные числа, использовать условие, в силу кото-
рого обе компоненты А имеют одинаковую четность, и доказать, что компоненты
частного — целые рациональные числа.
320.	Использовать решение предыдущей задачи.
321.	Применить решение задачи 312.
322.	Составить произведение данного числа на сопряженное с ним и при-
менить определение нормы.
323.	Применить определение нормы.
324.	Очевидно, что норма 1, —1, i, —i равна единице по определению нормы.
Пусть N (4) = 1, положить А = а + Ы и доказать, что либо а = ± 1 и b = 0,
либо а = 0 и b = ± 1.
325.	Применить определение нормы.
326.	Положить А = а + Ы, В = х + yi. Найти норму 4, норму В, норму
4 • В и сравнить произведение норм сомножителей с нормой произведения.
327.	Применить определение делимости и результат предыдущей задачи.
328.	Предположить противное и применить результат задачи 326.
329.	Применить результат задачи 322.
330.	Применить определение делимости и результат задачи 329.
331.	Применить определение делимости и результат задачи 329.
332.	Пусть р = а2 + Ь2, тогда р является нормой числа Гаусса 4 = а + Ы.
Пусть р = N (4) и 4 = а + Ы, тогда р = а2 + Ь2.
333.	Пусть N (4) = N (а + Ы) С Р- Это значит, что а2 + Ь2 < р при це-
лых рациональных а и Ь. Следовательно, абсолютная величина каждого из ком-
понент не превосходит корня квадратного изр. Ограниченных по абсолютной
величине целых рациональных чисел может быть лишь конечное число. Из них
можно составить лишь конечное число чисел Гаусса.
334.	Пусть 4 =И= 0 и 4 = а + Ы> тогда N (4) = а2 + Ь2 = р. Норма каж-
дого делителя 4 должна быть делителем числа р и потому она не больше числа
р (см. задачу 327). Но каждое натуральное число р имеет конечное число нату-
ральных делителей; следовательно, 4 имеет конечное число делителей.
335.	Применить результат задачи 329.
336.	Пусть 4 = а + bi. Рассмотреть три случая: а, b — четные, а, Ь — не-
четные, а, b имеют разную четность и для каждого случая составить норму 4.
337.	Доказать, что 45 — 4 делится на 5, положив 4 = а + Ы. Но 5 —
норма каждого из делителей. Тогда в силу задачи 329 4 5— 4 будет делиться на
каждый делитель.
338.	По условию 4 = Юс + q + (Юр + pr)i = 10 (с + pi) + q + pxi мож-
но представить в виде суммы двух чисел Гаусса, из которых первое делится на
каждый делитель, так как 10 делится на каждый делитель в силу задачи 331.
Следовательно, 4 будет делиться на те делители, на которые второе слагаемое бу-
дет делиться (см. 317).
339.	См. указание к предыдущей задаче.
340.	Доказать, что каждая компонента 4 делится на норму каждого дели-
теля, и применить результат задач 318, 331.
341.	Пусть первая компонента — целое рациональное число, т. е. ах + by =
а (х2 + у2) • р. Умножим обе части этого равенства на х и прибавим к его левой
части ау2 — ау2 = 0, тогда а (х2 + у2) + у (—ау + Ьх) = (х2 + у2) • рх. Тогда
сумма и одно из слагаемых делятся на х2 + у2, следовательно, и второе слагаемое
должно делиться на это число, но по условию х, у взаимно просты, следователь-
но, у и х2 + у2 также будут взаимно просты, следовательно, —ау + Ьх будет
делиться на х2 + у2, а это значит, что вторая компонента частного есть целое
рациональное число. Аналогично доказывается справедливость второго утверж-
дения, т. е. если вторая компонента частного есть число целое рациональное, то
таким же будет и первая его компонента.
342.	Число 4 делится на 3, 6 ± i, 1 + i, 2 + t, 3 — i и на все числа Гаусса,
которые из этих делителей получатся умножением на единицы. Число В делится
на 4 ± /, 2 + it 8 + 7i и на все числа, которые из них получатся умножением
на единицы.
273
343.	Подставим вместо X корень полинома, равный А. Тогда 0 « Ak +
+ С14Л"1 + ... + Ck-iA + С^. Сумма, равная нулю, и все слагаемые, кроме
последнего, делятся, очевидно, на А, Применяя свойство делимости (см. 317),
можно утверждать, что и Ck делится на А,
» Замечание. В задаче 334 было доказано, что каждое неравное нулю
число Гаусса имеет конечное количество делителей. Следовательно, все делители
числа можно найти. Подставляя эти числа в полином, можно найти все корни
полинома, каждый из которых является числом Гаусса. Так как целые рацио-
нальные числа являются числами Гаусса, то способом, указанным выше, будут
найдены и все целые рациональные корни полинома.
344.	Если А — корень полинома, то он делится на разность X — А и в ча-
стном получится полином, коэффициенты которого будут числа Гаусса:
Xk +	+ ... + Ck = (X - А) • (X*"1 + B1Xft-s + ... + В^).
Если в это равенство вместо X подставить по очереди 1, —1, i, —i, то, при-
меняя определение делимости, можно утверждать, что значение полинома Ф (1)
делится на 1 — 4, Ф (—1) делится на 1 + А и т. д.
345.	Применить результат задач 343 и 319.
346.	а) Только четыре единицы имеют норму, равную единице (см. решение
задачи 324). Следовательно, единица делится только на единицы. Подставляя их
по очереди в уравнение, найдем, что оно имеет два корня i, —i, каждый из кото-
рых есть число Гаусса.
б)	1, —1, 1 + 2г, 1 — 2i.
в)	i, —г.
г)	—1—г, —1 + г.
д)	G — i-
e)	1 + 3г, 1 — 3i.
ж)	Числа Гаусса не являются корнями этого уравнения. Решение задачи.
Найдем делители 4. Нормы делителей должны делить норму 4; следовательно,
только 1, —1, г, —г, 1 + г, —1 + h 1 — г, —1 — Л 2, —2, 2г, —2г, 2 + 2г,
—2 + 2г, 2 — 2г, —2 — 21, 4, —4, 4г, —4г могут быть корнями уравнения. Еди-
ницы не являются корнями уравнения (нетрудно проверить). Кроме того, если
в левую часть уравнения подставить —1, то получится 1. Это число, на основа-
нии задачи 344, должно делиться на 1 + 4, если число Гаусса, равное4, —ко-
рень уравнения. Следовательно, 1 + 4 должно равняться одной из единиц. Это
верно только для трех чисел: —2, —1 + г и —1 — г. Нетрудно проверить, что
оставшиеся три числа не являются корнями уравнения.
з)	i, I, —2i.
и)	—1 — г, —1 — I, 2 + 2г.	;
к)	—1 — 2г, —1 — 2f, 2 + i.
347.	1 + 2г, 1 — 2i, —2 + г, —2 — i — корни полинома четвертой степени.
Его можно разложить на произведение четырех множителей, каждый из которых
равен X — 4, где 4 — соответствующий корень полинома. 3Z, 3 + 31^3,
3 — Зг/3—три корня полинома третьей степени. Один, равный Зг, можно най-
ти, применяя результат задачи 343. Затем, разделив полином на разность X — 3i
и приравняв нулю частное, можно найти оставшиеся корни полинома, если ре-
шить квадратное уравнение. Следовательно, полином третьей степени можно
представить в виде произведения трех множителей первой степени.
349-a4’-i’l-
Указание. Положить 2Х = Y.
Указание. Домножить все члены уравнения на 2 и положить 2Х = Y.
Указание. Показать, что (1 + г)3= 2(—1+ г), и положить (1 + i)X =У.
274
-1 —/ —1—z
D—
Указание. Домножить на 4 и положить 2Х = У.
350.	Пусть Ф (0) — Ck = а + Ы и Ф (1) = at + 6rZ. Нормы этих чисел —
нечетные натуральные числа. Пусть число Гаусса А — корень полинома, тогда,
применяя результаты задач 343 и 344, можно утверждать, что Ф (0) = Ck делится
на Л и Ф (1) делится на 1 —Л. Следовательно, нормы этих чисел должны соот-
ветственно делиться на нормы чисел А и 1 — А (см. задачу 17). Следовательно,
нормы чисел Л и 1 — А должны быть числами нечетными одновременно, что не-
возможно благодаря результату задачи 336.
351.	Указание. Применить результат задач 350, 343, 336, 334, 327.
§7
353.	<?=5, числа: 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30; <?= 12,
числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, (10), (11), 10, 11, 12, 13, где (10) и (11) — одно-
значные числа, содержащие десять и одиннадцать единиц.
354.	10003, 102* 36?, 2113, 355. 100 1102, 11023, 212* 1233, 102* 537, 46*
42* 3810, 35п, 3212.
356.	Наибольшее однозначное число в троичной системе счисления содер-
жит две единицы. Наибольшее двузначное число в двоичной системе запишется
как 11 и будет содержать 2+1 = 3 единицы. Наибольшее пятизначное число
в пятеричной системе счисления запишется как 44 444 и будет содержать 54 • 4 +
+ 53 -4 + 52 -4 + 5- 4 + 4 = 3224 единицы.
357.	Нет, так как ни в семеричной, ни в пятеричной системе счисления нет
однозначных чисел для выражения 7, 8, 9 единиц.
361.	а) 114 023* б) 49 20412; в) 22 2123;	г) И (11)312; д) 50 232 666?;
е) 301 413 3335; ж) 855 (10) 2012; з) 41 414б; и) 15 476в; к) (10) 539п.
362.	а) Пятеричная, шестеричная, одиннадцатеричная, пятнадцатеричная
система счисления.
б)	Четверичная, семеричная, любая с основанием, большим 4, четырнадца-
теричная системы счисления.
в)	Восьмеричная, четвертичная, шестеричная, семеричная системы.
363.	а) 11 0113; б) 115 87510 : 12510 = 92710.
• 364. 121 221б; 220 042?; 14 71110; 37810; 1151* 171410.
365.	5; 6; 8. Имеем: 1610 = 31х; 1610 = Зх + 1; 1510 = Зх; х = 5.
366.	По первому условию задачи имеем: 304х = Зх2 + 4 = 53 + 2 • 52 +
+ 4-5+1, или Зх2 = 192, или х2 = 64, откуда х = 8. Аналогично во втором
случае х = 4.
367.	По условию задачи имеем: Зх6 + Зх5 + 2х4 + Зх8 + 4х = 57 895,
значит, Зх6 < 57 895, или х6 < 19 299, или х < 5, 18 ... В число 332 041 входит
цифра 4, следовательно, х = 5.
368.	Пусть х, у, k — цифры соответственно сотен, десятков и единиц иско-
у — х
мого числа. Тогда ЮОх + 10у + k = 81£ + 9у + х, или —= 8k — 10х.
Так как х, у, k — целые числа, то разность у — х должна делиться на 10,
что возможно при х = у. Откуда 8k — 10х = 0 и 4k = 5х. Но (4, 5) = 1, следо-
вательно, k = 5р, х — 4р и 0 < k < 10, т. е. 5р < 10. Значит, р равно или 0
или 1, но х — первая цифра трехзначного числа и х^0, следовательно, р = 1,
х = 4, k = 5. Искомое число 445.
369.	Удвоив число, предшествующее основанию системы счисления а, полу-
чим 2 (а — 1) = 2а — 2 = а + (а — 2), т. е. 2 (а — 1), по системе счисления
с основанием а оно записывается цифрами 1 на — 2. Имеем также (а — I)2 =
== а2 — 2а + 1 = (а — 2)а + 1, т. е. (а — I)2 — записывается по системе счи-
сления с основанием а цифрами а — 2 и 1.
275

370.	Учесть, что л10 — 1 = (а5 — 1) (аъ + 1) = (а + 1) • (а4 — а3 + а2 —
— а + 1) (а5 — 1) и что 9 999 999 999 = 1010 — 1.
На второй вопрос ответ отрицательный.
371.	Как известно, сумма квадратов п натуральных чисел выражается фор-
п(п + 1) (2п + 1)	п(2п2 + 3п+ 1) /	оч
мулои S= -------------------= ----------------- (см. задачу 3). Откуда S ==
6
6
=	231„.
с я(«+ 1)
372.	Сумма п первых натуральных чисел выражается формулой S—----— =
п , п
«= ~2 ' п + ~ * 1 (см. задачу 1). Если основание системы п, то эта сумма выра-
зится числом вида аа или ао (почему?).
373.	В системе счисления с основанием а = 2 для записи любого числа до-
статочно двух цифр: 1 и 0, следовательно, эта запись будет представлять собой
сумму различных степеней основания, т. е. 2 — %.
374.	Имеем: 144^ = 1 • k2 + 4k + 4 = (k + 2)2. Например, в пятеричной
системе счисления: 12| = (10 + 2)2 — 102 + 2 • 2 • 10 + 4 = 1443; в семерич-
ной системе счисления: 12? = (10 + 2)2 = 1447.
375.	См. задачу 374.
376.	Обозначим основание системы через k, тогда 16 324^ = &4 + 6 fe3+
+ 3ft2 + 2k + 4 = 125ft = (ft2 + 2k + 5)2, или 2k3 — life2 — 18ft — 21 = 0,
прибавив и вычтя по 3fc2 + 3kt получим (k — 7) (2k2 + 3k + 3) = 0, откуда
k = 7.
377.	По условию задачи имеем: А + В + С + 7 = (1 + 10 + 102 + ... +
+ 102™-1) • 4 + 2 (Г + 10+ ... + 10™) + 8 (1 + 10 + ... + Ю™"1) +7 =
4 (102™— 1)	2 (10™+1 — 1)	8 (10™—1)	4 • 102™+ 28 • 10™+49
=	9	9	+	9	+7—	g	—
/2- 10w + 7\2	,	2-10™+7
= ------------। ’НоД + В + С + 7 — число целое, следовательно,--------—
\ о /	3
число целое. Это число можно записать так:
т— 1
20 ... 07
3
т— 1
66?Гб9.
378.	Число, записанное 2т единицами, равно числу, записанному 2т де-
ю2™— 1 А	о 10™+!— 1
сятками, деленному на 9, т. е. А =-------. Аналогично В =--------------и
9	9
10™— 1
С «--------• 6. Установить вид числа А + В + С + 8.
379.	Преобразовать данное число к виду А = 23 • 210 (1623 + 1) +
+ 212 (1631 + 1) и использовать задачу 40, имея в виду, что 136 = 8 • 17.
380.	Установить сначала, что произведение цифр любого числа не больше
самого числа. Ответ: х = 12.
381.	Число рассматриваемого вида можно записать так: 1 + q2 + ... + q2k,
причем k — четное число. Имеем: q2k+2 — 1 = (q2 — 1) (1 + q2 + ... + q2k) =
«= (q — 1) (q + 1) (1 + q2 + ... + q2k). Если k — четное число, то (^+1)2 —
—1 = q2k+2 — 1 = (q — 1) . Q . (q + 1) . Qp Из доказанного следует, что
составными будут все числа вида 10 101, 101 010 101, 1 010 101 010 101 и т. д.
382.	Имеем: N — anan_Y ••• <haQ(ji где q — основание системы счисления-
an-i* •••> ai> ао—Цифры числа. По условию задачи имеем: N— (ап + ап-х+
+ ... + аг + а0) ~ т • d. Если N = qt то S = 1, где S — сумма цифр числа и
q — 1 = mdt откуда q = md + 1.
276
383.	Системы счисления с основаниями 4, 7, 10, 13 и т. д. для делимости на
3 и 10, 19, 28 и т. д. для делимости на 9.
384.	По задаче 382< основание системы счисления q должно удовлетворять
условию q = md+ 1. Найти искомые значения для q.
385.	а) Основание системы счисления должно иметь вид q = 5k + 1 (см. за-
дачу 382).
б) Из условия задачи следует также, что единица третьего разряда должна
делиться на 7, так как Nq = anan-i ••• fl2?2 + т- e- 92==7p, откуда q= 7a.
Следовательно, основание искомой системы счисления должно при делении на 5
давать в остатке 1 и делиться на 7. Наименьшим числом, удовлетворяющим ус-
ловию, будет число 21.
386.	апап.г ... аАа. Пусть основание системы счисления есть 13, тог-
да 10 = 3 • 4 + 1; 102 « 3 • 44 + 1; •••» т. е. = г2 — ... = гп= 1; для полу-
чения признака делимости на 3 имеем: Q == ап + аплл + ... + aQi т. е. если
ап+ an+i + ••• + ai + ао делится на 3, то и N делится на 3, и обратно. Анало-
гично для признака делимости на 4 имеем: 10 = 4 • 3 + 1; 102 => 4 • 33 + 1; ...,
т. е. Г1 = г2 а ... = гп =» 1, т. е. если ап + а/2+1 + ... + .аг + а0 делится
на 4, то N делится на 4. Если основание системы счисления есть 5, то признак
делимости на 3 получается следующим образом: г0 = 1; гг = 2; r2 = 1;г3«2,...,
Q я (а0 + а2 +...) + 2 (ах + а3 + Q' = «А +	+ ••• • Признак
делимости на 4 получается аналогично и есть делимость суммы цифр числа на 4.
Решение можно упростить, если использовать задачу 382.
388.	Имеется в виду, что число 13 дано в той же системе счисления, признак
делимости в которой на это число устанавливается. Имеем: N = апап_х... а0.
Если основание системы счисления есть 5, то признак делимости на 13 получится
из следующих рассуждений: 10б = 0 • 13 + 10; 10| => 13 • 3 + 1; Ю| = 13Х
ХЗО + 10 и т. д. Следовательно, по общему признаку делимости, если
(Oq + а2 + ...) + 10 (а±.+ а3 + .;.) = araQ + а3а2 + ...
делится на 13, то и N делится на 13, и обратно. Если основание системы счисления
есть 12, то признак делимости на 13 получается из следующих рассуждений:
а)	1312= 3 • 5. Признак делимости на 3 в двенадцатеричной системе счисле-
ния следующий: если aQ делится на 3, то и W делится на 3, и обратно, так как
основание системы делится на 3.
б)	Признак делимости на 5 в двенадцатеричной системе счисления получает-
ся при применении общего признака делимости и является следующим: если
+ 2 (Oj + аб + ...) + 4 (Оз 4~ ав + ...) + 3 • (flg + а7 + ...) + (аА + а8 + ...)
делится на 13, то и N делится на 13, и обратно.
38	9. Известно, что 987 654 312 : 123 456 789 =° 8. Показать, что аналогич-
ное соотношение имеет место и для любой системы счисления с основанием р > 2.
Учесть, что если alt a2i ..., йр^— некоторая перестановка значащих цифр в этой
системе счисления, то целое число, изображенное всеми цифрами системы, будет
иметь вид a-ipP-ъ + а2рр~2 + ... + ар_2+ Др-r Найти вид чисел в этой системе,
соответствующих числам 987 654 312 и наименьшему, записанному всеми знача-
щими цифрами системы счисления.
ГЛАВА II
§ I
,	„ a—k а
1. Сравнить дроби: --- и — .
b — k b
л „	„ a + k	а — k a a	a-[-k	a — k	а
2. Сравнить дроби---,------,----, ----- ,---- ,----с дробью — .
b b	b-\-k b — k	b + k	b — k	и b
277
3.	Увеличится на — аЬ; уменьшится на — ab.
4	4
4.	Сравнить выражения (а1+а2)Ь1»и	+ Ь2)а1 и им аналогичные.
5.	а) п = 8, п = 104; б) b =□ 45.
6.	1) а = 15, b = 3; 2) а = 3, b = 15.
Задача сводится к решению в натуральных числах уравнения 2аЬ = 5 (а 4“ Ь).
Имея в виду, что (2, 5) = 1, рассмотреть делимость ab на 5.
7.	а = 6, b = 2.
Задача сводится к решению в натуральных числах неопределенного уравне-
ния а (3 — Ь) = ЗЬ.
8.	Допустить противное и доказать, что неопределенное уравнение вида
а2 + 2а b — Ь2 = 0 не разрешимо в натуральных числах, если а < Ь.
9.	Принять во внимание, что 2! • 3 • 4 ... п= п!; 3! • 4 • 5 ... п= п\ и т. д.
И. Использовать признаки делимости на 3, 5, 9.
12.	Допустив обратное, получим, что числа п — 6 и п — 5 должны одно-
временно делиться на 3.
13.	Рассмотреть случаи, когда числа а и b взаимно простые, когда не взаим-
но простые, используя задачу 232, глава I.
х2 —Зх + 4	/х4-2\2	/т/7х\2	, Л
14.		—---== I ——I — I у Lg I ; х4* 2 может делиться на 7 толь-
ко в том случае, когда х не делится на 7, а 7х может делиться на 49 в том
случае, если х делится на 7. Аналогичны доказательства в остальных случаях.
х 4~ 1
15.	1) Числитель дроби —— , знаменатель х, i
меньшее 3.
х__з
2) Числитель дроби —-—, знаменатель х, где .
4
меньшее 7, дающее при делении на 4 остаток 3.
„	а 1
16.	По условию задачи имеем: —---—- = —-,
10а 4“ Ь 6а
_ b
где х — нечетное число,
х — натуральное число,
не
не
4 Л ' b Л
или ЮН------= 6а, т.
а
6а > 10, но 6а < 20, так как а и b меньше 10 и — < 10; следовательно, а — 2
а
или а — 3. При а = 2, b == 4; при а = 3, b = 24, что не соответствует условию
задачи. Искомая дробь ~ .
е.
1),
ап — 1. Установить, какие
Ы ‘ ‘	‘
11
10х 4- У < Юу + k, сле-
12 2-4 3-6
12 ’ 24 ; 36
ab 1
17.	Допустим, что число п существует, т. е. — = — . Преобразовав это
ab п
равенство, получим Юап = b (а — п), что невозможно (установить почему).
ab 1
18.	Пусть —	. Преобразовав это равенство, получим 10а = b (ап —
ab п
но (а, ап — 1) = 1, следовательно, 10 делится на
значения может принимать ап — 1. Искомые числа
л 19 26 16 49 Т1 10x4-У х
19.	— ; — : — ; — . Имеем: -----------= — ,
95 65 64 98	10y + k k
довательно, х С У! (10х + У)& = * (Юу 4“ &)> следовательно, k (у — х) делится
на 10, т. е. k = 5, или у — х = 5. Рассмотреть все случаи.
20. По условию задачи — —	; 9а 4- 2 = b (b + I); 9а = b (Ь 4~
b 9а 4- 2
+ 1) — 2; 9а делится на 3, следовательно, b (b 4~ 1) — 2 делится на 3, т. е.
b (Ь 4~ 1) = 3& 4~ 2, и, следовательно, b = Зп 4~ 1 (почему?), b 4“ 1 = Зп 4" 2.
Но b — число однозначное, следовательно, оно может иметь вид 1, 4, 7; b (Ь-\~ 1)=
= (Зп 4-1) • (Зп 4-2) = 9па4“ 9п4-2, т. е. 9а 4- 2 = 9п (п 4* 1) + 2 и
278
a == n (n + 1), но a — число однозначное, значит, a == 1 • 2 « 2 или a « 2 X
ci 2
X 3 — 6; b ф 1, так как 9a + 2 = b (b + 1) > 2; b Ф 4, так как тогда — = —
b 4
a 6	.
и — = — — сократимые дроби, значит, b = 7; а Ф 2, так как 9a + 2 = 20 не
b 4
6
делится на 7, значит, a = 6 и искомая дробь
9
21.	10^. Задача сводится к нахождению трехзначного числа, обладающе-
го указанным свойством. Таким числом оказывается 199. При этом отношение,
о котором говорится в задаче, преобразуется так, чтобы в выражении для него
была дробь, числитель которой не содержал бы одной из цифр искомого числа,
имеющейся в знаменателе этой дроби, т. е. если искомое число записать в виде
100х + 10у + z, то преобразуем отношение, о котором говорится в задаче, сле-
100x+10y + z . , / Их 4-у \
дующим образом:------------•-----=14-9 —----------— . Так как х, у, z—однознач-
ди 4- У 4- z	\х 4- у 4- 2/
ные числа (х =/= 0), то это отношение будет иметь наименьшее значение при z = 9.
Заменив в рассматриваемом отношении z на 9, преобразовать его аналогич-
ным способом.
§ 2
а b — а
22.	Пусть (a, b) — 1, тогда 1 — — = —-—.
b b
23.	Если (а, Ь) — 1, то (а, а, ± b) = 1, (b, а ± b) = 1 и (b, b — а) = 1.
24.	Если (а 4- b, а — b) = d > 1, то 2а делится на d, 2b делится на d, так
как 2a = (a 4" b) + (а — b) и 2b —(а 4“Ь)—(a — Ь), т. е. а делится на d и b
d
делится на d, если (2, d) = 1, или а и b делятся на ~ , если (2, d) = 2.
а
25.	Если — > 1 и (a, b) = d > 1, то а = Ьп + р и р делится на d, т. е.
b
Р	Р
дробь — сократима; если (a, b) = 1, то — несократимая дробь.
b	b
26.	Если (14a 4- 3, 21a + 4) = d, то la + 1 = (21a + 4) — (14a + 3) де-
лится на d; 14a 4“ 2 делится на d и 14a 4“ 3 делится на d, т. е. (14a + 3) —
14a 4-3
— (14a 4- 2) = 1 делится на d, что возможно, если d = 1, т. е. дробь -----
21a 4- 4
несократима.
a
Аналогично и для дроби -——.
2a 4-1
27.	При любом четном натуральном п дробь несократима, так как при этом
п3 — п	2п	/ о . .	.
значении п несократима дробь —------ = п — ------ , так как (2n, n2 4~ 1) = 1.
п2 + 1 п2 + 1
а2 + ab 4- Ь2	ab
28.	1) Преобразовать данную дробь к виду ------—----==а + Ь—--------
а 4“ о	а 4~ b
. аЬ
и решить вопрос о сократимости или несократимости дроби —— .
а b
2)	Данная дробь может быть сократима только на то же число, что и дробь,
ей обратная (почему?). Использовать указание к предыдущему пункту.
3)	См. решение задачи 13 данной главы.
29.	Преобразовать числитель дроби в произведение, а в знаменателе вы-
делить слагаемые, кратные одному из множителей числителя.
279
- 2я2—1 n + 1	n + 1
30.-----= n — -—— = n — --——---------—, но (n + 1, 2n + 2 — 1) = 1.
2м 4- 1 2м 1 2м 4-2 — 1
31.	5м2 4- 1 по условию делится на 2, следовательно, (м, 2) = 1; 5м2 4- 1
делится и на 3, поэтому 6м2 — (м2 — 1) делится на 3, т. е. м2— 1 =(м — 1)Х
Х(м4~ 1) делится на 3, значит, (м, 3) = 1.
32.	а1 — nab + b2 = (а + Ь)2 — (м 4- 2)аЬ (см. задачу 235).
33.	Имеем: (Ь 4- 1) (Юм 4- Ь) = (а 4- 1) (10Ь 4- а); 9 (а - Ь) = а2 - 62;
а 4~ b = 9.
§ з
a k .	.
34.	Если — 4- “ = А, где А — целое число и (а, Ь) == 1, (k, р) = 1, то
м р
ар 4“ bk — Abp; ар делится на Ь, но (а, Ь) = 1, следовательно, р делится на Ь.
Аналогично устанавливается, что b делится на р, значит, Ь = р\ отсюда а 4- k
делится на Ь.
б)	См. пункт (а) данной задачи.
a k
в)	— и — — данные дроби, искомое условие: а должно делиться на р, k
b	Р
должно делиться на Ь.
a	k	.
г)	— и — — данные дроби, искомое условие: а должно делиться на k, р
6	р
должно делиться на Ь.
. a k
35.	Пусть данные дроби есть у и — , причем (a, b)— 1, (£, р) = 1 и (6, р)=>
a k ар 4- bk
«=« 1. Имеем: — 4- — — —--------. Допустим, что (ар 4- kb, bp)= d > 1, тогда
о р Ьр
Ьр должно делиться на d, ар 4" kb тоже должно делиться на d, следовательно,
b или р должно делиться на d, так как (Ь, р) — 1. Если Ь делится на d, то bk и
ар делятся на d, т. е. (Ь, ар) делится на d, но (Ь, ар) == 1, так как (а, Ь) = 1 и
(6. р)
(ар + kb, bp} = 1".
36.	Г
наше предположение, что d > 1, неверное, т. е.
1, следовательно,
Несократима, так как (2м 4" b, а) — 1 и (2м 4* а 4* &) = 1.
а
Пусть имеем: —- —
b
а а (с — Ь)
с Ьс
а
Пусть данные дроби будут
Ь
a k
a(k — р) == bk, или " = -----, откуда
b k — р
и (k, k — р) — 1. Аналогично для случая разности а
39. Допустив противное, составить квадратное уравнение, корнями кото-
рого были бы эти дроби (теорема Виета), и доказать, что полученное уравнение
не может иметь дробных корней.
40. Выразив k через а, Ь и п, подставить полученное для k выражение в
37.
38.
а
= —, откуда с — 6 = 1 ис=64-1.
Ьс
k	a t k	ak
и — и пусть 4- — = — , тогда
р	b р	Ьр
а= kn b = k ~р, так как (а, Ь) = 1
k и р => а 4- Ь.
правую часть рассматриваемого равенства.
41.	Воспользоваться предыдущей задачей и учесть, что второе слагаемое
указанного в ней равенства есть правильная дробь.
42.	Учесть, что (а — Ь)2 > 0, если а Ь.
43.	Учесть, что ab = *— и ab 4* cd > 2 (см. задачу 42, глава II).
са
111	с
44.	— 4- — + “ =— ~~ • Использовать зависимость между корнями и
т п р	d
коэффициентами уравнения.
45.	Выполнить указанные преобразования.
280
хъ 2х — 2
46. Найти сумму данных дробей и преобразовать ее к виду —----------
найти сумму кубов данных дробей и преобразовать ее к такому же виду.
47. Пусть все дроби расположены в возрастающем порядке:
- = - , откуда «! = &!•-;
°2 al	al
, откуда a2 > b2  — ;
O2 Oj
7 > Г > откуда an > blt • - .
'n bi	.
Следовательно,
+ a2 + ••• +
+ ^2 + ••• + bn
ai
«i + o2+ ••• +an> — (*i + 62+ ••• + bn), откуда
bi
а1 Л
> — . Аналогично устанавливается и верхняя граница.
48. Пусть А — некоторое целое число; положив п — 22Л, получим:.
,111 1 1 1 / 1 1 \
1+ 2+I+7 + - +r^i+7 = 1 + “2 +(i+i) +
/1 2_ 1 ц /1	1
+ \5 + 6 + 7 + 8 / + - + 12й->+1 + 2^-‘+2 + - +
+ 22.4 _ ! + 2гл Ь
1,1, 11
но —ГТ? +—~ +	+ Г* > Т > так как каждый член этой суммы, кроме
п+1	п+2 2п 2	г
последнего, больше ~ , а всего членов п; следовательно, каждая из круглых
„ 1 111
скобок в полученном выражении больше — и тогда 1 + “ + у + ••• + — >
> 1 + ^+| + -+-| = л + 1.
2а '
§ 4
49.	1) Нет, так как всякое рациональное число обращается в конечную или
бесконечную периодическую систематическую дробь.
2)	В системе счисления с основанием 12 в конечные систематические дроби
обратятся те и только те обыкновенные дроби, знаменатели которых не содержат
множителей, отличных от 2 и 3 и их степеней; в чистые периодические дроби —
те и только те обыкновенные дроби, знаменатели которых не содержат множите-
лями числа 2 и 3 и их степени; в смешанные периодические — тс и только те обык-
новенные дроби, знаменатели которых содержат, кроме 2 и 3 и их степеней, дру-
гие множители.
1	2	7
Примеры. — = 0,412; — = 0,(4972)12; — = 0,2(9724)12.
□12	О12	2О12
3)	Конечной.
4)	Частное от деления двух конечных десятичных дробей выразится конеч-
ной десятичной дробью в том и только в том случае, если делитель будет иметь
множителями, отличными от множителей делимого, только 2 или 5 и их степени.
281
5,	6, 7). Периодическая дробь, так как множество рациональных чисел—поле.
1	1	1 Зп2 + б/i + 2
50.	— +	+	, о = '	। п / ।	» п (п 4- 1) (п + 2)
п п + 1 п + 2 п (п + 1) (п + 2)
делится на 3, *3п2 + 6п + 2 не делится на 3, следовательно, дробь обращается
в бесконечную периодическую; если п — нечетное число, то Зп2 + 6п + 2 не
делится на 2, но п (п + 1) (п + 2) делится на 2, значит, дробь обращается в сме-
шанную периодическую; если же п — четное число, то знаменатель делится на 4,
а числитель не делится на 4, т. е. дробь опять обращается в смешанную периоди-
ческую.
1	1	2	6п2 + 6п + 1 п „
51.	— +-------+--------= --------—------— ; 6п2 + би + 1
п п + 1	2/i + 1 n (n + 1) (2п+1)
не делится на 6, п (п + 1) (2n + 1) делится на 6.
52.	2n2 + 1 — число нечетное при любом натуральном п. Показать, что
число 2n2 + 1 не может иметь множителем число 5 (см. задачу 301, глава I).
а
53.	Рассмотреть алгоритм обращения дроби 7- в десятичную, имея в виду,
ft
что (a, ft) = 1, а < ft, получить равенство
а ---------------- rk
~ = ^, Я1Яг - Як +	. где Яи Яг.....Як~
неполные частные, полученные при делении на b соответственно 10а, Юг,...
al	а	ь
..., Юг^-р Затем получить выражения для ~ • —z и для — • 10*.
о 10*	ь
54.	По условию задачи знаменатель дроби b в каноническом разложении
содержит множители 2, 5 и множители, отличные от 2 и 5, т. е. имеет вид b —
b	а	а \ 5n~ka
=	2Л • 5* • р. Преобразовав дробь у к виду у — — •------ (если n>k)t уста-
новить, в какую десятичную дробь обращается второй множитель этого произ-
ведения, и использовать предыдущую задачу.
55—56. Представив данные дроби в виде обыкновенных дробей и сократив
их, получим обыкновенные дроби с разными знаменателями. Такие дроби в сум-
ме не могут дать целое число (см. задачу 34, глава II).
57. Пусть данные чистые периодические дроби получены при обращении
е а	с _
в систематические соответственно дробей — и в системе счисления с основа-
ft	а
нием q, причем (a, ft) = 1; (с, d) = 1; (ft, q) *= 1; (d, q) “ 1. Установить вид
ас
систематической дроби, полученной от обращения обыкновенной дроби -- ,
bd
имея в виду наибольший общий делитель знаменателя этой дроби и основания,
системы счисления q.
58—59. Представить систематические дроби в виде обыкновенных дробей,
выполнить указанные действия.
6°. 7 = Л, (ад... aA) = А +	; Ab 99... 9 +	... akb ==>
о	уу ... У
- -»	к
k
= 99 ...9а, но (ft, 9) = 1, следовательно, cqc^ ... аЛ делится на 9.
в
61. ~ = A,	О,...ре) = А +
е к
282
откуда
а • 99 ... 9 00 ... 0 = b • А • 99 ... 90 ... О + (аха2 ... алрхр2...	— аха2 ... апЬ,
е	k	е k
но сумма делится на 5, первое слагаемое тоже делится на 5, значит, и второе
слагаемое должно делиться на 5, но (5, Ь)=1, следовательно, аха2... аЛрх ...ре—
—аха2... ak делится на 5, т. е. оканчивается 0 или 5.
63.	Пусть А — нечетное число, не оканчивающееся 5,
дробь — обращается в чистую периодическую дробь, т. е.
тогда (Л, 10) = 1 и
у — 0, (abc ... k) =
/1 Xei 1,1 J
п
делится на А. Если
abc ... k ______________
=---------- и А • abc... k— 9 • И ... 1, откуда 9 • 11 ... 1
99 ...9
-	.	-	п	п
п
(9, Л) = 1, то 11 ... 1 делится на Л. Если (9, Л) = р > 1, то А должно быть
V—*
п
кратно 3 или 9, т. е. Л = ЗВ или Л = 9В, тогда 11 ... 1 должно делиться на В,
п
где В — нечетное число, не оканчивающееся на 5.
64.	Пусть данное число А является знаменателем некоторой обыкновенной
несократимой дроби. Если (Л, 10) = 1, то эта дробь обращается в чистую перио-
дическую десятичную дробь, которая, в свою очередь, может быть представлена
в виде обыкновенной дроби со знаменателем, состоящим из одних девяток, та-
ким образом, число Л — делитель числа, выраженного цифрой 9. Аналогичные
рассуждения проводятся и в остальных случаях.
65.	Пусть alt а2,... , ар, ар+1>..., а2р — цифры периода дроби, причем ар+1+
+	= ар+2 + а2 = ... = а2р + ар = 9. Составим обыкновенную дробь, соот-
ветствующую данной периодической.
1 = aJO2*-^ а2102*~2 + ... + ар10*+	+ ... + а2р х10 + а2„ =
п~	102^—1
= (10* ~ 1) (aJO*-1 + Д210^~2 + ... + gp.JP + ар)
102^ — 1	+
9 (IO**-1 + 10Р-2+ ... + Ю + 1) aJO*-1 + а210*~2 + ... + ар + 1
+	102Р— 1	“	10^+1
т. е. 10Р 4- 1 = п (aUOP-1 + аа10Р-г + ... + flp.jlO + ар + 1).
__________ k	k
66.	Пусть p — простое число и Л, (аха2... а2/2) = — . Периоды дробей —
Р	Р
102^
и -----одинаковы, следовательно, разность этих дробей — целое число, т. е.
р
\Q2nk — k = £(10”+ 1) • (10я — 1) кратна р. Но k не делится на р (почему?),
Ю« — 1 тоже не делится на р (почему?), следовательно, 10я + 1 делится на р,
10«&	£
10я& + k делится на р и ----+ — — целое число, или
__________________________Р Р	__________
Ааха2 ... ап, ап+1 ... а2Д (аха2 ... а2/г) + Л, (aYa2 ... а2п) — целое число, т. е.
0, ап+1 ...а2п (aYa2 ... а2п) + 0, (аха2 ... а2п) = 1, что возможно, если йх+ап+х=
= а2 + ап+2 = ... = а2п + ап= 9.
67.	Допустим, данная бесконечная дробь — периодическая и пусть а —
число цифр в периоде. Цифры периода могут быть либо все одинаковы, либо
различны. Если все цифры периода одинаковы, то получим, что только одна циф-
ра повторяется бесконечное число раз (цифра периода), а остальные девять цифр
283
повторяются конечное число раз (цифры до периода), что противоречит закону
составления данной дроби.
Если цифры периода различны, то пусть некоторая цифра b до периода пов-
торяется не более п раз, в периоде же она может повториться не более а — 1
раз, так как по допущению не все цифры периода одинаковы. Таким образом,
при сделанном допущении цифра b может повторяться не более А раз, где А —
наибольшее из чисел п и а — 1. По закону же образования данной дроби цифра
b может повторяться в ней неограниченное число раз.
§ 5
68. Допустить противное, т. е. что
данное число можно представить в виде
несократимой дроби.
Например, если
допустить, что У 12345,67 ==»
а
I9
где
(а, Ь) «= 1, то получим, что 100а2 1 234 567д2, т. е. а должно делиться на
1 234 567 и а « 1 234 567п, откуда 100 . 1 234 5672n2 « 1 234 567Ь2, т. е. Ь
должно тоже делиться на 1 234 567, что противоречит условию (a, b) = 1.
69.
70.
71.
Представить данное выражение в виде N “ 1 +
1
1+?Г
Использовать определения указанных действий.
а)	Привести примеры, подтверждающие справедливость утверждений,
например (У 2 — 5) (У 2 + 5) =» —23.
б)	Допустить противное и использовать задачу 70.
73.	Учесть, что переход от одной системы счисления к другой основан на
операциях, приводящих к рациональным числам.
74.	/5“ = 10.001...,; /2М «= 1,01...3.
75.	Допустить противное и провести рассуждения, аналогичные приведен-
ным в задаче 68.
76.	Если допустить противное, то придем к равенству вида пР *=* cP, где п —
основание логарифма, а — данное число, р, b — натуральные числа. По условию
задачи такое равенство невозможно (почему?).	х
77.	Если допустить противное, то придем к равенству рационального и ир-
рационального числа (показать это), что невозможно.
78.	Пусть а и b — рациональные числа, удовлетворяющие условию. Тогда,
допустив противное утверждению задачи, получим равенство а = b + k2 +
4~ 2)/rF • k (k — разность У а — УЬ), которое невозможно (почему?).
79.	а) Имея в виду, что р — число положительное, рассмотреть случаи а= 0,
а > 0, а < 0.
б)	См. пункт (а).
в)	Учесть, что для любого действительного числа а справедливы соотноше-
ния— |а| < а ^|а| .
г)	Учесть, что а = а — р + р.
80.	Учесть, что справедливость утверждения для п = 2 доказана в задаче
79, в.
ГЛАВА III
§ 1
i
2.	а) 0 +—; б) —1 4- 2t; в) —1 + г; г) 1 + 0».
О
3.	а) —1 + 21; б) 0 + 31; в) —4 + Qi; г) —	+ И; д) 2 + 21; е) 2 — 2i;
ж) Чг; 3) “4+
284
4.	а) Ф* = —35° + 26180°, где k = 0, ± 1, ± 2, б) 325°; в) нет.
5.	arg z =» — (р.
6.	Воспользоваться геометрической интерпретацией комплексных чисел.
| ?i| — | z2|= | zx+ z2|, если z2 = О или разность аргументов этих чисел рав-
на л + 26л, где k — целое число;
|Zi + 2г1 = lzil 4" I 2г1» если zi ~ или z2 = или разность аргументов
этих чисел равна 26л, где k — целое число.
7.	Воспользоваться геометрической интерпретацией комплексных чисел.
Тождество выражает теорему: сумма квадратов диагоналей параллелограмма
равна сумме квадратов его сторон.
8.	а) Окружность радиуса а с центром в начале координат; б) луч, выходя-
л
щий из начала координат под углом — к положительному направлению вещест-
8
венной оси.
9.	Комплексные числа, которые изображаются точками, лежащими вне кру-
га с центром в начале координат и радиусом, равным 5.
10.	а) Точки, лежащие внутри круга с центром в начале координат и радиу-
сом 3;
б)	точки, лежащие на окружности и вне круга радиуса 3 с центром в начале
координат;
в)	точки, лежащие внутри круга и на его границе с центром в точке (0,3)
и радиусом 5;
ж) точки, лежащие внутри кольца, ограниченного окружностями радиуса-
ми 2 и 3 соответственно с центром в (0, 0).
11.	а) На окружности радиуса 8 с центром в точке (0, 5);
б)	внутри круга и на его границе радиуса 4 с центром в точке (1, 1);
в)	на эллипсе с фокусами в точках (а, 0), (Ь, 0) и большой осью 5;
г)	на окружности радиуса 1 с центром в (0, 0);
д)	на прямой, перпендикулярной к отрезку, соединяющему точки (0, 0) и
^0, -—j и проходящей через середину этого отрезка;
е)	на прямой х — с и на полуплоскости, расположенной справа от нее;
ж)	на прямой у = с и на полуплоскости, расположенной снизу от нее;
з)	в полосе —1 < у < 0;
и)	в I координатном углу;
к)	все точки полуплоскости, расположенные правее прямой, параллельной
оси OY и проходящей через точку (1,5; 0) за исключением точки (3, 0);
л)	вне окружности радиуса 10 с центром в точке (+1, 0);,
м) часть кольца, ограниченного двумя лучами, выходящими из начала коор-
<гс л;
динат под углами — и — к положительному направлению вещественной оси и
2	4
окружностями с центром в точке (0, —1) и радиусами 2 и 1;
н) часть кольца, ограниченного двумя лучами, выходящими из начала коор-
л 4
динат под углами — и —- л к положительному направлению вещественной оси и
8	3
окружностями с центром в начале координат и радиусами 3 и 2 и часть окружно-
сти радиуса 3 между указанными лучами.
12.	Условию \г — Ы 3 удовлетворяют только числа, изображенные точ-
ками, которые лежат внутри и на границе круга с центром (0; 5) и радиусом 3.
Числу с наименьшим положительным аргументом соответствует точка касания
луча, выходящего из начала координат к границе этого круга.
12	16
5 + 5
(5л 5л\	/л .я'
cos — + i sin — I; ж) z =— 3 I cos — — i sin —
285
7	9	9 \
2 cos —• л + i sin — л I;
\	8	8 )'
л — а\
- jsin —— ; н) cos(—ф)+
< а < л z =
не является тригонометрической формой комплексного числа z, так как |z| не
может быть равен — 3 и коэффициент мнимой части выражения в скобках равен
, л .л	/ л . , . л\
— sin у , а не sin у. Представим число г в виде z = 31 — cos у 4- i sin у I.
Arg z есть такой угол ф, что
л ф ф л	л 6
cos ср =— cos — ; sin ф = sin — ; ф = Л— — = — Л.
т	7 т	7	7	7
/ 6л . . 6л\
Тригонометрическая форма z == 3 I cos у- -\-t sin у L
л . л	ч 29	. 29	'
з) cos — +/ sin у ; и) cos ~ л + i sin — л; к)
л /	л	л\	а/	л — а
л) 2 cos у I cos — + i sin у ; м) 2 sin у cos —~--------
О \	О	О/	2 \ Z	z
+ i sin (— cp); n) cos (л + <p) + i sin (л + <p); p) при I
а /	' а а\	л а / а+ 2л
= 2 cos — cos — 4- i si и — , при л < а < 2л z =— 2 cos — cos-----------
2 \	2	2/ н	2 \	2
, . . а+ 2л\
+ isin ----- 1
17.
18.
19.
20.
a) —2a — (a + lb)i; 6) 16 + 18k
a) b == —d;	6) a = —с и b —d.
a) b = 0;	6) a = 0.
Множество всех действительных чисел.
21. а) /б - /3-(34- /2)<; б) - 16- 6»; в)
/34-3/2	—34-/6
4	4
22.	a) х = 1,	б) х = 2,
у =2;	у——1.
23.	а) х — 1,	б) х = i,
y=i;	у = 1 — /.
24.	a) z — 3 + 4/; б) z — 3 + 4/.
25.	а) (—8, 1); б) (—2, —1); в) (—3, —1); г) (-5, 5).
Перемножить комплексные числа в тригонометрической форме.
Рассмотреть случаи: 1) п > 0; 2) п < 0 и воспользоваться задачей 26.
26.
27.
28.
29.
Заметим, что "если мнимые части чисел равны нулю, т. е. если эти числа
вещественные, то это утверждение неверно.
30.	а) Пусть z = х + iy — искомое комплексное число, тогда z = х — iy.
Из условия z2= z имеем: (х + /у)2 = х — iy. О т в е т: a) z1=— у + i К?..,
1	. 1Л 3
^2 =	i—2— ’	^4 ~ Н 6) zt — 0, z2 — 1, z3 — 1, z4 — t, Z5 — i.
31.	a) 1, если n — 4k; it если n = 4k + 1; —1, если n = 4k + 2; — Z, если
n = 4k + 3, где k — целое число;
б)	0.
32.	8.
33.	n = 4kt где k = 0, zb 1, ±2, ... .
. ч ль l 7/гл .	. Ikn \
34.	a) (1 — t)k = 22 cos--------1- 1 sin--- ;
\	4	4 /
6)	2 при n = 4k + 1,	2/ при n — 4k + 2, '
—2 при n = 4k + ЗЛ	-—2/ при n = 4k.
286
38.
36® a) 72 + 72/; 6) 1.	/
л
37. Убедиться, что |z|== 1, arg z = ± — , и воспользоваться формулой
О
,	Л ПК
Муавра. Ответ: 2 cos — .
3
з 8 / л л\
21 = ^C0Sy + ‘S,n5j’
4	81 / 2л . 2л\
— 77^ cos — + i sin — ,
2	256 \	9	9 )
A 2S6/	17	17 \
Воспользоваться формулой Муавра и формулой бинома Ньютона.
т
2 (-i^c^tg2^
.	к=0
tg ПХ =------------------------ .
2 (-1)* С^Х
fe=0
39.
40.
где т, е — такие целые числа, что
п — 1 t п — 1
—— — \<т< —— ,
2	2
п
2
п
41. —63. ’
42. Пусть arg z = ф. Тогда zx
44. a) sin——
. Зф	Зф\
sin у + I cos — I , I Zj =
ф I
= 2 sin — I. Рассмотреть три случая: 1) sin ф = 0; 2) sin ф < 0; 3) sin ф > 0.
Ответы: 1) zx = 0, arg zx не определен;
л 4- Зф Л	Зл + Зф
2) arg z1= —----; 3) arg z1=---— .
43. Воспользоваться формулами Муавра и бинома Ньютона.
. пх
sin ~'
2
X •----;
. X
sin —
2
. пх п + 1
sin — cos---X
2	2
б)———•
sin —
2
n	n
Обозначим T— 2 sin kx\ S == 2 cos
fe=l	ы
n	n
Тогда S + IT— (cos kx + i sin kx) =	a2*,
anan+l — —
x	x
где a = cos — + j sin — ; S + IT =-----------.
2	2	1
a — —
a
287
45. Очевидно, что zn = 1. Обозначим 1 + z+ z2 + ... + zn“1= S0 Тогда
Sz — z + z2 + ••• + zn-1 + zn = (S — 1) + 1 = S. Откуда S = 0, если z 1,
и S = ft, если z = 1.
2л£х
49. k — kxd, n — где и nx взаимно просты. Отсюда e = cos---------------- 4-
,	. 2k хл	„	o 2nek.
+ i sin-------- . Возводя 8 в степень e < n, e > 0, получим:	= cos-------- -|~
2nekr
+ i sin---* .
"i
_	2 ле/?.
Если 8е = 1, то -------= 2л s, где s — целое,
"i
kt€
или — = s, т. е. kre • пх, но kt взаимно просто с nt. Следовательно, е J пи
ni
что противоречит условию 0 < е < nt. Таким образом, 8«i =?^ 1 при 0 < е < пг.
При е = пх имеем:
8rti — cos 2nk± 4- i sin 2nkx = 1.
. ” n
8 — первообразный корень степени и. = — из единицы.
d
7	7
— л	4- 2/?л	—	л 4- 2/? л
6	6
52. a) aft= cos
+ i sin

—-------, где k — О, 1, 2, 3, 4.
5
2 ,
з -------------------- ~
5
б) 2 ^/Т8 cos	+ i sin + у /?л^ , где k — 0, 1, 2.
io,-/	12/? 4-1	12^+1 \
в у 2 cos---------л 4-1 sin--------л , где k — 0, 1
7 v \	60	60	)
53. Умножить обе части уравнения на х— 1:
2/?л 2kn
*k = COS — + 4’sin— ,
Л
6
4
9.
где k = 1, 2,
6.
§ 2
55.	Пусть z = а + bi, где a, b — действительные числа. Составить произве-
дение (х — z) (х — z).
58.	Использовать теорему Гельфонда-Шнейдера.
59.	cos Зф — 4 cos3 ф — 3 cos ф; cos 60° = 4 cos320° — 3cos 20°. Обозначим
cos 20° = х. Тогда cos 20° есть корень уравнения 8х3 — 6х — 1 = 0.
60.	Воспользоваться формулой sin Зф = 3 sin ф — 4sin^.
fit)
61.	Если — корень полинома над Й, то показать, что t— корень поли-
нома над Q.
62.	Степень г равна 2, z± = у ~ /7, z2 = у + ]/7.
63.	а) 3; б) 2; в) 2; г) 1.
м.7,-^2. 7,7,= --!—
1 г > 2	2	2	2	2
65.	z_£Q.	_
66.	z± — а + bi, z2= а — bi, степень z равна 2.
67.	а) Степень z равна 4, zx = у^З + ]/2,
г2 = /3 — У2, za=— J/3 + /2, z4=—/3 —/£
288
б) Степень	л -	1'2 J2 г равна 4, zt 		- т) — . 2 ~	Zs~~r+ т ’ -	/2	.} 2 2л ——   — 1  . 4	2	2
в) Степень	z равна 4,
?1 =— 1 +	-1 / LLLL  -1 / -1 V 2~+'У “>' '
г2 =— 1 +	1 / Г'2+l _ • -j/ V 2~1 У 2	V	2
=—1 —	П / /2+1	.	//2-1 V 2	1 У 2
Ч =- 1 —	, //2 + 1	, / /2-1 V 2	1 у 2
68. а) Степе	;нь z равна 2,
? = - 1 — б) Степень	,.-/2 7=Г2_.Г2 г равна 2,
Z1
-Тг^./г -
— 1 ' — ’ 2
69. a) a + ЬУ3; 6) a + by‘2 + Cy\ в) a + b}'2 + c)'+ 4- d) 10;
г) a + bi\ Д) a+^ by 3 "h^y 9 + d\ 27 4-	81; e) a + b]/ 2 + cy 3 -f- dj 6;
ж) a + by 2 4- Cy 3 + dy 9 + e у 648 + f у 72, где at b, c, dt e, f — произ-
вольные рациональные числа.
71.	a + bi, где a, b — действительные числа.
72.	a) He образует, так как, с одной стороны, а2 должно лежать в простом
расширении, а с другой стороны, а2 нельзя представить в виде двучлена а -ъ Ьа,
поскольку а — корень неприводимого над полем рациональных чисел полинома
х3 — 3; б) не образует.
74.	1= /2 + у 5.
75.	t = /2 + 7/3+ 2/.
76.	а) Рассмотрим полиномы f (х) = х3 — 5 и g (х) = х2 + х 4- 2. Выра-
зим наибольший общий делитель этих полиномов линейно через f (х) и g (х).
Имеем:
8 —	__ 2) f (х) — (х2 — Зх + 1) g (х). Подставим в это равенство х =»» /5.
Получим: 8 = (—> 25 + 3^ 5 — 1) (у 25 + у 5 + 2). Умножим числитель и
знаменатель на —у 25 + 3 уЛ5 — 1. Получим: , V_25,+у 5—LL .
10 Заказ 1089
289
2 ___ з _
б) — уг25+ у'5 —2; в) ~6 /25 + /5 +39 . г) _п^'7»+18/7—29^/7+
5	47
+ 48; д) —у 4 + 7 у'Т — 3, е) 2 + /2 + /6; ж) 1—j/"8 + 2^2 + 3^2;
з) (1 + /2-^2) (1 + yz4); n)-jT> 27 С/3 - 1); к) а (у 3 - V2) (/2 - 1).
77. а) —а3+ 2а2 + а — 3; б) —8а2 + 2а — 25; в) —а2 — 2а; г) —-;
— а3 + 2а2 — 4а + Ю ч	™
д) -------—--------; е) 8а2 4~ а 4~ 30.
18
§ 3
78.	Нет. 79. Нет. 80. Кольцо. 81. Нет. 82. Нет. 83. Кольцо. 84. Кольцо.
85. Кольцо. 86. Кольцо. 87. Нет. Например, З2 — 22 = 5 не принадлежит дан-
ному множеству. 88. Нет. Например, З2 — 3 = 6 не принадлежит данному мно-
жеству. 89. Поле.
90.	Нет. Например,	не принадлежит данному множеству.
X3 х- ' X3
5	1 бх + 2
91.	Нет. Например, --+ — =--------- не принадлежит данному мно-
х + 2 х х(х + 2)
жеству.
х2 -I— 2х -I— 1 х2 -I— 2х -4- 1
92.	Нет. Например, --j-------•-----j----— х4 + 4х2 + 1 + 4Х3 +
+ 2х2 + 4х не принадлежит данному множеству.
93.	Поле. 94. Кольцо. 95. Нет. Например, при а — 1, b = 0, а± = 0, bt = 1
имеем: У 2 • ]Лз = ‘Уб — не принадлежит данному множеству.
96.	Нет. Например,
(V2+ ИЗ + 1/6) (/2 + уз - /6) = 2 /6- 1
не принадлежит данному множеству. 97. Поле. 98. Поле.
99.	Нет. Например, i • i = —1 не принадлежит данному множеству.
ГЛАВА IV
§ 1
1.	/ («) [х + (2у — z)]3 + 2[х+ (2у — z)J2 — 3[х+ (2у — г)] + 5. Сгруп-
пировать члены, содержащие х2. Коэффициент при х2 будет равен 3 (2у — z) +
+ 2 = бу — 3z + 2.
2.	Прибавить и отнять 2abcd, сгруппировать по три члена.
3.	Перемножить многочлены, прибавить и отнять 2abmn, 2астр, 2bcnpt
сгруппировать члены и т. д.
4.	Представить данное выражение как сумму трех квадратов:
а4 — 2а2 Ь2 + &4 + с4 + d4 — 2с2 d2 + 2а2 Ь2 — \abcd +
+ 2c2d2 = (а2 — Ь2)2 + (с2 — d2) + 2 (ab — cd)2.
отсюда а2 — Ь2 = 0, с2 — d2 = 0, ab — cd — 0 и т. д.
5.	х + у = — z возвести в куб и т. д.
6.	Возвести а2 + Ь2 + с2 в квадрат, учесть, что а + Ъ = — С,
7.	Раскрыть скобки и сгруппировать члены, получим:
(ау — bx)2 + (az — cx)2 + (bz — су)2 = 0.
Выражение в каждой скобке равно 0.
290
8.	Имеем: а2 + b2 + с2 — ab — ас — Ьс — 0, у [(а — Ь)2 + (Ь + с)2 4*
+ (а — с)2] = О.
Для действительных a, b, с а — b — О, b — с — О, а — с = О, отсюда
а = b = с.
9.	Подставить вместо s его значение. Первая скобка будет равна:
(а + с) (а + Ь). Аналогично вторая: (Ь + с) (Ь + а) и третья скобка:
(с + а) (с + d) и т. д.
10.	Преобразовать, подставив вместо s его значение.
11.	Преобразовать данное выражение: (Зху + 2у) (5ху + 2х).
Положить (Зху + 2у) (Зху + 2х) = А2 — В2 — (А + В) (А — В),
отсюда ( А + В = Зху + 2х,
| А — В = Зху + 2у.
Решая данную систему, находим: А = 4ху + х + у, В — ху 4~ х — у;
следовательно, ху (Зх + 2) (Зу + 2) = (4ху + х + у)2 — (ху + х — у)2.
Остановить, единственное ли это решение.
12.	Положить данное выражение равным (ах + by + с) (ахх + ^у-г q).
Перемножить эти многочлены и приравнять коэффициенты при одинаковых
степенях х и у.
Или рассмотреть данный многочлен как квадратичную функцию относитель-
но х, найти ее корни.
13.	Ь2 (х4 — z4) + а2 (zl- у4) - Ь2 (х2 + г2) (х2 — z2) + a2(z2 + y^(z2-y2).
Подставить вместо х2 + z2 -- а2 и у2 + z2 = 62 и т. д.
14.	См. задачу 12.
15.	Положить данное выражение равным Ах3 4* Вх2 + Сх 4* D.
Легко заметить, что А - 1. Давая х значения, найдем В, С, D. Получим:
(х + 2) (х + 3) (х — 5) — х3 — 19х — 30.
Ь2
16.	Ь2 = 4ас, а > 0, так как с = — ,
4а
Ь2 (2ах + Ь)2
ах2 + Ьх + с — ах2 + Ьх + ~	-----•
4а 4а
Это будет полным квадратом в области действительных чисел, если а > 0.
17.	ах3 + Ьх2 + сх + d — (Ах + В)2, отсюда а ~ А3, b — ЗА2В, с — ЗАВ2,
d = В3; далее имеем: А = -уа, В = d. Откуда выводим требуемые условия
Ь — З^/Л/, с = 3^ad2. Это есть условие, необходимое и достаточное.
18.	А — =Р 4; В равно 8 или 0.
19.	а^ + а^Р-1 + ... + ар -= (bQxk 4-	+ ... + bk) (сох^ + qx^A-
+ ... + cq).
Полагая в этом тождестве х — 1, найдем:
«о + ai + ••• + ар ~ (^о +	+ ••• + ^k) (со 4" ci + ••• 4“
ао 4- ai 4" ... 4~ ар — т
§ 2
20.	(х — 1) (х 4" 1) (* 4- а) (х — а).
21.	(х + 1) (хг — х + а), если а >
22.	(х2 + х 4~ 3) (х2 — х + 3).
23.	(а — 2) (а + 2)2 (а2 — 2а + 4).
24.	(у + z) (х + У) (х + z).
25.	(х 4- У 4~ г) (ху + xz + yz).
26.	х (х2 + х + 1) (х2 — х + 1).
27.	(х— 1) (х+ 1) (х2 —х+ 3).
28.	(х2 + 2) (х2 + х + 1).
29.	(х — 1) (х2 4- х + 3) (х2 — х + 3).
30.	(х — I)3 (х 4- I)2 (х- 4-1).	.
10*
291
31.	(х2 + 2у2 — 2ху) (х2 4- 2vy 4- 2у2).
32.	(х2 Хх4- 1) (х3 — х2 -г 1). Прибавить и вычесть ха.
33.	(х2 4- * 4- 1) (х2 — х 4- 1).	_	_
34.	х44-2х24-1—2х2= (х24- I)2 —(/2х)2	=	(х2 4/2х 4 D X
Х(+-/2х+1)^
35.	х4 + 2 /3+ +3 — 2 /Зх2 + х2 = (х2 + /З)2 — х2 (2/3 — 1>=-
-= (х2 + /У+ X /2 /3— 1) (Х2+ Уз — хУ 2у 3 — 1).
36.	(х2 + У 2	+ хУ2/2+1) (х2 + У‘2— хУ2	/ 2+ 1).
37.	(х2 + /3	— хУ 2 /3 — 3) (х2+ /3+ хУ2	У 3 — 3).
38.	(х2 + 3) (х2 + Зх + 3) (х2 — Зх + 3).
39.	(1 — х) (1	4 х) (1 4 х1) (1 4- х 4- -х2) (1 — х 4*	х2) (1 — х2	4-	х4).
40.	f (х) = гр	(x)q (х) 4- г (х)\ ф (х) — гр (x)ql (х) 4-	(х),	если	г	(х)	4 Г1(х)=»
— 0, то / (х) 4 ф (х) делится на гр (х).
41.	f (х) 4 Ф (х) делится на х — 1, если f (1) 4 ф (1) = 0.
42.	Чтобы сумма двух многочленов делилась на х2 4 1, необходимо, чтобы
сумма остатков делилась на х2 4 1, т. е. (а 4* at)x 4 (b 4 Ьх)— 0, что возможно,
когда а = —av b = —Ь<.
43.	f (х) — гр (x)q (х) 4 г (х), ф (х) = гр (х)4- rt(x), f (х) ф (х) =
= гр(х)? (х) гр(х)^ (х) 4- гр (x)q{(x) г (к) 4- ф (x)q (х) rt(x) 4 г (х) rt (х).
Первые три слагаемых делятся на гр (х), следовательно, необходимо, чтобы
rt (х)г (х) делилось на гр(х).
44.	Один из многочленов должен делиться на х — 1, другой — на х + 1.
45.	f (х) = гр (х) (х — 1), ф (х) = гр, (х) (х — 2),
где гр (х) и грг (х) такие многочлены, что гр (2) 4 0, фг (1)	0.
46.	Делится, так как на двучлен (х — 2) делится каждое слагаемое.
47.	Делится. Положить х2 = у.
48.	Если т нечетное, то делится; если т четное, то не делится. Положить
х = 0.
49.	Преобразовать делитель: (ах 4 by) + (bx 4 ay)-
50.	Преобразовать делитель так, чтобы получились члены делимого
2х2 4“ 2у2 = (х2 — ху 4 У2) 4 (х2 4 ху 4 у2), а сумма пятых степеней делится
на сумму первых степеней.
51.	Делится, х2 — х -= х (х — 1) = (х — 0) (х — 1).
f (0) - (—1)2" 4- (—1)2/* - 2 - 0;
f (i) = (i + 1 — i)2« + (i __ i 4- \)2п — 2-0.
52. Делится.
2Х3 4 Зх2 4 х = х (2х2 4 Зх 4 1) = 2х (х 4 1) (х 4 “
/ (0) = О, / (-1) = О, f (- £) = 0.
53.	Рассмотреть все возможные случаи, т может иметь вид 3/г; 3k 4 1; 3fe 4 2.
2
54.	л = — — .
□
55.	При х = —у F (—у) = ау4 4 4Ьу6 4 У4, но F (—у) — 0, следовательно,
необходимо, чтобы а 4 4Ьу2 4 1 = 0. При х = — — у имеем: F — — yj =
=* ~у4 (13а 4 by2 4 1), но F^~- ~-yj=O, поэтому 13а 4 Ьу24 1 — 0- Решая
1	4
полученную систему двух уравнений, получим: а — — -д , b =	, .
17	17у2
56.	Обозначим х2 через у, получим. А у2'2-1 — yin~2 4 y2/*-3— ... -f- у—-1;
у2 ~ 1 - (у - 1) (у — 1). А (—1)= (—l)2,2-i — (-I)2"-2 4 ... 4 (—1) - I «
ж —2п. Не делится.
292
57. Помножить и разделить первый многочлен на х2 — 1, второй много-
член — на х — 1 и первое выражение разделить на второе. Разделится, если п —
нечетное число.
58.	Помножить и разделить первый многочлен на 1 — х4, второй ~ на
1 — х2 и т. д. Разделится, если п + 1 — нечетное число
59.	Частное данных многочленов помножить и разделить на х — 1. Условие
делимости /и -г 1 = k (п, + 1), где k — целое число.
60.	Не делится. Помножить и разделить первый многочлен на а4 — 1, вто-
рой многочлен — на а2 — 1 и т. д.
61.	х2 + 1 = (х + 0 (х — /). Найти значение данного многочлена при
х = i и х = —Л Если п — нечетное число, то разделится.
62.	Делится, х3 + х2 + х + 1 = (х2 + 1) (х + I). Корни этого многочлена
будут —1, /, —i. Найти значение рервого многочлена при значениях х = —1, i,
63.
Если п
Произведение преобразовать следующим образом: если п нечетное, то
- -П | _________________ Х2П
- = ~---Г=1+х2 + х4 + ....
X 1 —X2
1 _
А = !—-
1 — X
четное, то
1~хя \—хп 1—2хя + х2Я
А —	•	—
1 — X 1 + х	1 — X2
Непосредственным делением находим:
1 4" х2 + х4 + х6 + х8 + х10
/1 —xV
64.	(1 + х + х2 + ... + х22”1)2— -- I :
4-х12 4-... •
1 — 2хя + х222
1 — 2х 4- х2
Непосредственным делением находим:
1 + 2х 4- Зх2 4- 4х3 4- 5х4 4- бх5 4- 7х6 + ... .
65.	А = 9Я+1 — 222"1 = (9 — 2) (9я 4- 9й-1 .24-... + 2я).
66.	А — 8172X1 — 64я+1 (см. задачу 65).
67.	А	~	9	•	27п +	10	• 8я,	прибавить	и	отнять	9	•	8й	и	т.	д.
68.	А	=	9	•	32я +	2 •	82« = 11 • З222 +	2 • 8222	—	2	• 32я	и	т. д.
69.	А	=	5	•	5222 +	18	• 2п,	прибавить	и	отнять	5	•	2й	и	т.	д.
70.	А	=	З22242 (25я	—	12я)	и т. д.
71.	А = 121 • 1122 + 12 • 144", прибавить и отнять 12 • 11я (см. задачу 73).
72.	Если п — нечетное число.
73.	А = 49я — 16я - 264 — 33-(49— 16) (49я-J+49я"2.16 +4922‘3 Л62+...+
4- 1 б" 1) — 264 — 33 = 33 (49 — 1) (49я-2 + 49я’3 -г ... + 1) + {49я*2 • 16 +
+ 4922-3 • 162 + ... + 1622-1} — 264.
Все члены в фигурных скобках делятея на 8, следовательно, данное выраже-
ние делится на 264.
74.	А = 5 (41 + 8)яхх + 8й и т. д. Далее 5 • 8Я+1 + 8я = 41 • 8я.
75.	Данное выражение представить в виде А — Зп (4я — 1) — (4я —- Зп —
—1). 4я — 1 разложить на множители, а 4я = (3 + 1)я разложить по биному
Ньютона.
76.	1892 — 22 • И • 43. После преобразований данной суммы получим:
А = 43- 235 + 22 • З11 - 43 . 22 (233 + З11) = 43-4 (811 + З11) -= 43 • 4 • 11 X
х (gio — 8э . з + ... + З10).
77.	3 • 9я + 40п — 67 = 3 • 9я + 40п — 3 — 64 = 3 • (9я — 1) + 40п —
—64 = 3 - (9 — 1) (9я’1 + 9я-2 + ... + 9 + 1) + 40п — 64 = 3 • 8[ (8 + 1)я-4+
+ (8 + I)22"2 + ... + (8 + 1) + 11 + 40п — 64. Раскрывая скобки по биному
Ньютона, получим, что все члены каждого разложения, кроме последнего,
делятся на 8.
Обозначим их сумму через 8В, а сумма последних членов будет 1 + 1 + 1 +
+ ... + 1 = п. Следовательно, А = 3- 8-8В + 3-8п + 40п — 64 = 3 X
X 64# + 64п — 64 делится на 64.
78.	62я + Зях2 + 3я = 62Я + 9 ♦ 3я + 3я = 32я • 22я + 10 • 3я =*
«= 3я [3я • 22я + 10] = 3я [3я • 4я + 10| = 3я • 112я + 10] = 3я [12я — 1 +
+ 11] - 3я |(12 — 1) (12я-1 + 12я'2 + ... + 1) + 11| = Зя[ 1! (12я-1 + 12я-2 +
4- ... -г 1) — П]. Выражение в квадратных скобках делится на 11.
293
79.	A - 10" — 1 + 18/г - (10 — 1) (IO""1 + IO"'2 + ... +10 + 1) +
+ 18/i = 9 [IO""1 + 10"“2 + ... + 10 + 1 + 2/1]. Всякая степень 10 при
делении на 9 дает в остатке 1. Сумма остатков от деления на 9 всех членов будет
1+ 1 + ... +1, т. е. п — 1. Следовательно, остаток от деления всех членов на
9 будет п — 1 + 2/i + 1 = Зп, т. е. выражение, стоящее в квадратной скобке,
делится на 3, тогда все выражение разделится на 27.
80.	А = 49" — 48/1 — 1 = 49" — 1 — 48/1 = (49 — 1) [ 49"'1 + 49"’2 +
149/г-з + ... 4. 49 + 1]_48/i = 48К49"-1 — 1) + (49"~2 — 1) + ... + (49 — 1)]=
= 48 [48 (49"-2 + 49"-3 + ... + 1) + 48 (49"‘3 + 49"~4 + ... + 1) + 48].
Каждое слагаемое в квадратной скобке делится на 48; следовательно, все* произ-
ведение разделится на 482.
81.	(х + 2) (х — 1) (х2 + х + 6). Положить х2 + х	= у.
82.	(х — 1) (х + 2) (х — 3) (х + 4). Положить х2 +	х = у.
83.	(ах + 2Ь) (ах + а + Ь). Положить ах — у.
84.	(2х + у + z) (х + 2у + г). Данный многочлен представить	в	виде
(х + у + Z)2 + (х + у) • (X + у + г) + ху. Положить	X + у	+	z —	t	и	раз-
ложить полученный квадратный трехчлен на линейные множители.
85.	(х— 1) (х+ 2) (х2 + х + 5). Выражения в скобках отличаются на по-
стоянное слагаемое. Положить х2 + х + 1 = у, тогда х2+х+2=у + 1.
Полученный квадратный трехчлен относительно у разложить на множители.
86.	(х + 2) (х + 4) (х2 + 5х + 8). Положить х2 + 4х + 8 = у.
87.	(х + 2)2 (х2 + 6х + 4). Положить х2 + х + 4 — у.
88.	9 (х + I)2 (х2 + 4х + 1). Положить х2 + 6х + 1 = у.
89.	Соединить в группы множители 1 и 4, 2 и 3.
[(х + 1 )(х + 4)! [(X + 2) (X + 3)j - 24 - (х2 + 5х + 4) • (х2 + 5х + 6)-
— 24. Положим, х2 + 5х + 4 — v, тогда у2 + 2у — 24 —
=(у + 6) (у — 4) = (х2 + 5х + 10)(х2 + 5х) = х (х + 5) • (х2 + 5х + 10).
90.	(х+ 2) (х+ 6) (х2 + 8х + 10) (см. решение задачи 89).
91.	(х+ 8) (2х + 15) (2х2 + 35х+ 120). Соединить в группы крайние и
средние двучлены и положить х2 + 16х+ 60 = у. Разложить полученный квад-
ратный трехчлен относительно у на линейные множители.
.	92. Соединить в группы множители 1 и 4, 2 и 3. Положить х2 — 7х + 6 — у,
тогда у (у + 6) + 10 = у2 + бу + 10 - (у + З)2 + 1 > 0.
93.	(х2 + 5ах + 5а2)2.
94.	[х2 + (а + Ь)х +
+ ab, тогда У (У — ab) + /г ~ у2 — aby + /г, /г = —— .
4
95.	Делители свободного члена, взятые со знаком плюс или минус, могут
быть корнями соответствующего уравнения. При х = —2 F (—2) = 0. Следо-
вательно, данное выражение делится на х + 2. Затем к данному выражению при-
бавляем и отнимаем такие члены, чтобы каждые два рядом стоящих члена пред-
ставляли собой произведение некоторой степени х на (х + 2).
ab][x2 + (а + Ь)х] + Л; положим у = х2 + (а + Ь)х+
F (х) - х3 + 2х2 — 2х2 — 4х — 15х — 30 = х2 (х + 2) — 2х (х+2) —
- 15 (х + 2) = (х + 2) (х2 — 2х - 15) = (х + 2) - (х — 5) (х + 3).
96.	F (3) = 0. F (х) - х3 — Зх2 4- Зх2 — 9х + 2х — 6 = х2 (х — 3) +
4- Зх (х — 3) + 2 (х — 3) = (х — 3) (х + 1) (х + 2).
97.	(х — 1) (х + 3) (х + 7).
98.	(х — 1) (х + З)2.
99.	(х+ 1) (х+ 3) (х+ 5).
10Q. (х —3)2(х+ 5).	„	•
101.	Положить х = Зу • у3 — Зу2 + бу — 4 = (Зх г— 1) (Зх — 2)2.
102.	F (1) = 0, (х) = х4 — х3 + 2х2 - 2х + Зх —3 -= (х —1) (х3 + 2х +
). '
Ft (х) = х3 + 2х + 3;	(—1) = 0 и т. д.
F<x)=(x-l)(x+l)(x2-x+3).	-	-	-	•
103,	(х — 1) (х + 2) (х + 3) (2х — 1).
294
104.	(х — I)3 (2х + 5).
105.	(х + I)2 (х — 2)2.
106.	(х + 2)2 (х — З)2.
107.	(х — 1) (х + 1) (х + 5) (х — 3).
108.	F (х) = (х + 1) (27х3 — 27х2 + 18х — 4). Положить во второй скобке
Зх — у и разложить на множители многочлен у3 — Зу2 + бу — 4. Окончательно
(х -|- 1) (Зх — 1) (9х2 — бх + 4).
109.	(Зх — 1) (1 — х) (2х + I)2.
ПО. (а — 2)3 (а2 + 4).
111.	(а+ I)2 (а2 + 4)2.
112.	(х2 + ху + у2) (х — у + z).
113.	а2п (1 — ап — а*п) (1 + ап + а4").
114.	(х — у)2 (х+ 2у).
115.	А = х4 — х2у2 + 9х2у2 — 9у4 + бх3у—бху3 и т. д.
Окончательно А = (х — у) (х + у) (х + Зу)2.
116.	(х + у + 2) (ху + xz + yz).
117.	(х — у + z) (х + У + z) (х + у — z).
118.	(х2 — yz) (z2 — ху) (у2 — xz).
119.	—(а — Ь) (Ь —- с) (с — а) (а2Ь2 + а2с2 + Ь2с2 + а2Ьс + ab2c-\* аЪс2).
120.	(а + b)(b + с) (с + d).
121.	(а + Ь — с) (а — b + с) (а + b + с) (Ь + с — а).
122.	(х + У + z) (ху + xz Ь yz).
123.	(х — у)2 (х2 + ху + у2) (х + 2у) > 0.
124.	2 (х2 + у2) (х4 + 5х2у2 + у4).
125.	(х + у — 1) (х2 — ху + у2 +	х + у +	1).
126.	(х — у) (у — z) (х — z) (ху +	yz +	xz).
127.	(х + у + z) (х2 + у2 + z2).
128.	xyz (х — z) (х — у) (у — г).
129.	x2y2z2 (х — z) (х — у) (у — z)	(х +	У +	2).
130.	2. 131. х2 — 5х + 8. 132. бху (х + у) (х2 + ху + у2).
133.	7ху (х + у) (х2 + ху + у2)2.
134.	(х + у) (х - у)2 (х2 + у2) > 0.
135.	При а = Ь данный многочлен принимает значение, равное 0; следова-
тельно, он делится на (а — Ь), делится на (Ь — с) и (с — а), т. е. А — k(a — Ь)Х
X (Ь — с) (с — а). Частное k — постоянное число, так как все члены делимого и
делителя третьего измерения. Придавая a, Ь, с какие угодно значения, например
я =-0, Ь = 1, с — 2, получим: 6 = 2К, откуда /< = 3, следовательно, А =
= 3 (а — Ь) (Ь — с) (с — а).
Примечание. Нельзя придавать а, Ь такие значения, при которых
левая и правая части равенства обращаются в 0.
136.	При а = —Ь многочлен обращается в 0, следовательно, он делится на
а 4- Ь. Многочлен делится на а + с и Ь + с и т. д., т. е.
А = З(а-гЬ) (Ь + с)(с+а).
137.	(а + Ь) (Ь + с) (с + а).
138.	При а = 0, Ь = 0 и с — 0 многочлен обращается в 0. Следовательно,
А — /(abc. Полагая а= 1, b = 1, с — 1, получим: К = 4. Окончательно имеем:
А = 4а Ьс.
139.	4а Ьс.
140.	(х — у) (у — z) (z — х).
141.	—(а — Ь) (Ь — с) (с — а).
142.	(а + Ь)(Ь + с) (с + а).
143.	24 abc.
144.	При Ь = с многочлен обращается в 0, т. е. Р = 0, аналогично Р = 0
при а = с и а == Ь. Следовательно, многочлен делится на (а — Ь) (Ь — с) (с — а).
Данный многочлен четвертого измерения, следовательно, частное будет много-
членом первого измерения, т. е. Р - - (а — Ь) (Ь — с) (с — а) (Аа + ВЬ 4- Сс +
+ D), D = 0, так как в левой части все члены четвертого измерения, А = В —
С. Отсюда Р — А (а — Ь) (Ь — с) (с — а) (а + h + с). Полагая а = 0,
295
5=1, с = 2, найдем, что А = 1, тогда окончательно получим: Р = (а — д)Х
Х(Ь — с) (с — а) (а + Ь + с).
145.	(х — у) (у — z) (z — х) (х 4- у + г).
146.	2 (а — Ь) (Ь — с) {а - с) (а + b + с).
147.	12аЬс (а + b + с).
148.	3 (а — Ь) (Ь — с) (а — с).
149.	Р = [(2а + 2Ь + 2с)3 — (Ь + с)8] — [(с + а)3 + (а + Ь)3] = (2а + Ь +
+ с) А — (2а + b с)В — (2а + b + с) (А — В), т. е. данный многочлен
делится на 2а + b + с, делится на а + 2Ь + с и а -\-Ь + 2с, тогда Р = (2а +
+ b + с) (а + 2Ь + с) (а + b 4* 2с) К. Положив а— b = с = 1, найдем:
К - 3.
150.	При х = у многочлен обращается в 0, Р = 0, аналогично Р = 0 и при
х = z и у = z; следовательно, Р = (х — у) (у — z) (z — х) [Л (х1 2 + у2 + г2) +
+ В (ху + xz + У?)]. Полагая х = 0, у = 1, z — 2, получим: 5Л + 2В — 15.
Полагая х= 1, у = 2, z = 3, получим: 14Л + 11В ~ 15. Решая систему урав-
нений, находим: А = 5, В = —5. Следовательно,
Р — 5 (х — у) (у — z) (z — х) (х2 + У2 + Z2 — ху — yz — xz).
151.	5 (а + b) (а + с) (Ь + с) (а2 + Ь2 + с2 + ab + ас + Ьс) (см. решение
задачи 150).
152.	При а = 0, b = 0, с = 0 многочлен обращается в 0, следовательно,
Р — abc [Л (а2 + Ь2 с2) В (ab-\-bc + са)] и т. д.
Р = 80аЬс (а2 4* Ь2 + с2).
153.	—(а	—	Ь) (Ь —	с)	(с — а)	[а2 + Ь2 + с2	+	ab	+	ас	+	Ьс].
154.	—-(а	—	Ь) (Ь —	с)	(с — а)	(а + Ь + с)2.
155.	_	Ь) (Ь —	с)	(с — а)	[3 (а2 + Ь2 +	с2)	+	5	(ab	+	Ьс + са)].
156.	—(а	—	Ь)(Ь —	с)	(с — а)	(а + Ь+ с)2.
157.	При а = Ь, а = с, Ь = с многочлен обращается в 0; следовательно,
Р = (а — Ь) (Ь — с) (с — а) [Л (а3 + Ь3 + с3) + В (а2Ь + а2с + Ь2а + Ь2с +
4“ с2а + с2Ь) + Cabc], так как все члены в левой части шестого измерения, то
частное будет третьего измерения. Полагая а — 0, Ь = 1, с = 2, получим: ЗЛ 4-
4~ 2В ~ 5; полагая а = 0, Ь = 2, с — 3, получим: 7Л + 6В = 13, откуда
А — 1, В — 1. Полагая а = 1, Ь = 2, с = 3, найдем: С — —9. Следовательно,
Р = (а — с) (Ь — с) (с — а)[а3 4* Ь3 + с3 4* а2Ь + аЬ2 + а2с + Ь2с 4“ с2а +
+ с2Ь — 9аЬс].
158.	Р = К (а — b) (а — с) (а — d) (Ь — с) (b — d) (с — d). Полагая а = 0,
Ь = 1, с — 2, d = 3, найдем: К — —1.
159.	16 (а — Ь) (а — с) (а — d) (Ь — с) (Ь — d) (с — d).
160.	Р = (а — Ь) (а — с) (а — d) (b — с) (b — d) (с — d) • [Л (а3 + Ь3 +
+ с3 + d3) + В (a2b + а2с + a2d + Ь2с + b2d+b2a + c2d + с2а + с2Ь + d2a +
+ d2b + d2c) + С (abc + abd + acd + bed)].
Полагая: 1) a = 0, b — 1, c = 2, d = 3, имеем: ЗЛ + 4B + С = 1;
2)	а = 0, b —1, с = 2, d	—2, имеем: Л + ЗВ — 4С	—4;
3)	а ~ 0, b = 1, с = —3, d = 2, имеем: 14Л 18В — 6С = —6. Решая
систему, получим: Л = 0, В = 0, С = 1. Следовательно, Р = (а — Ь) (а — с)Х
X (а — d) (b — с) (Ь — d) (с — d) (abc + abd + acd + bed).
161.	При замене x на —(у + z) многочлен обращается в 0, следовательно,
он делится на х + у + z, т. е. Р = (х + у + z) [Л (х2 + У2 -т z2) + В (ху +
+ xz + yz)]. При х = 0, у = 1, z = 2 5Л + 2В = 3; при х = 0, у — 1, z — 1
2А + В = 1, откуда Л = 1, В = — 1. Тогда Р = (х + у + z) (х2 4- у2 4" z2 —
— ху — xz — yz).
§ 3
162.	х — 1. 163. Зх2 - х 4- 1. 164. х (х - 2). 165. 2х J I.
166.	(х2 + 1) (х+ I). 167. х (2х2 — Зх 1- 4) 16Я. П (а	1) (а ~ 1);
2)	Зх - у.
х — 1	2х2 — 2х — 3
169.	1) d (х) = х — I; А (х) =— —“ ; В(х)— -—~ ; 2) (dx) — 1,
1 » (х) (—х — 1)4“ /2 W (х3 + х2 — Зх — 2); d (х) найдем, используя ал-
горитм Евклида: делим f\ (х) на /2 (х); /2 W на первый остаток и т. д.
296
Чтобы найти многочлены А (х) и В (х), используем равенство d (х) ==
= h (х) А (х) + /2 (х) В (*) с неопределенными коэффициентами А (х) и В (х).
Приравниваем коэффициенты при одинаковых степенях х; решив полученную
систему, найдем А (х) и В (х).
170.	(х + 3) (х4 — 1). 171. (4х2 4- 3) (х — 2) (Зх + 1).
172.	(х — I)3 (х + 1) (х2 + 1). 173. (х — 2) (2х + 3) (Зх — 1).
174.	(х — 3) (х2 + Зх + 9) (х — 12) (х2 — 2). 175. (2х—1 )(х~-11)(х+9)(2х+1).
§ 4
181.
а — 3 а — b
Зх — 1	5х — 4
------- . 182. -------------
Зх + 1	х2-}- х +1
178.
. 183.
а2-! Л апЬп	х2 —- 1
---------. 179. --. 180. ----.
а4 —2а2+ 4 атЬт х2—х+1
3(х + 3)
X4 — X3 + 6х2 — 6х + 6
. Разложить
знаме-
натель на множители, представив его в виде х2 + 5х3 + 6 = (х2+ 1) + (5х3 + 5)
и т. д.
(х—I)2	а + b + с	а — 2Ь
184.		-------- 185. ---------. 186. ------- . Разложить числитель
х2 — Зх+1 а — b — с а + b — с
на множители:
А = а2 — ab + ас — 2ab + 2b2 — 2abc = (а — 2d) (а — b + с).
а + 2
187.	—— .
а —2
X2 — ху + у2
188.	----------—. Числитель и знаменатель помножить на х2 — у2.
(X — у)2
189.	(х2 — х + 1) (х4 — х2 + 1). Умножить числитель и знаменатель на
х4 — 1.
190.		. Умножить числитель и знаменатель на х2 — 1.
х + 1
X — 1
191.	. Умножить числитель и знаменатель на х2 — 1.
х2 —х+1
Примечание. Примеры 190, 191 можно решать непосредственным раз-
ложением на множители.
7	1
192.	а + b + с. 193. — (х2 + ху + у2). 194. — (х + у + z).
195.		, Преобразовать знаменатель:
(а + с — Ь) (с — а + b) и F
2 А2 + 2Ь2с2 + (а4 — Ь4 — 2а2Ь2) — с* = 2с2 (а2 + Ь2) — (а2 — Ь2)2 — с***
- с2 [а2 + b2 + а2 + b2 + 2ab — 2аЬ] - (а2 — Ь2)2— с4 =» с2[ (а + Ь)2 +
+ (а — Ь)2\ — (а2 — Ь2)2 — с* = и т. д.
196.	1. См. решение задачи 147.
b — d
197.		. 198. (х + у) (у + г) (z + х).
а — с
199.
203.
204.
пат + тап	х	(Ь + с + а)2
-----Z------ 200. -----------------------. 202. -—!!.
тат + пап	(х + 1) (х + 2) (х + 3)	2Ьс
b + c + d
а(а + b + с+ d)
1-й способ. Последовательно сложить первые два члена, к полученной
сумме прибавить третий член и т. д.
1 1 1
2-й способ.---------= — —--------- .
а (а - 1) а а + 1
297
1 1 _ 1
(я-г1)(я+2)	а+1 а + 2*
:i 1	1
(а 4 4) (а 4 5) а 4 4 а 4 5
205.
5
Сложив данные равенства, получим: ---------.
а (а + 5)
32
-----. Применить 1 -й способ предыдущей задачи.
9ПА 2Я+!	9П7 1	(а+ 1) (6+ 1) (С+ 1) (d+ 1) г
’ 2°7, L °8’-----------М---------------’ СМ’ 3адаЧУ 204'
210.	В левой части равенства имеем квадратный трехчлен; следовательно,
он может быть представлен в виде Ах2 4 Вх + С. При х = а имеем: а2 = Аа2 4
+ Ва + С; при х = b имеем: b2 = АЬ2 4 ВЬ 4 С; при х = с имеем: с2 = Ас2 4
4 Вс + С. Решая систему относительно А, В, С, находим: А — 1; В = 0; С = 0,
т. е. данное выражение равняется х2.
211.	Вынести за скобку ------------------ . В скобках получится квад-
(х—а)(х — Ь)(х— с)
ратичный трехчлен. Применяя способ, указанный в задаче 210, найдем: 4 = 0,
В 1, С = 0.
1	1	х	х — 11 у + 1	1 — х
212.	— . 213. 1— — . 214.  --. 215. ----------—-—. 216. -------------; .
217. 3(а2 + Ь2 + с2). 218.
Х“ — 1	ZX-f-y — J	l-f-X —Х‘
X — 1
-----. 219. а -4- b 4- с. 220. (а 4 b 4 с!2
221.	Умножить обе части равенства на разность дробей.
222.	Приравнять данные отношения числу k\ умножить первое равенство
на с, второе — на Ь, третье — на а и сложить.
223.	Воспользоваться производной пропорцией и заменить в правой части
b на ас.
2а	2b	2с	2Ь
224.	1 4- х = ——, 14- У =----,14-2=----------; следовательно,----- X
а 4 Ь b 4- с а 4 с	а 4 b
2с 2а а 4 b — (a — b) b 4 е — (Ь — с) с 4 а — (с — о)
X — * “7— =-------------Г4-------’-------Г4------*---------;------- и т- А-
Ь + с с4«	а-\-Ъ	&4с	с-\-а
225.	Воспользоваться производной пропорцией.
§ 5
1	2
226.	24. 227. 1. 228. 0,79. 229. 6-. 230. 2~. 231. 20,86. 232. 5,42. 233. 2,49.
Л	о
234. 2,36. 235. 2,90. 236. 12 . 237. 10^75. 238. —3/IT. 239. —2/ 5: 240. 8. 241. 3.
242. ^3/Г8. 243. 1 (2+ /б-/ГО). 244. (30-2/3^5 + Гб~-/7)
245. 3 (3/2-4) (3+/2 + /3) .
_________1__________________!__________
|"8Т + у'27 + 4+ * 8 4G 33 + 4 + /3+ 1)
=	4~1 . = _> 3- = £ 4 ^ ,-у_
М'зМ 4-2 6
298
247. 0,06. 248. a (/3 —/2) (/2 — 1). 249. 5/39.
240 Va-b(Va + Vb) tfa-b(Va-Vb) /5 (/6 4-1)
a — b	a — b	5
253. 1,79. 254. 0,15. 255. 0,918. 256. 0,234. 257. (y^TT 4- 4/8) (/IT 4- /8).
258.	(У 3 - 8/2) (4/3 4- V'2) (/3 4-/2).
259.	(Уз — /2) (Зу'З 4- 2/T4- 4).	260.	/2 )5 .
7°
261.	Знаки взять или верхние, или нижние. Положить: У А + У В +
+ ]/"д — У В = х. Возвести в квадрат, найти х, подставить. Аналогично най-
дем разность радикалов. Складывая и вычитая соответственно левые и правые
части равенств, докажем требуемое.
262.	3/7 — 2/3? 263. У2(УЗ+ 1). 264. 1^-(/34-1). 265. jA-J- У 5.
Нет смысла применять формулу. 266. У 2 + 1. 267. ]Лз — 1. 268. У 5 —- 2. 269. 1.
270. 0. 271. /64- У 2. 272. 2. 273. Ух+у+Ух — у, х > у > 0.
274. ]Лх+1 + Ух — 1 х>1.
275.	У b — а — Уа, если 2а\ У а — У b — а, если а^. b < 2а, а > 0.
о ]/-	2
276.	1)	----L при а > 2; 2) --- при 1 < а < 2. Применить формулу для
а — 2	2 — а
Va + Ув.	________
277.	У 5 — УЗ. 278. Применить формулу для ~У А 4- У В.
279. Положим "Кт + У а + J/ b 4- |/ с — У х + У У +_У г. Возведем__обе
части равенства в квадрат. Получим: х 4- у -j- z = т. Уху = У а, 2 Уxz =
= Уь, 2Ууг= У ~с. Решим систему относительно х, у, г:	.
у abc __ У abc	У abc
2с ’ У 26 ’ 2а ’
т. е. abc должно быть точным квадратом:
ab 4~ ас 4- Ьс
т = —-— .
2 У abc
280. 1 + /2 + /5. 281. 24- /^+/4-
19	__ _	_	_
282-	vs+mH-o'15-3’ ‘^+/з-г2).
283.	Второй множитель — СК (х + О2 + (У + О3 — У (* — О2 + (У — О2)*
284.	— = 7-=—=~=7<; А = аК, В = ЬК и т. д.
а b с d
285.	(У?— у‘у) (х 4- У). _
286.	(У х — У у) (х 4- Уху 4- У — 1)-	___
287.	Ух+ 1 (У X 4- 1 4- 1) [(X 4- I)2- (X 4- 1)/х 4- 1 4- 1].
288.	(/1 4- х — У1 — х) [2 4- /1 — х2 - У1 4- х — У 1 -х].
289.	х. Обозначить все выражение через у. Возвести в куб.
уЗ = хз _ зх зу. уз _ Зу „	_ з%) = 0; прибавить и вычесть х2у и ху2,
оазложить на множители
(у — х) (у2 4- ху 4- х2 — 3) = 0.
299
Уравнение относительно у имеет корень у = х. Цва др\гие корня мнимые-
290. (х— — )2. 291. Л. 292. хту'х™. 293. 1.
3,<	'	5	.
-	т-	2а
294. у- . 295. у0 . 296. —---------;	.
297.	Положить данное выражение равным у и возвести в квадрат, Если а > 2,
то у = 2 \а — 1. Если 1 С а 2, то у — 2.
298.	Если а2 > 4, то у = 2|z а2 - 2; если 2<^2<4, то у = 2 у 2.
299.	1Л(-2-+^ = 13/^=w =
'8	2
= -^/1+3]/5+3(/5)2+(/5)3 =	+ J'o)3— j(l + ]/5).
з------?-=_	3 /-------—	, г—
300 2у 2 + У 5 = У 16 + 8 У 5 = 1 + У 5
См. решение задачи 299.
301.	1 + УЗ. См. задачу 299.
302.	Общий метод. Положить 20-г 14’>/2 = (о + by 2)3.
Возвести в куб и приравнять рациональные и иррациональные члены в обеих
частях равенства: а3 д- 6аЬ2 — 2, Збг*2& 4- 2Ь3 ~ 14.
Решая систему уравнений, получим а — 2, b — 1. Или см. задачу 289.
303.	См. решение задач 289, 302.
з — о —
304.	а г b у 2 == — с у 4; возведем в куб и приравняем рациональные и
иррациональные члены в обеих частях равенства: а3 4- 2Ь3 — —4с3, Зя2Ь у 2 4"
+ ЗаЬ2 1 4 — 0, или За2Ь 4" За/?2 у 2 = 0, отсюда За2Ь = 0 или ЗаЬ2— 0. Тогда
з____________________________________	з _____	з___
а — 0 или Ь—0. Если а = 0, то b у 2 = —с । 4, или b = —с у 2, т. е. b = 0 и
с = 0. Если b = 0, то а = —с 4, откуда следует а = 0 и с ~ 0.
305.	х - 1. 306. — .
а
307.	— 1, если 0 < b < а\ 1, если а < b < 2а. 308. 2 У j х2.
j/x — 2
309.	—zzzzr • Разложить первые три члена на множители, х 2.
У X + 2	________=
310.	Применить формулу VА ± у В. 311. —1, | а I < 1 а 0.
о
312.	—	, х — действительное число.
313.	— 4ух, х > 0, х #= 4.
1/7	। х2 (х2 — fx4 — 1)
314.	J-L , X > 0. 315. -1-----------------— , I X > 1.
х + 1	2	1
316.
318.
319.
х 2 4~ 1
1,	если х > I; ------, если х < 1, | х | #= 1, х -
1 —х
,_______ 3
j/x — у (Зх 4- 2у — х2 — у2), х > у, х =/ — у.
320.	----, если а > b\ а + b > 0;
Уа — b
321. х2 > 4, если х > 2 или х < —2,
-	; если а>Ь, а-гЬ '0, аФ—Ь.
а — b
то Ух2 — 4 — дейсзвиitЛоное число.
322.
323.
r -L- 1 , ' х - 2
1) ----7 I, -------* если x > 2.
x — 1 F x -f_2_______
л x + 1	/ 2 — x
2) —-------- 11 --------если x < — 2.
x_— 1 | — x — 2
—t-13L Разложить по биному Ньютона (1 + Уа)5; (1 ~ Vo")5-
~1. 324. ----------—:-----. Вычислить сначала 1 — x2.
1 a
_	у 9и
325. Вынести в числителе и знаменателе за скобку Ут — х; ~ = —-— ,
т п2 -4- 1 ’
т + х	(п + 1 )-
т — х	(1 — п)2
1) если п > 1, то ответ п;
2) если 0 < п < 1, то ответ —.
п
1
326.	т при | т |	1; — при I т | < 1, т =£ 0.
/п
327.	JlHHL при т > л; У. при tn < п.
т—п	пт
т2	п2
328.	—, п > т; —п < tn.
п2	т2
b
329.	—Указание. Вынести за скобку в числителе и знаменателе
а
1	х	b	а + х	b + х
---------—•, но — = —, отсюда  -------=------- и т. д.
] х2 — а2	а	х	а — х	х — b
b (Ь — а)	у (а — Ь)2
330.	а — 6, а > Ь\ ---------, а < £ х2 — 1 = -------.
а	4аЬ
,	1 — ах
331.	а 4- Ь. 332. 1. Найти сначала --.
1 + ах .
333. 1. р'Г+2х +jK2+V3.
Применить формулу для VА + УВ.
22
334. -----. Вычислить сначала х + а и х 4~ Ь. 335. а (а — 1).
а — i _____________
1 L -1 /~ 1	1
О О I / Q	Q	I 1Л
336. а b |/ b — а . Положить х = у3; а - с3. 337. 0. 338.--------.
а2Ь2 4- 1
с4 — а2Ь2
339. -----------. Преобразовать первое равенство:
ху + у Ух2 + а2 + х У у2 4- Ь2 + У (х2 4- а2) (у^ + Ь2) = с2.
Подставить из второго равенства:
г + ху + Г (л2 + о2) (у2 + 62) = с2;
с2 — г = ху + Vz(x2 + а2) (у2	62)-
Возвести в квадрат последнее равенство. Затем возвести второе равенство в
квадрат и вычесть из первого второе полученное равенство.
301
ГЛАВА V
§ 1
1. а) х Ф ± 1;	2 и х> 3; —3	х 2; любое число; пустое множест-
во; х = а\ —2 < х< 0; О, х	—5, х > —2, х < —4.
б) х = 0; х > 2; х > 1; х < —1 и х > 5; любое число; х > —2; х > У^З.
•ГС	л	л
в) х ф (2k — 1) — + 1; х М= л/г — —; любое число; — — + ля;
2	4	4
л	л	л	л
— — + 2л/г < х < — + Глк; — — 4- nk < х < — -4- л/г.
2	2	2	4
2_
з
2_
з
2. 1 sg х < 4. 3. х -Д —2. 4. х= 1. 5. 2 С х 4, —4 х —2. 6. —4 <
< х < 4 и 4 < х 5. 7. х > 0. 8. —4 С^<1-9. х С 3 и х > 4. 10. 2 х
3,5 и 8. 11. х > 2. 12. х < 1; х =/= 0; 3 < х С Ю. 13. —3 < х < —1 и
х > 3. 14. 1 < х<2 их> 3. 15. 2 < х < 3, х —1, х = 0, х = 1. 16. Пустое
множество. 17. Пустое множество. 18. —3 х < 1 и 1 < х С 5. 19. —4 х < 1
и х > 1. 20. х < —1, 1 < х < 2, 2 < х < 3. 21. х > 3. 22. —1	х < 8.
23. х > 9. 24. х 2 и х > 3. 25. —2 < х с 1 и х > 4. 26. х < —2 и х > 2.
27. х < 2 и х > 5. 28. 1 < х < 2, 2 < х 3, х > 4. 29. х > 1. 30. х > 5 и
2
х #= 6. 31. —8 х < 1, х У= 32. —2 < х < 0, х > 1. 33. х < —6 и х > 2.
34. —3 <х<—у, 0<х<2, х>4. 35. —2 <х< !~К2.!,., kzK2! <х<1+К21.,
!±^.2L < X < 3. 36. х < —4, —4 < х <—2, 4 <х < 6, х > 6. 37. —2 < х <
«2, х	—5.. 38. nk < х < -^+лй. 39. х=2л7г. 40. х=-у + 2л/г, где
п — натуральное число. 41. -~ < х С 2. 42. 2 С х < 3, 3 < х 4. 43. 1 < х <
< 2, 2 < х < 2,5. 44. /2 С х < 2, 2 < х < 3.
§2
45. а) у > 3; б) у < 6. 46. а) у < ——; б) — — < у < 0. 47. а) у =£ 1;
4	4
1	1	3
б) у #= —2. 48. а) — — < у б) 0 < у 2. 49. а) 0 С у б) у > 0,
у ф 2. 50. а) у > 1; б) у 2. 51. а) Любое число; б) у > 0. 52. а) —5 у 5;
б) —13^ у 13. 53. а) - <уС 1; б) — < у < —. 54. а) — oo<y^lg3;
3	4	2
3	1
б) logj — < У < logJ —. 55. а) 0 < у < 2, у ф 1; б) —2 < у < 0, у — 1.
Г	Г
Л	л
56. а) 0 у Зл; б) — — С у С -.
§3
57. а) Четная; б) ни четная, ни нечетная; в) нечетная. 58. а) нечетная; б) ни
четная, ни нечетная; в) ни четная, ни нечетная; г) ни четная, ни нечетная.
59. а) Четная; б) четная; в) нечетная; г) нечетная. 60. а) Четная; б) нечетная.
302
61. а) Нельзя говорить о четности и нечетности данной функции, так как область
определения функции не симметрична относительно начала координат; б) четная;
в) нечетная; г) четная; д) нечетная; е) нечетная. 62. б) Четная.
§4
66. а) Если а > 0, то функция возрастает на промежутке (0, оо), убывает
/ 3	\
на промежутке (—оо, 0). б) Возрастает на промежутке I —, оо L убывает на про-
/ з\
межутке —оо, — . в) Возрастает на промежутке (—оо, 1), убывает на промежут-
ке (1, оо). 67. а) При а > 0 функция убывает, при а < 0 возрастает на промежут-
ках (—оо, 0) и (0, оо). б) Возрастает на промежутках (—оо, —1) и (1, оо), убы-
вает на промежутках (—1, 0) и (0,1). в) Функция убывает на промежутках (—оо, 0),
(0, оо). 68. а) Возрастает на промежутке (—оо, оо). б) Возрастает на промежутке
(—оо, оо). в) Возрастает на промежутке (—оо, оо). 69. а) Возрастает на проме-
жутке (—оо, оо). б) Убывает на промежутке (—оо, 0), возрастает на промежутке
(0, оо). 70. а) Возрастает на промежутке [ 0, оо). б) Убывает на промежутке
[—2, оо). в) Убывает на промежутке (—оо, 0), возрастает на промежутке (0, оо).
г) Возрастает на промежутке (—оо, оо). д) Возрастает на промежутке [0, оо).
71. а) Возрастает на промежутке (—оо, оо). б) Убывает на промежутке (—оо, оо).
в) Если а > 1, то возрастает на промежутке (—оо, оо); если 0 < а < 1, то функ-
ция убывает на этом промежутке, г) Возрастает на промежутке (0, со), убывает
на промежутке (—оо, 0). 72. а) Возрастает на промежутке (—оо, оо). б) Возраста-
ет на промежутке (0, оо), убывает на промежутке (—оо, 0). 73. б) Убывает на
промежутке (0, оо). в) Возрастает на промежутке (—5, оо). г) Убывает на про-
межутке (—ОО, 3).
ГЛАВА VI
§1
1. Равносильны. 2. Равносильны; не равносильны. 3. Не равносильны.
4. Равносильны. 5. Не равносильны. 6. Не равносильны; равносильны. 7. Равно-
сильны; равносильны. 8. Равносильны; равносильны. 9. Не равносильны. 10. Не
равносильны. 11. Не равносильны. 12. Равносильны. 13. Равносильны. 14. Не
равносильны. 15. Не равносильны. 16. Равносильны. 17. Равносильны. 18. Мо-
гут быть не равносильны. 19. Равносильны. 20. Не равносильны. 21. Равносиль-
ны. 22. Не равносильны. 23. Не равносильны. 24. Не равносильны. 25. Равно-
сильны. 26. Равносильны. 27. Равносильны. 28. Не равносильны. 29. Не равно-
сильны. 30. Не равносильны. 31. Не равносильны. 32. Равносильны. 33. Не рав-
носильны. 34. Не равносильны. 35. Равносильны. 36. Равносильны. 37. Равно-
сильны. 38. Равносильны. 39. Не равносильны. 40. Не равносильны. 41. Не рав-
носильны. 42. Равносильны. 43. Не равносильны. 44. Не равносильны. 45. Вооб-
ще говоря, не равносильны: [/ (х) + ф (х)] [f (х) — <р (х)] = 0; f (х) = —ср (х);
f W = <Р W-
46. Если k — нечетное число, то уравнения равносильны; если k — четное
число, то уравнения не равносильны. 47. Равносильны. 48. Равносильны. 49. Рав-
носильны, если f (х) > 0 и (р (х) > 0. 50. Если фх (х) + ф2 (х) не обращается в 0.
51. Уравнения не равносильны. Корень х = 2 первого уравнения не является
корнем второго уравнения. 52. Равносильны. 53. Неверно. 54. Уравнения не
равносильны; корень первого уравнения х — 0 не является корнем второго
уравнения.
§2
За
55. ----- при а Ф 3; нет решения при а —
а — 3
любое число при а ~ 1; нет решений при а = 0.
9
3. 56. ~ при а =£ 0 и а у= 1;
а
1
57. —• при m 0 и т 3;
т
303

а — 4Ь
а =^0. 60. ------- при а#=0 и а ^=2; любое число при а — 2,
— Ь = 0; нет решений при а = 2, Ь ~ или а — 0, b =£ 0. 61.
1
a + b
любое число при т = 3; нет решений при т = 0. 58. --- при а=£Ь и а^= ±1;
любое число при а = Ь или а — ± 1 и Ь ~= —а\ нет решений при | а | = 1, | Ь\=£ 1.
59. —— при Ь с; любое число при Ь = с и а=0; нет решений при Ь = с и
Ь — с
1
Ь = — или а =
2
2Ь — а
(^=тупри
1
а #= 1, Ь Ф 2; любое число при а = 1, Ь = ~ или а = 4, Ь — 2; нет решений
при а = 1, Ь — или а Ф 4, Ь = 2. 62.	э Л	„„
Н	2	(а2—4)(Z?2—9) r
бое число при а = ±2, а = ±3, Ь = ±а; нет решений при а = ±2, Ь ±2 или
а =/= ±3, Ь = ±3.
2
Z?2 —а2
§3
63. Нет решений. 64. 0,5 и —0,5. 65. 6 и —6. 66. 5 и —5. 67. 4 и —4. 68. 5
1	1	17	1
и -1. 69. —1. 70. —71. —. 72. 0 и 2. 73.	3. 74. 1 С х < 2. 75. 1; 5-.
3	3	19	2
2	2
76. 0; -. 77. —8; 2. 78. —4; 0; 2; 2-. 79. ±7; ±3; ±1. 80. -4; —2; 0; 2; 4.
5	3
§4
81. k = 5. 82. Д = Ь2 + с2 > 0. 83. а < —. 84. Д = п2. 85. Д =
20
/	q \2
«= п — “ I . 86. А =[ (а + I)2 + Ь2] [(а - I)2 + Ь2\ > 0. 87. А - (k — а)2 4-
\	п /
-h 4р2 > 0; корни равны, если k — п и р — 0. 88. А= у \(ab — ас)2 + (ab — Ьс)2 +
+ (Ьс — ас)2] > 0. 89. А = — [(а — Ь)2 + (а — с)2 + (Ь — с)2]	0; А = 0 при
а = Ь — с. 90. А — \(abx — baj2 + (сах— acj2 + (Ьс{ — ^с)2] С 0. 91. 1) а >
> 10; 2) —26- < а < — 5. 92. 1) а = —10, а = —22; 2) а = 2. 93. k = —18-
8
5	3
94.	т — 15. 95. р2— bq~m2, 96. а= 1; а =—2. 97.	а==
98.	с4 — Ь4 + 4ай2с = 0. 99. 262 — 9ас = 0. 100. —. 101. - и —2. 102. — -.
3	8	85
103. Предположим противное: оба уравнения имеют мнимые корни, тогда р\ —
— 4^ <0 и — ^Яъ < следовательно, р\ 4- Р^ — 4 (qr + р2) = р2{ +
+ Р2 — 2рхр2 ~ (Pi — Р2)2 < что невозможно. 104. q3 — qp2 + Р2 — 0.
105. Взять равенства аа2 4~ Ьа + с — 0; Аа2 + Ва + С = 0, где а — общий
корень. Исключить из этих равенств а2 и а. 109. 2q + р — 2 = 0. ПО. асх2 +
(2ас — Ь2)х + ас = 0. 111. а2х2 + а (Ь — с) х — Ьс = 0. 112. х2 — 15х +
4-53—0.	113. асх2 + (а + с) Ьх + Ь2 + (а — с)2 = 0.	114. а = ± 1.
Ь	ю
115.	— — (62 — 2ас}. 116. р4 - 3qp2 + q2. 117. —^66. 118. х2 — 343х + 81 = 0.
а3	9
119.
р2—2q 4р2— 87— 12р—18	,	- о л
120.	\ 121.	122. р3-4р7 123. 3pq^p3q\
Я7 ,	(47 — 6р т 9)2
2264
343’
304
124. р — 1, q — любое число; р ~ —2, q = —1.
0,707. 127. 3,608; —1,108. 128. —0,424; —7,076.
2а. 131. 2Ь ± а при а #= 2Ь. 132. а — 1; а — 2.
а — b при а =/= —Ь. 135.
Ь(2а-гЬ)
------~ и а при а=£ о;
а — Ь
125. 4,146; 0,682. 126. 1,154;
129. —0,234; —2,142. 130. 2;
133. а — с\ —2а. 134. а + Ь\
а при а = b 0; любое число
при а — b — 0.
а — 1	g + 1	1
136. ------ и —-------- при а Ф 0 и а Ф —2; — —- при а — 0;
а	а + 2	2
3
2
при а — —2. 137. — и —1 при b Ф 0; —1 при b = 0, а =/= 0; любое число при
b
а — 1 а
а — b — 0. 138. -- и —-----при а #= 0, а	—1; 0 при а — 0; 2 при а——1.
а а + 1
1 — т т 4- 1	,	1
139. ----~ и ;---- при т =#—2, т^\\ 0 при т = 1; — ~ при т=—2.
т + 2	1 — т	3
т —2п т + п	п 2	Л 4
140. ----и —------ при т п и т Ф—2п; — ~ при т = п =£ 0; при tu-
rn— п т 4~2п	3	3
— —2/г =/; 0; любое число при т = п = 0. 141. —; —	142. Нет решений. 143. 2;
3
4; —2; —4. 144. 2; 3; 4. 145. —2; 1. 146. 1—; 2. 147. х < — 2 и х > 2. 148. —1
< х 1. 149. 1	х 2. 150. 1. 151. х 2 и х > 3. 152. 2 < х 3. 153. 0; 1;
3	111
-1. 154. 1-; 2-; 3— 2-.
4	2	4	2
§5
155. а) Корни действительные; б) корни мнимые. 156. а)Х=0иХ = —
2_
з;
14	1
б) X = 0 и X = ”. 157. х4 — 5х2 + 6 = 0. 158. х4 — 14х2 +9 = 0. 159. q = -.
160. ±3; ±2. 161. ±/Тб; ±6/. 162. ~	6- ~.!.^2,.E+L+J;
I T^i ilM + l. 163. ±|/|; ±>- |/|; —(±1/)у3-----------------------
±>уе	,66. fe/2+l); /1 +
+	. J-2 ); 1 (1 - /5); 1 (1 +	. ^5 ).
166. 0; 5; ±tj/3;	167. х±0. Разделим обе части уравнения на х4. Поло-
1 - х2
жить -----= v — 1. Уравнение действительных корней не имеет. 168. а) 0;
х
5
б) 1; —1; в) ± 1; ±1,7; г) действительных корней нет. 169. —; —25.
170	73 ± 10 |/ 127
81
§6
171. ± 1; ~ 5 ±	172. ± i; -| 173. 3 ± 2 /2; 2 ± /3. 174. ± I;
2	2 3
305
—; — 2. 175. 3; — —;>76. •+• >; “1 — — • >77.	> ± 2 /2 »' 
2	_	35	2	_	3	5	__	3
. 178> 2±/5 \_±VYL. 179. /	3Л/У7;	1. 180. 1;
2	__	_	4	_2 3	4
-~1^^3;	7//44  181.	и т. д. 182. -1; х+ — =
2	15	2	х
-.-‘-А И н т. д. 183. — 2; i 184. - « + Гб ±/18 - 8 Г?
8	2 3	2	и
— 4 —/6 ± У18 + 8 /6
2
Воспользоваться формулой бинома Ньютона.
. ое	— а ± Ya2 — 4 ± V2а2 ± 2а Ya2 —4
185. ------------------------------.
2
3
186. р=±~. 188. 15х4 — 128х^+ 290х2 — 128х + 15=0. 190. 2; 1;
— 5 -fa /17 . 191. —4; 1; £+ /41, 192> 1; 2; 5;	193. 1; 3; 6. 194. 1/А;
_2	_	2.	2	Г 3
1/5; 3±?/6; ~9±»/21. 195. — 3; — —; 2; 5.
Г 3	3	6	5
§7
196. —1; 2; —1. 197. —3; —2; 5. 198. 1; ~1 1 ‘ /7 . 199. b _ 1 +
_ 42
± i 1/ А. 200. —2; —1 ± i. 201. —2; / A3, 202. — 2; / 1; — —.
V 2	2 3	2 3	2
ОАО ->4-/5+«У10 + 2/5 -1-/5 ±»У10-2У5
203’	4	'	4	’
204. 0; ±	 205. ±/; 0; 2; 4.
206. — —;	± 1 У1-9. 207. —; \f 1 ± * /15 .
3 |/	2	4 /	.	4
208.	± /2<‘; +/3Z; 2; —1 ± /X 209. —1. 210.	3.
3	2
211.	—1± i V2- —1. 212. 5; lA '2^23- 213. —а; а ± // ~ 4. 214. —а;
а ± УаГ+~2. 215. —2; —1 ± i. 216. 1— р; — y±j/l — —L_.
а + b	,_
217.	——; а, Ь. 218. с2; ± /б.
2
219 - + / У3-' ~(^ + 1’)±У(а + Ь)2-4ас
2	2 ’	2а
220.	а	~ 4. 221. 1; —4; —6; —1.
2
222.	—1; —5; 3; —1. 223. —1; 3; 1 ± </3? 224. —1; 0; ~ 1 ^У--
306
225 1 — 1: 7 • 1 ± г р95
4	’	^4	_
226. 2; 3; 5 г ^3 . 227. —3; 2; ~ 1 — ' У 15
2	2_
228. —6; — 6+ У5. 229. —6; 1; ~5 ± * ^39
230. ~5^ ^85,~	. 231. —2; —1; 0; I.
232. — —; 0- ~ 3 ± 1<65
2	4
§8
15	5	7
233. 17. 234. —. 235.	236. — — 0. 237. —; 7.
2	7	2	2
4
238. 1; 5. 239. 3; 4. 240. 5; —3. 241. —1 —; 2.
—	75
242. —; 5. 243. —. 244. ~ 7± К13. 245. —.
4	13_	2	_5
246. 2; 4; ZlZAJQ7. 247. 1; 2; ~ 9 ± ^73. 248. —2; 6; 3 ± /2Т. 249. 3.
_ 2	.	2	'
250. ‘Z1±_L1Z; ~ 1 ± ИГ 251. 2. 252. ±	± i/I 253. —1; 3; 1 + «У&
254. 4 при а Ф 0; любое число, кроме 1, при а ~ 0. 255. 5 при а ±5.
1	тп
256. —— при а + b Ф 0, аф Ь. 257. -------;-----; х #= т; х п\ х р.
а + b	т-\-п — р
её + b2
Любое число при т — п = р = 0; 0 при т = п = 0 и р =4= 0. 258. -------
а b
при а + Ь ф 0. Любое число при а = b — 0; нет решения при а + b = 0,
а = — b =/= 0. 259. + Ь. 260. 2а + с; —а — 2с. 261. а; b — 2.
Ьр — сп
262. —-------; ст =£ ар. 263. —а; b + 3.
тс — ар
264. а; b — 3. 265. ± а\ ± — (а 0).
а
266. 0; ± /а2 + Ь2. 267. ~±±_а. УА.
20 — 3k.	9	9
268. ------ при k и k Ф ± 1/ 12; нет решений при k ~ или k—
5k— 9	5	5
= ±1/12- 269. —а; —b при b ф —а, а ф 0; b ф 0; любое число, кроме 0, при
2Ь
b = —а Ф 0; нет решения при а = 0 или b = 0. 270. b — а, ---- при а^0,
а — о
b у= 0, b Ф ± а\ —2а при b = —а #= 0; 0 при b — а У= 0; нет решения при
а 4- b а — b
b = а — 0. 271.----, ------ при | а |	| b | и а Ф ± ЗЬ; 0,5 при а = ±5Ь\
а — Ь а + Ь
любое число, кроме 0 и 2, при а = b — 0; нет решений при а = ± b Ф 0.
а 4- b а — b
272. ------ и - при | а | Ф | Ь|; нет решений при а =* ± Ь. 273. —а; 5а;
а — b а b
при а#=0.
307
ГЛАВА Vli
1. (8,4,2). 2. (2; 1; 0, 5). 3. (1; —2; —1). 4. (1; 2; 3). 5. (1;—3. -2).
6. (1; 3; 5; 7). 7. (7; 3; 4; 2). 8. (1,5; 2; 3; 0,5). 9. (3; 2; 1; —1). 10. (9; /, 5. 3; 1).
,	d (b — d) г - d)
11. z = a + b 4- с; у = ab + ac + be; x = abc. 12. x = —---------------
a (b — a) (c — a)
и т. д.
— ab	— b	a
13.	x =---------------; у = ---; z— -----------------------------.
(6-l)(l~a)	(l-a)(fc-a)	(b-l)(&-a)
— abc	be
14.	x =---------------——; у =----------------------------- и т. д.
(a — 1) (d — 1) (с — 1)	>	(^-1)(6-с)(й-с)
15.	x = —(a + b + с); У — ab + ac 4- be; z = —abc.
16.	Сложим все уравнения, так как сумма коэффициентов у каждого неиз-
вестного одна и та же Получим: х 4- у -Ь z = 2 (а 4- b + с). Из этого уравнения
вычитаем первое: г ~ b т с. Аналогично находим: х = a -t- Ь; у — а 4“ с.
17.	(1; 2; 3; 4). 18. (2; 5; 7; 3). 19. (18; 12, 6; 0). 20. (0; 1; 2; 3). 21. (4; 3; 2; 1).
22. (1; 2, 3; —1).
23. Система имеет бесчисленное множество решений.
= 4 — 14хо 4~ 7х4,
х2 = — 14- 9х3 — 4х4, где х3 и х4 — любые действительные числа.
24. (1; 1; 1). 25. (1; 0;—1; 0). 26. Система несовместная. 27. (1;2;—2).
28. (5; 3; 4; 1; —3; —2). 29. (16; —1; —2; —3; —4; —5). 30. Так как Xi 4- х2 4-
4- х3 + ... + хп = 1, то х2 4- 2 — 1; х3 4- 3 = 1 и т. д. Откуда х2 = —1;
о	I	IX
Х3 = —2; ... ; х„ = 1 — п; х, = Ц------------.
31. Сложим все уравнения:
х, 4-х2-i-... + хи = 2 •
°i + °г ~Ь ••• 4~
(1 + «) п
Вычитая из второго уравнения первое, получим:
(п — 1)хх — х2 — х3 — ... — хп ~ а2 — av
или хг — (.*4 4~ *2 4~ ••• + *«) = а2 —- аГ Подставив значения хт 4~ х24- х3 4е
,	,	а2— а, 2(а14-а2 + ... + о„)
+ ... + х„, получим: Xj=----------1-------———----------- и т. д.
п	П2 (п 4" 1)
32.	Обозначим хх 4" х2 4~ х3 4- •.• 4~ хп через А, тогда
2хг — А ~ 2а,
4х2 — А = 4а,
. 2пхп — А = 2п а.
Сложив последние равенства, находим: А : А — 2пап.
Тогда хх = а (1 4" ^2Л1); х2 = а (1 4* п2п~2); ... ; хп = а 4- па.
33.	хг = 3; х2 = 5; х3 = 6; х4 = 6; х5 = 5; х6 = 3
йп	^п-1 I ап—о	••• а2 4~ а,
34.	х± -------------------------------- при п нечетном; если п четное, то
система будет неопределенной.
35.	Приравнять все отношения k : х = 206 — 1; у = 21 k — 1; х4-у=а
= 176, откуда
36.	(5; 10; 15; 20). Положить каждое отношение равным 6 и подставить в
последнее уравнение.
37	/15. 52. 59. 99\
кЗГ 31’ ЗГ 31/
308
as
Воспользоваться свойством производной пропорции.
38. х~
а + 6 — б? 4- d
as	ах	By	yz	би
-----—------------. Указание: — = — = — = —
оса 4- рб -1- ус 4- 6d-аа	$Ь	ус	dd
затем воспользоваться производной пропорцией.
40.	Преобразовать последние два уравнения:
у	у х	z X	у х	z
т	п	’ р	г ’ тр	пр’ тр	тг’
xyz	mps
— — — — — = k' х —.------------------
тр пр тг ’ тр + пр + тг
41.	а =£ 1,	система определенная;	а=	1, система	неопределенная.
42.	а = 0,	система определенная;	а —	0, система	неопределенная.
43.	а = 0,	система несовместная;	а —	—3, система неопределенная.
44.	а — 0	и а = 2, система несовместная.
45.
47.
48.
1
а = “Г, система несовместная; а = — 1,
система неопределенная.
46. а = —1, система неопределенная; а = —, система несовместная.
4
а = 0 и а = 1, система неопределенная.
а=0ио=1, система несовместная; а — — 1, система неопределенная
у произвольное ; а = 2, система неопределенная.
49. а — Ь, система неопределенная; а = b = 0, система неопределенная
(У = X).
50. а = b ==£ 0, система несовместная; а = 6 = 0, а = — 6, система не-
определенная.
51.	а ~ b и а = —Ь, система неопределенная.
52.	Единственное решение при р + п — 2т Ф 0; бесчисленное множество
решений при р + п — %т ~ 0.
53.	Единственное решение при 6 (а — 1)^0; бесчисленное множество ре-
шений при а = 1, b = —; в остальных случаях несовместна.
54.	Единственное решение при а Ф 0, 6 #= 0, с #= 0; бесчисленное множеств
во решений при а — 0, b 0, с Ф 0, b — с\ в остальных случаях несовместна.
55.	Система не может быть несовместной.
56.	а = 0, b ф 0, система неопределенная; а — b = 0, система неопреде-
ленная; с 4= 0, b = 0, система неопределенная.
57.	а = 0, b ф 0 ।
а 4= 0, b = 0 система неопределенная.
а = 0, 6 = 0 I
36 4-14а	56 4- 2а
59. Несовместны. 60. Совместны. 61. Несовместны. 62. Несовместны. 63. а =
= 0; а = — 1. 64. а = 4; а — + \ 12.
65. а = —1. 66. аг (63С2 — £3^2) “Ь ^2	^1^3) ^з (^2^1	^2^1)	0.
67. а = ±5; 6 = ±3. 68. Совместны.
69. а #=	0,	6	=4= 0,	а #=	0,
а	0,	6	= 0,	б? #=	0,
а =	0,	6	Ф 0,	с	0,
с —	0,	а	= 0,	6 =4=	0,
а =	0,	6	” - 0,	с	0,
система несозмесгная;
система со::лестная;
система нс?овмес!ная;
система нес вместная;
система соь естлая.
70. Система не может быть противоречивой, так как она имеет нулевые, реше-
ния. Xi ~ у2 = х3 = х4 — 0. Число неиз гстных больше числа уравнений, сле-
довательно, система имеет бесчисленное множество решений:
=== —/; х2 == 3/, v<j —	3/; х4 t.
309
71.	Принять ха за известную величину. Сложить первые два уравнения и
затем вычесть третье. Система несовместная.
72.	Система несовместная.
73.	Система неопределенная, хх == х2 = х3 == х4 — хь = /.
74.	т = 5.
75.
О, 1,
система несовместная;
система несовместная;
76.
77.
1, b = 1, система несовместная.
1, система неопределенная; а= —2,
1, система неопределенная; а= —3,
система несовместная,
система несовместная.
а =
а ~
а =
§4
115
78. 1; 1. 79. 7; 3. 80. 1; 1; 1. 81. 5; 3; 1. 82.	-. 83. 0; 0 и 3; 2. 84.1.
2 3 11
120 120 120
’ 61 : 111 19’
». г_—.
+ рг — РЯ
Преобразовать данные уравнения:
х + у_у + z __ z+ X____1
ху г' zy р' xz q'
Поделить почленно в левой части каждого уравнения; полученные уравнения
сложить и т. д.
— 2bc	— Zac	—2аЬ
87. х =	—» У = —;—» 2 = —Г~Г~•
b + с	а-]- с	а-\-Ь
Если х = 0; у — 0, то z произвольное; если х = 0; z — 0, то у произвольное;
если z — 0; у = 0, то х произвольное.
4
88. 15; 18; 55. 89. 10; 6; 7;
Преобразовать первые три уравнения:
х___ у_ _У -L — JL
5 “ 3; 6 ” 7; 21 ~ 4*
х	у	Z	U	, „
_	Подставив в последнее уравнение значения х, у, z, и>
30 18 21	4
найдем значение k.
3 6
90. 0;	Взять производную пропорцию.
23 23
1 1 1
91. х = ----------; у =-----------; г =-----------.
q + r—p	p—q + r	p+q—r
Разделить члены отношения в левой части первого равенства на xyz.
(82	13\	—
• 94- <2; -5>; (~4; 3>; <1 ± 2^3>:
2D 2D/
(3±3/3У 95. (I; 1); (1; 1); (-5±/Пб\. (-7±Гйб\ 9в> ?1= 2.
\	3	/	\	5	/ \	35	/
_ЗН
183*
97.	(4; 3); (3; 4); (—4; -3); (—3; —4).
98.	(±3; ±2); (±2; ±3). 99. (5; 1); (1; 5).	•	_
100.	(5; 1); (1;5); (3; 2); (2; 3). 101. (2; 1); (—1; —2); (1 ± У2; 1=F У2).
Положить ху ~ а, х — у — Ь.
102. (3;2); (-3;-2). 103. (-2;-4);
310
104.	(5; 3). 105. f—r; Положить — == а; —- — Ь.
\ 5 3 /	х у
106.	(3; 5). Положить х + 2у = а; у — 2х= Ь.
107.	(0; 0); (12; —3); (-3; 12); (17; 17). 108. (4; 1).
109.	(0; —2); (2; 0). 110. (4; 1); (1; 4).
...	Г ab ± У а2Ь2 — 4аЬ	-- /* ab ± а2Ь2 — 4аЬ
111. х= ± 1/ ---------------------; у = I/ -----------------------.
V 2Ь У “ У 2Ь
Положить х2 — /и; у2 = п и т. д.
х
112. (±3; ±1); (±0 ±30. Положить — = г и решить первое уравнение
r— г —	X + У
относительно z. 113. (±3у 2; ±у2.) Положить --= z и т. д. 114. (±2; ±1);
(=Т=2; ±1). 115. (14; —11); (11; —14). Положить (х + у)2 = а и т. д. 116. х — 0;
у = 0. Первое уравнение однородно относительно х и у. Рассмотреть случай,
когда х Ф 0, у Ф 0. Разделить на у2 (или на х2) и положить — = k. Решить
У
2	2/6
полученное уравнение k = 2 и k = следовательно, х= 2у и х= —у; —
3	3	\ 5
3\ /6 9\
~ 5/;U3’13/’
117. (±3; ±2); (+2)/2;	118. (3; 2); (—2; —3); (0; 0). 119. (0; 0);
/ 26	13\	г_
(2; 3);	120. (±3; ±1); (±2/2; ±/2).
\	5	5 /
121. ^±5j/^±122. (31; —9); (3; 5). Возможны два способа решения:
сведение к однородному или сложение обоих уравнений. 123. (1; 4); (—5; 4);
(5;—4); (—1;—4). 1-й способ. Сведение к однородному. 2-й способ. Умножить
первое уравнение на второе и вычесть второе. 124. ( ±|^8; ± уЛ2 );( ± Л/ ♦	;
	/3 \
	2 /
125. (±1;±2). 126.
ЗЛТ\
з,
• У = ь
у -1J. 128. (3; 2); (2; 3). 129. (±2; ±1); (Т 1; ±2). 130. (3; 1); (0; 0).
131. (± У2\ ± 8 )/2); (± 9; ± 7). Положить • х— а, ~~
• х~-а,
и т. д.
132.	(4; 2); (-2; —4); (0; 0). 133. (1; 3); (3; 1).
134.	(4; 2); (2; 4). Симметричные уравнения; выразить х + у их2 + у2 через
ху. Преобразовать второе уравнение к виду (х + у) + (х2 + у2 + 2ху) — 2ху —
= 26 и подставить значение х + у и т. д. 135. (3; 1); (1; 3); (—3; ± 2i\ —3 =р 20.
136.	(3; 5); (5; 3); (—3; —5); (—5; —3). Второе уравнение можно представить
в следующем виде:
х4 + 2х2у2 + у4 = 931 + х2у2,
(х2 + у2)2 = 931 + х2у2.
Подставить значение х2 + у2 из первого уравнения.
/4 2 \ '2 4
137.	(8; 4); (4; 8). 138. -; - ; (-; -
\ о о у \ о о
311
139. (5; —1); (—1; 5); (—4; —1); (—1; —4). Преобразовать второе уравнение:
(х + у)2 — (х + у) — 2ху = 22.
Подставить значение х у из первого уравнения.
140. (±5; ±3); (±3; ±5). 141. (2; 3); / —	—4I
—	\ 4 — /
142.	(4; 2); (2; 4); - 1 + j/L1; -1 Т ]/у).
143.	(6; 6); [	_3	1 +	1
L 2 __	2 J’
144.	(3; 1); у =	и т. д. Разделить второе уравнение на первое, по-
лучится:
1 + У2 + У4 _ _3
У + У3 ~ 2 ’
а — b ъг г
,45-^—И А-
146.	^—2 ± /ТЗ; ±
147.	(3; 1); (—1; —3). Предварительно преобразовать второе уравнение
Получится: х = у 13, у = — >/ 13.
Получится система уравнений: / х — у = 28,
I (х - у) (х + у) = 20.
Разделить одно уравнение на другое.
„8. (4; I); (I; 4>;	;
149.	(6; 3); (—3; -6); (2; 4); (—4; —2).
150.	(±1; гЬЗ); (±3; ±1); (=Н -+- 3Z); (±3ц AFf).
Преобразовать первое уравнение к виду
^г +['£+?? 4,25
Л + У/ X* — у)
(х — У\2
и положить —— = Z и т. д.
\* + у]
151.	(2; 3); (3; 2).	_	_
152.	(3; 1); (1; 3); (2 ± |/"у2 + j/y »).
153.	Преобразовать уравнение так, чтобы получилось симметричное урав-
нение относительно х2у2.
_ Ь2 Ч-1/^2 ! 16^2
х2у2 =-----—------J_---- и т. д.
8
154.	(1; 3); (3; 1); (2 ± 5t; 2 т 5/). Возвести обе части первого уравнения
в квадрат; 2ху перенести в правую часть. Снова возвести в квадрат, заменить
х4 + у4 через 82 и т. д.
155.	(12; 7); (10; 9). Предварительно положить х — 8 = а\ у — 5 — b и т. д.
156.	(±3; ±2); (±2; ±3). Возвести первое уравнение в квадрат и заменить
х4 4- у4 через 97.
157.	(±3; ±2); (±2; ±3). Из первого уравнения найти х2 + у2, из второго
уравнения (х2 + у2)2 и т. д.	_
158.	(1; 2); (2; 1); (—1 ± ]/2t; —1 Т } 2/). Известно, что х3 + У3 ~
— (х + у)3 — Зху (х + У); пользуясь этим равенством, преобразовать первое
уравнение; из второго уравнения найти х г У и т. д.
312
159.	(2; 1); (1; 2); (1; —2); (—2; 1). Преобразовать первое уравнение так,
чтобы в него входили только ху в соответствующих степенях; х4 ~г У4 (х-
4» у2)2 — 2х2У2, но X + у — 1 + ху и т. д,
160.	(±3; ±1); (±1; ±3.).
161.	(2; 1); (1; 2); (—3; 0); (0; —3); (1; —2); (2; —1) и т. д. Данные уравнения
можно привести к виду
(х + у)2 + (ху - I)2 = 10,
(х + у) (ху — 1) = 3.
Положить х + у — а, ху — 1 = Ь.
162.	(5; 2); (—2; —5). Разложить на множители левую часть первого урав-
нения и заменить х — у через 3; преобразовать:
(х4 + х2у2 + У4) + ху (х2 + у2) = 1031.
Возвести второе уравнение в квадрат и перенести —2ху в правую часть; снова
возвести в квадрат. Тогда х4 + х2у2 + у4 = 81 + Збху + Зх2у2. Подставить
значение х4 + х2у2 + у4 и т. д.
163.	(2; 1); (1; 2); (1 ± p/2f; 1 Т ]^2Q. Преобразовать первое уравнение:
х2у2 — ху (х + у) — (х + у) + (х2 + У2) — ху — 2. Из второго уравнения име-
ем: х + У = 5 — ху. Подставить значение х + У в первое уравнение.
164.	(0; 0); (3; 2); (—4; —12).
165.	Разложить на множители левые части уравнений и перемножить дан-
ные уравнения и т. д.
а — Ь
2
(0; 0); х = ±
2аЬ
а2 + Ь2
И т. д.
166. Разделить первое уравнение на
1 —У	1+у
----, второе на - и т. д.
1 —х	.1 —х
5
У~ 13’
167. (rb2; ±1);	-ч- 1^.
Зху + 2
241
Х1 “ 168’ Хг ~ ~ L
х
Преобразовать первое уравнение: —
X
—	. Подставить значение — во второе уравнение и т. д.
Зху — 2	у
168.	(±4; ±3).
169.	(0; 0); (±2; ±*1); (±1; ±2).
/ 25	5 \
170.	(2; 1); I— —; — — I. Преобразовать первое уравнение и заменить
\	6	3 /
4у2 = х + ху. Получится система:
J х = 7у — 5,
I 4у2 = х + ху.
/	24\ /	3 \
171-	(±4; ±3); (±3; ±4). 172. — 4;	; 3; ~ . Преобразовать второе
\	5 / \	5 /
уравнение х (х + 1) + (Зх + 5у) = 24 и положить х (х + 1) = а; Зх + 5у = Ь.
173.	(±2; ±1); (±1; ±2); (±2; Т1); (±1; ч=2).
174.	Преобразовать первое уравнение у2 (х — I)2 + 2у (х2 — 1) + 2х = а
и подставить у (х — 1) — Ь.
„ a~^b — b2 _ 2b(b + 1)
Х ~ 2 0+1) : У ~ а — Ь2 - 4& - 2 ’
175.	После преобразований уравнения примут вид:
— 2ху а2 — Ь2 — 1
первое уравнение ------------=--------------;
х2 + у2 + 1 а2 + ь2 + Г
313
второе уравнение
х2
Умножить данные уравнения на х ==
ние х во второе уравнение, получим:
Ь2 — а2 + 1
у = ±--------------;х
2а2 + 262 + 2
(а-/>)2 + 1
(а-Ь)2 + 1
• у. Подставив значе-
Ь2 — а2 + 1
(g--Z>)2+ 1
2а
176. (0; 0); (2; 1);
нения примут вид:
первое уравнение х
I. После преобразований урав-
= 4,5;
2
| = 10,25.
второе уравнение |х +	\ ' yj
Положить х + ~ — а; у + — = Ь.
х	у
177.	(3; — 1); (—1; 3). Остальные корни мнимые.
/ 5	\
178.	1±	±6; ±41.
179.	х = ± и т. д.
а
(	2
180.	(0; 0; 0); -- ,	,	------
k h \a + b-c a-b+с -a + b + c
2
2
b ' с )
1 1
—;--------z — гт------------и т- д-;
\ а
182. х= —7---------
а + b — с
кроме того, х = у = z = 0.
Преобразовать уравнения:
( (х + у) + (х + z) = а (у + х) (х + 2),
| (2 + У) + (У + X) = Ь (у + Z) (X + у),
I (х+ 2) + (2+ у) = С (у + г) (х+ г),
или
+ * х + у
1 . 1
у + Z
1
4-z-C‘
1
У + 2
6,
183. (0; 0; 0); (±/2; ± /2; ± /2J.
184. (0; 0; 0); х = у = z == L#-..UO5.
После преобразования получится:
х + — + у + — = I,
х	У
1	1
х + - + z + - = 1,
X	Z
1	1
У 4~ + z + — 1.
у	Z
314
185.	Х=±Л/	+	д.
у 2 \ b с а }
186.	(± 3; ± 2; ± 5). Перемножить данные уравнения.
а2
187.	х =--- ,	„ -===г и т. д. Сложить все три уравнения.
±	± о ± с
188.	х — ± 1/"и т д Сложить все три уравнения и найти ху, хг, yz.
все три уравнения; найти х + у 4- г
85 • 144
111
189. (2; 4; 6); (—2; —4; —6). Сложить
и т. д.	___
190. г = ±(£+^V^..
2ab
Разложить на множители левые части уравнений.
Положить х + У — 2= и,
X — у 4- 2 = V, у 4- 2 — X = (0. Найти u, vt а> и т. д. 191. (±10; ±7; ±4). 192. ; в следующем виде:	m	_ г—. Данные уравнения представить - + - = хг	ху	а ху	zy	b yz	хг	с 1 1 1
Сложить все три уравнения и решить относительно —, ——1
ху yz xz
(1	1 i	Г1	1	1 \	
		—’ 1	4~	— “*• I	— /п,
ху	2 '	\ а b	с /	
1	1	/1 . 1	1	
— 		—	1 +		= Лэ
х г	2	\а с		
1	1 ,	Г1	1	1 \	
—	— 1	т" 4"	ММ» —	1 = Р-
У*	2 ’	Ь с	а )	
193.
(9; 3; 1); (1; 3; 9).
194.	<±1; ±2; ±1>; (ЧрЧ: ±/г?'.
195.	У^-^Ь2. b У	а — Ь\ кроме того, (0; а; 0);
(а; 0; 0).
196.	(0; 0; 1); (1; 0; 0); (0; 1; 0). Возвести обе части первого уравнения в
квадрат и вычесть второе. Получится: ху + z (х + У) — 0- Заменить х 4- у из
первого уравнения ху = г2 — z; обе части уравнения х + У — 1 — 2 возвести
в куб;
х3 + У3 + Зху (у + х) — 1 — 3z + 3z2 — z3;
z3 + X3 4- у3 + Зху (у 4- X) - 1 - 3z 4- 3z2..
Подставить значение х3 4~ У3 + & из третьего уравнения и т. д.
315
197.	Преобразовать второе уравнение: (х + у)2 — 2ху + z2 — (х — у)3 —
2
—Зху (х + у) + z3, но х + у = — z; ху — Подставить значения х -г у н
ху. После преобразований получится уравнение z3 — 3z — 2 = 0, или (z 4~ 1) х
X(z2— z — 2) = 0, откуда zx = z2 = — 1; z3 = 2 и т. д. (2; —1; —1); (—1; 2; — 1);
(—1; —1; 2).
198.	Возвести первое уравнение в квадрат и вычесть второе: 4ху + 2xz 4-
+ 4yz — 228. Но xz = 4у2; следовательно, 4ху + 8у2 + 4yz == 228, или ху +
+ 2у2 + yz = 57, у (х 4- 2у 4~ z) = 57; у = 3 и т. д. (4; 3; 9); (9; 3; 4).
199.	(1; 2; 3); (2; 1; 3); (3; 1; 2) и т. д. Умножить первое уравнение на 2 и
сложить со вторым. Получатся системы:
[x4-y+z=6, и [x+y+z==— 6,
< ху + yz 4* xz “ 11,	< ху 4- yz 4- xz = 11,
(xyz = 6	(xyz = 6.
Воспользоваться обобщенной формулой Виета.
200.	Из первого уравнения вычесть второе; после преобразования получится:
(х — у) (х 4- У — z + 1) — 0. Откуда х = у и х4- у - ? + 1 = 0.
1)	Получается система: (х2 4~ xz = х 4" z,
(z2 + х2 = 2х,
откуда (z — х) (z 4- 1) = 0; z = х; z = — 1. При х = у — z или х = у и z — —1
решения будут: (0; 0; 0); (1; 1; 1); (1; 1; -1); (1; -1; 1); (-1; 1; 1).
2)	Если х + У — z 4" 1 — 0, то сложить первое и второе уравнения: х2 4~
+ У2 + (х 4- y)z = (х 4- у) + 2z. Подставить х 4“ У = z — 1. (х 4~ У)2 — 2ху 4*
+ z2, — 4z + 1 = 0. Из третьего уравнения имеем:
(z — I)2 — 2 (z — 1 — z2) 4- z2 — 4z 4- 1 = 0,
откуда (z — I)2 — 0 и т. д.
201.	Преобразовать третье уравнение: (х 4" у) (х2 — ху + у2) = 35z. Под-
ставив из первого уравнения х + у, получим: 5z (13 — ху) — 35, откуда ху =
— 13г — 7. Возвести обе части первого уравнения в квадрат и подставить значе-
25z2— 13z
ние х2 4“ у2 из второго уравнения, получим: ху = ----------; следовательно,
25z2 — 13z 4-14=0, откуда zr = 1 и z2 = — и т. д.
25
202.	(6; 3; 10); (3; 6; 10). Умножить первое уравнение на г; подставляя зна-
чения xyz из третьего уравнения, получим: xz 4~ yz = 90. Из второго и третьего
уравнений имеем: ху = 18 и z = 10. Получим систему:
(ху — 18,
|Х + у =г- 9.
,03 V --(«-* + с) ± У(а — Ь-(-с)г — 4а(а—Ь)
' ’	2 (а — Ь)
и т. д. Исключить z из второго и третьего уравнений и из первого и второго.
204	х = ±Vb + c±	Уа+~ь
2
Сложить второе и третье уравнения и т. д., получим систему:
(х 4- z)2 = b 4- с,
(у + Z)2 = а + Ь,
(х 4- у)2 = а 4- с,
205.	Сложив все три уравнения, получим: х 4- У 4- z = ± V а2 4- Ь2 4- с2.
Преобразовать первое уравнение:
(у 4- г 4- х) . (у 4- z — х) = а2.
316
Подставить значение х 4- У + z; y+z — х = --------------------—t
± У а2 + Ь2 4- с2
л	.	*2
Аналогично х + z — у ---------7=============-.
± У а2 + Ь2 + с2
,	с2
х + У - г = —-7=====-,
± У а2 4- Ь2 + с2
отсюда
Ь2 4-- с2
х = и т* д*
х 2 у а- 4- Ь2 4- с~
Если х + У + 2 = О, то я — & — с — 0; отсюда х = у = г = 0.
206.	Преобразовать уравнения:
х 4- У	67 — 1	х -J- z	а — 2	у 4~	z а —3
ху	а 4~ 1* гх	а 4- 2’ yz а 4- 3
Получится система:
1	1	2
+	— 1 — “ г»
х	у	a f	1
 -4-	-=	1	— —
z	у	а 4-	2
I	— —	i	6
( г у ~ а 4- 3‘
Откуда
2 (а 4- 1) (Д Ч- 2) (б? + 3)
а3 4- 6а2 4- За — 6
2(а-Ц)(а4~2)(а4-3)
а3 4* 2а' — а — 6
2 (а 4- 1) (а 4- 2) (а Ч 3)
а3 _ 2аз _ 13а __ б
207. х2 4- У2 — г2
2сху
г
212	2 2аУг
у2 4~ г3 — х2 —------,
х
2bxz
z2 4- х2 — у2 =------.
У
Сложить данные уравнения по два:
xyz = сх2 4- az2; xyz — су2 4~ bz2; xyz == ay2 + bx2.
Взяв первое и второе уравнения, первое и третье, получим:
1 у а (с —а + Ё)
V с(а — с + Ь)'
Из первого и второго и из второго и третьего уравнений можно получить!
у^г
л : ь<а~ьл-с)
У с (с 4- b — а)
317
Подставить значение х и у в первое уравнение:
2abc
Z =  -------—г-  
У ab (с — а + Ь) (а + с — Ь)
.	2аЬс
Аналогично у = —	....- —.....- ,
У ас (Ь + с — а) (а + Ь — с)
____________2abc__________
У Ьс (а + с — b) (а + Ь — с)
208. (2; 1); (1; 2). 209. (2; 1). 210. (3; 56); (2; 56); (-0,56; —1,56). 211. (—2; 3);
(1; —6); (3; —2). 212. (1; 2); (2; 1). 213. (3; 2); (—3; 2); (2; -3); (—2; —3).
214. (2; 0); (3; 1). 215. (0; 0); у j. 216. (0, 9; —0,2); (2,4; 3,9). 217. (3; 4); (4; 3);
(—3; —4); (—4; —3). 218. (2;~1).
ГЛАВА VIII
1. 1. 2. 16. 3. 4; 1. 4. 1; У4. 5. —343; 91 —. 6. 8; —8. 7. 5; —5. 8. 5; —5. 9. 0;
г	8	’
а; —а.
10.	х = 1, х = 3.
11.	Не имеет решения в области действительных чисел.
12.	Нет действительных корней.
13.	Не имеет корней.
14.	х = —7. Возвести последовательно в квадрат.
5а2 + Ь2
15.	х ~	. 16. х = 7. 17. Не имеет корней. 18. 4; —9.
19.	1; —4. Положить х2 + Зх — у2.
20.	1-й способ. Положить 8х = у2.
2-й способ, х2 — 4х + 4 + 8х — 8 У8х + 16 — 0,
(х — 2)2 + (/8х — 4)2 = 0.
Оба слагаемых, если рассматривать область действительных чисел, должны
равняться 0. хх = 2, У&х — 4 = 0, х2 = 2.
21.	х = 3. 22. х = 2. 23. х = 1. 24. Положить Ах2 + Вх = у, тогда У у + С +
+ У У + С1 = р.
(р2 + С-С1)2-4р2с
У	4рг
Х_—Вр± /б2р2 + Л[(р2+С-С1)2-4р2С]
*---------------------2Ар-------------------
25.	2=	Положить 9х2 + х — 2 = у2.
’	18
26.	V (/F+T —2)2 + V (/m — I)2' =1. 0 < х < 3.
27.	28. 4; —5. 29. Не имеет решений в области действительных чисел.
4
30. ----7=.. 31. В области действительных чисел не имеет решений. 32. 1. 33. 1. 34. 1.
х V 5_________
35. I / (1 +	] . 36. 4. 37. — 1; 1; 2. 38. Действительных корней уравнение
V \ 2 )
318
не имеет. 39. После преобразования получится: [x()/rx + 1)]2 —2 [х(Ух*+ 1)] +
2_
+ 1 = (х — Ь)2, откуда х = (1 — 6)3 .
40.	— Указание. 2х + 1 + х ]Лк2 + 2 = —(х + 1) Ух2+ 2х +3,
х < 0; возвести в квадрат.
8а — а3 _	„	-
41.		; а3 +а. Положить х — а = у3.
8
42.	Возвести в квадрат; перенести все члены в левую часть уравнения, при-
бавить и отнять х:
а + х — х2 —- У а + х — х = 0,
(У а -f-x 4- х) (Уа + х — х) — (У а + х 4- х) = 0,
(УЪ + х + х) (Уа + х — х — 1) = 0, откуда х = 0 при а = 0,
— 1 _i_ 1/4^ —3
х =------Г—|------- при а > 1.
43.	0 и 1 при а = 0, 2а+1 + /1 + 4а при д > 0
/2п/---------------------2/г,--------\2 (п /----п.---------\2
44.	Преобразовать:	1 + х- У I — х) + \И 1 + х — у 1 -xj =0,
откуда х = 0.
16
45-	25 •
46.	Решением будет множество действительных чисел х> —1.
47.	— 1<х<0. 48. В области действительных чисел уравнение не имеет кор-
ней. 49. 3. 50. ±4. 51. 2; 3. 52. 4. 53. В области действительных чисел уравнение
не имеет корней. 54. 0; 1. 55. а2. 56. 0. 57. Легко показать, что левая часть уравне-
ния равняется (У 1 + х)3 — (У 1 — х)3. Тогда (У 1 + х — У1 — х) (1 +_£_+
+У(1 -f-х) (1—х)+1 —х) = х; 2х=(У1 + х+	+ Х-У1-Х)
ит. д. х = 0.
58.	2 (/х + 1) (/х — 1) = (]/~х — 1) (]/2 —х+1); откуда хх=1; х2 = ±
2d
240	г______
59.	0; —. Умножить обе части уравнения на ]/1 + х+ 1.
289
60.	—. Умножить на 2. После преобразований получится: (Ух~+ Ух+2)2 +
4
+ 2(/^+/х+2)-8 = 0.	_______ з
61.	Возвести в куб. Заметим, что j/x + 45 — Ух — 16=1. После преобра-
зований получится: у (х + 45) (х—16) = 20; откуда получим: х± = 80; х2 =
= —109.
______________________________________________________ з ________
62. 4416. 63. 0; —19. Умножить обе части уравнения на У 8— х + У 27 + х.
64.	—---------Обе части уравнения д (х + а) Уа-^х — аУх3 возвести
frtf-уь2
в квадрат. __________________
/	(4/72 _ А3\3
65.	± “1 / а2_-________Умножить обе части уравнения на
V	27b*
зл----- у------
V а + + у а — х.
319
I 1	2 6
66.	0; L Возвести обе части уравнения в куб. 67. 0. 68. \Ь6 — а 6 J Поло-
жить х — у6; а —
69.	0; 1. Положить у х = z; — х = у. После преобразований получится:
у z2 4 /у2 = 1, откуда у х т 1 — х = 1.
- 63а _	з,.------	а + х
70.	0; —. Разделить на у а2—х2, и положить------ — у3.
65	а — х
ний
71.	Действительных корней уравнение не имеет.
/ 2_	2\2_
I 3	3 |3	Q
72.	\ b — а / . Положить х =
____________________________ V у3-
73.	—1; —2. Положить У1 + х = у. 74. 0.
,е (2 ± /3)" + 1	п ----j	Х4-1
75.	х = ------z------- Разделить на i х - I и положить ------= уп.
(2 ± } 3)” — 1	х — 1
О-	r-Г	П "---- “ Т-Г
х = -——------Положить у = у х + a; z — у х . После
получится: (у — z)2 (у 4- 2z) = 0.
77.	а. После преобразований получится: (ух ~ у4 ) 4 (у х—у/2Г)2—0.
5 +5^25	25 I 25-f-1
78.	хг =-----------; х2 ~— Положить (Зх — 5)3 = у5.
3	15^25
129 1094	/7Л-----
79.	—; ------. Разделить на (т х — 1
127 1093	т/—~ । 7 Г
76.
преобразова-
и положить
= У-
Ь2 — 2аЬ — а2
80’ ± 2 У 2ай —4
У*2	...
Возвести обе части уравнения в квадрат.
8,.^. 82.	(о + ч»
12
127
После преобразований получится:
а п_±1
~ х п
b х
а
* =——
83.
84.
85.
2п
(/Г ±	—о)"-2* „	2пг—
-----------—--------. Разделить на у хп и положить х
аЛ=2Г
После преобразований получится:
(Пг— Пг-\2 /т —	т,—\2 Л
\у х — у а у 4- К у * — уя/ =0, откуда х = а,
п
я—26
= У2Л.
86.	Вынести за знак радикала в первом члене х"-^1 , во втором члене
/ п п \n-yi
п	а	и+1 , n-М п~
После преобразовании получится: \х 4а /	== Ь, откуда
п п \П-Н
b —а /	, где b > а > 0,
320
87. a -h 6. Возвести обе части уравнения в куб.
89.	3; 2. Умножить на сопряженную величину знаменателя.
167
90.	—. Разделить на х — 2 числитель и знаменатель.
91.	81. 92. а А гтАА, 9з. о. 94. 62. 95. Действительных корней уравне-
ние не имеет.
96.	х — | 2 а |. Умножить на сопряженную величину знаменателя.
97.	“1/ LA_A = —. Возвести обе части уравнения в квадрат:
V 1—Ьх 1
х — ± — 1/~ ——- при я =5& 0, b =0= 0; 2а > Ь, а у= Ь.
а У b
98.	1. 99. 0; 1. Первая дробь равна (х —]/х)2+ (х — уТ) + 1, вторая
дробь х — ]Лх — 1. 100. х = 1 при —1 < а < 1 и а 00.
Л „ V1 + у х + /Г
101.	0. Положить— 	_------ = у.
у 1 - /г + уг
12
102.	5; — Разделить на (х2 — х — 4) и положить
X2 + X + 6
х2 — х — 4
а — Ь
юз.
х Ф 0; если т четное, то | х | < 1.
105.	Не имеет действительных корней.
25 _.	т /-;—
106.	--. Умножить на у х + у х.
107.	ПРИ « > 0. Освободиться от иррациональности в знаменателе.
108. ± ]Л2*. Привести к одному знаменателю.
Имеем:	'у/' 1 _ А = 0, откуда хх = 1.
11 Заказ 1089
321
Перенесем в правую часть уравнения второй и третий члены и возведем в
квадрат обе части уравнения; после преобразований получим: х — 1 Н-----—
— 2 л / J____—= 0. Умножим обе части уравнения на х, получим: (х2 — х) =»
у х
= 2 /х2 — х + 1 = 0, откуда х2 3 = —=-К„.
2
ПО. Умножив на сопряженную величину знаменателя, после преобразова-
нии получим:	+ х)3— (У а— х)3 = 3 У ах. Обе части уравнения возвести
в квадрат и упростить; снова возвести обе части уравнения в квадрат, после чего
получим: хх = 0; х2>3 = ± при а > о.
111. Умножить числитель и знаменатель левой части уравнения на 2, тогда
получится:
/2 + х-/х /	, /2 + х + /х
—--------— = а3 —zzzz--------
У2 + х + ]/х J /2-(-х — Ух
х =------ при 0 < а < 1.
2а
112. ±2. Перенести первый член уравнения в правую часть, дважды по-
следовательно после упрощения возвести обе части уравнения в квадрат.
113. 0; 1. 114. 4.'115. 4. 116. 2. 117. 1. 118. 3. 119. 3. 120. 4; —5.
121. Уравнение не имеет действительных корней.
122. 2. 123. 2. 124. 2. 125. 16; 30. 126. 27; 729; 1728. 127. (4; 1); (1; 4).
128. (8; 1); (1;8). 129. (27; 1); (— 1;—27). 130. (0; 0); (48; 16). 131. (±4; ±3); (±3;
/49 81\	/108	17\
±4).132. (16; 243); (81; 32). 133. (2; 8); (8; 2). 134. (25; 9);1 -; — I. 135.1—; И — I;
/20 16\
-; — . 136. (±5; ±3). 137. (1; 2); (2; 4). 138. (8; 2); (2; 8). 139. (4; 9); (9; 4).
\ о о /
140. (5; 3); (-5; -3); ( -	. 141. (±18; ±64). 142. (36; 25);
(25; 36). 143. (9; 7); (—9; —7).	_	_
144 /1 _!Л ( — 317 ± 45 /33 . 1015 Т 135 /33 \
\ 2 ’ 3)' \	32	’	48	)'
Подставить из второго уравнения Зу =» 4 — 6х в первое: У6х + 5 —
— У Юх —4= 1.
Положить 6х + 5 = а3, 10х —- 4 = Ь3 и исключить х. Тогда получим систему:
/5а3 — Зд3= 37,
\а —b — 1.
145.	(0; 0; 0);	1;
146.	(1; 1; 4); (1; 4; 1); (4; 1; 1). Возвести первое уравнение в квадрат и под-
ставить значение х + у + z = 6. Получим: Уху + У xz + У yz — 5	(4).
Второе уравнение возвести в квадрат и вычесть третье:
ху + xz + yz = 9.	(5)
Возвести уравнение (4) в квадрат и вычесть уравнение (5):
У xyz (У х	У у + У z) = 3, откуда У xyz — 2.
Получится система:
[X + у + Z = 6,
/ ху + xz + yz = 9,
{xyz = 4.
322
147.	Из третьего уравнения имеем:
g2	— а ±	—4Ь
2
Из второго уравнения	а х + у = — — Возвести первое уравнение
квадрат:	а2 — 4Ь ху =	. 7	16 —а ± 2Ь	—а Т 2Ь
*1,2 :	-	4	’ УМ- 4	•
ГЛАВА IX
1.	142 857. 2. Задача не имеет решения. 3. 35. 4» 25. 5. 54. 6. 59. 7. 46. 8. 23
5	17
и 45. 9. 18 и 14. 10. 438 и 102. 11. —. 12.	13. 473. 14. 453. 15. 246. 16. 432;
7	39
105; 20. 17. 24; 36; 40. 18. Числители дробей: 1; 5; 8. 19. 53; 23; 20. 20. 4884.
21. 320; 431; 542 и т. д. 22. 3; 6; 2; 12. 23. 10; 12; 18; 24. 24. 2463. 25. 8; 18/24; 35.
5
26. 41; 19; 11; 5. 27. 1909. 28. 32 и 23. 29. 47 и 74. 30. —.
8
2	3	12
31. —. 32.	33. 24. 34. 120. 35. 63. 36. 8281. 37. 83 и 38. 38. —. 39. 7 и 5.
9	5	25
2	1
40. 2 и 1. 41. 12. 42. у и 2р 43. 5 и 4. 44. 452. 45. 15; 12; 9. 46. 864. 47. 3;
4; 6. 48. 423. 49. 26; 6; 10. 50. 5; 3; 2. 51. 10; 5; 1. 52. 5478. 53. 453. 54. 18.
55. 777 777; 3333. 56. 3 080 103; 3 050 203; 3 020 303; 3 020 803; 3 030 703.
а — т — al
57. -------------э где /^0; любое число при Z = 0, т= п; нет решения
при I — 0 и т п.
58. 77 км. 59. 4 км. 60. 20 км. 61. 30 км/ч и 40 км/ч.
62. 4 км/ч и 3 км/ч. 63. 250м/мин и 200 м/мин. 64. 40 км/ч и 60 км/ч. 65. 720 км.
66. 20 км; 4 км. 67. 1,5 км; 1 км; 30 км. 68. 60 км/ч; 80 км/ч. 69. 8 км. 70. 60 км/ч;
40 км/ч; 10 км/ч. 71. 7,5 ч; 5 ч. 72. 4 км/ч. 73. 16 ч; 12 ч. 74. 18 км/ч; \2км/ч.
75. 45 км/ч; 60 км/ч. 76. 27 км/ч; 30 км/ч. 77. 30 км; 36 км. 78. 40 км/ч; 30 км/ч.
79.17,5 км/ч; 22 км/ч. 80. 4 -- км/ч.
О
81. 20 км. 82. 6 сек и 8 сек. 83. 375 сек. 84. 316 сек; 329 — сек. 85. 60 км.
37
86. 30 км/ч и 35 км/ч. 87. 105 км; 30 км/ч. 88. 5 км/ч; 3 км/ч. 89. 24 км/ч; 18 км/ч.
at	—d)
90.	36 км и 30 км. 91. 12 км/ч; 180 км. 92. -при с > а. 93. ----------- км;
с — a	v2 —
есйи v2= vt и d= то велосипедисты все время будут двигаться вместе;
если v2 < tip то встреча произойдет раньше (до пункта В); если = v% = 0, то
встречи не произойдет.
94.	—а< ++ 4asZ г
2а_________
95.	+^t_ км/ц
2t ___________________
96.	3 (s fa) + V 9(s- + t2v2 — bstv KMj4 по ГруНТОВой дороге.
6/
IP
323
n, d — Ы + V(d 4- Ы)2 4- 4aW ,
97.		!—r v	—!—L----------- км/ч—скорость велосипедиста.
98.	км/ч.
2/
99.	d ~~ Vй2-+ 4—км/ч при а > 0, d > 0, t > 0.
2а/__________________________
100.	±	+ У + ^апгп км/ч.
_____2п	1
101.	 У^ км/ч — скорость второго лыжника.
Если b — 0, то скорости равны.
102.	v = ~~С—УС	км/ч; если с > 0, то с > 16 (& — а);
если с < 0, то с < 16 (Ь — а).
103.	.т?	К.т2/г2 ~Ь км/ч; если п = 0, то т — 0; если пг — 0, то
п
be + ad
х = 0, что невозможно. 104. -------
2ас
(be — ad)(c + b — a — d)
105. Vi =----------------------
1 2т (b — d)(c — a)__________
bm — an ± У(bm— an)2 — 4abmn
bc — ad TJ
--------. Исследовать решение.
2ас
(Ьс — ad)(c -j- d — а — b)
2т (b — d)(c—a)
v2 =
ч.
106.		---------------------------------
2n_______________
107.	25 ~ + yj™_TP? + ^TP.L км/ч при a > 0, t > 0, 0 < p < s.
108.	15 дней и 30 дней. 109. 3 дня и 6 дней. ПО. 12 рабочих; 10 дней. 111. 75 дней
и 50 дней. 112. 92 л и 48 л. 113. 2 ч и 3 ч. 114. 6 ч; 9 ч\ 12 ч. 115.	6 дней;	12 дней;
4 дня. 116. 9 ч\ 12 ч\ 18 ч. 117. 3 ч\ 2,4 ч; 4 ч. 118. 50 г; 150 г; 200 г.	119.	ПО мин;
132 мин. 120. 24 дня и 36 дней. 121. 11 дней и 14 дней. 122. 15 ч;	10	ч; 6	ч.
123. 0,5 га. 124. 5 ч; 6 ч; 10 ч. 125. 13,5 ч; 18 ч; 27 ч.
2abc	2abc	2abc
126.		;	-----------;	----------.
Ьс + ас — ab ab -\-bc —ас ab + ас — Ьс
d — с
127.	-----, если d > с > 0, а > Ь > 0 или с > d > О, Ь > а > 0; любое
а — Ь
число, если а = Ь и с = d, Ь > 0, d > 0; нет решений, если а — Ьис =£ d, Ь > 0.
128.	а —-У.--^..-^— дней второй рабочий.
а(Уа +УТ) „	a(]^c' — yrb)
129.	-----zz----— Дней и ----—-----z— Дней.
]/с — Уь	уь + Ус
130.	если т = 0, то п = 0; если п = 0, то т = О,
120m
производительность труда рабочих одинакова._____
131.	+	гл. ап-У<№-№ап гл при а у 0>
2п	2п
п > 0, ап > 200.	______________
132.	n-^+/(n^.?08+4sm£ км первая бригада;
п + mt	m02H~ 4snd км ВТОрая бригада при т > 0, п > 0, <>0, s>n.
I
133.	30 г и 20 г. 134. 56-й и 66-й. 135. 84-й пробы; 10 г.
136.	60-й и 72-й. 137. 12 кг и 30 кг. 138. 40 т и 1232 т.
139.	500 кг, 400 кг, 100 кг. 140. 4; 4; 8. 141. 70; 80; 90. 142. 6 ведер и 4 ведра.
143.	700 г. 144. 30 л. 145. 10 бутылок.
ив. сорт_.
147.	Крепость второго сорта ~ [ а + d ± У (а + d)2 — 4 (be + da — ас) .
148.	(а — У ab) л, 149. а — Уab. 150.	, где а Ф р.
а — р
ГЛАВА X
§ 1
2. х=^а. 3. х—аа. 4. 18. 5. 48. 6. 27. 7. —. 8. а • Ь. 9. 20. 10. —.
8	b
_ cP	_
11. 52. 12. /6. 13. —. 14.144.15.4/3. 16. 4. 17. Ig2 = x, 1g 5 = у.
ь
IglO = lg2 + lg5 = 1, ху = 0,2104; lg2 = 0,301, lg5 = 0,699. 18. 3 = За;
1 —За .	1	1	зг— 1	2
; -1-2а;---а. 49. --------. 20. 1g /25 = - lg52 = - lg5 =
z	о	1 — а	□	о
2	2a	2a
=-(l-lg2)= j--. 21. 2-2а. 22. 1-y. 23.
а — 26 + 1	,	,	_ Ig6 а + 6 a + b
!85 -----------. 24. log, 6 - jL . -±-. 25.
3	18	, „ a ,	1
= iTTTn = TaK KaK log*5 = T- lo&2 = log«10 =
log410	3-f-2a	3	2
2a 12 — 4a	16
. 29. 8. 30. —.
52 . 72
lgl22,5 = lg
27. ------. 28.
1 — a
34. Взять за основание, например, число b.
26. Ig64 =
2а + 3
6 ‘
10 ’
log464 _
log410~
39.	Igy =  ----—;	Igz ==  -----—; исключить у, к = 10 g .
1 — Igx	1 — Igy
40.	а2 4- b2 + 2ab = 9ab и т. д. 41. logft а,
logx*	1
42.	-	* — —————————......................„   и т д
' logxaia2... ая logvax + log.v а2 + ... + logx an
43.	c2 — b2 = a2\ (c + b) (c — b) = a2.
Прологарифмировать при основании а и т. д.
46.	Первое отношение умножить и разделить на у, второе отношение — на х,
третье отношение •— на z; заменить у 1g х через lgxy и т. д. Применить производ-
ную пропорцию.
47.	0,8595. 48. 6,047. 49. 1,063. 50. 0,6348. 51. 0,2780. 52. 1,154. 53. 2,593.
54. 2,962. 55. 1,836.
§2
7	1	1
56.	-. 57. 0. 58. + 1. 59. — —. 60. -. 61. 1. 62. 3. 63. ±2. 64. Нет решений.
12	о	2
3
65. —1. 66.	67. «3,303; «—0,303. 68. 1; 2; 3. 69. —2; 1; 3. 70. 7; —1. 71. 2.
72. 10. 73. 2;	('g2 *S . 74. -. 75. 2 • nk ± —.
1g 3	6	3
325
76. ——-----------при а Ф Ь; если а = 1, то х = 2 о; если b = 1, то х
Igb — Iga
1	,	lg(a— b)
= —2a. 77. —— при m Ф 1 и m ф 0. 78.	79. 2. 80. 2. 81. 3.
a + b	lg(a + 0
82. 2. 83. —1. 84. 3. 85. 6. 86. 5. 87. 6. 88. 9. 89. 66. 90. 2; 3.
91. a 0,5642. 92.	°  93. Прибавить и отнять x2, тогда (y^2 + x) = (x + 3)8;
Z lg 2
x = 7Ц-. 94. 0. 95. — —. 96. —. 97. 7. 98. I/11!?. 99. 15. 100. 1.
lg 3	2	2	V Iga
1g 3 — 1g 8	lg 5	2 lg 60
101. -------102. 0; a 0,827. 103. 0,3. 104. 2. 105.	-7— « 1,969.
Ig3 — lg 2	lg7	3’ lg 8
106. 2. 107. 0. 108. ± rlg-19 ~;lg^ • 109. Разделить на 6х.	1	]§2.
Ig57 —lg37	A	lg3 —lg2
lg(1^5 4-1) lg2 Jn --------te2---- 112 n. j 11a a. * ~3|
lg 5
119. 0; —1, разде-
10.
--------Ig3 —lg2 	"2- * L * 
114. 5. 115.	7^-. 116. 7	117. 3; 11. 118.
lg 2 lg 2 lg3-lg2	2
lg6
лить на 32x. 120. 2. 121. 2; —2.122.	. 123. 0. 124. 1. 125.
Ig3
1. Положить 2х = у
и разложить на множители.
126.
127.
128.
1g 3
х = 0; х — —Левая часть уравнения есть куб.
__lg5
х = (*^5 + 0 — lg 2. Положить 2х = у.
1g 2
1; 2; 3. Положить Xх = у.
129.
IO-*2-*,
130.______________________
1g 5—1g 2
ся: 252Х = (4х —10х)2.
}g (1 + V11) _ j Разделить обе части уравнения на
2
x = Iff Ofdz 0 ~ После элементарных преобразований получит-
131.
132.
Ig3-lg2
lg(l + /5)-lg2’
lg a — lg
Разделить на

I i V
133. 2; —2. После преобразования получится: f ,-I +
______	k/2 + Гз/
+ (/2 + ]ЛзУ = 4.
134. 2. Разделить обе части уравнения на (2 ]Л2)Х.	_ *
1О1<1. Если Л/4—У^. = sina, то п/i±-KP- = cosa.
у 8	У 8	Г 8
Возможно при х — 2.
1g 2 — 1g 3	х/"~9
135. ;—т~77=-г?-— . Положить 1/	= у.
lg (V 5+0- lg2	уз }
8
326
136. 2. 137. —1. 138. 2. 139. 1. 140. Действительных корней нет. 141. хг = 2;
< — 1,8. 150. X]
1,4. 152. хг = -
= 1; х2 = —1.
х2 = 2.
153. xt = —2; х2 = 2. 154. хг = 0; х2 = 1. 155. хг = 0; 1,7 < х2< 1,8.
156. xj = 0; х2 = 1. 157. 3. 158. 0,5. 159. 4,5. 160. 2; 3. 161. 95; 5. 162. 54. 163. 29.
164. 9. 165. 48. 166. 8. 167. «10,39. 168. Уравнение действительных корней не
1 +ах
имеет. 169. Уравнение действительных корней не имеет. 170. 1g------ ==>
а
]g b	a Ig b	Г я 1g Ь — 10е 1
= lg-§—, 1 + ^=-^-, x=lg —----------------------- :1gа. 171. 1. 172. Her
с	10е	L 10е J
действительных корней. 173. 4.
1g 5	17 23
174. —	. 175. 5. 176. 10; 100. 177. 2. 178. 2. 179. —, —. 180. —5; 3.
1g 2	_	28 32
181. 3— 4,5. 182. -i; 7-/6; — 12L.~183. 1; 2. 184. —18. 185.
8	2	2	2	9
186. 11. 187. 2; 4. 188. 1; 5. 189. 100. 190. а > 0. Обозначить
а
log х	log 3
3 а = у; х = г логарифмировать по основанию a; logay = logflz и т. д.-
191. 3. 192. -к 193. 9; —1 + /10. 194. 1000; 0,001; 10; 0,1. 195. -~
2. 196. 10-*; 10. 197. 0,01; 0,1. 198. 10»; 10. 199. 5; ’/5 ..	200.	100; 0,1.
201. 1000; 0,1. 202. 10; 0,01. 203. 100; 0,01. 204. 0,0001; 10.
2
205.	у. 206. 1; 4. 207. 10; 0,1.
208.	log3 logj х — 1; logs х = 3; х = З3 = 27.
209.	Я 210. 81. 211. 16. 212. 27.
111	13
213.	ТТ7=-- 214. —; 16. 215. 4; 8. 216. 1; 5; —. 217. —.
/3 3/3	2	25	4
218 —35 ± V2W5 . —35 ± /345
4	’	4
219.	—. Уравнение имеет решение при log __ х < 0.
5	/5
220.	—. Область определения: logx/2x>0; х > 0; х^=1. logx 2 > 0
при 0 < х
Уравнение имеет решение только при log2 х < 0, т. е. 0 < х < 1. Следова-
тельно, 0 < х < —.
2
221.	—1; —8. Область определения х < 0. Производя преобразования,
обратить внимание на выражения под знаками радикалов и логарифмов. log2 /х2^
*og2 I х |.	___________
222.	m> Ig8; хм= 1О'”±Г1О^-8-1О^. m = lg8j x= 4.
327
223.	я > 4 — два действительных корня: х12= а — ' Q2 • а=4, х=2.
224.	b > 2 — два корня;
при b = 2 — один корень: х = а\
при b = —2 — один корень; х = —.
а
225.	а = — — одно решение: х = 2; 0 < а < — — два решения: х12 =
226. а = 0 — нет действительных корней;
— — <а<0* х -2а+* 1 * * * V ±/4Т+Т.
4	»	i,2	2
а > 0 — один корень: х =	+	+J_.
1
227. хг = Ь\ х2 = —. 228. х = а.
о
229. а > О, b > 0, с > 0, х = ас.
230. х = 2 ± У 4 — 1g п, 0 < х < 4; нет решений при п > 10 000, п < 1;
одно решение х — 2 при и = 10 000; два решения при 1 < п < 10 000.
231. х12=-а+^а2 + 4а; а>0.
‘,2	2
1 1
232. х1=	^	= а3у--
Т	/т ’
233. Х1= а; х2=	а . 234.	х =	а	п .__ _______________
235 х — апг	х	— ап.- п	_ 65 +/4833 .	_	65 +/4893
zoo. Xj. — и 1,	х2	— а 2,	— —	——"	—,	и2 —	— - -	 —.—	— *
8	8
2	—2
236. а > 1, xt = аа ; х2 = аа ; 0 < а < 1; нет решений.
У1 + 1.8.« + 1^.+ 1 _ /ife+JZ. - 1^±Д , «.
V loga * У loga х
237. хг = 1; х2 = у^; b > 0, а > 0.
238. а 10^, х1>2 = 1g а ± }^lg2 а — Ь2\ а < 10^; нет действительных
корней.
239.	= 1; 0,1 < х2 < 0,2.
240. 1,3 < хх < 1,4; —0,99 < х2 < — 0,98.
241. Нет действительных корней. 242. Нет действительных корней.
243. 1,4 < Xi < 1,5; 0,01 < х2 < 0,02. 244. 0,2 < х < 0,3.
245. Xi = 1; 0,33 < х2 < 0,34. 246. 1,8 < х < 1,9.
§3
249.
(3; 3); (4; 2). 250. (3; 4). 251. (2; 4); (—2;	252. (1; 4). 253. (7; 121).
V	5 -9 21g 5+ lg3
254. (3; 1). Перемножить оба уравнения. 255. (1; 2). 256. J/ у, ~	__jg g •
257.(3; 2). 258.	259. (2; 8). 260.	261.	(-2; 4).
328
262. (1; 1);	1/ У^)- 263* (7; 5). Из первого уравнения имеем: х +
\ О у Ztl ]
—	11	1 \
i = 2Х~У . 3 1 2 ; подставить во второе уравнение. 264. (4; 1). 265.	(— — V
/	266. (0; 6). Положить 5х = а; 2х+у = Ь. 267. (2; 3). В первом уравне-
\ 6 4 /
2
нии положить ху = 2. 268. 101; 	. Преобразовать второе уравнение: (у +
1g 102
+ 1)х=у —1.
4	4
269‘ х== lg(l +ую6 + 1) ~ 3’
_ 6х&
270. 5 9 = 58, х • у = 12; (х — у — 1) (х2 ± бу2 — 60) = 0;
( х — у — 1 — 0,
I ху = 12,
х2 + бу2 — 60 = 0,
ху = 12.
Решая эти две системы, получим: хх — 4, у^== 3; х3 4 = ± 6; х56 = ±2 уТГ;
х2= — 3, у2= — 4; у34= ±2; у3>в= ±_/б.
Г /- /~21	1\4 /т/21	1 \2 41
гл. (1. и 2>; [(У	272-	> >'• '*•
2; /2>. 273. 11; 1; 2); [ t"3/5 )‘	4 !'	™' (1б; 10,
L \ о /	\ О / Э J
275. (10; /10). 276. (2; 3). 277. (9; 7). 278. (7; 3). 279. (4; 2); (1; 1). -log** =
log24
= log2 у; х = у2.	280.	(3;3);	(-4;—4). log0 и + —-----= 2.
log0 и
281. ( х-у = ху, -1 -/5	-1 + /5 . „ _ 3 + /5 .
Ь±у=1, Х1 2------------**	2----У1------2----
3 —/5
у2= __L_
Проверить, какая система решений удовлетворяет данной системе уравнений.
(2 ±/10	—2 + /10\
10 2 ; 10	2	. 285. (а3;
/ \ а /
-; О»1 286. (32; 2); (2; 32).
а /
287. | х + у = а2,
( ху = Ь4,
«... -	7,,. -	ПР» а > „ К21
logo У 1 ,	4 г- 4	log, У
288.(81:16), log4y = —4 = ?log2y=log2/y; log16 у =	=
1 .	,	4г-
= - 10g2y = log2 у у.
Система примет вид:
х-Уу =77,
/х —Уу =7.
329
10 п ; 10 т ).
Из второго уравнения имеем:
1g х • Ig х	/ т \2 1g х tn
Igy • Igy	\ П / ’ Igy _ - Я *
Получаем систему:
г	т <
lgx = ± — 1g у,
lg*+ У Igy = тп + \.
290.	Преобразовать первое уравнение:
Ie Т(*уР = ю;
(ху)*у = ю1?^;
(ху)ху = ху;
(ху)*У-1 = 1.
Получится система уравнений:
(ху=1,	Л 1
1
*2 = Уз = 2-
первого уравнения имеем: х — у = 4; подставить во второе
9
^4
1
log —
р р
293.
Данные решения не удовлетворяют первому уравнению; система не имеет
решений.
291.	(20; 16). Из
уравнение.
/27
292.	(1; 1); -;
£
log "о
_(logp<?) logp<?; (logp?)
Прологарифмировать второе уравнение при основании р и подставить значе-
ние у в первое уравнение.
Г <7	р ”
294.
1 L
7 11 \р
2 : 2
295.
. Перейти к основанию а.
Подставить значение у в первое уравнение. После преобразований получится:
ах~г = b х . Прологарифмировать.
297. Прологарифмировать оба уравнения. Если а = Ь, то х = у. Если
1	1	г
а — то х = —. Система имеет бесчисленное множество решении.
д	у
/ а2 Ь2 \
298. (4; 1); (1; 9). 299. —; — .
\ b a J
330
ft* I 2 ь
ллл аф-а) Ь—а „	,
300.	с ; с Прологарифмировать первое уравнение при основании.
(1 з________\
-----; У 9 ; (1; 1).
^3	)
303.	Решая первое и второе уравнения, получим: х = 1. Тогда у =» 1 и г = 2,
или у = 2 и z = 1.
304.	Решая второе и третье уравнения, получим: х = 5. Подставив значение
х в третье и первое уравнения, находим: у = 7, z = 12.
305.	Преобразуя третье уравнение, получим: х — у — 4. Прологарифмиро-
вав первое и второе уравнения и решая их, получим: z = у2 и z = —; у =»
_________________	у*
— 1 dz У 1 “Ь 8а
»2 *
И т. д.
2
307. а > 0; х < 1; у < 1. Система имеет единственное решение:
х_ 1 — а — /а2 + 6а+ 1. а — 1 — /а2 + 6а + 1
2	’ У	2
308. Если а > 0, а Ф 1, то система имеет два решения: х = а, у — а2;
х — а2, у = а. Если а < —1, а —2, то система имеет два решения: х ~ —1 —
— а, у = (1 + а)2; х — (1 + а)2, у = — 1 — а. Если —1 а 0, то система
не имеет решений.
309. Xi= 1 а\3, ух= —; х2 = —, у2 = | а |».
I а I	। а ।
Логарифмируя второе уравнение, получим систему:
5-4
1g2 х + 1g2 у = -у Ig21 а |,
Igx- Igy = 21g | а|.
После преобразования получим:
1 Igx + lgy = 21g | о
I Igx • Igy =—31g2 | a| и т. д.
ГЛАВА XI
§1
Указания даются к одному из возможных способов доказательства неравен-
ства.
1	3
. 1. а2 + ab+ b2 = (а+ ~Ь)2 + -Ь2>0.
2	4
2. а2 — 2аЬ + Ь2 > 0, тогда а2 — ab + Ь2 > ab.
3. Сложить неравенства: а2 + b2 > 2ab, a2 + с2 > 2 ас, Ь2 + с2	2Ьс.
4. Сложить неравенства: а2 + 1 > 2a, Ь2 + 1 > 2d, с2 + 1 > 2с.
5. 2а 1 + а2 разделить на 1 + о2.
6. Сложить неравенства: а2 + Ь2 > 2ab, a2 + с2 > 2ас.
7. а2 + с2 > 2ас, ас = Ь2.
8. Сложить неравенства: а2 + b2 2аЬ, а2 + с2 > 2ас, Ь2 + с2 2Ьс.
Прибавить к обеим частям полученного неравенства 2аb + 2Ьс + 2ас,
1	1	_ b _ (a + d)(q-b)2
a b b2 a2	a2b2
10. Сложить неравенства: abc < abt abc < ac, abc < be.
331
a+b = a	b	a b
n- i + a + b	(1 + a) + b + (1 + b) + a_ 1 + a + 1 + b‘
12. Перемножить неравенства: 1 + at > 2 У alt где 1 < i n.
13. 1—x=y+z>2/yz>
1 — у = x + z > ЧУxz,
1 — z — x + у > 2Уху.
Перемножить эти неравенства.
a* + b*	b* + c* ,по а4 + с4
14., Сложить неравенства: —----> а2Ь2, — --> Ь2с2,	— ----
>
> а2С2.
Воспользоваться неравенством а2д2 + Ь2с2 + а2с2 ab2c + a2bc + abc2,
которое можно получить, сложив неравенства:
a2b2 + b2c2 , a2b2 + а2с2 а1 b2c2 -}-а2с2
--------------> ab2c, ------------> а2Ьс,---------------> abc2.
2	2	2
15.	а2 + ab + Ь2 0 (см. задачу 1). Умножить обе части этого неравенства
на (а — Ь)2.
16.	Сложить неравенства: (а2 — &2)2 > 0 и 2аЬ (а — 6)2 > 0.
17.	Перемножить неравенства:
а2 > а2 — (Ь — с)2 = (а + b — с) (а — b + с),
Ь2 > Ь2 — (а — с)2 = (Ь + а — с) (Ь — а + с),
с2 > с2 — (а — Ь)2 = (с + а — Ь) (с — а + Ь).
18.	Сложить неравенства а^ + а^ > 2а1а2, aj + а% > 2аха3, а% +	>
2а20з и прибавить к обеим частям полученного неравенства of + а% + а%.
19.	См. задачу 18. 20. См. задачу 18.
21.	4а4 — 4а3 + 5а2 — 4а + 1 = (а2 + 1) (2а — I)2 > 0.
22.	х5 + у5 — х4у — ху4 = (х — у)2 (х + у) (х2 + у2) > 0.
23.	Рассмотреть три случая: 1) х < 0; 2) 0 < х < 1; 3) х > 1. Для второго
и третьего случаев удобно преобразовать многочлен соответственно к виду
х8 + х2 (1 — х3) + (1 — х) и х5 + (? — 1) + х (х — 1) + 1.
24. (а + b + с)3 — (а3 + Ь3 + с3) = 3 (а + Ь) (а + с) (Ь + с) > (а +
+ Ь) (а + с) (Ь + с).
ал+4 (ал — 1) > 'а” — 1. ’
Обе части полученного неравенства разделить на 1 + а.
28. Сложить неравенства: 1	1
22-< — 2 ’
1
32	2 ~ 3 ’
1 1	£
Л2 < П — 1	и
29. Обе части неравенства aj + а| > 2аха2 разделить на аха2.
332
ad be	be -+ ad	a	b	c	d
31. ---!--- 4-----!----= — + — 4- — 4- — >4.
bd	ac	b	a	d	c
r2	1	v2	l	О	  1
32- TV 4 = ~i---------- и т- д- 33,	....- =Vx2 + 1 +	___- и Т. д.
1 + **	— 4- x2	Vх'2 + 1	/x2 + 1
X2 ‘
34.	Сложить неравенства: Xi + — >2, где 1 < i n.
xi	-
37.	Перемножить неравенства: a + b ab, b + c > 2 Уbe, a + c
>2/SL
38.	См. задачу 37. 39. Положить a + a = A, 6 + p = В и т. д.
40.	Умножить обе части неравенства а + b	2]/ab на УаЬ и т. д.
41.	Сложить неравенства: а + Ь > 2У ab;_b + с > 2У~Ьс, а + с 2Уас.
42.	Перемножить неравенства: а + 1 > 2У a, b + 1 > 2УЪ, а + с > 2 У ас,
Ь+с^2УЬс.
43.	См. задачу 42.
_	г	аг а»
44.	Сложить неравенства: у ata2 <--------— ,
1/----. ai + аз
У а\аз <	»
45. Сложить неравенства:
Н д.
V(4a + 1) - 1 < 4,1 %* +---.
/<«ГПГТ<^4±1..
46.
вертую
А + В >2]/ /45. Положить А — а + Ь, В = 2у аЬ. Возвести в чет-
степень.
48.
п,--------------
аха2...ап = У а^ а^ ... а^
п
51.
52.
п,-~----- 1 -t-Z-t-...	rt-f-1
V 1 • 2 ... п <------------=--------.
п	2
Число сомножителей в произведении 1 • 22 • З3 • ... • пп равно 1 + 2 +
... + n =----------. Среднее арифметическое этих сомножителей равно
п (п+О
Р-р 22 + 32 + - + ^2
1 + 2 + 3 +• ... + п
а + В + с
> a+b+c/l_ _1_	1 .
у аа ’ Ьь * ес
3	1
а + b + с а^ь^УааЬьс^
; а+ь+^ааььсс > у (« + ь +с)-
333
r___________ a — b + b 1	4
54.	Y(a — b) -b <----------------; -------------> —
Y 7	2	’ (a - b) b a2
1	4
# + ,	< 4 . > a + 2 > 3.
(a — b)b	a2
xy + 2	2
-----------------------= 1 + —•,	но x + у >
у / x у ху-------------ху
Г—	1	/	1 \ I 1 \
>2 Vxy, откуда — > 4..Следовательно, 1+—	1Ч-— >9,
ху	\ х / \ у)
56.	Применить неравенство а2 + Ь2 + с2 ab + Ьс + ас (см. задачу 3)
к выражениям: а3 + Ь8 + с8; а4Ь4 + а4с4 + 64с4. Обе части полученного не-
равенства а8 + Ь8 + с8 > a2b2c2 (ab + ас + Ьс) разделить
„ „ 1111
57.	Сложить неравенства: ->	----> —, ...
п + 1 2п п + 2 2л
К обеигл частям полученного неравенства прибавить
2п
1 1
58.	Легко видеть, что-;— ---— <-------- <
{п + k + 1) (п + k) (п + k)2
1 11 1
55.
на a3Z?V.
1
£
n + (n—1) 2ri
1
(n + k — l)(n±k)'
1
(и -р k -j- 1) (и &) a -j- k п -j- k -|- 1 (ji k — 1) (a -j- k) n -J- k — 1
1 „ 1 1 1 1 1
n + k‘ оэтому n + k n + /? + l<‘(n + fe)2<n + fe‘—1 n-yk' л0Л0
жить k соответственно равным 1, 2, ...» p и сложить полученные неравенства.
59.	Воспользоваться свойством среднего арифметического и среднего гео-
метрического положительных чисел, входящих в левую часть неравенства.
60.	3 (1 + а2 + a4) = (1 + а2 + а4) + (1 + а2) + (1 + а4) + (а2 + а4) >
> 1 + а2 + а4 + 2а + 2а2 + 2а3 = (1 + а + а2)2.
л+< ai+!.--+-» _
62.	а2 + Ь2 = (а + Ь)2 — 2ab=\ — 2ab\ а4 + 54 = (1 — 2аЬ)2 — 2а2Ь2. Имея
/а + Ь\2	1	/	1 \2	11
в виду, что ab < —— = — получим: а4 + Ь4 > 1 — 2- — — 2 • — = —-
\ 2 /	4	\	4/	16	8
k --------- А
63.	Воспользоваться неравенством у xyzt...v —.
k
64.	Произведение xmynzp...vr будет наибольшим при тех же значениях пе-
xmynzp...vr
ременных, при которых будет наибольшей дробь ---------------—-г, которую можно
tnmiinpp..,rr
xxyyzzvv
представить в виде произведения — ... — • —	... — ... — ... — ;
ттппрр г г
тир	г
сумма этих сомножителей равна х + у + ... + v = А, Следовательно, произве-
х	у	z	v
дение будет наибольшим при ~ = — = — = ... = —.
т	п	р	г
65. Пусть произведение k переменных положительных чисел равно постоян-
.	4	kr~r х + у + -..
ному числу xyz... t== Л. Воспользоваться неравенством у А <---.
k
х	х	у у t	t	„
66. х + j +	... +1 = - +...+ ~	“ +...+ - +...+ -	+...+	- .	Про-
m	m	n n r	r
tn	n	r
t x\m / У \n I t\r
изведение —	— •••"“ есть число постоянное, следовательно,
\т / \п ) \г j
334
сумма их будет наименьшей при равенстве сомножителей (см. задачу 65), т. е.
х	у	t
при — — = ... = —.
пг	п	г
67.	а : b — с : d. Пусть а — наибольшее, тогда d — наименьшее число.
а — b	с—d	а — b а а	а — b
-----=	. Откуда -= —; — > 1. Следовательно, ----- > 1 и
а с--------------------------------------------------------------с — dec	с — d
а — Ь > с — d, или а + d > b + с.
68.	Пусть х и у — измерения прямоугольника, х + у = А. Наибольшим ху
будет, когда х= у.
69.	Пусть a, bt с — измерения прямоугольного параллелепипеда, а + Ь +
3 — а + b + с т3
+ с = т\ у abc С----------; v —. Наибольший объем будет, когда а = b =*
пг
~ с~ т
7о. £ + 2 = -1.
7 ' 5	7
х
наибольшим при у =
х у
Сумма — и —• постоянна, поэтому произведение будет
7	5
У 2 u	20
— = —. Наибольшее значение равно ~.
5.7	7
•рЛ g
71.	2 1^6 при х =	72. 108 прих= —1. 73. СКа+ У~Ь)2 прих= Уab.
74. 0,5 при х = 1. 75. 4 при х = ±2.
§2
101.	Равносильны. 102. Не равносильны. 103. Не равносильны. 104. Не рав-
носильны. 105. Не равносильны. 106. Не равносильны. 107. Равносильны.
108. Не равносильны. 109. Не равносильны. ПО. Равносильны. 111. Равносиль-
ны. 112. Равносильны. 113. Не равносильны. 114. Равносильны. 115. Равносиль-
ны. 116. Не равносильны. 117. Не равносильны. 118. Не равносильны. 119. Рав-
носильны. 120. Не равносильны.
§3
121.	х > -- при а < 5; х < -- при а > 5; нет решения при а = 5.
5 — а	5 — а
пг + 2	1 пг + 2
122.	х >--- при п > —1; х <-------- при п < —1; любое число при
п + 1	«4-1
п = — 1 и пг < —2; нет решения при п = — 1 и m > —2.
3(1— т)	п 3(1—/л)	п
123.	х >	уу— при пг > —3; х <-у у при пг <—3; нет решения при
124. х > — при а > 0; х < — при а < 0; любое х при а = 0 и b < 0;
2а	2а
нет решений при а = 0 и Ь > 0.
125.	х > а + b при а > Ь; х < а Д- b при а < Ь; нет решений при а — Ь.
126.
а — 0 и
b (а — с)
——— при а у= 0; любое х при а — 0 и Ьс < 0; нет решений при
127.	х < — при а > 0; х > — при а < 0.
а	а
128.	х > а (а + 1) при а > 0; х < а (а + 1) при а < 0.
2	2
129.	х > / , .'ха ПР“ а > —1; •* <   при а < -1.
(а+1)2	(а+1)2
335
130. х> —1 прил>Ь>0. х<—1 при 0<а<Ь. 132. —7<х<7. 133. — — <х <
5
13	21	5л + 6
< - . 134. 20 <х<29,1. 135. х >-. 137. х < —— ]
4	5	л -г 3
3	2л — 3
а^—; нет решений при л^—3. 138. х > —----------
8 * 2л — 3	' 4m + 1
К л< 1,9; — < х <--------- при л < 1. 139. х>----— при
9 л—1	т+4
2т —3 л	2т —3	.
< X <-------- при — 4 < tn
т — 1
х < — при т = —4. 140.
5
1
несовместна при т — у,
3
)и — 3 < а < —; х < 3 при
8
при а > 1,9; х > — при
4m + 1
т — 1
5 т — 2	1
— < х <------ при — — < т
3 т—1 н 2
5	6
г > — при т > 1. 141. х < — т
и т > 2; нет решений при 0 < т < 2.
х > 1 при т = 1;
система
при т < 0
§4
142.	а) — 1 < х < 6; б) — 1 < х < 7.
5	1	1
143.	а)х< — — и х > 5; б) х < 4 ~ и х > 5
'	3	2	2
144.	а) х > 8; б) х — любое число.
1	2
145.	а) х > —1; б) х > —.	146. а) 0 < х < 3; б) х < 0 и х > —.
Л	□
4	2	10
147. —10 < х < — —. 148. —2,4 < х < 2. 149. х < - и х > 12. 150. 2 < х < —.
5	5	3
8
151. х < 1 и х > 3. 152. х < —8 и х > 2. 153. х < — —и х > 2. 154. О < х 6.
155.	х < —2,5, —1,5 < х < —0,5; 0,5 < х < 1,5; х > 2,5.
§5
156.	а) х < 2 и х > 3; б) любое число; в) нет решений; г) х < —7 и х > 2;
1	2
Д) — — < X < -; е) — 6 < X < — 3.
157.	а)1<х<2иЗ<х<4;б) —6 < х — 4 и —4 < х < —2.
158.	а) —3 < х < 0; б) любое число; в) х < — — и х > 1; г) —4 < х < 2.
1—/41	1+/41
159.	а) —1 < х < 2, х <-g-> х >---§--’	® < х < 4; в) х > 5 и
х < — г) х > 3 и х < —3; д) —2 < х < у; е) —1 < х < 2 и 3 < х < 6.
160.	а) х > 1 + /10 и х < 1— /10, —/3 < х < /3; б) —< х <
11+ /57	11
<---------4-----J в) х < 1 и х > 2; г) х < 1 и х > 2; д) х > уу.
161.	х < 0. 162. Любое число, если m =/= 0; любое число, кроме 0, если m = 0.
„	л	л	а	а
163.	х< — у и ПРИ х < у и х > — — при л < 0; х —
любое число, кроме х = 0, при а = 0.
336
164.	х < a (2/2 — 3) и x > — a (3 + 2/2) при a < 0; x <—a (3 + 2/2) и
x > — a (3 — 2/2) при a > 0; любое число, кроме x = 0, при a = 0.
165.	x — любое число, если а Ф 0; х — любое, кроме х = 0, если а = 0.
1СС _	„	_ 7.1 + /4а —7	\ — /4а=7	7
166.	x 2приа 4>	2(а — 2)	^х^	2(а —2)	пРи4<а<2;
. о 1 — /4а — 7	1+/47=7
х — 1 ПРИ а — 2; х 2(а 2)— и х > —%,  — ПРИ а > 2; нет реше-
. 7
нии при а < —.
7
167.	а < — —. 168. т > 1. 169. а < — 1.
4
_________7________1Л45	_
170. ___________________g2-< т < /12 — 4.
§6
171.	х < 2; 2х — 3<у <х — 1.
3	3
172.	х < —; у > —х +2; х ~ у > х — 1.
3
173. х > 20; ~ х + 2 < у < 2х — 8.
2	7
174.	Система не имеет решений. 175. х > 5; х + 2 < у < 2х — 3.
176.	Внутренние точки угла, образованного прямыми 4х + 5у = 9 и Зх +
+ 5у = 7 при х < 2.
177. Внутренние точки треугольника, координаты вершин которого (—3; —2);
178. х < — 4, у > — Зх — 4; — 4 < х < 4, у > 4 — х; х > 4, у > х —4.
179.	Внутренние точки треугольника, координаты вершин которого (0; 3);
(-2; 1); (2; 1). ,
180.	Внутренние точки квадрата, вершины которого (—1; 0); (0; 1); (1; 0);
(0; -1).
/	7 4 \
181.	Точки треугольника, координаты вершин которого —— ; — ;
182.	Точки четырехугольника, координаты вершин которого (1; 3); (2; 3);
—М-М-
3 I [ 4 У
183.	х > 1, 1 — х < у С 0.
184.	0 < х <	0 < у < х и ~<х<1, 0<у< —х + 1.
186.	Ординаты ограничены прямой у = х и параболой у = х2, 0 < х < 1.
. 1 /109	1 , /109
187.	Ординаты ограничены прямой и параболой; -g-——g— <х< -g--|--g—•
188. Внутри области, ограниченной параболами; —1 < х < 1.	_
5 — /17
189. Внутри области, ограниченной параболой и прямой; ---%---< х <
^5Ч--/Г7
2
337
1
190.	Внутри области, ограниченной гиперболой и двумя прямыми; — <
< х < 2.
191.	Внутри области, ограниченной параболой и прямой; 0 < х < 2.
192.	Внутри области, ограниченной параболами х = у2, х = —у2 и прямой
У = 4-
193.	_ /2 С х С /2; х2 < у < 4 — х2.
§7
199. —2 < х < 1, х > 3. 200. х < —3, —2 < х < 1, х > 3. 201. х < —3,
2 < х < 3. 202. —3 < х < —2, х > 2. 203. х > 7, 2 < х < 7, — 5 < х < — 3.
204. 2 < х < 4, х > 8. 205. Нет решений. 206. —2 < х < 1, 1 < х < 2.
207. —2 < х < 1 и х > 3. 208. х > 1.209. 0<х<1,2<х<3. 210. 1 < х < 2.
211. Нет решений. 212. Нет решений. 213. Любое число. 214. х <—3,
2	2
—2 < х < 2, х > 3. 215. х < —5, —2 < х < 2, х > 5. 216. х < — —, х > -.
5	5
217. х < —0,77, х > 0,77.
§8
220. При любом х, кроме х = 2. 221. —1,3 < х < — 1; 1 < х < 1,6.
222. х < —3, —2 < х < —1, х > 1. 223. х > 1. 224. 2,5 < х < 3, х > 4.
225. —3 < х < —1, х 3. 226. х < 1, 2<х<3, х> 5. 227. —1 < х < 1.
228. х < 1, х > 7. 229. При любом х, кроме х = ±1. 230. При любом х, кроме
г—	Г- 3
х — 1. 231. Нет решений. 232. х < —]/2, 1 < х < р 2, х > —. 233. —4 <
< х < — 3, — 2 < х < — 1, -^ < х < 3. 234. —3,4 < х < —2, 1 < х < 1,4,
х > 2. 235. —2 < х < — 1, 1< х < 2. 236. —1 < х < 1, 2 < х < 3, х > 4.
1	111	3	3
237. а) х > 7 и х < - -; б) - - <х < - , х < - - и х >	238.. а) 0 <
4	4	4	4	2	2
4	111,1,
<х<~;б)х> 1 их <—1. 239. а) х> —, б) —— < х < —. 240. х> —	ху-1.
5	6	6	6	2
3	1—]Л13	1 + 1<13
241. х > -р х#= 1- 242. х < —5 и х > 1. 243. -g- < х <---2----
244. х < —-— х> —х > 0. 246. х < —2чи х > — 1.
12	2	1
247. —5 < k < — 1.	248.	— < х < — при а > 0; — < х < ~ при а < 0.
а а	а а
2а — b	2а — b
249. х > —------ при а > Ь> 0 и а < b < 0; х < —--- при а > Ь,
а	а
6 < 0 и а < 6, 6 > 0.
2	2
250. х > — — а и х < — а при а > 0; — — а < х < — а при а < 0;
а	а
х < 0 при а = 0.
2	2
251. k < х < — k при k < 0; “7 k < х < k при k > 0.
О	О
3tn — 5	3tn — 5	„	_<
252. х <----------при tn > 1; х >---------при т < 1; нет решении при пг — 1
tn 1	tn -j- 1
и tn Ф —1.
338
253.	1 < х <--- и а + 1 < х при а > 1; 1 < х < а + 1 и х > —- при
а	а
О < а< 1; 1 < х < 2 их > 2 при а = 1; х < а + 1 и < х < 1 при а < —1;
а
а 4-1
о + 1 < х < 1 и х<---при —1 < х < 0; х<0и0<х<1 при а — —1;
а
нет решений при а = 0.
255.	т < — —.
2
§9
46	3
256.	х > 0. 257. х > 27 258. 1 < х < -. 259. - < х < 2.
260.	х > 1. 261. —х < 1. 262. —2 < х < 2.
9
263.	—4,5 < х < 0. 264. х С —2; 5 С х < 5 -.
265.	х < —2 и х > 14.
4
/3 ‘
267. 2 С х < 3. 268. —2 < х < 2. 269. х < —10 и х > 1.
270. х > —1. 271. Нет решений. 272. —< х < 3 — 2/3. 273. х > 34 +
-14-/13	5
+ 6	274. О <х <3. 275. х<—2 и —1< х <---------------. 276. — < х < 3.
О	-far
19 „	1
277. х = 5. 278. х > 5. 279. - < х < 9. 280. х < 0, 0 < х < - и х > 27.
о	2л
4	3	/73 + 5	1	— I а |
281. — — <х< — —, О <х< —77—. 282. - < х < 1. 283. —<х< | а\
и	□	14	z	/о
при а #= 0; нет решений при а = 0. 284. О < х < а при а > 0; 0 < х < 2а при
ab
а < 0. 285. —ab <х < 0. 286. О < х <------287. х < b при а Ь\ х < а при
а -|” а
,	1 4а2 * * 5 4- 1	1
а < Ь. 288. | а | < х при | а | > —;--— <х при | а | < —.
§ 10
289.	а) х > - б) —2 < х < 3.
4
290.	х < —1, 0 < х < 1, х > 1. 291. х < 0.
1g 2
292.	х < 2,5. 293. х>2 и х <^- -1.
2
294. О < х < 1. 295. х < 3. 296. х > 2 —.
О
297. х < 2.
9
298. х > 4. 299. х >5- .
2и
300.	-к	х <	35. 301. х	> 24. 302.	2/2 < х	< 6/3.
303.	х <	log3 2	и log3 4 <	х. 304. —10 < х < 10.
305.	х >	1	и х	< —2. 306. 0,01 < х	< 10 000.
307.	О <	х	< 0,0001 и х	10. 308. 1	< х < 3.
5
309. —3 < х < — 2 и х > 3. 310. х > —.
339
311.
312.
314.
316.
318.
319.
322.
324.
326.
328.
329.
330.
331.
3
-<%<2и7<х<8.
—1 < х < /— /3 и 1 + Уз < X + 3. 313. х < 2 и х > 9.
5 — /33	5 + /33	2
х <---------- и х >-----2---• 315. х < у и х > 1.
2 < х < 4. 317. 3 < х^ 5.
О .	. -3+/5 _ _
3 х	су ,	2	х < 1.
х > 0. 320. 3 < х< 4 и х > 6. 321. х < —2.
х > 10 и х ф 100. 323. 0 < х < 0,001; 1 < х < 100.
8 < х < 9. 325. х > 2.
12
х > 29 и 2"15 < х < 2'9. 327. х > — .
5
х > 2.
2	2
0 < х < ~ их>32.
2
х<22-^°а х>22+^.332. х>4их<-|.
333. log25 — 2<х< log23. 334. О < х < и х > 32.
335. 2 < х < 5, х #= 3,5. 336. 1 < х < 2.~337. 0<х<4их>64.
11	3	1
338.	—4 < х < —— < х < 4. 339. х< — 3 и — <х < 1. 340. 4— <
4 4	4	_	3
1	4	/19 — 1
< х < 7. 341. 2 < х <2-5- и х > 5. 342. -у < х < 8. 343. -—s-< х < 2 и
о	О	Z
„	/19+1
—3 < х < —----g--•
344. х < —2, 0 < х < 1, х > 1. 345. —2 < х < 1.
2
346. 2 < х < 3. 347. х > —
О
и х 1. 348. Нет решений.
349. у < х < 1. 350. 0< х < 1 и УЗ < х < 9.
351. х > 4 + У2 и 3 > х > 4 — У2. 352. 2 + У2 < х < 4.
353. —2 < х < —1, —1 < х < 0, 0 < х_< 1, х > 2.
354. 2<х<3их>4. 355. х < 4-/2 и 4 + /2 < х <6.
356. а2 < х и as < х < 1 при а > 1; 0 < х < а2 и 1 < х < а"8 при 0 < а <
< 1.
357. Нет решений. 358. х > 3 при 0<а<1;0<х<3 при а > 1.
359.	0<х<-- и 1 < х < У а4 при | а | > 1; — < х и У а4 < х < 1
а2	г	а2
при 0 < | а | < 1.
360.	1 < х < а при а > 1; а < х < 1 при а < 1.
361.	0 < х < — и я2 < х < а5 при а > 1;	а5 < х < а2 и х > — при
а	а
а < 1.
362.	— < х < 1 и х > а при а > 1; 0 <х <а и 1 < х < — при а < 1.
а	а
340
ГЛАВА XII
§1
2.	0,5; 1; 1,5; 2; ...; 5. 3. 2; 9; 16; ... . 4. да; За; 4а; 5а. 5. 5050. 7. ат+„ —
— агп_п = 2nd = А — В; d = —С/п = ±±_в
2п	2
9. Доказать методом математической индукции.
1 1 / 1 1 \
10»	= ,	— и т. д. 11. 55. 12. 1.13. —1; 3; 7; ... . Положить
d л2 /
п = 1 ип = 2. 14. 55. 15. 4; 12; 20;.... 16. ak = 106+ 1 ;S = 4380. 17. 2; 6; 10;....
18. а + а + 1 + а + 2 + ... + а + 2n = (n + I)4 — я4; а = 2я2 + п + 1.
19. па => х + (х + 2) + (х + 4) + ... + [х+ 2 (п — 1)]; х = n“-1— п + 1.
Положить а = 2; а = 3 и т. д.
л Г2а + Л(п—1)1	Г	1—а]
20. л4 = ——--------- n;d=:2 n2 + rt + l + ------ ;
L 2 J	[	n — 1J
должно быть целым числом. Бесчисленное множество прогрессий.
о [2a + d(n — 1)]	„ Г ,	1—а!
21. S = ----------- I л = л3; d — 2 л + 1 Н---;
L 2 J	L и —11
л	2(1—а)
а — целое число, следовательно, ----— должно быть целым
2(1-Д)
п — 1
числом.
22. х = ill дать значения л, равные 1, 2, 3, ... .
23.	л = 3. 24. Выразить Sx, S2 и S3 через разность и первый член прогрессии
и подставить их значения.
25.	Все дроби, заключающиеся между т и л, будут
Злг.	Злг + 1 ф	Злг + 2 .	Злг + 3 .	,	Зл — 2.	Зп — 1. Зп
Т’ 3 ’	3 ’	3 ’	*” ’ 3 ’	3~’ Р
Чтобы получить сумму всех несократимых дробей, необходимо из суммы
данных дробей вычесть сумму чисел пг\ т + 1; т + 2; ... ; л.
Искомая сумма будет л2 — лг2.
26.	Найти Sn и Зд и поделить одну сумму на другую; тогда получится: 2а =
= d и т. д.
27.	Найти сумму лг, п и т + л членов.
тт	лг2	d
28.	Из	отношения	— = —	наити а1 =	—.
Од Пй	2
/11\У	/12\х
34. Не могут. Действительно, И == 10</х; 12 = Ю4У; I “1 = 1 — 1 или
1Р
— = 10у"х, что невозможно.
12х
36. Первый член прогрессии должен быть целой степенью знаменателя про-
грессии.
37.
38.
40.
41.
k~nf~a	п~рГ b
К 7= у 7-
— = qn^P; ~ = qn~k; исключить q.
В С
Может при
а с
~Ь
но | b | = | с |; | с | = | d |.
q==
ad	а2
— = —; откуда — = 1,
b С
или а2 = &2; | а | = | b |; аналогич-
341

42.	Выразить левую часть через первый член и знаменатель прогрессии и т. Д.
46. ат = У АВ.
VI. ап^ = ап+2 — ал = anHq — и т. д. Подставить вместо q его зна-
Я
чение.
/	d\n	(	nd\
48. aqn = а 1 + — > а 1 + — = ап+1.
\	а /	\	а /
52.	Умножить на (а — Ь) и сгруппировать члены.
56.	Найти Sn, S2nt S3n и подставить в левую часть равенства.
, «-Vt- п—1/-—
b у b — а у а
59.	,	.	•
п— 1,-—	72—1/—
у о — у а
60.	1; 5; 25; ... или 25; 5; 1;... . 61. 2; 4; 8; ... или 8; 4; 2;... . 62. Возможно
при q = 2 ± УЗ и q = —1. 63. 1; 3; 9; ... . 64.	= 1; q — 2; п = 6.
65.	п = 5, х =	1 • х2 • х4 • ... • х2п = 64; х • х2 • ... • х2л-» = 32.
Поделить первое равенство на второе.
66.	2; 6; 18 или 18; 6; 2. 67. 1; 2; 4; 8 или 8; 4; 2; 1.
68.	2; 4; 8; 16.
— т2 ± п У2т2 — п2
69.	а =-------a-1  »------.
4	п2 — т2
70.	Раскрыв скобки и сгруппировав члены, получим:
Д.4Л+2____ |
71.	Неизвестные составляют геометрическую прогрессию 8; 4; 2; 1.
15 • 2п^	8
72.	хг = —---j-. 73. хх = —. Применить свойство производной пропорции.
1	1 1
74.	хх + — = х2 + — = ... = хл-|---.
хх	х2	хп
10	5 -
Последнее уравнение дает: nxj — — хх + л = 0; п < —. |Так как п — целое
3	3
число, то п “ 1. Таким образом, имеется одно уравнение: хЯ— =—.
хх 3
75.	Членами арифметической прогрессии не могут быть; членами геометри-
ческой прогрессии могут.
2л—2т / g—
q= V (Тб?‘
76.	Геометрическая прогрессия: q = 1; арифметическая прогрессия:
г--------------------- /я ------^\в
d — 0. 71.d — — 2а ± аУ 2 . 79. ---- атм.
У a J
80. 24; 27; 30; ... ; 54 и 24; 24; 24; ... ; 24. 81. а9=81; q = ± /3; л7 = 27. 82. 4;
4	20 100
12; 36 или — ; — —; —. 83. 2; 14; 98 или 38; 38; 38. 84. 27 или 3. 85. 2; 4; 8;
9	9	9
12 или 2~',	4; —.86. 1 ;4; 16; 64. 87. 8; 24; 40; 56. 88. 2 +/"2. 89. ! 1— 7/5
2’2 2 2	20
342
Ill tl
"• ? =	«*• 5?92- 2 (2 - V 2)- 93- ——°4- “i=6; я=к
У 2	^4	a — b — 1	3
11	о _ 1LLLLL
95. 3. 96. 1; T; .... 97. 16. 98. S => ^45; S = 32 . 54 . 38 • 516 • 332.564
4 16	”* •
Сгруппировать члены с основанием степени 3 и 5 и перемножить. 99. 64 • (— Г =з
1g 64 + 2	' 7
«= 0,01; п =---- ж 65,6. Необходимо взять 66 членов.
Ig8 - lg7
,10. s_ <“ + *>’ .
(a — x) 4ax
105.	P = (8 + 4 /2)a; S = 2a2.
102.	S = a2 / S'; P = 6a (2 + / J).
2	—	1
103.	P = — паУ 3; S = — ла2.
3	9
2/3r	2	8
104.	aL =---g--; a2 = уг. Поверхности кубов: 8r2; j/2;...; SKy6OB=12r2.
§2
п(д + 1) (2я + 1)
, 107. Один из возможных вариантов решения: п = 4k + 1.
я3 —я  я (я2 — 1) _ я(я + 1)(я—1) _ (2fe + 1) (2fe + 2) • 2fe
24 “	24	~	24	24	~
_ *(*+ >(-»* +В _+ 2! + 3, +... +
6
108. Представить Sn в следующем виде: Sn == (2 — 1) • 22 + (3 — 1) X
X З2 + (4—1) • 42 + ... + (и—1)п2. Раскрыть скобки, прибавить и отнять 1;
получится сумма кубов и сумма квадратов натуральных чисел.
n(n2—-1) (Зп + 2)
109. Прибавив и отняв учетверенную сумму квадратов п — 1 натуральных
чисел, получим:
_ я (4я2 — 1)
п 3
ПО. S„ = (1 + 1) • I2 + (2 + 1) • 22 + (3 + 1)  З2 + ... + (я + 1)я2.
Раскрыв скобки, получим:
__ n (n + 1) (п + 2) (Зп + 1)
343

111.	ak =□ k [n— (k ~ 2)][n-(fc-l)]= 63H2n+3)£2+(n+l)(n+2)fc.
Положив k равным 1, 2,...,n и сложив полученные равенства, получим:
_ n(n + l)(n + 2) (п + 3)
п	12
112.	Й_2й±а. .а i(?+p.
2	2	’	’ "	2
113.	1 = 1.
3 = 1+2.
6 = 1 + 2 + 3.
12-3
n (n + 1)
---2 ; =1+2 + 3+... + n.
r, n (n + 1) (л + 2)
Сложив по столбцам, получим: Sn —-------------------
114.	1 = 1.
4=1+3.
10 = 1 + 3 + 6.
n (n + 1) № + 2)
_ , ”(« + !)
2 • 3	^ । ^ । - । ••• т* 2
о п(п + \)(п + 2)(п + 3)
Сложив по столбцам, получим: Sn=-----------j—-—-— ------------.
115.	Одно из возможных решений: uk = 2k — 1 = k2 — (k — l)2. Полагая
k равным 1, 2, ..., n и сложив полученные равенства, получим: Sn = п2.
116.	uk = k (3k — 1) = 3fc2 — k; Sn = n2 (n + 1).
117.	uk = 3k2 — 3k + 1 = k3 — (k — I)3; Sn = n3.
118.	(2n — 1) + (2n — 3) + (2n — 5) + ... + 3 + 1 == n2
(2n - 3) + (2n - 5) + ... + 3 + 1 - (n - 1)2
3 + 1 -- 2"
1 = P
Сложить полученные равенства.
119.	ии = 4/?3 — 6/г2 + 4/г — 1 = /г4 — (6 — I)4; Sn = /Л
120.	Умножить обе части равенства на 2:
2Sn = 1 • 2 + 2 - 2 + 3 • 2 + ... + п • 2.
1 . 2 = 1 • 2,
2 • 2 = 2 • 3 — 1 • 2,
п - 2 = п (п + 1) — п (п — 1).
_ п (п + 1)
Сложив данные равенства, получим: 8п =-------------.
2	. П	(k + 1) * 6
121.	Умножйв данное равенство на 1*2-3, получим: ------------------------=
« k (k + 1) (k + 2) — (k — 1)6 (k + 1). Полагая k равным 1, 2, 3,... , /г и сло-
жив полученные равенства, получим:
п(п + 1)(п + 2)
122.	Умножив обе части равенства на 1 • 2 • 3 • 4, получим:
1 . 2 * 3 - 4 - uk = 4/г (k + 1) (k + 2) == k (k + 1) (k + 2) (k + 3)-
-(k - V)k (k +\)(k + 2);
n (n + 1) (n + 2) (n + 3)
1-2.3-4
344
123.	Умножив обе части равенства на 1 • 2 • 3 • 4 • 5, получим:
I • 2 . 3 • 4 . 5 • uk = k (k + 1) (k -f- 2) (6 + 3) (k + 4)—
-(6-1)6 (6+1) (6+2) • (6+3);
n(n + l)(n + 2)(n + 3)(n + 4)
o - — -
'/г —
123.45
1 = 1,
124.	2 • 3 = 2 (4 — 1)	=2-4 — 2,
2- 4- 5 = 2- 4 (6 — 1) = 2- 4- 6 — 2. 4,
2 • 4 • 6 •	• (2n — 2) (2n — 1) =
= 2 • 4 • ... • (2n — 2) • 2n — 2 . 4 • 6 • ... • (2n — 2).
Сложив полученные равенства, получим: Sn — 2п п\ — 1.
125.	1 • 2 = 1 • (3 —1) = 1 . 3 — 1,
1.3.4=1-3 (5 — 1) = 1-3.5 — 1-3.
Сложив полученные равенства, получим:
Srt=l .3.5-.... (2п - 1) (2n + 1) - 1.
126.	k + п — (п — 1) = k + 1. п (п + 1) (n + 2)‘... (n + k — 1) (п + k)
— (n — l)n (п + 1) ... (и + k — 1) = (k + l)n (n + 1) • (n + 2) ... (n + k —1).
Давая значения n от 1 до n и сложив полученные равенства, получим:
(k + l)Sn = п (п + 1) (п + 2) ... (п + k~ 1).
1 1111 1 11
127.	---= 1 — —; ----= — — —; ... ;------= —--------.
1-2	2 2-3	2	3 n(n+ 1) п п + 1
п
Сложив равенства, получим: Sn == ——.
п + 1
128.	Умножить обе части равенства на 2; 6-й член примет вид:
_______2____________1	1
(26 — 1) (26 + 1) “26 — 1"" 26 + Г
Полагая 6 равным 1, 2, 3, ... , п и складывая данные равенства, получим:
s = - п 
” 2п + Г
129.	Число сомножителей в знаменателе каждого члена равно 2, разность
между двумя соседними сомножителями равна 3, следовательно, надо 3 умножить
на (2 — 1), тогда каждое слагаемое можно представить в следующем виде:
1___j_/_l_	J_\
2.5~3\2"~5/’
1___1/1_И
5-8“ 3\5~~8/
1________£ / 1 _ 1 \
(Зп — 2) (Зп + 1) “ 3 \3п — 2 ~ Зп + 1 /’
-----’____________= 1 /_1_ о
(Зп — 1) (Зп + 2)_3 \3п — 1 Зп + ?!'
Sn = ~[-- —Л
3 \ 2 Зп +2/
345
13d. Число сомножителей в знаменателе равно 2, разность между соседними
сомножителями 7, следовательно, надо 7 умножить на (2 — 1), тогда каждый
член можно представить в следующем виде:
1	1 / 1	1 \
4 • 11 “ 7 \ 4	11/’
1	_ _1_ М _ П
И • 18“ 7 \11 “ 18/’
S =1/1— -L-
"	7 \ 4 7п + 4
131.	Число сомножителей в знаменателе 3, разность между двумя соседними
сомножителями 1, следовательно, надо 1 умножить на (3 — 1), тогда каждое
слагаемое можно представить в виде:
1 1/1 1 \
1-2-3 “ 2 \ 1 - 2	2-3 /’
___:I____1/1 __ 1 \
2-3-4 ~2\2-3~”3-4/
________1....../ * *1‘ * 2	1______\
л(п+1)(п + 2) “2\п(и + 1)"“ (п + 1)(и+2)	/
""	2 \ 1 • 2 (n + 1) (п + 2)
132.	Число сомножителей в знаменателе 3, разность между двумя соседними
сомножителями 4, следовательно, надо 4 умножить на (3 — 1), тогда
1 _ _£ / 1 _ ' 1 \
3-7-11 ” 8 \3-7 “”7- 11/’
1 _ _1_ / 1 __ 1 \
7 - 11 - 15“ 8 \7 • 11	11 - 15/
_____________1_____________(____________!___________________!________’
(4л — 1) (4л + 3) (4л + 7) “ 8 \ (4л — 1) (4л + 3)	(4л + 3) (4л + 7) t
	1 \
“	8 \ 3 • 7	(4п + 3) (4л 4- 7) )'
133.	Число сомножителей 4, разность между двумя сомножителями 1.
"	3 \ 1 • 2 • 3 (п + 1) (п. + 2) (л + 3) )'
134.	Число сомножителей 5, разность между двумя соседними сомножителя-
ми 1.
s = 1 /__!__________________________!_____________
"	4 \ 1 • 2 • 3 • 4 (л + 1) (л + 2) (л + 3) (я + 4) /'
135.	Число сомножителей 3, разность между двумя соседними сомножителя-
ми 5.
10 2 • 7	140
137. а. = 1 - р
___2___11
°2 “ 2 - 3 “ 2	2-3’
346
3	1
3	2-3-4	2-3	2-3-4
1
tz/z =--------—-----
1 • 2 • ... - n 2 - 3 • ... - (n+ 1)
S = lim Sn = lim 11 — —-—-—-———'j _ 1.
n -* oo n -► oo \
22 — I2 . 32 — 22
138. Sn =
22	1
~ P22— 1222	2332-- 2232
_l + ±	1
32	32
139. Sn -
+	——
T 2 \2n - 1 2n + 1
n2 \	£ "
2
£
= 2
1
140. ——
1
1
и2
2n + l
n2
2n —1
n —
2/t -j- 1
2-3... (n + 1)
42 — 32
(1 - 2)2	(2 - 3)2	(3 • 4)2 +
, 32	22	(n + I)2
’ n2(n + I)2 ~n2(n+ I)2
z n — 1 —--------——; Hm Sn — 1.
(n + I)2 (n + l)2n-.~
! .^/1 1\. ,
' + 2 \ 5 ~ 7 / + +
23	22 З2 32	, n2
— — — —I— --- —I—	-J— -- —
3	5^5	7 2n — 1
n2 _ (n — Ip \
2n — 1 2n — 1 /
n2 \ _ n (n + 1)
2n + l/ = 2(2n + l)‘
______ .	1 _1
2 + n2 + 2a + n2 + 32 n2 + (n — I)2 < n2
1 1
- —---4-... + —-—	-> 0 при n oo.
n2 + 1 n2 + 1	F
2	11	112
«'• ,— -^-77?»"»" 77-77-73?
#	2	2	4	4	4	8
Аналогично o , - = — ; —   ;
x2 + 1 x2 — 1 x4 — 1 x4 + 1 x4 — 1
2«	2rt	2rt+1
41" = X2'2 —1	x2rt+1= 1 ’
Сложив данные равенства, получим:
1	2Л+1	о 1
Sn = —Г - -Т»+Г~"Т-. Откуда S = — - .
1	/V	1	/V А
(n + 1)2—na
[«•(« + i)p=
_ '1 2
— 1 —’ 23	22
X8 — 1 ’
142.	Сгруппировать члены, в которые не входит разность прогрессии d, и
члены, в которые входит разность прогрессии d.
с П(П+1)Д (и — 1)п(п+ 1)д?
п ~	2	+	3
143.	Сгруппировать члены следующим образом: в одну группу — члены,
содержащие а, во вторую группу из оставшихся членов — члены, содержащие д,
и в третью группу — все остальные члены.
Г 2Ь + (и - 1) q	п (п 4- 1) (и — 1) п (2п — 1)
S„ = а ------д------- « + Ьр---------+ pq-------------------.
L ~	®
144.	Первый член: а . 1.
Второй член: а • 10 + а.
Третий член: а • 102 + а • 10 + а.
п-н член: а • Ю*"1 г а . Ю4-2 + ... + а . 10 + а.
347
sn = a (! + 10 4- Ю2 + ... + IO"-1) + a (1 + 10 + IO2 +... + IO"-2) + ... +
+ a (1 + 10) + a =	• (10« + IO"-1 + ... + 10 - n) =
_ a ( ю"*1 — 10 __ \
“10-l\ Ю-l j’
145.	370 368.
146.	Умножить обе части равенства на а и вычесть данное равенство.
пап	аП—*
Sn=a-1 — (a- I)2 *
.П (п+ 1)яп _ пап an — 1
п~ 2 (a -1) (а - I)2 + (а - 1)3‘
См. решение задачи 146.
148.	S5 = 351. Воспользоваться формулой предыдущей задачи.
149.	Умножить обе части равенства на а3 и вычесть данное равенство.
150.	S =	1	+ а +	а2	+	а3 +	...	+ а" + ... +
+ а +	а2	+	а3 +	...	+ ап + ••• +
+	а2	+	а3 +	•••	+ ап + ... 4"
+ а11 + ... +
Просуммировав по горизонталям, получим: S =------------------- .
(1 — а)2
151.	S = 2. См. задачу 150.
152.	S = (1 + а + а2 + а3 + ...) + (2a + 4a2 + 6a3 + 8a4 + ...)
1	1 4- a
~ -------+ 2a (1 + 2a + 3a2 + 4a3 + ...) = -
153. S = 1 + 2a 4- За2 + 4a3 + .	.. + (га	+ 1)а« + ..		.+
а + 2а2 + За3 + •	.. + пап		+..	. +
а2 + 2а3 + ..	. + (га —	- 1)ал	+.	
+ а3 + ..	• +(п-	2)а" .	+ .	.. +
Просуммировать по горизонталям: S =
154.	S == 1+ a+ a2+ a3 + ... +
+ 3a+3a2 + 3a3 + ...+
+ 5a2 + 5a3 + ...+
+ 7a3 +...+
Просуммировать по горизонталям: S = —
155.	S = ar + ar2 + ar3 + ar4 + ... +
+ abr2 + abr3 + abr4 + ... +
+ abr3 + abr1 + ... +
Просуммировать по горизонталям: S = —--.
156.	A2; ...; An — члены ряда.
Ay4jj A/lgj •••’,
Все А А равны между собой, так как АМХ = А2Л2 = ... = А Дл_2 = 0.
Следовательно, А2—	+ АЛР
Л3 = л2+ АЛХ = Л^гАЛр
Лл = Ла-У-*!) АА. ’
348
Сумма Sn — At= (n — 1) Лх 4- [1 + 2 + ... + (n — 1)] ДЛХ;
S, .„ Vi А^ д,,„
157.	Л_1;Д.41„,;5,,_„ + 2^_ЛШ>.
158.	A^ A2‘, A3 ; ... ; Ап‘
ДАХ; ДА2; ДА3; ...; кАп_]\
Д2АХ = Д2А2 — ... = Д2АЯ_2;
а2 = Ai + аах;
А3 — Л2 + ДА2 = А2 + ДАХ + Д2АХ;
А3 = А. + 2ДАХ + Д2АХ;
А4 = А3 + ДЛ3 = (Ах + 2ААХ + А2АХ) + \Аг + 2А2А2 = Ах + ЗААХ + ЗД2АХ,
ибо вторые разности равны между собой.
Аналогично j
А. = л 4- 4ДЛХ 4- Д2ЛХ; Ап = лх 4- (П -1) ДА 4-	дм1-
Следовательно, А. = А,,
Ai=Al + AAl, '
Л3 = 414-2ДД14-ЛМ1,
= л, + (» - 1)лл, + ,-!2—’)(" 2) дм,.
s„_„л, + ^44» дл, + [ 1 + 3 +... + <"-‘>("~г)]д.л,-
- »А +	ДА + ^"4^7 21А-А.
159.	Разности будут
А	ДА	Д2А	Д3А
13	2	0
4	5	2	0
9	7	2(	0
16.......................
S„ - „ А + ^11 д Л1 +	ДМ,;
Лх= 1; ДЛГ = 3; Д2ЛХ = 2.
е „ । «(«-О	п(п-1)(п-2)
Ои — ft “т~	• О
п	1*2	1 • 2•3
sn =	[6 + 9п -9 4-2(п- 1)(п - 2)] = J[2n* 4~ Зп 4- 1] =	+
О	О	1 • 2 • □
ГЛАВА ХШ
§1
1. 8t 2. 32 767. 3. Л"-\. 4. (т — I)2 (т — 2)... (т — п 4- 1). 5. 96. 6. 6.
7. 48. 8. 42. 9. а) Л* . Л®; б) А^ . Л®. 10. а) ЗЛ« ; б) (Л^ - А*) Л®.
11. Akn  Л"4Д. 12. Л"“* (Л^ — Л*). 13. 16. 14. 64. 15. 5; 20; 54; 90.
16. 10 000. 17. 756. 18. С|2. 19. 504. 20.	21. 20. 22. 46 376. 23. С|о • Р6;
349
c2n- cln • CL. 24. 651. 25. —. 26. 2 (6!)2. 27. 5! Al = 7200. 28. 15 368.
ZU ZU ZU	Л f
29. 175. 30. m\ n\\ m\ n\ (n + 1). 31. 2901. 32. 45. 33. 27. 34. 99. 35. 238. 36. 420.
37. 22. 38. 310. 39. 62. 40. 5Л§ = 125.
§2
r 53. 12. 54. 8! 55. r = 2; n =	17. 56. Найти C2f^ и	CJr	Заметим, что	(4п)!	=»
« 1 . 2 • 3 •	•	4n = 1 • 3 • 5 •	... • (4n — 1) (2 • 4 •	... •	4n) «
« 22Л Ц . 3 • 5 •	• (4n — 1)] •	(2n)!	(2n)!	1 • 2	. 3 .	... . 2n =• 1 .	3 • 5	X
X (2n — 1) • 2 • 4 • 6	*	- - -	-
57. Из равенства C'f
1 Из
m = 3; n = 6. 58. r = 14; n — 34. 59. 7. 60. Записать C2m + m =
m =• I, 2, 3,
писать С2т =
равенства
4n = 1 • 3 • 5 •	• (4п — 1) (2 • 4 • ...
... • (4п — 1)] • (2п)!	(2п)! = 1-2.3
‘ ~ ... . 2п = 1 • 3 • 5 • ... • (2п — 1) • 2Л (1 . 2 • 3 . ... . п).
=» 5 : 5 находим: п = 2/п.
= 5:3 находим: 8т — Зп = 6; отсюда
".	т+1 ПРИ
т—1 и сложить их результаты. 61. На С2. 62. За-
т2—т	, Л о
—-— при т = 1, 2, 3,..., zn, сложить результаты и использовать
~	— Зт2 + 2т
третье свойство сочетании. бЗ.Записать С^п=---------------при zn=l, 2, 3, ..., т9
сложить результаты и использовать третье свойство сочетаний. 64. Так как
гз 1 т т - 1
Ст + т' —
m-j-P то имеем:
1 .
'3
1	= Ч’
+з4=сь
+1 -з=с’.
^ + ь4=с»’
'4
С3
(/п^ 1) Кт
2	“ т*
Сложив полученные равенства, получим:
C^, = 1 • 1 + 1 • 3 + 2 • 3 + 2 • 5 + 3 • 5 + ... +	- 2).
65.	15. 66. 8. 67. 7. 68. x =» n + 2 ± У n + 2. Задача имеет решение при
п = k2 —2, где k — любое натуральное число, отличное от 1. При этом х =»
- k2 ± k. 69. 10.
’ §3
70.	« 1,018. 71. « 0,288. 72. 29 + 2781.
73.	2а6 — 30а462 + 30а2М — 2d6.
74.	(1 + 04Л+а	(2f)2ft+1 . В разложении будут члены, содержащие +Z или —t.
76. ШОхф'х. 77. 70х4у4. 78. Наибольший коэффициент если т == 2/г;
C2fe+1 и C2k+1> если m = 2fe + 1. 79. 12. 80. 240. 81. 495а4%-2. 82. 70 (1 — х2)2.
350
226 + 15	3_
S3, т —------~, наименьшее значение k = 6, тогда т = 21. 84. х.
85. 84г’. 86. С®6 Xs. 87. С^. 88. С°5. 89. Разложение будет *	 С"п.
1 _5
90. Cf2 • б’7. 91. 1000;	92. —264а3Ь7. 93. С^&’аг12. 94. С|2 . 95. 84х 2 .
96. 2; —1. 97.	2 = 5; х=2; у = 3. 98.	= 7;	п.г = 14.	99.	п =	7. 100.	60.
101.	Т14+1 = 36С24 . 102. — £9] Л 103. С?9 х3у2.	104. 26.	105. Т9;	Ты; Тп	и
гр	Ф 'Г	1Л-? ^+2	П	П — k	I
Л4;	Л5; Лв-	107. — = — , откуда	—— = ——п = - 1.	Трех
*k+i '/г+2	& + 1 _ k -р 2	_
равных членов не может быть. 108. C|q()/ 2)29. 109.	(]/2 )40 ()/3 )55.
ПО. 62л + Зл+2 + Зп = Зл (12л + 10) = 3” [(11 4- 1)л + 10] . 111. 32л+3 —
—24п + 37 = 27 • 9л — 24п + 37 = 27 (8 + 1)л — 24п + 37. 112.	32"+1 —
—5п = 3 (8 4- 1)л — 5п. Искомое выражение 32/2+1— Зп — (19n+3) = 32n+1—
—24п — 3. 113. После сокращения вынести за скобки п. 114. После сокращения
вынести за скобки п. 115. А = (С° +	+ С2 + ... + С”) + (Сп +	+
+ ... + п Сл). 116. Найти Ckn при k = 1, 2, 3, ..., п, вынести ~~ за скобки,
прибавить и отнять —-—. 117. Найти при 6 = 1,2, 3, ..., п, вынести -------
п + 1	п 4-1
за скобки, прибавить и отнять в скобках 1. 118. Взять (14*1)'* и (1—1)л и разло-
С* 2С^ ЗСЗ
жить по формуле бинома. 119. — = п; —- = п — 1; —~ — п — 3 и т. д.
С'п с2п
Сложить данные равенства. 120. (1 4- 2х)л разложить по формуле бинома и поло-
жить х = 1. 121. (1 4- разложить по формуле бинома, 1 перенести в левую
часть равенства, разделить обе части равенства на n+ 1. Положить х = 2.
122. Обозначить выражение в левой части через А и умножить обе части равенст-
ва на п! 123. Вынести за скобки —-—, затем прибавить и отнять 1 —-"-у--.
п 4- 1	1
Ляпин Сергей Евгеньевич,
Баранова Ирина Владимировна,
Борчугова Зоя Григорьевна
СБОРНИК ЗАДАЧ
ПО ЭЛЕМЕНТАРНОЙ АЛГЕБРЕ
Редактор Э. К. Викулина
Переплет художника О. М. Журавлева
Художественный редактор Е. Н. Карасик
Технические редакторы М. И. Сафронович
и И. В. Квасницкая
Корректор Н. И. Новикова
Сдано в набор 22/11 1973 г. Подписано к печа-
ти 15/XI 1973 г. 60x90l/ie. Бумага тип. № 2.
Печ л. 22. Уч.-изд. л. 22,60. Тираж 80 тыс. экз.
А10678.
Заказ 1089.
Издательство «Просвещение» Государственно-
го комитета Совета Министров РСФСР по де-
лам издательств, полиграфии и книжной тор-
говли. Москва, 3-й проезд Марьиной рощи, 41.
Саратовский ордена Трудового Красного Зна-
мени полиграфический комбинат Росглавпо-
лиграфпрома Государственного комитета Со-
вета Министров РСФСР по делам издательств,
полиграфии и книжной торговли, г. Саратов,
ул Чернышевского, 59.
Цена без переплета 63 к., переплет 21 к.
84 кои.