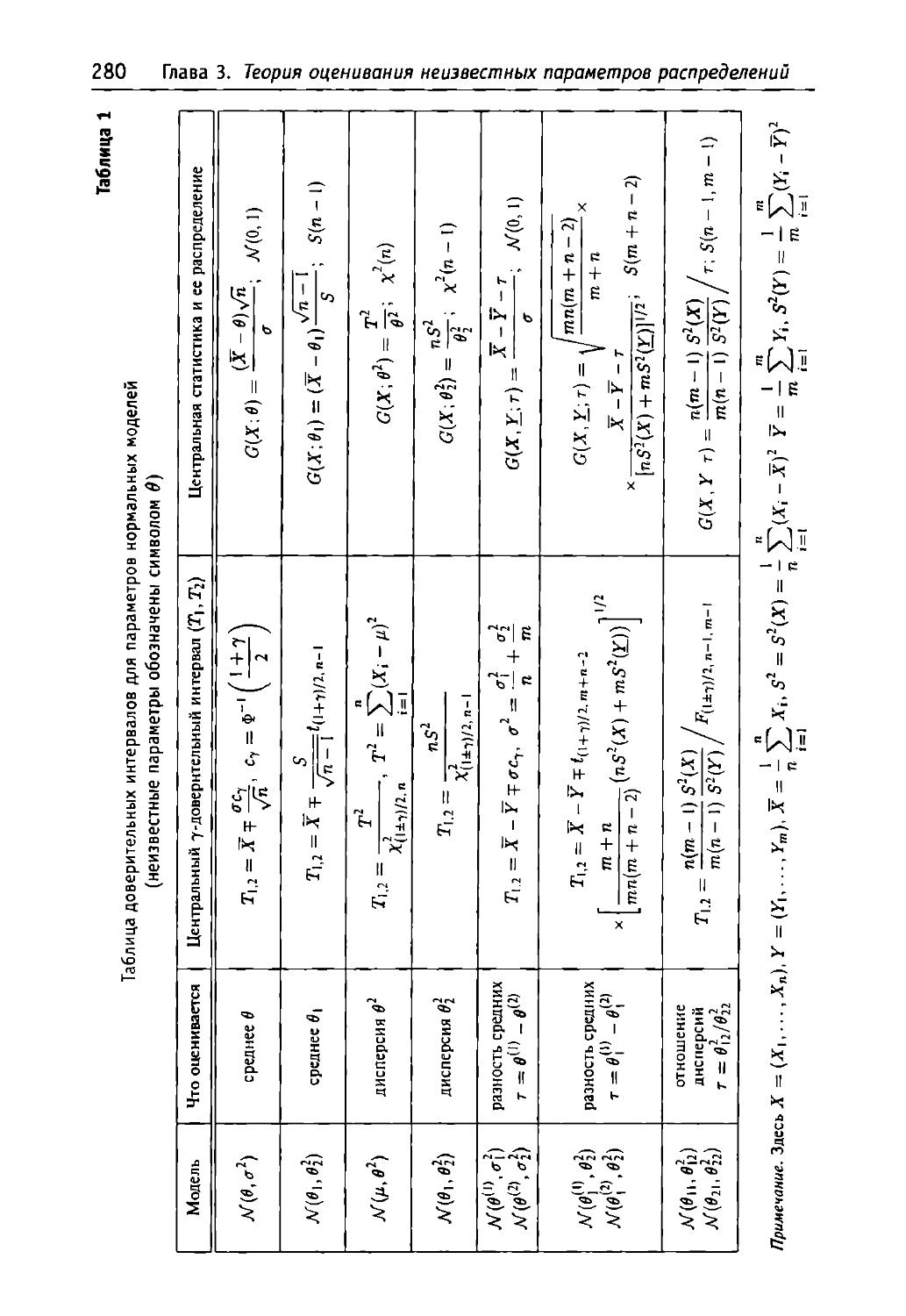
Автор: Ивченко Г.И. Медведев Ю.И.
Теги: теория вероятностей математическая статистика комбинаторный анализ теория графов математика статистика
ISBN: 978-5-382-01013-7
Год: 2009
Текст
ББК 22.172
Ивченко rриrорий Иваиович,
Медведев Юрий Иваиович
Введеиие в математическую статистику: Учебник.
М.: Издательство ЛКИ, 2010.
600 с.
Настоящая книrа представляет собой своеобраЗНbIЙ расширеННbIЙ учебник
по математической статистике. ДаННbIЙ учебник не оrpаничен рамками учебноrо
стандарта или вузовской проrpаММbI
он предназначен всем, кто интересуется
математикой вообще и, в частности, хочет узнать, что такое современная MaTeMa
тическая статистика, какие задачи и какими методами она решает, какие результаТbI
в ней уже накоплеНbI, какие проблеМbI в ней сеrодня актуалЬНbI; наконец, каковы
ее истоки, какой путь она прошла и какие ученые были ее творцами. По заМbIСЛУ
авторов, книrа простым и ДОСТУПНbIМ ЯЗbIКОМ рассказывает о математической CTa
тистике и одновременно обучает ей. Вся теория объясняется и иллюстрируется на
интереСНbIХ и тщательно подобраННbIХ примерах. Книrа может служить и задач
ником, так как содержит большой список упражнений для самостоятельноrо реше
ния, а также спраВОЧНbIМ пособием по математической статистнке, а в некоторых
аспектах
и по теории вероятностей.
Книrа будет интересна преподавателям, аспирантам и студентам естественных
и технических вузов, в которых изучается математическая статистика, научным
работникам, использующим в своей деятельности методЬ} математической стати
стики, а также самому широкому Kpyry любителей математики.
Издательство лки.
117312, Москва. пр-т ЩееТllдееятилетия Октября. 9.
Формат БО х 9011 б. Печ. л, 37,5. Зак. No 174Н.
Отпечатано В 000 "пк "Зауралье».
640022, Курrанекая обл., KypraH, ул. К. Маркса, 106.
ISBN 978----5-----382---01 О13
7
(Q Издательство ЛКИ, 2009
НАУЧНАЯ И УЧЕБНАЯ ЛИТЕРАТУРА
I
I ,
.,'" ""@""" ru
Каталor изданий вИнтернете:
http://URSS.ru
Тел.iфакс: 7 (499) 1З5---42
16
URSS Тел.iфакс: 7 (499) 1З5---42---46
5735 ID 71268
11111111111111111111111111
785382 010137
9
Все ПраВа заЩИЩСНbI. Никакая ЧаСтЬ "астоящей КI1иrи не может бblТЬ воспроизведена или
псредана в каКОЙ бы то ни бblЛО форме и КаКиМИ бbl то ни бblЛО средствами, будь то злек-
тронныс или мсханичеекие, включая фотокопирование И запись На маrНИТНblЙ ноеитеlIЬ,
а также размещение вИнтернете, есл" на то нет письменноrо разрсшеНI1Я владсльца.
Содержание
Предисловие
Введение
1. Что такое математическая статистика, ее предмет и задачи
2. Краткий исторический очерк развития
математической статистики
11
14
14
25
lЛава 1. (Вспомоrательная, но очень важная!) Основные распределеllИЯ
и их моделирование. 30
Введение 30
1.1. Основные дискретные модели математической статистики 31
1. Схема Бернулли и биномиальное распределение 31
2. Отриuательное биномиальное распределение 34
З. Распределение Пуассона 35
4. rиперrсометрическое распределение 37
5. РаспределеНllе Маркова Пойа _ 37
6. Полиномиальное распределение 39
7. MHoroMepHoe распределение Маркова Пойа 40
8. Распределение cTeneHHoro ряда. 42
1.2. Основные абсолютно непрерывные модели 43
1. Нормальное распределение 44
2. MHoroMepHoe нормальное распределение 47
З. rамма распределенис 51
4. Бета распредслеНlIе 53
5. Равномерное распределение 54
6. Распределение Стьюдента 55
7. Распределение Снедекора 56
8. Распределение Вейбулла 57
9. Распределение Парето 57
10. Распределение Дирих.ле 57
11. Преобразования случайных величин и векторов 58
1.3. Моделирование выборок из конкретных распределений 62
1. Предварительные замечания 62
2. Моделирование распределений Бернулли Bi(l, р)
и биномиальноrо Bi(k, р) 64
3. Моделирование отриuательноrо биномиальноro
распределения Bi (r,p) 64
4. Моделированис полиномиальных испытаний 65
5. Моделирование nyaccoHoBcKoro распределения П(л) . . . . . . . . .. 65
4
Содержание
6. Моделирование непрерывных распределений 66
7. Моделирование показательноrо
и связанных с ним распределениЙ 67
8. Моделирование нормальных слу'lайныx чисел 67
9. Метод суперпозиций 68
10. Моделирование uerlll Маркова 70
11. Метод Монте Карло 73
раж н М
IЛа8а 2. Первичиая обработка экспериментальных данных 89
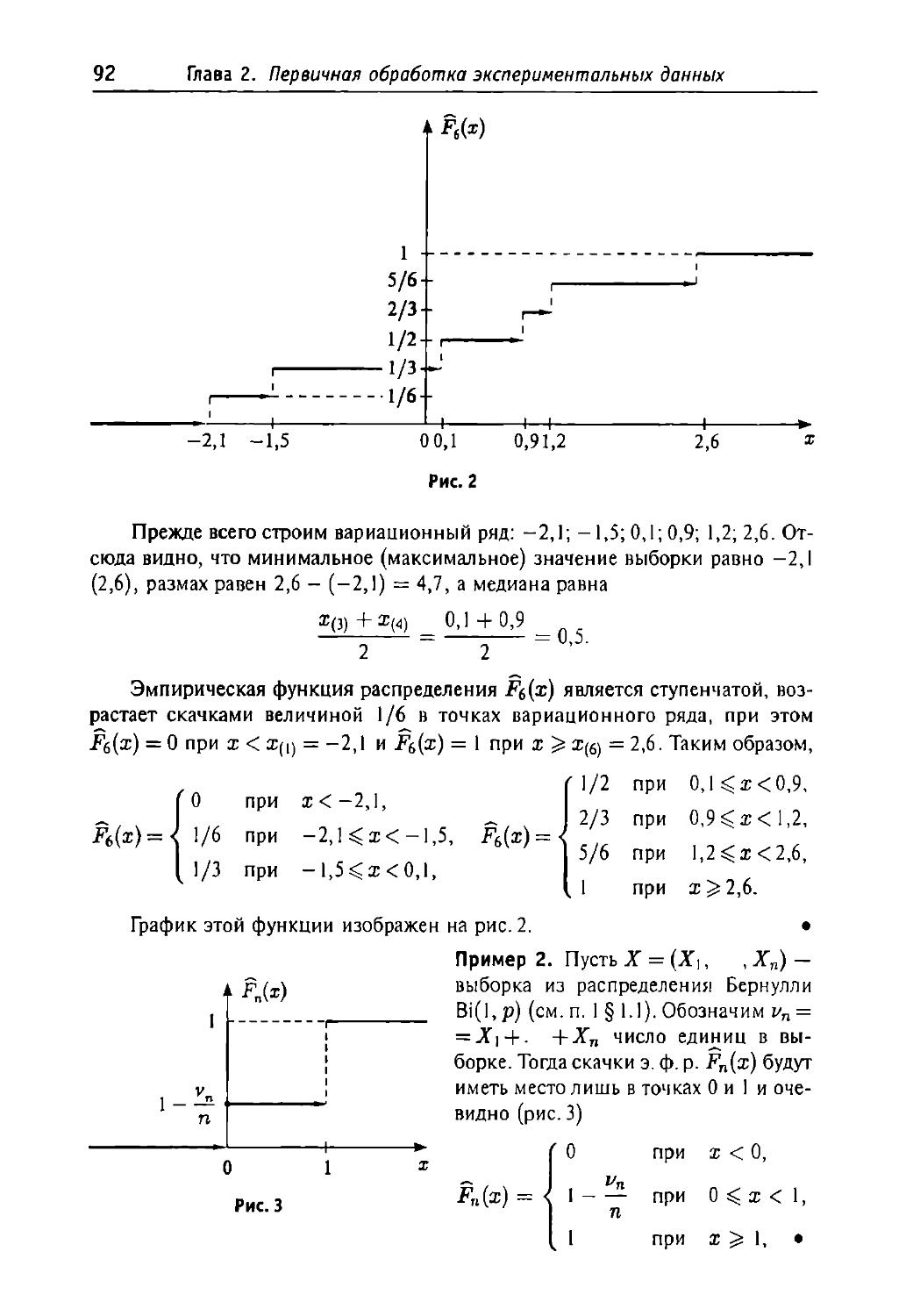
2.1. Вариационный ряд выборки, эмпирическая функция распределения
и rистоrpамма . 89
1. Порядковые статистики и вариационный ряд выборки 89
2. Эмпирическая функция распределения 90
3. Дальнейшие свойства э. ф. р. 96
4. Полиrон частот, rистоrpамма 100
5. Ядерные оценки теоретической плотности 103
2.2. Выборочные моменты: точная и асимптотическая теория 105
1. Выборочные моменты 105
2. Моменты выборочных cpeAHero и дисперсии 108
3. Сходимость по вероятности выборочных моментов
и функций от них 109
4. Асимптотическая нормальность выборочных моментов 114
5. Асимптотические доверительные интервалы
дпя теоретических моментов 117
2.3. MHoroMepHbIC данные 118
1. Эмпирическая функция распределения 119
2. Моменты 120
3. Большие выборки 121
4. Добавление: нормальная модель 122
5. Друrие корреляционные характеристики 125
2.4. Выборочные квантили и порядковые статистики 128
1. Теоретические и эмпирические квантили 128
2. Распределение порядковых статистик 130
3. Асимптотическая нормальность средних членов
вариационноrо ряда 133
4. Асимптотическое поведение крайних порядковых статистик 135
5. Асимптотическая теория дпя верхиих
экстремумов X(n m+I), т 1 138
2.5. Линейные и квадратичные статистики от нормальных IJыорокK 140
1. Лииейные и квадратичные статистики, условия их независимости 141
2. Распределения квадратичных статистик 143
3. Теорема Фишера 145
Упражнения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 150
Содержание 5
fлава З. Общая теория оценивания иеиэвестных пара метров распределений 159
3.1. СТf\тистические оценки и общие требования к ним 1 S9
1. Понятие статистической оценки и ее среднеквадратичная ошибка 1 S9
2. Несмещенные оценки Iб2
3. Оптимальные оценки Iб8
3.2. Критерии оптимальности оценок, основанные
на неравенстве Pao KpaMepa. Эффективные оценки 173
1. Функция правдоподобия, вклад выборки, функция информации 173
2. Неравенство Pao Крамера 175
3. Экспоненциальная модель 179
4. Критерий Бхапачария оптимальности оценки 181
5. К[Jитерии оптимальности в случае BeKTopHoro параметра 182
3.3. Достаточные статистики и оптимальные оценки 18б
1. Достаточные статистики и критерий факторизации 18б
2. Теорема Рао Блекуэлла Колмоrорова 191
3. Экспоненциальные семейства и достаточные статистики 193
3.4. Способы решения уравнения несмещенности 199
1. Модель степенноro ряда, оценнвание параметрических функций 200
2. Модели с выборочным пространством, зависящим от napaMeipa 8 204
3. Метод подrонки 207
4. rамма модель с неизвестным параметром масштаба,
оценивание параметрических функций 213
5. Друrие применения raмма модели для оцеиивания неизвестных
параметров 217
3.5. Оценки максимальноro правдоподобия . 219
1. Определение и при меры оценок
Мf\ксимальноrо правдоподобия (о. м. п.) 219
2. Принцип инвариантности для о. м. п. 223
3. МeiОД накопления для приближенноro вычисления о. м. п. 225
4. Асимптотические свойстоа о. м. п. 227
5. Асимптотические доверительные интервалы,
основанные на о. м. п. 234
3.б. Друrие методы н принципы построения оценок 239
1. Метод моментов. 239
2. Метод минимума хи квадрат 241
3. Модально несмещенные оценки 243
4. Медианно несмещенные оценки 245
5. Эквивариантные оценки 24б
б. Бf\йесовские и минимаксные оценки 2S0
7. Оцениванис по цеllЗурированным данным 2S8
3.7 Объединение и улучшение оценок 2б4
1. Объединение оценок 2б4
2. Улучшение оценок 271
3.8. Доверительное оценивание 27б
1. Построение доверительноrо интервала
с помощью центральной статиСТИКИ. . . . . . . . . . . . . . . . . . .. 277
б
Содержание
2. Построение ДОllерительноrо интервала с использованием
распределения точечной оценки параметра 281
3. Асимптотические доверительные интервалы 284
93.9. Оценивание при выборе из конечной совокупности 288
1. Оценивание среднеrо СОВОКУПНОСТИ 288
2. Оценивание состава совокупности 292
Упражнения 297
fлава 4. Проверка статистических rипотез 311
94.1. Основные понятия и общие ПРИНUИПbI теории ПрОllерки rипотез 311
94.2. Проверка rипотезы о виде распределения 318
1. Критерий соrласия Колмоrорова 318
2. Критерий соrласия хи квалрат К. Пирсона 320
3. Критерий хи квадрат для сложной rипотезы 327
4. Критерий квантилей 332
5. Критерий пустых ящиков 334
94.3. fипотеза и критерии однородности 340
1. Критерий однородности Смирнова 340
2. Критерий однородности хи квадрат 341
3. Друrие критерии в задаче о двух вы50рках 347
94.4. fипотеза независимости 350
1. Критерий независимости хи квадрат 351
2. Критерий Спирмена 357
3. Критерий Кендалла 358
4. Случай т признаков 359
94.5. fипотеза случайности 361
1. Критерий инверсий 362
2. Проблема датчиков и 050бщенный критерий хи квадрат 364
Упражнения 368
[Лава 5. Параметрические rипотезы 372
95.1. Общие положения 372
95.2. Вы50р из двух ПРОСТbIХ rипотез. Критерий Неймана Пирсона 374
1. Постановка задачи и предварительные соображения 374
2. Случай абсолютно непрерывных распределений 375
3. Критерий Неймана Пирсона в случае дискреТНblХ распредслсний 386
95.3. Сложные rипотезы 394
1. Р. н. м. критерии ПРОТИlJ сложных односторонних альтернатив.
Модели с монотонным отношением правдоподобия 394
2. Двусторонние альтернаТИВbI, р. н. м. несмещеННblС критерии 398
3. ЛокалЬНbIе наиболее мощныс критерии 403
4. Провсрка rипотез и ДOlJерительное оuеllивание 405
95.4. Критерий отношения правдоподобия 409
1. Метод отношения правдоподобия для общих rипотез . 409
2. КОП JUlя БОЛЫIIИХ выборок 417
3. ДIUIЫIС!\IIIИС аСИМПТОТI1'1сские свойства КОП .............. 421
Содержание 7
4. Сложная нулевая rипотеза 423
5. Доверительные области максимальноrо правдоподобия 42б
5.5. Проверка rипотез для конечных цепей Маркова 427
1. rипотеЗbl для конечных цепей Маркова 428
2. Критерий хи квадрат для простой rипотеЗbl 431
3. Критерий хи квадрат для сложной П1Потезы 432
4, Критерий отношения правдоподобия
для общих параметрических rипотез 43б
5. Критерий однородности 438
б. Оценивание порядка цепи 442
5.6. Понятие о последовательном анализе. Критерий Вальда. 443
1. Определение критерия Вальда 444
2. О числе испытаний до момента остановки в критсрии Вальда 445
3. О выборе flJаниц в критерии Вальда 446
4, О среднем числе наблюдений D критерии Вальда 448
Упражнения 451
lЛава 6. (Специальная) Линеiiная реrpессня н метод нанменьшнх квадратов 457
6.1. Модель линейной реrрессии 457
6.2. Оценивание пара метров модели линейной реflJессии 459
1. Метод наименьших квадратов 459
2. Оптимальность оценок наименьших квадратов 460
3. ОцеНИlJание остаточной дисперсии 462
4. Условные о. н. к. 463
5. Оптимальный выбор матрицы плана. 464
6. Примеры применения метода наименьших квадратов 465
7. ОртоrоналЬНblС мноrочлены Чебышева 470
6.3. Нормальная реflJессия 474
1. Модель нормальной реflJессии 474
2. Оценки максимальноrо правдоподобия (о. м. п.)
параметров нормальной реrрессии 475
3. Основная теорема теории нормальной реrреССИlI 47б
4. Доверительное оценивание параметров нормальной реrрсссии 477
5. Доверительная область для линейных комбинаций параметров t!.. 479
6. Система совместных доверитеЛЬНblХ интервалов 480
7. ДоверитеЛЬНblЙ интервал для отклика 481
8. Проверка адекватности модели 482
б.4. Общая линейная rипотеза нормальной реflJСССИИ 484
1. Понятие линейной rипотезы 484
2. F критерий для линейной rипотезы 484
6.5. Некоторые применения теории нормальной реflJСССИИ 490
1. rипотеза о параллельности линий реflJессии 490
2. fипотеза однородности для нескольких
нормальных выборок 493
3. Двойная классификация. Дисперсионный анализ 496
6.6. Статистическая реflJессия и проrнозирование. . . . ".. . " . " . . . " " .. 502
8
Содержание
1. Задачи статистическоrо проrноза 502
2. Условное математическое ожидание 503
3. Оптимальный предиктор и ero свойства 505
4. Из истории реrpессии 507
5. Линейный проrноз 508
6. Использование в проrнозе дополнительных переменных.
Алrоритм обновления проrноза 511
7. Проrнозирование стационарных временных рядов 514
Упражнения 520
fлава 7. Элементы теории решений. Дискриминантный аиализ 525
97.1. Статистические решающие функции.
Байесовское и минимаксное решения 525
1. Понятие решающей функции 525
2. Функция риска и допустимые решающие правила 526
3. Байесовское решение 527
4. Минимаксное решение 528
5. Оценивание параметров и проверка rипотез
с позиций теории решений 531
97.2. Классификация наблюдений 532
1. Задача классификации 532
2. Функция риска в задаче классификации 532
3. Байесовское решение 533
4. Минимаксное решение 535
97.3. Классификация наблюдений в случае двух нормальных классов 535
1. Байесовский подход 536
2. Минимаксный подход 537
97.4. Классификация нормальных наблюдений. Общий случай 538
1. Байесовский подход 538
2. Мl1нимаксный подход 540
3. Классификации наблюдений в случае неизвестных параметров 540
Упражнения 542
IЛаоа 8. Факторный анализ 546
98.1. Постановка задач факторноrо анализа 546
98.2. Неоднозначность решения в факторном анализе 548
98.3. Вывод уравнений максимальноrо правдоподобия 549
98.4. Итерационный метод нахождения факторных наrрузок 553
98.5. Проверка rипотеЗbJ о 'lИсле факторов 555
9 8.6. Центроидный метод 558
98.7 Оценка значений факторов 562
JjШIЩ 1). КОМПОllентный анализ
111 1I\I!:TilIIOIIKI ;ша'l компонентноrо анализа
_'} 1 I't'III lllIt' IICII(lIIIII,IX YIJallllclll1ii. rЛНUНbJС компоненты
I J. МСnllJl XOTCJIJIIIIII'II , . , , . . . , , , . , . . . . . . . . .
564
564
566
568
Содержание
9
Приложеиие
1. Нормальное распределение
2. Распределение Пуассона
3. Биномиальное распределение
4. Распределение х 2 (п)
5. Распределение Стьюдента S(n)
6. Распределение Снедекора S(nl, n2)
7. Критерий Колмоrорова
8. Критерий Смирнова
9. Равномерно распределеННblе СЛУ'lаЙНblе '1исла
10. Нормально распределеННblе N(O, 1) случаЙНblе числа
Литература
Путеводитель по моделям в при мерах и задачах
Именной указатель .... . . . . . . . . . . . . .
573
573
574
575
576
577
578
579
580
581
582
585
586
598
МатематичеСКQЯ статистика
является наукой о методах количественною анализа
массовых явлений, учитЬ/вающей одновременно
и качественное своеобразие этих явлений.
Б. В. rнеденко
Предисловие
Книса Ifеловеlfнее, lfecmHee, долzовечней и ответственней
любоzо друсосо источника информации.
В. А. Садовничий J)
Уважаемый Читатель! Эта книrа адресована тебе, поэтому мы хотим BHa
чале кратко пояснить ее суть и особенности, объяснить те идеи. которыми мы
руководствовались при ее написании. Прежде Bcero, это книrа для всех, т. е.
не для определенноro континreнта обучающихся по той или иной специаль
ности, Toro или иноrо профиля или направления, она не оrраничена рамками
определенноrо учебноrо cТ:JHдapTa или проrраммы, наконец, заранее YCTaHOB
ленными оrpаничениями по объему. Она для тех, кто по существу, а не для
(,rалочки» в ведомости, интересуется математикой вообще и, в частности, xo
чет узнать, что такое современная математическая статистика, какие задачи
и какими методами она решает, какие результаты в неЙ уже накоплены, какие
проблемы в ней сеrодня актуальны, наконец, каковы ее истоки, какой путь
она прошла, и кто был ее творцами (ведь история пауки так же важна, как
и сама наука). Итак, по замыслу, эта кни ra рассказывает о математической CTa
тистике, но одновременно и обучает ей, т. е. она может служить расшuреНltЫМ
учебником, как покрывающим стандартные вузовские проrраммы, предусмат
ривающие чтение (в том или ином объеме) курса математической статистики,
так и обеспеЧИIJающим возможность самообразования. Помимо этоrо, книrа
также может служить справочным пособием по математической статистике,
а в некоторых аспектах и по теории вероятностей. Из этой целевой YCTa
новки вытекают все ее структурные и содержательные особенности.
Наш деIJИЗ: просто о сложном! Мы стремились писать так, чтобы излаrае
мое было доступно каждому, кто знаком с начальными элементами математи
ческоrо анализа, линейной алrебры и теории lJероятностей. Причем помнить
их либо обращаться за нужными СlJедениями в соотвеТСТlJующие учебники
не обязательно, так как все необходимое напоминается (разъясняется) по xo
ду изложения соБСТlJенно статистической теории. Никаких сложных MaTeMa
тических конструкций и rромоздких доказательств! Вся теория объясняется
и иллюстрируется на интересных и тщательно подобранных примерах: (,при
изучении наук примеры полезнее правил» (И. Ньютон 2)). Для тех, кто имеет
1) Садовничий Виктор Антонович (р. 1939) российский математик, академик РАН, ректор
Mry им. М. В. Ломоносова (с 1992 [.).
2) Ньютон Исаак (1643 1727) анrлийский математик, физик, механик, астроном.
12
Предисловие
целью rлубоко освоить теорию статистическоrо вывода, приводится большой
список упражнений для самостоятельноro решения, т. е. книrа объединяет
одновременно и учебник, и задачник. Умение решать задачи означает как
знание теqрии, так и способность правильно этим знанием распорядиться,
т. е. привести теорию в действие, ведь «если действовать не будешь, ни к чему
ума палата,) (Шота Руставели )). Упражнения, как правило, сформулированы
так, что в самой формулировке уже заложен ответ, путь же к нему это и есть
тот творческий элемент, на котором можно узнать свои способности (знать
путь и пройти ею не одuо u то же). (,Подсказкой» здесь (при затруднениях)
Moryr служить соответствующие примеры из текста: на них можно освоить
необходимые лоrику и аналитическую технику.
Теперь несколько слов для преподавателей (/сак i?оворuли древние: doceпdo
discimus (лат.) уча, учимся сами). Одной из основных задач при препо
давании курса математической статистики является выработка у студентов
навыков обработки ремьных данных по соответствующим алrоритмам с при
влечением компьютерной техники при решении конкретных учебных задач.
В настоящее время rлубокое изучение теории математической статистики в OT
рыве от практики ее компьютерной реализации вообще невозможно. В то же
время сам характер этой дисциплины доставляет большой простор препо
давателю для орrанизации практической работы студенто!) с привлечением
компьютеров. Ключевым моментом при этом является моделирование на KOM
пьютере выборок из соответствующих распределений. Фактически на основе
любой «теоретической» задачи, в которой речь идет о том или ином статисти
ческом алrоритме анализа данных, преподаШlТель может поставить (и притом
в неоrpаниченном числе вариантов, варьируя конкретные значения парамет-
ров модели) соответствующую «практическую') задачу, формулируя в качестве
предварительноrо этапа задание смоделировать исходные данные с использо
ванием либо rOToBbIx таблиц случайных чисел, либо получаемых с помощью
специальных проrpамм. В дальнейшем, обрабатывая эти «экспериментarrь
ные» данные по соответствующему статистическому алrоритму, студент полу
чает возможность сравнить предсказание теории с известными ему исходны
ми параметрами, при которых моделировалась выборка. Подобный (,иrровой,)
элемент в орrанизации практической работы по курсу повышает интерес cтy
дентов к изучению теории. Вопросам моделирования конкретных распреде
лений уделяется в книrе существенное внимание.
Наконец, мы приводим в конце книrи достаточно обширный список ли
тературы как общеrо характера, так и специальных моноrрафий, в которых
более полно и rлубоко освещены различные аспекты статистической теории
и ее приложений; эта литература может быть использована для самостоятель
Horo и уrлубленноrо изучения отдельных вопросо!).
В приложении приведены краткие статистические таблицы, необходимые
для разбора примеров и решения задач, а также «Путеводитель по моделям
З) Руставели Шота rрузиtlСКИЙ поэт любви и красотЬ! XII в.
Предисловие
13
в при мерах и задачах», назначение KOTOpOro помочь быстро найти в тексте
нужное место, rде доказывается либо формулируется тот или иной KOHKpeт
ный факт (результат), относящийся к конкретной модели. Знак. в тексте
означает окончание доказательства. Знаком. отмечены ОКОН'lания примеров.
Нумерация формул, теорем, рисунков и т. д. В каждом параrрафе самостоятель
ная, при ссылках на материал друrоrо параrpафа указывается дополнительно
ero номер.
Наконец, еще одно пояснение об используемых обозначениях. По тексту
нам будут встречаться как скалярные, так и векторные величины, обозначае
мые в обоих случаях одним и тем же символом, например, f) скаляр и f) ==
== (f)l, , f)n) вектор. Эта их размерностная спецификация Bcerдa будет яс
на из контекста. Однако в ряде случаев (там, rде это диктуется содержательной
стороной вопроса), чтобы подчеркнуть мноrомерный характер некоторой Be
личины, мы будем дополнительно снабжать соответствующий символ чертой
снизу, например, == (Xl, ,Х n ) при n > 1, == ( l, , k) при k > 1 и Т.д.
Восточная мудрость rласит; «Если хотите увлечь вашим знанием cдe
лайте ero привлекательным. Настолько привлекательным, чтобы книrи вче
рашнеrо дня показались сухими листьями.). Мы стремились следовать этому
правилу. Насколько это нам удалось судить тебе, наш Читатель.
Мы выражаем сердечную блаrодарность нашим коллеrам и добрым TO
варищам: академику Ю. В. Прохорову, члену корреспонденту РАН Б. А. CeBa
стьянову и действительному члену Академии криптоrpафии рф В. П. Чистя
кову за постоянную поддержку нашей работы по математической статистике.
Авторы
Введение
...не пpOIJOpHblM достается успешный бе?, не храбрым победа,
не мудрым хлеб, и не У разум//ых бо атстIJО, и не искус-
ным блаzорасположение, 110 время и случай для IJcex их.
Екклесиаст (Библия. ВСТХIIЙ Завет. 9: 11)
Во всех изЬ/сканияхразума самое
трудное это начало.
Платон 1)
в любо}" начале волшебстIJО таится,
0110 нам IJ помощь, tJ I/ем заищта I/аша.
[. recce 2) и rpa в бисер
1. Что такое математическая
статистика, ее предмет и задачи
Итак, мы начинаем. Начинать же Bcerдa надо с определения предмета обсуж
дения. Наш пред ет современная математическая статистика. Как ее можно
определить кратко и, в то же время, понятно? Прежде Bcero это математи
ческая теория, а любую математическую теорию можно охарактеризовать ука-
занием области тех практических задач, к решению которых она при меняется.
Поэтому мы начнем с Toro, что при ведем несколько характерных примеров
таких задач, которые решаются методами математической статистики.
Пример 1. Имеется урна, содержащая шары двух цпетов, скажем, белые и чер-
ные. Пусть а число всех шаров, а( число белых из них и а2 == а аl
число черных шаров. Оба эти числа а! и а2 (или хотя бы только а[) нам
MO/Yl' быть неизвестны, и в этом случае может возникнуть потребность oцe
нить неизвестную долю р == al/a белых шаров в урне. Как поступить в этом
случае? Можно, например, извле'!Ь из урны все шары и ПОС'lитать число белых
среди них тоrда мы узнаем точно числа а и al, слеДОlJательно, и р == al/a.
Но такой <,тривиальный» эксперимент по разным причинам может быть Heocy
ществим (большой объем содержимоrо урны..... трудно ее исчерпать, (,дороrо.)
это стоит и т. п.). Поэтому в таких ситуациях обычно поступают следующим
1) Платон (427 347 до н. э.) древнеrреческий философ.
2) recce repMaH (1877 1962) немецкий писатель.
1. Что такое математическая статистика
15
образом: извлекают из урны некоторое число n шаров, подсчитывают число
наблюдавшихся в выборке белых шаров (обозначим ero т) и в качестве oцeH
/Си (приближенноrо значения) для неизвестной доли р == а,/а используют
величину fi == т/n долю белых шаров среди n извлеченных. Приведенное
описание TaKoro эксперимента еще не совсем полно, так как орrанизовать
выбор n шаров можно разными способами. Можно, например, извлекать ша
ры по одному последовательно, возвращая каждый раз вынутый шар обратно
(в этом случае rоворят о выборе с возвращением), а можно вынутый шар в урну
не возвращать (выбор без возвращения) в этом случае это то же самое, что
извлечь сразу комплект из n шаров (при n а); можно придумать и друrие
процедуры извлечения шаров из урны. Наконец, следует еще уточнить сам Me
ханизм отбора извлекаемых шаров, что делается уже с привлечением понятий
теории вероятностей и прежде Bcero понятия случайною выбора (но об этом
позже, см. при мер 1 в 1.1). Но во всех случаях возникает принципиаль
ный вопрос: будет ли <,эмпирическая,) оценка р отражать реальную картину,
т. е. будет ли она близка (в KaKOM TO смысле) к неизвестному нам истинному
значению р? Более TOro, если в наших возможностях по разному орrанизо
вать эксперимент (в этом случае rоворят об «активном» эксперименте), то
какая из соответствующих оценок будет «лучше,) (в KaKOM TO смысле)? Здесь
pe'IЬ идет, следовательно, о сравнении раlJJИЧНЫХ экс Статистические
периментов (способов действия) с позиций «качества,)
задачи оценивания
соответствующих оценок. На практике часто приходит
ся учитывать еще и затраты на проведение эксперимента, так что экономи
ческие аспекты также приходится включать при этом в Kpyr рассмотрения.
Ответ на все эти непростые вопросы, а тем самым и рекомендации, как наи
более рационально (rpaMoTHo) нам действовать в подобных ситуациях, дает
математическая статистика. .
Общее замечание. Использованный в этом примере язык урновой схемы «<урна
шары») является примером абстрактноЙ (математической) модели, подходяшей дня
описания мноrих реальных ситуаций (IJ биолоrии, демоrР<lфИИ, социолоrии, медици
не, психолоrии, линrвистике, экономике и т. д.). Под шарами в урне можно понимать
любую конечную совокупность объектов (элементов), которые (как в рассмотренном
примере) MOryт быть разбиты по некоторому альтернативному признаку (пол, воз
раст, состояние здоровья, доход, сорт, емкость и т. п.) на два непересекаюшихся
класса, и Torдa задача состоит в том, чтобы с помошью HCKOTOpOro статистическоro
эксперимента оценить долю определенноro класса во всей совокупности. Например,
совокупность это rраждане страны, избираюшие президента и разделившиеся
на два класса по признаку «за против», или партия каких то изделий, которые
MOryт быть исправными ИЛИ дефектными и т. д. В более общем случае исслсдусмыс
объекты Moryr бbIТЬ разбиты на больщее, чем 2, число классов (Torдa мыI будем ro
варить об урне с шарами, скажем, N различных цветов), и Torдa проблема состоит
в аценивании долей всех классов, составляющих исследуемую совокупность. Во всех
таких случаях язык урновых схем является универсальным экономным способом
описания исследуемой ситуации и им широко пользуются в современной математи
ческой статистике и теарии вероятностей.
16
Введение
Пример 2. Пусть требуется измерить некоторую величину а (например, диа
метр некоторой звезды). Поскольку на результаты измерений влияют мноrие
случайные факторы (точность настройки измерительноro прибора, поrреш
ность окруrления при считывании данных, психофизическое состояние опера
тора и т. д.), то результат i ro измерения X i можно записать u виде X j == a+ej,
rде ej случайна!! поrрешность измерения. СпраШИВ<lется, как по результа
там n измерений X 1 ,... ,х п оценить величину а, точное значение которой
нам неизвестно? Обычно в П1КИХ случаях в качестве оценки а используют
среднее арифметическое наблюдений
1
а == Х == (X, +
n
и математическая статистика позволяет обосновать разумность та Koro правила
оценивания. .
+Х П ),
Пример З. Пусть из некоторых соображений известно, что переменная У
линейно зависит от переменных х" '.,х т : У == Ао+А,х! + + Атхт
(в этих случаях rоворят, что У «реrpессирует» на XI, , х,.), причем коэф
фициенты Ао, AI' ,Ат неизвестны. При различных наборах (Xil, ,Xjr),
i == 1,2,. , п, измерены значени!! Yj == Ао + A,Xjl +. +A"Xjl' +ej, rде ei
ошибка измерения У при наборе (Xj', ,Xjl.)' Позначени!!м (Yi, Xil, .., Xir)
требуется оценить коэффициенты Ао, At, ,Ar. Задачи тaKOro типа назы
ваются ресрессионными, они часто встречаются, например, в экономических
исследованиях. Так, у может означать спрос на некоторый товар, который за
висит от ero цены (х ,). потребительскоrо дохода (Х2) и цен на конкурирующие
и дополняющие товары (Х), Х4, . . .), и эта зависимость в первом приближении
может быть реrрессионноro типа. Реrрессионные задачи составляют содержа
ние отдельноrо раздела математической статистики ресрессионноzo анализа.
Эти задачи будут рассмотрены в rл.6. .
Во всех предыдущих примерах речь шла об оце/(иваl/ии тех или иных па
раметров в соответствуюших математических модел!!х по результатам наблю
дений или измерений, т. е. на основе ЭМПUрU'lеских (опытных) данных. TaKoro
типа задачи, называемые общим термином «задачи оценки (или оценивания)
неизвестных параметров», составляют один из двух основных разделов MaTe
матической статистики. Добавим к сказанному еще следующее.
Иноrда нас интересует не точное значение неизвестноrо параметра, напри
мер, параметра а в примере 2, а требуется указать такой интервал а) а а2,
в котором с высокой rарантией (в статистике rоворлт «с высокой вероятно
стью», т. е. с вероятностью, близкой к 1) находится точное значение парамет
ра. Такой интервал (al, а2), rpаницы KOToporo также определяются по COOT
ветствующим эмпирическим данным, называют доверительным интервалом.
Такие задачи также относятся к задачам оценивания, но при этом rоворят
об интервальном (или доверительном) оценuваниu. Общая теория оценивания
излаrается в rл. З.
1. Что такое математическая статистика
17
Перейдем теперь к примерам задач друrоrо типа,
рассматриваемых в матемаТИ'lеской статистике. Но для
этоrо нам предварительно необходимо хотя бы кратко
напомнить некоторые элементы теории вероятностей. В качестве OCHoBHoro
пособия по теории вероятностей мы рекомендуем современный У'lебник для
технических пузо!] В. П. Чистякова (,Курс теории вероятностей» 1271.
в любой статистической задаче мы имеем дело с некоторым набором
исходных данных, которые получены в результате HeKoToporo эксперимента
(опыта): <<опыт вот У'lитель жизни !]е'lНЫЙ» (rёте 3)). Термин эксперимент
употребляется в статистике для обозначения любоrо процесса ПОЛУ'lения дaH
ных, все возможные исходы KOToporo MOryr быть указаны заранее и дей
ствительный ИСХОД KOToporo является одним из возможных. Обозначим эти
данные символом Х (это может быть число или вектор не которой размер
ности) и в дальнейшем будем называть их выборкой (синоним термина cтa
тuстuческuе данные). Реализации выборки Х обозна'lаются СООТDетствующей
строчной буквой х, а совокупность всех возможных реализаций обознача
ется Х := {х} и называется выборочным пространством. В математической
статистике рассматриваются такие эксперименты, исход которых случаен, так
что выборка Х является СЛУ'lайной вели'lИНОЙ с некоторым распределением
(функцией распределения) Fx на выборочном пространстuе Х.
Оrоворимся сразу, что в дальнейшем мы предполаrаем, что СЛУ'lайная Be
личина Х (или ее распределение Fx) является либо дискретной (и тоrда BЫ
борочное пространство состоит из KOHe'lHOrO или счетноrо числа ТО'lек), либо
абсолютно непрерывной (тоrда Х является евКJIИДОВЫМ пространством COOT
ветствующей размеренности или ero частью), эти два случая обы'lНО и Bcтpe
чаются в приложениях. В первом случае распределение выборки задается
вероятностями отдельных ее реализаций
Элементы теории
верОRтностей
f(x) := Р{Х := х}, х Е Х, L '(х) := 1,
хЕХ
во втором плотностью распределения '(х), т. е. такой неотрицательной
функцией на Х, что ДIIя л юбоrо параллелепипеда В С Х, т. е. множест!]а вида
В:= {х aj:( Х; bi, i := 1, ,r}, если х := (XI, ,x r ), выполняется
соотношение
Р{Х Е В} := f {(х) dx,
в
f f(x)dx== 1
Х
(эта формула сохранятся для любых квадрируемых или кубируемых MHO
жеств В). (Использование символа Р для обозначения вероятности события
является в настоящее Dремя общепринятым, поскольку во мноrих языках Ha
чальной буквой слова «вероятность» является Р probabi/ity в анrлийском,
3) rCTe Иоrанн ВолЬфrанr (1749 1832) немецКИl1 философ, ПОЭТ, ученый, естествоиспы-
ТАтель.
2 За.., 1748
18
Введение
probabi/i/e во французском, probabi/ifd в итальянском, probabilidad в испан
ском, probabilitas в латинском языке и т. д.). Обычно из контекста задачи
бывает ясно, о каком случае дискретном или абсолютно непрерывном
идет речь, поэтому мы ДJ1я единообразия используем одно обозначение f(x)
как для вероятности Р{Х == х} в дискретном случае, так и для плотности
распределения в абсолютно непрерывном, и для краткости в обоих случаях
будем называть функцию f(x) плотностью. Если функция f(x) из каких то
соображений задана, то мы будем rоворить, что задана вероятностная модель
эксперимента. В задачах теории вероятностей предполаrается, что вероятност
ная модель изучаемоrо явления полностью определена, и теория вероятностей
занимается разработкой методов нахождения вероятностей различных слож
ных событий (исходя из известных вероятностей более простых событий)
в рамках данной вероятностной модели. По этим вероятностям мы можем
в дальнейшем строить научно обоснованные проrнозы и тем самым рацио
нально планировать свои действия (если вы хотите насмешить [оспода Боzа,
расскажите ему о своих планах на завтра).
iI Статистическая Математическая статистика выделяется из теории
модель вероятностей в самостоятельную науку, хотя основные
методы и приемы рассуждений в ней остаются теми же.
Причиной 3Toro является именно специфичность задач, решаемых ею,
в известной мере они являются обратными к задачам теории вероятностей.
Дело в том, что на практике при изучении KOHKpeTHoro эксперимента pac
пределение Fx наблюдаемой случайной величины Х редко бывает известно
полностью. Часто можно априори (т. е. до опыта) утверждать лишь, что Fx
является элементом HeKoToporo заданноrо класса (семейства) распределений
:F == {Р} на выборо'IНОМ пространстве Х, так что F.x Е :F семейству апри
ори допустимых распределений выборки. Этот класс :F может в одних случаях
включать в себя все распределения, которые можно задать на .I (ситуация
полной неопределенности), в друrих же случаях он представляет собой HeKO
торое более узкое семейство распределений, заданное в той или иной явной
форме (что может отражать наличие определенной априорной информации
о характере изучаемоrо явления). Если задан класс :F допустимых распреде
лений выборки, то rоворят, что задана статистическая модель эксперимента.
Итак, статистическая модель описывает такие ситуации, коrда имеется
та или иная неопределенность в задании распределения Fx выборки (дaH
ных) Х, и задача математической статистики (в общем плане) состоит в том,
чтобы уменьшать эту неопределенность (насколько зто IЮЗМОЖНО), используя
информацию, доставляемую наблюдаемым исходом эксперимента (наблюдае
мой реализацией выборки Х). rоворят, что математическая статистика это
наука о статистических выводах: она уточняет (выявляет) структуру статисти
ческих моделей по результатам проводимых наблюдений. Методы, с помощью
которых это делается, называют статистическими методами.
Статистические Сказанноrо уже достаточно, чтобы писать задач-.и
IJТОрОro типа, решаемые математическои статистикои,
это задачи проверки статистических zипотез. Любое
rипотезы
91. Что такое математическая статистика
19
утверждение о виде или СDойстнах распределения РХ выборки Х называется
статистической сипотезой (обычно rоворят просто сипотезоti). В общем виде
задача проверки rипотез стаDИТСЯ так: выделяется некоторое подмножество
То С т и требуется по данным Х проверить, справедлиlЮ ли утверждение
Но ji'x Е То или же оно ложно. В этом случае Но называют основной (lIулевой)
rипотезой. Распределения F Е TI == Т\ТО, т. е. распределения из дополни
тельноrо (к то) подмножества допустимых распределений выборки, назы
ваются альтернативными, а утверждение Н\ РХ Е :F, альтернативной
zипотезой. Тоrда rоворят, что задача состоит в проверке rипотезы Но про
тип альтернативы Н\ (кратко: задача (НО, H 1 )) или внутри общей rипотезы
Н РХ Е Т == То U Т\ .
ПраDИЛО, соrласно которому мы, наблюдая Х, при Статистич ; ..,.
нимаем решение принять rипотезу НО как истинную критерий
либо отклонить ее как ложную (принять альтернатив
ную rипотезу H 1 ), называется статистическим критерием (или просто Kpи
терием). Математическая статистика и занимается разработкой рациональных
ПРИНЦИПОD конструирования таких правил (критериев) это и есть второй
тип статистических задач.
Теория это жернова, а опытные данные зерно, кото-
рое засыпается в эти жернова и перерабатывается ими.
Кельвин 4)
Добавим к сказанному еще следующее. На практике часто встречаются
ситуаЦIIИ, коrда эксперимент состоит в проведении повторных независимых
наблюдений над некоторой случайной величиной . Если ПРОRОДИТСЯ n Ha
блюдений, то выборка Х == (Х(,... ,Х n ) представляет собой n независимых
копий величины , т. е. предстаВляет собой n мерный случайный вектор,
компоненты KOToporo независимы и распределены так же, как (можно
также сказать, что Х; это результат i-ro наблюдения над ). В этом слу
чае функция распределения выборки имеет вид Fx(;r.) == F«XI)'" Р«Х n ),
;r. == (XI, .. ,Х n ), т. е. определяется распределением Р< наблюдаемой случай
ной величины , и rоворят, что Х == (X 1 ,..., Х n ) есть случайная выборка
обьема n из распределения (или из .c( ), .с == law (закон)). Статистическая
модель для повторных независимых наблюдений будет 11 дальнейшем обо
значаться кратко в виде Т == {Рд, т. е. указанием лишь класса допустимых
распределений исходной случайной вели'(ины (обычно индекс у Р< опус-
кается, если это не ПРИlЮдит к недоразумениям). Случайная выборка является
математической моделью независимых измерений, проводимых в одинаковых
условиях, и именно такие модели мы будем рассматривать 13 основном в по-
4) Кельвии (Томсон УИЛЬЯМ) (1 824 1907) анrлийскиЙ физик, почетный член ПетерБУРI'СКОЙ
академии lIaYK (1872), предложил абсолютную шкалу температур (шкала Кельвина).
2*
20
Введение
I.:Jlсдующем, хотя в ряде задач предположения о независимости и одинаковой
раСII!'сделенности компонент Х; не выполняются на это каждый раз будет
uбращатьсн внимание.
Теперь при ведем для иллюстрации несколько примеров конкретных cтa
тистических rипотеэ, чтобы продемонстрировать их разнообразие.
... .
,... Задачи проверки
rипотез
Пример 4 (rипотеэа о виде распределения).
Пусть произведено n независимых наблюдений над He
которой случайной величиной с неизвестной функ
цией распределения F{(x). rипотезой, подлежащей проверке, может быть
утверждение типа Но Р{(х) 0= Р(х), rде функция F(x) полностью задана,
либо типа Но P (x) Е уо, rде УО заданное семейство функций распре
деления. При этом обы'/но семейство УО задается в параметрuческом виде:
УО 0= {Р(х; е), (J Е е}, т. е. распределения из класса УО заданы с точностью
до значений HeKoToporo параметра В с областью возможных значений е. ro
ворят, что в этом случае известен тип распределения наблюдаемой случайной
величины, а неизвестен только параметр, от KOToporo зависит распределение.
Параметр (J может быть как скалярным, так и векторным, область (множе
ство) е ero допустимых значений называется nарамеmрl/ческuм множеством.
Если множество е состоит из одной точки, то соответствующее распределе
ние полностью известно, и в этом случае rипотеза Но называется nростой,
в противном случае rипотеза Но с//ожная. Эта терминолоrия общепринята
в математической статистике, и мы ею будем ниже пользоваться.
- Сложная rипотезо Например, наблюдается неотрицательная целочис
....-....: ленная случайная вели'/ина , скажем, число вызовов,
поступивших на телефонную станцию за фиксированное время t, и требу
ется по результатам наблюдений в n непересекающихся интервалах времени
(каждый длиной t) проверить rИl10тезу Но еЮ Е П(В), rде П(В) семей
ство всех пуассоновских распределений (здесь В > О любое положительное
число, т. е. е {В В > О}). Друrими словами, в данном случае речь
идет о rипотезе, что число вызовов 0= (t) имеет некоторое пуассоновское
распределение (список справочник основных вероятностных распределений
приводится ниже, в rл. 1). .
в качестве еще одной из возможных конкретизаций сформулированной
rипотезы рассмотрим ситуацию, описанную выше 8 при мере 2. В теории
измерений обычно считают, что общая ошибка измерения [j складывается
из большоrо числа частных ошибок, каждая из которых невелика. На OCHOBa
нии центральной предельной теоремы теории вероятностей можно предполо
жить, что результаты измерений Xj имеют нормальное распределение. Такое
предположение также является статистической rипотезой о виде распределе
ния наблюдаемых случайных величин. Поскольку нормальное распределение
определяется двумя параметрами: своими средним значением и дисперсией,
а rипотеза не фиксирует их значения (они MOryr быть произвольными), то
И В этом случае проверяемая rипотеза сложная.
1. Что такое математическая статистика
21
Наконец, при ведем конкретный при мер простой
rипотезы о виде распределения. Рассмотрим опыт, за
ключающийся в бросании иrральной кости. Здесь наблюдаемая случайная
величина { есть число выпавших очков; ее возможными значениями являют
ся числа 1,2,...,6, и если кость симметрична, то каждая ее rpaHb выпадает
с одной и той же вероятностью 1/6, т. е. Р{{ == k} == 1/6, k == 1,2, ,6.
Тем самым предположение (rипотеза) Но о симметричности кости однознач
но фиксирует распределение наблюдаемой величины, следовательно, в дaH
ном случае НО простая rипотеза о виде распределения. Спрашивается,
как по результатам n бросаний кости построить критерий, подтверждающий
или же опроверrающий rипотезу о симметричности кости? Такой критерий
в этой и аналоrичной задачах, известный как критерий х 2 (хи квадрат), мы
построим ниже, а сейчас при ведем связанный с данной моделью один за
бавный эпизод, изложенный Ж. Бертраном (1822 1900) в предисловии к ero
курсу «Исчисление вероятностей') (Париж, 1899): «Однажды в Неаполе пре
подобный rалиани увидел человека из Базиликаты, который, встряхивая 3 иr
ральные кости в чашке, держал пари, что выбросит 3 шестерки... Вы скажете,
такая удача возможна. Однако человеку из Базиликаты это удалось во второй
раз, и пари повторилось. Он клал кости назад в чашку 3, 4, 5 раз и каждый раз
выбрасывал 3 шестерки. "Черт возьми, вскричал преподобный, кости
налиты свинцом!" И так оно и было,).
Здесь в шутливой форме дан типичный пример статистическоrо вывода:
если бы кости были симметричны, то наблюдаемое событие (5 раз подряд BЫ
пали 3 шестерки) имело бы ничтожно малую вероятность (1/63)5:::::; 4,71.1O 1'
и, поскольку в эксперименте наблюдалось такое событие, вполне лоrично сде-
лать вывод, что априорная модель (симметричность костей) ложна.
Пример 5 (rипотеэа однородности). Одной из важных прикладных задач Ma
тематической статистики является задача проверки однородности исходных
статистических данных, т. е, rипотезы НО о том, что закон распределения
наблюдений оставался неизменным в течение всеro эксперимента. Формали
зация такой проблемы имеет следующий вид. Пусть имеются две независи
мые выборки Х == (Х" , Х n ) И у == (V 1 , .., У т ), описывающие один
и тот же процесс, явление и т. д., но полученные, скажем, в разное время
или в разных условиях, Требуется ответить на вопрос, являются ли эти BЫ
борки однородными, т. е. полученными из одноro и TOro же распределения,
или же закон распределения наблюдений от выборки к выборке менялся?
Если они однородны, то их можно объединить и работать с одной большой
выборкой объема n+т (заключающей в себе большую информацию, нежели
каждая выборка в отдельности), получая в итоrе более обоснованные (более
точные) статистические выводы о законе распределения наблюдений. Такая
задача может возникнуть, например, при контроле качества некоторой продук
ции, коrда по контрольным выборкам из различных партий надо установить,
не менялось ли ее качество от смены к смене или в результате изменения
технолоrическоrо процесса и т д.: если менялось (выборки неоднородны), то
»f
Простая rипатеза
22
Введение
производство надо остановить и подкорректировать технолоrический процесс.
Еще одна иллюстрация: поступающие в вуз абитуриенты разбиты на два по
тока. Как по результатам экзамена по одному и тому же предме1)' установить,
однородны ли оба потока? В таких ситуациях требуется проверить сипотезу oд
нородности Но FI(x) == Р2(Х), rде FI(x) и Р 2 (х) функции распределения
выборок Х и У соответственно (эти функции нам неизвестны или же прннад
лежат не которому заданному параметрическому семеЙству). В общем случае
можно рассматривать произвольное конечное число независимых выборок.
В современной статистике разработано большое число различных критериев
проверки rипотезы однородности, объединяемых общим термином критерии
однородности, и с этими критериями и их особенностями мы познакомимся
в rл. 4 ( 4.3). .
Пример б (rипотеза независимости). В эксперименте наблюдается ДBYMep
ная случайная величина == ( I, 6) с неИЗl:!естной функцией распределения
Р(х, у) и есть основания предполаrать, что компоненты I и 6 независи
мы. В этом случае надо проверить сипотезу независимости Но Р{(х. у) ==
== Р(, (Х)Р6 (у), rде Р{, (х) и Р(! (у) некоторые одномерные (иноrда rOBo
рят марсинальные) функции распределения. rипотезы TaKoro вида часто воз
никают в прикладных исследованиях, Korдa результаты наблюдений клас
сифицируются по двум признакам, I:! этом случае Но есть предположе
ние о независимости этих признаков. Так каждый сдающиЙ вступительные
экзамены в вуз аБИ1)'риент может быть классифицирован по двум призна
кам: {I Е {! (принят), О (не принят)} и 2 Е {I (мужчина), О (женщина)},
в этом случае rипотеза НО о независимости этих признаков означает OTCYТ
ствие дискриr,1Инации по половому признаку при приеме в вуз. Еще одна
иллюстрация: проведена частичная вакцинация населения против, скажем,
rpиппа; здесь признак I означает наличие (1), либо отсутстnие (О) прививки
ДJ1я KOHKpeTHoro индивидуума, а признак 6 состояние ero здоровья: здоров
(1) болен (О), rипотеза же независимости Но интерпретируется как неэф
фективность вакцины. rипотеза независимости может иметь и пара lетриче
ский вид, т. е. коrда априори постулируется, что распределение .c( I, 6) при
надлежит не которому паращтрическому семеikтпу :F == {Р(х, у; 8), 8 Е G}.
Если, например, :F является семейством всех днумерных нормальных pac
пределений, то rипотеза независимости в данном случае эквивалентна rи
потезе о некоррелированности признаков I и 6 (поскольку независимость
и некоррелированность ДJ1я нормальных случайных величин эквивалентны!).
В общем случае можно рассматривать k мерную (k 2) случайную величину
t == ( I, , k) И проверять rипотезу независимости ее компонент. Критерии
независимости будут рассмотрены в 4.4 книrи. .
Пример 7 (rипотеза случайности). В предыдущих при мерах априори предпо
лаraлось (постулировалось), что исходныеданные предстаВЛЯlOтсобой случай
ную выборку из HeKoтoporo распределения, т. е. компоненты вектора данных
Х == (X 1 , ... ,Х n ) независимы и одинаково распределены. Как правило, это
1. Что такое математическая статистика
23
предположение бывает оправдано, так как вытекает из самою характера зада
чи, и не подверraется сомнению. Но иноrда это исходное предположение само
нуждается в проверке, т. е. оно рассматривается как статистическая rипоте
за Но, называемая i!uпотезой случаЙllостu. Формализуется такая rипотеза сле
дующим образом. Пусть РХ(Хl, ,х п ) обозначает функцию распределения
выборки Х == (X I , ,Х п ). TOrдa ПОДJlежащая проверке rипотеза означает
утверждение Но FX(XI,"" х п ) == F(XI)'" F(x n ), rдe F(x) некоторая
одномерная функция распределения (она может быть полностью задана, либо
задано семейство, которому она принадлежит, либо никак не специфицирует
ся). Типичным примером ситуации, Korдa возникает необходимость проверки
rипотезы случайности является работа reHepaTopa (датчика) случайных чисел.
Под случайными числами мы понимаем последовательность {U I , и 2 ,. .} He
зависимых и равномерно распределенных на отрезке [О, I1 случайных величин.
Такие числа широко используются в различных областях: в статистике для
моделироuания случайных выборок из разлиЧНЫХ распределений (метод CTa
тистическоrо моделирования будет описан в 1.3), в криптоrрафии при по
лучении ключей для зашифрования информации, в численном анализе и т.Д.
В практических задачах последовательность {U 1 , и 2 ,...} строят либо с ис
пользованием rOToBbJx таблиц случайных чисел, либо rенерируют с помощью
специальных датчиков, встроенных непосредственно в ЭВМ, либо получают
проrpаммным способом по некоторому вспомоraтель П ..
( севдослучоиные
номуалrоритму в последнем случае получаются так Ha
. числа
зываемые псевдослучаuные числа, т. е. «очень похожие»
на случайные). Во всех случаях (особенно в последнем) требуется осуществ
лять контроль за «качеством,) вырабатываемой последовательности {Ui} (т. е.
чтобы эти числа БЬИJИ практически неотличимы от независимых равномерно
распределенных чисел), что в математическом плане сводится к проверке rи
потезы случайности (см. п. 2 4.5). .
Приведенные при меры не охватывают всех возни
кающих в приложениях задач проверки статистических
rипотез. Отметим еще один важный класс rипотез, KO
торые называются параметрuческuмu, это rипотезы об истинном значении
неизвестноrо параметра, определяющею заданное параметрическое семей
ство распределений (см. выше при мер 4). Если класс априори допустимых
распределений наблюдаемой случайной величины задан в параметрическом
виде, т. е. ею Е F == {Р(х; О), О Е е}, то в общем случае параметриче
ская rипотеза имеет вид Но О Е 80 С е, т. е. она определяется указанием
KOHKpeTHoro подмножества значений параметра О. Например, если F есть
класс всех нормальных распределений со средним 01 и дисперсией Oi (здесь
О == (01, 02», то утверждение Но 01 == 010, 02 == 020, rдe 010 и 020 заданные
числа, есть простая rипотеза о нормальном распределении наблюдений. rипо
теза же, выраженная равенством 01 == 010 И оставляющая значение дисперсии
2
02 неопределенным, сложная. Общая теория проверки параметрических
rипотез будет обсуждаться в rл. 5.
Параметрические "
rипотезы
24
Введение
,..
,. о современной Итак, математическая статистика решает две OCHOB
статистике ные проблемы:
1) оценивание различных параметров (характеристик)
распределений наблюдаемых случайных величин и
2) проверка различных rипотез о свойствах этих величин (их распределений)
и тем самым позволяет в итоrе подобрать подходящую вероятностную модель
изучаемоro эксперимента.
Помимо этorо, современная статистическая практика связана с MeToдa
ми сбора, обработки и интерпретации данных, планированием эффективных
и информативных экспериментов, принятием решений в условиях неопре
деленности и проrнозированием. Некоторые классы специфических задач
выделяются при этом в отдельные разделы (теории) так появляются Tep
мины «реrрессионный анализ», «дисперсионный анализ», «дискриминантный
анализ.>, «факторный анализ», «последовательный анализ», «компонентный
анализ'> и др. С некоторыми из них мы также познакомимся в дальнейшем.
Наконец, подчеркнем следующее. Практическая реализация COBpeMeH
ных статистических методов не возможна без интенсивноrо использования
компьютерной техники. Именно компьютерная реализация статистических
алrоритмов обработки информации делает их сеrодня одним из наиболее эф
фективных инструментов принятия рациональных решений в самых разных
областях человеческой деятельности (экономике, финансах, страховом деле,
медицине, социолоrи и т д.). Поэтому современный специалист статистик
должен как хорошо знать основы и методы теории статистическоrо вывода,
так и владеть навыками их практической реализации на компьютерах. Целям
подrотовки именно таких специалистов и служит настоящее пособие.
Итак, что же такое статистика? Некоторые понимают и исподьзуют ее, как
пьяный фонарный столб, т. е. не для освещения, а как опору, чтобы не упасть.
Широко известен, например, афоризм, что существует три вида лжи: ложь,
наrлая ложь и статистика. Но адресован он тем влиятельным лицам, которые
в уrоду своим политическим, финансовым и иным целям манипулируют CTa
тистическими данными, как им заблаrорассудится, и не имеет ничеrо общеrо
с наукой (.Математическая статистика.). На самом же деле, rоворя словами
анrлийскоrо статистика В. Томпсона, статистика это математическая
теория то;?о, как узнать нечто о мире через опыт.
«Давайте присядем на это бревно у дорощ zоворю я, и забудем бессер.
дечность и сквернословие этих поэтов. Настоящую красоту нужно искать в ве-
ликолепных рядах установленных фактов и общепринятых правил. В этом самом
бревне, на котором мы сидим, миссис Сэмлсон, Zоворю я, скрыта статистика
более прекрасная, чем любая поэма. Кольца показывают, что ему было шестьде-
сят лет. На 2лубине двух тысяч футов оно за три тысячи лет' превратил ось бы
в уzоль. Самая 2лубокая в мире уzoльная шахта находится 8 КиллиН2ворте, близ
Ньюкастла. В ящик длиной четыре фута, шириной три фута и высотой два фута
2. Исторический очерк развития математической статистики 25
восемь дюймов войдет тонна уzля. Если артерия nорезана, сажмите ее выше
раны. В носе человека тридцать костей. Лондонский Тауэр zорел в 1841 соду».
«Продолжайте, мистер Пратm, саворит миссис Сзмnсон. Эти мысли так
ориzинальны и приятны. Я думаю, ничеzо нет прекраснее зтой статистики».
О. rенри. Справочник rименея
«Вы еще не рассказали мне, заметила леди Наттзл, чем занимается ваш
жених».
«Он статистик», ответила Лзймия с неприятным ощущением обороняющеzося.
Леди Наттзл была, очевидно, застиzнута врасплох. Ей не приходило в zолову, что
статистики вступают в нормальные общественные отношения. Этот род людей,
как она предnолаzала, увековечен на некоторый второстепенный образ действий,
наподобие мулов.
«Но, тетя Сара, зто очень интересная профессия», сказала с жаром Лзймия.
«Я не сомневаюсь в зтом, ответила ее тетя, которая, очевидно, очень са.
мневалась. Выразить что-нибудь значительное в одних лишь цифрах, понятно,
настолько невозможно, что должен существовать бесконечный простор для хоро.
шо оплаченных саветов относительно таса, как зто сделать. Но не думаете ли
вы, что жизнь со статистиком была бы до некоторой степени, скажем, скучной?»
Лзймия молчала. Ей не хотелось соворить о поразительной zлубине змоцианальных
возможностей, котарую она открыла под цифровой внешностью занятий Эдварда.
«Дело не в цифрах, сказала ана наконец, а в том, что вы с ними делаете».
К. Мэндервил. Крушение Лэймии rёрдлнек
2. Краткий исторический очерк развития
математической статистики
Первыми крупными работами, относящимися к математической статистике,
были исследования Я. Бернулли 5) А. Муавра 6) и П. Лапласа 7) К. raycc 8) раз-
работал теорию ошибок наблюдений и, в частности, обосновал один из ее
основных принципов метод наименьших квадратов. Научное обоснование
закономерностей случайноrо рассеивания связано с именами русских MaTe
5) Бернулли Якоб (1700 1782) швейцарский физик и математик.
6) Муавр А6рахам де (1667 1754) франuyэcкий математик.
7) Лаплас Пьер Симон (1749 1827) крупнейший французский математик, физик, астроном,
почетный '1J1eH Петербурrской АН (1802).
8) raycc Карл Фридрих (1777 1855) великий немецкий ученый математик, физик, астро-
ном, почетный члеи Петербурrской АН (1824).
26
Введение
матиков П.Л. Чебышева 9), А.А. Маркова 10) и А. М.Ляпунова 11), значительно
уrлубивших результаты известных к тому времени классических исследований.
Зарождение мптематической статистики как отдельной математической
дисциплины относится к 20 30 M rr. ХХ в.
Ряд важнейших современных понятий и методов, оказавших большое
влияние на развитие современной теории математической статистики, пред
" " Р Ф 12)
ложил анrлиискии математик и статистик . ишер : метод максимальноrо
правдоподобия, дисперсионный анализ, понятия состоятельности, достаточ
ности, эффективности и др. Систематическое развитие теории проверки cтa
тистических rипотез началось с работ анrлийскоrо математика статистика
К. Пирсона 13) по критерию хи квадрат; он также внес большой вклад в раз
работку теОРИI:I корреляции и ее пременение к проблемам наследственности
и эволюции. Основной вклад в построение теории проверки статистических
rипотез внесли Ю. Нейман 14) и Э. Пирсон 15), сын К. Пирсона, которые ввели
понятия ошибок первоro и BToporo рода и показали общность и значение
метода отношения правдоподобия для построения критериев. Общая теория
статистических решающих функций, охватывающан как теорию проверки cтa
тистических rипотез, так и теорию оценивания, создана венrерским статисти
ком А. Вальдом 16)
Большую роль в развитии математической статистики сыrрали работы
17) I ) 19) 20) 21) С
r. Крамера , Э. Лемана , К. Рао ,М. Кендалла , А. Стьюарта , . Уилк
22) 23) 24)
са ,а также отечественных ученых А. Н. Колмоrорова ,Б. В. rнеденко ,
9) Чебышев Пафнутий Львович (1821 1894) выдаюшийся русский математик и мехаllИК.
10) Марков Андрей АндрееВll'1 (1856 1922) выдаюшийся русский математик, академик.
11) Ляпунов Александр Михайлович (1857 1918) Вblдаюшийся русский математик И мехаllИК.
12) Фишер Рональд ЭЙ1lмер (189().--1962) крупнейший анrлнЙскнй статистик, автор и иссле
дователь миоrих современных понятий в математической статистике,
13) Пирсон Карл (1857 1936) анrлийский математик-статистик, биолоr и философ.
14) Нейман Юрий (1894 1981) американский статистик.
I ) Пирсон Эroll Шарп (1895 1980) аНI'Лl1ЙСКI1Й статистик.
16) Вальд Абрахам (1902 1950) американский статистик BellrepCKOro происхождения.
17) Крамер rаральд (1893 1985) шведский статистик.
18) Леман Эрих (р. 1917) американский стаТИСТI1к.
19) Рао Кальямпуди Радхакришна (р, 1920) крупнейший ИII!\ИЙСКИЙ математик, статистик.
20) Кендалл Морис Джордж (1907 1983) анrлийский статистик.
21) Стьюарт Алан анrлийский статистик.
22) УИЛКС Самюэль СТJНIIИ (190б 1964) американский статистик,
23) КолмоrОРОIJ Аllдрей Николаевич (1903 1987) великий советский учеНblЙ, ОДИII из круп-
неЙших математиков хх в., акадеr.!ИК АН СССР, создатсль совремеltllОЙ аксиО tатики теории
вероятностей.
24) rнеденко Борис Владимирович (I912 1995) академик АН УССР, выдаюшиiiСЯ математик,
специалист по предельным теоремам теории вероятностей, истории математики, популяризатор
науки, замечательиый педаrоr.
9 2. Исторический очерк развития математической статистики 27
25) 26) 27)
Ю. В. Линника Е. Е. Слуцкоrо Н. В. Смирнова В. И. POMaHOBCKO
Щ 29) 30) 31)
ro Л. Н. 6ольшева ,Ю. 13. Прохорова ,А. А. БОРОDкова , Б. А. CeBa
стьянова 32), А. Н. Ширяева 33) и др.
Начиная с 50 x rr. ХХ в. в связи С появлением компьютеров лицо cтa
тистики изменилось. Если раньше отсутствие вычислительных возможностей
вынуждало статистиков использовать слишком упрощенные модели, даже ec
ли эти модели были не всеrда реалистичными, то теперь любое статистическое
решение. которое можно просчитать на компьютере за сравнительно неболь
шой отрезок времени, стало «доступным». Таким образом, сложные и TPYДO
емкие статистические методы вошли в повседневную пракТYlКУ. В это же время
статистика, в определенном плане, стала эмпирической наукой: за несколько
минут компьютеры MOryт порождать миллионы данных, используя которые
можно «проверять» новейшие методы.
Математическая статистика это непрерывно и интенсивно развива
ющаяся наука. В последние rоды появилось большое количество rлубоких
результатов, охватывающих, по существу, все основные направления COBpe
менной теории математической статистики. Достойный вклад в развитие HO
вых методов этой теории вносит отечественная математическая школа.
В наши дни математическая статистика переживает бурный этап постоян
Horo расширения областей праКТИ'Iескоrо примененил ее методов, блаrодаря
резкому росту арсенала средств, используемых исследователем. Внедрение
в статистическую практику вычислительной техники позволило при решении
задач математической статистики использовать методы статистическоrо Moдe
лированил (Монте Карло). Широкому распространению методов матеl\lати
ческой статистики способствовало создание больших универсальных пакетоI3
Ilрикладных статистических проrраМI\I, обеспечивающих быстрый и эффек
ТИВIIЫЙ компьютерный анализ больших маССИI30В статистической информа
25) ЛИННИК Юрий Владимирович (1915 1972) советский М<lтематик в области теории Bepo
ятности, теории чисел, статистики, академик АН СССР.
26) Слуцкий ЕRrений ЕвrеньеRИ'1 (1880 1948) выдаЮШI1ЙСЯ российский и советский матема-
тик, статистик и экономнст.
27) Смирнов Николай ВаСllЛЬеВИ'1 (1900 1966) члев-корреспондент АН СССР, крупнейший
спеuиалист 110 нрсдеЛЫIЫМ теоремам теории ВСРОЯТIIОСТСЙ и матемаТl1'lескоЙ статистики.
2К) Романовский BceBoJlon Иванович (1879 1954) русский, советский, узбеКСКИlI математик,
акадСЩIК АН Узбекской ССР
29) БOJ!ьшев ЛОП1н НиколаСDНЧ (1922 1978) советскиii математик, члеlI корреспондент АН
СССР
3О) Прохоров Юрий ВаСИЛЬеВИ'1 (р. 1929) советский математик, академик АН СССР OCHOR
ные труды по теории вероятностей, особенно по асимптотическим методам.
31) Боровков Александр AileKCeeUI1'1 (р. 1931) академик АН СССР, специалист в области
теории веРОllтностей и математической статистики.
32) CCBaCTbllHoR Борис Александрович (р. 1923) СОDетский матсматик, член корреСПOlшент
АН СССР.
ЗJ) Ширяев Аньберт Никодаевич (р. 1934) спеuиалист в области теории вероятностей и
математической статистики, член-корреспондент РАН.
28
Введение
ции. Именно в направлении соединения статистической теории и практики
ее компьютерной реализации заключается существо cOBpeMeHHoro этапа раз
вития методов статистическоrо анализа данных. Ибо (,Бесполезно вычислять
результат в такой форме, в какой потребитель не [отов ero использовать»
(Хэмминr).
Методы математической статистики, соединенные с возможностями co
временной компьютерной техники, широко и эффективно используются в
приложениях, ЯВJJяясь основой статистических методов исследования и KOH
троля MaccoBoro производства, статистических методов в области физики,
биолоrии, медицины, социолоrии, метеоролоrии; их также применяют при
обработке результатов статистическоrо моделирования в различных задачах
науки и техники.
В настоящее время статистические модели и методы иrрают все боль
шую роль при решении экономических, финансовых, социальных проблем,
а также различных проблем связи, телекоммуникации, защиты информации,
криптоrрафии и таких долrо считавшихся далекими от математики наук, как
психолоrия, линrвистика, криминалистика и т. д. Такие области науки, как
rидролоrия, климатолоrия, звездная астрономия, антрополоrия, также, OKa
зывается, не MOryт обойтись без методов математической статистики.
Без методов этой науки сеrодня невозможна разработка научно обосно
ванных проrнозов развития общества, включая проrнозы в политике, эконо
мике, социолоrии.
В заключение, для подтверждения тезиса о том, что история науки так же
важна, как и сама наука, приведем слова выдающеrося HeMeUKoro математика,
физика и философа, одноrо из создателей дифференциальноrо и интеrраль
Horo исчисления r. В. Лейбница 34). «Весьма полезно познать истинное проис
хождение замечательных открытий, особенно таких, которые были сделаны
не случайно, а силою мысли. Это приносит пользу не только тем, что воздает
каждому свое и побуждает друrих добиваться таких же похвал, сколько тем,
что познание метода на выдающихся примерах ведет к развитию искусства
открытия».
Все постоянство 8 зыбкости одной,
Все смутно пред 2лазами очевидца,
Я сложность вижу в истине простой,
Наукой правит случай не закон...
Ф. Вийон 35) . Баллада поэтическоrо состяэания
в Блуа (перевод Ю. А. Кожевникова)
Н) Лейбниц rотфрид Вильrельм фОН (1646 1716) выдющийсiI немецкий математик И фи
лософ.
35) ВИЙОН Франсуа (143 I после 1463) французский ПОЭТ и вор.
2. Исторический очерк развития математичесной статистики 29
Всему начала случай.
Старинная norOBopKa
..0 Памни, что случай плешив 36)
Б. rрасиан 37). Критикон
36) В античном изобразительном искусстве представлRЛИ аллеroрическую фиrypу Случая в виде
стояшеrо на колесе плешивоrо 'Iеловека с одной лишь прядью волос, за которую надо ero схватить,
пока не умчался.
37) rрасиан Бальтасар (1601 1658) испанский писатель.
rлава 1
(Вспомоrательная, но очень важная!)
Основные распределения
и их моделирование
Математические мадеЛll обьект
и орудие труда математиков.
К. А. Рыбников 11
Введение
Выше мы определили статистическую модель и ее отношение к Dероятност
ноЙ модели: в обоих случаях модель задается плотностью распределения f(x)
наблюдаемой случайной величины , а различие заключается в том, 'IТO мы
априори предполаrаем известным об этой плотности. В вероятностных задачах
эта плотность полностью известна, в статистических же она задается (пред
полаrается) с той или иной степенью неопределен ности, и статистик (,борется»
с этой неопределенностью. Часто мы предполаrаем известным вид плотности
j(x), а неопределенность выражается через те или иные параметры, от KOTO
рых зависит функция j(x) (выше такие модели названы парамеmрuческuмu) ,
В теории вероятностей наиболее часто встречаюшиеся законы распределения
(модели) имеют обшепринятос наименование и обозначение этот ('язык')
псреносится и на соответствующие статистические модели. Проиллюстрируем
это на одном конкретном примере.
Ф... Н ' . . Пусть из каких то соображений (например, OCHO
.,. ормольноя" '.' вываясь на центральной предельной теореме теории Be
модель
роятностей) постулируется, что .c( ) НОр lальное или
rayccoBcKoe распределение. Если обозначить через jl (мю) и и 2 (сиrма квад
рат) среднее и дисперсию нормальноrо закона, то сказанное в символьном
виде записывается так: .c( ) == N(jl, ( 2 ) (N большое круrлое является об
щепринятым обозначением нормальноrо закона распределения). В терминах
плотности j эта удобная лаконичная запись (,расшифровываетсн» так:
2 2 1/2 { (х р)2 }
j(x)==f(xljl,и )==(27rи) ехр 2и 2 , oo<x<oo (1)
1) РыБНИКО1J Константин АлексееВИ'1 (1913 2004) советский и российский математик, ис-
торик математики.
1.1. Дискретные модели математической статистики 3 1
(здесь oo < fL < 00, (7 > о и использовано стандартное обозначение exp{t} == e t ).
В вероятностных задачах, связанных с нормальным распределением, в этом
случае rоворят о нормальной .моделu параметры fL и (72 считаются извест
ными, и тем самым нормальная плотность J(xlfL, (72) полностью определена.
Если же один из этих параметров (или оба) априори неизвестен, то мы имеем
дело со статистической нормальной моделью. Неизвестный параметр модели
принято обозначать символом (J (тэта) , а область ero возможных значений е
(тэта большое), таким образом, в рассматриваемом случае мы имеем три Ba
рианта нормальной статистической модели:
1) N(e, (72), е == {е oo < е < оо}, известна дисперсия и неизвестно
среднее;
2) N (fL, е\ е == {(J о < е < оо}, и звестно среднее и неизвестна
дисперсия;
3) N(e., ei), е == {е == (е" ( 2 ) oo < е, < 00, 0< (J2 < оо}, оба пара
метра неизвестны.
Поскольку в дальнейшем мы будем иметь дело с конкретными моделями,
которые широко используются в практических приложениях, мы сначала при
ведем для напоминания и удобства изложения и последующих ссылок список
справочник основных вероятностных распределений, сопровождая их HeKO
торыми относящимися к теме комментариями. Это очень важный материал,
поскольку он является базоЙ для решения всех примеров и последующих задач.
1.1. Основные дискретные модели
математической статисти ки
Любая дорою начи//ается спервою шаса.
в этом параrрафе мы дадим определения и опишем необходимые нам в после
дующем основные свойства наиболее известных дискретных вероятностных
распределений (как одномерных, так и MHoroMepHbIx), а также проиллюстри
руем их использование IJ вероятностных и статистических задачах. Замечатель
ным фактом является то, что существует несколько распределений большой
общности, встречающихся в самых разнообразных задачах теории вероятно
стей и математической статистики. Прежде Bcero это биномиальное раСПре
деление, распределение Пуассона и нормальное распределение с первоro
мы и начнем.
1. Схема Бернулли и биномиальное распределение
Мадам, какова вероятность утром на улице встретить динозавра?
Одна вторая: ш/u встречу, или нет.
rоворят, что случайная величина { имеет распределение Бернулли с параметром
р (О < р < 1), если она принимает лишь два значения, обозначаемые обычно
32
rлава 1. Основные распределения и их моделирование
о и 1, и при этом
P{ =' 1} =' Р =' 1 P{ =' О}.
в терминах плотности f(x) это можно записать в виде
f(x) == f(xJp) =,p"ZqH, Х =' 0,1, q =' 1 р.
(1)
Бернуллиевская
модель
в символьных обозначениях сказанное выражается KpaT
ко так: L:.(() =' Bi(i, р) и называется бернуллиевской Moдe
ЛЬЮ. Фундаментальная роль этой модели в теории Bepo
ятностей и математической статистике ясна: она является подходящей MaTeMa
тической моделью для любоrо эксперимента с двумя исходами «<успех» «не
успех,»), т. е. простейшеrо статистическоrо эксперимента. Среднее и дисперсия
такой случайной величины есть
Е(=,р и Щ=,рq
(2)
(символ Е от анrлийскоrо expectation (математическое ожидание cpeд
нее значение), D от di5persion (дисперсия)). Если IJce случайные величины
последовательности {X 1 , Х 2 , ..} (конечной или бесконечной) независимы
и имеют одно и то же распределение Bi(I, р), то мы имеем nоследО(Jатель
ность испытаний Бернулли (или, кратко, бернуллиевскую последовательность),
называемую так по имени Якоба Бернулли (1654 1705) выдающеrося швей
царскоrо математика, впервые изучавшеrо такую схему (ero основополаrаю
щие труды в области теории вероятностей изложены в посмертно изданном
сочинении <.Искусство предположений.) (1713)).
Ao' Б Пусть {X 1 ,... ,Х n } бернуллиевская последова
иномиальная
' с. :"' ....... тельность с параметром Р . Тоrда сумма Х =' Х 1 +. . '+Х n
модель' "" .I,, jj
имеет биномиалыюе распределение с nарометрами пир,
что кратко записывается в виде:
L:.(x) =' Bi(n, р).
Эта случайная величина принимает, очевидно, лишь значения О, 1, ,n и
при этом
Р{Х =' х} =' f(xln,p) =' C pxqn "Z Х =' 0,1,
,n.
(3 )
Термин «биномиальное распределение» связан с тем, что вероятности (3) яв
ляются членами известноrо «бинома Ньютона»:
n
1 =' (р + q)n =' L C p"Zqn x
x o
Таким образом, биномиальная модель Bi(n, р) описывает распределение числа
«успехов» В n испытаниях Бернулли с неизменной вероятностью «уСПеха» р.
Здесь
ЕХ =' пр и DX =' npq.
(4)
1.1. Дискретные модели математической статистики ЗЗ
Полезно знать также следующее свойство биномиальноrо
распределения: если случайные величины X 1 , ,х/с
независимы и
С::.il.ОЙСТВО воспро '*
8t;. ИЭВОДИМОСТИ
.c(Xj) 0= Bi(nj,p), jo=l. ,k,
то
.с(Х. +
+ X k ) 0= Bi(n. +
+ n/с, р).
Это свойство биномиальноrо распределения Bi(n, р) называется васпроизво
димостью по параметру n.
Если параметр р нам неизвестен (а так на практике чаще Bcero и бывает!).
то мы имеем биномиальную статистическую модель
Bi(n, О), е 0= {О О < О < l}
(при n 0= 1 бернуллиевскую статистическую модель Bi(l, О».
Пример 1, Рассмотрим ситуацию, описанную в приме
ре 1 Введения. Если в данном эксперименте реализуется
схема выборо с возвращением, и если условия экспери
мента обеспечивают независимость извлечения каждо
ro очередноrо шара от результатов предыдущих извлечений (практически это
достиrается тщательным перемешиванием содержимоro урны перед каждым
очередным извлечением), то мы имеем бернуллиевскую модель Bi(l, О), rде
под «успехом» понимается извлечение белоro шара, для которой надо оценить
параметр О 0= а,/а по результатам n испытаний. В данном случае наблюда
емая случайная величина Х есть число белых шаров в выборке из n шаров,
которая имеет биномиальное распределение Bi(n, В). .
Примеры .,
биномиольной
модели
Пример 2. Рассмотрим подробно описанный в при мере 4 Введения эпизод
с преподобным rалиани. Здесь мы имеем эксперимент, состоящий в пятикрат
ном бросании трех иrpальных костей. Интересующая нас величина. характери
зующая один опыт, число выпавших шестерок на трех костях. Обозначим
ее . В свою очередь, она равна сумме трех бернуллиевских величин l, 6
и {з, rде i 1, если на i й кости выпала шестерка, и О в противном
случае (i 0= 1,2,3). Если исходить из тoro, что кости одинаковы (это обычно
не подверrается сомнению, хотя, на самом деле, это тоже rипотеза), то
случайные величины i, i 0= 1,2,3, имеют одно и то же распределение Бер
нулли Bi( 1, О), и они, ПО условию опыта, независимы. Тем самым их сумма
0= I + 6 + 6 имеет распределение Bi(3, (J), и над этой случайной вели
чиной произведено пять независимых испытаний, т. е. мы имеем случайную
выборку Х 0= (X 1 , , Х 5 ) из распределения Bi(3, О). Таким образом, мы по
строили биномиальную модель Bi(3, О) дЛЯ описания нашеro эксперимента,
и в рамках этой модели требуется про верить rипотезу симметричности костей
Но () 0= 1/6 (т. е. rипотезу о том, что каждая rpaHb выпадает с одинаковой
вероятностью 1/6). Как можно формализовать рассуждения преподобноrо?
Общее число выпавших шестерок Х 0= Х, + ... + Xs имеет биномиальное
3 За.., 1748
34
rла ва 1, Основньте распределения и их моделирование
распределение Bi(15, fJ), и по формуле (3)
Р{Х == 15} == j(151 [5, fJ) == fJlS
Следовательно, при справедливости rипотезы Но вероятность наблюдаемоrо
события, Т.е. Х == 15, равна 6 15 что ничтожно мало (!). Наверное, любой
разумный человек на месте преподобноrо усомнился бы в истинности rипо
тезы Но в данном случае (при таком наблюдаемом исходе эксперимента), .
Замечание. Обратим внимание на следующее. В данном случае, если отбросить
несущественные для математики эмоциональные нюансы (пари), а оставить лишь
физическую суть эксперимента (в ero ходе бbUЮ брошено 3 х 5 15 костей),
то можно сразу rоворить о случайной выборке объема n == 15, из распределения
Бернулли Bi(l, О) Х == (X 1 ,..., X 1S ), дЛЯ которой исследуется случайная вели
чина Х == Х ! + + X 1S общее число выпавших шестерок. Конечно, снова
.с(Х) == Bi(15,8).
2. Отрицательное биномиальное распределение
С бесконечной последовательностью испытаний Бернулли {X 1 , Х2, .} свя
зано еще одно важное дискретное распределение, которое обозначается Bi (r, р)
и называется отрицательным биномиальным распределением с параметрами r
и р (здесь r натуральное число). Это есть распределение числа «успехов»
(1), предшествующих T MY «неуспеху') (О), И оно задается вероятностями
j(xlr,p) == C:+x [pXqr х == 0,1,2, (5)
Заметим, что выражение для j(xlr, р) совпадает с X M членом разложения
функиии qr(1 p) ' В ряд по степеням р, т. е. отрииательноrо бинома (отсюда
и название):
00
1 == qr(1 p) ' == qr 2: C:+X IPX
х=о
rеометрическоя.! В частном случае r == 1 распределение Bi ( 1, р) Ha
модель , "". . , '11 зывается zеометрическим: это есть распределе ние '1 исла
. единии, предшествующих первому нулю в бернуллиев
ской последовательности. Формула (5) в этом случае принимает вид
f(xl1.p) == pXq, х == 0,1,2,
Если случайная величина имеет распределение Bi (r,p), то
(6)
Щ == тр
q
тр
и Щ == 2'
q
(7)
"tв{)й+ёТво"".roёпро '"'"
ИЗВОДИМОСТИ
Полезно знать также свойство воспроизводимости pac
пределения Bi (r. р) по параметру т: если случайные
величины Х[,..., X k независимы и
L{Xj) == Bi (rj,p), j == 1,..., k,
1.1. Дискретные модели математической статистики 35
то
.с(Х 1 +
+ X k ) Bi (r, +
+ rk, р).
Отсюда следует, что случайная величина с распределением Bi (r, р) можетбыть
реализована (построена) как сумма r независимых случайных величин с оди
наковым rеометрическим распределением Bi ( 1, р), этот факт используется
для моделирования случайных величин с отрицательным биномиальным pac
пределением (см. далее 1.3).
Если параметр р неизвестен, то имеем отрицательную биномиальную cтa
тистическую модель Bi (r, О), е {8 О < 8 < I} (при r 1 eOMeт
рическую статистическую модель Bi (l, В)). Эти модели часто используются,
например, при разработке математических методов контроля качества про
мышленной продукции.
Замечание. В формуле (5) бнномиальный коэффициент
z r(r+I)...(r+x l)
Cr+z 1 == I
Х.
определен при любом действительном т, а при r > О этот коэффициент положителен,
поэтому эта формула определяет распределение вероятностей при всех r > О и
О < р < 1, а не тольк при натуральных r При натураль Р
ных r распределение Bi(r, р) называют также распределенu- аспределение
Паскаля
ем Паскаля 2)
з. Распределение Пуассона
Случай ная величина { имеет распределение Пуассона 3) с параметром л (л > О),
если
Х!:
Р{{ х} J(хlл) == е Л , х 0,1,2, (8)
х!
что кратко записывается в виде .с({) п(л); при этом л Е{ Щ.
Пуассоновская модель П(Л) обычно описывает схему редких событии: при
некоторых предположениях о характере процесса появления случайных co
бытий число событий, происшедших за фиксированный промежуток времени
или в фиксированной области пространства, часто подчиняется пуассонов
скому распределению. Примерами Moryт служить число частиц радиактивноrо
распада, зареrистрированных счетчиком 8 течение HeKoToporo времени t, чис
ло вызовов, поступивших на телефонную станцию за время t, число дефектов
в куске ткани или в ленте фиксированной длины, число изюминок в кексе
и т. д. Наконец, распределение Пуассона дает хорошую аппроксимацию би
номиальноrо распределения для больших знач:ений n и малых значений р:
2) Паскаль Блез (1623 1662) Французский математик, механик, физик и философ, один из
основателей теории вероятностей.
З) Пуассон Симеон Дени (1781 1840) французский математик, механик и физик, иностран
НЬ1й почетнЬ1Й 'UleH nетербурrской АН (с 1826).
З.
36
rлава 1. OCHOBHble распределения и их моделирование
Bi(n, р) П(nр) , если пр невелико. Это свойство позволяет значительно
упростить вычисления в биномиальной модели при указанных условиях.
q Свойство воспро Распределение Пуассона воспроизводимо по своему
параметру, т. е, если Х] J , X k независимые слу
изводимости ( ) ( )
чайные величины и С X j == П >'j ,j == 1, ,k, то
.с(Х 1 + + X k ) == П(>'I + + >'1.).
Если параметр >. неизвестен, то имеем пуассоновскую стаmисmuческ.vю
модель П(8), е == {/':1 /':1 > О}
-t' Понятие распределения Пуассона впервые появилось в книre французскоro
ученоrо Симеона Дениса Пуассона (1781 1840) «Исследования о вероят
ности судебных приrоворов по уrоловным и rражданским делам», опубли
КОllанной в 1837 r. Пуассон обнаружил, что если в n испытаниях Бернулли
с вероятностью «успеха» р (см. п. 1) делать р все меньше и меньше и в то же
время увеличивать n так, что произведение пр == >. остается постоянным, то
вероятность (3) тощ что будет ровно х успехов, стремится к f(xl>') (см. (8)).
Следовательно, распределение Пуассона (8) является приближением для биноми
альноrо распределения (3). Возможность широкоrо применения и большая важ
ность пуассоновскоrо распределения не бьVlИ поняты современниками Пуассона,
более Toro, о нем почти полностью забыли. Однако после 1894 r. это распре
деление использовали при изучении cTpaHHoro феномена. За 20 лет между 1875
и 1894 п. в 14 различных каllалерийских корпусах rерманской армии бw\3 собрана
статистика траrических случаев, коrда солдат бьVl убит ударом копыта. Соrласно
280 (== 20 лет х 14 корпусов) наблюдениям, 196 солдат поrибли таким образом,
т. е. в среднем за [од >. == 196/280 == 0,7 Если бы число траrических исходов
подчинялось распределению Пуассона с параметром >. == 0,7, то можно было бы
ожидать, что при 280 наблюдениях в 139 случаях смертей нет, в 97 случаях
1 смерть, в 34 случаях 2 смерти и т. д. Д что показала статистика? В дей
ствительности данные бьVlИ соответственно 140,91, 32 и т. д.; практика и теория
оказались о столь хорошем соrласии, 'по вряд ли можно было ожидать большеro.
Это сравнение появилось в 1897 r. в моноrpафии Л. Борткевича «Закон малых
чисел». Пуассоновское распределение стало широко применяться лишь в ХХ D.
(по книrе 123, с. 34)).
... Р
,., аспредепение .
Эрr.анrа._
с распределением Пуассона связано еще одно ин
тересное дискретное распределение распределение
Эрланzа 4), задаваемое вероятностями
( N >.1. )
,N, с== LkТ
k=O
т. е. это усеченное сверху в точ:ке N пуассоновское распределение. В 1906 r,
Эрланr установил, что в некоторых случаях лучшее приближение (дЛЯ бино
миальноrо распределения) можно получить с использованием именно TaKoro
распределения.
>.k
eK==ckТ' k==O,l,
4) Эрланr Атнер Краруп (1878 1929) датский математик.
1.1. Дискретные модели математической статистики 37
Пример 3 (Дни рождения [25, с. 171 172]). Какова вероятность Рх Toro,
что в rруппе из 500 человек ровно х родились 1 января? Если эти 500 человек
выбраны случайно, то можно применить схему из 500 испытаний Бернулли
с вероятностью «успеха» р == 1/365. Для пуассоновскоrо приближения поло
жим л == 500/365 == 1,3699 Теоретические биномиальные вероятности (3)
и их пуассоновские приближения (8) приведены в следующей таблице.
х
@ЗI 4 C=J6l
Р. == f(xj500, 1/365) 0,253 0,3484 0,2388 0,1089 0,0372 0,0101 0,0023
Р. ::::: /(xI500/365) 0,2541 0,3481 0,2385 0,1089 0,0373 0,0102 0,0023
.
4. rиперrеометрическое распределение
Случайная 8еличина { имеет zuперzеометрuческое распределенuес параметрами
al, а2 и n, rде а(, а2 и n натуральные числа, причем
n а == аl + а2 .ею == Н(а), а2, n),
если
С Х cn x
Р{{ == х} == f(xla), а2, n) == й'с: 2 , х == О, 1,
а
,n.
(9)
Такое распределение возникает в следующей схеме. Рассмотрим ситуацию,
описанную в примере 1 Введения и предположим, что n шаров извлекаются
Hayzaa без возвращенuя. Тоrда, если обозначает число белых шаров в BЫ
борке, то эта случайная величина имеет распределение Н(а(, а2, n) (сра8НИ
с примером 1).
Заметим, что вероятность (9) отличны от нуля лишь при х a) и n x а2,
т. е. коrда целое х лежит в интервале mах(О, n а2) х min(n, al),
Если .с(о == Н(а(,а2, n). то ее первые два момента есть
па) nala2(a n)
E == и Щ== a2(a 1) (10)
5. Распределение Маркова Пойа
Обобщение понятия зачастую бывает
полезно для постижения есо сущности.
А. Н. Колмоrоров
Это распределение является обобщением одновременно и биномиальноrо,
и rиперrеометрическоrо распределений и возникает оно в следующей ypHO
вой схеме. Вновь вернемся к примеру 1 Введения и рассмотрим следующий
эксперимент. Из урны, содержащей первоначально а) белых и а2 == а а)
черных шаров, выбирается Hayraд (т. е. равновероятно) один шар, фиксиру
ется ero цвет и шар возвращается в урну с одновременным добавлением с
38
rлава 1. Основные распределения и их моделирование
новых шаров Toro же цвета. Затем из урны (содержащей теперь а + с ша
ров) снова производится случайное извлечение одноrо шара и повторяетсл
тот же процесс. Здесь С может быть любым целым числом и, в частности,
при с == О (новые шары не добавляются) мы имеем случайный выбор с воз
вращением, рассмотренный в примере 1, а при С == 1 (извлеченный шар
в урну не возвращается) схему случайноrо оыбора без возврашения, pac
смотренную в предыдущем п. 4 (в последнем случае процесс извлечения шаров
кончается через а шаrов из за отсyrствия шаров в урне). При С > О эта схема
выбора обладает эффектом последействия: если извлекается шар KaKoro To
цвета, то шанс (вероятность) извлечь шар такOI'О же цвета при следуюшем
испытании возрастает. Такая урновая схема может служить приближенной
моделью явлений, подобных эпидемиям, коrда осуществление некоторых co
бытий увеличивает шанс их повторения.
Пусть { обозначает число белых шаров, наблюдавшихся при n извле
чениях. Распределение вероятностей этой случайной величины называется
распределением Маркова Пойа (обозначается .e( ) == МП(n; а!, а2, С)), и оно
имеет вид
Р{{ == х} == f(xlal, а2, С; n) == C П(а! + jc)nf{(a2 + jc) jП(а + зс),
j O j=O j O
x==O,I, (11)
Если воспользоваться биномиальными коэффициентами и учесть, что для
любоro действительноrо а и натуральноrо х
х а(а 1)
Са ==
(а х + 1)
х!
и
О
Са == 1,
то формулу (11) при С =F о (Torдa числитель, и знаменатель в (11) можно
разделить на СП) можно записать также в любой из следующих двух форм:
f(xlaJ, а2, С; п) ==
С Х cn x
a,/c+x l a2/c+n x l
C:/C+n l
С Х С n .. Х
al/c a2/C
C a/c
( 12)
Подчеркнем, что из (11) при С == О мы получаем биномиальное распределе
ние Bi(n,p), р == al/a (как в примере 1 для схемы выбора с возвращением),
а из BToporo представления в (12) при С == I rиперrеометрическое pac
пределение H(al. а2, п) (как в п. 4 для схемы выбора без возвращения), так
что распределение Маркова Пойа включает в себя как частные случаи оба
эти распределения.
Если .ею == МП(п; al, а2. С), то среднее и дисперсия имеют вид
па!
E{==
а
и
nala2(a + сп)
щ==
а 2 (а + С) .
(13)
1.1. Дискретные модели математической статистики 39
Интересна история открьrrия этоro распределеиия. Впервые оно появляет
ся в работах выдющеrосяя PYCCKOro математика, акааемика А. А. Маркова
(1856 1922), который провел исчерпывающий анализ этоrо распределения
и опубликовал свои результаты в Известиях Петербурrской Акааемии наук
в 1917 r. Но, по видимому, эта публикация «осталась незамеченной" за рубежом,
так как, спустя 6 лет, в 1923 r. появляется работа Ф. Эrrенберrера и д. Пойа,
rдe вводится такое же распределение 11 доказываются для Hero некоторые част
иые результаты. С этих пор даиное распределение стало называться в зарубежной
литературе именем одноrо из ero авторов Пойа (вьщающийся американский Ma
тематик BeHrepcKoro происхождения (1887 1985)), хотя более исторически оправ
дано название «распределение Маркова Пойа",
б. Полиномиальное распределение
Полиномиальное распределение М(n; l!) с параметрами n и l!., rДе n Ha
туральное число, и Е==(Р',,, .,PN), O<Pi < 1, i== 1,.. .,N, РI +.. .+PN == 1,
это распределение случайноrо вектора!!. == (/11, .' . , /lN) С цеЛОЧИсленными
неотрицательными компонентами, удовлетворяющими условию
/1. + + /lN == n,
которое задается вероятностями
( n! Хl
Р{!!. == } == f In, Р) == Р,
х,! XN!
rДе == (XI, '., XN) произвольный вектор с целыми неотрицательными
координатами, причем Х. + + XN == n. Кратко это заПИСЫВается так:
.с(!!..) == М(n; l!.)' Название «полиномиальное распределение.) связано с тем,
что вероятность (14) представляет собой общий член в раlllOжении полинома
(р, + + PN)n по степеняМ Р" ,PN:
РХ;
(14)
1 == (р! +
) n '"' п! Хl
+ PN == L.J 1 , РI
х,. .. XN.
Xl+"'+XN n
РХ;
Здесь
E/li == npi, D/li == nPi(1 Pi) и
COV(/li, Vj) == nPiPj, i, j == 1, ,N, i"l- j.
Такое распределение возникает в схеМе полиномиальных
испытаний, т. е. независимых испытаний с N возмож
НbIМИ исходами, вероятности которых не меняются
от испытания к ИСПblтанию и равны Р., ,PN соответственно: если произве
дено n ИСПbIтаний и /li число реализаций в них i ro исхода, i == 1, , N,
то .с(!!..) == М(n; l!)' Если N == 2 (схема с двумя исходами), то Мь! имеем
схему Бернулли (см. п.1), для которой .c(/lI) == Bi(n,PI); с друroй стороны,
так как /12 == п V, и Р2 == I PI, то двумерный вектор (/1" п /11) имееТ
полиномиальное распределение М(n; PI, 1 Р,), эквивалентное, следователь
но, биномиальному распределению Bi(n, PI). Отсюда же ВbIтекаютследующие
свойства полиномиальноrо распределения:
(15)
Полиномиальные
испытания
40
rлава 1. Основные распределения и их моделирование
1) распределение каждой компоненты /lj вектора является биномиальным
Bi(n,pj), j == 1, ,N, и
q,h..,
,. Свойство воспро 1
изводимости,"
J
2) еС111 8ектора I'
,!6. независимы и L:( ;) == М(n;; Е)' i == 1,. , k, то
L:( I +
+ k) == М(n[ +
+ щ.; Е)
(воспроизводимость по параметру n),
Отметим еще, что часто вместо термина «полиномиальное,) используется
ero синоним «мультиномиальное».
В приложениях обычно вектор вероятностей Е. == (р[, ,Рн) неизвестен
в этом случае мы имеем полuномиольную статистическую модель М (n; О),
0==(01, ,он), С параметрическим множеством е == {О о < о; < 1,
i==I,...,N, 01+...+ен== I}.
Пример 4 (Обобщение примера 1 Введения). Имеется урна с шарами N раз
личных цветов, которые мы условно обозначим Аl, , Ан. Пусть aj число
шаров цвета Aj, j == 1, , N, и а == а[ + + ан общее число шаров
в урне. Рассмотрим следующий эксперимент: из урны по схеме выбора с воз
вращением Hayraд (т. е. равновероятно) извлекается n шаров (т. е. каждый раз
любой шар может быть извлечен с одинаковой вероятностью I/a и независи
мо от результатов предьщущих извлечений). Обозначим /lj число наблюдав
шихся Аj шаров, j == 1, ,N. Тоrда вектор == (У[, ,VN) будет иметь
полиномиальное распределение М(n;р) с пара метром р == (al/a,..., ан/а),
т. е. вектором долей цветов AI' ", А; Если этот вектор нам неизвестен, то
подходящей оценкой для Hero будет вектор относительных наблюдавшихся
частот !dn == (/lI/n," ,/lN /п), так как в силу (15) E /n == Е ([1 среднем
оценка /n совпадает со значением параметра Е)' в последуюшем мы дадим
cтporoe обоснование TaKoro правила оценивания (см. пример 1093.2). .
7. MHoroMepHoe распределение Маркова Пойа
Вновь обратимся к ситуации, описанной IJ при мере 4, и рассмотрим теперь
такой эксперимент: последовательно в каждый момент времени n == 1, 2,
из урны Harpaд извлекается один шар, фиксируется ero цвет и шар возврашает
ся обратно в урну с добавлением с новых шаров Toro же цвета, что и извлечен
ный шар (тем самым состав урны каждый раз увеличивается на с шаров, если
с > О, и уменьшается, если с < о; при с == О он остается неизменным, т. е.
в этом случае мы имеем схему выбора с возвращением, рассмотренную в при
мере 4). Вновь обозначим /lj число Aj шаров, наблюдавшихся при n извлече
ниях, j == 1, ,N. Torдa вектор == (Уl, ,ин) будет иметь распределение
n'
Р { и == Х } == .
I I
XI,-"XN.
пf 1 aj(aj + с) .. (aj + (Xj l)с)
a(a+c)...(a+(n I)c)
( 16)
1.1. Дискретные модели математической статистики 41
rде ;f == (Xl"" ,XN) произвольный вектор с целыми неотрицательными
координатами, причем Хl + + XN == n; множество таких векторов будем
обозначать K Nn . Это распределение называется мкоеомерным (N MepHbIM) pac
пределением Маркова Пойа с параметрами n, Q и с и обозначается символом
МП(n; Q, с), rде Q == (а), . .. , aN) вектор первоначальноrо состава урны.
Формула (16) является MHoroMepHbIM (N MepHbIM) аналоrом формулы (11)
и сводится к ней при N == 2. Если с :f=. О, то разделив числитель и знаменатель
в (16) на сп и используя, как и в п.5, биномиальные коэффициенты, этой
формуле можно придать еще две формы аналоrи форм (12):
N N
Pk ==;f} == !(;f!Q, с; n) == П C::/c+Xj J C /c+n 1 == П C j/c/ C a/c'
j l j 1
;f Е K Nn .
( 17)
Отметим три важных частных случая этих соотноше
ний. Если в формуле (16) положить с == О, то мы придем
к (14) с l!. == Q/a, т. е. распределение Маркова Пойа
Mn(n;Q, О) сводится к полиномиальному распределению М(n; gja). Далее,
если во втором представлении (17) положить параметр с == 1 (что COOTBeT
ствует схеме выбора без возвращения), то при n :;:;; а (иначе биномиальный
коэффициент с: обратится в О) получим распределение
N
P{ ==;f} == П с:; / C , ;f Е K Nn ,
j 1
которое является MHoroMepHbIM (N MepHbIM) аналоrом rиперrеометрическо
ro распределения (9) и сводится к нему при N == 2. Поэтому распреде
лени е, задаваемое вероятностями (18), называется мноzoмерным (N MepHbIM)
zиперzеометрuческuм распределением с параметрами Q и n. Оно обозначается
символически [.(!!.) == H(Q, n) и характеризует собой схему случайной BЫ
борки без возвращения объема n :;:;; а из конечной совокупности, состоящей
из а == а I + + aN элементов, разбитых по некоторому признаку на N
непересекающихся классов размерами соответственно а". ., aN (в данном
случае Vj интерпретируется как число наблюдавшихся в выборке элемен
тов j ro класса, j == 1, , N).
Наконец, если в первом представлении (17) все aj положить равными с,
то биномиальные коэффициенты в числителе станут равны 1, и мы придем
к формуле
Связь с друrими '"
распределениями
(18)
Р{!!. == J<.} == (C +n l) l
задающей равномерное распределение на множестве
KNn=={;f==(XJ,' ,XN) xi==0,1,2,.. ,i==l, ,N;XI+ +XN==n}:
число элементов (BeKTopoB;f) этоrо множества равно C +n l числу реше
ний уравнения Х) + + XN == n В. целых неотрицательных числах, и всем
им приписывается одинаковая вероятность.
42 rлава 1. OCHOBHble распределения и их моделирование
Таким образом, MHoroMepHoe распределение Марков Пойа включает в
себя в качестве чаСТНblХ случаев полиномиальное распределение, MHoroMepHoe
rиперrеометрическое распределение и равномерное распределение на множе
стве IC Nn.
Моменты Мп.рос
пределения
Если [,( ) == МП(n; ,c), то первые и вторые MO
менты случайноrо вектора Е == (//1, . . . , //N) имеют вид
а; aj(a aj)(a + сп)
E//j==n . D//j==n 2( ) , i==l, ,N, и
а а а+с
ajaj (а + сп)
cov(Vj, Vj) == n 2( ) ' i, j == 1, , N, i =1= j.
а а +с
Полное изложение теории этоrо распределения имеется в работе авторов
(.Об урновой схеме Маркова Пойа: от 1917 r. до наших дней,) (Обозрение
прикладной и промышленной математики. 1996. Т. З. Вып. 4. С. 484 511).
(19)
8. Распределение cтeneHHoro ряда
ЦеЛbIЙ класс дискреТНblХ распределений может бblТЬ построен по следующей
схеме. Рассмотрим ПРОИЗВОЛЬНblЙ степенной ряд
00
1(8) == L а(х)8 Х l О,
x '
с неотрицатеЛЬНblМИ коэффициентами (а(х) О для всех х l) иненулевым
радиусом сходимости R. Тоща при любом О Е е == (О, R) можно определить
дискретное вероятностное распределение с плотностью
ох
l(xJO) == а(х) 1(0) ' х == l, l + 1,
(20)
.
(эти числа неотрицательны и в сумме дают 1), TaKoro типа распределение и Ha
Зblвается распределением степенною ряда. Класс таких распределений весьма
Примеры обширен и включает в себя мноrие стандартные pac
распределений пределения. В частности, в Hero входят рас ределение
CTeneHHoro ряда Пуассона П(О) (см. (8)): для Hero 1(0) == е . == 00;
отрицательное биномиальное распределение Bi(r, в)
(см. (5)): для Hero 1(0) == (1 8) r, R == 1; ЛОi!арuфмическое распределение,
задаваемое вероятностями
ОХ / 1
l(xI8) == 1n ( ) '
х 1 О
х == 1,2,
(21)
для Hero
1 00 вх
J«(J) == 1п == ,, , R == 1
1 0 L.J x
x 1
И Т.д., а также соответствующие усечеННblе слева распределения.
1.2. Основные абсолютно непрерывные модели
43
Примечание. Усеченным называется распределение, у KOТOpOl'O некоторые значения
запрещены. Например, усеченным 8 нуле распределением Пуассона является распреде
ление, задаваемое вероятностями (сравни с (8))
е'"
f(xl(J)==ce o , x==I,2,...
х!
rде констаlПа с определяется из условия нормировки
(22)
00
L J(xJ(J) == 1,
",=1
и в данном случае она равна (1 e 8) 1
Если случайная величина имеет распределение
cтeneHHOro ряда (20), то ее первые два момента Haxo
дятся по формулам
== р(О) == O ; и Щ == а.2(о) == Ор!(О)
l1t
Моменты
(23)
(убедитесь, что формулы дня моментов в п. 2 и 3 являются частными случаями
этих выражений).
Важным свойством распределения cтeneHHoro ряда
является следующее: если случайные величины Х., . .. ,
Х П независимы и имеют ОДНо и то же распределение
(20), то их сумма Х == х, + .. + Х П также имеет распределение степенноrо
ряда, порождаемое функцией jrI (О), т. е.
ОХ
Р{Х == х} == jn(xIO) == ап(х) jn(O) ' Х == nl, nl + 1,...
Свонство воспро
изводнмости
(24)
rдe коэффициенты ап(х) определяются разложением
00
jn(O) == L ап(х)ОХ
z nl
t 1.2. Основные абсолютно непрерывные модели
Доросу осилит идущий.
в этом параrpафе мы продолжаем знакомство с основными вероятностными
распределениями и их свойствами, сосредоточившись теперь на случае абсо
лютно непрерывных распределений. Принцип изложения здесь тот же, что
и в предыдущем параrpафе о дискретных распределениях. Напомним, что тe
перь функция j(x) имеет смысл обычной ШIотности распределения, т. е. это
неотрицательная функция, удовлетворяющая условию нормировки
! /(х) dx == 1,
t:
44
rлава 1. Основные распределения и их моделирование
rде Е множество, на котором задано распределение наблюдаемой (изучае
мой) случайной величины .
1. Нормальное распределение
Это распределение уже встречалось нам ранее: ero формальное определение
дано во Введении к данной rлаве (см. (1). Роль нормальноrо распределения
(нормальной модели) в теории вероятностей и математической статистике
чрезвычайно велика и ее трудно переоценить. Нормальная модель возни
кает в таких статистических экспериментах, коrда на исход эксперимента
оказывает влияние большое число независимо действующих случайных фак
торов, каждый из которых лишь незначительно влияет на конечный резуль
тат (см. примеры 2 и 4 Введения). Для таких ситуаций имеется знаменитая
.. Ц ' -. теорема, называемая центральной пределыlOЙ тeope
ентральная "
'. ., ,', мои теории вероятностей (термин «центральная» OT
предельная теорема
ражает ее значимость, так ее впервые назвал Дьердь
Пойа), соrласно которой если {X 1 , Х 2 ,...} последовательность независи
мых одинаково распределенных случайных величин с положительной диспер
сией, то предельное при n ---+ 00 распределение нормированной надлежащим
образом суммы 8 п =о Х 1 +. + Х п является нормальным. Именно: при n ---+ 00
( 8 nр. )
I:. Jпa ---+ И(О, 1),
(1)
2
[де р. =о ЕХ), а =о DX 1 . Более Toro, известно, что при некоторых условиях
предельное распределение суммы Sn остается нормальным, даже если случай
ные величины X 1 , Х2, зависимы и неодинаково распределены. Возможно,
именно поэтому нормальный закон распределения возникает как подходящая
приближенная модель во мноrих областях исследований. Поэтому R KOHKpeT
ной практической задаче при построении соответствующей вероятностной
или статистической модели часто предполаrают, что распределение каждой
наблюдаемой величины приближенно нормально. В силу этоrо статистиче
ские методы, разработанные для нормальной модели, имеют весьма широкую
сферу применений и, следовательно, хорошо знать их очень важно. (ny
анкаре 5) KaK TO заметил с сарказмом, что все верят в универсальность HOp
мальноrо распределения: физики верят, потому, что думают, что математики
доказали ero лоrическую необходимость, а математики верят, так как считают,
что физики проверили это лабораторными экспериментами [23, с.49].)
Предельные теоремы Общее замечание. В (1) нам впервые встречается запись
типа 1:-(7)п) ---+ ((1]), которую мь) должны пояснить. Во мно"
rих задачах математической статистики (и теории вероятностей) рассматриваются
последовательности случайных величин {1]п, n =о 1, 2, ..}, сходящиеся в том или
ином смысле к некоторому пределу 7) (эта) (случайной величине или константе),
5) Пуанкаре Анри (1854 1912) Вblдающийся Франuузский математик, физик, астроном и
философ.
1.2. Основные абсолютно HenpepbIBHble модели
45
коrда n ---+ 00, в таких случаях rоворят о соответствующих предельных теоремах. Мы
будем использовать в дальнейшем лишь два простейших вида сходимости, без KOTO
рых нам совершенно невозможно обойтись: сходимость по вероятности и сходимость
по распределению, или (синоним) слабая сходимость. Напомним их определения. По
следовательность {I],,} называется сходящейся по вероятности к 1], если
lim P{II]" 1]1> е} == О V f > О,
".....00
р О .
что кратко записывается так: 1]" --------+ 1"/. чень важным при использовании этои cxo
" р Ф
димости является следующее своиство: если 1]" --------+ 1"/ и ункция rp непрерывна, то
р
rp(I],,) --------+ tp(1"/).
(2)
Под сходимостью по распределению (слабой сходимостью) [что кратко записывается
так: [,(1],,) ---+ [,(1"/) или "1" "1] пони мается сходимость соответствующих функций
распределения
Р,,(х) == P{I]" х}
к предельной функции распределения
Р(х) == P{I] х}
в каждой точке непрервности последней: F1I(X) ---+ Р(х), если в точке х функция
F(x) непрерывна. Известно, что из сходимости по вероятности следует слабая cxo
димость:
р
1]" --------+ 1"/ =} [,("1,,) ---+ [,(1]).
Примером сходимости по вероятности является знаменитый закон больших чисел:
если случайные веЛИЧИНbI "11,1]2, .. независимы, одинаково распределены и имеют
математическое ожидание EI]I == Р, то при n ---+ 00
1
("11 +
n
р
+ 1],,) --------+!J.;
(3)
примером же слабой сходимости является центральная предельная теорема (1). Эти
предельные теоремы (или, как rоворят, асимптотический подход) мы часто будем
использовать в дальнейшем в различных статистических задачах, но это не есть
«при хоть» математика, а «суровая» необходимость, ибо
Асимптотический подход зачастую eдиHcтBeH
ная возможность, открытая статистику в суровой
действительности.
Дж.Русас
Вернемся к нормальному распределению и про
должим обсуждение ero свойств. Уже отмечалось (но
выделим это особо ввиду важности данноrо свойства),
что если .ею == N(f.l, (12), то
Е{ == f.l и Щ == /12
"'f\Aоментьi"и СВОЙСТВО rf'
ВОСПРОИЗIIОДИМОСТИ
(4)
Далее, можно по казать, что всякая линейная комбинация нормально рас.
пределенных случайных величин также подчиняется нормальному закону.
46
rлава 1. Основные распределения и их моделирование
Пусть, в частности, случайные величины X 1 , ,Х" независимы и
.e(Xj) == N(JLi, (1;), z == 1, ,k.
Если Gl, . . . , а" и Ь постоянные, причем а; i- о хотя бы для одноrо значе
ния i, то
.е(а\Х\ + + а"Х" + Ь) ==
== N(alfJl + + akJLk + ь, ai(1i + + a (1Z).
(5)
в частности
.е(Х\ + + х,,) == N(JL, + + JL", (1; + + (1Z), (6)
т. е. нормальное распределение N(JL, (12) является воспроизводящим по пара
2
метрам JL и (1 одновременно.
Нормальное распределение со средним О и дис
персией 1 называется стандартным нормаЛЬНblМ pac
пределением, ero плотность и функция распределения
обозначаются через rp и Ф (фи малое и фи большое)
соответственно, так что
Стандартное
нормальное
распределение
1 ",1 / 2
'Р(х) == e
.Jii
'"
и Ф(х) == f rp(t) dt,
oo < х < 00.
(7)
oo
Эти функции протабулированы и для них имеются обширные статисти
ческие таблицы.
Наконец, отметим, что если .ею == N(JL, (12), (12 > О, то по свойству (5),
нормированная случайная величина ( == (, JL)/(1 имеет стандартное нормаЛ1,
ное распределение N(o, 1).
.... Л С нормальным распределением тесно связано одно
,. оrнормальное
ИНТересное распределение, называемое ЛОi!Нормальным.
распределение " "
I По определению, это распределение случаи нои вели
чины 1] == е{, rдe .ею == N(JL, (12). Для первых двух моментов 1] справедливы
соотношения
Е1] == ер+а! /2,
1 2 1
D1] == (е а I)e ,,+и
(8)
ИJ истории: нормальное распределение, ставшее краеуrольныM камнем
науки о случайном, бblЛО открыто французским математиком Абрахамом
де Муавром (1667 1754) в 1733 r., о чем он сообшил некоторым своим дpy
зьям. В 3 M издании своей книrи «Доктрина шансов. (1756) он так писал
о своем ОТКрblТИИ мировою значения: ....Возьму на себя смелость утверждать,
что это труднейшая проблема о случайном... (Де Муавр, как это ни странно,
не включил свое ОТКРblтие во 2 e издание книrи в 1738 [.; первое издание бblЛО
осушествлено в Анrлии в 1718 r., куда он переехал из Франции после отмены HaHT
CKOro эдикта, которblЙ предоставлял ryreHoTaM свободу вероисповедания) [231.
Некоторое время спустя нормальное распределение было снова открыто rayccoM
в 1809 r. и Лапласом в 1& 12 r. в связи с работами по теории ошибок наблюдений.
Лаплас дал первую (совершенную) формулировку центральной предельной Teo
ремЬ! и привел большое количество важНblХ приложений этоro распределения.
1.2. Основные абсолютно непрерывные модели
47
2. MHoroMepHoe нормальное распределение
Случайный вектор { == «(1, . . . ,(k) размерности k 2 имеет невырождеЮlOе
(или собственное) MHoZOMepHoe (k мерное) нормальное распределение с вектором
средних!!:.. == (PI, ,Pk) и матрицей вторых моментов (ковариаций)
Е == Ilcov«(j, (j)ll
(обозначается .ею == N(p, Е)), если ero плотность f( lp, Е) при всех ==
== (XI,'" , Xk) Е R k имее; вид
f( I!!:., Е) == (21r) k/2IEI I/2 ехр { ( !!:.)' E I( !!:.)}. (9)
.,
Элементы алrе6ры
Здесь приняты следующие обозначения, которые
будyr систематически использоваться и в дальнейшем:
R k это k MepHoe евклидово ПрОС11>анство, IAI == det А определитель
матрицы А lIaijll размера k х k, A I обратная матрица А, KOTO
рая существует, если матрица А невырождена (т. е. IAI i= О), при матричных
операциях векторы понимаются как вектор столбцы, знак' (штрих) озна
чает транспонирование, наконец, выражение х' A есть лаконичная запись
k
на языке ма11>ИЧНОЙ алrебры квадратичной формы L aijXjXj для вектора
,j 1
== (XI, , Xk) с матрицей коэффициентов А.
В (9) вектор!!:. == Е{ == (Е(I, . . . , E{k) может быть любой точкой R k , а KO
вариационная матрица Е произвольной симметрической (т. е. Е' == Е)
и положительно определенной (т. е. i Е > О, V;!2 i= Q) матрицей (ее назы
вают также дисперсионной матрицей и пишyr О( == Е). Напомним также, что
симметрическая положительно определенная матрица обязательно невырож
дена, и обратная к ней матрица также является симметрической положительно
определенной.
Таким образом, общее число параметров, которыми определяется HeBЫ
рожденное k MepHoe распределение N(!!:.., Е), с учетом симметричности MaT
рицы Е равно k+k(k+ 1)/2. Важнейшими свойствами
этоro распределения являются следующие:
1) некоррелированность компонент вектора { эквива
лент на их независимости и
Важнейшие .
свойства N(!!:.., Е)
2) сохранение свойства нормальности при линейных преобразованиях: если
'тl == L{, zae L произвольнйЯ (т х k) Maтpицa, то [,('Тl) == N(L!!:.., LEL') ,
т. е. новый случайный вектор 'тl имеет т MepHoe нормальное распределе
ние, параметры KOToporo вычисляются по очень простому правилу: вектор
средних E!l == L!!:., а дисперсионная матрица D'Тl == LEL'.
48
rлава 1. Основные распределения и их моделирование
Поскольку эти свойства MHoroMepHoro нормальноrо распределения чрез
вычайно важны, и поскольку не все читатели достаточно знакомы с MHoro
мерными распределениями, мы обсудим их несколько более подробно. Мы
.6I Х покажем, что на самом деле они очень просто ycтa
ороктеристические
Ф навливаются, если воспользоваться аппаратом xapaK
ункции
терисmических функций важнейшим инструментом
доказательства различных теорем теории вероятностей. Но сначала мы кратко
напомним их определение и некоторые из их основных свойств.
Характеристическая функция произвольной случайной величины (Beктo
ра) Х == (X 1 , ,Х,,), k? 1, определяется формулой
't'X
ФкЮ == Eel ,
rдe i мнимая единица, t == (t 1 ,. ,t,,), oo < tj < 00, j == 1, ,k, и
t' Х == tlX I + + t"X"
скалярное произведение векторов t и х.
Характеристическая функция всеrда существует, и для дискретной слу
чайной величины с плотностью f(';fJ == Р{ Х == }, Е Х, она вычисляется
по формуле
lJ1 кШ == 2: eit'if J(i),
(10)
;!
а для абсолютно непрерывной случайной величины с плотностью f(;К) она
есть интеrpал Рима на
Фк(t)== / eit'iff(;К)d , d == dx, .dx". (1I)
х
Соответствие, установленное формулами (10) и (11) между характеристи
ческой функцией Фх(t) и распределением случайной величины Х (ее плот
ностью J(;к)), являеТСя взаимно однозначным, т. е. по Ф кШ плотность f( )
восстанавливается (определяется) однозначно. Например, для одномерной
дискретной случайной величины Х с плотностью J(x), х == 0,1, 2, фор
мула обращения есть
11"
J(x) == / е itХФх(t) dt,
21r
(12)
"
если же случайная величина Х имеет плотность f(x) и функция Фх(t) аб
солютно интеrрируема, то формула обращения имеет вид
00
1 / itx (
f(x) == e Ф Х t) dt,
27r
( 13)
oo
Таким образом, различные свойства изучаемых случайных величин можно
формулировать как в терминах их плотностей, так и в терминах их xapaKTe
ристических функций.
1.2. OCHOBHble абсолютно HenpepblBHble модели
49
Перечислим теперь необходимые нам в последу
ющем свойства характеристических функuий. TaKO
вых Bcero два.
1. Линейное преобразование случайной Величины. Если случайный вектор У ==
== (Y 1 , . .. , У т ) получается из вектора Х == (Х), , X k ) с помощью ли
нейноrо преобразования У == L X +!!, rде L произвольная (тхk)-мат
рица и!! == (а), , а т ) произвольный вектор (L и !! постоянны), то
Свойства характери
стических функций
Фr.(t) == ei(!!iJ!xJL'O.
(14)
2. Критерий независимости. Если компоненты вектора Х независимы, то
Ф;r(t)==Фхl(t J ) 1l1 X .{t k ). (15)
Верно и обратное заключение: если имеет место разложение (15), то
компоненты X I , . .. , Xk независимы. Таким образом, представление (15)
является удобным для работы критерием независимости компонент BeK
тора Х.
После этоrо кpaTKoro экскурса в область теории вероятностей вернемся
к обсуждаемому MHoroMepHoMY нормальному распределению N( , Е) и дадим
ero новое (друrое) определение в терминах характеристической функции.
Случайный вектор { == ({" , {k) имеет k Mep Характеристическая"
ное нормальное распределение N( , Е), если ei!O xapaK функция N( , Е)
теристическая функция W Ш == Е ехр {i[{} имеет вид
1l1i.Ш == ехр {i ' /E }, Е я k
(16)
Это определение шире, чем определение (9) невырожденноrо распределения,
так к'ак здесь не требуется существования обратной матрицы E I Тем самым
определение (16) остается в силе и в случае вырожденной матрицы Е (т. е.
при JEI == О), в этом случае распределение N( , Е) называется вырожден
ным (или несобственным), и для Hero уже не существует k мерной плотности
типа (9). Мы не будем уrлубляться далее в эти тонкие вопросы, поскольку в по
следующем мы будем иметь дело лишь с невырожденными распределениями.
Подчеркнем лишь, что в любом случае остаются справедливыми формулы
Е{ == и D{ == Е == Ilcov({j, {j)ll
(17)
Если компоненты вектора { некоррелированы, т. е. COV({i, {j) == О при
i f=. j, то дисперсионная матрица Е становится диаrональной:
иf О
Е==
rде о} == Щj, j == 1, .. . , k,
4 Заказ 1748
о cтi
50
rлава 1. OCHOBHble распределения и их моделирование
и формула (16) принимает вид
) { . 1 ( 22
Ф' (t == ехр Z(tIJLI + + tkJLk) 2 {J"jt j +
k { и2 }
П ех р it'/I. 2t
Jt"J 2 J '
j 1
+ иЫ) }==
т. е. переменные t l , ,tk разделяются, и тем самым характеристическая
функция Ф Ш распадается в произведение одномерных характеристических
функuий компонент вектора {. По свойству (15) это означает независимость
компонент вектора . Итак, из некоррелированности нормалЬf!ЫХ случайных
величин следует их независимость, а поскольку из независимости случайных
величин (с любым распределением!) следует их некоррелированность, то тем
самым сформулированное ранее свойство 1) об эквивалентности этих двух
свойств ДJIЯ нормальных величин доказано.
Еще проще устанавливается свойство 2) о сохранении нормальности при
линейных преобразованиях. Действительно, если !l == L{, то характеристиче
екая функция вектора !l равна в силу (16)
Ф'!LШ == Eeit'!l == Eeit'L == Eei(L'O' == Ф' (L't) == ехр {it' (L ) t' (L LI)t},
что есть характеристическая Функuия нормальноro закона .лI(LJL, L LI).
Следствием этоrо свойства является следующий фундаментальный резуль
тат, который доказывается при помощи выбора соответствующей матриuы L:
совместное распределение любо о подмножества компонент вектора { является
нормалЬНblМ, u соответствующие подвектор векторц !!. и подматрица матриЦbl
будут вектором средних u дисперсионной матрицей это,о распределения.
MHoroMepHoe НОР\1альное распределение с HY
левым вектором средних ( == Q) и единичной дис
персионной матрицей
Стандартное MHoro-
мерное нормальное
распред ение
==1==11 :11
..
называется стандартным; о соответствующем случайном векторе также ro
ворят как о стандартном нормальном векторе. В этом случае компоненты
этоrо вектора являются независимыми стандартными нормальными случай
ными величинами, каждая из которых имеет плотность, указанную в (7).
В заключение отметим еше одно интересное
свойство нормальноro распределения. В алrебре дo
казывается, что любая симметрическая положитель
но определенная матриuа Е может быть приведена
Специальное линей
ное прео6разование
нормальноrо вектора
1:2. OCHOBHble абсолютна HenpepblBHble модели
51
с помощью ортоrональноro лреобразования, заданноro ортоroнальной матри
цей U (т. е. и 1 == и'), к диаrональному виду:
и'Еи Л 11:' :.11,
rдe Лj > О, j == 1, , k, собственные (или характеристические) числа Е.
Пусть теперь .е({) == N(f!:.., Е) и '1 == и' {. Torдa .e('!l) == N(U' f!:.., А), т. е.
вектор '1 будет иметь уже некоррелированные (следовательно, инезависимые)
компоненты. Далее, так как все Лj > О, то определена диаrональная матрица
л 1/2 О
1
A I/2 ==
О
\ 1/2
л/.:
Рассмотрим теперь случайный вектор
Q == A I/2('!1. U'I!.) == A I/2u'( f!:..).
Это будет также нормальный вектор с нулевым вектором средних (EQ == Q)
и дисперсионной матрицей А 1/2 АА 1/2 == :0., т. е. Q стандартны й нормаль
ный вектор. Таким образом, всесда можно указать линейное преобразованuе,
переводящее невырожденный (!) нормальный вектор в стандартный нормальный
вектор: для построения этоrо преобразования U надо решить линейную си
стему E!!j == Лj!!j' j 1, ,k, для определения собственных веКТОРО8
!!I' ,!!!.: И собственных чисел лl, , Л/.: дисперсионной матрицы Е, и TO
rда U == II!!, llill.
Мы оrpаничиваемся этим минимумом сведений о MHoroMepHoM нормаль
ном распределении, ибо сказано: «Не пытайся объять необъятное это He
возможно!», и переходим к следующему (после нормальноrо) по значимости
и широте применений непрерывному распределению, каковым является raM
ма распределение.
3. rамма распреАеllение
Случайная величина имеет 2амма расnределенuе с nараметрами а U л (а > О,
л > О): .ею == r(a, л), если ее плотность имеет вид
{ xJ. le z/a
f(xla, л) == О r(л)аJ.
при х;? О,
( 18)
при х < О.
Здесь r(л) rамма функция, определяемая соотношением
00
r(л) == ! tJ. le t dt, л> О.
о
( 19)
4*
52
rлава 1. OCHOBHble распределения и их моделирование
Полезно помнить следующие важные свойства этой функции:
r(л -+ 1) 0= лr(л), л> о, r(l) 0= 1,
следовательно, r(n -+ 1) 0= n! для всех натуральных n; далее r(lj2) == v:тr,
следовательно, для всех натуральных n значение r(n/2) также может быть
вычислено в явном виде; для больших значений л
Формула СН1рлинrа имеет место асимптотическая формула СтuрлиН2а 6 ):
r(л -+ 1) rv J27rл лЛе Л
(напомним, что «"'» есть символ аСИМПТОТИ'lеской эквивалентности: а '" Ь
при а, Ь ----7 00, если ajb ----7 1; формула Стирлинrа, иrрающая исключительно
важную роль в математике, была доказана в 1730 [., она yrверждает, '1ТО n!
приблизительно равняется J2rrn (nje)n; независимо от Стирлинra и раньше
Hero формулу для факториалов n! cJ1i(n/ е)П открыл Муавр, Стирлинr же
нашел вид константы с 0= .;2;).
В представлении (18) а называется параметром масштаба, а л napa
метром фоРМbI. Частные случаи raмма распределения r( а, л) при некоторых спе
циальныx значениях этих параме1рОВ имеют свои названия. Так, при л == 1 pac
Показательное пределение r(a, 1) называется показательным (или экс
поненциаЛЬНblМ) распределением с параметром масштаба
а, а r( 1, 1) стандартным nоказательным распределе
нием: оно задается плотностью f(X/1, 1) == e X х О.
Если n натуральное '1исло, то rамма распре
деление с параметрами а 0= 2 и л == n/2 называется
х 2 расnределением с n степенями свободы и обознача
ется r(2, n/2) == х 2 (n).
Наконец, при натуральных л r(a, л) называется распределением ЭрланZQ
порядка л. Это распределение суммы л независимых СЛУ'lайных вели'lИН с
одинакозыM показательныM распределением r( а, 1).
.... Приведем также вид соответствующей характери
Характеристическая
стической функции
функция и моменты
распределение
,
Распределение х.
Ф«(t) == Ее Щ
и моментов:
1
Ф«t) == (1 iаt)л ' t Е R'
и Ее == аЬr(л -+ ь)/r(л) при Ь > л, в '1астности,
Ц == ал, Щ == а 2 л.
(20)
(21)
6) Стирлинr Джеймс (1692 1770) шотландский математик.
1.2. OCHOBHble абсолютно HenpepblBHble модели
53
Важным свойством rамма распределения является ero
воспроизводимость по пара метру формы >.: если слу
чайные величины X 1 , , X k независимы и при этом
[,(X j ) == r(a, >'j), j == 1, , k, то
[,(Х[ + + Х п ) == r(a[, >'1 +... + >'k),
Свойство
воспроизводимости
Наконец, отметим следующее полезное свойство: если [,( ) == r(a, >'),
то для любой постоянной с> О .c( ) == r(ca, >'), в частности, если случай
ная величина имеет стандартное показательное распределение r(l, 1), то
[,(а{) == r(a, 1) ЭТО свойство используется в алrоритмах моделирования
(см. 1.3).
Модель rамма рапределения широко используется в задачах теории Ha
дежности и теории MaccoBoro обслуживания. Особую роль иrpает при этом по
казательное распределение r(a, 1). Этому распределению часто подчиняются
случайные длины интервалов между последовательными моментами нас1)'П
ления событий в, так называемых, пуассоновских потоках, времена «жизни')
различных технических устройств и т. д.
В задачах математической статистики rамма распрсделение иrpает боль
шую роль блаrодаря тесной связи с нормальным распределением, в частности,
там, rде рассматриваются квадратичные формы от нормальных случайных Be
личин. Наиболее ярким примером является х 2 (п) == r(2, nj2): это распре
2 2
деление суммы квадратов Х 1 + + х п , rде Х[, ,Х П независимые
стандартные нормальные случайные величины (см. упр.38).
Друrой важный результат состоит в следующем. Пусть (Х [, ... , х п )
случайная выборка из нормальноrо распределения N(Jl, (12). Обозначим
1 n
Х == Е X j
n j 1
n
2 1 2
И S == L)X j Х)
n j l
2
Torдa величинЫ Х и S независимы и при этом
"
Теорема Фишера
.с(Х) == N (Jl, : ),
( nв2 )
а .с
(12
== i(n 1).
(22)
Этот результат известен как знаменитая «теорема Фишера» (1925), и на нем
основывается orpoMHoe число важных результатов в статистике нормальных
моделей.
4. Бета распределение
Бета распределенuе Ве(а, Ь), а > О, Ь> О, задается плотностью
{ r(a + Ь) a [(1 )Н
f(xla. Ь) == (a)r(b) х х
при О х 1,
(23)
в остальных случаях.
54 rлзвз 1. OCHOBHble распределения и их моделирование
Если .ею =: Ве(а, Ь), то
а
E =:
а+Ь
аЬ
и щ
(а+Ь)2(а+Ь+ 1)'
(24)
В случае, коrда а =: Ь =: 1, бета распределение Ве( 1, 1) является равномерным
распределением на интервале (О, 1) (см. следующий пункт).
.6t С Один из наиболее важных случаев возникновения
"JI' вязь с [амма-
бета распределения выражается следующим утвержде
распределением _
нием: если случаиные вели'tины Х 1 и Х 2 независuмы и
имеют i!амма распределеиия r(a,'\I) и r(a, '\2) соответственно, то случайная
величина У =: X1!(X 1 + Х 2 ) имеет распределение Ве(ЛI, Л2)'
Отметим также, что нормирующий множитель в (23)
I
r(a)r(b) =: / xa I(1 х)Н dx
[(а + Ь)
о
называется бета фуН/сцией и обозначается
В(а Ь) == r(a)r(b)
, r(a + Ь)
(отсюда и название распределения Ве(а, Ь»).
5. Равномерное распределение
Равномерное распределение И(а, Ь), oo < а < Ь < 00, имеет постоянную плот
ность на интервале [а, Ь]:
1(xla, Ь) { а
Если .ею =: U(а, Ь), то
.e( = : ) =:U(о, 1) =: Be(l, 1)
при а:::; х :::; Ь,
(25)
в остальных случаях.
и
а + Ь (Ь а)2
Е{ =: ' Щ =: 12 (26)
Равномерное распределение И(а, Ь) описывает процесс «выбора точки
наудачу,) в интервале [а, Ь]. Так, если [а, Ь] интервал между последователь
ными отправлениями автобуса от остановки, то время ожидания пассажира,
не знающеrо расписания и пришедwеrо на остановку, есть случайная вели
'Iина с распределением И(а, Ь). Распределение и(о, 1) иrрает особую роль
в методах моделирования с помощью компьютеров случайных величин с за
ранее заданными распределениями (об этом подробно будет идти pe'lb в 1.3).
1.2. OCHOBHbfe абсолютно HenpepbfBHbfe модели
55
Такие методы широко используют для приближенных вычислений интеrpа
лов, решения дифференциальных и интеrpальных уравнений и т. д. (см. также
при мер 7 Введения).
б. Распределение (тьюдента
Стьюдент (Student) псевдоним анrлийскоrо статистика Уильяма Д. rocceтa,
впервые использовавшеrо это распределение в 1908 r. С 1899 r. он работал в
Дублине на пивоваренном заводе rиннесса, и ero начальник настоял на том,
чтобы rocceT писал под псевдонимом. По определению, распределением Стью
дента (синоним: t распределение) с n степенями свободы В(n) называется pac
пределение случайной величины (стьюдентова отношения)
t
n vx /n '
rде случайные величины ( и x независимы и при этом L.:(() == N(O, 1), а
L.:(x ) == х 2 (n). Плотность f(xln) этоrо распределения имеет вид
(27)
( n+ 1 )
I r ( X2 ) (n+')/2
f(xln) == ( ) 1 +
у1rn n n
r
2
oo < х < 00.
(28)
При ведем типичный статистический при мер, rAe
возникает это распределение. Пусть (Х" ,Х П )
случайная выборка из распределения N(()t, 8i) (т. е. pac
сматривается нормальная модель с неизвестными средним значением и дис
персией). Torдa в силу теоремы Фишера (см. (22)) стьюдентово отношение (27)
примет вид
,fii Х е, /
tn l == == yn(n 1)
82 nВ 2
n 1 е 2 2:)X i х)2
Статистический ..
пример){.
х е,
(29)
n
i 1
и при этом L.:(tn l) == В(n 1) (независимо от значения неизвестных пара
метров!).
Если случайная величина Х имеет t распределение В(n), то при n> 2
n
ЕХ == О и DX == .
n 2
(30)
в случае, KorAa n == 1, t распределение называется pac
пределением Коши 7) это распределение отношения
....
Распределение .
Коши
7) Коши Оrюстен Луи (1798 1857) французский математик, иностранный почетный член
Петербурrской АН (1831). Один из основоположников теории аналитических функций.
56
rлава 1. Основные распределения и их моделирование
двух независимых стандартных нормальных величин, оно имеет плотность
1 1
f(xll) == , oo < х < 00, (31)
тr 1 + х 2
ero характеристическая функция есть Ф(t) == e ltl и для Hero не существуют
моменты, в том числе и математическое ожидание.
Распределение Коши интересно своими связями с друrими распределе
ниями, возникает в некоторых фИЗИ'iеских задачах, связанных с блужданием
частиц, имеет ряд ориrинальных аналитических свойств. Например, по зако
ну Коши распределена функция tg 17. rдe случайная величина 17 равномерно
распределена на интервале [ тr /2, тr /2].
7. Распределение (недекора
По определению, распределением СнедеlCора с n и т степенями свободы (обо
значается В(n, т)) называется распределение случайной величины
x Х;" т X
Fn m == , (32)
, n т n Х;"
" 2 2
rде случаиные величины Х" И Хт независимы и име
!I!'P!j5ёiС: п реАе Л ёН ие"М ют i распределения с n и т степенями свободы COOT
ветственно. Часто это распределение называется также
F распределеllием или распределением Фишера.
ПЛотность f(xln, т) распределения В(n, т) имеет вид
( n ) П/2 r(T) Xn/2 1
f(xln, т) == т r (%) r ( ) (1 + nх/т)(п+т)/2'
х> О,
(33)
'С тистический
и f(xln, т) == О при х :::; О.
Это распределение иrpает в статистике важную
роль, так как отношение некоторых независимых KBaд
пример ,.i......j .,.., , ратичных форм от нормальных случайных величин под
чиняется F распределению. Вот один из COOTBeTCTBY
ющих примеров.
Пусть (X 1 , . .. , х п ) случайная выборка из нормальноrо распределения
N(f.tl. (7'2), а (Y 1 . . .. , У т ) независимая с первой случайная выборка из pac
пределения N(f.t2, (7'2). Torдa при n 2, т 2 и любых f.tl, f.t2 И (1.2
отношение
Fn l,т 1 ==
n
1 "" 2
(Xj X)
(n 1 ) .
I I
т
1 "" 2
(т 1) f:7' (Y j у)
(34)
1.2. Основные абсолютно HenpepbIBHble модели
57
будет иметь распределение В(п 1, т 1), что следует из теоремы Фишера
(см. (22».
Среднее и дисперсия случайной веЛИЧИНbI Fn,m имеют вид (при т> 4)
т 2т 2 (п + т 2)
EFn m == И DFn,m == ( )( )2 ' (35)
, т 2 n т 4 .т 2
8. Распределение Вей6улла
Распределение Вей6ума W (а, а, Ь) зависит в общем случае от трех параметров:
параметра сдвиеа (положения) а Е R I , параметра фОрМbI а > О и параметра
масштаба Ь > о и задается функцией распределения
F{(X)==l exp{ ( x a Y}, x a (36)
(F{(x) == О при х < а). Здесь
E ==a+br(l+ ) и Щ==Ь2[r(I+ ) r2(1+ )] (37)
Частный случай W(a, 1, Ь) известен как двухпараметричеСlCое пОlCазатель
lюе (экспоненциальное) распределение, а W(a, 2, Ь) как распределение Релея.
9. Распределение Парето
Случайная величина имеет распределение Парето 8) с параметрами Хо и а
(хо, а > О), если ее плотность такова:
{ при х Хо.
I(xlxo. а) I::'
(38)
в осталЬНbIХ случаях.
Это распределение применяется в качестве подходящей модели ДЛЯ широкоrо
класса эмпирических наблюдений, относящихея, например, к распределению
дохода, размера rородов или частоты слов в ЯЗbIке.
Если в (38) а > 2, то справедливы следующие формулы для перВbIХ двух
моментов:
ахо
E{==
a l
ах 2
и щ== о .
(а 1)2(a 2)
(39)
10, Распредепение Дирихпе
Распределение Дuрихле 9) D(g), rдe Q. == (а1, . .. , ak), а; > О, i == 1,
параметрический вектор, задается плотностью
'( I ) r(al + + ak) a, l ak 1 (
Х а Х 1 Х !. == х"
r(a,)...r(ak)
,k,
,Xk) Е &,
(40)
8) Парето Вильфредо (1848 192З) итальянский экономист и соuиолоr.
9) Дирихле Петер rycтaB (1805 1859) иемецкий математик.
58
rлава 1. Основные распределения и их моделирование
rде Е единичный симплекс:
Е == {f. О Xj 1, i == 1,
,k, х,+
+xk==I}.
Сравнение формулы (40) с формулой (23) для плотности бета распреде
ления показывает, что распределение Дирихле при k == 2 сводится к бета
распределению, поэтому распределение D(g) иноrда называют MHOlOMepHbIM
бета распределенuем.
Если L (i == (6, . . . , k)) == D(Q) , то первые и вторые моменты случай
Horo вектора i имеют вид (далее обозначено й == al + + ak):
Et aj Dt. Cti(Й ai)
..; == ' ... а 2 (й + 1) ,
Йjаj
COV( i, j)== а 2 (й+I) ' i=f-j,
при этом L( i) == Be(ai, а aj) (см. п. 4), i == 1, ,k.
(41 )
Замечание. Обратим внимание на то, что в данном случае координаты вектора { свя-
заны линейным соотношением I +... + k == 1, из KOTOpOro одна из них, скажем k'
может быть выражена через остальные: k == I I .. . k " Если, в соответствии
с этим, в (40) переменную Xk записать как 1 X, . .. Xk l, то f( IQ:) будет обычной
(k I) мерной плотностью распределения случайноro вектора ( " .. . , k 1)' которая
положительна в тех точках симплекса S С Rk 1 , rде О Х, 1, i == 1,.. ,k 1,
и О ::;:; Х, + + Xk 1 1. Именно при такой Иlперпретации формулы (40) Mbl по
лучаем при k == 2 представление (23). Далее, так как интеrpал от плотности f( I )
по симплексу S должен быть равен 1, то мы получаем формулу
/ "I I ak I ' ) ak ' r(ЙI)", r(Йk) ( )
X 1 ",Xk 1 (I XI ", Xk ' dXI...dxk l ( ) ' 42
rа'+"'+Йk
s
Формула Дирихле
известную в анализе как формула (uнте?рал) Дuрuхле (этот
интеrpал был впервые исслсдонан П. Дирихле в 1839 r.
и этим объясняется название распределения П( ).
11. Преобразования случайных величин и векторов
Мы завершаем разrовор об основных вероятностных распределениях техни
ческим, но совершенно необходимым для последующеro разделом, в котором
мы напомним некоторые формулы из теории вероятностей, которые часто ис
пользуются для нахождения явноrо вида распределений при преобразованиях
случайных величин. Выше мы уже встречались с примерами таких преобра
зований. Так, в п. 2 мы установили, как ВЫЧИСЛИТь распределение линейно
преобразованноrо нормальноro случаЙноrо вектора. Но есть и задачи (с ними
мы встретимся тоже), в которых необходимо иметь дело с преобразованиями
не линейными, а более сложными, как rоворят, функциональными. Поэтому,
хотя соответствующие формулы rораздо сложнее, но без них нам не обойтись,
и мы их здесь приведем для последующих ссылок на них.
1.2. OCHOBHble абсолютно непрерывные модели
59
Начнем с простейшеrо случая сдвиi! масштаБНОi!О npe
образования случайной величины {. Пусть { имеет He
прерынную функцию распределения F{(x) == Р{{ ::;; х}
Рассмотрим произвольное линейное преобразонание 17 == а{ + Ь, rдe а > о,
ь Е я' Torдa оченидно, что функция распределения преобразонанной слу
чайной величины 1/ равна
Сдвиr-масштабное
преобразование
( Х Ь )
F,,(x) == F{ .
Если, как и выше, через f(x) обозначать плотность исходной величины
и(х) F{(x)} , а через g(x) плотность преобразованной величины 1]
(g(x) == F (x)}, то в терминах плотностей предыдущее запишется так:
1 ( Х Ь )
g(x) == ! .
(43)
в этом случае Ь называют параметром caBUi!a (положения), а napaMeт
ром масштаба. В статистических задачах часто считается, что исходная плот
ность f нам известна, а параметры а и Ь (или один из них) неизвестны,
такую модель (43) называют сдвuюмасштабной: в этом случае наблюдаемая
случайная величина 1J предполаrается полученной с помощью HeKoToporo
линейноrо преобразоваllИЯ над «стандартной,) случайной величиной {, pac
пределение которой полностью известно. Таким образом, сдвиrомасштабная
модель является специальной формой общей параметрической модели. При
мерами сдвиrомасштабных моделей являются нормальная модель N(p., (72)
(здесь а == (), Ь == р., а стандартным является распределение N(O, 1), зада
ваемое формулами (7)), показательная модель r(a, 1) (здесь имеется только
один параметр масштаба а, а стандартным является распределение r(l, 1),
определенное в п. 3), равномерное распределение И(а, Ь) (здесь «стандартом,)
является U(О, 1)) и т. д. Сдвиrомасштабные преобразования часто использу
ются в задачах теории вероятностей и математической статистики.
Перейдем теперь к общему случаю произвольноrо
функциональноrо преобразования. Пустьслучайный BeK
тор Х == (X t , ,Х/,;) имеет абсолютио непрерывное
распределение с плотностью f('f), == (х[,..., Xk) Е
k ) /,;
Е S <;;; R и!! == (ht,... , h k S ----+ R произвольное взаимно однозначное
и rладкое (т. е. все частные производные дhi('f)/дХj непрерывны) преобра
зование,якобиан Koтoporo
Общее
функциональное
преобразование
.,
oh t ('f) дh k ('f)
oxl дх(
J(;f,) == det
oh l ('f) дh/,;('f)
дх/,; дХk
ба rлава 1. Основные распределения и их моделирование
не обращается на S в нуль. Тоща плотность распределения преобразованноrо
случайноrо вектора 1:. == МЮ == (hl ( Х ), , hk( X ») имеет следующий вид:
f (!l , (у) )
g(1/) == IJ(!l '( ») l ' J!. == (у"
, Yk) Е !l(S),
(44)
h '
rде
Частные случаи
обратное к !l преобразование: !l , (M ») == .
Эта «страшная» (в силу своей общности) формула
на самом деле чаще Bcero при меняется в более «про
зрачныXJ частных случаях, два из которых мы выделим особо. Если k == 1, то
речь идет о преобразовании случайной величины: У == h(X), rде h(x) вза
имно однозначная rладкая функция с необращающейся в нуль производной.
В этом случае формула (44) для плотности У принимает вид
f(h l(y»)
g(y) == Ih'(h '(y»)I'
(45)
. Линейное I
преоброзование
Для случая линейноrо преобразования: 1:. == А Х + !2.
при IAI == а =J. О формула (44) конкретизируется к виду
f(A '(y !2.»)
g(J!.) == lal
(для одномерноrо случая k == 1 формула (46) сводится к (43».
Эти два случая (k == 1 и линейное преобразование) чаще Bcero и Bcтpe
чаются в приложениях. В заключение приведем два иллюстративных (но по
лезных для дальнейшеrо) при мера использования этих формул.
Пример 1. Пусть.ею == И(О, 1), т. е. ( имеет стандартное равномерное pac
пределение, и 1]== In{. Здесь f(x) == 1, х Е (0,1), h(x) == In х, h'(x) == I/x,
h '(y) == e Y у > О, поэтому по формуле (45) плотность преобразованной
случайной величины 1] есть е Y, у > О. Таким образом, в данном случае
.е(1]) == r(l, 1), т. е. 1] имеет стандартное показательное распределение. Этот
факт используется при моделировании показательноrо распределения, о чем
будет идти речь в следующем параrpафе. .
(46)
. Получ--ение нормальных
случоиных величин
,из равномерных
Пример 2 (HeMHoro более сложный, но поучи
тельный и очень полезный!). Пусть случайные
величины Х, и Х 2 независимы и .c(Xj) == И(О, 1),
i == 1,2. Рассмотрим их прео бразование
У, == .J 21п Х ! siп (211" Х2), У 2 == .J 2 In Х, cos (211" Х 2 ) (47)
и найдем распределение пары У == (У" У 2 ). Здесь
у, == h l (х" Х2) == .J 21n х, sin (211"Х2),
У2 == h2(XI, Х2) == .J 21n х, cos (211"Х2),
(х" Х2) Е (0,1)2,
1.2. Основные абсолютно непрерывные модели
61
и все условия применимости формулы (44) выполнены. Имеем
ah l (XI,X2) sin(211' X 2)
аХI Х, y' 21n Хl '
ah 2 (xl, Х2) cos (211'Х2)
ах, Хl y' 21n XI '
ah l (Х" Х2) . /
а == 211'у 21n ХI cos (211' Х 2),
Х2
ah 2 (x" Х2)
а == 211' ''; 21" Х I si" (211' Х 2),
Х2
откуда находим якобиан J(XI, Х2) нашеrо преобразования: это определитель
si" (211'Х2)
xl -J 21" Х,
cos (211'Х2)
x, -J 21"x,
211'
J(Xl, Х2) ==
Хl
211' ''; 21n х, cos (211'Х2)
21l' ''; 21n Х, sin (211'Х2)
Поскольку совместная плотность пары (Х" Х 2 ) в данном случае есть произ
ведение равномерных плотностей на интервалах соответственно О < Х, < 1
и О < Х2 < 1, то f(XI,X2) == 1, (XI,X2) Е (0,1)2, И В силу (44) плотность
g(y" У2) преобразованной пары (Y 1 , У2) есть xl/211' Осталось выразить ХI
через (У" У2). В данном случае это очень просто, так как у нас
2 2 2
У, +У2 == !nxl.
Отсюда
XI == ехр { (Yi + yi) },
и окончательно получаем, что искомая плотность имеет вид
g(y" У2) == 2 ехр { (yi + Yi)}, (У', У2) Е R 2
Но это есть двумерная стандартная нормальная плотность (см. п. 2), т. е.
У == (Y j , У2)
является стандартным нормальным случайным вектором (ero компоненты
независимы и .с(У;) == И(О, 1), i == 1,2).
Таким образом с помощью «хитроrо» преобразования (47) мы можем по
лучать из независимых стандартных равномерно распределенных случайных
величин (т. е. в определенном плане простейших случайных величин) неза
висимые же стандартные нормальные случайные величины. Этот факт также
используется в алroритмах статистическоro моделирования (см. следующий
параrpаф). .
62
rлава 1. Основные распределения и их моделирование
Замечание. В связи с последним примером обратим внимание заинтересованноro
читателя на следующий нюанс. В данном случас нам не потрсбоllaJJОСЬ ВblЧИСЛЯТЬ
полностью обратное преобразование !! I('!l), т. с. находить обе обраТНbJе функции
XI == х,(у" У1) и Х1 = X1(YI, У1): поскольку плотность f здесь постоянна, а якобиан
J(XI' Х2) зависит лишь от XI, то достаточно знать лишь первую обратную функцию
XI = XI(Y', У1)' Подобное обстоятельство встречается достаточно часто в задачах,
связаННblХ с использованием ФОРМУЛbl (44). Позтому в конкретных задачах не надо
торопиться ВblЧИСЛЯТЬ !! '(-м): сначала надо ВblЧИСЛИТЬ якобиан J(;f) и получить
явное Вblражение для f( )/IJ( )I, а затем, в зависимости от вида зтоrо Вblражения,
уже решать задачу ero представления 'Iерез новую переменную '!! в общем, как
rоворили наши умные предки: .Festina lente.. торопись меменно (Октавиан ABryCT
(63 r. до н. Э. ]4 [. н. э.), римский император).
Дальнейшие свойства рассмотренных конкретных вероятностных распре
делений (как точные, так и асимптотические), а также связи tежду ними
обсуждаются в упражнениях в конце rлавы.
t 1.3. Моделирование выборок
из конкретных распределений
Точность результата не может быть
вЫluе точности исходных aalll/blx.
Для изучения и практической иллюстрации эффективности различных стати
стических процедур необходимо иметь наборы конкретных эксперименталь
ных данных, которые можно было бы рассматривать в качестве реализаций
некоторой случайной величины с известным законом распределения [( ).
ОбрабаТblвая эти данные по соответствующему статистическому алrоритму,
мы в этом случае получаем IЮЗМОЖНОСТЬ сравнить предсказание теории с из
веСТНblМИ нам параметрами этоrо распределения и тем самым «подверrнyrь
теорию практической проверке». Такой «иrpовой» элемент при орrанизации
практической работы по статистической обработке данных Повышает инте
рес и к изучению самой теории статистическоrо вывода. Для получения таких
исходных данных (выборок) широко используется метод статuстuчеСКОlО MO
делuрованuя, с помощью KOTOpOro, используя современные компьютеры, мож
но быстро «смоделировать» выборку Х == (Х". ,Х n ) из любоrо заданноrо
распределения [(О. Описанию соответствующих алrоритмоI3 моделирования
и посвящен настоящий параrраф.
1. Предварительные замечания
Обычно для получения реализации последовательности независимых случай
ных чисел с нужным нам распределением используют реализацию последо
вательности независимых и равномерно распределенных на интервале [о, 1]
случайных чисел
И О , U 1 , И 2 , .., .
(1)
1.3. Моделирование выборок из KOHKpeтHblX распределений б3
В свою очередь, для этоrо необходимо иметь практи '1'I"!!''.,р."..,) Датчики .,.
чески неоrраниченный источник, вырабатывающий по
следовательность (1), датчUlС случайных чисел. В co
временных компьютерах, как правило, имеются встроенные физические дaT
чики СЛУ'lайных 'Iисел, принцип работы которых основан на использовании
в Ka'leCTBe ИСТО'lников случайности быстро флуктуирующих шумовых про
цессов, вырабатываемых радиоэлементами. Отметим, что получаемые при
этом 'Iисла дискретные по своей природе, так как принимают значения
в пределах разрядности компьютера (так, при двоичном представлении 'Iисел
с N разрядами в ячейках случайное число может принимать 2 N возможных
зна'lений).
Однако, чаще Bcero в Ka'leCTBe 'Iисел (1) используют,
так называемые, псевдослучайные числа, т. е. детермини
рованные 'Iисла, ПОЛУ'lаемые по не которому алrоритму
и обладающие в той или иной мере свойствами СЛУ'Iайных 'Iисел, так сказать,
«похожие» на них. Имеются раЗЛИ<lные методы получения псеВДОСЛУ'Iайных
'Iисел, наиболее изоестным из которых является так называемый линейный
конzруэнтный метод, в котором полаrают И П == Zn/ffl, rдe {Zn} последо
вательность, определяемая рекуррентным соотношением
случайных чисел
Псевдослучайные .111{
числа
Zn+1 == aZ n + с (mod т), n == О, 1,2,
Zo на'lальное зна'lение, а, С, т натуральные 'Iисла (операция приве
дения чисел по модулю (mod) озна'lает, что если r == вт + l, о :( l < т, то
r (mod т) == 1). Числа {и п }, получаемые таким способом, конечно, не яв
ляются случайными (они детерминированные), но при специальном выборе
констант а, с, т и Zo свойства этих чисел «O'leHb похожи') на свойства по
следовательности (1) и потому их используют в качестве исходноrо материала
(т. е. в качестве последовательности (1)) для рещения модельных зада'l, иллю
стрирующих различные выводы теории. Приведем условия, которым следуют
при практическом выборе значений определяющих линейный конrpуэнтный
метод констант:
1) с и т взаиМНО простые числа;
2) Ь == а 1 кратно р для любоro простоrо р, являющеroся делителем т;
3) Ь кратно 4, если т кратно 4.
Но «правильный') выбор этих констант еще не «raрантирует» хороших
свойств псевдослучайных 'Iисел. Даже в датчиках, рекоме':!дованных для ши
pOKoro использования, нередко обнаруживаются существенные недостатки.
Поэтому «качество» псевдослучайных чисел требуется контролировать при
помощи различных статистических критериев (см. при мер 7 Введения), об
щая теория которых излаrается в rЛ.4 (см. п. 2 4.5).
После этих замечаний перейдем непосредственно к алrоритмам Moдe
лирования основных вероятностных распределений, описанных в предыд
щих параrpафах, считая, что в нашем распоряжении имеется неоrpаНИ'lенная
64 rлаоа 1. OCHOBHble распределения и их моделирование
последовательность (1) «простейших,) случайных величин с распределением
И(О, 1) (см. п. 5 1.2).
2. Моделирование распределений Бернулли Bi(l, р)
и биномиальноrо Bi(k, р) (см. п.1 1.1)
Чтобы получить реализацию бернуллиевской последовательности {X 1 , Х 2 , . . .},
rдe
Р{Х п == '} == 1 Р{Х п == О} == Р
при заданном р Е (О, 1), очевидно, достаточно положить
Х п == 1 (И п р), n == 1, 2,
(здесь и далее везде I(А) обозначает индикатор события А, т. е. I(А) == 1,
если А имеет место, и I(А) == О в противном случае). Действительно, незави
сим ость случайных величин {Х п } обеспечивается независимостью исходных
величин {И п } И
Р{Х п == I} == Р{И п р} == р дЛЯ любоrо n == 1,2,
Имея последовательность Бернулли {Х п } леrко смоделировать выборку
из биномиальноrо распределения Bi(k, р). Именно, поскольку
.с(Х 1 +
+ X k ) == Bi(k, р),
то положив
Х} == X(j l)k+l +
получим реализацию выборки (Х;,
+ X jk , j == 1, , n,
,X ) объема n из распределения Bi(k,p).
3. Моделирование отрицательноrо
биномиальноrо распределения Bi (r, р) (см. п. 2 1.1)
Поскольку число единицдо первоrо нуля в последовательности Бернулли {Х п }
имеет reометрическое распределение Bi (l,p), то, положив У == min{j О
ХН[ == О}, будем иметь .с(У) == Bi (l, р). Отсюда следует, что алrоритм MO
делирования выборки (У[, ,У п ) из распределения Bi (!, р) можно задать
формулами
1'; == min{j О XY; I+j+l == О}, i == 1, , n, Уа == О.
Далее, поскольку
.с(У[ + + У Т ) == Bi (r, р)
(свойство воспроизводимости отрицательноrо биномиальноrо распределения),
то смоделировать выборку (У(,. ,Y ) из распределения Bi (r, р) можно
(как и выше дЛя биномиальноrо распределения) по формулам
У} == Y(j I)r+1 + + Yjr, j == 1, ,n,
т. е. просуммировав числа {Y j } последовательными rpуппами по r подряд иду
щих чисел.
1.3. Моделирование Вblборок из KOHKpeтHblX распределений 65
4. Моделирование полиномиальных испытаний (см. п. б 1.1)
Пусть требуется смоделировать n независимых наблюдений над дискретной
случайной величиной { с распределением
Р{{ == [} == Р" l == 1, , N (Р\ + + PN == 1).
Разобьем отрезок [О, 1] на N интервалов &" , EN, rде
[1 == [O,PI], Е, == (РI + + рн, РI + + р,], 1 == 2, ,N
(так что &, имеет длину Р" l == 1, , N), и положим
N
X j == l1(Uj Е Е,), i == 1, ,n. (2)
' l
Так как Xj определяется только через Uj, то случайные веЛИЧИНbI {X j } неза
висимы и одинаково распределены, а
P{X j == [} == P{Uj Е е,} == 1&,1 == Р"
т. е. они распределены так же, как {. Таким образом, (Х 1,
из .ею.
, Х П ) выборка
Замечание. В случае ПРОИЗВОЛЬНblХ исходов al, ,aN СЛУ'lайную величину Х ; сле
дует определить по формуле
N
Х ; == L a[I(U; Е [1).
/=1
5. Моделирование пуассоновскоrо распределения П(л) (см. п. З 1.1)
Установим предварительно следующий факт.
Лемма, Определим случайную величину { равенством
{==max{j ПUj?е Л}, ),>0.
1=1
TorAa .ею == П(>.).
Доказательство. Перепишем определение { в эквивалентном виде
{ == тах {j
t 'п Uj ). }
1=1
(при j == О пустая сумма, как это обычно принято, считается равной О, а пустое
произведение полаrается равным 1). Torдa события
{{ < т} и { t 1 n Uj > л },
,=1
5 Заказ 1748
66 rлава 1. OCHOBHble распределения и их моделирование
очевидно, эквивалентны. Далее, в примере 1 в 1.2 было показано, что
.c( 1nU I ) == r(l, 1)
стандартное показательное распределение, а по воспроизводящему свойству
raмма распределения (см. п. 3 1.2)
.с( t1nUl) == r((,m)
; l
распределение Эрланса порядка т, поэтому (см. (18) 1.2)
{ т } 1 ; ос m l){
P{ < т} == Р I: (лИ; >.л == ( )' xm le x dx == I: е ЛI'
. т 1. О Т.
2 I л T
т 1.
Но это и означает (см. (8) 1.1), что случайная величина имеет распреде
пение П(.л). .
Из этой леммы следует, что выборку (X 1 ,
можно смоделировать по формулам
, Х n ) из распределения П(.л)
xk==max{j ПИхн+; е '\}, k==1,2.
' '
, п, Ха == о.
(3)
6. Моделирование непрерывных распределений
Для моделирования случайных величин с непрерывным распределением D
ряде случаев можно использовать следующий простой факт: если Р(х)
непрерывная и cтporo монотонно возрастающая функция распределения и
F I(y) обратная к ней функция (F I(F(x» == х), то Д)lя случайной вели
чины 1] == p 1 (И), rде .с(и) == Що, (), имеем
P{f1 х} == Р{И Р(х)} == F(x).
Таким образом, случайная величина 1] == F I (И) имеет функцию распределе
ния F(x), и если обратная функuия F I(y) может быть явно вычислена, то
F I (И;), i == 1,..., n, выборка из распределения F.
Замечание. Если функция Р(х) не является cTporo монотонной, то вывод остается
в силе, если под обратной функцией понимать
F I(y) == sup{x . Р(х) у}.
Заметим еще, что если (Х;, i == 1'..., п) выборка из HenpepbIBHoro
распределения F(x) , то (аХ; + Ь, i == 1, , п), rде а > О, Ь Е R 1 , будет BЫ
боркой из распределения сдвиrомасштабноrо типа F((x b)ja) (см. п. 11 1.2
9 1.3. Моделирование Вblборок из KOHKpeтHblX распределений 67
СООТllошение (43». Так, например, (аИ; +Ь, i == 1,... ,n) выборка из paH
HOMepHoro распределения И(Ь, а + Ь), а если L.:(Xj) == N(O, ]), т. е. {Xj}
стандартные нормальные числа, то L.:(iJ Xj+jl) == N(jl, iJ2); Н частности, чтобы
смоделировать выборку из распределения Коши (см. (31) 1.2), надо положить
Х ; == tg (7rUi I) == ctg (7fU j ). i == 1, ,n.
7. Моделирование показательноrо
и связанных с ним распределений (см. п. 3 1.2)
Чтобы смоделировать выборку (X 1 , ... . Х n ) из показательноrо распределения
r(a, 1), надо положить Х; alI1Uj, i == 1, ,n. Суммируя полученные
числа по т штук: Y 1 = Х 1 +. "+Х rn , У 2 == Хrn+1 + ..+Х2т, ,получим
выборку из распределения Эрланra r(a, т).
8. Моделирование нормальных случайных чисел (см. п. 1 1.2)
Большое число статистических задач связано с анализом выборок из нормаль
Horo распределения N(p" (1'2), при этом (см. замечание в п. 6) достаточно уметь
моделировать выборки из стандартноrо нормальноrо распределения N(O, ])
(см. (7) 1.2). В данном случае явной формулы для обратной функции ф l(у)
к стандартной нормальной функции распределения не существует, поэтому
описанный в п. 6 алrоритм моделирования неприrоден. Один из методов полу
чения стандартных нормальных СЛУ'IaЙНЫХ чисел из равномерных (1) состоит
в построении соответствующеrо явно вычислимоrо функциональноrо преоб
раЗQвания. Пример TaKoro преобразования нам уже встречался в примере 2
в 1.2 (см. там соотношения (47». Из полученноro в этом примере результата
следует, что каждая пара (U2I I, U 2k ). k == 1,2,..., чисел последовательности
(1) с помощью преобразования
X2k I == V 2 111 U2k I sil1 ( 27rU 2k),
Х2!.: == V 2 111 U2k I cos (27rU 2k )
(4)
порождает пару (X2k l, X 2k ) независимых стандартных нормальных чисел.
Друroй путь получения нормальных чисел из последовательности (1) paB
номерных чисел основан на использовании центральной предельной теоремы
теории вероятностей (см. соотношение (1) 1.2). В соответствии с этой тeo
ремой можно положить (см. формулы (26) 1.2, в соответствии с которыми
EU j == ]/2. DU; == ]/12)
U(k I)N+1 + +U kN N/2
X NK == V N / 12
k = 1,2,
(5)
Этот алroритм, очевидно. леrче реализуем, чем предыдущий, однако он при
водит лишь к приближенно нормальным числам, так как лишь в пределе при
S'
68
rлава 1. OCHOBHble распределения и их моделирование
N 00 распределение случайных величин X NK будет стандартным HOp
мальным N(O, ]). Но практически удовлетворительное приближение к pilC
пределению ./1/(0,1) получается уже при N == 12 это значение параметра N
в алrоритме (5) обычно и используют для конкретных вычислений.
9, Метод суперпозиций
В ряде СЛУЧilев моделируемое распределение может быть представлено IJ lJиде
смеси более простых распределений, и Torдa для моделирования TaKoro pac
. '( с """ пределения может быть использован метод суперпози
меси "
" ции, описанию KOToporo посвящен данный пункт. Но
;nа<;пnедеJ)ении. "
::s: ",,,,,r<l"""'. Ii сначала дадим определение смеси.
Пусть Р!.: О, L: Р!.: == 1, Fk(X) некоторые функции pac
k
пределения. Тоrда функция распределения
Р(х) == L: PkFk(X)
k
на] ывается смесью функций Р!.: (х) С весами Pk.
Аналоrично определяется смесь распределений IJ терминах Плотностей,
Пример 1, Функция распределения
11! !- - :
it7
1
{ х/2, О Х < 1,
Р(х) ==
1, Х 1,
.-
х
(см. рис. 1) является смесью с весами ]/2 функций
распределения paOHoMepHoro И(О, 1) и вырожденноrо
в точке Х == 1 распределений. .
Рис.l
-'l
Пример смеси
Пример 2. llYCTb распределение на [О, 1] задано плот
ностью вида
00
[(х) == L: ak xk с а!.: О.
k O
Тоrда так как
/ 1 а!.:
f(x) dx == L..J k + 1 == 1,
О k O
то положив Р!.: == ak/(k + 1), будем иметь
00
f(x) == L: Pk(k + l)x k .
k=O
Но
1.3. Моделирование Вblборок из KOHKpeтHblX распределений 69
(k + l)xA: == f(xlk + J, 1)
плотность бета распределения (см. (23) 1.2), следовательно,
00
'(х) == I: pA:f(xlk + 1, 1),
k O
т. е. такое распределение представляет собой смесь бета распределений
Be(k + J, 1) с весами Р}; == ak/(k + J). .
Теперь, чтобы смоделировать случайную величину,
функция распределения или плотность которой явлн
ются смесью, можно использовать метод суперпозицнн:
1) рэзыrpать значение дискретной случайной величины, принимающей зна
чение k с вероятностью Pk, k == о, 1, . (как в п. 4), допустим, что при
ЭТОМ было получено значение ;
2) смоделировать случайную величину с функцией распределения Fko (плот
ностью !k,J некоторым способом (скажем, методом обратной функции,
см.п.6).
Для произвольной непрерывной плотности '(х), заданной на отрезке [0,1],
можно использовать способ прнближениоrо моделировании методом суперпо
зиции, основанный на аппроксимации полиномами Берн Полиномы
10)
штеuна : Бернштейна
) "" ( k ) А: k n k
f n (х == f ;; СП х (1 х)
k O
Основой для этоrо служит известная в анализе
Метод 1It.
суперпозиции
Теорема Вейерштрасса 11) Если функция '(х) непрерывна на [О, 11.
то 'п(х) ---+ '(х) равномерно по х при n ---+ 00.
По этой теореме непрерывную на отрезке [О, 11
плотность '(х) можно равномерно приблизить плот
ностями IfOрмироваltНЫМИ полuномами Бернштейна
I
fп(x) == f ) , rдe d n == / 'п(х) dx,
О
Применение ..,.
теоремы
Вейерштрасса
10) Бернurrеiiн Cepreii Натанович (1880 1968) советский математик, академик АН СССР,
ВЬJДающийся спеuиалист по теории дифференuиальных уравнений, теории приближения Функ
uий мноrочленами И теории вероятностей.
11) Вейерштрасс Карл Теодор Вильrельм (1 8 15 1897) немеuкий математик, ВЬJДающийся
спеuиалист по математическому анализу, теории Функuий и линейной алrебре. Почетный член
Петер6урrcкой АН (1864).
70 rлава 1. Основные распределения и их моделирование
так как из равномерной сходимости /п(х) к f(x) следует сходимость
I
d n I /(х) dx == 1 при n 00.
О
Для моделирования случайной веЛИЧИНbI [п с плотностью fп(x) методом
суперпозиции представим lп(х) в виде
1п(х) == t /((k/n)) [(n + I)C Xk(1 x)n k]
k O n n + 1
Здесь в квадратных скобках стоит плотность f(xlk + 1, n k + 1) бета рас
пределения Be(k + 1, n k + 1) (см, п. 4 1.2), поэтому
I n
! " f(k/n)
1 == fn(x) dx == L..; ( ) '
О k O d n n + 1
откуда
1 n ( k )
d n == I: f .
k + 1 k O n
Следовательно, положив
Pk == / ( ) / t f ( ) ,
k O
получим представление
n
lr.(x) == I: Pk/(xlk + 1, n k + 1),
k O
которое позволяет .!Iрименить метод суперпозиции для моделирования слу
чайной веЛИЧИНbI n
10. Моделирование цепи Маркова
Методом статистическоrо моделирования можно моделировать и заВИСИМblе ис
ПblТЗНИЯ с ра3JIИЧНblМ характером зависимости. Мы рассмотрим ДlIЯ иллюстра
иии простеЙший тип стохастической зависимости маркоескую зависимость.
Напомним, что последовательность случайных величин {lIt,t == О, 1,2, },
принимающих значения из конечноrо множества Е == {I, 2, , N}, наЗbl
BaeMoro "ространстеом состQяний, является цепью Маркова, если для JIюБОI'О
t == О, 1,2, .. . распределение вероятностей случайной величины Vt+1 з.ависит
лишь от TOro, какое значение приняла предыдущая величина Vt, и не зависит
от более ранних величин V r , т < t. Формально это можно Вblразить через
УСЛОВНblе вероятности так:
P{Vt+1 == it+1lV r == i r , т:::; t} == P{Vt+l == it+IIVt == i t }, i t , it+1 Е [. (6)
1.3. Моделирование выборок из KOHKpemHblX распределений 71
Если при этом вероятности в правой части (6) не зависят от (,времени» t,
то цепь Маркова называется однородной. Обычно рассматривают только oд
народные цепи, которые являются подходящей моделью мноrих случайных
явлений; такую модель ввел в 1907 r. А. А. Марков, именем Koтoporo она
и называется.
Если 1LЛЯ однородной цепи Маркова {lIt} обозначить вероятность пере
хода из состояния i в состояние j через
Pij == P{ lI t+1 == jJlIt == i}, i, j Е е, (7)
то эти числа образуют матрицу переходных вероятностей Р == IIpijllf, элемен
ты которой обладают следующими свойствами:
N
Pij O, LPij==l, i==I,...,N;
j=1
Стохастическая .. .
. ..' '1. матрицо
такая матрица называется стохастической. Чтобы полностью определить цепь
Маркова, надо еще задать вектор начальных вероятиостей Р == (PI, . . . , PN),
rде Pi == P{vo == i}, i == 1'..., N. Зная вектор Р и матрицу Р можно леrко
вычислить совместное распределение величин 110,111, . . . , /lT при любом Т:
P{IIO == i o , 111 == i r , 112 == i 2 ,
IIT == i T } == PillPioi,Pi,ij
PiT '
(8) ,
Пусть теперь требуется смоделировать реализацию М
{ } оделирование 11It
однороднои цепи Маркова IIt, t == О, 1, ,Т с про .
u U u I епи
извольнои стохастическои матрицеи переходных Bepo . ц
ятностей Р == Ilpij[lf и вектором начальных вероятностей Р == (PI,. , PN)'
Для этоro мы используем модифицированный алrоритм моделирования поли
номиальных испытаний (см. ".4). Именно, построим сначала системуразби
ений отрезка [о, 1] на N интервалов в соответствии с вектором Р и строками
матрицы Р:
,,(О) == { ,,(О) ,,(О) } ,,(i) == { r(i) ,,(i) }
(... "1 '...'''N ' (... "'1 ,...,"N '
I r(O) I I (i) I .
rде "j ==Pj, e j ==Pij, J == 1,
i==I,...,N,
, N, и определим случайные величины
N
«О)(и) == "L,jI(U Е Е?)),
j=1
N
((i)(U) == L jI(U Е eji)).
j=1
(9)
i == 1, ,N,
rде случайная величина U равномерно распределена на отрезке [О, 1).
Так построенные случайные величины (() (дзета) будyr иметь распреде
ления на множестве t: == {I, 2, . . . , N}, задаваемые соответственно вектором
l!. и соответствующими строками матрицы Р:
P{((O)==j}==Pj, p{((i)==j}==Pij, j==I,...,N, i==I,...,N.
72 rлава 1. Основные распределения и их моделирование
После этоrо уже можно моделировать цепь с использованием случайных
чисел (1) по следующему алrоритму:
110 == (О) (и о ) ,
112 == (VI)(И 2 ),
11) == (VII)(И 1 ),
IIТ == ((VТ I)(Ит).
(10)
Действительно, здесь
Р{1I0 == j} == Р{(О) == j} == Р}
и
Р{lIн! == ЛII1 == i} == p{(i) == j} == Pij,
что и требовал ось.
_ Примеры модели
РОВQНИЯ цепи
Пример 3 (Случайное блуждание с поrлощением),
Частица, стартуя в момент t==O из точки k, O<k<N,
блуждает по целым точкам отрезка [о, N]. Пусть St
положение частицы в момент t == 0,1,2 (ВО == k). Если в момент t ча
стица находилась в точке l (SI == [) и при этом 1 1 N 1, то в
следующий момент t + I она может оказаться в точке 1 + 1 с вероятностью
p(P{St+1 == l+ IISI == [} == Р) и в точке l I с вероятностью q == 1 p(P{St+1 ==
== 1 IISI == [} == q); в точках О и N частица поrлощается и блуждание пре
кращается (P{SI+I == 0ISt == О} == P{St+1 == NISt == N} 1). Здесь мы
имеем однородную цепь Маркова {SI, t == О, 1,2, ..} с пространством COCTO
ян ий {О, 1,2, ,N}, вектором начальных вероятностей l!. == (О 010 о),
rде 1 стоит на (k + I) M месте, и матрицей переходных вероятностей Ilpijll ,
в которой РОО == PNN == 1, Pi,i+1 == Р, Pi,i J == q, если 1 i N 1, и Pij == О
при li j/ > 1.
Таким образом, блуждание частицы по целым точкам отрезка [о, N] с по
rлощением на концах описывается указанной специальной цепью Маркова.
Чтобы смоделировать такое блуждание, надо положить ВО == k, SI+I == St + X t + J
до тех пор, пока О < St < N, rде X I + 1 == 1, если Ut+1 р, И Xt+1 == 1,
если U t + 1 > Р; если же SI впервые станет равным О либо N, то процесс
прекращается. .
Пример 4 (Случайное блуждание с отражением). Пусть переходные вероят
ности Pi,i+), Pi,i ) для 1 i N I и Pi,j для li jJ > 1 остаются теми же
самыми. Если определить еще Роо == q, POI == Р, PNN == р, PN,N I == q, то
полученная цепь Маркова описывает блуждание частицы по целым точкам
отрезка [О, N] с отражением на концах. Моделирование тзкоrо блуждания
отличается от предыдущеrо случая только в конечных точках: при St == О
полаraем SI+I == SI + X I + 1 == X I + 1 , rде
{ 1, если U t + 1 Р,
XI+l ==
О, если U I + 1 > Р,
9 1.3. Моделирование Вblборок из KOHKpeтHblX распределений 73
а при 8t == N полаrаем 8t+, == 8t + Xt+l == N + Xt+l' rде
{ о, если U t + 1 р,
X t +, ==
если U t +! > р. .
11. Метод Монте Карло
Отметим еще один Kpyr задач, при решении которых можно эффективно ис
пользовать реализации случайных испытаний. Речь идет о, так называемом,
методе Монте Карло, или методе статистических испытаний (ero название
происходит от rорода Монте Карло в княжестве Монако, знаменитоro свои
ми иrорными домами). Этот вычислительный метод часто используется при
отыскании значений различных величин (определяемых, например, HeKOTO
рыми уравнениями или интеrpалами), коrда этим величинам можно при
дать вероятностную интерпретацию. Сущность метода Монте Карло состоит
в следующем: исходя из смысла вычисляемой величины а, подбирают такую
случайную величину , чтобы ее среднее значение совпадало с а: Е{ == а.
Далее моделируют выборку (X j , , х п ) из распределения Ц ) и в качестве
оценки для а используют выборочное среднее
1
Х == (X, +
n
+Х П ).
Обоснованием этоrо метода служит следующее
Утверждение. Пусть Х" ,Х П незаВИСИМblе наблюдения над случайной
величиной , E == а, D > О и Е{4 < 00. TorAa распределение случайной Be
n
C 2 1"" 2
ЛИЧИНbI Тп == уn(Х a)/8, rAe 8 == L.J(X; X) ,сходится при n -----+ 00
n ;=,
к стандартному нормальному распределению N(O, 1) (см. упр. 44 к rл. 2).
Отсюда следует, что если "1 заданное число, близкое к 1 (О < "1 < 1),
и величина с-у удовлетворяет равенству Ф(С-у) == (1 + "1)/2, rде Ф(х) CTaH
дартная нормальная функция распределения (см. (7) 1.2), то
P{JTnl < С-у} == Р{ ..;n 1; al < С-у} -----+ Ф(С-у) Ф( С-у)== 2Ф(С-у) 1 == "1
(11 )
(:щесь использовано равенство Ф( x) == 1 Ф(х), V х Е Rl).
Соотношение (11) означает, что ошибка в определении а этим методом
приблизительно с вероятностью "1 не превосходит C-y8/';n, коrда n ДOCTa
точно велико.
Пусть, например, требуется вычислить интеrpал
а == !.. / f(t,...., t r ) dt, ... dt r ,
(2)
V,
74
rлава 1. Основные распределения и их моделирование
rде область интеrpирования есть т мерНblЙ куб V r == {(t 1, , t r ) О tj 1,
i == 1, ,т} Очевидно, что положив здесь == f(U 1 ,... ,U r ), rде {Uj}
числа из последовательности (1), получим а == E . Таким образом, в каче
стве приближенноrо значения интеrpала (12) в данном случае можно взять
величину
1 n
Х == 2: Х", Х" == f(U(" I)rH
n "=1
Например, этим методом можно получить приближенное значение числа
I
е == J е Х dx + 1:
о
взяв, скажем, n == 100 paBHo epHЫX чисел {U j } Здесь точность метода леrко
оценить, сравнив значение оценки е с извеСТНblМ нам ТОЧНblМ значением
е == 2,71828 ...
,и",.),
k: == 1,
,n.
1 n
е == L е И ; + 1,
n j=1
Упражнения
Свои способности человек может узнать,
только попытU6шись приложить их.
Сенека 12)
о Пусть имеет распределение Бернулли Bi( 1, р). Показать, что Щ и O имеют
вид (2) 1.1, а характеристическая функция ф(t) == Ee il { == pe il + Ч. Убедиться в спра
веДIIИВОСТИ следующих формул:
1
Щ == -:-1/1'(0), Щ == 1/I1/(0) + (ф'(0))2
ж
( 1)
D Пусть Х имеет биномиальное распределсние Bi(n, р). Показать, что ее средиее
и дисперсия имеют вид (4) 1.1, а для ее характеристической функции 1/I(t) справед
ливо представление 1/I(t) == (ре;1 + ч)n nроперить справеДIIИВОСТЬ формул (1).
11 Доказать свойство воспроизводимости распределения Bi(n, р) по параметру n:
если X 1 " .. ,X k независнмые биномиальные случайные величины и J:.(X j ) == Bi(nj ,р),
j == 1'... ,k, то [(Х, + ... + X k ) == Bi(n. + ... + nk, р).
... УКQЗQние. Воспользоваться критерием независимости для характеристических функ.
ций (см. (15) 1.2) и результатом упражнения 2.
11 Доказать, что биномиальные вероятности f(xJn,p) (см. (3) 1.1) при юмене
нии х от О до n сначала монотонно возрастают, затем монотонно убывают, достиraя
наибольшеrо значения при х == т, [де m определяется неравенстваМI1 (n + I)p 1 <
< т (n + I)p; если же т == (n + l)р, то наибольшее значение достиraстсл дважды:
J(m I!n,p) == f(mln,p).
12) Сснека (4 [. до '1. э. 65 [. н. э.) древнеримский философ, воспитатель Нерона; по ero
приказу покончил жизнь самоубийством.
Упражнения
75
I Убедиться н том, что формула (5) 1.1 для плотности отрицательной биномиаль
ной величины может быть записана также в виде
f(xlr,p) == ( I)XC rpxq' х == 0,1,2,...
Указание. Воспользоваться замечанием о биномиальных коэффиuиснтах lJ конце
п. 2 1.1.
П Пусть .е(о == Bi (r,p). Показать, что ее характеристическая Функuия имест IJИД
ф(t) == Ee i /( == ( ) r
1 ре'/
и, ВОСПОЛЬЗ0ваВШИСh формулами (1), убедиться в справедливости формул (7) 1.1.
IJ Доказать свойство воспроизводимости распределения Bi (r, р) по параметру т:
если X 1 ,. .. ,Х !> нсзависимые случайные величины и
.e(X j ) == Вi(rj,p), j == 1,..., k,
то
.с(Х 1 +... + X k ) == Вi(r, +... + rk,p).
Указание. Воспользоваться критерием независимости для характеристических Функ
ций.
О Пусть в Gернуллиевской последовательности {X j , j 3 I} с пара метром р слу
чайная величина 7),' означает число испытаний до пояnления r ro нуля вк.лЮ'lИтельно.
Выписать плотносн величины 1/r И найти ее среднее и дисперсию.
Указание. 1/r == + т, те .ею == Bi (r, р).
D Пусть случайная величина ( имеет распрсделение Пуассона П(л). Показать, что
ее характеристическан функuия есть ехр {>.(e il I)} и по формулам (1) вычислить пер
вые два момента (.
IШ Доказать свойство воспроизводимости распределения П(>.): если X 1 , ... ,Х !>
независимыс пуассонооскис случайные пеличины с параметрами лl,'" ,>'k COOТBeт
ственно, то
.е(Х 1 + ... + X k ) == П(ЛI +
+ >'k),
Указание. Воспользоваться критерием незаlJИСИМОСТИ для характеристических функ
ций.
m Пусть СJJучайные величины Х, и Х 2 независимы и .e"(X j ) == п{лi) , i == 1,2.
Доказать следующий факт для' условноro распределения:
>'1
.c(X1IX 1 + Х 2 == n) == Bi(n,p) при р == .
ЛI +Л2
m Доказать следующую преДСЛhНУЮ теорему (теорему Пуассона) о СХОДИМОСПI би
номиальноrо распределения к пуассоновскому: если n """'7 00, а р """'7 О так, что
пр """'7 Л > О, то Bi(n,p) """'7 П(л), Т. с. (см. (3) и (8) 1.1) f(xln, р) """'7 f(х!Л),
Х == 0,1,2,.
Указание. Воспользоваться следующим свойством о непрерывном соответствии .меж
ду характеристическими функциями и распределениями случайных величин: пусть имеется
последооательность случайных величин {7)п} и последовательность {фп(t)} COOTBeT
ствую их характеристических функций, тоrда, если для любоro t фп(t) """'7 1jJ(t) при
76
rлава 1. Основные распределения и их моделирование
n -----+ 00 и ф(t) есть характеристическая Функuия некоторой случайной величины Т"/.
с В б б .. с
то 1/n 1/. ер но и о ратное, т. е. l1З сла 011 сходимости Т"/" 17 следует СХОДИМОСТI,
соответствующих характеристических функций.
В рассматриваемом случае воспользоваться упр.2 и 9 и пределом (1 + Cn Z )" -----+ сО"
если n -----+ 00, сп -----+ О, а nЕ n -----+ а > О.
IIJ Доказать следующее утверждение о сходимости отрицательноrо биномиальноrо
распределения к пуассоновскому: Вl(T,p) -----+ П(Л), если r -----+ 00, ар -----+ О так, что
тр -----+ л > О.
Указание. См. указание к упр. 12, использовать упр.6 и 9.
m Пусть независимые случайные величины X j , Х], имеют лоrарифмичсское
распределение (21) Э 1.1, а независимая от них величина У имеет распределение
Пуассона П(r In (1/(1 е»)). Определим случайную величину Z как сумму СЛУ'lайноro
числа у слаrаемых из последовательности {X j } Z == Х ! + Х] + + Х у , Z == о
при У == О. Доказать, что .c(Z) == Bi (r, е).
Указание. Установить сначала, что характеристическая функция суммы Х 1 + . . . + Х N
есть j"((}e it ) / fn (е), rде I(e) == ln (1 /(1 (}) (см. (21) и (24) Э 1.1), и применить формулу
полной вероятности; в итоrе получить, что EC ilZ == ((1 е)/(I ee;I))' (см. упр. 6).
IИ Установить справеД)IИВОСТЬ формул (1 О) Э 1.1 Д)Iя Е{ и O rиперrеометрической
случайной величины.
Указание. Воспользовавшись формулой свертки:
" С , C " ' С П
L.....J А В А+В
х
и равенством (далее используется обозначение (х),. == x(x 1) . (X T+ 1), (х)о == 1)
(x),C == (A),c = , получить общее представление Д)IЯ r ro факториальноrо момента
E ( t ) == ,, ( ) С;, C ! ' == ( ) С::; == (а[),(n), r == 1 , 2 , ...
, L.....J х, С:; а! , СЛ (а)т'
х
Далее использовать формулы Е{ == ЕЮj, Щ == E( )] + Е{ (ц)2
1m Пусть в (9) Э 1.1 а! ==ар, а2 == aq, q == ! р, о <р < 1 Убедиться в том, что при
а -----+ 00 I(xlap, aq, n) -----+ C:'pXqn X, т. е. rиперrеометрическос распределение H(ap,aq, n)
сходится к биномиальному распределению Bi(n, р), коrда а -----+ 00, а пир фиксиро
ваны.
Указание. Записать формулу Д)IЯ f(xlap, aq, n) в виде
хр(р I/a)... (р (х I)/а). q(q I/а) (q (n х I)/a)
f(xlap, aq, n) == С" (1 !/а) (1 (п I)/a)
и перейти здесь к пределу при а -----+ 00.
ID Оценка числа рыб в озере. Пусть а (неизвестное) число рыб в озере. Предполо
жим, что из озера вылавливают а! рыб, помечают их и выпускают обратно. При повтор
ном отлове n рыб среди них оказалось х помеченных. Считается, что результаты двух
отловов можно рассматривать как случайные бссповторные выборки из совокупности
всех рыб в озере. Тоrда вероятность тoro, что оторой улов содержит ровно х помечен
ных рыб, есть как раз rиперrеометрическая вероятность I(xlaj, az, n). На практикс
Упражнения
77
числа а" n и х наблюдаются. Спрашивается, как по этой информации оценить неиз
вестное число а рыб в озере? Можно, например, найти такое значение а, при котором
вероятность f(xla), а al, n) достиraет CBoero наибольшеro значения, поскольку для
TaKoro а наше наблюдение имеет максимальную вероятность. Это значение а назы
вается оценкой максимаnЬНО20 правдоподобuя для а. Рассматривая отношение
f(xla" а al, n)
f(xla),a 1 al,n)
(а al}(a n)
а(а а, n + х) ,
убедиться втом, 'по оценка а есть наибольшее целое число, не превосходящее nа,/х.
Так, например, при al == 1000, n == 1000 и х == 100 величина а == 10000.
ПJ Пусть целочисленный случайный вектор!!. == (11" , IIN) имеет полиномиаль
ное распределение М (n, р). Показать, что ero производящая функция
N
IfJШ == Е П t?
j=,
есть
IOШ == (p,t , + + PNtN)n t == (t"..., t N ),
а производящая функция подвеIqора IIk == (11" . .. , IIk), k < N имеет вид
\I'(t" + t n , 1,...,1) == (1 + tpj(t j ,)У
J=)
Получить отсюда, что
.c(II)) == Bi(n,PI)'
.c(1I21111==XI)==Bi ( n xI, Р2 )
1 Р,
и вообще
.c(lIjlll/ == Х/, l == 1,..., j 1) == Bi ( n Х) .. . хн'
2";;' j";;'N
m (Продолжение). Вывести формулы ддя смешанных факториальных моментов про-
из80льныIx порядков компонент вектора !!.:
Р} )
1 Р, Pj ' .
N or,+...+rN N
Е П (lIj )rj == ot") ot'N \1'(1, .. . , 1) == (n)rl ++rN П p;j
j=1 ,N j=,
В частности,
Ellj == npj, Ellj(lIj 1) == n(n I)pj, Ellillj == n(n I)pipj, i =1= j.
Получить отсюда формулы (15) 1.1.
m (Продолжение). Обозначим
{ Pi(I Pi) при i==j,
O'ij
PiPj при i =1= j,
и Ek == [[О'и Ilt, k :( N. Убедиться в том, что IEkl == det Ek == Р, .. . Pk(1 Р, ... Pk),
следовательно, IENI == О (отражение связи 111 + + IIN == n) и IEkl > О при k < N.
Проверить, что EN' , == Ilgij[lf ', rдe gii == 1!р; + I/PN, gij == l/PN, i =1= j.
78
rлава 1. OCHOBHble распределения и их моделирование
m Доказать воспроизводимость полиномиальноrо распределения М(n, р) по пнра
метру п: еСШI векторы X 1 , . .. ,X k независимы и [(X j ) == M(nj, ), i == 1'...' k, то
[(Х, +
+ X k ) == М(n, +
+ nk, р).
.. Указание. Воспользоваться критерием независимости ДJlЯ характеристических (или,
что то же самое, длн производящих) функций.
Общее эамечание, Ранее (в 1.2) мы напомнили определение и некоторые свойства
характеристических функций, которые используются для ИЗУ'lения свойств любых
СЛУ'lаЙных величин. Но при работе с дискретными случайными величинами часто
более удобно использование проиЗ80дящux функций, опреде
ляемых соотношением
Ф Ai
.,. Производящие .
фун кци И .118
<p{(z) == Ez{ == I>.p{ == Х},
Iz[ :( 1
х
(для мноrомерной случайной величины { == (€I ... k) производящая функция опре
деляется как 1p (ZI"" ,Zk) == Ezf' " _ z1'). Характеристическая функция -ф{(t) == ЕеЩ
выражается через ПрОIlЗВОДЯШУЮ функцию р:шенством -ф{ (t) == Ip{(e jt ) , и потому
свойства производящих функций аналоrичны СВОЙСТ!Jам характеРИСТИЧССКIIХ функ
цин. Например, критерий независимости звучит так: компонеllТЫ (дискретноrо) слу
чаЙноrо вектора Х == (Х " . .. ,X k ) незaIJисимы Torдa и только Torдa, Korna ero про
изводящая функция имеет вид
Ipx(Z"... ,z ) == 'Рх, (ZI) .. . <Рх. (Zk),
m Доказать, что между полиномиальным и пуассоновским распределениями суще
стоует следующая связь: если слу'шнные величины 1]1.... ,1]N незаВI1СИМЫ и [(1]j) ==
== П(Аj) , j == 1,. , N, то для их cOBMecTHoro условноrо распределения спраDедливо
представление
[(1]"...' 1]NI1]1 +... + 1]N == n) == M(n,PI,'" ,PN),
rAe
\
Pj==):, j==I....,N, Л==ЛI+...+А N .
.. Указание. Вычислить условную вероятность
P{'7I==XI. 1]N==XNI1]I+ +1]N==n}
и убедиться, что она имеет вид (14) 1.1.
m Пусть 8 схеме полиномиальных испытаний число испытаний есть случайная ве.
личииа У с распределением Пуассона П(л). Показать, что частоты исходов 1'1, ... ,VN
независимы и [(Vj) == П(ЛРj), j == 1,. .. ,N.
.. Указание. Используя упр. 18 и формулу полной lIеронтности, ОЫ'IИСШIТЬ совместную
производящую функцию частот V" . .. , VN; воспользоваться критерисм независимо
сти дЛЯ ПРОИJВОДЯЩI1Х функций.
m Показать, что ПРОИJводящая функция распределения cTeneHHoro ряда (20) 1.1
есть <p(z) == f(rJz)/ Л(}) и с ее помощью доказать формулы (23) 1.1 для моментов.
.. Указание. Через прОИJводящую функцию моменты находятся по формулам:
E€ == <p ()). щ == <p (I) + \p (I) (<p (I)(
Упражнения
79
m (Продолжение). Найти производящую функцию суммы Х) + + х n независи
MblX слаrаемых, имеющих одно и то же распределение cTeneHHoro ряда, и с ее помощью
установит[, формулу (24) 1.1.
m Исходя из вида характеристической функции нормальной случайной величины
с .ею == N(jl, (1"2):
ф(t) == ехр { itjl 2 t 2 }
И используя формулы (1), убедиться в справедливости формул (4) 1.2.
m с помощью характеристических функций установить свойство (5) 1.2 нормаль
ных случайных веЛИ'IИН.
m Показать, что если Х 1 и Х 2 независимые одинаково распределенные HOp
мальныe случайные величины, то их сумма Х) + Х 2 и разност[, Х, Х 2 независимы.
Указание. Вычислить соу(Х, + Х 2 , Х, Х 2 ) 1I убедиться в том, 'ПО она равна О.
Вообще, если Х., . . . , Х n случайная выборка из нормальноrо распределения N(!J., 0'2)
И Х == (l/n)(XI + .. . + Х n ), то Х и вектор (Х, Х, . .. 'Х n Х) независимы' так
как все ковариации соу(Х, X j Х) == О, i == 1,... ,n. Отсюда, между ПРО'IИМ, следует
независимость Х и 82 (см. (22) 1.2), так как 82 есть функция лишь от разностей
Xj X.i== I,....n...
m Пусть случайный вектор { == ( ., '" , k) имеет нормальное распределение
N(I!.. == lI(1"ijll ).
Доказать, что F{ == 1:., О{ == , т. е. Щj == Jlj, COV( j, j) == (1"jj, ,j == 1, ... , k.
Указание. Использовать общую формулу ДJlЯ моментов
д" +. "+'k
,Т. (О) "'+"'+'k E( t r , "k ) ....
д '1 д 'k .... { z \'1 .., \'k . ...
t) t
II!I (Продолжение). Показать, что подвектор , == ( I,' .. , ,), 1 ::; r < k, имеет HOp
мальное распределение N((!J.,. ,!J.,), Е, == II00ijll ).
Указание. Характеристическая функция подвектора {, есть
ф{(t l ,... ,t" О,... ,О),
rде ф{,(t l ,..., tt) дана в (16) 1.2. ..
IП Пусть Х == (Х" ,X ) стандартный нормальный вектор и U произволь
ная k х k ортоrональная матрица (т. е. и' == u I). Показать, что У == U Х также CTaH
дартный нормальный вектор.
m (Продолжение). Пустьтеперь L произвольиая тх k матрица и !! произволь
ный т-вектор. Показать. что т Beктop У == LX +!! имеет нормальное распределение
N(!!,LL').
m Пусть вектор == (V).... ,VN) имеет полиномиальное распределение М(n, Е.)'
rде О < Pj < 1, j == 1,..., N. Обозначим 1/; == (I/j npj)/Vn, j == 1'...' N,
1/' == (1/;, . .. , I/ ) (заметим, что 1/; +. .. + 1/;'; == О). Доказать центральную пределыlюю
теорему для полиномиальноro распредсления: если n ---t 00, то .е( I/' ) ---t N(Q, E N ),
rде дисперсионная матрица N указана в упр. 20.
80
rлава 1. Основные распределения и их моделирование
. Указание. Воспользоваться свойством о непреРblВНОМ соответствии между xapaK
теристическими Функuиями и распределеннями случаЙНblХ величин (см. указание
к упр. 12), которое справедливо также и для векторных случаЙНblХ величин, и YCTaHO
вить сходимость (используя упр. 18)
1 N 1 ( N ) 2 1
1im 1п IV . ( t ) == p t2 + p .t, == t'E N t.
""'0:> IC... 2 11 2 1 1 2
j 1 j 1
Замечание, Поскольку матрица EN Вblрождена (см. упр. 20), то предельное HOp
мальное распределение является несобственным, однако для любоrо подвектора
v' k == (v;, ,v;), k < N, будем иметь уже сходимость к собственному HOp
мальному распределению: [( 1/' k) ----+ N(Q, E k ). В частности, при k == 1 получаем
знаменитую теорему Муавра Лапласа о сходимости биномиальноrо распределения
к нормальному: .c(v;) ----+ N(O,PI(I р,)) или
.с ( 1/1 nРI ) ----+ N(O, 1)
.J np,(1 р,)
(поскольку [(1/1) == Bi(n,PI). см. упр.18).
m (Продолжение). Пусть теперь при n ----+ 00 вероятности Pj ----+ О, j == 1, ,N 1,
и при этом npj ----+ Л j , о < Л j < 00, j == 1,. , N 1. Это озна'lает, что при бол b
шом числе ИСПblтаний n ИСХОДbl с номерам и 1, 2, . ,N 1 будут IJстречаться редко
(в среднем .\"..., .\N I раз соответственно). Доказать, что компонеНТbI 1/1'... ,I/N I
будyr асимптотически незаВИСИМbI и прн этом .c(l/j) ----+ П(Л j ) , j == 1,... , N 1.
Указание. Установить сходимость для характеристических функций
N I
IVv'....vNjt l '. ,tN I) ----+ П ехр {Лj(е'lj I)}.
j 1
(см. упр.9 и 18).
IИ (Продолжение). Доказать, что распределение слу'шйной веЛичИНbI 1} == n I/N
сходится К распределению Пуассона П(.\I + + .\N I)'
. Указание. Заметить, что" == VI + + I/N I и воспользоваться упр. 10 (или преды
дущим результатом).
m Установнть справешlИВОСТЬ формул (21) 1.2 для момеНТОIJ rамма распределения,
предварительно получив представление (20) 1.2 для ero характеристической функции
и воспользовавшись соотношениями (1) в упр.l.
ID Пусть X 1 ,..., X k независимые случаЙНblе величины и .c(X j ) == r(a, .\j),
j == 1, ,k. Показать, что для любой постоянной с> О
.с (c(X 1 +... + X k )) == f(ca,.\, +
+ '\k),
. Указание. Воспользоваться свойствами характеристических функций.
lI3 Показать, что если X 1 , . .. , Х N незаВИСИМblе стандартные нормалЬНblе величи
Hbl, то .c(X +.. .+X ) == х 2 (n) == r(2, n/2). ОСНОВblваясь на uентральной предельной
теореме (см. (1) 1.2), установить, 'ITO при n ----+ 00
( Х 2 + + х 2 N )
.с I v'27i n ----+ N(O, 1).
Упражнения
81
... Указание. Сначала установить, что .e(X ) == r(2, 1/2), далее воспользоваться свой
ством воспроизводимости raмма распределения.
m Пусть X 1 , ,Х . независимые показательные случаЙНbJе величины с распре
делениями r(ai, 1), i == 1, , k, соответственно. Показать, что случайная величина
У == min{X 1 ,.. ,X k } имеет распределение r(I/al + + l/ak) I, 1)
... Указание. ВЫ'IИСЛИТЬ Р{У > у}.
!I!J Пусть k мерный нормальный вектор ( имеет собственное распределение N(p, ).
Доказать, что квадратичная форма
Q({) == ({ )' I({ !!.)
имеет распределение i(k).
... Указание, Рассмотреть линейное преобразование Z. == Л 1/2u' ({ ), переводящее
вектор { в стандартный нормальный вектор (см. п. 2 1.2), тоrда
Q({) == z.'z. == zi + + ZZ,
далее использовать упр. 38.
m Пусть о распределении случайных величин ( и Л (лямбда большое) известно,
что .е(л) == r(a, r), rде r целое, а условное распределение .е((lЛ == л) == П(>.).
По казать, что.ею == Вi(r,p) при р == а/(а + 1).
... Указание. Вычислить безусловные вероятности
/ "" >.k >.r 1
P{ == k} == e >' е Лfа dл, k == 0,1,
k l r(r)a r
о
и убедиться, что они имеют вид (5) 1.1.
m Пусть случайная величина ( имеет бета распределение Ве(а, Ь). Вычислить
Е(I О', r, s О, и получить отсюда формулы для Е{ и Щ (24) 1.2.
... Указание. Воспользоваться определением бета функции В(а, Ь) и свойствами raM
ма функции r(л) (см. п. 3 1.2).
m Пусть случайные величины Х 1 и Х 2 независимы и .e(X j ) == r(a, >'i), i == 1,2.
Доказать, что случайные величины У, == Х 1 + Х 2 и У 2 == X1/(X 1 + Х 2 ) независимы
и при этом .e(Y 1 ) == r(a, лl + Л2), а .е(У 2 ) == Be(>'I, >'2)'
... Указание. Применить формулу (44) 1.2 при вычислении совместной плотности
преобразованноrо вектора У == (Y 1 , У 2 ) И убедиться В том, что она есть произведение
марrинальных (одномерных) плотностей указанных raMMa и бета распределений.
m Пусть о распределении случайных величин ( и f) ИЗВестно, что
( al а2 )
.e(f}) == Ве 7' 7 '
rде а" а2 и с натуральные числа, а условное распределение .е({l1] == р) == Bi(n,p).
Показать, ,(то безусловное распределение ( есть распределение Маркова Пойа
МП(n; al, а2, с) (см. (11) 1.1); получить отсюда формулы (13) 1.1.
6 За"", 1748
82
rлава 1. Основные распределения и их моделирование
... Указание. Вычислить безусловные вероятности
I
Р { ' == Х } == С Х jP X ( 1 p) n X [(а/с) а,/Н ( I ) a2/C ld
" r(al/c)f(a2/ C )P р р,
о
а == al + а2,
и, воспользовавшись свойствами rамма Функuии, убедиться в том, что они имеют вид
(11) 1.1. При выlислениии моментов учесть, что r й факториальный момент биноми
альноro распределения Bi(n,p) есть (n),р' (см. ynp.19).
m Вывести формулы (26) 91.2.lU\Я моментов paBHoMepHoro распределения И(а, Ь),
а также получить вид ero характеристической функции
eilb e ita
w(t) == it(Ь а)
m Пусть (X 1 ,..., Х n ) СЛУ'lайная выборка из распределения И(а, Ь) и У
== min{X 1 ,..., Х n }, Z == max{X 1 ,... ,Х,,} Вывести вид совместной плотности слу
чайных величин У и Z:
{ n(n 1) ( ) n 2
z y
J(y, z) == О(Ь а)"
при а у < z Ь,
в остальных случаях.
Получить следующие формулы для моментов:
na+b
ЕУ ==
n+ 1 '
n(Ь а)2
ОУ == DZ ==
(n + 1)2(n + 2)'
а+nЬ
EZ ==
n+ 1 '
(Ь а)2
соу(У, Z) == ( 2( .
n + 1) n + 2)
11 Пусть случайная величина { имеет равномерное распределение U( rr/2, rr/2).
Показать, что случайная величина '1 == tg { имеет распределение Коши, зздаваемос
плотностью (31) 1.2.
... Указание. Сначала выписать функцию распределения F'/(X) == Р{17 Х}, диффе
ренцированием которой получить плотность.
m
а) Пусть X 1 и Х 2 незаоисимые стандартные нормальные случайныс uеличины.
Показать, что их отношение X 1 / Х 2 распределено по закону Коши.
... Указание. Плотность отношения ( == /17 двух нсзависимых СЛУ'lайных Be
личин, плотности которых J{ и Jq известны, вычисляется по Формулс
00
J,(y) == j J((xY)f./(x)lxl dx.
(2)
oo
б) Распределение Коши с параметром сдвиrа а (060зна'lается К(а» определяется
плотностью
1
1r I + (X' а)2'
х Е я l
Упражнения
83
(так что формула (31) 91.2 соответствует случаю а == О). Убедиться в том, 'по
характеристическая функция закона К(а) есть ехр {iat itI} и доказать следую
щий факт: если случайные величины X 1 ,... ,Х ,. независимы и .e(X j ) == K(aj),
j == 1, . . . , n, то .е(х) == К(й), rде черта означает среднее арифметическое.
m Провеr ить , что стьюдентово отношение t" (см. (27) 9 1.2) имеет моменты Et:
лишь при k < n, при этом моменты нечетноro порядка равны О, а
2" 1 . 3 . . . (2т 1 )n"
Ш N == при 2т < n.
(n 2)(n 4) ... (п 2т)
Получить отсюда формулы (30) 91.2.
... Указание. Учесть, что если .ею == N(O, 1), то E{2r+1 == О, Е{2" == 1 3... (2т 1),
а также формулы для моментов raмма распределения (см. п. 3 9 1.2).
m (Продолжение). Установить, что
( 1 ) ( n ' )
.е == Ве
1 + t /n 2' 2 .
... Указание. Воспользоваться упр. 43.
m
а) Показать, что если Х имеет распределение Снедекора В(n, т), то У == I/X
имеет распределение В(т, n).
б) Пусть t" имеет распределение Стьюдента В(n). Показать, что .e(t;.) == 8(1, n).
m Пусть F(x; n, т) функция распределения закона 8(n, т), а В(х; а, Ь)
ФУНКЦИЯ бета распределения Ве(а, Ь). Установить равенство
( nх n т )
F(x; n, т) == В т + nх ; 2'"2 '
х > О.
Получить отсюда выражение (33) 91.2 ДЛЯ плотности распределения 8(n, т). Найти
моменты этоrо распределения (35) 91.2.
... Указание. Записать соотношение (32) 9 1.2 в виде
т У
F,
", т n 1 У ,
x
rде У == , 2 '
Хп +Х,n
и воспользоваться упр.43, в силу Koтoporo .е(У) == Ве(n/2, т/2). Моменты выисля
ются по формулам
EF:, т == ( y E(X )rE(x ) r
используя далее формулы для момеитов rамма распределения.
liJ (Продолжение). Установить, что
( nр".т ) ( n т )
.е Be
т + nFn. "' 2' 2
6*
84
rлава 1. OCHOBHbfe распределения и их моделирование
ИI ПустьХ == (X 1 , ,Х/,Х/+!,. ,X 1 + m ) случайная выборка из показатель
Horo распределения r(a, 1) и
т Х 1 + + Х/
У ==
1 XI+I +.. +Х'+1II'
ДоказаТI>, что .с(У) == 5(21, 2т).
... Указание. Воспользоваться упр. 37, в силу KOToporo
.с ( (X! + .. . + X 1 ») == r(2, 1) == /(21)
и аналоrИ'lНО
.c( (XI+1 +
+ Х/+т») == х!(2т).
m Пусть случайная величина ( имеет Р<lспределение Вейбулла W(a, а, Ь) (с/./. (36)
1.2). Доказать формулы (37) 1.2 для Щ и щ.
m (Продолжение). Пусть (Х.,..., ХП) случайная выборка l1З распределения
W(a, а, Ь) и У == min{X 1 ,..., Хп}. Показать, что
( У а )
.с п'/О == W(I, а, О)
и ПОЛУ'IИ1Ъ отсюда следующие формулы для моментов У
ЕУ == а + Ь r (1 + ) п '{о ,
DY == ь 2 [r( 1 + ) r! (1 + )] n 2{o
... Указание. Вычислить Р{У > у}.
m Пусть { имеет распределение Парето с napaMCTpaMII хо 11 а: (C I. (38) 9 1.2). Для
каких натуральных значений k существуют моменты щk? Показать, что при а > 2
справеДЛИВbI формулы (39) 9 1.2 для и щ.
m (Продолжение). Доказать, что случайная оеЛl1'lина ТJ == In (иХО) имееТ показа
тельное распределение r(I/a:, 1) (см. п. 391.2).
... Указание. Примеиить формулу (45) 9 1.2 либо непосредственно вычислить функ
цию распределения Fq(t) == Р{ ТJ :( t}
ш Пусть о распределеиии случайных величин ( и ТJ lIЗоестно, что ( имеет pac
пределение Парето с параметрами ХО и а, а условное распределение ТJ при условии,
что ( == (J, является равномерным И(О, (J). Доказать, 'ПО условное распределение
.c((IТJ == х) есть распределение Парето с параметрами тах(хп, х) и а: + 1.
Упражнения
85
Указание. Если f{(O) и fq(x) есть марrинальные плотности веЛИ'IИН 11 Тf, а
fql{(xIO) плотность УСЛО8ноrо распределения .c('7I == О), то плотность f{lq(Olx)
условноrо распределения .сЮ'7 == х) вычисляется по фор
1) ) УСЛОВНblе .. \.
муле Байеса
f ( 8 I х ) == f{(O)fql{(xI8) .
q ( '
(3)
расп ределе н ия
и формула Байеса
при этом
f,,(x) == J f"I{(xI8)f{(8) dO
является нормирующим. множителем, не зависящим от переменной О условной
плотности f{lq(Olx), и потому вычислять ero явное значение в конкретной задаче
не обязательно (плотность любоrо распределения достаточно DЫЧИСЛЯТЬ с точностью
до нормируюшеrо множителя: f(x) == ер(х) р(х».
в нашем случае записать
f{(8) 8 a 11 (8 > хо), f"I{(xI8) == O 11 (О> х),
rде (напомним) 1(.) индикатор. ..
m Предположим, что X 1 , .. . ,X k независимые случайные величины и Х ; имеет
raMMa распределение r(a, i), i == 1, ... ,k. Пусть случайный вектор У == (Y 1 , .. . , Y k )
определяется соотношениями
Х;
у; == , , k.
X 1 + +X k
Доказать, что вектор У и случайная величина Х == Х) + + X k независимы и при
этом У имеет распределение Дирихле D( == ( I, , n») (распределение Х указано
в уПр. 37).
... Указание. Это упражнение является обобщением упр.43 и доказывается анало
rично. ..
m Доказать формулы (41) 91.2 для моментов распределения Дирихле D(g).
... Указание. Использовать формулу (42) 9 1,2 для интеrpала Дирихле и свойства raM
ма ФУIIКЦИИ. ..
m Пусть о распределении случайных векторов!!. == (VI,.", VN) и == ({I,.'., {N)
известНО, что .с({) == D(q/ с), rде q == (al. . . . , aN) и все а; и с натуральные числа,
а условное распределение .c( I{ == ) есть полиномиальное распределение M(n; )
(см. п. 6 9 1.1). Показать, что безусловное распределение вектора !!. есть N MepHoe
распределение Маркова Пойа МП(п; q, с) (см. П.7 9 1.1); получить отсюда формулы
(19) 9 1.1.
... Указание. Эта упражнение является MHoroMepHbJM обобшением упражнения 44 и
доказьшзстся аналоrично с использованием формулы (42) 9 1.2 для интеrрала Дирихле
и свойств raмма функции: в данном случае надо вычислить беЗУСЛОDные вероятности
P { == ;!;. } == "! I П N '; r(a/c) П N ajfc 1 d
, 1 Pj r( / ) r( / ) Pj PI
x l ' ... xN.. al с .. aN с ,
s }=I }=I
. dPN 1
13) Байес Томас (1702 1761) анrлийский математик веРОЯТНОСТI1ИК.
86
rлава 1. OCHOBHble распределения и их моделирование
(здесь область интеrрирования S определена 11 (42) Э 1.2, Р.... =с I Р, PN "
а =с а, + + а.... и f. (х" ,Х.у) ПРОИJВОЛЬН IЙ целочислеННblii вектор
с х, +.. . + Х.... =с n), и убедиться в том, что они имеют вид (17) Э 1.2. При ВbI'lислении
моментов Y'lecTb формулу для факториалЬНblХ моментов полиномиал ноrо распреде
ления (см. упр. 19).
Замечание. В этом упражнении речь идет о модели смеси вероятностных pacпpe
делений: в данном случае рассматривастся смесь полиномиальных распределений
М(n; р), rде I1ектор Р предполаrается слу'lайныM вектором, имеющим распределение
Дирихле, по этому .смсщивающему') распределению. Таким образом, установленный
результат можно сформулировать в этих терминах следующим образом: М/Юi!ОАlерное
распределе((//е Маркова Пойа является смесью полиномиальных распределениЙ по pac
пределению Дирш:ле.
Соответствующий «одномерны,)) результат упражнения 44 теперь ЗВУЧIIТ так: распре
деление Маркова Пойа МП(n; al, а2, с) является смесью биномиалЬНblХ распреде
лений Bi(n, р) по бета распределению: [(р) =с Ве(а,/с, а2/ с).
m Пусть о распределении случайных 1IeKTOpOB !!. =с (v" , VN) И { =с ({r, ,{N)
известно, что { имеет распределение Дирихле D(Q:) , а УСЛОIlное распределение
l(!!.I{ =с (J) есть полиномиальное распределение М(n; (J). ПоказаТI>, что условное pac
пределение
l({I!!. =с ) =с D(Q. + fJ
... Указание (см. указание к упр. 59). Если Х[, , Х.... целые неотрицательныс
числа, удовлетворяющие условию Х, +. .. + XN =с n, то в нашем случае условная плот
ность
а f J(J) o ' '
f I{( IO) (J '
OC;: ' , следовательно,
OXN
N
f{I ((JI ) ff,(O)f I{('f.I(J) O '+X, I ... O N+XN I
Замечание. В статистических приложениях часто предполаrаетс!!, что наблюдаемая
Вblборка (данные) Х имеет распределение из HCKoToporo парамеТРИ'lескоrо семейства
распределсний :F =с {F(x; О), О Е 8} (в данном случае Х =с !!. и :F =с М(n; О)
СопряжеННblе семейство vполиномиальных распределений), а о пара метре
семейства этоrо семеиства предполаrается, что он случаен, и ero aпpиop
ное распределенис ,[,(0) Е :F' заданному семеЙСТIIУ априор
распределении " п ( :F ' D( » С ..
HblX распределении и 11 нашем СЛУ'lае =с Q.. емеиство
:F' наЗblвается сопряжеНIIЫАI к семейству :F (обозначаетс!! :F' <:] :F), еСЛII при Х =с Х
апостериорное распределение пара метра .c(OIX =с х) Е :F' т. е. находится 11 том же
классе распределений, что и априорное распределение параметра. В этих терминах
полученный резул тат ЗIlУ'НIТ так: D(Q.) <:] М(n; О), т. е. распределение Дирихле сопря
жено к полиномиальному распределению.
АналоrИЧНblЙ результат мь! имели и в упр. 59: распределение Парето сопряжено к рав-
номерному распределению ЩО, О).
m Убедиться в справедливости также следующих yrверждений
(ниже Х =с (Х"... , Х n ) СЛУ'lайная I1ыборка и х =с х[ + + Х п ):
1) Ве(а, Ь) <:] Bi(т. О), при этом
.c(OI X =c ) =с Ве(а + х, Ь + nт х);
Упражнения
87
2) Ве(а, Ь) <1 Bi (r, О), при этом
.c(OI X == == Ве(а + х, Ь + nт);
3) r(a, >') <1 ЩО), при этом
.c(OI X == .f) == r ( па а+ 1 ' >. + х) ,
4) r(a, >') <1 r(o l, 1), при этом
.c(OI X ==.f) == r Cx: l ' >. + n);
5) N(p., 0.2) <1 N(O, ь 2 ), при этом
.c(Oj X == .f) == N(jjl' /7;), rде
р., == ( :2 + )/7;' /7; == ( ;2 + ) I
6) распределение Парето с параметрамн Ха и а сопряжено к равномерному pac
пределению И(О, О), при этом апостериорное распределение О при наблюдении
Х == .f есть распределение Парето с параметрами таХ(Ха, XI, ,Х п ) И а + n.
... Указание. При нахождении апостеРИОРНblХ плотностей (3) следовать указанию
к упр. 59.
m Пусть случайный вектор { == ('1,6) имеет двумерное собственное нормальное
распределение
N ( р." jj2), 11 /7; ра\(72 11)
Р(1", (1"2 /72
rде 1 < р == corr«( 1, (2) < 1. Доказать, что условное распределение
.с('21', == х) == N(M(x), (72),
rде условное среднее
/72
М(х) == Е(6", == х) == р.2 + p(x 11-1)
/7,
функция рарессиu '2 на ", являющаяся в данном СЛУ'lае линейной по х, а условная
дисперсия
(1"2 == D(Ы" == х) == (1 p2)(1"
не завис ит от х. Существуют ли друrие распределения .с({) , ОТЛИчные от нормальноrо,
обладающие такими же свойствами условноro распределения .с('21', == х)?
... Указание. Вычислить условную плотность величины 6 при условии '1 == Х по фор
муле 1<2I{, (ylx) == IЫ1(Х' у)/1{I (х) и убедиться в том, что она равна
1 { 1 2 }
ехр (y М(х)) .
Vh(1" 2(1"2
m (Обобщение на мноroмерный случай). Пусть Х == (Х"... ,ХН), У == Х т , r 2,
и совместное распределение
.с(Ж, У) == N (jj,.... , I1-r), 'f.; == II/7ijll ),
rдe матрица 'f.; не вырождена и 'f.; 1 == II/7ijll . Доказать, 'ITO
.c(YI X ==.f) == N(M( ), 1//7rr) ,
88
rлава 1. Основные распределения и их моделирование
rде
r 1 ir
M( ) == E(YIK == ) == IlT L:)x; Ili) и тт , == (Xi,'" ,хн).
i I (1
... Указание. Записав совместную плотность в виде (см. (9) ] .2)
fж.у(ХI,... ,хн,х т ) == Сехр { t (1i j (Xi lli)(Xj P-j)} ==
,,} I
[ T I ]
== С ехр { иТТ(х. 11.)1 + 2(х. Р-т) 2:>iT(Xi Ili) +
_=I
},
получить, что перемениая Х т войдет в ВbIражение условиой плотности fYIJ::(XTI )
в виде
{ тт ( . I ) 1 }
и iT Х; Р-;
ехр 2"" Х. р-. + L и .
.=1
m Оценить методом Монте Карло величину плошади а == "К/4 под дуrой единич
ной окружности х1 + у1 == 1, Х, у ): О.
rлава 2
Первичная обработка
экспериментальных данных
Дело Ifе в цифрах, а в том, что вы с IIИМИ делаете.
Данная rлава представляет собой общее введение в теорию выборочноro
(статистическоrо) метода. Здесь рассматривается ситуаuия, коrда исходные
данные (выборка) получаются в результате проведения повторных независи
мых наблюдений (измерений) над некоторой случайной величиной , закон
распределения которой в течение Bcero эксперимента остается неизменным.
Как уже отмечалось во Введении, в этом случае выборка представляет co
бой n мерный вектор Х == (X 1 ,. ,Х п ), rдe n число наблюдений (объем
выборки), а компоненты X j независимые копии наблюдаемой величины ,
т. е. имеющие такое же распределение, как и . в этом случае rоворят, что
Х == (Х" ,Х п ) есть случайная выборка (или просто выборка) из распреде
ления (или из .с (О ). в теории выборочноrо метода (или кратко: выборочной
теории) изучаются различные свойства случайной выборки и функций от нее.
В этой rлаве мы введем основные понятия выборочной теории, приведем
фундаментальные теоремы математической статистики, исследуем в точной
и асимптотической (т. е. при большом объеме выборки) постановках свойства
основных характеристик случайной выборки.
t 2.1. вариационный ряд выборки, эмпирическая функция
распределения и rистоrрамма
ВерlfО определяйте слова, и вы освободите
мир от половИIfЫ Ifедоразумеиий.
р. Декарт 1)
1. Порядковые статистики и вариационный РЯА выборки
Итак, пусть Х == (X 1 , ,Х п ) выборка из HeKoToporo распределения IЦ).
Произвольной реализаuии == (Х), . . . , Х п ) этой выборки можно поставить
в соответствие упорядоченную последовательность
Х(I) Х(2)
Х(п),
(1)
1) Декарт Рене (1596 1650) французскиЙ математик, физик.
90 rлава 2. Первичная обработка экспериментаЛЬНblХ данных
располаrая XI, ,Х n В порядке их возрастания, так что Х(I) == min{XI,' .. , Хn},
Х(2) второе по величине значение, Х(n) == maX{XI, , Х n }'
Обозначим через Х щ случайную величину, которая для каждой реализа
ции f. выборки Х принимает значение Хщ, k == 1, ,n. Так по выборке
Х определяют новую последовательность случайных величин Х(I), 'Х(n)'
называемых порядковыми статистиками выборки; при этом Хщ k я поряд
ковая статистика, а Х(I) и Х(n) экстремалыlеe (соответственно минималь
ное и максимальное) зна'lеllUЯ выборки, их разность р == х(n) X(I) называют
размахом выборки. Из определения порядковых статистик следует, что они
упорядочены по возрастанию их значений, т. е. они образуют возрастающую
последовательность
q...,
frta'р яд которая называется вариационным рядом выборки Х.
Симметричные относительно концов элементы после
довательности (2) Х(т) и X(n т+l) иноrда называют соответственно т M
минимальным и т M максимальным значениями выборки, или т ми нижним
и верхним экстремумами (т == 1,2, .). Важной характеристикой вариаци
oHHoro ряда выборки является ero медиана (или середина), которая равна
X(k+I)' если n == 2k+ 1, и (Хщ + X(k+J»)/2 при n == 2k. В дальнейшем под
термином «основные характеристики выборки» будем понимать совокупность
ее экстремальных значений, размаха и медианы.
Итак, вариационный ряд это расположенные в порядке возрастания
их величин элементы выборки. Подчеркнем, что для заданной реализации
f. == (XI, , X/I) выборки Х == (Х" ,Х n ) реализацией послеДОВ31'ельно
сти (2) является последовательность (1). Вариационный ряд является одним
из стандартных способов представления выборки.
X(I) Х(2)
Х(n),
(2)
2, Эмпирическая функция распределения
Введем теперь фундаментальное понятие математической статистики, KaKO
вым является эмпирическая функция распределеllия. Для этоrо определим CHa
4ала для каждоrо действительноrо Х случайную Dеличину j.Jn(X) , равную числу
элементов выборки Х == (X 1 , ,Х n ), значения которых не преlJОСХОДЯТ Х,
Т.е,
n
j.Jn(X) == 2: I(X j х),
i 1
(3)
1
и положим рn(х) j.Jn(x) это И есть эмпирическая функция распре
n
деления (далее используется сокращение э. ф. р.). соответствующая выбор
ке Х. Функцию распределения Р(х) наблюдаемой случайной величины
в этом контексте называют теоретической функцией распределения. По CBoe
му определению э. ф. р. случайная функuия: для каждоro Х Е я l значе
ние рn(х) случайная величина, принимающая значения О, 1/n, 2/n, . .. ,
2.1. ВариациОННblЙ ряд Вblборки, э. ф. р. u 2истосрамма 91
(п 1)/n, n/n '=' 1, при этом
{ k }
Р F7!(X) '=';: '=' Р{р,,(х) '=' k}.
С каждым X j , можно связать два события: {Xj х} и {Xj > х}. Вероятности
этих событий, очевидно, равны
р '=' P{Xj х} '=' F(x), q'=' P{X j > х} '=' 1 F(x).
Если событие {X j х} назвать успехом, то р" (х) является числом успехов
в n независимых испытаний Бернулли с вероятностью успеха р, поэтому
рп(х) имеет биномиальное распределение Bi(n, р) с р '=' F(x) (см. п. 1 1.1).
Следовательно,
{ ( k } k k () nk
Р Fn х) '=';: '=' CnF (х)(1 F х ) ,
k '=' О, 1, . . . , п.
(4)
Итак, э. ф. р. (как и вариационный ряд) HeKO
торая сводная характеристика выборки. Для каждой pe
ализации выборки Х функция Р,,(х) однозначно
определена и обладает всеми свойствами функции распределения: изменяется
от О до 1, не убывает и непрерывна справа. При этом она кусочно постоянна
и возрастает только в точках последовательности (1). Если все компоненты
вектора различны (в последовательности (1) все неравенства строrие), то
функция рn(х) задается, очевидно, соотношениями
Расп ределение "
э. ф. р.
Р.(х) { /n
при
при
при
х < Хр),
ХЩ Х < X(k+l),
х? x("j'
k '=' 1, .
,п 1,
т. е. в этом случае число скачков равно n и величины всех скачков равны I/n;
типичный rрафик функции Р,,(х) имеет вид, изображенный на рис. 1.
F..(X)
- - :
,
,
,
' . - I
,
,
, n
Х(1) Хщ О Х())
Х(п l) Х(п)
х
Рис. 1
Пример 1. Реализацией выборки Х (X 1 , ,Х6) являются следующие
данные: 1 ,5; 2,6; 1 ,2; 2,1; 0,1; 0,9. Найти ее основные характеристики и по
строить эмпирическую функцию распределения.
92 rлава 2. Первuчная обработка экспериментаЛЬНblХ aaHHblX
1
5/6
2/3
1/2
1/3
,...........!.- . 1/6
I
Р6(Х)
I
r----
I
2,1 1,5
х
00,1
0,91,2
2,6
Рис. 2
Прежде всею строим вариаuионный ряд: 2,]; 1,5; 0,1; 0,9; 1,2; 2,6. OT
сюда видно, что минимальное (максимальное) значение выборки равно 2,1
(2,6), размах равен 2,6 ( 2,1) == 4,7, а медиана равна
Х(з) + Х(4) 0,1 + 0,9
== == о 5.
2 2 '
Эмпирическая функuия распределения F6(Х) является ступенчатой, B03
растает скачками величиной 1/6 в точках вариаuионноrо ряда, при этом
Р6(Х) == О при Х < Хр) == 2,1 и Р 6 (Х) == 1 при Х Х(6) == 2,6. Таким образом,
0,1 x<0,9.
O,9 x< 1,2,
',2 x<2,6,
x 2,6.
rрафик этой функции изображен на рис. 2. .
Пример 2. Пусть Х == (X 1 , , х п )
выборка из распределения Бернулли
Bi(l,p) (см.п.1 S 1.1).Обозначим IIn==
==X 1 +. +Х " число единиu в BЫ
борке. Тоrда скачки э. ф. р. Рп(Х) будyr
иметь место лишь в точках О и 1 и оче
видно (рис. 3)
Р6(Х) == { /6
1/3
при
Х < 2,1,
2, 1 Х< 1,5,
1,5 x<0,1,
при
при
Рп(х)
I
1 У"
n
о
Рис. 3
F6(Х) == { :;: :::
1 при
х
{ О
v n
F,,(x) == :
при х < О,
при O X< 1,
при Х 1, .
2.1. Вариационный ряд выборки, э. ф. р. и 2UCmOi!paMMO 93
рв(х)
_ __ _ _ __ _ _M _ _ _ _____ ,
vN/n
--
V 2 --
n
V j
n
о
I
2
I
3
I I
N IN
.
Х
Рис.4
Пример 3. Пусть Х == (X 1 .. . ., Х,,) выборка из дис-
KpeTHoro распределенин .ею == (i, i2 1;;' ). Обозна-
n
LJИМ Vj == 2: I(X i == j) число реализаций исхода «j», j == О, 1,
i=1
вектор!!.. == (111'...' VN) имеет полиномиальное распределение М(n; l!. ==
== (Pl, ,PN» (см. П.6 91.1), а отдельная частота Vj биномиальное pac
пределение Bi(n, pj).
в данном СЛУLJае Э. ф. р. рn(х) будет иметь скачки лишь в точках 1,2, . , N
и при этом величина скачка в точке j есть
Э
. ф. р. для дискрет- .-.:
Horo распределения
,N, Torдa
. . . lIj
b.Fn(j) == Fn(J) Fn(J О) == , j == 1, ,N
n
Тем самым f1Jафик рn(х) будет иметь вид, указанный на рисА.
Здесь Р{ b.Fn(j) == о} == P(Vj == О) == (1 pj)n что мало при больших n,
т. е. в большой выборке CKaLJOK в точке j наверняка будет иметь место. Более
TOro, так как
N N N
Р{ U {ь.рnи) == О}} 2: P{ Pnи) == о} == 2:(1 pj)n О,
J=J J=l )=!
при n 00, то в больших выборках с вероятностью, близкой к 1, скаLJКИ
э. ф. р. Р,,(х) будут иметь место во всех точках 1,2, , N, а случайными будут
лишь величины этих скачков. .
Если же теоретическая функuия распределения Р{(х) == F(x) непре-
рывна, то с вероятностью 1 все элементы выборки Х == (X 1 , ... ,Х n ) будут
различны, и rрафик э. ф. р. рn(х) будет иметь вид, изображенный на рис. 1,
т. е. случайными теперь будут точки скачков, величины же скачков не случай-
ны и равны 1/n.
94 rлава 2. Первичная обработка экспериментаЛЬНblХ данных
Таким образом, ДIlИ выборок из дискретных и непрерывных распрсделе
ний характер соответствующих эмпирических функций распределения будет
различным. Тем не менее в любом случае э. ф. р. рn(х) с увеличением объема
выборки n сближается в каждой точке х с теоретической функцией распре
деления Р(х).
"""."С"-
.. СХОДИМОСТЬ ПО
вероятности,Э. ф. р.
A.: ''t. f
Теорема 1. Дпя любоrо х ( oo < х < (0) и любоrо
е > О при n 00
p{IFn(x) F(x)1 < е} 1,
р
т. е. Рп(х) Р(х) (сходимость по вероятности см. П.1 1.2).
Доказательство. Это утверждение является простым следствием упоминав
шеrося ранее закона больших чисел (см. (3) 1.2), так как, обозначив,
1/j == I(X j х), j == 1, ,n, мы получим последовательность независи
мых, одинаково распределенных случайных величин с математическим ожи
1 п
данием Е1]) == Р{Х) х} == Р(х), а Р,,(х) == l: 1]j. Таким образом,
n j 1
р
Рп(х) -----------7 F(x), что и утверждается lJ теореме. .
""G'ьр"iii: б=;ени1' Можно установить и скорость сближения э. ф. р.
дЛЯ Э. ф. р. Рп(х) с Р(х). Так как из (3) следует, что (см. (4) Э 1.1)
1
EF 7I (x) == Ejtn(x) == F(x),
n
1 1
DF7I(x) == "'2DjtJ'(x) == F(x)(l Р(х),
n n
(5)
то соrласно неравенству Чебышева (для любой случайной величины
P{I E I > е} Щjе 2 ) имеем для любоrо t > О
Р{ Jn I F 7I (x) F(x) I > t} F(x)(l F(x)) (6)
t '" 4t 2
(последнее неравенство следует из Toro, что Д1Iя любой функции распределе
ния F(x) имеет место оценка Р(х)(1 F(x») 1/4).
ПОЛ]"lенная оценка (6) универсальна, так как она не зависит ни от Teo
ретической функции распределения F(x), ни от точки х, ни от объема BЫ
барки n. В частности, из нее следует, что
Р{ IFn(X) F(x)1 > :п } 0,01.
2.1. ВариаЦИОННbfЙ ряд Вbfборки, э. ф. р. и zистоzрамма 95
Более TOro оценку можно полy'lить, если число Ha
блюдений n велико и в этой ситуации воспользовать
ся теоремой Муавра Лапласа о сходимости биноми
альноrо распределения к нормальному (см. замечание
к упр, 33 rл. 1): если О < F(x) < 1, то при n ----+ 00
( J.Ln(x) nF(x» ) N( )
l. ---------t 0,1.
yl nF(x)(1 F(x»
в терминах э. ф. р. рn(х) == J.Ln(x)/n это соотноше
ние можна переписать в следуюшем виде: обозна'IИМ
Wn(X) == v'1i(Fn(x) F(x») так называемый ЭМl1ири
ческии процесс, Torдa
l.(Wn(X») N(O, F(x)(1 F(x»).
Orcюда можно записать следующую цепочку соотношений:
""" . . 1 H ' ,
. . , "."" .,." ,"о еорема ..,.
Муавра ЛаплаСQ
для э. ф. р.
Э
мпирический
процесс
(7)
p{IWn(x)1 < t} == Р{ Рп(х) 5n < F(x) < рn(х) + };::::
;:::: Ф( ylF(X)( F(X)J Ф( ylF(X)( F(X)J ==
==2Ф ( t ) 1 2Ф(2t) 1.
yl F(x)(1 F(x»
Если мы хотим сделать правую часть равной заданному числу 'у, близкому к 1
(например, 'у == 0,99), то решив уравнение 2Ф (и) 1 == 'у, получим
t == ф I ( I+'У )
'У 2 2'
rде ф J обратная функция к стандартной нормаль
ной функции распределения (см. (7) 1.2). В итоrе
мы полy'lим соотношение
P{Pn(X) Jn <F(X) <рn(х)+ )n };:::'y, (8)
Доверительный ,
интервал для Teope
тической функции
распределения,
",- ",..J.;"-,,i.:-
которое означает, что )L'IЯ больших выборок с вероятностью, пр.uблизитель
но равной 'у, значение теоретической функции распределения будет отли
чаться от соответствующеrо значения эмпирической функции распределения
не больше, чем на t'Y/ Vп. Таким образом, в (8) определен случайный интервал
(F n (x)=ft 7 /vп) с центром в точке рn(х), который с высокой вероятностью 'у
накрывает значение теоретической функции распределения F(x), если в этой
точке F(x) i=- О. Такой интервал (рn(х) =f t 7 /vп) называется acUJ.ттomu
ческим 'У доверительнbIМ интервалом .lU1И F(x). Ширина этоro интервала при
96 rлава 2. Перsuчная обработка эксперuментаЛЬНblХ данных
больших n имеет порядок I/..Jn, т. е. это очень узкий интервал, с высокой
точностью локализующий значение F(x), если оно нам неизвестно. Напри
мер, при t-y == 2 величина 'у == 1 6 1O 5
Из этих рассуждений можно сделать следующий принципиальный BЫ
вод: если объем выборки большой, то э. ф. р. Рn(Х) в каждой точке х, rде
О < F(x) < 1, отличается от F(x) на величину порядка I/..Jn, т. е. Р,,(х)
сближается с F(x) с ростом n и тем самым э. ф. р. может рассматриваться
в качестве приближенноrо значения (оце//ки) теоретической функции pac
пределения F(x), если она нам неизвестна. Функцию рn(х) поэтому часто
называют cтaтucтUlfecKaUM аНйЛОi!ОМ Д1Jя F(x): рn(х) ::::: F(x).
Состоятельность Замечание. Указан ное в теореме 1 свойство сходимости
l'
3. ф. р. Рп(х) Р(х), n 00, наЗblвается в статистике СDОЙ
ством состоятеЛЬ/lости Э. ф. р. F.,(x) как оценки для Р(х).
Таким образом, теорема 1 утверждает, что э. ф. р. Р,,(х) является состоятельной OЦCH
кой для теоретической функции распределения Р(х) в каждой точке х.
З. Дальнейшие свойства э. ф, р.
(Этот материал для тех, кто хочет заrлянуТl. поrлу6же
в обсуждаемую проблематику)
Выше мы обсуждали одномерные свойства э. ф. р. рn(х), т. е. ее поведение
в фиксированной точке х, и ДЛЯ этоrо нам было достаточно знать лишь свой
ства биномиальноrо распределения Bi(n, F(x)). Более rлубокие особенности
э. ф. р. проявляются, если рассматривать ее поведение не в отдельной фикси
рованной точке Х, а в произвольной конечной системе точек XI < Х2 <... <
< XN I, т. е. если рассматривать случайный вектор (Fn(XJ), ,Fn(XN I))
Пусть хо == oo, XN == 00, точки xl, ", XN 1 таковы, что
0== F(xo) < F(x)) <
< F(XN J) < F(XN) == 1.
Обозначим
pj == D.jF == F(Xj) F(XH), i == 1, , N,
и введем случайные величины
N
J/j == D.ilLn == Jln(Xj) Jln(Xj l) == L I(XH < X j Xj), i == 1, ,N
j=J
Заметим, что lIi есть число реализаций событин A j == {Хн < Xj} в n He
зависимых испытаниях, а так как событин A J , ,AN образуют полную rpyn
пу попарно несовместных исходов с вероятностями их реализаций в отдельном
испытании PJ, ,PN соответственно, то случайный вектор!!. == (111' , IIN)
имеет полиномиальное распределение М(n; Р == (PJ, ,PN)) (см. п. 6 1.1).
Но из определения э. ф. р. следует, что
1 1
Fn(xj) == Jln(Xj) == (III +... + 11;), i == 1,... ,N,
n n
2.1. Вариационный ряд выборки, э. ф. р. и zucтozpaMMa 97
и тем самым MHoroMepHbIe свойства э. ф. р. Fп(х) опре ""'" MHoroMepHbIe .,
деляются полиномиальным распределением. Для поли свойства э. ф. р.
номиальноrо распределения известна центральная пре
дельная теорема о ero сходимости при n ----+ 00 к MHoroMepHoMY нормальному
распределению (см. упр. 33 к rл. 1), воспользовавшись которой мы сейчас леr
ко опишем поведен ие любых MHoroMepHbIx распределен ий э. ф. р. для бол ьших
выборок. Для этоro вычислим сначала приращения э. ф. р. Fп(х) и эмпири
ческоrо процесса Wn(X) == Jn(Fn(x) F(x») на интервалах (хн, Xi):
1 Vi
LljFn == LliJ.Ln == ,
n n
Ll i W n == Jn(LlJ?n Lli F ) == Jn ( Pi)
Следовательно,
1:(Ll 1 W n , Ll 2 W n ,.. ,LlNW n ) == 1:(Y , у;, ,у;").
Vj nPi
== У;
.;n
Последнее же распределение по упр. 33, rл. 1, сходится при n ----+ 00 к HOp
мальному распределению N(Q, E N ), rде дисперсионная матрица EN == II00ijllf
имеет элементы O'ij == pi(l5 ij Pj), l5 ij символ Кронекера (6 ij == 1, 6 i j == О,
i -1 Л.
Таким образом, совместное распределение любых приращений эмпири
ческоrо процесса (т. е. центрированной и нормированной э. ф. р.) асимптоти
чески (при n ----+ 00) нормально:
1:(Ll( W n , Ll 2 W n , ... , LlNW n ) --------7 N(Q, E N )
(9)
(это значительное усиление свойства асимптотической нормальности (7) эм
пирическоrо процесса в фиксированной точке).
Результату (9) можно придать следующую интепретацию. Обозначим WO(x)
случайную функцию (процесс), обладающую тем свойством, что
1:(Ll i WO, Ll 2 WO,
, Ll N WO) == N(Q, E N ),
т. е. совместные распределения всех ее приращений нормальны (такая функ
ция WO (х) называется i?оуссовскuм процессом, и она может быть конструктивно
определена, но это уже выходит за рамки нашеrо пособия). Тоrда (9) означает,
что при больших n эмпирический процесс Wn(X) Предельные распреде
б .-t
при лиженно устроен как rауссовскии процесс ления функционалов от
WO(x) Wn(X) WO(x). t;\л JW..'j .[ . процесса
Поэтому следует ожидать, что и распределения «хороших») функционалов g(.)
от эмпирическоrо процесса будут слабо сходиться к соответствующим распре
делениям g(WO):
1: (g(w n ») --------7 1: (g(WO») при n ----+ 00.
7 За.., 1748
98 rлава 2. Первичная обработка экспериментаЛЬНbfХ даННbfХ
Если это так, и если распределение предельноro функционала g(WO) можно
вычислить в явном виде, то на этом пути можно получать предельные теоремы
для распределений различных функционалов g(W n ) от эмпирическоrо про
иесса. Именно на этом пути получена знаменитая теорема А. Н. Колмоrорова
(1933) о предельном распределении максимальноrо отклонения
Dn == Dn(X) == sup IFn(x) F(x)1
oo<x<oo
(10)
э. ф. р. от F(x) на всей оси.
Теорема 2 (Теорема Колмоrорова), Если функция F(x) непрерывна, то при
любом фиксированном t > О
00
1im P{v'nDn t} == K(t) == L ( I)je 2j2t2
11.......00
j oo
(11 )
Распределение K(t), определенное в (11),
назьшается распределеllием Колмосорова, и оно не
зависит от вида теоретической функции распре
деления F(x).
При этом предельную функцию распределе
ния K(t), которая подробно протабулирована, можно с хорошим приБЛИЖе
нием использовать для Практических расчетов уже при n ? 20.
Теорему Колмоroрова обычно при меняЮТ ДJlЯ Toro, чтобы определить rpa
ниuы, в которых С заданной вероятностью находится rрафик теоретической
функции распределения F(x), если она неизвестна. Пусть для заданноrо
"( Е (О, 1) число t-y определяется уравнением К (t-,) == l' Тоrда из (11) имеем:
Распределение Колмоrо
рова и доверительная
зона дпя теоретической
функции распределения
Р{ v'nDn t-y} == Р{ рп(х) t-y/ v'n F(x)
рп(х) + t-yv'n для всех х} K(t-y) == 1
п.....оо
Таким образом, при больших n с вероятностью, близкой к 1, значения функ
ции F(x) Д11я всех х удовлетворяют неравенствам
Fn(x) t"{/Vп F(x) Fn(x) + t-y/';n.
Так как О F(x) 1, то эти неравенства можно несколько yroчнить:
тах{ О, Fn(x) t"{/ v'n} F(x) mil1{ рп(х) + t-,/ v'n, 1} (12)
Область плоскости, определяемая верхней и нижней rраницами в (12)
называется асимптотической "( доверuтелы/Ой зоной для теоретическоЙ функ
ции распределения. Для определення числовых значений t"{ при различных 'у
можно воспользоваться табулированными значениями функuии K(t), напри
мер, t o ,95 == 1,3581, to,')9 == 1,6216.
2.1. ВариациОННbJЙ ряд ВbJборки, э. ф. р. и ZUCт02pOMMa 99
Полезно знать также следующий результат, принадлежащий В. и. rли
венк0 2 ) (1933).
Теорема 3 (Теорема rливенко).
r{limD n ==O}==I.
n....оо
Друrими словами, максимальное отклонение эмпирической функции pac
пределения от теоретической функuии распределения на всей оси с вероят
ностью 1 будет сколь уrодно мало при достаточно большом объеме выборки.
Наконец, сформулируем еще один важный результат выборочной теории,
при надлежащий Н. В. Смирнову (1939), который раскрывает друrие свойства
эмпирических Функuий распределения.
Теорема 4 (Теорема Смирнова). Пусть Fln(X) И F 2т (x)
две э. ф. р., построенные на основе двух независимых
выборок объемов n и m из oAHoro и Toro же распреде
ления .ею, и
I
Э. ф. р. для ДВУХ
выборок
Dn,т == sup IF1n(x) F 2тn (x)l.
C(J<X<OO
(13)
TorAa, если теоретическая функция распределения Р(х) непрерывна, то для
любоrо фиксированноrо t > О
lim Р { J nт Dn.m t } == K(t),
n, Тn....C(J n + m
rAe функция K(t) определена в (11).
(14)
Эrу теорему обычно используют для проверки rипотезы однородности о том,
что две выборки получены из одноrо и Toro же распределения (см. пример 5
Введения и п. 1 4.3).
Подводя итоr обсуждению асимптотических свойств (свойств для боль
ших выборщ) эмпирической функции распределения, можно сделать сле
дующее общее заключение. То, что при больших n Fn(x) Р(х). находит
отражение в сл дующем фундаментал Б ЬН М принципе Фундаментальный
математическои статистики: для лю ои характери
принцип математиче
СТИки 9 наблюдаемой случайной величины , KO
скай статистики
торая есть некоторый функционал от теоретической
функции распределения Р(х) 9 == g(F), можно построить ее статuстuче
СКUЙ аналоz (оценку) 9n == 9 (р n ), и тоrда для больших n можно использовать
9n в качестве приближен Horo значения (оценки) для 9 9n g.
2) rливенко Валерий Иванович (1 896 1940) российский математик, специалист в области
теории вероятностей и математическоro анализа.
7'
100 rлава 2. Первичная обработка экспериментаЛЬНblХ даННblХ
4, Полиrон частот, rИСТоrрамма
ПОМИМО вариационноrо ряда и эмпирической функции распределения суще
ствуют и друrие способы наrлядноrо представления статистических данных,
облеrчающих работу с ними. Так, если наблюдаемая в эксперименте случай
ная величина { дискретна и принимает значения al, а2, .. то более наrляд
ное представление о ее законе распределения дадут относительные частоты
11; == II r /n, rде IIr число элементов выборки Х == (X I . , Х n ), приняв
n
ших значение a r : IIr == L I(X j == a r ), т == 1,2, В этом случае, соrласно
j=l
закону больших чисел, при n 00 11; Р{{ == a r }, т == 1,2, т. е. 11;
сближается с ростом n с теоретической вероятностью Р{{ == а,.}, и потому,
по крайней мере для больших выборок, относительные частоты 11,: можно
рассматривать в качестве приближенных значений (оценок) для неизвестных
вероятностей Р{{ ==a r }.
Познавательная ценность теории вероятностей обусловлена тем,
что массовые случайные явления в своем совокупном действии ca
здают стРО2ие закономернасти. Сама панятие математическай
вероятнасти было бы бесплодно, если бы не находило свое20 осу.
ществления в виде частоты появления какоzo либо результата
при МНО20кратнам повторении аднорадных уславий.
А. Н. Колмоrоров
V r Исходные данные дискретноrо типа
4 обычно записывают в виде последователь
3 ности пар {(ar, II r )}, rде IIr > О, или в виде
2 таблицы
] ,
a r 111 112
О 2 3 4 5
называемой статистическим рядом (под
. черкнем, что в этом случае Lr IIr == n).
V r Наrлядным представлением таких дaH
1/3 ных является поли20Н частот, который
1/6 представляет собой ломаную с вершинами
в точках (а т , II r ), т == 1,2, (см. рис.5).
1/12 Можно рассматривать также статисти
О 2 3 4 5 a r ческий ряд {(ar, II,:)} (здесь Lr 11; == 1) и
РИс.5 соответствующий полиrон относительных
частот.
2.1. Вариационный ряд выборки, э. ф. р. и Zucт02paMMa 101
Пример 4. Наблюденные значения целочисленной величины { ДI1я 12 опытов
оказались равными 5, 1, 4, О, 1, 4, 3, 5, О, 5, 5, 2. Статистические ряды и
полиrоны частот этих данных таковы:
1
a r
.
v r
Для непрерывной случайной величины {, обладаю
щей непрерывной плотностью f (х), также можно пост
роить по соответствующей выборке Х == (Х], . . . , х п )
статистический аналоr fn(x) ДI1я плотности f(x), который называется zucmo
zраммой. Для этоrо используется метод zpyппUpOBKU, в соответствии с которым
область Д возможных значений { разбивается на некоторое число N непе
N
ресекающихся интервалов д" . . . , ДN (так что Д == U Дr ), подсчитывают
r l
,Х П , попавших в соответствующие ин
М
етод rруп пировки
И rистоrромма
числа Vl,
тервалы:
,VN наблюдений Х"
N
I/r == L I(X j Е дr), r == 1,
j=1
И строят кусочно постоянную функцию
N
, N (так что L V r == n ) ,
T '
V r
fn(x) == nlДrl при х Е дr, r == 1,
(здесь IДrl длина интервала Дr). То, что построенная по такому правилу
rистоrрамма lп(Х) действительно «похожа» на теоретическую плотность f(x),
следует из закона больших чисел, соrласно которому при n -----1 00 относитель
ная частота vr/n сближается с теоретической вероятностью
,N
(15)
Р{{ Е Дr} == / f(x) dx.
6..
Но этот интеrрал по теореме о среднем равен f(аr)IДrl, rде а с не которая
внутренняя точка интервала дс (при малом Дr В качестве а с можно взять,
например, середину интервала). Таким образом, при больших n и достаточно
«мелком» разбиении {Дr} !п(х)::::: f(a r ) при х Е дr, Т.е. rистоrpамма 1п(х)
будет достаточно хорощо приближать трафик плотности f(x), следователь
но, fn(x) можно рассматривать в качестве статuстuчеСКО20 аналоzа (оценки)
f . ·
102 rлава 2. Первuчная обработ/(а Эl<сперuментаЛЬНbfХ aaHHbfX
Рис. б
Наряду с rистоrpаммой, в качестве приближения для не известной тeope
тической ПЛОТIIОСТИ '(х) можно использовать кусочно линейный rрафик,
.. v ..
Полиroн частот называемыи полUi'ОНОМ частот, и которыи строится так:
если построена rистоrрамма fп(x), то ординаты, COOT
ветствующие серединам интервалов rруппировки, последовательно соединяют
отрезками прямых (см. рис. 6). Построенный таким образом кусочно линей
ный rpафик также является статистическим аналоrом теоретической плотно
сти. rруппированные данные удобно представлять в виде соответствующеro
статистическоrо ряда {(a r , V r )}, rде a r середина r ro интервала rpуп
ПИрОlЗки.
Метод rpуппировки применяется и для дискретных данных, коrда, Ha
пример, множество возможных значений наблюдаемой случайной величины
счетно (как для пуассоновской или rеометрической величины). Относитель
ные частоты V r /n 13 любом случае являются статистическими аналоrами (oцeH
ками) для теоретических вероятностей P{ Е .6. r }.
Метод rруппировки наблюдений удобный и часто более экономный
способ записи информации, содержащейся в выборке. Если, напри мер, n == 104
а точность измерений наблюдаемых значений на интервале (О, 1) сравнима
с 0,1, то ясно, что практически бесполезно знать все 104 измерений, а ДOCTa
точно указать лишь 10 частот Vl, , VIO попадания в интервалы
( Т 1 Т ]
.6. r == ю' 10 '
r == 1,
10,
т. е. знать лишь rисmrрамму выборки. Однако, этот способ обладает и очевид
ными недостатками, связанными снекоторой неопределенностью в способе
разбиения {.6. r } и частичной потерей информации при оrрублении данных
(ведь фактически мы все наблюдения, попавшие в интервал .6. r , заменяем
на среднюю mчку a r этоrо интервала). Поэтому rистоrрамму используют
практически лишь на предварительном этапе анализа статистических данных.
Пример 5. Наблюдения над непрерывной случайной величиной , окруrлен
ные с точностью 10 2, оказались равными 0,59; 0,16; 0,44; 0,48; 0,90; 0,19;
0,65; 0,42; 0,35; 0,84; 0,28; 0,63; 0,54; 0,12; 0,18; 0,67; 0,94; 0,63; 0,33; 0,03.
Построим rистоrpамму и полиrон частот этих данных, взяв в качестве интер
валов rруппировки
( Т 1 Т )
.6. r == ю' 10 '
r == 1,.. , 10.
2.1. Вариационный ряд выборки, э. ф. р. и zucтozpaMMa 103
3
2
1
о 2 3 4 5 6 7 8 9 10
Рис. 7
Частоты интервалов здесь равны
т
Е
20
V r
I
16rl == 1O nl6rl == 2, поэтому по формуле (15) значение rИС1'оrраммы f20(X)
в T M интервале 6r равно v r /2. Вид rистоrpаммы и полиrона частот указан
на рис. 7 .
5. ЯдерНlolе оценки теоретической плотиости
(3тот материал также для желающих заrлянуть поrлубже в проблему
оценивания теоретической плотности)
Один из современных подходов в задаче оценивания не известной Teope
тической плотности f(x) основан на использовании так называемых ядернbIX
оценок, т. е. оценок вида
1 п ( Х X j )
f,,(x) == 2:: k
пап j 1 а п
(16)
при соответствующем выборе ядра k(t) и последовательности чисел а п О
при n 00. в качестве ядра k(t) здесь выбирают rладкие оrpаниченные
плотности (например, равномерную плотность на интервале ( ]/2, 1/2)), что
обеспечивает хорошее сближение 1п(х) с f(x) при n 00. Будем далее
считать, что выполняется условие
d 2 == J k 2 (t) dt < 00
(17)
и а п О при n 00 так, что пап 00 (например, а п == n (} О < а < 1).
Torдa можно показать, что при этю< условиях для непрерывной и orpa
ниченной плотности f(x) > О при n 00
С( у'nа п (1п(х) Е1п(х))) N(O, о.2(х)) ,
( 18)
104 rлава 2. Первuчная обработка эксперuментальных данных
rде
а 2 (х) == d 2 f(x);
при этом
1 ( x ) 1 ! ( X t )
Efn(x) == E k == k f(t) dt ==
а n а п а n а п
! k(z)f(x ar,z)dz ------+ f(x),
так как
! k(z) dz == 1.
Таким образом, (18) означает, что !n(x) сближается с f(x) при n ------+ 00:
ОТЮlОнение !n(x) от Efn(x) (которое, в свою очередь, близко к f(x)) имеет
порядок I/ ";na n , который мал при больших n,
Доказательство утверждения (18) состоит в применении uентральной Пре
дельной теоремы к сумме (16) независимых и одинаково распределенных
слаrаемых в «схеме серий», т. е. коrда слаrаемые (а. следовательно, и их pac
пределение) зависят от числа n (оно выходит за рамки нашеrо пособия, и мы
ero опускаем).
Вопрос об оптимальном выборе «свободных» параметров а п и функuии
(ядра) k(t) зависит здесь от свойств rладкости теоретической плотности f(x).
Так, если f(x) имеет непрерывные производные порядка 2т > 2, то мож
но выбором а п и k(t) добиться скорости сближения !n(x) с f(x) порядка
n 2m/(4m+l) при n ------+ 00.
п . . ... . На практике часто используют «прямоуrольные,)
." ..е, УШl!IЬ=;;Шес ",, ядра:
k(t) { '
1 1
t
2" "2'
в противном случае.
8 таком случае !n(x) == vn(x)/(na n ), rде
n ( )
а п а п
V ( x ) =='" [x X- x+
n L...J 2" 1" 2
i 1
[ аn а п ]
число наблюдений в интервале х 2' х + 2
Имеются также результаты вида:
Р { lim supl!n(x) f(x) I == О } == 1
п----+оо х
(при соответствующих условиях на '(х), k(t) и а п ) и вида
Р{ supl!n(x) f(x)1 > Е п } "" оп,
:/:
2.2. Выборочные моменты: точная и асимптотическая теория 105
позволяющие рассчитывать асимптотические доверительные зоны дпя f(x),
основанные на ядерной оценке 1п(х) вида (16).
! 2.2. Выборочные моменты:
точная и асимптотическая теория
Пусть Х == (Х" ,Х п ) выборка из распределения.ею и F(x) и Рп(х)
соответственно теоретическая и эмпирическая функции распределения. На
Рп(х) можно смотреть как на функцию распределения некоторой дискретной
случайной величины, принимающей n значений: Х" ,Х п С вероят
ностями, равными I/n (если какое либо значение встретится в выборке k
раз, то этому значению соответствует вероятность k/n). Об этом распреде
лении rоворят как об эмпирическом или выборочном распределении (отсюда
и термин эмпирическая функция распределения дпя Р п (х». Как дпя исходноrо
распределения .e( ) вводятсЯ различные числовые характеристики (MaTeMa
тическое ожидание, или среднее, дисперсия, моменты и т. д.), так и для эм
пирическоro распределения, связанноrо с выборкой Х, вводятся аналоrичные
характеристики, называемые эмпирическими (или выборочными): выборочное
среднее, выборочная дисперсия и Т.д. Таким образом, эмпирическая (или выбо
рочная) характеристика является статистическим анаЛОi!ОМ соответствующей
теоретической характеристики, аналоrично тому, как эмпирическая функ
ция распределения Рп(х) является статистическим аналоrом теоретической
функции распределения F(x). В общем случае, если 9 == Eg(O есть HeKOTO
рая теоретическая характеристика наблюдаемой случайной величины , то ее
статистический аналоr, т. е. соответствующая эмпирическая (или ныборочная)
характеристика, lJычисляется по формуле
1 n
9п == 'L g(Xi).
n i=1
(1)
1. Выборочиые моменты
Наиболее важными характеристиками случайной величины являются ее MO
k ( ) },
менты O:k == E , а также центральные моменты JLk == Е 0:, (Korдa они
существуют). Их статистическими аналоrами, вычисляемыми по COOTBeTCTBY
ющей выборке Х == (Х" , Х n ), являются выборочные моменты COOTBeT
ственно обычные
п
1", k
О:;, == L.J X j
n j=1
(2)
и центральные
n
1 '" ( ) },
JLk == L.J Xj 0:) .
n i=1
(3)
106 rлава 2. Первичная обработка экспериментаЛЬНbJХ даННbfХ
..
Выборочное
среднее
....
Выборочная
дисперсия
Особенно важны моменты nepBoro и BTOpOro порядков.
При k == 1 величину а) называют выБОРОЧНblМ средним и
обозначают стандартным СИМВОЛОМ Х (черта означает cpeд
нее арифметическое):
1 n
X==al== LXj. (4)
n j 1
При k == 2 вели'lИНУ Р2 называют выборочной дисперсией и
также обозначают стандартным символом в2 == в\х):
n
2 1" 2
S == Р2 == L..,.{Xj Х)
n j l
(5)
Таким образом, выборочные среднее и дисперсия являются статистическими
аналоrами теоретических среднеrо (математическоro ожидания) Ц и диспер
сии D , Korдa они существуют.
Между выборочными а!; и выборочными центральными Т!; моментами
сохраняются те же соотношения, что и между теоретическими обы'lНЫМИ а."
и центральными J1.k моментами. В общем случае при k ? 2 из (3) имеем по
формуле бинома Ньютона
k
р" == L( 1)' Cr Х' a" r,
, O
т. е. выборочные центральные моменты являются мноrочленами от обычных
выборо'lНЫХ моментов. В 'Iастности,
n
2 2 1" 2 2
S == а2 Х == L...J Х ; Х ,
n i 1
(6)
р) == аз з.ха2 + 2Х З ,
Р4 == 54 4Х аз + 6х2а2 зХ 4
Если выборочные данные представлены в виде статистическоrо ряда
{(a r ,1J r )} (коrда наблюдаемая величина дискретна или коrда применяется
метод rpуппировки), то выборочные моменты ВЫ'lисляются по формулам
1""
а." == L...J arv r ,
n
r
в частности,
1" ( ) "
J1." == L...J а . а.1 1J r ;
n
r
1"
a.1 ==а== L...J ar/J r ,
n
r
(7)
2 1" 2 1"
Р2 == S == L...J (а . а) V r == L...J
n n
r r
2 2
а . /J r а .
92.2. ВblБОрОЧНblе MOMeHmbl: точная и асимптотическая теория 107
в этом случае для упрощения вычислений исходные данные часто удобно
преобразовать, положив Ь т == (а т а)/с, rдe сдвиr 7i есть значение а т с MaK
симальной частотой V r И единица масштаба с > О произвольна. Средние
2 2
ii и Ь, и дисперсии S (а), S (Ь) соответственно исходных и преобразованных
данных связаны при этом соотношениями
ii == сЬ + а, в2(а) == с 2 в2(ь).
(8)
Пример 1, Вычислим выборочные среднее и дисперсию по исходным и rруп
пированным данным, приведенным в примере 5 2.1. По формулам (4) и (6)
имеем
9,37 2
Х == 20 0,468, S 0,067.
Далее, середины интервалов D. r в данном случае равны а т == r . 0,1 0,05,
при этом 7i == а7 == 0,65; кроме Toro, здесь удобно выбрать в качестве едини
цы масштаба с == 0,1. Таким образом, статистический ряд преобразованных
по формуле b r == (a r а)/с == (т . О, 1 0,7) 10 == r 7 данных имеет вид
Е
V r 20
2: br/J r == 37,
37
Ь == == 1 85
20 '
и, следовательно, ii == 0,65 0,185 == 0,465.
Аналоrично,
L b;v r == 201,
r
1 201
в2(ь) == L b;v r jj2 == 1,852 6,628
n 20
r
и, следовательно, в2(а) 0,066. .
При мер 2. Проводились опыты С бросанием одновременно 12 иrральных KO
стей, при этом наблюдалось число { костей с числом очков 4, 5 или 6. Данные
ДЛЯ n == 4096 опытов приведены в таблице, rде V r . обозначает число опытов,
в которых наблюдалось значение == r (т == О, 1, . 12)
r 9
V r 257
Е
4096
Назовем успехом выпадение на одной кости 4, 5 или 6 очков вероят
ность этоro равна 1/2, тоrда наблюдаемая случайная величина { равна числу
успехов в 12 испытаниях Бернулли с вероятностью успеха 1/2, т. е { имеет
биномиальное распределение Bi( 12, 1/2). По формулам (4) 1.1 теоретическое
среднее есть E == 6, а теоретическая дисперсия О{ == 3.
Вычислим теперь выборочное среднее и дисперсию для приведенных
данных. Здесь мы имеем дело со статистическим рядом {(т, v r )}, поэтому
108 rлава 2. Первичная обработка экспериментаЛЬНblХ aaHHblX
вычисления производим по формулам (7) (8), предварительно преобразовав
данные, положив b r == r 6 (поскольку здесь а == 6). Статистический ряд так
преобразованных данных имеет вид
b r
V r
Здесь
L brv r == 569,
569
Ь == 4096 0,14
r
и, следовательно, аl == а + ь 6,14.
Аналоrично,
L b;V r == 12083
r
и Д2 == 5 2 (ь) == L b;v r il 2,93.
n
r
в данном случае различие между теоретическими и выборочными моментами
незначительно. .
Выборочные моменты это функции от выборки Х, т. е. они являются
случайными величинами, поэтому важно знать их вероятностные свойства,
т. е. уметь находить их распределения (которые иноrда называют выборочными
распределениями) и изучать различные характеристики этих распределений.
Рассмотрим сначала некоторые характеристики выборочных среднеrо и дис
персии.
2. Моменты выборочных среднеrо и дисперсии
Так как Xj независимы и распределены так же, как , то
1 n
ЕХ == L EX j == E == а 1,
n j 1
n
1 L 1 J1.2
DX== DХj== Щ== .
n 2 . n n
, I
(9)
Рассмотрим теперь выборочную дисперсию 52 (см. (5)). Положив
1'; == Xj а}, i == 1, , n,
запишем (5) в виде
n n
2 1", 2 1", 2 2
S == L.,.. (у; У) == L.,.. 1'; У
n i 1 n i 1
( 10)
Поскольку Е1'; == О, ЕУ/ == J1.2 и ЕУ;Vз == ЕУ;ЕVз == О (i -1 Л, то
n n
2 1 L 1 L 2 J1.2
ЕУ == EY;Yj == Е1'; == .
п 2 n 2 n
j,j l i 1
2.2. Выборочные моменты: точная и асимптотическая теория 109
Отсюда и из (10) находим
2 n 1
ЕВ == P2.
n
Среднее выбороч JIIIt:
ной дисперсии
(11)
Перейдем к вычислению DS 2 ИЗ (10) находим
1 ( n ) 2 2 n
(в2)2 == n 2 L 1';2 ;; у2 L 1';2 + у4
I l I l
(12)
Так как случайные величины У"... ,У n независимы и Е1'; == О, то в пра
вой части равенства
4 1
ЕУ ==
n 4
n
L E1';Yj Y kYi
,k,I 1
отличны от нуля только n слаrаемых Er;4 == JL4 И c cI == 3n(n 1) слаrаемых
Е1';2 у ] == JL , i 1= j. Поэтому
4 1 ( 2 ) JL4 + 3(n I)JL
ЕУ == 4 nJL4 + 3n(n 1)JL2 == 3 .
n n
Аналоrично находим
2 E( tr;2)2 == JL4+(: I)JL ==E( Y2 tr;2).
I ] I I
с учетом этих соотношений из (12) и (11) по формуле
ов 2 == E(S2)2 (Ев 2 )2
DS 2 == JL4 JL 2 (JL4 2/LП + JL4 3JL ==
n n 2 n 3
r"Д сперси'; ;;;'Тб р; .,.
.. ,. ной ... . . Аиспеnсии ,
' '''' ' ' i1I ''''''''''
получим
(n I)2 ( n 3 2 )
== Р4 JL2 .
n 3 n 1
( 13)
Аналоrично можно находить моменты и более высоких порядков, хотя
с увеличением порядка вид формул и их вывод усложняются.
З. Сходимость по вероятности выборочных моментов и функций от них
В этом пункте мы проанализируем свойства выборочных моментов, опреде
ленных равенствами (2) и (3), для больших выборок, т. е, их асимптотиче
ское поведение при неоrpаниченном 1I0зрастании объема выборки n. Чтобы
подчеркнуть зависимость моментов аА; и ДА: от объема выборки, будем их
110 rлава 2. Первичная обработка экспериментаЛЬНblХ даННblХ
в дальнейшем снабжать индексом n, т. е. писать &n!.: и 'iink' Первые два MO
мента случайной величины &n!.: соответственно равны (везде далее предпола
raeM, что все соответствующие моменты наблюдаемой случайной величины {
существуют)
n
1", k k
ЕЙnk == L...J EX i == Е{ == Ctk,
n i l
n
1 '" k 1 k 1 ( 2!.: ( "' ) 2 )
DЙnk == "2 L...J DX j == щ == Е{ Е{
n j 1 n n
2
а2!.: й!.:
n
(14)
На основании неравенства Чебышева (напоминание см. перед форму
лой (6) 2.1) отсюда следует, что для любоrо е > О при n ----+ 00
P{I&nk Ctkl < е} 1,
(15)
т. е. выборочный момент &n!.: сходится по вероятности при n ----+ 00 к COOTBeT
ствующему теоретическому моменту й",. Тем самым &nА: можно использовать
в качестве приближенноrо значения (оценки) для Ctk, Korдa число наблю
дений n достаточно велико. Аналоrичное утверждение справедпиво и для
выборочных центральных моментов: 'iink J.Lk, И вообще для любых выбо
рочных характеристик, которые имеют вид непрерывных Функuий от конеч
Horo числа величин &n!.: (центральный момент 'iink, как показано выше в п. 1
(см. (6), выражается через &nl, ,&n'" в виде мноrочлена степени k). Этот
вывод является следствием следующей общей теоремы о сходимости Функuий
от случайных величин,
Теорема 1. Пусть случайные величины 1}l (n), ,'Т7r'(n) сходятся по вероят
ности при n ----+ 00 к некоторым постоянным Cl, ,C r соответственно. TorAa
ДЛЯ любой непрерывной функции Ip(XI,.. , X r ) случайная величина
«(n) == ip(1}I(n),
,1}r(n)) Ip(CI,
, C r ).
Доказательство. Поскольку ip непрерывна, то дпя любоrо е > О найдется
О == о(е) такое, что lip(X),. ,X r ) Ip(C" ,cr)1 < е при IXj cil < о,
i == 1, ,Т. Введем события В ; {llli(n) Cij < О}, i == 1, ,Т Torдa
событие В == В) Br влечет событие
с== {I((n) Ip(CI,
,с,.)1 <е}
Отсюда
Р{С} Р{В} == 1 Р{В} ==
== 1 P{B)U...UB r } 1 L,:P{B i }.
j 1
(16)
92.2. Выборочные моменты: точная и асимптотическая теория 111
р
Далее, из сходимости 7li(n) Cj имеем, что Д!1я данноro 6 и любоro
-у> о найдется nj == ni(r) такое, что
P{B j } == P{I17i(n) Cil ): 6} < !..
Т
при n ): nj. Пусть по == тах{ n), .. . , n r }, Torдa при
одновременно все неравенства P{B j } < -У/Т, i == 1,
из (16) получим
Р{ I(n) tp(C, , .. . , C r ) I < ё} ): 1 'у при n): по.
n ): ПО выполняются
, т. Следовательно,
Но это и означает yrверждение теоремы. .
I Замечание. Очевидно, что для справедливости теоремы l достаточно потребовать
непрерывности функции rp только в не которой окрестности точки (с"... ,c r ).
В частности, теорема 1 дает, что выборочная дисперсия 82 (см. (5)) cxo
дится по вероятности к теоретической дисперсии
JL2 == Щ 82 JL2.
Однако, в отличие от формулы (14), rдe математи
ческое ожидание Qnk совпало с соответствующим
теоретическим моментом O!k, в (11) правая часть
смещена относительно JL2. Если вместо в2 ввести величину
....-ф
Подправленная
выборочная дисперсия
n
2 n 2 1 "" 2
80 == B == L..,.(Xi Х) ,
n [ n [
i 1
(17)
то для нее получим
E8J == JL2, DSJ == ( n: 1 у ов 2 ( [8)
Из неравенства Чебышева и формул (18) и (13) следует, что для любоrо
ё > О при n 00
p{lsJ JL21 < ё} 1, ([9)
2 р 2 (
т. е. 80 ---------+ JL2. Таким образом, подправленная выборочная дисперсия 80 в \7)
уже будет иметь математическое ожидание, совпадающее с теоретической
дисперсией JL2, сохраняя при этом свойство сходимости по вероятности к JL2
с ростом объема выборки (что вполне естественно, поскольку поправочный
коэффициент n/(n [) \ при n 00).
Теперь настало время ввести несколько новых понятий, которыми широко
оперирует современная математическая статистика это понятия cmaтиcmи
/Си, несмеще1lносmu и состоятельности.
Любая случайная величина Х являющаяся функцией от
выборки Х == (X 1 , ... , Х П ): т == Т(Х), называется статистикой,
Определение 1
112 rлава 2. Первичная обработка экспериментаЛЬНblХ данных
Примерами конкретных статистик являются выборочные моменты Qk
и выборочные центральные моменты /ik, статистикой являетсs! выборочная
характеристика gn В (1). Приведем еше два примера конкретных статистик,
используемых в различных статистических задачах.
При исследовании свойств rpафика плотности распределения непрерыв
ной случайной величины часто рассматривают такие характеристики, как KO
эффицuенты асимметрии '/'1 и эксцесса '/'2, определяемые формулами
J.L)
'/'1 == '
Jl2
J.L4
'/'2 == 2 3.
Jl2
(20)
Если rрафик плотности симметричен относительно нуля, то '/'1 == О И
по значению '/'1 судят о степени откпонения от симметрии. Аналоrично, для
нормальноrо распределения '/'2 == О, поэтому о кривых плотности с '/'2 == О
rоворят, что они имеют нормальный эксцесс. Если же '/'2 > О ("i'2 < О), то rOBo
рят, что эксцесс кривой плотности положителен (отрицателен). Если задана
выборка Х == (X 1 , ,Х n ) из абсолютно HenpepBHoro распределения .L:(o,
то выборочные коэффициентbl aCU/llMempuu 1nl и эксцесса 1n2 определяются как
статистики
Jl n3 Jin)
"Уnl == )/2 == sз И
Jln2
Эти статистики как непрерывные функции от выборочных моментов в си
лу теоремы 1 сходятся по вероятности при n -----t 00 К соответствующим Teo
ретическим характеристикам (20).
Статистика Т == Т(Х), используемая в качестве при6ли
женноrо значения для некоторой (неизвестной) теоретической характери
стики 9 : Т g, называется несмещенной в среднем (или просто несмещен
ной) оценкой 9 (для g), если выполняется условие
Jin4 3
'/'п2 == s4 .
(21 )
Определение 2
Е Т(Х) == g.
(22)
Свойство несмещенности интуитивно примекательно: оно означает, что
по крайней мере «8 среднем.> используемая оценка приводит к желаемому
результату. Поэтому в конкретных задачах оцениваниSJ 'lacTo ишyr именно He
смешенную оценку. С примерами несмещенных оценок мы уже выше [Jстреча
лись. Так, первое соотношение (5) 2.1 означает, что эмпирическаSJ ФункциSJ
распределения Рn(Х) ямяется несмешенной оценкой теоретической функции
распределения F(x) в каждой точке х Е RI; аналоrично, ввиду (14) выбороч
ный момент ank является несмешенной оценкой для теоретическоrо MOMeH
та Q:k, а ввиду (18) статистика 85, определенная в (17), SJВЛSJется несмешенной
оценкой теоретической дисперсии J.L2. Выборочная же дисперсия 82 в качестве
оценки для J.L2 == O свойством несмещенности не обладает: она имеет смеще
ние Е8 2 Jl2 == J.L2/n (см. (11)), которое стремится к О при n -----t 00 такие
оценки называются аcuмптотuчески несмещеннымu. Тем самым выборочная
8 2 - о.,.,
дисперсия является лишь асимптотически несмещеннои оценкои Jl2. ,очно
2.2. Выборочные моменты: точная и асимптотическая теория 113
так же и друrие выборочные центральные моменты 'jink (см. (3)) являют
ся асимптотически несмещенными оценками ДJIЯ теоретических центральных
моментов Jlk, поскольку ДJIЯ них известно, что Е 'jink Jlk ----7 О при n ----7 00.
Статистика Тn == Tn(X 1 ,. . . ,Х n ) называется состоятель
ной оценкой для теоретической характеристики g, если Тn 9 при n----7 00.
Таким образом, состоятельность в статистике это эквивалентное поня
тие ДJIя сходимости по вероятности. Оно означает, что для выборок большоrо
объема значительная разница между значениями оценки и оцениваемой xa
рактеристики маловероятна, и потому разумно (по крайней мере ДJIЯ больших
выборок) принять статистику Тn за приближенное значение не известной xa
рактеристики у. Состоятельность является обязательным требованием для лю
боrо правила оценивания. Подчеркнем, что это свойство оценок имеет асимп
тотический характер и связано лишь с большими выборками (с увеличением
информации, доставляемой выборкой, точность оценки должна возрастать!).
В отличие от этоro свойство несмещенности никак не связано с числом Ha
блюдений. Отметим также, что все выборочные моменты (как обычные, так
и центральны)) являются состоятельными оценками соответствующих Teope
тических моментов, выборочные коэффициенты асимметрии и эксцесса (21)
также являются состоятельными оценками соответствующих теоретических
характеристик (20).
Наконец, подчеркнем, что для про верки СОСТОЯ "'>:У"/о>"О''i'',,",",' Критерий .,
тельности некоторой несмещенной оценки Тn для 9 состоятельности
достаточно убедиться, что ее дисперсия DTn ----+ О при
n----7 00, так как в этом случае по неравенству Чебышева
{ } отn
р [Тn gl > е ----7 О, \:j е > О. (23)
е
На основании этоrо критерия и ввиду (5) 2.1 можно заключить, что эм
пирическая функция распределения рn(х) ЯWlяется состоятельной оценкой
теоретической функции распределения Р(х) в любой точке х Е R 1
Ввиду особой практической важности оценивания теоретических среднею
01 == E и дисперсии Jl2 == O суммируем полученные выше результаты (9),
(18) и (19) в форме отдельной теоремы.
Определение 3
Теорема 2. Вblборочное среднее
1 n
Х == :L Xj
n j 1
и статистика
n
В5 == "(Xj х)2
n ] L.,..
j 1
являются несмещеННblМИ и состоятельными оценками соответственно для E
иЩ.
8 За..] 1748
114 rлава 2. Перsuчная обработка эксперuментальных данных
Пример З. Рассмотрим ситуацию, описанную в примере 1 1.1. В данном
случае речь идет об оценивании теоретическоrо среднеl'О (J == E (доли белых
шаров в урне) 13 схеме Бернулли Bi( 1, (J) по выборке Х == (X 1 , , X,J, rде
Х ) == 1, если в j M испытании извлечен белый шар, и X j == о в противном
случае. Здесь выборочное среднее
1 Х
Х == (XI + + Х,,) == ,
n n
rде Х число наблюдавшихея белых шаров, является несмещенной и COCTO
ятельной оценкой (J == а,/а. .
4. Асимптотическая иормальность выборочных моментов
Продолжим исследование свойст13 выборочных моментов для больших выбо
рок и оБСУДIIМ теперь асимптотическое при n ----+ 00 поведение их выборочных
распределений. Но сначала введем некоторые дополнительные обозначения
и определения для удобства дальнейшеrо изложения (см. Общее замечание
вп.19 1 ,2).
Если распределение случайной величины 1/" сходится при n ----+ 00 к pac
пределению случайной величины 1/ и при этом [,(1/) == N(p, 0"2), то будем
писать [,(1/п) ----+ N(p, (12). Далее иноrда будем rО130рИТЬ, что случайная Be
2
личина 1/п асuмпmоmuческu нормальна с nараметраМII рп И (1п или, короче,
асuмnmоmческu нормальна N(pn, (1 ), и записывать это следующим образом:
[,(1/п) '" N(pn, O" ), если [, ( 1/п ;п Рп ) ----+ N(O, 1).
Найдем сначала асимптотические распределения выборочных моментов
n
апl: (см. (2». Величина nап!: == L xf является суммой независимых одина
i 1
2k
ково распределенных случайных 13еличин. Если конечен момент 021: == E
то к этой сумме можно применить центральную предельную теорему теории
( ( ) k k 2
вероятностей см. соотношение 1) Э 1.2 . Так как EX j == Ok. DX j == 02!. О!.
(см. (14», то величина
пап!.: ПО!.:
ап!. О!.
) n(а.2!.: ol) ) (021: oz)/n
асимптотически нормальна N(O, 1). Таким образом, справедлива следующая
теорема.
Теорема З. Если конечен теоретический момент 02k, то при n ----+ 00 вы60-
( 02!.: 02. )
рочный момент Оп!. асимптотически нормален N a.k, n k
2.2. Выборочные моменты: точная и асимптотическая теория 115
Полезность этой теоремы состоит в том, что она позволяет оценивать для
больших выборок вероятности заданных ОТКТlOнений значений выборочных
моментов от теоретических. Действительно, из этой теоремы имеем, что при
любом фиксированном t > О и n ----t 00
t
Р { Iank йkl < t } ----t ! e x2/2dx == Ф(t) ф( t) == 2Ф(t) 1
V а2!.: az v 211'
t
(обозначения см. в (7) 1.2).
В частности, из теоремы 3 следует, что если теоретическая дисперсия
11-2 == D существует, то при n ----t 00 выборочное ореднее К == anl асимптотиче
ски нормально И(а, ,11-2/n). Отметим в этой связи, что если [.(0 ==И(аl ,11-2),
то случайная величина Х, как сумма независимых нормальных случайных Be
личин, также нормальна с параметрами аl и 11-2/n (см. соотношение (5) 1.2),
Т.е, в данном случае [.(Х) == И(а" 11-2/n) при любом n.
Справедлив также более общий результат об асимптотической нормально
сти любоrо конечноrо числа выборочных моментов ank. Но для доказательства
этоro надо знать мноroмерный вариант центральной предельной теоремы, KO
торый формулируется следующим образом.
Мноrомерная центральная предельная теорема. Пусть T MepHыe случайные
векторы !1 == (1}kl, ,1}kr), k 0= 1,2, независимы, одинаково pacnpe
делены и имеют конечные моменты
ai == E1}ki, b ij 0= COV(1}ki, 1}kj) , i, j == 1, ,Т.
TorAa при n ----t 00
.c(nl,
,(nт) ---------t N(Q, в 0= IIbijll ),
rAe
,. . (1}'i + + 1}ni пai)
<,щ vn
(определение MHoroMepHoro нормальноrо распределения дано в n. 2 1.2).
i == 1,
, т
Рассмотрим теперь вектор 4п == (anl, , а"т), составленный из произ
вольноrо числа т первых выборочных моментов. Обозначим
O= (а"
,a r ) == Е4п и == 1I00ijll , rдe O'ij 0= ai+j G:iG:j,
Леrко убедиться, что дисперсионная матрица DAn == (l/n)L: (см. упр. 21). BBe
дем, далее, векторы 'ТlJ. == (X k , xf,. , Х[), k == 1,.. ,n, они являются
независимыми и одинаково распределенными, так как X 1 ,... ,Х n незави
симы и одинаково распределены, при этом Еъ. == , D'ТlJ. == L:. Осталось
заметить, что пАп 0= 1} +... + 1] , и применить к этой сумме мноrомерную
I n
8.
11б rлава 2. Первичная обработна экспериментаЛЬНblХ aaHHblX
центральную предельную теорему:
( пА па )
.с N(O, Е)
или, что эквивалентно, .с(д.n) '" N(Q., (l/n)E).
Таким образом, справедлива следующая теорема о совместном распреде
лении выборочных моментов.
Теорема 4. Если конечен теоретический момент a2r, то при n ----+ 00 COBMecт
ное распределение выборочных моментов (anl"" ,a nr ) асимптотически HOp
мально N(Q. == (al, ,a r ), (l/n)E).
Эта теорема полезна больше не сама по себе, а своим важным следствием,
которое мы приводим без доказательства. Именно, справедлива
Асимптотическая HOp
мальность функций от
выборочных моментов
Теорема 5. Для любой дифференцируемой функ
ции ер от т nepeMeHHblx
.с (v'n( ер (д.n) <p(Q.))) N(O, ( 2 )
при условии, что и 2 == Q'EQ > О, rAe
Q == grad <p(Q.) == ( д; ) ,
дep( ) ) I
аХ . ;f !!
Более тощ если и 2 == и 2 ({а.}) непрерывная функция от теоретических
моментов {а.} и и == и 2 ({а n .}) (т. е. моменты а. заменены соответствую
щими выборочными моментами а n .), то
с ( v'n ep(д.n)и <p(Q:) ) N(O, 1).
(24)
Из теоремы 5, в частности, следует, что асимптотически нормальными
являются и центральные выборочные моменты /ink, поскольку они являются
непрерывными функциями (мноrочленами) от обычных выборочных MOMeH
тов. Например, соответствующее утверждение для выборочной дисперсии S2
формулируется следующим образом (см. упр.23).
Асимптотическая
нормальность выбо
рочной дисперсии
Теорема б. Если конечен теоретический момент /14,
то при n ----+ 00 выборочная дисперсия S2 асимпто
тически нормальна N(/12, (/14 /1 )/n). Более Toro,
.с ( y'ri(S2 /12) ) N(O, 1).
V /in4 S4
(25)
2.2. Выборочные моменты: точная и асимптотическая теория 117
5. Асимптотические доверительные интервалы
для теоретических моментов
Теоремы предыдущеrо пункта, в особенности теорема 5 в варианте (24), ис
пользуются в статистике для построения доверительных интервалов для Teo
ретических моментов. С примером доверительноro интервала мы уже встреча
лись в п. 2 2.1, rде был построен асимптотический 'У доверительный интервал
для теоретической функции распределения F(x) в произвольной точке х, rде
F(x) -1- О. Дадим теперь общее определение доверительноrо интервала. Пусть
нас интересует некоторая теоретическая характеристика 9 наблюдаемой слу
чайной величины и имеется выборка Х 0= (Х" ,Х П ) из .ею.
'У доверuтельным интервалом для 9 называется такой
случайный интервал т(х),т 2 (х)), Т,(Х) < Т 2 (Х), который содержит
внутри себя (накрывает) неизвестное значение 9 с вероятностью, не MeHb
шей 'У:
Р{Т(Х) < 9 < Т 2 (Х)} 'У. (26)
Здесь T1(X) и Т 2 (Х) некоторые статистики (функции от выборки), Ha
зываемые соответственно нижней и верхней доверительными lраницами, а 'У
задаваемый заранее доверительный уровень, который обычно выбирается ДOCTa
точно близким к 1 (например, 'У 0= 0,9; 0,95; 0,99 и т. д.). Длина T2(X) T, (Х)
TaKoro интервала характеризует точность локализации оцениваемой xapaKTe
ристики 9, а величина 'У отражает «степень rотовности мириться с возмож
ностью ошибки,), т. е. является показателем надежности доверительноrо ин
тервала.
Если выполнено условие (26), то практически это означает, что в большом
числе независимых применений TaKoro правила оценивания мы можем оши
биться, yrверждая, что 9 Е (т,(х), Т 2 (Х)), примерно в (1 1')100 % случаях.
Общая теория доверительноrо оценивания будет обсуждаться позже
(см. rл. 3 3.8), а сейчас мы продемонстрируем такой подход в оценива
нии теоретических моментов. При этом, поскольку мы будем основываться
на предельной теореме 5, то речь будет идти о построении асимптотических
доверительных интервалов.
Итак, пусть нас интересует характеристика 9 0= rp(Q) , Q 0= (о:, ,O:r),
rде rp заданная непрерывно дифференцируемая функция. Тоrда на OCHOBa
нии (24) мы можем записать следующую цепочку соотношений:
Определение 4
Р{ lrp(An) 91 < } 0= Р{9 Е (rp(An) =F ji )}
Ф(е-у) Ф( ) 0= 2 Ф(е-у) 1 0= 'У, (27)
если 0= ф I(1 +1')/2)
Но это и означает, что (rp(An) =F иn/yТi) есть асимптотический 'Y дo
верительный интервал для 9 0= rp(Q). Центр этоrо интервала находится в слу
чайной точке 'Р(А п ), а ero длина равна 2 и п/ yТi, т. е. при больших объемах
118 rлава 2. Первичная обработка экспериментаЛЬНblХ даННblХ
выборки это достаточно узкий интервал, обеспечивающий высокую точность
локализации оцениваемой характеристики g 'P(Q:). Таким образом, мы
имеем общее решение доверительноrо оценивания произвольных (непрерыв
но дифференцируемых) функций от любоrо конечноrо числа теоретических
моментов. На практике нам обычно бывают нужны более частные случаи oцe
нивания отдельных моментов прежде Bcero среднеrо и дисперсии наблюда
емой случайной величины . Поэтому выпишем еще в явном виде несколько
конкретизаций этоrо общеrо решения.
Пример 4. Рассмотрим задачу построении доверительноrо интервала IU1я про
k
извольноrо теоретическоrо момента а!.: == E k 1. В этом случае, BMe
сто использования общеrо алrоритма (27), проще непосредственно исполь
зовать теорему З, заменив в ее формулировке асимптотическую дисперсию
(а2!.: ai)/n ее оценкой (а n ,2!.: a;k)/n' в итоrе это даст искомый асимп
тотический 'У доверительный интервал IU1я а!.: вида
...
Доверитепьный ИН
тервал для cpeAHero
( аn" 1= с, а n , 2!.: n a;tk) .
Полаrая здесь k == 1, получим соответствующий
интервал IU1я теоретическоrо среднеrо аl == Е{:
(28)
( с,В )
X1= ,;n "
(29)
.
Пример 5. Чтобы построить асимптотический 'У доверительный интервал IU1я
теоретической дисперсии JL2 == D , надо просто воспользоваться резулыа
Доверитепьный ИН том (25): искомый интервал есть
тервал для диспеРСИИ,1
(В2 1= С, V Цn4 : В4 )
(За)
.
2.3. MHorOMepHbIe данные
ВысиlOЯ математика проще эле.менmарной в то.М СМblсле, что
исследовать непроходимую чащу леi!че с самолета, нежели пеUl
ком (но ддя этОi!О надо иметь самолет и уметь им Уl1равлять. .
Иноrда наблюдаемая в эксперименте случайная величина представляет собой
вектор некоторой размерности k 2: { == ( I, , k), В этом случае BЫ
бор ка из .ею есть совокупность k MepHbIx векторов {Х/ == (X/l, ., X/ k ),
1 == 1".., п} и обработка таких MHoroMepHbIx данных уже более трудоемка,
2.3. МН020мерные данные
119
так как помимо обычных выборочных моментов здесь надо вычислять эм
пирические (выборочные) аналоrи для смешанных теоретических моментов,
среди которых важнейшим для приложений является второй смешанный MO
мент или ковариация.
Чтобы не заrpомождать изложение техническими деталями, рассмотрим
подробно лишь простейший случай k == 2. Итак, пусть наблюдается двумерная
случайная величина == (6,6) и {Х 1 == (Х II , Х 12 ), l == 1,. ., ,n} повторные
независимые наблюд ния над ней. Обозначим F(XJ. Х2) == P{ ! :::;; XI, 6 :::;; Х2)}
(теоретическую) функцию распределения, Ц == (E I, Е6) ==!!:. == (р), Р2)
вектор средних и D j == o-j, j == 1, 2, cov(6, 6) == 0'12 вторые центральные
моменты вектора {. Как в данном случае по выборочным данным построить
эмпирические (выборочные) аналоrи этих характеристик?
1. Эмпирическая ФУНКЦИЯ распределения
Эмпирическая функция распределения определяется по аналоrии с OДHOMep
ным случаем формулой
1 n 1 n
рn(х), Х2) == L I(X II :::;; XI, Х 12 :::;; Х2) == L 1}1. (1)
n n
1=1 /=1
в (1) {1}I == I(X II :::;; Х" Х/ 2 :::;; Х2)} независимые одинаково распреде
ленные случайные величины, принимающие значения О и 1, т. е. бернуллиев
ские величины, причем
Е1}I == P{X 11 :::;; Х), X I2 :::;; Х2} == F(XI, Х2),
D1JI == Р(Хl, Х2)(I Р(х), Х2))'
Отсюда и из (1) следует, что
1 n
ЕРn(Хl, Х2) == L E'Тl/ == F(xJ, Х2),
n
I )
(2)
т. е. э.ф. р. рn(х), Х2) является несмещенной оценкой дЛЯ F(XI, Х2) при лю
бых XI, Х2.
Далее
1 n 1
DFn(x), Х2) == 2 L D1JI == F(XI, Х2)(I Р(х), Х2)), (3)
n /=1 n
что стремится к нулю при n 00, т. е. Fn(XI, Х2) является состоятельной
оценкой для F(Xj, Х2).
Таким образом, здесь имеется полная аналоrия с одномерным случаем
(см. (5) 92.1).
120 rлава 2. Первuчная обработна энсперuментальных данных
2. Моменты
Обратимся теперь к моментам. Обозначим Xj == (X 1j ,.. ,X nj ), j == 1, 2, BЫ
борочные данные ДfJя j й координаты вектора { == ({), 6) и пусть , 8}
соответствующие выборочные среднее и дисперсия, вычисляемые по форму
лам (4) (5) 2.2.
Torдa X j является эмпирическим аналоrом ДfJЯ теоретическоrо среднеrо
8 2 2
J.Lj == E{j, а j ДfJЯ дисперсии (7j == D{j
Выборочная Выборочная же (эмпирическая) ковариация аналоr
теоретической ковариации
ковариация
(712 == COV( I, Ы == Е({I J.L1)(6 J.L2) == E 16 J.LIJ.L2
определяется формулами
I n I n
812 == 2)Хll X 1 )(X 12 Х 2 ) == L X/lX 12 X 1 X 2 . (4)
n n
I ) I I
Выборочный
коэффициент
корреляции
Соответственно, выборочный (эмпирический) коэффи
циент корреляции аналоr теоретическоrо коэффициен
та корреляци и
COV({I, Ы
р == P( I, Ы == corr( I, Ы == .JЩ I D6
определяется формулой
812 ( )
Рn == 8) 82 ' 5
Исследуем некоторые свойства этих новых выборочных характеристик.
В 2.2 мы установили, что выборочная дисперсия не является несмещенной
оценкой теоретической дисперсии, но леrко построить статистику уже являю
щуюся несмещенной оценкой дисперсии (см. формулы (17) (18) 2.2). Анало
rичный факт имеет место и ДfJЯ выборочной ковариации. Именно, справеДfJива
Лемма. Статистика
n 1 n
812 == "(Х ll X 1 )(X12 Х2)
n l n ]L.,.
' I
является несмещенной оценкой теоретической ковариации (712 == COV({I, 6).
(6)
Доказательство. Введем случайную величину 1} == {) +6. Выборочные дaH
2 2
ные для нее есть Х/ == Х ll + Х12, l == 1, . . . , n, а ее дисперсия D1] == (71 + (7 + 2(712.
Построим несмещенную оценку ДfJЯ D1]: это есть статистика
n n
1 L 2 1" ( ) 2
(X/ X) == L.,. (Xll X))+(X12 X2) ==
n 1 n ]
' l ' I
92.3. MHOi!OMepHbIe данные
121
ппп
I L 2 I L 2 2 L
== (Хп X 1 ) + (X 12 Х 2 ) + (ХII X 1 )(X/ 2 Х).
n ' n 1 n '
/ I / I / I
В этом разложении
1 2
(n 1) 6(X/j X j )
/ I
есть несмещенная оценка для о';, j == 1, 2, следовательно, последнее слаrае
мое несмещенная оценка для 20'12. .
В общем случае для k мерной наблюдаемой величины { == ('1, " ",,) с
Е{== == (J.ll",' ,JL") и дисперсионной матрицей D{ == Е == II00ij == COV('i, ЫII
выборочные моменты первоrо и BToporo порядков вычисляются по формулам
n n
1" 2 1" 2
Xj == ;, 6 X/j, 8j == -; 6(X/j Xj)
I 1 / I
1 n
8 ij == L(X/ i Xi)(X1j Xj), i 1- j.
n
/ I
Таким образом, здесь мы имеем вектор выборочных средних ( , , X k )
и выборочную дисперсионную матрицу Е == 118ij" ' rде 8 ii == 8;, i == 1, , k.
Вектор выборочных средних будет несмещенной оценкой для вектора Teo
ретических средних == (JL 1, , J.l/J, т. е. ЕХ; == JLi, i == 1, . . . , k, а подправ
ленная выборочная дисперсионная матрица n/(n l)Е несмещенной oцeH
кой дЛЯ Е: Е(n/(n I)Е) == Е (это равенство следует понимать поэлементно).
3. liольшие выборки
Обсудим теперь асимптотические свойства введенных новых эмпирических
характеристик, предполаrая, что теоретические ковариации существуют. Тоrда
по закону больших чисел при n -----+ 00
1 n
L X/iX/j E('i'j),
n
/ I
Р 2 Р
но также и Xj E'j, 8j D'j. Следовательно,
по теореме 1 Р.2
р
8 ij O'ij
,. '1<
Состоятельность
...
выборочных ковари "'"
аций и коэффициен
тов корреляций
8 ij Р ( )
и Pij == 8i 8 j Pij == Р 'i, 'j ,
i 1- j. (7)
Таким образом, выборочные ковариации и коэффициенты корреляций
являются состоятельными оценками соответствующих теоретических ковари
аций и коэффициентов корреляций (конечно, если все теоретические диспер
сии 0'; > О).
122 rлава 2. Первичная обработка экспериментаЛЬНblХ aaHHblX
Можно также по казать, что E'Pij Pij ---------7 О при n ----+ 00, т. е. P;j являются
лишь асимптотически несмешенными оценками ДI1я Pij.
4. Добавление: нормальная модель
Предположим, что наблюдается двумерная нормальная случайная величина:
L:((I,6) ==N ( (J1.I'J1.2)' 11 O' РО', 2 0'2 11) , Ipl < 1
PO'I0'2 0'2
(см. п. 2 1.2), и требуется по соответствующей выборке рассчитать довери
тельный интервал ДI1я теоретическоrо коэффициента корреляции р.
Это можно сделать на основании результата Р. Фищера (1915 r.), который
показал, что если от выборочноrо коэффициента корреляции Рn, определен
Horo в (5), перейти к новой статистике
1 1 +Рп
Zn == In ,
2 1 Рп
то уже для небольших объемов выборки n статистика Zn будет распределена
приблизительно нормально, со средним значением и дисперсией, заданными
приближенными выражениями
EZ ,. + Р
n " 2(n I)' rде
1 1 +р 1
( == 1п , и DZ n .
2 l p n 3
Дрyrими словами, L:(vп-=з(zп ()) ---------7 N(O, 1) при n ----+ 00.
Отсюда, так же, как и в п. 5 2.2, мы можем построить асимптотический
')' доверитеЛЬНblЙ интервал для (: (Zп=FС-у/Vn:=З), с-у == ф 1 ((1+')')/2) По
скольку функция ( == ((Р) в (8) монотонно возрастает, то разрешая уравнения
(8)
с;
((р) == Zn =F v'n 3
-7 До ;рите ьны '
интервал для Р
относительно р, мы получим асимптотический ')' дo
верительный интервал ДI1я caMoro коэффициента KOp
реляции р:
( Cl ( Zn ) , CI ( Zn+ ))
vn=з vn=з
(здесь С' обратная функция к О. Поскольку в этом алrоритме число n
предполаrается большим, то в (9) можно оrраничиться лишь пеРВblМИ двумя
членами разложения в ряд Тейлора 3) функции C'(Zn + еп), еп ---------7 о, И ис
рЕ b:.."f ==
(9)
)Тейлор Брук (1685 1731) анrлийский математик и философ, в 1712 r. нашел общую
формулу разложения функций в степенной ряд, носящую ero имя.
2.3. MHOZOMepHbIe данные
123
пользовать приближенный интервал
'Y (C1(Zn) =f vn 3 :t CI(t)lt z)
e 2Z . 1 ( 4Gye 2Z . )
== l=f
e 2Z . + 1 (e 4Z . I)Jn=3 .
При больших n это достаточно узкий интервал, окружающий точку
(e 2Z . J )/(e 2Z .. + 1). В свою очередь, если значение статитстики Рn мало,
тоrда Zn Рn, И интер!Jал (1 О) может быть заменен приближенным интерва
лом == (Рn =f Gy/ vn 3 ), который уже является симметричным интервалом
с центром в точке Рn. Построенный интервал может быть использован
также для ПрО!Jерки rипотезы Но, состоящей в том, что р == ро, rде ро
некоторое малое заданное число. В частности, при ро == О rипотеза Но будет
означать независимость компонент I и 6 наблюдаемой двумерной нормаль
ной случайной величины { == (6,6), поскольку в данном случае некоррели
рованность (ро == О) эквивалентна независимости (см. п. 2 1.2). Рассуждаем
при этом мы так. Если rипотеза Но р == ро верна, то
(10)
p{ су СУ }
Pn <PO<Pn+ 1
yn 3 yn 3
или, что то же,
P{lpn Роl vn 3 } 1 1== а.
При достаточно малом значении а (при I близком к 1) событие 'Рn Роl
ey/ практически невозможно, и если для данной выборки обна
руживается, что Ipn pol ey/ , то мы должны отклонить rипотезу
о равенстве р == ро, как противоречащую данным. В противном случае rИ
потеза считается соrласующейся с данными, и она принимается. При этом
мы можем ошибиться, отклонив rипотезу НО, если она верна, но вероятность
этоrо приблизительно равна а, т. е. мала.
Обычно такую методику применяют для пров рки _ " rипотеза"
zипотезы независимости Но: Р == О (понятие общеи rи ."., "
) независимости
потезы независимости см. в примере 6 Введения, и в
этом случае правило принятия решения формулируется следующим образом:
задаемся малой вероятностью а ошибочно отклонить истинную rипотезу Но
(а называется уровнем значимости) и определяем число су == ф I ((1 + 1) /2) ,
1 == 1 а. Далее по имеющейся выборке вычисляем значение статистики
Рn по формуле (5), и если окажется, что 'Рn! ey/ , то rипотеза Но
отверraется, в противном случае, т. е. при IP"nI < ey/ , она принимается.
Таким образом, здесь мы встретились с конкретным примером проверки
статистической rипотезы, общая теория которых будет детально обсуждаться
в rлА.
124 rлава 2. Первuчная обработка эксперuментаЛЬНbfХ aaHHblX
Замечание, Плотность fn,p(r) статистики РП имеет вид [15, с.436): при n> 2
1
f (r) '= n 2 (1 2 )(n I)/2 ( 1 r2)(n 4)/2 1 xn 2 dx , Irl < 1,
П,р 1т Р (1 prx)n 1
о
т. е. зависист лишь от пир, и при р '= о (т. е. при независимости I И 6)
( n 1 )
f ( т ) '= r 2 ( 1 2 ) (n 4)/2
п,О ( n 2 ) r ,
v'7Тr
2
Irl < 1.
Если (при р'= О) раССМотреТЬ преобразование
рп
Тп '= v n 2 '
V 1 p
то, используя формулу (45) 1.2, нетрудно убедиться R том, что статитсти
Ка Тп имеет распределение Стьюдента S(n 2) (это мы оставляем читателю
в качестве простоrо упражнения на применение формулы преобразования
(45) 1.2). Поскольку функция у '= vn=2 xj при Ixl < 1 MOHO
тонно возрастает от oo до 00 , то отсюд а следует, что события {ITnl > t,,}
и {Ipn I > z,,} при Za '= t"j V n 2 + t эквивалентны. Поэтому, если при
заданном а, О < а < 1, число t a выбрано так, чтобы выполнялось условие
P{ITnl > t a } '= а, то будет выполняться также условие P{lpnl > z,,} '= а.
На этом факте, аналоrично предыдущему, можно предложить следующий ал
rоритм для проверки rипотезы независимости Но р О, который уже
«работает» при любом числе наблюдений n > 2. Пусть задан малый уровень
значимости а. Torдa, поскольку плотность распределения Стьюдента (см. (28)
1,2) симметрична относительно нуля, то, обозначая функцию распределения
закона S(n) через Sn(X), из цепочки соотношений
ос
а'= p{JTnl > t a } '= 2 / f(xln 2) dx '= 2(1 Sn 2(ta))
t.
получаем, что t" определяется уравнением
а I ( а )
Sn 2(ta) '= 1 2' т. е. t(t '= Sn 2 1 2 '
rде S; 2(') обратная функция к Bn 2(X)'
Далее вычисляем п о имеющи мся данным значение рп, И если окажется,
что Ipn I > Za '= t(t/ V n 2 + t , то мы отверrзем rипотезу Но как проти
воречащую данным, поскольку вероятность тaKoro события при rипотезе Но
(равная, по предыдущему, а) мала при малом а, В противном случае, т. е. при
Ipn I Z", rипотеза НО принимается. Вероятность ощибочно ОТКJlОНИТЬ при
этом истинную rипотезу Но в точности равна а.
2.3. MHOZOMepHbIe данные
125
5. Друrие корреляционные характеристики
В теории статистической реrpессии (о которой подробно будет идти речь в rл. 6
6.6) важную роль иrpают, помимо обычных корреляций (коэффициентов
корреляций corr( , 1J) == p( , 1J», друrие, более сложные корреляционные
характеристики совокупности изучаемых случайных величин. Здесь мы дадим
их определения и построим их эмпирические (выборочные) аналоrи.
Итак, пусть имеется совокупность случайных величин У и Х == (X 1 ,
, Х р ), связанных не которой стохастической зависимостью, причем Х дo
ступно наблюдению (измерению), а значение У непосредственно измерить
невозможно (например, У связано будущим). Torдa возникает задача предска
зания (проrноза, оценки) величины У по информации, доставляемой измере
нием величин Х" ,Х р , которые в этом контексте называются предсказЬ/
вающими nеременнЬ/ми. Функция от предсказывающих переменных tp( X ), KO
торую используют В качестве оценки для У' Ip( X ) >:;; У, называют предиктором
величины У по Х. Задачей разработки методов построения наилучших (в Ka
KOM TO смысле) предикторов занимается теория статистической рарессии.
Для измерения точности предиктора Ip обычно используется cpeдHeKвaд
ратичная ошибка (с. к. о.)
L\(tp) == E(tp( X ) у)2
Предиктор, минимизирующий с. к. о. В заданном классе
предикторов L называется оnтимаЛЬНblМ предиктором, или
nрОi!НОЗОМ (в классе L), и обозначается си мволом tp *
tp' == arg min L).(Ip),
'PEL
.,f
Проrноз
(11 )
ero с. к. о. есть
L\' == L\(tp') == E(tp'( X ) у)2 == i nf L E(Ip( X ) у)2 (12)
'РЕ
Таким образом, в общем случае задача построения наилучшеrо (в cpeд
неквадратичном смысле и в заданном классе предикторов L) проrноза для
величины У по Х сводится к решению экстремальной проблемы (11) (12).
Часто оrраничиваются классом линеЙНblХ пpeдиK Линейный проrноэ.
торов, т. е. коrда L есть класс линейных функций: ./Ij
L == {у' tp( ) == /30 + /3,Хl +. + /3рХр} в этом случае оптимальный предик
тор всеrда существует (при условии существования вторых моментов и HeBЫ
рожденности дисперсионной матрицы Е == О Х ) и имеет вид:
У р ' == \I"( X ) == /30 + /3 Х 1 +... + /3;Х р ==
==/30+ O/ X ==EY+ "( X EX ), (13)
rде
/3* == E '!!, Q == соу(У, Х) == (соу(У(, X J ),
,cov(Y 1 , Х р »)
и
/3 . == ЕУ /3 *'ЕХ'
о ,
126 rлава 2. Первuчная обработка экспериментальнЬ/х даннЬ/х
при этом ero с. К. о.
* == O" Q' IQ, O" == DY. (14)
Таким образом, как сам оптимальный предиктор, так и ero с. к. О. BЫ
ражаются в данном случае лишь через первые и вторые моменты системы
случайных величин (У, Х ).
Множественный В изложенной теории линейноro nроrноза особую
Р ОЛЬ иr р ает величина
коэффициент
корреляции
2 Q/ 'Q 2 *
РУХ == == Р (У, tp ( Х )),
ау
(15)
называемая множественнЬ/м коэффициентом корреляции; она является eCTe
ственной мерой зависимости между У и Х (мерой точности ПрОi'llоза) и с ее
помощью можно сравнивать различные совокупности предсказывающих пе
ременных в конкретных задачах. Сorласно (15) множественный коэффициент
корреляции между У и совокупностью Х == (Х" ,Х р ) равен квадрату
обычноrо коэффициента корреляции между У и оптимальным линейным
предикторомдля У по Х. Чем ближе P x к 1, тем меньше с. к. о. * (см. (14)),
а при P K == 1 с. к. о. * == О, т. е. пр;ноз абсолютно точен: в этом случае
У == ср* ( Х ), т. е. У функционально связана с Х.
в практических приложениях теоретические моменты системы слу'шйных
величин (У, Х) обычно неизвестны, поэтому все сведения, необходимые для
построения оптимальноrо предиктора, получают в результате обработки CTa
тистических данных, которые представляют собой выборку из распределения
.с(У, Х ). Оценив по такой вспомоrательной выборке (по результатам прошлых
измерений Х и У) первые и вторые моменты, как это описано выше в п. 2,
« ЭМПИРИ'iеский .. jl И заменив этими оценками теоретические характери
,',. стики J1.0 == ЕУ, !!:. == ЕЖ, Q и , строят эмпирический
предиктор
предиктор
....... ........,
* ( X ) == {З * + {З х
tp о ,
Д* == '(1,
.......* ...... ......."'1.......
{ЗО == /1-0 !!:.'
( 16)
который и используют для предсказания в друrих случаях (в будущих изме
рениях). Точность эмпирическоro предиктора (16) оценивается эмпирическим
множественным коэффициентом корреляции
a' I(1
..-.2
рук == В2(у)
( 17)
(в формулах (l6) (17) == (BOI' , SOp) , == IISij 11/;, индекс «O»COOТBeTCTBY
ет У). Множественный коэффициент корреляции P K принято записывать
2
в виде PO(I...p)'
Еще одна полезная корреляционная характеристика возникает при pac
смотрении следующеrо вопроса. Корреляцин между двумя величинами, CKa
жем, в нашем случае, меЖдУ У и Х р , характеризуется коэффициентом кор-
92.3, MHozoMepHble даННblе
127
реляци и РОр соп(У, Х р), который иноrда называется также полным Ka
эффициентом корреляции У и Хр. Если рассматривать У и Х р совместно
с остальными р 1 величинами X 1 ,..., Xp I, то можно считать, что изме
нение величин У и Х р вызывается в какой то мере изменением остальных
величин, Спрашивается, как в такой ситуauии измерить непосредственную
связь У и Х р , ИСКJJючая, так сказать, влияние промежуточных переменных
Х 1, , Х p I? ДЛЯ этоrо служит частный коэффици Ч У фф
Qстныи коэ и OIIt
ент корреляции величин У и Х Р относительно X 1 ,.
" циент корреляции
Xp l, обозначаемыи символом POp(I...p I)' Для ero BЫ
числения поступают следующим образом. Строят оптимальные линейные пре
дикторы !U1я У и Х р, основанные на лромежуточных переменных Х 1, . . . .
Xp l, по алrоритму (13), Т.е.
y'==/3 +/3;Xl+', +/3; IXp 1
и
Х . · . х · Х
р==ао+аl 1+...+ap 1 p l,
и рассматривают <<остатки.) еl == У У' и е2 == Х р х; тем самым ИСКJJюча
ется влияние «общих факторов.) X 1 , . .. , Xp 1 на рассматриваемые перемен
ные У и Х р ). После этоrо вычисляется обычный коэффициент корреляции
p(el, е2) между этими остатками, который и есть частный коэффициент KOp
реляции POp(l...p l) величин У и Х р относительно X 1 , ,Xp l' В теории
линейноrо проrнозирования доказывается, что
р Ор
POp(l...p l) == (рООррр) 1/2 '
(18)
rде IIpi j ll == Ilpijll 1 и
Pij == p(Xi,X j ), i,j ==0, 1,
,р (Х О == У).
Из (18) следует, что частный коэффициент корреляции определяется че
рез обычные коэффициенты корреляции системы величин У, X 1 . , Х р .
следовательно, ero эмпирический аналоr строится заменой IJ (18) теоретиче
ских корреляций Pij на выборочные корреляции Pij, определенные в (7):
Op
Р
Pop(I...p l) == (p OO p PP )I/2'
(19)
Из формул (17) и (19) видно, что эмпирические множественный и част
ный коэффициенты корреляций представляют собой непрерывные функции
от выборочных вторых моментов, поэтому по теореме 1 2.2 на основании
соотношений (7) можно заключить, что они являются состоятельными oцeH
ками соответствующих теоретических характеристик.
Пример 1. Рассмотрим случай р == 2. Здесь предиктор У' == /3 + /3 X 1 . rде
соrласно (13) /3; == cov(Y, X1)!DX 1 == РоI 0"0 И /3'0 == ЕУ /3;EX 1 .
0"1
128 rлава 2. Первичная обработка экспериментаЛЬНbfХ данных
Аналоrично, предиктор Х; == a + a;X 1 , rдe
. соу(Х 2 , X 1 )
al==
DX I
а2
== PI2 ,
аl
ао == ЕХ 2 a;EX 1 .
Следовательно, остатки имеют вид
еl == у у. == у ,в;Х 1 /3 , е2 == Х 2 Х; == Х 2 а;Х, ао,
а их с. к. О, по (14) равны Del == a (1 P l) и De2 == (ji(! P 2)' Далее непо
средственно вычисляем
cov(el, е2) == соу(У /3;X 1 , Х 2 a;X 1 ) == (РОl P01PI2)(10(12,
( ) cov(el' е2) Р02 P01Pl2 (20)
Р е I е2 == ==
, Dе l Dе 2 / (1 p ,)(1 РТ2)
С друrой стороны, обращая корреляционную матрицу Ilpijll и вычисляя
элементы
02 Р02 P01PI2 00 1 РТ2 22
Р == IPijI Р == 1P:iI' Р
по формуле (18) приходим к тому же результату (20).
Вычислим, наконец, оптимальный предиктор (13).
Здесь
1 P I
Ipijl '
11 1
1; аl
Р12аl (12
Р 12 (j (j i ' а2 11 ' ( )
== POI(10(jl, Р02аоа2
и в итоre находим
/3; == (10 РОl Р02Р12
(11 1 РТl
/3; == аО Р02 POIPl2
а2 1 РТl
Таким образом,
<p.(X 1 , Х2) == ЕУ + /37(Х 1 EX 1 ) + /3;(Х 2 ЕХ 2 )
с указанными коэффициентами /37 и /3;. Множественный же коэффициент
корреляции (15) здесь имеет вид
2 2 2
2 РОI + Р02 РОI P01Pll
РО(I2) == 1 2
Pl2
(21 )
.
2.4. Выборочные квантили и порядковые статистики
1. Теоретические и эмпирические квантили
Важный класс характеристик наблюдаемой (скалярной) случайной величи
ны составляют квантuлu. По определению, р квантйль (р это решение
уравнения F((p) == р, о < р < 1, rде Р(х) функция распределения . Если
2.4. ВblБОРОЧНblе квантили и nорядКОВblе статистики 129
функция F(x) cтporo возрастает, то однозначно определена обратная к ней
функция F l, И Torдa (р == F l(p). В общем случае, Д1IЯ произвольной непре
рывной справа функции F обратная к ней функция. Квантильная .,f'
определяется равенством ........ функция
F I(p) == inf{x F(x) р} (1)
и называется квантильной функцией.
Итак, в любом случае (ДIIЯ любой функции распределения) р квантиль
случайной величины { (или ее распределения) есть (р == F I (р), т. е. значение
квантильной функции (1) в точке р Е (О, 1) (см. рис. 1)
F(x)
I
(р, о
х
Рис. 1
Рп(х)
k
........ .
n
р
: k 1
, n
X(k l)
Хщ
ж
Рис. 2
Статистическим аналоrом Д1IЯ (р (выборочной, или эмпирической, p-KвaH
,!,uлью) (п, р называется р-квантиль эмпирической функции распределения
рп(х) , построенной по выборке Х == (X 1 , ,Х П ) ИЗ .ею. Эти новые вы-
борочные характеристики просто выражаются через порядковые статистики
выборки (см. п. 1 э2.1).Действительно (см. рис.2), если (k l)/n < р k/n,
I
или k 1 < пр k, то (п,р == F;; (р) == Хщ. Поэтому, если число пр целое,
т. е. пр == k, то ,p == Х(пр); если же число пр дробное (т. е. k 1 < пр < k), то
uелая ero 'IaCTb [пр] == k 1 (т. е. k == [пр] + 1) и потому (п,р == XOnpl+ 1 )' Итак,
{ Х (I 1+ 1 ) при П Р дробном,
(п,р == F;;I(X) == пр (2)
Х(пр) при пр целом.
9 яка, 1748
130 rлава 2. Первuчная обработка эксперuментаЛЬНblХ данных
...
Выборочная
медиана
' . . При р == 1/2 квантиль ('/2 называется теоретиче
.,...." СКОЙ медианой, a , 1/2 выборо'fНОЙ медианой (несколь
ко отличается от определения медианы вариационноrо
ряда в П.I 2.1); при Р == 1/4 и 3/4 соответствующие квантили иноrда назы
ваются квартилями, соответственно нижними и верхними.
Итак, поскольку, ввиду (2), выборочные квантили по существу есть COOT
ветствующие порядковые статистики выборки, то дальнейший разrовор будет
вестись в терминах именно порядковых статистик.
2. Распределение порядковых статистик
Предположим, что распределение случайной величины абсолютно непре
рывно и f(x) == F'(x) ее плотность. Найдем функцию распределения
Fk(X) == Р{Хщ :::;; х} и плотность 9k(X) == FL(x) произвольной порядковой
статистики Хщ (k == 1, ,n) выборки Х == (X 1 , ,Х П ) из .ею.
Событие {Хщ :::;; х} означает, что не менее k элементов выборки Х име
ют значения, не превосходящие х, но это есть событие {ILn(X) k} (см. (3)
2.1), следовательно, эти два события эквивалентны. Как показано в п. 2 2.1,
случайная величина ILn(X) при любом Х Е R 1 распределена по биномиально
МУ закону Bi(n, F(x)) Отсюда имеем
п
Fk(X) == P{J.ln(x) k} == L C pr(x)(l p(x))n
" !.;
В частности, из (3) имеем, что распределения экстремумов имеют вид
F,(x) == Р{Х(I) :::;; х} == I (1 р(х))п.
Fn(x) == Р{Х(п) :::;; х} == Fn(x).
(3)
-'lt,..
Неполная
бета Функция
Таким образом, '1 любой модели функции распределе
ния порядковых статистик леrко выписываются. Далее,
правую часть (3) можно записать через так называемую
непОЛ/lУЮ бета Функцию
z
[(а + Ь) / a ' ( b 1
B(z; а, Ь) == r(a)r(b) t 1 t) dt, о:::;; z :::;; 1,
о
которая представляет собой функцию распределения закона Ве(а, Ь) (см. п. 4
1.2). Именно, интеrрироваНl1ем по частям нетрудно установить формулу
(4)
z
B(z;k,n k+I)== ( ) ! ) f tH(I t)n kdt==
k l!n k!
о
,1
L C zr(l z)n r,
r-k
(4')
2.4. Выборочные квйнтили и порядковые статистики 131
из которой следует, что формуле (3) можно придать
также вид
Ф ..
ункция распреде-
ления Хщ
Fk(X) == В(Р(х); k, n k + 1). (5)
Неполная бета Функция подробно протабулирована, поэтому представ
ление (5) полезно для проведения численных расчетов, связанных с порядко
выми статистиками.
До сих пор ниrде не предполаraлосьсуществование плотности f(x) ==F' (х),
поэтому предьщущие формулы справедливы для любых распределений .с({).
Если же { имеет плотность распределения f(x), то
соотношение (5) можно продифференцировать по х Плотность распре- ..,.
и получить в итоrе, что плотность 9/,;(Х) == Р{(х) Cy , = :JJ ;
ществует и имеет вид
n! /,; 1 n /,; (
9/,;(Х) == (k I)!(n k)! F (х)(l Р(х» !(х). 6)
Можно также выписать совместную плотность для любоrа числа поряд
ковых статистик (см. упр. 31). Укажем, например, вид двумерной плотности
gkr(X\, Х2) для пары порядковых статистик (X(k), X(r), 1 :( k < r :( n:
n!
9kr(X" Х2) == (k l)!(r k l)!(n т)! Х
XFk I(XI)(F(X2) F(XI»)r H(1 F(X2»n r f(XI)!(X2) (7)
при ХI < Х2 И равна нулю в остальных точках.
Приведем, наконец, вид совместной плотности всех n порядковых CTa
тистик:
91.. .n(XI' ... , Х n ) == n!f(x,) ... f(x n ), Х, < Х2 <
< Хn.
(8)
Рассмотрим один важный для последующеrо и поучительный при мер
работы с порядковыми статистиками.
Пример 1. Пусть Х == (X 1 , .. . ,Х n ) выборка из стандартноro показатель
Horo распределения r(l, 1) (см. п.3 1.2) Т.е. коrда плотность f(x) == e X
х > О. в этом случае совместная плотность всех n порядковых статистик
Х(I), . .. , Х(n) по формуле (8) есть
( ) I X] ... Xn
91..." xl, .. . ,Х n n.е ,
о < х\ < Х2 <
< Хn.
(9)
Y r == (n r + I)(X(r) Х(н),
r == 1, . . . , n, Х(О) == О,
..
Спейсинrи показа-
тельной Вblборки
Рассмотрим новые статистики
называемые cпeйcинzaмu, и найдем их совместное распределение. Для этоrо
надо лишь воспользоваться соотношением (44) 1.2. В данном случае якобиан
9-
132 rлава 2. Первичная обработка экспериментаЛЬНblХ даННblХ
преобразования YI == nХ, У2 == (n 1)(Х2 Xl),
очевидно, n!, т. е. постоянен, а
Уn == Х N Xn ' равен,
n
n
n
2: У, == 2:(n r + I)(xr ХН) == 2: Xr.
,=1 ,=1 ,=1
. Моменты порядковых
статистик показатель
ной выборки
Следовательно, lUIя совместной плотности rp(YI,' . . ,Уn) преобразованных CTa
тистик имеем в виду (9) представление
'Р(Уl, ,yn)== 91...n(Xl" ,Х n ) ==e YI ''' Yn
n.
Но это означает, что статистики Y 1 ,... ,У n независимы и имеют одно и то же
стандартное показательное распределение r( 1, 1). (!)
Отсюда можно сделать следующие интересные выводы. Выразим исход
ные порядковые статистики Хщ через спейсинrи У 1 , , У n :
k
'" У ,
X(k) == L.J n r + 1 ' k == 1,
'='
Тем самым Хщ представляется в виде линей
ной комбинации независимых случайных величин,
поэтому, в частности,
' .:it.:,<.t.-.ill:iiJiI.
k 1
ЕХщ == '" EY r ,
L.Jn r+1
,=l
k 1
DX(k) == 2: ( )2 DY r .
'= 1 n r + 1
Но среднее и дисперсия закона r(1, 1) равны 1 (см. (21) 1.2), поэтому
k 1 n 1 n
ЕХ(ч == 2: n r + 1 == 2: """;" DX(k) == 2: "72'
'=' '=n k+1 J j=n k+1 J
В частности, ШlЯ максимальноrо значения выборки Х(n) эти формулы
принимают вид
,n.
(10)
(11 )
n 1 n 1
ЕХ(n) == 2:""";', DX(n) == 2: . (12)
j=l J j=1 J
Если объем выборки n ----+ 00, то, используя известные асимптотические
формулы из анализа:
n 1
2: "7 == In n +с+ 0(1), с == 0,5772. константа Эйлера 4),
j=1 J
4) Эйлер Леонард (1707 1783) rениальный швейцарский математик, механик, физик и аст.
роном, академик Петер6урrской АН.
2.4. Выборочные квантили и порядКОВblе статистики 133
n 1 71"2
L == 6 +0(1),
j l J
заключаем, что в среднем х(п) неоrpаниченно Dозрастает как ln n, D то время
как дисперсия DX(n) --------+ 71"2/6, т. е. имеет конечный предел. .
Замечание. В рассмотренном примере нам удалось, «иrpая,) на специфических oco
6енностях показательной модели, вычислить в явном виде моменты (среднее и дис
персию) порядковых статистик. Но это исключительный случай. Вообще же проблема
отыскания моментов порядковых статистик весьма сложна и ее удается решить лишь
ДJlя некоторых моделей 1:(0 (см. упр. 32 данной rлавы и упр.46, 56 rл. 1), в отличие
от проблемы получения их распределений. Подчеркнем, что для выборочных MOMeH
тов D этом аспекте все наоборот.
Перейдем теперь к исследованию асимптотических
свойств порядковых статистик для больших выборок
(при n ----+ 00). Поскольку число порядковых статистик
равно объему Dыборки и, следовательно, неоrраничен
но растет вместе с n, то было бы наивным надеяться на то, что все они
будут иметь однотипные асимптотические свойства. И, действительно, эта
проблема распадается на две самостоятельные задачи: асимптотика «средних,)
членов вариационноrо ряда (2) 2.1 и предельные распределения «крайних,)
порядковых статистик. Прежде Bcero поясним эту терминолоrию.
Под средними членами вариационноrо ряда выборки объема n при n ----+ 00
понимаются порядковые статистики Хщ, номера которых k == k(n) удовле
творя ют УСЛОDИЮ k/n ----+ р при некотором р, О < р < 1. Таким образом, это
такие члены вариационноrо ряда, которые расположены «далеко» ОТ ero KOH
ЦОВ. Крайние же порядКОВblе статистики эm члены вариационноrо ряда,
расположенные в ero концевых законах, т. е. статистики X(r) при r оrpани
ченных и X(n s+ 1) при S оrраниченных.
Асимптотические
свойства порядко
вых статистик
3. Асимптотическая нормальность средних членов. вариационноrо ряда
Зафиксируем некоторое р, О < р < 1, и рассмотрим порядковую статистику
Хщ с k == [пр]. Справедлива следующая теорема о ее асимптотическом pac
пределении.
Теорема 1. Если в некоторой окрестности точки (р плотность f(x) непре
рывна вместе с производной и f((p) > О, то при n ----+ 00
.с (X(lnpl)) '" N ( (р, n (p) ) , q == 1 р.
!
(13)
Доказательство. Рассмотрим случайную величину
1Jn == (Хщ (p)f((p) !Е
VPi
134 rлава 2. Первичная обработка экспериментальных aaHHblX
и покажем, что ее плотность 'Рn(х) сходится при n ----+ 00 к стандартной HOp
мальной плотности lf1(x) == (211'(1/2e X'/2 (см. (7) Э 1.2). По формуле 43 Э 1.2
из (6) имеем
'Рn(Х) == JЧ- f I((p)gk(tn), rде t n == (р + f( p) JЧ- .
Запишем If1n(x) в виде про изведения А 1 (п)А 2 (п)А з (п), rдe
п! fpq k 1 n !. f(tr.)
AI(n) == (k l)!(n k)! V p q А2(П) == f((p) ,
Аз(п) == ( F n) ) н ( 1 :(tn) ) n !.
и найдем предел каждоrо из этих трех множителей при n ----+ 00 и k == [пр].
Простым упражнением на применение формулы Стирлинrа дЛЯ rамма функ
ции (см. п. 3 1.2) является установление предела AI(n) ----+ (211') 1/2 (OCTaB
ляем это читателю). Далее, А2(П) ----+ 1 в силу непрерывности функции f(x).
Наконец, поскольку F((p) == р, из тейлоровскоrо разложения в точке (р
F(t n ) == р + х fpq + x2pq f'((p) + O ( )
V 2п f2((p) n
нетрудно получить, что Iп Аз(п) ----+ x2/2. В итоrе это дает нужный предел
'Рn(х) 'Р(х). . .
jI, Состоятельность
выборочных
квантилей ,
3i1мечание. Ввиду связи (2) между порядковыми статисти-
ками и выборочными квантилями соотношение (1 З) спра-
ведливо также и при замене X(lnl'lJ на (".1':
( pQ )
.с (", 1') N (1" пр(р) .
(14)
Отсюда можно сделать вывод о том, что выборочная р квантиль (,'.1' является асимп-
тотически несмещснной и состоятельной оценкой теоретической р квантили (1"
СправедЛИВ более обший результат (МНОlомерная предельная нормальная
теорема): если в некоторых окрестностях точек (Р;' i == 1, ,Т, rде О < РI <
< Р2 < < Pr < 1, плотность f(x) непрерывна вместе с производной И по
ложительна, то при n ----+ 00 совместное распределение выборочных квантилей
(n,р;, i == 1, , т, асимптотически нормально с вектором средних значений
((pl' .., (р,) и матрицей вторых моментов
1 r
Ilиijlli,
n
rде
Pi(I Pj)
0'1) ==
!((p.)f((p,)
2.4. Выборочные квантили и порядковые статистики 135
Пример 2. Найдем асимптотическое распределение
выборочной медианы (",1/2 для выборки из нормаль
Horo распределения N(/1, /72). Соотношение (14)
для выборочной медианы из любоrо распределения
с плотностью f(x) принимает вид
.с ((п, 1/2) "'" N (1/2' 4nj2 (1/2) ).
Распределение
выборочной медианы
в нормальной модели
(15)
Если же f(x) имеет вид, указанный во Введении к rл. 1, то леrко видеть,
что функция f(x) симметрична относительно точки /1, поэтому (1/2 == /1,
а f(/1) == 1(V21Т/7). Подставляя эти значения в (15), получим
.с(,", 1/2) "'" N (р" :2 ). (16)
Для сравнения отметим, что соответствующее выборочное среднее Х при
любом п нормально N(/1, /72 jn). Таким образом, обе статистики Х и (",1/2
являются состоятельными оценками теоретическоrо среднеrо /1, но Х имеет
меньшую дисперсию, поэтому выборочному среднему следует отдать предпо
чтение как более точной оценке. Систематически вопросы сравнения точности
различных оценок одной и той же теоретической характеристики будут pac
сматриваться в rл. 3. .
Итак, средние члены вариационноrо ряда для больших выборок из дocтa
точно rладких распределений являются асимптотически нормальными (как и
выборочные моменты, см. п. 4 2.2), и ИМИ можно оценивать теоретические
квантили любых уровней р, О < р < 1, Совершенно иначе устроены асимп
тотические распределения крайних порядковых статистик, к рассмотрению
которых мы теперь переходим.
4. Асимптотическое поведение крайних порядковыx статистик
Относительно асимптотическоrо поведения порядковых статистик, находя
щихся на разных краях вариационноrо ряда, справедливо следующее общее
утверждение.
Теорема 2. Для выборки из абсолютно непрерывноrо распределения стати
стики X(r) И X(fI S+I) при любых фиксированных т, s 1 и п 00 асимп
тотически независимы и при этом
.c(nF(X(r))) r(l, Т),
.с(п(1 F(X(n S+I)))) r(l, s)
(17)
(определение rамма-распределения r(a, л) см. в п. 3 91.2).
1Зб rлава 2. Первuчная обработка зксперuментальнЬ/х данных
Доказотельство. Пусть Х П (каппа) и 1Jп обозначают рассматриваемые пре
образованные статистики:
Х П == nР(Х(Т») , 1Jn == n(1 F(Х(П S+I»))'
(] 8)
Вычислим сначала якобиан преобразования YI ==nF(XI), У2 ==n(] Р(Х2)):
очевидно, он есть J(XI, Х2) == n2 f(XI)f(X2). с учетом этоrо, по формуле (44)
].2 и с использованием формулы (7) для совместной плотности ({JП(УI, У2)
преобразованных статистик х п и 1Jп имеем следующее представление:
Ут, п s+ 1 ( F 1 ( ) , p 1 (1 ) )
({Jn(Yl,Y2) == ( ( )) ( ( )) ==
n2fF 1 fF I I
, ( ) " 1 ( ) s 1 ( ) n T
n. У2 ] УI + У2
(r l)!(n r s)!(s ,)!n 2 ппп
в условиях теоремы при любых фиксированных YI, У2 > О
n!
k I,
(n r s)!n '+3
(1 УI + n У2 ) п r s
e YI Y2,
что в итоrе дает
yk le YI
If'n(Yl. У2) ( ])!
s 1 Y2
У2 е
(s I)! .
Но это и означает, что в пределе случайные величины Х п , 1Jn (следовательно,
и Х(т). Х(п S+l») независимы и имеют указанные в (17) rамма распределения,
которые являются в данном случае распределениями Эрланra соответственно
порядков r и s. .
Обратим внимание на следующие моменты. Во первых. предельные pac
пределения крайних порядковых статистик не являются нормальными (в отли
чие от средних членов вариационноrо ряда). BO BTOPЫX, теорема 2 определяет
вид предельных распределений не самих порядковых статистик, а некоторых
функций от них, определенных в (18). Конечно, если эти уравнения можно
явно разрешить, т. е. получить явные представления
Х I ( х п )
(т) == F --;.
Х(П S+I) == F I (1 ),
(]9)
то можно получить предельные распределения и самих статистик Х(Т)' Х(П S+I)
через предельные распределения х п , 1Jп. В качестве иллюстрации такой ВОЗ
можности рассмотрим следующий при мер.
2.4. Выборочные квантuлu u порядковые стотистики 137
При мер з. Пусть .ею == r(l, 1) стандартное
показательное распределение. Здесь
Распределение верхних 'Ii"
экстреМУМОБ для
показательноi1 модели
:Z:
Р(х) == J e tdt == 1 е Ж, х О,
О
И леrко находим
F I(t) == In (1 t), 0< t < 1.
Следовательно, в силу (19) X(n S+I) == 1п n In т}п. Отсюда по теореме 2
00
P{X(n 3+1) Iп n х} == Р{17п е Ж} J 1rH(y) dy, (20)
e '
rде обозначено 1rk(t) == е Itk / k!, k == О, 1, 2, это обозначение будет ис
пользоваться и в дальнейшем. Интеrpированием по частям интеrpал в (20) MO
жет быть вычислен в явном виде, что при водит к окончательному результату:
s 1
P{X(n s+l) In n х} L 1rk(e :Z:), oo < х < 00. (21)
k=O
В частности, для максимальноrо значения выборки Х(П) (21) принимает вид
Р{Х(П) In n х} e e '
oo < х < 00.
(22)
Напомним, что ранее, в примере 1, были получены асимптотические значения
среднеrо и дисперсии статистики Х(П)'
Предельное распределение в (22) называется дважды экспоненциальным,
ero среднее и дисперсия равны соответственно с (константа Эйлера) и 1r 2 /6,
так что для
с == lim ( t 1п N )
п---+оо J
j=1
имеем одно из возможных интеrpальных представлений:
00
с== J xexp{ x e :Z:}dx
oo
(значение с вычислено с 260 десятичными знаками). .
Однако, в явном виде обратную функцию F I(t) удается выписать лишь
в редких случаях, поэтому теорема 2, вообще rоворя, оставляет открытым BO
прос о предельных распределениях для самих минимальных и максимальных
значений выборки (или нижних и верхних экстремумов). Кроме тoro, эта Teo
рема не охватывает случай выборок из дискретных распределений (но факт
138 rлава 2. Первuчная обработна эксперuментаЛЬНblХ данных
асимптотической независимости для них также имеет место). Общее рещение
вопроса о возможных предельных распределениях для крайних порядковых
статистик в больших выборках дается классической теорией экстремальных
зна'1ений, основной вклад в которую внесен отечественными математиками
Б. В. [неденко (1941 1943) иН. В.Смирновым (1949) (о нем см. в p.l). Пол
ное И:1JIожение этой теории выходит за рамки настоящеrо пособия, поэтому
мы оrpаничимся лишь общим описанием основных ее результатов.
5. Асимптотическая теория для верхних экстремумов X(n m+l), m 1
Общая задача ставится так: пусть при некотором выборе нормализующих
констант а n > О и Ь N имеет место сходимость
Р { X(n m+l) Ь N :::; Х } _______________ Gт(x),
а n n"-+ОО
(23)
rде Gm(x) некоторая невырожденная (т. е. имеющая более чем одну точку
роста) функция распределения. Нужно ответить на следующие два вопроса:
1) какой может быть предельная функция распределения Gm(x)? и
2) при каких условиях на общую функцию распределения F(x) случайных
величин Х" . ., , Х n И каких а n и Ь N будет выполняться соотношение (23)
для каждой возможной функции Gm(x)?
....
,... Распределения экстре
мальныx значений
Вот полные ответы на эти вопросы.
1) Gm(x) может быть лишь одноrо типа из следующих трех, называемых
распределениями экстремальных зна'1ений: (обозначения см. в (20»
л,m)(х) { Oт ' при х:::; о,
а> о;
1 L'/!Ax a) при Х > о,
r O
л m)(х) { ' .,(Ixl") при х:::; о, а> о; (24)
при х > о,
т l
л т)(х) == L 1!'r(e X), oo < х < 00.
r O
Если выполняется (23) с С m == л}m) то rоворят, что функция распреДе
ления F(x) принадлежит области притяжения типа л m)
2.4. Выборочные КВGнтили и порядковые статистики 139
2) Необходимыми и достаточными условиями при
Нaд1Iежности функции распределения F(x) об
ласти притяжения каждоrо из этих трех типов
являются (ниже используются обозначения XF
1П == inf{x F(x) 1 Ijn}):
тип А\т):
XF == 00 И
. 1 F(tx) a
11т == х
t oo 1 F(t)
при этом а п == 1П, Ь П == о;
тип A т):
Области притяжения ""
экстремаЛЬНblХ типов
sup{x F(x) < I},
Vx > О,
XF < 00 И
. I F(xF tx) а
11т == Х, V х > о,
ц.о 1 F(XF t)
при этом а п == XF /'" Ь П == XF;
тип A т): при всех Х Е R I существует
. 1 F(t + xg(t)) x
11т == е
фр 1 F(t)
rде
Хр
J 1 Р(и)
g(t) == du'
1 F(t) ,
t
при этом а п == у(,п), Ь п ==,п.
Если F(x) не относится ни к одной из указанных трех катеrорий, то
соотношение (23) не может быть выполнено ни при каком выборе KOH
стант а п и ь п '
З) Если существует f(x) == F'(x), то достаточными
условиями принадлежности F(x) к COOTBeTCTBY
ющим областям притяжения являются:
тип л\т): f(x) > О мя всех конечных х хо и
. tj (t)
11т ( ) == а: > о;
Ноо 1 F t
Условия принадлеж .,.
насти к экстремаль
HblM типам
(25)
тип A т) f(x) > О в некотором конечном интервале (хо, XF), f(x) == О
при Х > XF И
. (XF t)f(t)
11т == а: > о;
ttxp 1 F(t)
тип A т) J'(x) < О в некотором интервале (хо, XF) (XF 00), f(x) == О
при Х XF И
. f'(t)(1 F(t))
11т 2( ) == l.
фр f t
(26)
(27)
140 rлава 2. Первичная обработка экспериментаЛЬНblХ даННblХ
Замечание, Аналоrичная теория существует и ДIIЯ нижних экстремумов Х(т), т 1
фиксировано; при этом, поскольку Х(т) == X(n m+I)' [де X(I) Х(П) есть
вариационный ряд выборки ( X 1, . . . , х п ), то результаты для Х(т) получаются
простой переформулировкой соответствующих результатов ДIIЯ верхних экстремумов.
Интересующихся деталями мы отсылаем к обзорной статье 5) rде имеются также
дополнительные сведения и комментарии по этой проблеме.
Приведенный выше пример 3 относится к области притяжения типа Аз.
К такому же типу относится и следующий пример (далее мы оrраничиваемся
лишь максимумом Х(П) И пишем Aj вместо АУ)).
..... Пример 4 (Нормальное распределение).
'" Примеры роспреде Пусть Р(х) == Ф(х) (см. (7) Э 1.2). Здесь Хр == 00 и
лений зкстремумов 1 Ф(х) rv ip(x)/x при Х 00, при мени м критерий
(27) и при выборе
а п == (21п n) 1/2 Ь" == (21n n)I/2 (2In n) 1/2(ln ln n + 1n 4п)
2
имеем:
t:-( X(n : Ь п ) Аз. .
Пример 5 (Распределение Парето, см, п. 9 1,2). Здесь Р(х) == 1 (хо/х)а
х > хо, и применим критерий (25), при этом а п == /п == хоп I/а, Ь" == О.
Следовательно, по (24)
p{/ I Х(П) :::; х} e x D х> О.
Таким образом, распределение Парето с параметрами хо и а принадлежит
области притяжения типа А, с данным параметром а. .
Пример б (Равномерное распределение). Пусть Р(х) == х, О :::; х :::; 1. Здесь
Хр == 1 и применим, очевидно, критерий (26) с а == 1, при этом а п == 1/n,
Ь" == 1. Таким образом, в данном случае имеем предел типа А 2 (см. (24)):
Р{n(Х(П) 1) :::; х} е Х х < О.
С примерами статистических применений экстремальных значений выборки
мы встретимся в rл. 3. .
! 2.5. Линейные и квадратичные статистики
от нормальных выборок
Выше (см. п. 1, 2 1.2) уже rоворилось о той исключительной роли, которую
иrpает в приложениях математической статистики нормальная модель. Раз
личные свойства нормальных случайных величин обсуждались в 1.2 и сфор
мулированы в форме упражнений 26 32, 38,40 к rл. 1. Здесь мы установим еще
5) Ивченко Т. и. ПредеЛЬНblе распределения экстремальных характеристик Вblборок // Обозре-
ние прикладной и ПРОМblшленной математики. 1997. Т. 4. ВblП. 3. С. 443 469.
2.5. Линейные и квадратичные статистики
141
несколько общих результатов ДIIЯ нормальных выборок, относящихся к ли
нейным и квадратичным формам от нормальных случайных величин, которые
иrpают важную роль в статистике нормальной модели.
1. линейныe и квадратичные статистики, условия их неJависимости
Пусть Х == (X 1 , ,Х n ) выборка из стандартноrо нормальноrо распреде
ления #(0, J). Рассмотрим квадратичную форму
n
Q == L aijXiX j == Х'АХ, А == Ilaijl17, А' == А,
;,j 1
n
И т линейных форм t k == L bkiX;, k == !, .. ,т, или в матричных обозна
; I
чениях t == Бх. Здесь Б прямоуrольная (тхn) матрица и t == (t l , ,t m ).
Далее будем обозначать через О матрицу с нулевыми элементами и через ]["
единичную матрицу порядка n.
Следующая лемма дает критерий независимости статистик Q и t.
Лемма 1. Если БА == О, то статистики Q и t независимы.
Доказательство. Матрица А действительна и симметрична, поэтому. как
известно из алrебры, можно найти такую ортоrональную матрицу И (т. е.
ии' == :nn), что И'А И == Л. Здесь Л диаrональная матрица с элементами
ЛI, ,л n , являющимися корнями характеристическоrо уравнения
det (А л][n) == О.
Столбцами :!!I ,
':!!" матрицы И являются собственные векторы матрицы А:
А:!!; == Лi:!!j, i == !,. ,n.
Пусть r paHr матрицы А (т. е. число линейно независимых ее строк)
и ЛI, ,Л r отличные от нуля характеристические числа. Эквивалентной
формой записи
А == или'
(1)
является, так называемое, спектральное представление
матрицы А:
r
А == L Л; Ы!;
j 1
(напомним, что при матричных операциях векторы понимаются как BeKTOp
столбцы). По условию леммы
Спектральное
представление
маТРИЦbl
(2)
r
О == БА == L Л;(В1f;)i.
j 1
142 rлава 2. Первичная обработка экспериментаЛЬНbfХ даННbfХ
Умножим это равенство на вектор J},j справа. В силу ортоrональности соб
ственных векторов ( J},j == о при i -1- j) получим
BY:.i == О, i == 1, , r. (3)
Рассмотрим теперь случайный вектор (t"... ,t m , y:'/IX' ,y:' X). Этот
вектор распределен по нормальному закону, поскольку является линейным
преобразованием нормальноrо вектора Х (ведь при линейных преобразова
ниях нормальность сохраняется, см. П.2 1.2). В то же время из представле
ния (2) имеем
r
Q == Лi(хlJ},;) (у:.;х) == Лi(у:';х)2
i ' i '
Следовательно, утвеРЖдение будет доказано, если показать, что случайные
величины t" ,t m некоррелированы с x, i == 1, , r (тота эти две
rpуппы величин будут независимыми, см. п. 2 1.2). Обозначая через!i строки
матрицы В (i == 1, ,т), в силу соотношений (3) имеем
COv ( ti и'.х ) == с оу ( Ь'.х и'.х ) == E ( b'Xиl.X ) E ( b'X ) E ( иl.X ) ==
, } ' } I ) I )
== E(!iXX'y:') == E(XX')J},j == Q;Jl.nY:.j == '.!!:] == О. .
(4)
Установим теперь аналоrичный критерий независимости двух квадратич
ных форм Q, == X X и Q2 == Х'ВХ.
Лемма 2. Если АВ == ВА == О, то статистики Q, и Q2 независимы.
Доказательство. Пусть ДIIя матрицы А справеДIIИВО спектральное представ
ление (2), а аналоrичное предстаапение ДIIя В имеет вид
s
В == '"' II J 'v .v'. S == rank В.
J J'
j 1
По условию,
о == АВ == ЛilljУ:.i( j)1!j.
i.j
Умножив это равенство слева на ц;., а справа на lli, получим J}, :!1J == О,
k == 1, , т, l == 1, S, т. е. векторы Y:.l' ,J},r ортоrональны всем BeK
торам :!!." ,1!а' Отсюда, как и выше, имеем, что случайные величины У:.;Х
и :!!.jx некоррелированы, а так как они совместно нормально распределены,
то и независимы. Но
r
Q, == Лi( х)2.
i='
Q2 == IIj(1!jX)2,
j='
следовательно, Q, и Q2 независимы. .
2.5. ЛинеЙНblе и квадратичные статистики
143
2. Распределения квадратичных статистик
Среди квадратичных статистик от выборки Х == (X 1 ,..., Х n ) из.ею ==N(O, 1)
простейшей является сумма квадратов X +. . .+X , о которой нам уже извест
но (см. п. 3 1.2 и упр. 38 к rл. 1), что ее распределение есть х 2 распределение
с п степенями свободы: .e(X + .. + X ) == х 2 (п). Что можно сказать о pac
пределении произвольной квадратичной формы Q == Х/АХ с действительной
симметричной матрицей А? Этот вопрос мы и рассмотрим в данном пункте.
Обозначим tr А след (track) квадратной матрицы А, т. е. сумму ее диаrональ
ных элементов. Имеет место следующее общее утверждение.
Теорема 1. Если матрица А идемпотентна (А 2 == А), то .e(Q) == х 2 (т), rAe
r == tr А == rank А.
Доказательство. Пусть для А справедливо представление (2). Torдa, так как
ненулевые характеристические числа матрицы А 2 равны )..:, i == 1, . . . , Т, то,
в силу идемпотентности А, ).., == ==)..r == 1 и потому (см. (4))
Q == ( x)2
i 1
Из ортонормированности собственных векторов !!I"" ,1!r следует, что слу
чайные величины X, i == 1,..., т, независимы и нормальны N(O, 1), сле
довательно, .e(Q) == х 2 (т). Наконец, используя непосредственно проверяемое
равенство tr (АВ) == tr (В А) , из формулы (1) находим
tr А == tr (И'ИЛ) == tr Л ==).., +
+ Л r == Т. .
Замечание. В качестве следствия этоrо результата докажем упражнение 40 к rл. 1.
Примснив алrоритм п. 2 1.2, построим прео6разование %.. == л I/2и'( р,), пе
реводящее вектор { с .ею == N(I!.'}:) в стандартный нормальный вектор f Тоща
{ I!. == ил'/2%.. и, следовательно,
Q({) == ({ I!.)'}: I({ !!.) == z' лl/2и'}: lилl/2 == ' ,
таккаки'}: lи == л 1 По теореме 1 .e(Q({)) == x 2 (k), посколысуединичная матрица
lk является идемпотентной и tr lk == k.
Таким образом, при некоторых условиях на матрицу квадратичной формы
2
от стандартноrо нормальноrо вектора она распределена типично по закону Х
Но что будет, если нормальный вектор Х == (Х 1, , Х n ) не является CTaH
дартным? В таких случаях возникает новое распределение для квадратичных
статистик от Х, являющееся обобщением распределения хи квадрат. Добавим
зто важное распределение к списку уже имеющихся.
144 rлава 2. Первuчная обработка экспериментальных данных
Пусть X 1 , ,Х n независимые нормальные случайные величины и
при этом .c(Xi) == N(/Li, 1), i == 1,. , n. Тоrда, как мы знаем, сумма
n
:L)X i /Li)2
i 1
имеет распределение i(n). Однако часто бывает необходимо знать распреде
ление суммы квадратов самих случайных величин Xi. Распределение случай
... Н Ь ной величины u 2 == X + + X называют HeцeH
ецентрал ное
2 траль//ым распределением xи Kвaдpaт с n степенями
Х распределение 2 2 2
свободы и параметром нецентральности'\ == Рl + рn
и обозначают символом х 2 (n; ,\2): .с(u 2 ) == х 2 (n; ,\2). Плотность этоrо pac
пределения имеет вид
n/2 l 00 ( \ 2 ) j
Х n.,\2 == е (х+л2)/2 "'" ХI\
f( 1,) 2 n / 2 j!2 2j r(j + nf2) , х > О, (5)
а первые два момента равны
Еu 2 == n +,\2 Du 2 == 2(n + 2,\2),
(6)
Если параметр ,\2 == О, то i(n; ,\2) == i(n), Т.е. нецентральное распре
деление i переходит в обычное (центральное) распределение i
в качестве иллюстрированноrо примера ситуаций, rде возникает HeцeH
тральное распределение хи квадрат. докажем следующее утверждение.
Лемма 3. Пусть n мерный нормальный вектор У имеетсобственноераспреде
ление N(f!:.., Е). Тоrда статистика Q == Y'E ly имеет распределение х 2 ( n; ,\2),
\ 2 ' l
rде л == f!:.. I; f!:...
Доказательство. Рассмотрим вектор Х == л 1/2 u 'y, rде U ортоrональная
матрица, приводящая I; к диаrональному виду (см. п. 2 1.2): И'ЕИ == Л.
Тоrда .с(Х) ==N(J!:., :n'n). rде J!:. == л 1/2U'f!:..' Далее, у == uл l /2 Х и потому
Q == х' лI/2U'I; luлI/2 Х == х' Х == X +... + X ,
поскольку U'I; IU == Л Следовательно,
.с( Q) == .с(х; +
+x ) ==х 2 (n;,\2),
rде
\2 I ' uл 1 / 2 л 1 / 2 u ' ' l
л == f!:.. f!:.. == f!:.. f!:.. == f!:.. '" f!:..'
поскольку UЛ IU' == I; I. .
2.5. Линейные и квадратичные статистики
145
3. Теорема Фишера
Наиболее часто используемыми статистиками от нормальных выборок явля
ются выборочное среднее
1 n
Х ::= 2:: X i
n i l
и выборочная дисперсия
n
2 1" 2
8 ::= L.)X i Х)
n i I
Первая из них является линейной, а вторая квадратичной функцией от
X 1 , . , ХП' Полученные в предыдущих пунктах результаты позволяют весьма
просто доказать знаменитую теорему Р. Фишера (1925).
Теорема 2 (Теорема Фишера). Пусть Х ::= (Х"..., х п ) выборка из
2 2
.с(о ::= #(J1., ff ). TorAa статистики Х и 8 независимы и при этом
.с(Х) ::= # (jl, :2 ). а .с ( ;2 В2) ::= i(n 1).
Доказательство. Перейдем к стандартным нормальным случайным вели
чинам
Xi J1.
Y;::= , i::= 1, ,n.
ff
Torдa леrко проверить, что
n
1 X jl
У ::= 2:: у; ::=
n i 1 ff
и в2(у)::= 82(;) .
ff
2
Поэтому достаточно показать, что У и S (У) независимы и при этом
.c(-.,fii У) ::= #(0,1), а .с(nв 2 (у))::= i(n 1).
Рассмотрим n мерный вектор столбец!!. ::= (I/n, . . . , '/n)' и (n х n) MaT
рицу В ::= II!!.. .. !!.II. Леrко проверить, что У::= t{Y, а
n8 2 (у) ::= (У ВУ)'(У ВУ).
Orcюда n8 2 (У) ::= У'АУ, rдe матрица А::= Jl. n В идемпотентна и tr А ::= n 1.
Теперь !!.' А::=!!.' !!.' В ::=!!.' !!.' ::= о и, следовательно, по лемме 1 статистики У
2
И 8 (У) независимы. Далее, закон распределения У очевиден (см. (5) 9 1.2),
а закон распределения n8 2 (у) следует из теоремы 1. .
10з.коз 1748
146 rлава 2. Первичная обработка экспериментаЛЬНblХ aaHHblX
Замечание. Так как для распределения i(n 1) среднее и дисперсия равны COOT
ветственно n 1 и 2(n 1) (см. п. 3 1.2), то из доказанной теоремы слсдует, что
ДЛЯ нормальных выборок
о 2n 1
ES == (J
n
n '
DS 2 == 2(J4-----,-----
n-
(7)
(сравни с соответствующими формулами (11) и (1 З) 2.2 ДЛЯ выборки из произволь
HOro распределения, при этом используйте формулу (20) 2.2 для эксцесса 12 и тот
факт, что для нормальноrо распределения 12 == О).
При ведем несколько важных примеров статистических применений Teo
ремы Фишера.
Пример 1 (Оценивание парамеТРО8 нормальной модели). Рассмотрим за-
дачу построения доверительных интервалов (см. определение (26) & 2.2) ДJlЯ
неизвестных параметров ()! и 8i общей нормальной статистическоЙ модели
N(8,,8 ).
"""' Д Доверительный интервал ДJlЯ дисперсии 8 MO
оверительный интер
Жет быть построен На ОСнове Toro факта, что выбо
вол для дисперсии 2 2
рочная дисперсия S == S (Х) для выборки Х
== (Х" ,х n ) из распределения N(8" 8 ) имеет по теореме 2 следующее
распределение:
.с ( n8 2 ) == х2(n 1)
(независимо от значений неизвестных параметров!). Поэтому, обозначая через
X ,n ' р квантиль распределения i(n 1) и выбирая при заданном ДОDери
тельном уровне 'у два числа QI и а2 так, чтобы а, + а2 == 1 'у, будем имеТь
{ 2 nS 2 2 }
'у == р X""n 1 < 8i < XI ",.n 1 ==
{ nS 2 2 nS 2 }
== р 2 < 82 < ---т----------- .
Xl a1,n 1 X",.n '
(8)
2
Но это И означает, что 'У доверительным интервалом ДJlЯ 82 является ин
тервал
( 2 nS 2 , ;S2 ) , аl + а2 == 1 "(. (9)
X' a2,n ' Xal.n j
На самом деле это целое семейство интервалов, так как при заданном 'у
числа а, и а2 можно выбрать разными способами. На практике обычно реко-
мендуют выбирать их так, чтобы были одинаковыми вероятности попадания
величины nS 2 / 8i левее и правее указанных R (8) rpаниц:
{ nS2 2 } { nS2 2 } 1 'у
Р 8i Xa"n 1 == р 8i ;;:: X, ""n 1 == ,
2.5. ЛинеЙНblе и квадратиЧНblе статистики
147
т. е. 01 == 02 == (1 "'1)/2. В это случае интервал (9) называют центраЛЬНblМ
"'1 доверитеЛЬНblМ интервалом, и он имеет вид
( nS2 nS 2 )
2 '2 .
X!:\'-I,n 1 XiТ,n '
в частности для выборки объема n == 1 О и доверительноrо уровня "'1 == 0,9 из таб
лии квантилей х 2 распределения имеем Хб,О5;9 == 3,3251, Хб.95;9 == ]6,9] 90, по
этому центральный 0,9 доверительный интервал для Bi имеет вид (0,59] IS 2 ,
3,007 S2)
Рассмотрим теперь задачу доверительноrо oиe
нивания среднеrо 01 Как уже отмечалось в п. 6 1.2
в связи с обсуждением распределения Стьюдента,
в силу теоремы Фишера стьюдентово отношение (см. (29) ] .2)
Х Bl
t n ,==
S
2
имеет при любых значениях парамеТРОIJ 6, и 62 распределение Стьюдента
S(n 1), при этом оно симметрично относительно нуля (см. (28) 1,2). Поэто
му, обозначая через tp,n ' р квантиль распределения S(n 1), из (11) имеем
"'I==P { ltn ll<t!..:tJ.n I } ==P { X ;' t!..:tJ.n ,<BI<X+ ;' t!..:tJ.n I } '
2' yn 1 2' yn 1 2'
т. е. "'I доверительным нтервалом для 61 является симметричный относитель
но случайной точки Хинтервал
( Х =F tw n ' ) .
2' yn I
(10)
Доверительный интер
вал для cpeAHero
(11 )
(12)
в частности, из таблиц квантилей распределения Стьюдента имеем
tO,975; 9 == 2,262, поэтому для выборки объема n == 10 и доверительноrо уровня
'у == 0,95 этот интервал имеет вид (Х =F О, 754S).
Иноrда необходимо знать оценку OДHOBpeMeH
2
но и дlJя среднеrо О, и для дисперсии В2' т. е. He
обходимо оценить пару 6 == (6" т), т == 6i. в этом
случае требуется построить такое случайное (т. е. за
висящее от выборки Х) подмножество 9 1 (Х) в R == {В == (В" т) oo <
< ВI < 00, Т > О}, которое бы с заданной вероятностью "'1 накрывало неиз
вестное значение О, т. е. чтобы выполнялось соотношение
''' '''' ' 'До1iе'р еrn.нci:i 'If'
область для cpeAHero
и дисперсии
Р{В Е 9 1 (Х)} == "f.
( 13)
Такое подмножество может быть построено на основании уже полученных
результатов. Именно, сопоставим каждой паре В == (В" т) подмножество BЫ
борочноrо пространства
{ rn I n 2 " }
Н(В)== V IX 611<t,t < S <t ,
10.
148 rлава 2. Первичная обработка экспериментаЛЬНblХ данных
rде
t == == ф , ( l+'УI ) I 2
С-у, 2 ' t == Х '..::12. 1 '
1 ,n
i == 8\1l) и 'у 1'у2 == f.
Torдa в силу независимости Х и 82
t ll 2
== Х '+7' n l '
1 '
( { rn } { , n 2 II }
Р{Х Е Н 8)} == Р V :;:-IX 811 < С-у, р t < :;:-8 < t == /О'2 == f.
Но условие {Х Е Н(8)} эквивалентно условию {8 Е у,(Х)}, rде
{ n ns 2 ns 2 }
Y1(:f) == 8 == (81, т): т > (x 8'((2' tiI < т < т .
Область Y1(:f) представляет собой часть полуплоскости R , оrраничен
б ( II ) 2 jt 2 2 . t ll 2 jt '
ную пара олои т == х и1 n и двумя прямым и Т == ns I и т == ns
(см. рис. 1). Таким образом, построена 'У доверительная область У1(Х) дЛЯ
пары 8 == (8\, 8f), удовлетворяющая (13). · т
Пример 2 (Задача сравнения двух средних).
Среди ПРИЮ1адных задач встречаются такие, при
решении которых приходится сравнивать средние
двух независимых выборок. Для тaKOro cpaBHe
ния полезно иметь доверительный интервал для
разности соответствующих выборкам математи
ческих ожиданий. В случае нормальных выборок
такой интервал можно леrко построить на OCHO
вании теоремы Фишера.
Пусть Х == (X 1 ,. . . , X 71 ) и у == (У\, .. ,v,1l) две независимые выборки,
причем первая из распределения И(8 1), O ), а вторая из и(о 2), 8i). Ta
ким образом, соответствующие модели различаются только своими средними
и требуется оценить их разность Д == 8\1) 0\2) Эту задачу называют задачей
сравнения двух средних. Построим выборочные средние Х: У и выборочные
дисперсии 8 2 (х), 8 2 (у) этих выборок. Из независимости выборок и в силу
теоремы 2 эти четыре статистики независимы. Кроме Toro,
81
х
Рис.l
( X 8 1) ) == ( ) ( Y 8\2) ) == ( )
L 8 N о, ,L 8 N о, ,
2 n 2 т
-C( 82(X)) == х 2 (n 1), -C( 82(y)) == х 2 (т 1).
Отсюда (см. (5) 1.2)
( Х 8(1) У 8(2) )
L I 1
82 82
( X Y Д ) .r ( 1 1 )
== L == JV О +
82 'n т
2.5. ЛинеЙНblе и квадратиЧНblе статистики
149
или
L ( Jmn X Y 6. ) ==N(o,I),
т + n (}2
а также (см. п 3 1.2, свойство воспроизводимости х 2 распределения)
L ( S2(X) + S2(y) ) == х 2 (т + n 2).
02 02
Следовательно, стьюдентово отношение (27) 1.2 имеет в данном случае
вид
J тn Х у 6.
t т + n ()2
т+n 2
nS 2 (X) + mS 2 (y)
() (т + n 2)
x y 6.
.J nS 2 (X) + mS 2 (y) ,
(14)
и оно имеет распределение Стьюдента В(т + n 2)
при любых () I), () 2) И O . Основываясь на (14),
r доверительный интервал для 6. строится так же,
как и интервал (13) в предыдущем примере: он име
ет вид
ДоверитеЛЬНblЙ
интервал дпя разности
двух средних
( [ ] 1 /2 )
т+n 2 2
X Y=FtWт+n 2 ( ) (nS (X)+mS (У)) .
2 . тn т + n 2
( 15)
.
Пример 3 (Доверительный интервал ДЛЯ отноwения дисперсий двух HOp
мальных моделей). Рассмотрим ситуацию, коrда Х == (Х" .. . , Х п ) BЫ
бор ка из распределения И(О11, () 2)' а У == (Y 1 , , У т ) из распределения
И(О21, () 2) И пыборки независимы. Требуется оценить отношение т == O;2/() 2
неизпестных дисперсий. Построим выборочные дисперсии в2(х) и в2(у).
По условию они независимы, а по теореме Фишера
L ( В2(Х) ) == i(n 1), L ( п: В2(у) ) == х 2 (т 1).
012 ()22
Поэтому мы можем построить статистику Снедекора (32) 1.2, которая в дaH
ном СЛ)"lае принимает пид
n(т 1) В2(х) 1
Fn I,m 1 == т(n 1) S2(y) ;:. (16)
Эта статистика имеет распределение Снедекора B(n 1, т 1) при любых
2 2
значениях пара метров ()II, ()12' 021, (}22 J поэтому, обозначая через Рр, n 1, т 1
150 rлава 2. Первuчная обработка экспериментаЛЬНbJХ aaHHblX
р квантиль распределения В(п 1, т 1) и задаваясь доверительным YPOIJ
нем 1, из (16) будем иметь
1== Р{ F(I 1)/2.n I,т 1 < Fn I,rп 1 < F(I+1)/2'n l.m l} ==
{ п(т 1) В2(х) 1
== Р т(п 1) В2(у) F(I+1)/2.n l.rп 1 < т <
< п(т 1) В:(Х) 1 } .
т(п 1) S (У) F(1 1)/2,n l,rп 1
.. Доверительный интер
вол для отношения
дисперсий
Тем самым построен центральный 'У довери
тельныЙ интервал для т: он имеет вид
( п(т 1) В2(х) 1
т(п 1) В2(У) F(I+1)/2.n l.rп l'
п(т 1) В2(Х) 1 )
( 17)
т(п 1) В2(у) F(I 1)/2,rH,т 1
в частности, из таблиц квантилей распределения Снедекора имеем
F O ,95; 8,8 == Fo d5: 8,8 == 3,44, F од 12,12 == Fo d5; 12.12 == 2,69,
поэтому О,9 доверительный интервал для выборок объемов n == т == 9 есть
( О,29В 2 (Х) з,44S 2 (Х) )
В2(у) , В2(у) ,
а для выборок объемов п == т == 13
( О,37В 2 (Х) 2,69В 2 (Х) )
В2(у) , В2(у)
.
Упражнения
Там, <де есть (ЮЛЯ, BcezJa есть JOPOi?O.
Хадсон 6)
о Пусть IIn число успехов в n испытаниях Бернулли с вероятностью успеха р,
О < р < 1. При больших n выllислитьb rpаницу О-т такую, чтобы событие IlIn/n pl О-т
имело вероятность::::: "1. Укладываются ли в эти rpаницы при "1 == 0,98 результаты
следуюшеro эксперимента (эксперимент Бюффона 7»): при n == 4040 бросаниях монеты
наблюдалось 2048 выпадений <,rерба.?
6) Хадсон анrлийскиit альпинист XIX в.
7) Бюффон Жорж Лун Леклерк (1707 1788) французский естествоиспытатель, почетный
член Петербурrcкой АН (1776).
Упражнения
151
... Указание. Применить теорему Муавра Лапласа (см. замечание к упр. 33 rл. ]).
D (Продолженuе). Смоделировать выборку объема n ] 000 из распределения
Bi(l, 2/5) и проверить аналоrично предьwущему, укладываются ли в указанные rpани
цы реЗУЛJ,таты полученных экспериментальных данных. Построить rрафик, соединив
прямыми последовательные точки
( I/k )
k, k '
k == ]00,200,..
]000.
11 Смоделировать выборку из биномиальноrо распределения Bi( 4, ] /3) _ Постро
ить rpафик частот l/r/n, [де 1/,. число опытов, в которых наблюдалось значение
r == О, 1,2,3,4, и вычислить выборочные среднее, дисперсию и коэффициенты асим
метрии и эксцесса. Найти д из условия P{IX all д} == 0,998 и сравнить с ним
вычисленное по экспериментальным данным отклонение выборочноrо среднеrо от Teo
реТИ'Jескоrо аl
... Указание. Воспользоваться теоремой 3 9 2.2.
11 Смоделировать выборку из полиномиальноrо распределения М(500;р; ]/5,
i == ], , 5), и, рассматривая эти данные как наблюдения над случайной величи
ной , принимающей значения 2, ], О, 1,2, построить полиrон частот и вычислить
выборочные среднее и дисперсию. Найти {) из условия
P{IX all tI} == 0,98
и сравнить с ним наблюденное значение отклонения IX а 11.
g Смоделировать выборку объема n == 100 из показательноrо распределения r( 1, ]).
Вычислить ее основные характеристики, построить эмпирическую функцию распре
деления и rистоrрамму, вычислить выбороч ные моменты aj, j == ],2, и сравнить их
с теоретическими значениями.
D Пусть X N1 , ,X Nn приближенно нормальные N(J.L, €Т 2 ) числа, каждое из KO
TOpbJX получено суммированием N равномерно распределенных на (О, ]) слаrаемых.
Получить три реализации (при N == 2,4, ]2) выборок с n == ]00, J.L == О, и2 == 1. Для
каждой выборки построить эмпирические функции распределения и rистоrраммы;
получить оценки J.L и €Т 2 ; вычислить 3 й и 4 й выборочные центральные моменты
и сравнить их с истинными значениями теоретических моментов.
О СмодеЛИРОlJать выборку объема n == 500 из paBHoMepHoro распределения И(О, ]2).
rруппируя данные по интервалам Е , == (т, r + ]], r == О, ], 1], построить полиrон
частот и сравнить ero с rрафиком функuии f(x) == с, О < х < 12. Рассматривая
!JIуппированные частоты как результаты наблюдений над дискретной случайной вели
чиной, принимающеЙ значения, совпадающие с серединами соответствующих интер
валов, вычислить выборочные среднее и дисперсию и сравнить их с теоретическими
значениями.
D Для данных при мера 2 в 92.2 построить rpафик частот l/r/n И сравнить ero с rpa
x2 /2
фиком функции се . . вычислить выборочные коэффициенты асимметрии и экс
цесса; найти {) из условия Р{ IX а I1 {)} == 0,998 и сравнить с ним вычисленное
по приведенным данным отклонение выборочноrо среднеrо от теоретическоrо аl
D (Продолже//uе). В том же эксперименте наблюдалась также случайная величина ,
равная числу костей с 6 очками. Соответствующие данные приведены в таблице:
152 rлава 2. Первичная обработка экспериментаЛЬНblХ даННblХ
r О 1 2 3 4 5 6 ) 7
lI r 447 1145 1181 796 380 115 24 8 4096
Ответить на те же вопросы, а также вычислить выборочные среднее и дисперсию.
... Указание. Считать, что .е(О == Bi (12, 1/6).
lliI Наблюдались показания 500 Hayraд выбранных часов, выставленных в витринах.
Пусть r номер промежyrка от r ro часа до (т + I) ro, r == О, 1, .. 11, а lI r число
часов, показания которых ПРИНaдI1ежат T MY промежyrку. Результаты таким образом
сrpуппированных наблюдений оказались следующими [15, с.4591:
r О 1 2 3 4 5 6 7 8 9 10 11
V r 41 34 54 39 49 45 41 33 37 41 47 39 500
а) Построить полиrон частот и сравнить ero с rpафиком функции f(x) == С, 0< х < 12.
б) Рассматривая эти данные как независимые наблюдения над дискретной случай
ной величиной С принимающей значения, СО!lпадающие с серединами COOTBeT
ствующих интервалов (Т. е. значения 0,5; 1,5;... , 11,5), вычислить выборочные
среднее и дисперсию.
в) Принимая, что в п. б) случайная величина' имеет равиомерное распределение,
найти 5 из условия P{IX all 5} == 0,98 и сравнить с ним наблюдавщееся
значение ОТКJlонения 'Х а 11.
m При про ведении n == 2608 опытов по наблюдению числа а частиц (О, излучае
MbJX радиоактивным веществом за определенный период времени, получены следую
щие дан ные (V r число ОПЫТО!l, ДlJя которых число, == т, r == О, 1, . . .):
r
о 2
57 203 383
3 4 5
525 532 408
10
10
11
4
) 12
2 2608
1/,
Построить rрафик частот vr/n И вычислить выборО'JНЫС среднсс и диспсрсию.
m Пусть ( O,8; 2,9; 4,4; 5,6; 1, 1; 3,2) наблюдавшиеся значения случайной !le
личины,. Вычислить основные характеристики выборки, построить эмпирическую
функцию распределения и убсдиться в том, чтО Р 6 ( 5) == 1/6, Рб(О) == 1/2, Р6(4) == 5/6.
m в эксперименте наблюдалась целочисленная случайная веЛИ'lина . CooтвeTCTBY
ющие выборочные значения оказались равными: 3, О, 4, 3, 6, О, 3, 1. Вычислить OCHO!l
ные характеристики выборки, построить эмпирическую функцию распредсления и про
верить, что РхО) == 3/8, Р8(3) == 3/4, Р8(5) == 7/8.
m Коrда функция Рn(х) будет имсть скачки размера лишь I/n (или, что эквива
лентно, будет иметь ровно n скачков)?
ВJ Пусть х] < Х2. Чему равна вероятность P{Fn(XI) == Р n (Х2)}?
m Пусть P{ == j} == Pj, i == 0,1,..., N, и Х == (Х], ,Х n ) выборка из .е(О.
Найти вероятность Р{FnШ РnИ О) == k/n} Рассмотреть случай .ею == Bi(N,p).
m Пусть Х == (X 1 , ,Х n ) выборка из HenpepbJBHoro распределения F. Какому
распределению будет соответствовать выборка У == (Y 1 , ... . У n ), rде 1'; == Р(Х;)?
[ Замечание. Если случайная величина Х имеет функцию распределения Р(х) и Р(х)
непрерывна, то переход к новой случайной величине У == Р(Х) называется преоб
разованuем Смирнова.
Упражнения
153
m Пусть Х выборка из paBHoMepHoro распределения И(О, 1) и F непрерывная
и cTporo монотонная функция распределения. Положим У; == F '(X;), i == 1, ., n.
Из KaKoro распределения будет выборка У?
m Пусть в точках Х; выполняются условия О < F(Xj) < 1, i == 1,. , k. Рассмотрим
события А; == {F(xj) Е (Fn(xj) 'f trJ Jn) }, [де (рп(х;) 'f trJ";n) аСИМnТОТИ'lе
ский 1; доверитсльный интервал для Р(х;), определенный в (8) 2.1. Доказать, что вe
роятность одновременноrо осуществления событий AI' , Ak удовлетворяет условию
k
Р(А 1 n...nA k ) Е1;.
; ,
Замечание. Система интервалов
{ ( t r ; )
Fn(Xj) 'f vn '
i==I,''''k}
называется системой совместных доверительных интервалов для F(x;), i == 1, . . . , k.
Е!] Пусть XI < Хl заданные точки на числовой прямой, такие, что О < F(x,)
F(X2) < 1. Доказать формулу
) F(x,)(I F(Xl))
cov(Fn(x.). F n (X2) == .
n
... Указание. Представить случайную величииу
Lln(x" Х2) == Рп(Х2) Iln(X.)
(см. (3) 2.1) о виде суммы независимых индикаторов
n
I1п(х" Хl) == L I(х) < Х ; Х2)'
i 1
m Пусть Х == (X 1 , ... ,Х П ) выборка из HeKoTo(Joro распределения [( ), для KO
Toporo сущсствует момент а2, == Ее ' Доказать, что дисперсионная матрица всктора
Ап == (а n ", .. ,Ci nr ) первых r выборочных моментов имест вид
DAn == Ilcov(Ci nj , Cinj)lI == .!.lIai+j a;ajll .
n
m Доказать, что соу(х, вl) == рз(n 1)/n 2 Рассмотреть случай .ею == N(Il, /12).
m Доказать теорему 6 2.2 об асимптотической нормальности выборочной диспер
сии. Убедиться в том, что при n ----+ 00 Ев 1 /1.2, Ds 2 (1l4 /1. )/n.
... Указание. Учесть, что в 2 == <P(Onr, а n2 ), [де <р(Х" Х2) == Х2 Х; (см. (6) 2.2), и
применить теорему 5 9 2.2.
m Пусть al i= О, Р2 < 00. Доказать, что при n ----+ 00 .e(X I) N ( , )
а, а,п
... Указание. Применить теорему 5 2.2.
m Убедиться в справедливости следующих yrверждений о распределении выбороч
Horo среднеro для выборки Х == (Х.. .. . . Кп) из соответствующих распределений:
а) lЩ == [(а, л) => .е(nХ) == r(a, nл),
154 rлава 2. Первuчная обработка эксперuментальных данных
б) .ею == Bi(k, р) .е(nХ) == Bi(nk, р),
в) .ею == П(л) .е(пХ) == П(nл),
r).ею == Bi (r,p) !(nХ) == ВI(nT,p).
... Указание. Воспользоваться свойством воспроизводимости рассматриваемых pac
пределений (см. 1.1 и 1.2).
m (Продолжение). Убедиться в том, что для выборки из распределения Коши К(а)
(см. упр. 48 (б) rл. 1) .е(Х) == К(а).
m Пусть в эксперименте наблюдается двумерная случайная величина { == ({I, {2)
и (X'I, Х'2)' i == 1'... ,n, соответствующие выборочные данные. Для упрощения
вычислений выборочноrо коэффициента корреляции Рп (см. (5) 2.3) часто бывает
удобно предварительно преобразовать исходные данные с помощ ю HeKoToporo ли
нейноro преобразования:
X'I al
1';. == ь , '
Xi2 a2
у. , ., == i == l '
. Ь 2 '
,n,
( 1)
rде al, а2 действительныс, а b l , Ь 2 положительные числа. Доказать, что при лю
бом выборе а" а2, Ь" Ь 2
р,,(Х) == р,,(У).
m Вычислить выборочный коэффициент корреляции для следующих данных n == 26
наблюдений над величиной { == ({I, 6), записанных в виде статистическоro ряда:
{I 23,0 24,0 24,5 24,5 25,0 25,5 26,0 26,0 26,0 26,5 26,5 27,0 27,0 28,0
6 0,48 0,50 0,49 0,50 0,51 0,52 0,49 0,51 0,53 0,50 0,52 0,54 0,52 0,53
v. 2 4 3 2 1 ] 2 I 2 1 1 2 1 3
... Указание. Произвести линейное преобразование (1), выбрав al == 26,0, ы == 0,5,
a2==O,50,b 2 ==O,OI.
Ответ: Р26 == 0,793.
m Используя независимые равномерно распределенные на [0,1) случайные числа {U i },
построить последовательно сть пар сл учайных чисел
X il == V 21" И 2Н sin (2л U 2i ),
X i2 == V 21" И 2Н cos (2л и 2 ;), i == 1,2, ,50,
вычислить для этих данных выборочный коэффициент корреляции и проверить rипо
тезу независимости Но: р== О, используя как точный, так и асимптотический алrорит
мы, описанные в п. 4 2.3 (см. п. 8 1.3).
m Доказать, что совместная функция распределения двух порядковых статистик X(r)
И Хи (1 r < s n) при х < у имеет вид
I
Frs(x, у) == L: L: i! '!(п :'i .)! Fi(X)[F(y) F(x)]j[1 F(y)]n i j
.=. j=max(O.s i) J J
n
" ;
и
Р..(х,у) == P{X(s) у} == Р,(у) при х у.
Упражнения
155
Указание. Использовать эквивалентность событий
{X(r) :::; Х, Х(.) :::; У} и {Jln(X) т, Jln(Y) S},
а также тот факт, что случайные величины
111 =о Jl,,(x), 112 == Jln(Y) Jln(X), 11] =о n Jln(Y)
(при Х < у) имеют полиномиальное распределение M(n;PI,p2,P]), rдe PI =о Р(х),
Р2 =о Р(у) Р(х), Р] =о 1 Р(у). Если же Х У, то событие {Хи :::; Х, X(j) :::; у} ==
=о {X(s) :::; У}.
m Пусть распределение .с(о абсолютно непрерывно и ero плотность Р'(х) == f(x).
Выnести следующую формулу для совместной плотности порядковых статистик X( I)'
.'.,Х(Ч (l:::;k l < <kr:::;n):
n!
9k...k,(X" ,х,) == (k ) ( k ) (k k )'( k) Х
I 1 ! k 2 J 1 1... r r J 1 . n ,!
Х Fkl j(XI)(F(X2) F(XI»)kl kl 1
(F(x r ) F(xH)( k' I I(1 F(XT»)n k, f(xj) .. f(x,)
при xl < х) < < х, и равна нулю в остальных точках.
Получить отсюда формулы (7) и (8) 2.4.
... Указание. Записать вероятность события {X(k;) Е (Х; +dxj), i =о 1, ,т} при бес
конечно малых dXj, i == 1,..., т, и, разделив ее на dXI .. . dx r , получить в пределе
пр и dXj , О, i =о 1,... , т, nид искомой плотности.
m Убедиться в том, что для случая .с(о == И(О, 1) распределения порядковых cтa
тистик имеют вид (при 1 :::; k < 1 :::; n)
.с(Хщ) =о Be(k, n k + 1), .с(Хо) X(k) =о Ве(1 k, n 1 + k + 1)
(см. п. 4 1.2). Вывести отсюда формулы для моментов
k k(n k + 1) k(n 1 + 1)
ЕХщ == n + l ' DX(k) == (n + 1)2(n + 2) ' соУ(Хщ , X(I) == (n + I)2(n + 2) '
... Указание. Используя формулу (44) 1.2, найти совместную плотность вели'lИИ
У ! Хщ и У 2 =о X(l) Хщ, интеrpированием которой получить марrинальную
плотность величины У2' При вычислении моментов использовать формулы (24) 9 1.2,
а также формулу D(X(I) Хщ) == DX(I) + DX(k) 2 соУ(Хщ , X(l)'
m (Продолжение). Используя эти результаты, получить формулы для моментов экс
тремумов выборки из ПрОИЗRольноrо paBHOMepHoro распределения И(а, Ь), приведен
ные в упр. 46 rл. 1 (см. П.5 9 1.2).
m Пусть Х == (X 1 , ... ,Х П ) выборка из распределения с плотностью f(x)
== (1/2) cos х, \xl :::; 7r /2. Вывести формулу
11"
ЕХ ( 1 2 2n+ICn )
(п) 2 2п .
Доказать, что при n , 00
ЕХ(п) == Л(1 +o( ))
и
{ .;n ( 11" ) } x2
Р 2 Х(п) "2 :::; Х , е ,
х < О.
156 rлава 2. Первичная обработка экспериментальных aaHHblX
... Указание. Воспользоваться тождеством
L C kCtx2k == ТПС п
k
И также применить критерий (26) 9 2.4.
m Пусть Х == (X J , ,Х,,) выборка из распределения Коши (см. (31) Э 1.2).
Показать, что при n 4 00 И а п == tg (1r/2 1r/n) n/1r
P{a;JX(n) х} --------t e l/x х > О.
... Указание. Применить критерий (25) 92.411 учесть, что liш t(1r /2 arctg t) == 1
1"'00
IИ Пусть Х == (Х.,... ,Х п ) выборка из усечеННОlО nоказателЬНОlО распределения,
задаваемоrо функцией распределения
Р(х) == k(1 e X), О х хо, k == (1 e XU) I,
при некотором конечном хо > О. Показать, что при n 4 00
Р{n(е ХО 1) I(X(n) хо):( х} --------t е Х , х < О.
... Указание. Применить критерий (26) 9 2.4.
I Замечание. Обратим внимание на то, что здесь мы имеем предельное распределение
типа А 2 (см. (24) 92.4), в отличие от примера 3 в 92.4, [дс для оБЫ'Iноrо показатель
Horo распределения (т. е. при хо == 00) мы имеем предел типа Аз.
m Пусть функция распределения наблюдаемой случайной величины ( имеет вид
{ 1 e J / x
Р(х) == 1
при х < О,
П[)II Х О.
Доказать, что ДIIЯ распреде,1ения максимальноrо значения выборки объема n из .с(о
при n 4 00 выполняется соотношение
Р { Х(п) Ь" :( Х } e e ' oo < х < 00,
а"
rдс а п == (Inn) 2, Ь" == I/(Inn).
... Указание. Применить критерий (27) 9 2.4.
Ш Пусть Х == (X 1 , .. . ,Х,,) стандартный нормальный вектор (т. е. выборка из
стандартноrо нормальноrо распределения N(O, 1)). Рассмотрим три квадратичные
формы от Х:
n
I 2
Q2 == (XI +...+Х,,),
n
n
QI == Lxl,
i=1
Q) == Е(Х; xi
i=1
Применив теорему 1 92.5, убедиться в справеДIIИВОСТИ следующих соотношений:
,C(QI) == i(n), ,C(Q2) == X 2 (1), ,C(QI) == х2(n 1).
... Указание. Получить представление QI == X'D.nX, Q2 == х'вх, rде в == III/nll
Qз == Х'АХ, [де А == 1" В.
Упражнения
157
m Пусть .С(У) == И(р., 'r.), l'r.l =1= О и Q == (У р.)' А(У р.), [де матрица А УДО8Ле
ТlJоряет условию A'r.A:: А. Доказать, что .c(Q) == i(m), [;е т == tr (A'r.). Получить
отсюда yrверждение теоремы 1 2.5 и упражнения 40 к rл. 1.
.... Указание. Запись У в виде У == + ВХ, [де Х стандартный нормальный вeK
тор (см. п. 2 1.2), тоrда Q == Х'А,Х, [де матрица AI == в' АВ идемпотентна. Далее
применить теорему 1 2.5. .
lIiJ (Продолжение). Доказать следующее обобщение леммы 3 2.5: квадратичная фор
ма Q == У'АУ имеет распределение :e(r; . ,2), [де r == rank А и . ,2 == !!.' A . В 'laCTHO
сти, при А == 'r. ' величина r == n и л? == !!.''r. I!!. (лемма 3).
.... Указание. Использовать то же преобразование У == ВХ, 'ПО и в доказательстве
леммы 3. Тоrда Q == Х'В'АВХ и здесь матрица А, == В'АВ идемпотентна и rank А, ==
== rank А. Далее, как и при доказательстве теоремы 1 2.5, привести Q к сумме KBaд
ратов незаоисимых нормалl>НЫХ вели'IИН. .
m Пусть Х == (Х". , Х,,) выборка из распределения И(О, 1) и квадраТИ'I
ная форма Q == х' Х разложена на сумму ДВУХ квадратичных форм Q == Q 1 + Q2, [де
Q, == Х'А,Х 11 rank А ; == nj, i == 1,2. Доказать, 'lТo если n, + n2 == n, то Q 1 И Q2
независимы и I(Qi) == x 2 (ni), i == 1,2.
.... Указание. Проверить, 'ITO матрицы А) и А 2 идемпотентны и А, А 2 == О .
l зам чан е. СправеД)lИ боле ильное yrверждение: если Q :: QI + . .. + Qk, [де
Q, XAiX, rank А ; nj, 1,..., k, то "l + + nk n <==> QI,''', Qk
независимы и L(Q.) == x 2 (nj), i == 1,..., k.
m Пусть Х == (X 1 ,... ,Х П ) выборка из нормальноro распределения И(р., 0'2).
Показать, что функция распределения статистики 1] == (Х 1 Х)/( vn:I'S) имеет вид
P (11) == 1 1/2В (1 112; (n 2)/2, 1/2) при 0<11 < 1 и P (11) == 1 P ( 11) ддя
1 < 11 < О (здесь В(х; а, Ь) неполная бета функция, см. п. 2 2.4).
.... Указание. Получить сначала представление
У 1
1]== ,
J Y? +. ., + yn2 1
[де случайные величины Y 1 , ,Yn ' независимы и нормальны И(О, 1). Далее BOC
пользоваться упр. 52 к rл. 1. .
m Пусть имеется выборка объема n из двумерноrо собственноrо нормальноro pac
пределения (см. п. 4 2.3) и (X 1 , Х 2 ), (8 , 812, 8j) и РП соответствующие выбороч
Hble характеристики.
а) Доказать, что (X 1 , Х 2 ) 11 (8 , 8'2. 8п независимы;
б) пусть Q == n(X 1 P.I, X2 J.'2)''r. 1 (X 1 p.I, X2 p.2)' доказать, что I(Q) == х 2 (2);
в) пусть n > 2 и ТВ == Jn 2 рв/( ';1 Pf, ), доказать, что ЦТ,,) == S(n 2).
.... Указание. а) см. замечание к упр. 28 rл. 1; б) см. замечание в п. 2 2.5; в) см. заме
чание в п. 4 2.3. .
158 rлава 2. Первичная обработка экспериментаЛЬНblХ данных
m Пусть Х == (Х,..... Х П ) выборка из распределения [Ю, ==Il, Щ==а' > О,
4 < 00 И Х, s2 соответствующие выборочные среднее и дисперсия.
Доказать, что при n 00
[(Т" = Jn(x Il)/S) N(O, 1).
... Указание. Воспользоваться центральной предельной теоремой, сходимостью
р р
S/a I и следующим фактом: [(11п) [(11), (" I => [("11") [(11).
rл а в а 3
Общая теория оценивания
неизвестных параметров распределений
Оценивать значит создавать. Именно оценка придает
ценность и драюценность всем оцененным вещам. Лишь
через оценку появляется ценность: и без оценивания был бы
пуст орех бытия.
Ф. Ницше 1) Так rоворил Заратустра
Настоящая rлава посвящена общей теории статистических оценок oд
ной из основных проблем, решаемых математической статистикой, как это OT
мечено в общем Введении. Здесь в рамках произвольной параметрической CTa
тистической модели излаrаются основные подходы к построению эффектив
ных оценок для неизвестных параметров модели и функций от них. PaCCMaT
риваются два традиционных подхода к решению этих задач: точечное и интер
вальное оценивание (более общо оценивание с помощью доверительных
множеств), а также некоторые друrие современные концепции оценивания.
При точечном оценивании в основном рассматриваются несмещенные oцeH
ки, и за меру их точности принимается величина дисперсии оценки. Основное
внимание уделяется методам построения оптимальных оценок, при этом pac
сматриваются случаи как скалярноrо, так и BeKTopHoro параметров. Излаrают
ся различные подходы Д)lЯ построения доверительных интервалов и довери
тельных множеств, в том числе принцип отношения правдоподобия один
из наиболее универсальных современных принципов решения мноrих CTa
тистических задач. Рассматриваются также вопросы оценивания при выборе
из конечных совокупностей. При решении рассматриваемых задач использу
ются как точный, так и асимптотический (Д)lЯ больших выборок) подходы,
что диктуется, в основном, спецификой конкретной анализируемой ситуации.
3.1. Статистические оценки
и общие требования к ним
1. Понятие статистической оценки и ее среднеквадратичная ошибка
Это понятие уже встречал ось нам в rл. 2. Там rоворилось, что значение эмпири
ческой функции распределения Fn(x) в каждой точке Х можно рассматривать
1) Ниuше Фридрих (l844 1900) немецкий философ, поэт мыслитель.
160 rлава з. Теория оценивания неизвестных параметров распределений
в качестве приближенноrо значения (оценки) для теоретической функции pac
пределен ия Р(х) наблюдаемой в эксперименте случайной веЛИ'IИНЫ , а раз
личные выборочные характеристики (моменты ak и I1k (см. (2) (3) 2.2),
квантили (n, р (см. (2) 2.4) и т. Д.) как оценки соответсТl3УЮЩИХ теорети
ческих характеристик распределения (( ). При этом использование термина
«оценка,) обосновывалось тем, что для выборок большоrо объема значитель
ная разница между значениями выборочной и теоретической характеристик
маловероятна, и поэтому разумно (по крайней мере для больших выборок)
приншь выборочную характеристику за приближенное значение COOTBeTCTBY
ющей теоретической характеристики, коrда последняя неизвестна. Таким об
разом, в этот термин вк.ладывался определенный асимптотический смысл при
n ----+ 00 (напомним, что n это объем выборки Х == (Х), ,Х n ) из pac
пределения (О). Выражением этоrо «разумноro» свойства оценки является
понятие ее состоятельности (см. определение 3 в 2.2) одноrо из основных
понятий теории оценок.
В то же время при применении теории оценивания на практике обы'l
но приходится строить приближенные значения дли различных неизвестных
теоретических характеристик изучаемой модели при конечных (и часто Becь
ма умеренных) объемах выборки, и при этом обосновывать соответствующие
рекомендации с точки зрения каких либо критериев оптимальности. Общие
методы решения подобных задач развиты в теории оценивания неизвестных
параметров распределений, которой и посвящена настоящая rлава.
Итак, пусть задана статистическая модель :F == {F} для схемы повтор
ных независимых наблюдений над некоторой случайной веЛИ'IИНОЙ и Х ==
(X 1 , ,Х n ) есть выборка из распределения (( ) Е:;: В дальнейшем pac
сматриваются различные функции Т == Т(Х) от выборки, сами являющиеси
случайными величинами (т. е. для которых при всех t определены вероятности
рти) == Р{Т(Х) :(; t}). Если при этом фУНКЦИfl Т не зависит от неизвестноrо
распределения наблюдаемой величины С то ее приня
Статистика и оценка то называть статистикой (см. определение 1 D 2.2).
Часто требуется по выборке Х сделать те или иные зак.лючения об истинном
значении 90 некоторой (неизвестной) характеристики 9 9(0 наблюдае
мой случайной величины. Прежде Bcero под этим понимается задача оценить
это значение 90, т. е. построить такую статистику Т(Х), значение которой
t == T( ) при наблюдавшейся реализации выборки Х можно было бы
считать разумным (в KaKOM TO смысле) приближением для 90: t 90. В этом
случае rоворят, что статистика Т(Х) оценивает 9 или, что Т(Х) есть оцеliка
9 (для у) и часто подчеркивают это обозначением 9 == Т(Х). Так в общем
виде формулируется задача тОlfеlfНОсО оценивания неизвестных параметров pac
-1' пределений.
Точность оценки Ясно, что для оценивания заданной характери
стики 9 можно использовать различные оценки и,
чтобы выбрать лучшую из них, надо иметь критерий сравнения качества (точ
насти) оценок. В свою очередь, и подобные критерии MOryт быть разными
3.1. Статистические оценки и общие требования к ним 161
(в зависимости от целей, ДJJЯ которых строится оценка, удобства исполь-
зования критерия и т. п.), но любой критерий определяется выбором мер/"
точности оценок (меры близости оценки к истинному значению оцениваемой
характеристики). Кроме Toro, обычно класс рассматриваемых в конкретной
задаче оценок оrраничивают некоторыми дополнительными требованиями.
Таким образом, если определен некоторый класс оценок тg (в задаче оцени-
вания g) и выбрана мера точности, то оцен ка Т Е Тg, оптимизирующая эту
меру, называется оптимальной (в классе Тg).
Итак, для построения теории оптимальноrо оценивания прежде Bcero на-
до доrовориться о мере точности оценок, т. е. уточнить смысл приближенноrо
равенства Т(Х) g. Если статистика Т(Х) используется для оценивания
величины g, то одной из разумных мер расхождения между ними является
(Т(Х) g)2, или квадратичная ошибка. Но так как эта величина случайная, то
для измерения точности оценки Т используется сред- С ...
2 реднеквадратичная
неквадратичнаяошибка (с. к. о.) t:.(T) == Е(Т(Х) у) 6
оши ка оценки
rде Е, как и ранее, знак математическоrо ожида
ния. С. к. о. наиболее распространенная и традиционно используемая в при
кладной математической статистике мера точности оценок, хотя, в принципе,
можно было бы использовать и друrие меры точности, например, среднюю
абсолютную ошибку EIT( Х) 9 1, однако здесь мы сталкиваемся с серьезными
аналитическими трудностями вычисления этой меры в конкретных задачах.
Мера t:.(T) по рождает и соответствующий критерий оптимальности оценок:
оценка, минимизирующая с. к. о. В заданном классе оценок Тg, называется -s::."
оптимальной в среднеквадратичном смысле (в классе Оптимальная оценка '*
Ту) и обозначается символом Т' (или g*, чтобы под
черкнуть, что эта оценка ДJJЯ g):
Т' == arg min t:.(T);
1'EТg
(1)
ее с. к. о. есть
t:.* == t:.(T*) == Е(Т*(Х) g)2 == inf Е(Т(Х) g)2
TEТg
(2)
Таким образом, в общем случае задача построения наилучшей (в средне-
квадратичном смысле и в заданном классе оценок 79) оценки для характери-
стики 9 по выборке Х сводится к решению экстремальной проблемы (1) (2).
Ниже эти общие положения конкретизируются в рамках произвольной
параметрической модели :F == {Р(х; О), О Е 8} (см. пример 4 Введения).
Если модель :F параметрическая, то любая теоретическая характеристика яв
ляется функцией от параметра модели О, и в таком случае речь идет об оце-
нивании параметрических функций, для которых будем использовать обозна
чение т(О) (тау от тэта).
Подчеркнем, наконец, следующее довольно очевидное, но весьма важное
обстоятельство. При оценивании заданной параметрической функции т(О)
11 За... 1748
162 rлава з. Теория оценивания неизвестных nараметр08 распределений
A'
,. Необходимое усло
!3ие оценивания
необходимо, чтобы область значениЙ соответствующей
оценки Т(Х) совпадала с областью значений т(О):
{t: t == l'(Х), f. ЕХ} == {т: т == т(О), О Е е}, (3)
так как в противном случае оценка может давать значенrlЯ вообще не принима
емые оцеНИllаемой lIеЛИЧИНОI1 (оценка будет лишена практическоrо смысла!).
Напомним, что в (3) .I обозначает выборочное пространство (совокупность
всех возможных реаЛJ1ЗациЙ выборки Х), а G параметрическое множество
(совокупносп, всех допустимых значений параметра модсли О).
2. Несмещенные оценки
Одно из центральных понятий математическоЙ статистики понятие He
смещенной оценки уже было введено в 2.2 (соотношение (22)), rдe также
даны краткие комментарии и соответствующие примеры. Здесь мы обсудим
это ПОНЯТ1lе с общих позиций 11 более детально.
Любая Оllенка Т == Т(Х) является случайной l3еЛl1ЧИНОЙ, поэтому об
щим требованием к ней является достаточно высокан степень концентрации
ее распределения около истннноrо значения оцениваемоЙ характеРIIСТИКИ.
Че:'1 выше степень этоЙ концентрации, Te 1 лучше (точнее) соответствующая
оценка. Выражением этоrо lJ определенной стеПСIШ и являетсн условие He
смещенности. Дадим ero более детализированное (11 контексте обсуждаемоЙ
проблематики) и общее определение, Но сначала условимся о некоторых дo
полнительных обозначениях.
В случае параметрической модели :F == {Р(х; О), О Е е} распределение
вероятностей на выборочном пространстве Х, отвечающее пара:\1етру О, обо
значается символом Р6. Аналоrично, индекс О при СJIМllOлах математическоrо
ожидания Е, дисперсии D и Т. д. будет означать, что соответствующие нели
чины вычисляются для распределении Р/I. Например, Е6Т(Х), D/lT(X)
обозначения СООТIJСТСТВУЮЩИХ MOMeHTOIJ статистики Т(Х) в случае, коrда
ФУl1КUl1Я распределения выборки Х == (Х 1, , Х 7 ,) есть
Fx(f.; О) == F(xJ, О) Р(х", О)
("ли плотность fx(f.; О) == f(x!, О) f(x 7l ; О)). ПРI1 этом для единообразия
иноrда будет использоваться сокращенная запись через интеrpал Стилтьеса 2):
Е6 Т (Х) == J T(f.) dFx(f.; О).
Здесь интеrpал понимается как n мерный интеrрал по IJССМУ выборочному
пространству Х, который в случае абсолютно непрерЫIJНОЙ 10дели вычисля
етея как обычный интеrpал Римана
J T(XJ,
, Xn)!(Xl: О)
f(x,,; О) dXI
dx n ,
2) СТlUПьес To ac ЯII ( Л.) (1856 J894) rоллаllДСКИЙ математик и астроном.
3.1. Статистические оценки и общие требования к ним 163
а в случае дискретной модели как соответствующая сумма
ЕТ(х" . . . , xn)f(Xi; В)
'(х п ; В).
Этоro уже достаточно, чтобы перейти к точным формулировкам.
Статистика Т == Т(Х) называется несмещенной в среднем
(или просто несмещенной) оценкой для заданной параметрической функции
т(8), если она удовлетворяет условию Условие .,.
ЕеТ(Х) == т(8), V {J Е е.
(4)
несмещенности
Об условии (4) rоворят как об условuи несмещенносmи. Если оно не выпол
няется, то величина
Ь(В) == ЕеТ(Х) т(6)
назыоается смещенuем оценки Т(Х). Таким образом, можно также считать, что
несмещенные оценки это такие оценки, для которых смещение Ь(В) == О,
V {J Е 8. В общем случае среднеквадратичная ошибка
Ь.(Т; О) == Ее(Т(Х) т(в»2
оценки Т == Т(Х) выражается через дисперсию оценки и ее смещение сле
дующим образом
Ь.(Т; В) == DeT + ь 2 (о).
(5)
Следовательно, дЛЯ несмещенных оценок с. к. о. совпадает с дисперсией
оценки.
В конкретных задачах часто оrpаничиваются рассмотрением лишь класса
'т,- несмещенных оценок дЛЯ т == т(В):
'т,- == {Т(Х) ЕеТ(Х) == т(О) , V 8 Е 8}.
Функция т(6) называется оцеliиваемой, если класс т;.
не пуст, т. е. если существует хотя бы одна несмещенная
оценка для т(В). Про любую несмещенную оценку мож
но сказать, что «О среднем» она приводит к желаемому результату. К тому же,
как это будет показано далее, дЛя несмещенных оценок можно построить
достаточно ПрОС1)'ю и практически полезную теорию, о которой критерием
точности оценки является ее дисперсия.
О ...
цениваемые
функции
Неснолько СЛОВ о философии «CpeaHeZO». В пользу среднеro» можно при
вести следующие рассуждения из книrи BeHrepcKoro математика rабора Ce
кея «Парадоксы В теории вероятностей и математическоЙ статистике» [23].
Уравнивание противоположных значениЙ и отклонений о "среднем", т. е.
СУМ ИрОDание набдюдений в одно значение, имеет давние традlЩIIИ. Эсхил писал
в траrедии "эвмениды'' .. Бо!)' всеrда середина любезна, и меру чтит божество",
а последователи Кl1Тайскоro философа Конфуция roворят, что "в неПОДDИJКНОСТИ
среднеro (= Чжун Йюн) ссть величайшее совершенство" Математически поня
тие "среднеrо" можно интерпретировать различными способами (арифметическое
среднее, reометрическое среднее, медиана и т.д.). Однако в статистических при
менениях в течение долroro времени крайне важную роль нrpало арифметическое
164 rлава з. Теория оценивания неизвестных параметров распределений
среднее. Уже в первых выдющихсяя результатах в теории вероятностей и MaTeMa
тической статистике изучалось арифметическое среднее статистической выборки
и росло понимание важности ero использования».
Однако условие несмещенности в среднем не следует абсолютизировать: в HeKOTO
рых случаях требование несмещенности (4) может оказаться слишком «жестким»
И привести к нежелательным результатам. Так, может оказаться, что несмещен
ные оценки (в данной модели и для данной параметрической функции) вообще
не существуют (т. е. класс -ТТ == r2i пустое множество), а 11 друrих случаях,
хотя и имеются, но практически бесполезны. Н иже эти общие положения ил
люстрируются примерами. Но предварительно отметим, что существует также
и критическая философия «среднеrо,). Так имеет место (и некоторыми актив
но используется) такой прием искажения истины, как использование «средних
цифр,) (как заметил Ленин, «нет ничеrо rлупее так называеМblХ "средних цифр",»,
коrда понятие среднеro используется как синоним типичноrо. Примерами таких
подмен MOryr служить средний доход населения, средняя температура больных
в некоторой больнице, среднее количество осадков за несколько сезонов в He
котором реrионе (в области N в прошлом rоду была летом засуха, и все поля
выrорели, а этим летом прошли ливни. которые все смыли с полей, но в среднем
количество осадков за два сезона 8 пределах нормы, или: в некоторой стране
есть Bcero лишь несколько очень боrатых семей и большое количество бедных, чьи
доходы соответственно Of1JOMHbl и малы, поэтому здесь средний доход вовсе нети
пичен). Таким образом, средние характеристики часто вводят в заблуждение. Как
отмечается в [231, <.средний человек одна из них». Неудивительно, что иссле
дования бельrийскоro ученоrо Л. А. Ж. Кетле по этому вопросу стали источником
rорячих споров. Худшее в «среднем человеке» не ero серость, а возникающие про
тиворечия. Например, средний рост не соответствует среднему весу и т. д. Только
по одной этой причине можно усомниться в справедливости слов Дж. Рейнольдса
(nepBoro президента Королевской академии художеств в Лондоне), коrда он CKa
зал, что «в среднем источник прекрасноrо,).
Перейдем к обещанным примерам, оттеняющим различные нюаНСbJ He
смещенности в среднем.
Что примера лучше действует?
Что людьми сильней ворочоет?
А. С. Пушкин. Бова (1814)
/
Пример 1 (Несмещенное оценивание в схеме Бернулли). Пусть
Х == (Х(, ,Х п )
выборка из распределения Бернулли Bi(l, О), т. е. Х ; принимает значения
О и 1 с вероятностями f(x; О) == ОХ(1 о)Н х 0,1 (см. п. 1 1.1).
Опишем класс оцениваемых функций в рассматриваемой модели и найдем
соответствующие несмещенные оценки. Для этоro запишем ДI1Я произвольной
статистики Т( Х ) ее математическое ожидание:
Е//Т(Ю ==
I:
T(iJf(x,; 8)
f(x n ; 8) ==
i!i. (XI," .,Х.)
3.1. Статистические оценки и общие требования к ним 165
n
L T( )oExo (1 o)n Ex; == L Or (1 o)n L T( ).
! r O !:Ex; r
Здесь правая часть представляет собой полином от О степени не выше n,
следовательно, в данной модели несмещенные оценки можно строить лишь
для параметрических функций т(О), являющихся полиномами степени не BЫ
ше n числа наблюдений. Отсюда, в частности, следует, что для функций
вида т(О) == o a а > О и т(О) == ОЬ Ь > n, несмещенных оценок по выборке
объема n не существует.
Пусть теперь
n
т(О) == L aj
j O
произвольный полином степени n (или ниже, если старшие коэффициенты
а; равны нулю). Построим сначала несмещенную оценку дпя отдельной сте-
пени fY при j n. Из упр. 19 к rл. 1 имеем, что если случайная величина v
имеет биномиальное распределение Bi(n, р), то дпя ее j ro факториальноrо
момента при j n справедпива формула E(V)j == (n)jr В нашем случае
статистика Х == X 1 + + Х П имеет распределение Bi(n, О) (см. п. 1 1.1),
следовательно, Е8(Х); == (n)jtY. Это означает, что статистика (X)j/(n)j явля
етея несмещенной оценкой дпя oj при любом j n. Отсюда, в свою очередь,
имеем, что несмещенной оценкой полинома т(О) является статистика
т == Т( Х ) == t aj(X)j .
j O (n);
Итак, в бернуллиевской модели Bi(l, О) класс оцениваемых параметри-
ческих функций по n наблюдениям совпадает с классом полиномов степени
не выше n, и дпя любой такой функции т(О) ее несмещенная оценка т дается
формулой (6). .
Пример 2. Пусть .ею Е П(О) семейство пуас Отсутствие несмещен- -.f'
соновских распределений (см. п. 3 1.1) и n == 1, ной оценки в пуассо
т. е. произведено одно наблюдение Х над пуассо >"новской модели
новской случайной веЛИ4ИНОЙ. Требуется оценить
параметрическую функцию т(О) == 1/0.
Если Т(Х) несмещенная оценка т(О), то условие (4) принимает вид
00 ох 1
L T(x)e 81 == , v () > О.
х=о Х. ()
(6)
или
00 (}х+1 00 or
L T(x)-------r == е 8 == I: " V О> О.
x o Х. r=O r.
lбб rлава з. Теория оценивания неuзвестных параметров распределений
Очевидно, что функция Т(х), удовлетворяющая последнему условию и He
зависящая от (), как это требуется в соответствии с определением понятия
оценки, не существует, т. е. в данном случае несмещенных оценок ДJIЯ т(())
OO H .
Ф. Несмещенные оценки
в отрицательной
биномиальной модели
Пример З. Пусть .ею Е Bi (r, 8) семейство OT
рицательных биномиальных распределений (см. п. 2
1.1) и n == 1. Построим несмещенную оценку ДJIЛ
параметрической функции т. (8) == ()" rде s ? I
целое число. Здесь условие несмещенности (4) принимает вид
00
Е T(x)f(xlr, ()) == Ts(()), V () Е (О, 1),
", o
или
ос ос
Е Х Х 8" Е C j () s+j
T(x)Cr+X I() == ( ) r+ J ' 1 ,11 8 Е (О, 1).
1 () r
X O j O
Но из тождественноrо равенства двух степенных рядов следует равенство их
коэффициентов при соответствующих степенях (). Следовательно, функция
Т(х) здесь однозначно определена, и она есть
{ Опри х < s,
т. ( ) C +; H н .
r,s Х С '" П Х J
+ I при х;;:: s
r "' . Х + r j 1
J o
(Здесь учтено, что при Ь < О C == О).
Таким образом, несмещеннал оценка ДJIя Та(()) существует, единственна
и имеет вид
П Н X j
Та == Tr,s(X) == . I(Х ;;:: s).
. Х+т з 1
з О
Обратим внимание на то, что эта оценка может принимать нулевое зна
чение (при Х < s), которое не принадлежит области значений функции Ts(())
(ведь О < Ts(()) < 1 при О < 8 < 1), тем самым ДJIЯ нее не выполняется
условие (3). Если же r == 1, то оценка T1,s(X) вообще принимает лишь два
значения:
(7)
Х? s,
не при надлежащие области значений функции Ts(()), т. е. такая оценка лише
на какоrо либо практическоrо смысла. Этот при мер показывает, '!то иноrда
принцип несмещенности может привести к бесполезному результату. .
Пример 4 (Общая нормальная модель, оценивание дисперсии). Пусть
{ О,
T 1 ,5(X) == 1,
х < s,
X==(X1....,X n ), n;;::2,
3.1. Статистические оценки и общие требования к ним 167
lIыборка I1З нормальноrо распределения М(О1, oi) (оба параметра неиз
вестны). Требуется оценить парамеТРИ'lескую функцию т( О) == т( 01,82) == 8 .
Мы уже знаем (см. теорему 292.2), что несмещенной оценкой теоретической
дисперсии является (в любой модели!) статистика
n
2 1 2
Во == n 1 L..,..(X i Х) ,
i 1
при этом (см. замечание к теореме Фишера в 92.5, соотношение (7))
2 ( n 2 ) 28
DeBo == D s == .
n 1 n 1
(8)
Ниже (см. 3.2, ПРИ\1ер 9) будет показано, что по критерию минимума
2
дисперсии оценка иа является оптимальнои среди всех несмещенных оценок
функции т(О) == O !:! модели М(О1, O ), т. е. ф(л)
ее дисперсия (8) меньше дисперсии любой 2
й2
друrОI1 несмещеннои оценки величины 172' 71 I
Рассмотрим теперь класс оценок вида
2
ТА == ЛSа. Так как
ЕеТА == лЕеsJ == лО ,
2
n+1
,
.
,
,
.
.
л
то 13 этом классе имеется лишь единственная
несмещенная оценка т(О), соответствующая
2
значению л == 1, т. е. оценка so.
Вычислим среднеквадратичную ошибку
произвольной оценки ТА:
n 3 n 1
n+! >" ТI+l
Рис. 1
А(Т А ; О) == Ее(ТА 0 )2 == Ее [л(sJ Oi) + (..\ l)оп 2 == л2DеsJ + (л 1)20 .
Отсюда из формулы (8) получим
А(Т А ; О) == 1jJ(л)О .
2..\2
1jJ(л) == + (л 1)2
n 1
Здесь функция ф(л) есть парабола, rрафик которой изображен на рис. 1. Функ
ция 1jJ(л) достиrает MHНlIMY\1a при л' == (n 1)/(n + 1) и 1jJ(л*) == 2/(n + 1).
Отсюда. учитывая (8), имеем
204 204
А(ТА'; О) == < == A(SJ; О).
n+ 1 n 1
Таким образом, по критерию минимума с. к. о. оптимальноЙ в классе Т == {ТА}
является оценка
n
.2 1 2
ТА' == Л So == L..".(Xi Х) .
n+ 1.
1 1
(9)
168 rлава з. Теория оценивания неизвесmных параметров распределений
Эта оценка смещенная, но она точнее оценивает теоретическую диспер
сию O модели N(O(, O ), чем несмещенная оценка Вб. Найдем еще смещение
Ьп(О) оценки Т).,.:
2 . 2 20
Ьп(О) == ЕТ).,. 02 == (л 1)02 == .
п+1
Это смещение мало при большом объеме выборки п и Ьп(О) -----1 О при п -----1 00,
т. е. Т).,. асимптотически несмещенная оценка.
Отметим дополнительно, что при любом л Е (Сп З)/(п + 1), 1) оценка
Т)., имеет меньшую с. к. о., нежели TI == Вб, но в классе несмещенных оценок
2
Во оптимальная оценка.
Этот пример показывает, что не может быть единственноrо критерия,
по которому следует сравнивать все оценки, как не существует единственной
оценки данной теоретической характеристики, подходящей ДlIЯ всех случаев.-
Статистичесние задачи не имеют
однозначных ответов.
Э.Леман
З. оптимальныe оценки
Требование несмещенности в силу сделанных выше замечаний нельзя paCCMaT
ривать как универсальное. Тем не менее во мноrих встречающихея на практике
случаях оно уместно и обоснованно и далее мы будем рассматривать в OCHOB
ном именно несмещенные оценки.
Итак, пусть требуется оценить заданную параметрическую функцию т == т(О)
В модели F == {Р(х;О), О Е е} по соответствующей выборке Х == (Х". . " Х п ).
Обозначим 7;. класс всех несмещенных оценок Т == Т(Х) ДlIЯ т(О) И предпо
ложим, что он не пуст (что это не Bcerдa имеет место, rоворит нам пример 2
выше). Дополнительно предположим, что дисперсии всех оценок из класса
7;. конечны: D6T == Ев(Т т(0»)2 < 00, VT Е 7;. и V () Е е. в этом случае,
как отмечено выше (см. соотношение (5)), мерой точности оценок является
их дисперсия.
Замечание. Напомним, что в теории вероятностей для любой случайной веЛИЧИНbi {
с конечной дисперсией мерой разброса» ее значений BOKpyr среднеrо значения
р. == щ служит стандартное отклонение (J" == , а знаменитое правило «трех
сисм» rласит, что значение { попадает в отрезок [11- З(J", Р. + 3и] с вероятностью,
мало отличающейся от 1. Так, для нормальной N(1I-, 0"2) величИНЫ
Р{р. З(J" { 11-+ 3и} == р{1 {: р. 1 З} == Ф(З) Ф( З) == 2Ф(З) 1 :::0:0,997,
т. е. попадает в отрезок [1I-'f 30'] с вероятностью, лищь HeMHoro отличающейся от 1.
Итак, пусть Т' и Т оценки из класса 7;.. Если
DoT* DoT, V () Е е,
(1 О)
3.1. Статистические оценки и общие требования к ним 169
со строrим неравенством хотя бы при одном (), то по критерию минимума дис
персии следует отдать предпочтение т', как более точной оценке. Если усло
вие (10) выполняется дI1я любой оценки Т Е Т" то т' называют несмещенной
оценкой с равномерно минимальной дисперсией (сокращенно, н. о. р. м. д.). Ta
кую оценку т' (коrда она существует) будем для краткости называть также
оптимальной и иноrда обозначать т' чтобы подчеркнуть, что она относится
к функции т«(}).
Итак, оптимальной (среди несмещенных) яв
ляется оценка т' Е Т" дI1я которой выполняется
условие
Условие оптимальности
несмещенной оцеНКI1,
!ii }
DOT' == inf DoT, V () Е е. (11)
ТЕт.
Требование равномерной (по параметру ()) минимальности дисперсии
весьма сильное и не всеrда имеет место. Может оказаться, что из двух HeCMe
щенных оценок ТI и Т 2 дисперсия DIITj минимальна (в ЮIассе Т,) для одних
значений параметра (), а дисперсия DoT2 для друrих значений (). В таких
случаях с помощью одноrо критерия минимума дисперсии эти оценки cpaB
нить нельзя. Однако это требование выделяет оптимальную оценку в классе т,
однозначно, если такая оценка существет, о чем rоворит следующая теорема.
Теорема 1. Пусть Ti==Tj(X), i == 1, 2, двеоптимальныеоценки для т==т«(}).
Тоrдэ т, == Т 2 3).
Доказательство. Рассмотрим новую оценку ТЗ == (Т ! + Т 2 )/2. Ясно, что
ТЗ Е Т, и
1
DоТ з == (DoTl + DoT2 + 2 COVo (Т), Т 2 )).
4
(12)
Воспользуемся известным в теории вероятностей неравеНСТIЮМ Коши
Буняковскоrо: для любых случайных величин 171 и 172 С конечными диспер
сиями
ICOV(17I' 172) I .J D1]ID1]2'
причем знак равенства имеет место только если 171 и 172 линейно связаны.
Отсюда и из (12), положив DoTj == DIIT2 == V == V«()), получим
1
DоТ з 2(V+ Iсоуо(Т),Т 2 )!) V.
(13)
Поскольку Tj, i == 1, 2, оптимальные оценки, то v == DIITj DIIТЗ,
откуда DоТ з == V, т. е. Т3 также оптимальная оценка. Но так как в He
равенствах (13) имеют место знаки равенства, то СОУII (T j , Т 2 ) О и, более
Toro, COVo (Т" Т2) == DIITI == V. Следовательно, Тl и Т2 линейно связаны,
3) Здесь и далее равенство статистик понимается в том смысле, что
Ре{Х Е { : TI( );O; T2( )}} == О, '71) Е е.
170 rлава з. Теория оценивания неизвестных nараметр08 распределений
т. е. Tl == kT 2 + а. Из условия несмещенности оценок имеем 7 == k7 + а,
т.е. а == (1 k)7, и следовательно, TI 7 == k(T 2 7). Здесь коэффициент
k == k (fJ) определяется цепочкой равенств
V == СОУе (TI, Т 2 ) == Ее(Т! 7)(Т 2 7) == kEe(T2 7)2 == kDeT2 == k.u.
Отсюда имеем k == 1, следовательно, TI == Т 2 . .
Приведем пример существования оптимальной оценки в конкретной MO
дели,
Пример 5 (Бернуллиевская модель, оценивание параметра). Пусть
х == (Х" ,Х n )
выборка из.ею Е Bi(l, О) и требуется оценить параметр е.
Здесь Е8 Xj == О, поэтому выборочное среднее Х является несмещенной
и состоятельной оценкой () (см. теорему 2 2.2). Однако Х не единственная
несмещенная оценка О. Например, всякая статистика
1 n
Т == L bjXj при ы +
n.
, I
+ Ь N == n
также является несмещенной оценкой о. При этом, так как (см. (2) 1.1)
1 n ь 2 Ь 2
DuT == 2" '" Ь;8(I 8) O(I (}) о при n ----7 00
n n
, I
(здесь Ь == тах Ibjl), то оценка Т также и состоятельна. Таким образом, такие
I
оценки так же «хороши», как и Х.
Итак, в данной задаче класс т; содержит MHoro
оценок и потому возникает вопрос о выборе cpe
ди них наилучшей. Покажем, что в данном слу
чае оптимальная оценка Т' существует и при этом
.
т == х. Поскольку DuX == 8(1 8)/n, то в co
ответствии с определением (11) достаточно показать, что для любой оценки
т Е т.,. выполняется неравенство
Оптимальность
вы60рочноrо cpeAHero
в бернуллиевской
модел и
8( 1 О)
D8T ,V 8 Е (О, 1).
n
(14)
в данном случае распределение выборки задается плотностью (см. при
мер 1)
L(;f,; 8) == 02: Х О(I 8)n 2:x;, ;f, == (XI,..., Х п ).
( 15)
Так как
1 == L Ц?::.; 8) и 0== ЕвТ(Х) == L T(?::.)L(;f,; О),
1
3.1. Статистические оценки и общие требования к ним 171
то, дифференцируя эти тождества по О, получим
aL('!1.; О) д [п L('!1.; О) ( . ) ( д 'П L(X; О) )
О дО дО L '!1., 8 Е{I дО '
!.
L ( ) д In L('!1.; О) ) ( ( ) д 'п L(X; О) )
I == Т Х L ( x' , О == Ей Т Х .
дО . дО
;!i.
Отсюда можно записать
[ alnL ( X'O )]
1 == Е{I (Т(Х) О) дО'
и, соrласно неравенству Коши Буняковскоrо,
2 ( alnL ( X'8 )) 2
1 :::;; Е{I(Т(Х) 8) Е{I дО '
Но Ев(Т(Х) 0)2 == О{lТ, поэтому из последнеrо неравенства следует, что
1
О{lТ ? , I;j О Е (О, 1).
( д Iп L(X; О) )
Е{I дО
В рассматриваемом случае (см. (15))
alnL(X;O) 1 n [ ( N ) 1 n
дО == 8" Х; 1 О n Х; == 00 О) (X; О),
( 16)
поэтому
( дIПL(х,О) ) 2 [ [ n ] 2
Е{I дО == 02(1 0)2 Е{I (X; О)
n n
== 02(1 O)2 0BXI == 0(1 O) ' (17)
Отсюда и из неравенства (16) получаем соотношение (14).
Учитывая важность для приложений бернуллиевской модели Bi( 1, О),
сформулируем полученный результат в виде теоремы. .
Теорема 2. Относительная частота произвольноrо события в n независимых
испытаниях является опти мал ьной несмещенной оценкой для вероятности
этоrо события.
Как следствие этой теоремы отметим, что значение эмпирической функции
распределения Рn(Х) в каждой точке х является оптимальной несмещенной
оценкой ДЛЯ значения в этой точке теоретической функции распределения
Р(х).
172 rлава 3. Теория оценивания неuзвестных параметР08 распределений
-f' Приведем следующую юмористическую историю, приналлежащую Д. Пойа
[20) и показывающую, как не следует интерпретировать частотную концеп
цию вероятности. Д p Тел (доктор телепатии), закончив осмотр пациента,
покачал rоловой. «Вы очень серьезно больны, сказал он, из десяти
человек с такой болезнью выживает только один». Пациента эта информация
изрядно испуrала, и д p Тел начал ero успокаивать: (,Но Вам очень повезло, что
Вы пришли ко мне, сэр. У меня уже умерли от этой болезни девять паuиентов,
так что Вы выживете».
Установим следующее важное СВОЙСТВо оптимальных оценок.
Теорема 3. Пусть Т,* и Т; оптимальные оценки функций Т) == TI (О) И
Т2 == Т2(8) соответственно. TorAa статистика Т* == a1T 1 * + а2Т2* является оп
тимальной оценкой функции т == аl ТI + а2Т2 для любых постоянных аl и а2.
Доказательство. Установим сначала следующее свойство оптимальных oцe
нок, представляющее самостоятельный интерес: д/!я любой статистики 'Ф == 'Ф( Х)
с Е(J'Ф == о, v о Е е (такая статистнка 'Ф(Х) называется несмещенной оценкой
нуля), выполняется равенство СОУо (T 1 *, 'Ф) == о, v о Е е, т. е. оптимальная
оценка некоррелирована с любой несмещенной оценкой нуля.
Для доказательства рассмотрим статистику i\ == Т; + >''Ф. При любом >.
это несмещенная оценка TI, поэтому В силу оптимальности оценки Т)*
Doi\ == D(JT,* + >.2 D (J'Ф + 2>' СоУо (T 1 *, 'Ф) D(JT,*, V 8 Ее. (18)
Отсюда следует, что СОУе (T 1 *, 'Ф) == О, так как в противном случае при>. == >'0 ==
== СОУо (T 1 *, 'Ф) /D(J'Ф левая часть (18) была бы равна D(JT 1 * coy (T 1 *, 'Ф) /D(J'Ф,
что меньше, чем D(JT 1 * , при СОУе (T 1 *, 'Ф) i- о (см. рис. 2).
>'0
).
Рис. 2
Перейдем непосредственно к доказательству теоремы. Пусть Т про
извольная несмещенная оценка т Torдa 'Ф == Т* Т будет несмещенной
оценкой нуля и, по предыдущему, СОУе (T i *, 'Ф) == о, i == 1,2. Отсюда
О == а) СОУе (Т,*, 'Ф) + а2 СОУе (Т2, 'Ф) == СОУо (Т*, 'Ф) == D(JT* СОУе (Т*, Т),
т. е.
D(JT* == СОУе (Т*, Т) .j D(JT* . D(JT или D(JT* D(JT, V О. .
9 3.2. Критерии оптимальности оценок по Pao KpaMepy 173
Таким образом, в конкретных задачах, коrда оцениваемая параметриче
ская функция т(О) раСКJJадывается в сумму более простых функций Ti(O),
задачу построения оптимальной несмещенной оценки Д1Jя т(О) можно CBO
дить К аналоrичной задаче Д1Jя ее слаrаемых Ti(O).
В заКJJючение этоrо параrpафа рассмотрим один конкретный пример при
менения полученных результатов.
Пример б. Рассмотрим ситуацию, описанную в при
мере 1 Введения, и предположим, что в эксперимен
те реализуется схема выбора шаров с возвращением.
Тоrда, как показано в при мере 1 1.1, мы имеем дело
со схемой (моделью) Бернулли Bi( 1, О), rде неизвестная вероятность (,успеха»
О alja доля белых шаров в урне. По теореме 2 доля Xjn наблю
давшихся белых шаров при n извлечениях (относительная частота ('успеха»
== извлечение белоrо шара) является оптимальной несмешенноЙ оценкой о:
0* == Х/n. Таким образом, преД1Jоженная в при мере 1 Введения интуитивная
оценка на самом деле оказывается наилучшей с рассматриваемых позиций
несмещенности и оптимальности. .
Перейдем теперь к общим методам построения оптимальных несмещен
ных оценок.
ОПП1мальная оценка
вероятности «успеха»
В схеме Бернулли
tf
t 3.2. Критерии оптимальности оценок, основанные
на неравенстве Pao KpaMepa. Эффективные оценки
Чтобы продвинуться вперед, нам необходимо ввести несколько новых важ
ных понятий, которыми оперирует теория оптимальных оценок. С этоrо мы
и начнем.
1. Функция правдоподобия, вклад выборки, функция информации
Пусть, как обычно, f(x; О) плотность наблюдаемой случайной величины ,
Х==(Х". .,Х n ) выборкаизL( )Е.1'=={F(х;О),ОЕе} и;!с== (xJ,.. ,х n )
реализация Х. Функция L(;!C; О) == f(xl; О) f(x n ; О) является, очевидно,
плотностью случайноrо вектора Х. Рассматриваемая при фиксированном ;!с
как функция пара метра О L(;!c; О) называется функцией правдоподобия (иноrда
об L(;!c; О) rоворят как о правдоподобии данных).
В дальнейшем предполаrается, что L(;!c; О) > О при всех ;!с Е Х и О Е е,
и дифференцируема по параметру О. Пусть сначала параметр (J скалярныЙ.
С
лучаиная величина Вклад выборки
( ) д lп L(X; О) д 111 f(X i ; О)
у Х; О == дО == L; дО
i l
называется вкладом выборки, а i e слаrаемое в правой части (1) называется
вкладом i CO наблюдения, i == 1, , n. В дальнейшем предполаrается, что
0< Ее у2 (х;о) <00, 'tjOEe. (2)
(1)
174 rла8а З. Теория оценивания неизвестных параметров распределений
в последующем изложении нам неоднократно придется дифференциро
вать по 8 интеrралы типа
/ T(; )L(;f; 8) d;к
(интеrpирование ведется по всему выборочному пространству 1:) и предпола
[ать при этом, что можно менять порядок интеrрирования и диффернцирова
;.: ния. Модели, для которых все перечисленные условия
Реryлярные модели выполняются, называются кратко реi!улярными. OTMe
тим, в частности, общее необходимое условие реrуляр
ности, состоящее в том, что выборочное пространство 1: не должно зависеть
от неизвестноro параметра 8.
Рассмотрим некоторые своЙства вклада V (Х; 8) ДЛЯ реryлярных моделей.
Bcerдa имеет место тождество (по 8)
/ L(;f; (}) d;f == 1 (d;к == dXl dx n )
(здесь и далее везде для дискретных моделеЙ интеrрирование заменяется CYM
мированием). Так как модель реrулярна, то, дифференцируя это тождество
по 8, получим
/ д 111 L(;к; 8) / д 1п L(;к; 8) ( ) (
0== dx== Lx;() dx==EпV Х;8 ) .
а8 д8 и
Таким образом, для реryлярной модели
E o V(X;8) ==0, V8EG.
Далее, в силу предположения (2) и (3) определена функция
i n (8) ==D o V(X;8) ==E O V 2 (X 8),
(3)
(4)
;.:
Информация Фишера
которая носит название информации Фишера о па
раметре (), содержащеЙся в выборке Х. Величину
i((}) == i, (8) == Ео ( д 111 ; ; 8) У
(5)
называют также количеством информации, содержащейся в одном наблюдении.
Из (1) имеем
n )
д 'п f(X i ; 8)
i n (8) == DoV(X; 8) == 2: D( д(} == ni(8),
, 1
(6)
т. е, количество информации, содержащейся в выборке, возрастает I1p0l10pциo
I/а//ЬНО объему выборки.
Если плотность f(x; (}) дважды дифференцируема по (), то продиффе
ренцировав при n == I тождество (3) еще раз, получим
f а2 111 f(x; (}) f( . 8 ) d + / ( д 111 f(x; ()) ) 2 f( . 8 ) d == О
д8 2 Х, Х д(} Х, х ,
3.2. Критерии оптимальности оценок по Pao KpaMepy 175
т. е. (см. (5))
i(O) == Ее ( {}2 ln {; О) ) .
(51)
Пример вычисления информации Фишера для бернуллиевской модели
Bi(l, О) имеется (} 3.1 (формула (17)): для этой модели i(O) == 1/(0(1 О)).
Рассмотрим еще один при мер вычисления функции i(O) для нормальной
модели N(O, (1'2). Здесь вклад одноrо наблюдения
( . ) {} 'п f(X i ; О) Х! О {}2 'п f(XI; О) ( 7 )
V Х i, О дО (1'2 ' {}О2 и 2 '
откуда по формуле (5') получаем i(O) == (1' 2. Вид функции i(O) для ряда CTaH
дартных моделей приведен в табл. 1.
Табпица 1
м одеЛl, N(8, (12) N(p., 82) r(8, л) Bi(k,8) Bi (r,8) П(8) К(8)
i(8) 2 28 2 Л8 2 k/(8(1 8)) r/(8(1 8))2 8 I 1/2
и
(определение указанных моделей см. в 1.1 1.2, общая модель Коши К(О)
определена в упр. 48 (б) к rл. ]).
Приведем еще пример нереrулярной модели.
Пусть .ею Е ЩО, О). Здесь из тождества
Нереryлярность JIIt:
равномерной модели
/J
f dOX = I
о
не следует, что
/J
f dx == О
дО О '
о
так как при дифференцировании интеrpала по верхнему пределу появляется
еще одно слаrаемое. В данном случае причина нереrулярности заключается
в том, что выборочное пространство (интервал (О, О)) зависит от неизвестноrо
параметра О.
2, Неравенство Pao KpaMepa
В случае реrулярных моделей для дисперсий несмещенных оценок можно
установить абсолютную нижнюю rраницу, что и будет показано в настоящем
пункте. Рассмотрим задачу оценивания некоторой параметрической функции
т(О) в реrулярной модели :F == {Р(х; О), О Е е} со скалярным параметром О.
Предположим, что класс Т-Т несмещенных оценок т(О) не пуст, и функция
т(О) дифференцируема. Torдa имеет место следующее утверждение.
176 rлава з. Теория оценивания неизвестных параметров распределений
Теорема 1 (Неравенство Pao KpaMepa). Для любой оценки Т:: Т(Х) Е т;.
справедливо неравенство
[7"'(8) ]2
D8 T ni(8) .
(8)
Равенство здесь имеет место TorAa и только TorAa, KorAa Т линейная Функ
ция вклада выборки, т. е.
Т(Х) 7"«(}) :: a(8)V(X; (}),
(9)
[де а«(}) некоторая функция от 8; в этом случае
D8T :: а(8)7"' (8).
( 10)
Доназательство, По условию
ЕоТ(Х):: / T( )L(;f; (}) d :: 7"(8), V 8 Е е.
(11 )
Модель;: реryлярна, поэтому, дифференцируя это тождество по 8 и учи
тывая (1), (3), получим
, / д Iп L(x; (})
Т (О) :: T(;f) д8 L( ; 8) d;f ==
:: E8(T(X)V(X; (}») :: cov8(T(X)V(X; 8»). (12)
Используя неравенство Коши Буняковскоrо и определение (4), из это
[о состояния получаем оценку [Т' ((})]2 :::;; i n «(})D8T причем равенство здесь
имеет место лишь в случае, коrда (при каждом ()) статистика Т(Х) и BКI1aд
выборки У(Х; 8) линейно связаны, т. е. имеет место (9). Отсюда, во первых,
имеем неравенство (8), так как i n «(}):: ni(8), а, BO BTOpЫX, подстаоляя пред
ставление (9) в (12) имеем т'«(}) :: a I(8)D8T, Т.е. приходим к (10). .
Замечание, Если Т == Т(Х) оценка со смещением Ь(8) и функция Ь(/1) диффе
ренцируема, то, используя вместо соотношения (11) тождество
I T(g;)L(;f.; 8) d;r == т(8) + Ь(8),
с помощью аналоrичных рассуждений можно установить неравенство (также назы
ваемое неравенством Pao Крамера)
[т'(8) + Ь'(8)] 2
овт ?:
ni(8)
обобщающее (8).
..
Эффективные оценки
Если существует оценка Т' Е т;., для которой
rpаница Pao KpaMepa (8) достиraетсЯ, то ее назы
3,2. Критерии оптимальности оценок по Pao KpaMepy 177
вают эффективной. Эффективная оценка является оптимальной, и, соrласно
теореме 1 3.1, она единственна. Из теоремы 1 следует, что критерием эффек.
тивности оценки является представление (9). Будем называть этот критерий
оптимальности оценки критерием Pao Kpaмepa. Для эффективной оценки,
т. е. УДОВllетворяющей представлению (9), ее дисперсия может быть вычислена
также по формуле (10).
Отметим следующее обстоятельство. Вклад выборки V(X; 8) однозначно
определяется моделью. Поэтому предстаВllение (9) (коrда оно имеет место)
единственно и, следовательно, эффективная оценка может существовать толь
ко ДЛЯ одной определенной параметрической функции т(8) и не существует
ни для какой друrой функции параметра 8, отличной от ат(8) +Ь, rде а и Ь
константы.
С примером эффективной оценки мы уже встречались в примере 1 3.1.
Там мы имели предстаВllение 8( 1 8) / n V (Х; 8) == Х (} , т. е. а( 8) == 8( 1 8) / n,
т(8) == 8, и потому статистика Х в модели Bi( 1,8) ЯВllяется эффективной
оценкой параметра 8. Рассмотрим еще несколько примеров на применение
критерия Pao KpaMepa,
Пример 1. Пусть Х выборка из нормальноroраспределения N(8,(J"2). ИЗ (7)
2
следует, что в данном случае (J" /nV(X; 8) == Х 8, т. е. по критерию Pao
Крамера выборочное среднее Х в модели N(8,0'2) ЯВllяется эффективной
оценкой (} и D8X == и2/ n , что совпадает с нижней rpаницей в (8). .
Пример 2. Пусть Х == (Х], . . . ,Х n ) выборка из .ею Е N(p" (2). Здесь
L(X; 8) == ( 8)n ехр { 2:2 Т*(Х)}' Т*(Х) == t(Xi р,)2,
и потому
V ( X' 8 ) == д lп L(X; 8) == !!...Т* ( Х )
, д8 83 (} ,
(}3
V(X; 8) == Т*(Х) (}2
n
Но это по критерию Pao KpaMepa означает, что статистика Т*(Х) ЯВllяется
эффективной оценкой т(8) == 82 и D 8 T* == 2(}4/ n . .
Назовем эффективностью оценки Эффективность ,.
Т == Т(Х) Е т; отношение оценки
[т'(8)]2
е(Т) == е(Т; 8) == D8 T . ni(8) (13)
Из неравенства (8) следует, что О е(Т) 1, а для эффективной oцeH
ки т* ее эффективность е(Т*) == 1. Таким образом, эффективность оценки
это отношение минимально возможной дисперсии в классе всех несмещен
ных оценок т; к дисперсии данной оценки Т Е Т;.
12 Заказ 1748
или
178 rлава з. Теория оценивания неизвестных параметров распределений
Важным понятием в теории оценок является также асимптотическая эф
фективность, которая является аналоrом понятия эффективности для боль
ших выборок (при n ----+ 00). Оценка Тn(Х), Х == (Х" ,Х n ), для т(8) при
n ----+ 00 может оказаться асимптотически нормальной:
.сО(Тn (Х» '" N (Т(8), O"j 8» )
4 Асимптотическая
эффективность
оценки
даже в тех случаях, коrда ООТn не существует. АСИМI1
тотuческой эффектUВllостью такой оценки назовем пе
личину
[т'(8)Р 2
ео(Тn; 8) == O"T(8).
Оценку T называют асuмптоmическu эффективной, если eo(T ; 8) == 1.
Таким образом, в этом СЛУ'Iае за среднее и дисперсию оценки ТN мы прини
маем среднее и дисперсию аппроксимирующеrо 'lOрМaJlЫlOrо закона распре
деления.
(14)
Пример 3 (продолжение примера 2). Рассмотрим еще одну несмещенную
оценку функции т(8) == 82 именно, оценку 56 (см. (17), (18) 2.2). Как сле
дует из (7) 2.5, для нее DosJ == 284j(n 1), а функция информации вданном
случае есть i(8) == 28 2 (см. табл. 1). Следовательно, по формуле (13) эффек
тивность e(SJ) == (n I)jn < 1. Таким образом, статистика sJ не является
эффективной оценкой теоретической дисперсии (таковой ЯIlляется указанная
в при мере 2 статистика Т*), но она асимптотически эффеКТИ[Jна. .
Пример 4 (продолжение примера 1). Рассмотрим в качестве оценки 8 AЫ
БОрОlШУЮ медиану (;.,1/2' Как показано в примере 2 2.4
( 71'0"2 )
.со ((;.,1/2) '" N (J, 2n '
поэтому асимптотическая эффективность (14) в данном случае есть
ео ((n,
2
; 8) == 0,637.
71'
...
...... Сверхэффективные
Эффективной же оценкой является выборочное среднее Х Это означает, что
при больших n статистика Х для выборки объема n' == o,6 n оцеНИlJает Ис
тинное значение О2С такой же точностью, что и статистика (n, 1/2, независимо
от значений 8 и (J"
Интересно отметит!>, что при нарушении усло
вий реrулярности дисперсия оценки при n ----+ 00 MO
жет убывать значительно быстрее, чем rраница Pao
Крамера в (8), т. е. Moryr существовать «сверхэффек
тивные» оценки. .
.21"i ""'M
93.2. Критерии оптимальности оценок по Pao KpaMepy 179
Пример 5. Рассмотрим нереryлярную модель И(О, О). Из упр. 46 к rл. 1 полу
чаем, что максимальное значение выборки Х(П) имеет моменты
п
ЕеХ(п) == О,
n+l
по 2
DaX )
и (" (n + 1)2(n + 2)'
т. е. Тп == (п + 1)/nX(n) несмещенная оценка О, а ее дисперсия
(р
DeTn == n(n + 2)
убывает с ростом n как n 2 в то время как rраница Pao Крамера убывает
I
как n ·
Пример б. Пусть требуется оценить неизвестный параметр сдвиrа О распре
деления Вейбулла W(O, а, Ь) (см. п. 8 Э 1.2). Из упр. 56 к rл. 1 получаем, что
несмещенная оценка () по выборке объема n есть
Т" == X(I) br(! + )n I/O,
rдe X(I) минимальное значение выборки. Эта оценка имеет дисперсию
DeTn == DeX(I) == ь 2 [r( 1 + ) r 2 (! + ) ]п 2/a,
порядок которой n 2/o может быть сколь уrодно высоким при достаточно
малых а < 2. В данном случае модель также нереrулярна, поскольку ее
выборочное пространство зависит от О. .
З. Экспоиенциальная модель
Введем важный класс параметрических моделей, называемых экспоненцuаль
ными, ДJlЯ которых всеrда существует эффективная оценка некоторой пара
метрической функции. По определению, модель Т=={Р(х;О),ОЕ8} экс
nоненцuйльнйЯ, если плотность f(x; О) имеет вид
f(x; О) == ехр {А(())В(х) + С(О) + D(x)}.
(15)
Мноrие статистические модели удовлетворяют этому условию. В частно
сти, это известные нам модели N((), (1'2), N(p" 02), r(O, л), Bi(k, О), Bi (r, ()),
П(()) , приведенные в табл. 1. Модель Коши К(О), очевидно, не экспоненци
альная, а равномерная модель И(О, О), хотя и удовлетворяет условию (15), но
не является реryлярной.
Вклад выборки ДJlЯ экспоненциальной модели равен
n [ 1 n С'(О) ]
V(X; ()) == А'(О) 2:: B(Xj) + nCI(O) == пА' (О) 2:: B(Xj) + А'(О) .
, I , I
12*
180 rлава з. Теория оценивания неuзвестных параметров распределений
Это равенство можно записать в виде (9), если положить
n
.. 1", (
Т == Т (Х) == в Xj),
n j 1
С'(О)
т(О) == А'(О) '
1
а(О) == пА' (О) .
(16)
Зфф ' ' вные
оценки в экспонен
циальныx моделях
По критерию Pao KpaMepa заключаем, что стати
стика т' является эффективной оценкой для парамет
рической функции т(8), при этом соrласно формулам
(lO)и(16)
. т' (О)
D8 T == nА'(О) ' (17)
Верно и обратное: если эффективная оценка для не которой функции т(О)
существует, то модель является экспоненциальной. Действительно, интеrрируя
по 8 равенство (9), получаем
lп L(X; 8) == Аl (8)Т(Х) + С\ (О) + DI (Х).
Отсюда следует, что плотность f(x; 8) должна иметь вид (15).
Таким образом, эффективные оценки существуют для некоторых функций
т(8) только в случае экспоненциальных моделей.
Для перечисленных выше шести реrулярных экспоненциальных моделей
вид функции т(8), эффективной оценки т' дJlя нее и соответствующей дис
персии (17) приведены в табл. 2.
Таблица 2
Модель
т(О)
т'
О8 Т '
N(e, (,-2) I " (12
е х 0= L Х ;
n ' I n
N(J-t,(J2) (}2 I " , 2(}4
L(X i p.)
n ' I n
Х (}2
r(e, >.) (J
>. >.n
Bi(k, ()) Х (}(I О)
(J
k kn
ВI(T, О) () Х ()
rn(1 (})2
' () r
Х ()
П((}) ()
n
3.2. Критерии оптимальности оценок по Pao KpaMepy 181
Отметим также, что для реryлярных экспоненциальных моделей функцию
информации i(O) можно вычислять по формуле
С' ( О ) А" ( () )
i(O) == т'(О)А'(О) == А'(О) С"(О), (18)
что следует из сравнения rpаницы Pao KpaMepa в (8) с (17) и вида т(О) в (16).
4. Критерий Бхапачария оптимальности оценки
Неравенство Pao KpaMepa (8) дает неулучшаемую rpаницу дисперсии HeCMe
щенных оценок (для реrулярных моделей) в тех случаях, коrда существует
эффективная оценка. Однако, если такой оценки не существует (представ
ление (9) не имеет места ни для какой статистики т(х)), то можно найти
лучшую (т. е. БОльшую) нижнюю rраницу для дисперсии несмещенных oцe
нок. Основное условие достижения нижней rраницы дисперсии в HepaBeH
стве Pao KpaMepa состоит в существовании оценки т, для которой разность
т т(()) является линейной функцией от
alnL 1 BL
де == L дО
(для краткости мы пишем просто L вместо L(X; ())). Предположим, что такой
оценки не существует, но зато имеется оценка т', для которой т' т(О)
1 aL 1 д 2 L 1 a r L
линейная функция от , д 2 ' . . L дО :
L дО L О r
r L(i) . aiL
т' т(О) == L ai(O)L' L(I) == aO i ' (19)
i l
при некотором r 2. Torдa т' оптимальная оценка для т(О). Этот крите
рий оптимальности, обобщающий критерий Pao KpaMepa, называется Kpи
терием Бхаттачарuя.
Практически этот критерий используют так: учитывая старшие ПрОИЗВОk
ные функции правдоподобия, подбирают такую их линейную комбинацию,
чтобы получить представление вида (19); при этом последовательно полаrа
ют r 2,3, Если при не котором значении r это удается сделать, то
получающаяся при этом пара т(О) и т' == Т'(Х) и есть соответственно па
раметрическая функция и оптимальтная оценка для нее (случай r == I в этой
методике соответствует критерию Pao KpaMepa).
Мы не будем при водить точных формулировок (ввиду их rромоздкости),
а оrраничимся лишь примером, иллюстрирующим изложенную идеолоrию.
Пример 7. Рассмотрим модель И(О, 0.2) и оценим функцию т(()) == 02 Мы
уже знаем (см. пример 1), что оптимальной оценкой для среднеrо О является
выборочное среднее
1 n
Х == L X i .
n i l
182 rлава з. Теорuя оценusания неизsестных параметров распределений
Конечно, было бы ошибкой оценивать 02 посредством r Найдем здесь оп
тимальную оценку с помощью критерия Бхатrачария.
Здесь
I { I n }
L(X;O) == ( 2) /2 ехр 2 2:)х; 0)2
211'а n 2а .
. I
и непосредственно проверяется, что
I [ 20а 4 (1 ) а4 (2 )] 2 а 2 2
L + L Х О
L n n 2 n
. 2 2 /
По критерию Бхапачария отсюда следует, что статистика Т == Х а n
оптимальная (т. е. несмещенная с равномерно минимальной дисперсией) oцeH
ка для т(О) == 02 Несмещенность этой оценки проверяется непосредственно:
. 2 а 2 2 а 2 а 2 2 а 2 2
ЕеТ == ЕеХ == DeX + (ЕеХ) == + О == О .
ппп n
5. Критерии оптимальности в случае векторноrо параметра
Выше рассматривался случай скалярноrо параметра, однако все введенные
понятия и критерии оптимальности непосредственно переносятся на случай
BeKTopHoro параметра () == (81, , О,.). В этом случае под окладом выборки
понимается вектор == (V 1 , v,.), rде
v,. == V, ( X' О ) == д '" L(X; О) i == l '
, 1, a8 i '
,Т,
.... И Ф
,.. н ормационная
матрица
а аналоrом функции информации (4) является инфор
мацион//ая матрица Фишера
In(О) == De == IIE8( Vj)II .
Информационную матрицу одноrо наблюден ия
1(0) == ЦО) == Ilgijll
можно вычислить по формулам
.. .. ( ) ( aln!(XI;O) aln!(XI;O) ) ( a211l!(Xl,0) )
У,) Y') 8 Ee дО; aO j Ее aOiaO j
(последнее равенство справедливо для дважды дифференцируемых по па
раметрам О" ,Or функций (плотностей) !(х; О)). Для схемы повторных
независимых наблюдений In (О) == nl(O), т. е. здесь имеется полная аналоrия
со случаем скалярноrо параметра (см. (6)). В определении реrулярной модели
здесь дополнительно предполаrается, что матрица 1(0) неlJырождена при всех
О Е е.
Предположим, что ищется оценка для дифференцируемой 'IUСЛО80Й функ
ции т(8). Torдa имеют место следующий МНОеомерный анаЛОе нера8енст8а Pao
Крамера и соответствующий критерий оптимальности.
(20)
(21)
93.2. Критерии оптимальности оценон по Pao KpaMepy 183
Теорема 2. Если модель :F реryлярна, то для дисперсии любой несмещенной
оценки Т == Т(Х) функции т(8) справедливо неравенство
1 и 2 ( О )
nllт Q'((J)I I(8)Q(8) == , 'V() Е е,
n n
(22)
rAe
( дт(О)
!!(О) == grad т(О) == '
дт((}» ) .
д8 с
Равенство здесь имеет место TorAa и только TorAa, KorAa
Т(Х) т(8) == L ai ((})\'i (Х; (})
i=l
(23)
при некоторых функциях aj((}), i == 1, ,Т.
По аналоrии со случаем скалярноrо параметра назовем несмещенную
оценку т' == т' (Х) Д1Iя т((}) эффектив1l0Й, если ее дисперсия совпадает при
всех (} с правой частью неравенства Pao KpaMepa (22). Аналоrично вводится и
асимптотическая эффективность ео(Тn) для асимптоти Асимптотическая
чески нормальных N (т(8), cr (8)ln) оценок Т'I == Т" (Х), зффективность
Х == (XJ,. ,Х,,). ФУНКЦИИ т(О):
и;' ( 8)
ео(Тn; О) == ( ) . (24)
и т 8
Оценка Т" называется асимптоmически эффективной, если ео(Тn) == 1,
т. е. если ее асимптотическая дисперсия cr ((})/n совпадает с rраниuей Pao
Крамера (22). С применением этоrо понятия мы встретимся HeMHoro позднее,
в 3.5.
Из теоремы 2 следует, что критерием эффективности (а значит, и опти
мальности) оценки Т является представление (23). Приведем при мер исполь
зования этоrо критерия.
При мер 8 (Общая нормальная модель, оценивание cpeAHero). Пусть
Х == (X 1 , , Х,,)
выборка из НОР\lальноrо распределения N((}I' (} ) (оба пара'.4етра неизвест
ны). Требуется оценить теоретическое среднее т((}) == 8!. Как мы уже знаем,
выборочное среднее Х ncerlla является не мещенной оценкой теоретическоrо
средНеrо. Покажем, что в данном случае Х оптимальная оценка. Для этоrо
достаточно убедиться, что справеДllИВО представление
(}i
VI(X; (}) == Х (}1,
n
и применить критерий (23).
184 rлаоа з. Теория оценивания неизвестНblХ параметров распределений
Ранее (см. пример 1) было показано, что Х
оптимальная оценка теоретическоrо среднеrо и для
модели N«(J, (1'2) (с известной дисперсией). Таким
образом, статистика Х наилучшим образом oцeHи
вает неизвестное среднее I/ормальной модели независимо от mOi!O, известна диc
персия или нет. .
Пример 9 (Общая нормальная модель, оценивание дисперсии), В ситуации
предыдущеrо примера 8 оценим T(8)o=8i. Мы уже знаем (см. пример 4 93.1),
что несмещенная оценка S имеет дисперсию 28i/(n 1), n ? 2. Сравним
эту дисперсию с rраницей Pao KpaMepa в (22). Для этоrо вычислим сначала
информационную матрицу для модели N(8 1 , 8i). Здесь
1 { (х 8,)2 }
j(x; 8) 0= ехр 2
V 27r(J2 2()2
И по формулам (21) имеем
9'1 0= Е в 82"2 0= 8:;2 } 11
9'2 = 921 = 282"З Ев (Х, (1) = о, => 1(8) = 8 2
922 = З82"4 Ев (Х 1 8,)2 82"2 = 282"2
Отсюда находим, что правая часть внеравенстве (22) равна 28i/n, что меньше,
чем DeS . Таким образом, S не является эффективной оценкой. Это, KO
нечно, еше не означает, что существует более точная (с меньшей дисперсией)
оценка, нежели S . Мы покажем, что в дан ной задаче rpаница Pao Крамера
в (22) не достиrается ни для какой несмещенной оценки 8i, но оптимальная
оценка (н. о. р. м. д.) существует, и это S .
Для этоrо мы воспользуемся аналоrом крите
рия Бхапачария для BeKTopHoro параметра, который
имеет следующий вид: если при некотором целом
s ? 2 и коэффициентах с. с.(О) имеет место
представление
Оптимальность
выборочноrо cpeAHero
в нормальной модели
2:2"211
(25)
Оптимальное оцени
вание дисперсии
в нормальной модели
1 [ 8L 82 L 8 s L ]
T T=L LCi 88i + C;j 88i88j +."+ L.Ci''';' 88 il .88;, ' (26)
I ",) ,,1,
то статистика Т = Т(К) есть оптимальная оценка функции т 0= т(8).
В нашем случае
oL 0= д In L 0= t(X; 8,)2 0=
L д82 882 82 ; , 82
n
0= "' ( К. Х ) 2 + 2: ( Х 8 ,) 2
(JЗ I 83 8 '
2 ; , 2 2
3.2. Критерии оптимальности оценок по PQo KpQMepy 185
18 2 L 8 2 1nL ( 8InL ) 2 n2 2 n
L 8(J2 == дr + д8 == 04 (Х 01) (J2 '
I I 1 2 2
Отсюда
1 ( oi 8 L oi 82 L ) 1 2 2 2 2
== L..,.(X i Х) 02 == 50 (J2
L n 1 802 n(n 1) 80 n 1 i=1 '
И по критерию (26) 55 оптимальная оценка (Ji.
Итак, в задаче оценивания дисперсии т(8) == oi в модели И(81, 8i) имеет
место более точная, чем (22), rраница для дисперсии несмещенных оценок
функции т(О):
204
D/lT ;
n 1
· 5 2
при этом равенство достиrается для статистики Т == о.
.
Замечание. При оценивании caMoro параметра (вектора) (J == ((JI, ... ,(Jr) в качестве
оценкн высryпает векторная статистика 'l. == 'l.(X) == (T1(X)...., Tr(X) , и Torдa
свойство ее несмещенности определяется равенствами EoTj(X) == (Jj, i == 1,... ,Т,
или в векторной форме: Ee'l.(X) == В, V В, а аналоrом неравенства (22) является
следующее неравенство для дисперсионной матрицы Do'l. == JICOYe (T j , Ti)II :
Do'l. 1;; 1 (В).
(27)
Здесь неравенство А В между матрицами (одинаковой размерности) означает, что
матрица А В является неотрицательно определенной, т. е. для любоrо вектора f
соответствующей размерности Вblполняется условие f' (А B)f О или f' Af f' Bf.
Пример 10 (ПолиномиалЬНilJI модель, оценивание параметрическоrо вектора).
В приложениях часто возникает модель с конечным числом N 2 возможных
исходов (которые можно считать числами 1,2, ,N), вероятности которых
PI, .., PN неизвестны (Р] +.. '+PN == 1) полиномиальная модель М(n; Е),
l!. == (Pl, ,PN) (см. п. 6 1.1). Здесь в качестве неизвестноrо параметра
следует взять вектор 0== (Pl, ,PN I), поскольку PN == I PI PN I'
Друrими словами, в данном случае речь идет об n испытаниях X 1 , , Х п над
дискретной случайной величиной { с плотностью f(x; О) == Р//{{ == х} == Рх,
х == 1, , N. Записав функцию I (х; О) с помощью индикаторов в виде
N N I
'( . О) П I(x=j) П ( . ; ) I(X=j)
х, Pj PN Р} PN
j=1 j=1
(28)
N
(так как 2: I(х == j) == 1), получим
j=1
8 2 1п '(х; О) == { I(х == i)pj2 + I(х == N)p,/, z == З,
2 i,j==I,...,N I.
8Pi 8 pj I(х == N)PN , i i= j,
186 rлава з. Теория оценивания неизвестных параметров распределений
.. Информационная
матрица для nолино
миальной модели
Отсюда по формуле (2)) найдем информационную
матрицу /(0) == 119ijllf l:
.. ( OZln/(X 1 ;8) ) { pjl+p//, 2==),
91) EII орор' I
1 ) PN, ii=j.
(29)
Непосредственными вычислениями можно убедиться (это мы оставляем чи
тателю в качестве упражнения), что
1/( 8) I == (РI
PN(1 > о И / 1(8) == Il00ijllf 1 == I;N I,
rде
п-.. { Pi(l Pi), 2 ==],
V,)
PiPj, i f. j,
Если теперь в качестве оценки Дl1я (J l3Зять вектор относительных частот
n
исходов ,2, ,N 'I.. == (vl/n' , vN I/n), rде Vj 2: /(X i == Л,
;=1
j == 1,... , N (как это предполаraется в примере 4 в 1.1), то, во первых, это
будет несмещенная оценка, а, BO BTOpЫX, ее дисперсионная матрица, в силу
соотношений (15) 1.1, есть DII'I.. == l/nI;N 1 == l/nI I(8), т. е. Дl1я этой
оценки внеравенстве (27) достиrается равенство. Следовательно, 'I.. есть эф
фективная (оптимальная) оценка 8. .
3.3. Достаточные статистики и оптимальные оценки
Рассмотренные в предыдущем параrрафе критерии оптимальности оценок
имеют сравнительно оrраниченную применимость. Во первых, они требуют
жестких условий реrулярности исходной модели и, BO BTOpЫX, в ЛУLlшем слу
чае позволяют находить оптимальные оценки для отдельных параметрических
функций т(8). Более эффективным способом построения оптимальных oцe
нок является использование достаточных статистик, рассмотрению которых
и посвящен настоящий параrраф. Достаточность является одним из важней
ших понятий в математической статистике. Ввел ее Р. Фишер в 20 e rr. ХХ в.
выдвинув идею о том, что Дl1я статистическоrо анализа, касающеrося неизвест
ных параметров, не всеrда нужно знать все элементы выборки в отдельности,
а достаточно знать лишь некоторые функции от выборки, называемые ДOCTa
точными статистиками.
1. Достаточные статистики и критерий факторизации
По определению, статистика Т == Т(Х), скалярная или векторная, называ
ется достаточной для модели F == {Р(х; 8), 8 Е 0} (или для пара метра 8),
если для любоro события А С Х условная вероятность РII{Х Е А I Т(Х) == t}
9 з.з. ДостатОЧНblе статистики и оптимаЛЬНblе оценки 187
не зависит от е. Это свойство статистики Т означает, что она содержит всю
информацию о пара метре е, имеющуюся в выборке. Действительно, Bepo
ятность любоrо события, которое может про изойти при фиксированном Т,
не зависит от е, следовательно, оно не может нести дополнительной инфор
мации о неизвестном параметре е. Эквивалентное определение достаточности
в терминах плотности выборки Х == (X 1 , , Х n ) формулируется так: стати
стика Т достаточна, если условная плотность L( lt; е) случайноrо вектора Х
при условии Т(Х) == t не зависит от параметра е. Сама выборка Х, очевидно,
является достаточной статистикой (Ре(Х Е AIX == ) при любом е есть либо
1, если Е А, либо О в противном случае), но обычно стремятся найти дo
статочную статистику наименьшей размерности, представляющую исходные
данные в наиболее сжатом виде, в этом смысле rоворят о МUllимальной дocтa
точной статистике. При наличии достаточной статистики все статистические
выводы об исследуемой модели в конечном итоrе формулируются в терминах
этой статистики; следовательно, минимальная достаточная статистика дает
оптимальный способ представления исходных данных, что особенно важно
при обработке больших массивов статистической информации.
Практически достаточные статистики находят на OCHO
вании следующеrо утверждения, которое называется Kpитe
рием факторизации.
Критерий JIIO;
факторизации
Теорема 1 (Критерий факторизации). Для Toro чтобы статистика Т(Х) была
достаточной для параметра е, необходимо и достаточно, чтобы функция прав
доподобия L( ; е) выборки имела вид
L( ; е) == g(T( ); e)h( ),
(1)
rAe 9 и h неотрицательные функции, и h не зависит от е.
Доказательство, Доказательство приведем только для дискретной модели.
Если статистика Т достаточна, то при любом t из области значений T(i)
функция L(; .lt; е) не зависит от е и ее можно записать в виде h(ь t). Пусть
Ре{Т(Х) == t} == g(t; 8) и T( ) == t; тоrда событие {Х == } {Т(Х) == t},
поэтому
L( ; 8) == Ре{Х == } == РО{Х == , Т(Х) == t} ==
== Ре{Т(Х) == t} РО{Х == I Т(Х) == t} ==
== g(t; e)L( lt; е) == g(T( ); 8)h( ; t),
т. е. имеем представление (1).
Обратно: пусть имеет место разложение (факторизация) (1). Тоrда при
любом таком, что T( ) == t,
Ре{Х == ,T(X) == t}
L( lt; е) == Ре{Х == I Т(Х) == t} == Ре{Т(Х) == t}
188 rлава з. Теория оценивания неизвестных параметров распределений
==
L( ; о)
L( ';O)
g(t; O)h( )
g(t; O)h( ')
==
h( )
h( ') ,
,,-': T(;f.')=t f!: T(;!')=t ;!': T(i)=t
Т. е. не зависит от О. Если же таково, что T( ) f.t, то, очевидно, L(;!Clt;O) ==0.
Таким образом, при любом условная вероятность L(;!Clt; О) не зависит
от О. .
Отметим, что всякая эффективная оценка является одновременно ДOCTa
точной статистикой, так как (см. (9) 3.2) из представления
Т(Х) т(О) == а(О) 8 1" L(X; О)
80
следует форма (1) дl1я L( ; О). Итак, эффективная оценка существует толь
ко Torдa, Korдa имеется достаточная статистика. Но последняя может суще
ствовать и при отсyrствии эффективной оценки, т. е. условие достаточности
является менее оrpаничительным, чем условие существования эффективной
оценки.
Заметим также, что если Т достаточна, то таковой же является и любая
взаимно однозначная функция от Т. Действительно, если Н == rp(T) , и rp
взаимно однозначная функция, то существует обратная функция
tp 1 Т == rp I(H)
и из представления (1) имеем
L( ; О) == g(tp I(H); O)h( == gl(H; O)h( ),
т. е. Н достаточная статистика.
Примерами достаточных статистик дl1я ряда моделей со скалярным пара
метром являются (с учетом сделанноrо замечания) эффективные оценки т'
приведенные в табл. 2 3.2. Рассмотрим еще несколько примеров нахождения
достаточных статистик для моделей с векторным параметром и дl1я Hepery
лярных моделей.
При мер 1 (Общая нормальная модель, достаточная статистика для нее).
Функцию правдоподобия дl1я модели N(OI' O ) можно записать в виде
1 { 1 2 п(х 8 1 )2 }
L( ; О) == (211"о2)п/2 ехр 202 L...-(Xi х) 202 '
2 2 .=1 2
(2)
откуда по критерию факторизации (1) зак.лю<шем, что в данном случае ДOCTa
точной статистикой является пара
2
Т == (T 1 , Т2) == (Х, S )
или пара
( х t X j 2 ) ,
.=1
поскольку они однозначно определяют друr друrа.
.
3.3. ДостатОЧНblе статистики и оптимаЛЬНblе оценки 189
Пример 2 (Двухпараметрическая покаэатеllьная модель, достаточная стати-
стика для нее), Рассматривается частный случай W(OI, 1,02) модели Вей
булла (см. П.8 1.2) с плотностью
1
f(x; О) == О 2 e (x 81)/82, Х 01 (о == (fJ 1 , (2) О 1 Е R 1 О 2 > о). (3)
Запишем плотность с помошью индикатора:
f(x; ()) ():;le (x 81)/82I(x ( 1 ),
тorдa функция правдоподобия выборки Х == (X 1 ,... ,Х П ) примет вид
L( ; О) == ir f(Xi; ()) == о:;" ехр { t Xi; О) } fr I(х; 01),
;=1 ;=1 2 ;=1
Здесь
n
П I(x; fJ 1 ) == I(х; fJ j , i == 1,
;=1
, п) == I(m,in Х; fJ 1 ) == I(x(l) fJ 1 ),
I
поэтому
L( ; О) == о:;" ехр { (Х" (1) }I(X(1) (1),
Отсюда по критерию факторизации следует, что достаточной статистикой для
параметра fJ == (fJ 1 , (2) является пара (Х(I), Х). Как будет ясно из дальнейше
ro, удобнее мя работы оказывается пара
Т == (T I , Т 2 ) == (X(I), Х Х(I)),
которая также является достаточной статистикой. .
Пример 3 (Равномерная модель, достаточная статистика для нее).
Пусть Х == (X 1 , ,Х П ) выборка из paBHoMepHoro распределения U(О, 8),
8 > О неизвестно. Записав плотность paBHoMepHoro распределения (см. П.5
1.2) с помошью индикатора: f(x; 8) == O II(O х О), получим МЯ функ
ции правдоподобия выборки представление
n n
L(;f; 8) == П f (Х;; 8) == 8 n П I(О Х; 8) == () n I(х(п) 8)I(x(I) О).
;=1 i=1
Отсюда следует, что в данном случае достаточной статистикой является
максимальное значение выборки Х(П)'
Аналоrично, для обшей равномерной модели U(OI, (2), 81 < 82, можно
записать
L( ; О) == (82 01) nI(81 X(l) Х(п) (2),
следовательно, статистика
Т == (TI, Т 2 ) == (Х(I)' х(п))
достаточная для 8 == (81, (2),
.
190 rлава з. Теория ОЦенивания неизвестных параметров распределений
Пример 4 (Равномерная модель (продолжение)). Рассмотрим модель
И(а(О), Ь(О)) ,
rдe а(О) < Ь(В), VB, заданные непрерывные функции скалярноro параметра О.
Как и в предыдущем примере З, можно записать
L(;f; В) == (Ь(В) а(В) n I( а(В) Хщ Х(п) Ь(В) (4)
Следовательно, двумерная статистика Т == (Х(I), Х(п)) является достаточ
ной ДflЯ В. Выясним теперь, нельзя ли здесь найти одномерную, т. е. более
экономную, достаточную статистику. Индикатор в (4) равен I тоrда и только
Torдa, коrда
{Х(I) а(О), Ь(О) Х(п)}' (5)
Пусть а(В) t, Ь(В) ,J.. с возрастанием fJ Тоrда условие (5) ЭКlIивалеНТIIО
условию
{о a '(x(J)), В b l(x(n»)} {:::::::> {В T,(;f) == mil1(a l(x(I))' b l(x(n)))}.
Таким образом, соотношение (4) можно записать в виде
L(!.; О) == (Ь(е) а(В) n I(T,(;f) В),
откуда следует, что
Т, == T1(X) == mil1(a '(X(l)), b I(X(n)))
одномерная достаточная статистика ДflЯ В.
Аналоrично, если а(В) ,J.., Ь(е) t с возрастанием В, то одномерная ДOCTa
точная статистика также имеется и имеет вид
Т 2 == Т 2 (Х) == max(a I(X(l)), b I(X(n))).
Этими двумя СЛУ'I3ями исчерпываются ситуации, коrда в модели U (а(В), Ь(О) ,
существует одномерная достаточная статистика. Обратим внимание на то, что
как TI' так и Т 2 являются функциями исходноЙ дuумерной достаточной CTa
тистики Т == (X(l), Х(п))' Это обстоятельство имеет общий характер, т. е.
мuuuмальная достаточная статистиlCа есть ФУUICI{ИЯ любых друсих достаточ
ных статистиlC.
В частности, ДJlЯ равномерной модели с нулевым средним И( В, В) oд
номерная достаточная статистика Т2 принимает вид
Т 2 == тax( Xp), Х(п)) == max(jX(I)I, IX(n)I),
а ДЛЯ модели И(О, () + 1) одномерноЙ достаточной статистики не существует..
Пример 5 (Модель Коши). Для модели К(е) (см. упр. 4& б) к rл. 1) функция
правдоподобия выборки Х == (X I , , х п ) имеет вид
I n 1
L ( x.(} ) П
, 71"" i l 1 + (Х; 0)2'
И здесь нельзя найти статистику Т, дающую факторизацию (1), размерность
которой была бы меньще n. ·
3.3. ДостатОЧНblе статистики и оптимаЛЬНblе оценки 191
2. Теорема Рао Блеку]лла Колмоrорова
Прежде Bcero напомним определение условноro математическоrо ожидания.
Пусть Х и У две случайные величины и р(х), q(y) ИХ плотности.
Обозначим f(x, у) совместную плотность величин Х Условная плотность
и У, Torдa функция
f
f(x, у)
p(xly) == q[ij)'
определенная там, rде q(y) > О, называется условной плотностью величиНbI Х
при условии, что У == у. Далее, обозначим
h(y) == E(XIY == у) ==
{ Е х p(xly),
== J х p(xly) dx,
если
Х дискретная случайная
величина,
если
Х непрерывная случайная
величина.
По определению, случайную величину h(Y) называют условным MaTe
матическим ожиданием случайной величины Х при фиксированном значе
нии У Имеет место следующая формула полноrо математическоrо ожидания
E(E(XIY)) == ЕХ
(6)
(предполаraется, что среднее значение ЕХ существует).
Роль достаточных статистик в теории оценивания раскрывает следующее
утверждение.
Теорема 2 (Теорема Рао Блеку]лла Колмоrорова). Оптимальная оценка,
если она существует, является функцией от достаточной статистики.
Доказательство. Пусть Т == Т(Х) достаточная статистика и Т! == Т, (Х)
произвольная несмещенная оценка заданной параметрической функции т(О).
Рассмотрим функцию
H(t) == E8(T,IT == t) == / TIC )L( lt; О) d'f..
Эта функция не зависит от О, так как условная плотность L( lt; О) от парамет
ра не зависит. Далее, статистика Н (Т(Х)) является также несмещенной oцeH
кой т(О). Действительно, по формуле полноrо математическоrо ожидания (6)
Е 8 Н(Т) == Е8 (Е 8 (Т 1 IT)) == ЕоТ, == т(О).
Наконец, справедливо неравенство
D8H(T) D8 T , , '110,
192 rлава з. Теория оценивйния неизвестных параметров распределений
причем равенство имеет место в том и только в том случае, коrда TI == Н(Т).
Для доказательства этоrо заметим, что
ОеТ, == Eo[Tt H(T)+H(T) T(8)] 2 == Ее [ТI H(T)]2 +ОеН(Т) ? ОоН(Т),
поскольку, в силу (6),
E[Tt Н(Т)] [Н(Т) т(8)] == Е [(Tt Н(Т))Н(Т)] ==
== Е{ Н(Т)Е[ (Tt H(T))IT]} == Е{ H(T)[E(TtIT) Н(Т)]} == О.
Таким образом, дrIЯ любой несмещенной оценки функции т(8), не являю
щейся функцией от достаточной статистики, всеrда можно указать несмещен
ную оценку, которая зависит от достаточной статистики и имеет дисперсию
меньшую, чем исходная оценка. Следовательно, оптимальную оценку надо иc
кать среди функций от достаточной статистики. .
При отыскании явноrо вида оптимальных оценок важную роль иrра
ет свойство полноты достаточной статистики. По определению, достаточная
,. Полная достаточная статистика Т == Т(Х) называется полной, если дrIЯ
статистнка всякой функции rp(T) из Toro, что
Eorp(T) == О, '1/ 8, (7)
следует rp(t) == О на всем множестве значений статистики Т.
Теорема З. Если существует полная достаточная статистика, то всякая функ
ция от нее является оптимальной оценкой cBoero математическоrо ожидания.
Доказательство. Пусть Т == Т(Х) полная достаточная статистика и Н(Т)
произвольная функция от Т. Обозначим
ЕеН (Т) == т(8).
(8)
Из условия полноты следует, что Н(Т) единственная функция от Т, yдo
влетворяющая соотношению (8), так как если бы была еще какая нибудь
функция Н,(т), удовлетворяющая (8), то мы бы имели, что
Ев [Н(Т) HI(T)] == О, '1/8,
откуда H1(T) == Н(Т).
По теореме 2 оптимальную оценку дrIЯ т(8) надо искать в классе функ
ций, зависящих от Т. Но Н(Т) единственная функция от Т, несмещен
но оценивающая т(8); следовательно, она и является искомой оптимальной
оценкой. .
Подведем итоr. Итак, пусть в рассматриваемой модели
:F == {F(x; 8), 8 Е е}
существует полная достаточная статистика Т (т. е. уравнение (7) имеет един
ственное (нулевое) решение) и требуется оценить заданную параметрическую
функцию т(8). Torдa:
з.з. ДостатОЧНblе статистики и оптимаЛЬНblе оценки 193
1) если существует какая то несмещеllная оценка т( fJ),
то существует и несмещенная оценка, являющаяся
функцией от Т; можно так же сказать, что если
нет несмещеННblХ оценок вида Н(Т) (т. е. уравнение
(8) не имеет решения), то класс 1;- несмещеннbIX
оценок T(fJ) пуст;
2) оптимальная (т. е. н. о. р. м. д.) оценка, KOi!aa она существует, Bcei!aa явля
еmся функцей от Т, и она однозначно определяется уравнением (8);
3) оптимальную оценку т' можно искать по формуле
'I'1.Построе'ние.'Опти:' .,
мапьных оценок
т' == Н(Т) == Ee(TIIT),
исходя uз любой несмещенной оценки Т, функции T(fJ).
В конкретных задачах при отыскании явноro вида оптимальных оценок
критерий (9) используется редко, так как вычисление условноrо математиче
cKoro ожидания обычно сопряжено со значительными аналитическими тpyд
ностями. Чаще решают непосредственно уравнение (8), которое в развернyrой
форме для абсолютно непрерывной модели имеет вид
(9)
/ H(T)g(t; fJ) dt == T(fJ), V fJ Е е,
(10)
rде g(t; fJ) плотность статистики Т (для дискретной модели интеrpирование
в (10) заменяется суммированием L: н (T)g(t; fJ)). Это уравнение в дальней
t
шем будем наЗblвать урав1lением несмещенности. Ero можно решать различны
ми способами (см. дальнейшие примеРbl в 3.4), например, разлаrая правую
и левую части в рЯДbl по степеням fJ (в случае аналитических функций T(fJ)
и g(t; fJ)) и приравнивая соответствующие коэффициенты.
Дальнейшее обсуждение роли достаточных статистик в теории оптималь
Horo оценивания будет посвящено раЗЛИЧНblМ примерам их применения в KOH
кретных задачах. Но прежде мы вьщелим один ваЖНblЙ класс параметрических
моделей, для которых вопросы о виде достаточной статистики и ее полноте
решаются весьма просто. Это модели экспоненциальноrо типа, которые нам
уже встречались ранее (в п. 3 3.2) для случая скалярноro пара метра. Дадим их
определение для общеrо случая r MepHoro параметра fJ == (fJ 1 , ,fJ r ), r 1.
3. Экспоненциальные семейства и достаточные статистики
Модель, задаваемая плотностью вида (сравни с (15) 3.2)
f(x; fJ) == ехр {t (JjBj(x) + C(fJ) + D(x) }
J I
(или приводимой К такому виду заменой параметров) называется T пapaMeт
рическим экспоненциалЬНblМ семейством. В качестве примера можно указать
13 За.а, 1748
(11)
194 rлава з. Теория оценивания неизвестных параметров распределений
нормальную модель N(O" Oi), дли которой
{ х2 OIX O }
/(х;О)==ехр 2+2 2 II1(02Vh) ,
202 02 202
что приводится К виду (11) заменой о; == o:;2 O =: OrO:;2
Если имеет место (11), то по критерию факторизации статистика
т == (T r ,
n
,ТТ), rде Tj == Tj(X) == L Bj(X i ), j == 1,
i 1
, Т, (12)
является достаточной для параметра О == (Or, , от), 11 она будет полной,
если раЗ lерность параметрическоro множества е pa!JH<I r (т. е. е содержит
некоторый r мерный параллелепипед).
Так, указанные в табл. 2 3.2 оценки т' ,шляются llOЛНЫМI1 достаточными
статистиками для соответствующих моделей; для модели же N(OI, (5) полной
достаточной статистикой является в соответствии с (12), пара ( Xi, X?) или
,
эквивалеНТН<lЯ ей пара (Х, S ) (см. прнмер 1).
Пример б (Оценивание нормальной функции распределения).
Пусть ЦО =: N(O, (12), т. е. наблюдается нормалЬН<lЯ случайная веЛИ'lина
с известной дисперсией rт 2 и неизвестным средним О Требуется по выборке
Х == (X 1 , ,Х n ) оценить вероятность т(О) == Р В {( хо} в заданной точ
ке хо. Как мы знаем (см. замечание к теореме 2 3.1), коrда у нас нет никакой
априорной информации о теоретической функuии распределения Р{(х), то
оптимальной несмещенной оценкой для F{(xu) является значеНllе н точке хо
ЭМПИРII'lеской функции распределении
1 n
Рn(ХО) == L I(X i ::;; хо).
n i 1
Но D нашем случае вид оцениваемой функции нам известен:
{ ( о хо О } ( хо О )
т(О) == F,(xo; О) == Ре ::;; == ф
( 13)
(см. n.l, (7) 1.2), поэтому, примення изложенную теорию достаТО'lНЫХ cтa
тистик, МЫ построим более точную оценку, учитываюшую имеющуюси <lПрИ
орную информацию о модели, в которой мы работаем.
Именно, как отмечено выше, выборочное среднее Х нвлнетсн здесь пол
ной достато'lНОЙ статистикой, 11 если мы uозьмем в качестве исходной HeCMe
щенной оценки функции (13) простейшую статистику
TI == I(Х 1 ::;; хо) ЕвТ, == Ре(Х, ::;; хо) == т(О),
то оптимальная оценка Iожет быть найдена по формуле (см. (9))
т' == Eo(T1IX) == РО{Х 1 xulX} == PO{X 1 Х хо XIX}.
3.3. Достаточные статистики и оптимальные оценки 195
Здесь (см. упр.28 к rл. 1) случайная величина Х I Х не зависит от условия
Х, поэтому указанная условная вероятность совпадает с безуслооной оероят
ностью Р@{Х 1 Х хо Х}. НО линейная функция Х 1 Х от нормальной
выборки распределена по нормальному закону со средним
E@(X 1 У) == Е@Х 1 Е@У == О О == О
и дисперсией
( " ) [( ) 2 ]
n 1 1 n 1 n 1 2 n 1 2
De(XI X)==D@ Xl 2..:Х; == + (J" == (J"
n n i 2 n n 2 n
поэтому
т' == Р@{Х 1 У хо У} ==
{{;!; Хl У {;!; хо Х }
==Рв ==
n 1 (Т2 n I (J"
== Ф( {;!;х о Х ).
Обратим внимание на то, что оптимальная (н. о. р. м. д) оценка для функ
ции (13) получается не просто заменой неизвестноrо параметра О на дo
ст аточную с татистику Х, но введением еще и дополнительноro множителя
J n/(n 1) в aprYMeHT функции Ф, доrадаться до такой «экзотики» из Ka
ких то друrих соображений представляется весьма проблематичным. .
Еще более «экзотичен» результат следующеrо примера, полученный с ис
пользованием таких же идей А. Н. Колмоrоровым в 1950 r. в более общей
задаче.
( 14)
При мер 7 (Задача Колмоrорова). Пусть по выбор
ке Х == (X 1 , ,Х П ), n > 2, из нормальноrо pac
пределенил N(OI, O ) (оба параметра неизвестны)
требуется оценить значение теоретической функ-
ции распределения F«(x; О) в заданной точке хо, т. е. параметрическую функ
цию (сравни с (13))
{ Ol XO OI } ( XO OI )
т(О) == F«(xo; О) == Рв == Ф .
Оценивание функции ..,.
распределения 8 общей
нормальной модели
( 15)
Следуя изложенной выше идеолоrии, будем искать оптимальную HeCMe
щенную оценку в виде (9), rде в качестве исходной несмещенной оценки снооа
возьмем индикатор ТI == I(X 1 ха). В данном случае полной достаточной
2
статистикой является, как мы знаем, Т == (Х, S ), поэтому можем записать
{ ХI Х I }
т' == Ee(T1IT) == Рв{Х 1 xolT} == Р vn=Js ио Т ,
( 16)
13*
196 rлава з. Теория оценивания неизвестных параметров распределений
rде
ХО x
ио == ио(Т) == .
Vn=Js
Если бы случайная величина
XI X
'Т/==
Jn=1 s
не зависела от условия Т, то правая часть (16) была бы равна FfJ(uo) , rде
вид функции распределения FfJ(и) указан в упр.42 к rЛ.2. Таким образом,
нам остается установить независимость статистик 1J и Т. Для этоro сделаем
небольшое отсryпление и добавим еще кое что из теории (изложенноrо выше
нам не хватает).
...
... Свободные
статистики
Статистика U == И(Х) называется свободной,
если ее распределение не зависит от параметра () Е е (в про
извольной пара метрической модели F).
Теорема 4 (Теорема Басу). Пусть Т(Х) полная достаточная статистика,
И(Х) свободная статистика. TorAa Т(Х) и И(Х) независимы.
Доказательство. Пусть А произвольное измеримое (т. е. для KOToporo
определены выписываемые далее вероятности) событие. Torдa вероятности:
условная It'A(T)==Pg{UEAIT} и безусловная 'УА==Ре{ИЕА} не за
висят от () по условию теоремы, при этом Eglt' А (Т) == 'У А. Следовательно,
обозначая g(T)==It'A(T) 'YA, имеем Egg(T) ==0, 'V(). Из полноты Т следует,
что g(T)==O, Т.е. безусловная 'УА и условная It'A(T) вероятности совпадают.
Но это и означает независимость статистик Т(Х) и И(Х). .
Вернемся к нашей задаче и заметим, что если ввести нормированные слу
чайные величины Yi==(Xi ()I)/()2, i == 1, ,n, которые имеют уже cтaH
дартное нормальное распределение -лf(о, 1) (т. е. не заlJисящее от параметра ()),
то леrко проверить (это мы оставляем в качестве npocToro упражнения для
читателя), что статистика 'Т/ в терминах величин У; сохранит свой вид:
У 1 y
1J == vn=IS(Y) ,
1 n
rде в2(у) == L(Y; у)2
n i 1
Отсюда следует, что распределение статистики 11 не зависит от пара метра MO
дели () == (81,82), значит, она является свободной (!) статистикой, и по теореме
2
Басу 1J и Т == (Х, S ) независимы (!).
Отсюда и из (16) имеем т' == FfJ(иo), Используя результат упр. 42 к rл. 2,
можем записать явный вид этой оценки через неполную бета функцию:
3.3. Достаточные статистики и оптимальные оценки 197
{ 1 ( 2 n 2 1 )
1 B ] ио(Т); . .
. . ( ) 2 2 2
т T Т
1 ( 2 n 2 1 )
B I и о( Т ) '
2 . 2 '2 '
если 0< ио(Т) < 1,
если 1 < ио(Т) < О.
с помошью индикаторов этой формуле можно придать следуюший оконча
тельный вид: н. о. р. м. Д ДЛЯ функции (15) является статистика
. [ ] ( 2 n 2 1 )] ( )
т 1 "2B 1 ио(Т); ' "2 1 Х < Хо +
] ( 2 n 2 1 )
+ B 1 иo(T); , I(X Хо).
222
(17)
Это и есть знаменитый результат А. Н. Колмоrорова.
.
Наш следующий пример относится к оцениванию в полиномиальной
модели М(n; !!) (см. при мер 10 в 3.2).
Пример 8 (Полиномиальнаи модель: оценивание параметрических
ций), Записав плотность f(x; 8) (см. (28) 3.2) в виде
N ' ( ) !(X=j) { N ' }
f(x;8) PN П Pj exp LI(x j)ln Pj +lnPN ,
. 1 PN . 1 PN
J= J
видим, что она приводится к виду (11) заменой
8j ln( : ), j I,...,N I.
функ
(18)
Таким образом. эта модель уклаДblвается в схему r параметрическоrо (при
r N 1) экспоненциальноrо семейства, и, следовательно, для нее полной
достаточной статистикой является вектор r (Tl. . TN ,), rде
n
Tj L I(Xi j) Vj
i='
число реализаций исхода «j» В выборке Х (X 1 ...., Х n ), j 1,... ,N 1.
Заметим, что число реализаций исхода «N» есть VN n V\ VN l ,
а распределение полноrо случайноrо вектора == (VI, . . . , VN) есть полино
миальное распределение М(n; р!, .., PN)'
Из изложенной в п. 2 теории следует, что в данной модели несмешенные
оценки существуют лишь для таких параметрических функций, которые име
ют вид ЕвН('[), или, что то же самое, вид EBH( ). Но (см. (14) 1.1)
E8H( ) ==
L
Н( ) n! х, XN
X"...,XN I IP, ".PN'
Х!.... XN.
X,+...+XN n
198 rлава з. Теория оценивания неизвестных параметров распределений
и при любой функции Н правая часть здесь представляет собой полином
от Pl, , PN степени не выше n. Следовательно, оцениваемымИ (т. е. для
которых существуют несмещенные оценки) параметрическими функциями
в данной модели являются лишь полиномы степени не выше n от Р!, . . . ,PN
Так, из упр. 19 к rл. 1 следует, что несмещенной оптимальной оценкой функции
т(8) == p ' .. . Р'; при ТI + + TN n является статистика
. (1I1)r, (IIN )rN
т ==
(n)r,+ ..Нн
(напомним, что (а)", == а(а 1) (а k + 1), (а)о == 1). Оценки для произ
вольных полиномов (степени не выше n) можно строить с помощью линейных
комбинаций этих статистик на основе теоремы 3 3.1.
Как частный случай этих результатов при N == 2 имеем соответствующие
выводы для бернуллиевской модели. В примере 1 в 3.1 были построены
несмещенные оценки для произпольных полиномов степени не выше n (n
объем выборки) от параметра (J модели Bi( 1, О) (соотношение (6) в 3. 1).
Эти оценки представляют собой функции от полной достаточной статистики
Х == х! + + х n числа «успехов» n n испытаниях, следовательно они
являются оптимальными (н. о. р. м.д). .
В заключение этоrо параrpафа при ведем пример достаточной статистики,
не являющейся полной.
Пример 9. Пусть произведено одно наблюдение над дискретной случайной
величиной Х с распределением
'(х; 8) == { :Х (1 8)2
при x== I,
при х == О, 1, 2, . . . ,
(J Е (О, 1).
Тоrда Х достаточная, но не полная статистика. Действительно, пусть
<р(х) заданная на множестве { I, О, 1,2, . ..} функция, удовлетворяющая
условию Ео<р(х) == О, '11 (J Е (О, 1). Это условие можно записать в виде
00
If'( I)8( 1 o) 2 + I: <р(х)8 Х == О
х=о
или, так как
00
00
<р(О) + I:[<p(x) + x<p( I)](Jx == О.
Х=!
(1 8) 2 == I:(x + I)8 X
х=о
Но этому условию удовлетворяет любая функция, для которой <р(0) О,
<р(х) == x<p( I), х == 1,2, Т.е. значение 1f'( I) можно задать произ
вольно. Следовательно, в данном случае критерий полноты не выполняется,
поэтому уравнение несмещенности не будет иметь однозначноrо решения,
g 3.4. Способы решения уравнения несмещенности
199
Рассмотрим, например, задачу оценивания функции т(в) == (1 в)2 Непо
средственно можно убедиться в том, '!то любая статистика Т == Та(Х), ще
Та(Х) == { 1
ах
при Х == О,
при Х == 1, 1, 2,
а произвольно, является несмещенной оценкой т(в) (проверку этоrо мы
оставляем читателю в качестве npocToro упражнения). .
i 3.4. Способы решения уравнения несмещенности
А .математику уже затем y ить следует,
что она ум в порядок приводит.
М. В. ЛОМОНОСОD 4)
Настоящий параrраф посвящен применению теории достаточных статистик
при отыскании оптимальных несмещенных оценок в конкретных задачах.
Ключевым моментом при этом является отыскание решения уравнения He
смещенности (10) 3.3. Имеются классы статистических моделей, для которых
разработаны специфические методы решения уравнения несмещенности, поз
воляющие получать явные выражения для оптимальных оценок произвольных
оцениваемых параметричеСКllХ функций. Изложение этих методов и cocтaB
ляет содержание данноrо параrрафа. Подчеркнем, что прежде чем решать
уравнение несмещенности, необходимо в каждой КОНКретной задаче:
а) определить достаточную статистику Т == Т(Х);
б) найти ее распределение: FT(t; В) == Рв{Т(Х) ::;; t} или плотность g(t; в);
в) проверить, обладает ли она свойством полноты, т. е. решить однородное
уравнение (7) 3.3 и убедиться, что оно имеет единственное (нулевое)
решение.
Только убедившись, что в рассматриваемой модели несмещеннаи оценка
нуля единственна, можно приступать к решению уравнения несмещенности
для заданной параметрической функции т(в). По этой проrpамме мы и будем
в дальнейшем действовать.
Но прежде сделаем одно полезное замечание. В KOHKpeT
ной задаче, найдя полную достаточную статистику Т == Т(Х),
полезно вычислить ее среднее J.l(B) == Е@Т(Х), т. е. опреде
лить тем самым ту параметрическую функцию, для которой сама статистика Т
является оптимальной оценкой. Может оказаться, что J.l(B) == kB, т. е. линейно
зависит от паращтра В рассматриваемоЙ модели. Тоща оптимальной oцeH
кой в' для параметра В будет, очевидно, статистика в' == T(X)jk. Например,
Полезное 011{
замечание
4) ЛОМОНОСОВ Михаил Васильевич (1711 1765) русский учеНЫЙ ЭНUllклопедист 11 мыслитель,
ПОЭТ, акапеми к Петербурrcкой А Н.
200 rлава з. Теория оценивания неизвестных параметров распределений
пусть модель F :=: и(о; 8) равномерное распределение с неизвеСТНblМ пра
вым концом носителя (носителем распределения наЗblвают то множество,
на котором соответствующая плотность f(x; 8) > о), Как показано в при
мере 3 3.3 достаточной статистикой в этом случае является максимальное
значение х(n) выборки Х :=: (X 1 ,... ,Х n )' То, что эта статистика полна, будет
n
установлено чуть ниже (см. при мер 3), а так как ЕеХ(n) == 8 (см. упр. 46
n+1
. n+ 1
к rл. 1), то отсюда следует, что 8 == X(n) оптимальная оценка 8.
n
1. Модель CTeneHHoro ряда, оценивание параметрических функций
Эта модель, охватывающая большое число конкретных дискретных распреде
лений, введена и описана в п. 8 9 1.1. Из вида плотности (20) 9 1.1 следует,
что она относится к экспоненциальному семейству (см. п. 3 3.3) и потому
обладает полной достаточной статистикой Т == Т(Х) :=: X 1 + + хn. Pac
пределение этой статистики указано в (24) 9 1.1. Следовательно, здесь у нас все
rOToBo, чтобы приступить к основной проблеме решению уравнения HeCMe
щенности. Предположим, что требуется оценить параметрическую функцию
т(8), представимую в виде сходящеrося на е CTeneHHoro ряда:
00
т(8) == :L bjeJ
j=r
Torдa из формулы (24) 9 1.1 следует, что в данном случае уравнение HeCMe
щенности ЕеН(Т) == т(8) принимает вид
00 00 00
:L H(t)a n (t)8 t == [n(8)т(8) :=: :L а n (х)8 Х :L b j 8 j ==
t=nl z=nl j=r
00 k nl
== :L 8 k :L bjan(k j). (1)
k=nl+r j=r
Поскольку это тождество по 8, приравнивая соответствующие коэффициенты,
находим
H(t)a,,(t) { F bja,,(t j)
при t?nl+T,
при t < nl + т.
.:
Общее решение
Отсюда получаем, что оптимальная оценка т. для функ
ции т(8) имеет вид
T nl
т. == Н(Т) :=: a;I(T) :L bjan(T j) I(Т ? nl + т). (2)
j=r
3.4. Способы решения уравнения несмещенности 201
Это чрезвычайно общий результат, поскольку здесь функция f(O), зада
ющая модель, и оцениваемая функция т(О) произвольные аналитические
функции на е. Вьщелим особо важные специальные случаи решения (2).
Пусть т(О) == f(O). Torдa в исходном соотноше СпециаЛЬНblе случаи 'If'
нии (1) правая часть есть паромеrрических
00 ф к й
fn+J(O) == L an+l(x)B X
x (n+I)1
И потому оптимальная оценка f' этой функции есть
f . == а п + 1 (Т) I ( T ( + 1 ) l )
а п (Т) 7 n .
Если Tr(O) == Or то из (2) следует, что
. ап(Т т)
Tr == () I(T nl + т).
а п Т
(3)
(4)
Пусть теперь т(О; х) == ох / f(O), х 1, т. е. речь фактически идет об oцe
нивании теоретической плотности f(xIO) (см. (20) 91.1). В этом случае ис
ходное соотношение (1) запишется в виде
00
L H(t)an(t)Ot == ох fn I(O) == ох L an I(j)iY,
t nl j (п 1)1
откуда аналоrично предыдущему имеем
. an I(T x) (
т (х) == () 1 Т (n I)l + х).
а п Т
(5)
В частности, оптимальная оценка f'(x) теоретической плотности f(xIO)
получается умножением правой части (5) на коэффициент а(х):
an I(T х)
f*(x) == а(х) () I(T (n I)l + х), х [. (6)
а п Т
Наконец, если требуется оценить параметрическую функцию вида
TV'(B) == Ее<Р({) == L <p(x)f(xIO),
x 1
то оптимальная оценка получается заменой в правой части этоrо равенства
теоретической плотности f(xIO) ее оценкой (6):
T (n l)1
. "'"'" . ( ) "'"'" ( ) ( ) an I(T х)
Tf(J == L...J <р(х)! х == L...J <р х а х ( )
а п Т
x 1 x 1
(7)
202 rлава з. Теория оценивания неизвестных параметров распределений
Отметим также, что по критерию для экспоненциальной модели (см. п. 3
3.2) выборочное среднее Х == Т(Х)!n является эффективной (значит, и оп
тимальной) оценкой теоретическоrо среднеro (см. (23) !} 1.1) () l' (())! f(8), и это
есть единственная эффективная оценка в модели cTeneHHoro ряда.
Итак, ДlIЯ важноrо класса дискретных распределений типа cTeneHHoro
ряда можно строить оптимальные оценки для произвольных пара метрических
функций, представимых в виде cTeneHHoro ряда от ().
Рассмотрим несколько конкретных примеров на применение полученноrо
общеrо результата.
Пример 1 (Пуассоновекая модель, оценивание параметрических функций).
Пусть Х == (Х" ,Х п ) выборка из распределения [( ) Е П(()). Оценим
параметрическую функцию Тс,!(8) == 8 С e !B при заданных t < n и r О
целом. Здесь (см. п. 8 1.1) f(()) == еВ, значит,
f " (()) == е " В == (n() , )Х , ( ) nХ '- О
т. е. а'l Х == , Х,:; .
X O Х. х!
ДЗJJее,
( 8 ) == ()С e tB == ()С ( t8)i == ( t)j ()j
Т С ,! " ( . Т ) ' '
. O . . J .
.= )=С
Т.е.
( t)j r
b j == (j т)! ' j т.
Поэтому по формуле (2)
. Т! т ( t)j r nT j
Tr,t == nТ L (j т)! (Т j)! I(T т) ==
)=С
T c
Т! L i i T r i
== ( ) т CT "( t) n I(T т) ==
T т!n .
.=0
С С 1 ( ) T c
== т! т т n t
n
Общий результат
Этому результату можно придать следующую OKOH
чательную форму:
( ) T
. r 1 t
Тс! == T!C7' 1
, n с n
(8)
Подчеркнем, что в данном случае оцениваемая функция т(8) зависит
от двух свободных параметров: t < n и целоrо r О. Придавая этим пара
метрам конкретные значения, можно из (8) получать са остоятеЛЬНblе инте
ресные результаты.
3.4. Способы решения уравнения несмещенности
203
j' == (1 + ) т
Специальные
случаи
Так, при r == О, t == 1 функция Tr,t(O) == f(O) И из (8)
имеем оценку
соrласуюшуюся с обшим результатом (3).
При t == 1 функция Tr,t(O)/r! == е доr/r! есть теоретическая вероятность
Ро{( == т} == f(rIB) и для нее из (8) имеем оптимальную оценку
1 ( l ) T r
/' (т) == C 1 r == О, 1, , т
n r n
Если, например, требуется оценить вероятность
k
7(0) == Р/I{( ::;; k} == I: f(rIB),
r O
то оптимальной оценкой будет статистика
{ k 1 ( 1 ) T r
k CT 1
т' f'(r) ' n' n
при Т > k,
при т::;; k.
Наконец, при t == О из (8) имеем вид оптимальной оценки ДЛЯ Tr(O) == Or
т; == Т! С Т == т(т 1) (Т r + 1) (T)r (9)
n r n r n r
В частности, оптимальная оценка caMOro параметра В есть выборочное
среднее: ВО == Т /n == Х, что соrласуется с результатом, указанным в табл. 2
3.2. .
При мер 2 (Отрицательная биномиальная модель, оценивание параметриче-
ских функций). По выборке Х == (X 1 ,... ,X,J требуется оценить параметри
ческую функцию T$,t(O) == 05(\ O)t t < nт, модели Bi (r, О). Здесь (см. п. 8
1.1)
00
/п(о) == (1 O(nr == I: C:r+z IOz
x O
Т.е. ап(х) == C r+z l' Х == О, 1,2, а
ос
/n(O)T$,t(O) == 05(1 O) (nr t) == I: C:,H+H0 5 + i
i O
Следовательно, уравнение несмещенности (1) запишется в виде
00 00
I: Н(х)ап(х)ОХ == I: C r t+HB5+i,
x O i O
204 rлава з. Теория оценивания неизвестных параметров распределений
откуда находим, что
Общий результат
cx .
Н(х) == nr t+Z H .
Cnr+z 1
.....с ";;: Ьт.:;"tлу и Это значительное усиление результата примера 3
З.I. В частности, полаrая s == 1, t == О, получим вид
оптимальной оценки по n наблюдениям для параметра В:
cT 1 Т
в' · nr+T 2
== TI,O == СТ nт + т 1
nr+T 1
Таким образом, оптимальная оценка Ts', t имеет вид
cT '
· Н(Т) nr+T s t 1
Ts,t т
Cnr+T 1
(10)
(i 1)
(сравни с (7) 3.1 при s == 1).
Кроме TOro, поскольку (см. п. 2 1.1) L,e(T) Bi(nr, О), то ЕеТ
== nrO/(1 О), Т.е. статистика Т/nт == Х/т является оптимальной оценкой
ДJ1я параметрической функции Т(В) == В /(1 В), что соrласуется с результатом,
указанным в табл. 2 3.2. .
2. Модели с выборочным пространство м, зависящим от параметра (J
Пусть носителем распределения наблюдаемой случайной величины { является
отрезок [а, В] и теоретическая плотность имеет вид
f(X;0)==QI(B)M1(x), a x B (12)
(вне отрезка [а, В] плотность равна нулю). Здесь функция QI(B) > о для всех
(} а и дифференцируема, кроме TOro, Dblполняется условие нормировки
В е
! f(x; В) dx == 1, т. е. ! М 1 (х) dx == Q,I(B) '
а а
Дифференцируя это тождество по В, имеем
Q; (В)
M1(B) == QT(O)
этим соотношением связаны функuии М 1 и QI В (12).
Пусть теперь дана выборка Х == (X 1 , , х п ) из указанноro распределе
ния. Записав функцию правдоподобия с помошью индикаторов в виде
n
n
n
L(;f; В) == П f(x;; В) == Q (B) П M1(x;) П I(a Х; О) ==
i=l i=l i=1
n
== Q (B) I(x(n) О) П М 1 (Xi) I(x(I) а),
;=1
3,4. Способы решения уравнения несмещенности 205
по критерию факторизации получаем, 'по достаточной статистикой в данной
модели является Т == Х(П) максимальное значение выборки. Найдем ее
распределение: при t Е [а, 01
t n
FT(t; О) == Р,{Т t} == P { t} == Q (O) (/ M1(x) dX)
а
Q (O)
Q (t)'
откуда для плотности 9)(t; О) == F (t; О) получаем представление
( t. О ) == nQ (8)Q (t) == nМ 1 (t)Qf (О) [ 1
9) , Q +)(t) Q7 I(t)' t Е а, О .
Для проверки полноты статистики Т надо убедиться в том, что HeCMe
щенная оиенка нуля в этой модели единственна, т. е. решить однородное ypaB
нение Е8'Р(Т) == о, "1 О а. В нашем случае оно эквивалентно уравнению
(13)
,
/ 'P(t)MI(t)Q: n(t) dt == О, "1 О а.
а
Дифференцируя это тождество по 8, получаем 'Р(О)М) (8)Q: n(0) == о, "10 а,
откуда 'Р(О) == О, "1 О а. Таким образом, свойство полноты здесь имеет Me
сто, и можно приступать к решению уравнения несмещенности для заданной
параметрической функиии т(О):
8
/ H(t)gl(t; О) dt == т(О), "1 О а.
(14)
а
Далее мы считаем, что функция т(8) дифференцируема. Переписав ypaB
нение (14) с учетом (13) в виде
,
/ I n т(О)
n H(t)M)(t)QI (t) dt == Qf(O) ,
а
"10 а,
и продифференцировав это тождество по 8, получим
nН ( О ) М ( O )Q I n ( O ) == T'(O)QI(O) nT(O)Q (O)
) I Q +)(O)'
или
Н(О) == T'(O)QI (О) nT(O)Q'1 (О) == т(8) + т'(О) == т(О) + т'(О) .
nM1(0)Qi(0) nM1(0)QM) nf(O; О)
»f
Общий результат
в итоrе, мы имеем следующий общий результат:
в модели (12) оптимальной оценкой для произвольной
206 rлава з. Теория оценивания неuзвесmных параметр08 распределений
дифференцируемой функции 7(8) является статистика
. ( ) 7' (Х(1I))
7 := Н Х(1I) := 7(Х(п)) + f(X . Х )
n (11)' (п)
(15)
Замечание. Если рассмотреть «симметричную,} модель (неизвестен леВblЙ конец HO
сителя распределения):
f(x; О) == Q2(0)M)(x), О х Ь,
( 16)
то аналоrИЧНblМИ рассуждениями можно установить, что полной достаточной стати
стикой теперь явдяется минимальное значение Вblборки X(I), ее плотность имеет вид
Q (O)
Y2(t; О) == nM 2 (t) Q I (t) ' t Е [О, Ь],
(17)
а оптимальной оценкой ддя произвольной дифференцируемой функиии т(О) явля
ется статистика
. (Х ) T'(X(I))
Т T (1)
nf(X(I),X(1)
Проверку этих yrверждений мь, оставляем читателю в качестве упражнения, а далее
мь! проиллюстрируем изложенную теорию несколькими примерами.
( 18)
Пример 3 (Равномерная модель, ОЦенивание параметрических фУНКЦИЙ).
Пусть .ею Е И(О,8), 8 > О. ЭТо модель вида (12) с а := О, Q,(8) == 1/8,
M1(x) == 1, поэтому для нее «работает» результат (15). В частности, если
7r(8) := 8 r То оптимальная оценка 1U1я этой функиии по n наблюдениям есть
Xr l
. r т (п) n + т r
7r := Х(п) + X( )
nf(X(n); Х(п) n n
(19)
(раньше, см. введение к данному параrрафу, мы установили этот результат для
т == 1). Обратим внимание на То, <!то здесь аl := E8 := 8/2, и, следовательно,
оптимальная оценка для теоретическоrо среднеrо аl есть
. 1. n + 1
аl == 71 == x(n),
2 2n
а не выборочное среднее Х(!). При этом
1 82
D8X := D8 := ,
n 12n
а в силу упр. 46 к rл. 1
. (n + 1)2 Х (n + 1)2
D 8 a l 4n 2 D8 (п) 4n 2
nо 2
(n + 1)2(n + 2)
82
4n(n + 2) .
Следовательно, эффективность выборочноrо среднеrо по отношению к опти
мальной оценке равна
D8a 3
:= < при n 2.
D8 X n + 2
3.4. Способы решения уравнения несмещенности 207
Этот пример показывает, что не всеrда выборочное среднее наилучшим обра
зом оценивает теоретическое среднее модели. .
Пример 4 (Покаэательная модель с параметрами сдвиrа, оценивание пара
метрических фУНКЦИЙ). Пусть плотность наблюдаемой случайной lJеличи
ны есть f(x; О) == е (x II), х О. Требуется оценить тт(О) == от по выборке
объема n. Это модель вида (16) с Ь == 00, Q2(O) == ее М 2 (х) == e X поэтому
по формуле (18)
· Х Т T X T 1
ТТ == (1) (1)
n
(20)
.
Пример 5 (Приведенное покаэательное распределение, оценивание пара
метрических фУНКЦИЙ). Приведенное к отрезку [8, Ь! показательное распре
деление задается плотностью f(x; О) == e X I(e /I e b), х Е [О, Ь]. Это pac
пределение имеет вид (16), поэтому, применяя (18), получим, что оптимальной
оценкой произвольной степени параметра тт(О) == ОТ является следующая cтa
тистика от выборки объема n:
* Х Т X T I (1 e X(II b )
ТТ (1) (1) .
n
(21)
.
З, Метод подrонки
Здесь pe'lb будет идти о весьма простом, но очень эффективном в ряде случаев
приеме решения ураlJнения несмещенности ЕеН(Т) == т(О). Предположим,
что т(О) > О ДJ1я всех О Е е, Torдa можем записать тождество
[ Н (Т) ]
Е/I т(О) == 1,
или
/ H(t)g(t; О)
Т(О) dt == 1.
Пусть здесь (ключевой момент!) имеет место факторизация
g(t; 8)
т(О) == и(t)gl(t; 8),
rде функция gI(t; О) принаДJ1ежит тому же семейству плотностей, что и плот
ность g(t; е) полной достаточной статистики Т. Torдa мы имеем тождество
(22)
/ H(t)и(t)gl(t;O)dt: 1,
которому удовлетворяет (в силу полноты статистики Т) единственная функ
ция H(t) == и I(t). Это дает решение исходноro уравнения несмещенности:
Т* == и I(T) (ДJ1я дискретной модели, в этих рассуждениях интеrpирование
надо заменить суммированием). Таким образом, если в конкретной задаче yдa
ется установить факторизацию (22), то мы тем самым получаем одновременно
и вид искомой оптимальной оценки ДJ1я т(О). Продемонстрируем эффектив
ность TaKoro приема соответствующими примерами.
208 rлава з. Теория оценивания неизвестных параметров распределений
Пример б (Нормальная модель с неизвестным средним, оценивание параме-
трических функций). Пусть Х == (Х"..., Х П ) выборка из L({) EN«(I, ( 2 ).
Здесь, как мы уже знаем, полной достаточной статистикой Т является выбо
2
рочное среднее Х и Le(X) == N«(I, и (n), т. е.
g(t; (1) == f(J"2Jn(t; (1) == С:( 2 ) 1/2 ехр { 2:2 (t (I)2}.
Рассмотрим сначала задачу оценивания теоретической fUlОтности 1'«(1) == f (J"2 (х; (1)
в произвольной точке х. Здесь уравнение факторизации (22) принимает вид
f(J"2/n(t; (1) С { n 2 I 2 }
==уnехр (t (I) + (x (I) ==
f (J"2 (х; (1) 2а 2 20'2
==';nex p { n (x t)2 n 2 ( t (n I)(I+x ) 2 } ==
2(n l)а2 2(n 1)0'2 n
I ( (n I )(I+Х ) 2 n I 2
== f(J"l (х; t)f(J"l/n t; n ,rде аl == a ,
т.е.
и(t) == f;i'(x; t), а gl(t; (1) == f(J"i/n (t; (n (I + х )
Таким образом, gl(t; 8) является нормальной плотностью TaKoro же вида,
как и g(t; 8), и тем самым решением уравнения несмещенности
! H(t)g(t; (1) dt == 1'«(1)
""о'птимаjigjfti;(о'ценlta '
нормальной плотности
является функция H(t) == и l(t) == '(J"'(х; t) HOp
I 2
мальная плотность со средним t и дисперсией 0'1
В итоrе имеем, что оптимальной оценкой теорети
ческой плотности '(J"'(Х; О) является статистика
· С --
пециальныи случан
'*(х) == '(J"'(х; Х).
I
(23)
Отсюда можно вывести следующее важное за-
ключение: если оценивается пара метрическая функ-
ция вида
1'(8; 0'2) == ЕефЮ == ! ф(х) f o-l (х; О) dx.
(24)
то оптимальная оценка для нее получается по формуле
1'. == ! ф(х)f.(х) dx == ! 1/J(x)f(Jl(x; Х) dx == т(Х; a ), (25)
т. е. в выражении для т(8; ( 2 ) надо прОСТо заменить параметр О на статистику
2 2 2
Х, а величину а на аl == «n 1)(n)O' .
3.4. Способы решения уравнения несмещенности 209
Так, если -ф(х) == e itx то получаем характеристическую функцию
2 it { . 172 2 }
т(О; и ) == Еее { == ехр ztO 2t
(см. УПр.26 к rл. 1), следовательно оптимальной Оптимальная оценка .,
оценкой для нее является статистика нормальной характери
{ 2 } стической функции
т' == ехр itX I t 2 (26)
В качестве еще одноro KOHKpeтHoro при мера возьмем функцию -ф(х) == х 2
Тоrда из (24) имеем
т(О; (72) == Еее == De + (Ee ) 2 == 172 + ()2
и, следовательно, в силу (25), т' == иi + Х 2 или (02). == т' и2 == Х 2 и2 /n
оптимальная оценка ДJlЯ 02
Наконец, если взять 'Ф(х) == I(х Ха), то
2 ( Ха (1 )
т(О; и ) == Ре{{ Ха} == Ф
и по формуле (25)
. ({!; Ха Х )
т ==ф
n 1 и
"' ''''О' i1 тимальная 7 0ценка' ..,
нормальной функции
t распределения
с этим результатом мы уже встречались в примере 6 3.3 (см. там COOTHO
шение (14»). .
Пример 7 (Биномиальная модель, оценивание параметрических функций).
Пусть требуется по выборке Х == (Х"..., х п ) из биномиальноrо распре
деления Bi(k, О) оценить параметрическую функцию Тт, 5(0) ()' (1 0)5
rдe r, s заданные неотрицательные целые числа такие, что r + s kn.
Поскольку модель Bi(k, ()) входит в экспоненциальное семейство, то стати
стика Т == Х 1 + . . . + х n является достаточной и полной, и ее распределение
Ее(Т) == Bi(kn, о) (см. п. 1 1.1). В данном случае уравнение факторизации
(22) запишется в виде
C t nt r (1 O) kn t s C t (c t r ) I c t r пt r (1 п ) kn r
kл[7 kn kn r s kn r 5[7 [7
Т. е. здесь 91 (t; (1) == Ck r sOt r (1 O)kn r (t r) биномиальные вероят
( ) t ( t r ) I
ности В точках t == r, r + 1, , kn s, а функция и t == C kn Ckn r s
Значит, оптимальная оценка функции Тт, 5«() есть
CT r
· 1 (T) kn r s
Тт, s и т
' C kn
(27)
14 Зака, 1748
210 rлава з, Теория оценивания неизвесmных параметрО8 распределений
в частности, при r == 1, S == О получаем оптимальную оценку пара метра В:
2' I
. . C!:n I т 1
В == Т1,о == ст == kn == "k X
"'"
этот результат мы уже и ели в 3.2 (см. табл. 2). .
Пример 8 (Оценивание размера конечной совокупности: выбор с возвра
щением). Пусть в урне находятся занумерОllанные числами 1,2, ,() шары,
110 их число (j нам неизвестно. По схеме случайноrо выбора с возвращением
из урны ИЗllлекается n шаров и при этом каждый раз фиксируется номер из
меченноrо шара. Пусть Х == (Х"... , Х n ) номера извлск,шшихся шароu.
Требуется по этой информации оценить общее число шаров в урне () и, более
общо, ПрОЗIЮЛЬНУЮ степень тт((}) == о" rде r > n (целое). Если обозна
чает номер случайно извлеченноrо шара, то распределение этой случайной
величины задается вероятностями
1 1
f(x; ()) == Pe{ == х} == о' х == 1, ,о, или f(x; В) == OI(x В).
Отсюда ДJ\Я функции правдоподобия имеем представление
n
L( ;(}) == Пf(Хi;В) ==(TnI(maxxi ()) ==(} "I(x(ll) (}),
I
i 1
По критеРИЮ факторизации отсюда делаем "ывод, что максимальный наблю
давщийся номер Х(n) является достаточной статистикоЙ для параметра ().
Найдем ее распределение. Имеем
Pe{X('I) t} ==Ре{Х ; t, i== 1,
( t ) "
,n}== -ё
t ().
Следовательно,
( (} t ) n ( t () I ) n
g(t; ()) == Ре{Х(n) == t} ==
t == 1,2,
,8.
(28)
Убедимся теперь!3 полноте статистики Х(n)' Для этоrо запишем УРiшнение
несмещенноro оценивания нуля:
е
L 1p(t)g(t; (}) == О, 'v () 1
t 1
Полаrая здесь последовательно () == 1, (j == 2, очеIlИДНО, получим, что
!p(I) == !р(2) == == О, т. е. этому УСЛОВИЮ удовлетворяет лишь нулевая
(на множестве значений статистики Х(n) функция, следовательно, статистика
Х(n) полная.
Для оценивания функции тт((}) == оТ применим метод подrонкн. Здесь
уравнение факторизации (22) записывается !3 виде
t n (t I)n == t" (t 1)11 [( ! ) n+т ( ) n+T ]
вn+т t n + r (t 1 )"+т О () ,
3.4. Способы решения уравнения несмещенности
211
т. е. новая плотность
( 8 t ) ,,+т
91 (t; 8) ==
с 1 ) ,,+т
имеет такой же вид, как и g(t; О). а функция
tn (t l)n
U ( t )
t n + 1 ' (t I)n+r
Следовательно, оптимальная оценка для 7,.(8) есть
хn+т (х I ) n+т 1 ( 1 X l ) n+r
* I ( Х ) (n) (n) Х ' (n) ( 29 )
7, ==и (11) == Х " ( Х I ) n == (n) 1 ( 1 X I ) n .
(11) (n) (n)
Отметим, что если х(n) велико, то, воспользовавшись приближением
( X l ) k kX 1
1 (n) ::::: 1 (n)'
формуле (29) можно придать приближенную форму
. n+т r
7, ::::: X(n)'
n
В частности, оптимальная оценка числа 8 шаров в yp
не имеет вид
O ""C'""""'КQ'
птимальная оценк . .
число шаров в урне
:<J;"N
( 1 ) n+1
. * 1 1 Х(,,) n + 1
8 == 7) == Х(n) ( I)n ::::: X(n)' (ЗО)
\ 1 Х(n) n
Иrровую интерпретauию этой задачи дает В. Феллер [25, с. 240], пред
лаrая для оценки числа зареrистрированных в rороде автомобилей встать
на перекрестке и записывать номера Х], ,Х n проезжающих автомобилей.
Если в rороде имеется 1000 машин и производится случайная выборка объема
n == 10, то математическое ожидание максимальноrо наблюденноrо реrистра
ционноrо номера ЕвХ(n) ::::: (nf(n + 1))8 приближенно раlJНО 9\0.
Иллюстрauией статИСТИ'lеской процедуры (30) являются следующие pe
зулыаты, полученные моделированием с помощью таблиц СЛУ'lайных чисел:
при 8 == 10 000, n == 10 значения оценки (ЗО) ДI1я десяти неззвисимых выбо
рок оказались равными (с ТО'lностью до единицы) 10549,9841,10486, 10891,
10462, 1087З, 8789,10753,9960, 10287 Эти данные свидетельствуют о xopo
шем качестве оценки (ЗО). .
Замечание. Мы знаем, что оценка (30) имеет наименьшую дисперсию среди всех
несмещеННblХ оценок О. Но какова величина этой дисперсии ОоО*? На практике,
чтобы судить о точности оценки, важно уметь оценивать ее дисперсию по имеющимся
данным (по выборке). В таких случаях оптимальную несмещенную оценку о' для
ОоО' можно построить по формуле
D* == (0')2 (02)*.
(31)
*
212 rлава з. Теория оценивания неизвестных параметров распределений
Действительно, так как Eвf}' == В, Е8(в2)' == е2 то
EвD' == Е8(о')2 Е8(в2)' == Ее(в')2 (;2 == Е8(/п2 (E8/J')2 == D8(j",
а поскольку D' есть функция от полной достаточной статистики, то D' еСть н. о. р. м. д.
Так, в рассматриваемом случае на основании (29) имеем
[( I ( I X I ) n+' ) 2 1 ( I X ' ) n+2 ]
, , 2 . 2 (п) (п) I 2
D == (т,) 72 == х(п) 1 (1 x( p" 1 (1 x( )" ;:::: n 2 Х (П)
(приближенное равенство справедливо при больших значениях х(п))'
Замечание. В данной модели теоретическое среднее есть
I 8 (j + 1
0:, == E8 == (j L Х ==
х==l
и оптимальной оценкой Д/lЯ Hero является статистика 0:; == (7,' + 1)/2, но не uыбо
рочное среднее J{ (1).
Пример 9 (Оценивание размера конечной совокупности: выбор без воэвра
щения). Предположим, что в ситуации предыдущеrо примера производится
случайный выбор без возвращения n шаров или, что то же самое, извлекается
сразу комплект из n шаров, причем все С; возможных вариантов выбора
равновероятны. Снова пусть х(п) обозначает максимальный наблюденный
номер. Torдa Х(П) будет также полной достаточной статистикой и
cn 1
g(t; О) == Р8{Х(п) == t} == ----пl , t == n, n + 1, ,О. (32)
8
Здесь метод подrонки удобен дl1я оценивания параметрических функций
вида
Tr(lJ) == (8 + 1) (() + т) == (();! т)! , т > n (целое). (33)
Записав уравнение факторизации (22):
Ctn II(C:) l(}! ......!!....... (t 1)! Ctn:/ ll
(() + т)! n + r (t + r 1)! С;:: '
имеем, что
cnH 1
( t О ) t+r l
91; == с п + ,
8+,
плотность TaKoro же вида, как и g(t; (}), а функция
n (t 1)!
и(t)
n+т (t+T 1)!
Следовательно, Оптимальная оценка дl1я функции Tr(O) имеет вид
. l n+т (X(n)+r I)!
Т' == и (Х(П) == (Х(П) 1)!
3.4. Способы решения уравнения несмещенности 213
n+т
== X(n)(X(n) + 1)
n
(Х(П) + r 1).
(34)
Если х(п) велико, то формуле (34) можно придать приближенную форму
* n+r r
Tr ::::: X(n)'
n
т. е. получаем такой же результат, как и в предыдущем примере для схемы
выбора с возвращением.
В частности, оптимальная оценка числа () шаров
в урне есть
О ....ф
птимольноя оценка
числа шаров в урне
* * n + 1
() == Т) 1 == Х(П) 1
n
(сравни с (30)), а оптимальная оценка для дисперсии DoO* имеет вид (см. (31)
и (33)
D* == (()*)2 (82)* == (Т; 1)2 т'; + 3TI* 1 == (тп 2 + TJ* Т';.
Учитывая (34), окончательно находим
(35)
* Х(п)(Х(п) n)
D == 2 .
n
.
Замечание, Поскольку (34) есть несмещенная оценка для (33), то мы имеем общую
формулу для рассматриваемой модели:
n
ЕеХ(n)(Х(n) + 1)... (Х(n) + r 1) = (8 + 1) (8 + т). (36)
n+т
в частности,
n
ЕеХ(n) == n + 1 (8 + 1),
2 n
ОоХ(n) == X(n)(X(n) + 1) X(n) (ЕоХ(n)) == (n + 1)2(n + 2) (8 + 1)(8 n).
Учитывая (35), можем также записать
D о* (n + 1)2 D Х (о + 1)(8 n)
о n 2 о (n) n(n + 2)
Следовательно, оптимальная оценка для т(О) = DOX(n) есть
. n 2 . (Х(n) n)
т = o =
(n + 1)2 Х(n)(n + 1)2'
4. raMMa MOAeпb с неизвестным параметром масштаба,
оценивание параметрических функций
Определение и основные свойства модели r((), л), rде 8 > О неизвестный
парамеЧJ масштаба (парамеЧJ формы л далее считается известным) приведе
ны в п. 3 1.2 (см. также пример 1 в 2.4 о свойствах порядковых статистик
214 rлава з. Теория оценивания неизвесmных nараметров распределений
ДIIЯ выборки из r(l, 1)). Отдельные результаты об оценивании для этой MO
дели нам уже встречались ранее. Так в табл. 2 3.2 указана эффективная
(следовательно, оптимальная) оценка для caMoro пара метра О это стати
стика Х/>.. Там же отмечено, что r(O, >') это модель экспоненциальноro
Типа, и для нее полной достаточной статистикой является сумма наблюдений
Т == Т(Х) == Х) + . + Х,.. По воспроизводящему свойству raмма распреде
ления .св(Т(Х)) == r(O, n>.), т. е. (см. (18) 1.2) плотность статистики Т есть
tn)., 1 e t/B
g(t; О) == f(tlO, п>.) == [(n>.)оn)., ' t? о. (37)
Основываясь на этих фактах, в данном пункте мы решим задачу оптималь
Horo оценивания произвольных параметрических функuий для этой модели.
Мы начнем с построения оценки дЛЯ параметрической функuии
Тт,х(О) == ОТ e x/B т > п>., х? о. (38)
Здесь два свободных пара метра: r и х, поэтому (38) на самом деле задает
двухпараметрическое семейство функциЙ от (J. Для отыскания оптимальной
оценки т;' з; мы воспользуемся методом подrонки. Уравнение факторизации
(22) этоrо метода в данном случае принимает вид
tn),, lе (t з;)/В r(n>. + т) tn),, 1
r(n>,)OnA+T r(n>.) (t х)nА+Н f(t xlO, n>. + т), t? х,
Т.е. 91(t; О) == f(t xJ8, n>. + т) rамма плотность вида (37), а функция
r(n>. + т) t,.)., )
и(t) == r(n>.) (t X)1I).,+T J (t ? х).
A
Общий результа. Следовательно, искомая оптимальная оценка есть
. 1 r( n>.) (Т х )'IЛ+Т I
Тт,з; == и (Т) == r(n>. + т) Tn)" 1 I(Т? х). (39)
Выделим важный частный случай этоrо результата. Если в (38) положить
r == >. (при n ? 2) и домн ожить функцию Т )."З;(О) на Iножитель x)., '/r(>.),
то получим теоретическую плотность f(xl(J, >.). Следовательно, из (39) полу
.. .
.,. Оптимальная оценка чаем оптимальную несмещенную оценку / (х) для
rамма плотности теоретической плотности rамма модели r(o, >'):
.
Специальный случай
. r(nл) x),, I(T x)(n I»,, 1
/ ( х ) == I ( Т Х ) .
r(Л)r(n 1)>') Tn)" l "
(40)
В свою О'lередь, этот результат можно применить
для оценивания параметрических функций вида
00
т(О) == Е/lIfIЮ == J lfI(x)f(xI8, >') dx
о
3.4. Способы решения уравнения несмещенности 215
оптимальная оценка дЛЯ ,(8) ПОЛУ4ается просто заменой в этом интеrpале
теоретической плотности f(xI8, л) ее оценкой (40). В итоrе имеем
00 т
/ r ( n'\ ) TI n>' /
" == ( x )f ' ( x ) dx == ( x ) x>' I ( T X ) (n ))>. ) dx
rp r('\)r((n 1)'\) I(J ,
О U
4ТО после замены переменных х ----+ хТ приводит к формуле
I
т' == [(п'\) / lP(xT)x>' )(1 x)(n I)>' 1 dx. (41)
f('\)r((n 1),\)
О
Пример 10, Пусть по Вblборке Х == (Х), ",Х n ), п 2, из.ею Е r(8,л)
требуется оценить преобразование Лапласа
т(8) == E/le t == (1 + fJt) >.
при t> о. По формуле (41) имеем
I
, r(пл) / xlT >' ) (1 ) (n I ) A 1 d
7' == е х х х.
rщr((п 1)'\)
u
Этот интеrpал можно вычислить, разложив экспо
xlT Ф "
ненту е в ряд и воспользовавшись ормулои для
бета функции В(а, Ь) (см. п. 4 1.2). В итоrе получим
,. == r(n'\) f r('\ + j) ( tT/
r('\) j O j!r(n'\ + j)
Оценивание ,.
прео6разовання
Лапласа
(42)
.
Пример 11 (Оценивание функции надежности). Функцией надежности Ha
Зblвается вероятность 7'с(8) == РеЦ с} == E8I( с), rдe с> О заданное
число. Чтобы построить оптимальную оценку для 7'(8) по п 2 наблюдениям
Haд , нужно вычислить интеrрал в (41) при 'Р(х) == l(х с), Т.е.
{ r(n'\) / ) x>' I(1 x)(n I)A 1 dx при Т> с
т; == rщr((п 1)'\) ,
с/Т
О при T
Используя неполную бета функцию B(z; а, Ь) (см. (4) 92.4), этой формуле
можно придать вид
,; == [1 B( ;'\, (п 1)'\) ]I(T > с).
(43)
216 rлава з. Теория оценивания неиэвестных параметров распределений
Выделим частный случай этоrо результата при л == 1: в этом случае
тс(в) == е c/B и
( ) n l
т; == 1 f I(Т > с).
(44)
.
Пример 12 (Нормальная модель с неиэвестной дисперсией: оценивание па-
раметрических функций). Полученные для rамма "lОдели результаты можно
при менять и к друrим моделям, именно, к таким, в которых соответствующая
достаточная статнстика имеет rамма распределение: ведь ключевым моментом
выще при выводе оценки (39) было то, что достаточная статистика Т == Т(Х)
имела rамма распределение r(B, nл). Продемонстрируем это на примере ис-
следования нормальной модели N(f.L, ( 2 ). Эта модель экспоненциальноrо
типа, и как отмечено в п. 3 3.3 (см. табл. 2 3.2) ПQ1lНОЙ достаточной стати-
стикой д;1Я нее является
n
Т == I:(X i /li
i l
Для нее, очевидно, ЕвТ == nDBX 1 == nв 2 и потому оптимальной оценкой
для в 2 теоретической дисперсии модели является Т /n, что соответству-
ет результату, указанному в табл. 2 3.2. Но теперь мы можем продвинyrь
ся значительно дальше и построить оптимальные оценки д;1Я произвольных
функций от параметра О, Для этоrо найдем сначала распределение статисти
ки Т. Заметим, что .cB((X j /l-)/O) == И(О, 1), V i, следовательно (см. упр. 38
к rл. 1), ..св (Т /fi) == х 2 (n) == r(2, n/2). Отсюда имеем (см. п. 3 1.2), что
.св(Т) == r(2B 2 , n/2). Поэтому все полученные выше результаты для raMMa
модели заменой () 4 2в 2 , Л 4 1/2 переносятся на рассматриваемую модель.
Например, рассмотрим параметрическую функцию т(В) == (2B 2 )r Ее оп
тимальная оценка получается из (39) при х == О, л == 1/2 и имеет, следова
тельно, вид
. . О - б """" v ' .. . н
" JIII> щии результат" .
J
для модели N(/l-. B )
. r r(n/2)
т == Т
r(n/2 + т) ,
причем r здесь любоедеЙСТl3ительное число, боль-
шее (n/2). В частности, любая степень (}k при
k > n оценивается статистикой
k. ( T ) k/2 r(n/2)
(О) == '2 r((n + k)/2) '
(45)
При k == 2 имеем отмеченный выше результат для дисперсии в 2 по
СКОЛЬКУ r(n/2 + 1) == (n/2)r(n/2). .
Пример 13 (Общая нормальная модель: оценивание функций от дисперсии),
Использованную 1J предыдущем примере идеолоrию можно применить и в
более общей ситуации, Korдa оба параметра нормальной модели неизвестны.
3.4. Способы решения уравнения несмещенности 217
Итак, пусть Х == (X I , ,Х n ), n 2, выборка из .сю == N(O), O ). Для
этой модели полной достаточной статистикой является пара
т == (T 1 , Т 2 ) == (х: I=(X i Х У )
,=)
(см. пример 1 в 3.3, а также п. 3), при этом по теореме Фишера (см. п. 3 2.5)
.ce(T2/0 ) == ;е(n 1) == r(2, (n 1)/2), Т.е. .с8(Т 2 ) == r(20 , (n 1)/2). По
этому, если т(О" (2) == Т(О2), т. е. параметрическая функция зависит только
от теоретической дисперсии, то дЛя ее оценивания можно применить извест
ные результаты дЛЯ rамма модели с учетом замены О 20i, А (n 1)/(2n).
В качестве кон KpeTHoro примера, как и выше,
k
рассмотрим задачу оценивания степени 02 при
k > n + 1. Полаraя в (39) r kJ2, х == О,
пА == (n 1)/2 получим вид искомой оптималь
ной оценки
Об
щий результат
ДЛЯ модели N(OI, oi)
(Ok)*== ( T2 ) k/2 r«n I)/2) .
2 2 r«n+k I)/2)
в частности, при k == 2 эта оценка принимает вид
(46)
n
Т 2 1 I: 2 2
== (Х; Х) == 80,
n 1 n 1 .
\=1
и мы приходим К уже известному нам из примера 9 3.2 результату, что
статистика 8J является оптимальной несмещенной оценкой теоретической
дисперсии O нормальной модели N(8[, oi). Однако результат (46) rораздо
более общий. .
5. Друrие применения rамма модели
ДЛЯ оценивания неиэвеСТНblХ параметров
В ряде случаев дЛя наблюдаемой случайной величины ( с плотностью f(x; О)
можно подобрать такое функциональное преобразование 17 == h«(), что преоб
разованная величина 7J будет иметь rамма распределение с неизвестным па
раметром масштаба, и тоrда задача оценивания для исходной модели f(x; 8)
может быть решена с использованием изложенных в п. 4 результатов ДЛЯ raM
ма модели. Несколько таких примеров будут рассмотрены в данном пункте.
Пример 14 (Бета распределение). Пусть имеет плотность
f(x;O)==Oxe l, xElo,lj, 0>0,
т. е. (см. п.4 1.2) .сеЮ == Ве(О, 1). Рассмотрим преобразование 1/ == 1" (,
Torдa по формуле (45) 1.2 найдем, что плотность g(y; О) случайной величи
ны 17 есть g(y; 8) == 8e ey, у О, т. е. .с 8 (17) == r(8 1, 1). Следовательно, если
218 rлава з. Теория оценивания неизвестных параметров распределений
имеется выборка Х '= (X 1 ,
,Х п ) из .соЮ, то статистика
n
т == L 'П Xi
i 1
имеет распределение r(8 1, п), и D терминах этоН статистики ожно строить
оптимальные оценки для параметрических функций от 8 I , исполыун резуль
таты п. 4. .
Пример 15 (Распределение Вей6улла). Пусть имеет плотность
f( п ) а a I x. / o
Х;!7 == ОХ е х ;? О,
т. е. (см. п. 8 1.2) .соЮ == W(O, а, B 1 / O ). Torдa аналоrИ'IНО предыдущему
примеру имеем .co( a) == r(B, 1), СлеДОDательно, статистика
n
т '= L ХУ
i 1
имеет распределение r(8, п) и ('работают.) нсе результаты П.4. .
При мер 16 (Распределение Парето). Пусть плотность наблюдаемой случай
ной lIеличины имеет вид
в
'(х; В) == 8+1' х;? 1, 8> О
х
(см. п. 9 1.2). Тоща .c8(111 ) == r(B I, 1), и мы имеем ситуацию примера 14
с достаточной статистикой
n
T'=LII1X i .
i=1
Пример 17 (Распределение Лапласа). Это распределение задается плотно
стью
.
e lxl/o
'(х; О) '= 28' х Е R 1 О> О.
Нетрудно убедиться в том, что здесь .со(IЩ r(O, 1) (это Ы оставляем
в качестве упражнения читателю), поэтому мы имеем ситуauию при мера 15
с достаточной статистикой
n
т == L IXil.
i l
.
я слышу, и я забываю.
Я вижу, и я запоминаю.
Я делаю, и я понимаю.
Китайская пословица
3.5. Оценки МQксимальноzо правдоподобия
219
3.5. Оценки максимальноrо правдоподобия
Оптимальность это еще не все; оптимальность
лишь одна стОрОllа очень сложной карmины.
Э.Леман
Метод оценипания, основанный на использовании достаточных статистик,
наряду с сильными сторонами обладает и своими слабостями. Прежде всеro
это спязано с тем, что этот метод ориентирован на построение HecMeuцeH
ных оценок, а, как уже отмечал ось выше, HecMeuцeHHыe оценки не Bcerдa
сушествуют или практически мало приrодны; в таких случаях приходится
использовать CMeuцeHHыe оценки. Далее, даже при наличии HecMeuцeHHЫx
оценок этот метод не всеrда приводит к однозначному решению (достаточная
статистика не IJсеrда обладает спойством полноты), и, следовательно, в Ta
ких случаях для выбора ОКОН'lательной оценки необходимо приплекать те
или иные дополнительные соображения. Наконец, при реализации метода
достаточных статистик мы часто сталкипаемся с трудными аналитическими
задачами, связанными с решением уравнения несмеuценности (10) 3,3, и этот
метод часто приводит к сложным для практическоrо использования форму
лам для оптимальных несмешенных оценок (см. например, формулу (17) 3.3
для оценки нормалЬНОЙ функции распределения (15) 3.3). В таких случаях
предпочтение может быть отдано друrим методам, которые приводят пусть
не к оптимальным, но зато просто конструируемым и леrче пычислимым
оценкам (особенно, если они по эффективности мало уступают оптимальным
оценкам). Такими преимуuцествами в ряде случаев обладают оценки макси
мальноrо прапдоподобия, которым посвяшен настояuций параrраф.
1. Определение и примеры оценок
максимальноrо правдоподобия (о. М. п.)
Одним из наиболее универсальных и эффективных методов оценивания неиз
вестных параметроп распределений является метод максuмаЛЬНОi?О пpaBдoпo
добия, КОТОРЫЙ и приводит к оценкам маКСU.l1аЛЫIOi!О правдоподобия (далее мы
будем использовать для них сокрашенное обозначением о. м. п.). Этот метод
получил распространение в 20 e п. ХХ в. блаrодаря работам анrлийскоrо cтa
тистика Р. Фишера (хотя у Hero были и предшественники). Суть этоrо метода
состоит в следуюuцем.
Пусть, как обычно, имеется пыборка Х == (X 1 , ,Х n ) из HeKoToporo
распределения .ею Е :F == {F(x; (}), () Е е} и L(f.; (}) функция правдопо
добия (см. п. 1 3.2). Если для двух значений {}I, {}2 пара метра {} выполняется
условие L(f.; ()l) > L(f.; ()2), то rоворят, что значение {}I «более правдопо
добно,), чем ()2 (при {} == {}! «вероятность получить реализацию f. больше.),
чем при {} == ()2). Наиболее правдоподобное значение параметра при данной
реализации f. выборки Х обозначается O'(f.) , а статистика о' == О(Х) и есть
о. м. п. для параметра {}. Таким образом, по определению, O(f.) это Ta
220 rлава з. Теория оценивания неuзвестных параметр08 распределений
кая точка параметрическоro множества е, в которой функция правдоподобия
L(if,; е) достиrает максимума:
L(f; 8(if,») L(;r; е), v е,
или L(if,; 8(if,)) == sup L(f; е).
IJ
(1)
Если Д11я каждоro if, из выборочноro пространства Х максимум L(;r; 8)
достиrается во внyrpенней точке е и функция L(;r; е) дифференцируема по е,
то 8(х) удовлетворяет уравнению
oL(if,; 8) д In L(f,; 8)
де == о или д8 == О.
q Уравнения .... Для BeKTopHoro пара метра 8 == (е" . . . , e r ) это ypaBHe
правдаподобия ние заменяется системой уравнений
д In L(;f; 8) == О
o8j ,
i == 1,
, Т.
Эти уравнения называются уравнениями правдоподобия.
.
Свойства о. м. п.
Отметим следующие свойства о. м. п.
1) Если сущестlJует эффективная оценка Т(Х) для скаляр//Оzо параметра е,
то 8 == Т(Х). Это очевидное следствие критерия эффективности Pao
Крамера (9) 3.2:
дlпL(х;е) == ( ( ) )
ае а(е) Т Х е .
2) Если имеется достаточная статистика Т(Х), а о. м. п. существует u eдиl/
ствеНlIO, то она является функцией от Т(Х). Действительно, из представ
ления (1) 3.3 следует, что в данном случае максимизщия L(;f; 8) CBO
дится К максимизации g(T(f,); е) по 8. Следовательно, 8(if,) == 8'(T(;r)).
Примерами о. м. п. 8' Д11я ряда моделей со скалярным параметром явля
ются приведенные в табл. 2 3.2 соответствующие эффективные оценки. Так
2
Д11я моделей N(8, (J" ), r(8, 1), Bi(l, е), П(е) о. м. п. 8 == Х. Рассмотрим еще
несколько примеров нахождения о. м. п.
Пример 1 (Общая нормальная модель, о. м. п, ее параметров).
Пусть L(O Е N(8" 8 ). Функuия правдоподобия Д11Я этой модели указана
в примере 1 в 3.3. Обозначив
n
s2 == 2::(X j х/
n j l
запишем ее в виде
2 N / 2 { [ (Х 8,)2 1 ( S2 ) S ] }
L(f; е) == (21res) ехр n 2ei + 2 ei 1 1n е 2 .
(2)
3.5. Оценки маКСUlofальноzo правдоподобия
221
Воспользуемся теперь элементарным неравенством In а :::;; а 1, V а > О,
из KOToporo следует, что 'П а 2 :::;; а 2 1 или In а :::;; (а 2 1)/2; знак равенства
достиrается только при а == 1. Учитывая это, имеем, что выражение в KBaд
ратных скобках в (2) всеrда неотрицательно и обращается в нуль лишь при
8. == Х, 82 == s. Но это означает, что B( == (81( ' 82( ») == (х, s). Таким об
разом, вданном случае о. м. п. существует, единственна и при этом 8 == (.х, S),
rде S2 выборочная дисперсия. Отметим также полезный факт, что
( ) 2 "/2
sup L( ; 8) == L ; 8( ) == (211'es )
(J
(3)
Подчеркнем, что полученная о. м. п. 8== (8;,82) == (Х, S) функция дo
статочноЙ статистики Т == (T 1 , Т2) == (Х, 32), определенноЙ в примере 1 Э 3.3..
Пример 2 (Мноrомерная нормальная модель, о. м. п. ее параметров). Пред
положим, что наблюдается мноroмерная случайная величина == ( I, , k).
распределенная по невырожденному нормальному закону N( , I;), rде вектор
k
средних значений!!:. == (PI, ,J.tk) и дисперсионная матрица I; == 11 O'ij 111
неизвестные параметры (см. п. 2 Э 1.2). Здесь общее число неизвестных пара
метров (с учетом симметричности матрицы I;) равно k + k(k + 1)/2. Пусть
Х == ( Х l' , Х п ) выборка из .с({), т. е. L независимые k MepHbIe
случайные величины с fUютностью, указанной в (9) Э 1.2. Найдем оценки па
раметров () == (Р, Е) такой модели по методу маКСИМ3!lьнЬrо правдоподобия.
В данном случае функция правдоподобия
n
L( ; 8) == П f( I , Е) ==
' I
== (211') kn/2IEI n/2 ехр { Ё( )'E !( !!:.)}. (4)
/ I
Пусть == ( ! +
динатно), TOrдa
+ n)/n (сложение векторов производится ПОКоор
n n
L( )'I; I ( JL) == L( Ю'I; I ( ю + n@ )'I; I @ ) (5)
/ ! ' I
(здесь == (Х!, .., Xk), rдe Xj среднее арифметическое j x координат
векторов I' ' n)' Введем также выборочную дисперсионную матрицу
1 n k
I;( ) == L( Ю( )' == IISijll1
n
, !
(см. П.2 Э 2.3). Воспользовавшись равенством
i Ву.. == tr (ВУ), У == -v..-v..'
222 rлава з. Теория оцениванuя неuзвестных параметров распределений
и линейностью оператора tr (nзятия следа от матриuы), получим
71
:L( f)'E I( Ю == n tr (E IEC )).
1 1
(6)
Учитыпая равенства (5) и (6), перепишем формулу (4) 11 ниде
L(;f; В) == (27r) kn/2 ехр { [@ !:)'E /@ !:) + tr (E IE(;r)) + ln IEI] }
Отсюда следует, 4ТО максимизаuия по () Функuии правдоподобия эквива
лентна минимизauии по !: и Е функции
'Ф(;f; !:' Е) == (f !:)'E ) @ !:) + [tr (E ) E(;f)) k ln I E ' E(;r) 1]
(постоянные k и ln IE(;r) I введены здесь дJ1я упрощения дальнейших пре
образопаний). Обозначим л), ,Лk собственные 4исла матрицы E 1 E(;r)
(все они положительны), TOrдa след (tr) этоЙ матриuы ранен сумме
Л, + + Лk. а ее определитель произведениlO Лj Лk, (;леДО'l<пельно,
можем записать, что
k
ф(;f; !:. Е) == (f !:)'E ) @ р) + :L (Лj 1 111 Лi).
j 1
Поскольку E ' положительно определенная матриuа и а 1 111 а О,
V а> О, из последнеrо соотношения ПОЛУ4аем Ф(;f; , Е) О, причем paBeH
ство имеет место только при р == f, Л) == Лk == 1, Т.е. при Е == E(;f).
НО это означает, что о. м. п. параметроп!: и Е НIIЛНЮТСЯ соответственно стати
стики Х == (X 1 , ,х\) и Е(Х) == IISjjll Как показано в П.2 2.3. вектор
пыБОР04НЫХ средннх Х == (х" ,X k ) является несмещенной оuенкой дJ1я
пектора == (PI, ,Pk), несмещенной же оuе)IКОЙ дJ1H Е нuляется подправ
ленная выборочная дисперсионная матриuа (n/(n 1))Е(Х). .
Пример 3 (Равномерная модель, О. м. п. ее параметра).
Если Х == (Х" . Х n ) выборка из paHHoMepHoro pac
пределения И(О, О), то из формулы дJ1я L( ; О), ПОЛУ4енной
n при мере (3) 3.3, следует, что L(;r; В) монотонно убывает
по () дJ1Я В Х(п), а при () == Х(п) Функuия прандоподобия
достиrает максимума (см. рис. 1). Таким образом, о. м. п.
() В == Х(п) , т. е. совпадает с достаТ04НОЙ статистикой. 8 этой
точке функция прапдоподобия разрывна, поэтому производ
нан L(;f; В) по (J в этой точке не существует. Таким образом,
в данном СЛУ4ае о. м. п. не япляется решением уравнения правдоподобия. Это
характерно дJ1я ситуauий, Коrда выБОР04ное пространстпо ,;( зависит от неиз
BecTHoro параметра.
L(x(n); (})
о х(n)
Рис. 1
3.5. Оценки максимальною правдоподобия
223
Если же Х выборка распределения И(8,8 + 1), то из формулы (4)
Э 3.3 имееr.1 L( ; 8) == /(8 X(I) х(п) 8 + 1). Отсюда следует, что любое
8 Е [Х(П) 1, X(l)] маКСИМlПирует функцию правдоподобия; таким образом,
здесь о. м. п. не единственна. В качестве решения можно выбрать, например,
8 == (X(l) + Х(П) 1)/2; в этом случае 8 функция достаточной статистики
Т == (X(I), Х(П)) (см. пример 4 в Э 3.з). .
Пример 4 (Двухпараметрическая покаэательная модель, о. м, п. ее парамет
ров). Эта модель определена в примере 2 в Э 3.3. Из полученной там формулы
L( ;(}) == 8:;П ехр { ; (T,( ) +T2( ) ( 1 )} I(TI( ) 8,) (7)
следует, что при любом 82 максимум по О, достиrается при О, == Т, ( ) == Х(,),
и он равен ехр { n(ln 82 + T2( )/82) }; максимум же последнеrо выражения
по 82, как леrко видеть, достиrается при 82 == T2( ) == Х X(I)' Таким об
разом, о. м. п. 8 == (8,,82) == (X(I), Х X(I)) , т. е. совпадает с достаточной
статистикой Т == (Т" Т 2 ) == (Х(,), Х Х{I))' .
2. Принцип инвариантности для о. м. п,
Важным свойством оценок максимальноrо правдоподобия является их инва
риантность относительно преобразований параметра. Это означает, что если
q q(8) произвольная функция 8 (8" ,8 r ), взаимно однознач
но отображающая параметрическое множество е рассматриваемой модели
в множестно Q == {q == (q" , qr)} С R r то о. м. п. q == q(8). ДеЙСТI3итель
но, поскольку q взаимно однозначное отображение, существует обратная
функция 8 == 8(q). Тоrда
supL( ;8) == supL( ;8(q)),
дЕе qEQ
и если максимум по 8 функции L( ; 8) достиrается в точке 8, то максимум
по q функции L ( ; 8(q)) имеет место в точке q, удовлетворяющей уравнению
О@ == 8, Т.е. в точке q== q(O).
Соrласно этому, в каждой конкректной задаче можно IJыбрать в каче
стве исходной наиболее удачную параметризацию, а о. м. п. получать затем
с помощью соответствующих преобразований. Таким образом, в методе MaK
симальноrо правдоподобия по существу достаточно построить лишь оценку 8
параметра модели, а оценки различных параметрических функций получают
ся как результат подстановки 8 == 8 в оцениваемую функцию. Отметим, что
в методе достаточных статистик наилучшая несмещенная оценка ищется дrlЯ
каждой функции т(8) независимо.
Продемонстрируем эффективность принципа инвариантности примерами.
224 rлава з. Теория оценивания неuзвестных параметр08 распределений
Пример 5 (Общая нормальная модель, о. м, п. функции распределения).
Пусть в условиях примера 1 требуется оценить параметрическую функцию
т(8) == РО{{ ХО} == ф ( Ха 81 )
(см. пример 7 в 3.3). Поскольку о. м. п. (j == (,Х, В), то по принципу инвари
антности о. м. п.
(7)
( Ха Х )
т == т(8) == Ф
(сравни с оценкой Т. в при мере 7 в 3.3, соотношение (17)). .
Пример б (Двумерная нормальная модель, о. м. п. ее параметров), Пусть
Х/ == (X II ,X 12 ), 1 == 1, ,n, независимые наблюдения над двумерной
случайной величиной == ({I, 6) с распределением
N (0,0), 11:;2 р;211).
rде и2 > О И Р Е ( I, 1) неизвестны. Здесь теоретическая плотность есть
(далее 8 == (и2, р))
1 { xi + x рх 1 Х2 }
f(x\, Х2; 8) == 2K и2 ехр 2и2(1 р2) + (72(1 р2)
(8)
(это частный случай общей формулы (9) 1.2). Найдем о. м. п. 0=2 и р. Здесь
плотность сложным образом зависит от параметров, поэтому удобно перейти
к новым параметрам q == (ql,q2), положив ql == ql(8) [2(72(1 /)] I
q2 == q2(8) == р[(72(l /)] \ Тоrда формула (8) перепишется в виде
f(Xl, Х2; q) == ехр {ql(X 2 + у2) + q2XY + Т(Ч)},
27r
rде T(q) == (1/2) (п (4q q ). Отсюда сразу получаем, что уравнения правдо
подобия для нахождения о. м. п. ql и q2 имеют вид
t(X;1 + Х;2) == дт(q) == ;ЧI 2 '
n / I дql 4ql q2
t X/IX/2 == д д т(q) == 4 2 Ч2 2 '
n / \ q2 ql q2
(9)
Но
2 2ql
(7
4q q '
q2
Р ==
2q\ '
3.5. Оцен/(и ма/(симальноzо правдоподобия
225
поэтому из соотношений (9) находим, что
n
2 1 "" 2 2 )
(J == L..,.(X/ 1 + X 12 ,
2п
/ I
n
2 L X/ 1 X/ 2
/ I
(10)
р== I1
L(ХЛ + Х?2)
/ I
.
Пример 7 (Лоrнормапьное распредепение, о. м. П. параметрических функ
ций). Пусть Х == (X 1 , ,Х n ) выборка из лоrнормальноrо распределе
ния, т. е. (см. п. 1 1.2) X i == еУ; , rде [е(:1';) Е N((}j, (} ). Построим О. м. п. ДJ1я
теоретических среднеrо и дисперсии этоrо распределения, т. е. (см. (8) 1.2)
ДJ1я функций
71((}) == ехр {(}I + (); }
2
И 72((}) == (е 1 1) ехр {2(}I + (}2}.
(11 )
k
Прежде Bcero отметим, что моменты ЕеХI можно вычислить следующим
образом. Поскольку характеристическая функция случайной величины У ! есть
(см. упр.26 к rл.l)
. { (}2t2 }
ф(t) == Eee'tY, == ехр it(}, + '
то
k kY; ( k ) { k2t2 }
ЕеХI == Еее I == Ф i == ехр kB, + 2 .
Orсюда ДJ1я 71((}) == ЕеХI и 72(0) == DeXI == EeX (EeXI)2 имеем Пред
ставления (11). Перейдем теперь к ПОС'J1l0ению оценок. Мы уже знаем о. м. п.
(61, 62) == (У, S(Y)), но Torдa по принципу инвариантности искомые о. м. П.
71 И 1) строятся сразу в соответствии с формулами (11):
{ S2(Y) }
71 == ехр У + '
72 == 712(e S2 (y) 1).
.
З. Метод накопления для приближенноrо вычисления о, м. п.
Оценки максимальноro правдоподобия в явном виде не всеrда удается полу
чить; в таких случаях прибеrают к приближенным методам решения ypaBHe
ний правдоподобия (коrда такие уравнения можно составить). Мы опишем
один из таких методов, который называется методом Ha М
етод накопления .-:
копленuя Фишера. Он заключается в следуюшем. Пусть Ф
ишера
О скалярный параметр и функция правдоподобия
L((}) == L(;!;.; (}) дважды дифференцируема по (). Разложим функцию вклада
V«(}) == V(;!;.; О) (см. (1) 93.2) в ряд Тейлора в окрестности точки (}о, BЫ
бранной в качестве начальноrо приближения для 6(;!;.) == 6, и вычислим это
15 За... 1748
226 ';lава З. Теория оценивания неизвестных параметров распределений
разложение при 8 == 8:
V(e) == V(Oo) + (О Oo)VI(o*),
(12)
*
rде О .некоторая промежуточнаяточка между О и 00' Но V(O) == о по опре
делению о. м. п. О, поэтому из (12) имеем
V (00)
0== 00 VI(O*)
Если заменить теперь в этом равенстве 0* на 00 и VI(Oo) на Ев V'(X; (0) ==
== ni(Oo) (см. соотношение (51) 3.2), то получим первое приближение
V(Oo)
01 == 00 + ni(Oo)
Теперь этот процесс можно повторить, взяв в качестве HOBoro начальноrо
приближения 01 и т. д. Таким образом, (k + 1) e приближение по методу
Ф
,. Рекуррента метода накопления вычисляют рекуррентно по ормуле
накопления
V(8/.;)
0/.;+1 == О/.: + ( {] ) '
nz и/.:
k == О, ,2,...
( 13)
Процесс вычислений продолжают до достижения желаемой точности:
101.:+1 0/.:1 < е. Важным в этом методе является выбор начальной точки 00.
Обычно в качестве 00 берут значение какой нибудь леrко вычисляемой co
стоятельной оценки (см. определение 3 в п. 3 2.2); тоrда все три точки 00,
*
О и О при больших объемах выборки n будут находиться вблизи истинноrо
значения пара метра. Метод накопления, как правило, быстро приводит к цe
ли, хотя в некоторых случаях этот процесс может и не сходиться.
Пример 8 (Модель Коши, оценка параметра по методу накопления), Пусть
Х == (х l ,... ,Х П ) выборка из распределения Коши К(О) (см. упр. 48 (б)
к rл.l).
Здесь функция вклада
n Xj О
V(O) == 2 1 + (Xi 0)2
И получить точное решение уравнения правдоподобия V(O) == о невозможно.
Функция информации i(O) для модели К(О) равна 1/2 (см. табл. 1 3.2),
поэтому последовательность (13) принимает в данном случае вид
2
(}/.:+I == 8/.; + V(8/.;), k == 0,1,2,...
n
В качестве начальноro приближения 80 здесь можно взять выборочную Me
диану , 1/2, которая в силу соотношения (15) 2.4 является состоятельной
оценкой теоретической медианы (1/2, совпадаюшей в данном случае с (). .
3.5. Оценки максиf.ЮЛЬНОi?О правдопод06ия
227
При мер 9 (Модель степенноrо ряда, метод накопления для нее). Эта модель
апределена в П.8 91.1. Из фармулы (20) 1.1 имеем для функции вклада
представление
V(O) == :0 In (е nх l n(O) Ц a(Xi») == п: n ( == n х :(O) ,
rде р,(0) теаретическое среднее (см. (23) 91.1). Таким образом, уравнение
прапдопадобия У(О) == о здесь имеет пид
р,( О) == х.
Вычислим функцию информации i(8). Имеем (см. (4), (5) 3.2)
. 2 1 2 1 0'2(0) р,'(0)
z(O) == E/JV (х,;О) == 02 Е в(Х, р,(0») == 02 D /JX, == 7" == о'
rде 0'2(0) теаретическая дисперсня (см. (23) 91.1). Если урапнение (14)
нельзя решить точно, то для приближенноrо определения значения о. м. п. О
можно применить метод накопления.
В частности, для усеченноro п нуле распределения Пуассона (см. (22)
91.1) функция 1(0) == еВ 1 и уравнение (14) принимает вид 0== х(1 e B).
1 (1 + O)e B
а функция инфармации равна i(O) == ( (J 2
О 1 с)
(14)
.
4. Асимптотические свойства о. м. п.
Метод максимальнаrа правдопадобия и вазникающие в нем аценки макси
MaтJbHora прапдоподобия никак не связаны с абсуждавшимися ранее свой
ствами несмещеннасти и оптимanьности аценок. Более Taro, в paCCMOTpeH
ных выше при мерах пычисления а. м. п. мы абнаружили, чтО' а. м. п. не всеrда
являются несмещенными аценками. Так из примера 1 следует, чтО' а. м. п. дис
персии O нармальной модели N(O" O ) является выборачная дисперсия 82,
каторая, как мы знаем, является смещеннай оценкай (см. п.3 9 2.2), OДHa
ка ее смещение Е и в 2 Oi == oi/n убывает с растом объема выбарки, т. е.
ана является асимптатически несмещенной. Тем самым, можнО' сказать, чтО'
свойстпа этой аценки «улучшаются» С упеличением числа наблюдений п. Это
абстаятельство имеет весьма общий характер, именно, Б 6 .,
" ольшие Bbl арки
О. м. п. обладают хорошими асимптотическими cвoиcтвa
ми для больших выборок. МажнО' сказать, что ширакае использование этих
аценок связано именно с их асимптатическими свайстпами, праявляющими
ся при неоrpаниченном накоплении данных.
О роли асимптатическою падхода (предельных теорем) в теарии пераят
настей и математической статистике уже вкратце rаварилась ранее (см. абщее
замечание в п. 1 1.2). Добавим еще к этаму, чтО' асимптатический подхад поз
валяет исследапать единым методам различные задачи и палучать при этам
достаточна общие результаты. Эти результаты 8 дanьнейшем Maryr использа
15*
228 rлава з. Теория оценивания неизвестных параметров распределений
ваться в задачах с выборками конечноrо объема, и TOrдa они рассмаlpИIJаются
как приближенные. Иноrда асимптотический подход ивляется еДИНСТIJенным
математическим подходом, позволяющим в конкретной статистической за
даче предлаrать некоторые процедуры и исследовать их свойства. При этом
(что очень существенно!) окончательные результаты удается получить в про
стой и наrлядной форме, и (что не менее важно) именно асимптотический
подход позволяет вскрыть rлубокую математическую сущность проблемы. Из
ложение асимптотической теории оценок максимапьноrо правдоподобия и co
ставляет дальнейшее содержание этоrо параrpафа. Чтобы подчеркнуп, зави
симость рассматриваемых ниже статистик от объема выборки, будем отмечать
их индексом n.
Коrда rоворят об асимптотических СВОЙСТIJах оценок (или СIJойствах для
больших выборок), то прежде Bcero имеют в виду их состоятельность. Это
СIJОЙСТВО нам уже встречалось ранее (см. определение 3 !J п. 3 2.2 и KOMMeH
тарии к нему). Дадим el'o общее определение в рассматриваемом контексте
и сформулируем простой, но важный, критерий состоятельности, обобщаю
щий критерий (23) 2.2.
Пусть Х == (X 1 ,. . ., Х n ) выборка из распределении .ею Е :F == {Р(х; 8),
В Е е}, rде параметрическое множество е в общем случае некоторый He
вырожденный открытый интервал в R r По определению, оценка Т" == Тn(Х)
для заданной параметрической функции т(В) назыllетсяя состоятелыlOй, если
при n ----+ 00
Р, )
Тn --------+ т(В ,
"18 Е е,
( 15)
т. е., каково бы ни было истинное значение парамеlpа 8, оценка Т" сходится
по вероятности (относительно распределения РО) к истинному значению oцe
ниваемой функции. Подчеркнем еще раз, что свойство состоятельности в CTa
тистических задачах ивляется обязательным для любоrо праIJила оценивания.
Е
,. Критерий состоя- ели статистика имеет конечную дисперсию, то
тельности оценки имеет место следующий критерий состоятельности.
Теорема 1. Пусть ЕоТn == т(В) + сп, DoT" == ОП и С11 == СП (В) ----+ О, б n ==
== б n (8) ----+ О при n ----+ 00 для всех 8 Е е. Тоrда Тn состоятельная оценка
функции Т == т(8).
Доказательство, Поскольку
JTn EoTnl ==1(T n т) + (Т E8Tn)l ITn тl IE8Tn TI,
событие {[Т" тl с} влечет событие {ITn EoTnl с [cnl}. Отсюда
по неравенству Чебышева имеем
po{ITn тl с} :::; P 8 {IT n ЕоТnl с [cnl} :::; (с б nl)2 ----+ О
при n ----+ 00 и всех 8 Е е. .
3.5. Оценки максимальноzо правдоподобия
229
С помощью этой теоремы во мноrйх случаях леrко доказывается состоя
тельность конкретных оценок.
Сейчас будет своевременным привести список
справочник основных предельных теорем теории
вероятностей о сходимости функций от случайных
величин, которые интенсивно используются в раз
личных статистических задачах, связанных со схемой (,больших выборок.
(пример одной из таких теорем нам встречался в п. 3 2.2 (теорема 1)).
предельные теоремы
теории вероятностей
Основные ,
Справочник предельных ,еорем (обозначения см. в п. 1 t 1.2)
р р
10 Если 1]n 1] И функция rp непрерывна, то "'(1]n) ---------+ '1'(1]), а также
"'(1]n) "'(1]).
20 Пусть {1]n, (n}, n 0= 1,2'...' последовательность пар случайных Be
личин. Torдa
р р р
а) 1]n (n о, (n ( ===} 1Jn (;
р с с
б) 1]n (n о, (n ( ===} 1Jn (;
с р р
в) 1Jn 1]. (n о===} 1]n(n о;
с р с
r) 1]n 1], (n С 0= сопst ===} 1Jn + (n 1] + С,
с с
1Jn(n С1], 1]n/(n 'fJ/ C при С i= о;
р с
д) 1]n (n о, (n (,
р
функция rp непрерывна ===} ip(1]n) "'«(n) о.
з О Пусть Тn == Тn (Х) оценка скалярноrо параметра 8 такая, что
l-e (';n(T n 8)) N(O, 0'2(8))
(или, '/то то же, l-е(Тn) '" N(8, О'2(8)/n)) при n 00 и всех 8 Е е. Пусть,
далее, функция rp дифференцируема и ip' i= о. Тоrда
l-е(.;n(ip(Тn) ip(8))) N(o, Irp'(8)]20'2(8)); (16)
кроме Toro, если "" (8) и 0'(8) непрерывны, то
( ",(Тn) "'«()) )
Le .;n ip'(Tn)O'(Tn) N(O, 1).
40 (аналоryrверждения з0 для случая BeKTopHoro параметра 8 == (81,.. ,8 r )).
Пусть 'l.n 0= (T 1n , ,Trn) оценка пара метра 8, удовлетворяющая
условию Le(';n('l.n 8)) N(Q, Е(8)) при n 00 и всех 8 Е е. Тоща для
любой дифференцируемой функции '1' от r переменных
(17)
l-e( ';n(rp(1:n) ",(8))) И(О, v 2 «()))
( 18)
230 rлава 3. Теория оценивания неизвестных параметров распределений
при условии, что v(O) =1= о, rдe
v 2 (0) == 1].1 (O)L(O)1].(O) И Q(O) == ( д; ) ,
arp(o» ) .
дОт '
если, кроме Toro, функция rp непрерывно дифференцируема, и все элементы
дисперсионной матрицы (O) непрерывны по (), то
{е ( yIn(rp n) rp(())) ) N(O, 1).
(19)
Вернемся к оценкам максимальноro правдоподобия и сформулируем их
основные аСИМПТОТИ'lеские свойства. Будем предполаrать, что модель :F яв
ляется реrулнрной в смысле 3.2, а функция праlJдоподобия Ln(f.; 8) при
всех n 1 и ;f Е :r имеет лишь один локальный максимум по 8, лежа
щий внутри е, и притом достижимый (Т. е. о. м. п. 8п существует и совпадает
с локальным максимумом). Кроме TOro, плотность f(x; О) трижды дифферен
... Асимптотические цируема по О и при этом существует не зависящая от О
свойства о. м. п.: функция М(х) такая, что для всех О Е е
I дЗ In f(x; О) I
aO i дО) aO k М(х), ЕвМ({) < 00 (i,j, k == 1'...' т).
Теорема 2. П сть выполнены перечисленные условия. TorAa:
1) о. м. п. 8п является состоятельной оценкой пара метра о;
2) эта оценка асимптотически нормальна, именно, при n ---+ 00
{е( vn(8n ()) N(Q, 1 1(0»),
(20)
rAe 1(0) информационная матрица модели, определенная в (21) 3.2;
кроме тощ если т(8) непрерывно дифференцируемая функция от О
и :;:;1 == т(8п) ее о. м. П., то при n ---+ 00
.се (vn(r,; T(O»)) N(O,O';(o)),
(21 )
если
0';(0) =1= О, rAe 0';(0) == !/(0)1 1(0)!!.(0), 1].(0) == ( д; ) ,
более тощ если функция 0';(8) непрерывна по 8, то
Le ( yIn(r n =Т(8)) ) ---+N(o,l);
О'т(Оп)
З) является асимптотически эффективной оценкой т(О) (в смысле П.5
р.2».
дт(О) )
д()т '
(22)
3.5. Оценки максимаЛЬНО20 правдоподобия
231
Выделим специально случай скалярноrо параметра, ввиду ero особой pac
пространенности в приложениях. Для этоrо случая соотношения (2U} (22)
принимают соответственно вид
С 8 (J1i(8 n В») N (о, i( ) ) ,
( 'Т'(8)Р )
C 8 (J1i(T n т(В»)) N о, i(8)
(23)
(24)
и
L, ( JП , ) #(0, 1) 125)
Т/(В n ) i(B,,)
(здесь i(B) функция информации, определенная в (5) и (5') 3.2, и т' (8) -::? ().
Доказательство. Приведем доказательство асимптотической нормальности
(23). Для этоrо разложим функцию вклада V,,(B) == Vn(X; В) В рид Тейлора
в окрестности истинной точки В и вычислим это разложение в точке 6"
, ' 211.
0== Уn(В,,) == Vn(B) + (В,. В)Уn(В) + (Bn В) У ,. (В ),
2
rде В. некоторая промежyroчная точка между (J и 8... Это равенство можно
записать в виде
с Vn(B) ( V (B) )
Уn(Вn В) == vii i(B) n i(B) + Е,.
(26)
rде
I вl IV '(B')I 18n (JI n .
'Еn' 2ni(B) '" 2i(B) n М(Х).
Поскольку 8п В, из условия на функцию М на ОСНОlJани и свойства 20 в)
р
следует, что Еn О. к величине
' ( 82 In f(X j ; (J)
V" В) 8В2
n n j 1
применим закон больших чисел, соrласно которому (см. (5') 3.2) эта Be
личина сходится по вероятности к i(B), следовательно, все выражение в
знаменателе в (25) сходится по вероятности к 1. К случайной же величине
Vn(B) == ( t д!п f(X j ; (J» ) 1
Jn i((J) j 1 80 Jn i(O)
применима центральная предельная теорема, по которой в силу соотношений
(3) и (5) 3.2 при n 00 эта величина асимптотически нормальна N(O, i l(o».
232 rлава з. Теория оценивания неUЗ8естных параметр08 распределений
Отсюда и из (26) по свойству 20 r) следует, что такое же предельное распре
деление имеет и vn (оп О).
Утверждения (24) и (25) следуют из (23) на основании свойства з0
Наконец, утверждение об асимптотической эффективности оценки т п
следует из Toro, что величина ео(7';,; 8) в (14) 3.2 тождественно равна 1. .
.... ''''
.,.. Комментарии
к свойствам о. м, П.
Добавим некоторые комментарии к изложенным pe
зультатам. Факт асимптотической нормальности о. м. п.
это очень сильный результат. Например, утвержде
ние (24) rоворит о том, что для больших выборок распределение о. м. п.
Т п концентрируется BOKpyr истинноrо значения оцениваемой параметриче
ской функции т(О) (предельное распределение имеет среднее значение т(О)),
и степень этой концеН11Jации, характеризуемая асимптотической дисперсией
[т'(О)Р
( ) ,возрастает с ростом объема выборки n. Это можно интерпретировать
ntO
так, что оценка 7';, является асимптотически несмещенной и среди всех таких
оценок обладает наименьшей асимптотической дисперсией, т. е. она является
асимптотически эффективной. При этом, однако, надо иметь в виду, что сама
оценка Tn может вообще не иметь моментов, т. е. т(О) может не быть асимпто
[т'(8)р
тическим значением среднеrо Евтн, а ( ) асимптотическим значением
n t 8
D ( " с.
дисперсии ВТ п В теории вероятностеи известно, что из сходимости 1]п 1],
вообще rоворя, не следует сходимость соответствующих моментов).
Рассмотрим, например, задачу оценивания параметрической функции
т(О) If() в пуассонвской модели П(О). Здесь, как уже отмечалось в п. 1,
о. м. п. 'о == х: поэтому О. м. п. Т п == 1/ х: и дня нее соотношение (24) прини
мает вид
LB(Vn(Tn O I)) N(O,8 J), 'V(»O.
"в
В то же время [в(nХ) == П(nО) (см. п. 3 1.1), откуда Рв{Х == О} == е > О.
Таким образом, с положительной вероятностью Х принимает нулевое значе
ние и поэтому статистика Т п ни при каком n не имеет конечных моментов.
Тем не менее ДIlЯ больших выборок (при n -----t 00) среднее и дисперсию
аппроксимирующеrо нормальноrо закона распределения можно трактовать
как среднее и дисперсию самой оценки и rоворить о ее свойствах несмещен
ности и оптимальности в асимптотическом смысле.
Далее, определение асимптотически эффективной оценки предполаrает,
что невозможно построить оценку с меньшей асимптотической дисперсией.
Как правило, это имеет место для реrулярных моделей, удовлетворяющих
условиям, при которых справедлива теорема 2, хотя существуют и исключения,
как это видно из приводимоrо ниже при мера 10. Для нереrулярных моделей
(коrда неприменимо неравенство Pao KpaMepa) асимптотическая дисперсия
о. м. п. может иметь порядок, больший n l. Так, из результатов примеров 5
3.5. Оценки максuмаЛЬН020 правдоподобuя
2ЗЗ
3.2 и 3 следует, что для равномерной модели И(О, О) О. м. п. ОП == Х(n) имеет
2
дисперсию, порядок которои n
Пример 10 (Нормальная модель с неизвестным средним, сверхэффективная
оценка ее параметра). Пусть Х == (Х" ... , Х n ) выборка из N(O, 1). Тоrда
о. м. п. ОП == Х и [,е(Оn) == N(O, I/n). Рассмотрим оценку
{ Х при IX'? аn,
Тn
ЬХ при IXI < аn,
rде константа а n -----+ О, но v'ria n -----+ 00 при n -----+ 00. Найдем предельный закон
распределения этой оценки. Имеем
Р8{ v'ri(Tn O) :( х} == Рn Р8{ v'ri(X O) :( х}+(I Pn) Р8{ v'ri(bX 8) :( Х},
rде
Рn == P8{IXI ? аn} == Ф( v'ri(0 а n ))+
{ I при 181 > О,
+ Ф( J7i(8 + аn))
n oo О при О == О.
Таким образом, при n -----+ 00 для 181 > о и О == О соответственно имеем
[,e(v'ri(Tn 8)) N(o,I), [,o(v'riTn) N(0,b2)
или [,8 (Тn) "" N (о, o-j.(о)/n) , rде
{ I при 101 > о,
o-j. (8) == Ь 2
при 8 == О.
Следовательно, ее асимптотическая эффективность (14) 3.2 (см. табл. 1 3.2)
есть
1 { 1 при 18[ > О,
ео(Т II ; 8) == aj.(8) == b 2 при 0==0.
При 'ы < 1 ео(Тn; 8) ? I со строrим неравенством в точке 8 == О, т. е. Тn
сверхэффективная оценка. Причина этоro заключается в данном случае в Ha
рушении непрерьшности функции o-j.(О) в нуле.
Точки О, в которых ео(Тn; О) > 1, называют точ
камu сверхэффектUВlfостu. В рассматриваемом примере
это точка 8 == О. Как показал Ле Кам (1953) множество
точек сверхэффективности не более, чем счетно, поэтому явление сверхэф
фективности не иrрает существенной роли в теории оценивания. Известны
также дополнительные условия реryлярности на статистическую модель, KO
торые исключают это явление. Так, С. Р. Рао доказал, что для этоro достаточно
потребовать равномерности по параметру 8 в предельном соотношении
[,8(Т n ) "" N (Т(8), O-j. 8) ), V О Е е.
Сверхэффективная .
оценка
234 rлава з. Теория оценuвания неизвестных параметр08 распределений
Приведем пример, иллюстрирующий роль свойства реryлярности модели:
при ero нарушении о. м. п. не являются асимптотически нормальными. .
Пример 11 (Равномерная МОАель, распределение О. м. п. ее параметра).
Пусть Х == (Х [, , Х п ) выборка из распределения ЩО, 8). Torдa о, м. п.
8 п == X(/I) , а как было показано в 2.4, экстремальные значения выборки
не являютсл асимптотически нормальными. В частности, в рассматриваемом
случае, из примера 6 2.4 имеем (поскольку [0((/8) == Що, 1))
po{n( I) x} ex х<о.
.
в заключение этоrо пункта применим изложенную теорию о. м. п. К по-
линомиальной модели M(n;PI,'" ,PN) (см. при меры 10 в З.2 и 8 в З.3).
Пример 12 (Полиномиальная модель, о. м. п. для нее). Здесь функция прав-
до подобия
N
L(B) == П p i, 8 == (Pl," ,PN I),
i=1
поэтому уравнения правдоподобия имеют вид l/i/Pi VN /PN == О, i == 1,. .,
N 1. Они определяют единственное решение pi == Vi/n, i == 1,. .. ,N 1,
максимизирующее функцию правдоподобия, следовательно, о. м. п. 8/1 ==
== (v)/n, ,vN I/n), т. е. выражается через полную достаточную статистику
(V), ,1IN I) (см. пример 8 в З.З). Подчеркнем, что о. м. п. вероятностей Pi
являются относительные частоты Vi/n реализаций соответствующих исходов
в n испытаниях. Информационная матрица модели вычислена в примере 10
в 3.2, rде также указана обратная к ней матрица r. N 1. В данном случае все
условия реryлярности выполняются, следовательно, по теореме 2
[о( vп(8 п 8)) ---4 N(Q, EN I) при n 00,
(27)
или
( V. П Р '
r * , I
ч!!.=..;n ,
i== 1,.. ,N 1) N(Q,r.N I)'
Этот результат есть центральная предельная теорема для полиномиальноrо
распределения M(n;PI, ,PN), сформулированная в упр.33 к rЛ.I. .
5. Асимптотические доверительные интервалы,
основанные на О. м. п.
Основное значение утверждения теоремы 2 об асимптотической нормально-
сти оценок максимальноrо правдоподобl1Я состоит в том, что оно позволяет
сконструировать универсальный алrоритм построения доверительных интер-
валов и доверительных множеств (в случае DeKTopHoro параметра) как дЛя
caMOro параметра модели, так и для произвольных достаточно хороших пара-
метрических функций. С подобной задачей мы уже встречались в п. 5 2,2,
3.5. Оценки максимальноzо правдоподобия
235
rде на основании теоремы об асимптотической нормальности выборочных MO
ментов и функций ОТ них бьиlИ построены асимптотические доверительные
интервалы Дf1я теоретических моментов и функций от них. Общее определе
ние , доверительноrо интервала Дf1я заданной теоретической характеристи-
ки наблюдаемой случайной величины дано в (26) 2.2. Коrда мы работаем
в рамках параметрической модели :F == {Р(х; О), О Е е}, ТО оно конкрети
зируется следующим образом: 'У доверительным интервалом для параметри
ческой функции т(О) называется такой случайный интервал (T1(X), Т 2 (Х») ,
ТI < Т2, который удовлетворяет условию
Pe{Tl(X) < т(О) < Т 2 (Х)} " v О Е е.
(28)
Расчет таких интервалов на основе теоремы 2 (в этом случае мы будем rоворить
об асимптотических доверительных интервалах) осуществляется по той же
схеме, что и в п. 5 2.2. Именно, на основании (22) имеем, что при n 00
и всех (J
если с.у == ф I«l + ,)/2). Переписав это COOTHO
шение в Dиде
{ vnJTn т(О) I }
Ре < с.у Ф(с.у) Ф( с.у) == 2Ф(с.у) I =="
О'т(Оп)
Асимптотический дове-
рительный интервал:
общее решение
.
Jt'
{ с.уО'т(Вп) ( ) с.уО'т(Вп) }
Р д Т'I vn < т О < тп + vn "
(29)
получим, что (Тп =F c.yO'r(Bn)/v'n) И есть искомый асимптотический , ДOBe
рительный интервал для т(О). Центр этоrо интервала находится в случай-
ной точке Тп == т(вп), являющейся о. м. п. для т(О), и он имеет случайную
ДlIину 2c.yO'r(B n )/v'n. При этом, поскольку Тп асимптотически эффектив
ная оценка т(О) , то построенный интервал будет асимптотически кратчайшим
среди всех подобных интервалов, порождаемых аналоrичным образом друrи
ми состоятельными и асимптотически нормальными оценками функции т(О).
Выделим также представляющие самостоятельный интерес частные случаи об
щеrо результата (29).
Если О скалярный параметр, то из (23) сле
дует, что асимптотически кратчайшим , довери
тельным интервалом Дf1я Hero является интервал
Асимптотический ДOBe Jt'
рительный интервол:
сколярный парометр
( с.у С.У )
ОП , оп + ,
V n i(Bn) V n i(Bn)
с.у == ф l С:' )
(30)
Более Toro, если т(О) непрерывно дифференцируемая функция и т'(о) i- о,
то (Тп =FC-ут'(Вп)/ vni(В п » ) аналоrичный интервал для т(О).
236 rлава з. Теория оценивания неизвестных параметров распределений
Преобразование,
стабилизирующее
дисперсию
Если функция т выбрана так, что
т'(О) J r;;;;;
Y'i(В) == а == const, или т(О) == а V i(O) dO,
(31 )
то в этом случае асимптотическая дисперсия о. м. п. Т п не зависит от неиз
BeCTHoro параметра (такую функцию называют преобразованием, стабилизuру
ющим дисперсию) и вид соответствующеrо интервала значительно упрощается:
(т п 4 ac,!,JТi) , т. е. он имеет фиксированную длину. Так как функция т MO
нотонна (ведь т'(О) -1- О), то неравенства
ас, ас,
т п ..;n < т(О) < т п + ..;n
можно разрешить относительно О и получить 1' доверительный интервал для
caMoro параметра О. Например, если т' (О) > О, то
1 ( ас, ) 1 ( ас, )
т т п ..;n < о < т т п + ..;n ,
(32)
rде т l обратная функция к т Использование таких интервалов в ряде слу
чаев предпочтительнее, нежели (30).
Продемонстрируем эти общие принципы Прl1мерами.
Пример 13 (Общая нормальная модель, доверительный интервал для Teo
ретической функции распределения). Построим приближенный (асимпто
тический) доверительный интервал для парамеТРИ'lеской функции т(О)
== Ф (Ха Ol)!02) в модели N(OI, O ) (см. (7)). О. м. п. Т п указана в при мере 5,
поэтому нам достаточно вычислить величину (J;(O) 13 (21). Информационная
матрица нашей модели вычислена в примере 9 в 3.2 (соотношение (25)).
Используя этот результат находим
2 ( ) == [( дТ(О) ) 2 ( 8T(O) )] 2== [ (Xa OI)2 ] { (Xa OI)2 }
(J т О дО 1 + 2 дО 2 02 271' 1 + 20i ехр O
Итак, искомый 1' доверительный интервал есть
(т(Оп) =F с,1") ) ,
rде Оп == (Oln, 02n) == (.Х, S). .
При мер 14 (Доверительный интервал для параметра модели степенноrо
ряда), Функция информации i(O) для этой модели вычислена в примере 9.
Используя этот результат и общее соотношение (30), имеем для искомоrо
асимптотическоrо r доверительноrо интервала для О представления
( ) ( оп )
Оп =F с,у == Оп =F С, (J(On)";n ,
(33)
g 3.5. Оценки максимаЛЬНО20 правдоподобия
237
rде Оп решение уравнения р(8) == Х, а р(8) и (]'2(8) теоретические
среднее и дисперсия соответственно. .
Пример 15 (ПуаССОНО8СКая модель, доверительный интервал для параметра).
Поскольку пуассонвская модель является моделью типа степенноro ряда и для
нее р(8) == (]'2(8) == 8, то из (33) имеем, что в данном случае асимптотиче
ский 'У доверитеЛЬНblЙ интервал для (J есть (х =F ey Jx/n ) Далее, ypaB
нению (31) удовлетворяет здесь функция т(О) == ..;о при а 1/2 (ведь
i(8) == 1/8, см. табл. I 3.2), а соответствующий интервал дIIЯ нее есть
(УХ =F ey/(2Vn)). Отсюда по формуле (32) получаем друrой доверитель
НblЙ интервал дIIЯ 8:
((Л 2 У (Л+ 2 У)'
КОТОРblй совпадает с преДblДУЩИМ, если пренебречь членами порядка n I .
Пример 16 (rеометрическая модель, доверительный интервал для пара-
метра). Оценим парпметр (J rеометрической модели Bi (l, 8). Это также MO
дель типа cTeneHHoro ряда, поэтому применимо общее решение (33). Здесь
(см. (7) 1.1) р(О) == 8/(1 8), (]'2(8) == 8/(1 0)2 решением уравнения
правдоподобия р(8) == Х является о. м. п. Оп == Х /( 1 + х), поэтому искомый
'Y-доверитеЛЬНblЙ интервал имеет вид
(о. Н.,(I о.) {; ) с: х 'f "' V п(1 X)' )
.
Пример 17 (Бернуллиевская модель, асимптотический доверительный ин-
тервал ДЛЯ параметра). В рассматриваемом случае о. м. п. -вп == Х и функция
информации i (8) == [8(1 8)] I (см. табл. 1 3.2), поэтому из (30) имеем,
что (X=Fey J X(I Х)/n ) асимптотический 'У доверительный интервал
дIIЯ 8 Решением уравнения (31) является здесь функция т( 8) == arcsin ..;о при
а == 1/2, поэтому соответствующий интервал дIIЯ нее есть (Т(Х) =F 2 )
Если воспользоваться соотношениями (32) и при этом пренебречь членами
порядка n 1 то получим преДblдущее решение для 8 (это мь! npeдllaraeM
про верить читателю самостоятельно). .
В случае BeKTopHoro параметра 8 == (81," ., 8r) Доверительные области: ..,.
может представлять практический интерес довери мноrомерный параметр
тельное оценивание caMoro этоro вектора. В этом
случае нужно указать такое случайное (т. е. зависящее от Вblборки Х) под
множество Q7(X) в параметрическом множестве е рассматриваемой модели,
238 rлава 3. Теория оценивания неuзвестных параметров распределений
которое накрывает истинное значение неизвестноro параметра О с вероятно
стью, не меньшей заданноrо доверительноrо уровня,. т. е. чтобы выполнялось
соотношение, аналоrичное (28):
Ро{О Е Q'Y(X)} " 'r/ О Е е.
(34)
Такое подмножество Q1(X) С е называется , доверuтелы/йй областью для О.
В случае реryлярных моделей, удовлетворяющих условиям теоремы 2, для
больших выборок леrко построить приближенные доверительные области,
основанные на оценках максимальноrо правдоподобия. Для этоro надо BOC
пользоваться следующим утверждением, представляющим собой асимптоти
ческий вариант результата, сформулированноro в упр.40 к rл. I (см. также
Замечание в п. 2 2.5): если ДТIЯ k MepHoro случайноro вектора выполняет
n
СЯ асимптотическое (при n ----t 00) соотношение С({ ) '" N(/l ,Еn) и IEnl i О
n n
при всех n, то
с( ({n JE I ({n !!.J) X2(k).
В силу этоrо утверждения из (20) имеем, что квадратичная форма
(35)
Qn(O) == n(о n O)I(O)(ii n О)
(36)
при всех () имеет предельное при n ----t 00 распределение i(r). Более тo
ro, если информационная матрица 1(0) непрерывна по О, то на основании
утверждения 40 можно заключить, что в (36) [(О) можно заменить на [(о n )
с сохранением при этом формы предельноro распределения. Итак, при BЫ
полнении указанноrо условия имеет место предельное соотношение
Lo ( Qn (О) == n(Оn о)' I(Оn)(Оп О)) х2 (т).
(37)
Пусть, как обычно, X ,r обозначает , квантиль распределения х2(т). Тоrда
из (37) имеем, что при n ----t 00
РО{ Qn(O) :;:;; X;,r} ,.
(38)
/, 'АСим';;"ici +: 'ескиЙ" Be
...
,.. рительныи эллипсоид для
параметра реryлярной
модели
Определим теперь область Q'Y(X) С е условием
Q1(X) == {о Qn(O):;:;; X , r} (39)
Это есть некоторый случайный эллипсоид с цeH
тром в точке ОП и, по построению, при n ----t 00
Ро{О Е Q1(X)} == РО{ Qn(O) :;:;; X ,r} "
т. е. Q'Y(X) есть асимптотическая , доверительная область ДТIЯ О
Пример 18 (Доверительная область для параметров полиномиальной MO
дели). Если в полиномиальной модели M(n;PI, ,PN),O==(Pl," ,PN I),
число испытаний n велико, то для одновременноro оценивания неизвестных
3.6. Друzие методЬ! и принциПbl построения оценок 239
вероятностей Pi можно воспользоваться изложенной асимптотической теори
ей. Все предварительные вычисления нами уже проведены в при мере 12 и при
мере 10 в 3.2, используя которые вычисляем квадратичную форму в (37):
N I N I
Qn(8) == n L (jj; Pi)(Pj Pj)PN 1 + n L(iJi Pi)2Pi 1 ==
',j 1 i=1
[ N I ] 2
)lIi nPi)
I I
/lN
+ I: (/li nPi)2 == t (lIi nPi)2
i 1 /li i 1 /li
(40)
При этом параметр r в (37) равен здесь N 1. В результате искомая область (39)
может быть записана в виде
У,(Х) == У i С1д == { (Pl,
N ( ) 2 N }
/li nPi 2
,PN) L . X"N I'LPi==l.
i=1 i=1
(41)
Эrа область представляет собой пересечение N MepHoro эллипсоида с центром
в точке!!.. == (/11, , lIN) С rиперплоскостью РI + + PN == 1.
Если N == 2, то речь идет об оценивании параметра бернуллиевской
модели Bi(l, 8) по n испытаниям, и леrко видеть, что область (41) сводится
к интервалу, построенному в примере 17. .
t З.б. Друrие методы и принципы построения оценок
ПравилыlO в философии рассматривать сходство
даже в вещах, далеко отстоящих дру;! от друzа.
Аристотель 5)
Кроме рассмотренных в предьщущих параrpафах общих подходов дЛЯ оцени
вания неизвестных параметров распределений на практике используют и дpy
rие методы построения оценок. В настоящем параrрафе мы лишь кратко
затронем соответствующие проблемы, чтобы показать их мноrообразие и oд
новременно расширить rоризонты дЛЯ 'Цiтателя.
1. МеТОА моментов
Исторически первым общим методом точечноrо оценивания неизвестных па
раметров является метод моментов, предЛоженный К. Пирсоном (1894). Cyrb
этоrо метода состоит в следующем.
Пусть, как обычно, Х == (X 1 ,..., Х П ) выборка из распределения
.ею Е F == {F(x, 8), 8 Е е}, rдe 8 == (81, ,8r) и е R r Предположим,
5) Аристотель (384 322 rr. ДО н.э.) древнеrpeческий философ, ученый-энuиклопедист.
240 rлава з. Теория оценивания неизвестных параметров распределений
что у наблюдаемой случайной величины существуют первые r моментов
k
O:k == E k == 1, ,Т ОНИ ЯВЛЯЮТСЯ функциями от не известных парамет
ров В: O:k == O:k(B). Рассмотрим соответстоующие выборочные моменты (;k
(см. п. 1 2.2) и составим систему уравнений относительно В:
O:k(lJ) == (;k, k == 1,. , r
(1)
Предположим, что эта система однозна'IНО разрешима и обозначим ее реше
ние == (X) == It'j((;I, ,(;r), i == 1, ,Т Тоrда '8 j , ,8,. и есть оценки
.... О параметроо BI, , IJ r по методу моментов. Если функ
..,. ценки по методу .
" ции It'j, t == 1, ,Т, непрерывны, то из состоятельно
моментов ' ::i;;.'.
сти выборочных моментов (см. п. 3 2.2) по теореме 1
2.2 следует, что статистики ё;(х) являются состоятельными оценками IJj:
при n ----+ 00
р
Bj(X) lt'j(O:I,' ,00r)==lJj, i==I,.. ,Т
Таким образом, метод моментов при определенных условиях приводит к co
стоятельным оценкам; при этом уравнения (1) во мноrих случаях просты
и их решение (8 отличие, например, от метода максимальноrо правдоподо
бия) не связано с большими вычислительными трудностями.
При мер 1. Пусть .ею Е N(IJ) , IJ ). Зд есь О:! == Е{ == IJ\, B == Щ == 0:2 O: ,
поэтому '81 == (;1 == х: '82 == J (;2 (;i == 8, т. е. ('81,82) совпадает с оценками
максимальноro правдоподобия ( , 8;) == (Х; 8) (см. пример 1 3.5). .
Пример 2. Пусть .ею Е U(B 1 , IJ 2 ), Здесь
ВI + IJ 2 lJi + IJ)IJ 2 + IJ
0:1 == ' 0:2 == 3
и система (1) имеет решение 81 == Х v3 8, '82 == Х + v3 8. Эти оценки
не являются функциями достаточной статистики (Х(!), х(n)) (см. пример 3
3.3), поэтому они мало эффективны. .
Пример 3 (rамма модель, оценивание параметров методом моментов), Пусть
.ею Е r(B\,B 2 ) (см. п.3 1.2). Здесь е == {В == (1J 1 ,B 2 ) IJ j > О, i == I,2}
и O:k == Btr(1J 2 +k)jr(B 2 ) == IJtB2(1J2+1) (1J2+k 1), 13 частности, 0:1 == 1J 1 1J 2 ,
0:2 == IJтВ2(1J2 + 1). Система (1) имеет здесь решение
( ) (;2 (; 82 (;i Х 2
Вl Х == в 2 (х) == 2 8 2 .
0:1 х' 0:2 0:1
rамма модель с двумя незвестными параметрами весьма сложна ДЛЯ анализа
какими нибудь друrими известными нам методами, метод же моментов быст
ро приводит К простым формулам для оценок ее параметров. .
Отметим, что метод моментов неприменим, коrда теоретические моменты
нужноrо порядка не существуют (например, для распределения Коши). Кроме
Toro, оценки метода моментов, вообще rоворя, мало эффективны, поэтому
З.б. Друzuе методЬ! u nринциnЬ! построения оценок 241
их обычно используют лишь в качестве первых приближений, основываясь
на которых можно находить последующие приближения с БОльшей эффек
тивностью.
2. Метод минимума хи нвадрат
Систему различных методов построения оценок можно получить, KOHCTPy
ируя тем или иным способом меру D отклонения эмпирической функции
распределения -Рп(х) от Р(х; О) истинной (но неизвестной) теоретической
функции распределения выборки. В любом случае такая мера является функ
цией от выборки (данных) Х и неизвестноrо параметра о: D == D(X; О). Если
такая мера сконструирована, то в качестве оценки параметра 8 естественно
взять значение, минимизирующее меру D: О(Х) == arg miп D(X; О).
(J
Одной из наиболее известных таких мер является предложенная К. Пирсо
ном мера xи Kвaдpaт. Эта мера конструируется следующим образом. Разобьем
множество & возможных значений наблюдаемой случайной величины на N
непересакающихся подмножеств (<<интервалов»)
[" ... ,&н ([ == &, U. U &н, [i n &з == g, i i= j),
и пусть Vj число элементов выборки Х == (Х" .. . , Х п ), попавших в ин
тервал [j:
n
Vj == 2:I(Xi Е [j), j == 1,..., N (VI +
i='
Обозначим, далее, через Pj(O) теоретическую вероятность попадания в &з:
+ VN == n).
Pj(O) == Pe{ Е [j} == f dF(x;O), j == 1.... ,N (Р,(О)+...+РН(О) == 1).
f.j
Поскольку относительная частота Vj/n попадания в интервал [j явля
ется состоятельной оценкой вероятности pj(8), то одной из возможных мер
отклонения эмпирических (выборочных) данных от теоретических значений
может быть мера
N 2
D== СЗ( Рз(О»)
J=l
rде С" , Сн некоторые «веса».
Если здесь положить «веса» С] == n/Рз(О) , то мы и получим меру хи квад
рат:
N 2 N ( ( ») 2 N 2
2 n ( Vj ) Vj nPj 8 v j
Х == 2: р. ( О ) ;: pj(8) == пр (О) :L пр (О) n. (2)
J= I J ]=1 J J= 1 J
Выбор именно таких «весовых» коэффициентов в D оправдан тем, что, как это
будет показано позже (см. П.2 и 3 Э 4.2), полученная при этом мера хи квад
рат (2) обладает следующим замечательным свойством: ее асимптотическое
lБЭа..э 1748
242 rлава з. Теория оценивания неизвесmНbfХ nараметров распределений
распределение для больших выборок (при n (0) зависит лишь от числа N
интервалов (подмножеств) разбиения и является стандартным распределени
ем хи квадрат.
Оценка по методу
2
минимума Х
Оценку 8, полученную из условия обращения меры
i в минимум, называют оценкой по методу минимума
2
Х При достаточно общих условиях эта оценка оказы
вается состоятельной, асимптотически нормальной и асимптотически эффек
тинной (как и оценка максимальноro правдоподобия).
Для нахождения указанной оценки надо решить систему уравнений
N 2
L QPj(O) == о k == 1,
. РЧо) дО!: '
з 1 J
Однако это трудно сделать даже в простейших случаях, поэтому, учитывая,
что
, r
(о == (О"
,8r}) .
V' Р
1 j==I,...,N,
nPj (()) n.....оо '
эту систему обычно заменяют более простой системой
N
,, opj(8) == О,
L..J ( ) k== 1,. ,Т,
j=1 Pj 8 88k
решение которой находить, как правило, rораздо проще. Оцен\<и парамет
ров 8, получающиеся как решение системы (3), называют оцеНКОАfИ по видo
2
измененному методу минимума Х ; для больших выборок их асимптотические
свойства остаются такими же, как сказано выше.
Замечание. В описанном методе оценивания параметров используются не сами Ha
блюдения X 1 ,... , Х П ' а лишь 'Iзстоты !!. == (VI, .. . , VN) попадания элементов BЫ
барки в соответствующие подмножества &1, ." '&N Такой «'l3стотный,) способ пред
стаоления статистических данных называют методом сруппировки наблюдений, а под
множества [1,' .. ,[N подмножествами (или интервалами) rруппировки. При этом
. распределение вектора частот!!. == (VJ, . . . , V N) является, очевидно, полиномиальным
, распределением М (n; Р1 (О), ,PN(O)) (см. п. 6 1.1). В этом контексте вероятность
N
P{v==h}=L(I)(h'O)== n! П рhj(О) hl+ +hN==n, (4)
8 , hl!...h N '. ] ,
]=!
(3)
называют частотной функцией правдоподобия в методе zpynпupoBKlI наблюдений (в oт
rl
личие от обычной функции правдоподобия L(;f.; О) П f(Xi; О)). Если искать
;=1
оценку параметра О по методу максимальноrо правдоподобия, основываясь на функ
цИИ L(J) (!!; О), т. е. искать ее точку максимума, решая систему уравнений
д In L(I)(!!; О)
aO k ==0, k==I,...,r,
то, как леrко видеть, эта система сводится к системе (3).
9 З.б. Друzие методbl и принциПbl построения оценок 243
3. Модально несмещенные оценки
До сих пор мы в основном рассматривали несмещенные оценки, т. е. такие
статистики О(Х), которые удовлетворяют условию (если оценивается сам па
раметр 8)
Евб(Х) == (J, V (J Е в.
в силу TOro, что математическое ожидание случайной величины часто Ha
зывают средним значением, несмещенную оценку б(Х) называют также He
смещенной в среднем. Однако в статистике используются и друrие понятия
несмещенности, в частности, модальной несмещенности и медианной He
смещенности, в основе определений которых лежат такие характеристики
статистической оценки, как соответственно мода и медиана. Их мы кратко
и обсудим в этом и следующем пунктах. Остановимся сначала на понятии
модальной несмещенности.
Пусть Х случайная величина с плотностью f(x), х Е R 1 . Любая точка
максимума функции f(x) называется модой случайной величины Х (ее закона
распределения). Если плотность зависит от параметра: f(x) == f(x; (J), (J Е в,
то и мода, вообще rоворя, зависит от (J. Если мода единственна, то распре
деление величины Х называют унимодаль//ым. Унимодальные распределения
иrpают важную роль в теории вероятностей и математической статистике.
Примерами таких распределений являются нормальное, показательное, Пуас
сона, Коши и др. распределения.
Пусть оценка О(Х) параметра (J имеет унимодальное pac
пределение и x((J) (каппа от тэта) ero мода. Если x((J) == (J при всех
(J Е е, то О(Х) называется модально несмещенной оценкой параметра (J.
Такие оuенки MOryr оказаться предпочтительнее друrих при некоторых
функциях потерь. Здесь уместно сделать общее замечание о терминолоrии,
используемой в общей теории оuенинания. В этой теории при выборе крите
рия качества (или точности) оuенки исходят из некоторой неотрицательной
функции L(б, (J), измеряющей расхождение между пара метром (J и ero oцeH
кой О == б(Х) такая функция называется функцией потерь. Средние потери
ЕвL(б, (J) == R(Й, (J) называются функ.циейриска (или просто риском) оценки б,
и риск является мерой точности оценки. Если L(O, (J) == (б (J)2, то rоворят
о квадратичной функции потерь, Torдa квадратиЧНblй риск Н(о, (J) == Ев(о (J)2
есть среднеквадратичная ошибка (с. к. о.). Иноrда используются и друrие
функции потерь, например, L(o,(J) == 115 (JI или L(й,6) == (1 бj(J)2, или
L(й,(J) == (б 1 (J 1)2 И Т.д.
Пример 4. Пусть Х == (X 1 , , Х n ) выборка из
нормальноrо распределения N((J,0'2). В качестве
оценки дЛЯ 6 возьмем оптимальную несмещенную
2
оценку б(Х) == Х Поскольку Ев(Х) == N((J, о' jn), а нормальное распре
деление является унимодальным, причем ero мода x((J) совпадает с MaTeMa
тическим ожиданием (J, то в данном случае х(6) == 6 при всех (J и потому
1 "
Примеры модально .000:
несмещенных оценок
244 rлава з. Теория оценивания неизвесmных параметров распределений
обычная несмещенная оценка Х является здесь одновременно и модально
несмещенной оценкой 8. .
Пример 5. Пусть Х == (Х.,... , Х п ) выборка из paBHoMepHoro распределе
ния И(О, 8). Покажем, что статистика о(Х) == Х(n) максимальное значение
g(t. 8) выборки является модально несмещенной оценкой
, парамеlpа 8. Плотность статистики X(JI) следует из об
щеrо соотношения (13) & 3.4 при а == О, QI(8) == 1/8,
М 1 (х) == 1 (см. пример 3 в & 3А) и имеет вид
ntn 1
g(t; О) == вn /(0 ::;; t ::;; 8).
Так как (см. рис. 1) при любом 8>0 функция g(t; 8)
имеет единственны й максимум в точке х (8) == 8, то CTa
тистика Х(n) является модально несмещенной оценкой
дЛЯ О. Для сравнения напомним (см. при мер 3 13 & 3А), что оптимальной He
смещенной оценкой для 8 является статистика 8' == ((п + 1)/n)X(n). .
Пример 6 (Покаэательное распределеиие, модально несмещенная оценка
параметра). Пусть Х == (X 1 , ,Х n ), п :;:: 3 выборка из показательноrо
распределения r(O, 1) (см. п.3 & 1.2). Рассмотрим статистику
о
Рис. 1
8
n
Oc(X)==CLXi. с>О.
i=1
Из свойств raмма распределения имеем, что
.с 8 ((ЦХ)) == r(cO, п),
т. е. плотность статистики (ЦХ) есть (см. (18) & 1.2)
xn le x/c8
f(xJc(}, п) == r(n)(c8)ТI ' х:;:: О.
Здесь функция f(xlc8, п) имеет при любом О единственный максимум в точке
х == х(8) == сО(п 1), следовательно, при с == I/(n 1) статистика
1 n
ос(Х) == v n == '" X i
п 1 L..,.
i=l
будет модально несмещенной оценкой 8.
Мы знаем, что при квадратичной функции потерь несмещенная в среднем
оценка Х является оптимальной несмещенной оценкой для 8 (см., например,
таБЛ.2 в 3.2). Сравним теперь риски этих двух оценок, V N И Х: относительно
функции потерь L(б,8) == (o 1 8 1)2 Используя формулы для моменто13
rамма распределения (см. п. 3 & 1.2), неЧJУДНО получить (это мы оставляем
читателю в качестве упражнения), что
щХ 8) == Е8 ( ) 2 ==
п+2
(п l)(n 2)02'
3.б. Друzие методЬ! и nринциnЬ! построения оценок 245
( I 1 ) 2
R(V n .8) == Ео V n 'о
1
(n 2)0'
Отсюда имеем R(V n , О) < R(X, 8), V О> О, т. е. при такой функции потерь MO
дально несмещенная оценка имеет равномерно меньший риск, нежели оценка,
несмещенная в среднем. .
4, Медианно несмещенные оценки
Определение медианы для произвольноrо распределения F было дано в п. 1
2.4 это р квантиль (р при р == 1/2. Пусть Х == (X 1 , . .. ,Х П ) выборка
из распределения с плотностью f(x; 8). е Е е, и пусть б(Х) некоторая
оценка параметра О. Обозначим ее медиану т(О).
В таком СЛУ'lае, если
т(О) == О при всех О Е е,
то статистика б(Х) называется медuйнно несмещенной оценкой е.
Пример 7. В условиях примера 6 рассмотрим CTa
тистику Х(1) минимальное значение выборки.
Ее плотность по формуле (6) 2.4 имеет вид
9 (х ' е ) == !?: e nX/O х О
1, е . "".
поэтому, решая уравнение
х
== J gl(t; О) dt == 1 e nX/O
о
найдем медиану
Показательно "
распределение:
оценивание параметра
1
т(О) == o In 2.
n
Следовательно. статистика б(Х) == nX(I)/(ln 2) яапяетея медианно несмещен
ной оценкой е. Найдем распределение этой статистики. Так как (см. (18) 1.2)
.cO(X(I») == r( , 1), то [о(о(Х)) == r C:2 ' 1).
т. е. распределение б(Х) от n вообще не зависит и потому ее с. к. о. не cxo
дится к О при n 00, более Toro, о(Х) вообще не является состоятельной
оценкой. .
rамма-модель "
оценивания параметра
Разницу между различными понятиями не.
смещенности можно про иллюстрировать на при-
мере raмма модели r(e, Л) (см. п. 3 1.2). Ес.ли
рассмотреть статистику Т(Х) == Х 1 +. .. + х п , то, так как .со(т(х)) == r(e, пА),
ее плотность есть
tn>' 1
( . п ) t/O t О
9 t,!7 r(nл)оп>' е , .
246 rлава з. Теория оценивания неизвесmных параметров распределений
х rп ЕТ
Рис. 2
rрафик этой плотности, а также мода х, медиана т и среднее значение
ЕТ изображены на рис.2. Здесь ЕвТ == nЛ8, т.е. Т/(nл) несмещенная в
{)g(t; О)
среднем оценка О. Мода х статистики Т находится из урапнения == о
и равна О(n).. 1), откуда следует, что модально несмещенной оценкой пара
метра О будет статистика а(Х) == Т/(n).. 1). Медиана же т статистики Т
является корнем уравнения
т
1 J 1
tn>' ' е t/8 dt ==
r(n)..)on>' 2'
о
т/8
или r( л) J tn>' le t dt == 2""
о
Отсюда следует, что т пропорционально о: т == ОА(n),,) , rде А(n),,) KOH
станта, не зависящая от О, следовательно, медианна несмещенной оценкой О
будет статистика JI(X) == Т/А(n),,).
.. Параметр сдвиrа:
эквивариантная
оценка
5. Эквивариантные оценки
В некоторых случаях класс рассматриваемых оценок параметра О разумно
оrpаничить заранее некоторым условием инвариантности относительно тoro
или иноrо преобразованияданных. Рассмотрим, например, задачу оцениванин
параметра сдвuzа, т. е. коrда плотность наблюдаемой
случайной величины имеет вид f(x; О) == f(x О),
rде f известная функция (здесь х Е R 1 О Е R').
В этом случае для любой константы с
Р/I{Х; + с х} == Р/I{Х ; Х с} ==
x c х
J f(t О) dt == J f(и с 6) dи == Р8+с{Х ; х}.
oo
oo
Поэтому разумно рассмотреть в качестве оценок параметра О статистики
т == Т(Х" ... , х п ), инвариантные относительно сдвиra, т. е. удовлетворя
З.б. Друzие методы и принципы построения оценок 247
ющие условию
Т(Х) + с,
, Х п + с) == Т(Х) + с.
:(5)
Оценки параметра сдвиrа В, удовлетворяющие условию (5), называются эк
вивариантl/Ь/ми оценками.
Леrко видеть, что статистики Тl (Х) == Х и Т2(Х) == 1/2(X(l) + Х(n)) яв
ляются эквивариантными оценками параметра сдвиra (). Действительно, ДJlЯ
любоro числа с
1 n
T1(X 1 + с,..., Х п + с) == 2)X i + с) == Х + с == T1(X) + с,
N.
1=1
Т2(Х' + с,
I
,х n + с) == ((Хщ + с) + (Х(n) + с)) == Т2(Х) + с.
2
Статистики же Т з (Х) == в2 И Т 4 (Х) == Х(n) X(l) условию (5) не удовлетво
ряют.
Покажем теперь, что с. к. о. R(T, В) == Ев(Т(Х) в)2 любой эквивари
антной оценки Т == Т(Х) не зависит от оцениваемоrо параметра сдвиrа В.
Действительно,
n
R(T,lJ) == / (T( в)2 П f(Xi В) d?2 ==
i=1
n n
== / т 2 (ХI O,..., Х П O) Пf(Хi B)d?2 == / T2( ) Ц f(xi)d == R(T,O).
1=1 1=1
в свете этоrо представляется естественным в качестве оценки параметра сдви
ra выбрать такую эквивариантную оценку Т, которая минимизирует с. к. о.
R(T, О) в классе всех эквивариантных оценок параметра сдвиrа (). Такая oцeH
. п 'If
ка, называемая оцеюсоu иmмена, существует и имеет вид Оценка Питмена
n
/ В Ц f(X 1 ()) dB
В * 1=1
n n
/ п f(Xi ()) d()
1=1
(6)
Таким образом, оценка Питмена (6) является наилучшей в смысле минимума
квадратичноrо риска (с. к. о.) несмещенной эквивариантной оценкой пара
метра сдвиrа ().
Пример 8 (Оценка Питмена для cpeAHero нормальноrо распределения).
I ) '
Пусть .ею Е N((), 1), т. е. f(x; В) == r-; e (x B -/2 Здесь неизвестный пара
v 2п
метр (среднее) является параметром сдвиra, поэтому оценка Питмена (6) ДJlЯ
248 rлава з. Теория оценивания неизвестных параметров распределений
Hero есть
00 n
J () ехр { 2)X j ()2 } d()
I I
()* oo
п....... 00 n
J ехр { (Xi О)2} d(J
OQ
00
J 8 ехр { n 2 + n() l' } d()
oo
00
J ехр { n 2 + n() l' } d(J
oo
=:
00
J ()exp{ (() 1')2}d()
=: Х,
oo
00
J ехр { (() 1')2} d()
oo
т. е. () совпадает с выборочным средним Х: которое является эффективной
оценкой () (см. табл. 2 3.2). .
Пример 9 (Оценка Питмена для параметра САвиrа paBHoMepHoro распреАе
пения). Пусть Х =: (X 1 , .., х п ) выборка из pa[jHoMepHoro распределения
И(() 1/2,()+ 1/2),T.e. здесь [(х;() =: I«(J 1/2::::; х::::; ()+ 1/2) =: I( 1/2::::;
::::; х () ::::; 1/2), следовательно, 8 является параметром сдвиrа. Поскольку
n ( 1 1 )
П f(X i ;8) =: 1 "2::::; X(I) ()::::; х(п) ()::::;"2 =:
1=1
=: 1 ( Х(П) ::::; () ::::; X(I) + ) , (7)
то оценка Питмана (6) принимает здесь вид
X(I}+I/2
J 8 d(J
. X(.) 1/2
()п =:
X(I)+1/2
J d()
Х(n) 1/2
1 ( Х(I) + у ( Х(П) у 1
"2 ( 1 ) ( 1 ) =: "2(Х{I) + Х(П),
X(l) +"2 Х(П) "2
(8)
т. е. совпадает с несмещенной оценкой максимальноrо правдоподобия 1f (из (7)
следует, '!То любое 8 Е [Х(П) 1/2, Х(I) + 1/2] максимизирует функцию прав
доподобия, а средняя ТО4ка этоrо интервала (8) в силу упр.46 к rл. 1 является
несмещенной оценкой О). .
3.6. Друzuе методы и nринциnы построения оценок 249
Замечание. Можно показать, что оценка Питмена (6) может быть получена по фор
муле
8 == Т(Х) Eo(T(X)IY),
rде Т(Х) произвольная эквиваРllантная оценка, У == (Х) х п , .. . , Xn 1 х п )
И Ео символ матемаТИ'lескоrо ожидания Ее при 8 == о; при этом вид оценки 8:
от выбора Т(Х) не зависит.
Рассмотрим теперь аналоrичный подход в за
даче оценивания параметра масштаба, т. е. коrда
теоретическая ПЛОТНОСТЬ имеет вид
., '" 6 ' a '"
р"раметра масштаба
'(х;(}) == f( ),
(} > О неизвестный параметр масштаба, а f известная функция. В этом
случае для любой константы с > О
х/с
Pe{cXj х} == Ре{ Xj } == / f(t; 8) dt ==
oo
х/с х
== / f( ) dt == J c f( ) dи == Pce{X j х},
oo oo
т. е. изменение масштаба измерения данных в С раз эквивалентно в данном
случае изменению параметра в с раз. Поэтому в задаче оценивания парамет
ра (} ДЛЯ таких моделей разумно рассматривать в качестве оценок статисти
ки, инвариантные относительно изменения масштаба, т. е. удовлетворяющие
условию
Т(сХ) == T(cX 1 ,..., сх п ) == сТ(Х).
(9)
Статистические оценки параметра масштаба 8, удовлетворяющие условию (9),
также называются эквиварuантными оценками.
При мерами таких статистик являются Х: S, (Хр) + Х(2))/2. в задачах
оценивания параметра масштаба естественной функцией потерь является
I ( Т ) 2
L(T, (}) == 02 (Т (})2 == О 1
(1 О)
Таким образом, если измерять качество оценок с помощью функции риска
Я(Т, 8) == ( 2 ) Ее(Т (})2
которая представляет собой нормированную с. к. о., то оптимальная (т. е.
минимизирующая эту меру точности) эквивариантная оценка параметра
250 rлава з. Теория оценивания неизвестных параметров распределений
..
.,.. Оценка Питмена
параметра масштаба
масштаба в, называемая также оценкой Пuтмена,
существует и имеет вид
в ==
00 n
/ 2 П f(X i ; в) d(J
о , I
00 n
/ 3 П f(Xi; в) d(J
о , l
/ 00 1 n ( X i )
вп+2 П f (i d(J
о I I
00
/ в пl + з iI f ( " ) d(J
о , l
(11 )
Пример 10 (Оценка Питмена для параметра масштаба paBHoMepHoro распре
деления). Пусть Х (X j , , Х n ) выборка из распределении И(О,8),
в> О, Т.е.
1 1 ( х )
f(x; О) == 1(0 (х (в) == 1 О ( ( 1
О (J (J
Здесь f(x) == 1(0 ( х ( 1) равномерная плотность на 10, 1] и
n ( х. )
П f i == I(Х(п) ( 8).
I I
Поэтому по формуле (11) находим, 'по оценка Питмена для параметра О есть
. / 00 dO ( / 00 d8 )
вп== вп+2 оп+з
Х(.) Х(.)
п+2
== п + 1 Х(n).
(12)
Мы знаем (см. пример 5), что наилучшей несмещенной оценкой (J относи
тельно квадратичноЙ функции потерь L(T, 8) == (Т 8)2 illJляется статистика
((п+ 1)/п)Х(п). Поэтому оценка Питмена (12) является смещенной, но она
наилучшая в классе эквивариантных оценок пара метра (J относительно функ
ции потерь (1 О). .
б. Байесовские и минимаксные оценки
В этом пункте мы познакомим читателя с основными элементами весьма по
пулярноrо и IJ то же время неоднозначно воспринимаемоrо специалистами так
Байесовский подход называемоrо байеСОВСКОlО подхода (метода) в стати
стике. Оценки неизвестных пара метров распределе
ний, получаемые этим методом, носят название байесовскuх оценок. При бай
есовском подходе предполаrается, что параметр (J изучаемой модели
F == {Р(х; 8), О Е 8}
это случайная величина с некоторым распределением на параметрическом
множестве е, задаваемом плотностью 1!"(в). (В таких случаях будем исполь
зовать одно и то же обозначение О как для случайной величины, так и для
3.6. Друzие Meтoabl и прuнцuпbl построения оценок 251
принимаемоrо ею значения, полаrая, что это не вызо
вет затруднений при чтении). Это распределение .с(о)
называют aпpuopHblM распределением параметра и счи
тают известным. Итак, можно предстамять себе, что до на'Jала наблюде
ний над случайной величиной с .c( ) Е :F производится дополнительный
эксперимент, в котором разыrpывается (моделируется) значение случайноrо
параметра с заданной плотностью 11'(0), О Е е, и затем уже с полученным зна
чением О моделируется выборка Х == (Xt. , х п ) из распределения F(x; О).
Если мы исходим при оценивании параметра из заданной функции потерь
L(T, О), то мы можем усреднить соответствующий риск R(T, О) == E8L(T, О)
оценки Т == Т(Х) по априорному распределен ю параметра и тем самым ..,
вычислить полную среднюю потерю (усредненныи риск) Бойесовский риск
Априорное роспре
деление порометро
r(T) == f R(T, 0)11'(0) dO,
( 13)
которую мы несем при использовании статистики Т в качестве оценки неиз
BecTHoro параметра О Величина r(T) в (13) называется баиесовским риском.
Таким образом, при таком подходе оценка характеризуется одним числом
байесовским риском и, следовательно, все оценки MOryr быть упорядочены
в соответствии со значением этой характеристики. Оптимальной является
оценка Т' минимизирующая байесовский риск r(T): Байесовскоя .,
o" el!, KO п.э.е9!!' ет о
( ] 4 ) ' f i9 oi1 МJ.O Lal """.
Т' == arg min r(T);
7'
Т' и называется байесовской оценкой для О. Подчеркнем, что Т' зависит от
выбора априорноrо распределения 11', поэтому для различных априорных pac
пределений пара метра соответствующие байесовские оценки будyr, вообще ro
воря, различны, D этом состоит основной недостаток байесовскоrо подхода.
Рассмотрим теперь вопрос о том, как практически находить байесовские
оценки Т' Основой ДЛЯ этоrо служит теорема Байеса, соrласно которой aпo
стериорное распределение параметра при наблюдении Апостериарное .,
Х == ;f задается условной плотностью роспределение
( I ) f(;f; 0)11'(0)
11' O;f f(;f) ,
( 15)
rде
!(;f) == Ef(;f; О) == f !(;f; 0)11'(8) d8, или !(х) == L !(;f; Oi)1I'(Oj),
если О принимает дискретные значения {8j}. Тоrда байесовская оценка Т'
это оценка, минимизирующая апостериорный риск
E(L(T, O)IX ==;f) == f L(T, 0)1I'(OI;f) dO.
(16)
252 rлава з. Теория оценивания неизвестных параметр08 распределений
Действительно, если Е (L(T*, O)IX == ) E(L(T, O)IX == ), то по формуле
полноro математическоrо ожидания
т(т*) == EL(T*,О) == E[E(L(T*,O)lX)] Е [E(L(T, 8)IX)] == EL(T, О) == т(т).
/
Апостериорное
среднее параметра
Для случая квадратичной функuии потерь
L(T, О) == (т 0)2
байесовская оценка т* вычисляется особенно просто:
т' == Е(8IХ) == / 01Т(8IХ) dO,
(17)
т. е. она совпадает с апостериорным средllим параметра.
Это леrко следует из uепочки соотношений
Е [(О т(х))2IХ] == Е [(8 Т*(Х) + Т*(Х) Т(Х)) 2 1х ] ==
:о D(OIX) + (Т*(Х) т(х))2 D(OIX);
минимум здесь достиrается при Т :о т*, и он раIЗен апостериорной дисперсии
параметра D(OIX). Отсюда также следует, что т(т*) :о ED(OIX).
СопряжеННblе Важную роль IЗ теории баЙеСО\JСКИХ оценок иrрают co
пряжеНllые априорные распределения 1:.(8), т. е. кота апо
аПРИОРНblе
стериорное распределение пара метра 1:.(OIX == ) принад
распределения
лежит тому же семейству распределений, что и 1:.(8). При
меры сопряженных семейств приведены IЗ упр. 64 к rл. 1 (см. также замечание
к упр. 63 rл. 1). Для сопряженных априорных распределений задача вычисле
ния байесовской оценки (17) значительно упрощается.
Пример 11 (Байесовская оценка вероятности успеха в схеме Бернулли),
Пусть Х == (X 1 , ,Х n ) выборка из распределения Бернулли Bi( 1,8) и
Х == X 1 +.. .+Х n наблюдавшееся, число «успехов,>. Тоrда 1:.в(Х) == Bi(п, О)
и, как мы знаем, оптимальной несмещеНI-IОЙ оценкой О при КIЗадр,пИЧНОЙ
функции потерь является статистика Т:о Х /n == х (см. табл. 2 3.2). Пред
положим теперь, что параметр 8 случайная величина с априорным распре
делением типа бета распределения Ве(а, Ь) (см. п. 4 1.2), при этом парамет
ры а и Ь считаются известными. Соrласно упр. 64 к rл. 1, бета распределение
Ве(а, Ь) является сопряженным к семейству бернуллиевских распределений
Bi(l, О), и при этом для апостериорноrо распределения параметра О справед
ливо соотношение
1:.(OIX :o ) == Ве(а + х, Ь + n Х),
rде Х == Хl +.. + Х п . Отсюда по формуле (24) 1.2 имеем, что апостериорное
среднее (17), а тем самым и байесовская оиенка параметра О, есть IЗ данном
случае
* а+Х
т ==
а+Ь+n
( 18)
.
3.6. Друzuе методЬ! и принципЬ! построения оценок 253
Если априорная информация об оцениваемом параметре 8 отсутствует
или байесовский подход вообще неприменим, для построения оценки мож
но использовать так называемый минuмаксный подход, при котором за меру
точности оценки Т принимается максимальное значение ее риска, или MaK
сuмальный риск,
т(Т) == тах R(T, 8).
в
Оценка, минимизирующая максимальный рис , назы
вается мuнuмаксной оценкой О и обозначается Т:
т == arg min(T).
т
fV ' Мин имо..ксt:tо r ,.
оценка
(19)
в общем случае вопрос об отыскании такой оценки весьма трудный, но в ряде
случаев она может быть найдена так: предположим, что существует априорное
распределение 1r(O) > О, дЛЯ KOToporo соответствующая байесовская оценка
Т; имеет постоянный риск: R(T;, О) == а == const. Torдa Т == Т;.
Действительно, предположим, что существует оценка Tl' для которой
m(T 1 ) < т(Т;). Очевидно, что для любой оценки Т и любоrо априорноrо pac
пределения 1r параметра 8 справеДllИВО неравенство т(Т) т(Т) (см. (13»,
а ДIlЯ оценки Т; здесь имеет место равенство. Отсюда имеем
r(Tl) m(T 1 ) < т(Т;) == т(Т;),
что противоречит байесовости оценки Т;. Следовательно, т(Т;) т(Т) для
любой оценки Т, и потому Т; минимаксная оценка.
Добавим к этому, что такое распределение 1r(8) Наименее 6лаrопри tf'
называется ffaUMeHee бласоприятным априорным pac ятное априорное
пределеffuе параметра, и оно часто находится в сопря распределение
женном семействе.
Замечание, Эrот термин отражает следующую особенность TaKoro априорноrо pac
пределения. Пусть 1[' любос друrое априорное распределение и т;, COOTBeT
ствующая ему байесовская оиенка. Torдa
т(Т;,) == J ЩТ;, , 8)1[' (8) d8 J ЩТ;, 8)7!" (8) d8 == а == т(Т;),
т. е. 1[ такое априорное распределение, которое причиняет статистику ffоибольшие
неизбежные средние потери.
Пример 12 (Минимаксная оценка вероятности успеха в схеме Бернулли).
В ситуации примера 11 вычислим функцию риска, т. е. с. к. о. байесовской
оценки (18). Поскольку эта оценка смещенная (несмещенной является оценка
Х/n), то, соrласно формуле (5) 3.1, ее с. к. о. равна сумме квадрата смещения
( ) . а + пО О а 8(а + Ь)
Ь 8 == ЕвТ О == ==
а+Ь+n а+Ь+n
и дисперси и
. nO(1 8)
D Т ==
в (а+Ь+n)2'
254 rлава з. Теория оценивания неизвестных параметров распределений
Т.е.
( . ) ( ' ) 2 [a 8(a+b)12+n8(1 8)
R Т, е Ее Т е ( )2 .
а+Ь+n
(20)
Чтобы получить минимаксную оценку, надо найти такое априорное распре
деление Ве(а, Ь), 1UIя KOToporo эта функция риска не зависит от 8. Из (20)
леrко находим, что это имеет место при (а + ь)2 == n и 2а(а + Ь) == n, т. е.
при а == Ь == ,Jii/2. Следовательно, минимаксная оценка 8 в данной задаче
существует и имеет вид
Х + V1i/2
Т==
n+vn '
(21)
а ее риск равен
1
R(T, 8) == т(Т) == (а + Ь + n)2 == 4n(1 + 1/.fii)2 . (22)
Для сравнения рассмотрим риск оптимальной несмещенной оценки Т == Х/n.
Имеем
8( 1 8)
R(T, 8) == DIIT == ,
n
а
R(-, В)
8( 1 8) 1
т(Т) == тах == > т(Т).
е n 4n
[рафик функций риска оценок Т и Т приве
дены на рис. 3. Из рисунка видно, ..::!ТО зона пред
ПО'lтения минимаксной оценки Т перед oцeH
кой Т имеет вид
т
{8 ЩТ, 8) < R(T, 8)} == {8 Е ( T е п ) },
о
1/2
8
rде
Рис.З
е п == 1/2 V 1 (1 + ) 2
Если n велико (n ----+ 00), то е п ----+ О, и эта зона предпочтения сужается точке
е == 1/2. Таким образом, при большом числе наблюдений n оценка Т TO'l
нее оценки Т лишь для незначительной зоны значений параметра 8. Для
большинства же значений параметра 8 более точной является несмещенная
оценка Т == Х/n. .
Изложенная выше теория байесовскоrо и минимаксноrо оценивания OT
носится к случаю скалярноrо параметра, но все ее основные положения пере
носятся и на случай векторноro параметра 8 == (81,.'.' 8т). Если 1UIя оценки
З.б. Дpy иe Memoabl и принципbl построения оценок 255
'[ (T 1 , , Tr) параметра О ее точность измеряется
с помощью квадратичной функции потерь
Квадратичная "'1:
функция потерь
L('[, О) == 1'[ 812 == 2)Т; 8;)2.
i t
т. е. квадратичным риском R('[.8) Е81'[ 012, то байеСО8ская оценка
r* == arg min т('[), rде байесовский риск т('[) == ER('[, 8), есть вектор апо
r
стериорных средних '[* == E(OIX), а минимаксная оценка f. == arg min т('[) ,
z:
rде m('[) == mах R('[, 8), есть такая байесовская оценка r*, для которой риск
8
постоянен: R('[',8) == const.
Пример 13 (Байесовская и минимаисная оценки параметров полиномиаль
Horo распределеНИJl). Пусть наблюдается целочисленный случайный BeK
тор!:!. == (v). ,VN), имеющий полиномиальное распределение М(п;р ==
== (Pt, ,PN)) (см. п. 6 1.1), параметры Е. KOToporo неизвестны, т. е. здесь
Е.==8Е9=={8==(8" ,ON) 8; O,i==I,.. ,N,8t+ +8 N ==I}.
Предположим, что вектор Е. случаен и ero априорное распределение есть
распределение Дирихле D(Q:) с известными параметрами Q. == (0:"..., O:N)
(см. п. 10 1.2). Распределение Дирихле сопряжено к полиномиальному pac
пределению и при этом для апостериорноrо распределения параметра Е. спра
ведливо соотношение .c(r.I!:!. == == D(Q. + ) (см. УПр. 63 к rл. 1). Отсюда
с учетом формул (41) 91.2 имеем, что байесовская оценка параметра Е. есть
вектор
O:+V
1:.' == E(PI!:!.) ==
о:+п
(23)
(здесь а == а) + + aN, п == VI + + VN)' Напомним, что наилучшей
несмещенной оценкой для Е. является статистика Е.* == !:!./п (см., например,
пример 10 в р.2).
Вычислим функцию риска оценки (23). Для этою удобно переписать пред
ставление (23) 8 виде
r* == ШЕ.' + (1 ш) ,
rде
а
л
,
О:
n
ш==
О: + п'
(24)
показывающем, что точка r* Е 9 лежит на отрезке, соединяющем точки l!.*
и . Из (24) имеем
R(r*, 8) == Е 8 1'[* 012 == Е81ш(р' О) + (1 ш)( 0)12 ==
2
== ш 2 Е 8 1Р* 0[2 + (1 ш)21 012 == (1 1(12) + (1 ш)21 812
п
256 rлава з. Теория оцеНUВQния неизвестных параметров распределений
Если здесь == f == (I/N, . .. , I/N), то ПОЛУ'lим
0-2 n nN 0-2
R(',f*,8) == ( )2 1812 + ( )2 .
о-+n N о-+n
Отсюда следует, что при о- == ..;ii риск R(',f*, 8) будет постоянным и равным
N 1
[N(..;ii + 1)]2'
Но это означает, что D( Vnf) наименее блаrоприятное априорное распре
деление, а минимаксной оценкой является статистика
v'п * 1 ( Vj + v'п/N
T== p + e==
v'п+I v'п+I n+v'п'
j == 1,
,N).
(25)
.
в предыдущих примерах 12 и 13 удалось найти наименее блаrоприятное
априорное распределение параметра модели и тем самым леrко построить
минимаксную оценку. Но такое распределение не всеrда существует, и в таких
случаях для отыскания минимаксной оценки может быть полезным следую
щий критерий.
Лемма, Пусть {1rk} некоторая последовательность аПРИОРНblХ распределе
ний параметра и {Тп последовательность соответствующих байесовских
оценок. Если существует оценка ТО, для которой функция риска удовлетворя
ет условию
R(To, 8) lim т(Т;) , V (),
k.....oo
то То есть минимаксная оценка: То == т
Доказательство, Для любой оценки Т выполняется цепочка соотношений
т(Т) == s p R(T, ()) ? J Н(Т, ()) 1r k(8) d() ? т (Тп.
Отсюда следует, что
т(Т) ? lim т(Т;) ? R(Тo, 8), V (), т. е. т(Т)? т(Т о ). .
k.....oo
I Замечание. Очевидно, что в этих распределениях lirn может быть заменен на lim sup.
Пример 14 (Минимаксность ВbJ60рочноrо cpeAHero для нормальной Moдe
ли). Пусть Х == (Х), ,Х n ) выборка из распределения N((), ь 2 ) (ь 2 из
вестно). Покажем, что статистика Х: являющаяся оптимальной несмещенной
оценкой О относительно квадратичной функции потерь L(T, ()) == (Т ()}2
(см. табл. 2 3.2), есть также и минимаксная оценка для (). Для этоrо мы CHa
чала найдем байесовскую оценку Т* для 8 относительно априорноrо распре
деления .с(()) == N(JL, (72), являющеrося сопряженным к семейству N((), ь 2 )
3.б. Друzие методbl и принципbl построения оценок 257
(см. упр.64(5) к т.!). Используя результат этоrо упражнения, сразу находим
2 ( 1 N )
0'1 == 0'2 + ь2
* 2 ( р n )
т == E(8jX) == 0'1 0'2 + ь 2 Х ,
(26)
при этом байесовский риск
т(т*) == ED(8[X) == О'Т.
Можно Проверить (это мы оставляем читателю в качестве упражнения),
что функция риска оценки т* имеет вид
n0'4 [ ( n0'2 ) 110'2 ] 2
R(T*, 8) == Е8(Т* 8)2 == t! + t! ] () + t"0'/
(27)
и здесь нет априорноrо распределения (в сопряженном семействе), для KOTO
poro Н(Т*, ()) == const. Поэтому применим критерий минимаксности, сформу
лированный в лемме. Для этоrо рассмотрим последовательность априорных
распределений {N(p, O'k)}, rдe O'k -----t 00 при k -----t 00, Соответствующие бай
есовские оценки в силу (26) есть т; == 0' k(pO';:2 + nЬ 2 х) И их байесовские
риски удовлетворяют соотношению
* 2 ( 1 N ) ь2
r(Tk) == O'lk == "' k 2 . + L' .
v !r k oo n
Подчеркнем также, что т; х при k 00. Но для оценки То == Х ФУНКЦИЯ
риска есть
2 ь2 *
R(X, 8) == Е 8 (Х ()) == D8X == == lim r(T k ),
n k oo
следовательно Х == т минимаксная оценка 8, и она является пределом
при k -----t 00 байесовских оценок т; . .
1 n
Замечание. Таким образом, выборочное среднее Х == L Х ; является «образцо-
n j 1
вой оценкой неизвестноrо теоретическоrо среднеro 8 в нормальной модели N(8, ь 2 ):
оно является несмещенной оценкой с равномерно минимальной дисперсией, а TaK
же минимаксной оценкой при квадратичной функции потерь. Естественно поставить
вопрос, сохраняется ли свойство оптимальности выборочноrо среднеrо в MHoroMep
ном случае. Как показал К. Стейн (1956), ответ на этот вопрос отрицателен. Точнее,
рассмотрим k мерную нормальную модель N(8 == (81, .. . , 8 k ), b 2 D. k ) (т. е. (см. п. 2
1.2) наблюдается k мерный вектор { == ( I, , k) С независимыми (для простоты)
нормальными N(8 j , ь\ j == 1, ,k, компонентами) и предположим, что по соот-
ветствующей выборке Х/ == (X/I,' .. ,X'k), l == 1,... ,n, оценивается не известный
вектор средних 8 == ((}I, ,8 k ) при квадратичной функции потерь
k
L(r, 8) == Ir (}1 2 == L(T j (}j)2
j 1
17 Закаа 1748
258 rлава з. Теория оценивания неuзвестных параметров распределений
Тоrда (см. п. 2 2.3) вектор выБОРОЧНblХ средних Х == (Х" . . . ,X k ), [де
1 n
X j == L X/ j , j == 1,..., k,
/ I
будет несмещенной оценкой для вектора О 11 ее функция риска равна
k
'''' k,
Н(Х, 8) == EeIX 81 == L..., DoXj == Ь.,
j 1 n
т. е. не зависит от О. Постоянность функции риска подсказывает, что рассматривае.
мая оценка является Мl1нимаксной при любой размеРНОСТI1 k. Но, оказывается, что
при k > 2 она может быт cTporo улучшена. Именно, в 1961 [. Джеймс и Стейн пред.
ложили следующую простую оценку для математическою ожидания мноroмерноro
нормальноro распределения (при k З)
О' == ( 1 (k 2)Ь 2 ) х
IXI 1
и показали, что ее риск Н(О', О) < н(Х, О), т. е. оценка О' равномерно лучше, чем
Х (rоворят также, что оценка Х является lIедопусmuмой, см. П.2 7.1). ОТКРblтие
Стейна, явившесся сюрпризом, показывает, 'ITO даже тоrда, коrда рассматривается
классическая проблема оценивания (т. е. оценивание среднеro значения нормальноrо
распределения), выоро'lное среднее зто не единственная оценка, которую следует
прииимать во внимание.
7. Оценивание по цензурированным данным
До сих пор рассматривались методы оценивания, использующие информа.
цию, доставляемую полной выборкой Х == (X J , . .. , х п ). Однако, на практи.
ке возникают задачи оценивания и по неполной выорке,' т. е. KorAa некоторые
наблюдения либо отсутствуют, либо о них имеется лишь 'Iастичная инфор
мация, в таких случаях rоворят о цензурuроваl/llЫХ данных. Типичными
примерами цензурирования являются следующие ПЛ<1НЫ испытаний на на.
дежность: берется контрольная партия из n однотипных ищелий, BpeMeHa
жизни" которых независимые одинаКОlJО распределенные случайные вели.
чины, и наблюдаются либо моменты отказов за заданное времн t (l тип цен.
зурирования), либо моменты первых т( < n) отказов (1] тип цензуриронаНИfJ).
В обоих случаях достиrается экономия времени на пропедение эксперимен.
та (получение исходных данных), что бывает важным ф<1КТОрОМ н реальных
условиях. В общем случае] тип цензурирования определяется заданием TaKoro
интервала (t l ,t 2 ), что наблюдаются лишь значения Х; Е (t(,t 2 ), а 1] тип
заданием двух целых чисел rJ, Т2 О, таких что наблюдаются лишь значения
порядковыx статистик Хщ при Т) + 1 k n Т2 (если соответствующее
оrpаничение с какой.нибудь одной стороны отсутствует, то rоворят о "ростом
цензурировании).
Рассмотренные выще методы MOryr быть применены и к цензурированным
данным. ПРОИЛЛЮСlpируем это на примере оценивания пара метров О == (0(, Oz)
нормальной модели N(O., oi) при простом цензурировании.
З.6. Друzие методbl и принципbl построения оценок 259
Пример 15 (1 тип цензурирования). Пусть из n наблюдений фиксируются
лишь те, которые при надлежат интервалу (t, 00). Пусть таких наблюдений OKa
залось N, а их самих обозначим У == (У" , У N) (таким образом, n N О
наблюдений потеряно). Тоrда функция правдоподобия данных, ОLJеоидно,
имеет вид (далее u == (t 0,)/02)
N
L(1/.; О) == С::фП N(u)(vЪrО2) N ехр { 2:(у; OI)2 } ==
202 i 1
N n N ( ) N { N 2 N ) 2 }
== СП Ф (и) V21f02 ехр 28 2(У 81 ,
202 202
rде
N
i == 2:(у; у)2
N.
, I
Отсюда следует, что в данном слуLJае достаточной статистикой ЯRЛяется тройка
2
(N.Y,S (У».
Будем искать оценки параметров О == (81' (2) по методу максимальноro
правдоподобия. Для этоrо запишем уравнения правдопод06ия
д Iп L(1/.; О) N n N Ф'(и)
дО I == O (у (1) Ф(u) == О,
д Iп ц'!!.; О) N ( 2 2 ) N (n N)u Ф'(и)
== 8 + (у О,) == О.
дО 2 O 02 82 Ф(и)
Если обозначить А(и) == (и N)ф'(u)/(NФ(и», то эти уравнения приводятся
к виду
у О, == 02А(и), i + (у (1)2 == 8 (I + иА(и». (28)
Учитывая, что 8 2 и == t 01 == t У + 02А(и), т. е. 02 == (у t)j(A( и) и),
из nepBoro уравнения (28) имеем
О, == у л(у t), ,\ == А(и)
А(и) u
(29)
Далее, так как
(у (1)2 8 иA(и) == O A(и)(A(и) и) == '\(у t)2,
из 8Тороro уравнения (28) следует, что
8 == 82 + >.(у t)2 (3О)
Но также 8 == (у t)2 j(A(u) и)2, поэтому
82 == (у t)2 [ 1 А(и) ] == (у t)2 1 А(и)(А(и) и) .
(А(и) и)2 А(и) u (А(и) и)2
17*
260 rлава з. Теория оценивания неизвестных параметров распределений
Отсюда
52 1 А(и)(А(и) и)
1==
(у t)2 (А(и) и)2
(31)
Теперь, вычислив по данным величину 1, из урапнения (31) находим значе
ние и, затем>. == Л(и) в (29) и, наконец, из (29) и (За) значения 8\ и 82. Тем
самым однозначно определяются о. м. п. 8\,82.
Отметим, что если N == n, т. е. наблюдается полная выборка, то А(и) == О,
следовательно, л == О, и мы приходи м к обычным о. м. п. 8. == У, 82 == S(Y)
(см. при мер I в 3.5). .
Пример 16 (11 тип цензурирования). Пусть наблюдению доступны лишь по
рядковые статистики X(k) при k > Т для заданноrо Т ;;:: 1. Обозначим
У == (У\,..., YN) == (X(r+!), ,Х(n)), N == n Т, тоrда из п. 2 р.4 имеем,
что плотность распределения вектора У (функция правдоподобия данных)
есть
n! r ( Y\ 8\ )( ) N { 1 2 }
L('P..; 8) == Т! Ф v 27r8 2 ехр 282 (У; 8\)
2 , I
Отсюда следует, что достаточной статистикой является вданном случае тройка
2
(X(r+\), У, S (У), а метод максимальноrо правдоподобия ПРИВ0ДИТ к тем же
уравнениям (28) с заменой t на УI == Х(,.+\) И и на и' == (У! (1)/82. .
Рассмотрим еще один практически важный пример.
Пример 17 (Оценивание параметра масштаба покаэательноrо распределе
ния по цензурированным данным). Пусть для выборки Х == (X j , , Х n )
из показательноrо распределения .ею Е r(8, 1) (см. п. 3 1.2) доступны Ha
блюдению лишь первые r порядковые статистики X(J), ,X(r). Рассмотрим
класс линейных оценок
r
Tr == L >'Хщ
k l
для параметра 8 и найдем в нем оптимальную несмещенную оценку (т. е.
н.о.р.м.д.). Для этоrо прежде !!cero заметим, что .ее(О8) == r(l, 1) CTaH
дартное показательное распределение, поэтому, воспользовавшись результа
тами при мера 1 2.4, запишем представление
k 1';
Хщ == о L . ,
i 1 n 'l+ 1
rде {1';} независимые случайные величины с распределением r(l, 1).
Статистика Tr при этом примет вид
r k у. r У;Л
Tr == 8 Лk .' == о "
L...J L...J n 2+1 L.,.n i+1'
k=\ i=\ i=1
3.6. ДрУluе методы u принципы построения оценок 261
r
rдe Л j == 2: Лk, i == 1,
k j
, т. Отсюда, учитывая, что ЕУ; == DY; == 1, имеем
r Л j
E8 T r == () 2: . ,
. n z+1
' '
r Л 2
2" j
D8 T r == () (n i + 1)2 '
' '
Условие несмещенности теперь принимает вид
r л-
" 1 == 1
n i+1 ·
' '
и при этом условии надо минимизировать по л l .... . Л r сумму
r М
F(Л,.,,,,л r )==" ( : )2 '
n t+l
1==1
r r
Так как сумма L X при условии L Xj == 1 обращается в минимум при
j 1 j ,
Х, == == X r == I/r (показать!), то в нашем случае оптимальный выбор Л i
таков: л; == (n i + I)/т, i == 1, ,Т Тем самым оптимальная оценка
существует и имеет вид (далее учитывается, что У; == (n i+ I)(Хщ Х(н»)/(),
i==l, .т,Х(о)==О)
r
. 1" 1 n T
Tr == L.)n i + I)(X(i) Х(Н») == (X(1) +... + X(r») + Хи
r j , r r
и
(}2
D8 T ; == .
r
Подчеркнем, что при r == n (наблюдается полная выборка) т: == Х, т. е. мы
приходим к эффективной оценке ДЛЯ () (см. табл. 2 3.2). .
Дальнейший материал для тех, кто хочет расширить и уrлу6ить свои
представления об обсуждаемой проблематике. Мы дадим общие определения
Й
современных моделе неполных данных и приведем Модели неполных »?
OCHoBH le результаты о соответствующих oцe Kax неиз ' '''''"'''' ' '''"''''' ' ;, данных
вестнои функции распределения наблюдении.
Итак, пусть {Xj} независимые одинаково распределенные случайные
величины (н. О. р. с. в.) с общей функцией распределения F(t) == Р{Х, t},
которая неизвестна и должна быть оценена по соответствующей выборке
с неполными данными. Опишем сначала наиболее распространенные модели
неполных данных.
Модель 1 (цензурированные данные). Задана последовательность н. О. р. С. в.
{T j }, независимая от {Х;}, и предполаraется, что исходные данные (выборка)
262 rлава з. Теория оценuвания неизвестных параметров распределений
имеют вид (X j , б j ), i == 1,..., n, rдe
X j == Х ; Л Т ; (Л == min), б j == I(Х; :;;; Tj).
(32)
Таким образом, пара (X j , 1) означает, что наблюдается X j == X j , если же дано
(X i , О), то это означает, что наблюдается X j == T j , а об X j известно лишь, что
X j > T j . Можно также сказать, что в этой модели о результатах некоторых
наблюдений известна лишь частичная информация типа, что Х ; > Т ; (о такой
модели иноrда rоворят как о правоцензурuрованных данных).
С. в. {Tj} называются цензурuрующuмu переменными. .
Модель 2 (усеченные данные). Здесь задается последовательность н. о. р. с. в.
{tj}, не зависящая от {X j }, и предполаrается, что Х ; наблюдается лишь
в случае, Korдa X j tj. Таким образом, вданной модели выборка предстаIJJIяет
собой n пар (Х;,т с х; tj, i 1, ,п. Эта выборка порождается
большей выборкой (X j , tj), i == 1, ,т(п), rдe
т(п) == min{ т t I(X j t j ) == п}
, I
(33)
Здесь речь идет о левоусеченных данных (случай усечения справа: Х ; наблю
дается лишь в случае Х ; :;;; tj, сводится к предыдущему умножением Х, и tj
на 1). Таким образом, здесь о наблюдениях с Х; < tj вообще нет информа
ции. С. В. {t;} называются усекающими переменными. .
Модель 3 (смешаннаи). В этом случае данные подверrаются как цензуриро
ванию, так и усечению. Имеются последовательности {Tj} (цензурирующие
переменные) и {t j } (усекающие переменные), не зависящие от {X j } и между
собой и состоящие из независимых С. В., которые с положительной вероят
ностью Moryr принимать значения OO (расширенные с. в.). Здесь исходные
данные (выборка) имеют вид (Х;, бi, ti) с X j O t j , i == 1,.. n, которые
порождаются больщей выборкой (X j , T j , tj), i == 1, ,т(n), rде
т(n) == min{ т t I(Х; ЛТj t j ) == п} (34)
, l
Если здесь положить все Tj 00, то получим усеченную модель, а при
t j == oo цензурированную. .
Оценивание Функ Оценки теоретической функции распределения F(t)
ции распределения в таких моделях данных носят название product liтit
(p. f.) оценок и их конструкции имеют следующий вид.
Для модели 1 рА оценка рn (Каплан иМейер, 1958)
определяется равенством
.6/
..,., Оценка
Каплана Мейера
п{ !lNn(S) }
1 Fn(t) == ss.t 1 Yn(S) ,
'"
(35)
!i З.6. Друzuе методЬ! и принципЬ! построения оценок 2БЗ
rдe О/О =' О, I::1N n (s) Nn(s) Nn(s О) величина скачка в точке s
(так что 13 (35) произведение берется по точкам скачков функции Nn(s)).
n
n
Nn(s) =' L I(X j s Л T i ) == L I(i j s, jjj == 1),
j 1 i 1
n
n
Yn(s) == L I(X j Л T i ;? s) == L I(X j ;? s),
i=1 j 1
Асимптотические (при n -----t 00) СlIойства оценки Fn(t) аналоrичны свой
CTBa классической эмпирической функции распределения (см. п. 2 и 3 2.1),
например, имеет место аналоr теоремы rливенко
Р { lim sиp I Fn(t) F(t)1 =' О } =' 1.
П.....ОО t
Для модели 2 p. f. оценка p (Линден Бэлл, 1971)
определяется равенством
...
Оценка
Линден Бэлла
"Ii:;l.ll :.с... f'...,....v.... ..::н.- ".
1 F;(t) == П { I Ln(8) } ,
s t Rn(s)
'"
(36)
rAe
n
n
Ln(8) =' L I(X; s),
j l
Rn(s) == L I(X j O ;? s ;? tп.
j 1
Оценка p обладает хорошими асимптотическими свойствами, в частно
сти, свойством состоятельности, KorAa с. в. tj имеют непрерывную функцию
распределения. Для случаев, KorAa t; не ямяются н. о. р. с. в., а также для
дискретных с. в., для обеспечения состоятельности оценки Лей и Йинr (1991)
предложили модифицированную p. f. оценку рп:
п{ I::1Ln(s) а }
1 Fn(t) == 1 Rn(8) I(Rn(s);? сп) ,
" !
(37)
rAe с> О и О < а < 1 заданные числа.
Для модели 3 ими же предложен модифицированный вариант оценки рп:
, п{ I::1L (s) I а }
1 Fn(t) == ',(! 1 щ.(8) I(Rn(s);? сп) ,
"
(38)
rAe
n
L (s) == L I(Xj s, бj == 1),
i 1
n
R (s) == 2: I(X; ;? 8 ;? ti).
i=1
Асимптотические свойства этих p. /. оценок и дальнейшие детали их теории
можно найти в работах: Loi Т. L., Yiпg Z. Estimating а distIibиtion function
254 fлава з. Теория оценивания неизвестных параметров распределений
with truncated and censored data // Ann. Statist. 1991. V. 19. NQ 1. Р 417 442;
GiI/ R. D. Glivenko Cantelly for Kaplan Meier // Math. Meth. Statist. 1994. V.3.
NQ 1. Р. 76 87.
9 з. 7. Объединение и улучшение оценок
Настоящий параrраф посвящен важным вопросам построения на базе уже
имеющихся оценок (дпя не которой теоретической характеристики или па
раметра) новой оценки, обладающей большей точностью, нежели исходные
оценки. Здесь можно выделить два аспекта:
1) проблема объединения информации, получаемой в разных эксперимен
тах, и построение итоrовой оценки с большей точностью, нежели оценки,
порождаемые соответствующими экспериментами, и
2) проблема «улучшения.) имеющейся оценки с целью построения на ее
основе новой оценки с большей точностью. Ниже будут изложены He
которые общие подходы в решении этих проблем и даны практически
полезные иллюстрации их применения в конкретных задачах.
1. Объединение оценок
В качестве введения в общую проблематику рассмотрим простейшую ситу
ацию, коrда имеются две независимые и несмещенные оценки Т, и Т 2 He
KOToporo параметра () и их дисперсии DT i == 17';, i == 1,2, известны. Как
на их основе построить более точную новую несмещенную оценку? PaCCMOT
рим ЮIасс линейных комбинаций
1:::. == {Та о:Т, + (1 0:) Т2, о:::; о: :::; 1}.
Все они несмещенные оценки:
ЕТа == o:ETI + (1 0:) ЕТ 2 == о:() + (1 0:) () == ()
и
DTa == 0:2U" + (1 0:)2U" == ф(о:).
Найдем о: из условия обращения дисперсии DTa в минимум, т. е. решая
уравнение ф'(о:) == о. Отсюда находим точку минимума
2
. 17'2
о:
O'f + O'
iI W"(5бти нени€{ Ч "'l',;" ,i'
незовисимых оценок
и, следовательно, оценку с минимальной дисперсией
(в классе 1:::.)
. 17'2 U"f
Т == Та' == 2 2 Т) + 2 2 Т2;
U" + 0'2 0'1 + 17'2
(1)
з. 7. Объединение и улучшение оценок
2б5
ее дисперсия
2 2
D T * 11' 1 11'2 . ( 2 2 )
=о 2 2 < mш 11'1,11'2 .
11') + 11'2
т. е. это более точная несмещенная оценка, нежели исходные оценки T j , Т 2 .
Пример 1 (Нормальное распределение, объединение оценок).
Пусть Х =о (Х 1, ,Х n ) и У =о (Y 1 ,... , У т ) две независимые выборки
из одноrо и Toro же нормальноrо распределения N(()I' ()i) (оба параметра
неизвестны). Мы знаем (см. теорему 2 Э 2.2), что
1 n
Х =о L: Х ;
n i l
n
2 1 L: 2
И So(X) =о (Х ; Х)
n 1 .
, I
2 2
несмещенные оценки соответственно дпя 81 и ()2 И аналоrично У и ВО (У).
Мы также знаем (см. теорему Фишера и соотношение (7) в Э 2.5), что эти
четыре статистики независимы и
DX =о ()i , DY =о ()i , DS 2 (X) =о 2 DS (Y) =о 2 .
n т о n l' т 1
Отсюда и из (1) получаем, что объединенная оценка для ()) есть
* DY DX
8=0 Х+ У=о
I DX + DY DX + DY
n т 1 ( " т )
=o X+ Y=o L:Xi+L:Yi ,
n+т n+т n+т i 1 i 1
т. е. среднее арифметическое всех данных, и при этом D8 =о 8i/(n+m). Aнa
лоrи'lНО имеем, что объединенная оценкаДIJЯ теоретической дисперсии ()i есть
(2)
2* n 1 2 т 1 2
(()2) =о ВО(Х) + 2 Во(У) =о
n+т 2 n+т
1 [ n 2 m 2 ]
=о n + т 2 (X; Х) + (Y; У) ,
и при этом D(()i)* == 281/ (n + т 2).
В общем случае, коrда оценки коррелированы:
corr(Tl, Т 2 ) =о р, дпя дисперсии их линейной комби
нации Та имеет место соотношение
(3)
.
Объединение Koppe .-.:
ЛИрОВQННЫХ оценок
DTa =о (il1' + (1 0:)211'i + 20:(1 O:)PI1')11'2 == ф(о:),
И решение уравнения ф' (о:) =о О есть
* 11'2(11'2 PI1'I)
о: 2 2 '
11') 2pl1'I11'2 + 11'2
2бб rлава з. Теория оцеНUВGния неизвестных парометров распределенuй
в итоrе имеем, '1ТО в классе t1 существует единственная оценка с минимальной
дисперсией
. 0'2(0'2 PO'I) ТI + 0',(0'1 Р0'2)Т2
Т == Та' == 2 2
0'1 2рО') 0'2 + 0'2
и ее дисперсия есть
(4)
0'20'2(1 р2)
от' == '2
О'т 2РО')0'2 + O'i'
'1то сводится К результату (1) при Р == О.
Перейдем к общей постановке проблемы объединения оценок. Пусть
Tl, ,Tk несмещенные оценки некоторой вели'lИНЫ g, ПОЛУ'lенные в k
экспериментах. Обычно на практике это оценки, построенные по COOТBeT
ствующим независимым выборкам Xj == (Xjl, ,Xjnj)' j == 1, ,k, т. е.
Tj == Tj(X j ), j == 1, ,k, и тоrда они представляют собой независимые слу
чайные вели'lИНЫ с ETj == 9 и некоторыми дисперсиями, которые мы будем
обозна'lать DTj == a}/nj, j == 1, , k. Такой вид дисперсии имеют в случае,
2 .
коrда Tj == X j == (X j1 + + X jn ) /nj и DX ji == O'j' Z == 1, , Щ, но такое
обозначение мы сохраним для них и для случаев, коrда оценки Tj MoryT зада
ваться и каким ли60 друrим образом. Требуется по оценкам Tj, j == 1, , k,
построить более точную оцен ку для g, нежели любая из этих исходных оценок,
учитывая при этом различные специфические условия, моryщие иметь место
на практике, KaK TO: дисперсии известны либо нет. В более общем случае ис
ходные оценки MOryт быть коррелироваными, и Torдa MOryт возникать допол
нительные предположения об их смешанных вторых моментах (ковариациях).
Возможны и дальнейшие различноrо типа детализации общих ситуаций, свя
занные, например, с условием несмещенности оценок Tj (в принципе, это
исходное условие может также нарушаться, т. е. оценки Tj Moryт быть He
однородными и в смысле математическоrо ожидания, а не только в смысле
дисперсии). Таким образом, эта проблематика весьма мноrоплановая, и мы
далее дадим описание оптимальных алrоритмов построения итоrовой оценки
лишь при простейших естественных предположениях.
1) Некоррелировонные оценки с известными дисперсиями. Предположим, что
дисперсии DTj (т. е. величины О'}, j == 1, . , k) исходных оценок известны,
и эти оценки некоррелированы. Итоrовую оценку величины 9 будем искать
в классе линейных несмещенных оценок вида
TQ. == alT 1 +
+ akTk == Q.'r,
(5)
rде
Q. == (al"", ak), О) +
+ ak == 1, r == (T 1 ,
, T k ).
При этом в качестве критерия точности оценки TQ. будем считать ее диспер
сию. Таким образом, нашей целью будет построение несмещенной оценки
с минимальной дисперсией (н. о. м. д.) В классе оценок (5).
3.7. Объединение и улучшение оценок
267
в принятых обозначениях и при сделанных предположениях дисперсия
произвольной оценки (5) равна
2
20'1
ОТ а == аl +
nl
Минимум правой части (6) по при условии
2
20'k
+ak '
nk
(6)
k
2:Щ==1
j 1
находится методом неопределенных множителей Лаrpанжа 6), соrласно KOTO
рому надо найти абсолютный минимум функции
k 2 2 k
F( , л) == 2: a O'j л (L aj 1).
J l J J I
Решая систему уравнений
aF( , л)
д ==0, j==l,...,k,
aj
леrко находим, что минимум достиrается при
aF( , л)
дл == о,
. nj 2
aj == aj == 2 В, j == 1'... . k,
O'j
в 2 == (Е ; ) (7)
) I J
Объединенная оценка ..,.
при ОТС У1: !!, .I'\ е,в; ,
Таким образом, в рассматриваемом случае
н. о. м. д. Т' существует и имеет вид
Т' == TQ.' == a TI +
k
. 2 Щ .
+ akTk В L...J 2Tj.
0'.
j 1 J
(8)
при этом из (6) и (7) следует, что
0'2
ОТ' == в 2 < min 2 == т!п OT j (9)
J Щ J
(как и должно быть: ведь DT' есть минимум среди всех линейных комби
наций (5), включая и сами исходные оценки Tj). Отметим также очевидное
неравенство:
2
2 1 O'j
В :( тах
k j nj
2) Обьединение оценок с неизвестными дисперсиями. Более реалистичной
является ситуация, Korдa дисперсии объединяемых оценок неизвестны. Для
6) Лаrранж Жозеф Луи (1736 1813) французский математик, механик и астроном, почетНblН
член Петербурrской АН (1776).
268 rлава з. Теория оценивания неизвестных параметров распределений
этоrо случая мы будем предполаrать, что оценки Tj порождены независимыми
выборками Xj == (X jl , . . . , XjnJ Tj == X j , и при этом нам известны также
выборочные дисперсии
".
2 1 2:: 1 2
Sj(X) == (Xji X j ) ,
N.
J i 1
j == 1,... ,k.
в рассматриваемом случае естественно поступить следующим образом: за
менить в формулах (7) и (8) неизвестные дисперсии о} их оценками s]
Объединенная оценка и в итоrе взять в качестве объединенной оценки
в случае неизвестных следующую оценку со случайными «весами»:
дисперсий Т Т + + Т (10)
== йl I Qk k.
rде веса
nj 2
Qj == '"""2 В
S.
J
j == 1,
, k,
в 2 == ( t n )
j 1 s)
(11 )
Однако исследование свойств оценок вида (10) значительно усложняется.
Так, если в случае известных дисперсий о} дисперсия объединенной оценки
(8) не превосходит дисперсии любой исходной оценки Tj, то такое YТBep
ждение для оценки (10), вообще rоворя, уже перестает быть верным. Но, как
показывают соответствующие исследования, такое явление может происхо
дить лишь при небольших объемах выборок. В случае же больших выборок,
т. е. при minj nj ---+ 00. свойства оценок (10) будут «достаточно хорошими».
Приведем соответствуюшую предельную теорему, дающую условия, при KO
торых оценка (10) является состоятельной и асимптотически нормальной.
Теорема 1. Пусть объемы выборок удовлетворяют условиям:
Щ == /j(n)n, 1'j(n) ---+ /j > О при n ---+ 00, j == 1,
, k,
( 12)
( ) 8 2 2 2
k фиксировано и, кроме Toro, Е X ji 9 :( с < 00, О < Q. :( Oj :( о" < 00,
j == 1,..., k. TorAa величина (Т g)/ в при n ---+ 00 асимптотически HOp
мальна с параметрами (О, 1): L((1' g)/B) ---+ N(O, 1).
Из этой теоремы следует, что ДТIЯ больших выборок (12) при достаточно
широких условиях оценка (10) обладает хорошими асимптотическими свой
ствами: она является асимптотически несмещенной, состоятельной (так как
в 2 ---+ О при n ---+ (0) и, более тoro, она позволяет построить для величины
9 асимптотический 'У доверительный интервал. Действительно. так как при
n ---+ 00
{ 11' gl }
р < с-у ---+ Ф(С-у) Ф( С-у) == 2Ф(С-у) 1 == /,
Ij 3.7. Объединение и улучшение оценок
269
rде / Е (О, 1) заданный доверительный уровень и е-, == ф I((1 +/)/2), то
отсюда следует, что интервал
1(n) == (т =F е-,В) (13)
является аСИМnТОТИ"lеским / доверительным интервалом для g:
P{g Е 1(n)} / при n 00.
Дальнейшие УТО"lнения свойств оценок (1 О)
можно сделать, если дополнительно предположить,
что выборки Х} извлечены из нормальных COBO
куnностей N(g, о}), j 1, ,k. Вместо CMe
8 2 " 2
щенных оценок j теоретических дисперсии 0'1
будем использовать несмещенные оценки
2 n} 8]
8 jo == .
nj 1
Torдa формулы (1 0) (11) заменяются на формулы
то == aloT) +
+ akOTk,
rде (в условиях (12))
;:;;. /j(n) B 2 З . == 1, k
.....зо 8 2 О, ., ,
jO
Объединенная оценка
в случае НОРМОЛЬНblХ
Вblборок
(14)
k
Вб == ( /j ) )
j l 8 jo
( 15)
Покажем, "ITO в данном случае оценка То является несмещенной. Действи
тельно, так как для нормальных выборок по теореме Фишера (см. теорему 2
2
2.5) статистики X j и 8 jo независимы, то независимы Tj и ajo, Но Torдa
k k k
ЕТо == EajoET j == 9 Eajo == gE ( 'L ajO) == g, (16)
J I з==l з 1
k
поскольку ajO == 1.
j==1
Вычисление дисперсии оценки (14) более сложно, и мы приведем для нее
лишь асимптотическую формулу в условиях (12).
Теорема 2. Если для нормальных выборок выполняются условия (12) и
О 2./ 2 2
<!!.. 0'1 (j < 00,
то
Вб [ ojo(1 O jO) ] o( )
DTo 1 + L.J + 5/2'
n n j==1 /j n
(17)
270 rлава з. Теория оценuвонuя неизвестных параметров расnределенuй
rAe
k
В5 == (2: ; )
) I )
'У) 2
а jO == 2 Во, j == 1,
(Т )
, k.
Таким образом, по крайней мере ДJlЯ нормальных выборок точность He
смещенной объединенной оценки (14) асимптотически (в условиях (12» тa
кая же, как и ДJlЯ оптимальной объединенной оценки (8) в случае известных
дисперсий.
3) Обьединение коррелированных оценок. В общем случае наличия Koppe
ляuий Pij == corr (T i , Tj) между исходными оценками Т., , Tk дисперсия
оценки (5) имеет вид
k 1 1: 1 1
DT == '" ao'coY( ' Т-)== '" D"a.o. == o/Da== Q(Q) (18)
L...J 1) 1, J n L...J IJ') n n ,
,з 1 i,j .
rде
PijUjUj
Dij==ncov(Ti,Tj)== ' nj=='Yjn, i,j==I,...,k.
y'Yi'Yj
Считая матрицу D == IIDijll известной и невырожденной, будем минимизи
ровать квадратичную форму Q(Q) при оrpаНИ'lении
k
2: a j==l.
j 1
Снова применяя метод неопределенных множителей Лаrpанжа, введем функцию
k
F(g:, А) == Q(Q) А (2: а) 1)
J I
И найдем ее точку минимума, решая систему уравнений
oF(g:, А)
д ==0, i==I,...,k,
Oi
k
Е0} == 1.
j>=1
Эта система имеет вид
oQ(Q) k
== 2 I: Dijoj == А, i == 1,
а, j 1
k
,k, I:aj==l,
з l
или в матричной форме
л
Dg:== "21,
k
2:0]==1,
з 1
3.7. Объединение и улучшение оцеНОI<
271
rде 1 вектор столбец из единиц. Отсюда
А
а== D II
2 ,
А
I'a == I'D I 1 == 1.
2
Таким образом,
== (1' D ll) I и !;! ==!;!* == (!' D ll) l D Il-
Это и есть оптимальный 8ыбор !;!* коэффициентов линейной комбинации (5)
с учетом наличия корреляций между исходными оценками {Tj}. Запишем
этот результат в более явном виде. Для этоrо обозначим
k
O I == IIDijll , Wi == L: Dij,
j 1
k k
W == L: W i == L: Dij,
i 1 i,j 1
( 19)
Wi
H
, W'
Torдa
W == 1'D 11,
I'D I
!;!*' == W == (H 1 , . . . , H k )
()бъединенноя
оценка в случае
наличия корреляций
ин. о. М.д.
k k
. ., ""' I ""'
Т == TIJ.' ==!;! 'l. == L..J HjTj == W L..J WjTj.
j l j 1
(20)
При этом (см. (18)
1 I 1 I
ОТ. == a*'Oa. == I'D IDD II == I'D II == ( 21 )
n nW2 nW2 nW
Оценка (20) точнее оценивает g, нежели любая из исходных оценок Tj.
2. Улучшение оценок
Выше мы акцентировали внимание на использовании несмешенных (или асимп
тотически несмещенных) оценок и искали среди них оценку с наименьшей
дисперсией, как наиболее точную. Однако в реальных ситуациях 8 ряде случаев
требование несмещенности итоrовой оценки не является <'естественным», бо
лее Toro, использование смешенных оценок может оказаться даже предпочти
тельным, если в качестве критерия точности оценок использовать cpeДHeKBaд
ратичную ошибку (с. к. о.). Один при мер TaKoro рода мы уже встречали ранее
в связи с задачей оцеНИ8ания дисперсии общей нормальной модели (см. при
мер 4 в 3.1). В общем случае, пусть Т есть несмещенная оценка с равномерно
минимальной дисперсией для некоторой параметрической функции т == т(О),
О Е е, но нас не устраивает ее точность, хотя оценка Т и является наилучшей
272 rлава з. Теория оценuвания неизвестных параметров распределений
среди несмещенных оценок. Спрашивается, можно ли с помощью Т постро
ить оценку с меньшей с. к. о.? Ясно, что такая оценка, если она существует,
будет смещенной, тем самым, доryуская смещение оценки, мы стремимся
увеличить точность (уменьшить квадратичный риск == С. к. о.). Итак, в этой
проблеме платой за более высокую точность оценки является отказ от условия
ее несмещенности. Рассмотрим, коrда и как этоrо удается ДОСТИЧЬ.
С помощью оценки Т введем класс оценок
т == {Т>, == лТ, л Е R'}.
Torдa с. к. О. произвольной оценки Т л из этоrо класса есть
Ев(Т>, т(о»2 == Ев [л(Т т(О» + (л I )т(О)] 2 == Л 2 DBT + (л I )2т 2 (о)
и минимум этоrо риска достиrается при
т 2 (0) (ЕвТ) 2
л == лт(О) == 2( ) == Е (О, 1).
DBT + r О ЕвТ
Если лт(8) == л' == const (не зависит от 8), то при всех О Е е
Ев(Т).. т(о»2 < Ев(Т>, т(о)2 == DBT,
(22)
т. е. Т л ' искомая оценка, причем она является смещенной (именно так
было в примере 4 в 3.1)).
В общем случае, коrда лт(О) не является тождественной константой.
введем два числа
(1). ) (2) )
л т == mf лт(О и л т == sup лт(8 .
в 8
Torдa, если л с > О при некотором с Е R I то оценка ТО) == л с(т с) + с
будет иметь меньшую с. к. о., чем оценка Т; если же л с < 1, то лучшей
(более точной) оценкой будет т(2) == л с(Т с) + с. Достаточным условием
существования какой то одной из оценок т(1) или т(2) является выполнение
неравенства
(23)
D8 T
е 'v 8 Е е, ( 24 )
[Е8(Т с)]2 "" ,
при некоторых с Е R\ И е> О (с и е не зависят от О).
Доказательства, Докажем это, например, ДlIЯ sup. Имеем (О ДlIЯ сокращения
записи опускаем)
DT Е(т(2) т)2 == DT Е [л(2) (Т т) + (с r)(1 ).(2))]2 ==
== (1 л (2) 2) DT (1 л (2) ) 2 (с т) 2 > О {::::::?
(так как л(2) < I и DT == D(T с)
(1 + л(2))[Е(Т с)2 (Е(Т с))2] > (1 ).(2) [Е(Т с)]2 {::::::?
З. 7. Объединение и улучшение оценок
273
{:::::::} (1 + >. c)( 1 лт с(О» > (1 л Jлт с(О) {:::::::} 2лт с(0) < 1 + л с,
что очевидно, так как Лт с(О) (; л с < 1. .
Пример 2, Пусть наблюдения производятся над rеометрической случайной
величиной {' == (+ 1 с Lвю == Bi (l, 1 1/0) (см. п. 2 1.1), т. е.
1 ( 1 ) X
РВ{(==Х}==а 1 B
х==I.2,..., 0>1.
Тоrда, в соответствии с формулами (7) 1.1,
Е//( == Е//( + 1 == о( 1 ) + 1 == о, D//(' == D//( == 0(0 1).
Пусть Х == (X 1 , ,Х П ) соответствующая выборка. Поскольку paCCMaT
риваемая модель относится к семейству моделей степенноrо ряда, то (см. п. 1
n
3.4) сумма наблюдений 2.:: Xi является здесь полной достаточной стати
i 1
стикой И потому выборочное среднее Т == Х есть н. о. р. м.д. дЛя О. В данном
при мере условие (24) принимает вид
D//T 0(0 1) I 1 11 О> 1,
[Е//(Т с)]2 == n(О с)2 c 1 r Е: == ;'
и, следовательно, оценка, имеющая меньщую с. к. о.
как (см. (22»
[Ев(Т 1)]2
ЛТ 1 (О) == (Т )2
Е// 1
чем Т, существует. Так
(o 1)2
D//T + (О 1)2
==
1
О
1+
n(О 1)
< 1,
а (см. (23»
(2) 1 n
Л Т I == sиp Л1' I ( О ) == / ,
//>1 1+1 n n+1
то искомая оценка есть
т(2) == л (2) ( Т 1 ) + 1 == nХ + 1 .
T l n+ 1
Конечно, эта оценка уже не будет несмещенной, но ее с. к. о.
(25)
« (2) ) 2 O(O I) O I O(O I)
Е// Т О == ( )2 < D//T == .
n+1 n+1 n
(26)
.
На практике иноrда сталкиваются с противоположной ситуацией, коrда
имеется смещенная оценка оп(Х), Х == (X I ,.. ., Х п ), дЛя пара метра О, а усло
вия задачи требуют использования несмещенной оценки или хотя бы оценки
183акаэ 1748
274 rлава з. Теория оценивония неизвестных парометров распределений
с меньшим смещением, чем у дп(Х). При этом экспериментатор даже ro
тов пойти на увеличение риска оценки, лишь бы уменьшить ее смещение.
Общий прием, с помощью KOToporo можно уменьшать смещение исходной
смещенной оценки, носит название метода «склодною Ifожа» Uackkl1ife metl10d
(анrл.)). Суть ero состоит в следующем.
Метод Рассмотрим оценки On(i)(X), основанные на BЫ
борках объема n 1, ПОЛУ'lенных из Х в результате
исключенин i ro наблюдения:
«складноrо ножа»
On(i)(X) == On l(X),
Построим оценку
,Xi l, Хн),
,Х П ), i == 1,
n.
01 == n(5n(Х) (n I)O(l)(X),
I n
O(l)(X) == L On(i)(X).
n i l
(27)
Можно показать, что если смещение исходной оценки о(п)(Х) имеет вид
а, а2
Еоп(Х) В == -;;; + n 2 +
2
то смещение ЕВI В == O(I/n ) оценки 01 уже не содержит членов порядка
O(I/n), т. е. оценка 01 устраняет смещение порядка I/n. При этом 130 мноrих
случаях дисперсии оценок О) и оп(Х) приблизительно одинаковы, а диспср
сию DO j можно оценить по формуле
n I n 2
Е(ОТI(i)(Х) O(l)(X))
n i 1
Оценка 01 называется ОЦ€llКОЙ «екладНО20 IIOЖО» первою порядка. Метод
«складноrо ножа.) дает хорошие результаты при устранении смещения оценок
максимальноrо правдопобия (о. м. п.), которые, как правило, оказываются
смешенными; при этом оценка О) имеет такое же аСИ lПтотическое распреде
ление, как и исходная о. м. п. (см. соотношение (23) 3.5).
Пример З. Пусть Х == (X j , ,Х П ) выборка из нормальноrо распреде
ления .лf(В 1 , 8i) и надо оценить 8i. В качестве оценки можно использовать
выборочную дисперсию
2 I n 2
S == L(X i Х) ,
n i )
которая является о. м. п. Дl!И Bi (см, при мер I в 3.5). Но эта оценка смещена
( 1:'2 n S 2 4
несмещеннои оценкои является статистика uO == ,см. пример
n 1
в 3.1) и ее смещение есть
2 2 n I 2 2 8i
EeS В 2 == Ee S 82 == .
n n
9 3.7. Объединение и улучшение оценок
275
Чтобы уменъшить смещение, применим формулу (27). Так как
2 1 n 2 1 ( n ) 2
Оп(Х) ==8 == n X; n 2 I:Xi
, I I I
то
( ) I ( 2 2 2 2 )
On(i) Х == Х 1 + + хн + Xi+1 + .. . + Х"
n 1
(n 1)2 (Х 1 + + ХН + Xi+1 +... + хп)2 ==
== ( X2 X2 ) 1 [( х. ) 2 2X Х. +Х 2 ]
n ] L....J J I (n 1)2 L....J J I L....J J l'
j 1 j 1 j J
откуда
1 n
O(I)(X) == I: On(i)(X) ==
n i 1
1 n 1 [ n ( " ) 2 ]
== I: Хl ( )2 I: xi + (n 2) I: Х ; .
n i 1 n n 1 i 1 j 1
Подставляя Оп(Х) И О(l)(Х) в формулу (27), имеем
n 1 ( n ) 2 J n I n
81 == " Хl I: Х ; I: х; + " x j 2 +
L....J n. n. n(n 1) L....J
, I , I , I , I
n 2 ( n ) 2 1 n 2 1 ( n ) 2
+ "х. " Х. " Х-
n(n 1) f:; I n 1 f:; I п(n 1) f:; I
n
1" 2 2
== n 1 L....J(X i Х) == So,
j 1
т. е. мы устранили смещение порядка I/n и пришли к наилучшей несмещен
ной оценке 8б (см. пример 9 в Э 3.2). .
В случае, Korдa необходимо устранять смещение
Обобщенная оценка ...
И более высоких порядков, чем O(I/n), используют
обобщенную оценку «складною ножа» k 20 порядка
«cкnaAHoro ножа»
k k . k
8k == :! ( I)i CL (1 ) O(j)(X) ,
, O
rде О(о)(Х) == Оп(Х), O(I)(X) среднее значение оценок On(i)(X) , построен
ных по выборкам объема n 1 с пропущенным i M наблюдением (как выше
в (27)), О(2)(Х) среднее от оценок опил(Х) при выборках объемами n 2
(пропущены i e и j e наблюдения) и т. д. Оценка 6k устраняет смещеliие
k
вплоть до членов порядка J/n , k == 1,2, ... .
18*
276 rлава з. Теория оценивания неизвестНbJХ параметров распределений
t 3.8. Доверительное оценивание
До сих пор мы акцентировали внимание на точечных оценках параметра О ис
следуемой модели F == {Р(х; О), О Е 6} и функций от Hero. Любая точечная
оценка представляет собой функцию Т == Т(Х) выборки Х == (Х 1, , Х n),
т. е. является случайноЙ величиной, и при каждой реализации;!;, выборки Х
эта функция определяет единственное зна4ение t == Т(;!;,) оценки, принимае
мое за приближаемое значение оцениваемой характеристики. При этом надо
принимать но внимание, 4ТО в каждом конкретном СЛУ4ае значение оценки
может отличаться от зна4ения параметра, поэтому желательно было бы знать
и возможную поrрешность, возникающую при использовании предлаrаемой
оценки, например, указывая такой интервал (или область в случае BeKTopHoro
параметра), внутри KOToporo с высокой (т. е. близкой к 1) вероятностыо 'у
находится истинное значение оцениваемоrо параметра. При таком подходе
rоворят об интервальном или доверителЬ/юм оценивонии. Основная цель при
этом состоит в том, 4тобы при заданном доверительном уровне, построить
кратчайший интервал, обеспе4ивающий наиболее Т04НУЮ локализщию oцe
ниваемой характеристики.
С подобноrо рода задачами мы уже встречались paliee (см. П.2 Э 2.], п. 5
2.2, П.4 Э 2.3, П.3 Э 2.5, П.5 Э 3.5). Общее определение , доверительноrо
интервала дано в П.5 Э 2.2 (соотношение (26», в СЛУ4ае парамеТРИ4еских
моделей в П.5 Э 3.5 (соотношение (28», там же (соотношение (34» дa
но определение и , доверительной области для BeKTopHoro параметра. Для
удобства дальнейшей работы воспроизведем это определение здесь еще раз
в СЛУ4ае оценивания скалярноrо параметра О При интеРIJ<UIЬНОМ оценивании
ищут две такие статистики T j == 1i(X), i == 1,2, что ТI < Т2, дЛЯ которых
при заданном доверительном уровне, выполняется условие
Р@{Т,(х) < О < Т 2 (Х)} " v О Е е.
(1)
Иноrда рассматривают одностОРО/lllllС доверительные uитервалы, COOTBeTCTBeH
но верхний (вида О < Т 2 (Х» и liUJlCIIlIU (Вlща Т)(Х) < О), определяемые
условиями, аналоrИ4НЫМИ (1), в которых опускают соответствующую вторую
rраницу. Вместо (1) иноrда также пишут
Ре{ (} Е (T1(X), Т 2 (Х»} ,.
АналоrИ4НО определяетсн доверительный интервал для отдельной компо
ненты (например, (1) В СЛУ4ае MHoroMepHoro параметра О == (01, , Or):
P@{T1(X) < (), < Т 2 (Х)} " v О Е е.
Перейдем теперь к ИЗJ10жению общих приемов построения доверительных
интервалов в произвольных парамеТРИ4еских моделях (во встречавшихся нам
ранее примерах мы имели дело лишь с нормальными либо аСИМПТОТИ4ески
нормальными распределениями).
3.8. Доверительное оценuвание
277
Пусть модель :F == {F(x; 8), 8 Е 6} абсолютно непре
рывна и существует случайная величина С(Х; 8), за
висящая от выборки Х == (Х), ,Х,,) и от парамет
ра 8 и такая, что: 1) ее распределение не зависит от 8 и 2) при каждом
Е Х функция C( ; 8) непрерывна и cтporo монотонна по 8 такую
случайную величину называют цешnраЛbJlOU статистикой (для 8). Аналоrич
но определяется центральная стати
стика для отдельной компоненты (Ha
пример, 81) MHorOMepHoro параметра
8 С(Х; 81), а также для скалярной
параметрической функции т == '1(8)
(() может быть как скаляром, так и BeK
тором) С(Х; т). Далее будем pac
сматривать для краткости лишь случай
скалярноrо параметра (для BeKTopHO
ro параметра все рассуждения анало
rичны).
ПУСТЬДlJя модели F построена цeH
тральная статистика С(Х; 8) и !с(9)
ее плотность распределения. Функция
!с(9) от пара метра 8 не зависит [условие 1)), поэтому для любоrо 'у Е (О, 1)
можно выбрать величины 91 < 92 (мноrими способами) так, чтобы
92
Р е {9! < С(Х; 8) < 92} == f !с(9) d9 == 'У.
91
1. Построение доверительноrо интервала
с помощью центральной статистики
Центральная
статистика
G(Б(})
92
Тiж)
(}
Рис, 1
(2)
Определим теперь два числа Ti( ), i == 1, 2, Е Х, rдe Tl( ) < T 2 W, как
решения относительно 8 уравнениЙ
C( ; 8) == 91,92 (3)
(однозначность определения этих чисел обеспечивается условием 2), нало
женным на функцию C( ; 8)). Torдa неравенства 91 < С(Х; 8) < 92 экви
валентны неравеНСТ[lам TI( ) < () < T2( ) (см. рис. 1) 11, следовательно, (2)
можно переписать в виде
Po{TI (Х) < 8 < Т2(Х)} == 'У, V О.
ТаКI1М образом, построенный интервал (Т 1 (Х), Т2(Х)) в соответствии с (1)
явлнется 'У доверительным интервалом дЛЯ О.
На практике, 'lТобы устранить неопределенность в выборе чисел 91 и 92
В (2), рекомендуется выбирать их так, чтобы выполнялись равенства
J !с(9) d9 == J JG(9) d9 == 1 ; 'у ;
oo 92
(4)
278 rлава з. Теория оценивания неизвестных параметров распределений
...
Центральный довери
тельный интервал
в этом случае соответствующий доверительный ин
тервал называют центральным.
С применением изложенной методики мы уже
встречались ранее в 2.5 (п. 3) в связи с обсуждением
теоремы Фишера. Так в при мере 1 в 2.5 была построена центральная CTa
тистика G(X; 8i) == nS 2 /8i для дисперсии 8i нормальной модели N((MJi),
с помощью которой был получен центральный r доверительный интервал
(1 О) дЛЯ 8 . Аналоrичный интервал для среднеrо 81, указанный в (12), был
построен с помощью центральной статистики tn 1 Jj (11). Друrие иллюстра
ции этой методики дают при меры 2 и 3 2.5. Но все это было осуществлено
с учетом специфики нормальной модели, т. е. в достаточно частном (хотя
и важном) случае.
В то же время можно выделить целый класс моделей, для которых цeH
тральная статистика всеrда существует и имеет простой вид. Именно: если
функция распределения Р(х; 8) наблюдаемой случайной величины непре
рывна и монотонна по параметру 8, то можно положить
n
G(X; 8) == 2:: 111 F(X j , 8).
j 1
(5)
Действительно, условие 2) здесь обеспечено предположением о свойствах
функции Р(х; 8), а так как преобразование Смирнова", == F( ; 8) порожда
ет случайную величину с равномерным распределением И(О, 1) (см. Уl1р. 17
к rл. 2), т. е. .cs(1J) == И(О, 1) не зависит от 8, И, в свою очередь, .с( 111 ",) ==
== r(l, 1) (см. пример 1 в 1.2), то слаrаемые в (5) независимы, и каж
дое из них имеет стандартное показательное распределение r(l, 1). Отсюда
по воспроизводящему свойству raмма распределения (см. п. 3 1.2) имеем
Lo(G(X; 8» == r(l, n), т. е. G(X; 8) центральная стаТИСТИК<I с плотностью
(см. (18) 1.2) fc(g) == 9n le g jr(n) , 9> О. Следовательно, соrласно изло
женной выше общей методике, Д1Jя построения r доверительноrо интервала
для 8 мы должны определить числа 91 < 92 из условия
9' 00
1 / n I 9 1 / n 1 9 1 r
[(n) 9 е dg == r(n) 9 е dg == 2
о
и, решая относительно 8 уравнения
(6)
n
2:: 111 F(X i ; 8) == 9; (i == 1,2),
i 1
(7)
найти корни Tj(X) < Т 2 (Х). В итоrе мы построим центральный r довери
тельный интервал (T 1 (X),T 2 (X» для 8.
Добавим некоторые комментарии к изложенному алrоритму. Обозна
чим r p , n р-квантиль распределения r(I, n), тоша условия (5) означают, что
3.8. Доверительное оценuванuе
279
gl == r(l 'Y)/2,n, g2 == r(I+'Y)/2.n и, следовательно, ДlIЯ определения g, и g2
можно воспользоваться известными таблицами квантилей rамма распределе
нин r(l, n). Очевидно, что наибольшая трудность в применении методики
к конкретным задачам заключается в нахождении корней уравнений (7).
Рассмотрим несколько важных примеров использования центральных
статистик при построении доверительных интервалов.
Пример 1 (Доверительный интервал для параметра равномерной модели).
Пусть по выборке Х == (X 1 , ,Х П ) из распределения ЩО,8) требуется
построить доверительный интервал ДlIЯ параметра 8 Здесь F(x; 8) == х/8,
О х 8, т. е. функция распределения непрерывна и монотонна по 8 при
8 > о, и центральная статистика (5) принимает вид
n
а(Х;8) == LlпХ i +nlп8.
i 1
Леrко видеть, что решениями уравнений (7) являются здесь
{ 1" }
Tj(X) == ехр gj + L 111 Х ; , j == 1,2,
n n i 1
rдe g! == r(l 'Y)/2,n, g2 == r(I+'Y)f2,n, а искомый интервал есть (Tl( ), T2( »'
Центральная статистика может быть не единственна. Так, в обсуждаемом
примере можно указать еще одну центральную статистику, а именно, из п. 2
3.4 (соотношение (13» следует, что плотность статистики Х(П) == шах X i
] I n
имеет здесь вид
n
gl (t; 8) == tn l t Е [о, О].
ОП
Отсюда по формуле (45) Э 1.2 леrко получить (задача!), что
.со ( ( X n) У) == Що, 1), V О > о.
Таким образом, случайную величину (X(n)/fJ)n также можно использовать в
качестве центральной статистики ДlIЯ оценивания 8. Соrласно общей методи
ке (соотношения (2) (3). ,/, доверительным ДlIH О является любой интервал
вида
( Х(П) Х(П» )
/ ' / ' О < g 1 '/';
(g +")')1 n gl n
центральным среди них является интервал, соответствующий значению g ==
== (1 ,/,)/2, наименьшую же длину имеет интервал при g == 1 ")', Т.е.
интервал (Х(П), Х(п)/(I ")')I/n) (показать!). .
Пример 2 (Аоверительный интервал для cpeAHero нормальной модели).
Пусть по выборке Х == (X I , ,Х П ) из распределения N(O, 0.2) (0.2 извест
но) требуется построить доверительный интервал ДlIЯ неизвестноrо cpeДHe
ro fJ. Поскольку .со(Х) == N(8, (12/ n ) или .со (-Jii(Х 8)/(1) == N(O, 1), то
280 rлава 3. Теория оценивания неизвестных параметров распределений
...
:&
о::
\1:1
{!
.",
....
....
о
::Е
)(
:о
з:
..,(1)
:ij ::Е
::Е О
CLC:::
о о
з: ;
'" s
о v
CL
:u
::Е
"' :т
CLro
"' %
с: ..,
а: О
:::t'8
'" :;;
о CL
;:а
'" ::Е
CLro
'" CL
.... "'
з: с::
S Q)
)( :о
:о %
з: ....
.., v
с; Q)
'" '"
.... ..,
S S
Q.Q)
'" %
"'
О
"'
::$
:s
с;
'"
Q) I
s N !:
з: ...:
Q) I
о; I х
Q) ci 1
:'! N
Q. ci +
с: I I !: (;)
u
" .. $
Q. I Ni>< .. + + ....
Q) . . 'i>< .... '--.......
Q) I !: !: .
s .. 1:>. N I c
'" q;- Nhl ь
'" ь INN I Е с!
:: 1 11 q,
... I
u I .... I
:: I N 11 11 I
... 11
'" 1::;' q, !: I 1
t; 11 NN -;::- I !: $
q, .... +
'" q, 11 с5' I >.i I E
'" I
з:
.о с5' 11
с5' .. (5 <::, -;::-
(5
з: (5 .Е.. :>.
Q) х
::r
(5
-,
Е N Nb'1 !: ,.............. .
............... 'i ........
IN g ...:
I I + N I
"
Q. " ::i I Ntr)
1:! Nb"! "
+ !: -;::
з: -;:: "r.--H .
s -, .:!: I 11 N + :!!
':: е< "
:а 11 11 N b -;:: ::;. '--.......
з: tr) I +
.о -;::
о; >-- N h -fl ;.. '" 5:1
Q) <.> <.>
.... I . ь ft
з: t""
Q. ;[I " ft 1:>.
Q) 11 N
.. н-- I 1 I
о h -;:: "! I
"1 I
;.... ft -fl е::;- I I I I
'>: 1:.:: 11 N I 11 + + е:$
:а 11 "! 11 11 N е: !: !:
з: е::;- е::;-
.о "! N 11
!: N
е::;-
з: х
'" >< ><
t "' "'
q, <ь' X N '=N
q, 5 ... 5
'" со: з: s q,
Q) Q) s :: Q. I Q. I u ---..
S Q) Q) u u u u Q) Q. N
з: з: з: Q. Q. .о=- 3 QJN
!:! :'! :'! Q) u .... О с: q,
с:: с: u ... u i5 11
о Q. Q. u u О 11 о 11
о u u S S з: ;!; о "1 ....
"1 "1 ..,
.... " .... '" ....
Q. Q.
.о NN ""b b ..-..&.........-..&....... N N
N N... N..;' q, q, N f""'.&.......
о; ... ... q,
Q) ь . . . . .
... ... ::i. q, N N = N
:::Е '"Ъ ....... q, q,
N
,:::-
I
8
· ("J
I !:
11
С
....
tr)
.hJ
IE
11
1:>'
I
J
3:
"("J]
I
11
'"
11
N
"("J]
I
11
I
11
:>.
"
11
:.::
.о
u
u
"1
...,
..
"
>:
'"
..
..
З.8. Доверительное оценuвйние
281
центральной статистикой для О является здесь G(X; О) == Vn(X O)/(Т. YpaB
нения (4) принимают в данном случае вид Ф(91) == (1 1)/2, Ф(92) == (1 +1)/2
и при этом 91 == 92 (так как Ф( х) == I Ф(х)). Будем использовать привыч
ное нам обозначение с-у == Ф 1 (( 1 +,) /2) (см. (27) 2.2), TorAa 92 == 91 == С-у,
и, решая уравнения (3), леrко находим центральный , доверительный интер
вал для (): (Х::т: С-уи / vn). Это симметричный относительно случайной точки
Х интервалдлины2С-уи/vn. в чаСТНОСТИ,длядоверительноrо уровня 1 == 0,99
величина с-у == 2,5758, для 1 == 0,998 с-у == 3,0902 и Т.д. Значения с-у для раз
личных 1 можно извлечь из таблиц квантилей cтaHAapTHoro нормальноrо pac
пределения N(O, 1). Доверительный интервал для cpeAHero при неизвестной
дисперсии (Т2 построен нами раньше в примере 1 IJ 2.5 (соотношение (12))..
Пример 3 (доверительный интервал ДЛЯ дисперсии нормальной модели).
Дnя модели N(JL, (2) (JL известно) также леrко найти центральную статистику
для r == т(О) == 02:
1 n
G(X; т) == (Xj р.)2
r j 1
Действительно, так как LO«X i р.) /В) == N(O, 1), то LO(X j р.)2 /т) == x 2 (1)
(см. упр. 38 к rл. 1) и потому LO(G(X; О) == х 2 (п). Если Х;, n есть р квантиль
распределения х 2 (п), то решениями уравнений (4) являются 91 == X I 'Y)/2,n И
92 == Xf'+'Y)/2,n' Разрешая относительно r уравнения G(X; т) == 9i (i == 1,2),
"" О 2
получаем центральныи 1 доверительныи интервал для дисперсии r == :
( n n )
(Xi JL)2 (Xj JL)2
j 1 j 1
2 ' 2
Х(1+'У)/2, n XP 'Y)/2, n
(сравни с решением (10) 2.5 для случая неизвестноrо среднеrо JL). ·
Учитывая важность нормальной модели, особую роль ее в приложениях,
приведем сводную таблицу (см. табл. 1) доверительных интервалов для ее
napaMeтpoR (в различных постановках), объединив результаты примеРОIJ 2, 3
и полученные ранее в 2.5 (примеры I 3).
2. Построение доверительноrо интервала с использованием
распределения точечной оценки параметра
Если уже имеется некоторая точечная оценка Т == Т(Х) для параметра (J
и известна ее функция распределения FT(t; В), то доверительный интервал
282 rлава з. Теория оценивания неuзвестНbfХ параметров распределений
.
Непрерывная модель
для & можно построить, основываясь на этой функ
ции. Предположим сначала, что распределение oцeH
ки Т непрерывно и функция FT(t; 8) непрерывна и монотонна по 8. Пусть за
дан доверительный уровень / Определим при каждом & Е е числа t; == ti(O),
i == 1,2, rде t, < t2 И
PB{t] < Т(Х) < t 2 } == F T (t 2 ; О) FT(t l ; &) == /.
(8)
Чтобы данная процедура была однозначной, рекомендуется выбирать эти
числа так, чтобы выполнились условия
1 /
FT(t l ; &) == 1 FT(t2; &) == ,
2
(9)
т, е. речь идет о построении централыfсоo доверительноrо интервала. Обозна
чим через 1)1 подмножеСТl30 е х е 1)1 {(О, о') t1(0) < &' < t2(&)}
(рис. 2). Тоrда РВ{ (В, Т(Х») Е 1)1} == /, V О Е е. Определим теперь при фик
сированном ()' сечение 1)1(&') множества 1)1 1)1(0') == {о (&, о') Е 1)1}
И рассмотрим случайное множество 1)1(Т(Х») с е. Событие О Е 1)1(Т(Х»)
происходит Torдa и только Torдa, KOrдa Т(Х) Е (t l (&), t 2 (&» и, следователь
но, при каждом О имеет вероятность / Таким образом, построено случайное
множество 1)1(Т(Х» , которое накрывает истинное значение параметра О
с вероятностью /. Если это множество является интервалом, то тем самым
построен (центральный) / доверительный интервал дли &. Это будет так, ec
ли кривые о' == ЦО), i == 1,2, являются монотонными одноro типа (т. е.
одновременно либо возрастают, либо убывают), 'ПО обеспечивается условием
непрерывности и монотонности функции FT(t; О) по О (рис. 3).
Таким образом. при сделанных предположенинх множество 1)1(0') при
каждом о' предстаnлнет собой интервал; следовательно, определены ero концы
01(0') < &2(0'), а тем самым и соответствующий / доверительный интервал
(T1(X), Т 2 (Х» ДЛЯ О, rде Т;(Х) == О;(Т(Х», i == 1,2.
Построение диаrpаммы придает наrлндный смысл этоЙ методике. Диаrрам
му стронт по вертикали (длн любой абсциссы О находнт из (9) соотuетстuующие
О' t,(O)
rт(t; 8)
О (01< 02)
t\(O\) t l (B 2 )
t
РИс.2
Рис. 3
3.8. Доверительное оценивание
283
ординаты t l и t 2 ); (,читают,) же ее по ЮрUЗ0нтаЛll, т. е. для наблюдавшейся op
динаты t == T(;f) (;f раелизация выборки Х) «считывают,) две величины 81
и 82 И утверждают, что 8 Е (01, (2), Таким образом, если (,читать» диаrpамму
по вертикали, то rpаницы области Р"( описываются парой переменных точек
(О, t 1 ) и (О, t 2 ), таких что выполняются условия (9). Если же «читать.) диа
rpaMMY по rоризонтали, то rраницы Р"( можно эквивалентно описать парой
переменных точек (t, (1) и (t, 82), взяв за независимую переменную наблю
даемое значение t оценки Т(Х). Torдa соотношения (9) можно переписать
в терминах этих величин так: если функции t;(8) возрастают (см. рис. 2). что
соответствует убыванию по О функции FT(t; О), то
' ,
1 FT(t; (1) == FT(t; (2) == '
если же функции t;(8) убывают, что соответствует возрастанию по О функции
FT(t; 8), то
I ,
FT(t; (1) == 1 FT(t; (2) == .
Итак, алroритм построения центральноrо , доверительноro интервала
для 8 в случае, Korдa функция распределения FT(t; 8) оценки Т == Т(Х)
непрерывна и монотонна по О, состоит в следующем. Пусть t == T(;f)
наблюдавшееся значение оценки. Решая относительно 8 уравнения
1 , 1 +,
F T( t. О ) ==
, 2' 2 '
(10)
находим два числа 01 < 02. Далее утверждаем, <!то 8 Е (8 j , (2), Приведенная
теория rарантирует, что при" близком к 1, вероятность ошибки в случае
применения этоro правила равна 1 ,
Ан -
алоrичные рассуждения можно провести и для Дискретная модель
случая дискретной модели. Единственное отличие
состоит в том, что из за ступенчатости функции распределенин Fl'(t; О) !J co
отношении (8) можно, вообще rоворя, обеспечить лишь выполнение Hepa
венства
P8{t l < Т(Х) < t2} == F T (t 2 о; 8) FT(t l ; О) " (11)
поэтому вместо условий (9) следует ввести условия
1 ,
F T (t l ;8) ,
2
' ,
1 FT(t2 о; 8) '
(12)
rдe t, наибольшее, а t 2 наименьшее значения Т, удовлетворяющие
этим неравенствам. Кривые о' == Ц8), i == 1,2, в данном случае являются
ступенчатыми (рис. 4) и при «считыванию) величин 8;(0'), i == 1,2, следует
брать крайнюю правую точку отрезка пересечения rоризонтальной прямой
с левой кривой и крайнюю левую точку с правой кривой (Korдa линия
пересечения попадает на rоризонтальные «ступеньки,) кривых).
8'
284 rлава з. Теория оценивания неизвестных параметров распределений
1 ,
FT(t; 8) == 2'
l ,
1 FT(t о; 8) == 2;
t наблюдавшееся значение оценки Т.
Замечание. Часто вместо центральноro доверительноrо интерnала в дискретном слу
час рекомендуется строить множество V 1 по принципу включения D Hcro значений
статистики Т с наибольшими (при каждом 8) вероятностями их появлсния. В случас
применения этоro метода вместо условий (11) (12) rpаницы t j == Ц8), 1,2,
определяются из условия
8'
8
Рис. 4
Алrоритм построения центральноrо
, доверительноrо интервала для 8 в дис
кретном случае в основном тот же, что
и для HenpepbIBHoro, только вместо ypaB
нений (1 о) надо решать относительно 8
уравнения
( 13)
8
Pe{t l < т < t 2 } == Е Ро{Т == t} ? 1;
'I<I<'!
при этом в сумму должны быть включены значения t с наибольшими вероятностями
их появления, а интервал (t l , t 2 ) должен быть наименьшим, УДОDлетворяющим этому
условию. В рядс случаев, коrда распределение стаТИСТИКII Т асимметрично, такой
способ позволяет получить более короткис доверительныс I1нтервалы.
(14)
3. Асимптотические доверительные интервалы
В pSlДe случаев, кота имеется состоятельная и асимптотически нормальная
оценка Тn == Тn(Х), Х == (Х". ,Х у ,), для параметра 8, можно построить
асимптотический (при больших n) довсрительный интервал. С примерами
построения таких интервалов мы встречались в п. 5 2.2, п. 4 2.3 и п. 5 3.5.
В общем случае, пусть при n ---+ 00 имеет место соотнощение
C8(Vn(T,, 8)) N(O,и2(8)), '</8 Е 8,
причем асимптотическая дисперсия и 2 (8) непрерывна по 8. Тоrда в силу (17)
3.5
( уп(Тn 8) )
С 8 и(Т n ) N(O, 1),
откуда следует, что при n ---+ 00 и всех 8
'r:/ 8.
{ vnlTn 81 }
Р8 и(Т,,) < С, == 2Ф(с,) 1 =="
если с-у == ф I((1 +,)/2). Переписав это соотношенис в виде
{ C-уи(Тn) с,и(Т n ) }
Р8 Т" ,fii < 8 < Тn + vn "
3.8. Доверительное оценивание
285
получаем, что (T'I =F e-,q(Тп)/ ) асимптотический 1' доверительный ин
тервал для 8. Это симметричный относительно центральной точки Т п интер
вал шириной 2e.yq(Tn)/ , поэтому он будет тем уже, чем меньше асимп
тотическая дисперсия оценки тп, т. е. чем выше асимптотическая эффектив
ность ТП (в смысле п. 5 3.2). Следовательно, асимптотически кратчайший
доверительный интервал будет по рождаться асимптотически эффективной
оценкой. Если исходная модель:F {Р(х; 8), 8 Е е} реrулярна, то пе
речисленными свойствами обладают оценки максимальноrо правдоподобия
(см. п. 4 3.5). Поэтому построенные в п. 5 3.5 доверительные интервалы
являются асимптотически оптимальными (кратчайшими).
Проиллюстрируем изложенные общие принципы при мерами.
Пример 4 (Доверительный интервал для параметра 6ернуллиевской модели).
Пусть требуется построить доверительный интервал ДJlЯ параметра 8 модели
Bi(I,8). Если имеется соответствующая выборка Х == (X 1 , , х п ), то, как
мы хорошо знаем, оптимальной несмещенной оценкой дли 8 являетси BЫ
борочное среднее Т == Х. Статистика Т принимает значения вида k/n,
k == 0,1, ,n, при этом (см. П.1 1.1)
n k
P1{ ; 8) == Ро{т } == Ро{ X i k} == C;'8 r (1 8)n r
Здесь
d ( k. ) k k ( R k 1
PT ;8 == nCn 18 1 8) <О при k<n,
d8 n
так что при k < n функция FT(k/n; 8) монотонно убывает по 8. Следова
тельно, применима описанная в п. 2 методика, соrласно которой при Т == k/n
центральным 1' доверительным интервалом для 8 нвляется интервал (81, (2),
rде 8) и 82 определяются в соответствии с уравнениями (13), которые в дaH
ном случае принимают вид
( ) n
k 1 r r n ,. 1 l'
1 Fr ; 81 == 2: С п 81 (1 (1) == '
r k
k
( k ) '""' r O r ( ) n r 1 l'
Р т ;;,;82 == СП 2 1 82 == ;
r O
(15)
при этом, если наблюдалось Т == 1 (т. е. k == n), то принимают 82 == 1, а при
т == о (т. е. k == О) полаrают 81 == О.
Практически rраницы 81 и 82 вычисляют, используя ИХ связь с кванти
лями бета распределения (см. п. 4 1.2). Именно, по формулам (4) ( 4') 2.4:
n
2: C;'8 (I 8,)n r == В(8,; k, n k + 1),
,' k
286 rлава з. Теория оценивания неизвестных параметров распределений
t n
L C 8;(1 (2)n T == 1 L C 8;(1 В2)n " == 1 В(8 2 : k + 1, n k).
T O r k+.
Поэтому уравнения (15) можно переписать в виде
I ,
В(8.; k,n k + 1) == ,
2
1+,
В(8 2 ; k + 1, n k) == """2
(16)
ДоверитеЛЬНblЙ
интервал для параметра
модели Bi(l, ) ""J.. .:
Следовательно, если обозначить z(p; а, Ь) p KBaH
тиль бета распределения Ве(а, Ь), т. е. решение
уравнения B(z; а, Ь) == р, о < р < 1, то из (16)
имеем (заменяя k на nТ)
( 1 , )
81 == Z """2; nТ, n nТ + 1. '
( 1+, )
02 == Z """2 ; nТ + 1, n nТ
< 17)
Доверительные интервалы (81, (2) рассчитаны для широкоro диапазона зна
чений n при 'у == 0,9; 0,95; 0,99 (см. [3]).
Если число наблюдений n велико, то для быстроrо нахождения прибли
женноro доверительноrо интервала для 8 можно воспользоваться асимптоти
ческой теорией, изложенной в при мере 17 в 3.5. .
Пример 5 (доверительный интервал для параметра пуассоновской модели).
Как и в nредьщущем примере, здесь оптимальной несмещенной оценкой для О
является статистика Т == Х (см. при мер 1 в 3.4), принимающая значения
k/n, k == 0,1,2, .; при этом (см. п. 3 1.1) L8(nT) == П(n8), поэтому
( k ) { k } k n8 (n8)'.
F T ;;;;8 ==Р8 T ; == 2:e 7'
T O
Здесь
d ( k ) nB (n8)!,;
F- T . () == ne < о
d8 n' k!'
т. е. функция FT(k/n; 8) монотонно убывает по 8 Соrласно общей методике,
если наблюдалось Т == k/n, то центральным , доверительныM интервалом
для 8 является интервал (81,82), rде ()I и 82 определяются соответственно
уравнениями
( k 1 ) 2: 00 n8, (nвl)r 1 ,
I FT '81 == е ==
n ' Т! 2'
r k
k
F T ( n k; ()2 ) 2: e nB2 (n8 2 У == 1 ' .
r O Т! 2
В данном случае rpаницы 81 и 82 можно выразить через квантили хи квадрат
распределения. Для этоrо получим сначала вид ФУНКЦИl1 распределения Сn(х)
{l8)
3.8. Доверительное оценивание
287
закона х 2 (n) (см. п. 3 91.2) при n == 2k. Обозначая для краткости '1r T (t) ==
t t T j ' О 1
е Т., Т , ,"', имеем
/ <XJ k ' x/2 / 00 k 1
1 G 2k (2л) == k e l )!2 k dx == 1I'ни) dt == L 1I'т(Л)
2.\ А т=О
(интеrpал леrко вычисляется интеrрированием по частям). Отсюда находим,
что
k ' <XJ
G 2k (2л) == 1 L 1I'т(Л) == L 1I'r(Л).
,=О r=k
( 19)
С учето (19) уравнения (18) можно переписать теперь в виде
1 ,
G2k(2nOI) == ,
2
1+,
G 2 k+2( 2n0 2) == .
2
(20)
2
Следовательно, если Х Р n обозначает р квантиль
2 '
распределения Х (n), т. е. решение уравнения
Gn(x) == р, то из (20) имеем (заменяя k на nТ)
'Д ;ери; ; ный »f
интервап дпя параметра
модепи П(О)
] 2
О, == 2n XP 1)/2. 2nТ ,
1 2
О 2 == 2n ХР+1)/2, 2nТ+2
(21)
Как и в предыдущем примере, Дf1я больших объемов выборки можно про
сто рассчитать приближенный доверительный интервал, воспользовавшись
асимптотической теорией оценок максимальноrо правдоподобия, что проде
лано уже в примере 15 93.5.
В данной модели можно построить асимптотический доверительный ин
тервал для О и друrим способом, а именно, воспользовавшись нормальной ап
проксимацией ДJ1Я выборочноrо среднеrо: LU(X)""" N(O, О/n) (см. теорему 3
92.2 с учетом Toro, что для nyaccoHoBcKoro распределения П(О) среднее и дис
персия равны (}, см. п. 3 91.1). Отсюда можем записать, что при больших n
{ vnlX 01 } { 2 O }
, ::;:: РО JO < С 1 == РО (Х О) < ==
== Р о { 02 20 ( Х + ; ) + Х 2 < О } == Р 8 {Т, < О < Т 2 },
rдe
( q C ) '/2
TI2==X+ =F x +
, 2n n 4n 2
Таким образом, (Т" Т 2 ) друrой приближенный , доверительный ин
тервал для О С точностью до членов порядка 1/n этот интервал эквивалентен
интервалу (Х =F C-у vХjn ), полученному в примере 15 в 3.5. .
288 rлава з. Теория оценивания неизвесmных параметров распределений
Пример б (Доверительное оценивание квантилей). Пусть по выборке Х
== (X 1 , , Х n ) из непрерывноrо распределения с неизвестной функцией pac
пределения Р(х) требуется построить доверительный интервал для р кванти
ли (1' при заданном р Е (О, 1) (см. п. 1 2.4). Точные доверительные интервалы
в этой задаче можно строить, основываясь на формуле (5) 2.4. Именно, под
ставляя в эту формулу х == (1' И учитывая, ЧТо Р(р) == р, получим
Р{Хщ (р} == В(р; k, n k + 1) = 71,
т. е. порядковая статистика X(k) является нижней 71 доверительной rраницей
д.nя (1" Аналоrично,
Р{Х(l) > (р} == ] В(Р; [, n l + 1) = 72,
т. е. Х(l) верхняя 72 доверительная rраница дЛЯ ()I' Наконец, так как
X(k) < X(l) при k < [, то
Р{Хщ < (1' < X(l)} == ] Р{(р Хщ} Р{Х(l) ()'} ==
== В(р; k, n k + 1) В(р; [, n l + 1) == 71 + 72 1 = 7
Это означает, что (Хщ, Х{/)) 7 доверительный интервал д.nя (1" .
3.9. Оценивание при выборе из конечной совокупности
1. Оценивание cpeAHero совокупности
В прикладных исследованиях часто приходится иметь дело со следующей си
туацией. Имеется конечная совокупность и == {Uj, ,и n } из N объектов,
каждый из которых характеризуется некоторой величиной х(и), и Е U. Зна
чения xi == х( Ui), i == 1, , N, неизвестны, и требуется оценить их сумму
N
Т == T(;f) == :L Xj, ;f == (XI,
, XN),
(1)
j l
или, что то же, величину J1. == T(;f)/N, называемую средним совокупности и
(можно рассматривать и друrие функции от ;f, под.nежащие оценке).
При этом предполаrается, что в силу объективных причин (большой раз
мер совокупности или большая стоимость наблюдения и т. п.) мы не можем
наблюдать все объекты с их соответствующими х значениями, а обследова
ниюдоступна лишь не которая часть из них (выборка), выбираемая по HeKOTO
рому случайному закону. Математическая формализация сказанноrо состоит
в следующем.
Назовем выборкой S любую конечную упорядоченную последователь
ность объектов из и, т. е.
S==(Ui"
, Щп(.))' i Е {I,
,N}.
Здесь n(s) есть объем выборки в, который может быть как фиксирован
ным, так и меняться от выборки к выборке. В первом случае rоворят о BЫ
3.9. Оценивание при выборе из конечной совокупности 289
борках фиксированноrо объема n. Если все элементы выборки разли'IНЫ, то
rоворят о 6ыборе без 60звращенuя (в этом случае n(в) :( N), в противном слу
чае (допускаются повторения объектов в выборке) о выборе с 60звращенuем.
Множество всех выборок обозначается через S и называется выБОрОЧI/ЫМ пpo
странст60М. Если на S задана вероятностная мера Р, при писывающая каждой
выборке s Е S вероятность р(в) ее извлечения (2:: р(в) == 1), то rоворят,
sES
, '" - ( ) '"
что задан выuорочныu план в. п. , подразумевая под Выборочный план
этим тройку А == (И, В, Р). Итак, мы можем наблю
дать лишь некоторую совокупность объектов из и, BЫ
бираемую в соответствии с заданным в. п. А.
Далее, мы рассматриваем f. == (XI, ,XN) как параметрическую точку
1З R N И определяем оценку дЛЯ T(f.) как функцию е{в, f.) на S х R N , которая
зависит от f. только через те Xj, для которых u; Е s (таким образом, е(в, f.) ==
== е(в, f.'), если Х; == Х; дЛЯ lЗсех и; Е в). Друrими словами, оценка есть
функция выбранных объектов и их наблюденных х значений. Мы будем pac
сматривать класс t: == [(А) всех несмешенных оценок:
[=={e(B,
2:: р(в)е(в, f.) == T(i), 'i f. Е R N },
sES
(2)
и искать в нем наилучшую (опmимальную) оценку, т. е. оценку, для которой
дисперсия
De(s,f.) == L р(в) [е(в, f.) T(iJ]2
.ES
минимальна для 'i f. Е R N Оптимальная оценка, вообще rоворя, не всеrда
существует, и в таких случаях для сравнения различных оценок используется
понятие допустимой оценки. По определению, оценка е(в, f.) (для T(f.))
наЗЫlJается допустuмой (в классе Е(А)), если не существует Допустимые .,f'
друrой оценки el(S,f.) Е [(А) , дЛЯ которой
оценки
Det(S,f.):( De(s,f.), 'if. Е R N
со строrим неравенством хотя бы в одной точке f..
Ясно, 'по недопустимые оценки должны быть oTBeprHyrbI. С друrой CTO
роны, обычно класс допустимых оценок является весьма широким и никакие
две допустимые оценки еl и е2 уже несравнимы (по значению дисперсии),
N
так как для них существуют непустые множества X t , Х 2 С R с условием
Del < De2, f. Е X 1 ,
и
De2 < Det, f. Е Х 2 .
Поэтому lЗыбор оценки из класса допустимых должен проводиться с учетом
дополнительных соображений.
193.0.,1748
290 rлава з. Теория оценивания неизвестных параметров распределений
q......
. Оценка
rорвица Томпсона
Наиболее употребительными оценками дЛЯ T( )
являются оценки rорвица Томпсона ё(s, ), которые
определяются следующим образом. Обозначим
1f(u) == Р(и Е s) == I: p(s)
$: s "
(3)
вероятность включения в выборку объекта и Е и (сумму вероятностей всех
выборок, содержащих и), и предположим, что в. п. А таков, что 7r(U) > О,
'r/ и Е U. Torдa, по определению,
х(и) х(и)
e(s, == L.J 7r(U) == L, I(и Е s) 7r(U) .
"Е$ 11
(4)
Так как
EI(u Е s) == Р(и Е s) == 7r(U),
то
Её(s, ) == I: х(и) == T( , т. е. ё(s, ) ЕЕ.
"
Нетрудно заметить, что оценка rорвица Томпсона является единственной
линейной несмещеНIIОЙ оценкой для Т, т. е. оценкой вида
L а(и)х(и) == L I(и Е s)a(и)x(u).
IIEs
11
Действительно, условие несмещенности означает, что
L x(u)a(U)7r(U) == L х(и), "i/ Е R N
"
"
Полаraя здесь == (О.. . 010.. . О), rде 1 стоит на i M месте, имеем
a(Uj)7r(Uj) == 1,
1
т. е. a(Uj) == ( ) '
7rUj
i == 1,
,N
I Замечание. Если рассматривать класс всех несмещенных оценок е(А) для в. п. А
с условием 1I'(и) > О, v и Е И, то можно лншь доказать, что ё(s, является допу
стимой оценкой.
.. Выбор без
возвращения
На практике чаще Bcero используются выборочные планы
фиксированною объема и для выбора без возвращения с paв
номерной мерой на S (выборочный nлаи А*). В этом случае
множество S состоит из (N)n == N (N 1) (N n + 1) всех упорядочен
ных комбинаций дЛины n из раlПИЧНЫХ элементов и и p(s) == I/(N)n,
"i/ s Е S. Нетрудно видеть, что ДJlЯ любоro ФИКСИРОlJанноrо элемента и cy
ществует n(N I )n I различных выборок из S, содержащих этот элемент,
поэтому
( ) n(N ] )n I
7r и (N)n
n
N
3.9. Оценивание при выборе из конечной совокупности 291
Следовательно, для в. п. А* оценка rорвица Томпсона принимает вид
N
ё(в,;!;.) == L: х(и), (5)
n
tlEs
)
т. е. N ё(a, ) есть обычное выборочное среднее х наблюденных х значений.
Из предыдущеrо следует, что для в. п. А* х есть оптимальная линейная оценка
для CpeaHei!O совокупности р. Вычислим дисперсию этой оценки. Так как
1 ( N ) 2 I I N
х 2 ==2 LI(щЕS)Хi ==2LI((ui,tLj)ES)X;Xj+2LI(uiES)X
n n . . n .
;=1 '#<) .",,1
и
) п(п I)(N 2)n 2 п(п 1)
EI((u;,tLj)ES ==Р((и;,Щ)ЕВ)== (N)" == N(N I) '
i fj,
то
N
2 2 n 1 I 2 2
Dx == Еж Р == nN(N 1) L.J. XjXj + nN L....J Xi Р ,
'#<) .=1
что леrко при водится к виду
( 1 1 ) 2
Dx == ;; N (1,
N
2 I 2
rдс (1 == N ) L....J (Х; р)
i=1
(6)
Величина (12 называется дисперсией совокупности U.
2
И ноrда требуется оценить не только среднее р, но и дисперсию (1 COBO
кynности U. По аналоrи со случаем бесконечной совокупности рассмотрим ".
в качестве оценки для (f величину Оценка дисперсии совокупности
'(;2 == ;;:2(а, == (x(и) х)2 (7)
n I L....J
uEs
v П 2
И наидем ее математическое ожидание. ерепишем (f в виде
N
и2 == I(и; Е S}((Xi р) (х р»)2 ==
n I L....J
i=l
N
I L 2 n 2
== I(и; Е S)(Xi р) (x р)
n ' n l
i=1
Torдa с учетом предыдущих соотношений имеем
N
2 n ) 2 n 2
Е(1 == L....J (Х; Р Dx == (1
(п l)N . n 1
.=\
т 2 2
.аким образом, (1 есть несмещенная оценка для (f .
19'
292 rлава 3. Теория оценuвания неизвестных параметров распределений
Замечание. СправедllИВ более СИЛЬНblЙ результат: "(i есть оптимальная оценка и2
в классе ваех несмещеННblХ квадраТИЧНblХ оценок, т. е. оценок вида
L а(и, v)(x(и) x)(x(v) х).
n, .Е.
2. Оценивание состава совокупности
Часто составляющие совокупность и объекты классифицируются по HeKOTO
рому признаку (например, полу, возрасту, если И биолоrическая популяция,
уровню качества, если И партия промышленных изделий и т. д.) на задан
ное число k классов (слоев) И],.. ,U k (И == И} U U U k , U j n U j == i25,
Расслоенная i i- j) IJ таких случаях rОIJОрЯТ о расслоенной совокупности.
Размеры клаССОIJ N 1 , , N k (состав СОlJОКУПНОСТИ) явля
совокупность
ются неИЗlJестными параметрами, которые должны быть
оценены по результатам соответствующеrо выборочноrо эксперимента. Что
касается размера N == N 1 + + N k всей совокупности И, тО lJ одних случаях
он может быть известен, lJ друrих же также представляет собой неИЗIJестный
параметр. Например, в задачах статистическоrо (IJыборочноro) контроля Ka
чества продукции И представляет собой партию некоторых изделий, каждое
из которых может классифицироваться По альтернаТИlJНОМУ признаку «ис
правно дефектно»; в этом случае число классов k == 2, размер N всей партии
известен и, следовательно, речь идет об оценивании размера лишь OДHO
ro класса, например, числа дефектных изделий в партии. При изучении же
биолоrических популяций (например, популяции рыб в некотором водоеме),
в социолоrических исследованиях, анализе TeKCTOlJ 8 линrвистике и т. д., как
правило, общий размер совокупности неизвестен и также подлежит оцени
ванию по результатам IJыборочноrо обследования. Задачи, связанные с oцe
ниванием состава конечных совокупностей, обширнан и мноrообразная
область прикладных статистических исслеДОlJаний, достаточно полно OTpa
женная в обзоре Ивченко и Хонова 7) Здесь же мы в качестве иллюстрации
лишь кратко коснемся некоторых из этоrо Kpyra вопросов.
Выборочный 1) Рассмотрим сначала задачу выборочною контроля.
контроль Пусть имеется ппртия из N изделий, содержащая HeKOTO
рое (неизвестное) число D дефектных изделий, D Е {О, 1,
"N}. Чтобы оценить параметр D или, более общо, некоторую заданную
функцию от Hero r(D), случайным образом без возвращения из всей партии
извлекается п( < N) изделий, каждое из которых провернется на доброкаче
ственность. Пусть Xi == 1, если i e ПРОIJеряемое изделие дефектно, и X i == О
В противном случае, i == 1, , п. Положим d == Х 1+' . . + Х п общее число
обнаруженных в выборке Х == (X 1 , , Х n ) дефектных изделий. Тоrда d
полная достатОЧllая статистика.
7) Ивченко [. И. Хонов С. А. Статистическое оценивание состава коне'lНОЙ совокупности / /
Дискретная математика. 1996. Т. 8. N! 1. С. 3 40.
3.9. Оценивйние при выборе из конечной совокупности 293
Донйзотельство. Вычислим функцию правдоподобия
PD(X == ), == (Х(,..., Х n ), Х. == 0,1,
наших данных. По формуле умножения вероятностей можем записать
PD(X == ) == PD(X 1 == x,)P D (X 2 == x21X 1 == Xl) Х
Х PD(X n == XnlXi == Xi, i == 1, ,n 1).
Леrко видеть, что здесь
PD(Xj == X jIX; == Х;, i == 1, ,j 1) ==
{ D N X' . Xj l при Х) == I, }
J+l
D X1 Xj l
I при Х} ==0
N j+ 1
(D xl Xj I)Xi. ) 1 X'
. (N D J + 1 + Х( + + Xj l ]
N J + 1
Отсюда
PD(X == ) == DX1(D XI)X2
(N D (1 XI))' X2
Х
(D Х, xn l)Xn(N D)l XI Х
( ) 1 X
N D (n 1 ХI xn ') n
(N)n
Наконец, воспользовавшись формулой
(l(l .':1)C2
(l .':1
) С l!
.':n ' n == (l
.':)
.':n)!'
.':. == О, 1,
которая леrко устанавливается, например, индукцией по n, окончательно
находим
D!(N D)!(N n)! C =
PD(X == ) == (D d)!(N D n + d)!N! C . (8)
Соrласно критерию факторизации (1) Э 3.3, это означает, что d достаточная
статистика для параметра D.
Чтобы убедиться в ее полноте, требуется доказать, что если EDrp(d) == О
при D == О, 1, , N, то rp(k) == О при k == О, 1, . min(n, D) == n 1\ D при
всех возможных D, т. е. при k == О, 1, , n. Но статистика d имеет известное
rиперrеометрическое распределение (см. П.4 91.1):
c k Cn k
PD(d == k) == f(k; D) == D c: D , k == 0,1, ,n 1\ D, (9)
N
поэтому предыдущее условие имеет вид
nлD
L l{J(k)f(k; D) == О, D == О, 1,..., N.
k O
294 rлава з. Теория оцеНUВDНUЯ неuзвестных параметров распределений
Полаrая здесь последовательно D == О, D == 1 и т. д., получим
cp(k) == О, k == 0,1,
,1 . .
Пусть теперь r(D) ПОДl1ежащая оцениванию функuин параметра D,
Torдa оптимальная несмещенная оценка для нее это решение уравнения
несмещенности
EDT(d) == T(D), D == О, 1, ,N
Но при любой функции Т левая часть здесь представлнет собой полином от
D степени n, поэтому, если T(D) не есть полином степени n, то это
уравнение решения не имеет, и, следовательно, ДI1Я таких функций T(D)
несмещенных оценок не существует, Если же Tj(D) == (D)j, j n, то BOC
пользовавшись формулой ДI1я факториальных моментов rИllерrеометри"еско
ro распределения: ED(d)j == (D)j(n)j/(N)j, сразу же получаем вид оптималь
ной оценки факториальной степени (D){ т; == (d)j(N}j/(n)j. Оценки для
произвольных полиномов
n
T(D) == I: aj(D)j
j O
можно строить с помощью линейных комбинаций статистик т; на основании
теоремы 3 3.1. В 'Iастности, T == dN/n оптимальная оценка caMOro
параметра D. а т' == d(n d)(N)2/(n)2 оптимальная оценка функции
r(D) == D(N D) при n 2.
Для сраlJнения приведем вид оценки максимальноrо правдоподобия Па
раметра D, которая получается максимилизацией по D правоЙ ,.асти (8):
jj == Id(N + I)/n] (здесь 'а] целая часть числа а).
2) Задача выборочною контроля (продолженuе). В некоторых системах CTa
тистическоrо контроля качества продукции поступают следующим оБР<JЗОМ.
Если число d обнаруженных в выборке дефектных изделий удовлеТВОРSlет He
равенству d k o , rде ko задаваемый заранее lIекоторый уровень (ko < n),
то они заменяются на исправные, после чеrо вся партия принимается. Если же
d > k o , то контролю подверrаются все N изделий, и все дефектные изделия
заменяются на исправные. Пусть случаЙНi1Н величина есть число обнзру
женных при описанном способе действин дефектных изделий (подчеркнем,
что это более "боrатая,) статистика, чем d). Тоща для любой (!) параметриче
ской функции T(D) можно построить несмещенную оценку вида T( ), т. е.
являющуюся функцией от , причем такая оценка единствеllна.
Доказательство. Так как распределение статистики имеет, очевидно, вид
(см. (9»
PD( == k) == f(k; п), k == О, 1,... , k o ,
n
Pп( == п) == I: f(k; D) == F(ko; п) (при D > k o ),
k kll+l
3.9. Оценивание при выборе из нонечной совонупности 295
то условие несмещенности в данном случае выrлядит так:
ko
EDT({) == L T(k)J(k; D) + T(D)F(ko; п) == т(п), D == О, 1, . .. , N.
k O
Но при n ko вероятности J(k; п) == О дЛЯ k > D, поэтому отсюда получаем
систему уравнений
v
L T(k)f(k; п) == т(п), D == О, 1,... ,ko.
k O
Эrотреуrольная система, в которой диаrональные коэффициенты J(D; п) i= О.
Следовательно, при любой правой части значения T(k), k == 0,1, ,k o ,
отсюда однозначно определяются. Для значений же т > ko полаrаем
ku
т(т) L T(k)J(k; т)
Т ( т ) k O
F(ko; т)
что возможно, так как F(ko; т) # о при т > ko. .
Если т(п) == п, то (так как Evd == DnjN) функция Т имеет вид:
kN
T(k) == при k == О, 1, . . . ,ko и
n
N k"
т :Е kJ(k; т)
n
Т(т) == k=O при т > !СО. (10)
F(ko; т)
В частности, если положить здесь ko == n (КОН'flX.Jль всей партии не преду
сматривается), то это решение сводится к полученному в предыдущей задаче:
ТЮ == т/'
Рассмотренный пример иллюстрирует тот факт, что наличие дополнитель
ной информации позволяет получать более сильные статистические выводы. ,
.,
3) Схема повторносо вьюора. Пусть из совокуп Повторный Вblбор
ности и, размер которой N и размеры ее классов
N), .. . ,N k неизвестны, по схеме случайноrо выбора с возвращением из
влекается п объектов и при этом фиксируется, к какому классу принадЛе
жит наблюдавшийся объект. В результате подсчитывается число Jljr объектов
класса U j , появившихея В выборке по r раз каждый, и тем самым исходная
статистическая информация об исследуемой совокупности представляется Ha
бором данных {Jljr, j == 1, ..., k; r == 1, , п}. По этой информации тpe
буется оценить неизвестный параметрический вектор N == (N], ,Nk) и,
вообще rоворя, произвольную функцию т(ю от Hero. Показано 8), что В дaH
!) Ивченко r. и. о некоторых задачах статистическоrо ВЫ80да дЛЯ расслоенных СО80КУПНО
стей // Теория вероятностей и ее применеНИII. 1984. Т. 29. N.! 1. С. 113 118.
296 rлава з. Теория оценивания неизвестных пораметров распределений
ной схеме полной достаточной статистикой является !l == (1/1, .. ,1/k), rде
n
1/) == L Pjr
r 1
число различных наблюдавшихся объектов класса Uj, j == 1, , k. Таким
образом, задача построения оптимальной несмещенной оценки для r( N ) CBO
дится к выяснению условий разрешимости и отысканию при этих условиях
явноrо вида решения уравнения несмещенности
E!;LT(!l) == r( N ), V N -1= Q.
(11)
Обозначим через Aj оператор сдвиrа на единицу j й переменной:
Ajf('f) == Л'!!. + j),
'f == (XI'
, Xk),
е. == ( О
) '
,0,1, О,
, О),
[де 1 стоит на j M месте, через 1 тождественный оператор: 1 f ('f) == f ('f)
и положим 6j == Aj 1 (6j называется оператором разности по j й пepe
меннай). Torдa, если возможные значения вектора N оrpаничены условием
N == N[ +... +N k n, уравнение (11) разрешимо для любой Функuии r( N )
и при этом оптимальной оценкой для r( N) является статистика
* (6i'
r ==
6k' ( I)1/I)f(Q)
61/0 П
(12)
[де
1/ == 1/1 +
+ 1/k, f('f) == (х! +
+ Xk)nr('f)
и
Оптимальная
оценка размера
совокупности
6 r t n == 2) I)' jC!(t+j)n
j=O
в частности, оптимальная оценка для размера N всей
совокупности имеет вид
61/0 n + 1
N* ==
61/0 П
( 13)
Если же N -1= Q априори может быть любым целочисленным вектором,
то уравнение (11) разрешимо лишь для функций вида r( N ) == f( N )/N n [де
f( ) полином степени n, удовлетворяющий условию f(Q) == О. Для
любой такой функции оптимальная оценка имеет вид (12). В частности, He
смещенные оценки существуют лишь для полиномов степени n от долей
[3j == Nj/N, j == 1, ,k, а оптимальной оценкой для величины I/N (KOTO
рая всеrда существует при n 2) является статистика
( )*
61/0n [
61/0 П
( 14)
Упражнения
297
Упражнения
я занимался до сих пор решением ряда задач,
ибо при изучении наук примеры полезнее правил.
Исаак Ньютон
D Пусть в урне находится а шаров, из которых al белые и а2 == а al
черные. Общее число шаров а известно, а неизвестным и подлежащим оцениванию
является число al белых шаров или, 'по то же самое, их доля р == al/a. Опыт
заключается в извлечении без возвращения n, шаров n < а, причем предполаrается,
что любая из с: комбинаций шаров может быть извлечена с равной вероятностью.
Пусть Х обозначает число белых шаров в выборке и Рп == Х/n. Найти Ер" и D Рп,
и обосновать использование случайной величины Рп В качестве оценки дЛя р. Сравнить
с результатом при мера 6 в 3.1.
.... Указание. Использовать тот факт, что Х имеет rиперreометрическое распределение
H(al,a2,n) (см.п.4 1.1).
D (Продолжение). Рассматривается модель Маркова Пойа извлечения шаров из yp
нь, (см. П.5 91.1). Пусть, по прежнему, Х есть число белых шаров в выборке объе
ма n, т. е. L:(X) == МП(n; al, а2, С), и пусть С > О. Убедиться в том, 'по доля белых
шаров в выборке Рп == Х/n является несмещенной, но не состоятельной оценкой для
p==al/a.
.... Уназание. Воспользоваться формулами (13) 91.1.
IJ Рассматривается ситуация, описанная в п. 791.1 (мноrомерная модель MapKOBa
Пойа для урны с N цветами шаров). Используя формулы (19) 91.1, убедиться в том,
что вектор относительных наблюдавшихся частот цветов в n извлечениях dn ==
== (v,/n,. .. ,l/N /n) является несмещенной оценкой дЛя вектора == (al/a,... ,aN /а)
долей цветов в урне в стартовый момент.
EI Пусть Х == (X 1 , ,Х П ) выборка из некотороro распределения L:Ю, для KO
Toporo среднее аl == Е известно. Требуется оценить неизвестную дисперсию Р2 == O .
I n
Убедиться в том, что статистика Тп(Х) == L(Xi Q:1)2 является несмещенной и co
n i J
стоятельной оценкой Р2, если Е 4 < 00.
11 В каких случаях статистика Тп(Х) == ..jan2/2 является состоятельной оценкой
теоретическоrо среднеro Q:I? Убедиться в том, что это имеет место, в частности, для
моделей [(8, 1) и N(8, 8\ 8 > О.
.... Указание. Воспользоваться состоятельностью выборочноro момента ап2'
П По n независимым наблюдениям X 1 ,... , Х ,. над случайной величиной требу
ется оценить неизвестную вероятность р == P{ Е Ll}, rде интервал Ll задан. Положим
n
l/n == L I(Х ; Е Ll)
i 1
число попаданий в интервал Ll. Показать, что статистика Т,. == vn/n несмещенная
и состоятельная оценка р. При каком значении р дисперсия DTn будет максимальной?
298 rлава з. Теория оценивания неизвестных параметров распределений
D Пусть случайная величина принимает значения 1'2'...' N с некоторыми (He
известными) вероятностями Pi,'" ,P:v соответственно. Над произведеl10 n незави
симых наблюдений и пусть V r означает число тех из них, коrда наблюдался исход .т»
(т == 1,... ,N, VI + + V:v == п). Доказать, что относительная частота V; == vr/n
является несмещенной и состоятельной оценкой дли вероитности Pr.
. Указание. Воспользоваться тем, что случайная веЛИ'lина 1/, имеет биномиальное
распределение Bi(n, р,.); применить иеравенство Чебышева.
D Пусть g оценкаДilЯ теоретической характеристики 9 и О < Dg < 00. Убедиться
в том, что статистика g2 не янляется несмещенной оценкой мя g2 и вычислить ее
смещение.
D По выборке Х == (X 1 , ... ,Х.) из распределения c( ) построить несмещенную
оценку ero характеристической ФУНКЦИl1 (х. ф.) ф(t) == Е e il (
. Указа.ние. Рассмотреть эмпирическую х. ф.
II!J По результатам n испытаний оценивается не известная вероятность .успеха.> (J
в схеме Бернулли Bi(I, 8). Обозначим Т. число успехов в этих испытаниях и pac
смотрим класс оценок вида Т == (То + о)/(n + {3). Вычислить среднеквадратичную
ошибку Т, убедиться в том, что при а == v'n/2, {3 == v'n она равна [4( JП + 1 )2] I
И сравнить эту ощибку с риском .обычной» оценки то/п.
m (Продолжение). Убедиться в том, что в Кдассе оценок вида Н(т.) несмещснная
оценка для параметрической функции т(е) == 0'(1 e)' при целых s, t О существует
лишь при s + t :::;; n и при этом условии она сдинственна и имеет вид
Н(т.) == (т,,).(n T,,)t , rде (а), == а(а 1) (а r + 1).
(n)Ht
. Указа.ние. Исподьзовать тот факт, что Се(Т.) == Bi(n, 8).
m Пусть Х == (X 1 , ... ,Х О ) выборка из биномиальноrо распределения Bi(k,8)
и Т == Х 1 +.. .+Х". Описать Кдасс оцениваемых параметрических функций, т. е. таких,
ДЛЯ которых сущеСТIlУЮТ несмещенные оценки вида Н(Т); построить несмещенную
оценку для Tj (е) == е}
. Указание. Воспользоваться свойством воспроизводимости распределени!! Bi(k,8)
(см. n.1 1.1) и результатом при мера I в 3.1.
m Пусть произведено одно наблюдение Х над пуассоновскоИ случайноИ ВСЛИ'IИНОЙ
с неизвестным параметром е. Показать, 'по Т(Х) == (X)j несмещенная оценка дли
Tj(8) == oj (j == 1,2,...), а ДЛЯ функций т(е) == 8 a при а > О несмещенных оценок
не существует. Построить неемещенную оценку для т(е) == (8 + I) I
m По одному наблюдению над дискретноЙ случайной величиной с распределе
нием
e e е'
f(x;fJ)== , х== 1,2,...
1 e " х!
(урезанное в нуле пуассоновское ра.сnределенuе), требуется оценить функцию т(О)
== I е 8 Убедиться в том, что статистика
{ 2 при 'leTHOM,
тю ==
о в пporивном случае
единствеиная несмещенная оценка T(II), но она практически бесполезна.
Упражнени1l
299
х 1
m Показать, что Т(Х) == L"7 единственная несмещенна.а оценка функции
;=1 I
7(8) == I" (1 8) в модели Bi (I, 8) при одном наблюдении,
m в модели И(р., 82) требуется оценить 7(8) == (}2 по выборке объема n. Показать,
что ыборочная дисперсия в2 имеет меньшую с. к. о., чем несмещенная оценка T ,
указанная в упр. 4, но в классе несмещенных оценок Т.. точнее, чем B == (n/(n I»S
Ш Доказать, что статистика
Л 1 ..
Т..(Х) == I L 'Х; рl
n ;=1
несмещенная и состоятельная оценка параметра О модели N(p, 82).
m Дана выборка Х == (Х" Х 2 , Х]) из нормальноro распределения N(O, 82). Рас-
смотрим статистику
1
Рт(Х) == 2T 1(lxi Т),
rде Т == Т(Х) == (Xi + xi + Х;) 1(2, которая как функция nepeMeHHoro Х предстааляет
собой плотность равномерноro распределения и( T, Т). Убедиться в том, что РТ(Х)
при любом Х является нссмещенноЙ оценкой теоретической плотности.
. Указание. Учесть, что [в(т 2 /0 2 ) == i(з). ..
Ш Пусть Х == (X 1 , . . . , Х..) Ь1борка нз распределения N(p., 82) и
..
Т == 2)X i р.)2
;=1
Провсрить, что несмещеиной оценкой для функции 7k(8) == 8 k при любом k > n
является статистика (см. (45) 3.4)
. ( Т ) k(2 r ( )
Tk== 2 r( n k )'
Сравнить оценку 7; с оценкой, указанной в упр. 17.
. УКQЗQние. Использовать тот факт, что f:. e (T/8 2 ) == х 2 (n), и формулу для моментов
raмма распределения (см. п, 3 1.1). ..
EiJ Доказать, что в общей нормальноЙ модели N(8 1 , 8 ) несмещенной uценкой для
функции Tk(8) == O по выборке объема n при k > n + 1 является статистика (см. (46)
3.4)
( nS 2 ) k/2 r( )
2 r( n+ I )'
[де в2 выборо'lНая дисперсия. Рассмотреть случай n == 2 и в.ычислить смещение
статистики 'Х) Х 2 1 как оцеики (}2-
... Указание. Учесть, что по теореме Фишера le(nS 2 /8i) == i(n 1). ..
т; ==
300 rлава з. Теория оценивания неизвесmных nараметров распределений
m Пусть Х == (X 1 , ,Х n ) Вblборка из rамма распределения r(/J, л) и Т ==
== Х 1 + + ХN' Убедиться в том, что статистика
. r r(лn)
Т, == т r(лn + r)
несмещенная оценка функции тт(е) == е' при любом r > лn (см. (39) 3.4).
... Указание. Воспользоваться свойствами rамма распределения (см. п. 3 1.2).
m По Вblборке Х == (X 1 , ,Х n ) из paBHoMepHoro распределения u(е, 2е) TpC
буется оценить параметр О. Доказать, что в классе оценок вида Т == aX(I) + fЗХ(ra} ,
а, {3 О, оптимальная несмещенная оценка сеть
. n+ I (
Т == X(I) + 2Х(n));
5n + 4
вычислить ее дисперсию.
... Указание. Воспользоваться результатами ynp. 46 к rл. 1.
m Оценивается параметр /J распределения U(О, О) по выборке Х == (X 1 , ,Х,,).
Убедиться в том, что статистики TI == (n + l)fnX(n), Т 2 == 2Х и Тз == (n + I)X(I)
несмещенные. Какая из них предпочтительнее?
m Пусть Х == (X 1 , ,Х n ) выборка из U(/J 1 ,02), Доказать, что статистики
TI == (Х(,)+Х(n»)/2 и Т 2 == (n+l)/(n I)(X(n) X(i») несмещенные и состоятельные
оценки функций 7'1 (О) == (01 + е2)/2 и Т2(О) == е 2 /J 1 соответственно.
m Показать, что для лоzuстuческоzо распределения, задаваемоro плотностью
'(х; О) == e x+8(1 + e x+e) 2, Х, О Е R 1
несмещенной и состоятельной оценкой параметра О является выборочное среднее Х.
m Является ли выборочное среднее состоятельноЙ оценкой параметра О модели
Коши К(О)?
... Указание. Использовать упр.48(б) к rл. 1.
m Проверить, что количество информации i(O) дIIя соответствующих моделеЙ имеет
указанныЙ в табл. 1 93.2 вид.
m Установить результатьr, указанные в табл. 2 93.2.
m Рассматривается задача оценивания функции т(О) == о2 В модели r(/J, л) по BЫ
борке Х == (X 1 ,..., Х,,). Воспользовавшись критерием Бхаттачария, показать, что
статистика Т' == n/(л(лn + 1))X 2 является оптимальной, но не эффективной oцeH
кой 7'(е).
lIiI Пусть Х == (X 1 ,..., Х,,) Вblборка из обратною zayccoscK020 распределения,
задаваемоrо плотностью
( Л ) 1/2 { Л(Х р.)2 }
'(х; л, 11-) == 2'1!"Х З ехр 2/ 2X '
х > О,
л > О, р. =J=. о.
1) Убедиться в том, что Х оптимальная несмещенная оценка параметра р. в лю
бом случае, известен или нет параметр л. Получить отсюда, что EX 1 == 11-.
DX r == р.З / л.
2) Найти эффективную оценку л 1 при известном 11-.
Упражнения
301
Указание. Воспользоваться общими результатами для экспоненциальной модели
и критерием Бхаттачария.
III Доказать непосредственно полноту достаточной статистики Т 0= Х 1 +.. ,+Х ,. дЛЯ
биномиальной модели Bi(k, О). Получить отсюда, что в данном случае несмещенные
оценки существуют лишь для ПОЛИНОмов
т(8) 0= L ajO j
j=O
при r С kn, при этом оптимальная оценка имеет вид
т' 0= t aj(T)j .
j=U (kn)j
Указание. Воспользоваться свойством воспроизводимости распределения Bi(k, О).
m Доказать полноту достаточной статистики Т == Х 1+ .. + Х ,. для пуаССОНОDСКОЙ
модели П(8). Показать, что оптимальной несмещенной оценкой для сходящеrося при
"' . . "' aj(T)j
всех 8 > О cTeneHHoro ряда т(О) 0= ajOJ является статистика т 0= ...............
. . nJ
J O J
Указание. Воспользоваться СВОйством воспроизводимости распределения П(О).
m Показать, что оптимальной оценкой параметра О, урезаиноro D нуле пуассонов
CKOro распределения (упр. 14) по соответствующей выборке Х == (X 1 ,. ,Х n ) явля
ется статистика т' == T{1nOT I /({1nОТ) при т 0= Х ! + .. . + Х N ) n + 1 и т' 0= О при
т == n, [де
n
{1nOk 0= 2.) I)n rC rk
,'=0
Указание. Воспользоваться общим результатом ш\я модели cтeneHHoro ряда.
m Доказать, что оценки, указанные в упр, 19,20 и 21 оптимальны..
2 2
aII Показать, что в модели N(O, "(о ) достаточной является статистика Т == (Х, s ),
но она не полна.
Указание. Вычислить среднее функции
(Т ) 0= S2(n + "() yz
!(J (n 1)"(
m По результатам n) 2 независимых измерений диаметра 01 Kpyra построить оп
тимальную несмещеиную оценку
т' 0= ?!:. ( Х 2 S2 )
4 n '
11'
ero площади т(О) == o , считая поrрешности измерений нормальными N(O,Oi)
4
случайными величинами.
m Доказать, что в упр.23 статистика TI оптимальная несмещенная оценка О.
Рассмотреть класс оценок Т л == ЛТ 1 И убедиться в том, что в нем имеются оценки
с меньщей с. к. о" чем у оценки T 1 , оптимальным же по критерию минимума с. к. о.
является выбор л' == n(n + 2)/(n + 1/.
302 rлава з. Теория оцениванuя неuзвестных параметров распределений
IEI Доказать, что Т == (Х(I), Х(n) полная достаточная статистика ДJlЯ модели
и(81, 82) и обосновать оптимальность оценок в упр. 24. Построить оптимальные oцeH
ки мя 8, и 82.
... Указание. Воспол ЬЗОШlТься упр.46 к rл. ]. ..
m Рассматривается доухпарамстрическая показатеЛl,ная модель W(O" 1,02) (см.
пример 2 в 3.3). Основываясь на том факте, что здесь достаточная статистика
т == (T 1 , Т 2 ) == (Хр) , Х Хр))
полна, убедиться в том, что оптимальными несмещенными оценками параметров MO
дели являются соответственно
, Т 2 1
01 == Т, ( ) == (nX(I) Х)
n 1 n 1
. n
82 == l Т2;
n
при этом
. 8 ,8
Do8, == ,Do82 ==
n(n ]) n 1
... Указание. Используя результаты примера 1 в 2.4, представить Т I и Т 2 через по
казательные спейсинrи У" , У n : У, == n(ТI О,) /02' У2 + .. . + У , == nТ2/8 2 , rJ!e
У . == (n r + l)(X(r) X(r I))/82' r 2. Отсюда, в частности, следует, что Т, и Т 2
независимы, ..
1m Убедиться в том, что оптимальная несмещенная оценка параМСТ[1<1 8 раСПJ1еделс
n
ния Вейбулла W(O, а, е'/О) по выборке Х == (Х" ... , Х n ) есть Т /n, rде т == 2::= xf
i=1
... Указание. См. пример 15 3.4. ..
m Доказать непосредственно, вычислив Ее6n 11 De6n, асимптотическую несмещен
ность и состоятельность о. м. п. 6n параметра О нормальноii модели N(p, 02) Н найти
ее предельныii при n ----+ 00 закон распределения; вычислить асимптотическую эффек
тивность оценки ТВ в упр. ]7.
[ 1 n ] 1(2
... Указание. Выразить Вn == ;; 2::=(х ; р)2 через оптимальную несмещенную
,::::;;(
оценку т,' в упр. ]9; ПРl1менить к оценке Т, центральную предельную теорему. ..
m Убедиться в том, что о. м, п. В п параметра 8 в модели N(8, 28) имеет вид В п ==
1 "
== 1, rде Т" == 2::= Xi, и доказать ее состоятеЛI,НОСТь.
n ;=1
... Указание. Применить к Т, закон больщих чисел. ..
m Имеется выборка (X i . Y i ), i == ],... , n, из двумерноro нормальноrо распределе
ния
N(O,o),II I\), (JE( I,]).
COCT3BfIТb уравнение праодоподобия мя о. м. П. ВN 11 убедиться 11 том, что ее асимпто
тическая дисперсия равна (1 02)2 / (n( 1 +02)). Рассмотреть 11 качестве альтернаПIВНОЙ
оценки КОЭФФlщнента корреЛЯЦИl1 8 Dыорочныый коэффициент корреляции
] "
Т, == 2::= XiYj
n ;=1
Упражненuя
зоз
и доказать, что ero асимптотическая эффективность есть
( 1 82 ) 2
ео(Тn; iJ) == 1 + iJ2
. Указание. При вычислении моментов использовать характеристическую функцию
(см. указание к упр. 29 rл. 1).
m Пусть х == (Х,.... ,Х n ) Вblборка из распределенuя Кептайна, задаваемоrо
плотностью
(x) { 1 2 }
f(x;8)== r:c ехр (J 2(9(x) 81) . 8== ((Jl,(J2),
v 2rr8 2 2 2
[де у(х) некоторая дифференцируемая монотонно возрастающая Фуикция (при
у(х) == х имеем нормальное распределение N((JI, 8i)). Убедиться в том, что справед
ливо следующее обобщение результата при мера 1 в 3.5: о. м. п. 8 == \9, Т), [де
1 n
'9 == L g(Xi).
n i l
2 1 1
Т == L....(g(X i ) 9)
n i l
Является ли 9 эффективной оценкой 81? Показать, что при известном значеиии 81 == а
эффективной оценкой ei Я8ЛЯется статистика
2 1 п 2
Т\ == L(g(X;) а)
n.
, I
(ср. с соответствующими результатами для нормальной модели, см. примеры 1, 2 и 8
3.2).
m Найти о. м. п. 8 п параметра е отрицательной биномиальной модели 81(т, 8)
и вычислить ее асимптотическую дисперсию.
. Указание. Использовать общие результаты примера 9 в 3.5 для модсли CTeneHHoro
ряда.
m Пусть D полиномиальном распределении М(n; РI , . . . ,PN) вероятности исхо
дов имеют вид Р; == pi(8), i == 1,..., N, rде 8 общиЙ неювестный (скалярный)
параметр. СостаВИТI) уравнения метода наКОПЛСНlIЯ для приблИJКСННОro Dыlисленияя
о.М.п.8.
m Показать, что асимптотическая эффективность выборочной медианы в модели
Коши К(8) (см. пример 8 в 3.5) равна 8/rr 2 == 0,8...
. Указание. Воспользоваться теоремой 1 2.4 (соотношение (15»).
m Убедиться в асимптотической несмещенности и состоятельностн О. м. п. 0" == Х(п)
пара метра 8 равномерной модели И(О, 8) (см. примеры 3 и 11 3.5). Доказать непо
средственно, что при n 00
Р в { n(о; 0,.) :::; t} ...-.....t 1 e 1 t О.
. Указание. Использовать упр.23, а также 46 к rл. 1.
304 rлава з. Теория оценивания неизвестных параметров распределений
m Показать, что в случае модели И(8 1/2, (J + 1/2) любое значение
(J Е [Х(.) ,X(I) + ]
является о. м. п. 8.. Какая точка этоrо интервала является несмещенной оценкой 8?
... Указание. Записать О. м. п. в виде
8.==a(X(.) )+(I a)(X(IJ+ )' aEIO,II,
и найти а из уравнении несмещенности.
liJ Рассматривается ссмейетво распределений Вейбулла W(/:/, а, Ь) с неизвеСТНblМ
параметром сдвиrа. Убедиться в том, что при О < а ::;:; 1 о. м. п. 0" == X(I) асимптоти
чески иесмещена и состоятельна, а ее закон распределения не является нормалЬНblМ
при n ---+ 00.
... Указание. Использовать результаТbI при мера 6 3.2 и упр. 56 к rл. 1.
m Случайная величина , характеризующая срок службы элементов электронной
аппаратуры, имеет распределение Релея W(O, 2,,;0) (см. упр.40). Убедиться в том,
'!то о. м. п. В. == Tjn, т. е. совпадает с оптимальной несмещенной оценкой /:/
m По выборке Х == (X 1 ,... ,Х.) из rамма распределения r(8, л) требуется oue
нить функцию т(8) == /:/ I Показать, что о. м. п. Т п == лj Х, убедиться u ее асимп
тотической несмещенности и состоятельности, а также установить, что при n ---+ 00
.со(т,,) N(lj/:/, Ij(лn8 2 ).
... Укозание. Использовать упр.21.
m Доказать, что для распределения Лапласа с nараметром сдвиса, задаваемоrо плот
ностью f(x; 8) == (lj2)e lz OI, х, 8 Е R 1 , О. м. п. 8" совпадает с выборо',ной медианой
и установить ее асимптотическую нормальность: .с о (8п) N(8, n I).
m Убедиться в асимптотической несмещенности и состоятельности о. м. п. В. ==
== (BI.' В 2 .) парамстров двухпараметрической показательной модели (см. пример 4
в 3.5).
m ПреобразованиR, стабилизирующие дисперсию. Установить следующие, полеЗНblе
аппроксимации для распределений специалЬНblХ функций от О. м. п.:
д;lя модели Bi(k,8):
.со (arcSin Iiп) N(arCSin,;o, 4 n )'
д;lя модели П(8):
х
8 .
· Т'
.со (Д,) N(,;o, 4 ). В. == Х;
д;lя модели N(j1., (2):
.со(lп В.) N (In 8, 2 )'
д;l1I модели r(8, л):
[ 1 · ] 1/2
0" == ;; f;(x; j1.)2
.со(l" 8 п ) .лr(IП 8, >. ),
х
е п == .
л
Упражнения
305
... Указание. СМ. П.5 (соотношение (31») р.5.
m Обоедllнеlluе статиСlIIиlfескоu UllформаЦIlU. Пусть X j == (X jl , ,X jnj )' j == 1,
, k, незэвисимые выоркии из распределений N((Jjl' (J ), j == 1,... , k, COOTBeT
2
ственно и X j , 8j соответствуюшие выборо'lныe средние и дисперсии. Доказать,
что "о == (X 1 ,..., X k , (2) О. м. п. ДЛЯ (J == ((JII,..., (Jkl, 02). rдe
2 1 k 2
(J2== Lnj8j, n==nl+ +nk:
n j=1
несмешенной же оценкой для обшей дисперсии O является статистика
Щ == ( ) 6;2
n k
... у'l(азание. Использовать пример I в 3.5, записав функцию правдоподобия для всех
данных в виде
2 "/2 { 1 2 [ 1 ( t2 ) t ] }
L == (21ret ) ехр 2(J2 L.J nj(xj (Jjl) n 2" 'ii I 111 о- '
2 j= I 2 2
rде
2 1 2
t == L.J n]Sj'
n j=1
m Показать, что 'У-доверительный интервал ДЛЯ параметра (J модели N((J, (J\ (J>O.
по выборке Х == (X 1 , ... ,Х п ) имеет вид
( Х Х ) ==ф I ( 21 )
1 + :/ ..;n ' ] c / ..;n , С 1 2'
Получить аналоrичный результат для случая (J < О.
... Указание. Использовать тот факт, что .co(vn(X (J)/(J) == .N(O, 1).
m Пусть Х == (X 1 ,... . Х п ) IIыоркаa из распределения N((J, 0-2).
1) УбедИ1ЪСЯ IJ том, '!то любой интервал вида
( 0-92 (J"91 )
6. 1 (Х) == Х ..;n ' х ..;n ,
[де 91 < 92 любые 'lисла, удовлетворяюшие условию Ф(g2) Ф(gl) == "1. явля
стся 1 довеРl1тельным интервалом для параметра (J. Доказать, что кратчайший
из этих интероалов есть 6.;(Х) == (X'f о-с.,/ Jn).
2) Сколько необходимо произвести наблюдений n == n(l, 1), чтобы точность лока
лизации параметра, т. е. длина интервала 6.;(Х) , была равна заданной величи-
не '? Проверить, что при aдaHHЫX n и 1 доверительный уровень 1 == 'У(n, 1) ==
== 2Ф(lvn/(20-» 1.
... Указание. Использовать резудьтаты при мера 2 в 3.8.
20 За.а) 1748
ЗОб rлава з. Теория оценивания неuзsестНbfХ параметров распределений
m Доказать, что 'У-доверительным IlНтеРIJалом для среДllеквадраТИ'lноrо отклоне-
ния (J модели N(j1.,(JJ) является любой интерIJал б')"( ) (T/a2,T/al), rде
2 '
т L...,(X j J1.)
i=1
а числа а, < а) выбираются из условия
/ 01 , 'У
xkn(x-) dx "2'
О,
rде kll(t) плотность распределения х 2 (n). Определить кратчайший в этом классе
интервал б;(Х).
... Указание. Использовать то, что {д(т 2 /(2) /(n).
eiJ Доказать, что нижний и верхний 'У-доверительные интервалы для среднеro (JI
модели N((J" (Ji) по выборке Х (Х"... ,Х П ) имеют соответственно ВIIД
( Х t')",/l 'S < (JI )
Jn=l
( е: < Х + t')".n ,S )
Jn=l
... Указание. См. пример I u 2.5, rдc постросн двусторонний интерuзл для е,
m (Продолжеllие). ПостроиТl, односторонние 'У ДОВСР'1ТСЛl,ныс интерuзлы для дис-
персии о;:
( nВ) < О; ) и ( (Ji < )
х;...- - X -')",n-'
(двусторонний центральный 'У доверительный интервзл указан в (10) 2.5).
m Пусть Х (Х" '" ,Х,,) 11 У (Y 1 ,... , У т ) дне незаIJI1Сllмые выборки, при-
'leM первая fIЗ распределении N(e('), 0';), а вторая IIЗ N((J(2) , а;). Показать, что
центральныii 'у доверllтельный интервал для разносТl1 среДНI1Х r e(l) е(2) имеет
вид, указанный в табл. I 3.8.
m Пусть Х (Х], .., Х..) и У (У], . .. , у,,,) IIсзаDllсимые выборки l1J рас-
преДСЛСНIIЙ f«(J" 1) и f((J2, 1) соответственно. Доказать, 'по нентральный 'У довери-
тельный интерва для отношения r О2/е] имеет ВIIД
( F(I ')")/ '" 2... У , F1]+')")/j:'" 2т У ) ,
rде Fp.r,. р квантиль распределения Снедекора S(r, s).
... Указание. Использовать тот факт, что {д(Т Х /у) В(2n,2т) (см. упр. 54 к r,1. 1).
m УбсдlПЬСЯ в ТO , что 'У-доuсрительный интерuзл для Пilра етра СДIJI1rа показа-
тельноrо распределения: f(x; О) e цд. х О, по n наблюдениям имест оид
(Х(I) + ( ) In(I 'Y), X 1 ]))
KaKOi'I оид будет иметь здесь центральный 'У доверитсльный интерозл?
Упражнения
307
... Указание. НаЙти распределение статистики Х(IJ == min X j и учесть, ,(то собblтие
I:::;i:::;n
{Х(IJ 8} является достоверным.
raiJ Рассматривается модель упр.40. Убедиться 8 том, 'ПО централЬНblЙ 'У ДО8ери
тельный интервал для параме1l'а 8 имеет вид
( ,2Т , 2 2Т ) .
X(I+1)/2. 2п X(I 1)/2. 2п
В частности, при а == 1 имеем соответствующее решение для модели r(8, 1).
... Указание. Y'lecTb, что [.8(ца /8) == i(2) (см. пример 15 в 3.4 и п. 3 1.2).
m Рассматривается модель упр. 39. УЧИТblвая, что
( 2nТ 2 ) 2
[.8 о; == r(2, n 1) == Х (2(n 1)),
т. е. 2nTz/8z центральная статистика для 02 (см. указание к упр. 39), убедиться в том,
что
( 2nТ2 2nТ 2 )
z '2
X(I+11/Z. 2(n l) X(I 1)/Z. Z(n l)
есть центральный 'У ДО8еритеЛЬНblЙ интервал для 82. Далее, так как
[.Н Cn(T 2 81) ) == r(2, 1) == i(2)
и стаТИСТИКI1 TI и Т] независимы, то
2n(T 1 (1) 2nТ]
202 2(n I)О)
(n I)(T 1 (1)
Т]
центральная статистика для 81, имеющая распределение Снедекора 8(2, 2(n 1)).
Следовательно, централЬНblЙ 'У доверитеЛЬНblЙ интервал для 81 есть
( Т] Т2 )
TI n 1 1'(I+l')/2.z.2(n l), TI n 1 F(I 1J/Z,2.2(n I) .
z
I!II Протозuрова//uе будущuх наблюде1/UЙ. Пусть n, Х и 8 объем, ВblбоРОЧНblе
среднее и дисперсия выборки из распределения N(8 1 , 8i). Показать, что с вероятно
стью r результат следующеrо, (n + I) ro испытания Xn+1 попадет в интервал
(х т tЩ:z!.П 18
(n + 1) )
(n 1) ,
[де lp.n p KBaHТlIJJb распределения Стьюдента S(n).
... Указание. Учссть, 'ПО
[.(
(n 1) (Х X n + I ) ) == 8(n 1)
(n + 1) 8
(следствие теоремЬ! 2 2.5).
20*
308 rлава з. Теория оценивания неизвестных параметров распределений
m Пусть Х 0= (Х" ,Х,,) ВbIборка из нормалЫlOrо распределения N(p., ()2).
Показать, что приближеННbJе (при больших п) 1 доверительные интервалы дю, Ilара
метра () 11 функции т«()) 0= In () имеют вид соответственно
( с.у )
О" 1 1= -I2Тi
(In О" 1= Jin ),
rде
[ I n ] 1/2 ( 1 + )
ОП == (Xi р.)2 И С, == ф 1 Т .
Получить из oтoporo результата друrой интервал для ().
... Указание. Использовать результат, указаННbIЙ в упр. 55.
m Доказать, 'ITO в слу'ше 60ЛhШИХ ВbIборок асимптотичеСКII кратчайшиЙ 1 ДOBe
ритеЛЬНbIЙ интервал дI1Я Ilараметра () модели r(O, л) имеет вид хл I(1 1= C,/fu) ,
а аналоrи'IНЫН интсрвал для функции т«()) == 1п О есть (1п 0" 'F С,/ V>:;;) (см. упр. 55).
Получить из [jToporo результата друrой интервал дЛЯ О.
i!I По IIbIборке Х == (Х" ... , Х n ) из распределения Bi( 1, ()) построить асимптоти
ческий (при n ----+ 00) 1 доверитеЛЫIЫЙ ннтервал для () основываЯСh на нормальной
аппроксимации
L ( .,fii(X () ) N(O 1)
O '
(теорема Муавра Лапласа). Сравнить полученное решение с решением, указаННblМ
в Ilримере 17 в 3.5.
m Показать, что асимптотическиЙ 'У довернтельный интервм для параметра 1) OT
Рlщательной биномиальной lOдели ВI(r, О) имеет вид
1/2
С:Х 'F C 7 [ n(rr: X )J ] )
(ср. с результатом примера 16 3.5).
... Указание. Воспользоваться общим реЗУЛhтатом (33) Э 3.5 для модели степенноrо
ряда 11 формулами (7) Э 1.1.
liJ ПоказаТh, ЧТО оценкой по методу моментов параметра 1) paBHoMepHoro распрс
деления И(О, () является статистика 8 == 2Х и исследовать ее на несмещенность,
состоятеЛhНОСТU и эффективность (см. упр.23).
m УбеДИТhСЯ в том, '11'0 оценка по методу моментов параметра 8 распределения
И( (), (}), О > О, есть 8 == .
m Пусть Х == (X 1 , . . . , Х ,,) выборка из распределения Лапласа с плотностью
f(x; ()) == ( )e OIXI, () > О.
Показать, '1то оценка () по методу моментов ест!. 7f == у'2/0. 2 .
Ш Найти мстодом моментов оценки парамстров ()I и ()2 «Дllоiillоrо,) распределения
Пуассона, задаваеМОl'О вершпностями
1 ( o ()f b, 8f )
Po{ == х} == е I . + е - .
2 х! х'
х == О, 1, 2, ... ,
о < ()I < ();.
Упражнения
309
m Пусть Х(I) < < Х(Т) цензурированные данные для n наблюдений (т :( n)
11 модели упр. 39 и У; == (n i + I)(X(i) Х(Н)) , i == 2,... ,r. Показать, что
У 2 + +У Т 1 ( Т )
61 == У == == '" Хи) nХ(I) (n r)X(r)
r 1 r 1 L..J
i== I
и 6) == Х(l) f /n несмещенные оценки соответственно для (J1 и 01 И вычислить
их дисперсии
01
D 8 6 1 == (r 1) '
(при r == n имеем результат упр. 39).
... Указание. Перейти к веЛИ'lИне {о == ({ OI)/(}1 И использовать пример lu 9 2.4.
m Рассматривается задача оценивания неизuестной вероятности «успеха» О по Ha
блюдснию числа «успехов» Х В n испытаниях Бернулли. Пусть функция потерь имеет
BIIД
O;r
D 8 6) == (r 1)n 1
_ (6 (J)1
L(r'i, О) == 0(1 О) '
а априорное распределение параметра f.((J) == И(О, 1). Доказать, 'ITO байессовская
оценка есть О'(Х) == Х/n относительная частота «успеха,>, И она же является ми
нимаксной; при этом байессовский риск т(6') == I/n.
... Указание. Вычислить апостериорный риск (16) 93.6 и убедиться в том, что он ми
нимизируется при о(Х) == Х /n, при этом функция риска R(6', О) == I/n не зависит
от О.
m Пусть ИСПblтания Бериулли продолжаются до получения T ro .неуспеха,> и Х
чнсло .успехов» n этих ИСПblтаниях, т. е. [8(Х) == ВJ(T, (J). Убедиться в том, 'ITO если
функция потерь Ц6, О) == (15 (})1, а априорное распределение [(()) == Ве(а, Ь), то
байессовскан оценка всроятности .успеха» О есть
а+Х
6'(Х) == Е (OIX) == Ь
а+ +т+Х
... Указание. Использовать УПр. 64 (2) к rл. 1 и ФОРМУЛbl (24) 1.2.
Ш По выборке Х == (X 1 ,.. ,Х n ) из пуассоновскоro распределения П(О) оценива
ется параметр О при квадраТИ'IНОЙ функции потерь L(6, О) == (6 (})1 и априорном
распределении [(О) == r(a, л) Показать, что байессовская оценка имеет вид
' ( . а(л + Х)
6 Х) == ,
nа+ 1
Х == X 1 + .. . + Х п ,
и ее риск есть т(6') == ла 1 /(nа + 1). Определить оrrrимальный объем выБОрКII при
цене с> О одноrо наблюдения (т. е. МИНИМlIЗирующий общие потери т(6') + сп).
... Указание. Использовать упр. 64(3) к rл. 1 и формулы (21) 9 1.2.
m (Продолжение). Убедиться в том, что если функция потерь L(o, О) == (о (})1/(J,
то байессовская оценка при л + Х > 1 имеет вид
а
6'(Х)== (Х+Л 1)
nа+ 1
и ее риск т(й') == а/(nа + 1).
310 rлава з. Теория оцениsания неизвестных параметров распределений
m Рассматривается задача оцеНI1ВЗНИЯ параметра 8 пока"Jательноrо распределеНИII
с плотностью Лх; е) == ee eE х? О, (J > О, ПО выборкс Х == (X 1 , ,Х п ). ПусТl>
функция потерь L(5,8) == (б 8 J)2 и априорное распределение [(е) == r(a, А),
А> 2. ДоказаТl>, что байссовскаи оценка имеет вид
I ( 11 )
б'(Х) == (А ) а L Х ; + I
а +n ' .
, I
и ее риск r(5') == [а 2 (А + n ')(А ')(А 2)] 1 Убсдиты:я '1 том, что оптимальное
число наблюдений при цене с > О одноrо наблюдения раино
, 1
n == A+I.
a v c(A I)(А 2)
... Указание. И пользовать упр. 64 (4) к rл. 1 и формулы для моментов r"'MMa pacnpe
деления (п. 3 1.2). .
m Пусть Х == (X 1 ,..., Х п ) выборка JIЗ paUHoMepHoro распредсдеНlНl U(О, е),
rде априорное распределение параметра (J есть распредеЛСlll1С Пареl'О с параметра\lИ
X и а > 2 (см. п. 9 1.2). Убедиться l' том, 'по ПрJl кuаЩJаТИ'lноi1 функиии ПОТС[JI,
байесовская оценка () имеет ВJlД
' ( n+а (
6 Х) == так Хо, Х(п)),
n+o: '
Х(II) == тах X j ,
l i 1I
и ее риск r(б') == ax /I(o: 2)(n + о: 1)21. Определить оптимwll>ныH объем выборки
при цене с> О одноrо наблюдеНIIИ.
... Указание. Использовать упр. 64 (6) к [п. 1 и формулы (39) 1.2. .
ED Убедиться в том, 'ПО байесовская оценка параметра (J нормал ноro распре
делеНИII N((J, ь 2 ) при квадратичной ФУНКЦИI1 потсрь и аПРflOРНОМ раСПРСДСЛСНflИ
[(е) == N(p,и 2 ) есть б'(Х) == р, и ее риек r(б') == и; (обозначения упр.64 (5)
к rл. 1), а ОППJмальное число наблюдений при цене с> О одноrо наБДЮДСНlI1I равно
n' == b(c 1/2 Ьи 2).
... Указание. Использовать упр.64 (5) к [п. 1. .
rлава 4
Проверка статистических rипотез
...УзловЫ,1I вопроса", "штl?матlllfескоii статистики является
вопрос: кйк далеко MOi'ym (JI1IКЛОltяться велиlfШtЫ, вЫЧllслеJlные
1/0 выБОрl\е, от соответствующих идеальных значении?
Б. Л. Ван дер 8арден 1)
Эта rлава представляет собой введение в теорию проверки статистиче
ских rипотез. Здесь Dlюдятся основные понятия этой теории (статистической
rипотезы, статистическоrо критерия, КРИТИ'lеской области, функции мощ
ности И др.) И на примерах решения задач проверки типичных и наиболее
распространенных 11 приложениях статистических пшотез излаrаются общие
принципы построения и исследования критериев соrласия. Значительное (]ни
ание уделяется методу rруппировкн наблюдений с последующим примене
нием классическоrо критерия хи квадрат.
4.1. Основные понятия и общие принципы
теории проверки rипотез
Как отмечзлось в общем Введении, математическая статистика, помимо oцe
нивания неизвестных парамеТРОIl распределений, занимается еще и проверкой
статистических rипотез, т. е. различных предположений о виде или СВОЙСТl3ах
распределений наблюдаемых случайных величин. Общее понятие стаТИСТl1че
ской rИllOтезы (далее будем rо(]оритьдля краткости просто rипотезы) и приме
ры Тl1ПИ'IНЫХ 11 наиболее распространенных rилотез приведены 80 Введении.
Поэтому здесь мы оrpаничимся лишь кратким напоминанием ОСНО8Ных фак
тов, необходимых нам для развития этой темы.
Пусть Х данные (выборка), Х == {х} выборчное пространство,
:F == {F} совокупность априори допустимых распределений Х. [i'x He
известное истинное распределение данных Х, Fx E:F В общем случае задача
про верки rипотез ставится так: выделяется некоторое подмножество :Fo с :F
допустимых распределений и требуется по данным Х про верить, справед
ЛI1ВО ли yruеРЖдение Но Fx Е :Fo или же оно ложно. В этом случае Но
называется основнои (нулевой) lипотезои. Распределения F Е FI == F\:Fu Ha
зыаютсяя альтернативными, а У'шеРЖдеНl1е НI Fx Е :F 1 альтернативноu
1) Ван дер Варден Бартел Лендерт (1903 1996) rОЛJlандский математИК статистик И ал
rебраист.
312
rлава 4. Проверка статистических zипотез
zuпотезой. В этом случае pe'lb идет о проверке rипотезы НО против альтер
нативы НI или о задаче (НО, Н,); иноrда также rоворят, '{то rипотеза НО
проверяется внyrри общей rипотезы Н РХ Е F 0= Fo U FI' Если подмно
жестrю Fo(FI) состоит из одноrо элемента, то rипотсза Но (альтернатива Н,)
называется простой, в противном случае сложной.
Правило, соrласно которому мы, наблюдая Х, принимаем решение при
нять rнпотезу Но как истинную либо отклонить ее как ложную (т. е. при
нять альтернативную rипотезу H 1 ) наЗЫIJается статистическим критерием
(или просто критерием).
СтаТИСТИ'lеские rипотезы MOryr быть самые разные. В простейших СЛУ'lа
ях проверяемая rипотеза может однозна'lНО фиксировать распределение РХ,
НО типично она указывает лишь тот класс допустимых распределений, KO
торому, по предположению, принадлежит истинное распределение данных.
В некоторых случаях класс F это все распределения на выборочном про
странствех, тоща альтернативная rипотеза Н, 0= Но (<<не НО») никак не KOH
кретизируется, и здесь речь идет просто о соzласии данных Х с нулевой
rипотезой НО (соrласуются ли данные Х с rипотезой НО I1ЛИ же они ее
опроверrают) соответствующие критерии называютсл критериЯА1U СО2ласия.
В друrих случаях класс всех допустимых распределений данных является за
данным парамеТРИ'lеским семейством F 0= {Р(х; 8), 8 Е 8}; здесь rипотезы
имеют вид Но: 8 Е 80 С 8, а Н, : 8 Е 810= 8\80, и называются пapaMeтpи
ческими. О соответствующих критериях также rоворлт как о параметрическuх
критериях. В любом случае «хороший,) критерий должен учитывать специ
фику проверяемой rипотезы: в непараметрическом случае он должен быть
универсальноrо типа, т. е. обнаруживать любые отклонения от Но, в парамет
рическом же СЛУ'lае он должен быть направлен на обlJаружеllие конкретных
(в рамках рассматриваемой параметрическоi1 модели F) отклонений от Но.
Но любой стаТИСТИ'lеский критерий строится по следующей схеме.
Поскольку критерий это правило, которое ДJНI каждой реализации х
выборки Х должно приводить К одному из двух решений: принять rипоте
зу Но или отклонить ее (принять альтернативу Н,), то каждому КРl1терию
соответствует некоторое разбиение выборочноrо пространства Х на два вза
имно дополнительных множества Хо и ХI (ХОПХI 0= "', XOUXI 0= х), rде ХА
состоит из тех точек Х, мя которых НО принимается, а Х I из тех, мя KOTO
рых НО отверrается (принимается H 1 )_ Таким образом, Хо это область при
нятия rипотезы НО, а Х, область ее отклонения, которую принято называть
критической областью. Тем самым, любой критерий проверки rипотезы НО
однозначно задается соответствующей критической областью х" и о таком
критерии часто rоворят как о «критеРИl1 Х,». Итак, критерий Х, имеет вид
I НО отверraетсл {:::=> Х Е Х) .1
Как в конкретной задаче (Но, H 1 ) выбирать крИТИ'lескую область XI? Это
делается на основе постулируемоrо в математической статистике слеДУlOщеrо
4.1. OCHOBHble понятия и принципЬ! теории проверки i'ипотез 313
общею принципа принятия решения: если в экспери
менте наблюдается маловероятное при спраuедЛИВО
сти rипотезы Но событие, то считается, что l'ипоте
за Но не соrласуется с данными (или противоречит им), и в этом случае она
отверrается (отклоняется); в противном случае считается, что данные не про
тиворечат Но (или соrласуются с ней), и H принимается.
В соответствии с этим принципом критическая область Х 1 должна быть
выбрана так, чтобы была мала вероятность Р{Х Е XIIHo}, т. е. условная
(при условии, что Но справедЛипа) пероятность попадания значения выбор
ки Х n область Х 1 Поэтому при построении критерия задаются заранее
некоторым малым числом а (например, а =о 0,001; 0,01; 0,05 и т.д.) И нала
raют условие
Общий ПрИНЦИП ....
принятия решений
Р{Х Е XIIHo}::;; а.
(1)
Если выполнено (1), то rоворят, что критерий Х, имеет уровень значимо
сти а и подчеркивают это обозначением X 1 =о X 1a . Ясно, что условием (1)
критическая область X 1a определяется неоднозначно, и чтобы устранить эту
неопределенность, надо ввести дополнительное понятие ошибок критерия.
Следуя любому критерию Х'о. мы можем принять правильное решение
либо совершить одну из двух ошибок: ошибку 1 ro рода, OTBeprHYB НО, Korдa
она верна, или ошибку 2 ro рода, приняв Но, коrда она ложна (ошибка l ro
рода совершается, коrда наблюдение Х попадает n критическую область Х'а,
в то время как верна rипотеза Но: вероятность этоro есть как раз левая часть
(1), а ошибка 2 ro рода коrда Х Е X 1a =о Х оа , но rипотеза Но не верна).
Введем теперь фундаментальное понятие теории проверки статистических
rипотез понятие функции мощности критерия. По Функция МОЩНОСТИ
определению, функцией мощности критерия Х!а Ha критерия
зывается следующий функционал на множестве всех
допустимых распределений :F =о {Р} выборки Х
W(F) =о W(F; X 1a ) =о Р{Х Е XlaIF}, F Е :F
(2)
Друrими словами, W(F; X 1a ) это вероятность попадания значения выбор
ки Х в критическую область Х la, коrда F ее истинное распределение.
Через функцию мощности леrко выразить вероятности обоих типов ошибок,
свойственных критерию Xl a . Именно, вероятность ошибки I ro рода есть
W(F) при F Е :;:0, а 2 ro рода 1 W(F) при F Е :F 1 . Иноrда удобно
записывать эти веро5lТНОСТИ в симполическом виде: P{H1IHo} (вероятность
ошибки l ro рода) и P{HoIH]} (вероятность ошибки 2 ro рода).
Естественно стремиться построить критерий так, чтобы свести к минимуму
вероятности обоих типов ошибок. Однако при фиксированном объеме выбор
ки сумма вероятностей ошибок обоих типов не может быть сделана как уrодно
малой (это cBoero рода принцип неопределенности при проверке rипотез). По
этому рациональный принцип выбора критической области формулируется сле
ДУЮЩИМ образом: из всех критических областеЙ Х'а (т. е. удовлетворяющих
314
rлава 4. Проверна статuстuчеснuх 2uпотез
условию (1)) выбираетсн та, для котороЙ вероятность ошибки 2 ro рода ми
нимальна, т. е. при условии
W(F; X 1o ) а, 'v F Е ТО,
(3)
надо минимизировать (за счет выбора X 1o ) величину I W(F; X 1o ), 'V F Е T 1 ,
или, что ЭКlJивалентно, максимизировать мощность W(P; Х 1а ), 'V F Е Tl.
Итак, при заданном уровне значимости а наилучшим среди всех крите
риев X 1a является тот, который обладает наибольшей мощностью при альтер
нативах. Если для двух критериев X O и X 10 имеют место соотношения
W(F; X a) W(F; X 1a ),
W(F; X a) ) W(F; X 1a ),
'V F Е ТО,
'V F Е TI,
и
(4)
то roворят, что критерий X O равномерно МDЩllее критерия X 1 ,,; если (4) BЫ
/. полняется для любоro критерия X 1a , то Xia называется рав/юмерl/О наиболее
,( р МОЩНblМ критерием (р. н. м. к.) В задаче (НО, H 1 ). Р. н. м. к.
. Н. M к. идеал, но он не Bcerдa достижим. Поэтому u конкретных за
дачах зачастую приходится оrpаничиваться более умеренными требованиями
к критериям Мннимальным таким требованием является свойство lIесмещен
' iI. Несмещенность 1I0сти, которое означает, что одновременно с (3) должно
выполняться условие
!<ритерия
W(F; X 1a ) > а, 'V F Е TI'
(5)
т. е. при любом альтернативном распределении данных мы должны попадать
в критическую область с большей вероятностью, нежели при нулевой rипотезе.
В случае «больших выборок.), т. е. KorAa Х == (X j , ,Х,,) есть случайная
выборка объема n из HeKoToporo распределения .c( ) и n 00, критерий
.. Состоятельность должен обладать свойствОМ состоятеЛЫlOстu (чтобы под
черкнуть зависимость от n пишем W r1 ):
критерия
Wn(F; X 1a ) 1, 'V F Е Т 1
(6)
Это СIJОЙСТВО очень важно. Оно означает, 'по, если истинной яuляетсн HeKO
торая альтернатива, то при большом числе наблюдений мы будем попадать
в критическую область с вероятностью, бл I1ЗКОЙ к 1, т. е. отклоняя нуле
вую rипотезу НО, мы будем принимать правильное решение. Таким образом,
можно I:казать, что состонтельный критериЙ «улавливает» любые отклонения
от нулеIЮЙ rипотезы, KorAa они имеют место, если число наблюдений (объем
lJыборки) неоrраниченно возрастает.
. .. «Близкие» Более тонкие свойства состоятельноrо критерия lЗы
ражаются IJ терминах «близких,) альтернатив, т. е. Korдa
вместо фиксированной альтернативы F Е T 1 , paCCMaT
РИlJается последовательность альтернаТИIJНЫХ распределений {Fr1} , «сближа
ющихся» (в том или ином смысле) с ТО, и исследуется поведение мощности
Wn(Fn; X 1o ) при n 00. в этом случае условие (6), вообще rоворЯ, уже
альтернативы
4.1. OCHOBHble понятия и nринциnbl теории проверки шnотез 315
не будет иметь места, и оно заменяется на условие
Wn(Fn; X 1a ) "(, а < "( < 1. (7)
Если последовательность (,близких» альтернатив {F,J такова, что при HeKO
тором "( Е (а, ]) выполняется (7), то такие альтернативы называются (,поро
rOBbIMI1»; они определяют тот (.пороr чувствительности» критерия X 1a К OT
клонениям от нулевой rипотезы НО, коrда критерий еще «реаrирует,) на такие
отклонения: он способен различать распределения F Е Fo и Р1! Е FI С ошиб
ками Wn(.F') ::::; а и I W n (Р п ) ::::; ! "(. Однако в конкретных задачах такое
полное исследование асимптотических свойств критериев не всеrда осуще
ствимо ввиду аналитических трудностей.
В теории часто оказывается полезным paCC:\10T
рение так называемых рандомuзированных критериев.
Korдa при наблюдении Х == х rипотеза Но отклоня
ется с некоторой вероятностью (x) и принимается с дополнительной вероят
ностью ! (x). В этом случае функции rp(x) Е 10, 1] называется критической
функцией, а функция мощности «критерия » определиется равенством
Рандомизированные -:
КРl1терии
W(F; ) == E( (X)IF) == / rp(x) dF(x).
Если функция принимает лишь два значения О и 1, т. е. является инди
каторной функцией HeKoToporo подмножества выборочноrо пространства, то
получаем предыдущую схему нерандомuзuрованноlO критерия с КРИТllческой
областью X 1 == {х rp(x) == !} они обычно и прушениются на llрактике.
В приложениях обычно критическая область за Тестовая статистика ·
дается с помощью некоторой статистики Т :.= Т(Х),
которая <,измеряет» отклонение эмпирических данных от соответствующих
(rипотезе но) rипотетических значений и распределение которой при спра
uедлИIЮСТИ rипотезы Но должно быть известно (точно или ХОПI бы прибли
женно, т. е. дпя больших выборок). Если r == {t == Т(х), х Е Х} простран
ство значений этой статистики, то критическая область критерия может быть
задана непосредственно в этом пространстве как некоторое подмножество
"а С Т, которое должно удовлетворять условию
Р{Т(Х) Е "oIF} ::::; а, V F Е Fo.
(8)
т. е. включать все маловероятные при rИllотезе Но значения Т. Решающим MO
ментом для расчета критерии (т. е. обеспечения (8)) является проблема OTЫCKa
ния распределения статистики Т(Х) при rипотезе Но. В частности, если Но
сложная rипотеза. то желательно, чтобы распределение Т(Х) было одним
и тем же для всех F Е Fo. Чтобы вычислить полностью функцию мощности
W(F; Т) == Р{Т(Х) Е "oIF}, F Е F, а тем самым исследовать и вероятность
ошибки 2 ro рода, надо знать распред<'_lение Т(Х) также и при альтернативах
F Е Fl' что представляет собой, как правило, весьма трудную задачу. Итак,
в терминах выбранн ой статистики Т =-= Т(Х) критерий им еет вид:
rHo отверrается -{::::::} Т(Х) Е "0,1
316
rлава 4. Проверка статистических 2ипотез
rдe при заданном уровне значимости а критическая область a УДОllлетворяет
условию (8). Статистика Т наЗЫIlается статистикой критерия "ли тестовой
статLlстикой, а сам критерий называетси «критерием a»'
П Наконец, отметим, что для параметрических задач,
араметричеСКQЯ Korдa допустимые распределения данных Х идентифи
..8 f1. i.>;. ."iИ;..м.. цируются параметром О, МИ функции мошности ис
пользуется обозначен ие
W(O) == W(O; Xlo) == Ре{Х Е XI(r}, () Е е,
(9)
а проблема построения наилучшеrо критерия в задаче
Но О Е е о , НI () Е 0, == е\0 0
при уровне значимости Q формулируется так:
W(O; Xlcr) а,
..
Общие замечания
v о Е е о ,
w(O; Х,а) тах,
VO Е 8"
( 10)
в заключение этоro введения сделаем несколько об
щих замечаний. В конкретных задачах выбор уровня
значимости критерия до некоторой степени произволен и свизан с практи
ческой стороной вопроса. Так, часто ошибочное принитие или отклонение
rипотезы Но связано с материальными затратами. Если принятие rипоте
зы Но в то время, Korдa она неверна (ошибка 2 ro рода), приводит к большим
затратам, Torдa как отклонение истинной rипотезы НО (ошибка 1 ro рода)
приводит к небольшим потерим, то ясно, 'ITO желательно сделать как можно
меньшей вероятность ошиБЮ1 2 ro рода, допуская сравните.1ЬНО БОЛl,шие зна
чения а. Обычно мя а выбирают одно из следующих стандартных значений:
0,005; 0,01; 0,05; мя этих значений рассчитывают соответствуюшие таблицы,
используемые при проведени\\ различных испытаний.
Далее, в отличие от теории оцеНИlJания неизоестных параметров распре
делений, коrда МЯ характеризации качества соответствующих оценок ДOCTa
точно было уметь вычислять, как прапило, лишь neplJbIe два момента ис
пользуемых статистик, II теории проне[жи rипотеJ требуется знание ncero
распределения статистики КРllтерия: как минимум при нулеlJОЙ rипотеJе
(чтобы рассчитать критическую область), а вообще же rоворя и при альтер
нативах (чтобы оценить мошность). В этой связи отметим, что для Dыборок
фиксированноrо объема (ИЛl1, как roBOpHT, случан "малых ныборок») эта про
блема не l\сеrда поддается практическому решению, поэтому при проверке
. . д д
БОЛЫJ..Iие выборки ПlllOтез часто примениется асимптат'1ескии па ха ,пред
полаrающий неоrpаниченнос возрастание объема n IJbI
борки Х == (X 1 , ,Ха), Т.е. проблема решаетсн для случая «больших BЫ
борок». Асимптотический подход широко используется при расчете статистн
ческих критериев, часто позволяя исследовать единым методом различные
задачи и получать весьма общие результаты, При этом финмьные реЗУЛl)таты,
как правило, имеют простую и наrлядную форму, удобную для практическl1X
расчетов. Эти результаты в дальнейшем MorYT использоваться и для выборок
4.1. OCHOBHble понятия и прuнципЬ! теории проверки lипотез 317
конечноro объема, давая приближеНl-iое решение задачи. Асимптотический
подход «зачастую еДИНСТIJенная IЮЗМОЖНОСТЬ, открытая статистику в cy
ровой действительности,) (дж. Русас) и с ero применением мы неоднократно
будем встречаться D дальнейшем.
Наконец, отметим, что важным показателем каждоro критерия яwщется
трудоемкость практической реализации соответствующеro алrоритма. На прак
тике, Korдa требуется быстро получить ответ, предпочтение нередко отдается
просто реализуемому критерию, даже если он не является оптимальным в тeo
ретическом смысле. При этом ТИПИчной является ситуация, коrда МЯ одной
и той же задачи имеется несколько разработанных критериев, каждый flJ KOTO
рых обладает определенными сr:ецифическими достоинства и, среди которых
не последнее место занимает простота ero практической реализации.
Далее изложенные принципы применяются при решении описанных во
Введении задач проверки типичных статистических ПJПотез.
Из истории (по книrе r. Секея [23]). Трудно сказать что то определенное
о TO I, KorAa предпринимались первые попытки проверять статистические
rипотезы. Б. В. rнеденко в своей Книrе [81 отмечает, что учет населения,
проведенный в древнем Китае в 2238 r. до н. Э., показал, что доля po
дившихся мальчиков составляла 50 %. Джон Арбутнот (1667 1735), анrлийский
математик, врач и писатель, был первым, кто (в 1710 [.) заметил, что rипотеза
о равном соотношеНI1И родившихся мальчиков и девочек должна быть опроверr
нута, так как соrласно демоrрафическим данным за 82 rO.J,a (доступным в то время)
малЬ'111КОВ к<lждый [од рождалось больше, чем девочек. Этот факт заинтересовал
П. Лапласа. В 1784 [. он с удивлением обнаружил, что в нескольких различных
районах доля родившихся малЬЧИКОв приблизительно равнялась 22/43, а в Пари-
же это отнощение было равно 25/49, что меньше 22/43. Лаплас был заинтриrован
таким различием, но вскоре нашел .iL1Я Hero разумное объяснение: в обшее число
РОДIIВШИХСЯ В Париже включались также все подкидыши, а насе.1ение из приrо
родов предпочитало подкидьшап. младенцев одноrо пола. Коrда Лаплас исключил
подкидышей из общеrо числа родившихсл, доля lIоворожденных мал(,чиков стала
близкой к 22/43.
В 1734 r. французская академия присудила Даниилу Бернулли (1700 1782)
швейцарскому физику и матсматику премию за исследование по орбитам пла
нет. С ПОМОЩI.ю HeKoтoporo критерия проверки rипотез Бернулли пытался пока
зать, что схожесть орбит Шlанет Jlвляется далеко не случайной (в ero модели каждая
орбита соответствует некоторой точке на единичноЙ сфере, и Бернулли проверял
rипотезу о равномерном распределеНИI1 этих точек). В 1812 [. Лаплас исследовал
похожую проблему. Он пытался применить статистические методы для решения
вопроса о том, какую нз rипотез следует принять: являются ли кометы обычными
элементами Солнечной системы или они Bcero лишь «незванныe roсти,). В по
следнем случае уrлы между орбитами комет и эклиптикоЙ были бы ра8номерно
распределены на интервале от О до 1[/2, что как раз COBnaд<leT С математической за
писью предположения Лапласа (он обнаружил, что кометы не являются обычными
элементами Солнечной системы). Основоположниками современноЙ теории про
верки статистических rипотез были К. Пирсон, Э. Пирсон, r. Фишер и Ю. Ней
ман. Большой вклад fj ее стаНОВ. ение и развитие внесли r. Крамер, Р. фон Мюее,
А. Н. KO.1MoropoB, Н. В. Смирнов и друrие ученые, работавшие позднее.
318
rлава 4. Про верна статистических шпотез
Хотя это может пОКQзаться парадоксом,
вся наука основана на идее аппроксимации.
Бертран Рассел 2)
! 4.2. Проверка rипотезы о виде распределения
КлаССlIка это та, что все хатеЛII бы
пРО'lUтать, 110 "иКl110 '1итать "е хочет.
Марк Тое н З)
Мы начинаем изложение основных результатов теории проверки rипотез с pac
смотрения классической задачи о виде распределения наблюдений (см. при
мер 4 Введения). В простейшем ее варианте задача ставится так: пусть Х ==
== (X j , ,X'I) выборка из распределения .ею с неИЗflестной функцией
распределениР. P (x), о которой выдвинyrа простая rипотеЗ<l Но Р(х) ==
== Р(х), rде функция Р(х) полностью задана. Здесь альтернативные pac
пределен ия никак не конкретизируются, т. е. допустимыми распределениями
данных (выборки Х) ЯflЛЯЮТСЯ любые распределения на выборочном про
странстве Х == { == (XI, ,х п )} (априори может быть ясен лишь тип
распределения Р( абсолютно непрерывный либо дискретный, что опреде
ляется обычно физическоЙ природоЙ наблюдаемой случайной величины {).
Следовательно, вданном случае альтернатива Н, == Но «<не Но,», И речь идет
просто о соrласии данных и rипотезы Но. Наиболее известными (классиче
скими) критериями соrласия 1) данной задаче ЯflЛЯЮТСЯ критерий КолмоrОрОlJа
и критерий ХИ КlJадрат.
1, Критерий соrласия Колмоrорова
. Статистика Этот критерий применяют lJ тех случаях, коrда функция
Р(х) непрерывна. Статистика критерия определяется
Колмоrороао
формулой
Dn == Dn(X) == sup 1F,,(x) F(x)l,
oo<x<oo
(1)
т. е. представляет собой максимальное отклонение эмпирической функции
распределения Рn(х) , построенной по выборке Х, от rипотетической (т. е.
определяемой rипотезой Но) функции распределения Р(х). То, что это «pa
зумная» статистика для проверки rипотезы Но, следует из известных нам
свойств э. ф. р. рп(х). Так, мы знаем (см. теорему 2 3.1 и комментарий
2) Рассел Бертран Артур УИЛЬЯМ (1872 1970) анrлиЙскиЙ математик, философ, ЛОП1К, co
циолоr, обшествеНIIЫЙ деятель.
З) Тоен Марк (Сэмюэль Ленrхорн Клеменс) (1835 1910) знаМСIIИТЫЙ ,шерикаНСКllii писа
тель.
4.2. ПровеРКQ zипотезы о виде распределения
319
к ней), что при каждом х 8еличина рп(х) является оптимальной несмещен
ной оценкой для Р(х), и эта оценка состоятельна (см. комментарий к формуле
(23) 2.2), т. е. с увеличением объема выборки n происходит сближение рп(х)
с Р(х) (если, конечно, rипотеза Но справедлива). Поэтому, по крайней Me
ре при больших n, в тех случаях, коrда rипотеза Но истинна, значение Dn
не должно сущеСТ8енно отклоняться от нуля. Отсюда следует, что критиче
скую область критерия, oCHoBaHHoro на статистике Т == Dn, следует задавtlть
8 виде Тi('( == {t t('(}, т. е. БОЛl,шие значения Dn надо интерпретировать как
свидетельство против проверяемой пшотез!.! Но. Критическая rраница t a при
заданном уровне значимости а рассчитывается при этом на основании тeo
ремы Колмоrорова (см. теорему 2 2.1). Именно, если n достаточно велико
(уже при n 20), то положив t cr == Ла./.Jii, [де (см. (11) 2.1) К(Л а ) == 1 а,
будем иметь
P{D" Е ТialHo} == Р{ .JiiDII лаlН о } ;:::: I К(.\..) == а, (2)
т. е. по краЙней мере для больших выборок условие (8)
женно выполняться.
Тем ca 1ЫM критерий соzласия Кол.wоzoрова форму
лируется следующим образо:.1: если n 20 и при BЫ
бранном уровне значимости а число Л а определено
соотношением К(Л а ) == 1 а, то
I Но отвер.'ается {:::::=? .JiiDn Ла.1
4.1 будет прибли
..
Критерий
Колмоrорова
(3)
Следуя этому правилу, можно ошибочно отклонить rипотезу Но, коrда она
верна, с вероятностью, приблизительно равной а. Этот критерий состоятелен
(альтернативой здесь является любое непрерывное распределение Р{ ф- Р).
'#
Дополним сказанное некоторыми комментариями. КомментаРИl1
Прежде Bcero подчеркнем, что распределение статисти
ки Dn при rипотезе Но не зависит от вида функции Р(х). Этот факт имеет
принципиальное значение, так как имея таблицы значений функции Колмо
[орова K(t), мы имеем возможность рассчитывать критерий (3) для проверки
rипотезы относительно произвольной непрерывной функции распределения
Р(х). Такие подобные таблицы имеются в книrе 131, [де также даны детальные
практические рекомендации по их использованию.
Далее, по своей сути критерий Колмоrорова (3) является асимптотиче
ским (т. е. он «работает» лишь ДI1я больших выборок), поскольку в основе
ero лежит предельная теорема 2 2.1. Но помимо вывода предельноrо резуль
тата (см. (11) 2.1) Колмоrоров (1933) дал рекуррентные соотношения для
конечных n, которые затем были использованы для табулирования точноrо
распределения статистики Dn. Поэтому для расчета точных значений кри
тической rраницы t a в случае малых 8ыборок также можно ВОСПО.llьзоваться
соответствующими таблицами, информация о которых имеется в 112, с.бll].
320
rлава 4. Проверка статистических шпотез
Наконец, отметим, что ДI1Я практических вычислений статистики пп по
лезна эквивалентная (1) формула п п == Пlах( п: , п;;), rAe
( k ) ( k 1 )
п: == тах Р(Х(I,;» I п;; == тах Р(Хщ)
' I.: JI п 1 I.: fl п
и Х(I) :::;; Х(2) :::;; :::;; Х(П) вариациоi'!НЫЙ ряд выборки Х.
Замечание. Описанную методику проверки rипотезы о виде распределения наблю..
даемой случайной веЛI1'1ИНЫ можно распространить 11 на случай провеРКI1 сложноЙ
rипотсзы Но Р{(х) Е То == {Р(х;(), () Е 8}, [де То заданное параметрическос
семеЙство распрсдслсний (комментарии см. jj ПРl1мере 4 I3uеДСНI1Я). В этом случае
вместо (1) используют тестовую статистику
Ь" == sup IFn(x) Р(х; 0,,)1,
'X)<X<OO
rде 'Оп оценка максимальноro праuдоподобl1Я параметра В Если семсИство То
рсrулярно (см. п. 4 3.5), то известно ,ICIIМПТОТИ'lсское (при n , 00) распределение
статистики Ь,,, которым можно воспользоваться длн раС'lеПl соответствующей Kp11
тической rраницы критерия. Однако это распредеЛСlше имеет уже отлl1чный от (11)
2.1 и rораздо более с. ожныli IIИД, отражающий спеЦИфИ'lеские свойства ссмейства
Т о ; тем самым раC'lСТ соответствующеrо критерия зна'lительно усложняетсн 4 )
2. Критерий соrласия хи квадрат К. Пиреона
Одним из наиболее универсальных методов ПрОlJерки различных статисти
ческих rипотез является метод xи Kвaдpaт (х 2 ). В этом методе работают
с дискретными данными, но поскольку любые исходные данные можно CBe
сти к дискретным методом IРУППИРОВКИ наблюдений, как это описано в П.2
9 З.6, т. е. перейти от исходноЙ Dыборки Х (Х" ,Х П ) К частотам
== (1I1,', ,1IN) попадания ее элементов в соответствующие подмножества
rpуппировки [1, , [N, то тем самым метод х 2 можно применять к данным
любой природы, в том числе и MHoroMepHbIM (подчеркнем, что описанный
в п. 1 критерий КолмоrОрОlJп «работает» лишь с выборками из HenpepbIBHoro
одномерноrо распределения).
Итак, пусть в эксперименте наблюдается дискреТJiан случайная вели
чина , принимающая зна'lения 1,2, I N с некоторыми веронтностями
Р" ,PN (р, + + PN == 1). Если произведено п независимых испытаний
над , т. е. имеется выборка ( " , n). то пусть
п
lIj == I: I( i == Л, j == 1, , N,
i '
соответствующие частоты исходов (1I, + + lIN == п). TorAa вектор
!!. == (111' , lIN) имеет полиномиальное распределение М (п; Р" , PN)
4) Тюрцн Ю. Н. о предельном распределеНИl1 статистик КОJlмоrОрОН СМИрllова /UIЯ СЛОЖfIOН
rипотезы // ИЗВ.АН СССР. Сер. Матем. 1984. Т48. N26. с.1314 134З.
4.2. Проверка i!uпотезы о виде распределенuя
321
(см. п. 6 1.1). В методе i работают именно с данными !!.., а проверяемые
rипотезы формулируются в терминах вектора вероятностей Р =о (Pl, ,PN).
По сути это параметрическая модель, так как она определяется конечным
числом параметров (PI, ,PN I), Рассмотрим сначала задачу проверки про
стой rипотезы в рамках этой модели.
Итак, пусть по НQблюдению вектора частот!!.. =о (V1, , VN) требуется
проверить простую rипотезу Но =о l!..0 rде ЕО =о (р7, ,P"rv) заданный
вероятностный вектор (О < Р} < ], j =о 1, , N, Р7 +- ..+P"rv =о 1). К. Пирсон
В 1900 r. предложил использовать в качестве меры отклонения эмпирических ,
'-
данных (относительных частот !!../n) от rипотетических значе М 2 .
ний l!..0 меру хи квадрат (см. (2) 3.6) ера Х
N ( 0 ) 2
X =о X (!!..) =о L: Vj Pj
j 1 nPj
N v2
=о L: ......L n
np .
j 1 J
(4)
На этой тестовой статистике и основывается знаменитый критерий i к. Пир
сона. В основе этоrо критерия лежат следующие очевидные соображения. Если
rипотеза Но справедлива, то, поскольку относительная частота Vj/n события
{{ =о j} является состоятельной оценкой ero вероятности Р} (j == 1, .. . , n).
при больших n разности IVj/n pjl должны быть малы, следовательно, и зна
чение статистики X не должно быть слишком большим. Поэтому eCTeCTBeH
но задать критическую область для rипотезы НО в виде a =о {X > t a },
rде критическая rраница t a при заданном уровне значимости а должна быть
выбрана из условия
P{X > ЦН о } =о а.
(5)
Такой критической областью и определяется критерий i rлавная проблема
здесь ВЫ'lИсление rраницы t a в (5), для чеrо надо знать распределение
-ir2 о 2
статистики .л п при нулевой rипотезе Но. Точное распределение .с(Х п IHo)
неудобно для расчета критерия, нодля больших объемов выборок n статистика
X имеет при rипотезе НО простое предельное распределение, не зависящее
от rипотезы (т. е. от Е О )' Именно, справедливо следующее утверждение.
Теорема 1. Если О < Р} < 1, j =о 1, . N, то при n ----4 00
.c(X IHo) ----4 X\N 1).
Доказательство. Как показано в примере ]2 3.5, при сформулированных
. ( . . )
условиях вектор нормированных частот!!.. =о VI, , VN 1 . rде
. Vj пр;
Vj =о ..;n
j=o],...,N;
21 За... 1748
322
rлава 4. Проверна статистических i!ипотез
имеет в пределе невырожденное нормальное распределение .лf(Q, tN l), rде
..... 11 О Ол О ° II N 1
l...N I== (1ij==Pi(lij PiPj I
дij символ Кронеккера. Отсюда на основании соотношения (34) 3.5 можно
заключить, что при n 00
t:.(Qn == !!. tNI I IHo) X2(N 1).
С друrой стороны, из (4) имеем
N I ( . ) 2 ( .
о 2 '" V j V I +
Х п == L.J +
j 1 Pj
+ v' ) 2
N I
P'N
.' t ·
==!!.п !!.",
rде матрица
i == Ilgijll l == tN 1
(см. пример 10 в 3.2). Таким образом, X == Q". .
На практике предельное распределение i(N 1) можно использоватьдля
расчетов с хорошим приближением уже при n ;;:: 50 и Vj ;;:: 5, j == 1, ,N.
При выполнении этих условий можно записать, что
rде FN I(t)
полаrан
о J
P{X > tolHo} 1 FN I(tcr),
функция распределения закона /(N 1). СлеДОl3ательно,
I FN I(ta) == а,
т. е.
2
t o == XI cr. N
(напомним, что X ,r обозначает р квантиль распределения /(т)), получаем
асимптотический вариант критерия / задаваемый критической областью
о 2 2
{Х" > XI o,N I}'
Таким образом, КJlассический критерий соrласия / имеет следуюший
вид: пусть объем выборки n и наблюдавшиеся значения вектора частот
!!. == (V), ,VN) удовлетворяют условиям n ;;:: 50, Vj ;;:: 5, V j; тоrда при
заданном уровне значимости а
I о 2' I
Но отверraется <:==} {Х" > XI o.N I},
(6)
.. Кр\.1reр Й-х1:
о 2
rде статистика Х п определена 13 (4).
Сделаем несколько общих замечаний. Критерий co
2
rласия Х применяется в тех случаях, коrда в каждом
испытании наблюдается одно из N несовместных собы
тий А!, .., AN И заданы частоты появления этих событий в n (независимых)
испытаниях (можно rоворить также, что наблюдается дискретная случайная
Комментарии
4.2. Провернй zипотеЗbf о виде распределения
323
веЛИ'lИна == номер реализуемоrо в испытании события). Если же исходные
данные предстамяютсобой выборку из HeKoToporo непрерывноrо распределе
ния, то, ПРИ\lеняя предварительно метод rpуппировки наблюдений, приходят
к рассмотрению дискретной схемы, в которой в качестве событий Aj pac
сматриваются события { Е [j}, rде [1, ,[N интервалы rруппировки.
Недостатком метода НDЛяется то, что при rруппировке данных происходит
некоторая потеря информauии. Кроме TOro, остается еще вопрос о выбо
ре числа интервалов N и их виде (более детально эти вопросы освещены
в [12, rл. 30]). Однако критерий i имеет и свои достоинства: при ero приме
нении нет необходимости учитывать точные значения наблюдений (бывают
случаи, коrда исходные данные имеют не числовой характер, см. пример 2
ниже); несомненными преимуществами критерия являются ero простота, Ha
rлядность и универсальность.
2
При ведем несколько примеров практическоrо применения критерия Х
Пример 1. При n == 4040 бросаниях монеты Бюффон
получил 1/1 == 2048 выпадений rерба и 1/2 == n 1/1 == 1992
?
выпадений решки. Проверим, используя критерий X
совместимы ли эти данные с rипотезой Но о симметричности монеты, т. е.
'ПО вероятность выпадения rерба р == 1/2. Здесь N == 2, p == p 1/2
и по формуле (4) имеем
,0,2 (1/1 np )2 (1/2 nР'2)2 (1/1 np )2 6
Аn== + == ==оп.
np np np Р'2 '
2
Пусть уровень значимости Q == 0,05. Из таблиц распределения хнаходим
2
ХО,95; 1 == 3,841. Следовательно, данные не противоречат rипотезе Но. .
Пример 2 [12, с.563]. В экспериментах с селекцией ro Эксперимент
роха Мендель (см. ниже) наблюдал частоты различных Менделя
видов семян, получаемых при скрещивании растений
с круrлыми желтыми семенами и растений с морщинистыми зелеными ce
менами. Эти данные и значения теоретических вероятностей, определяемые
в соответствии с теорией наследственности Менделя, приведены в следующей
таблице:
Эксперимент -:
Бюффона
Семена
Частоты I/j
Вероятности pj
Круrлые и желтые 315 9/16
Морщинистые и желтые 101 3/16
Круrлые и зеленые 108 3/16
Морщинистые и зеленые 32 1/16
Е n == 556 1
21*
324
rлава 4. Проверка статистических zuпотез
Следует проверить rипотезу Но о соrласовании частотных данных с Teope
.2
тическими вероятностями. Вычисления по формуле (4) дают здесь Х п =' 0,47
Из таблиц распределения х\З) следует, что npl1 любо уровне значимости
а 0,90 критерий (6) не oTBepraeT rипотезу, так что между наблюдеНИЯМI1
и rипотезой имеется очень хорошее соrласие. .
-!' Из истории науки. С именем монаха авryстинскоrо монастыри rperopa MeH
деля;) снизан поучительныЙ эпизод из истории наУ'IIШХ открытиii. В 1866 [.
Мендел!> открыл законы классическоi1 reHeTIIKI1. Но открыт!> м,що их
нужно доказать. И он провел серию опытов на растении с назваНl1ем лст
ре6l1нка. Почему из тысячи видов он остановился именно на этом растении,
сказать трудно. Факт u том, что опыты не удалис!>, и монах сделал вывод, что
ero законы неверны. Впоследствии выяснилось, что Мендель выбрал неудачный
объект исследований. Но дело было сделано имя монаха и ero заКОНbI предали
забвению. В 1900 r. эти же законы были заново открыты cpU'jy тремя ботаНl1ка
ми Xyro де Фризом, Карлом Koppehco:l-! и Эрихом ЧермаКО:l-!. КазШlOсь бы, 11М
ничеrо не мешало закрепить за собой лавры первооткрыватслсЙ. Но с непомер
ным усердием они принялись рыться в научных архивах и нашли забытые стат!>и
о ('правилах Менделя'>. Ученые не прекратили поиск, а, наоборот, уrлубились
в HerO. И пришли к неожиданному выводу: их' законы за 30 лет до них ОТКрЬиI
тот самый монах 11З авrустинскоrо монастыря. Что ботаники делают дальше? Все
просто: они признают за собой «приоритст ВТОР I',ноro открытия", а законы Ba
рекают именем выдающеrося монаха.
Предмет математики настолько серьезен, что полезно
не упускать случая сделать ею неМНО20 занимательным.
Б. Паскаль
Рассмотрим, наконец, пример, коrда rипотетическое распределение яв
ляется непрерывным.
Пример 3. Использун данные, приведенные в упр. 10 к т.2, проверим co
rласуют"я lIИ они с rипотезой НО о том, что показания часов равномерно
распределены на интервале (О, 12). Здесь N =' 12 и при rипотезе НО р; =' 1/12,
j =' О, 11. Значение статистики (4) есть 10,000, а, например, X .95; 11
=' 19,675, поэтому следует признать, что соrласие предположенин с опытными
данными хорошее. .
..
'Jr, Состоятельность
J
критерия X .....
2
Дпя критерия Х можно провести полное J1ссле
дование предельноro при n ...... 00 поведения ero МОШ
ности при альтернативах. В рассматриваемой методике
rипотезы характеризуется вектором р =' (Pl, ,PN) вероятностей, с KOTO
рыми появляются 8 каждом испытании собblТИЯ А J, , AN, поэтому для
5) Меllдель rperop Иоrаllll (1 822 IB84) аОСТРИЙСКIIЙ еС1еСТООИСl1ытатель, ОСIIOВОIЮ/IOЖIlI1К
учения о наследственности.
4.2. Проверка 2ипотезы о виде распределения
325
функции мощности критерия (6) будем использовать обозначение
{ 02 2 }
Wn ) == р Х N > XI o,N IIE ' (7)
а о соответствующей rипотезе будем rоворить для краткости как о rипотезе р.
В этих обозначениях полученный выше результат записывается Б виде:
Wn O) а при n 00.
Установим теперь следуюший результат.
Теорема 2. Для лю60rо вектора Ei=E O выполняется условие Wn ) 1 при
_ 2
n 00, т. е. критерии Х является состоятельным.
02
Доказательство. Вычислим среднее и дисперсию статистики Х N при про
извольной rипотезе Е. Для этоrо перепишем формулу (4) в виде
12 == (У) nр))2 2 (1I) nр})(р} Р;) , n (Pj р;)2
n Q + L.J о r L.J о
j 1 nPj j 1 Pj j 1 Pj
Так как
E(VjIE) == nPj, E[(lIj npj)2IE] == D(vjIE) == npj(1 Pj).
то
Е ( 1 2 1 ) (Pj pj)2 + pj(l pj)
пР n.L..J О .L..J О .
j 1 Pj j 1 Pj
о 2 1 О )
Отсюда. в частности, имеем Е(Х n Р == N 1. Этот результат соrласуется
с асимптотическим результатом теоремы 1, поскольку среднее предельноrо
распределения i(1V 1) равно N 1 (см п. 3 1.2). Аналоrично можно
вывести и формулу дJ1Я дисперсии:
02 (n ')(n 2) 2
D(Xnlp) == 4 (R З2 R 2I ) +
n
n 1 2 1 2
+ 2 (ЗR22 2R21RII R 21 ) + (RI2 R II ),
n n
(8)
(9)
rде
N pk
R ks == L .
j l Pj
N
Если Е == Е" то R ks == L(Pj)k S И из (9) имеем
j 1
. 2 О 1 ( 1 2 )
D(XnIE ) == 2(N 1) +;;, Li N 2N + 2 2(N 1)
j 1 Р)
32б
rлава 4. Проверка статистических zипотез
при n ----+ 00, что также соrласуется с теоремой 1. Если же r. -:F Е О ' то из (8) и (9)
следует, что при n ----+ 00 среднее и дисперсия статистики K при rипотезе r.
имеют порядок роста n. С учетом этоrо из (7) по неравенству Чебышева (при
t == Xi a.N ') имеем
I Wn ) p{K t/E} == Р{ 'K E(k IE)1 ;) IE(k IE) t/I Е}
D(k lp) ( 1 )
(E(k IE) -=- t)2 == о;; ·
..
Тем самым, если rипотеза Но неверна, а истин
ной является некоторая альтернатива р, то критерий
(6) обнаружит это с вероятностью. бл иэкой к 1, KO
rдa п велико. Но что будет, если альтернатива р «мало
отличается» от Е О ' т. е. если Е == Е(n) ----+ Е О при n ----+ оо? Что собой пред тавля
ют [j данном случае «noporoJJbIe.) альтернативы, т. е. для которых выполняется
условие (7) 4.1, которое в наших обозначениях заПl1шется lЗ виде
«Близкие» альтерно
тивы и мОЩНОСТЬ
1
критерия .
Wn (n» ----+ 'У, Q: < 1 < 1?
Ответ на эти вопросы дает следующее утверждение.
Теорема З. Пусть альтернатива имеет вид
Е(n) == Е О + J-п ,
rAe == (/3., , fЗN) -:F Q фиксированный вектор, задающий отклонение
N
от rипотезы НО (L (3j == о) TorAa при n ----+ 00
j 1
N (.12
)./==L
j ! pj'
rAe FN I(t; л 2 ) функция нецентральноrо распределения хи квадрат
W'I (n» ----+ 1 FN I(Xi a,N I; ,.\2),
( 10)
i(N 1; л 2 )
(см п. 2 25).
Доказательство. Как и при доказательстве теоремы 1, можно по казать, что
при rипотеэе Е(n) распределение вектора нормированных частот
( lIj nPj(n) . )
.;n , J == 1,...,N I
4.2. Проверка 2ипотезы о виде распределения
327
сходится при n -----+ 00 к нормальному распределению N(Q, t N 1), Но
. Vj пр} Vj npj(n)
Vj == ..;n == vn + {3j,
поэтому
.c(. .I (n)) -----+ N( N / N I)' N I == ({31, .., {3N I),
А так как
Х ' 2 .,..... I.
n == 2.,N I ,
то по лемме 3 2.5 (точнее, на основании асимптотическоrо варианта этой
леммы)
.c(X IE(n)) -----+ i(N 1; ,\2),
rде
N {3 2
>.2 == ltNI I N L
j 1 Pj
(проверяется непосредственно). Отсюда и из (7) следует (10). .
то б v 2 v
,аким о разом, критерии Х ('реаrирует» на отклонения от нулевои rи
потезы, имеющие при больших n порядок n 1/2 это И есть о«пороrовые.,
альтернативы для данноrо критерия; более близкие альтернативы, т. е. откло
няюшиеся от Но на величину o(n I/2) (в этом случае >.2 -----+ О), критерий
не отличает от НО, так как в таких случаях Wn(P(n)) -----+ а (вероятность по
падания в критическую область при альтернативе асимптотически такая же,
как и при основной rипотезе); для более же удаленных альтернатив (т. е. при
>.2 -----+ 00) критерий остается состоятельным: Wn(P(n)) -----+ 1.
Тем самым при простой rипотезе Но удается провести исчерпываюшее
исследование асимптотических свойств критерия i для больших выборок.
з. Критерий хи квадрат для сложной rипотеэы
Сложные rипотезы для полиномиальноro распределе
нин .1\,f(n; ) в обшем случае имеют следуюший вид:
»f
Сложные rипотезы
Но Е == [!.(8), () == (()I,
,8r) Е е, r < N 1.
Таким образом, при rипотезе Но вероятности исходов являются некоторыми
функциями от неизвестноrо параметра 8 с множеством возможных значе
ний е. Чтобы построить критерий проверки такой rипотезы по наблюдению
вектора частот == (VI, , VN) можно, по аналоrии с предыдущим случаем,
поступить следующим образом. Построим статистику, аналоrичную (4),
2 ( ) (Vj npj(8))2
Х П О L.J .(8)
. ПР )
J I
328
rлава 4. Проверка статистических i!ипотез
Эта статистика зависит от неизвестноrо параметра 6, поэтому непосредствен
но использовать ее нельзя требуется предварительно исключить неопреде
ленность в 6. Для этоrо заменяют 6 некоторой оценкой Оп == 0., (!!.) и получают
2 2
В итоrе статистику Х 7I == Xпи n). Это уже функция только от наблюдений!!.,
следовательно, ее значение можно однозначно вычислить для каждой реали
зации вектора !!.. Однако, чтобы рассчитать соответствующий критерий, надо
2
знать распределение Х П при rипотезе Но (хотя бы приближенно). Положение
осложняется тем, что теперь величины Pj(On) уже не постоянные, а представ
ляют собой функции от наблюдений !!., поэтому теорема 1 к статистике X
2
неприменима. Более Toro, следует ожидать, что распр еление Х п будет, BO
обще rоворя, зависеть от способа построения оценки 6п.
2
Проблема нахождения предельноrо (при n ---+ 00) распределения дЛЯ Х П
при этих усложненных условиях была решена американским статистиком
Р. Фишером в 1924 [. Он показал, что существуют методы оценивания па
раметра 6, при которых это предельное распределение имеет простой вид,
а именно, является распределением x 2 (N 1 т). В частности, это будет
иметь место при использовании оценки максимальноrо правдоподобия
N
е п == arg тах П (pjUn)Vj
8 j 1
или, что то же самое, оценки по видоизмененному методу минимума хи
квадрат (см п. 2 3.6), которая является решением системы уравнений (3) 3.6.
В этом случае для построения критерия используется теСтовая статистика
N 2
X == x (en) == l: (V] n р !..(6 п ))
j I npj(6 n )
(11 )
Сам критерий рассчитывается на осноnании следующеrо утверждения.
Теорема 4. Пусть функции pj(6), j == 1, , N. удовлетворяют условиям:
N
1) l:pj(6) == 1, '</6 Е 8;
j=1
2) pj(6) с > О, '</ j, и существуют непрерывные про из водные
apj(6) a 2 pj(6)
, , k,l == 1, ,т;
д6/,; д6/,; д6/
3) (N х r) матрица Ilapj(6)/a6/,;1I имеет paHr r для всех 6 Е 8. Тоrда
.c(i IHo) ---+ X2(N 1 Т),
2
rде статистика Х п определена в (11).
4.2. Проверка i!ипотезы о виде распределения
329
Доказательство этой теоремы можно найти в 1JIII!I8.'1K 2 .,
[15, c.462 4701. При выполнении условий теоремы 4 ., рите ии Х для
сложнои rипотезы
критерии имеет вид:
'НО отверraется {:::::::} XT > X ".N I T.I (12)
(здесь а заданный уровень значимости и предполаrается, что n 50 и
1/j 5, Vj).
Этот критерий можно применять также в следующей общей ситуации.
Пусть задана выборка Х == (Х"... , х п ) из HeKoToporo распределения .e( ),
о котором требуется проверить rипотезу Но .ею Е Fo, rде Fo == {F(x; О),
О Е е} заданное пара метрическое семейство. Проведем rруппировку Ha
блюдений, основываясь на интервалах [1, ,[N ([i n [j eJ, i f. з,
[, U U [N == [ множество возможных значений ), т. е. подсчитаем
частоты
n
1/j==I:I(X i E[j), j==I,...,N,
i l
и rипотетические вероятности
Pj(O) == p{ Е EjlHo} == / dF(x; О), j == 1, ,N
tj
Решив далее систему (З) З.6, найдем оценку Оп И вычислим значение CTa
2
тистики Х П В (1 ]). Если выполнены условия теоремы 4, то применяется
критерий (12). Следуя этому критерию, можно ошибочно отклонить rипоте
зу НО, коrда она верна, с вероятностью, приближенно равной а.
Пример 4. Среди 2020 семей, имеющих двух детей, 527 семей, в которых два
малЬ'lика, и 476 Две девочки (в остальных 10]7 семьях дети разноrо пола).
Можно ли с уровнем значимости а == 0,05 считать, что количество мальчи
ков в семье с двумя детьми ( ) биномиальная случайная величина? Здесь
речь идет о проверке rипотезы Но .e( ) Е Bi(2, О), поэтому rипотетические
вероятности исходов имеют вид
ро(О) == P{ == О} == (1 0)2,
р,(О) == P{ == ]} == 20(1 О),
Р2(О) == P{ == 2} == 02
Отсюда в соответствии с (3) 93.6 получаем уравнение для нахождения оценки
параметра О
t IIjpj (О) == 21/0 + 1 20 111 + 21/2 == О,
j O Pj (О) 1 О О( 1 О) О
решая которое, находим
1/1 + 21/2
Оп ==
2n
ззо
rлава 4. Проверна статистических 2ипотез
в данном случае 110 == 476, 11) == 1 О 17, 1/2 == 527, n == 2020, поэтому 'Оп == 0,513.
Далее вычисляем значение статистики (11):
2 1
X == 2: (lIj np (Oп» == 0,116,
j O npj(On)
2 1
И этот результат надо сравнить с XI a, ,. Поскольку Хо,3; 1 == 0,148, при любом
уровне значимости Q 0,7 rипотез принимается. .
При мер 5 (Пуассоновская модель, критерий х2 для нее), Пусть произво
дится n независимых наблюдений над неотрицательноЙ целочисленной слу
чайной величиной . Требуется проверить rипотезу Но .ею Е П(О). Здесь
множество [ возможных значений есть {О, 1,2, .}, т. е. бесконечно, по
этому надо предварительно провести rруппировку наблюдений. В качестве
соответствующих «интервалов,) выберем [j == {j I}, j == 1, , N 1,
[N == {N 1, N,...} при некотором N ) 3 (Torдa N 1 I > О). rипотети
ческие вероятности при таком способе rруппировки будут равн ы (см. (8) 9 1.1)
Pj(O) == f(j 110), j == 1,
00
,N 1, PN(O) == 2: f(xIO),
x N 1
rдe
e вox
f(xIO) == .
х!
Уравнение для нахождения оценки 'Оп R данном случае имеет вид (см. (3) 93.6)
N I . 1 IIN f ( ')f(xIO)
'" ( 1 ) 11' + x N 1 == О
6 О J 00 .
j ( 2: f(xIO)
x N (
Отсюда
[ N ) IIN f X f (X I 6) ]
2:(j 1)lIj + x:: )
j ) 2: f(xI8)
x N l
Здесь первый член в квадратных скобках равен сумме всех наблюдений X j
таких, что Xj N 2, а последний член приближенно равен сумме наблю
дениЙ, оказавшихея большими N 2. Таким образом. в качестве прибли
женной оценки для О можно взять выборочное среднее: 'Оп == Х (напомним,
что обычная оценка максимальноrо правдоподобия для параметра О в модели
П(О) точно равна Х см. п. 1 93.5).
1
o==
n
4.2. Проверка zипотезы о виде распределения
331
Теперь находим
! e XXj '
(j l)!
Pj == Pj(On) == e X t ::
k N 1
при j == 1, ,N 1,
при j == N,
и (при больших выборках) rипотеза Но отверrается на уровне значимости а
Torдa и только тоrда. коrда
N ( ) 2
/lj nPj 2
> Xl o N 2'
ПР' '
j . )
Пример б (Нормальная модель, критерий х2 для нее). Пусть Но rипотеза,
состоящая в том, что выборка Х == (Х" ,х n ) получена из нормальноrо
раСIJределенил N(fJ i , fJi) (здесь fJ == (fJ 1 , fJ 2 )). Зададим интервалы rруппировки
в виде E: j == (aj l, щ], j 1, ,N, N > 3, rде ао == oo, aN == 00,
uj == аl + () I)h, j == 1, . N 1, al, h некоторые фиксированные
величины. В таком случае, обозначив для краткости
1 { (X fJl)2 }
g(x; fJ) == r-c ехр 2 '
V 211' 2fJ 2
.
имеем
Pj(fJ) == / g(x; fJ) dx, j == 1, ,N
fJ 2
[j
Система (3) 3.6 в данном случае состоит из следующих двух уравнений:
N
/I ( jfJ ) / (х fJ1)g(x: fJ) dx == О,
} , Р} [.
)
t /ljfJ [ 2 / (х O,)2g(X; 8) dx / g(x; 8) dx] == О.
j ' Р) () 2 < [ .
)
N
Поскольку L /lj == N, эти уравнения можно привести к виду
j 1
N / xg(x; 8) dx N / (х 8.)2g(X; 8) dx
8. == /I /j ,fJi == L /I/')
n j 1 / g(x; fJ) dx n j ' / g(x; 8) dx
tj {j
2
Разрешая эту систему относительно 8, , 82, можно найти оценки 8, и fJ 2 .
332
!лава 4. ПроверКQ статистических 2Uпотез
При малом h можно получить практически приемлемые приближенные
значения дrlЯ этих оценок. Предположим сначала, что /)) == /)N == О (левее
точки а, и правее точки aN I == а) + (N 2)h нет выборочных точек).
Заменяя интеrралы по областям [} произведением подынтеrралl,НОЙ функции
в средней точке Zj на длину I[j I == h для j == 2, , N 1 получим следующие
приближения:
N I
2 1" 2
02 L....J /)j (Zj (}I)
n
j 2
Если крайние интервалы не пусты, но содержат малую часть выборки, то
можно использовать приближения
N I
1"
(}I L....J/)jZj,
n j 2
1 N
(}I L /)jZj,
N.
J I
N
2 1" 2
02 L....J /)} (Zj (}I)
n j 1
rAe ZI == а), ZN == aN ).
С учетом этих допущений можно считать, что если проверяемая rипо
тез Но верна, то статистика (11) распределена приближенно (при больших
выборках) по закону X 2 (N 3), и на этой основе рассчитывать COOTBeTCTBY
ющий критерий (12). .
4. Критерий квантилей
Методхи квадрат можно применятьдля построения критериевсоrласия и в за
дачах Apyroro типа, Korдa нулевая rипотеза фиксирует некоторые частные
характеристики функции распределения Р{ (х) наблюдаемой случайной вели
чины . Рассмотрим типичную ситуацию TaKoro рода, Korдa rипотеза имеет
вид Но F{((j) == Pj, j == 1, ,N 1, rAe oo < (1 < < (N I < 00
И О < РI < < PN I < 1 заданные числа, т. е. Но это rипотеза о том,
что распределение .с(о имеет заданные квантили (j для заданных уровней Pj
Это сложная rипотеза: соответствующий ей класс распределений :1'0 включает
все распределения с указанными квантилями.
Пусть имеется выборка Х == (X 1 , ,Х n ) из HeKoToporo HenpepbIBHoro
распределения .c( ), о котором выдвинута такая rипотез Но. Построим крите
рий типа х2 для проверки зтой rипотезы. Для этоrо положим [.j == ((j l, (jl,
j == 1,... ,N, (о == oo, (N == 00, И пусть /)j число выборочных точек X i ,
принадлежащих интервалу [j. Тем самым мы1 имеем схему rpуппировки дaH
HblX с естественными (т. е. порождаемыми самой пронеряемой rипотезой)
интервалами. Torдa
.c( == (/)1,"., vN)IH o ) == М(n; Е О == (р7
,р",у») ,
rде Р; == Pj Pj I, j == 1, , N, Ро == О, PN == 1, и rипотеза Но ЭКlJивалент
на утверждению, что вероятности исходов в построенной полиномиальной
схеме равны заданным числам Р7 .., ,р",у. Следовательно, для проверки зтой
94.2. Проверка i!ипотезы о виде распределения
333
rипотезы можно использовать построенный в п. 2 критерий х 2 (6). В данном
контексте этот критерий называют критерием квантилеu.
При N == 2 и РI == 1/2 соответствующий критерий называют критерием
знаков. В этом случае Но это rипотеза о том, что выборка Х извлечена
из распределениSl .c( ) с медианой (" а тестовая статистика (4) принимает вид
х;' == (Vl y + (V2 y == (VI y (13)
rде 111 число выборочных точек X j в интервале ( oo, (,], или, что то же
самое, число отрицательных разностей X j (" i == 1, ,n (отсюда и назва
ние критерия).
На практике критерий знаков чаще Bcero применлют в следующей ситуа
ции. Пусть (X j , Y i ), i == 1,... ,n, независимые наблюдения над двумерной
случайной величиной { == ( I, 6). Требуется проверить rипотезу Но о ТОМ,
что компоненты 6 и 6 независимы и одинаково распределены, т. е. что
P (x, у) == Р(х)Р(у), rде Р(х) некоторал (неизuестная) одномерная функ
ция распределения. Чтобы построить соответствующий критерий, поступают
следующим образом. Составим разности Zj == Xi , i == 1,..., n. Если
rипотеза Но верна, то P{Zj < О} == P{Zj > О} == 1/2, и тем самым rипотеза
сводится к утверждению, что выборка (Zl,'", Zn) извлечена из распреде
ленил, медиана KOTOpOro равна О. В этом случае V, равно числу отрицатель
ных Zj, а статистика (13) для больших выборок распределена при rипотезе Но
, 2 ( ) li Jf
приближенно по закону Х 1 . ем самым при уровне Критерий знаков
значимости а асимптотическии вариант критерия зна
ков имеет вид
Но отверrается {:::::::} (Vl у > xi o,
(14)
Замечание. Из (13) видно, что критерий знакоп по существу основывается на стати
стике V" которая имеет при rипотезе Но биномиальное распрсделенис Bi(n, 1/2).
поэтому на самом деле здесь речь идет о провсрке простой параметрической rипотезы
опараметре биномиальноro распределеНl1Я Bi(n, В), именно, rипотезы Но (J == 1/2.
В основе критерия (14) леЖl1Т нормальная аппроксимация .c(viIHo) Н(n/2, n/4)
(теорема Муавра Лапласа), из которой и следует, что
.с ( (VI i YIH O ) х 2 (1) при n 00.
При малых выборках критерий знаков как частный случай критериев ШlЯ общих пара
метрических rипотез в биномиальной модели Bi(n,8) будет раСС'lитан позже (в rл. 5)
при изложении общей теории проверки параметрИ'lеских rипотез. Вообще же крите
рий знаков (,старый и знаменитый.) (Я. raeK иЗ. Шидак), он применяется уже очень
давно, по крайней мере не позже, чем с 1925 r. (Р. Фишер); детальное обсуждение
ero праКТИ'lескоrо использования можно найти в книrе [26, с. 5& 65), rде приведена
и соответствующая обширная библиоrpафия
ЗЗ4
rлава 4. Проверка статистических zипотез
5. Критерий пустых ящиков
В этом пункте мы кратко коснемся еще одноrо COBpeMeHHOro подхода к задаче
проверки простой rипотезы Но о виде распределения, связанноrо с методом
rpуппировки наблюдений. Как уже отмечалось в п. 2, при rруппировке Ha
блюдений (в случае выборки из непрерывноrо распределен ин) происходит
неизбежная потеря информация, так как вместо самих наб_1юдений исполь
зуются лишь частоты попадания в интервалы rруппировки. Этот HeДOCTa
ток метода можно уменьшить, устраивая (,более мелкое., разбиение носите
ля распределения наблюдаемой случайной веЛИ'IИНЫ, т. е. уuеЛИ'lивая число
интервалов rpуппировки N. Однако, Torдa критерий х 2 становится TpyдoeM
ким, так как подсчет и обработка большоro (при больших N) числа частот
111, . . . , IIН требует больших вычислительных затрат. Следует также иметь в ви
ду И то обстоятельство, что теорема 1 о предельном распределении статистики
K справедлива лишь при фиксированных значениях параметров N и pj,
j == 1, , N, и ее уже нельзя использовать для расчета критической rраницы
критерия, если N 00. Выход из этой противоречивой ситуации можно най
, 2
ти, сконструировав более простые, нежели Х,р тестовые статистики и доказав
для них предельные теоремы, учитывающие одновременное неоrpаниченное
возрастание параметров n и N. Одной из таких простых статистик является
число пустых (т. е. не содержащих ни одной выборочной точки) интервалов
РО == ро(n, N) (мю ноль). Критерий, основанный на этой статистике, назы
вают критерием пустых ящиков, ero мы и опишем. (Если интерпретировать
интервалы rруппировки как ящики, а испытания как бросание в них дроби
нок, то ро(n, N) есть число пустых яшиков после бросания n дробинок
отсюда и название критерия.)
Для HeKoToporo упрощения мы конкретизируем нулевую rипотезу
Но Р{(х) == Р(х),
считая, что Р(х) == х, О х 1; таким образом, Но это rипотеза о том,
что наблюдаемая случайная величина имеет равномерное распределение
на отрезке [О, 11. (На самом деле это не есть сужение проблем Ы, так ка к с по
мощью преобразования Смирнова (см. упр. 17 к rл. 2) 1] == Р(О мы всеrда
можем перейти от слу'шйной величины с абсолютно непрерывным pac
пределением F к равномерно распределенной на отрезке [о, 1] uеличине 1].)
Далее, обычно в методе rpуппировки рекомендуется интервалы Е" , EN
выбирать равновероятными при нулевой rипотезе, т. е. чтобы все р) I/N,
поэтому далее мы полаrаем Ej == ((j I)/N,j/N], j == 1,..., N.
Итак, пусть V" ,VN частоты попадания элементов выборки Х ==
== (X I ,..., Х n ) из HeKoToporo абсолютно HenpepbIBHoro распределения на
[о, I1 в эти интервалы. Определим индикаторные СЛУ'lайные величины 1]j ==
== I(Vj == О), j == 1, , N, Torдa, очевидно, JLO == 1]1 + + 1JN Вычисли",
первые два момента этой статистики ШlЯ произвольноrо распределения Ha
блюдений Р{, д я KOToporo
F{(j/N) F{((j I)/N) == Pj, j == 1,... ,N
4.2. Про верка zипотезы о виде распределения
335
Имеем
N N
Еро == L Е1]) == L Р{1]) == l},
j l j l
N N
Dpo == L D1]j + 2 L cov(1]j, щ) == L P{1]j == I}(I P{1]j == I}) +
j 1 i<j j l
+ 2 L [P{1Ji == 1]j == I} Р{1]; == I}P{1]j == I}]
i<j
ИСПblтания независимы. поэтому
P{1Jj == I} == P{Vj == О} == (1 pj)n
Р{1]; == 1]j == I} == Р{У; == Vj == О} == (1 Р; pj)n
il-j
Следовательно,
N
E/l o == L(I Pj)" D/l o == 2 2..:о Р; pj)n + E/l o (E/l o )2 (15)
j l i<j
С помощью метода неопределеННblХ множителей Лаrpанжа (см. о нем в п. I (1)
3.7) леrко проверить, что среднее E/l o как функция парамеТР08 Pl, ,PN
достиrает минимума при Pj == 1/ N, j == 1,... , N, т. е. при нулевой rипотезе.
В этом случае ФОРМУЛbl (15) принимают вид
E/l o == N ( 1 )"
( 2 ) " ( I ) n 2 ( 1 ) 2"
D/l o == N(N 1) 1 N + N 1 N N 1 N
(16)
Таким образом, при любом отклонении от нулевой rипотезы, таком, что
вероятности попадания в интервалы rруппировки не все равны I/N, статисти
ка /lo имеет тенденцию увеличиваться, т. е. (,слишком большие» значения /lo
«свидетельствуют,) против rипотезы Но. Отсюда следует, что критическую об
ласть критерия следует задавать в виде
{/lo(n, N) > t,,(n, N)}.
( 17)
Для нахождения критической rpаницы t,,(n, N) надо знать распределение
статистики /lo при rипотезе Но. Точное ее распределение известно и имеет
вид 114, с. 10],
N k ( . ) n
k . . k + J
P{/lo(n, N) == klHo} == С л, 2) I)JC k 1
J O
ЗЗб
rлава 4. Проверка статистических zипотез
однако использовать ero дли практических расчетов при больших n и N
(что и представляет наибольший интерес для приложений) неудобно. Поэто
му при больших значениях n и N для расчета критерия (17) естественно
воспользоваться предельными теоремами. Одна из необходимых нам таких
теорем, дающая вид асимптотическоrо распределения /.Lo при любом абсо
лютно непрерывном распределении наблюдений Р( (а не только для нулевой
rипотезы Но : Р«(х) == х, о:::; х :::; 1) формулируется следующим образом.
Обозначим через
j/N
Pj == / f(x) dx, j == 1, ,N,
(j I)/N
веронтности попадания наблюдений в интервалы rРУППИРОI\КИ для распреде
ления с плотностью J(x) и будем предполаrать, что все допустимые плотности
f(x) > о, х Е [о, 1], и непрерывны.
Теорема 5. Пусть n, N 00 так, что nfN р > о. TorAa
[,(/.Lo(n, N)!f) rv N(Nm(f), N(12(J)),
rAe
1
т(1) == / e pf(x) dx,
о
1 1 2
(12(1) == / e pf(X)(1 e pf(X)) dx р [/ J(x)e pf(x) dx]
о о
( 18)
Для нулевой rипотезы f(x) == 1, х Е 10,1], поэтому утверждение Teope
мы 5 принимает вид
( /.Lo(n,N) Ne P I ) N( )
[, НО о, 1 .
..j Ne /)(1 (1 + p)e p)
Этот результат уже позволяет приближенно рассчитать критическую rpаниuу
в (17) при больщих n и N и заданном уровне значимости а. В самом деле,
из (19) следует, что если в (17) положить
(19)
tQ(n,N)==Ne P+to ..j Ne p(I (I+p)e p), ф( tо)==а, (20)
то при n, N 00, n/N р > о критерий (17) будет иметь в пределе уровень
значимости а.
.... К
ритерий
пустых ящиков
Итак, асимптотический (при больших n, N и 1 fN ==
== Р > о) вариант критерия пустых ящиков имеет следую
щи й вид:
4.2. Проверка zипотезы о виде распределения
337
I Но отверraется Jlo(n, N) > ta(n, N),I (21)
rде ta(n, N) дано в (20). Следуя этому правилу, можно ошибочно oT8eprHYJ'b
истинную rипотезу Но F{(x) == х, О х 1, с вероятностью, приближенно
равной а.
Теорема 5 позволяет также исследовать предельное поведение МОЩНОСти
W N (/) критерия (21) и при произвольной альтернативе, задаваемой плотно
стью '(х) 1: 1, х Е [о, 1]. Действительно, в условиях этой теоремы
W N (/) == P{Jlo(n, N) > ta(n, N)If} ==
== Р { Jlo(n, Nm(f) > Za(N) l j } :;:::'Ф(Zа(N)), (22)
N 17(!)
rдe
т(!) e P 170
za(N) == ../N 17(!) t a 17(/) '
175 == e P(1 (1 + p)e P).
Воспользуемся, далее, известным в теории вероятностей неравенством Йен
сена 6), справедливым для любой случайной величины 'т1 и любой выпуклой
вниз функции g(x) g(E1]):::;; Eg(1]) с равенством ТОлько в случае, коrда
'т1 == сопst (предполаrается, что указанные математические ожидания суще
ствуют, для выпуклой вверх функции g(x) неравенство заменяется на про
тивоположное); для неотрицательной величины 'т1 и g(x) == ln х это Hepa
венство принимает вид In Е'Т1 E1n 1] или Е'Т1 ехр {Eln 'Т1}. Полаraя здесь
'т1 == е Р!Ю. rде.ею == И(О, 1), получим неравенство (см. (Ig))
1
т(!) ехр { p / '(х) dx} == e P
о
таК как j(x) функция плотности на [0,1]; равенство здесь имеет место
только в случае '(х) == const == 1, т. е. при нулевой rипотезе. Итак, для любой
альтернативной плотности '(х) =/:. 1 разность т(!) e P > О, и потому
величина za(N) в (22) при N ----+ 00 неоrpаниченно Состоятельность .,.
возрас.тает. Это, в свою очередь, в силу (22) означает, ;"'. критерия пустых
что 11т W N(f) 1, т. е. критерий пустых ящиков . ' ящиков
N oo '
является состоятельным.
Итак, если выполнены условия теоремы 5, то мощность критерия пустых
ящиков при любой фиксированной альтернативе стремится к 1. Однако, если
при изменении n и N изменяется также и альтернатива, сближаясь с нуле
вой rипотезой Но, то мощность критерия уже необязательно будет сходиться
к 1 это зависит от скорости сближения альтернативы с нулевой rипотезой.
Теорема 5 дает возможность ответить и на вопрос о том, с какой скоростью
6) Йенсен ИоrаНI1 Людвиr (1859 J925) датский математик, труды по математическому aHa
лизу, rеометрии.
22 3а.., 1 748
ЗЗ8
rлава 4. Проверна статистических zипотез
может про исходить это сближение, чтобы критерий (21) обладал еще спо
собностью «реаrировать» на альтернативу. В данном случае альтернатипами
являются любые абсолютно непрерывные распределения на [О, 11, отлича
«Близкие» ющиеся от paBHoMepHoro распределения И(О, 1); сле
довательно, «близкую» альтернативу Fn можно задать
плотностью
альтернаТИВbI
!п(х) == 1 + а(n)Ь(х),
(23)
rде а(n) ----+ О при n ----+ 00, а Ь(х) произвольная непрерывная функция,
удовлетворяющая условию
I
f Ь(х) dx == О.
о
Здесь а(n) и определяет скорость сближения (в смысле поточечной сходимо
сти) альтернативной плотности 1" с плотностью при нулевой rипотезе.
Следующее утверждение является простым следствием теоремы 5.
'М6щно& ; критери; Теорема б, Если в соотношении (23) положить
,']J: .)( "! , , '"""",," а (n) == n 1/4,
то при n, N ----+ 00, n/N ----+ р> о мощность WN(/n) удовлетворяет предель
ному соотношению
WN(fn) ----+ Ф(Ll(ь 2 , р) t a ),
(24)
rде
Ь2 3/2
д(ь 2 р) == р
, 2 .J еР 1 Р ,
1
ь 2 == / ь 2 (х) dx.
О
Из этой теоремы следует, что критерий пустых ЯЩИК08 позволяет отличать
от rипотезы Но альтернативы, сближающиеся с ней со скоростью n I/4 Более
близкие альтернативы вида (23) (т. е. при а(n)n 1/4 ----+ О) этот критерий асимп
тотически (в условиях теоремы 6) не отличает от Но (т. е. W N (/11) ----+ а), а для
более удаленных альтернатив (т. е. при а(n)n'/4 ----+ 00) он сохраняет свойство
состоятельности (т. е. WN(/n) ----+ 1).
Дальнейшие результаты
Критерий пустых ящиков приплекателен своей простотой и достаточно широ
ко известен (по крайней мере с работы Ф.Дейвид 1950 r.). Подробное изложе
ние относящихся к нему результатов и историю вопроса можно найти в книrе
114, rл.5], rдe также рассмотрены и обобщения этоro критерия. «Критерий
пустых ящиков может быть полезен при проверке rипотезы о paBHOMepHO
сти распределения каких либо объектов в оrpаниченной части пространства,
4.2. Проверка zuпотезы о виде распределения
339
например, звезд в части космическоro пространства, особей какой либо био
лоrическоЙ популяции в ее ареале и т. п.') [14, с. 101. в то же время очевидно,
что статистика ро включает далеко не всю информацию, содержащуюся IJ BЫ
борке Х == (X 1 , , Х п ). Более полно эта информация может быть учтена,
если конструировать тестовые статистики вида Симметрические .
п статистики
2..: СтРт,
T O
rде
N
Рт == Itr(n, N) == 2..: 1 (lIj == т)
з )
число частот 111, ,IIN, принявших значение r == о, 1, ,n, а Со, С),
Сп некоторые «lJeca,), выбираемые из тех или ИНblХ условий оптимальности.
Статистики TaKoro вида наЗblваются симметрическими статистиками в схеме
zpyппupOBKU наблюдений, а порождаемые ими критерии симметрическими
критериЯА1U. Обшие результаты для симметрических критериев. обобщающих
критерий пустых ящиков, изложены в работах авторов 7) Здесь же мы лишь
отметим, что в условиях теоремы 6 наибольшую асимптотическую мощность
среди всех симметрических критериев имеет известный ..,;f'
нам критерий х 2 , тестовая статистика KOTOpOro (см. (4» Критерий х 2
в рассматриваемом случае принимает вид
N п
K == N "II? n == N "т 2 рт n.
n цз n ц
j 1 T O
Критическая rpаница для этоrо критерия, превышение которой при водит к OT
клонению rипотезы НО, имеет асимnтотически вид ta(n, N) == N + t'kV2N,
ф( tj) == а, а предельная мощность при «noporOBbIX» альтернативах равна
Ф(ь\/j)1i t a )
Интересно сравнить, насколько уступает по мощности критерий пустых
яшиков простейший симметрический критерий оптимальному (но TPy
доем кому) критерию i Из (24) следует, что
д(ь 2 . р) == ь 2 2 е(р), rде е(р) == р
v "2 V 2(eP I р)
Как функция от рвеличина е(р) монотонно убывает от I при Р == о до О
при р == 00, т. е. при малых значениях р == n/N критерий пустых ящиков
2
по мощности мало уступает критерию Х Некоторые численные значения
функции е(р) указаны в следующей таблице:
7) Ивченко r и. Медведев Ю. И. Разделимые статистики и проверка rипотез. с.'lучай малых
выборок 11 Теория вероятностей и ее примеиения. 1978. Т. 23. NJ 4. С. 796 806: l1вченко [.I1.,
Медведев Ю. И. Разделимые статистики и проверка rипотез для rрynпированных данных 11 Теория
вероятностей и ее ПРИl.1енения. 1980. Т. 25. NJ 4. С. 549 560.
22"
340
rлава 4. Проверка статистических 2ипотез
р 0,05 0,10 0,15 0,20 0,30 0,40 0,50 0,60 0,70 0,80
е(р) 0,992 0,983 0,975 0,967 0,950 0,933 0,917 0,900 0,884 0,865
Р 0,90 1,00 1,10 1,20 1,30 1,40 1,50 1,60 1,80 2,00
е(р) 0,851 0,834 0,818 0,802 0,786 0,769 0,753 0,738 0,706 0,675
4.3. rипотеза и критерии однородности
..
Задача о двух Вblборках
о rипотезе однородности и ее прикладном значе
нии подробно рассказано в примере 5 Введения.
Ее простейший вариант, который часто называют также задачей о двух выбор
"ах, формулируется следующим образом. Пусть Х == (X j , , х п ) выборка
из распределения .с({) снекоторой (неизвестной) функцией распределения
Р ! (х), а У == (Y i , ,У т ) выборка из распределения С('Т/) снеизвестной
функцией распределения Р 2 (х). rипотезой однородности ЯВJlяется утвержде
ние Но F1(x) == Р 2 (х). Это одна из основных проблем непараметрической
статистики, для решения коmрой разработано большое '1исло соответствую
щих критериев од//ородности. Некоторые из них будут описаны и обсуждены
в этом параrрафе.
1. Критерий однородности Смирнова
-- Статистика СМИрНОf>а Этот критерий является одним из первых кри
териев однородности в зада'lе о двух выборках
из непрерывных распределений (1939 r.). Ero тестовой стаП1СТИКОЙ является
D I1 ,т == sup 1.F\I1(x) Р 2т (Х) I ,
oo<x<oo
rде Fln(X) И Р2rn(Х) ЭМПИРИ'lеские функuии распределения, построен
ные по выборкам Х и У соответственно. Статистика Dn, т «сама наПfJаши
вается» 1} Ka'leCTBe разумной тестовой статистики ДJ1я rипотезы OДHOpOДHO
сти Но. Ведь, как мы знаем (см., например, п. 1 4.2), ЭМПИРИ'lеская функuия
распределения является оптимальной оценкой ДJ1И теоретической функции
распределения, и с увеЛИ'lением объема выборки они сближаются, поэтому
в случае справедливости rипотезы Но функции Fin(X) И Р2rn(Х) оценивают
одну и ту же неизвестную функцию распределения. Тем самым в этом случае
(по крайней мере при больших n и т) статистика Dn, т не должна существен
но отклоняться от нуля. Отсюда следует, '1т слишком большие зна'lениЯ эmй
статистики следует расценивать как свидетельство против rипотезы НО и по
тому разумно выбрать КРИТИ'lескую область в виде Тю == {Dn,т > ta(n, т)}.
Критическую rpаницу ta(n, т) при заданном уровне значимости а находят
на основании известноrо при rипотезе НО предельноrо (при n, т ----+ (0)
распределения статистики Dn, т, даваемоrо теоремой Смирнова (см. тeope
му 4 2.1). На основании этой теоремы при больших n и т можно положить
4.3. rипотеза и критерии однородности
341
tcr(n, т) == V I/n + I/m Лcr, rдe К(Л а ) == 1 o:. Действительно, в этом случае
Р{ Dn,m > V * + Л "IН О } ==Р{ v n:тт Dn,m > лаlно} I К(Л,,) ==0:.
Итак асимптотический (при больших n и т)
вариант критерия однородности Смирнова имеет вид:
»f
Критерий Смирнова
отверrается {::=:} Dn т > Л" V + 1 , 1
' n m
rде К(Л а ) == 1 0:, K(t) функция распределения Колмоrорова (см. (II)
2.1). Вероятность ошибочно OTIJeprHyrb при этом истинную rипотезу НО
приблизительно равна а. Отметим также, что этот критерий состоятелен (аль
тернативой здесь является любая пара непрерывных распределений (F 1 , Р 2 )
такая, что F1(x) фF 2 (х)).
Подчеркнем, что критерий (1) проверки неизменности функции распре
деления не зависит от KOHKpeTHoro вида функции. Для приложений это имеет
важное значение, так как истинное распределение наблюдений, как правило,
бывает неизвестно, а интерес представляет вопрос о том, не изменялось ли
это распределение от выборки к выборке. Для применения критерия Смир
нова необходимо лишь выполнение условия непрерывности, которое обычно
бывает ясно из физической природы изучаемоro явления и не требует специ
альной проверки.
Отметим также, что практически значение статистики Dn, т peKOMeндy
ется вычислять по формуле Dn,m == max(D:'m, D;;,m), rде
'Н о
(1)
+ ( r ) ( s 1 )
Dn,m == mах F1n(Y(r)) == mах F 2m (X(s)) ,
l r ffl m l s n n
( T 1 ) ( 5 )
D;;,m == mах F1n(Y(r)) == mах Р 2т (Х(8))
I r ffl m I s n n
и Х(1) Х(2) х(n) , У(1) У(2) У(т) порядковые статистики
выборок Х и У соответственно. В книrе [3, с. 88 891. приводятся детальные
практические рекомендauии по применению (расчету) критерия Смирнова
в том числе и в случае малых выборок, .-де имеются и соответствующие
таблицы для численных расчетов.
2. Критерий однородности хи квадрат
Этот критерий применяют к анализу данных, имеющих дискретную CТPYKТY
ру, конкретнее, коrда в опытах наблюдается некоторый переменный признак,
принимающий конечное число N 2 различных значений. Но к такой схеме,
как мы знаем (см. п. 2 4.2), можно свести любую друryю модель, при меняя
предварительно метод rpуппировки данных, поэтому метод хи квадрат при
меним на самом деле к анализу данных любой природы, т. е. является в этом
342
rлава 4. Провер/(а статистических zипотез
смысле универсальным. Кроме Toro, с помощью этоrо метода можно анали
зировать одновременно любое конечное число выборок.
Итак, пусть осуществлено k серий независимых наблюдений, состоящих
из nl. . . . , nk наблюдений соответственно, и ПУСТЬ!4 == (ViI,' . . ,ViN) часто
ты исходов i й серии, а р. == (Pil,..., PiN) их вероятности (i == 1,... ,k).
'"4
Torдa lUпотеза однородности означает утверждение, что вероятности нсходов
не менялись от серии к серии, т. е.
НО :Е! ==
== '!!.k == l!. == (р"
,PN),
(2)
rде Р некоторый (неизвестный) вектор вероятностей (Рl + + PN == 1).
Чтобы построить критерий проверки этой I"Ипотезы, поступают следу
ющим образом. Поскольку при rипотезе Но каждый из lJeKTOpOB частот
!!.i, i 1,... ,k, распределен по полиномиальному закону M(ni; '!!.), то
E(Vij I Но) == niPj, j == 1, , N, и в качестве меры отклонения эмпирических
данных от их rипотетических (при rипотезе Но) значений можно выбрать
статистику (см. п.3 4.2)
k
х 2 (р) == '" х 2 (р)
nl.. .n L....J n; '
i=1
rде
Х;;(р) == (Vij n iPj )2 ,
niPj
заменив здесь неизвестные параметры Р их оценкой маКСИ;\lальноrо прав
доподобия, которая вычисляется в предположении истинности проверяемой
rипотезы но:
Е == arg тах П p;;j == arg тах П p 'j
i,j 1'. j
k
rде V.j == L Vij.
i=1
.. Тестовая статистика
в задачах OДHOpOД
... рсти o J ""1i "
Таким образом, в этом случае (при rипотезе Но) все данные можно объ
единить в одну 8ыборку объема n n! + + nk с частотами исходuв
v." , V.N, следовательно (см. пример 12 3.5),
Pj == v.j /n, j == 1, , N. В итоrе мы получаем TeCTO
IJУЮ статистику критерия однородности хи квадрат
k N 2
2 2 L L 1 ( n;V.j )
х x n V..
n'...nk n,...nk(E) . . ')
. 1 . 1 n,v. ] n
.= )=
(3)
2
С помощью которой и строится критическая область критерия: {X ni . ..п, > t,,}
Для нахождения критической rраницы t(l при заданном уронне значимости а
используется следующий предельный результат [15, с. 4831, аналоrичный Teo
реме 4 4.2: при 1!.j 00 (i == 1, ,k)
.c(i ''''nkIHo) i((k I)(N 1)).
в силу 3Toro результата при больших ni можно полаrать t a == X (l,(k I)(N ')'
4.3. rипотеза и критерии однородности
343
Итак, асимптотический (при больших ni)
вариант критерия имеет вид:
,f
К 2
ритерии однородности Х
Но отверrается {=:::}
2 2
Хп,...n. > Xl a,(k l)(N I)'
(4)
2
rде статистика Х п ,.. .п. вычисляется по формуле (3). Вероятность ошибочно
отклонить при этом истинную rипотезу (2) приблизительно равна а, если n
достаточно велико.
Эту же методику можно использовать и ДI1я провер
ки rипотезы о том, что rипотетические вероятности Pj
имеют заданную параметрическую форму: Pj == pj(8) ,
j == 1, ,N. Такая СИ'l)'ация возникает, например, коrда требуется проверить
rипотезу о том, что k серий наблюдений произведены над одной и той же слу
чайной величиной с распределением из заданноrо параметрическоrо семей
ства :F == {F(x; 8), fJ Е е}. В этом случае предварительно проводится rруп
пировка наблюдений с N интервалами и вычисляются оценки Pj == р;СО) , rде
Парометрические _
rипотезы
'jj == arg тах П (pj (fJ)) v.j
О .
J
Число степеней свободы в предельном (ДI1я статистики X ,.. .П. (Е) при rипоте
зе но) распределении х2 заменяется при этом на k(N 1) т, rде r == dim е
(dimention размерность) (предьщущая ситуация соответствует случаю r ==
==N I).
Критерий однородности х2 (4) является состоятельным, т. е. с вероят
ностью, стремяшейся к I при n 00, он «улавливает.> любые отклонения
от нулевой rипотезы (2), при которых вероятности появления исходов от ce
рии к серии не сохраняют постоянноrо значения.
Для случая двух выборок (k == 2) статистика (3) принимает, как нетрудно
проверить, следующий вид
N 2
2 ,,1 ( Vlj V2 j )
Х п ,П2 == ni n 2
. j 1 Vlj + V2j nl n2
Если положить U/j == Vlj/(Vlj+V2j), U/ == nl/(nl +n2), то последнее выражение
преобразуется к виду, более удобному ДI1я практических вычислений:
N
Х "п! == U/(I U/) (2:U/ jV i j nlU/)
J I
(5)
Выделим также важный ДI1я приложений частный случай двух исходов
(N == 2), которые можно обозначить А и А. fипотеза однородности (2) в этом
случае есть утверждение, что событие А имеет во всех испытаниях одну и '1)' же
(хотя и неизвестную) вероятность реализации р. Здесь оценкой для Р является
344
rлава 4. Проверка статистических шпотез
относительная частота появления события А во всей совокупности данных:
k
1"
р:= I q := L..J IIjl,
n i=1
rде IIjl число появлений события А в испытаниях i й серии, а статистика (3)
принимает вид
k ( ;;:;'\2 k 2
2 " l/iI njpJ " I/ il Е
Х п ,.. .В, L..J L..J n .
pq j=1 nj pq j=1 nj q
(6)
" ,r ' ",. Рассмотрим здесь детальнее случай двух выборок
Е'Та i5Лl1ца,«2 х 2». (n := 2). Для наrлядности в этом случае данные сводят
в так называемую таблицу (.2 х 2» (ДBa Ha ДBa):
А А L:
(1 ) //11 //11 //10 == nl
(2) //21 //11 //1. == nl
L: //01 //.1 n
в этих обозначениях запишем тестовую статистику (3) в виде
2 (I/ij I/j.l/.j/n)2 Ll j
Хп,В! n L..J = n L..J .
,j:1 I/j.l/.j ,j=ll/j.lI.j
Рассмотрим разности Lljj := I/jj I/j.l/.j/n, i, j := 1,2. Леrко видеть, что все
суммы
2: Ll ij = L Llij := О.
j
Например,
111.1/., 1/,.1/.2 1/,.
Ll 11 + Ll 1 2 := 1/11 + 1/12 := 1/,. (I/.l + 1/.2) := 111. 1/1. == о.
ппп
Таким образом, все четыре величины Llj j равны по модулю и потому
2 3 л 2
2 2 " == n L..11' .
X R1R1 := nLl ll L..J
,j=ll/j.lI.j 1/1.1/2.//.11/.2
Далее,
( 1111 )
nLl ll == 1/,. (I/I. + 1/2.) (1111 + 1/21)
1/1.
поэтому, обозначая
( 1/11 1/21 )
:= 1/1.1/2. ,
1/1. 112.
( 1/21 )
ZR'Rl
nl n2
4.3. [ипотеза и критерии однородности
345
получим
2
X 2 == nlll.!l2. ( V2' ) 2
п,П2 == Zn,n!'
V.,V.2 V,. V2.
Представление (7) подсказывает идею использовать Zn,n! В качестве дpy
rой тестовой статистики в рассматриваемой задаче. Эта статистика является,
2
очевидно, более информативной, чем статистика Хп,п!, так как знак Zn'n2
может нести дополнительную информацию о характере альтернативы в тех
случаях, коrда rипотеза Но неверна (знак тестовой статистики указывает
на направление отклонения альтернативы от Но). Действительно, если обо
значить через Р; вероятность реализации А в испытаниях i й серии (i == !, 2),
то .c(Vil) Bi(ni, Pi) и E(vlI /n, 1I2'/n2) == р, Р2. Следовательно, при
альтернативе вида H р, > Р2 статистика Zn,Rl будет иметь тенденцию
смещаться вправо от нуля. а при альтернативе Нl р, < Р2 влево. Ta
ким образом, статистику Zn'n2 естественно использовать в задачах проверки
rипотезы Но против «односторонних,) альтернатив HI+ или H, т. е. в зада
+ 2
чах (Но. Н, ) и (Но. H, ), в то время как статистика Хп,п! «работает» лишь
в задаче (но, Н, == H U H 1 ), т. е. при обшей (двусторонней) альтернативе
HI Р. f:. Р2.
Для построения соответствующеrо критерия надо исследовать распре
деление статистики ZR,R! при нулевой rипотезе. Мы будем рассматривать,
как обычно, схему больших выборок, т. е. предполаrать, что n" n2 -----+ 00.
Тоща на основании теоремы Муавра Лапласа .c(vi,/n;!Ho) '" N(p, pq/n;) ,
i == !, 2, а так как случайные величины V" и V2' независимЬ! по условию, то
при rипотезе НО
(7)
L ( V2' ) '" N ( o, npq ) .
n) n2 n'n2
Следовательно, статистика
( VII V2' )
(п,п! == ;;- v npq == Zn'n2 n2pq
при rипотезе Но асимптотически нормальна с параметрами О и 1:
L(n,n! JHo) '" N(O, !).
р р
Но при rипотезе Но v.,/n Р, V.2/n q (ведь относительная частота
исхода в n независимых испытаниях является СОСтоятельной оценкой ero
вероятности), следовательно,
V.IV.2 Р
].
n pq
Отсюда следует (см. справочник предельных теорем в п. 4 3.5, yrверждение
20 (r», что при rипотезе Но предельные распределения статистик Zn,n! И (п,п!
совпадают. Итак, при n" n2 -----+ 00
L(Zn'n2IHo) -----+ N(O, 1).
34б
rлаоа 4. Проверко статистических zипотез
Пусть теперь требуется проверить rипотезу однородности Но р, == Р2
против правосторонней альтернативы H р, > Р2. Из предыдущих рассуж
дений следует, что критическую область разумно выбрать в виде {Zn]n) > t a },
так как большие положительные значения статистики Znln) естественно pac
сматривать как свидетельстnо в пользу альтернативы н,+ Далее, поскольку
при больших nl и n2 P{Zn]It) > talHo} 1 ф(t а ) == ф( tа), то при YPOB
не значимости а критическая rраница приближенно определяется условием
Ф( tа) == а, т. е. t a == ф l(а) == ф I(1 а) есть квантиль уровня 1 а
стандартноrо нормальноrо распределения.
Замечание, Поскольку ДJJЯ любой rипотеЗbl, задаваемой вероятностями PI, Р2 при
nJ,n2 00
r.( V II V21 ) .r ( PIQI + Р2Чl )
/V РI Р2, ,
nl n2 nl n2
то аналоrИЧНblМИ рассуждениями можно показать (это мы оставляем читателю в ка-
'lecTBe упражиения), что ДJJя «близкой,) альтернативы
PI Р2
/PIiiI ,fii.'
при nl, n2 00 так, что nl /n 1, ВblПОЛНЯется предельное соотношение
H
а> О,
.с(ZП]П2Щ:) ....., N( a Vi (1 1),1)
Этот результат позволяет вычислять предельную мощность nOcтpoeHHOro критерия
при таких альтернативах:
P{Zn]n2 > toIH,:} ....., Ф(а (,).
Пример 1. Поступающие в вуз абитуриенты разбиты на два потока по 300
человек в каждом. Итоrи экзамена по одному и тому же предмету на каждом
потоке оказались следующими: на I M потоке баллы 2, 3, 4 и 5 получили
соответственно 33, 43, 80 и 144 человека; соответствующие же данные для
BToporo потока 39, 35, 72 и 154. Можно ли при уровне значимости а == 0,05
считать оба потока однородными? Здесь k == 2, N == 4 и статистика (5) при
2
нимает значение 2,18. Критическая же rт>аница ХО,95; 3 == 7,82. Таким образом,
2 2
Хп]п) < ХО,95; 3, т. е. соrласие rипотезы однородности с данными хорошее. ·
Пример 2 [15, с.484]. В таблице на с.347 приведено число детей, родив
шихся в Швеции в течение k == 12 месяцев 1935 r.
Оценкой для вероятности рождения мальчика является
45 682
p== ==05175.
88 273 '
По формуле (6) получаем X ", .П]) == 14,986 с 11 степенями свободы. Посколь
ку X ,95: 1I == 19,7, то можно считать (при уровне значимости а == 0,05), что
данные совместимы с rипотезой о постоянной вероятности рождения маль
чиков по месяцам. .
4.3. [ипотеза и критерии однородности
347
Пол ребенка
МеСЯЦbl == n,
Мальчики Девочки
1 3743 3537 7280
2 3550 3407 6957
3 4017 3866 7883
4 4173 З7l1 7884
5 4117 3775 7892
6 3944 3665 7609
7 3964 3621 7585
8 3797 3596 7393
9 3712 3491 7203
10 3512 3391 6903
11 3392 3160 6552
12 3761 3371 7132
== I/.j 45 682 42591 88273 == n
З. Друrие критерии 8 эаАаче о АВ УХ Вblборках
Кроме двух описанных критериев однородности разработаны и друrие MeTO
ды, основанные на различных принципах. Далее при водится краткий обзор
некоторых из них, применяемых в случае двух выборок из непрерывных pac
пределений.
а) Критерий знаков. Простой для проверки однородности критерий, не
требующий сложных вычислений, представляет собой описанный в п. 4 4.2
критерий знаков. Основным недостатком этоrо критерия является «неэконом
ное» использование информации, содержащейся в результатах наблюдений,
поэтому ero обычно рекомендуют применять только на стадии предвари
тельноro анализа. Кроме TOro, этот критерий можно использовать лишь Д1Iя
выборок одинаковоrо объема.
б) Критерий пустых блоков. Целый класс критериев однородности можно
построить исходя из следующих соображений. Рассмотрим вариационный ряд
выборки Х: X(l) < Хщ < < Х(n} (поскольку выборка из непрерывноrо
распределения, то с вероятностью 1 все порядковые статистики будут различ
ны, см. п. 2 2.1). Он порождает естественное разбиение оси Ох на интервалы
(Х(Н) , X(i}], i == 1, .,. , n + 1 (Х(О) == oo, X(n+l} == 00), которые называют
ся выборочными блоками. Пусть (r == (r(n, т) число этих блоков, каждый
из которых содержит ровно r элементов второй выборки У == (У" , У;n),
r == О, 1,. ,т. Тоrда в качестве тестовой статистики можно взять, вообще
rоворя, произвольную линейную комбинацию L Cr(r. в частности, простей
r
шая такая статистика (О число блоков, не содержащих ни одноrо элемента
второй выборки, порождает критерий пустых БЛОК08. Основой Д1Iя построе
348
rлава 4. ПрО8ерка статистических zипотез
rкР:; рJй""-
пустых блоков
!S.!i:.oj;" "
ния И расчета этоrо критерия в случае больших выборок является следующий
результат [24, с.453]: если n, т 00 так, что т/n р > о, то
.с ((о(n, т)lН о ) rv N ( , ( nр2)3 ) .
1 +р 1 +р
Отсюда получаем асимптотический вариант критерия
пустых блоков: при уровне значимости а i!Uпотеза одно-
родности Но отвеРi?ается тОi?да и толЬ/со тОi?да, КОi?да
n с: р
(о(n,т) > 1 +р +уn (1 +р)3/2 t();,
Этот критерий является состоятельным против альтернатив (F 1 , F 2 ), Fl F2,
удовлетворяющих следующему условию: функuил F2(FI I(и)), и Е 10, 11, имеет
производную g(и), отличную от 1 на множестве положительной лебеrовой
меры.
в) Критерий серий. В ряде случаев особый интерес представляют такие
отклонения от нулевой rипотезы Но FI(x) == F 2 (x), коrда одно распределе
ние сдвинуто относительно друrоrо, например, Korдa F! (х) > F 2 (x), в этом
случае rоворят, что случайная величина 1] с распределением F 2 «стохастически
больше,), чем {, распределение которой есть Fl (при каждом х величина 1]
с б6льшей вероятностью превосходит х, <leM О. Простой критерий, хорошо
«улавливающий,) такие отклонения, можно построить следующим образом.
Объединим обе выборки Х и У в одну (Х". ,Х n , У" У т ) и построим
вариационный ряд этой объединенной выборки. После этоrо заменим все
элементы выборки Х буквой С, а все элементы У буквой С. В результате
получим некоторую последовательность n букв С и т букв С Число всех
таких последовательностей равно C +т и интуитивно ясно, что при rипоте
зе Но (элементы обеих выборок Х и У должны «IJести себя одинаково,») все
возможные последовательности равновероятны. Описанные выше ОТКIIонения
от Но при водят К тому, что с повышенной вероятностью будут наблюдать
ся последовательности, в которых элементы одноrо вида имеют тенденцию
смещаться к какому нибудь краю последовательности (в приведенном выше
примере буквы С смещаются к правому краю). Одной из статистик, с по
мощью которой можно количественно охарактеризовать степень перемеши
вания в получаемой последовательности букв С и С, является число серий
W(n, т). Серией называется участок последовательности, состоящий из под
ряд идущих одинаковых букв и оrpаниченный с обеих сторон (или с одной
стороны, если речь идет о концах последовательности) букваМII друrоrо ви
да. Число серий будет мало, если одинаковые буквы rpуппируются IJ одном
месте, поэтому в данном случае следует задать критическую область в виде
{W(n, т) ta(n, т)}. Такой критерий, предложенный в 1940 r. Вальдом
и Вольфовитцем, и называется критерием серий.
Асимптотический (для больших выборок) вариант этоrо критерия можно
рассчитать на основании следующеrо утверждения [24, с. 459]: если n, т 00
ф( t();) '= а.
(8)
4.3. rипотеза и критерии однородности
349
так, что т/п р > О, то
( 2nр 4n р2 )
.c(W(n, m)IH o ) "" N 1 + р ' (1 + р)3 .
При этих условиях критерий серий формулируется следу
ющим образом: при уровне значиА10сти а щпотезу oдHopoд
ности Но отверсают тисда и только тОсда, КОсда
2nр 2р
W(n, т) :;С; ..;n ( ) 3 / 2 ta, ф( tа) == а.
1 +р 1 +р
.,
Критерий серий
(9)
Этот критериЙ ЯlJляется состоятельным против тех же альтернатив, что и pac
смотренный в п. б) критерий пустых блоков.
r) Рансовые критерии. Иноrда исходная статистическая информация MO
жет быть задана не числовыми значениями наблюдений, а отношением по
рядка между ними (типа «больше меньше»). Особенно часто это имеет Me
сто в психолоrических исследованиях. В таких случаях наблюдения ранжи
руют, т. е. упорядочивают по степени их предпочтения. Номер места, KOTO
рое занимает конкретное наблюдение в таком упорядоченном ряду, называют
раНi?OА1 этоro наблюдения. Таким образом, с caMoro нача р"
ла информация может быть задана ранrами наблюдений; анrи
статистические методы, которые применяют в таких ситуациях, называют
раНi?Oвыми методами, статистики, являющиеся функциями только paHroB,
раНi?Oвыми статистиками, а критерии, основанные на таких статистиках,
раllCовыми критериями.
PaHroBbIe методы можно применять и в тех случаях, коrда заданы чис
ловые значения наблюдений, т. е. выборка Х == (Х[,... , Х n ), так как при
этом всеrда можно УПОрЯДО'Jить элементы выборки, построив ее вариацион-
ный ряд. В этом случае paHroM i ro наблюдеНf\Я X j является номер места Rj,
которое занимает X j в вариационном ряду Хр) :;С; Х(2) :;С; :;С; Х(n)' Teo
рия paHroBbIx критериев является важной и хорошо разработанноЙ областью
современноЙ математической статистики, она весьма полно изложена в [7].
В этом пункте мы рассмотрим в качестве иллюстрации лишь один при мер
paHroBoro критерия однородности критерий Вилкок Критерий '11t
сона, предложенныЙ впервые Вилкоксоном (1945) дЛЯ BЫ
Вилкоксона
борок одинаковоrо объема и распространенныЙ на случай
выборок разных объеМОIJ Манном и Уитни (1947).
Рассмотрим, как и в предыдущем случае, объединенную выборку (X 1 , . . . ,
Х n , Y 1 , ,У т ) И построим ее вариационный ряд. Пусть R j paHr величи
ны X j В этом ряду (i == 1, , n) и Т == R, + + Rn сумма номеров
мест, которые занимают в общем вариационном ряду элементы выборки Х.
Ранroвая статистика Т и есть тестовая статистика критерия Вилкоксона.
Введем случайные величины Zrs == I(X r < Y s ) и положим
n m
u == Щn, т) == L L Zrs,
r l s 1
(10)
350
rлава 4. Проверна статистuческuх i!uпотез
так что U есть общее число тех случаев, коrда элементы выборки Х предше-
ствуют в общем вариационном ряду элементам выборки У Можно показать,
что статистики Т и U связаны линейным соотношением
п(п + 1)
т +И == пт + ,
2
поэтому критерий Вилкоксона эквивалентен критерию, основанному на CTa
тистике И, называемому иноrда критерием MaHHa YитHи,
Для любой пары (F 1 , Р 2 ) абсолютно непрерывных распределений среднее
значение статистики U есть
00
ЕИ == пт EZ ll == пт Р{Х, < У,} == пт J FI(X)f2(X) dx == апт, (11)
OQ
следовательно, при нулевой rипотезе, т. е. при FI == Р 2 . ЕИ == пт/2. Таким
образом, с позициЙ статистики U альтернативы можно характеризовать вели
чиной параметра а в (11): а < 1/2, либо а> 1/2, либо а i= 1/2. Для расчета
критерия можно использовать следующий результат для случая больших BЫ
борок [24, с.467]: если п, m ---t 00, то
С(И(п, т)lН о ) rv N( n , пт(п 2т + 1) )
(это предельное распределение можно с хорошим приближением использовать
уже при п, m 4, n + m 20).
Основываясь на этом результате уже можно рассчитать асимптотический
вариант критерия соrласия для rипотезы Но. Критическая область имеет раз
личный вид в зависимости от целей, для которых строится критерий. Если хо-
тят получить критерий, состоятельный против алы-ернатив (F 1 , Р 2 ) с а < 1/2,
то критическую область следует задать в виде {И(п, т) ta(n, т)}, [де при
при больших n и m и заданном уровне зна',имости Q критическая rраница
имеет вид
) пт J nm(n + m + 1)
ta(n, т t a , Ф( to) == а.
2 12
Случай а > 1/2 сводится к рассмотренному перестановкой Р, и Р2. Наконец,
критерий, состоятельный против двусторонних альтернатив: а 1= 1/2, задается
двусторонней критической областью
{I ( ) пт l J nm(n+m+ 1) }
U n m > t /2
'2 12 а
4.4. rипотеэа неэависимости
В данном параrpафе будут рассмотрены несколько вариантов проверки rипо-
тезы независимости, описанной в при мере 6 Введения. В этом случае дан-
ные представляют собой независимые наблюдения (Xi, У;), i == 1'...' п,
4.4. rипотеза независимости
351
над не которой двумерной случайной величиной { == ({ 1, 6) с не известной
функцией распределения Р{(х, у), о которой требуется про верить rипотезу
Но Р{(х, у) == Р{,(х)Р 6 (у), rде Р{;(х), i == 1, 2, некоторые одномерные
функции распределения.
1. Критерий неэависимости хи-квадрат
Простой критерий соrласия для rипотезы независимости Но можно постро
ить, основываясь на методике хи-квадрат. эту методику применяют для дис
кретных моделей с конечным числом исходов, поэтому условимся считать,
что случайная величина {l принимает конечное число s некоторых значений,
которые будем обозначать а(, , a s , а вторая компонента 6 k некото-
рых значений b 1 , , b k . Если данные имеют друryю структуру, то их пред-
варительно rpуппируют отдельно по первой и второй компонентам. В этом
случае множество возможных значений {l разбивается на s непересекаю
щихся интервалов E l}, ,E l), множество значений {2 на k интерва-
лов E 2}, , Ek 2 } И тем самым множество значений двумерной величины
{ == ({l, {2) разбивается на N == sk прямоуrольников Е?) х ЕУ}
Пусть Vij есть число наблюдений пары (ai, bj) (число элементов выборки,
принап.лежащих прямоyrольнику ((1) х ЕУ>, если данные rpуппируются), так что
k
2: 2: Vij == n.
i l j 1
Результаты наблюдений удобно для наrлядности
расположить D Dиде таблицы сопряженности двух
признаков (в приложениях {( и 6 обычно озна-
чают два признака, по которым производится классификация результатов
наблюдений, и тоrда НО есть rипотеза о независимости этих признаков):
" 'lЪб; а н ()crй.1 ".
двух приэнаков
{I 6 Е
ы 1 Ь 2 .. b k
О, 1111 1112 IIlk 111.
02 1121 1122 112k 112.
О. 11. I V s 2 .............. IIsk V..
L 11.1 11.2 lI.k n
ПУСТЬРij == P{ I == ai, 6 == b j }, i == !, ,s, j ==!, ,k. Torдa rипотеза
независимости означает, что существует s + k постоянных Pi., p.j таких, что
s k
2: Pi. == 2: p.j ==! и Pij == Pi.P.j.
i l j 1
352
rлава 4. Проверка статистических 2ипотез
Поскольку наблюдения независимы по условию, то '{астоты (lIij, i == 1, ., s,
j == ), . . . , k) распределены по полиномиальному закону И при rипотезе Но Be
роятности исходов Pij имеют указанную специфи'{ескую структуру (они опре
деляются значениями r == s + k 2 неизвестных параметров Pi., i == 1,. . ., s 1,
P'j, j == 1, .. . , k 1). Следовательно, rипотеза независимости в данном слу
'{ае является специфической формой сложной rипотезы ДJIЯ полиномиальной
модели, рассмотренной в п. 3 4.2. Чтобы применить критерий хи квадрат (12)
4.2, надо сна'{ала найти оценки максимальноrо правдоподобия для определя
ющих рассматриваемую модель неизвестных параметров при справедливости
rипотезы НО, т. е. максимизируя в данном слу'{ае функцию правдоподобия
П ( . . ) V;j П и" П v.j
\YI'P,) Pi. P.j
i,j j
по параметрам Pi., p.j. Отсюда, как и в п. 2 4.3, имеем
....... Vi.
Pi. == ,
n
lI.j
p.j == ,
n
т. е. это обы'{ные оценки параметров полиномиальных распределений
[.(111"'" ,lIs.) == М(n; PI', . Ра.)
и
[.(V., , ..., V.k) == М(n;р."
,P.k).
...
Тестовая статистика для
rипотезы независимости
С учетом этоrо тестовая статистика (11) 4.2 при
нимает вид
( ) 2 s k 1 ( ) 2
2 lIij nPi.p.j Vi.V.j
Х П == L....- == n L....- Vij
. . nPi.p. ) ' . , . , lIi.Vo ) ' n
1,) I )
(1)
с '{ИСЛОМ степеней свободы
N 1 r == sk 1 (s + k 2) == (s I)(k 1).
4,. Критерий _
независимости Х
Итак, асимптоти'{еский (при больших п) оариант
2
критерия независимости Х при заданном уровне зна
'{имости Q имеет вид
I 2 2 I
НО отверraется Х п > Х ' a, (a J)(k 1)'
(2)
2
rдe Х п вы'{исляется по формуле (1).
Пример 1 [12, с.781], Каждый из n == 6800 индивидуумов классифициро
вался по двум признакам: цвету rлаз ( l) и цоету волос (6), при этом для I
было определено 3 катеrории (al, а2, аз), а для 6 4 катеrории (Ь,. Ь 2 , Ь з , Ь 4 ).
Данные эксперимента приведены в таблице
9 4.4. rипоmеза независимосmи
353
I 2 2:
Ь 1 Ь 2 Ь} Ь 4
аl 1768 807 189 47 2811
а2 946 1387 746 53 3132
а} 115 438 288 16 857
.2: 2829 2632 1223 116 6800
Здесь значение статистики (1) равно 1075,2, а, например, x ,999; 6 == 22,S,
поэтому rипотезу Но о независимости этих признаков следует отклонить;
вероятность ошибки при этом значительно меньше а == 0,001 .
В приложениях часто каждый из признаков {I и 6 ," Алы рнативные -.f'
имеет альтернативную структуру, т. е. S == k == 2. Ти _ признаки
пичным примером является классификация сдающих
вступительные экзамены в вуз абитуриентов по признакам «принят (А)
не принят (1).) и «мужчина (В) женщина (В)>>. Для таких ситуаций мож
но провести более rлубокий анализ соответствующих статистических данных,
которые удобно представлять D виде следующей таблицы «2 х 2» сопряжен
ности признаков.
1\6 I(B) О(В) 2:
I(A) 1111 1112 111'
О(А) 1121 1112 111.
2: 11'1 11.2 n
Структура таблицы здесь такая же, как и таблицы «2 х 2,) в случае про
верки однородности (см. п. 2 4.3), поэтому ее анализ во MHoroM аналоrичен
(хотя ее содержание имеет совсем друrой смысл!). Так, совершенно аналоrич
но можно установить, что статистика (1) имеет вданном случае представление
2 2
Х" == Zn, rде
Zn == ( V21 ) nV..V2.
VI. V2. V.1V.2
Поскольку статистика Zn является знакопеременной, ее знак может нести
дополнительную информацию, указывая «направление» отклонения от нуле
вой rипотезы, и, следовательно, основываясь на ней, можно построить «более
тонкий» критерий.
Установим предварительно следующую связь статистики $" с выборочным
коэффициентом корреляции Р" (см. (5) 2.3) для наших данных: Zn == ';nPn.
Доказательство. Действительно, пусть (X i . 1';), i == 1,..., n, независи
мые наблюдения над (6. {2) и Х == (X 1 ,..., х п ), У == (Y 1 ,... , У П ). Тоrда,
23 З.к.з 1748
354
rлава 4. Проsерка статистических zuпотез
очевидно, выборочные средние есть Х VI./n, У == v.l/n, выборочные
дисперси и равны
n
8 == '" хl Х 2 == Х(l Х) == VI.V2. ,
n
i=1
n
8i == '" У? у2 == У(1 У) == V.I/J.2 ,
n п 2
;=1
наконец, выборочная ко вариация (см. (4) 2.4)
1 n /JII VI.V.I
812 == '" XiY; Х у == ==
n n п 2
;=1
1 [ ] VI.V2. ( /JII /J2I )
== 2" VII(VI. + vz.) VI.(VII + V21) == .
n n VI. v2.
Отсюда имеем
РП == 812 == ( V21 )
8182 V,. V2.
Zn
.;N ' ·
в частности, отсюда следует (см. п. 3 2.3), что при n 00
Zn Р
.;n р == соп(6, 6).
Найдем, наконец, предельное (при n ----+ 00) распределение статистики Zn
при rипотезе Но. ДЛН этоrо введем случайную lJеличину
(3)
1 n
(п == L(X i Р(А))(У; Р(В)). (4)
у' пР(А)Р(А)Р(В)Р(В) i=1
Если rипотеза Но справедлива, то X i и У; независимы и потому
E(X i Р(А))(У; Р(В)) == E(X i P(A))E(Y i Р(В)) == О,
D(X; Р(А))(У; Р(В)) == E(X i Р(А))2(у; р(в))2 ==
== E(X i Р(А))2 Е (у; р(в))2 ==
== DXiDf'; ==
== Р(А)Р(А)Р(В)Р(В),
при этом слаrаемые в (4) независимы и одинаково распределены по условию.
Следовательно, случайная величина (п представляет собой нормированную
сумму независимых одинаково распределенных слаrаемых и к ней можно
применить центральную предельную теорему (см. (1) 1.2), соrласно которой
n ----+ 00 .c((nIHo) ----+ N(O, 1).
94.4. rипотеза независимости
355
Далее, так как
n n
)X; Х)(У; У) == 2)X i Р(А))(У; Р(В)) п(Х Р(А))(У Р(В)),
i 1
i=1
то
n
2)Х ; Х)(У; У)
812 i 1
Zn == v'ri ==
8(82 V nX(1 Х)У(1 У)
[ (п y'n(Х Р(А)) У Р(В) ] [ A)P( B)P( ) ] 1/2
V P(A)P(A) V P(B)P(B) X(I X)Y(I У)
По теореме 3 92.2 об асимптотической нормальности выборочных MO
ментов при n ----+ 00
( y'n(X P(A)) ) -лr( )
С- ----+ 0,1,
V P(A)P(A)
р р
а по закону больших чисел Х --------? Р(А), У --------? Р(В). Следовательно, при
n----+ 00
y'n(Х Р(А)) У Р(В) р
--------+ О,
V P(A)P(A) V P(B)P(B)
[ A)P( B)P( ) ] 1/2 1
Х(l Х)У(1 У) ,
и потому предельные распределения Zn И (п совпадают (см. справочник
предельных теорем в П.4 93.5). Итак C-(Zп!Но) ----+ -лr(о, 1) при n ----+ 00.
Эти результаты уже дают возможность построить и рассчитать критерий
проверки rипотезы независимости НО, основываясь на статистике ZN' Альтер
нативы здесь можно характеризовать величиной коэффициента корреляции
р == corr({I, 6), для KOТOporo нетрудно получить предстамение (это мы OCTaB
ляем читателю в качестве простоrо упражнения)
1/2
Р(АВ) Р(А)Р(В) [ ( I ( 1 )] [ Р (В)Р(В) ]
Р == == Р А В) Р А В
V P(A)P(A)P(B)P(B) Р(А)Р(А)
(5)
Рассмотрим, например, правостороннюю альтернативу H р > о (или,
что ввиду (5) эквивалентно, P(AIB) > P(AIB)), означающую положительную
коррелированность признаков {I и 6 (или положительную сопряженность
событий А и В А в паре с В встречается с большей вероятностью, чем
р
в паре с В). Torдa при rипотезе Но (см. (3)) Zn --------+ О, если n ----+ 00, а при
23'
35б
rлава 4. Проверка статистических 2ипотез
альтернативе H Zn 00, поэтому естественно рассматривать слишком
большие значения Zn как свидетельство в пользу альтернативы HI+ Следо
вательно, если рассматривается задача (НО, Н)+), то критерий следует задать
крuтической областью вида {Zn > t a } При этом P{Zn > talHo} Ф( tа),
т. е. t a == ф I(1 а) есть (1 а) квантиль стандартноrо нормальноrо pac
пределения N(O, 1). Итак, в задаче (Но. H Р > О) д.ля больших выборок
критерий при уровне значимости а имеет вид: если Zn ::;; t a == ф I(1 а), то
cuпотеза НО принимается, в противном случае она отклоняется (принимается
альтернатива НN.
Аналоrично рассматривается симметричная задача (Но. Н,:р<О): здесь
критическая область имеет вид {Zn < ta}, ф( tа) == а. Общий же критерий
независимости х 2 проверяет Но лишь против двусторонней альтернативы HJ ==
== H U Hl : р i=- О, и он задается в данном случае двусторонней критической
областью {IZnl>ta/2}=={i >xi a,)} (см. (2)), поскольку t /2 == Xi a,l'
Замечание, Можно показать, что если в задаче (НО, Н() <,близкая» альтернатива
задается условием
+ а
H 1n Р == р(n) == VТi '
а> О фиксировано. то .c(ZnIHI ) ----t N(a, 1) и, следовательно, мощность крите
рин {Zп > t a } удовлетворяет предельному соотношению
P{Zn > taIHI } ----t Ф(а t a ).
Пример 2. Имеются следующие данные о приеме в вуз (А принят, В
мужчина):
в в Е
А 97 40 137
А 263 42 305
Е 360 82 442
Проверим rипотезу о независимости при знаков ('результат» и «пол.) про
тив альтернативы H P(AIB) > P(AjB). Здесь
Z == ( 40 ) 360.82.442 == 3 86
n 360 82 137 305 "
2 2
а Zn == 14,89. В то же время, например, ХО999'I == 10,8. Это означает, что rипо
теза о независимости признаков должна б lТ oTBeprHyra (вероятность COBep
шить при этом ошибку меньше 0,00 1) в пользу альтернативы
Н, P(AIB) < P(AjB)
(этот факт можно интерпретировать как отсyrствие дискриминации в OTHO
шении женщин при приеме в вуз). .
4.4. rипотеза независимости
357
Пример З. в следующей таблице приведены 818 случаев, классифицирован-
ных по двум признакам: наличию прививки против холеры (А) и отсутствие
заболевания (В):
в в Е
А 276 3 279
А 473 66 539
Е 749 69 818
Проверим rипотезу Но о независимости признаков А и В против аль
тернативы HI+ об ИХ положительной сопряженности (т. е. об эффективности
вакцинации). Здесь
( 276 3 ) 749 69.818
Z == 5 4S
n 749 69 279 539 "
2 2
а Zn == 29,70. Так как ХО.999; 1== 10,8, то rипотеза Но должна быть oTBeprHyra,
а поскольку ф 1(0,999) == 3,09, то принимается альтернатива HJ+ Вероят
ность ошибочно отклонить Но в пользу H при этом меньше 10 3 .
2. Критерий (пирмена
На практике для проверки rипотезы независимости часто используют ранroвые
критерии (см. п.3 (r) 4.3). Наиболее известным из них является критерий
Спирмеnа, называемый по имени знаменитоrо психолоrа, который ввел ero
в ]904 r. Он основывается на коэффициенте ранroвой корреляции р, опреде
ляемом следующим образом.
Обозначим через Rj paHr Х; среди наблюдений Х.,... , Х N (т. е. номер
места, занимаемоrо величиной Х; в вариационном ряду Х(I) Х(n));
аналоrично, пусть В; paHr У; среди наблюдений Y 1 ,..., Уn. Тем самым
исходные данные (Xi. У;), i ==], ., n порождают n пар paHroB (R;,8i),
i == 1, .. . , n. Переставив эти пары в порядке возрастания первой компоненты,
обозначим полученное множество пар через (1, T 1 ), , (n, Тn)' Статистика
Сп ирм е на р определяется теперь как коэффициент корреляции двух множеств
paHrOB (R 1 , ,Rn) и (81, , Вn):
р==
n
I)R; ii)(8 i В)
i l
[ n n ] 1/2
:L::(R; Щ2 :L::(8 j 8)2
i 1 j 1
(здесь R и 8 соответствующие арифметические средние). Но (R 1 . . .. , Rn)
и (81, , 8n) некоторые ререстановки множества (1,2, ,n). поэтому
n
R==8==.!.:L:: i == n+l ,
n . 2
, l
358
rлава 4. ПровеРКQ статистических шпотез
ппп ( ) 2
2 2 2 'n+1
2)R; R) == (S; S) == I> n 2
. l . l . l
n(n 2 1)
12
так как
.2 n(n + 1)(2n + 1)
L.Jt 6 .
; I
ii 'с+' тистика
Спирмен.?
Отсюда
12 n ( n+I )( n+l )
р == n(n2 1) I: R i 2 В , 2
, I
12 n ( n+I )( n+l )
== n(n 2 1) Е i 2 Т , 2 .
(6)
Таким образом, р линейная функuия paHrOB Т;. Часто IIСПОЛЬЗУЮТ также
формулы
6 n 6 n
р == I n(n 2 1) I:(R; в;)2 == 1 n(n 2 1) I:(T j i)2 (7)
' I ' I
совпадение которых с (6) проверяется непосредственно.
При полном соответствии paHroB (R; == В;, i == 1, ,n) статистика
р == 1, а при противоположных paHrax (Т; == n i + 1, i 1, , n)
р == 1, вообще же 1 Р 1. Далее, если rипотеза Но верна, то Ер == О,
Dp == I/(n 1), поэтому значения р, близкие к крайним, рассматривают
как свидетельствующие против Но, и, следовательно, критическую область
К критерия Спирмена задают в виде 7ia == {Ip! > la(n)}
""'" ритерии
С е Для определения числовоrо значения критическои rpани
пирм на
цы la(n) при заданных объеме выборки n и уровне зна
'IИМUСТИ а используют таблицы табулировзнноrо распределениSI статистики
р при нулевой rипотезе, рассчитанные для n == 2, ,30 (в [31 приведена
таблица ДЛЯ n == 4( 1) 10). Для больших n можно воспользоваться асимптоти
ческим результатом 1.:( VnpIHo) И(О, 1). Отсюда следует, что если выбрать
la(n) == lo/2/Vn, ф( tа/2) == а/2, то при больших n
Р{р Е 7ioIHo} == Р{ vnlpl > ta/2IHo} ;:::; 2Ф( taj2) == а,
т. е. уровень значимости критерия приблизительно раВен а.
3. Критерий Кендалла
Друrой известн ый ран rовый критерий предложен М. Кендаллом (1938) и OCHO
ван на статистике
2
Т== n(n 1) ВТ,
n 1 n
ВТ == L L sign (Tj Т;),
; I j ;+1
(8)
4.4. rипотеза независимости
359
rде sign а == 1, если а > о, и 1, если а < О. Если rипотеза Но верна, то
О7 == 2(2п + 5) и С(7I Н о) '" N ( O, 9 4 п )
9п(п 1)
Е7 == о,
при п ""'""* 00. Отсюда следует, что при больших n критическую область следует ,
»r
выбрать в виде Критерий Кендалла
{ 2ta/2 }
a == 171 > 3J1i .
Для n == 4( 1) I О критическая rpaH ица критерия Кендалла рассчитывается с по
мощью таблицы, приведенной в [3]. Например, при п == 9 критической об
ласти {171 О,5} отвечает вероятность ошибки nepBoro рода 0,076.
Практически статистику Кендалла 7 рекомендуется вычислять по фор
муле
4N
7 == 1
п(п 1) ,
rде N число тех пар индексов (i, Л, i < j, для которых т; < Tj. Дей
ствительно, обозначим дополнительно через N! число тех пар индексов (i, Л,
i < j, для которых Т ; > Tj. Тоrда, очевидно, В.. == N N 1 , а N + N 1 ==
== п( п 1) /2 общее число пар (i, Л, i < j Складывая эти два равенства,
получаем В.. == 2N п(n 1)/2. Отсюда и из (8) получаем указанное пред
ставление для 7
4. Случай m признаков
В этом пункте мы опишем типичную практическую ситуацию, в которой для
анализа данных при проверке rипотезы независимости эффективно применя
ются paHroBbIe методы. Рассмотрим совокупность индивидуумов, обладаюших
таким признаком, который, может быть, и не поддается точной количествен
ной оценке, однако позволяет сравнивать индивидуумы друr с друroм. Таким
образом, в результате подобноrо сравнения всю совокупность можно «paH
жировать», приписав каждому индивидууму порядковый номер, COOTBeTCTBY
ющий итоriМ сравнения с остальными индивидуумами. Если индивидуумы
MOryт обладать не одним, а двумя и более признакам и, то для исследования
их влияния друr на друrа обычно рассматривают выборку из n независимых
индивидуумов и ранжируют их по каждому признаку отдельно. Пусть количе
ство исследуемых признаков есть т 2, тоrда результаты ранжировок по этим
признакам можно записать в виде (т х n) матрицы, i я строка которой
TII TI2 Tln
я== Т21 Т22 Т2n
Т т ! Т т 2 Т тn
содержит результаты ранжировки по i MY признаку (i == 1, ., т), а столбцы
соответствуют индивидуумам, принадлежащим исследуемой выборке (таким
360
rлава 4. Проверка статистических zuпотез
.N
Коэффициент
конкорданции
образом, Tij это порядковый номер j ro индивидуума при сравнении ero
с друrими индивидуумами по i MY признаку).
В качестве единой выборочной меры связи т при
знаков Кендалл и Бэбинrrон Смит ([939) предложи
ли коэффициент СОi!ласованности W, называемый также
коэффициентом конкорданции (conc6rdance соrласие,
соответствие, конкорданция):
12 n [ т т(n+ 1 ) ] 2
W == т 2 (n ] n) Sw, SW == L Tij 2
J I I I
Если по матрице R вычислить коэффициент р Спирмена (см. (6) (7))
для каждой из т(т [) /2 пар признаков, то арифметическое среднее таких р
будет равняться (mW I)/(т 1). В частности, если т == 2, то Р == 2W [.
Коэффициент W принимает значения из отрезка [о, ]] и используется
в качестве тестовой статистики для проверки rипотезы Но о независимости
признаков (признаки называются независимыми, если для любоrо столбца
матрицы R ранrи Tlj, T2j, ,Tmj являются независимыми случайными Be
личинами). Если rипотеза Но верна, то
(9)
[
EW ==
т'
2(т 1)
DW ==
т 3 (n [)
и распределение W удовлетворительно аппроксимируется бета распределе
нием [3, с. 97 98]; в [з] имеются также таблицы дI1я расчета критерия при
n == 3, т == 3(1)10; n == 4, т == 3(1)6 и n == 5, т == 3. Например, при n == 5
и т == 3 критическая область критерия независимости трех признаков зада
ется неравенством {W 0,733}, если уровень значимости есть а == 0,038.
Приведем несколько иллюстративных примеров расчета критерия, опи
рающеrося на коэффициент ранrовой корреляции р Спирмена.
Пример 4. В следующей таблице указана относительная оценка знаний по Ma
тематике и литературе 8 учеников, занумерованных числами от ] до 8, причем
лучшим знаниям соответствует меньщий paHr:
Ученик (i)
Рзнr знаний по математике (R j ) 5 2 1 7 8 4 6 3
PaHr знаний по литературе (Sj) 4 3 2 1 7 6 5 8
Проверим по критерию Спирмена rипотезу Но о независимости между
успехами по математике и литературе против альтернативы Н,+ успехи по Ma
тематике и литературе положительно коррелированы.
В данном случае в пользу альтернативы rоворят «большие,) значения CTa
тистики р, поэтому В задаче (НО, Нп критическую область разумно взять
в виде одностороннеrо неравенства {р > ta(n)}. При n == 8 и, например,
94.5. rипотеза случайности
Збl
а == 0,1 критическая rpаница tQ(n) == 0,4762, а величина р, вычисленная
по формуле (7), равна
р == 1 83 8 (12 + 12 + 12 + 62 + 12 + 22 + 12 + 52) == 1 08 == == 0,1667.
Так как р < tO,l (8), У нас нет оснований oTBepraTb rипотезу независимости. .
При мер 5. Относительная оценка знаний математики и физики в rруппе из 7
учеников дала следующие результаты (R j paHr по математике, Sj paHr
по физике i ro ученика):
i 1 2 3 4 5 6 7
R j 5 7 1 4 2 3 6
S; 4 6 3 5 1 2 7
Проверим с уровнем значимости а == 0,05 rипотезу НО о независимости
между успехами по математике и физике. В данном случае критическая область
критерия Спирмена имеет вид {Ipl > to,os(7)} и вычисления дают
6105
Р == 1 73 7 == 1 28 == 0,8022.
t O ,05 (7) == 0,7450,
Следовательно, rипотеза Но отверrается.
.
.,
Важное замечание
в заключение этой темы подчеркнем, что выше
рассмотрена rипотеза независимости НО в ее самой
общей форме, без каких либо дополнительных априорных предположений
(за исключением предположений типа непрерывности распределения наблю
дений). В то же время такая rипотеза может возникать и в рамках параметри
ческих моделей, т. е. коrда априори предполаraется, что все допустимые pac
пределения наблюдений при надлежат заданному параметрическому семейству
распределений. Если, например, мы работаем в рамках двумерной нормальной
модели, то rипотеза независимости эквивалентна предположению о равенстве
нулю коэффициента корреляции. Критерий проверки такой rипотеЗbl, TeCTO
вой статистикой KOToporo является выборочный коэффициент корреляции,
рассмотрен ранее в п. 4 92.3-
t 4.5. rипотеэа случайности
Хаос ужас БОi!ов.
Древнее ВbIскаЗbIвание
в раЗЛИЧНbIХ статистических задачах исходные данные Х == (Х" , Х n ) ча
сто рассматривают как случайную выборку из HeKoToporo распределения .c( ) ,
т. е. считают компоненты Xj вектора данных Хнезависимыми и одинаково
Зб2
rлава 4. Проверкй статистических zипотез
распределенными случайными величинами. Но иноrда это исходное предпо
ложение само нуждается в проверке как специальная статистическая rипотеза
(см. при мер 7 Введения). Такая rипотеза, называемая 2ипотезой случайности,
записывается в виде
Но Fx(x),
,х п ) == F(x))
F(x n ),
rде F(x) некоторая одномерная функция распределения. Мы рассмотрим
некоторые подходы к построению критериев соrласия ДJJЯ ПрОDерки такой
rипотезы.
1. Критерий инверсий
Предположим, что вектор Х имеет непрерывное распределение. Если rипо
теза НО верна, то компоненты вектора Х «раlJноправны,> И поэтому данные
не должны быть ни в каком смысле упорядочены. Друrими словами, ситу
ацию, соответствующую rипотезе НО, можно охарактеризовать как «полный
хаос», или «полныЙ беспорядок». При отклонениях от НО исходные данные
имеют тот или иной порядок, проявляются связи. Следовательно, при про
верке НО надо основываться на тестовых статистиках, измеряющих степень
(.беспорядка,> данных. Одной из таких естественных статистик является число
/. инверсий в выборке, которое определяется следующим образом.
.. Инве сии _ Построим вариационный ряд Х(I) < < Х(П) BЫ
Р. барки Х. rоворят, что компоненты X j и Xj образуют
инверсию, если i < j, НО Xi стоит правее Xj в вариационном ряду, т. е. Ha
блюдению с меньшим номером соответствует большее значение. Пусть 1/;
число инверсий, образованных компонентой X j (в вариационном ряду ле
вее Х; стоит 1/; элементов выборки с б6льшими номерами), i == 1, , n 1.
Тоrда Т" == Тп(Х) == 1/) +... + 1/n 1 общее число инверсий ДJJЯ выборки Х.
Статистика T'I является естественноЙ мероЙ «беспорядка» среди наблюдений
и ее можно использовать ДJJЯ проверки rипотезы Но. Крайние случаи, коrда
вариационный ряд имеет вид
Х) < Х 2 < < Х" или Х" < Xn ) < < Х),
естественно рассматривать как свидетельства «полноrо отсутстпия беспоряд
ка», т. е. противоречащие rипотезе Но. В первом из этих случаев статистика Т"
принимает минимальное значение, равное О, а во втором она максимальна
и равна
n(n 1)
(n 1) + (n 2) + + 1 == 2 .
Таким образом, малые значеНИЯ Т" и значения, близкие к n(n 1)/2, eCTe
ственно рассматривать как критические ДJJЯ rипотезы Но. Чтобы высказать
более определенные суждения о виде критерия инверсий, надо исследовать
распределение статистики Т" при справеДJJИВОСТИ rипотезы Но.
Из соображений симметрии ясно, что при rипотезе Но любое из n! 01'
носительных расположений элементов выборки в соответствующем вариа
ционном ряду имеет одинаковую вероятность l/n! Случайная величина 7Ji
4.5. rипотеза случайности
363
определяется расположением компоненты X i по отношению к Xi+I"" ,х n
В вариационном ряду и не зависит от относительноrо расположения послед
них между собой, т. е. 1Ji не зависит от 1]i + 1, , 1Jn 1, i == 1, .. ,n 2. Но это
означает, что случайные веЛИЧИНbI 1]1, ,'Т/n l взаимно незаВИСИМbI.
Далее, 1Ji может с одной и той же вероятностью I/(n i + 1) прини
мать значения О, 1, , n i, поэтому ее производящая функция имеет вид
(см. замечание в упр.21 к rл. 1)
n i
\Oj(Z) == L P{1]i == r }zr == (1 + Z + ... + zn i),
n +1
r O
а производящая функция статистики Тп вид
" I п 1
EZTn == L Р{Т п == r}Zr == П \Oi(Z) == П(1 + Z +... + Zr).
r j 1 n. r 1
Отсюда имеем (см. указание к упр. 24 rл. 1)
n i
E1Ji == \0;(1) == '
" 2 (n i)(n i + 2)
D1]j == \Oj (1) + E1]j (E1]i) == ,
12
n(n 1)
ЕТn == L.J Е'Т/i == 4 '
j 1
(1)
n(n I)(2n + 5)
DTn == L.J D1]j == .
. 72
. I
Итак, среднее значение статистики Тn при нулевой rипотезе совпадает с ce
рединой промежyrка 10, n(n 1)/2J, и в критическую область 7ia следует ,
ВКJJючать все целые точки этоrо промежyrка, ДOCTa К - -
ритерии инверсии
точно удаленные от середины, т. е. можно положить
{I n(n 1) 1 }
'ТJa == Т п 4 > ta(n) .
(2)
Критическую rpаницу ta(n) при заданном уровне значимости а выбирают
из условия Р{Т п Е 'ТJaIHo} а или, '1ТО эквивалентно,
{ n(n l) n(n I) }
Р 4 ta(n) Тn 4 + ta(n) 1 а
(3)
иа(n) это минимальное число, удовлетворяющее данному соотношению).
Соотношениями (2) (З) и определяется критерий UHlJepcиu. Распределение
статистики Тn протабулировано для значений n == 2(1)12 (соответствующая
Зб4
rлава 4. Проверка статистических zuпотез
таблица приведена в [3]) и может быть использовано для расчета критерия (2).
При n > 10 можно использовать нормальное приближение
.c(TnIHu) N(ET n , DTn),
rде ЕТn и DTn указаны в (1). В таких случаях можно приближенно полаrать
t 3/2
()
t a n 6 '
а
Ф( ta / 2) ==
2'
2. Проблема датчиков и обобщенный критерий хи квадрат
В примере 7 Введения была сформулирована проблема контроля «качества.)
последовательностей, вырабатываемых датчиками (rенераторами) случайных
или псевдослучайных чисел, которая кратко называется nроблемой датчиков.
Научная и практическая значимость этой проблемы очень высока, так как
спрос на такие датчики, а также на сами случайные последовательности в Ha
стоящее время непрерывно возрастает (появляются даже научно производ
ственные фирмы, занимающиеся производством и продажей больших масси
вов случайных чисел; например, с 1996 r. в мире распространяется компакт
диск «The Marsaglia random number CDROM», содержащий 4,8 млрд «истинно
случайных» бит).
1f Эта проблема имеет большую историю. Еще в начале хх n. СЛУ'lайные
последовательности цеЛblХ чисел имитировалИСЬ с ПОМОЩЬЮ простейших
случайных экспериментов: бросание монеты или иrpальной кости, извле
чение шаров из урны, раСКЛailblвание карт, рулетка и т. д. В 1927 r. Л. Типпе
том впервые были опубликоваНbI таблицы, содержащие СВblше 40000 случаЙНblХ
цифр, «произвольно извлечеННblХ из отчетов о переписи населения». В 1939 [.
М. Дж. Кендалл и Б. Бэбинrтон Смит с ПОМОЩЬЮ специально сконструированноrо
механическоro устройства [енератора случаЙНblХ чисел создали таблицу, вклю
чающую 10' случаЙНblХ цифр. В ]946 [. американский матемаТIIКДЖОН фон Ней
ман впервые предложил компьютеРНblЙ алrоритм rенерации случайных чисел.
В 1955 [. компания RAND Corporation опубликовала получившие широкую попу
ЛЯРНОСТЬ таблицы, содержащне 106 случайных цифр, сreнерированных на ЭВМ.
Таблицы случайных чисел можно найти в каждом сборнике статистиче
ских таблиц. Так в [з] приведена таблица, содержащая 12500 цифр от О до 9.
Эrи данные можно рассматривать как реализации независимых и одинако
во распределенных случайных величин, принимающих значения О, 1,2, ,9
с одной и той же вероятностью, равной 0,1. Каждая пара таких цифр пред
ставляет собой реализацию случайной величины, которая может принимать
любые целочисленные значения от 00 до 99 с одинаковыми вероятностями,
равными 0,01. Аналоrичный результат получится, если цифры сrруппировать
по три, четыре и т. д.
Если каждую rpуппу из k цифр) рассматриваемую как целое число, YMHO
жить на lo k то получим реализации случайной величины С принимаю
щей k разрядные значения от О до (1 lO k) С одинаковыми вероятностями,
94.5. [ипотеза случайности
Зб5
k
равными 1 О Такое распределение вероятностей близко к равномерному pac
пределению И(О, 1), причем разность соответствующих функций распределе
k
ния не превосходит 1O Следовательно, реализации можно рассматривать
как реализации случайных величин, равномерно распределенных на отрезке
10, 1 j. Эти реализации и называют обычно равномерно распределенными слу
чайными числами. Из этих чисел с помощью алrоритмов, описанных в 1.3,
можно построить (сreнерировать) случайные числа с любым друrим распре
делением, отличным от paBHoMepHoro распределения и(о, 1).
Итак, в математическом плане, основное требование к датчику случайных
чисел состоит в том, что вырабатываемая им последовательность 6,6,...
должна быть в статистическом смысле неотличима от последовательности
независимых и одинаково распределенных случайных величин, т. е. должна
соответствовать rипотезе случайности Но (соrласовываться с ней). Теперь мы
уточним постановку задачи, которую будем обсуждать далее.
Пусть задана последовательность из n случайных величин (выборка)
1,6,
, n,
(4)
принимающих значения из конечноrо множества (алфавита) [; == {1, 2, . . . ,N},
отоситеш.НО которой требуется проверить rипотезу Но о том, что эти слу
чайные величины в совокупности независимы и равномерно распределены
на множестве [;, Т.е. P{ i == j} == I/N, j == 1, ,N, i == 1,2, rипо
теза Но это есть rипотеза об идеальном датчике: если rипотеза Но верна,
то датчик, вырабатывающей последовательность (4), реализует ('идеальную»
схему независимых испытаний с равновероятными исходами. Но идеальных
датчиков не существует; более тоro, как отмечено в примере 7 Введения
(см. также п. 1 Э 1.3), часто датчик вырабатывает последовательность (4) про
[раммным способом (т. е. эти числа :.1oryт быть даже детерминированными),
но тоrда эти числа должны быть «практически неотличимы» (или очень по
хожи») от независимых и равновероятных чисел. В математическом плане это
понимается так: выборка (4) не должна опроверl'ать rипотезу Но никаким тe
стом. Практически же идyr на следующий компромис: определяется некоторая
совокупность статистических критериев (тестов) и, основываясь на выборке
(4), подверrают rипотезу НО проверке по каждому из этих контрольных тестов.
Если rипотеза НО успешно проходит такое тестирование, то она принимается
как истинная, и числа (4) рекомендуются для использования в COOTBeTCTBY
ющих целях как независимые и равномерно распределенные на множестве [;
случайные числа. Общепринятый в настоящее время стандартный набор таких
тестов сформулировал д. Кнут (1969) и он имеется в книrе /131, однако работа
по совершенствованию методов тестирования случайных и псевдослучайных
последовательностей продолжается. В качестве примера одноro из подходящих
для проверки rипотезы Но тестов мы подробно опишем критерий типа хи
квадрат, основанный на подсчете частот s цепочек в последовательности (4).
Идею Построения этоro теста можно объяснить следующим образом. По
скольку rипотеза Но простая (она однозначно фиксирует распределение
Збб
rлава 4. Проверка статистических zuпотез
наблюдений (4)), то, в принципе, для ее проверки можно было бы исполь
зовать классический критерий х 2 , описанный в п. 2 4.2. Но этот критерий
«работает» лишь при условии независимости наблюдений (4): он состоятелен
против альтернатив, которые учитывают изменение лишь вероятностей появ
ления исходов, но сохраняют предположение о независимости наблюдений.
Но ведь именно это предположение о независимости и требуется подверrнyrь
проверке! Поэтому критерий х 2 Пирсона не решает эту проблему. Сохраняя
идеолоrию метода хи квадрат (сравнение эмпирических частот некоторых co
бытий с их rипотетическими вероятностями с помощью меры хи квадрат),
можно попытаться сконструировать тест, «реаrирующий» на альтернативы TO
ro или иноrо типа зависимости между данными (4), рассматривая вместо
частот отдельных исходов в последовательности (4) частоты цепочек исходов
некоторой фиксированной длины s 2, причем цепочки должны быть пе
/, рекрывающимися. Точное определение таково: s цепочкой (или S i!раммой)
S называется любая подпоследовательность последова
цепочки
тельности (4), состоящая из s подряд идущих ее членов.
Таким образом, из (4) можно образовать следующие s цепочки: ( J, , s),
(6, ' S+I), ,( n s+J,' , n), Bcero n s + 1 цепочек, Пусть теперь
z == (i l is) любая 8 мерная комбинация элементов множества Е, всех
различных таких комбинаций N S В методе хи квадрат используются часто
ты s цепочек и (8 + l) цепочек, подсчитываемые по следующим формулам:
n s+'
II[ == L I( t == i J , t+1 == i 2 ,
t=1
t+э 1 == is),
n 6
/I[j == L I( t == i"
t=1
(напомним, что I(A) есть индикатор события А). При этом достаточно BЫ
числить лишь частоты {II[) (их число равно N S + 1 ), так как можно положить
(5)
t+s ' == i s , t+s == j),
jE&
N
II[ == L /I,j
j=1
(на самом деле последняя сумма может на 1 отличаться от 11[, но на излаrаемых
далее асимптотических результатах это никак не сказывается).
Далее, при rипотезе Но (все j независимы и равномерно распределены
на &)
n a n
Ev .== "-'
1] Ns+1 Ns+1
(асимптотическое равенство справедливо при n -----t 00 И фиксированном 8)
И аналоrично EII, "-' n/N s , поэтому для проверки Но можно сравнивать
эмпирические частоты lI'j с, например, IIJN при помощи «стандартной»
4.5. rипоmеза случайности
Зб7
статистики хи квадрат:
X ,HI l.:
(,j) Е [.+1
(V,j 1/"{ / N)2
v,/N
(6)
Обоснованием именно такой конструкции тестовой статистики является сле
дующий асимтотический результат [29].
Теорема 1. Пусть rипотеза НО, означающая, что последовательноаь (4) по
лучена по схеме независимых испытаний с N равно вероятными исходами,
справедлива. TorAa статистика (6) имеет предельное (при n 00) распре
деление 'J/(NS(N 1)). Соответавующий критерий, задаваемый при уровне
значимости а критической облааью
{X ,Hl > Xi a,N'(N [)}' (7)
состоятелен против альтернатив, при которых последовательность (4) представ
ляет собой однородную зрrодическую цепь Маркова порядка s или меньше.
Здесь нам встретились некоторые новые понятия, которые мы должны
пояснить, прежде чем комментировать этот результат. Понятие цепи MapKO
ва нам уже встречалось ранее. Именно, в п. 10 1.3 приведено определение
простой (т. е. порядка 1) однородной цепи Маркова. Обобщение на произволь
ный порядок s выrлядит следующим образом (сравни с (6) 1.3): при любых
k > s и i), , i k Е Е условная вероятность P{ k == i k I т == i т , т < k}
не зависит от значений i m для т < k S, т. е. вероятности, с которыми k
принимает возможные значения, зависят лишь от значений s предыдущих
случайных величин последовательности (4). В этом случае rоворят, что цепь
Маркова управляется переходными вероятностями
Pi,...i.:j == P{ k == j I k s == i[,
k 1 == is}.
(8)
Если эти переходные вероятности не зависят от «временю> k, то цепь называ
ется однородной. Чтобы полностью определить вероятностный закон, управля
ющий цепью Маркова порядка s, нужно еще задать начальное распределение
цепи, т. е. вероятности P{ k == i k . k :( s}. Наконец, цепь Маркова является
Эрi!одИlfеской, если ДlIи любых i 1 , ,is Е Е существуют пределы
lim P{'t == i"
t---+oo
t z } Р -
..t+s 1 s "'"
(9)
не зависящие от начальноrо распределения цепи; эти пределы Pi"...,i. назЫ
ваются стационарными вероятностями комбинаций i == и[, . ., , is). При этом
для эрrодичности цепи достаточно, чтобы все переходные вероятности (8)
были положительны (в цепи возможны все переходы).
Цепь Маркова порядка s это специфическая, но в то же время весьма
общая модель зависимых (,на rлубину s,» испытаний, подходящая для описа
ния мноrих реальных процессов, поэтому в обсуждаемой проблеме датчиков
Зб8
rлава 4. Проверка статистических zипотез
подобные, как rоворят, марковские альтернативы представляют особый инте
рес, и качество тех или иных критериев для проверки rипотезы случайности Но
прежде Bcero проверяют именно на таких альтернативах: критерий должен
быть состоятельным против марковских альтернатив. Теорема 1 и утверждает,
что обобщенный критерий х 2 . определяемый соотношениями (6) (7), с этих
позиций является вполне подходящим тестом для rипотезы случайности: если
мы хотим КОНТРОЛИРОlJать отклонения от нулевой rипотезы типа марковской
зависимости до порядка 8 включительно, то мы должны использовать частоты
(8+ 1 ) цепочек в исходной последовательности (4) для конструирования TeCTO
вой статистики (6). Сама же тестовая статистика и основанный на ней крите
рий (7) вполне приемлемы с позиций трудоемкости практических вычислений.
Упражнения
Если действовать не будешь,
ни " чему ума палата.
Шота Руставели
D Среди n 10000 чисел О, 1, ,.. ,9 числа, не превосходящие 4, встретились
5089 раз. Проверить по критерию / Пирсона rипотезу о равноверятности чисел при
уровне значимости а == 0,05. При каком уровне значимости эта rипотеза отверrается?
D Смоделировать выборку объема n == 1000 из распределения Бернулли Bi( 1, 3/5)
и проверить по критерию XZ соответствие данных теоретической модели.
.... Указание. Использовать, например, таблицу случайных чисел и алroритм п. 2 1.3.
11 При n == 4000 независимых испытаниях события AI' Az, Аз, составляющие пол
ную '"Руппу, осуществились соответственно 1905, 1015 и 1080 раз. Проверить, соrласу
ются ли данные при уровне значимости 0,05 с rипотезой Но р, == 1/2, pz == Рз == 1/4,
rде Р; == Р{А;}
.... Указание. Применить критерий XZ с критической rpаницей X .95;Z == 5,99.
11 в десятичной записи числа 1[ среди первых 10002 знаков после запятой цифры
0,1, ,9 встречаются соответственно 968, 1026, 1021,974,1014, 1046, 1021,970,948,
1014 раз. Прооерить по критерию х 2 rипотезу о равновероятности .слу'lайны.. чисел
О, 1, ... ,9. При каком yp0[JHe значимости эта rипотеза отверrается?
g Используя таблицу значений какой либо функuии (С05 Х, е Х , In хит. д.) выписать
100 цифр, выбирая из каждоro значения функции второй знак справа, и проверить
для такой оыборки по критерию / rипотезу о равновероятности цифр О, 1, ,9 при
уровне значимости 0,01.
DI Соrласуются ли данные, приведенные в примере 2 в 2.2 с rипотезой о сиММет
ричности костей? Ответить на такой же вопрос в отношении данных, приведенных
в упр. 9 к rл. 2.
D Смоделировать выборку объема 100 из распределения Bi(3, 1/2) и проверить co
ответствие полученных данных теоретической модели.
.... Указание. Использовать алrоритм п. 2 1.3.
Упражнения
Зб9
D Смоделировать выборку объема 100 из paBHoMepHoro распределения И(О, 1) и про
верить по полученным данным rипотезу о равномерности распределения по критериям
Кол MoropOBa и х 2
D Смоделировать выборку объема n == 100 из показательноrо распределения r(i. 1)
и, сrpуппировав полученные данные по N == 4 равновероятным (при rипотезе Но
F(x) == 1 е Ж х О) интервалом, про верить по критерию i rипотезу НО при
уровне значимости а == 0,1.
... Указание. Использовать алroритм п. 7 1.3.
lIiJ Проверить по критерию Колмоrорова соответствие данных, полученных в упр.6
к rл.2, rипотезе о нормальной распределенности чисел.
m в reнетической модели Фншера [2, с.79) считается, что вероятности появления
потомства, классифицируемоro по четырем типам, имеют вид PI (8) == (2 + 8)/4,
Р2(8) == pJ(8) == (1 fJ)/4, Р4(8) == 8/4, fJ Е (0,1) неизвестныйпараметр. Построить
критерий i соответствия этой модели реальным данным.
m При 8000 независимых испытаниях события AI. А 2 И A J , составляющие полную
rpуппу, осуществились соответственно 2014, 5012 и 974 раза. Верна ли при уровне
значимости 0,05 rипотеза: P{AI} == 0,5 28, Р{А 2 } == 0,5 + fJ, Р{А з } == 8, rде
8 Е (О, 1/4)?
111 Проверить rипотезу Но L:( ) Е П(8), 8 > О неизвестный параметр, для
данных, приведенных в упр. II к rл. 2.
... Указание. В качестве оценки пара метра принять выборочное среднее.
m Через равные промежутки времени в тонком слое раствора золота реrестри
ровалось число { частиц золота, попавших в поле зрения микроскопа. По данным
наблюдений, приведенных в следующей таблице (Vj число ОПьrrов, для которых
{ == i, i == О, 1, 2, . . .), проверить rипотезу пуаССОНОБОСТИ Но L:({) Е П( 8), fJ > О
неизвестный параметр, оцениваемый выборочным средним.
i О 1 2 3 4 5 6 7 Е
V' 112 168 130 68 32 5 I 1 n == 518
I
m в течение эпидемии rpиппа среди 2000 контролируемых индивидуумов одно за
болевание наблюдалось у 181 человека, а дважды болели rpиппом лишь 9 человек.
Соrласуются ли при уровне значимости 0,05 эти данные с rипотезой, соrласно KOТO
рой число заболеваний отдельноrо индивидуума биномиальная Bi(2, 8) случайная
величина?
m Исходя из формул (8) (9) 4.2, убедиться в том, что среднее и дисперсия стати
.2 о / t=
стики Х п при «близких.) альтернативах вида Е(п) == l!. +!!.. уп, f!..1 Q, имеют при
n 00 следующие асипмтотические представления:
E(.t IE(n)) == N 1 + t Р! +o( ),
j=1 Р I
D(.t IE(n)) ==2(N 1)+4t fi! +o( )n ) .
]=1 Р I
24 Зака, 1748
370
rлава 4. Проверка статистических 2ипотез
ID Исходя из формул (15) Э 4.2, получить, что при
pj==pj(n)== (1+ 4 )' j==I,...,N и
n
n, N 00, N . р > О,
e Pb2(N)
Ep,o(n,N)==Ne P+Vii//2 (1 +0(1)),
2
тах Ibjl::; с < 00
l j N
N
1
b 2 (N) == N L Ь;,
j 1
Dp,o(n,N) ==Ne P(1 (1 +p)e P)(1 +0(1)).
m Следующая таблица содержит данные о смертности среди матерей, родивших
первоro ребенка, в четыре различные периода времени [2, с. 102] (n) ЧI;IСЛО матерей,
Vj число смертных исходов):
nj 1072 1133 2455 1995
Vj 22 23 49 33
По критерию однородности х 2 с двумя исходами проверить rипотезу Но о том, что
в уровнях смертности между этими периодами не существует различия.
m Смоделировать выборку объема n == 200 равномерно распределенных чисел (X i ).
С помощью критерия Смирнова проверить, что две подвыборки (X 2i , i == 1, 100)
и (X 2i + J , i == О, 1,.. . , 99) являются выборками из одноrо и Toro же распределения.
m Смоделировать последовательность (X j , i == 1,2, ]00) случайных величин,
с равными вероятностями принимающих значения ], 2, 3, 4, 5. ОбраЗОJJать из этой
последовательности двс выборки (Х 2 " i == 1,2, ,50) и (X 2i + J , i == 0,1, ,49)
и провсрить для них rипотезу однородности.
... Указание. Использовать алrоритм п. 4 1.3.
m Пусть случайные величины 'fJ1,"', 'fJN независимы и [,(Тjj) == Щ8 j ), j == 1,.. , N,
[де параметры 8) неизuестны; дополнительно известно, что 'fJ1 + + 'fJN == n. По-
строить при этом условии критерий х 2 дJlя проверки rипотезы однородности
Но 81 ==
== 8 N .
... Указание. Воспользоваться упр. 22 к rл. 1.
m Из 300 абитуриентов, поступивших в вуз, 97 человек имели 5 в школе и 48
получили 5 на вступительных экзаменах по тому же предмету, причем только 18 человек
имели 5 и в школе, и на экзамене. С уровнем значимости 0,1 проверить rипотезу
о независимости оценок 5 в школе и на экзамене.
m Используя данные, полученные в упр. 20, обраЗОJJать последовательность. пар
(X2j l, X 2i ) , i == 1,2, ,50, и проверить по этим данным rипотезу независимости.
m Можно ли с уровнем значимости 0,001 С'lИтать, что последовательность чисел
1,05; 1,]2; 1,37; 1,50; ],51; 1,73; 1,85; ],98 является реализацией случайноrо вектора, все
8 компонент KOToporo независимые одинаково распределенные непреРЬ!JJные слу-
чайные величины?
... Указание. Применить критерий инверсий.
m Смоделировать выборку из 100 равномерных псевдослучайных чисел. С помощью
статистики Т п числа инверсий проверить rипотезу случайности ДJlЯ этих данных.
Упражнения
371
m Доказать, что число инверсий Т п в случайной выборке объема n из непрерывноrо
распределения распределено асимптотически нормально Н(n(n 1)/4, n] /36).
... Указание. Используя производящую функцию EZTn (см. П. 194.5), перейти к xa
рактеристической функции и убедиться в том, что при n ----t 00
{ ( n(n 1) ) 6 } { t 2 }
Еехр it Т п 4 n]j2 ----t ехр 2
rлава 5
Параметрические rипотеэы
Статистика это искусство уточнять то,
что является неизвестным.
Пара метрические rипотезы, рассматриваемые в настоящей rлаве, это
rипотезы об истинном значении неизвестноrо пара метра, определяющеrо
априори заданное параметрическое семейство распределений. Здесь изложены
и продемонстрированы на конкретных при мерах основные принципы постро
ения оптимальных или асимптотически оптимальных (для больших выборок)
критериев про верки таких rипотез, в основе которых лежит метод отношения
праВДОllодобия Ю. Неймана и Э. Пирсона. Отдельные параrpафы посвящены
последовательному анализу А. Вальда и статистическому анализу конечных
цепей Маркова.
5.1. Общие положения
Важный класс статистических rипотез составляют rипотезы о параметриче
ских моделях. В этом случае априори постулируется, что класс :F допустимых
распределений наблюдаемой случайной величины { является некоторым пара
метрическим семейством :F == {Р(х; О), О Е 8}, т. е. все допустимые распре
деления идентифицируются соответствующим параметром О (О" ,Or)
со значениями из параметрическоrо множества 8 R r поэтому rипотезы
..w П О распределении [(о, по существу, относятся к неиз
,. араметрические l)
вестному пара метру 11 и называются парамеmрuческuми.
rипотеЗhl
" Примерами параметрических rипотез являются yrBep
ждения:
1) Но О == 00, rдe 00 Е 8 некоторое фиксированное значение параметра;
2) Но О( == 02 == == Or;
3) Но 9(0) == 90, rде g(O) некоторая (в общем случае векторная) функ
ция, 90 фиксированное значение.
В общем случае основная (нулевая) параметрическая rипотеза задается
указанием HeKoToporo подмножества 80 С 8, элементом KOToporo является,
по предположению, неизвестное истинное значение параметра О, что записы-
вается в виде Но О Е 80. Точки О Е 8, == 8\80 называются альтернатива
ми, а yrверждение Нl О Е 8) альтернативной rипотезой. Таким образом,
в параметрическом случае альтернативная rипотеза конкретизируется и имеет
такОЙ же вид, как и основная rипотеза Но. Друrими словами, в данном случае
95.1. Общие положения
373
отклонения от основной rипотезы имеют вполне определенный вид, orpa
ниченный рамками рассматриваемоrо параметрическоrо семейства. Следова
тельно, и соответствующий статистический критерий должен быть направлен
на выявление именно таких отклонений от НО, учитывать их специфику.
Следует ожидать, что наличие такой значительной априорной информации
о допустимых распределениях наблюдений (данных) должно привести к бо
лее сильным выводам, найти свое отражение в свойствах соответствующих
параметрических критериев.
Общие принципы построения критериев, изложенные в 94.1, относятся и
к рассматриваемому случаю. Напомним кратко, что если в задаче (НО: () Е во,
Н) О Е e l ) примен яется некоторый «критерий Х!О», т. е.
I Но отверraется {::::::::} Х Е Х!О, I
rде х исходные данные и при заданном уровне значимости а критическая
область X 1a удовлетворяет условию
W(8) == W(8; X 1a ) == Ре{Х Е Х)а} а, 'rJ 8 Е во (1)
(функция w(o; Х!а), 8 Е в, называется функцией мощности критерия Х!а),
то проблема максимум состоит в построении TaKoro критерия X a' для KOToporo
при произвольном Х)О, удовлетворяющем (1),
W(8; X a) W(8; Х!а) при О Е во и
W(8; X a) W(8; Х!а) при () Е e l .
(2)
Такой критерий X a (коrда он существует) называется равномерно
наиболее мощным критерием (р. н. м. к.) В задаче (НО, Н!).
Равномерно наиболее мощный критерий не всеrда существует, поскольку,
как правило, критерий, максимизирующий мощность при определенной аль
тернативе 8 Е e 1 , зависит от этой альтернативы, и экстремальная задача (2)
при оrраничении (1) имеет решение только в некоторых специальных случаях.
С примерами таких ситуаций мы встретимся в дальнейшем.
Часто оrpаничиваются рассмотрением подкласса несмещеннbIX критериев,
для которых одновременно с (1) выполняется условие
.,f
Р. н. М. К.
W(O) а, 'rJ8 Е в!.
(3)
в ряде задач, для которых р. н. М. к. не существуют, MOryт иметь место р. н. м.
несмещенные критерии.
Наконец, напомним, что в случае рандомизиро Р _
аНДОМИЗl1рованныи
BaHHoro критерия, задаваемоrо критической функ _ . . . .. _
( ) критерии
цией tp х , функция мощности критерия "Р» опре
деляется равенством
W(O) == W(8; tp) == Eetp(X) == / "Р(х) dFx(x; 8).
(4)
Излаraемая ниже теория параметрических критериев базируется на методе
отНОшения правдоподобия, предложенном Ю. Нейманом и Э. Пирсоном (1933)
374
rлава 5. Параметрuческuе zuпотезы
в качестве основы общеrо метода построения критериев. В основе этой теории
лежит знаменитая (фундаментальная) лемма Неймана ПирСОl/а, дающая вид
наиболее мощноrо критерия в задаче различения двух простых rи потез. С этоrо
результата мы и начнем (в случае, коrда множество 81 состоит из одной точки,
т. е. альтернатива Н! простая, вместо р. н. м. к. используется термин наиболее
мощный критерий).
5.2. Выбор И3 двух простых rИпотез.
Критерий Неймана Пирсона
1. Постановка эадачи и предварительные соображения
Рассмотрим простейший частный (но иrpающий принципиальную роль в по
следующей теории) случай, Коrда обе rипотезы Но и Нl простые. Форма
лизуется это так: постулируется (априори предполаrается), что допустимыми
распределениями наблюдаемой случайной величины являются лишь два за
данных распределения (две функции распределения) ро(х) и Р[ (х) и требуется
по выборке Х (Х), ,Х n ) из.ею проверить rипотезу Но P (x) ро(х)
против альтернативы НI Р((х) == F1(x). Чтобы подчеркнyrь, что это частный
случай параметрических rипотез, можно рассмотреть семейство распределе
ний вида Р(х; О) (1 о)ро(х) + ОР[ (х), [де параметрическое множество 8
состоит из двух точек: 8 {О, I} и проверяемая (основная) rипотеза есть
Но 8 80 О, а альтернатива Н) () 81 1. Тоща Р,(х) Р(х; (Ji),
i О, 1, и речь идет о выборе одноrо из этих распределений в качестве
истинноrо.
Соrласно изложенному выше общему принципу, задача построения наи
лучшеrо (наиболее мощноrо) критерия 1: 0 сводится в данном случае к pe
шению экстремальной задачи максимизации по 1:[0 мощности W((JI, 1:[а):
W(8 1 ; 1:[а) Ре, {Х Е 1: lo } == тах
(1)
при оrpаничении
W((Jo; 1:(0) == Р@о{Х Е 1: lo } а.
Нетрудно понять, как надо строить оптимальную критическую область X o.
Рассмотрим правдоподобие данных L(if; О) f (xI; О) f(x n ; О) при каждой
из rипотез Но и Н[ (см. П. 1 93.2). Torдa, например, Д1IЯ непрерывных данных
проблема (1) запишется D виде
W(8 o ; 1: la ) f L(;т;.; (0) dif == а,
А'а
W(8 1 ; Х[а) f L(;т;.; (}I) dif тах,
А'а
(2)
5.2. Критерий Неймана Пирсона
375
т. е. среди всех областей Х la надо выбрать ту, для точек которой правдопо
добие L( ; (1) будет наибольшим в сравнении с L( ; (0), Следовательно все
выборочные точки == (Хl, , Х П ) надо ('упорядочить» соответственно Be
личине отношения Отношение Jf
n
правдоподо6ия
п f(Xi; 81)
( ) Ц ; (1) i 1
lх== ==
Ц ; (0) n
П f(Xi; 80)
i 1
(3)
и затем включить в X a все те из них, для которых Ц ) ? С, а rpаница С == Са
должна быть выбрана так, чтобы обеспечить первое условие в (2). Функuия
l( ) в (3) называется отношением правдОflодобия, она и порождает тестовую
статистику Т(Х) == I(Х) критерия Неймана Пирсона в рассматриваемой
задаче (Но. H 1 ). Таким образом, критерий Неймана Пирсона основывается
на статистике отношения flравдОflодобця
( L(X;81)
1 Х) == L(X;8 0 )
К р ите р ий Неймана Пи р сона ·
;iIIЩ
l(;f) ? Са}.
и задается критической областью
X a == { == (хl, .., х п )
То, что такая конструкция приводит к оптимальному критерию, и yrверждает
фундаментальная лемма Неймана Пирсона.
2. Случай а6солютно непрерывных распределений
Прежде чем давать ее точную формулировку, условимся о некоторых соrлаше
ниях. Рассмотрим сначала случай абсолютно непрерывных распределений Fo
и Р 1 И будем считать, что соответствующие плотности /о(х) и fl (х) удовле
Тlюряют условию /j(x) > О, j == О, 1 (это исключает тривиальные ситуации,
коrда при одной из rипотез некоторые значения х «запрещены», И следова
тельно, наблюдая в опыте такие значения, мы однозначно определяем, какая
из rипотез верна). Определим теперь функцию
'Ф(с) == Po{I(X) ? С} == f Ц ; (0) d
!.' l(!.) c
(для сокращения записи пишем Pj вместо Р в ;, i == О, ], и P;{S} вместо
Ре;{Х Е S}). С ростом С эта функция может только убывать, кроме TOro,
(0) == ]. Далее,
1 ? P 1 {I(X) ? С} == f L( ; (}1) d ? с / L( ; (0) d == С'ф(с),
l.' l(;r) c
l.: l(iJ c
37б
rлава 5. Параметрuчеснuе zuпотеЗbf
поэтому ф(с) Ijc, т. е. ф(с) --4 О при С --4 00. Будем предполаrать, что
существует такое значение С == Са, что ф(с а ) == а (в частности, это всеrда
имеет место, если функция ф(с) непрерывна). Torдa для соответствующеrо
множества Х;а == { [( ) Са} имеем
W(8 0 ; X a) == Po{1: a} == / L( ; (0) d == Ф(Са) == а. (4)
Xio
Справедливо следующее yrверждение.
Теорема 1 (Лемма Неймана Пирсона). При сделанных предположениях
критическая область 1: a задает наиболее мощный критерий для rипотезы
Но Р{(х) == ро(х) относительно альтернативы Н, Р{(х) == р,(х) среди
всех критериев уровня значимости а.
ДОКQJOтельство. Рассмотрим любой друrой критерий 1: la, так что
W(Bo; X 1a ) == P O {1: la } == / L( ; (0) d == а.
1: 1.
(5)
Из формул (4) и (5) получаем
PO{X a XlaX a} == а Po{X'aX a} == PO{X 1a X1aX;a}'
Соrласно определению множества Х7а' вне этоrо множества l( ) < Са, т. е.
caL(!.; (0) > L(!.; (1),
поэтому
PI{X a XlaX a} CaPO{X a X'a1: a} ==
== CaPO{X 1a 1:la1: a} > P,{X 1a XlaX a}'
Прибавляя к обеим частям этоro неравенства Р) {1: 'aX a}' получим
P,{X a} == W(O,; 1: a) > W(8,; X 1a ) == Р 1 {X 1a }. .
Замечание. Конечно, Оптимальный критерий должен удовлетворять условию HeCMe
щенности (3) !\ 5.1. Покажем, что критерий Неймана Пирсона Х;а обладает этим
свойством. Пусть в (4) Са > 1. Torдa
W(8 1 ; Х;а) == I L( ; 8,) d Са I L( ; 80) d == аСа> а.
л ra х o
Если же Са:::; 1, то
W(8); Х;а) == 1 Pj{X:a} > 1 с"Ро{Х: а } 1 РО{Х:а} == РО{Х;а} == а.
Следовательно, в любом случае W(8.; х;а) > а.
5.2. Критерий Неймана Пирсона
377
Рассмотрим теперь вопрос о расчете критерия Х;а, т. е. о вычислении
критической rpаницы Са (см. (4» и вероятности ошибки 2 ro рода
{3 == fЗ(а, n) == 1 W(8[; X a)'
Точное вычисление этих основных параметров критерия возможен в том слу
чае, коrда распределение тестовой статистики [(Х) известно как при rипоте
зе Но, так как при альтернативе НI (см. примеры ниже). Но это не всеrда
осуществимо, поэтому часто для решения этой задачи применяется асимпто
тический подход (при объеме выборки n ---+ 00), основанный на использова .,.
нии центральной предельной теоремы (UПТ). Использование ЦПТ
Обозначим
z. 1n 't(X j ) i == l '
, 10(Xj)'
тorдa Sn == ZI +.. ,+Zn есть сумма независиМЫХ одинаково распреленных при
каждой rипотезе случайных величин и событие {l(X) :;:: Са} можно записать
в виде {Sn:;:: Inc a }. Обозначим, далее,
,n,
J fl(x) 2
aj == EeZI == fj(x) 1" ( ) dx, (1'j == DejZ[, j == О, 1
) 10 х
(предполаraется, что эти моменты существуют). Из неравенства In t t 1,
t > О, и представления
J [ fl(X) ( fl(X) )]
ао == fo(x) I" fo(x) fo(x) 1 dx
следует, что ао О, и аналоrично, аl :;:: О. Будем далее считать, что ао < О,
al > О и (1'] > О, j == 0,1. Тоrда при n ---+ 00 на основании ЦПТ(см. (1) 1.2)
L./Jj(Sn) rv N(naj, n(1']), j == О, 1.
Отсюда следует, что для больших выборок для расчета критерия Неймана
Пирсона можно воспользоваться нормальной аппроксимацией для суммы SN.
Имеем
{ Sn nао In Са nао }
a==Po{Sn:;::lnca}==P O :;:: ::::::ф( tа).
n(1'о n(1'О
Inca==naO+ta(1'oVn, Ф( tа)==а, (6)
А .... J.fc...",
симметрическии: вор OHT" .
критерия Неймона Пирсонg,
,.\ff;
если Са выбрано так, что
Соотношение (6) рещает вопрос о приближенном определении критической
rpаницы в критерии Неймана Пирсона в случае больщих выборок.
Аналоrично, с учетом (6) для вероятности ошибки 2 ro рода {3(а, n) при
больших n можем записать
{ Sn nа[ ао а! (1'0 }
{3(а, n) == PI{Sn < In Са} == р! < vn + ta .
n(1'1 (1'[ (1')
(7)
378
rлава 5. Параметрические zuпотеэы
Здесь (ао al)Vn ----t oo при n ----t 00 И прямое применение ЦПТ дЛЯ
вычисления этой вероятности при больших n становится уже некорректным
/ (из UПТ ожно лишь заключить, что {3(а, n) ----t О при n ----t 00); rоворят,
/
'" Б что в данном случае значение суммы Sn находится
ольшие уклонения .
в зоне больших уклонении (от cpeAHero значения nal
при рассматриваемой rипотезе H 1 ). Таким образом, для определения значения
{3(а, n) при больших n необходимо использовать более rлубокие (нежели
ЦПТ) результаты из теории суммирования независимых случайных величин
так называемую теорию больших уклонений. Применение этой теории к нашей
задаче дает в типичных случаях следующий результат [5, с.289]: при n ----t 00
1 { t2 }
{3(а, n) '" .J2rn ехр nао + .,fiiaot o ,
ао 2 n 2
(8)
т. е. ошибка {3 убывает экспоненциально с возрастанием числа наблюдений n,
если при этом rипотетические распределения Fo и Fl остаются фиксирован
ными (т. е. фиксированы параметры aj, а], j == О, 1).
«Близкие» rипотезы Однако, можно представить себе более слож
ную ситуацию, коrда вместе с ростом числа наблю
дений n изменяются и распределения Fj, j == О, 1 , т. е. их параметры щ, а]
являются некоторыми функциями от n: aj == aj(n), а] == а](n). TorAa COOT
ношение (1) позволяет ответить на вопрос о том, для каких (,близких,) rипотез
критерий Неймана Пирсона 1:;0 имеет невырождающуюся в пределе мощ
ность, т. е.
W(8); 1:;0) == 1 {3(а, n) ----t 1, а < r < 1.
Это будет так, если, например,
J7i(ao(n) al(n))
----t 6 < О, ао(n)"'" al(n):
al(n)
в этом случае из (1) имеем r == Ф(6 t o ).
Таким образом, мы можем сделать следующий принципиальный вывод:
при больших выборках наиболее мощный критерий Неймана Пирсона спо
собен различать rипотезы, сближающиеся со скоростью порядка l/.,fii (pac
стояние между rипотезами измеряется взвешенной разностью средних значе
ний случайной величины Z == [п (fl Ю/ fоЮ) при этих rипотезах).
Пример 1 (Критерий Неймана Пирсона АЛЯ cpeAHero нормальной модели),
Пусть о нормально распределенной случайной величине с известной дис
персией а 2 и неизвестным средним 8 имеются две rипотезы: Но 8 == 80 и
Н)+ : () == 8l (для определенности будем считать, что (}о < 81), Если Х == (X 1 ,
... ,Х n ) выборка из .c( ) и {f ее реализация, то отношение правдопо
добия имеет вид
(9)
l( ) == ехр { 2 2 t[(Xi 81)2 (Xj ()0)2]} ==
, )
5.2. Критерий Неймана Пирсона
379
{ n n 2 2 }
== ехр (81 Оо)х (O) 80)
а 2 2а 2
инеравенство l(;f,) с эквивалентно неравенству
2 1" с 81 + 80
x a + .
n(8) 80) 2
которое удобно "ере"исать в виде
Vn а vn
(x 80) vn( 8 ) 1" с + (81 80) == t(c).
17 n 8) о 217
2
Так как Leo(X) == N(8 0 , 17 /n), то отсюда имеем
{ vn }
1fJ(c) == Peo{I(X) с} == Ре" 7(Х (0) t(c) == Ф( t(с».
При с> О функция t(c) непрерывна, поэтому непрерывна и функция 1fJ(c),
и для любоrо о: Е (О, 1) однозначно определена величина сй, rде t(C a ) == t a .
а Ф( tй) == 0:.
Таким образом, в данном случае крите
рий Неймана Пирсона задается критиче
ской областью
К Н П
рl1Терий еймана ИрСQна
о;!..,....""", ......л...I! З? Ааче (НО, иt)
*+ { Vn(x 80) }
х 1й ;f, t c} ,
а
Ф( ta) == 0:.
(10)
Подчеркнем следующие важные обстоятельства: в данном случае критическая
область наиболее мощноrо критерия {1(X) Сй} оказалась выраженной
через выборочное среднее Х достаточную статистику для модели N(8, ( 2 )
(см. п. 1 3.3), а сама критическая область (10) не зависит от KOHKpeTHoro
значения альтернативы 01 (> 80),
2
Вычислим мощность критерия (10). Так как Le,(X) == N(OI, 17 /n), то
W(O); Х;:) == Р/I, { Х 80 + ::п tй} ==
== Ре { Vn CK 81) Vn (8 1 8o)+ta } ==
1 а 17
==Ф( :п (81 00) tй). (11)
в частности, отсюда видно, что W(8); X :) > ф( tй) == о: (несмещенность).
Аналоrично, при 8. < 80, т. е. в задаче Критерий Неймана Пирсона .,.
(Но, Hl )' критическая область наиболее в задаче (НО, Hl )
мощноro критерия имеет вид
X == {"'" .;n х: 80 ta}, ф( tй) == 0:, (12)
380
rлава 5. Параметрические zuпотезы
лх; fJ)
Q
о
fJ o
fJ o + t.!!.. fJ ,
"'n
:е
Рис. 1
а ero мощность
W(8!; X ;;) == Ф ( (80 8,) t O ).
Из (11) следует, что вероятность ошибки 2 ro рода критерия (10) равна
.+ ( С 8\ Во )
13 == 13(0, n) == 1 W(8,;X 10 ) == Ф t a уn .
( 13)
Наrлядной иллюстрацией этих результатов служит рис. 1.
Рассмотрим следующую задачу. Пусть заранее заданы вероятности оши
бок о и 13. Определим, каким должно быть минимальное число n' == n'(а, {3)
наблюдений, необходимых для Toro, чтобы ошибочные заключения моrли
быть сделаны с вероятностями, не превосходящими а и {3
Из (13) следует, что {3(о, n) с ростом n убывает к нулю, поэтому искомое
число n' есть наименьшее из тех n, для которых (3(0, n) ::;; (3. Для определе
ния n имеем два уравнения:
( 8) 80 )
ф( tа) == о и Ф t a .;n == {3.
Пусть (р обозначает р квантиль стандартноrо
#(0, 1) , T. е. Ф(р) == р. Torдa
81 80
to == (о, t o ,;n == ({З,
(7"
нормальноrо распределения
2 (о + (0)2
Т.е. n == (7" (8, (0)2.
iI Число наблюдений
в критерии
.Неймона Пирсона
Но n должно быть целым числом, поэтому надо по
л ожить
. == [ 2 (0 + (0)2 ] + 1 ( 14 )
n и (8, (0)2 '
rде [а] целая часть а. Отсюда следует, что при фиксированных ошибках а
и {3 число необходимых наблюдений пропорционально дисперсии и 2 и об
ратно пропорционально квадрату разности между rипотетическими средними.
5.2. Критерий Неймана Пuрсона
381
Если, например, о == fЗ == 0,001, то (а == (jЗ == 3,09 и из ФОРМУЛbl (14) имеем
. 38,20'2
n == (01 00)2 + 1.
При 0'2 == 1, 01 00 == 1 значение n. == 39. Таким образом, если требуется
различить rипотеЗbl с указаННblМИ параметрами, то только при числе ИСПblта
ний, не меньшем 39, можно быть уверенным в том, что, следуя критерию (10),
будет принято ошибочное решение с вероятностью, не большей 0,001.
Наконец, здесь леrко решается и вопрос о поведении «Близкие» ..,.
критерия при «близких» альтернативах (см. конец п.2).
Пусть, например, решается задача (но, нп и рассматри
ваются «близкие» альтернаТИВbI вида
HI 0== Oln == 00 + Еn,
rде Еn t о при n -----7 00. Тоrда из (11) имеем
. *+ ( V1i )
W(Oln, X 1a ) ф En t a -----------1
альтернативы
1, если v'nEn -----700,
1 == Ф ( t a ), а
если Еn == V1i ' а> О,
-----------1
а если En==O( ).
Orcюда следует, что в данном случае «пороroВblе» альтернативы имеют вид
а
Oln == 00 + .;N '
а> О константа; более близкие альтернаТИВbI (Oln 00 == o(l/v'n)) от Но
асимптотически не отличаются, а более далекие (v'n(Oln 00) -----7 00) улав
ливаются критерием с вероятностью, стремящейся к 1 при n -----7 00, коrда они
вернЬ! (т. е. против таких «близких» альтернатив критерий сохраняет свойство
состоятельности). Итак, для больших выборок критерий Неймана Пирсона
X : (как и критерий X; (12)) способен различать rипотеЗbl, сближающиеся
со скоростью 1 / v'n .
в качестве важноrо приложения этих результатов по II\II8Ir'Сравнение ..,.
строим критерий для проверки rипотеЗbl о равенстве cpeд двух средних
них двух незаВИСИМblХ нормалЬНblХ выборок. Более KOH
кретно, речь идет об известной нам задаче сравнения двух средних (см. пример 2
2.5) в следующем варианте: пусть Х и У ВblБОРОЧНblе средние двух He
заВИСИМblХ Вblборок объемов n и т из распределений N(OI' O' ) И N(02, O' )
соответственно (дисперсии 0'; извеСТНbI) и требуется проверить rипотезу о pa
венстве средних Но: Ь, == 01 (}2 == О против альтернативы HI+ : Ь, == ь'о > О.
382
rлава 5. Параметрuческuе 2uпотезы
в качестве тестовой статистики здесь естественно взять Т == (Х Y)/(J",
rде (J"2 == (J";/n + l7i/m (см. таблицу в п. 1 3.8). Леrко находим, что распре
деление этой статистики при обеих rипотезах имеет вид: [(TIHo) == N(O, 1),
[(TIHn == N(/1o/l7, 1), таким образом, вданном случае речь идет о различе
нии двух простых rипотез о среднем нормальноrо распределения с единичной
дисперсией по одному наблюдению над случайной величиной Т. Следователь
но, можно воспользоваться вариантом критерия Неймана Пирсона (10) при
n == 1. В итоrе имеем, что искомый критерий имеет вид х;: == {Т t a },
Ф( tа) == а, а вероятность ошибки 2 ro рода (см. (13)) fЭ == Ф(t а /10/17). .
Пример 2 (Проверка rипотез АЛя дисперсии нормальноrо распределения).
Пусть Х == (Х" , х п ) выборка из распределения N("", 82) ("" известно),
о котором выдвинуты две простые rипотезы Но 8 == 80 и HI 8 == 8, < 80.
Чтобы построить критерий Неймана Пирсона для различения этих rипотез,
найдем сначала статистику отношения правдоподобия
n
П e (X; !J)'/2Bi
. , v'21r8,
l(X) == I
П e (Xi !J)'/2BJ
i 1 ../ii8 0
( 8 ) n { 82 82 }
8 ехр 858;' Т ,
n
Т == I:(X; ",,)2
i 1
Здесь [в(Т/8 2 ) == i(n) (см. пример 3 3.8) инеравенство l(X) с экви
валентно неравенству Т:>:; t, поэтому при уровне значимости а критическая
rpаница t == t a определяется из условия
а == Р{Т :>:; talHo} == р" ( ),
rде Fn(t) функция распределения закона х2(n). Отсюда ta./ 8 5 == Х;,п
2 ( ) v v
а квантиль распределения Х n и искомыи критерии имеет вид
X == {Т :>:; 05 X ,n}'
Ero мощность
( * ) { 2 2 I } ( 2 85 )
w 8,; Х'а == Р Т:>:; 80 Ха,п НI == р" Ха,п о; .
Аналоrично находим, что при 8, > 80 критерий имеет вид
Х;: == {Т 8 Xi a,n}
и имеет мощность
( *+ ) ( 2 8б )
W8 1 ;X'a ==1 Fn X' a'n 8; .
.
5.2. Критерий Неймана Пирсона
383
Пример 3 (MHoroMepHoe нормальное распределение, критерий Неймана
Пирсона для вектора средних). Пусть == ( ),... , {k), k ;?; 2, нормаль
ный случайный вектор, имеющий при rипотезе H i распределение N(!!:..(i), ),
i == О, 1 (общая дисперсионная матрица известна и предполаrается невырож
денной, см. п. 2 1.2). Построим критерий Неймана ПирсонадЛЯ различения
rипотез НО и НI по одному наблюдению Haд .
В данном СЛУ'Iае отношение правдоподобия в соответствии с (9) 1.2 есть
f( IJL(I), ) { 1 [( ( 0 ) ' I ( О ) ( 1 ) ' I ( 1 ) ] }
l( == == ехр ;f JL ) (;f JL ) ( JL ) ( JL) .
f(;fI!!:..(O), ) 2
Непосредственно проверяется, что выражение в квадратных скобках равно
(!!:..(О) !!:..(I»' I(!!:..(O) + !!:..(I» 2(!!:..(0) !!:..(I»' I;f,
поэтому обозначив
Q == 1 (!!:..(О) i»,
критическую область критерия ХI == {l(;f) ;?; с} можно записать в виде
ХI (с) == { Q' Q'(!!:..(O) + !!:..(I» ::;; С) == Iп с} (15)
Рассмотрим случайную величину
У == Q' Q' (JL(O) + JL(I».
2
Как линейная функция от эта величина распределена по нормальному
закону при обеих rипотезаХ, следовательно, чтобы найти ее распределения
L:(YIH i ), i == О, 1, достаточно определить только ее первые и вторые моменты.
Имеем
E(YIH i ) == Q' JL(i) Q' (JL(O) + JL(I» == { pj2 при == О,
2 pj2 при z == 1,
rде
р == Q'(!!:..(O) !!:..(I» == (!!:..(О) !!:..(I»' I(!!:..(O) !!:..(I», (16)
а
D(YIHi) == D(Q'{IH i ) == Q'r,Q == р, i == 0,1.
Таким образом, L:(YIH i ) == N(( 1)ip/2,p), i == О, 1,
величина р, определенная в (16), называется расстоянием
Махаланобиса 1) между распределениями N(f!:.(i), r,), i == 0,1
Р ояни " ..,
Мохапано6исо
1) Махаланобис Прасанта Чандра (1893 1972) индийский экономист, статистик. Иностр.
член АН СССР (1958).
384
rлава 5. Параметрuческuе 2uпотезы
(или между rипотезами Но и Н). Отсюда находим вероятности ошибок l ro
и 2 ro рода критерия Xi(C):
( С) Р/2 )
а(с) == Р{У cllHo} == Ф VP .
( Cl+P/2 )
{3(с) == Р{У > c11H 1 } == ф VP .
(17)
Если задан уровень значимости (вероятность ошибки I ro рода) а, то крити
ческая rpаница СI в (15) должна быть взята в виде
Р
Сl == 2' + ..jp (". Ф( (а) == а.
В итоrе получаем, что в рассматриваемой задаче (Но, H 1 ) критерий Неймана
Пиреона при уровне значимости а задается критической областью
X " == { Q' ( !!:.(о) ..jp (,,}
и ero мощность равна Ф(..jp + (,,).
( Ig)
.
Замечание. ИзлаrаеМblЙ ПОДХОД к построению оптимальноrо критерия в зацаче раз
личения двух простых rипотез, связаННblЙ с именами Неймана и Пирсона, является
общеПРИНЯТblМ (классическим) вариантом, но он не есть единственно ВОЗМОЖНblЙ.
Друrой вариант, также основаННblЙ на сравнении правдоподобий данных при pac
сматриваеМblХ rипотезах, представляет следующее yrверждение.
Теорема 2. Пусть по наблюдению Х требуется различить два распределения
с плотностями /о(Х) (rипотеза но) и /.(х) (rипотеза Н). Рассмотрим класс
критериев вида
Xl(C) == {х /,(х) с/о(х)}, С> О, (19)
и пусть а(с) и {3(с) соответствующие вероятности ошибок l ro и 2 ro
родов. TorAa
{3(с) 1 {3(с)
1) 1 а(с) С а(с) ,
2) а(с) + {3(с) 1,
3) min(a(c) + {3(с» == a(l) + {3(I),
с
4) если Х есть случайная выборка объема n и
/ /1 (х)
/о(х) lп /о(х) dx == (j < О.
то вероятности О'п И {3п ошибок оптимальноrо критерия Х) (1) удовле
творяют условию О'п, {3п ---+ О при n ---+ 00.
5.2. Критерий Неймана Пирсона
385
Доказательство.
1) Утверждение следует из очевидных соотношений
а(с) == / /о(х) dx / /l(X) dx == (l {3(с»,
Х,(с) .1:,(С)
{3(с) == / /I(X) dx с / /о(Х) dx = с(l а(с», Хо(с) == jl(c).
.1:0(С) :1:0(С)
2) Пусть с > 1, Torдa, используя первое из предыдущих соотношений, имеем
1
а(с) + (3(с) (1 (3(с» + {3(с) < 1.
с
При с 1 используем второе неравенство:
а(с) + (3(с) а(с) + c(1 а(с» 1.
З) Пусть с > 1. Тоrда исходим из соотношения
а(с) + {3(с) == / /о(Х) dx + / /I(X) dx == 1 / (f1(X) /о(Х» dx.
.1:,(С) .1:0(С) :1: ,(С)
Очевидно, X1(c) X J (I) и на множестве X1(1) разность /I(X) 'о(Х) о.
Следовательно,
/ (f1(X) /о(Х» dx / (/I(x) /о(Х» dx,
Х,(с) .1:,(1)
откуда а(с) + {3(с) a(l) + (3(I).
При с < I рассуждаем аналоrично, исходя из соотношения
а(с) + (3(с) == 1 / ио(х) /J(X» dx.
.1:0(С)
4) Пусть
n
Х == (X 1 ,.... Х п ), /j( ) == п /j(Xi). j == 0,1.
i t
Рассмотрим статистику
I fJ(X i )
Тп(Х) == L..J In I (х . ) .
n i 1 )0 .
Если верна rипотеза НО, то на основании закона больших чисел при
n 00
Тп(Х) Е(1П : 'НО) == / fo(x) 1n : dx == о,
25 За",,] 1748
38б
rлава 5. Параметрические zuпотезы
при этом, соrласно неравенству Йенсена (о нем см. в п. 5 4.2), Bcerдa
6:::; О. Далее, из (19) следует, что в данном случае множество ):1(1) можно
записать в виде
):1(1) == {f. == (XI,..., Х n ) : Tn(f.) О},
поэтому при fJ < О.
а п == Р{Тn (Х) OIHo} :::; Р{ IТn(Х) 61 1611Но} --------+ О,
(20)
если n ----+ 00. В силу симметрии (если поменять ролями Но и H 1 ) также
и fЗn ----+ О. .
Таким образом, если в концепции Неймана Пирсона, вместо минимиза
ции вероятности ошибки 2 ro рода при фиксированной вероятности ошибки
I ro рода, исходить из минимизации суммы вероятностей ошибок, то мы
придем к оптимальному критерию ):1(1) вида (19) (или (20»). При этом при
бесконечно большой выборке критерий ):1(1) Рa3lIичает rипотезы Но и Н)
(в случае 6 < О) безошибочно.
Пример 3 (Продолжение). В этой задаче критерием, минимизирующим CYM
МУ вероятностей ошибок, является (см. (15»)
):.(1) == {f. !!' :::; !!'(f!..(O) + f!..(I))},
(21 )
и эта сумма равна в силу (17)
a(l) +fЗ(l) == 2Ф( V; ).
.
3. Критерий Неймана Пирсона
в случае дискретных распределений
Аналоrичные рассуждения можно провести и для дискретных распределений,
для которых вероятности Jj(Z/;) > О, j == О, 1, для всех Zk ВОЗМОЖНblХ зна
чений наблюдаемой случайной величины . Общий принцип здесь остается
прежним: «упорядочивают» выборочные точки f. == (XI"'" Х n ) в COOTBeT
ствии с величиной отношения правдоподобия
n
П !1(Xi)
( \ L(f.; (1) i=1
1 ;f} == ==
L(f.; (0) П N
!O(Xi)
i=1
и включают в критическое множество ):, максимальное число их, соrласую
щееся с требованием
:Е L(f.; (0) :::; а.
!ЕХI
5.2. Критерий Неймана Пирсона
387
Однако в отличие от непрерывноro случая здесь в силу дискретности, вообще
rоворя, уже нельзя получить точное значение а за счет выбора rpаницы с
в неравенстве Ц ) с, определяющем множество X I : может быть так, что,
включив в Х ! очередную точку мы еще не достиrнем уровня о, а включив
следующую превзойдем ero. Детальнее это можно объяснить следующим
образом. Обозначим < l/,: < lk+1 < возможные значения статистики
I(X). Тоща при заданном уровне а можно определить такое k == k(a). что
L: L( ; во) < а L: L( ; во).
(22)
;!i:/(!J /HI
;!i:l(;!i) lk
Если здесь в правой части имеет место знак равенства, то полаraя
X a == { : l( lk(a)}
и повторяя рассуждения, проведенные в п. 2, можно показать, что критическая
область X a является оптимальной, т. е. основанный на ней критерий
I Но отверrается {::::::} I(X) Е X a I
(23)
имеет наибольшую мощность при альтернативе Нl среди всех критериев ypOB
ня значимости о.
Пусть теперь в (22) имеют место строrие неравенства (так чаще Bcero и
бывает). Обозначим
aj == L: L( ; lJj), j == О, 1,
;!i:/<!) /HI
(24)
Pj == Pj{I(X) == lk} == L: L( ;(Jj), j == О, 1.
;!i : /<!)=/k
Тоrда соотношение (22) можно записать в виде 00 < а < Оо+Ро. Чтобы в этом
случае построить критерий с уровнем значимоСТИ о, надо использовать прием
рандомизации, т. е. ПОС1Упить следующим образом. Коrда выполняется paBeH
ство Ц ) == lk(a), произвести дополнительный случайный эксперимент с ДBY
мя исходами ii и R, вероятности которых равны соответственно (о ао)!ро
и I (а ао)!ро (дrlя этоrо можно воспользоваться алroритмом п. 2 1.3),
и OTBeprHyrb rипотезу Но, если наблюдается ii, и принять Но в против
ном случае. Если же l(f.) > lk(a), то rипотезу Но следует oTBeprHyrb, а при
l( ) < l/':(a) принять. Друrими словами, мы С'J1!ОИМ рандомизированный
критерий с критической функцией
{I при 1 (f.) > lk(a),
a oo 1 (f.) == l/':(a). (25)
'P.( == при
ро
О при l( < lk(a).
25-
388
rлава 5. Параметрuческuе zuпотезы
Вероятность ошибки I ro рода тaKoro критерия в соответствии с (24) равна
a ао
P{HIIHo} == Ео'Р'(Х) == Po{l(X) > lk(a)} + Ро{ЦХ) == lk(a)} ==
Ро
a ао
== ао + ро == а,
Ро
т. е. критерий 'Р* имеет уровень значимости в точности равный а. Ero мощ
ность вычисляется аналоrично:
*. (а ао)Рl
W(8 1 ; 'Р ) == E1'P (Х) == а( + .
Ро
Покажем, что это наиболее мощный критерий в задаче (но, H 1 ) Pac
смотрим произвольный критерий 'Р с уровнем значимости а Ео'Р(Х) == а,
и обозначим х:!: == { : 'P'(iJ 'P( ) О} (знак +( ) соответствует HepaBeH
ству> «». Если Е х+, то 'P'( ) > О и поэтому L( ; (1) lkL( ; 00); если
Е x , то 'P( < ] и, следовательно, L( ; (1) lkL( ; (0), Таким образом,
2:('P'( ) 'P( ») (L( ; 01) lkL( ; (0») == L + 2: О.
1. EX+ EX
Orсюда дIIЯ разности мощностей получаем
Е('Р'(Х) E1'P(X) == L('P'( ) 'P( »)L( ;81)
lk L ('P'( ) 'P(iJ)L( ; (0) ==
J.
== lk(Eo'P'(X) Ео'Р'(Х») == lk(a а) == О,
Т.е. W(8(; 'Р*) W(8 1 ; 'Р).
И [ак, в дискретном случае также Bcerдa можно построить наиболее мощ
ный критерий с заданным уровнем значимости а, но такой критерий, вообще
rоворя, является уже ращомизированным. Отметим, что рандомизация бы
вает необходима лишь на поrpаничном множестве { Ц ) == lk(a)} и только
в том случае, коrда желательно иметь вероятность ошибки I ro рода paB
ной точно а. На практике предпочитают в таких случаях (т. е. коrда в (22)
имеют место строrие неравенства) несколько изменить уровень значимости
так, чтобы отпала необходимость в рандомизации, т. е. заменить а на MeHЬ
ший уровень ао (см. (24» и использовать нерандомизированный критерий
X ao == {l( lk(a)+I} вида (23), который, по предыдущему, является наи
более мощным критерием уровня значимости ао «а). Можно также ис
пользовать еще один нерандомизированный критерий X a' == {l( ) lk(a)}
С б6льшим уровнем значимости а' == ао + Ро. Далее мы проиллюстрируем эти
общие положения несколькими примерами.
95.2. Критерий Неймана Пирсона
389
Пример 4 (6ернуллиевская модель, проверка простых rипотеэ). Пусть о He
известной вероятности ('успеха') В в бернуллиевской модели Bi(l, О) имеются
две простые rипотезы: Но В == 00 и H О == 01 > 00. Здесь для любой точки
== (Хl"", х п ), Xj Е {О,I}, i == 1,..., n, правдоподобие
L( ; B j ) == 0.1(1 Oj)n r, j == О, 1,
n
rде r == T( == L Xj наблюдавшееся число «успехов,), а их отношение
j 1
'( == [ B I (1 Bo) ] r ( ) n
00(1 (1) 1 Во
Функция I{'(О) == О!( 1 О) возрастает на интервале (О, 1), поэтому при BI > Во
l{J(fJ1)!I{'(B o ) > 1 и неравенство Ц ) с эквивалентно неравенству
( "" \ 1" с nРl
r ,
Р
rдe
( ) ( Вl(1 Во) )
РI 1" 1 00 ' р In Во(1 ( 1 ) .
Следовательно, критическая область критерия Неймана Пирсона выражает
ся в данном случае через статистику т(Х) и имеет вид
X == { T( Та}. (26)
Далее, поскольку .c(r(X)IHo) == Bi(n, (0), то для определения при заданн!>м
уровне а критической rpаницы Та имеем в соответствии с (22) условие
n n
0:0 == L C:B (I oo)n т < а L C::O(f(1 Bo)n т == 0:' (27)
m r.+1 m r.
Если здесь в правой части имеет место знак равенства (о: == 0:'), то тем
самым критерий (26) полностью определен; подчеркнем, что он не зависит
от альтернативы 01, от нее зависит лишь мощность критерия
n
W(OI; X :) == Р{т(Х) TaIHI} == L C:Or(l Bl)n т
m==r a
Чаще Bcero, однако, при заранее заданном а в (27) имеет место случай
cтpororo неравенства (а < а'); следовательно, критерий, определяемый кри
тической областью (26) будет иметь уровень значимости несколько б6льший,
чем а, а именно, равный а' В данном случае можно использовать также
наиболее мощный критерий {т(Х) Та + I} с уровнем значимости ао < а.
Если бы в данной ситуации требовалось построить критерий с уровнем
значимости, точно равным а, то следовало бы прибеrнyrь к рандомизации
и поступить следующи'м образом. Положив
ро == Р{т(Х) == ralHo} == C .O .(I Bo)n ro == а' ао,
390
rлава 5. Параметрические zuпотезы
задать критическую функцию (см. (25»
{ 1 при T( ) > Та,
О 00
'P ( == при T( ) == Та,
ро
О при T( ) < Та,
(28)
Т.е. условиться отверrзть rипотезу НО, если T( ) > Та, И принимать ее, если
T( ) < Та; если же T( ) == Та, то Но отверraется с вероятностью (о Оо)/Ро
и принимается с дополнительной вероятностью (о' о) /Ро. Тоrда вероятность
ошибки 1 ro рода тaKoro рандомизированноrо критерия равна
P{HIIHo} == EBolp (X) ==
О 00 о 00
== Рво{т(Х) > Та} + Рво{т(Х) == Та} == 00 + ро == о.
ро Ро
Мощность этоro критерия вычисляется по формуле
W(OI; 'P ) == EBI<P (X) ==
n ( О ) ro ( I О ) n r.
L с:о;п(1 (1)n т + (о (0) i 1 01
rn ro+1 О О
Случай 0\ < 00 рассматривается аналоrично, при этом критическая об
q ласть имеет вид {T( Та}.
Большие выборки Для случая больших выборок (n ----+ 00) по теореме
Муавра Лаnласа
.св(т(Х» "'" N(nfJ, n8(1 О»,
поэтому условие (27) можно заменить приближенным условием
( n(Jo Т а )
Рво{т(Х) Та} Ф == о,
V n(JO(! 00)
Т.е.
n80 Та
== (а'
V n8 0(1 (0)
Отсюда получаем асимптотический вариант критерия Неймана Пирсона в
нашей задаче
X ; == {т(Х) nОо (а ! n80(1 оо)}, Ф«(а) == о. (29)
Вычислим, наконец, мощность критерия (29) при ",близкой» альтернативе
+ 6
Н 1п 8==О1п==8 о + y'тi '
б> О.
5.2. Критерий Неймана Пирсона
391
Имеем
W(8 1n ) == Р8,. {r(x) п80 (o yl n8 0 (1 8 0 )} ==
{ r(X) п8 1п t5
== р 81. (о
у п8 1п (1 8 1п ) y 8 1n(1 8 1п )
Ф ( t5 +(0 )
у 80( 1 80)
Пример 5 (Пуассоновская МОАепь, проверка простых rипотеэ). Рассмотрим
задачу различения двух простых rипотез H j 8 == 8j, i == О, 1, О < 80 < 81, для
пуассоновской модели П(8). Схема рассуждений здесь такая же, как в преды
дущем примере. Статистика отношения правдоподобия есть
I(X) == ( : ) т. еп(8о 81) , ТП == t X j ,
j I
80(1 (0) }
8 1п (1 8 1п )
.
'т. е. выражается через достаточную статистику модели П(8) (см. п. 1 З.З),
при этом L8(T n ) == П(п8) (см. п. 3 1.1). В терминах статистики ТП критерий
задается критической областью вида {ТП t o }, rде критическая f1)аница t o
при уровне значимости а определяется условием
ао == e nllo (п8 0 )т < а е П80 (п80)т == а'
L.J т! L.J т!
ffl to+l m to
При а == а' оптимальный критерий имеет вид X o == {ТП t o }; если же а < а' ,
то можно использовать нерандомизированные наиболее мощные критерии
X o' == {ТП t o } И X oo == {ТП t o + l} с уровнями значимости COOT
ветственно а' > а и ао < а. В случае а < а' можно построить также
рандомизированный критерий с уровнем значимости в точности равным а:
ero критическая функция 'P (T) имеет такой же вид, как (28) в предьщу
щем примере (с учетом обозначений, принятых в (ЗО), В частности, здесь
, n80 (n8 0 )t o )
РО == а ао == е .
t o !
В любом случае мощность вычисляется по формуле
00 ( п8 ) т ( 8 ) to
W(8 1 ) == '" e nll, + (а ао).....!. е п(81 8о)
L.J т! 80
m to+l
(30)
Если n 00, то по центральной предельной Teope
ме L8 (ТА) '" N (п8, п8), и рассуждая как в предьщущем
примере, получим, что асимптотическая форма критерия Неймана Пуассона
имеет вид {ТА п80 (o }. а ero мощность при близкой альтернативе
81 == 8 1п == 80 + fJjvlтi, fJ > О, удометворяет предельному соотношению
Iim W(8 1n ) == Ф ( + (о ) .
п--+оо V 80
tf
Большие выборки
392
rлава 5. Параметрические zuпотеЗbf
Подчеркнем, что в любом случае вид оптимальной критической области здесь
также не зависит от альтернативы 01. .
Пример б (Полиномиальная модель, проверка простых rипотез). Пусть по
наблюдению вектора частот исходов!!. == (Vl, .., VN) В n ИСПblтаниях требу
ется различить две простые rипотеЗbl о векторе вероятностей исходов в по
линомиальной модели М(n; О) (см. п. 6 1.1): Но 8 == l!. == (Pl, ,PN)
И Нl О == q == (ql, . . . , qN) (все О < Pi, qi < 1). Здесь статистика отношения
правдоподобия
l(!D == ft ( qi ) V;
i l Р,
поэтому, переходя к лоrарифмам, запишем критическую область наиболее
мощноro критерия в виде
N
X == {Тп == Vi In ( ;; ) l}. (31)
Для расчета критической rpаНИЦbl и мощности тэкоrо критерия можно BOC
пользоваться центральной предельной теоремой дпя полиномиальноrо pac
пределения (см. упр. 33 к rл.I), справедпивой при n ..... 00. Тестовая статисти
ка Т" в (31) как линейная функция асимптотически нормальноrо вектора !!.
будет иметь асимптотически нормальное распределение при обеих rипотезах
(см. п. 2 1.2), поэтому нам нужно вычислить лишь средние и дисперсии
статистики Тп при rипотезах Но и Hl. Из формул (16) 1.1 имеем
N ( qi )
E(TnIHo) == n L Pi ln = nао,
' l Р,
N ( qi )
E(TnIHI) == n L qi]n = пaj,
' l Р,
N
D(TnIHo) == n LPi(1 pi) ln 2 ( Qi. ) n LPiPj ln ( qi ) ln ( qj )
.=1 Р. . j Р, Р]
[ N N 2 ]
== n Pi In 2 ( ;; ) ( Pi ln ( ;: ) ) = nb ,
(32)
и аналоrично
N N 2
D(TnIHl) == n [ q. ]п 2 ( ;: ) ( Qi ln ( ;:) ) ]
Ь 2
== n ).
.
Большие Вblборки
Таким образом при больших n можно воспользо
ваться нормальной аппроксимацией
.L:(TnIHi) '" N(nai, nЬ;), i == О, 1,
5.2. Критерий Неймана Пирсона
393
с указанными в (32) параметрами. Отсюда уже стандартными рассуждениями
получаем, что асимптотический (при n ----+ 00) вариант критерия (3 1) при
уровне значимости а есть
N
Xra == { L: vj !п q ? nао +..;n Ь О ta } , ф( tа) == а. (33)
i 1 PI
Для вероятности ошибки 2 ro рода получаем соотношение
{ Тn nа! ао аl Ь О I }
fЗn == P{HoIHl} == Р VnЬ ! :::;..;n + ь;t а Н ! .
(34)
По неравенству Йенсена ао < О, аl > О, поэтому, если rипотезы фиксиро
ваны, а n ----+ 00, то отсюда лишь следует, что fЗn ----+ О. Более определенные ,
зак.лючения можно сделать, рассматривая «близ Б
« лиэкие» альтернаТИВbI
кие» альтернативы, которые в данном случае удоб " ;, "" ' ' ,
но задать в виде
qi == qi (n) == Р; ( I + ), i == 1,. " N,
тах 16 i l :::; с < 00,
i
N
L: Pi 6 i == о.
i 1
в этом случае из формул (32) имеем (поскольку !п (1 + е) == е .02/2 + 0(.0)))
N
qj
аl ао == L:(qi Pi) !п ==
i l Р;
1 n ( 6; ( 1 ) ) 1 N 2 ( 1 )
== vn Pi 6 i vn + о;:; == ;:; Pi 6 i + О n3/2 '
N
2 2 1 '"" 2
Ь О rv Ь 1 rv L.J Pi6i .
2n .
I I
Поэтому, обозначив
N
62 == L:р;б;.
i I
из (34) получим, что при n ----+ 00
fЗn ---------+ Ф( J2 6 + t a ),
сам же критерий (33) может быть записан в виде
{ 62 6 }
Xra == Тn? "2 + v'2 t a .
.
394
rлава 5. Параметричесние zипотезы
5.3. Сложные rипотезы
Случаи, Korдa основная и альтернативная rипотезы являются простыми, Bcтpe
чаются в приложениях сравнительно редко. На практике чаще имеют место
ситуации, Korдa обе rипотезы (или по крайней мере одна из них) сложные.
В этих случаях равномерно наиболее мощные (р. н. м.) критерии существуют
только если модель:F == {Р(х; В), В Е 8} обладает определенными свойства
ми. Рассмотрим некоторые наиболее типичные случаи.
1. Р. н. м. критерии против сложных односторонних альтернатив.
Модели с монотонным отношением правдоподо6ия
Пусть проверяется простая rипотеза Но () == (}о против сложной альтернативы
Н! : В Е 81 == 8\ {Во}. Построим критерий Неймана Пирсона Xro == xro, ((}о (}J)
ДJlя фиксированной альтернативы Вl Е 81, как это описано в 5.2. Если этот
критерий (т. е. вид соответствующей критической области) зависит от (}I, то
это значит, что не существует критической области, которая была бы наилуч
щей для всех (), Е 81' Друrими словами, в этом случае не существует р. н. М. к.
Однако может оказаться, что критерий Xro((}o, (}l) не зависит от конкретной
альтернативы ВI Xro(Bo, ( 1 ) == xro(Bo). Torдa соответствующая критическая
область максимизирует мощность при любой допустимой альтернативе и по
этому Xro(Bo) является р. н. м. к. В задаче (Но () == Во, НI В Е 81),
Такие случаи уже встречались нам в 5.2. Так, в примере 1 (COOTHO
щение (10)) построен критерий Неймана Пирсона в задаче (Но () == (}l,
НI () == ()! > (}о) для нормальной модели N(B, (1'2), который оказался не зави
сящим от альтернативы В) , следовательно, этот критерий x : является р. н. м.
критерием при сложной правосторонней альтернативе Hl+ () > Во- Аналоrич
но, р. н. м. критерием при сложной левостОРОl1l1ей альтернативе Н! В < (}о
в этой модели является критерий (12). Такие же заЮlючения можно cдe
лать о критериях, построенных в при мерах 2,4,5. Таким образом, здесь мы
имеем примеры существования р. н. м. критериев проверки простой rипоте
зы Но при сложных односторонних альтернативах в случае скалярноro па
раметра. Если же в этих задачах рассматривать полный класс альтернатив
НI == Н)+ U Н! В f= Во, то р. н. м. к. не существует, так как при альтернати
вах В > (}о и () < Во критерии различаются.
Рассмотренные примеры характерны следующими двумя обcroятельствами:
1) в каждом из них статистика отношения правдоподобия l(X) зависит от
данных Х через достаточную статистику соответствующей модели (Ha
пример, в примере 1 это выборочное среднее Х: в примере 2 выбо
рочная дисперсия (с точностью до коэффициента) и т.д.);
2) l(X) является монотонной функцией от достаточной статистики, в силу
чеrо, неравенство l(X) с, определяющее оптимальную критичеСI<;:УЮ
область, эквивалентно аналоrичному (одностороннему) неравенству ДJlя
соответствующей достаточной статистики. Эти факторы имеют общую
природу, и они приводят К следующему общему результату.
5.3. Сложные zuпотезы
395
Предположим, что 8 скаляр и альтернатива Нl односторонняя (т. е.
либо Нl == Н, 8 < 80, либо HI == HI+ 8 > (0), основная же rипотеза
Но 8 == 80 простая. Пусть, далее, семейство F == {Р(х; 8), 8 Е 8}
обладает достаточной статистикой Т == Т(Х) (см. теорему I 3.3) и статистика
отношения правдоподобня
( ) g(T(X); (1)
1 Х ==
g(T(X); (0)
является монотонной функцией от Т (Torдa roворят, что Монотонное
модель :F обладает монотонным отношением npaвдoпoдo отношение
6ия, мноrие стандартные модели таковы, например, правдоподобия
:F == N(8, (j2), N(j1., (2), Bi(k, 8), П(8), Bi (r, 8), r(8, ),».
Torдa в задаче (но, Н]) существует р. Н. м. критерий, совпадающий с критерием
Неймана Пирсона при произвольной фиксированной альтернативе из Hl.
Докозотельство. Пусть, например, Нl == HI+ И при фиксированном 81 > 80
отношение g(T; (1)/ g(T; (0) t по т. Построим критерий Неймана Пирсона
в задаче (80, (1), В данном случае неравенство [(Х) с {==::} Т(Х) ct,
причем rpаница с: определяется лишь распределением
Р(х; (0) P/lo{T(X) ct} == а.
Таким образом, критерий X : == {Т(Х) с:} не зависит от конкретной алъ
тернативы 81 > 80, следовательно, он есть р. н. м. к. для задачи (Но, н)+).
Если g(T; ( 1 )/g(T; (0) -t. по Т, то неравенство для Т заменяется на проти
воположное. Аналоrично рассматривается и случай левосторонней альтерна
тивы Н, .
Замечание, Можно доказать [16, с. 101], что для моделей с монотонным отношением
правдоподобия р. н. м. критерий в задаче (Но: 8 == 80, HI+ 8 > (0) является OДHOBpe
МеННО р. н. м. критерием проверки сложной rипотезы Но (J 8о против HI+ TOro же
уровня значимости. Аналоrичное утверждение справедливо и для двойственной про
блемы про верки сложной rипотезы НО : (J 80 против левосторонней альтернативы
Н! 8 < 80'
В частности, для экспоненциальной модели, введенной в п. 3 3.2, плот
ность которой имеет вид
'(х; 8) == ехр {А(8)В(х) + С(8) + D(x)},
( 1)
статистика
n
Т(Х) == I: B(Xj)
j l
является достаточной и
l( ) == ехр {( А(8) А(80) )Т(Х) + п( С(8 1 ) С(8 0 ») }.
Следовательно, если функция А(8) cтporo монотонна, то l(X) монотонная
функция Т, поэтому для такой модели всеrда существует р. н. м. К. против
39б
rпaBa 5. ПараметричеСl<uе zипотезы
односторонних альтернатив. Вид критических областей указан в следующей
таблице
н,+ О > 80 HI (J < 00
А(8) t Т(Х) с: Т(Х) :::; с;;
А(8) .j. Т(Х) :::; с: Т(Х) с;;
Пример 1 (Выборочный контроль: биномиальный выбор). В процессе про
изводства изделия обычно подверrают выборочному статистическому KOHтpO
лю. Предположим, что каждое изделие независимо от друrих может оказать
ся дефектным с некоторой одной и той же, но неизвестной вероятностью 8
(О < () < 1) и исправным с дополнительной вероятностью 1 8 Пусть для KOH
троля взято n изделий и результат описывается вектором Х == (X 1 , ,Х n ),
rде X j == 1, если i e изделие дефектно, и Xj == О в противном случае. Часто
бывает нужно проверить rипотезу НО 8 80, rде 80 некоторая кри
тическая доля брака (если rипотеза НО истинна, то процесс производства
необходимо приостановить и усовершенствовать для уменьшения доли бра
ка). При сделанных предположениях число т(Х) == Х) + + Х N дефектных
изделий в выборке имеет биномиальное распределение Bi( n, О), к которому
применима изложенная выше теория. Следовательно, существует р. н. М. кри
терий про верки rипотезы НО против альтернативы H) () < ()о, который
задается критической областью вида {т(Х) Та}. Критическая rpаница Та
вычисляется здесь так же, как в при мере 4 5.2. .
Пример 2 (Обратный биномиальный выбор). В условиях предьщущеrо при
мера иноrда применяют друrой план контроля, который называется обратным
биномиальным выбором. В этом случае испытания продолжают до получения
заданноrо числа т <'успехов» (здесь под .успехом» понимается обнаружение дe
фектноro изделия). Пусть У; число испытаний между (i 1) M и i M .успе
хами». Torдa Y 1 , .., У Т независимые rеометрические случайные величины:
РО{У 1 == у} == ()( 1 О)У
у == О, 1, 2, . . . ,
т. е. У == (Y 1 , , У Т ) выборка из распределения Bi (I, 1 О) (см. п. 2 1.1),
которое является распределением экспоненциальноrо типа (1) с
Tr(Y) == L У; и А(О) == In (1 О).
i==1
Так как А(8) убывающая функция О, то в задаче (НО () 00, Hl (J < ()о)
р.Н. м. к. существует и имеет вид (см. таблицу) {Tr(Y) c }. Этот вывод co
ответствует и интуитивному представлению, так как при больших значениях (J
естественно ожидать, что r й «успех» наступит достаточно быстро, поэтому
большие значения Т естественно трактовать как свидетельствующие против
rипотезы Но (в пользу альтернативы н,). Для расчета крнтнческой rpаницы
5.3. (ложные zипотезы
397
используют тот факт, что L@(Tr(Y)) == Bi (T, 1 О), следовательно, при задан
ном уровне значимости а rpаница C определяется условием (см. (6) 1.1)
00 00
ао == L C:+X I(1 (1 (10)1: < а :::; L C;+X l(1 (1 (10)1: == а/ (2)
1: C; + I
х==с;
Дальнейшие рассуждения такие же, как в примерах 4 и 5 5.2. Если а == а/,
то критерий нерандомизированный и есть X; == {Tr(Y) C } Если же
а < а', то можно использовать любой из нерандомизированных критериев
Х;;;' == {Tr(Y) C } или x; o == {Tr(Y) C + 1} с уровнями значимости
соответственно а/ и ао, либо строить рандомизированный критерий с помо
шью критической функции Ip в (28) 5.2 (с учетом обозначений, принятых
в (2), в частности, здесь РО == а' ао == C C; 100(1 оо)с;;).
Особенно прост будет критерий при т == 1, т. е. коrда тестовой статисти
кой является У 1 число испытаний, предшествуюших появлению первоrо
дефектноrо изделия. В этом случае условие (2) записывается в виде
ао == (1 (10)C;;+1 < а:;;; (1 (10)С;; == а',
поэтому при уровне значимости а == (1 (}o)s при заданном целом s 1 кри
терий задается критической областью X; == {У; s} и ero мощность при
произвольной альтернативе (}l < (10 есть
00
W(OI) == Ре,{У; 5} == L (}I(l (}I)Y == (l (}I)S
11=
Наконец, при больших т можно воспользоваться центральной предель
ной теоремой и получить нормальную аппроксимацию для распределения
статистики Tr(Y) , именно (см. (7) 1.1), при т ---+ 00
( 1 (1 1 0 )
Le(Tr(Y») IV N ТВ' тт .
Эта аппроксимация позволяет просто рассчитать асимптотический вариант
критерия. Имеем
( T(I (1o) (}oC;; )
РВО {Tr(Y) Са} Ф
у т(1 (10)
== а,
откуда
1 (}о у' т(1 00)
Са == T (о (}о ,Ф((а) == а.
В итоrе получаем, что при больших Т и заданном уровне значимости а кри
терий имеет вид
. { 1 (10 y'T (I (}o) }
X 1a == Tr(Y) T (о (}о '
398
rлава 5. Параметрические zuпотезы
и ero мощность W r «(},) при «близких» альтернативах вида (}I == B 1r == (}О б / JТ,
6 > О, удовлетворяет предельному соотношению
lim Wr(B\r) == Ф ( + (о ) .
Т---+QO ВО 1 ВО
(3)
.
Пример 3 (Покаэатепl.ная модель, р. н. м. К. дЛЯ односторонних rипотеэ).
Предположим, что время (,жизни,) HeKOToporo техническоrо устройства есть
случайная величина , распределенная по показательному закону r(B, 1)
(см. п. 3 1.2) с неизвестным параметром В > О. Пусть Х 1, . . . ,Х n Bpe
мена «жизни» n контрольных устройств, и по этой информации требуется
про верить rипотезу НО () ВО при альтернативе Н! В < Во. Так как MO
дель r(B, 1) входит в экспоненциальное семейство (1) (для нее А«(}) == I/B
и Т(Х) == Х. + + Х n » то В нашей задаче р. н. м. критерий существует
и задается критической областью вида {Т(Х) с}. Это также ожидаемый
результат, так как параметр В есть среднее значение и потому малые значе
ния Т(Х) естественно интерпретировать в пользу альтернативы.
Заметим далее, что из свойств raмма распределения вытекает COOTHO
шение
1:.11 ( 2T X» ) == х 2 (2n)
и, следовательно, rpаницу критической области можно определить по табли
цам квантилей распределения i(2n). Именно, так как
{ 2Т(Х) 2 }
Рllо Хо,2n == а,
то при уровне значимости а р. н. м. к. В нашей задаче имеет вид
. { ( ) ВО 2 }
Xl o == Т Х "2 Хо ,2n .
Мощность этоrо критерия при произвольной альтернативе В\ < (}о вычисля
ется по формуле
{ 2Т(Х) (}о 2 } ( (}о 2 )
W«(}\) == P el ()\ Хо,2n == F2n е;-Хо,2n ,
rде F 2n (t) функция распределения закона i(2n). .
2. Двустороннне аl1l.тернативь., р, н. м. несмещенные критерии
Как уже отмечалось выше, даже для моделей экспоненциальноrо типа (1)
с монотонным отношением правдоподобия при двусторонней альтернативе
Нl == Hl U HJ+ () =1= (}о «() скалярный параметр) р. н. м. критерия, вооб
ще rоворя, не существует. В задачах с такими альтернативами) т. е. в задаче
(НО В == Во, Н\ В =1= (}о), обычно поступают следующим образом: исполь
зуют статистику Т(Х), с помощью которой строятся р. н. м. критерии против
5.3. Сложные zипотеэы
399
односторонних альтернатив H и Н+, И задают критическую область в виде
'xlo == {T( c J U {T( ;;:: c J, Т.е. объединяют две соответствующие
односторонние критические области с уровнями значимости аl и а2 таки
ми, что аl + а2 == а. Таким образом, получается целое семейство критериев
с уровнем значимости а (условие а == аl + а2 оставляет одну степень свобо
ды). В этом семействе обычно и находится оптимальный критерий. Прежде
чем формулировать соответствующие общие утверждения рассмотрим xapaK
терный иллюстративный пример.
Пример 4 (Нормальная модель с неизвестным средним, двусторонняя аль-
тернатива). Рассмотрим применение описанной методики к задаче (НО: () == (}о,
НI : () =f. (}о) в модели N«(J, 0.2). Из примера 1 5.2, как отмечено в начале п. 1,
следует, что р. н. М.к. уровня значимости аI при левосторонней альтернативе
Н, (J < ео имеет вид (12) 5.2 (с заменой а на al), ар. н. М.к. уровня зна
чимости а2 при правосторонней альтернативе Н(+ () > 00 вид (10) 5.2
(с заменой а 4 а2). Следовательно, при произвольных al, а2 таких, что
а[ + а2 == а, объединенная критическая область
{ .j1i(x (}о) .j1i(x (}о) }
,х(о == :f to, либо t 02
О О
задает критерий уровня значимости а в задаче (Но. H I ). Интуитивно предпо
чтителен выбор «симметричноrо» критерия, т. е. Korдa аl == а2 == aj2; в этом
случае получаем критерий
{ .j1ilx Bol }
,х 10 == ;f: о ;;:: t a /2 .
(4)
(5)
По кажем, что этот критерий один обладает свойством несмещенности cpe
ди всех критериев вида (4). Мощности односторонних критериев указаны
в при мере 1 5.2, откуда получаем для мощности произвольноrо критерия (4)
выражение
W(8; 'xlo) == Рв{Х Е 'x J + Рв{Х Е X ) ==
== ф ( v: д t ol ) + Ф ( v: д t (2 ) == ф(д),
д == в (}о.
Исследуем поведение функции ф(д). Ее первые две производные равны
ф'(д) == [exp { ( ": д t a2 Y} ехр { ( ": д + toIY}],
11 n [ ( .j1i ) { 1 ( .j1i ) 2 }
Ф(Д)== о2..;Т:К t02 b. ехр 2 д t02 +
+ (t a , + д ) ехр { ( д + t a , У} ]
400
rлава 5. Параметрuческuе zuпотеэы
Отсюда
ф' (д) == о {=::}
..;n ..fii
tOl A==tal+ fj.
(J" (J"
{=::}
t a , t o ,
Д == До == (J" 2Vn '
а
11 n ( ) { I 2 }
Ф (до) == (J"2..f2ii t o , + t 01 ехр "8 (t OI + t a1 ) .
При малых 0'1 и 0'2 величины t a , и t Ol положительны, следовательно,
Ф"(До) > О, т. е. до точка минимума функции ф(Д). Поскольку До == О
{=::} а, == 0'2 == 0'/2, а 1/1(0) == Ф( tаl)+Ф( tОl) == 0'1 +0'2 == а (все критерии
(4) имеют уровень значимости а), то лишь для симметричноrо критерия (5)
выполняется условие несмешенности W(8; X 1o ) > а, 'rj 8 i- 80' В остальных
случаях, т. е. при а) i- й2, критерий X 10 при некоторых альтернативах бу
дет иметь мощность меньшую а, т. е. будет смещенным (см. рис. 1). Таким
образом, среди всех критериев вида (4) лишь симметричный критерий (5)
несмещенный и, следовательно, ему надо отдать предпочтение.
-ф(Д)
До < О О До>О
t:J.
Рис. 1
Критерий (5) на самом деле обладает наибольшей мощностью среди всех
несмещенных критериев уровня значимости а, т. е. является р. н. м. HeCMe
щенным критерием. Это утверждение является следствием приводимой ниже
теоремы 1 об общем виде р. н. м. несмещенноrо критерия. .
Пусть е интервал действительной оси и 80 внутренняя точка е.
Пусть, далее, допустимые распределения абсолютно непрерывны и функ
ция правдоподобия L(;f; 8) имеет во всех внутренних точках е ПрОИЗ80ДНУЮ
aL(;f; (})/д8 == LI( ; 8) такую, что ILI( ; 8)1 M(;f) , rде M(f.) интеrри
руемая функция на выборочном пространстве Х (Torдa
:8 / L( ; 8) d == / LI ( ; 8) d
s 5
ШIя любоro подмножества S Х). Определим, наконец, множество
i la == { : L( ; 81) ?: cL( ; (0) + c)L, (;f; 8 0 )},
(6)
5.3. СлОЖНblе 2uпотезы 401
rдe 01 -1- 00 и постоянные с О и СI определяются из условий
P8 u {i 1a } == J L( ; (0) d == а, P'8u{i1a} == J LI( ; (0) d == О. (7)
х'о
X 10
Теорема 1. Если определенное в (6) множество не зависит от 01, то X 1a есть
р. н. м. несмещенный критерий уРОВНЯ значимости а ДЛЯ про верки простой
rипотезы Но 0==00 против двусторонней альтернативы НI 0-1-00'
Доказательство. Рассмотрим любой несмещенный критерий X 1a про верки
rипотезы Но О == 00. Так как мощность W (00; X 1a ) == а и производная
функции МОЩНОсти по О существует, то W'(Oo; X 1a ) == О. Как и в доказатель
стве теоремы 1 95.2, запишем равенство
P 8u {i 1a Xlai 1a } == а P8o{Xlaila} == P 8o {X 1a X,ai 1a }; (8)
кроме Toro из (7) имеем
Р'80 {Х 'а X1ai 1a } + и {x1ai 1a } == о
и аналоrично
P u{Xla xlai 1a } + P'8u{X 1a i 1a } == О,
Т.е.
P'8u{i 1a X1ai 1a } == u{Xlaila} == P'Uo{Xla X1ai 1a }. (9)
Из определения (6) множества Х 'а И равенств (8) и (9) получаем следующую
цепочку соотнощений:
Р8,{Х ,а Х,аХ ,а } cp 8u {i 1a Х,аХ ,а } + ctP'8u{i 1a x1ai 1a } ==
== cP8u{Xta Х,аХ ,а } + CI o{Xla Х,аХ ,а } P 8 ,{X 1a X1ai 1a }.
Отсюда следует, что p 8 ,{i 1a } Р 8 , {X 1a }, Т.е. критерий Х'а имеет наиболь
шую мощность среди всех несмещенных критериев Toro же уровня значимо
сти а при альтернативе 01. Но по условию, множество X ta не зависит от 01 ,
поэтому этот критерий ЯRJ1яется р. н. м. несмещенным критерием против лю
бой против любой допустимой альтернативы 01 -1- 00. .
I Замечание. Аналоrичное yrвержденне справешlИВО также И ШlЯ дискретных моделей
с теми же оrоворками, что и при построении критерия Неймана Пирсона в 5.2.
При мер 4 (продолжение). Применим доказанный результат к критерию (5).
Здесь
n
LI ( ; О) == 2 (х O)L( ; О),
(7
следовательно, неравенство в (6) эквивалентно неравенству
L( ; (1) п(х (0)
L( (0) :;-- С + С! (72 '
(10)
26 Зака. 1748
402
rлава 5. Параметрuчеснuе 2uпатезы
которое леrко привести к виду
ехр { MT(J2) 2 } с + c',T(J2),
(11 )
rде
y'1i(B 1 во) I Сl y'1i
М == , СI == .
(J" (J"
Неравенство, противоположное (11), эквивалентно неравеНСТlЗам
( \ y'1i(x (0)
T ==
(J" ,
t( ,) ::;; T(J2) ::;; t(2)
( 12)
Статистика Т(Х) при нулевой rипотезе имеет стандартное нормальное pac
пределение N(O, 1), симметричное относительно нуля. Отсюда и из (10) сле
дует, что дЛЯ обеспечения BToporo из соотношений (7) необходимо, чтобы ин
тервал (12) был симметричен относительно нуля. Это означает, что t(2) == t(l)
Для одновременноrо выполнения и первorо из соотношений (7) надо поло
жить t(2) == to./2, rдe Ф( to./2) == а/2. Таким образом, условия (7) выполняются
тоща и только Torдa, коrда область (6) имеет вид i\, == {J2 IT(J2) I to./ 2 },
т. е. мы пришли к (5). Следовательно, по теореме 1 критерий (5) является
р. н. м. несмешенным критерием в задаче (НО В == 00, Н, О =f=. (0), Функция
мошности этоrо критерия
( y'1i(B Oo) ) ( y'1i(Oo o) )
W(o; 3:10.) == Ф (J" t C1 /2 + Ф (J" t C1 /2
симметрична относительно точки В == 00, в которой она имеет минимум,
равный а. При О -1= 00 мошность cTporo больше а и стремится к 1 при
О ::!:оо. В соответствии с теоремой 1 rрафик этой функции лежит выше
соответствуюшеrо rрафика любоrо друrоrо несмешенноrо критерия в данной
задаче (все rpафики проходят через точку (00, а)).
Сравним функцию мошности W(o; i 1a ) С функциями мощности COOTBeT
ствующих односторонних р. Н. М.к W(O; 3:;:;) и W(O; 1:;:) (рис. 2). Функция
w(O; Х,о.) всеrда заЮJючена между этими двумя функциями (они изображены
W(B; Х'а)
1
+
о
Во
в
Рис. 2
5.3. [ЛОЖНbJе zuпотезы
403
на рисунке пунктирными линиями с соответствующим знаком), за исключе
нием точк fJ == fJo, в которой все три rрафика совпадают. Это означает, что
критерий 1:]а всеrда менее мощный, чем один из односторонних критериев
1: или 1:; , но всеrда более мощный, чем друrой односторонний критерий..
Более полно теория р. н. м. несмещенных критериев изложена в [16, rл. 4].
З, Локальные наиболее мощные критерии
На практике особый интерес представляют малые отклонения от нулевой
rипотеЗbl Но fJ == fJo. В этом случае при исследовании свойств критерия
можно оrpаничиться только анализом локальноrо поведения ero функции
мощности W(fJ) в окрестности точки ()о. При таком подходе часто удается
построить локаЛЬНblй наиболее мощный (л. н. м.) критерий, даже Torдa, Korдa
р. н. м. критерия не существует.
Пусть fJ скалярный параметр и выполнены условия реrулярности,
сформулированные перед теоремой 1. Кроме Toro, будем считать, что ДI1я
любой критической области 1:[" функция мощности W(fJ) W(8; 1: la )
(W (fJ o ) == а) допускает разложение в ряд Тейлора в окрестности точки fJ O :
(fJ fJ)2
W(fJ) == а + (fJ fJO)W'(fJ o ) + о WIl(fJ O ) + (13)
2
Пусть теперь rипотеза Но fJ == 80 проверяется против правосторонней
альтернаТИВbI HI+ fJ > fJ o . Torдa для получения л. н. м. односторОНнеrо
критерия необходимо максимизировать величину
W' (fJ o ) == f LI (f.; fJO) df.
,;('0
при оrpаничении
W(fJ o ) == I L(f.; fJo) df. == а.
,;(10
Повторяя рассуждения, использованные при доказательстве теоремы I 5.2,
можно получить, что оптимальная критическая область имеет вид
+ { LI(f.; fJ o ) + }
.:r IO f. L(f.; 80) ;): С" ,
rде rpаница ct определяется условием W(80; .:rt) == а.
Аналоrично, критическая область
(14)
{ L](f.;fJo) }
х,,, == f. L(f.; fJ o ) Са '
задает л. н. м. критерий В случае левосторонней альтернаТИВbI HI fJ < fJ o .
При двусторонней альтернативе НI () i= fJ o необходимо ввести дополни
тельное условие несмещенности критерия: W'(fJ o ) == о; тоrда л. н. м. кри
терием является критерий, максимизирующий WIl(fJ O ) коэффициент при
26*
( 15)
404
rлава 5. Параметрические 2uпотезы
(О 00/ в разложении (13). Как и при доказательстве теоремы 1 выше, можно
показать, что в этом случае оптимальная критическая область имеет вид
:!IO == { : L2( ; (0) cL( ; (0) + c,LI( ; оо)},
( 16)
rдe
( ) д L 1 ( ; О)
L Х' О ==
2 , дО
и константы С и с, определяются условиями W(Ou) == 0:, WI(Ou) == О.
Пример 5 (Нормальная модель, л. н. М, критерий для cpeAHero). Рассмотрим
ту же задачу, что в примере 4, и построим в ней л. н. м. критерий. Здесь
(см. (10»)
[ n2 n ]
L2( ; О) == (7'4 (х 0)2 и2 L( ; О),
поэтому
LI( ;Oo) N ( п ) L2( ;O(l) n2 ( ) 2 n
Х ио Х 00
L( ; (0) и2 'L( ; (0) и4 и2 .
Следовательно, область (16) задается условием T2( ) kIT( ) + k 2 (Т опре
делено в (11). Чтобы было выполнено условие несмещенности, эта область
должна быть симметричной (поскольку распределение статистики Т(Х) при
rипотезе Но симметри'шо относительно нуля), 'по имеет место только при
k l == О. Таким образом, условие можно переписать в виде IT( ) I k. Наконец,
из условия W(Oo) == о: находим k == t o / 2 , rде Ф( tа/2) == 0:/2. Окончательно
получаем, что область (16) имеет вид {ITI t a / 2 }, т, е. результат совпадает
с полученным в примере 4. Это ожидаемый результат, так как л. н. м. HeCMe
щенный критерий должен СОlшадать с р. Н. м. несмещенным критерием, коrда
последний существует. .
Вернемся к случаю односторонних альтернатив и проанализируем более
подробно условия в (14) ( 15). Вспомнив определение вклада выборки V(X; О)
(см. (1) 3.2), можем записать
L,( ; (0) д д
) == д 1п L( ; (0) == L.J д 'п f(Xi; (0) == Y( ; (0),
L(;[; 00 О i=' ()
Как показано в п. 1 3.2, ./U1Я реrулярных моделей
Ево V(X; (0) == о, D8 0 V(X; (0) == ni(Oo),
rдe i(O) информauия Фишера (см. (5) (5') 3.2). Если n велико, то, по
центральной предельной теореме,
( У(Х; (0) )
.еВа ...;. '" #(0.1),
ш(Оu)
следовательно, для больших выборок при вычислении rраниц в (14) (15)
можно использовать нормальную аппроксимацию (17): в (14) полаrать
( 17)
Ij 5.3. СЛОЖНblе 2uпотеЗbl
405
с; :::::: to. Vni«()o) , а в (15) полаrать C :::::: ta Vni(Bo) , rде ф( tо.) == 0'. Тем
самым получено общее асимптотическое решение задачи построения л. н. м.
односторонних критериев для больших выборок.
При меняя прием объединения двух односторонних критических областей,
можно построить и асимптотический двусторонний критерий
{IV(X; Bo)1 t a / 2 vni(B o ) }
(18)
проверки rипотезы Но В == ВО против альтернативы НI В i=- Во.
V(X; Во)
Из свойства симметрии предельноrо распределения статистики
yfii
вытекает, что критерий (1 8) несмещенный и не существует друrоrо HeCMe
щенноrо критерия, который имел бы асимптотически большую мощность.
Друrими словами, критерий (18) является асимптотически л. Н. М. несмещен
ным критерием в задаче (Но В == ВО, Н, В =F Во).
Построенный приближенный критерий (18) совпадает с полученным
в при мере 5 точным критерием для нормальной модели N(B, 0'\ OCHOBaH
ным на статистике
( ) yfii(X Во)
т Х ==
о' '
поскольку в этом случае
( . ) yfiiT(X)
V Х, ВО ,
о'
а i(B) == 0' 2 (см. табл. 1 3.2).
Пример б (Модель Коши, л. н. м. критерий ДЛЯ нее). Пусть требуется прове
рить rипотезу Но В == ВО против альтернативы Н, В =F ВО дЛЯ модели Коши
К(В) (см. указание к табл. 1 3.2). Используя результаты примера 8 3.5,
получим, что при больших n л. н. м. несмещенный критерий имеет вид
{ 2 V2 [ n Х; ()о I }
1:10. == vrn f; 1 + (Х; Во)2 t a / 2 .
.
4. Проверка rипотез и доверительное оценивание
Между задачами про верки rипотез о пара метре В и ero доверительным оцени
ваением имеется тесная связь, позволяющая просто получать решение одной
из этих задач, KOrдa решение друrой известно. Это делается с помощью сле
дующих рассуждений.
Рассмотрим для произвольноrо ВО Е е какой либо критерий 1:10. == 1: la (Bo)
проверки простой rипотезы Но В == Во. Пусть 1:00.(ВО) == i]a(Bo) область
принятия rипотезы Но. Тем самым в выборочном пространстве 1: задано ce
мейство подмножеств {1:0а(В), ВЕе}. Определим теперь при каждом Е 1:
подмножество g'Y( ) С е, r == 1 0', положив g'Y( ) == {В : 1:0а(В) 3 }.
406
rлава 5. Параметрические zuпотезы
Таким образом, IJ параметрическом МНОЖССТlJе е получаем семейсТIJО п()д
множеств {9')"( ), Е х}
Рассмотрим случайное множеСТIJО 91 (Х). События
{8 Е g')"(X)} и {Х Е ХОа(8)}
эквивалентны, так как по построению каждое из них влечет за собой дpy
[ое, поэтому их нероятности при каждом В СОlJпадают. Но, по построению,
Ре{Х Е хоо(8)} == 1 а, следовательно, Ре{8 Е 9')"(Х)} 1 а, т. е.
у')"(Х) нвляется l' доверительноЙ областью для В (см. напр., соотношение
(33) 3.5). Эти рассуждения можно и обратить, именно, если имеется ce
мейство 1' доверительных областей {9')"( ), Е х} для 8, то множество
Хо, lJ == { ВО Е У1 ( )}, а == 1 1', определяет область принятия rипотезы
Но 8 == Во с уровнем значимости а.
Таким образом, задача построения ДОlJеритеJlЬНОЙ области ДIlя параметра 8
(доверительноrо интервала, если В скалярный параметр) и задача ПрОIJСрКИ
простой rипотезы о 8 взаимно обратны. При этом р. н. м. критерий (коrда он
существует) соответствует наикратчайшей доверительной области и наоборот.
Проиллюстрируем этот принцип несколькими полезными Прllмерами.
Пример 7 (Нормальная модель, оптимальный доверительный интервал для
среднеrо). Рассмотрим модель N(8, 0"2) (0'2 известно). В примере 4 построен
оптимальный (р. н. м. несмещенный) критерий (5) в задаче (НО В == 80,
Н 1 : 8 -1- 80), Здесь
хо,,(В) == { vnl: 81 < t a / 2 }' ф( tО/2) == а/2,
и множество g')"( ), l' == 1 а, имеет вид
t oj2 O' t oj2 O' }
x <8<x+ .
n n
Следовательно, интервал (Х =f ta/2 О' /-/ii) является наикраТ'lайшим среди
всех (1 а) доверительных интервалов для неизвестноrо среднеrо закона
N(8, 0'2) это значительное усиление результата примера 2 3.8 (подчеркнем,
что t a / 2 == Cl o)'
Далее, так как р. н. м. критериЙ против правостороннеЙ алы-ернативы
Н 1 + 8 > 80 задается критической областью (1 О) 5.2, то
{ v'nlx 81 } {
g1"( ) == 8 О' < t O / 2 == 8
хо а (8) == {.f. v'n(: 8) < t a }, Ф( ta) == а,
и потому МНОЖССТIJО y')"( ) {8 8 > x taO'/-/ii} Отсюда имеем наи
лучший односторонний (нижний) (1 а) доверительный интервал ДIlЯ В:
(Х tao"/v'n, 00). Аналоrично, исходя из (12) 5.2, получаем наилучший
верхний (1 а) доверительный интерВал для 8: ( oo, Х + t a O'/v1i). 8
5.3. [ЛОЖНblе zuпотеЗbl
407
Пример 8 (Оптимальный доверительный интервал для дисперсии нормаль
ной модели). В примере 3 Э 3.8 был построен центральный { доверитель
ный интервал для неизвестной дисперсии модели N(p" (}2). В то же время
в упр. 12 к данной rлаве указан вид р. н. м. несмещенноrо критерия для rипо
тезы Но () == (}о противдвусторонней альтернативы НI () -1- (}о, откуда имеем
n
ХОа(8) == {;!С 82X J,n < Т(;!С) < (}2X a2.n}, Т(;!С) == l)Xi р,)2
i 1
Следовательно, множество 9')" (;!С) , 'у == I 0:, имеет здесь вид
9')" (;!С) == { 82 (;!с) < 82 < Т 2 (;!С) } .
XI a2'n Ха"п
Эrо означает, что наикратчайший (1 0:) доверительный интервал для 82 есть
( (X) , T X) ) ,
XI a2, Ха"п
rде (X ,.n' Xi al'n) указаны в упр. 12. Следовательно, центральный интервал
в данном случае не является наилучшим. При ведем краткую таблицу значениЙ
пар (X I'n; XT al.n) и (X I ')")/2,n; X I+')")/2,n) для 'у == 1 о: == 0,95:
n (X I' n; X al. n) ( 2 . 2 )
X(I 1)/2.'" X(I+l)/2.n
2 (0,08; 9,53) (0,05; 7,38)
5 (0,99; 14,37) (0,83; 12,83)
10 (3,52; 21,73) (3,25; 20,48)
20 (9,96; 35,23) (9,59; 34,17)
.
"
Методику, устанавливающую связь между за «Мешающий" пораметр
дачами доверительноrо оценивания и проверки
rипотез, можно применять и в более общих ситуациях, коrда требуется oцe
нить лишь подвектор (}(I) параметрическоrо вектора () ((}Cl), 8(2)) (о 8(2)
в таком случае rоворят как о «мешающем» параметре), а также коrда интерес
представляет заданная параметрическая функция т(8).
Пусть, например, имеется семейство { доверительных областей 9r(;!C) для
8(1), т. е. семейство подмножеств параметрическоro множества
8(1) == {(}Cl) ((}О) , (}(2)) Е 8},
удовлетворяющих условию
Ро{8О) Е 9')"(Х)} ) {, 'V 8.
408
rлава 5. Параметрuческuе 2uпотеЗbJ
Определим для фиксированноrо 11 1) подмножество
1:0, I , == {;f 9,(;f) Э 8 1)}
В выборочном пространстве 1:. Torдa по построению
P(8 1),8(2)){X Е 1:0,1 ,} == P(8,\'I,/112)){I1 I) Е 9,(Х)} l'
или
P(/1 I),/1(2)){X Е :fo, I ,} :( 1 ")'.
Следовательно, область 1: la == 1:0, I , Q' == 1 1, задает критерий уровня
значимости о: для проверки rипотезы Но 11(1) == 11 1) (это rипотеза сложная,
так как остаWlяет неопределенным значение ,Р». Как и выше, можно про
вести обратные рассуждения: от задачи ПрОIJерки rипотезы перейти к задаче
доверительноrо оuенивания.
Пример 9 (проверка rипотез для параметров общей нормальной модели).
В примере 1 2.5 построены доверительные интервалы для неизвестных cpeд
Hero 111 и дисперсии 11 в модели N(I1[, 11 ). Используя результат (12) из этоrо
примера и описанную методику, сразу получаем критерий проверки rипотезы
о среднем Но 11, == 11'0 (112 произвольно) против альтернативы HI 111 i- 1110:
{ Ix 11101 }
1: 1a == ;f уп 1 S(;f) tl a/2,n 1 . (19)
Известно [16, с.225], что критерий (19) является оптимальным (р. н. м. He
смещенным), поэтому и доверительный интервал (12) 2.5 является наикрат
чайшим. О
Аналоrично, используя результат (9) 2.5, получаем следующий критерий
для проверки rипотезы о дисперсии Но (}2 == 1120 (11, произвольно) против
альтернативы НI 112 i- 1120:
1:10 == {;f пв 2 (;[;,):( l1 oX "n 1 либо nS 2 (;f) l1 oX l}, (20)
2 2 8 v 1
rдe XOI,n 1 И XI al,n 1 те же, что в при мере с заменои n на п .
Критерий (20) также р. н. м. несмещенный [16, с. 224], поэтому и COOT
ветствующий доверительный интервал (9) 2.5 наикратчайший (он не COB
падает с центральным интервалом (10»). .
Пример 10 (rипотеза о равенстве средних ДВУХ нормальных моделей).
Рассмотрим ситуацию, описанную в примере (2) Э 2.5. Используя постро
енный там доверительный интервал для разности средних == 11(l) 11(2)
получаем критерий проверки rипотезы о равенстве средних Но == О, KO
торый определяется критической областью
X la == {(;f,,!!) Ix У"I tl a/2,n+т 2
n+т }
( 2) (nS2(;f) + mS 2 (y))
nт n+т
(21 )
5.4. Критерий отношения правдоподобия
409
Эта область задает р. н. м. несмещенный критерий [16, с. 234], тем самым и
соответствующий доверительный интервал для !1 является наиболее точным.
Если же теоретические дисперсии известны, то, используя результат, YKa
занный в таблице 3.8, получаем, что критерий имеет вид
1:10 == { ( , у) Ix yl ? (l o/2
(Т2 (Т2 }
.......!.+ ,
n т
Ф((р) == р.
(22)
.
5.4. Критерий отношения правдоподобия
1. Метод отношения правдоподобия ДЛЯ общих rипотез
Одним из наиболее универсальных методов построения критериев про верки
сложных параметрических rипотез является метод отflОIUel/ия правдоподобия,
суть KOToporo состоит в следующем. Для проверки rипотезы Но () Е 90 С 9
против альтернативы HI () Е 9, == 9\90 вводится статистика отношения
правдоподобuя
sup Ln(X; О)
ВЕ8,
Л n ==Л n (Х,9 0 )== supLn(X;O) ' X==(X j ,
ВЕ 8 о
представляющая собой естественное обобщение на случай сложных rипо
тез статистики I(X) Неймана Пирсона (см. (3) 5,2); как и в критерии
Неймана Пирсона в случае простых rипотез, здесь в критическую область
включаются большие значения этой статистики.
В литературе, однако, традиционно в качестве тестовой стати коп-
стики В задаче (Но, H I ) используют несколько отличную статистику
, Х n ),
sup Ln(X; ())
( ) ВЕ8о
Л N ==лn Х;90 == supLn(X;O) ,
"Ее
которая предпочтительнее Л N С позиций практических вычислений, и крити
ческую область задают в виде
(1)
1:1 == { : лn( ; 90) с}.
(2)
Критическую rpаницу с в (2) выбирают так, чтобы критерий имел заданный
уровень значимости а:
Р,,{х Е 1: j } == Р"{Лn(Х; 90) с} а, '<:j () Е 90.
(3)
Соотношениями (1) (3) определяется критерий отношения правдоподобия
(КОП) в задаче (Но () Е 90, НI () Е 91),
Как было показано в Э 5.2, метод отношения правдоподобия в случае про
стых rипотез Но и НI приводит К оптимальному критерию. В общем случае
410
rлава 5. Параметрuческuе 2uпотеЗbJ
сложных rипотез это свойство оптимальности не выполняется. Тем не Me
нее этот метод широко применяют, получая удовлетворительные решения
во мноrих практических задачах. Кроме TOro, как будет показано ниже, при
некоторых естественных условиях реrулярности на исходную статистическую
модель :F == {F(x; О), () Е 8} КОП обладает свойством асимптотической
оптимальности дI1я больших выборок.
При мер 1 (КОП для cpeAHero нормальной модели). Продемонстрируем из
ложенный метод на уже рассмотренной в примере 9 5.3 задаче о среднем
(Но 81 == 810, HI 81 i= (10) дI1я нормальной модели N(8(, 8 ). Здесь
е == {8 == (81, (2) 81 Е R(, 82 > О} полуплоскость, 80 == {8 81 == 810,
82 > О} полупрямая. В соответствии с (1) мы должны вычислить аб
солютный супремум sup L(X; ()) и условный (при rипотезе НО) супремум
ВЕе
sup L(X; 8) функции правдоподобия выборки Х. Но такие задачи мы уже
8Е е о
решали при нахождении оценок максимальноrо правдоподобия (о. м. п.) для
пара метров модели в 15. Так, в примере 1 3.5 мы нашли, что
sup L(X; 8) == L(X; (j == (Х: 8)) == (27re82) n/2,
ВЕе
n
2 1 2
8 == L.J(Xi Х)
N.
, I
Условный же супремум есть (см. табл. 2 3.2)
sup L(X; О) == sup L (Х, (810, (}2)) == L (х; «()10, ВО)) == (27reBJ(n/2,
ВЕе , 82
rде
n
Вб == L(X; (10)2
n i 1
2
О. м. п. для дисперсии 82 при rипотезе Но; при этом леrко видеть, что
2 2 2
80 == 8 + (Х (10)
Отсюда имеем
( В2 ) n/2 ( t2 ) n/2
Ап == ......Q. 1 + .....Е.=.!...
В2 n 1
инеравенство {Ап :::; с} {::::::} {ltn 11 t} Но статистика tn 1 есть стьюденто
во отношение (см. (29) 1.2), соответствующее rипотезе Но, т. с. .c(tn IIHo) ==
== В(n 1). Таким образом, статистика tn 1 при rипотезе НО И:о.1еет распреде
ление, не зависящее от «мешающеrо.) параметра 82, а именно распределение
Стьюдента с n 1 степенями свободы. Тем самым мы можем рассчитать крити
ческую rpаницу t при заданном уровне значимости а: t == tl (j/2. n 1, И В итоrе
прийти к критерию (19) в примере 9 5.3. Таким образом, в данном случае
метод отношения правдоподобия приводит к оптимальному критерию, .
X 810
tn l ==yn 1 В '
5.4. Критерий отношения правдоподобия
411
rp(t) == te
о
Рис. 1
Пример 2 (КОП для дисперсии нормальной модели). Рассмотрим, к какому
результату приводит аналоrичный подход в задаче о дисперсии (Но: 82 == 820,
НI : 82 =1= (20) нормальной модели N(()l' 8 ). Абсолютный супремум sиp L(X; 8)
ОЕ8
здесь тот же, что и в предыдущем примере, поэтому достаточно вычислить
условный супремум sиp L(X; 8). В данном случае
ВЕе"
80 == {() == (()" (2) 82 == 820, 81 Е R I },
т. е. надо найти о. м. п. В ) ДJlЯ модели N(8 j , 8 0) с известной дисперсией
и затем вычислить L (Х; (BI, (20»)' НО ВI == J{ (см. табл. 2 3.2), а из пред
ставления (2) 3.3 для функции правдоподобия L(X; 8) следует, что
sup L(X; 8) == L (Х; (.Х, ()20)) == (211'8 0) n/2 ехр { 82 } .
ВЕе" 2820
Отсюда имеем (см. (1))
( е8 2 ) П/2 { nВ2 } ( Tn+1 п/2 82
n 8 o ехр "2 8 0 Trj е ), Тп == Тп (Х) == 8 0 '
и (см. рис. 1) неравенство {ЛП с} {:::::::} {Т" t 1 либо Т" t2}, Таким обра
зом, КОП в данном случае имеет вид
:IIO == { 82( ) () otl либо 82( ) 8i o t2}.
Для вычисления критических rраниц t 1 и t2 воспользуемся теоремой Фишера
(теорема 2 2.5), соrласно которой
( n 2 ) 2
[,0 (} 8 :о:: Х (n 1).
Следовательно, мы имеем уравнение
а == Р{Х Е XI"IHo} == Fn l(ntl) + I Fn l(nt2),
412
rлава 5. Параметрuчес/{uе zuпотезы
[де Pn I (t) функция распределения закона i(n 1). Полаraя 11'1 ==Pn I(nt l ),
11'2 == 1 Fn l(nt2), будем иметь nt l == X "n l' nt 2 == X /)2.n l' И тем самым
X 1 /) == { nB2( ) O oX ,.n 1 либо nB2( ) 0 OX /)2.n I},
11'1 + 11'2 == а.
Здесь I1'] и 11'2 MorYT быть любыми положительными числами, в сумме дa
ющими а, поэтому мы имеем на самом деле целый класс критериев уровня
значимости а. Эту неопределенность можно устранить, исследуя получен
ные критерии на несмещенность. Для этоrо вычислим функцию мощности
W(02) == W(02; X 1a ), Снова воспользовавшись теоремой Фишера, получим
{ n 2 8 o 2 } { n 2 8 й 2 }
W(B 2 ) ==PIJ B 5 O X/)I,n 1 +PIJ 8 5 () XI /)2,n 1 ==
( (} o 2 ) ( O o 2 )
== Pn 1 O X/)I,n 1 + 1 Pn 1 oi XI /)2,n 1
Чтобы обеспечить несмещенность: W(8 2 ) а при В2 i- 820 (напомним, что
W (820) == а), надо решить уравнение w' (020) == О, т. е. (далее F 1 (t) == kn I (t))
X " n I kn 1 (X " n 1) == X /)2' n 1 kn 1 (Х Й2' " )).
Вместе с условием 11'1 + 11'2 == а последнее ураонение однозна'IНО определяет
выбор пары (11',,11'2), а тем самым и (X "n l' X /),.n I), обеспечивающих
несмещенность критерия X 1 /). В итоrе мы приходим к критериlO (20), указан
ному в примере 9 5.3, т. е. и D данном случае метод приводит к оптимальному
критерию.
Если рассмотренные примеры носили суryбо иллюстративный характер
(мы получили в них уже известные решения, следуя новому методу), то два слс
дующих ПрИ 1ера по существу демонстрируют IЮЗМОЖНОСТИ метода отношения
Задачи ДЛЯ мноrих праrщоподобия. В них будут рассмотрены типичные.
так называемые, задачи для MHOZUX выборок, ДЛЯ реше
Вblборок
НИЯ которых этот метод особенно эффективен. .
Пример 3 (rипотеза однородности для нескольких нормальных выборок).
Пусть имеется k 2 независимых выборок Xj == (X jl , , XjnJ, при этом
Xj выборка из нормальноrо распределения N(B 1j , (} ), j == 1, , k (все па
раметры О == (811, , 8 1k , (2) неизвестны). Требуется про верить zипотезу oд
нородности Но BII == 012 == == Olk (при rипотезе Но все выборки
из одноrо и Toro же распределения И(О), O ) с некоторыми (неизвестными)
параметрами). Построим КОП для проверки этой rипотезы. Обозначим X j ,
5] выборочные среднее и дисперсию j й выборки, j == 1,. , k, и положим
n == nl + .. + nk общее число наблюдений,
k
1",
Х == щ X j
n j 1
9 5.4. Критерий отношения правдоподобия
413
2
среднее всех данных, В выборочная дисперсия всех данных:
k n-
2 1,,'\...2... 2
в == L.J L.J(X jj Х)
n. .
J I , I
наконец,
2 1 2
Во == L.J njBj'
n.
J ]
Пусть Lj == Lj(8Ij, (2) обозначает функцию правдоподобия для j й BЫ
борки, т. е. (см. (2) 93.3)
L. == ( 27r8 2 2 ) nj /2 ех р { nj в 2 ( Х- 8 ] . ) 2 } . I k
J 282 J 282 J J ' J == ,"', .
2 2
(4)
Поскольку выборки независимы, то функция правдоподобия всех данных есть
k k
L(e) == П L j (8]j, (2) == (27r8i) n/2 ехр { 2 2 Вб 2 2 2: nj (X j (}lj)2 } ==
j l 2 2 j 1
2 n '2 { 1 2 [ 1 ( В5 ) Во J }
== (27reB o ) I ехр 282 L..J n;(X j 8 1j ) n 2 82 1 lл 8 .
2 j ] 2 2
(5)
Рассуждая далее как в при мере I 93.5, убеждаемся в том, что показатель
экспоненты в (5) BcerAa O и знак ('==» {:::::::} (}Ij == Х;, j == 1, , k, (}2 == Во.
Таким образом,
sup L(8) == L(X"
о
При rипотезе же Но все данные это одна выборка объема n из нормальноrо
распределения N(()I, () ), поэтому условный супремум L(8) совпадает в дaH
ном случае с безусловным супремумом примеров I и 2, т. е. равен (27reB 2 ) n/2
Отсюда находим статистику отношения правдоподобия (1) (л статистику)
,X k , Во) == (211'еВб) n/2
(6)
( nв2 ) n/2
tnjB]
J ]
в общем случае произвольноrо числа выборок k «работать» с этой статистикой
трудно и общее решение (вид КОП) будет получено нами позже в рамках co
ответствующей асимптотической теории для больших выборок. Но в частном
(важном) случае двух выборок (k == 2) можно продвинуться дальше и полу
чить явный вид КОП.
( В2 ) n/2
>.
n,.. .n. Вб
(7)
414
rлава 5. Параметрuческuе юпотезы
.
Две выборки
Итак, пусть далее k == 2. Запишем разложение
2 ";
2 2
nВ == L..J L..J(X ji Х) ==
j 1 i 1
'" ( ) 2 " ( ) 2
n2 n]
== L X)i Х) + ;-(Х, Х 2 ) + L X 2i Х 2 + ;-(Х 1 Х,)
' ] , I
2 2 n'n2 2
== n,В] + n2В2 + (X] Х 1 )
n
Тоrда из (7) имеем
\ ( n]n2 (Х'; Х2)2 )
л" "2 1 t-- 2 J
I n n]В] + n2 В :;'
( t2 ) "/2
1 ,, 2
== +
n 2
(8)
rде
nln2(n 2)
tn 2 == (X 1 Х 2 )
11'(nIS + n 2 вп
имеет при rипотезе Но распределение Стьюдента В(n 2) (см. пример 2 2.5,
соотношение (14) при д == о с учетом принятых здесь обозначений). Из (8)
следует, что неравенство {ЛП'n2 :( с} эквивалентно неравенству {ltn 21 ) t},
КОП дпя двух а так как .c(t" 2IHo) == В(n 2), то при уровне значимо
выборок сти (\' КРИТllчеСКЮI rраниuа t == t 1 ('(/2, ,, 2, И мы получаем
вид КОП в данном случае:
X1(l == {ltn 21 ) tl (l/2,n 2}, (9)
Но такой критерий (с точностью до обозначений) мы уже получили ранее
в примере 10 (соотношение (21). Таким образом, jj случае проверки rипотезы
о равенстве средних двух нормальных выборок КОП совпадает с оптимальным
критерием. .
Пример 4 (rипотеэа о равенстве дисперсий нормальных выборок). Пусть
B , ,Si выборочные дисперсии, построенные по независимым BЫ
боркам объемов nJ, ,n,.. из соответствующих нормальных распределений
N(8]j, 8 j), j == 1, ,k. Построим КОП дЛЯ проверки rипотезы о равенстве
дисперсий Но 821 == == 8 2k .
Пусть Lj(8Ij, 8 2j ) Функuия правдоподобия для j й выборки, j == 1,. .., k,
k
а L == П L j (8]j, 8 2 j) для всех данных. Как и в предыдущем примере 3
j )
находим, что условный (при rипотезе Но) супремум L дается формулой (6).
БезусловныЙ же (абсолютный) супремум L равен
k k
П sup Lj((J]j, (J2j) == П (21reS]) nj/2.
j ' з '
95.4. Критерий отношения правдоподобия
415
Таким образом, в данном случае л статистика (]) имеет вид
k k 52 n /2
Лп,...п. == ( В/ ) n/2 П(5])Пj/2 == Ц ( 8; ) J
О J I J I О
Анализ общеrо случая мы отложим до следующеrо параrрафа, rдe будут ДOKa
заны общие предельные теоремы для больших выборок, а сейчас оrpаничимся
частным случаем двух (k == 2) выборок. В этом случае (10) Д 6 ."
ее вы орки
можно преобразовать следующим образом
( n5 ) n,/2 ( n5i ) п,/2
Лn,n, == 2 52 52 S2
. n]5 1 + n2 2 nl 1+ n2 2
nn/2 5'2
n,/2 n,/2 ( ) n,/2 ( ) n,/2
n l n 2 5 + n2 5i '!!25 + 51
nl n2
nn/2 ( n5 2 ) n l /2 ( n52 ) n/2
]+
n,/2 n,/2 N 2 5 2 N 2 52
n] n 2 2 2
nl/2 ( nl ] ) n/2
== С Fn, I,n, 1 ] + n2 ] Fn, I,n, 1
(10)
rдe
nl(n2 I)5
Fnl l,n, 1 == ( ])5 2
n2 nl 2
имеет при rипотезе Но распределение Снедекора 5(nl !,n2 1) (см. п. 7 1.2).
При этом (см. рис. 2) нераоенство {Лп,п, с} {FlI, I.'I, 1 CI либо
Fn, I,n, 1 ? С2}, СI < С2. Обозначая Fn,m(t) функцию распределения закона
5(n, т), для определения критических rраниц с] и С2 при заданном уровне
значимости а имеем уравнение
а == P{Fnl I,n, 1 СI либо Fnl l,n, 1 ? С2I Н о} ==
== Fnl ],n, 1 (CI) + ] Fnl l,n, I(C2),
<р(Р) == pR'I!(l + ap(12
с
С\
F
Рис.2
416
rлава 5. Параметрuческuе 2uпотезы
..
;;1iI
Следовательно, если С) =о Fa, ,п, \, n2 l аl квантиль pac
пределения В(n, 1, n2 1), а С2 =о F) al.nl l. n2 1, то при
любых 0'1 и 0'2 таких, что а) + 0'2 =о а, КОП имеет вид
1:\0 == {FПI \'П2 1 Fal,n, I,n2 1, либо Fnl I'n2 1 F\ 02'ПI I,П2 \} (11)
(сравни с упр. 16, rдe построен критерий при 0'1 == 0'2 =о 0'/2 методом об
ращения центральною доверительноrо интервала для отношения теоретиче
ских дисперсий). Чтобы критерий вида (11) был несмещенным, надо BЫ
числить функцию мощности W(8 2 \, (}22) и потребовать выполнения уc.rIOвия
W(8 21 , (22) а при 821 1- 822 (при нулевой rипотезе W(8 2 , (2) =о а). Для
этоrо заметим, что по теореме Фишера l(nisl/8ii) =о i(ni 1), i == 1,2,
и потому отношение Снедекора в общем случае произвольных дисперсий 821
и 822 имеет вид (см. п. 7 1.2)
n\B / n2Si n\(n2 I)S 8 2
F == e l(nl 1) 8 2(n2 1) =о n2(n, I)Si 8 ) '
при этом .c.(F) =о В(nl 1, n2 1). С учетом этоrо для функции мощности
критерия (11) при произвольной альтернативе 8 =о (821, (22): 821 1- 822 имеем
представление
W(8 21 , 022) =о Р8{FПI ),П2 1 С, либо FП1 ).Пl 1 С2} ==
( 8i2 ) ( 8i2 )
=о F'II I,n, \ cl 8il + 1 Fn, I,n2 \ C2 8 i\
Условие несмещенности можно записать как равенство нулю производной
правой части по т == 8i2/8il при Т == 1 (ниже fn, I'''2 I(t) == F , I.", )(t)):
C\fn, I'nl I(C\) == c2fnl l,nl \(C2),
( 12)
Этим равенством вместе с условием й'+0'2==0' rраницы С) и С2 (следова
тельно и 0'1. 0'2) определяются уже однознач но, тем самым мы получаем He
смещенный критерий вида (11), который янляется оптимальным [16, с. 230]. .
в рассмотренных примерах удалось найти точное распределение статисти
ки (1) (точнее, некоторых взаимно однозначных функций от нее) при нулевой
rипотезе, что и позволило рассчитать соответствующие критерии. Такое об
стоятельство характерно Д)lя нормальной модели. Для друrих моделей точное
распределение Л П удается найти не всеrда, поэтому для малых выборок Me
тод отношения правдоподобия не всеrда позволяет получить решение зада'JИ
(рассчитать КОП). В то же время для больших выборок при достаточно об
щих условиях можно рассчитать асимптотический вариант КОП и установить
ero асимптотическую оптимальность. Далее излаrаются основные элементы
асимптотической теории критерия отношения правдоподобия Д)lя больших
выборок.
5.4. Критерий отношения правдоподобия
417
2. КОП для больших выборок
Будем далее предполаraть, что выполняются условия реryлярности. обеспе
чивающие существование, единственность и асимптотическую нормальность
о. м. п. -вп == (Oln, ,Отп) параметра 0== (01, . . - , ОТ) (см. п. 4 Э 3.5). PaCCMOT
рим сначала случай простой нулевой rипотезы (далее пишем Ln вместо L).
Теорема 1. Пусть требуется проверить простую rипотезу Но О == 00, rAe
00 == (010,' ,ОтО) заданная внутренняя точка параметрическоrо множе
ства е. TorAa при n 00 и при выполнении указанных условий реryлярности
КОП задается асимптотически критической областью
Л/а == {f. == (Х/,
, х п ) 21п Лn(f.; 00) x7 a, т},
( 13)
т. е. при n 00
Ро,,{Х Е .I 1a } == Ро" { 21п ЛП(Х; 00) X7 a,T} а.
Доказательство. Достаточно установить, что IЗ условиях теоремы
.св" ( 21n ЛП(Х; 00)) х 2 (т).
(14)
Если справедлива rипотеза Но, то в силу состоятельности О. м. п. ОП ее зна
чение при больших n находится вблизи точки 00, поэтому для In Ln(Oo) ==
== In Ln(X; 00) можно записать разложение Тейлора относительно точки 00:
1 a21nLn(f} )
1п Ln(Oo) == In Ln(On) + L.J д д (Ojn Ojo)((}jn (}jo),
2 . . о; (}j
1,)=1
.
rде О н е которая промежуточная точка между 00 и (}п. Отсюда следует, что
2111 Л П == 2[1п L/8n) 1п Ln((}o)] ==
I a2Ln(0 ) с r.:
дО дО. Vn(Ojn Ojo)vn(Ojn Ojo),
;,j / n ')
р . р
Так как ОП (}о, то и оп 00, а поскольку вторые производные функции
правдоподобия, по предположению, непрерывны по О, то по теореме ] 2.2
при больших n величина
(15)
1 д 2 1п Ln((} )
n aOjaO j
будет мало отличаться от величины
д 2 1п Ln(Oo) {)2 In j(X k , 00)
n дО,д(}, n дО дО. '
') k / 1)
27 Заказ 1748
418
rлава 5. Параметрuческuе zuпотеЗbf
которая на основании закона больших чисел, в свою очередь, будет мало
отличаться от среднеrо
( 821п f(X 1 ; (0) )
E8 u 8()j8()j .
Таким образом, матрица предельных (при n 00) значений коэффици-
ентов квадратичной формы в (15) совпадает с информационной матрицей
I(()o) (см. (21) 3.2). Далее, по теореме 2 Э 3.5 (соотношение (19)) случайный
вектор 1] == vn("Вп (0) имеет при rипотезе Но такое же распределение,
п
как нормальный N(Q, I I(Bo)) случайный вектор !l: Таким образом, правая
часть (15) имеет в пределе такое же распределение, как и квадратичная форма
Q == !J..' I(()o)!J... Но, по теореме 1 Э 2.5 (см. замечание к ней), L:(Q) == х 2 (т),
что и доказывает (14). .
Замечание. Предельные распределения статистик 2 In л п и Q II) == ,./ /(0,.)7] при
нулевой rипотезе совпадают (следует l1З хода предыдущих рассужде й), п ;тому
КОП (13) асимптотически эквивалентен критерию вида
(1) {Q (I) 2 }
1: la n XI a.T .
(16)
Если здесь матрицу /(8 и ) заменить на близкую к ней при больших n матрицу /(0,),
то получим еще один критерий, асимптотически эквивалентный (13):
{ I 2 }
Ila == n(Оп оо) /(Ои)(О. оо) XI aJ .
( 17)
Замечание. Из доказательства асимптотической нормальности о. м. п. следует (см. co
отношение (26) Э 3.5), что IJ случае одномерноro параметра предеЛЬНЬJе распределения
C V.(Ou)
7]п == v n(О" (0) и Vпi(Ou) при rипотезе Но совпадают. В случае lJeKTOpHoro пара
I !:.п(оо)
метра этот вывод остается в силе, если вторую статистику заменить на / (Ои) ,jii ,
alnLII(O) .
[де (см. П.5 93.2) .!С,,(8) == (Vj,,(O), ,Vrn(O» и V;II(O) == дО; , z == 1, ,r
Отсюда и из предыдущеrо замечания следует, что при rипотсзе Но статистики Q IIJ
и Q 2) == !:. (80)/ I (Ou)!:.n(OO) имеют одно и то же предельное распределение х 2 (т),
n
поэтому КОП асимптотически эквивалентен также критерию вида
(2) {Q (2) 2 }
X 1a == n XI a,,' .
( 18)
Достоинством ЭТОrО варианта критерия ЯDляется то, что при ero использовании
не требуется вычислять о. м. п. Jn И ero, следоваТельнО, целесообразно при менять
в тех случаях, коrда явный вид О" получить невозможно.
Итак, в задаче проверки простой rипотезы Но О == 00 против сложной альтерна
ТИВЬJ HI 8 Е 8\{Ou} все четыре критерия (13), (16), (17) и (18) аСИМnТОТИ'lески
эквивалентны, т. е. уровень значимости каждоrо из них стремится к а при n ----t 00.
5.4. Критерий отношения правдоподобuя
419
Рассмотрим важный ДТIЯ приложений пример применения изложенных
результатов к полиномиальному распределению М (n; Е == (р" ,PN)).
При мер 5 (Метод отношения правдоподобия для полиномиальноrо распре-
деления). Все необходимые вычисления для данноrо распределения прове
дены ранее в при мераХ 10 3.2 и 12 3.5. Используя их, находим, что л ста
тистика (1) для проверки простой rипотезы Но l!. == Е О имеет вид
N
П о";
р'
J N о у'
Лn(рО) == з=1 == П ( n Р з ) ]
п ( ) у; з 1 Vj
J=I
Отсюда
N
о L Vj
2Iплn(р)==2 v.ln .
J np
з=1 )
Заметим, что в данном случае вектор
r= ( V\ о
11 ==Jn(8n (Jo)==vn PI,
n n
( v' npo )
== !!..* == ) Jn ) . j == 1, ,N 1 ,
а 1(80) == t,.) 1 (эти обозначения использовались в доказательстве теоремы 1
94.2), поэтому квадратичная форма
Q , 1(8 ) *''''' \ * Х '2
n == '!1 n о '!1n ==!!.. z...N I!!.. == n
(см. (4) 4.2). Далее для квадратичной формы Q I) в (16) имеем представление
(см. (29) 3.2)
VN I О )
PN I ==
n
[ N \ ( ) ( 2 N I ( ) ( ) ]
(1 n n У) о n Vi о Vj о
Qn) == n Vj + YN ;: pj) + i 1 VN ;- Pi ;: Pj ==
if-j
== (v) nр;)2
L.J У'
j=1 ]
Наконец (см. (28) 93.2)
\'jn((J) == t д 1" f(X i ; 8) == t ( I(X i == j) I(Xi == N) ) == Yj YN ,
i=1 OPj i=1 Pj PN Pj PN
j==I,....N I,
27-
420
rлава 5. Параметрические i!uпотезы
и потому
Q 2) =: 1C (OO)tN l1Cn(Oo) ==
n
=: r L I: ( 11: lJ ) 2pj(1 pj) I: ( lJ: II ) ( lJ lJ ) pip; ]
n j 1 Pj PN i,j 1 Pi PN Pj PN
i",j
=: [ I: ( lJj nP) IIN ;0 пр';. ) 2 Р) ( Е ( lJ: lJ ) р; ) 2 ]
j l} N j 1 Р} Рн
Далее простыми преобразовзниями с учетом равенств
N I N I
L lJj =: n lJN, L Р) =: 1 Р;'
j l j 1
(2) , 2
приходи м к представлению Qn == ХN'
Таким образом, в рассматриваемой задаче критерий можно строить, ис
пользуя любую из тестовых статистик
N
21n Лnч!.О) == 2 L IIj 111 IIjo ,
j 1 ПР)
N ( 0 ) 2
Qn == Q 2) == X == L lJj Pj , (19)
j 1 пр)
N ( 0 ) 2
Q ) =: L lJj lJ Pj
j 1 J
Если справедлива rипотеза Но l!. =: ЕО, то в пределе при n 00 все эти cтa
тистики имеют одно и то же распределения i(N 1), поэтому при заданном
уровне значимости а критическую rраницу выбирают равной Xi a,N 1 Cтa
тистика X (статистика хи квадрат К. Пирсона) нам уже встречалась ранее
в п. 2 4.2, rдe она была введена из друrих соображений. В 4.2 (теорема 1)
, 2
было получено то же самое предельное распределение статистики Х N при
v v 2
нулевои rипотезе и построен асимптотическии вариант критерия соrласия Х
(см. (6) 4.2). Здесь эти же результаты получены как простое следствие метода
отношения правдоподобия применительно к полиномиальному распределе
нию. Таким образом, для полиномиаш.ноrо распределения оба метода: метод
хи квадрат и метод отношения правдоподобия, асимптотически эквива
лентны. С позиций практических применений классическая статистика X
предпочтительнее (проще вычисляется) статистики 21п лт.{f!.О), но по cpaB
нению со статистикой Q I) У нее преимуществ нет. .
5.4. Критерий отношения правдоподобuя
421
З. Дальнейшие асимптотические свойства КОП
В этом пункте мы рассмотрим поведение КОП при альтернативах в случае
больших выборок. Прежде всею мы покажем, что этот критерий состоятелен,
т. е. для любой фиксированной альтернативы О 1= 00 ero мощность
Wn(O) == РО { 21" лп(Х; (0) x o,T} ---------t 1 при n ----+ 00. (20)
Донозательство. Для простоты рассмотрим случай скалярноrо пара метра
(т == 1).
Пусть 01 f. Во произвольная фиксированная внyrpенняя точка е.
Запишем статистику Л П (Х; (0) == л п (00) В виде
Ln(OI) Ln(Oo)
лп(В о ) == ( O ) == Л п (ОI)lI п (Оо, (1),
Ln (оп) Ln 1
Отсюда
2111 лп(Оо) == 21п лп(В 1 ) + nvn(Bo, ( 1 ),
(21)
rде
v n (8 0 ' (1) == In /ln(Oo, ( 1 ) == [In Ln(BI) In L n (8 o )] ==
[ 1 n 1 n ]
== 2 ;;, t1 1 " f(Xi; (1) ;;, f; 1" f(Xi; (0) .
Введем функцию Н(В) == Ео, 111 f(X i ; О). На основании закона больших чи
сел, при rипотезе О == 01 И n ----+ 00
1 n Р"
L In f(X i ; OJ;) ---------t H(8J;), k == 0,1.
n i l
Далее имеем
Н И) (О) == Е ( aj In f(X 1 ; О) )
О, дОЗ ,j == 1, 2.
Отсюда (см. (3) и (5') 3.2) H'(B 1 ) == о, H"(Ol) == i(BI) < О. Это означает,
что в точке В) функция Н(О) имеет максимум, поэтому случайная величина
v n (80' (1) сходится по вероятности к положительному числу 2[H(81) H(Oo)].
По теореме 1, LO, ( 2111 лп(В))) ---------t x 2 (1), следовательно, из (21) имеем, что
при альтернативе В) статистика 2 'П Л П (00) по вероятности неоrраниченно
возрастает при n ----+ 00. Отсюда следует соотношение (20) при О == О). .
Таким образом, для КОП (13) функция мощности Wn(O) сходится при
n ----+ 00 к функции
{ а при В == 80,
((В) == 1 при О f. 80'
422
rлава 5. Параметрuчеснuе zипотезы
«Близкие» Можно также исследовать поведение мошности КОП
альтернативы и при «близким альтернативах, т. е. KOrдa альтернатива
81 == 01 (n) ----+ 00 при n ----+ 00. Приведем (без доказа
тельства) результат, даюший вид предельноrо распределения тестовой стати
стики в (13) при «noporoBbIx» альтернативах.
Теорема 2. Пусть близкая альтернатива имеет вид
о
Ol(n) == 00 + Jn '
rAe == (о". ., Or) фиксированный ненулевой вектор, задающий отклоне
ние альтернативы от нулевой rипотезы. TorAa в условиях теоремы 1 при n ----+ 00
.с о ,(") ( 2In '\"(Х; (0») х 2 (т; ,\2), ,\2 == I 1(00)!2. (22)
(определение нецентральноrо распределения хи квадрат см. в п. 2 2.5).
Из этой теореМЫ следует, что для близких альтернатив вида
о
81 (n) == 80 + Jn
мощность КОП удовлетворяет при n ----+ 00 соотношению
W" (8 1 (n») == Ро,(") { 2111 '\"(Х; (0) xi (l.r'}
1 Fr(Xi a.r;,\2), (23)
rдe Fr(t;,\2) функция распределения закона х 2 (т;,\2).
Для более близких альтернатив (случай ,\2 ----+ О или Jn(О,(n) (0) ----+ Q)
мощность стремится при n ----+ 00 к уровню значимости а, т. е. такие альтерна
ТИВbI по КОП асимптотически от нулевой rипотезы не отличаются. Более же
далекие альтернативы (случай ,\2 ----+ 00 или Jn(8 1 (n) (0) ----+ 00) критерий
улавливает с вероятностью, стремяшейся к 1 при n ----+ 00, коrда они верны,
поскольку для таких альтернатив мощность стремится к 1. Эти выводы СПра
веДЛИВbI и для критериев (щ ( 18).
Пример 5 (продолжение). Для близких альтернатив
р(n) == рО + ,
Jn
N
L,Вj == О,
j 1
мощность любоro из критериев, основанных на тестовых статистиках, указан
ных в (19), равна в пределе (при n ----+ 00) указанной в соотношении (10) 4.2
величине. Это утверждение является специализацией общеrо результата (23)
для полиномиальной модели. .
5.4. Критерий отношения правдоподобuя
423
4. (ложная нулевая rипотеэа
Все важные асимптотические свойства КОП сохраняются и дnя случая слож
ной нулевой rипотезы. Мы оrpаничимся лишь формулировками COOTBeTCTBY
ющих yrверждений, отсылая интересующихся деталями доказательств к ори
rинальной работе на эту тему 2)
Пусть требуется проверить сложную rипотезу Но О Е 80 С 8, т. е.
подмножество 80 не сводится к одной точке. Альтернативная rипотеза
Н) О Е 8\80 также сложная. Рассмотрим типичную ситуацию, коrда 80
евКJlИДОВО подпространство размерности меньшей, чем размерность Bcero па
раметрическоro множества 8 (напомним, что 8 либо все T MepHoe евКJlИ
дово пространство R r при не котором r 2, либо еro подмножество той же
размерности т). Пусть s == dim 80 (от dimension (анrл.) размерность), так
что s < r == dim 8; тоща значение параметра () Е 80 можно выразить в виде
функции HeKoтoporo новоro параметра О == (01,... ,os) с соответствующим
множеством возможных значений ь., т. е. 80 имеет параметрическое пред
ставление в терминах пара метра а:
80== {0==(01' ,Or) ()==h(o), 0==(01, ..,os) ЕЬ.}. (24)
В общем случае будем предполаraть, что функции h(6) == (hl(O), ,hr(O))
удовлетворяют следующим стандартным условиям реryлярности: они трижды
непрерывно дифференцируемы и paHr матрицы их производных Ilah j (о) / aO j 11
равен s всюду в ь..
Опишем также друrой, эквивалентный, способ задания нулевой rипо
тезы. Обозначим через 0(2) совокупность тех координат вектора О, KOTO
рые являются взаимно однозначными функциями от о. Пусть дnя простоты
0(2) == (Or S+I' ,Or). Torдa О можно выразить через 0(2) 0== 0(0(2)). Если
теперь ввести функции Hj(O) == Oj h j (0(0(2))), j == 1, .. . , r s, то rипотеза
Но О Е 80 примет вид
НО Hj(()) == О, j == 1,
,Т s.
(25)
Тем самым rипотезу Но можно задать указанием HeKoToporo числа связей
(оrpаничений) на координаты параметрическоro вектора () == (81'.... Or).
В приложениях часто встречается случай, коrда 80 задается как цuлиН
дрuческое подМl/ожество 8, например,
80 == {о (J == (010,' ,(Jr s.O, (Jr
,()r)},
(26)
rде ()jO, i == 1, , r s, некоторые фиксированные значения координат
01, ,Or s, а остальные координаты (Jr s+l, . .. ,()' (их число есть s) явля
ются свободными параметрами (их принято называть «мешающими» парамет
рами). Если 80 имеет вид (26), то rипотезу Но () Е 80 называют ЛUllеUIIОU.
2) Davidsoп R., Lever W The limiting distriЬutiоп of the likelihood ratio statistic under а class of 'осаl
altemati s / / Sankhya, А. 1970. У. 32. N2 2. Р. 209 224.
424
rлава 5. Параметрuческuе zuпотеЗbf
Пусть проверяемая rипотеза задана в форме (24). Если функцию прав
доподобия данных (выборки Х) рассматривать при этой rипотезе, то она
является функцией HOBoro параметра о: Ln(X; О) == Ln(X; h(6» и при BЫ
полнении всех сформулированных условий реrулярности о. м. п. б n параметра
О будет обладать стандартными асимптотическими свойствами (см. теорему 2
3.5), а А статистика (1) может быть записана в виде
( . Ln (Х; h(б n »)
лnХ,ео) .
Ln(X; оп)
Для больших выборок (при n ----+ 00) справедливы следующие результаты:
1) .с( 21п лn(Х; 8o)IHo) х2(т s);
2) КОП, основанный на критической области
1: 1a == { 21IlАn( ;8о) X a.r s},
(27)
(28)
состоятелен.
Применим эти результаты к анализу л статистик (7) и (1 О), выведенных
нами ранее в задачах для мноrих нормальных выборок.
Пример б (продолжение примера 3). В примере З, очевидно, dim е == k + 1,
dim 80 == 2, а 2 1п Anl"'n' == n(ln 82 111 В5), поэтому асимптотический
вариант КОП (28) имеет вид
X 1a == {n(1п в2 111 В5) X a, k I}' (29)
.
Пример 7 (продолжеиие при мера 4). Здесь общее число неизвестных пара
метров равно 2k == dim 8, а число параметров. определяющих rипотезу Но,
равно k + 1 == dim 80, т. е. в (28) r s == 2k (k + 1) == k 1; тестовая же
статистика в силу (10) есть
k
21п Anl"'n' L nj(111 В5 'п в1).
j=1
в итоrе критерий (28) принимает в данной задаче вид
k
Лl а == { nj(ln В5 'п в]) ? X a'k I}'
J=I
(ЗО)
.
Пример 8 (rипотеэа однородности для схемы Бернулли). Пусть X 1 , ,X k
выборочные средние дl1я независимых выборок объемов nl, ,nk из
совокупностей Bi(l, (1), , Bi(l, (Jk) соответственно. Построим асимптоти
ческий (при nl, .., nk ----+ 00) вариант КОП D)1Я rипотезы однородности
Но : О! == . . . == (Jk.
5.4. Критерий отношения правдоподобuя
425
Обозначим через Lj(8j) == 8?Х;(I 8j)nj(' X;) функцию правдоподобия
для j й выборки, j == 1, .. . , k. То rдa , в силу независимости выборок, функ
ция правдоподобия для всех данных есть L(81'" , (},,) L,(8 1 ) L,,(8,,).
Далее, так как о. м. п. параметра бернуллиевской модели совпадает со cpeд
ним арифметическим выборки (см. п. 1 3.5), то отсюда имеем
" " ,,
тах L((}l,' ,8,,) == П maxLj(8 j ) == П Lj(Xj) == П X;jXj (1 Xj)nj(I Xj),
8".. .,8. 8j
j ' j=' j l
а при rипотезе Но
maxL(8, ,8) == mах(}nХ(1 (})nO X) == Х nХ (1 X)n(' x),
О 8
rде n == n, + + n", Х == (n1X, + + n"х,,)/n выборочное среднее
всех данных. Отсюда имеем, что в данном случае статистика отношения прав
доподобия имеет вид
ХnХ(1 x)n(1 X) k ( X ) njXj ( 1 Х ) Щ(l Х;)
Л n ,. .n. == " == п х 1 Х
П X; j X j (1 Xj)ni(' Xj) J=l J J
j '
Наконец, здесь dim е == k, dim е о == 1, следовательно, критерий (28) прини
мает вид
"
:r jO == { 2 z= nj [Xj(1n Xj 1п Х)+
J '
+ (1 Xj) (In (1 Xj) 1п (1 х))) xi O," I}' (31)
Напомним, что эту задачу мы уже решали в п. 2 4.3, и полученный там кри
терий однородности х 2 , основанный на статистике (6), записывается в наших
обозначениях в виде
:r == { Х == "" n ( Х' Х ) Х . } . .
'" "..,". Х(l Х) J 'r i .,Н
Пример 9 (rипотеэа ОДНОрОДНОСТИ ДЛЯ пуассоновских выборок). Пусть X j ==
==(Xj j , ,X jnj ), j == 1,...,k, независимые выборки из совокупностей
П(8 1 ), , П(8,,) соответственно. Требуется по этим данным проверить rипо
тезу однородности Но 81 == == (}". Схема решения здесь такая же, как
в предыдущем примере. Используя те же обозначения и учитывая, что в дaH
ном случае
Lj(8 j ) ==
n8 - (} nj х;
е 1 ] .
J
n-
]
П х ..'
JI'
i '
j == 1,
,k,
42б
rлава 5. Параметрuческuе 2uпотезы
найдем, что
ХпХ
k
П Х;;
j 1
(напомним (см. п. 1 3.5), что здесь о. м. п. вj == X j , а при rипотезе Но о. м. п.
(j == Х), Если nj, , nk 00, то асимптотический вариант КОП (28) при
нимает в данном случае вид
л
n....nj,:
k ( x ) nix;
==п
j 1 X j
k
X 1a == { 2 L.: njXj (In xj Iп Х) x7 a, k l}'
J I
(32)
.
5. Доверительные области максимальноrо правдоподобия
Изложенные результаты дают возможность получить общее решение задачи
доверительноrо оценивания параметров распределений ДI1Я общих параметри
ческих моделей. При этом используют общую методику, изложенную в п. 4 Э 5.3.
Далее будем предполаrать, что выполняются стандартные условия реrулярно
СУИ, формулируемые в аСИМПТОТИ'lеской теории КОП.
Рассмотрим КОП уровня зна'lИМОСТИ а == 1 'Y дnя произвольной простой
rипотезы, фиксирующей зна'lение параметра В == (B 1 , , Вт). Соrласно (J 3),
в СЛУ'lае больших выборок область принятия этой rипотезы имеет вид
Хо-у == { 21п лп( ; В) < x .T}
Отсюда имеем, что
9-у(Х)=={В 21IlЛп(Х;В)<Х ,r}
(33)
есть асимптотическая 'У доверительная область дnя параметра В. Определен
ное таким образом случайное подмножество параметрическоrо множества е
называется (асимптотической) доверительной областью максимальною пpaвдo
подобия. Таким образом, множество (33) строител на основании статистики
отношения правдоподобия
( . ) Ln(X; В)
лпХ,В
Ln(X,Bn)
и ВКЛЮ'lает в себя все значения параметра, при которых функция правдопо
добия Ln(X; В) близка к своему максимальному значению Ln(X; 8;1), или,
как rоворят, все достаточно правдоподобные зна'lения пар!метра. в 'Iастности,
наиболее правдоподобное значение параметра о. м. п. ОП всеrда принад
лежит 9-у(Х) (см. рис. 3).
Приближенную доверительную область максимальноrо правдоподобия
можно построить и дnя произвольной совокупности координат параметри
чеСКОrО вектора В при наличии мешаюших параметров. Пусть, например,
требуется оценить координаты в(1) == (BI,'" , Br s) (остальные координаты
5.5. Проверка 2uпотез для конеЧНblХ цепей Маркова 427
1::1
>-Т/К; ())
е"
о ()
9 1 (Ю
Рис. 3
в(2) == (Or s+l,"', ОТ)) являются мешающими параметрами). В этом случае
следует рассмотреть линейную rипотезу относительно (l(I) (см. предыдущий
пункт), вычислить статистику
sup Ln (Х; (в(I), 0(2)))
лп(Х; в(I)) == 8(2)
Ln(X;On)
и на основании (28) положить
Q,(X) == {0(1) 21n лп(х; (l(I)) < X ,r s}'
Это и есть искомая асимптотическая '}' доверительная область для (l(l) так
как из (27) (28) следует, что при n 00
PII{O(l) Е Q-r(Х)} == Р8{ 2111Лп(Х; (l(I)) < X;,r s} --------+ '}', V{l Е е.
! 5.5. Проверка rипотез для конечных цепей Маркова
Изложенные выше подходы к про верке rипотез для ситуаций, коrда исходные
статистические данные (выборка) представляют собой результаты последо
вательных независимых наблюдений над некоторой случайной величиной,
можно применять и для моделей с зависимыми наблюдениями. Одной такой
весьма общей и важной для приложений моделью является цепь Маркова He
KOToporo порядка s :;::, 1, определение которой дано в п. 2 4.5. В данном пара
rpафе на примере этой модели мы обсудим специфические проблемы провер
ки rипотез для зависимых испытаний и приведем некоторые общие результаты
для соответствующих критериев типа хи квадрат и отношения правдоподобия.
Полное освещение этой темы имеется в [9].
428
rлава 5. Параметрuческuе 2uпотезы
1. rипотеЭbl ДЛЯ конеЧНblХ цепей Маркова
Пусть задана последовательность из n случайных величин (выборка объема n)
'1,6,...,'n,
(1)
принимающнх значения из конечноro множества (алфавита) Е == {I, 2,. . . ,N},
и пусть априори предполаraется, что эти случайные величины связаны в oд
нородную цепь Маркова порядка s 1 (это предположение будем далее
назыатьb общей rипотезой 1ls). Точные определения всех этих понятий дано
в п. 2 4.5 после теоремы 1. Вероятностный закон, управляющий последова
тельностью (1). задается переходными вероятностями (см. (8) 4.5)
Pa:j == P{ k == j I k s == i J ,
k 1 == i s }, z == (i),
, i s ),
(2)
и начальным распределением P{ k == i k , k 8} (которое, однако, в излаrа
емой ниже асимптотической (при n ----t 00) теории не иrрает никакой роли,
и потому мы на нем не будем акцентировать внимание, понимая под rипоте
зами утверждения лишь о переходных вероятностях (2)). Тем самым, можно
сказать, что модель (rипотеза) 1ls определяется значениями NS+ 1 величин
{Ра:) Различные утверждения, фиксирующие вид или значения переходных
вероятностей (2), называются rипотезами о цепи Маркова.
Пусть, например, {Pl:j} некоторые заданные значения величин P':j'
Torдa утверждение НО Р') == P :j' i l , ,is, j Е Е, есть простая rипотеза
о цепи Маркова, однозначно фиксирующая переходные вероятности цепи (2).
В свою очередь, в зависимости от вида этих вероятностей P -j rипотеза
нО может означать и цепь порядка 8 (общий случай) и более частные
случаи, состоящие в том, что цепь имеет меньший порядок r < s (если
pi".. .,i.:j == pi, ,+", ..,i.:j, т. е. зависимость (,на rлубину,) 8 (8 т) == т) или даже
образует последовательность незаl3ИСИМЫХ испытаний (если p[:j == pj, т. е. нет
зависимости от прошлоrо); в последнем случае при р) == I/N, j == 1, ,N,
Н О u
rипотеза означает схему независимых испытании с равновероятными ис
ходами (именно такую rипотезу мы рассматривали в п. 2 4.5 в связи с !1pO
блемой датчиков).
О
Часто проверяемая rипотеза Н определяется не полным заданием пере
ходных вероятностей (2), а указанием лишь их функциональной зависимости
от HeKoToporo параметра (J == ((JJ, ,(Jk) с соответствующей областью воз
можных ero значений 6, являющейся открытым подмножеством k MepHoro
k
евклидова пространства R :
но == Н О (6) Pi:j == p,:j(6), (J Е 6.
(3)
В этом случае мы имеем дело с про веркой сложной rипотезы Н О (6) внутри
более общей сложной rипотезы 1ls. В частности, проверяемая rипотеза MO
жет заключаться в том, что последовательность (1) является цепью Маркова
5.5. Проверка 2uпотез для конеЧНblХ цепей Маркова 429
порядка, меньшеrо s, но без указания точных значений переходных вероят
ностей, Например, пусть
Pi],. ..,i.:j (О) == Oi. ,+],.. (4)
rде О. > О таковы, что
N
L Oi. r+],,, .i.:j == 1, iS T+""" is Е &,
j 1
т. е. сами переходные вероятности являются неизвестными параметрами и
при этом зависимость от прошлоrо имеет «rлубину» r (здесь параметр k ==
== NT(N 1)). В этом случае проверяемая rипотеза состоит в том, что цепь
имеет порядок r < s. Если r == О, то имеем rипотезу о независимости испы
таний при конкурирующей rипотезе типа марковекой зависимости порядка s.
Сделаем теперь следующее общее замечание. В п. 2 4.5 (соотношение (5))
были введены важные эмпирические характеристики выборки (1) частоты
V. j появления комбинаций (zj) == (i[ isj), называемых (s+ 1) цепочками,
в последовательности (1):
n .
V'j == L 1((t == i" (t+1 == i 2 ,
t l
(t+s ' == i s , (t+s == j).
(5)
Число всех таких (s + l) цепочек равно N S +1, так как каждый символ i"
i s , j пробеrает все множество е == {1, 2, ,N}. Однако не все COOTBeTCTBY
юшие частоты V. j будут отличными от нуля. Так, если переходная вероятность
P'j' определенная в (2), при некоторых l, j равна нулю, то комбинация (zj)
не может появиться в выборке (1), и потому V,j == О. Конечно, в силу слу
чайности, lJij может принимать нулеlJое значение и при P,:j > О, но в теории
эрrОДИ4еских цепей Маркова доказывается, 4ТО в больших выборках (при
n 00) вероятность TaKoro события близка к нулю, и потому можно С4Итать,
что для больших выборок с вероятностью, близкой к 1, v. j > О{=::} P.:j > О.
С учетом этоrо заме4ания будем далее оrраНИ4иваться рассмотрением лишь
тех комбинаций ил, для которых P.:j > О. Множество всех таких комби
наций обозна4ИМ e +' а ero объем tf == le +ll. в 4ЗСТНОСТИ, если все
переходные вероятности Рц > О, то
&;+1 == t: H1 == f х
х & и rf == les+11 == N s + 1
J
8+ 1 раз
Далее, если проверяемая rипотеза задана в парамеТРИ4еском виде (3), то
множество
& +I == ((lj) P.:j((J) > О}
может, вообше rОIJОрЯ, зависеть от параметра О и тем самым для каждоrо
значения О быть своим. Этот нереryлярный случай мы будем в дальнейшем
430
r1laBa 5. ПараметрuчеСl<uе cuпотезы
исключать из рассмотрения; более Toro, мы будем предполаrать выполненным
следующее общее условие реryлярности.
,.
Условие реryлярности А
Условие А.
1) Множество t:g+ 1 == {(ТЛ p,j(()) > О} не зависит от О и обладает сле
дующим свойством: любая цепь Маркова с переходными вероятflостями Pi:j
такими, что P':j > О {::::::} (ТЛ Е t:g+ 1 , является Эр20дической;
2) функции P,:j(O) трижды непрерывно дифференцируемы по о;
Il aP,)(}) II О
3) матрица дОт размера (d х k) имеет paнz k всюду в 0.
Обозна'IИМ теперь H класс эрrодических цепей Маркова порядка s, для
переходных вероятностей которых выполняется условие p,:j > О {::::::} (ТЛ Е t:g+ 1
В силу условия А (п. 1) это цепи, в которых возможны такие же переходы
z """"'7 j, как и при rипотезе н О (0), но вид переходных вероятностей при
этом никак не конкретизируется (за исключением необходимоrо условия cтo
N
хастичности L РЦ 1, V Т). Если справедлива некоторая альтернатива
j 1
Н Е Н' \1-l : для не которой комбинации (Тл if. t:g+ 1 переходная вероят
ность P,j > О, то, как отмечено выше, P{V'j > OIH} """"'71 при n """"'7 00. Но при
rипотезе н О (0) событие {V,j > О} невозможно, и потому появление в BЫ
борке (1) комбинации (ТЛ свидетельствует о том, что rипотеза Н О (0) ложна.
Таким образом, альтернативы Н Е 1is \ H , по длинной реализации цепи (1)
улавливаются с вероятностью, близкой к 1, и потому проблема, собственно.
состоит в различении rипотезы НО (0) и альтернатив из класса 1i .
Наконец, выделим еще один тип задач для цепей Маркова, возникающих
в приложениях. Иноrда требуется проверить нулевую rипотезу НО внутри бо
лее узкоro класса rипотез, нежели общий класс 1is. Формализация подобных
ситуаций выrлядит следующим образом. Пусть априори постулируется, что
мы имеем дело с цепью Маркова вида (3), а проверяемая rипотеза есть YТBep
ждение н О (8 0 , 8) () Е 80, rде 80 заданное подмножество 8, при этом
dim 80 == r < k. Обычно подмножество 80 задается с помощью новой пара
метризации в терминах HeKoToporo параметра д == (151, ,д,.) с множеством
возможных ero значений ь., rдe Ь. заданное открытое подмножество r Mep
Horo евклидова пространства Н' В этом случае 80 есть образ Ь. при некотором
отображении h == (h" . ,h k ):
80 == {(} () == h(д) == (h,(д),.. ,hk(б)), б Е ь.} (6)
в дальнейщем мы будем предполаrать, что отображение h удовлетворяет CTaH
дартным условиям реryлярности:
Условие В. Функции h(t5) == (h l (15), .. . , h k (15»)
триJ/fдbl HenpepblBHO дифференцируеМbI в D.. и
5.5. Проверка zuпотез для конечных цепей Маркова 431
'1i'
Усповие реryпярноcrи В
rank " а б) " == r всюду в D...
Из изложенноrо видно, насколько более разнообразны MOryт быть rипо
тезы, подлежащие проверке, в рамках марксовской модели зависимых испы
таний в сравнении со схемой независимых испытаний. Тем не менее знакомые
уже нам стандартные (можно даже сказать классические) методы хи квадрат
и отношения правдоподобия позволяют построить удобные ДТlЯ применений
критерии про верки всех таких rипотез.
2. Критерий хи квадрат для простой rипотеЭ"1
Пусть требуется про верить простую rипотезу
НО Р':j == Pl:j > о {::::::} Щ) Е [;+ I
В соответствии со сказанным в п. 1, будем рассматривать в цепи (1) лишь те
комбинации (Ij), дЛЯ которых Plj > о, т. е. при (Ij) Е [;+1 В методе хи
квадрат сравниваются наблюдаемые частоты {V,j' (lj) Е [;+ J} С соответствую
шими «rипотетическими частотами» {V,Pl:j} и в качестве тестовой статистики
используют статистику
Проcrая rипотеза
для цепи Маркова
X .S+1 == L
(,j)E[ +]
(V'j V, Pl)2
V , ' p .
':]
(6')
N
(здесь V'j вычисляются по формуле (5), а v, == L V'j' см. замечание к форму
j 1
лам (5) 4.5). Расчет соответствующеrо критерия производится на основании
следуюшеrо утверждения [29].
Теорема 1. Еспи справедлива rипотеза НО, то статистика (6') имеет в пре
деле при n ----+ ос> распределение x 2 (d> N S ). Соответствующий критерий,
задаваемый при уровне значимости а критической областью
{X ,S+I > Х; (}.ао ю},
состоятелен против любой фи ксированной апьтернативы Н Е lls.
(7)
Выделим важный частный случай, коша все пе
реходные вероятности p[:j > О. Torдa [;+1 == [5+ I ,
dO == N S + I И критерий (7) принимает вид
2
Критерий Х
,"" ;, .9 .
432
rлава 5. Параметрuческuе zuпотеЗbf
{ ( V"' V' p ) 2 }
2 · J · i:j 2
Xn.S+1 == 2: V" . > XI a,N'(N I)
(ij)E['+' · Р.:;
(7')
с частным случаем критерия (i), коrда все Pl:j == IjN, мы уже встречались
в п. 2 4.5 при обсуждении проблемы датчиков случайных чисел.
3. Критерий хи квадрат для сложной rипотезы
Рассмотрим теперь проблему пронерки сложной rипотезы н О (6) вида (3)
внутри общей rипотезы lls и будем предполаrать выполненным условие pe
ryлярности А. Критерий соrласия для rипотезы Н О (6) строится по аналоrии
со случаем простой rипотезы, т. е. с использованием стандартной статистики
типа ХИ К13адрат
X .S+I(O) == 2:
(ij) Е[,;+ ,
(Vij V, Pi:j (О) )2
viPi:j(O)
Конечно, эту статистику еще нельзя использовать для построения критерия,
так как она зависит от неизвестноrо параметра О. Но если параметр О пред
варительно оценить по данным (5), т, е. заменить ero некоторой оценкой
8n == en({Vij}), и затем заменить функции Pi)O) оценками р'-; == Pi:j(8n),
то мы придем уже к настоящей тестовой статистике
(Vij vi PiY
2 2
ХП,Нl == Xn,s+I(On) == L..J
(ij)E[,;+1
Vi Pij
(8)
Это достаточно сложная для pacLleToB, а rлавное для исследования ее pac
пределения статистика, но тем не менее для таких статистик имеется хорошо
разработанная асимптотическая (при n ----+ 00) теория, которая утверждает,
что если оценки 8n получаются по методу максимальноrо правдоподобия, то
статистика (8) имеет при rипотезе Н О (6) предельное распределение i, как
и в случай простой rипотезы. Отличие проявляется лишь 13 числе степеней
свободы предельноro распределения, которое уменьшается на величину, paB
ную числу оцениваемых параметров, определнющих rипотезу Н О (6). То есть
в данном случае имеется полная аналоrия с теорией метода ХИ КRадрат для
схемы независимых испытаний.
Приведем ключевые элементы этой теории. Рассмотрим функцию прав
доподобия выборки (1) при rипотезе НО (6), т. е. вероятность наблюденной
реализации цепи в предположении, что rипотеза нО(е) истинна:
Ln(O) == Р{,...Ц,+, (О) Р6.. '{'+':{'+2(0)
Р{п ....{п ,:{..(О) == п (Pi)O))/I,j
(ij)EE + ,
(9)
5.5. Проверка zuпотез для конеЧНblХ цепей Маркова 4ЗЗ
По аналоrи и со случаем независимых испытаний назовем оценкой максималь
HOro правдоподобия (о. м. п.) 8n пара метра 8 решение системы уравнений
д 1" Ln(8)
д8 т
" дРц(8) О
L..J т 1,
( " ) ,,+, Pi:j(8) 88 т '
'} Е"о
,k.
(10)
Относительно существования, единственности и свойств решения системы (10)
известно следующее утверждение [29].
Теорема 2. Пусть выполнено условие д, TorAa с вероятно тью, стремящейся
к 1 при n ----+ 00, система (10) имеет единственное решение 8n, являющееся co
стоятельной оценкой параметра 8. Более Toro, если 80 есть истинное значение
8, то нормированный случайный вектор vп(8 n ВО) распределен асимптоти
чески нормально с центром в нуле и матрицей вторь'& M6'WlIiTOB T 1 (80), rAe
' С'
Т(8) IIE e ( д In P{la :{'+1 (В) д 1" P{la:;:{.+, (В) ) 11
Эта теорема аналоr хорошо известных утверждений об асимптотиче-
ских свойствах о. м. п. для схемы независимых испытаний; она указывает
метод оценивания неизвестных параметров для цепей Маркова.
Наконец, основой Д,l\Я построения и расчета критерия проверки rипотезы
нО(е) служит следующее утверждение.
Теорема З. Пусть выполнено условие Д и Pij Pi:j(8 n ), rAe 8n О. м. п.
параметра 8. TorAa, если rипотеза Н О (8) справедлива, то определенная в (8)
2
статистика Xn,s+1 распределена в пределе при n ----+ 00 по закону
i(d O N S k),
а критерий, основанный на критической области
2 2
{Xn,S+1 > XI Q,,jO N' k}'
(11 )
имеет асимптотически уровень значимости а и является состоятельным против
любой фиксированной альтернативы Н Е 1ls-
О
Пример 1 (rипотеза о ПОРRАке цепи Маркова). Пусть rипотеза Hr означает,
что наблюдаемая последовательность (1) представляет собой цепь Маркова
порядка т, в которой разрешены все переходы. Требуется построить критерий
проверки этой rипотезы внyrpи общей rипотезы 1ls (допускается марковость
порядка s > т). в этом случае нулевая rипотеза задается так, как указано в (4),
т. е. неизвестными параметрами , определяющими H , являются положитель-
28 Зак", 1748
434
rлава 5. Параметрuческuе zuпотезы
ные числа ()i' '+I'" образующие параметрический вектор fJ размерности
k == Nr(N 1).
Найдем о. м. п. Д)lя этих параметров. Поскольку координаты вектора fJ
удовлетворяют линейным связям (условию стохастичности)
N
Е fJi, .. .i,:j == 1, V is r
j 1
, is Е Е,
то мы имеем задачу на условный экстремум. Введя множители Лаrpанжа
!\ == (Лi и +,... (is r+I,"', is) Е E r ),
СВОДим задачу к отысканию абсолютноrо максимума функции
F(fJ,!\) ==
Е
v . . . ln fJ. . .
*1, r+I.' .I.J S. r+I" .1,:]
i. ,.+ J '" . .,Ё, ,)
Е
л.
',
. ( fJ. . . 1 )
...1, I. ,.+I...I.:J '
J I
i' r+l"
rде символ * на месте недостающих индексов в комбинации (i l
чает, что по этим индексам произведено суммирование.
Для этоrо мы должны решить систему уравнений
i.j) озна
aF(fJ, )
a()i. ,+ ,. .i,:j
v. . .
.tI, r+I...I.fJ Л. О' . . f
fJ. I. ,+I'. == , Zs r+I,...,Zs,J Е ,
1. r+l"
N
Е (}i, ,+I...i.:j == 1,
j 1
Отсюда леrко находим решение 8" == (8;' '+I."
Zs r+ 1,
,is Е Е.
Zs r+l,
,i.,j Е Е):
8. . _ V.i, ,,+I' .i,j
2. r+I" .1,:1 lJ .
.1, ,,+I'
Zs r+l,
,is,j Е Е,
( 12)
которое rоворит о том, что оценками переХОДНblХ вероятностей при rипотезе
H являются наблюденные относительные частоты соответствующих перехо
.... К 2 ДОВ В последовательности (1). В итоre получаем,
,.. ритерии Х для rипотезы
М что статистика (8) в данном случае имеет вид
о порядке цепи аркоеа
2 ""
Xn,s+l.r == L..J
(lj)E!'+1
( v v . . . ) 2
i. *1. r+I" .1.1
v
ij V . .
*I' "+I.' .',.
v, v. . .
1* *I. ,.+I.' .1.]
( 13)
v.
*I' I"'+I" .
о
и если rипотеза Hr справедлива, то при n ----+ 00 эта статистика имеет пре
дельное распределение X 2 ((N S Nr)(N 1)).
5.5. Проверка 2uпотез для конеЧНblХ цепей Маркова 435
Выделим важный частный случай r == О, соответствующий rипотезе Hg
о независимости случайных величин в последовательности (1), KOrдa в качестве
альтернатив допускается марковость порядка 5. В этом случае Pi:j == ()j > о
и == v.j/n, поскольку
v. == 2: Vij == n.
ил
Таким образом, для проверки rипотезы независимости
Hg внутри общей rипотезы 1is служит статистика
Критерий
2
независимости Х
2 ""
Xn,s+I,O == L....J
иЛЕ['+ I
( V O ' v,.v.j ) 2
') n
vi. v. j
(14)
n
Если rипотеза Hg справедлива, то статистика (14) при n ----7 00 имеет распре
деление i(N S I)(N 1)). .
Пример 2 (rипотеза о циклическом случайном блуждании). Предположим,
что в длинной реализации (1) простой (5 == 1) цепи Маркова наблюдались
лишь переходы i ----7 i:f: I (при i == 1 значение 1 1 интерпретируется как N,
при i == N значение N + 1 интерпретируется как 1). Таким образом, здесь
множество &б == {(i, i:f: 1), i == 1,2, ,N} разрешенных переходов состоит
из dO == 2N элементов и не совпадает с множеством &2 всех пар (i, j). Пусть
требуется проверить rипотезу
нО Pi:i+l == е, Pi:i 1 == 1 (),
rдe () Е (О, 1) неизвестный параметр (это и есть rипотеза о циклическом
случайном блуждании). Проверим, что в данном случае выполнено условие А.
Рассмотрим произвольную (простую) цепь Маркова с матрицей переходных
вероятностей вида
О PI2 О
Р21 О Рв
О РЗ2 О
р==
О
PNI О
О PIN
О О
о
PN I:N 2 О
О PN:N I
PN I:N
О
N
rдe все Pi:i:J::.1 > О. Леrко видеть, что Р состоит только из положительных эле
ментов. Это означает, что за N шаrов с положительной вероятностью из лю
боrо состояния можно достичь лю60rо друrоrо состояния цепи, что является
28'
4Зб
rлава 5. Параметрuческuе zuпотезы
достаточным условием эрrодичности. Таким образом, п. I условия А здесь
выполняется, а п. 2 и 3 очевидны. Следовательно, для построения критериf.l
Н О v v
про верки rипотезы можно восполыlватьсяя изложен нои выше теориеи.
Для этоrо найдем прежде Bcero оценку (}п для параметра ().
Обозначим
N
и == L Vi,i+1
j 1
число переходов «вперед,) (i ---+ i + 1) в выборке (1). Тоrда функция правдо
подобия (9) запишется в данном случае в виде
Ln ((}) == (}и (I (}У и
и уравнение
д In Ln((}) == О
д(}
имеет единственное решение 8" == и/n. Отсюда, в силу теоремы 3, имеем,
что статистика
(",,'+1 "' )' + t
и
V'
I
n
rде Vj == Vi,i 1 + Vj,i+l, распределена в пределе при n ---+ 00 по закону /(N 1),
если rипотеза НО справедлива. Следовательно, при уровне значимости а кри
терий для rипотезы нО имеет вид
N
2 "
Х п, 2 == L....J
j 1
(Vj,H Vi(1 ) у
Vi (1 )
i 1
' Н О
. отверraется
{::=:}
2 2 I
{Х п ,2 > XI a,N I}'
(15)
Если бы нужно было про верить соответствуюшую простую rипотезу о цик
лическом блуждании: () == (}О, rде (}О Е (О, 1) заданное уисло, то в COOTBeT
ствии с п. 3 следовало бы воспользоваться статистикой (см. (6'))
х 2 (Vi,i+l Vj(;lO)2 (Vj,H vi(1 (}0))2
п, 2 L....J II'(}О + L....J V' ( 1 (10 ) ,
j 1 ' j 1 I
( 16)
которая при справедливости про веря ем ой rипотезы распределена при n ---+ 00
по закону x\N). ·
4. Критерий отноwения правдоподобия
АЛя общих параметрических rипотез
Рассмотрим, наконец, проблему про верки rипотезы н О (8 0 , 8), rде 80 задано
в виде (6) и при этом выполнено условие D Torдa функция правдоподо
бия (9) при rипотезе н О (8 0 , 8) становится функцией от H080ro параметра 6:
5.5. Проверка zuпотез для конеЧНblХ цепей Маркова 437
Ln(h(o)) , и система уравнений
BlnLn(h(O)) ::: '" v aj apa}(h(O)) :::O
aO l (lj +IPa:}(h(O)) BO l ,1:::1,...,r, (17)
О
будет иметь состоятельное решение ОП, если rипотеза Н (80,8) справедлива.
Общий принцип построения критерия отношения правдоподобия (КОП) дЛЯ
проверки rипотезы н О (8 0 . 6) остается таким же, как и в случае независимых
испытаний: строится статистика отношения правдоподобия (л статистика)
Ln (h(5n))
л n == Ln(8n) ,
(18)
rдe 8" решение системы (10), и критическая область задается в виде
{л n < Са}, тде при заданном уровне значимости а критическая rраница
Са выбирается так. чтобы выполнялось условие
Р6{>..n < Са} а, V () Е 60. (19)
Основой для расчета тaKoro критерия служит следующая теорема [29].
Теорема 4. Пусть выполнены условия А и В. TorAa, если rипотеза н О (80, 6)
справедлива, то при n ----+ 00 статистика
[ ( )] '" Pij(8n)
21п л n == 2 In Ln(8n) In Ln h(on) ::: 2 L.J Vij In ( )
Р '. h ( on )
(Ij)Ee + I 1:)
(20)
имеет предельное распределение X\k r); если 00 истинное значение
параметра О, то статистика
[ О )] '" Pi:j{h(5n))
2 \п Ln(h(On)) InLn(h(O) == 2 . L.J Vij In '..(h(OO))
(ij)El +1 Р,.)
(2\)
распределена в пределе при n ----+ 00 по закону x 2 (r); при этом статистики
(20) и (21) асимптотически независимы.
Итак, при заданном уровне значимости а КОП про верки rипотезы
Н О (8 0 , 8) 8 Е 80 внyrpи общей rипотезы н О (6) : 8 Е 6 имеет для больших
выборок вид
н О (80.8) отверrается { 2IПЛn>Х а,k r}' (22)
При этом, напомним, r::: dim 80 < dim 8 == k.
Аналоrично с помощью статистики (2\) строится критерий проверки про
стой rипотезы О ::: 00 внутри rипотезы: О Е !J..
438
rлава 5. Параметрuческuе 2uпотезы
Пример 3 (продолжение примера 2). Предположим, что класс цепей, в KO
торых разрешены лишь переходы в соседние состояния (i ----+ i:!: 1), выделен
условием цикличности: Pi;i+1 == о, О Е (О, 1), и требуется при этом проверить
простую rипотезу нО : О == 00 в силу теоремы 4, в этой задаче надо восполь
зоваться статистикой (21), которая в обозна'lениях при мера 2 имеет в данном
случае вид
и 1 и/n
Т п == 2и 111 + 2(n и) ln u .
nи 1 О
(23)
Если rнпотеза нО истинна, то эта статистика аСИМПТОТИ'lески (при n ----+ 00)
распределена по закону x2(1), откуда и следует соответствующий критерий:
{Т п > X a,I}' ·
5. Критерий однородности
В этом пункте мы рассмотрим применение метода отношения правдоподобия
к еще одной общей статистической проблеме проверке rипотезы OДHOpOД
НОСТИ для мноrих выборок в маРКО8СКОЙ модели. В общем виде эта проблема
формулируется следующим образом.
Пусть (T) == { iT)}, Т == 1, ,v, независимые марковские цепи по
рядка s с одним и тем же пространством состояний Е == {I, .. ,N} и одним
и тем же множеством возможных переходов
,,3+ I ( Й ) О ( :; J ' ) Е " 0 5+ \
"о Р .:j и > {::::=} . "
8 == (81,
, (}k) Е е.
в дальнейшем предполаrается выполненным стандартное условие реrуляр
ности А. Обозна'lИМ 'Iерез 8(Т) Е е зна'lение параметра 8, порождаюшеrо
процесс (T) (так что (T) управляется переходными вероятностями P.:j ((}(Т)) ,
) (1) (v)
Т 1, .., V . Зна'lения (} ,..., (} неизвестны и, вообще rоноря, различ
ны. Эту модель будем называть общей rипотезой Н, ее размерность ('Iисло
определяющих ее параметров) dim 1i == vk. Предположим теперь, "то мы
располаrаем выборкой из каждоrо процесса, так "то наши исходные стати
СТИ'lеские Данные есть
с(Т)
"\ '
, :) , т == 1,
, V.
(24)
По этой информации требуется построить критерий проверки 2uпотезы oдltO
родности нО (}(I) == == (}(v) внутри rипотезы Н. Размерность этой rипотезы
есть k, и она (rипотеза) озна'lает, "то наблюдаемые процессы (T) являются
независимыми реализациями одноrо и TOro же MapKoBcKoro процесса из
описанноrо выше класса процессов; друrими словами, в этом отношении Ha
ши данные (24) однородны.
Схема применения Л метода в данном случае выrлядит следующим обра
зом, Выпишем функцию правдоподобия данных (24) при rипотезах 1i и нО.
5.5. ПровеРКG zuпотез для конеЧНblХ цепей Маркова 439
Поскольку выборки независимы, то в соответствии с (9) имеем
Ln,.. .п. (B I),
V
,B(v) == П Lnr(B(T),
T I
Ln r (В(Т) ==
п
(с)
(Pi:j (В(Т)) v ij
(25)
(,ла;+'
Ln(8)==Ln,...n.(B,...,8)== П (p,:j(8)('j,
(,j)E[ +1
rдe 11}:) число наблюдаемых комбинаций (zj) в выборке с номером т
']
v
(см. (5», 1Iij == .L: 11/;) и n == n, + + n т , Далее, исходя из (25) и (26),
T I
мы оцениваем неизвестные параметры В(Т) т == 1, , V, при rипотезе 11.
и 8 при rипотезе нО по методу максимальноrо правдоподобия, решая
соответствующие уравнения типа (10). Пусть соответствующие о. м. п. есть
J:), т == 1, ,v, и п' Torдa тестовая статистика (л статистика) имеет вид
(26)
[ ( (I) (v) ]
21п Лп,...п. == 2 'П Ln,...n. Оп" ,ОП. ) ln Ln(On) ==
v ( (T) )
== 2 ""' ""' 1I (T) In ( РI:j 8::...' ) , (27)
L.J L.J '] . ( 8 )
T I (,j)E[ +' Р.'] n
а сам критерий однородности формулируется следующим обр азом:
Iн О отверraется {::=> { 2IПЛПI...п.>t}.1 (28)
Обоснованием этой методики является следующая теорема об асимптотиче
ском распределении статистики (27), дающая одновременно и способ вычис
ления критической rpаницы t в (28).
Теорема 5. Пусть выполнено условие Д и n) nv 00 так, что nт/n л т ,
О
0< л т < 1, т == 1, ,v. TorAa, если rипотеза однородности Н справедли
ва, то статистика (27) распределена в пределе по закону i(k(v 1», rAe
k(v 1) == dim 11. dim нО
Основываясь на этой теореме, при выполнении ее условий мы выбираем
в (28) при заданном уровне значимости а величину t как квантиль уровня
1 а распределения i(k(v 1»: t == Xi a,k(V I)' и TOrдa
Р{ 2IПЛп,...п. > Xi a,k(v I)IHO} a_ (29)
440
rлава 5. Параметрические zипотезы
Соотношениями (27) (29) полностью определен состоятельный в классе 1l
критерий однородности в общем случае произвольной параметрической MO
дели и произвольноrо числа выборок.
Выделим важный специальный случай описанной общей схемы, коrда
rипотеза 1l задана указанием лишь множества E +I возможных переходов
без конкретизации вида переходных вероятностей Pi:j' (Zj) Е E +I В этом
случае сами эти вероятности являются неизвестными параметрами модели; их
число (с учетом условия стохастичности Е Pi:j == 1, 'rj i Е [S) дЛЯ каждоrо
j
процесса (T) есть cf N J , т. е. dim 1l == v( dO N J ), а dim нО == fJ N S
а их о. м. п. являются наблюденные относительные частоты соответствующих
переходов (см. пример 1):
(т)
(T) V ij
Pi:j == ---Тт)' т == 1,.. , v,
V,
,о
V,.
')
Pi:j == ,
Vjo
(lЛ Е t: +l
Отсюда имеем, что в рассматриваемом случае статистика (27) принимает вид
(т)
() v,. vio
21п Лп,...п. == 2 Е Е V i ; In т'
T I (lЛЕЕ +1 V i * Vij
v
(3О)
и при rипотезе однородности НО она имеет предельное (в условиях теоремы 5)
распределение х2((а? NJ)(v 1)).
Замечание. Можно показать, что в рассматриваемой задаче тестовая статистика (ЗD)
асимmотически эквивалентна статистике типа хи квадрат
I: I: (v,;' _,;';;;;)' (31)
т= I (ij)Ec.;+' V,(T) Vij
'. vi.
Пример 4 (Модель случайноrо блуждания, проверка rипотеэ однородности
для нее). Рассмотрим класс простых цепей Маркова, множество разрешен
ных переходов в которых имеет вид как в примерах 2 и 3:
t: =={(i,i:!:I), i== 1,2, ,N}.
Пусть мы имеем v независимых выборок 13 этой модели и {v j (TlfoJ}' т == 1,. .., v,
соответствующие наблюденные частоты переходов. Можно рассмотреть
следующие четыре rипотезы. Прежде Bcero это общая rипотеза 1l, соrлас
но которой каждая из наблюдаемых цепей управляется своей матрицей пере
ходных вероятностей, вид которой указан в примере 2; если обозначить р(т)
матрицу процесса (T), то эту rипотезу будем обозначать (p(I), , p(V)). rипо
тезу, соrласно которой p(J) == . .. == p(v) == Р, обозначим (Р). Далее, выделим
5.5. Проверка 2uпотез для конеЧНblХ цепей Маркова 441
общую rипотезу о UИКJIическом СЛУ'-IaЙНОМ блуждании (см. пример 2) и обо
значим 0(1), ,O(v) значения соответствующих параметров для наблюдаемых
процессов такую rипотезу обозначим (0(1), , o(v). Наконец, rипотезу,
соrласно которой 0(1) == == O(v) == О, обозначим (В). Таким образом, (Р)
это общая rипотеза однородности, а (О) rипотеза однородности дrIя модели
ЦИКJIическоrо случайноrо блуждания. Соотнощения между этими rипотезами
можно изобразить следующей диаrpаммой:
(р(1), . .. , p(v»
/
(Р) е (0(1), ,O(v)
/
(О)
Здесь каждое ребро представляет собой статистическую проблему про
верки rипотезы, являющейся началом ребра, внутри более общей rипотезы,
Я13ляющейся ero концом. Например, ребро а соответствует проверке rипотезы
(о) внутри rипотезы (0(1),. ,O(v). Из пяти проблем а, Ь, с, d и е пробле
мы а, с и е это проблемы однородности.
Выпищем для каждой rипотезы оценки параметро13, максимальное значе
ние лоraрифма функции правдоподобия и ее размерность (т. е. число степеней
свободы) (см. табл.).
rипотеза
о. М.п.
тах ln L
Е
{ (т) v (т)
(р(l), ,рИ) /li'( 1 } 2:2: (т) /l ij vN
/l ij ln W
11.. T I (ij)аб /l j .
(8(1),. . ,8(v)) { ::) } v [и(т) ( и(т) ) ]
2: и(т) ln + (n т и т ) In I v
1'==1
(Р) { /li'Ш } /1- -
2: '] N
/lij In
11,. /1'
(ij)E[J ..
(8) u u ln ; + (n и) ln (1 ;)
n
Здесь в дополнение к введенным ранее обозначениям положено
N
и(т) == '"" II(T) и U == U(I) + . . . + u(v).
L...J 1..+1
i 1
442
rлава 5. Параметрuческuе 2uпотезы
Чтобы построить критерий для соответствующей проблемы (см. диаrpам
му), надо взять строки этой таблицы для двух соответствующих rипотез и BЫ
числить разность между выражением в третьем столбце выше расположенной
строки и соответствующим выражением нижней из этих двух строк; будучи
умноженной на 2, эта разность дает соответствующую тестовую статистику.
Число степеней свободы в предельном распределении х2 для этой статистики
(если справедлива более узкая, т. е. ниже расположенная rипотеза) равно раз
ности размерностей рассматриваемых rипотез. Например, асимптотический
(в условиях теоремы 5) критерий однородности для проверки rипотезы (В)
внутри rипотезы (0(1), ,O(v)) (проблема а) имеет (при уровне значимо
сти а) вид
{2 ( [и(T) In ::) -+ (n т и(т)) In (1 '::) )]
[иln;-+(n и)ln(l ;)]) >XT a,v l} (32)
Если же мы хотим про верить ту же rипотезу (В) внутри общей rипотезы
(р(1),..., p(V)) (проблема е), то надо использовать критерий
v (т)
{ 2 (l: l: Vi? In V )
T I (ij)Et:J V j .
[иln*-+(n и)ln (I )]) >XT a,vN I} (33)
Отметим также, что критерии для проблем Ь и d по существу построены
в примере 2, а критерий для проблемы с есть частный случай критерия, по
рождаемоrо тестовой статистикой (30). .
б, Оценивание порядка цепи
Важнейшим параметром марковской модели является порядок цепи. В при
ложениях этот параметр, как правило, неизвестен и потому представляет
большой теоретический и практический интерес вопрос о ero оценивании
по наблюдаемой реализации цепи (1). Один из возможных подходов к этой
проблеме состоит в использовании построенноrо в при мере 1 критерия про
верки rипотезы о порядке цепи. Основываясь на тестовой статистике (13)
можно предложить следующий алrоритм последовательноrо типа для опреде
ления порядка цепи в рамках модели 1{..
с сзмоrо начала мы задаемся некоторым достаточно большим значением
s и априори предполаrаем, что наблюдаемая последовательность (1) ЯDляет
ся реализацией некоторой однородной эрrодической цепи Маркова порядка
не выше s. Подсчитав частоты Vrj' i == (i l , .., i.), (8+ I) цепочек в последо
2
вательности (1), с помощью статистики Xn,S+I,O (14) мы проверяем rипотезу
5.6. Последовательный анализ. Критерий 8альда 443
независимости Hg r == О (т истинный порядок цепи, r :::; s). Если при
уровне значимости а: rипотеза Hg принимается, т. е. наблюдается событие
{ 2 2 }
Ао == Xn,S+I,O:::; ХI о,(NЧ)(N J) , (34)
то процедура заканчивается на I M шаrе и принимается решение, что r == О.
в противном случае, т. е. если наблюдается противоположное к (34) событие,
2
выполняется 2 й шаr процедуры, а именно, с помощью статистики Х n , s+1, 1
(13) проверяется rипотеза H r == 1 (цепь имеет порядок 1). Если rипотеза
о
Нl принимается, т. е. наблюдается событие
{ 2 2 }
Аl == Хn,эН :::; Xl (),(N' N)(N I) , (35)
то процедура заканчивается на 2 M шаrе и принимается решение, что r == 1.
Если же наблюдается дополнительное событие .AI' то выполняется следу
ющий, 3 й шаr процедуры, состоящий в проверке rипотезы Hf r == 2:
2
вычисляется статистика X",.+I,2 (13) и ее значение сравнивается с критиче
2
ским уровнем XI o,(N' N2)(N I)' Если наблюдается событие
2 2
А 2 == {X n ,S+I,2:::; Xl O,(N' Nl)(N I)}' (36)
то процесс заканчивается принятием решения r == 2, в противном случае
процесс продолжается аналоrичным образом и т. д. Действуя таким образом,
мы можем остановиться на KaKOM TO значении r :::; s 1, либо, проделав s
шаrов и отклонив на S M шаrе rипотезу H r == s 1, делаем заключение,
чтоr s.
Таким образом, обозначая через т* оценку для истинноrо порядка цепи,
можем записать итоr в следующей форме:
т* == min{r rипотезаН принимается} ==
{ 2 2 }
== min r Xn,S+I,r:::; Xl a, (N' N')(N I) ,
(37)
* * о
если r :::; s 1, и r s, если все rипотезы Hr' r :::; s 1, последовательно
отверrаются. Отметим также следующее из (37) соотношение
*
Р{т >т}==Р{АоА\ Ar}==
{ 2 2 }
==Р Xn,S+I,t>XI o,(N' Nt)(N I),t==O,I,...,r,
т:::; s 1.
(38)
5.6. Понятие о последовательном анализе.
Критерий 8альда.
в примере I 5.2 при рассмотрении задачи о выборе одной из двух rипотез
о среднем нормальной модели была установлена связь между числом необхо
димых наблюдений и значениями вероятностей ошибок I ro и 2 ro родов а:
444
rлава 5. Параметрuческuе 2uпотезы
и fЗ (соотношение (14) 5.2). Это число n. можно рассчитать заранее (до про
ведения испытаний), и оно не зависит от исходов самих испытаний (от pea
лизации выборки). Альтернативой к правилам проверки rипотез, основанным
на выборках фиксированноrо объема, являются последовательные правила
(критерии), коrда вопрос о числе необходимых испытаний решают в про
цессе их проведения, и это число зависит от результатов испытаний, т. е.
само является случайной величиной. Последовательные правила впервые бы
ли предложены А. Вальдом (1943), и их изучение составляет предмет важноrо
раздела математической статистики последовательною анаЛиза. В данном
параrpафе на примере различения двух простых rипотез о распределении Ha
блюдаемой случайной величины { мы кратко обсудим основные особенности
последовательности критериев. С общей теорией последовательноrо анализа
можно ознакомиться в [6] и [28].
1. Определение критерия 8альда
Пусть, как обычно, Xj наблюдавшаяся реализация случайной величины {
в i M испытании, i == 1,2, и
n
L jn == L(x,
,х n ; (Jj) == п fj(xj)
j 1
функция правдоподобия для первых n испытаний при rипотезе Hj () == (}j,
j == О, 1 (напомним, что fj(X) плотность распределения { (или вероят
ность в дискретном случае) при rипотезе Hj, и испытания предполаrаются
независимыми). Соrласно теории Неймана Пирсона (см. 5.2) наилучшая
процедура проверки rипотезы Но против альтернативы Н, состоит в приня
тии или отклонении rипотезы Но в зависимости от Toro, меньше или больше
отношение правдоподобия L,n/ Lon не которой выбранной rраницы С, при
этом объем выборки n фиксируется заранее и не зависит от наблюдений. Oд
нако если объем выборки сделать зависяшим от исходов испытаний, то можно
добиться выиrрыша в среднем числе испытаний до принятия окончательноrо
решения. Эта идея реализуется в определяемом ниже последовательном Kpитe
риu отношения правдоподобия, который принято называть по имени ero автора
критерием Вальда.
Зададим две положительные константы Ао < 1 < А ! и будем проверить
испытания (наблюдения над {) до тех пор, пока не будет впервые нарушено
какое нибудь из неравенств
L 1n
Ао < < A j . (1)
Lon
Если в момент прекращения испытаний (момент остановки) L,n/Lon Ао,
то принимается rипотеза НО, если же Lln/ Lon ;?: А" то принимается rи
потеза H j . Такая последовательная процедура характеризуется, как обычно,
вероятностями ошибок I ro и 2 ro родов а == P{HIIHo} и fЗ == P{HoIHI}'
а также средним числом Ej(V) == E(IIIHj) испытаний V до момента остановки
5.6. ПоследоватеЛЬНblЙ анализ. Критерий Вальда 445
(j =' О, 1). Если вероятности ошибок а и {3 заданы, то любой критерий с Ta
кими ошибками называют критерием силы (а, (3). В классе критериев данной
силы (а, {3) предпочтительным являетсл тот, который требует меньшеro числа
наблюдений. Критерий, минимизирующий одновременно Eo(v) и Е ) (v) Ha
зывают оптимальным. Таким свойством оптимальности и обладает критерий
Вальда. В частности, этот критерий требует в среднем меньше испытаний,
чем критерий Неймана Пирсона с такими же вероятностями ошибок (а, {3).
Эти и друrие свойства критерия Вальда рассмотрены ниже.
2. О числе испытаний до момента остановки в критерии 8альда
Пусть плотности fj(X) > О, j =' О, 1, и н етождественны. Это означает, что
определена и невырождена случайная величина Z == 1" (!)( )/fоЮ); будем
предполаrать, что существуют E8Z f= О и D/JZ == (1"2(в) > О (В =' ВО, ( 1 ).
Обозначим также Zi =' [п (!1(X i )/ !O(Xi)) , i =' 1,2, ., rдe X j , Х 2 ,
последовательные независимые наблюдения Haд . Torдa Z" Z2, являются
независимыми наблюдениями над Z, и если Z" Z2, наблюдавшиеся
реализации этих величин, то в этих обозначениях процедура проверки rипотез
заканчивается принятием Но или НI при первом п, при котором нарушается
какое нибудь из неравенств
ао =' ln Ао < Zl +
+ Zn < In А ! =' а" ао < О, а) > О.
(2)
Критерию можно дать следующую наrлядную rеометрическую интерпрета
цию. Рассмотрим блуждающую на плоскости частицу, находящуюся в началь
ный момент в начале координат, ордината которой в каждый целочисленный
момент времени t =' 1, 2, получает приращение Zt. Torдa ордината частицы
в момент t =' п будет равна Zl + + Zn И блуждание продолжается, пока
траектория частицы впервые не выйдет за пределы полосы, оrраниченной
двумя rоризонтальными прямыми на уровнях ао и а) (см. рис. 1).
Выход траектории на верхнюю (нижнюю) rраницу приводит к принятию
rипотезы Н ! (Но). Прежде Bcero возникает естественный вопрос, не может ли
EZJ
Принимать НI
a l
t
О
а о
Принимать Но
Рис. 1
446
rлава 5. Параметрuческuе i?uпотезы
блуждание продолжаться бесконечно долrо, в этом случае проиесс провер
ки rипотез никоrда бы не закончился. Ответ на этот вопрос дает следующее
yrверждение.
Теорема 1. Критерий Вальда с вероятностью 1 заканчивается за конечное
число шаrов, т. е. lim РО{У > п} == О (О == 60, (1),
n OO
Доказательство. Зафиксируем некоторое число r и введем случайные вели
чины
1/1 == Z! + + Zr, 1/2 == Zr+1 + + Z2r,
Torдa событие {у > rk}, эквивалентное событию ао == ZI + + Zj < а),
i rk, включается в событие ао < 1]1 + + 1]j < al, j k, которое,
в свою очередь, включается в событие l1/jl < Ь == al ао, j k. Случайные
величины 1/j независимы и одинаково распределены, поэтому
РВ{У> rk} Po{l1]jl < Ь, j k} == pk(6),
(3)
rде
р(6) == po{I1/11 < Ь} == РВ{1]; < ь 2 }.
Но
r
Е в 1]; De1]1 == 2:: DeZj == то.2(О),
i 1
2
что может быть сделано больше, чем Ь , если выбрать
r > тах ( cт2 :o) ' cr2 :1 J .
Отсюда следует, что выбором r можно обеспечить неравенство р(6) < I (так
2
как в противном случае распределение величины 1] было бы сосредоточено
на интервале (О, ь 2 ) и ее среднее было бы меньше, чем ь 2 ). Переходя в Hepa
венстве (3) к пределу при k ---+ 00, получаем
lim Ре{У > п} == lim РВ{У> rk} == О. .
n OO k oc
Итак, в критерии Вальда число испытаний V до момента остановки с Be
роятностью 1 принимает конечное значение. Справедливо и более сильное
yrверждение, а именно: все моменты случайной велu'1UНЫ v конеЧНbI. В част
ности, конечны и средние значения Ео(У) и EI(v); вычисление этих величин
при заданных ошибках (а, /3) рассмотрено ниже в П.4.
з. о выборе rраниц в критерии Вальда
Установим теперь замечательную связь rpаниu Ао и АI В (1) с вероятностями
ошибок а и {З.
5.6. ПоследоватеЛЬНblЙ анализ. Критерий Вальда 447
Теорема 2. rраницы Ао и А] критерия Вальда силы (а, fз) удовлетворяют
неравенством
f3 , 1 {3
Ао ? A == , А! А) == ;
1 а а
при этом, если rраницы Ао и АI В (1) заменить их оценками A и A , то сила
полученноrо критерия будет равна (а', р'), rде
, а f3 1:::;::L I I
а , и а +fз а+fЗ.
1 f3 I a
(4)
(5)
Доказательство. Обозначим через ХОп (X 1n ) множество тех результатов Ha
блюдений (XI, . Х п ), для которых процедура заканчивается на n M шаrе
принятием Но (соответственно H 1 ), например,
Хоп == {(ХI
Llk
,Х п ) Ао < L < A J . k == 1,
Ok
L 1n }
, n 1, Ао .
LОп
в силу теоремы 1, ДJ1Я О == 00,01
00
00
00
:L Pe{v == n} == :L Ре{Хоп} + :L Pe{Xln} == 1.
n ] п=' п=]
Далее имеем
00 1 00
а == P{HIIHo} == :L P/lu{X 1n } А :L Ре, {X 1n } ==
n 1 I п 1
1 1 f3
== (I P{HoIHI}) == ,
AI АI
так как в точках множества X 1n выполняется неравенство Lon L]n/AI'
Аналоrично получаем
00
00
f3 == P{HoIH,} == :L Ре, {Хоп} Ao:L Peu{XOn} ==
n 1 n 1
== Ао(1 P{HIIHo}) == Ао(1 а),
поскольку в точках множества ХОп выполняется неравенство L 1n АоLОп.
Тем самым неравенства (4) доказаны.
Рассмотрим теперь критерий 8альда с rpаницами A и A , определен
ными в (4), и пусть а' и р' ero ошибки. Torдa на основании доказанноrо
ДОЛЖНЫ выполняться неравенства
f3 fз'
>-
1 а r 1 а"
1 f3 1 fз'
.
а а
448
rлава 5. Параметрические zuпотезы
Отсюда имеем
{3' (1 а'){3 ,
1 a 1 a
Складывая неравенства
{3'(I а) {3(I а') и а(1 {3') O"(I {3),
(1 {3')а а
a' .
1 {3 1 {3
получаем, что
!
Комментарии
{3' а {3 а'
или
а' + {3' 0'+ {3. .
На практике теорему 2 используют следующим об
разом. Если требуется построить критерий 8альда силы
(а, {3), то rраницы в (1) полаraют равными cooTBeTCTlJeHHO A и A'I' как опре
делено в (4). В этом СЛУ'Iае последнее неравенство в (5) rарантирует, '{то сумма
действительных ошибок а' и {3' TaKoro критерия не превосходит суммы а + {3
заданных ошибок. Далее, обычно а и {3 не превышают О, 1, поэтому из осталь
ных неравенств (5) следует, что разность между действительными и заданными
ошибками в этих случаях незна'lительна. Таким образом, можно утверждать,
что такой специальный выбор rраниц в критерии ВалЬда приводит к более
СИЛЬНОМУ критерию.
Отметим в этой связи интересную особенность последовательноro кри
терия по сравнению с обычными критериями, основанными на выборках
фиксированноrо объема. В обычном критерии при определении критической
rpаницы при заданном уровне зна'lИМОСТИ и вычислении мощности надо знать
распределение тестовой статистики и при нулевой rипотезе, и при альтерна
тиве. При расчете же критерия Вальда не 80зникает проблемы отыскания
распределений. Действительно, rpаницы A и А') зависят только от заданных
ошибок а и {3, а отношение Lln/ Lon можно вычислить на основании Ha
блюдаемых данных. Необходимость отыскания распределений при использо
вании последовательноrо критерия возникает только при исследоuании числа
наблюдений v до момента остановки.
4. О среднем числе наблюдений в критерии 8альда
Установим предварительно одно интересное равенсТIJO, назьшаемое mожде
сmвом Вальда. Пусть Sv == Zl + + Zv ордината блуждающей частицы
Тождество Вальда в момент остановки (см. п. 2), тorдa
Ев(Sv) == Ев(Z)Ев(v).
(6)
Докозательство. Введем СЛУ'Iайные величины Y 1 , У 2 , rдe У n == 1, если
решение не принято до n ro шаra, и У n == О в противном случае, Torдa,
очевидно, У n есть функция только ZI, . .. , Zn I и, следовательно, не зависит
от Zn, И можно записать
00
Sv == Е YnZ n '
n 1
5.6. ПоследоватеЛЬНblЙ анализ. Критерий Вальда 449
Отсюда по свойству математическоrо ожидания, (E( 1])) == E( )E(1J), если слу
чайные величины и 1] независимы) имеем
00
00
00
Ee(Sv) == L Ee(YnZ n ) == Ee(Z) L Ее(Уn) == Ee(Z) L Р6{У n == 1}. (7)
n '
n 1
n 1
Событие {У n I} эквивалентно событию {v п}, а так как для любой
целочисленной положительной случайной величины >< (каппа) справедлива
формула
00
Ех == L Р{>< п} (показать!),
n 1
то из (7) следует тождество Вальда (6). .
Пусть теперь заданы значения ошибок а и fЗ. Как показано в п. З, прак
тически при малых а и j3 rpаницы в (2) можно заменить соответственно на
, А , j3 , А , I I j3
ао == In о == ln и аl == In ,== п .
I а а
(8)
При малых а и /3 ширина интервала (a , a ) велика, а величина E6(Z) от а
и fЗ не зависит и, по предположению (см. п.2), конечна. Поэтому можно
пренебречь эффектом превышения суммой Sv rраницы в момент остановки,
т. е. положить Sv aj, если принимается rипотеза Hj, j == О, 1. Друrими
словами, можно считать среднее значение суммы Sv приближенно равным co
ответствующей rpанице a или а'., Из этих рассуждений и тождества (6) имеем
E6u(V)E6u(Z) == Eeu(Sv) a P{HoIHo} + a',P{H,IHo} == (1 a)a + аа',.
Аналоrично
Ее, (v)Ee, (Z) == Ее, (Sv) a P{HoIH,} + a P{HIIHI} == jЗа + (1 /3)a .
Таким образом, Ej(V) == Eej (v) можно вычислять по следующим приближен
HbIM формулам:
( ) (1 a)a + aa
Ео lJ Eo(Z) ,
Е ( v ) fЗа + (1 jЗ)а
I E,(z)'
(9)
rде a или а'l определены в (8).
Пример 1 (критерий 8аЛЬАа АЛЯ нормальной модели). Построим и рассчи
таем критерий Вальда для задачи различения двух простых rипотез о среднем
нормальной модели, которая рассмотрена в примере 1 5.2 с позиций теории
Неймана Пирсона. Здесь
Zj == 'п I1 (Xj) == (Xj 00)2 (Xj 01)2 == 81 80 ( Xj 80 + 8' ) (10)
10 (Xj) 20'2 0'2 2
29з...аJ 174
450
rлава 5. Параметрические zuпотезы
и критерий 8альда силы (а, (3) определяется в данном случае следующим
образом. Наблюдения продолжаются до тех Пор, пока впервые не нарушится
какое нибудь из неравенств
(12 /3 n n (12 1 /3
In < I: Xj (Oo + 01) < 111 ;
01 Во 1 а. 2 ВI Во а
I I
если нарушается левое (правое) неравенство. то принимается rипотеза Но (Н().
Вычислим среднее число наблюдений до момента остановки. Из (10) имеем
{ (01 00)2
E, ( Z ) == OI Bo ( (J. (JO+(JI ) == 2(12
} (12 J 2 (01 00)2
2(12
при j == О,
при j == 1.
Orсюда и из (9) находим
2(12 [ /3 1 (3 ]
Eo(v) ( о )2 (1 а) In + а Iп ,
Вl О 1 а а
EI(V) (О 2(1 )2 [ /3 Iп + (1 (3) Iп 1 (3 ] ,
I O I a а
Для критерия Неймана Пирсона с теми же ошибками а и (3 необходимое
число испытаний n. определяется формулой (14) 5.2. Отсюда имеем
Если Q' == /3. то (о
Eo(v) 2 [ (1 а) 111 + а Iп I /3 ]
n. ((" + (р)2 1 а а'
EI(v) 2 [ (3ln +(I /З)IП ' (3 ]
n. ((о + (р)2 1 а а
/3 l fЗ
(р, In == 111 И из соотношений (11)
1 a а
(11)
следует, что
Eo(v) EI(v) 1 2а Iп 1 а == 'Ф(а).
n. n. 2(J а
( 12)
При а == 0,05 квантиль (о == 1,645 и 'Ф(а) == 0,49, т. е. экономия наблюдений
при последовательной процедуре составляет приблизительно 50 %.
Более определенные выводы о сравнении критериев Вальда и Неймана
Пирсона можно сделать при а == fЗ О. В этом случае (" oo и, если
воспользоваться известной асимптотической формулой ДIIЯ нормальной функ
ции распределения Ф(х) [3, с. 10]:
e x2/2
Ф( X) == (I + о( 1)), Х 00,
ху21!'
( 13)
Упражнения
451
то на основании (13) можно записать асимптотическое равенство (вместо
точноrо равенства Ф((а) == а)
1 + 0(1) e ( /2 == а.
(а ,д:i
Решением этоrо уравнения, как нетрудно убедиться непосредственной под
становкой (проделайте это самостоятельно!), является
2 1 1
(а == 21п lп lп [п 411" + 0(1).
а а
Отсюда и из (12) следует (это мы оставляем читателю в качестве упражнения
на асимптотические вычисления), что при а ----+ О
(а) == ( I In(ln(l/a» ln411"+0(1) ) .
'ф 4 + 21п (I/a)
(14)
Представление (14) rоворит о том, что при ошибках а == {3 ----+ О последователь
ная процедура 13 среднем приблизительно в четыре раза экономнее оптималь
ной процедуры с фиксированным объемом выборки. .
.@( Последовательный критерий отношсния правдоподобия А. ВалЬда (1943)
стал важным открытием в статистике, позволиошим (в ТИПИЧНЫХ ситуаци
ях) на 50 % уменьшить среднее число наблюдений (при тех же вероятностях
ошибок). Насколько это важно для приложений roворит тот факт, что в [o
ды второй мировой войны открытие ВалЬдЗ было объявлено «секретным.., и ero
основная книrа «Последовательный анализ» была опубликована ЛИшь в 1947 [.
rод спустя Вальд и Дж. Волфовиц доказали, что методы, отличные от последова-
тельноro критерия отношения правдоподобия, не дают тзкоrо уменьшения числа
элементов выборки. В настояшее время тсория последооательноrо анализа ВалЬда
ЯDЛяется частным СЛ)"iаем обшей теории стохастических процессов с остановкой,
изложенной в (281.
Упражнения
Величайшая цель образования /te знание, а действие.
rерберт Спенсер З)
D Пусть Х == (X 1 ,..., Х П ) выборка из показательноrо распределения r(B, 1)
(см. п.3 9 1.2), о котором требуется проверить простую rипотезу Но (J == Во против
альтернативы Н, (J == BI' Убедиться в том, что здесь наиболее мощный критерий
выражается через достаточную статистику
п
т == Х;
;=1
З) Спенсер rерберт (1820 1903) анrлийский философ и социолоr.
29.
452
rлава 5. Параметрuческuе 2uпотезы
и имеет при 80 < 8. вид
.+ { 80 2 }
Ilo == Т '2 XI o,2n ,
а при 80 > 81 вид
. { 80 2 }
Ilo == Т '2 Хо,2J1
Получить также следующие выражения для мощностей:
( . .+ ) ( 8о 2 )
W 8,,1:10 == 1 F2n в; X' 0,211 ,
. ( 8о 2 )
W(81,1:lo)==F2J1 В;Хо,2П,
rде F 2n (t) ФУНКЦИЯ распределения закона х 2 (2n).
... Указание. Воспользоваться соотношением [,о(2Т/8)
свойств rамма распределения.
D Пусть для распределения Коши 1С(8) с плотностью
i(2n), вытекающим из
1 1
{(х; 8) == ;;: I + (х 8)2'
XER 1
проверяется rипотеза Но (J == о против альтернативы HI 8 == ,. Показать, что при
уровне значимости
l' I
а == arct g ;:::: о 352
2 11' 2 '
наиболее мощный критерий по одному наблюдению имеет вид
1:;0 == { х > }
и ero мощность равна
l' 1
"2 + ;;: arctg "2 ;:::: 0,648.
Если же
1
а == (arctg 3 arctg ') ;:::: 0,148,
11'
то критерий имеет вид
х;о == {' х 3}
и имеет мощность
I
arctg 2 ;:::: 0,352.
11'
IJ Убедиться в том, что наиболее мощный критерий для различения двух простых
rипотез о симметричном относительно нуля распределении наблюдаемой СЛУ'lайной
величины Но .ею == И( а,а) и 81 .ею == N(O, (7'2) (а и (7' известны) имеет
для больших выборок следующую аСИМПТОТИ'lескую форму
. { п 2 n ) 2а 2 m }
Ilo == f;x; за +(озv '5 '
... Указание. Воспользоваться цеmрапьной предельной теоремой при отыскании pac
пределен ия тестовой статистики.
ф{(о) == а.
Упражнения
453
D в последовательности независимых испытаний с двумя исходами вероятность
.успеха> равна р. Построить критерий проверки rипотезы Но Р = о против аль
тернативы HI Р = 0,01 н определить наименьший объем выборки, при котором
вероятности ошибок I ro и 2 ro родов не превышают 0,01.
g По схеме примера 4 5.2 построить и рассчитать критерий Неймана Пирсона
различения двух простых rипотез в биномиальной модели Bi(k, (J). Показать, что для
выборки Х = (Х"... . Х п ) большоrо объема этот критерий в задаче (Но (J = 80.
HI+ (J = 81 > 80) имеет асимптотически вид
X : = { Xj ;;:, knBo (о J knB o(1 во)}, Ф«(,,) = а,
и ero мощность Wn«(JI) при .близких> альтернативах вида
д
(J, = 8,п = Во + ...;n ' z; > О,
удовлетворяет соотношению
lim W n (8 In ) = Ф ( z; ( k (J ) + (о ) .
п оо у
... Указание. Воспользоваться теоремой Муавра Лапласа. .
П Чтобы проверить rипотезу НО : 8 '= (Jo против альтернативы Н I (J = (J, (О < (Jo <
< BI < 1) в схеме Бернулли с неизвестной вероятностью .успеха> (J, осуществлен
эксперимент, в котором наблюдается число «успехов>, предшествующих первому .He
успеху>. Построить наиболее мощный критерий при уровне значимости а = (Jg, rде
s 1 заданное целое число, и убедиться в том, что вероятность ошибки 2 ro рода
этоrо критерия /3 = 1 в:
... Указание. Использовать тот факт, что наблюдаемая случайная веЛИ'lина Х имеет
распределение !В(Х) '= 81(1, О) (см. п.2 1.1). .
D Доказать формулу (3) 5.3 для мощности критерия обратноrо биномиальноrо
выбора.
EiJ Убедиться в том, 'по построенный в упр.5 критерий Неймана Пирсона для
биномиальной модели Bi(k, О) является р. н. м. критерием в задаче (Но (J (Jo,
HI+ В> Во).
... Указание. Воспользоваться свойством модели с монотоииым отношением правдо
подобия. .
g Пусть в схеме Бернулли с неизвестной вероятностью .успеха> (J испытания про
должаются до получения r ro .неуспеха> и Tr наблюдаемое число .успехов>.
Построить р. н. м. критерий проверки rипотезы Но В ОО против альтериативы
н,+ (J > ОО и показать, что при r ---+ 00 ero аСИМПТОТИ'lеская форма есть
",.'+ '= { '" >- r(Jo (a.,;rёo } (
""Ia .Lr"" 1 8o ,Ф(а)=а.
... Указание. Воспользоваться свойством модели с монотонным отношением правдо
подобия и применить центральную предельную теорему к сумме Tr = X 1 + + Xr.
rде X 1 ,..., X r независимые reометрические 81(1, О) случайные величииы. .
454
rлава 5. Параметрuчеснuе zuпотезы
IШ Убедиться в том, что построенные в упр. I критерии Неймана Пирсона х;:
и x; являются одновременно р. н. м,к. В задачах соответственно (НО () ()о,
Н I + (J> (Jo) и (НО (J) ()о, HI (J < ()о).
m (выборочный контроль). Пусть партия из N изделий содержит неизвестное число ()
дефектных изделий, (J Е {О, 1, . .. ,N} Чтобы проверить rипотезу НО () (Jo против
альтернативы HI+ () > ()о, берут на контроль случайную выборку из n « N) изделий
и каждое из них проверяют. Основываясь на статистике Т обнаруженнос в выборке
число дефектных изделий, построить р. н. м. критерий.
.... Указание. Убедиться в том, что распределение статистики Т (rиперrеометрическое
распределение Н((), N (), n), см. п. 4 1.1) имеет монотонное отношение правдопо
добия.
m Рассматривается задача (НО (J == (Jo, HI (J i= ()о) для нормальной модели
с неизпестной дисперсией N(/-L, ()\ Используя результаты примера 2 5.2 и прием
объединения односторонних критических областей, показать, что р. н. м. несмещенный
критерий имеет в данном елучае вид
X 1a == {т () X "n} U{T) () X; al.n},
rHe t, == X " n И t 2 == X; al. n определяются условиями (ниже kn(t) == p (t) плот
ность распределения х2(n»)
t,k,,(t l ) == t 2 k n (t 2 ), аl + 02 == о.
3на'lения (x ,.n' X; al,n) для Q == 0,05 и n == 2, 5,10,20,30,40,60 см в [12, с. 2751.
m Рассматривается задача (п u () == (Jo, Н, () i= ()о) для показательной моделИ
r((), 1). Используя результаты упр. 1 и прием объединении односторонних критических
областей (см. также пример 3 5.3), показать, что р. н. м. несмещенный критерий имеет
в данном случае вид
Х'а == {т Х;"'2П} U{ Т) X; al.2,,},
[де t l == Х;,.2П и t 2 == X; a1,2n определяются условиями (см. упр.12)
t l k 2п (t l ) == t 2 k 2 ,,(t 2 ), QI + а2 == а.
m Проверяется rипотеза Но () == ()о против общеН 3J11,тернативы HI () i= ()о
для моделИ Bi(k, (). Показать, что для больших выборок л. н. м. несмещенный крите
рий (18) 5.3 имеет пид
{ IT kn()ol }
) t"/2 ,
y! kn()o( I ()о)
n
T==I:X j ,
j;:::1
и ero мощность при альтернативах вида () == ()п == (Jo + б/.,[ii удовлетворяет предель
НОМУ соотношению
lim W«()n) == Ф ( б () ( k () ) t a / 2 ) + Ф ( б ( k t a / 2 ) .
.1400 y y
.... Указание. См. табл. I в 3.2.
Упражнения
455
m Убедиться в том, что в задаче (НО В =О ВО, HI В i= Во) дr1я пуассоновской
модели П(В) Л. н. м. несмещенный критерий для случая больших выборок имеет вид
{ ltxi nBol ta/2}'
а ero мощность при локальных альтернативах вида В =О ВN =О ВО + o/..;n удовлетворяет
предельному соотношению
W(Bn) =О Ф( Jno t ал ) + Ф( Jno tал).
... Указание. Использовать общий результат (18) 5.3 и табл. 1 в 3.2.
m Основываясь на результате, полученном в примере 3 2.5 (соотношение (17)),
убедиться в том, что дr1я проверки rипотезы о равенстве дисперсий двух нормальных
моделей можно использовать критерий
{ n(т 1) S2C )
Х,а=о ( ' ): т(n l) S2('!!) FI,n l,m 1 либо
n(т 1) S2( )
PI
т(n 1) S2( ) r
н}.
ID Убедиться в том, что в условиях упр.63 к rл.3 критерий проверки rипотезы
однородности НО т =О Bl/BI =О 1 имеет вид
Х 10 =О { ( , Jf) Р а / 1 ,1n, 2т либо FI I' 2n, 2т }
И вычислить ero мощность при произвольной альтернативе т i= 1.
m Обращая построенный в упр. 64 к rл. 3 доверительный интервал, получить следу
ющий критерий для rипотезы Но В == ВО при альтернативе Н) В i= Во:
.Ilo == { X(I) Во либо X(I) Во In а}
Вычислить функцию мощности 3Toro критерия и убедиться в ero несмещенности.
m Используя результат при мера 1 3.8, показать, что критерий проверки rипотезы
Но В =О ВО дЛЯ paBHoMepHoro распределения И(О, В) имеет вид
X 1a =О { Х(n) Boa l / n либо X(1I) Во};
вычислить ero функцию мощности и убедиться в том, что он несмещенный.
II!J Обращая построенный в упр. 65 к rл. 3 доверительный интервал, получить, что
критерий для проверки rипотезы Но В =О ВО В модели Вейбулла W(O, >., в 1 / Л ) имеет
вид
{ Во 2 } U { ВО 2 }
Х)а== Т(ТХо,,2n T TX) 02,2n' al+a2==a.
Чтобы получить несмещенный критерий, величины X ,.1n И X; a2' 111 выбираются
так же, как в упр. 13.
m Обращая построенные в упр. 66 к rл. 3 доверительные интервалы для параМетров
двухпараметрической показательной модели W(B 1 , 1, ( 1 ), построить критерии провер
ки rипотез Но BI == ВIU И Но В 2 == В 20 .
m Построить КОП дЛЯ rипотезы Но В == ВО в биномиальной модели Bi(k, В)
и убедиться в том, что ero асимптотический (дr1я больших выборок) вариант совпадает
с локальным наиболее мощным критерием, построенным в упр. 14
456
rлава 5. Параметрические zипотезы
... Указание. Воспользоваться общей теорией КОП для полиномиальноrо распределе
ния (пример 5 5.4).
ПJ Построить коп для rипотезы Но (J == 00 в пуассоновской модели П«(J) и y6e
диться В том, что в случае больших выборок он совпадает с локальным наиболее
мощным критерием, указанным в упр. 15.
... Указание. Воспользоваться тем, что при n 00 предельные распределения при
rипотезе Но статистик 21" Аn и Q ) == V';«(Jo)/ni(Oo) в (18) 5.4 совпадают
m Пусть наблюдается реализация длины n простой однородной эрroдической цепи
Маркова с множеством C == {(ij)} пар разрешенных переходов i j и rf == 1t' I.
Показать, что КОП для простой rипотезы нО, фиксирующей матрицу переходных
вероятностей ро I!pi j l!f rде Plj > о <=> (ij) Е [ , имест аСИМnТОТИ'lескИ (при
n (0) вид (сравни с критерием (7) 5.5)
{ "'" lIij 2 }
2 L.J lIij 1" > XI Q,d" N ..
lI. p .
(i])E[J · 1]
m Пусть rипотеза НО означает, что случайные величины
I, ... ' n независимы и одинаково распределены на множеСТilе [ == {I, 2, . ,N},
а при rипотезе 11.1 эти случайные величины связаны в простую однородную цепь Map
кова, в которой возможны любые переходы i j Показать, что при n 00 коп
для проверки rипотезы независимости НО внyrpи rипотезы 11.1 задается критической
областью
{ nllij 2 }
2 L..J Vij 1" > Xl Q,(N I)1
i,j=1 lJ..lI. j
(сравни с критерием (14) 5.5).
rлава б
(Специальная)
Линейная реrрессия
и метод наименьших квадратов
Статистика. это физика чисел.
П. Диаконис
Эrой rлавой мы начинаем серию специальных rлав, посвященных pac
смотрению специфических задач, решаемых математической статистикой, KO
торые объединяются тем или иным общим признаком (связанным чаще Bcero
с областью их практических приложений), и выделяемых в отдельные разделы
(теории). Настоящая rлава посвящена pezpeccUOHHOMY й/tализу (см. пример 3
общеrо Введения) чрезвычайно важному ПРИК1lадному разделу современной
математической статистики. В ней рассматривается практически важный слу
чай неодинаково распределенных наблюдений с одинаковыми дисперсиями,
коrда их средние имеют вид линейных функций от неизвестных параметров
(так называемая схема линейной pezpeccuu). Излаrаются К1Iассический метод
наименьших квадратов (метод Eaycca MapKoвa) для оценивания параметров
модели и ero оптимальные свойства, рассматриваются вопросы ero практи
ческоrо применения. В рамках нормальной модели дается полное решение
задач доверительноrо оценивания произвольных линейных функций пара
метров реrpессии и про верки линейных rипотез для них. Дается применение
модели нормальной реrpессии к задачам дисперсионноro анализа. Излаrаются
элементы теории статистической реrрессии и корреляции.
6.1. Модель линейной реrрессии
До сих пор рассматривались ситуации, коrда исходные статистические дaH
ные (выборка) Х == (X 1 ,... ,Х П ) представляли собой результаты повторных
независимых наблюдений над некоторой случайной величиной (ИСК1lючени
ем является 5.5, в котором наблюдения предполаrались связанными в цепь
Маркова), в такой случайной выборке компоненты Xj независимы и одинако
во распределены: Fx; == F{, i == 1, . . . , n. Однако в реальных ситуациях такие
предположения выполняются далеко не всеrда. Например, имеется обшир
ный Kpyr прикладных задач, в математической модели которых естественно
предположение, что средние значения наблюдений Х ; представляют собой
линейные функции от неизвестных параметров fl == ({3I,..., {3k), а вторые
458 rлава б. Линейная реzрессия u метод наименьших квадратов
моменты удовлетворяют тем или иным дополнительным условиям. В таких
случаях rоворят о модели линейной pezpeccuu.
Более конкретно, здесь речь идет об изучении таких случайных экспе
риментов, Korдa на их исход влияют некоторые неслучайные переменные
(факторы) ZJ, ,Zk, значения которых MOryr меняться от опыта к опыту.
Например, ZI, ,Zk MOryr быть входными характеристиками прибора, при
задании которых наблюдается соответствующий «отклик» как исход экспери
мента. В друrих случаях значения фаКТОРО!J для каждоrо опыта MorYT быть обу
словлены не зависящими от исследователя причинам и (как правило, это имеет
место, например, в экономических исследованиях). Но в любом случае стати
стические данные состоят при этом из множества наблюдавшихея значений
<<откликов» Х" , Х П И соответствующих значений факторов, т. е. имеют вид
( . (i) (i) ) . .
Xi, ZI ,..., Zk ,Z 1, , n, при этом всеrда предполаrается, что k < n.
Часто можно считать, что факторы ZI, , Zk оказывают влияние только
на среднее значение «отклика», при этом математическое ожидание исхода
i ro опыта имеет вид
k
ЕХ; == "Е {3jzJi) == (i)' , (i) == (z i)
j '
и)
,Zk ),
т. е. яuляется линейной функцией неизвестных пара метров == ({3" ,{3k)
(напомним, что при матричных операциях !JeKтopbI понимаются как BeKТOp
столбцы). Друrими словами, случайную величину X j , описывающую резуль
тат i ro опыта, можно представить в виде
X j == (j)/f3 + ':j, i == 1,
,n,
(1 )
rде tj случайная «ошибка», распределение которой не зависит от парамет
ров и E': j == О. Если ввести (kхn) матрицу Z == II (') (n)lI, составленную
из векторов столбцов ;.(j) (она называется матрицей плана), и вектор «оши
М бок,> .: == (':1, ,':п), то в матричных обозначениях
атрица ппана
предыдущие равенства принимают вид
х == z' f3 + f,
Ef == Q.
(1 ')
Далее, обычно предполаrают, что <<ошибки,> ':1, ,':п (или, что то же самое,
случайные наблюдения Х" , Х п ) некоррелированы и имеют одинаковые
дисперсии DX j == D':j == и2 > О, i == 1, , n, rде и2 обычно неизвестно.
В этом случае матрица вторых моментов вектора наблюдений Х имеет сле
дующий вид:
D( X ) == D(f) == E(ff') == и211п,
(2)
rде 11n единичная матрица порядка n. Соотношениями (1) (2) и опреде
ляется модель линейной pezpeccuu. Параметры fЗl, ,{3!.: называются коэффи
2 . д .
цuентами pezpeccuu, а u" остаточноu uсперсиеu.
6.2. Оценивание параметров модели линейной ресресcuи 459
в описанной схеме переменные Z" ,Zk MOryт быть функционально
зависимы. Так, все Zj MOryт быть функциями oAHoro переменноro t, например,
Zj == aj(t), rAe aj(t) полином степени i > 1, в этом случае rоворят
о параболической ресрессии.
В более общем случае возможны корреляции между наблюдениями Х;,
Torдa вместо условия (2) вводится условие D( ) == (iG. Если ма1l'ица G из
вестна и невырождена, то, положив, У == G I/2 Х , получим, что так преобра
зованные данные удовлетворяют модели (1) (2) (напомним, что при линейном
преобразовании J::. == L X первые и вторые моменты случайноro вектора пре
образуются следующим образом: Е(У) == LE( X) , D(J::.) == LD( X )L'). Таким
образом, самостоятельноrо изучения заслуживает только стандартная модель
(1 ) (2).
В излаrаемой далее теории определяющую роль иrpает (k х k) матрица
A==Z W
Эта матрица BcerAa нео1l'Ицательно определена и положительно определена
TOrдa и только TorAa, KorAa rank Z == k, т. е. KorAa ее строки линейно незави
симы. Действительно, квадратичная форма {' А{ == t' ZZ't == (Z't)' (Z'{) о,
v{ == (t" ,t k ), причем равенство нулю возможно только при Z't == Q.
в свою очередь, это равенство эквивалентно равенству t';'1 + + tk == О,
rдe;." , ;'k столбцы матрицы Z' Таким образом, равенство нулю (А{ при
некотором t -j. Q имеет место только в случае линейной зависимости векторов
;." . . . , ;'k' т. е. при rank Z < k. В дальнейшем мы будем BcerAa предполаrать,
что "-1a1l'ица А не вырождена (или, что эквивалентно, rапk Z == k). Случай
вырожденной матрицы А более сложен ДIlЯ анализа и соответствующие pe
зулыаты можно найти в [21, rл. 4]; полное изложение теории реrрессионноro
анализа с ее мноroчисленными теоретическими и практическими нюансами
имеется в 122].
6.2. Оценивание парамеТРО8 модели линейной реrрессии
Рассмотрим прежде I1cero задачу точечноrо оценивания параметров (3" ,fЗk
И и2 модели (1) (2) 6.1.
1. МеТОА наименьших кваАратов
Общим методом оценивания неИЗIlестных коэффициентов реrрессии (31, . . . ,
(3k является разработанный К. rayccoM (1809) и А. Марковым (1900) (о нем
см. в п. 5 1.1) метод наименьших квадратов, в соответствии с которым oцeH
ки этих параметров находят из условия обращения в минимум квадратичной
формы
8@) == S( X ;f}) == ( Х Z'f})'( X Z'I}) == f.'f.,
(1)
представляющей собой сумму квадратов <<ошибок» в (1) 6.1. Точку !!. ==
== (Ь 1 , .. . , Ь k ), удовлетворяющую равенству 8(Ю == miп 8((3), называют oцeH
!!.
460 rлава 6. Линейная реzрессия и метод наименьших квадротов
..
О. н. К.
кои наименьших квадратов (о. н. к.) пара метра 13 == (13\,
И обозначают!!. == .
,13k)
Теорема 1. Если матрица А в (3) 6.1 не вырождена, то о. н. к. !!. существует
и определяется равенством
jj ==!!. == A \ Z X .
(2)
Доказательство. Пусть 13 == !!. + , Torдa
S(f!.) == ( Х z'!!. Z'Ю'( Х z'!!. Z'Q) == (Х Z'!!.)'( X Z'f2) + 'A ,
поскольку
( Х Z'!!.)' Z' + 'Z( X Z'!!.) == 2 X' Z' 2!!.'A == о.
Таким образом,
В(!!.) == В@ + Q' A В@
(3)
и равенство достиraется лишь при == Q. Следовательно, Q единственная
точка минимума квадратичной формы (1). .
Замечание. Практически о. н. к. (J == arg min 8((3) находят, решая систему уравнений
I!..
aS(f!) == О . == 1 k
J(3j ,} , "
.., .
.,.. Нормальные,'
уравнения :.
которые называются нормаЛЫlыми уравнениями метода наи
меньших квалратов.
в ряде случаев интерес представляют не сами параметры 131,. ,13k, а их
некоторые линейные комбинации, т. е. новый параметрический вектор t ==
== (t j , ,t m ), т k, связанный с f!. соотношением t == Tf!., rде Т задан
ная (т х k) матрица. В этом случае о. н. к. f для определяется равенством
f == T , rде определено в (2); представление f через исходные данные,
следовательно, имеет вид
f==TA 'Z X .
(4)
2. Оптимальность оценок наименьших квадратов
Исследуем свойства полученных в п. 1 оценок. В общем случае будем pac
сматривать задачу оценивания вектора t == Т!!. в Юlассе линейных оценок,
т. е. оценок вида! == L X , являющихся линейными функциями от наблюде
ний Х == (X 1 ,... ,Х п ).
6.2. Оценивание параметров моделu лuнейной pezpeccuu 461
Теорема 2. Пусть матрица А не вырождена. TorAa для произвольноrо BeK
тора == Т!.!.. о. н. к. Т, определенная равенством (4), является несмещенной
оценкой с минимальной дисперсией в классе всех линейных несмещенных
оценок ; при этом
О(Т) == (f2TA IT' == (f2 D .
(5)
Доказательство. Из (4), (зj и (1') 6.1 имеем
Еа) == Т А 1 ZE( Х ) == Т А J Z Z' {3' == Т!.!.. == ,
т. е. I линейная несмещенная оценка . Пусть l == L X произвольная
линейная несмещенная оценка , т. е.
ЕЮ == LE( X ) == LZ'!J.. == T!J...
Это равенство должно, по определению несмещенности, выполняться для
любоrо !J.., поэтому отсюда следует, что
L z' == Т
(6)
Из (2) 6.1 находим
О(О == LD( X )L' == (Т2 LL'
(7)
Наша цель минимизироватьдисперсии оценок lJ, ,1т, т. е. диаrональные
элементы матрицы LL'. Для этоro запишем тождество, следующее из (6):
LL' == (Т A ! Z)(T A I Z)' + (L Т A l Z)(L Т A lZ)'
Здесь в правой части каждое слаrаемое имеет вид Н н', откуда следует He
отрицательность диаrональных элементов. Но от L зависит только второе
слаrаемое, поэтому диаrональные элементы матрицы DЮ в (7) одновременно
достиraют минимума тorдa и только Torдa, коrда L == Т А ) Z. Соответствую
щая оптимальная оценка имеет вид r == Т А 1 Z Х == Т, т. е. совпадает с о. н. к.
(4). Наконец, формула (5) следует из (7), если подставить вместо L найденное
оптимальное рещение. .
2 J
В качестве npocToro следствия теоремы 2 получаем, что о(ш == (f А ,
или
cov(fjj,1i j )==a 2 a jj , i,j==l,...,k, rде lIaijll==A l==llaijll 1 (8)
Замечание. Если матриuа Т имеет вид Т == АА, то формулы (4) и (5) принимают
соответственно вид
t == AZ Х , оа) == (J2 ЛАЛ' ,
т. е. необходимость в Dыислениии обратной матрицы А 1 ДЛЯ нахождения О. н. К. И ИХ
вторых моментов отпадает.
Итак, теорема 2 позволяетрещить задачу построения оnтимальныхлиней
ных (по наблюдениям Х ) оценок для произвольных линейных комбинаций
коэффициентов реrpессии это оценки наименьших квадратов.
462 rлава б. ЛинейнаR pezpeccUR и метод наименьших квадратов
З. Оценивание остаточной дисперсии
Из (1) и (2) 6.1 имеем
n
ЕВ«(!) == L Ecl == n17 2
i 1
Далее, учитывая (8) и определение следа (tr ) матрицы (см. п. 2 2.5), найдем
k
E( !!)'A( f!) == L aijE(A /3i)(Дj /3j) ==
,j 1
k
2,", .. 2 I 2 2
q L.. aija ' ) == 17 tr (AA ) == 17 tr:n' k == k17
Ц I
Orсюда и из представления (см. (3))
В((!) == S( ) + ( f!)' A( (!)
(9)
следует, что
ЕS(Ш == (n k)17 2 ,
т. е. несмещенной оценкой Д)1Я остаточной дисперсии 172 является статистика
1 (Х Z/jj)'( X zljj)
и2 == B(/3) ==
n k n k
( 10)
,
Вектор l1. == х Q f!. называют остаточным вектором, а ero компоненты
1Ii, i == 1'...' n, остатками. Таким образом, полученный результат (1 О)
можно сформулировать так: оценка и2 равна сумме квадратов остатков, пoдe
ленной на n k (разность между числом наблюдений и числом коэффициентов
реrpессии /3i).
2
Приведем также друrое выражение Д)1я q , которое понадобится нам в
дальнейшем. Используя представление (2), запишем остаточный вектор в виде
и == (:n.n Z'A I Z) X == В Х == B(Z'fi + ) == Bf. (11)
Непосредственно проверяется, что матрица В [j (11) симмеТРИ'lна и идем
потентна (в 2 == В); следовательно, вместо (10) можно использовать представ
ление
"(;2 == X/BX == c'Bc (12)
n k n k '
показывающее явную зависимость оценки q2 от наблюдений.
Наконец, из (11) непосредственно вытекают следующие свойства остаточ
Horo вектора И (их проверку мы оставляем читателю в качестве упражнения):
Е(Ш ==Q, D(Ш == и2в == D( X ) D(Z/ ), Е иl == Q (13)
6.2. Оценивание параметров моделu лuнейной pezpeccuu 4БЗ
(в последнем соотношении Q обозначает нулевую (k х п) матрицу, т. е. co
стоящую сплошь из нулей, следовательно, о. н. к. ji И остаточный вектор ld.
некоррелированы: cov(jij, щ) == О, i == 1,..., k, j 1,..., n).
4. Условные о. н. к.
Выше мы рассмотрели случай, коrда вектор {3 == ({31, ,{3k) априори Mor
быть произвольной точкой еВЮlИдова пространства k (на ero значения не Ha
кладывалось никаких оrpаничений). Однако в ряде практических задач допу
стимые значения {3 бывают оrpаничены теми или иными условиями. Типичная
модель с оrраничениями на {3 имеет вид
T == tJ,
(14)
rде Т не которая заданная (т х k) матрица (т ( k) и O == (t lO , ,tmo)
заданный вектор такой, что система (14) совместна. Друrими словами, усло
вие (14) означает, что допустимые значения коэффициентов реrpессии {31,
{3k удовлетворяют т заданным линейным оrpаничениям
jli == tjO, j == 1,
,т,
(14')
rде 'I' , :п строки матрицы Т. Естественно предполаrать, что оrpани
чения (14') линейно независимы (иначе можно перейти к меньшему числу
уравнений, исключив линейно зависимые). Таким образом, в дальнейшем
будем считать, что rапk Т == т (случай т == k, однозначно фиксирующий
вектор {3, в последующих рассуждениях формально допускается).
Рассмотрим задачу оценивания параметров {3 в этой усложненной ситу
ации. Обозначим
ST == miп S({3)
fl; Tfl t,
и назовем условной оценкой наименьших квадратов (у. о. н. к.)
T То значение Ii (удовлетворяющее условию (14)), при
котором этот условный минимум достиraется: ST == S( _T)'
(15)
Условная 8{
_.о.н.к.
Теорема З. Пусть IAI i=- о и rank Т == т. Тоrда
lT == A ITD I(T O),
rAe 73 обычная о. н. к. (2) и матрица D определена в (5).
(16)
Доказательство. Из (16) непосредственно видно, что T T == o, т. е. вектор
T удовлетворяет условию (14). Запишем теперь раlЛожение (см. (1»)
S(fl) == [ х Z' T + Z'@T )]' [ х Z' T + Z/( T )] ==
464 rлава б. Линейная реi!ресcuя и метод наименьших квадратов
== B( T) + 2( T )'(z x Alr) + ( T )' A( T f!).
Так как (см. (2)) A == z x , то из (16) имеем
Z X АfЗт == T'D I(T o).
Учитывая также, что T( 1' Ш == o T , получаем окончательное представ
пение для B( ), справедливое для всех :
B( ) == B( T) + 2(k ТШ'D I(т t o ) + ( T Ш'А( т ). (17)
Пусть теперь удовлетворяет условию (14). Тоrда средний член в (17) обра
щается в О, и мы получаем, что для таких
B( ) == B( T) + (lr ш' A( T ) B( T)
(сравни с (3)), причем равенство достиrается только при fi == T' .
Замечание, Полаrая о (9) f!.. == 'Л-т И учитывая, 'ПО, в силу (16),
(Д 13 )' А(Д fj )== (т13 tU)'D IT A I AA I т' п 1 (тД tu)==(Tjj tll)' п 1 (тр tlJ),
T T
получаем следующее представление услооноro минимума ST == S(jj ) через абсо
T
лютный минимум S( ):
ST == S( ) + QT,
I I
QT == (т!!.. to) п (Т!!.. o).
(18)
5. Оптимальный выбор матрицы плана
Рассмотрим «активный,) эксперимент, коrда значения факторов ZI, , Zk для
каждоrо опыта выбираются исследователем. Покажем, как в этом случае оп
тимально задать матрицу плана Z == II Y) f(n) 11 , rде i й столбец f(i) есть
комбинация значений факторов для i ro опыта (i == 1, .. . , п). В качестве кри
терия оптимальности естественно использовать величину дисперсий оценок
13i, т. е. величины a ii в (8); TOrдa задача сводится к выбору такой матрицы Z,
чтобы диаrональные элементы матрицы A ' == (ZZ') I были Минимальны.
Если значения факторов выбирать произвольными, то все элементы MaT
рицы A ' можно сделать одновременно как уrодно малыми, так как если Z
заменить на aZ, то A ' заменится на A I/a2....... Q при а....... 00. Чтобы ис
КJ1ючить этот случай, предположим, что значения факторов можно менять
в оrраничеННblХ областях, именно: наложим оrраничения вида
n
I L( (i) ) 2 2
Z.Z.== z. ==а ) '
} } } ,
i 1
j== t,...,k,
(19)
( (1) (n» ) б - Ф . 1 k
rде 2fj == Zj ,..., Zj на ор значении n уровнеи актора Zj, J ==, ,
(строки матрицы Z), а a , ... ,ak задаНные положительные константы.
6.2. Оценивание параметров модели линейной pezpeccuu 465
Теорема 4. При оrраничениях (19) имеют место неравенства
(7"2
DjЗj 2' j == 1,. , k,
a j
и минимум достиrается TorAa и только TorAa, KorAa векторы "
rональны, т. е. : j == о при i f= j.
' k OpTO
Доназательство. Пуст'ь j == 1. Запишем матрицу А == Z z' в виде
А == II ' I " '
rдe == ( ; I'"'' I)' Torдa, на основании формулы обращения матриц,
а" == [FI/IAI. Далее, умножая определитель IAI справа на определитель,
равный 1, получаем следующую формулу:
[AI== I 1 Q' II l l Q 1 == 1 ; , Q'F IQ
Q F p Q D.k 1 Q
Отсюда, учитывая соотношения (19) и (8), имеем
2 11 21РI (1'2 (1'2
D{31 == (1' а == (7" IAТ == а7 Q'F 'Q a '
так как Q' F IQ О. Знак равенства имеет место только при Q == Q (поскольку
подматрица F положительно определенной матрицы А также положительно
определена), т. е. при : I == О, i == 2, , k. Доказательство для друrих j
можно получить простой пере нумерацией факторов. .
В заключение отметим, что для оптимальной матрицы плана Z матрица
А == Z Z' является диаrональной с элементами ajj == аЗ == j' j == 1, .., k,
поэтому в этом случае нет проблемы ее обращения: о. н. к. И их вторые MO
менты имеют вид
j X
f3 j == ,.....,
z.z.
J J
I == IFI( " J Q'F 'Q).
(1'2
Df3' ==
J z'.z.'
J J
cov(JJi, liJ) == О,
i f= j.
(20)
б, Примеры применения метода иаименьших квадратов
Пример 1 (ПростаR реrрессия, оценивание параметров). Проиллюстрируем
общую теорию на примере важноrо для практических приложений случая
простой pezpeccuu, коrда число параметров k == 2, т. е. == ({31, (32) , а векторы
,;,,(i) имеют вид ,;,,(i) == (1, ti), i == 1,..., n. Тоrда
EXi=={3,+{32ti, i==l,...,n, (21)
т. е. среднее значение наблюдений является линейной функцией одноrо фак
тора t Так, t может быть температурой, при которой производится экспери-
мент, дозой лечебноro препарата, возрастом обследуемых лиц и Т, д., и речь
за Заказ 1748
4бб rлава б. Линейная реzрессuя и метод наименьших квадратов
идет об изучении связи между откликом (исходом эксперимента) и фактором t
на основании результатов реrистрации n пар измерений (X i , t i ), i == 1, , n,
rде Х; наблюдается при значении t; фактора t. Прямую r.p(t) == (31 + (32t,
соответствующую (21), называют линией pezpeccuu, а коэффициент (32 ее
наклоном.
В данном случае ма11JИЦЫ z, А и столбец r == z Х равны:
t 1
t n
n
А==
2: t i
2: t i
2: t ;
( 2: Х ; )
у==
2: tiXi
z==
Будем предполаrать, что не все ti одинаковы (тorдa rank Z == 2), тоща
n
IAI == n 2: t; (2: tj) 2 == n 2:и; [)2 > О,
i 1
rдe, как обычно, черта сверху означает арифметическое среднее, и
A l == 11 2: t n n[ 11 '
IAI n[
A 'Y == ( X2:t [2: tiXi ) ( (3 (3 = 2 ' )
IAI 2:tiXi n[X
В результате несложных преобразований запишем оценки jЗl и (32 В более
удобном для вычислений виде (проверить!)
2:(ti t)(X i Х)
132 == "" 2 '
L-(t; t)
Дl == Х [732'
(22)
Вторые моменты этих оценок образуют ма11JИЦУ (7"2 A I (см. (8», поэтому
2: t; 2 (7"2
D(3, == 2 а D.82 == 2 '
n 2:(ti t) 2:(ti t)
t 2
cov(f3" (32) == "" 1\2 (J"
L-(t i t/
Наконец, в силу (22),
S( ) == 2:(X i 73) 7i2ti)2 == 2: [(X i Х) 732(ti [)] 2 ==
"" 2 -;;2 "" 2
== L-(Xi Х) .82 L-(t; t)
(23)
6.2. Оценивание параметров модели лuнейной pezpeccuu 467
" 2 Ф
инесмещенная оценка для остаточнои дисперсии и вычисляется по ормуле
2 S( )
и == . .
n 2
Пример 2 (Параболическая реrрессия). Пусть j й фактор Zj является поли
номом aj(t) степени j 1 от общей переменной t; Torдa
] == (aj(t l ),
,aj(t n )). j == 1,. ,k,
набор ero значений для n уровней, а
(j) == (al(tj),. ,ak(tj)), i == 1,..., n,
комбинация значений факторов ZI, . . . , Zk ДI1я i ro опыта. Таким образом,
матрица плана Z == II (I) (n)11 определяется выбором n точек t l , , t n
значений общеrо фактора t для n опытов. В этом случае среднее значение i ro
наблюдения Xj имеет вид
k
EX j == ",(tj; f!) == L /3jaj(tj), i == 1, ... ,n. (24)
j 1
Определенная здесь функция ",(t; f!) представляет собой полином (параболу)
степени k I и называется кривой параболической рарессии.
Опишем типичную СИ1)'ацию, коrда имеет место схема параболической pe
rpессии. Предположим, что имеется теоретическая зависимость вида Х == ",(t; (З)
между переменными t и Х, причем значения t и Х получают из наблюдениЙ.
Задача состоит 8 определении по экспериментальным данным неизвестных
параметров /31, ,/3k, входящих В это уравнение. Каждое измерение Х при
заданном t дает уравнение, связывающее неизвестные параметры, и если бы
измерения величины Х производились без поrpешностей, то для определе
ния параметров /31, , /3k было бы достаточно k измерений. Однако точные
измерения на практике чаще 8cero невозможны, поэтому для заданных значе
ний t соответствующие значения Х известны с какими то поrрешностями, т. е.
реально вместо точноrо значения Xj == ",(tj; /3) мы имеем случайный результат
X j == ",(tj; /3) +!j, rде !j ошибка измерёНия. Если условия эксперимента
обеспечива т отсутствие систематической ошибки (Ее; == О), равноточность
(D!j == (72 i == 1, ,n) и некоррелированность (cov(!j, !j) == О, i i- j)
результатов измерений, то приходим к схеме реrрессии вида (24).
Чтобы исключить влияние поrрешностей измерений, нужна дополни
тельная информация. Для этоrо проводят большое число измерений n > k
и полученные экспериментальные данные обрабатывают по методу наимень
ших квадратов. В результате находят не точные значения коэффициентов
(ЗI, . . . , /3k, а определяют их о. н. к. fil' . ., ,д;.. в данном случае этому методу
можно дать следующую rеометрическую интерпретацию (см. рис. 1).
Нанесем на плоскости (t, х) наблюдавшиеся точки (tj, Xj), i == 1, , n.
Torдa значения f!..* неизвестных коэффициентов f!.. подбирают так, чтобы co
ЗО
468 rлава б. Линейная реzрессия и метод наименьших квадратов
х
*
,
,
.
,
.
.
t l
t 2
t"
t
РКС.l
ответствующий эмпирический rpафик х == !p(t; /3*) «наилучшим образом» про-
ходил около наблюдавшихся точек. Если в качестве критерия оптимальности
взять велкчину
n
2:(X j cp(tj; {i*))2
i=1
сумму квадратов отклонений эмпирическоrо rрафика в точках t 1 , , t n
от наблюдавшихся значений X 1 , ,Х П , то приходим К методу наименьших
/3 *
квадратов с решением == {i.
Формально такой же вид имеет и классическаSJ задача математическоrо
анализа приближений функций.мноrочленами. В этом случае данные (ti, X j ),
i == 1, .. , n, интерпретируют как пары соответствующих абсцисс и ординат
rpафика изучаемой функции и задача состоит 11 подборе UllmерполяциО/l/lО20
МНО20члена вида !p(t; (i), который давал бы наилучшее приближение в среднем.
n
т. е. минимизировал бы величину 2:(X j !p(t; ю)2
j=J
.
Приt;lер 3 (Численная иллюстрация [11]). ПРИllедем пример lIычисления
оценок пара метров {i. Пусть требуется определить неизвестные коэффици-
енты (/3.. /32. /33) функциональной зависимости
x(t) == /3 J + t/32 + t J /3J.
Будем nредполаraть, что в точках tj == 2 + 3i/n, i == 1, ,n, измерены
значения функции x(t). Ошибки измерений €j, i == 1,..., n, будем считать
2
независимыми и нормально распределенными с &i == О, D€j == и В этом
случае имеем линейную модель
Xi == x(tj) + €j == {31 + ti{32 + tt{3J + €j, i == 1, . n.
Пусть {31 == 3, {32 == 1, {33 == 1, и 2 == 0,04. Смоделируем €j Д/Jя n == 25
и n == 100, используя алroритмы п. 8 и 6 1.3, и найдем соответствующие X j .
6.2. Оценивание параметров моделu лuнейной pezpeccuu 469
х
3,5
з
х = ж(t) = /31 + /3 2 t + /3зt
/
3.0
2.5
0.5
t
0,0
0.5
1,0
Рис. 2. (n = 25)
х
3,5
х
х
э
ж = x(t) = /3, + /3 2 t + /3эt
з
х = x(t) = /3, + /3 2 t + /3)t
3,0
2.5
0.5
0,5
1,0
0.0
Рис. З. (n = 100)
470 rлава б. Линейная реzрессия и метод наименьших квадратов
Решая систему нормальных уравнений
8 "
8(.j l:)Xi /31 ti/32 t1/3з)2 == о, j == 1,2,3,
I-'J , l
2
найдем оценки /31' /32, /33, а также (j :
2
1) ДJlЯ n == 25: /31 == 2,983; /32 == 0,828; /33 == 0,895; (J' == 0,034;
2
2) ДJlЯ n == 100: /3, == 2,992; /32 == 1,007; /33 == 1,001; (J' == 0,046.
На рис. 2 и 3 приведены соответствующие rрафики x(t) и x(t) == lil +
3
+ t/32 + t /33, знаком 181 отмечены резуЛ!,таты измерений (t i , Xi). .
7. Ортоrональные мноrочлены Чебышева
В описанной в примере 2 схеме предполаrалось, что мноrочлены aj(t) заданы.
. I
В частном случае aj (t) == e и Torдa
k
rp(t; fi) == L /3jt H
j l
(это имеет место в примере 1). В друrих случаях (например, в задачах интер
поляции) мноrочлены aj (t) можно выбрать достаточно произвольно, и тоrда
критерием их выбора является простота соответствующих вычислени Как
отмечалось в п. 5, наиболее просто рещается задача вычисления о. н. к. /3 при
диаrональной матрице А == ZZ': в этом случае (см. (20))
"
L aj(ti)Xi
i 1
/3j == " j == 1,
L a;(ti)
i l
,k.
(25)
Условием диаrональности матрицы А является ортоrональность векторов
j == (aj(t 1 ),.. ,aj(t,,)):
"
j r == L aj(ti)ar(ti) == о, j -1= r
i 1
(26)
Мноroчлены, удовлетворяющие условию (26) называют ортошнальнымu MHO
сочленами Чебышева.
Покажем, что при заданных t 1 ,... ,t" такие мноrочлены Bcerдa можно
построить. Без потери общности можно предполаrать старщий коэффициент
aj(t) рапным 1, таким образом, а, (t) == 1, a2(t) == t + с, ... . Из условия (26)
6.2. Оценивание nараметр08 модели линейной pei!peccuu 471
при j == 1, r == 2 имеем
n
n
0== L a2(ti) == L ti + nС,
i l i l
т. е. с == i. Тем самым, второй MHoro'UleH Чебышева есть a2(t) == t [.
Выведем теперь общую рекуррентную формулу, позволяющую вычислять
следующий мноroчлен по двум предыдущим, этим и будет доказано cy
ществованием всех мноrочленов системы Чебblшева. Предположим, что для
HeKoToporo т 2 мнorочлены aI(t),... ,ar(t) уже построеНbl. Рассмотрим
ПРОИЗВОJlЬНЫЙ мноrочлен ф(t) степени, меньшей т Ero можно однозначно
представить в виде
r
ф(t) == L 1s a s(t).
s l
Действительно, из условия ортоrональности (26) при j == 1,
,т имеем
n n
L ф(ti)аj(ti) == 1) L а] (ti),
i I i 1
т. е. эти равенства однозначно определяют коэффициенты 11, . .. . 1т, Отсюда,
в частности, следует, что если ф(t) мноrочлен степени, меньшей т 1, то
n
L фj(ti)ат(ti) == о.
{ I
(27)
Рассмотрим теперь MHOrO'UleH степени т следующеrо вида
a(t) == (t + 1)a T (t) + fЗаr I(t).
Если j < т 1, то в силу (27)
(28)
n
n
n
L aj(ti)a(ti) == L(t i +1)aj(ti)a T (ti) + fЗ L aj(ti)aT I(ti) == О
i l i 1 i 1
(так как степень мноrочлена (t + 1')aj(t) равна j < т 1), т. е. при любых по
СТОЯННblХ fЗ и l' мноrочлен (28) ортоroнален мноrочленам аl (t), .. . , aT 2(t).
Выберем эти ПОСТОЯННblе так, чтобы он бblЛ ортоrонален также aT 1 (t) и aT(t).
Для этоrо ДОЛЖНbl выполняться следующие условия:
n
n
n
L aT I(ti)a(ti) == L tiaT I(ti)aT(ti) + fЗ L a; I(ti) == о,
i 1 i==1 i l
n
n
n
L aT(ti)a(t i ) == L tia;(t i ) + l' L a (ti) == о.
i I i==I i 1
472 rлава б. Линейная реzрессия и метод наименьших квадратов
Отсюда находим 13 и 'У:
tiar l(t;)ar(t;)
fЗ== L.J 2 '
;=1 aT 1
'у == t t;a;;t i ) ,
;=1 а т
(29)
rде
n
aJ==LaJ(ti), j==1,2,...
;=1
При таком выборе постоянных 13 и 'у мноrочлен (28) ортоrонален всем MHoro
членам al(t),... ,ar(t), следовательно, он является следующим мноrочленом
ar+l(t) системы Чебышева. Тем самым, получен алrоритм построения систе
МЬ) ортоrональных мноrочленов Чебышева. В дополнение к указаННblМ ранее
двум первым мноrочленам al(t) и a2(t) при ведем явный вид тpeTbero MHoro
члена аз(t), который следует из (28) и (29):
( n ) n
] 2 1
аз(t) == (t t) t 2 L t;(t; t) L t;(t; t) ==
а 2 ;=1 n ;=1
( n ) 2
1 з а 2
== (t t) t t 2 L(t; i) .
а 2 ;=1 n
(3О)
Итак, если в схеме параболической реrpессии (24) мноrочлены aj(t) яв
ляются ортоrоналЬНblМИ мноrочленами Чебышева, то о. н. К. j3j вычисляются
по формулам (25), а соответствующее значение 8( ) == mll1 8(13) таково:
fJ
8( ) == t ( Х; t j3jaj(t;) у
.=1 )=1
n k n k
== L хl 2 L 1i j L aj(t;)X; + L а)т ==
;=1 j=1 ;=1 j=1
n k
== L хl L а;Щ. (3])
;=1 j=1
Отметим следующее важное обстоятельство. Как видно из формулы (25),
о. н. к. /3j определяется только мноrочленом aj(t) и не зависит от параметра k
схемЬ) (24). Кто позволяет упростить задачу построения интерполяционноrо
мноrочлена более высокой степени, если требуется повысить точность интер
поляции. Так, предположим, что Дl!Я заданноrо k построен интерполяцион
НblЙ мноrочлен
k
rp(t;j3I' ",/3k) == L1i j a j (t),
j=1
6.2. Оценивание nараметров модели линейной pezpeccuu 473
однако значение s(73I"'. ,73k) в (31) еще велико, т. е. точность приближения
исследуемой функции мноrочленом степени k 1 недостаточна. Torдa строят
интерполяционный мноrочлен степени k вида
k+l
Ip(t; 731, . .. , 73k' lh+ 1) == L 73 j aj(t),
j 1
т: е. добавляя следующий, (k + I) й мноrочлен Чебышева аНl (t) с коэффи
циентом lh+I' вычисляемым по формуле (25) (при этом предыдущие коэф
фициенты 731' . .. ,1ik остаются прежним и). Далее вычисляют
s(1iI' .. . ,lh+ 1) == s(fjl' ,73k) a + IЩН (32)
и если точность приближения, достиrнутая с помощью мноrочлена k й CTe
пени недостаточна, то можно подбирать далее мноrочлен (k + 1 ) й степени
и т_д., пока не достиrнем желаемой точности.
Пример 4 (Численнаи иллюстрации [11]). В OCHOBax химии» Д. И. MeHдe
леев 1) при водит следующие данные о количестве (х) азотно натриевой соли
NaNO), которое можно растворить в ]00 r воды в зависимости от темпера
турь' (t):
t j О 4 10 15 21 29 36 51 68
Х; 66,7 71,0 76,3 80,6 85,7 92,9 99,4 113,6 125,1
Построим по этим данным приближенную эмпирическую формулу вида
х == !3, + !32t, описывающую зависимость между рассматриваемыми величи
нами. Здесь речь идет о линейной зависимости, поэтому это схема простой
реrрессии, рассмотренная в примере ]. Используя формулы (22), получаем
731 == 67,5,132 == 0,87 Таким образом, линейная приближенная формула имеет
вид
х == 67,5 + 0,87t.
(33)
отклонений, вычисленная по формуле (23),
При этом сумма квадратов
равна 11,1.
Установим, как повышается точность приближения, если в качестве ин
терполяционноrо мноroчлена использовать квадратичную параболу. Запишем
искомый мноrочлен в каноническом виде:
Ip(t; ) == !31al(t) + !32a2(t) + !3заз(t),
rде aj(t) мноroчлены Чебышева (напомним, что аl (t) = 1, a2(t) == t l ==
== t 26, а аз (t), указан в (30)). Результат (33) можно записать в каноническом
1) Менделеев Дмитрий Иванович (1 834 1907) выдюшийсяя русский химик, разносторонний
ученый, педаrоr; OTKpbU1 периодический закон химических элементов (1869) один ИЗ осиовнbIX
законов естествознания.
474 rлава б. Линейная реzрессия и метод наименьших нвадратов
виде так:
х == 90,12al(t) + 0,87a2(t),
и достаточно вычислить по формуле (25) jЗ3' В данном случае
аз(t) == (t 26)(t 40) 451,1,
поэтому значения аз(t j ) таковы: 588,9; 340,9; 28,9; 176, 1; 356, 1; 484, 1;
484; 491, 1; 176, 1; 724,9. Отсюда
a == 2: a (tj) 1,6 106 2: аз(tj)Хj 2,2 103
и по формуле (25) l3з 1,4 1O 3. поправка в (32) а Щ 3,0. Таким
образом, учитывая мноroчлен аз(t), мы незначительно увеличиваем точность
аппроксимации, и в качестве удовлетворительной эмпирической зависимости
можно принять формулу (33). .
Общее замечание. Метод наименьших квадратов применяют такжс n случаях, Korдa
зависимость ЕХ; от не является линейной. Пусть
Х; == f(tj;(J"... ,fЗk) + E:j, i == 1, ,n,
rде Ее; == О, DE:; == (12, СОУ(Е:;, Е: j) == О, i '" j. Тоrда о. н. к. параметров миними
зируют ПО выражение
n
Q@ == L (Х; f(t;; fЗl,... ,fЗk))2
;=1
и для их отыскания надо решить систему уравнений
aQ(f3)
д fЗ; == О, i == 1, . .. , k.
t 6.3. Нормальная реrрессия
1. Модель нормальной реrрессии
До сих пор делались предположения только о первых и вторых моментах
наблюдений (см. условия (1') и (2) 9 6.1). Развитая при этих минимальных
предположениях теория наименьших квадратов позволяет получать только
точечные оценки для параметров (3" , (3k И их линейных комбинаций.
Чтобы получать более сильные утверждения (строить доверительные интер
валы и проверять различные rипотезы) необходимо сделать дополнительные
предположения о виде распределения наблюдений Х == (Х" ,Х П ) или,
что то же, вектора «ошибок,) f. == (е 1, , e 7l ) (см. (I) ( 1') 9 6.1). Чаще Bcero
предnолаrается, что этот вектор имеет нормальное распределение, т. е. в дo
полнение к (\') и (2) 9 6.1 nолаrается, что
.c(f.) == N(Q, (Т2:п. п ).
(1)
6.3. Нормальная реzрессuя
475
в этом случае rоворят о 1/0рмальной pezpeccuu. Отметим, что условия (1') (2)
6.1 и (1) можно объединить и записать в виде
.с( Х ) == N(Z'r!.., 0' 2n n).
(2)
Общие свойства MHoroMepHoro нормальноrо распределения изложены в п. 2
1.2. Подчеркнем, в частности. что условие (2) означает, что компоненты
2
вектора Х независимы и имеют одинаковые дисперсии о' , но их средние,
вообще rоворя, различны.
2. Оценки максимальноrо правдоподобия (о. м. п.)
параметров нормальной реrрессии
Нормальная модель (2) определяется (k + 1) MepHЫM параметром
() == «(3),
. (3J.:, 0'2).
область возможных значений KOToporo представляет собой евклидово полу
пространство
е == {О oo < (3j < 00, j == 1, ,k, 0'2> О}.
Если f == (ж 1. ,Х n ) наблюдавщаяся реализация вектора m функция
правдоподобия этих данных имеет вид (см. соотнощение (9) 91.2)
L(f; О) == (21!'0'2) n/2 ехр { 2 2 S(f; r!..) }, (3)
rде квадратичная форма S(;f; r!..) определена в (1) 96.2.
Найдем о. м. п. пара метров О, которые максимизируют функцию L(;f, (}).
Из (3) следует, что при любом 0'2 > О максимизация L(f, О) по r!.. эквивалентна
минимизации по r!.. квадратичной формы S(;f; r!..). Таким образом, для модели
нормальной pezpeccuu о. н. К. совпадает с О. м. п. этих параметров .
Замечание. Из теоремы 2 6.2 следует, что о. н. К. являются оптимальныии в клас
се линеЙНblХ оценок. Для схемы нормальной реrpессии справешlИВО более сильное
утверждение: О. Н. к. являются оптимальными в классе всех (не только линеЙНblХ) не-
смещенных оцеиок рассматриваемых пара.метрических функций.
Н " 2 2 П (3)
аидем теперь о. м. п. о' для остаточнои дисперсии о' одставив в
2
вместо r!.. оценку r!.. и пролоrарифмировав, получим, что (j это то значе
2
ние о' , которое минимизирует выражение
S(fJ)
+ n 1" 0'2
о'
Отсюда имеем
2 S( )
,..
v .
n
(4)
476 rлава б. Линейная реzрессия и метод наименьших квадратов
Ранее было показано (см. п. 3 6.2), что п общем случае несмещенная оценка
для (]"2 имеет вид S( )/(n k), поэтому о. м. п. "(i оказывается смещенной
и ее смещение
Еи2 (]"2 Е ( n : k (;2) (]"2 ( n : k 1) (]"2 (]"2
убывает по модулю с ростом числа наблюдений n. Таким образом, оценка (4)
является лишь асимптотически несмещенной (что вообще характерно для
о. м. п.).
З. Основная теорема теории нормальной реrрессии
Все дальнейшие выподы теории нормальной реrрессии базируются на следу
ющей важной теореме.
Теорема 1. Случайные величины (j и S«(j) S( X ; (J), а также S«(j) и Q
S(f!) S( ) независимы; при зтом
2 1
[о(ю N(f!., (]" А ),
( S«(j» ) 2
[о (]"2 х (n k).
[o( ) X2(k).
(5)
Доназательство, Введем нормиропанный вектор (,ошибок» f* f/ и' L(f*) ==
N(Q,]l.n) (см. (1». Тоrда (см. (1') 6.1)
Х Z/f!. + (]" *
а равенство (2) 6.2 примет вид
(6)
fЗ 1 *
f!. +(]"A Zf
Из представления (12) 6.2 следует, что
S@ е*' Ве.
(]"2
Наконец, из тождества (3) 6.2 имеем следующее предстамение для Q:
(7)
(8)
Q == S(f}) . S(ff.) == (ff. f!.)' A(ff. Ю.
(9)
Незаписимость и s(ff.) следует теперь из предстаuлений (7) и (8), леrко
проперяемоrо факта А I ZB A 1 Z(l n Z/ A l Z) == о и леммы 1 2.5.
Далее, из представления (9) имеем, что Q зависит от данных Х лишь через
ff.; следовательно, n силу незаписимости и S(ff.) случайные величины Q
и S@) также независимы. Первая часть теоремы доказана.
6.3. Нормальная реzрессия
477
Докажем теперь yrверждения (5). Так как линейная функция HOp
мальноro вектора (см. (7», то также нормальный вектор, а ero первые
и вторые моменты вычислены 8 п. 2 6.2 и имеют указанный в (5) вид.
Закон распределения Q/(72 устанавливается на основании представления
(9), факта нормальности вектора fj и замечания к теореме I 2.5.
Наконец, закон распределен s(jJ)/(72 следует из представления (8) и
теоремы 1 2.5, поскольку матрица В идемпотентна и
tr В == tr:n' n tr(Z'A IZ) == n tr(ZZIA I) == n tr:D. k == n k. .
Следствие 1. Из nepBozo соотношения в (5) следует, что для любоzо j == 1, . . . , k
[, ( 1ij {3j ) == .лf ( О 1 )
/J rr;JJ '
(7уа
(10)
и 1i j не зависит от S( ). Поэтому из определения закона Стьюдента (п. 6 91.2)
и из теоремы I следует, что при любом (J
( (j)
(е tn k == (f3j {3j)
n k )
a jj S( ) == S(n k).
(1])
Следствие 2. Из определения заКОlfа Снедекора (п. 7 91.2) и теоремы I имеем,
что при любом (J
( n k Q )
(е Fk n k == == S(k, n k).
, k S(Ш
(12)
4. Доверительное оценивание параметров нормальной реrрессии
Построим доверительный интервал для коэффициента реrpессии {3j. Из (10)
2 ..
следует, что статистика (3j имеет распределение .лf({3j, (7 а п ), поэтому здесь
мы имеем задачу оценивания неизвестноrо среднеro нормальноrо закона с He
известной же дисперсией (так как (72 неизвестно) по наблюдению над случай
ной величиной 1i j . На основании (11) стьюдентово отношение t k является
центральной статистикой для {3j (см. п. I 3.8), поэто Доверительные
{3
му 'у ДОDерительныи интервал для j строится по схеме интервалы дпя IIC'
примера I 2.5 и имеет вид (сравни с (12) 2.5). коэффициентов
g;@ реrрессии
( ajj )
{3j =f t(H1)f2, n k n k S(Ш. (13)
Чтобы построить доверительный интервал для остаточной дисперсии (72,
2
воспользуемся вторым соотношением в (5), из KOTopOro следует, что S({3)/(7
соответствующая центральная статистика. Искомый 'у доверитеm.ный
478 rлава б. Линейная реi!ресcuя и метод наименьших квадратов
ДоверитеЛЬНblе
интерваЛbl ДЛR . 'с
остаточной ",./1
дисперсии .i1lllli8
интервал строится здесь по схеме при мера I 2.5 и име
ет вид (сравни с (10) 2.5)
( B( )
2 '
X(I+7)/2. n "
B( ) )
2 .
X(l 7)/2, n "
(14)
и ноrда требуется оценить весь параметрический вектор (3 == ((31, , (3k).
k
т. е. построить доверительную область 97 11 еВКI1идоrюм пространстпе IR
наКРЫllающую точку fi с заданной вероятностью 'у. Такую область мож
но построить, основываясь на результате (12). Действительно, если F7. ". n "
есть 'У квантиль распределения S(k, n k), то из (9) и (12) следует, что при
любом ()
'у == Рв{Fk.n k < F7.k.n k} == Рв{fi Е 9 7 ( Х )}. (15)
,., ДоверитеJlЬНQR,. rде
06ласть.liiiillll { k }
9'У( Х ) == fi (fi fi)/A(fi {!) < n k S({!)F7,k," k
Тем самым построена искомая 'У доверительная область дЛя fi: это BHyтpeH
ность эллипсоида с центром в точке , rраница Koтoporo задается уравнением
, 2 k
(fi fi) A(fi fi) == а 7 ( Х ) == n k S(I!)F7' ", n k. (16)
Пример 1 (Простая реrрессия, доверительное оценивание параметров),
Построим 'У доверительный интервал дЛя наклона (32 простоЙ реrрессии
(см. пример 1 6.2). Из (10) и (22) (2З) 6.2 следует, что это интервал
1J2 =F t(l+'Y)/2, ,, 2
S (iЗ)
n
(n 2) L:(ti [)2
i 1
Аналоrично, из (15) (16) и формул примера 1 6.2 имеем, что BHyrpeHHocTb
эллипса
n
2 21 L: 2 2
((31 (31) + 2t((31 (31)((32 (32) + (fЗ2 (32) t; == ( 2) S((3)F7,2.n 2
n nn
; l
в плоскости перемеННblХ ((3 1, (32) с вероятностью 'у содержит неизвестную
точку fi. ·
6.3. Нормальная реzрессuя
479
5. Доверительная область для линейных комбинаций параметров
Пусть требуется оценить одновременно т ::;; k линейных комбинаций t ==
== (t 1 , ,t m ): t == Tfi, rде Т заданная (т х k) матрица и rankT == т.
Torдa из теоремы] следует, что о. н. к. I == T имеет распределение N(t, q2D),
rде матрица D определена в (5) 6.2. Отсюда по теореме \ 2.5 (см. замечание
к ней) следует, что квадратична форма
QT == а O/D la t)
(17)
имеет следующее распределение:
1:8 ( ) == i(m).
При этом QT как функция 13 не зависит от В(Д) (теорема \). Следовательно,
статистика Снедекора имеетв данном случае вид
n k QT
F. k
т,n ' т B( )
и при этом 1:8(Fm,n IJ == В(т, n k). Отсюда, как и в
случае оценивания {3, получаем следующий 'У довери
тельный эллипсоид для t:
д ;р ; ьный tf
эплипсоид
9t-у( Х ) == {t (t T )/D I(t T ) < n: k S( )F-y, m,n k }. (18)
При Т == lk полученное решение сводится к (15).
Отметим некоторые частные случаи общеro решения (\8). При т == \
речь идет об оценивании одной линейной комбинации,1' fi == л,.81 +. . '+Лk.8k.
В этом случае эллипсоид (\8) вырождается в интервап
(,1/ =t=t('+-Y)/2'n k (,1'A I,1) : ),
поскольку F-y, J,n k == tll+'Y)/2,n k (показать, используя упр. 5\ (б) к rл. 1).
Пусть матрица Т имеет следующую структуру: в каждой строке только
один элемент отличен от нуля, при этом в r й строке на месте jr стоит
единица, r == \,... ,т, 11 < 12 < < jm' Тоrда Т.8 == (.8j" ,.8jJ == .8(т)
и, следовательно, речь идет об одновременном оценивании части координат
вектора fi. В этом случае матрица D представляет собой минор
(19)
A I ( .
Зl,
, jm) == А(т)
матрицы А l получающийся вычеркиванием всех строк и столбцов с HO
мерами, отличными от 1(,... ,1т, и из (\8.) получаем, что 'У доверительный
480 rлава б. Линейная реzрессия и метод наименьших квадратов
эллипсоид для подвектора fi(т) имеет вид
9Т7( Х ) == {fi(т) (fi(т) Q(т))'A I(т)(fi(т) (т)) <
< n: k S( )F,r,m'n k}'
(20)
Пример 2 (Доверительный интервал для ординаты линии реrрессии).
Пусть IJ схеме простой реrрессии (см. при мер 1 Э 6.2) требуется оценить зна
чение линии реrрессии (()(t) == 13\ + /32t IJ произвольной точке t. Используя
обозначение
2 1 2
S (t) == L,(ti t)
n i 1
из формул примера 1 Э 6.2 получаем, что при !\ == (1, t)
>"А lл == [ 1 + (t [)2 ]
n s2Ш
,..... .......
Кроме тощ ij5(t) == !\ == х + (t t)/32. Отсюда и из (19) окончательно имеем,
что искомый , доверительный интерlJал имеет uид
( Х + (t [)'в2 t(J+7)/2,n 2 п(п I 2/( ) [1 + (ts (:{ ] ) ·
б. Система совместных доверительных интервалов
В конкретных практических задачах построение доuерительных эллипсоидо!)
в (15) и (18) трудная вычислительнан задача. Поэтому предпочтительнее
иметь результат, сводящий проблему к построению системы доверительных
интервалов для отдельных компонент oueHHBaeMoro параметрическоrо BeK
тора, с заданной вероятностью одновременно накрывающих соответствующие
компоненты. В таких случаях rоворят о системе совместнЬ/х доверительнЬ/х
интервалов. Расчет такой системы осноuыuается на следующем интересном
утверждении из теории квадратичных форм.
Теорема 2. Пусть В положительно определенная матрица и t,!\ BeKТOp
столбцы. Тоrда
, (!\'О2
t Bt == тax .
!\B !\
(21 )
Доказательство. Представим В в виде В == Н н' Это всеrда можно cдe
лать, выбрав Н == и л l / 2 , rде и ортоrональная матрица, приводящая В
к диаrональному виду Л. Положим теперь Х == H't, r. == H I!\; Torдa
х' у == (!\, х' х == t' Щ, r.'r. == !\' B '!\.
6.3. Нормальная реzрессuя
481
По неравенству Коши Буняковскоr02) ( Х'У) 2 ( Х'Х ) (У 'В , причем знак
«==,) {:;> векторы Х и r линейно зависимы. Отсюда и из предыдущих COOT
ношений имеем ( /02 а'щ)( /в I ) или {щ ( / )2/( /B ' ). .
Положим теперь в соотношении (21) ==?. IJ.., в == А; тоrда соотноше
ния (15) (16) можно записать в виде
{ I ' @ (3) I } { I I I }
'}'==Ро m;x ( 'A I /2 <а,А Х ) ==Ро (f!.. f!..) <и'Y( X ; )'\7' ,
rде
и'Y( X ; ) == a'Y(X)( /A I )'/2 (22)
Таким образом, для любоrо () выполняется соотношение
Pи{ '?. и'Y( X ; ) < 'IJ.. < / + и'У( Х ; ), \7' } == '}'. (23)
Тем самым для всех (!) линейных функций I (3 указана система совместных
доверительных интерnалОIJ с доверительным уровнем ')'. Если требуется oцe
нить конечное число линейных комбинаций 'IIJ.., , IJ.., то из (23) имеем
следующий результат:
r , "
P/J1. rlJ.. и'У( Х ; r) < rlJ.. < rlJ.. + и'У( Х ; r)' r == 1,.
,т} '}'.
(24)
Пример 3 (совместные доверительные интервалы для коэффициентов ре-
rрессии), Пусть 1 т k и Л r == (О О 1 О О), rде 1 стоит на месте jr,
r == 1, , т. Torдa t!,.1J.. == (3j" A ' . == aj,j, и на основании (24)
{(.вj,=fа'У( Х ) j.j.), Т== 1, ,т}
система совместных доверительных интервалов уровня "( ДIIЯ координат
(3j" , /3jm При т == k получаем решение ДIIЯ всех коэффициентов perpec
сии/3"...,(3". ·
7. Доверительный интервал ДЛЯ отклика
На практике большой интерес представляет предсказание будущих значений
ОТКJlика Х при тех или иных заданных значениях факторов Z" . . . , z". В этом
случае речь идет о построении доверительноrо интервала для значения Х, OT
КJlика Х, соответствующеrо фиксированным значениям Z'I, , Z." факторов:
"
Х, == 2..= (3jz.j + е. == ыJ.. + е,.
j '
(25)
Предположим, что мы уже оценнли вектор /3 по n наблюдениям Х ==
== (Х" .., Х n ) И что е, не зависит от == (el, . . ,е n ) и .с(е.) == И(о, (12).
2) Буняковский Виктор Яковлевич (1804 1889) русский математик, специалист по теории
вероятностей, теории чисел и математическому анализу.
31 з,." 1748
482 rлава 6. Линейная реzрессия и метод наименьших квадратов
,
Torдa мы можем использовать оценку Х. == .fЗ, которая на основании Teo
ремы 1 имеет нормальное распределение:
LB(X.) == И( : , 0'2 :A 1 .).
(26)
Но также
LB(X.) == N( :!i, 0'2)
и Х. не зависит от Х.. Отсюда следует, что
( 2 I l )
LB(X. Х.) == N О, о' (1 + .A .) .
(27)
Это дает нам возможность построения стьюдентова отношения
Х. Х.
tn k ==
O' v 1 + A l .
8(Д)
О'2(n k)
(Х. x.)
V 8( )(l + A l .)
/ ..-' Д
оверительный
интервал АЛЯ отклика
и получения следующеrо 1' доверительноrо интер
вала для Х..
(Х. =F t(1+'Y)/2, n k
8(Д) 1 + A l . )
n k
(28)
Пример 4 (Проrноэирование в схеме простой реrрессии). Пусть в схеме
простой реrрессии требуется построить 1' доверительный интервал для OT
клика Х. в точке t.. Используя обозначения примера 2, находим, что интер
вал (28) принимает вид
( х + (t. Е)Д2 =F t(1+'Y)/2, n 2
( 1 ( (t. [)2 )) 8( ) )
l+ 1+
n s2(t) n 2
(29)
Подчеркнем, что этот интервал отличен от соответствующеrо интервала для
ординаты cp(t.) (см. пример 2): он шире, что естественно, так как СЛУ'lайная
флуктуация е. вносит дополнительную неопределенность в проблему. .
8. Проверка адекватности модели
В практических ситуациях при подборке подходящей модели типа модели
нормальной реrрессии (2), важным является вопрос проверки адекватности
модели, который может быть конкретизирован так: все ли факторы, оказы
вающие существенное влияние на отклик Х, учтены в модели (2), или же
действительное число факторов больше k? Если модель (2) справедлива, то,
как показано в 6.2, статистика (j2 (см. (10) 6.2) является несмещенной
оценкой для остаточной дисперсии 0'2 Если же реальная модель имеет на ca
мом деле больше коэффициентов (факторов), то оценка (j2 будет смещенной
и при этом E(j2 > 0'2 В этом случае использование модели (2) может привести
к неправильному предсказанию отклика. Поэтому при проверке адекватности
6.3. Нормальная ре2рессuя
483
основное внимание уделяется недопущению модели с меньшим числом KO
эффициентов (факторов), чем требуется.
Чаще Bcero процедуры проверки адекватности модели состоят в cpaB
2 о о о * 2 о
нении оценки (1" с независимои от нее друrои оценкои (1" для остаточнои
2 2 * 2
дисперсии (1" Если (1" соизмеримо с (1" влияние неадекватности можно
считать незначительным и модель (2) принимается; если же 0:2 существенно
* 2
больше (1" то этим влиянием (неадекватности) нельзя пренебречь, и модель
надо скорректировать, добавляя новые коэффициенты.
*2
Чтобы получить независимую оценку (1" надо провести в неизменных
условиях (т. е. при некотором фиксированном значении факторов ZI, , Zk)
серию независимых опытов, в результате которых получим выборку значений
отклика (Y 1 , ,У т ). В этом случае наблюдения У\, У т будут незави
симы ми одинаково распределенными нормальными случайными величинами
с дисперсией (1"2 и несмещенная оценка для (1"2 по этим данным имеет вид
т т
*2 1 "" 2 1 ""
(1" == L..,.(Yj У) У == L..,. 1';,
m I т
j 1 j 1
(30)
а ее распределение есть
.c( т I 2) ==x2(т I). (31)
Следовательно, тестовой статистикой для про верки rипотезы адекватности
Но Е0: 2 == (1"2 (32)
является дисперсионное отношение Фишера
0:22
Fn k, т 1 == ... (33)
(1"
Если rипотеза адекватности (32) истинна, то стаmстика Fn k, т \ имеет
распределение Снедекора с n k и т 1 степенями свободы:
.c(Fn k, т IIHo) == В(n k, т 1). (34)
Следовательно, алrоритм проверки aдeKBaTHO Алrоритм проверки
сти реrрессионной модели состоит в следующем: адекватности модели
1. После оценивания реrрессионных коэффициентов IJ.. == (/31, ,f3k), Т.е.
2
получения о. н. к. == (/3\, . , /3,,), вычисляют значение оценки о: в (10)
6.2 для остаточной дисперсии (1"2
2. Проводят серию новых опытов r == (У!, , У т ) И по (30) получают He
2
зависимую оценку для (1"
3. Вычисляют дисперсионное отношение (33).
4. При заданном уровне значимости а (напр., а == 0,05) и числах степеней
свободы n k и т 1 по таблицам распределения Снедекора определяется
величина Fr:
P{Fn ",m 1 > Fr} == а.
31'
484 rлава б. Линейная реzресcuя и метод наименьших квадратов
5. Сравнивают величины Fn k,m ' (см. (33)) и р т и делают OДl1H из двух
выводов:
А. Если Fn k.m 1 р т , модель считается адекватной.
Б. В противном случае модель неадекватна и надо изменить ее структуру, BBe
дя дополнительные коэффициенты, и заново собрать данные. Например,
если полином первой степени (простая реrрессия) оказался HeaдeKBaT
ным, то надо перейти к модели второй степени и т. д.
i 6.4. Общая линейная rипотеза нормальной реrрессии
1. Понятие линейной rипоте]ы
При применении схемы нормальной реrрессии на практике часто I30зникает
необходимость проверить те или иные rипотезы о значениях коэффициентоIЗ
реrрессии fЗ" ,l3k. В общем виде задача формулируется следующим обра
зом: по наблюдениим Х == (Х" , х n ) требуется проверить rипотезу НО,
соrласно которой коэффициенты 13".. ,fЗk удовлетворяют некоторым за
данным оrpаничениям, локализующим их допустимые значения !J некотором
/. подмножестве Во Е R k Если эти оrpаничения линейные, то rоворят о линей
Л нои rипотезе. Для линейной rипотезы подмножество Во
инеиная rипотезо
является линеиным подпространсТlЮМ вида
Во == {/!.. т/!.. == t o }'
(1)
rдe Т заданная (т х k) матрица (т k), rапk Т == т, t o заданный BeK
тор и предполаrается, что система Т/!.. == tJ совместна. Таким образом, в общем
случае линейная rипотеза записывается в виде НО fi Е Во. В любом случае
это сложная rипотеза, так как она оставляет произвольным значение пара
метра и 2 В терминах общеro параметра модели () == (/!.., и 2 ) можно записать
НО В Е е о == {В fi Е Во, и 2 > О}.
Примером конкретной линейной rипотезы яuляетсSl утверждение
(2)
НО fЗ2 == (320,
задающее конкретное значение наклона линии реrрессии в модели простой
реrpессии (см. пример 1 6.2).
2, F-критерий для линейной rипоте]..1
Чтобы построить критерий проверки rипотезы НО, воспользуемся уже из
вестным нам решением задачи доверительноrо оценивания (см. п. 5 6.3)
и принципом соответствия между проверкой rипотез и доверительным oцe
ниванием (см. п. 4 5.3). НаПОМНИ.\1 общую схему этоrо соответствия.
Пусть в не которой модели:F== {Р(х;(}), () Е е} построена система 'Y дo
верительных областей {g7C ), Е 1:} для параметрической функции 9 == g((}).
б.4. Общая линейная 2ипотеза нормальной pezpeccuu 485
Тоrда подмножество выборочноrо пространства, задаваемое условием
Х Ой == { 90 Е 9')"(п}, а == I 1,
определяет область принятия rипотезы НО 9 == 90 с уровнем значимости 0:.
В нашем случае, соrласно (17) I 8) 6.3, 1 доверительная область мя
== т{3 имеет вид
9 == { t QTiK,O < p . }
т')" S(I!.( X » n k ')",m.n k ,
поэтому область принятия rипотезы НО : == O с уровнем значимости о: == I 1
задается условием
{ QT( , to) т }
Х Ой == S(lJ » < n k F')",m,n k .
tf
F крнтерий
Отсюда имеем, что критерий для 2ипотезы НО : /3 Е ВО
(см. (1» задается критической областью
{ n k QT( ,tO) }
Х!о == S('l.( » ? F! u,m,n k
(3)
Выпишем явное выражение дJ1Я тестовой статистики критерия (3). В co
ответствии с (17) 6.3 она есть
F == n k QT( t o ) == n k (T t.o)' D I(TQ Ы
т В(Ш т B( )
(4)
и большие ее значения являются критическими МЯ проверяемой rипотезы.
Построенный критерий называют F KpuтepueM.
Приведем и друrой подход к построению критерия (3), проливающий
дополнительный свет на ero существо. Рассмотрим о. н. к. I тД мя t
и составим вектор отклонений Т (3 t.o. Если rипотеза НО не верна, то
весьма вероятно, что эти отклонения велики. Будем измерять степень OT
клонения величиной QT( X , t.o). Torдa, поскольку математическое ожида
ние квадратичной формы можно преобразовать следующим образом (ниже
l: == О(1::.) == Ilcov(Y" Yj)II):
Е( У' вю == l: b ij Е (1'; Y j ) == l: b ij cov(Yi, Y j ) + l: b ij Е1'; EYj ==
i,i i,j i,i
== tr (Bl:) + E(r.')BE (Y ),
I
УЧИТblвая (5) 6.2, имеем при r. == т!!.. t.o, в == п
I и 2 I , 1
EQT( X , t.o) == tr (1т) + E(T/3 t o ) D Е(Т/3 t.o) ==
т т т
2 1 ( ) ' ! ( ) 2
== (J' + т/3 o D т/3 t o ? (J' ;
т
486 rлава б. Линейная реzрессия и метод наименьших квадратов
знак равенства имеет здесь место только при Т/3 === t o , т. е. при справеДllИВОСТИ
rипотезы Но. С друrой стороны, как мы знаем з п. 3 6.2, S( )I(n k) He
смещенная оценка ДIlИ (J"2 всеrда, т. е. безотносительно к истинному значению
fЗ. Поэтому у отношения F в (4) числитель в среднем больше знаменатели,
коrда rипотеза Но ложна, и потому большие значения F естественно pac
сматривать как свидетельствующие против rипотезы Но. Из этих рассуждений
также следует, что статистика F явлиется отношением двух независимых и He
смещенных (при rипотезе Но) оценок для остаточной дисперсии (J"2 С такой
. Дисперсионное дисперсионное отношение интерпретацией свнзан
термин, используемый иноrда ДIlи статистики F.
отношение Для вычисления статистики F можно использовать
также формулу
п k ST S( )
p
т S(f}) ,
( 5)
которая следует из (18) 6.2. Таким образом, дисперсионное отношение F
можно выразить непосредственно через условный ST (при условии T(i === t o )
и абсолютный s(jj) минимум исходной квадратичной формы S(fЗ). в KOH
кретных задачах условный минимум ST зачастую находят непосредствен
но, поэтому представление (5) более удобно ДIlЯ практических расчетов,
нежели (4).
Пример 1 (Простая реrрессия, rипотеза о наклоне ее линии реrрессии).
Рассмотрим rипотезу Но /32 == /320, фиксирующую значение наклона линии
реrpессии (см. при мер 1 6.2). В данном случае т == 1 и условный минимум
(при rипотезе Но)
n
ST == miп z)x; /320t; /31)2
{З, i 1
находится непосредственно: он достиrается при fЗl == Х /320t (черта сверху,
как обычно, означает среднее арифметическое) и ero значение, учитывая COOT
ношения (22) (23) 6.2, можно записать в виде (проверить самостоятельно!)
n
ST == S( ) + (Д2 /320)2 (t; [)2
i l
По формуле (5) имеем, что в данном случае дисперсионное отношение равно
n
2 1 '""" 2
F == (п 2)(/32 /320) S( ) f:1(t; t) ,
(6)
а критическая rраница в (3) выбирается равной FI Ct.I. n 2. Так как
2
FI Q,1,n 2 == tl Ct/2,n 2
6.4. Общая лuнейная zuпотеза нормальной pezpeccuu 487
(см. замечание к формуле (19) 6.3), то F критерий в рассматриваемом случае
сводится к критерию
Но отверrается {:::::}
s(ю
l.д2 .д201 tl a/2.n 2 n
(п 2) 2::(t; i)2
\ i l
(7)
rде в(Д) определено в (23) 6.2).
Отметим, что к этому результату можно прийти также и обращая довери
тельный интервал для /32, построенный в примере 1 6.3).
В том случае, KOrдa /320 == О, речь идет о про верке значимости влияния
фактора t на исход эксперимента, и если rипотеза НО 132 == О отверrается, то
rоворят, что реrpессия значима и влиянием фактора t пренебреrать нельзя.
Добавим к этому следующее. Как леrко видеть из соотношений (22) (2З)
6.2, можно записать также представление
] 2
(Х; X)(ti i)
s(jj)== (Xj xi [L: (I R2) (Xi xi
ц L.:(tj t)2 Ц
(8)
rде
2::(X i X)(t i i)
R
j L.:(X; х)2 2::(ti i)2'
есть выборочный коэффициент корреляции между Х и t.
Из (8) следует, что чем больше значение R 2 (чем ближе оно к 1), тем
меньше B( ), т. е. тем лучше подобранная прямая реrрессии соответствует
наблюдениям. Тем самым, если rипотеза Но 132 == О отверrается, то вели-
чина 1 R 2 является мерой соzласuя подобранной прямой реrpессии данным
наблюдений.
Наконец, F статистика (6) при 1320 == О С учетом (8) (9) может быть за
писана в виде
(9)
п2 2
(п 2)132 ц(ti t) (п 2)R 2
р== ==,
(1 R2) L.:(X i Х)2 1 R2
(10)
т. е. может быть выражена через R 2 , а критерий (7) для rипотезы (32 == О может
быть записан соответственно в виде
{ IRI }
у'(1 Ю)/(n 2) tl a/2.n 2 .
(11)
.
488 rлава б. Линейная реzрессия и метод наименьших квадратов
Пример 2 (Критерий значимости реrрессии). В приложениях теории линей
ной реrpессии обычно первый коэффициент /31 выделяется, т. е. полаraется
первый фактор Z, == 1 (как в схеме простой реrрессии (21) 6.2). В этом слу
чае наблюдаемая переменная Х зависит от k 1 фактора Z2, , Zk И часто
бывает желательно удостовериться, является ли их влияние на Х значимым.
Итак, если априори предполаrать, что модель имеет вид
(i) (i)
X i == /3, + /32 Z 2 + + /3k Z /,; + €i, i == 1,
,n,
( 12)
то речь идет о проверке rипотезы Но /32 == == /3!.: == О. Если rипотеза Но
отверrается, то rоворят, что реrpессия значима и факторами Z2, , Zk нельзя,
вообще rоворя, пренебречь (в то же время следует иметь в виду, что отклонение
rипотезы Но вовсе не означает, что модель (12) действительно адекватна).
В данном случае rипотеза Но имеет вид Tfi == Q, rде т == IIQ Jl./,; III
матрица размера (k 1) х k и paHra k 1, так что применима общая теория
F критерия с т == k 1 и
n n
ВТ == min L(Xi /3,)2 == L(X i х/ == х' Х nх 2
{З, i ' i 1
Кроме Toro, величину B( ) в силу соотношений (1 O) ( 12) 6.2 можно записать
также в виде
B( ) == X' (Jl. n Z'A IZ) X == х ' х 'Z X .
(1 З)
Следовательно, F статистика (5) имеет в данном случае вид
,
n k fЗ Z Х nх 2
p== "
k 1 х' Х fi Z Х
(14)
а F критерий для rипотезы НО (Т. е. критерий для «всей.) реrpессии в целом)
задается критической областью {Р FI a,k I,n k}, rде а заданный ypo
вень значимости.
Полезной мерой степени соответствия аппроксимирующей реrрессии
,
Х == Z fi имеющимся данным Х == (X I , . . . , Х n ) является выборочный MHO
жественный коэффициент корреляции R/,; 1. Он определяется как коэффици
ент корреляции между данными {Х" ,Х n } и их оценками {Х\, ,Х n }:
Rk 1 ==
n
L(X i Х)(Х; Х)
i 1
(15)
n
n
L(X; Х)2 L(X; Х)2
; I
i '
б.4. Общая линейная zuпотеза нормальной pezpeccuu 489
2
Величину Rk 1 обычно называют коэффициентом дe
терминации.
Покажем, что
Коэффициент
детерминации
n
Q\ 2 "'" 2
S({iJ == (1 R H ) L.,..(Xi Х)
i 1
Доказательство. Действительно, рассмотрим первое уравнение системы HOp
мальных уравнений 8S({i)/8fЭl == о: оно имеет вид
(16)
"'" ( (i)
L.,.. X i fЭ I fЭ2 Z 2
(i» )
fЭkZk == О
или 2:(X i X i ) == о, т. е. Х == X i . С учетом этоrо имеем
i
"'" 2 "'" 2 "'" 2 "'" 2
L.,..(Xi Х) == L.,..(X i Xi + X i Х) == L.,..(X i X i ) + L.,..(Xi Х)
i i i
(17)
поскольку (см. (2) 6.2)
L(Xi Xi)(Xi Х) == L(X i Х,)Х; == ( Х х)' Х == х' Х r Х ==
i i
== X' Z'A IZ X X' Z'A IZZ'A 'Z X == О.
Из (17) следует, что
Q\ "'" 2 "'" 2 "'" 2
S(fiJ == L.,..(X i X i ) == L.,..(X i Х) L.,..(Xi Х)
( 18)
Далее,
2:(X i X)(Xi Х ) == L(Xi X)(Xi Х) ==
i
== L(X i Х ; + X i Х)(Х ; Х) == L(X i х)2,
i i
поэтому (см. (15»
L(Xi х)2
R 2 i
k 1 == L(Xi х)2'
( 19)
Теперь соотношение (16) непосредственно следует из (18) и (19). .
Из равенства (16) видно, что чем ближе значение RI I к 1, тем лучше
,
аппроксимирующая поверхность Х == Z {3 соответствует данным наблюде
ний. Отметим, что при k == 2 (один фактор) мы получаем соответствующие
490 rлава б. Линейная ре рессия и метод наименьших квадратов
результаты при мера 1. Так, коэффициент R 1 == R (см. (9», а равенство (16)
COOTBeTCTDyeT равенству (8). Можно также по казать, что аналоrом представ
ления (10) является здесь следующая формула для статистики (14):
R 2
F==(n k) k
1 Rk 1
(20)
.
6.5. Некоторые "рименения теории
нормальной реrрессии
Изложенная в предыдущем параrрафе теория проверки rипотез о коэффи
циентах реrрессии имеет широкое применение. К схеме реrрессии Moryr
быть сведены мноrие rипотезы о математических ожиданиях нормальных co
вокупностей, которые зачастую имеют форму, на первый озrляд, отличную
от рассмотренной выше. Некоторые из таких задач рассматриваются в этом
параrрафе.
1. rипотеэа о параллеЛl.ности линий реrрессии
Предположим, что имеется r ? 2 rpynn независимых наблюдений x i)
XA ) i == 1, " ,Т, распределенных нормально с общей (неизвестной) диспер
. 2
снеи (J" и средними
E x (i) (i) (3 (i) + (3 (i) t (i)
j JLj I 2 j
j == 1, .. ,ni , i == 1, . . . , Т.
(1)
Друrими словами, имеется r различных схем простой реrрессии (пример 1
96.2) и проверяемая rипотеза Но состоит в том, что все линии реrрессии (1)
имеют один и тот же наклон, т. е.
Н (3 (l)
О 2
(3 (Т)
2
Такая rипотеза может встретиться, например, при проверке равенства несколь
ких скоростей роста, при сравнении нескольких способов обработки и т. д.
Покажем, что рассматриваемый случай можно свести к схеме общей ли
ней ной rипотезы. Положим
f!.. == ((31,
X(I) х(2)
, nl 1 1)
n == nl + + n т ,
, (32т) == 2 ((3 I), (3 I), (3 2), (3 2)
(2) (Т)
,XnJ""'X 1
,ХА:») ,
( (1)
Х==(Х',...,Х П )== X 1 '
(3 (Т) (3 (Т» )
, I ' 2
и введем матрицу Z размера 2т х n, составленную нз векторов столБЦО8 (i)
вида
z == " (') . . . (nl) (nl + 1) .. . (11) 11 ==
6.5. Применения теории нормальной pezpeccuu
491
I
t(l)
,
О
О
I
t(l)
п,
О
О
о
о
I
t(2)
1
о
о
I
t(2)
П1
о
о
I I
t(r) t(r)
I (п.)
В этих обозначениях вектор Х распределен по нормальному закону
N(Z/ , 0'2:п. п ). Таким образом, имеем частный случай (при указанном выборе
(i» схемы нормальной реrpессии. Проверяемую rипотезу можно записать
в виде Но /34 /32 == == /32r /32 == О, т. е. она задается (r 1) M ли
нейным соотношением между коэффициентами реrpессии и, следовательно,
для ее проверки можно применить F критерий 6.4. Для этоrо надо найти
абсолютный 81 == s(ij) И условный ST (т. е. при rипотезе Но) минимумы
квадратичной формы
n
S(/3) == " (X i (i)//3)2 == " (X(i) рУ»)2
J J
i 1 i,j
(2)
НаХОЖдение 8, сводится к минимизации выражения
8( ) == L 8(i),
i 1
rде
п;
s(i) == L (Xji) /3\i) /3 i)tji») 2 i == 1, , r,
j 1
т. е. достаточно найти минимум каЖдОЙ квадратичной формы s(i) отдельно.
В несколько отличных обозначениях эта задача решена в примере I 6.2,
поэтому из (22) и (23) 6.2 имеем, что минимум S(i) достиrается при
(i) (i) (i) (i)
""'1 ""'I ""'2 ""'2 '
rдe
п;
L (хУ) X(i») (tY) t<i»)
(i) j 1
/32 ==
п;
L (tY) j<i») 2
j 1
ji/i) == X(i) j(i)ji2(i)
(3)
492 rлава 6. Линейная реzрессия и метод наименьших квадратов
n. п.
(i) 1 (i) (i) 1 (i)
(здесь Х == L.J X j t == L.J t j и при этом предполаraется, что
n, j 1 n, j 1
для любоro i == 1,..., Т не все числа t\i) ,t } одинаковы). Таким образом,
в данном случае
r n.
81 == :L L [(хУ) x(i)) 2 i32(i) 2 (tJi) l(i)) 2]
i 1 j 1
Введем следующие обозначения:
(4)
1Jj
sf(t) == L (tji) l(i)/
j l
п;
s (X) == L (хУ) x(i)) 2
j 1
(5)
п;
Si(X,t)==L(xji) X(i))(tJi) l(i)), i==l, ,Т
j l
(с точностью до множителя это выборочные дисперсии и ковариация MHO
жеств (x!i), ,ХШ) и (t\i) , .. ,t !)). Тоща из (3) и (4) следует, что 81 можно
записать в следующем, удобном для вычислений, виде:
8 [ 2 ( Х ) sHX,t) ]
1 L.J S, s2(t ) '
, I I
(6)
Для вычисления 8 т надо минимизировать по .8 I)
L (хУ) .8 i) .82 t ji)) 2
i,j
т. е. приравнивая нулю все ее частные производные по этим параметрам. He
посредственным дифференцированием можно ПрОJJерить (это мы оставляем
читателю в качестве npocToro упражнения), что при любом фиксированном
(32 минимум достиrается при .в!i) == b\i) == хи) (32t<i) i == 1, ,Т, и сумма
квадратов при этом равна
L [(x;i) X(i)) (32 (tY) l(i)) ] 2
i,j
(3 (r)
, 1 ,.82 сумму
Минимум же последнеrо выражения достиrается при
L (Xji) X(i)) (tji) [1i))
(3 Ь i,j
2== 2==
L (t}i) l(i)/
SI(X,t)+ +Sr(X,t)
s (t) + .. . + s;'(t)
i,j
6.5. Применения теории нормальной рецессии
493
(см. (5», и он равен
r [t S,(X, t)]2
ВТ == I> (X) 1 lr
i==1 L s;(t)
i 1
(7)
В данном случае параметры k и т в (5) 6.4 равны соответственно 2т и r 1,
поэтому статистика F в силу соотношений (6) и (7) принимает вид
t sl(;, t)
i 1 Si(t)
[t Si(X,t)]2
, I
r
n 2т
p==
T l
L sl(t)
i==1
r r 2 ( Х )
L Si (Х) L Si 2 ,t
i l i==1 Si(t)
(8)
В итоrе имеем, что при заданном уровне значимости а F критерий мя про
веряемой rипотезы Но задается критической областью {Р) FI a,r l,n 2r},
2. rипотеза однородности для нескольких нормальных выборок
В примере 3 5.4 была сформулирована общая rипотеза о равенстве средних
значений нескольких нормальных выборок. Такая rипотеза часто возника
ет в приложениях, например, при сравнении нескольких различных способов
обработки или процедур, условий, размещений и т. п. с целью выяснения, вли
яют ли различия между ними на интересующий исследователя исход. Вообще
подобная проблема имеет место каждый раз, коrда интересуются влиянием
на исход эксперимента KaKoro To одноro фактора. Если число различных зна
чений этоrо фактора (число уровней, на которых может находиться фактор)
равно k, то nj число наблюдений, соответствующих j MY уровню факто
ра, а ХШ == (X jl , . . . ,xjnJ сами наблюдения (результаты эксперимента).
В этом случае rоворят также об одинарной классификации исходов.
В примере 3 5.4 мы исследовали эту проблему (проверка rипотезы oд
нородности) с позиций критерия отношения правдоподобия, но получили
окончательное решение лишь МЯ случая двух (k == 2) выборок (см. критерий
(9) 5.4). Общее же решение МЯ произвольноrо числа выборок было полу
чено лишь МЯ случая больших выборок (см. критерий (29) 5.4). Теперь же
мы в состоянии получить общее решение д.lJЯ произвольноrо числа выборок
и произвольных их объемов, если воспользуемся теорией F критерия. Для
этоrо сведем рассматриваемую схему к схеме реrpессии.
494 rлава б. Линейная реzресcuя и метод наименьших квадратов
Положим Х (X j , , Х n ) ( x (I), , х(Ч), n nl+ + nl.:,
и введем ма11>ИЦУ плана
I 1 О О
О О 1 О О
Z == II (I) (n,) (ТI'+') (n)11 ==
.. ....... .а.о...
О О
rде в j й С11>оке единицы стоят на местах nl +. .. +nj 1 + 1, nl +.. . +nj,
j == 1,... . k (по == О). Тоrда Х" .. . , Х n независимы (по условию) и
( ) N( (i)' Z )
L Х ; == IJ., (Jz ,
i == 1,... , n,
IJ. == (811,
,811.:),
Таким образом, мы имеем здесь частный случай (с указанной матрицей пла
на Z) схемы нормальной реrpессии, в которой требуется проверить rипотезу
Но 8,z 81l == ==8'1.: 811 ==О(Нозадается(k I) млинейнымсоотноше
нием между коэффициентами реrpессии). Следовательно, можно применить
теорию F критерия. Для этоro надо вычислить абсолютный S, и условный ST
(при rипотезе но) минимумы квадрати'lНОЙ формы
S == :L(X ji 81j)2
i,j
Так как
2 2
S == L)X jj Xj) + nj(X j 8 1j )
i. j j
".
1 I
Xj == X jj ,
n'
J i '
то при отсyrствии оrраНИ'lений на 811,.' ,811.: минимум достиrается при
8 1 j == , j == 1, ,k, и равен
S, == :L(X jj X j )2
i.j
1.:
:LsJ,
j 1
п;
2 2
Sj == (Xji X j )
i 1
(9)
Далее имеем
ST == in :L(Xj j ( 1 )z
I ..
1, J
Здесь можем записать разложение
2 z 2
(Xjj (1) == (Xji Х) + n(Х (1)
i,j
i,j
k
' J ( ' )
Х == X ji == njX J ,
n i,j n j 1
6.5. Применения теории нормальной pezpeccuu
495
отсюда следует, ,[ТО
k
Вт =о )Xji х/ =о В, + Е nj(XU) х/
i, j l
и минимум достиraется при 81 == х:
Таким образом, вданном случае статистика F принимает вид (см. (5) 6.4)
(10)
k
Е nj(x(j) Х)2
F =о n k j 1
k 1 k
s;
j 1
(11)
а F критерий ДIIЯ rипотезы однородности Но задает
ся при уровне значимости а критической областью
{F ? FHI",k l,n k}, Нетрудно убедиться в том, что
ДIIЯ случая двух выборок (k == 2) полученное решение С80ДИТСЯ к (9) 5.4.
Отметим, что соотношение (10) можно интерпретировать как разложение
полной суммы квадратов отклонений наблюдений от общеrо среднеrо (,пол
ной изменчивости») на сумму КlJадраТОIJ отклонений каждой величины Xij
от соответствующеrо rpynnoBoro среднеro значения (,изменчивость внутри
[рупп») и сумму квадратов отклонений rpynnoBblx средних от общеrо cpeДHe
ro ((изменчивость между rpуппами»). При этом, если rипотеза Но истинна,
То (см. формулу (11) 2.2)
"" 2 2
ЕВ т =о Е L...J(X ji Х) =о (n 1)02'
- ...
.' . ,F критерий
. 'однородности
i.j
k k
ЕВ) =о Е Es] =о E(nj I)O =о (n k)8 ,
j 1 j 1
k
Е Е nj(XU) Х)2 =о ЕВ т EBI =о (k I)O .
j )
Отсюда следует, что (при нулевой rипотезе но) каждая из статистик
1 "" 2
Q =о n 1 L-.J(Х ji Х) ,
1, J
QI =о k 1 Е nj(x(J) х)2,
j
Q2 =о ""(Xi" X(j)2
n k J
;,j
496 rлава б. Линейная ре2ресcuя и метод наименьших квадратов
является несмещенной оценкой дисперсии O , и F критерий можно считать
критерием совместности независимых оценок Q, и Q2 (статистику F мож
но записать в виде F == QI/Q2) Такое разложение изменчивости исходных
данных и ero интерпретация характерны для дисперсионною анализа разде
ла математической статистики, объединяющеrо совокупность статистических
приемов, широко применяемых в самых разнообразных экспериментах, IJ KO
торых наблюдения тем или иным способом классифицируются (разбиваются
на rруппы или классы) IJ соответствии со значениями некоторых сопyrствую
щих факторов.
З. Двойная классификация. Дисперсионный анализ
Рассмотренный в предыдущем пункте случай является простейшей схемой
дисперсионноrо анализа (один фактор), в которой решение получается с по
мощью методов реrpессионноrо анализа. Рассмотрим применсние реrресси
oHHoro анализа еще к одной, имеющей большое практическое значение, схеме
дисперсионноrо анализа, коrда число факторов, IJЛИЯЮЩИХ на исход экспе
римента, равно ДIJУМ.
Предположим, ,,то исход эксперимента заlJИСИТ от значений двух факто
pOIJ R и С, причем фактор R может находиться на r УРОIJНЯХ R I , , Rr,
а фактор С на s УРОIJНЯХ C 1 , , C s . Пусть, далее, при каждой возможной
комбинации уровней обоих факторов ПРОИЗIJОДИТСЯ ровно одно наблюдение:
X ij при комбинации (R i , C j ), i == 1, ,т; j == 1, ,S. При этом наблю
дения {Xij} независимы и распределены нормально с одинаковыми диспер
2
сиями (j И средними значениями
EX ij == ij == J.L + а; + /3j,
( 12)
rдe
r
Е а; == L fЗj == о.
i 1 j=1
Условия (12) и (13) означают, что оба фактора действуют независимо (в этом
случае rоворят, что они аддитивны). Действительно, если обозначать через а'
и /3' действия факторов R и С соответственно, то аддитивность означает, что
t: ' /3 , Е ...../ fЗ ' ,...../ fЗ fЗ ' fЗ '
..ij == а; + j- сли положить теперь J.L == а + ,а; == а; а, j == j
(черта сверху, как обычно, означает среднее арифметическое), то получим
соотношения (12) ( 13).
Такую схему удобно представить IJ lJиде прямоуrольной таблицы из r
строк, соответствующих уровням R 1 , ,Rr и s столбцов, соотвеТСТIJУЮЩИХ
УРОIJНЯМ С" ,C s . Случайную величину X ij называют реаi?ирующей: она
описывает реакцию, ВЫЗЫlJаемую комбинацией (R i , C j ) факторов R и С
Из (12) следует, что EX ij при любых i и j окаЗЫlJается при УСЛОIJИИ (13)
линейной функцией от r + s 1 неизвестных коэффициентов J.L, ai, fЗj Таким
образом, здесь мы также имеем частный случай схемы нормальной реrрессии
(13)
6.5. Прuмененuя теории нормальной pezpeccuu
497
и, следовательно, можно применить разви'l)'Ю Вblше теорию. Все ее положе
ния, как мь! знаем, базируются на анализе квадратичной формы
s
s == I: I:(X ij ij)2
i 1 j 1
(14)
В данном случае удобно преобразовать Э'l)' форму следующим образом.
Обозначим
1 I:
Х == Х..
.. TS.. ')'
1,)
1 S
Х. " Х.
1. 8 6 1).
) I
1 r
X j == L: Xij.
Т i J
Torдa, УЧИТblвая (12), имеем
S == I:(Xij f.L (1i /3j)2 ==
i, j
== '""" [( Х" Х. Х . + Х ) + ( Х. Х (1. ) +
L...i 1) 1. ,) .. ,. .. I
i,j
+ (К.) х.. /3j) + (Х':. JL)]2 ==
== '""" ( Х.. Х. Х. + Х ) 2 + S " ( Х Х (1. ) 2 +
L...i 1) 1. .) .. L...i 1. .. 1
i,j
+ т I:(X j Х. /3j)2 + TS(X. JL)2, (15)
j
так как все попарные произведения после суммирования дадут нули.
Оценки наименьших квадратовдnя коэффициентов реrpессии это зна
чения параметров, обращающие квадратичную форму (14) в минимум, поэто
му из (15) сразу получаем, что в данном случае эти оценки таковы:
Ji == Х., ai == X i . Х.., 13з == Х з Х.. (16)
Из (15) и (16) также имеем, что минимальное значение формы S равно
. '""" 2 '""" 2
81 == тт S == L...i(Xij ij) == L...i(X ij X i . Х. З + х..}
i, j i,j
Найдем дисперсии полученных оценок (16). Так как
lr IS
Х.. == L: Xl. == L: X. t ,
r 1 1 8 t J
(17)
то
T I l L s l I I:
а' == X. Х 1 /3 . == X. X t .
1 1. .,) .) .
r r I i 8 S t#=j
2
Но X 1 ., l== 1,...,т, независимы и DX1.==(J" /8; аналоrично, X. t , t==I,...,s,
2
независимы и DX,t == (J" /Т; следовательно,
32 За.., 1748
498 rлава б. Линейная реi!рессия и метод наименьших квадратов
Daj == ( (T 1)2 + T , ) ст 2 == T 1 (12,
т 2 т 2 S тв
s 1 2 (12
DfЗ' == (1 DJ1. == .
) rs тв
( 18)
Доверительные
интервалы
в соответствии с обшей теорией (см. п. 4 6.3) отсюда
находим, что 1 ДОllерительными интерlJалами для пара
метров jl, O'i И fЗj являются соответственно (в данном
случае параметр n k в (13) 6.3 равен rs (т + s 1) == (т I)(s 1))
(Ji =f t(J+'Y)/2. (r l)(s 1)
( aj =f t(I+1)/2,(H)(S I) V TB(: 1) )'
31 )
rs(r I)(s 1) ,
(д] =f t(J+'Y)/2,(HHH) V rs(: 1) )'
rдe Ji, aj, jjj и 3, определены в (16) и (17).
Отметим также, что 3 1 /(т I)(s 1) несмешенная оценка (12
Проверка rипотез Рассмотрим теперь задаllУ проперки наиболее ин
тересных в исследуемой схеме rипотез. Пусть требу
ется проверить rипотезу Hci l ) о том, что фактор R не влияет на исход испы
таний, т. е.
(1)
Но 01 ==
== От == О.
( 19)
Так, например, rлавным интересующим исследователя фактором может быть
фактор С, соответствующий, скажем, различным способам обработки, в то
время как R соответствует классификации по месту, rде производятся наблю
дения. В этом случае rипотеза HJI) соответствует предположению о том, что
эта вспомоrательная классификация не влияет на результаты эксперимента и,
следовательно, может не приниматься во внимание.
Следуя общей теории F критерия (см. 6.4), вычислим сначала 3т ми
нимальное значение квадратичной формы (14) при rипотезе HJI) ИЗ (15)
и (17) имеем
т
3 т == 31 + s 2:(X j , x:i
i 1
поэтому статистика F (см. (5) 6.4) имеетвданном случае вид (при т == T 1)
"' ( Х Х ) 2
1. ..
j 1
F == s(s 1) 2 '
"' ( Х . Х. Х . + х )
IЗ 1, .) ..
(20)
j,j
6.5. Применения теории нормальной pezpeccuu
499
а F критерий уровня значимости а для rипотезы H I) задается критической
обл астью
(1)
X 10 == {Р FI a.r I,(r l)(s I)}'
Аналоrично рассматривается rипотеза
(21)
Н (2) fЗ
О I
== /3. == о.
(22)
о несущественности влияния на исходы испытаний BToporo фактора С. Здесь
критическая область имеет вид
(2)
..\.10
s
( x. x ) 2
,) ..
j \
т(т I) 2 F\ cr.s
(Xij Xi. X,j + Х..>
i.j
I)
(23)
Наконец, критерий уровня значимости а для rипотезы
(3)
Но al ==
== a r == /3\ ==
== /3. == о
о независимости результатов испытаний от влияния обоих факторов задается
критической областью
Х (3)
10
5 ( X' х ) 2 + r ( X х ) 2
,. .. .) ..
(т 1)(5 1) i 1 j 1
T+5 2
( X" х x .+Х ) 2
') ,. .) ..
i,j
FI o.
r+s 2.
(r I)(s 1)
Найдем, наконец, доверительные области для раз
ЛИЧНblХ '1'упп параметров модели (12). Пусть требуется
построить r доверительную область g l) для эффектов
al, ,a r фактора R. Соrласно принципу соответствия между проверкой
rипотез и доверительным оцениванием (см. п. 4 5.3), 'lТобы построить g I),
надо рассмотреть соответствующую rипотезу
(24)
Доверительные
""'1" "";"" области
НО а; == aiO, i == 1, . .. ,т (t а;о == о).
i 1
Критическую область уровня значимости cl == 1 r ДIIя нее можно получить
из (20) (21), заменяя Xij на Xij CliO; она имеет вид
{ r 2 1 2 }
L(Xi. X.. aiO) F7,r I,(H)(H) ( 1) L(Xij Xi. X.j+X..) .
i 1 S S i,j
32'
Отсюда следует вывод, что
500 rлава б. Линейная реi!рессия и метод наименьших квадратов
g l) { (0(.
r
,ОТ) L о; == О И
; I
т }
2 1 2
2:(0; Х i, + Х..) < F7,r I,(T I)(s l) ( 1) 2:(X ij X i , X,j + Х..)
. I 88 ..
I 1,)
Здесь неравенство определяет BHyтpeH
ность шара в пространс е па метров
(01, ,ОТ) С центром (X 1 . Х..,
КТ, К..) IJ rиперплоскости 2: а; == О.
Так, если r == 2, ТОДО13ерительная область
отрезок биссектрисы 02 Ol, яв
а[ ляющийся диаметром некоторой окруж
ности с центром на этой биссектрисе
(см. рис. 1).
Аналоrично строится доверительная
РИс.l область для эффектов /31,' I (3s BToporo
фактора.
fи Српретация в заключение дадим интерпретацию paCCMOTpeH
нои схемы, характерную для дисперсионноrо анализа.
Положим в разложении (15) все о; и (3) равными нулю, а J1. == Х:,. в резуль
тате получим соотношение
Во == 2:(X ij Х:У == 8 2:(K i . Х:У + r 2:(X: j x:i + BI,
С,) j
которое можно интерпретировать как разложение полной измен'\ивости 80
на три компоненты:
2
Во. == r L)X. j Х..)
j
Компонента В.о описывает изменчивость, обусловленную первым факто
ром R, компонента 80. вторым фактором С. Компонента же В.. есть
сумма квадратов величин с нулевыми средними:
2
8.0 == S L...,(X i , Х..)
и
В.. == BI'
(25)
Е ( Х-' К. К. + К ) == II + о. + /3 . ( 11 + о. ) ( ll + {З . ) + IJ == О
1) 1. .) .. ,... 1 J ,... 1 ,... J ,... ,
поэтому она не может быть связана с факторами R и С. (Напомним, '!то Be
личина Q == В../(т 1)(8 1) является несмещенной оценкой дисперсии (12.)
Вели'lИНУ В.. принято называть «ошибкой», подчеркивая тем самым, что она
связана со случайностью результатов наблюдений, а не с каким либо pacxo
ждением в их средних.
6.5. Применения теории нормальной pezpeccuu 501
Вычислим, наконец, Е8.0 и Е8 0 .. Из (16) и (18) имеем
E(X X ) 2 E 2 D (E ) 2 r 1 2 2
j, .. == aj == aj + aj == (Т + aj.
Т8
Отсюда и из (25) следует, что
r
Е8. 0 == (r l)cт2 + 8 L а;. (26)
i 1
Аналоrично находим
Е8 0 . == (8 l)cт2 + r L {3f.
j 1
Из (26) имеем, что при rипотезе (19) величина
Q 8.0
l r 1
может служить несмещенной оценкой дЛЯ (Т2. Аналоrично, из (27) заЮlючаем,
что
(27)
Q2 ==
8 1
несмещенная оценка (Т2, коrда справедЛива rипотеза (22).
Теперь F критерий (21) дЛя rипотезы HJI) (19) можно интерпретировать
как критерий совместности двух независимых оценок Ql и Q для (12 (стати
стика (20) в этих обозначениях равна отношению QI/Q). Аналоrично можно
интерпретировать и критерий (23) для rипотезы HJ2) (22) (ero тестовой CTa
тистикой является Q2/Q).
Обычно составляющие этой двухфакторной модели объединяют в следу
ющую таблицу дисперсионною анализа:
Источник Степень Сумма Среднее суммы Отношение
дисперсии свободы квадратов квадратов Снедекора
В F
строки T I В. о Q .0
I .0 Q
r 1
В F. Q2
столбцы s 1 Во. Q о.
2==
s 1 о. Q
(r I)(s 1) В
ошибка В.. Q == ..
(r l)(s 1)
Первое отношение Снедекора F. o служит Д!1я проверки rипотезы H ')
о том, что все aj равны нулю, второе для проверки rипотезы HJ2) о paBeH
стве нулю всех {3j.
502 rлава б. Линейная реzрессия и метод наименьших квадратов
6.6. Статистическая реrрессия и проrнозирование
ОчеllЬ трудllО чтО ,1Uбо предСКilЗЫfiilll1Ь,
110 особеlflfО трудllО предсказывать будущее.
Китайская пословица
1. Задачи статистическоrо проrноза
В различных областях '1еловеческой деятельности '1асто возникают ситуации,
коrда по имеющейся информации (данным) Х требуется предсказать (спро
rнозироuать, оценить) некоторую величину У, стохастически сuизанную с Х
(т. е. Х и У имеют некоторое совместное распределение .с(Х, У)), но которую
непосредственно измерить невозможно (например, У может относитьси к бу
дущему, а Х к настоящему). Так, например, может предстаlJЛЯТЬ интерес
проrноз успеваемости первокурсников очередноrо набора по оценкам, полу
ченным ими на вступительных экзаменах. Здесь Х было бы средним баллом
этих студентов на вступительных экзаменах, а У средним баллом по ито
rзм, скажем, первой сессии; при этом совместное распределение .с(Х, У)
можно в принципе определить (оценить) по аналоrичным данным за про
шлые rоды. Или: можно ли, зная рост отца (Х), предсказать рост ero сына
(У), если у выбранных случайно из большой популяции людей эти характери
стики (Х, У) имеют известный (нормальный) закон распределении'! Такой же
характер имеют задачи проrнозировании поrоды по результатам cooТl3eTcTBY
ющих атмосферных измерений, селекционирования новых видов растений
и жиuотных, определения возможностей индивидуумов в определенных обла
стях с помощью соответствующей системы контрольных тестов и т. д. Особо
важное значение проrнозироuание имеет н таких областях, как индустрии, эко
НОМИКа, коммерция (проrнозирование экономических показателей, динамики
цен на тот или иной продукт, курса акций на KaKoe TO время IJперед и т. д.).
Во всех этих слу'шях речь идет о uеличинах, недоступных непосредственному
наблюдению (измерению) в данный момент и которые надо оценивать (про
rнозировать) с помощью доступных измерению сопутствующих величин.
В общем случае Х озна'lает некоторую соuокупность {X 1 , Х 2 , .} Ha
блюдаемых случайн ых нели'lИН, которые в рассматриваемом контексте назы
ваются предсказывающими (или nрО2Ноз//ыми) переменными, и задача состоит
в построении такой функции <р(Х) ОТ этих величин, которую можно было бы
использовать в качестве оценки для проrнозируемой lJеличины У <р(Х) У
(т. е. чтобы она была в KaKOM TO смысле «близка.) к У); такие функции назы
ваются nредикторами величины У по Х. Задачей разработки методов постро
ении оптимальных (в том или ином смысле) предиктов занимаетси теория
статистической рарессии (или, что то же, стохастическою nРО2ll0зuровш/Uя).
Для построения этой теории прежде всеro требуется УТО'lНИТЬ смысл при
ближенноrо равенства <р(Х) ::::;; У Если <р(Х) используется для предсказания
величины У, то одной из разумных мер расхождения между ними ЯIJлиеТС51
)
квадратическая ошибка (<р(Х) Y) , но так как lJеЛИ'lина У неизвестна,
6.6. Статистическая реzрессия u проzнозирование 503
то для измерения Т04НОСТИ предиктора tp используется среднеквадратическая
ошибка (с. к. о.) C:.(tp} == E(tp(X} у}2 Предиктор, минимизирующий с. к. о.
В заданном классе предикторов Ф, называется оптималыlмм nредuкторОJII, или,
кратко, nрО2НО30М (в классе Ф), и обозначается симво ПроrНQЗ '*
*
лом tp :
tp* == arg min (tp);
I'ЕФ
(1)
ero с. к. о. есть
* == (tp*) == E(tp*(X) у}2 == inf E(tp(X} у)2
I'ЕФ
(2)
Таким образом, в общем случае зада4а построения наИЛУ4шеrо (в cpeДHe
квадратическом смысле и в заданном классе предикторов Ф) предиктора для
веЛИ4ИНЫ У по Х сводится к решению экстремальной проблемы (1} (2). Как
будет ясно из дальнейшеrо, основным аналитическим инструментом решения
этой проблемы является аппарат условных распределений, поэтому мы пред
варительно напомним некоторые факты и формулы из теории вероятностей,
которые будут использоваться далее.
2, Условное математическое ожидание
Напомним, 4ТО мы оrpаничиваемся рассмотрением лишь абсолютно непре
рывных либо дискретных распределений С(Х, У} и используем общее обозна
чение /ху (х, у) для СОRместной плотности в первом случае и совместной
uероятности Р{Х == х, У == у} во втором, называя в любом СЛУ4ае функ
цию /ху(х, у) плотностью. По совместному распределению С(Х, У) можно
определить условное распределение C(YIX == х) веЛИ4ИНЫ У при заданном
значении Х. Так, в абсолютно непрерывном случае это распределение задает
ся условной плотностью
/ху(х, у)
!Ylx(ylx) == /х(х) ,
rде
/х(Х} == J /ху(х, у) dy
марrинальная плотность Х (для дискретных распределений последний
интеrpал заменяется соответствующей суммой). В предположении существо
вания соответствующих моментов мы можем вычислить среднее и дисперсию
этоrо условноrо распределения: условное математическое ожидание
М(х) == E(YIX == х),
(3)
Ф у кци"яре rрессии "
называемое функцией ресрессиu У на Х, и условную
дисперсию
D(YIX == х) == Е[(У м(х)2 I Х == х].
(4)
504 rлава б. Линейная реzрессия и метод наименьших нвадратов
Так, Д/JЯ абсолютно непрерывных распределений
М(х) == / YfYlx(ylx) dy == / Yfxy(x, у) dy fx x) '
D(YjX == х) == ! (у м(х))2 fYlx(Ylx) dy;
в случае же дискретных распределений интеrралы в этих формулах заменяются
соответствующими суммами.
В соответствии с (3) и (4) можно рассматривать случайные величины
М(Х) и D(YIX), которые при Х == х принимают значения соответственно
М(х) и D(YIX == х). Обозначим
O' == DY, O' == DM(X), O' x == ED(YIX). (5)
Torдa имеют место следующие полезные формулы:
ЕУ == E[E(YIX)] == ЕМ(Х), (6)
ОУ == DE(YIX) + ED(YIX), или O' == O' + O' x. (7)
Соотношение (6) называют формулой пОЛНОlО математическоzо ожидания,
а (7) формулой разложения дисперсии.
Формула (6) проверяется непосредственно: например, для абсолютно He
прерывных распределений из определения М(Х) имеем
ЕМ(Х) == / M(x)fx(X) dx == / (1 yfYix(ylx) dY) fx(x) dx ==
/ У(/ fxy(x, у) dx) dy == 1 yfy(y) dy == ЕУ
Формула же (7) получается с использованием определения (4) и формулы
полноrо математическоrо ожидания (6) из цепочки равенств
DY == Е(У Еу)2 == Е[(У М(Х) + (М(Х) Ем(х))]2 ==
== Е{ Е[(У м(х)2 I х]} + DM(X) +
+ 2Е{ Е[(У М(Х))(М(Х) ЕМ(Х)) I Х]} ==
== ED(Y/X) + DM(X),
поскольку
Е[(У М(Х))(М(Х) ЕМ(Х)) I х] ==
== (М(Х) ЕМ(Х))Е[(У М(Х)) I х] == О.
Отметим важное следствие формулы (7):
O' == DE(YIX) O' == ОУ,
(8)
6.6. Статистическая реzресcuя и проzнозuрование 505
причем равенство в (8) выполняется лишь в случае, коrда
o" x == ED(YIX) == Е{ Е[(У м(х))2 I Х]} == Е(У м(х))2 == О,
Т.е. KOrдa У == М(Х) (У является функцией Х).
Примеры вычисления условных средних и дисперсий в мноrомерной HOp
мальной модели указаны в упр. 65 и 66 к rл. 1; подчеркнем, что в зтих примерах
функции реrpессии М(х) являются линейными по х, а условные дисперсии
от х не зависят. Приведем еще один иллюстративный при мер вычисления
условных среднеrо и дисперсии.
Пример 1. Пусть U 1 И И 2 независимые показательные с пара метром Mac
штаба а> О случайные величины (см. п. 3 1.2). Положим
Х == И 2 , У == И 1 + U 1 U 2 .
Torдa
М(х) == E(YIX == х) == Е[(I + x)U 1 ! == а(1 + Х),
D(YIX == х) == О(I + x)U11 == а 2 (1 + х)2
Следовательно, М(Х) == а(1 +И 2 ), D(YIX) == а 2 (1 +и 2 )2 и потому
0"1 == DM(X) == аОИ2 == а 4 ,
o" x == ED(YIX) == а 2 Е(1 + и 2 )2 == а 2 (1 + 2а + 2а 2 ). .
3. ОПТИМ311ЬНЫЙ предиктор и ero свойства
Решение экстремальной проблемы (1) (2) существенно зависит от задания
класса Ф, в котором ищется проrноз. Если класс Ф есть класс всех функций
It'(X) , то ответ на вопрос о существовании и виде оптимальноrо предиктора
(проrноза) It'* (Х) дает следующее утверждение.
Теорема 1. Оптимальный предиктор It'* в классе всех функций Ф == {It'} cy
ществует и совпадает с функцией реrресси и У на Х, т. е.
It'* (Х) == М(Х) == E(YIX);
(9)
этот предиктор имеет максимальную корреляцию с У среди всех предикторов.
Доказательство. По формуле полноro математическоrо ожидания для любой
функции It' Е Ф
Е[(У М(Х»(М(Х) It'(X»)] ==
== Е{ Е[(У М(Х)(М(Х) \О(Х») I Х]} ==
== Е{ (М(Х) It'(X»)E[(Y М(Х») I Х]} ==
== Е{ (М(Х) It'(X») (М(Х) М(Х») } == О,
506 rлава б. Линейная реzрессия и метод наименьших квадратов
поэтому для С. к. о. предиктора 'Р можно записать следующую цепочку COOT
нощений:
Д('Р) == Е('Р(Х) у)2 == Е[('Р(Х) М(Х)) + (М(Х) у)]2 ==
== E(Ip(X) м(х))2 + Е(М(Х) у)2 ? Е(М(Х) у)2 == Д(М).
Знак равенства достиrаетси здесь лищь при 'Р == М, следовательно, 'Р' == М.
Отсюда также следует, что минималЬНШJ ошиБК;1 предсказания д' в (2)
может быть записана в виде (см. (4) (5))
д' == Д(М) == Е(У м(х))2 == Е{ Е[(У M(x))21 Х]} == ED(YIX) ==О'}Х,
( 10)
Переходя к доказательству второй части теоремы, прежде Bcero заметим,
что для произвольноrо предиктора rp с учетом (6) имеем
СОУ('Р(Х). У) == E(It'(X) EIp(X)) (У ЕУ) ==
== Е{ E[(Ip(X) Е'Р(Х))(У ЕУ) I х]} ==
== Е{ ('Р(Х) Еср(Х))Е[(У ЕУ) I Х]} ==
== Е('Р(Х) EIp(X)) (М(Х) ЕМ(Х)) == СОУ('Р(Х), М(Х)).
В дальнейшем для сокращения записи apryMeHT Х будем опускать и для любых
случайных величин {,{I, 6 будем использовать стандартные обозначения
COV( I, Ы
O'l == щ, P({I, Ы == corr({i, 6) == .
(7(, O' )
При It' == М полученное выше равенство дает
соу(м; У) == соу(М, М) == O' ? о,
откуда
О'м
р(М, У) ==
О'у
Используя это И то, что Ip({I, ЫI 1, имеем
2 соу 2 ('Р, У) соу 2 ('Р. М) (7 2 2 2
Р (ср, У) == 2 2 == 2 2 2 == Р (Ip, М)р (А1, У) р (А1, У).
O' O'y O' O'M (7у
Таким образом, Р(М; У) ? Ip('P, У)! дЛЯ любою Предиктора 'Р. .
.. Корреляционное Квадрат максимальноrо значения коэффициента
отношение корреляции /(М, У) имеет специальное обозначение
1]i,x и называется корреляцuо//ным отношение.М. Из пре
дыдушеrо и (7), (10) для Hero можно записат(, следующие представления:
2 2 Л'
2 2 О'м О'ух L1 )
1]ух == р(М, У) == sup Р ('Р, У) == 2 == 1 == 1 ----т. (11
ЕФ О'у О'у О'у
6.6. Статистическая ре2рессия и пРО2Нозирование 507
ОТ , * 2
сюда следует, что 'Т/УХ ----7 1, если ошибка проrноза.l ----7 О, И 'Т/УХ == О,
если y'leT Х не уменьшает ошибки проrноза (.l' == lТ X == lТ ). Таким обра
2 б
зом, корреляционное отношение 1]ух представляет со ои меру зависимости
между У и Х (или меру точности проrноза, так как .l' == lТ (1 1] x )),
и по этой мере можно сравнивать различные совокупности проrнозных пе
ременных в конкретных зада'lах: значения этой меры при надлежат интервалу
10, 11, чем ближе l1 x к 1, тем точнее проrноз У по данному Х, а 1] x == 1 тоrда
и только тоща, Korдa У == М(Х), т. е. коrда У функционально связано с Х.
Пример 2 (Проrноз в нормальной модели). Пусть совместное распределение
пары (Х, У) есть нормальное распределение с ЕХ == J1.X, ЕУ == J1.y, DX == ui,
DY == lТ , corr(X, У) == р, Ipl < 1. Тоrда (см. упр.65 к rл. 1) проrноз У по Х
имеет вид
/ту
М(Х) == Е(У[Х) == J1.y + p(X J1.x), (12)
lТx
Eroc.K.o..l* == lТ X == (1 p2)/Т < /Т (см. (10)), а корреляционноеот
ношение 'Т/ x == 1 .l'/lТ == / (см. (II), т. е. равно квадрату коэффициента
корреляции Х и У. .
4. Из истории реrрессии
Терми н «реrрессия» был предложен Фрэнсисом rалыоном З) и основан на сле
дующем наблюдении. rалыон IIЗмерял рост отца (Х) и сына (У), выбранных
случайно из большой популяции людей. Если предположит!', 'ПО
L(x,Y)==N((J1.,J1.),II::2 р;21J)
р>О
(здесь J1. среднее роста мужчин по популяции, lТ 2 дисперсия роста
по популяции), ТО в соответствии с (12), проrноз роста сына у отца, чей
рост Х, есть
М(Х) == J1. + р(Х J1.) == (1 р)р. + рХ (13)
и совпадает с E(YIX) средним ростом сыновей, чьи отцы имеют рост Х.
Из (13) следует, что проrноз М(Х) ближе к среднему по популяции J1., чем
рост отца Х. если рост отца Х 1 > J1., то M(X 1 ) < Х} у высоких отцов
сыновья будут, как правило, меньшеro роста, т. е. наблюдается ('реrpессия
к среднему.). Но эта тенденция компенсируется «проrрессией К среднему»
среди сыновей отцов небольшоrо роста: если Х2 < J1., ТО М(Х 2 ) > Х 2
(см. диаrpамму), и тем самым парадокса не получается популяционное
среднее остается постоянным.
М(Х 2 ) M(X 1 )
1. . 1.
Х 2 J.1. Х.
З) rалЬТОII Фрэнсис (1822 1911) анrлийский психолоr и биалоr, один из создателей евrеНИКII.
508 rлава б. Линейная реzрессия и метод наименьших квадратов
При этом дисперсия предсказанноro значения
ОМ (Х) == О(рХ) == р2 а.2
2
меньше дисперсии (J" реальных отцов.
Здесь уместно сделать следующее замечание, имеющее общий характер.
На практике (и у rальтона) точное распределение L(X, У) обычно не из
вестно и линия реrрессии М(Х) строится приближенно по оценкам ji и р
Эмпирический на основе большой выборки (X j , 1';), i == 1, ,n,
из rенеральной совокупности, и в итоrе используют
проrноз
эмпирический пРQ2/tоз
М(Х) == (1 P)Ji + рХ
(детальнее об этом речь будет идти позже).
Итак, если коэффициент корреляции описывает зависимость между двумя
случайными величинами одним числом, то реrрессия выражает эту зависи
мость в виде функциональноrо соотношения и поэтому дает более полную
информацию. Вначале реrpессионный анализ применялся в биолоrии; между
1920 и 1930 rr. он начал интенсивно использоваться в экономике, что привело
к возникновению новой области науки эконометрики; в настоящее время
реrpессионный анализ интенсивно используется практически во всех обла
стях науки, так как анализ величины У, определяемой по друrой величине Х,
коrда У измерить трудно, а Х достаточно леrко, весьма важен.
5. Линейный проrноз
Итак, при минимальных предположениях о совместном распределении С(Х, У)
величин Х и У (требуется лишь существование вторых моментов) мы имеем
универсальное решение ДJJЯ проrнозирования У по наблюдению над Х, дa
ваемое функцией реrрессии (9). Однако здесь имеются две трудности:
1) для вычисления проrноза М(Х) == E(YIX) надо абсолютно точно знать
закон распределения С(Х, У) и
2) явное вычисление М(Х) может оказаться трудной аналитической задачей
и проrноз может оказаться слишком сложной функцией, мало приrодной
для конкретных расчетов.
Однако обеих этих трудностей можно избежать, если сузить Kpyr поис
ков наилучшеrо предиктора до класс L простейших, а именно, линейных
предикторов Ip( X ) == {30 + {3' Х (здесь мы считаем, что Х == (Х" , Х р )
и f!.. == (/31,"', {3р)). Для эт о случая решение экстремальной проблемы (1)
дается следующим утверждением.
Теорема 2. Пусть L == {Ip Ip(IO == /30 + {3' Х } есть класс всех линейных
предикторов У по Х . Torдa оптимальный линейный предиктор (линейный
б.б. Статистическая реzрессия и пР02нозuрованuе 509
n роrноз)
If'i == arg min 6(1f')
'(JEL
tf
Линейный nроrноз
дается соотношением
* ( Х ) == ЕУ + a/1:; I ( X Е Х ) == {3 . + {3 '/ Х
If'L о '
(14)
т. е.
{3 == ЕУ Q'1:; IE X == ЕУ f!..*' EX , f!..' == E lQ,
[де Q == соУ(У, Х ) == (соу(У, X 1 ), ,соУ(У, Х р )), Е == D( X ) и nредnолаrа
ется, что 'ЕI -# о. Этот nредиктор имеет максимальную корреляцию с У среди
всех линейных nредикторов.
Доказательство. Пусть ер произвольный линейный предиктор. Torдa ero
с. к. о. 6('Р) может быть записана в виде
Ll(If') == Е(У {30 f!..' X )2 == Е[(У ЕУ) Ь f!..'( X Ею]2 ==
== DY + ь 2 + {311:;{3 2{31 Q,
rдe обозначено Ь == {зо ЕУ + f!..' EX (проверяется непосредственно, что мы
оставляем 'lитателю в качестве простоrо упражнения).
Пусть теперь f!.. == f!..* + , rдe f!..* указано в (14) и t! произвольный
вектор. Torдa (также проверяется непосредственно)
ь 2 + f!../1:;f!.. 2f!..'Q == ь 2 + 'E f!.."Q f!..*'Q
и равенство здесь достиrается лишь при Ь == о, Q == Q (поскольку невырож
денная дисперсионная матрица является положительно определенной). Таким
образом,
6(1f') DY f!..*IQ == a Q1E IQ == 6('P ), (15)
т. е. предиктор If'i (14) обладает в КI1acce L минимальной с. к. о. Первая часть
теоремы доказана.
Далее, из определения векторов Q и f!..* следуют равенства
соУ(У, f!../ Ю == f!..1 Q == f!..' Ef!..*
соу(У, f!..*'Жj == f!.."1:;f!..' == D(f!..*1 Х ) О.
(16)
Из последнеrо равенства также имеем
с оу ( У {3 *' Х )
2 2 ( У (З *'Х ) == , == {3 *'1:; {3 '
аур ' D(f!..*I X )
Воспользуемся неравенством Коши Буняковскоrо (для любых векторов Q И!!.
(Q/ !!.) 2 (Q' Q)(!! !!.)) в виде
(f!..IEf!..*)2 == (f!../1:;1/2 E l/2f!..*)2 (f!..'Ef!..)(f!..*'1:;f!..*),
(17)
510 rлава б. Линейная ре2ресcuя и метод наименьших квадратов
TOrдa из (16) и (17) получим
2 2 I соу2(у, ' Х ) (13 ЕfЗ ) 2 ;
( У fЗ Х ) == ' *2 fЗ *'Е fЗ *== " ( У fЗ *'Х )
иур , == D( f X ) fЗ'ЕfЗ '" иур ' .
Отсюда следует, что для любоro предиктора ер Е L
..
МножествеННblЙ
коэффициент
корреляции
p(Y, " Х ) == р(У, ep ( X )) jp(Y, ep( X ))I. .
Из этих рассуждений (см. формулу (15)) следует,
что в теории линейноrо проrнозированин особую роль
иrрает величина
2 /E If!
РУХ == ,
иу
которая имеет специальное название множествеНI/ЫЙ коэффицие/fт корреляции.
Эта величина зависит только от вторых моментов совокупности переменных
( Х , У) и представляет собой обобщение квадрата обычноrо коэффициента
корреляции на случай MHoroMepHoro Х (если Х есть скалярнан величина Х,
т. е. р == 1, то р}х == / (Х, У)). Таким образом, P X это мера корреллшlОН
ной заоисимости У от вектора Х . Через эту Mepy c. к. о. линеЙноrо проrноза
ep можно записать в виде (см. (15))
( 18)
/l == /l(ep;,) == и (1 P K)'
( 19)
, *
откуда следует, что чем ближе рук к 1, тем TO'IHee проrноз ер/,. Множествен
ный коэффициент корреляции иrрает в теории линейноrо проrнозирования
такую же роль, как корреляционное отношение l] x (см. (11)) в общей теории
проrнозирооания. Для P K можно записать аналоrичную (11) цепочку COOT
ношений:
13 *'ЕfЗ * /l*
P X == == р2(у' ep ) == Sllp /(У, ер) == 1 , (20)
и у .pEL и у
2
откуда, в частности, видно, 'ПО рук равеи квадрату оБЫ'lНО20 коэффицие/fта
корреляции между У и оптималыlмM ЛИllеЙI/ЫМ предиктором для У
. 2 2
Поскольку L С Ф, то из (11) и (20) следует, что пук рук, а 11 тех случа
ях, коrда функция реrрессии М( Х ) линейна (Torдa она являетсн линейным
проrнозом), ошибки /l* и /l совпадают, слеДОl3ательно, l] x р}х. По
этому в общем случае разность п K P x. может служить мер-;й откл нения
реrpессии от линейности.
Итак, в условиях теоремы 2 линейный проrноз ep ( Х ) дЛЯ У также всеrда
может быть построен, при этом для ero ПЫ'lислеНИ!1 достаТО'IНО знать лишь
первые и вторые моменты распределения [,( Х , У), Т.е. минимальную инфор
мацию об этом распределении. На практике обычно используют линейные
проrнозы, а необходимые для этоro моменты оцениваютсн по результатам
96.6. Статистическая реzрессия и проzнозuрование 511
прошлых наблюдений над Х и У Заменив в (14) точные значения MOMeH
TOU (Korдa они неизвестны, а так обычно и бывает) их оценками, как это
описано в п. 5 2.3, мы получаем эмпuрuцескuй предикmор ( X ) (см. (16)
2.3), который и используется дЛя проrНОЗl1рованин будуших значений У
Также по прошлым наблюдениям оценивается множественный коэффициент
корреляции P K (см. формулу (17) 2.3), что дает возможность оценить с. к. о.
(19), т. е. точность проrноза.
Примерами линейноrо проrноза являются проrноз 11 нормальной модели
(см. пример 2, соотношение (12), и упр. 25), а также проrнозы, указанные
в при мере 1 и упр. 23, 24: во всех этих случаях функция реrрессии М(Х)
линейна, следовательно, она, как абсолютно оптимальный предиктор (в COOT
ветствии с теоремой 1), и является линейным проrнозом. То, что функция pe
rрессии не Bcerдa оказывается линейной, демонстрирует следующий при мер.
Пример З. Пусть модель [(Х, У) задается следующим образом:
[(У) == Ве(а, Ь)
бета распределение (см. п. 4 1.2), а
L(XIY == у) == Bi (r, у)
отрицательное биномиальное распределение (см. п. 2 1.1). Тоrда по форму
ле Байеса (см. соотношение (3) п упр. 59 к rл. 1) условная плотность fYlx(Ylx)
есть
f ( 1 ) fY(Y)/xly(xly) '" Н (I ) I "' (1 ) r a+"' I (1 ) b+r 1
YIX У Х == == У У У У == У У ,
fx(x)
т. е. L(YIX == х) == Ве(а + х, ь + r) и потому (см. (24) 1.2)
а+Х
М(Х) == E(YIX) == а + Ь + r + Х
Это есть проrноз У по Х в классе всех функций tp(x), и он не является
линейным. .
6. Использование в проrнозе Аополнительных переменных.
Алrоритм обновления проrноза
При практической реализации теории линейноrо проrНОЗИРОllания возникают
следуюшие важные вопросы: 1) как из множества всех факторов {X j }, влияю
щих на проrнозируемую величину У, выделить наиболее существенные, или,
друrими словами, как упорядочить проrнозные переменные по степени их
важности в проrнозе У'! 2) если решен I-й вопрос, следовательно, мы имеем
упорядоченный ряд факторов Х} >-- Х 2 >-- >-- Xl' 1 >-- Хl' >-- то сколь
кими факторами оrpаНI1ЧИТЬСЯ в построении предиктора tp ? 3) наконец, как
рационально действовать при расчете проrноза, чтобы избежать чрезмерных
затрат?
512 rлава б. Линейная ре2рессия и метод наименьших нвадратов
Хорошо постовить вопрос зночит
уже наполовину решить ezo.
Д.И.Менделеев
Чтобы ответить на эти вопросы, исследуем предварительно, как изменя
ется ТО4НОСТЬ проrноза при увеличении 'Iисла проrнозных перемен ных. Усло
вимся далее кодировать переменные Х ; их индексом (,i», i == 0,1,2, при
2 22 2 * ()
этом ХА == У, тоrда О'у == 0"0, РУК == PO(I.. 'р)' а для с. к. О. ДL D 19 будем ис
пользовать обозначение O" (I.. .р). в этих обозначениях формула (19) примет вид
2 2 ( 2 )
0"0(1.. .р) == сто 1 PO(I.. .р) .
Пусть по факторам Х (X 1 ,., Xp l) построен линейный проrноз
<p ( X ) == Yp* l (см. (14), rде Х есть вектор размерности р 1); ero с. к. о. есть
2 2 ( 1 2 ) Е Х
O"O{I.. 'p l) == 0"0 PO(I'''p I)' сли добавить в проrноз новое переменное р,
то С. к. о. HOBoro предиктора ; == <P (XI, ,Х р ) станет равной 0'5(1' ..р) ==
== 0'6 (1 P (l" .р»). Следовательно, относительное уменьшение ошибки про
rноза при добавлении p ro переменноrо будет равно
0'2 0"2
O(I"'p l) O(l...p)
0'2
O(I..p 1)
2 2
РО(I"'р) PO(I...p l) 2
2 == POp(l"p I).
1 PO{l..p 1)
(21)
..
Частная корреляция
Определенную в (21) величину POp(l"p l) называют
частной корреляцией между У и Х р , исключающей
влияние «nромежуточнbIX» nеременных X 1 ,... ,Xp 1 Из (21) следует, что
0"2 0"2 ( I 2 )
O(I"'p) O(I"'p l) POp(I."TH) ,
(22)
и если частная корреляция POp(l.. 'p l) мала, то учет Х Т } мilЛО что добавляет
в проrноз. При р == равенство (22) принимает вид cтJ(I) == ст6(1 P61)'
т. е. наибольшую точность простейший nредиктор Y 1 * имеет, если фактор Х 1
имеет наибольшую корреляцию с У.
Отсюда вытекает следующий принцип упорядочения факторов по степе
ни их важности в проrнозе: в качестве nервО20 фактора Х I выбирается фактор
с наибольшей корреляцией с У; в качестве следующе20 по важности фактора Х 2
выбирается фактор с наuбольшей 'tастной корреляцией с У, исключающей вли
янuе X 1 , и Т.д., т. е. частная корреляция POp(I...p l) ямяется инструментом
упорядочения предсказывающих переменных по степени их важности в про
rнозировании У.
Отметим некоторые свойства частной корреляции. Обозначим
Pij == p(X i , X j ), i, j == О, 1, ..., р, р == Ilpijllg и p ' == Ilpijll .
6.6. Статистическая реzрессия и пРО2Нозирование 513
Тоrда
рОр I Р02 Ро] PI2
POp(J.. 'p 1) == (23)
рООррр p 2 J (I P5J)(1 P 2)
Далее, построим линейный проrноздля Х р по переменным Х == (X 1 , ., .
Xp l):
, · ,1 , 1 ( у\
Х р == йо + Q Х , Q == Е Q, !!. == соу Х р . КJ,
, ., ( )
йо == ЕХ р Q ЕХ , Е == D Х ,
и рассмотрим остатки е I == У Yp' J И е2 == Х р х;. Тоrда можно показать,
что
POp(I,,'p l) == p(el, е2), (24)
т. е. частная корреляция это обычный коэффициент корреляции между ocтaт
ками, получающимися вычитанием из У и Х р их оптимальных линейных пpeдиK
торов, основанных на X I , , Xp 1 (так ИСЮlючается влияние общих факторов
X I , ,Xp 1 на переменные У и Х р ).
Остатки е, являющиеся ошибками соответствующих проrнозов, обладают
следующими свойствами:
1) они имеют нулевое среднее, так как
У . /3 ' /3 .1 ( ( ))
Ее] == Е EYp 1 == ЕУ о Е Х == О см. 14 ;
2) следовательно, Del == Е(У Yp' 1)2 == ' == O'G(i"'P I);
3) cov(/3' X ,ei) == coy(/3' X ,Y /3" X ) == /3'Q /3'E/3' == /3'Q /3'!! == О,
т. е. они некоррелированы с проrнозными переменнымй:' Это свойство
можно проинтерпретировать также так: оптимальный линейный предиктор
концентрирует в себе всю корреляцию У с прОZНОЗIIыми пepeMe/IНЫMи.
На изложенном выше основан следующий эф Алroритм 06HOB .,
фективный алrоритм обновления проrноза для У при
пения проrноза
добавлении в проrноз дополнительноrо переменноrо.
Пусть построен проrноз (см. (14))
Yp' 1 == tp (XI"" ,Xp l) == /3 + " x , Х == (X 1 , ,Xp I),
И будем искать новый предиктор Yr: при добавлении в проrноз новой пере
менной (фактора) Х р в виде линейной комбинации /30 + /3' Х + /3ре2. Torдa
для определения коэффициентов надо минимизировать с. к. о.
Е((У /30 ' Х ) /3ре2)2 ==
== Е(У /30 f!..' х )2 + /3;и;! 2/3р cov(el' е2) ==
( 'у\2 ( cov(el,e2) ) 22 cov 2 (el,e2)
== Е У /30 /3 КJ + /3р 2 и е2 2
О' е2 и е2
зз 3аказ 1748
514 rлава б. Линейная ре2рессия и метод наименьших квадратов
(поскольку
соу(У /30 ' Х , е2) == соу(е" е2) + COY(Yp' I ' Х , е2) == соу( е" е2»,
Отсюда следует, LITO оптимальные значении ДЛЯ /30 и /3 == (/3" . . . , /3p ,)
прежние (см. (14», а оптимальный uыбор /3" такои (см.(24»:
* соу(е" е2) О"е, (Те,
/3" == 2 ==p(el,e2) ==POp(l' .,H)
О"е! О"е] О"е]
(25)
Таким образом, новый проrноз может быть вычислен по формуле
У; == Y; l + /3;е2 == Yp* 1 + 13;(X p Х,:) ==
p ,
== 13 a 13; + L,(13: a:13,:)X i + 13;X p . (26)
i '
т. е. предыдущие коэффициенты (перед переменными X 1 , , Х,н) пересчи
тываются, а коэффициент при новой переменной Х р раВен 13; (см. (25». При
этом ошибка HOBoro проrноза вычисляется по формуле (22).
Фактически это есть реккурентный алrоритм построеНИSI проrноза: мы
начинаем с простеЙшеrо предиктора.
Y 1 * == 13 + 13 X 1 ,
. 0"0
/31 ==POI , /30 == ЕУ /3 EXI'
0",
(27)
2 2 2 ( 2 )
ero с. к. о. о" е, == 0"0(1) == О"() I РО, . и последоuательно добавляем новые пе
ременные Х 2 , Х), (по степени убывания их значимости) с пересчетом
по формуле (26) на каждом шаrу коэффициентов предыдущей линейной KOM
бинации, пока не достиrнем желаемой точности проrноза, что контролируется
формулой (22) (см. также при мер 1 в п. 5 2.3).
7. Проrнозирование стационарных временных рядов
Наиболее важные применения теории линейноrо проrноза связаны с nporHo
зированием ста/(ионаРIlЬ/Х случайllЬ/Х Ilроцессов. Под этим термином мы будем
понимать последовательность случайных величин {Xt. t Е Z}. Z множе
ство ВСех целых чисел, УДОIJлетворяющих следующим условиям:
EX t == т == COl1st, cov(Xt+k' X l ) == Rk' V t.
(28)
Таким образом, для стационарной последовательности {X t } среднее любоrо
ее члена остается постоянным, а ковариации между ее членами заIJИСЯТ лишь
Временной ряд от разности их номеров. Параметр t обычно трактуется
как (дискретное) время, а последовательность {X t } назы
вают epeMeHHblJtt рядом. Величину Rk в (28) обычно называют автОКО8арuацuей
с задержкой (ласом) k, а всю последовательность {Rk} ':'00 a8тOKoвapиaцu
анной функцией или, кратко, автОКО8арuацией. Отметим следующие очевидные
6.6. Статистическая реzресcuя u проzноэирование 515
ее свойства:
Ro == ОХ, == (72 == const,
Rk
COlT(Xt+k. Х,) == == Pk,
Ro
IRkl Ro, R k == Rk, P k == Pk,
.t Ri jCiCj == .t CiCj cov(X i , X j ) == о( t CiXi)
I,J I l,з 1 , I
Определенный в (29) коэффициент корреляции Pk обычно называют aв
токорреляцuей с задержкой k, а всю последовательность {Pk} oo aвтOKOp
реляционной функцией или, кратко, автокорреляцией (в технической литературе
используется также термин коррелоzраМАlа). Последнее свойство в (29) называ
ется свойством положительной определенности автоковариации. В дальнейшем
предполаrается, что матрица R(n) == IIRi jIl7 не вырождена при любом n 1.
Сделаем еще одно дополнительное предположение, при котором модель
BpeMeHHoro ряда обладает хорошими свойствами реryлярности. Именно, будем
считать, что выполняется условие
(29)
О,
Vn.
00 00
2: IRkl ==Ro+22:IRkl <00.
k oo k 1
(3О)
Если имеет место (30), то можно рассмотреть преобразованuе Фурье 4) aBТOKO
вариации {Rk}:
1 00 1 1 00
f(л) == Е Rk cos kл == Ro + Е Rk cos kЛ,
271' k oo 271' 11' k 1 (31)
л Е [ 11',11'].
Условие (30) обеспечивает равномерную сходимость ряда (31) к непрерывной
функции, и ero сумма f(л) называется спектральной плотиостью BpeMeHHoro
ряда {Х,}. Коэффициенты сходящеrося ряда Фурье, . . .Спектральная tf
как известно, однозначно определяются ero суммой _ плотность
по формулам
1r
Rk == f f(л) cos kл dл, k Е Z.
(32)
11'
Соотношения (31) (32) показывают, что спектральная плотность f(л) (коrда
она существует) и автоковариация {Rk} находятся во взаимно однозначном
соответствии, поэтому стационарный временной ряд {Х,} можно описывать
в терминах любой из этих двух функuий.
4) Фурье Жан Батист Жозеф (1768 IB30) французскиЙ математик, один ИЗ основополож
ников математической фИЗИКИ, почетный член Петербурrской АН (1829).
ЗЗ'
516 rлава б. Линейная реzрессия и метод наименьших квадратов
Модель стационарноrо BpeMeHHoro ряда является удобной для исследо
вания и в то же время подходящей для описания мноrих реальных процессов.
В рамках этой модели, в частности, достаточно просто решаются задачи про
rнозирования, что и является нашей целью в этом пункте. В общем виде задача
ставится так: построить оптимальный линейный предиктор (проrноз) для зна
чения Xt процесса в момент t, предполаrая, что известно некоторое число
n 1 предыдущих значений Xt "" ,Xt n. Покажем, как адаптируется
разработанная выше общая теория линейноrо проrнозирования к модели CTa
ционарноrо BpeMeHHoro ряда. Для простоты будем считать, что т == EX t == О,
в противном случае Xt нужно просто заменить на Xt т. В этом случае
по теореме 2 n проrноз Xt*n для Xt имеет вид
n
Xt == 13 ,Хн +... + 13 nXt n == L 13 jXH'
j 1
rде 13 j, j == 1,... , n, минимизируют относительно 13,. ,13n cpeДHeKBaдpa
тическую ошибку проrноза Е ( Xt -t 13jXt j) 2 Соrласно (14), коэффици
J '
енты 13* == CB I' '/3 n) оптимальноrо n предиктора определяются вданном
n
случае автоковариацией {Rk} процесса {X t } по следующим формулам:
(33)
: == R I(n) , Q == cov(Xt. (Хн,..., Xt n)) == (Я"
, я,.).
(34)
Если обозначить R I(n) == IIRijll , то в координатной записи решение имеет
вид
n
/3 . "'" R ij R '
n) L..J \,
i '
j == 1,
,n.
(34')
Наконец, с. к. о. 6 *(n) проrноза Xt*n. соrласно соотношениям (18) ( 19) и (29),
есть
6*(n) == E(X t х;n)2 == ЯО Q'R I(n)Q.
(35)
Если воспользоваться следующей формулой для разложения определителя:
I I == IAI(a ftA If)
(здесь А квадратная невы рожденная матрица, Q и векторы столбцы
и а скаляр) и положить здесь А == Я(n), а == Ro, Q == == , то формуле
(35) можно придать вид
*( ) == IR(n + 1)1
n IR(n)l'
(35')
Соотношениями (33) (35') полностью решается задача построения и pac
чета линейноrо проrнозз в модели стационарноrо BpeMeHHoro ряда.
6.6. Статистическая реi!рессия и пРОi!нозирование 517
Рассмотрим, наконец, как конкретизируется в дaH Обновление ..,.
ном случае алrоритм обновления проrноза, если мы хотим
проrноза
добавить в проrноз дополнительное наблюдение Xt n 1
(см. соотношение (26)). Прежде Bcero мы должны построить еще один n про
rноз по тем же переменным Xt 1, . . . , Xt n ДIIя величины Xt n 1 (так сказать,
проrноз в прошлое). В силу специальной структуры стационарноrо BpeMeH
Horo ряда (корреляции между ero членами зависят лишь от разности COOTBeT
ствующих моментов времени) этот «обратный') предиктор Xt' n I имеет те же
коэффициенты, что в (33), но переменные должны быть взяты в обратном
порядке:
Xt' n 1 == f3 IXt n + + fЭ пХн (36)
(в этом леrко убедиться и формальными выкладками, повторив рассуждения,
использованные при выводе (33), что мы рекомендуем читателю проделать
самостоятельно). Далее мы рассматриваем остаток е п == Xt n 1 Xt' n l'
который некоррелирован с переменными Xt 1, , Xt n И имеет дисперсию
и;n == '(n), указанную в (35'). Наконец, новый (n + I) предиктор Xt n+1
ДIIя X t , учитывающий дополнительную, (n+ I) ю переменную Xt n l, имеет
вид
Xt*.n+1 == Xt*n + fЭ +I,П+lеп,
\37)
rдe (см. (25) и (36))
* cov(X t , е п ) Rn+! {З !Rn fЗ пRI
f3n+l,n+1 == и n == '(n) (38)
при этом {3 +!.п+! есть частная корреляция Xt с Xt n l, исключающая вли
яние всех промежуточных переменных Xt 1, . . . , Xt n.
Подставив н (37) выражения (33) и (36), получим явное представление
(n + I) проrноза Xt "+' через проrнозные переменные Xt l, . .. , Xt n l:
n
Xt n+1 == 2)f3 j {3 +1.n+I{3 ,n j+I)XH + {3 +1.n+IXt n+ (39)
j=1
Этими соотношениями (36) (39) и решается проблема обновления проrноза
в модели BpeMeHHoro ряда: мы видим, что добавление к n проrнозу Xt*n
В (37) HOBoro члена {3 +I. "+I е п вносит поправки в старые коэффициенты при
переменных Xt I,' ,Xt n. Таким образом, если записать (n + I) проrноз
в стандартной форме типа (33)
"+I
Xt*.n+1 == L{3 +1.jXt j, (40)
j=!
то мы получаем, сравнивая (40) с (39), следующие рекуррентные уравнения
ДIIЯ вычисления ero коэффициентов:
{з н j == fЗ j {3 H n+If3 , n j+I' j == 1, ... , n, (41)
rде {з н п+ 1 указано в (38).
518 rлава б. Линейная реzрессия и метод наименьших квадратов
Наконец, формула (22) Д!1я с. к. о. обновленноrо проrноза конкретизиру
ется в данном случае к виду
6,*(п + 1) == 6,* (п)(1 ,8 "n+J)'
(42)
Если задать еще соответствующие величины Д!1я nepBoro шаrа (п == 1):
* R,
f311 == Ro '
6,*(1) == ' НО
Ro R,
RI I == Ro(1 ,8'71)
Ro
(43)
(см. соотношения (34) и (35') Д!1я п == 1), то мы имеем эффективный peKyp
рентный алroритм построения проrноза в модели стационарноrо BpeMeHHoro
ряда. Именно: начиная с соотношений (43), далее для n > 1 по уравнениям
(38) и (41) последовательно вычисляем коэффициенты проrнозадо требуемоrо
порядка, а уравнение (42) позволяет на каждом шаry контролировать ошибку
соответствующеrо предиктора.
Замечание, Мы рассмотрели проблему проrнозирования на один шаr вперед (при из
вестных зиачениях Xt j, j == 1'2'...' оцеиивается Х,). Но, очевидно, на том же
пути можно рассчитать соответствующий проrНОЗ и на любое число щаrов вперед,
Т, е. построить предиктор дЛя Xj+k ПО наблюдениям над ХН, ,X' n для любоrо
конечноrо k > о: дЛя этоrо в алrоритме DbI'lИсления предиктора (33) достаточно
лишь заменить вектор!! ==!!u == (RI,'" ,R,.) на вектор !!J.. == (Rk+I, ,Rk+n)'
Замечаиие. Представляет также интерсс вопрос об асимптотическом (при п 00)
повсдснии ощибки (35') пропюзз (33), т. е. при неоrраНИ'lенно возрастающем числе
проrНОЗИblХ переменных. Если д'(п) О при п 00, то проrноз (33) ЯIIЛЯетсSl
асимптотически ТОЧНblМ. Обозначим л"j, j == 1'... , n, собственные числа маТРИЦbl
ковариаций R(n). Можно показать, что д'(п) e k , [де
I n
k == lim LIПЛ"j'
r,l.......oo n
j=1
Таким образом, проrноз Х,',. является асимnтотически ТОЧНblМ k == oo. Если же
k > oo, то, как установил А. Н. Колмоrоров (1941),
lim д'(п) == ехр { 'П 271" + j " 'п f(л) dл } ,
n OO 271"
[де f(л) спектральная пЛОТность процесса {Х,}, определенная в (3 1).
Мы оrpаничиваемся этим общим введением в теорию стохастическоrо
проrнозирования и отсылаем заинтересованноrо читателя к книrе [4], rде дa
но более детальное изложение этой теории и ее применений к анализу ряда
важнЫХ для приложений конкретных моделей временных рядов (как стацио
нарных, так и нестационарных), а также подробно описана и проиллюстри
рована ее компьютерная реализация в системе STATISТlCA.
6.6. Статистическая реi!рессия и nрОi!Нозирование 519
Если знать, что ждет нас впереди, то
стоит ли переживать это заново?
Конфуций 5)
в заключение мы рассмотрим несколько примеров расчета проrнозов
в конкретных физических моделях.
Пример 4 (Проrноэирование в схеме бесповторноrо выбора), Имеется урна
с а шарами, аl из которых белые и а2 == а а, черные. Шары извлекаются
по одному последовательно, равно вероятно и без возвращения. Пусть {(п)
обозначает число белых шаров в выборке объема п, п < N Построим проrноз
(k) ДI1я (п + k) при известном (п), 1 k а п. .
Решение. Если (n) == s, то в урне после пизвлечений осталось а n ша
ров, из которых аl s белые, а остальные а п al + s черные.
Далее из этой остаточной урны должно быть извле'lено еще k шаров, поэто
му (см. п. 4 1.1) число (n + k) s белых шаров в этой дополнительной
выборке имеет rиперrеометрическое распределение Н(аl s, а2 п + s, k).
По формуле (10) 1.1 математическое ожидание этой случайной величины,
аl s
Т.е. E( (п + k) s I (n) == s), равно k . Но проrноз
a n
(k) == E( (п + k) I (п»),
поэтому отсюда имеем
(k) == (n) + k(al (n» ==
a n
== ( 1 ) {(п) + аl Е [ (п), al], . (44)
a п a n
Пример 5 (Проrноэирование в схеме nOBTopHoro выбора). В урне имеется N
шаров, занумеРОl)3ННЫХ числами 1,2, ,N. Шары извлекаются по одному
последовательно, раВНОl3ероятно и с возвращением. Пусть Х(п) обозначает
число различных шаров в выборке объема n. Построим проrноз X (k) для
Х(n + k) при известном Х(п). .
Решение. Пусть Х(п) == в. Обозначим i l , , iN s номера шаров, не Из
влекавшихся ни разу в первых п извлечениях, и положим 1j == 1, если шар
с номером ij будет извлечен хотя бы один раз при следующих k извлечениях,
и Ij == О в противном случае. Тоrда, О'lевидно,
N s
Х (п + k) == s + 2: 1j
j 1
5) Конфуций (551 479 до н. э.) древнекитайский МblCлитель.
520 rлава б. Линейная реzрессия и метод наименьших квадратов
и
E(Ij I Х(п) == s) == P{Ij == I I Х(п) == s} ==
k
== I P{Ij == 01 Х(п) == s} == 1 (1 )
откуда
k
E(X(n+k)IX(n)==S)==S+(N S)[I (1 ) ]
Таким образом, окончательно имеем
X (k) == Е(Х(п + k) I Х(п)) ==
== Х(п) + (N Х(п)) [1 (1 ) k] ==
== (1 ) k Х(п) + N [1 (1 ) k] Е [Х(п), N).. (45)
Предвидеть значит управлять.
Б. Паскаль
Упражнения
Приступай к решению своих проблем правильно и начинай с от-
ветов. Tozaa, вОЗМОЖllO, одl/ожды ты lIauJeUlb zлавl/ЫU вопрос.
р. ван rулик. Отшельник в жураВЛИНblХ перьях
(в книre .Убийства в китайском лабиринте»)
D Убедиться в том, что система нормалЬНblХ уравнений метода наименьших квад-
ратов
aS({3)
{)(37 == о, j == 1, . . . , k,
имеет вид Afi == zж., rде А == ZZ'
11 Получить следующие ЯВНblе ФОРМУЛbl для О. н. к. (см. (2) 6.2) при k == 2:
ДI ==
[ П ппп ]
" (i)2" (i) X . " (i) (i)" ( i) X .
Z2 ZI I ZI Z2 Z2 I
;==1 i 1 i=J i::1
[ (i>2 (;)2 ( (i) (j» 2 ]
ZI Z2 ZI Z2
i=1 i=1 i=!
Упражнения
521
[ щ2 (i) X . (i) и) (j) X . ]
L...J z 1 L...J Z2 I L...J ZI Z2 L...J Z 1 I
132 =: (=1 ;=1 ;==1 i=1
[ (i)2 щ2 ( (j) (j» ) 2 ]
L...J Z I L...J Z2 L...J Z 1 Z2
;=.1 ;=1 (=)
Получить отсюда при (j) == (z i), Z ') == (1, t i ) формулы (22) 6.2
11 Проверить непосредственно несмещенность о. н. к. (22) 6.2 в модели простой
реrpессии и найти условие их состоятельности, т. е. условие, при котором DA 4 О
при n 4 00 (j == 1, 2).
11 Показать, что для состоятельности оценки 0:2 в модели простой реrpессии ДOCTa
точно, чтобы DS( )/n2 4 О при n 4 00, [де s( ) дано в (23) 6.2. Проверить, что
в случае нормальной реrpессии это условие выполняется.
1':1 Значения функции x(t) == /31 + /32t + /3]t 2 измерены в точках tj (i == 1, '" ,n):
Xj==X(tj)+Ej, EEj==O, DEi==/12 COV(Ej,Ej) ==0, i::j.j.
Найти: 1) о. Н. к. 731' Р2, 73]; 2) ЕД, DД, cov(73i, 73 j ).
а (Продолжеl/ие). Убедиться в том, что статистика
ь
J == J x(t) dt,
а
rде x(t) == 731 + t + p]t 2 , является несмещениой оценкой интеrpала
ь
J == J x(t) dt;
а
получить формулу
] (Ь a)i+j
DJ == L . . соv(fЗi, /3j).
ц I &}
iJ Смоделировать наблюдеиия Х ; == fЗ 1 + /32ti + Ei, i == 1, . . . , n, если n == 100, fЗ I == 2,
/32 == 1, t j == 2i/n, Е; независимые равномерно распределенные на [ I,386; 1,386]
случайные величины. Построить rрафики функций x(t) == 2 + t, x(t) == PI + P2t
на отрезке [0,2]; отметить также точки (t j , X j ), i == 1,..., n.
... Указание. См. замечание в п. 6 1.3.
D Выполнить такое же зацание, как в упр. 7, но с Е; распределениыми нормально
с Ее; == О, DE, == 0,16.
... Указание. Использовать алrоритмы П.8 н 6 1.3.
а В предыдущем упражнении получить следующие общие формулы дЛЯ 1 довери
тельных интервалов параметров /3., fЗ2 И /12:
(Р' 'I,.,)f"' '
n ]
s@ L t;
п(п 2) ,; '
522 rлава б. Линейная ре2рессия и метод наименьших квадратов
[д, ",,,)p,. ,
s@
s(fJ) ]
71
(n 2) f;(t, [)2
s@
2
Х( 1 +1)/2. n 2
< и 2 <
2
X(I 1)f2.n 2
и рассчитать их численные значения ПО результатам модеЛИРОВ<lНИЯ при 'у == 0,9 и
"1 == 0,95 (Вblражение ДIIИ S( ) указано 13 формуле (23) 96.2). Построить также 'Y дo
верl1тельный эллипс 91 ( Х ) ДIIя вектора (/31, /32), УКа3анныН 11 примере I 96.3.
m По данным независимых раВНОТОЧНblХ измерений (X j , t j ), i == 1, , n, значений
некоторой линейной функции x(t) == /31 + /32t (поrpешности измерений подчиняются
нормальному распределению N(O, 0'2) с неИЗllсетной дисперсиеil) построить довери
теЛЬНblЙ интервал ДIIЯ веЛИЧИНbI
а
I x(t) dt (а задано).
o
Провести соответствующие Вblчисления для следующих данных: (2,96; 2), (3,20; 1),
(3,41; О), (3,63; 1). (3,79; 2) при а == 2 и доверительном урооне 'у == 0,95.
... Указание. Воспользоваться преДblДУЩИМ упр.
m Координаты a(t) движущейся равномерно 11 прямолинейно точки (т. е. a(t) ==
== а(О) + vt) о моментЬ! t == 1,2,3,4,5 оказались соответственно равны 12.98; 13,05;
13,32; 14,22; 13,97 Предполаrая поrpешности измерений незаВИСI1МblМИ и нормаль
ными N(O, и 2 ), построить 0,95 доверительный эллипс для вектора (а(О), v), rде v
CKOpOCТl, точки.
... Указание. Использовать результат примера 1 6.3.
m Смоделировать наблюдения X j == /31 + /32t + (3)t 2 + Cj, i == 1, , n с fЗl == 8,
fЗ2 == 1 О, fЗ.l == 2, n == 100, t j == 1 + 2ijn, Cj незаоиеимые равномерно распреде
ленные на отрезке [ 1 ,386; 1,386] случаЙНblе величины. Построить rрафики Функций
x(t) == /31 + /32t + /33t2 и x(t) == 131 + 132t + 133t2 на отрезке [1, 31.
m Выполнить такое же задание, как в упр. 12, в случае нормально распределенных
С; с Ес; == О, DCj == 0,16.
m В предыдущем УПр. построить "1 доверитеЛЬНblе интерll<lЛЫ ДIIЯ параметроо /31,
/32, /3з и и 2 , 'а также систему совместных доверительнЬ1Х интервалоо уровня "1 ДIIЯ
fЗl, /32, /3) (см. пример 3 6.3).
m В четыехуrольникеe ABCD результаты независимЬ1Х и равноточных измерений
уrлов АВО, ОВС, АВС, BCD, CDB, BDA, CDA и DAB (в rpaдycax) COOT
ветственно таковы: 50,78; 30,25; 78,29; 99,57; 50,42; 40,59; 88,87; 89,86. Считая, 'ПО
ошибки измерений распределены нормально N(O, 0'\ найти о. н. к. уrлов /31 == ABD,
fЗ2 == DBC, /3з == CDB и /34 == ВОА. ПостроитьО,95 доверитеЛЬНЬ1jj интервал для 0'2.
Упражнения
523
... Указание. В данном случае речь идет о следующей модели нормальной реrрессии:
X 1 ==/3I+':), Х 2 ==fЗ2+':2' Х)==jЗl+/32+':)' Х4==180 jЗ2 fJ)+':4,
X j == (З) + ':5, Х 6 == fЗ4 + .:&, Х 7 == (З) + /34 + ':7, ХН == 180 fЗ] fЗ4 +':8
(Х; результаты указанных последовательных измерений).
m Используя представление (8) 6.2), установить формулу
t k
Е оД; == и 2 tr A ) == (]"2 Е лj]
j=) j=1
rде Лj собственные числа матрицы А; вывести отсюда критерий состоятельности
о. н. к. jjj: min Лj ----t 00 при n ----t 00.
}
... Указание. Использовать следующие факты из тсории матриц: собственные числа
матрицы A I являются обратными значениями собственных чисел А и след А равен
сумме ее собственных чисел.
ID Убедиться в том, что интервалы
(д Д; т [ n k S@F1,k.n k(aii 2a ij + a jj )] 1/2), 1::; j < i ::; k,
образуют систему совместных доверительных интервалов уровня 'у для разностей
fЗ; /3j, i > j.
m Построить систему сооместных довсрительных интервалов для средних значений
всех наблюдений X 1 , ,Х " В модели нормальной рсrpессии.
... Указание. Положить в соотношении (24) 6.3) r == f(r) r == 1'... ,n.
m Пусть имеются k предметов, оеса которых fЗ), ., . ,fJk неизвестны. Для определе
ния этих весов взвеШl1ваются комбинации предметов: каждая операция (ювешивание)
состоит в том, что несколько предметов кладут на одну чашу пеСОII, несколько
на друrую и добавляют разновес для приведения весов u раuновесие. В результате по
лучают соотношения
() (i)
fJ)z/ + + /3tZt == Х;
(для i ro взвешивания, i == 1,. ,n), rде ZY) == 1, 1, О в зависимости от Toro, ле
жит j й предмет на левой чаше весов, на правой или uообще не участвует в данном
(i M) взвешивании, а Х; добавляемый вес. Считав поrрешности измерений незави
симыии и нормальными N(O, (]"2), оценить веса четырех (k == 4) предметов по данным
следующей таблицы восьми (п == 8) взвешиваний:
/31
/32
/3)
/34
Х; 20,2 8,1 9,7 1,9 19,9 8,3 10,2 1,8
1 1 1
1 1 1
I I I
I I 1
I 1
1 1
1 I
I I
1
I
1
I
(содержимое внутренней части таблицы образует матрицу плана Z == Ilf(l) f(R)11
( (1) (8). )
С ортоrональными строками fj == Zj ,..., Zj ), J == 1, 2, 3, 4 . Вычислить вторые
524 rлава 6. Линейная ре2рессия и метод наименьших квадратов
моменты оценок, а также найти оценку для (Т 2 Построить систему совместных ДOBe
рительных интервалов для fJl, .. . ,fЗ4 С доверительным уровнем 0,95.
... Указание. Воспользоваться теоремой 4 9 6.2.
fI!J Построить F критерий (6) 96.4, используя результат при мера I 96.3 и принцип
соответствия между проверкой rипотез и доверительным оцениванием (см. П.2 96.4
и П.4 95.3).
m Убедиться в том, что для случая двух выборок F критериЙ однородности, по
строенный в п.2 96.5, совпадает с критерием (9) 9 5.4; в случае же произвольноrо
числа выборок л статистика (7) 95.4 и F стаТИСТl1ка (11) 96.5 связаны соотношением
( k I ) n/2
л пl ... п . == n k F + I
m Доказать формулу (20) 96.4, выражаюшую F стаТI1СТИКУ критерия значимости
реrpессии через коэффициент детерминации R I'
DJ Пусть .с(Х) == п(л) распределение Пуассона с параметром Л, а .c(YIX == k) ==
== Bi(k, р) биномиальное распределение с параметрами k ир. Показать, что
М(Х) == E(YIX) == рХ, М(У) == E(XIY) == лq + У q == 1 р,
D(YIX) == рчХ, D(X I У) == лq
и, следовательно, uf,x == лрq, uiy == лq.
m (Продолжение). Показать, что .с(У) == П(лр) и потому и , == лр, ui == л. Полу-
чить отсюда, что для обоих проrнозов М(Х) и М(У) их корреляционные отношения
совпадают и равны р.
m Используя результат упр. 66 к rл. 1, построить проrноз У по Х в общей нормаль
ной модели и убедиться в том, 'ПО корреляционное отношение в этом СЛУ'lае имеет вид
1 1 ( TT ) I
1JYK == U Т7 .{J"
ЕВ Построить линейный проrноз 1p (X) в модели, описанной в примере 3 96.6.
m Пусть величина У имеет распределение Парето с параметрами Хо > О и а > 2
(см. п.9 91.2), а .c(XIY == у) == ЩО, у) равномерное распределение на' [О, у).
Убедиться в том, что проrноз У по Х в классе всех функций Ip(X) имеет вид
а+ I . Х5
М(Х) == E(YIX) == тах(хо, Х) и ero с. к. О. == а(а 2)
... Указание. См. решение аНЗJIоrи'lНОЙ задачи в примере 3 9 6.6.
m Доказать формулу (23) 96.6 для случая р == 2.
m Получить вид проrноза У 2 ', указанный в примере I п.5 92.3, как результат об
новления проrноза 1';' (см. (27) 96.6) по аЛl'ОрИТМУ (26) 96.6.
Каждая истина проходит через три инстанции:
«какая чушы), «в этом что-то есты и «кто же
этоzо не знает»!
Триада rумбольдта 6)
6) rумбольдт Вильrельм (1767 1835) немецкий ученый, философ и rосударственный деятель.
rлава 7
Элементы теории решений.
Дискриминантный анализ
Дело не в том, что О/Щ не видят решения.
Дело в том, что они I/е видят проблемы.
r. к. Честертон 1)
Острие булавки (из сборника
«Скандальное происшествие с отцом Брауном.»
Эта небольшая rлава представляет собой краткое введение в одно из Dаж
ных направлений современных статистических исследований теорию CTa
тистических решающих функций. Здесь излаrаются основные идеи и HeKOTO
рые результаты этой теории в рамках двух традиционных подходов к приня
тию решения байесовскоrо и минимаксноrо. Общие идеи иллюстрируются
практически важным примером решения задачи классификации наблюдений
по нескольким классам. Подробно исследуется ряд ситуаций, характеризую
щихся предположением о нормальном законе распределения наблюдений.
! 7.1. Статистические решающие функции.
Байесовское и минимаксное решения
1. ПОНJlтие решающей функции
Во мноrих случаях конечную цель статистическоrо анализа можно выразить
в форме решения о том или ином поведении или действии. Так, при выбо
рочном контроле продукции следует принять одно из двух решений: принять
партию изделий или забраковать ее; врач, анализируя симптомы болезни,
должен отнести ее к одному из конечноrо числа стандартных видов, т. е.
принять одно из конечноrо числа возможных решений; анализируя данные
наблюдения за некоторым случайным процессом с постоянным, но неизвест
ным средним, требуется принять решение о величине воздействия на процесс
(ero коррекции) для приведения среднеrо, например, к нулю; это воздействие
может быть выражено некоторым действительным числом t и, следовательно,
здесь число решений бесконечно. Во всех этих случаях решение принима
ется на основании анализа наблюдения х над соответствующей случайной
величиной Х и, следовательно, представляет собой некоторую функцию о(х)
1) Честертон rилберт Кит (lg7 19З6) анrлнRский писатель.
526 rлава 7. Элементbl теории решений. ДискриминантНblй анализ
на выборо'/ном пространстве Х == {х}, область значений которой MHO
жество возможных D данной ситуации решений D {d}. Таким образом,
б(х) это правило, ставящее в соответствие каждому результату наблюденин
х Е Х решение d == б(х) Е D, которое должно быть принято. Функцию б(х)
называют решающей функцией (или решаЮЩI/М правилам, или процедурой) , и ее
следует выбирать 11 соответствии с некоторыми требованиями оптимальности.
Принципы решения этой задачи развивает теория статистических решающих
функций (теория решений), разработанная А. Вальдом (1950). Ниже кратко из
лаrаются некоторые основные идеи и результаты этой теории.
2. Функция риска и допустимые решающие правила
Пусть заданы класс распределений (модель) :F == {Р(х; О), О Е е}, которому,
по предположению, прИНaдJlежит (неизвестное) распределение наблюдаемой
случайной величины Х, и множество решений D {d}, которые можно
принимать на основании наблюдения над Х. Чтобы получить критерий выбо
ра решающей функции, надо сравнить результаты использования различных
правил б. Введем для этоrо неотрицательную фу"кцию потерь L(d, О), опреде
ленную на прямом произведении D х е, rдедля каждых d Е D и О Е е число
L(d, О) О интерпретируется как убыток или потеря от принятия решения d,
_ коrда Х имеет распределение Р(х; О). Тоrда для всякоrо пра
Риск "' вила б можно определить ФУlIкцию риска (или просто риск)
R(б, О) == ЕеL(б(Х), О),
( 1)
представляющую собой средние потери от применения решающеrо правила б,
коrда истинным распределением наблюдений является распределение Р(х, О).
Функция риска дает критерий сравнении различных решающих правил,
а именно, если для двух правил б' и 15 выполняется неравенство
R(5', О) R(б, О), V О Е е,
(2)
со строrим неравенством хотя бы для одноrо значения О, то правило (/ пред
почтительнее 5, так как использование 51 при ВОДИТ в среднем к меньшим
потерям. С друrой стороны, решающие праDила 151 и 152 Moryт оказаться He
сравнимыми по критерию (2), если R(15 1 , О) < R(б 2 , О) дЛЯ некоторых значе
ний О, а для остальных значений О имеет место обратное неравенство. Чтобы
выбрать в такой ситуации одно из двух правил, необходимо привлекать дo
полнительные соображения.
_ Недопустимые Таким образом функция риска позволяет лишь час
решающие ПрОВИЛQ тично упорядочить все решающие правила 5. Х -----------+ D,
тем не мене, она позволяет «отсеять» заведомо пло
хие праl1Ила. Назовем правило 5 недопустИМЫI>I, если существует правило б'
предпочтительнее б в смысле (2). Решающее правило, не явлнюшееся He
допустимым, называется допустимым. Ясно, что все недопустимые правила
должны быть oTBeprHYТbI, так как для каждоrо из них можно найти более оп
тимальное (в указанном смысле) правило. Если класс допустимых решающих
7.1. Статистические решающие функции
527
правил состоит из единственноrо правила, то оно и является оптимальным
решением. Но обычно этот класс достаточно широк и никакие два решающие
правила из множества допустимых несравнимы (по критерию (2)). Поэтому
д.lIя дальнейшеrо упорядочения допустимых правил и выбора среди них луч
шеrо привлекают дополнительные соображения. Для решения этой задачи в
статистике традиuионно при меняют два подхода: 6айесовскuй и минш.lаксный.
3. Байесовское решение
При байесовском подходе дополнительно предполаrается, что пара метр О
это случайная величина с некоторым известным распределением, задаваемым
плотностью 11'(0) и называемым aпpUOpHbIftl распределе
нием. В этом случае можно усреднить риск (1) по этому
априорному распределению и тем caMblM подсчитать
полную среднюю потерю (усредненный риск)
....
Априорное .oot:
роспределение
т(6) == I R(6, 8)11'(0) dO
(3)
(если О принимает дискретные значения, то интеrрал заменяется суммой
'" . R(6, 8j)1I' (Oj) ), которую мы несем при использовании решающеrо прави
1 _ ,
ла 6. Величина т(6) в (3) называется 6аиесовскимриском Байесовский риск
правила 6. Таким образом, при таком подходе каждое
решающее правило характеризуется одним числом и, следовательно, все pe
шающие правила MOryr быть упорядочены в соответствии со значения ми этой
характеристики. Оптимальной является процедура, минимизирующая байе
совский риск т(6):
6* == arg miп 6;
6
она называется 6айесовским решением. Подчеркнем, что
6* зависит от выбора аПриорноrо распределения 11':
6' == 6;, поэтому для различных априорных распре
делений параметра соответствующие байесовские pe
шения будут, вообще rоворя, различны.
Байесовское решение о' находят на основании тeo
ремы Байеса, соrласно которой апостериорное pacпpeдe
ление параметра при условии Х == х задается условной
плотностью
(4)
...
Байесовское .tt
8i1i11ii1i1f. реш е н и е
Теорема Байеса ..
или
( I ) f(x; 0)11'(0)
11' О Х f(x) ,
f(x) == Ef(x; О) == I f(x; 0)11'(0) dO,
f(x) == f(x, Oi)1I'(Oi)
(5)
rде
528 rлава 7. Элементbl теории решений. Дискриминантный анализ
в дискретном случае. Torдa равенство (3) можно записать в виде (в абсолютно
непрерывном случае)
т(о) == / (/ L(o(x), B)f(x; В) dx) 11'(8) d8 ==
== / (/ L(o(x), В)1I'(8Iх) dB) f(x) dx ==
== J f(x)E [L(o(X), В) I Х == х] dx
(6)
(в дискретном случае интеrpалы заменяются соответствующими суммами).
Из соотношения (6) следует, что оптимальной является такая процедура, Koтo
рая при каждом х миnимизuрует средние потери относителыlO апостериорною
распределения 1I'(8Iх).
Ал , Таким образом, для заданноrо априорноrо распре
rоритм , _ деления параметра 11'(8) алroритм нахождения байесов
cKoro решения имеет следующий вид:
а) для Х == х по формуле (5) находят апостериорное распределение 1I'(Blx);
б) после этоrо для каждоrо возможноrо решения d Е D вычисляют среднюю
потерю E[L(d, О) I Х == х] относительно этоrо апостериорноrо распреде
ления;
в) в качестве искомоrо выбирают решение с минимальной средней потерей.
Отметим, наконец, что байесовское решение, построенное для любоrо
распределения 11'(8) > О, является допустимым. Действительно, пусть о'
соответствующее байесовское решение и предположим, что существует проце
дура О, для которой R(o, 8) R(o', О) со строrим неравенством на множестве
значений 8, имеющем положительную (относительно распределения 11') Bepo
ятность. Torдa, очевидно, для соответствующих байесовских рисков (3) имеет
место неравенство т(о) < т(о'), что противоречит определению байесовскоrо
решения.
4. Минимаксное решение
При отсутствии априорной информации о () применяют прием упорядочения
допустимых решающих правил по максимальному значению функции риска
Я(о,8) (или максимальному риску)
т(о) == sup R(o, 8),
8
И из двух правил предпочтительным считают правило с меньшим максималь
1' ным риском (отсюда термин «минимаксное»). Правило "б, минимизирую
.. Минимакс щее т(о), называется минимаксным решающим правилом:
(7)
l == arg mill т(о).
о
(8)
7.1. Статистические решающие функции
529
Таким образом, минимаксное правило
избавляет от чрезмерных потерь: наихудший
ожидаемый ущерб ДI1я Hero минимален. Но
принцип минимакса не Bcerдa блаrоразумен.
Так, на рис. 1 приведены rрафики функций
риска ДI1я двух правил 5} и 62, откуда видно,
что правило 52 хуже 6} ДI1я большинства зна
чений О, но предпочтительнее 01 по прин
ципу минимакса.
В общем случае вопрос о существовании и строении минимаксноrо пра
вила достаточно трудный и здесь не рассматривается. Отметим один слу
чай, Korдa удается просто установить минимаксность HeKoToporo решающеrо
правила. Именно: предположим, что существует априорное распределение
параметра 11'(0) > О, ДI1я KOToporo функция риска соответствующеrо байесов
CKOro правила а; постоянна: R(5;, О) == а == const (такое распределение 11'
называется наименее бла оприятным априорным Наименее блarоприятное
распределением). Torдa 5 тr минимаксное pe априорное распределение
шение.
Действительно, D противном случае существовала бы процедура а, ДI1Я KOTO
рой максимальный риск т(а) < а. Но это означало бы, что R(o, О) < Щ5;, О),
V е, в противоречие с допустимостью байесовскоrо решения.
Пример 1 (бернуллиевская модель, решающие правила для нее).
Пусть Х бернуллиевская случайная величина, причем вероятность «успеха,)
(J может быть либо О} == 1/3, либо е2 == 1/2. Таким образом, здесь Х == {О, 1},
е == {1/3, '/2} и '(х;О) == ОХ(1 О)Н, х == 0,1. Пусть, далее, множество
решений D состоит из двух элементов d l и d 2 , а функция потерь L(d, О)
задается следующей таблицей:
d l d 2
(Jj О 2
82 3 I
R( 6, 8)
62
8
Рис, 1
в данном случае ДI1я каждоrо х Е Х возможны только два решения,
а множество Х содержит две точки, поэтому Bcero имеются четыре решаю
щие функции Ok, k == 1,2,3,4, а именно: 5,(0) == d l , 15,(1) == d l ; 52(0) == d},
52(1) == d 2 ; 15з(0) == d 2 , 5)(1) == d,; 54(0) == d 2 , 154(1) == d 2 . По формуле (1),
которая в данном случае принимает вид
R(Ok, е) == L( 5 k (O) , е) (1 О) + L( 5 k (I), о) О, О == О}, 02,
находим четыре вектора риска (R(5 k , (1), R(Ok, (2)), k == 1,...,4, числовые
значения которых соответственно равны (0,3), (2/3,2), (4/3,2), (2, 1). Здесь
процедура 5) недопустима, так как 152 предпочтительнее, а среди допусти
мых процедур 61, 152 И 64 две последние обладают минимаксным свойством:
т(6 2 ) == т(5 4 ) == 2 < т(5)) == 3.
343;о.а, 1748
530 rлава 7. Элементbl теории решений. ДискриминантНblй анализ
Пусть теперь на множестве е {О), 02} задано некоторое априорное
распределение 11': 11'(0)) == а, 11'(02) == 1 а, О а 1. Найдем COOTBeТCТBY
ющее байесовское решение 6'
l u способ. В соответствии с определением (3) вычислим байесовские
риски
1'(6;) == R(r5;, О,)а + R(6;, (2)(1 а)
дЛЯ ДОПУСТИМЫХ правил (i == 1,2,4):
1'(151) == 3(1 а),
4
1'(152) == 2 за,
1'(64) == а + 1.
rрафики этих функций от а изображены на рис. 2, из KOToporo видно, что,
если а 3/7, то m.in 1'(15;) == 1'(154), Т. е. в соответствии с (4) здесь 15' == 64;
I
если 3/7 < а 3/5, то min7'(6;) == 1'(152) Т.е. здесь 15' == 152; наконец, 15' == r5[
I
при а > 3/5.
Жирной линией на рис. 2 изображен rpафик байесовскоrо риска р(а) == 7'(15')
как функции а это выпуклая ломаная линия, являющаяся нижней rpанью
семеЙСТlJа линейных функций {7'(r5;), i == 1,2, 4} Такая картина характерна
для байесовских решений в задачах, n которых параметр О принимает ровно
два зна'lения, а множество D состоит лишь из конечноrо числа решений.
1'(6) 2 й способ. Вычислим апостериор
ное распределение (см. (5))
(о . , ) == f(x; 0;)11'(8;)
11' I х '(х)'
Имеем
о
з 1 3
7'25'
а
а(1 O[)
11'(8110) == 1(0) ,
( 1 ) (1 а) (1 (2)
11' 020 1(0) ,
(8)
11'(8111) == 1(1) '
(1 a)82
11'(0211) == '( 1) .
Рис. 2
Средняя потеря относительно этоrо апостериорноro распределения при х == О
для решения 15 (О) == d l равна
E[L(d l , О) I Х == О] == L(d l , 01 )11"(8110) + L(d l ; (2)11'(0210) ==
3(1 a)(l (2) 3(1 а)
1(0) 2/(0) ,
7.1. Статистические решающие функции
531
а для решения 0(0) == d 2 она равна
2а(l O,) (1 a)(l (2) (3+5а)
1(0) + 1(0) == 6/(0) .
Сравнивая эти потери, находим, что при а 3/7 потери дЛя решенияz d 2
меньше, т. е. 0* (О) == d 2 , если же а > 3/7, то 0* (О) == d l
Аналоrичный анализ Дl]я случая, коrда х == 1, дает: если а 3/5, то
0'(1) == d2, И 5'(1) d) при а > 3/5. Тем самым получены значения
байесовскоrо решения 5*(х) в каждой точке х == О, I при любом априорном
распределении параметра.
Конечно, оба способа, хотя и в разной форме, дают один и тот же pe
зультат, так как (см. рис. 2) при а 3/7
6'(0) == d 2 == 04(0),
при а > 3/7
0*(0) == d) == (НО) == 01(0),
И аналоrично, при а 3/5
0* ( 1) == d 2 == 52 ( 1) == 54 (1),
при а> 3/5
5*(1) == d l == 51(1).
.
5, Оценивание параметров и проверка rипоте]
с позиций теории решений
Рассмотренные в предыдущих rлавах задачи оценивания и проверки rипотез
также можно сформулировать в терминах прннятия решений. Рассмотрим, Ha
при мер, задачу точечной оценки скалирноrо параметра В. Выбор статистики
Т(Х), оценивающей О, можно трактовать как решающее праIJИЛО, соrласно
которому принимается решение d t оценить параметр величиной t == Т(х),
если наблюдается Х == х. В этом случае функция потерь может быть, напри
мер, L(d t , О) == w(lt (1), rде w cTporo возрастающая функция ошибки
It 01. Если, IJ частности, выбрать (jJ(Z) == z2 то функция риска оценки Т
(квадратичный риск)
R(T, О) == Ев(Т(Х) в)2
(9)
совпадает со среднеквадратической ошибкой Т. В rлаве 3 рассматривалась,
в основном, проблема построения оценок, минимизирующих квадратичный
риск (9) в классе несмещенных оценок, это оценки (; равномерно мини
мальной дисперсией. В п. 6 3.6 достаточно подробно обсуждалсл байесовский
и минимаксный подходы в проблеме оценивания, rде по ходу изложения об
суждались и некоторые дополнительные аспекты этой теории.
Рассмотрим теперь интерпретацию задачи проверки rипотез в терминах
теории решений. Предположим, что требуется проверить rипотезу Но О Е 80
при альтернативе Н, . О Е 8, == 8\8о. Тоrда любой критерий есть решающее
'34*
532 rлава 7. Элементы теории решений. Дискриминантный анализ
правило с двумя решениями: d o (принимать Но) и d l (принимать H I ). Здесь
естественно считать, что потеря равно О, если принято правильное решение.
Тоrда функuия потерь должна удовлетворять условиям L(d o , О) == О, '<1 О Е е о ,
и L(d., О) == О, '<10 Е е.. Если дополнительно принять, что потери от He
правильноro решения равны 1, т. е. L(d o , О) == 1, '<1 О Е е" и L(d l , О) == О,
'<1 О Е ео, то при такой простой функции потерь для любоro решающеro пра
вила 6 функция риска будет иметь вид (см. (1))
{ Ро{6(Х) == d 1 } == P{HIIHo}
R(6, О) ==
Ро{6(Х) == d o } == P{HoIHl}
при О Е е о ,
при О Е e J ,
т. е. ее значения совпадают с вероятностями ошибок l ro и 2 ro родов.
t 7.2. Классификация наблюдений
1. Задача классификации
В этом параrpафе мы рассмотрим один частный, но предстаlJЛЯЮЩИЙ боль
шой практический интерес случай, коrда параметрическое множество модели
F == {Р(х; О), О Е е} состоит из конечноrо 'Iисла точек: е == {Oj, ,Ok},
т. е. имеется Bcero k распределений Fi(X) == Р(х; Oi), i == 1, , k, одно из KO
торых является истинным всякий раз, коrда производится наблюдение над Х
с С(Х) Е F В этом случае задача состоит в том, чтобы по наблюдению над Х
решить, какое из этих k распределений истинно. С позиций теории решений
в данном случае множество решений D == {d" .., dJJ, rде решение d j озна
чает, что в качестве истинноrо распределения выбирается F i , i == 1, ,k.
Типичная ситуация, KOrдa возникает подобная задача, может быть описа
на следующим образом. Пусть множество исследуемых объектов разбито на k
классов или rpупп Н" , Hk. Каждый объект характеризуется набором Х
числовых параметров, которые непосредственно Moryт быть измерены. Пред
полаrается, что Х случайная величина, а принадлежность объектов к раз
ным классам выражается в том, что для объектов из класса H i эта случайная
величина имеет распределение F j , i == 1'... , k. Задача состоит в том, чтобы
по наблюдению над Х определить тот класс, к которому принадлежит COOT
ветствующий объект, или, что то же самое, какое из распределений F J , ,Fk
истинно. Такие задачи называют задачами классификации, идентификации или
дискриминации (от анrл. discrimination различение) и их решение составляет
содержание дискриминантНО20 анализа одноrо из разделов современной Ma
тематической статистики. Мы рассмотрим общие принципы решения таких
задач с позиций теории решений и проиллюстрируем их на примерах наибо
лее важных моделей таких ситуаций.
2. Функция риска в 1адаче классификации
Пусть 6 == 6(х) произвольное решающее правило в рассматриваемой задаче:
6: Х D. Torдa оно порождает разбиение выбороч Horo пространства Х == {х}
7.2. Классификация наблюдений
5ЗЗ
на k взаимно непересекающихся областей W 1 , . , . , Wk, rдe
Wj == {х о(х) == dj}, i == 1,
, k.
(1)
Таким образом, множество W j С Х включает все такие точки х, коrда при
наблюдении Х == х в качестве истинноrо выбирается распределение F j .
Пусть, далее, на D х 0 задана функция потерь L(d, 8), определяющая
потери, от неправильной классификации, т. е. заданы числа L(d j , (Jj) == l{jli) ,
i, j == 1, ,k, rде l(jli) убыток, который имеет место в случае, коrда объ
ект i ro класса отнесен к j MY (j 1= i). В данной задаче естественно считать,
что потеря равна нулю, если выбрано правильное решение, т. е. l(iIi) == о,
i == 1,..., k. Torдa функция риска (1) 7.1 представляет собой k мерный
вектор Е(о) == (R1(o),... , Rk(O)), rде
k
Rj(o) == R(o, (Jj) == EI/,L(o(X), (Jj) == Е l(jli)p(jli), (2)
j 1
rде p(jli) == РI/.{Х Е W j } вероятность Toro, что объект i ro класса отнесен
к j MY классу. Можно сказать, что Rj(б) средние потери, которые имеют
место при классификации по правилу О произвольноrо объекта i ro класса.
Задача состоит в построении оптимальноrо (т. е. с наименьшими потерями)
решающеrо правила о.
З. БайеСО8ское решение
Пусть задано априорное распределение:!!. == (11'1, ,1I'k) на 0 == {Оl ,(Jk},
т. е. известно, что произвольный наблюдаемый объект принадлежит к клас
су H j с вероятностью 11', i == 1, ,k (11'1 + + 1rk == 1). Тоrда байесовский
риск (3) 97.1 на основании (2) равен
k k k
r(o) == Е Rj(o)1rj == Е Е l(jli)p(jli)1rj.
j 1 j 1 j 1
(3)
в соответствии с общим алrоритмом построения байесовскоrо решения (см. п. 3
97.1), т. е. правила О, минимизирующеrо риск (3), по формуле (5) Э 7.1 находим
апостериорные вероятности классов при условии Х == х:
1I" ( х ) == /;(Х)1I'; i == 1,
I k
Е 1I'sfs(x)
s 1
, k.
(4)
Далее, если принять решение отнести объект с характеристикой х к j MY
классу (т. е. если б(х) == d j ), то для TaKoro правила средние условные (при
534 rлава 7. Элементы теории решений. Дис/(риминантный анализ
условии Х == х) потери равны
k
Е[ЦО(Х), О) I Х == х] == L L(d j , Оi)1Тi(Х) ==
i 1
k
L l(jli) 1Т i !;(Х)
;=1
k
L 1Т s !s(Х)
s=1
(5)
Наконец, решение dj должно быть выбрано так, чтобы минимизировать (5).
. В итоrе мы приходим к следуюшей формулировке
, .P ",..k'"i;''''' ОПТИМ,Ulьноrо способа действия: если наблюдалось Х == Х,
то надо определить минимальную сумму
k
hj(x) == L l(jli) 1Т i!i(Х), j == 1,
, k,
(6)
i l
и отнести обllект к классу с номером, равным номеру этой минимальной CYMMbI
(если минимум достиrается при нескольких значениях j, то можно взить
любое из них, например, минимальное).
Итак, имеет место следующее утверждение.
Теорема 1. Оптимальное (байесовское) решающее правило 0* в задаче клас
сификации определяется следующим разбиением выборочноrо пространства
x==WI*U UW;:
W i * == {х h;(x) == mil1 hj(x)}, i == \,
I J k
, k,
(7)
rAe функции ltj(X) определены в (6) и i минимальное значение индекса,
удовлетворяющее указанному услови ю.
Рассмотрим частный случай, коrда l(jli) == \, j i i. Torдa
k
hj(x) == L 1Тi!i(Х) == 1Тj!j(Х) + L 1Тi!i(Х)
;Fj i 1
и условие в (7) принимает вид
1Тi !;(х) == тах 1т I (х).
I j k J J
(8)
Величины 1Тj!j(Х) пропорциональны апостериорным вероятностям классов
(см. (4»), поэтому в данном случае байесовский принцип сводится К следу
ющему: относить объект с характеристикой х к тому классу, апостериорная
Принцип максимума вероятuость которою максимальна. Такой
принцип называют принципом максимума
апостериорной вероятности
апостериорной вероятности. Этот принцип
7.3. Наблюдения в случае двух нармальных классов 535
используют во всех случаях, коrда потери l(jli) либо неизвестны, либо их
трудно оценить числом.
Выделим случай двух классов (k == 2), т. е. коrда объекты классифициру
ются по альтернативному признаку. Здесь
hl(x) == l(112)1I'2/2(X), h 2 (x) == l(211)1I'1/I(X),
следовательно, решение d) (отнести объект с характеристикой х к первому
классу) принимается Torдa и только Torдa, коrда l(ll2)1I'2f2(X) l(211)1I"Ifl(X),
Таким образом, байесовское правило 0* имеет в данном случае следующий вид:
о*(х) == { dl
d 2
при Х Е W 1 *
при Х Е W
W1*== { X /2(X) 1I'Il(211) }
/1 (х) 11'2 l( 112)
(9)
а соответствующий ему вектор риска (R,(o*), R 2 (0*)) в соответствии с (2)
равен
(ФII)Ре,{Х Е W 7},l(lj2)PII 2 {X Е W j *}).
(10)
4. Минимаксное решение
Если априорные вероятности классов неизвестны, то дЛя построения решаю
шеrо правила используют минимаксный подход (см. п. 4 Э 7.1), в соответствии
с которым ищется правило 6, минимизирующее тах Ri(O) (см. (2)). В ряде
l l n
случаев минимаксное правило О удается построить, определив наименее бла
rоприятное априорное распределение :!r == (11"" ,11'/,:), при котором дЛя
соответствующеro байесовскоrо решения 0* все компоненты вектора риска
11(0') одинаковы, в этом случае 6 совпадает с решением 0*
Например, в случае двух классов из (10) следует, что 11'1 (11'2 == l 11"1) надо
определить из условия
* *
l(2jl)P II ,{X Е W 1 } == l(112)PII2{X Е W 1 }.
(11 )
Отсюда видно, что даже в этом простейшем случае дЛя произвольных распре
делений F i задача построения минимаксноrо решения достаточно сложна.
В следующих параrрафах эти вопросы рассмотрены детальнее дЛя случая HOp
мальных распределений.
t 7.3. Классификация наблюдений
в случае двух нормальных классов
Предположим теПерь, что в эксперименте наблюдается нормальный случай
ный вектор Х == (Х 1 , ,X r ), распределенный дЛя объектов из класса Нl
по закону N(J.l(I), Е), а ДJ!Я объектов из класса Н 2 по закону N(J.l(2) , Е),
причем векто;, l!:.(I), l!:.(2) и матрица Е известны (IEI f О). Таки образом,
536 rлава 7. Элементbl теории решений. ДискриминантНblй анализ
здесь предполаrается, что имеет место случай двух нормальных классов, раЗJIИ
чающихся только средними значениями, и задача состоит в том, чтобы по Ha
блюдению над вектором Х решить, какое из ЭТИХ двух распределений истинно.
Найдем байесовское и минимаксное правила в данной ситуации.
1. Байесовский подход
В этом случае предполаraется, что заданы потери [( 112) и l(211) от принятия
неправильноrо решения и априорные вероятности 11'1 и 11'2 (11'1 +11'2 == 1) клас
сов НI и Н 2 соответственно, тем самым определена константа
... Д
искриминантная
функция
с==1п [ 1I'2 l (112) ] .
1I' I l(211)
В соответствии с (9) область W 1 * наилучшей классификации в пользу класса
НI определяется неравенством 1п (11 (;!;) / 12 (!f.)) ? с, которое в соответствии
с соотношением (9) & 1.2 принимает в данном случае вид
[(!f. t:(2))'E 1 (!f. t:(2)) (!f. t:(I))'E 1 (!f. t:(I))] ? с
или, если положить Q == E 1 (t:(I) t:(2)) ,
Q'!f. '(t:(I) + t:(2)) ? с. (1)
Линейную функцию rp( ) == Q'!f. называют диCKpиMи
НОllmной функцией. Таким образом, области наилучшей
классификации определяются в данном случае дискри
минантной функцией rp( ): наблюдение Х == относится к классу Н, тоrда
и только Torдa, коrда
rp(!f.) ? сl == С + Q' (t:(I) + t:(2)).
Если потери l(i IЛ неизвестны или их трудно оценить числом, то применяют YKa
занноеправило классификации сl(ф) == Ц211) == l,т.е.вэтомслучае(см. (1))
W 1 * == { '!f.? 'п ( : ) + Q'(i) + t:(2)) } (2)
Замечание. Ранее (см. пример 3 в 95.2 и ero продолжение там же) мы уже paCCMa
тривали задачу различения двух нормальных распределений N(p." > , Е) с позиций
критерия Нсймана Пирсона, Korдa минимизируется вероятностьошибки 2 ro рода
при фИКСИРОDанной вероятности ошибки I ro рода (критерий (18) 5.2), и с позиций
минимиззции суммЬ! вероятностей этих ошибок (КРlПсрий (21) 5.2). Тсперь же мь!
получили НОВblЙ, более СИЛЬНblЙ, результат с позиций теории решений, УЧИТblвающий
как наличие дополнительной априорной информации о rипатетических распределе
ниях (априорные вероятности 11", и 11'2 классов HI и Н 2 ), так и более детализирован
ное описание последствий от ошиБОЧНblХ решений (задание потерь l(jli». в част
ности, полученное здесь решение (2) соответствует критерию (21) 5.2 и сводится
к нему при 11', == 11"2 == 1/2, т. е. в случае априори равновероятных классов Н, и Н 2 .
7.3. Наблюдения в случае двух нормальных классов 537
2. Минимаксный ПОДХОД
Найдем теперь минимаксное решение 15, которое используется в случае He
известных априорных вероятностей классов. Для этоrо вычислим вероятно
сти ошибочных КIIассификаций p(jii) == P{HjIH;}, i,j == 1,2, i =1= j, для
произвольноro байесовскоro правила, задаваемоrо условием (1) (константа с
теперь произвольна, так как априорное распределение :1[ == (11'1, 11'2) произ
вольно), и из условия (11) 7.2 найдем наименее блаroприятное априорное
распределение. Соответствующее этому априорному распределению байесов
ское решение (1) и является искомым минимаксным решением 'J'.
Для этоrо можно воспользоваться ВЫ4ислениями, проведенными в при
мере 3 5.2. Именно, если ввести случайную величину
у == [!' х [!' ( (1) + (2)),
то из формул (16) 5.2 получим, что
.c(YIH 1 ) ==лr( ,р), .c(YIH 2 ) ==лr( ,p). (з)
rде
р == ( (l) (2))/ ) (l!.(I) l!.(2))
есть расстоянне Махаланобиса между распределениями
лr(!!:..О), ) и N(l!.(2), ).
Отсюда находим вероятность ошибочной КIIассификации:
р(211) == Р{Н 2 IН)} == Р{У < clHI} == Ф ( с ./2 ) ,
р( 112) == Р{Н] [Н 2 } == Р{У с[Н 2 } == Ф ( с :;/2 ) .
Следовательно, уравнение (11) 7.2 для определения наименее блаrоприятно
ro апроирноrо распределения (11'1, 1 11']), или, 4ТО эквивалентно, константы с,
имеет вид
(4)
l(2 1 1)ф( С:2 ) == l(I12)Ф( С:;/2 ).
(5)
Итак, если априорные вероятности КIIaccoB неизвестны, то минимаксное
правило КIIассификации определяется разбиением Х == wt u w 2 ', rде
W I ' == { : / [!' (!!:..(I) + (2)) с}, W; == W , (6)
и константа с выбирается из условия (5).
Отметим, что если l(211) == l(112), что решением уравнения (5) является
с == О, а так как
с == Iп [ 1I'2 l ( 112) ]
1I' I l(211) ,
538 rлава 7. Элементbl теории решений. Дискриминантный анализ
то в этом случае имеем, что наименее блаrоприятное априорное распределение
является равномерным: 1Т) == 1Т2 == 1/2. Для этоrо случая области наилучшей
классификации W t * (6) и (2) совпадают и, как отмечено в замечании п. 1,
мы приходим к критерию (21) 5.2, так смыкаются подходы байесовский
и минимаксный с подходом, основанным на минимизаиии суммы вероятно
стей ошибок l ro и 2 ro рода. Отметим также, что в этом случае вероятность
ошибочной классификации произвольноro объекта равна Ф( /р/ 2 ) , следова
тельно, чем более далекими (в метрике р Махаланобиса) нвлнются «rипотезы»
HI И Н2, тем меньше веронтность ошибочной классификации правила (6).
7.4. Классификация нормальных
наблюдений. Общий случай
в этом параrpафе мы рассмотрим примене !Ие изложенной в 7.2 теории
к общему случаю нескольких классов, заданных мноroмерными нормальными
распределениями. Предположим, что эти распределения различаются только
своими средними, и пусть N(I!..(i), Е) распределение наблюдений Х мя
объектов из класса Н; (i == 1, , k). Кроме тоro, все иены ошибочных клас
сификаиий будем считать равными единиие: l(jji) == 1, j f.= i.
1. Байесовский подход
Пусть заданы априорные вероятности 1Т; ==Р{Н;}, i== 1,... ,k (1Т) +.. .+1Тk == 1)
принадлежности произвольно выбранноrо объекта соответствующим классам.
Torдa байесовское решение можно получить с помощью приниипа максимума
апостериорной вероятности (см. (8) 7.2), в соответствии с которым области
классификации имеют вид
W i * == { ;f
rде (см. (9) 1.2)
1 { 1 ( (;) ) ' I ( (i) ) }
JiС;f) (21ТУ/2IЕII/2 ехр 2 ;f !:!:.. Е ;f !:!:.. '
J ' ( x ) 1Т-
.2 ' I
J() /'" ,J ,
. х 1Т-
J ,
,k, j ,Н},
z == 1,.
, k,
i == 1,
, k.
Отсюда, как и в п. 1 7.3, получаем, что
КлассиФикаЦИОННblе ФУНКЦИИ
W j * == {;f U;j(;f) С; Cj, j == 1,
k, j f.= i},
(1)
rдe С; == ln (I/1Тi), i == 1,
,k, и
( ) ( Ji (;f) ) , 1, ( (i) (Л )
иij ;f == In Jj(;f) == !!ij;f 2!!ij!:!:.. +!:!:.. '
!!ij == E I (!:!:..(;) !:!:..(j)) , i, j == 1'...' k, i f.= j.
(2)
(})
7.4. Классификация нормальных наблюдений. Общий случай 539
Отметим, что каждая lCЛассификационная функция иjj( ) связана только
с i й и j й совокупностями, иjj( ) == Ujj( ), при этом все они линейные
функции наблюдений . Следовательно, области W j ' оrpаничены rиперплос
костями.
Вычислим, наконец, вектор риска l1. == (RI' ", R k ) этоrо байесовскоrо
правила. В соответствии с формулой (2) 7.2 в данном СЛУ'lае
Я ; == 2:= p(jJi) == 1 р(ф) == 1 / fj( )d ==
j
== 1 p{Ujj(X) c; Cj, j == l,...,k, j 1=i I Hj}, (4)
поэтому надо знать распределение случайноrо вектора
U j == (Ujj(X), j==l,...,k, j1=i)
при rипотезе Н;. Чтобы найти это распределение, введем матрицу
Е; == II!!il " !!ikll,
составленную из векторов столбцов Qij' j == 1, , k, j 1= i, определенных
в (3). Тоrда из формулы (2) следует, что вектор и ; получается из Х с помощью
линейноrо преобразования вида U j == Е;Х +!4 Следовательно, по свойству 2)
в п. 2 1.2 (сохранение нормальности при линейных преобразованиях)
.c(L[iIHi) == N(E:!!:.(i) + Qi' E:EE i ). (5)
Отсюда имеем, что j я координата вектора средних E( U iIH j ) равна
а' . JL (i) a'. (JL (i) + JL (j) == а'.. (Jl (i) JL (j) == Pij
IJ 2 '} 2 IJ 2 '
rде pjj (!!:.(i) !!:.(j)'E 1 (!!.(i) !!:.(Л) расстояние Махаланобиса между
i M и з м классами (или между распределениями N(!!:.(i),E) и N(!!:.(j),E)),
а и, s) й элемент дисперсионной матрицы I; EEi, равный скалярному про
изведению j й строки матрицы I; (т.е. вектора !!;j) на s й столбец матрицы
EEi (Т. е. E!!is == (!!:.'i) !!:.(s)), имеет вид
Pijs == (!!:.(i) !!:.(j)'I; I(f!:.(i) !!:.(а).
Тем самым распределение (5) полностью определено. Оно является невырож
денным (IE)::Ei I 1= О) Torдa и только Torдa, коrда Е; матрица полноro
paHra, т. е. коrда rank Е; == k I (это имеет место, в частности, Korдa векторы
средних значений !!:.(I) , , !!:.(k) линейно независимы и r == dim Х k 1).
В этом случае существует плотность gi('!!) нормальноrо распределения (5) и
формулу (4) можно записать в виде
Ri == I р(ф) == I / / gj(!!) d!!, i == 1, .., k (6)
Ci Cl Ci CIt
540 rлава 7. Элементbl теории решений. ДиснриNинантНblЙ анализ
Х 2
W 1
(1)
..,!!:
(З) ,-
t!:. "',
.
W 2
.
W)
X 1
'.. (2)
t!:.
Рис. 1
(здесь интеrpал имеет кратность k 1, так как среди разностей Cj Cj OTCYТ
ствует разность Cj е;).
в качестве примера рассмотрим случай трех классов (k == З), задаваемых
двумерными нормальными распределениями (т == 2).
В данном случае области W j * i == 1, 2, З, имеют соответственно вид
W 1 * == { == (XI, Х2) иI2( ) С! С2, Ulз(:r) С! Сз},
W; == { == (XI, Х2) иj2( ) < С! С2, U23(:r) С2 Сз},
Wj == { == (Х" Х2) и'J( ) < С( Сз, и23(!.) < С2 Сз}
Эти области должны исчерпывать всю плоскость, поэтому линии, задаваемые
уравнениями Uj2( ) == СI С2, иlЗ( ) == С! CJ и U2З(; ) == С2 С), должны
пересечься в одной точке (см. рис. 1).
2. Минимаксный ПОДХОД
Если априорные вероятности 11'" . . . , 1I'k классов неизвестны, то области клас
сификации ищутся в виде (1), rде неопределенные константы Ci > О, i ==
== 1,... , k, следует выбирать из условия равенства всех компонент вектора
риска R == (R" .. ,R k ), которое в силу (6) приводит к равенствам
p(lll) == р(212) ==
== p(klk).
(7)
Эти равенства однозначно определяют разности Cj Cj (по крайней мере в
принципе), а тем самым и области (1) минимаксноrо правила классификации.
З. Классификация наблюдений в случае неизвестных параметров
Выше предполаrалось, что все допустимые распределения наблюдений пол
ностью известны. Однако в приложениях эти распределения часто бывают
известны лишь с точностью до значений некоторых параметров (например,
!!:.(i) , i == 1, .. . , k, или , или одновременно всех этих параметров) . В таких
7.4. Классификация нормаЛЬНblХ наблюдений. Общий случай 541
случаях можно решать задачи классификации при наличии дo
полнительных, как rоворят, обучающих выборок ( x i), .. , X !)
из соответствуюших распределений N(p,(i), ), i == 1,..., k.
Эти выборки можно использовать для оценки соответствуюших не известных
параметров и, заменив неизвестные параметры их оценками, поступать далее,
как и в случае полностью известных распределений, получая в итоrе эмпuрu
ческие (приближенные) правила классификации.
Если неизвестны средние f!:.(i) то их заменяют оценками
Обучающие .-:
выборки
П;
Ji(i) == '"""" X (.i)
nL.J)
I j 1
средними арифметическими выборок. Дисперсионная матрица (коrда
она неизвестна) оценивается выборочной дисперсионной матрицей (см. П.2
2.3); при этом так как матрица , по определению, общая Д)1я всех классов,
то мя ее оцениваНЮI следует использоnать информацию, доставляемую всеми
выборками. Эту информацию объединяют следующим образом. Построим
по i й выборке ( x i) ", к.;:!) выборочную дисперсионную матрицу
Пi
(i) == '"""" (X (i) (i) ) (X (i) (i) ) ' . 1 k
n. L.J ) f!:. ) !:!:. ' z == ,..., ,
I j 1
ni (i)
Torдa (см. п. 2 2.3) матрица l.J Д)1я любоrо будет несмещенно
(ni 1)
оценивать . Отсюда
k k
Е L ni (i) == L(ni 1) == (n k) , n == nl +
+nk,
i 1
i 1
и, следовательно, выборочная матрица
k
1 L (i)
== n'
k l'
n .
i 1
построенная с учетом всех данных, является также несмещенной оценкой
матрицы .
Построив эти оценки неизвестных параметров, далее можно ввести oцeH
ки КlIассификационных функций щз( ) (см. (2))
иij( ) == gj gj (E(i) + Е т ), j == I (ЕЮ Е Ш ),
и использовать их Д)1я построения эмпирических областей классификации
W i == { : иij( cj СЗ' j == 1,
заменяющих в данном случае области (1).
,k, j -# i}, i == 1,... ,k,
542 rлава 7. Элементы теории решений. Дискриминанmный анализ
в качестве обоснования этой методики можно привести следующие
«асимптотические» рассуждения. Предположим, что объемы обучающих BЫ
борок велики (nj --------7 00, i == 1,... ,k). Тоща оценки (i) i == 1, ,k, и Е,
как мы знаем (см. п. 3 2.3), сходятся по вероятности соотвеТСТlJенно к !!:.(i)
i == 1, ,k, и Е. Отсюда следует, что j сходится по lJероятности к Q.jj' а
j ( (i) + (j)) к Q. j (!!:.(i) + !!:.(j)) (см. теорему 1 2.2). Следовательно, npe
дельное распределение Ujj(X) совпадает с распределением Uij(X), поэтому
для достаточно больших обучающих выборок эмпирические КlIассификаци
онные функции Uij(:J2) можно использовать так же, как если бы были точно
известны распределения совокупностей.
Упражнения
НиКОсда lIе ставьте задачу, решение
котороЙ вам неuзвесml/О.
Праоило Берке
Зllаlluе ответов великое nреимущество.
Арабская ПОСЛОВlща
D Пусть ((Х),= Bi(l,e), <:1== {(l1 == 1/3, (1) ==2/3}, множеСТlюрешений D'= (d"d)}
и функция потерь задана таблицей
d l d)
(JI О I
(J2 2 О
1) Определить осе допустимые решающие правила в данной ситуации и убедиться
о том, что 6'= (6(0),6(1)) '= (d l , d 2 ) минимаКСliая процедура.
2) Убедиться о том, что для априорноrо распределении 11'(81) '= а, 11'(8)) '= 1 а,
а Е 10, 11, байесовское решение имеет следующий вид: 15' (О) '= d) при а :( 1/2,
15'(0) '= d l при а > 1/2 и b*(I) == d) при а 4/5, b'(I) '= d l при а > 4/5.
Построить rрафик байесовскоrо риска р(а) '= r(b*) как функции а.
<0lIl Указание. См. решение в примере 1 Э 7 1.
В Пусть .с(Х) '= Bi(J, 8), е'= {Оl '= 1/4,8) '= 3/4}. D '= (d l , d), d)} и Функuия
потерь задана таблицей
d, d) d)
(11 О 1 1/2
(1) 4 О 1/2
1) Убедиться в ТОМ, что байесовское решение д' == (15'(0),15'(1)) при априорном
распределении 11"((11) '= а Е [О, 1), 11'«(1)) == 1 а, имеет вид: Ь' '= (d), d)) при
Упражнения
543
а 1/4; o'(d J , d)) при 1/4 < а 7/10; о' == (d " d)) при 7/10 < а 3/4;
д' == (d l , d J ) при 3/4 < а 21/22; о' == (d" d,) при а> 21/22.
2) Показать, что байеСОIIСКИЙ риск р(а) == r(o') есть
1
а при О а ,
4
1 +4а 1 7
при <а:<:
8 4 '" 10'
4 3а 7 3
р(а) == при <a ,
4 10 4
11 10a 3 21
8 при 4' < а 22 '
4(1 а) 21
при 22 < а 1.
Построить rpафик функции р(а), а Е [О, 1].
... Указание. Сравнить средние потери E(L(d, fJ)lx) относительно апостериорноrо pac
пределения, указаННbIе 11 следующей таблице.
d l d 2 d J
1 a 3а 1 +2а
ж==о
1(0) 4/(0) 8/(0)
3(1 (l) а 3 2а
ж==1
1(1) 4/(1) 8f(l)
IJ Пусть .с(Х) == Bi(l,fJ), е == {ОI.fЧ, D == {dl,d)} и функция потерь L(d,fJ)
задана таблицей (а, Ь > О).
d, d 2
е, О а
е) ь О
Рассмотреть два случая: 1) е 1 2/3, е) == 1/2; 2) О, == 3/4, е) == 1/2. Убедиться
в том, что в обоих случаях множества ДОПУСТИМbIХ решающих правил совпадают, но
для случая 2) при любом апроиорном распределеиии пара метра байесовское решение
предпочтительнее.
... Указание. Воспользоваться решением упр. 1.
11 Пусть .с(Х) == Bi(3,0), е == {8 1 == 1O 2 е) == 10 1}, D == {dl,d)} и функция
потерь L(d, е) задана таблицей
d, d)
О, О 2
е) 1 О
544 rлава 7. Элементbl теории решений. ДискриминантНblй анализ
Рассмотреть три решающие правила о; == (6;(0),6;(1).0;(2), Oj(3»): О, == (d" d 2 , d 2 , d 2 ),
02 == (d l , d" d 2 , d 2 ), 0з == (d" d., d l , d 2 ) и убедиться в том, что минимаксное решение
l == 01 И m(б) == 0,792,
1:1 Пусть [(Х) == В'i( 1, О), е == {Ol, 02}, D == {d" d 2 } и функция потерь задана таб
лицей, указанной в упр. 3. Рассмотреть решающие функции
{ d' при x==O,I,...,i I,
О;(х) == . .
d 2 при x==t,t+l,
i == 1,2,... ,
и убедиться в том, что при аО, :::;; Ь(l (2) минимаксное решение 1; == 01 Построить
l при а8, > Ь(l (2),
.... Указание. Получить сначала вектор риска ШlЯ i й процедуры:
л; == (R(oj, (1), R(Oj, (2») == (a8 , Ь(l 8;»).
1'1 Убедиться в том, что если в условии упр.5 заменить [(Х) на пуассоновский
закон П(8), то 1; == О, при а(l e ol) :::;; Ьe 02, а соответствующий вектор риска есть
(а(l e OI), Ьe 02).
iJ Предположим, что наблюдается случайная величина Х, распределенная по HOp
мальному закону с неизвеСТНblМ средним 8 и известной дисперсией и2 множество
решений D == {d l , d 2 , d з } И функция потерь L(d, О) задана таблицей
d l d 2 d з
О
8<0 о 2
8==0 О
8>0 2 О
Рассмотрим решающие функции вида
{ dl при Х < а,
ОIlb(Х) == d 2 при а х :::;; Ь,
d) при Х > Ь,
Убедиться в том, что функция риска имеет вид
а < о < Ь.
(8 a) C Ь) 8 < О,
Ф +Ф при
(J (J
ЩО.Ь, 8) == Ф(;) +Ф( ) при 8 == О,
(a o) C 8)
Ф +Ф при /J > О,
q (J
и построить ее rpафик при Ь == a.
liJ Предположим, что е == {О, J}, D == {d} == [0,1] и функция потерь имеет вид
L(d,8) == Id 81 а , а 1. Рассмотрим класс решающих функций нида о(х) == const
(т, е, решение принимается без предваритеЛЬНblХ наблюдений), Убедиться D том, что
Упражнения
545
в этом классе байесовское решение d' , соответствующее априорному распределению
7f(0) == а Е [О, 1], 71"(1) == I а, при а> 1 имеет вид
, [ ( а ) I/(a I) ] 1
d == 1+
1 a
если же а == 1,10 d' == О при а > 1/2, d' == 1 при а < 1(2, а при а == 1(2 в Ka'lecTBe d'
может быть взято любое d Е [О, 1].
Уназание. Установить сначала, что байесовский риск есть
r(d) == atf1 + (1 а)( I d)a .
D Рассматривается задача оценивания неизвестной вероятности ('успеха. В по Ha
блюдению числа (,успехов.) Х в n испытаниях Бернулли (таким образом, здесь .с(Х) ==
Bi(n, 8), е == D == [О, 1]). Пусть функция потерь имеет вид
(d 8)2
L(d, В) == 8(1 8) '
а априорное распределение параметра является равномерным и(о, 1). Показать, что
байесовское решение есть б' (х) == х/n, и оно же является и минимаксным, при этом
r(б') == 1(n.
1m Предположим, что по наблюдению Х оценивается параметр В paBHoMepHoro
распределения U(Й,8), при этом параметр случаен и имеет априорную плотность
7f(B) == Be O 8 > О. Убедиться в том, что байесовская оценка при квадратичной
функции потерь имеет вид б' (Х) == Х + 1, а се риск r(б') == 1.
Уназание. Записать среднюю апостериорную потерю для решения d в виде инте
rpала
00 00 00
E[L(d, В) 1 х == х] == / (d 8)27f(Blx) dB / (d в)2е O dB / (d х t)2e t dt
о z О
И продифференцировать по d. .
m Рассмотрим задачу оценивания скалярноro параметра 8 при функции потерь
L(d,8) == Id 81, d, В Е я 1 Доказать, что при наблюдении Х == х байесовское
решение б'(х) при любом априорном распределении параметра .с(В) есть медиана
апостериорноrо распределения L(8Ix), т. е. такое 'IИСЛО, что
' } I { " I
P{8(dlx 2' Р 8 d x} 2'
Уназание. Установить неравенство E(IB dllx) E(IB d'llx), 'r/ d Е я 1 .
m (Продолжение). Пусть оценивается среднее модели Jf(B, ь 2 ), Korдa [(8) ==N(p.,o.2).
Используя упр.64 (5) к rЛ.1 и введенные там обозначения, убедиться в том, что байе
совская оценка по выборке Х == (Х I ,... ,Х П ) из N(B, ь 2 ) имеет вид
б'(Х) == i ( :2 + nь )
и ее риск равен r(6') == EIB б' (X)I == OI-l2fi (сравии с упр. 83 к rл. 3).
Уназание. Воспользоваться формулой полноrо математическоrо ожидания (см. (6)
96.6). .
З5 Заказ' 748
rлава 8
Факторный анализ
Если Kтo тo способен предсказать, чем закончатся
ею исследования, то зта проблема I/е очень zлубока
и, можно сказать, практически не существует.
А. Шильд
эта rлава, как и последующая, посвящена изложению методов исследо
вания и объяснения структуры корреляционных матриц систем случайных
величин. Такие исследования важны при анализе и интерпретации результа
тов эксперимента. Их целью в первом случае является выявление небольшоrо
числа скрытых общих факторов, оказывающих решающее влияние на резуль
таты эксперимента, во втором определение небольшоrо числа линейных
комбинаций наблюдаемых переменных, объясняющих их суммарную диспер
сию. В обоих случаях такое исследование позволяет лучше понять природу
случая, порождающеrо данные, и достичь более экономноrо их представле
ния, что важно при обработке больших массивов информации.
8.1. Постановка задач факторноrо анализа
При исследовании сложных объектов собирают статистику оБЫ<IНО по боль
шому числу различных характеристик объекта, стремясь при этом y'lecTb как
можно больше. Однако это стремление приводит, как правило, к обратному
эффекту, именно, с одной стороны, получается оrромный массив информа
ции, который трудно (а практически зачастую и невозможно) проанализи
ровать математическими методами, а с друrой стороны, получается «засоре
ние,) данных большим количеством несущественных характеристик, которые
не несут в себе никакой существенной информации об исследуемом объек
те, но по которым собирается большая (и часто дороrостоящая) статистика.
В этих ситуациях естественно встает задача отделить существенные xapaKTe
ристики от несущественных, отыскать те общие факторы, наличием которых
можно объяснить те или иные закономерности, действующие в множестве cy
ществеННbJХ характеристик, и тем самым «сжать информацию, т. е. записать
ее в терминах меньшеrо числа переменных. Конечно, все эти и аналоrичные
задачи можно математически cTporo формализовать и решить лишь в рамках
определенной модели. Одной из таких моделей, достаточно хорошо действу
ющей во мноrих реальных ситуациях, является модель факmОРIIОi!О аllGлuза.
Основной задачей факторноrо анализа является экономное описание экс.:-
периментальных данных. Он «объясняет» корреляционную матрицу системы
8.1. Постановка задач факторноzа анализа
547
случайных величин (далее пишем кратко с. в.) XI,"', X r (т. е. наличие
корреляций между ними) наличием небольшоrо числа обших rипотетических
переменных или факторов, от которых зависят XI, , Xr. В обшем виде MO
дель факторноrо анализа выrлядит следующим образом:
Х. =о '1'1(11," ,/k)+el,
(1)
X r =о 'l'r(ll,
, Л) + e r ,
rде 'Р; известные функции k переменных, 11, .., Ik И el, ,e r с. в.,
причем el, ,e r независимы как между собой, так и от 11, ,lk.
Если в представлении (1) число k значительно меньше Т, то С. в. Х 1, . . . ,
X r связаны между собой лишь через небольшое число с. в. 11, ,Л. С. в.
el,", ,e r не участвуют в этой связи и каждая из них влияет лишь на COOT
ветствующую компоненту вектора =о (Xl,..., X r ). Переменные 11,... ,Ik
называются общими факторами (они отражают "
те причины факторы, которые обуславливают Общие и частные факторы
зависимость между XI, .., X r ), а переменные el,'" ,e r называются част
ными факторами (они отражают локальные причины факторы). Определение
общих факторов и выявление их смысла в конкретной ситуации является важ
ной прикладной задачей. Решение ее позволяет: 1) объяснить природу зави
симости наблюдаемых с. в. Х.,... ,X r , 2) отделить существенные переменные
(зависящие от 1.,... , 'k) от несущественных (не зависящих от 1" , Ik)
3) более экономно записать информацию в терминах 11,'", Ik, а не самих
с.в. XI, ,X r (при k«r).
Дополнительно к (1) в факторном анализе обычно
принимаются следующие допущения.
1. Модель (1) линейна, т. е.
ХI =о lllfl +
,.
Линейная модель
+ llklk + el,
(2)
X r =о lrlll +
+ lrklk + e r ,
или в матричном виде (напомним, 'по при матричных операциях векторы
понимаются как вектор столбцы)
=о Lf + f.,
rде L =о IIlij 11 прямоуrольная матрица размера r х k; l =о UI, . . . , Л),
f. =о (el, , e r ).
2. Факторы 11, .. , /k независимы.
3. Все факторы, как 11, .. . , Л, так и еl, .. . , e r распределены по нормаль
ному закону, при этом будем предполаrать, что '; распределено по CTaH
дартному закону N(O, 1), i =о 1, , k, а ej по закону N(O, Vj),
j=ol,.. ,Т.
35"
548
rлава 8. Факторный анализ
Матрица наrрузок
Коэффициент lij IJ (2) называется lIаzрузкой i й
переменной на j й фактор (или наrрузкой j ro факто
ра в i й переменной). Матрица L = 111ijll называется
матрицей наlРУЗОК.
Обычно наrрузки lij и осmаmОЧIlЬ/е дисперсии V, являются неизвестными
параметрами модели (2), так же, как и число общих факторов k, и их надо
оценить по наблюдениям над с. в. !. = (XI. ... , Х т ). Иноrда еще ставится BO
прос оценки значений самих факторов 11, .., Ik по результатам наблюдений.
Эти задачи мы и рассмотрим далее.
Исторически факторный анализ возник из нужд психолоrии. Он исполь
зовался для Toro, чтобы определить относительно небольщое число тестов,
ответы на которые давали бы как можно более полное описание способно
стей человека. Однако в последнее время факторный анализ все более ши
роко используется в социолоrии, экономике, медицине, rеолоrии и мноrих
друrих областях. Широкому распространению методов факторноrо анализа
в последнее время способствовало развитие средств вычислительной техники.
Это связано с тем обстоятельством, что практическая реализация положений
теории факторноrо анализа связана, как правило, с весьма трудоемкими BЫ
числениями, что будет ясно из последующеrо изложения.
8.2. Неоднозначность решения в факторном анализе
Задачи факторноrо анализа имеют ту специфику, что ни наrpузки, ни факто
ры в модеЛИ (2) 8.1 не Moryт быть определены однозначно. ДеЙСТDительно,
пусть Н произвольная ортоrональная матрица размера k х k. Рассмотрим
случайный вектор i ' ) = Н 1.. в силу основных предположений модели (2)
8.1 (компоненты вектора L незаl3ИСИМЫ и распределены каждая по закону
N(O, 1)) и в силу ортоrональности Н имеем (см. упр. J 1 к rл. 1), что KOM
поненты вектора i l ) также независимы и распределены каждая по закону
N(O, 1). В этом случае представление!. = L[ + f можно записать в виде
!. = (LH')(H п + = L 1 [(I) + ,
rде LI = LH' Отсюда следует, что компоненты вектора [(I) также ЯВJIяются
общими факторами модели (2) 8.1, но с друrой матрицей наrрузок.
Ортоrональное преобразование Н определяет некоторое вращение в про
странстве факторов, и таким образом, (общие) факторы определяются с точ
ностью до вращения; при этом соответственно изменяются и наrpузки на
факторы.
Это свойство часто используется для преобразования фаКТОРОIJ, получен
ных в каком нибудь практическом исследовании. Вращение обычно подби
рают так, чтобы коэффициенты наrрузок удовлетворяли тем или иным СIJОЙ
ствам, например, чтобы определенные переменные имели как можно большую
8.3. Вывод уравнений максимальноzо правдоподобия 549
наrpузку на один фактор и нулевые или почти нулевые наrрузки на друrие
факторы.
Во всяком случае в факторном анализе возникает еще одна задача BЫ
бор вращения (ортоrональной матрицы Н) факторов и интерпретация фак
торов, получаемых после тaKoro вращения (по коэффициентам наrрузок на
факторы).
Выбор вращения факторов производится совместно со специалистом в
той области, из которой возникла конкретная задача (статистике часто пpи
надлежит первое слово, но никоzда последнее!). Иноrда можно избежать про
извол во вращении факторов, если из дополнительных соображений известно,
что некоторые элементы матрицы наrpузок L должны быть равны нулю (т. е.
некоторые переменные Xj не зависят от некоторых факторов fj).
8.3. ВЫВОД уравнений максимальноrо правдоподобия
Обозначим через С == IICjj II матрицу вторых моментов с. в. == (XI, , X r ).
Torдa из (2) 8.1 следует, что
k
Cjj == DXj == 2: l;j + Vj,
j=1
(1)
k
cij == cov(Xj, Xj) == EXjxj == 2: ljsljs, i i= j,
s=1
или в матричном виде
с == LL' + V,
( 1')
те V 11: :11 д""он""на, _атрн", оcr.пoчных днсперснй. Мат-
рица С обычно неизвестна и ее оценивают по выборке.
Пусть (I), , (п), n Т, независимые наблюдения над с. в. . По
строим дЛя этой системы с. в. выборочную ковариационную матрицу (см. п. 2.
2.3)
n
А == Ilajjll == 2: (I) (I)I
n 1=1
(напомним, что у нас вектор средних значений известен и равен нулю; если бы
вектор средних был неизвестен, то в качестве А надо было бы взять матрицу
n+1
А == lIajj II == 2: ( (I) ) ( (I) ш') ,
n
1=1
и Torдa с учетом зтих обозна<lений все последующие выводы сохраняют свою
силу). Наша цель использовать информацию, содержащуюся в А, дЛЯ по
лучения оценок параметров ljj и Vj. Для этоro мы воспользуемся методом
550
rлава 8. Факторный анализ
максимальноrо правдоподобия. Соrласно этому методу оценки lij и Vi опре
деляются из условия, чтобы совместная плотность элементов выборочной
ковариационной матрицы, вычисленная в наблюденной «точке,) А == Ilaijll ,
т. е. функция правдоподобия, имела наибольшее значение. Воспользуемся сле
дующим результатом.
Если случайный вектор ;r. == (XI, ,Х,,) распределен по нормальному
закону N(Q, С), то совместное распределение элементов матрицы А == lIajjll,
Распределение., 'j{ называемое распределением Уишарmа и обозначаемое
Уишарта .... W(r, n, С), имеет плотность вероятностей
,(Т, n)ICI n/2[AI(n r I)/2 ехр { % L: ai/ j }, (2)
',}
.. [
rде lIe'JII == C и -У(Т, n) множитель, зависящий только от r и n. Отметим,
что это распределение сосредоточено на множествс положительно определен
ных матриц А == Ilajjll размерности r х Т Сумма в (2) может быть записана
также как tr(AC \ Отметим также, 'по W(I,n,o.2) есть не что иное, как
распределение (0.2 jn)i(n) (см. п. 3 1.2), так что распределение Уишарта
2
есть мноrомерныи аналоr распределения Х
Опуская члены, не зависящие от С, из (2) получаем, что о. М. п. для ljj
и Vj это те значения lij и Vj. которые доставляют минимум функции
L == IJlICI + 2.: ai/ j
i,j
(3)
Чтобы получить соответствующие уравнения, мы должны продифферен
цировать (3) по lij и Vj И прираuнять все частные ПРОИЗВОДНblе нулю.
Будем обозначать большими буквами Cij алrебраические дополнения
элементов C;j в матрице С. Тоrда поскольку
IC[ == 2.: CijC ij == 2: Cjj, C ij
}
то
дlСI е.
дс" ,},
']
Если при этом матрица С симметрична, то из C ij == Cj j следует, что при i 1= j
alCI
== 2C j j.
vCjj
Отсюда также следует, что если элементы Cij ЯRllЯЮТСЯ функциями ОТ Z[, ,Z ,
то
alCI '" alCI дСij '" С .. aCij
'}
aZ t . . дСij aZ t . . дZ t
',] ',]
8.3. Вывод уравнений максимальноzо правдоподобия 551
Используя эти формулы и учитывая соотношение (1), ПОЛУ4ИМ:
дlп/С/ C jj jj
== ICТ ==с i == I,....r,
д Iп ICI == L C ts IJCts == L c ts IJCts + L c tt IJCtt == 2 L cSjlsj, (4)
дlц t,s 'СI дljj t<s дlij t дl;j s
i==I,...,r, j==l, ,k,
поскольку
: :; == { 'jj
при t =1= i,
при t == i,
и при t =1= s
{ Опри t =1= i, s =1= i,
IJCts [. t == i ,
IJl. SJ при
I} 1
tj при S == Х.
Вычислим теперь 4астные производные по ljj и Vi от c ts == Cts/IC[.
Так как дифференцировать 'СI мы уже умеем (см. (4)), то достаТ04НО
найти производные от C ts . Эти производные можно вычислить, воспользо
вавшись разложением C ts по элементам HeKoToporo столбца (CI V , С2и,'" ,с,.и)
без элемента Ctv (здесь V =1= в):
(5)
C ts == L cfJ"C ts , "и,
"
rдe C ts , ии обозна4ает апrебраИ4еское дополнение элемента С ии В C ts . Отсюда
IJC ts
д == Cts,ij,
Vj
IJC ts == L
дlij ". "
"Ft,"FS
если t =1= i, s =1= i,
IJC ts дС ии
дс и " дl jj
L
дс".
Cts,,,v IJ 1'
']
(6)
", v
"Ft, "#-S
Если воспользоваться теперь соотношением
C ts , "vlCI == CtsC"v CtvC"s,
формулами (5) и (4), то из (6) можно ПОЛУ4ИТЬ, что
ad s == ( IJCts C ts д 1п jC[ ) IC I , == cit csj
IJVj IJVj IJVi
и анапоrИ4НО
ad s "" C ts , j" "" C j " "" "t sj
IJl.. == 2 L..J l"jiCI 2C ts L..J l"j ICI 2 == 2 L..J lujc с ,
1) иср> " и
t =1= i.
552
rлава 8. Факторный анализ
Таким образом, окончательно получаем, что
1 aL '" иi '" иt si
2 == L.J lиjC L.J lиjC ats C
1] и t,s,и
aL ii '" it si
== С L.J С ats С
aVi t
,s
(7)
(8)
Нетрудно заметить, что правая часть (7) есть элемент j й строки и i ro столбца
матрицы
L'C I L'C IAC l,
а правая часть (8) есть i й диаrональный элемент матрицы
c 1 C IAc 1
Таким образом, уравнения максимальноrо правдоподобия для определе
ния оценок параметров lij и Vi имеют вид
L'c 1 L'C lAC 1 == О, (9)
diag(C 1 c 1 AC I) == О, (10)
rде diag М обозначает матрицу, содержащую только диаrональную часть MaT
рицы М При этом С имеет IJИД (1').
Выще мы IJидели ( 8.2), что матрица L определяется с точностью до YMHO
женин справа на ПрОИЗIJОЛЬНУЮ ортоrональную матрицу (это также IJИДНО и
из уравнений (9) (10), поскольку при умножении L справа на произвольную
ортоrональную матрицу величина С остается неизменной). Чтобы зафикси
ровать L (зафиксировать направление в пространстве факторов), мы добавим
к (9) ( 1 О) еше одно условие. Именно, мы будем требовать, чтобы матрица
J == L'v IL (10')
была диаrональной с диаrональными элементами, расположенными в порядке
убывания.
Уравнения (9) (]0) можно значительно упростить. Для этоro умножим
сначала (9) справа на С. В результате мы придем к уравнению
L' L'C lA == О. (11)
Далее, поскольку матрица V == С LL' диаrональная с положительными эле
ментами и поскольку в силу (] 1)
V(C I C I Ac l) == :n' r Ac 1 LL'C I + LL'C I Ac l == :n' r Ac l
то уравнение (10) эквивалентно уравнению
diag(:n' r AC [) == О. (12)
Аналоrично имеем:
(:n' r AC I)v == С А LL' + AC ILL' == с А
8.4. Итерацuонныu метод нахождения факторных наzрузок 553
и потому (12) эквивалентно уравнению
diag( С А) == о.
Из (13) следует, что для всех i Cji == aji и в силу (1)
k
vj == ajj 2: l;jo
j 1
Таким образом, оценки для остаточных дисперсий Vj Moryr быть найдены по
формуле (14), коль скоро будyr получены оценки для факторных наrpузок ljj.
Приведем уравнение (11) к виду, более удобному для практическоrо pe
шения. Воспользуемся для этоrо тождеством
(13)
(14)
c 1 == V I V I L(l k + J) I L'V I
( 15)
Чтобы убедиться в ero справедливости, умножим правую часть на С == LL' + V:
lr ==:п. r + V ILL' v IL(:п.k + J) IL' v IL(:П'k + J) IL'V ILL' ==
==:п. r + V ILL' v IL[(:п.k +J) I +(l k +J) IJ]L' == n r ,
что и требовалось. Умножив далее (15) слева на L', получим:
L'C 1 == L'v 1 L'V IL(].k + J) IL'V 1 ==
== [lk J(:п. k + J) I]L'V I ==
== [(llk+J)(llk+J) 1 J(lk+J) I]L'V 1 ==
== (nk + J) I L'V I (16)
Подставив (16) в (11), придем к уравнению
L' == (:п.1.: +J) IL'v IA.
Умножив теперь обе части этоrо равенства слева на J 1(11.: + J). будем иметь:
L' +J IL' == J IL'v IA.
или
L' == TIL'V I(A V).
(17)
t 8.4. Итерационный метод нахождения факторных наrруэок
Уравнение (17) 8.3 можно записать в виде
JL' == L'v I(A V).
( 1)
Отсюда следует, что элементы J являются собственными значениями, а
строки L' соответствующими собственными векторами маlpИЦЫ v l (А V).
На этом и основан итерационный метод решения уравнения (17) 8.3.
554
rлава 8. Факторный анализ
Этот метод описывается следующим образом. Обозначим через [; i ю
строку матрицы L/ и предположим, что у нас есть начальные приближения
L(i) и V(i) для L и V соответственно. Пусть f;(I) обозначает i ю строку L(J)'
Тоrда на первом шаry процедуры мы находим
/ [ / 1Т 1
BeKTop CтpOKY 1 == I(I) Y(J)
/ / А [ /
oeKTop CTPOKY !!1 == 1 ЦI)'
число h 1 == !! I
И R качестве 2 ro приближения к {I принимаем BeKTop CтpOKY
/ 1 /
{Ц2) == '!!I'
Если У нас более одноrо фактора (k 2), мы делаем второй шаr: находим
последовательно
, [ ' 1Т 1
oeKTop CтpOKY 2 == 2( 1) У (1)
число j21 == !!МЦ2) ,
/ ' А [ ' . 1 /
Beктop cтpoкy !!2 == !!!.2 2(1) }21 I(2)'
/
число h 2 == !!2 2
И В качестве BToporo приближения к {; принимаем BeKTop CТPOKY
/ 1 /
[2(2) == v%. '!!2'
Для тpeТbero фактора (k 3) последовательно находим:
/ [ / I
BeKTOp cтpoкy з == З(I) 1)
два числа jЗI == ;fI(2) И jЗ2 == ;f2(2)'
, ' А [ ' . [ / . 1 /
BeKTop CтpOKY !!з == з З(i) JЗ1 l(2) ЗН 2(2)'
число h З == !!; З
и в ка4естве BToporo приближения к {; принимаем BeKтop CTPOKY
/ 1 /
f З (2) == "jhJ '!!З'
и т. д. Если у нас k факторов, то делаем k таких шаrов. Таким образом, в конце
этоrо цикла мы получим второе приближение L(2) дЛЯ L. Матрицу V(2) мы
находим, подставляя элементы матрицы L(2) в уравнение (14) Э 8.3.
Матрицы L(2) и V(2) можно использовать как начальные в новом цикле
и получить следующие приближения L(з) и V(З) и т. д. Установить условия cxo
димости описанноro итерационноrо процесса не представляется возможным,
однако, на практике оБЫ'IНО процесс сходится и притом довольно быстро (хотя
известны при меры, коrда сходимость очень медленная или вообще oTCyrCTBY
ет последнее происходит, как правило, из за плохоrо выбора наЧaJ1ьноrо
приближения). Вопроса о выборе начальноrо приближения мы еше коснемся
несколько позже (в Э 8.6).
8.5. Проверка zипотезы о числе факторов
555
t 8.5. Проверка rипотеэы о числе факторов
в предыдущей теории предполаrалось, что нам точно известно число k об
щих факторов. Однако, на практике это число обычно неизвестно и всякое
предположение о ero значении должно быть подверrнyrо про верке как стати
стическая rипотеза.
Итак, предположил, что мы из некоторых соображений приняли, что чис
ло общих факторов есть некоторое фиксированное число k (например, k == 1).
Обозначим эту rипотезу Но. Друrими словами, НО есть предположение, что
ковариационная матрица С (размером r х т) может быть представлена в виде
суммы диаrональной матрицы V с положительными элементами и матрицы
LL' paHra k (см. (1) g 8.3). Для дальнейшеrо потребуем, ЧТобы выполнялось
соотношение
(r k)2>r+k.
(1)
Общая же rипотеза Н, внутри которой мы должны проверить НО, не делает
никаких предположений о матрице С (кроме, конечно, положительной опре
деленности). Для проверки НО внyrpи Н мы применим MeTOД (метод OT
ношения правдоподобия, см. g 5.4).
Соrласно л методу мы должны вычислить статистику л n , равную OT
ношению максимума функции правдоподобия (2) g 8.3 по множеству па
раметров 80, составляющему rнпотезу НО, к максимуму этой же функции
по множеству параметров 8, составляющему rипотезу Н Если при этом объ
ем выборки n 00, то при rипотезе Но
[( 21п n) X 2 (t),
rде t == dim 8 dim 80 (см. п. 4 5.4).
В нашем случае максимум функции правдоподобия при rипотезе Но дo
стиrается при С == LL + V, rде оценки L и V определяются уравнениями
(17) и (14) 8.3. При rипотезе же Н, очевидно, наилучшей оценкой для С
является выборочная матрица ковариаций А, поэтому из (2) 8.3 следует, что
n/2
Л N == C : ) ехр { т; tr (AG I)},
или
( IGI I )
2Iплn==n Iпщ+tr(АС ) T.
Вычислим теперь число степеней свободы t в предельном законе х2 Ч ис
ло независимых пара метров (элементов матрицы С) при rипотезе Н равно,
очевидно, т(т + 1)/2, следовательно,
(2)
т(т + 1)
dim 8 == .
2
556
rлзва 8. Фа/(торный анализ
Далее, число всех пара метров в представлении (1') 8.3 равно r + rk, однако,
вследствие неопределенности, I!озникающей из возможности вращения фак
торов, мы в 8.3 накладывали еще условие (10/), фиксирующее однозначно
матрицу L. Это условие накладывает еще k(k 1)/2 оrраничений на эле
менты L и V, и потому действительное число независимых параметров при
rипотезе Но равно
k(k 1)
dim 80 == r + rk .
2
Таким образом, число степеней свободы
r(r+l) k(k I)]
t== r(k+I)+ == [(r k)2 (r+k)].
222
В силу предположения (1) число t положительно.
Итак, если объем выборки n велик, то статистика (2) распределена при
ближенно по закону х2 (t), rде t дано в (3).
Этот результат позволяет стандартным образом орraнизовать проверку
соrласия экспериментальных данных и rипотезы Но о наличии точно k общих
факторов.
/
_ Критерий ДЛЯ rипотезы
о числе факторов
(3)
Проверка rипотезы осуществляется следую
щим образом. Задаваясь вероятностью а откло
нить rипотезу НО, Korдa она верна (уровень ]Ha
чимости критерия), по таблицам распределения X 2 (t), rдe t дано в (3), опре
2
деляем квантиль XI a,t из условия
{ 2 2 }
Р Х (t) > XI a,t == а.
Далее, для данноrо k методом 98.3 Вblчисляем С == LL' + 11 и определяем
значение статистики 21п л п в (2). Если это значение оказалось больше. чем
xT a,l, то мы отверrзем rипотезу Но и rоворим, что в факторной модели
2
необходимо не менее k + 1 факторов. Если же 211l Л П XI a, I то, как
обычно, можно лишь сказать, что опыт не onpoBepraeT rи потезу.
_ Практические На практике число факторов и оценки L и V находят
рекомендации так. Из априорных соображений определяют предполаra
емое число факторов k и для этоrо числа методом 8.3
определяют L и V После этоrо проверяют rипотезу о наличии ровно k факто
ров. Если rипотеза отверrается, то заново вычисляют L и v уже для k+ 1 фак
тора и снова проверяют rипотезу о наличии k + 1 фактора и т. д., пока не полу
2
чим впервые 21п л n < Xl o,t. Параметры L, V и число факторов в момент
остановки и принимаются за параметры нашей факторной модели (2) 8.1.
В заключение приведем некоторые соображения, несколько улучшающие
описанный критерий и упрощающие ero практическое применение.
Прежде Bcero рекомендуется заменить множитель n в (2) на
I 1 2 ( )
n ==n 6(2r+5) 3k. 4
8.5. ПроверКQ zипотезы о числе факторов
557
Было замечено, что при этом распределение статистики (2) более точно ап
2
проксимируетсн Х распределением.
Далее, если бы уравнения д1Iя оценок были решены mочно, то тоща co
rласно (12) 8.3
I
tr (АС ) == tr lr == т
и, следовательно, статистику (2) можно было бы заменить на
,ICI ' I I
n In ТAI == n (п С AI.
Используя теперь (1]) и (15) 8.3, можно получить, что
СНА == JL r + C I(A С) == JL r + V I(A С).
Действительно, поскольку из (]6) и (1]) 8.3 «<крышки.> для краткости опус
каем)
V IL(JLr + J(IL'V IA == V IL(JLr + J) IL'C,
то в силу (]5) 8.3 имеем:
(v 1 C I)A == (V l C I)C,
(5)
или
V I(A С) == C I(A С).
Обозначив через
1
Iltijll == т == V (А С),
статистику (5) можно представить теперь в виде
n' In 11r + TI.
(6)
(7)
Поскольку матрица y 1 диаrональная, а диаrональные элементы матрицы
А С соrласно (]3) 8.3 равны нулю, то диаrональные элементы матрицы Т
также равны нулю. Далее, при больших n разности aij j, как правило,
невелики, и потому в разложении определителя IJL r + TI можно опустить
члены, содержащие произведения более двух этих разностей. С учетом этих
соображений мы получаем следующее приближенное равенство
:L (aij j)2
ViVj
11r + TI 1
:L tijtji == ]
l i<j r
l j<j r
Наконец, статистику (7) можно приближенно заменить статистикой
(aij Cij)2
n' L
l i<j r
VjVj
(8)
Статистикой (8), вместо (2), обычно пользуются на практике. Вычисление
выражения (8) неизмеримо проще, чем вычисление (2), и использование CTa
тистики (8), как правило, приводит к хорошей аппроксимации, даже Korдa
сделано сравнительно мало итераций и точные о. м, п. L и v еще не найдены.
558
rлава 8. Факторный анализ
8.6. Центроидный метод
в этом параrрафе мы опишем один из приближенных методов определения
факторных наrpузок, который часто используется на практике. Этот метод
по существу своему является итерационным и носит название цеllтроидllОZO
метода. Оценки, получаемые этим методом, обычно бывают близки к О. м. п.
и достаточны для мноrих практических целей. Но как правило, peKOMeHДY
ется использовать эти оценки в качестве начальноrо приближения в методе
максимальноrо правдоподобия (см. 8.4).
... Факторные _ Введем понятие факторных дисперсий. Назовем
дисперсии" факторнымu дисперсиями диаrональные элементы MaT
рицы LL' Следовательно, факторными дисперсиями
с. в. Xl, ,X r являются те части общих дисперсий, которые вносят факторы
!!, , !k. Из (1) 8.3 следует, что факторной дисперсией с. в. Х; является
2 2
число lil + + lik'
Дадим описание центроидноro метода, одновременно иллюстрируя ero на
примере. В этом методе обычно рассматривают выборочную корреляционную
матрицу. Перед началом анализа надо знать начальные значения факторных
дисперсий. В качестве таковых выбираются максимальные по модулю значе
ния элементов в столбцах корреляционной матрицы (без учета диаrональных)
и ими заменяют единицы на диаrонали этой матрицы. Так получаемую MaT
рицу обозначим Ао.
В качестве иллюстративноrо примера мы будем рассматривать следующую
корреляционную матрицу (мя r == 6), в которой уже проделана отмеченная
выше первоначальная процедура
1 2 3 4 5 6
1 0,439 0,439 0,410 0,288 0,329 0,248
2 0,439 0,439 0,351 0,354 0,320 0,329
3 0,410 0,351 0,410 0,164 0,190 0,181
4 0,288 0,354 0,164 0,595 0,595 0,470
5 0,329 0,320 0,190 0,595 0,595 0,464
6 0,248 0,329 0,181 0,470 0,464 0,470
В данном случае все корреляции положительны, но если бы это было
не так, то прежде чем действовать дальше, мы должны были бы изменением
знака у одной или более переменных XI, ,X r постараться минимизировать
число отрицательных корреляций (при изменении знака у Х; изменяются
знаки у элементов i -й строки и i ro столбца корреляционной матрицы; при
8.6. Центроuдный метод
559
этом диаrональный элемент остается неизменным). Эrим мы достиrаем Toro,
чтобы суммы по столбцам были бы как можно больше.
После этой операции с изменением знаков (в нашем при мере этоro делать
не надо) вычисляют суммы по столбцам и полную сумму всех элементов
матрицы Ао. Числа, получаемые делением сумм в соответствующих столбцах
на квадратный корень из полной суммы, и являются первыми оценками для
наrpузок на первый фактор.
При этом, если бы мы меняли знаки у некоторых переменных, то у co
ответствующих наrрузок мы должны были бы изменить знаки на обратные.
В примере
Суммы 2,153 2,232 1,706 2,466 2,493 2,162 == 13,212
Наrpузки на 1 й фактор 0,592 0,614 0,469 0,678 0,686 0,595 == 3,635
Обозначим через [ == (lll, [21, ,lrJ) так полученную строку наrpузок
и вычислим первую остаточную матрицу Ао lll'l (исключим влияние пер
Boro фактора из первоначальной матрицы). В примере Ао lll'1 имеет следу
ющий вид:
D
2
3
4
5
6
1 0,086 0,076 0,132 0,113 0,077 0,104
2 0,076 0,062 0,063 0,062 O,IOI 0,036
3 0,132 0,063 0,190 0,154 0,132 0,098
4 0,113 0,062 O,154 0,135 0,130 0,067
5 0,077 O,IOI o, 132 0,130 0,124 0,056
6 0,104 0,036 O,098 0,067 0,056 0,116
в матрице Ао l\l'1 уже обязательно будут отрицательные элементы,
поскольку суммы по столбцам в ней Bcerдa равны Нулю. Поэтому перед
следующим этапом в Ао lll'1 надо проделать описанную выше процеду
ру с изменением знаков как минимум у одной переменной (минимизируя
число отрицательных знаков). В нашем примере число отрицательных знаков
в Ao l\l'1 можно сделать нулем, если изменить знак у переменных Х4, Х5 и Х6.
Затем снова в диаrональные клетки Ао lll ставим максимальные по модулю
значения элементов соответствующих столбцов (но это лишь на первом цикле
итерационноrо процесса; на последующих же циклах замены Диаrональных
элементов не производятся). Так получаемую матрицу обозначим AI' В при
мере А 1 имеет вид:
560
rлава 8. ФакторнЬ/й анализ
0,132 0,076 0,132 0,113 0,077 0,104
0,076 0,101 0,063 0,062 0,101 0,036
0,132 0,063 0,190 0,154 0,132 0,098
0,113 0,062 0,154 0,154 0,130 0,067
0,077 0,101 0,132 0,130 0,132 0,056
0,104 0,036 0,098 0,067 0,056 0,116
Далее с матрицей А 1 проделывается то же, что и с матрицей Ао: находятся
суммы по столбцам и полная сумма, извлекается квадратный корень из полной
суммы и на это число делятся суммы в столбцах. Получаемые числа (с учетом
восстановления знаков) и есть первые оценки наrpузок на второй фактор:
f == (lI2, l22, ... ,lr2)'
в при мере мы должны взять наrpузки для Х4, Х), Х6 со знаком минус.
СуммЬ! 0,634 0,439 0,769 0,680 0,628 0,477 1; == 3,627
НaJ1>УЗКИ на 2 й фактор 0,333 0,231 0,404 O,357 О,ЗЗО 0,251 ,ft == 1,904
После этоrо рассматривается матрица А J f2f , с ней проделывается та же
процедура, что и с матрицей Ао f1f; и Т.д. пока не исчерпаем всех факторов
и не получим полностью матрицу L == Illijll (i == 1, ,т; j == 1, ,k).
Здесь так же, как и в методе максимальноrо правдоподобия ( 8.5), действует
правило, оrpаничивающее число факторов k условием т + k < (т k)2 Так,
в нашем при мере мы должны оrраничиться вторым этапом, так как значение
k == 3 уже не удовлетворяет этому условию.
Суммируя теперь по строкам квадраты элемеНТОIJ этой матрицы:
k
d. " l .
I L..J I)'
j I
получим новые оценки для факторных дисперсий. На этом первый цикл ите
рационноrо процесса заканчивается. Только нужно у переменных, менявших
знак, вернyrься к первоначальным знакам. Полученными факторными дис
персиями можно воспользоваться для следующей итерации: в i ю диаrональ
ную клетку исходной выборочной корреляционной матрицы надо подставить
полученное число d j , i == 1, ,k, и повторить тот же процесс и Т.д. Сходи
масть на практике описанноro процесса очень быстрая.
8.6. Центроuдный метод
561
Для нашеrо при мера первые оценки матрицы наrpузок и факторные дис
персии имеют вид
0,592 0,333 d l == 0,461
0,614 0,231 d 2 == 0,430
L== 0,469 0,404 d, == 0,383
0,678 0,357 d 4 == 0,587
0,686 О, 330 d s == 0,580
0,595 0,251 d 6 ==0,417
Описанная п!)оцедура отыскания факторных наrpузок
имеет наrлядную reометрическую интерпретацию. Отож
дествим наши наблюдаемые переменные х" . , Х Т С BeK
торами, выходящими из начала координат r MepHoro пространства, косинусы
уrлов между которыми равны соответствуюшим корреляциям, а ДIIины co
ответствующим стандартным отклонениям. Далее, если направления, которые
приписаны переменным, уже найдены, то мы изменением, если необходимо,
их знаков сделаем как можно больше корреляций положительными; тоща BeK
торы будут иметь тенденцию к rpуппировке в одном направлении в пучок и их
сумма будет иметь наибольшую ДI1ину. Эта сумма и принимается за первый
фактор, а в качестве наrpузок переменных Х" . . . ,Х т на этот фактор при
нимаются ДI1ины проекций соответствующих векторов на суммарный вектор.
После этоrо исключается влияние nepBoro фактора (как это описано выше)
ИДlJя первой остаточной матрицы строится новая rеометрическая lOдеЛl) 11 т.Д. ,
Для центроидиоrо метода, так же как и ДlJЯ метода MaK К 2 .,
2 ритерии Х
симальноrо правдоподобия, существует критерий типа «х
Дl!Я больших выборок.) Дl!Я проверки rипотезы о наличии ровно k факторов,
т. е. критерий значимости остатков после исключеttия k факторов. Прибли
женная статистика этоrо критерия, которая обычно используется на практике,
имеет вид
rеометрическая ..
интерпретация
n ( '" х 2 . + '" Х"Х .. )
2 11 '] JI ,
i i<j
rде Ilxijll == х == V I(Ao LJ IL'V IAo). Здесь Ао == А V, J == L'V 'L
(вообще rоворя, не диаrональная). Число степеней свободы в предельном pac
пределении х 2 здесь равно 1/2((т k)2 r k) Эта rипотеза проверяется
точно так же, как и в случае получения оценок методом максимальноrо прав
доподобия.
Общая схема применения факторноro анализа
на практике имеет следующий вид. Сначала с помо
щью центроидноrо метода получают первоначаль
ные факторные наrpузки и факторные дисперсии. С помощью критерия ДIIЯ
центроидноrо метода уточняют необходимое число факторов. После этоro
центроидные наrрузки используют в методе максимальноrо правдоподобия
Зб 3..., 1748
Общая схема 1IIt.
факторноrо анализа
562
rлава 8. Факторный анализ
в качестве первоro приближения. Вообще, методу максимальноrо правдопо
добия следует отдать предпочтение, так как в настоящее время он является
единственным методом, дающим эффективные оценки факторных наrpузок.
8.7. Оценка значений факторов
Решение вопроса о числе общих факторов и о получении наrpузок на факторы
по переменным составляет основу факторноrо анализа. Однако на практике
часто представляет интерес и задача приближенной оценки значений самих rи
потетических факторов по наблюденным значениям переменных Х 1, , X r ,
после Toro, как каким либо методом уже решена первая задача. Здесь мы
рассмотрим один из простых методов решения этой задачи.
В этом методе оценки 1;, , j;. факторов находятся из условия обраще
ния в минимум величины
r 2
I: e j ,
j l Vj
которую в силу (2) 8.1 можно записать также в виде
r k 2
I: ( Xj I: lijfj ) .
. . V,
, l J I
(1)
.fiЛ"' ' '"'.'"" .,., . < Таким об р азом , здесь минимизи ру ется взвешенная
.,. етод минимизоции
сумма квадратов остатков в модели (2) 8.1, поэтому
метод называется методом мuнuмuзаЦIiU остатков.
Дифференцируя (1) по fj и приравнивая частные производные нулю,
получаем следующую систему уравнений:
остатков
r k r
I: I: lisljj f. == I: ljj Xj, j == 1, ,k,
j 1 B l V, i 1 V,
или в матричной форме
LIV ILf == LIV l .
(2)
Полаrая
J == L'v IL,
находим, что оценки факторов по данному методу равны
Z == J l L'V I .
(3)
Таким образом, оценки факторов являются линейными функциями от наблю
даемых переменных.
Интерпретация факта может оказаться
важнее самою факта.
g 8.7. Оценка значений факторов
56З
.lf 3аКJIючительные замечания. В заключение отметим, что в факторном aHa
лизе в силу неоднозначности решения (см. 8.2) весьма существенную
роль иrpает проблема интерпретации результатов исследования (бывает:
мысль, достойная оваций, nОlибнуть может от интерпретаций). В каче
стве иллюстрации этоro приведем результаты одноro KOHKpeTHoro исследования
в области социолоrии 1), описанные в книrе [18, с. 98 99]. Известный специалист
в области факторноro аналнза Кэттел исследовал показатели, характеризующие
уровень культурноro развития наций. Было Вblбрано 72 количественно измеряе
MblX показателя ДЛЯ анализа культурноrо уровня 69 наций. В их число входили все
показатели, которые, по мнению автора, характеризуют культуру нации. Среди
них оказались число лауреатов Нобелевской премии, число зареrистрированных
проститyrок, число секретных доrоворов, число революций за 100 лет, минималь
ный Dозраст вступления в брак, потребление сахара на душу населения, процент
HerpoB, отношение разводов к бракам, процент самоубийств и т. д. Анализу было
подверrнуто 2556 корреляционных связей. ОкончатеЛЬНblе результаты были пред
ставлеНbI 12 факторами. Автор пытался дать ОСМblсленную интерпретацию каж
дому фактору, рассматривая ero наrруженность исходными переменными. При
этом использовались весьма вычурные формулировки для обозначения факто
ров, например: <<просвещенное изобилие в противовес удручающей бедности ,
.осмысленное трудолюбие в противовес эмоциональности , «консервативность
И патриархальная стабильность в противовес безрассудной боrеме» и Т.д.
.Результаты TaKoro исследования, может быть, и любопытны в KaKOM TO СМblсле,
но нам кажется, что они все же не имеют большоro эвристическоrо значения,
вряд ли, исходя из подобных исследований, можно вьшвинуть содержательные
rипотеЗbl о развитии КУЛЬТУрbl. Нам представляется неудачной сама ПОПblтка
создания модели, всесторонне и полно описывающей такую сложную и плохо
орrанизованную систему. Видимо, факторный анализ имеет смысл применять
к всестороннему описанию более простых систем, [де леrче вьшвиraть rипотезы,
подлежащие дальнейшему обсуждению [18]. И еще: .Если roворить о критиче
ской оценке факторноro анализа, то следует вспомнить довольно старое, очень
резкое, но, вероятно, не совсем справедливое замечание о том, что, пользуясь этим
методом, получишь то, что туда внесешь . Но, хотя этот метод и не дает однознач
Horo решения, он все же nOMoraeT исследователю формулировать реалистичные
rипотеЗbl об исследуемой системе, обостряет ero интуицию, упрощает итоrовый
алrоритм проведения эксперимента, помоrая отсеивать множество «ШУМОВblХ» по
казателей и выделять наиболее существенные характеристики изучаемоrо объекта
или процесса. В качестве литературы по теории и приложениям факторноrо aHa
лиза можно указать книrи [17, 19].
Пuсанье KHUl занять е без конца, их
чтенье утомительна для тела.
1) Ca/te/l R. В. The Dimenlions of Cullural Pal1ems Ьу Faclorizalion of Nalional Characlers //
1. Abnor. and Socia! Psychology. 1949. У.44. Р. 443 469.
rлава 9
Компонентный анализ
Не дОРОеll на.М дНII, не жаль нам их нимало,
Чтоб то, чем дорожим, росло и созревало
Цветок Лll пестуем в саду, еде сладко дЫШllМ,
Ребенка ли растим иль к"uж:е'lКУ МЫ птием.
Фридрих Рюккерт 1)
! 9.1. Постановка задач компонентноrо анализа
Компонентный анализ или, иначе, метод lла8НbJХ компонент так же, как 11 фак
торный анализ, исследует структуру ковариационных (или корреляционных)
матриц систем случайных величин (с. в.). Однако лишь только в этом и COCTO
ит их формальное сходство. Если для факторноrо анализа важны корреляции
между переменными, которые он объясняет НaJ1I1'lием HeKoToporo числа об
щихдля всех переменных факторов, то в компонентном анализе интересуются
исключительно дисперсиями переменных и их линейных комбинаций. При
этом [j компонентном анализе не делается фактически никаких предположе
ний о наблюдаемых с. в. Х" . . . ,Х Т , В то время, как длн факторноrо анализа
существенным является линейность и нормальность ero модели (см. (2) 98.1),
которая, если и не верна, то хотя бы приближенно отражает суть дела.
В компонентном анализе ищется такое линейное преобраЗО13ание
Хl == 111fl +
+ 1 1'.f" ,
(1)
Х Т == lrlfl +
+ lITI",
или в матричной форме
';f == L [, ( 1 ')
rде ';f == (Х1' ,Х Т ), [ == (/1, ,Ir) векторы столбцы и L == 111ijll
квадратная матрица размером r х т, в котором С. 13. 11, ,fr некоррелиро
ваны и нормированы (E/i == О, Dfi == 1, i == 1, ,т; всеrда для простоты
предполаrается, что EXi == О, i == 1, ,т).
Представление исходных с. в. Х(, ,Х,. В виде (1) имеет ряд преиму
ществ. Действительно, в этом случае их дисперсии весьма просто выражаются
1) Рюккерт Фридрих (1788 1866) немецкиii ПОЭТ, np3M3Typr.
9.1. Постановка задач компонентНОi!О анализа
565
через коэффициенты lij:
2
DXj == liJ +
+ [Тт, i == 1,
,Т.
(2)
Ввиду (2) суммарная дисперсия с. в. Х),
, Х . равна
r r r
L DXi == L IТl + . . . + L [;"
i l i l i-l
(3)
поэтому. величину l;j можно назвать вкладом компоненты Ij в дисперсию пе
ременной Xj, а величину l;j +. . . +l;'j вкладом компоненты Ij в суммарную
дисперсию. Далее, предположим, что вклад компоненты Ir н суммарную дис
персию мал. Тоrда можно пренебречь влиянием компоненты Ir, и вектор
== (XI, ,Х т ) характеризовался бы в этом случае не r случайными чис
лам и XI, ,х,. а лишь r I случайными числами 11, , I,. ). Вообще,
если бы суммарный вклад компонент 11.:+), ,Ir в суммарную дисперсию,
равный 13 силу (2) и (3)
,.
L L li j ,
j k+l i=1
был мал настолько, что им можно было бы пренебречь, то это означало бы, что
влиянием компонент Л+I, ,1" можно пренебречь, и следовательно, вектор
характеризовался бы не т параметрами, а лишь k параметрами 11, ,л.
Иноrда такое исследование nOMoraeT лучще понять природу случая, порожда
ющеrо случайный вектор . Кроме этоrо, при этом удается (,сжать.) l1НфОр
мацию, т. е. достичь экономии в описании изучаемоrо объекта (описывать ero
меньшим числом параметров).
Как будет показано ниже, отыскание представления (J) эквивалентно
определению r таких нормированных линейных комбинаций У" ,ут пе
ременных XI, ,Х,. (т. е. сумма квадратов коэффициентов равна 1), что для
каждоro k == 1, т Yk имеет наибольшую дисперсию среди всех нормиро
ванных линейных комбинаций при условии некоррелированности с преды
дущими комбинациями YI, , Yk )- Такие линеЙНblе комбинации Уl, . . . , у.
называются i!лавнымu компонеитами системы с. в. Х), , Хт.
Следовательно , пе р вой rлавной компонентой ·
. JЛОВНЫ,е КО"'!90ненты
переменных Х), ,х . называется нормированная
линейная комбинация этих переменных, обладаю
щая максимальной дисперсией.
Второй rланной компонентой называется нормированная линейная KOM
бинация, обладающая максимальной дисперсией при условии некоррелиро
ванности с первой rлавной компонентой.
Третьей rлавной компонентой наЗblвается нормированная линейная KOM
бинация с. в. Х),. ,Х Т , обладающая максимальной дисперсией при условии
некоррелированности с первой и второй rлавными компонентами и т. д.
5бб
rлава 9. КомпонентНblй анализ
Для практики обычно наибольший интерес представляют те переменные
или их линейные комбинации, которые имеют большие дисперсии, поскольку
именно такие комбинации и Hecyr в себе максимум информации о степени
изменчивости Toro или иноrо показателя или признака. В практических ис
следованиях, коrда число рассматриваемых переменных, которые требуется
обработать, слишком велико, стремятся выделить относительно небольшое
число их линейных комбинаций с большими дисперсиями, а линейные KOM
бинации с малыми дисперсиями отбрасываются, как несущественные. Таким
образом, достиrается сокращение числа исследуемых переменных.
Ввиду этоrо отыскание rлавных компонент и выделение из них тех, KOTO
рые удовлетворительно объясняют суммарную дисперсию, представляет боль
шой практический интерес. Метод rлавных компонент был предложен еще
в 1901 r. К. Пирсоном и позднее вновь открыт и детально разработан Хотел
линrом 2) (1933 r.). Этот метод хорошо изложен в книrе 111.
t 9.2. Решение основных уравнений. rлавные компоненты
В этом параrpафе мы полу'lИМ представление (1) 9.1 для любой системы с. П.
XI,'" ,Х т . Предположим, что известна ковариационная матрица А этих С. в.
(если ковариационная матрица неизвестна, но даны незаписимые наблюдения
наде. в. == (Xl, ,Х т ), то во всех нижеследующих рассуждениях надо под А
понимать выборочную ковариационную матрицу).
Обозначим через U ортоroнальную матрицу, с помощью которой А при
водится к диаrональной матрице
Л(
о
А==
(1)
о
>'т,
в которой элементы расположены в порядке убывания, т. е. >., > >'2 > >
> >. > о (мы предполаrаем для простоты, что все >'i различны и положи
тельны, что для большинства праКТИ'lеских ситуаций обы'lНО выполняется).
Таким образом,
А == и'АU.
(2)
Фактически >'!; есть k e по величине собственное значение матрицы А, а k й
столбец !!k матрицы И соответствующий собственный вектор, так что
A!!k == >'k!!k' k == 1, , т, (3)
что является эквивалентной записью соотношения (2).
Рассмотрим теперь новые переменные 'н- == (YI, ,Ут), задаваемые pa
венством
'н- == U/ . (4)
2) ХотеJ!JJинr rаралЬд (1895 1973) американский статистик и экономист.
9.2. Решение OCHOBHblX уравнений. rлаВНblе KOMпOHeHmbl 567
Вычислим их ковариационную матрицу В. Поскольку EXj == О, то ЕУI == ==
== EYr == О и потому
В == Е(1!..1!..') == Е(и' 'и) == и'E( ')и == и' Аи == л.
Из этоro соотношения следует, что с. в. у" , Yr некоррелированы и DYk == "\k,
k == 1, ,Т.
Покажем теперь, что У! есть нормированная комбинация с наибольшей
дисперсией. Пусть
у' == CIXI,+
, + CrX r == ' , == (CI,
, Ст),
, 2
== С( +
+ с;. == 1,
есть произвольная нормированная линейная комбинация X OB. Тоrда из (4)
следует, что
· ' и ., ·
у == '!!. == '!!. == CIYI +
+ C;Yr, O == U'f.
При этом ., O == 1, поскольку при ортоrональном преобразовании длина BeK
тора не меняется. Отсюда
r r
Dy' == L с;2..\; == ..\1 + L c;2(..\j "\1),
i 1 i 2
поскольку
r
.2 02
СI == 1 L..J Cj
i 2
Это выражение, очевидно, достиrает максимума при С; == == С; == О, так
как ..\1 > ..\; при i 2.
Аналоrично, У2 представляет собой нормированную линейную комбина
цию, некоррелированную с УI и имеющую наибольшую дисперсию (из TOro,
что у' == L C;Yj некоррелирована с у" следует С; == О, а далее при меняются
предыдущие рассуждения) и Т.д.
Таким образом,
УI == !! == UIIXI + и21 Х 2 + + UrlX r
есть первая rлавная компонента переменных Х 1, , X r И ее дисперсия равна
первому собственному значению ..\1 (здесь и далее U == IIЩjl1 и :ц;. k я
строка матрицы и'),
У2 == !!; == UI2 X I + и22 Х 2 +
+ U r 2 X r
есть вторая rлавная компонента и ее дисперсия равна второму собственному
значению ..\2 и т. д. Вообще
Yk == :ц;. == Ulk X , + иU,Х2 + + UrkXr (5)
есть k я rлавная компонента и ее дисперсия равна k MY по величине соб
ственному значению ..\k'
568
rлава 9. КомпонентНblй анализ
. rлавны
компоненты (ВИД)
Итак, нахождение rлавных компонент и их дис
персий сводится, по существу, к нахождению собствен
ных значений и собственных векторов ковариационной
матрицы А. При этом k я rлавная компонента имеет дисперсию, равную k MY
по величине собственному значению, а коэффициенты ее линейной комби
нации являются компонентами соответствующеrо собственноrо вектора А.
Чтобы получить теперь представление (1) 99.1, достаточно пронормиро
ватьс.В. У" ,Ут в (4).
Положим
1 1,
Л =о ...;>:; Yk =о ..;>:; '!lk ' k =о 1, r (6)
Тоrда с. В. ft, ,fr будут некоррелированы и нормированы (DЛ =о 1).
В матричной записи (6) имеет вид
L =о Л 1/2"!!... =о Л 1/2и' .
(7)
Это равенство выражает L через . Чтобы выразить через [, умножим
(7) слева на И Л '/2 Поскольку ии' =о Jl. r , то это дает
=о И Л 1/2 f
Сравнивая (8) с (1) 99. 1, получаем, что
L =о И Л '/2
(8)
(9)
Тем самым получено представление (1) 99.1.
Итак, с. в. 11, ,1,. в (1) 9 9.1 это суть нормированные rлавные KOM
поненты переменных Х1, , Хт, При этом k й столбец f k матрицы L равен
lk =о v>:;.'!lk
и при этом
l l[,; =о Лk'!l '!lk =о Лk =о lik + + l;k'
Таким образом, вклад компоненты Л в суммарную дисперсию с. в. Х1, , Х Т
равен как раз ),k. Следовательно, зная собственные значения матрицы А,
мы леrко можем найти и долю, вносимую каждой компонентой IJ суммарную
дисперсию, равную в силу (3) 99.1 ЛI + + Л r =о tr (Л) =о tr (А).
9.3. Метод Хотеллинrа
Как следует из 99.2 в компонентном анализе основная задача состоит в BЫ
числении собственных значений и собственных lJекторов КОlJариационной
матрицы А. В настоящее время для этой цели используются ЭВМ. Имеется
несколько способов решения этой задачи. Мы приведем здесь итерационный
метод, разработанный Хотеллинrом.
9.3. Метод Хотеллuнzа
569
Пусть !!(о) любой вектор, не ортоrональный к первому собственному
вектору !!I (обычно в качестве компонент начальноrо вектора !!(О) peKOMeH
дуется брать числа, приблизительно пропорциональные суммам элементов
соответствующих столбцов матрицы А). Определяем последовательно
1
, !!щ, i == О. 1, 2, . . .
!!(i)!!(i)
!!(i) == AQ(H)' i == 1,2,
Тоrда имеют место следующие соотношения:
1 ', ,2
1т !!(i)!!(i) == 1\1,
.....00
Нт i) == :f:!!I'
.....00
Q;==
(1)
(2)
(3)
(4)
Докажем (3) и (4). Поскольку А == И ли', то A i == И лiu'
Si == (!!(i)!!(i)( 1/2, из (1) и (2) получим, что
Q(i) == SiAQ(H)'
При меняя последовательно несколько раз (5), найдем, что
i) == tiAif!(o) == tД лiи' !!(о),
rде ti = SOS( ... Si. Из (1) и (6) следует, что
, Ь t 2 , ил 2i u '
1 == Q(i)!!(i) == i !!(О) !!(о).
Соотношение (6) можно записать также в виде
Полаraя далее
(5)
(6)
(7)
i ( 1 ) ; ,
Q(i) == tiлlU л U !!(о).
(8)
Но
о
,1im ( ,1 Л ) i Iiт
.....00 ,1'\1 i....oo
( y
о
о
=с,
о
( : Y
о
о
так как >'j/ >'1 < 1 при j > 1. Таким образом,
.liт и ( ,1 Л ) iu,!!(о) == ИСU'!!(О) == II!!I,Q.. .,QIIU'!!(o) == !!I!!'!!(O) = (!!I.!!(O))YI
......00 ,1'\1
(9)
(здесь символом Q обозначается нулевой столбец матрицы).
37 з..., 1748
570
rлава 9. Компонентный анализ
с учетом (9) из (7) имеем:
1 == .Iim (tjл )2 Нт (о)u ( л ) 2iu, (о) == (Y;Q(O))2 .Iim (tiл )2
1---+00 1---+00 Л 1 1---+00
Таким образом,
. 2 I
.Iim (tjЛ ) == 2 ' (10)
НОО (м',!!(о))
поскольку, по предположению, м'&(о) i= о. Из (8) с учетом (9) и (10) следует,
что
. I ( ' )
.llm == :f:,......... YIQ(o) МI == :f:YI'
1---+00 !!, Q(O)
Далее из (2) с учетом этоrо соотношения и соотношения (3) 9.2 следует, что
.lim (i) == :f:AYI == :f:ЛIМ1'
1---+00
Отсюда
., \ 2 , \ 2
.Ilm !!(i)!!{i) == ЛIУllli == Лl.
1---+00
Таким образом, соотношения (3) и (4) доказаны.
Чтобы найти второе собственное число и соответствующий собственный
вектор, рассмотрим матрицу
А 2 == А ЛIМlм'l'
Тоrда, если i i= 1, то
А 2 !!; == А!!; ЛI(У;!!i)Уl == Лi!!;,
поскольку !!; == о, и
А 2 Мl == Ам! Л, (y',Yl)Ml == Л1УI ЛIУl == О,
поскольку !!'1!!I == 1.
Таким образом, Ml' М2" ., У , являются собственными векторами матри
цы А2, а соответствующие собственные значения равны О, >'2' , >'Т' Сле
довательно, >'2 наибольшее собственное значение матрицы А2, а !!2
соответствующий собственный вектор. Для определения У2 и Л2 можно, сле
довательно, применить к А 2 описанный выше процесс последовательных при
БЛЮКенИЙ. После этоrо можно определить матрицу
Аз == А 2 ).2М2У;
и методом последовательных приближений определить >'з и УЗ как ее наи
большее собственное значение и соответствующий собственный вектор и Т.Д.
" Практические Имеется несколько способов, позволяющих COKpa
тить объем работы в методе последовательных приближе
рекомендации ний. Один из них состоит в том, что матрицу А возводят
9.3. Метод Хотеллuнzа
571
в некоторую степень, а затем уже при меняют метод последовательных при
ближений. Так, можно пользоваться матрицей А 2 , положив
]
I Q(;).
(i){!(i)
Этот процесс сходится вдвое быстрее, чем процесс, определяемый формула
ми (1) и (2). При использовании А 4 == А 2 А 2 сходимость получается вчетверо
более быстрая и т. д. Отметим при этом, что А 2 симметрическая матрица,
поэтому при ее вычислении достаточно определить лишь т(т+ 1)/2 ее элемен
тов. Для контроля вычислений можно использовать равенства tr (А) == tr (Л) ..,.
и А == LL', rдe L определено в (9) 9.2. Прнмер Джефферса
2
{!(i) == А H)' !!(i) ==
Приведем один коикретный пример применения метода rлавных компо
нент. В работе Джефферса З) этот метод был применен в следующей задаче
классификаuии. Объектом исследования служили летающие тли. Нужно
бьuIO разбить этот вид насекомых на подrpуппы по варьируемости их MOp
фолоrнческих признаков. Было измерено 19 различ HblX признаков, которые оказа
лись весьма сильно коррелированными между собой; так коэффиuиенты парных
корреляuий по мноrим признакам достиraли значений 0,90..;- 0,99. Компонент
ный анализ показал, что можно оrpаничиться двумя первыми rлавными компо
нентами, на которые приходится 85,5 % от общей дисперсии. Первая компонента
задается различием в размерах насекомых, DТорая в значительной степени связана
с числом яйuекладок.
rрафи"ески результаты предстаалены на рис. 1 (результаты наблюдений представле
ны на плоскости, задаваемой двумя первыми компонентами). Здесь ясно видно, что
обследованных насекомых можно разбить на четыре хорошо раЗЛИ'lИмые rpуппы.
++t++ компонента 1
++++ +tJ+
+ компонента 2
+++
+
.t+t t
+++
++
'_Со 1
J) JeJJers J. N. R. Two Сзsе 51udies in lhe Аррliсаtюn of Principal Componen! Anal)'5is /1 Аррl. Stat.
1967 16. N! 3. Р. 225 236.
37*
572
rлава 9. Компонентный анализ
-'l&,
.,. rеометрическая
интерпретация
Вообще, rеометрически нахождение rлаВНbIХ KOM
понент сводится к переходу к новой ортоrональной си
стеме координат: первая координатная ось ищется так,
чтобbI соответствующая ей линейная форма извлекала возможно большую
дисперсию, далее ищется ортоrональная ей ось, которая делает то же самое
с оставшейся дисперсией и т. д.
Ao' 3 В заключение отметим, что как фаКТОРНbIЙ, так и
.,. аключител _ ные.,
, компонентныи анализ это математические (стати
замечания. v
. стические) методы, OCHOBaHHbIe на линеИНbIХ моделях
и (в первом случае) нормальном законе распределения, и служащие лишь
средствами, облеrчающими исследователю проникновение в тайны природы.
Природа же надежно охраняет свои тайны:
Природа с красоты своей
Покров а снять не позволяет,
И ты машинами не вынудишь у ней,
Чеzо твой дух не yzoaaem.
В. С, Соловьев 4)
(Перевод из траrедии rёте «Фауст»)
ЧтобbI проникнyrь в них, надо или ставить активный эксперимент, что
всеrда трудно, или научиться их отraдывать. Факторный анализ и метод rлав
ных компонент и служат этой цели. Возникнув сто лет назад в основном
из нужд психолоrии и социолоrии, эти методы в настоящее время находят все
более широкое применение как некоторые вспомоrательные приемы анализа
данных в задачах caMoro разноrо характера.
... нет ничеzо лучше, кок наслаждаться человеку
делами своими: потому что это доля ezo; ибо
кто приведет ezo посмотреть но то, что будет
после неzo?
Екклесиаст (Библия. Ветхий 3авет. 3:22)
Пусть не корят меня, что я не сказал ничеzо
HOBOZO: ново уже само расположение материала;
исроки в мяч бьют по одному и тому же мячу,
но не с одинаковой меткостью.
Б. Паскаль
4) Соловьев Владимир Серrеевич (1 B53 1900) русский релиrиозный философ и поэт.
Припожение
Что виделось вчера как цель zлозом твоим,
Для завтрашнеiО дня оковы;
МЬiСЛЬ толь/,о пища мыслей 'IOВЫХ,
НО zолод их неутолим.
Эмиль Верхарн 1)
1. Нормальное распределение
Ср
Квантили распределения: р == ! e z)/2 dж == Ф«(р)
oo
р I (р р I (р р I (р
0,50 0,000 0,68 0,468 0,86 1,080
0,51 0,025 0,69 0,496 0,87 1,126
0,52 0,050 0,70 0,524 0,88 1,175
0,53 0,075 0,71 0,553 0,89 1,227
0,54 0,100 0,72 0,583 0,90 1,282
0,55 0,126 0,73 0,613 0,91 1,341
0,56 0,151 0,74 0,643 0,92 1,405
0,57 0,176 0,75 0,674 0,93 1,476
0,58 0,202 0,76 0,706 0,94 1,555
0,59 0,228 0,77 0,739 0,95 1,645
0,60 0,253 0,78 0,772 0,96 1,751
0,61 0,279 0,79 0,806 0,97 1,881
0,62 0,305 0,80 0,842 0,98 2,054
0,63 0,332 0,81 0,878 0,99 2,326
0,64 0,358 0,82 0,915 0,999 3,090
0,65 0,385 0,83 0,954 0,9999 3,720
0,66 0,412 0,84 0,994 0,99999 4,265
0,67 0,440 0,85 1,036
По тексту используются также обозначения су =о ф 1 ((1 + 'У)/2) , т. е. су == (1+1)/2,
И t o == ф l(а) Т.е. t o == <:o == (I o; при этом t O / 2 == CI o'
1) Верхарн Эмиль (1855 1916) бельrийский поэт и npaMaтypr.
574
Прuложенuе
2. Распределение Пуассона
ао )"k
Значения функции Е k! е Л
k=ж
0,1 0,2 0,3 0,4 0,5 0,6
О 1,000 1,000 1,000 1,000 1,000 1,000
1 0,095 0,181 0,259 0,330 0,394 0,451
2 005 018 037 062 090 122
3 001 003 008 014 023
4 001 002 003
0,7 0,8 0,9 1,0 2,0 3,0
О 1,000 1,000 1,000 1,000 1,000 1,000
1 0,503 0,551 0,593 0,632 0,865 0,950
2 156 191 228 264 594 801
3 034 047 063 080 32З 577
4 006 009 014 019 143 353
5 001 001 002 004 053 185
6 001 018 084
7 005 034
8 001 012
4,0 5,0 6,0 7,0 8,0 9,0
О 1,000 1,000 1,000 1,000 1,000 1,000
I 0,982 0,993 0,998 0,999 1,000 1,000
2 908 960 983 924 0,997 0,999
3 762 875 938 970 986 994
4 567 735 849 918 958 979
5 371 560 715 827 900 945
6 215 384 554 699 809 884
7 111 238 394 550 687 793
8 051 IЗЗ 256 401 547 676
9 021 068 153 271 408 544
10 008 032 084 170 283 413
11 003 014 043 099 184 294
12 001 005 020 053 112 197
13 002 008 027 068 124
14 001 004 013 034 074
15 001 006 017 042
Прuложенuе 575
4,0 5,0 6,0 7,0 8,0 9,0
16 001 002 008 022
17 001 004 011
18 002 005
19 001 002
20 001
3, Биномиальное распределение
95 % доверитеЛЬНblе пределы (81, (2) дIIЯ лараметра 8:
РеС8! < (J < 82) == 0,95.
4 5 6 7 8 9 10 11 12
О 0,98 0,84 0,71 0,60 0,52 0,46 0,41 0,37 0,34 0,31 0,29 0,27
0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00
1,00 0,99 0,91 0,81 0,72 0,64 0,58 0,53 0,48 0,45 0,41 0,39 0,36
0,03 0,01 0,01 0,01 0,01 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00
2 1,00 0,99 0,93 0,85 0,78 0,71 0,65 0,60 0,56 0,52 0,48 0,45 0,43
0,16 ОМ 0,07 О.os 0,04 0,04 0,03 0,03 0,03 0,02 0,02 0,02 0,02
3 1,00 0,99 0,95 0,88 0,82 0,76 0,70 0,65 0,61 0,57 0,54 0,51 0,48
0,29 0,19 0,15 0,12 0,10 0,09 0,08 0,07 0,06 0,06 0,05 0,05 0,04
4 1,00 1,00 0,96 0,90 0,84 0,79 0,74 0,69 0,65 0,61 0,58 0,55 0,52
0,40 0,29 0,22 0,18 0,16 0,14 0,12 0,11 0,10 0,09 0,08 0,08 0,07
5 1,00 1,00 0,96 0,92 0,86 0,81 0,77 0,72 0,68 0,65 0,62 0,59 0,56
0,48 0,36 0,29 0,25 0,21 0,19 0,17 0,15 0,14 0,13 0,12 0,11 0,10
6 1,00 1,00 0,97 0,93 0,88 0,83 0,79 0,75 0,71 0,68 0,65 0,62 0,59
0,54 0,42 0,35 0,30 0,26 0,23 0,21 0,19 0,18 0,16 0,15 0,14 0,13
7 1,00 1,00 0,97 0,93 0,89 0,85 0,81 0,77 0,73 0,70 0,67 0,64 0,62
0,59 0,47 0,40 0,35 0,31 0,28 0,25 0,23 0,21 0,20 0,18 0,17 0,16
8 1,00 1,00 0,98 0,94 0,90 0,86 0,82 0,79 0,75 0,72 0,69 0,67 0,64
0,63 0,52 0,44 0,39 0,35 0,32 0,29 0,27 0,25 0,23 0,22 0,20 0,19
9 1,00 1,00 0,98 0,95 0,91 0,87 0,84 0,80 0,77 0,74 0,71 0,69 0,66
0,66 0,56 0,48 0,43 0,39 0,35 0,32 0,30 0,28 0,26 0,24 0,23 0,22
576 Прuложенuе
12
10 1,00 1,00 0,98 0,95 0,92 0,88 0,85 0,82 0,79 0,76 0,73 0,70 0,68
0,69 0,59 0,52 0,46 0,42 0,38 0,35 0,33 0,31 0,29 0,27 0,26 0,24
11 1,00 1,00 0,98 0,95 0,92 0,89 0,86 0,83 0,80 0,77 0,74 0,72 0,69
0,72 0,62 0,57 0,49 0,45 0,41 0,38 0,36 0,34 0,32 0,30 0,28 0,27
12 1,00 1,00 0,98 0,96 0,93 0,90 0,87 0,84 0,81 0,78 0,76 0,73 0,71
0,74 0,64 0,57 0,52 0,48 0,44 0,41 0,38 0,36 0,34 0,32 0,31 0,29
Приме'lQние. Значения 82 набраНbI в первых строках, значения 81 ОО вторых.
2
4. РаспреАеление Х (n)
х;, "
Квантили распределения: р == 2n/2r n/2) / хn/2 lе ж/2 dx
о
0,999
1 0,016 0,148 0,455 1,07 2,71 3,84 6,63 10,8
2 0,211 0,713 1,39 2,41 4,61 5,99 9,21 13,8
3 0,584 1,42 2,37 3,67 6,25 7,82 11,3 16,3
4 1,06 2,20 3,36 4,88 7,78 9,49 13,3 18,5
5 1,61 3,00 4,35 6,06 9,24 11,1 15,1 20,5
6 2,20 3,83 5,35 7,23 10,6 12,6 16,8 22,5
7 2,83 4,67 6,35 8,38 12,0 14,1 18,5 24,3
8 3,49 5,53 7,34 9,52 13,4 15,5 20,1 26,1
9 4,17 6,39 8,34 10,7 14,7 16,9 21,7 27,9
10 4,87 7,27 9,34 11,8 16,0 18,3 23,2 29,6
11 5,58 8,15 10,3 12,9 17,3 19,7 24,7 31,3
12 6,30 9,03 11,3 14,0 18,5 21,0 26,2 32,9
13 7,04 9,93 12,3 15,1 19,8 22,4 27,7 34,5
14 7,79 10,08 13,3 16,2 21,1 23,7 29,1 36,1
15 8,55 11,7 14,3 17,3 22,3 25,0 30,6 37,7
16 9,31 12,6 15,3 18,4 23,5 26,3 32,0 39,3
17 10,09 13,5 16,3 19,5 24,8 27,6 33,4 40,8
18 10,9 14,4 17,3 20,6 26,0 28,9 34,8 42,3
19 11,7 15,4 18,3 21,7 27,2 30,1 36,2 43,8
20 12,4 16,3 19,3 22,8 28,4 31,4 37,6 45,3
Приложение 577
0,3 0,5 0,7 0,9 0,95 0,99 0,999
21 13,2 17,2 20,3 23,9 29,6 32,7 38,9 46,8
22 14,0 18,1 21,3 24,9 30,8 33,9 40,3 48,3
23 14,8 19,0 22,3 26,0 32,0 35,2 41,6 49,7
24 15,7 19,9 23,3 27,1 33,2 36,4 43,0 51,2
25 16,5 20,9 24,3 28,2 34,3 37,7 44,3 52,6
26 17,3 21,8 25,3 29,2 35,6 38,9 45,6 54,1
27 18,1 22,7 26,3 30,3 36,7 40,1 47,0 55,5
28 18,9 23,6 27,3 31,4 37,9 41,3 48,3 56,9
29 19,8 24,6 28,3 32,5 39,1 42,6 49,6 58,3
30 20,6 25,5 29,3 33,5 40,3 43,8 50,9 59,7
Прuмечанuе. При больших n (n> 30) для вычисления квантилей х;.п можно исполь
зовать приближенное соотношение Х;,п:::: (р + v'2n"=I//2, rде (р дано D табл.l.
5. Распредепение Стьюдента S(n)
(n+ 1) I
r р.П ( 2) (n+I)/2
К""""" р","р,,""". Р (n) J 1 + : "'
vrn r oo
2
0,950 0,975 0,990 0,995
1 3,078 6,314 12,706 31,821 63,657
2 1,886 2,920 4,303 6,965 9,925
3 1,638 2,353 3,182 4,541 5,841
4 1,533 2,132 2,776 3,747 4,604
5 1,476 2,015 2,571 3,365 4,032
6 1,440 1,943 2,447 3,143 3,707
7 1,415 1,895 2,365 2,998 3,499
8 1,397 1,860 2,306 2,896 3,355
9 1,383 1,833 2,262 2,821 3,250
10 1,372 1,812 2,228 2,764 3,169
11 1,363 1,796 2,201 2,718 3,106
12 1,356 1,782 2,179 2,681 3,055
13 1,350 1,771 2,160 2,650 3,012
14 1,345 1,761 2,145 2,624 2,977
15 1,341 1,753 2,131 2,602 2,947
16 1,337 1,746 2,120 2,583 2,921
578 Прuложенuе
0,900 0,950 0,975 0,990 0,995
17 1,333 1,740 2,110 2,567 2,898
18 1,330 1,734 2,101 2,552 2,878
19 1,328 1,729 2,093 2,539 2,861
20 1,325 1,725 2,086 2,528 2,845
21 1,323 1,721 2,080 2,518 2,831
22 1,321 1,717 2,074 2,508 2,819
23 1,319 1,714 2,069 2,500 2,807
24 1,318 1,711 2,064 2,492 2,797
25 1,316 1,708 2,060 2,485 2,787
26 1,315 1,706 2,056 2,479 2,779
27 1,314 1,703 2,052 2,473 2,771
28 1,313 1,701 2,048 2,467 2,763
29 1,311 1,699 2,045 2,462 2,756
30 1,310 1,697 2,042 2,457 2,750
ПримеЧQНUJI.
1. Для малblХ значений р квантили tp,n находятся по формуле tp,n ;:::: tl p,,,.
2. При n > 30 можно использовать приближенное соотношение t p ,,, ;:::: (р, rде (р
дано в табл. 1.
6. Распределение Снедекора S(n.. n2)
Значения функции Рр, п" nj:
( nl + n 2 ) F.
( n ) ",/2 r P J 'n"n! ( N ) (n,+n,)/2
р == .....!. x",/2 I 1 + .....!.Х dx
n2 r ( I ) r ( 2 ) О n2
при р == 0,95 ир == 0,99. "ЛеВblе. rpаНИЦbl доверитеЛЬНblХ интервалов находятся
из условия FJ p,nl'''! == Pp !,,,,
100
161 200 216 225 234 239 242 244 248 252 253
4052 4999 5403 5625 5859 5981 6056 6106 6208 6302 6334
2 18,51 19,00 19,16 19,25 19,33 19,37 19,39 19,41 19,44 19,47 19,49
98,49 99,01 99,17 99,25 99,33 99,36 99,40 99,42 99,45 99,48 99,49
3 10,13 9,55 9,28 9,12 8,94 8,84 8,78 8,74 8,66 8,58 8,56
34,12 30,81 29,46 28,71 27,91 27,49 27,2"3 27,05 26,69 26,35 26,23
При ложе ни е 579
6 8 ]0 12 20 50 100
4 7,71 6,94 6,59 6,39 6,16 6,04 5,96 5,9] 5,80 5,70 5,66
21,20 18,00 16,69 15,98 15,2\ ]4,80 ]4,54 14,37 ]4,02 ]3,69 13,57
5 6,6] 5,79 5,41 5,19 4,95 4,82 4,74 4,68 4,56 4,44 4,40
]6,26 13,27 12,06 11 ,39 10,67 10,27 10,05 9,89 9,55 9,24 9,]3
6 5,99 5,14 4,76 4,53 4,28 4,15 4,06 4,00 3,87 3,75 3,71
13,74 ]0,92 9,78 9,15 8,47 8,10 7,87 7,72 7,39 7,09 6,99
8 5,32 4,46 4,07 3,84 3,58 3,44 3,34 3,28 3, ]5 3,03 2,98
1] ,26 8,65 7,59 7,0] 6,37 6,03 5,82 5,67 5,36 5,06 4,96
10 4,96 4,10 3,7] 3,48 3,22 3,07 2,97 2,91 2,77 2,64 2,59
10,04 7,56 6,55 5,99 5,39 5,06 4,85 4,71 4,4\ 4,12 4,0]
12 4,75 3,88 3,49 4,26 3,00 2,85 2,76 2,69 2,54 2,40 2,35
9,33 6,93 5,95 5,4] 4,82 4,50 4,30 4,]6 3,86 3,56 3,46
20 4,35 3,49 3,10 2,87 2,60 2,45 2,35 2,28 2,12 1,96 1,90
8,]0 5,85 4,94 4,43 3,87 3,56 3,37 3,23 2,94 2,63 2,53
30 4,17 3,32 2,92 2,69 2,42 2,27 2,]6 2,09 1,93 1,76 1,69
7,56 5,39 4,51 4,02 3,47 3,17 2,98 2,84 2,55 2,24 2,13
50 4,03 3,]8 2,79 2,56 2,29 2,]3 2,02 1,95 1,78 ],60 ] ,52
7,]7 5,06 4,20 3,72 3,]8 2,88 2,70 2,56 2,26 ],94 1,82
100 3,94 3,09 2,70 2,46 2,19 2,03 1,92 1,85 1,68 1,48 1,39
6,90 4,82 3,98 3,5] 2,99 2,69 2,5] 2,36 2,06 ],73 1,59
200 3,89 3,04 2,65 2,41 2,\4 1,98 \,87 1,80 ],62 1,42 1,32
6,76 4,71 3,88 3,4] 2,90 2,60 2,4] 2,28 1,97 1,62 \ ,48
1000 3,85 3,00 2,61 2,38 2,10 1,95 ],84 ] ,76 1,58 1,36 1,26
6,66 4,62 3,80 3,34 2,82 2,53 2,34 2,20 1,89 1,54 1,38
Примечание. Значения Р О ,95; п,. П2 набраны в первых строках, значения Р О ,99; п" П2 во
вторых.
7. Критерий Колмоrорова
Значения функции Ар: р == P(Dn == sup IFn(x) F(x)1 > Ар)
z
0,0]
1 0,950 0,975 0,995 ]9 0,271 0,301 0,36]
2 776 842 929 20 265 294 352
580
Прuложенuе
I 0,10 0,05 0,01 I 0,10 0,05 0,01
3 636 708 829 25 238 264 317
4 565 624 734 30 218 242 290
5 509 563 669 35 202 224 269
6 468 519 617 40 189 210 252
7 436 483 576 45 179 198 238
8 410 454 542 50 170 188 226
9 387 430 513 55 162 180 216
10 369 409 489 60 155 172 207
11 352 391 468 65 149 166 199
12 338 375 449 70 144 160 192
13 325 361 432 75 139 154 185
14 314 349 418 80 135 150 179
15 304 338 404 85 131 145 174
16 295 327 392 90 127 141 169
17 286 318 381 95 124 137 165
18 279 309 371 100 121 134 161
8. Критерий Смирнова
Значения вероятности P{Dnn :<; k/n), rде Dnn == suplF 1n (х) Р2п{Х) 1.
х
11
1 1,000
2 0,667 1,000
3 400 0,900 1,000
4 229 771 0,971 1,000
5 127 643 921 0,992 1,000
6 069 526 857 974 0,998 1,000
7 037 425 788 947 992 0,999 1,000
8 020 340 717 913 981 998 1,000 1,000
9 01\ 270 648 874 966 993 0,999 1,000 1,000
10 006 213 582 832 948 988 998 1,000 1,000 1,000
11 003 167 521 789 925 979 996 0,999 1,000 1,000 1,000
12 002 131 464 744 900 969 992 999 1,000 1,000 1,000
13 001 102 412 700 874 956 987 997 1,000 \,000 1,000
14 000 079 365 657 845 941 981 995 0,999 1,000 1,000
15 000 062 322 614 816 925 974 992 998 1,000 1,000
16 000 048 284 574 785 907 965 989 997 1,000 1,000
17 000 037 249 535 755 888 955 984 995 0,999 0,999
18 000 028 219 497 725 868 944 979 993 998 999
Прuложенuе
581
1 2 3 4 5 6 7 8 9 10 11
19 000 022 192 462 694 847 932 973 991 997 999
20 000 017 168 429 664 825 919 966 988 996 999
21 000 013 147 397 635 804 905 959 984 995 998
22 000 010 128 368 606 782 891 951 980 993 998
23 000 008 112 340 578 759 876 942 975 991 997
24 000 006 098 314 551 737 860 932 970 988 996
25 000 004 085 290 525 715 844 922 964 985 994
26 000 003 074 267 499 693 828 911 958 982 993
27 000 003 064 246 474 671 811 900 952 978 991
9. Равномерно распределеННI.lе случайные числа
6548 1 I 76 74 17 4685 0950 5804 77 69 7445
80 12 4356 35 17 7270 80 15 4531 8223 7445
7435 0998 1777 4027 72 14 4323 6002 10 19
6991 6268 0366 2522 9148 3693 68 72 0337
0989 3205 05 14 2256 85 14 4642 7567 8893
3407 2768 5036 6973 61 70 6581 3398 8556
4557 1824 0635 3034 26 14 8679 9074 39 82
0205 1656 9268 6657 48 18 7305 3852 4789
05 32 5470 4890 55 35 7548 2846 8287 0975
0652 9647 78 35 8083 4282 6093 5203 4476
22 10 9405 5860 9709 3433 5050 0739 9823
5072 5682 4829 4052 4201 5277 5678 51 98
1374 67 00 78 18 4754 06 10 6871 1778 1749
3676 6679 51 90 3647 6493 2960 91 10 6242
91 82 6089 28 93 78 56 1368 2347 8341 1329
6847 9276 8646 1628 3554 9475 0899 2345
2694 0368 5870 2973 41 35 53 14 0333 4045
85 15 7479 5432 9792 6575 5760 0408 81 19
11 10 0020 4012 8607 4697 9664 4894 3937
582 Прuложенuе
1650 5344 8440 21 95 2565 4365 1770 8293
1009 7325 3376 5201 3586 3467 3548 7607
3754 2048 0564 8947 4296 2480 5240 3732
0842 2689 53 19 6450 9303 2320 9025 6047
9901 9025 2909 3767 07 15 3831 13 11 6509
1280 7999 7080 1573 6147 6403 2366 53 53
8095 9091 17 39 2927 4945 6606 5747 17 56
2063 6104 0200 8229 1665 31 06 0108 0582
1595 3347 6435 08 03 3606 8526 9776 02 89
8867 6743 9704 4362 7659 6357 3321 35 75
9895 1168 77 12 17 17 6833 7379 6457 5376
При.мечанuя.
1. Приведенные в таблице цифры можно рассматривать как реализации незави
симbIX одинаково распределенных случайных величин, принимающих значения
О, 1, . . . , 9 с одннаковой вероятностью IO l
2. Если взять из этой таБЛНЦbl непересекающиеся rpYnnbI ИЗ, скажем, четырех цифр
бl, б2, аз, а4 и образовать из ник 'Iисла вида 0,а 1 а,(а з а 4 ' то эти числа можно pac
сматривать в качестве значений (с точностью 10 ) равномерно распределеннык
на [О, 11 случайных величнн.
10. Нормально распределениые Лf(О, 1) случайные числа
0,486 0,856 O,491 1,983 I,787 0,261
0,256 0,2]2 0,2 ]9 0,779 0,105 O,357
0,065 0,415 O,169 0,313 1,339 1,827
1,147 O,121 1,096 0,181 1,041 0,535
0,]99 0,246 1,239 2,574 0,279 2,056
1,237 1,046 o ,508 1,630 0,]46 0,392
1,384 0.360 0,992 0,116 1,698 2,832
0,959 0,424 0,969 1,141 1,041 0,362
0,731 1,377 0,983 1,330 1,620 I,040
0,717 O,873 1,096 1,396 1,047 0,089
1,805 2,008 1,633 0,542 0,250 O,166
],186 1,180 1,114 0,882 1,265 0,202
0,658 1,141 1,151 1,210 0,927 0,425
0,439 0,358 1,9З9 0,891 0,227 0,602
1,З99 0,230 0,385 0,649 O,577 0,237
Прuложенuе 583
0,032 0,079 0,199 0,208 1,08З O,219
0,151 0,376 0,159 0,272 0,31З 0,084
0,290 0,902 2,273 0,606 0,606 0,747
0,873 0,437 0,041 0,307 0,121 0,790
0,289 0,513 1,132 2,098 0,921 0,145
0,291 1,221 1,119 0,004 0,768 0,079
2,828 0,439 0,792 1,275 0,375 1,656
0,247 1,291 0,063 1 ,793 O,513 0,344
0,584 0,541 0,484 0,986 0,292 0,521
0,446 1,661 1,045 1,363 1Щ6 2,990
0,034 2,127 0,665 0,084 0,880 1,473
0,234 O,656 0,340 0,086 0,158 0,851
0,736 1,041 0,008 0,427 0,831 0,210
1,206 0,899 0,110 O,528 0,813 1,266
0,49] 1,114 1,297 1 ,433 1,345 0,574
1,334 1,278 0,568 0,109 0,515 0,566
0,287 O,144 0,254 0,574 0,451 1,181
0,161 0,886 0,921 O,509 1,410 0,518
1,346 0,193 I,202 0,394 1,045 0,843
1,250 0,199 0,288 1,810 1,378 0,584
2,923 0,500 0,630 O,537 0,782 0,060
1,190 O,318 0,375 I,941 0,247 0,491
0,192 O,432 I,420 0,489 I,711 I,186
0,942 1,045 O,151 0,243 0,430 0,762
1,216 0,733 0,309 0,531 0,416 1,541
0,499 0,431 1,705 1,164 0,424 0,444
0,665 0,135 0,145 0,498 0,593 0,658
0,754 0,732 0,066 1,006 0,862 0,885
0,298 1,049 1,810 2,885 0,235 0,628
1,456 2,040 O,124 0,196 0,853 0,402
0,593 0,993 O,106 0,116 0,484 1,272
1,127 1,407 1,579 1,616 1,458 1,262
O,142 0,504 0,532 1,381 0,022 0,281
0,023 0,463 0,899 0,394 0,538 1,707
0,777 0,833 0,410 0,349 1,094 0,580
0,241 0,957 1,885 0,371 2,830 0,238
0,022 0,525 0,255 0,702 0,953 0,869
0,853 1,865 O,423 O,973 1,016 1,726
O,501 0,273 0,857 0,465 1,691 0,417
0,439 0,035 0,260 0,120 0,558 0,056
584 Приложение
0,627 0,561 0,471 I,029 2,O15 O,594
1,108 2,357 0,310 0,479 O,623 1,047
1,726 1,956 0,610 2,709 0,699 I,347
0,524 O,281 0,220 0,057 0,481 0,996
O,573 0,932 0,738 о,ЗОО O,586 1,023
0.579 0,551 0,359 0,326 0,884 O,298
O,120 0,418 O,094 1,114 0,457 1,064
0,191 0,074 1,501 1,068 0,798 0,162
0,071 0,524 0,031 О,772 O,768 0,129
3.001 0,479 0,402 0,226 0,023 1,204
1,066 1,097 1,752 0,329 1,256 0,318
0,736 0,916 0,291 0,085 1,701 1,087
O,342 1,222 0,933 0,130 0,674 0,899
O,188 1,153 0,450 0,244 0,072 1,028
1,395 1,298 0,512 O,882 0,490 1,304
1,531 0,349 0,059 0,415 1,084 0,958
0,443 0,292 0,539 1,382 0,318 0,243
1,409 O,883 0,229 0,129 0,367 0,095
1,730 O,056 0,078 2.361 O,992 I,488
0,266 0,757 0,194 1,078 0,529 0.з61
Законы статистики везде одинаковы, продолжал Николай Пет
рович солидно. Утром, например, zocmeu бывает меньше, потому
что публика еще исправно; но чем больше солнце поднимается
к зениту, тем наплыв делается сильнее. И, наконец, ночью, по вы-
ходе из театров это почти целая орzия!
И заметьте, пояснил Семен Иванович, каждый день, в одни
и те же промежутки времени, цифры Bcezaa одинаковые. Нолеба
ний никаких! Такава незыблемость законов статистики!
М. Е. Салтыков-Щедрин 2)
Случай всеzда именует себя Боzом, Kozaa он
не хочет подписываться своим именем.
Д, Франс 3)
2) Салтыков Щедрин Михаил Евrpафовнч (IB26 1889) велнкий русский писатель сатирик.
3) Франс Анатоль (Hacr. имя Анатоль Франсуа Тибо) (1844 1924) франuузский писатель,
нобелевский лауреат (1921).
Литература
1. Андерсон Т. Введение в мноrомерный статистический анализ. М.: Физматrиз, 1963.
2. Бuкел П., Доксам К. Математическая статистика. Т 2. М.. ФиС, 198з.
З. Большев Л. н., СмиРllов Н. В. Таблицы математической статистики. М.: Наука, 1983.
4. Боровиков В. П. ИвчеllКО r If. Проrнозирование в системе STAT1SТICA в среде
Windows. М.. ФиС, 2006.
5. Боровков А. А. МатсмаТИ'lеская статистика. М.: Издательство Физико матемаТИ'lе-
ской литературы, 2007.
6. Вальд А. Последовательиый анализ. М.: Физмапиз, 1960.
7 [аек Я., Шuдак З. Тсория ранroвых критериев. М.: Наука, 1971.
8. [иедellКО Б. В. Курс тсории вероятностей. 9 e изд. М.: Издатсльство ЛКИ/URSS,
2007.
9. Ивченко r и., rлибо'/еllКО А. Ф., Иванов В. А., Медведев Ю. И. Статистический анализ
дискретных случайных послсдовательностей. М.. МИЭМ, ]984.
10. Ивченко r и. Медведев Ю. И. Математическая статистика. 2 e изд. М.: Высшая
школа, 1992.
11. Ивченко {. и., Медведев Ю. И. Чистяков А. В. Задачи с решениями по математи
'IССКОЙ статистике. М.: Дрофа, 2007.
12. Ке//далл м., Стьюарт А. Статистические выводы и связи. М.: Наука, 1973.
13. Кнут Д. Искусство проrpаммирования. М.: Мир, 2004.
14. Колчин В. Ф., СевастЬЯllов Б. А. Чистяков В. П. Случайные размещеиия. М.: Наука,
1976.
15. Крамер r Математические методы статистики. М.. Мир, 1975.
16. Леман Э. Проверка статистических rипотез. М.: Наука, 1979.
17. ЛоулиД, Максвелл А. Факторный анализ как статистический метод. М.: Мир, 1967.
18. Налимов В. В. Теория эксперимента. М.: Наука, 1971.
19. Окунь Я. Факторный анализ. М.: Статистика, 1974.
20. Пойа Д Математика и правдоподобные рассуждения. М.: Книжный дом .Либро-
KOM»/URSS, 2010.
21. Рао К. Р. Лине"ныс стаТИСТИ'lеские методы и их применения. М.: Наука, 1968.
22. Себер Дж. Линейный реrрессионный анализ. М.: Мир, 1980.
23. Секей r Парадоксы в теории вероятностей и математической статистике. М.: Мир,
1990.
24. Уилкс С. МатемаТИ'lеская статистика. М.: Наука, 1967.
25. Феллер В. Введсние в теорию вероятностей и ее приложения. Т. 1, 2. М.: Книжный
дом (.Либроком.>/URSS, 2010.
26. Холле//дер М., ВульфД Непараметрические методы статистики. М.: Фи С, 1983.
27. Чистяков В. П. Курс тсории вероятностей. 7 e изд. М.: Дрофа, 2007
28. Ширяев А. Н. Статистический последовательный анализ. М.: Наука, 1976.
29. Billings/ey Р. Statistical inference for Markov processes. The University of Cllicago Press,
1961.
3830...1748
Путеводитель по моделям
в примерах и задачах
Смелость начало дела, но случай хозяин конца.
Демокрит 1)
Назначение llaHHoro путеводителя помочь читателю быстро наiiти в тексте
нужное место, rlle доказывается либо формулируется тот или иной конкретный факт
(результат), относящийся к конкретной модели (в скобках указаны соотвстствующие
координаты, при этом, например, «упр. 3.10 означает упражнение 10 к rл. 3). Модели,
как правило, занумерованы в той последовательности, в которой они встречаются в TeK
сте, также в такой последовательности перечисляются и относящиеся к ним фаКТbI.
1. Бернуллиеsская модель Bi(l, р)
определение и свойства (9 1.1, п. 1, упр. ].1)
реализация в урновой схеме (9 1.1. прим. 1 и 2)
моделирование (9 1.3, ".2)
эмпирическая функция распределения для нее (92.1, прим.2)
оценивание доли белых шаров в урне (92.2, прим.3)
эксперимент Бюффона с бросанием монеты (упр. 2.1, 94.2, прим. 1)
обработка эмпирических данных (упр.2.2)
оценивание параметрических функций (93.1, прим. ,упр. 3.10, 3.11)
оптимальность DыБОрО'lllоrо cpellHero при оценивании парамстра (93.1, прим.5)
оптимальная оценка доли белых шаров в урне (93.1, ПрIlМ. 6)
эффективность выбоРО'lНоrо cpellHero (93.2, п. 2)
достаточная статистика для нее (93.2, табл. 2)
о. м. п. пара етра (93.2, табл. 2)
асимптотический доверительный интервал для параметра (93.5, прим. 17, упр. 3.70)
байесовская оцеика параметра (93.6, прим. 11, упр. 3.77)
минимаксная оценка параметра (93.6, прим. 12)
доверительны интервал для пара метра (93.8, прим. 4)
критерий соrласия х 2 для нее ( пр. 4. 1, 4.2)
критерий Неймана Пирсона (95.2, прим. 4, упр. 5.4)
р. н. м. к. при односторонней альтернативе (95.3, п. 1)
КОП для rипотеЗbl однородности (95.4, прим. 8)
решающие правила в ней (97.1, прим. 1, упр. 7.1,7.2,7.3).
1) Демокрит (ОК. 460 [. до Н. Э. roд смерти неизв.) древнеrреческий фи,lосоФ атомист.
Путеводитель по моделям в примерох и задачах
587
2. Бииомиальная модель Bi(n, р)
определение и свойства ( I.I, п. 1, ynp.I.2, 1.3, 1.4,2.25)
реализация в урновой схеме ( I.I, прим. 1 и 2)
дни рождения, эмпирические данные ( 1.1, прим.3)
моделирование ( 1.3, п.2)
аппроксимация распределением Пуассона (упр. 1.12)
условные распределения компонент полиномиальноro вектора (упр. 1.18)
моменты (упр. 1.19)
нормальная аппроксимация, теорема Муавра Лапласа (упр. 1.33)
связь с распределением Маркова Пойа (упр. 1.44)
эмпирические данные в опыте с бросанием костей ( 2.2, прим.2)
обработка эмпиричсских данных (упр. 2.3, 2.8, 2.9)
информация Фишера для нее ( 3.2, табл.1)
эффективная оценка для параметра (Р.2, табл. 2)
достаточ ная статистика для нее ( 3.2, табл. 2, упр. 3.31)
оценивание параметрических функций ( 3.4, прим. 7, упр. 3.12, 3.31)
о. м. п. параметра ( 3.2, табл. 2)
преобразование о. м. п., стабилизирующее дисперсию (упр, 3.55)
проверка rипотезы соrласия ( 4.2, при t. 4, упр. 4.7,4.15)
р. н. м. к. при односторонней альтернативе ( 5.3, прим. 1, упр. 5.8)
критерий Неймана Пирсона (упр. 5.5)
л. н. м. несмещенный критерий (ynp.5.14)
КОП для простой rипотезы (упр. 5.22)
проrноз в ней (упр. 6.23,6.24)
решающие правила IJ ней (упр.7.4, 7.9)
95% Hыe доверительные интервалы для пара метра (прилож. табл. 3).
Э. Отрицательная биномиальная модель Вi (r, р)
определениеисвойства( 1.1,п.2,упр.I.5, 1.6, 1.7,1.8, 1.14, 1.41,2.25)
как частный случай модели CTeneHHOro ряда ( 1.1, ".8)
моделирование ( 1.3, п.3)
аппроксимauия распределением Пуассона (ynp.I.13)
оценивание параметрических функций ( 3.1, прим. 3, 3.4, прим.2)
информация Фишера для нее ( 3.2, табл. 1)
эффективная оценка для параметрической функции ( 3.2, табл. 2)
достаточная статистика ДIIЯ иее ( 3.2, табл. 2)
о. м. п. параметра (упр. 3.45)
асимптотический доверительный интервал ДIIИ параметра (упр. 3.71)
байесовская оценка параметра (ynр. 3.78)
р. н. м. к. при одиосторонней альтернативе ( 5.3, прим. 2, упр. 5.9).
38"
588
Путеводитель по моделям в примерах и задачах
4. rеометрическая модель Вi(l, р)
определение и СUОЙСТIJа ( 1.1, п. 2)
моделирование (9 1.3, п. 3)
достаточная статистика МЯ нее (93.2, табл. 2)
о. м. п. параметра и основанный на ней доверительный ннтервал (93.5, прим. 16)
улучшенная оценка параметра (93.7, прим.2)
оценивание параметрической функции (упр. 3.15)
р. н. м. к. при односторонней альтернативе (95.3, прим. 2)
критерий Неймана Пирсона (упр. 5.6)
решающие правила в ней (упр. 7.5).
5. Пуассоновскзя модель П(.\)
определение и свойства (9 1.1, п. 3, упр. 1.9, 1.10, 1.11. 1.13, 1.14, 1.41, 2.25)
дни рождения, аппроксимация (9 1.1, прим.3)
усечение в нуле (91.1, п.8)
как частный случай модсли CTeneHHOro ряда (9 1.1, п.8)
моделирование (9 1.3, п.5)
теорема Пуассона дJJiI биномиальноro распределения (упр. 1.12)
аппроксимация дJJЯ полиномиальноrо распределения (упр. 1.34, 1.35)
оцениuание парамеТРИ'lеских функций (93.1, пр им. 2, 93.4, прим. 1, ynp.3.13,
3.14,3.32, 3.33)
информация Фишера дJJЯ нее (93.2, табл. 1)
эффективность выБОРО'iноrо среднеrо (93.2, табл. 2)
достаточная статистика дJJЯ нее (93.2, табл. 2, упр. 3.32)
о. м. п. параметра (93.2, табл. 2)
о. м. п. для yce'leHHoro D нуле распределения (93.5, прим. 9)
доверительные интервалы для параметра (93.5, прим. 15, 93.8, прим. 5)
преt;6разование о. м. п., стабилизирующее дисперсию (упр. 3.55)
метод моментов для двоiiноrо распределения Пуассона (упр. 3.75)
байесовская оценка параметра (упр. 3.79, 3.80)
проверка rипотезы соrласия ДIIЯ нес (94.2, ПрIlМ. 5, УПр. 4.13, 4.14)
rипотеза одородноети для нее (упр. 4.21, 95.4, прим. 9)
критерий Неймана Пирсона (95.2, прим. 5)
р. н. м. к. при односторонней альтернативе (95.3, п. 1)
л. н. м. несмещенный критерий (упр. 5.15)
КОП ДЛЯ простой rипотезы (упр. 5.23)
проrноз в ней (упр. 6.23, 6.24)
решающее правило в ней (упр. 7.6)
зна'lения функuии Р{( ;;3 х} (прилож. табл. 2).
Путеводитель по моделям 8 примерах U задачах
589
б, rиперrеометрическая модель Н(а(, az, n)
определение и свойства, реализация в УРНОIIОЙ схеме ( 1.1, п.4)
мноrомерный вариант ( 1.1, п.7)
моменты (упр. 1.15)
аппроксимация биномиалЬНblМ распределением (упр. 1.16)
о. м. п. для параметра а al + а, (упр. 1.17)
р. н. м. к. при односторонней ЭUJьтернаТИllе (упр. 5.11)
проrноз в ней (96.6, прим.4).
7. Модеяь Маркова Пойа МП(n; а(. az. с)
определение и свойства, реЭUJИЗация в урновой схеме ( 1.1, п. 5)
Мllоrомерный вариант ( I.I, п. 7, ynp.I.62)
как смесь БиномиэuJьныIx распределений (У'lР. 1.44)
оцениваНllе параметра Р аI/(Й' + а1) (упр.3.2)
оценивание MHoroMepHoro параметра (упр. 3.3)
8. Полиномиальная модель М(n; Р(. . .. ,PN)
определение и свойства ( I.I, п.6, ynp.I.18, 1.21)
моделиро ание ( I.3, ".4)
моментЬ! (упр. 1.19, 1.20)
связь с пуассоновским распределением (упр. 1.22)
случайное число испытаниЙ (упр. 1.23)
центральная предельная теорема для нее (упр. 1.33)
пуассоновская аппроксимация (упр. 1.34, 1.35)
связь с распределением Маркона Пойа (упр. 1.62)
эмпирическая ФУНКlЩЯ распределения для нее (92.1, прим. 3)
обработка эмпирических данных (упр. 2.4)
информационная матрица для нее ( 3.2, прим. 10)
оценивание параметрическоrо вектора (93.2, прим. 10, упр. 3.7)
оценивание параметрических функций (93.3, прим. 8)
О. м. п. параметрическоro вектора ( 3.5, прим. 12)
асимптотическая доверительная область для параметров (93.5, прим. 18)
байесовская оценка пара метров ( 3.6, прим. 13)
минимаксная оценка параметров (93.6, прим. 13)
о. м. п. пара метра в модели М (п; Р, (О), .,. ,PN(O)) (упр.3.46)
про верка rипотеЗbl в эксперименте Менделя (94.2, прим.2)
проверка rипотезы о равновероятности классов ( 4.2, прим. 3)
критерий соrласия х 2 для нее (упр. 4.3, 4.4, 4.5, 4.6)
критерий соrласия х 2 для сложной rипотеЗbl (упр. 4.11, 4.12)
критерий Неймана Пирсона ( 5.2, прим.6)
КОП для простой rипотеЗbl (9 5.4, при ,'1. 5).
590
Путеводитель по моделям в примерах и задачах
9, Модель cтeneHHoro ряда
определение и свойства (э 1.1, п. 8)
производящая функция и моменты (упр. 1.24, 1.25)
оценивание параметрических функций (э 3.4, п. 1)
о. м. п. параметра (э 3.5, прим.9)
аснмптотический доверительный интервал для параметра (э 3.5, прим. 14)
10. Конечная совокупность
занумерованные элементы, оценивание параметрнческих функций (э 3.4, прим.8
и 9)
оценивание среднеrо, оценки rорвица Томпсона (э 3.9, п. 1)
выборочный контроль (э 3.9, ".2)
оценивание состава (э 3.9, п. 2)
оцеНИll3ние доли белых шаров в урне (упр. 3.1)
проrнозирование в схеме nOBl'OpHOrO выбора (э 6.6, прим.5).
11. Цепь Маркова
определение и моделирование (э 1.3, п.l0, э4.5, ".2)
случайное блужданне (э 1.3, прим. 3 и 4)
обобщенный критерий х 2 дI1Я контроля марковской зависимости (!\ 4.5, п.2)
проверка rипотез (э 5.5)
критерий х 2 дI1Я простой rипотезы (э 5.5, ".2)
критерий х 2 для сложной rипотезы (э 5.5, 11.3)
rипотеза о порядке цепи Маркона (э5.5, прим. 1)
rипотеза о циклическо случайиом блуждании (э 5.5, прим.2 и 3)
КОП для общих параметрических rипотез (э 5.5, п. 4)
критерий однородности (э 5.5, п. 5)
критерии однородности в модели циклическоro блуждания (э 5.5, прим. 4)
оценивание порядка цепи (э 5.5, п. 6).
12. Нормальная модель N(p., /7(2)
опредсление и свойства (введение к rл. \, \.2, п. 1, упр. 1.26, \.27, 1.28)
моделирование ( 1.3, П.6 и 8)
независимость выборочных среднеrо и дисперсии (упр. 1.28)
связь с распределением Коши (упр. 1.48)
сопряженность к нормальному распределению (упр. \.64(5))
распределение выборочной медианы в больших выборках (э 2.4, прим.2)
распределение BepXHcro экстремума в больших выборках (э 2.4, прим. 4)
доверительное оцениваение среднеrо (э 2.5, прим. 1, Э 3.8, прим. 2,
упр. 3.58, 3.60, Э 5.3, прим. 7)
доверительное оцениоаение дисперсии (э 2.5, прим. 1, Э 3.8, прим.3, упр. 3.6\,
Э 5.3, прим.8)
доверительная область для параметров (э 2.5, прим. \)
задача сравнения двух средних (э 2.5, прим. 2, упр. 3.62)
Путеводитель по моделям 8 примерах и задачах
591
доверительный интервал для отношения дисперсий ( 2.5, прим. 3)
таблица доверительных интсрвалов ( 3.8, п. 1)
доверительный интервал для параметра 8 модели N(8, 02) (упр.3.57)
доверительный интервал для параметра 8 модели N(p., (2) (упр.3.59)
асимптотические доверительные интервалы в модели N(p., (2) (упр. 3.68)
обработка эмпирических данных (упр.2.6)
распределение статистики 1/ == (х, х) / ( Vn=J s) (упр.2.42)
асимптотическая нормальность статистики Т п == vn(X /J)/ s (упр.2.44)
оцеНИllание дисперсии модели N (81' 8i) ( 3.1, прим.4)
информация Фишера для нее ( 3.2, табл. 1)
эффективность выорочноrоo среднеrо ( 3.2, прим. 1, табл. 2)
эффективная оценка дисперсии ( 3.2, прим.2 и 3, табл.2)
асимптотическая эффективность выборочной медианы ( 3.2, прим.4)
оптимальная оценка для 82 в модели N(8, (12) ( 3.2, прим.7)
оптимальное оценивание среднеro модели N(8 1 , oi) (93.2, прим.8)
оптимальное оценивание дисперсии модели N(8 1 , 8i) (93.2, прим.9)
информационная матрица для модели N(8 j , 8 ) ( 3.2, прим.9)
достаточные статистики для нее ( 3.2, табл. 2, 3.3, прим. 1)
оценивание теоретической функции распределения ( 3.3, прим. 6 и 7)
оценивание пара метрических функций в модели N(8, (12) (93.4, прим.6)
оценивание параме1l'ических функций в модели N(,L, 82) (93.4, прим, 12,
упр. 3.I7 3.19, 3.34)
оцениваНllе пара метрических функций в модели N(o,oi) ( 3.4, прим. 13,
упр.3.20, 3.34, 3.36)
о. м. п. параметров ( 3.5, прим. 1)
о. м. п, функции распределения (93.5, прим.5)
о. м. п. cpellHero и диспеРСИl1 лоrнормальноro распределения ( 3.5, прим. 7)
сверхэффеКТИlIная оценка параметра модели N(8, 1) ( 3.5, прим. 10)
асимптотический доверительный интервал для функции распределения ( 3.5,
прим.13)
метод моментов для нес (93.6, прим. 1)
модально несмешенная оценка среднеrо ( 3.6, прим.4)
оценка Питмена (эквивариантная) среднеro ( 3.6, прим. 8)
минимаксность выборочноrо среднеrо ( 3.6, прим. (4)
оценивание по цензурированным данным для нее ( 3.6, прим. 15 и (6)
объедlшение оценок ( 3. 7, прим. 1, упр. 3.56)
оценка «складноro ножа» дисперсии ( 3.7, прим. 3)
состоятельная оценка параметра модели N(O, 8\ о> О (упр.3.5)
сравнение оценок дисперсии в модели N(p., 02) (ynp.3.16)
достаточная статистика в модели N(8, "'(82) (упр.3.35)
о. м. п. параметра модели N (/J, 02), асимптотические свойства (упр. 3.41)
592
Путеводитель по моделям в примерах и задачах
О. м. п. парамеrра модели N(8, 28) (упр. 3.42)
преобразование о. м. П., стабилизирующее дисперсию, в модели N(p., 81)
(упр. 3.55)
проrнозирование БУДУЩllХ наблюдений (у пр. 3.67)
байесовская оценка пара метра 8 модели N(8, ь 1 ) (упр. 3.83, 7.12)
критерий соrласия х 1 по rpуппировзнным данным ( 4.2, прим.6)
критерий Колмоrорова (ynp.4.10)
критерий Неймана Пирсона ДЛЯ срсднеro модели N(8, 0'1) ( 5.2, прим. 1)
критерий Неймана Пирсона для дисперсии модели N(p., 81) ( 5.2,
прим.2)
р. н. м. к. при односторонних альтернативах ( 5.3, п. 1)
р. н. м. И л. н. м. несмещенные критерии при двусторонней альтернативе для
модели N(8, 0'1) ( 5.3, прим. 4 и 5)
р. н. м. несмещенный критерий при двусторонней альтернативе ДЛЯ модели
N(p., 82) (УПР. 5.12)
р. н. м. несмещенный К[Jитерий для срсднеrо модели N(8 1 , 8i) при двусторонней
альтернативе ( 5.3, прим. 9)
р. н. м. несмещенный критерий ДЛЯ дисперсии модели N(8 1 , 8i) П[JИ двусторонней
альтернативе ( 5.3, прим. 9)
rнпотеза о равенстве средних доух моделей ( 5.3, прим. 10)
КОП для среднеrо модели N(8), 8 ) ( 5.4, прим. 1)
КОП ДЛЯ дисперсии модели N(8), 8i) ( 5.4, прим.2)
КОП для rипотсзы о равенстве средних ( 5.4, прим. 3 и 6)
КОП ДЛЯ rипотезы о равенстве дисперсий ( 5.4, прим.4 и 7)
критерий Вальда (последовательный) ДЛЯ модели N(8, 0'1) ( 5.6, ПрIIМ. 1)
rипотеза о равенстве дисперсий двух моделей (упр. 5.16)
F критерий однородности для средних ( 6.5, п. 2, упр. 6.21)
метод наименьших квадратов (упр. 6.8 6.11, 6.13 6.15, 6.17 6.19)
решающие правила для нее (УП[J. 7.7)
квантили распределения N(O, 1) (прилож. табл. 1)
реализации случайных N(O, 1) '(исел (ПРI1ЛОЖ. табл. 10).
13. Двумерная нормальная МОАель
N( (P.I, Р.2)' IIp:I CТ2 p {211)
условное марrинальное распределение n ней (упр. 1.65)
асимптотический доверительный интервал для р ( 2.3, п.4)
rипотсза независимости Но р == О ( 2.3, п.4)
обработка эмпирических данных (упр. 2.29)
распределение выборочных моментов (упр. 2.43)
о. м. п. пара метров модели N((O, 0),11;;2 р;211) ( 3.5, прим. 6)
Путеводитель по моделям в при мерах и задачах
593
оценивание коэффициента корреляцин модели N (О, o),II II) (упр.3.43)
проrноз в ней ( 6.6, прим.2).
14. Мноrомернзя нормальная модель N(l:!:.' :Е)
определение и свойства ( 1.2, упр. 1.30)
моменты (упр. 1.29)
линейные преобразования (упр. 1.31, 1.32)
центральная предельная теорема для полиномиальной модели (упр. 1.33)
распределение квадратичных форм (упр. 1.40, 2.38 2.41)
условное марrинальное распределение в ней (упр. 1.66)
о. м. п. ее параметров ( 3.5, прим. 2)
оценка Джеймса Стейна вектора средних ( 3.6, прим. 14)
критерий Неймана Пирсона для вектора средних ( 5.2, прим.3)
критерий для вектора средних, минимизирующий сумму вероятностей ошибок
( 5.2, продолжение прим. 3)
нормальная реrpесия, о. м. п. ее парамс1Т'ОВ ( 6.3, п. 2, упр. 6.4)
доверительный интервал дЛя наклона простой р rреССIIИ ( 6.3, прим. 1)
доверительный эллипс ДJlЯ пара метров простой реrрессии ( 6.3, прим. 1)
доверитсльныii интсрвал ДJlЯ ординаты линии реrреССIIИ ( 6.3, прим.2)
совместные доверитсльные интервалы дЛя коэффициентов реJ1}CССНИ
( 6.3, прим. 3)
rипотеза о наклоне линии реrрессии ( 6.4, прим. 1, упр.6.20)
критерий знаЧllМОСТИ реrрессии ( 6.4, прим.2, упр. 6.22)
rипотеза о параллельности линий реrpессии ( 6.5, п. 1)
дисперсионный анализ при двойной классификации ( 6.5, п.3)
проrноз в ней (упр.6.25)
классификация наблюдений по двум классам ( 7.3)
классификauня наблюдений по k 2 классам ( 7.4)
распределение Уишарта (выборочной ковариационной матрицы) ( 8.3).
15. rамма модель r(a, Л)
определение и свойства ( 1.2, п. 3, упр. 1.36, 1.37, 1.41, 1,43, 2.25)
связь с распределением Дирихле (упр. 1.60)
сопряженность к распределению Пуассона (упр. 1.64(3))
сопряженность к показательному распределению (упр. 1.64(4))
информация Фишера ДJlЯ нее ( 3.2, табл. 1)
эффективная оценка для парамстра а ( 3.2, табл. 2)
достаточная статистика ДJlЯ нее ( 3.2, табл. 2)
оценивание параметрических функций ( 3.4, прим. 10, 11, упр. 3.21, 3.29, 3.34)
метод моментов дЛя нее ( 3.6, прим. 3)
модально несмешснная оценка параметра а ( 3.6, прим.7)
медианно несмешенная оценка пара метра а ( 3.6, прим. 7)
о. м. п. в ней (упр.3.52)
594
Путеводитель по моделям в примерах и задачах
преобразование о. м. п. стабилизирующее дисперсию (упр. 3.55)
асимптотические ДОllерительные интерllалы 11 ней (упр. 3.69)
16. Показатепьная ()кспоненциальная) МОАель r(a, 1)
определение и свойстоа (91.2, ".3)
моделирование ( 1.3, п. 7)
распределение нижнеrо экстремума (упр. 1.39)
связь с распределеНllем Снедекора (упр. 1.54)
связь с распределением Парето (упр. 1.58)
порядковые статистики и спейсинrи (92.4, прим. 1)
распределение верхних экстремумов в больших выборках ( 2.4, прим. 3, упр. 2.36)
обработка эмпирических данных (упр. 2.5)
приведенное к отрезку [8, Ь] распределение [(1, 1), оцеНИllание пара метрических
функций ( 3.4,прим.
оценивание функции надежности ( 3.4, прим. 11)
о. м. п. параметра ( 3.2, табл. 2)
модально несмешенная оценка параметра ( 3.6, прим. 6)
медианно несмещенная оценка параметра ( 3.6, прим. 7)
оценивание пара метра по цензурированным данным (93.6, прим. 17)
состоятельная оценка параметра (упр. 3.5)
доверительный интервал ДlJЯ отношения пара метро о двух моделей (упр.3.63)
доверительный интервал ДlJЯ параметра (упр. 3.65)
байесовская оценка параметра (упр. 3.81)
критерий соrласия х 2 для нее (упр.4.9)
р. н. М. к. при односторонней альтернативс ( 5.3, прим. 3, упр. 5.10)
критерий Неймана Пирсона (ynp.5.1)
р. н. м. несмещенный критерии при двусторонней альтернативе (упр. 5.13)
rипотеза OДHOPOДHOCТII (упр. 5.17)
функция реrpессии (96.6, прим. 1).
17. Двухпараметрическая показательная МОАель W(a, 1, Ь)
определение и свойства (9 1.2, п.8)
достаточная стйтитстика ДЛЯ нее ( 3.3, прим. 2)
оценивание параметрических функuий в модели W(8, 1, 1) (9).4, прим. 4)
о. м. п. параметров (9).5, прим. 4, упр. 3.54)
ОlIТималЬНЬJе несмещенные оценки параметров (упр. 3.39)
доверительный интервал ДlJЯ парамстра модели W(8, 1,1) (упр.3.64)
доверительные интервалы для парамеТРОIl (упр. 3.66)
оценивание параметров по цензурированным данным (упр. 3.76)
несмещенный критерий при двустороннеЙ альтернативе ДlJЯ модели W(8, 1, 1)
(упр. 5.18)
критерии проверки rипотез Hu 81 == 810 И Но 82 == 8 2о для модели W(8i, 1.82)
(упр.5.21).
Путеводитель по моделям 8 примерах и задачах
595
18. Распределение XM KBaApaT х 2 (п) == r(2, П/2)
определение и свойства ( 1.2, п. 3, упр. 1.38)
центральная предельная теорема ДJIЯ Hero (упр. 1.38)
как предельное распределеНllе статистики хи квадрат К. Пирсона ( 4.2, п2)
кнантили (прилож. табл. 4).
19. Равномерная модель и(а, Ь)
определение и свойства ( 1.2, п. 5, упр. 1.45)
преобразование к п()к зательному распределению ( 1.2, прим.1)
преобразование к норМоеЬНОМУ распределению ( 1.2, прим.2)
моделирование ( 1.3, п.6)
совместное распределение и моментЬ! экстремумов (упр. 1.46)
СВЯJь с распределением Коши (упр. 1.47)
распределение BepxHero экстремума в больших Вblборках ( 2.4, прим.6)
обработка эмпирических данных (упр. 2.7, 2.10)
распределение ПОРЯДКОВblХ статистнк и их моментЬ! (упр. 2.32, 2.33)
сверхэффективная оценка параметра модели И(О, 8) ( 3.2, прим. 5)
доt-таТОЧН<lЯ статистика для модели и(о, 8) ( 3.3, прим.3)
достаточная статистика для модели и(а(8), Ь(8» ( 3.3, прим.4)
оценивание параметрических функций в модели И(О, 8) ( 3.4, прим. 3)
оценивание параметрических функций в модели и(81, Oz) (упр. з.24,3.38)
о. м. п. параметра в моделях И(О, О) и И(О, о + 1) ( 3.5, прим. 3)
о, м. п. пара метра в моделях И(О 1/2, О + 1/2) (упр.3.49)
аСИМПТОтические свойства о. м. п. параметра !! модели и(о, 8)
( 3.5, прим. 11, упр. 3.48)
оценки параметров по методу моменто!! (93.6, прим. 2, упр. 3.72, З. 73)
модалЬНО несмещенная оценка параметра модели И(О, 8) ( 3.6, прим. 5)
оценка Питмена (эквивариантная) параметра модели И(О 1/2,8 + 1/2)
( 3.6, прим.9)
оценка Питмена (ЭКВИllариантная) пара метра модели И(О, 8) ( 3.6, прим. 10)
до!!ерительный интервал для параметра модели И(О, О) ( 3.8, прим. 1)
оценнвание параметра модели и(о, 28) (упр.3.22)
сравнение оценок параметра в модели И(О,8) (упр.3.23, 3.37)
байесовская оценка пара метра модели И(О, О) (упр. 3.82, 7.10)
критерии СОI'ласия для нее (упр. 4.8)
rипотеза однородности для нее (упр.4.19)
rипотеза случайности для нее (упр.4.25)
критерий Неймана П ирсона различения равномерной и нормальной моделей
(упр.5.3)
несмещеННblЙ критерий при двусторонней альтернативе в модели И(О, О)
(упр.5.19)
метод наllменьших квадратов для нее (упр.6.7, 6.12)
реализации случаЙНblХ чисел (прилож. табл. 9).
596
Путеводитель по моделям в примерах и задачах
20. Бета-распределение Ве(а, Ь)
определенис и свойства ( 1.2, ".4)
как чаСТНblЙ случай распределения Дирихлс ( 1.2, п. 10)
смеси ( 1.3, прим. 2, п.9)
моментЬ! (упр. 1.42)
связь с rаМ"1а распределением (упр. 1.43)
связь с распреДСJ1ением Маркова Пойа (унр. 1.44)
связь с распределением Стьюдента (упр. 1.50)
связь с распределением Снедекора (упр. 1.52, 1.53)
сопряженность к биномиальному распределению (упр. 1.64(2»)
оценивание параметрических функций в модели Ве(е, 1) ( 3.4, прим. 14)
проrноз ( 6.6, прим. 3, упр.6.26)
21. Распределение (тьюдента В(n)
определение и свойства ( 1.2, п. 6)
моменты (упр. 1.49)
связь с бета распределением (упр. 1.50)
квантили (прилож. табл. 5).
22, Распределение Коши К(а)
определение и свойства ( 1.2, п. 6, упр. 1.48(б), 2.26, 3.26)
моделирование ( 1.3, ".6)
распределение BepXHero экстрсмума в больших Вblборках (упр.2.35)
информация Фишера ДЛЯ Hero ( 3.2, табл. 1)
достаТО'lная статистика ДНЯ Hero ( 3.3, ПрIfМ. 5)
О. м. п. пара метра, мстод накопления ( 3.5, прим.8)
асимптотическая эффективность выборО4НОЙ медианы (упр. 3.47)
л. н. м. нссмещенный критерий при двусторонней альтернатипс ( 5.3, прим.6)
критерий Неймана Пирсона (упр. 5.2).
23. Распределение (недекора (F-распределение) В(n, т)
определенне и свойства ( 1.2, п. 7, упр. 1.51(a»
связь с распределением Стьюдента (упр.I.5I(б»)
связь с 6ета распределением (упр. 1.52, 1.53)
связь с показательным распределением (упр. 1.54)
квантили (прилож. табл. 6).
24. Распределение Вейбулла W(a, а, Ь)
определение и свойства ( 1.2, п. 8, упр. 1.55)
распределение нижнеro экстрсмума (упр. 1.56)
сuерхэффективная оценка параметра ( 3.2, прим.6)
оценивание параметрических функций ( 3.4, прим. 15, упр.3.40)
о. м. п. параметра е в модели W({/, а, Ь) (упр.3.50)
о. м. п. параметра (/ в модсли W(O,2, .;о) (упр.3.51)
Путеводитель по моде/lЯМ в примерах и задачах
597
доnеритеЛЬНblЙ интерnал ДЛЯ параметра О модели W(O, а, Ol/a) (упр.3.65)
несмещенный критерий при двусторонней альтернативе ДЛЯ модели
ИТ(О, а, Ol/U) (Уllр.5.20).
25. Распределение Парето
определенис и свойства (9 1.2, п. 9, упр. 1.57)
связь с показатеЛЬНblМ распределением (упр. 1.58)
сопряжеюlOСТЬ к равномерному распределению (упр. 1.53, 1.64(6))
распределение oepXHero экстремума в бодьших ныоркахx (92.4, прим. 5)
оценивание парамеТРИ'lеских функций (93.4, JJprIM. 16)
проrноз (упр. 6.27).
26. Распределение Дирихле D(O:i. . . . , 0k)
опредедение и соойства (9 1.2, п. 10, упр. 1.61)
как смешивающая Mep<l в модели Маркова Пойа (упр. 1.62)
сопряженность к полиномиальному распределению (упр. 1.63).
27. Распределение Паскаля (91.1, п.2)
28. Распределение Эрланrа (9 1.1, п.3)
29. Распределение лоrарифмическое (9 1,1, ".8)
30. Распределение лоrнормальное (91.2, п. 1)
31. Распределение Релея (91.2, п.8)
32. Распределение Колмоrорова (92.1, п.3, прилож. табд. 7)
33. Распределение дважды экспоненциальное (92.4, п.4)
34. Распределение Лапласа (93.4, прим. 17, упр.3.53, 3.74)
35. Распределение лоrистическое (упр.3.25)
36. Распределение обратное rayccoBcKoe (упр.3.30)
37. Распределение Кептайна (упр.3.44)
38. Распределение Уиwарта (98.3)
Только терпеливый закончит дело,
а торопливый упадет.
Саади 2)
Это не конец, и даже не начало нонца.
Но, возможно, это конец начала.
У.Черчилль))
2) Сзадlt (121O 1292) великий персидский поэт.
Э) ЧеР'IЮUJЬ Уинстон (187 1965) анrлийский политическиЙ деятель.
Аристотель 239
Большев Лоrllll Николаевич 27
Байес Томас 85, 251, 511, 527
Басу Дебабрата 196
Бернулли Даниил 317
БернуJlЛИ ЯкоG 25, 31 34, 36, 37, 39,64,74,
91,92,107,114,150,164,173,252,253,
298, 309, 368, 424, 453, 545
Бернштейн Серrей Натанович 69
Бертран Жозеф Луи Франсуа 21
Блекуэлл Дэвид 191
Боровков Александр Алексеевич 27
Борткевич Л. 36
Буняковекий Виктор Яковлевич 171, 176,
481,509
Бхаттачария 181,182,184,300,301
Бэбинrтон Смит Б. 360, 364
Бюффон Жорж Луи Леклерк 150, 323, 586
Вальд Абрахам 26, 348, 372, 443 451, 526,
593
Ван дер Варден Бартел Лендерт 311
ВейБУJ!JJ ВалоЦllИ 57, 84. 179, 189,218,302,
304, 455, 598
Вейерштрасс Карл Теодор Вильrельм 69
Верхарн Эмиль 573
Вийон Франсуа 28
ВI1ЛКОКСОI1 ФрЭl1К 349, 350
Волфовиц Джекоб 451
raeK Я. 333
rальтон Фрэнсис 507, 508
raycc Карл Фридрих 25, 46, 457, 459
rенри О. (Уильям Сидни Портер) 25
recce repMaH 14
rhe Иоrанн ВолЬфraнr 17, 572
rливенхо Валерий Иванович 99, 263
rнеденко Борис Владимирович 26
rорвиц 290, 291, 590
rрасиан Бальтасар 29
rулик Роберт ван 520
rумбол!'дТ Вильrельм 524
Дейвид Ф. 338
Декарт Рене 89
Именной указатель
Демокрит 586
Джеймс 258, 594
Джефферс 571
Диаконис ПСрСII 457
Дирихле Петер rycTaB 57, 58, 85. 86. 255,
594, 597, 598
Йенсеи Иоrаtlll Людвиr 337, 386, 393
Й инr 263
Каплан 262
КеЛЬВI1II (Томсон Уильям) 19
Кендалл Морис ДжордЖ 26, 358 360, 364
Кептайн 303, 599
Кетле Ломбер Адольф Жак 164
Кнут Дональд 365
КОЛ'о10rоров Анлрей НиколаеВl1'1 26, 37. 98,
100,191,195, 197, 3I7 320, 341,369,518.
579, 592, 599
Конфуций 163,519
Коши Оrюстен Луи 55,56,67,82, 154, 156,
169, 171, 175, 176, 179, 190, 226, 240, 243,
300, 303. 405, 452, 481, 509, 591, 596, 597
Крамер rаБРl1ЭЛЬ 26. 173. 175 1 84, 220. 232,
317
Кэттел РэймOJ IJJ Бе[тард 563
Лаrранж Жозеф Луи 267, 270, 335,434
Ламас Пьер CflMOII 25,46,80,95.151,215,
218,304,308,317,333. 345, 390,453,587,
599
Ле Кам 233
Лей 263
ЛейбflИЦ rотфрид Вl1льrельм 28
Леман Эрих 26, 168, 219
Линден Бэлл 263
Линник Юрий ВладИМИРОВИ'J 27
Ломоносов МИХ31111 ВасильеRИ'! 199
Ляпунов Александр Михайлови'! 26
Mal!H rенри 349, 350
Марков Андрей АlJдреевич 26, З7 42, 70 72,
81,85,86,297,367, 372, 427 431,
433 435. 440, 442, 456, 457. 459, 587,
589 591, 597, 598
Махаланобис Прасанта Чандра 383. 537 539
Именной УНйзатель
599
Мейер 262
Мендел
еD Дмитрий Иванович 473, 512
Мендель rperop Иоrанн 323, 324, 590
Мизес rаральд Рихард фон 317
Муавр Абрахам де 25, 46, 52, 80, 95,151,
308, 333, 345, 390, 453, 587
Мэндерви,1 К. 25
Нейман ДжОн фон 317, 364
Нейман Юрий 26, 372
384, 386, 389
391,
394,395,401,409,444,445,449,450,453,
454, 536, 587
590, 592, 594, 595, 597, 598
Ницше Фридрих 159
Ньютон Исаак 11, 32, 106, 297
Октавиан ABrycт 62
Парето Вильфредо 57, 84, 86, 87,140,218,
310, 524, 595, 598
Паскаль Блез 35, 324, 520, 572, 599
Пирсон Карл 26, 239, 241, 317, 320, 321, 366,
368, 420, 566, 596
Пирсон Эrон Шарп 26, 317, 372
384. 386,
389,390,394,395,401,409,444,445,449,
450,453,454, 536, 587
590, 592, 594, 595,
597, 598
Питмен 247
2S0, 592, 596
ПЛатон 14
Пойа Ды:рдь 37
42, 44, 81, 85,86, 172,297,
587,589,597,598
Прохоров Юрий Васильевич 13, 27
Пуанкаре Анри 44
Пуассон Симеон Дени 31, 35,36,42,43,75,
76, 78, 80, 227, 243, 308, 391, 524, 574,
587,588,594
Пушкин Александр Серrеевич 164
Рао Кальямпуди Радхакришна 26, 173,
J75
184, 191,220,232,233
Рассел Бертран Артур Уильям 318
Рейнольдс Дж. 164
РомановскиЙ Всеполод ИваНОВИ'1 27
Русас Дж. 45, 317
Руставели Шота 12, 368
Рыбииков Константин Алексеевич 30
Рюккерт Фридрих 564
Сами Муслихат
Дин 599
Сil.l108IIИ'IИЙ Виктор АНТОНОВИ'I 1I
Сщтыков-Щелрин Михаил Евrрафович 584
C
I"lcTbIlllon Борис Александрович 13.27
С
ксй raGop 163, 317
Сшека 74
Слуцкий Евrений ЕвrенЬеВИЧ 27
Смирнов Николай Васильевич 27, 99, 138,
152, 278, 317, 320, 334, 340, 341, 370, 580
Снедекор Джордж 56, 83, 149, 150,306, 307,
415,416,477,479,483,501,578,595.597,
598
Соловьев DладюlИР Серrеевич 572
Спенсер rерберт 451
Спирме" 357, 358, 360, 361
Стейи К. 257, 258, 594
СТlUпьес Томас Ян ("1,1.) 162
Стирлинr Джеймс 52, 134
Стьюарт Алан 26
Стьюдент (Уильям Д. rocceт) 55,83, 124,
147, 149, 307, 410, 414, 477, 577, 597, 598
ТВСН Марк (Сзмюэль Ленrхорн Клеменс)
318
Тейлор Брук 122,225,231,403,417
Типпет Леонард 364
ТОМПСОJl В. 24, 290, 291, 590
Уилкс Самюэль Стэнли 26
Уитни 349, 350
Уишарт 550, 594, 599
Феллер Вильям 211
Фишер Роальд Э. 26, 53, 55
57, 122,
145
149, 167, 174", 175, 182, 186,217,219,
225,265,269,278,299, 317,328,333,369,
404,411,412,416,483,587,588,591,594,
597
Франс Анатоль (Анатоль Франсуа Тибо) 584
Фурье Жан Батист Жозеф 515
Хадсон 150
Хотеллинr rаральд 566, 568
Хэмминr Ричард }-Зсли 28
Чебышев Пафнутий Львович 26, 94, 110,
111, 113, 228, 298, 326, 470
473
Черчилль УИIIСТОН 599
Честертон rилберт Кит 525
Чистяков Владимир Павлович 13, 17
Шидак 3. 333
Шильд А. 546
Ширяев Альберт Николаевич 27
Эrrепберrер Ф. 39
Эйлер Леонард 132, 137
Эрланr ArHep Краруп 36,52, 66,67, 136,599
Эсхил 163