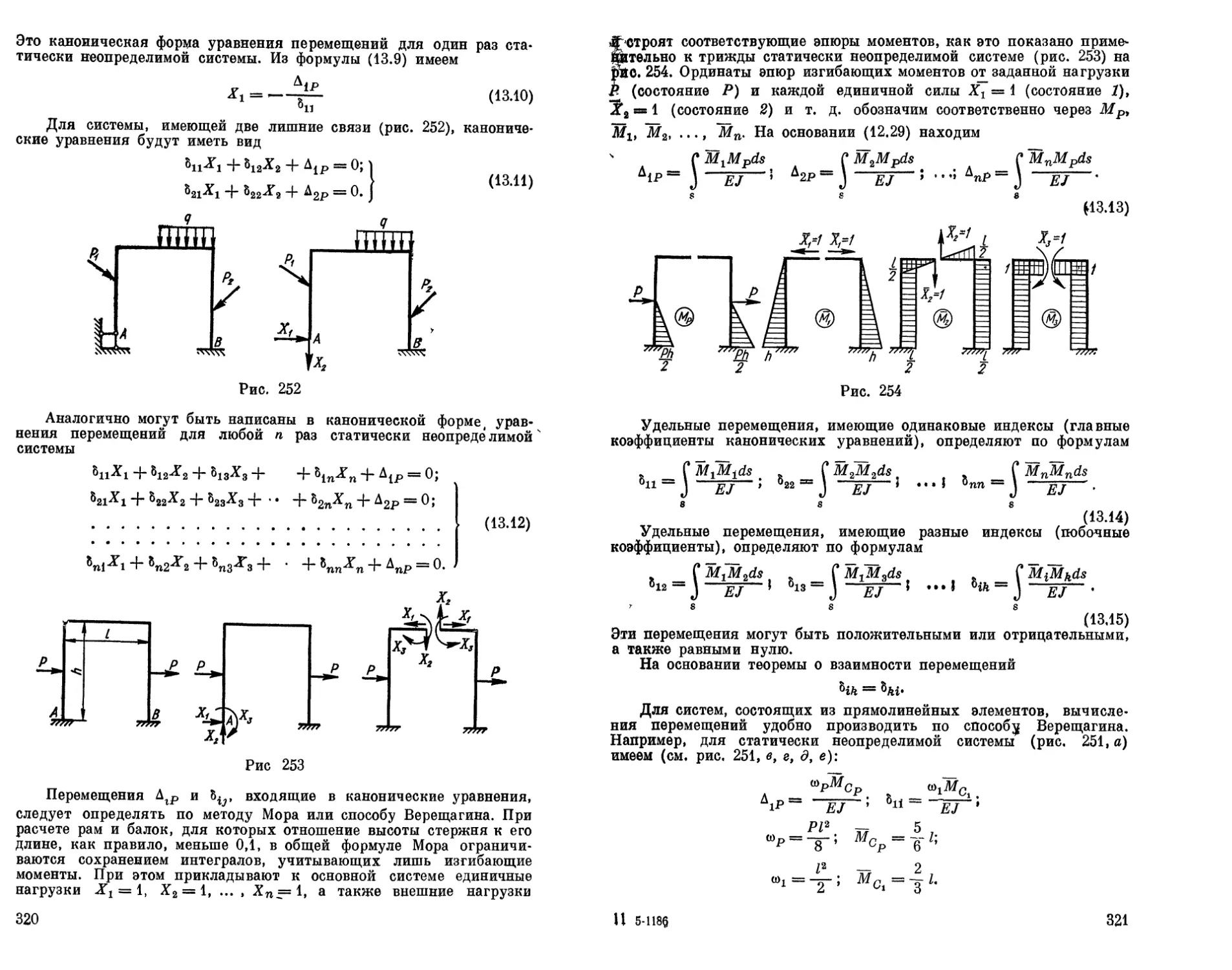
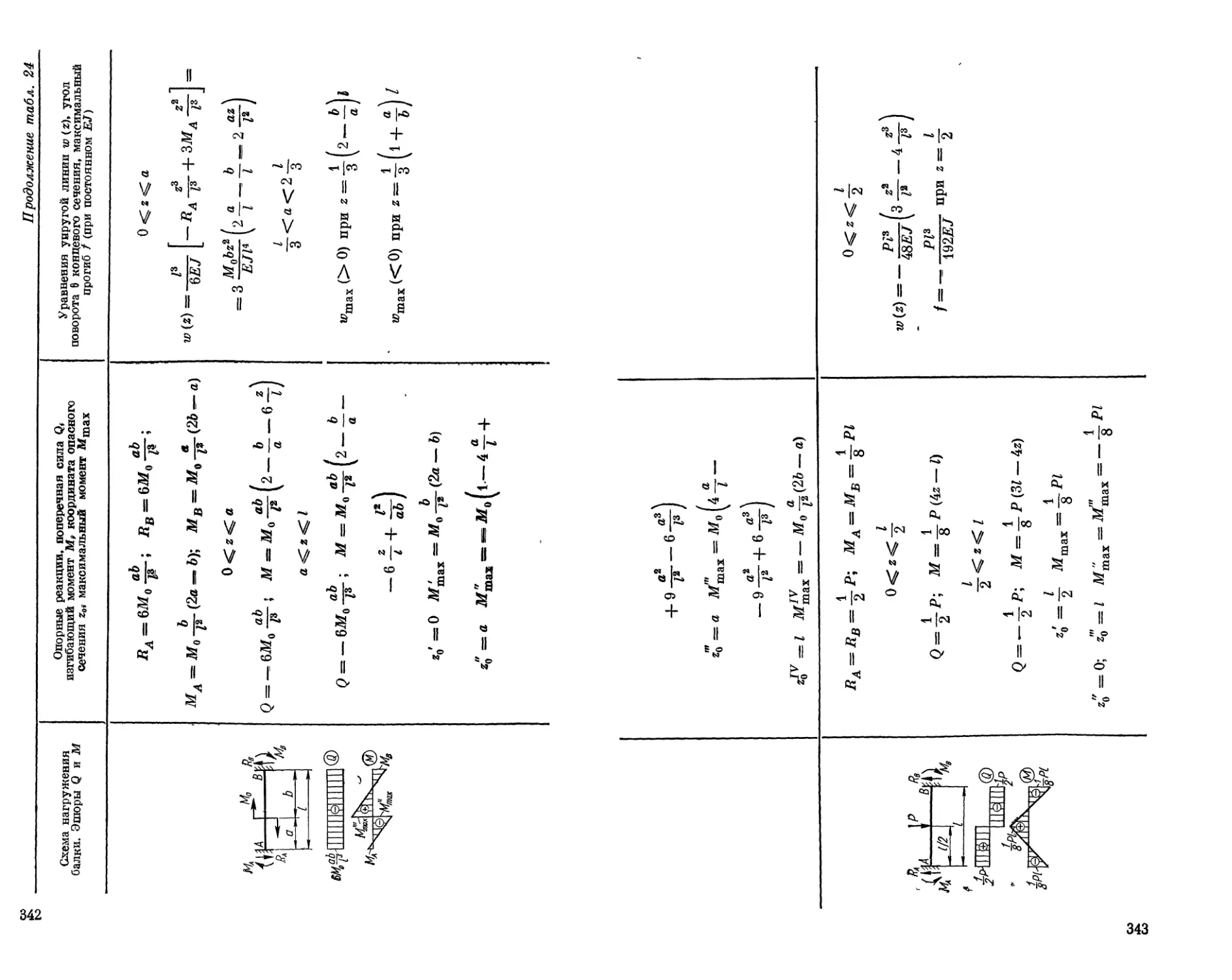
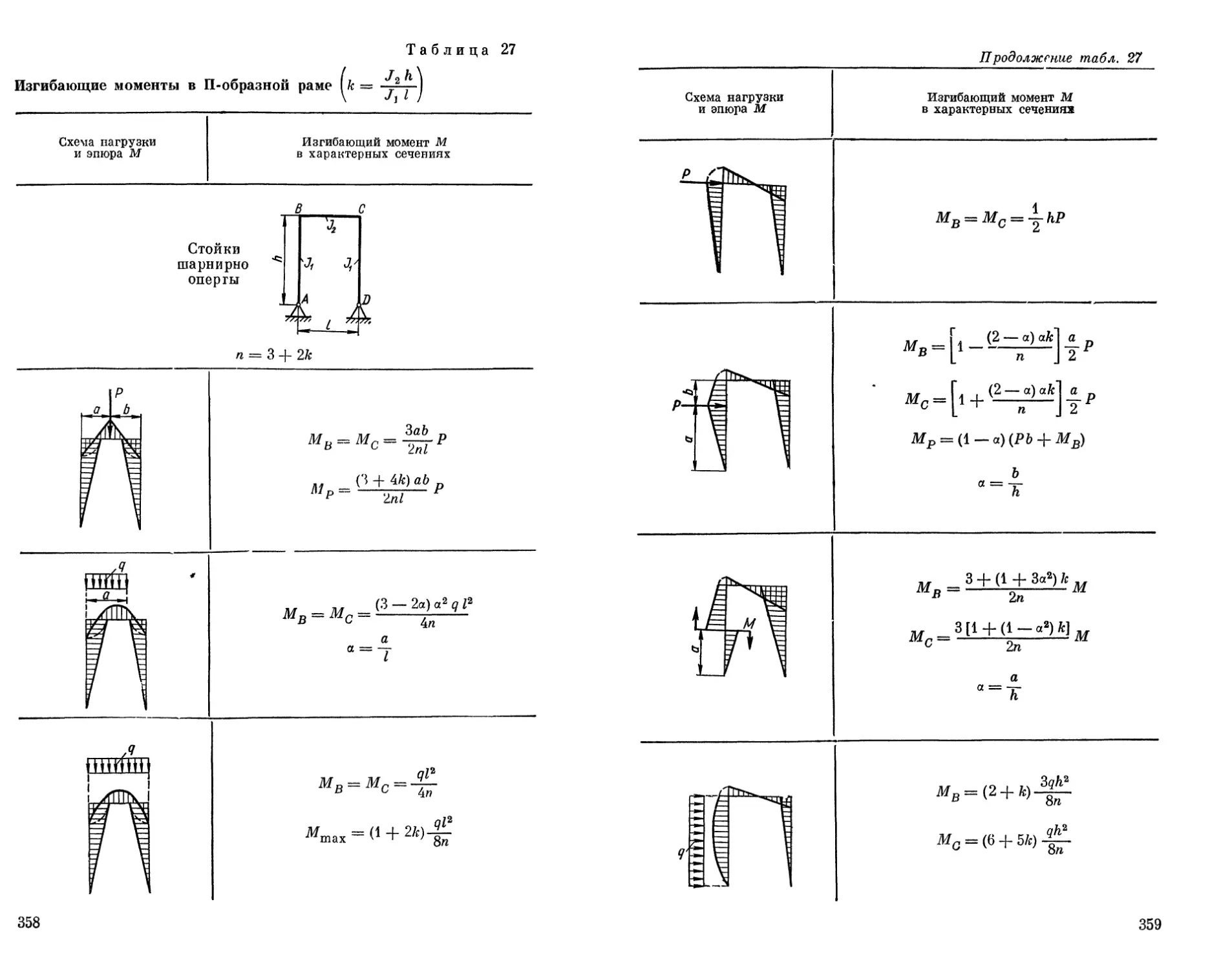
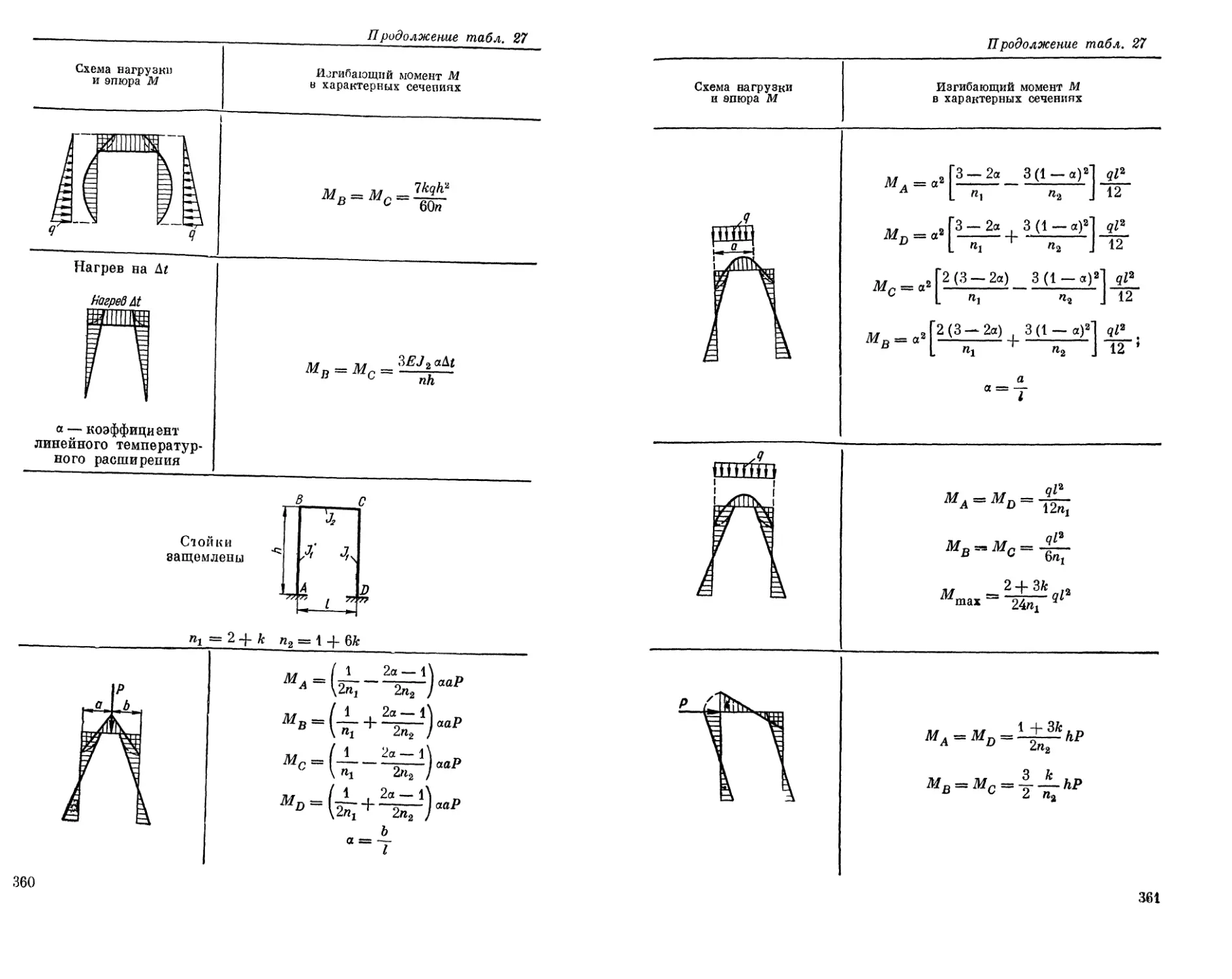
Текст
Г.С ПИСЛРЕЙКО Л г.
АП ЯКОВЛЕВ < е
BBMAIBEEB ' *
й
*№$
Л
'=т=’
СПРАВОЧНИК J|
ПО СОПРОТИВЛЕНИЙ
Л4АТЕРИАЛОВ •*
__________
4
Г. С. ПИСАРЕНКО,
А. П. ЯКОВЛЕВ,
В. В. МАТВЕЕВ
СПРАВОЧНИК
ПО СОПРОТИВЛЕНИЮ
МАТЕРИАЛОВ
ИЗДАТЕЛЬСТВО
«НАУКОВА ДУМКА»
КИЕВ —1975
605(083)
П34
УДК 539.3/4+539.1+620.17(031 J
В справочнике приведены сведения по основным вопросам курса
сопротивления материалов для высших технических учебных заве де
ний, а также данные по результатам расчета достаточно широкого
круга наиболее типичных элементов конструкций.
Предназначен для инженеров различных специальностей, стал
кивающихся в практической деятельности с расчетами на проч
ность, и студентов высших технических учебных заведений, может
быть полезен также преподавателям и аспирантам.
Рецензент доктор техн, наук П. М. в А Р В А К
Редакция справочников
00001-175
М221(04)—75 '
CJ Издательство «Нау^ •
)75 г.
ПРЕДИСЛОВИЕ
Сопротивление материалов является одной из ос*
новных общеобразовательных инженерных дисциплин
и играет существенную роль в формировании инженера
почти любой специальности. Особенно большое значе-
ние сопротивление материалов имеет для механических,
машиностроительных и строительных инженерных спе-
циальностей.
Введение в учебную программу высших технических
учебных заведений новых дисциплин, отражающих со-
временное состояние науки и техники, при ограниченных
сроках обучения привело к существенному сокращению
количества лекционных часов по курсу сопротивления
материалов. Восполнение появившихся в результате это-
го пробелов в знании студентами втузов сопротивления
материалов может быть достигнуто в известной мере за
счет самостоятельного изучения ими необходимых разде-
лов этого важного для будущего инженера курса кпо
соответствующим учебникам.
В Советском Союзе многократно издавались учебники
по сопротивлению материалов С. П. Тимошенко,
Н. М. Беляева, В. И. Феодосьева и многие другие. Вместе
с тем имеется большая заинтересованность в справочнике
по сопротивлению материалов, отражающем с достаточ-
ной полнотой современное состояние науки о прочности,
как со стороны большой армии инженеров-производствен-
ников и конструкторов, так и со стороны учащихся и на-
учных работников. К сожалению, такого справочника
ни в нашей стране, ни за рубежом нет, а существующие
краткие справочники по сопротивлению материалов
и строительной механике носят специализированный
характер и подают материал по ряду важнейших разделов,
базируясь на различных подходах, применяемых в раз-
ных курсах сопротивления материалов. Авторы поста-
вили перед собой цель создать справочник по сопротивле-
нию материалов, который бы обладал достаточной пол-
нотой и универсальностью, отражал современнее состоя-
ние науки о прочности и основывался на едином подходе
к подаче справочного материала, увязанного с соответ-
ствующим теоретическим курсом. В качестве последнего
был принят учебник Г. С. Писаренко, В. А. Агарев^,
А. Л. Квитки, В. Г. Попкова, Э. С. У майского «Сопротив-
ление материалов», изд. 3, Киев, «Вища школа», 1973,
в котором нашел отражение многолетний опыт препода-
вания сопротивления материалов в Киевском политехни-
ческом институте и опыт использования двух предыдущих
3
изданий этого учебника студентами многих высших учеб-
ных заведений нашей страны.
Перед справочным материалом в виде окончательных
формул, таблиц и графиков в каждой главе кратко изла-
гаются основные теоретические предпосылки. При этом
формулируются исходные гипотезы, соответствующие
правила, теоремы и даются важнейшие заключения
и рекомендации. Для облегчения пользования справоч-
ными данными на с. 698 приведен перечень таблиц,
содержащихся в книге.
Мы надеемся, что настоящий справочник будет поле-
зен не только инженерам-конструкторам и производствен-
никам всех специальностей, встречающимся в практиче-
ской деятельности с расчетами на прочность, но будет
с успехом использован также студентами, аспирантами,
преподавателями и научными работниками.
Глава 1
ВВЕДЕНИЕ
§ 1. Наука о сопротивлении материалов.
Изучаемые объекты
Сопротивление материалов — наука об инженерных методах
расчета на прочность, жесткость и устойчивость элементов сооружений
и машин.
Прочность — способность конструкции, ее частей и деталей выдер-
живать определенную нагрузку, не разрушаясь.
Жесткость — способность конструкции и ее элементов противо-
стоять внешним нагрузкам в отношении деформации (изменения формы
и размеров). При заданных нагрузках деформации не должны превы-
шать определенных величин, устанавливаемых в соответствии с требо-
ваниями к конструкции.
У стойчивость — способность конструкции и ее элементов сохра-
нять определенную начальную форму упругого равновесия.
Для того чтобы конструкции в целом отвечали требованиям проч-
ности, жесткости и устойчивости, необходимо придать их элементам
наиболее рациональную форму и определить соответствующие раз-
меры.
Сопротивление материалов решает указанные задачи, основываясь
как на теоретических, так и на опытных данных, имеющих в этой
науке одинаково важное значение.
В теоретической части сопротивление материалов базируется
на теоретической механике и математике, а в экспериментальной —
на физике и материаловедении.
Сопротивление материалов является наиболее общей наукой
о прочности машин и сооружений. Без фундаментального знания
сопротивления материалов немыслимо создание различного рода ма-
шин и механизмов, гражданских и промышленных сооружений, мостов,
линий электропередач и антенн, ангаров, кораблей, самолетов и верто-
летов, турбомашин и электрических машин, агрегатов атомной энерге-
тики, ракетной и реактивной техники и др.
Сопротивление материалов не исчерпывает всех вопросов механи ки
деформированного тела. Этими вопросами занимаются такие смежные
дисциплины, как строительная механика стержневых систем, теория
упругости и теория пластичности. Однако основная роль при решении
задач на прочность принадлежит сопротивлению материалов.
При всем разнообразии видов конструктивных элементов, встре-
чающихся в сооружениях и машинах, их можно свести к сравнительно
небольшому числу основных форм. Тела, имеющие эти основные формы,
и являются объектами расчета на прочность, жесткость и устойчивость.
Это стержни, пластинки и оболочки, массивные тела.
Стержнем, или брусом, называется тело, у которого один размер
(длина) значительно превышает два других (поперечных) размера
(рис. 1). В инженерном деле встречаются стержни с прямолинейной
(рис. 1, а) и криволинейной (рис. 1, б) осями. Как прямые, так и кри-
вые стержни могут быть постоянного (рис. 1, а) или переменного сечения
5
(рис. 1, в). Примерами прямых стержней являются балки, оси, валы.
Примерами кривых стержней могут служить грузоподъемные крюки,
звенья цепей и т. п. Стержни со сложным профилем поперечного сече-
ния, у которых толщина стенок значительно меньше габаритных раз-
меров сечения, называются тонкостенными (рис. 1, г).
Оболочка представляет собой тело, ограниченное двумя криво-
линейными поверхностями, расположенными на близком расстоянии
друг от друга, т. е. тело, один размер которого (толщина) значительно
меньше двух других. Геометрическое место точек, равноудаленных от
Рис. 1
Рис. 2
обеих поверхностей оболочки, называется срединной поверхностью.
По форме срединной поверхности различают оболочки цилиндрические
(рис. 2, а), конические (рис. 2, б), сферические (рис. 2, в) и др. К обо-
лочкам относятся тонкостенные резервуары, котлы, купола зданий,
обшивки фюзеляжей, крыльев и других частей летательных аппара-
тов, корпуса судов и т. п.
Если срединная поверхность оболочки представляет собой плос-
кость, то такая оболочка называется пластиной (рис. 2, г). Пластины
могут быть круглыми, прямоугольными и иметь другие очертания.
Толщина пластин, как и оболочек, может быть постоянной или пере-
менной. Пластинами являются плоские днища и крышки резервуаров
(рис. 2, д), перекрытия инженерных сооружений, диски турбомашин
и т. п.
Массивным называется тело, у которого все три размера — ве-
личины одного порядка. Это •— фундаменты сооружений, подпорные
стенки и т. п.
В сопротивлении материалов, как правило, задачи решаются про-
стыми математическими методами с привлечением ряда упрощающих
гипотез и использованием данных эксперимента; решения при этом
доводятся до расчетных формул, пригодных для использования в ин-
женерной практике. Основным объектом, рассматриваемым в сопротив-
лении материалов, является прямой стержень.
6
§ 2. Виды деформаций. Понятия о деформированном
состоянии материала
Реальные тела могут деформироваться, т. е. изменять свои форму
и размеры. Деформации тел происходят вследствие нагружения их
внешними силами или изменения температуры. При деформации тела
его точки, а также мысленно проведенные линии или сечения переме-
щаются в плоскости или в пространстве относительно своего исходного
положения.
При нагружении твердого тела в нем возникают внутренние силы
взаимодействия между частицами, оказывающие противодействие внеш-
ним силам и стремящиеся вернуть частицы тела в положение, которое
они занимали до деформации.
Различают упругие деформации, исчезающие после прекращения
действия вызвавших их сил, и пластические, или остаточные, дефор-
мации, не исчезающие после снятия нагрузок. В большинстве случаев
для величин деформаций элементов конструкций устанавливают опре-
деленные ограничения.
В сопротивлении материалов изучаются следующие основные виды
деформаций, растяжение и сжатие, сдвиг (или срез), кручение, изгиб.
Рассматриваются также более сложные деформации, получающиеся
в результате сочетания нескольких основных видов деформаций.
Растяжение или сжатие возникает, например, в случае, когда
к стержню вдоль его оси приложены противоположно направленные
силы (рис. 3). При этом происходит поступательное перемещение
сечений вдоль оси стержня, который
при растяжении удлиняется, а при « р
сжатии укорачивается. Изменение пер- xgr .х /&ГУ
воначальной длины стержня I, обозна-
чаемое AZ, называется абсолютным уд- у^у\уу'уу'у'г
линением (при растяжении) или абсо-
лютным укорочением (при сжатии). р
Отношение абсолютного удлинения И
(укорочения) AZ к первоначальной дли- Рис. 3
не I называется средним относитель-
ным удлинением (укорочением) на длине I или средней линейной
относительной деформацией участка и обозначается обычно еср:
AZ
£«Р~ I
Истинное линейное относительное удлинение, или относительная
линейная деформация в точке, определяется как относительная дефор-
мация участка при I О
г
£ — 1Ш1 .
М 1
На растяжение или сжатие работают многие элементы конструк-
ций: стержни ферм, колонны, штоки поршневых машин, стяжные
болты и др.
Сдвиг, или срез, возникает, когда внешние силы смещают два
параллельных плоских сечения стержня одно относительно другого
при неизменном расстоянии между ними (рис. 4). Величина смещения
As называется абсолютным сдвигом. Отношение абсолютного сдвига
к расстоянию между смещающимися плоскостями (тангенс угла 7)
7
называется относительным сдвигом. Вследствие малости угла у можно
принять
tg7~7=_
Относительный сдвиг является угловой деформацией, характеризующей
перекос элемента.
На сдвиг, или срез, работают, например, заклепки и болты, скреп-
ляющие элементы, которые внешние силы стремятся сдвинуть друг
относительно друга.
Кручение возникает при действии на стержень внешних сил, обра-
зующих момент относительно его оси (рис. 5). Деформация кручения
Рис. 4
сопровождается поворотом поперечных сечений стержня друг относи-
тельно друга вокруг его оси. Угол поворота одного сечения стержня
относительно другого, находящегося на расстоянии Z, называется
углом закручивания на длине I, Отношение угла закручивания ф к дли-
не I называется относительным углом закручивания
•ч-
На кручение работают валы, шпиндели токарных и сверлильных
станков и другие детали.
Изгиб (рис. 6) заключается в искривлении оси прямого стержня или
в изменении кривизны кривого стержня. Происходящее при изгибе
перемещение какой-либо точки оси стержня выражается вектором,
начало которого совмещено с первоначальным положением точки,
а конец — с положением той же точки в деформированном стержне.
Рис. 6
В прямых стержнях перемещения точек, направленные перпендику-
лярно к начальному положению оси, называются прогибами. Обозна-
чим прогибы буквой де, а наибольший прогиб — буквой /. При изгибе
также происходит поворот сечений стержня вокруг осей, лежащих
в плоскостях сечений. Углы поворота сечений относительно своих
начальных положений обозначим буквой ф.
На изгиб работают балки междуэтажных перекрытий, мостов,
оси железнодорожных вагонов, листовые рессоры, валы, зубья шесте-
рен, спицы колес, рычаги и многие другие детали.
8
Описанные выше простейшие деформации стержня дают пред-
ставление об изменении его формы и размеров в целом, но ничего
не говорят о степени и характере деформированного состояния матери-
ала. Исследования показывают, что деформированное состояние тела,
вообще говоря, является неравномерным и изменяется от точки к точке.
При этом деформированное состояние в точке тела полностью опре-
деляется шестью компонентами деформации: тремя относительными
линейными деформациями 8», 8у, и тремя относительными угловыми
деформациями ^ху> Чхг? ^yz'
§ 3. Основные гипотезы
Для построения теории сопротивления материалов принимают
ряд гипотез о структуре и свойствах материалов, а также о характере
деформаций.
1. Гипотеза о сплошности материала. Предполагается, что мате-
риал полностью заполняет занимаемый им объем. Атомистическая тео-
рия дискретного строения вещества во внимание не принимается.
2. Гипотеза об однородности и изотропности. Предполагается,
что свойства материала одинаковы во всех точках и в каждой точке —
во всех направлениях. В некоторых случаях предположение об изо-
тропии неприемлемо. Так, анизотропными являются древесина, свой-
ства которой вдоль и поперек волокон существенно различны, а также
армированные материалы.
3. Гипотеза о малости деформаций (гипотеза относительной жест-
кости материала). Предполагается, что деформации малы по сравнению
с размерами деформируемого тела. На этом основании пренебрегают
изменениями в расположении внешних сил относительно отдельных
частей тела при деформации и уравнения статики составляют для
недеформированного тела. В некоторых случаях от этого принципа
приходится отступать, что оговаривается особо.
4. Гипотеза о совершенной упругости материала. Все Теда пред-
полагаются абсолютно упругими. В действительности реальные тела
можно считать упругими только до определенных величин нагрузок,
и это необходимо учитывать, применяя формулы сопротивления мате-
риалов.
5. Гипотеза о линейной зависимости между деформациями и на-
грузками. Предполагается, что для большинства материалов справед-
лив закон Гука, устанавливающий прямо пропорциональную зависи-
мость между деформациями и нагрузками.
Как следствие гипотез о малости деформаций и о линейной зависи-
мости между деформациями и усилиями, при решении большинства
задач сопротивления материалов применим принцип суперпозиции
(принцип независимости действия и сложения сил). Например, усилия
в любом элементе конструкции, вызванные различными факторами
(несколькими силами, температурными воздействиями), равны сумме
усилий, вызванных каждым из этих факторов, и не зависят от порядка
их приложения. Это же справедливо и в отношении деформаций.
6. Гипотеза плоских сечений. Предполагается, что мысленно про-
веденные плоские сечения, перпендикулярные к оси стержня, в про-
цессе его деформирования остаются плоскими и перпендикулярными
к оси.
Эти, а также некоторые другие гипотезы позволяют решать широ-
кий круг задач по расчету на прочность, жесткость и устойчивость.
Результаты таких расчетов обычно хорошо согласуются с данными
эксперимента,
9
Глава 2
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Сопротивление стержня различным видам деформаций часто за-
висит не только от его материала и размеров, но также от очертаний
оси, формы поперечных сечений и их расположения относительно
направления действующих нагрузок. Рассмотрим основные геомет-
рические характеристики поперечных сечений стержня, отвлекаясь
от физических свойств изучаемого объекта. Этими характеристиками
являются: площади поперечных сечений, статические моменты, моменты
инерции, моменты сопротивления, радиусы инерции.
§ 4. Статический момент площади.
Центр тяжести площади
Рассматривая произвольную фигуру (поперечное сечение стержня),
связанную с системой координат хОу (рис. 7), по аналогии с выраже-
нием для Момента силы относительно какой-либо оси можно составить
выражение для момента площади, которое
называется статическим моментом. Так, произ*
ведение элемента площади dF на расстояние у
от оси Ох
dSx — ydF
называется статическим моментом элемента
площади относительно оси Ох. Аналогично
dSy = xdF — статический момент элемента пло-
щади относительно оси Оу. Просуммировав эти
произведения по всей площади, получим статические моменты пло*
щади соответственно относительно осей х и у.
Sx = ydF*f Sy — § xdF. (2.1)
F F
Размерность статического момента — единица длины в кубе (напри-
мер, см?).
Пусть хс и ус — координаты центра тяжести фигуры. Продолжая
аналогию с моментами сил, на основании теоремы о моменте равнодей*
ствующей можно написать следующие выражения:
Sx — ГУс*> — Гхф
где -площадь фигуры.
Координаты центра тяжести равны
___________________Sy t _______Sx
(2.2)
(2.3)
10
Для вычисления статических моментов сложной фигуры ее разби-
вают на простые части (рис. 8), для каждой из которых известна пло-
щадь (Fi) и положение центра тяжести (^, у^). Статические момен-
ты всей фигуры относительно осей Ох и Оу соответственно будут
равны
г«=п
$х = Р1У1 + F2y2 4" • • • + FпУп = 2 &
г=1
*
г«=п
Sy — F]%1 4" F2х2 4” • • • 4" Fпхп = У, FjX{.
(2.4)
Из формул (2.3) и (2.4) определяем
координаты центра тяжести сложной фи-
гуры
г=п i^n
2 &о 2
*С р i=n ' VC р
2 Fi 2 Fi
1=1 г=^1
(2.5) Рис. 8
§ 5. Моменты инерции плоских фигур
Осевым, или экваториальны Mt моментом
инерции площади фигуры называется интеграл произведений
элементарных площадок на квадраты их расстояний от рассмотри-
Рис. 10
Рис. 11
ваемой оси. Так, моменты инерции произвольной фигуры (рис. 9)
относительно осей х и у соответственно равны
Л = ^y*dF-, (2.6)
F F
Пользуясь этими формулами, вычислим моменты инерции для
простейших фигур.
U
Прямоугольник (рис. 10). Учитывая, что элементарная
площадка dF == bdy, найдем
h
2
С С Ъ№
\y*dF~ \ y2bdy = ~.
F h
2
Очевидно,
^-72 *
Треугольник (рис. 11). Учитывая, что b (у) ~ -^(h — у),
dF = ~(h~y) dy, момент инерции относительно оси х выразим как
h
Круговой сектор (рис. 12). Учитывая, что dF = pdcpdp
и у ~ р sin с?, определим момент инерции относительно оси х:
0 т
sin 2а"]
р2 sin2 ippttydp = -у- [(P — a) —
F
Полярным моментом инерции площади фигуры
относительно данной точки (полюса О) называется интеграл произве-
дений элементарных площадок на квадраты их расстояний р от по-
люса (рис. 9):
/p-JpW. (2.7)
F
Если через полюс проведена система взаимно перпендикулярных
осей а?, у, то р2 = х2 + У2* Из (2.6) и (2.7) будем иметь
Jp-Jx+Jy- (2-8)
Круг (рис. 13), Учитывая, что dF = 2лр dp, полярный момент
инерции будет: г
Jp= JpW = 2nJp3dp = ^.
F Й
12
или
г _ тс^4
“ 32 •
Из (2.8) очевидно, что для круга
г - Г —
Jx - Jy- — --g4 •
Отметим, что величины осевых и полярных моментов инерции всегда
положительны.
Центробежным моментом инерции назы-
вается интеграл произведений элементарных площадок на их расстоя-
нця от координатных осей х, у.
Jxy = J xydF. (2.9)
F
В зависимости от положения осей центробежный момент инерции
может быть положительным или отрицательным, а также равным
нулю. Оси, относительно которых центробежный момент инерции равен
нулю, называются главными осями инерции. Две взаимно перпендику-
лярные оси, из которых хотя бы одна является осью симметрии фигуры,
будут ее главными осями. Это следует из того, что в этом случае каж-
дой положительной величине xydF соответствует такая же отрицатель-
ная величина по другую сторону оси симметрии (рис. 14) и их сумма
по всей площади фигуры равна нулю. Главные оси, проходящие через
центр тяжести сечения, называются главными центральными осями.
Размерность моментов инерции — единица длины в четвертой степени
(например, <ш4).
§ 6. Моменты инерции сложных сечений
При вычислении моментов инерции сложных сечений последние
обычно разбивают на отдельные простые части, моменты инерции кото-
рых известны. Из основного свойства интеграла суммы следует, что
момент инерции сложной фигуры равен сумме моментов инерции ее
составных частей. Определим момент инерции сложцой фигуры (рис. 15)
относительно оси х, разбив ее на простые части I, II, III, имеющие
соответственно площади FI? Fn, Fln:
Л = JyW+ J У У><№,
FI fxl FHI
Рис. 15 Рис. 16 Рис. 17
13
или
+ + (2.10)
Заметим, что в случае, когда в сечении имеется отверстие, последнее
удобно считать частью фигуры с отрицательной площадью. Так, мо-
мент инерции относительно оси х сечения, показанного на рис. 16, будет
Т __ Я тП _
j х J х 12 •
§ 7. Моменты инерции относительно параллельных осей
Пусть известны моменты инерции фигуры относительно централь*
ных осей х, у
Jx= § y2dF; Jy=^x*dF-, Jxu=^xydF. (2,11)
F F F
Требуется определить моменты инерции относительно осей х19 ylt
параллельных центральным (рис. 17):
~ § VidF> = У ZidF\ JXiyt — J ViVidF. (2.12)
F F F
Координаты любой точки в новой системе х1О1у1 можно выразить
через координаты в прежней системе хОу так:
= ж 4- b; z/i = у + а. (2.13)
Так как статические моменты площади относительно центральных
осей равны нулю, формулы (2.12) с учетом (2.13) окончательно могут
быть представлены в виде:
= Л +
Jy~Jy +
= + (2-15)
' Следовательно: 1) момент инерции относительно любой оси равен
моменту инерции относительно центральной оси, параллельной дан-
ной, плюс произведение площади фигуры на квадрат расстояния между
осями; 2) центробежный момент инерции относительно любой системы
прямоугольных осей равен центробежному моменту инерции относи-
тельно системы центральных осей, параллельных данным, плюс произ-
ведение площади фигуры на координаты ее центра тяжести в новых
ъсях. Необходимо отметить, что координаты а, Ъ, входящие в формулу
(2.15), следует подставлять с учетом их знака.
* § 8. Зависимость между моментами инерции
1 при повороте координатных осей
Пусть известны моменты инерции произвольной фигуры отнсси-
•ельно координатных осей х, у (рис. 18):
Jy^\x4F\ Jxy-=\xydF. (2.16)
F F F
Требуется определить моменты инерции относительно осей xlt уъ повер-
нутых относительно осей х и у на угол а против часовой стрелки, счи-
тая последний положительным:
Jyi= (2.17)
F F F
Координаты произвольной элементарной площадки в новой сис-
теме (а?10ух) могут быть представлены
системы (хОу) следующим образом:
s ОС = ОЕ -J- AD = х cos а у sin а;
уг = ВС = BD — ЕА = у cos а — х sin а.
G
Окончательно находим:
J = Jx COS2 а + Jy sin2 а — Jxy sin 2а;
=3 Jу cos2 а-f-Jx sin2 а + Jxy sin 2а,
С
JXlyt ~ Jxy COS 2а »-»(J у Jx) sin 2а. (2,20)
Отметим, что формулы (2.19) и (2.20), полученные при повороте
любой системы прямоугольных осей, естественно, справедливы для
центральных осей. Складывая почленно (2.19), находим
+ Jyt = + Jv — Jp-
Следовательно, при повороте прямоугольных осей сумма осевых момен-
тов инерции не изменяется и равна полярному моменту инерции от**
носителъно начала координат.
При повороте системы осей на угол а == 90° имеем:
= А>’ = JX{yi = — Jxy-
§ 9. Определение направления главных осей инерции»
Главные моменты инерции
Наибольший практический интерес представляют главные цеп*
тральные оси, относительно которых центробежный момент инерции ра-
вен нулю. Обозначим главные центральные оси буквами и, г. Очевидно,
Juv ~ 0*
V Для определения положения главных цен-
V" s тральных осей произвольной несимметричной
[ \ фигуры необходимо центральные оси а?, у по-
/ \V веРнУть на такой угол а0 (рис. 19), при котором
\ —j л центробежный момент инерции относительно
\ J нового положения осей станет равным нулю
JXiyt = JUV = 0.
Рис. 19 Из форм лы (2 20) получим
JX1V1 Jxu cos 2ao ~ 2" "~ Sin 2a° = °*
откуда
tg2a0 = 72^r. (2.21)
Jy -- Jx
Получаемые из (2.21) два значения угла a0 отличаются друг от
друга на 90° и определяют положение главных осей.Как легко видеть,
меныпий из этих углов по абсолютной величине не превышает .
Обычно пользуются меньшим углом. Проведенную под этим углом
(положительным или отрицательным) главную ось обычно обозначают
буквой и. Напомним, что отрицательный угол а0 откладывают от оси х
по ходу часовой стрелки.
Рис. 20
На рис. 20 приведены некоторые примеры обозначения главных
осей в соответствии с указанным правилом. Начальные оси обозначены
буквами х и у. Значения главных моментов инерции можно получить
из общих формул <2.19), приняв a =» a0:
Ju =* Jx cos2 a0 + J у sin2 a0 — Jxy sin 2a0;
J v = J у cos2 a0 + Jx sin2 a0 4- Jxy sin 2a0.
(2.22)
^Сложим и вычтем последние выражения. С учетом (2,21) будем иметь:
1
, Ju"\"Jv— Jx~]-Jy>
, Ju Jv~ (Jx J у) cos 2a0 2JXy sin 2a0 == (Jx Jy) .
* Cub
^Решая совместно последние уравнения относительно Ju и JV) получим
А = 4 [(7х + + (/* “ 'созЪ;
1 Г 1
А> = V (Jx + Jy) (Jx^Jy) '
Очевидно, при Jx>Jy, Ju>J&
(2.23)
Q
Г
Учитывая, Ц соответствии с (2.21), что
1
cos 2а0
= ±/l + tg22a0 = ±l/ 14
4/1,
____лу__
(Jx-Jy)2
выражения (2.23) для главных моментов могут быть записаны в виде
Ju = У КЛ + Jy) ±V(Jx- Jy)2 +
J^i l(A + Jy) T V(Jx - Jy)2 + iJly],
(2.24)
причем верхние знаки следует брать при Jx>Jy и нижние — при
Jx <^i J у
Таким образом, формулы (2.21), (2.23) и (2.24) позволяют опреде-
лить положение главных осей и величину главных центральных мо-
ментов инерции.
Если теперь вместо произвольной начальной системы центральных
осей хОу принять систему главных осей, то формулы перехода к повер-
нутым осям (2.19) и (2.20) упростятся:
J = Ju cos2 а + sin2 а;)
* 1 (2.25)
Jyi = Jv COS2 a + Ju sin2 a, J
/ад1 = у(^и-А)зт2а. (2.26)
Отметим, что главные моменты инерции обладают свойством
экстремальности. В этом легко убедиться, продифференцировав выра-
жения (2.19) по переменной а.
Плоскости, проведенные через ось стержня и главные оси инерции
его поперечного сечения, называются главными плоскостями*
§ 10. Графическое представление моментов инерции.
Понятие о радиусе и эллипсе инерции
Вычисление моментов инерции по (2.23) — (2.26) можно заменить
их графическим определением. При этом принято различать две задачи:
прямую и обратную.
При решении прямой задачи определяются моменты инерции отно-
сительно произвольной центральной системы осей я?, у по известным
главным моментам инерции Ju и Обратная задача состоит в оты-
скании главных моментов инерции по известным моментам инерции
JXt Jy к Jxy относительно произвольной центральной системы осей
я, у-
Прямая задача. Определить моменты инерции Jx, Jy> JXy
относительно осей х и у (рис. 21, а) по Ju и Jv относительно глав-
ных осей, направление которых известно. Для определенности поло-
жим Ju > Jv.
Выберем прямоугольную систему координат в некоторой геомет-
рической плоскости (рис. 21, б). По оси абсцисс будем откладывать
осевые моменты инерции Joc (Ju, Jv, JXf J у и т. д.), а по оси орди-
нат центробежные J^{Jxy и т. п.).
17
В соответствующем масштабе откладываем вдоль оси абсцисс
отрезки О А и ОВ, равные главным моментам инерции. /Отрезок АВ
1
делим пополам, так что ВС = АС = у (А А)- Из точки С описы-
ваем радиусом С А окружность, называемую кругом инерции. Тогда
для определения момента инерции относительно оси х, проведенной
под углом а к главной оси и, из центра круга проводим под углом
2а луч CDX. Положительные углы откладываем против часовой
стрелки. При этом оказывается, что ордината точки Dx равна цеятро-
Рис. 21
бежному моменту инерции Jxyi а абсцисса — осевому моменту инер-
ции Jx относительно оси х. Чтобы получить значение момента инер-
ции Jy относительно оси у, перпендикулярной к оси х и, следова-
тельно, проведенной под положительным углом 0 = а + ~ к главной
оси и, проводим из центра круга луч СВУ под углом 20 — 2 -f-
+ . Легко видеть, что он является продолжением луча CDX.
Абсцисса точки Dy равна моменту инерции ордината KyDy-+
центробежному моменту инерции с обратным знаком (—Ау)> что
соответствует центробежному моменту инерции относительно осей,
повернутых на 90°. Отметим, что двум взаимно перпендикулярным
осям соответствуют две точки круга (Dx и Dy)t лежащие на одном
диаметре.
Проведем из точки Dx ось я, параллельную соответствующей
оси на рис. 21, а. Точка М ее пересечения с кругом называется по*
люсом круга инерции (главная Точка или фокус круга инерции).
Легко показать, что линия, соединяющая полюс с любой точкой круга,
дает направление оси, представленной на диаграмме данной Точкой.
В частности, линия МА дает направление главной оси и. Линия
МВ параллельна главной оси и.
Обратная задача. Известны моменты инерции JXt Jyi Jxy
Площади сечения бруса относительно системы центральных осей х, у
(рис, 22, а). Определить положение главных осей инерции и величину
18
главных моментов инерции. Для определенности построения примем
Jx> Jy 0
В геометрической плоскости (рис. 22,6) строим точки Dx и Dy,
соответствующие моментам инерции относительно осей х и у. Абсциссы
этих точек являются осевыми моментами инерции: ОКХ ~ Jx, ОКу =
= Jy\ ординаты — центробежные моменты инерции Jxy, причем
Рис. 23
KXDX — Jxy\ KyDy = — Jxy. Так как обе точки принадлежат одному
диаметру, то соединив их, получим центр круга инерции С, из кото-
рого описываем окружность радиуса
CDX — CDy—У + Jxy.
пересекающую ось абсцисс в точках А и В. Очевидно, что абсциссы этих
точек (ОА и ОВ) являются искомыми главными моментами инерции
/и 0
19
Для определения направления главных осей построим фокус
круга инерции. С этой целью из точек Dx и Dy проведем линии, соот-
ветственно параллельно указанным осям, до пересечения с кругом
в точке М. Соединив затем фокус с точками А и В круга, получим
направление главных осей и и v (рис. 22, б). Графическое решение
обратной задачи соответственно для четырех случаев, изображенных
на рис. 20, показано на рис. 23, а, б, в, г.
Момент инерции фигуры относительно какой-либо оси можно
представить в виде произведения площади фигуры на квадрат некото*
рой величины, называемой радиусом инерции:
F
(2,27)
где ix — радиус инерции относительно оси х.
Из (2 27) следует, что
(2.28)
Аналогично радиус инерции относительно оси у
(2-29)
Главным центральным осям инерции соответствуют главные
радиусы инерции
iv=y (2.30)
Построим на главных центральных осях инерции плоской фигуры
эллипс с Полуосями, равными главным радиусам инерции, отклады-
вая при этом вдоль оси и отрезки,
равные а вдоль оси р — отрезки,
равные iu (рис. 24). Такой эллипс, назы-
ваемый эллипсом инерции, обладает тем
замечательным свойством, что радиус
инерции относительно любой централь-
ной оси х определяется как перпенди-
куляр ОА, опущенный из центра
эллипса О на касательную к нему,
параллельную оси х. Для получения
точки касания достаточно провести
параллельно данной оси х любую хорду.
Точка пересечения эллипса с линией,
соединяющей центр О и середину хор-
ды, является точкой касания. Измерив
отрезок О A — ix, находим момент инер-
ции по формуле
Jx = Fil
20
§ 11. Моменты сопротивления
Осевым моментом сопротивления называется
отношение момента инерции относительно данной оси к расстоянию
до наиболее удаленной точки поперечного сечения:
W* = . (2.31)
26пах
Размерность моментов сопротивления ~ единица длины в кубе (мм39
см3 или м3).
Практическое значение имеют моменты сопротивления относи-
тельно главных центральных осей» которые обычно называются просто
моментами сопротивления,
1. Для прямоугольника (рис. 10):
ж=т! <2-32>
«'•“-й—т- <233)
2. Для круга (рис. 13):
Wx = Wy = W = -^ = *-£ = —. (2.34)
3. Для трубчатого сечения с внутренним диаметром д и наруж-
ным — D:
Wx=Wv = W=A = K (Д4 ~ di} = g (1 - «4). (2.35)
X// OuU O4i
где
а = А. (2.36)
Полярным моментом сопротивления назы-
вается отношение полярного момента инерции к расстоянию от по-
люса до наиболее удаленной точки сечения:
(2-37)
Ртах
В качестве полюса принимается центр тяжести поперечного сече-
ния стержня.
1. Для круга (рис. 13)
^=4=?=^- <2-з8>
2. Для трубчатого сечения
"> <2-3’)
21
J 12. Порядок расчета
При анализе геометрических характеристик плоских фигур любой
сложности важнейшей задачей является определение положения глав-
ных осей и величин главных моментов инерции. Можно рекомендовать
следующий порядок определения положения главных осей и величин
главных центральных моментов инерции сложного профиля, состоя-
щего из простых частей, характеристики которых легко определить.
1. Проводим произвольную прямоугольную систему осей. Разби-
ваем фигуру на простые части и определяем по (2.5) положение ее цен-
тра тяжести.
2. Проводим начальную систему центральных осей я, у таким
образом, чтобы наиболее просто можно было вычислить моменты
инерции частей фигуры относительно этих осей. Для этого определяем
моменты инерции частей фигуры относительно своих центральных
осей, проведенных параллельно осям а?, у, используя при этом формулы
перехода к параллельным осям (2.14) и (2.15). Таким образом, полу-
чаем значения Jy и Jxy-
3. Определяем по (2.21) угол наклона главных центральных осей,
причем ось, проведенную под меньшим углом (положительным или
отрицательным), обозначаем буквой и, а перпендикулярную к ней —
буквой V.
4. По формулам (2.24) определяем значения главных центральных
моментов инерции Ju и
Пример. Определить положение главных центральных осей
и вычислить главные моменты инерции для поперечного сечения
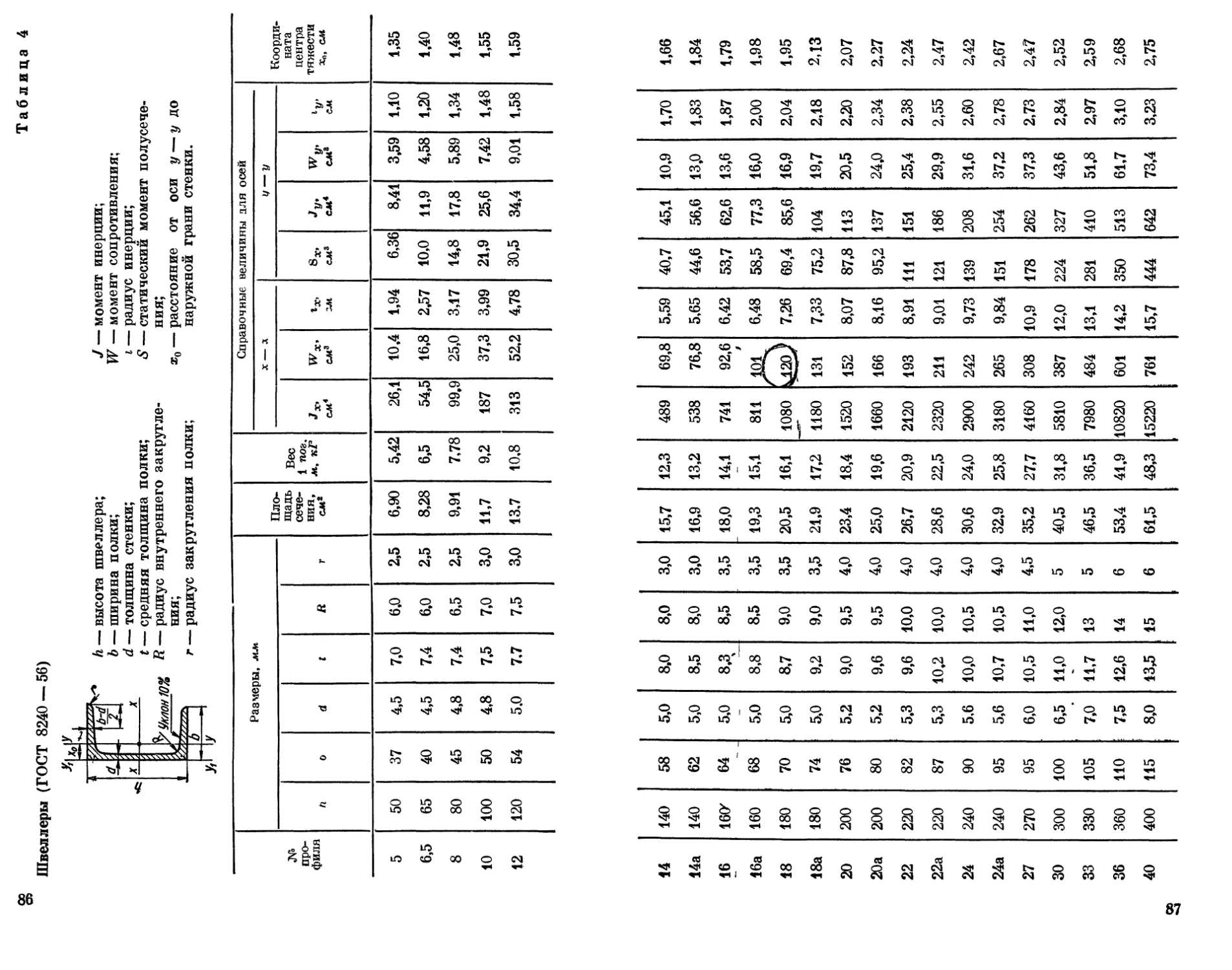
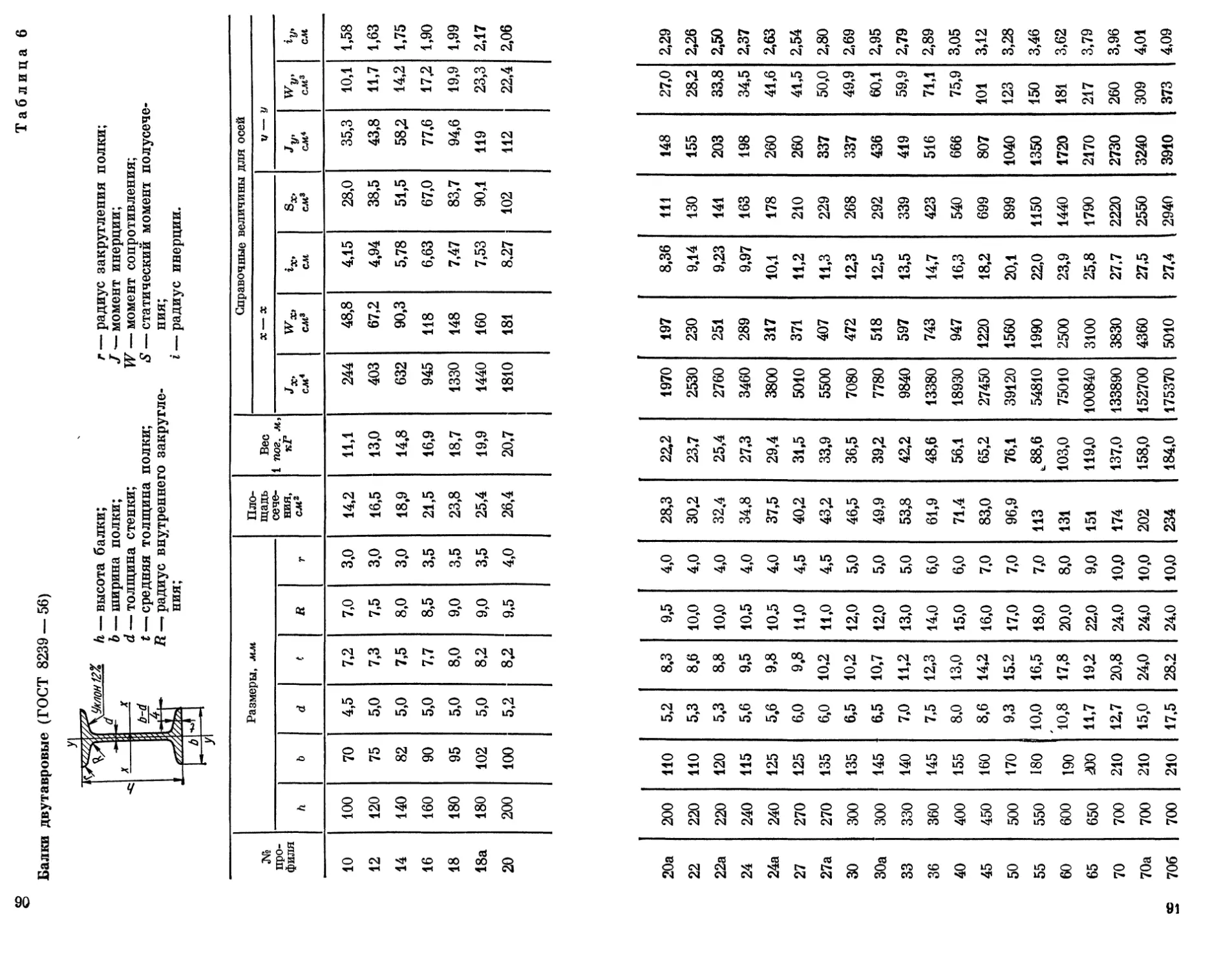
(рис. 25, а), которое состоит из неравнобокого уголка № 14/9 (ГОСТ
8510—57) и швеллера № 24 (ГОСТ 8240—56).
Рис. 25
Решение. Через центры тяжести С± и С2 уголка и швеллера
проводим центральные оси уг и я2, Уз» параллельные их сторонам.
Поскольку х2 — ось симметрии швеллера, она и ось у2 являются его
главными центральными осями. Главная центральная ось yQ уголка
образует с его центральной осью угол а.
Для уголка Fi = 22,2 см2; JXl — 146 см4; Jyt = 444 см4;
22
= <Лп1п = 85,5 см4; tg а = 0,409; а = 22° 15'; координаты центра тяже-
сти хс == 4,58 см, ус = 2,12 см.
Для швеллера F2 = 30,6 см2; Jx* = 2900 см4; Jyz = 208 см4;
JXiVi = 0; координаты центра тяжести хс = 2,42 см; ус = 12 см.
Найдем главный момент инерции JXq и центробежный момент
инерции J уголка:
Jx = == 444 + 146 — 85,5 = 504.5 см4;
XLlciX 1 7
JXiVi = — sin 2 (9°° - «) = J-X*~ Jy° Sin2a =
504,5 — 85^5 0,701 = 146,7 cMi
£
Расстояния между центральными осями уголка и швеллера равны:
между осями arx и х2
12,00 + 2,12 = 14,12 см;
между осями и у2
14,00 — 2,42 — 4,58 = 7,00 см. '
Определим координаты центра тяжести С всей фигуры в системе
осей х2, у2:
22,2 • 7,00 9 о. . 22,2 . 14,12 к о.
~ 22,2 + 30,6 ~ 2,94 СМ’ Ус ~ 22,2 + 30,6 ~ 5,94 см'
Центр тяжести С должен лежать на прямой что необходимо
проверить на рисунке. Через центр тяжести С проводим центральные
оси хс и ус, параллельные проведенным ранее центральным осям
уголка и швеллера. В системе центральных осей хс, ус координаты
центров тяжести уголка и швеллера равняются:
xCi =» 7,00 — 2,94 =* 4,06 см; yCi =*= 14,12 — 5,94 =. 8,18 см;
хсл см\ Ус2 = 5,94 см.
Вычислим осевые и центробежный моменты инерции всего сечения
в системе произвольных центральных осей хс, ус:
JXq - 146,0 + 22,2 • 8,182 + 2900 + 30,6 • 5,942 = 5607,6 см4;
jVq 444,0 + 22,2 • 4,Об2 + 208,0 + 30,6 • 2,942 = 1282,4 см4;
Jxc ус ~ 146,7 + 22,2 ’ 4,06 8,18 + 30,6 ’ (^2>94) ’ Н5’94)
= 1417,3 см4.
По формуле (2.21) находим угол а0 наклона главных центральных
осей х и у относительно произвольных центральных осей хс и ус\
%Jxryr 2 1417 3
tg 2a0 =. - 0,66;
2a0 = 33е 20'; a0 = — 16° 40'.
Поскольку угол a0 отрицательный, главная центральная ось и откла-
дывается относительно произвольной центральной оси хс по часовой
стрелке, а поскольку /Х(, > Jy^ то ось и является осью, относительно
которой момент инерции будет максимальным.
23
5607,6-1282,4? ! Ш7)32
Главные моменты инерции определим по формуле (2.24):
г 5607,6 + 1282,4
•'и, и 2 2
= 3445,0 ± 2585,6 см4;
= Jmax = 6030,6 см4 = 6030,6 • 10-3 м4;
Jv = Anin = 859,4 см* = 859>4 • 10~? ж4-
Проверка. Должны удовлетворяться условия
Jxq + vq ~ Ju~V J v и /и« = 0.
В данном случае имеем
J*G + Jvc 5607,6 + 1282,4 = 6890,0 = Az + А> = 6030,6 +
+ 859,4 = 6890,0 см4;
Геометрические характеристики плоских сечений
Форма сечения Площадь сечения F Координаты крайних точек сечения
Квадрат 1/ S'=ht h ^ = 2/! = -2
х_ р о X
* л
У Любая цеЕ ось — глав] [тральная эая
Квад рат п У У - М олый _ Xi~ Д
X
V/.
% %
% %
Люба ось — // л
У 1Я цег »глав; [трал] цая ьная
24
dxc yc
Лю = 2 ®in -|- Jxquq cos 2% =
= 5607'6—1282'4 . (—0,55) + 1417,3 • 0,836 =
= —1189,4 + 1184,9 = — 4,5 cm*.
4 5
Относительная ошибка составляет 100 = 0,4%, что допу-
стимо.
На рис. 25, б показано построение круга инерции для графического
решения этой же задачи.
Геометрические характеристики различных плоских сечений,
а также сечений прокатных профилей приведены в табл. 1—8.
Таблица 1
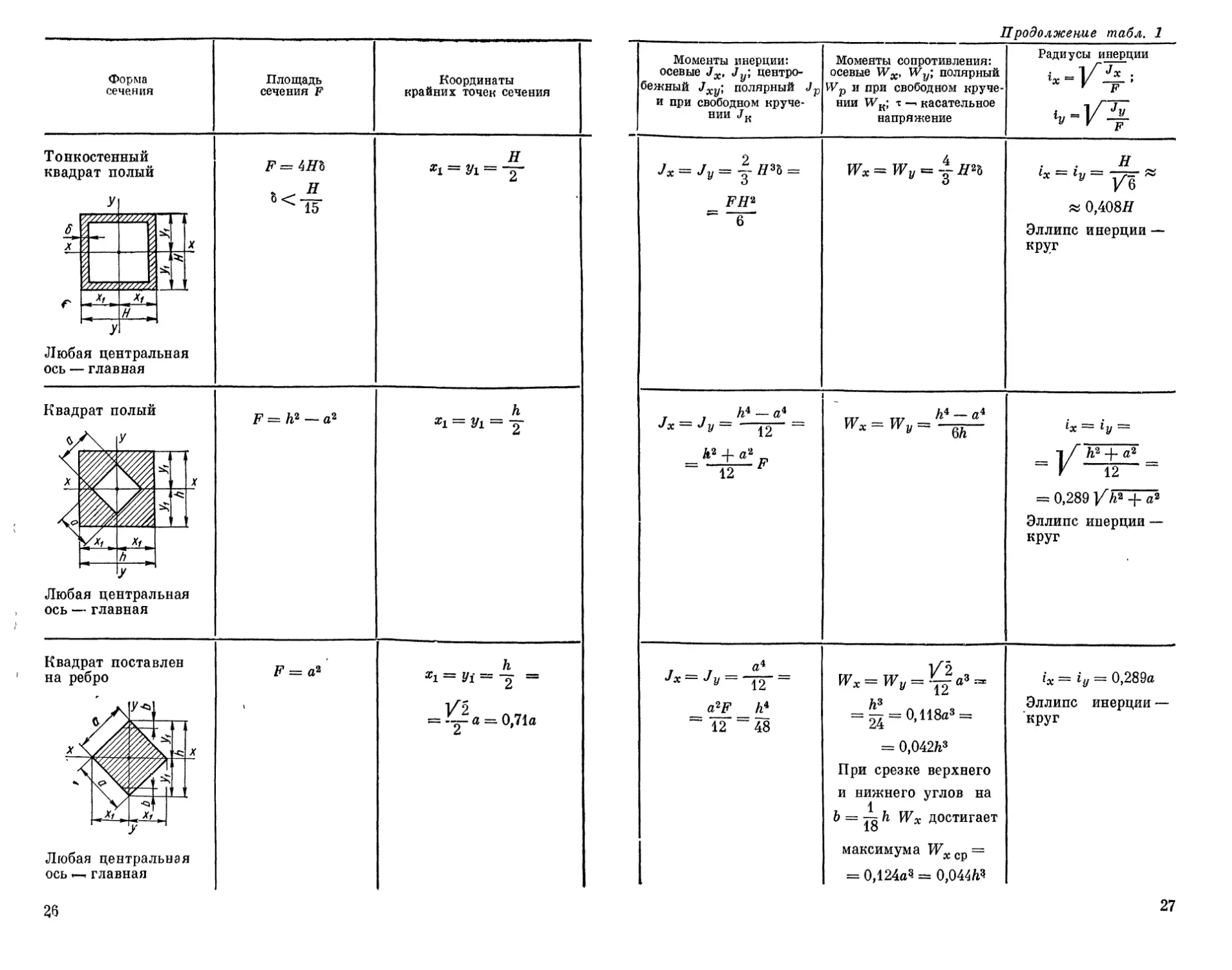
Моменты инерции! осевые J х, центро- бежный Jxy; полярный Jp и при свободном кручении JK Моменты сопротивления: осевые Wx, wy} полярный Wp и при свободном кру- чении WK; т — касательное напряжение Радиусы инерции *»-О
_ _ №F J* = Jv 12 12’ h* h?P Jx2— з — з ’ JK = 0,1406ft4 h3 Wx = Wy~~, WK = 0,208&3 Tmax посередине сторон, в углах т = 0 h = 0,289Л Эллипс инерции •— круг
j -j “ 12 F TV _TV Hi~hi Wx-Wy- ей 1х = 1у = - l/~ga+^ ~ Г . 12 = 0,289 /Я2 4-Л1* Эллипс инерции — круг
25
Форма
сечения
Тонкостенный
квадрат полый
Любая центральная
ось — главная
Квадрат полый
Любая центральная
ось — главная
Площадь сечения F Координаты крайних точек сечения
Т V ь. « н *1 = 2/1 = —
F = № — а2 h = = Т
Квадрат поставлен
на ребро
F = а2
Любая центральная
ось главная
h
xi = Vis=~2 =
= ~?а = 0,71а
Ci
26
Продолжение табл. 1
Моменты инерции: осевые Jx, Jy; центро- бежный Jxy; полярный Jp и при свободном круче- нии JK Моменты сопротивления: осевые Wx, Wy; полярный Wp и при свободном круче- нии WK; т касательное напряжение Радиусы инерции
2 JX=JV = v Н*Ъ = и ~ 6 4 Wx = Wy = -?rH4 о н Ь-1у-у=г№ « 0,408Я Эллипс инерции круг
j -j Jx — J у — ' |2 “ + °* „ = "12 F h4 — а4 Wx-Wy~ Qh 1х 1у — •— 1/" “Н Я2 _ “Г 12 ~ = 0,289 ]/Ла + а2 Эллипс инерции — круг
j -j _^L- 12 - a2F A* ~ 12 ~ 48 h3 = т^ = 0,118a3 = = 0,042fc3 При срезке верхнего и нижнего углов на 1 b = ^8 h Wx достигает максимума V7xcp = = 0,124а3- = 0,044^3 ix— iy~ 0,289а Эллипс инерции — круг
27
Форма
сечения
Площадь
сечения F
Координаты
крайних точек сечения
F = а2 — Ь2
Квадрат полый по-
ставлен на ребро
Любая центральная
ось — главная
Прямоугольник
F = bh
b
Xl~ 2
H
f 2
Ya== 0,71а
h
= T
Оси x^-x и у —у —
главные централь-
ные
28
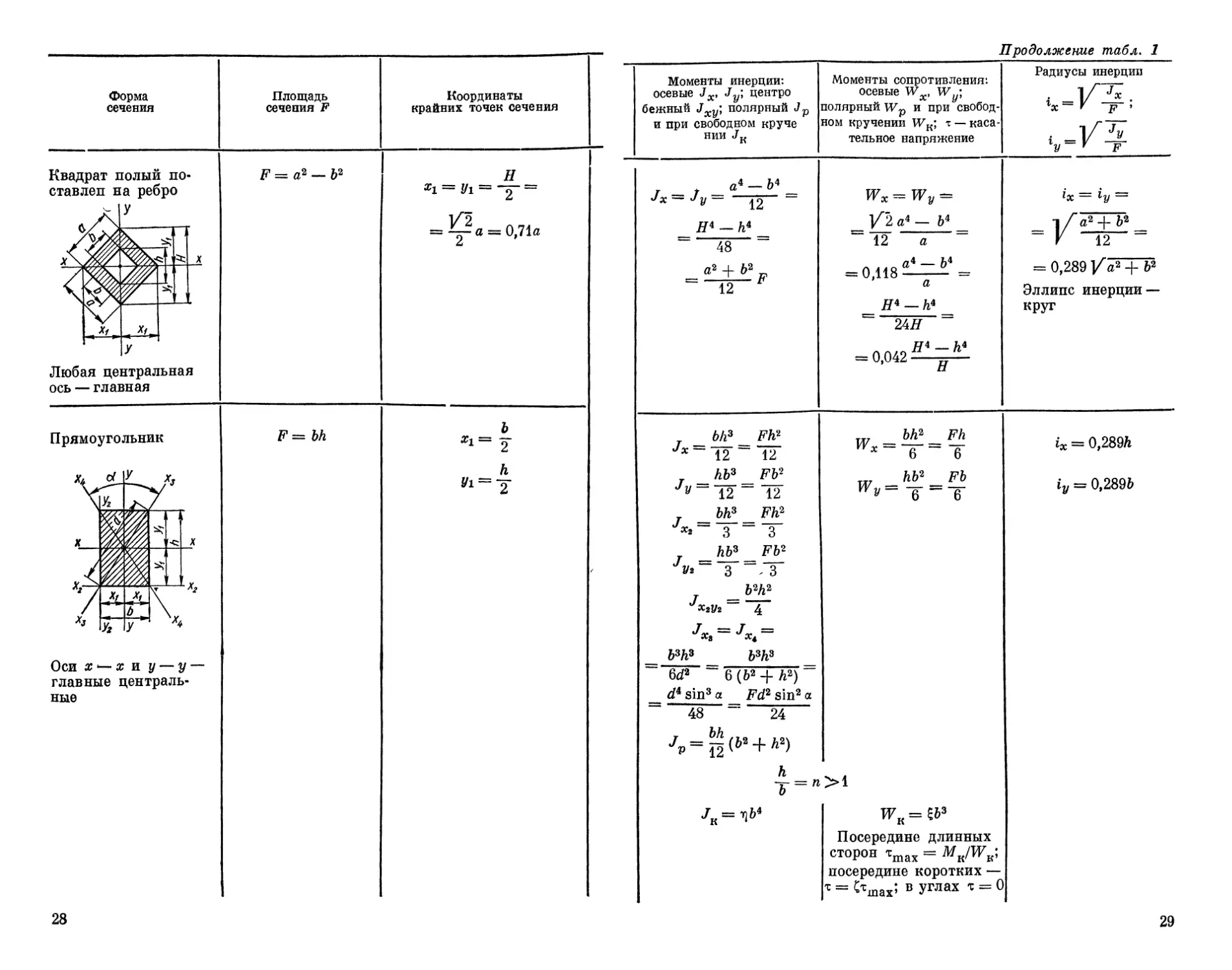
Продолжение табл, 1
Моменты инерции: осевые Jx, Jy; центро бежный Jxy] полярный и при свободном круче нии JK Моменты сопротивления: осевые Wx, Wy; полярный Wp и при свобод- ном кручении ТУК; т — каса- тельное напряжение Радиусы инерции i =у^.. i =У А У F F
J -J at-bt- Jx— Jy — 12 — Я4 — h* ~ 48 ~ а2 + Р = "12 р = Wy = _ У‘2 а* — Ь4 “12 а “ = 0Д18 а __ H^ — h\ 24Я “ = 0,042^1 а ^х—1у~ — 1/* — У 12 “ = 0,289 /а2 + Ь2 Эллипс инерции — круг
bh3 Fh2 hb3 Fb2 Jy-~12 ~ “12 _ bh3 Fh2 3 ” 3 _hb3_Fb2 3 “ - 3 _b2h2 Jx2y2 4 J = J = •*3 X4 №h3 _ &ЗДЗ _ 6<P ~ 6 (ь2 + Л2)_ _ s’n3 a _ sin2 “ 48 ~ 24 4 = й(Ь2 + Л2) h T —" JK=^ w bh2 Fh ^ = V=1- w hb2 Fb Wv= -Q =T >1 WK = tf>3 Посередине длинных сторон tmax = Мк/Жк; посередине коротких — т = ^тах? в Углах т = 0 ix = 0,289/г iy = 0,2896
29
Форма сечения Площадь сечения F Координаты крайних точек сечения
п 1 1,5 2 3 4 6 8 10
5 0,208 0,346 0,493 0,801 1,150 1,789 2,456 3,123
0,1404 0,2936 0,4572 0,7899 1,1232 1,789 2,456 3,123
с 1,0 0,8588 0,7952 0,7533 0,7447 0,7426 0,7425 0,7425
Прям полых оуголъ I > ник F=BH — bh Л* Il II fcq 1хэ| to
ж 777 X
X 7/
7/ 1
77 %.
-Л. £ л Г/
Оси х— главные У х и цех у- upaj -у — тьные
Тонкости уГОЛЬНИ! энный прямо- £ полый И F = 28 (В + Н) 5< 15 45 Н м к- II II tj| tq w| to
х_ 2^2? _х
7 ?77< / >
//
В
Оси х главн] ' J ые X и цев Ур- етральные
30
Продолжение табл. 1
Моменты инерции: осевые Jx, Jy\ центро- бежный Jxy\ полярный Jp и при свободном круче- нии JK Моменты сопротивления: осевые Wx, Wy\ полярный Wp и при сво- бодном кручении VVK; т — касательное напряжение Радиусы инерции • 1/^. { „1/ гУ Y F
h T = n>i
JK =-!(»-0,63) bi 1 И\==у(п-0,63) &3 = -А ь В точках длинных сто- рон, за исключением концов, ттах; посере- дине коротких сторон т = 0,7 425ттах; в углах т == 0
BH3 — bh3 Jx ~ 12 HB3 — hb3 Jy-~ £2 ’ « я II II 64 Св Со tjj ГО " ГО “ Со I ЙЗ | _ -if BH3 - bh^ lx~ V 12 (BH-bh) . _ -if HB* — hb* ly~ V 12(BH-bh)
8 11 II | 09 1 09 co ^4 + + 3 II II 1 09 1 <09 го|Сп w|tg ^GO tt;| to + + ix = 0,2897/ X x V в + н iy = 0,2895 X x V h + b
31
Форма
сечения
Площадь
сечения F
Координаты
крайних точек сечения
Прямоугольник
Оси X — X и у — у —
F = b(H — h)
b
= T
H
y^T
главные центральные
Прямоугольник с
круглым отверстием
Оси х — х и у — у ~
главные центральные
Прямоугольник
с двумя отверстиями
F=bh
zd2
2
/ d2 \
= bh (1-1,57-—=—)
\ bh J
b
xi = T
h
У1=2
b
X1~ 2
h
У^ = -2
32
Продолжение табл, 1
Моменты инерции: осевые Jx, Jy; центро- бежный Jxy; полярный Jp и при свободном круче- нии JK Моменты сопротивления: осевые Wx, Wyi полярный Wp и при сво- бодном кручении Wrf т — касательное напряжение Радиусы инерции 1/” Jx lx “ V -fT 5 i «1ЛА. гУ“ У F
Ъ3 Wx=~A <яз--а8) Wy=~{H-h) ix = __ 7 f H3+Hh+h^ _ V 12 =0,289 ^ff3+ffh+h3 iy = 0,289fc
__ 1 Ibh3 rcd4\ _ Jx ~ 4 \ 3 16 } “ -^G-059-^ - 12 ^1 0,59 T 1 / hb3 nd4\ Jy ~ 4 \ 3 16/~ - 12 ^1 0,59 hb3 j _ 1 (bh3 wi*\ Wx ~ 2h \ 3 16 / ~ = ^(1_0,59^) 0 \ vrr / 1 I hb3 nd4\ __ Wy ~ 2b \ 3 16 / ~ 6 \ hb3 / ix = 0,289ft X / d4 / 1—0,59^3 4zl/ bh3 X 1/ d2 f 1— 0,785 4г- f bh iy = 0,2896 X f 1-0,785 r bh
J -^fl- Jx ~ 12 L1 d4 I -U8-^(l + 1 4ft Я +1MJ T hb3 It 4,ad*} Jу — ir Л o 11 — 1,18 ttx 1 * 12 \ hb3/ ТЛ7 6A2|\ и^ = -в-[1- d4 I +i6-S-)l “ /J TJZ hb2 (4 ^l/=—^1- -l,18-£-) hb3 1 ix = 0,289ft X 1-1,18 и>x v 4+isg) 1-1,57-^- iy = 0,289Ь X , /1-1,18-£ 7
2 5-1186
33
Форма сечения Площадь сечения F Координаты крайних точек сечения
Прямоуго. с полукрз вырезами У пьник тлыми F = bh — nr2 £ to[ Sr to| с-
X X
% .<5
Xi
J' У-У — тральные
Оси х главш 1 У — х ле в и 1,ен
Прям с повер] % >уго ауть ль ник [Й 1У - F=bh 1 yi = (h cos a + b sin a) 1 xt = {b cos a — h sin a)
_Х
-t Xf г
1у
Узкая прямоуголь- ная полоса F= It a + b Уо= 2 h {/i = -2
к Сз| 1
34
Продолжение табл. 1
Моменты инерции: осевые Jx, Jy; центро- бежный Jxyi полярный Jp и при свободном круче* нии JK Моменты сопротивления: осевые Wx, Wy\ полярный Wp и при свобод- ном кручении WK; т — касательное напряжение Радиусы инерции ,-K5
bh3 яг4 12 4 hb3 Г ^ = ^--2[о,11Н + , 4rVl + ~2 \"2 3i/ J + to 3 I « Дл. <н* * № О- г-^-, II g. I М 1 to ОО лх Ь> + 1 Ь> h> и и •Л*
Лс = ^(Ь2 cos2 а 4- + &2sin2a) •fy = jg(fc2sin2a + + b2 cos2 a) Jxy=g(62-h2)sin2a ff'=“x x cos2 a s*n2 a h cos a 4~ b sin a Wy = b~X X s*d2 a ~b ft2 cos2 a b cos a — h sin a ix — - Гcos2 a -|- _ I/ + &2 sin2 a F 12 ~ 1 /" h2 cos2 a + = 0,289 у 4- 62 sin2 a 1 /"fe2 sin2 a + = 0,289 К +52cos2a
_ Ztft2 _ Fh? Jx~ 12 ~ 12 =-§-(a2 + a6 + 62) ту _ ^Ж8 = ^(а2 + а& + Ь2) ix = 0,289fc
2*
35
Форма сечения Площадь сечения F Координаты крайних точек сечения
СИА тав НИИ гметр р из ов нтчный дву- прям оу го ль- F — ah b (Н — h) Н to] Ьц 1^1
V//, г ?ж_ 5? X
g
№1
Oci гла П7
X — вные 4 -X и цент у — у— ральные
Дв? X |Гтавр У1 о,, F=aH + + 26 (c + q) 1 Ь = ^(В-а) flq [eq 11 11 &
*1^ р _х
т
J1
~fz
у!
Сил ние вив шет5 ИЗ ] :ов )ИЧН01 трямс в сече- >уголь- F=BH— bh я ^=т
фз!
Щр|
Ось цен 41 | X — трал: X— I ьная 41 главная
86
Продолжение табл. 1
Моменты инерции: осевые Jx, Jy; центро- бежный Jxy; полярный Jp и при свободном круче- нии JK Моменты сопротивления: осевые Wx, Wy; поляр- ный Wp и при свободном кручении VVK; т — касательное напряжение Радиусы инерции ix=y?“.; X Г Р 1 i =1/А гУ У р
ah3 Ъ ^-^+r2(H3-h3) a3h b3 и . Jy ~ 12 + 12 h) ah3 Wx ~ 6Н + T1Z a3h 1 № 1х -1/+ ъ {Н3 — Ъ3) V 12 [afe+б (Я—fc)] гу = _]/ a3h+ b3 (H — h) V 12[ah+b
Л = 1[вЯ3- /у = А[ВЗ(Я-Л) + + M3 + ^(B4-a4)] h — hA ““ 2b Для стандартных дву- тавров 1 “~"б' и'-“тя4ш’- Жг/ = -^-[в3(Я-Л) + + М3 + -|(В4-а*)] <ё“ h" II II Ф1
_ _BH3~ bh3 Jx 12 BH3—bh3 Wx~ 6Н 1/ Bff3 ~ bh? lx~ V 12 (BH^bh)
37
Форма сечения Площадь сечения F Координаты крайних точек сечения
Симметри ние из пр ников ши иное сече- ямоуголь- F^BH+bh н У^~2Г
Дик ь № 2 2 2 Ось х— х центральн Е яг дуй в. 2 — гла ая -J—л вная
Крестовин % TT22Z а И F = Hb + (B — b)h в Ж1 = Т н Vi = —
7,777771'.. X
-Л
J)
в „
у
КрестовнЕ стенная х pJ|LJ га тонко- F=hb + (b — V)b 51 и to| ю| о
Г 1*; J ч
Jfrj Lx,~—
ь *
У
38
Продолжение табл. 1
Моменты инерции: осевые Jx, Jy; центро- бежный Jxy; полярный Jp и при свободном круче- нии JK Моменты сопротивления: осевые Wx, Wy; полярный Wp и при свобод- н ом кручении V7K; т — касательное напряжение Радиусы инерции
_ _ВН* + Ь№ Jx~ 12 х 6Н . _ -1/ BH*+ b№ lx r 12 (BH+bh)
Т _ ьн* + (В — Ъ) № ЬН*+(В-Ь)К> kh И6* и и <tK J3>
Jx 12 Лй3 + (Я —Л) 63 И Л - 6Я hB» + (H-h) №
Jv~ 12 QD
Л = Л [&38 + 88(Ь-&)] fe38 + 83 (6_8) х~ 6h J38 +8s (fe_8) Wy- - gj kk kk II II -J*
39
Форма сечения Площадь сечения F Координаты крайних точек сечения
Неси Двутг угол! ь мметричный 1вр из прямо- эНИКОВ F=bC1 + й (h Вс Ъ± — Ъ — а Вг = В —а В xi=T 1 2/i = -2 X 4z аН^+B^+b^ (2Я-С1)
2
с Т X
X
А аЯ 4-В1С 4-Ь1С1 у[ = н — yt h = yt —с hi = у/— Q
Оси а главн Ж; ж 7
Bl л, А X X,
/9 у — У ~~ (тральные
У ? — ые X и цев
Симм из пр етрич •ямоу У :ный та ГОЛЫШ! |£ вр сов Уг F=(B^b)c+bh В , 1 2/х — 2 X (В — Ь) с° 4- bh2 х (B~b)c-[-bh yi = h — у^
Z Xi -XJ
7/
* < X
У
40
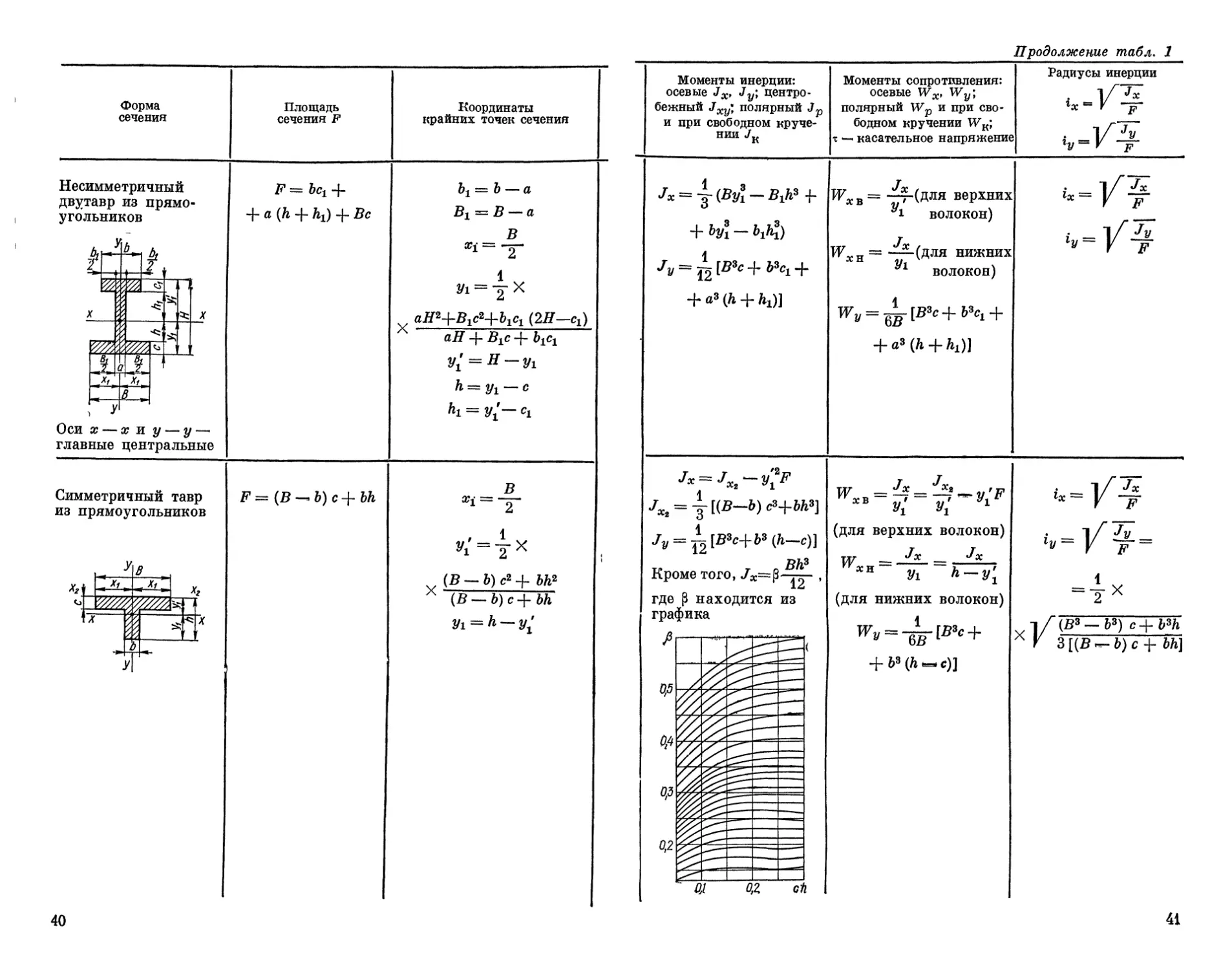
Продолжение табл. 1
Моменты инерции: осевые Jx, Jy; центро- бежный Jxy; полярный Jp и при свободном круче- нии JK Моменты сопротивления: осевые Wx, Wy; полярный Wp и при сво- бодном кручении WK; т —< касательное напряжение Радиусы инерции 1/" Jx V ~р i _]/ гу— V F
Jx = ~(By31 — B1h3 -ь + by3l-b1h3) Jy = ^[B3c+^C1 + + a»(h + h1)] Wx в = -^7-(для верхних волокон) ТГХН = —(для нижних волокон) ^=6F[B3c+63ci + + a8 (ft + MJ я II II
JXi = ^[(B-b) сЗ+ЬЛЗ]
I
Jv = ±\B3c+b3(h-c)]
“ у[ Уг 1 ix~ V Ф
(для верхних волокон) «Г* II II
V¥xn~ V1 h-y^ 1
(для нижних волокон) “2Х
1/(Д8 —ьз) c+b3h Х V 3 [(В — Ь) с -f- bh]
+ 6’(Л »=.«)]
41
Форма
сечения
Площадь
сечения F
Координаты
крайних точек сечения
Несимметричное се-
чение из прямоуголь-
ников
F = аН + Ьс
аН2 + be2
2(aH-\-bc)
= H — yt =
ЛНг -Ь be (2Я — с)
2 (аН Ьс)
F = Bh-\-
-±2b(H~h)
Bh? + 2Ь (Н* — №)
Vi ~ 2 [Вй + 2b (H — h)]
y[=H^
Устой с обратными
стенками
F = BH-^±bh
У1 =
ЗВН2 — h2 (Ь + 2а)
6ВЯ — ЗЛ (а + Ъ)
= У1
42
Продолжение табл. 1
Моменты инерции: осевые Jx, Jy, центробежный поляр- ный Jv и при свободном кручении JK Моменты сопротивления: осевые Wx, Wy} полярный Wp и при сво- бодном кручении WK; т — касательное напряжение Радиусы инерции 1/" Jx • 1х « У ”рг ’ •«-/5
/« = у(2^-^ + + w'fi WXB=" хн уг (для нижних волокон) w — — Jx жв = у; ~н-У1 (для верхних волоков) И,ЖН>»7ЗСВ ix== V
II + II 5 К *Ь Оз ' to *5 1 + to to> Г 1 ? tS а- II J? ~~~ М to " X z to I ? м 1 , “ з: м в- + « “ + + 05 Wx=-^- У1 (для нижних волокон) (для верхних волокон) Wy = В3Н— (H—h) (B—2by ~ 6В «• 8’ 11 X
1 .4 и4 8 Х jto И О- СО Оз — II °- О- 1 СО ю 11 + 4^1 ‘ S’ 1 5 х (для нижних волокон) (для верхних волокон) WV~ 6 h b' — a? 24В b — а II II
43
Форма
сечения
Площадь
сечения F
Координаты
крайних точек сечения
F = <(26-t)
Равнобокий уголок
xi= Viв
h» 4-1 (6 — t)
2 (26-t) '
= h «•= а?, = 6 •=• у.
Равнобокий уголок
F = t (27г = 4)
h -j” t — 2с
V1 vr~
, h? + ht — t2
1----7=
1 (2/г-О/2
Неравнобокий уго-
лок
_ 62 + Att
X1 '^(b+h,)
= 6 — »! =
b2 + (26 — t)
- 2(6 + 6,)
_ h2 + b^
^-Zih + bi)
y[ = h — у, =
62 + 6,(26—0
2(6 + 6,)
44
Продолжение табл. 1
К" ” Моменты инерциц: осевые Jx, Jy; -центро- бежный полярный Jp и при свободном круче* нии JK Моменты сопротивления: осевые Wx, Wy; полярный Wp и при сво- бодном кручении WK; t — касательное напряжение Радиусы инерции гх - V -р-; i ]/~Jy lv У ~
+ Т + = ± i i =. «Uy < • у 7 te ‘Л is J 7^5» s 1 ~ - ^7^7 В "S 1) и 1 + 1 “7 j ,S + Т7х = ТГг, « v Vi (для левых и нижних волокон) *1 (для правых и верхних волокон) lmin lvt = “/у1
jx=4 [2c4 - -2(c-«)4 + / t \31 + ЦЛ-2с+-^) J h* — (h — t)4 Jy ~ " 12 W = ХВ у г (для верхних волокон) И7хв = — жв Vi (для нижних волокон) [ф II II >(Н .J3» »
Jx ~ "3" (Л —’ 3/1)3 + + fy/i~ &1 (3/Л —/)3] jу ~ [J ( & — #1)3 + 4- hx[ — hi (Xi — J)3] bbihhit Jxv~' МТ+М- __ bbxhhxt 4 (Л + bi) ^xB=-^7- хв у{ (для верхних волокон) ^н = — хн У1 (для нижних волокон) W = «п (для правых волокон) W = Xi (для левых волокон) ix = ]/ = 0.29Л 'у = У = 0,326
45
46
П родолжение табл, 1
Моменты инерции: осевые Jx, центро- бежный J^y, полярный Jp и при свободном круче- нии JK \ Моменты сопротивления осевые Wx, Wyi полярный Wp и при сво- бодном кручении VTK; т —* касательное напряжение Радиусы инерции
Ьйз _ (Ь — — 2t)3 Jx~ 12 ht* + 6Z&2 (6 — ix) + + 2t (6 -. tr)3 Jy ~ 12 J _Jx COS2 a —J у SID2 я Л2 cos 2a _ Jycos2a—sin2a ~~ cos 2a tg2“- JX-JV wx = - bh3-(b~‘t1)(h'-2t)3 Wy = kt* + 6tb2 (b — tj) + + 2t(b-tl)3 6 (26 — tj) Ь"1ь ЬФ II II
bh3 Fh2 Jx~ 36 “ 18 bh3 _ Fh2 12 6 bh3 _ Fh2 Jx>~ 4 ’ ~ 2 bh (b2 <— Jy~ 36 F (62 — ~ 18 t h^i+xr) у* - 12 •^ = 52 XW1 + ж1) “гра = ^(3№2 + ж? + 4) Для равностороннего треугол роной b н высотой h _ hb3 _FW, Jy Jvl 48 24 ’ h3 h* - K~ 15/3 25,981 _ 3 fe4 M ~ 80 /3 ~ 46,188 W X H 12 (для нижних волокон) w = ^в 24 (для верхних волокон) __ bhjb^^x/x^ Wy^ ~ 36*! (для правых волокон) _ 5fe(62 —x/art) ^л“" 36*; (для левых волокон) 1ьника со сто- РИ = W — — fryn гг у л 12 ’ WK = 0,05&3 = fe3 _ № ~ 7,5/З-12,99 “ h Посередине сторон тта\’ в Углах т = 0 h 1х = “ = 3/2 = 0,2357/г 1 1у — г— X 3]/2 X /&2 Хх = = 0,2357 X х 1/б2 -= х{ xt - Ь 1/”3 1у~ 6 V 2 “ = 0,2046
47
Форма сечения Площадь сечения F Координаты крайних точек сечения
Прямо угоды Zr х2 угольный 1ИК ' у А *1 к*/г 7 Ъ г Уг У тре- X *2 •st |см II Йм Л О ^•|со <м|со ^[со <м|со JI II II II н н £ "S
48
Продолжение табл. 1
Моменты инерции: осевые Jx, Jy; центро- бежный полярной Jp и при свободном круче- НИИ JK \ Моменты сопротивления: осевые Wx, Wy; полярный Wp и при сво- бодном кручении WK; — касательное напряжение Радиусы инерции гх — V р » i -У11. гу — у р
\ Для равнобедренного т нием Ь, высотой h и угд /к = ^ЛЬ«е-=°Д05Ь4 реугольника с основа- юм при вершине а < 15° Игк = -Длб2_ 0,10563= К 12 — ” ъ В точках длинных сторон вблизи основа- ния *стах; в углах т = 0
_ ____ bh3 F№ х~~Зб"= “18 7 _ bh3 _ Я™ х>~~ 12 ~ j. bh3 Fh2 Х>~~~Т г ~ b3h - Fb* Jy 36 “ 18 _ b3h _ Fb3 Jv*~ 12 ~ ПГ T b3h3 Jxy - 72 _ W Jx2y2 — "24 = &2fe2 Jxsy2 *“ g J — — (Л24-Ь21 — ^g2 p ~~ 36 ( ~ 36 'c* = h? + b* А>а = ^’+»!) = bhc3 ~ 12 4в = й<3/12 + 62) W = ЛН 12 (для нижних волокон) ггхв 24 (для верхних волокон) W = — YVyn 12 (для левых волокон) W — —- 1/п“ 24 (для правых волокон) ix = .Ь. = 0,2357Л 3/2 Ъ ly~zV2~ = 0,23576
49
Форма
сечения
Площадь
сечения F
/Координаты
крайних точек сечения
Трапеция
F = ^(bt + b)h
_ 4-261
У1~ 3(64-м
, 26 +
Ul~ 3(6 4-6i
Ось х х цент-
ральная
Для равнобедренной
ним + bQ = Ь
2/1 “3(2б1 + 60)й
6
®1--2
Для трапеции в виде
сотой Л>4Ь
5С
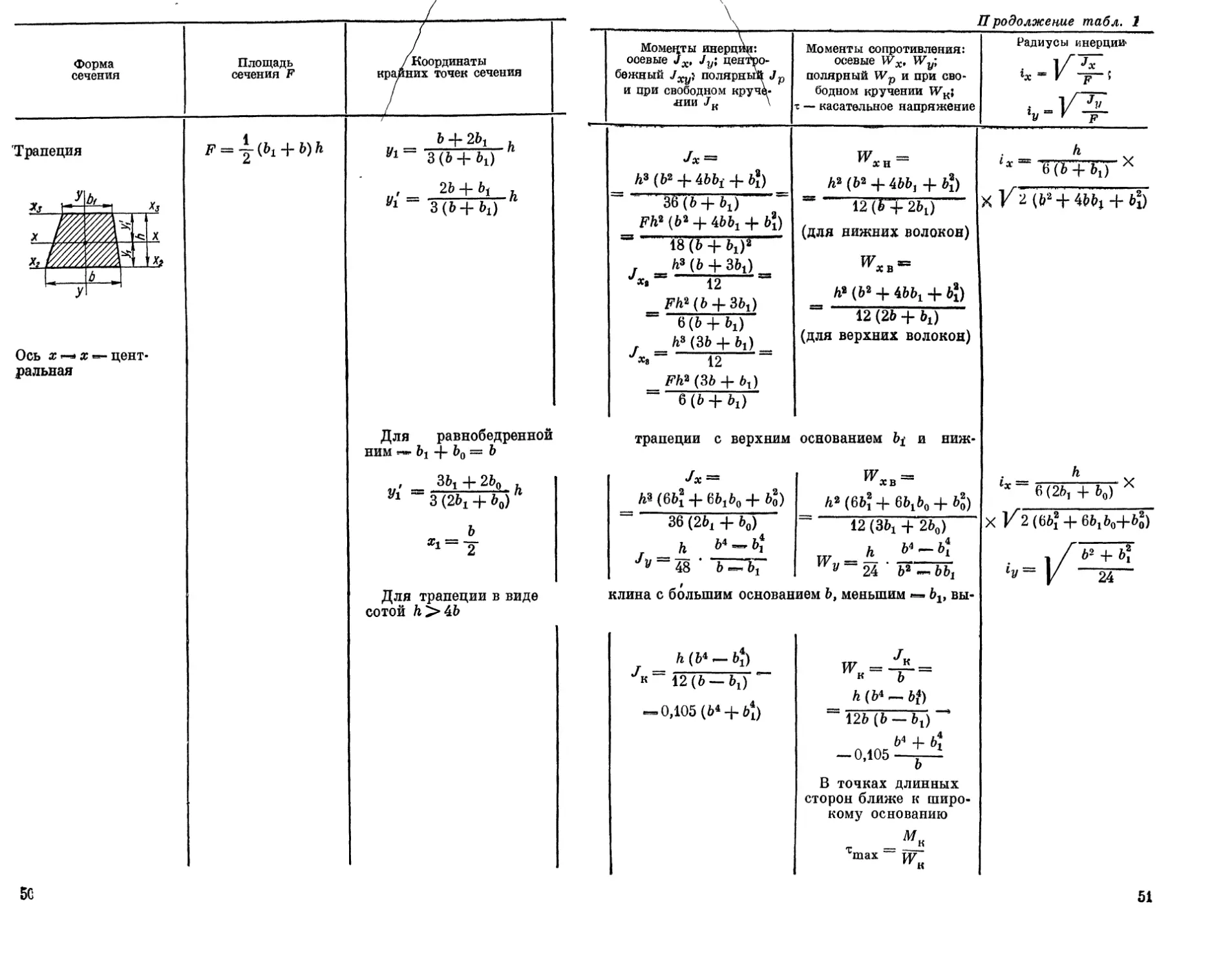
П родолжение табл. 1
Моменты инерции: осевые Jx, Jy; центро- бежный полярный Jp и цри свободном круче- нии JK \ Моменты сопротивления: осевые Wx, Wy, полярный Wp и при сво- бодном кручении WK; т — касательное напряжение Радиусы инерции • 1/7*- lx “ V ~р~ ! i =1/3£ гУ V F
= Л3 (Ь2 4- 4bbj 4- b{) Mlb+bJ Fh2 (b2 4- ibbt 4- bi) e 18(Ь4-М8 , b3 (b + 3&1) Jx> “ 12 F№(b + 3bi) ~ 6(&4-M h* (3b 4- bl)... »»“ 12 Fh2(3b + bi) 6(&4-M трапеции с верхним h?- (6b? 4- 6btb0 4- b20) W — хи h2 (Ъ2 4- 4ЬЬ, 4- b}) 12($Н-2М (для нижних волокон) h2 (Ъ2 4- 4ЬЬХ 4- Ь?) “ 12 (25 + bt) (для верхних волокон) основанием Ь± и ниж- h2 (6b? 4- 6blbo4-6o) h 1х “ Ьх) х X /2 (Ь2 4-4bbj 4-Ь?) h 1х~ 6(2Ь, 4- Ьо) Х xK2(6b?4-6b1b04-b?) ! / ь* + ь? ‘У - |/ 24
36 (2bi 4- b0) _ h V-b] Jy~ 48 b — bi клина с большим основан b(b4 — bi) 4- 12(b —bt) " — 0,105 (b4 4- bi) 12 (3bj 4- 2b0) ш - h ^““24 W-bbt нем b, меньшим — blf вы- Жк = -7Г = н b h (5* ~ 5f) 125(b —&i)~" 54 + &J — 0,105—j—1 b В точках длинных сторон ближе к широ- кому основанию т =^к Tmax w к
51
форма сечецил Площадь сечения F координаты крайних то^ек сечения /
Полый I У )омб F =у (а& —«А) 2? Л* II II to| О- to|
_х
/У
% L.
« а
У
Круг У] г, 2 w 0,785d2 Х1 — У1 — d ~ 2
X X
_ xf
2г , ьная
Люба ось — У я Ц61 глав гграл ная
Кольцо F_ 4 D Х1 = У1 = -^
Любая центральная
ось —»главная
52
Продолжение табл. 1
Моменты инерции: осевые Jx, Jy, центро- бежный Jxy\ полярной Jp и при свободном круше- нии Моменты сопротивления: осевые Wx, Wy; полярный Wp и при сво- бодном кручении VHK; х — касательное напряжение Радиусы инерции -jT'> гу У
ab3 — ajf J* = 48""- а3Ь — Jv~ "" 48 п&3 ** л^Ь^ W*~ 246 а3Ъ — alb± Wy ~ 24a . - f а^ — а^ — у 24 (ab — aj&J 1 Г а3Ь^ afbi lv-y ^(ab — aibi)
nd^ яг4 Jx Jv~64~T~ _ Fd3 _ Fr3 ~ 16 “ 4 ~ ж 0,05d4 я 0,785r4 7p=/K = 2/a = 2/y = Old4» 32 2 иД ~ я 1,57г4 T7K=P7V = ^ = ^» я 0,ld3 x 0,785r3 УУР "к 16 2 » 0,2d3 « 1,57т-3 Во всех точках пери- метра ттах ,, d г ix=^iy = 1: = -I Эллипс инерции ~ круг
г _ г - К - dl) J Jx — Jy— 64 — лР4 = 64 = _ F (D3 + d3) _ “ 16 ~ FD2 = 16 d+«2)« и 0,05D4 (1 — a4) J p ~ Jк = __ л (P4 — d4) __ 32 = ^(l-a4)« »0,lP4(l=a4) Wx = Wy = _n(Di — d<) _ ~ 32Z) 7lZ)3 =—_(1-a4)« ж 0,W3 (1 — a4) _ л (P4 — d4) _ - 16D ~ kD3 ,, — 16 ~ я 0,2В3 (1 — a4) Во всех точках наруж- ной окружности тшах 1х — 1у~ = ~/D3 + d2 = = ^-/1 + а3 Эллипс инерции — круг
53
Форма сечения Площадь сечения F 7 Координаты крайних точек сечения
Круг с ческим л неконцснтри- отверстием У< p =₽ (1 92) d D ^i= —
1 X*. i Jg ж $w V *° •* 1 __ as D l-a»(l-2fr) »t“ 2 ' " 1 —a8' , D l—«8(l + 20) "i“T' "i-a8" “ й a ₽ = -p
U r’
У1
Круг с круговым вырезом — «
У X
х ХС
с d 4R„
У
Тонкс л 1 эстен ь< У ное i : ода 50ЛБЦ0 F = nbd d xi = yi=‘-2=zr
Люба ось — к dz 2Г X J [ьная
У я це: - глаз нтрал зная
54
Продолжение табл. 1
\
\
Моменты инерции: осевые Jx, Jy; центро- бежный Jxy; полярный Jp и при свободном круче- нии JK Моменты сопротивления? осевые Wx, Wy; полярный Wp и при сво- бодном кручении WK; т — касательное напряжение Радиусы инерции
Jx~~ 64 -*61‘ r nD* Jy = ~u 1 — a4 — x2ft2 — a2/ (1»«4) Wx~ 32 Х (1—а2) (1—а4) —16а2р2 Х 1— а2(1 + 2^) (для верхних волокон) w*~ 32 X (1—а2) (1—а4) —16й2р2 Х 1 —а2(1 — 2₽) (для нижних волокон) ттг к/)3 .. Жу= 32 (1-а4) D / 1 + а2 — X 1 / / п 1/ _!6 А- F \1 — а/ “ 1^1 + а2
r T JK = 0 fciB4 0,005 0,1 W в На дне 0,2 _ д3 : ~ к2 выреза 0,4 т тах 0,6 0,8 1 1,5
1,57 1,56 1,56 1,46 1,22 0,92 0,63 0,38 0,07
/c2 0,64 1,22 1,22 1,23 1,31 1,52 1,91 2,63 7,14
i и Й и a SSL I « । co n ” 2 QO oo К 'll fcj g в s и и §? 7 и s co C> I* co C5 *g a sa S •» a И „ K 11 II тл7 тсМ2 Wx = Wy = -j- = = лбг2 « 0,7858d2 J/JZ = W ~ rcdrf2 р ге к 2 = 2я8г2 » 1,576с!2 Во всех точках пери- метра ттах d "1 /•— 1 V 2/2 = — » 0,353d /2 Эллипс инерции <== круг
55
Форма сечения Площадь сечения F Координаты крайних точек сечения
Круговое незамкну- тое тонкостенное кольцо te—S d+ 8 «1 = Vi = —
У х $ X
У d
Полу» 2L :руг У1 _ ltd2 тег2 ^=- = Тя и 0,393d8 11 со| *• « « а I » Н II Р й WIM tola, и © *1* II £ К II “ to
X
Л?|
_ Xi _ 1 Xi _
а=2г _
у!
Четверть круга
__ яг2
« 0,785г8
^ = 2/1 =37*0.424'’
xi = V1 ~ °’576г
56
Продолжение табл. 1
Моменты инерции: осевые центро- бежный Jxy; полярный Jp и при свободном круче- нии JK Моменты сопротивления: осевые Wx, Wy; полярный Wp и при свободном кручении WK; т — касательное напряжение Радиусы инерции 1/" Jx гх~ V ~р~~ 5 i гУ F
__ icdB3 = “У рр- — — (^dB)2 ~ к 3rcd+l,8B ~ icdB2 * Т~ В точках внутреннего и наружного контуров сечения 3tcJ + 1,8В _ _ <г — 1 М тах (тсб/В)2 к
d* / Я 8 \ ~ Jx ~ Чб" VT 9я/ « 0,00686d4 и 0,11г4 Ju = JX2 = 128 — Т — Fd2 _ Fr2 ~ — "Т? 4 ~ « 0,0246d4 « 0,393г* Wx « 0,0324d3 ж 0,259г3 (для нижних волокон) Wx « 0,0239d3 « 0,191г3 (для верхних волокон) тт_ nd3 тег3 « 0,05d3 « 0,393г3 ix « 0,132d d lv —
J «0,0714г4 Лтах Л « 0,0384г4 ^min Л2 = ^«0'0549'-1 J — J — « Jy3~ 16 « 0,196г4 ^ЗД, = -0.0165г* J — — ‘'здз ~~ 8 wx = w„ = Л2 Уг _ тс2г3 9тс2 —. 64 “48 Зтг —4 х 0,923г3 (для верхних и правых волокон) wx = W„ = Хц уг ТС2Г3 = w^2-64^ я 1,245г3 (для нижних и левых волокон) iv ж 0,302г *max i f «0,221г 2/min
57
Форма
сечения
Площадь
сечения F
Координаты
крайних точек сечения
Круговой сектор
F = = аг2
s — 2га
_ 7Ш°
“ = 18бт
-Оси х — х и у у ~
главные центральные
6
= Г sin а
2г sin а
~ зГ- ~
= 38,2^2-2
а0
, /. 2 sin а\
у1 =Ч1—&Н
Ь = 2г sin а
Круговой сегмент
— sin 2а)
ка°
Х== 180*
&
^=2-
b — 2r sin а
______4г sin3 а
3 (2а — sin 2а)
_ / 4 sin3 а
1 — \ 3 2а — sin 2а
—COS а I
у1 = г (1 —
4 sin3 а
3 2а <— sin 2а
58
Иродолжение табл. 1
Моменты инерции: осевые Jx, Jy} центробежный полярный Jp и при свобод- ном кручении JK Моменты сопротивления осевые Wx, Wy} полярный Wp и при свободном кручении с — касательное напряжение Радиусы инерции 1 -1/'^х 1Х "К -р- > { _1/ 'у V
А = |2а -|- sin 2а — о \ 32 sin2 а^ _ Уа / ~~ Fr2 1 = “з— 1 2а sin 2а »—- 8а \ 32 sin2 а\ г 9а ) JXt = -у- (2а + sin 2а) /•4 Jy = — (2а sin 2а) == Fr2 — (2а — sin 2а) оа г3 жх = 4-х о 0 32 sin2 а 2а + sm 2а — . 2 sin а 1 з7- (для верхних волокон) Зг3а /9 х 16 Sin а \ , . „ 32 sin2 а\ + sm 2а * т 9а / (для нижних волокон) ___ о 2а — sin 2а Wy = г3 . у sin а 1Х = -у X Г А , sin 2а Х1 / 2а 1/ 16 sin2 а Г 9а2 г я / . sin 2а 1У- 2 Г" 2а
Jx = 4- (2а — sin 2а -I- О + 4 cos а sin3 а) = Fr2 1 =-(<+ 4 cos а sin3 а\ 2а — sin 2а / 7*4 / Jy = — 12а — sin 2а — cos а sm3 а} == о / - 4 V 3Х cos а sin8 а 2а - sin 2а / Jxt = “§- (2“ — — sin 2а cos 2а) ”'=£ (для нижних волоков) "'"V (для верхних волокон) г3 / Wy = -S-. 2а- * 8 sm а \ sin 2а <— 4 • з \ -х- cos а sm3 а I м / ix = у X Т Г л , 4 cos а sin3 а Х|/ 1+ 2а-sin 2а = “2~ X 1 Г, 4 cos а sin3 а Х г 3 2а — sin 2а
59
Форма сечения Площадь сечения F Координаты крайних точек сечения
Полукольц > У] 0 u(P2-d2) 8, - И 2х = -8-(1-*2)« к 0,3932)2 (1 — а2) d а~ D «С! а 1 J Р w N> w * to я м Ъо й й ” b Ь « 5 +v ° + - К 71 + ? + S Нь « “ + + « + *• + ' « * р "Г 1 р “ 8 II
X
х2 ил a Jr
'*1 г
Ъ -
У
Сектор кольца |-ЛУ|.Х'.| — 7Л2 (1 — а2) 7С7° 7== 18(7 Г а~ 7Г со с» >—7* в а X Г“ X 1 1 =- \ Д !“ X £_ 'Я J j " !- М СО “в .9 СО |<М * ** «к « 1 1 1 II и|ю ’Н т-ч СЧ we, »- -1" х к "Vх ' ;; eq |со II 5^. 5 (1 'а? X
.1 л?
3/1 >.
У
во
Продолжение табл. 1
Моменты инерции: осевые Jx, Jy\ центробежный полярный Jp и при свобод- ном кручении JK Моменты сопротивления: осевые Wx, Wy; полярный Wp и при сво- бодном кручении V7K; т — касательное напряжение Радиусы инерции
Jx » 0,00686 (Р4 — d4) — 0,0177P2d2 (D — d) Dd ~ = 0.00686P4 (1 — a4 — - 2,54a2 14-a/ . n (P4 — d4) Jy 128 ~ = (1 — «*) » и 0.0246P4 (1 — a4) Wx « 0,00686Р3 X (1-а4) (14-а)- — 2,54а2 (1—а) Х 0,288 (1 + а) — — 0,212а2 (для верхних волокон) Wx « 0,0324Z>3 X (1-а4) (! + «)- — 2,54а2 (1—а) 1 а + а2 (для нижних волокон) _ itD3 /Л 4Ч 64 (1 «4)и «0,05Р3(1—а4) '-=/т ii/ = -i/P24-d2 = = /1 4- «а
Rl — rA I Jx = (27 + , . n 32sln!7\ =^<1+“2)^+ , . „ 32 sin2-A + SUJ27 _ J Я4 — r4 JXI=~^^+ 4- sin 2y) = R4 = g- (1—a4) (27 + sin 27) R4 M Л,= ^Ц-^(27- — sin 27) = R4 = " (l-a4) (2-f- — sin 27) = (14-a2) x X (27 — sin 27) = Jx у1 (для верхних волокон) (для нижних волокон) R3 ^ = ^-(1-а4)Х 27 —sin 27 sin 7 R Г (14- а2) х х1/ х1+т?~ 1/ ' г ^16 sin2 7^ Г 972 / i -Ах 1у~ 2 Х (1-Н2)(1-
61
Форма сечения Площадь сечения F Координаты крайних точек сечения
Сектор ТО1 ного колы _ *1 _ , акосте ца л х, ~ ш- к F = 2агЪ _ ка° e~ Tso3 Xf = г sin а sin а У! = г а , Л sin а\ И = г 1 1 \ а / г, 1 sin а \ . у = г cos а I 1 \ а /
к gbfaC— L
S <3 S2r
Круг л с лыской л
_х
< <5
У1 h г~ d I [> 0,5
iKpyr <сегме >и сш СО С] нтам) гзу Y > _ Xf резан! и свер VЛ/г 1ЫМИ »ху a) b = d cos а h = d sin а d2 F ~ (2а + sin 2а) 5) b = у; h = 0,866rf F = 0,74d2 в) b = у; h = 0,943d F = 0,773d’ <сг «с: 5i О II О II ^1 о* П *•5 ьо| Й ьо| SX g- «^1 a- Си Р
Л - JL. X
с
ь л |
i > °
У
62
П родолжение табл. 1
Моменты инерции: осевые Jx, Jy; центробежный полярный Jp и при свобод- ном кручении Моменты сопротивления: осевые Wx, W^» полярный Wp и при свободном кручении ГИК« т — касательное напряжение Радиусы инерции »-O
/ Jх == "' п п 1 2а -|~ sin 2а 4 sin2 а\ __ а ] Fr2 I = —7— I 2а 4- sin 2а *— 4а \ 4 sin2 а\ « / &г3 Jy — — (2а — sin 2а) = Fr2 = (2а sin 2а) ТТ7 бГ2 Wx W -у X „ . . о 4 sin2 а 2а + sin 2а — 1 а /~ О sin2a
л 8Ша 1 . а (для верхних волокон) &г2 Л , . о 4 sin2 а 2а + sm 2а а / 4> “J- — xl / a 1/ s*n2 a r a2
X . sin а —- «—> cos а а (для нижних волокон) &г2 2а — sin 2а Wy^2‘ Sina“
я"'' II II о| Jo о , ч*- ~ 1 * " II w _ d8(2,6a-l) к 8 (0,3a+ 0,7) В середине плоского среза ттах; в углах — т = 0
r d4 ( sin 4а\ Л= 32 4“/ \ r d4 1 . sin 2а . ^=-ЗГ(“+_2~-1’ sin 2а cos2 а \ 1 з / Jx == 0,0395d4 Jy = 0,0485d4 Jx = 0,0461d4 Jy = 0,(W4 ттг d3 ( sin 4a\ Tv* = Та~>— a т— 16 sm a \ 4 / Tj/ d3 I . sin 2a ^=16 (“+—+ si n 2a cos2 a \ + з / Wx = 0,0912d3 Wy = 0,097d3 Wx = 0,0978d3 Wy = 0,098</3 <m. r«. <m. г». и « « « « II II II II II II 11 11 О О О О 8 К й Л; >: S & 2 £ ф|
63
Форма сечения Площадь сечения F Координаты крайних точек сечения
Круг со срезанными сегментами с четы- рех сторон р = — (1 _ь 12 V 3 /3 \ __ q бд/^2 xt = у± = 0,433d
'Ji 1
у 1 1 к - —X Z /
.X/ 1
> J
у! •«
Правильш угольник У ай шести- F = 0,866d2 = = 2,598Я2 чз |<м II
х_. А. _х
У
Правильш угольник У2. > яй восьми- ^1 F = 0,828d2 = = 4,828с2 d = У1 — ~2
X 1 __х
Н-у| \у2
Правильнз угольник нами % J ЫЙ МНС с п ст* ‘Тг _ <Г *1 )ГО- оро- -f-x 1 F = — па2 ctg а = = nr2 tg а = паг н = ~— 2 S1D а а 2 tg а
64
Продолжение табл. 1
Моменты инерции: осевые Jx, Jy\ центробежный Jxy, полярный Jp и при сво бодном кручении JK t Моменты сопротивления осевые Wxt Wy; полярный Wp, и при сво- бодном кручении WK; — касательное напряжение Радиусы инерции х г F г — гУ У р
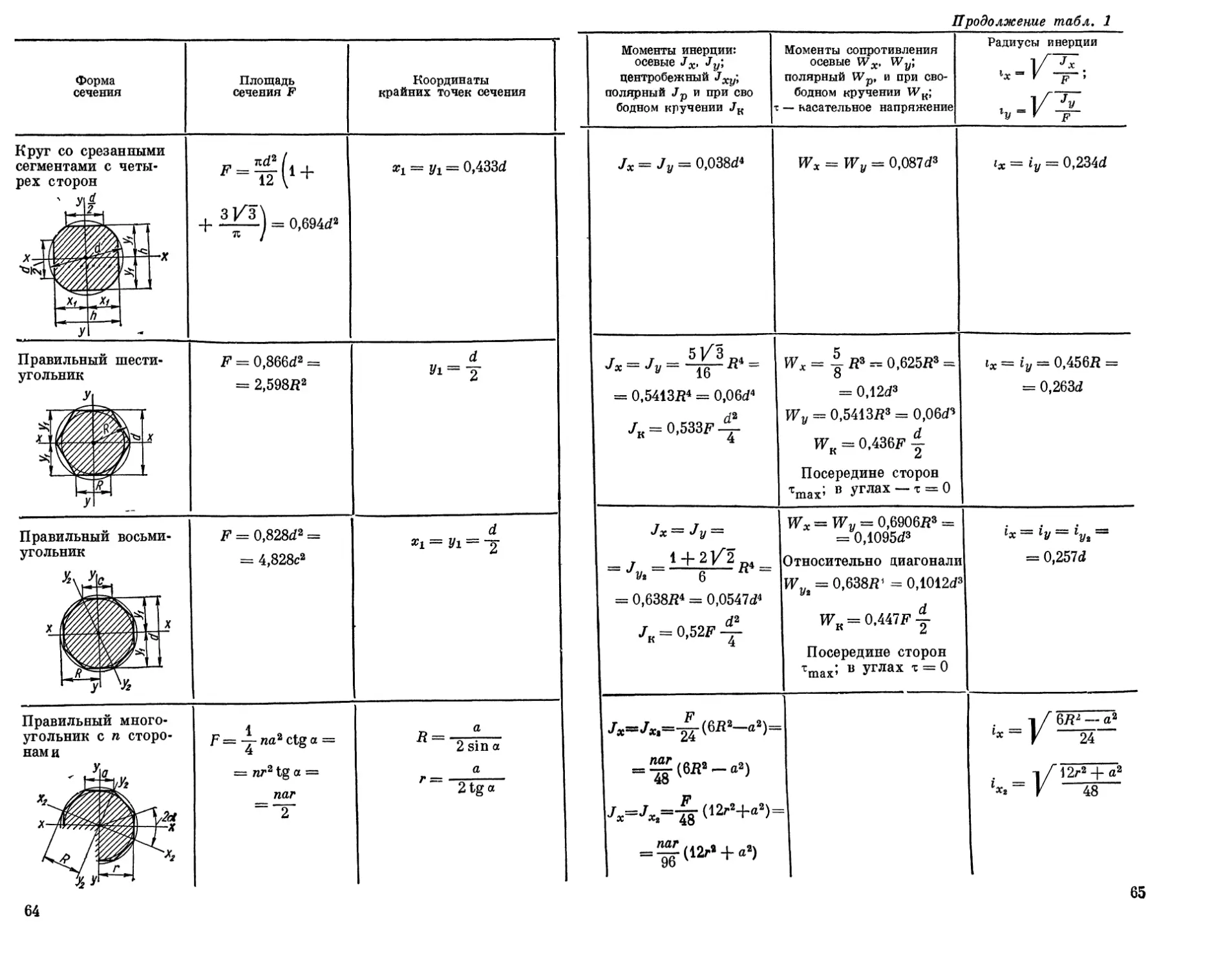
Jx = J у = 0,038с!4 Wx = Wy = 0,087</3 ix = iy = 0,234d
j -j Jx — J у — It — = 0,5413В4 = 0,06d4 K 4 к Wx = Я3 == 0.625Я3 = = 0,12</3 Wy = 0.5413Я3 = 0,06с/3 WK = 0.436F 4 z Посередине сторон ттах; в Углах ~ ’ = 0 ix = iy — 0,456В = = 0,263d
/x == Jy — = 7 _1+2/2 JVi 6 K = 0,638B4 = 0,0547d4 d2 = 0,52F 4- K 4 wx = Wy = 0,6906Я3 = = 0,1095d3 Относительно циагонали W,, = 0,638Л’ = 0,1012с/3 Уг VFK = 0,447Fy Посередине сторон ттах’ “ т = 0 ix — iy = iyi = == 0,257d
Jx=/X1=-^-(6K2-a2)= = ^(6Яа-аа) 4o ^=^,=-J-(12r2+«2)= = ^(12r’ + aa) УО 1/ 6ДЛ —aa lx ~ r 24 -l/12ra + a2 ~ V 48
65
Форма сечения Площадь сечения F Координаты крайних точек сечения
Круговое сечение с одной шпоночной канавкой F^K4-bt 4 d Xi = Уг = у
Круговое сечение
с двумя шпоночными
канавками
— 2bt
Т
d
2
d
^«2
Мостовой бык
с закруглениями
F — bh + —
b + h b /4 ! Ч
*1 = -у- = ~2 (1 + а)
= bh ~ а
h
г=т
II
ь
Оси х^—х и У — у —
главные центральные
h
^=2
а
66
Продолжение табл. 1
Моменты инерции: осевые JJу} центробежный Jxy; полярный Jp и при свободном кручении JK Моменты сопротивления: осевые Wxt Wyt полярный Wpf и при свободном кручении WK; г —• касательное напряжение Радиусы инерций
r nd* bl (d — t)* W - bt ~ W
л ' 64 4 nd* bi (d — t)2 32 4 Л ~ 32 2d. bt(d-ty « 16 _ 2d
t nd* bi(d — z)2 w ~ — О2
Л ~ 64 2 ~ nd* bt (d — i)2 " ~ 32 ' 2 1 л ~ 32 d w ~ bt ~ *)а к ~ 16 d
, bh3 Л , 3л \ Jx~ 12 V + 16“/ 1 h№ i jу = 17(1 + 0,165a8 + + Зла (0,5 + 0,212a)2] ^ = -б(Й^)|1 + 4- 0,165a8 4- 4-Зла (0,5 4-0,212а)2] %- II 11 •2^
3*
67
Эллипс
Форма
сечения
Площадь
сечения F
F = nab
Координаты
крайних точек сечения
Оси х^х и у «= у
главные центральные
а
~Ь
х± = Ъ
Vi==a
68
П родолжение табл. 1
Моменты инерции: осевые Jx, центробежный полярный и при свободном кручении JK Моменты сопротивления: осевые Wx, Wy] полярный Wp и при свободном кручении WK] т — касательное напряжение Радиусы инерции « 1/~ Jx 1х= V ~р~ ’* {«ул. гУ у F
II “ Ч „ и4, "а" я II II II || Г л>| •Ч л-1 а й я й 1g 1 » “ 00 СО и i « , “ел | ел II II + », Ьу |Ьу Лч II 1 11 II а и * “ Wx = к 0,785а2б х 4 Wy = и 0,785аб2 у 4 vv к ~ 2 По концам малой оси Мк 2^к тшах — ЙГ лб2а По концам большой оси &ттах т а <3 |<М Л |<м II II Л* .л*
/ К 3 ( П _ Jx~ Ъа \8 ’“9л/“ ~2Fa ( 8 9л2 ) лаб3 F& Jv-~8~~T Wx~-^ba — д j (для нижних волокон) , 2 1 8 \ ba21 — 1 '8 (для верхних волокон) w - каЬ2 - ^у- 8 ~ « 0,392а б2 о» ,, “leg ' ' |сч .1 е |сч II
69
Форма сечения Площадь сечения F Координаты крайних точек сечения
У
Оси X — X И —2/ — главные центральные ©•j а «1 = п> 1
ai _ а .Л ъ = «<1
70
Продолжение табл. 1
Моменты инерции: осевые Jx, Jy, центробежный полярный Jp и при свободном кручении JK Моменты сопротивления* осевые Wx, Wy; полярный Wp и при свободном кручении WK; г — касательное напряжение Радиусы инерции { -ДТП. гУ~ у
Jx=ja8^_„_j= \16 9к2/ /»-Чй-й)= == 4Р&2 (~ — - 4 \16 9ла/ W = xmin 3 , 2/*2 4\ = ТЬа (16—э) (для нижних волокон) W = Ущ1П = -4аЬ(16—э) (для правых волокон) II S 7 jgl* to
Л = -^(а8Ь-а?Ь1)« ~ .1 а2 (а 36) 5 Л = |(«Ь3-^)~ « -J Ь* (Ъ + За) 8 Приближенные значе если отношения В : ах г тс&4гс3 .. 4Ч JK == ~~ 2 ГГ (1 а ) К П2 + 1 к a3b>— afbi «Г* $Г' II II
rr X — /' **>* 4 а « а (а -(- 3&) & Л ab3*-ax&J ^-4 Ь « »±-Ь(6 + За)8 НИЯ J и W пригодны, [ & : &! малы пЬ3п /А АЧ жк= 2 (1-а4) В конце малой полуоси Мн »г —— — ... • тах Жк ’ в конце большой полу- тшах
п При малой толщине можно принять равно- мерное распределение напряжений по сеченик т— м« 2П )
71
Форма сечения Площадь сечения F Координаты крайних точек сечения
Пара сегме боли* нт *3 •> веский 1 х} 4j II со| to 5 II II II сл| СО сл| to to| <3- >-
с X
<2 7М< -Х2
X/ Х1
> b'
' .У
Парабо полусе] X / лический гмент У\ p-bh д* л* 11 "l II JI сл| W сл| Ы> сУ сл SI w а- >• о- °*
и Я X
ЯЕ я <3
уГ
Кругов ник л ОЙ х,\ треуг *!. ОЛЬ* F = 0,215г2 ^1= 2/1 = 0,223г = 0,777г
-V
X X
Уз
Полое сечение в виде чечевицы || a | g II » |CM be ° " » |cm "° о -|- a « -f- II N II I - s J; + ‘gi* и и ^1 =
г > _ X1 _ , Xf~ X = ]/ (5+Л) (г+Ц^) Ъ + h h= —
_ ь
V У оу
72
Продолжение табл. 1
Моменты инерции: осевые Jx, Jy; центробежный Jxy; полярный Jp и при свободном кручении JK Моменты сопротивления осевые Wx, Wy, полярный Wp и при свободном кручении WK; х — касательное напряжение Радиусы инерции х ' р i 1У У
. 8 ... 12J7ia ^=175^- 175 j *’~105 “ 35 , 2 ... 3Fh2 JXi=^bh2^ — _ hb3 _ Fb2 Jy~ 30 — 20 Wx = ^bh* оо (для нижних волокон) (для верхних волокон) w hbi ^ = 15- |ео CM |1Q || II
, 4 ... 12F/i2 '‘“175**’- 175 wx , =ibh2 xmin 35 (для нижних волокон) и»» CM [lq II
=/у = 0,00755г4 JXt = 0,003г4 ^. = /„. = 0,0181^ 4, = 0,0121г4 Р7Х 4 = 0,0097г3 x8min L , =0,187r жеШ1П
•4 = Л [2a (2 + 4- cos 2a)3 sin 2a] = Fr2 = [2a (2 4“ cos 2a) *~=- «=» 3 sin 2a] Jy = л*3& (2a «==. sin 2a) = Fr2 = £_(2a-.sin2a) w „ == Jk — Х Vi 8+Л iFy = А. «1 lx —rx Г 24-cos 2a 3 sin 2« 1/1 sin 2a '« = ' У 2“"~ =
73
Форма сечения Площадь сечения F Координаты крайних точек сечения
Волне (вол hi параб Дугам X 1 •сГ стое д об о ли* и) < железо разован гескими £ - X, _ь * Ы X V + &4 V si* + g + I’0, 2 Й X "1 " ч| SI 1 "Неч1 1 см XI. ci ^1 + | II II II * J, II | •о1
/I +V <+(?)’] ж 4- 8 (26 + 5,: о Zfi)
Станд катни ребро Форм; ные, i арт! й ш 1ЫЙ про [веллер 1- на ввя» h S/i = y
с 2
2 7777b.
улы ht а приближен- и
Волнисто (волны о дугами к »е желез бразова] РУга) ю аы F = 2s(y+ЛХ) hl = h ~ т 6 «I —у 6 + 8 У1= —
х_ s_x
—< dfe X-
~ л, ’ J __ п| л 6 Г << 4*
74
Иродолжение табл. 1
Моменты инерции, осевые Jx, Jy\ центробежный полярный Jp и при свободном кручении <7К Моменты сопротивления: осевые Wx, Wy', полярный Wp и при свободном кручении WK; с — касательное напряжение Радиусы инерции
, 1280 1 8 а==-2Г’ Т — Ь^) = = (Ml — Ml'8) = 16 . , , 8 '8\ । = 1051Чй-У1) + 4-2,68 (%+ гЛ) [У — _ х h + Ъ i — ]/" ^Jx ~ х ~ г 8 (2&4-5.2Л) ~ « 1,35 X 1 / х V 8 (26 4- 5,26)
. 5 (КЬ9 , Ml, 1 Jx== 4 I 16" 1 6fcl + 4- 2 4- 3 Aij УУх h+Ъ
_6 (6-|-5)3 Jx~- 1й2' - W ~(^+5)3 х 81 > —/т
73
Форма - сечения Площадь сечения F Координаты крайних точек сечения
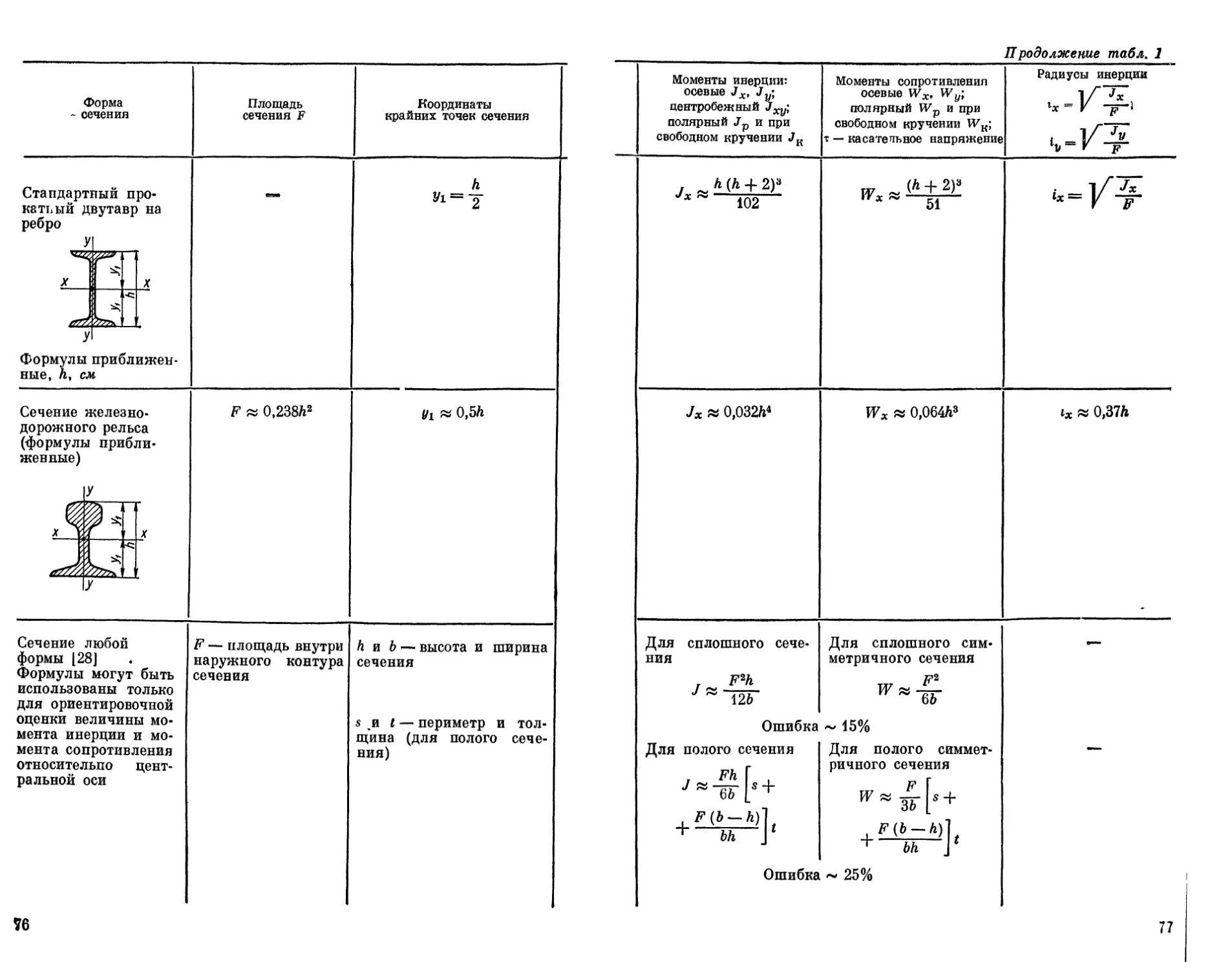
Стандарт катьый д ребро У ный про- вутавр на II ьо| 5г-
X п X
с
У Формулы ные, h, cj приближен- и
Сечение > дорожног (формулы женные) келезно- о рельса прибли- F » 0,238ft2 yi « 0,5А
Л %) X
j с
И
Сечение любой формы [28] Формулы могут быть использованы только для ориентировочной оценки величины мо- мента инерции и мо- мента сопротивления относительпо цент- ральной оси F — площадь внутри наружного контура сечения Аид — высота и ширина сечения s и t — периметр и тол- щина (для полого сече- ния)
w
П родолжение табл. 1
Моменты инерции: осевые Jx, Jy\ центробежный Jxy; полярный Jp и при свободном кручении JK Моменты сопротивления осевые Wx, Wy\ полярный Wp и при свободном кручении WK; т — касательное напряжение Радиусы инерции
..А (А+ 2)» Jx ~ 102 х ~ 51 -=/¥
Jx w 0,03264 Wx » 0.064А3 0,376
Для сплошного сече- ния F2h ~ 126 Для сплошного сим- метричного сечения F2 W » —— е—
Ошибка - 15%
Для полого сечения j Fh Г , 7 ~ ~бГ [х + , У(»-А)1. 1 bh у Для полого симмет- ричного сечения F Г , ^(А-А)]. + bh ]*
Ошибка ~ 25%
11
Таблица 2
Угольники равнобокие (ГОСТ 8509^—57)
b«— ширина полки;
d—.толщина полки;
R—«радиус внутреннего закругления;
г — радиус закругления полки;
J —момент инерции;
i —»радиус инерции;
«« расстояние от центра тяжести
до полки.
№ про- филя Размеры, мм Площадь профиля, см2 Вес 1 пог. м, кГ Справочные величины для осей
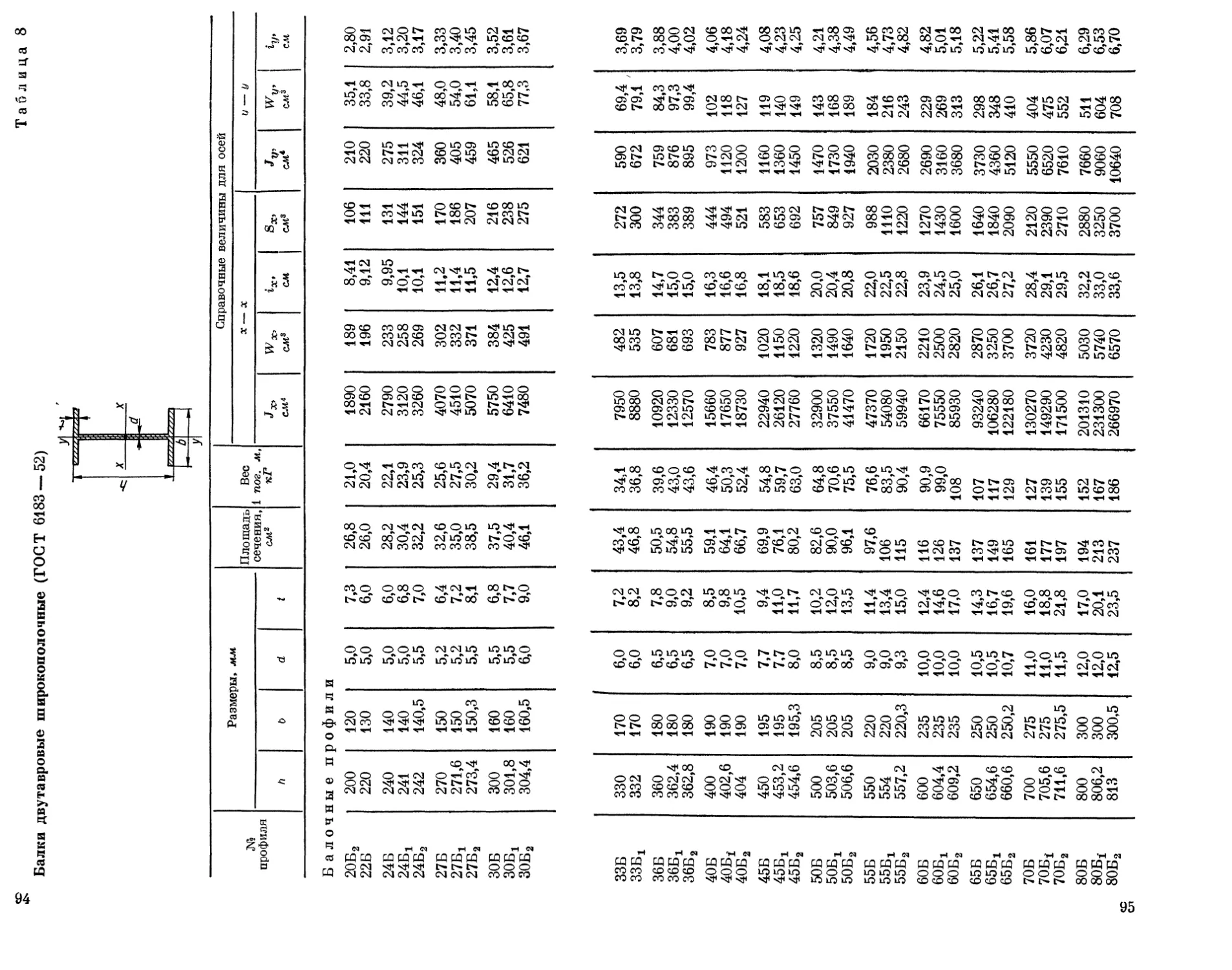
b d R г X —• X *0 — Х9 ?/о— У о xt — xt Ui
Jx, см4 в шах см' max ^х0» см min Jy9' см4 min 5 в
2 20 3 3,5 1,2 1,13 0,89 0,40 0,59 0,63 0,75 0,17 0,39 0,81 0,60
4 1,46 1,15 0,50 0,58 0,78 0,73 0,22 0,38 1,09 0,64
2,5 25 3 3,5 1,2 1,43 1,12 0,81 0,75 1,29 0,95 0,34 0,49 1,57 0,73
4 1,86 1,46 1,03 0,74 1.62 0,93 0,44 0,48 2,11 0,76
2,8 28 3 4 1,3 1,62 1,27 1,16 0,85 1,84 1,07 0,48 0,55 2,20 0,80
3,2 32 3 4,5 1,5 1,86 1,46 1,77 0,97 2,80 1,23 0,74 0,63 3,26 0,89
4 2,43 1.91 2,26 0,96 3,58 1,21 0,94 0,62 4,39 0,94
3,6 36 3 4,5 1,5 2,10 1,65 2,56 1,10 4,06 1,39 1,06 0,71 4,64 0,99
4 2,75 2,16 3,29 1,09 5,21 1,38 1,36 0,70 6,24 1,04
4 40 3 4 5 1,7 2,35 3,08 1,85 2,42 3,55 4,58 1,23 1,22 5,63 7,26 1,55 1,53 1,47 1,90 0,79 0,78 6,35 8,53 1,09 1,13
3 2,65 2,08 5,13 1,39 8,13 1,75 2,12 0,89 9,04 1,21
4,5 45 4 5 1,7 3,48 2,73 6,63 1,38 10,50 1,74 2,74 0,89 12,10 1,26
5 4,29 3,37 8,03 1,37 12,70 1,72 3,33 0,88 15,30 1,30
3 2,96 2,32 7,11 1,55 11,3 1,95 2,95 1,00 12,4 1,33
5 50 4 5,5 1,8 3,89 3,05 9,21 1,54 14,6 1,94 3,80 0,99 16,6 1,38
5 4,80 3,77 11,20 1,53 17,8 1,92 4,63 0,98 20,9 1,42
3,5 3,86 3,03 11,6 1,73 18,4 2,18 4,80 1,12 20,3 1,50
5,6 56 4 6 2 4,38 3,44 13,1 1,73 20,8 2,18 5,41 1,11 23,3 1,52
5 5,41 4,25 16,0 1,72 25,4 2,16 6,59 1,10 29,2 1,57
4 4,96 3,90 18,9 1,95 29,9 2,45 7,81 1,25 33,1 1,69
6,3 63 5 7 2,3 6,13 4,81 23,1 1,94 36,6 2,44 9,52 1,25 41,5 1,74
6( 7,28 5,72 27,1 1,93 42,0 2,43 11,2 1,24 50,0 1,78
4,5 6,20 4,87 29,0 2,16 46,0 2,72 12,0 1,39 51,0 1,88
5 6,86 5,38 31,9 2,16 50,7 2,72 13,2 1,39 56,7 1,90
7 70 6 8,0 2,7 8,15 6,39 37,6 2,15 59,6 2,71 15,5 1,38 68,4 1,94
7 9,42 7,39 43,0 2,14 68,2 2,69 17,8 1,37 80,1 1,99
8 10,70 8,37 48,2 2,13 76,4 2,68 20,0 1,37 91,9 2,02
5 7,39 5,80 39,5 2,31 62,6 2,91 16,4 1,49 69,6 2,02
6 8,78 6,89 46,6 2,30 73,9 2,90 19,3 1,48 83,9 2,06
7,5 75 7 9 3 10,10 7,96 53,3 2,29 84,0 2,89 22,1 1,48 98,3 2,10
8 11,50 9,02 59,8 2,28 94,9 2,87 24,8 1,47 113,0 2,15
9 12,80 10,10 66,1 2,27 105.0 2,86 27,5 1,46 127,0 2,18
5,5 8,63 6,78 52,7 2,47 83,6 3,11 21,8 1,59 93,2 2,17
6 а Q 9,38 7,36 57,0 2,47 90,4 3,11 23,5 1,58 102,0 2,19
8 80 7 9 О 10,80 8,51 65,3 2,45 104,0 3,09 27,0 1,58 119,0 2,23
«м со - 8 12,30 9.65 73,4 2,44 116,0 3,08 30.3 1,57 137,0 2,27
Продолжение табл 2
№ про- филя Размеры, мм Площадь профиля, см2 Вес 1 пог. м, кГ Справочные величины для осей
b d R 1 X — X Х0 Хо Vo — Vo X, — xt Ui
Ji 3s О Ji и • S И Ss max CM mln CM‘ mln iVo, cm I о 5 Q
6 10,6 8,33 82,1 2,78 130 3,50 34,0 1,79 145 2,43
9 Qfi 7 10 3,3 12,3 9,64 94,3 2,77 150 3,49 38,9 1,78 169 2,47
уи 8 13,9 . 10,90 106,0 2,76 168 3,48 43,8 1,77 194 2,51
9 15,6 12,20 118,0 2,75 186 3,46 48,6 1,77 219 2,55
6,5 12,8 10,1 122 3,09 193 3,88 50,7 1,99 214 2,68
7 13,8 10,8 131 3,08 207 3,88 54,2 1,98 231 2,71
8 15,6 12,2 147 3,07 233 3,87 60,9 1,98 265 2,75
10 100 10 12 - 4 19,2 15,1 179 3,05 284 3,84 74,1 1,96 333 2,83
12 22,8 17,9 209 3,03 331 3,81 86,9 1,95 402 2,91
14 26,3 20,6 237 3,00 375 3,78 99,3 1,94 472 2,99
16 29,7 23,3 264 2,98 416 3.74 112 1,94 542 3,06
4 4 но 7 А О Л 15,2 11,9 176 3,40 279 4,29 72,7 2,19 308 2,96
11 8 12 4 17,2 13,5 198 3,39 315 4,28 81,8 2,18 353 3,00
8 19,7 15,5 294 3,87 467 4,87 122 2,49 516 3,36
9 22,0 17,3 327 3,86 520 4,86 135 2,48 582 3,40
12,5 125 10 12 14 4,6 24,3 28,9 19,1 22,7 360 422 3,85 3,82 571 670 4,84 4,82 149 174 2,47 2,46 649 782 3,45 3,53
14 33,4 26,2 482 3,80 764 4,78 200 2,45 916 3,61
16 37,8 29,6 539 3.78 853 4,75 224 2,44 1051 3,68
9 24,7 19,4 466 4,34 739 5,47 192 2,79 818 3,78
14 140 10 14 4.6 27,3 21,5 512 4,33 814 5,46 211 2,78 911 3,82
12 - 32,5 25,5 602 4,31 957 5,43 248 2,76 1097 3,90
10 31,4 24,7 774
11 34,4 27,0 844
12 37,4 29,4 913
16 160 14 16 5,3 43,3 34,0 1046
16 49,1 38,5 1175
18 54,8 43,0 1299
20 60,4 47,4 1419
18 180 11 12 16 5,3 38,8 42,2 30,5 33,1 1216 1317
12 47,1 37,0 1823
13 50,9 39,9 1961
14 54,6 42,8 2097
20 200 16 18 6 62,0 48,7 2363
20 76,5 60,1 2871
25 94,3 74,0 3466
30 111,5 87,6 4020
22 220 14 16 21 7 60,4 68,6 47,4 53,8 2814 3175
16 78,4 61,5 4717
18 87,7 68,9 5247
20 97,0 76,1 5765
25 250 22 24 8 106,1 83,3 6270
25 119,7 94,0 7006
28 133,1 104,5 7717
30 142,0 111,4 8177
4,86 1229 6,25 319 3,19 1356 4,30
4,95 1341 6,24 348 3,18 1494 4,35
4,94 1450 6,23 376 3,17 1633 4,39
4,92 1662 6,20 431 3,16 1911 4,47
4,89 1866 6,17 485 3,14 2191 4,55
4,87 2061 6,13 537 3,13 2472 4,63
4,85 2248 6,10 589 3,12 2756 4,70
5,60 1933 7,06 500 3,59 2128 4,85
5,59 2093 7,04 540 3,58 2324 4,89
6,22 2896 7,84 749 3,99 3182 5,37
6,21 3116 7,83 805 3,98 3452 5,42
6,20 3333 7,81 861 3,97 3722 5,46
6,17 3755 7,78 970 3,96 4264 5,54
6,12 4560 7,72 1182 3,93 5355 5,70
6,06 5494 7,63 1438 3,91 6733 5,89
6,00 6351 7.55 1688 3,89 8130 6,07
6,83 4470 8,60 1159 4,38 4941 5,93
6,81 5045 8,58 1306 4,36 5661 6,02
7,76 7492 9,78 1942 4,98 8286 6,75
7,73 8337 9,75 2158 4,96 9342 6,83
7,71 9160 9,72 2370 4,94 10401 6,91
7,69 9961 9,69 2579 4,93 11464 7,00
7,65 11125 9,64 2887 4,91 13064 7,11
7,61 12244 9,59 3190 4,89 14674 7,23
7,59 12965 9,56 3389 4,89 15753 7,31
00
Таблица 3
ос
to
Угольники неравнобокие (ГОСТ 8510—57)
В — ширина большей полки;
Ъ — ширина меньшей полки;
R — радиус внутреннего закругления;
г — радиус закругления полки;
J — момент инерции;
i — радиус инерции;
гг0, Уо — расстояние от центра
тяжести до полок.
№ профиля Размеры, мм Площадь профиля, см2 Вес 1 пог. м, кГ Справочные величины для осей
В ъ d R г х — х у— у xi — xi У1 — У1 и — и Угол наклона оси tg а
5 й 3 •гВ § 5 •J53 сс § g н «О g о ф в К „ В ф в о Л В tr Н 5а см* в g 2 н *8 - o°?S3 о ф В к - S ф в О CU в tr н и 3 о я a s min
2,5 1,6 25 16 3 3,5 1,2 1,16 0,91 0,70 0,78 0,22 0,44 1,56 0,86 0,43 0,42 одз 0,34 0,392
3,2 з 3,5 1,2 1,49 1,17 1,52 1,01 0,46 0,55 3,26 1,08 0,82 0,49 0,28 0,43 0,382
"2" 32 20 4 1,94 1,52 1,93 1,00 0,57 0,54 4,38 1,12 1,12 0,53 0,35 0,43 0,374
4,2 5 3 4,0 1,3 1,89 1,48 3,06 1,27 0,93 0,70 6,37 1,32 1,58 0,59 0,56 0,54 0.385
40 25 4 2,47 1,94 3,93 1,26 1,18 0,69 8,53 1,37 2,15 0,63 0,71 0,54 0,381
4,5 3 1,7 2,14 1,68 4,41 1,43 1,32 0,79 9,02 1,47 2,20 0,64 0,79 0,61 0,382
2,8 45 28 4 5 2,80 2,20 5,68 1,42 1,69 0,78 12,1 1,51 2,98 0,68 1,02 0,60 0,379
5 3 5,5 1,8 2,42 1,90 6,17 1,60 1,99 0,91 12,4 1,60 3,26 0,72 1,18 0,70 0,403
35 50 32 4 3,17 2,49 7,98 1,59 2,56 0,90 16,6 1,65 4,42 0,76 1,52 0,69 0,401
5,6 3 3,16 2,48 10,1 1,79 3,30 1,02 20,3 1,80 5,43 0,82 1,95 0,79 0,407
3,6 56 36 4 6,0 2,0 3,58 2,81 11,4 1,78 3,70 1,02 23,2 1,82 6,25 0,84 2,19 0,78 0,406
5 4,41 3,46 13,8 1,77 4,48 1,01 29,2 1,86 7,91 0,88 2,66 0,78 0,404
4 4,04 3,17 16,3 2,01 5,16 1,13 33,0 2,03 8,51 0,91 3,07 0,87 0,397
6,3 5 2,3 4,98 3,91 19,9 2,00 6,26 1,12 41,4 2,08 10,80 0,95 3,73 0,86 0,396
4£ 63 40 6 7,0 5,90 4,63 23,3 1,99 7,28 1,11 49,9 2,12 13,10 0,99 4,36 0,86 0,393
8 7,68 6,03 29,6 1,96 9,15 1,09 66,9 2,20 17,90 1,07 5,58 0,85 0,386
у 4,5 5 5,07 3,98 25,3 2,23 8,25 1,28 51,0 2,25 13,6 1,03 4,88 0,98 0,407
о 70 45 7,5 2,5 5,59 4,39 27,8 2,23 9,05 1,27 56,7 2,28 15,2 1,05 5,34 0,98 0,406
5 6,11 4,79 34,8 2,39 12,5 1,43 69,7 2,39 20,8 1,17 7,24 1,09 0,436
7,5 7е» 50 6 8 2,7 7,25 5,69 40,9 2,38 14,6 1,42 83,9 2,44 25,2 1,21 8,48 1,08 0,435
5 / о 8 9,47 7,43 52,4 2,35 18,5 1,40 112 2,52 34,2 1,29 10,90 1,07 0,430
8 5 5 6,36 4,99 41,6 2,56 12,7 1,41 84,6 2,60 20,8 1,13 7,58 1,09 0,387
80 50 6 8 2,7 7,55 5,92 49,0 2,55 14,8 1,40 102 2,65 25,2 1,17 8,88 1,08 0,386
5,5 6 7,86 6,17 65,3 2,88 19,7 1,58 132 2,92 32,2 1,26 11,8 1,22 0,384
9 90 56 9 3 8,54 6,70 70,6 2,88 21,2 1,58 145 2,95 35,2 1,28 12,7 1,22 0,384
00 оо 53 8 11,18 8,77 90,9 2,85 27,1 1,56 194 3,04 47,8 1,36 16,3 1,21 0,380
Продолжение табл. 3
g
№ профиля Размеры, мм Площадь профиля, еле8 Вес 1 поа, ле, кГ Справочные величины для осей
В ь d R Т X — X У — У Xi — Х1 У1 — У1 и — и Угол наклона оси tg а
Jx, еле4 •Э Jyt еле4 5 Iy * н PH §5 S V 2 и й . £§£££ 5 О н Я 5 s о Ф Я X „ CU и я® и min Ju, см4 min iu, см
6 9,59 7,53 98,3 3,20 30,6 1,79 198 3,23 49,9 1,42 18,2 1,38 0,393
1U 100 63 7 10 3,3 11,10 8,70 113,0 3,19 35,0 1,78 232 3,28 58,7 1,46 20,8 1,37 0,392
6,3 8 12,60 9,87 127,0 3,18 39,2 1,77 266 3,32 67,6 1,50 23,4 1,36 0,391
10 15,50 12Д0 154,0 3,15 47,1 1,75 333 3,40 85,8 1,58 28,3 1,35 0,387
6,5 11,4 8,98 142 3,53 45,6 2,00 286 3,55 74,3 1,58 26,9 1,53 0,402
11 110 70 7,0 10 3 3 12,3 9,64 152 3,52 48,7 1,99 309 3,57 80,3 1,60 28,8 1,53 0,402
7 8,0 13,9 10,90 172 3,51 54,6 1,98 353 3,61 92,3 1,64 32,3 1,52 0,400
7 14,1 11,0 227 4,01 73,7 2,29 459 4,01 119 1,8 43,4 1,76 0,407
8 16,0 12,5 256 4,00 83,0 2,28 518 4,05 137 1,84 48,8 1,75 0,406
12 5 10 19,7 15,5 312 3,98 100,0 2,26 649 4,14 173 1,92 59,3 1,74 0,404
125 80 12 11 3,7 23,4 18,3 365 3,95 117,0 2,24 781 4,22 210 2 69,5 1,72 0,400
14 140 90 8 12 4 18,0 14,1 364 4,49 120 2,58 727 4,49 194 2,03 70,3 1,98 0,411
9 10 22,2 17,5 444 4,47 146 2,56 911 4,58 245 2,12 85,5 1,96 0,409
16 9 22,9 18,0 606 5,15 186 2,85 1221 5,19 300 2,23 НО 2,20 0,391
10 160 100 10 13 4,3 25,3 19,8 667 5,13 204 2,84 1359 5,23 335 2,28 121 2,19 0,390
12 30,0 23,6 784 5,11 239 2,82 1634 5,32 405 2,36 142 2,18 0,388
14 34,7 27,3 897 5,08 272 2,80 1910 5,40 477 2,43 162 2,16 0,385
18 180 НО 10 14 4,7 28,3 22,2 952 5,80 276 3,12 1933 5,88 444 2,44 165 2,42 0,375
11 12 33,7 26,4 1123 5,77 324 3,10 2324 5,97 537 2,52 194 2,40 0,374
11 34,9 27,4 1449 6,45 446 3,58 2920 6,50 718 2,79 264 2,75 0,392
ZU 200 125 12 14 4,7 37,9 29,7 1568 6,43 482 3,57 3189 6,54 78^ 2,83 285 2,74 0,392
12,5 14 43,9 34,4 1801 6,41 551 3,54 3726 6,62 922 2,91 327 2,73 0,390
16 49,8 39,1 2026 6,38 617 3,52 4264 6,71 1061 2,99 367 2,72 0,388
12 48,3 37,9 3147 8,07 1032 4,62 6212 7,97 1634 3,53 604 3,54 0,410
25 250 160 16 18 6 63,6 49,9 4091 8,02 1333 4,58 8308 8,14 2200 3,69 781 3,50 0,408
16 18 71,1 55,8 4545 7,99 1475 4,56 9358 8,23 2487 3,77 866 3,49 0,407
20 78,5 61,7 4987 7,97 1613 4,53 10410 8,31 2776 3,85 949 3,48 0,405
00 Сл V
Таблица 4
Швеллеры (ГОСТ 8240 — 56)
h — высота швеллера;
b — ширина полки;
d — толщина стенки;
t — средняя толщина полки;
R — радиус внутреннего закругле-
ния;
г — радиус закругления полки;
J —момент инерции;
W — момент сопротивления;
i — радиус инерции;
S — статический момент полусече-
ния;
®о — расстояние от оси у — у но
наружной грани стенки.
№ про- филя Размеры, мм Пло- щадь сече- ния, CJW2 Вес 1 пог. м, кГ Справочные величины для осей Коорди- ната центра тяжести Хо, СМ
X — Л и —У
п О 4 t R г •?х» см4 wx, см3 гх, зм 8Х, см3 7 У’ см* см8 1У’ см
5 50 37 4,5 7,0 6,0 2,5 6,90 5,42 26,1 10,4 1,94 6,36 8,41 3,59 1,10 1,35
6,5 65 40 4,5 7,4 6,0 2,5 8,28 6,5 54,5 16,8 2,57 10,0 11,9 4,58 1,20 1,40
8 80 45 4,8 7,4 6,5 2,5 9,91 7,78 99,9 25,0 3,17 14,8 17,8 5,89 1,34 1,48
10 100 50 4,8 7,5 7,0 3,0 11,7 9,2 187 37,3 3,99 21,9 25,6 7,42 1,48 1,55
12 120 54 5.0 7,7 7,5 3,0 13,7 10,8 313 52,2 4,78 30,5 34,4 9,01 1,58 1,59
14 140 58 5,0 8,0 8,0 3,0 15,7 12,3 489 69,8 5,59 40,7 45,1 10,9 1,70 1,66
14а 140 62 5,0 8,5 8,0 3,0 16,9 13,2 538 76,8 5,65 44,6 56,6 13,0 1,83 1,84
16 16(У 64 5,0 8,3 8,5 3,5 18,0 14,1 741 92,6 6,42 53,7 62,6 13,6 1,87 1,79
16а 160 68 5,0 8,8 8,5 3,5 19,3 15,1 811 6,48 58,5 77,3 16,0 2,00 1,98
18 180 70 5,0 8,7 9,0 3,5 20,5 16,1 1080 ^20} 7,26 69,4 85,6 16,9 2,04 1,95
18а 180 74 5,0 9,2 9,0 3,5 21,9 17,2 1180 131 7,33 75,2 104 19,7 2,18 2,13
20 200 76 5,2 9,0 9,5 4,0 23,4 18,4 1520 152 8,07 87,8 ИЗ 20,5 2,20 2,07
20а 200 80 5,2 9,6 9,5 4,0 25,0 19,6 1660 166 8,16 95,2 137 24,0 2,34 2,27
22 220 82 5.3 9,6 10,0 4,0 26,7 20,9 2120 193 8,91 111 151 25,4 2,38 2,24
22а 220 87 5,3 10,2 10,0 4,0 28,6 22,5 2320 211 9,01 121 186 29,9 2,55 2,47
24 240 90 5,6 10,0 10,5 4,0 30,6 24,0 2900 242 9,73 139 208 31,6 2,60 2,42
24а 240 95 5,6 10,7 10,5 4,0 32,9 25,8 3180 265 9,84 151 254 37,2 2,78 2,67
27 270 95 6,0 10,5 11,0 4,5 35,2 27,7 4160 308 10,9 178 262 37,3 2,73 2,47
30 300 100 6,5 11,0 12,0 5 40,5 31,8 5810 387 12,0 224 327 43,6 2,84 2,52
33 330 105 7,0 11,7 13 5 46,5 36,5 7980 484 13,1 281 410 51,8 2,97 2,59
36 360 110 ; 7,5 12,6 14 6 53,4 41,9 10820 601 14,2 350 513 61,7 3,10 2,68
Й 40 400 115 8,0 13,5 15 6 61,5 48,3 15220 761 15,7 444 642 73,4 3,23 2,75
Таблица 5
£
Швеллеры (ГОСТ 8240 — 56*)
h — высота швеллера;
Ъ — ширина полки;
d — толщина стенки;
t— средняя толщина полки;
R — радиус внутреннего закругле-
ния;
г — радиус закругления полки;
J момент инерции;
W — момент сопротивления;
i — радиус инерции;
S — статический момент полусече-
ния,
а?0 — расстояние от оси у — у до
наружной грани стенки.
№ про- филя Вес 1 пог. м, кГ Размеры, лии Пло- щадь сече- ния, см2 Справочные величины для осей Коорди- ната центра тяжести х0, см
X— X у — У
h b d t R r JX’ см4 wx, см3 гх» см см3 JV’ см4 wv> см3 V см
5 4,84 50 32 4,4 7,0 6 2,5 6,16 22,8 9,10 1,92 5,59 5,61 2,75 0,954 1,16
6,5 5,90 65 36 4,4 7,2 6 2.5 7,51 48,6 15,0 2,54 9,00 8,70 3.68 1,08 1,24
8 7,05 80 40 4.5 7,4 6,5 2,5 8,98 89,4 22,4 3,16 13,3 12,8 4,75 1,19 1,31
10 8,59 100 46 4,5 7,6 7 3 10,9 174 34,8 3,99 20,4 20,4 6,46 1,37 1,44
12 10,4 120 52 4,8 7,8 7,5 3 13,3 304 50,6 4,78 29,6 31,2 8,52 1,53 1,54
14 12,3 140 58 4,9 8,1 8 3 15,6 491 70,2 5,60 40,8 45,4 11,0 1,70 1,67
14а 13,3 140 62 4,9 8,7 8 3 17.0 545 77,8 5,664 45,1 57,5 13,3 1,84 1,87
16 14,2 160 64 5,0 8,4 8,5 3,5 18,1 747 93,4 6,42 54,1 63,3 13,8 1,87 1,80
16а 15,3 160 68 5,0 9,0 8,5 3,5 19,5 823 103 6,49 59.4 78,8 16,4 2,01 2,00
18 16,3 180 70 5,1 8,7 9 3,5 20,7 1090 121 7.24 69,8 86,0 17,0 2,04 1,94
18а 17,4 180 74 5,1 9,3 9 3,5 22,2 1190 132 7,32 76,1 105 20,0 2,18 2,13
20 18,4 200 76 5,2 9,0 9.5 4 2X4 _1520_ 152 __8,07 87.8 ИЗ 20,5 2,20 2,07
20а 19,8 200 80 5,2 9,7 9,5 4 25,2 1670 167 8,15 95,9 139 24,2 2,35 2,28
22 21,0 220 82 5,4 9,5 10 4 26,7 2110 192 8,89 110 151 25,1 2.37 2,21
22а 22,6 220 87 5,4 10,2 10 4 28,8 2330 212 8,99 121 187 30,0 2,55 2,46
24 24,0 240 90 5,6 10,0 10,5 4 30.6 2900 242 9,73 139 208 31,6 2,60 2,42
24а 25,8 240 95 5,6 10,7 10,5 4 32,9 3180 265 9,84 151 254 37,2 2.78 2,67
27 27,7 270 95 6,0 10,5 11 4,5 35,2 4160 308 10,9 178 262 37,3 2,73 2,47
30 31,8 300 100 6,5 11,0 12 5 40,5 5810 387 12,0 224 327 43,6 2,84 2,52
33 36,5 330 105 7,0 11,7 13 5 46,5 7980 484 13,1 281 410 51,8 2,97 2,59
36 41,9 360 110 7,5 12,6 14 6 53,4 10820 601 14,2 350 513 61,7 3,10 2,68
40 48,3 400 115 8,0 13,5 15 6 61,5 15220 761 15,7 444 642 73,4 3,23 2,75
8
Таблица 6
Балки двутавровые (ГОСТ 8239 — 56)
h — высота балки;
b — ширина полки;
d — толщина стенки;
t—-средняя толщина полки;
Я —радиус внутреннего закругле-
ния;
г — радиус закругления полки;
J'—момент инерции;
W — момент сопротивления;
£ — статический момент полусече-
ния;
i — радиус инерции.
№ про- филя Размеры, мм Пло- щадь сече- ния, см2 Вес 1 пог. м, кГ Справочные величины для осей
X— X V — У
h 6 а t R г JX’ CJH4 см3 *х» см 8». СМ3 Jy, СМ4 Wy. см3 см
10 100 70 4,5 7,2 7,0 3,0 14,2 11,1 244 48,8 4,15 28,0 35,3 10,1 1,58
12 120 75 5,0 7,3 7,5 3,0 16,5 13,0 403 67,2 4,94 38,5 43,8 11,7 1,63
14 140 82 5,0 7,5 8,0 3,0 18,9 14,8 632 90,3 5,78 51,5 58,2 14,2 1,75
16 160 90 5,0 7,7 8,5 3,5 21,5 16,9 945 118 6,63 67,0 77,6 17,2 1,90
18 180 95 5,0 8,0 9,0 3,5 23,8 18,7 1330 148 7,47 83,7 94,6 19,9 1,99
18а 180 102 5,0 8,2 9,0 3,5 25,4 19,9 1440 160 7,53 90,1 119 23,3 2,17
20 200 100 5,2 8.2 9,5 4,0 26,4 20,7 1810 181 8.27 102 112 22,4 2,06
20а 200 НО 5,2 8,3 9,5 4,0 28,3 22,2 1970 197 8,36 111 148 27,0 2,29
22 220 НО 5,3 8.6 10,0 4,0 30.2 23,7 2530 230 9,14 130 155 28,2 2,26
22а 220 120 5,3 8,8 10,0 4,0 32.4 25,4 2760 251 9,23 141 203 33,8 2,50
24 240 115 5,6 9,5 10,5 4,0 34,8 27,3 3460 289 9,97 163 198 34,5 2,37
24а 240 125 5,6 9,8 10.5 4,0 37,5 29,4 3800 317 10,1 178 260 41,6 2,63
27 270 125 6,0 9,8 11,0 4,5 40,2 31,5 5010 371 11,2 210 260 41,5 2,54
27а 270 135 6,0 10,2 11,0 4,5 43,2 33,9 5500 407 11,3 229 337 50,0 2,80
30 300 135 6,5 10,2 12,0 5,0 46,5 36,5 7080 472 12,3 268 337 49,9 2,69
30а 300 145 6,5 10,7 12.0 5,0 49,9 39,2 7780 518 12,5 292 436 60,1 2,95
33 330 140 7,0 11,2 13,0 5,0 53,8 42,2 9840 597 13,5 339 419 59,9 2,79
36 360 145 7,5 12,3 14,0 6,0 61,9 48,6 13380 743 14,7 423 516 71,1 2,89
40 400 155 8,0 13,0 15,0 6,0 71,4 56,1 18930 947 16,3 540 666 75,9 3,05
45 450 160 8,6 14,2 16,0 7,0 83,0 65,2 27450 1220 18,2 699 807 101 3,12
50 500 170 9,3 15,2 17,0 7,0 96,9 76,1 39120 1560 20,1 899 1040 123 3,28
55 550 180 10,0 16,5 18,0 7,0 113 .88,6 54810 1990 22,0 1150 1350 150 3,46
60 600 190 '10,8 17,8 20.0 8,0 131 103,0 75010 2500 23,9 1440 1720 181 3,62
65 650 а)о 11,7 19.2 22,0 9,0 151 119,0 100840 3100 25,8 1790 2170 217 3,79
70 700 210 12,7 20,8 24,0 10,0 174 137,0 133890 3830 27,7 2220 2730 260 3,96
70а 700 210 15,0 24,0 24,0 10,0 202 158,0 152700 4360 27,5 2550 3240 309 4,01
S 706 700 210 17,5 28.2 24,0 10,0 234 184,0 175370 5010 27,4 2940 3910 373 4,09
<О <0 CO Балки двута вровьи У / у Таблица 7 i (ГОСТ 8239 — 56*) '^\^<лон12% h — высота балки; г — радиус закругления полки; х Ь — ширина полки; J — момент инерции; ' d — толщина стенки; W — момент сопротивления, : t — средняя толщина полки; 6* — статический момент полусече- rj Н R — радиус внутреннего закругле- ния; ния; i — радиус инерции.
№ про- филя Bee 1 пог m. кГ Размеры, мм Пло- щадь сече- ния, см2 Справочные величины для ocef
X — X у ~~ y
ь R г Jx> сма g 3 lx* см Sx. CM3 Jv.t CM* wv CM3 гУ’ CM
10 12 14 16 18 18a 20 20a 22 22a 24 24a 27 27a 30 30a 33 36 40 45 50 55 60 65 70 70a 706 9,46 11,5 13,7 15,9 18,4 19,9 21,0 22,7 24,0 25,8 27,3 29,4 31,5 33,9 36,5 39,2 42,2 48,6 56,1 65,2 76,8 89,8 104,0 120,0 138,0 158,0 184,0 100 120 140 160 180 180 200 200 220 220 240 240 270 270 300 300 330 360 400 450 500 550 600 650 700 700 700 55 64 73 81 90 100 100 110 110 120 115 125 125 135 135 145 140 145 155 160 170 180 190 200 210 210 210 4,5 4,8 4,9 5,0 5,1 5,1 5,2 5,2 5,4 5,4 5,6 5,6 6,0 6,0 6,5 6,5 7,0 7,5 8,0 8,6 9,5 10,3 11,1 12,0 13,0 15,0 17,5 7,2 7,3 7,5 ’ 7,8 8,1 8,3 8,4 8,6 8,7 8,9 9,5 9,8 9,8 10,2 10,2 10,7 11,2 12,3 13,0 14,2 15,2 16,5 17,8 19,2 20,8 24,0 28.2 7,0 7,5 8,0 8,5 9,0 9,0 9,5 9,5 10,0 10,0 10,5 10,5 11,0 11,0 12,0 12,0 13,0 14,0 15,0 16,0 17,0 18,0 20,0 22,0 24,0 24,0 24,0 2,5 3,0 3,0 3,5 3,5 3,5 4,0 4,0 4,0 4,0 4,0 4,0 4,5 4,5 5,0 5,0 5,0 6,0 6,0 7,0 7,0 7,0 8,0 9,0 10,0 10,0 10,0 12,0 14,7 17,4 20,2 23,4 25,4 26,8 28,9 30,6 32,8 34,8 37,5 40,2 43,2 46,5 49,9 53,8 61,9 71,4 83,0 97,8 114,0 132,0 153,0 176,0 202,0 234,0 198 350 572 873 1290 1430 1840 2030 2550 2790 3460 3800 5010 5500 7080 7780 9840 13380 18930 27450 39290 55150 75450 101400 134600 152700 175370 39,7 58,4 81,7 109,0 143,0 159,0 184,0 203,0 232,0 254,0 289,0 317,0 371,0 407,0 472,0 518,0 597,0 743,0 947,0 1220,0 1570,0 2000,0 2510,0 3120,0 3840,0 4360,0 5010,0 4,06 4,88 5,73 6,57 7,42 7,51 8,28 8,37 9,13 9,22 9,97 10,10 11,20 11,30 12,30 12,50 13,50 14,70 16,30 18,20 20,00 22,00 23,90 25,80 27,70 27,50 27,40 23,0 33,7 46,8 62,3 81,4 89,8 104,0 114,0 131,0 143,0 163,0 178,0 210,0 229,0 268,0 292,0 339,0 423,0 540,0 699,0 905,0 1150,0 1450,0 1800,0 2230,0 2550,0 2940,0 17,9 27.9 41,9 58,6 82,6 114,0 115,0 155,0 157,0 206,0 198,0 260,0 260,0 337,0 337,0 436,0 419,0 516,0 666,0 807,0 1040,0 1350,0 1720,0 2170,0 2730,0 3240,0 3910,0 6,49 8,72 11,5 14,5 18.4 22,8 23,1 28,2 28,6 34,3 34,5 41,6 41,5 50,0 49,9 60,1 59,9 71,1 85,9 101,0 122,0 150,0 181,0 217,0 260,0 309,0 . 373,0 1,22 1,38 1,55 1.70 1,88 2,12 2,07 2,32 2,27 2,50 2,37 2,63 2,54 2,80 2,69 2,95 2,79 2,89 3,05 3,12 3,26 3,44 3,60 3,77 3,94 4,01 4,09
Таблица 8
Балки двутавровые широкополочные (ГОСТ 6183 — 52)
№ профиля Размеры, мм Площадь сечения, см2 Вес 1 пог. м, кГ Справочные величины для осей
X — X и — У
h b d 1 см4 wx> см3 ^х* см 8Х, CJH3 см4 wy, СМ3 см
Б а л о ч ные профили
20Б2 200 120 5,0 7,3 26,8 21,0 1890 189 8,41 106 210 35,1 2,80
22Б 220 130 5,0 6,0 26,0 20,4 2160 196 9,12 111 220 33,8 2,91
24Б 240 140 5,0 6,0 28,2 22,1 2790 233 9,95 131 275 39,2 3,12
24БХ 241 140 5,0 6,8 30,4 23,9 3120 258 10,1 144 311 44,5 3,20
24Б2 242 140,5 5,5 7,0 32,2 25,3 3260 269 10,1 151 324 46,1 3,17
27Б 270 150 5,2 6,4 32,6 25,6 4070 302 11,2 170 360 48,0 3,33
27БХ 271,6 150 5,2 7,2 35,0 27,5 4510 332 11,4 186 405 54,0 3,40
27Б2 273,4 150,3 5,5 8,1 38,5 30,2 5070 371 11,5 207 459 61,1 3,45
ЗОБ 300 160 5,5 6,8 37,5 29,4 5750 384 12,4 216 465 58,1 3,52
30Бх 301,8 160 5,5 7,7 40,4 31,7 6410 425 12,6 238 526 65,8 3,61
30Б2 304,4 160,5 6,0 9,0 46,1 36,2 7480 491 12,7 275 621 77,3 3,67
ЗЗБ 330 170 6,0 7,2 43,4 34Д 7950 482 13,5 272 590 69,4 , 3,69
ЗЗБХ 332 170 6,0 8,2 46,8 36,8 8880 535 13,8 300 672 79,1 3,79
36Б 360 180 6,5 7,8 50,5 39,6 10920 607 14,7 344 759 84,3 3,88
36БХ 362,4 180 6,5 9,0 54,8 43,0 12330 681 15,0 383 876 97,3 4,00
36В2 362,8 180 6,5 9,2 55,5 43,6 12570 693 15,0 389 895 99,4 4,02
40Б 400 190 7,0 8,5 59,1 46,4 15660 783 16,3 444 973 102 4,06
40Бх 402,6 190 7,0 9,8 64,1 50,3 17650 877 16,6 494 1120 118 4,18
40Б2 404 190 7,0 10,5 66,7 52,4 18730 927 16,8 521 1200 127 4,24
45Б 450 195 7,7 9,4 69,9 54,8 22940 1020 18,1 583 1160 119 4,08
45БХ 453,2 195 7,7 11,0 76,1 59,7 26120 1150 18,5 653 1360 140 4,23
45Б2 454,6 195,3 8,0 11,7 80,2 63,0 27760 1220 18,6 692 1450 149 4,25
50Б 500 205 8,5 10,2 82,6 64,8 32900 1320 20,0 757 1470 143 4,21
50Бх 503,6 205 8,5 12,0 90,0 70,6 37550 1490 20,4 849 1730 < 168 4,38
50Б2 506,6 205 8,5 13,5 96,1 75,5 41470 1640 20,8 927 1940 189 4,49
55Б 550 220 9,0 11,4 97,6 76,6 47370 1720 22,0 988 2030 184 4,56
55БХ 554 220 9,0 13,4 106 83,5 54080 1950 22,5 1110 2380 216 4,73
55Б2 557,2 220,3 9,3 15,0 115 90,4 59940 2150 22,8 1220 2680 243 4,82
60Б 600 235 10,0 12,4 116 90,9 66170 2210 23,9 1270 2690 229 4,82
60Бх 604,4 235 10,0 14,6 126 99,0 75550 2500 24,5 1430 3160 269 5,01
60В2 609,2 235 10,0 17,0 137 108 85930 2820 25,0 1600 3680 313 5,18
65Б 650 250 10,5 14,3 137 107 93240 2870 26,1 1640 3730 298 5,22
65БХ 654,6 250 10,5 16,7 149 117 106280 3250 26,7 1840 4360 348 5,41
65Б2 660,6 250,2 10,7 19,6 165 129 122180 3700 27,2 2090 5120 410 5,58
70Б 700 275 11,0 16,0 161 127 130270 3720 28,4 2120 5550 404 5,86
70Бх 705,6 275 11,0 18,8 177 139 149290 4230 29,1 2390 6520 475 6,07
70Б2 711,6 275,5 11,5 21,8 197 155 171500 4820 29,5 2710 7610 552 6,21
80Б 800 300 12,0 17,0 194 152 201310 5030 32,2 2880 7660 511 6,29
80Бх 806,2 300 12,0 20,1 213 167 231300 5740 33,0 3250 9060 604 6,53
80Б2 сс 813 300,5 12,5 23,5 237 186 266970 6570 33,6 3700 10640 708 6,70
СЛ
со о Продолжение it \абл. 8
Справочные величины для осей
гаамсры, Площадь Вес „ „ ,, - сечения. 1 поз. лг. • * - у . —
профиля h Ь | t см2 кГ Jx, Wx, ix, Sx, Jy, Wy, гу,
CM4 CM3 CM CM3 CM4 CM3 см
90Б 900 325 13,5 17,8 232 182 297810 6620 35,8 3810 10200 628 6,63
90Б, 906,8 325 13,5 21,2 254 200 342900 7560 36,7 4310 12150 748 6,91
90Б2 915 325,5 14,0 25,3 286 224 401370 / 8770 37,5 4970 14560 895 7,14
100Б 1000 350 14,5 20,0 279 219 443090 ' 8860 39,8 5100 14320 818 7,16
100Бх 1009 350 14,5 24,5 311 244 522550 10360 41,0 5890 17530 1000 7,51
100В2 1010 400 15,0 25,0 344 270 595810 11800 41,6 6650 26690 1330 8,81
ЮОБз 1017 401 16,0 28,5 382 300 676480 13300 42,1 7490 30660 1530 8,96
Ю0Б4 1023,6 402,5 17,5 31,8 424 333 758760 14830 42.3 8360 34600 1720 9,03
lOOBj 1031’ 404 19,0 35,5 469 368 851050 16510 42,6 9330 39070 1930 9,12
100Б» 1039 406 21,0 39,5 522 410 956290 18410 42,8 10430 44130 2170 9,19
100Б, 1047,6 408 23,0 43,8 578 454 1070370 20440 43,0 11620 49680 2440 9,27
Колонные профил и легкие
27Л 275,6 220 6,0 9,2 55,9 43,9 8040 583 12,0 319 1630 148 5,40
27Л, 278,4 220 6,0 10,6 62,1 48,7 9220 662 12,2 362 1880 171 5,51
27Л2 281 220,5 6,5 11,9 69,2 54,3 10430 742 12,3 407 2130 193 5,54
ЗЗЛ 336,8 260 7 0 10,6 77,2 60,6 16500 980 14,6 537 3110 239 6,34
33 Л, 340 260 7,0 12,2 85,5 67,1 18800 1110 14,9 607 3580 275 6,47
ЗЗЛ2 343 260,5 7,5 13,7 95,1 74,6 21330 1240 15,0 681 4040 310 6,52
40Л 408 300 8,0 12,5 106 82,9 33080 1620 17,7 888 5630 375 7,30
40 Л, 412 300 8,0 14,5 118 92,3 33130 1850 18,0 1010 6530 435 7,45
40Л2 415,2 300,8 8,8 16,1 131 102 42710 2060 18,1 ИЗО 7310 486 7,48
50Л 508,6 340 9 7 14,5 145 114 69110 2720 21,8 1500 9500 559 8,09
50Л, 513,4 340 97 16,9 161 127 79770 3110 22,2 1710 11070 651 8,28
50Л2 517,6 340,6 ЮЛ 19,0 179 140 89950 3480 22,4 1910 12520 735 8,37
60Л 608,6 400 11*4 16,7 199 156 135130 4440 26,0 2450 17820 891 9,46
5-1186
60Лх 60Л2 613,8 618,6 400 400,6 11,4 12,0 19,3 21,7 220 243 173 191 154550 173960 ) ’ * J 5040 5620 716,5 26,8 2770 3090 20590 23260 1030 1160 9,68 9,79
70Л 711,6 420 13,0 21,8 270 212 250200 7030 30,4 3880 26930 1280 10,0
70Л! 718,4 420,3 13,3 25,2 301 236 287620 8010 30,9 4410 31200 1490 10,2
70Л2 724,0 421,8 14,8 28,0 335 263 322980 8920 31,0 4940 35040 1660 10,2
Колонные профили тяжелые
20Т 203 200 6 8,8 46,3 36,4 3640 359 8,86 197 1170 117 5,03
20Тх 205,4 200,5 6,5 10,8 52,2 40,9 4180 407 8,95 224 1340 134 5,08
20Т2 208 201 7 11,3 58,4 45,9 4770 459 9,04 253 1530 152 5,12
24Т 249 240 6,5 10,5 65,2 51,2 7810 628 10,9 343 2420 202 6,09
24ТХ 252 240,5 7 12 73,7 57,8 9010 715 11,1 392 2780 231 6,15
24Т2 255 241 7,5 13,5 82,2 64,5 ‘ 10240 803 11,2 442 3150 261 6,19
24Т3 258 241,5 8 15 90,7 71,2 11500 891 11,3 492 3520 292 6,23
ЗОТ 312,4 300 8 13 101 79,2 19060 1220 13,7 666 5850 390 7,61
ЗОТ, 315,4 301 9 14,5 ИЗ 88,8 21540 1370 13,8 749 6590 438 7,64
30Т2 318,4 302 10 16 125 98,3 24070 1510 13,9 833 7350 487 7,66
ЗОТ3 322,4 303 11 18 141 110 27450 1700 14,0 943 8350 551 7,71
30Т4 326,4 304 12 20 156 122 30930 1900 14,1 1050 9370 616 7,75
40Т 417 400 10 17 174 137 59120 2840 18,4 1540 18140 907 10,2
40Тх 421 401 И 19 195 153 66760 3170 18,5 1730 20420 1020 10,3
40Т2 425 402 12 21 215 169 - 74570 3510 18,6 1930 22740 ИЗО 10,3
40Т3 429 404 14 23 239 188 83220 3880 18,6 2140 25290 1250 10,3
40Т4 433 406 16 25 264 207 92080 4250 18,7 2360 27900 1370 10,3
40Т5 441 406,5 16,5 29 299 235 107940 4900 19,0 2730 32480 1600 10,4
40Тв 449 408 18 33 338 265 125170 5580 19,2 3130 37370 1830 10,5
40Т, 457 410 20 37 380 298 143510 6280 19,4 3550 42530 2070 10,6
40Т3 465 412 22 41 422 331 162610 6990 19,6 3980 47820 2320 10,6
40Т, 475 415 25 46 478 375 188050 7920 19,8 4550 54850 2640 10,7
4ОТ1о 489 400 28 53 531 417 215600 8820 20,1 5140 56600 2830 10,3
40Ти 501 403 31 59 594 466 248150 9910 20,4 5820 64460 3200 10,4
40Т12 513 407 35 65 663 521 283730 11060 20,7 6570 73170 3600 10,5
40Т13 527 412 40 72 746 586 328350 12460 21,0 7480 84130 4080 10,6
40Т14 541 417 45 79 831 652 376070 13900 21,3 8440 95770 4590 10,7
Глава 3
ВНЕШНИЕ И ВНУТРЕННИЕ СИЛЫ.
МЕТОД СЕЧЕНИЙ.
ЭПЮРЫ ВНУТРЕННИХ СИЛ
§ 13. Классификация внешних сил
Внешними силами, или нагрузками, называются силы взаимодей-
ствия между рассматриваемым элементом конструкции и связанными
с ним телами. Если внешние силы являются результатом непосред-
ственного, контактного взаимодействия данного тела с другими телами,
то они приложены только к точкам поверхности тела в месте кон-
такта и называются поверхностными силами. Поверхностные силы
могут быть непрерывно распределены по всей поверхности тела или
ее части. Величина нагрузки, приходящаяся на единицу площади, назы-
вается интенсивностью нагрузки, обозначается обычно буквой р и имеет
размерность кГ/см2, кГ/м2 или Т/м2. По ГОСТу 9867—61 в Между-
народной системе единиц физических величин (СИ) единицей силы
является ньютон (н). Это сила, которая сообщает покоящемуся телу
массой в 1 кг ускорение, равное 1 м/сек?. Размерность ньютона —
кг м/сек2.
1 кГ = 9,81 н\ 1 н = 0,102 кГ.
Единица давления — ньютон на квадратный метр (н/м2). В инже-
. кГ н н
первых расчетах можно принять 1 « 10
Нагрузка, распределенная по поверхности (рис. 26, а), приведен
ная к главной плоскости (рис. 26, б), т. е. нагрузка, распределенная
по линии, называется погонной нагрузкой, обозначается обычно бук-
вой q и имеет размерность кГ/см, кГ/м или Т/м. Характер изменения q
по длине обычно показывают в виде эпюры (графика) q.
В случае равномерно распределенной нагрузки (рис. 26, а) эпюра
q прямоугольная (рис. 26, б). При действии гидростатического давле-
ния эпюра q треугольная (рис. 26, в).
Рис. 26
Равнодействующая распределенной нагрузки численно равна пло-
щади ее эпюры и приложена в ее центре тяжести. Если нагрузка
распределена на небольшой части поверхности тела, то ее всегда за-
меняют равнодействующей, называемой сосредоточенной силой Р
(кГ или Г).
98
Встречаются нагрузки, которые могут быть представлены в виде
сосредоточенного момента (пары). Моменты М (кГ • см или Т • м)
обозначают обычно одним из двух способов (рис. 27, а, б) или в виде
вектора, перпендикулярного к плоскости действия пары. В отличие
от вектора силы вектор момента изображают в виде двух стрелок или
волнистой линией (рис. 27, в, г). Вектор момента принято считать
правовинтовым.
Силы, не являющиеся результатом контакта двух тел, а прило-
женные к каждой точке объема, занятого телом (собственный вес,
силы инерции), называются объемными или массовыми силами.
Рис. 27
В зависимости от характера приложения сил во времени разли-
чают нагрузки статические и динамические. Нагрузка считается ста-
тической, если она сравнительно медленно и плавно (хотя бы в течение
нескольких секунд) возрастает от нуля до своего конечного значения,
а затем остается неизменной. При этом можно пренебречь ускорени-
ями деформируемых масс, а следовательно, и силами инерции.
Д инамические нагрузки сопровождаются значительными ускоре-
ниями как деформируемого тела, так и взаимодействующих с ним тел.
Возникающими при этом силами инерции пренебречь нельзя. Дина-
мические нагрузки делятся на мгновенно приложенные, ударные и
повторно-переменные.
Мгновенно приложенная нагрузка возрастает от нуля до макси-
мума в течение долей секунды. Такие нагрузки возникают при воспла-
менении горючей смеси в цилиндре двигателя внутреннего сгорания,
при трогании с места железнодорожного состава.
Ударная нагрузка характерна тем, что в момент ее приложения
тело, вызывающее нагрузку, обладает определенной кинетической
энергией. Такая нагрузка возникает, например, при забивке свай
с помощью копра, в элементах кузнечного молота.
П овторно-переменна я нагрузка характерна своей непрерывной
периодичностью. Такие нагрузки испытывают при работе штоки, валы,
оси железнодорожных вагонов, колеблющиеся элементы конструк-
ций и др.
§ 14. Внутренние силы. Метод сечений.
Эпюры внутренних сил
Между соседними частицами любого тела (кристаллами, молеку
лами, атомами) всегда имеются определенные силы взаимодействия,
или внутренние силы, которые стремятся сохранить тело как единое
целое, противодействуя всему, что может изменить взаимное располо-
женно частиц, т. е. деформировать тело.
Внешние силы, наоборот, всегда стремятся вызвать деформацию
тола.
Величина внутренних сил, действующих между двумя какими-
либо частицами, в нагруженном и ненагруженном теле будет различной.
4* 99
6
Рис. 28
дой стороне сечения получим
В сопротивлении материалов не принимаются во внимание внут-
ренние силы, действующие в ненагруженном теле, а рассматриваются
только те дополнительные внутренние силы, которые появляются
при нагружении тела. Эти дополнительные внутренние силы взаимо-
действия, возникающие в результате нагружения, часто называют
усилиями.
Для выявления внутренних сил, возникающих в теле под нагруз-
кой, в сопротивлении материалов пользуются методом сечений.
Смысл этого метода состоит в том, что нагруженное тело (рис. 28, а}
мысленно рассекают некоторой плоскостью на две части А и В. Для
того чтобы каждая из этих частей
находилась в равновесии под дей-
ствием приложенных к ней внеш-
них нагрузок, необходимо действие
отсеченной части заменить некото-
рой системой внутренних сил в се-
чении. Эти силы и явятся силами
взаимодействия между частями тела»
А и В» Внутренние силы, действу-
ющие в сечении со стороны части
А, в соответствии с третьим зако-
ном Ньютона равны по величине
и противоположны по направлению
внутренним силам, действующим
в сечении со стороны части В
(рис. 28, б).
Как всякую систему сил, внут-
ренние силы, распределенные па
сечению, можно привести к одной
точке (например, к центру тяжести
сечения), в результате чего на каж-
главный вектор и главный момент
внутренних сил в сечении (рис. 28, в). Применительно к стержню
последний обычно рассекают плоскостью, перпендикулярной к оси
(рис. 29, а). Если главный вектор и главный момент спроектировать
на ось стержня z и главные центральные оси сечения у и х, то на
каждой стороне сечения получим шесть внутренних силовых факторов
(рис. 29, б): три силы (N, Qy, Qx) и три момента (Mz, Му, Мх). Эти
величины называются усилиями и моментами в сечении стержня.
Рис. 29
Как видно из рисунка, N вызывает продольную деформацию стерж*
ня (растяжение или сжатие); Qy и Qx — сдвиг сторон сечения соот-
ветственно в направлении осей у и х\ Mz вызывает кручение стержня;
Му и Мх — изгиб стержня в главных плоскостях xz и у?. Поэтому
для усилий и моментов в сечении приняты следующие названия:
100
N — продольная, или осевая (направленная вдоль оси),
сила\
Qy и Qx — поперечные (реже — перерезывающие) силы;
Mz = Мкр — крутящий момент;
Му и Мх •— изгибающие моменты.
Можно дать следующие определения перечисленным компонентам
внутренних усилий: продольная сила N предсргавляет собой
сумму проекций всех внутренних сил, действующих в сечении, на нор-
маль к сечению (или на ось стержня)) поперечные силы Qy
и Qx — это суммы проекций всех внутренних сил в сечении На глав;
ные центральные оси сечения у и х соответственно; крутящий
момент Мг (или Мкр) — это сумма моментов всех внутренних
сил в сечении относительно оси стержня) изгибающие мо-
менты Мх и Му — это суммы моментов всех внутренних сил
в сечении относительно главных центральных осей инерции сечения
х и у соответственно.
Для практического вычисления усилий и моментов в сечении сле-
дует иметь в виду, что: N численно равна алгебраической сумме про-
екций всех внешних сил, действующих на одну из частей (левую или
правую) рассеченного стержня, на ось стержня (на нормаль к сече-
нию); Qy — то же на ось у; Qx — то же на ось х; Мкр численно равен
алгебраической сумме моментов всех внешних сил, действующих
на одну из частей (левую или правую) рассеченного стержня, относи-
тельно оси стержня; Му — то же относительно оси у; Мх — то же от-
носительно оси х.
Таким образом, метод сечений позволяет найти в£е усилия и мо-
менты в любом сечении стержня при действии любой нагрузки.
Для этого необходимо сделать следующее:
1. Найти главные центральные оси поперечного сечения стержня.
2. Провести мысленно поперечное сечение стержня в том месте, где
нужно найти усилия и моменты.
3. Вычислить усилия N, Qy, Qx и моменты Мкр, Му, Мх как
алгебраические суммы проекций и моментов внешних сил, действую-
щих на одну из частей (левую или правую по отношению к сечению)
рассеченного стержня, обычно на ту, где проекции и моменты вы-
числяются проще.
Усилия и моменты в разных сечениях одного и того же стержня
В общем/ случае различны. Графики (диаграммы), показывающие,
как изменяются усилия и моменты при переходе от сечения к сечению,
называются эпюрами усилий и моментов.
При построении эпюр рекомендуется пользоваться следующими
правилами:
1. Ось (базу), на которой строится эпюра, всегда выбирают так,
Итобе она была параллельна оси стержня (или совпадала с ней).
2. Ординаты эпюр, выражающие в выбранном масштабе значение
усилия или момента, откладывают от оси эпюры по перпендикуляру.
г 8. Эпюры принято штриховать
ЛИВИЯМИ, перпендикулярными к базе. М#р>0
Положительные значения усилий или '\\
моментов откладывают вверх от базы, I
отрицательнее —- вниз. I/ "жЖ \J
4. На эпюрах проставляют числа,
покаеывахрщие величины характерных
ординат, а в поле эпюре в кружочке
ставят знак усилия. Рис. 30
101
При построении эпюр продольных сил и крутящих моментов
рекомендуется пользоваться следующими правилами в отношении
их знаков:
1. Продольная сила N считается положительной, если она вызы-
вает растяжение, и отрицательной, если вызывает сжатие»
2. Крутящий момент Мкр считается положительным, если при
наблюдении с торца вдоль оси рассматриваемой части он действует
по часовой стрелке (рис. 30).
Рис. 31
Примеры построения эпюр продольных сил показаны на рис. 31,
32, 33 (at — arctg 7^; а2 = arctg 7F2; 7 — объемный вес). Эпюра кру-
тящих моментов для трансмиссионного вала, схема которого приве-
дена на рис. 34, а, показана на рис. 34, б. На рис. 34, в показано на-
правление максимального положительного момента в сечении рас-
сматриваемого вала.
Прежде чем перейти к построе-
нию эпюр поперечных сил и изги-
бающих моментов при изгибе ба-
лок — к разделу сопротивления ма-
териалов, имеющему весьма суще-
ственное значение для понимания поведения элементов конструкций
под нагрузкой, напомним некоторые исходные основные понятия,
связанные с балками.
§ 15. Балки и их опоры
Балками называют прямолинейные стержни, работающие на из
гиб. Плоским изгибом балки называется такой изгиб балки, при кото-
ром вое заданные силы лежат в одной (силовой) плоскости (рис. 35, а),
102
причем эта плоскость совпадает с одной из главных плоскостей балки.
При расчете балку принято заменять ее осью (рис. 35, б), все
нагрузки должны быть приведены к этой оси, а силовая плоскость
будет совпадать с плоскостью чертежа.
Все многообразие существующих опорных устройств балок схе-
матизируется в виде следующих трех основных типов опор.
Рис. 36
Шарнирно-подвижная опора (рис. 36, а), в которой может возни-
кать только одна составляющая реакции направленная вдоль
опорного стержня.
Шарнирно-неподвижная опора (рис. 36, б), в которой могут возни-
кать две составляющие — вертикальная реакция RA и горизонтальная
реакция Н А.
Защемление (иначе жесткое защемление или заделка), где могут
быть три составляющие — вертикальная (RA) и горизонтальная (Ял>
реакции и опорный момент МА (рис. 36, в).
Все реакции и моменты считаются приложенными в точке А —
центре тяжести опорного сечения.
a 6 6
Рис. 37
Балка, показанная на рис. 37, а, называется простой или одно-
пролетной, или двухопорной, а расстояние I между опорами — про*
летом.
Консолью называется балка, защемленная одним концом и ле
имеющая других опор (рис: 35, б), или часть балки, свешивающаяся
103
за опоры (часть ВС на рис. 37, б и части АС и BD на рис. 37, в). Балки,
имеющие свешивающиеся части, называются консольными.
Балка называется статически определимой, если число неизвест-
ных опорных реакций не превышает трех; в противном случае балка
статически неопределима. Балки, изображенные на рис. 35 и 37,
статически определимы, а балка, изображенная на рис. 38, а, назы-
вается неразрееной и является статически неопределимой, поскольку
имеет пять неизвестных опорных реакций: три — в опоре А и по од-
Рис. 38
ной — в опорах В и С. Поставив, например, в любых двух сечениях
первого пролета балки шарниры (точки D и Е на рис. 38, б), получим
статически определимую шарнирную балку, ибо каждый такой про-
межуточный шарнир к трем основным уравнениям статики прибавляет
одно дополнительное уравнение, поскольку сумма моментов относи-
тельно центра шарнира от всех сил, расположенных по одну сторону
от него, равна нулю.
§ 16. Вычисление реакций
Для того чтобы можно было приступить к построению эпюр,
необходимо знать все внешние нагрузки, включая реакции, которые
предварительно должны быть определены.
При определении реакций рекомендуется придерживаться следую-
щей последовательности, которую мы проиллюстрируем на примере
простой балки (рис. 37, а)\
1. Обозначив опоры буквами А и В, три неизвестные реакции
ЯА, RB и НА определим из следующих уравнений равновесия:
сумма проекций всех сил на ось балки равна нулю
Sz = °-
откуда находим ЯА;
сумма моментов всех сил относительно опорного шарнира А
равна нулю
2>л = о,
откуда находим RB\
сумма моментов всех сил относительно опорного шарнира В
равна нулю
М=0'
откуда находим RA.
2. Для контроля можно использовать условие равенства нулю
суммы проекций на вертикаль
или условие равенства нулю суммы моментов относительно какой-
либо точки С, отличной от А и В, т. е.
2мс=0.
104
Рис. 39
Рис. 40
Я
Рис. 41
Рис. 42
3. Если в результате вычисления какая-либо реакция окажется
отрицательной, то па рисунке необходимо изменить ее направление
на обратное по сравнению с направлением, принятым в начале рас-
чета.
4. Если нагрузки, действующие на балку, перпендикулярны
к оси балки, то НА = 0 и уравнением SZ = 0 не пользуются.
Поперечная сила
векторы стремятся вращать
§ 17. Усилия и моменты в сечениях балки
При плоском изгибе вся нагрузка расположена в главной плос-
кости стержня zy (рис. 35, а), и поэтому она не дает проекций на ось х
и моментов относительно осей z и у. Следовательно, в любом сечении
балки
Qx=Mz=M^=My = b,
и отличными от пуля будут три величины — N, Qy и MXf KOTO-
" " Л [ м.
Эти усилия действуют в сече-
ниях рам и кривых стержней. В бал-
ках же при нагрузке, перпендику-
лярной к оси, равной пулю будет
продольная сила N — 0. Поэтому
в балках приходится иметь дело
с поперечной силой Q и изгибающим
моментом М.
При построении эпюр попереч-
ных сил Q и изгибающих моментов
М принимают следующие правила
^знаков:
Q в сечении положительна, если ее
части рассеченной балки по часовой
стрелке (рис. 39, а).
Изгибающий момент М в сечении положителен, если
он вызывает сжатие в верхних волокнах балки (рис. 39, а).
Очевидно, поперечные силы и моменты, показанные на рис. 39, б,
имеют отрицательные знаки. Эпюры поперечных сил и изгибающих
моментов для балок, нагруженных по различным типичным схемам,
приведены на рис. 40—44.
§ 18. Дифференциальные зависимости при изгибе балок.
Некоторые особенности эпюр Q и М
Рассмотрим балку с произвольной нагрузкой (рис. 45, а). Между
интенсивностью q распределенной нагрузки, поперечной силой Q
и изгибающим моментом М, действующими в некотором сечении, суще-
ствуют следующие дифференциальные зависимости, которые легко
Рис. 45
106
могут быть выведены из условий равновесия элемента, выделенного
из балки (рис. 45, б):
(3.2)
dQ
-dl = q'
~T = Q;
dz
d*M
dz2 -Я- (3.3)
В тех случаях, когда на рассматриваемом участке действует
« кГ • см
равномерно распределенный момент интенсивностью т —
(рис. 45, в), формула (3.2) принимает вид
^ = Q + m. (3.4)
Соотношения (3.1) — (3.4) называются дифференциальными зави-
симостями при иа?ибе. Они позволяют установить некоторые особен-
ности эпюр поперечных сил и изгибающих моментов.
1. На тех участках, где нет распределенной нагрузки, эпюра Q
ограничена прямыми, параллельными базе, а эпюра М, в общем слу-
чае,— наклонными прямыми (рис. 46).
(3.1)
;шшпн1
в^
с я ЗГ
' Ч^ГГТТГта*
Рис. 47
£
7
а
ЯШШ
ШШ1
!аГ®ж
б
Рис. 48
2. На тех участках, где к балке приложена равномерно распреде-
ленная нагрузка, эпюра Q ограничена наклонными прямыми, а эпюра
М — квадратичными параболами (рис. 47). При построении эпюры М
на сжатых волокнах выпуклость параболы обращена в сторону, про-
тивоположную направлению действия нагрузки q (рис. 48, «, б).
3. В тех сечениях, где Q = 0, касательная к эпюре М параллельна
оси эпюры (рис. 47, 48).
4. На участках, где Q> О, М
возрастает, т. е. слева направо
положительные ординаты эпюры
М увеличиваются, отрицатель-
ные — уменьшаются (участки А С
и ВЕ на рис. 46 и 47): на тех
участках, где(?<0, М убывает
(участки CD и DB на рис. 46 и
47).
5. В тех сечениях, где к
балке приложены сосредоточен-
ные силы:
а
107
а) на эпюре Q будут скачки на величину и в направлении прило-
женных сил (на рис. 46 и 47 эти скачки отмечены жирными линиями
со стрелками);
б) на эпюре М будут переломы (рис. 49), причем острие перелома
направлено против действия силы.
6. В тех сечениях, где к балке приложены сосредоточенные моменты,
на эпюре М будут скачки на величину этих моментов, на эпюре Q
никаких изменений не будет.
7. Если на конце консоли или в концевой опоре приложен сосре-
доточенный момент, то в этом сечении изгибающий момент равен внеш-
нему моменту (сечения С и В на рис. 50).
8. Эпюра Q представляет собой диаграмму производной от
эпюры М. Значит, ординаты Q пропорциональны тангенсу угла на-
клона касательной к эпюре М (на рис. 43 а = £ = arctg-~).
Эпюры поперечных сил и изгибающих моментов для балок с раз-
личным закреплением концов приведены в табл. 9.
§ 19. Построение эпюр для статически определимых рам
Рамами называются системы, состоящие из стержней, соединен-
ных жесткими узлами. Вертикальные стержни рамы принято называть
стойками, горизонтальные — ригелями. Жесткость узлов устраняет
возможность взаимного поворота скрепленных в узле стержней, т. е.
в узловой точке углы между их осями при деформации остаются не-
изменными.
Ось рамы представляет собой ломаную линию, однако каждый
участок ее можно рассматривать как балку. Поэтому построение
эпюры для рамы сводится к построению эпюр для каждого входящего
в нее стержня как для балки. Однако в отличие от обыкновенных
балок в сечениях стержней рамы, кроме изгибающих моментов М и по-
108
перечных сил Q, обычно действуют еще и продольные силы N. По-
этому для рам необходимо строить эпюры М, Q и N.
Для N и Q сохраняются ранее принятые правила знаков: N >*0,
если продольная сила вызывает растяжение; Q > 0, если вектор силы
вращает части рассеченной рамы по часовой стрелке.
Для изгибающих моментов специальных правил знаков не уста-
навливают, а при составлении выражений для М принимают по соб-
ственному усмотрению какой-либо момент положительным.
При построении эпюр положительные ординаты N и Q отклады-
вают с внешней стороны, а отрицательные — внутрь контура рамы.
Эпюры М для рам условимся строить на сжатых волокнах. Построе-
нию эпюр должно предшествовать определение неизвестных реакций.
Пример построения эпюр #, Q и М для рамы-консоли, нагружен-
ной по схеме, приведенной на рис. 51, а, показан на рис. 51, б, в, г.
§ 20. Построение эпюр для кривых стержней
В поперечных сечениях плоского кривого бруса могут действовать,
как и в рамах, три силовых фактора: #, Q и М. В случае, когда ось
кривого стержня очерчена по дуге окружности, положение любого
сечения удобно определять при помощи полярной системы координат,
и тогда продольная и поперечная силы и изгибающий момент будут
функциями угла ф — #(ф), (?(ф), М(ф).
Для N и Q остаются ранее принятые правила знаков; эпюры М,
как и в случае рам, строим со стороны сжатых волокон.
Пример построения эпюр 2У(ф), @(ф) и М(ф) для кривого бруса-
консоли, нагруженного по схеме, приведенной на рис. 52, а, когда
2V (<р) = (cos ф + 0,5 sin <р) Р;
Q (?) = (sin — 0,5 cos ср) Р;
ЛГ (ср) = (1 г— cos ср — 0,5 sin <р) PR
показан на рис. 52, б, в, г.
Если на кривой стержень действует равномерно распределенная
нагрузка, при вычислении jV, Q и М полезно иметь в виду следующую
теорему: равнодействующая равномерно распределенной нагрузки, при-
ложенной к дуге любого очертания, равна произведению интенсивности
нагрузки на длину хорды, стягивающей эту дугу, перпендикулярна
этой хорде и проходит через ее середину.
Эпюры 7У(ф); ()(ф) и М(ф) для кривого стержня, нагруженного
по схеме, приведенной на рис. 53, а, показаны на рис. 53, б, в, г.
109
На участке 0< <р < а #(ф), Q(q>) и М(ф) определялись соответ-
ственно по формулам:
2V (?) = — Pi sin -у = — 2qR sin2 — qR (1 — cos ?);
Q (?) = Px cos = 2qR sin cos = qR sin ?;
Zu Zu Zu
M (?) = Pl = 2qR2 sin2 -2- = qR2 (1 — cos <f>),
Zj
где равнодействующая распределенной нагрузки q на дуге, соответ-
ствующей углу ф, Pv = 2qR sin .
Рис. 53
На участке а < ? < р
ДГ (?) = — Р2 sin (? ~“ у) = 2qR sin ~ sin (? — y
Q (?) = P2 cos ^? — yj = 2qR sin cos ^? — уj ;
(?) = p2 cos (? —= 2(1R2 sin у sin (? ~ y)
где равнодействующая распределенной нагрузки q на дуге, соответ-
ствующей углу а, Р2 = 2qR sin ~ .
Zu
110
§ 21. Дифференциальные зависимости при изгибе
плоских кривых стержней
Дифференциальные соотношения между q, Q, N и М, которые
могут быть выведены из условий равновесия элемента, выделенного
из произвольно нагруженного кривого стержня (рис. 54 и 55), имеют
вид
При выводе указанных зависимостей было предположено, что изги-
бающий момент считается положительным, если он вызывает сжатие
внутренних волокон стержня (волокон, расположенных на вогнутой
стороне), а распределенная нагрузка положительна, если она направ-
лена к центру кривизны стержня. Зависимости (3.5) — (3.10) позво-
ляют проверить правильность составления выражений для 2У(ф)»
<?(ф) и М(ф). Выражения для внутренних усилий в кривом стержне
для различных случаев его нагружения приведены в табл. 10 и И.
111
§ 22. Построение эпюр внутренних сил
для пространственных стержней
В рамных системах, оси составляющих стержней которых не
лежат в одной плоскости, а также в плоских системах, находящихся
под воздействием пространственной нагрузки, могут действовать
в сечениях стержней все шесть внутренних силовых факторов:
Qy, Qx, Mz, Му, Мх (рис. 29, б), В этом случае эпюры изгибающих
моментов по-прежнему строят на сжатых волокнах, причем ориентира'
вать их следует так, чтобы плоскость эпюры совпадала с плоскостью
Рис. 56
а
действия пары того изгибающего момента, для которого она построена^
Знак изгибающего момента вводится произвольно и притом только
в случае необходимости записать соответствующее уравнение.
Рис. 57
" ’ Для продольных сил и крутящих моментов сохраняются прежние
правила знаков. Эпюры N и Мкр могут быть ориентированы как
угодно, но их ординаты всегда откладываются по нормали к оси
стержня.
Поперечные силы в сечении считаются положительными, если
их направление совпадает с положительным направлением у и х,
112
В качестве иллюстрации приведем для ломаного стержня
(рис. 56, а, б) результаты построения эпюр внутренних силовых фак-
торов (рис. 57).
Рис. 58 Рис. 59.
Эпюры внутренних сил для пространственно нагруженного криво-
линейного стержня (рис. 58), построенные на основании зависимостей
Миз (?) = му (?) = (PR + МА) sin Т;
Мкр (?) = Mz (?) = (PR + МА) cos т - PR,
при Р = 200 кГ; МА = 2000 кГ • cm;'R = 30 см приведены на рис. 59.
§ 23. Напряжения в сечении
В сечениях нагруженного стержня возникают непрерывно распре-
деленные внутренние усилия (рис. 60, а), равнодействующими кото-
рых являются главный вектор R и главный момент М, приложенные
в центре тяжести сечения. Проекции R и М на главные центральные
оси х, у и ось стержня z дают величины компонентов внутренних уси-
лий N, Qy, Qx, Му, Мх и Mz.
Рассмотрим бесконечно малый элемент площади dF (рис. 60, б)
с произвольными координатами х, у. В силу малости элемента можно
Рис. 60
считать, что внутренние усилия распределены на нем равномерно,
а равнодействующая их dR приложена в центре его тяжести. Следо-
вательно, при приведении этих усилий к центру тяжести элемента dR
будет являться главным вектором силы, а главный момент, очевидно,
будет равен нулю.
113
Проекциями dR на оси z, у, х будут элементарные силы dN, dQy,
dQx. Разделив эти величины на площадь dF, получим выражения для
внутренних усилий, приходящихся на единицу площади, называемых
напряжениями в точке (у, х) поперечного сечения стержня:
dN dQy dQx
a==dF’ Zx = -dF-
(3.11)
где о — нормальное напряжение, ту, тх — касательные напряжения.
Размерность напряжений — сила, деленная на квадрат длины
{кГ/мм\ кГ/см? и т. д.).
Таким образом, напряжением называется внутренняя сила, отне-
сенная к единице площади в данной точке рассматриваемого сечения.
Полное напряжение в точке может быть выражено через нормаль-
ное и касательные напряжения:
₽ = = + + <ЗЛ2>
Учитывая (3.11), нетрудно установить общие зависимости между
напряжениями а и т, с одной стороны, и компонентами внутренних
усилий с другой:
^= padF; (3.13)
F
Qy=\ ^ydF-, (3.14)
F
Qx = ( WF; (3.15)
F
My=^ xadF; (3.16)
F
Mx == J yzdF\ (3.17)
F
Mz = MKP = j (ytx + xty) dF — ytdF, (3.18)
F F
где ______________
dF ' \dF/'\dF/ r
p — расстояние от центра тяжести сечения до липни действия dQ
(рис. 60, в).
Зависимости (3.13) — (3.18) называются статическими уравне-
ниями. В общем случае расчета, когда закон распределения напряже-
ний по сечению не известен, их применять нельзя. Например, зная
величину изгибающего момента Му в сечении, нельзя найти нормаль-
ные напряжения, пользуясь формулой (3.16). Однако если, пользуясь
теми или иными соображениями, удается установить, как распреде-
ляются по сечению о или т, то тогда по формулам (3.13) — (3.18)
можно найти и сами величины напряжений.
Выводы формул для определения напряжений целесообразно про-
водить по следующей схеме:
114
1. Рассматривается статическая сторона задачи — записываются
те из уравнений (3.13) — (3.18), которые необходимы для вывода.
2. Рассматривается геометрическая сторона задачи — на основа-
нии опытных данных записываются геометрические уравнения, уста-
навливающие зависимость перемещений точек стержня от их поло-
жения в сечении.
3. Рассматривается физическая сторона задачи — на основании
опытных данных записываются уравнения, выражающие зависимость
между напряжениями и деформациями (или перемещениями).
4. Производится синтез, т. е. совместно решаются уравнения,
полученные в п. 1—3, и путем исключения деформаций (пли переме-
щений) получаются формулы, выражающие напряжения через усилия
или моменты в сечении.
§ 24. Условия прочности и жесткости
Основной задачей сопротивления материалов является определе-
ние надежных размеров поперечного сечения детали, подверженной
тому или иному силовому, температурному или другому воздействию.
Такие размеры могут быть определены из расчета на прочность, жест-
кость или устойчивость. Основным является расчет на прочность.
Физически очевидно, что материал не в состоянии выдерживать
сколь угодно большие напряжения. Поэтому величины наибольших
напряжений из условия надежности работы детали должны быть
ограничены некоторыми допустимыми значениями. Эти значения на-
зываются допускаемыми напряжениями и обозначаются 1а] или [т].
Если известны допускаемые напряжения и имеются формулы,
выражающие напряжения через усилия и моменты в сечении, то прин-
ципиально можно рассчитать на прочность (подобрав необходимые
размеры, при которых напряжение не будет превышать допускаемые)
любую деталь.
На практике встречаются три случая расчета на прочность:
1. По известным нагрузкам требуется для выбранного материала
найти необходимые размеры поперечного сечения детали, обеспечиваю-
щие ее надежную работу (проектировочный расчет).
2. Известны материал и размеры детали. Требуется выяснить,
может ли эта деталь выдержать заданную нагрузку (проверочный
расчет).
3. Известны материал, размеры детали и схема ее нагружения;
требуется найти допустимую величину нагрузки.
В основе всех этих расчетов лежит условие прочности
атах<Н или ттах<М-
выражающее тот факт, что наибольшие напряжения — нормальное,
касательное или эквивалентное (см. гл. VI), действующие в опас*
ной точке, не должны превышать допускаемого напряжения.
Аналогично проводится и расчет на жесткость, только вместо
условия прочности используется условие жесткости, ограничивающее
величину деформаций (или перемещений). Однако даже в том случае,
когда выполнен расчет на жесткость, всегда необходимо проводить
проверочный расчет на прочность и, если он дает отрицательный
результат, следует принять размеры, полученные из расчета на
прочность.
115
g Таблица 9
Опорные реакции, поперечные силы и изгибающие моменты в статически определимых балках
а. b _ RB = 0 V ° « II V о о 0 < a M = 0 z< a+ b a, -}- b z I M = — — В a S + £ В A II C- to и A H* L A V II ° v KI A 1 A £ i “ к
Л 4 r Rs Ms J®
F"" • / J в
I ..I.. ЛШ A
т В* R, © ® ml яв = о MB = ml 0 <z С I Q = 0 O^z^l M-^mz Zq — I = —
/Н
_ z J
А p Re 4 Ms © ® Pl RB^P MB~Pl 0 < z<Z P 0<z<Z M = — Pz 20= I M = — Pl max
Kz J В *~*4
llllllllll ML!
Продолжение табл. 9
Схема нагружения балки, эпюры Q и М Опорные реакции Поперечная сила Q Изгибающий момент М Координата опасного сечения г0 и максимальный момент ^тах
А udz f J ЯВ=2 Pi i=l мв = 2 Pibi ь=1 bi === I — (Li о=-2^ j=l м=-2 p^z~aj) /=1 1 ^тах ~ ZJ г=1
А . ;J7 1ш£цц -^1 ©S-®^ PB~ .. <7*2 Мв~ 2 0<2</ Q=—qz 0<Z<Z .. <?z2 М~ \ Zo = l м — Щах 2
ъ> 1 4 Со 1 ► S to to to 1 II _ to|’Q 0<z<Z 0=—^ v 21 Q<z<l M — q4 Ы Zo I м =-q- iV1 max 6
o>ta.®4'S.<§)
А рЩтргг^и So to II 4* 0<z<Z 0<z^l z0= I
qL 2 sL? 3 «3=^ I z lz2\ <? ql г 21*) M 2 V2 3 Z3/ ЛТ M — —, -— iV1 max з
<£)
Продолжение табл. 9
Схема нагружения балки, эпюры Q и М Опорные реакции Поперечная сила Q Изгибающий момент M Координата опасного сечения z0 и максимальный момент ЛГтах
А g . Не ч мв © Ча о] |со §j<n 2, 05 II :§Г 0<z«< а 0<z<a м = -^ 6a a^z^l „, Qa( 2 \ M = e=T^-Ta) Zo = Z Л>г Яа 2 \ ^тах 2 \ 3 Л/
,z J
v 2а а< z< 1 Q=~q-%
liiSLUB
5>
Ч' А ю © я © S: а II Ьв Ч| у 4-S 001 S* Q^z^a 0 ^/2—--'l У — 2 г a a2} a z I Ы *« ioT4 1 e x--— ян ICQ <3 |cQ 8 । - 1 У/ "m IW8 V - ** «’I §J<^I V §> v 0 r <3 « J II 11 i z0 = Z М 1У1тах— 2\ 3J
*** / . Wllliai
А 1 k 1 11 ! *“1ъ м1~ о < Z < у z Z 4Ы <2 = -</z[-| + + (±__Г)_ + \ Z 2/ / 4 \ 2*1 /_Z 1 ] — \Z "2/J । + I' w| >6* ts5| ® '^т~' ~lN *• 'в д 11 А 1 to! N Л м|-о . -А; | ~ “К м1~ t J 1 w| У Zq = Z ^тах ”4
: 1 i
„ 4t + <?2 >
rb-~—l
Р
MB = (2qi + q2,)-Q-
0<z<Z
<?=—<7jZ —
0<z<Z
«—“4-
^2 Ql -3
----6T^
Zq - I
Mmax^-(2qt +
P
+ 42)~q-
I
Продолжение табл 9
Схема нагружения балки, эпюры Q и М Опорные реакции Поперечная сила Q Изгибающий момент M Координата опасного сечения z0 и максимальный момент Mmax
А 7? - 1 г 3 Mg \12 R -ql Rb~~3 ,, qP Мв~ 12 0<z<Z V 3Z2 0<z<Z <?z4 M s= 12Z2 Zq == I м ~—3!— max ^2
' 4U2L-Z) Lz Яг Як У°в i§: *> щ to « “ w> b? 1 ** *S- 0<z< I fz2 1 ’~T Р/ 0< z <J n. ql2 [z3 z4 \ 3 V3 4Z4 / Zq == Z м =-^ max 4
IRHTII1K ч Mg @ ®,г 4
ИГ ТТЛВ' •
|
Jg'-'r-p: 1? i-Ж, Г F ч ®,г 3 д' ql Л, ql2 Мв~ з ^<Z<1 / __2 зЛ ~ 3 13г 0< z< Z 3 \ Z3 р) Zq — I М =:—^- л шах з
Мо 1 |Ai <В RA = RB = ~у 0<z<Z <?=-4° Q^z^l M = ^S(l-Z) и zo = O ^max
^zx ШЖПТйГЬь»
Ra~ Re ~~
AT i - М2
Z
0<z<Z
мд~м2
м = мх
мг — м2
I
I мг > м2
Zq — 0; Afmax “
II Mt < M2
Zq = If ^max == M2
123
to
Продолжение табл. 9
Схема нагружения балки, эпюры Q и М Опорные реакции Поперечная сила Q Изгибающий момент M Координата опасного сечения z0 и максимальный момент Mmax
л 1 м. ,||П||| wim R, т: J 1 . М2 Г © 1® — RB = Mi + M2 1 0<z<Z z. Mt + M2 I O^z^l Л/r IM Ч" Мп М = М1-^ —— - z ь I Mi>M2 zo = O; ЛГшах = Л/1 II Afi<M2 2o = I» J^niax ~~ ' ^2
а Г Ь - R -R КА — КВ~ 1 0 ^z^Z Q^.z^a T I I a<~ — 2
Ai ц> \Rb В л Mo „ мо
% гз *• ». t Q = ~- M j^z b a z^l zo — -^max =Mo — II a>~ z0 = fl? ^max “ Mq
№ 1 & fcw © M = ^(l—z) ь
1
^a. c Ra-Rb- Mi + M^ I 0<z<Z n Mt + M2 v I 0^ a M = _M1+M2z a + b м = — У2 z + Mi a -(- b <z< I ^max — наибольшее абсолютное значение момента в сечениях С и Л
Ra' I 'pF ^M2
r~ z H I 7>
НШИ11ШШ
^Re'4
-
. О , b >1 ft ft to II II ft ft ^1» <3 1 «Н V V a. V/ II V/ Q O' s \ _ e м и ~ 1 V/ •°l V/ - t* Оч Ы « p V II V a. ® IS! e II z0 = a _ ab Мщах ~ & ~1
Л Pb T г ' & i © Pa ®
L I
Ш1
zfltll |lll|l[e]|||||
:Ж
О
Продолэ&ение табл, О
1 1 1
qb (2с + Ь) Ка 21 qb (2а 4- Ь) 21 0<z<a _ qb (2с + b} “ 21 а z а -|- Ъ z — а\ Ъ / а b z 1 qb (2а + Ь) * 21 * . L » * §- + к Д 11 о м о- "S' * §- Л bo I А О- I ~ + Z0 “ » -1 а К ? /Л - /Л * + + а ~ 12^ с- *=“ I • м . , b(2c+b) z° ~ a + - 21 ~ Мъж-<1Ь J [e + , H2c+&)] 1 4Z J
+ I-*» а |<м S- <*> §J- II II с$ 0< 2< а <? = <7а(^ + 1 а] a^z^. 1 v 2/ 0 <С z«J а М = qa2 (-£• + j у Аъ б\ Z Z2 1 + ~Т] ~а 2а2 \ a^z^l iV1 2 V IJ a L a\ Z° “ 2 \2 / / “ « ( а Л = Tl.T+b) м 2--I ‘“max g V 0
Продолжение табл. 9
Схема нагружения балки, эпюры Q и М Опорные реакции Поперечная сила Q Изгибающий момент М Координата опасного сечения z0 и максимальный момент ЛГтах
А) Л Ra _ Q ~ . b , С * Ч йз I + || <? $ £ йЗ 1 II II § ч ч< Щ h ‘°- ЙЗ ЙЗ ЙЗ <4 1 1 *° '*'?? ’ ? + ч V | V | е г " о V/ i v/ У + V «Я II О о f V/ * + ~ 1 сз «о О- II О' х . &: • х 11 + И + II Д * ? о s, § s» * V “ *^/лм|«/л t^i/A । +V5 1 х ~ sP * < * I Я>0 R zt-a- — Мтах- 2 (““’ 91) II Я<0 z0 = c + 42 м — (с -I- R) ^тах- 2 \с+ q2 )
шн И ^9 Lgj 1, 77 Zr fc °9 R @ Qc* S
' 1
l&Ib. 1
NJ III 1Щ r
Па в ^^гтГНТШТ ® -f ^.|с© "с>[оо II II cq 0<z<Z Q = —(1 = 3-) V 6 \ l2j 0 <С 2 < 1 м=^(±^\ 1М 6 \ 1 Z3/ z0 = -2- = 0,5774/ /з М = *-— тах 9/3 = 0.06429Z2
t Z 7? * I
_ Zq ~ ж
1 1
5 1186
1 1
% p# RA = ^l+^i A 6 o<; z<c i П —- 7? . — 7. -1- 0<z<Z M = R.z — + 1 = Л , Z° i-kl O-, &
;'Ж Вт
А % _ z в,. t © DA p ?i + Zq2 , RB= b 1 » S’ H ** Г» <N О - 1 я TH ч О 1 + У A, Q +^Т23 M =21L max 6 A (1 — k)2 где к = ~ Qi
i ^Тг>ч^
^«lurai
wS®
я _/!+*+*
O' c _ ^3 Co s 1 ? * «Й 11 Ct co 1 1 1 *£" .в, I~ ?// u |~» e V Й- F V 1 • ы 1 N 1 V/ II V/ 8-h° o o O- e || « О 1 0 <: z<C a ,, qc2 M~ 61 z a^z^l M = ^±- 6 L i (z —a)3l 20 = e + cj/^- Afmax = -^-(“ + +4с/5)
/?А. ds SL2.1 61 J t f^g q
77Л I
1111©11 IlTTr^
- Zo Hb1
‘б&5с'/ы)
со
о
Продолжение табл 9
Схема нагружения
балки, эпюры
Q и М
Опорные
реакции
Поперечная
сила Q
Изгибающий
момент М
Координата опасного
сечения zQ
и максимальный
момент Мтах
я, qa2 t.
^max з~
2 a\W
3 ll
. ч(1 + с)
А 6
, _<?0 + а)
В-----—
0< z «С а
с____
V 6 1 fl
а «С I
qc Г/ 4~
6 [ c
-3^1
c2 J
0 za
M = W£+f_4)
6 \ a a? J
a^z<l
M qc(i — z) p + a _
6 [ c
U-z)2l
c2 J
I a > c
-if a(l—c)
z°- V з
^iriax ~______
-if a(l — c)
9 V 3
II a <fc
?(z + fl) l/~c(l — a)
~ 9 V 3
1 1 1 1
a Q==R*-q~f(2-^) az^l 0 a M = Ra > z — 6 \ a j
Р_?1Д2 —q2b2 Q = — Rb 4" a^z^ I
6Z ?2 (Z —z) / _ M = RB (Z — z) —
1 2 \ _ ?z(Z —Z)2 /„ I — z\
I — z\ 6 V ъ 1
b )
R - 0<z<Z O^z^l
ff _ qi hb —4- У 12 k I3 J . ql2 [ z z4 \ 12 К Z I4 J
1 Я>0
Zq — a
^max 3? 4~
Ц
Ы fl<0'2_
2Rb
<h
мшах = м-
-4* ..
* 9tOa
M = 4;--Ra =
О
-т + м
Zq — a
z0 = 0,63Z
Wmax=0,0394<?/^
Продолжение табл. 9
Схема нагружения балки, эпюры Q и М Опорные реакции Поперечная сила О Изгибающий момент М Координата опасного сечения z0 и максимальный момент Л^щах
А % 9. i yffCrnr 1 1 & & to {ь II II w|“2. w|-g. + м |« N I1-* С© v । чй? V/ ~lco + о 'O'l00 II о ^<z<l ql2 [ z z3 М ~~ 3 \~Т 2 I3 + + —) 1 ’ Z° — 2 5 ^max “ 4§
* z x z' * D © %
I
1^ГПТгъ^
- ?0 .
I J _J & t> ЙЗ So g; to > II 1 w ‘S, tss •£, K> i 4 0<z<Z (? = 4(1-2-у)- ДМ $<z<l ql2 ( z z2\ 2 \l I2) 1 Ш Zq=z-~ — 2 ql >max = 4- + (ДМ)2 М. + Mt 1 2ql2 2
Al т Ь м, НШШПШИ1 © Rs ® M2
Z ~ 1, *
_ Zp _ Xf$£>T
IzQI *4~ а
^тах ~ М
Zq — I
Q = -P^
I Z I а
Q = P
M=—P~z
Z z I —|— a
M — — P (Z -j- a — z)
----Pa
Продолжение табл, 9
co
4^.
co
СП
Схема нагружения балки, эпюры Q и М Опорные реакции Поперечная сила Q Изгибающий момент M Координата опасного сечения z0 и максимальный момент ^max
Ц п 1Л>, to 4 to Il II k? + «*• ‘ to « к 1 + г *Q 0<z<Z . <?-£(*- * Zl \ _ a2 _ 9 \ Z2 lj I < z < I + a Q = q(l + a — z) 1 । Ji 1 « u « « «1- , + 4- " J MH V * v 1 « Y 1 и ii § S; » и и-, I II - - || Y и 0 ~ V' ~ 11 ii - 00 “ 1 + 1 ~ 4- “ 1 4 г x x ^ca LC1 s£^l co
1ШМШПШ11 \® ®
ь_ T' J
7
и 2
q~8p- г г \
qa2 21 34 ® 7? UA- 2/ +24) a / 0< z^ I Q=.-^L V 21 I z I -|- a Q = q (i + a — z) 0<z< I qa2 z M—2~l l^Z<L l-\~a M-. 9(Z4~a — z)2 2 z0 == I M max 2
4, _ 2'
1 a
qa
HrilllHIIIIIll
1 1 1
.a L , с ? RA = RB = P 0<z< a Q = -P a^z-^a-\~l 9 = 0 a4-Z^z<Z-|*2a 9 = P 0 z a M = — Pz a z a 1 M^ — Pa "i z I 4" 2л M = — P (I 4- 2a — z) о z0 Z 4" a M = — Pa lvlmax. ~ ru>
к Р' IP ' X if^ йр "r
7 LA ) !P
Е L
Ч llWBIB г
№ ,4 & 11 bo Ci ГГ' 1' b>|~ * -|“ to 11 О c> » H II + II » •q 7* . A •z: A । « || A 1 to h* Д . N ?U\ ф + о I A & *«Ы " to _L. N © 14- ►.!»». - tc ! 0<z<a M = -q-f a<; z <: a +1 M = ^[(14-24)x {a g2 1 x \T—T; i2 J a + Z=Cz^Z-|-2a 1 M = -v?(Z4-2a-z)2 it 01 |<M e ' 4- M i ,a I .a I s-h 1 -H II 1 7 * v * 11 Л и o-l^ V и о (1 « § « и a II 8 £
к ПИШИППШ1ИШШ © ®
Z 4 1 - Z' 7
а / 1 /
M'S. । &K. ^Ths
"s4^p 4° ’!> _ -t
2£72.£7 d4 z'
'SlAir № ^2 2^
Продолжение табл. 9
Схема нагружения балки, эпюры Q и М Опорные реакции Поперечная сила Q Изгибающий момент М Координата опасного сечения z0 и максимальный момент Мтах
Р- Р Ил р' -ря * II СВ СВ 11 II II •ti с-1 g а + с-1» /О » о ° II Л II Л и Ы 1 Ы «7. л । л 1 * «я Г» <ЧЛ « CL V/ I V/ Ь, ' V 11 V/ О « 1 II IS I с^> Ъ == 1 М ' ^Р — max — II c<Z Ъ Zq = а ^тах ~
tyr. jzJ. ь . J . с е
_ • z - -
IIIIIII-1IIIIIII
1 © \раТ
1
Таблица 10
Изгибающий момент Mt нормальная N и поперечная Q силы
в консольном круговом стержне при нагружении в его плоскости
Схема /V Q M
г Р sin <р + + Т COS Ср P COS cp — « T sin cp Mq + PR sin cp — TR (1 — cos cp)
Р Г / v\\ Р COS (а — <р) + +т sin (а — —?) P sin (a — — <?) — — T COS (a — — ?) MQ PR [cos (a — *- cp) — COS a] — — TR [sin a, — — sin (a — cp)]
к qR (1—cos^) qR sin cp qR2 (1 — coscp)
q=const Ц qR sin ср -qR(l - — cos 9) — qR2 (cp — sin cp)
a=const J) 0 /пЯср
<38
Таблица 11
Изгибающий Миз и крутящий Мкр моменты в консольном
круговом стержне при нагружении, перпендикулярном
его плоскости
Глава 4
МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛА
ПРИ РАСТЯЖЕНИИ И СЖАТИИ
§ 25. Напряжения и деформации при растяжении и сжатии
Напряженное состояние осевого растяжения или сжатия харак-
терно тем, что и?» шести компонентов внутренних усилий только про-
дольная сила N не равна нулю. Рассмотрим стержень, нагруженный
осевыми силами (рис. 61). Для произвольного сечения п—п статиче-
ская сторона задачи выражается уравнением
N = j* adF. (4.1)
F
Геометрическая сторона задачи определяется гипотезой плоских
сечений (гипотезой Бернулли), основанной на данных экспери-
мента: поперечные сечения стержня, плоские до деформации, оста-
ются плоскими после деформации, перемещаясь поступательно вдоль
оси стержня. Из этого следует, что все волокна элемента длиной I уд-
линяются на одну и ту же величину AZ и их относительные удлинения
8 одинаковы:
£ == ~ = const. (4.2)
Физическая сторона рассматриваемой задачи определяется зако-
ном Гука, выражающим линейную зависимость деформаций от на-
пряжений
£ = , ИЛИ <J = #£, (4.3)
где Е— коэффициент пропорциональности, называемый модулем
упругости при растяжении или модулем Юнга. Е имеет размерность
4/ п
Рис. 61
I
напряжения (кГ/см2, кПми2 и т. д.) и является одной из физических
констант материала (см. табл. 12). Учитывая, что Е = const, а согласно
(4.2), (4.3) и о = Е& = const, из (4.1) находим
» = (4.4)
140
При растяжении а положительно, при сжатии — отрицательно» Фор-
мула (4.4) справедлива для сечений, достаточно удаленных от мест
приложения сосредоточенных нагрузок. Вблизи приложения нагру-
зок имеет место более сложный закон распределения напряжений.
При определении напряжений при растяжении и сжатии, как
и при других видах деформаций, необходимо пользоваться вытекаю-
щим из эксперимента положением, носящим название принципа
С ен-Венан а: если тело нагружается статически эквивалентной
системой сил, т. е, такими силами, у которых главный вектор и глав-
ный момент одинаковы, и при этом область приложения нагрузок
невелика по сравнению с размерами тела, то в сечениях, достаточно
удаленных от мест приложения сил, напряжения мало зависят от
способа нагружения.
Этот принцип можно проиллюстрировать примером приложения
эквивалентных нагрузок, приведенным на рис. 62. Один и тот же
стержень, закрепленный верхним концом, нагружается на свободном
конце статически эквивалентными нагрузками, равнодействующие
которых выражаются величиной вектора Р. Исследования показывают,
что напряжения в сечении, достаточно удаленном от места приложения
нагрузки, практически оказываются во всех трех случаях одинако-
выми.
Относительная деформация ойределяется через продольную силу
на основании (4.3) и (4.4) следующей формулой:
8 = -йг (4-5)
Hit1
а полная деформация стержня длиной I рля однородного материала
(£ ss const) при одинаковой по длине силе N формулой:
т
ЕЕ
Д/ = а =
(4.6)
’ Формула (4.6) выражает закон Гука для абсолютных удлинений.
Произведение ЕЕ в знаменателе формулы называется жесткостью
поперечного сечения стержня при растяжении (сжатии) и имеет
ЕЕ
размерность силы, а величина с= —~
называется жесткостью стержня при рас-
тяжении (сжатий), ее размерность —
сила, деленная на длину,
В том случае, когда продольная сила
и поперечное сечение стержня по длине
не постоянны (рис. 63), полное удлинение
стержня определяется по формуле
Д/ =
J EF (z)
О
(4.7)
Растяжение и сжатие сопровождаются также изменением попе-
речных размеров стержня (рис. 64, а, б). Абсолютные поперечные
деформации стержня определяются формулами
Да = ах — а;
Д& = bi — b.
141 I
Относительные поперечные деформации (при растяжении отрица-
тельные, а при сжатии положительные) определяются формулой
, Да Д2>
£ .—- —— '
а Ъ
Метку относительной поперечной и относительной продольной
деформациями при простом растяжении и сжатии в пределах примени-
мости закона Гука существует постоянное отношение, абсолютная
величина которого называется
коэффициентом Пуассона и
обозначается буквой ц
(4.8)
О S Коэффициент Пуассона —
рис, 64 безразмерная величина и для
всех изотропных материалов
(см. табл. 12) лежит в пределах 0—0,5 (для пробки близко к нулю;
для каучука близко к 0,5; для стали ц « 0,3).
Учитывая, что е и е' всегда имеют противоположные знаки, по-
лучим
£ == — |Х£ = — у, — .
(4.9)
При расчете стержней, работающих на растяжение или сжатие,
условие прочности следует записывать для опасного сечения, которое
характеризуется максимальным значением 2Vmax на эпюре осевых сил
г — тах
гтах р lGJ’
(4.10)
где [aj — допускаемое напряжение на растяжение [о+ ] (при расчете
на растяжение) или допускаемое напряжение на сжатие [о_] (при рас-
чете на сжатие).
По формуле (4.10) могут быть решены задачи трех типов: подбор
размеров поперечного сечения стержня; проверка прочности; опреде-
ление допускаемой нагрузки.
В некоторых случаях стержни рассчитывают исходя из условия
жесткости
J ILb \Z)
(4.11)
где — изменение размеров детали; [ AZ1 — допускаемая величи-
на изменения размеров.
Расчет из условия жесткости всегда должен быть дополнен расче-
том на прочность. Если окажется, что условие прочности не удовлет-
воряется, то размеры стержня должны быть взяты исходя из условия
прочности.
142
§ 26. Испытание материалов на растяжение и сжатие
Испытание на растяжение. Основным видом исследования меха-
нических свойств материалов является испытание на растяжение. Оно
проводится на специальных испытательных машинах, создающих по-
степенно возрастающую нагрузку на испытываемый образец и осуще-
ствляющих в процессе нагружения регистрацию величины действую-
щей на образец силы и его деформации.
Чаще всего применяют цилиндрические образцы (рис. 65, «),
а при испытании листового материала — плоские образцы (рис. 65, б).
Для цилиндрических образцов выдержи-
вают определенное соотношение между
расчетной длиной образца 10 и диаметром
образца d0. Обычно 10 == 10 d0 (длинный
образец); реже l0 5d0 (короткий образец).
Учитывая, что диаметр d0 связан
с площадью сечения образца Fo форму-
лой
4> = V ^9=1,131/FO,
связь между расчетной длиной Zo и пло-
щадью поперечного сечения образца Fo
можно выразить для длинного образца
зависимостью
Z0=U,3/f0, (4.12)
для короткого —
10 = 5,65
В качестве основных образцов при испытании на растяжение
применяют цилиндрические образцы с диаметром d0= 10 мму рас-
четной длиной Zo = 100 мм и /0 = 50 мм. Допускается применение
и других пропорциональных
образцов, в которых вы-
держаны соотношения разме-
ров в соответствии с фор-
мулой (4.12).
Диаграмма растяжения.
При испытании материала на
растяжение современные ма-
шины позволяют автоматиче-
ски получить записанный в
определенном масштабе график
зависимости деформации об-
разца от нагрузки, или так
называемую диаграмму растя-
жения. Типичный вид диаг-
раммы растяжения в коорди-
натах Р — &1 для малоугле-
родистой стали приведен на
рис. 66.
На диаграмме имеется ряд характерных участков и точек, соот-
ветствующих различным стадиям деформирования образца.
143
Точка А характеризует наибольшую (предельную) нагрузку Рпц|
до которой соблюдается линейная зависимость между нагрузкой и
удлинением образца; точка В соответствует наибольшей нагрузке Руп,
при которой образец сохраняет упругие свойства, т. е. при разгрузке
еще не наблюдается остаточная деформация, точка С соответствует
нагрузке Рт, при которой образец деформируется без возрастания
нагрузки, или, как говорят, материал начинает «течь», образуя на
диаграмме так называемую площадку текучести CD,
г--—-—------у После стадии текучести материал снова приобре-
/ | тает способность увеличивать сопротивление даль-
L-----------1 нейшей деформации. Точка Е соответствует мак-
симальной (предельной) нагрузке Ртах, после ко-
Рис. 67 торой начинается местное сужение образца в виде
шейки (рис, 67), в результате чего происходит па-
дение нагрузки. Точка F соответствует нагрузке Рк, при кото-
рой образец разрушается.
Пользуясь указанными характерными нагрузками, взятыми из
диаграммы растяжения, и зная площадь сечения испытуемого образца
Fo, определяют основные характеристики прочности материала:
р
апц ~ — предел пропорциональности}
a = ^22
уп
предел упругости}
предел текучести;
ов = —— предел прочности, или временное сопротивление;
напряжение в момент роарыва.
’, Поскольку при растяжении сечение образца непрерывно меняется,
особенно в период нагружения, характеризуемый участком диаграммы
DEF, значения ов и ок имеют достаточно условный характер. Осо-
бенно условным является напряжение ок, так как начиная с нагрузки
Ртах происходит образование шейки и в момент разрыва сечение образ-
ца в шейке оказывается существенно меньше начальной площади
сечения образца Fo.
Для материалов, диаграмма растяжения которых не имеет резко
выраженной площадки текучести, предел текучести условно опреде-
ляют как напряжение, при котором остаточная деформация состав-
ляет величину, установленную ГОСТом или техническими условиями.
По ГОСТу 1497—61 эта величина остаточной деформации составляет
0,2% измеренной длины образца, а условный предел текучести от
обозначается а0 2.
Учитывая, что практически трудно установить начало отклонения
от закона пропорциональности и начало появления первых остаточных
деформаций, вводят также понятие условного предела пропорциональ-
ности и условного предела упругости.
144
Под условным пределом пропорциональности понимают наимень-
шее напряжение, при котором отклонение от линейной зависимости
между напряжением и деформацией достигает некоторой заданной
величины (порядка 0,002%).
Под условным пределом упругости понимают наименьшее напря-
жение, при котором остаточная деформация достигает заданной вели-
чины (обычно 0,001% — 0,05%). Условный предел упругости отме-
чается индексом, соответствующим заданной величине остаточной
деформации, например <*о,оо1 и а0,05-
При испытании образцов на растяжение определяют также харак-
теристики пластичности, к которым относится относительное удли-
нение
в = 4^- • 100, %
^0
и относительное сужение
ф = . 100, %,
где
= Fo ^mirr
Кроме указанных выше
характеристик механических
свойств материала (прочности и
пластичности), данные о которых
для различных материалов при-
ведены в Приложении 1, опре-
деляются еще энергетические ха-
рактеристики материала. Оказы-
вается, что диаграмма растя-
жения дает информацию и об этих его свойствах. Так, ее площадь
характеризует работу, затраченную на растяжение образца. Ра-
бота, затраченная на растяжение образца до деформации (рис. 68),
равна
Л, = J (Р + dP) « С Pdk,
О о
что соответствует площади О АВ CD MN диаграммы, а работа, затра-
ченная на разрыв образца, определяется площадью всей диаграммы
OABCDEFG.
В пределах упругости работа деформации выражается площадью
заштрихованного треугольника (рис. 69, а) и при удлинении образца
Д/ и соответствующей ему силе Р равна
РЫ
Луп 2 ’
а удельная работа деформации равна
__ ^уп РМ G&
“уп у
145
и выражается площадью заштрихованного треугольника диаграммы
в координатах 0—8 (рис. 69, б).
Диаграмма напряжений. Поскольку диаграмма растяжения ха-
рактеризует не только свойства металла, но и размеры образца, то ее
принято перестраивать в относительных координатах <г—8. Такая
диаграмма, построенная на основании диаграммы растяжения (рис. 66)
и называемая диаграммой напряжений, представлена на рис. 70.
На этой диаграмме точки О, а, &, с, d, е, / соответствуют точкам О, Л,
С9 D, Е, F первичной диаграммы растяжения (рис. 66).
Рис. 69
Рис. 70
Из диаграммы напряжений (рис. 70) видно, что
tg а == = Е,
т. е. модуль упругости при растяжении численно равен тангенсу угла
наклона прямолинейного участка диаграммы напряжений к оси
абсцисс. В этом — геометрический смысл модуля упругости при
растяжении.
Заметим, что нисходящий участок ef диаграммы напряжений
(рис, 70) носит условный характер из-за значительного различия
между сечением шейки и первоначальной площадью сечения образца
1200
800
400
кГ/см*
о UOOZs
Рис. 72
FQ, на которую делят соответствующие усилия, взятые из диаграммы
растяжений для получения ординат диаграммы напряжений на
участке ef.
Примерный вид диаграммы напряжений для различных материа-
лов приведен на рис. 71. Кривые 1, 2,31 4 соответственно характерн-
ее
зуют механические свойства бронзы (<гв = 2470 кГ/см2\ 6 = 36%),
углеродистой стали (<гв = 3580 кГ/см2\ 6 = 38%); никелевой стали
(ов = 7150 кГ/см?\ 6 = 54%); марганцовистой стали (<гв = 9160 кГ/см2',
6 = 30%).
Диаграмма напряжения для чугуна, являющаяся типичной для
хрупкого материала, приведена на рис. 72.
Если относить усилия, действующие на образец в каждый момент
времени нагружения, к истинному значению поперечного сечения
в соответствующий момент времени, то мы получим диаграмму истин-
ные напряжений (рис. 70, пунктирная линия).
Р
Рис. 73
Рис. 75
Испытание на сжатие. Испытание материалов на сжатие произ-
водится на специальных прессах или универсальных испытательных
машинах. Для испытания изготовляются образцы в виде цилиндров
небольшой высоты (обычно высота составляет от одного до трех диа-
метров) или кубиков. При испытании на сжатие трение, возникающее
между сжимающими плитами испытательной машины и торцами об-
разца, оказывает существенное влияние на результаты испытания
и характер разрушения испытуемого образца.
При сжатии цилиндрического образца из малоуглеродистой стали
последний принимает бочкообразную форму (рис. 73). Диаграмма сжа-
тия, полученная для этого материала, приведена на рис. 74.
На рис. 75, а показан характер разрушения при сжатии образца
из камня при наличии сил трения между плитами машины и торцами
образца. При уменьшении сил трения путем нанесения на торцы слоя
парафина характер разрушения того же образца может быть проиллю-
стрирован рис. 75, б.
147
Вид разрушенного при сжатии чугунного образца показан на
рис. 76, а соответствующая диаграмма сжатия на рис. 77.
Диаграммы сжатия при испытании кубика древесины показаны
на рис. 78 (кривая 1 — при сжатии вдоль волокон, кривая 2 — при
сжатии поперек волокон).
§ 27. Концентрация напряжений
Концентрация напряжений — местное повышение напряжений
в элементах конструкций, обусловленное резкими переходами в попе-
речных сечениях, связанными с наличием отверстий, выкружек, кана-
Рис. 80
вок, надрезов и т. п., называемых концентраторами. На рис. 79 пока-
заны графики распределения напряжений в сечении растягиваемой
полосы, ослабленном круглым отверстием (рис. 79, а) и полукруглыми
выкружками (рис. 79, б).
Степень концентрации напряжений характеризуется так называе-
мым коэффициентом концентрации
шах
а =------
°н
(4.13)
где атах — максимальное напряжение в месте концентрации, ан —
номинальное напряжение, определяемое по формуле
где N — нормальная сила в ослабленном сечении; — площадь
ослабленного сечения, называемая площадью нетто.
Иногда номинальное напряжение определяют по формуле
N
(^15)
z бр
где F6p — площадь сплошного сечения (без учета ослабления ее нали-
чием концентратора), или площадь брутто.
При концентраторах, занимающих незначительную часть сечения
148
(например, при малых отверстиях), номинальные напряжения, опре-
деляемые по формулам (4.14) и (4.15), практически будут одинаковыми
При определении максимальных напряже-
ний в зоне концентратора расчетным путем
коэффициент концентрации, вычисленный по
(4.13), называется теоретическим коэффици-
ентом концентрации. Например, в случае ма-
лого круглого отверстия (рис. 79, а) <х = 3, а
в случае полукруглых вырезов (рис. 79, б) а «
«2 В действительности коэффициент концен-
трации реальных элементов конструкций, эффек-
тивный коэффициент концентрации kt опреде-
ляемый экспериментально, оказывается мень-
ше теоретического (а > k). Обычно расчеты на
прочность с учетом концентрации напряжений
проводят на основании знаний величин теорети-
ческих коэффициентов концентрации, значения
которых для случая растяжения круглых
стержней с различной формой концентраторов
приведены на рис. 80 и ниже.
Рис. 81
Вид концентратора напряжений а
Полукруглая выточка при отношении к диаметру стержня Галтель при отношении радиуса галтели стержня Переход под прямым углом Острая V-образная выточка Нарезка дюймовая Нарезка метрическая Отверстие, при отношении диаметра к диаметру стержня от 0,1 до 0,33 Риски от резца на поверхности изделия ее радиуса к диаметру отверстия 0,1 0,5 1,0 2,0 0,0625 0,125 0,95 0,5 1,2- 2,0 1,6 1,2 1,1 1,75 1,50 1,20 1,10 2,0 3,0 2,0 2,5 2,0 -1,4
Более полные данные о коэффициентах концентрации приведены
в Приложении 2.
Высокая концентрация напряжений особенно опасна для элемен-
тов конструкций, изготовленных из хрупких материалов, так как
при достижении в зоне концентрации напряжений, равных пределу
прочности материала, последний начнет разрушаться. В случае плас-
тичного материала концентрация напряжений менее опасна, пос-
кольку при достижении в зоне концентратора напряжения, равного
пределу текучести пт, произойдет перераспределение напряжений
по схеме, показанной пунктирными линиями на рис. 81.
§ 28. Допускаемые напряжения
Определив механические свойства материала путем проведения
соответствующих испытаний образцов, можно найти, какие напряже-
ния являются безопасными для работы конструкции, т. е. установить
149
допускаемые напряжения. Очевидно, допускаемое напряжение должно
быть меньше опасного для данного материала напряжения, составляя
некоторую его часть. Примем
(4.16)
где [а]—допускаемое напряжение; а0— опасное напряжение; п —
коэффициент запаса прочности.
Для деталей, изготовленных из пластичных материалов, опасным
напряжением следует считать предел текучести а0 = ат, из хрупких—
временное сопротивление а0 = ав.
Выбор коэффициента запаса прочности п, показывающего во
сколько раз допускаемое напряжение меньше опасного, зависит от
состояния материала (хрупкое, пластичное), характера приложения
нагрузки (статическая, динамическая, повторно-переменная), а также
от таких общих факторов, как неоднородность материала, неточность
в задании внешних нагрузок, приближенность расчетных схем и фор-
мул и т. п.
Величина запаса прочности зависит также от того, какое напряже-
ние мы считаем опасным (ат или ав).
Для пластичных материалов при статической нагрузке, когда
<зо = °т; п =
г
"т
запас прочности принимают равным
«т = 1,4 н- 1,6.
При статических нагрузках в случае хрупких материалов,
когда а0 = ав; п = пв,
[а] =----,
"в
запас прочности принимают равным
пв = 2,5 — 3,0.
Иногда и для пластичных материалов допускаемые напряжения опре-
деляют по временному сопротивлению, величину которого практи-
чески определить проще. Тогда
г 1 __ СТв
° ~ «в ’
Учитывая, что ат = (0,5-г-0,7) ов; /гв = 2,4-г-2,6.
Иногда допускаемые напряжения на растяжение обозначаются
[а+], а на сжатие — [а_]. Хрупкие материалы сопротивляются сжа-
тию лучше, чем растяжению, и для них [а^-] <С
При статических нагрузках в случае однородных хрупких мате-
риалов следует учитывать концентрацию напряжений и расчет вести
по наибольшим местным напряжениям
°тах = а°н < [°]-
Ориентировочные значения допускаемых напряжений при статических
нагрузках для различных материалов приведены в табл. 13.
150
Таблица 12
Модули упругости и коэффициенты Пуассона
Наименование материала Модуль упругости Е . 10-®, кГ/см2 Модуль упругости G . 10-6, кГ(см2 Коэффициент Пуассона Р<
Чугун серый, белый 1,15 —1,60 4,5 0,23—0,27
Ковкий чугун 1,55 — «—•
Углеродистые стали 2,0—2,1 8,0—8,1 0,24—0,28
Легированные стали 2,1— 2,2 8,0—8,1 0,25—0,30
Медь прокатанная 1,1 4,0 0,31—0,34
Медь холоднотянутая 1,3 4,9 —
Медь, литье 0,84 — —
Фосфористая бронза ка- таная 1,15 4,2 0,32—0,35
Латунь холоднотянутая 0,91—0,99 3,5—3,7 0,32—0,42
Корабельная латунь ката- ная 1,0 0,36
Марганцовистая бронза катаная 1,1 4,0 0,35
Алюминий катаный 0,69 2,6—2,7 0,32—0.36
Алюминиевая проволока тянутая 0,7 — «м
Алюминиевая бронза, ли- тье 1,05 4,2 мчи
Дюралюминий катаный 0,71 2,7
Цинк катаный 0,84 3,2 0,27
Свинец 0,17 0,70 0,42
Лед 0,1 0,28—0,3
Стекло 0,56 2,2 0,25
Гранит 0,49 — —
Известняк 0,42 — —
Мрамор 0,56 — —
Песчаник 0,18 ——
Кладка из гранита 0,09—0,1 — —
из известняка 0,06
из кирпича 0,027—0,030 — —
Бетон при пределе проч- ности 0,16—0.18
100 кГ/см2 0,146—0,196 — ——
150 кГ/см2 0,164—0,214 — —
200 кГ/см2 0,182—0,232 — —
Дерево вдоль волокон 0,1 —0,12 0,055 —
Дерево поперек волокон 0,005—0,01 — —
Каучук 0,00008 — 0,47
Текстолит 0,06—0,1 —— __
Гетинакс 0,1—0,17 — —
Бакелит 0,02 —0,03 — 0,36
Висхомлит (ИМ-44) 0,040—0,042 — 0,37
Целлулоид 0,014—0,028 — 0,33=0.38
151
Таблица 13
Ориентировочные величины основных допускаемых напряжений
на растяжение и сжатие
Наименование материала Допускаемые напряжения, кГ/слг2
на растяжение на сжатие
Чугун серый в отливках 280—800 1200—1500
Сталь ОС и Ст. 2 1400 1400
Сталь Ст. 3 1600 1600
Сталь Ст. 3 (в мостах) Сталь углеродистая конструкцией- 1400 1400
ная (в машиностроении) Сталь легированная конструкцион- 600—2500 600—2500
ная (в машиностроении) 1000—4000 1000—4000
и выше и выше
Медь 300—1200 300—1200
Латунь 700—1400 700—1400
Бронза 600—1200 600—1200
Алюминий 300— 800 300— 800
Алюминиевая бронза 800—1200 800—1200
Дюралюминий 800—1500 800—1500
Текстолит 300— 400 300-400
Гетинакс 500— 700 500—700
Бакелизированная фанера 400— 500 400-500
Сосна вдоль волокон 70—100 100—120
Сосна поперек волокон — 15—20
Дуб вдоль волокон 90—130 130—150
Дуб поперек волокон — 20—35
Каменная кладка ДО 3 4—40
Кирпичная кладка до 2 6—25
Бетон 1—7 10—90
Глава 5
НАПРЯЖЕННОЕ И ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ
§ 29. Напряжения в точке.
Главные площадки и главные напряжения
Напряжения являются результатом взаимодействия частиц тела,
появляющегося при нагружении его внешними силами. Действию
внешних сил, стремящихся изменить расположение частиц тела или
вызвать их смещение, препятствуют возникающие при этом в теле
напряжения. Они ограничивают это смещение некоторой малой вели-
чиной. В одной и той же точке напряжения в разных направлениях,
как правило, будут различными и только в отдельных случаях нагру-
жения они могут быть одинаковыми.
Рассматривая напряжение в точке А нагруженного тела, отнесен-
ной к малым площадкам (рис. 82), принадлежащим двум разным сто-
ронам сечения 1—I, проведенного через эту точку, легко убедиться,
что если под действием внешних нагрузок площадки стремятся отойти
одна от другой или сблизиться, то между ними возникают соответ-
ственно растягивающие или сжимающие нормальные напряжения о,
если площадки стремятся сдвинуться одна относительно другой, то
в них возникают касательные напряжения т; если же одна площадка
стремится отойти от другой, оставаясь ей параллельной в каком-
нибудь произвольном направлении, то в такой площадке одновре-
менно возникают и нормальные а и касательные т напряжения, а их
результирующей является полное напряжение pt вектор которого
совпадает с этим направлением. Перемещение площадок в этом случае
может быть геометрически разложено на два перемещения: взаимное
удаление и сдвиг.
В общем случае, выделим в окрестности рассматриваемой в
нагруженном теле точки элементарный обьем материала в виде
бесконечно малого параллелепипеда (рис. 83). На его гранях влияние
удаленной части тела должно быть заменено соответствующими
Рис. 83
напряжениями или их составляющими (нормальными и касательными
напряжениями), как показано на рисунке.
При изменении ориентации граней выделенного элементарного
153
параллелепипеда напряжения на его гранях также будут изменяться.
Всегда можно найти такую ориентацию элемента, при которой в его
гранях касательные составляющие напряжений будут отсутствовать.
Те площадки, по которым не действуют касательные напряжения,
называются главными площадками, а нормальные напряжения на этих
площадках — главными напряжениями. Можно доказать, что в каж-
дой точке любым образом нагруженного тела всегда имеется по крайней
мере три главные взаимно перпендикулярные площадки, т. е. пло-
щадки, в которых отсутствуют касательные напряжения. Направле-
ния, параллельные главным напряжениям, называются главными
направлениями напряженного состояния в данной точке. Главные
напряжения принято обозначать од, о2, о3; при этом полагают, что
между указанными напряжениями существует следующее соотношение
(понимая его в алгебраическом смысле):
С1 с2 аз-
Напряженное состояние, в котором только одно из главных напря-
жений (любое из трех) не равно нулю, а два других равны нулю, назы-
вается одноосным или линейным (рис. 84, а). Если два главных напря-
жения отличны от нуля, а одно равно нулю, то такое напряженное
состояние называется двухосным или плоским (рис. 84/). Случай на-
пряженного состояния, при котором все три главные напряжения от-
личны от нуля, называется трехосным или объемным (рис. 84, в),
Кроме того, различают однородное напряженное состояние тела,
при котором в каждой точке какого-либо сечения и всех параллельных
ему сечений напряжения одинаковы, и неоднородное напряженное
состояние, при котором в разных точках любого сечения рассматри-
ваемого тела или других параллельных ему сечений напряжения
различны.
§ 30. Линейное напряженное состояние
С линейным напряженным состоянием мы встречаемся, главным
образом, в стержнях, испытывающих растяжение или сжатие, хотя
некоторые элементы испытывают линейное напряжение и в стержнях,
подвергающихся изгибу или сложному нагружению.
При растяжении стержня (рис. 85, а) нормальное напряжение
в площадке F определяется формулой
N Р
F ~ F е
154
Касательные напряжения в этой площадке равны нулю. В любой
площадке Fa (рис. 85, б), внешняя нормаль к которой па образует
с направлением а угол а, полное напряжение ра равно
ра = — = -у COS а = о cos а.
Нормальные и касательные напряжения в площадке Fa будут
аа = ра cos а = a cos2 а; (5.1)
та = ра sin а = sin 2а. (5.2)
Нормальные напряжения аа поло-
жительны, если они растягивающие;
касательные напряжения та положи-
тельны, если они стремятся повернуть
рассматриваемую часть элемента отно-
сительно любой точки, взятой внутри
ее, по часовой стрелке (аа и та на
рис. 85, б положительны).
Согласно формулам (5.1) и (5.2)
рис. 85, а) та = 0; аа = а, а при а =
Рис. 85
при а = 0 (площадка I на
(площадка II) та = аа = 0.
Следовательно, площадки I и II являются главными; главные
напряжения будут
= а; а2 = с3 — 0.
При сжатии ах == а2 = 0; а3 = — а.
Касательные напряжения согласно (5.2) достигают своей наи-
большей величины при а = + 45° и равны
а
та max = *2~ ’
На основании (5.1) и (5.2) легко убедиться, что нормальные
и касательные напряжения в площадке F$, перпендикулярной
к площадке Fa, т. е. в площадке, внешняя нормаль к которой обра-
зует угол 0 = a + 90° с направлением напряжения а, будут
ар — a cos2 0 = a cos2 (а + 90°) = a sin2 а; (5.3)
Тр = у sin 20 = ~ sin 2 (а -|- 90°) = — ~ sin 2а. (5.4)
§ 31. Плоское напряженное состояние
При плоском напряженном состоянии, когда на элемент по его
двум взаимно перпендикулярным граням действуют напряжения
«1 и а2 (рис. 86), нормальные и касательные напряжения, действую-"
щие на площадке (а), внешняя нормаль к которой па образует с на-
155
правлением напряжения угол а, определяются соответственно по
формулам
аа = oj cos2 а + о2 811)2 а» (5.5)
-- °2 • п
т = .1---? sin 2a.
(5.6)
Из этих формул могут быть получены выражения для определе-
ния нормальных и касательных напряжений в площадке (0), перпен-
дикулярной к площадке (а), т. е. в пло-
щадке, внешняя нормаль к которой обра-
зует угол f (90° — а) с направлением
с1:
= °i sin2 а + а2 cos2 а; (5.7)
Тр = « —sin 2а. (5.8)
Складывая левые и правые части
уравнений (5.5) и (5.7), находим:
°а Н” С(3 = С1 4“ С2> (5.9)
т. е. сумма нормальных напряжений,
взаимно перпендикулярным площадкам, инва-
риантна по отношению к наклону этих площадок и равна сумме
главных напряжений*
Из (5.6) и (5.8) следует, что как и при одноосном напряженном
состоянии, касательные напряжения достигают наибольшей величины
при а = +45°, т. е. по площадкам, наклоненным под углом 45° к глав-
ным площадкам, и равны
90-d7g
/
ha
111
Л
с\
£
й
A I D
Uf
Рис. 86
действующих по двум
\ о(_ _
= (5.10)
Сравнивая (5.6) и (5.8), находим, что
= (5.11)
Это равенство выражает закон парности касательных напряжений,
который может быть сформулирован так: если по какой-либо площадке
имеется некоторое касательное напряжение, то по перпендикулярной
к ней площадке непременно будет действовать касательное напряже-
ние, равное по величине и обратное по знаку*
Экстремальными значениями для нормальных напряжений явля-
ются величины главных напряжений.
На всех наклонных площадках нормальные напряжения имеют
промежуточные между и о2 значения.
Одно и то же напряженное состояние элемента может быть пред-
ставлено главными напряжениями ах и а2 (элемент ABCD, рис. 86
и 87, а) или напряжениями в наклонных площадках %, та, ар, Тр
(элементы abed на рис. 86 и 87, б).
В теории напряженного состояния различают две основные за-
дачи.
Прямая задача. По известным в точке главным площадкам
и действующим в них главным напряжениям требуется определить
156
нормальные и касательные напряжения по площадкам, наклоненным
под заданным углом к главным площадкам, т. е. по напряжениям,
действующим на гранях элемента АВ CD (рис. 88), определить напря-
жения в гранях элемента abed.
Обратная задача. По известным нормальным и касатель-
ным напряжениям, действующим в двух взаимно перпендикулярных
площадках, проходящих через данную точку, требуется найти глав-
ные направления и главные напряжения. Иначе говоря, дан элемент
Рис. 87
Рис. 88
abed (рис. 88) с действующими по его граням нормальным и касатель-
ным напряжениями; требуется определить положение элемента АВ CD,
т. е. угол а0, и найти главные напряжения.
Обе задачи могут решаться как аналитически, так и графически.
§ 32. Прямая задача при плоском напряженном состоянии.
Круг напряжений
Аналитическое решение прямой задачи дается формулами (5,5) —
(5.8).
Графически аа, та; можно определить по известным глав-
Рис. 89
пым напряжениям и а2 (рис. 89, а) с помощью так называемого
круга напряжений (круга Мора), построенного в координатах а, т
157
яа отрезке АВ как на диаметре, равном разности главных напря-
жений <*1-302 (рис. 89, б). Действительно, проведя от центра круга
напряжений (точки С) луч CD под углом 2а до пересечения
с окружностью, мы получим точку Da, координаты которой будут
характеризовать соответственно напряжения aa и та:
ОКЛ = OC + CDa cos 2а = cos 2а =
Z Li
= ах cos2 а + а2 sin2 а = аа;
ад£ = CDesin 2а = ~-? Sin 2а = Та.
Легко показать, что точка Dp характеризует напряжения
ар, тр в площадке (р), перпендикулярной к площадке а,
окъ = ОС — СКа = °* — 01' ~ °2 COS 2а =
= ах sin2 а + а2 COS2 а =
= та= V
Точки Da и Dp, характеризующие напряжения на двух взаимно
перпендикулярных площадках (а) и ф), всегда лежат на концах од-
ного диаметра.
Построенный круг Мора полностью описывает напряженное со-
стояние элемента, изображенного на рис. 89, а. Если менять угол а
в пределах от —90° до 4-90°, то наклонные площадки (а) и (р) займут
последовательно все возможные положения, а точки Da и Dp опишут
полный круг. В частности, при a = 0, когда грани ef и ет станут
главными площадками и по ним будут действовать те же напряжения,
что и в гранях элемента abed, точка Da совпадет с точкой А, а точка
Dp — с точкой В.
Для определения положения полюса на круге напряжений, как
и в случае круга инерции, проведем из точки Da линию, параллельную
оа (в нашем примере горизонталь, рис. 89, б), до пересечения с окруж-
ностью. Искомый полюс — точка М. Полюс М можно было бы найти,
проведя из точки Dp линию, параллельную напряжению Ор, т. е.
проведя вертикаль. Можно доказать, что линия, соединяющая полюс М
с любой точкой круга, параллельна направлению нормального напряже-
ния на площадке, которой эта точка соответствует. Так, например,
линия МА параллельна главному напряжению ох, а линия МВ парал-
лельна главному напряжению о2.
§ 33. Обратная задача при плоском напряженном состоянии
При практических расчетах часто приходится решать обратную
задачу — определять at и а2 по известным аЛ, та, ар, tp (рис. 90, а).
Пусть аа > ар; та > 0. Очевидно, круг напряжений в координатах
о, т (рис, 90, б) мы легко построим, зная положение двух диаметрально
158
противоположных точек круга Da и D^ координатами которых явля-
ются соответственно оа, та и При этом абсциссы точек пересе-
чения круга с осью а — О А и ОВ — дадут соответствующие величины
главных напряжений и а2.
Для определения положения главных площадок найдем полюс
и воспользуемся его свойством. С этой целью из точки Da проведем
линию, параллельную линии действия а а, т. е. горизонталь. Точка М
пересечения этой линии с окружностью и будет полюсом. Соединив
Рис. 90
(5.12)
точку М с точками А и В, получим направления главных напряже-
ний ах и а2. Положение главных площадок, очевидно, будет перпен-
дикулярно к направлениям главных напряжений. На рис. 90, а вну-
три исходного элемента выделен элемент, ограниченный главными
площадками, на гранях которых показаны главные напряжения ох
и а2. Из рассмотрения круга напряжений можно получить аналитиче-
ские выражения главных напряжений ах и о2 через оа, та,
«X = у [ва + ”, + V(°а — °р)2 4- ;
’2 = J [°а + — V (°а — °?)2 + 4т«] .
Из рис. 90, б следует также, что
МК^ МК$
tg а =---= , ----=-------— -------------.
АК$ ОА — ОКр ^1 —
Эта формула и определяет единственное значение угла
который нужно повернуть нормаль па, чтобы получить направление
алгебраически большего главного напряжения. Заметим, что отри-
цательному значению а соответствуют углы, отложенные по часовой
стрелке, и что если одно из главных напряжений, вычисленное по
формулам (5.12), окажется отрицательным, то напряжения следует
обозначать не ог иа2, аахиа3; если же оба главные напряжения
окажутся отрицательными, то они должны быть обозначены о2 и аз*
(5.13)
а0» на
159
§ 34. Объемное напряженное состояние
Объемное, или трехосное, напряженное состояние в сопротивле-
нии материалов рассматривается редко. Поэтому мы здесь укажем
лишь на некоторые основные моменты теории объемного напряжен-
ного состояния.
7 Рассмотрим случай объемного напряженного состояния (рис. 91),
когда по граням выбранного кубика действуют все три главных на-
пряжения
<3i > <*2 > <*3 =£ О-
Рис. 92
Очевидно, в площадке /, параллельной нормальные и касательные
напряжения не будут зависеть от сх, а только от напряжений о2 и аз
и во всех подобных площадках будут характеризоваться кругом на-
пряжений Lj с диаметром а2—о3 (рис. 92). В площадке ZZ, парал-
лельной а2, нормальные и касательные напряжения будут характери-
зоваться кругом напряжений £п с диаметром ах—о3 и, наконец, в
площадке ZZZ, параллельной напряжению о3, нормальные и касатель-
ные напряжения будут характеризоваться кругом напряжений Zni с
диаметром ох—а2.
Во всех указанных площадках метод определения оа, та и
не будет отличаться от рассмотренного выше метода решения прямой
задачи для плоского напряженного состояния.
Можно доказать, что если провести площадку, не параллельную
ни одному из главных напряжений, то нормальное оа и касательное та
напряжения в этой площадке могут быть определены по формулам
аа " а1 cos2 а1 + а2 cos2 а2 + °з cosa аз5
Г-д 2 g 2
та = у ах cos2 ах + а2 COS2 а2 + а3 COS2 а3 — ста »
(5Л4)
где ах, а2, а3 — углы, которые образует нормаль к рассматриваемой
площадке с направлениями сх, а2> о3.
Доказывается также, что точка Z)a(aa, та)» характеризующая
напряженное состояние в произвольно наклоненной площадке, будет
всегда лежать в заштрихованной области (рис. 92) или на границе ее»
если площадка параллельна одному из главных напряжений.
Из рассмотрения кругов напряжений (рис. 92) видно, что ттах,
характеризуемое точкой D на окружности и действующее в пло-
щадке, параллельной главному напряжению а2, наклоненной к напря-
160
жениям <4 и с3 под углом а = 45®, равно радиусу большого круга.
Следовательно, при объемном напряженном состоянии
ттах = ~"2 з • (5.15)
В случае площадки, внешняя нормаль к которой образует с на-
правлениями «1, а2 и о3 одинаковые углы = а2 = а3 == а, назы-
ваемой октаэдрической площадкой (поскольку она параллельна грани
октаэдра, который может быть образован из куба), когда
cos2 + cos2 а2 + cos2 а3 = 1;
COS2 а = ,
о
формулы (5.14) примут вид
= °1 + °2 + ®3 = .
ОКТ 3 иср’
1^2-1 /~г~. ГТ 2
ТОКТ = ~3~ V ®1 + °2 + ®3 ~ °1°2 — °2а3 — °3®1 =
= у V(°1 - ®з)2 + (®2 - °з)2 + (®з - °1)2 • (5.17)
Касательное напряжение, определенное по формуле (5.17), назы-
вается октаэдрическим. Октаэдрическое нормальное напряжение пред-
ставляет собой как бы среднее напряжение для данного трехосного
напряженного состояния.
При оценке прочности материала в условиях сложного напряжен-
ного состояния часто используется некоторая фиктивная величина
напряжения называемая интенсивностью напряжения и связанная
с токт зависимостью
3
/2 Х°кт
§ 35. Деформации при объемном напряженном состоянии.
Обобщенный закон Гука
Базируясь на гипотезе о том, что материал следует закону Гука,
а деформации малы, можно получить зависимости между напряжени-
ями и деформациями в общем случае объемного напряженного состоя-
ния. При этом будем исходить из зависимостей (4.3) и (4.9), получен-
ных ранее для линейного напряженного состояния.
Рассмотрим деформацию прямоугольного параллелепипеда раз-
мерами аХЬхс (рис. 93, а) под действием главных напряжений
а2, с3 (полагаем, что все они положительны) по трем его граням,
параллельных соответственно ребрам а, 6,
Удлинения ребер соответственно будут
пые деформации в главных направлениях
Да Д&
£1 = у; *2-т; *3~--
с.
Да, Д&, Де, а относитель-
Дс
6 5-1186
161
^пть результат дей-
^пример,
Каждое из этих относительных удлйн^н'й'Й
ствия всех трех напряжений аг, а2 и4 о3. При* *19)
ei = ei + ei'+ ei'«
где согласно (4.3) и (4.9/
Учитывая (5.20), можно записать (5.19) в виде:
Ч = ->-!л->-!л->=4-[а1-1х(^ + аз)Ь (5’21>
И/ Uj th И/
Аналогично могут быть записаны и выражения для е2 и е3 как
/ («1, а2, а3). В результате обобщенный закон Гука для изотропного
материала выразится следующими соотношениями;
1
(а1 — Р (^г + <*з)1;
, 1 ।
с2 ~ [а2— Р (*1 + аз)1;
(5.22)
£3 = -g-[a3 —Р (С1 + а2)]« !
Заметим, что сжимающие напряжения следует в формулы (5.22)
подставлять со знаком «минус». Очевидно, в случае плоского напря-
женного состояния, в частности при о2 = 0, обобщенный закон Гука
(5.22) будет иметь вид
£i = —ра3);
е2 =-----(а1 + аз);
1 /
ез -= (сз “ Pai)-
162
Закон Гука справедлив не только для главных деформаций,
но и для вычисления относительных деформаций по любым трем вза-
имно перпендикулярным направлениям, поскольку при малых дефор-
мациях влиянием сдвига на линейную деформацию из-за его малости
можно пренебречь. Поэтому относительные удлинения в направлении
действия напряжений аа, (рис. 93, б) равны:
1 1
£a = -g-(°« — !«₽);
Объемная деформация представляющая собой относительное
изменение объема v0 — abc, после приложения к нему напряжений
а2, <*з определяется с точностью величин второго порядка мало-
сти формулой
£v — —= ei + е2 + £з (5.23)
или через напряжения с учетом (5.22) формулой
£t?=—(<?i + <?2 + аз)- (5.24)
В частности, При равномерном всестороннем сжатии, когда «х =
=с= (j2 == <73 == р,
=----, (5.25)
Ё
где К = 3 (1 — 2|Л) ’ •
Величина Я называется модулем объемной деформации. Из (5.24)
видно, что при деформации тела, материал которого имеет коэффициент
Пуассона ц = 0,5 (например, резина), объем тела не меняется.
§ 36. Потенциальная энергия деформации
Потенциальной энергией деформации называется энергия, кото-
рая накапливается в теле при его упругой деформации. Когда под
действием внешней статической нагрузки тело деформируется, точки
приложения внешних сил перемещаются и потенциальная энергия
нагрузки убывает на величину, которая численно равна работе, совер-
шенной внешними силами. Энергия, потерянная внешними силами,
не исчезает, а превращается, в основном, в потенциальную энергию
деформации тела (незначительной частью энергии, рассеиваемой
в процессе деформации, главным образом, в виде тепла, при этом пре-
небрегают).
Приращение потенциальной энергии U деформируемого тела
р^вцо уменьшению потенциальной энергии нагрузки Uu и численно
равнр работе Ар, совершенной внешними силами, т. е.
27 = Лр. (5.26)
Таким образом, потенциальная энергия деформации численно равна
работе внешних сил, затраченной при упругой деформации тела.
6* 163
В случае простого растяжения (рис. 94)
£7 =
РМ
2
удельная потенциальная энергия
U PM os
“ “ v ~ 2FI ~ 2 ’
(5.27)
Рис. 94
где у —объем тела; F —площадь поперечного сече-
ния.
Учитывая, что s == -=г , получим
а
q2
U = ^-. (5.28)
В случае объемного напряженного состояния,
когда потенциальная энергия деформации опреде-
ляется суммарной работой главных напряжений oj,
а2, <*з на соответствующих перемещениях elt s2, е3
(рис. 95), на основании (5.28) удельная потенциаль-
ная энергия выражается формулой
и-~2
qlSl । q2g2 1 q3g3
2'2’
Воспользовавшись обобщенным законом Гука, можем исключить
деформации. Получим
w = -rirgr* [qi + q2 + сз 2р. (<Ji<J2 + q2q3 + q3qi)]• (5.29)
При деформации упругого тела (рис. 95)
изменяется, вообще говоря, не только его объем,
но и форма (например, кубик превращается
в параллелепипед). Поэтому полную удельную
потенциальную энергию деформации и можно
представить в виде двух слагаемых:
u = uv + иф,
где uv— удельная потенциальная энергия изме*
нения объема;
иф — удельная потенциальная энергия изме-
нения формы.
Можно показать, что
Рис. 95
«Ч>=Ц^(‘1 + ’2Ч-с3)*; (5.30)
1 + Р* г 2 1 2 I 2 / । ।
“Ф = ~31Г — ( qlq2 + q2q3 + q3ql)]
= Mr K’l - °2)2 + (°2 - °s)2 + (’3 - ’l)2]-
(5.31)
Глава 6
КРИТЕРИИ ПРОЧНОСТИ
§ 37. Основные теории прочности
Важнейшей задачей инженерного расчета является оценка проч-
ности детали по известному напряженному состоянию, т. е. по извест-
ным главным напряжениям в точках тела. Наиболее просто эта задача
решается при простых видах деформации, в частности при одноосном
напряженном состоянии, так как в этом случае значения предельных
(опасных) напряжений легко установить экспериментально. Напом-
ним, что опасным напряжением для пластичных материалов является
предел текучести, а для хрупких — временное сопротивление.
Таким образом, условие прочности при одноосном напряженном
состоянии (рис, 96, а) принимает вид
°i <[’+]; 1. (б-1)
где [а*] и [а_]—допускаемые напряжения соответственно при
растяжении и сжатии.
В случае сложного напряженного состояния, когда два или все
три главных напряжения ах, о2, °з не равны нулю (рис. 96, б), пре-
дельное (опасное) состояние для одного и того же материала может
иметь место при различных предельных значениях главных напряже-
ний в зависимости от соотношения между ними. Поэтому эксперимен-
тальная проверка опасного состояния из-за бесчисленного множества
возможных соотношений между ах, о2, аз и трудности осуществления
экспериментов практически исключается.
Другой путь решения поставленной задачи заключается в выборе
критерия прочности (критерия предельного напряженно-деформи-
рованного состояния). Для этого вводится гипотеза о преимуществен-
Рис. 96
Рис. 97
ном влиянии на прочность материала того или иного фактора. При
этом предусматривается возможность проверки выбранного критерия
прочности сопоставлением данного сложного напряжеррого состояния
с простым, например с одноосным растяжением (рис. 97, а, б), и уста-
новления такого эквивалентного напряжения, которое в обоих слу-
165
чаях дает одинаковый коэффициент запаса прочности. Под по*
следним в общем случае напряженного состояния понимают число п,
показывающее, во сколько раз нужно одновременно увеличить все
компоненты напряженного состояния (ot, о2, аз)» чтобы оно стало пре-
дельным:
ООО
Gj — HQ-1) G2 — — П&&,
Выбранные таким образом гипотезы называют механическими
•теориями прочности. Ниже рассмотрены основные критерии (теории
прочности).
Критерий наибольших нормальных напряжений (первая теория
•прочности). Предполагается, что опасное состояние тела, находяще-
гося в условиях сложного напряженного состояния, определяется
.уровнем наибольшего нормального напряжения
о
GX = а+ I
шли т > (6.2)
1°з1 = Д- J
•Условие прочности с коэффициентом запаса п имеет вид
I ZR ox
*йли > (6.3)
Из I <[*-!> J
аде
’ Эта теория подтверждается на практике только для весьма хруп-
ких и достаточно однородных материалов (стекло, гипс, некоторые
-виды керамики).
Критерий наибольших относительных линейных деформаций
(вторая теория прочности). За критерий предельного состояния при-
нимают наибольшую по абсолютной величине линейную деформацию,
я1, е. условие разрушения:
I Emax I = е°‘ <6-4)
'Условие прочности имеет вид:
₽0
Етах=Е1 <[*] = —• <6-5)
-Учитывая, что [е] = -Цг-, а также, что
1
«1 = -g- 1’1 — И (°2 + «з)1.
’условие прочности (6.5) можно представить в виде:
«1 — Iх («2 + ®з) < [°1- (6.6)
!Как видно из (6.6), с допускаемым напряжением нужно сравнивать
<166
не то или иное главное напряжение, а их комбинацию. Эквивалентное*
напряжение в этом случае будет равно
®экв II = «1 — Н (°2 + °з)- (6-7)»
Эта теория имела довольно широкое распространение, но опытное-
подтверждение получила только для весьма хрупких материалов.
Критерий наибольших касательных напряжений (третья теория»
прочности). Предполагается, что опасное состояние нагруженного*
тела определяется уровнем максимального касательного напряжения.
Условия разрушения и прочности соответственно имеют вид:
хтах = т°» (6.8>
ттах И = ~ • (&9)
Так как
условие прочности (6.9) для главных напряжений запишется так:
«1 — (6.10)
а эквивалентное напряжение по третьей теории прочности опреде-
лится формулой
°ЭКВ III = с1 с8-
Эта теория дает хорошие результаты для материалов, одинаково
сопротивляющихся растяжению и сжатию. Недостатком третьей тео-
рии является то, что она не учитывает среднего по величине главного
напряжения а2, которое оказывает определенное, хотя в большинстве
случаев и незначительное, влияние на прочность материала. Считая!
предельным состоянием для пластичных материалов предел текуче-
сти, условие (6.8) можно представить в виде
— °з = °т- (6.12>
Это условие удовлетворительно описывает начало пластической
деформации разупрочняющихся материалов, для которых характерна*
ее локализация.
Критерий удельной потенциальной энергии формоизменения (чет-
вертая теория прочности). Предполагается, что опасное (предельное^
состояние нагруженного тела определяется предельной величиной,
накопленной удельной энергии формоизменения. Последнюю можно»
определить при простом растяжении в момент начала текучести
иф max мф ~ иф. т* (6.13))
Условие прочности будет
иф max < ^мф1* (6.14)
Полагая, что материал следует закону Гука вплоть до наступле-
ния предельного состояния, на основании (5.31) при простом растя-
жении в момент начала текучести (^ = оа=аа = 0) имеем:
__ 1 Ч~ 2
МФ-т ~ ЗЕ °т‘
467
Условие (6.13) после подстановки (5.31) и значения Ыф т из
последнего равенства примет вид
+ а2 + °3 — (а1°2 + а2а3 + аЗа1) = °Т»
ИЛ0 _______________________________________________ . (6.15)
У [(«1 - <Ч)2 + («2 ~ °з)2 + (°3 - °1)2J = ОТ.
Условие прочности (6.14) будет иметь вид
У у К’1 ~ °2)2 + - Оз)2 + (°3 - °1)21 < -V = [О]• (6.16)
Эквивалентное (расчетное) напряжение по четвертой теории
прочности определится формулой
°8КВ IV = У J [(’1 - °2)2 + (°2 - Оз)2 4- (Оз - «!>«] . (6.17)
Расчетное уравнение четвертой теории прочности можно полу-
чить исходя из критёрйя пдстоянства октаэдрических касательных
напряжений
токт max 1хокт1*
' ’ Такая трактовка освобождает рассматриваемую теорию прочности
от ограничений, связанных с областью применимости закона Гука,
и дает возможность установить не только начало пластической дефор-
мации, но и начало разрушения.
Четвертая теория прочности применима для пластичных материа-
лов, одинаково сопротивляющихся растяжению и сжатию.
Критерий Кулона — Мора. Этот критерий основан на предположе-
нии, что прочность материала в общем случае напряженного состоя-
ния зависит, главным образом, от вели-
чины и знака наибольшего ох и наимень-
шего Оз главных напряжений (погреш-
ность, связанная с тем, что не учитывается
о2, обычно не превышает 12—15%). Исходя
из этого предположения, любое напряжен-
ное состояние можно представить одним
кругом Мора, построенным на главных
напряжениях и ст3.
Если при данных о^ и а3 нарушается
прочность материала, то круг, построен-
ный на этих напряжениях, называется предельным. Меняя соотно-
шение между ах и о3, получим для данного материала семейство пре-
дельных окружностей (рис. 98). Огибающую ABCDE семейства
предельных кругов можно с достаточной степенью точности заменить
прямыми, касательными к кругам Мора, построенным для растяже-
ния, с диаметром, равным временному сопротивлению при растя-
жении ов, и для сжатия — с диаметром, равным временному сопротив-
лению материала при сжатии ов сж (рис. 99).
Очевидно, рис, 99 может быть перестроен в масштабе допускае-
168
мых напряжений (рис. 100). Диаметр круга для растяжения равен
1С+] = * а для сжатия — [с_] = ~^СЖ" •
Из рассмотрения подобия треугольников О^О^а и OtO$b находим
Эквивалентное напряжение по рассмотренной теории Мора
%нв. м “ ai [а*] ’Сз' (6.19)
Теория прочности Кулона — Мора позволяет установить сопротив-
ление разрушению материалов, обладающих разным сопротивлением
растяжению и сжатию (хрупких материалов). Она имеет сущест-
венное преимущество перед первой и второй теориями, которые на
практике еще иногда применяются.
Следует подчеркнуть, что хрупкое или пластичное состояние мате-
риала определяется не только его свойствами, но и видом напряжен-
ного состояния, температурой и скоростью нагружения. Как показы-
вают опыты, пластичные материалы при определенных условиях
нагружения и температуре ведут себя как хрупкие, а хрупкие матери-
алы, при определенных напряженных состояниях, могут вести себя
как пластичные.
§ 38. Понятие о некоторых новых теориях прочности
Условие перехода материала в предельное состояние можно выра-
зить в виде некоторого уравнения
F(ab ^-0, (6.20)
которое может быть представлено предельной поверхностью в трех*
мерном пространстве, где по осям декартовой системы координат от-
кладываются главные напряжения.
Так, предельная поверхность, соответствующая условию появле-
ния массовых пластических деформаций, по теории удельной потен-
циальной энергии формоизменения (6.15) имеет вид
(С1 _ О2)2 + (С2 _ аз)2 + (Сз - С1)2 _ 2%а = 0. (6.21)
Предельная поверхность (6.21) представляет собой круговой цилиндр
с осью, равнонаклоненной к координатным осям (рис. 101, а), и ра-
диусом г »
169
Для плоского напряженного состояния, когда одно из главных
напряжений равно нулю, условие (6.21) дает эллиптическую предель-
ную кривую (рис. 101, б).
Критерию наибольших касательных напряжений соответствует
предельная поверхность в виде правильной шестигранной призмы,
вписанной в цилиндр. Критерию наибольших нормальных напряжений
соответствует куб с ребрами, равными
о0. Заметим, что все точки, распо-
ложенные внутри области, ограни-
ченной предельной поверхностью,
соответствуют напряженным состоя-
ниям с коэффициентом запаса
прочности п>1, а напряженные
состояния, представленные точками,
лежащими вне области, ограничен-
ной предельной поверхностью, име-
ют коэффициент запаса прочности
и < 1.
Новейшие теории и основывают-
ся на выборе различных вариантов
формы предельной поверхности, при которой можно наиболее полно
учесть особенности сопротивления данного класса материалов в
условиях сложного напряженного состояния.
Критерий прочности Ягна — Бужинского. Предельная п оверх-
ность (6.20) принимается в виде полинома второй степени, симмет-
ричного ко всем трем главным напряжениям,
(а1 — са)2 + (с2 — аз)2 + (С1 — сз)2 + а (С1 + в2 + аз)2 +
(®i ^2 ®з) ~ (6,22)
где
. ь_ 1-1^1)...
la+]la-J [C+][G-J
При этом [04.], [а_], [т] определяются из опыта для данного мате-
риала при испытании соответственно на одноосное растяжение,
сжатие и чистый сдвиг.
Очевидно, теория прочности Ягна—-Бужинского позволяет учесть
не только различие в сопротивлении материала растяжению и сжатию,
но также и сопротивление сдвигу.
Критерий прочности Писаренко—Лебедева. К числу новых теорий
следует отнести теорию, предложенную Г. С. Писаренко и А. А. Лебе-
девым [14], которая основана на предположении о том, что наступление
Предельного состояния обусловлено способностью материала оказы-
вать сопротивление как касательным, так и нормальным напряжениям.
Критерий прочности предлагается искать в виде инвариантных к на-
пряженному состоянию функций касательных напряжений, например
октаэдрических касательных напряжений, и максимального нормаль-
ного напряжения.
При атом критерии прочности может быть записан в виде
W + W1®1 < ^2- (6>23)
Выражая константы т1 и т2 через предельные напряжения при
одноосном растяжении и сжатии cL (в частности, через <?р
и <jb сж), условие (6.23) приводим к виду
3
+(*-*)
170
или, переходя к интенсивности напряжений, к виду
хсг + (1~х)а1<о0> (6.24)
Для материала, находящегося в пластичном состоянии, когда
34. = cjL; X == 1, выражение (6.24) преобразуется в критерий проч-
ности, соответствующий теории формоизменения; для хрупких
материалов, когда X = О, выражение (6.24) преобразуется в первую
теорию прочности. При 0<Х<Л, что соответствует большинству
реальных конструкционных материалов, предельная поверхность по
уравнению (6.24) будет представлять собой равнонаклоненную к глав-
ным осям фигуру, в которую вписана шестигранная пирамида, соот-
ветствующая теории Кулона—Мора, и выражаемая формулой (6.19).
Теория, представленная критерием (6.24), хорошо согласуется
с данными эксперимента для широкого класса достаточно однородных
конструкционных материалов.
Для материалов, обладающих существенной структурной неодно-
родностью (отдельные виды металлокерамики, графиты, пенопласты,
каменное литье и т. п.), предложено условие
xai + (1 — х) (6.25)
Qi "4- Со “4~ л
1 де J ~ ———- — параметр напряженного состояния, Л—параметр
аг
структуры материала, среднестатистическое значение которого для
указанного класса материалов составляет 0,7—0,8.
Уточненное значение параметра А можно определить, используя
данные испытаний на кручение:
4= ?—/Зх
1 — X ’
°+
где у = — ; тк — предельное напряжение при кручении.
тк
Критерий прочности Фридмана. Этот критерий базируется на рас-
смотрении диаграмм механического состояния, которые строят исходя
из того, что, в зависимости от типа напряженного состояния, материалы
могут разрушаться от растягивающих напряжений (путем отрыва)
и от касательных напряжений (путем среза). Соответственно этому
различают две характеристики прочности — сопротивление отрыву
£от, представляющее собой величину нормальных напряжений на
поверхности разрушения в первом случае, и сопротивление срезу £к,
представляющее собой величину касательных напряжений во втором
случае. Обе характеристики прочности 50Т и не зависят от типа
напряженного состояния. Кривые деформации также не зависят от
напряженного состояния.
Нарушение прочности путем отрыва описывается второй теорией
прочности
сэкв и = ci (а2 + аз) = ^ОТ’ (6.26)
а нарушение прочности второго вида — третьей теорией прочности
= (6-27)
171
Диаграмма механического состояния состоит из двух диаграмм
(рис. 102) — диаграммы в координатах ттах, о9кв п = £от и
диаграммы ттах, 7тах- На диаграмму наносят предельные линии,
соответствующие пределу текучести при сдвиге тт, сопротивлению
срезу tK и сопротивлению отрыву S0T. Отклонение линии сопротив-
ления отрыву вправо выше предела текучести соответствует возрас-
танию сопротивления отрыву с появлением остаточных деформаций.
Для характеристики типа напряженного состояния вводится
сб
РГ
К
я
ко
S
t
а
£
С
>6
g
коэффициент мягкости
т
max
°экв II
(6.28)
Различные напряженные состоя-
ния изображаются на диаграмме
лучами, тангенсы углов наклона
которых равны а.
При всестороннем растяжении
(°1 = °2 = °з)
и луч совпадает с осью абсцисс. При простом растяжении (г, = с;
о2 = а3 = 0) имеем
ттах=^-| °8КвП=°; « = °.5-
При простом сжатии (сгх = о2 = 0; а3 == — а)
о . 1
Tmax ~2 ’ сэкв II ~~ > а •
Принимая р = 0,25, находим а = 2,
Рассматривая лучи, отвечающие различным типам напряженного
состояния материала, можем приближенно установить вид разруше-
ния и выбрать, следовательно, подходящую теорию прочности. ’ ’
Из рассмотрения на диаграмме луча 1 видим, что он раньше всего
пересекает линию сопротивления отрыву. Следовательно, материал
разрушится путем отрыва без предшествующей пластической дефор-
мации. Луч 2 пересекает сначала линию текучести, а затем линию
сопротивления отрыву. Следовательно, при данном напряженном
состоянии разрушению путем отрыва предшествует пластическая
деформация. Для напряженного состояния, характеризуемого лучом 5,
разрушение происходит после пластической деформации путем среза.
В случае, когда луч сначала пересекает линию сопротивления
отрыву, следует пользоваться теорией Кулона—Мора, первой или
второй теорией прочности. Если же сначала пересекается линия пре-
дела текучести, то расчет прочности должен производиться по третьей
или четвертой теории прочности.
Таким образом, диаграммы механического состояния, с известным
приближением, отражают тип разрушения в зависимости от вида на-
пряженного состояния.
Заметим, что лучи, изображающие напряженное состояние, явля-
ются прямыми лишь до достижения предела текучести.
В заключение настоящей главы приведем в виде таблицы сводку
рассмотревших и других теорий прочности, встречающихся в сопро-
тивлении материалов (см. табл. 14).
172
5 J сб И 4) сб И II &
L 3< j s о В и В § В + с Pd о > || © ' 1 °
I о a g ф н сб в II
в в о н
р Л А
! 1 о ф
л
J •«* t> в Л в m
• •* tt «
1 о
) co и § В о
+ и н о
el В
i U ф В
1 t + 3 в
vH ё я
О ф в
о « н
1 г-ч |eo 8. я сб §
4 ф В И ф 1 о р в о § о
В г© о
Ри о в
И «
сб 4~© о
I4 И Ф о rf
Ф • в
1 В в
w ф
& й
1 1 о 1 и 1 в сб
& t> со О &
Q Сб + В о
Я & Ph ei « О В о О о
lb >> в
H M в:
О 61 о
w сб о
I 1 co >> S О + 61 61 в pd в
в и о
Ц В В
1 1 ф & KO (01- в ф е
о о *
по об ’гн |<М Ф 1 о I © g О |р § II о " § ~
немые № в
и и J 1
ф ф Ф те ©
£ й ° г
1 Pd В в 1
ц Pd & II
о в
ре- йх ов, ые § §
нш л® Pd м п
® о Н Фн Л sd ф и 2 s д Л В в w ф Е |
й S в о S -г о В 2 о
« б и § В н Pd °
§ и §sgs ф со § n S
имеча 5 * О ф go S § g § О я Ф о в « ф в
© § в § 2 я Н R О К В ф м В я ’5 & в
В о В §•§ g § 8 S ьм Ои В сб у Сб PdH
g g 2 -и Й a S M s s£S§M В В ф В Ь о в яЕ&
j5 ® g g g ч ч ь я й в в
ция ным рди- иче- а я в 5 ьО ф я О о и S
гатерпрета остранстве эний смещен чала коо ’идростат косоуг ипед с о шонакло ТНЫМ OCJ
Геометрическая i критерия в пр напряж< уб с центром, гносительно на ат в сторону г кого сжатия 'авносторонний пый параллелен имметрии, pai ой к координа
К о в о Рч « о В
h « и +
для ЭКЕ апряже кв гч се и о и g И сч о zL
№ со Ф о @2 Ф о § § S о» 1 о*
к и § Е II
Выр ле! 0 0 СО о
S 1аи- эрмаль- 1жений - Лейб- зывают гебша— рий наи- [их линей- деформаций отта—Грас- называют Сен-Венана)
I а К со РЗ « и & 1 И и S ф « &S и н S
g В я J S § В й И у В И о й Й В Сб ® йю иЬ-я gcu Крите б опыт пых (Мари гофа, также
173
Продолжение табл 14
»jx Критерий Выражение для эквива- лентного напряжения стэкв Геометрическая интерпретация критерия в пространстве напряжений Примечания
Критерий наи- больших каса- тельных напря- жений (Кулона) аэкв = а1 сз Правильная шестигранная призма, равнонаклоненная к координатным осям Удовлетворительно описывает пре- дельное состояние пластичных мало- упрочняющихся материалов (отпу- щенные стали), для которых харак- терна локализация пластических де- формаций
Критерий окта- эдрических каса- тельных напряже- ний или удельной энергии формоиз- менения (Губера— Мизеса—Генки) сэкв = Круговой цилиндр, описан- ный вокруг призмы, интер- претирующей критерий мак- симальных касательных на- пряжений Хорошо описывает предельное со- стояние широкого класса пластичных материалов (медь, никель, алюминий, углеродистые и хромоникелевые стали и т. п.)
Критерий Куло- на—Мора а9КВ = °1 — Шестигранная равнснакло- ненная к координатным осям пирамида Применяется для установления пре- дельного состояния достаточно одно- родных материалов, по разному со- противляющихся растяжению и сжа- тию
Критерий Ягна — Бужинского + -5' л 1 + 1 "р~. 1 ° II -9- о —ч 11 е Э- । 1 to 1 1 1 1 СО 1 СО ~ II 1 1 м II + г й ' X Равнонаклоненная к главным осям поверхность вращения. Однозначной геометрической интерпретации не имеет Применяется в тех же случаях, что и критерий Кулона — Мора. При Go = Go совпадает с критерием окта- эдрических касательных напряжений
Критерий Балан- дина аэкв — 3 (1 — X) аср + 2 + —= Go Параболоид вращения, рав- нонаклоненный к коорди- натным осям Является частным случаем критерия Ягна — Бужинского \при т«=|/ 3 J
Критерий Бот- кина — Миролю- бова аэкв = 3 (1 — X) аср 4- +4(i+x) «{ & Круговой конус, равно- наклоненный к координат- ным осям Применяется в тех же случаях, что и критерий Кулона — Мора. При ° о = % совпадает с критерием окта- эдрических касательных напряжений
Критерий Друк- кера — Прагера %кв = (1 + /х) ’< — + 1 +/х + /1 _ /х\2 о^р \1 -J— ]ЛХ/ Сто Двуполостный параболоид вращения, равнонаклоненный к координатным осям Удовлетворительно описывает пре- дельное состояние сравнительно пла- стичных материалов, для которых Х>0,3
Продолжение табл. 14
Критерий Выражение для эквива- лентного напряжения °экв Геометрическая интерпретация критерия в пространстве напряжений Примечания
Критерий С. Д. Волкова с = 2 4- g2 4- g3 — 2р. (o1 q2 -j- + °2аз 4“ g3qi) 4- t qi~-q3 1 2 Предельная поверхность не исследована Критерий получен на основе 'анализа модели микроскопически неоднород- ной среды в предположении, что критическое касательное напряжение в плоскости скольжения зависит от нормального напряжения в этой плоскости и от среднего напряжения. Xs, р, X, С — константы материала, определяемые из опытов при различ- ных напряженных состояниях, напри- мер при одноосном растяжении, одно- осном сжатии, чистом сдвиге и двух- осном равномерном растяжении
Критерий Писа- ренко — Лебедева Сэкв 4“ (1 ЗС) Коническая поверхность, описанная вокруг пирамиды Кулона — Мора. В сечении октаэдрической плоско- стью — равносторонний кри- волинейный треугольник Хорошо описывает предельное со- стояние широкого класса достаточно однородных конструкционных мате- риалов. При а* = а0 преобразуется в критерий октаэдрических каратель- ных напряжений. В случае, когДги < (весьма хрупкие материалы), результаты вычислений практически совпадают с данными расчета по кри- терию наибольших нормальных на- пряжений
Критерий Писа- ренко—Лебедева аэкв "1“ 3<?ср + (1-Х)аМ Oi Предельная поверхность рав- нонаклонена к координат- ным осям. В сечении окта- эдрической плоскостью — равносторонний криволиней- ный треугольник Хорошо описывает предельное состоя- ние неоднородных материалов (хруп- кие металлокерамические композиции, графит, хрупкие термореактивные пластмассы, различные горные порода^ пенопласты и т. п.). Среднестатисти- ческое значение лараметраЛ для ука- занных материалов составляет 0,7—0,8
Критерий В. А. Кузьменко 1 аэкв — а аР где 2(1 —<7) + <72(3 — — 2?) + 1,33 (1 — — 2^)(1—Q)2 2(1-<?) + д2(3-’ -2g) 4-С (1- — 2g) (l-g)a + + xg2(l-2g) _ gjq2 4~ q2q3 + q3ql . X 2,2,2 » gl 4“ q2 4“ q3 . _ 4 £f + e2 + e3 1 £1| 4- I s2 |+| Ssl Предельная поверхность при q = 0,5 — круговой цилиндр, соответствующий критерию удельной энергии формоизменения. При измене- нии q цилиндр деформируется Предельное состояние ‘ считается ре- зультатом развития докритического значения деформаций сдвига, связы- ваемых с пластическим течением, и деформаций растяжения, связываемых с образованием и раскрытием трещин в деформируемом материале. Критерий хорошо описывает пре- дельное состояние материалов, плас- тичность которых значительно зависит от условий деформирования. Параметр состояния q изменяется от 0 (хрупкое состояние) до 1 (пластичное состояние)
Глава 7
РАСТЯЖЕНИЕ И СЖАТИЕ
§ 39. Расчет стержней на растяжение (сжатие)
с учетом собственного веса
Напряжение в любом сечении стержня постоянного сечения под
действием внешней растягивающей силы (рис. 103, а) с учетом соб-
ственного веса может быть определено на основе гипотезы плоских
сечений по формуле
здесь
N (z) = Р +
где F — площадь сечения; 7 — удельный вес.
Очевидно,
|Л'(2)1таХ=-Р + ^
P + tFl Р , ,
. °max =---------р-----=—+
Условие прочности будет
р
сшах = “р" + < [а]
или
При Р =0
стах ~ 1^
а условие прочности принимает вид
11 < [«]•
178
Отсюда предельная длина, при которой стержень не должен разру-
шаться от действия собственного веса,
а критическая длина, при которой стержень будет разрушаться от
собственного веса,
I — °в
*кр “ •
Перемещение любого сечения, находящегося на расстоянии z от
свободного конца стержня, к которому приложена внешняя сила Р
(рис. 103, а), определяется по формуле
м.>-<«>
J ПГ J ПГ ihv ZZi
z z
Перемещение нижнего конца стержня, очевидно, будет равно
полному удлинению стержня и определится формулой
, л? Pl . У*
(г)«-0 — Дг — рр + 2Е •
Учитывая, что вес
стержня Q = ^lFt получим
&l=PL + ^L
EF 2EF •
(7.4)
Эпюры осевых
рис. 103, б, в, г.
сил, напряжений и перемещений показаны на
§ 40. Стержень равного сопротивления растяжению (сжатию).
Ступенчатый стержень
Стержнем равного сопротивления растяжению (сжатию) назы-
вается такой стержень, в каждом поперечном сечении которого»
напряжения одинаковы и равны допускаемому.
Площадь поперечного сечения такого стержня
(рис. 104) изменяется по закону
F(z) = F<>e^, (7.5)
где Fq = ----минимальное сечение стержня
М
в месте приложения нагрузки; 7 — удельный
вес; z — текущая координата; е — основание
натуральных логарифмов.
Наибольшая площадь сечения
Рис. 104
7? _j£
р _____р е [CTJ _ ? е М
*max~^oe [а] *
(7.6)
179
Вес стержня Q определяется из условия Р -f- Q±= [a] Fmax, от-
— Р, или с учетом (7.6) Q — Р (efo —1).
стержня равного сопротивления
куда Q = [a] Fmax
Относительное укорочение
Ы
сжатию е 5= -~г-,
Л
а абсолютное укорочение
Дг=е/=-И-ь (7.7)
&
Стержень равного сопротивления действию
осевых сил является оптимальным с точки зрения
рационального использования материала, что суще-
ственно в случае большой длины стержня.
Ступенчатый стержень состоит из отдельных
участков (ступеней) с постоянной площадью попе-
речного сечения в пределах каждого участка. Он
занимает промежуточное положение между стерж-
нем постоянного поперечного сечения и стержнем
равного сопротивления
Сечение любого и-го участка при длинах уча-
стков 1Ь Z2, Z3, ••• > •••» и сечениях соответ-
ственно Flt F2t F3t ..., Fn, ... , Fm (рис. 105) мо-
жет быть определено по формуле
, ___________Р [д]ге~г______
п (М--Л)(М--Л) •••
(7.8)
то
Если длины всех участков одинаковы:
11 — ^2 — h — • • • — Zn — • • • — Im-------------------f
(7.9)
где т — число ступенек в стержне; I — длина стержня.
§ 41. Статически неопределимые конструкции
Статическц неопределимыми называются конструкции, в эле-
ментах которых усилия не могут быть определены из уравнений
статики. Кроме уравнений статики при решении статически неопре-
делимых задач необходимо использовать также уравнения, учитываю-
щие деформации элементов конструкций.
» ’ Все статически неопределимые конструкции имеют так называе-
мые лишние связи в виде закреплений, стержней или других элементов.
Лишними такие связи называются потому, что они не являются необ-
ходимыми для обеспечения равновесия конструкции и ее геометриче-
ской неизменяемости, а обусловливаются требованиями к прочности
и жесткости конструкции. Число лишних неизвестных, или степень
статической неопределимости системы, устанавливается разностью
180
между числом \ неизвестных, подлежащих определению, и числом
уравнений статцки.
При одной лишней неизвестной система называется один раз или
однажды статически неопределимой, при двух — дважды статически
неопределимой и т. д. Конструкции, показанные на рис. 106, a, 6t
е, д, е, являются однажды статически неопределимыми, а конструкция,
приведенная на рис. 106, в,— дважды статически неопределимая.
Решение статически неопределимых задач проводят в четыре
этапа.
1. Статическая сторона задачи. Составляют урав-
нения равновесия отсеченных элементов конструкции, содержащие
неизвестные усилия.
2. Геометрическая сторона задачи. Устанавли-
вают связь между деформациями отдельных элементов конструкции,
исходя из условий совместности деформаций. Полученные уравнений
называются уравнениями совместности деформаций.
3. Физическая сторона задачи. В уравнениях
совместности выражают деформации элементов конструкций на основа-
нии закона Гука через действующие в них неизвестные усилия.
4. Синтез. Решают совместно полученные уравнения относи-
тельно искомых неизвестных усилий.
’ Ниже приведен пример расчета один раз статически неопредели-
мой трехстержневой системы-подвески (рис. 107, а),
1. Статическая сторона задачи (рис. 107, б)
2 X = N3 sin а — N3 sin а = 0; (7.10)
2 У = iVi + JV2 cos а + ?V8 cos а — Р = 0. (7.11)
Из (7.10) находим:
(V3=^a;
(7.12)
181
из (7.11) находим:
Ni + 2N2 cos a = P. (7.13)
2, Геометрическая сторона задачи (рис. 107, в)
Д23 = Д/2 = Д/х cos a. (7.14)
3. Физическая сторона задачи
(7.15)
Рис. 107
4. Синтез. Подставляя (7.15) в (7.14), получим
7V2Z2 Njh
EF2 EFi
cos a.
(7.16)
Решая совместно (7.16) и (7.13), находим
1 -|- 2 — cos2 a
П С2
Р — COS a
Cl
1 + 2 — cos2 a
(7.17)
где
Усилия и N2 оказались зависящими от соотношения жесткостей
стержней. Поэтому при проектировочном расчете вычислить их можно,
задавшись некоторым отношением жесткостей стержней. В этом одна
из особенностей расчета статически неопределимых стержневых систем.
182
§ 42. Расчет гибких нитей
Гибкой нитью называется стержень, способный сопротивляться
только растяжению. Из шести компонентов внутренних сил для гиб-
кой нити только осевая сила не равна нулю.
К гибким нитям относят провода электрических и телеграфных
сетей, цепи висячих мостов, тросы канатных дорог и т. п. Точки под-
веса гибких нитей могут находиться как на одном, так и на разных
уровнях (рис. 108, а, б),
Основной нагрузкой гибкой
нити из материала с удельным
весом 7 и с площадью попереч-
ного сечения F является собст-
венный вес провода с интенсивно-
стью ?п = 7 А Однако нагрузка
в гибкой нити может создаваться
не только собственным весом
провода, но также некоторыми
другими факторами, например
давлением ветра, весом льда при
обледенении проводов. Эти на-
грузки также предполагаются рав-
номерно распределенными по
длине нити. Интенсивности этих
нагрузок обозначим соответствен
но и дп.
Толщина корки льда в зави-
симости от климатического райо-
на принимается равной 0,5—
2,5 см.
Давление ветра в горизонтальной плоскости будет
или
4В = ka<lCKd' (7.18)
где р — давление; d — диаметр провода с учетом его увеличения
за счет обледенения; £ = 1,2 — аэродинамический коэффициент;
а = 0,85 — коэффициент неравномерности ветра; дСк — скорость на-
пора. Выражая последнюю через скорость ветра в метрах в секунду,
a d — в метрах, найдем интенсивность ветровой нагрузки:
q* = 636 • 10-W [кГ/м]. (7.19)
Суммарная интенсивность нагрузки на гибкую нить может быть
определена по формуле
9 = К(?п + <?л)г + <7*. (7.20)
Плоскость действия суммарной нагрузки, совпадающая с плос-
костью провисания нити, не будет вертикальной.
Гибкая нить относится к классу однажды статически неопредели
мых систем.
183
Приведем основные формулы, применяемые при расчете гибкой
нити в общем случае, когда точки подвеса нити находятся на разных
уровнях (рис. 109, а).
Обычно распределенную нагрузку q, действующую на провод,
заменяют статически эквивалентной нагрузкой д, распределенной
вдоль пролета длиной к
Полагая нить идеально гибкой, можно считать растягивающие
усилия в любом сечении нити касательными к кривой провисания нити.
В точках закрепления А и В усилия, действующие в нити, равны реак-
циям опор ТА и Тв. Представляя реакции опор в виде горизонтальных
(Я) и вертикальных (R) составляющих, из рассмотрения статической
стороны задачи найдем*
2г = -ял + яв = 0; 2.у = -/^яв+?! = о;
&
откуда ЯЛ=ЯВ=Я; (7.21)
во“4+ят' (7.22)
я«-4— (7.23)
184
Из рассмотрения равновесия части нити (рис. 109, б) находим
2г = -Я + Тг(г) = 0;
2^==--RA + <7z + 7’J/(2) = 0.
откуда
7^) = Я;
(7-24)
(7.25)
Н — горизонтальная составляющая усилия, одинаковая во всех сече-
ниях, называется натяжением нити.
Суммарное растягивающее усилие в любом сечении нити
Т (Z) = K^(Z) + ^(Z) = 4- [я у + ? (4“г)]2 (7>26)
и максимально при z = 0, т. е.
Т’тах = ]/ Я* + + Я А)2 • (7.27)
г ~ Для пологих нитей (длина которых по кривой провисания мало,
не более чем на 10%, отличается от длины пролета) разница между
Гтах и Н невелика. Поэтому с достаточной для практики точностью
расчет нити на прочность ведут по величине натяжения Н.
Уравнение кривой провисания нити найдем, приравняв на осно-
вании совершенной гибкости нити изгибающий момент нулю:
М (z) = RAz - Ну - -4 = 0.
откуда с учетом (7.22) получим
I ql . h\ qz* -
^=(1я+7Г--2я- (7-28)
т. е. кривая провисания нити имеет аналитическое выражение
параболы.
Заметим, что если задачу решать точно, считая нагрузку распре-
деленной равномерно по длине нити, а не по пролету, то кривая про-
висания будет цепной линией. Правая часть уравнения (7.28) является
первым членом разложения уравнения цепной линии в ряд Маклорена
по степеням z. Использование приближенной формулы (7.28) на прак-
тике дает вполне удовлетворительные результаты.
Положение нижней точки подвешенной нити, координаты которой
обозначены z = а; у = f (рис. НО, а), определим, приравняв нулю
производную правой части уравнения (7.28):
dy ql h gz
dz - 2H I H
185
откуда
I . Hh
z = a = _L4----=-
2 <fl
(7.29)
Подставив (7.29) в (7.28), найдем наибольшее провисание нити
Различают три характерных случая расположения низшей точки
кривой провисания нити.
1, Низшая точка кривой провисания находится в пределах про-
лета, т. е. а < I (рис. 110, а). Согласно (7.29) это будет иметь место,
когда
(7.31)
2. Низшая точка кривой провисания находится вне пролета,
?. о. а > I (рис. 110, б). Это будет при условии
*><-• <7-32)
3. Низшая точка кривой провисания совпадает с нижней точкой
подвеса, т. е. а == I (рис. 110, $). Для этого случая необходимо, чтобы
я=тг- <’33>
Во всех трех случаях координаты а и /' низшей точки определя-
ются по формулам (7.29) и (7.30).
Установим зависимость между натяжением Н и стрелой правы-
сания J. Подставляя в (7.28) z — и t/ = —- + / (рис. 111), найдем
/--g- <7.34)
186
или
Я = (7.35)
Натяжение нити, выраженное через наибольшее провисание най-
дем из решения квадратного уравнения (7.30) относительно Я:
Я=-^-[/'~4±//'(/'-Л)].
Если низшая точка кривой провисания находится в пределах пролета,
то перед корнем берется знак «минус», если вне пролета — знак
«плюс».
Рассматривая геометрическую сторону задачи, установим связь
между длиной подвешенной нити 5, пролетом /и величиной провиса-
ния /. Длину элемента нити, учитывая малое провисание, можно выра-
зить следующей зависимостью: j
1
dS = Vdz^ + dy* = Г1 + ] 2 dz s [1 + ~ №Y1 dz. (7.36)
L \ / J L \ “z / j
Подставляя производную от выражения (7.28) ~ в (7.36) и инте-
грируя по всей длине, найдем
S=Z + 2& + 4 <7-37)
или, учитывая (7.35),
s-, + tt + -s- <7-38>
Удлинение подвешенной нити от растяжения равно
Д5 = .У-£=г + ^ + -^--Д (7.39)
где L — длина пеподвешенной нити.
Из рассмотрения физической стороны задачи устанавливают зави-
симости изменения длины нити от растягивающего усилия и от изме-
нения температуры.
Принимая для пологих нитей за расчетное растягивающее усилие
натяжение Я и заменяя длину нити расстоянием между точками под-
веса найдем удлинение нити по формуле
. _ Я/j HI ...
EF~ EF cos )
Температурное удлинение нити определяется формулой
A1S(-aZ1(t-t0) = -JT(«-t0), (7.40а)
vUv р
187
где а — коэффициент линейного расширения материала нити; Го —
температура в момент подвешивания нити; t— температура, для
которой проводится расчет нити.
Суммарное изменение исходной длины нити
№ = Д5Н + &St = + —2Ц- (I —t0). (7.41)
а * 1 №cosfP cosp v '
Приравнивая правые части (7.39) и (7.41), выражающие одну
и ту же величину удлинения подвешенной нити, найдем:
т___7f Я213 । Ь2_____HI________г*______t \ /у 421
L 1+ 24Я2 + 2Z EFcosp cos р о)' <7,42)
Совместное рассмотрение уравнений (7.35) и (7.42) позволяет
определить натяжение нити Н и стрелу ее провисания /. Опреде-
лив Я, по формуле (7.27) можно найти Гтах, а зная последнее,—
проверить прочность по формуле
0 = _£ша2_ (7.43)
или с учетом (7.35)
Введя понятие удельной нагрузки
7— р л
получим условие прочности (7.44) в виде
° = , (7.45)
Заметим, что при расчете электрических проводов сечение провода F
'определяется из электрических соотношений, а затем выполняется
проверочный расчет по формуле (7.45).
Большой практический интерес представляет частный случай
расчета нити, когда точки подвеса находятся на одном уровне, т. е.
при
cos р — cos 0 = 1; h — 0; RA — RB = е
Как и в общем случае, останутся в силе формулы (7.34) и (7.35), а урав-
нение совместности деформаций (7,42) примет вид
г 7 1 Я213 HI
L~l + 24Я2 al
(7.46)
’ На практике часто приходится учитывать влияние на напряжение
и стрелу провисания нити изменений температуры и нагрузки. Пусть
188
требуется определить изменение напряжения и стрелы провисания
в состоянии и, характеризуемом параметрами #n, qn, in, Нп~
« , по сравнению с первоначальным состоянием т в момент
О/П
л р
подвеса нити, характеризуемом параметрами qm, fm> Нт = •
О/7П
Решение поставленной задачи может быть получено, если выра-
зить длину L нити для состояний т и п в соответствии с (7.46):
qmi3 Hmi
L 1 + 1 (t,n *o)’
m
T , , <№ Hnl
L~l + ~24H*
n
Приравняв правые части этих уравнений и введя замену
Ят _ . jTn __ ___ Нт . _ _Нп
" р — 7т» ^7 — \п> ат — р , ~ ,
окончательно получим
аП ^7”2 — г,/ 2 Ь(7.47)
24ап
Зависимость (7.47) иногда
Она может быть представлена
называют уравнением состояния
в виде
нити.
№е
(7.48)
или, учитывая, что
. _ 1тР .
Чп12
Sfn
в виде
fn “ [ fm + g- al2 — ’gy—] tn ~ = 0- (7.49)
При различных уровнях точек подвеса уравнение состояния
нити соответственно примет вид
3 7m^4
fn- fm + ^l3
(^n — ^m)
COS p
64 Efm COS p fn
A 7n^4 _ Q
64£cosP
(7.50)
189
Кубическое уравнение (7.49) или (7.50) относительно /п удобно
решать графически. Так, записав его в виде —а/п —0 или
fn — afn + bt где а и Ъ — известные числа, строят графики
V = fn и у = afn +6.
Абсцисса точки пересечения получаемой при этом кубической
параболы с прямой линией и дает значение искомого провисания fn
(рис. 112).
При расчете нити на прочность необходимо учитывать случаи
наиболее неблагоприятных сочетаний ветра
У к и обледенения, вызывающих максимальные
7 напряжения в ней.
уу Из уравнения состояния (7.47) следует,
г Л s' / что в случае малых пролетов при I -+ О
S'Ъ / сп = Gm *4“ (tm — tn)>
JiS т. е. изменение напряжении зависит главным
. --------образом от изменений температуры.
fn . ж J В случае больших пролетов при I -+ оо
получим
Рис. 112
®п
7п
7m
т. е. напряжение в основном зависит от нагрузки.
Критической длиной нити /кр называется такая длина, при кото*
рой напряжение в нити одинаково в обоих опасных состояниях (как
при наибольшей нагрузке — состояние м, так и при наинизшей тем-
пературе— состояние тп), т. е. когда
°п — — [ °]*
(7.51)
Полагая, что tn соответствует температуре обледенения (обычно
to6 = —5°С), при которой 7n = 7max’ а соответствует наинизшей
температуре при которой на цить действует только собствен-
ный вес 7, т. е. = 7Х, найдем критическую длину нити ZKp из
(7.48) с учетом (7.51):
/24а (t0Q *min)
" - -
7шах 71
Сопоставляя расчетный пролет I е критическим /кр, можно убе-
диться, что при I < ZKp наибольшие напряжения будут при наиболее
низкой температуре, а в случае I > /кр наибольшие напряжения в
нити будут при наибольших нагрузках.
Глава 8
сдвиг
^ет на срез
§ 43. Сдвиг. Раъ _ „ тл
а тем, что из шести составляющих
Деформация сдвига характера г°мента М отлична от нуля
главного вектора силы! R и главного Mv. все остальные равны
только одна поперечная сила ((или а -
нулю. ^осы
Примером сдвига или среза может служить деформация ни..,
при резке ее ножницами (рис. ИЗ, а, б). Практически деформаций
сдвига в чистом виде получить трудно, так' как о Па обычно cdripVBb^'-
дается другими деформациями, и чаще всего деформацией1 и^Гйбй
При нагрузке по схеме, показанной нас рисунке, нй участке Ъс, *
очевидно, поперечная сила
Q = P, (&!)’*
g связь между касательными напряжениями т и поперечной’ силой^
будет
I tdF = Q. (8.2)
F
Принимая касательные напряжения т по площади поперечного»
сечения F распреД&нЬнными равномерно (рис. 114), на основании
(8.2) найдем
или, учитывая (8.1),
Р
F ‘
т =
(8.3У
Рис. fl4’
Допущение о равномерности распределения касательных напря°"
жений по сечению является весьма условным, поскольку в силу за-,
кона парности касательные напряжения у верхней и нижней граней'
191
равны нулю. Однако принятое допущение широко используется на
практике при расчете болтов, заклепочных и сварных соединений,
шпонок и т. п.
§ 44. Чистый сдвиг
Случай плоского напряженного состояния, когда по четырем
граням выделенного элемента действуют только касательные напря-
жения (рис. 115), называется чистым сдвигом. Найдем величину глав-
Рис. 115
ных напряжений применительно к схеме нагружения, приведенной
на рис. 115, а. Для этого, имея в виду, что в данном случае аа ®
s= Ор == 0; та = т; тр = т, строим круг напряжений (рис, 115, б),
из которого следует, что
— — с3 = т. (8.4)
Средние напряжения в главных площадках, совпадающих с фасад-
ной гранью, а2 = 0. Главные площадки наклонены к граням элемента
под углом 45°. Под действием касательных напряжений элемент
abed, имевший форму квадрата со стороной а, превратится в ромб
Рис. 117
a'b'c'd'. Деформация чистого сдвига заключается в изменении пря-
мых углов. Представляя для наглядности элемент, находящийся
в условиях чистого сдвига, закрепленным по одной из граней (рис. 116),
найдем
As
192
Учитывая малость угла, можем принять tg 7 « 7, тогда относи-
тельный сдвиг
Зависимость между нагрузкой и деформацией при сдвиге видна
из диаграммы сдвига (рис. 117), которая может быть получена по*
добно диаграмме напряжений при испытаниях на растяжение.
Очевидно, в пределах линейной зависимости между 7 и т справед-
ливо соотношение
7 = -у или т = Gy, (8.6)
где G — коэффициент пропорциональности» который называется
модулем упругости при сдвиге или модулем упругости второго рода
и имеет размерность кГ/см2 (или кГ/мм2). Формулы (8.6) выражают
закон Гука при сдвиге, записанный в относительных координатах»
Из рис, 116 видно, что удлинение Д/ диагонали АС = I == а]^2 равно:
/ д/ = ССг cos f ~ -—-А « CCi cos 45° = ,
1 1^4 2/ 1 у2
Л а относительное линейное удлинение диагонали (в направлении сг)
Д/ As 7
^пли, учитывая (8.6),
е = ^. (8.7)
Применяя обобщенный закон Гука к чистому сдвигу (рис. 116),
^находим
Йз сопоставления правых частей
Е
равенств (8.7) п (8.8) получаем
Е
При [Л = у ч- ~ G — (0,375 ч- 0,4) Е.
Используя (8.5), выразим абсолютный сдвиг As через Q = Ft:
а ч Qa
— g а~ GF ’
т. о.
As =
Qa
GE
(8.10)
7 5 1186
193
Формула (8.10) выражает закон Гука при сдвиге в абсолютных еди-
ницах-
Потенциальная энергия деформации при сдвиге определяется
формулой
_ ksQ Q*a .
2 2GF
Удельная потенциальная энергия деформации при сдвиге
__ U __ Q*a
U V 2GFaF 2G
где V — объем элемента.
Главные напряжения при чистом сдвиге (рис. 115, а) равны:
01 = т; о2 _ 0; о3 =—~ т.
Условия прочности при чистом сдвиге запишутся;
цо цервой теории прочности
= т < [а]; (842)
цо второй теории прочности
«i — p-as <14
Подставляя значения главных напряжений, находим
(ваз.
Для металлов [1^0,25—0,42, поэтому [т] = (0,7 4- 0,8) [<?].
По третьей теории прочности
< [а].
Отсюда
г < = [т] (8.14)
и допускаемое напряжение
М = 0,5 [gJ.
Цо четвертой теории прочности
2 । 2 г 1.
+ —о1°з< М;
Следовательно,
[т] = -М. и 0,6 [а].
1 /3
194
Отметим, что при расчетах деталей из пластичных материалов
(болты, заклепки, шпонки и т. п.) наиболее подходящей является
последняя формула.
§ 45. Некоторые примеры расчета на срез
Расчет болтовых и заклепочных соединении. При расчете болтов
на срез (рис. 118, а) условно принимают распределение внешних сил,
Рис. 118
действующих на болт, и касательных напряжений в сечении среза
соответствующим схеме, приведенной на рис. 118, б.
Условие прочности болта на срез может быть записано в виде
т-------------------------2_ гт1
Tmax “ р l -I
или, учитывая, что Q — Р (рис 118, в), a F ==
4Р
Tmax =
Отсюда определим диаметр болта
''-/-ТПГ- <8Л5>
При расчете болтовых или заклепочных соединений следует учи*
тывать, что нагрузка, приложенная к элементам соединения, помимо
среза вызывает смятие контактирующих поверхностей. Под смятием
понимают пластическую деформацию, возникающую на поверхности
контакта.
Расчет на смятие проводят приближенно, поскольку закон распре-
деления давления по поверхности контакта в точности не известен.
Обычйо принимают нелинейный закон распределения давления
7*
195
(рис. 119, а), считая, что давление пропорционально проекции dF}
площадки dF цилиндрической поверхности на диаметральную плос
кость
q dF
~ dFr ‘
Рис. 119
Максимальное напряжение смятия для цилиндрической поверхности
равно
Р Р
°см~ ^см ~ М*
где FCM = bd —- площадь проекции поверхности контакта на диамет •
ральную плоскость (рис. 119, б).
Условие прочности на смятие имеет вид:
= (8-16)
Допускаемые напряжения на смятие устанавливаются опытным
путем и принимаются равными
[асм1 = (2 — 2,5) [а_].
На основании (8.16) можно определить необходимый диаметр
болта:
(8Л”
Из двух диаметров, найденных по формулам (8.15) и (8.17), следует
взять больший, округлив его до стандартного значения.
Так как болты и заклепки ослабляют соединяемые листы, послед-
ние проверяют на разрыв в наиболее ослабленных сечениях, В случае
одного болта условие прочности будет иметь вид
’=г^7= ЧЬ-d) <[°+L
где b — ширина листа.
196
Рассмотрим заклепочное соединение, заклепки которого испыты-
вают двойной срез (рис. 120).
Полагая, что растягивающая сила N равномерно распределена
между заклепками, найдем, задавшись диаметром заклепок d и толщи-
ной листа 6, число заклепок i из условия прочности на срез
4
2 ТУ
1 nd2 [т]
или из условия прочности
смятие
Л . .
асм ““ ibd
Расчет сварных соединений. На срез принято (также условно)
рассчитывать и некоторые сварные соединения. Наиболее распростра-
нены соединения в стык и соединения с помощью угловых или валико-
а
5
Рис. 121
fl
вых швов. Соединения в стык применяются, когда соединяемые листы
находятся в одной плоскости. При толщине листов б < 8 мм кромки
листов не обрабатываются (рис. 121, а); при б » 8-4-20 мм кромки
листов скашиваются и сварка производится с одной стороны. При этом
получается V-образный шов (рис. 121, б); при & 20 мм кромки ска-
шиваются с двух сторон. Получается Х< образный шов (рис. 121, в).
Расчет таких швов проводится на разрыв. Расчетную толщину шва
принимают равной толщине листа Ь (наплавы не учитываются).
Соединения с помощью угловых швов применяют в случаях,
когда соединяемые листы параллельны или перпендикулярны. К ним
Рис. 122
Рис. 123
относятся соединения внахлестку, с накладками и тавровые. Если
направление шва перпендикулярно к действующему усилию, то шов
называется лобовым. Швы, параллельные усилию, называются флан-
говыми или боковыми. Применяются также косые швы (рис. 122),
направленные под некоторым углом к действующей, силе. На рис. 123
197
показано соединение листов внахлестку лобовыми швами, на рис. 124—
соединение с накладками, приваренными фланговыми швами, на
рис. 125 — тавровое соединение.
Обычно при расчетах сварных швов наплывы не учитывают,
а считают, что в разрезе угловой шов имеет
равнобедренного треугольника (рис. 126, а, б).
Разрушение шва будет происходить по его
минимальному сечению, высота которого
т — Ъ cos 45° « 0,78.
Рис. 124
форму прямоугольного
Рис. 125
Расчетная площадь сечения шва длиной I составит
F — ml = 0,78/.
Расчет швов, как и заклепок, условно ведется в предположении рав-
номерного распределения напряжений по сечению шва. Некоторые
значения допускаемых напряжений при расчете сварных соединений
конструкций, изготовленных из Ст. 3, приведены в табл. 15.
Расчет лобового шва. Учитывая, что сопротивление стали срезу
ниже, чем сопротивление растяжению, составляющей нормальных
напряжений в лобовом шве пренебрегают и расчет швов производят
условно на срез, предполагая, что касательные напряжения равно-
мерно распределены по площади сечения ABCD (рис. 126). При рас-
чете лобовых швов соединения внахлестку учитывают оба шва — верх-
ний и нижний. Их общая площадь
F = 2т/= 2 • 0,78/= 1,48/.
Условие прочности запишется в виде
Z ~ ~F~ = 1,46/ *
Расчетная длина торцевого шва /р определится формулой
I - р (
р 1.48 [г8] • (
Расчетная длина шва /р в связи с непроваром в начале и в конце шва
обычно принимается на 10 мм меньше действительной /:
/р = / — 10 мм.
Расчет фланговых швов. Фланговые швы наиболее распространены
ша практике. Они менее жестки, чем лобовые, из-за большей протя-
498
женности металла в направлении действия силы. Фланговые швы
всегда ставятся парами. Они работают на срез в биссекторных сечениях
(рис. 127). Площадь среза двух швов
F = 2 • 0,7d (Z — 10 мм) = 1,4Ь (Z — 10 мм).
Условие прочности на срез:
= — = Р
F 1,4b (I — 10л«л«) ‘
Длина шва определяется формулой
р
I = " л 7ГГ"1 + 10 мм‘
М& [тэ]
Расчет врубок. К числу соединений, прочность которых опреде-
ляется в основном из условия среза, относятся врубки, используемые
для соединения деревянных элементов конструкций (рис. 128). Древе-
сина является анизотропным материалом, его механические свойства
зависят от направления силовых воздействий относительно ориента-
ции волокон.
Так, для сосны предел прочности вдоль волокон равен 400 кПсм\
поперек волокон — 50 кГ/см2, для дуба соответственно 500 кГ/см*
и 150 кГ/см*. Вследствие различной сопротивляемости древесины-
вдоль и поперек волокон приходится принимать разные допускаемые
напряжения для различных направлений действия сил.
/11*
Рис. 128
Некоторые данные о допускае-
мых напряжениях для сосны и дуба
приведены в табл. 16.
В качестве примера рассмотрим
расчет соединения стропильной ноги
со стропильной затяжкой (рис. 128).
Угол между осями стропильной
ноги и затяжки обозначим а, а силу,
действующую вдоль стропильной
ноги, — #. Сечение стропильной
ноги F = hb. Конец затяжки испы-
тывает скалывание вдоль волокон под действием горизонтальной
проекции силы N
Ni = N cos а.
199
Длину части затяжки ху выступающей за врубку, определим из
условия
• __
max FCK Ъх
откуда
fck == Ьх >
а
Л\ N cos а
Необходимая площадь смятия врубки
[а ] •
I CMJ
Глубина врубки
_ TV cos а
Ы’см!
Таблица 15
Допускаемые напряжения для сварных соединений, kVIcm2,
Вид деформации Обозначение Ручная сварка (электроды с тонкой обмазкой) Автоматическая и ручная сварка (электроды с толстой обмазкой)
Растяжение [’*1 1000 1300
Сжатие [°9 1 1100 1450
Срез 800 1100
Таблица 16
Допускаемые напряжения для древесины
Вид деформации Обозна- чение Доп ускаемое напряжение, кГ/см2, для
сосны дуба
Растяжение [<* + ) too 130
Сжатие вдоль волокон и смятие торца 1*-] 120 150
Смятие во врубках вдоль волокон [асм5 80 110
Смятие перпендикулярно к волокнам (на длине бодее 10 см) 1 qCM^ Тс 2 24 48
200
Продолжение табл, 16
Вид деформации Обозна- чение Допускаемое напряжение, кГ/см2, для
сосны дуба
Скалывание во врубках вдоль волокон м 5—10 8—14
Скалывание локон во врубках поперек во- 6 8
Изгиб 2 [»J 120 150
Скалывание при изгибе 20 28
Примечание. При смятии (или скалывании) под углом а к направле-
нию волокон допускаемое напряжение имеет промежуточное значение между
1асмЗ и Гасм1 те или М и [th и может быть определено по условной формуле
Т Т
Сасм1
1 । /
| [асм^_те
1 2
—11 sin8 а
Глава 9
КРУЧЕНИЕ
§ 46. Напряжения и деформации при кручении
Напряженное состояние кручения характеризуется наличием
в стержне единственного внутреннего силового фактора — крутящего
момента Mz = Мкр (рис. 129), т. е. момента, действующего в плос-
кости поперечного сечения стержня (остальные компоненты внутренних
сил равны нулю):
Qx = Qy = N = 0; Мх = Му == 0.
Стержень, работающий на кручение, называется валом, Экспери-
ментально установлено, что при кручении вала длиной I двумя крутя-
щими Моментами Мк, приложенными по концам вала, последний
будет закручиваться, т. е. одни сечения вала будут поворачиваться
относительно других, в то время как длина вала останется неизменной.
Рассматривая кручение вала, нагруженного по схеме, приведенной
на рис. 139, легко заметить, что угол поворота ср любого сечения,
находящегося на расстоянии z от места задел-
ки вала, будет тем больше, чем больше z и кру-
тящий момент Мк. Если закручивать вал
вплоть до его разрушения и представить
зависимость ср = /(Мк) графически, то полу®
чим диаграмму кручения, вид которой для
пластичного материала приведен на рис. 131.
На этой диаграмме, как и на диаграмме растя-
жения, можно заметить ряд характерных учас-
тков и точек (1,2,3): Мпц — величина крутя-
щего момента, до которой сохраняется линей-
ная зависимость между ср и ЛГК; Мт — мо-
началу текучести; Мъ — величина крутящего
момента, вызывающего разрушение. Обычно интересуются значениями
202
моментов и деформациями, соответствующими линейному участку
диаграммы кручения, для которого справедлив закон Гука.
Крутящий момент в некотором сечении вала, являющийся равно-
действующим моментом касательных напряжений тр, действующих
в элементарных площадках dF, расположенных на расстоянии р от
центра сечения, можно выразить уравнением
Характер распределения касательных напряжений тр по сечению
устанавливается из геометрической картины деформации вала при
кручении, представленной на рис. 132. Опыт показывает, что рас-
стояния между сечениями скручиваемого вала
не меняются, а продольные линии предвари-
тельно нанесенной сетки принимают винтовой
характер. При этом прямые углы сетки иска-
жаются, как и в случае чистого сдвига. По-
следнее обстоятельство является свидетель-
ством того, что выделенный элементарный
объем любого слоя материала вала находится
в условиях чистого сдвига. Вследствие того,
что радиусы, проведенные в торце сечения,
остаются прямыми, нижележащие слои по
мере приближения к центру испытывают мень-
шую деформацию сдвига. Согласно экспери-
ментальным данным сечения, плоские до де-
формации вала, остаются плоскими и после
деформации, поворачиваясь одно относитель-
но другого на некоторый угол ф. В этом
смысл гипотезы плоских сечений, на основа-
нии которой строится элементарная теория
кручения стержней.
Для наружного слоя выделенного эле-
ментарного участка вала длиной dz (рис. 133)
Рис. 133
будут справедливы
соотношения, полученные ранее применительно к чистому сдвигу,
т. е.
* b'b
rdy
dz
203
_ ’ d®
Величина — относительный угол закручивания, имеет размер-
яя ~
ность см""1 и обозначается обычно 0.
Связь между относительным сдвигом и относительным углом
закручивания примет вид
7 = 0г. (9.2)
Выражая сдвиг 7 в наружных волокнах вала через напряжения,
в соответствии с законом Гука при сдвиге найдем связь между каса-
тельными напряжениями в крайних волокнах тг и относительным
углом закручивания 0
тг=б?0г. (9.3)
Учитывая, что радиусы сечений остаются прямыми, можно по анало-
гии с (9.3) установить связь между касательными напряжениями
в сечении стержня на расстоянии р от центра сечения и относительным
углом закручивания
tp=G0p. (9.4)
Подставляя (9.4) в (9.1), найдем
Мкр= G6 p2dF=G6Jp
F
Отсюда получим формулу для определения относительного угла за-
кручивания вала
а —
“ dz ~ GJp
(9.5)
где GJp — жесткость поперечного сечения стержня при кручении,
имеет размерность кГсм2.
Полный угол закручивания вала длиной I равен
f Ml
J GJp GJp
(9.6)
(9.7)
где GJp/l — жесткость вала при кручении, имеет размерность кГсм
(размерность момента).
Подставив значение 0 из (9.5) в (9.4), определим касательное
напряжение тр в любой точке сечения стержня
__ ^крР
Jv '
Максимальное касательное напряжение, очевидно, будет
т - МкрГ
max г j >
v
204
или
xmax ~~
^кр
Wp
(9.8)
где Wp s= —2— полярный момент сопротивления (см. (2.38)).
Для сплошного круглого вала диаметром d полярный момент
сопротивления определяется формулой (2.38) и
_ 16МКР
хтах — •
(9.9)
Для трубчатого круглого вала Wp определяется по (2.39) и
_ 16Мкр
max - '
d
где а =—отношение внутреннего диаметра вала к наружному.
Условие прочности при кручении вала записывается в виде
Мко
ттах — 1ХЬ (9.11)
Отсюда момент сопротивления вала при кручении должен быть
(9.12)
На основании (9.9) диаметр круглого сплошного вала определим
из условия
* / 16MKD
d>V (9.13)
а на основании (9.10) наружный диаметр трубчатого вала при
заданном а — из условия
’ / 16М~
D>V <9Л4>
Если крутящий момент выразить через мощность /V, л. с.
и число оборотов в минуту п, то получим
лг
= 71620 —, кГсм> (9.15)
КР п
и формула (9.13) примет вид
<9Лв)
205
а формула (9.14) запишется так:
д>71'4КМ0~^-
Если мощность К задана в киловаттах (1л. с. =0,736 кет), крутя-
щий момент может быть выражен формулой
ЛГ = 21^2. А = 97360 — кГсм. (9.18)
к₽ 0,73b п п
Помимо расчета на прочность, валы рассчитывают также и на жест-
кость, ограничивая относительные углы закручивания некоторой
допускаемой величиной [6]:
вЮах = 477<[9]’ (9Л9)
откуда полярный момент инерции, обеспечивающий допускаемую
жесткость, определится формулой
Мкп
О-ёй- (9-20)
Отсюда диаметр сплошного круглого вала должен быть
£/ 32М„_
d>V <9-21)
а наружный диаметр D трубчатого вала при заданном а
Z>>1/______32Мкр____ (9.22)
я (1 — а«) G [0] 1 1
Рис. 134
Поскольку в поперечных сечениях вала действуют касательные
напряжения, распределенные согласно (9.7) по линейному закону
(рис. 134, л), то, в силу закона парности касательных напряжений,
и в диаметральных сечениях вала должны возникать касательные
напряжения, равные по величине, но обратные по знаку (рис. 134, б)«
206
По площадкам, расположенным под углом 45° к сечениям, в кото-
рых действуют максимальные касательные напряжения, действуют
главные нормальные напряжения, равные по величине касательным
напряжениям в данной точке сечения, как показано на рис. 135.
В связи с этим характер разрушения (сдвиг или отрыв) вала при кру-
чении будет зависеть от способности материала сопротивляться дей-
ствию касательных или нормальных напряжений. Так, при кручении
деревянных валов с продольным
..........................jg-p......................расположением волокон послед*
/ ' \---------------------/г\\ ние будут разрушаться от каса-
II \Мк\ ^\/ III ч тельных напряжений, действую-
' и j i I X 11 \/Л щих вдоль волокон (трещины
*4/^ V' / продольные) (рис. 136). При кру-
\? 7 У|У чении чугунных валов разруше-
J * ние наступит под действием нор-
мальных растягивающих напря-
Рис. 135 жений, максимальное значение
которых имеет место в сечениях,
идущих по винтовой линии и пересекающих образующие под углом
45°, как показано на рис. 137,
Рис. 136
Рис. 137
§ 47. Кручение стержней некруглого сечения
При кручении стержней некруглого сечения (прямоугольных, тре-
угольных, эллиптических и др.) гипотеза плоских сечений неприме-
нима. Точные расчеты на кручение таких стержней могут быть полу-
чены методами теории упругости. Окончательные формулы для опре-
деления максимальных касательных напряжений ттах, относительного
угла закручивания 0 и полного угла
В этих формулах «7К и WK — неко- Рис. 138
торые геометрические характери-
стики, которые условно называют моментом инерции и моментом со-
противления при кручении и размерность которых соответственно
см4 и см3 (см. табл, 1).
207
Распределение касательных напряжений по прямоугольному сече-
нию стержня приведено на рис. 138. Наибольшие напряжения возни-
кают в наружных слоях посредине длинной стороны сечения (точки С
и D). Определяются они по формуле (9.23), где
Жк = а^2 (9.26)
(Л — длинная сторона; Ъ — короткая сторона прямоугольного се-
чения).
Напряжения посредине короткой стороны (в точках А и В) могут
быть выражены через тшах:
т ~ Vmax* (9.27)
Относительный угол закручивания определится по формуле (9.24),
где выражение для момента инерции при кручении JK будет
JK = $hb\ (9.28)
* h
Коэффициенты а, ₽ и 7> зависящие от отношения у, приведены
ниже
h Ъ 1 1,5 1,75 2,0 2,5 3,0
а 0,208 0,231 0,239 0,246 0,256 0,267
0,141 0,196 0,214 0,229 0,249 0,263
* 1 1,000 0,859 0,820 ' 0,795 0,766 0,753
h Ь 4,0 6,0 8,0 10 00
а 0,282 0,299 0,307 0,313 0,333
0,281 0,299 0,307 0,313 0,333
* 7 0,745 0,743 0,742 0,742 0,743
Условия прочности и жесткости при расчете на кручение стерж! я
прямоугольного сечения соответственно имеют вид:
Мко
ттах ~ а^2 И? (9.29)
о ____ кр Г fi 1
max “ 1
(9.30)
При кручении стержней, сечения которых представляют собой
равнобедренную трапецию, приближенные значения ттах и 0 могу г
быть получены путем определения указанных величин для стержня
208
с сечением эквивалентного прямоугольника, который строится по
схеме, приведенной на рис. 139.
При кручении стержня сложного замкнутого сечения, состоящего
из прямоугольных элементов (рис. 140), момент инерции равен
Рис. 139
Рис. 140
где п — 1, 2, 3, ... — номера составных простых частей рассматри-
ваемого сечения.
Так как угол закручивания для всего сечения и для каждой его
части один и тот же
Мкп Мкп Мкп мкр„
~ GJ ~ GJ ~ GJ GJ ’
к Ki Кг
то крутящие моменты, воспринимаемые каждой частью сечения,
будут пропорциональны их жесткости:
J„G
м — М —— = М —-i- :
«Pi ywKP j^g жкр ’
M = M : М — М
ШКр2 КР ’ ’ ’ • ’ mKPn МкР Jk ’
Соответственно наибольшее касательное напряжение в каждом п-м
элементе сечения будет
Мкп М / \ М / \
__ крп _ J кр / КП \ кр [ кп \
кп WK ~~ I JK
Kn Kn \ K
Очевидно,
к \ WK
к \ кп
где
_ ^кр ( кп \ _ ^кр
ШаХ 4 Ик / “ WK ’
к \ Kn/max к
(9.32)
И7 —--------!
к / 4
I к?г
\ WK /
\ кп /шах
Для стержня эллиптического сечения (рис. 141)
(9.33)
w - —
rrK- 16 >
к
(9.34)
209
тде Ъ и h соответственно размеры малой и большой осей эллипса.
Наибольшие касательные напряжения ттах возникают в наруж-
ных точках сечения, лежащих на малых полуосях, и определяются
по формуле
(9.35)
_________________________ ^кр _
ттах ~ |7к - ^b2h *
Напряжения в наружных точках, лежащих на больших полуосях,
равны
. ттах
т =-----
т
h
где тп = -&-
Условный момент инерции эллипса при кручении
Рис. 142
При кручении замкнутых тонкостенных профилей (рис. 142),
в которых стенка настолько тонка, что касательные напряжения по ее
толщине можно считать одинаковыми, равными напряжениям посре-
дине толщины стенки и направленными по касательной к срединной
линии стенки, касательные напряжения можно определять по фор-
муле Бредта:
М
t - КР
2юд
где о — площадь, охватываемая средней линией тонкостенного сече-
ния; 6 — толщина стенки.
Если толщина стенки профиля по контуру будет неодинакова,
то максимальное касательное напряжение в тонкостенном замкнутом
стержне определится формулой
_ Мкр
тах 2“Ьт1п
Относительный угол закручивания тонкостенного стержня
с неодинаковой толщиной стенки определится формулой
ds
4Gu)2 У Ъ
(9.39)
где s — длина замкнутого контура.
210
Полный угол закручивания стержня длиной I будет
__Ж ds
4tr(o2 j В
(9.40)
Формула (9.39) может быть записана в виде
где
При постоянной толщине стенки по контуру формула (9.39)
примет вид
й
4G«>«&
В частности, для круглой тонкостенной
трубы с радиусом срединной линии R при
В = const
т =
2nR
"Т“
Согласно
(9.37) и (9.41)
^кР
2nR4 ’
^кр
2nR3bG ’
(9.41)
При кручении тонкостенных стержней открытого профиля
(швеллер, двутавр, уголок) (рис. 143) можно воспользоваться теорией
расчета на кручение стержней прямоугольного сечения. В этом слу-
чае профиль разбивают на прямоугольные элементы, толщина h кото-
рых значительно меньше их длины Ь. Согласно данным, приведенным
на стр. 208, > 10, а = р = у.
Тогда для составного профиля на основании (9.31)
/К=11т26"/1п’ (9Л2>
где т] — некоторый поправочный коэффициент, учитывающий схемати-
зацию, связанную с заменой реального профиля прямоугольниками.
Ниже приведены значения коэффициентов т) для типичных профилей:
для уголкового Сечения т) = 1,00;
для двутаврового сечения ц — 1,20;
для таврового сечения т| = 1,15;
для швеллерного сечения р = 1,12.
В тонкостенных открытых профилях длину контура принято
обозначать через s, а толщину — через б. При этом формула (9.42)
примет вид
п
211
Максимальные касательные напряжения в незамкнутом про-
филе определяются по формуле
§ 48. Расчет винтовых пружин
(9.44)
Рис. 144
Цилиндрические винтовые пружины. Приближен-
ные формулы для определения напряжений, возникаю-
щих в винтовой пружине с малым шагом при ее растяже-
нии или сжатии (рис. 144), могут быть получены из рас-
смотрения внутренних усилий, действующих в сечении
витка (рис. 145), заменяющих влияние
шейной нижней части растягиваемой пружины. Под
действием поперечной силы Q == Р и крутящего
момента, равного произведению растягивающего
усилия на средний радиус R пружины Мкр = PR,
в сечении витка возникают две группы касательных
напряжений: напряжения от среза, которые условно
примем распределенными равномерно и равными
, _ Q _ 4Р
Т — F ~ nd2 ’
и напряжения от кручения, максимальное значение
которых
мысленно отбро-
Рис. 145
Q=P
" _ Мкр 16РЯ
тшах— - nd3 ’
где d — диаметр поперечного сечения проволоки пружины.
Характер распределения напряжений т' и т", действующих в се-
чении витка, показан соответственно на рис. 146, а и 146, б. Из кар-
тины распределения напряжений следует, что в наружных волокнах
витка, расположенных со стороны оси пружины (точка Л), напряже-
ния т' и т^ах совпадают по направлению. Поэтому максимальные
напряжения в пружине будут
_ 4Р 16РЯ
хтах т • ттах — ’ г6/з
16Р7?! , d\ ,Q/K4
или “'max = -^з- V + 4R ) • (9’45>
При расчете пружин большого среднего радиуса R из тонкой про-
d .
волоки, когда ут- < 1, максимальное напряжение с достаточной
степенью точности можно определить по формуле
_ 16РД
хтах— ^3 ’
212
На практике при расчете пружин в формулу (9.46) вводят попра-
вочный коэффициент k, учитывающий как влияние перерезывающей
силы, гак и некоторые другие факторы (изгиб стержня пружины, про-
дольные деформации и т. п.). В этом случае формула (9.46) примет вид
ттах ~ (9.46а)
V д
Рис. 146
0,615
т
Значение поправочного коэффициента k зависит от отношения радиуса
пружины R к радиусу витка г и определяется по формуле
, 4m —
k = ----------------
4m —
R
где т = —.
Г д
Значения коэффициента k для различных соотношений
приведены ниже:
А.3456789 10
Г
$АТ)
k 1,58 1,40 1,31 1,25 1,21 1,18 1,16 1,14
Удлинение (или осадка при сжатии) пружины определяется по формуле
. 64Р/?3м
Gd*
(9.48)
где п —число витков пружины.
При расчете пружин на прочность в случае статической нагрузки
допускаемые напряжения на срез следует выбирать в зависимости от
диаметра проволоки, из которой изготовлена пружина. Для закален-
ной пружинной стали при диаметре проволоки d = 6 мм [т] =
= 50 кГ/мм*\ при d == 10 мм [т] = 40 кГ/мм2\ при d — 12 мм [т] =
= 35 кГ/мм\ для хромоникелевой стали при d == 12 ™ 16 мм [т] ==»
= 70 кГ/мм\ для фосфористой бронзы с G = 4,4 105 кГ/см? при
d = 16 мм [т] = 13 кГ/мм2.
В случае изменяющихся нагрузок указанные значения [т] должны
быть уменьшены примерно на 30%, а при непрерывной работе пру-
жины в условиях переменных нагрузок — на 60%.
Часто при расчете амортизационных пружин (пружин для смягче-
ния резких толчков) за основу берут кинетическую энергию Т, кото-
рую должна поглощать пружина (рессора) при эксплуатации.
213
При таком (энергетическом) подходе объем пружины при задан-
ном допускаемом напряжении [т] определяется по формуле
г_ 4GT
№ •
Конструируя пружину по найденному объему, следует выбрать
ее размеры 7?, d и п с таким расчетом, чтобы при проверке осадки пру-
жины X не было закрытия зазоров между витками.
Конические винтовые пружины. На практике приходится встре-
чаться с коническими пружинами (в виде усеченного конуса). Если
R± и R2 — соответственно минимальный и максимальный радиусы
концевых витков пружины, то максимальное касательное напряжение
может быть определено по формуле (9.45) или (9.46) после замены
радиуса R величиной большего радиуса R2:
__ 16РД2
"'max — •
Осадка конической пружины определяется по формуле
Х = + (Ъ + Ъ).
§ 49. Концентрация напряжений при кручении
Максимальное напряжение в зоне концентраторов (надрезов»
выточек, отверстий, резьбы и т. п.) при кручении можно найти по форг
муле
ттах ~ а?тн’
где тн — номинальное напряжение, вычисляемое методами сопро-
тивления материалов, в частности, для круглого вала радиуса г по
формуле
ах — коэффициент, показывающий, во сколько раз в месте концентра-
тора возрастет номинальное напряжение. Коэффициент ах опреде-
ляется методами теории упругости
или экспериментально на упругих
моделях и обычно называется тео-
ретическим коэффициентом кон-
центрации.
На рис. 147 приведены графики
72р\
зависимости ах = / I — I для различ-
ных соотношений (рис. 148).
Для случая кручения трубчатых
тонкостенных валов с малыми попе-
речными отверстиями (рис. 149, а)
коэффициент концентрации около
отверстия равен четырем.
Действительно, выделив вокруг
отверстия главными площадками,
по граням которых будут действо-
вать нормальные напряжения а = т
214
(по площадкам ab и cd — растягивающие, а по площадкам ad и
be — сжимающие), некоторый элемент (рис. 149, б) и представив
картину напряжений у отверстия от растягивающих напряжений
Рис. 150
(рис. 150, а) и от сжимающих напряжений (рис, 150, б), раздельно
находим в точках т (см. § 27)
°тах = За 4- а = 4<з;
в точках п = — °-За = — 4а.
Поскольку Мкр а = а — т — “ Wp ’
то о = 4а - 4 Мкр max н * рур •
Таким образом, в рассматриваемом случае коэффициент концентра-
ции = 4.
215
Глава 10
ИЗГИБ
§ 50. Нормальные напряжения при плоском изгибе
Расчетные формулы для определения нормальных напряжений
при изгибе обычно выводят из рассмотрения плоского чистого из-
гиба (рис, 151, а).
Рис. 151
Чистый изгиб характерен тем, что из шести компонентов внут-
ренних усилий только Мх не равен нулю, а
N = Qx = Qy = 0; Му = Mz = 0.
Условие равновесия, связьь
вающее напряжения и внутренние
усилия в поперечном сечении
балки (рис. 151, 6) (опускаем
индекс х у момента), будет иметь
вид
\<sydF=M. (10.1)
F
Геометрическая сторона за-
дачи вытекает из рассмотрения
картины деформации той же
балки (рис. 152).
Наблюдая за деформацией сетки, предварительно нанесенной на
балку (рис. 152, а), легко заметить (рис. 152, б), что продольные линий
сетки при чистом изгибе искривляются по дуге окружности, контуры
поперечных сечений остаются плоскими кривыми, пересекая продоль-
ные линии под прямыми углами. Это свидетельствует о том, что при
чистом изгибе поперечные сечения остаются плоскими и, поворачиваясь^
становятся нормальными к изогнутой оси балки,
216
В сжатой области (сверху) волокна укорачиваются, а в зоне рас-
тяжения удлиняются. Зона растяжения и зона сжатия в сечении балки
разделяются нейтральным слоем с радиусом кривизны р. Длина ней-
трального слоя при изгибе остается неизменной.
Относительное удлинение некоторого волокна, находящегося на
расстоянии у от нейтрального слоя (рис. 153, а), при чистом изгибе
найдем из рассмотрения деформации
участка балки длиной dz (рис. 153, б):
(р + У) ^9 — dz
dz
е =
(р + у) rfe —prfe __ £
pt/O р
(10.2)
5
Рис. 153
Подставив (10.2) в физическое уравнение (закон Гука)
(10.3)
1
выразим нормальное напряжение а через кривизну у:
а = -у- у. (10.4)
Далее подставив (10.4) в (10.1), получим
1 Л4
р EJx ’
(10.5)
а подставив (10.5) в (10.4), найдем формулу для определения нормаль-
ного напряжения в любом слое сечения балки на расстоянии у от
оси х\
Из анализа формулы (10.6), называемой формулой Навье, следует,
что изменение напряжений по высоте сечения подчиняется линейному
закону; напряжения максимальны в слоях с координатой утах, а ми-
нимальны (равны нулю) при у = 0, т. е. в нейтральном слое.
217
Подставляя <s из (10.6) в условие N == j adF = 0, найдем, что»
F
ydF = = 0. Отсюда следует, что нейтральная линия сечения
F
(ось х) проходит через центр тяжести сечения.
В случае прямоугольного сечения балки с высотой h
м h
_ MVmox _ 2 _ М
°max Jx - jx ~ Wx
(10.7),
где Wx = —— = —~ называется моментом сопротивления сечения
^max Л
2
при изгибе (см. § 11).
Рис. 154
Очевидно, для любого сечения, имеющего горизонтальную ось
симметрии (рис. 154), возможен единственный момент сопротивления
при изгибе в плоскости yzt определяемый по формуле
--—
^тах
Рис. 155
Если сечение не имеет горизонтальной оси симметрии (рис. 155),
следует различать два момента сопротивления
4 , Jx
Wx - —— и W^== —А~
^тцх 2/щах
218
Эпюра нормальных напряжений а в последнем случае не будет
симметричной, как для сечений с горизонтальной осью симметрии,
а будет иметь вид, показанный на рис. 155 и 156.
Формулы для определения нормальных напряжений, полученные
из рассмотрения чистого изгиба, оказываются с достаточной степенью
точности пригодными для определения
нормальных напряжений в общем
случае изгиба, когда Q не равно нулю.
§ 51. Касательные напряжения
при изгибе
бтах
Рис. 156
В общем случае поперечного изгиба
(рис. 157, д), когда в сечениях стержня,
S3 изгибающего момента М, дей-
т также поперечная сила Q,
в сечении балки возникают не только
нормальные а, но и касательные напря-
жения т, равнодействующая которых
равна Q.
Вывод формулы для определения
касательных напряжений в сечении основан
методе сечений, диф-
и поперечной силой
на
ференциальной зависимости между моментом
и законе парности касательных напряжений.
Рис. 157
Рассматривая условия равновесия элемента А1т1т2А2 (рис. 157, а,
б, в, 5), выделенного сечениями А А2В2 и ть т2 из балки, нагру-
женной сосредоточенной силой Р (рис. 157, д), найдем:
(10.8)
219
где
Т = t'bdz\
Nt=^'dF = №dF=-j-Sx(y);
J J J X J X
F F
(10.9)
(10.10)
JV2 = 4.c'dF = f (J?.+ dJtf) dF = M± dM (1011)
J J X J X
F F
Подставляя (10.9) — (10.11) в (10.8) и учитывая закон парности
касательных напряжений, получим формулу Журавского для опреде-
ления касательных напряжений при поперечном изгибе балки про-
извольного сечения
, QSX {у)
' Wx’
(10.12)
где Sx(y) — статический момент относительно нейтральной линии
той части площади F(y)t которая расположена ниже или выше рас-
сматриваемого слоя материала на расстоянии у от нейтрального слоя
балки; Ь(у)^ ширина сечения в рассматриваемом слое материала.
Характер изменения касательных напряжений по высоте балки в об-
щем случае зависит от формы сечения балки.
Поскольку в рассматриваемом сечении Q и Jx постоянны (а в слу-
чае прямоугольного сечения и ширина Ь постоянна), то, как видно из
формулы (10.12), закон изменения касательных напряжений в сечении
будет определяться законом изменения статического момента Sx(y).
В частности, рассматривая статический момент площади CinlmyA1
(рис. 157, г), находим
_. . _ . . bh2 I.
S(y)^F(y) 3/ц,т=-8- |^1
4у2 \
/г2 )
(10.13)
т. е. статический момент по высоте сечения изменяется по параболи-
ческому закону. Очевидно, по такому же закону по высоте балки
изменяются и касательные напряжения, достигая максимума при
у = 0:
тшах
Ф^тах
bJx
Q ™
v 8 _ 3 Q
, bh3 ~ 2 F ’
Ь12
(10.14)
где F = bh — площадь сечения балки.
В наиболее удаленных от нейтральной линии точках в наруж-
ных волокнах ;/ = ± у и т = 0.
Эпюра касательных напряжений для прямоугольного сечения
220
балки, построенная на основании формулы (10.12) с учетом (10.13),
приведена на рис. 158. При этом
X = J2_
2bh
Рис. 158
Рис. 159
Из формулы (10.15) видно, что максимальные касательные
напряжения в стержне прямоугольного сечения, действующие
в нейтральном слое, отличаются от средних напряжений, которые
- х Q
могли быть получены по формуле тс == , в полтора раза, т. е
Tmax ““
(10.16)
Для круглого сечения (рис. 159) формула Журавского для верти-
кальной составляющей полного касательного напряжения может быть
записана в виде
4(9 / v2 \
Закон изменения т по высоте и в данном случае оказывается пара-
болическим. В наиболее удаленных от нейтральной линии точках
А (при у = ± R) т = 0. Наибольшее касательное напряжение будет
в точках нейтральной линии (при у = 0):
t _А_2___________133_2_
“ах ~ з ~ 1>0й р •
Эпюра т для круглого поперечного сечения, построенная на осно-
вании формулы (10.17), приведена на рис. 159.
Формулу для выражения максимальных касательных напряже-
ний применительно к поперечному сечению любой формы по аналогии
с (10.14) можно в общем виде представить так:
(«>.18)
где k — коэффициент, зависящий от формы сечения. Так, например,
для прямоугольника к = 1,5, для круга k = 1,33.
221
Эпюры нормальных и касательных напряжений, построенные
соответственно на основании формул Навье и Журавского для дву-
тавровой балки № 12 (Jx = 4^3 см4; 8тах= 38,5 см3) при М =
» 200 кГм и Q = 1 т, приведены на рис. 160. Наблюдаемые на эпюре т
перепады объясняются резким
& изменением ширины балки при
Рис. 160
переходе от полки к стенке.
§ 52. Расчет на прочность
при изгибе
При изгибе балки в общем
случае, когда М =£ 0 и Q =# 0
(рис. 161, а), из-за неравно-
мерности распределения нор-
мальных и касательных на-
пряжений отдельные элементы
материала находятся в усло-
виях различного напряженного состояния (рис. 161, б). При этом
только наружные волокна (элементы 1, 2, 12, 13, 14) находятся в уело-
№,1т
*л=Ч/г 4г
Рис. 161
виях линейного напряженного состояния (растяжения или сжатия),
все остальные выделенные по высоте балки элементы (3—И) нахо-
дятся в условиях плоского напряженного состояния, причем элементы
222
(6, 7, 8) нейтрального слоя находятся в условиях чистого сдвига.
Характерно, что при деформации изгиба максимальные значения нор-
мальных и касательных напряжений оказываются в разных точках
сечения. В точках, где а максимально (наружные волокна балки),
т = 0, и, наоборот, там, где т максимально (нейтральный слой), <з = 0.
Таким образом, логично рассматривать два условия прочности»
относящиеся к различным точкам балки:
а) по нормальным напряжениям
______^Лпах f i
°max ~ pF
(10.19)
б) по касательным напряжениям
^max^max _ г ,
%ах = ----bJ---
(10.20)
Обычно из условия прочности по нормальным напряжениям
(10.19) определяют размеры балки принятой формы поперечного
сечения
М
(10.21)
а потом проверяют, удовлетворяет ли выбранное сечение балки усло-
вию прочности по касательным напряжениям (10.20).
Однако такой подход к расчету балок, особенно балок с опти-
мальной формой сечения, обеспечивающей минимальный вес и необхо-
димую прочность (двутавровые, тавровые, швеллерные и другие про-
фили), еще не гарантирует прочность балки. Во многих случаях в се-
чениях балок имеются точки, в которых одновременно действуют
болыйие нормальные напряжения (мало отличающиеся от максималь-
ных) и большие касательные напряжения.
В частности, такое сочетание 9 и т имеет место при изгибе двутавро-
вой балки в зоне перехода полки в стенку (рис. 160). В таких случаях
возникает необходимость проверки балки на прочность по главным
напряжениям.
В общем случае плоского напряженного состояния, испытывае-
мого элементом материала балки (например, элемент 5 на рис. 161, б),
на который действуют оа = а, определяемое по формуле Навье, та =»
= тр = т, определяемое по формуле Журавского, и при = 0, глав-
ные напряжения находят по формулам (см. § 33):
’I = 4 [в + /’3 + 4т»];
«и
а2 = 0;
5з=у1°-1/Га2 + ‘4т21-
(10.22)
Зная главные напряжения, можно по различным теориям проч-
ности выразить эквивалентные напряжения, которые не должны пре-
вышать допускаемые.
223
Таким образом, условия прочности по различным теориям могут
быть представлены в виде (см. § 37)
%кв I = 4-1° + + 4т21 < [°]; (ю.гз)
°экв II = 0>35° + °>35 Ко2 + 4т2 < [о] (при р. = 0,3); (10.24)
°9Кв Ш = + < [»]; (10.25)
°экв IV = /з2 +3т2 < [0]; (10.26)
°8кв М = Цг 3 + < [о], (10.27)
где
т —
k±L
l*_J *
При проверке прочности балок по главным напряжениям часто
возникает необходимость знать не только величины главных напря-
жений в той или иной точке, но и их направления.
В частности, это необходимо при конструировании железобетон
ных балок, в которых арматуру следует располагать таким образом,
чтобы она сопротивлялась действию растягивающих напряжений.
В любой балке можно построить ли-
Рис. 162
нию, касательная к которой в каж-
дой точке будет характеризовать
направление главных напряжений.
Такая кривая называется траекто-
рией главных напряжений. Траекто-
рии главных напряжений зависят от
вида нагрузки и условия закреп-
ления балки.
Очевидно, через каждую точку
балки проходят две траектории
главных напряжений, соответственно
<уг и о3, пересекающиеся между
собой под прямым углом. В железо-
бетонных балках обычно стремятся
располагать арматуру в направлении
траектории главных растягивающих
напряжений (рис. 162).
§ 53. Концентрация напряжении при изгибе
При изгибе, как и в случае растяжения или кручения, в местах
резкого изменения размеров или формы поперечного сечения возни-
кает концентрация напряжений. При статических нагрузках концен-
трация напряжений в деталях, изготовленных из пластичных материа
лов, не является опасной благодаря перераспределению напряжений
в зоне концентрации за счет текучести материала. В случае хрупких
материалов, когда не приходится рассчитывать на перераспределение
224
напряжений и ограничение максимальных напряжений пределом теку-
чести, концентрацию напряжений следует учитывать и при статиче-
ских нагрузках. Допускаемые максимальные напряжения в зоне кон-
центратора не должны достигать временного сопротивления материала,
являющегося в данном случае предельным.
Влияние концентрации, возникающей в месте резкого изменения
диаметра вала (рис. 163, а), мо-
жет быть учтено введением неко-
торого коэффициента концентра-
ции а:
атах “ и,
Р1
где ао ® =?, найденное для вала
н W
с диаметром, равным меньшему
диаметру рассматриваемого вала
(рис. 163, б) при отсутствии
концентратора.
Значения коэффициента кон-
центрации а для различных со-
D
отношении диаметров и ра-
диусов закруглений в галтели г,
найденные методами теории упру-
го Q D . _
гости для -г- = 3 и —г = 1,5,
а а
Рис. 163
приведены в виде графика а = (рис. 164).
Максимальные напряжения в зоне концентратора в пластине
с двусторонней выточкой гиперболической формы при чистом изгибе
в плоскости пластины (рис. 165) могут быть определены по следующей
формуле, полученной методами теории упругости:
max
8 5-1186
223
где
ЗМ ,>
°н = -тг-лт (& — толщина пластины).
н 2а*о
На рис 166 приведен график зависимости cmax oi отношения
. На рис. 167 даны зависимости теоретического коэффициента
концентрации а для различных отношений ширины пластины Н
к ее ширине h в месте выточки радиуса р от отношения .
На рис. 168 даны графики распределения напряжений в зоне
концентратора в виде эллиптического отверстия в широкой пластине
при чистом изгибе в ее плоскости для случая, когда ~ = 25, По мере
226
удаления от дна выточки, а также в направлении вдоль оси у напря-
жения быстро убывают. Штриховой линией показано распределение
напряжений, вычисленных по элементарной теории изгиба путем
учета ослабления сечения отверстием.
Наибольшее напряжение, возникающее у дна выточки, можно
определить по формуле
атах ~~ сн G р ) ’
где
ЗЛП .
°н “2б..... (° — толщина пластины).
Рис 169
Зависимость от отношения — графиче-
шал р
ски представлена на рис. 169.
Для круглого отверстия атах = 2о. При
Р 00 °тах *
В случае глубокой круговой выточки на
теле вращения (рис. 170) наибольшее напря-
жение при изгибе возникает у дна выточ-
ки, где материал находится в условиях объемного напряженного
состояния. На рис. 170 показано распределение всех трех главных
напряжений (сг, с2 и а3), а на рис. 171 дано распределение напряжений
и о2 У Дна выточки в зависимости от
отношения — при различных коэффи-
циентах Пуассона.
В случае мелких выточек на деталях
вращения величина коэффициента концент-
рации зависит, главным образом, от отно-
шения радиуса закругления г к диаметру
выточки. На рис. 172 приведен график за-
(г \
-jl для этого случая.
Весьма распространенными концент-
раторами в работающих на изгиб дета-
лях машин являются различного рода
поперечные отверстия. Концентрация
в этом случае зависит от отношения
диаметра поперечного отверстия d к диа-
метру детали D, в которой это отверстие
сделано. Зависимость коэффициента кон-
d
центрации а от — приведена в виде
графика на рис. 173.
Рис. 170 В заключение заметим, что при изгибе
возможна не только концентрация нор-
мальных напряжений, но и концентрация
касательных напряжений в местах резких переходов, в частности
в сечении 1—1 двутавровой балки (рис. 174, а, б). Однако
вследствие закруглений в местах перехода стенки в полку конвент-
8*
227
рация напряжений снижается и вместо эпюры, показанной на
рис. 174 б, имеет место эпюра, покачанная на рис. 174, е.
Рис. 173
§ 54, Дифференциальное
уравнение изогнутой оси
балки (упругой линии)
В инженерной практике при-
ходится проводить расчет балок
при изгибе не только на проч-
Рис. 174 ность, но и на жесткость, или де-
формативность.
Деформативностъ балки в данном сечении характеризуется про-
гибом w и углом поворота 0. Информацию о w и 0 как функциях коор-
динатной оси, совпадающей с осью балки, можно получить, зная
уравнение изогнутой оси балки (упругой линии).
Упругой линией называется плоская кривая, форму которой при-
нимает ось балки при плоском изгибе, На рис. 175 и 176 упругие
линии изображены тонкими линиями.
228
Уравнение упругой линии легко получить» вная выражение кри-
визны через изгибающий момент M(z) в данном сечении и изгибную
жесткость EJ поперечного сечения балки (см. § 50)
и выражение кривизны через координаты точки в данном сечении
w и г, известное из курса высшей математики:
d2w
dz2
_М2р
dz / J
(10.29)
Имея в виду знаки для М и - в зависимости от действия моментов
и расположения координатных осей (рис. 177), можно приравнять
правые части выражений (10.28) и (10.29), приняв в обоих случаях
229
знак «плюс». Тогда точное уравнение изогнутой оси балки получим
в виде
(10.30)
d2w
dz2 _ М (z)
Г. , / dw УР “ EJ
L1 + \dr) j
В связи с малостью деформации балки (о>тах = (0,01 —0,001) I и
/ dw\2
в Формуле (10.30) можно пренебречь членом » О2.
Тогда дифференциальное уравнение (10.30) можно переписать
в виде
d2w __ М (z)
(10.31)
Это п есть то исходное (приближенное) дифференциальное уравнение
изогнутой оси балки, решая которое можно получить уравнение
упругой линии w = / (z) и уравнение угла поворота 6 = = fa (z).
Проинтегрировав уравнение (10.31) первый раз, найдем
е (г) = 4г = (* + К- (Ю.32)
az J
Проинтегрировав второй раз, получим
w (z) = f dz f dz + Ctz + Ct, (10.33)
J J
где Сг и C2 — постоянные интегрирования, которые должны быть
найдены из граничных условий (условий на концах балки).
Если балка имеет на конце заделку (рис. 178), то прогиб
и угол поворота в ней равны нулю:
wB = 0; = 0.
Для балки на двух шарнирных опорах (рис. 176) равны нулю
прогибы на этих опорах:
wA = 0; wB = 0.
Учитывая дифференциальную зависимость между изгибающим
моментом М (z) и распределенной нагрузкой (см. § 18)
выражение упругой линии (10.31) можно записать в виде;
<‘ом>
230
Рис. 178
В этой форме дифференциальное уравнение применяют обычно при
расчете балок на упругом основании, а также при рассмотрении коле-
баний балок.
Для иллюстрации нахождения уравнений упругой линии w =
= /(z) и угла поворота 0 = f(z), а также определения максимальных
прогибов wmax и углов 0юах (представляющих наибольший практиче-
ский интерес) путем интегрирова-
ния дифференциального уравнения
(10.31) рассмотрим несколько при-
меров.
Для консоли постоянного попе*
речного сечения при действии сосре-
доточенной силы Р на свободном
конце (рис. 178) изгибающий момент
на расстоянии z от конца будет
М (z) = Pz,
а дифференциальное уравнение изо-
гнутой оси консоли (10.31) примет
вид
d2w _
dz2 “ IT'
Pz
После двукратного интегрирования будем иметь
= "" ПЁТ + C1Z + с*
Ct и С2 определим из граничных условий:
при z = I w = 0;
при z = I 0=0.
Из второго условия получим
C1 2EJ '
из первого условия получим
3EJ •
Уравнения прогиба и угла поворота следующие:
Р73 Г 7 / 7 VI
w(2) = ~ wi2~3t + vtj j; <10-35)
(10.36)
231
Максимальные значения w и 8 имеют место на свободном конце
балки в точке А:
л Р1*
wmax 1л 3ej ’ (10.37)
fi -fl Pl*
max — 2EJ ’
(10.38)
Отрицательное значение fA свидетельствует о том, что прогиб направ-
Ж7
Рис. 179
лен в сторону, противоположную
положительному направлению оси и>\
положительное значение 8 показы-
вает, что поворот сечения происхо-
дит против часовой стрелки.
В случае изгиба балкщ шар-
нирно опертой по концам и несущей
равномерно распределенную наарузку
q (рис. 179), выражение изгибаю-
щего момента будет
а дифференциальное уравнение
изогнутой оси балки (10.31) примет
вид
d*w
dz*
-ld.$Lz
EJ \ 2
Проинтегрировав дважды, получим
0 (z\ — - — -Ql , z2 _ -A- z3 _J_ r .
( ' dz ~ iEJ 6EJ +
al
W 12EJ z3 ~ 24£/ + ClZ ^1 2’
Граничные условия следующие:
при z = 0 w = 0;
при z = I w == 0.
Из первого условия находим w (0) = С2 — 0;
из второго условия имеем
1 ~ ’
Подставив значения С± и С2 в выражения для w (z) и 6 (г),
получим уравнение упругой линии и уравнение угла поворота
(10.39)
232
Максимальное значение прогиба будет посредине пролета
“’max — f — — 384 "gj" • (10.40)
Максимальные значения угла поворота будут на опорах
•<»>-•. —& = <,М1>
~ ев-
Уравнения изогнутой оси балки, значения максимальных проги-
бов и углов поворота опорных сечений для различных схем нагруже-
ния простейших балок приведены в табл. 20.
При определении перемещений отдельных сечений балки в ряде
случаев удобно использовать графоаналитический метод, основанный
на аналогии между дифференциальным уравнением упругой линии
(10.31) и дифференциальной зависимостью (3.3), связывающей изгибаю-
щий момент и интенсивность распределенной нагрузки. Указанная
* М (z)
аналогия позволяет вычисление прогиба w по известному
вести так же, как определение М (z) по q (z). Ордината эпюры
М (z), деленная на EJ, рассматривается как некоторая фиктивная
нагрузка
/ч М (z)
^Ф EJ ’
В этом случае искомые прогиб w(z) и угол поворота 0(z) опреде-
ляются соответственно как изгибающий момент Мф(г) и поперечная
сила Q$(z) в сечении z фиктивной (взаимной) балки от фиктивной
нагрузки, равной эпюре M(z) действительной балки
w(z) =
Мф (и) .
EJ 1
(10.42)
0(z)
ж EJ ’
Фиктивная (взаимная) балка имеет длину участков, равную длине
участков действительнрй балки, а опоры выбирают таким образом,
чтобы удовлетворить условиям деформации действительной балки.
Сочетания опорных закреплений действительной и фиктивной балок
приведены в табл. 17.
Последовательность определения деформаций следующая. Строит-
ся эпюра изгибающего момента действительной балки; выбирается
соответствующая схема фиктивной балки; фиктивная балка нагру-
жается эпюрой изгибающего момента действительной балки; в выбр'ан-
ном сечении фиктивной балки определяются фиктивные изгибающий
момент Мф(г) й поперечная сила Q$(z) и по формулам (10.42) вычисля-
ются значения прогиба и угла поворота в выбранном сечении*.
• Приведенный выше графоаналитический метод, или метод Мора, основан-
ный на идентичности дифференциальных уравнений, не является единственно
возможным. Недавно были сформулированы и другие аналогии, позволяющие
заменить нахождение силовых и деформационных факторов в одном (заданном)
стержне нахождением деформационных и силовых факторов в другом (фиктив-
ном, взаимном) стержне (см. Дополнение, стр 610).
233
При вычислении M$(z) и Q$(z) в случае сложной конфигурации
эпюры изгибающего момента действительной балки, представляющей
фиктивную нагрузку, ее разбивают на отдельные простейшие фигуры
(см., например, рис. 240), площади и положения центров тяжести
которых известны (табл. 23).
§ 55. Определение перемещений в балках по методу
начальных параметров
Определение перемещений методом непосредственного интегриро-
вания дифференциального уравнения упругой линии в случае балок
с большим числом участков, каждый из которых характеризуется
своим выражением изгибающего момента, сопряжено со значитель-
ными трудностями, связанными с определением произвольных постоян-
ных интегрирования. При интегрировании дифференциальных урав-
нений для п участков приходится иметь дело с двойным числом nocio-
яниых интегрирования/Добавив к двум основным условиям на кон-
цах балки 2(п—>1) условий непрерывного и плавного сопряжения всех
участков упругой линии, можно составить 2п уравнений для опреде-
ления этих произвольных постоянных.
Задача становится весьма трудоемкой уже при трех участках.
Технику определения постоянных интегрирования можно существенно
упростить, сведя ее к отысканию всего двух неизвестных прогиба
и угла поворота в выбранном начале координат. Этот метод, называе-
мый методом начальных параметров, основан на следующих исходных
положениях:
1. Начало координат выбирают в крайней левой точке рассматри-
ваемой балки и оно является общим для всех участков.
2. Выражение для изгибающего момента M(z) составляют путем
вычисления моментов сил, расположенных слева от рассматриваемого
сечения, взятого на расстоянии z от начала координат.
3. При включении в уравнения внешнего сосредоточенного мо-
мента М, приложенного на некотором расстоянии а от начала коорди-
нат, его умножают на множитель (z—а)0, равный единице.
4. В случае обрыва распределенной нагрузки (например, в сече-
нии z = d, рис. 180, б) ее продлевают до конца рассматриваемого
участка, а для восстановления фактически действующей на балку
нагрузки вводят компенсирующую нагрузку обратного направления
(экстраполированную дополнительную нагрузку и нагрузку, ее ком-
пенсирующую, принято показывать пунктиром).
5. Интегрирование уравнений на всех участках производят без
раскрытия скобок.
При таком подходе выражение изгибающего момента на любом
участке представлено через все силовые факторы, действующие слева
от рассматриваемого сечения, включая изгибающий момент Мо и по-
перечную силу Qo, действующие в сечении, совпадающем с началом
координат. Величины Мо и Qq так же, как и прогиб и угол поворота
0О в начале координат, называются начальными параметрами. Изги-
бающий момент для балки, показанной на рис. 180, а, при выборе
начала координат в точке К на расстоянии z (в четвертом участке
балки) будет*
М (Z) = Мо + Qoz + М (z - а)0 + Р (г - b) + qc + к ,
234
где
, t л Qd Яс
к = tg Р = ~d^c •
После подстановки изгибающего момента в дифференциальное
уравнение (10.31), двукратного его интегрирования и определения
постоянных интегрирования, которыми оказываются начальные
параметры
(71 = 0О и С2 == w0,
уравнения 0 (z) = fa (z) и w (z) = f (z) в самом общем виде могут
быть записаны так:
•(,>“е- + -Ег["»ТГ+ S
(10.43)
235
» w = «>, + V + -Jj- [«.-J + S +
+ Si<i=*_s^]. (10.44|
л Полученное уравнение (10.44) обычно называют универсальным
уравнением упругой линии, имея в виду» что оно может быть приме-
нено при любых расчетных схемах балок.
В уравнения (10.43) и (10.44) подетавляют нагрузки, расположен-
ные слева от рассматриваемого сечения; знаки слагаемых определя-
ются знаком соответствующих силовых факторов. Итак, определение
перемещений по методу начальных параметров в конечном итоге сво-
дится к определению величин начальных параметров Qq, Мо, 0о и ^о-
При этом статические начальные параметры Qq и Мо находятся из
условия равновесия балки, геометрические начальные параметры 0О
и w0 определяются из условий на опорах. Для определения начальных
параметров Q() и Мо могут быть использованы данные табл. 9, а для
определения параметров 0О и данные табл. 20.
Воспользуемся полученным универсальным уравнением для
определения прогибов консоли (рис. 181, а, б) в точках z = а и z =?= 2 а.
Уравнение упругой линии на участке, где приложена нагрузка <?,
будет иметь вид
aj(z) = wo4-0oz + -gj-
[»2 «3 лг4 *1
Из условия равновесия балки
находим
мй~мА~-^
Qq Ra
Так как начало координат совпа-
дает с заделкой, то геометрические
начальные параметры —- прогиб и
угол поворота в начале координат—
равны нулю:
w0 = 0; 0о = 0.
Уравнение прогибов на первом
участке АС будет
qa2 z2
qaz?
qz*
1Г
При z а
qa*
wc-‘~'HET'
236
Уравнение прогиба на втором участке СВ будет
, ч 1 Г qa* z2 , г3 z4 , (z—-а)4
2~ 21 +qa 31 Qir + q~Tl . •
Положив z = 2а, получим для прогиба свободного конца
Iqa4
Wb ~ 2AEJ ’
Определив прогибы и углы поворота, можно проверить жесткость
балки или подобрать ее сечения из условия жесткости:
“’max = / < И-
Допускаемые величины прогибов (/] устанавливаются из условий
эксплуатации или экспериментальных данных,
В случае расчета перемещений для балок с промежуточным шар-
ниром универсальные уравнения (10.43) и (10,44) должны быть запи-
саны в виде:
е (г) =х е0 4 a {Z - г)* 4- -Ij- [м0 ~ + 2 М + Q„ +
’-SfeT^-4]’ <10-45)
M<> 2! + 2j M 21
1
w (z) = w0 + 0O3 + a (z e) 4- -gy
у I?
iimnni
(10.46)
Я Р
я
1ПШП
Рис. 182
£
___/
&
I
Рис. 183
где a — угол, на который отличаются углы поворота стержней, при»
мыкающих к промежуточному шарниру, т. е.
6 Мл + а==е(е)Пр>
где в(в)пр —угол поворота правого стержня в точке * (рис. 180);
8 («)а — угол поворота левого стержня в том же шарнире S.
Слагаемые с сомножителем (г — /) < 0 при расчете не учитываются,
237
Взаимный угол наклона а является дополнительной неизвестной
величиной в уравнениях (10.45) и (10.46). Как и начальные параметры
ю0 и 0О, угол а определяется из условий на опорах. В зависимости от
расчетной схемы балки возможны два основных случая составления
опорных условий.
1. Угол а может быть определен из условия равенства нулю про-
гиба на правой опоре (рис. 182).
2. Угол а определяется совместно с 0О из условия равенства нулю
прогибов на опорах В и С (рис. 183) путем решения системы двух
алгебраических уравнений.
§ 56. Расчет балок переменного сечения
на прочность и жесткость
Ступенчатые стержни. При расчете на прочность ступенчатого
стержня, изготовленного из пластичного материала, условие проч-
ности будет иметь вид
max г
max “
(10.47)
Для стержня из хрупкого
материала следует учитывать кон-
центрацию напряжений в местах
сопряжения двух сечений разного
диаметра. В этом случае условие
прочности должно записываться
в виде
М
0таХ = ааН=“17-<[а1>
(10.48)
где а — теоретический коэффи-
циент концентрации напряжений
(см. Приложение 2). В обеих фор-
мулах W — момент сопротивле-
ния ослабленного сечения.
При определении деформации
ступенчатой балки (рис. 184, а)
необходимо записать дифферен-
циальное уравнение изогнутой
оси балки для каждой из ступе-
ней, изгибные жесткости попереч-
ных сечений которых соответствен-
но равны EJt1 EJ2, EJ3\ . t.:
d2w M (z) t d2w _ M (z) d2w __ M (z)
dz^TTT’ dz2 “ EJ2 ' dz2 ~~ EJ3 ’
Заменим ступенчатую балку эквивалентной балкой постоянного
сечения с моментом инерции JOt равным моменту инерции одного из
участков балки, например второго Jo == /2. Умножив числитель и
знаменатель правой части дифференциального уравнения (10.49)
для произвольного участка п на получим
d2u> М (z) <70_ М (z) _ М (z) _
238
где pn = -~р--коэффициент приведения. В примере, приведенном
Jn
3
на рис. 184, : J3 1:3 :2 и = 3; р2 « 1; ₽з«« у •
Так как изгибающий момент является линейной функцией нагруз
ки, то для каждой части балки вместо умножения на коэффициент
приведения изгибающего момента можно умножить на этот коэффи-
циент все внешние нагрузки данной части вместе с внутренними усили-
ями Q и М в местах сопряжения различных ступеней (рис. 184, б, в).
Соединив отдельные части друг с другом и просуммировав внутренние
усилия на стыке, мы получим балку постоянного сечения с изгибной
жесткостью EJQ, нагруженную приведенными внешними нагрузками
(т. е. нагрузками, измененными в раз). При этом в местах сопря-
жений будут наблюдаться скачки поперечных сил и изгибающих мо-
ментов, соответственно равные
= Q1 (р2 pi); Дф2 = Qz (?з Рг)»
В местах стыка частей балки надо приложить дополнительные
сосредоточенные "силы и сосредоточенные моменты, определяемые при-
веденными формулами.
Полученная таким образом эквивалентная балка (рис. 184, г)
будет иметь упругую линию, полностью совпадающую с упругой
линией заданной ступенчатой балки (рис. 184, а).
Перемещения такой балки можно определить, интегрируя диффе
ренциальное уравнение.
d2w __^пр
dz2 EJq
где Мпр — момен!? приведенных внешних нагрузок и дополнительных
нагрузок Д(> и ДМ, определяемый, как и в обычной балке, нагружен-
ной по схеме рис. 184, г. Для определения w и 0 можно воспользо-
ваться также универсальными уравнениями (10.43) и (10.44) метода
начальных параметров, рассматривая приведенную балку, как балку
постоянного сечения с изгибной жесткостью поперечного сечения FJ0.
Балки с непрерывно меняющимся по длине сечением. Бели раз-
меры сечения стержня непрерывно изменяются по дайне, то формулы,
полученные на основании гипотезы плоских поперечных сечений,
становятся неверными, как и сама гипотеза. Однако, как показывают
результаты расчета методами теории упругости, в том случае, когда
угол наклона образующей поверхности стержня-к его оси не превы-
шает 15—20°, распределение нормальных напряжений по высоте се
чения можно принимать линейным^ ТсФдй, естественно, можем ис
пользовать обычное условие прб^йости и дифференциальное уравне
ние упругой линии
amax ~ Jy (z) (10.52)
d2w М (z)
dz2 ” EJ (z) ’
239
Погрешности при вычислении касательных напряжений по фор-
муле Журавского
т QS(y)
(10.54)
в данном случае будут ббльшими, чем при вычислении нормальных
напряжений по формуле Навье:
_ М (z) у
(10.55)
Формулу (10.53), выражающую дифференциальное уравнение
изгиба балки переменного сечения, можно записать в виде;
d2w ^пр
HzT ~ EJ0
(10.56)
где Мпр (z) == (z) — приведенный изгибающий момент, смысл
которого отличен от Мпр, входящего в формулу (10.51); Jo— момент
инерции какого-либо сечения, обычно наибольший или наименьший.
Балка, момент сопротивления которой меняется пропорционально
изгибающему моменту от внешних нагрузок, называется балкой рав-
ного сопротивления изгибу. Рассчитывается такая балка по формуле
И/(г)=4-Т-)- (10.57)
В балке равного сопротивления изгибу максимальные напряже-
ния в любом сечении одинаковы и равны допускаемым [а]. Примером
балки равного сопротивления может служить консоль с постоянной
шириной Ь и переменной высотой h(z) (рис. 185), определяемой из фор-
мулы (10.57). Тогда
Рис 185
{ 6 - [а] “ [а] ’
откуда
Н2) = (10.58)
Следовательно, высота балки меняется по
параболическому закону, достигая максиму-
ма в месте закрепления
h0 — h(l)—]/~ VI
Поскольку согласно (10.58) в месте приложения силы (z = 0) h (0) = 0,
то высота концевого сечения определяется из условия среза:
3 Р __ 3 Р
ттах~ 2 F ~ 2 bh
240
откуда
ЗР
2b [тJ
Балки параболического очертания (весьма выгодные с точки
зрения экономии материала) из-за сложности изготовления применя-
ются весьма редко. На практике часто применяют балки равного
сопротивления изгибу, имеющие по-
стоянную высоту h и переменную ши-
рину b(z) (рис. 186).
Закон изменения ширины b (z) най-
дем из (10.57). Тогда
г
Рис. 186 Рис. 187
ЗР
6(z)= [а] 2-
I
При s=»-s-
°0 \ 2 / 2А2 [а] ‘
Максимальный прогиб такой балки равного сопротивления изгибу
определяется на основании (10.56). По известным Jo, J (2) и их
отношению
Л ______ &0 _
J (z) ~ b (z) 2z
241
молено наити приведенный момент
W W ~ j (z) Jo - 2 j (2) 4 -
Подставляя Мпр в (10.56), получим
d2w __ Pl
dz2 4EJQ
Интегрируя это уравнение дважды, находим
CZ ~fl W - £J0 \ 4 Z + C
1 / Plz2
w(2) = ^(~8~ + C12 + C2
Постоянные интегрирования Ct и C2 определяются из условий
w (0) = 0;
Отсюда
с2 = о.
о
Тогда
w (z) ---
Рис. 188
1 I Pl 9 Pl2 '
EJq \ 8 2 8 2
а
, (Л р/3
“’max ~ w \ 2 / ~ 32£/0 ’
Отсюда видно, что максимальный прогиб
балки равного сопротивления изгибу в полто-
ра раза больше прогиба балки постоянного
сечения с изгибной жесткостью EJh.
Приведенная теория с достаточной степе-
нью приближения может быть использована
при расчете рессор (рис. 187, а, б, в, г).
При этом ширину концевых сечений
балки определяют из условия среза
(см, рис. 188, а, б).
откуда
Тшах р ~
. ~ Р
242
Формулы для определения размеров поперечного сечения и макси-
мального прогиба балок равного сопротивления приведены в табл. 18.
В табл. 19 даны уравнения упругой линии и углов поворота попереч-
ных сечений консольной балки переменной высоты для некоторых
случаев ее нагружения.
§ 57. Расчет на изгиб с учетом сил инерции
Действие сил инерции следует учитывать при расчете элементов
конструкций, испытывающих большие ускорения. Примером может
Рис. 189
служить спарник АВ (рис. 189), соединяющий две оси, одна из кото-
рых (OJ является ведущей. Любой элемент длины спарника, описы-
вающий окружность радиуса г с угловой скоростью со, испытывает
центростремительное ускорение со2г. Интенсивность возникающей по
длине спарника распределенной нагрузки будет:
где F — площадь поперечного сечения спарника; 7 — удельный вес
материала; g ускорение силы тяжести.
Наиболее опасным положением спарника будет крайнее нижнее
положение А^В^ при котором нагрузки от сил инерции ди и от соб-
ственного веса qG суммируются:
9щах = <?и + 9С = + 7** = 7^ (1 + •
Рассматривая спарник как балку на двух шарнирных опорах,
найдем максимальный изгибающий момент
м _ Ятах12 _
штах“- g “ 8 V g
и наибольшее напряжение
__ ^тах _ F уР L , <п2г
°тах ~ w — W 8 \ g
Силы инерции необходимо учитывать также при расчете шатуна
поршневой машины (рис. 190). Шатун испытывает инерционную рав-
номерно распределенную нагрузку, меняющуюся по линейному за-
кону, как показано на рисунке. Максимальная интенсивность нагрузки
243
будет в точке А, когда кривошип составляет с шатуном угол, рав-
ный 90°,
2
чтах g * ’
где г — радиус кривошипа.
Максимальный изгибающий момент в шатуне (при рассмотрении
его как шарнирно опертой балки), как известно, будет на расстоянии
-4= от точки В\
/з
__ ^тах*2
тах~ 9/3 ’
а максимальное напряжение
^шах
Q SX2 .....
max jy
Подставляя значение <7тах# найдем
а =
тах~ 9/ЗИ^ “ 9/ЗЖ*
§ 58» Касательные напряжения при изгибе балок
тонкостенного профиля. Центр изгиба
Формула Журавского дает верные результаты в случаях, когда
ширина балки (сечения тп На рис. 191) достаточно мала по срав-
нению с высотой Л.
В сеЧенйях mxni полок тонкостенного профиля (рис. 191, б, а, д)
напряжения т, параллельные усилию Q, настолько малы, что ими
Рис. 191
можно пренебречь. Но в этих полках возникают касательные напря-
жения тп, перпендикулярные усилию Q. Учитывая малую толщину
полки t, можно считать, что касательные напряжения тп по толщине
полки распределены равномерно. Тогда их величина определится по
формуле
, (*)
п 7Г'
(10.59)
244
найденной из рассмотрения условия равновесия части полки двутавро-
вого сечения длиной dz (рис. 192), где статический момент
с/ \ М \ h
(10.60)
Из сопоставления формул (10.59) и (10.60) видно, что закон распреде-
ления касательных напряжений по ширине полки определяется зако-
ном изменения статического момента
S (х), т. е. тп распределяются по линей-
ному закону.
Эпюры касательных напряжений,
^построенные для двутаврового сечения
№ 20 при Q = 10 000 кГ, приведены на
рис. 193.
Касательные напряжения в полках
тонкостенных профилей существенно вЛйя-
ют на характер нанряженного состояния
стержня и вид его деформации.
Если сечение имеет две оси
симметрии и силовая плоскость про-
ходит через одну из них (рис. 194, а),
то в сечении возникают равнодей»
ствующие усилия в стенке Тот
и в полке Тп (рис. 194, б). В силу
симметрии полок усилия Гп вза-
имно уравновешиваются на каждой
полке.
Иначе обстоит дело, если глав-
ная центральная ось, перпендику-
лярная к нейтральной линии, не яв-
ляется осью симметрии (рис. 195, а).
Касательдые напряжения в стенке
и полках приводятся соответственно
к усилиям Гст и Гп (рис. 195, б).
При этом вертикальными касательными напряжениями в полках
пренебрегают. Поперечная сила
<? = Уог
При этом она не проходит через центр тяжести, а будучи равнодей-
ствующей силы Тот и двух сил Та, создающих пару, смещена на
245
некоторое расстояние xG (рис. 195в б) и пересекает нейтральную
линию в точке С.
Смещение хс можно определить из условия
откуда
Жс==_£е!_ (Ю.6О
Учитывая, что
Ь—х0 Ь—эс0
rn = ‘ j Va:== j =
— (*^о" ~~(Xo~~d)
Ь—х0
Q^-X.-xyt-^ Qt(h t}(b dy
J t
— (^0—
формулу (10.61) можем записать в окончательногм виде:
t{h_ty{b-dy £
с~ kJ 2 •
Смещение равнодействующей относительно центра тяжести сече-
ния на расстояние xG + я0, как это следует из схемы, приведенной
на рис. 196, а, приводит к тому, что внешняя нагрузка Р, действую-
щая в плоскости zy, вызывает в сечении балки не только переменный
по длине изгибающий момент M(z) = Pz, но также крутящий момент
(рис. 196, б) Мкр = Р(#о 4- хс) за счет смещенности поперечной силы
Q = Р (являющейся равнодействующей усилий Гст и Тп). Вследствие
этого балка будет не только изгибаться, но и скручиваться (рис. 196,г).
Для предотвращения скручивания на практике используют сим-
246
метричные сечения из двух шнеллеров или выносят точку приложения
нагрузки из главной плоскости так, чтобы она проходила через точку С
(рис. 196, г).
В этом случае участок балки длиной z полностью уравновесится
силами Р, Q (z) = Р и моментом М (z) » Pz и кручения не будет. По-
этому точку С называют центром изгиба или центром жесткости.
Рис. 196
Центры изгиба всех сечений балки расположены на прямой, которая
называется осью жесткости балки (рис. 196, б). Очевидно, для стерж-
ней с двойной симметрией ось жесткости балки совпадает с осью, на
которой размещены центры тяжести сечений.
§ 59. О расчете балок на упругом основании
При рассмотрении балки на сплошном упругом основании
(pnq. 197) предполагается, что реакция основания в каждой точке про-
порциональна упругому прогибу w в этой точке.
Обозначив коэффициент пропорциональности, имеющий размер-
Рис. 197
Рис. 198
ность —SEfL- t буквой а, получим, что интенсивность реакции осно-
(длина)2 J
вания равна aw.
Таким образом, при заданной внешней распределенной нагрузке
q(z) полная распределенная нагрузка, действующая на балку, будет
р (z) = q (z) — aw (z). (10.62)
247
Расчет балок на упругом основании представляет собой статиче-
ски неопределимую задачу. Интенсивность реакции основания связана
с деформацией балки, поэтому при решении задач сначала необходимо
найти упругую линию балки. Дифференциальное уравнение изогну*
той оси балки согласно (10.34) можно записать в виде
= -4- [<? (*) ~ ™ (*)]• (10.63)
Если распределенная нагрузка отсутствует, g(z)=O (рис. 198),
уравнение (10.63) примет вид
й-”» I»-64'
Выберем начало координат на левом конце рассматриваемого
участка, где начальными параметрами будут: wQ, 60> и Qq. Введя
обозначение
{L имеет размерность длины) и заменив независимую переменную z
безразмерной абсциссой
5 L ’
уравнение (10.64) перепишем в виде
d*W 1 / л
_ 4-4^ = 0.
Общее решение этого уравнения:
w = (\е^ cos 8 + Сsin £ + С3е~~^ cos £ + sin 5.
Взяв соответствующие производные от (10.65), выразим
них М и 0:
(10.65)
через
= 0£ == (cos 5 — sin 5) + С2^ (cos 5 + sin 8) —
— C3e~z (cos 6 4- sin 5) + C^e-l (cos £ _ sin £);
(10.66)
(С sin £____С cos 8_____С е~^ sin £ I
+ C4e^cosS); (10.67)
= ~' — *“2 (cos 5 + sin 5) — C2e5 (cos 6 — sin $) —
— C3e“’E (cos 5 — sin $) — (cos 5 — sin $)]. (10.68)
248
Положив в (10.65) — (10.68) £=0, получим выражения для
начальных параметров:
м>о = + <?3;
£0О = Ci + С2 — Cz + С4;
LW0 = _(— 2С2 + 2С4) EJ-,
L*Qq = — (2Ct — 2С2 — 2С3 — 2С4) EJ.
Решив систему этих четырех линейных уравнений относительно
постоянных интегрирования, получим выражение последних через
начальные параметры в виде:
г w° | £6о I L3%
“ 2 + 4 + 8EJ '
Г £6о . L2M« , £8<Ч
°2 ~ 4 + kEJ + 8EJ 5
г, __। .
сз - 2 4 -г 8EJ ’
/Д £»М0 , L3Q0
* it ikEJ "Г 8EJ •
Подставив выражение постоянных интегрирования в (10.65) —
(10.68), найдем
w (z) = »aYt (5) + /ДУ2 (5) 4- Ya (?) + Yt (5);
в (z) = в0У, (5) + У2 (5) + Уя (5) - У4 (6);
aJ ihj Lt
М (z) = MgYi (?) 4- LQgYg (5) - a.&WgYg ($) - а£М0У4 (I-);
Q (г) = QbYt (?) - «LwgYg (?) - а2?0оУ3 (?) - MgYi (g),
Lj
где Ух, У2, У3, У4 — функции А. Н. Крылова*;
Ух ($) == ch $ cos g = (И + cos $;
У2 (ё) = v (ch 5 sin 5 + sh 5 cos 5) =
di
= [(^ + sin 5 + — e”~^) cos
У3 (S) = у sh 6 sin $ = у (e^ — ^) sin £ j;
1
^4 (£) == у (ch £ sin £ sh $ cos 6) =
== У t(*e + e^) sin $ cos $].
* Значения этих функций приведены в Приложении 4. Более подробные
таблицы имеются в [Ъ 15].
249
При дифференцировании функций Крылова имеют место следующие
важные зависимости:
LYi == —4У4; £У2=Ух; 1У3'== У2; LY\ = У3.
В общем случае (рис. 199), когда на отрезке Oz действует
сосредоточенный момент Mi в точке с абсциссой сосредоточенная
сила Pi в точке с абсциссой bi
Рис. 199
и равномерно распределенная на-
грузка qc на участке от z = с до
z = d, общие уравнения для ш, О, Q
и М будут иметь вид:
w(z) = waYA + V-y2(r) +
if / 7 \ I Z \
4- —J+
\ Zj /
—rS’1 [>"(№)-<1Ш»
о W = V1 (1) + -17 {+ (1) + ^£2уз (1) -
- woy4 j + l 2 Л/{У2 + i2 X PiY* (г-=^) +
+ £3 X 4 y4 ; (10,70)
M (z) = Moyt f J-j + Q0LY2 - a^w0y3 ) - aZ, 360У4 +
+ S ^y> (^)+L X+£2 X 4y* -
-y8(z-=M|; (10.71)
\ /.
Q (z) = £(71 (-£ )- aiw„y2 ) - а£*60У., (-J ) - ^2- У4 ) -
—4 S M^y4 + X p*y> (Чг) +
JU 4ети \ La / \ Lj /
+ zj?i[y!(^!j-y2[^j], (10.72)
Таким образом, при известных начальных параметрах wQi 0О>
и ()0 величины w (z), 6 (2), М (z) и Q (z) могут быть определены
в любом сечении с координатой z по формулам (10.69) — (10.72).
Начальные параметры в каждом конкретном случае могут быть
определены из условий на концах балки. Эти условия для различных
случаев закрепления балки при совмещении начала координат с левым
ее концом представлены ниже.
250
Условия на концах балки Левый конец (2 = 0) Правый конец (*= 0
Левый конец Правый конец W 8 м Q и 8 м Q
Свободен Свободен — — Мо Со — — М, Qi
Свободен Оперт — м0 Со 0 — —
Свободен Заделан — — м„ Со 0 0 — —
Оперт Оперт 0 —- м. — 0 — —
Оперт Заделан 0 — Мо — 0 0 — —
Заделан Заделан 0 0 — — 0 0 — —
Mi и Qi — соответственно внешние сосредоточенные момент и сила
на правой опоре.
При выборе начала координат на левом конце однопролетной
балки два начальных параметра всегда известны. Для определения
двух других параметров необходимо решить систему двух алгебраиче-
ских уравнений, составленную из условий закрепления правого конца
балки.
§ 60. Изгиб балок, материал которых
не следует закону Гука
Диаграммы растяжения и сжатия для Материалов, не следующих
закону Гука (чугун, камень и др.), показывают, что напряжения
растут медленнее деформаций и отставание роста напряжений от де-
формаций значительнее при растяжении, чем при сжатии (рис. 200).
В этом случае нейтральная линия не проходит через центр тяжести
поперечного сечения, а смещается в сторону центра кривизны оси
балки (рис. 201). По известному радиусу кривизны нейтрального
слоя р на основании гипотезы плоских сечений относительное удлине-
ние волокна, находящегося на расстоянии у от нейтрального слоя,
как и прежде, определяется известной формулой
р
(10.73)
Поэтому прежде всего следует найти положение и радиус кри-
визны нейтрального слоя.
251
Рассмотрим балку прямоугольного сечения из материала, не сле-
дующего закону Гука (рис. 202). Учитывая, что для многих материалов
зависимости 8 = /(о) при растяжении и сжатии могут быть представ-
лены в виде
₽ _ ь -П. __ k т
ер “ Vp’ сж ~
(10.74)
где ftp, /гсж, п и т — величины, характе-
ризующие физические свойства мате-
риала, положение нейтрального слоя
можно определить из условий
^2 = J «/2? = 0;
F
J 'ydF~M~Q
tlf, flji
b (J °p^-J ’саЛ)=0; (10.75)
о о
Л1
*>(( acmVdv) = M‘ (10.76)
о 0
На основании (10,74) и (10.73)
1 1
p W M
Подставляя (10.77) в (10.75) и (10.76) и интегрируя, соответственно
получим
1 1
« / fel V Й т ( h2 \тк -о-
«+1 \ frpp; 1 т+1 vw / 2
1 1
П \П I ГП 1 / ^2 \ Ш 72 пл
2re + 1 \ fcpP / 2m + 1 *cffip j
(10.78)
(10.79)
Учитывая, что /ix 4- /i2 = h, из последних двух уравнений найдем
р, ht и h29 а затем по формулам (10.77) — напряжения ор 0 aCJK
Можно решить и обратную задачу: определить наибольший
допускаемый изгибающий момент по допускаемым напряжениям
растяжения [ор] или сжатия [асгк]. При этом, пользуясь формулами
(10,77), определяют напряжения в крайних волокнах
/ \п
гр)шах ~ °х \ fcpp J 1
1
(ссж)тах °2
т
. (10.80)
/^2 \
/
252
На основании (10.80) выражения (10.78) и (10.79) можно предста-
вить в виде
п . т , л
—— Gihi-----------т-г- а2п2 = 0;
1 1 1 т + 1 J 2
(10.81)
Ь°^ + 2^ГТ 4’2^ = М‘ (1°-82)
<672 -f- 1 6772 -f- 1
Кроме того, из уравнения (10.80) следует, что
a"fcp
^2 С2^СЖ
(10.83)
Пользуясь соотношением (10.81) — (10.83) и учитывая, что
hr + можно по известному [ар| или [асж] определить поло-
жение нейтральной оси и допускаемое значение изгибающего мо
мента [М]
В случае, когда материал еле
дует закону Гука, но модули уп-
ругости при растяжении 2?р и сжа-
тии £сж неодинаковы (обычно
^сж>^р)» эпюРа нормальных на
пряжений будет иметь вид, приве-
денный на рис. 203, а максималь-
ные напряжения при известном
действующем изгибающем моменте
М для стержня прямоугольного се-*
чения будут определяться по фор-
мулам
(10.84)
В случае, когда напряжения определяются через относительные
деформации в крайних волокнах, найденные с помощью тензомет-
ров, формулы (10.84) лучше представить в виде
ЗМ
асж~ М2
есж
ер
£р
есж
°Р~ Иг2
(10.85)
253
Таблица 17
Схемы действительных и соответствующих им фиктивных балок
254
Таблица 18
Балки равного сопротивления изгибу
255
g Таблица 19
Уравнения упругой лжннж ж угла поворота поперечных сечений консольной балки переменной высоты
Схема балки и нагрузки Уравнение упругой линии Уравнение угла поворота
I Z 1 " Г |n j 2 l а /7 ч а 1 EJrs L a+"z 1 2(«+г) 1 22? {l -z> 2L\ PL3 Г 2г-j-a _ 21 +al EJ0 L2(a4-«)2 27? J
ИИИ111 < ”2£j0 (2а1и a + z («+ *)Hn (« + *)-U~ 2£2 (I — «•) + (a4-z)ln£ — a2 / 1 1\ r\ 2 \ a + z L ) pL3 f. L 2EJ0 [ a 4-2 /1 1 \ — 2a — i- + \a + z L / , J i O] + a \2 (g + z)2 2Z,2 /]
I ' I
со
5-1186
N>
сл
^°£3_ Jq/t (л _l_ za [in (a -4- z} — 11 — 3aL In L — 3a In L _L (I z\ J.
GE J I ' z GE J Ql L a+z IV ZJ T
'^ГПСД I J — 3a2 In —; h(3aln£+r L 9 г 2 ) (^ 2)“b a 4~ z \ Ь ALr / / 1 + 3a2 -4 \a + z 1 \ L )
4 /7^ / 1 1 \ 4-T[Z2-(a + z)2]+ 2 (e + /—£ ) + 3ab a3 / 1 Т\(« + г)а 1 L2/J
< u-Л M£S F z . 1 21 +al ML3 Г 1 -Л1
I , 1 EJa [ 2L2 1 2 (g + zj 2£2 J EJa L 2 (a + Z)2 2L3 J
Таблица 20
Уравнения упругой линии, максимальные прогибы и углы поворота концевых и опорных сечений
статически определимых балок постоянного поперечного сечения
Схема балки Уравнение упругой линии w (z) и максимальный прогиб / Угол поворота 6
М°А ,w К z 0<2</ мор /. а2 Wz~ 2EJ \ l] t Mttla n 2КЛПрИг-0 fl Moi е==ЁГ при z = 0
— в 1
* И 0<z<a U>z 4т 1(^1 + - Z>2 ~ (“ - z)2 “ - M2 (a + b -;z)2] a z < a + b wz = o|t[(^i + ^2) (Z-z)2-M2(« + 6-z)2] a + &<z</ + zY z 2EJ V / 1 0==Л_[(м1 + л/2)г- th J -Mia-M2 («4-6)1 при z = 0
_а*
•
<0 * f - 2EJ [(Л/1 + Jf2) Z« — Mi«2 — M2 (a + 6)2] при z = 0
,w ^Fcrcccd I j z 0 z << I ml3 Г z . / zVl Wz &EJ [ 31 + k 11 J f~ 3EJ п₽иг-° A — ml‘ 0 “ 2EJ при z — 0
i tn О w Z z 0<z<Z _ Pl4 L o^./zVl Wz 6Ej{2 3Z+U/J pp t = ~ 3ES При г“° a Pl2 0'“ 2EJ при z = 0
Продолжение табл» 20
Схема балки Уравнение упругой линии w (z) и максимальный прогиб / Угол поворота 6
w Г к g 1 Z? р ' z 7| 2 1 1 ^04^* 1 ” СЗ • *Т CQ N | | о «0 I « *>! С£5 —ыч СО S'"*» О V V/ Н II N N 7 In V ;i v 1Л ср » ° 1Г "Р « ” со лЬ 1 1 1го II со 1ч». 53 3" s₽ 50 II II S* } Pbz ® ~ 2EJ при 2=0
Г Л 1ШНШ Z \_z 0<z< 1 _ Гч / 2 _L ( Z VI Wi ~ 24£J[3 4 I +\ I / J 8£J nPaz=0 n_ 0_ HE J при 2=0
। I
w(z) =
0<2<6
qP |\ , я3 , «4
24EJ [ 4 Z3 “Г“7Г —
^4 Tq z а3 , а4
24EJ [ 4 /3 + /4 -
___?1V (z — 6)41
Z3 / I + Z4 Z4 J
. № О л а*\
I 24£J \3 4 Z3 + Z4 / ПрИ Z “ °
12QEJ
_z_ z5
i +
ql*
1&ej при z = °
при 2=0
9 = -24Ё7 праг = 0
Продолжение табл, 20
Схема балки Уравнение упругой линии w (z) и максимальный прогиб / Угол поворота В
i fTrrr^ I ; Z 0 2 Z /X (ал ЛК Z 1 к Z<L w^>— 120E/V 15 г+5 г* ) . И А ' = -12сГ ~ЁТ “Риг = ° 9 = ~&Т ПРИ z = 0 oihJ
w ^ггГГ^ ;Z 0< а •»=-т£Ж5-5т+4)- <^(r я±-1.ч д2>! г 1 гй 1 1 fl ffi °. a 4-4— 'l 9 24EJ V 8 I '*'3 I2 ) при z==0
g J Z z — 5Jb 8 +3 l2 j i 4- a2/3 j f qal* /_ _ a . a3 \ A ' ЗоМ5 5г+/3)прИг-0
О z^a
"W--
fl qal3 ( а
я2\
14
при z = O
1№EJ (20“10Т 2 ?) ПРН г — 0
_ __ 109?Z4 Г 140 z 32 z5 ]
192022,7 109 ’ I +109 ’ Z5 J
гг(з)
__ IWql* 140 z
192022/ 119 ‘ I +
fl 7 ql*
9==96 ~ЁТ пРиг = °
32
109
64
109
10,9?Z4
19222J при г-О
Продолжение табл, 20
Схема балки Уравнение упругой линии w (z) и максимальный прогиб / Угол поворота 6
,1 И* Л 9K_j< тптптЕм Z Д'- 0 < z w(z)— 49nffz 11?1 + 4?2 5(3<h+<72) I + z4 z5 1 + 5?i + (^2 — <7i) -j5“j 9= ^2W T ?~lS ПРИ 2 = 0
W ^м0 z L - f- ® z I t \ Z —4— _L w (z) QEJ V I 3 I* + Z3 / M„l2 I w 16EJ “РИ Z 2 f = — 0,0642 при z = 0.422Z EJ n MqI 9 3EJ п₽иг-° A M^l , 9- 6EJ nPH2~Z
I
0<z<7
w (z)=~~£j [(2лл+м*)т-
-ЗМ^+^-Л^)-^
6 = _ . \ ZE J , MJ\ +--0ЁТ) °₽BZ = 0
0 = J^iL4 GE J 1 MJ 3EJ п₽и z — г
0<Jz<e
V /, а2 а 13 а®\ а
6EJ [12~~1 ~8 ' УГ) при2 = —
MJ*
3EJ
а о “3^
Ч---2-^-1 при 2 = а
й _ MJ / „ а а2 \
е-“'бжгг~6т+3-^;
при 2=0
л __ М^1 11 _ а а2\
“ EJ \3‘ 7 Ч- /? '
при z = а
6=-^®L(l—.3—)
ZEJ V I* )
w =
при z = I
П родолжение табл. 20
Уравнение упругой линии w (z)
и максимальный прогиб /
Угол поворота О
Схема балки
U?(z) =
0<z<Z/2
PZ3 z Л z3 \
48SJ V Z Z3 /
р/з I
' AQJ? T z ~9~
TqEj npHZ=:0
PZ2
6 = 16£V ПрИ z ~1
0 z a
, Pa262 Q z , z z3
W (z) = — —r7~ [A-r T---5T
4 ' ЬЕЛ \ a b a2b
Pba
6ЕЛ
(a + 2b) =
w(z)
Pa2b2 \9 l — z l — z (l — z)*
SEJl [/ b + a ab2
w = — Mipf (3/2 — 462) °₽и 2 = 4
PZ3
w~~~ ZE J
ры2У1 i/T ь3?
/ = У l1-^) ПРИ2==
2
| при z = a
PZ2 ( b b9 \
QEJ \T Z3 /
при z — 0
Pa
6ЕЛ
(Z2 —a2)
при z = Z
w(z)
Pa3
§EJ
AI z
a / a
z3
a3
w^-------firl3
'qEj l \ a } a a3
(z — a)3
a3
Pa^
w --------
6^J
b_
a
при z == a
PP z_g3^
24EJ \ I 4 Z? J
I
при z = у
a Pa (a -j-b)
2EJ
e ==Pa(a-|-&)
2EJ
при z^O
при z = I
0<z<Z
iiV q
i
2iEJ
5ql* I
384EJ при z — у
A V4
9==~’йЁГ npnz = O
® = 24Е/ ПРИ z = 1
о
Продолжение табл, 20
00
Уравнение упругой линии w (z)
и максимальный прогиб /
Угол поворота 0
Схема балки
to
О z «с а
24£J \ I Р
ab* 1 Ь3 Ъ3\
+ /з + 2 Р Р /
при z = О
d^c + Lb
I* J
tiling
w(s) =
qa4
2Ш
)2
Z
a
й_____
’ - 6EJ
w(z) =
a2l2
При 2 = 0
qa4
1AEJ
.Ji!!
a2l2
z4 (z — a)4
аЧ аЧ
12EJ \ 2Z2 /
при z — I
qa3l (, „а , п a2 \
“’==_'24£7'(4“7T + 3-p-J при2=«
qP
3&)EJ
f = —0,00652-^- при z = 0,5193/
£iJ
e==—зёбЁ7“ п₽нг=-о
fl _ 8qls ,
в — 360£Z п₽и z ~ 1
О
Продолжение табл. 20
Схема балки Уравнение упругой линии w (z) и максимальный прогиб f Угол поворота 6
ъ¥| s S 7Г 1 7 S3 T 8 “ CO rx w ^3 1 g* Is 1 сл 4 » to ° CO r---' j Д » о H» a 1 сл *» ¥ ' 1 a । * I A »L, 1 A -f- u 1 V \ t» « ~ 4S CO ~ 4 « ° t » ‘1 ts» ' ,1 a 1 ® = ~-чЙ7(40“45Т + oOUjD J \ I 4- 12 -Ja-j при z = 0 fl 9g2^ L о “2\ «- 90£Z I5 3 ej при z =I
X ^ггГШ j. ^o _ b 1 7 J 0 <C z a ~w - -S- f (10 -3 -Й - - •» -4-1 obUzV l\ г ] a al* J a z I qa&l 17 & \ z w 360EJ Ц10 3 7^) a ~ я_ ЯЬ’-l Ло 3 z>2>| 360Я/ kW z2 / ‘ при z = 0
w — 10+ 3<L-a)6] 1U al2 b*al J fl (20 15 b I 3-^1 «“ збо£/ \ ° 1 + e) при z = I
qa62i Pn ZWEJ \ Ь 44 H ~l — 13 -jT} при 2 = a
f 61_ ql4 I -ЁТ при2= 2 e iL. при z — 0 при z = Z
1 5760 ~ 30^/ ft °” ЗОЯ/
ol* I5
w(z)-- ^EJ
f_____UL.
' 120EJ
z __ z3 2 Z5
7 ~ Р ' 7 ’ ¥
I
при Z = у
5 ql*
при2 = °
. 5 qls ,
« = 192 £/ ПРИ2 = /
го
Продолжение табл. 20
Уравнение упругой линии w (z)
и максимальный прогиб /
Угол поворота 6
Схема балки
ЬЗ
Pal2 I z z3
W^~ QEJ \l ~~~F
, Pal2 [z za {I 4- a) {z — I)3
w W = -6Ё7" [-—FT ---------
Pal2
ггтят = 0,0642При z = 0,578Z
шах j
Pa2
(I 4- а) при z = 14- a
w
,W
гр
а
а
z
6
aZ3
Ра2 Г 2 z3
w (z) ------I (3Z + la} - 3 (Z + а) — +
Ра2 9
w (2) = ~ ~ЬЁГ l(3z +2а) ~3 (z + а) т +
23 (2--I
I2
A Pal П
в = -6£Г прИ2 = 0
Pal .
—SET пр’ z~‘
—Й~<2, + 3“>
при z = 14- а
0 =
а Pal
6:=-2ЁГ ПрИ2 = а
PaZ .
, = “-2£T-,npHZ = a + Z
Pa(a-HZ) Л
8= 2Ef- ПРИ 2=0
6
w
Ра2
(3Z + 2а) при z = 0 и z = И 2а
0x4 J
, Ра? I
1=~Щ- приг = а+у
6==
Ра (а + Z) о
—2Е}-- при z = 2а + Z
. qa2l2 I z z3
w^— \2EJ \T ~ Zs
w(z)
<7«3Z И , . о а 'i , (. ,
__H4 + 3-r)-4l1 +
а___zV
I "~Т/
b=iSj п₽иг=°
2
а
a z
Т I
О
' = n₽H2 = z
= +
qa2l2 I
w= 32ЁГ °рИ г== У
при z = I + а
“'max = °>0321 при 2 = °'577Z
UjJ
w
qa$
'2AEJ + За) прих = /+а
to
03
to ___________Продолжение табл, 20
Схема балки Уравнение упругой линии w (z) и максимальный прогиб / Угол поворота 9
ГЛ 1 14- । + 1 ”Г |<М CM «e|s, 'Zp || II п 1 И и м Н । 1 4- »1 °" и1 Л ТТ? т , в « - г + + Л ч- =-1” 1 "м 2t "^Г“ч £2 1 V, V •* ® ~ е 1 ~|« V К , ~ is । + us Il 'в 1^4 1°° S3 II ® г*» О II и 2 1 <м — Л II — Si ц * 5 1 II й - qP (< — ? аЙ 6 2iEJ V 2 Z2 / при z — 0 1 ь = _^3. .(1+ 24£J V 1г 1 при Z = 1 6 = _-^-(4 —+ 4-^-1) 24£J \ I3 1 I3 ) при z = Z 4- а
1
2UEJ
о<: z< а
ql3
~2AEJ
а2
Z2
О
1 — 6
а z а -j- I
....
ВШЙНН1
2zz|// 77&Т7
-° -\Л L г[-,а -
— lYi К ®2 Q а3^ а
24EJ |Д Z2 6 “К/ Т
. а3 \
— 4 I при z = О
ql3 /1 а2 \
— 4£/ \ 6 Р ) ПрИ 2 ~ а
z
«Ф)
W =
при z = а +1
90/3 fl ft q2 О. аЙ
24£7 V Z2 ~1?)
при z = 0 и z = l +2а
—-4^.1
24EJ \ Z2 I3 )
при z = I + 2а
ql4 I 5 а2\ , I
W 1QEJ \24~ FJ при z = ® + у
Глава 11
СЛОЖНОЕ СОПРОТИВЛЕНИЕ
мх
$
Рис. 204
Под сложным сопротивлением подразумевают различные комбина-
ции простых напряженных состояний (растяжения, сжатия, сдвига,
кручения, изгиба). В общем случае нагружения бруса (рис. 204, а)
в его поперечных сечениях действуют
шесть компонентов внутренних усилий1
(N> Qx, Qv, Мх, Му, Мкр) (рис. 204, б),
связанные с четырьмя простыми деформа-
циями стержня: растяжением или сжа-
тием, сдвигом, кручением и изгибом.
На основании гипотезы о независимом
действии сил напряженное состояние
жесткого стержня определяют путем сум-
мирования напряженных состояний, вы-
званных каждым видом простого нагруже-
ния в отдельности.
Аналогично деформации (перемеще-
ния) могут быть определены путем сло-
жения деформаций (перемещений), вы-
званных каждым компонентом нагрузки
в отдельности.
Принцип суммирования действия сил,
или принцип суперпозиции, применим во
всех случаях, когда деформации малы,
а материал подчиняется закону Гука. На
практике редко встречаются случаи, ког-
да в стержне возникают все шесть ком-
усилий, обычно приходится иметь дело с раз-
внутренних
их комбинациями.
понентов
личными
§61. Сложный и косой изгиб
Сложный, или неплоский, изгиб вызывается внешними силами,
действующими в разных плоскостях, проходящих через ось балки
(рис. 205, а). Изогнутая ось балки в этом случае не является пло-
ской кривой.
Если все нагрузки, вызывающие изгиб, действуют в одной пло-
скости, не совпадающей ни с одной из главных плоскостей, то изгиб
называется косым (рис. 206, а).
Обычно сложный или косой изгиб приводят к двум плоским
изгибам, для чего нагрузки, действующие в произвольных продоль-
ных плоскостях, раскладывают на составляющие, лежащие в главных
плоскостях zy и zx (рис. 205, б, 206, б). При этом в сечении возни-
кает четыре компонента внутренних усилий: QXi Qy, Мх и Му.
276
Напряжения в точках любого сечения, расположенных в первом
квадранте системы координат ху (рис. 207, а), при одновременном
действии Мх и Му определяются формулой
п _ Мху Мух
9 Т » Т •
J X у
(11.1)
Применяя эту формулу в общем случае, следует учитывать знаки
при координатах х и у.
Рис. 205
Рис. 206
277
При косом изгибе (рис. 208) имеют место зависимости
Мх = М cos а;)
* л# • (Н.2)
Му = М sm а,)
где М — изгибающий момент в данном сечении в силовой плоскости
рр (рис. 207, б).
Формула (11.1) может быть записана в виде
(Н.З)
Уравнение нейтральной линии получим из (11.1), приняв а=0:
а = ^2 + = о. (11.4)
«/х J у
Уравнение (11.4) является уравнением прямой линии, проходящей
через начало координат. Положение нейтральной линии определяется
тангенсом угла ее наклона р (рис. 207, б) к главной оси х:
а?0 м х J у
Строя векторную диаграмму моментов (рис. 208), определяют
угол а наклона силовой плоскости рр (плоскости действия момента)
tga = ^. (11.6)
Тогда угол наклона нейтральной линии (11.5) может быть представ-
лен формулой
tgf> =---£-tga. (Н-7)
J и
278
из которой видно, что в общем случае сложного изгиба, когда
Jx Jy, нейтральная линия не перпендикулярна к силовой линии.
Поскольку при косом изгибе отношение Му к Мх, характери-
зуемое tg а (11.6), постоянно по всей длине стержня, угол наклона
нейтральной линии р также постоянен, т. е. упругая линия распо-
ложена в одной плоскости п^п (рис. 208), называемой плоскостью
изгиба.
Проверка прочности при сложном напряженном состоянии осу-
ществляется на основании данных о наибольшем суммарном напря-
жении. Очевидно, при сложном изгибе атах будут в точках, наи-
более удаленных от нейтральной линии (точки А и В на рис. 209).
Рис. 208
Рис. 209
В данном случае в точке А возникают наибольшие растягивающие
напряжения, в точке В — наибольшие сжимающие напряжения.
Условия прочности будут иметь вид:
G = G .
wmax А
М*УЛ.МУХА'.
Ч---г— < 1а+Ь
J у
cmin = аВ =
мхУв ,
----7------Т~ К 1 -I'
JX J у
(11.8)
(11.9)
Jх
В случае косого изгиба (рис. 207, б) условия прочности запишутся
в виде:
sin а ув cos а\
стах “ ^Апах I j ।
\ У v х I
(хп sin а COS а\
7~у * Jx /
В частности, для прямоугольного сечения, когда
(11.10)
(11.11)
•Ту
Ув Уй
хв
формулы (11.10) и (11.11) могут быть представлены так:
., /sin а , cosa\ г _
°шах — “ ^тах у (11.12)
я. /sin а , cos а\ _ ,.л .оч
cmin °£> “* ^max Н~ уух j [°—!♦ (11.13)
Определение размеров сечения в случае неплоского
изгиба
подбора, задаваясь различными отношениями
моментов сопротивлений. Касательные на-
пряжения могут быть определены по фор-
муле Журавского
_ Qy$x, - ____QxSy
v ~ Jxb ’ х - Jyh •
Перемещения определяются по принципу
независимости действия сил. Если w — про-
гиб в направлении главной оси у\ v «- прогиб
в направлении главной оси х (рис. 210), то
дифференциальные уравнения изгиба в пло-
скостях yOz и xOz будут иметь вид
= EJy^^My. (11.14)
Уравнения (11.14) решают любым известным
способом как для простого изгиба.
прогиба в любом сечении балки может быть
Величина полного i л
получена геометрическим суммированием прогибов в разных плос-
костях по формуле
(11.15)
§ 62. Изгиб с растяжением
Совместное действие изгиба и растяжения (сжатия) имеет место
при: продольно-поперечном действии нагрузок; внецентренном растя-
жении (сжатии).
Сложный изгиб с растяжением (сжатием) прямого бруса. В об-
щем случае (рис. 211, а), когда на брус действуют продольные
и поперечные силы, пересекающие ось бруса, в сечении возникают
усилия Мх, Му, Qx, Qy, а также продольное усилие в направлении
оси z~Nz (рис. 211,6). Нормальные напряжения в произвольной
точке при этом определяются формулой
NZ . Мх , Му
(11.16)
Полагая напряженное состояние в опасной точке линейным (прене-
брегаем при этом касательными напряжениями), условие прочности
запишем в обычном виде
° max
(11.17)
280
Для сечения с двойной симметрией формула (11.16) примет вид
с N 4 М* 4 МУ
F Wx х Wy '
В случае изгиба в плоскости zy
в + м*
±~~ F ± wx *
Эти формулы применяются также при
рам и арок малой кривизны.
расчете на прочность плоских
Внецентренное растяжение (сжатие)
прямого бруса. Ядро сечения. На прак-
тике часто изгиб сочетается с растяжени-
ем (сжатием), что обусловлено внецентрен-
ным приложением нагрузки, параллельной
оси стержня, когда равнодействующая
Р не совпадает с осью балки (рис.
212). Обозначим координаты точки при-
ложения равнодействующей хр и ур,
а расстояние этой точки до оси z, называемое
эксцентриситетом, — е. Внутренние усилия
в любом сечении равны:
N = Р\ Му = Рхр\ Мх = PyPi
а напряжения в произвольной точке сечения
определяются формулой
N . Му . Мх ...
^=-г + -77ж+—у'
или
Р I XpF ypF \
+ + (11.20)
Г \ у J Х /
Рис. 212
Эту формулу можно выразить также
через радиусы инерции
Р Л . хр . Ур \
\i+~fx + -tV •
\ /
(11.18)
(11.21)
281
Уравнение нейтральной линии и = 0 находим из (11.21):
хр
Ур
— Уо = ‘“I-
1х
(11.22)
Отрезки, отсекаемые нейтральной линией на осях у и х (рис. 213),
найдем из (11.22), положив хо = О, !/о = О,
.2
Ун
.2
1х
Ур
(11.23)
Из (11.23) следует, что нейтральная линия пересекает координатные
оси в точках, принадлежащих квад-
ранту, противоположному тому, в ко-
тором находится точка приложения
силы Р.
Условия прочности для точек
с наибольшими растягивающими и
наибольшими сжимающими напряже-
ниями (соответственно точек Л и В
на рис. 213) можно записать в виде:
°тах “ ° А — р И Н ХА 4"
\ 1У
Ур \
+ -ГУА <Р+1; (11.24)
1х /
Р Л Хр
ст1п — ----рГ I 1 хв
\ 1у
(11.25)
Эпюры напряжений приведены на рис. 213.
Для стержня прямоугольного сечения условие прочности удобно
представить следующим образом:
_ _ [ Мх | Му Г 1
атах “ F ~г Wx "Г Wy
(11.26)
Формулы (11.24) — (11.26) справедливы и в случае, когда силаР
является сжимающей, при условии, что нет опасности потери устой-
чивости.
Расстояние нейтральной линии от центра тяжести и величины
зон сечения, испытывающих растягивающие и сжимающие усилия,
зависят от эксцентриситета е. Очевидно, одна из зон может отсут-
ствовать (при растяжении — зона сжатия, при сжатии — зона растя-
жения), а нейтральная линия не будет пересекать сечение.
Представляет большой практический интерес, особенно при вне-
центренном сжатии колонн из материалов, плохо сопротивляющихся
растяжению (например, кирпичной кладки), знать то максимальное
значение эксцентриситета, при котором в сечении не будут возни-
кать напряжения растяжения, т. е. нейтральная линия будет каса-
тельной к сечению.
282
Область вокруг центра тяжести сечения, внутри которой прило-
жение силы Р вызывает во всех точках поперечного сечения напряжения
одного знака, называется ядром сечения. Для определения ядра
сечения необходимо задаваться различными положениями нейтраль-
ной линии, проводя ее касательно к контуру и нигде не пересекая
его (рис. 214), и вычислять координаты соответствующих точек при-
ложения силы по следующим, вытекающим из (11.23), формулам:
.2 .2
*₽ =—(Ц-27)
ун Хв
Вычисленные таким образом точки и определят контур ядра сечения.
Рис. 214
Рис. 215
При повороте нейтральной линии относительно некоторой
неподвижной точки контура сечения, например точки А, точка при-
ложения сйлы перемещается вдоль некоторой прямой, например
2—3.
Для построения ядра сечения какой-либо фигуры, например
прямоугольника (рис. 215), необходимо рассмотреть ряд положений
нейтральной линии, совпадающих со сторонами сечения. Совместив
нейтральную линию со стороной CD (положение 1—1), получим:
z/H = -?£-; ян= оо ; тогда на основании (11.27)
где
,2_ Jx № 52 ф .2_ А _ bh3 _ Я2
1X~ F ~ i2bh ~ 12 ; ly ~ F ~ 12bh ~ 12 *
Таким образом, мы определим координату точки 1 ядра сечения.
Совмещая положение нейтральной линии со стороной AD (положение
2—2), аналогично получим
h
ян=^- —
283
а координатами точки 2 ядра будут
9
ур=°;
*н
А
6 •
Задаваясь соответствующими положениями нейтральной линии 3—3
и 4—4, по аналогии определим координаты точек ядра 3 и 4.
В табл. 21 приведены форма и размеры ядра сечения для раз-
личных сечений брусьев.
§ 63. Изгиб с кручением
Круглый вал. Совместное действие изгиба и кручения является
наиболее характерным случаем нагружения валов. В этом напряжен-
ном состояний имеют место пять компонентов внутренних усилий:
^кр — Му, Мх\ Qy и Qx*
При расчете валов сначала строят эпюры изгибающих моментов
Мх и Му, результирующего момента М, а также крутящих момен-
Рис. 216
Рис. 218
284
тов Л/кр и устанавливают опасное сечение (рис. 216, а, б, в, е, д).
Результирующий изгибающий момент определяют по формуле
м = 1/м2 + мъ.
V X ‘ у
(11.28)
По известным М и Мкр в опасном сечении определяют макси*
мальные нормальные и касательные напряжения в опасных точках
сечения (рис. 217) по формулам:
м 1А/2 + м2 °тах = 1Г= W (11.29) Л/ V
Главные напряжения в наиболее опасной точке (точка В на ряс. 218)
будут (см. § 52)
ai = y (a + V<a2 + 4:T2); а2 = 0; а3 = (а — ]/а2 + 4т2). (11.31)
Для проверки прочности элемента, выделенного у опасной точки,
следует воспользоваться одной из формул соответствующей теории
прочности:
°экв М - Цр ’ + < И; (11.32)
°вкв IV=/’8 + 3x2<[o], (11.33)
где
Формула (11.32) пригодна при лг<1 для хрупких материалов и при
тп = 1 для пластичных материалов.
Подставляя в формулы (11.32) и (11.33) выражения для напря-
жений и учитывая, что Wp = 2W, получим
%кв м = ~уу [“— + М* +
+К мкр + <+<] < [°]; (Н.34)
%кв IV = V0.75М2р + м2 + М2 < [,]. (11.35)
Вторые сомножители в этих формулах представляют собой приведен-
ные моменты Мпр, действие которых эквивалентно совместному
285
действию моментов Мх, Му и Мкр в соответствии с принятыми
теориями прочности
«п. м - +<+«'. «1 «*>
Мпр IV = К°-75Мкр +М*+Му = К0-75Мкр + М* (11-37)
Аналогично для других теорий прочности получим:
мпр I = у + /< + Мр + Мкр] ’ (1Г38)
мпр П = 0.35 ]/Мх + Му + °-65 V +м*у + (11-39)
а
S
Рис. 219
эпюры MXt Му и Мкр
(при р, = 0,3);
Мпр Ш = ]/^+^ + <р. (11-40)
Условия прочности (11.34) и (11.35)
можно выразить одной формулой
МПГ)
°Экв = пГ<[а]-
Отсюда
М
(11.42)
laJ
а диаметр вала определим из условия:
(11.43)
Приведенные формулы полностью при-
менимы и при расчете валов кольцевого
сечения.
Брус прямоугольного сечения. При
нагружении бруса прямоугольного сече-
ния системой сил Р± и Р2 (рис. 219, а),
вызывающих в сечении моменты Мх, Му
и Мкр, расчет проводят по следующей
схеме. Внешние силы раскладывают на
составляющие, приводя их к оси вала.
Для нахождения опасного сечения строят
(рис. 219,6). Установив по эпюрам опасное
сечение 1—1, расположенное левее точки приложения силы Р2, нахо-
дят опасную точку в нем, для чего строят эпюры напряжений от
всех силовых факторов (рис. 220, а, б, в, г, д, е):
аг(Мя); аг(Л/й); zxz{Qx)- zyz(QvY, z (Мкр).
286
Эпюра т (Мкр) для длинной стороны контура имеет максимум,
который обозначим ттах(^кр)- Наибольшую ординату эпюры т (Мкр)
на короткой стороне обозначим ттах(^кр)' Эти напряжения можно
Рис. 220
рассчитать по известным формулам кручения брусьев прямоуголь-
ного сечения (см. § 47):
ттах (-^кр) ~ TL “ ТЛГ “ а/^а »
ттах (^кр) ТМ ХК 7ттах (^кр)*
В данном случае атах от изгиба не совпадают с ттах от круче-
ния, поэтому для выявления самой опасной точки приходится рас-
сматривать сочетание напряжений в нескольких точках. Обычно
бывает достаточно трех точек: одной из угловых (Л или С) и точек
посредине длинной (точки L или N) и короткой (точки М или К)
сторон прямоугольника. Так, для точек С, L, К будем иметь:
_ Мх Му
с Wx Wy
. — f 3 Qx .
L~ ahb* х 2 bh '
т Оу.
к 7 ± 2 bh '
(11.44)
(11.45)
(11.46)
287
Обычно касательные напряжения от поперечных сил Qx и Qy
малы и ими можно пренебречь.
Эквивалентные напряжения в точках L и К согласно IV теории
прочности и теории Кулона—Мора равны:
в точке L
WIV = V + з < [’]; (11-47)
1_та-мж
’экв М- 2 Wx + 2 ' \ wx / }'4 \ ahb* / < f J’
(11.48)
в точке К
if ( Ми V п /* V
°экв IV = У у ууу I + 3 V ahb2/ (11.49)
1 —/пМт/ , i + ml f f Му \2 , ,/*Кср? Г1 /ллк^
WM— 2 Wy 2 У \ Wy ) +4\*ahb2) С11’50)
Таким образом, наиболее опасная точка определяется только
в результате вычисления эквивалентных напряжений во всех трех
точках (С, L и К) по формулам (11.44), (11.47) — (11.50). При этом
в каждом конкретном случае положение наиболее опасной точки
зависит от соотношения моментов Мх, Му и Мкр.
Общий случай действия сил на брус. Если в сечении стержня
действуют осевая сила Nz, изгибающие моменты в главных плоско-
стях Мх и Му, а также крутящий момент Мкр, то условие прочно-
сти, например по IV теории прочности, в точке К (рис. 220, а)
будет
if ( Му Nz\2 /*м™\2
%кв iv = У +-/)+3 г < к
аналогично в точке L
1/"Гм2 ЯГ? I м«г, V
%kbiv=у НЙ-+-Г-)+зЬ^7<м- (11-52)
288
Таблица 21
Форма и размеры ядра сечения
Поперечное сечение;
ядро сечения
(заштриховано)
Размеры ядра сечения
h
h
Х2 — Уъ — "д" »
rmin = 0.0589Л
Прямоугольник
Равнобедренный
треугольник
b h
Xl - T: У1 ~И :
ь h
= з ; Ун - -3 ;
________bh
'min — 6 _|_ Аа
Ь h h
X1 - 8": U1 _ 12 ’ Уг ~ Т *
„ , /3,,
При h = b (равносторонний треуголь-
ник)
_ 6 _/з.
— 8 . У1 — 24 Ь> — 12 Ь
Ядро подобно
поперечному сечению
Ю 5-П86
289
Продолжение табл. 21
Поперечное сечение,
ядро сечения
(заштриховано)
Размеры ядра сечения
Ядро — ромб
b (bh —* bthi) '
4 feh3 — brf
t'ia='6 h(bh—bihl) ‘
При h = b и ht = b± (полый квадрат)
[/ h
1 + Ш J
rmin — 0,22567?.
Восьмиугольник
Если восьмиугольник полый (радиусы
описанных окружностей: наружной — /?2,
внутренней — Rlf толщина стенки равна
0,924 (Я2 —/?!)), то
Гт1п = 0,2256й2 1
Ядро — восьмиугольник
Г =
D
8
290
Продолжение табл. 21
Поперечное сечение;
ядро сечения
(заштриховано)
Размеры ядра сечения
Полый круг
Ядро — круг
Тонкостенная труба
D
4
г =
Ядро — круг
10*
Глава 12
ОБЩИЕ ТЕОРЕМЫ ОБ УПРУГИХ СИСТЕМАХ.
ОБЩИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
§ 64. Обобщенные силы и перемещения
Встречающиеся в задачах сопротивления материалов и строи-
тельной механики внешние нагрузки весьма разнообразны и обычно
Рис. 221
представляют собой группу сил. Работу группы постоянных сил
можно представить в виде произведения двух величин
4 = РДр, (12.1)
в котором множитель Р зависит только от сил группы и называется
обобщенной силой, а Др зависит от перемещений и называется
обобщенным перемещением.
Таким образом, под обобщенной силой будем понимать любую
нагрузку (сосредоточенные силы, сосредоточенные моменты, распре-
деленные нагрузки), которая способна совершать работу на соответ-
ствующем обобщенном перемещении.
Так, рассматривая работу системы сил, действующих на стер-
жень (рис. 221), будем иметь
А = РДХ — РД2 = Р (Д2 — Д2) = РДр,
где Р — обобщенная сила; Др = Д1— Д2 = Д/ — обобщенное переме*
щение.
Работа системы сил (рис. 222)
4 = Р AAt 4- Р • ВВХ = Р (ОА + OB) dy = Pady = Mdy.
Здесь обобщенной силой является момент М == Ра, а соответствую
щим обобщенным перемещением — угол поворота
292
Для системы сил (рис. 223) обобщенной силой является момент М,
а обобщенным перемещением — изменение угла а между элементами
АВ и CD, т, е.
Др = -р dy2.
Обычно принято обозначать обобщенные перемещения (как
линейные, так и угловые) буквами Д и & с соответствующими двой-
ными индексами. Первый индекс указывает точку и направление
перемещения, второй — силовой фактор, вызвавший это перемещение.
Например, Дрр означает перемещение точки приложения силы Р пФ
направлению ее действия, вызванное той же силой Р (рис. 224, а),
Дмм— перемещение точки приложения момен-
та М в направлении действия момента, выз-
ванное этим моментом (рис. 224, б).
Для обозначения полного перемещения,
вызванного несколькими силовыми факто-
рами, при Д сохраняют только первый ин-
декс. Так, полный прогиб и угол поворота
конца балки (рис. 225) соответственно выра-
зятся формулами:
Др = Дрр + др(3 + ДрМ; 1
— ^мр + ^mq + ймм-1
Перемещения,- вызванные единичной силой (Р = 1) или единич-
ным моментом (М — 1), принято обозначать буквой & и называть
удельным перемещением. Если единичная сила Р = 1 вызвала пере-
мещение &р, то полное перемещение
Др, вызванное силой Р, будет
Рис. 224
И
Отсюда размерность удельного перемещения
р]
размерность обобщенного перемещения
размерность обобщенной силы
(12.4)
Если силовые факторы, действующие на систему, обозначить
соответственно Хъ Х2, Х3 и т. д. (рис. 226), то перемещения по
направлению каждого из них можно выразить формулами
Д2 = Д1р -|- -|~ X2S12 + *3*w f
Д2 = ^2р 4“ *1&21 4~ *2*22 4“ *3*23» (12»5)
Д3 = &ЗР + *1*31 4” *2*32 + *3*33»
293
где
Xi^u — Au; X2^i2 = ^12» ^1з — ^13’ • •,
Xi^mi ” A mi*
Размерность перемещений можно установить, умножив
последнее равенство на Хт. При этом выражение XmXfimi = Хтктг
имеет размерность работы (кГсм), ъткуць получим
rSs 1 кГ см
Рис. 226
Например, в формуле (12.5) размерность
Ri3] =
пГ см ' __ кГ см _ 1
[XJ [Х3] кГ • кГ см ~~ кГ
§ 65. Работа внешних сил
Из рассмотрения картины деформации упругого элемента
(рис. 227, а) в пределах закона Гука, представленной в координатах:
обобщенная сила Р — обобщенное перемещение А (рис. 227,6), сле-
дует, что приращение силы dP вызывает бесконечно малое переме-
щение dA. Работа внешних сил при этом, если пренебречь беско-
нечно малыми второго порядка, равна
dA = (Р + dP) db « Pdb.
294
Полная работа, совершенная статически приложенной обобщен-
ной силой Р, вызвавшей обобщенное перемещение Д = РЪрр, вы-
ражается формулой
р Р
С С С ъррр*
Л = I Pd^ = Pd (РЪрр) = PbppdP == ;
д о о
ЪРР pi да _ РА
А~ 2 ~ 2ЪРР ~ 2
(12.6)
Таким образом, действительная работа при статическом действии
обобщенной силы на упругую систему равна половине произведения
окончательного значения силы на оконча-
тельное значение соответствующего пере-
мещения.
При действии на упругую систему
нескольких обобщенных сил Р1} Р2, . ,. ,
Pi (рис. 228) работа деформации равна
полусумме произведений окончательных
значений обобщенных сил на соответст-
вующие окончательные суммарные обоб-
щенные перемещения
а=4 S<12-7)
Рис. 228
и не зависит от порядка нагружения
системы.
§ 66. Работа внутренних сил
При упругой деформации в элементах
деформируемого тела развиваются внутренние
силы — силы упругого сопротивления (рис. 229).
Эти силы также совершают работу. Поскольку
направления упругих сил (показаны пункти-
ром) противоположны перемещениям (на
которых они совершают работу), вызываемым
внешними силами (показаны сплошными
линиями), то работа внутренних сил всегда
от рицательна.
Работа внутренних сил N, Q и М, воз-
никающих в элементе стержня длиной ds (рис. 229), совершаемая
осевой силой N на перемещении
A (ds)
Nds
ЕЕ *
моментом М на перемещении
Mds
295
и поперечной силой Q на перемещении
Qds
^ds « к Qp, (12.8)
может быть выражена формулой
aw - M*ds ~ N*ds k Q2ds
W 2EJ 2EF k 2GF'
(12.9)
Интегрируя (12.9) в пределах каждого стержня и суммируя резуль-
таты по всем стержням системы, получим формулу для работы
внутренних сил в случае плоского изгиба
S S S
0 0 о
Заметим, что выражение (12.8) получено из условия
dWQ
lds=—
где
dWQ^= I
F
F
«2
Q*ds ( Sx
2GJi \ Ь2
х и
F
kv 2GF '
F Г SldV
ky = * . 1 —p---коэффициент, зависящий от формы сечения.
J F
В частности, для прямоугольного сечения b х h\
г — on, Jх — |2 ’
4у2\
& ;
X —
1,2;
ft/2
. 9 С А-
о
32
для круглого сечения к == ; для прокатных профилей приближенно
F
к*=—-} где Fc—= площадь стенки; F — полная площадь сечения.
296
Для чистого сдвига когда
,тт_ 1 f , w Qids Q2ds
dWQ-~^\ ^dsdP = ----
F
В том случае, когда в стержне действует крутящий момент
МКр, при котором элементарный участок стержня закручивается на
угол
где &7К жесткость поперечного сече-
ния стержня при кручении, элемен-
тарная работа внутренних сил за счет
кручения равна
d^KP = -4^Kprf? =
- 2GJ* ’
а полная работа внутренних сил в стержне длиной I будет:
1
2 GJV
(12.11)
В общем случае (рис. 230), когда в сечении стержня действуют
все шесть силовых факторов (N, Qx, Qy, Мх, Myf М2 = Мнр), работа
внутренних сил (сил упругости) будет определяться по формуле:
f Mds W = — 1 —- J 2EJX s fM^ds J ^Jy J 2G7k 8 8
_ P N*ds _ r J ^EF J 8 8 , Qxds C, Qyds kx 2GF J ky 2GF (12.12) 8
Формула (12.12) справедлива и для стержней малой кривизны.
§ 67. Применение начала возможных перемещений
к упругим системам
Применительно к упругим системам начало возможных переме-
щений можно сформулировать так: если система находится в равно-
весии под действием приложенной нагрузки, то сумма работ внешних
297
и внутренних сил на возможных бесконечно малых перемещениях точек
системы равна нулю
2 + Wim —
(12.13)
чина и направление внешних и
ними. Поэтому при вычислении
где — внешние силы; Д$ш — возможные перемещения точек при-»
ложения этих сил; 2 Pi^imв работа внешних сил; == работа
внутренних сил.
В процессе совершения системой возможного перемещения вели-
внутренних сил остаются неизмен-
работ следует брать не половину,
а полную величину произведения
соответствующих сил и перемещений.
Учитывая малость деформаций
и их линейную зависимость от
нагрузок, в качестве возможных
перемещений можно принимать
упругие перемещения, вызванные лю*
бым видом нагрузки и происходя-
щие без нарушения связей. Работа
внешних и внутренних сил на воз-
можных перемещениях называется
возможной или виртуальной работой.
Рассмотрим два состояния пло-
ской системы, находящейся в рав-
новесии: состояние а, при котором
система деформируется обобщенной
силой Ра (рис. 231, а), и состояние Ь системы, деформируемой силой
Рь (рис. 231,6).
Перемещения состояния b могут рассматриваться как возможные
для состояния а и, наоборот, перемещения состояния а являются
возможными для состояния Ь.
Йоэтому работа Ааь сил состояния а на перемещениях состояния
а
Рис. 231
b и работа АЬа состояния Ъ на перемещениях состояния а соответст-
венно равны
АаЬ — Р a^abi
Aba ~ ?b&ba>
(12.14)
(12.15)
298
Работа внутренних сил состояния а (рис. 232, а — штриховые
линии) на перемещениях, вызванных нагрузкой состояния Ъ (рис.
232, а, б), может быть найдена из рассмотрения работы внутренних
сил при деформировании элемента стержня длиной ds (рис. 233).
Рис. 233
Ниже приведена схема определения работы внутренних сил.
Внешнее усилие, действующее на элемент (рис. 232, б) Деформация элемента (рис 233) Работа внутренней силы состояния а на перемещениях состояния b Работа внутренней силы состояния а в системе стержней
Яь (Д^)ь = Nbds = EF ~Na(Ms)b = NgNbds ЕЕ V4 С NaNbds 2-1 J EF
Qb (7</з)6 = ^Qa^ds)b^ _ J k QaQbds
... ,.Qbds GF к QaQbds “ GF s
Мь Wb = _ Mbds ~ EJ — Ma (d<f)b = MaMbds ~ EJ yi C MaMbds 2j j EJ s
Таким образом, полное значение возможной работы внутренних
сил стержневой системы будет
S S
S
299
Подставляя (12.14) и (12.16) в (12.13), получим общее выражение
начала возможных перемещений для плоской упругой стержневой
системы
MaMbds
EJ
^^NgNbds j
s
s
(12.17)
Если в качестве возможных принять действительные перемеще-
ния Да, вызванные заданной нагрузкой Ра, то выражение (12.17)
примет вид
(12.18)
или
где
Таким образом,
s
s
Л2
А + W = 0,
Nads
ЕЕ
0.
ка>
(12.19)
(12.20)
(12.21)
А =
представляет собой действительную работу внешних сил в процессе
статической деформации, а
представляет собой работу внутренних сил в процессе статической
деформации.
Из уравнения (12.20) следует, что действительные значения
работы внешних и внутренних сил равны по величине и противо-
положны по знаку.
300
§ 68. Теоремы о взаимности работ и перемещений
Рассмотрим упругую систему в двух состояниях: в состоянии 1
(рис. 234, а) и в состоянии 2 (рис. 234,6). На основании принципа
возможных перемещений для первого состояния получим
+ <12-23>
] aj ) а Г J Сгг I
8 8 8
для второго состояния
р2д21 2jLJ ej j
S 3
+ f к 2^1= о. (12.24)
ar J Сгг I
Так как выражения для работ внутренних сил в обеих формулах
одинаковы, то из (12.23) и (12.24) выводим равенство
^12 = ^2 • ^21* (12.25)
Формула (12.25) выражает теорему о взаимности работ (теорему
Бетти): возможная работа внешних (или внутренних) сил состояния 1
на перемещениях состояния 2 равна возможной работе внешних (или
внутренних) сил состояния 2 на перемещениях состояния 1.
В частном случае, когда Рг ® 1; Р2 = 1 (рис. 235), на основании
(12.15) получим соотношение
812 = 821) (12.26)
выражающее теорему о взаимности перемещений (теорему Максвелла):
перемещение точки приложения первой единичной силы по ее направле-
нию, вызванное действием второй единичной силы, равно перемещению
точки приложения второй единичной силы по ее направлению, вызван-
ному действием первой единичной силы.
§ 69. Общие формулы для определения перемещений.
Метод Мора
Общие формулы для определения перемещений легко получить,
пользуясь началом возможных перемещений, если в качестве вспо-
могательного состояния принять систему, нагруженную в точке,
301
перемещение которой^ нас интересует, соответствующей единичной
обобщенной силой -ЗГ| = 1, которая должна совершать работу на
возможном перемещении, каким является интересующее нас переме-
щение Д^р под действием внешних нагрузок.
Обозначив усилия, вызванные системой внешних сил SP
(рис. 236, а), через Мр, Np, Qp, а усилия, вызванные единичной
силой Xi = 1 (рис. 236, б),«— через Ni, Qi, начало возможных
перемещений для вспомогательного состояния (принимая в качестве
возможного действительное перемещение) можно записать в виде
Г f MiMpds f NiNpds C QiQpdsl
1 AtP = 2jLJ EJ j"""W J GF J
8 S 8
(12.27)
Рис. 236
Очевидно, в самом общем случав, при наличии всех шести ком-
понентов внутренних сил, формулу (12.27) можно записать в виде
«’“ZjjL EJx + ~Ё7Г + G/k 4
8
,к A-к ^А-
+ kx~GF +ky~GF +
GF "И EF lds'
(12.28)
Формула (12.28) является наиболее общей и применима также для
расчета стержней малой кривизны. Определение перемещений по
формулам (12.27) и (12.28) называют способом Мора или способом
перемножения епюр,
В большинстве случаев при определении перемещений в балках,
рамах и арках по методу Мора в формуле (12.27) можно пренебречь
влиянием продольных деформаций и сдвига, учитывая лишь переме-
щения, которые вызываются изгибом. Тогда формула (12.27) для
плоской системы может быть записана следующим образом:
д»р Zj j FJ
8
(12.29)
302
ДгР
При пространственном нагружении формула Мора принимает вид
Г M*Mpds f MyM^ds Г M^M^dsl
+ } gj;.....]• (12>30)
3 S 8
При расчете шарнирных ферм, образованных из прямых стерж-
ней, в формуле Мора сохраняется член, содержащий лишь продоль-
ную силу: _
VI NiNp
гР~ Jj ЕЕ 1‘
Формула (12.31) носит название формулы Максвелла.
Порядок определения перемещений по методу Мора.
1. Строится вспомогательная система и нагружается единичной
нагрузкой в точке, где требуется определить перемещение. При
определении линейных перемещений в заданном направлении прикла-
дывается единичная сила, при определений угловых перемещений —
единичный момент.
2. Для каждого участка системы выписываются выражения сило-
вых факторов в произвольном сечении заданной (Мр, Np, Qp)
и вспомогательной (М$, Ni, Qi) систем.
3. Вычисляются по всем участкам системы интегралы Мора. При
расчете плоских балок, рам и арок используется формула (12.29),
при расчете ферм — формула (12.31).
4. Если вычисленное перемещение имеет положительный знак,
то это значит, что его направление совпадает с направлением еди-
ничной силы. Отрицательный знак указывает на то, что действитель-
ное перемещение противоположно направлению единичной силы.
В табл. 22 приведены выражения интеграла Мора для наиболее
распространенных случаев сочетания эпюр М| и Мр при изгибе.
§ 70. Перемещения, вызванные изменением температуры
Предположим, что элемент стержня ds нагрет внизу до темпера-
(12.31)
Рис. 237
туры £н и наверху — до tB (рис. 237, а, б), а также, что по высоте
сечения температура изменяется по линейному закону. Тогда удли-
нения верхних и нижних волокон рассматриваемого элемента равны:
дв (ds) = atB ds; |
Дн (ds) = atads, /
где a коэффициент линейного температурного расширения.
(12.32)
303
Удлинение по оси неравномерно нагретого элемента и взаимный
угол поворота его крайних сечений высотой h равны:
4В 4“
(Ms)t = а в2 ? ds; (12.33)
Д„ (ds) — Д„ (ds) t„ —t_
(rf?), = _2----> .h B = a -2L—2. ds. (12.34)
Для определения перемещения любой точки К системы в любом
направлении i — i, вызванного разностью температур, выбираем
вспомогательную систему и_нагружаем ее соответствующей обобщен-
ной единичной нагрузкой Xi = 1 (рис. 237, в). Принимая интересую-
щее нас перемещение за возможное, запишем в соответствии
с (12.27) формулу возможных перемещений применительно к рас-~
сматриваемому случаю:
д« = S J Mi (*р)( + S J ЛГ*
8 8
(12.35)
Учитывая (12.33) и (12.34), получим
д«=X У —4'^"ds+X Уds- <12-36)
Формула (12.36) применима и для расчета брусьев малой кривизны.
В фермах, где действуют только продольные усилия, темпера-
турные перемещения определяются по формуле
д{( = 2^«/.
(12.37)
где t ----~------температура по оси стержня.
§ 71. Вычисление интеграла Мора
по способу Верещагина
Интеграл Мора J M^Mpdz для случая, когда эпюра от заданной
нагрузки имеет произвольное, а от единичной — прямолинейное
очертание (рис. 238), оказалось удобным определять графо-аналити-
ческим способом, предложенным А. Н. Верещагиным.
Примем следующие обозначения: Q — площадь эпюры Мр от внеш-
ней нагрузки; С —центр тяжестй» эпюры; MQ — ордината эпюры от
единичной нагрузки под центром тяжести эпюры Мр,
304
Очевидно,
М pdz = dQ
(дифференциал площади эпюры);
M{ = ztga;
У MjMpdz — tga j* zdQ;
1 i
У zdQ =r zc2; tg a zq =
i
MiMpdz = QMC.
Рис. 240
Общая формула перемещений для систем, состоящих из прямо-
линейных элементов
у-i Р M^Mpdz
Д1₽ = 2jр
запишется в виде:
SQMp
-ЁТ- (1238>
Это и есть формула Верещагина. Вычисление по этой формуле
производится по участкам, на каждом из которых прямолинейная
эпюра должна быть без переломов (рис. 239).
В тех случаях, когда обе эпюры (М^ и Мр) прямолинейны,
можно умножать площадь одной из них на ординату другой эпюры,
расположенную под центром тяжести первой. Сложная эпюра Мр
может быть разбита на простые фигуры (рис. 240), для каждой из
которых легко определить координату центра тяжести. При этом
площадь каждой фигуры умножают на ординату единичной эпюры под
305
ее центром тяжести, обозначаемую через % (вместо MCh). Формула
Верещагина в этом случае примет вид
2d
fe==l, 2, 3.,
EJ
(12.39)
В табл. 23 приведены площади и координаты центров тяжести
некоторых элементарных фигур.
При учете кручения в соответствующий член общей формулы
(12.38) будет входить жесткость на кручение GJK. Если эпюры Мр
и М^ противоположны по знаку, то результат их умножения имеет
знак минус.
Общая формула Верещагина применима и при расчете стержней
переменного сечения. В этом случае интеграл Мора записывается
в виде:
где J(z) — момент инерции площади произвольного сечения; JQ -=*
момент инерции определенного (характерного) сечения.
Йазовем величину
М = Mr.______-2-
пр ШР J(Z)
приведенным изгибающим моментом в текущем сечении» Теперь
интеграл Мора может быть записан в виде
а формула Верещагина «
-^-2, Ц2И)
где Snp==площадь эпюры Мпр; MG — ордината единичной эпюры
под центром тяжести приведенной эпюры.
§ 72. Потенциальная энергия деформации
В соответствии с законом сохранения энергии работа внешних
сил при деформировании упругой системы не пропадает, а трансфор-*
мируется в потенциальную энергию деформации, которая может
проявиться в виде работы, совершаемой внутренними силами при
306
разгрузке. Так, при частичной разгрузке (рис. 241) балка, несколько
выпрямляясь и приподнимая ос1авшую часть груза, совершает опре-
деленную работу.
Пренебрегая при статическом нагружении кинетической энер-
гией, а также потерями энергии на внутреннее трение, изменение
температуры, магнитные и электрические явления, имеющие место
при деформации, можно утверждать, что уменьшение потенциальной
энергии груза равно изменению потенциальной энергии деформации,
накопленной упругой конструкцией, т. е.
U^Up,
где U — приращение потенциальной энергии деформации; Up —
уменьшение потенциальной энергии груза.
Уменьшение потенциальной энергии
груза численно равно действительной
работе внешних сил при нагружении тела.
Следовательно, потенциальная энергия
деформации численно равна работе внеш-
них сил при нагружении системы или
работе внутренних сил, совершенной
в процессе разгрузки. Согласно (12.12),
потенциальная энергия деформации в об-
щем случае может быть определена фор-
мулой
1 { Mlds
TJ — А-- I
и~А~ 2 .) EJK
i ССл
2 J GJ
6 K
1
2 J Т77
1 I №ds
2" J EF
8
1 L , 1 L
2 J GF 2 J v GE •
8 8
(12.41)
Поскольку потенциальная энер-
гия деформации является квадра-
тичной функцией обобщенных сил
(или обобщенных перемещений), она
всегда положительна.
§ 73. Теорема Кастильяно.
Теорема Лагранжа
Рассмотрим упругую систему
(рис. 242), статически нагруженную
произвольной нагрузкой Q и некотор(
мещение точки приложения силы Р
Рис. 242
й обобщенной силой Р. Пере-
по ее направлению и от ее дей-
ствия будет Арр, а перемещение той же точки под действием сил
Q будет Арр. При полном перемещении рассматриваемой точки,
равном Др = Арр Арр, потенциальная энергия упругой системы
выразится формулой
и =~P^pp + P^pQ + Uqq,
307
где (7qq—энергия, накопленная в результате деформации системы
только силами Qt численно равная работе сил Q на вызванных ими
перемещениях.
Так как Дрр = PSpp, то вышеприведенную формулу можно запи-
сать в виде
tf = -i-p%P+PaPQ+erQQ. (12.42)
Продифференцировав это выражение по силе Р, получим
== РЪрр 4- Дрр = дРР + дР(Э = ДР.
Таким образом,
ДР = -^г- (12.43)
Перемещение точки приложения обобщенной силы по направлению
ее действия равно частной производной от потенциальной энергии по
этой силе. В этом состоит теорема Кастильяно.
Заметим, что вторая производная от потенциальной энергии по
силе (обобщенной) согласно формуле (12.42) равна:
адр . ......
Qp ^рр (12.44)
и имеет существенно положительную величину.
Для плоской стержневой системы формула (12.41) примет вид
CM*(s)ds CN2(s)ds C,Q2(s)ds
U-]~EJ + } 2EF +}k~2GF-’ (12,45)
8 S S
где M (5), N (s), Q (s) — усилия в сечении стержня.
Применяя правило дифференцирования по параметру, находим
Л _ ди __ С м (*) ds дМ 00 ! f N (*) ds dN (*)
p dP EJ dP + J EF dP +
8 8
4^’ (i2-46)
s
или, пренебрегая влиянием на величину перемещений осевых
и поперечных сил, будем иметь
CM(s)<ls дМ (s)
Лр J ~Ё7----------эр~- (1247)
8
Если при определении перемещений точки по условию задачи
нет соответствующей обобщенной силы, ее вводят в виде фиктивной.
308
Составленное выражение для потенциальной энергии деформации
дифференцируется по этой силе, после чего она приравнивается нулю.
Если представить потенциальную энергию деформации как
квадратичную функцию независимых перемещений Дъ Д2, • • • , Ап»
то оказывается, что частная производная от потенциальной энергии
по любому перемещению равна силе, действующей по направлению
перемещения, т. е.
= Pi- (12-48)
В этом состоит теорема Лагранжа.
§ 74. Теорема о минимуме потенциальной энергии
Заменим в статически неопределимой системе (рис. 243, лишние
связи соответствующими реакциями Xt, Х2г Х3... (рис. 243, б), которые
будем рассматривать как независи-
мые друг от друга внешние нагруз-
ки, и вычислим по методу Кастильяно
соответствующие перемещения Дъ
Аа, А3, • ••
Зная заранее, что указанные
перемещения равны нулю, мы имеем
право записать
л ди а л ди
41 ~ дХ, “°’ 4’ ~
0;
Рис. 243
где U — U (Xlt Х2, , Р) — полная потенциальная энергия
деформации системы.
Легко убедиться, что равенства
дЦ
дх.
= 0;
2£_=о-
дХг °’
-^- = 0 ..
дх3 и-
(12.49)
выражают условия экстремума функции U. Нетрудно видеть, что
этот экстремум является минимумом. Доказательством последнего слу-
жит положительный знак вторых производных, которые, согласно
(12.44), выражают перемещения &и, S22> Ь33, ... , являющиеся сущест-
венно положительными величинами:
dW d4J d*U
дХ* ~ 11’ дХ22 ~ 22’ дх} ~ :
Таким образом, в статически неопределимых системах лишние
неизвестные усилия принимают такие значения, при которых потен-
циальная энергия деформации имеет наименьшее значение (теорема
Менабреа). Эта теорема известна также как теорема о наимень-
шей работе, так как вместо потенциальной энергии можно говорить
о численно равной ей работе внешних сил. Из нее следует, что при
добавлении в упругую систему каких-либо связей потенциальная
энергия системы всегда уменьшается.
309
Таблица 22
о __
Выражения интеграла Мора I MiMpdz для различных сочетаний эпюр и Мр{1 -=» основание площади эпюры)
Эпюра \ ЛГг Эпюра \ Мр \ ^ипЯПй‘ А-гпШП)4
Л IB III 1
\dl г Ц fit Ц
о -J-fe ffe" Ч- 2fe3) Z ^h(2ht—hl)l ^hh(l + i)l
"[ППЛп^ ~ыч 4-ш о -g- h (2hj 4- h2) I ~-h(h2-2h1)l Lhh [1+^)1
4гттттгШТЖ 1 1 i 1 -1 (fej + 2й2) Ы 1 1 -g- [fcj- (2hr 4- h2) 4- -f” h2 (2^-2 ~b ^i)] I i -g- (fej (fe2 — 2fej) + + h2(2h2 — h^] I i ±[(1+P)fe1 + + (1+*) h2]hl
уШ 1- (1 + a) hhl l[(l + ₽)fe, + 4~ (1 4~ a) ^2] i g-L(l+«)*2- - (1 + ₽) M hl ^hhl при a = a
у (fe2 — hr) hl 1 -g- (2h2 — hl -g- [h2 (2Й2 4~ ^1) — (2hi 4-^2)] 1 - -g- [h2 (2h2 — ht) — — h. (h2 — 2jit)]l l[(l+'a)fe2- -(H-P)AJW
hh$l — hh^l Ал^+мр/ ^hlfit-hi) p/ 4-(3-3a- 6P к при a < a, hh (Q a2\ —n— 1 j * 6 \ ap / при a > a
1 1 1
co
h 4 ^h{ht + Zh2)l Afecs^-fet)/ ~hh(l+a + a2)l
— hhl О lw 1 - 12 ^1) ^Md + F+P2)/
1 - <N |co 1 _ y hhl yfe(fe2 — hi) I 4- (1-Рф) hhl 0
z£<nT co| to i h (3^ + 5^)/ 1л(5Лг-3»;)/ l(5-p-₽2)W
Л _]TUk 0 — Ш 4 ^fc(5fei+3£2)Z ^fe(3fe2—5^) 1 ~ (5 — a — a2) hhl
Л 4. h2 — ^(^ + /12 + 4-47i)Z lfe(fea + 2fe)/ 4 _ -g- (hih^ 4- ^hh0 + -j- ^2^2) 1 - -g- (Z&2^2 *4“ 4ЛЛ-0 =— h^hx) I (! + ₽) + + ^2 (1 + a) + + 2Л3(1 + «T)]feZ
_ 42 ~ 'h
Таблица 23
Площади и координаты центров тяжести некоторых элементарных
фигур
Эпюра М Площадг 2 Координаты центра тяжести
гС 1—
lh 2 <м |со I
. zt l-Zc
II ив (^1 + ц 1 2 ~Ь 2^2 1 3(^ + м fe2 4~ ] з (^i Ч" ^2)
?С г _ I'Zc .
— 1
|я Ь _ lh 2 а 4~ 1 Ь + 1 3
J
- l'Zc г
1
Ква/] па ——=ессц ?с (рат ipa6( ЩЦ 1 ичн зла R l~Zc :ая 1 lh 3
314
Продолжение табл. 23
Эпюра М Площадь 2 Координаты центра тяжести
гс l — zc
Кубическая парабола lh ~1 Li
Ъ , 1-% 1 ~Т 5 * 1 5
п оловина кв ной пара' .иИЦ at Zc - - 1 адратич- 5 олы l-Zcr ^-Ih О 1' 001 со <**
Квадрати парабо Z [чная ла м Zc м * т'4 т' т'
Квадратичная
парабола
а/
-|- За [а 4" /)]
I ва31 4- 8а/2 + З/3 .
г° ~ 4 За2/ + За/2 + /3 ’
_ I 6а2/4- 4а/2 4-/3
1 Zc~~£ За2/ 4- За/2 4- I3
Глава 13
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
§ 75. Основные этапы расчета статически
неопределимых систем
Статически неопределимыми называются системы, силовые фак-
торы в элементах которых не могут быть определены только из
уравнений равновесия твердого тела. В таких системах имеется
больше связей, чем это необходимо для равновесия. Таким образом,
Рис. 245
соответ-
лишних
усилий
неопре-
кйЛ Я
777777,
А
ft
часть связей в этом смысле является как бы лишней, а
ствующие усилия являются лишними не известными. По числу
связей или лишних неизвестных
устанавливают степень статической
делимости системы.
На рис. 244, а приведена статически
определимая система, а на рис. 244, б — один
раз статически неопределимая. На рис. 245, а
показана дважды статически неопределимая
балка, полученная из статически определи-
мой системы (рис. 245, б) в результате уста-
новки двух шарнирных опор в точках
В и С. На рис. 246 показана дважды стати-
чески неопределимая плоская рама.
Статическая неопределимость может быть
результатом не только введения дополни-
тельных связей, но также и условием образования системы. Приме-
ром может служить рама (рис. 247, а), в которой реакции опор
НА, Вв легко определяются из условий равновесия, но послед-
ние не позволяют найти все силовые факторы в ее элементах. Раз-
резав раму на две части й рассматривая равновесие одной из них
Рис. 246
316
(рис. 247, б), мы устанавливаем, что эта рама представляет собой
систему шесть раз статически неопределимую, так как каждый
замкнутый (бесшарнирный) контур является три раза статиче-
ски неопределимым.
Установка шарнира на оси стержня (рис. 248, а) (одиночный
шарнир) обращает в нуль изгибающий момент в этом сечении и,
следовательно, снижает степень статической неопределимости на
единицу. Шарнир, включенный в узел (общий шарнир), где схо-
дятся п стержней (см., например, рис. 248, б, в), снижает сте-
пень статической неопределимости на п — 1, так как заменяет
Рис. 248
(рис. 248, г). Степень ста-
($) может быть определена
(13.1)
собой столько же одиночных шарниров
тической неопределимости плоских систем
по формуле
s = 3/с — ш,
где к— число замкнутых контуров, ш — число шарниров в пересчете
на одиночные. Основание (земля) рассматривается как стержень
бесконечной жесткости (EJ = оо).
При расчете статически неопределимых систем можно в качестве
неизвестных принимать как силы или силовые факторы, так и пере-
мещения или деформационные факторы. В первом случае имеем так
называемый метод сил, во втором — метод перемещений.
Расчет по методу сил проводят в такой последовательности.
1. Устанавливают степень статической неопределимости.
2. Путем удаления лишних связей заменяют исходную систему
статически определимой, называемой основной системой. Таких систем
317
можно построить несколько, соблюдая при этом условие их геомет-
рической неизменяемости.
3. Основную систему нагружают заданными внешними силами
и лишними неизвестными усилиями, заменяющими действие удален-
ных связей, в результате чего получают &квивалентную систему.
4. Для обеспечения эквивалентности исходной и основной систем
неизвестные усилия должны быть подобраны так, чтобы деформации
основной системы не отличались от деформации исходной статически
неопределимой системы. Для этого перемещения точек приложения
лишних неизвестных по направлению их
действия приравнивают нулю. Из полу-
ченных таким образом уравнений опреде-
ляют значения лишних неизвестных уси-
УФ д
1П11ПШШ1П11
Рис. 249 Рис. 250
лий. Определение перемещений соответствующих точек можно
производить любым способом, однако лучше использовать при этом
наиболее общий метод Мора или способ Верещагина.
5. После установления значений лишних неизвестных усилий
производят определение реакций и построение эпюр внутренних
усилий, подбор сечений и проверку прочности обычным способом.
Рассмотрим пример расчета статически неопределимой системы
(рис. 249, а). Приняв реакцию опоры В за лишнюю неизвестную Xl9
получим основную систему в виде консоли, нагрузив которую рас-
пределенной нагрузкой q и усилием придем к эквивалентной
системе (рис. 249, б). Дополнительным уравнением перемещений
будет равенство нулю прогиба в точке В:
= 0. (13.2)
Полный прогиб Д) можно представить как сумму прогибов от внеш’
ней нагрузки (рис. 249, в)
<“>
и от неизвестной реакции X, (рис. 249, г)
Аи ~ 3£/ '
318
Уравнение (13.2) можем записать в виде
Д1 ss Д|р Ди = О, (13.5)
или
8EJ т 3EJ
Отсюда находим искомую реакцию
Xi = ~ql. '(13.6)
Из уравнения статики легко найти остальные
обычным способом построить эпюры Q и М, как
это показано на рис. 250.
В табл. 24 приведены расчетные формулы
для определения опорных реакций, поперечной
силы Q, изгибающего момента М и перемещений
для основных случаев нагружения стати-
чески неопределимых однопролетных балок,
а в табл. 25 — для случаев смещения опор
и неравномерного нагрева балок.
§ 76. Канонические уравнения метода сил
Дополнительные уравнения перемещений,
выражающие равенство нулю перемещений по
направлениям лишних неизвестных, удобно
составлять в так называемой канонической форме,
т. е. по определенной закономерности. Покажем
это на примере решения простейшей статиче-
ски неопределимой системы (рис. 251, а).
Выберем в качестве основной системы кон-
соль; в качестве эквивалентной системы полу-
чим консоль, нагруженную внешней силой Р
и лишней неизвестной (рис. 251,6). Допол-
нительное уравнение перемещений, выражающее
равенство нулю перемещения точки В от сил
Р и Xlt будет
реакции, а затем
Д!«Д(Р, Хх) =0.
На основании принципа независимости дей-
ствия сил запишем
(13.7)
е
Дх = Д1РДц, (13.8)
Рис. 251
где Д1Р — перемещение от заданной нагрузки Р
(рис. 251, в); Апперемещение от силы Xlt Обозначив перемещение
от Х1==1 по ее направлению через (рис. 251,6), получим
Дц = &1Л.
Уравнение перемещений (13.8) примет вид
Mi + Ajp == о.
(13.9)
319
Это каноническая форма уравнения перемещений для один раз ста-
тически неопределимой системы. Из формулы (13.9) имеем
Aj р
=-------- (13.10)
Для системы, имеющей две лишние связи (рис. 252), канониче-
ские уравнения будут иметь вид
^ii^i + ^12-^2 4- &ip = 0;]
. Y , . т . Л п (13.11)
Ь21Л1 + б22^2 Т ^2Р = О. J
Аналогично могут быть написаны в канонической форме, урав-
—------—- »— —.г раз статически неопреде лимой 4
нения перемещений для любой п
системы
12)
Перемещения ДгР и входящие в канонические уравнения,
следует определять по методу Мора или способу Верещагина. При
расчете рам и балок, для которых отношение высоты стержня к его
длине, как правило, меньше 0,1, в общей формуле Мора ограничи-
ваются сохранением интегралов, учитывающих лишь изгибающие
моменты. При этом прикладывают к основной системе единичные
нагрузки 2^ = 1, Х2 = 1, ...» Хп = 1, а также внешние нагрузки
320
^строят соответствующие эпюры моментов, как это показано приме-
нительно к трижды статически неопределимой системе (рис. 253) на
рйо. 254. Ординаты эпюр изгибающих моментов от заданной нагрузки
В (состояние Р) и каждой единичной силы Xt = 1 (состояние 7),
5*а == 1 (состояние 2) и т. д. обозначим соответственно через
®i, М2, • • •, На основании (12.29) находим
Удельные перемещения, имеющие одинаковые индексы (главные
коэффициенты канонических уравнений), определяют по формулам
С МrM±ds . С M2M2ds С MnMnds
11 J EJ » “ J EJ 5 •• • J »nn — J EJ
8 S 8
(13.14)
Удельные перемещения, имеющие разные индексы (побочные
коэффициенты), определяют по формулам
CM^M2ds CMjM3ds . CM^Mkds
°12 —J EJ * “I»-J ej 5 •••! ®ift —J EJ 1
r 8 S S
(13.15)
Эти перемещения могут быть положительными или отрицательными,
а также равными нулю.
На основании теоремы о взаимности перемещений
bik = hi*
Для систем, состоящих из прямолинейных элементов, вычисле-
ния перемещений удобно производить по способу Верещагина.
Например, для статически неопределимой системы (рис. 251, а)
имеем (см. рис. 251, в, г, д, е):
_“₽>сР
Д1р~ EJ ' 511 “ EJ ’
”р-Т'
.. = 4; мс,^г.
И 5-118§
321
Следовательно,
а 5 р/3 х
Д1Р “ 48 ‘ EJ ’ 611 ~ 3EJ *
Из формулы (13.10) находим
Д1Р 5
Л1~“- Bn^ie^*
Если учитывать влияние разности температур, то порядок расчета
сохранится прежним, а свободные члены канонических уравнений
при этом будут представлять собой перемещения в основной системе
не только от заданной нагрузки, но и от изменения температуры:
+ &12^2 + • • * 4- \п%п 4" \р 4" дц = 0;
(13.16)
+ Чах2 4-----1- ^Ппхп + дпР + ^nt == °’
где &it — перемещение в основной системе по направлению силы Х^
вызванное разностью температур.
После определения коэффициентов и свободных членов Д$р и
решаем систему канонических уравнений (13.16) и находим лиш-
ние неизвестные Х2, ... , Хп. Далее обычным способом строим
эпюры внутренних сил (2V, Q и М). Построения удобно производить
методом суммирования по схеме
М == + М2Х2 4---h мр\
Q~Qixi + Q^+ — +Qp1
(13.17)
Отметим, что вид канонических уравнений остается неизменным
при любом возможном варианте основной системы, изменяется лишь
смысл лишних неизвестных и геометрический смысл перемещений.
В табл. 26, 27, 28 приведены расчетные формулы для определе-
ния изгибающего момента в характерных сечениях некоторых видов
статически неопределимых рам для простейших случаев их нагру-
жения.
§ 77. Многоопорные неразрезные балки.
Уравнение трех моментов
Нераарезными называются балки, лежащие более чем на двух
опорах (см., например, рис. 255, а). Число лишних связей в нераз-
резной балке, а следовательно, и лишних реакций равно числу про-
межуточных опор. Иногда крайняя опора выполняется в виде
защемления. В этом случае степень статической неопределимости
балки увеличивается на единицу.
При выборе основной системы за лишние связи целесообразно
принимать не промежуточные опоры и лишние неизвестные реакции
322
в них (рис. 255, б), что привело бы к излишне громоздким вычис-
лениям при определении лишних неизвестных, а изгибающие моменты
в опорных сечениях. В этом случае, очевидно, основной системой
будет система однопролетных балок, соединенных на опорах шарни-
рами. Тогда эквивалентная система при расчете по методу сил будет
представлять собой ряд простых шарнирно-опертых балок, нагру-
женных заданной нагрузкой и неизвестными изгибающими моментами
по концам (рис. 256):
« Xf, М2 = Х2; ... 5 в ^п-М • • •
Дополнительное уравнение перемещений для каждой промежу-
Рис. 255
Рис. 256
точной опоры должно выражать условие равенства нулю взаимного
угла поворота опорных сечений смежных балок. Поскольку
каждая из двух опорных балок основной си-
стемы под действием внешних нагрузок в про-
лете и концевых моментов деформируется
независимо от другой, то торцы двух смежных
балок, примыкающих к одной опоре, например п-й
(рис. 257), могут поворачиваться на некоторый
угол Д£ев и Д°рав. Так как в исходной статически
неопределимой неразрезной балке каждая пара
таких сечений представляет собой одно сечение,
то из условий сплошности их взаимный угол пово-
рота должен быть равен нулю. Отсюда для каждой
промежуточной опоры
Рис. 257
п
ДП = Д"ев + дпра* « 0.
(13.18)
Так как основная система состоит из отдельных, не связанных
между собой однопролетных балок, то при раскрытии условия (13.18)
11*
323
достаточно рассмотреть примыкающие к n-й опоре два пролета 1п
и Тогда условие (13.18), записанное в канонической форме,
будет иметь вид
Snf п-1 Хп-1 + ЪппХп + Ъп9 п-НХп-Н + ДпР °- (13.19)
Рис. 258
В соответствии с построениями, приве-
денными на рис. 258, а, б, в, г,
г
Рис. 259
s______L
nn - EJn ’
1 /I __
2 3 ~
2 3
^Лн-i
in . _S±A-
ZEJn 3^Jn+1
(13.22)
»n,n+l-^re+)
^n-M
6^n+1
(13.23)
1
2 3 ~
Подставляя (13.20) — (13.23) в (13Л9), получим
^n—1 (’у- +
Jn \ J n
^n+1 \ , v ^n^l
zqrr "+•
/» / wn^n I
b 77" +
^n-bl^n+l
^n4-l^n+l ,
(13.24)
324
Заменив обозначение лишних неизвестных Xi на получим урав-
нение трех моментов
Jn \ J п
1п+* \л.М Zn+1 -
7 I + Mn+1 j
Jn-M / n-M
6 । tdna'n
\ Jn^n
। ^4-1^+1
•Лг-Н^п-Н
(13.25)
При расчете неразрезных балок составляют столько уравнений
трех моментов, сколько имеется промежуточных опор. Решив полу-
ченную систему уравнений, определяют лишние неизвестные моменты
Mi на опорах. Зная концевые моменты эквивалентной системы, все
дальнейшие расчеты выполняют обычным методом, как при расчете
любой статически определимой системы.
Для балок постоянного сечения (.7 = const) уравнение трех
моментов (13.25) упрощается:
(ln + ln.±i) + ^n4-lZn4-l в
((дп0'п
\ In
(13.26)
1п^\ I
Уравнения трех моментов для второй и предпоследней опор нераз-
резной балки, очевидно, будут содержать только два момента.
Уравнения трех моментов используются и при расчете неразрез-
ной балки, один конец которой жестко заделан. В этом случае
составляют уравнение трех моментов также для защемленного конца,
ставя там как бы промежуточную опору, и в сторону заделки вводят
фиктивный пролет. Если заделан левый конец балки, в уравнении
трех моментов должны быть положены равными нулю Мп__^, 1п,
а член 6 будет отсутствовать. Если не все опоры неразрезной бал-
ки находятся на одном уровне, а имеет место смещение некоторых
опор, то в балке могут возникнуть значительные начальные напря-
жения. Эти напряжения зависят от разницы в уровнях опор и жест-
кости балки, увеличиваясь пропорционально указанным величинам.
Влияние смещения опор на напряженность неразрезной балки
может быть оценена следующим образом. Пусть имеет место картина
смещения опор, приведенная на рис. 259. Углы поворота левого
и правого пролетов относительно опоры п будут
У1 Уп-11 Уп-j-i Уп
0п = ------, о = —---------------
Ч-м
Угол поворота считаем положительным, если сечение поворачивается
по часовой стрелке. Очевидно, взаимный угол поворота торцевых
сечений на опоре п
— ®п4-1
(13.27)
325
Теперь каноническое уравнение при расчете на смещение опор,
в котором роль ДпР играет Дп, примет вид
n—1 + + Дп = 0. (13.28)
В случае балки постоянной жесткости, с учетом (13.21)—(13.23)
и (13.27), уравнение трех моментов (13.28) окончательно можем запи-
сать в виде
Mn^ln + 2Мп (ln + Zn+1) + = - QEJ (0п+1 - 0п). ,
(13.29)
Если, кроме смещений опор действуют внешние нагрузки, в правой
части уравнения (13.29) должны быть сохранены члены, содержа-
щиеся в правой части уравнения (13.26).
§ 78. Расчет статически неопределимых
криволинейных стержней
При расчете статически неопределимых упругих систем, содер-
жащих криволинейные стержни, так же, как и при расчете любых
статически неопределимых систем, рекомендуется пользоваться кано-
ническими уравнениями метода сил. Однако в этом случае переме-
щения, входящие в канонические уравнения, следует вычислять не
по способу Верещагина, а по методу Мора.
В качестве примера рассмотрим круговое кольцо постоянного
поперечного сечения, растягиваемое двумя равными и противопо-
ложно направленными силами Р (рис. 260, а). Эта система, как
и всякий замкнутый контур, является трижды статически неопре-
Рис. 260
делимой. Выберем основную систему, разрезав кольцо по сечению А2
(рис. 260, б). Из условия симметрии следует, что поперечная сила
в этом сечении Х2 = 0. Разрезав кольцо по диаметру -— Л2
(рис. 260, в), из условий равновесия отсеченной части находим зна-
Р
чение нормальной силы == -g- . Неизвестный изгибающий момент
найдем из рассмотрения эквивалентной системы (рис. 260, е).
Каноническое уравнение перемещений, выражающее условие
равенства нулю взаимного угла поворота граней в сечении Л2, будет
&1Л + д1р==0, (13.30)
326
где
ds
~~ЁГ~} (13-31)
s
8n=f^^. (13.32)
J nJ
8
При этом Мр и Mt согласно рис, 261, а, б могут быть выражены
формулами:
IJ PR ч /л тс I
Мр =---2" (i — cos<р) 10<ср с уI;
= —1.
Подставляя выражения для Мр и МА
в (13.31) и (13.32), получим:
2
л _z f РВ2(1 —coscp)dcp
------------------2EJ--------=
О
Рис. 261
2РЯ2 / и
EJ \2
2
С Rdy 2тс7?
8и = 4]-ЁГ = -ЁТ-
о
Теперь уравнение (13.30) может быть переписано так:
2nR , 2PR*(n
EJ + EJ \ 2
откуда
2P7?2 (4“’1)
=--------^4-----0Д82Р/?. (13.33)
Таким образом, изгибающий момент в сечении А
МЛ=^№2РЕ
и направлен в сторону, противоположную принятой ранее.
327
Изгибающий момент в произвольном сечении можно выразить
формулой
пп
м (<f) = -y (1 = cos<f) + 2ИД?
максимальный момент
Мтах = Мв = ^0,318РЛ.
Поперечная сила в любом сечении выражается формулой Q (^) ®
Рис. 262
= 0,5Р sin ср; осевая сила N (<р) = 0,5Р cos ср. На рис. 262 приведены
эпюры М, Q и N.
В табл. 29 приведены расчетные формулы для определения уси-
лий и перемещений в различных случаях нагружения кольца.
§ 79. Определение перемещений в статически
неопределимых системах
После определения значений лишних неизвестных усилий
и построения эпюр перемещения в статически неопределимых систе-
мах можно найти обычными способами. При этом в каждом конкрет-
ном случае следует использовать тот метод, который наиболее просто
приводит к результату. Например, прогибы и углы поворота сечений
статически неопределимых балок, несущих сложную нагрузку, реко-
мендуется определять по методу начальных параметров. Метод Мора,
являющийся универсальным, обычно используют при определении
перемещений в балках, рамах и фермах.
Используя формулу Мора
S S S
следует рассматривать окончательные эпюры М, AT, Q от силовых
факторов статически неопределимой системы, а также эпюры
Ni, Qi от единичного силового фактора, соответствующего искомому
перемещению. При этом для установления эпюр Ni и Qi целесо-
328
образно единичную нагрузку прикладывать к основной статически
определимой системе.
В качестве примера вычислим взаимные перемещения точек
— А2 и В±^ В2 соответственно в горизонтальном и вертикальном
направлениях для статически неопределимой системы, представляю-
щей собой одноконтурную раму, под действием сил Р, приложенных
по схеме, приведенной на рис. 263, а. Прежде всего определим лиш-
ние неизвестные этой трижды статически неопределимой системы.
Выберем основную систему, разрезав одну из стоек по оси симметрии
(рис. 263, б). Вследствие симметрии нагрузки в месте разреза попе-
речная сила Х2 = 0. Из рассмотрения условий равновесия половины
рамы (рис. 263, в) находим
2Х3 = Р; Х3=4-
Лишний неизвестный момент определится из следующего кано-
нического уравнения:
+ д1р = 0- (13.35)
Здесь Д1Р— перемещение в направлении действия усилия Xi от
р
сил Р и = —.
&
329
Для определения перемещений Д^р и строим соответствую-
щие эпюры (рис. 263, г, д) и, пользуясь способом Верещагина,
находим
А1Р
МгМр ds 2
~Ej[
EJ
8
Pli _ Pli
ds _
EjT~~
8
Подставив (13.36) и (13.37) в (13.35),
2Z2
EJt ф EJ2 ’
(13.36)
(13.37)
имеем:
4£J, -0:
*1 =
1
A (h. । A
•Л
Pii
При lt = l2 = l и J± = J2 = J
На рис. 263, e, ж, в построены эпюры М, Q и N для рассмотрен-
ной рамы.
Для определения взаимного перемещения точек А2 в гори-
зонтальном направлении прикладываем к основной системе в этих
Рис. 264
точках единичные силы (264, б) Xi = 1. Перемножая эпюру Мр,
которую удобнее представить в виде, показанном на рис. 264, а, на
эпюру Mif находим (при Zx = Z2 = Z и = J2 = J).
A2 ~ Дг
8
MiMpds i I Pl* I
EJ ~~ ~EJ \ 16” “2 +
PZ2 Z PZ2 I \ PZ3
+ 8 2 32 *4/ 64EJ '
330
Чтобы определить взаимное вертикальное перемещение точек Вг — В2,
прикладываем к основной системе в этих точках единичные силы
Xk ® 1 (рис. 264, в). Перемножая эпюры Мр и 7Й&, находим
л Л V С MhMp ds ! ( Р12 I
йВ!-В2 - - 2j J ~Ё7 -'ёГПб' У"
8
PZ2 I 9 Z2 Р1 5 Р/3
16 6 * + 8 ‘ 16 ) ~ 192 ’ EJ
В случае действия на статически неопределимую систему темпе-
ратуры к перемещениям основной системы, нагруженной найденными
липшими неизвестными, следует добавить температурные перемеще-
ния. При этом формула (13.34) с учетом (12.36) примет вид
8 8 8
+ S f Nia (<н *в) ds + V f Mia Vя ~4 ds, (13.38)
8 8
где Mti Nt, Qt ** эпюры от лишних неизвестных, обусловленных
изменением температуры.
В табл. 24, 25, 29 приведены выражения для перемещений
в статически неопределимых однопролетных балках и кольце для
различных случаев их нагружения.
§ 80. О расчете пространственных рамных систем
Как известно, в самом общем случае в сечении стержня действуют
шесть внутренних силовых факторов: Nz, Qx, Qy, MXt My и Mz.
Для неподвижного закрепления,
сечения нужно наложить шесть связей
усилия в которых могут быть найдены
из шести уравнений равновесия твер-
дого тела.
Рис. 265 Рис. 266
Количество связей в пространственной системе, превышающее
указанное число, дает степень статической неопределимости. Так,
пространственная рама, показанная на рис. 265, а, является системой,
шесть раз статически неопределимой, так как из уравнений равно-
весия можно определить лишь реакции одной жесткой опоры. Один
из вариантов основной системы вышеуказанной рамы приведен на
рис. 265, б. Для определения шести неизвестных усилий необходимо
решить шесть канонических уравнений обычного вида.
331
Пространственная рама, показанная на рис. 266, а, является
системой 24 раза статически неопределимой. Основная система
(рис. 266, б) содержит четыре разреза, в каждом из которых имеем
шесть неизвестных усилий.
В конструкциях встречаются плоские рамы, подверженные дей-
ствию пространственных нагрузок. В плоских рамах, нагруженных
перпендикулярно к их плоскости (рис. 267, а), силовые факторы,
характеризующие работу рамы в ее же плоскости, равны нулю. С ле-
Рис. 267
довательно, из шести неизвестных (рис. 267, б) три равны нулю,
т. е. Х4 = Х5 = Хв = 0 (рис. 267, в). Это обстоятельство упрощает
расчет плоских рам.
При расчетах плоских рам пространственные нагрузки расклады*
вают на составляющие, действующие в плоскости рамы и перпенди-
кулярно к ней, и, используя принцип независимости действия сил,
рассчитывают систему отдельно для каждой из нагрузок, действую*
щих в разных плоскостях.
В качестве примера приведем расчет по методу сил рамы, пока-
А
D
Рис. 268
занной на рис. 267, а. Из соображений
симметрии выберем основную систему
в виде, приведенном на рис. 268. Этот
вариант удобнее, чем приведенный на
рис. 267, в, так как крутящий момент
Х2 и поперечная сила Х3, т. е. косо-
симметричные силовые факторы, оказы-
ваются равными нулю. Неизвестный
изгибающий момент Хг легко опреде-
лить из канонического уравнения
5цХ1 + Д1р = 0. (13.39)
Для определения перемещений Д1Р и строим эпюры изгибаю-
щих и крутящих моментов для Р-го (рис. 269, а) и единичного Х± = 1
(рис. 269, б) состояний. Эпюры крутящих моментов показаны
штриховыми линиями.
Пренебрегая влиянием осевых и поперечных сил, формулы Мора
для определения перемещений запишем в виде
+ (1М)
в ё в К
332
Учитывая, что единичные эпюры ограничены прямыми линиями,
перемещения Д1Р и можем определять по способу Верещагина
Ы f
£
Рис. 270
где
1 □_ б -Д/1 . А_
1 + b GJK I.
1+
Окончательные эпюры М, Мкр и Q приведены на рис. 270.
333
gg Таблица 24
Опорные реакции, поперечные силы, изгибающие моменты и перемещения в статически неопределимых
однопролетных балках
Схема нагружения
балки Эпюры Q и М
Опорные реакции, поперечная сила Q, изгибающий
момент М, координата опасного сечения zo,
максимальный момент Мтах
Уравнения упруг©й линии w (z), угол
поворота 0 концевого сечения, максимальный
прогиб / (при постоянном EJ)
3 Л — я 1 7» я
^А~ rb~~2 ~1~ ’ = ~2
«>&)=* —~4ЁТ
0<z I
I г3 _____2 -z2 I z 'j
\ Z8 i2 1- i]
4 Мо1* 1 ,
/в“'27£Т ПРИ z = TZ
й Мч1 л
е = - -щ-при 2 = 0
R _д И-
“а-ив- 2 I \
О С z < а
Мв - 2 V /2 J
w(z) =
MQl2 Г 1 Л а2 V z3
--ЁТ М1-т-Д-ё
^тах — М* 2 ' I (1 /2 )]
z0 = ^тах “ Z2 )
а < z I
t ч M0Z2 Г 1 Л а2 \ / Z3
w (z) ” £J [ 4 V Z2 Д /3
9 z1^ 1 / z2 , a2^ , z]
l) 2\Z2't'Z2/'1’Zj
M0Z / а 1 3 a2 \
® — EJ V I 4 4 ' Z2 /
при z = 0
при a <Z 0,275Z j ^тах ' ^тах I
при а — 0,5771 ^тах == О
Продолжение табл. 24
Схема нагружения
барки. Эпюры Q и М
Опорные реакции, поперечная сила Q,
изгибающий момент М, координата опасного
сечения z0, максимальный момент Мтах
Уравнения упругой линии w (z), угол
поворота Q кенцеввго сечения, максимальный
прогиб / (при постоянном EJ)
= = м^Р1
О < Z < 1/2
м~ър*
Z/2<z<Z
— 11 р; М = р[~ — 1
16 ’ \2 11
z0 =d Л^тах = Jg Pl
f = — 0,0093 - - - при z = Q,4A7l
EJ
РГ*
0=-32£7 приг = °
7 Pl3 I
w ~ 768EJ п₽и 2 — 2
R P a2 /„ a
BA==T "Fl3~T
0<z<6
co
P b fc2\
«В--2- • 7^---iF/>
MB = ^(Z + &)
w(z)
Pl3
6EJ
O-— •—fs--V M-— -(з^-lz
У “ 2 Z2 \ I I ' ~ 2 Z2 Г IГ
I 2 Z2 V IJ 11 ’
M — Pa
z— b
a
z0 — d ^fmax —
при a = 0,6342 наибольшее значение
^max = 0.174PZ
при a = 0,4231 наибольшее значение
2Итах = — 0,193PZ
Pa3b3 (За + 4M
W =-------12PZ7----при 2=6
fc<z<Z
a2z
при a == 0,586Z наибольший прогиб
при z = b
Pl3
/ =-0,0098
л J
. ( **
4EJ\ I3
при 2 = 0
Продолжение табл, 24
Схема нагружения
балки. Эпюры Q и М
Опорные реакции, поперечная сила Q,
изгибающий момент М, координата опасного
сечения zq, максимальный момент Мтах
Уравнения упругой линии w(z), угол
поворота 0 концевого сечения,
максимальный прогиб f (при постоянном EJ)
^A = 4?Z’‘ ^B = 4?Z; МВ = 4<?'/!!
0<Z<Z
хл ,/ 3 z \ л, _ (3 1 z
“Тр M-qlz^8-2‘ t
z0 — l Л/max = — — <;Z2
< = уZ Mmax = i2§
0<z<Z
f s ql* К z4 z3 z\
W(^ = 48EJ V Z« 3 Z8 + I /
1 = “ 185AV П₽И 2 = 0,421Z
9==^8lJ ПрИ2 = 0
I
05
co
CD
Rs ' '0ч, w « “H ,—. * : «is i ,—, 13 I % M II f ” 1” ” Iм «, %- * ф T Л .‘h -» ..cm §. n|~ '~T‘* *~~,x । * и V '^r' *1** Ч« II -1 s Л « I1 + s II ы V Z-—n l~ “ a cqV .. cm (CM тч|см В й? о ~ ~ J . 5 яф «н 7 о •s. ' su лЬ 11 II * ® г IS II ’•’ Is4 N ' « 'V ii § i ’’J «&• rv 05 II 1 ql* ' 2S9,8EJ ПрЛ Z ~ 0,5Z
, £ *0/2, z / 8
e£, w| > 6i W
Продолжение табл. 24
Схема нагружения балки. Эпюра Q и М Опорные реакции# поперечная сила 0, изгибающий момент М, координата опасного сечения zQl максимальный момент Afmax Уравнения упругой линии w (2), угол поворота 9 концевого сечения, максимальный прогиб / (при постоянном EJ)
/О II °; - Т 1 ~ ib л м. О to еГ Л II Л й А ! । н & i и Л " а, «л 'a ‘Jjp й> а" 1 " «1* * *1 • о • W f== 419EJ пРиг-°^ ql^ 1 ю= 426Л£7при2=2
в 2 \
<г 15
15^ М
rA — mql’ RB- 40ql’ MB — 120 qli
0<z<l
„ /11 z , 1 z2 \
~ ql \40 ~ I + 2 Z2 / ’
M f11 z 1
2 \20 I 3 Z2 /
7
20 = Z ^max “ |20
2O'=O,329Z M'ax = =g
i----- 327,8K7 ПРИ 2 ~ °’402Z
ql* I
w ?A9EJ при 2 2
* M p * M p
ra = ra+-T’ RB~RB--r
*
* f l\ , ^B12 I
w w \ 2 / 16£/ при 2 2
Параметры co знаком * соответствуют
статически определимой балке на двух
опорах (см. рисунок)
Продолжение табл, 24
Схема нагружения
балки. Эпюры Q и М
Опорные реакции» поперечная сила Qf
изгибающий момент М? координата опасного
сечения zoi максимальный момент Мтах
Уравнения упругой линии w (z), угол
поворота 8 концевого сечения, максимальный
прогиб / (при постоянном EJ)
«А = 6М0-^-; RB = 6M0^-;
МА^М(1~(2а^Ъ)-, Мв = МаЛ-(2Ь~-а)
O^z^a
Q = _6M0-^; М = Л/0-^-(2-±-6-|)
а z I
Q = — 6M0-^; М = Мй^2-^_
с 2 i И
zo==O Л/тах — Мо (2а — Ь}
<^ = ^„(1.-4^ +
О z а
73 Г z3 «2 1
w = ИЕ7 Ra ~1-г + >1Ма -p-j =
_ M^bz2 ( a b az \
~ ° EJP \ I ~ I ~l* ]
i<a<2i
“’max (> °) ПРИ z = 4 (2 ~ t)1
“’max«°) ПРИ z==4(1 + t) 1
+ 9
aa
К
К —
6 I3 >
z0 — а I ”y
У /2 -Г b Z3
4V=Z M^al = -M0^(2b-a)
= = 2ИД = М£ = 1Р/
0<z<-i
Q = lp; M = lp(4z-Z)
Z о
4<г< i
£л
Q = ~^-P-, M = ±P(3l-tz)
Z о
2o = ~2 ^max = "g
zo — 9’ zo — ^max = -^max = Я
, ч Pt'S к zt , zS
w^~ ifcEJY I3 I3 .
' Pla I
- W2EJ при 2 — 2
Продолжение табл. 24
Схема нагружения
балки. Эпюры Q и М
Опорные реакции# поперечная сила Q, изгибающий
момент координата опасного сечения z0#,
максимальный момент 2Итах
Уравнения упругой линии w (z)# угол
поворота 0 концевого сечения, максимальный
прогиб / (при постоянном EJ)
Co
Си
иА — г---р---> КВ — F --р---’
= Ра ; Мв = РЪ
0< zа
— Л
v (Lu J
U^Z^l
Q = _pf(3b + a>. м-р, Ь2 Г3а + 6-
V /3 , ж- в а у а1 г
г2 (г —а)_ 1
" 62а J
<=0 М^ = -Р^
*<>' = “ ^шах = 2^
z9 I Afmax — — Р р ,
если a << Ь ) ^max I ^max I -^max I»
если а >» Ь | -^max I ^max > । ^max I
4
наибольшее значение | ^^ax I 27
I
при a = -y
0<z<a
w(z) =
РаЬ2 z2 f ~Dz b
QEJ I2 \ I ~ ~a
a>b
2 P a3b2
3 EJ ' (3a 4- b)2
2al
* 3a-}- b
a<b
2 P a2b3
3 EJ (3b 4- a)2
, 2Ы
^z = l~Zb + -a
Pa3 b3
w — -зкЖнрИ2 = а
0<z<2
/ч PzU Л_
w{z)^^1aej Vе* l]
, Pl3 I
3S^EJ ПРИ Z 2
Продолжение табл. 24
Схема нагружения
балки. Эпюры Q и М
Опорные реакции, поперечная сила Q, изгибающий
момент М, координата опасного сечения z0,
максимальный момент 1Итах
Уравнения упругой линии w (z), угол
поворота 6 концевого сечения, максимальный
прогиб / (при постоянном EJ)
__ 7ql*
3840EJ
I
при z = у
—20?Z; Rb~ 2Oql’ МА зо ' мв 20
0<z<Z
_ 1 , ( 3 22 \ _9 ( 3 Z
~ ql \1б~ I2)’ M~ql \2О ' "Г ~
__ 1 Zd ____ 1 \
^"6 “К““зб/
zo = 0 ^max = ’
% =0,548Z <ax = g
f—при г=°-525/
-----WT при г== т
МА = <20л - 9*е); мв = (2вв - 9*д)
*(1\ (Ма + Мв)12
= —ГёЖТ-----
I
при Z = у
Параметры со знаком * соответствуют
статически определимой балке на двух
опорах (см. рисунок)
Таблица 25
Расчетные формулы, учитывающие смещение опор и изменение температуры в статически неопределимых
балках (при постоянном EJ)
Схема балки Опорные реакции# поперечная сила Q и изгибающий момент 2И, координата опасного сечения z0 и величина максимального момента ЛГтах Уравнение упругой линии w (zk угол поворота 0 концевого сечения и максимальный прогиб /
wu JSZ <цл| 4 1 -— в I ШН.Ш Z?r ® fa й -3^2. й -3EJto. М 3EJf» UA 1Ъ~’ КВ— > Д2В= Z2 о<2<г О__ЗК>%. ЗД//Й у- /3 , м- l3 z , .. 3EJfB Zq 1 Л^тах — j2 0< 2<Z «>w=-4(2-3t+4) f — — fo при 2—0 0 = при Z == 0
A <5£JJ Z о» к © ® 7 H > A L -1 ^Г-' 11 3EJ\. 3&7e0. M SEJ^ KA 12 , К В — 12 • iUA i~ O^z^l M^3-^(l-z) 20 = 0 Mmax = ^ 0<z</ if z z^ z^ \ U7 (z) = — 0o-J ^2 ~ — 3 4- J 0,1930o l при z = 0,422Z 0 = — 0O При 2 = 0 1 0 = ~ 0O при z = I
1 I
п „ i2EJ , л, SEJ
Кд *В — /о» Мд — fQ
0<z<Z
Л 12&Л .. 6EJ i
Q— £3 /о» j2 fo ( 4 2
, Л Л/Г, &EJ ,
zo 0 ^тах — р fo
n 1 7LT" ^EJ .
Zo — I -^max---------/о
W (z) = — /о f1 — (з — 2 у 1 -~-
j — — при z = О
£
&
llllIlMlllllhO^
со
R — R -6^eo- M
KA — UB — /2 ’ MA ~~ » ----1
I z*^ z
w(z) == — 0o / Hr — 2"jF + ~i
6EJ6O. QEJ6,
4— , — z
3 49o , 1
f-—~vl при Z=T
zq — 0 Л^тах
2о — I ^тах
4EJ0O
I
2£J0O
I
0 = — 0О при z = О
8
Продолжение табл, 25
Схема балки
Опорные реакции, поперечная сила Q
и изгибающий момент М, координата опасного
сечения z0 и величина максимального момента Мтах
Уравнение упругой линии w (z), угол
поворота 9 концевого сечения и максимальный
прогиб /
По высоте сечения
балки температура из-
меняется линейно
_ _ Sa&tEJ __ ZaAtEJ
щшшшп©
.. 9Ы
0<£<Z
C/Ml2! Z z2
w^— 4Л I / 2 /2
, aAt'l2
f==wT^
3
О _ ЗаД^7
2hl
„ SaktEJ
M=-2hT-*
А П
0 = “7=— при Z = 0
2o ^max
ZaLtEJ
2A
z3 \
Ж/
(a — коэффициент линейного темпера-
турного расширения материала
балки;
At — разность температур верхнего и
нижнего волокон балки)
По высоте сечения
балки температуре
изменяется линейно
; 4. Ав В\
f)
—---©
ЯЛ^ЯВ = О;
мЛ = мв =
abtEJ
h
0<z<Z
w (z) = 0
z
Л a&tEJ
Q = 0; М == —-— = const
(а — коэффициент линейного темпера-
турного расширения мате риала
балки;
At — разность температур верхнего
и нижнего волокон балки)
Продолжение табл, 26
Схема нагрузки
и епюра М
Изгибающий момент М
в характерных сечениях
Вертикальное смещение
опоры С
Вертикальное смещение
опоры А
Значения М те жег что и при верти-
кальном смещении опоры Ct но с обрат-
ными знаками
Нагрев на Де
., о EJ, [. . h2 \ .
Мв “ 1 + “ТГ0^
а nh \ I2 ]
акоэффициент
линейного температур-
ного расширения
352
Продолжение табл. 26
Схема нагрузки
и эпюра М
Изгибающий момент М
в характерных сечениях
Ригель шарнирно оперт,
стойка защемлена
А
п ~ 4 + ЗА:
А n D п
пл Гл О + а)1 п Ь
Мр = а 1--------------—!— аР', а = -—
L п J 2
пл °i* пл
А Ап ’ В 2п
Мл = [2 + (2 + ЗЛ)а]7г. Р
я _ ЗаА: (1 — а) Ь п а
Мр =-------i----— Р\ а = -г-
в п h
Мр = аЬР — аМА — (1 — а) Мр
Г 2 1
МА = а (2 — За) — — (1 — а) (За — 1) \М
кМ п
Мв = 3(1^а)(3а^1)— ; а = |
12 5-1186
353
Продолжение табл. 26
Схема нагрузки
и эпюра М
Изгибающий момент М
в характерных сечениях
Горизонтальное
смещение опоры С
МА=.в(2 + Зк}-^.
Вертикальное
смещение опоры С
мА = &
Мв = 12
% j
nl2
^2 /
nl2
Вертикальное
смещение опоры А
Значения М те же, что и при верти-
кальном смещении опоры С, но с обрат-
ными знаками
Поворот опоры А
па угол 0
»л-12(1 + 4>^«
354
Продолжение табл. 26
Схема нагрузки
и эпюра М
Нагрев на Д/
Изгибающий момент М
в характерных сечениях
а — коэффициент
линейного темпера-
турного расширения
6 7г(3 + 4 + тг)“а‘
Мв=6^-2(з4-2-^-)аДг
” nh\ I2 ]
Ригель и стойка защемлены
12*
п =51 4- к
Л
шпшз
I _ I
М мь = —-Р
А 2п 9 b п
Mc = [(2-a)fcH-2(l-a)]gp
Мр = ааР — аМR — (1 — a' Мс; a = ~
Ма~ 24/, 1 Мп~ 12ге
МС = (2+
35Э
Продолжение табл. 26
Схема нагрузки и эпюра М Изгибающий момент М в характерных сечениях
tj Р— <3 МА = [1 + а(Ц-2/с)]^Р м “±<kz^p в л л/ aMl-«)fe a=a G 2л h
ь л МА = [а (2 — За) — (1 ~ а) (3а ~ М Л L j к V Мв = (1—а) (За—1)^. Мс = (1-а)(За-1)^; а = ^
.(з + з»,.. м
в 12л
24л
М ^l2
МС“~“24Г
Горизон!альное
смещение опоры С
A/A = 3(l + 2fc)4^i
в nhl
мс = з^
G nhl
356
Продолжение табл, 26
Схема нагрузки
и эпюра М
Изгибающий момент М
в характерных сечениях
Д/ _ 3 ^^2 /
МА-6 п12
М — g ^2 /
Вертикальное
смещение опоры С
Вертикальное
смещение опоры А
iWc=3(2+J;)-^i
Значения М те же, что и при верти-
кальном смещении опоры С, но с обрат-
ными знаками
МА = (3 + 4к) 9
м =2^9
" nl
Mc = ^f 9
G nl
Нагрев на Дг
zttffl
мА = -^4.(2 + А +
А nh \ к 1£
мв =
^=-^[* + (2 + *)-£]^
а — коэффициент
линейного темпе-
ратурного расширения
357
Таблица 27
Продолжсние табл. 27
Изгибающие моменты в П-образной раме
Схема нагрузки
и эпюра М
Изгибающий момент М
в характерных сечениях
Схема нагрузки
и эпюра М
Изгибающий момент М
в характерных сечениях
Стойки
шарнирно
оперты
1
ив-ис=|ы>
L /& j £*
(2 — а) аЛ1 а р
n
Мр = (1-а)(РЪ + Мв)
h
3 + (1 + За2) к ..
Т 2».... М
м 4i + (i-^k}M
мв=(2+к)-^
MG = (Q + 5k)^-
358
359
П род о лжение табл. 27
Продолжение табл. 27
Изгибающий момент М
в характерных сечениях
Схема нагрузки
и эпюра М
Изгибающий момент М
в характерных сечениях
Схема нагрузки
и эпюра М
Нагрев на At
мв = мс =
в с 60п
м - Л3~2а 3(1-“)2]
А~ L~
мв = мс = -£72.aAt
1S с nh
3(1 —я)2] <?Z2
n2 J 12
ЛГс = а2 2(3-,2а)
с [ «1
3(1-
пг
,[2(3 — 2а) , 3(1 —а)2] ql2 .
В “ “ 1~------+-----“1 Т2"‘
а — коэффициент
линейного температур-
ного расти репия
Стойки
защемлены
д/ _д/ ___
MA-MD- 12ni
Мв « Мс = 4^-
в и 6ггх
24- 3fe 2
ma» 24»! 4
MR = Mr = ~ — hP
B b 2 n2
360
361
Продолжение табл. 27
Схема нагрузки
и эпюра М
Изгибающий момент 1И
в характерных сечениях
А I ^2
а[1 + а(1 + ft)]) а п
'Г nx / 2
I ____ Г3 С1 — а)^ а (1 — а) &1 а р
~1 П2 П1 J 2
D ( «2
a[l+a(l + fe)]l а р
пх / 2
г __ ГЗ (1 — а) к а (1 — a) fol а р
С L П2 ’ ni J 2
t а (2 — За) к / бак Д1 М
2mx у П-2 / J 2
a(2— 3a)fc_ / 6afc _ Л1M
2п± \ и2 /] 2
362
Продолжение табл, 27
Схема нагрузки
и эпюра М
Изгибающий момент М
в характерных сечениях
(к + 3 , 1 + 4^ qh2
А \ 6nj п2 / 4
_/l + 4fe 3 + ^ qh2
D \ n2 6n2 ) 4
,, . - 8 4- 37с qh2
л_ j.. qh2
М ту =2 Mq " 757г--------
В ° ЗОП!
Нагрев на Д«
Нагрев At
ж „д = 3(1+цу,.дц
А и k^h
ил ъя 3EJ2 a&t
а — коэффициент
линейного температур-
ного расширения
звз
Таблица 28
Изгибающие моменты в замкнутой раме
к = ; Р = Ф ; п = 1 + р + 6/с; т = (2 + к) + 4 (3 + 2*)
J1 I J з /с
Схема нагрузки
Изгибающие моменты в узлах рамы
(положительные моменты вызывают растяжение
с внутренней стороны рамы)
.. /4 J 1 -1— 2<I\Pl
МА, D — “ “) I — + ~ I ’
9 \ III rl j и
A, D
с = —я(1—«)
2fc + Зр j
. кт
Р1
2
Pl'
2 ;
MA,D = «&-a)p(^r±
PZ
2
МА. D = “ 1“ (1 + fc) - (2 + fe)l T
1 } Ph
T2.[l + 3fc(2-a)]}^
MB, C = “ 1“ (fc + p) + p] ±
±.L{3ak + p^™
a
a~T
364
П родолжение табл. 28
Схема нагрузки
Изгибающие моменты в узлах рамы
(положительные моменты вызывают растяжение
с внутренней стороны рамы)
,q
пиши
„ 2* + Зр
М О = МГ =-• -Г--
ВС 12 кт
А и . Мт
.. .. 3 + 2k gl2
МА = md — —t— p~hr;
A u km 12
q-
|ишии
М=МС = — JL
во m 12
^A,D = «2
3 (1 — a)21 qP
n I 12
fiir
[1
— (3~2a)(2* + 3p)±
Q
±4(1-“)*
а
а=т
365
Продолжение табл. 28
Схема нагрузки
Изгибающие моменты в узлах рамы
(положительные моменты вызывают растяжение
с внутренней стороны рамы)
I
[1
(2*4-3)
— (1 — а)2
и
2 P-2a-L
Мвс = _«2р1——±
, 3(1 — и)21 ql2 а
±—п |-ЁГ; а = ~1
,_______(3 + к 1 +4fc\ qh?
Л, D ( (jm n / 4
, — /fe + 3p 2*4-p) gfe2
C ( 6m — n j 4
мл = мв = мс = л/0 =
Л2
1 + k ql2
1 + k 12 ПРИ 72 ~Ja
366
Продолжение табл, 28
Схема нагрузки
Изгибающие моменты в узлах рамы
(положительные моменты вызывают растяжение
с внутренней стороны рамы)
Ma=Md = 8 +3ft т q№ 60
мв = мс = 1 + 2к т qh,2 р_60"
„ Зр + 2к+ 1)М
МА, D~~"P
MBtC~
3 4-2Л
кт
± п) 2
/2-М~ 1\М
кт + п ] 2
367
Усилия и перемещения при нагружении кольца в его плоскости
N, Q, М — нормальная и поперечная силы и изги-
показаны положительные направления для усилий,
растай ия угла <р); by — изменения диаметра кольца
личению диаметра); Е — модуль упругости материала;
Схема Q 1
qR 0
р 1 Y Р sin ср 1 -% Р cos <р
’Р
2Р °<?<Г Р (0,3183 cos ср 4- sin ср) Р • 0,3183 • cos ср 0<?< у — Р (0,3183 sin ср — — COS ср) л — Р • 0,3183 sin ср
с
368
Таблица 29
баюший момент в сечении кольца, определяемом углом ср (на рисунке
действующих па впереди лежащее сечепие кольца в направлении воз-
в направлении осей х и у (положительное значение соответствует уве-
F, J — площадь и момент инерции сечения кольца.
м 8
0 . * 4R2 bx — by — x * EF
— PR (о,3183 — у sin <pj PR3 ILJ PR3 by = 0,149 ihj
0<<р<у
PR (0,3183 cos ср + sin ? — 0,8183)
О
PR (0,1817 + 0,3183 cos <р)
^ = -0,1366-—
IhJ
PR3
by = 0,1488
369
Схема N Q
0<C <p <ct 0< ?< «
P (0,3183 sin2 a cos tp + P (cos cp —
+ sin cp) 0,3183 sin2 a sin <p)
a <C ср тс a ср тс
P • 0,3183 sin2 a cos cp — P 03183 sin2 a sin cp
0<«p<a 0<<(p a
P [0,3183 cos cp (sin2 p — P [0,3183 sin cp (sin2 a *—
IPi |P — sin2 a)] — sin2₽)]
• /?7\ d 1 a cp < p «<?< P
Tw T P [0,3183 cos cp (sin2 p — P [0,3183 sin tp (sin2 a *-
Pf TP — sin2 a) + sin cp] — sin2 P) + cos cp]
p cp < я p< f < я
P [0,3183 cos cp (sin2 p — P [0,3183 sin cp (sin2 a —
— sin2 a)] — sin2 p)]
370
Продолжение табл. 29
м 5
PR3 Г 1 8x=-gJ-[y (sin2a + 2) +
0<^ ср а 4-0,6366 (a sin a 4- COS a — 1) —
PR [0,3183 (a sin а + COS а 4- + SIB2 а COS ср —- 1) — — sin а 4- sin ср] — 2 sin a j
а ср к PR3 Г 1 = “#7“ T (s,n a cos a
PR [0,3183 (а sin а 4- + COS а 4- sin2 a cos ср — 1)] 4~ ct) 4~ 0,6366 (a sin a 4“
4- COS a — 1) — sin aj
0 ср а
PR [0,3183 (Р sin р 4- cos р — — a sin а — COS а — sin2 a cos tp 4“ PR3 Г 1 = EJ [ 2 (sm2 a + S1“2 +
4- sin2 3 cos cp) — sin p 4- sin a] 4- 0,6366 (p sin p4-cosp —
a < cp<p — ot sin a — cos ct) 4- 1 — 2 sin P)
PR [0,3183 (p sin p 4- cos p — — a sin a — COS a — sin2 a COS cp 4~ PR3 Г 1 By = -EJ- 1 2 (sin ₽ COS ₽ +
4- sin2 p cos cp) — sin p + sin <p] 4- P — sin a COS a — a) 4"
P < <p + 0,6366 (P sin P4-C0SP —
PR [0,3183 (p sin p 4- cos p — — a sin a — COS a) 4»
— a sin a 4- COS a — sin2 a cos cp 4~ 4* sin a — sin p]
4- sin2 p cos cp)]
371
Схема /V Q
0<Г ср << а Р [0,3183 (а — — sin а COS а) — 1] cos ср а ср тс Р • 0,3183 (а — — sin a cos а) COS ср 0 < ср < а Р [0,3183 (sin а COS а — «— а) -|- 1] sin ср а ср <L тс Р • 0,3183 (sin а ♦ cos а — — а) sin ср
\р р I л /р Д \ р 0 ср а Р 5— COS ср 2 sin а т 0 < ср а Р гг“.:— sm ср 2 sin а т
°^~п ><. ✓р ^\р
0<^ ср <^тс /И 0,6366 cos ср к 0<ср <тс Л/ 0,6366 sin ср R
лсС
372
Продолжение табл, 29
м &
0< ср <а PR [0,3183 (sin а — а cos а 4- 4- а cos <р — sin а cos а cos ср) — — COS <р 4- COS а] а ср тс PR • 0,3183 (sin а — a cos а + 4- а cos ср — sin а cos а cos ср) pt?3 Г 5х = ^Т- 0,6366 (sin а — EJ [_ 1 1 — а cos а) 4- — (sin а cos а — а) I; ZU J PR* Г Ъу = ЛД- 0,6366 (sin а — EJ L — а cos а) 4- cos а 4- 4-3-sin2 а —1^|
0< ср< а PR ( cos ср 1 \ 2 \ sin а а / при ср = 0, 2а, 4а, ... д/(+) — 13 max~ 2 \sin а а/ При ср 5= а, За, ... ^max “ ~ 2 ("7 с1£ а) Радиальное перемещение точки приложения силы от центра РВ3 Г 1 /а 2EJ [ sin2 а \ 2 sin 2а \ 11 + 4 / а J Радиальное перемещение в точ ках ср = 0, 2а, 4а, ... (к центру) PR* (2 1 а cos а \ \EJ \ а sin а sin2 а /
о<?<| MQ ^0,6366 cos ср.— тс “2 М0 ^0,6366 cos 4- О о II II и «о «о 1 1
373
Схема N Q
0 cp к M ----- 0,6366 sin a cos cp R 0 cp u Д# 0,6366 sin a sin q R
P = 2qR sin a |P 0<; cp << a — qR 1 ~ sin3 a cos cp + \O7t 0< cp< a I D/1 . 3 . qR o~ sin3 a sin cp — \3k — sin a cos cp^
1 ] + sin a sin cp j a ср к a ср я
ШЕИ /1 —- qR hr~ sin3 a cos cp + \3k t + sin2 cp^ D/1 . з . дЯ 1 sm3 a sin cp — — sin cp cos cpj 1
374
Продолжение табл. 29
м б
0< ср <а Мо [0,3183 (2 cos ср sin а + а) — 1] а <р «с MQ [0,3183 (2 cos ср sin а + а)] "М п* ъх = ~Ё7~ <°-6366а — sin °) М R* Ъу = (0,6366а + cos а — 1) EJ
0 С ср а М (0) — gR2 £sin а sin ср — 1 1 — sin3 а (1 — cos ср) а <Р 11 М (0) + qR2 sin3 а (1 <— cos ср) — (sin2 а + sin2 ср) j M(0) = 9fl2[l + ysin*a + , i ( . 1 . , •4 sin а a sin2 а — к \ 2 sin3 а 3 . а \1 5 т- sin a cos а «—Т1 3 4 4/J __ 2q /?4 Г 1 sin a sin2 а ж EJ [4 2 1 2 sin3 a 1 I a . , 12 kU Sln“ + , з . ,i . 2 Yl + -4- sin a cos ct + ~ a sin2 a 1 x 2g/?4 Г 1 sin2 a
v ” EJ [12 1 4 a sin a sin2 a cos a ~ 4 12 COS a 1 /a sin2 a 6 Д 2 + , 3 . , a \1 -4- -7- sin a cos a + -7- sin a 4 4 /J
375
Схема N ° 1
0 <С ? а — QT?[sina sin ср 4- + (14- cos а) COS ср] — О < ср а
Р » 2qR sin а *— N (тс) COS ср — qR [sin а cos ср — — (1 + COS а) sin ср] —
- а < у п
<5 — qR(l + COS а) — — N (тс) cos <р + N (тс) sin 9 а < <Р < тс
N (я) = — (- — ТС — sin а + а cos а) qR sin ср 4- N (тс) sin ср
39ч б < ср < а — qR sin2 ср 0<Г ср а qR sin ср cos ср
j *V/ а < ср тс — а а <р те — а
Щ W — qR • sin а • sin ср qR sin а cos ср
376
Продолжение табл. 29
м d
0 с р а gB2j^sina sin р 4~ (1 + cos а) cos р— тс ?Я4 L 2a 8*~ EJ Г x + 2 sin a 3 sin a
1 1 (тс _ а + sin а) 4“ тс J 7V (тс) R • cos р а р < тс Г 1 1 qR* cos р — ~ (sin а «— а) | 4- 4- N (тс) • R > cos ср * тс 2 тс cos a a cos a\ 2 2/ 0 < а<^тс x /9 2a i 8*="£742-v + ,2 sin a a sin a \
тс 2 /
0< р < а Af (0)-^sm2? а р тс — а М (0) — qR* ^sin а . sin ср — 5 qR* f . sin3 a . Bx= EJ [ S.na 3 + 1 -| (a 4“ 3 sin a COS a 4“ TC 4- 2a sin2a)j 8y = 2^_fsin2a — tLJ l sin2 a cos a
М(0)_,Я-[1(| + о 2 cos a 2 тс sin a
4- а sin2 а 4- ~ sin a cos aj — 1 ’ 2 1 — yrfa 3 1 3 1 2 1 (2a sin2 a 4- 3 sin a X TC X COS a 4- a)j
377
Глава 14
РАСЧЕТ ПЛОСКИХ КРИВЫХ БРУСЬЕВ
§ 81. Определение напряжений в брусьях
больший кривизны
К кривым брусьям относятся грузоподъемные крюки, проушины,
звенья цепей, ободы шкивов и колес, арки и т. п. Оси этих брусьев
являются плоскими кривыми. В поперечных сечениях плоского кри-
вого бруса в общем случае действуют три внутренних силовых фак-
тора М, Q и N, правило определения которых такое же, как и в
брусьях с прямой осью. Дифференциальные зависимости между М,
Q и q были приведены в § 21.
Рис. 271
Представляют большой практический интерес кривые брусья,
имеющие продольную плоскость симметрии (рис. 271, а, б), в кото-
рой обычно действуют внешние нагрузки.
Распределение нормальных напряжений в поперечных сечениях
кривых брусьев иное, чем в брусьях с прямой осью. Это различие
при прочих равных условиях тем больше, чем больше кривизна бру-
са, характеризуемая отношением высоты поперечного сечения h
кривого стержня к радиусу кривизны R его оси. В связи с этим
378
принято различать брусья малой кривизны, у которых > ь
h 1
брусья большой кривизны, у которых
XI О
При изгибе брусьев малой кривизны нормальные напряжения
с достаточной степенью точности можно определять по формуле Навье
(10.6), выведенной для балок с прямой осью. Максимальные напря-
жения, подсчитанные по формуле Навье для бруса прямоугольного
hi
сечения с отношением -р- — т?, отличаются на 2% от напряжений
xi 1 <3
вычисленных по формулам для бруса большой кривизны; при
hi о cn/ h 1
-F = 7?i~na 3,5%; при — = на 7%
R 10 Я 5
Рассмотрим случай чистого изгиба бруса большой кривизны
(h 1 \
-р->-р-1 (рис. 271). Предполагаем, что радиус гн нейтрального
jfl о /
слоя неизвестен и не совпадает с радиусом R оси стержня
Рис. 272.
При выводе формулы для определения нормальных напряжении
в брусе большой кривизны исходят из тех же гипотез, что и при
выводе формулы Навье, т. е. пользуются гипотезой плоских сечений
и гипотезой о том, что продольные волокна материала не давят
друг на дргуа. Выбираем направление осей сечения х и у, как пока-
зано на рис 271 (при этом ось х считается совпадающей с нейтраль-
ной линией, положение которой пока не известно). Направление у
к центру кривизны принято за положительное.
Рассмотрим статическую сторону задачи и напишем условие равно-
весия применительно к элементу бруса (рис. 272, а), оставшемуся
379
после удаления отселенных частей. Для нашего случая, когда в сече-
нии действует один силовой фактор будем иметь
a dF == 0;
ay dF = М.
(14.1)
(14.2)
В силу симметрии
Му = ах dF = 0.
F
Рассмотрим геометрическую сторону задачи. Относительное удли-
нение произвольно выделенного элементарного участка АВ, находя-
щегося на расстоянии у от нейтральной линии (рис. 272,6) и полу-
чившего в результате деформации удлинение i/Д dy, равно:
у
(гн — У) '
(14.3)
где (гн — у) dy — длина элемента до деформации.
Из рассмотрения физической стороны задачи, определяемой зако-
ном Гука
а'=£е =- —О—, (14.4)
d<f> Гн — у
условие (14.1) перепишем в виде
d<P J rH - У
F
Так как
Е-¥^о,
dy
то
( ydF
hH-y
= 0.
(14.5)
Из (14.2) находим
ay dF
Г V2dF
d<f JrH — у
F
(14.6)
380
Так как
у2 dF
С У* + '„!/ ~ г„У
} Г-~У
F
Ь^+г(Л^-=-?х + °.
или
Г -fl ЛЕ»
\ JL!i!L = — Sx = — (— е) F = eF, (14.7)
рп У
можем представить (14.6) так:
E&dv „ п.
——- eF = М.
dcp
Отсюда
(14-8)
d<? eF
где е.— расстояние от нейтральной линии до центра тяжести; F —
площадь поперечного сечения.
Рис. 273
а
Подставив (14.8) в (14.4), найдем формулу для определения нор-
мальных напряжений при изгибе
или
Му
eF (гп ~ у) ’
Му
Sx (гн — у) ’
(14.9)
(14.10)
381
г ;е М — изгибающий момент в сечении; Sx — статический момент
площади сечения кривого бруса относительно нейтральной линии.
Из анализа (14.9) пли (14.10) видно, что нормальные напряжения
по высоте распределяются по гиперболическому закону (рис. 273,6).
Абсолютные величины напряжений в крайних волокнах сечения
бруса согласно (14.9) определятся по формулам
_ Mht . __ Mh2
01 ~~ FeR1 9 °2 FeR? 9
(14.11)
где Rx и R2 — соответственно радиусы кривизны внутренних и внеш-
них волокон кривою бруса; ht и h2— расстояния от нейтральной
линии до этих волокон Знак напряжения определяется по направ-
лению изгибающего момента в сечении
Формулы (14 9)—(14.11) могут быть использованы, если известна
входящая в эти формулы величина е или радиус нейтрального слоя
гн, поскольку
е = Н-гв,
(14.12)
где Л— радиус слоя, в котором расположены центры тяжести сече-
ний бруса Радиус гн определим из уравнения (14.5).
Произведя замену переменных: г = гн — у или у = гн — г, пере-
пишем уравнение (14.5) в следующем виде:
( ydF
J/H-*
или
Отсюда
(14.13)
Так как для прямоугольного сечения F = bh (7г — высота сечения;
д—ширина сечения); dF~bdr, формула (14.13) может быть записа-
на в виде
н
h ___ h
In J? 2,303 Ig^'
zti щ
(14.14)
Воспользовавшись рядом
r R+i
. /io i
In = In---r = In--r
R1 R h 1 h
R~2 l~2R
h L i 11h У, 11 h\* ।
Я L + 3 \2Rj + 5 \2R) +
382
будем иметь
В первом приближении
(14.15)
Во втором приближении
_ A/А
е~ 122? I 15\2Я.
(14.16)
На основании (14.13) аналогичным путем можно получить выра-
жение для е в случае других форм поперечного сечения. В табл. 30
приведены радиусы кривизны rR нейтрального слоя для сечений
различной формы. Из (14.12) по известным гн могут быть опреде-
лены п величины е. Для некоторых форм поперечного сечения <
можно определить по табл. 31.
§ 82. Расчет на прочность
Условие прочности для стержня малой кривизны, когда в ею
сечении действуют изгибающий момент и нормальная сила (рис. 273, а)
имеет вид
М , N г 3
°тах ~ И7 ‘ ° ’
(14.17)
где F — площадь сечения; W — момент сопротивления сечения (см.
§ И).
Для стержня большой кривизны на основании (14.9) условие
прочности будет
Му 7V
°тах ре (Гн _ у) -I" р
(14.18)
При этом нужно рассматривать точки сечения, в которых сум-
марные напряжения от изгиба и растяжения будут наибольшими
(рис. 273, б, в, е). Для этих точек в формулу (14.18) следует под-
ставлять у = или у = h2 и соответственно rR — у — Ri или
гн — У = Яг-
383
Если брус большой кривизны изготовлен из материала, для
которого допускаемые напряжения на растяжение [а+] и сжатие [а__]
различны (некоторые чугуны, пластмассы и др.), то условия проч-
ности должны выполняться для крайних точек сечения как в растя-
нутой, так и в сжатой области.
§ 83. Определение перемещений
Для определения перемещений в стержнях любой кривизны
удобно пользоваться методом Мора (§ 69).
В стержнях малой кривизны можно пренебречь продольной
деформацией и деформацией сдвига и в случае плоского изгиба
пользоваться формулой Мора в виде
АгР“
MiMp ds
eJ
(14.19)
При плоском изгибе бруса большой кривизны деформация эле-
мента от действия усилий Мр и Np состоит из удлинения Д (ds)
отрезка ds оси и относительного поворота dO сечений, ограничива-
ющих элемент (рис. 274, а, б). Взаимный угол поворота сечений
Дб/ср = вызванный изгибающим моментом, можно определить из
(14.8), где eF = | | = S,
Мр dy Мр ds
= ~ES~ = ESR0 '
Угол поворота сечений, вызванный осевыми силами вследствие
неодинаковой длины волокон элемента (рис. 274, б), равен
^2 =
N pds
ТЁЩ'
Полный угол поворота составляет
М pds
dft = d0x 4- d02 = pen "b
Npds
EFRo'
(14.20)
Удлинение элемента в результате действия осевых сил
Д (ds)1
Np ds
EF '
384
Удлинение, вызванное поворотом сечения на угол dOp
Д (ds)2 =» е _ ESR^
Mpds Mpds
e~~EFR^'
Полное удлинение осевого волокна
TV р ds р ds
Д (ds) = Д (^)i + Д (ds)2 = . (14.21)
Подставляя (14.20) и (14.21) в формулу возможных перемещений,
находим общую формулу для определения перемещений бруса боль-
шой кривизны
в
MiMp
~ESR^
NiMp+ MiNP JViNp CiQpl
EFR0 + EF + k GF J <14’
Обычно на практике пренебрегают влиянием поперечной силы,
в результате чего последнее слагаемое в (14.22) отсутствует.
В табл. 32, 33 приведены выражения для определения переме-
щений свободного конца консольного кругового стержня постоянного
поперечного сечения при различных схемах его нагружения, а в
табл. 34 — значения определенных интегралов, часто встречающихся
при определении перемещений в кривых стержнях.
13 5-1186
385
Таблица 30
Радиус кривизны нейтрального слоя гн для сечений
различной формы
Сечение
(С — центр тяжести)
Прямоугольник
380
Продолжение табл. 30
Сечение
(С — центр тяжести)
~h ^3^3
bt lng+b2ln J+Mn§
___4~ ^^2^2_
мп^+2Мп*_д.
13*
387
Продолжение табл. 30
Значение коэффициента k в формуле е = kR
Сечение
R
а
k
Прямоугольник
1,2 0,305
1,4 0,204
1,6 0,149
1,8 0,112
2,0 0,090
2,2 0,077
2,4 0,065
2,6 0,055
2,8 0,047
3,0 0,041
3,5 0,028
4,0 0,021
6,0 0,0093
8,0 0,0052
10,0 0,0033
388
ITродолжение табл. 31
Сечение
Тавр
— 4&2J ^1 ~ ^2 — 4,5&2j
а = R — 7?! = 2,04&2
R а k
1,2 0,418
1,4 0,299
1,6 0,229
1,8 0,183
2,0 0,149
2,2 0,125
2,4 0,106
2,6 0,091
2,8 0,079
3,0 0,069
3,5 0,052
4,0 0,040
6,0 0,018
8,0 0,010
10,0 0,0065
Двутавр
— 6&2; *3 — 4&2;
Л.-£ = 2&2, Л2 = 3&2, ^3 ==: ^2,
а = R — = 2,3462
б)
&£ — — 3&2J ^1 — ^3 — ^2>
Л.2 = 462,’
а = R —- Ry = 3&2
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
3,0
3,5
4,0
6,0
8,0
10,0
0,409
0,292
0,224
0,178
0,144
0,120
0,103
0,089
0,077
0,067
0,049
0,038
0,018
0,010
0,0065
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
3,0
3,5
4,0
6,0
8,0
10,0
0,408
0,285
0,208
0,160
0,127
0,104
0,088
0,077
0,067
0,058
0,041
0,030
0,013
0,0076
0,0048
389
Продолжение табл. 31
Сечение а k
В) h± = &з — 6&2; = h3 — b2; h2 = 462 и а — R — Ri — 3&2 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3,0 3,5 4,0 6,0 8,0 10,0 0,453 0,319 0,236 0,183 0,147 0,122 0,104 0,090 0,078 0,067 0,048 0,036 0,016 0,0089 0,0057
1 У 'рапеция Ьг^ 1,2 1,4 1,6 1,8 2,0 2,2 0,336 0,229 0,168 0,128 0,102 0,084
С 2,4 2,6 2,8 3,0 3,5 4,0 6,0 8,0 10,0 0,071 0,061 0,053 0,046
ь, 1 5* с е
У ct
а) 61 = t = 2Ъ2; i — R fe = ( -я. 1- 3) 0,033 0,024 0,011 0,0060 0,0039
б) а = bl = я — 462; h Я,= 2&2 5&2; , = 0,4й 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3,0 3,5 4,0 6,0 8,0 10,0 0,352 0,243 0,179 0,138 0,110 0,092 0,078 0,067 0,058 0,050 0,037 0,028 0,012 0,0060 0,0039
390
Продолжение табл. 31
Сечение
Треугольник, у которого
3
h — -~Ь и а = Л — 7?i =
о х
R а k
1,2 0,361
1,4 0,251
1,6 0,186
1,8 0,144
2,0 0,116
2,2 0,096
2,4 0,082
2,6 0,070
2,8 0,060
3,0 0,052
3,5 0,038
4,0 0,029
6,0 0,013
8,0 0,0060
10,0 0,0039
Круг
1,2 0,224
1,4 0,151
1,6 0,108
1,8 0,084
2,0 0,069
2,2 0,058
2,4 0,049
2,6 0,042
2,8 0,036
3,0 0,030
3,5 0,022
4,0 0,016
6,0 0,0070
8,0 0,0039
10,0 0,0025
Кольцевое сечение
D = 2d и а = — = d
1,2 0,269
1,4 0,182
1,6 0,134
1,8 0,104
2,0 0,083
2,2 0,068
2,4 0,057
2,6 0,049
2,8 0,043
3,0 0,038
3,5 0,028
4,0 0,020
6,0 0,0087
8,0 0,0049
10,0 0,0031
391
Таблица 32
Перемещения свободного конца консольного кругового стержня постоянного сечения при нагружении
в его плоскости (w9 v, 6 — вертикальное, горизонтальное и угловое перемещения соответственно)
Схема W 0
1IV 1Р — cosa) + „ / a sin 2a\ +рдЬ~— )- __TR (1 —COS a)2j Д2 Г rj 1 —^0 (a —Sin a) — + TR (y a — 2 Sin a + ~j [ЛГ0а4-РЛ (1 — cos a)— — TR (a — sin a)]
# г j р Мо'Лт V R2 Г — Mo (sin a — a cos a) + / 1 з \ 4- PR a 4- 4-a COS 2a т-sin 2a 1— ’ \ 2 4 / __ / 3 n — TR cos a — — cos 2a — \ 4 1 • 9 Л1 x- a sin 2a 7- 2 4 /J л2Г V— — MQ(a sin a — 14- COS a)— — PR (cos a cos 2a — \ 4 1 1 \ — у “Sin 2a — —j 4- + TR (a 1- a cos 2a -f- 3 \1 4- -7- sin 2a — 2 sin a I 4 / j S-AM'fl + PR (sin a- — a cos a) — TR (a sin a — — 1 4- cos a)]
I
qR*(i — cos a)2 EJ 2 qR4 /3 n . , sin 2a\ £/(2“ 2S1““+ 4 J qR9. — (a-sma)
q^const^ w V
q* const if <*/~ V qR4 / a . sin 2a\ — ^y+acosa-sma-— qR4 la2 , sin2a\ — ^y-asma+ j #Z?3 / a2\ — (^l-cosa- ~j
m=const 3\ w V mR3 . ^=rr (sin a - a cos a) Hi J -тгг (1 — COS a — a sm a) mR2 a2 1T‘*2
Таблица 33
СО
Перемещения свободного конца консольного кругового стержня постоянного сечения при нагружении
в перпендикулярной плоскости (К — отношение жесткостей сечения при изгибе EJ и кручении GJK)
Схема Перемещение, перпендикулярное к плоскости WV Угол поворота вокруг оси v Угол поворота вокруг оси w
j w р V РЯ»/14-ЗХ < *— 1 • 9 яД 2 «-H-4-sm2a- — 2k sin aj PRZ(\ — 1 . . 1 + X EJ (—sm2a+-T-a — k sin a j рх?2Гх-1 . 2 , EJ[— Sln a + + X (1 — COS a)j
EJ I 4 Sin2“+ 2 “ — k sin a^ iH“H+~sin2aJ M0R X —1 . 2 EJ 2 “
\ I '
4м м0й2Гх —i . . . EJ [— sin2a + + X (1 — COS a)j M0R X-l EJ 2 SП “ ^oB/'l + X X—1 . „ \ "gj V 2 “ 4 sm2“J
(pconst ) V ^[(1 — COS a)2 + + k (a — sin a)2] </Я2Г gj 1 (* + 1) (1 — cos a) — j — (1 — cos 2a) — — ka sin a J Д + 1) (sin a — Д + , X—1 . „ , ] H 7— sin 2a — ka cos a 4 I
Таблица 34
Значения определенных интегралов, часто встречающихся
при определении перемещений в кривых стержнях
Интеграл Пределы интегрирования
от 0 до a n K от 0 до у от 0 до ~ ОТ 0 ДО тс
У sin ср dcp 1 — COS a 0,293 1 2
У COS ср dcp sin a 0,707 1 0
§ sin2 ср dcp 1 . o . a — sin 2a + у 0,143 0,785 1,571
J cos2 cp dcp 1 . o . a J Sin 2a + — 0,643 0,785 1,571
J sin2 cp cos cp dcp sin3 a 0,333
T“ 0,118 0
1 — COS3 a 0,667
§ cos2 cp sin cp dcp 3 0,216 0,333
J sin 2cp dcp 1 cos 2a 2“ ~ 1 2 1 0
J cos 2cp dcp 1 • 9 у Sin 2a j_ 2 0 0
У sin cp cos cp dcp sin2 a 0,5
“IT 0,25 0
У cp sin cp dcp sin a — a cos a 0,152 1 3,141
j* cp COS cp dcp COS a + a sin a — 1 0,262 0,571 —2
J cp sin2 cp dcp 1 4- (a2 — a sin 2a) — (COS 2a — 1) 0 0,0833 0,868 2,47
У cp COS2 cp dcp 1 — (a2 -f- a sin 2a) -f- 1 + g-(cos 2a — 1) 0,226 0,368 2,47
j* cp sin 2cp dcp sin 2a a cos 2a 0,25 0,785 —1,571
4 2
У cp cos 2cp dcp 1 У (cos 2a-l) + 0,143 —0,5 0
, a sin 2a
+ 2
j* sin (a — cp) sin cp dcp sin a a cos a 0,076 0,5 1,571
2 2
j* cos (a — cp) sin cp dcp a sin a 2 0,278 0,785 0
396
\
А л а в а 15
РАСЧЕТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ
И ЙРАЩАЮЩИХСЯ ДИСКОВ
§ 84. Толстостенный цилиндр, подверженный
внутреннему и наружному давлению
2г,
2Л
Цилиндр считается толстостенным, если толщина его стенки
больше одной десятой его среднего радиуса. Рассмотрим толстостен-
ный цилиндр, находящийся под действием внутреннего (рх) и наруж-
ного (р2) давлений (рис. 275); и г2 — соответст-
венно внутренний и наружный радиусы цилиндра.
Вследствие осевой симметрии цилиндра и нагрузок
напряжения и деформации в цилиндре будут так-
же симметричны относительно его оси.
Двумя сечениями, перпендикулярными оси
цилиндра, выделим кольцо единичной длины
(рис. 275). Из этого кольца вырежем элемент abdc
(рис. 276, а) двумя плоскостями, проходящими че-
рез ось цилиндра и образующими между собой угол
d6, и двумя цилиндрическими поверхностями ра-
диусами г и г-}-dr (рис. 276,6). По граням этого
элемента будут действовать радиальные <зг и тан-
генциальные а0 напряжения, заменяющие воздей-
ствие отброшенной части цилиндра и удовлетво-
ряющие условиям равновесия элемента. Очевидно,
с0 и аг будут главными напряжениями.
Определение = f (рп р2> >*) и а0 = (рх, р2, г)
начнем с рассмотрения статической стороны задачи
и составим уравнения статики в соответствии с
принятой системой координат (рис. 276, в): рис. 275
2^ = 0; 2У = О-
Рис. 276
Благодаря симметрии элемента второе условие удовлетворяется
тождественно, а первое после подстановки выражений для усилий
примет вид
2 % = — Qrr + (cr + daT) (г + dr) dft — 2 L0 dr sin = 0.
397
гг . ^6 do J
Принимая sin -у = -у и отбрасывая величины второго порядка
малости, получим /
cfor | л
r_ + or_oe==0.
Это уравнение содержит два неизвестных напряжения ае и аг.
Для их определения необходимо рассмотреть геометрическую и физи-
ческую стороны задачи, что позволит представить уравнение (15.1) в
перемещениях.
Обозначим радиальное перемещение цилиндрической поверхности
радиуса г через и (рис. 276, а); тогда перемещение цилиндрической
поверхности радиуса г + dr будет и + du. Относительное удлинение
элемента длиной dr выразится формулой
du
’
(15.1)
(15.2)
Относительное удлинение в тангенциальном (окружном) направ-
лении будет равно:
е _ (r + “) rffl —rrffl _ (15.3)
0 rd0 г
Рассматривая физическую сторону задачи, представим зависимости
между напряжениями и деформациями в соответствии с обобщен-
ным законом Гука применительно к плоскому напряженному состоя-
нию в следующем виде:
Е , ,
Ог=пг72(%+1ле9);
Л
Е , ,
Учитывая (15.2) и (15.3), получим
_ (^и t и \ .
Qr ““ { |1’2 \rfr “Г Т/ ’
Е (и , du\
С0~1 — р.2 \ г I* dr) ‘
(15.4)
Подставив (15.4) в (15.1), получим дифференциальное уравнение
в перемещениях
Й + - ?--------Т=°- (15.5)
dr2 ' г dr г2
Записав это уравнение в виде
1|’1 1Ы] = 0
dr [г dr J
после двукратного его интегрирования найдем общее решение:
и = С\г + С2 у. (15.6)
где Ct и С2 — постоянные интегрирования, определяемые из гранич-
ных условий. В нашем случае такими граничными условиями будут:
(аг)г=п = Pi и (аг)г_Г2 = —р2.
398
Цодставив (15.6) в (15.4), найдем
\ Е» Г Л _ 1
\ = (1 + р*) Сг - С2 ;
\ 1 - Г L r2 J
°е = Г=У(1 + н)С1+ Ц^<?2].
Подставляя граничные условия в (15.7), получим
—— т-----Т2 С1 + Iх) G----Г~ £»]»
1 г L Гх J
-Р2=г-^ к+с* - с*1 •
1 —И L r2 J
(15.7)
(15.8)
Решив совместно эти уравнения, найдем
2 2
1 — р. r 2Р2 .
— р 2 2 ’
Е ?2 — ?1
r 1 + р. Г1Г2 (Pl Р2)
Ь ?2 ~ П
Подставив значения постоянных Сх и С2 в (15.6)—(15.8), найдем
окончательные формулы для определения радиального перемещения и
и напряжений (формулы Ляме):
1 — р. Г1Р1 1— Г2Р2 1 + Р- в -ч- в 2 2. ч Г1?2 (Pl — Р2) 1 ' 2 2 г ’ Г 2 — Г (15.9)
Г1Р1 r2P% rlr2 (Pl Р2) 1 (15.10)
аГ — 2 2 2 2 ?2 — Г1 Г2 — Г1 Г2
^1Р1 — Г2Р2 Г1Г2 (Р1 — А) 1 (15.11)
а0 — 2 2 । 2 2 Г 2 ~ Г2 — ГХ Г2 ‘
Сложив (15.10) и (15.11), убеждаемся, что
<Jr + 00 = const,
следовательно,
ez = — -g- (о, + Че) = const>
т. е. поперечные сечения цилиндра при деформации остаются пло-
скими. Формулы (15.9)—(15.11) праведливы для бесконечно длин-
ного цилиндра и годятся для использования в сечениях цилиндра,
достаточно удаленных от днищ, если таковые имеются.
При наличии осевых нагрузок N, действующих на цилиндр,
в частности при наличии днищ, в его стенках возникают осевые
напряжения
_ TV _ N
(15.12)
399
При этом в (15.9) появляется слагаемое
Ди = —р. г,
а напряжения аг и а9 не изменяются. /
В частном случае, когда отсутствует наружное давление (р2 = О,
pt == р), формулы для определения напряжений и перемещений в
толстостенном цилиндре можно записать в виде
2 , 2 ч
°Г — 'г" 2 г2 1 Р» (15.14)
г2 — Г1 \ г /
Г1 / Г2 \
»е = -5—2 Н+я- ₽; (15.15)
'’г — \ г 1
2 2 2
1 — [1 Г1Р , 1+(Л W 1
и е 2 е 2 2 г ' (15.16)
Л Г2 — гх г2 — Г1 г
При этом
(ar)max = (аг)г=гх “
/х _ ( \ _ L±± (15.17) (аб)тах \аб)г=Г! j А;2-Р»
где
гг
Радиальное перемещение внутренней поверхности, т. е. увели-
чение внутреннего радиуса, равно:
Г1 /1 + к2
Ир-
(15.18)
Для наружной поверхности цилиндра имеем:
(аг)г==Г2 — 0;
= (15Л9)
Рис. 277
Эпюры напряжений для рассмат-
риваемого случая при к = — = 0,5
Г2
приведены на рис. 277, а. Напряже-
ния вдоль радиуса изменяются по
гиперболическому закону. Опасные
точки (точки наибольших напряже-
ний) находятся на внутренней по-
верхности цилиндра при г = i\.
Из анализа (15.17) следует, что
при г2 °о и к -> 0
(Ог)г=Г1 Р’ Р*
Используя, предположим, третью теорию прочности, имеем
%квШ = а1'-сз<[4 (15.21)
400
В рассматриваемом предельном случае (к -> 0)
\ °i = (°е)г=г1 = Р< °з = (®г)г=Г1
условиеусрочности (15,21) примет вид
откуда
2 ’
Таким образом, цилиндр с весьма толстой стенкой не допускает
внутреннего давления, большего определенной величины, т. е. уве-
личение толщины стенки цилиндра не всегда является эффективным
способом увеличения прочности.
Рассмотрим частный случай, когда отсутствует внутреннее дав-
ление (p1 = 0i р2 = р). Формулы (15.9)—(15.11) примут вид
2 2
ЪЪР 1
2 2 ’ «
Ч Г
(15.22)
(15.23)
(15.24)
Как видно из (15.23) и (15.24), оба напряжения в этом случае
сжимающие, причем | а0 |> ] аг |. На внутренней поверхности
(’r)r=rt = 0; (15.25)
К (15-26)
(«)г-г, = -^ Р. (15.27)
На наружной поверхности цилиндра
МГ.Г, = -Р-,
(°e)r-rt=—г^рр; (15-28)
(»)г=г, = - % - И Р. (15.29)
Эпюры напряжений аг и а0 при к = — = 0,5 приведены на
рис. 277,6. Наибольшее по абсолютной величине напряжение а0 ока-
зывается на внутренней поверхности цилиндра; эти точки и являются
опасными. Положив в формуле (15.22) = 0 и г = г2, получим вели-
чину перемещения наружной поверхности для сплошного цилиндра:
(“)г=г2 = -ф(1-(4
(15.30)
В табл. 35 приведены расчетные формулы для толстостенных
цилиндров при различных схемах нагружения.
401
§ 85. Расчет составных цилиндров
С целью получения более равномерного распределения напряже-
ний по толщине стенки и разгрузки внутренних слоев за счет луч-
шего использования наружных, цилиндры делают составными путем
одевания с натягом одного цилиндра на другой (обычно с помощью
горячей посадки). В таких цилиндрах величина допускаемого внут-
реннего давления может быть значительно больше, чем в цельном
цилиндре, что используется при изготовлении орудийных стволов.
При посадке одного цилиндра на другой с натягом окружные
напряжения во внутреннем цилиндре являются сжимающими, а в
наружном — растягивающими. Эпюра напряжений, возникающих после
посадки, представлена на рис. 278, а.
Под действием внутреннего давления в таком составном цилиндре
возникают напряжения, определяемые по формулам (15.14) и (15.15)
Рис. 278
как для цельного цилиндра и характеризуемые эпюрами, показан-
ными на рис. 278, б. Просуммировав эпюры напряжений, приведен-
ные на рис. 278, а и рис. 278, б, мы получим действительную эпюру
(рис. 278, в), имеющую место в составном цилиндре при внутреннем
давлении.
Из суммарной эпюры видно, что напряжения в стенке составного
цилиндра распределены более равномерно, чем в сплошной стенке
(эпюра показана пунктиром), поэтому в составных цилиндрах имеет
место более рациональное использование материала, чем в сплошных
цилиндрах.
При расчете составных цилиндров основным является установле-
ние величины давления рс на поверхности их контакта при заданном
патяге S, представляющем собой разность между наружным диамет-
ром внутреннего цилиндра I и внутренним диаметром наружного
цилиндра 77 (рис. 279). Очевидно, уменьшение наружного радиуса
внутреннего цилиндра Uj и увеличение внутреннего радиуса наруж-
ного цилиндра ип равны половине натяга:
i«ii+iuni=4- <15-31)
Учитывая, что S весьма мал по сравнению с радиусом поверх-
ности контакта, будем считать, что г21 = г1П = гс (гс — радиус по-
верхности контакта составного цилиндра).
Контактное давление рс будет наружным для внутреннего ци-
линдра и внутренним для наружного цилиндра.
402
юзначим
Радиальное перемещение контактной поверхности внутреннего
цилиндра определяем по формуле (15.29):
го /1 + \
(15 32)
Рис. 279
Подставляя абсолютные значения этих перемещений в (15.31),
имеем
ГС + \ . rc/1 + fe2| \ *
откуда, решив уравнение относительно рс, находим
5
_________________2 __________
Р°~ r/i + k[ \ Гс/1+^ V
2Ц1-Л’ |Х7+ Е2 \i_fe|+1X2J
(15.34)
Если составляющие цилиндры изготовлены из одного материала,
формула упрощается и принимает вид
(!-$(!-$
Р° V d + ^d-^ + d + ^d-^) ' ( }
По найденному значению рс = /(5) определяют начальные напря-
жения во внутреннем (формулы (15.23), (15.24)) и наружном (фор-
мулы (15.14), (15.15)) цилиндрах. Формулы (15.34) и (15.35) справед-
ливы, если напряжения не превышают предела пропорциональности.
При появлении при посадке пластических деформаций фактические
усилия рс будут меньше расчетных.
403
§ 86. Температурные напряжения в толстостенных цилиндрах
В случае неравномерного нагрева толстостенных цилиндров в них
развиваются температурные напряжения. При расчете температурных
напряжений полученные ранее уравнение равновесия (15.1) р геомет-
рические соотношения (15.2) и (15.3) останутся без изменений, а фи-
зические зависимости будут несколько иными.
Обозначив через t (г) повышение температуры, зависящее от
текущего радиуса г, и через а — коэффициент линейного расширения,
а также, приняв значения модуля Е и коэффициента Пуассона р
соответствующими средней температуре стенки, запишем обобщен-
ный закон Гука в виде
~о) + & (?) = const;
1
e«' = -g-(®r —p°z—pae) + atW;
i
ee = (’0 ~ И’г — !“>•) + ««(>•)•
(15.36)
Решив эти уравнения относительно напряжений, получим
Е
°2 = (1 + [J.) (1 — 27) К1 “ + *“9 — (! + Iх)at (г)1; (15-37)
Е
°г = (1 4_ jx)(1 __ 2{*) К1 “ + 1X60 + 1*2~ + at <15'38)
Е
= (i + и) (1 — 2pJ «1 — Р) *9 + Р^г + р^ — (1 + р) at (г)]. (15.39)
Имея в виду, что
*г = ё И ев = 4> (15.40)
после подстановки в уравнение (15.1) выражений (15.38) и (15.39)
найдем
cZ2iz 1 du и __ 1 р dt (г)
dr2 г dr г2 1 — ра dr
(15.41)
Зная закон изменения температуры i = /(r), из уравнения (15.41)
можно определить перемещение.
Переписав (15.41) в виде
d (цг)1 ___ + Iх (г)
dr L г dr J ~ 1 — р ' dr *
после двукратного интегрирования этого уравнения получим
г
= у • ^at(r)rdr+C1r + ^ .
Г1
(15 42)
Постоянные интегрирования С± и С2 определим из условий для
аг на внутренней и наружной поверхности цилиндра
(’r)r.rt = 0; (ar)r=r2 = 0. (15 43)
404
Внеся \(15.40) и (15.42) в (15,38), будем иметь
г
Е Г 1 -|- р. 1 f . t \ J I C*2 . {A "I
ar = r~;— — -o- | at (r) r dr + 4—------£ + £z
1 + p. L 1 — P r2 J 1 — 2р. r2 1 — 2р. zj
T1
Подставив это выражение в (15.43) и решив полученную при этОхМ
систему двух уравнений относительно постоянных интегрирования,
найдем
Г2
_(l + fA)(l_2p,) 1 С
Ci — ’ 2 " 2 2 \ cti (г) г ar pez,
г2 ?
Сг =7"Ц ’ Т—2 \ at &>r<ir.
i-V- rt-rjn
После подстановки (15.40) в (15.37)*=(15.39) с учетом (15.42) и най-
денных значений С± и С2 получим
г Л 2 2 ГЛ
Е Г 1 С ri С 1
аг = т— —\ at (г) г dr + -j—-2 \ at (r)rdr ; (15.44)
i — PL r J v 2 T ^1) * v J
Г1 Г1
r I 2 2 ГЛ
E Г 1 C r —r! C
°® = 1---Й 72’ 1 at r dr + 72--------2ГЧ 1 at rdr^at W; (15.45)
1 —J (ra_r)r2J
П Г1
r*
аг = —[ 22,X i I at (r) r dr + (1 — p.) — at (r)] . (15.46)
1 — Iх Lr2 — r, J J
Неизвестная величина e2, входящая в последнюю формулу, в слу-
чае свободного расширения цилиндра может быть найдена из условия
отсутствия в поперечном сечении цилиндра продольной силы:
2к г2
J j a2rdrd? = 0 (15.47)
0 Г!
или
Ге
У azr dr == 0.
Г1
Подставляя в последнее равенство выражение для (15.46), найдем
2 С
^ = 1-----2 \ at (г) г dr.
r2—ri J
п
С учетом полученного выражения формула (15.46) примет вид
г2
Е / 2 С , \
°2 = 1---- Н-----2 1 a-t (г) г dr —at (г) . (15.48)
l-fX^-r^J I
405
/
(15.49)
ГС
Вычислить интеграл \ at (г) г dr и определить напряжения воз-
Г1
можно, если известен закон изменения температуры t(r) по толщине
стенки.
При линейном законе изменения температуры
',2 — ',i
где Т — ti — t2l h и t2 — температура на внутренней и наружной
поверхностях цилиндра соответственно.
Подставив (15.49) в (15.44), (15.45) и (15.48), после интегрирова-
ния найдем
г з / 2 \ з 3~|
Г1 I riNra —'i
г2, \ г2 ) »2 -2
3 / 2'
rl I Г1
%г "Ь Тг' Н 2 1~2
г \ Г /Г2 — Г1.
ЕаТ
°г 3(1 —p.)(r2 —/-j)
_ ЕаТ
3(1-!л)(г2-г1)
ЕаТ
°2“ 3 (1 — р.) (г2 — Z|)
Напряжения у внутренней поверхности
(сг)г=>Г1 = 0’
ЕаТ
3r
(15.50)
3 3
'’2— fl
~2
(15.51)
(15.52)
2 2
r2 — rl
цилиндра при г = гг будут
3r,
(°e)r=r, - (’^)г=г, 3(1-р)(г2-Г!)
У наружной поверхности при г = г2
Ыг=г2 ~ 0»
/ \ \ ЕаТ L
(®е)г=га — (°z)r=ra — 3 (1 — [Л) (г, — rt) I дГг
2 2
(15.53)
2 (4—г?)]
(15.54)
2 2
'•г —'•i
Эпюры распределения температурных напряжений по толщине
стенки цилиндра с отношением к =
на рис. 280, а.
=s 0,5 при jx = 0,3 приведены
Г2
406
В случае логарифмического закона изменения температуры в стенке
толстостенного цилиндра
(15.55)
In ~
Г1
После подстановки (15.55) в (15.44), (15.45), (15.48) и выполнения
интегрирования формулы для определения напряжений аг, ае и а2
соответственно будут иметь вид
аг =
ЕаТ
2(1 —ц) In
ri
EaT
2(1 -pc) In J
a =_^_
2(1 —p.)ln-~-
2 / 2\ П
1 r2 i Г1 I л Г2 1 i r2
to r “b 2 2 I »2 ) to ~~~ i
r Л \ r* ] riJ
2 / 2 \ “I
2 2 I 1 «2 1 Ш »
1 — In —-
(15.56)
(15.57)
(15.58)
У внутренней поверхности цилиндра при г = г1 напряжения
(аг)г=п “ О»
ЕаТ
2(1—(л) In —
2/,
2 2
г2~~~ >1
In . (15.59)
У наружной поверхности при г = г2
(ar)r=r2 ~ 0;
ЕаТ
<’е) т=т, ~ ^\=тг
2(1 — р.)
2r 1 - ]
1-----г1п^-. (15.60)
Эпюры распределения температурных напряжений по толщине
стенки цилиндра с отношением к = — = 0,5 при ц = 0,3 в случае
Г2
изменения температуры по логарифмическому закону представлены
на рис 280, 6.
Вблизи торцов цилиндра напряжения, определяемые с помощью
приведенных формул, могут иметь место лишь в том случае, если
торцы будут нагружены поверхностной нагрузкой, изменяющейся в
соответствии с формулой для аг.
§ 87» Расчет вращающихся дисков
Вращающийся диск обычно испытывает растяжение под дейст-
вием центробежных сил, являющихся для него основной нагрузкой,
а также изгиб. При неравномерном нагреве в нем могут возникнуть
и температурные напряжения. Обычно нагрузка и температурное
поле симметричны относительно оси диска, вследствие чего напря-
жение является функцией расстояния от оси вращения.
Рассматривая тонкий плоский диск постоянной толщины h,
можно считать, что напряжения по его толщине распределены равно-
1 _ 2 In
2rl I 'd
2 2 П ». I *
>2 ~ П Г1 J
1
407
мерно, а напряжения, параллельные оси диска, отсутствуют (а2 = 0).
Таким образом, задача определения напряжений в диске сводится к
так называемой плоской задаче теории упругости, а именно к задаче
о плоском напряженном состоянии.
1
Если диск, удельная масса материала которого равна у, вра-
щается с угловой скоростью то массовые силы, действующие на
выделенный элемент диска (рис. 281, а), могут быть представлены
равнодействующей (рис. 281,б), лежащей в срединной плоскости
элемента и равной
Рис. 281
Запишем условие равновесия элемента, спроектировав все силы на
ось х:
+ (15.61)
Геометрические и физические уравнения при расчете дисков
такие же, как и в задаче Ляме ((15.2)—(15.4)). Поэтому дифферен-
циальное уравнение (15.61) в перемещениях с учетом (15.4) примет
вид
Л . 1 du и 1 — р-2 7 2
ТтН----3-----2 — ——ёг- — w Л (15.62)
dr2 г dr г2 Eg
Переписав (15.62) в виде
dfl d (w)l _ 1 — |ла 7
dr [г dr j E g
и проинтегрировав его последовательно дважды, найдем
« = + (15.63)
Подставив (15,63) в (15.4) будем иметь
= + -р2'2; (15-64)
Ое = С1-^-Ц^ 1 <№, (15.65)
° 1 г2 8 g
где _
С1==г^Л1; (15-66)
1 — р. А "Г г
408
Постоянные и С2 (следовательно, Сг и С2) определяются из гра-
ничных условий. Для диска с центральным отверстием в общем слу-
чае имеем следующие условия на внутреннем (г == т^) и внешнем
(г = г2) контурах:
(аг)г=Г1 в ап»
(аг)г=г2~ аг2-
В соответствии с (15.64) эти условия дают два уравнения:
^ = ^ + -2-------8~ 7 Г1’
/nt ^*2 3 4“ р. 7 „ 2
’^ = ^1 + 4--^ f “%
Г2
Решая совместно эту систему двух уравнений, находим:
2 ?2 С1 2 2 СГ2 7*2 — ?! 2 2 ^2 — 2 2 СГ2 7*2 Г1 2 Г1 2 2 аГ1 * Г2 — >1 2 2 Г1Г2 О g (15.67) (15.68)
3+ |Л 7 8 g 9 2 2
2 г2 Г d — Г1
В случае, когда = 0 и аг, = °’
С*! = .1^ 8 g (ri + rl)> (15.69)
G = 3 + р- . х 8 g п 2 2 (О2Г1Г2. (15.70)
Подставив последние значения Сг и С2 в (15.64) и (15.65), получим
(22 .
2 . 2 Г1Г2
>•1 +^— 7г--г ): (1571)
Г , 2 2.
ав=1--1<й2[(3 + (л)^ + г1 + ^-2]-(1+3|л)г2]. (15.72)
Обозначив
ri 7. г . 3 + |х у о 2 1 + 3{Л
-^- = Л; — = р; = (15.73)
r2 r2 ° g О ~Г* Iх
можем записать:
409
Напряжение ог положительно и достигает наибольшей величины
при р = Vk = j/" :
(ar)max = c(l-fc)2- (15.75)
Напряжение аб также положительно при всех значениях р и
достигает максимума при р = к:
+ (15.76)
Из сопоставления (15.75) и (15.76) следует, что всегда имеет место
неравенство (ао)тахХ0г)тах- Поэтому условие прочности должно
быть записано (например, по IV теории) в следующем виде:
’экв IV = (Мтах = * [2 + (1 - /п) Л2] < [а]. (15.77)
В случае хрупкого материала следует пользоваться теорией Ку-
лона—Мора, которая при а3 =а2 = 0 приводит к той же формуле
(15.77).
Формулы для определения напряжений в сплошном диске (г1==0)
на основании (15.64) и (15.65) будут иметь вид
аг = сг — ^4-^ • — “2г2; (15.78)
о 8
= 4 (15-79)
Если внешняя нагрузка на наружном контуре (г = г2) отсутст-
вует, т. е. сГ2 = 0, то согласно (15.78) находим
с, (15.80)
Подставив (15.80) в (15.78) и (15.79), будем иметь
ог = с(1 — р2); (15.81)
а0 = с(1 — /пр2). (15.82)
Оба напряжения положительны и увеличиваются с приближением
к центру диска. В центре диска при р = О
(^)тах-(»е)тах = ^ = Ц^ (15.83)
Согласно (15.3) радиальное перемещение
и = е0 • г. (15.84)
Так как
ее = -£- (а8 ~
и = (ае — [Лаг). (15.85)
410
Для определения перемещения на наружном контуре диска в фор-
мулу (15.85) необходимо подставить значения г = г2; о0 = а02; ar=ar^
В случае неравномерного нагрева диска к напряжениям, вызван-
ным центробежными силами и контурными нагрузками (если таковые
имеются), следует прибавить температурные напряжения. Темпера-
турные напряжения определяются так же, как и в толстостенном
цилиндре, поэтому уравнение равновесия (15.61) при со = 0 будет
совпадать с уравнением (15.1):
Г Л
^ + сг-’9=°.
(15.86)
Относительные деформации с учетом температурного расширения
определяются следующими выражениями:
ег = (°г—) + а« (г);
1
ео =+ “«('•)•
(15.87)
Решая совместно эти уравнения относительно напряжений, найдем
СТГ =-2 [ег н- — (1 +р-)а« (г)];
Е
°0 = 1----7? [£6 + — С1 + Iх) at (r)J-
1 fX f
(15.88)
Учитывая (15.2) и (15.3), получим
Е \du , и ,t . . . . |
=jTzp т - о+1х)at wj;
Е Ги I du .. , . t . J
°о = ТТ^Г2[у + ^-(1 + (х) “'WJ-
(15.89)
При линейном изменении температуры вдоль радиуса диска
Г — Т\
t(r) — T------ последние выражения принимают вид
(15.90)
Модуль упругости Е и коэффициент Пуассона ц полагаем постоян-
ными, не зависящими от температуры, и равными их значениям при
средней температуре диска.
411
Подставляя (15.90) и (15.91) в уравнение равновесия (15.86), будем
иметь
(15.92)
с?г2 1 г dr г2 r2^rt v
Записав это уравнение в виде
А Га . d (цг)] = А+± аТ
dr [ г dr J г2 — гг 1
после двойного интегрирования получим выражение для перемещения
» = В1Г + у
+
1 + р
3 (г2 — гх)
аГг2.
(15.93)
Подставив (15.93) в (15,90) и (15.91), для напряжений найдем
т
Т7--------г аЕг\
3 (г2 — rj
сг —
£2
Г2
а ~ В2 2
Т
Г2~~~ Г1
аЕг,
(15.94)
(15.95)
где
в1=т^\в^
aTrt ,
г2 —'ЧГ
в2~т^в2.
Постоянные В± и В2 могут быть определены из граничных условий
при г = Гр (аг)г=Г1 = аГ1 = 0 и при г = г2; (ог)г=.Г2 = о.
Напряжения от центробежных сил и температурные напряжения
следует просуммировать. В случае линейного изменения температуры
вдоль радиуса, сложив правые части выражений (15.64) и (15.94),
а также (15.65) и (15.95), будем иметь
со2?*2
т
з (г2 — гО
аЕг,
°e = D
L
г2
14-Зр- 1
8 ’ g
2 Т
со2г2 — -5- ---------------аЕг,
3 г2 — 7*!
п I Е
^ = #+7^
3 + Р*
8
1
S
где D == б?! 4- В/, L = С2 + В2 —- новые постоянные, которые надле-
жит определить из граничных условий.
412
413
Продолжение табл, 35
Глава 16
РАСЧЕТ ТОНКОСТЕННЫХ ОБОЛОЧЕК
§ 88» Расчет тонкостенных оболочек
по безмоментной теории
К тонким оболочкам могут быть отнесены цистерны, водонапор-
ные резервуары, воздушные и газовые балоны, купола зданий,
герметические перегородки в самолетах и судах, аппараты химиче-
ского машиностроения, части корпусов турбин и реактивных двига-
телей и т. п.
Рис. 282
Рассмотрим элемент оболочки, показанный на рис. 282, а, б.
В общем случае в сечениях, которыми выделен элемент, будут дей-
ствовать погонные (отнесенные к единице длины сечения) усилия
(рис. 282, а) и моменты (рис. 282, б): нормальные усилия ATj. и N2,
касательные (сдвигающие) усилия Si и 52; поперечные силы Qi и
изгибающие моменты и М2; крутящие моменты Mi кр и М2 кр.
Учет всех перечисленных силовых факторов при расчете оболо-
чек приводит к весьма сложным исходным дифференциальным урав-
нениям, решение которых даже для простых случаев сопряжено
с большими математическими трудностями. Во многих случаях исход-
ные уравнения могут быть существенно упрощены. Этого можно
достичь исходя из самого характера задачи. Во-первых, если обо-
лочка представляет собой тело вращения и нагрузка симметрична
относительно оси оболочки, то задача называется осесимметричной
и в этом случае во всех сечениях, образованных плоскостями, прохо-
дящими через ось симметрии, и ортогональных им сечениях имеют
место равенства
М1кр = Л72кр = 51 = 52 = 0; Q1==0 (или (?2 = 0).
Во-вторых, если по виду оболочки, характеру нагрузки и закрепле-
ний можно по тем или иным соображениям прийти к выводу, что
какие-либо усилия или моменты всюду малы по сравнению с осталь-
415
ными усилиями или моментами, то принимают допущение, что эти
усилия и моменты равны нулю. Например, часто полагают, что
кр = М2 кр = 0; Qr = Q2 = О,
и в результате приходят к так называемой безмоментной теории
оболочек.
В частности, безмоментной теорией оболочек пользуются при
определении напряжений в резервуаре (рис. 283), представляющем
собой осесимметричную оболочку. Будем считать, что меридиональ-
ные сечения срединной поверхности оболочки образуют плавные кри-
вые, а толщина оболочки h является малой по сравнению с радиу-
сами кривизны. Тогда в случае закрепления краев резервуара таким
Рис. 283
образом, что на них могут действовать только усилия, касательные
к меридиональным кривым, можно считать, что оболочка находится
в безмоментном напряженном состоянии.
Резервуар, показанный на рис. 283, заполненный (полностью или
частично) газом, жидкостью или сыпучим веществом, в котором
давление одинаково во всех точках плоскости, перпендикулярной к
оси резервуара, представляет собой оболочку, находящуюся не только
в безмоментном, но и в осесимметричном напряженном состоянии.
Выделим из рассматриваемой оболочки прямоугольный криволи-
нейный элемент ABCD, проведя два близких осевых сечения и два
ортогональных к ним и к поверхности оболочки сечения. Обозначим
длины граней элемента через dsx и ds2 (рис 284). В гранях элемента
соответственно будут действовать растягивающие усилия (в случае
внутреннего давления) TV2 dsr и N± ds2. Здесь и N2 соответственно
нормальные усилия, приходящиеся на единицу длины контура эле-
мента,
N2 = im.h, (16.1)
где Qf — окружное (широтное или кольцевое) нормальное напряжение,
направленное по касательной к окружности радиуса р; = pi; —
меридиональное нормальное напряжение, направленное по касательной
к меридиану с радиусом рт = р2.
Рассмотрим условие равновесия элемента, спроектировав па нормаль
OOi (рис. 284) внутренние усилия, действующие по контуру элемента,
416
а также давление р, действующее на выделенный элемент площадью
dsi ds2:
2N1ds2 sin sx sin 4- (N2 + dN2) dst sin — pds^s^—O
Учитывая малость углов d^t и dcp2 п пренебрегая величинами
второго порядка малости, находим
Ni .N2
— 4—- = р.
Pl Р2
(16.2)
Учитывая также (16.1) и то, что р< == Pi и рш = р2, на основании
(16.2) получим
at । Gm __ _Р
Pt Pm h
(16.3)
Уравнение (16.3) называется уравнением Лапласа. Для определе-
ния двух неизвестных и ат одного уравнения Лапласа недоста-
точно. Второе уравнение легко можно получить из рассмотрения
условий равновесия нижней части оболочки радиуса г, отсеченной
конической поверхностью A[D}B1 (рис. 285):
TV2 cos а • 2кг — ркг2, — — <2р = О,
где Qm— вес жидкости или сыпучего тела, находящейся в рассмат^
риваемой части резервуара; — собственный вес рассматриваемой
части резервуара.
Рис. 286
(16.4)
Отсюда погонное усилие в рассматриваемом сечении стенки будет
I + Qp .
2 2 COS а 2кг cos а
Зная №, меридиональное нормальное напряжение от согласно (16.1)
определим из формулы
а — pr I
m ~ 2h cos а 2кг1г cos а
(16.5)
Так как задача определения напряжений в степках резервуара
решалась в предположении, что напряжения по толщине стопки рас-
пределены равномерно, не было необходимости рассматривать 1еомет-
рическую и физическую стороны задачи, т е. в принятой постановке
задача о расчете тонкостенных сосудов оказалась статически опре-
делимой.
14 5-1186
417
Нормальные напряжения <st и cm, действующие в площадках,
где отсутствуют касательные напряжения, очевидно, являются глав-
ными. Что касается третьего главного напряжения, направленного
по нормали к поверхности оболочки, то оно на внутренней поверх-
ности равно р, а на наружной — нулю (при внутреннем давлении).
Поскольку в тонкостенных оболочках в и а2 = значительно
больше р, последним по сравнению с и ст пренебрегают, т. е. о3
полагают равным нулю.
Следовательно, будем полагать, что материал оболочки находится
в плоском напряженном состоянии. Поэтому при расчете на проч-
ность в зависимости от состояния материала следует пользоваться
соответствующей теорией прочности. Так, по IV теории прочности
условие прочности будет иметь вид
аэкв IV = + — wZ < [’]• (16.6)
Ниже приведены расчетные формулы для резервуаров различных
форм.
Сферический баллон заполнен газом, давление которого
равно р. Подставляя в (16.3) значения — =
найдем
2 — -^
R ~~ h*
или
0==31 = 02 = g. (16.7)
Условия прочности по первой, третьей и четвертой теориям проч-
ности приводятся к виду
’0KBiv = 2T<M. (16.8)
Цилиндрический баллон заполнен газом, давление которого
равно р (рис. 286).
В этом случае
Pi ~ Pm = °0*
Из (16.3) находим
Напряжение ат в стенке баллона, отдаленной от его торцов, опре-
делим по формуле (16.5) (положив (?ж — = 0; а = 0):
(16.10)
или
1
ст — ~2
Сферический резервуар (рис. 287) наполнен жидкостью
(или сыпучим телом) с плотностью 7. В этом случае
pi = рт = Л; r — R sin ср; Н —R (cos <р — cos р);
р = = чД (cos <р — cos р).
418
Из уравнения Лапласа находим
<4 + °т = (COS <р — COS р). (16.11)
Воспользовавшись формулой (16.5), в которой
<?ж = t^ABC = V | (ЗЯ ~ Яс) = R3 (1 - COS (2 +
+ cos<p), (16.12)
Рис. 287
положив в ней = 0 и а = 90° ср, найдем
*fR2 Г1 + cos ср + cos2 ср ~ cos pl
°т~ h L 3(1 +cos?) 2 j *
Затем из (16.11) определим
__ V?2 Г 2cos2 ср 2cos ср — 1 cos р
а* h~ [ 3 (1 + cos ср) 2 J ’
Максимальное напряжение будет в точке G где ср = О,
__ _7д2(1 —cos₽)
ci*max °*max 2h
(16.13)
(16.14)
(16.15)
На краю оболочки, при ср = р
/о\ /о\ 2 —cos Р—cos2 Р
’«•(₽)“ ®=тг" ~1+'сМ— • <16Л6>
Сферический купол радиуса R и с толщиной стенки h
изготовлен из материала с плотностью у (рис, 288). Вес единицы
площади оболочки q = Нормальная составляющая
qn = q cos ср = cos <р
играет роль давления, приложенного к поверхности, и в уравнении
Лапласа (16.3) следует полагать р == -~qn> а в уравнении (16.5) р=0.
Учитывая, что р/ = рт = Rf из уравнения Лапласа находим
+ °; = ^ = cos ?• (16.17)
14*
419
Используя формулу (16.5), в которой
<2р = 4s лев == thSACB = ih2nRHc = -'Kl-H2 (1 — cos ?),
т. e.
<?p = 2n^hR2 (1 — cos cp);
r = R sin cp; a = 90° — cp; p = 0,
а также учитывая, что в сечении АВ вес части АС В вызывает сжа-
тие, найдем
Тогда из уравнения (16,17) имеем
„ 1 — cos ср — cos2 ср
Ч = yR т— . (16.19)
1 1 1 + COS ср V '
Меридиональные напряжения всюду сжимающие и возрастают
по мере удаления от вершины купола к краю. Кольцевые напряже-
ния в верхней части купола отрицательные (сжимающие); при
ср = 51° 50' они обращаются в нуль, а при ср> 51° 50' становятся
растягивающими. Приведенные результаты верны, если устройство
купола таково, что в нем могут возникать только реакции, направ-
ленные по касательной к меридиональной кривой.
§ 89. Распорные кольца в оболочках
Если в некотором сечении AAt оболочки (рис. 289) имеется пере-
лом, то касательные к меридиональной кривой слева и справа от
точки А образуют между собой угол 180° — («1 + а2)- Погонные уси-
лия, вызванные меридиональными напряжениями amt и оШ2 (рис. 290)
в сечениях ВВ± и СС1} бесконечно близких к ААТ (образованных
коническими поверхностями OtBBt и О2ССГ, нормальными к средин-
ной поверхности оболочки), будут равны и amJi29 где и h2 —
толщина частей оболочки 1 и 2.
Из условия равновесия кольца ВВ^С имеем:
cos ai = amJi2 cos a2 2rcr,
или
COS ai = COS a2.
420
Таким образом, проекции этих усилий на ось оболочки взаимно урав-
новешиваются. В то же время сумма проекций указанных усилий на
плоскость ААг (рис. 291) дает погонное радиальное усилие
9 = sin ах + amJi2 sin <х2, (16.20)
которое можно рассматривать как местную нагрузку, сжимающую
оболочку и могущую вызвать в оболочке значительный изгиб, j
Рис. 292
Чтобы уменьшить изгиб, в резервуарах часто устанавливают
кольца жесткости, или распорные кольца (рис. 292), которые и вос-
принимают на себя радиальные усилия q по схеме, приведенной
на рис. 293. В кольце возникают только сжимающие напряжения,
и условие прочности для кольца будет иметь вид
(16.21)
1 к
где 7?к— радиус срединной поверхности кольца; FK — площадь по-
перечного сечения кольца; q погонная нагрузка, действующая на
кольцо, определяемая по формуле (16.20).
Иногда вместо распорного кольца в месте излома создают мест-
ное утолщение оболочки, загибая края днища резервуара внутрь
оболочки, или, например так, как показано на рис. 294.
В табл. 36 приведены расчетные формулы для определения на-
пряжений и перемещений в тонкостенных оболочках.
421
Таблица 36
Расчетные формулы для определения напряжений и перемещений
в тонкостенных оболочках
р — давление; д —погонная нагрузка; и ц— меридиональное и
окружное нормальные напряжения (положительные при растяжении);
h — толщина оболочки; R радиус срединной поверхности в попе-
речном сечении оболочки; Е, р., чм — соответственно модуль упру-
гости, коэффициент Пуассона и удельный вес материала оболочки;
w — перемещение в направлении нормали к поверхности (направление
от оси или центра оболочки считается положительным); 7 —удель-
ный вес жидкости.
Схема
Формулы
Сферическая оболочка.
Равномерное внутрен-
нее давление
pR t pR2 ч
®»П — — 2Л ’ w~ 2Eh
Сферическая оболочка,
полностью заполненная
жидкостью и опертая
по кольцу радиуса
R sin а0
Внутреннее давление р = 4R (1 — cos а)
а< а0
°тп
2 cos2 а
1 + cos а
чТ?2 {
= «Г 5 — 6 COS а 4
2 COS2 а
1 + cos а,
°т
54
2 cos2 а
1 — COS а
1R2 (
а/=1/ц1-6соза
2 cos2 а
1 — COS а\
422
Продолжение табл, Зв
Схема
Формулы
Сферический резер-
вуар, наполненный
жидкостью. Кромки
свободно оперты
Внутреннее давление р — yR (cos ср — cos р)
— Г 1 + CQS ? + cos2cp cos З]
Ст~ ~F[ 3(1+cos?) 2 ]
__ 7Z?2 Г—1 + 2 cos ср + 2 cos2 ср cos pl
s' ~т[ 3(1+cos?) 2 J
при ср == О
?/?а 1 — cos р
°тп — ' 2 ° max
при ср = р
_ — — cos Р — cos2 3
«Ш-—д' ' 6(1 + COS0)
Изменение радиуса круга на контуре
д 7^2 sin Р (1 + Р1) (2 — cos а — cos2 а)
_« — . 6 (1 + cos а)
Сферический купол под
действием собственного
веса. Кромки свободно
оперты
W* . __ n 1 — cos — cos2 ср
1 + COS ср * а/1 + COS Ср
= 0 при <р = 51° 50'
с/ < 0 при 0 < а < 51° 50'
а; > 0 при а > 51а 50'
Сферический купол.
Равномерное нормаль-
ное давление. Кромки
шарнирно оперты на
упругое кольцо. Мате-
риалы оболочки и коль-
ца одинаковы
Вдали от краев при Н >> ЮЛ
ст — at —
pR
2h
Напряжения в опорном кольце
pR2 sin а
°к 2
cos а — 0,39
V Rh
R sm а
F + 0,39ft/7?A
где F площадь сечения опорного кольца
423
Продолжение табл. Зв
Схема
Длинная цилиндриче-
ская оболочка с дни-
щами. Равномерное
внутреннее давление
Формулы
Вдали от краев
pR pR
°m~2h’ “ Т ~ "max
Цилиндр, заполненный
жидкостью. Верхние
края свободно оперты
7 (Я — х) R
2Г; °t==------h-----
Длинная коническая
оболочка. Равномерное
внутреннее давление
Вдали от краев
рх tg а рх tg а
~т 2h~ 1 Qt~ h
3pz2 tg2a
W ~ ih'E ’
424
Продолжение табл, 36
Схема
Формулы
Коническая оболочка
под действием собст-
венного веса. Края
свободно оперты
Вдали от краев
7м • ® 7м •' х • sin2 “
; а/ = 1 ----
2 COS а COS а
Радиальное перемещение края (х = I)
Д = tg a [sin2 а — у)
Л \ Z /
При sin а
Д =0
Коническая оболочка,
полностью наполненная
жидкостью. Края сво-
бодно оперты
ат
2h cos а
=
7У tg«
h cos а
(Я-*)
3i#2tga 3 „
сттпях = ~ ПРИ Х~-гН
max 167г. cos а r 4
c*max
__ 7g2 tg а
~ COS а
H
при X = —
Изменение радиуса круга на контуре
д = _^1*р£_“
r COS а
425'
Продолжение табл. 36
Схема
Цилиндрическая обо-
лочка с коническим
днищем, заполненная
жидкостью
Формулы
Напряжения в днище
_ ___ 7 tgа ( TJ I ТТ \
т ~ 2k cos а з )
ух tg а . ГТ , „
Ч = У—2- (Я + Я *= х)
1 Л cos а4 1 к ’
Як
Если Я > -х- , то
О
’«max == 2/г cos а + т) Нк ПРИ х = Hi
Нк
Если Н < -у-, то
О
Зч tg а . , __ чо
°mmax == i'H’' 6-№ + Я„)8 ПРИ
max 16Д cos а 4 1 к'
Q
*=|(Я + Я„)
Если Я>.ЯК, то
7 tg а в Я 4“ Я.
%nax e 7i~---№ + Я )2 ПРИ х -----о—
‘max 4Д cos а \ । к' 2
Если Я< Як, то
c*max == 1 ПРИ
‘max fa cos а к г к
Цилиндрическая обо-
лочка со сферическим
днищем, заполненная
жидкостью
Напряжения в днище
yR
°mmax = (Н + НС> °РИ х == 0
°<-g я + яс->
ж (37? — а?)1
~3 (2Я —а:)]
’«max = (Я + Яс) при ж = О
Для полусферического днища (Яс = R)
yR
°wmax c*max + R) ПРИ я = О
426
Продолжение табл, 36
Схема
Формулы
Торовая оболочка. Рав-
номерное внутреннее
давление
аячпах
— PR 2fl + 8*п ?
°т “ 27г а + R sin tp
pR (2а — R) тс
= ПРИ<Р = —"2
* 2h
pR2 Га.. „ . , ,. ч 1
(1-2h) + (1-h)costJ
Значения am и at достаточно точны при
w =
Глава 17
РАСЧЕТ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ
СОСТОЯНИЯМ
§ 90. Основные понятия о предельном состоянии
Приведенные выше методики расчета на прочность стержней,
балок и конструкций были основаны на оценке прочности материала
в опасной точке, т. е. проводился расчет по допускаемым напряже-
ниям. Опасным, или предельным, состоянием конструкции считалось
такое ее состояние, при котором наибольшее местное напряжение
достигало опасной величины — предела текучести (для пластичного
материала) или временного сопротивления (для хрупкого материала).
Состояние всей остальной массы материала во внимание не прини-
малось.
В то же время при неравномерном распределении напряжений,
например при изгибе, кручении, в статически неопределимых кон-
струкциях, изготовленных из пластичных материалов, появление
местных напряжений, равных пределу текучести, в большинстве слу-
чаев не является опасным для всей конструкции в целом.
В связи с этим возникла необходимость в новом подходе к оценке
прочности конструкций по ее предельному состоянию.
Под предельным состоянием конструкции понимают такое ее со-
стояние , при котором она теряет способность сопротивляться внеш-
ним воздействиям или перестает удовлетворять предъявляемым к ней
эксплуатационным требованиям.
Различают три вида предельных состояний: а) по несугцей спо-
собности (прочности, устойчивости и усталости. При достижении
этого состояния конструкция теряет способность сопротивляться
внешним воздействиям или получает такие остаточные изменения,
при которых она перестает удовлетворять предъявляемым к ней
эксплуатационным требованиям; б) по развитию чрезмерных дефор-
маций от статических или динамических нагрузок, при которых в
конструкции, сохраняющей прочность и устойчивость, появляются
необратимые деформации или колебания чрезмерной амплитуды, так
что конструкция перестает удовлетворять предъявляемым к ней
эксплуатационным требованиям; в) по образованию и развитию тре-
щины, когда в конструкции, сохраняющей прочность и устойчивость,
появляются крупные трещины, вследствие чего дальнейшая эксплуа-
тация конструкции становится невозможной (потеря требуемой водо-
непроницаемости, опасность коррозии из-за повреждения отделочного
слоя и т. п.).
Методы расчетов по предельным состояниям широко применяются
при проектировании строительных конструкций и позволяют вскрыть
резервы прочности, не используемые при расчетах по допускаемым
напряжениям, и уменьшить вес конструкции.
Ниже рассмотрены некоторые примеры расчета по предельным
нагрузкам конструкций, изготовленных из пластичных материалов,
имеющих площадку текучести на диаграммах растяжения, сжатия
и чистого сдвига. С целью упрощения расчетов эти диаграммы
(рис. 295) схематизируются таким образом, что участок прямой, выра-
428
/жающий закон Гука, непосредственно переходит в горизонтальную
/прямую без плавного перехода (рис. 296). Этим самым принимается
'равенство между пределами пропорциональности и текучести. Длина
горизонтального участка диаграммы не ограничивается, т. е. материал
считается идеально пластичным, не упрочняющимся. Такая диаграмма
носит название диаграммы II рандтля.
Замена реальных диаграмм схематизированной диаграммой Пранд-
тля приемлема для материалов типа алюминия и вполпе допустима
для материалов, имеющих диаграммы с ограниченной длиной пло-
щадки текучести (рис. 297).
Предельное состояние конструкции, определяемое значительной
пластической деформацией, наступит в начале упрочнения материала
и предельная нагрузка может быть вычислена по пределу текучести.
Рис. 295 Рис. 296 Рис. 297
Для сложного напряженного состояния существуют различные
теории перехода материала в пластичное состояние Наиболее просто
расчеты выполняются при использовании теории пластичности Сел-
Всиана, согласно которой пластичное состояние материала при слож-
ном напряженном состоянии наступает тогда, когда наибольшие
касательные напряжения достигают предельного значения — предела
текучести при сдвиге
Tmax " V (17.1)
Исходя из изложенных выше положений, рассмотрим некоторые
характерные случаи расчета по предельному состоянию.
§ 91. Расчеты при растяжении и сжатии
При растяжении и сжатии напряжения распределяются равно
мерно по площади поперечного сечения стержня. Поэтому расчеты
па прочность статически определи-
мых систем по допускаемому напря-
жению и по предельному состоянию
дают один и тот же результат
В случае статически неопределимых
систем результаты расчетов будут
различны. Это легко показать на
примере расчета на растяжение трех-
сторжиевой подвески (рис. 298), на-
груженной силой Р. Площади попе-
речных сечений стержней одинаковы;
материал пластичный с пределом те-
кучести ат.
Рис. 298
При расчете рассматриваемой однажды статически неопределимом
системы по допускаемому напряжению, согласно данным §41, мри
429
~ —— - •
1 l+2cos3a’
N3 = N3
COS2 a
1 + 2 COS8 a •
(17.2$
(17.3)
Очевидно, всегда > N2 = 7V3, т. е. большее усилие возникает
в среднем стержне. Следовательно, в среднем стержне будет и наи-
большее напряжение, равное
__ Nt _ 1 Р
°тах — р ~ 1 + 2 cos3 a ’ F
Запас прочности при этом будет равен:
5т 1 + 2 cos3 a
% = —="+>-----------F'r
° max ♦
(17.4)
(17.5)
При расчете рассматриваемой подвески по предельному состоянию
усилие в среднем стержне при появлении в нем пластической дефор-
мации будет
(17.6)
При этом согласно (17.2) внешняя нагрузка
Р1Т = (! + 2 соз3 а) 2%,
(17.7)
а усилия в крайних стержнях рассматриваемой системы, превратив-
шейся в статически определимую систему, будут
P-FcT
ДГ2 = = -------?.
2 3 2 cos a
(17.8)
Несущая способность конструкции выдержать нагрузку Р>
будет исчерпана, когда напряжения в крайних стержнях достигнут
предела текучести, а соответствующая этому моменту нагрузка со*
гласно (17.8) будет равна:
ЯГ — дг — Fe — Рщ) F<3t
Откуда
Рпр =” С1 + 2 cos а) Fct-
(17.9)
^1т » F •
Запас прочности при расчете по предельному состоянию
Рпр (1 + 2 cos a) Fст
% ” р —
(17.10)
P
Из сопоставления (17.5) и (17.10) видно, .что пцр>пт. Например,
Лпп
при a = 30° отношение —“==1,19. Таким образом, расчет по пре-
ПЧ}
дельному состоянию позволил выявить скрытый запас прочности
конструкции.
430
§ 92. Расчет при кручении
При кручении стержней сплошного круглого сечения касатель-
ные напряжения в упругой области на расстоянии р от центра сече-
ния (рис. 299) определяются по формуле (§ 46)
Рис. 299
(17.11)
(17.12)
Рис. 300
Опасное состояние стержня при расчете на кручение по допус-
каемым напряжениям определяется появлением пластических дефор-
маций в крайних волокнах, когда крутящий момент
Мкр = Мт = ттТ7р. (17.13)
При этом стержень сохранит способность воспринимать возрастающий
крутящий момент вследствие роста напряжений до уровня предела
текучести ч:т (рис. 300) в точках, лежащих ближе к центру сечения
(рис. 301, а).
При расчете по предельному состоянию, при котором пласти-
ческие деформации распределены по всему сечению (рис. 301, б),
крутящий момент равен (рис. 301, в)
481
Величина
1У = ^р(пл) (17.16)
называется пластическим моментом сопротивления при кручении. Тогда
^пр “ тт ^р(пл)‘ (17.17)
Отношение предельного момента Мпр к моменту определяе-
мому по формуле (17.13), будет
Рис. 302
^пр______Wp (ПЛ)______nd3 -16_______4
МТ ~ WP “ 12 • Кб/з - 3 ’
или
4
Мпр = уМт-1,ЗЗМт.
Таков скрытый запас прочности скру-
чиваемого круглого стержня, который об-
наруживается при переходе от расчета по
допускаемым напряжениям к расчету по
предельному состоянию.
В случае статически неопределимой
системы, приведенной на рис. 302, а, б, в
запас прочности при расчете по предель-
ному состоянию оказывается в 1,78 раза больше запаса прочнос-
ти, получаемого при расчете по допускаемым напряжениям.
§ 93. Расчет при изгибе
При изгибе нормальные напряжения по высоте сечения распре-
делены неравномерно (рис. 303, а) и па расстоянии у от нейтральной
линии определяются по формуле Павье (10.6)
Максимальные напряжения па краю сечения
М
сшах ~ jy >
432
где W — момент сопротивления при изгибе, который, например,
для балки прямоугольного сечения шириной b и высотой h равен*
Опасная величина изгибающего момента при расчете по допускае-
мым напряжениям будет (если пределы текучести при растяжении
и сжатии одинаковы)
Мт «= отЖ. (17.18)
При этом балка способна воспринимать возрастающий изгибающий
момент. По мере увеличения изгибающего момента по сравнению
с Мт пластическое состояние материала распространяется в направ-
лении нейтральной оси (рис. 303, б) вплоть до полного исчерпания
несущей способности балки. Предельное состояние наступит тогда,
когда текучесть распространится по всему поперечному сечению
(рис. 303, в), после чего дальнейшая деформация балки будет происхо-
дить без увеличения изгибающего момента. В рассматриваемом попе-
речном сечении образуется так называемый пластический шарнир,
который передает изгибающий момент, равный предельному изги-
бающему моменту, определяемому для сечения, симметричного отно-
сительно нейтральной оси, по формуле
Мпр= [ = 2 р^=’т'2^тах> (17.19)
F F/2
где 5тах — статический момент площади половины поперечного сече-
ния отпосительпо нейтральной оси.
Величину 26’тах принято называть пластическим моментом сопро-
тивления и обозначать И7ПЛ. Тогда
^ПР = %И/ПЛ. (17.20)
Отношение
характеризует степень увеличения запаса прочности балки при пере-
ходе к расчету по предельным нагрузкам. В случае балки прямо-
угольного сечения
W
1 г пл_
W "
bh2
4
bh2
= 1,5.
6
Для двутавровых прокатных балок в среднем — 1,18.
W
В табл. 37 сведены расчетные формулы для определения пласти-
ческих моментов сопротивления для некоторых сечений балок.
433
Таблица 37
Продолжение табл. 37
Пластические моменты сопротивления для некоторых
сечений балок
Сечение
Пластические моменты сопротивления
Пластические моменты сопротивления
^пл---j- 5 ^пл ~
4 — ?уЗ
Жпл - 3 (Ьа — &1)2 Р + &2
17пл = 25х; Жпл « (1,144-1,18) Wx
^пл = (2 - /2) « 0.09776А2;
^пл « 2,36ЖМ
<73
^пл = > ^пл ~
434
Глава 18
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
§ 94. Устойчивое и неустойчивое упругое равновесие
В системе, находящейся в деформированном состоянии, равно-
весие между внешними нагрузками и вызываемыми ими внутренними
силами упругости может быть не только устойчивым, но и неустой-
чивым.
Упругое равновесие устойчиво, если деформированное тело при
любом малом отклонении от состояния равновесия стремится возвра-
титься к первоначальному состоянию и возвращается к нему после
прекращения внешнего воздействия, нарушившего первоначальное
равновесное состояние. Упругое равновесие неустойчиво, если де-
формированное тело, будучи выведено из пего каким-либо воздейст-
вием, продолжает деформироваться в направлении вызванного
отклонения и после прекращения воздействия в исходное состо-
яние не возвращается. Между этими двумя состояниями равнове-
сия находится переходное состояние, называемое критическим. При
критическом состоянии деформированное тело находится в безраз-
личном равновесии: оно может сохранять первоначально приданную
ему форму, по может и потерять ее от самого незначительного
воздействия.
Устойчивость формы равновесия деформированного тела зависит
от величины приложенной к нему нагрузки. Нагрузка, превышение
которой вызывает потерю устойчивости пер-
Р>Ркр воначалъной формы тела, называется крити-
Г ческой нагрузкой и обозначается через Ркр.
На рис. 304, а, б, в показаны возможные
|\ случаи деформирования стержня в зависи-
I \ мости от сжимающей нагрузки: при Р <
j I < Ркр — форма равновесия остается устойа
। / чивой (рис. 304, а); при Р = Ркр — состояние
I / безразличного равновесия, когда стержень
может занимать одно из трех показанных
сплошной и пунктирными линиями по ложе-
в ний (рис. 304, б); при Р>*Ркр стержень те-
Р с 304 ряет Уст°йчивость> выпучивается, т. е. пря-
гис‘ 6 4 молинейная форма равновесия перестает быть
устойчивой (рис. 304, в).
Достижение нагрузками критических значений равносильно раз-
рушению конструкции, так как пезстойчивая форма равновесия
неминуемо будет утрачена, что практически связано с неограничен-
ным ростом деформаций и напряжений. Разрушение обычно происхо-
дит внезапно от изгиба и при малых значениях сжимающих напря-
жений, когда прочность элемента на сжатие еще далеко нс исчерпана.
Для обеспечения определенного запаса устойчивости необходимо,
чтобы удовлетворялось условие
р < [Л,
(18.1)
436
где Р — действующая нагрузка; [Р] =—допускаемая нагрузка, которая
при коэффициенте запаса устойчивости тгу равна:
р
[Р] = -^
пу
(18.2)
Таким образом, при расчете упругих систем (в частности, таких
типичных систем, какими являются сжатые стержни) на устойчи-
вость прежде всего необходимо уметь определять величину крити-
ческой силы Ркр.
Ниже мы рассмотрим основные формулы
для определения критических нагрузок при
сжатии длинного тонкого стержня или при
так называемом продольном изгибе.
§ 95. Формула Эйлера для определения
4 критической нагрузки сжатого стержня
Предполагая, что критическая сила Ркр
не вызывает в стержне напряжений, превы-
шающих предел пропорциональности, и что
имеют место только малые отклонения от
прямолинейной формы, значение критической
силы Ркр для сжатого стержня длиной Z,
закрепленного по схеме, приведенной на
рис. 305, а, можно определить из следующего
приближенною дифференциального уравнения
изогнутой оси балки (§ 54):
рт d2 w (z) __, ч
EJmin —£z2 ' =
а 5
Рис. 305
(18.3)
где Jmin — наименьший момент инерции сечения стержня (при
потере устойчивости прогиб произойдет перпендикулярно^ к оси
наименьшей жесткости); М (z) — изгибающий момент, равный
М (z) = г— Pw.
(18.4)
Подставив (18.4) в (18.3), получим
ИЛИ
d2 w
dz2
-f- к2 w = 0,
(18.5)
где
= -----
^Anin
(18.6)
437
Решением полученного однородного дифференциального уравне-
ния (18.5) будет
w = A sin kz + В cos kzf
где А и В — постоянные интегрирования — определяются из гранич-
ных условий. В частности, для случая шарнирного закрепления кон-
цов сжатого стержня (рис. 305, а), граничные условия будут:
» («) 1г=о = °! w lz=i = °-
Из первого граничного условия следует, что В = 0, поэтому
w (z) == A sin kz. (18.7)
Из второго условия получаем
A sin kl = 0.
Так как
А ^=0,
то
sin& = 0. (18.8)
Корень этого уравнения kl может иметь бесконечное число значений:
О, тс, 2тс, ... , птс, т. е.
kl = птс,
где п — произвольное целое число.
Очевидно, первый корень kl = 0 должен быть отброшен, так как
он не соответствует исходным данным задачи. Таким образом,
кЧ* == п2тс2. (18.9)
Учитывая (18.6) и (18,9), находим искомое критическое значение
усилия Р
Это выражение впервые было получено Эйлером и называется фор-
мулой Эйлера.
Наименьшее значение критической силы Р*р, получаемое при
п == 1 и kl = тс, равно:
т тс2 2?«7mln
^Р = ——• (18.11)
Уравнение изогнутой линии при малых деформациях согласно
(18.7) имеет вид
w(s) = Д81П—г".
438
Значение А характеризуется величиной максимального прогиба
. . imz . „
wmax = А К0ГДа sm т" == 1 • Следовательно,
4
, . Ttnz
w = У sin —.
4
(18.12)
Максимум w (z) имеет место при таком значении z, для которого
т. е.
или
Наименьшее
гс
нулю, равно
откуда
dw t пъ mtz
= у cos —
dz г I I
Ttnz
cos —=
I
0.
= 0,
значение аргумента, при котором косинус
следовательно,
nrcz ГС
I ~ т*
I
2~ 2п
равен
(18.13)
Рис. 306
Из (18.12) или (18.13) следует, что п рав-
но числу полуволн синусоиды, умещающихся
на длине изогнутого стержня (рис. 306). Если
n = 1, то z = ~-, и максимальное значение
прогиба wmax = / имеет место посредине
стержня. Это соответствует основному случаю,
305, б, когда после потери стержнем устойчивости при минимальном
значении критической силы Р*р на его изогнутой оси умещается
показанному па рис.
только одна полуволна синусоиды.
§ 96. Влияние условий закрепления концов стержня
на величину критической силы
Влияние условий закрепления концов стержней на величину
критической силы легко выяснить путем сопоставления вида изогну-
той оси стержня при различных случаях закрепления с формой
изогнутой оси в основном случае, т. е. при шарнирном закреплении
обоих концов стержня.
Стержень длиной I с одним жестко аакрепленным, а другим сво-
бодным концом (рис. 307, а). При потере устойчивости стержень нахо-
439
дится в таком же состоянии, как и половина стержня длиной L = 21
с шарнирно закрепленными концами (рис. 307,6). Это значит, что в
рассматриваемом случае
р! ___ 7x2 ^min _ 7x2 ^min
кр — (2Z)2
(18.14)
4Z2
При этом изогнутая ось стержня (рис. 307, а) имеет вид половины
п 1
полуволны синусоиды. Значит, п = —..
Рис. 307 Рис. 308
Стержень длиной I с двумя жестко закрепленными концами
(рис. 308). При потере устойчивости средняя часть стержня будет
иметь такую же форму, как и стержень длиной L == с шарнирно
закрепленными концами, т. е.
(18.15)
В
HP “ / j \ 2 — /2
\2j
этом случае образуется две полуволны: средняя, длиной £ =
и две крайних половинки полуволны, длиной —. Значит, п = 2.
Стержень, длиной I с одним жестко закрепленным концом,
а другим шарнирно опертым (рис. 309). После потери устойчивости
440
правая часть стержня СВ будет иметь вид полуволны синусоиды.
Из сравнения рис. 309 и рис. 307, б находим, что участок СВ имеет
длину £ = 0,7/, а следовательно,
т л2 £Jmin
ркр==-(оЖ- <1816)
Из сопоставления (18.11) и (18.14) — (18.15) следует, что в общем
случае указанные формулы могут быть представлены в виде
к2
РКР=~(^)“ ’ (1817)
где vl = /— приведенная длина стержня; I — фактическая длина
стержня; v — коэффициент приведения длины.
При шарнирном закреплении обоих концов стержня v = 1; если
один конец стержня жестко закреплен, а другой свободен, = 2;
если оба конца жестко закреплены, v = ; если один конец жестко
закреплен, а второй шарнирный оперт, v = 0,7.
Приведенные случаи закрепления концов стержня на практике
в чистом виде встречаются редко. Наиболее распространены случаи
закрепления, когда один конец стержня жестко заделан, а другой
упруго оперт или когда оба конца упруго закреплены.
Рассматривая первый из указанных случаев (рис. 310), легко
заметить, что после потери устойчивости упруго опертый конец пере-
мещается в вертикальном направлении па величину /в, при этом
возникает упругая реакция пропорциональная отклонению fB
и равная
7?в = с /в,
где с — коэффициент жесткости опоры В.
Дифференциальное уравнение упругой линии при этом будет
иметь вид
= С1*18)
ИЛИ
= (18.19)
где
4 Р
7.2 _ КР
Переписав уравнение (18.19) в виде
+ = + (1820)
az \ *кр / У кр
441
находим его решение:
U) = С sin kz + D cos kz + fB fl = ~— fB z. (18.21)
\ *кр / "кр
Постоянные интегрирования и критическую нагрузку определим
из граничных условий:
при z = О
w(0)=ipa = 0, (18.22)
^) = 6(0)=0; (18.23)
при Z = I
w(l)=wB = fB. (18.24)
Из (18.22) находим
\ *кр /
Для использования (18.23) вычислим производную (18.21):
= кС cos kz RD sin kz +
az r*Kp
откуда при z = 0 получаем
гкр
или
*кр
Подставив полученные значения С и D в (18.21), найдем
«Ф) =—т4— fB state *-/в(1--------Z|coste-f-
Л'/кр \ *кр /
+ /в (1 “ 0 + 4s- (18-25)
\ *кр / ^кр
Используем граничное условие (18.24). Положив в (18.25) z = Z, найдем
W (0 = — -ТБ— /в sin kl *“ /в I1 11cos kl +
ЛГКР \ Кр /
\ кр / кр
442
или
•—~— sin kl — [ 1 —» — I ] cos kl О,
*Ркр I Ркр 1
tgkl = kl\l
(18.26)
Если из этого уравнения найти наименьшее значение к, то тем самым
будет найдено наименьшее значение критической нагрузки
PKp = ^^min-
Рассмотрим два предельных случая. Положив с = 0, находим
к
tg/cZ = оо; kl = ,
т. е. приходим к расчетной схеме, когда один (левый) конец жестко
заделан, а другой (правый) свободен (рис. 307, а). Величина крити-
ческой силы в этом случае определяется формулой (18.14).
“ГС
Положив с=оо, из (18.26) находим tg&Z = &Z; kl — -^ и вели-
чину критической силы (18.16), которая соответствует случаю, когда
один конец стержня жестко заделан, а другой шарнирно оперт (рис.
309).
Следовательно, изменение коэффициента упругости с от нуля до
бесконечности может быть учтено коэффициентом приведения v, кото-
рый при этом будет изменяться в пределах от 2 до 0,7.
Значения коэффициента приведения длины v, а также коэффи-
циента устойчивости \ = &LZ1 для центрально сжатых стержней
постоянного и переменного поперечных сечений для различных слу-
чаев их нагружения и закрепления приведены в табл. 38. В табл. 39
даны значения критических нагрузок для полосы и некоторых дву-
тавровых балок.
§ 97. О потере устойчивости при напряжениях,
превышающих предел пропорциональности материала
Формула Эйлера была получена из дифференциального уравнения
упругой линии, поэтому ею можно пользоваться лишь в случае,
если справедлив закон Гука, т. е. пока критическое напряжение,
возникшее в сжатом стержне при критической нагрузке Р*р, не пре-
вышает предела пропорциональности
— ^кр <• а
кр р апц*
Представив критическое напряжение в виде
_ Ркр ~2Е
°кр F F(yl)2 (\а ’
443
. . / *^min _ о
где i ~ imin = I/ —--------наименьший главный радиус инерции
площади сечения стержня (§ 10), или
т&Е
скр = -х2-> (18-27)
где
Х==—— (18.28)
lmin
— безразмерная величина, называемая гибкостью стержня, из (18.27)
видим, что критическое напряжение зависит только от модуля упру-
гости Е и гибкости X.
Построив график зависимости a = f(X) (рис. 311) —- гиперболу
Эйлера, — можно убедиться, что для
данного материала (с известным мо-
дулем Е) формула (18.27) справед-
лива, начиная с определенного зна-
чения гибкости, которое может быть
найдено из условия
_п2Е
акр х2 Спц
Определим предельную гибкость
Хпред, ниже которой формулой
(18.27) пользоваться нельзя:
^Е
апц
\тред
Так, например, для стали марки Ст. 3, модуль упругости которой
Е = 2 106 кГ /см2, апц « 2000 кГ/см\
уГ ^Е__-|/3,142 2 106
А<Апред~ У опц ~ ' 2000
100,
т. е. формулой Эйлера (18.27) можно пользоваться на участке гипер-
болы, показанной на рис. 311 сплошной линией, при гибкости X
не менее 100.
Однако, как показывает опыт, и на участке, где ^<Хпред, при
напряжениях в стержне, больших апц, при которых формула Эйлера
дает завышенные значения критических напряжений (участок гипер-
болы Эйлера, показанный на рис. 311 пунктиром), стержень может
потерять устойчивость. В этом случае значение критического напряже-
ния может быть вычислено согласно опытным данным Ф. С, Ясин-
ского для различных материалов по эмпирической формуле
акр = а^ЬХ. (18 29)
Для чугуна пользуются квадратизной зависимостью
скр = а + с^'
(18 30)
444
Значения постоянных коэффипиептов а,
материалов приведены ниже.
Ъ и с для некоторых
Материал хпред а ь с
Ст. 2, Ст. 3 100 3100 11,4 —
Ст. 5 100 4640 32,6 —
Сталь 40 90 3210 11,6 —.
Кремнистая сталь 100 5890 38,2 —
Дерево (сосна) 110 293 1,94 —
Чугун 80 7760 120 0,53
При некоторых значениях гибкости Хо величина окр, вычисленная
по формулам (18.29) или (18.30), становится равной предельному
напряжению при сжатии, т. е. для пластичных материалов
с — <3 •
кр т>
для хрупких материалов
скр
Стержни, у которых Х<Х0, называют стержнями малой гибкости
и рассчитывают только на прочность. Для стали марки Ст. 3, напри-
мер, при 40 < X < 100 график зависимости окр = f (X), полученный на
основании формулы (18 29), представляет собой наклонную прямую
SM (рис. 311), а часть графика NS при 0<Х<40 может рассматри-
ваться как горизонтальная линия.
Таким образом, график <ткр = f (X) для стали марки Ст. 3 состоит
из трех участков: горизонтального участка NS, соответствующего
а “ °т’ наклонного участка SM при 40 < X < 100 и гиперболы Эй
лера при X > 100 (правее точки М).
§ 98. Расчет сжатых стержней на устойчивость
при помощи коэффициентов уменьшения
основного допускаемого напряжения
Центрально сжатые стержни с малой гибкостью (Х<Х0) сохра-
няют несущую способность при условии, что критические напряже-
ния не превышают опасного напряжения, т. е. что
%р<ао>
где для хрупких материалов а0 — для пластичных материалов
а0 == от. Несущая способность стержней малой гибкости определяется
прочностью материала.
В случае стержней с большой гибкостью опасным состоянием
следует считать момент возникновения в сжатом стержне напряже-
ний, равных окр. Поэтому для обеспечения работоспособности стержня
необходимо выполнение следующего условия устойчивости:
скр Iе'у
(18 31)
445
где [°ly — допускаемое напряжение на устойчивость, определяемое
по формуле
Здесь пу коэффициент запаса устойчивости, который из-за возмож-
ной эксцентричности приложения нагрузки, искривления стержня
и неоднородности материала принимается всегда несколько больше
основного коэффициента запаса прочности (пу>*п0). Для стали
пу sa 1,8 -т- 3,0; для чугуна пу «= 5,0 ч- 5,5; для дерева пу = 2,8 ч- 3,2.
Чем больше гибкость, тем меньшим принимают иу.
На практике при расчете на устойчивость принято пользоваться
не допускаемым напряжением на устойчивость [о]у, а допускаемым
напряжением на сжатие [о__] с соответствующим поправочным коэф-
фициентом f, значение которого может быть установлено из отно-
шения _ Скр . Пр I3-] «у С0 ‘
Отсюда Ыу = ^- • У О0 «у
или Ыу = Я°-]( (18.32)
где ? —_““Р_ . А., (18.33) °0
Здесь — коэффициент уменьшения допускаемого напряжения на
сжатие, или коэффициент условного допускаемого напряжения.
В табл. 40 приведены значения <р для различных гибкостей.
Таким образом, учитывая (18.32), расчетную формулу на устой-
чивость (18.31) теперь можем переписать в виде
°тах<[°1у = ?[’-!
ИЛИ
N
(18.34)
г брутто
Различают два вида расчета на устойчивость: поверочный и проек-
тировочный.
При поверочном расчете исходят из известных размеров и формы
поперечного сечения стержня и прежде всего определяют наименьший
446
осевой момент инерции Jmln, площадь F, вычисляют минимальный
радиус инерции
______1/" 'Ли in
Jmin — г F ’
а также гибкость
х = Х.
lmin
Затем, зная гибкость, находят по таблице коэффициент <р, определяют
допускаемое напряжение на устойчивость
[о]у == ср [а
Р
сравнивают действительное напряжение о = — с допускаемым
брутто
напряжением на устойчивость [а]у и выясняют, удовлетворяется
ли условие
При проектировочном расчете исходят из условия
» = (18.35)
тл брутто
Необходимое сечение определяется формулой
^бруТТО = -36)
Кроме искомой площади F6pyTT0 в последнем соотношении неизвест-
ным является также коэффициент ср. Поэтому при подборе сечения
приходится пользоваться методом последовательных приближений,
варьируя величину коэффициента <р. Обычно при первой попытке
принимают <рх = 0,54-0,6. При принятом срх по формуле (18.36) опре-
деляют Ебрутто и подбирают соответствующее сечение. Зная сечецие
и определив Jmln, imln и X, устанавливают фактическое значение
коэффициента <р/. Если значительно отличается от ср1э то и напря-
жение будет отличаться от допускаемого. Тогда следует повторить
расчет, т. е. предпринять вторичную попытку, приняв среднее по
величине значение между коэффициентами <р$ и ср/:
f0 -
В результате второй попытки устанавливают Если требуется
третья попытка, то расчет повторяют при
,о _Л2+?2'
?з = —
и т. д, Обычно на практике удается обойтись двумя-тремя попыт-
ками.
447
§ 99. Выбор материала и рациональной формы
поперечных сечений сжатых стержней
Для стержней большой гибкости (Х> Хпред), когда %р<^пц,
модуль упругости Е является единственной характеристикой, опре-
деляющей сопротивляемость стержня потере устойчивости. Тогда,
очевидно, для стальных стержней, работающих на сжатие, у которых
практически Е меняется мало, нецелесообразно применять сталь
повышенной прочности. Что касается формы поперечного сечения, то
рациональной будет такая форма, при которой при определенной
площади величина наименьшего радиуса инерции imin является
наибольшей.
Введем безразмерную характеристику
?min
Vf
которую назовем удельным радиусом инерции. О рациональности того
или иного сечения можно судить на основании данных, приведенных
ниже.
Сечение К
/
Трубчатое I а = -—
\ нар
Трубчатое (а = 0,7 — 0,8)
Уголковое
Двутавровое
Швеллерное
Квадратное
Круглое
Прямоугольное (h = 2b)
2,25—1,64
1,2 —1,0
0,5 —0,3
0,41—0,27
0,41-0,29
0,289
0,283
0,204
Анализ приведенных данных
Рис. 312
всех направлениях, т. е. чтобы
возможности одинаковыми.
показывает, что наиболее рацио-
нальными являются трубчатые
сечения, столь же рациональны
коробчатые тонкостенные сечения.
Наименее рациональными являют-
ся сплошные прямоугольные сече-
ния.
При проектировании стерж-
ней, несущая способность кото-
рых определяется сопротивлением
потере устойчивости, следует
стремиться к тому, чтобы стер-
жень был равпоустойчивым во
шные моменты инерции были по
§ 100. Продольно-поперечный изгиб
Изгиб стержня называется продольпо-попсречпьш, если в его
поперечных сечениях возникают изгибающие моменты как от про-
дольных, так и от поперечных нагрузок (рис. 312).
448
Вычисление полного изгибающего момента Мп в поперечных
сечениях производят с учетом прогибов оси стержня:
|Mn(z) | = | M(z) | + | Swn(Z) J, (18.37)
где M(z) — изгибающий момент от действия поперечной нагрузки;
Su?n(z) — изгибающий момент от действия осевой нагрузки 5. Определе-
ние величины полного изгибающего момента Mn(z) осложняется тем,
.что в этом случае нельзя пользоваться принципом независимости
действия сил.
Рассмотрим приближенный метод определения изгибающего
момента Mn(z). Он основан на допущении, что изогнутая ось балки при
поперечной нагрузке принимает форму синусоиды, т. е.
w(z) « г sm -у-.
(18.38)
При наличии продольной силы также приближенно принимают, ято
«’nW® fnsin—•
(18.39)
Такое допущение позволяет получать достаточную точность для
шарнирно опертой балки при действии поперечных нагрузок, направ-
ленных в одну сторону, особенно, если деформация балки оказы-
I l\ f
вается симметричной относительно ее средины, где wn I у I = fn.
Дифференциальные уравнения упругой линии при поперечном
и продольно-поперечном изгибе соответственно запишем так:
d2 w(z) __М (z),
dz2 ~ EJ '
(18.40)
«’„(г) M (z) Su>n(z)
dz2 ~ EJ EJ
(18.41)
Исключив из уравнений (18.40) и (18.41) М (z) и учтя допущения
(18.38) и (18.39), будем иметь
/г л d2 I • S , . nz
dz2 (sm I / EJ ^Sm I ’
15 5-1186
449
После дифференцирования получим
и2 .9
= (18.42)
Обозначив
^=РЭ, (18-43)
из уравнения (18.42) найдем выражение для прогиба посредине про-
лета балки при продольно-поперечном изгибе
-----Ц- (18.44)
'-К'
Формула (18.44) дает удовлетворительные результаты, когда сжи-
мающая сила S не превышает 0,8Р*р. Предполагая, что изгибающие
моменты пропорциональны прогибам, в соответствии с (18.44) можно
получить простую приближенную формулу для определения изги-
бающего момента при продольно-поперечном изгибе в виде
М
(18.45)
гэ
Тогда величина максимальных напряжений в сечении стержня опре-
делится формулой
°max р "I
или с учетом (18.45) формулой
_ £ , М
amax j? + / е ’
w 1-4-
\ 9 t
(18.46)
(18.47)
Из формулы следует, что принцип независимости действия сил
здесь не имеет места.
В табл. 41 приведены уравнения изгибающего момента и упру-
гой линии для некоторых случаев продольно-поперечного изгиба
балок постоянного поперечного сечения.
450
Сб
er
s
я
о
сб
н
Коэффициент устойчивости т) 9,8696 20,199 2,4674 9,8696
Коэффициент приведения длины •» чем 669*0 04 Я-М
CL CL 'CL
Б
•II -Н одр 1 1 04 СО |
16*
rts сл Продолжение табл. 38
к с Схема стержня и его нагружения Коэффициент приведения длины » Коэффициент устойчивости т)
5 4 1 ЦЕ^р 2 2,4674
6 1 1ЛР 0,5 39,4784
7 1 1 '^Р 0,699 20,199
| 1
а 1 а 1
8 *р 0 0,1 0,2 о,з 0,4 0,5 0,6 0,7 0,8 0,9 2 1,87 1,73 1,6 1,47 1,35 1,23 1,13 1,06 *1,01 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 2,4674 2,832 3,283 3,845 4,551 5,438 6,511 7,726 8,874 9,637
а 1 а 1 у
9 —М“. ^р 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 2 1,85 1,7 1,55 1,4 1,26 1,11 0,975 0,852 0.757 0 о,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 2,467 2,883 3,414 4,105 5,021 6,26 7,99 10,39 13,59 17,24
Продолжение табл, 38
с Схема стержня Коэффициент
с и его нагружения ’ приведения длины v
2
Коэффициент устойчивости т/
P2/Pi P2/Pi *1
0 1 0 9,8696
0,25 0,95 0,25 10,93
0,5 0,91 0,5 11,92
0,75 0,89 0,75 12,46
1 0,87 1 13,04
2 0,82 2 14,68
В общем случае при
10
^кр (^1 ^2^кр
р.
Продолжение табл. 38
№ п. п. Схема стержня и его нагружения Коэффициент приведения длины ? Коэффициент устойчивости tj
14 —
а 1 Р2 pt
0 I 0,-1 0?2 0,-5
гр, г ^кр = "Ь ^2)кр 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,714 2,714 2,710 2,703 2,688 2,665 2,635 2,599 2,557 2,513 2,467 2,961 2,960 2,953 2,936 2,904 2,856 2,793 2,715 2,636 2,551 2,467 3,701 3,698 3,679 3,622 3,525 3,384 3,211 3,020 2,821 2,641 2,467
а 1 р2 Pt
* 1 2 1 5
0 0,1 0,2 0,3 4,935 4,930 4,880 4,712 7,402 7,377 7,207 6,769 14,80 14,68 13,78 11,70 27,14 26,66 23,19 16,82
0,4 4,470 6,074 9,187 11,57
0,5 4,136 5,268 7,060 8,210
0,6 3,759 4,497 5,504 6,048
0,7 3,385 3,830 4,376 4,660
0,8 3,040 3,280 3,551 3,685
0,9 2,734 2,832 2,936 2,986
1,0 2,467 2,467 2,467 2,467
Продолжение табл. 38
1
18 / ^кр = кр 0,434 52,5
19 а I- / ^КЭ ~ ^Кр 1,122 7,839
20 3 1 1 / а ^кр ~ 0,723 18,9
21 сл со L ‘ : ^кр “ (^)кр ?? 0,577 1 29,64
Продолжение табл, 38
№ п п Схема стержня и его нагружения Коэффициент приведения длины * Коэффициент устойчивости ц
22 z J ^кр “ (9^кр 0,366 73,65
23 11 е |Ь__. а.* Г qt\ \ 2 /кр 0,560 31,47
24 <7 ? ' 1 17 ’С i JL ~ / \ аТ~к ГТ а \ ! к 11 11 к \i СТ 0,694 20,49
05 1 _
25 2 1 2 . / р ( \ кр \ 2 /кр 1.486 4,47
26 "° « h 1 \ JU J\ ds ! \ 1 *1 \ 7 1,388 5,123
27 q; и® < S | / JU J / Я I / *о J—Uk 0,782 16,126
d to Продолжение табл, 38
1 № п n Схема стержня и его нагружения Коэффициент приведения длины v Коэффициент устойчивости ц
28 п 7С2 EJ Для п = ql: —— п о 9,87 0,25 8,62 0,50 7,40 0,75 6,08
1,0 4.77 2;0 — 0.66 3,0 — 4,94 4,0 — 9,87 5,0 —14,80 При больших значениях п коэффициент и; может оказаться отрицательным и для устойчивости равновесия стержня к нему должна быть приложена растягивающая сила Р
I I__________________________________________________________________________________________________________1
29 < ! тт , *2 EJ При п = ql: 4гг
п *1
0 0,25 0,50 0,75 1,0 2,0 3,0 4,0 5,0 2,47 2,28 2.08
]. 1 1,91 1,72 0,96 0,15 —0,69 —1,56 См. примечание к схеме 28
30 J е—а Л ! J а: •/
0,2 0,4 0,6 0,8 1
0,01 0,1 0,2 0,4 0,6 0,8 1,0 0,153 1,47 2,80 5,09 6,98 8,55 к2 0,27 2,40 4,22 6,68 8,19 9,18 к2 0,598 4,50 6,69 8,51 9,24 9,63 к2 2,26 8,59 9,33 9,67 9,78 9,84 к2 к2 к2 к2 к2 тс2 к2 к2
а Л
। k "L- -1
/
— — Продолжение табл. 38
В В Схема стержня и его нагружения Коэффициент приведения длины v Коэффициент устойчивости 7)
31 — а : t
0?2 0Л 0,6 0,8 1,0
✓ 0,01 0,1 0,2 0,4 0,6 0,8 1,0 0,614 5,87 11,1 20,2 27,7 34,0 4л2 1,08 9,48 16,3 24,9 30,6 35,3 4те2 2,39 15,5 20,5 26,3 31,1 35,4 4тс2 8,48 17,1 21,1 27,5 32,5 36,4 4л2 4л2 4тс2 4л2 4л2 4л2 4л2 4л2
_ а
1
32 1 Л _ J Р —• Приближенно 2 4К7 • 1 Lzi? J 1 J Л теа1 2Л67-[— + -Г- — М/, Msm d Некоторые конкретные значения тр
а
7
а! 1 0 0,1 0,2 0,5 1,0 2,0 5,0 10 20 50 100
0 2,467 2,243 2,056 1,645 1,234 0,8225 0,411 0,2243 0,1175 0,0484 0,0247
0,1 2,467 2,285 2,126 1,761 1,367 0,944 0,4894 0,2714 0,1436 0,0595 0,0301
0,2 2,467 2,325 2,197 1,881 1,52 1,093 0,5919 0,3350 0,1793 0,0749 0,038
0,3 2,467 2,363 2,262 2,013 1,692 1,277 0,7293 0,4237 0,2302 0,0971 0,0494
0,4 2,467 2,396 2,327 2,141 1,879 1,499 0,9174 0,5498 0,3064 0,1309 0,067
0,5 2,467 2,423 2,379 2,256 2,068 1,756 1,178 0,7462 0,4268 0,1860 0,0958
0,6 2,467 2,444 2,420 2,350 2,235 2,025 1,531 1,052 0,633 0,2848 0,1482
0,7 2,467 2,457 2,446 2,415 2,356 2,256 1,950 1,530 1,018 0,488 0,2588
0,8 2,467 2,464 2,461 2,453 2,440 2,402 2,297 2,106 1,730 0,9991 0,5592
0,9 2,467 2,467 2,466 2,465 2,465 2,459 2,446 2,424 2,374 2,189 1,746
1,0 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467
Gn=l
EJ Г /
Ркр = т] . Приближенно т) = 2,467 : 11 —
— •'i v v — ^1/ л_из — ^2 v_2_2/_
Ji I2 I \ Л I2 1
(л 1 U an—
‘ V M-i ’ * 11
Продолжение табл. 38
I № п. п. Схема стержня и его нагруженйя Коэффициент приведения длины v Коэффициент устойчивости tq
34 р = к₽ \ 4 /.кр —
Л J Число участков с различными моментами инерции
2 3 4 5 10
0,2 0,4 0,6 0,8 1,0 5,2 9,88 14,0 17,4 20,5 6,32 10,9 14,6 17,8 20,5 6,48 11,1 14,7 17,8 20,5 7,32 11,2 14,76 17,9 20,5 7,4 11,2 14,8 18,0 20,5
♦♦
35 - -—-< ₽ «Р 4 /кр — J 1 J Число участков с различными моментами инерции
2 3 4
0,2 0,4 0,6 0,8 1,0 18,1 31,2 41,0 49,4 54,8 21,8 34,2 42,4 49,5 54,8 22,8 34,3 42,4 49,5 54,8
•
Момент инерции сечения изменяется вдоль оси по закону 7(г) = /0(а + Нп
п
1 2 3 4
0 од 0,2 0,4 0,6 0.8 1,0 3,67 4,67 5,41 6,78 7,78 8,85 7U2 0,25 3,59 4,73 6,39 7,70 8,83 к2 3,24 4,52 6,28 7,64 8,83 к2 ЗД2 4,41 6,24 7,64 8,83 л2
п = 1 — сплошной стержень прямоугольного попереч-
ного сечения постоянной высоты; ширина сечения
меняется по линейному закону
п — 2 — пирамидальный стержень, составленный из
четырех угловых поясов, соединенных решеткой (или
обшитых тонкими листами)
п = 3 -т- стержень прямоугольного сечения постоянной
ширины, когда высота сечения меняется по линей-
ному закону
п = 4 — сплошной пирамидальный (конический)
стержень
П родолжение табл. 38
1 № п п Схема стержня и его нагружения Коэффициент приведения длини » Коэффициент устойчивости rj
37 •— Момент инерции сечения изменяется вдоль оси по закону J (z} = Jo (а -J- bz)n
J* n
0,5 1 Ь5 2 3 4
0 0,1 0,2 0,4 0,6 0,8 1,0 7,86 7,97 8,31 8,76 9,3 тс2 5,78 6,48 7,01 7,87 8,61 9,27 тс2 5,78 6,58 7,69 8,54 9,25 тс2 1,0 5,4 6,37 7,61 8,51 9,24 к2 5,01 6,14 7,52 8,5 9,23 тс2 4^81 6,02 7,48 8,47 9,23 тс2
38 1 4 J. J/V Р — Момент инерции сечения изменяется вдоль оси по закону J (z) — Jo (а 4- bz)n
J*
1 1 2 1 3 1 4
Li—F 1 0,1 0,2 0,4 0,6 0,8 1,0 20,35 26,16 31,03 35,42 4тс2 14,39 18,93 25,54 30,79 35,35 4те2 13,7 18,49 25,34 30,71 35,33 4тс2 13,3 18,23 25,23 30,68 35,32 4к2
39
Момент инерции сечения крайних участков изме-
няется вдоль оси по закону J(z) = = Jq (а + bz)n
«Л а • /
~Г 0 0,2 Ои j 0.6 | 0,8 п
0 5,78 7,04 8,35 9,36 9,8 1
1,0 1,56 2,78 6,25 9,59 2
0,01 5,87 7,11 8,4 9,4 9,8 1
3,45 4,73 6,58 8,61 9,71 2
2,55 3,65 5,42 7,99 9,63 3
2,15 3,13 4,84 7,53 9,56 4
0,1 6,48 7,58 8,63 9,46 9,82 1
5,4 6,67 8,08 9,25 9,79 2
5,01 6,32 7,84 9,14 9,77 3
4,81 6,11 7,68 9,1 9,77 4
0,2 7,01 7,99 8,9 9,73 9,82 1
6,37 7,49 8,61 9,44 9,81 2
6,14 7,31 8,49 9,39 9,81 3
6,02 7,2 8,42 9,38 9,8 4
0,4 7,87 8,59 9,19 9,7 9,85 1
7,61 8,42 9,15 9,63 9,84 2
7,52 8,38 9,1 9,62 9,84 3
7,48 8,33 9,1 9,62 9,84 4
0,6 8,61 9,12 9,55 9,76 9,85 1
8,51 9,04 9,48 9,74 9,85 2
8,5 9,02 9,46 9,74 9,85 3
8,47 9,01 9,45 9,74 9,85 4
0,8 9,27 9,53 9,69 9,82 9,86 1
9,24 9,5 9,69 9,82 9,86 2
9,23 9,5 9,69 9,81 9,86 3
9,23 9,49 9,69 9,81 9,86 4
— Продолжение табл. 38
( 1 о 1 № п п Схема стержня и его нагружения Коэффициент приведения длины v Коэффициент устойчивости
— Момент инерции сечения крайних участков изме- няется вдоль оси по закону J (z) = Jo (я 4- bz)n
а * / п
0 0,2 0,4 0,6 0,8
i J Jk 0,2 0,4 0,6 0,8 20,36 18,94 18,48 18,23 26,16 25,54 25,32 25,23 31,04 30,79 30,72 30,68 35,4 35,35 35,33 35,32 22,36 22,25 20,88 20,71 27,8 27,35 27,2 27,13 32,2 32,02 31,96 31,94 36,0 35,97 35,96 35,96 23,42 22,91 22,64 22,49 28,96 28,52 28,4 28,33 32,92 32,77 32,72 32,69 36,36 36,34 36,32 36,32 25,55 24,29 23,96 23,8 30,2 29,69 29,52 29,46 33,8 33,63 33,56 33,54 36,84 36,8 36,8 36,78 29,0 27,67 27,24 27,03 33,08 32,59 32,44 32,35 35,8 35,64 35,6 35,56 37,84 37,81 37,8 37,8 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
а 1
1
Q = Qo
*—’ Момент инерции сечения изменяется вдоль оси по ll — z\n закону J (z) = J1—— 1
п 0 1 2
7,839 5,78 3,67
—’ Момент инерции сечения изменяется вдоль оси по // — z\n закону J (z\ —-—1
п 0 1 2 3
16,1 13 9,87 6,59
— Момент инерции сечения изменяется вдоль оси по 1 1 ’— z\ закону J (z) = J1—— 1
Л 7П
2 3 4 5
0 1 2 3 4 27,3 23Д 18,9 14,7 10,2 41,3 36,1 30,9 25,7 20,2 52,1 45,8 39,5 33,0 63,6
Продолжение табл. 38
472
Продолжение табл. 38
Схема стержня и его нагружения Коэффициент приведения длины v Коэффициент устойчивости
45 J а а> При т = ——2 (Z — а) (1 — а) и п = —~ Pi а
л2 Р = — кр ( ^min >а)2
0 0,4 0,8 1,2 1,6 П При Ру = Рг = Р 0 J== J2 == J ' EJ — 4 Z2
р . ”agJ кр (у/)2
а а
1 I
0 0,699 0 20,19
0,1 0,646 0,1 23,63
0,2 0,593 0,2 28,09
о,з 0,539 0,3 33,96
0,4 0,487 0,4 41,68
0,5 0,439 0,5 51,12
0,6 0,41 0,6 58,84
0,7 0,412 0,7 58,92
0,8 0,436 0,8 51,97
0,9 0,467 0,9 45,27
1,0 0,500 1,0 39,48
Продолжение табл» 38
Схема ртержня и его нагружения Коэффициент приведения длины v Коэффициент УСТОЙЧИВОСТИ 7)
46 При т = — t/j (Z — а) Р2 G — «) и п = —Ц- - Рг а
Р -ТС2Д7т1п
W (уа)2
При Рг = Р2 = Р и Ji = J2 = J
Р ^EJ EJ
«Р (yl)2 I2
а Т а 1
0 0,5 0 39,48
0,1 0,463 0,1 46,13
0,2 0,426 0,2 54,45
0,3 0,391 0,3 64,56
0,4 0,362 0,4 75,22
0,5 0,35 0,5 80,76
0,6 0,362 0,6 75,22
0,7 0,391 0,7 64,56
0,8 0,426 0,8 54,45
0,9 0,463 0,9 46,13
1,0 0,5 1,0 39,48
474
Продолжение табл, 38
47
Схема стержня
и его йагружения
Коэффициент
приведения длийы ?
Коэффициент
УСТОЙЧИВОСТИ 7]
«Т «^2 О
При т = —; / . • и п =
— a) а
7С2
р_________mm
КР (va)2
При Pt = Р2 = Р И J, = J2 = J
Р - "* EJ _ EJ
«Р (vZ)2 “71 Z2
а т V а ~Г
0 1,0 0 9,87
0,1 0,933 од 11,83
0,2 0,868 0,2 13,11
0,3 0,804 0,3 15,26
0,4 0,746 0,4 17,72
0,5 0,699 0,5 20,19
0,6 0,672 0,6 21,88
0,7 0,668 0,7 22,14
0,8 0,679 0,8 21,4
0,9 0,693 0,9 20,55
1,0 0,699 1,0 20,19
475
Продолжение табл. 88
Схема стержня
и его нагружения
Коэффициент
приведения длины »
Коэффициент
УСТОЙЧИВОСТИ 7)
р *2EJ EJ
»Р= (vZ)2 Z2
а 7 V а Г *1
0 1,0 0 9,87
од 0,925 0,1 11,53
0,2 0,85 0,2 13,65
0,3 0,776 0,3 16,37
0,4 0,704 0,4 19,9
0,5 0,636 0,5 24,42
0,6 0,575 0,6 29,82
0,7 0,53 0,7 35,1
0,8 0,507 0,8 38,41
0,9 0,501 0,9 39,4
1,0 0,5 1,0 39,48
476
Продолжение табл. 38
Схема стержня и его нагружения Коэффициент приведения длины v Коэффициент устойчивости ц
49 р,^ J, £3% При т = 71 /2 ^2 h Р ^=z ^mln «р ~ (vZr)2 Значения v находят из графиков, построенных для схемы 47
j-j- 37 Q I] 2
При т± = - ° - и тг = - + 7
71 t0 Ji 42
^min
FKP — (V/J2
477
Продолжение табл. 38
Схема стержня
и его нагружения
Коэффициент
приведения длины v
Коэффициент
УСТОЙЧИВОСТИ 7]
52
Р = к2
КР- (^0)2
При т — ------
A h
Р2 ^2
И П==Р^1
Р . A/min
КР - (VZJ2
Значения находятся из
графиков, построенных
для схемы 48
54
f'O
р ___к* ^min
КР- (W0)2
478
Продолжение табл. 38
479
Продолжение табл. 38
480
Продолжение табл 38
Схема стержня
и его нагружения
Коэффициент
приведения длины
Коэффициент
УСТОЙЧИВОСТИ 7)
62
кр ~
63
Si I
So I
мм/ ♦** ****
'1 '2 Ц »
П (S1 + s2) EJ
Некоторые конкретные
данные при:
п = 0
16 5 1186
481
Продолжение табл, 38
Схема стержня
и его нагружения
Коэффициент
приведения длины v
Коэффициент
УСТОЙЧИВОСТИ Т]
63
8
6
4
2
Q
2 4 6 8
482
Продолжение табл. 33
Схема стержня
и его нагружения
Коэффициент
приведения длины v
Коэффициент
УСТОЙЧИВОСТИ 7]
0,5 < v < 2
Некоторые конкретные
данные
2,4424 39,48
65
0,7 < v < оо
Некоторые конкретные
данные
0<v)<20,14
Sil s2l
т^~ЕГ m^EJ
?i r2 I3
(S1 + s2) EJ
«•**. «**«
16*
483
Продолжение табл. 38
Схема стержня
и его нагружения
Коэффициент
приведения длины v
Коэффициент
УСТОЙЧИВОСТИ Т|
0,5 < v < 1
Конкретные значения v
могут быть взяты из
графика, построенного
для схемы 50
Если т1 = т2 = т =
Г2 I3
(S1 + s2>‘ EJ
«***
9,8696 < <39,48
1 < N < OO
Конкретные значения
могут быть взяты из
графика, построенного
для схемы 63 (случай
п == 0)
Если т1 = т2^=т,=
(si + si) EJ
0<т] <9,8696
484
П родолжение табл, 38
485
Продолжение табл, 38
Схема стержня и его нагружения Коэффициент приведения длины v Коэффициент । УСТОЙЧИВОСТИ 7)
7( ) гп^гп; т2*п*м Н /. ,т- /п^л=оо;/л^/п р ' ,^г S1 1 mi - 'ЕГ; So 1 ГП2==='еТ *««* 0,5 < v < 0,7 Конкретные значения v могут быть взяты из графика, построенного для схемы 54 п — (Sj -I- s2) EJ »»* 20,14 < tj < 39,48
71
$ т^оо;п=0;т2-т р
l<v<2
Некоторые конкретные
данные
т — 511
l~ EJ ’
So I
~ЁГ ''
Г1 гг I3
(«1 -|- s2) EJ
л* ****
2,4424 9,8696
п =
486
Продолжение табл. 38
Схема стержня
и его нагружения
Коэффициент
приведения длины v
Коэффициент
УСТОЙЧИВОСТИ 7}
0,7 < n < 1
Конкретные значения
могут быть взяты из
графика, построенного
для схемы 52 с учетом,
Si I
что т1 = ; т2 =
_ $2 ,
" ТГ’
9,8696 <i]< 20,14
П I3
(si 4* sa) EJ
73
2 < v < oo
Некоторые конкретные
данные
m —sil.
mi~EJ’
rir^3
n~(st+ s2) EJ
* * * * *
О < 7} <2,4424
у» _ S1 .
1- EJ ’
___ S2 I
тз~~ЁТ'
Необходима также про-
верка устойчивости по
формуле
Р --^г* I
Г1 + г/
$ $ ф
За расчетное принима-
ют наименьшее значе-
ние Ркр
9,8696
487
Продолжение табл, 38
Схема стержня Коэффициент Коэффициент
и его нагружения приведения длины v УСТОЙЧИВОСТИ 7]
(г — коэффициент жест- кости упруго-переме- щаюгцейся опоры)
76
При числе пролетов
п ~ 2 значения \ могут
быть взяты из гра-
фика, построенного для
схемы 69.
При п = 3
Р~ Р
г — коэффициент же-
сткости упруго-пере-
мещающейся опоры
г/3
EJ
488
Продолжение табл. 38
Схема стержня и его нагружения Коэффициент приведения длины v Коэффициент устойчивости
77 При .числе пролетов п = 2
п — 4
г — коэффициент же-
сткости упруго-пере-
мещающейся опоры
Н3
EJ
489
Продолжение табл. 38
Схема стержня и его нагружения Коэффициент приведения длины v Коэффициент УСТОЙЧИВОСТИ К)
78 Д К X Значения \ могут быть взяты из графика, по- строенного для схе- мы 52. При этом т = _ si ~ 2EJ (s — коэффициент же- сткости упруго-повора- чивающейся опоры) es
79 4 , Р Значения v могут быть взяты из графика, по- строенного для схе- мы 54. При этом т = (s — коэффициент же« сткости упруго-пово- рачивающейся опоры)
* J и Jt — наибольший и наименьший моменты инерции поперечного сечения
соответственно.
* * Предполагается, что имеется несколько участков одинаковой длины?
причем разности между моментами инерции соседних участков одинаковы.
* ** ri и г 2 — коэффициенты жесткости левой и правой упру го-перемещаю-
щихся опор.
* *** 8, и 8г - коэффициенты жесткости левой и правой упруго-поворачи-
вающихся опор.
* **** с — коэффипиент жесткости упругого основания (коэффициент
постели), равный отношению реакции основания к его осадке.
490
Критические нагрузки для полосы и некоторых
Типы опор:
В горизонтальной и
вертикальной плоско-
стях == заделка
Таблица 39
двутавровых балок*
В горизонтальной
плоскости заделка,
в вертикальной —
шарнир
В горизонтальной
плоскости шарнир,
в вертикальнойза-
делка
В горизонтальной
плоскости шарнир,
в вертикальной —
направляющие
В горизонтальной и
вертикальной плоско-
стях — шарниры
Схема Критическая нагрузка
1 М = — кр 21 При потере устойчивости плоскость дей- ствия пары сохраняет неизменную ориента- цию в системе подвижных осей, жестко связанных с перемещающимся торцовым се- чением
^КР — 12 \S I LJ)
. _ 4,0135
при а = 0 Ркр = —р-
Р11
Если высота консольной полосы меняется
------3 Ь Ь II / 4 2 Ь
I по закону h = ho |/ 1.—j~ , где Ло — высота
полосы у основания, z — текущая координата
вдоль полосы, то mS п 1 кр ~ т 1 1 | 1,333 12 14 ) 2,4 J 2,81 J 3,21 ) 3,61
* S = j/^EJ GJK , где EJ — наименьшая жеса кость при изгибе;
GJ г— жесткость при круяении.
491
Продолжений табл, 39
Схема
Критическая нагрузку
Р = ^
кр 12
Коэффициент к берется из таблицы.
/2 2GJ*
При этом % = ’ где & ~~жест"
кость одной из полок двутавра при изгибе
в ее плоскости
х I 0,1 | 1 | 2 | 3 I 4 I 6 I 10 I 24 | 40
к j 44,3] 15,7] 12,2] 10,7] 9,7б| 8,69| 7,58] 6,19) 5,64
гг /а 1 4,013
При % > 40 к = -----—j—
5,566
гкр — /2
кр
12,856*
Z* 2
Л
< I
Если высота консольной полосы меняется
п Г 7
по закону h = h01/ 1 <— — » где hQ — высота
полосы у основания, z— текущая коорди-
ната вдоль полосы, то (WKp == -р-
' n I 1 | 1,333 I 2 [ 4
т I У,6 | 10,4 ] 11,2 I 12,8
qQl \ 26,56
2 /кр ~ Z2
д0 в корне
492
Продолжение. табл. 39
Критическая нагрузка
, А 15,95S
(^)кр /2
„nS
^кр i
где к — высота балки, D—жесткость одной
из полок двутавра при изгибе в ее плоско
сти
EJ 4- GJ
М = -------------£ 4-
«Р 2/? “
S2
R2
Нижний знак определяет критическое зна
чение момента, направленного противо-
положно показанному на схеме
Р — __
кр /2
а: /( 0,05 | 0,1 | 0,15 I 0,2 | 0,25
к I 111,6 I 56,01 J 37,88 I 29,11 | 24,1
а : /| 0 3 [ 0,35 | 0,4 I 0,45 I 0,5
к I 21,01 j 19,04 I 17,82 | 17 15 | 16,94
Ркр = (s — 3,48 4
КР \ / /
493
Продолжение табл. 39
Критическая нагрузка
Схема
__________________Продолжение табл. 39
Критическая нагрузка
_к^/ '
«Р — /2 /
/2 2^К
При х — • —— t где h «= высота балки,
D — жесткость одной из полок двутавра при
изгибе в ее плоскости, значения к будут
.. 2*5
^кр I
х 0,4 4 8 16 32 64 160 400
к 86,4] 31,9] 25,6 21,8 19,6 18,3] 17,5 17,2
р 44’55
кр /2
Й0кР =
28,315
/2
>_____kS_
КР"“ /2
(^)кр /2
При х = , где h — высота балки,
D^~ жесткость одной из полок двутавра
при изгибе в ее плоскости, значения к
будут
/2 267
При ^==’р- • ’—д- , где —высота балки;
D — жесткость одной из полок двутавра при
изгибе в ее плоскости, значения к будут
х | 0,4 | 4 | 8 | 16 | 32 | 64 1128 | 320
А: 1268 j 88,8| 65,5] 50,2] 40,2,34,1| 30,7| 28,4
х 0,4 4 8 16 32 64 1281400
к 143 53 42,6 36,3 32,6 30,5 29,41 28,6
Если при опрокидывании нагрузка остается
параллельной первоначальному направле-
нию, то
/ оч EJ
(7^2 Q 2)2
Если при опрокидывании нагрузка остается
направленной к исходному центру кривизны,
то
кр R* / ЖГ“
02/и2+62-££-
\
р _2£
кр ~ /2
а ’.I | 0,1 | 0,2 ( 0,3 | 0,4 | 0,5
"V| 117153,2) 35,2| 28,5126,7
, 48,6S
W‘)kp ~ ~~р
495
404
Продолжений табл. 39
Схема
Критическая нагрузи:
(^КР [2 1
При х = К > где — высота балки,
D — жесткость одной из полок двутавра при
изгибе в ее плоскости, значения к будут
х | 0,4 | 4 | 8 | 16 | 32 | 96 [ 128 1400
к j 4881161 j 119 j 91,3| 73,0| 58,0| 55,8| 51,2
р ~ —-
ГКР /2
a :l I 0,1 I 0,2 I 0,3 I 0,4 I 0,5
к j 608 j 155180,9| 58,б| 53,0
(^)кр
129,15
Z2
„ mEJ
(^КР /J2
Нагрузка остается параллельной своему
первоначальному направлению
6 | тс : 41 к * 21 тс 11,063^1 1,1тс|1,24тс
T40I Too
Р = - --
Кр /2
а: ZI 0,1 I 0,2 | 0,3 I 0,4 I 0,5 I 0,6 I 0,7 I 0,8 10,9
к I 65,8| 34,7| 25,8| 22,8| 22,9| 25,7| 32,9| 50,7|1 И
. Л _ 39,6S
(^)кр /2
496
Продолжение табл. 39
СхеД1
Критическая нагрузка
р
Кр ~ /2
а : I I 0,1 [ 0,2 | 0,3 I 0,4 I 0,5 I 0,6 I 0,7 I 0,8 10,9
к I 77,5| 41,5| 31,5| 28,9| 30,5| 37,1] 53,9| 104 |376
* I
, л 57,2$
(^Кр /2
р
кр /а
а : I | 0,1 | 0,2 I 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 10,9
* 179,6| 43,2| 33,7| 31,9| 35,1145,1) 70,3| 1491 625
(^)кр =
64,6$
I*
№ SSS
Кр /2
а : /I 0,1 [ 0,2 I 0,3 I 0,4 I 0,5 I 0,6 I 0,7 I 0,8 10,9
к 1138 J 67,1 / 47,0| 40,1] 39,9] 46,2| 64,2| 1191 422
497
498
Продолжение табл. 39
Схема
Критическая нагрузка
Л. и и
1ШШШГ
✓
уГ II [ II ГК
Вертикальные перемещения опорных сече-
ний предполагаются невозможными
(во
кр
98,7S
Р -Л
кр- (3
а : /I 0,1 I 0,2 I 0,3 I 0,4 I 0,5 I 0,6 I 0,7 I 0,8 10,9
к 13991118167,8| 52,б| 50,2| 57j| 82,2| 1611 621
q
и пиит
i" 'i '
120.6S
/2
499
Коэффициенты условного допускаемого напряжения на сжатие <р
Материал Гиб
0 10 20 30 40 50 60 70 80
Сталь
Ст. 0 Ст. 2 Ст. 3 Ст. 4 1,00 0.99 0,97 0,95 0,92 0,89 0,86 0,81 0,75
Ст. 5 НЛ-1 1,0 0,98 0,95 0,92 0,89 0,86 0,82 0,76 0,70
НЛ-2 1,00 0,98 0,95 0,93 0,90 0,83 0,78 0,71 0,63
8,5KCH® 1,00 0,97 0,95 0,91 0,87 0,83 0,79 0,72 0,65
Чугун
СЧ 12-28 СЧ 15-18 СЧ 15-30 СЧ 15-32 СЧ 15-36 1,00 0,97 0,91 0,81 0,69 0,57 0,44 0,34 0,26
СЧ 18-36 СЧ 21-40 СЧ 21-44 СЧ 24-44 СЧ 28-48 1,00 0,95 0,87 0,75 0,60 0,43 0,32 0,23 0,18
Алюминиевый сплав
АМг 1,00 0,973 0,945 0,917 0,87 0,77 0,685 0,603 0,53 0,387 0,387 0 269
АМгб 1,00 0,973 0,946 0,89 0,77 0,64 0,542 0,458
АВТ1 1,00 0,996 0,992 0,90 0,78 0,66 0,557 0,463
Д16Т 1,00 0,999 0,998 0,835 0,70 0,568 0,455 0,353
Каменные и армокаменные 1,00 0,99 0,96 0,91 0,85 0,78 0,72 0,65 0 58
элементы -
Железобетон 1,00 1,00 1,00 1,00 1,00 1,00 0,83 0,73 0,6^
Бетон тяжелый 1,00 1,00 0,96 0,90 0,84 0,76 0,70 0,63 0,57
Бетон легкий 1,00 1,00 0,95 0,86 0,73 0,68 0,59 0,52 0,46
Дерево (сосна, ель) 1,00 0,99 0,97 0,93 0,87 0,80 0,71 0,61 0,49
500
Та б л и ц a 40
кость X
90 100 110 120 130 140 150 160 170 180 190 200
0,69 0,60 0,52 0,45 0,40 0,36 0,32 0,29 0,26 0,23 0,21 0,19
0,62 0,51 0,43 0,38 0,32 0,28 0,26 0,24 0,21 0,19 0,17 0,16
0,54 0,45 0,39 0,33 0,29 0,26 0,23 0,21 0,19 0,17 0,15 0,14
0,55 0,43 0,35 0,30 0,26 0,23 0,21 0,19 0,17 0,15 0,14 0,13
0,20 0,16 ’— •— — — — — — —
0,14 0,12
0,465 0,415 0,365 0,327 0,296 0,265 0,235
0,322 0,28 0,243 0,213 0,183 0,162 0,148 .. -
0,312 0,252 0,21 0,175 0,15 0,129 0,113 —
0,212 0,172 0,142 0,119 0,101 0,087 0,076 — — —— — —
0,53 0,48 0,43 0,38 0,35 0,32 0,29 — —• — — —
0,57 0,52 г— ,— — •—— — — — <— — ,—
0,51 0,45
0,38 0,31 0,25 0,22 0,18 0,16 0,14 0,12 0,11 0,10 0,09 0,08
501
to
Таблица 41
Уравнения изгибающего момента М(z) и упругой линии io(z) для некоторых случаев продольно-поперечного
изгиба балок постоянного поперечного сечения (fc= 1/ —)
\ у EJ/
Схема балки
и ее нагружения
w (Z)
izf / \ Р [sh U 7
Л/ (z) = — —-- sh kz —
к (jshfc/
e (a) sh к (z — a) J
„ж f ч P sh kb , ,
M (a) = ---------—- sh ka
к sh kl
e (a) == О при z a
e (a) = 1 при z > a
P / shfcfc v 7 (л a\ ,
( ~ EJk* t sh kl Sh kz ~~ V T) kz ”
*— e (a) [sh к {z — a) — k(z — a)]|
z ч P f sh kb , , (л a \ )
w~ EJk3 (shlT shka~(1 ~~i) ka\
M(z) = MpLg-Sh*z-
L sh kl
e (a) chk(z — a) j
И/Г / \ 71Г СЬЛб , ,
M (a) — M - sh ka
shkl
e(a)=^0 при z < a
e (a) = 1 при z>> a
M f ch kb , - z
W(2)— EJk* ( sh kl Shkz T~~
e (a) [ch к (z — a) — 1]|
Г ch v , a 1
“’(a)==-W [TO-Shfto-Tj
СЛ 2 Продолжение табл. 41
Схема балки и ее нагружения М(2) W (Z)
q И'HHHHU ? 1 м (/) = 'k^chkl (1 ~ ch kl - kl sh kl)
kl ch*(z“4
w(2)= K7F
sm kb . ,
—— sm kz —
sm kl
P ( sm kb . , , [л
w(z) = -ггттц-1-----—77 smh+ 1--------у I kz +
v 1 EJkA ( sm kl \ И
— e (a) sin к (z
e (a) [sin к (z — a)
, _ , x P sm kb . ,
M (a) = -----r-yy- sm ka
v к sm kl
e (a) = 0 при z < a
e (a) = 1 при z >> a
P ( sin kb . r ,
“’^=-ЁЖ\—snrslQka + V“
M(z} — M\ . гт- sin kz —
L sm kl
— e (a) cos к (z — a) j
cos kb . ,
M (a) = M . sm ka
' sm kl
e (a) = 0 при z < a
e (a) = 1 при z > a
M
W(Z)_ EJk^
cos kb
sin kl
T , Z
sm kz + -y -•
— e (a) [1 — cos к {z — a)]
w^- EJk*
cos kb
sin kl
sm ka + у
M(z) = ^- 1
8
Схема балки
и ее нагружения
М (z)
Продолжение табл. 41
w (z)
J * 1
cos к I z — -g-
Id
cos 2
, / 1
cos к I z x-
\ I
kl
C0S~T
cos к I — cos kb
sm kl
sin kz —*
— cos kz + 1
а
w^=z EJW
1
ял-/ /x 9 [cos&Z— cosZrb . T
M <* >=I—И—sm kz -
— cos kz J- cos к (z — a)
, ,, 4 q ( smkz z\
A:2 \ sin kl I J
1 sinZrZ
Mmax при z = T arc cos -j-r-
o Продолжение табл, 41
Схема балки и ее нагружения М. (z) w(z)
р J Z /И(?Ч_ - Р Sinfcz e=s
ч 1 г ( ' к cos kl
ч * м . 1 т Z м м (2) = cos & (J 2) cos kl
J1 N* ЕЕПНШ _z Д Z М (0 = "7.2 g 11 ~~ C0S к2 cos kl «— kl sin kl) •ЧЯВГ
1 * —1—
q
+ 2 V И
I l\ g { kl kl , k2l2\
w\2) EJk1 2 tg 4 + 8 )
Глава 19
УПРУГИЕ КОЛЕБАНИЯ
§ 101. Классификация механических колебаний
Все колебательные процессы, с которыми приходится встречаться
в физике и технике, можно классифицировать в соответствии с зако-
ном, по которому некоторая величина, характеризующая колебатель-
ный процесс, изменяется во времени. Такую классификацию можно
назвать кинематической в широком' смысле этого слова. Колебания
могут быть периодическими и непериодическими. Кроме того, имеется
широкий промежуточный класс так называемых почти периодических
колебаний.
Периодические колебания описываются периодической функцией,
значение которой повторяется через определенный отрезок времени Г,
называемый периодом колебаний, т. е.
/(« + Г) = /(0
при любом значении переменной t.
Непериодическими называются функции, не удовлетворяющие
этому условию.
Почти периодические функции определяются условием
I/1G + *)-fi (0 |<е
при любом t, где т и е — определенные постоянные величины. Оче-
видно, что если £ очень
Рис. 313
по (19.1), только знак
(плюс).
мало по сравнению со средним значением
модуля функции ft (i) за время t, то поч-
ти периодическая функция будет близка
к периодической, в которой т будет почти
периодом.
К наиболее распространенным перио-
дическим колебаниям относятся гармони-
ческие, или синусоидальные, колебания.
Непериодические колебания гораздо
разнообразнее периодических. Такие коле-
бания чаще всего являются затухающими
(рис. 313, а) или нарастающими (рис. 313, б)
синусоидальными колебаниями. Затухаю-
щие колебания математически могут быть
представлены выражением
х = A~bt cos (art + ср), (19.1)
где А, b и toпостоянные величины;
t — время.
Нарастающие гармонические колебав
ния математически описываются аналогич-
при bi должен быть заменен на обратный
510
Строго говоря, название затухающие гармонические (или сину-
соидальные) колебания не совсем логично, так как гармонические
колебания не могут затухать. Тем не менее на практике этим назва-
нием пользуются.
Классификация колебательных процессов по внешним признакам
не является достаточной, а потому она должна быть дополнена клас-
сификацией колебаний по основным физическим призна- п
кам рассматриваемых колебательных систем. -v/z/z
При исследовании колебательных движений упру-
гих систем важно знать, какое число независимых пара-
метров определяет положение системы в каждый данный
момент времени. Число таких параметров называется чис- <
лом степеней свободы,
В простейших случаях положение системы может
быть определено одной величиной. Такие системы вазы- рдД
ваются системами с одной степенью свободы, Колебатель- ii
ная система, состоящая из груза Q, подвешенного на пШ
пружине (рис. 314), будучи устроена так, что возможны —;•
только вертикальные перемещения груза, является систе- ъ
мой с одной степенью свободы. Ее положение в любой
момент времени может быть определено одним пара- г
метром — перемещением по вертикали. Рис. 314
Примером системы с двумя степенями свободы может
служить невесомая балка, несущая две массы (рис. 315). Здесь неза-
висимыми параметрами, определяющими положение системы в любой
момент времени, могут служить перемещения масс тх и т2 относи-
тельно положения равновесия. Увеличивая число сосредоточенных
масс колеблющейся балки, переходим в пределе к балке с распреде-
ленной по всей длине массой — колебательной системе (рис. 316)
с бесконечным числом степеней свободы.
Классификация механических кол ебаний
/77/ т2 может быть проведена и по другим признакам.
в частности, принято различать следующие
четыре типа колебаний: собственные колебания,
вынужденные колебания, параметрические колеба-
Рис. 315 ния и автоколебания.
Собственными (или свободными) называются
колебания, возникающие в изолированной системе вследствие внешнего
возбуждения («толчков»), вызывающего у точек системы начальные
отклонения от положения равновесия, и продолжающиеся затем благо-
даря наличию внутренних упругих сил, восстанавливающих равновесие.
Необходимая энергия, обеспечивающая процесс колебаний, поступает
извне в начальный момент возбуждения колебаний. Период колебаний
Рис. 316 Рис. 317
(время одного полного колебания) или частота колебаний (величина,
обрат ная периоду) зависит от самой системы. Частота колебаний явля-
ется вполне определенной для данной системы и называется собственной
частотой колебаний системы. Собственные колебания из-за потерь энер-
гии в системе практически всегда являются затухающими, хотя при
анализе собственных колебаний потерями энергии часто пренебрегают.
511
Вынужденными называются колебания упругой системы, происхо-
дящие при действии на систему (в течение всего процесса колебаний)
заданных внешних периодически изменяющихся возмущающих сил. Ха-
рактер колебательного процесса при этом определяется не только
свойствами системы, но существенно зависит также от внешней силы.
Примером вынужденных колебаний могут служить поперечные коле-
бания балки (рис. 317), вызываемые неуравновешенной массой ротора
установленного на ней работающего электромотора.
Вынужденные колебания происходят с частотой возмущающей
силы и поддерживаются за счет непрерывного поступления энергии
извне. При совпадении частоты возмущающих сил с частотой собст-
венных колебаний системы наступает явление резонанса, характерное
резким возрастанием амплитуды вынужденных колебаний, представ-
ляющим опасность для работы рассматриваемой механической коле-
бательной системы.
Параметрическими называются колебания упругой системы, в про-
цессе которых периодически меняются физические параметры системы—
величины, характеризующие массу или жесткость системы. При этом
внешние силы не влияют непосредственно на колебательное движе-
ние, а изменяют физические параметры системы. Примером парамет-
рических колебаний могут служить поперечные колебания массы на
вращающемся стержне некруглого сечения, имеющем разный эква-
ториальный момент инерции относительно взаимно перпендикуляр-
ных осей.
Автоколебаниями, или самоколебаниями, упругой системы назы-
ваются незатухающие колебания, поддерживаемые такими внешними
силами, характер воздействия которых определяется самим колеба-
тельным процессом.
Автоколебания возникают в системе в отсутствие внешних перио-
дических воздействий. Характер колебаний определяется исключи-
тельно устройством системы. Источник энергии, покрывающий потери
энергии в системе в процессе ее колебаний, составляет неотъемлемую
часть системы. Таким образом, автоколебания отличаются от собст-
венных колебаний, являющихся затухающими, тем, что они не зату-
хают. С другой стороны, автоколебания отличаются от вынужденных
и параметрических колебаний, вызываемых внешними силами, харак-
тер действия которых в обоих случаях задан, тем, что они являются
самовозбуждающимися, так как процесс колебаний здесь управляется
самими колебаниями.
Примером автоколебаний может служить вибрация частей само-
лета (флаттер), когда источником дополнительной энергии, поддер-
живающей колебания системы, является энергия воздушного потока,
а также трепетание флага на ветру.
Классификацию колебаний принято также проводить по виду
деформаций упругих элементов конструкции. В частности, примени-
тельно к стержневым системам различают продольные, поперечные и
крутильные колебания.
При продольных колебаниях перемещения всех точек упругого
стержня направлены вдоль оси стержня. При этом имеет место дефор-
мация удлинения или укорочения стержня, т. е. продольные коле-
бания можно называть колебаниями растяжения — сжатия.
При поперечных (изгибных) колебаниях основные компоненты пере-
мещений (прогибы) направлены перпендикулярно оси стержня.
При крутильных колебаниях имеют место переменные деформации
кручения. Возможны также изгибно-крутильные колебания, т. е.
колебания, при которых одновременно имеют место переменный изгиб
и кручение.
512
§ 102. Свободные колебания систем
с одной степенью свободы
Простейшей колебательной системой с одной степенью свободы
может служить груз, подвешенный на вертикально расположенной
пружине (рис. 318).
Дифференциальное уравнение колебаний груза
Q получим, взяв сумму проекций всех сил (вклю-
чая силы инерции согласно принципу Даламбера)
на вертикальную ось, в виде
Отсюда
или
Q + сх — ----~ — о.
— х 4- сх = О,
g
Рис. 318
х + — О,
(19.2)
где х — вертикальное перемещение груза от поло-
d*x
жения статического равновесия; х = ; t — время; с — жесткость
пружины; g— ускорение силы тяжести; о) — угловая частота собст-
венных колебаний
“2 = 4 = 5L; (19.3)
V ист
&ст = — удлинение пружины при статическом действии груза Q,
Решением уравнения (19,2) будет
х — A cos tdt + В sin to;, (19.4)
где A is В — постоянные интегрирования, зависящие от начальных
условий.
Если заданы начальная координата груза xQ и начальная скорость
г0 = х при t = 0, то из (19,4) определим
Л=я0;В = -^. (19.5)
Полагая
х0 = a sin а и = a cos а, (19.6)
решение (19.4) можно представить в виде
х — a sin (coi + а)>
где а — амплитуда колебаний, определяемая формулой
Величина а называется фазой колебаний, а величина а — сдвигом
фазы. На основании (19.6) а может быть определено из условия
17 5-1186
513
Угловая частота колебаний (число колебаний, совершаемое в
течение сек) на основании (19.3) будет
»-/4 <19-7)
или
.-/1,
Q
где т = ----масса подвешенного груза.
Зная круговую частоту, можно определить период колебаний
= ? = = <19-8>
Число колебаний в секунду, т. е. секундная частота, выражае-
мая в герцах, определится формулой
1 (О
' = Т = 2< (19.9)
При колебаниях груза, подвешенного на конце пружины, пред-
ставляющей собой стержень длиной I с жесткостью поперечного
сечения на растяжение ЕЕ и жесткостью
ЕЕ
с~~ ’
собственная частота колебаний согласно (19.7) определится формулой
-/4=Я?- <*9-*»>
т, Q
Имея в виду, что — = т, можно записать:
Рис. 319
Из формул (19.10) и (19.11) видно, что частота соб-
ственных колебаний системы при неизменной массе
возрастает с увеличением жесткости и уменьшается
с увеличением массы при неизменной жесткости.
Отношение частот собственных колебаний грузов,
прикрепленных к концам двух разных стержней,
обратно пропорционально корню квадратному из
отношения статических удлинений стержней.
Примером системы с одной степенью свободы
может служить также колебательная система, со-
стоящая из массивного диска, прикрепленного к
нижнему концу жестко закрепленного верхним кон-
цом вала (рис. 319). Если к диску в его плоскости
приложить и внезапно удалить пару сил, то воз*
никнут свободные колебания кручения вала вместе
с диском. Обозначим крутильную жесткость вала
(крутящий момент, вызывающий закручивание вала на один радиан)
через с:
Gnd*
С~1 32’
(19.12)
514
где G — модуль упругости при сдвиге; d — диаметр вала; I длина
вала.
Воспользовавшись принципом Даламбера (инерцией массы стержня
пренебрегаем), получим дифференциальное уравнение крутильных
колебаний диска, приравняв крутящий момент с<р, действующий
в валу при его закручивании на угол ср, моменту сил инерции массы
диска:
(19.13)
где J — момент инерции диска относительно оси стержня, перпенди-
кулярной плоскости диска.
Для диска постоянной толщины /г, изготовленного из материала
с удельным весом 7, получим
_ rcZWrr __ QD2
J “ 32g ~ 8g *
(19,14)
где D — диаметр диска; вес диска.
Для диска переменной толщины h (р)
Обозначив
D/2
/==7 j л (р) 7P3rfP"
о
U)
(19.15)
(19,16)
уравнение (19,13) перепишем в виде
(19.17)
Общее решение этого уравнения будет <р = A cos + В sin сог. (19.18)
Период колебаний рассматриваемой системы
Те—= 2x1/"—.
О) г с
(19.19)
+ =
Для стержня постоянного диаметра d с учетом (19.12) имеем:
(19,20)
а секундная частота колебаний
В табл. 42 приведены собственные настоты колебаний систем
с одной степенью свободы.
17*
515
§ 103. Вынужденные колебания систем
с одной степенью свободы при гармоническом возбуждении
Уравнение вынужденных колебаний системы с одной степенью
свободы (рис. 318) получим, если в (19.2) кроме сил инерции ~х
и сил упругости, действующих на груз Q, учтем влияние периоди-
ческой возмущающей силы Р cospt:
~~ х “И сх — Р cos pt. (19.22)
Обозначив
= ю‘2; (19.23)
Pgcos pt _ q cog (19.24)
где p — угловая частота возмущающей силы, приведем уравнение
(19.22) к виду
х 4- оРх = q cos pt. (19.25)
При р малом по сравнению с <о членом х можно пренебречь и счи-
тать, что имеет место только статическая деформация, максимальное
значение которой
ЖСТ •
(19.26)
Для определения динамической деформации необходимо решить
уравнение (19.25). Решение уравнения (19.25) будет состоять из суммы
общего решения однородного уравнения (при q cos pt = 0)
х = A cos + В sin (19.27)
и частного решения уравнения (19.25)
х — С cos pt. (19.28)
Подставив (19.28) в (19.25), найдем
С = (19.29)
Тогда общее решение уравнения (19.25) будет
х = A cos art 4- В sin wr 4- -2 ^2 cos PL (19.30)
Первые два слагаемых правой части (19.30) характеризуют свобод-
ные колебания, которые обычно быстро затухают; последнее характе-
ризует вынужденные установившиеся колебания с угловой частотой р
( т , р \ 7
^с периодом Л= ~ или / = Щ] и амплитудой С = -а • Ампли
туда вынужденных колебаний существенно зависит от соотношения
516
собственной со и вынужденной р частот колебаний и может быть
охарактеризована так называемым коэффициентом нарастания колеба-
ний или коэффициентом динамического усиления
8 = — = q = 0)2 = 1
Р »ст <02 — Р2 • <02 Ю2 _ р2 Р2
<й2
ИЛИ
где
Как видно из (19.31), при малом отношении
Р -> 1 и С -> а?ст. Когда же частота вы-
нужденных колебаний р -> со, т. е. ~ 1, то
С -> оо. Когда р = со, имеет место состояние
резонанса. Соответствующая частота возму-
щающей силы р == ркр при этом называется
критической. График зависимости |Р| = / j ,
приведенный на рис. 320 и представляющий
собой так называемую амплитудную кривую
ту дно-частотную характеристику, позволяет
дение колебательной системы в зависимости
свободных со и вынужденных р колебаний.
резонанса, или ампли-
проанализировать пове-
от соотношения частот
§ 104. Свободные колебания системы с одной степенью
свободы с учетом сопротивления, пропорционального скорости
Уравнение свободных колебаний системы с одной степенью сво-
боды (рис. 321, а) с учетом сопротивления, пропорционального ско-
рости движения колеблющегося
груза, получим из рассмотрения
условий его динамического равно-
весия:
= О)2 — п2.
Q — О-х — ах — Q 4- сх,
или
х + 2пх + w2# — 0, (19.33)
где а — коэффициент пропорцио-
нальности; ах — сила сопротивле-
ния.
В уравнении (19.33)
ш2=^-;2п = ^. (19.34)
(19.35)
517
Решение уравнения (19.33) будет
х = e~~nt (Л sin + В cos (19.36)
где е = 2,718.
Период затухающих колебаний рассматриваемой системы
(19.37)
Т 2к 2тс
/со2— п2 ’
где п — коэффициент, характеризующий демпфирующую способность
колебательной системы. Из (19.36) видно, что из-за множителя
амплитуда колебаний с течением времени уменьшается«— колебания
затухают. Постоянные интегрирования А и В в решении (19.36) опре-
деляются из начальных условий. Так, полагая, что при t = 0 х = а?0;
х = Xq, находим
В == Xq; А = — (#о + яя0).
о)1
В этом случае решение (19.36) может быть представлено в виде
’nt ~ sin + xQ ^cos ~ sin (Oxijj , (19.38)
В частном случае, когда Л = 0, т. е. когда
х = е
хо । пхо __ Q
«х ' (Di
уравнение (19.38) примет вид
х = cos (Oxi.
Графически это уравнение представлено на рис. 321,6. Уменьшение
амплитуды следует геометрической прогрессии. Действительно, при
i = 0; i = Т; t = 2Т и т. д. амплитуды соответственно имеют значения:
а0 = х0; «х = хое^пТ; а2 = х^2пТ и т. д.
— = — == ... = = епТ
а1 а2 ak+i
откуда
1ц = in enT = пТ = 8. (19.39)
«Л+1
Величина b называется логарифмическим декрементом колебаний и
обычно является основной характеристикой затухания колебаний, или
характеристикой демпфирующих свойств колебательной системы.
Методы определения характеристик демпфирования колебательных
систем и данные по демпфирующим свойствам конструкционных
материалов приведены в [11].
§ 105. Вынужденные колебания систем с одной степенью
свободы с учетом сопротивления, пропорционального скорости
Согласно данным предыдущих параграфов дифференциальное
уравнение вынужденных колебаний системы, приведенной на рис. 321, а,
при действии внешней возмущающей силы Р sin pt должно быть запи-
сано в окончательном виде:
х + 2пх + (о2# = q sin pi, (19.40)
518
где, как и ранее,
К =
(19.41)
решения
(19.42)
(19.43)
= q = %.
Q 4 Q
Общее решение уравнения (19.40) будет состоять из суммы
однородного уравнения (19.33)
х = e~~nt (A sin -|- В cos со1(),
где (ох = ]/(d2 — п2, и частного решения уравнения (19.40)
х = К sin pt + L cos pt.
После подстановки (19.42) в (19.40) найдем
д (щ2 _ р2) . г __________2?рп
— р2)а + 4р2я2 ’ (<о2 — р2)2 4р2п2
Тогда общее решение уравнения (19.40) будет иметь вид
х == e^nt (A sin <охг -f- В cos с^г) —
2р<рг , । <7(ю2 — р2) .
— -7-5---ГЛ ". • /"-2-2 C0S Pf + Т2^-2ТГТ~ГТ^ sm Р*- (19.44)
(о)2 — р2)2 + 4р2п2 ' (о)2 — р2)2 + 4pW ' '
Поскольку со временем свободные колебания, характеризуемые
членом, содержащим множитель e^nt, затухают, то при установив-
шихся колебаниях вынужденные колебания системы будут характе-
ризоваться последними двумя членами правой части решения (19.44),
пропорциональными q. Период незатухающих колебаний будет
гр
Г1 = 7-
Если ввести следующую замену:
________ад q,n
(Ш2 _ р2^ + ip2n2 - Л sin a,
д (юа — р2)
(19.45)
-------... .о-т = 21 cos а,
(со2 — р2)2 + 4р2га2
то решение для вынужденных колебаний может быть представлено
в виде
х = 21 (cos a sin pt — sin а cos pt) = 21 sin (pt — a),
где амплитуда 21 и угол сдвига фаз а на основании (19.45)
определяется соответственно формулами:
.... д---------;
У (со2 — р2)2+4р2№
. 2рп
tg a = -5-^—2 .
О)2 -------
(19.46)
и
(19.47)
(19.46)
(19.48)
(19.49)
При to > р угол а будет положительным и люшшшш ,
Л тс . , тс
Оа< —. При <о < р получим -к-<а<я, т. е. вынужденные коле-
41 *
меныпим
т. е.
519
бания отстают от возмущающей силы больше, чем на -g-. При р—<о;
tg а = оо, т. е. колебательная система занимает свое среднее положение
в тот момент, когда возмущающая сила имеет максимальное значение.
Имея в виду, что
находим
д ... gPQ -Р . .
со2 Qcg с ст’
(19.50)
(19.51)
где бст — деформация пружины при статическом приложении ампли-
тудного значения возмущающей силы.
Учитывая (19.51), выражение для амплитуды вынужденных коле*
баний 9( (19.48) можем представить в виде
где 1 — коэффициент, зависящий от демпфирующей способности
колебательной системы.
При Т\ > Т 91 -> Ьст; при Тг Т 91 оо.
Коэффициент нарастания амплитуды р в рассматриваемом случае
равен:
р-1
^ст
или, с учетом (19.52),
(19.53)
1_________
э2\2 4р2п2
о2/
Амплитудные резонансные кривые р = /1^~^для различных зна-
чений у показаны на рис. 322, а график, выражающий зависимость
приведен на рис. 323.
а
520
§ 106. Критическая скорость вращения вала
Число оборотов, при котором вращающиеся валы, попадая в резо-
нанс, становятся динамически неустойчивыми, в результате чего moi ут
возникнуть недопустимо большие колебания, называется критическим.
Можно показать, что таким критическим числом оборотов вала явля-
ется число оборотов в секунду, соответствующее собственной частоте
его поперечных колебаний.
Рассмотрим вращение диска, насаженного на вал (рис. 324, а).
Центр тяжести диска С практически всегда не совпадает с осью
вращения на некоторую величину е. Центробежная сила, действую-
щая на вал при вращении диска весом Q с
угловой скоростью р, будет
Т = -у Р2 (W + ё),
где w —прогиб вала в месте посадки диска.
Реакция вала в месте приложения силы Т
Р == cw,
где сего изгибная жесткость. В случае постоян-
ного сечения жесткостью EJ, при размеще-1
нии диска посредине шарнирно опертого вала Я
4&EJ Рис.
Z3 ’
Из условия равновесия очевидно, что Р =» Т. Подставив
и Р их выражения, найдем:
(w + е) р2 = cw
с =
S
324
вместо Т
или
е
w =
(19.54)
р2 Q
Имея в Ьйду, что собственная частота поперечных колебаний вала
уравнение (19.54) можно представить так:
(19.55)
(19.56)
— 1
р2
Из (19.56) следует, что критическая скорость, при которой w-» оо,
будет ' __
= <19-57)
При Ркр^60 центр тяжести диска будет располагаться между линией,
соединяющей опоры, и искривленной осью вала (рис. 324, б), и урав-
нение для определения прогиба запишется так:
-2. е) pt — CWi
521
откуда
1 _ i___
P2Q P2 „
Из (19.58) следует, что с увеличением р прогиб w -> et т. е. при очень
больших скоростях центр тяжести диска достигает линии, соеди-
няющей опоры, и изогнутый вал вращается вокруг центра тяжести
диска С,
§ 107. Свободные колебания упругих систем
с несколькими степенями свободы
При рассмотрении колебаний упругих систем с несколькими сте-
пенями свободы дифференциальные уравнения движения во многих
случаях можно получить, как и в случае системы с одной степенью
Рис. 325
свободы, пользуясь принципом Даламбера. Так, для системы с двумя
степенями свободы, показанной на рис. 325, а, состоящей из двух
масс и тп2 и двух пружин с жесткостями ct и с2, положив, что
массы могут перемещаться при отсутствии трения только в горизон-
тальном направлении вдоль оси х, а также обозначив перемещение
массы тг и т2 соответственно через хг и x2i будем иметь, что на
массу т1 действуют силы натяжения пружин — и с2 (х2 — хх),
а также сила инерции — Уравнение движения массы будет
—qXjL 4“ с2 (х2 х1) гп1х1 = 0,
или
/ftjffj. + С1Х1 С2 (Х2 — Х1) = (19.59)
Схема сил, действующих на г-ю массу, в общем случае показана на
рис. 325, б.
На массу т2, кроме силы инерции, действует только сила натя-
жения второй пружины — с2 (х2 — #x) и уравнением ее движения буде^
m2i’2 + С2 (х2 ^1) =* 0- (19.60)
Уравнения движения (19.59) и (19.60) можно было бы получить
несколько иным способом. Действительно, можно считать, что име-
ются две связанные между собой пружины (рис. 325, о), которые под-
вергаются действию сил инерции — и — т2х2, приложенных в точ-
ках / и 2. Тогда первая пружина нагружается силой—— т2х2,
а вторая — силойт2х2. Перемещение первой массы при этом будет
равно удлинению первой пружины:
<—т1х1 — т2х2
а перемещение второй массы
7П2#2 Aft 2^2 т2Х2
•to Xi =*• --- =S 1 * ~ <=!== ' •
С2 Cj с2
522
Преобразовав последние уравнения, получим систему дифференциала
ных уравнений, эквивалентных (19.59) и (19.60):
~ (19.61)
^2С1С2 + С2 (^1^1 + ^2^) + ^^2^2 = °- (19.62)
Наиболее общим способом составления дифференциальных урав-
нений является известный из теоретической механики способ, осно-
ванный на применении уравнений Лагранжа второго рода, которые
при отсутствии сил сопротивления и внешних возмущающих сил
имеют вид
dt ~ дх1 ~ dxi ’
(19.63)
(i = l, 2, 3, ... , n),
где T и U *== соответственно кинетическая и потенциальная энергия
системы.
Применительно к системе, приведенной на рис. 325, а, будем
иметь
•2 -2
т^хг т2х2
г = ~ + ~5
от
— = тп^:
d /дТ ,
dt =^1’
аг \дх1'
эи
д^ГС1Х1
С2(^2 —^1)\
2 2
дТ ОТ А дТ А
дх2 ~ ™2*2’ ^1 ~ ~ *
d (дТу
dt \di2j
С2 \х2 * ^1)» — С2 \Х2 Х1)*
Уравнение (19.63) примет вид
^1^1 + С1Х1 С2 (Х2 xi) =
^2Х2 + С2 (Х2 х1) == 0.
(19.64)
Уравнения, полученные из уравнений Лагранжа, оказались полностью
совпадающими с таковыми, полученными на основании принципа
Даламбера. Такое совпадение имеет место всегда.
Решение уравнений (19.64) ищем в виде:
= Xj sin (cot + a)|
x2 = X2 sin («г 4- a),
(19.65)
где Х1Э X2, <»> и a — постоянные, которые должны быть выбраны так,
чтобы удовлетворялись уравнения (19.64). Подставив решения (19.65)
в уравнения (19.64), найдем
(ci + с2 — — Кс2 = °;
^Ххс2 + Х2 (с2 — /п2со2) = 0.
(19.66)
и
1 /712^2 9
523
В этих уравнениях неизвестными являются Xj, Х2 и <о. Частоту со
определим из (19.66), полагая, что Xj #= 0 и Х2 =£ 0. Это возможно
тогда, когда определитель однородной системы относительно Хх и Х2
будет равен нулю:
I ci 4- с2 — —с2 I _ 0
I —с2 с3 — m2o>2 J 9
или
_ fct + ft , \ + _£lft. _ 0
\ mj тп2/ W1?n2
Отсюда
ф2 = £ /ft_+5 , _ft \ T i/’ j pi + ^2 . c2V
*•2 2 \ m, m2/ V i \ mi m2) тгт,'
Соответственно могут быть определены две собственные частоты:
Двухчастотный колебательный процесс в соответствии с (19.67)
можно записать так:
а?! = Хп sin ((Ojf 4- at) 4- Х12 sin (a)2£ 4~ az)»
х2 = Х21 sin (<0^ + aj) 4- Х22 sin (со2? + а2).
(19.68)
Первый индекс при X показывает номер координаты, а второй — номер
слагаемого в строке, или номер частоты. Из (19.66) имеем
. 2
Х2 _ gl + С2 ~~ , Х2 _ С2
с2 М с2 — т2(л2 ’
или в соответствии с принятой индексацией
। 2
V >-21 С1 + Сз ~ mi0>1
'21 — г- —----------------;
Лц с2
V ____ ^22 __ g2
Л22 — 7-------------5 *
Л12 с2 — m2a)2
Тогда уравнения (19.68) могут быть записаны так:
sb (w^ + 04) + Х12 sin (a2t + a2); j
^2 ~ ^21^11 sin -|~ 04) 4“ ^22^12 sb (w2i 4- a2). /
Значения Xn, X12, и a2 определятся из начальных условий. Так»
например, полагая при t = 0 ' _
(0) == 0; х2 (0) = 0;
а?1(0) = 0; я2(0) ==р0>
из (19.69) найдем
Xn sin 04 4- Х12 sin a2 = 0;
X21Xn sin at 4- X22^i2 sin a2 = 0;
X11<D1 cos 04 4- X12(d2 cos a2 = 0;
^21^11^1 cos 04 4- X22X12(D2 COS a2 = Vq.
524
Отсюда, поскольку «р w2, и известны, найдем
„ „ П- 1 - ₽» 1 .1 _ {’О 1
°’ ~ ~ Х21-Х2В ’ А12 - <0, Х22-Х21 •
Подбирая начальные условия так, чтобы было равно нулю, полу*
чим одночастотные колебания, описываемые одной гармоникой:
а?ц = kn sin (а)^ + о^);
^21 = “Wii sin (М + «1)<
Колебания, описываемые одной гармоникой, называются первыми нор-
мальными колебаниями.
Очевидно, при условиях, когда Xp = 0, колебания будут проис-
ходить по второй форме. Вторые нормальные колебания будут опи-
сываться формулами
*12 = ^12 sin (<М + «2);
#22 = ^22^12 Sin (<М + а2)«
Число нормальных форм колебаний и равное ему число собствен-
ных частот совпадают с числом степеней свободы колебательной
системы.
В табл. 42 приведены собственные частоты колебаний систем
с двумя степенями свободы.
$
Рис. 326 Рис. 327
Характерными колебательными системами со многими степенями
свободы являются упругие валы с насаженными на них дисками
(рис. 326, а). Рассмотрим крутильные колебания такого вала.
Пусть Jlt J2i J3, . .. , Jn — моменты инерции масс дисков отно-
сительно оси вала; • • • » ?п — углы поворота дисков при
колебаниях; с1? с2, с3, ...» сп — жесткости при кручении различных
участков вала:
1 Ц '
где — полярный момент инерции площади сечения вала; Ц — дли-
на соответствующего участка.
Тогда величины крутящих моментов, возникающих в сечениях
различных участков вала при взаимном повороте дисков, соответст-
венно будут — ср2); с2(ср2 — ср3) и т. д. (рис. 326,6). Кинетическую
и потенциальную энергии системы с п степенями свободы (пренебре-
525
гая моментом инерции массы вращающегося вала по сравнению с мо-
ментами инерции дисков) можно представить в виде
где
гааП , -2
1=1 ।
г—п
i=l
(19.70)
Подставляя (19.70) в уравнения Лагранжа (19.63), получим сле-
дующую систему дифференциальных уравнений свободных крутиль-
ных колебаний вала с п степенями свободы:
+ ci (?х — <р2) = 0;
Л?2 + с2 (?2 — ?з) —Q(?i — ?2) = 0;
j3?3 + С3 (?3 — ?<) с2 (?2 ?з) = 0;
>(19.71)
/п—i?n—1 + сп—1 (?п—1 ?п) ~~ сп—2 (?п—2 — ?n—i) — 0;
Jп?п сп—i (?n—i ?п) ~ 0. J
Суммируя эти уравнения, будем иметь
+Л?2 4” * ”
откуда
+ Л<?2 +-----F А?п == const,
т. е. момент количества движения системы вокруг оси вала при
свободных колебаниях остается постоянным. Обычно момент коли-
чества движения принимают равным нулю и тем самым исключают
из рассмотрения любое вращение вала как твердого тела и рассмат-
ривают только колебательное движение, вызываемое скручиванием
вала.
Решение уравнений (19.71) ищем в виде
= Xt cos (ы 4- а);
ср2 = Х2 cos (ок + а);
?n = ^n cos(wt + a).
Подставляя (19.72) в (19.71), будем иметь:
— cr (Xt — Х2) == 0;
J2^2^2 4~ С1 (^1 — ^2) —* С2 (^2 — \j) Ф
Jn^n^ 4~ СП~-1 (^П—1 - ^п) = 0-
(19.72)
(19.73)
Исключая из этих уравнений Хх, Х2, ... , Хп, получим уравнение
частоты.
526
(19,74)
Так, в случае трех дисков (рис. 327) система уравнений (19.73)
примет вид
— сг (Хх — Х2) = 0;
<72Х2<02 Ч" (^1 \й) — (Xg — Х3) 5=5 Ф
/3Х3о2 -j- с2 (Х2 — Х3) == 0.
Сложив эти уравнения, получим
+ J2X2 + J3X3 = 0. (19.74а)
Из первого и третьего уравнений системы (19.74) найдем
X, = ; Хз = • (19.75)
1 JjU)8 я— Ci d J3Q)2 — С2
Подставив (19.75) в (19.74а), получим
1J 2^3 _
С1С2
~г I а»7з 1Jз ।
ci с2 / ~г
+ (А + ^2 + А) == 0* (19.76)
Решая это уравнение относительно о>2, можно получить два корня
(Di и (о|, соответствующие двум главным видам колебаний. Подставив
затем (01 и (о2 в уравнение (19.75), получим отношения амплитуд
Л2
и для двух главных видов колебаний и тем самым установим
Л3
состояние системы во время колебаний. Указанные два вида колеба-
ний для трехмассовой колебательной системы представлены на рис. 327
диаграммами I и II соответственно для одноузловой и двухузловой форм
колебаний.
В качестве другого примера системы со многими степенями
свободы рассмотрим поперечные колебания упругой балки, несущей
ряд сосредоточенных точечных масс
(рис. 328). Прогибы в местах приложе-
ния масс тп2, ... , тп могут быть
выражены через силы инерции в следу-
ющем каноническом виде:
mz ms тп
...
Рис. 328
1^1 — —tf&lWl&H — (^2^2^12 — ’ * ’
™2 = —^1^1^21 — Z7?2W2^22 — • • • —ZWnWnB2n;
— W2WgBn2 * ’ ‘
где (см. § 69)
о
(индексы ik при 5 выражают перемещения в направлении i, вызван-
ные единичной силой, действующей в направлении /с); M^(z), Мд (/Л^
изгибающие моменты, вызванные соответственно единичными силами
Pt = — =1; Рд = — = 1.
527
Коэффициенты 8^ удобно определять по формуле Верещагина
(§ 71):
EJ '
где Q — площадь эпюры Mi (или ее ласти); — ордината эпюры
расположенная против центра тяжести площади эпюры Q.
Для системы с одной степенью свободы на основании (19.77) бу-
дем иметь уравнение с одним неизвестным
Это уравнение эквивалентно известному уравнению
mw + cw = О,
поскольку
Для системы с двумя степенями свободы неизвестные функции
прогиба и w2 согласно (19.77) выразятся так:
w1 == — m2w2b12\
w2 = — m2w2S22.
В общем случае при решении уравнений (19.77) функцию прогиба
следует искать в виде
wi = \ sin (coi 4- a). (19.78)
Подставляя (19.78) в (19.77), найдем
Xi — 1) + Х27И2512о)2 4- • • • + ХптпЬ1Псо2 = 0; ’
X1?n1S21a)2 4- Х2 (m2?)22a)2 — !)-}-••• 4~ Xnmnb2na>2 = 0;
4- X2wi2Sn2co2 4- ... 4- \n (тпЪпп(л2 — 1) = 0. t
(19.79)
При наличии колебаний амплитуда Х$ не обращается в нуль,
если определитель, составленный из коэффициентов системы уравне-
ний (19.79) при Х|, равен нулю:
/П^цСО2 — 1
Л?1&210)2
m1Sniw2
Ш2&120)2.............
пг2522со2 —1 . . .
^2^?22^2.............
тпЪ1п(л2
= 0. (19.80)
Написав этот определитель в развернутом виде, будем иметь
1 — а±(1)2 4" + • • • + (—1)п ап(л2п = 0, (19.81)
где «г — коэффициенты при различных степенях угловой частоты со.
Из (19.81) можно найти выражения для частот <о2,
(a>i > w2 > • • . > ton).
528
Общее решение системы уравнений (19.79) будет
wi = sin (wx£ 4* ai) 4" sin ~b #2) 4~ • * ’ 4~ ^in sin 4~ an)»
или
w± = ku sin (idit 4- ®i) 4“ ^12 sin (ю2г 4- «2) 4- • ‘ • 4- sin (t*W 4“ an)‘>
Wz == ^21 sin (a)j£ 4* ai) 4- ^22 sin (o)2i 4" аг) 4~ ’ ‘ • 4“ ^2n sin (<on£ 4“ an)>
Wn = )'ni sin (a)xi 4~ ai) 4~ ^n2 sin (<o2£ 4“ аг) 4~ * ’ * 4" ^nn sin (<oni 4~ an)-
В частном случае системы с двумя степенями свободы уравнени
(19.79) и (19.80) будут иметь вид
кх (wi^nw2 — 1)4“ X2m2812o)2 = 0;
Х17п^21ю2 4- Х2 (тп2В22со2 — 1) = 0;
I'Mn*)2 —1 w2S12a)2 I ф
| wx?)21(o2 w2S22(o2 — 1 j
или
6)4 (&11&22 — b?2) ^1^2 — 0)2 (^UW1 4- ^22^2) 4-1=0-
Решив последнее уравнение, получим выражения для частот и со2:
4” ^/~ (^11 4~ S22 --^(^11^22 &12)2 “2 I
т \ т^/
-.Л---------!—---------Га 4-5 ~2 —
^=1/ 2(8и822 -В^)т2
~ (8u + 822 ^) — 4(8п822 -812)2—“ .
§ 108. Продольные и крутильные колебания стержней
При продольных колебаниях стержня все его частицы дви-
жутся параллельно оси. При выводе дифференциального уравнения
продольных колебаний стержня рассмотрим
условие динамического равновесия участка
стержня длиной dz (рис. 329, а), ограничен-
ного сечениями а и Ь. Обозначив перемеще-
ние сечения а через и, а сечения Ъ — через
, ди .
— dz, найдем усилия, действующие в се-
(JZ
чениях а и Ъ имея в виду, что относитель-
ди
ное удлинение е = о-
EFV>
dz
Nb~EF
ди д (ди\
dz dz \dz/ Z
529
Сила инерцйи элемента стержня длиной dz при общей массе
стержня пг и длине I будет
_ w д2и
РЯ~ I ’ dtidz'
Тогда, пользуясь принципом Даламбера, условие динамического
равновесия элемента стержня запишем в виде
Уь-Уа = Ри,
или
, пг д2и .
dz~Twdz-
Сократив на dz и заменив на р (плотность материала), пред-
ставим дифференциальное уравнение продольных колебаний стержня
в виде
д2и д2и
(19.82)
где
(19.83)
Е
Обозначив — = а2, уравнение (19.82) запишем так:
д2и 9 д2и
Я?'
Решение уравнения (19.33), следуя методу Фурье, ищем в виде
и = ZT, (19.84)
Z = /iW; Т = /2(г).
Продифференцировав уравнение (19.84) по z и е, получаем
dt2 Z dt2 ; dz2 dz2 ’
Подставив (19.85) в (19.83), имеем
Z -d?-aTd^'
(19.85)
или
1 d*T_ a2 d2Z
Т ' dt2~ Z ' dz2'
Приравнивая правую и левую части последнего уравнения к одной
и той же постоянной величине «2, получим два обычных уравнения
второго порядка:
dt2
<FZ__ <o*
dZ*~~ a* •
Частными решениями этих уравнений соответственно будут
Т — cos cot; sin ш(;
(D (1)
Z = cos — z\ sm — z.
a 1 a
(19.86)
(19.87)
(19.88)
530
Для получения общего решения уравнения (19.86), составленного
из частных решений (19.88), необходимо учитывать граничные усло-
вия стержня. Так, если оба конца свободны, то должны удовлетво-
ряться следующие условия:
=°; fir) =0' <19-89)
\dz/z=o \dz/z=4
Подстановкой решений (19.88) в (19.86) и (19.87) убеждаемся, что
решение sin — z уравнения (19.87) следует исключить, как не соот-
ветствующее первому условию (19.89).
Для обеспечения второго условия (19.89) необходимо, чтобы вы-
полнялось равенство
sin у I = 0. (19.90)
Полученное уравнение частоты будет удовлетворено при
— I == l1Zt
а
где i = 1, 2, 3...
Частоту основного тона колебаний будем иметь при 1 = 1:
ait % Е
в1=Т=7Г Т* (19,91)
Соответствующий период колебаний
= (19.92)
Форма этого вида колебаний показана на рис. 329, б кривой 1,
для которой
— (0-« Z ~ nz
Zt =3= Cl COS —i- = C1 cos .
a 4
Форма второго вида колебаний, для которого
л гг 2^2
— = 2к и Z2 = CS cos—-
а I
приведена на рис. 329, б (кривая II).
Общий вид частного решения уравнения (19.83) при i-й форме
колебаний будет
iitz ( . ntat , — . inat [ /лс\
и = cos — I Ai cos -y + Bi sm у-1. (19.93)
Наложением подобных частных решений любое продольное коле-
бание стержня можно представить в виде
Siitz / . inat , п . inat\ z.nn/.
cos — I Ai cos y- + Bi sm -у I, (19.94)
z—1, 2,3...
где произвольные постоянные Ai и Bi должны выбираться из началь-
ных условий.
531
Например, пусть при t = 0 (m)(„0 = /(z); (u')/=0 = Л (z). Тогда
из (19.94) при 4 = 0 находим
I == 00
S. (TtZ
Ai cos — ;
l==l
1 t \ V1 1па ъ i^z
ft И = 7, — Bi cos —.
откуда, используя метод Фурье, найдем
. 2 ( 4 inz ,
— у \ f (z) cos — dz;
0
г» 2 ( , z . ikz ,
1/1 C0S Т dz-
iita J ь
0
Крутильные колебания стержня (например, цилиндрического)
легко охарактеризовать посредством вычерчивания волнистой линии
на развернутой поверхности
стержня (рис. 330, а). Обозначим
угол закручивания сечения, на-
ходящегося на расстоянии z, отно-
сительно неподвижного сечения
через ф, а угол закручивания се-
чения с координатой z + dz —
Эф
через dz (рис. 330, б). Тогда
„ , g. dy
элемента длиной dz будет , а
OZ
а
Рис. 330
dz
5
относительный угол закручивания
крутящие моменты (см. § 46) в сечениях стержня с крутильной жест-
костью GJp, ограничивающих элементарную его длину dz слева и
справа, соответственно будут:
Gj/Л и +
н dz * \dz 1 dz2 /
Приравнивая равнодействующую этих крутящих моментов моменту
б2ср
инерции вращения элемента длиной dz, равному pdp dz, где р —
плотность материала, получим дифференциальное уравнение кру-
тильных колебаний стержня
_ d2cp d2cp
GJpS-pz = pJp-^£Zz,
или после сокращения на Jp и dz:
<9z2 ~ P dt2'
(19.95)
Q
Обозначая — через а2, уравнение (19.95) можно представить в
виде
д2? _ „2 д2?
dt2 ~ dz2 •
(19.96)
532
Решение уравнения такого вида рассмотрено выше для 'случая про
дольных колебаний стержня
В табл. 43 приведены частотные уравнения и собственные формы
продольных и крутильных колебаний стержней при различных гра-
ничных условиях.
§ 109. Поперечные колебания призматических стержней
Дифференциальное уравнение поперечных колебаний стержня
получим из рассмотрения условий динамического равновесия эле-
мента dz (рис. 331), выделенного из произвольно закрепленного
стержня.
Проектируя все силы, действующие на рассматриваемый элемент
(включая в соответствии с принципом
Даламбера силы инерции) на верти-
кальную ось w, будем иметь
Q — qt dz — Q — dz = 0.
откуда
= (19.97)
где Q — поперечная сила; qi — интен-
сивность сил инерции массы
<7« = Р2?-^5 (19.98)
(Р—площадь поперечного сечения; р — плотность материала; w—
поперечное перемещение; t — время).
Подставив (19.98) в (19.97) найдем уравнение поступательного
движения элемента колеблющегося стержня:
(19.99)
dt2 dz
Для получения уравнения вращательного движения элемента
стержня в плоскости wz сложим угол поворота сечения 0, вы-
званный изгибом, с углом сдвига 7, обусловленным действием
поперечной силы:
(19.100)
В силу известной связи между изгибающим моментом М и
углом поворота 0 (§ 54)
M = (19.101)
и между поперечной силой Q и углом сдвига 7 для принятой в на-
шем случае системы координат (§ 66)
&7FG (19.102)
(/с —коэффициент, учитывающий форму сечения стержня) выражение
для Q в соответствии с (19.100)—(19.102) может быль представлено
так:
Q = (19.103)
533
Так как момент инерции вращения массы рассматриваемого эле-
мента равен
026 С 2 , 020 С 2 020^
^2 J У J =
уравнение вращательного движения элемента на основании принци-
па Даламбера может быть записано в виде
п, дМ , тдЧ
Qdz--^dz--------fJ^dz
или после сокращения на dz и подстановки (19.101) — следующим
образом:
kGF \<9z *“ fJ dt2 ~~ °'
Продифференцировав это уравнение по z, получим
+ = (19.104)
\ 0z2 dz) dz3 r dz dt2 4
Подставив (19.103) в (19.99), будем иметь
pF^-fcGFfe’-~)==°. (19.105)
dt£ \dz2 dz) v
Исключив из (19.104) и (19.105) угол 0, получим дифференциальное
уравнение свободных поперечных колебаний стержня
/ Е\ d2w d2w pV№> .„.
EJ dz* ~ P7 + kG) dz2 dt2 + ?F dt2 + kG dt2 ~ °' <19Л06>
Если пренебречь силами инерции вращения элемента и влиянием
на прогиб поперечной силы, уравнение (19.106) можно представить
в виде
£7S+₽FS=°-
(19.107)
Простейшим периодическим решением уравнения (19.107) является
так называемое главное колебание, в котором функция прогиба колеб-
лющегося стержня изменяется с течением времени по гармониче-
скому закону
w = ср (z) sin (о>г + а). (19.108)
Функция ср (z), устанавливающая закон распределения макси-
мальных отклонений точек оси стержня, называется формой главного
колебания или собственной формой.
Для получения уравнений собственных форм подставим (19.108)
в (19.107) и после сокращения на sin(a)Z4-a) получим
^2-^ = 0, (19.109)
где
к2 = р-~ . (19.110)
Общее решение уравнения (19.109) имеет вид
ср (z) = A cos kz + В sin kz + С ch kz + D sh kzt (19.111)
или, будучи выражено через функции Крылова, значения которых
приведены в Приложении 3, записывается так:
? (з) = CXS (kz) + С2Т (kz) + C3U (kz) + C4V (kz).
534
Здесь Л, В, С, D (или Clt С2> С3, — постоянные интегриро-
вания, определяемые из условий закрепления стержня. Так, напри-
мер, для шарнирно-закрепленного стержня (рис. 332) условия на
концах будут:
при z = 0 (0) = 0; у" (0) = 0;
при z = I ср (I) = 0; (Z) = 0.
Исходя из этих условий и из (19,111), будем иметь
А + С = 0; В sin kl + D sh kl = 0;
—Л 4- C = 0; —В sin kl 4* D sh kl = 0,
откуда
A == C = D = 0,
В sin kl == 0.
Но так как В =£ О, следовательно, sin kl « 0. Из полуденного частот*
ного уравнения находим
kjl = /те
(/ = 1, 2, 3, ...).
Из равенства
4 __ рВо>? _ WCO •
~ Е J ~ EJ
определим собственную круговую частоту
<19л,2)
период _
7 —— —1/* —
/ате г EJ
и частоту колебаний, гц, __
'-Т = 2Т>/“- <19л13>
Уравнение собственных форм коле-
баний стержня будет
cpi (г) = В sin . (19.114)
I
Первые три собственные формы коле-
баний балки на двух опорах показаны
на рис. 332.
Общее решение дифференциального
уравнения (19.107) применительно к рас-
сматриваемой балке на двух опорах мо-
жет быть записано в виде-
Рис. 332
w (х, г) = 2j (<Ч cos (ojt + bi sin u)|t) sin -j- , (19.115)
i-1
где ai и bi должны быть подобраны из начальных условий (при t=«0),
Частотные уравнения и их корни, а также уравнения собственных
форм поперечных колебаний стержней при различных закреплениях
их концов приведены в табл. 44. Корни частотных уравнений попе-
535
речных колебаний стержней на упругих опорах приведены в табл. 45;
стержней с сосредоточенными массами—в табл. 46. В табл. 47
приведены значения некоторых интегралов, встречающихся при рас-
четах поперечных колебаний стержней. к
Если колеблющийся стержень испытывает действие продольной
сжимающей силы N, то дифференциальное уравнение упругой линии
имеет вид
„ Td2W , , , . пт
EJ—2 = M (z) — Nw.
После двойного дифференцирования и замены согласно принципу.
d2lM d2w
Даламбера = — pF получим дифференциальное уравнение
свободных поперечных колебаний стержня
d^w d2w d2w
dz* dz* ‘ dt2
Собственная форма колебаний определится в этом случае выражением
ср (z) == A cos кгг + В sin krz + С chk2z -}- D sh k2z,
где
Величина к определяется по формуле (19.110).
Выражения для собственных частот поперечных колебаний стерж-
ней, нагруженных продольными силами, приведены в табл. 48.
§110. Закон сохранения энергии при колебаниях
пенью
Рис. 333
(19.116)
одной сте-
Из принципа сохранения энергии при колебаниях вытекает, что
сумма кинетической и потенциальной энергии колебательной механи-
ческой системы в любой момент времени остается постоян-
ной (энергетическими потерями пренебрегаем), т. е.
Т + U == const.
В частности, применительно к системе с
свободы (рис. 333), для которой
т = i3;
и = ~,
уравнение (19.116) примет вид
= const>
(19.117)
где с — жесткость пружины.
536
Правая часть уравнения (19.117) зависит от начальных условий.
Полагая, например, что при t = Q перемещение (я)/==0 = *о> а началь-
ная скорость = 0, будем иметь
2
Q • 2 , сх2 СХ0
гг +т = Т’
(19.113)
т. е. при колебаниях сумма кинетической и потенциальной энергий
остается равной начальной энергии деформации пружины, растянутой
на величину х0.
Из анализа уравнения (19.118) видно, что в момент, когда колеб-
лющийся груз находится в среднем положении (х = 0), энергия
системы определяется кинетической энергией
'2 2
^шах _ схо
2g “ 2 ’
(19.119)
Уравнение (19.119) может быть использовано для определения
частоты колебаний. Действительно, положив
х == х0 cos со?; i?max == л*оо),
после подстановки значения х и £тах в (19.119) будем иметь
7-1 2 9. 2
Qxq®* сх0
~~2Г =~29
откуда
2 £?
<O2 = -q
И __ _________
<«“>
что совпадает с полученной ранее формулой (19.3).
Заметим, что, исходя из уравнения (19 117), выражающего закон
сохранения энергии при колебаниях, легко получить дифференциаль-
ное уравнение движения колеблющегося груза. Для этого достаточно
уравнение (19.117) продифференцировать по времени t и произвести
соответствующее сокращение.
§ 111. Некоторые приближенные методы определения
собственных частот колебаний упругих систем
Способ Рейлея. Частота колебаний определяется из рассмотре-
ния баланса энергии системы при определенных допущениях относи-
тельно деформирования колебательной упругой системы. В частности,
для учета массы пружины в колебательной системе с одной степенью
свободы (рис. 333) делается допущение, что масса пружины мала по
сравнению с массой подвешенного груза Q, форма колебаний не
зависит существенно от массы пружины и с достаточной точностью
можно принять, что перемещение любого ее поперечного сечения на
расстоянии т] от закрепленного конца такое же, как если бы пружина
была невесомой, и равно ~ (Z—длина пружины).
537
При весе единицы длины пружины q, кинетическая энергия эле^
мента пружины длиной dr\ будет
а полная кинетическая энергия всей пружины выразится интегралом
I
т С Я (? 1 {dx\
T^}2g\~'dt) T-
О
Это значение кинетической энергии пружины следует прибавить
к кинетической энергии груза
_ Q{dx\*
Q~2g\dt) •
Тогда полная кинетическая энергия будет
Выражение потенциальной энергии останется прежним:
t^ = V-
Ci
Теперь условие сохранения энергии колеблющейся системы может
быть представлено в виде
1 (dx\2(- ql\ , ex2 сх*
2i\zt] V?+t/ + t==t-
Сравнивая это уравнение с (19.118), находим, что для оценки
влияния массы пружины на частоту собственных колебаний нужно
к весу груза прибавить одну треть веса пружины. Таким образом,
круговая частота определяется формулой
"= / “9Л21>
3
Рассмотрим колебания груза, расположенного посредине балки
(рис. 334). Следуя методу Рейлея, полагаем, что вес балки ql мал
сравнительно с грузом Q и что кривая про-
гиба балки при колебаниях имеет такую
же форму, как и кривая статического про-
гиба. Обозначив через / перемещение гру-
за Q при колебаниях, получим выражение
поперечного перемещения любого элемента
балки длиной dz и весом qdz, находяще-
гося на расстоянии z от опоры (стр. 266):
w==/3zC_ (19.122)
Кинетическая энергия самой балки
Z/2
. _~q_ Ud£ 17 ql_ (df\*
6 2g J \dt 1“ j 35 2g ’
0
538
Кинетическая энергия груза
Q (dd\*
*~2g\dt] ’
Полная кинетическая энергия системы будет
, 17 ,
Ф ™ , Ф 359i (4f\*
Т-Тг + Т„-—
выражением для потенциальной энергии
(19.123)
Пользуясь известным
деформации изгиба
а также учитывая, что
\M*dz
J 2EJ ’
О
_ _ _ „ d^w
m^ej^.
dz2
где для рассматриваемого случая согласно (19.122)
d2w___ 24
dz*-----
найдем:
?/2
Т7 о CEJ(24A\ 24EJ 42
и=2 ]тЬ/2) Л=—'•
Условие сохранения энергии при колебаниях теперь примет вид
Л , 17 ,
+ 35 А2
т + и
/2 = const.
2g
Продифференцировав последнее уравнение по времени I, после сокра-
щения получим
rf2/ 48&7
dt* + Z3-
(19.124)
—V' = 01
или, введя понятие приведенного прогиба Ьпр,
17
8 —________ __ 73
п*> 48£J
(19.125)
дифференциальное уравнение колебаний груза на балке с учетом
массы последней (19.124) окончательно можно представить в виде
—+ —/ = О
539
Отсюда круговая частота колебаний груза согласно (19.120) опреде-
лится формулой
(19.126)
Из (19.125) следует, что для учета массы балки при определении
частоты собственных колебаний груза, расположенного посредине
17
балки, достаточно к весу последнего прибавить = 0,483 веса балкп.
ао
17 I
Величина — называется приведенной массой балки.
35 g
Используем метод Рейлея для определения частоты поперечных
колебаний стержня с сосредоточенными массами (рис. 328). В этом
случае предполагается, что кинетическая энергия системы опреде-
ляется только поступательным перемещением масс, а потенциальная
энергия обусловлена только изгибом стержня Полагая, что все массы
колеблются синфазно с одинаковой частотой, перемещение сечения
балки с абциссой z в функции времени можем описать синусоидаль-
ным законом
(2, t) — w (z) sin (оц 4- а),
где w (z) — функция, определяющая форму колебаний.
Скорость перемещения оси балки будет
dtp (z, t}
и (z, f) = • т —- = uw (z) COS (wf + a),
pmax = °>w
Максимальное значение кинетической энергии п масс равно
i=n
7’=-! У (19.127)
<==1
где wi — амплитудное значение прогиба в месте г-й сосредоточенной
массы.
Максимальная потенциальная энергия деформации балки
I
о
(19.128)
Приравнивая правые части уравнений (19.127) и (19.128) и решая
полученное уравнение относительно to2, найдем
(О
I
EJ
б
г = п
г=1
(19.129)
540
В случае непрерывно распределенной массы формула Рейлея для
приближенного определения квадрата круговой частоты (19.129) при-
мет вид
i
С (dI 2w\2
\ EJ dz
J \ <№]
0,2 = £------------, (19.130)
J mw2 dz
О
где
g *
Если действительная форма колебаний w(z) известна, формула (19.129)
дает точное значение частоты. Обычно функция прогиба w(z) заранее
не известна и ею, следуя методу Рейлея, приходится задаваться.
Способ Ритца является дальнейшим развитием способа Рейлея.
В уравнение упругой линии колеблющейся системы вводятся неко-
торые параметры, величина которых подбирается таким образом,
чтобы частота основного тона была минимальной. Так, например, при
поперечных колебаниях стержня функция прогиба выбирается в виде
ряда
w (z) = arwY (z) + a2w2 (и) + . .. , (19.131)
каждый член которого должен удовлетворять граничным условиям,
а коэффициенты ряда аг, а2, а3, ... должны выбираться из условия
минимума частоты:
д
да1
(19.132)
I
§ mw2dz
о
Продифференцировав это выражение и разделив результат на
j* mw2 dz, с учетом (19.130) получим
0
(19.133)
Таких уравнений будет столько, сколько членов в ряде (19.131). По-
лученная система уравнений однородна относительно коэффициентов
а2, а3, . . . , О"п,.
Приравняв определитель этой системы нулю, получим частотное
уравнение Этот метод позволяет найти не только низшую частоту
собственных колебаний, но и значения высших частот, хотя и с
меньшей точностью.
541
Способ Бубнова—Галеркина. Применим этот способ при реше-
нии, например, задачи о поперечных колебаниях стержня перемен-
ного сечения, описываемых дифференциальным уравнением
Д [к/ (г) ^1 - т = 0. (19.134)
dz2 [_ dz2J dt2
Решение этого уравнения можно найти с помощью подстановки
w = Z (z) • Т (t),
используя которую получим дифференциальное уравнение для опре-
деления функции прогиба Z(z):
-m^Z = 0. (19.135)
Согласно способу Бубнова—Галеркина действительная кривая про-
гиба, выражаемая функцией Z(z), заменяется некоторой приближен-
ной функцией ф (2), удовлетворяющей граничным условиям задачи.
Функция ф (г) должна быть ортогональна исходному дифференциаль-
ному оператору. С этой целью образуем интеграл
1
J [ю- (2) (z)} ф (z) dz = 0. (19.136)
о
Отсюда, в частности, может быть получена формула Рейлея
I
( lEJ(z)^ (z)]"ty(z)dz
to2 = ~——у-----------------------, (19.137)
С тпф2 (z) dz
0
Если представить ф (z) в виде ряда
ф (z) == а1ф1 (z) + а2ф2 (z) -I- (19.138)
и рассмотреть каждое из слагаемых ф$ (z) как возможное перемеще-
ние, то вместо (19.136) получим соотношение, выражающее равенство
нулю виртуальной работы:
I
§ {(£J(z)|"(z)]'' —пи»2ф(г)} |i(z)<lz = 0. (19.139)
е
Таких равенств можно записать столько, сколько слагаемых имеет
принятое для ф (г) выражение (19.138).
Каждое из уравнений (19.139) однородно и содержит неизвестные
коэффициенты alt а2, а3, ... в первой степени. Приравняв нулю опре-
делитель системы уравнений (19.139), получим частотное уравнение,
из которого может быть определена угловая частота собственных
колебаний.
542
Таблица 42
Собственные частоты колебаний систем с одной и двумя
степенями свободы
т —масса груза; с-—жесткость упругого элемента; /-—длина стерж-
ня; G— модуль упругости при сдвиге; EF — жесткость поперечного
сечения стержня при растяжении; GJp — жесткость поперечного сече-
ния стержня при кручении; EJ— жесткость поперечного сечения
стержня при изгибе
Схема колебательной системы Число степе- ней свобо- ды Собственная частота /, гц
/ = А 1/_£1£2_
7 2я Г т 4- с2)
543
Продолжение табл, 42
Схема колебательной
системы
Число
степе-
ней
свобо-
ды
Собственная частота /, гц
/ = _1_ 1/
’ 2ъаЪ V т (aJ2 4- bJt)
при — J
i -i /аЖл
' 2каЬ г т
при J\~ J2~ J и а = & = -i
2 1/зЖ/
кг ml3
544
Продолжение табл, 42
Схема колебательной
системы
Число
степе-
ней
свобо-
ды
Собственная частота /, ец
/ -|/“ ЗЕЛ
' nab V та (За + 46)
1 при а = 6 — -~
8_ 1/Ш
' “ тс Г 7/пР
/==1
' тсб V т (За 4- 46)
a JI 6
, __ _J_ 1 f 2
2тс6 V т (aj9 4 6Jr)
1 при = Уг = J
\/ }'EJ
2тс6 т (а 4 Ь)
18 5-1186
54J
Продолжение табл. 42
Схема колебательно1 системы Число степе- ней свобо- ды Собственная частота /, ец
cf Ъ с3 Ш2 С2
1/ (с1+сз I сг+езУ .с1с2+с1сз+с2сз
V \ пг1 т2 / тхт2
при ct = с2 — с и гпг == zn2 == /п
277/ П72 С2 /П3
шшп
— - - **
2
11/ 1[(^.±Л± ci + м х
V 2 1 \тп1 ' т2 т9 / +
1/ (^+^+Ei±^)-4ciC2I!li±^l
г \т1 тп3 тп2 / т1 т2 т3 J
при сх = с2 = с и т^ = т2 = т3 = т
546
П родолжение табл. 42
Схема колебательно!
системы
Числи
степе-
ней
свобо-
ды
Собственная частота Л гц
— моменты инерции масс дисков
относительно оси’ вала
При Cjl — ^2 И — J2 =—~ J
_ 1 cs с2.+ с8\
.2-& V 2 11“~ + ~
'с1+<>з । са+сзУ ЛСг+С1<>3+с2с3]
i Л Л /~4 71Л J-
2
А, А — моменты инерции массы дис-
ков относительно оси вала
при et = с2 — с и Jx — J2 — J
18*
547
Таблица 43
Частотные уравнения и собственные формы продольных и крутильных колебаний стержней постоянного
сечения
сл CD Схема закрепления стержня Частотное уравнение Корни частотного уравнения * j Собственная фор- ма колебаний
1 sin kl = 0 k(l ~ in i = 1, 2, 3, ... cp (z) = С COS kz
1 г cos kl = 0 fci/ = y(2i-l) i = l, 2, 3, ... y(z) = C sin kz
/ Afg к 1 _ г\ sin kl = 0 fyl = in i = 1, 2, 3, ... cp (z) — C sin kz
550
Продолжение табл. 43
*-------------------
Схема закрепления
стержня
Частотное уравнение
Корни частотного уравнения *
Собственная фор-
ма колебаний
.7, kl
tg kl —----
а
cl
При продольных колебаниях а = — ;
гЬг
- cl
при крутильных колебаниях а = —г-,
Gjp
где Fys.Jp — площадь и полярный момент
инерции поперечного сечения стержня;
с — жесткость опоры относительно про-
дольных или крутильных перемещении
? (z) = С sin kz
mJ
pfMJp h
I
Igkl = a kl При продольных колебаниях a = ; т при крутильных колебаниях a = , где т — масса груза; J — момент инерции массы груза относительно оси стержня; F — площадь сечения; Jp— полярный мо- мент инерции сечения стержня a 0 0,5 1.0 10 оо Ф (z) = С cos kz
кг1 тс 4,26 4,50 4,69 3 2 Я
Ф (z) = С sin kz
pESfy $
I
kl tgkl — a
rr « PFl
При продольных колебаниях a == ; при
крутильных колебаниях a = ,
где m — масса груза; J — момент инерции
массы груза относительно оси стержня;
F — площадь сечения; Jp— полярный мо-
мент инерции сечения стержня
СЛ Продолжение табл. 43
Схема закрепления стержня Частотное уравнение Корни частотного уравнения * С°маТко™бания°Р‘
Продольные колебания
/ £ \2 I &
mim2 \pF/ 4J tg kl ~ + pF = °’
крутильные колебания
tgw-(j1 + /2) А = о,
pjp
т19 т2— массы грузов; J19 J2—моменты
инерции массы грузов относительно оси
стержня; F — площадь сечения; Jp — по-
лярный момент инерции сечения стержня
* Собственные частоты определяют по формуле /• = а, где а m J/ для продольных и а =
лебаний. р
? (2) =
= С ^cos kz —
—к sin kz)
?Jp 1
1/" G
||/ — для крутильных ко-
r р
Таблица 45
Корни частотных уравнении поперечных колебаний
стержней постоянного сечения на упругих опорах *
Схема закрепления стержня
График для определения
коэффициентов kl
Асимптота J
А ! при KL = Л
° 50 ЮО
* Собственные частоты определяют по формуле 1
где т « pF.
ffi.l/EJ - к*1/~~
г pF "" 2п V т’
554
П родолжение табл. 46
—
Схема закрепления стержня
\
График для определения
коэффициентов hl
555
Таблица 46
Корни частотных уравнений поперечных колебаний
стержней постоянного сечения с сосредоточенными
массами т*
Схема стержня
График для определения
коэффициентов М
tpFEJ т
т .PfiJ.. т-
(feZ)2 ] Л FJ
2к V pF
Собственные частоты определяют по формуле / ==
556
\ Таблица 47
Значения некоторых интегралов, встречающихся при расчетах
поперечных колебаний стержней (cpi — t-я собственная форма
колебаний)
V Схема закрепления стержйя г 1 1 I <Р: dx 1 J 0 -М 0 1 1 § )2 dx 0 1 13 J dx о .
1 0,6366 0,5 4,9343 48,705
2 0 0,5 19,739 779,28
3 0,2122 0,5 44,413 3945,1
4 0 0,5 78,955 12468
5 0,1273 0,5 123,37 30440
1 0,8445 1,0359 12,775 518,52
2 0 0,9984 45,977 3797,1
1—I 3 0,3637 1,0000 98,920 14619
4 0 1,0000 171,58 39940
5 0,2314 1,0000 264,01 89138
1 0,6147 0,4996 5,5724 118,80
2 —0,0586 0,5010 21,451 1250,40
i 3 0,2364 0,5000 47,017 5433,0
4 —0,0310 0,5000 82,462 15892
5 0,1464 0,5000 127,79 36998
1 1,0667 1,8556 8,6299 22,933
к 2 0,4252 0,9639 20,176 467,97
1 3 0,2549 1,0014 77,763 3808,5
4 0,1819 1,0000 152,83 14619
5 0,1415 1,0000 205,52 39940
557
Таблиц/ 48
Собственные частоты поперечных колебаний стержней постоянного
сечения, нагруженных продольными силами /
Схема стержня
Собственная частота колебани]
. 0,562 т/ EJ (. , 5N13}
_ 0,5621/EJ / «у/’ \
h—irV +
WZ2 \
i^EJ!
Г л\а в а 20
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ ДЕЙСТВИЮ
ПОВТОРНО-ПЕРЕМЕННЫХ НАПРЯЖЕНИЙ
§112, Явление усталости материалов
Усталостью материалов (в частности, металлов) называется явле-
ние разрушения при многократном повторении нагружений. Способ-
ность материалов сопротивляться разрушению при повторно-перемен-
ных напряжениях называется выносливостью
материала.
Усталостное разрушение наблюдается
при наличии одной из следующих особен-
ностей нагружения:
1) при многократном нагружении одно-
го знака, например, периодически изме-
няющегося от пуля до максимума (рис.
335, а);
2) при многократном нагружении, пе-
риодически изменяющемся не только по
величине, но и по знаку (знакопеременное
нагружение), когда на выносливость мате-
риала одновременно оказывают влияние и
повторность и переменность нагружения.
При этом различают симметричное нагру-
жение (рис. 335, б) и несимметричное
(рис. 335, <?, г).
Для разрушения от усталости недо-
статочно переменности напряжений. Не-
обходимо также, чтобы напряжения имели
определенную величину. Максимальное на-
пряжение, при котором материал способен
сопротивляться, не разрушаясь, при любом
произвольно большом числе повторений нагружений, называется
пределом выносливости или пределом усталости.
Усталостный излом металла имеет
характерный вид (рис. 336). На нем
обычно можно наблюдать две зоны:
одна из них (Л) гладкая, притертая,
образовавшаяся вследствие постепен-
ного развития трещины; другая (В) —
крупнозернистая, образовавшаяся при
окончательном изломе ослабленного
развившейся усталостной трещиной
сечения детали. Зона В у хрупких 4 ма-
териалов имеет крупнокристалличе-
ское, а у вязких — волокнистое строе
ние.
Механизм образования трещин при
повторно-переменном напряжении весь-
Рис. 336. ма сложен и не может считаться пол-
Рис, 335
559
ностью изученным. Из несомненных положений теории усталости
можно отметить следующие: /
1) процессы, происходящие в материале при повторно-переменном
нагружении, носят резко выраженный местный характер; Г
2) решающее влияние на явление усталости до образования пер-
вой трещины оказывают касательные напряжения, вызывающие пла-
стические сдвиги и разрушение путем среза. Развитие усталостных
трещин ускоряется при наличии растягивающих напряжений и у
пластичных, и, в особенности, у хрупких материалов (типа чугуна),
в которых появление трещин отрыва значительно повышает чувстви-
тельность к растягивающим напряжениям.
Предел выносливости определяют экспериментально на соответ-
ствующих испытательных машинах путем испытания партии образцов
из данного материала в количестве не менее 6—12 штук. Предел
выносливости зависит от многих факторов, в том числе от формы и
а
t
5
Рис. 337
размера образца или детали, способа ее обработки, состояния поверх-
ности, вида напряженного состояния (растяжение — сжатие, кручение,
изгиб), закона изменения нагрузки во времени при испытании, темпе-
ратуры и т. п
В большинстве случаев переменные напряжения, вызывающие
разрушение от усталости, представляют собой функцию времени
а == / (г) с периодом, равным Т. Совокупность всех значений напряжений
за один период называется циклом напряжений (рис. 337, а). На вели-
чину предела усталости оказывают влияние максимальные (Ртах) и
минимальные (рт1П) напряжения цикла. Основной характеристикой
цикла является коэффициент асимметрии цикла
r = (20.1)
Ртах
Различают также среднее напряжение цикла (рис. 337, б)
Ртах Pmin
Рс — 2
и амплитуду цикла
Ртах' Pmin
Ра- 2
(20.2)
(20,3)
560
\
Сиднее напряжение цикла может быть как положительным, так
и отрицательным; амплитуда цикла определяется абсолютной вели-
чиной (без учета знака).
В соответствии с (20.2) и (20.3), очевидно,
\ /’max = Pc + Р&> Pmin ~ Рс ^а*
Наиболее опасным является так называемый симметричный цикл
(когда Рщах = “Pmin и рс = 0), при котором
Pmin Л
г =--------- —1.
Ртах
Предел усталости при симметричном цикле обозначается через
При пульсирующем цикле, когда pmin = 0,
Ртах
а предел выносливости обозначают через р0. При постоянной нагруз-
ке, когда Pmax Pmin Р’
г — — = 1.
Р
В самом общем случае при коэффициенте асимметрии г предел
усталости обозначают через рг. В частном случае, например, при
г = —0,5 предел усталости обозначают р_0 5- Циклы» имеющие оди-
наковые характеристики г, называют подобными. Характеристика цикла,
или коэффициент асимметрии, может меняться от — оо до -j-оо (см.
табл. 49).
Следует иметь в виду, что в случаях, когда речь идет об уста-
лости при растяжении — сжатии или изгибе, вместо обозначений ра,
Рс» Ро» Ртах’ Pmin и т’ А* необходимо использовать обозначения
соответственно аа, ас, а0, amax, amin и т. д.» а в случае рассмотрения
сопротивления материалов действию повторно-переменных касатель-
ных напряжений (при циклическом кручении) следует применять
обозначения та, тс, т0, ттах, Tmin и т. д.
§113. Методы определения предела выносливости.
Диаграммы усталости
При испытании материала на выносливость чаще всего исполь-
зуют гладкие цилиндрические образцы диаметром 7—10 мм.
В зависимости от вида действующих в образце повторно-пере-
менных напряжений (растяжения — сжатия, переменного изгиба,
переменного кручения), а также характеристики цикла (коэффициен-
та асимметрии г) значения предела выносливости будут различными.
Поэтому, ставя перед собой цель получения предела выносливости
материала, следует заранее указать, при каком виде деформации
(изгибе, кручении и т. п.), а также при каком характере изменения
напряжений за цикл, т. е. при каком значении г, требуется опреде-
лить предел выносливости.
В соответствии с поставленной задачей выбирают испытательную
Минину. Для испытания на усталость при изгибе применяют машины
561
Рис. 338
(рис. 338), в которых циклические симметричные напряжения в/испы-
туемом образце возникают за счет вращения образца, нагруженного
укрепленным на конце с помощью шарикового подшипника трузом.
Число оборотов в минуту таких машин обычно составляет около 3000
(50 гц). Современные усталостные машины,
в частности машины с магнитострикцион-
ными вибраторами для испытания при
растяжении — сжатии, позволяю^ произво-
дить испытания при частотах порядка
10000—20000 гц.
При испытании партии образцов с
целью определения предела выносливости
необходимо обеспечивать в отдельных
образцах различные напряжения для выяв-
ления закономерности изменения числа циклов до разрушения при
тех или иных уровнях напряжений.
Обработка получаемых экспериментальных данных осуществляется
путем построения кривых усталости^ часто называемых кривыми Вел-
лера (рис. 339).
Рис. 340
Кривая усталости строится по точкам в координатах: максимальное
напряжение цикла ртах (атах или ттах) — число циклов до разру-
шения N. Каждой точке соответствует один разрушившийся образец,
проработавший N циклов с заданным ртах.
По мере снижения напряжения образцы выдерживают до разру-
шения все большее число циклов, а кривая усталости ртах = / (N)
как бы приближается к некоторой асимптоте, параллельной оси
абсцисс N. Число циклов, при котором кривая усталости практи-
чески начинает совпадать с асимптотой, может быть принято за базу
испытания на усталость, т. е. за такое число циклов, превышение
которого при данном напряжении практически не должно приводить
к разрушению образца. Таким образом, базой испытания на выносли-
вость называется наибольшее число повторно-переменных нагружений,
существенное превышение которого не должно приводить к усталостным
разрушениям испытуемого образца при данном напряжении.
Для черных металлов (сталь, чугун и т. п.) в инженерной прак-
тике за базу испытания принимают 10 млн. циклов; для цветных
металлов (медь, алюминий и т. п.)-*база испытания в 5—10 раз
больше, чем для черных металлов.
В некоторых случаях, особенно для цветных металлов, кривая
усталости в координатах N, р медленно стремится к асимптоте, по-
этому базу испытания приходится выбирать значительно большей.
В таких случаях вообще трудно говорить об истинном, так называемом
физическом пределе усталости, поскольку таковой практически отсут-
ствует. Говорят об условном пределе усталости, понимая под ним
562
максимальное напряжение, при котором не происходит разрушение
при Осуществлении определенного наперед заданного числа циклов,
принимаемого за базу испытания.
КрЬме построения первичных диаграмм усталости, в координатах IV,
атах nPF растяжении — сжатии и изгибе или в координатах N, ттах
при крушении эти диаграммы строят также в полулогарифмических
координатах 1g ЛГ, атах (рис. 340) или 1g JV, ^тах« В этом случае пре-
дел усталости будет характеризоваться ординатой горизонтального
участка кривой усталости.
Как показывают многочисленные испытания на усталость, для
некоторых материалов можно заметить следующие соотношения между
пределами выносливости при симметричном цикле, полученными при
изгибе t кручении и растяжении — сжатии на гладких
образцах. Для стали = 0,7а^ , для чугуна = 0,65а^, =
= 0,8а^; для сталей и легких сплавов х = 0,55*3^. Замечено так-
же, что для стали существуют следующие соотношения указанных
пределов выносливости с временным сопротивлением при растяжении:
— 0,28ав; = 0,4ав; т_х s= 0,22ав. Для цветных металлов
<^ = (0,24 — 0,5) ав.
Диаграмма предельных напряжений. Для характеристики сопро-
тивляемости материала повторно-переменным напряжениям при раз-
личной асимметрии цикла строится так называемая диаграмма пре-
дельных напряжений (рис. 341) в координатах omax> amin~'°c (®иа'
грамма Смита).
Рис. 342
Ординаты кривой С АВ диаграммы соответствуют значениям пре-
делов усталости (максимальным значениям напряжения) при различ-
ной асимметрии цикла, которые берутся из первичных диаграмм
усталости.
Тангенс угла наклона луча, проведенного из начала координат
до пересечения с предельной кривой САВ и образующего угол 3
с осью абсцисс ас, будет:
qmax __ а щах _ 2
qc qmax 4" атт 1 4" г
(20.4)
563
I
„ Диаграммы предельных напряжений обычно ограничивают в/верх-
ней части пределом прочности или пределом текучести материала.
Примерный вид диаграммы предельных напряжений, ограниченной
пределом текучести тт, для случая циклического кручения/ приве-
ден на рис. 342. /
Диаграммы предельных напряжений можно строить такя^е в коор-
динатах аа — ас (диаграмма Хейя). В этом случае (рис. 343) тангенс
угла 3, образованного лучом, проведенным из начала координат,
с предельной кривой будет выражаться так:
qmax qmin____ 1 —г
qmax 4” qmin ' 4“ r
(20.5)
Для оценки сопротивляемости
напряжениям при сложном напря-
женном состоянии, например при
совместном действии циклического
изгиба и кручения, используют
соответствующие усталостные ма-
материала повторно-переменным
шины, позволяющие получать интересующее нас напряженное со-
стояние.
На рис. 344 приведены результаты экспериментов с гладкими
образцами при различном сочетании переменных нормальных (о) и
касательных (т) напряжений при симметричном цикле. Через
и обозначены пределы выносливости соответственно только при
изгибе и только при кручении, а иа и та — предельные амплитуды
при одновременном действии изгиба и кручения. Экспериментальные
данные группируются около кривой, которая с достаточной степенью
точности может быть аппроксимирована для конструкционных сталей
дугой круга (рис. 344, кривая 1), описываемой уравнением
/ qa \2 / \2
тЧ + Л <20-6)
\а-1/ \Т_4/
Для высокопрочных сталей и чугунов экспериментальные данные
располагаются ближе к эллиптическим дугам (рис. 344, кривая 2).
В случае симметричного цикла с соблюдением синхронности и
синфазности напряжений условие прочности в амплитудах главных
напряжений в соответствии с третьей теорией прочности запишется
так:
(а1)а-(’з)а = а-1> (20-7)
а по четвертой теории прочности — в виде:
К’1)а “ W + К’з)а “ <оз)а]2 + 1(’з)а - (°1)аГ = 2в1Г (20-8)
564
При сложном напряженном состоянии, характеризуемом совмест-
ным действием циклического изгиба и кручения, условие прочности
(20.8), с учетом соотношения будет иметь вид
”И°«+(йГ^==°-1- (20<9)
Это условие совпадает с выражением (20.6), вытекающим из экспери-
ментальных данных.
§ 114. Влияние на предел выносливости материала
конструктивно-технологических факторов
Влияние концентрации напряжений. Наибольшее влияние на
предел выносливости оказывает концентрация напряжений, степень
которой характеризуется теоретическим коэффициентом концентрации
а (см. § 27). Как показывают опыты, предел усталости образцов с кон-
центраторами напряжений оказывается больше вычисленного
через теоретический коэффициент концентрации а, т. е.
Поэтому наряду с теоретическим коэффициентом концентрации вве-
дено понятие эффективного, или действительного, коэффициента кон-
центрации к. Эти коэффициенты обозначены так: для нормальных
напряжений
для касательных напряжений
где и — пределы выносливости, полученные при действии
циклических нормальных и касательных напряжений на гладких
образцах; а^1к и т_1к — пределы выносливости образцов с концентра-
торами напряжений.
Практически оказалось удобнее определять эффективный коэффи-
циент концентрации через так называемый коэффициент чувстви-
тельности материала к концентрации напряжений
__j
<7 = 7—Г • (20.10)
который зависит от материала, а также от коэффициентов qQ\ к°;
а0 -—при нормальных напряжениях илиqz; kx; az—при касательных.
Для определения коэффициента чувствительности q в литературе
имеются графики (рис. 345). Зная q, а также теоретический коэффи-
циент концентрации напряжения а, можно определить согласно
(20.10) эффективный коэффициент концентрации к по формуле
&=^1 + <7(« — 1). (20.11)
565
Для материала, чувствительного к концентрации напряжения,
когда q 1, к -> а. Для материала, не чувствительного к концен-
трации напряжения, когда q -> 0, к -> 1.
Влияние концентрации напряжений при сложном напряженном
состоянии оценивается на основе испытания образцов с концентра-
торами и получения соответствующих диаграмм (рис. 346), которые
аналогично диаграммам, приведенным для гладких образцов (рис. 344),
описываются эллиптической зависимостью
(V / \2
—) +( —) =1, (20.12)
а-1к/ Ь~1к/
где 1к, 1к — пределы усталости при симметричном цикле для
образцов с концентраторами только при изгибе и только при круче-
нии соответственно; оак, ?ак — амплитудные значения напряжений
при одновременном синхронном и синфазном изменении напряжений
при сложном напряженном состоянии и различных сочетаниях пере-
менных нормальных и касательных напряжений.
Влияние размеров (масштабный фактор). Эксперименты пока-
зывают, что с увеличением размеров образца предел выносливости
падает. Это снижение обычно учитывается с помощью некоторого
коэффициента, обозначаемого, например, применительно к нормаль-
ным напряжениям так:
е = <2=1к,
° («-iJd.*
где (а_х)^0 — предел выносливости гладкого лабораторного образца
диаметром б£о = 7-г-1О мм\ (s—Jd— предел выносливости рассматри-
ваемой детали диаметром Поскольку (a_i)d < (а—i)d0> то> оче"
видно, коэффициент влияния абсолютных размеров еа«<1.
При наличии концентратора влияние масштаба оценивается так
же, как и для гладких образцов с помощью коэффициента еак:
(20.13)
=
(20.14)
где (a_1K)d и (a^1K)d —пределы выносливости детали и лаборатор-
ного образца соответственно. На рис. 347 приведены кривые зависи-
566
надреза).
мости е = / (d) Здесь кривая 1 соответствует детали из углеродистой
стали без концентратора; кривая 2 — детали из легированной стали
(ав = 100 ч-120 кГ/мм?) при отсутствии концентратора и из углеро-
дистой стали при наличии концентратора; кривая 3 соответствует
детали из легированной стали при наличии концентратора; кривая 4—
для любой стали при весьма большой концентрации напряжений
(например, при концентраторе типа
Снижение предела усталости
с увеличением размеров особенно
сильно выражено у неоднородных
материалов. Так, например, с уве-
личением размера образца из се-
рого чугуна с 5 Ч- Ю мм до 50 мм
снижение <jb и может достиг-
нуть 60 ч-70%. Для углеродистой
стали увеличение диаметра образ-
ца с 7 мм до 150 мм приводит к
снижению предела выносливости
примерно на 45%.
Кроме эффективного коэффи-
циента концентрации (kG)d для
образца вводя! понятие эффектив-
ного коэффициента концентрации напряжений для детали (&а)д, учи-
тывающего одновременно и размеры и концентрацию:
Если (ka)d определяется на образцах достаточно большого диа-
метра (когда дальнейшее увеличение диаметра мало влияет на (k(S)d)i
то
(^~(e^(a_1K)d (ео)/
(20.15)
(20.16)
Рис. 348
Влияние концентраторов
напряженного состояния. При циклическом кручении, например, коэф-
фициент концентрации оказывается более низким, чем при изгибе
при той же форме концентратора Это видно, в частности, из рис. 348
и 349, на которых приведены значения эффективных коэффициентов
Рис. 349
напряжения существенно зависит от вида
567
с поверхности, а плохое
концентрации для ступенчатых валов с галтелью соответственно для
изгиба и кручения. Соотношение между кх и kQ может быть пред-
ставлено формулой
На рис. 350 приведены графики, характеризующие эффективные
при растяжении —»сжатии. Из графи-
ков (рис. 348 и 350) видно, что значе-
ния эффективных коэффициентов при
растяжении —- сжатии несколько пре-
вышают таковые при изгибе. Более
полные данные о коэффициентах кон-
центрации и чувствительности к кон-
центрации напряжений приведены в
Приложении 2.
Влияние состояния поверхности.
На предел выносливости существенное
влияние оказывает состояние поверх-
ности детали или образца. Это объяс-
няется тем, что на поверхности почти
всегда имеют место дефекты, связанные
с качеством ее механической обработ-
ки, а также с коррозией под влиянием
окружающей среды. Поэтому усталост-
ные трещины, как правило, начинаются
ство последней приводит к снижению
предела усталости.
Влияние качества механической обработки поверхности на вынос-
ливость можно оценить некоторым коэффициентом 1, который
равен отношению предела выносливости испытуемого образца с опре-
деленной обработкой поверхности к пределу выносливости тщательно
Рис. 351 Рис. 352
отполированного образца. На рис. 351 приведена зависимость коэф-
фициента р от предела прочности для различных видов обработки
поверхности стальных образцов. Кривая 1 соответствует полирован-
ным образцам; кривая 2 — шлифованным; кривая 3—образцам с тон-
кой обточкой; кривая 4— образцам с грубой обточкой; кривая 5 — с
наличием окалины. Из графика видно, что при грубой обточке пре-
дел выносливости снижается на 40%, а при наличии окалины — на 70%.
Влияние коррозии в процессе испытания на предел выносливости
при ротационном изгибе показано в виде графиков на рис. 352, где
по оси ординат отложено значение коэффициента
_К
к ~ '
568
выражающего отношение предела выносливости корродированного
образца к пределу выносливости полированного образца апо
оси абсцисс — временное сопротивление материала исследуемых образ-
цов. Кривая 1 характеризует влияние коррозии в пресной воде при
наличии концентраторов напряжений; кривая 2 — в пресной воде при
отсутствии концентраторов и в морской воде при наличии концентра-
ции; кривая 3~-в морской воде при отсутствии концентрации.
Влияние пауз. На предел выносливости имеют влияние /паузы
(перерывы нагружения). Иногда за счет пауз число циклов до разру-
шения увеличивается на 15—20%. Увеличение числа циклов тем
больше, чем чаще паузы и чем они длительнее (последний фактор
влияет слабее).
Влияние перегрузок (нагрузок, больших предела выносливости)
на величину предела выносливости зависит от характера перегрузок.
При малых перегрузках до определенного числа циклов усталостная
прочность повышается, при больших перегрузках после определен-
ного числа циклов — понижается.
Влияние тренировки. Если создавать в образце напряжения не-
много ниже предела выносливости, а затем постепенно их увеличи-
вать, то сопротивление усталости материала может быть су щественно
повышено. Это явление, называемое тренировкой материала, широко
используется в технике. Особого эффекта можно достигнуть при
постепенном увеличении перегрузки. При этом упрочнение можно
получить при сравнительно кратковременных тренировках (порядка
50 000 циклов), но при сильных перегрузках.
Влияние температуры. Применительно к обычным конструкцион-
ным материалам повышение температуры приводит к снижению пре-
дела выносливости, а снижение температуры — к повышению выносли-
вости как гладких образцов, так и образцов с концентраторами.
Для стали при температуре выше 300° С с ее повышением на
каждые 100° С предел усталости падает на 15—20%. Однако для
некоторых сталей с повышением температуры от 20 до 300° С наблю-
дается некоторое повышение предела усталости. Это повышение,
по-видимому, связано с физико-химическими процессами, протекаю-
щими в материале под одновременным воздействием температуры
и циклических напряжений. Влияние концентрации напряжений на
выносливость, как правило, с повышением температуры уменьшается.
При понижении температуры от 20 до —190° С предел выносли-
вости у некоторых сталей увеличивается более чем вдвое, хотя удар-
ная вязкость при этом существенно падает.
§ 115. Расчет на прочность при повторно-переменных
нагрузках
При простых видах деформации детали, работающей при сим-
метричном цикле, например при циклическом растяжении — сжатии
или изгибе и фактически действующем знакопеременном напряже-
нии аа, запас прочности можно определить по формуле
п — -------
где —предел выносливости детали при растяжении-сжатии
или изгибе, который может быть определен по пределу выносливости
лабораторных полированных образцов (^__i)cZ0> с учетом эффективного
коэффициента концентрации (&a)d> масштабного фактора еа, состояния
569
поверхности и среды, характеризуемых, соответственно, коэффициен-
тами 3 и рк, по формуле:
/ \ == (c—i)d
В случае сложного напряженного состояния согласно (20.9)
или согласно (20.6)
2 2
G Т
а । а
°—lK)d (т—1k)cZ
Тогда, имея в виду, что
(°—1к)й
и — --------------------------------------
(Т—1к)д
та
на основании (20.17) будем иметь
2 2 “Г 2 9
П
откуда запас прочности при сложном напряженном состоянии опре-
делится формулой
(20.18)
В случае определения запаса прочности при асимметричном цикле
и любом виде циклического нагружения (изгиб, растяжение *— сжа-
тие, кручение) можно исходить из
схематизированной диаграммы пре-
дельных напряжений для гладких
образцов (рис. 353), представив ее
в виде прямой, проходящей через
точки Л и В с координатами О,
г и -у-, а0, уравнение которой
£
имеет вид
атах = а—1 “I °с = 1 Н*
“2
, (л 2а,—ао\
+ 1------1---- а
\ / °
или
’тах = ’-1 + (1-Ф>с> (20-19)
где — коэффициент чувствительности материала к асимметрии
цикла равен:
ф = —
(20.20)
570
При действии касательных напряжений уравнение предельной
кривой максимальных напряжений по аналогии с (20.19) будет иметь
вид
(20.21)
тхпаХ = г-1 + (1-К) ’с-
Значения коэффициентов и для
сталей с различным вре-
менным сопротивлением приведены ниже:
ав, кГ1шл? фо Фх
35—55 0 0
52—75 0,05 0
70—100 ОД 0,05
100-120 0,2 0,10
120—140 0,25 0,15
Предельная амплитуда напряжений для гладкого образца ца
основании (20.19) может быть выражена формулой
°а = °тах ~ °с = °-1 ~ Mr
Предельная амплитуда напряжений для детали (oaK)d будет
. °а
(0^"(Чд" (Мд
(20.22)
а уравнение кривой предельных напряжений для детали (рис. 354)
может быть записано в виде
(°max)d = (aaK)d + °с = + f1 — (fc^] ’с- <20'23)
Для определения запаса прочности детали, напряжение в которой
на диаграмме предельных напряжений (рис. 355) характеризуется
точкой М с координатами аа, ас, необходимо найти координаты
точки N, находящейся на пересечении луча, выходящего из начала
координат, с кривой предельных напряжений для детали. Координаты
571
точки АГ определятся из совместного рассмотрения уравнений кривой
(линии) AN предельных напряжений для детали
(’max, «)d = + f1 ~ ’с (20.24)
и уравнения луча
(20.25)
с
где штрихами обозначены текущие координаты.
Ордината точки N, лежащей на пересечении прямых AN и ON,
будет одна и та же, т. е.
или
(Мд
(атах, к)й атах»
а
f max r
а =------ а ,
0 °C
откуда находим абсциссу точки N:
ас =
a-i
ст-1 ас
—
l’wL’c
Учитывая, ЧТО а_ = — а _, ПОЛУЧИМ
а Шал и *'•'
, ’-1 • °C
(^а)датах ас (^а)д ^ааС
(20.26)
а° (Мд ’а + Фа’о’
Подставляя это значение s'o в (20.25) и обозначая эту ординату
(’max) неРез (’гк)<р получим
, к ст—iqmax
Таким образом, окончательное выражение для запаса прочности
запишется так:
_ (агк)й
max
Аналогично при кручении
п.
(20.27)
(Мд’а + Vc
(20.28)
(Мдта + Мо '
При сложном сопротивлении и несимметричном цикле запас проч,
ности может быть определен по формуле
П — г.... ,
1/2 < 2
где по и пх находят, соответственно, по формулам (20.27) и (20.28).
Выбор запаса прочности при расчетах на действие повторно-
переменных напряжений зависит от точности определения усилий
и напряжений, от однородности материала, качества обработки детали
572
и других факторов. При повышенной точности определения напря-
жений (в частности, с использованием тензометрирования), однород-
ном материале и качественной обработке принимают запас прочности
п = 1,3 -т-1,4.
Для обычной точности определения усилий и умеренной одно-
родности материала п — 1,4 -г-1,7. При пониженной точности опре-
деления усилий и напряжений, а также при пониженной однород-
ности материала п = 1,7-т-3,0.
Остановимся на порядке проектировочного расчета на выносли-
вость, например, штока поршневого двигателя, когда даны нагрузки,
действующие на проектируемую деталь (Ртах и Pmin); задан мате-
риал, т. е. известны ав, от, фа; известна технология обработки
детали; известен тип концентратора (предположим, задан диаметр
поперечного отверстия в детали S) и требуется определить размеры
детали. При решении поставленной задачи прежде всего устанавли-
вают опасное сечение детали, которым, очевидно, будет сечение в
месте концентратора. Так как соотношения диаметра отверстия кон-
центратора и диаметра самой детали неизвестны, следует задаться
теоретическим коэффициентом концентрации а0 и для данного мате-
риала по известному (ав) из графика (рис. 345) при данном % опре-
делить коэффициент чувствительности материала к концентрации
напряжений qat а затем по формуле
найти значение эффективного коэффициента концентрации. Из гра-
фика (рис. 351) находят значение коэффициента р, характеризующего
качество обработки поверхности. Задавшись коэффициентом е, учиты-
вающим размеры, определяют эффективный коэффициент концентра-
ции детали
(Мд - •
Затем, задавшись коэффициентом запаса прочности па, по формуле
п a-i _______________________________
(^)д°а”НЛ ч ^max ^min . . ^max “b ^min
(Мд----------------------2----+ ---------2-----
находят площадь поперечного сечения детали
„г р ___________________р р । р
[(Мд а*2....тш+та г иш
и ее диаметр
По окончании расчета необходимо проверить правильность выбран-
ного коэффициента s по графику (рис. 347) при известном теперь
диаметре детали d. В случае резкого расхождения полученного зна-
чения е с принятым ранее расчет необходимо уточнить.
В случае проверочного расчета известны форма и размеры детали
(предположим, речь идет о круглом ступенчатом стержне, подвержен-
ном осевой повторно-переменной нагрузке с заданной асимметрией
цикла); заданы максимальный диаметр d и радиус закругления г
в месте сопряжения разных диаметров вала; известен материал детали
573
(св, ат, a_s) и качество ее механической обработки. Требуется опре-
делить допускаемое усилие, которое может воспринимать деталь.
Решать поставленную задачу следует в таком порядке:
1. Установить теоретический коэффициент концентрации %, поль-
зуясь, например, графиком, приведенным на рис. 350.
2. По графику (рис. 345) найти коэффициент чувствительности
к концентрации напряжений qa.
3. Определить эффективный коэффициент концентрации
4. По графику (рис. 347) найти коэффициент влияния абсолютных
размеров е.
5. По графику (рис. 351) определить коэффициент р, учитывающий
качество обработки поверхности.
6. Найти эффективный коэффициент концентрации напряжений
для детали
\ °)Д
7. Задаться коэффициентом запаса прочности па
8 Определить амплитуду напряжений, исходя из формулы
п - - °-1
° (Мд’а + U,’
„ _ °-1 1
а п %
(Чд + +. V
Обычно для некачественных сталей == 0, тогда
а =—
а ММд
9 Определить допускаемое амплитудное усилие
Р = F о
а m,D а 4 п0(/с3)д
10. Найти среднее усилие
р = р L+..C
И. Определить максимальное и минимальное усилия цикла
р = р 4- р •
max г а ~ с’
Р = р г
mm г max ' •
Наконец, рассмотрим порядок определения запаса прочности
для вращающегося круглого трубчатого вала с поперечным от-
верстием для смазки В, испытывающего переменный изгиб при
симметричном цикле с заданным ^тах = совместно с пере-
менным кручением с ^Икртах при известной асимметрии цикла г.
574
Известен наружный D и внутренний d диаметры вала, материал вала
(°в» ат’ °—п т—1)’ а также качество механической обработки поверх-
ности вала.
Задачу следует решать в таком порядке:
1. Определить номинальные напряжения в вале от изгиба и кру-
чения (§ 46, 50):
__ ^тах ,
аш 1\ ~ ЦТ ’
о = а .а =: О*
1 итах’ ис ’
М
__ КР max
max — |ур
Tmin = ГТтах
Ттах Tmin
а“ 2
Ттах “Ь Ттт
Тс- 2 •
2. Определить коэффициент концентрации при изгибе при изве-
стном (рис. 173).
3. Определить по графику (рис. 345) при найденном аа и извест-
ном % коэффициент чувствительности к концентрации напряжений qg
и найти эффективный коэффициент концентрации при изгибе
*а = 1 + <7а (% — !)•
4. Выбрав по графику (рис. 347) е, а по графику (рис. 351) р,
определить эффективный коэффициент концентрации для детали
(‘•)Д = 7Г
5. Определить запас прочности при изгибе по формуле
а—1 °—1
И - — -
° (Мдаа + Ъс (к,)д °а
(так как для рассматриваемого случая ас = 0).
6. Установить коэффициент концентрации при кручении ах>
а также, приняв qx « qgi определить эффективный коэффициент кон-
центрации при кручении
кх — 1 + (“т — !)•
Приняв те же значения е и р, что и при изгибе, найти эффек-
тивный коэффициент концентрации для детали при кручении
К
(Мд = 7Г-
575
7. Определить запас прочности при кручении
Пг== (Мд^а + 'Ьс ’
8. Вычислить общий коэффициент запаса прочности
Мт
Таблица 49
Характеристики циклов повторно-переменного нагруженця
Наименование цикла ртах; pmin Pmax+Pmin PC= 2 Pmax~Pmin Pa- 2 Pmin r= Ртах
Постоянный положи-
тельный
Pc ~ Ртах ~
\Р Ли ах “ ~ Лит 0 r = 4-l
4 Pa^°
Несимметричный
положительный
Лпах >0 Pc>° O<r<4-1
Лтп >0 pa*°
1 _ 1/
Пульсирующий
положительный 1
Z Лпах >о Pc = ~2 Лпах г = 0
Лиш = 0 _ £ P& 2 ^max
Несимметричный
tP Лпах >0 Pc>°
/~х si —1 <r<0
Pmin <0 Pa
576
П родолжение табл. 49
Наименование цикла Pmax; Pmin Ртах+Ртт ₽с- 2 Pmax—Pmin Ра“ 2 e Рт1п Ртах
Симметр! 1ЧНЫ 4 й / 1 Ртах ”~Pmin Pmin 0 53 <? II II •а о В Ю И г = —1
j 1 Несимметч Р с шчный Ртах > 0’ Pmin < Q Ртах < 1 Pmin | Рс<0 Ра — oo<Zr<Z—1
Пульсирующий отрицательный р t Ртах = 0 Pmin < 0 _ 1 Р° ~ 2 Рпйя 1 . Ра 2 । Рпип1 Г = «—00
1 Несиммет{ отрицате; Р шчный тьный t "Q Чз 0 в S' Я А А ° о Рс<° Ра^0 +1<г<+оо
Постоянный отрицательный И t Ртах Pmin^O /’max ~ Pmin = = Рс<° Ра = 0 г = -|-1
1
19 5-1186 5 77
Глава 21
РАСЧЕТ НА УДАРНУЮ НАГРУЗКУ
§ 116. Расчет на удар при осевом действии нагрузки
Влияние ударного действия нагрузки на величину деформации
или напряжения принято оценивать коэффициентом динамичности
g
*д = Г> <21Л>
ст
где Вст — деформация упругого элемента (рис. 356, а), при статиче-
ском приложении нагрузки Q (при постепенном увеличении нагрузки
от нуля до ее конечного значения); Ьд — де-
формация (рис. 356, б) при ударном приложе-
нии нагрузки (предположим, при падении
груза Q с высоты Н).
Динамическая деформация может быть
выражена через статическую формулой
&д = ^д&ст-
По аналогии установим связь между дина-
мическим и статическим напряжениями:
сд ~ ^д°ст = У ‘
К—л
(21.2)
Чтобы воспользоваться формулой (21.2),
необходимо знать коэффициент динамичности
ка-
коэффициента динамичности исходят из допу-
При определении я л
щения, что связь между усилиями и деформациями сохраняется оди-
наковой как при статической Рст, так и при динамической нагруз*
ках, т.
е.
5ст = —
8Д = -’
Д с
EF
где с —-у — жесткость стержня.
Вывод формулы для определения коэффициента динамичности
базируется на законе сохранения энергии. Изменение потенциальной
энергии положения груза Т при его падении с высоты Н и прохож-
дении пути Н + Ьд будет
Т = (?(Я + ЬД).
(21.3)
578
Потенциальная энергия деформации стержня, накопленная при
ударе, может быть выражена формулой
1
= 2- рд8д = Т- <2Ы)
На основании закона сохранения энергии запишем
Т = ия
или
с8д
-^ = <2(Я + 8Д), (21.5)
Имея в виду, что &ст = , уравнение (21.5) можно представить так:
^-2Вст.8д~28ст Я = 0.
Отсюда определим неизвестную динамическую деформацию
6д = 8ст±У5ст + 28стЯ-
Удерживая в соответствии с физическим смыслом задачи знак плюс,
последнюю формулу можем представить в виде
8д = 5ст(1+1Л + |^). (21.6)
\ иСТ/
Таким образом, в соответствии с (21.2) находим выражение коэф-
фициента динамичности: ____
к =1+1/1+^. (21.7)
°ст
Если учесть, что Н = (у — скорость падающего груза в начале
2g
удара), получим _____
*д = 1+/1 + ^-. (21.8)
2Н То Qv2
Так как z—= 77—, где То = QH — кинетическая энергия па
°СТ СТ
4
дающего груза к моменту соударения; Z7CT =х ~ (?&ст — потенциаль-
ная энергия деформации стержня при статическом приложении на-
грузки Qt коэффициент динамичности можно также выразить формулой:
Ад = 1 + Р<1 + ^2-- (21.9)
Г и ст
При Я = 0 &д = 2. Поскольку, как правило, Н > &ст, то в Выраже-
нии для кд можно пренебречь единицей по сравнению со вторым
слагаемым. Тогда получим
+ 1+ /?- = ! +(21Л0)
А т Ост F СТ ' М ст
19*
579
Динамическое напряжение при ударе согласно (21.2)
+ (2i.li)
\ ' %т/ Г ' IF
Динамическая нагрузка при ударе
Рд = onF = k^F = Q (1 + )/1 + . (21.12)
Из анализа формулы (21.11) видно, что при равномерном распреде-
лении напряжений по длине стержня, т. е. когда стержень имеет
постоянное сечение, величина динамических напряжений зависит не
только от площади поперечного сечения стержня F, как это имеет
место при действии статической нагрузки в статически определимых
системах, но и от его длины I и модуля упругости материала Е. При
этом, чем больше объем материала, подвергаемого удару упругого
стержня, тем меньше возникающие в нем динамические напряжения.
С другой стороны, снижение напряжений при ударе в стержне
с выточкой может быть достигнуто путем уменьшения объема упру-
гого элемента за счет уменьшения площади утол-
щенной части и увеличения тем самым деформа-
тивности стержня. Этой же цели можно достиг-
нуть, взяв материал с более низким модулем
упругости; выравняв площади поперечного сече-
ния по длине стержня; увеличив длину стержня;
а также путем включения буферных пружин.
Учет массы стержня, испытывающего удар,
может быть осуществлен в предположении, что
после смятия и снижения скорости груза на
первом этапе от v до vlf равной скорости дви-
жения верхнего сечения стержня в начале второго
этапа удара, скорость нижележащих сечений умень-
шается по линейному закону, падая до нуля
в нижнем сечении (рис. 357), т. е. скорость в
любом сечении стержня на расстоянии х от
нижнего конца будет
1>(ж)
Соответствующая кинетическая энергия элементарною участка
стержня длиной dx в рассматриваемом сечении будет
Q
Рис. 357
I
2
”1
^Fl
т
а полная кинетическая энергия ударяемого стержня может быть
выражена формулой
т d
°~2g ’ I2
О
ИЛИ
т i
3 2g’
где Qg = yFl — собственный вес ударяемого стержня.
580
Выразим потерю энергии на смятие материала в месте соударе-
ния груза и стержня в течение первого этапа удара (когда скорость
изменяется от и = 2g Н до i^) формулой
ДГ == — — f— 4- -^1) = -2_ Гр» _ (1 . (21.13)
2g \2g^3-2g) 2g Г ^3Q/J-
Эту же потерю энергии можно выразить так:
дг=I(р -1,1)2 +1 § (° -1,1)2=р -2wi+** 0+§>)]•(21-и)
Приравняв правые части формул (21.13) и (21.14) и решив получен-
ное уравнение относительно v19 найдем
*1 ----V-77r- (21.15)
14-11°
ф 3 Q
Таким образом, кинетическая энергия, которая при ударе переходит
в энергию деформации ударяемого стержня, будет
-2g+3' 2g - / ±£p\-
2g V + 3 Q]
Подставив в (21.9) вместо Го полученное значение Г, выразим
коэффициент динамичности формулой
(21.16)
ст
или
кп
Лд = 1
(21.17)
Qu2
(1 4^ у Uct
v2 Qc
Учитывая,что » Я; HQ = Го, а также, обозначив = р, фор- .
мулу (21.17) перепишем в виде
*д=1
1 +
(21.18)
Максимальиое напряжение при ударе определится формулой
°д ~ ^даст сст I 1
То
1 +
или
сд — °ст
2EFH
ц_1££
+ 3 Q
581
Значения коэффициента, учитывающего массу ударяемого эле-
мента, для некоторых частных случаев приведены в табл. 50.
§ 117. Напряжение при скручивающем ударе
В случае ударного кручения, осуществляемого, предположим, по
схеме, приведенной на рис. 358, максимальные динамические напря-
жения в вале определятся по фор-
Здесь Н — высота падения груза; Q — вес падающего груза, Я —
радиус кривошипа; I — длина вала; J р, Wp — полярные момент
инерции и момент сопротивления сечения вала.
Динамические напряжения, возникающие в вале при резком
торможении быстро вращающегося маховика (рис. 359), имеющего
запас кинетической энергии То,
можно найти, также исходя из за-
кона сохранения энергии
ТО = С7Д, (21.21)
где С/д — потенциальная энергия
деформации вала при ударном кру-
чении.
Имея в виду, что
^кр.
2GJp ’
1
U — ~~М ф ==
Д 2 кр.дтд
(21.22)
и учитывая, что
, — МКР- ,?
Дтах Wp
или
ж тж7
кр. Д ТДтах Р 16 Тдтах ’
можно записать
и.
т* nW Т* IF
г Дтах Дщах
WGJp 2“ 4G
(21.23)
582
Подставив (21.23) в (21.21) и решив полученное уравнение отно-
сительно искомого максимального динамического напряжения, получим
<2,-24>
где кинетическая энергия маховика весом Q, вращающегося с угло-
вой скоростью (о, определится формулой
Т
о
j
2 \Л/
J 2 Т
“1 w ’ / =
QD2
8g
(V — диаметр маховика).
§118. Расчет на удар при изгибе
Максимальные динамические напряжения при ударном изгибе
могут быть определены по формуле
аД max ^дасттах
где _____
*д = 1+]/1 + у-
г /ст
(/ст — статический прогиб в месте удара, зависящий от схемы нагру-
жения и условий опирания).
В случае удара посредине балки с
изгибной жесткостью сечения EJ
(рис. 360) получим
/ a =
'от 48£J ’ CTmax W 4Т7 ’
а максимальные динамические напря-
жения в этом случае будут
а =Ь =_21Г1_1.
дтах д сттах 4РИ [
т/"д . 96ЯК7]
V 1+~оН'
Обозначив QH — То, будем иметь
, =Я(1 + 1/1 +
Дтах 4Ж\ V
Рис. 360
(21.25)
96Т0£/|
Q4* j*
Условие прочности в этом случае запишется так:
W (‘ + /* + ТЯ?) < (•«!• <2,-2«>
где
(^д-» запас прочности с учетом динамической нагрузки, ат— предел
текучести материала балки).
583
Учесть массу ударяемой балки можно, применив методику, рас-
смотренную при продольном ударе. Будем полагать, что в конце
первого этапа удара скорость балки в месте падения груза равна vt.
Qv{
Кинетическая энергия груза, очевидно, будет равна —. Предполо-
жим также, что при ударе и при статическом приложении нагрузки
(в нашем случае посредине пролета балки) изогнутая ось балки
может быть описана одним и тем же уравнением
Ql3
где f = — стрела прогиба балки.
Обозначив величину максимального прогиба посредине балки
через wmax, величину прогиба в сечении на расстоянии z от левого
конца балки определим по формуле
а скорость движения этого сечения — из выражения
dw 1/0,2 /
Кинетическая энергия элемента балки dz9 находящегося на рас-
стоянии z от левого конца балки, будет
а кинетическая энергия всей балки определится формулой
Z/2
2 f /«Чпах? 1 3 . . 3)2 . _ 17 1FZ ЛЧпахУ
б .) гД~/ Z» (<5Zz 4г) <й-35 •
О
Поскольку в конце первого этапа удара скорость посредине балки
равна 1?х, т. е.
dw^n^
max
dt “ ь
то кинетическая энергия балки в начале второго этапа удара будет
r8 = g (21.27)
Выразив потерю энергии на смятие в месте удара за первый
этап в виде
Qv^ (<М 17 yFl Л Q Г 2 аЛ 17 jFZn
ДГ~-2Г V2? + 35 V V_2Fl- Ч +35 Q /] ’
584
или
+ .15)], ,209)
а затем, приравняв правые части уравнений (21.28) и (21.29) и решив
полученное уравнение относительно vt, найдем
Кинетическая энергия системы (балка —груз), которая должна
трансформироваться в энергию деформации балки при ударе, опре-
делится формулой
„ 2
T_Qvi 17 yFl 2 Qv2 1
2g + 35 ' 2g Vi ~ 2g . , 17 iFl'
1+35 V
Обозначив
T _n„
формулу (21.31) можем переписать в виде
у»_________Л)
17 4FI ‘
1 ' 35 V
(21.31)
(21.32)
Максимальное динамическое напряжение согласно формуле (21.25)
после замены в ней Го на Т определится так:
°Л =hU1+V14'
Дтах 4Ж \ т
эвтяЛ
Q4* )’
или с учетом (21.32)
а
Дтах
1 +
96T0EJ
\ ии /
(21.33)
_ ь в - V*
Д сттах ~ 4Ж
где
fcn = l +
(21.34)
585
Таблица 50
Значения коэффициента а, учитывающего массу ударяемого
элемента в формуле коэффициента динамичности
1+j/'1±BCT(l+a.₽) 1+ j/'1 + gBCT(14-a. Р)
Н — высота падения ударяющего тела; и — скорость ударяющего тела
в момент начала удара; &ст — деформация ударяемого упругого эле-
мента при статическом приложении силы, равной весу ударяющего
тела; £ = , где Q9J1 — вес ударяемого элемента, Q — вес ударяю-
щего тела; g —ускорение силы тяжести
Схема упругого элемента
и характер его нагружения
1/3
Fi + Ft + VFiFt
67
336
586
Продолжение табл. 60
Глава 22
КОНТАКТНЫЕ НАПРЯЖЕНИЯ
§ 119. Основные понятия и формулы для определения
контактных напряжений и деформаций
Напряжения и деформации, возникающие при взаимном нажатии
двух соприкасающихся тел, называются контактными. Материал
в месте контакта, не имея возможности
свободно деформироваться, находится
в объемном напряженном состоянии
(рис. 361). Контактные напряжения
имеют чисто местный характер и весьма
быстро уменьшаются по мере удаления
от места соприкосновения. Контактным
напряжениям следует уделять сущест-
венное внимание при расчете на проч-
ность таких деталей, как шариковые
и роликовые подшипники, зубчатые
колеса, колеса подвижного состава,
рельсы и т. п.
Впервые правильное решение ос-
новных задач о контактных напряжениях и деформациях было про-
ведено методами теории упругости в 1881—1882 гг. Г. Герцем.
Ниже приведены некоторые формулы для определения контакт-
ных напряжений и деформаций, полученные при следующих пред-
положениях:
1) напряжения в зоне контакта не превышают предела упругости;
2) площадки контакта малы по сравне-
нию с поверхностями соприкасающихся
тел;
3) силы давления, распределенные по
поверхности контакта, нормальны к этой
поверхности.
Сжатие шаров. Радиус круговой пло-
щадки а (рис. 362), образующейся в месте
контакта при взаимном нажатии силой Р
двух шаров с радиусами R± и и моду-
лями упругости материала соответственно
Ег и Е2, определяется по формуле
а = 0,88
1
jL. (22.1)
1
Нормальные (сжимающие) напряжения на площадке контакта
распределены по полусфере. Наибольшее напряжение, имеющее место
588
в центре площадки контакта, может быть определено по формуле
Р EfEl
а3 = „ а 1 = „ 1,5-4- =-0,388 4Р---------
тах ’па2 (£ _|_ е )2
(Ях + Я2)г
Rl-Rl
(22.2)
Два других главных напряжения в центре площадки равны:
а1 = а2 = — 0,8|стах|.
Благодаря объемному напряженному состоянию материала
в центре площадки контакта, при котором все три сжимающие
Р
Рис. 363
Рис. 364
напряжения практически одинаковы, материал здесь может выдер-
живать без появления остаточных деформаций весьма большие дав-
ления, составляющие, например, согласно четвертой теории прочно-
сти величину атах = 5ат. Для стали, у которой спц = 10000 кГ1 см2,
°тах Достигает 50 000 кГ/см2.
Наиболее опасная точка в зоне контакта расположена на оси z,
на глубине, равной примерно половине радиуса площадки касания.
Главные напряжения в этой точке равны:
С1 = О2 = ₽- о,18атах; а3 = - о,8атах, (22.3)
где стах определяется по формуле (22.2).
Наибольшее карательное напряжение в опасной точке
ттах 1 2 3 0’3 ^тах* (22.4)
Максимальные напряжения, возникающие в площадке при дав-
лении шара на вогнутую сферическую поверхность с радиусом Т?2
(рис. 363), получим по формуле (22.2), заменив в ней знак при R2
на обратный:
® / EiE22
omax = 0,3881/ 4Р--------
шах V (Ey + Е,)
(R2-R1)2
RfRl
(22.5)
589
При давлении шара радиусом = R на плоскость (рис. 364),
напряжения определим по формуле (22.5), приняв в ней Л2= оо;
® / £? El 1
.„„-ода|/ —
(22.6)
Сжатие цилиндров. При взаимном сжатии равномерно распреде-
ленной нагрузкой q двух цилиндров, соприкасающихся параллель-
ными образующими (рис. 365), ширина прямоугольной площадки
контакта определяется по формуле
(22.7)
Наибольшее напряжение, действующее в точках оси площадки каса-
ния, определяется формулой
- U7 f - 0,413 /2, -jbA- (22,3)
Опасная точка в зоне контакта находится на оси z на глубине,
равной 0,45. Главные напряжения в этой точке имеют следующие
значения:
01 = —0,180ашах;
о2 = 0i288amax
о8 = — °,780атах.
(22.9)
Максимальное касательное напряжение в опасной точке
ттах 0>Затах.
(22.10)
590
Изменив в формуле (22.8) знак при Л2 на обратный, получим напря-
жение в случае давления цилиндра на вогнутую цилиндрическую
поверхность
5-й. (22.1!)
При взаимном давлении цилиндра радиусом Rt = R и плоскости,
приняв в (22.8) Я2 = оо, найдем
(22.12)
Приведенные выше формулы получены при коэффициенте Пуас-
сона р = 0,3. Однако в практических расчетах они пригодны и при
других значениях р.
В общем случае контакта двух тел из одинакового материала,
сжимаемых силой Р в направлении оси z (рис. 366) и касающихся по
плоскости АВ, при радиусах кривизны первого тела рх и р/; второго
тела р2 и р2' (полагаем, что р1<р/; р2 < р2) полуоси образующейся
эллиптической площадки контакта определяются формулами:
(22.13)
(22.14)
где р— коэффициент Пуассона.
Ниже приведены значения коэффициентов аир как функций
вспомогательного угла ф, вычисляемого по формуле
(22.15)
где ср — угол между главными плоскостями кривизны тел, в которых
лежат радиусы pi и р2. Знаки в формуле (22.15) выбираются так,
чтобы соэф был положительным.
591
фО а Р ф® а Р
20 3,778 0,408 60 1,486 0,717
30 2,731 0,493 65 1,378 0,759
35 2,397 0,530 70 1,284 0,802
40 2,136 0,567 75 1,202 0,846
45 1,926 0,604 80 1,128 0,893
50 1,754 0,641 85 1,061 0,944
55 1,611 0.678 90 1,000 1,000
Наибольшее напряжение в центре площадки контакта
атилт = ----г
шах тсаб
(22.16)
Наиболее опасная точка расположена на оси z на некоторой глубине,
зависящей от отношения —.
а
Максимальное касательное напряжение не зависит от указанного
отношения и равно
ттах ” 0»32°тах-
(22.17)
Как следует из приведенных формул, контактные напряжения
зависят от упругих свойств материала и не являются линейной
функцией нагрузки, так что темп их роста отстает от темпа увеличе-
ния сжимающей нагрузки. Это объясняется тем, что с увеличением
нагрузки увеличиваются и размеры площадки контакта. В табл. 51
приведены расчетные формулы для определения параметров контакта
двух тел (коэффициентов А и В уравнения эллипса касания, раз-
мера площадки контакта, наибольшего контактного напряжения
атах и взаимного сближения Д) Для упрощения вычислений по при-
веденным формулам в табл. 52 даны значения входящих в них коэф-
фициентов па, пь, пр, в зависимости от отношения А и В.
§ 120. Проверка прочности
при контактных напряжениях
Проверку прочности при контактных напряжениях следует произ-
водить по третьей или четврртой теории прочности:
%кв ш =ai —
1 / 1
®экв IV = У 7 I (°1 — °s)2 + («г — °з)2 + (®з — «1)2 < [«]•
592
Подставив в эти формулы ах, а2» аз» выраженные через атах в центре
площадки контакта, запишем условия прочности в виде
аэкв=татах<[°1- (22.18)
откуда
amax < т М fа]конт»
где [<*]конт = допускаемое напряжение для наибольшего напря-
жения в месте контакта. Значения коэффициента т в зависимости от
Ъ
соотношения полуосей эллиптической площадки — приведены ниже
ъ.
а
аэкв III
т » ———
стэкв IV
т —----------
сттах
1 (круг) 0,620 0,620
0,75 0,625 0,617
0,50 0,649 0,611
0,25 0,646 0,587
0 (полоса) 0,600 0,557
Можно рекомендовать следующий порядок расчета на прочность
элементов конструкции в местах контакта:
1. Определить главные радиусы кривизны контактирующих тел
Pi> Р1> Ра, р2Г ’ а также угол у между их главными плоскостями
кривизны.
2, Вычислить по формулам (22.13) и (22.14) с учетом (22.15)
размеры полуосей эллиптической площадки контакта.
3. По формуле (22.16) определить отах, а в случае круглой
и прямоугольной площадок контакта по формуле (22,2) или (22.8)
соответственно, не определяя размеров площадки.
4. Расчет на прочность можно производить по формуле (22.18),
находя значения т по вышеприведенной таблице. При этом рекомен-
дуется исходить из четвертой теории прочности.
5. Для роликовых и шариковых подшипников Нконт =
== 35000 ч- 50000 кГ/см2 для рельсовой стали — 8000 ч-10000 кГ/см2.
В табл 53 приведены наибольшие допускаемые давления
на площадке контакта при первоначальном контакте по линии
(тп, = 0,557) и статическом нагружении В случае первоначального
контакта в точке значение [о]конт следует увеличить в 1,3 ч-1,4
раза.
593
Расчетные формулы для определения параметров контакта двух тел
Схема касания
Коэффициенты уравнения эллипса касаний
А В
Размеры площадки контакта
Два сфериче-
ских тела
*1 + ^2 7?i + Т?2 2R1R2 a = b~ 0,9086 X d Г 2 . ,2. х 1/ Р -^2) г 1~г *'2 \ Ь2 / Если 2?! = /?2 == И а = 6 = 1,1091/4 ТГЙГ F С' «! -j- П2
Шар и сфери-
ческое углуб-
ление
Т?2 Rj Т?2
2Z?i R2 2RtR2
R%^> 7?1
a~b~ 0,9086 x
Если Er = E2 = Ё
7?i7?2
T?2 — 7?x
594
Таблица 51
Наибольшее напряжение, «тах
Сближение соприкасающихся тел, Д
0,8255 X
и = р.2 = 0,3, то
0,388 тЛ РЕ2 .
1
тах т = "3 атаХ;
max = 0,133стах
1,231
2?! + /?2
2?i R2
ш
0,5784 X
0,8255 X
и = рь2 = 0,3, то
тахт = Аатах
max Ci = 0,133ста_
*- ' JlluX
595
Схема касания
Сферическое
тело и плос-
кость
Коэффициенты
уравнения эллипса
касания
А | В
1 1
2R 2R
Размеры площадки контакта
а = b = 0,9086 X
Если Ег = Е2 — Щ
Сферическое
тело и цилиндр
Если Ег == Е2 = Е
д = 1,397пь1/4~2ДД1+2Д
Т Ja £Jti2 -j- /ц
596
Продолжение табл. 51
Схема касания
Коэффициенты
уравнения эллипса
касания
Размеры площадки контакта
Сферическое
тело и цилинд-
рический же-
лоб
1
а = l,145na X
b — 1,145«ь X
Если Ег = Е2 = j
Сферическое
тело и круго-
вой желоб
(шариковый
подшипник)
7?з
598
Продолжение табл 51
Наибольшее напряжение, °шах Сближение соприкасающихся тел, Д
0,365пр X 0,655пд X
з Г /2Д2-Д1У 1/ р V д1д* 1 х I/ Т \ я, + е2 ) и [л1 = |л2 = 0,3, то X 1 / Р2 2Д2-Д1 + 1-112 |/ ЯХЯ2 Ях 1 Ег )
0,245пр"|/ РЕ2 pfo РД^ * \ •**! “2 / 0,977ид У (-У]
0,365пр X 0,655пд х
еи 1 со еч сч OS i + J. ” -к + । е* тч I 1 diit а, X X X ъ ьэ ьо 1 1 -г - + х
И Р-! = Р-2 = 0,3, ТО
з Г /2 1 1 V
0,2&р]/ РР
2 1 1
Ях я2 + Я,.
599
Схема касания Коэффициенты уравнения эллипса касания А | В Размеры площадки контакта
a = 1,145тго X
Роликовый
подшипник
1 / 1
2 \P2
4 2 л 2
t — Н 1 — р-2
E.
b = 1,1457гь X
E
Да_____
1 1
я3 я4
4 2 л 2
1 — Pi , 1 — Ра
Если Et — E2~ E
a = l,397no
P
E
1_ 1 1___1_
Ri + Я,+ Я, Я4
b = l,397nb
p
E
600
Продолжение табл, 51
Наибольшее напряжение, ®тах
Сближение соприкасающихся тел, Д
и |лх = |Л2 = 0,3, то
0,245пр х 0,977лд х
3 Г /1 1 1 1 \2 а? - <4 «1 cq а* я а. |ft) '
601
Схема касания Коэффи уравнена касг А тшенты я эллипса 1НИЯ В Размеры площадки контакта !
Цилиндры со
взаимно пер-
пендикуляр-
ными осями
1
2Ra
1
2Я2
а = l,145na X
b = 1,145пь X
Пр^
а = b — 0,9086 X
Если Ег = Е2 = Е
Л ОЛГ, R1R*
Ь-1,397», j/-/
Г & п.% ~f- £1^
Пр«
а = Ъ = 1,109-~
602
Продолжение табл. 51
Наибольшее напряжение, «щах
Сближение соприкасающихся тел, Д
0,365np X
0,655пд X
R1 — R% — R
WTlnb
1 /!?]*№
У \EJ R1R2
603
Схема касания Коэффициенты уравнения эллипса касания А | В — —— Размеры площадки контакта
Полуширина полоски контакта
Цилиндры
с параллель-
ными осями
1/ 1
2 \ R
1
R*
Р Rt r2 Р - н
I Rt+RA Е,
Ь « 1,128 х
2,
При?
Ь = 0,798 X
2
Р-1
'2
Если Ег~ Е2~ Е
6 = 1,522 J /2_ Д1Д2 IE + При
6 = 1,076
604
ITродолжение табл, 51
Наибольшее напряжение, атах
0,5642 X
7?! — /?2 — R
и у-х == р.2 = 0 А то
Сближение соприкасающихся тел, Д
[, 2 , х
(in ^14-0,407) +
/^1 \ о ]
1 — 1W, 2R, , Л ,м
In 4-0,407
е2 \ Ъ 1
Г(1п -^-4-0,407) X
nl b J
iA 2 А 2\ П
/1 — Р-1 . 1 — ^2\ I
Х\ Et + Е2 /J
0,418
PER1-\-R2
I Я1/?2
0,5796 - J- (in 4- 0,814)
— /?2 — R
0,591 У
Р I 4R2 \
0,5796-jg-(h 4- 0.814J
605
Схема касания
Коэффициенты
уравнения эллипса
касания
Размеры площадки контакта
А В
Цилиндр
и цилиндриче-
ская впадина
с параллель-
ными осями
1 / 1
2 \ Я/
rJ
Полуширина полоски контакта
b = 1,128 X
Если Ег = Е2 — Е
b = 1,522
Я1 Я2
/?2 — R1
Цилиндр
И плоскость
1
2П
Полуширина полоски контакта
д = 1,131 X
Если Ег = Е2 = Е
Два тела, огра-
ниченные
криволиней-
ными поверх-
ностями и
соприкасав-
шиеся до де-
формации в
одной точке
Большая полуось эллипса
Малая полуось эллипса
Р — нагрузка, Е —•> модуль упруго-
сти; р. — коэффициент Пуассона;
1 и 2 — индексы, соответствующие
первому и второму телам; —
сумма главных кривизн поверхно-
стей соприкасающихся тел в месте
первоначального контакта
606
Продолжение табл. 51
Наибольшее напряжение, атах Сближение соприкасающихся тел, Д
Г R2 — R1 0,5642-1 / М г / 1 — н 1— ;л2 Г Ех 1 Е2
и Р-1 = 1Х2 = 0,3, то
РЕ R2 — R.
I
1,82(1 - In b)
и H-i = ^2 = 0,3, то
Уменьшение размера диаметра ци-
линдра между двумя сжимающими
его гранями (с учетом контактных
и общих деформаций цилиндра)
Р I 4Я\
ДП= 1,159-~г 0,41 + In^H
IE \ Ъ /
1
2 Х
607
Таблица 52
Численные значения коэффициентов na, пр, пд
А В Пв пь Пр Лд
1,0000 1,000 1,0000 1,0000 1,0000
0,9623 1,013 0,9873 0,9999 0,9999
0,9240 1,027 0,9742 0,9997 0,9997
0,8852 1,042 0,9606 0,9992 0,9992
0,8459 1,058 0,9465 0,9985 0,9985
0,8059 1,076 0,9318 0,9974 0,9974
0,7652 1,095 0,9165 0,9960 0,9960
0,7238 1,117 0,9005 0,9942 0,9942
0,6816 1,141 0,8837 0,9919 0,9919
0,6384 1,168 0,8660 0,9890 0,9889
0,5942 1,198 0,8472 0,9853 0,9852
0,5489 1,233 0,8271 0,9805 0,9804
0,5022 1,274 0,8056 0,9746 0,9744
0,4540 1,322 0,7822 0,9669 0,9667
0,4040 1,381 0,7565 0,9571 0,9566
0,3518 1,456 0,7278 0,9440 0,9432
0,3410 1,473 0,7216 0,9409 0,9400
0,3301 1,491 0,7152 0,9376 0,9366
0,3191 1,511 0,7086 0,9340 0,9329
0,3080 1,532 0,7019 0,9302 0,9290
0,2967 1,554 0,6949 0,9262 0,9248
0,2853 1,578 0,6876 0,9219 0,9203
0,2738 1,603 0,6801 0,9172 0,9155
0,2620 1,631 0,6723 0,9121 0,9102
0,2501 1,660 0,6642 0,9067 0,9045
0,2380 1,693 0,6557 0,9008 0,8983
0,2257 1,729 0,6468 0,8944 0,8916
0,2132 1,768 0,6374 0,8873 0,8841
0,2004 1,812 0,6276 0,8766 0,8759
0,1873 1,861 0,6171 0,8710 0,8668
0,1739 1,916 0,6059 0,8614 0,8566
0,1603 1,979 0,5938 0,8507 0,8451
0,1462 2,053 0,5808 0,8386 0,8320
0,1317 2,141 0,5665 0,8246 0,8168
0,1166 2,248 0,5505 0,8082 0,7990
0,1010 2,381 0,5325 0,7887 0,7775
0,09287 2,463 0,5224 0,7774 0,7650
0,08456 2,557 0,5114 0,7647 0,7509
0,07600 2,669 0,4993 0,7504 0,7349
0,06715 2,805 0,4858 0,7338 0,7163
0,05797 2,975 0,4704 0,7144 0,6943
0,04838 3,199 0,4524 0,6909 0,6675
0,04639 3,253 0,4484 0,6856 0,6613
0,04439 3,311 0,4442 0,6799 0,6549
0,04237 3,373 0,4398 0,6740 0,6481
0,04032 3,441 0,4352 0,6678 0,6409
0,03823 3,514 0,4304 0,6612 0,6333
608
Продолжение табл, oz
А В па пь Пр Пд
0,03613 3,594 0,4253 0,6542 0,6251
0,03400 3,683 0,4199 0,6467 0,6164
0,03183 3,781 0,4142 0,6387 0,6071
0,02962 3,890 0,4080 0,6300 0,5970
0,02737 4,014 0,4014 0,6206 0,5860
0,02508 4,156 0,3942 0,6104 0,5741
0,02273 4,320 0,3864 0,5990 0,5608
0,02033 4,515 0,3777 0,5864 0,5460
0,01787 4,750 0,3680 0,5721 0,5292
0,01533 5,046 0,3568 0,5555 0,5096
0,01269 5,432 0,3436 0,5358 0,4864
0,009934 5,976 0,3273 0,5112 0,4574
0,007018 6,837 0,3058 0,4783 0,4186
0,003850 8,609 0,2722 0,4267 0,3579
Таблица 53
Допускаемые давления на площадке контакта при первоначальном
контакте по линии и статическом нагружении
Марка металла Временное сопротивле- ние, кГ/мм* Твердость по Бринелю Допускаемое максимальное давление на площадке контакта [°1конт» кТ7слс8
Сталь
30 48—60 180 8500-10500
40 57—70 200 10000—13500
50 63-80 230 10500—14000
50Г 65—85 240 11000—14500
15Х 62—75 240 10500—16000
20Х 70—85 240 12000—14500
15ХФ 160—180 240 13500—16000
ШХ15 г—» — 38000
Чугун СЧ21-40 96 180—207 8000—9000
СЧ24-44 100 187—217 9000—10000
СЧ28-48 НО 170—241 10000—11000
СЧ32-52 120 170—241 11000—12000
СЧ35-56 130 197—255 12000—13000
СЧ38-60 140 197—255 13000—14000
20 5-1186
609
Дополнение
ДЕВЯТЬ НОВЫХ АНАЛОГИЙ В СОПРОТИВЛЕНИИ
МАТЕРИАЛОВ
В работах [30,31] предложены девять новых аналогий, базирую-
щихся на идентичности дифференциальных уравнений в задачах
нахождения для стержней продольных сил и продольных перемеще-
ний при осевом растяжении — сжатии, угловых деформаций и угло-
вых перемещений при кручении, угловых деформаций и сдвиговых
линейных перемещений при сдвиге, обобщенных поперечных сил
и изгибающих моментов, углов поворота и прогибов при изгибе.
Ниже формулируются эти аналогии.
Аналогия 1. Задачи нахождения продольных сил и перемеще-
ний при осевом растяжении — сжатии стержня эквивалентны задачам
нахождения обобщенных поперечных сил и изгибающих моментов при
изгибе взаимной балки. Условия эквивалентности и взаимности
таковы:
п (х) — 9 (*) (Д-1)
ЕЕ (х)
N (х) * <?* (®) (Д.2)
ЕЕ (х)
и (х) 2; М (я). (Д.3)
Здесь п(х) — интенсивность распределенной продольной нагрузки;
q (х) — интенсивность распределенной поперечной нагрузки; N (х) —*
продольная сила; EF (х) — жесткость при растяжении — сжатии;
Q* (х) — обобщенная поперечная сила, Q* (х) = Q (х) + т (х), и (х) —»
продольное перемещение; М (х) — изгибающий момент; т (а?) — интен-
сивность распределенной моментной нагрузки.
Аналогия 2. Задачи нахождения продольных усилий и переме-
щений при осевом растяжениисжатии стержня эквивалентны зада-
чам нахождения угло$ поворота и прогибов при изгибе взаимной балки.
Условия эквивалентности и взаимности таковы:
п (х) у М (х) (Д.4)
EF (х) EJ(x)_'
N(x) , Ч а (х)\ ЕЕ (х) v л (Д-5)
u(a?) £ w(x). (Д-6)
Здесь EJ (х) — жесткость при изгибе; а (х)—угол поворота; w (х) —
прогиб.
610
Аналогия 3. Задачи нахождения угловых деформаций и линей-
ных сдвиговых перемещений при сепарированном сдвиге стержня экви-
валентны задачам нахождения продольных сил и продольных перемеще-
ний при растяжении •- сжатии взаимного стержня.' Условия эквива-
лентности и взаимности таковы:
9 (ж) Л п (Д-7)
GF(x) * EF (х) '
N (х) . (Д-8)
EF (ж) ’
£ и (х). (Д.0)
Здесь GF (х) — жесткость при сдвиге; к — коэффициент, характери-
зующий неравномерность распределения касательных напряжений по
высоте сечения; 7 (х) относительный сдвиг (угловая деформация);
v{x) — сдвиговое линейное перемещение.
Аналогия 4. Задачи нахождения угловых деформаций и линей-
ных сдвиговых перемещений при сепарированном сдвиге стержня экви-
валентны задачам нахождения угловых деформаций и угловых переме-
щений при кручении взаимного стержня. Условия эквивалентности
и взаимности описываются формулами:
q(х) к ткW
GF(x) GJ*(x) ;
7 (*) £ в (а?),
v (a?) <Р (*)•
(Д.Ю)
(Д.Н)
(Д.12)
Здесь /пк (х) — интенсивность распределенной крутящей нагрузки;
GJK W жесткость при кручении; 0 (о?)—угловая деформация (отно-
сительный угол ^закручивания); ср (а?)—угловое перемещение (угол
закручивания).
Аналогия 5. Задачи нахождения крутящих моментов и углов
закручивания при кручении стержня эквивалентны задачам нахождения
обобщенных поперечных сил и изгибающих моментов при изгибе взаим-
ной балки. Условия взаимности и эквивалентности таковы:
т«№ / X GJK (х) * q (Ж)’ (Д-13)
М (а;) GJk(x} (Д14)
<Р (®) Z м (х). (Д15)
Здесь Мк (а?) крутящий момент.
2С*
611
Аналогия 6. Задачи нахождения продольных сил и переме-
щений при растяжении — сжатии стержня эквивалентны задачам
нахождения крутящих моментов и углов закручивания при кручении
взаимного стержня. Условия взаимности и эквивалентности таковы:
п (®) тк (®)
EF (х) GJK (х) '
N (х) мк(х)
EF (х) * GJK(x) :
и (®) +- <Р («)•
(Д-16)
(Д-17)
(Д18)
Аналогия 7. Задачи нахождения угловых деформаций и линей-
ных сдвиговых перемещений при сепарированном сдвиге стержня экви-
валентны задачам нахождения обобщенных поперечных сил и изгибаю-
щих моментов при изгибе взаимной балки Условия эквивалентности
и взаимности таковы:
(Д-19)
(Д20)
(Д-21)
Аналогия 8. Задачи нахождения угловых деформаций и линей-
ных сдвиговых перемещений при сепарированном сдвиге стержня экви-
валентны задачам нахождения углов поворота и прогибов взаимной балки.
Условия взаимности и эквивалентности выражаются формулами:
g (ж) ^М(х).
GF EJ ’
v(xyZw (х)\
7 (») $ « (»)•
(Д-22)
(Д-23)
(Д-24)
Аналогия 9. Задачи нахождения крутящих моментов и углов
закручивания при кручении эквивалентны задачам нахождения углов
поворота и прогибов взаимной балки при изгибе. Условия взаимности
и эквивалентности таковы:
Шк{х) М(х)
GJK(x) *- EJ (х) ’’
(Д-25)
Мк(»)
G7K(®)
3.а (»).
(Д-26)
sWJ м (»);
(Д-27)
612
Проиллюстрируем некоторые аналогии примерами, взятыми из
указанйых статей.
Пример 1. Тяжелый призматический стержень находится под
действием силы тяжести, представляющей собой осевую равномерно
распределенную нагрузку интенсивностью п (а?) — ^F (рис. 367, а).
Здесь F — площадь поперечного сечения; 7 — объемный вес. Покажем
для этого случая применение аналогии 1. В заданном стержне гра-
ничные условия таковы: при а? = 0 и = 0 и при а? =±= Z и = 0. В соот-
ветствии с (Д.З) взаимный стержень должен быть выбран так, чтобы
Рис. 867
изгибающие моменты по концам равнялись нулю. Этому условию
удовлетворяет балка на двух опорах (рис. 367, б). В соответствии
- F*t 7
с (Д.1) фиктивная нагрузка для этой балки q (х) = —~----------2”’
где Е— модуль упругости. Теперь достаточно для этой взаимной
(фиктивной) балки построить от фиктивной нагрузки две эпюры:
поперечных сил (рис. 367, в) и изгибающих моментов (рйс. 36), г).
Первая эпюра в соответствии с (Д.2) представляет эпюру продольных
N (х)
сил , вторая — эпюру продольных перемещении.
Пример 2. Тяжелый призматический брус закреплен у верх-
него конца (рис. 368, а) и находится под действием собственного
веса. Покажем и на этом примере применение аналогии 1. Граничные
условия здесь таковы: при х == О N = 0 при х = I и~0. В этом
случае взаимная балка должна быть выбрана так, чтобы поперечная
сила на одном конце и изгибающий момент на другом равнялись
нулю. Соответствующая балка показана на рис. 368, б. Эпюра Q (х)
N (х}
(рис. 368, в) соответствует эпюре , а эпюра М (х) (рис. 368, г)
соответствует эпюре и (х).
Пример 3. Для стержня, показанного на рис. 369, а, применим
аналогию 2. В соответствии с (Д.6) граничные условия во взаимной
балке должны быть таковы, чтобы по концам прогибы равнялись
нулю. Этим условиям удовлетворяет балка, показанная на рис. 369, б.
613
7 М
В соответствии с (Д.4) = -ттг представляет собой моментную
iii thJ
нагрузку, а потому эпюры Q(x) (рис. 369, в) и М (х) (рис. 369, г) от
этой нагрузки будут эпюрами углов наклона и прогибов, которые
N (х) . ч
в свою очередь являются эпюрами —- и и(х).
Пример 4. Защемленный с двух концов круглый вал закру-
Рис. 368
Рис. 369
чивается равномерно распределенными крутящими моментами интен-
сивностью (рис. 370, а). Покажем на этом примере приложение
аналогии 5. Граничные условия в заданном стержне таковы: при
= 0 !р = 0 и при х—1 9 = 0. В соответствии с (Д.15) во взаимном
стержне на концах изгибающие моменты должны равняться нулю.
Взаимная балка показана на рис. 370, б. Фиктивная нагрузка
614
q(x) = . В соответствии с (Д.14) и (Д.15) опюра Q(x) соответ-
«ZldT (•£)
ствует — (рис. 370, в), а эпюра М (х) — эпюре углов закручива-
ли
ния ср (х) (рис. 370, г).
Пример 5. Ступенчатый вал (рис. 371, а) закручивается двумя
сосредоточенными моментами. Взаимная балка постоянного попереч-
Рис. 370
Рис. 371
ного сечения, по продольным размерам и схеме нагружения соответ-
ствующая исходному валу, но с приведенными значениями длин,
т. е. с различным масштабом приведенных участков, показана на
рис. 371,6. Здесь Jp и Jp — полярные моменты инерции сечений
вала слева и справа. Теперь для решения задачи осталось построить
две эпюры Q и М (рис. 371, в, г).
Подобным образом могут быть применены для решения задач
и другие аналогии. Приведенные аналогии значительно расширяют
возможности эффективного использования материала справочника. Ряд
данных, относящихся к одному виду напряженно-деформированного
состояния стержня, может быть с помощью аналогий использован
при рассмотрении других видов деформаций.
615
физико-механические свойства материалов
(для ориентировочных расчетов)
ав —предел прочности при растяжении (для дерева —вдоль волокон);
ос —предел прочности при сжатии (для дерева —вдоль волокон);
си —предел прочности при изгибе;
тв —предел прочности при кручении;
тср — предел прочности при срезе (для дерева —вдоль волокон);
%ц — предел пропорциональности при растяжении;
ат —предел текучести при растяжении;
Материал Предел прочности, кГ/мм* Предел текучести, пропор- циональности, кГ/мм2 Предел выносливо сти, кГ/мм2
ГОСТ 380 — 60 об: Углеродистые ыкновенного
Ст. 1 св = 32 — 40 от = 18 ю счел 1 1 1 СМ СО ОО II IIII & r-i тн 7 1 1 1 О Р о
Ст. 2 ав = 32 —40 ат = 19—22 Q а о | 1 1 Jr i_l м II II U t-Л- 1-Л. 00 •<! Ю WW 05
Ст. 3 ов = 38 — 47 "т = 21 — 24 а__1р = 12 —16 ^ = 17 — 22 T_t = 10 — 13
Ст. 4 ов = 42 —52 ат = 24 —26 с_1 = 19 —25
Ст. 5 ов = 50 — 62 ат = 26 - 28 см ооо см со 1 1 1 ь* см со II II II Р, 14 7 „U о
Ст. 6 <зв = 60 — 72 ат = 30-31 м 1 II II II h^to СП СП СО 1 1 1 to со to СП
специального
ГОСТ 5520 — 62
15К 20К II II Ё 00 II II to to СО 1 1 to ьо СП со
616
Приложение 1
со 1 — условный предел текучести при растяжении (деформация 0,1%);
°т. с — пРеДел текучести при сжатии;
°т. и предел текучести при изгибе;
а_1р — предел выносливости при растяжении;
сиг —предел выносливости при изгибе;
г —предел выносливости при кручении.
Относи- тельное удлинение (относи тельное сужение), % Твердость по Бри нелю, кГ/лш2 Ударная вязкость, кГм/см3 Модуль упругости Коэффи циепт Пуассона Удельный вес, г/слх3 Коэффициент линейного расширения. х10’грау
стали
качеств а***
28 110 — — — — —
26 116 — — — — —ч
21—23 131 7—10 — — — —*
19—21 143 6-8 —— — — в—4
15-17 170 — «в—• ! —i
н а з н а \ чения ’— в. л 1 — г—Э
23 — 7—8 — — ч
22 — 6—7 — г
6
Материал Предел прочности, кГ/мм2 Предел текучести, пропор- циональности, кГ/мм2 Предел выносливости, кГ/мм2
ГОСТ 6713 « 53 Ст. 3 мост. М16С и* wQ II II СО СО 00 00 II II Ю tO СО Ф* *—
ГОСТ 1414 « 54 А12 А40Г в°в° II II о to 3 1 w У —
качествен
ГОСТ 1050 = 60 10 а = 34 — 42 В °т = 21 ггГ н н *О IIII II t-Sb оо а» to 11 1 t^tO to to СП
20 ав = 42 —50 °т = 25 CD (М СО ч* СМ’*-* 1 11 см ь-о "ГН II II II О. «Ч гН 7 J J о
30 ов = 50 — 60 °т = 30 °—1р = 17-21 а , =20 — 27 T—j ==11 — 14
40 ав = 58 70 °т = 34 СМ О7> см оо^ 1 11 оо со II II II ТЛ' о
45 ав = 61 - 75 °т = 36 ггГ м м *о II Ik II h^to h* СП СП CD 1 и ю со to ОФ* СП
50 ав = 64 = 80 °т = 38 CD НО ч-< СМ СО СМ 1 11 о t"-CD (М СМ^н II II II cu r-i ft 7 J J о
60 ов = 69 — 90 = 41 &3S3 1 11 <М ^00 CM II IIII Си т-1 1-1 1JJ и
зог ;в = 55 - 70 °т = 32 а_, = 22 — 32
60Г *в = 71 ат = 42 о_1р = 25 —32
618
Продолжение приложения 1
Относи тельное удлинение (относи- тельное сужение), % Твердость по Бри нелю, кГ/мм2 Ударная вязкость, кГм/см2 Модуль упругости £(<?), X10-"4 кГ/мм2 Коэффи- циент Пуассона Удельный вес, 0/см3 Коэффициент линейного расширения* Х10‘ -Ц- град
22 (50) 7—10
22 (50) — 7—10 — — —
22 (36) 160 2,02 — 11,9—14,2
14 (20) 207 — — — —
ные***
31 (55) — — 1,90 1— 7,83 11,6-14,6
25 (55) — — 2,02 — 7,82 11,1—14,4
21 (50) — 8 — 7,82 12,6—15,6
19 (45) — 6 2,135 — 7,81 12,4—14,6
16 (40) — 5 2,04 — 7,81 11,6—14,7
14 (40) — , 4 2,20 — 7,81 12,0—14,1
12 (35) — 2,08 — 7,80 11,1—14,6
20 (45) — 8 2,17 — 7,81
И (35) — — 2,109 7,81 11,6—14,6
619
Материал Предел прочности, КГ/ЛМС2 Предел текучести, пропор- циональности, кГ/мм2 Предел выносливости, кГ/мм2
ГОСТ 5058 — 65 Легированные
15ХСНД ГОСТ 4543 — 61 Ов = 64 — 66 ат = 39-42 = 31 T_i = 16
20Х <jb = 72 - 85 е, = 40 - 65 а а 1 1 II II ьо со СО QO
40Х ав = 73 — 105 от = 65 — 90 Г1° 1 М Н II II II ЬО СО ьэ ь* ЬО 1 1 1 ЬО со огоо
45Х ав = 85 — 105 ат = 70 - 95 с_х = 40 — 50
ЗОХМ ав = 74 — 100 от = 54-85 5 о- СО со со сч II II II Q, i-Ч ГЧ 7»',' о
40ХН ов == 100 — 145 ат = 80 — 130 °—1р = 31—42 а_х = 46 — 60
12ХНЗА ав =з 95 140 а, = 70 —110 а_х = 42 — 64 т_! = 22 — 30
20ХНЗА % = 95 — 145 ат = 85 — 110 Ю„-ч-ч <х> со со СЧ II 11 7 1 О Р
40ХНМА св = 110 — 170 ат = 85 — 160 Г iQ II II М СП м о со -ч 00 о
ЗОХГСА св = 110— 170 ат = 85 — 150 а_1 = 48 — 70 т_! = 28 — 40
Нержавеющие жаро
ГОСТ 5632 ~ 61
1X13 (ЭЖ1)
sB-61
<*т==41
= 37
620
Продолжение приложения 1
Относи тельное удлинение (относи- 1 тельное сужение), о/ /о Твердость по Бри- нелю, кГ/мм? Ударная вязкость, кГм/см2 Моцуиь упругости в (G), х 10—4 кГ/мм2 Коэффи- циент Пуассона Удельный вес, г/слг3 Коэффициент линейного расширения, ХЮ6—1—. град
стали***
18—21 — 7,11 2,07 — 7,74 мак 11,3
— — — 2,185 (0,808) — 7,85 13,4—14,8
9(45) 187—219 5 2,109 (0,8015) — 7,82 12,8
— — 2,130 — 7,82 12,3—14,4
— 1— — 2,040 — 7,82 11,8
— — — •— — — е—
— — Z 2,040 (0,815) — 7,85 11,0—14,5
— — — 2,040 — 7,85 11,7
прочные < стали '— 1,980 (0,830) — 7,85 11,0
22 (60) — 1 2,2 — 7,75 10,1-12,25
621
Материал Предел прочности, кГ]мм2 Предел текучести, пропор- циональности, кГ/мм2 Предел выносли- вости, кГ/льм.2 /
2X13 (ЭЖ2) (закал- ка с 1000—1020° С на воздухе, отпуск при 720—750° С) % =72 ат = 52 = 37
1Х17Н2 (ЭИ268) (за- калка с 1030° С, от- пуск при 680° С) % = 96 ат = 77 а—! = 49
1Х18Н9Т (ЭЯ1Т) % = 58 ат = 24 = 20 — 24 т:-! = 13,5
Х12Н22ТЭМР (ЭИ696М, ЭПЗЗ) (прокатка, старение 730° С, 16 « + + 630° С, 16 ч) ав = 135 ат = 104
ГОСТ 5632-31 Жа ростойкие и жаро
Х20Н77Т2ЮР (ЭИ437Б) (аустени- тизация при 1080° С) с охлажде- нием на воздухе, старение при 750° С, 16 ч) ов = 92 —109 зт = 66
ЖС6К (закалка с 1210—1220° С с ох- лаждением на воз- духе, отжиг при 950° С, 2 ч) ав = 100 —107 вт = 88 — 94 '—
Тугоплавкие
Вольфрам (нелегиро-
ванный*****)
Сплавы вольфрама,
W — 15Мо*****
W — 2Nfr*****
W — 3,6Та*****
% =10,7
^ = 17,5
*в = 23,4
% = 35
622
Продолжение приложения 1
Относи- тельное удлинение (относи- тельное сужение), % Твердость по Бри нелю, кГ/мм2 Ударная вязкость, кГм/см2 Модуль упругости £(<?), х 10“”4 кГ/мм2 Коэффи- циент Пуассона Удельный вес, г (см2 Коэффициент линейного расширения, Х10’—Ц- град
21 (65) — 6—17 2,2 7,75 10,1
17 (59) — ‘— 2,0 — 7,75 10,3
70 (80) — 28 2,0 — 7,9 16,6—18,6
20 (46) — — — — ==»
прочные < 11—24 (10—21) сплавы 3,5 2,0 — 8,2 12,7
1,5—7
(8—16)
металлы [
49 (76) — — 4,2 (1,5) 0,3 19,3 4,45
27 (78) — — — — —
9 (25) — — — — — •—
15 (8) — — —• —~~
Материал Предел прочности, кГ/мм2 Предел текучести, пропор- циональности, кГ/мм2 Предел / выносливо- 1 сти, кГ/мм2 \
Молибден ’в = 78 от = 7б —
Сплавы молибдена
нм Л 20°С ВМ4 11800° С ’в = 80 ов = Ю от = 68 —
вм-2 2о:с % = 75 >— —
11800° С ав = 9 —— —
( 20° С sB = 43 —60 в —
вм-з
11800° С зв = 12 — 13,5 е— —
Ниобий ав = 77 От = 60 —
Сплавы ниобия
вн-2 ( 20°с ’в = 75 ат = 70 —
(1500° С °в = 8-10 — —
вн-з( 200 с ав = 75 —80 — —
11500°С ав=12,5 — —
ВН-4 ( 2°О°С ав = 81 ат = 73 —
(1500° С % = 17 Серый
ГОСТ 1412 — 54
СЧ 12-28 Q Q Q я о и II II II оо о 5 —• *—
СЧ 15-32 8° OQ BQ II II II II ГО СО О •£* ЬО Си сл
СЧ 18-36 S g о II II II Д О S ООО iQL II II СО "о Си
624
Продолжение приложения 1
Относи- тельное удлинение (относи- тельное сужение), % Твердость по Бри- нелю, кГ(мм2 Ударная вязкость, кГм/см2 Модуль упругости Е (G) X 10—4 кГ/мм2 Коэффи- циент Пуассона Удельный вес, г/слг3 Коэффициент линейного расширения, хю’—L- град
20 — —- 3,3 (1,22) 0,31 10,2 5,6
10 — — 3,3 — 10,3
45 — — 1,85 — — —
10 (30) — 0,2 3,33 — — —
18 — — 1,85 — — —
2,8 (0,7— 40) — — 3,25 — — —
40-50 (6,5) — — — —
20—25 (25-35) — 37 1,06 (0,88) 0,39 8,57 7,1
18—28 — 27 1,06 — 8,66 6,25
— — — — — — —
16—20 (40—70) — 30 — — — —
40—43 —— —— —— —— ——
16 (33) — 5—7 — — — —
24 (30) — — — — — —
чугун
— 143—229 — 0,8-1,5 (0,45) 0,23—0,27 6,8—7,1 10—12
— 163—229 — 0,8—1,5 (0,45) 0,23-0,27 6,8—7,1 10—12
— 170—229 — 0,8-1,5 (0,45) 0,23-0,27 7,0—7,2 10—12
625
Материал Предел прочности, кГ/мм2 Предел текучести, пропор- циональности, яГ/льм,2 Предел выносливо- сти, кГ/jwai2
СЧ 21-40 ю о оо с\] ог М II II II II о° os р“ °т = 0,75ов Г г II II 00 о
СЧ 24-44 о о М о II1 II II о о S а О О О Р ат = 0,75ав м о СО II II II 7 o' J t>
СЧ 28-48 оа В° oQ BQ II II II II СО Ц>. Н*. К> СП 00 О 00 % = 0,75ав °-1р = 7.5 сг_х = 15 — И
СЧ 32-52 й § 8 8 II II II II а о S а О О О Р от = 0,85ав Г г Г А* « 1II II СЛ
СЧ 35-56 a Q Q Q и а о и II II II II Щ М W О О О Сп ат = 0,85ав Г 1° I •-* I-* II II II сл
СЧ 38-60 со о о со CQ sfi СО *<Г| II 'll 11 11 ои о° ьВ Ра ат = 0,85ав == 15 ^ = 11,5
Белый чугун Q а а S Q И II II II ООО 1 L 1 ООО •—
Жаропрочный
ГОСТ 2176—43
Х28 ’в = 35
аи = 55
Х34 ав = 40
’и = 50
626
Продолжение приложения 1
Относи- тельное удлинение (относи- тельное сужение), % Твердость по Бри- нелю, кГ/мм2 Ударная вязкость, кГм/см2 Модуль упругости х 10—4^кГ/мм2 Коэффи- циент Пуассона Удельный вес, г/см2 Коэффициент линейного расширения, хю«-5-_ град
— 180=207 0,9 0,85 (0,45) 0,23—0,27 7,2—7,3 10—12
’— 187—217 0,9 1,1 (0,48) 0,23-0,27 7,25—7.4 10—12
1,0—1,2 170—241 1,0 1,2 (0,52) 0,23—0,27 7,3—7,4 10-12
1,0—1,2 187—255 1,0 1,3 (0,56) 0,23—0,27 7,3—7,4 10—12
1,1—1,3 197=269 1,1 1,45 (0,64) 0,23—0,27 7,3-7,4 10-12
1,2—1,4 207—269 1,0 1,6 (0,7) 0,23—0,27 7,4—7,6 10—12
'— 300—700 0,1-0,5 \ 1,6-1,8 «— 7,5 ±0,2 8±2
чугун
— 220—270
250—320
627
Продолжение приложения 1
Материал Предел прочности, кГ/мм2 Предел текучести, пропор- циональности, кГ]мм2 Предел выносливо- сти, кГ/мм2 Относи- тельное удлинение (относи- тельное сужение), % Твердость по Бри- нелю, кГ/мм2 Ударная вязкость, кГм/см2 Модуль упругости E(G), X 10"“4 кГ/лил2 Коэффи- циент Пуассона Удельный вес, г/см3 Коэффициент линейного расширения, Х10в—1— град
ГОСТ 1215—59 Ферритный КЧ 30-6 КЧ 33-8 КЧ 35-10 КЧ 37-12 Перлитный КЧ 45-6 КЧ 50-4 КЧ 56-4 КЧ 60-3 КЧ 63-2 ГОСТ 7293—54 ВЧ 45-0 ВЧ 50-1,5 о о ю о о о о to to о г- ю со 00 о ю ’ГН Illi 1111 Л ЮО^ОЮОООО О 05 СО СО £2 Ь* Ю Г- 00 О Ш о 04 CQ со о СО to со to Г* <35 to CO'<fCOOOHOcOc0tQCOCOtQoQ Ю Г- Ю tO СО СО Л II II Л II II Л II II Л II И Л Л и II Л Л Л II II II II II II II II овоари ОЯоНнО о“оянш о“ е>°о®ри „» e.ee>°t>S,p“ ь" о° о® р“ о о to С т- ~ О о: 1“ 1~ Е^ с ? ! 1 1 т- ?! О ?! ?! с ?! ?! Г? С! С! | СЧ СО Х|< ! | 1 Jg О II II II II II И II II II II II II 1 II II II 1 1 1 II Н ОЬ о Я j о s вь О я О Я о я "f. cP о“ j j (Г / ° Ковкий ’-)Р= 7 o_i = 12 Т—1 = 11 °-1р = 8 a_i = 13 Т_! = 12 °-1р = 8 = 14 Т—1 = 13 0-1р= 8 c__i = 14 т-1 = 13 °-1р =11 0-1 = 18 Т_1 = 16 Чугун с шарД а_1==18 — 20 G-! = 20 — 22 «_! = 17-21 чугун >6(7) >8(9) > 10(11) >12(13) >6 >4(3,5) >4 >3 >2 ВИДНЫМ I 0,4—1,4 1,5—3,0 < 163 <149 <149 <149 <241 <241 <269 <269 <269 фафитом 207—269 207-255 1,2 1,3 1,4 1,6 0,8 0,5-1,5 1,5—3 1,55 (0,63) 1,6 (0,64) 1,66 (0,65) 1,98(0,73) 1,74 (0,68) 1,3—1,6 (0,7) 1,3 (0,775) 0,23 0,25 0,27 0,36 0,28 7,2 7,21 7,22 7,24 7,3 7—7,5 7—7,5 10,5 10,3 10,2 10 10 10,6—11,4 10,6—11,4
A2R
629
Материал Предел прочности, кГ/мм2 Предел текучести, пропор- циональности, кГ/мм2 Предел выносливо- сти, кГ/мм2
ВЧ 60-2 sQ oQ «q II II II II 1111 ь*. tO Сл О О О ат = 42—55 СО СО СЧ 1 1 fr- ю ЧН яви >11 II o' J
ВЧ 45-5 ша я° <? аа II II II II С5 00 £* О Си О СИ III] to rfs <J Q Сл Сл Сл О СЛ от = 32-42 О_1 = 18^20
ВЧ 40-10 sQ ов II II II to 1 ] 1 to *4 to Сл О О Сл ст = 30 — 40 о , == 25 *" 28 *-1 = 19,8
Цветные
Алюминиевые сплавы
ГОСТ 4784-65 АМцМ °в тср = 13 = 8 ат = 5
АМг2М ав = 19 ат = 8
тср = 12,5
АМг2П ав = 25 ат = 21
= 15
ср
АМгб °в = 32 ат = 17
АМгбМ °в = 30 °т = 15
Д1 (0) °в = 21 °т = 11
Д1П (3 и ЕС) °в = 41 ат = 25
тср = 27
no Р°> % = 22 °т = 11
До \(3 и ЕС) св = 46 °т = 30
a_i = 5*
а-! = 12*
= 12,5*
= 7,5*
== 12,5*
630
Продолжение приложения 1
г — Относи- тельное удлинение (относи- тельное сужение), % Твердость по Бри- нелю, кГ/мм2 Ударная вязкость, kFjw/cjw2 Модуль упругости Х10^4 кГ/мм2 Коэффи- циент Пуассона Удельный вес, г/см3 Коэффициент линейного расширения, град
' 2—3 255—285 1,5—3 1,8 (0,8) «-а 7—7,5 10,6—11,4
. 5—10 173—207 2,5—8 1,3 (0,7) — 7—7,5 10,6—11,4
10—20 156—179 5—7 1,6 (0,75) — 7—7,5 10,6—11,4
металлы
деформируемые
23 (70) 30 — 0,71(0,27) 0,3 2,73 24
23 (64) 45 0,71 (0,27) 0,3 2,67 23,8
6 60 — 0,71 (0,27) 0,3 2,67 23,8
24 »—= —— 0,7 «— 2,64 24,7
18 —• 0,71 (0,27) 0,3 2,64 24,7
18 (58) 45 0,71 (0,27) 0,31 2,8 22,9
15 (30) 115 3 0,71 (0,27) 0,31 2,8 22,9
15 (50) 50 0,71 0,31 2,8 22
105 — 0,71 0,31 2,8 22
631
Продолжение приложения 1
Материал Предел прочности, кГ/мм2 Предел текучести, пропор- циональности, кГ/мм2 Предел выносливо- сти, кГ/мм2 Относи- тельное удлинение (относи тельное сужение), % Твердость по Бри- нелю, кГ/лш2 Ударная вязкость, кГм/см2 Модуль упругости £'(<?)> х 10-’4 кГ/мм2 Коэффи- циент Пуассона Удельный вес, г/см3 Коэффициент линейного расширения, х10“—Ц- град
Д16, Д16П плакированные листы % = 44 а = 29 18 (30) 105 —
(3 и полу- ЕС) г(3 и ЕС) ав = 52 т от = 38 = 14* 11 (15) 131 —
фаб- рика- (О) тср Ов о CQ 1 СЧ СЧ СЧ II II о_= 10 с-1= 9* 18 (30) 42 — > 0,71 (0,27) 0,31 2,78 22,7
ты ЦСЗ) % = 43 т <*т = 23 13 (15) — —
плакированные листы О
(3 и ИС) °В = 46 % = 41 — и — —
профили (3 и ИС) % = 42 — 50 зт = 40-44 —— 7 — —
АК4-1 = 43 ст = 28 а__х = 13»* 13 (26) 120 — 0,72 (0,27) 0,33 2,8 19,6-24,8
ВД17 В °в = 49 ат = 33 s-i = 16,5* 20 115 — 0,71 (0,27) 0,31 2,75 23,6—26,9
л сплавы литейные
Алю миниевыа
ГОСТ 2685—63
АЛЧ литой в землю термообработка Т5 термообработка Т7 литой в кокиль (термообработка Т5) О t— СО СЧ СЧ О СЧ СЧ -ГН СЧ СЧ сч со СЧ II II II II II II II ft a ft д о я и д га о О Р о р о о р сч оо ео сч сч II II II II J = 5,6* а_х = 5,6* a__i = 6,5* 1,0 0,5 1,2 0,5 80 100 90 120 0,3 . 0,72 (0,27) 0,33 2,75 22,3—24,4
АЛ2 литой в землю литой в металли- ческую форму литой под давле- нием оо со сч сч ян СЧ сч II и II II а дога д ОРО и ®т = 8 ®т = 9 «т =12 а_х = 5,5** а_х = 7** 6 5 1,8 50 55 0,8 . 0,7—0,72 (0,27) 0,33 2,65 21,1—23,3
АЛЗ литой в землю термообработка Т5 литой в металли- ческую форму термообработка Т5 г— о сч о- СЧ сч сч II II II II ОИОВО° ов 4» II II II II tO kA. ГО Ю -о № — 2 3 4 3 70 75 70 80 0,22 0,45 0,7—0,72 (0,27) 0,33 2,7 22—24
633
632
Материал Предел прочности, кГ/лш8 Предел текучести, пропор- циональности, кГ/мм2 Предел выносливо- сти, кГ/мм*
АЛ8 (термообра- °в ==30 °т = 17 с_1 = 5*
ботка Т4) литой в землю литой в металли- гср % = 23 = 33 °т = 18
ческую форму АЛ9 литой в землю Св = 20 О = 11 = 4,5*
(термообработка Т4) литой в землю тер Св II II to US Сл т °т = 21
(термообработка Тб) литой в металличе- тср с = 12 = 23
скую форму (тер- мообработка Тб) АЛИ (термообра- в % = 22 °т = 15 — 6,5
ботка Т2) АЛ13 литой в землю °в = 17 °т = 9 0—1 = 4*
литой в металли- тср Св = 14 = 20 °т = 10
ческую форму АЛ15В литой в землю % = 15
термообработка Т5 °в = 20 ’— —
литой в металли- °В = 18 — —
ческую форму термообработка Т5 °в = 22 — >—
АЛ19 (литой в землю) термообработка Т4 °в = 32 °т = 16 S-! = 7**
термообработка Т5 °в = 37 °т = 22 о^ = 7*
ВТ1 °в = 61 °т = 47 Титан и erd а__! = 26
ОТ4 °в = 70 — 85 °т = 55 — 65
634
Продолжение приложения 1
Относи- тельное удлинение (относи- тельное сужение), % Твердость по Бри- нелю, кГ/мм2 Ударная вязкость, к Гм/см2 Модуль упругости х 10— * кГ/мм2 Коэффи- циент Пуассона Удельный вес, a/cAi8 Коэффициент линейного расширения, Х10«—1— град
12 75 1
. 0,7—0,72 0,33 2,55 24,5—25,6
15 80 — (0,27)
6 55 —
2 75 . 0,7—0,72 0,33 2,66 23—24,5
(0,27)
5 70 —
2 80 — — — 2,94 24,4
3 65 0,5 1 0,7—0,72 0,33 2,6 20
5 70 — | (0,27)
— 70 —
<— 80 — 0,7—0,72 0,33 2,7 22—24
0,5 70 — (0,27)
0,5 85 —
9 90 — 1 0,7—0,72 0,33 2,78 19,5—21,9
5 100 — J (0,27)
сплавы
20—30 (>45) 150—180 >7 1,121 (0,411) 0,32 4,5 8
10—40 229—302 3,5—6,5 1,1 (0,4) — — 4,55 8-9,8
(25—55) — 1,2
635
Предел Предел текучести, Предел
Материал прочности, кГ/мм2 пропор- выносливо-
циональности, сти, кГ/мм2
кГ/мм2
ВТ8 ав =105—118 Зт =95-110 а_х = 50
гср = 65-70 %ц = 75- 85
ВТЗ-1 ав = 95—120 зт =85 — 110 = 48
*ср> 65 °пц = 70- 85
ВТ14 ав = 95 — 120 — S5-ЦО —
Медные
Лату
ГОСТ 1019—47
Л68 мягкая СЧ о СО СЧ II II с Ра °ОЛ= 9,1 а_д = 12
твердая ав =66 °о,1 ~ §2 = 15
ЛА77-2 мягкая ’в =^0 <*т =14
твердая °в =65 — —
ЛМц 58-2 мягкая °в = 40 ат =15,6
твердая ®в =70 — —
ЛС 59-1 мягкая О о СЧ II II с « о О Р от = 14 —
твердая °в =65 ат =45 = 16
ЛК80-3 мягкая °в =30 ат =20
твердая °в =60 — —
, Продолжение приложения 1
Относи тельное удлинение (относи- тельное сужение), % Твердость по Бри- нелю, кГ/мм2 Ударная вязкость» кГм/см2 Модуль упругости Е(6), х 10~4 кГ/мм2 Коэффи- циент Пуассона Удельный вес, г/см3 Коэффициент линейного расширения, хЮв —L- град
9—15 (30—55) 310—350 3—6 1,1 (0,425) 0,3 4,48 8,3—9,1
10—16 (25—40) — 3-6 1,15 (0,43) 0,3 8,6 4,5
6-10 (25-35) 255—388 2,5—5 1,15 1— 4,52 8—8,7
сплавы
ни
55 (70) 55 17 1,1 — 8,6 19
3 150 — 1,15 — — —
55 60 20 1,05 8,6 18,3
12 170 — — — — —
40 85 12 1,0 8,4 21,2
10 175 — — — — —
45 (44) 90 2,6—5 1,05 (0,35) — 8,5 20,6
16 140 — — — — —
58 100 12 0,98 8,5 17
4 180 — — — — —
636
637
Материал Предел прочности, кГ/лии2 Предел текучести, пропор- циональности, к Г/мм2 Предел выносливо сти, кГ/мм2
Б ронаы
Бр 0-10 % = 25 — —
Бр. ОЦ8-4 Бр ОЦС 6-6-3 ав = 20 ат =4—5 —
ГОСТ 613—65 литье в землю ав = 15 ат = И —
литье в кокиль ств = 18 = 8-10 —
тср = 22 °пц = 5
Бр. ОФ 10-1
литье в землю % = 20 — 30 = 25 — 35 % = 14 °пи ~ 8 — 9 —
литье в кокиль % "т =20 —
тср = 34 спц = 13-14 Бронаы
ГОСТ 493 — 54
Бр. А5 литье в кокиль аВ = 28 °т = 7 —
мягкая деформи- руемая °в = 38 о.г =16 а__г = 13,4**
твердая деформи- ав = 80 ат =50
руемая Зпп = 48
Бр. АМц 9-2
литье в кокиль °в = 40 ат =20 °пц = 11
мягкая деформи- руемая ав = 40 =30 —
твердая деформи- руемая св = 60 ат =50 q 1 -- 21****
Бр, АЖМц 10-3-1,5 ав = 56 ат =21 —
литье в кокиль = 38 °пц = ^7
мягкая деформи- ’в = 61 =19 —
руемая твердая деформи- °в = 60 — 70 '— а__! = 28****
руемая
638
Продолжение приложения 1
Относи- тельное удлинение (относи- тельное сужение), % Твердость по Бри- нелю, кГ/мм2 Ударная вязкость, кГм/см2 Модуль упругости E(G), X10—4 кГ/мм2 Коэффи циент Пуассона Удельный вес, г/см9 Коэффициент линейного расширения, Х10’—Ц- град
оловянные
И 80 — 3 — — —
4 ~ 75 — — — — —
6 60 — 8,82 17,1 -18,2
4 (6—10) 60 2—3 0,9 — — —
3(3) 80—100 0,6 0,754 — 8,58 17—22
* 7—10 (10) 90—120 0,9 1,03 — 8,76 17
алюминиевые
55 (48) 65 16
65 (70) 60 И 1 — 8,2 15,6
4 200 — 1,1 — — —
20 (25— 27) 90—120 7 0,92 — — —
25 110—130 — 1,05 — — —
4-5 (55) 160—180 — — — 7,6 17—20
22 (25— 27) 130 6—8 1 — — —
32 (55) 125—140 — 1,05 — — —
9—12 160—200 — — — 7,55 16—20
639
Материал Предел прочности. кГ/мм2 Предел текучести, пропор- циональности, кГ/мм2 Предел выносливо- сти, кГ/мм2
Бр АЖС 7-1,5-1,5 Бр. АЖ9-4 литье в кокиль мягкая деформи- руемая твердая деформи- руемая ГОСТ 493—54 Бр. КМцЗ-1 мягкое состояние твердое состояние МА1 листы прутки МАЗ полосы прутки ВМ654 прутки прутки (ИС) полосы профили поковки штамповки яааааа »QortaQ =° .f'W »°«Q а° в° oQ II II II II II || II II || II II II II || II II II || || II СО СО СО со го СО tO Ю I-* Ю ю О СО м СП СП to <-* 4Х СП со СП ОО СО W ф 4S СП СП СП О ° СП СП || •О СП О =20 °пц = 18 а, =22 °пц = 12.7 «т =35 ®т =10-20 ат =10-20 Магни ат =12 ат =14 ат =17 ат =22 ст =30 °пц = I4-5 от =28 «т =29 °пц = 13 «т =29 ат =25 =26 G_x = 21**** а_х = 18,5**** Бронза а_1х=11—16 евые сплавы s-i = 7,5** = 7,5** a_j = 15**
640
Продолжение приложения 1
Относи- тельное удлинение (относи- тельное сужение), % Твердость по Бри- нелю, кГ/лии2 Ударная вязкость, кГм/см2 Модуль упругости E(G), ХЮ—4 кГ/мм2 Коэффи- циент Пуассона Удельный вес, г/см3 Коэффициент линейного расширения, X10s-l— град
j 18 — — — — — —
10—20 120—140 6,3 1,12
(25—30)
40 (33) но 8 1,12 0,49 7,5 16,2—17,1
5 160-200 — 1,16
кремнии пая
25—45 70—90 |13—17 1,04 8,4 15,8—20
5—10 170—190
дефор мируел [ ы е
8 45 0,5 0,4
4(6) 45 0,6 0,4 |о,34 1,76 22,3—32
15 (23) 1 0,43
|о,34 1,8 26,1—31,2
12 60 — 0,43
9(24) 60 —
9(24) — 0,9
10 (25) — — > 0,43 034 1*8 20,9-22,6
10 — —
12 г — —
14 55 —
21 5-1183
641
Материал Цредел прочности, к/ /шл1 Предел текучести, прспрр пионаЛьйостм, кГ/мм2 Предел выносливо сти, кГ/мм*
Магниевый сплав
МЛ6
литой a Q Н Q 5 « О се II II II II н- М н. СП СП С“ °т =11 = 8,5**
термообработка Т4 От = 10 = 9,5**
термообработка Тб % =26 ’ср"16 От = 14 = 8,5**
Свинец ГОСТ 3778 — 65 % = 1,5 — —1.8 (дефор- мированный и О) ат =0,5-1 = 0,42***
Цинк ГОСТ 3640 — 47 ав =6,4 ат =1.0 J
Никель ,в =40 — 55 ат= 6 —20 —
ГОСТ 849 — 5Ь (мягкое состояние) (мягкое состояние)
ов =50 — 100 (твердое состояние) ат = 28 — 90 (твердое состояние)
Мельхиор МНЖМц 30-0,8-1 (МН 70-30) ГОСТ 492 — 52
мягкое состояние ов = 35 — 45 ат = 14 —
твердое состояние ав = 55 — 65 ат = 54 —
Нейзильбер МНЦ 15- 20 ГОСТ 492 — 52
мягкое состояние ав = 40 — 45 ст= 14 = 12 — 14
твердое состояние ав = 60 — 72 ат = 59 —
Монель НМЖМц 28-2,5-1,5 ГОСТ 492 — 52
мягкое Состояние ав = 50 — 60 ат = 20 = 17
твердое состояние ав = 70 —85 ат = 65 - 75 = 26
642
Продолжение приложения 1
Относи тельное удлинение (относи- тельное сужение), % Твердость по Бри- нелю, Ударная вязкость, кГ-м/см2 Модуль уПр^ГОСТИ х 10—кГ/мм2 Коэффи- циент Пуассона Удельный вес, г/сж3 Коэффициент линейного расширения, х10«-1— град
литейный
1.5 (2,5) 55 0,2 (0,16) —
5(12) 60 0,3 0,42 (0,165) 0,33 1,81 26,1—27,7
1(3) 80 0,15 (0,165) 0,33
35—50 (90—100) (литой) 60-70 (дефор- мирован- йый) 20(50) 3,8—4 (литой) 20 20.6—2,3 (О) 0,15—0,18 0,53 — 11,34 7,133 28 39,7
30—50 (мягкое состоя- ние) 2—15 (твердое состоя- ние) 90—120 (О) 125—220 (нагарто- ванный) — 1,8-22,7 (0»73) — 8,9 13,3—16,3
40-50 3—5 70 190 — | 1,54 — 8,9 16
40—50 2-3 70 160 — | 1,26 — 8,7 16,6
30-50 (65) 3—5(50) 110—140 140-220 — | 1,82 — 8,8 14-15
643
Материал Предел прочности, кГ/мм2 Предел текучести, пропор- циональности, кГ/мм2 Предел выносливо- сти, кГ/мм2
Пластические
I
Стеклопласты ГОСТ 10087 — 62, ГОСТ 10292 — 62, ГОСТ 2910 — 67, ГОСТ 10316 — 62 на основе ткани oQ wQ II II II ю W О Q 1 1 1 СО СЛ О О °пп = 12,2-26 2=1 = 0,22 — 0,25 ав
на основе нитей, ав = 30 — 50 — 2=1 = 0,25 — 0,28
ориентированных ас = 23 — 46 ав
в двух взаимнопер- а =40 — 42
пендикулярных на- правлениях и
Текстолиты (на ос- ав = 4,5 —И ат = 7—8 2=1 = 0,25 — 0,3
нове хлопчатобу- а = 12 — 25 ав
мажных тканей) ГОСТ 5 — 52, с аи = 7,5 - 16 а-1р = 2
ГОСТ 2910 — 67, ГОСТ 5385 — 50 тв s= 9 — 10
Древесные пластики ав = 14 — 30 — 2=1 = 0,25 —0Л
ГОСТ 8697 — 58 ас = 12 — 18,5 аи == 16,5 — 28 %
Гетинакс (на основе ав == 6 — 10 — ’ °—1р — 5,8
сульфатной бумаги) а=4 — 14 ==1 = 0,2 — 0,3
ГОСТ 2718 — 66 и % = 3,5 — 4,9
Фибра (на основе ав = 5-7 — 2=1 = 0,2 — 0,3
специальных сор- а = 8 — 14 %
тов бумаги) ГОСТ 6910 — 54 С аи = 6—9,5
Волокниты (наполни- % = 3 - 13 — 2=1 = 0,25 — 0,3
тели: а =10 —15 ’в
хлопковые очесы, асбоволокно, стек- ловолокно) с аи = 4-13
644
Продолжение приложения 1
Относи- тельное удлинение (относи- тельное сужение), % Твердость по Бри- нелю, кГ/мм2 Ударная вязкость, кГм/см 2 Модуль упругости Е (G), х10—4 кГ/мм2 Коэффи- циент Пуассона Удельный ъес, г/см3 Коэффициент линейного расширения, хю*—L- град
массы
— 27—38 0.5—5,25 0,18—0,22 (0,035—0,04) 0,035— 0,622 1,4—1,85 0,45—8.3
— 28-52 0.5—5,25 0,24—0,35 0,035— 0,622 1,7—1,9 0,45—83
— 30 035 0,04—0,1 (0,25) — 1,3—1,45 3.3—4,1
— 18—20 0.17—0,8 0,12—0,34 — 1,2—1,4 —
— 25—30 (8—20) х X 10~2 0,1—0,18 (0,008— 0,025) — 1,3—1,4 20
— 10 — (0,07) — 1,1—1,25 —
— 18—35 (15-65) х X ю~2 0,05—0,118 — 1,35—1.9 —
645
Материал Предел прочности, кГ/мм2 Предел текучести, пропор- циональности, кГ/мм2 Предел выносливо- сти, кГ/мм2
Термореактивные пресспорошки (на- полнители: древесная мука, кварцевая мука, слюда) ГОСТ 5689 — 66, ГОСТ 9359 — 66 ав = 2,5 — 6,9 %-7-30 аи = 4,5 — 10 — —1 = 0.3 — 0,4 ’в
Органическое стекло (на основе полиме- ров и сополимеров метакриловой кис- лоты) ГОСТ 10667 — 65, ГОСТ 9784 — 61 ОО °- о см £2 ’ч-i *"• IO J. ОО II II II со о s t> О о ^=1=0,1—0,16 °В
Термопласты линейные полимеры с различной сте- пенью кристаллиза- ции неармированные Фторлон-4 (фторо- пласт-4) ГОСТ 10007 — 62 Капрон А, Б, В Полиамидная смола 68 ГОСТ 10589 — 63 О ОО I I I см ю || । । । 7е? см см. о qO о °- ° ’ • С | 6 О тН о Q II II II 1 II II II II II II II II II II II о= о° о= „« о° о= О» о° оа ъ о° — ?=1 = 0,15 — 0,2 °в
646
Продолжение приложения 1
Относи- тельное удлинение (относи- тельное сужение), % Твердость по Бри- не лю, кГ/мм2 Ударная вязкрсуь, кГм/см2 Модуль упругости Ё ;G), х 10—4 кГ/мм2 Коэффи- циент Пуассона Удельны^ Вес, 8/CAt3 Коэффициент линейного расширения, Х10» -1— град
— 10—60 0,03^0,8 е— '— 1,3—2,7 (0,22—7)х10
2,5—23,2 12—25 (4—33) х X «г» 0,027—0,041 — 1,18—1,2 46—120
*—- 3—16 — 0,0015—0,007 — 0,92—2,1
1,5—14 — (0,16— -2.2) х X Ю~2 0,00037— 0,002 (0,00015— 0,00019) ’— 0,02—0,6 (3,5—7,8) X Х10
300—350 3—6 *— 0,0047— 0,0085 ’— 2,19—2,35 (8—25) х 10
150—200 10—12 1,5—1,6 0,0144 (0,0045— 0,0048) — 1,1—1,14 (6—15) х 10
100 10—15 — 0,012 — 1,11 (10—12) х Ю
647
Материал Предел прочности, кГ/мм2 Предел текучести, пропор- циональности, кГ/шл,2 Предел выносливо- сти, кГ/мм2
Винипласт ГОСТ 9639 61 % ==4-6 а0 = 8 —16 <хи = 8-12 — —
Полиэтилен высокой плотности (низкого давления) SF хГ OQ 1 f 7 СЧ 00 1 сч сч сч II II II «os ООО — —
Полистирол блочный ГОСТ 9440 — 60 о ** ° Й ГС —ч О II II И о“ о° оВ — —
Другие
Лед -- — —
Каучук натуральный ав==1,6—3,8 — —
Стекло ГОСТ 10135 — 62 о о сч ю о . 12 । М ю LO II II II О“ ов — —
Базальт ос = 25 —30 — —
Гранит ав==0,3 ас=12-26 — —
Известняк ас = 5,0 — 15 — —
Песчанник ав = 0,2 ас = 4-1,5 — —
Мрамор ас=10 —18 — —
Кладка из гранита, известняка, кир- пича ав = 0,02 — 0,05 ас==0,25- 0,9 — —
Бетон । ас = 0,5-4,8 । — —
64$
Продолжение приложения 1
Относи- тельное удлинение (относи- тельное сужение), % Твердость по Бри- нелю, кГ/мм2 Ударная вязкость, кГм/см2 Модуль упругости Е (G), х 10~4 кГ/мм2 Коэффи- циент Пуассона Удельный вес, г/см8 Коэффициент линейного расширения, XlO’-l— град
10—100 13—16 0,5—0,8 0,03—0,04 0,354 1,3—1,4 (6—7)Х10
250—900 4.5—5,8 — 0,005—0,008 — — 0,94—0,96
0,4— 0,7 14—15 0,16—0,2 0,012—0,032 1,05—1,1 60
материалы
— — — 0,1 (0,25— 0,03) — 50,7
600—700 «— — (0,6-1) X Х10~4 0,47 0,91 (1,8-2,8) X X 10«
— —• 0,015— 0,025 0,48—0,85 (0,022— 0,032) 0,18—0,32 2,2—8 0,5—15
— — — — 2,7—3,3 —
— — — 0,49 — 2,5—2,8 —
— — — 0,42 — 1,8—2,6 —
— — — 0,18 — 2,1—2,8 —
— — — 0,56 — 2,5—2,8 —
— — 0,09—0,1 0,06 0,027—0,03 — — | 4—7
— — — 0,146—0,232 0,16—0,18 — 10—14
649
Материал Предел прочности, кГ/мм2 Предел текучести, пропор- циональности, кГ/мм2 Предел выносливо сТи, кГ/мм2
Cocjia обыкновенная (15% влажности) ав = 9,31—11,5 ас = 4,27—4,66 аи = 7,36—8,77 трп = 0,62-0,73 °пц = 6>1 °пц = 3’1 —
Ель обыкновенная (15% влажности) СЧ СО СЧ Г- СМ СЧ С© Ч-Н Ь* О 1111 Г* но СЧ о °q *2 *5 Г. « С II || II II »И ОЯ & Q Q § € II II Ю СП Vi о —
Береза обыкновенная (15?4 влажности) ав = 16,1 — 21 ас = 4,37—5,33 аи = 9,67—10,84 V =0.85-1,33 °пц = ЗУ| —
Тополь (15% влаж- ности) § qq wQ II и II II О о ОО оо ui о Ь ф <1 о l-Jb — —
Акация (15% влаж- ности) ’в = 16.9 ас = 6,65 аи= 13,92 тср = 1,25 — 1,4 — —
Бук кавказский (15% влажности) ав = 12,91 ос = 4,74 аи = 9,53 г ср = 0,99—1,31 апц = °Пц = 2,9 —
Ясень (15% влажно- сти) •S1 BQ с? и° II II II II С£> JX Q0 СП Jx г . 1 I 1 1 •“* СП bi 05 00 сл сх> %ц=7,4 апп — 2,7
650
Продолжение приложения 1
Относи- тельное удлинение (относи- тельное сужение), % Твердость по Бри- нелю, кГ/мм* Ударная вязкость, кГм/см2 Модулх упругости Е (G), х 10—4 кГ/мм? Коэффи- циент Пуассона Удельный вес, г/см3 Коэффициент линейного расширения, 8рад
— 1,99—2,7 0,18—0,23 0,102—0,145 (0,0055) 0,49 0,48—0,54 Вдоль воло- кон 3,7; поперек волокон 63,6
— 1,82—2,52 0,18—0,19 0,11 (0,0055) 0,44 0,46 Вдоль воло- кон 5,4; поперек волокон 34,1
— 2,98—3,92 0,41-0,54 0,15—0,184 (0,0065) 0,41 0,64—0,73 Вдоль во- локон 2—5
— 1,73—2,5 0,19 0,13 (0,0055) — 0,46 Вдоль во- локон 2—5
— 6,19—8,81 0,92 0,09—0,16 (0,0045— -0,0065) — 0,75—0.81 Вдоль во- локон 2—5
—- 3,79-5.71 0,39 0,127 (00065) 0,58 0,68 Вдоль воло- кон 2—5
— 5,34—7,32 0,3—0,43 0,124—0,15 (0,0065) 0,43 0,66—0,71 Вдоль воло- кон 2—5
651
Материал Предел прочности, кГ/мм2 Предел текучести, пропор- циональности, кГ/мм2 Предел выносливости, кГ/мм2
Дуб (15% влажно- сти) а = 12,88 % = 5,2 аи = 9.35 г.п =0,85—1.25 ср ° -Э g s II II to co —
Липа сти) (15% влажно- 00 o' 00 1 io оо _ £2 СЭ 00. СО t" О II II II II о° о® £ 1O II II H ЕГ c c о t> —~
Ольха сти) (15% влажно- оа Q Q Q S О И II II II II -J СС со Й * ** *** **** ***** 00 Ъ о° -q W О оо СП — —•
Клен сти) (15% влажно- % = 5,2 ои = 10,53 г =1,13-1,29 — 1
* Предел выносливости получен на базе 5 x10е циклов.
** Предел выносливости получен на базе 2х107 циклов.
*** Предел выносливости получен на базе 107 циклов.
**** Предел выносливости получен на базе 10е Циклов.
***** сгв, относительное удлинение и относительное сужение приведены для
Состояние материала: О — отожженный; 3 — свежезакаленный; ЕС — естественно
Термообработка: Т2 — отжиг; Т4 - закалка; Т5 — закалка и кратковременное
Т7 — закалка и стабилизирующий отпуск.
652
Продолжение приложения 1
Относи- тельное удлинение (относи- тельное сужение), % Твердость по Бри- нелю, кГ/мм2 Ударная вязкость, кГм/см2 Модуль упругости £(G), х IO—* кГ/мм2 Коэффи- циент Пуассона Удельный вес, г/см3 Коэффициент линейного расширения, xlO»—L. град
— 4,63—6,53 0,46 0,073—0,151 (0,0065) 0,43 0,76 Вдоль волокон 4,9; поперек волокон 54,4
— 1,56—2,34 0,28 0,09 (0,0045) — 0,51 Вдоль волокон 5,4; поперек волокон 44,1
— 2,48-3,67 0,25 0,132 (0,0055) ’— 0,53 Вдоль волокон 2-5
— 5,06—6,9 0,37 0,118 (0,0055) — 0,7 Вдоль волокон 2—5
температуры 1650° С
состаренный; ИС — искусственно состаренный.
(неполное) искусственное старение; Тб — аакалка и полное искусственное старение;
653
Приложение 2
Коэффициенты концентрации и чувствительности к концентрации напряжений
№ п/п Схема нагружения элемента конструкции или детали Теоретический коэффициент концентрации напряжений а Эффективный коэффициент концентрации напряжений р Коэффициент чувствительности к концентрации напряжений 4 О — 1
1 Валы, оси с галте- лями г Л 11 ! □ “ « 8 Z 1 £ Z £ 33 | При d = 30 — 50 мм и = 2 а 1 1 1 1 1 1.8 — — — Для стали ав, т кГ/мм* 1 2 3 4 d 9
40 0,2—0,5 0,27—0,32
1 L-Г Растяжение — сжатие £21 1 1 Г 1.0
5' 80 0,2—0,5 0,59—0,65
О Q2 Ofi r/d
0 0,2 0,4 0,6 r/d
Для стали 1 — ав — 120 кГ/мм2 2 — ав = 80 кГ/мм2 3 — ов = 40 кГ/мм2 120 0,2—0,5 0,82—0,93
1 1 1
Для стали
1 — ав = 120 кПмм*
2 — gb == 100 кГ)мм2
3 — ав == 80 кГ/мм?
4 — ав = 40—60 кГ 1мм?
При-^-<2
еэ Сл со Продолжение приложения 2
.в в Схема нагружения элемента конструкции или детали Теоретический коэффициент концентрации напряжений а Эффективный коэффициент концентрации напряжений р Коэффициент чувствительности к концентрации напряжений р-1
D d т ~Т ав КГ/ММ2
< 5® | 80 | > 100
1,05 0,02 0,05 0,10 0,15 0,20 1,70 1,48 1,28 1,20 1,16 1,88 1,57 1,33 1,23 1,20 2,05 1,63 1,36 1,25 1,22
1Д 0,02 0,05 0,10 0,15 0,20 2,00 1,64 1,37 1,27 1,20 2,24 1,70 1,42 1,31 1,24 2,47 1,75 1,45 1,34 1,27
1,25 0,02 0,05 0,10 0,15 0,20 2,12 1,81 1,47 1,35 1,30 2,68 1,97 1,54 1,40 1,32 3,10 2,10 1,60 1,43 1,34
1,5 0,02 0,05 0,10 0,15 0,20 2,42 1,91 1,53 1,38 1,33 2£6 1,61 1,44 1,36 2,20 1,67 1,48 1,38
Для чугуна
при d = 12 мм р = 1,15
при d — 50 мм р = 1,25
3.
Валы, оси с галте-
лями
При d = 30 — 50 мм
Для сталей при = 1,4
Кручение
1 — % — 120 кГ/мм2
2 — ав = 60 кГ/мм2
3 — ав = 40 кГ/мм2
При ~-<1,4 pv = l + 4?-l)
Продолжение приложения 2
№ п/п Схема нагружения элемента конструкции или детали Теоретический коэффициент концентрации напряжений а Эффективный коэффициент концентрации напряжений р Ко эффгциент чувствительное! i» к концентрации нодряжений 9 ~~ а — 1
Значения n находятся из гра-
фика
При d — 30 — 50 мм и = 2
При = 2 для сталей
ав, кГ/мм1 2 7 1Г а
50 0,025 0,05 0,075 0,1 0,125 0,15 0,7 0,65 0,63 0,6 0,57 0,5
120 0,025 0,05 0,075 0,1 0,125 0,15 0,82 0,8 0,8 0,77 0,77 0,76
I
I
1 — ов = 120 кГ/мм?
2 — ов = 50 кГ/мм2
При -у <2
f3v = l + ^-l)
Значения v находятся из гра-
фика
Для сталей
D d г ав, кГ/мм2
< 50 80 > 100
0.02 1,24 1,29 1,33
0,05 1,15 1,18 1,20
1,05 0,10 1,08 1,10 1,12
0,15 1,06 1,08 1,09
0,20 1,05 1.06 1,07
Продолжение приложения 2
№ п/п Схема нагружения элемента конструкции или детали Теоретический коэффициент концентрации напряжений а ' Эффективный коэффициент концентрации напряжений 3 Коэффициент чувствительности к концентрации напряжений 4 а— 1
Для сталей
D d г d св, кГ/мм2
< 50 80 > 100
1,1 0,02 0,05 0,10 0,15 0,20 1,40 1,25 1,12 1,09 1,06 1,52 1,28 1,16 1,12 1,08 1,62 1,30 1,18 1,14 1,10
1,25 0,02 0,05 0,10 0,15 0,20 1,64 1,40 1,20 1,15 1,09 1,73 1,45 1,27 1,20 1,13 1,80 1,48 1,32 1,24 1,16
1,5 0,02 0,05 0,10 0,15 0,20 1,76 1,48 1,24 1,19 1,10 1,97 1,56' 1,32 1,25 1,18 2,14 1,62 1,38 1,29 1,24
4. Валы, оси с выточ- ками
Растяжение — сжа-
тие
Схема определения ис-
ходной величины а пока-
зала пунктиром
Для чугуна — 1,1 —1,4
Для сплава МЛ4 (~ = 0,1 —
— 0,121 — 1,4 — 1,8
Для сплавов МА2, МАЗ, МА5 —
1,7 — 2
Для сплавов АЛ5, АЛ7, АЛ8,
АЛ9 —1,3 —1,8
Для сплавов Д16, АК2, АК8 —
1,6 —1,8
Для сталей р находят из таб-
лицы, приведенной для схемы 5
Для сплава МЛ4 (-4-= 0,1—
\а
—0,12 — 0,4 —0,8
Для сплавов МА2, МАЗ,
МА5 — 07 — 1
Для сплавов АЛ5, АЛ7,
АЛ8, АЛ9 —0,3 —0,8
Для сплавов Д16, АК2,
АК8—0,6 —0,8
5. Валы, оси ками . .. V С Е 1ЫТОЧ-
м\ : (1 И
М 1 /
Изгиб
Схема определения иско-
мой величины а показана
пунктиром
32
Для стали
при d = 30 — 50 мм и ~ = 1
#кГГТтт-ЬЕ
О 0J 02 О^гЦ
1 — <jb — 100 кГ/мм2
2 — св = 50 кГ/мм2
Для сталей при ав < 50 кГ/мм2
i т
Г d а
0,02 0,6
0,05 0,69
0,5 0,10 0,74
0,15 0,75
0,20 0,75
Продолжение приложения 2
№ п/п Схема нагружения элемента конструкции или детали Теоретический коэффициент концентрации напряжений « Эффективный коэффициент концентрации напряжений р Коэффициент чувствительности к концентрации напряжений * а — 1
При у- ¥= 1
t г d 9
₽,= Значения графика V = ! + »(₽-!) v находятся из 1,0 0,02 0,05 ОДО 0,15 0,20 0,5 0,59 0,72 0,74 0,75
2,0 0,02 0,05 0,10 0,15 0,20 0,45 0,57 0,72 0,72 0,74
0,5 $25
1 1 2t/r
Некоторые значения р Для сталей при ав = = 80 кГ/мм2
t т 1 d ав, кГ/мм?
1 г г d
< 50 80 > 100
0,5 0,02 0,05 ОДО 0Д5 0,20 1,77 1,72 1,59 1,45 1,37 2,02 1,87 1,69 1,53 1,41 2,22 1,98 1,77 1,59 1,45 0,5 0,02 0,05 0,10 0,15 0,20 0,78 0,83 0,84 0,84 0,85
1,0 0,02 0,05 ОДО 0,15 0,20 1,85 1,80 1,65 1,50 1,45 2,12 1,96 1,76 1,58 1,48 2,35 2,10 1,85 1,65 1,50 1,0 0,02 0,05 0,10 0,15 0,20 0,66 0,71 0,84 0,85 0,86
2,0 0,02 0,05 ОДО 0,15 0,20 1,92 1,86 1,70 1,54 1,48 2,21 2,03 1,82 1,63 1,52 2,46 2,10 1,92 1,70 1,54 2,0 0,02 0,05 0,10 0,15 0,20 0,59 0,69 0,84 0,85 0,87
Для сталей при 100 кГ/мм2
t т т d 9
0,5 0,02 0,05 0,10 0,15 0,20 0,9 0,93 0,94 0,95 0,95
1Д> 0,02 0,05 0,10 0,15 0,20 0,8 0,82 0,94 0,94 0,94
2,0 0,02 0,05 0,10 0,15 0,20 0,71 0,8 0,93 0,94 0,94
Продолжение приложения 2
№ п/п Схема нагружения элемента конструкции или детали Теоретический коэффициент концентрации напряжений а Эффективный коэффициент концентрации напряжений р Коэффициент чувствительности к концентрации напряжений 4 а —1
Для серого чугуна при ав = Для сплавов [d = 8 мм;
= 29 кГ/мм2
При d = 8 мм и = 0,3.3 -^- = 1.25 — 1,5) а /
МЛ4 -0,4-1
Ат-т-Н" —п МА2, МАЗ, МА5 — 0,7 — 1
7,4-4- АЛ5, АЛ7, АЛ8, АЛ9—
у О — 4, 0 — 0,3
L ГЫ 0 0,1 0,2 £tfr/d, Д16, АК2, АК8 — 0,5 — 1
При ЙГЙ^О.ЗЗ ₽v = v₽
Значения v находятся из
графика
V-
0,95 -
ПЯ5\ I I I I I I I _
0 0,1 0,2 03^
Для сплавов I d = 8 мм\ =
= 1,25 —1,5 j
МЛ4«—1,4 —2
МА2, МАЗ, МА5 —1,7—2
АЛ5, АЛ7, АЛ8, АЛ9 — 1 — 1,3
Д16, АК2, АК8 —1,5 —2
6.
Валы, оси с выточ-
ками
Кручение
—I— Ж ЙЙ
? f 0 12 3456 7Щ2О
Схема определения иско-
мой величины а показана
пунктиром
Для сталей Для сталей. при ав 50 кГ/мм2
i г Т ов, кГ/мм2
< 50 80 > 100
0,5 0,02 0,05 0,10 0,15 0,20 1,46 1,43 1,36 1,27 1,22 1,61 1,52 1,42 1,32 1,25 1,73 1,60 1,46 1,36 1,27 t ~г~ Г т Q
1.0 0,02 0,05 0,10 0,15 0,20 0,64 0,74 0,81 0,91 1.00
1,0 0,02 0,05 0,10 0,15 0,20 1,51 1,48 1,39 130 1,27 1,67 1,58 1,47 1,35 1,29 1,81 1,66 1,51 1,39 1,30
2,0 0,02 0,05 0,10 0,15 0,20 0,49 0,72 0,76 0,77 0,96
2,0 0,02 0,05 0,10 0,15 0,20 1,56 1,51 1,42 1,33 1,29 1,73 1,62 1,50 1,38 1,30 1,87 1,71 1,56 1,42 1,32
Продолжение приложения 2
£ с _1_ Схема нагружения элемента конструкции или детали Теоретический коэффициент концентрации напряжений а Эффективный коэффициент концентрации напряжений р Коэффициент чувствительности к концентрации напряжений 1
t г г d а
при ав = 80 кГ/мм?
1,0 0.02 0,05 0,10 0,15 0,20 0,84 0,89 0,98 1,06 1,07
2,0 0,02 0,05 0,10 0,15 0,20 0,47 0,73 0,91 0,91 1,00
при ав 100 кГ/мм2
1,0 0,02 0,05 0,10 0,15 0,20 1,01 1,02 1,06 1,14 1,15
2,0 0,02 0,05 0,10 0,15 0,20 0,76 0,84 1,00 1,00 1,07
7. Валы, оси ками 60 Х7/ с выточ- При d — 8 мм; = а = 1,02 — 1,6 г = 0,05 мм; = 0,006; d — = 4 — 4,5; « = 4,5 — 6 г Для сплавов МЛ4 —1,8 — 4,3 МА2, МАЗ, МА5 — 1,9 — 2,5 АЛ5, АЛ7, АЛ8, АЛ9 — 1—1,4 Д16, АК2, АК8 —1,1 —2,6 Для сплавов МЛ4 —0,2 —0,8 МА2, МАЗ, МА5 — 0,25 — — 0,26 АЛ5, АЛ7, АЛ8, АЛ9 — — 0 — 0,07 Д16, АК2, АК8 —0,03 — — 0,27
Л7 ( 4
Изгиб
8. Валы, оси с попе- речными круглыми отверстиями 2,0 При -^- = 0,1—0,33 Для сталей Для сталей — 0,7 *—1,0
р 22 Т
1 . 4
1 Li 1,8 1,4 4
1
1 п li ।
1 1
Изгиб 0 6Q 80 100 бв,кГ/ммг
Продолжение приложения 2
При других величинах ав сле-
дует применять поправочный
коэффициент ё, который нахо-
дится с помощью нижеприве-
денного графика
9.
Валы, оси с попе-
речным круглым
отверстием
Кручение
Верхняя граница соответствует
высоколегированным чугунам,
нижняя — малолегированным
чугунам
Для сталей при d = 30 — 50 мм
и 4 = 0.05—0.25
и
7,3-^-==-----
I I I L.L1Z
40 SO 80 100
Некоторые числовые значения р,
соответствующие графику, при-
ведены в таблице
о
о
Продолжение приложения 2
№ ц/п Схема нагружения элемента конструкции или детали Теоретический коэффициент концентрации напряжений а Эффективный коэффициент концентрации напряжений 3 Коэффициент чувствительности к концентрации напряжений 4 «-1
I
а ~Т ств кГ/мм2
50 60 80 100
0,05— —0,25 1,75 1,78 1,83 1 92
Для серого чугуна с = 22 кГ/мм2 и при ~ — °в = 0.1
Р /,4 1,2 1,0 Л L
) 20 30 ft) d)MM
I
10.
Валы, оси с одной
и двумя шпоночны-
ми канавками
Изгиб
Для расчетов: при одной шпо-
ночной^ канавке
ясР bt(d—tY
0 ~ 32 2d
при двух шпоночных канавках
~ nd6 Ы (d — ty
0 ~ 32 d
где Жи — момент сопротивле-
ния сечения при изгибе.
Для сталей
kFJmm* 0
50 1,5
60 1,6
70 1,72
80 1,8
90 1,9
WO 2,0
Продолжение приложения 2
11 № п/n | Схема нагружения элемента конструкции или детали Теоретический коэффициент концентрации напряжений а Эффективный коэффициент концентрации напряжений 3 Коэффициент чувствительности к концентрации напряжений п Р-1 9 а — 1
Кручение Для расчетов: при одной шпо- ночной канавке ~ nd3 bt(d — t)2 ~ 16 2d ‘ при двух шпоночных канавках ltd3 bt (d — t)2 ~ 16 d где WK — момент сопротивле- ния сечения при кручении. Для сталей
ав, кГ/ММ2 0
- 50 60 70 80 90 100 1.4 1,5 1,6 1,7 1,8 1,9
/
ю
to
5-1186
11.
Валы, оси со шли-
цевыми (зубчаты-
ми) участками
Изгиб
Для сталей при расчетах в слу-
чае прямобочных шлицев мо-
мент сопротивления сечения
определяют по формуле
где d— внутренний диаметр;
6 — поправочный коэффициент,
равный:
для легкой серии 1,09 — 1,16;
для средней серии — 1,14 —
1,27;
для тяжелой серии — 1,14 —
1,39
Меньшие значения 6 соответ-
ствуют большим d
Для эвольвентных шлицевых
соединений WH определятся
как для сплошного круглого
сечения с диаметром, равным
диаметру делительной окруж-
ности
5$ Продолжение приложения 2
| № п/п Схема нагружения элемента конструкции или детали Теоретический коэффициент концентрации напряжений а Эффективный коэффициент концентрации напряжений 3 Коэффициент чувствительности к концентрации напряжений ~_Р-1 а — 1
Кручеййе Для прямобоких шлицев а = 2,5 — 3,2 Для эвольвентных шли- цев а = 1,2 —1,5 Для прямобоких шли- цев — 0,5 —1,2 Для эвольвентных шли- цев — 0,8 — 3,0
ств* кГ/мм2 3
Прямоуголь- ные шлицы (ГОСТ 1139— 53) Эвольвентные шлицы (ГОСТ 6033— 51)
40 50 60 70 80 90 100 120 1,35 1,45 1,55 1,60 1,65 1,70 1,72 1,75 1,35 1,45 1,55 1,60 1,65 1,70 1,72 1,75
ств» кГ/мм2 3
Прямоуголь- ные шлицы (ГОСТ 1139 — 53) Эвольвентные шлицы (ГОСТ 6033 — 51)
40 50 60 70 80 90 100 120 2,10 2,25 2,35 2,45 2,55 2,65 2,70 2,80 1,40 1,43 1,46 1,49 1,52 1,55 1,58 1,60
•
12. Некоррегированные
шестерни эволь- вентного профиля с углом а = 20° при нагрузке, при- ложенной к верши- не зуба
сл
При количестве зубьев
2 = 20-4-80
Момент сопротивления сечения > с прямобокими шлицами при кручении 17к = 217и Для эвольвентных шлицевых соединений Т7К определяется как для сплошного круглого сечения с диаметром, равным диаметру делительной окруж- ности
р=1 + г(а-1) Для сталей
Продолжение приложения 2
с?
№ П/П Схема нагружения элемента конструкции или детали Теоретический коэффициент концентрации напряжений а Эффективный коэффициент концентрации напряжений р Коэффициент чувствительности к концентрации напряжений а — 1
1 — = 0,124 — 0,222 т 2 — 2С = о,124— 0,17 т 3 — = 0,258 — 0,36 т 4 — = 0,305 — 0,317 т 5 — -^- = 0,55 т в ^- = 0,495 — 0,6 т Здесь: s — толщина осно- вания зуба в опасном се- чении; 1 — плечо дейст- вия изгибающей силы, т модуль зацепления; г( — радиус закругления вершины зуба инстру- мента Для чугуна — 1,2 — 1,3 1 — =0,8 °в 2 — =0,7 °в 3 — — = 0,6 °в ®т 4 — = 0,55 % 5— -^—=0,4 — 0,5 °В
1 1
1 1
13. Болтовые соедине- ния при растяже- нии — сжатии для d = 12 мм Для сталей
ав> кГ/ммг ?
метрическая резьба дюймовая резьба
40 60> 80 100 3,0 3,9 4,8 5,2 2,2 2,9 3,5 3,8
14. Прямоугольная ступенчатая полоса с z P=14-g(a — 1) Значения q могут быть взяты из графика, при- веденного для схемы 12
& 111
Растяжение — сжа- тие Я 0,2 Ofi Ofir/t>
3
Продолжение приложения 2
№ п/п Схема нагружения элемента конструкции или детали Теоретический коэффициент концентрации напряжений а Эффективный коэффициент концентрации напряжений р Коэффициент чувствительности к концентрации напряжений . Р-1 q а — 1
15. Прямоугольная ступенчатая полоса V. ₽ = 1 + д(а —1) Значения q могут быть взяты из графика, приве- денного для схемы 12
of 1,5 to L Д
ДА
М (-1 Изг иб . л —
9 » Ег
? 0,2 Ofi 0,6 г/А
16. П рямоуго льная пластина с отвер- стием d В а Для сталей Для ст d В алей ств, кГ/мм2
0 0,1 0,2 о,з 0,4 0,5 Для сплавов = 40 мм] d = 2,5- 3,0 3,03 3,14 3,36 3,74 4,32 МА2, МАЗ, 1 : 1 6 ММ] ТО -3
60 80 100
л 1,6 1,2 VIA5, Д16, лщине h -
0 0,1 0,2 0,3 0,4 0,5 1 о,з 0,3 0,28 0,25 0 22 0,18 0,1 — 0,4 0,39 0,36 0,34 0,29 0,24 0,53 0,48 0,47 0,44 0,4 0,35 0,29
ежа-
к ( < *
Растяженв тие у* [е — Ю 50 70 90 110 бв, кГ/мм2 АК2, АК8 при В — = 1,5 — 5 мм 1,2 —1,8
i |
Прямоугольная
пластина с отвер-
стием
Для сталей
Некоторые значения q при
B/h = 3 и -^- = 0,1—0,9
Для стали с ав =
= 60 кГ/мм2 — 0,37 — 1,46;
ав = 80 кГ/мм2 — 0,5 — 2
ав = 100 кГ/мм2 — 0,63 —
— 2,5
Изгиб
18.
Прямоугольная
пластина с боко-
выми вырезами
Растяжение — сжа-
тие
о
со
Для сплавов МА2, МАЗ, МА5, Д16, АК2, АК8 при В = 40 мм]
d = 1 — 6 мм] h~ 1,5 — 5 мм
1,6 —2,5
1,3 —1,8
Р = 1 + <7(а-1)
j_______0,2 —1,3________
Значения q могут быть
взяты из графика, приве-
денного для схемы 12
Продолжение приложения 2
£ с £ Схема нагружения элемента конструкции или детали Теоретический коэффициент концентрации напряжений а Эффективный коэффициент концентрации напряжений 0 Коэффициент чувствительности к концентрации напряжений Л 0~1 q “ а — 1
19. Прямоугольная пластина с боко- выми вырезами (Way 7,0 ГЕ 0 0,2 ОА 1.25- — 0,5 г/Ь ₽ = l + s(« —1) Значения q могут быть взяты из графика, приве- денного для схемы 12
Изгиб
Прямоугольная
пластина с боко-
выми вырезами
Для сплавов МА2, МАЗ, МА5, Д16, АК2, АК8 при В — 12 мм\
г = 16 мм; h = 0,5 мм
2 1,5 — 2 0,5 — 1
Изгиб
21. Полоса с односто-
ронним или с двух- Для сплавов МА2, МАЗ, МА5 при г = 0,02 0,05 мм; ? — 3 «= 15;
сторонним надрезом
Растяжение — сжа-
тие или изгиб
0,03 — 0,07
Профиль с входя-
щим углом
Изгиб
Элемент конструк-
ции с входящим
углом
Изгиб
7 — легированная
(% = 90 кГ/мм2)
2 — углеродистая
(ав = 50 — 70 кГ/мм2)
Для чугуна с св = 29 кГ}мм2
Для стали с ав =
= 90 кГ/мм2
0,1 — 0,3 I 0,33 — 0.47
Для стали с ав =
= 50-4-70 кГ1мм2
0,1—0,6 I 0,2 — 0,35
Продолжение приложения 3
Приложена е 3
Функции Крылова S, Т, U, V
1
S (kz) яь-х- (ch kz + cos kz);
A
1
T (kz) = у (sh kz + sin kz);
1
U (kz) = -5- (ch kz — cos kz);
1
V (kz) = — (sh kz sin kz),
причем
S' (kz) = kV (kz); S" (kz) = k4J (kz); S'" (kz) = №T (kz);
T' (kz) = kS (kz); T" (kz) = k?V (kz); T'" (kz) = k*U (kz);
V (kz) = kT (kz); U" (kz) = №S (kz); U'" (kz) = №V (kz);
V'(kz) = kU (kz); V" (kz) = k*T (kz); V"' (kz) = k*S (kz)
kz
kz 8 (bz) Т(М U (kz) V (kz)
0,00 1,00000 0,00000 0,00000 0,00000
0,01 1,00000 0,01000 0,00005 0,00000
0,02 1,00000 0,02000 0,00020 0,00000
0,03 1,00000 0,03000 0,00045 0,0Q000
0,04 1,00000 0,04000 0,00080 0,00001
0,05 1,00000 0,05000 0,00125 0,00002
0,06 1,00000 0,06000 0,00180 0,00004
0,07 1,00000 0,07000 0,00245 0,00006
0,08 1,00000 0,08000 0,00320 0,00009
0,09 1,00000 0,09000 0,00405 0,00012
0,10 1,00000 0,10000 0,00500 0,00017
0,11 1,00001 0,11000 0,00605 0,00022
0,12 1,00001 0,12000 0,00720 0,00029
0,13 1,00001 0,13000 0,00845 0,00037
0,14 1,00002 0,14000 0,00980 0,00046
0,15 1,00002 0,15000 0,01125 0,00056
0,16 1,00003 0,16000 0,01280 0,00068
0,17 1,00003 0,17000 0,01445 0,00082
0,18 1,00004 0,18000 0,01620 0,00097
0,19 1,00005 0,19000 0,01805 0,00115
0,20 1,00007 0,20000 0,02000 0,00134
0,21 1,00008 0,21000 0,02205 0,00155
0,22 1,00010 0,22000 0,02420 0,00178
0,23 1,00012 0,23000 0,02645 0,00203
0,24 1,00014 0,24000 0,02880 0,00231
0,25 1,00016 0,25000 0,03125 0,00261
0,26 1,00019 0,26001 0,03380 0,00293
0,27 1,00022 0,27001 0,03645 0,00328
0,28 1,00026 0,28001 0,03920 0,00366
0,29 1,00029 0,29001 0,04205 0,00407
T (kz)
U (kz) V (kz)
0,30 1,00034 0,30002 0,04500 0,00450
0,31 1,00038 0,31002 0,04805 0,00497
0,32 1,00044 0,32003 0,05120 0,00546
0,33 1,00049 0,33003 0,05445 0,00599
0,24 1,00055 0,34004 0,05780 0,00655
0,35 1,000625 0,35004 0,06125 0,00715
0,36 1,00070 0,36005 0,06480 0,00778
0,37 1,00078 0,37006 0,06845 0,00844
0,38 1,00086 0,38006 0,07220 0,00915
0,39 1,00096 0,39007 0,07605 0,00989
0,40 1,00106 0,40008 0,08000 0,01067
0,41 1,00117 0,41009 0,08405 0,01149
0,42 1,00129 0,42011 0,08820 0,01235
0,43 1,00142 0,43012 0,09245 0,01325
0,44 1,00156 0,44014 0,09681 0,01420
0,45 1,00171 0,45015 0,10126 0,01519
0,46 1,00186 0,46017 0,10581 0,01625
0,47 1,00203 0,47019 0,11047 0,01731
0,48 1,00221 0,48021 0,11522 0,01844
0,49 1,00240 0,49023 0,12007 0,01961
0,50 1,00260 0,50026 0,12502 0,02084
0,51 1,00280* 0,51029 0,13007 0,02211
0,52 1,00304 0,52031 0,13522 0,02344
0,53 1,00329 0,53024 0,14048 0,02481
0,54 1,00354 0,54038 0,14583 0,02624
0,55 1,00381 0,55042 0,15129 0,02773
0,56 1,00410 0,56046 0,15684 0,02927
0,57 1,00440 0,57050 0,16250 0,03037
0,58 1,00471 0,58054 0,16825 0,03253
0,59 1,00505 0,59060 0,17411 0,03424
0,60 1,00540 0,60074 0,18006 0,03601
0,61 1,00577 0,61070 0,18612 0,03784
0,62 1,00616 0,62076 0,19228 0,03973
0,63 1,00656 0,63082 0,19853 0,04169
0,64 1,00699 0,64089 0,20489 0,04369
0,65 1,00742 0,65097 0,21136 0,04578
0,66 1,00790 0,66104 0,21791 0,04793
0,67 1,00830 0,67112 0,22458 0,05013
0,68 1,00891 0,68121 0,23134 0,05248
0,69 1,00945 0,69130 0,23820 0,05477
0,70 1,01000 0,70140 0,24516 0,05718
0,71 1,01059 0,71150 0,25223 0,05967
0,72 1,01120 0,72161 0,25939 0,06223
0,73 1,01183 0,73173 0,26666 0,06486
0,74 1,01249 0,74185 0,27403 0,06756
0,75 1,01318 0,75198 0,28149 0,07034
0,76 1,01390 0,76211 0,28906 0,07319
683
682
П родолжение приложения 3
Продолжение прилож ения 3
kz S (kz) Т {kz) U {kz) V (kz) kz S (kz) T (kz) U (kz) V(ftz)
0,77 1,01465 0,77226 0,29674 0,07612 1,23 1,24 1,09550 1,09865 1,25348 1,26444 0,76196 0,77385 0,78658 0,79936 0,31099 0,31867 0,32647 0,33439
0,78 1,01542 0,78240 0,30451 0,07913 1,25 1,10187 1,27545
0,79 1,01623 0,79256 0,31238 0,08228 1,26 1,10518 1,28648
0,80 1,01707 0,80273 0,32036 0,08538 1,27 1,28 1,10856 1,11203 1,29750 1,30866 0,81.228 0 82531 0,34245 0,35064 0,35896
0,81 0,82 1,01794 1,01884 0,81290 0,82309 0,32844 0,33662 0,08862 0,09194 1,29 1,11557 1,31980 0,83845
0,83 1,01978 0,83328 0,34490 0,09535 1,30 1,11920 1,33097 0,85163 0,86507 0,36741 0,37600 0,38471 0,39357 0,40256
0,84 1,02075 0,84348 0,35329 0,09885 1,31 -1,12292 1,34218
0,85 1,02175 0,85380 0,36177 0,10242 1,32 1,12673 1,35343 0,87855
0,86 1,02280 0,86392 0,37036 0,10608 1,33 1,13062 1,36471 0,89214 0,90585
0,87 1,02388 0,87415 0,37905 0,10983 1,34 1,13460 1,37604
0,88 1,02500 0,88440 0,38785 0,11366 1,35 1,13867 1,38740 0,91966 0^41169 0,42096
0,89 1,02615 0,89465 0,39674 0,11758 1,36 1,14283 1,39881 0,93336
1,02735 0,90492 0,40573 0,12159 1,37 1,14709 1,41026 0,94764 0,43035 0,43991 0,44959
0,90 1,38 1,15144 1,42175 0,96180
0,91 1,02858 0,91520 0,41483 0,12570 1,39 1,15588 1,43329 0,97607
0,92 1,02986 0,92549 0,42404 0,12990
0,93 1,03118 0,93082 0,43335 0,13418 - 1,40 1,16043 1,44487 0,99047 0,45933
0,94 1,03254 0,94612 0,44275 0,13856 1,41 1,16507 1,45655 1,00497 0 46941
0,95 1,03395 0,95645 0,45227 0,14303 1,42 1,16982 1,46817 1 01959 0,47952 0,48980
0,96 1,03540 0,96679 0,46188 0,14761 1,43 1,17466 1,47990 1,03434
0,97 1,03690 0,97716 0,47161 0,15297 1,44 1,17961 1,49167 1,04920 0,50021
0,98 1,03845 0,98753 0,48143 0,15704 1,45 1,18467 1,50349 1,06417 0,51078
0,99 1,04005 0,99793 0,49136 0,16190 1,46 1,18984 1,51537 1,07926 0,52149
1,00 1,04169 1,00833 0,50139 0,16687 1,47 1,19510 1,52728 1,09448 0,53237
1,48 1,20048 1,53926 1,10981 0,54339
1,01 1,04338 1,01876 0,51152 0,17193 1,49 1,20597 1,55130 1,12526 0,55456
1,02 1,04513 1,02920 0,52176 0,17710
1,03 ' 1,04693 1,03953 0,53211 0,18237 1,50 1,21157 1,56338 1,14083 0,56590
1,04 1,04878 1,05014 0,54256 0,18774 1,51 1,21729 1,57553 1,15653 0,57738
1,05 1,05068 1,06064 0,55311 0,19322 1,52 1,22312 1,58773 1,17235 0,58903
1,06 1,05264 1,07116 0,56377 0,19880 1,53 1,22907 1,59999 1,18828 0,60083
1,07 1,05466 1,08169 0,57454 0,20449 1,54 1,23514 1,61231 1,20435 0,61279
1,08 1,05673 1,09225 0,58540 0,21029 1,55 1,24132 1,62469 1,22053 0,62492
1,09 1,05887 1,10283 0,59638 0,21620 1,56 1,24769 1,63714 1,23679 0,63720
1,06106 1,11343 0,60746 0,22222 1,57 1,25407 1,64965 1,25327 0,64965
1,10 - 1,58 1,26063 1,66222 1,26983 0,66226
1,11 1,06333 1,12405 0,61865 0,22835 1,59 1,26732 1,67486 1,28652 0,67504
1,12 1,06562 1,13469 0,62995 0,23460
1,13 1,06800 1,14536 0,64134 0,24095 1,60 1,27413 1,68757 1,30333 0,68800
1,14 1,07044 1,15605 0,65285 0,24742 1,61 1,28108 1,70034 1,32027 0,70112
1,15 1,07295 1,16677 0,66446 0,25401 1,62 1,28815 1,71319 1,33734 0,71441
1,16 1,07552 1,17750 0,67619 0,26071 1,63 1,29536 1,72608 1,35453 0,72786
1,17 1,07816 1,18828 0,68801 0,26753 1,64 1,30271 1,73910 1,37186 0,74149
1,18 1,08087 1,19908 0,69995 0,27447 1,65 1,31019 1,75216 1,38932 0,75530
1,19 1,08365 1,20990 0,71200 0,28153 1,66 1,67 1,31782 1,76530 1,40690 0,76928
1,08651 1,22075 0,72415 0,28871 1,32558 1,77852 1,42462 0,78344
1,20 1,68 1,33348 1,79181 1,44248 0,79778
1,21 1,08934 1,23163 0,73641 0,29601 1,69 1,34154 1,80519 1,46046 0,81229
1,22 1,09243 1,24254 0,74878 0,30344
685
681
Продолжение приложения S
k2 8 (kz) Т (kz) U (kz) V(M Продолжение приложения 3
kz S (kz) T (kz) U (kz) V(fez)
1,70 1,34974 1,81864 1,47858 1,49683 0,82699 0,84186
1,71 1^35808 1,83219
1,72 1,36657 1,84581 1,53523 0,85692 2,17 1,93612 2,57392 2,50011 1,74813
1,73 1,37522 1,85952 1,53375 0,87216 2,18 1,95373 2,59337 2,52594 1,77326
1,74 1,38401 1,87331 1^55242 0,88759 2,19 1,97158 2,61300 2,55198 1,79865
1,75 1,39297 1,88820 1,57122 0,90321 1,81431
1,76 1,40208 1,90117 1,59016 0^91903 2,20 1,98970 2,63208 2,57820
1,77 1,41135 1,91524 1,60924 0,93502 2,21 2,00807 2,65279 2,60464 1,85022
1,78 1,42078 1,92940 1,62846 0^95120 2,22 2,02671 2,67296 2,63126 1,87640
1,79 1,43038 1,94366 1,64783 0,96759 2,23 2,04560 2,69332 2,65810 1,90285
2,24 2,06476 2,71388 2,68513 1,92956
1,80 1,44013 1,95801 1,66734 0,98416 2,25 2,08420 2,73462 2,71237 1,95655
1,81 1,45006 1,97246 1,68699 1,00093 2,26 2,10390 2,75556 2,73982 1,98381
1,82 1,46015 1,98697 1,70679 1,02191 2,27 2,12387 2,77670 2,76748 2,01135
1,83 1,47042 2,00166 1,72673 1ДО507 2,28 2,14412 2,79804 2,79536 2,03916
1,84 1,48086 2,01642 1,74682 1/Э5244 2,29 2,16465 2,81958 2,82345 2,06725
1,85 1,49147 2,03128 1,76706 1,07001 2,09563
1,86 1,50225 2,04625 1,78745 1,08778 2,30 2,18547 2,84133 2,85175
1,87 1,51322 2,06133 1,80798 1,10576 2,31 2,20657 2,86329 2,88027 ’ 2,12429
1,88 1,52437 2,07652 1,82868 1,12394 2,32 2,22795 2,88546 2,90902 2,15324
1,89 1,53570 2,09182 1,84952 1,14233 2,33 2,24964 2,90785 2,93798 2,18247
2,34 2,27161 2,93045 2,96717 2,21200
1,90 1,54722 2,10723 1,87051 1,16093 2,35 2,29388 2,95328 2,99659 2,24182
1,91 1,55892 2,12276 1,89166 1Д7974 2,36 2,31645 2,97634 3,02624 2,27193
1,92 1,57081 2,13841 1,91297 1,19877 2,37 2,33932 2,99962 3,05612 2,30234
1,93 1,58290 2,15418 1,93443 1,21800 2,38 2,36250 3,02312 3,08624 2,33306
1,94 1,59518 2,17006 1,95605 1,23745 2,39 2,38598 3,04686 3,11658 2,36406
1,95 1,61265 2,18608 1,97783 1,25713
1,96 1,62032 2,20222 1,99977 1,27701 2,40 2,40978 3,07084 3,14717 2,39539
1,97 1,63319 2,21849 2,02187 1,29712 2,41 2,43389 3,09506 3,17800 2,42700
1,98 1,64626 2,23489 2,04415 1,31745 2,42 2,45832 3,11952 3,20907 2,45895
1,99 1,65954 2,25142 2,06707 1,33800 2,43 2,48307 3,14423 3,24039 2,49119
2,00 2,44 2,50814 3,16919 3,27196 2,52375
1,67302 2,26808 2,08918 1,35878 2,45 2,53354 3,19439 3,30378 2,55664
2,01 1,68671 2,28337 2,11193 1,37828 2,46 2,56927 3,21986 3,33585 2,58983
2,02 1,70062 2,30181 2,13487 1,40102 2,47 2,58535 3,24558 3,36817 2,62335
2,03 1,71474 2,31889 2,15797 1,42249 2,48 2,61174 3,27156 3,40076 2,65720
2,04 1,72907 2,33611 2,18125 1,44418 2,49 2,63848 3,29781 3,43360 2,69136
2,05 1,74362 2,35347 2,20470 1,46611
2,06 1,75840 2,37098 2,22832 1,48827 2,50 2,66557 3,32433 3,46672 2,72587
2,07 1,77360 2,38864 2,25212 1,51068 2,51 2,69300 3,35113 3,50010 2,76070
2,08 1,78861 2,40645 2,27609 1,53332 2,52 2,72079 3,37820 3,53374 2,79584
2,09 1,80405 2,42441 2,30024 1,55620 2,53 2,74893 3,40555 3,56765 2,83137
2,10 2,54 2,77742 3,43318 3,60175 2,86722
1,81973 2,44253 2,32458 1,57933 2,55 2,80627 3,46110 3,63632 2,90342
2,11 1,83565 2,46081 2,34910 1,60269 2,56 2,83549 3,48931 3,67107 2,93995
2,12 1,85179 2,47925 2,37380 1,62630 2,57 2,86507 3,51780 3,70061 2,97683
2,13 1,86817 2,49785 2,39868 1,65017 2,58 2,89502 3,54660 3,74144 3,01408
2,14 1,88479 2,51661 2,42375 1,67428 2,59 2,92535 3,57571 3,77705 3,05167
2,15 1,90165 2,53554 2,44902 1,69865
2,16 1,91876 2,55464 2,47447 1,72327 2,60 2,95606 3,60511 3,81295 3,08962
2,61 2,98714 3,63483 3,84915 3,12793
686 2,62 3,01862 3,66486 3,88565 3,16660
П родолжение приложения 3
Продолжение приложения 3
kt S (Л г) Т (kz) U (kz) V (kz)
2,63 3,05047 3,69521 3,92235 3,20564
2,64 3,08273 3,72587 3,95955 3,24505
2,65 3,11538 3,75186 3,99696 3,28483
2,66 3,14843 3,78818 4,03469 3,32499
2,67 3,'18188 3,81984 4,07273 3,36552
2,68 3,21755 3,85182 4,11108 3,40645
2,69 3,25001 3,88415 4,14926 3,44775
2,70 3,28470 3,91682 4,18877 3,48944
2,71 3,31980 3,94985 4,22810 3,53152
2,72 3,35533 3,92321 4,26717 3,57401
2,73 3,39128 4,01695 4,30777 3,61688
2,74 3,42767 4,05105 4,34811 3,66017
2,75 3,46449 4,08550 4,38879 3,70384
2,76 3,50175 4,12034 4,42982 3,74794
2,77 3,53945 4,15554 4,47120 3,79244
2,78 3,57760 4,19112 4,51293 3,83736
2,79 3,61619 4,22709 4,55503 3,88271
2,80 3,65525 4,26345 4,59748 3,92847
2,81 3,69476 4,30020 4,64030 3,97465
2,82 3,73493 4,33735 4,68330 4,02127
2,83 3,77520 4,37490 4,72705 4,06832
2,84 3,81612 4,41285 4,77098 4,11582
2,85 3,85751 4,45122 4,81530 4,16375
2,86 3,89940 4,49001 5,86000 4,21212
2,87 3,94176 4,52921 4,90510 4,26095
2,88 3,98461 4,56884 4,95059 4,31028
2,89 4,02796 4,60891 4,99648 4,35996
2,90 4,07181 4,64940 5,04277 4,41016
2,91 4,11617 4,69034 5,08947 4,46082
2,92 4,16103 4,73173 5,13658 4,51195
2,93 4,20640 4,77357 5,18410 4,56355
2,94 4,25230 4,81586 5,23206 4,61563
2,95 4,29875 4,85862 5,28042 4,66820
2,96 4,34567 4,90181 5,32923 4,72124
2,97 4,39315 4,94553 5,37846 4,77478
2,98 4,44117 4,98970 5,42814 4,82881
2,99 4,48972 5,03435 5,47825 4,88335
3,00 4,53883 5,07949 5,52883 4,95838
3,01 4,58850 5,12513 5,57985 4,99392
3,02 4,63872 5,17127 5,63133 5,04998
3,03 4,68950 5,21791 5,68327 5,10655
3,04 4,74085 0,26556 5,73569 5,16364
3,05 4,79277 5,31272 5,78858 5,22126
3,06 4,84527 5,36090 5,84195 5,27942
3,07 4,89836 5,40963 5,89580 5,33810
3,08 4,95204 5,45888 5,95014 5,39734
3,09 5,00631 5,50868 6,00498 5,45711
688
kz S (kz) T (kz) U (kz)
3,10 5,06118 5,55901 6,06032 5,51744
3,11 5,11666 5,60990 6,11616 5,57832
3,12 5,17275 5,66135 6,17252 5,63976
3,13 5,22931 5,71336 6,22936 5,70177
3,14 5,28678 5,76594 6,28678 5,76435
3,15 5,34475 5,81910 6,34471 5,82751
3,16 5,40316 5,87284 6,40317 5,89125
3,17 5,46257 5,92717 6,46217 5,95657
3,18 5,52245 5,98209 6,52171 6,02049
3,19 5,58298 6,03762 6,58182 6,08601
3,20 5,64418 6,09375 6,64247 6,15213
3,21 5,70603 6,15050 6,70369 6,21885
3,22 5,76855 6,20787 6,76349 6,28621
3,23 5,83161 6,26588 6,82800 6,35417
3,24 5,89564 6,32451 6,89080 6,42277
3,25 5,96021 6,38379 6,95384 6,49199
3,26 6,02535 6,44372 7,01848 6,56185
3,27 6,09145 6,50431 7,08322 6,63236
3,28 6,15813 6,56555 7,14857 6,70352
3,29 6,22552 6,62747 7,21454 6,77533
3,30 6,29364 6,69006 7,28112 6,84782
3,31 6,36248 6,75334 7,34833 6,92095
3,32 6,43206 6,81732 7,41619 6,99478
3,33 6,50238 6,88199 7,48460 7,06928
3,34 6,57345 6,94737 7,55383 7,14448
3,35 6,64527 7,01346 7,62363 7,22036
3,36 6,71786 7,08027 7,69410 7,29696
3,37 6,79121 7,14782 7,76524 7,37425
3,38 6,86534 7,21610 7,83706 7,45226
3,39 6,94026 7,28513 7,90957 7,53099
3,40 7,01597 7,35491 7,98277 7,61045
3,41 7,09247 7,42546 8,05666 7,69065
3,42 7,16978 7,49676 8,13028 7,77159
3,43 7,24790 7,56885 8,20661 7,85326
3,44 7,32685 7,64172 8,28266 7,93573
3,45 7,40662 7,71539 8,35945 8,01893
3,46 7,48723 7,78986 8,38697 8,10291
3,47 7,51858 7,86514 8,51535 8,18768
3,48 7,65099 7,94124 8,59427 8,27322
3,49 7,73415 8,01816 8,67407 8,35956
3,50 7,81818 8,09592 8,75464 8,44671
3,51 7,90309 8,17453 8,83599 8,53466
3,52 7,98888 8,25398 8,91813 8,62343
3,53 8,07556 8,33431 9,00107 8,71302
3,54 8,16315 8,41550 9,08482 8,80346
3,55 8,25164 8,49717 9,16938 8,89472
3,56 8,34104 8,58054 9,25478 8,98685
689
Продолжение приложения 3
п г родолжение приложения 8 kz S (kz) T (kz) U (kz) V (kz)
kz S (kz) Т (kz) U (kz) V(fez)
4,03 4,04 13,75435 13,89955 13,67275 13,81102 14,38500 14,52242 14,44882 14,59335
8,43137 8,61440 9,34100 9,07982
3,57 4,05 14,04622 13,95074 14,66122 14,73228
3,58 8,52264 8,74917 9,42807 9,17367 4,06 14,19435 14,09195 14,80144 14,88658
3,59 8,61485 8,83485 9,51599 9,26838 4,07 14,34395 14,23464 14,94306 15,03530
3,60 8,70801 8,92147 9,60477 9,36399 4,08 4,09 14,49506 14,64767 14,37883 14,52455 15,08613 15,23065 15,18545 15,33703
3,61 8,80213 9,00902 9,69442 9,46048
3,62 8,89772 9,09751 9,78495 9,55788 4,10 14,80180 14,67179 15,37663 15,43007
3,63 8,99330 9,18696 9,87637 9,65618 4,11 14,95747 14,82058 15,57408 15,64456
3,64 9,09035 9,27738 9,96870 9,75541 4,12 15,11470 14,97095 15,67304 15,80055
3,65 9,18845 9,36878 10,06193 9,85557 4,13 15,27350 15,12288 15,82351 15,96304
3,66 9,28747 9,46116 10,15608 9,95666 4,14 15,43386 15,27641 15,97551 16,11703
3,67 9,38754 9,55453 10,25115 10,05869 4,15 15,59533 15,43157 16,12905 16,27755
3,68 9,48864 9,64891 10,34717 10,16168 4,16 15,75942 15,58835 16,28415 16,43962
3,69 9,59077 9,74430 10,44414 10,26564 4,17 15,92464 15,74676 16,44082 16,60324
10,54206 10,37057 4,18 16,09150 15,90648 16,59909 16,76844
3,70 9,68159 9,84072 4,19 16,26001 16,06860 16,75896 16,93522
3,71 9,79819 9,93819 10,64095 10,47648
3,72 9,90349 10,03670 10,74082 10,58339 4,20 16,43020 16,23204 16,92046 17,10363
3,73 10,00986 10,13626 10,84169 10,69130 4,21 16,60208 16,39721 17,08360 17,27121
3,74 10,11732 10,23690 10,94355 10,80023 4,22 16,77568 16,56409 17,24841 17,44530
3,75 10,22587 10,33861 11,04643 10,91017 4,23 16,95099 16,73272 17,41490 17,61862
3,76 10,33552 10,44141 11,15033 11,02116 4,24 17,12806 16,90312 17,58307 17,79360
3,77 10,44630 10,54533 11,25526 11,13318 4,25 17,30687 17,07529 17,75297 17,97028
3,78 10,55819 10,65034 11,36124 11,24627 4,26 17,48746 17,24926 17,92458 18,14867
3,79 10,67123 10,75649 11,46878 11,36041 4,27 17,66985 17,42505 18,09795 18,32878
11,47564 4,28 17,85405 17,60266 18,27309 18,51064
3,80 10,78540 10,87377 11,57638 4,29 18,04008 17,78214 18,45002 18,69425
3,81 10,90074 10,97221 11,68555 11,59195
3,82 11,01725 11,08180 11,79582 11,70935 4,30 18,22794 17,96367 18,62874 18,87964
3,83 11,13493 11,19255 11,90719 11,82786 4,31 18,41767 18,14670 18,80929 19,06683
3,84 11,25380 11,30449 12,01969 11,94750 4,32 18,60928 18,33183 18,99168 19,25583
3,85 11,37389 11,41763 12,13329 12,06826 4,33 18,80280 18,51889 19,17594 19,44667
3,86 11,49518 11,53198 12,24803 12,19017 4,34 18,99823 18,70790 19,36207 19,63935
3,87 11,61769 11,64754 12,36393 12,31322 4,35 19,19558 18,89887 19,55010 19,83392
3,88 11,74145 11,76434 12,48099 12,43745 4,36 19,39491 19,09182 19,74005 20,03037
3,89 11,86646 11,88238 12,59922 12,56285 4,37 19,59620 19,28677 19,93194 20,22872
12,00166 12,68944 4,38 19,79949 19,48374 20,12579 20,42901
3,90 11,99271 12,71864 4,39 20,00479 19,68277 20,32162 20,63121
3,91 12,12024 12,12224 12,83926 12,81723
3,92 12,24905 12,24407 12,96109 12,94623 4,40 20,21212 19,88385 20,51945 20,83545
3,93 12,37917 12,36722 13,08415 13,07645 4,41 20,42150 20,08701 20,71931 21,04164
3,94 12,51059 12,49167 13,20844 13,20797 4,42 20,63296 20,29229 20,92120 21,24985
3,95 12,64333 12,61744 13,33398 13,34063 4,43 20,84651 20,49968 21,12516 21,46007
3,96 12,77740 12,74453 13,46079 13,47460 4,44 21,06217 20,70922 21,33120 21,67235
3,97 12,91283 12,87299 13,58888 13,60966 4,45 21,27996 20,92093 21,53935 21,88670
3,98 12,04960 13,00280 13,71825 13,74637 4,46 21,49991 21,13483 21,74963 22,10315
3,99 12,18775 13,13398 13,84893 . 13,88421 4,47 21,72204 21,35094 21,96236 22,32170
13,98094 14,02366 4,48 21,94635 21,56927 22,17665 22,54240
4,00 13,32730 13,26656 4,49 22,17288 21,78587 22,39345 22,76524
4,01 13,46823 13,40053 14,11427 14,16384
4,02 13,61057 13,53593 14,24895 14,30565 691
690
П родолжение приложения 3
Продолжение приложения 3
kz S (kz) Г (kz) и (kz) 7(М kz S (kz) Т (kz) U (kz) V (kz)
4,50 22,40166 22,01274 22,61246 22,99027 35,52149 35,88107 36,48849
4,51 22,63270 22,23791 22,83371 23,21750 23,44695 23,67865 4,97 36,13585
4,52 22,86602 22,46540 23,05722 4,98 36,50253 35,88467 36,23810 36,84908
4,53 23,10165 22^69524 23,28303 4,99 36,87284 36,25155 36,59878 37,21326
4,54 23,33965 22,92744 23,51114 23^1962 36,96314 37,58106
4,55 23,57990 23,16204 23,74159 24,14888 5,0 37,24680 36,62214
4,56 23,82259 23,39905 23,97439 24,38796 5,1 41,19599 40,54105 40,81801 41,46686
4,57 24,06766 23,63850 24,20957 24,62888 5,2 45,55370 44,87495 45,08518 45,75840
4,58 24,31766 23,88041 24',44916 24 87166 5,3 50,36263 49,66682 49,80826 50,49909
4,59 24,56510 24,12481 24,68719 25'11733 5,4 55,67008 54,96409 55,03539 55,73685
5,5 61,52834 60,81919 60,81967 61,52473
4,60 24,81752 24,37172 24,92967 25,36541 5,6 67,99531 67,29004 66,21974 67,92131
4,61 25,07242 24,62117 25,17463 25,61593 5,7 75,13504 74,44067 74,30033 74,99136
4,62 25,32984 24,87318 25^42210 25,86892 5,8 83,01840 82,34183 82,13288 82,80633
4,63 25,58980 25,12777 25,67210 26,12438 5,9 91,72379 91,07172 90,79631 91,44562
4,64 25,85233 25,38498 25,92467 26,38236 100,37773 100,99629
4,65 26,11746 25,64483 26; 14981 26^4288 6,0 101,33790 100,71687
4,66 26,38520 25,90734 26,43757 26,90597 6,1 111,95664 111,37280 110,97337 111,55491
4,67 26,65559 26,17254 26,69797 27,17164 6,2 123,68604 123,19521 122у68950 123,22830
4,68 26,92865 26,44046 26,96103 27,43994 2х 134,37338 133,87245 133,37338 133,87245
4,69 27,20440 26,71113 27,22678 27,71087 6,3 136,64336 136,15092 135,64350 136,13411
6,4 150,96826 150,46912 149,97508 150,35257
4,70 27,48287 26,98456 27,49526 27,98448 6,5 166,77508 166,39259 165,79749 166,17747
4,71 27,76410 27,26079 27,76799 28,26079 6,6 184,24925 183,92922 183,29902 183,61768
4,72 28,04810 27,53985 28,04045 28,53982 6,7 203,55895 203,30357 202,64457 202,89872
4,73 28,33490 27,82177 28,31729 28,82160 6,8 224,89590 224,70860 224,02740 224,21449
4,74 28,62454 28,106555 28,59693 29,10618 6,9 248,47679 248,35764 247,66106 247,77920
4,75 28,91704 28,39327 28,87944 29,39356 273,82956
4,76 29,21242 28,68490 29,16483 29,68378 7,0 274,53547 274,48655 273,78157
4,77 29,51072 28,97852 29,45314 29,97686 7,1 303,33425 303,28381 302,64970 302,62707
4,78 29,81197 29,27513 29,74440 30,27285 7,2 335,16205 335,25434 334,55370 334,46067
4,79 30,11619 29,57477 30,03855 30,57176 7,3 370,33819 370,50003 369,81211 369,64954
4,80 7,4 409,21553 409,44531 408,77698 408,54660
30,42341 29,87746 30,33591 30,87363 7,5 452,18406 452,92446 451,73742 451,54146
4,81 30,73367 30,18325 30,73367 31,17849 7,6 499,67473 500,03281 499,42347 499,06489
4,82 31,04699 30,49215 30,93959 31,48637 7,7 552,16384 552,58097 552,01042 551,58780
4,83 31,36340 30,80420 31,24607 31,79729 7,8 610,17757 610,64966 610,12361 609,65112
4,84 4,85 31,68295 32,00565 31,11943 31,43787 31,55569 31,86847 32,11130 32,42842 5 2 643,99272 644,49252 643,99272 643,49252
4,86 32,33153 31,75955 32,18445 32,74868 7,9 674,29767 674,81986 674,34367 673,82102
4,87 32,66063 32,08450 32,53670 33,07212
4,88 32,99298 32,41277 32,82615 33,39876 8,0 745,16683 745,73409 745,31233 744,74473
4,89 33,32862 32,74438 33,15194 33,72865 8,1 823,49532 823,95189 823,73886 823,28200
4,90 33,66756 33,07936 8,2 910,06807 910,70787 910,40722 909,76714
33,48105 34,06181 8,3 1005,75247 1006,41912 1006,18385 1005,51695
4,91 34,00976 33,41774 33,81353 34,39828 8,4 1111,50710 1112,18393 1112,02639 1111,33933
4,92 34,35554 33,79570 34,14942 34,73810 8,5 1228,39125 1229,09140 1228,99326 1228,29291
4,93 34,70464 34,10486 34,48879 35,08128 8,6 1357,57558 1358,28205 1358,25430 1357,54765
4,94 35,05718 34,45367 34,83153 35,42788 8,7 1500,35377 1501,05950 1501,10242 1500,39658
4,95 35,41320 34,80602 35,17782 35,77792 8,8 1658,15549 1658,85342 1658,96658 1658,26850
4,96 35,77275 35,16195 35,52765 36,13145 8,9 1832,56070 1833,42607 1833,42614 1832,74284
692
693
Продолжение приложения 3
Продолжение приложения 4
kz S (kz) Т (kz) U (kz) V(fez)
9,0 2025,31545 2025,97701 2026,22658 2025,56489
9,1 2238,34934 2238,98270 2239,29706 2238,66360
9,2 2473,79487 2474,39373 2474,76971 2474,17079
9,3 2734,00871 2734,56071 2735,00094 2734,44255
9,4 3021,59536 3022,10755 3022,59505 3022,08297
Зтс 3097,41192 3097,91193 3098,41197 3097,91193
9,5 3339,43314 3339,89411 3340,43031 3359,96926
9,6 3690,70306 3691,11321 3691,68775 3691,27754
9,7 4078,92063 4079,26590 4079,88299 4079,53766
9,8 4508,47103 4508,25298 4508,90146 4508,61946
9,9 4982,14802 4982,35202 4983,03721 4982,32136
10,0 5596,19606 5506,34442 5507,03599 5506,88844
Приложение 4
Функции Крылова для расчета балок постоянного сечения
на упругом основании
£ Ji Л J* J<
0 1 0 0 0
0,010 1,0000 0,01000 0,00005 0,00000
0,020 1,0000 0,02000 0,00020 0,00000
0,05 1,0000 0,0500 0,0013 0,00002
0,10 1,0000 0,1000 0,0050 0,0002
0,20 0,9997 0,2000 0,0200 0,0014
0,30 0,9987 0,2999 0,0450 0,0045
0,40 0,9957 0,3997 0,0800 0,0107
0,50 0,9895 0,4990 0,1249 0,0208
0,60 0,9784 0,5974 0,1798 0,0360
0,70 0,9600 0,6944 0,2444 0,0571
0,80 0,9318 0,7891 0,3186 0,0852
0,90 0,8931 0,8804 0,4021 0,1211
1,00 0,8337 0,9668 0,4945 0,1659
1,10 0,7568 1,0465 0,5952 0,2203
1,20 0,6561 1,1173 0,7035 0,2852
1,30 0,5272 1,1767 0,8183 0,3612
1,40 0,3656 1,2217 0,9383 0,4490
1,50 0,1664 1,2486 1,0620 0,5490
u/2 0,0000 1,2546 1,1507 0,6273
1,60 —0,0753 1,2535 1,1873 0,6615
1,70 —0,3644 1,2322 1,3118 0,7863
1,80 —0,7060 1,1789 1,4326 0,9237
1,90 —1,1049 1,0888 1,5464 1,0727
2,00 —1,5656 0,9558 1,6490 1,2325
2,10 —2,0923 0,7735 1,7359 1,4020
2,20 —2,6882 0,5351 1,8018 1,5791
2,30 —3,3562 0,2335 1,8408 1,7614
5 Jt J 8 J<
2,40 —4,0976 -0,1386 1,8461 1,9461
2,50 -4,9128 —0,5885 1,8105 2,1293
2,60 —5,8003 —1,1236 1,7256 2,3065
2,70 —6,7565 —1,7509 1,5827 2,4725
2,80 —7,7759 —2,4770 1,3721 2,6208
2,90 —8,8471 —3,3079 1,0838 2,7443
3,00 —9,9669 —4,2485 0,7069 2,8346
3,10 —11,1119 —5,3023 0,2303 2,8823
3,20 —12,2656 —6,4711 —0,3574 2,8769
3,30 —13,4048 —7,7549 —1,0678 2,8068
3,40 —14,5008 —9,1507 —1,9121 2,6589
3,50 —15,5198 —10,6525 —2,9014 2,4195
3,60 —16,4218 —12,2508 —4,0459 2,0735
3,70 —17,1622 —13,9315 —5,3544 1,6049
3,80 —17,6875 —15,6761 —6,8343 0,9969
3,90 —17,9387 —17,4599 —8,4909 0,2321
4,00 —17,8498 —19,2524 —10,3265 —0,7073
4,10 —17,3472 —21,0160 -12,3404 —1,8392
4,20 —16,3505 —22,0755 —14,5274 —3,1812
4,30 —14,7722 —24,2669 —16,8773 -4,7501
4,40 —12,5180 —25,6373 —19,3743 —6,5615
4,50 —9,4890 —26,7447 —21,9959 —8,6290
4,60 —5,5791 —27,5057 —24,7117 —10,9638
4,70 —0,6812 —27,8274 —27,4823 —13,5732
4,80 5,3164 —27,6052 —30,2589 —16,4604
4,90 12,5239 —26,7239 —32,9814 —19,6232
5,00 21,0504 —25,0565 —35,5775 —23,0525
5,10 30,9997 —22,4661 —37,9619 —26,7317
5,20 42,4661 —18,8057 —40,0350 —30,6346
5,30 55,5317 —13,9201 -41,6826 —34,7246
5,40 70,2637 —7,6440 -42,7727 —38,9524
5,50 86,7044 —0,1901 —43,1593 —43,2557
5,60 104,8687 9,7544 —42,6775 -47,5558
5,70 124,7352 21,2199 —41,1454 —51,7563
5,80 146,2448 34,7564 —38,3640 —55,7429
5,90 169,2837 50,5203 —34,1198 —59,0363
6,00 196,1881 70,6079 —27,4846 —62,7889
6,10 221,8019 91,4992 —19,4005 —65,1503
6,20 245,5231 112,5249 —10,2356 —66,4981
2tc 267,7468 133,8725 0 —66,9362
6,30 272,2487 138,4120 2,2886 —66,9175
6,50 324,7861 198,1637 35,7713 —63,3105
7,00 413,3762 386,8072 180,1191 —13,2842
7,50 313,3700 580,6710 423,9858 133,6506
5/2* 0 643,9927 643,9926 321,9964
8,00 —216,8647 628,8779 737,3101 422,8713
8,50 —1479,3701 241,4136 981,0984 860,3917
9,00 —3691,4815 —1010,8800 834,8607 1340,3007
3* —6195,8239 —3097,9120 0 1548,9560
9,50 —6660,9594 —3581,4756 —250,9959 1539,7410
10,0 —9240,8733 —7616,1462 —2995,7095 812,3636
694
ЛИТЕРАТУРА
1. Ананьев И. В. Справочник по расчету собственных колебаний упругих си-
стем. ОГИЗ — Гостехиздат, М., 1946.
2. Биргер И. А., Шорр Б. Ф., Шнейдерович Р. М. Расчет на прочность дета-
лей машин. Справочное пособие. «Машиностроение», М., 1966.
3, Варвак П. М. Варвак А. П. Пять новых аналогий в сопротивлении матери-
алов.— Проблемы прочности, 1972, 1.
4. Варвак П. М.> Варвак А. П, Четыре новые аналогии в сопротивлении мате-
риалов.— Проблемы прочности, 1972, 10.
5. Иванов В. Ф., Никитин Г. В. Справочник по строительной механике, т. If
Изд-во КУБУЧ. Л., 1933.
6. Любошиц М. И., Ицкович Г. М. Справочник по сопротивлению материалов.
«Вышэйшая школа», Минск, 1969.
7. Материалы в машиностроении, т. 1. Цветные металлы и сплавы. «Маши-
ностроение», М., 1967.
8. Материалы в машиностроении, т. 2. Конструкционная сталь. «Машино-
строение», М., 1967.
9. Материалы в машиностроении, т. 3. Специальные стали и сплавы. «Маши-
ностроение», М., 1968.
10. Материалы в машиностроении, т. 4. Чугун. «Машиностроение», М., 1969.
11. Материалы в машиностроении, т. 5. Неметаллические материалы. «Маши-
ностроение», М., 1969.
12. Михайлов-Михеев П. В. Справочник по металлическим материалам Турби-
не- и моторостроения. Машгиз, М.~Л., 1961.
13. Писаренко Г, С., Яковлев А. П., Матвеев В. В. Вибропоглощающие свойства
конструкционных материалов. Справочник. «Паукова думка», К., 1971.
14. Писаренко Г. С. и др. Сопротивление материалов. Гостехиздат УССР К.,
1963.
15. Писаренко Г. С. и др. Курс сопротивления материалов. Изд-во АН УССР,
К., 1964.
16. Писаренко Г. С., Лебедев А. А. Сопротивление материалов деформирова-
нию и разрушению при сложном напряженном состоянии. «Паукова дум-
ка», К., 1969.
17. Прочность. Устойчивость. Колебания, т. 1. Под редакцией И. А. Биргера
и Я. Г. Пановко. «Машиностроение», М., 1968.
18. Прочность. Устойчивость. Колебания, т. 2. Под редакцией И. А. Биргера
и Я. Г. Пановко. «Машиностроение», М., 1968.
19. Прочность. Устойчивость. Колебания, т. 3. Под редакцией И. А. Биргера
и Я. Г. Пановко. «Машиностроение», М., 1968.
20. Рудицын М. Н., Артемов П. Я., Любошиц М. И. Справочное пособие по
сопротивлению материалов. Госиздат БССР, Минск, 1958.
21. Рудицын М. Н., Артемов П. Я., Любошиц М. И. Справочное пособие по
сопротивлению материалов. «Вышэйшая школа», Минск, 1970.
22. Серенсен С. В., Ногаев В. П., Шнейдерович Р. М. Несущая способность
и расчеты деталей машин на прочность. Машгиз, М., 1963.
23. Справочник по технической механике. Под редакцией академика
А. Н. Динника. ОГИЗ, М.— Л., 1949.
24. Справочник по строительной механике корабля. Под редакцией академика
Ю. А. Шиманского, т. 2. Л., 1958.
25. Справочник проектировщика промышленных, жилых и общественных зда-
ний и сооружений. Под редакцией А. А. Уманского. Гос. изд-во литера-
туры по строительству, архитектуре и строительным материалам. М., 1960.
26. Справочник машиностроителя, т. 6. Под редакцией Э. А. Сателя. «Маши-
ностроение», М., 1964.
27. Справочник машиностроителя, т. 3. Под редакцией академика АН УССР
С. В. Серенсена. Машгиз. М., 1963.
28. Технический справочник железнодорожника, т. 2. Технические расчеты,
Гострансжелдориздат, М., 1950.
29. Трощенко В. Т. Усталость и неупругость металлов. «Наукова думка»,
К., 1971.
30. Справочник по сопротивлению материалов. «Буд1вельник»,
31. Химушин Ф. Ф. Жаропрочные стали и сплавы. «Металлургия», М., 1969.
696
ПЕРЕЧЕНЬ ТАБЛИЦ
Таблица 1. Геометрические характеристики плоских сечений 24
Таблица 2. Угольники равнобокие (ГОСТ 8509 — 57) ... . 78
Таблица 3. Угольники неравнобокие (ГОСТ 8510 — 57) . . . 82
Таблица 4. Швеллеры (ГОСТ 8240 — 56)................ 86
Таблица 5. Швеллеры (ГОСТ 8240 — 56*)............... 88
Таблица 6. Балки двутавровые (ГОСТ 8239 — 56)....... 90
Таблица 7. Балки двутавровые (ГОСТ 8239 — 56*)...... 92
Таблица 8. Балки двутавровые широкополочпые
(ГОСТ 6183 — 52)......................................... 94
Таблица 9. Опорные реакции, поперечные силы и изгиба-
ющие моменты в статически определимых
балках...................................................116
Таблица 10. Изгибающий момент М, нормальная W и попе-
речная Q силы в консольном круговом стержне
при нагружении в его плоскости...........................138
Таблица И. Изгибающий 7Ииз и крутящий Л4кр моменты в
консольном круговом стержне при нагружении,
перпендикулярном его плоскости...........................139
Таблица 12. Модули упругости и коэффициенты Пуассона . . 151
Таблица 13. Ориентировочные величины основных допуска-
емых напряжений на растяжение и сжатие ... 152
Таблица 14. Критерии предельного состояния изотропных
материалов (при статическом нагружении) ... 173
Таблица 15. Допускаемые напряжения для сварных соедине-
f ний...........................................200
Таблица 16. Допускаемые напряжения для древесины . . . 200
Таблица 17. Схемы действительных и соответствующих им
фиктивных балок..........................................254
Таблица 18. Балки равного сопротивления изгибу...............255
Таблица 19. Уравнения упругой линии и угла поворота по-
перечных сечений консольной балки переменной
высоты...................................................256
Таблица 20. Уравнения упругой линии, максимальные про-
гибы и углы поворота концевых и опорных се-
чений статически определимых балок постоян-
ного поперечного сечения.............................. . 258
Таблица 21. Форма и размеры ядра сечения.....................289
Таблица 22. Выражения интеграла Мора § M^pdz для раз-
личных сочетаний эпюр М{ и Мр............................310
Таблица 23. Площади и координаты центров тяжести неко-
торых элементарных фигур ................................314
697
Таблица 24. Опорные реакции, поперечные силы, изгибающие
моменты и перемещения в статически неопреде-
лимых однопролетпых балках .............................334
Таблица 25. Расчетные формулы, учитывающие смещение
опор и изменение температуры в статически не-
определимых балках (при постоянном EJ) . . . 348
Т а б л и ц а 26. Изгибающие моменты в Г-образной раме...351
Таблица 27. Изгибающие моменты в П-образной раме .... 358
Т а б л и ц а 28. Изгибающие моменты в замкнутой раме .... 364
Таблица 29. Усилия и перемещения при нагружении кольца
в его плоскости ........................................368
Т а б л и ц а 30. Радиус кривизны нейтрального слоя гн для сече-
ний различной формы.................................... 386
Таблица 31. Значение коэффициента к в формуле е = kR . . 388
Таблица 32. Перемещения свободного конца консольного
кругового стержня постоянного сечения при на-
гружении в его плоскости .... .......392
Таблица 33. Перемещения свободного конца консольного кру-
гового стержня постоянного селения при нагру-
жении в перпендикулярной плоскости......................394
Т а б л и ц а 34. Значения определенных интегралов, часто встре-
чающихся при определении перемещений в кри-
вых стержнях............................................396
Таблица 35. Расчетные формулы для толстостенных цилинд-
ров ....................................................413
Таблица 36. Расчетные формулы для определения напряже-
ний и перемещений в тонкостенных оболочках 422
Т а б л и ц а 37. Пластические моменты сопротивления для неко-
торых сечений балок .... .... 434
Таблица 38. Коэффициенты v и 7} для определения критиче-
ской нагрузки центрально сжатых стержней по
формуле Ркр = = т) -р- ................451
Таблица 39. Критические нагрузки для полосы и некоторых
двутавровых балок ......................................491
Таблица 40. Коэффициенты условного допускаемого напря-
жения на сжатие ср......................................500
Таблица 41. Уравнения изгибающего момента М(г) и упругой
линии w(z) для некоторых случаев продольно-
поперечного изгиба балок постоянного попереч-
ного сечения ...........................................502
Таблица 42. Собственные частоты колебаний систем с одной
и двумя степенями свободы...............................543
Т а б л и ц а 43. Частотные уравнения и собственные формы про-
дольных и крутильных колебаний стержней по-
стоянного сечения.......................................549
Т а б л и ц а 44. Частотные уравнения и собственные формы по--
перечных колебаний стержней постоянного се-
чения ..................................................553
Т а б л и ц а 45. Корни частотных уравнений поперечных колеба-
ний стержней постоянного сечения на упругих
опорах..................................................554
Т а б л и ц а 46. Корни частотных уравнений поперечных колеба-
ний стержней постоянного сечения с сосредото-
ченными массами tn......................................556
698
Таблица 47. Значения некоторых интегралов, встречающихся
при расчетах поперечных колебаний стержней
(<pz — i-я собственная форма колебаний) .... 557
Таблица 48. Собственные частоты поперечных колебаний
стержней постоянного сечения, нагруженных
продольными силами ........................................558
Таблица 49. Характеристики циклов повторно-переменного
нагружения.............................................576
Таблица 50. Значения коэффициента а, учитывающего массу
ударяемого элемента в формуле коэффициента
динамичности...............................................586
Таблица 51. Расчетные формулы для определения параметров
контакта двух тел......................................594
Т а б л и ц а 52. Численные значения коэффициентов na, tib> npt 608
Таблица 53. Допускаемые давления ла площадке контакта
при первоначальном контакте по линии и ста-
тическом нагружении....................................... 609
ОГЛАВЛЕНИЕ
Предисловие................................................ 3
Глава 1. Введение ......................................... 5
§ 1, Наука о сопротивлении материалов. Изучаемые
объекты..................................... 5
§ 2. Виды деформаций. Понятия о деформированном
состоянии материала........................ 7
§ 3. Основные гипотезы ....................... 9
Глава 2, Геометрические характеристики плоских сечений 10
§ 4. Статический момент площади. Центр тяжести пло-
щади .............................................................................................. 10
§ 5. Моменты инерции плоских фигур................................... 11
§ 6. Моменты инерции сложных сечений. 13
§ 7. Моменты инерции относительно параллельных осей 14
§ 8. Зависимость между моментами инерции при пово-
роте координатных осей............................ 14
§ 9. Определение направления главных осей инерции.
Главные моменты инерции........................... 15
§ 10. Графическое представление моментов инерции,
Понятие о радиусе и эллипсе инерции ...... 17
§ 11. Моменты сопротивления.................. , . 21
§ 12. Порядок расчета............................................................................. 22
Глава 3. Внешние и внутренние силы. Метод сечений.
Эпюры внутренних сил................................ 98
§ 13. Классификация внешних сил.................. 98
§ 14. Внутренние силы. Метод сечений. Эпюры внутрен-
них сил.......................................... 99
§ 15. Балки и их опоры...........................102
§16. Вычисление реакций.........................104
§ 17. Усилия и моменты в сечениях балки..........106
§ 18. Дифференциальные зависимости при изгибе балок.
Некоторые особенности эпюр Q и М ................106
§ 19. Построение эпюр для статически определимых рам 108
§ 20. Построение эпюр для кривых стержней........109
§ 21. Дифференциальные зависимости при изгибе плос-
ких кривых стержней..............................111
§ 22. Построение эпюр внутренних сил для простран-
ственных стержней................................112
§ 23. Напряжения в сечении .......................ИЗ
§ 24, Условия прочности и жесткости..............115
700
Глава 4. Механическпе характеристики материала при
растяжении и сжатии ................................140
§ 25. Напряжения и деформации при растяжении и сжа-
тии .......................................... < . 140
§ 26 Испытание материалов на растяжение и сжатие . 143
§ 27. Концентрация напряжений....................148
§ 28. Допускаемые напряжения.....................149
Глава 5. Напряженное и деформированное состояние . . . 153
§ 29. Напряжения в точке. Главные площадки и глав-
ные напряжения...................................153
§ 30. Линейное напряженное состояние.............154
§ 31. Плоское напряженное состояние..............155
§ 32. Прямая задача при плоском напряженном состоя-
нии. Круг напряжений.............................157
§ 33. Обратная задача при плоском напряженном состоя-
нии .............................................158
§ 34. Объемное напряженное состояние............160
§ 35. Деформации при объемном напряженном состоя-
нии. Обобщенный закон Гука.......................161
§ 36. Потенциальная энергия деформации..........163
.Глава 6. Критерии прочности..........................165
§ 37. Основные теории прочности.................165
§ 38. Понятие о некоторых новых теориях прочности. . 169
Глава 7. Растяжение и сжатие.........................178
§ 39. Расчет стержней на растяжение (сжатие) с учетом
собственного веса............................. 178"
§ 40. Стержень равного сопротивления растяжению
(сжатию). Ступенчатый стержень ..................179
$ 41. Статически неопределимые конструкции.......180
§ 42. Расчет гибких нитей........................183
Глава 8. Сдвиг ......................................191
§ 43. Сдвиг. Расчет на срез......................191
§ 44. Чистый сдвиг...............................192
§ 45. Некоторые примеры расчета на срез..........195
Глава 9. Кручение........................................202
§ 46. Напряжения и деформации при кручении .... 202
§ 47. Кручение стержней некруглого сечения.......207
§ 48. Расчет винтовых пружин.....................212
§ 49. Концентрация напряжений при кручении.......214
Глава 10. Изгиб ........... . . ....................216
§ 50. Нормальные напряжения при плоском изгибе . . 216
§ 51. Касательные напряжения при изгибе..........219
§ 52. Расчет на прочность при изгибе.............222
§ 53. Концентрация напряжений при изгибе.........224
§ 54. Дифференциальное уравнение изогнутой оси балки
(упругой линии)..................................228
§ 55. Определение перемещений в балках по методу
начальных параметров........................... 234
701
§ 56. Расчет балок переменного сечения на прочность
и жесткость.......................................238
§ 57. Расчет на изгиб с учетом сил инерции........243
§ 58. Касательные напряжения при изгибе балок тонко-
стенного профиля. Центр изгиба . .... 244
§ 59. О расчете балок на упругом основании...... 247
§ 60. Изгиб балок, материал которых не следует закону
Глава 11. Сложное сопротивление.................... . . 276
§ 61. Сложный и косой изгиб.......................276
§ 62. Изгиб с растяжением.........................280
*§63. Изгиб с кручением............................284
Глава 12. Общие теоремы об упругих системах. Общие
методы определения перемещений ..........................292
§ 64. Обобщенные силы и перемещения...............292
§ 65. Работа внешних сил..........................294
§ 66. Работа внутренних сил .................... 295
§ 67. Применение начала возможных перемещений
к упругим системам......................... . 297
§ 68. Теоремы о взаимности работ и перемещений . . . 301
§ 69. Общие формулы для определения перемещений.
Метод Мора........................................301
§ 70. Перемещения, вызванные изменением температуры . 303
§ 71. Вычисление интеграла Мора по способу Вереща-
гина .............................................304
§ 72. Потенциальная энергия деформации............306
§ 73. Теорема Кастильяно. Теорема Лагранжа.........307
§ 74. Теорема о минимуме потенциальной энергии . . . 309
Глава 13. Статически неопределимые системы.............316
§ 75. Основные этапы расчета статически неопредели-
мых систем........................................318
§ 76. Канонические уравнения метода сил...........319
§ 77. Многоопорные неразрезные балки. Уравнение трех
моментов ....................................... 322
§ 78. Расчет статически неопределимых криволинейных
стержней .........................................326
§ 79. Определение перемещений в статически неопреде-
лимых системах....................................328
§ 80. О расчете пространственных рамных систем . . . 331
Глава 14. Расчет плоских кривых брусьев..................378
§ 81. Определение напряжений в брусьях большой кри-
визны 378
§ 82. Расчет на прочность.........................383
§ 83. Определение перемещений................. 384
Глава 15. Расчет толстостенных цилиндров и вращающихся
дисков............................................. 397
$ 84. Толстостенный цилиндр, подверженный внутрен-
нему и наружному давлению 397
§ 85. Расчет составных цилиндров..............402
702
§ 86. Температурные напряжения в толстостенных ци-
линдрах ...............................................404
§ 87. Расчет вращающихся дисков..................407
Глава 16. Расчет тонкостенных оболочек..................415
§ 88. Расчет тонкостенных оболочек по безмоментной
теории..........................................415
§ 89. Распорные кольца в оболочках...............420
Глава 17. Расчет конструкций по предельным состояниям . 428
§ 90. Основные понятия о предельном состоянии .... 428
§ 91. Расчеты при растяжении и сжатии............429
§ 92. Расчет при кручении........................431
§ 93. Расчет при изгибе..........................432
Глава 18. Устойчивость сжатых стержней..................436
§ 94. Устойчивое и неустойчивое упругое равновесие . . 436
§ 95. Формула Эйлера для определения критической
нагрузки сжатого стержня..........................437
§ 96. Влияние условий закрепления концов стержня на
величину критической силы.................. . ... 439
§ 97. О потере устойчивости при напряжениях, превы-
шающих предел пропорциональности материала . 443
§ 98. Расчет сжатых стержней на устойчивость при
помощи коэффициентов уменьшения основного
допускаемого напряжения...........................445
§ 99. Выбор материала и рациональной формы попереч-
ных сечений сжатых стержней.......................448
§100. Продольно-поперечный изгиб ...........448
Глава 19. Упругие колебания...................................510
§ 101. Классификация механических колебаний.......510
§ 102. Свободные колебания систем с одной степенью
свободы................................... .......513
§ 103. Вынужденные колебания систем с одной степенью
свободы при гармоническом возбуждении.............516
§104 Свободные колебания системы с одной степенью
свободы с учетом сопротивления, пропорциональ-
ного скорости.....................................517
§ 105. Вынужденные колебания систем с одной степенью
свободы с учетом сопротивления, пропорциональ-
ного скорости.....................................518
§ 106 Критическая скорость вращения вала...............521
§ 107. Свободные колебания упругих систем с несколь-
кими степенями свободы . . . .....................522
§ 108 Продольные и крутильные колебания стержней . . 529
§ 109. Поперечные колебания призматических стержней 533
§ 110 Закон сохранения энергии при колебаниях .... 536
§ 111. Некоторые приближенные методы определения
собственных частот колебаний упругих систем . . 537
Глава 20. Сопротивление материалов действию повторно-
переменных напряжений ............................. 559
§112. Явление усталости материалов.....................559
§ ИЗ . Методы определения предела выносливости. Диа-
граммы усталости..................................561
703
§ 114. Влияние на предел выносливости материала кон-
структивно-технологических факторов.................56Ц
§115. Расчет на прочность при повторно-переменных
нагрузках..........................................56
Глава 21. Расчет на ударную нагрузку.......................57
§116. Расчет на удар при осевом действии нагрузки. . 57<
§117. Напряжение при скручивающем ударе............581
§ 118. Расчет на удар при изгибе...................58<
Глава 22. Контактные напряжения.........................588
§ 119. Основные понятия и формулы для определения
контактных напряжений и деформаций................58$
§ 120. Проверка прочности прй контактных напряжениях 592
Дополнение. Девять новых аналогий в сопротивлении мате-
риалов ................................................. 611
Приложения .............................................61JP
1. Физико-механические свойства материалов . . . 61^
2. Коэффициенты концентрации и чувствительности
к концентрации напряжений.......................654
3. Функции Крылова S, Г, U, V..................682
4. Функции Крылова для расчета балок постоянного
сечения на упругом основании ................ 694^
Литература................................................696
Перечень таблиц.......................................... 698^
Писаренко Георгий Степанович
Яковлев Анатолий Петрович
Матвеев Валентин Владимирович
СПРАВОЧНИК ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
Редактор Е. А. Воронько. Художественный редактор В. М. Тепляков. Оформле
ние художника В. Ф. Ковальского. Технический редактор Б. М. Кричевская
Корректоры Л. М. Тищенко, А. И. Разбицкая. *
Сдано в набор 28.1 1974 г. Подписано к печати 8.IV 1975 г. БФ 00999. Зак 5-1Ь
Изд. № 328. Тираж 76 000. Бумага машинно-мелованная для книг в перенлет
Ко 7, бумага №'2 для книг в переплете № 5. Формат SlxlOSVsa* Условно-пе’
листов 36,96. Учетно-изд. листов 33,3. Цена 2 руб. в переплете >7 и 1 ру(
80 коп. в переплете № 5.
Издательство «Наукова думка», Киев, Репина, 3. ",
Отпечатано с матриц Книжной фабрики им М В Фрунзе республиканского п{
изводственного объединения «Полиграфкнига», Госкомиздата УССР, ХарьК
Донец-Захаржевская, 6/8 на Харьковской книжной фабрике «Коммунист» реет
бликанского производственного объединения «ПолитаФкнига» Госкомизда
УССР. Харьков, ул Энгельса, U