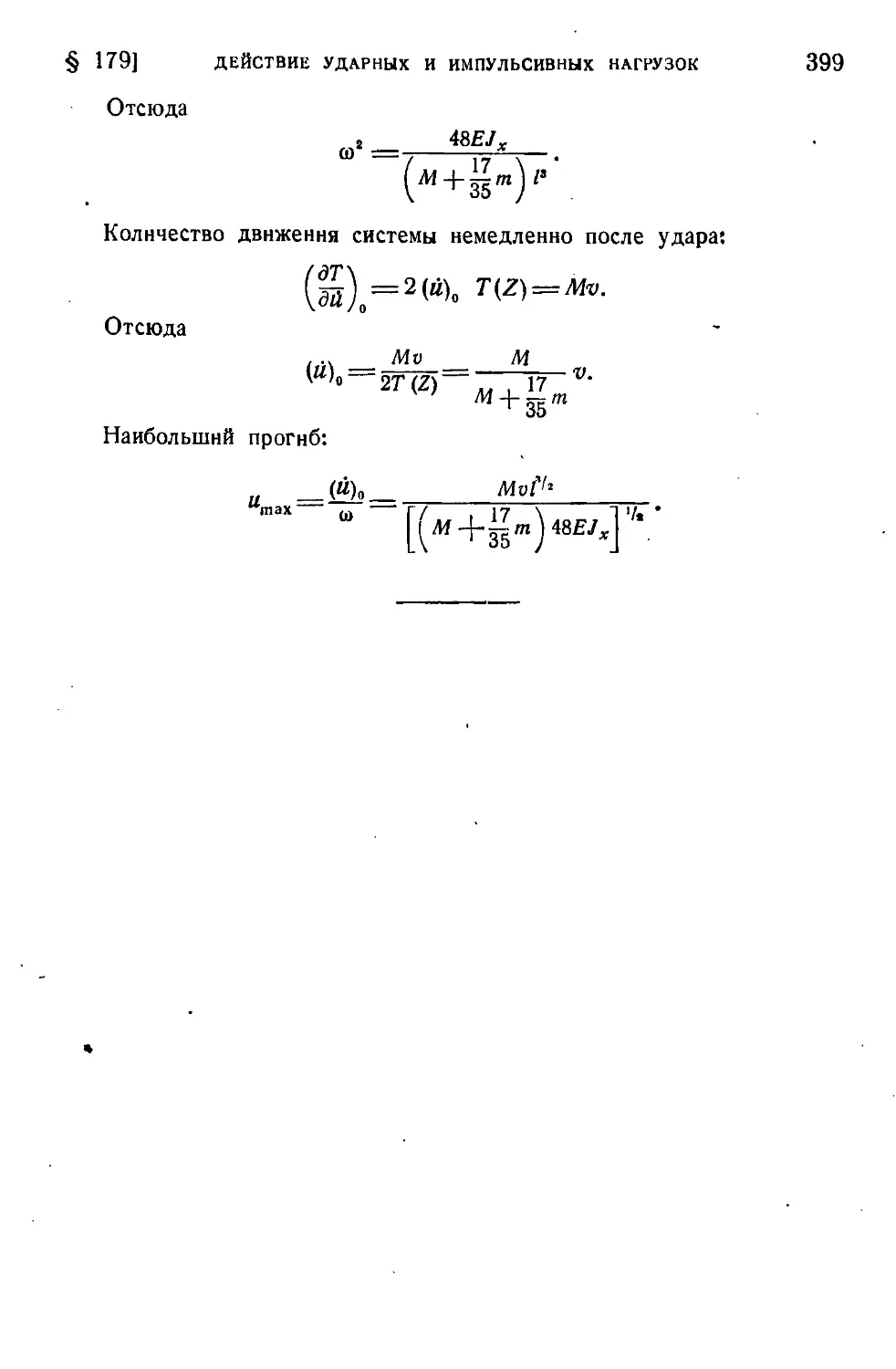
Автор: Работнов Ю.Н.
Теги: сопротивление материалов механика деформируемых тел упругость деформация
Год: 1962
Текст
Ю. н. РАБОТНОВ
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Допущено Министерством высшего и среднего специального образования РСФСР » в качестве учебного пособия для университетов
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 196 8
6.05
Р 13
ОГЛАВЛЕНИЕ
Предисловие ..................................................... 9
Глава 1. Основные понятия.....................................11
§ 1. Задали и содержание сопротивления материалов...........11
§ 2. Сопротивление материалов и теоретическая механика .... 13
§ 3. Статически неопределенные задачи.......................14
§ 4. Внешние силы...........................................15
§ 5. Принцип отвердения.....................................16
§ 6. Недопустимость замены системы сил статически эквивалентной ........................................................17
§ 7. Однородное тело .......................................19
§ 8. Внутренние силы . .....................................20
§ 9. Напряжение.............................................21
§ 10. Простейшие типы напряженного состояния................22
§ 11. Простейшие виды деформации.......................... 24
§ 12. Упругость и пластичность..............................25
§ 13. Закон Гука..........................-............... 26
§ 14. Диаграмма пластичности ...............................27
§ 15. Тела изотропные и анизотропные........................29
Глава II. Растяжение — сжатие....................................31
§ 16. Стержни и стержневые системы .........................31
§ 17. Принцип Сеи-Веиана и гипотеза плоских сечеиий.........32
§ 18. Напряжения и деформации при растяжении ...............34
§ 19. Расчеты на прочность при растижеиии и сжатии..........36
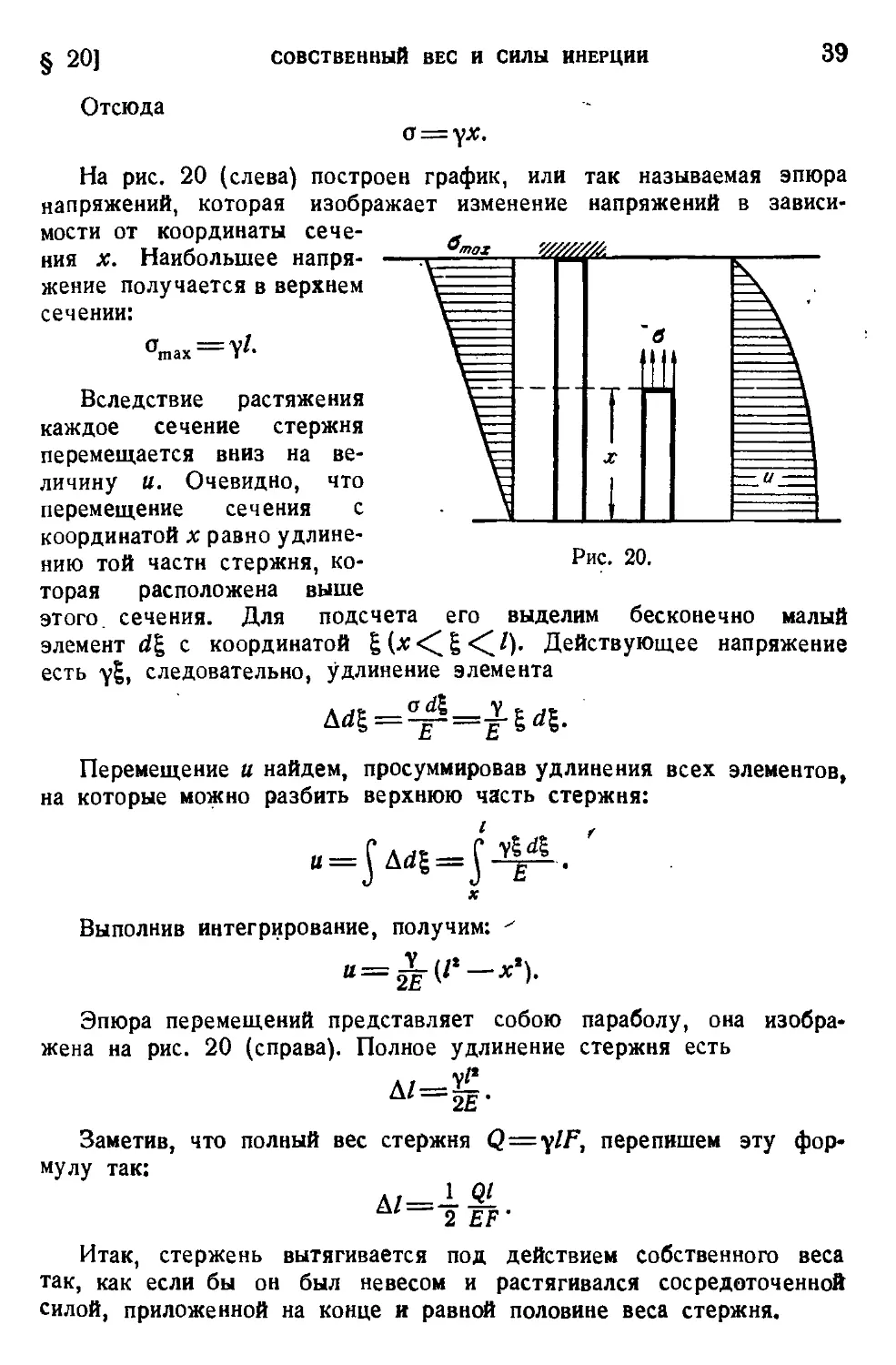
§ 20. Собственный вес и силы инерции........................38
§ 21. Стержни переменного сечения...........................42
§ 22. Перемещения узлов стержневых систем...................43
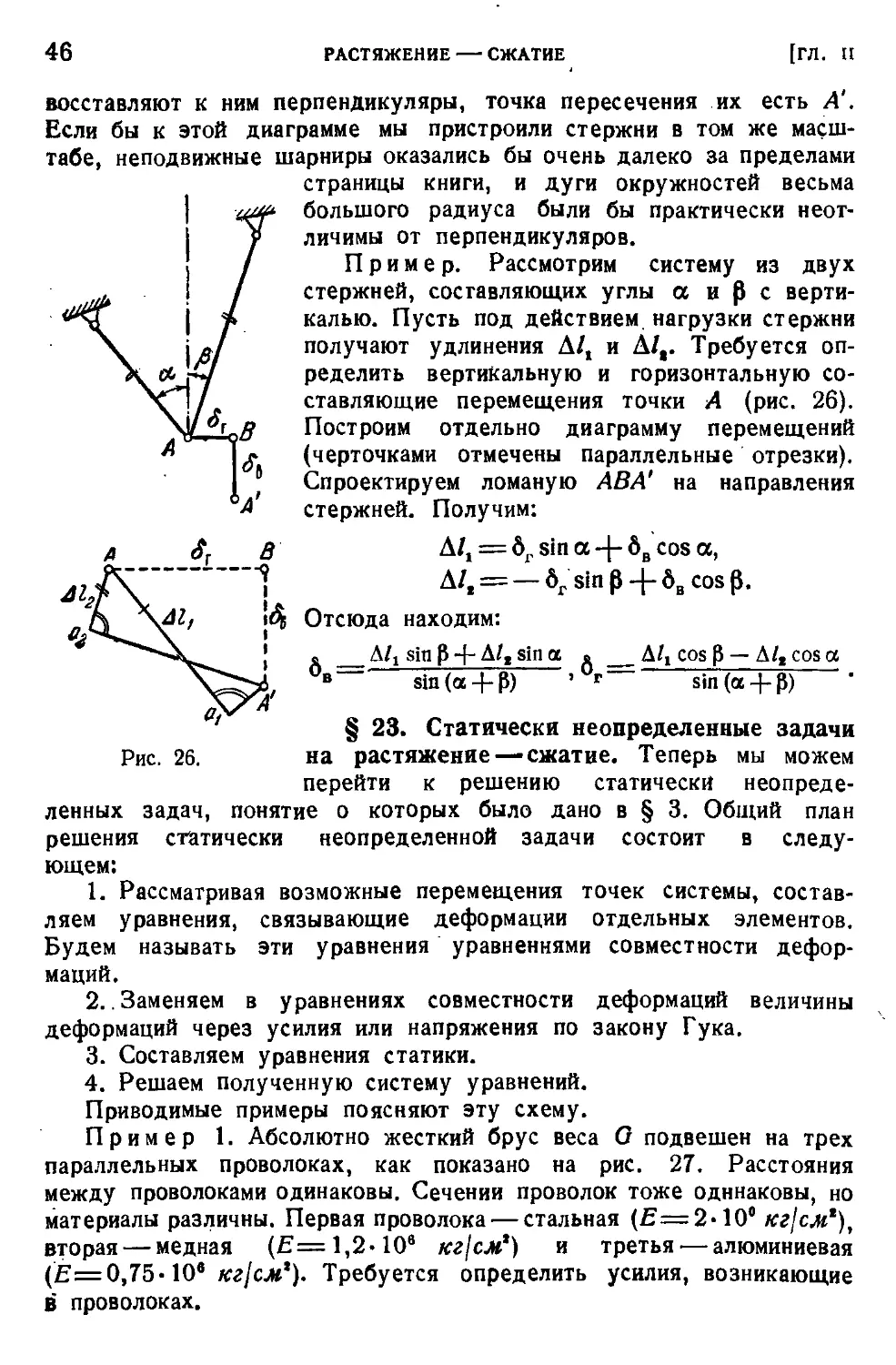
§ 23. Статически неопределенные задачи иа растяжение — сжатие . 46
§ 24. Температурные и монтажные напряжения..................49
§ 25. Общие соображения о расчете стержневых систем .,......52
§ 26. Расчет статически неопределимых систем по допускаемым ' нагрузкам ...................;............................54
§ 27. Остаточные напряжения после пластической деформации . . 57
§ 28. Потенциальная энергия растяжения ................... 59
§ 29. Напряжения при ударе............................ 61
1
4
ОГЛАВЛЕНИЕ
§ 30. Распространение упругих воли в стержнях . ...............63
§ 31. Концентрация напряжений...................................66
§ 32. Нелинейные задачи иа растяжение — сжатие.................70
Глава III. Сложное напряженное состояние.............................72
§ 33. Напряжения иа косых площадках при растяжении .... 72
§ 34. Напряжения при двухосном растяжении...............74
§ 35. Круговая диаграмма Мора...........................74
§ 36. Общий случай плоского напряженного состояния-......76
§ 37. Определение напряжений на произвольной площадке .... 79
§ 38. Пространственное напряженное состояние ..................79
§ 39. Главные напряжения.................................81
§ 40. Главные касательные напряжения....................83
§ 41. Октаэдрическое напряжение....................... 85
§ 42. Закон Гука для главных осей.......................87
§ 43. Изменение объема при упругой деформации................ 88
§ 44. Чистый сдвиг............................................ 89
§ 45. Деформация элемента объема в общем случае ....... 91
§ 46. Условие пластичности Треска — Сен-Венана..........92
§ 47. Условие пластичности Мизеса............................. 95
§ 48. Условия пластичности для плоского напряженного состояния 96
§ 49. Потенциальная энергия’ упругой деформации ...............99
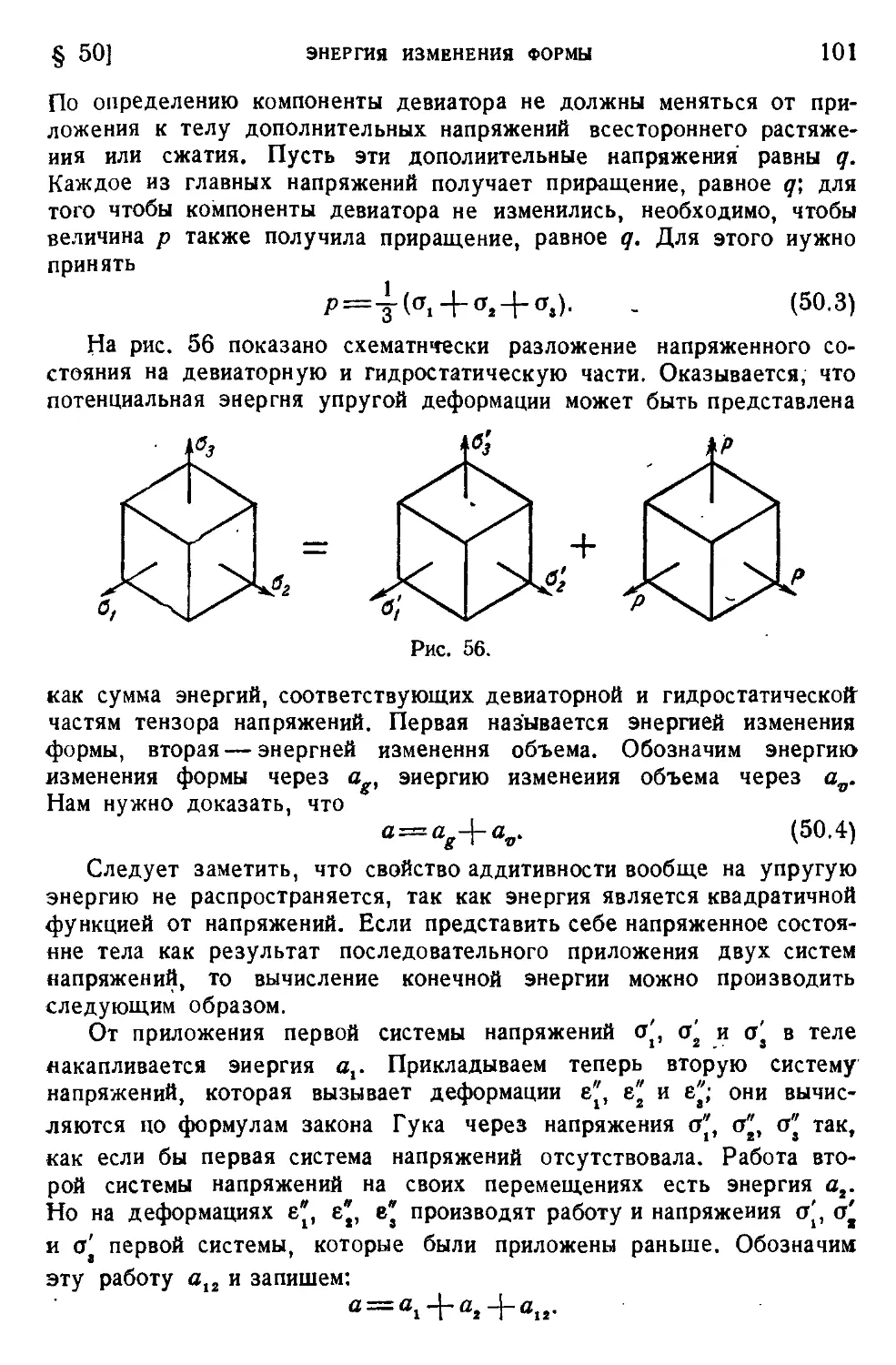
§ 50. Энергия изменения формы ................................100
Глава IV. Некоторые примеры расчета йа прочность....................104
§ 51. -Расчеты иа прочность изделий сложной формы.............104
§ 52. Безмоментные оболочки вращения..........................105
§ 53. Местные напряжения в безмоментных оболочках.............109
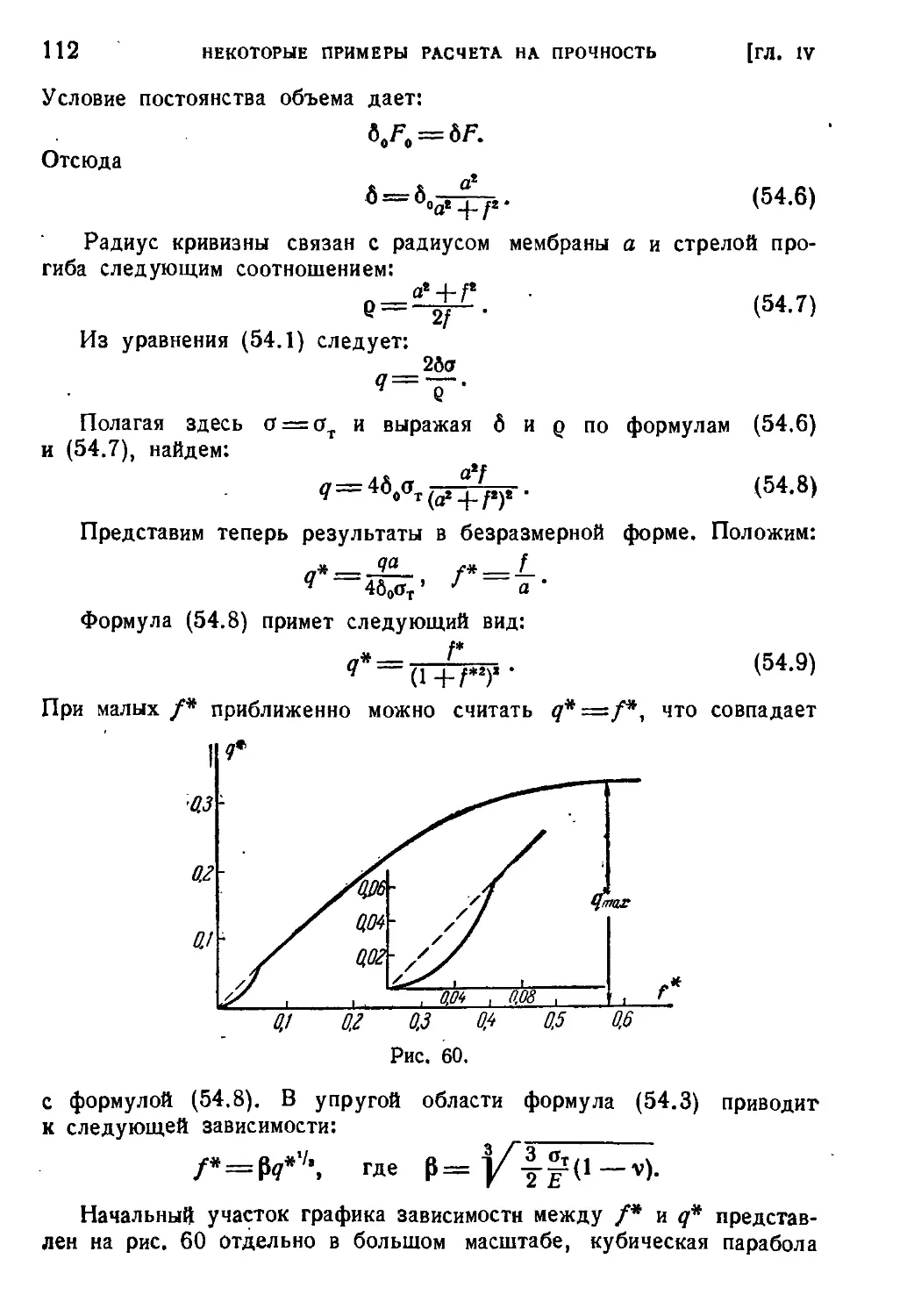
§ 54. Большие прогибы мембраны.................................НО
§ 55. Условные расчеты.........................................113
§ 56. Некоторые дальнейшие примеры условных расчетов ' .... 116
§ 57. Расчет сварных соединений ....................•..........118
Глава V. Физические основы прочности металлов и сплавов...........122
§ 58. Задачи испытания материалов.............................122
§ 59. Статические испытания иа растяжение......................123
§ 60. Исследование металлов в области малых деформаций .... 126
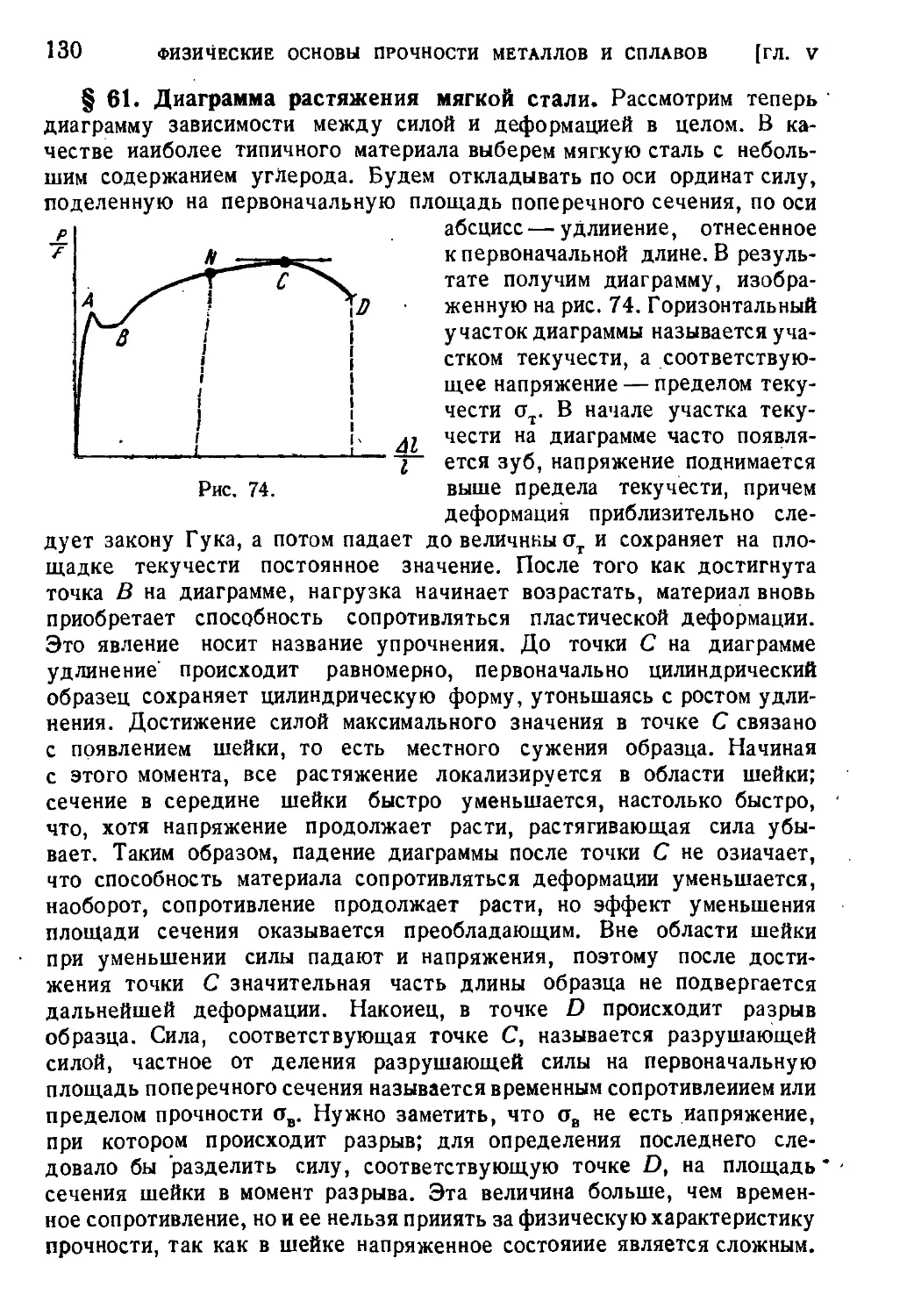
§ 61. Диаграмма растяжения мягкой стали.......................130
§ 62. Опыты иа сжатие.........................................132
§ 63. Строение и упругая деформация металлических кристаллов . 134
§ 64. Типичные кристаллические структуры металлов ............135
§ 65. Пластическая деформация монокристаллов..................139
§ 66. Прочность кристаллов и сопротивление пластическому деформированию ..................................................141
§ 67. Дислокации..............................................143
ОГЛАВЛЕНИЕ 5
§ 68. Движение и равновесие дислокаций ........................................................................................145
§ 69. Источники дислокаций.................................................................................................. 147
§ 70. Границы блоков.....................................151
§ 71. Деформация поликристаллических металлов и сплавов . . 152
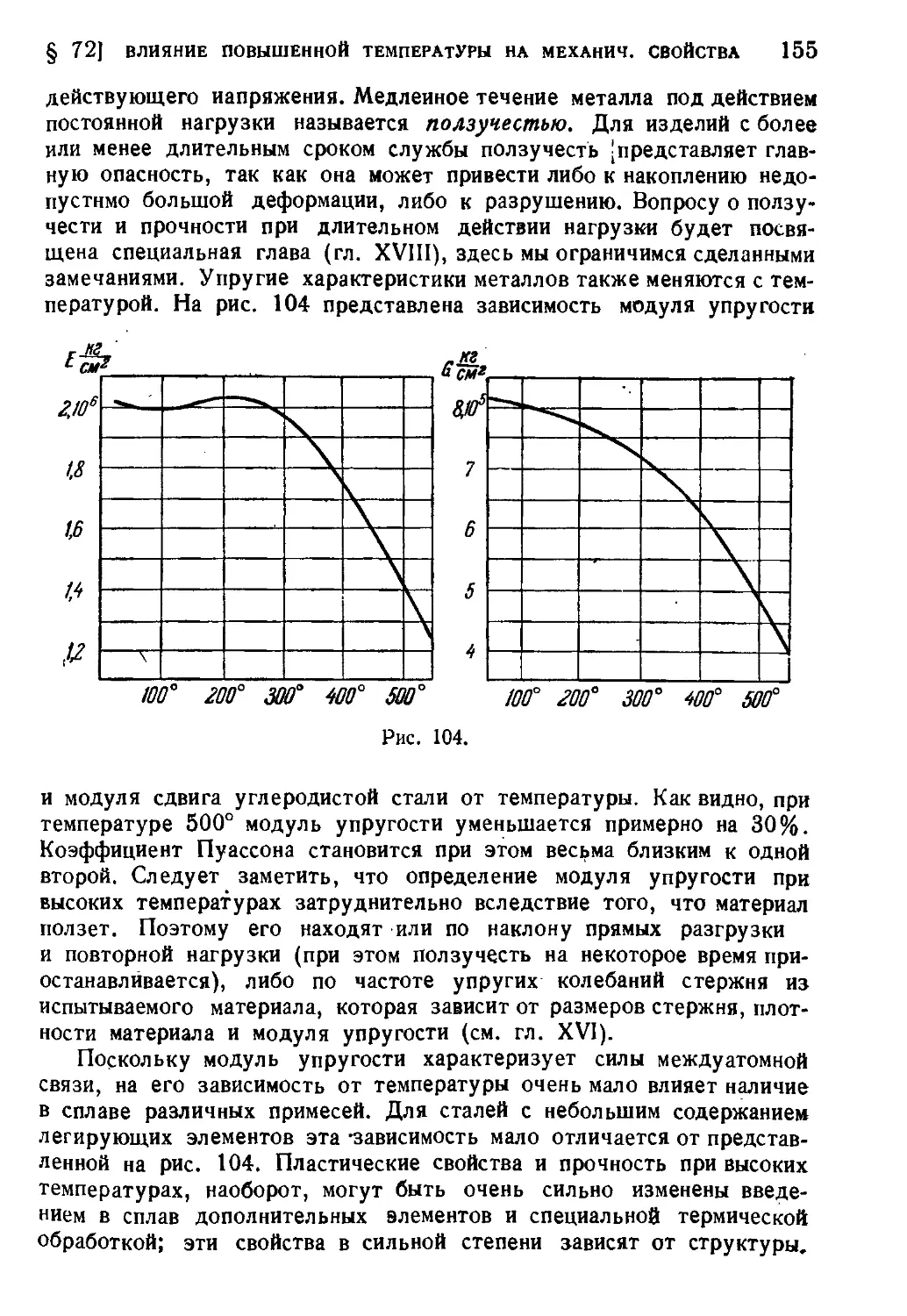
§ 72. Влияние повышенной температуры на механические свойства 154
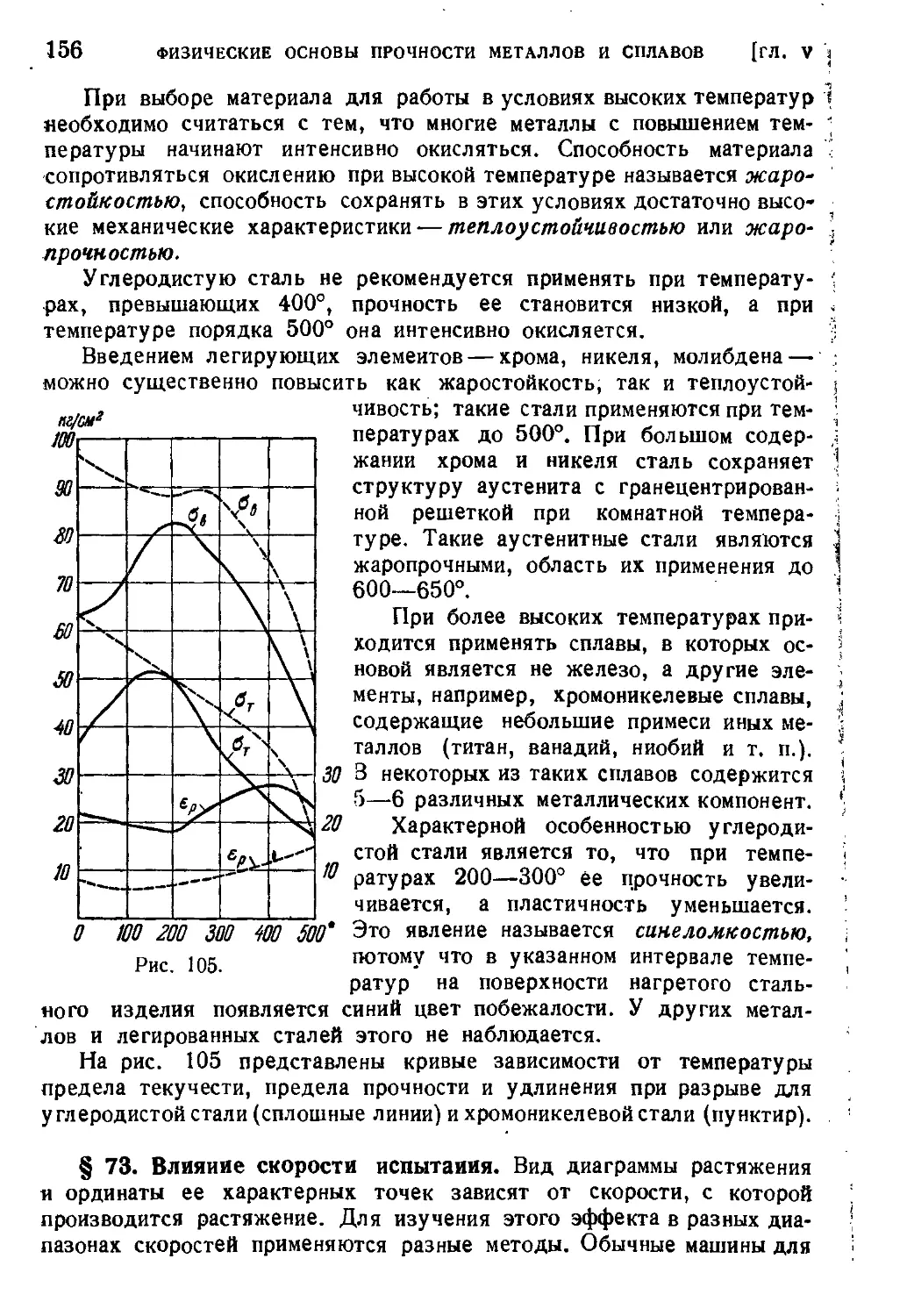
§ 73. Влияние скорости испытания......................... 156
§ 74. Испытания на твердость ..................................................................................................159
Глава VI. Теории пластичности, нелинейной упругости и последействия 161
§ 75. Основные принципы построения теории пластичности .... 161
§ 76. Ассоциированный закон течения......................162
§ 77. Течение при условии пластичности Сен-Венана и Мизеса . . 164
§ 78. Закон упрочнения ....................................................................................................... 165
§ 79. Деформационная теория пластичности . . . ...............................................................................167
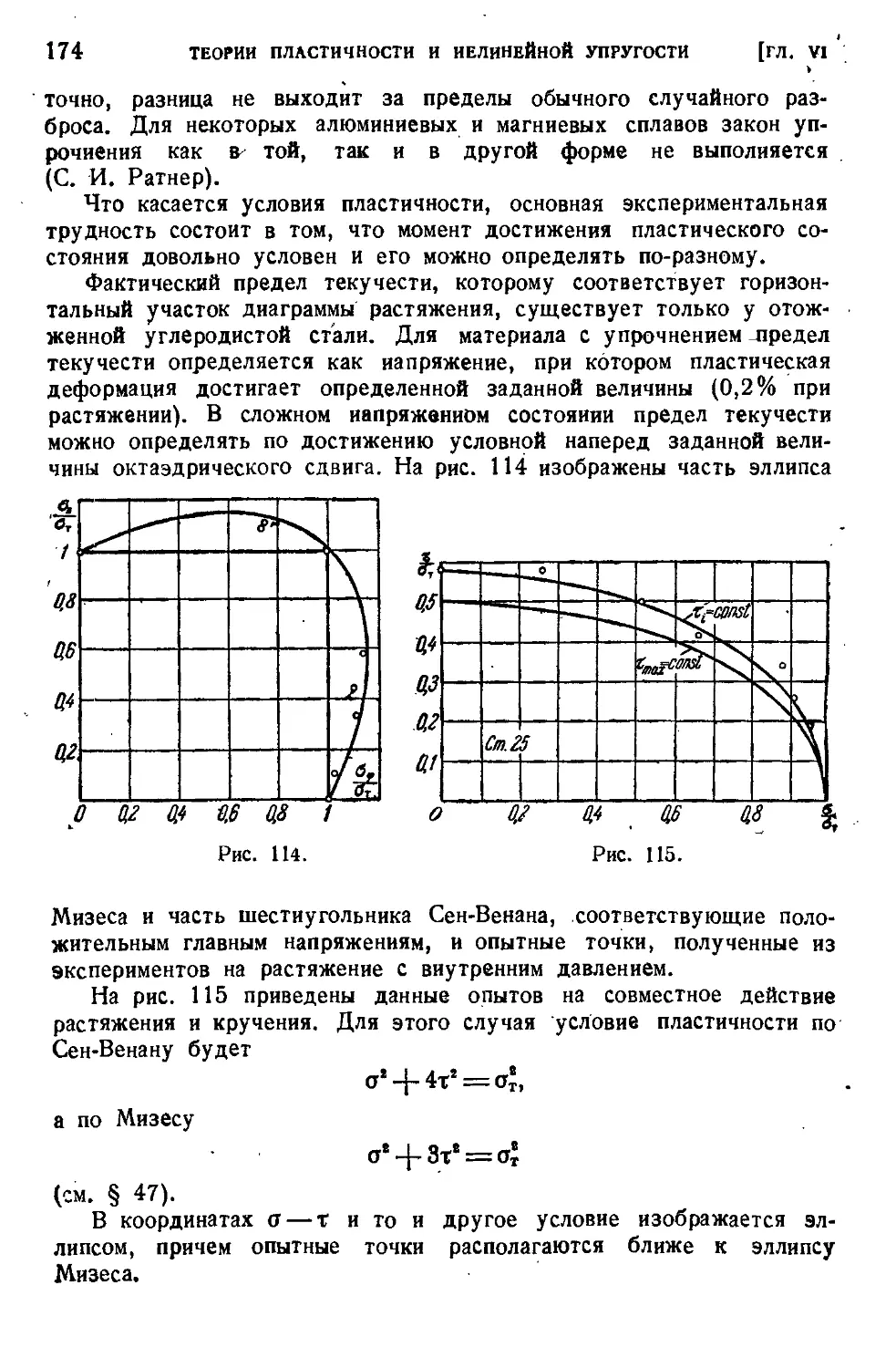
§ 80. Экспериментальная проверка теорий пластичности.....170
§ 81. Конечная деформация ................................................................................................... 175
§ 82. Нелинейно упругое тело.............................176
§ 83. Высокоэластические деформации......................178
§ 84. Упругое последействие..............................180
§ 85. Некоторые свойства вязко-упругого тела.............182
§ 86. Принцип суммирования Больцмана — Вольтерра.........184
Глава VII. Кручение ..................................................................................................................186
§ 87. Кручение стержней круглого сечения........................................................................................186
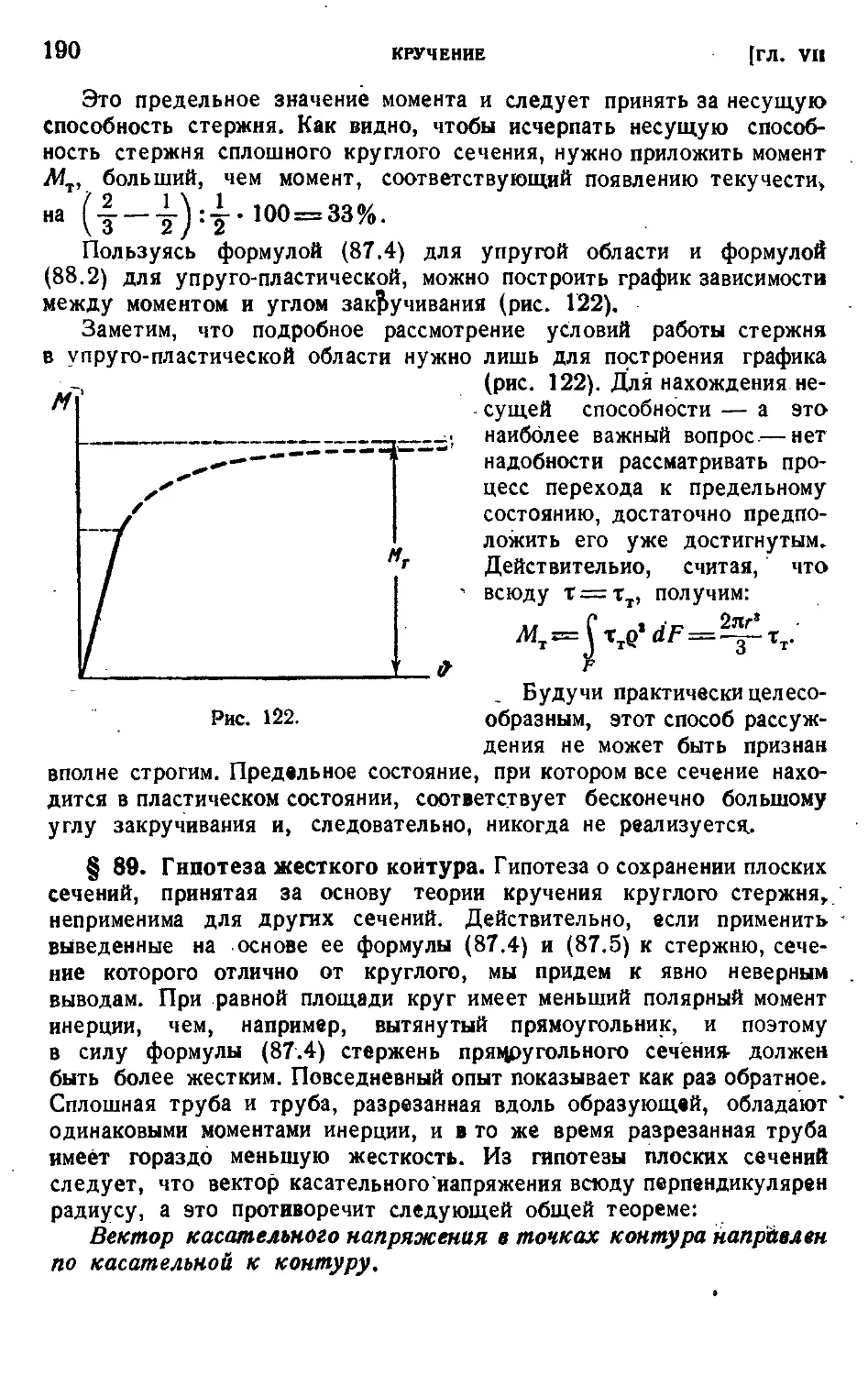
§ 88. Упруго-пластическое кручение стержня круглого сечения • 188
§ 89. Гипотеза жесткого контура.................................................................................................190
§ 90. Кручение тонкостенных стержней замкнутого профиля ... 192
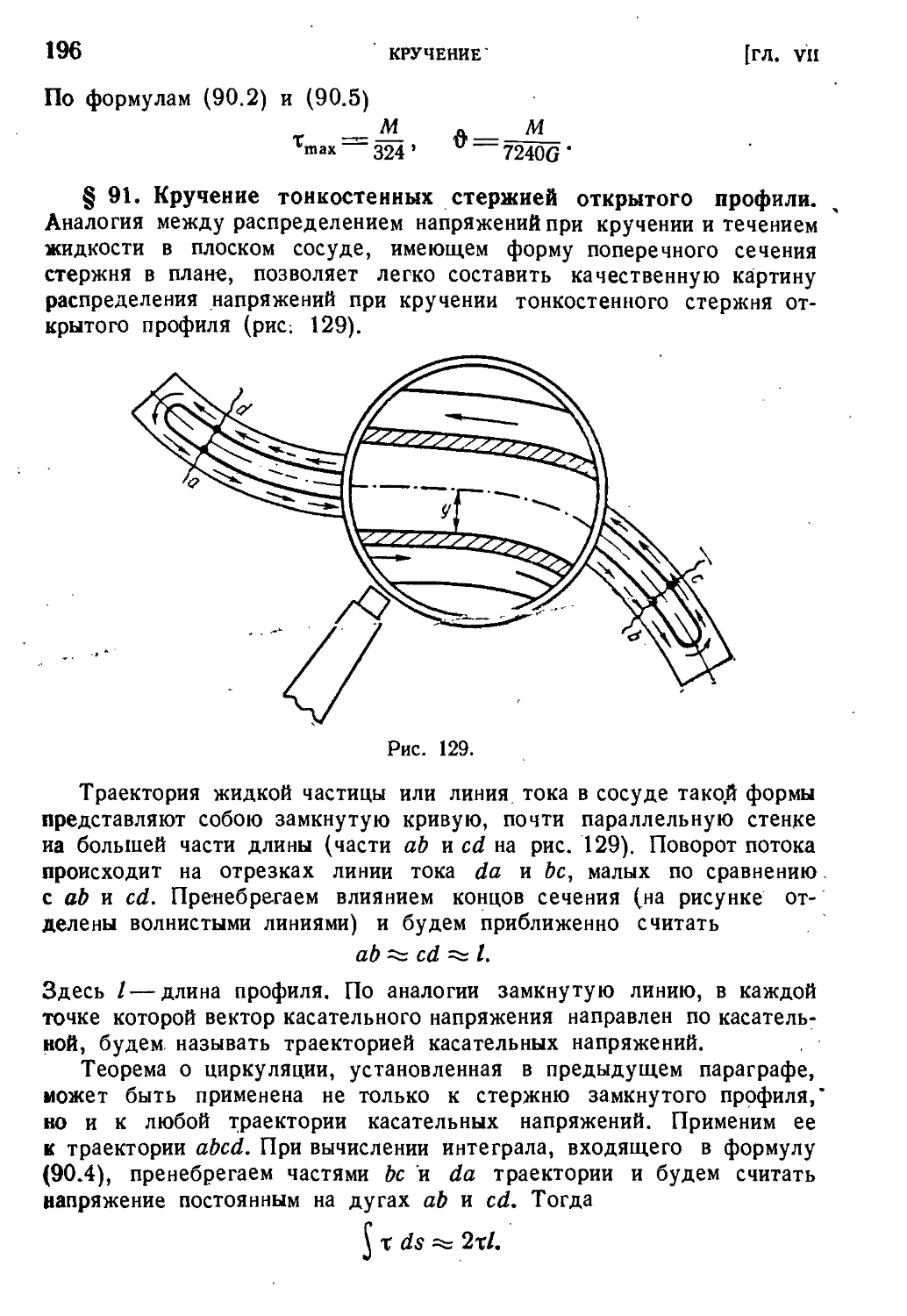
§ 91. Кручение тонкостенных стержней открытого профиля ... 196
§ 92. Кручение упругих стержней сплошного профиля...............................................................................199
§ 93. Опытное исследование кручения.............................................................................................201
§ 94. Предельное состояние закрученного стержня из вдеально-пластического материала.....................................204
Глава VIII. Теория моментов инерции...................................................................................................207
§ 95. Основные определения. 207
§ 96. Общие теоремы о моментах.........................................208
§ 97. Преобразование статических моментов и моментов инерции при параллельном переносе осей..............................210
§ 98. Вычисление моментов инерции...............................................211
§ 99. Преобразование моментов инерции при повороте осей . . . 214
§ 100. Главные оси и главные моменты инерции................................................215
Глава IX. Напряжения мри изгибе.......................................................................................................219
§ 101. Действие поперечных сил на балку..........................................................219
§ 102. Гипотеза плоских сечений и принцип Сен-Венана.221
§ 103. Нормальные напряжения при изгибе..........................................................223
§ 104. Изгибающие моменты и перерезывающие силы..........................................225
6
ОГЛАВЛЕНИЕ
§ 105. Дифференциальные соотношения между интенсивностью нагрузки, перерезывающей силой и изгибающим моментом. Эпюры.......................................................226
6 106. Расчет на прочность при изгибе по допускаемым напряжениям .......................................... . ........229
§ 107. Упруго-пластический изгиб.............................231
§ 108. Несущая способность стержня прн изгибе................233
§ 109. Принцип Сен-Веиаиа.................................. 236
§ ПО. Виецеитрениое растяжение — сжатие.....................237
§ 111. Ядро сечения .........................................239
§ 112. Несущая способность внецеитреиио сжатогр стержня ... 241
§ 113. Расчет составных балок................................243
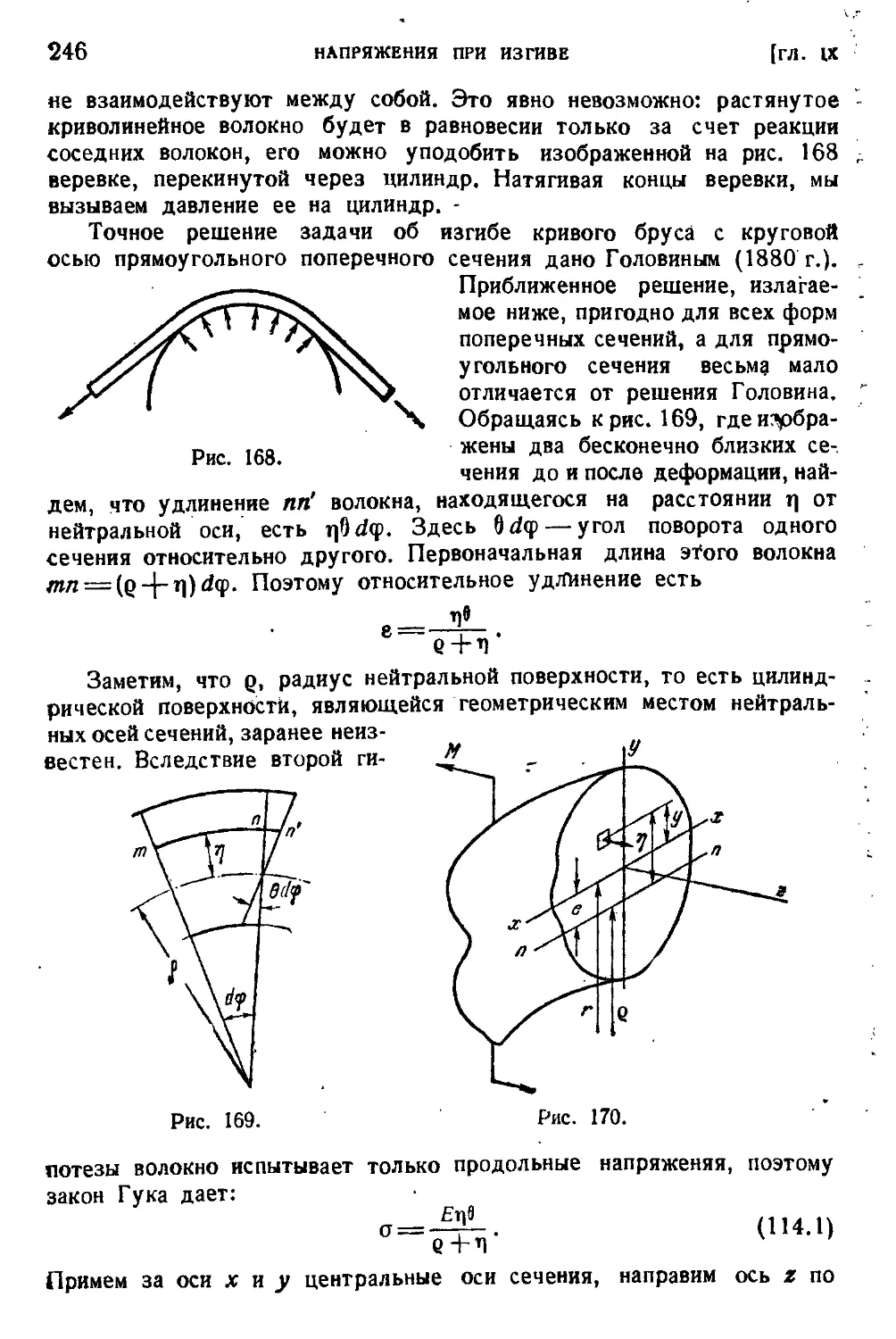
§ 114. Изгиб кривого бруса...................................245
§ 115. Нахождение нейтральной оси в кривом стержне...........248
Глава X. Деформации при изгибе....................................250
§ 116. Дифференциальное уравнение изогнутой оси.............250
§ 117. Пределы применимости приближенной теории . . . ... . .251
§ 118. Интегрирование уравнения изгиба .....................253
§ 119. Примеры определении прогибов ........................255
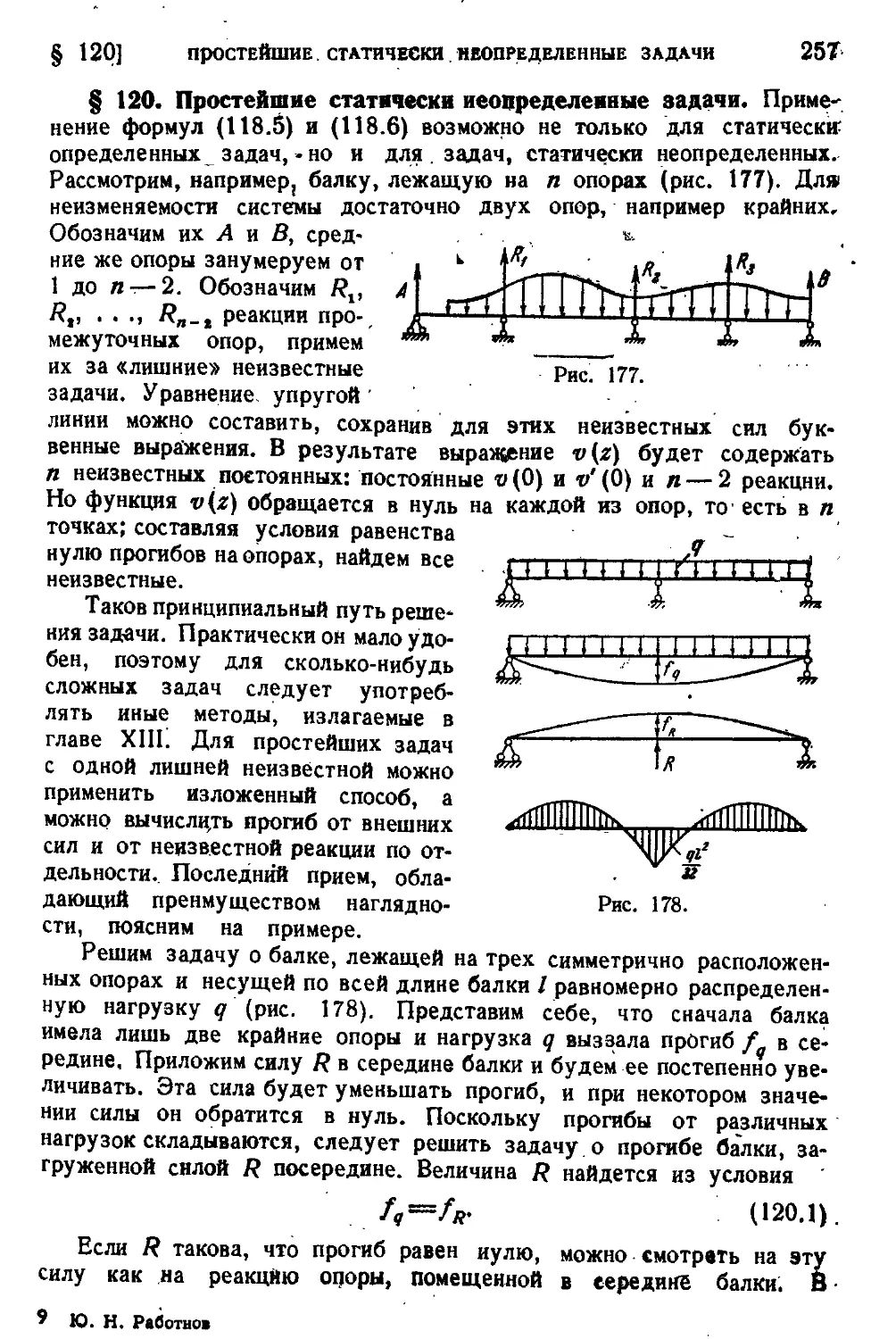
§ 120. Простейшие статически неопределенные задачи..........257
§ 121. Расчет статически неопределимых балок по способу допускаемых нагрузок.......................................... 258
§ 122. Изгиб стержней переменного сечения. Графоаналитический метод..................................................260
§ 123. О решении линейных дифференциальных уравнений с постоянными коэффициентами..................................263
§ 124. Продольно-поперечный изгиб............................266
§ 125. Изгиб балки иа упругом основании......................270
Глава XI. Изгиб и кручение тонкостенных стержней ..............275
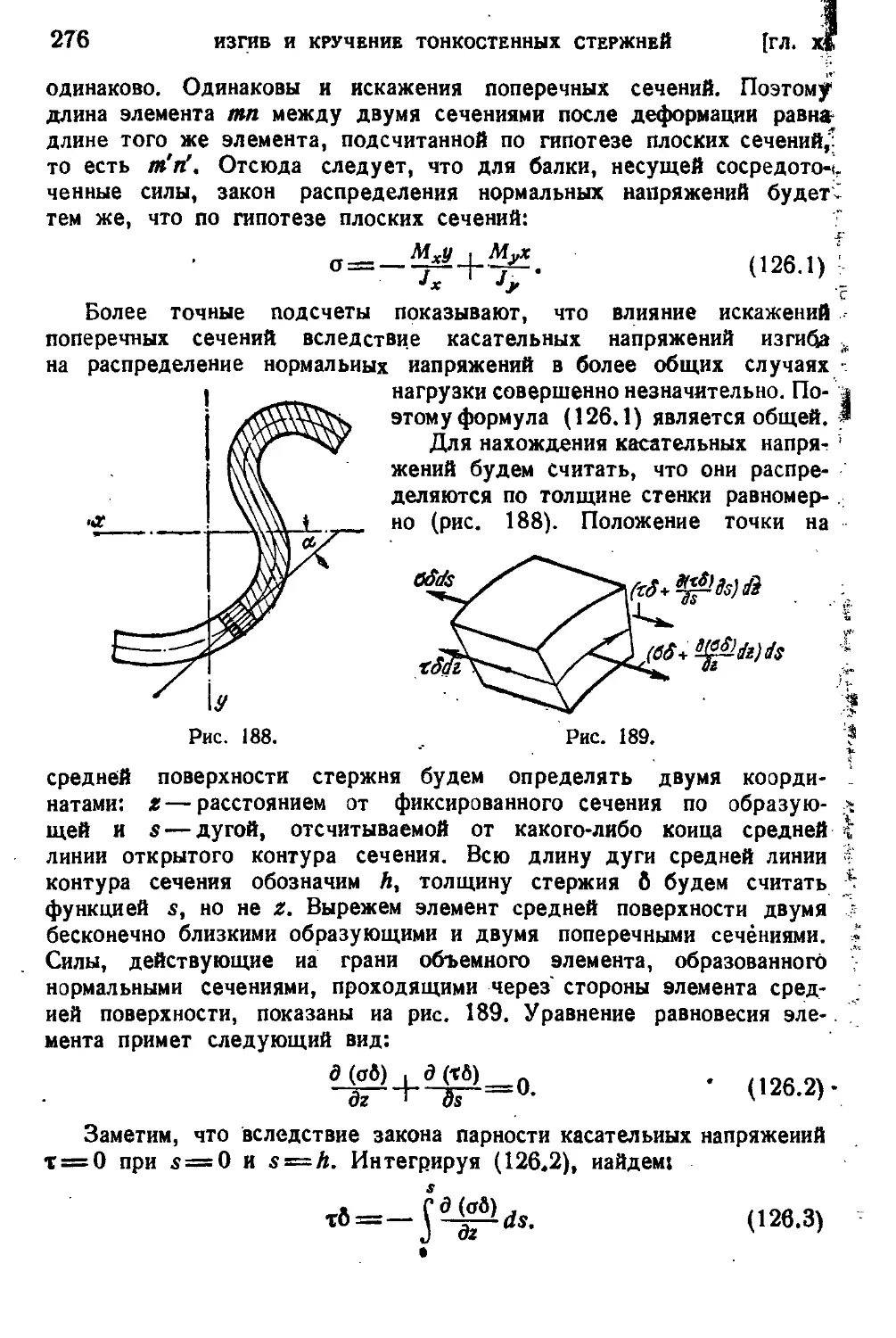
§ 126. Нормальные и касательные напряжения при изгибе .... 275
§ 127. Касательные напряжения при изгибе в плоскости симметрии 277
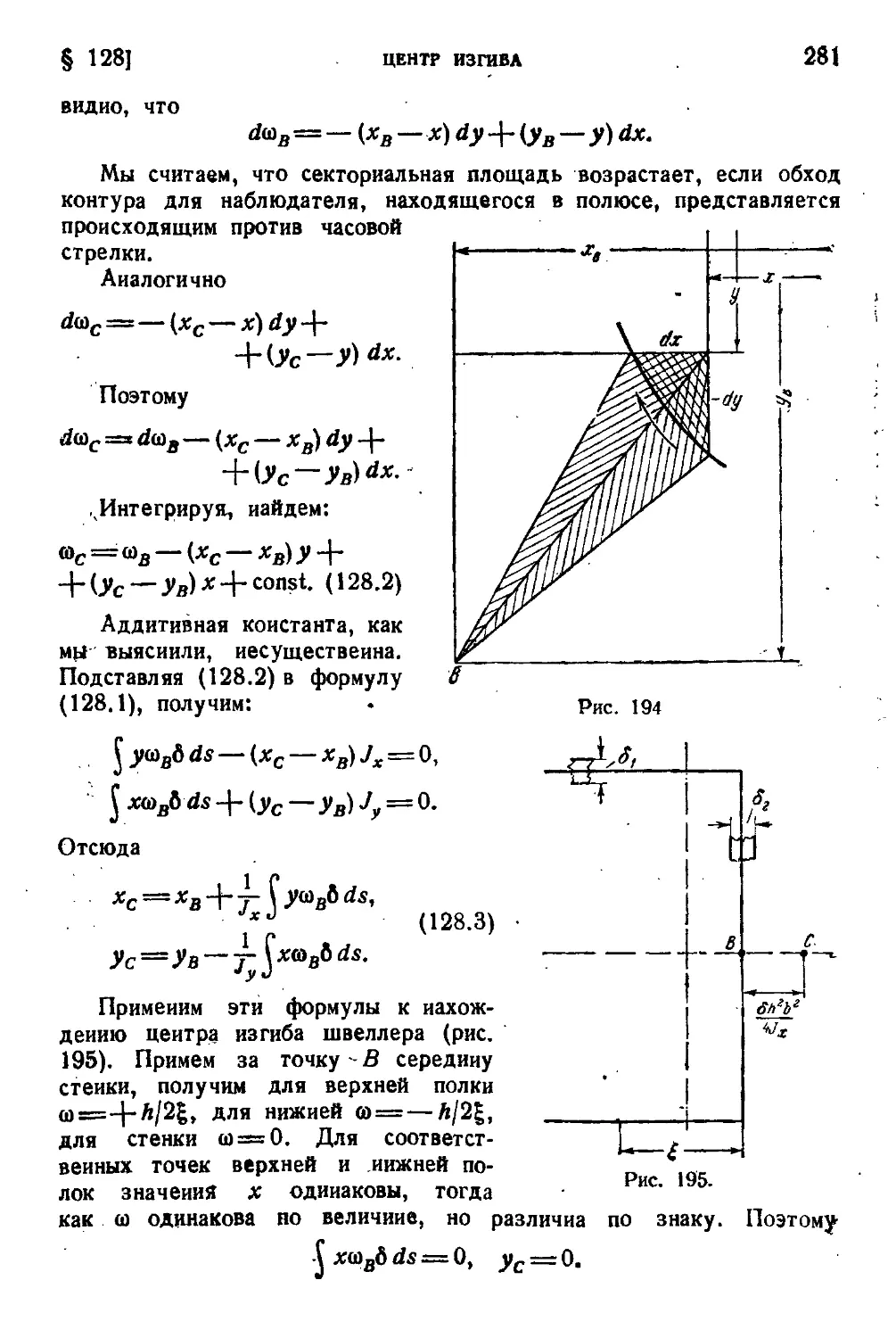
§ 128. Центр изгиба..........................................279
§ 129. Дополнительные напряжения при кручении................282
§ 130. Закон секториальиых площадей..........................283
§ 131. Уравнение стесненного кручения........................286
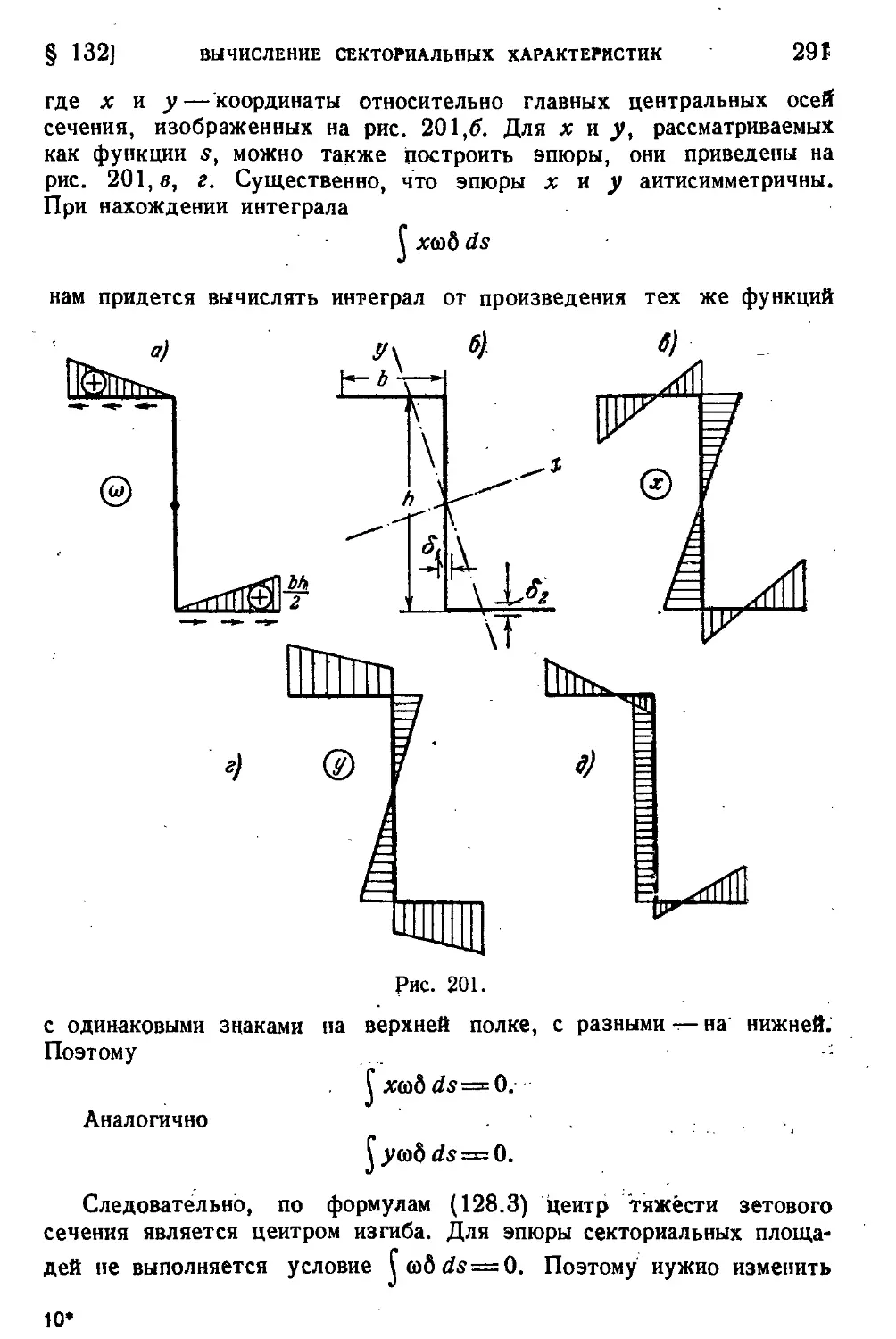
§ 132. Вычисление секториальиых характеристик................288
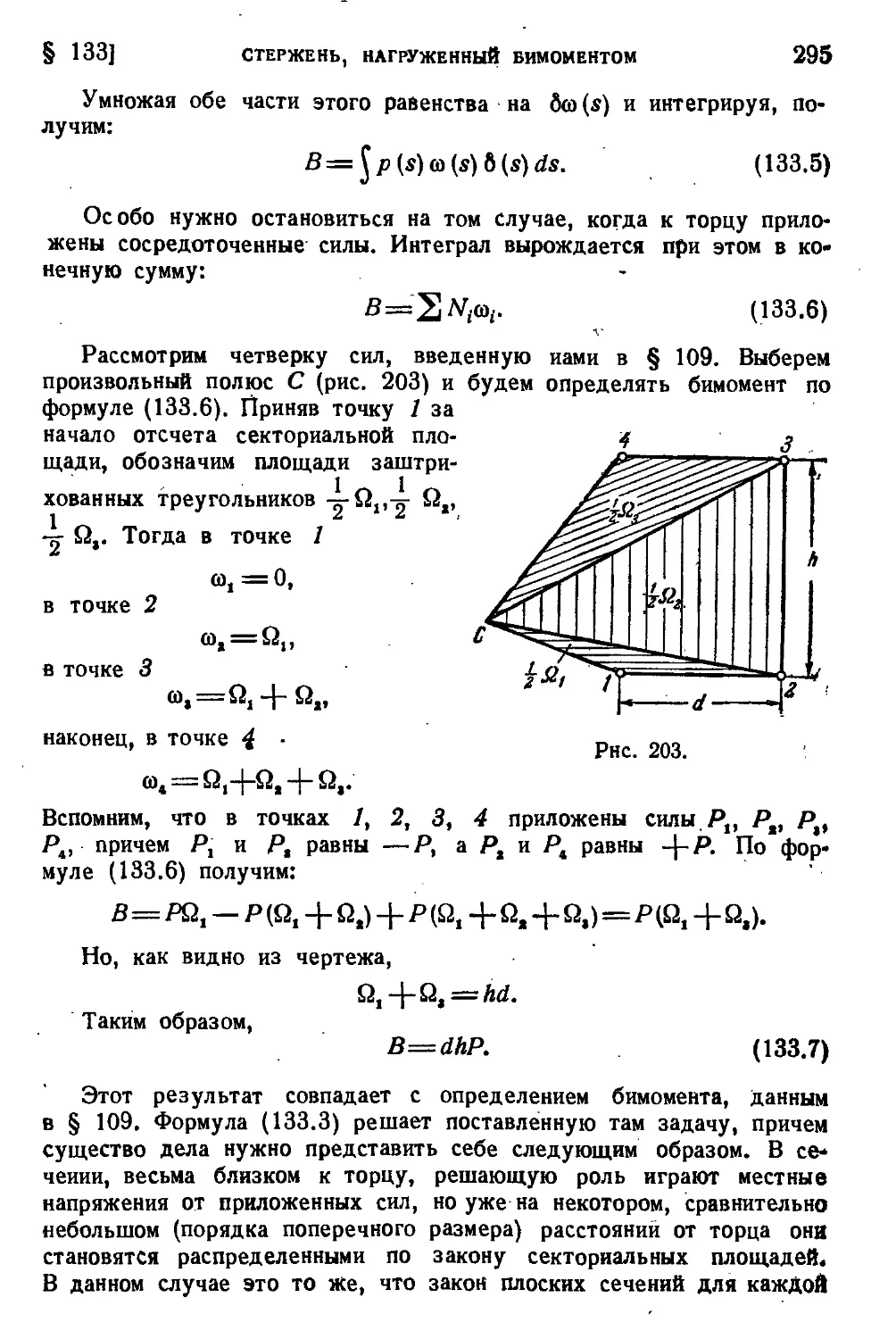
§ 133. Стержень, нагруженный бимоментом .....................293
§ 134. Некоторые примеры стесненного кручения................296
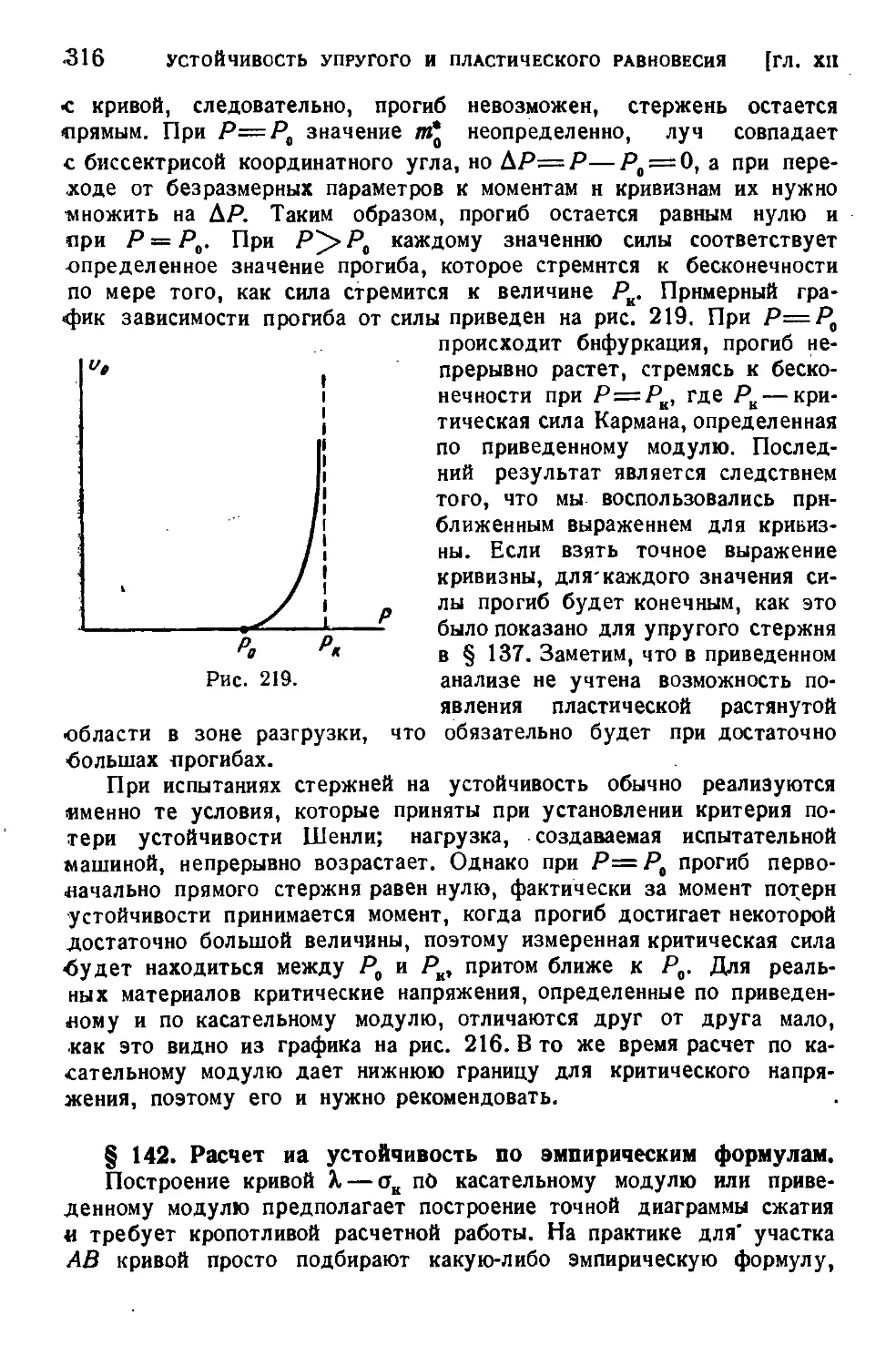
Глава XII. Устойчивость упругого и пластического равновесия . . . 300
§ 135. Постановка вопроса об устойчивости...................300
§ 136. Устойчивость сжатого упругого стержня................301
§ 137. Эластика Эйлера......................................302
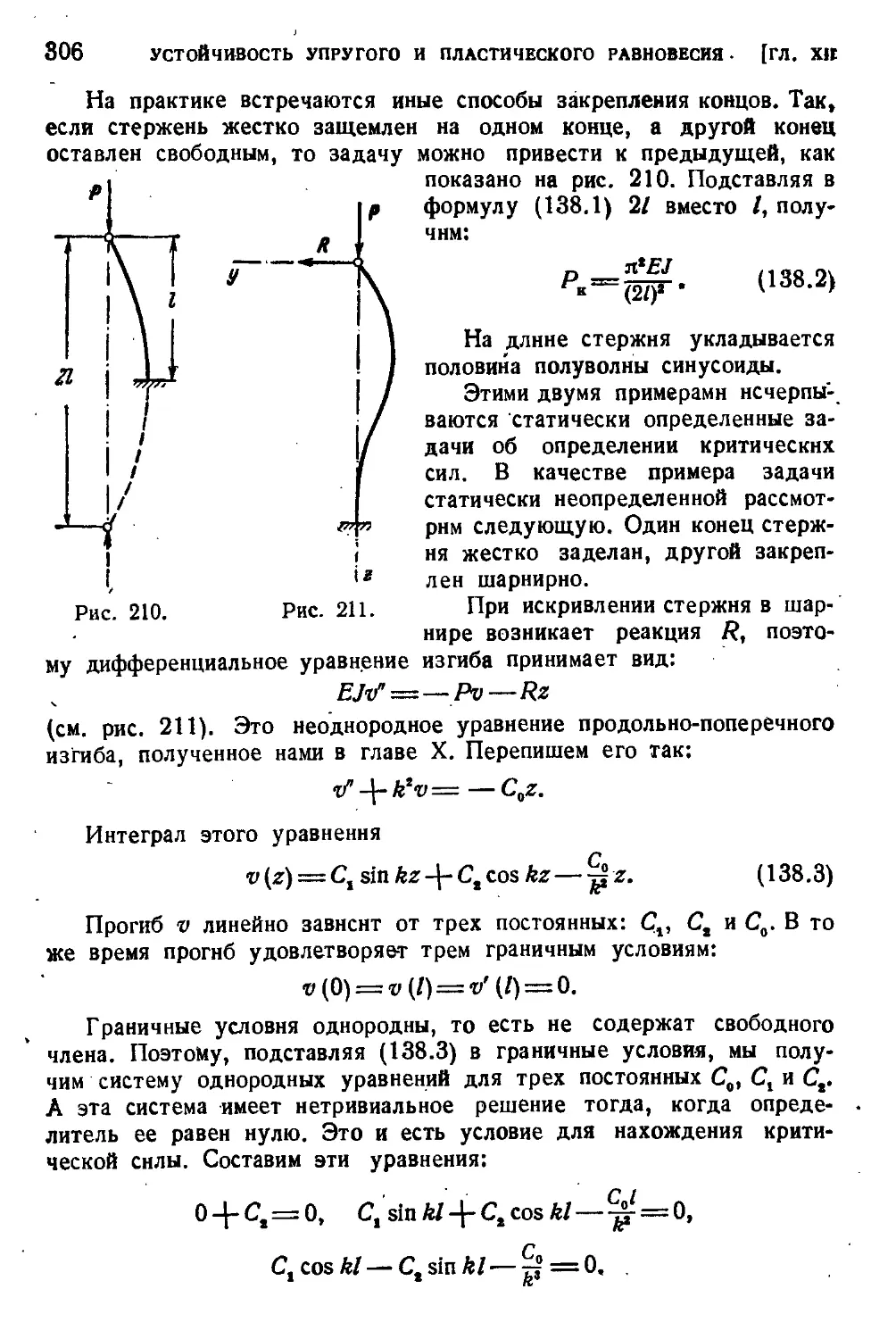
§ 138. Критические силы при иных видах закрепления стержня . 305
§ 139. Потеря устойчивости за пределом упругости.......... 307
ОГЛАВЛЕНИЕ 7
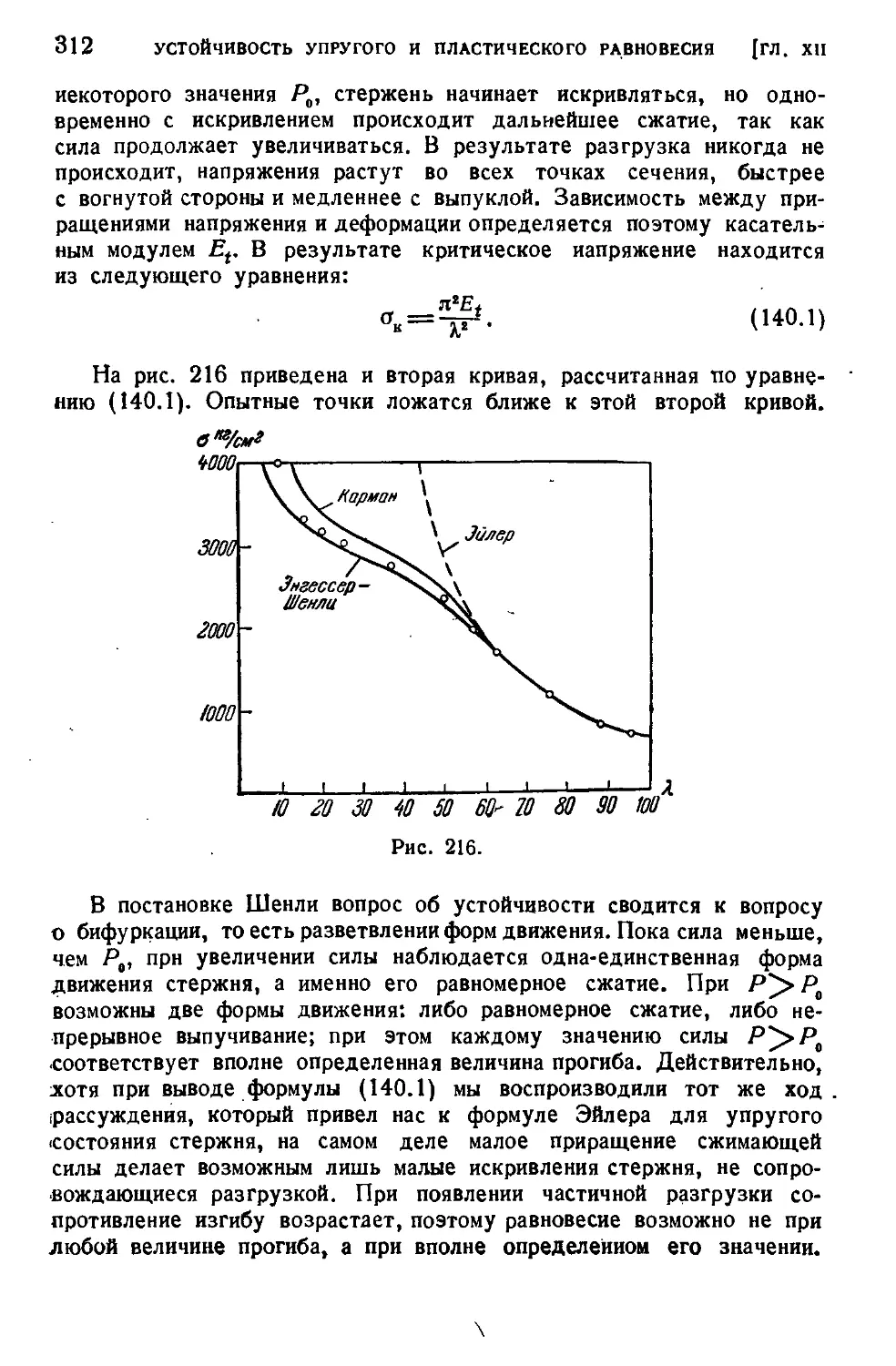
§ 140. Потеря устойчивости за пределом упругости (продолжение) 311
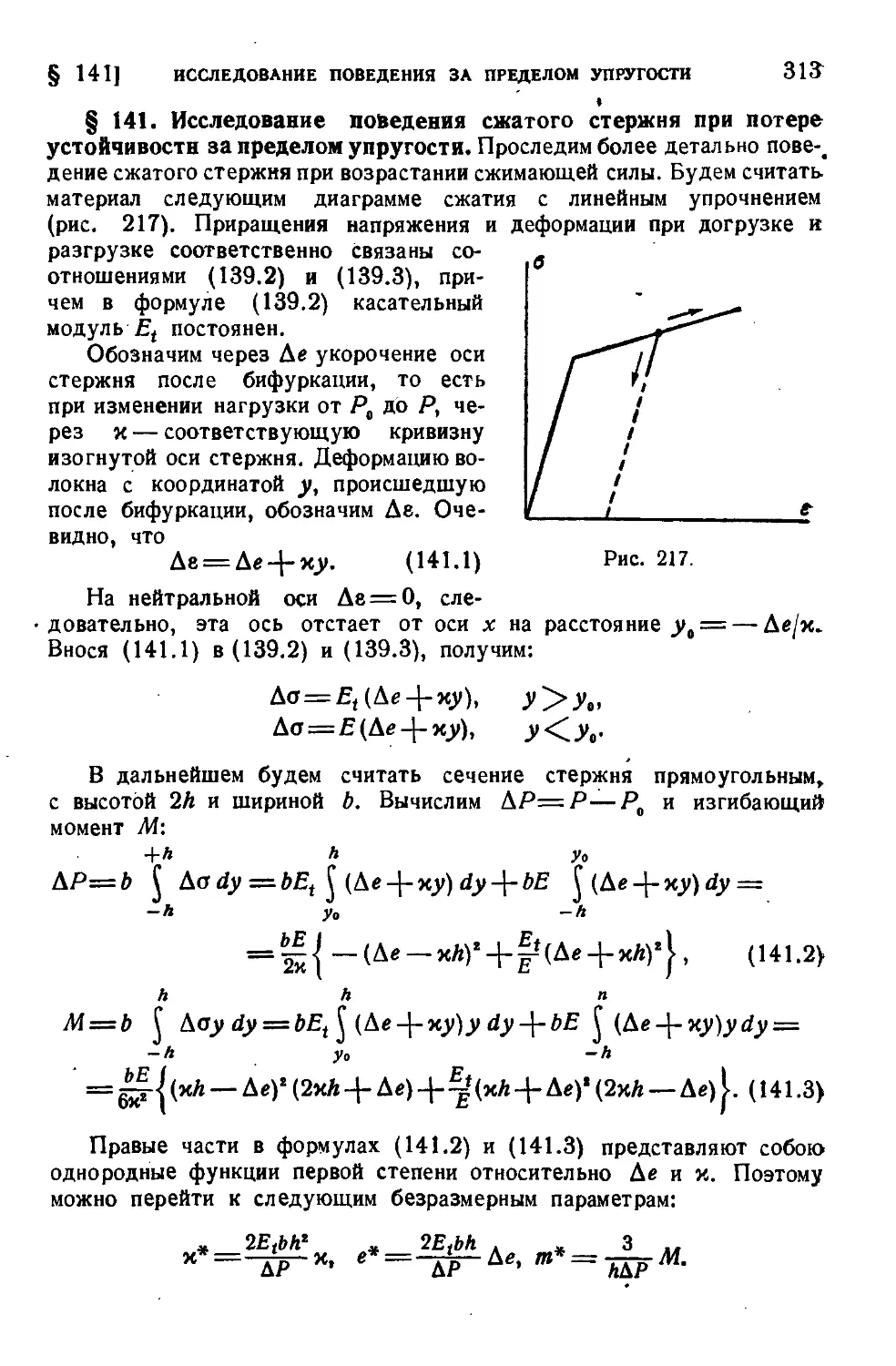
§ 141. Исследование поведения сжатого стержня при потере устойчивости за пределом упругости..........................313 •
§ 142. Расчет иа устойчивость по эмпирическим формулам .... 316
Глава ХШ. Трубы и диски ........................................318
§ 143- Толстостенные трубы. Дифференциальные уравнения равновесия и совместности ....................................318
§ 144. Упругое состояние трубы. Формулы Ламе . ............320
§ 145. Пластическое состояние трубы........................322
§ 146. Вращающиеся диски. Упругое состояние................326
§ 147. Диск равного сопротивления .................328
§ 148. Предельное равновесие вращающегося диска ...........329
Глава XIV. Общие теоремы сопротивлении материалов...............331
§ 149. Обобщенные силы и обобщенные перемещения............331
§ 150. Начало возможных перемещений для деформируемого тела 332
§ 151. Теоремы Лагранжа и Кастильяио..................'. . . 334
§ 152. Линейные упругие системы.......................... 336
§ 153. Теорема о взаимности работ........................ 338
154. Теорема Кастильяно для линейных упругих систем .... 339
§ 155. Расчет винтовых пружин..............................341
§ 156. Теорема о минимуме энергии..........................342
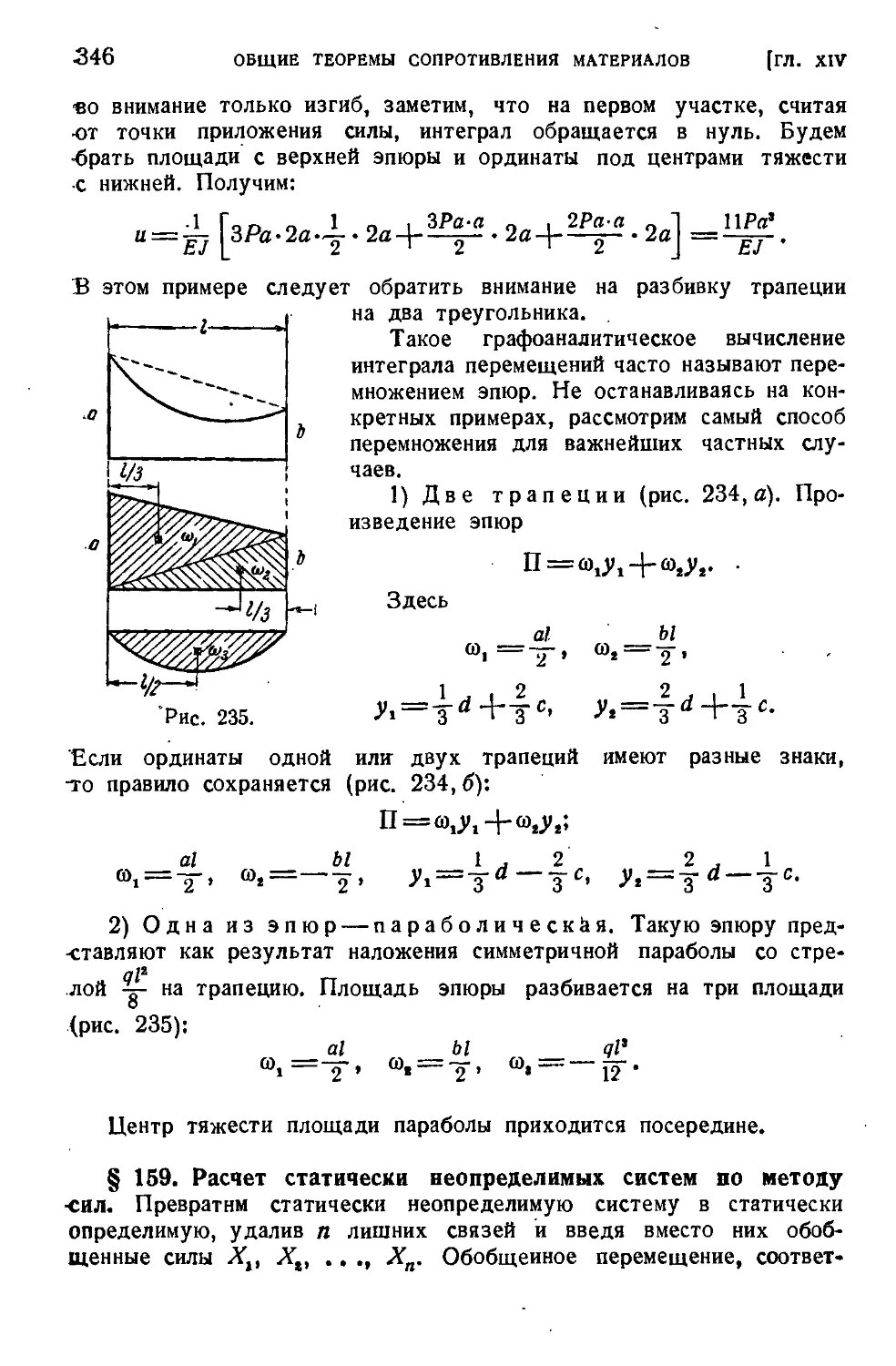
§ 157. Интеграл перемещений................................343
§ 158. Графоаналитический способ вычисления интеграла перемещений .................................-...................345
§ 159. Расчет статически неопределимых систем по методу сил . . 346
§ 160. Уравнение трех моментов ............................348
Глава XV. Теория предельного равновесия ........................352
§ 161. Жестко-пластическое тело ...........................352
§ 162. Поверхности иагружеиия..............................354
§ 163. Истинное и допустимые состояния элемента ...........355
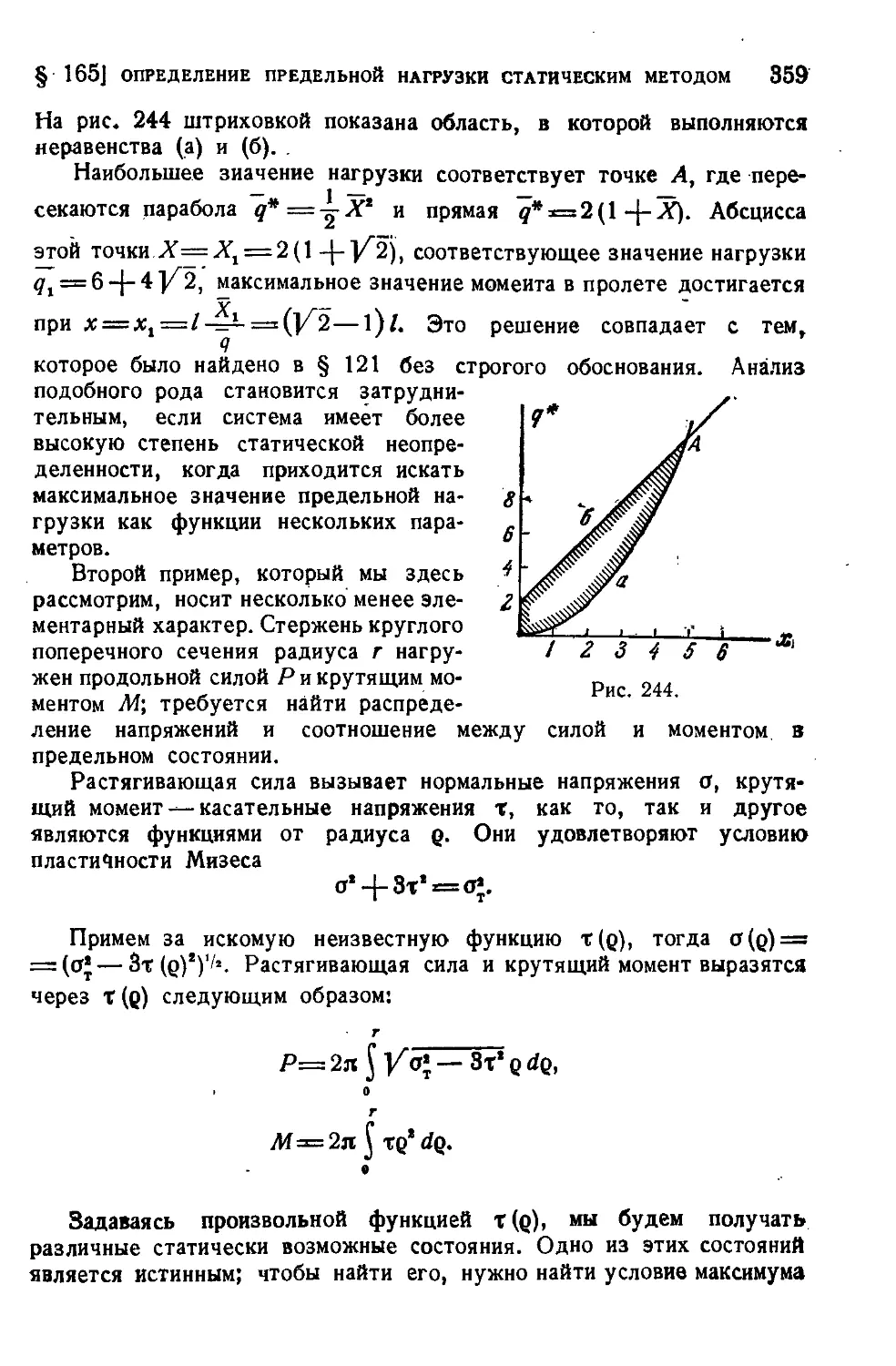
§ 164. Статический метод определения предельной нагрузки . . . 356
§ 165. Примеры определения предельной нагрузки статическим методом................................................... 358
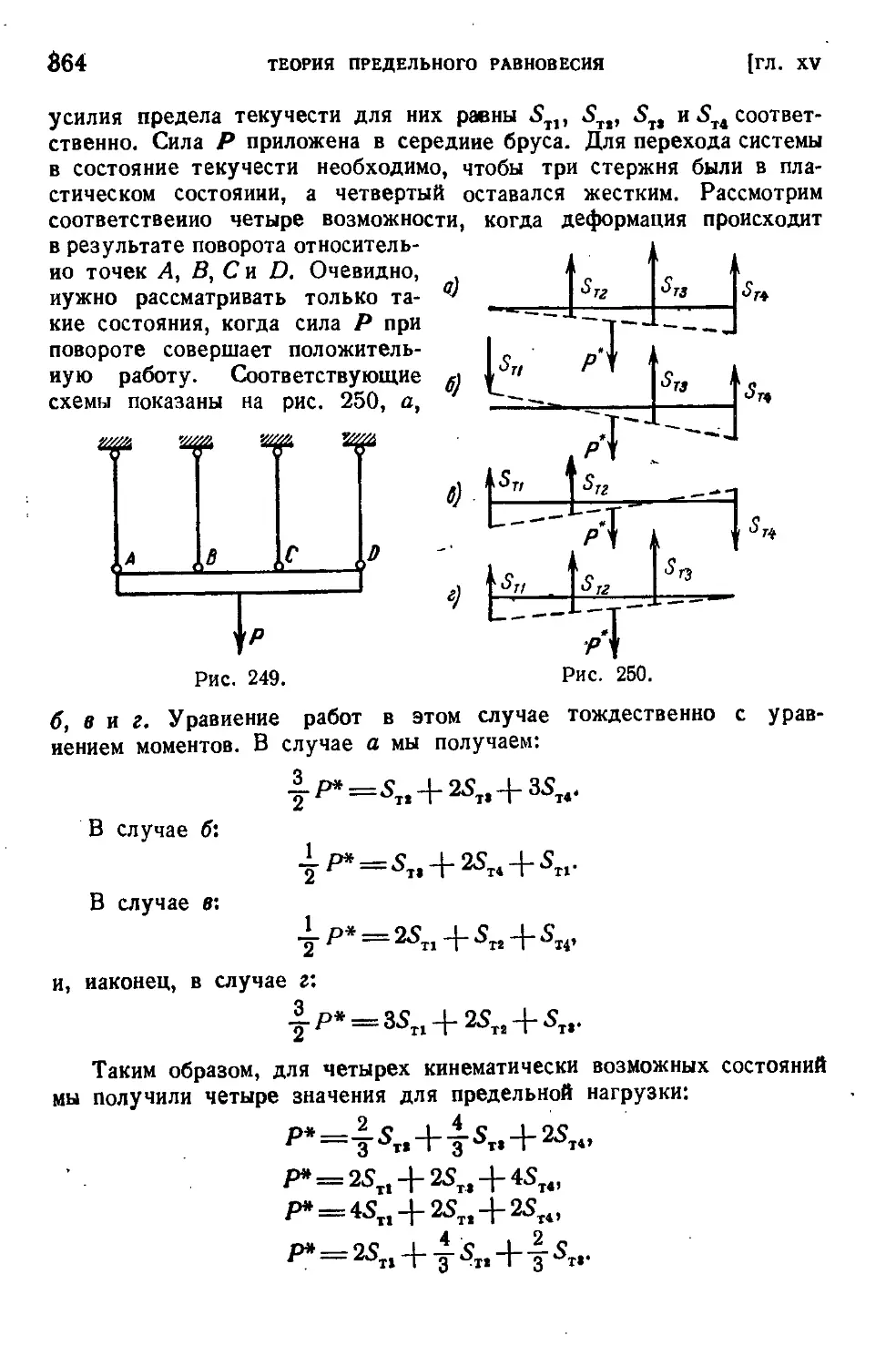
§ 166. Кинематически возможные состояния...................360
§ 167. Кинематический метод определения предельной нагрузки . 362
§ 168. Примеры определения предельной нагрузки кинематическим методом . . . .......................................... 363
§ 169. Предельное равновесие пластинок.....................366
Глава XVI. Динамические задачи сопротивлении материалов .... 370
§ 170. Колебания систем с конечным Числом степеней свободы . . 370
§ 171. Собственные частоты и главные формы колебаний .... 372
§ 172. Представление произвольной конфигурации системы через главные формы. Главные координаты..........................376
§ 173. Формула и способ Релея..............................378
§ 174. Нижние оценки для частоты основного тона............380
8
ОГЛАВЛЕНИЕ
§ 175. Продольные колебания стержней ....................... 381
§ 176. Поперечные колебания стержней . . ...................386
§ 177. Колебании балок постоянного сечения ..................389
§ 178. Способ Релея — Ритца в применении к поперечным колебаниям стержней...............................................391
§ 179. Действие ударных и импульсивных нагрузок на упругие системы .......................Г............................396
Глава XVII. Теории прочности .....................................400
§ 180. Постановка вопроса о прочности.......................400
§ 181. Хрупкое и пластическое разрушение....................4QJ
§ 182. Теория прочности Мора .............................. 402
§ 183. Механизм хрупкого разрушения ........................407
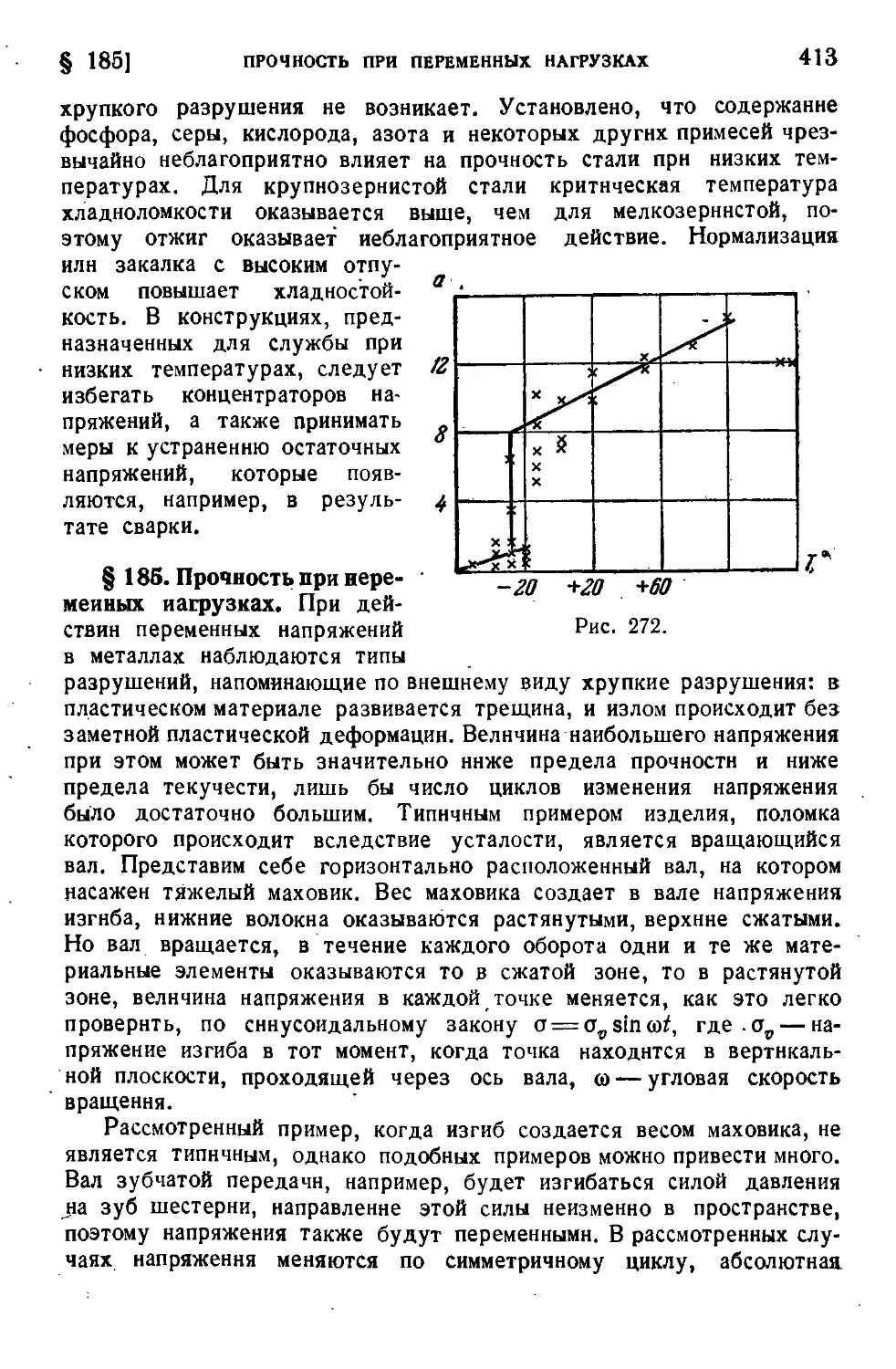
§ 184. Прочность при низких температурах.................. 411
§ 185. Прочность при переменных нагрузках ..................413
§ 186. Природа усталостного разрушения .....................416
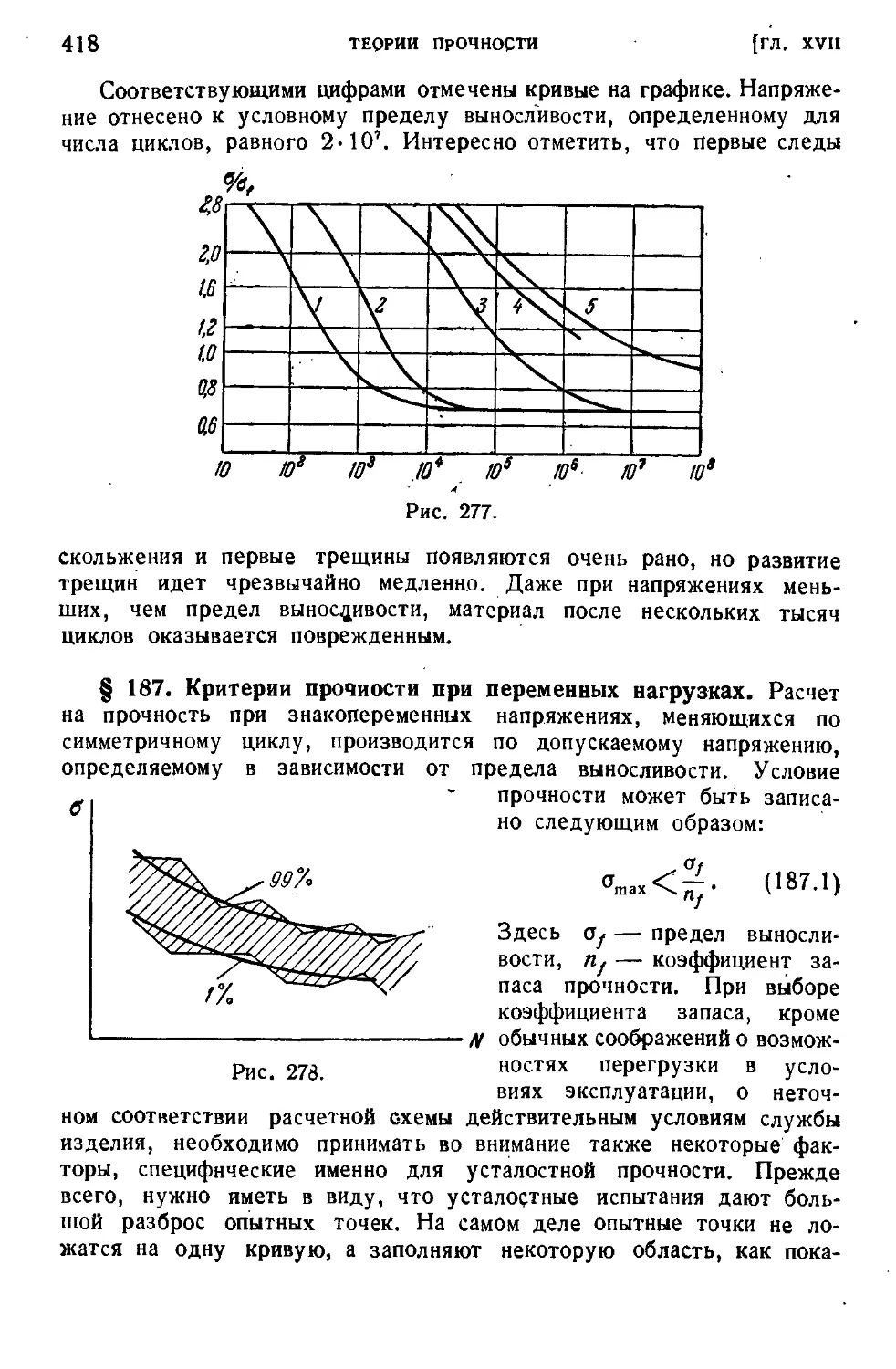
• § 187. Критерии прочности при переменных нагрузках '........418
§ 188. Влияние концентрации напряжений на усталостную прочность .................................................... 422
§ 189. Усталостная прочность при сложном напряженном состоянии ...................................................... 424
Глава XV1I1. Ползучесть и длительная прочность....................427
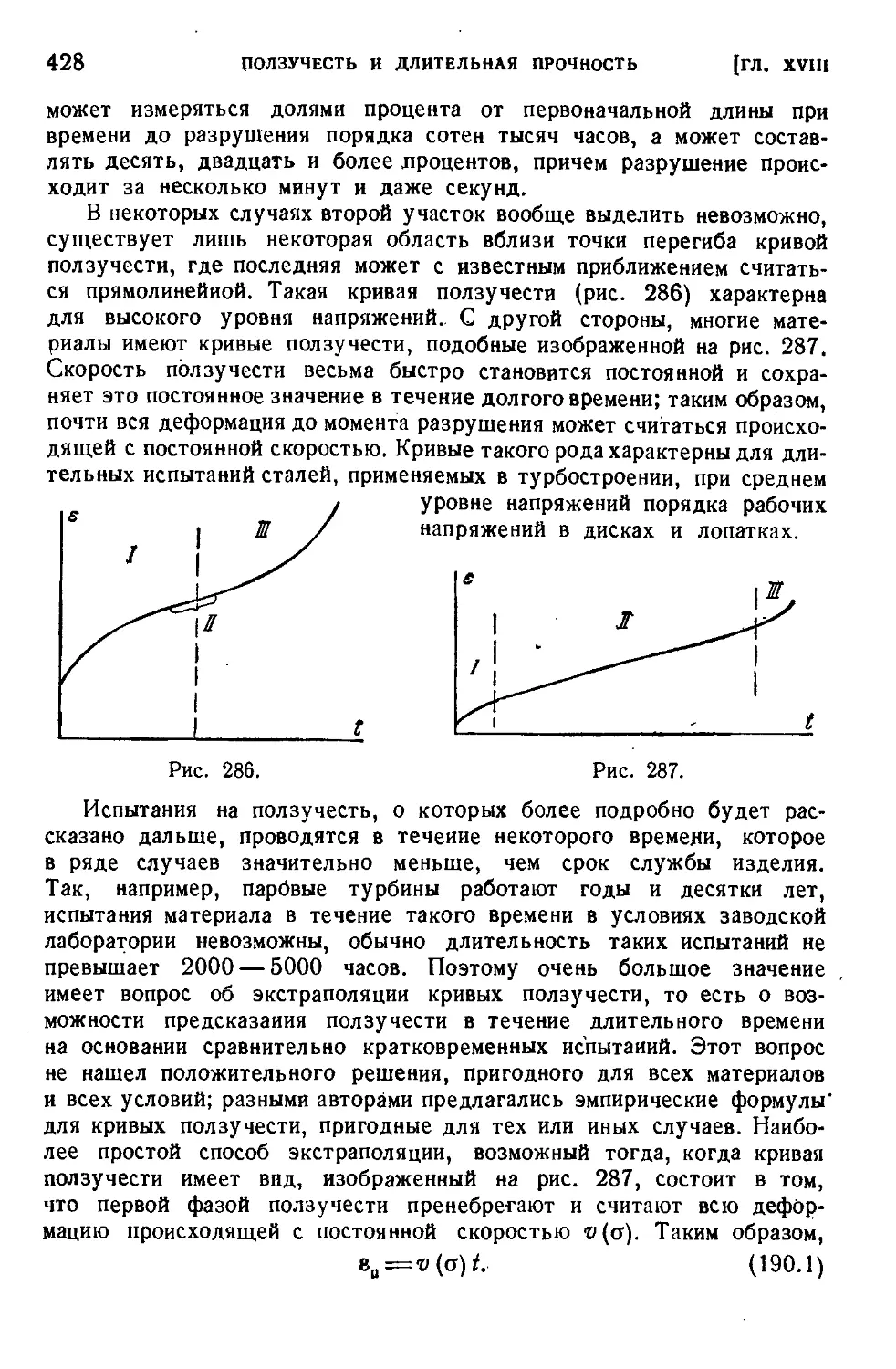
§ 190. Ползучесть металлов...................................427
§ 191. Процесс ползучести .................................. 430
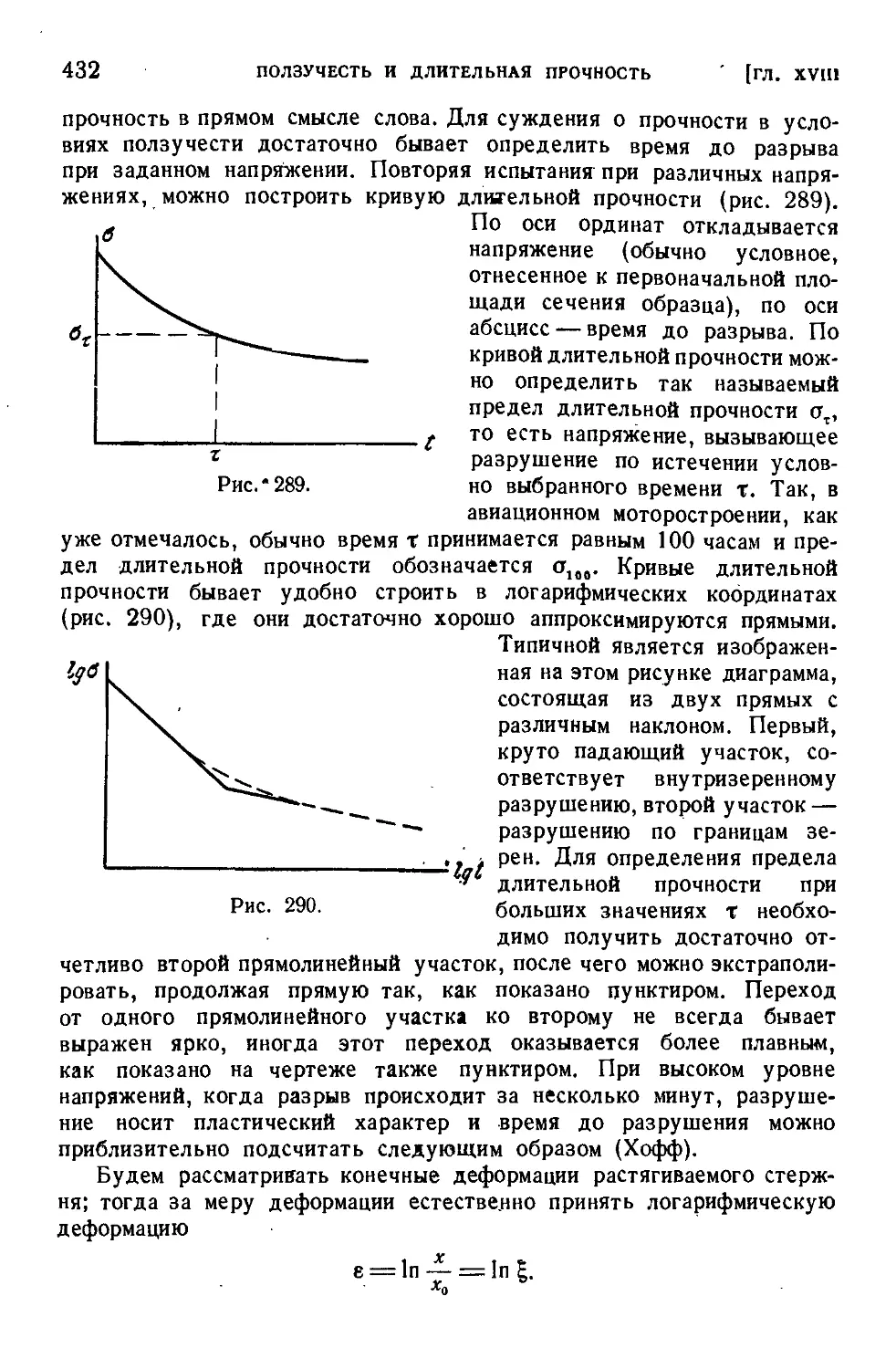
§ 192. Длительное разрушение ......... 431
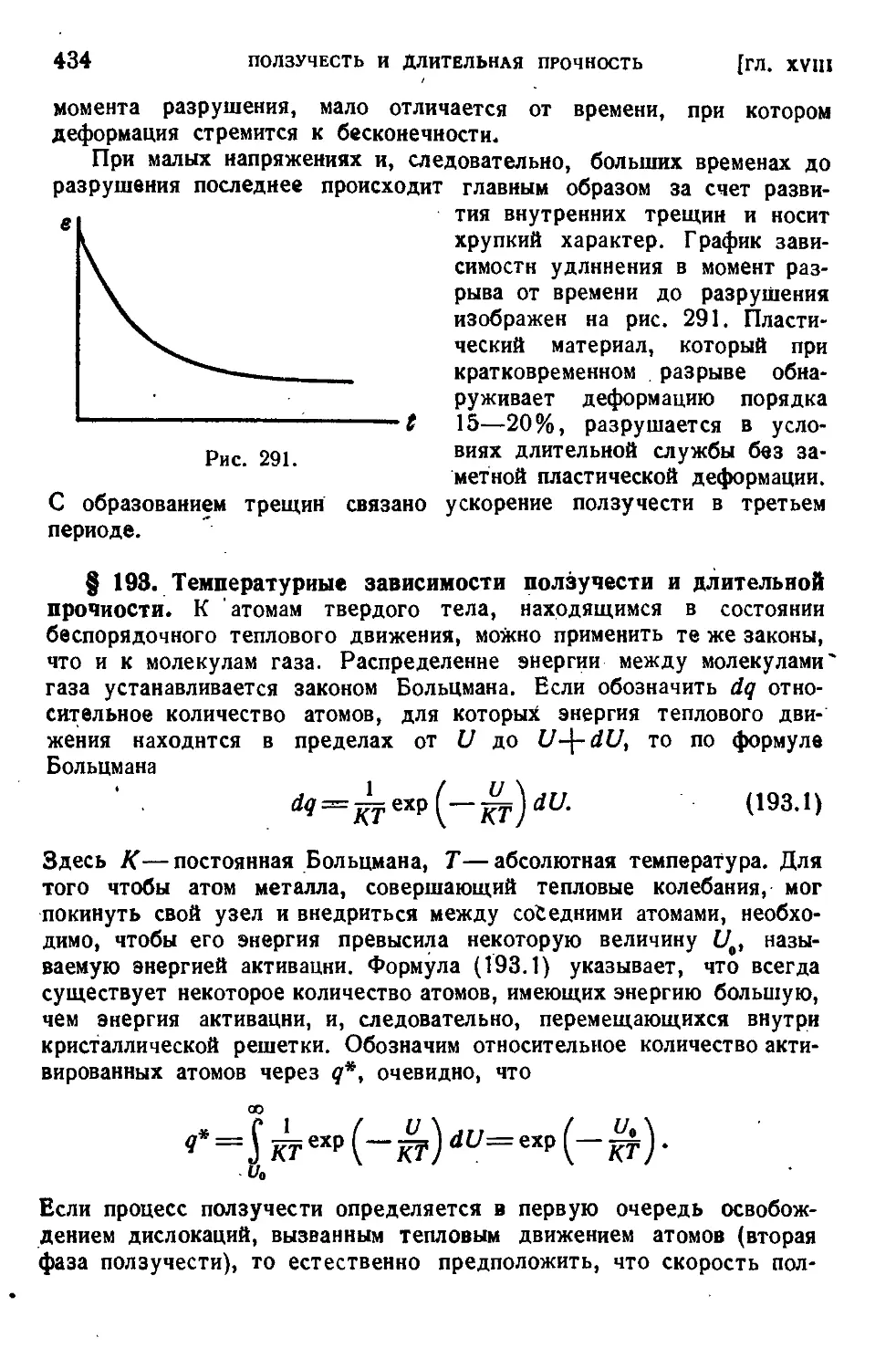
§ 193. Температурные зависимости ползучести и длительной прочности ......................................................434
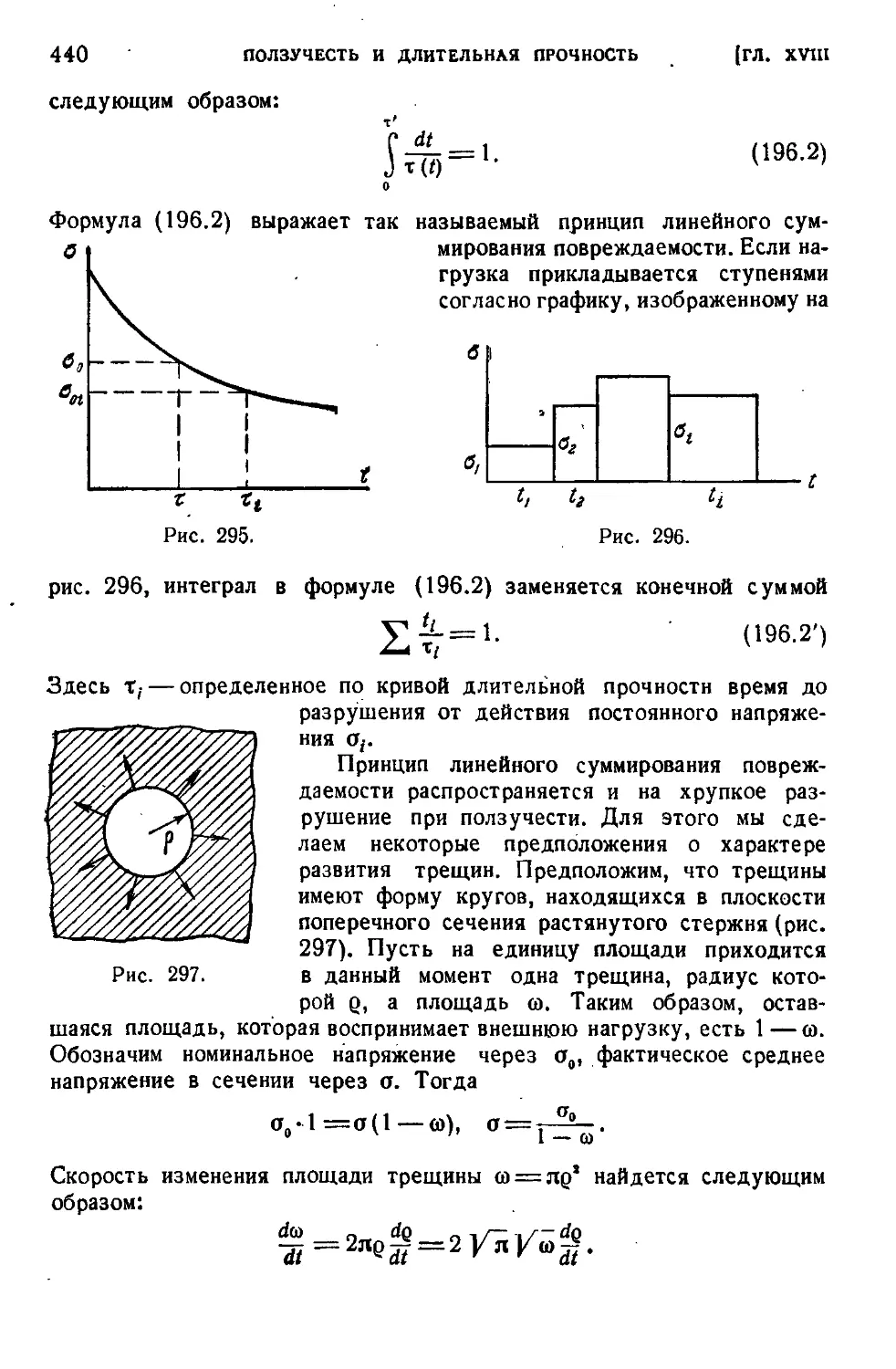
§ 194. Феноменологические теории одномерной ползучести ..... 436
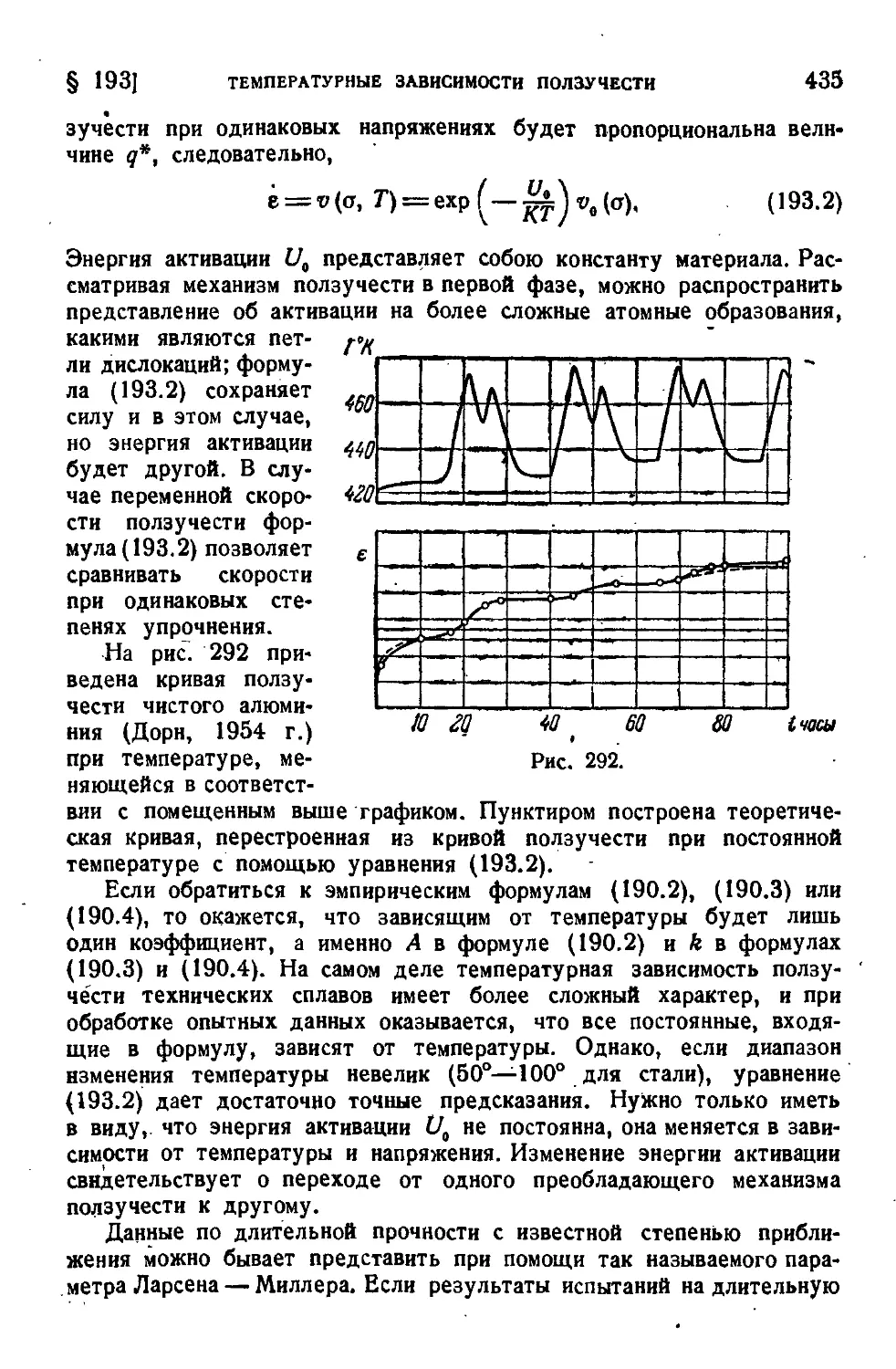
§ 195. Релаксация напряжений ...........437
§ 196. Длительная прочность прн переменных нагрузках.439
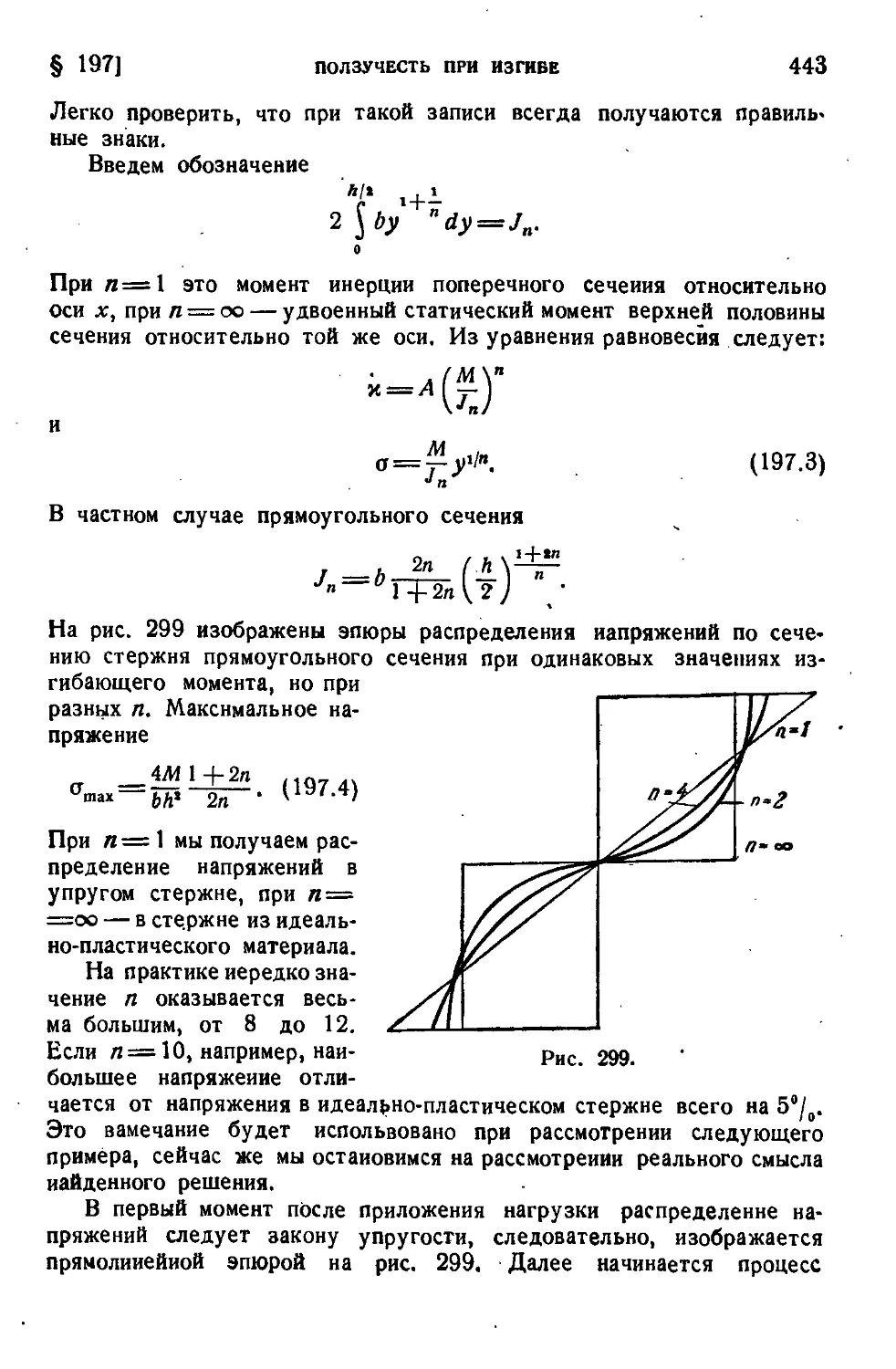
§ 197. Ползучесть при изгибе................................442
§ 198. Критическое время сжатого стержня .......445
§ 199. Ползучесть и длительная прочность при сложном напряженном состоянии...............................................448
§ 200. Вращающиеся диски в условиях ползучести...........449
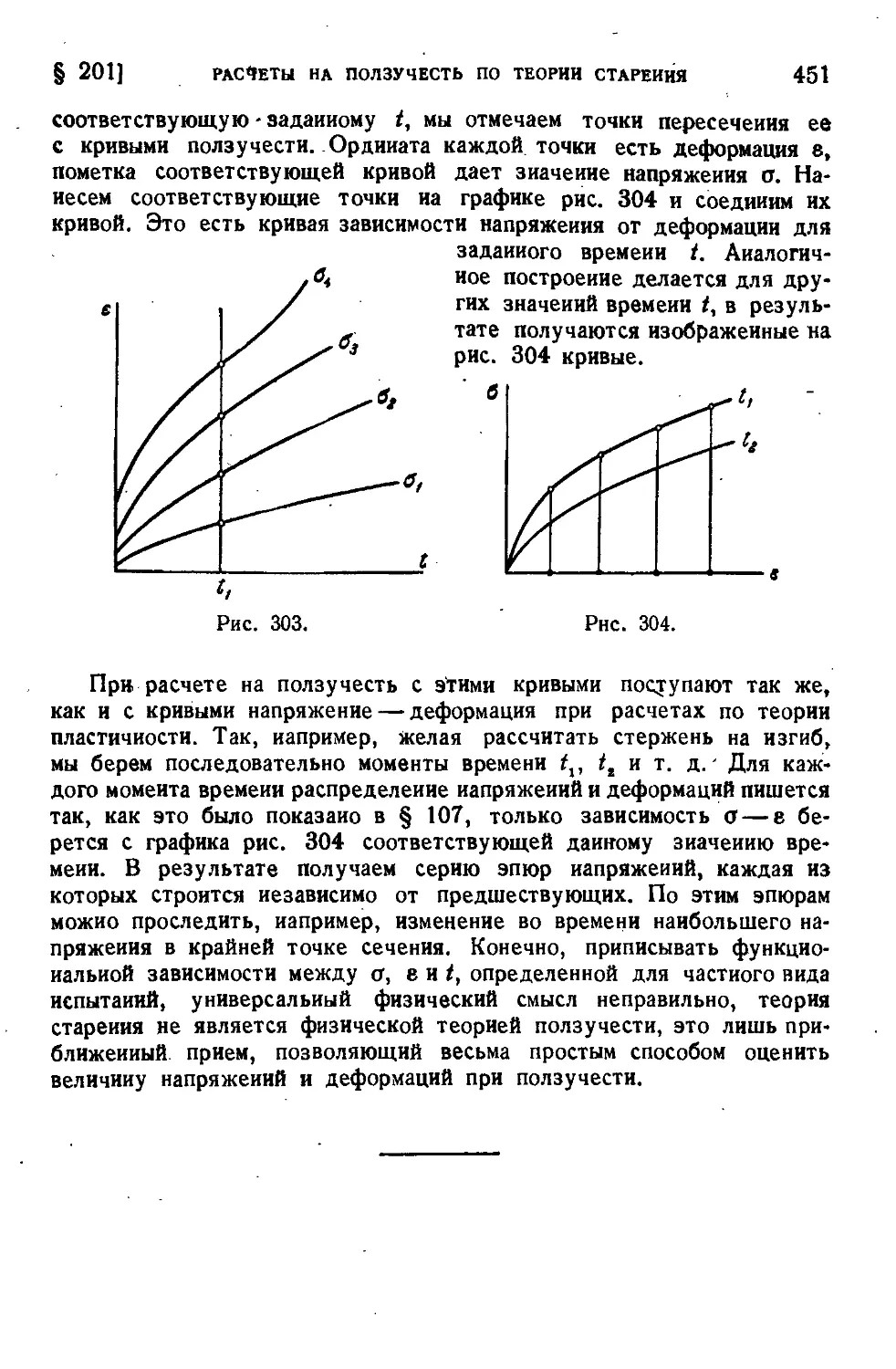
§ 201. Расчеты на ползучесть по теории старения ...........450
Предметный указатель..............................................452
ПРЕДИСЛОВИЕ
Основой при составлении этой книги послужили лекции, читавшиеся автором в Московском государственном университете и выпущенные в 1950 г. издательством Московского университета. За истекшие двенадцать лет в учении о прочности материалов и конструкций достигнут значительный прогресс, многие точки зрения изменились, существенно расширился объем сведений и представлений, полагаемых в основу методов расчета на прочность частей машин и сооружений, усовершенствовались и сами расчетные методы.
Достижения теории упругости, теории пластичности и механики материалов стали широко применяться в практике проектирования. Однако основная тенденция развития сопротивления материалов, на наш взгляд, состоит в расширении его физической базы, усложнении и усовершенствовании простейших моделей деформируемого тела, применительно к которым развиваются те или иные расчетные схемы. Поэтому автору казалось совершенно необходимым написать заново главу о физических основах прочности на основе дислокационных представлений, уделить значительно большее внимание основам теории пластичности, посвятить специальный раздел теории предельного равновесия. Вопросы динамики, включая теорию упругих колебаний, действие ударных и импульсивных нагрузок и начальные сведения о распространении волн, также являются, на взгляд автора, необходимой частью современного курса сопротивления материалов. Расчеты на прочность при высоких температурах поставлены в настоящее время на надежную основу, и в книгу включена соответствующая глава.
Значительной переработке подверглись и остальные разделы, носящие более традиционный характер.
В то же время автор сознательно не акцентировал внимания на изложении расчетных методов более специального характера, ограничившись наиболее простыми, непосредственно вытекающими из общих принципов и иллюстрирующими их прямое применение. Конечно, прн расчете сложных статически неопределимых систем — ферм, балок и рам — следует пользоваться теми или иными частными приемами, позволяющими существенно упростить и рационализировать
10 ПРЕДИСЛОВИЕ
вычислительную работу и получить необходимый результат наиболее коротким путем, но эти приемы излагаются в курсах строительной механики, и читатель, владеющий основами общей теории, в случае необходимости всегда сможет их изучить.
В области усталостной прочности идет непрерывное усовершен- • ствование и уточнение расчетных методик, связанное с дифференциацией коэффициента запаса, более полным использованием непрестанно-пополняющегося экспериментального материала и учетом многообразных факторов, влияющих на усталостную прочность. И здесь автор ограничился изложением общих принципов.
В настоящее время при серьезном подходе к расчету на прочность более или менее ответственных изделий приходится использовать огромный опыт, накопленный в соответствующих отраслях техники, и обращаться к специальным руководствам и справочникам.
Перенесение всего справочного материала в общий курс невозможно, да и не имеет смысла.
Исходная точка зрения автора состояла в том, что сопротивление материалов — это раздел механики деформируемого твердого тела, непрерывно обогащающий свое физическое содержание, использующий результаты смежных наук и вовлекающий в круг своих задач изучение новых явлений. «
Автор выражает глубокую благодарность многочисленным друзьям, сообщившим свои замечания по первой книге и оказавшим помощь советами при составлении настоящего руководства.
Ю. Н. Работное
ГЛАВА I
ОСНОВНЫЕ ПОНЯТИЯ
§ 1. Задачи и содержание сопротивления материалов. Учение о сопротивлении материалов, или, как обычно говорят, «сопротивление материалов», представляет собой главу механики, имеющую дело с реальными твердыми телами. Практическая цель, которую ставит перед собою сопротивление материалов, — это расчет на прочность частей машин и сооружений, поэтому изучаемыми В сопротивлении материалов объектами являются не какие угодно тела, а части машин и сооружений, изготовленные из тех материалов, которые в данное время применяются в технике. В процессе эксплуатации машина или сооружение подвергается действию разного рода сил. Все реальные тела под действием сил деформируются, то есть изменяют свою форму и размеры. Если силы достаточно велики, тело может разрушиться, то есть распасться на части. Для того чтобы часть конструкции могла выполнять свои функции, необходимо, чтобы была обеспечена прочность ее при рабочих условиях. Под нарушением прочности мы будем понимать либо фактическое разрушение, либо появление недопустимо больших деформаций. Иногда в этих случаях говорят о расчете иа прочность и иа жесткость, понимая под прочностью в узком смысле слова гарантию от разрушения, под жесткостью — ограничение деформации. Мы будем понимать термин «прочность» в дальнейшем, если это особо не оговорено, в широком смысле слова.
Что такое допустимая и недопустимая деформация — это вопрбс, который в каждом отдельном случае решается особо в зависимости от той конструктивной функции, которую выполняет данная часть сооружения. Так, если мост прогибается под действием силы веса проходящего поезда на несколько сантиметров, то этот прогиб ничтожно мал по сравнению с пролетом моста, длина которого измеряется десятками метров; его Считают допустимым. С другой стороны, прогиб станины или шпинделя токарного станка в одну десятую миллиметра от силы, действующей на резец, исключает возможность сколько-нибудь точной обработки детали и совершенно недопустим.
Свойства реальных материалов, применяемых в технике, сложны и разнообразны, однако основные понятия механики применимы к ним
12
ОСНОВНЫЕ понятия
[гл. 1
в полной мере. Разрушение изделия означает преодоление внутренних сил связи между его частями; для суждения о возможности разрушения необходимо знать эти силы, а нахождение снл является предметом механики.
Изделия, вообще говоря, могут разрушаться н не от действия механических сил, а от других причин. Они могут корродировать, растворяться, расплавляться при высокой .температуре. Стойкость материалов по отношению к немеханическим воздействиям не относится к предмету сопротивления материалов.
В основе механики лежат опытные факты, устанавливающие простейшие, фундаментальные свойства тех тел, с которыми имеет дело та или иная глава механики. На основании этих фактов формулируются некоторые законы, описывающие свойства изучаемых тел с той или иной степенью приближения, то есть устанавливающие некоторые соотношения между механическими величинами — силами, перемещениями, скоростями. Эти законы могут быть чисто эмпирическими, а могут вытекать из тех или иных физических соображений, например, являться результатом изучения внутренних процессов, происходящих в структурных элементах тела при его деформации. Поэтому сопротивление материалов тесно связано с физикой твердого тела и так называемым механическим материаловедением, изучающим на опыте те свойства материалов, которые важны для суждения о прочности.
Для современной механики характерно расширение ее физической базы, более полный учет всех свойств реальных тел — твердых, жидких и газообразных, которые изучает механика. Эта же тенденция определяет современное развитие сопротивления материалов. Те относительно простые схемы, которые полагались в основу расчетов несколько десятков лет тому назад, недостаточны для анализа современных конструкций; повышение рабочих параметров машин во многих случаях лимитируется возможностью создания прочной конструкции, и от материала приходится требовать, чтобы он работал на пределе, в то же время должна быть достаточная уверенность в надежности конструкции. Большое значение приобрели расчеты на прочность конструкций, подверженных действию динамических нагрузок, высоких температур, больших давлений; появились многочисленные новые' материалы с физическими и механическими свойствами, отличными от свойств привычных и хорошо изученных старых материалов. Поэтому учение о прочности представляет в настоящее время весьма обширную и разветвленную область знания, изложение всех ее аспектов и соответствующих методов и результатов в одной книге совершенно невозможно. При решении многообразных и сложных вопросов прочности для новых конструкций инженеру всегда приходится обращаться к помощи специальной литературы. Сопротивление материалов в обычном понимании слова — это лишь первый концентр сведений по механике деформируемого тв^рдо¥б_тела, а именно изло
§ 2] СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ И ТЕОРЕТИЧЕСКАЯ МЕХАНИКА 13
жение общих принципов, лежащих в основе учения о прочности, и методов расчета типовых, простейших элементов конструкций, встречающихся проектировщику на каждом шагу в его практической деятельности.
§ 2. Сопротивление материалов и теоретическая механика. Механика имеет дело с равновесием и движением материальных точек и систем материальных точек. Материальная точка представляет собою простейший идеальный объект механики, не существующий в природе, это некоторая абстракция, оказывающаяся полезной для перехода к реальному телу, которое можно представлять себе как систему материальных точек. В то же время представление о материальной точке может оказаться достаточным для решения некоторых вопросов механики. Так, размеры планет настолько малы по сравнению с расстояниями их от Солнца, что планеты можно считать материальными точками, не имеющими размеров, и рассчитывать с очень большой степенью точности траектории их движения.
Теоремы механики, относящиеся к каким угодно системам материальных точек, носят чрезвычайно общий характер; для их конкретизации необходимо знать природу взаимодействия между отдельными точками системы. Это взаимодействие осуществляется либо внутренними силами, либо геометрическими связями. Для построения механики реальных сред — твердых, жидких и газообразных — законы механики приходится дополнять физическими законами или гипотезами о взаимодействии между точками, составляющими систему. Простейшим гипотетическим телом является абсолютно твердое тело, то есть система материальных точек, расстояния между которыми неизменны. Абсолютно твердое тело не существует в природе, но, создавая эту абстракцию, мы сохраняем из всего многообразия свойств реального тела одно, а именно наблюдаемую в известных условиях относительную неизменяемость формы и размеров. Объектом теоретической механики по существу являются именно материальная точка и абсолютно твердое тело*). Для тех явлений, когда деформации тела несущественны и ими можно пренебречь, Выводы теоретической механики^ оказываются точными и вполне достаточными. Так, например, в кинематике механизмов обычно бывает возможно пренебречь деформациями звеньев, которые изготовляются весьма жесткими, поэтому скорости и ускорения, вычисленные по правилам механики твердого тела, точно соответствуют действительным. Реакции статически определимых балок, усилия в стержнях статически определимых
*) Здесь мы имеем в виду традиционное понимание термина «теоретическая механика», нашедшее отражение в учебны-^. программах и большинстве учебных пособий, В действительности, конечно,,, механика сплошных сред — твердых, жидких и" газообразных — это тоже «теоретическая механика».
14
ОСНОВНЫЕ понятия
[гл. I
ферм находятся из уравнений статики так, как если бы части соответствующих конструкций были жесткими.
Но постановка вопроса о расчете иа прочность и жесткость для абсолютно твердого тела лишена смысла, так как оно, по самому значению термина, не может ни деформироваться, ни разрушаться. В то же время существуют задачи статики обычного характера, например об определении реакций связей, в которых предположение о неизменяемости формы и размеров приводит к абсурду, они принципиально не могут быть решены без допущения возможности деформаций. Это так называемые статически неопределенные задачи.
§ 3. Статически неопределенные задачи. Так называются задачи
статики, в которых число неизвестных превышает число уравнений равновесия. Простейший пример статически неопределимой системы изображен на рис. 1. Тяжелый однородный стержень веса О, кото-
рый мы будем считать абсолютно жестким, подвешен на трех симметрично расположенных -нерастяжимых нитях. Для трех натяжений Tlt Tt и Tt статика дает только два уравнения:
Л + Л+т’.=о. (3-1)
1\ = Т,. (3.2)
Задача оказывается неопределенной. Легко
рис. 1. понять, что эта неопределенность связана
именно с гипотезой о нерастяжимости нитей.
Представим себе, что средняя нить короче крайних на сколь угодно
малую величину е. Тогда вся тяжесть груза приходится на среднюю
нить, крайние нити не натянуты:
Т1 = Т1 = 0, Tt = G.
(Случай А)
Если, наоборот, средняя нить длиннее крайних на величину е, то она свободно провисает, и груз G распределяется поровну между двумя крайними нитями. В этом случае получаем следующее решение, удовлетворяющее уравнениям статики:
Tl — Tl = ^-G, Т, = 0. (Случай Б)
Чтобы перейти от случая А к случаю Б, нужно изменить длину средней нити на бесконечно малую величину 2е. Значит, бесконечно малое изменение длины одной из нитей влечет за собой конечное изменение всех натяжений. Это физически абсурдно. Так как нельзя себе представить реальные нити строго одинаковой длины, то всегда должен осуществляться либо случай А, либо случай Б. Вопрос же о том, что будет, если нити строго математически равны между собой, принципиально неразрешим и не должен ставиться для идеальных, то есть нерастяжимых нитей.
ВНЕШНИЕ СИЛЫ
15
§ 4]'
Для бруса, подвешенного, на реальных нитях, вопрос о-натяжениях решается немедленно. Предположим, что нити имеют одинаковую толщину и сделаны из одинакового материала. Под тяжестью груза нити вытянутся, вследствие симметрии системы брус останется горизонтальным, значит, увеличение длины каждой нити будет равно одной и той же величине.
Естественно предположить, что у одинаковых нитей равным удлинениям соответствуют равные натяжения. Отсюда
7’, = 7’t=7’1. ‘ (3.3)
Последнее уравнение вытекает не из законов статики, а из рассмотрения деформаций системы. Решая его совместно с уравнениями статики, получим
т1==л=Г1=|0.
Теперь, если средняя нить короче крайних на малую величину е, нат'яжение ее больше, чем натяжение крайних на малую величину ДГ. При в, стремящемся к нулю, ДТ стремится также к нулю.
В дальнейшем мы встретимся с многочисленными примерами статически неопределимых систем и рассмотрим общие методы их расчета.
§ 4. Внешние силы. Обычно изучение механики начинается с механики твердого тела, и некоторые основные принципы формулируются именно для этого простейшего случая; поэтому нам следует остановиться на тех особенностях, которыми отличается применение понятий и аксиом статики к деформируемым телам. Начнем с основного, первичного понятия, а именно понятия силы, определение которого выходит за рамки наших задач.
В теоретической механике обычно вводят сначала сосредоточенные силы. После этого дается понятие о силах массовых, или объемных, то есть непрерывно распределенных по объему тела, и силах поверхностных, действующих на часть площади поверхности. Однако сосредоточенных сил в природе не существует, все реальные силы — это силы взаимодействия между телами. Мы называем их «внешними» по отношению к каждому из взаимодействующих тел. Силы взаимодействия могут проявляться на расстоянии (тяготение, магнитная сила) или при непосредственном соприкосновении. В первом случае силы непрерывно распределены по объему, во втором — по поверхности. Рисуя вектор силы тяжести, приложенный к центру тяжести тела, мы заменяем действительную силу тяжести, распределенную по объему, фиктивной силой, поступая так на основании аксиом и теорем статики твердого тела. Таким образом, приложенная в центре тяжести сила веса есть фикция. Этой фикцией можно пользоваться, например, при определении реакций изгибаемой балки, если число уравнений статики достаточно для
16
ОСНОВНЫЕ ПОНЯТИЯ
[гл. *
их нахождения. Но изгиб балки под действием собственного веса и под действием сосредоточенной силы, равной ее весу, но приложенной в центре тяжести, будет различным.
Прн рассмотрении давления двух соприкасающихся тел принято считать, что в точке касания ограничивающих эти тела поверхностей возникает сила взаимодействия. На самом деле соприкасающиеся тела деформируются в месте касания, и сила передается от одного тела к другому не в точке, а по площадке. Размеры этой площадки могут быть очень малы, но всегда конечны. В сопротивлении материалов замена одной системы сил другой, статически ей эквивалентной, недопустима и понятие сосредоточенной силы теряет смысл. Поэтому при формулировке задач всегда следует иметь в виду реальное осуществление заданной нагрузки и быть крайне осторожным в упрощении силовых схем. Только в том случае, когда сила является результатом непосредственного соприкосновения двух тел и площадка контакта весьма мала по сравнению с размерами тел, мы не будем вводить в рассмотрение величины этой площадки,'говоря, что на тело действует сосредоточенная сила, равная равнодействующей давлений по площадке контакта.
Делая такое упрощение, мы можем достаточно точно определить деформации в частях тела, удаленных от площадки контакта, но должны отказаться от рассмотрения состояния его в непосредственной близости от этой площадки.
Таким образом, в сопротивлении материалов сосредоточенная сила есть равнодействующая давления, действующего по весьма малой площадке. Только в таком смысле мы будем понимать этот термин.
§ 5. Принцип отвердения. Деформируемое твердое тело может рассматриваться как изменяемая система материальных точек. Поэтому те аксиомы статики, которые относятся к изменяемой системе, сохраняются в сопротивлении материалов. В частности, к деформируемому твердому телу применима аксиома отвердения, которую формулируют так: равновесие системы не нарушается от наложения лишних связей. Мысленно превращая деформируемое тело в абсолютно твердое, мы налагаем на него лишние связи. Значит, равновесие деформируемого тела не нарушается, если его превратить в абсолютно твердое. После этого для него можно составлять уравнения статики твердого тела, которые, таким образом, сохраняют силу и в сопротивлении материалов.
При применении принципа (аксиомы) отвердения необходимо предположить, что сначала тело получает деформацию, а потом, для определения реакций связей, его можно превращать в абсолютно твердое.
Рассмотрим, например, балку (рис. 2), лежащую на трех опорах и нагруженную двумя сосредоточенными силами (термин «сосредоточенная сила» нужно понимать в том смысле, как это разъяснено
§ 6] НЕДОПУСТИМОСТЬ ЗАМЕНЫ СИСТЕМЫ СИЛ ЭКВИВАЛЕНТНОЙ 17 выше). Если считать балку абсолютно твердой, те вопрос об определении реакций лишен смысла. В действительности под действием сил балка прогнется, как указано на рис. 2 пунктиром. Только после изгиба в опорах возникнут совер- .
шенно определенные реакции. К |
Представим себе, что после де- у----------77
формации балка стала абсолютно жесткой. Величины реакции от этого рис 2.
не изменились, ио мы получаем право составлять уравнения равновесия обычным способом. Конечно, в данном случае этих уравнений недостаточно для нахождения реакций.
Из принципа отвердения вытекают два свойства фундаментальной важности:
1) реакции связей в статически неопределимых системах удовлетворяют уравнениям статики, составленным так, как если бы система состояла из абсолютно жестких элементов;
2) в системах, статически определимых, реакции определяются так, как если бы элементы системы были абсолютно жесткими.
§ 6. Недопустимость замеиы лентной. Мы уже отметили, что сил производят на деформируемое
системы сил статически эквива-статически эквивалентные системы тело различное действие. Поэтому
в сопротивлении материалов не имеют места теоремы статики твердого тела, относящиеся к эквивалентности различных систем сил. Так, силу нельзя переносить вдоль линии ее действия и при задании силы необходимо учитывать точку ее приложения. Рассмотрим, например, три одинаковых стержня, нагруженных осевыми силами, как показано на рис. 3.
В первом случае сила приложена на конце и растягивает весь стержень. Во втором — сила приложена посередине и растягивает только верхнюю, заштрихованную часть стержня. В третьем случае сила действует непосред-
ственно на заделку и совершенно не растягивает стержня.
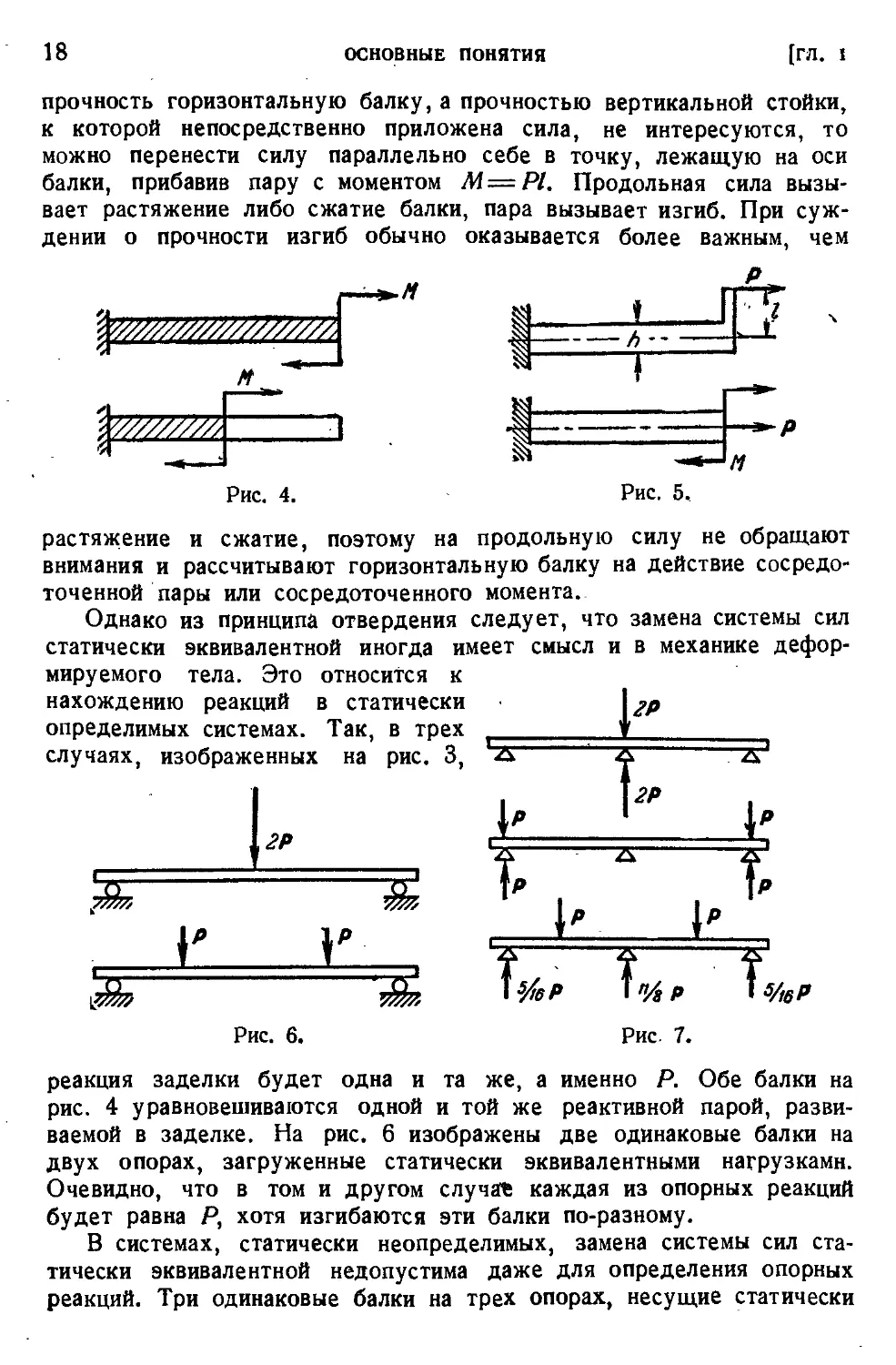
В сопротивлении материалов пару сил нельзя переносить в ее плоскости, и мы говорим о точке приложения пары, б сосредоточенной паре или сосредоточенном моменте. Это ясно из рис. 4, на котором изображены две балки, защемленные на одном конце (замурованные в стену) и нагруженные парами сил. В первом, случае изгибается вся балка, во втором — только заштрихованная половина.
Понятие сосредоточенного момента, или сосредоточенной пары, нуждается в пояснении. Реальная задача обычно соответствует схеме, изображенной на рис. 5. Ясно, что если требуется рассчитать на
18
ОСНОВНЫЕ понятия
[гл. I
прочность горизонтальную балку,а прочностью вертикальной стойки, к которой непосредственно приложена сила, не интересуются, то можно перенести силу параллельно себе в точку, лежащую на оси балки, прибавив пару с моментом М—Pl. Продольная сила вызывает растяжение либо сжатие балки, пара вызывает изгиб. При суждении о прочности изгиб обычно оказывается более важным, чем
растяжение и сжатие, поэтому на продольную силу не обращают внимания и рассчитывают горизонтальную балку на действие сосредоточенной пары или сосредоточенного момента.
Однако из принципа отвердения следует, что замена системы сил статически эквивалентной иногда имеет смысл и в механике дефор
мируемого тела. Это относится к нахождению реакций в статически определимых системах. Так, в трех случаях, изображенных на рис. 3,
Рис. 6.
Рис. 7.
реакция заделки будет одна и та же, а именно Р. Обе балки на рис. 4 уравновешиваются одной и той же реактивной парой, развиваемой в заделке. На рис. 6 изображены две одинаковые балки на двух опорах, загруженные статически эквивалентными нагрузками. Очевидно, что в том и другом случае каждая из опорных реакций будет равна Р, хотя изгибаются эти балки по-разному.
В системах, статически неопределимых, замена системы сил статически эквивалентной недопустима даже для определения опорных реакций. Три одинаковые балки на трех опорах, несущие статически
§ 7]
ОДНОРОДНОЕ ТЕЛО
19
эквивалентные нагрузки, будут испытывать со стороны опор разные реакции. Пример этого приведен на рис. 7. В первом случае вся сила воспринимается средней опорой и реакции крайних опор равны нулю; во втором — на средней опоре не возникает реакции, реакция каждой из крайних опор есть Р. Для рассмотрения третьего случая нужно воспользоваться теорией изгиба. Метод решения такого рода задач будет изложен в дальнейшем; на чертеже приведены найденные в результате решения величины этих реакций, по */,, Р на крайних опорах и "/,Р на средней опоре.
§ 7. Однородное тело. В механике, в отличие от физики, реаль-
ное тело заменяется идеальным однородным телом, сохраняющим некоторые простейшие свойства реальных тел, но лишенным индивидуальной структуры. Дело в том, что изделия, применимые в технике,
настолько велики, что размеры структурных элементов материала по сравнению с ними могут считаться пренебрежительно малыми. Однородным телом мы будем называть такое, которое обладает одинаковыми свойствами, какие бы ни были его размеры. Предположение об однородности противоречит представлениям физики о корпускулярном
строении вещества; действительно, уменьшая
лучим в конце концов в его объеме один атом или же окажемся в пространстве между атомами. У большинства материалов, применяемых в технике, существует неоднородность в масштабах гораздо больших. Все металлы, например, имеют кристаллическую структуру. В чистых металлах кристаллиты состоят из одного вещества, в сплавах иногда оказываются перемешанными кристаллиты разных компонент.
Предположим, что из металла изготовлены образцы в форме кубиков, размеры ко
размеры тела, мы по-
торых того же порядка, что и размеры кри-
сталлитов. Тогда, очевидно, свойства кубика 1 (рис. 8), вырезанного на стыке трех кристаллитов, будут отличаться от свойств кубика 2, вырезанного из целого зерна. Но если размеры образца велики по
сравнению с размерами зерен, так что в каждом образце их содержится очень много, то индивидуальные различия между образцами, вырезанными из разных частей тела, сглаживаются, и свойства практически перестают зависеть от объема образца (лишь бы он был достаточно велик).
Изделия, применимые в технике, велики по сравнению с размерами кристаллических зерен, поэтому материал этих изделий считают однородным. Таким образом, свойство однородности, например, стали
20 ОСНОВНЫЕ ПОНЯТИЯ [гл. I
или бронзы является относительным. Зерна чугуна и сплавов, применяемых для литья, крупнее, но и детали, из них изготовляемые, обычно более грубы. Такой материал, как бетон, заведомо неоднороден: он состоит из щебня или гравия, скрепленного цементной массой. Но размеры бетонных сооружений велики по сравнению с размерами камней, входящих в его структуру, поэтому практически и бетон следует считать однородным.
Свойство относительной Однородности в сопротивлении материалов приводит к понятию сплошной среды, поэтому в дальнейшем мы будем часто выделять бесконечно малый элемент тела и рассматривать его деформации, перенося на бесконечно малый объем те свойства, которые установлены в результате опытов над образцами больших размеров. Этот прием позволяет применить в сопротивлении материалов методы анализа бесконечно малых, без которых построение современной теории вряд ли было бы возможно.
§ 8. Внутренние силы. Связность тела в недеформированном состоянии обусловливается тем, что между его атомами существуют силы взаимодействия и каждый атом находится в равновесии под действием приложенных к нему сил. Внешние силы вызывают дефор-/р мацию тела, следовательно, меняются между-р 1 р атомные расстояния, меняется взаимное распо-
\ ложение атомов, меняются и силы взаимодейст-
уч. I ' ) вня между атомами. Изменение сил взаимо-
/ \ \У действия между атомами вследствие деформации
_---мы будем называть внутренними силами, со-р / провождающими деформацию. Однако не да-
лее как в предыдущем параграфе мы отказа-Р^\/ Ца лись от представления об атомном строении тела,
wi заменив реальное тело гипотетическим одно-
С , родным телом. Поэтому меру внутренних сил
нам придется вводить формальным способом.
'Pf Сплошное однородное тело не имеет в своем
Рис. 9. . составе взаимодействующих частиц, сплош-
ность его обеспечивается внутренними связями. Разрушим мысленно эти связи, рассечем тело некоторой поверхностью на две части. Согласно аксиоме связей, они могут быть заменены силами действия оставшейся части иа отброшенную. Проведем рассуждения более подробно. На рис. 9 изображено произвольное твердое тело, на которое действуют внешние силы А, л, Pt,...,Pn, вызывающие его деформацию. Часть этих сил (и даже все силы) может быть реактивной. Будем обозначать совокупность внешних сил символом (Ре) *). Если тело находится в покое, силы должны удо-
') Индекс е — начальная буква латинского слова exterus — внешний..
НАПРЯЖЕНИЕ
21
§ 9] влетворять условиям равновесия. Случай движения, согласно принципу Даламбера, можно привести к предыдущему .включив в совокупность (Ре\ непрерывно распределенные по объему силы инерции.
Из принципа отвердения следует, что условия равновесия этой системы сил те же, что и для тела абсолютно твердого: главный, вектор и главный момент равны нулю. Запишем это символически: (Ре) = 0.
Рассечем мысленно тело какой-либо поверхностью (например,, плоскостью) на две части, отбросим одну из этих частей, например правую, и рассмотрим оставшуюся, в данном случае левую. Некоторые внешние силы оказываются при этом отброшенными вместе с правой частью.
Обозначим совокупность внешних сил, приложенных к левой половине тела, символом (Ре)л. Оставшаяся часть, находящаяся под действием сил (Ре)я, не будет в равновесии; система сил (Ре)х может оказаться уравновешенной только случайно. Нарушение равновесия происходит здесь от нарушения внутренних связей между левой я правой частями тела. Согласно аксиоме связей действие отброшенной правой половины на оставшуюся левую может быть заменено приложенными к сечению (на чертеже заштриховано) силами реакции правой части на левую. Эти силы и являются внутренними силами, которые не обнаруживаются до тех пор, пока не сделано сечения и не отброшена одна часть тела. Таким образом, способ воображаемых сечений позволяет обнаруживать внутренние силы и рассматривать их как внешние по отношению к оставшейся части тела. Совокупность внутренних сил в сечении мы будем обозначать символом (/>) *). Внутренние силы нужно представлять себе непрерывно распределенными по сечению, поэтому обычное изображение вектора для этих сил не годится и иа чертеже они никак не показаны.
Так как правая часть тела отброшена только мысленно, то левая часть на самом деле остается в равновесии, а для этого надо, чтобы действующие на нее внешние силы и возникающие в сечении внутренние -силы были уравновешены. Запишем это так:
(^)л+(Л)=о.
§ 9. Напряжение. Мера внутренних сил для данной точки деформированного тела дается физической величиной, которую называют напряжением. Имея в виду исследование Внутренйих сил в малой области, окружающей точку М (рис. 10), мы проведем через эту
точку сечение, отбросим верхнюю часть тела и заменим действие ее
на нижнюю внутренними силами. Выделим в сечении площадку Д/7,
контур которой окружает точку М. Результирующую ^внутренних
*) Индекс i — начальная буква латинского слова infernus — внутренний.
22
ОСНОВНЫЕ ПОНЯТИЯ
[ГЛ. I
сил, действующих на эту площадку, представим вектором ДА Разделим теперь ДР на ДР. В результате получим новый вектор в*, направленный так же, как ДР.
Назовем в* средним напряжением на площадке ДР, Теперь начнем уменьшать площадку ДР, но так, чтобы точка М все время оставалась внутри площадки. Как говорят, будем стягивать площадку к точке М. При этом вектор а* будет меняться по величине и на
при безграничном уменьшении площадки к некоторому вектору в. Предел отношения результирующей внутренних сил на площадке Др к величине площадки при стягивании ее в точку М называется истинным напряжением в точке М. Применяя обычную символику, можем написать:
«»lim (tj).
Вектор напряжения а имеет размерность: сила, деленная на площадь. Обычно в технике напряжение измеряют в килограммах на квадратный сантиметр илинаквадратныймиллнметр. напряжения в точке Af, мы рассекаем тело
правлению, стремясь
Чтобы найти вектор
плоскостью, проходящей через точку М. Но через точку М может проходить сколько угодно различных сечений. Определяя вектор а для той же точки Af, но для другого сечения, мы получим иной результат. Таким образом,, беря различные сечення, проходящие через данную точку, можно определить бесконечное множество относящихся к этой точке векторов напряжений. Совокупность всех векторов напряжений для всех площадок, заключающих в себе точку,
характеризует напряженное состояние в точке.
Будем рассматривать напряженное состояние в точке как единое целое, как некоторую физическую величину; эта физическая величина носит более сложный характер, чем те, с которыми обычно имеют дело в механике, и называется тензором напряжений. Оказывается, что напряженное состояние, или тензор напряжений, определяется заданием шести скалярных величин, или. компонент тензора, подобно тому как вектор определяется заданием трех скалярных величин — его проекций на оси. Изучение напряженного состояния в точке является одной из основных задач нашего курса.
§ 10. Простейшие типы напряженного состояния. Не задаваясь целью дать общее изложение механики сплошной среды, мы не будем развивать общей теории напряженного состояния, как это делается обычно в курсах теории упругости н теории пластичности, хотя почти
§ 10]
ПРОСТЕЙШИЕ ТИПЫ НАПРЯЖЕННОГО СОСТОЯНИЯ
23
&
Рнс. 11.
сечения. Такое напряжен-иазывается чистым растя-
все элементы этой теории будут в дальнейшем сообщены. Для уяснения принципов, а также для решения важнейших задач нам будет достаточно отправляться от простейших типов напряженных состояний, переходя от иих к более сложным.
Заметим, прежде всего, что вектор напряжений естественно разложить иа две составляющие: направленную по нормали к площадке, на которой действует напряжение, и лежащую в этой площадке. Назовем первую составляющую нормальным напряжением, вторую — касательным. Их скалярные величины обозначаются соответственно ант. Если нормальное напряжение направлено по внешней нормали к поверхности выделенной части тела, то его считают положительным и называют растягивающим напряжением; если по внутренней — его считают отрицательным и называют сжимающим. При первоначальном рассмотрении типичных видов напряженных состояний бывает, удобно ввести понятие об однородно# напряженном состоянии, то есть ие меняющемся от точки к точке. Для однородного напряженного со
стояния в* = в независимо от величины площадки и ее ориентации, поэтому операция предельного перехода для отыскания напряжений оказывается излишней.
Представим себе призматическое тело, к основаниям которого приложены нормальные усилия, равномерно распределенные по площади оснований с интенсивностью а иа единицу площади (рис. И). Тогда в любом плоском сечеиии, перпендикулярном оси призмы, напряжения будут направлены по нормали и постоянны во всех точках -
ное состояние жением.
В качестве рим прямоугольный параллелепипед с измерениями а, Ь, с (рис. 12). Предположим, что иа верхнюю грань действуют равномерно распределенные касательные усилия, параллельные ребру а, интенсивность которых иа единицу площади есть г. Для того чтобы главный вектор системы внешних сил был равен нулю, к нижией грани должны быть приложены противоположно иаправлеииые силы той же интенсивности. Усилия, действующие на горизонтальные грани, каждое из которых статически эквивалентно силе xab, составляют пару с плечом с. Момент этой пары есть xabc.
второго примера рассмот-
24 ОСНОВНЫЕ ПОНЯТИЯ [гл. I
Чтобы уравновесить его, приложим к грани cb вертикальные равномерно распределенные касательные усилия т' и к противоположной грани — противоположно направленные касательные усилия. Они приводятся к паре x'cba. Из условий равновесия получаем:
х = х'.
Это соотношение называют законом парности касательных напряжений. Более точная его формулировка будет следующей: составляющие касательного напряжения на двух взаимно перпендикулярных площадках, перпендикулярные линии их пересечения, равны между собой.
В любом плоском сечении, параллельном одной из граней ab или Ъс, будут действовать постоянные касательные напряжения г. Такое напряженное состояние называется чистым сдвигом. Как чистое растяжение, так и чистый сдвиг реализовать довольно трудно, в особенности это относится к чистому сдвигу; однако напряженные состояния, изображенные на рис. И и 12, представляют собою основные элементы, из которых строятся напряженные состояния оамого «ложного характера.
§ 11. Простейшие виды деформации. Призма, находящаяся под действием равномерно распределенных по ее основаниям растягивающих напряжений, будет равномерно растягиваться в направлении оси. Если выбрать отрезок pq какой-либо образующей прямой или другой прямой, параллельной образующей, длина которого до деформации была /, после деформации длина его увеличится, станет равной /-1-Д/. Величина 8 = -^- называется относительным удлинением. Очевидно, что если материал однороден, величина 8 не зависит от того, как выбран отрезок длины I и какова эта длина, иначе говоря, не зависит от базы измерения.
Опыт показывает, что поперечные размеры призмы при растяжении уменьшаются. Если длина отрезка, перпендикулярного оси, была до деформации равна /п после деформации она стала равной /j-j-AZj. Величина = представляет собою относительное поперечное сокращение.
Величины 8 и ъ' имеют всегда противоположные знаки.
Параллелепипед, находящийся под действием касательных напряжений, претерпевает деформацию иного характера, ребра его не меняют своей длины, а первоначально прямой угол искажается, как показано иа рис. 12. Такая деформация называется деформацией сдвига, за меру ее принимается’ величина, на которую изменился первоначально прямой угол; на чертеже эта величина обозначена буквой у.
§12] УПРУГОСТЬ И ПЛАСТИЧНОСТЬ 25
Мы связали деформацию растяжения с напряженным состоянием чистого растяжения и деформацию сдвига с напряженным состоянием чистого сдвига, хотя это и не вполне очевидно. Существуют тела столь сложной структуры (некоторые кристаллы), что растягивающие напряжения вызывают в них сдвиг и, наоборот, касательные напряжения связаны с удлинениями. Однако для сопротивления материалов такие тела интереса не представляют.
§ 12. Упругость и пластичность. Понятия напряженного и деформированного состояний, введенные в предыдущих -параграфах, носят первое — чисто статический характер, второе — геометрический, и еще ничем ие связаны с реальными свойствами тела. Напряжения и деформации могут существовать не только в твердом теле, но и в жидкости, в газе и вообще в любой сплошной среде. В реальных твердых телах напряжения и деформации оказываются связанными между собой определенными зависимостями, которые могут быть установлены лишь из опыта. Надежное установление этих зависимостей является основной задачей при построении теории сопротивления материалов. Различные материалы обладают различными свойствами, зависимости между напряжением и деформацией оказываются для них различными. Поэтому при пользовании теми или иными формулами сопротивления материалов необходимо следить за тем, чтобы свойства тех тел, к которым эти формулы применяются, соответствовали основным предпосылкам, положенным в основу при их выводе.
По характеру зависимости между напряжениями и деформациями тела можно условно, имея в виду цели расчета, различать: тела упругие и тела пластические.
Упругостью мы будем называть свойство тела, выражающееся в однозначной зависимости между силами, действующими на тело, и его деформациями. В частности, упругое тело после снятия действовавших на него -нагрузок возвращается в исходное состояние. Как говорят, оно не получает остаточных деформаций. Этот факт содержится в определении упругости.
В противоположность упругости пластичность состоит в том, что тела получают деформации, зависящие не только от конечных значений действующих на них сил, но и от порядка их приложения. В частности, если пластическое тело было подвергнуто действию сил, то после удаления их оно в первоначальное состояние не приходит, сообщенные силами деформации сохраняются, полностью или частично, и после прекращения действия этих сил.
Свойства упругости и пластичности являются не абсолютными, а относительными. Например, стальная пружина, которая выпрямляется полностью, будучи согнута небольшой силой, под действием большей силы получает такой прогиб, который полностью уже не восстанавливается. Значит, для стали малые деформации упруги, а большие —
26 ОСНОВНЫЕ ПОНЯТИЯ . [ГЛ. 1
пластичны. В то же время всякое пластическое тело восстанавливает некоторую, пусть небольшую, часть своей деформации. Следовательно, в нем, наряду со свойством пластичности, существует и свойство упругости.
Изучение поведения упругих тел произвольной формы под действием произвольных сил служит задачей специальной дисциплины, называемой теорией упругости. Иногда употребляют термин математическая теория упругости, подчеркивая этим та, что, поскольку закон упругости предполагается известным, определение напряжений и деформаций является строго поставленной математической задачей интегрирования некоторых систем дифференциальных уравнений. Методы теории упругости, при всей их общности и точности, еще недостаточны для суждения о прочности реальных конструкций. С другой стороны, строгая постановка вопроса об определении напряжений и деформаций методами теории упругости часто приводит к непреодолимым математическим трудностям. Сопротивление материалов тесно связано с теорией упругости и широко использует ее результаты, но нельзя считать, что это упрощенная теория упругости. Пользуясь более простыми математическими методами, сопротивление материалов ставит более широкую задачу, а именно суждение о прочности элементов конструкций с возможно более полным учетом реальных свойств материалов.
Наряду с теорией упругости, притом значительно позже, возникла теория пластичности, изучающая с общих позиций поведение тел под нагрузкой в области пластических деформаций. Развитие теории пластичности в сильной степени повлияло на развитие теории сопротивления материалов, и начальные сведения по теории пластичности включены в эту книгу.
§ 13. Закон Гука. Наблюдения показывают, что для большинства упругих тел, таких, как сталь, бронза, дерево и др., величины деформаций пропорциональны величинам действующих сил. Типичный пример, поясняющий это свойство, представляют пружинные весы, у которых удлинение пружины пропорционально действующей силе. Это видно из того, что шкала делений у таких весов равномерна. Как общее свойство упругих тел закон пропорциональности между силой и деформацией был впервые сформулирован Р. Гуком в 1660 г. и опубликован в 1678 г. в сочинении «De potentia restitutiva» *). В современной формулировке этого закона рассматривают не силы и перемещения точек их приложения, а напряжение и деформацию.
Так, для чистого растяжения полагают:
о е=£«
•) <0 восстанавлввающей силе».
§14] ДИАГРАММА ПЛАСТИЧНОСТИ _ 27
Здесь 8 — относительное удлинение любого отрезка, взятого в направлении растяжения. Например, если ребра изображенной на рнс. 11 призмы до приложения нагрузки были а, b и с, как показано на чертеже, а после деформации они будут соответственно а', b', с', d — а тогда 8=—-— .
Постоянная Е, имеющая размерность напряжения, называется модулем упругости или модулем Юнга.
Растяжение элементов, параллельных действующим напряжениям or, сопровождается сокращением перпендикулярных элементов, то есть уменьшением поперечных размеров стержня (на чертеже — размеры Ь и с). Относительная поперечная деформация , b' — b с’ — с 8=—=—
будет величиной отрицательной. Оказывается, .что продольная и поперечная деформации в упругом теле связаны постоянным отношением:
8' = — V8.
Безразмерная величина v, постоянная для каждого материала, называется коэффициентом поперечного сжатия или коэффициентом Пуассона. Сам Пуассон, исходивший из теоретических соображений, которые оказались впоследствии неверными, считал, что v = 1/4 для всех материалов (1829). На самом деле значения этого коэффициента различны. Так, для стали v = 0,3.
Заменяя в последней формуле 8 выражением а/Е, получим:
, vo 8_—
Закон Гука не является точным законом. Для стали отклонения от пропорциональности между or и 8 незначительны, тогда как чугун или резина явно этому закону не подчиняются. Для них 8 = ф(ог), причем ф (or) может быть аппроксимирована линейной функцией разве лишь в самом грубом приближении.
В течение долгого времени сопротивление материалов занималось лишь материалами, подчиняющимися закону Гука, и приложение формул сопротивления материалов к другим телам можно было делать только с большой натяжкой. В настоящее время нелинейные законы упругости начинают изучаться и применяться к решению конкретных задач.
§ 14. Диаграмма пластичности. Свойства пластичности проще всего уяснить на примере чистого растяжения такого материала, как мягкая малоуглеродистая сталь. Предположим, что стержень находится в условиях простого растяжения (рис. 11) и напряжение от растет. При этом стержень растягивается, сохраняя призматическую форму.
28
ОСНОВНЫЕ понятия
[гл. 1
Будем изображать зависимость между а и е на графике (рис. 13), построение которого очевидно. В действительности при растяжении стержня напряжения распределяются по сечению не вполне равномерно, а призматическая форма образца нарушается *). Поэтому график, подобный изображенному на рис. 13, удается построить лишь для деформаций, не превышающих нескольких процентов. До точки А зависимость между а и е следует закону Гука. После точки А диаграмма становится криволинейной, в точке В она имеет горизонтальную площадку, называемую площадкой текучести. На площадке текучести деформация происходит без увеличения нагрузки. Начиная с точки С, диаграмма снова идет вверх. Часть диаграммы, расположен-
ная правее точки С, называется областью упрочнения. Однозначная всюду, кроме площадки ВС, зависимость между а и е устанавливается диаграммой пластичности только при условии непрерывного возрастания а или е. Представим, что мы довели нагружение до точки М на диаграмме и начали уменьшать нагрузку. Процесс разгрузки будет изображаться прямой МР, параллельной первоначальному упругому участку диаграммы. Этот результат можно истолковать в том смысле, что полная деформация, изображаемая абсциссой точки М на диаграмме пластичности, состоит из двух частей — пластической деформации епл и упругой деформации о/£: о । е £ ।
При снятии нагрузки упругая пропорциональная в каждый момент
исчезает, а пластическая остается. На чертеже деформация изображается отрезком ОР, а отрезок PN собою упругую деформацию, соответствующую напряжению в точке М диаграммы.
Таким образом, существенная особенность пластических материалов состоит в том, что процессы нагрузки и разгрузки описываются для них различными законами.
Иногда диаграмму изображенной на рис.
Рис. 14.
деформация, напряжению, пластическая представляет
пластичности заменяют идеальной диаграммой, 14, а именно считают:
а=Ее (е=^ет),
а—ат (е>ет).
*) Подробнее об этом см. в главе V.
§ 15] ТЕЛА ИЗОТРОПНЫЕ И АНИЗОТРОПНЫЕ 29
Постоянная ат называется пластической постоянной или пределом текучести, ет = ^, Идеальная диаграмма позволяет с достаточной для целей практики точностью решать вопрос о прочности и жесткости конструкций из малоуглеродистой стали, обычно применяемой в строительном деле,
Совершенно аналогичным образом рассматривается зависимость между сдвиговой деформацией и касательными напряжениями.
В реальных телах возможны и более сложные виды связи между напряжениями и деформациями, существенно зависящие от времени действия нагрузки. К рассмотрению некоторых из таких зависимостей мы вернемся впоследствии в связи со специфическими задачами прочности при высоких температурах и некоторыми другими вопросами (гл. V, VI, XVIII).
§ 15. Тела изотропные и анизотропные. Рассмотренные выше свойства упругости и пластичности устанавливаются в результате опытов, произведенных над образцами. Для некоторых материалов, как, например, сталь, медь и другие металлы, прессованные пластики, бетон, эти свойства будут одинаковыми для образцов, вырезанных из тела в различных направлениях. Такие тела называются изотропными. Но древесина, например, обладает в силу своей структуры разными свойствами в разных направлениях; образец, вырезанный вдоль волокна, покажет при испытании на растяжение или сжатие совершенно иные свойства, чем образец, вырезанный в поперечном направлении. Такие материалы, которые обнаруживают разные свойства в разных направлениях, называются анизотропными.
Единичные кристаллы металлов всегда анизотропны, потому что атомы образуют в иих кристаллическую решетку правильного строения и степень густоты расположения атомов для различных направлений различна. Изотропия поликристаллического металла объясняется тем, что кристаллические зерна чрезвычайно малы по сравнению с образцом и расположены в беспорядке; таким образом, все ориентации зерен равновероятны и в среднем для всех направлений свойства оказываются одинаковыми. Обработка давлением — ковка, штамповка, протяжка, волочение — создает определенную ориентацию зерен, поэтому, например, свойства проката в продольном н поперечном направлениях будут различными. Такая анизотропия в меньшей мере относится к упругим свойствам, чем к пластичности и прочности. Модуль упругости для продольных и поперечных по отношению к направлению проката образцов почти одинаков, тогда как характеристики прочности, например сопротивление разрыву, различны.
Иногда материал искусственно создается анизотропным. Так, например, стеклопластики представляют собою ткань из стеклянного волокна или просто слои стеклянного волокна, пропитанные полимерным
30 ' ОСНОВНЫЕ ПОНЯТИЯ [гл. I
материалом. Стеклянное волокно обладает высокой прочностью, полимер связывает его в сплошную массу. Очевидно, что такая масса хорошо сопротивляется растяжению в направлении волокон, если же вырезать из нее образец наискось, перерезав волокна, то растягивающая нагрузка будет восприниматься не высокопрочными волокнами, а относительно слабым связывающим материалом и прочность окажется небольшой.
При изучении поведения плит или стержней из армированного бетона, пластинок, подкрепленных ребрами, и тому подобных конструкций часто бывает возможно учитывать работу арматуры и ребер при помощи осредненных характеристик, заменяя, например, бетонную плиту, армированную в одном направлении, сплошной плитой из воображаемого материала, обладающего разными свойствами для разных направлений, то есть анизотропного. Такая анизотропия называется конструктивной.
ГЛАВА II
РАСТЯЖЕНИЕ — СЖАТИЕ
Ряс. 15.
§ 16. Стержни и стержневые системы. В этой главе мы будем заниматься простейшими задачами сопротивления материалов, то есть такими задачами, в которых величины напряжений определяются совершенно элементарными способами. Простейшим видом напряженного состояния нужно считать растяжение или сжатие. Оказывается, что растяжение и сжатие реализуются весьма часто почти в чистом виде в конструкциях, элементами которых служат стержни. Стержнем называется тело, одно измерение которого велико по сравнению с другими. Стержни могут иметь постоянное или переменное сечение, а также могут быть прямыми или криволинейными.
Понятие прямолинейного стержня нуждается в некотором уточнении. Представим себе плоскую фигуру (рис. 15, а), движущуюся параллельно себе без вращения так, что центр тяжести ее скользит по оси zz, перпендикулярной плоскости фигуры. Контур ее опишет в пространстве боковую поверхность стержня, ось
Если фигура, двигаясь вдоль оси zz, одновременно около оси, получается так называемый естественно закрученный стержень (рис. 15, б). Примером естественно закрученного стержня служит спиральное сверло.
Если фигура, двигаясь вдоль оси, одновременно меняется сама, меняет свою форму и площадь, но так, что центр тяжести все время остается на оси zz, мы получим стержень переменного сечения с прямолинейной осью.
zz называется осью
стержня. вращается
32
РАСТЯЖЕНИЕ---СЖАТИЕ
[ГЛ. II
Примеры стержней переменного сечения приведены на рис. 15, в, г, д (в— клин, г — конический стержень, д — стержень в форме тела вращения).
Стержни встречаются как основные элементы огромного большинства инженерных конструкций. Мостовая ферма, схематически изображенная на рис. 16, состоит из отдельных стержней, соединенных
Рис. 16.
между собою заклепками или сваркой. Такие детали машиностроения, как болт, ось, вал, шатун, тоже являются стержнями. Поэтому расчет стержней и стержневых систем — это первоочередная задача сопротивления материалов. Для решения ее приближенные методы вполне достаточны.
§ 17. Принцип Сен-Венана и гипотеза плоских сечений. Будем говорить, что стержень растягивается, если к торцам его приложены системы сил, статически эквивалентные одной силе, действующей -по
оси стержня, как это показано на рис. 17. На рисунке действующие нагрузки изображены в виде сил, приложенных в центрах тяжести торцов стержня, но эти сосредоточенные силы здесь совершенно условны. На самом деле нагрузка прикладывается к концу стержня каким-либо реальным способом; на рис. 18 схематически изображены некоторые из таких возможных способов передачи нагрузки на стержень.
В машинах для испытания на разрыв круглый образец либо захватывается губками с насечкой (рис. 18, б), либо имеет головку (рис. 18, в). На рис. 18, г изображен конец тяги, снабженный нарезкой. На этот
конец навертывается гайка, опирающаяся на плоскость плиты, в которой просверлено отверстие для тяги. Растягивающее усилие передается от гайки к тяге, распределяясь по виткам нарезки.
Подобных конкретных случаев передачи растягивающего усилия стержню можно указать очень много, все они будут различны, и,
§17] ПРИНЦИП СЕН-ВЕНАНА И ГИПОТЕЗА ПЛОСКИХ СЕЧЕНИЙ 33
казалось бы, все их нужно изучать по отдельности. Однако при расчете стержней на растяжение не считаются с индивидуальными особенностями, зависящими от конкретного способа приложения нагрузки, а принимают во внимание только равнодействующую всех сил, приложенную к каждому из концов стержня. При этом руководствуются правилом, которое принято называть принципом Сен-Венана, по имени французского ученого (1797—1886), который дал точное решение
Рис. 18.
задач о кручении и изгибе стержней и при этом сформулировал принцип, носящий его имя и приложимый не только к растяжению— сжатию, но также к кручению, изгибу и многим другим задачам сопротивления материалов и теории упругости. Формулировка этого принципа в применении к рассматриваемой задаче . может быть следующей:
Способ приложения силы к торцу стержня сказывается лишь в непосредственной близости к торцу.
Несколько расплывчатая формулировка (неясно, что значит «непосредственная близость») объясняется тем, что этот принцип не есть Положение, строго доказанное для самого общего случая. Многочисленные опыты и теоретические исследования неизменно обнаруживали весьма быстрое затухание по мере удаления от торца тех напряжений, которые связаны с неравномерностью распределения усилий по торцу,— так называемых местных напряжений. Практически, если поперечные размеры стержня одного порядка, эти местные напряжения становятся неощутимыми на расстоянии от торца порядка поперечного размера. В тонкостенных стержнях дело может обстоять иначе (см. главу IX, § 109 и гл. XI).
Это значит, что для всех изображенных на рис. 18 случаев напряженное состояние будет различным только в незаштрихованной части. Напряженное состояние в части стержня, удаленной от конца (на чертеже заштриховано), будет во всех случаях одним и тем же состоянием простого растяжения, напряжения во всех точках становятся при этом одинаковыми, направленными по нормали к поперечному сечению стержня. Область, близкая к месту приложения силы, будет
2 Ю. И. Работное
34 РАСТЯЖЕНИЕ---СЖАТИЕ [ГЛ. II
областью местных напряжений, учет которых составляет особую задачу. Поскольку в соответствии с принципом Сен-Венана напряженное состояние в средней части 'стержня не зависит от способа приложения силы, оно будет тем же самым, что и в простейшем случае, изображенном на рис. 11, когда к торцам приложена равномерно распределенная нагрузка, параллельная оси стержня. Это напряженное состояние однородно, во всех точках поперечного сечения напряжения равны и параллельны оси стержня. Каждый элемент объема деформируется совершенно одинаково, торцы изображенной на рис. 11 призмы после приложения нагрузки раздвинутся, но останутся плоскими и параллельными между собой. Этот факт — сохранение плоских сечений при растяжении — иногда кладут в основу всей теории как фундаментальную гипотезу плоских сечений, формулируемую так:
Сеченая, перпендикулярные оса стержня и плоские до деформации, остаются плоскими а перпендикулярными оси после деформации.
Конечно, плоскими остаются только такие сечения, которые удалены от места приложения силы на расстояние, порядок которого не меньше порядка поперечного размера.
Все изложенное относится также и к случаю сжатия, который формально отличается от случая растяжения только изменением направления силы. Фактическая разница между растяжением и сжатием гораздо глубже, потому что при сжатии может возникнуть новое явление — потеря устойчивости. Центрально сжатый прямой стержень, длина которого значительно больше поперечных размеров, может сохранять прямолинейную форму лишь тогда, когда сжимающая сила меньше некоторого критического значения. При небольшом эксцентриситете приложения силы или при малом искривлении оси стержня, неизбежном в действительности, сжимающая сила, хотя бы и меньшая критической, вызывает не только сжатие, но и изгиб. При этом эффект изгиба часто оказывается гораздо больше, чем эффект сжатия. С этим обстоятельством нужно считаться при расчете сжатых стержней, ему будет посвящена одна из глав нашего курса. Здесь же мы не делаем принципиальной разницы между растяжением н сжатием, будем лишь приписывать растягивающим напряжениям знак плюс, сжимающим — минус.
§ 18. Напряжения и деформации при растяжении. Рассмотрим стержень, к концам которого приложены растягивающие силы, как показано на рнс. 17. Чтобы определить внутренние силы или напряжения, мысленно рассечем стержень плоскостью тп, перпендикулярной оси стержня (не слишком близко к концу), и отбросим одну часть, например верхнюю. Оставшаяся нижняя часть изображена на том же чертеже справа. Согласно сказанному выше действие верхней части на иижнюю можно заменить нормальными напряжениями <т,
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ
35
§ 181 ----------------------- --------
равномерно распределенными по сечению тп. Сделаем это и составим условие равновесия нижней части с^е#жня; тогда получим: aF —
Здесь F— площадь поперечного сечения.
Отсюда
-4-
Это основная формула для напряжений при растяжении.
Сделаем замечание, относящееся к знакам. Знак внешней силы устанавливается по отношению к той или иной системе координат; таким образом, он совершенно условен- Нельзя сказать, положительна или отрицательна сила Р на рис. 17, так как на чертеже отсутствует ось координат; выбирая положительное направление оси вверх или вниз, можно приписать силе Р тот или иной знак. Однако, уславливаясь считать растягивающие напряжения положительными, а сжимающие — отрицательными, мы придаем знаку напряжения определенный физический смысл, не зависящий от выбора той или иной системы отнесения. Растягивающие напряжения принято изображать стрелками, выходящими наружу из объема рассматриваемой части тела. Таким образом, правило знаков для напряжений следующее:
Положительное направление нормальных напряжений определяется внешней нормалью к поверхности, ограничивающей рассматриваемую часть тела.
Если на стержень действуют сжимающие силы (рис. 19), в сечении можно нарисовать или сразу сжимающие напряжения, обозначив их (— а), или, что удобнее, положи
тельные напряжения а. Тогда из уравнения равновесия ответ получится с правильным знаком. В данном случае условие равновесия будет
— CF— Р=0.
Отсюда
Р а = -Т.
Это основная формула для напряжений при сжатии.
Формулы для напряжений при растяжении и сжатии можно объединить:
о=±4-.
Здесь Р— абсолютная величина внешней силы, знак плюс или минус выбирается по смыслу задачи.
2*
36
РАСТЯЖЕНИЕ — СЖАТИЕ
[гл. II
При расчете стержневых систем оказывается удобным ввести понятие о внутренней силе, или усилии, в стержне М=-|-.Р в случае растяжения и ^=—Р в случае сжатия. Тогда в любом случае
Переходя к определению деформаций, заметим, что для части стержня, находящейся в условиях чистого растяжения, справедливо равенство
С другой стороны, по закону Гука
Но так как а = , то
или
Если стержень растягивается, то W положительно, Д/ также положительно и представляет собою удлинение. При сжатии, когда N отрицательно, отрицательное Д/ является укорочением. Можно записать формулу для удлинения так:
А/ , Р1
Д 1~~ 1 EF*
Здесь Р—абсолютная величина внешней силы, знак выбирается по смыслу.
§ 19. Расчеты на прочность при растяжении и сжатии. Величину напряжения в растянутом или сжатом стержне обычно принимают за основной критерий для суждения о прочности той конструкции, элементом которой служит данный стержень. Поэтому расчет фермы, например, сводится к тому, чтобы определить усилия во всех элементах и, зная площади сечений, найти напряжения по формуле
N
Величину действующего напряжения мым допускаемым напряжением, которое в прямых скобках; условие обеспечения
сравнивают с так называе-принято обозначать буквой о прочности будет
§19] РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ РАСТЯЖЕНИИ Н СЖАТИИ 37
Допускаемое напряжение выбирается в зависимости от материала и условий службы данного сооружения. Если речь идет о пластическом материале, например стали, то, очевидно, допускаемое напряжение не должно превышать предела текучести. В то же время допускаемое напряжение нельзя принимать равным пределу текучести, необходимо иметь некоторый запас прочности на случай перегрузок в процессе эксплуатации, неточного изготовления стержня (сечение меньше, чем предусмотрено чертежом), отклонения свойств примененного материала от тех свойств, которые установлены при испытании образца, и так далее. Поэтому для пластических материалов принимают:
Здесь лт— коэффициент-запаса прочности по отношению к пределу текучести; этот коэффициент всегда больше, чем единица. В строительных металлических конструкциях, например, обычно лт = 1,5.
Хрупкие материалы, такие как чугун, бетон, естественные и искусственные камни и другие, ие обнаруживают заметных остаточных деформаций, они разрушаются сразу, лишь только напряжение достигнет величины так называемого предела прочности илн временного сопротивления ств. Для таких материалов
1 J «в
Здесь лв— запас прочности по отношению к временному сопротивлению.
Вообще, если принять условно за разрушающее напряжение то напряжение, при котором становится невозможным выполнение конструктивной функции изделия, то допускаемое напряжение есть результат деления разрушающего напряжения иа коэффициент запаса прочности.
Вопросу о рациональном выборе коэффициента запаса прочности посвящена обширная литература. Важность его чрезвычайно велика, так так снижение коэффициента запаса означает экономию материала и расширение технических возможностей. Мы вернемся к этому вопросу впоследствии, а пока заметим, что для строительных конструкций нормы допускаемых напряжений узаконены и являются обязательными при всяком строительном проектировании.
В машиностроении, вследствие большого разнообразия применяемых материалов и типов нагрузки, узаконенные общеобязательные нормы отсутствуют, однако отдельные ведомства, крупные заводы и проектные организации обычно имеют свои нормы допускаемых на* пряжений, которые вырабатываются с учетом производственного опыта.
38 РАСТЯЖЕНИЕ--СЖАТИЕ [ГЛ. II
Если допускаемое напряжение [а] известно, то расчет на прочность сводится к обеспечению выполнения неравенств:
р
у [о]р (при растяжении), р
7г^[<т]сж (при сжатии).
Заметим, что расчет на прочность при сжатии по приводимой формуле действителен только для коротких стержней; желая рассчитывать по этой формуле длинные стержни, нужно значительно уменьшать величину допускаемого напряжения (см. гл. ХИ, § 142).
§ 20. Собственный вес и силы инерции. Предыдущие формулы относятся к стержням постоянного сечения, нагруженным силами на концах. Может случиться, что силы распределены непрерывным образом по поверхности или объему стержня. Так, например, замурованный в стену стержень, если вытягивать его за конец, встречает сопротивление со стороны скрепляющего его со стеной цемента по всей поверхности заделки. Пример распределенной по объему силы — это сила тяжести. При рассмотрении динамических задач о напряжениях в движущихся стержнях можно, согласно принципу Даламбера, вводить непрерывно распределенные по объему силы инерции. Во многих случаях ввиду малости деформаций достаточно определять кинематические элементы движения так, как если бы тело было абсолютно жестким. Таким образом ускорения, а следовательно, и силы инерции могут быть найдены заранее. Способ решения таких задач, которые можно назвать квазистатическими, ничем не отличается от способа решения статических задач сопротивления материалов. Специфика динамических задач обнаруживается тогда, когда нельзя пренебречь силами инерции, происходящими от движения, связанного с деформацией. Таковы, например, задачи о колебаниях стержней и о действии ударной нагрузки.
Рассмотрим некоторые примеры статических задач с распределенными внешними силами.
а) Напряжения и деформации от собственного веса. Рассмотрим стержень, подвешенный за верхний конец и растягиваемый собственным весом (рис. 20). Отсекая мысленно часть стержня на расстоянии х от нижнего конца, приложим в сечении равномерно распределенные силы с интенсивностью а, которые уравновешивают вес части стержня, имеющей длину х. Уравнение равновесия будет
cF—yFx = 0.
Здесь у—удельный вес материала стержня, F—площадь поперечного сечения.
§ 20]
СОБСТВЕННЫЙ ВЕС И СИЛЫ ИНЕРЦИИ
39
Отсюда
а —ух.
На рис. 20 (слева) построен график, или так называемая эпюра напряжений, которая изображает изменение напряжений в зависи-
мости от координаты сечения х. Наибольшее напряжение получается в верхнем сечении:
°max = W-
Вследствие растяжения каждое сечение стержня перемещается вниз на величину и. Очевидно, что перемещение сечения с координатой х равно удлинению той части стержня, ко
Рис. 20.
торая расположена выше
этого, сечения. Для подсчета его выделим бесконечно малый элемент с координатой &(х<^^<^/). Действующее напряжение есть у£, следовательно, удлинение элемента
Перемещение и найдем, просуммировав удлинения всех элементов, на которые можно разбить верхнюю часть стержня:
»=W-P^-'
X
Выполнив интегрирование, получим:
а= 2Ё х
Эпюра перемещений представляет собою параболу, она изображена на рис. 20 (справа). Полное удлинение стержня есть
Заметив, что полный вес стержня Q=ylF, перепишем эту формулу так:
Д/=1 О'
2 EF'
Итак, стержень вытягивается под действием собственного веса так, как если бы он был невесом и растягивался сосредоточенной силой, приложенной на конце и равной половине веса стержня.
40
РАСТЯЖЕНИЕ---СЖАТИЕ
[ГЛ. 11
Для металлических конструкций напряжения и деформации от собственного веса обычно незначительны, и с ними можно не считаться, за исключением особых случаев (например, расчет канатов шахтных подъемников или буровых штанг). В бетонных и каменных
сооружениях, для которых допускаемые напряжения низки, напряжения от собственного веса существенны и часто являются главными.
б) Вращающийся стержень. Совершенно аналогично решается вопрос о напряжениях в стержне с площадью поперечного сечения F, вращающемся с угловой скоростью (0 около оси z, перпендикулярной оси стержня (рис. 21).
Мысленно отрезая кусок стержня на расстоянии х от оси, состав-
ляем для него уравнение равновесия. Центробежная сила Р этого куска длиной I — х равна
со«1Г(/-х)Ц^.
ё £
Приравнивая ее внутренней силе в сечении oF, найдем:
—X*).
Наибольшее напряжение будет в том сечении, которое проходит через ось вращения:
______уаЧ1___ук* °max 2g ~ 2g'
Здесь через « обозначена окружная скорость конца стержня. Таким образом, для каждого материала может быть допущена определенная скорость вращения стержня, зависящая от допускаемого напряжения и удельного веса материала.
в) Напряжения в склейке. Полоска из упругого материала толщиной h приклеена к жесткому основанию, как показано на рис. 22. От действия силы Р в полоске возникает напряжение ст0. Касательные напряжения т в слое клея уравновешивают силу Р. Сделаем предположение о том, что касательное напряжение в склейке пропорционально относительному смещению склеенных элементов. Сечение тп с координатой х получает горизонтальное перемещение в, сечение pq с координатой x-\-dx получает перемещение и-{-du, и согласно Сделанной гипотезе:
1 = ^,
§ 201
СОБСТВЕННЫЙ ВЕС И СИЛЫ ИНЕРЦИИ
41
Здесь k — коэффициент пропорциональности, зависящий от толщины слоя клея и его физических свойств.
Рассмотрим теперь равновесие элемента, выделенного сечениями тп
и pq. Если напряжение в левом сечении есть а, то напряжение в правом сечении есть a-{-da. Будем считать ширину полоски равной единице, тогда площадь ее сечения есть h и разница сил в се-
чениях тп и pq равна h da. Эта сила уравновешивается касательным напряжением г на площади склейки, равной dx. Таким образом, hda=xdx
или da т dx h *
Р
Заметим, что du есть абсо- Рис- 22-
лютнойудлинение отрезка dx, du _
следовательно, его относительное удлинение е=-т- и по закону Гука
Внесем в уравнение равновесия выражения для а и для г. Получим: с d’a k Е dx? h
£
Введем обозначение а’ = тт и перепишем дифференциальное уравне-Un
ние следующим образом: d’a • п
Общий интеграл его: и — A sh ах В ch ах.
Граничные условия будут следующие: при х — 0 а = 0; при х=1 <т = а0; но а пропорционально первой производной от и, следовательно, fdu\ ________________________g /da \ __а±
\dx J х=» ’ \dx /хг=1 Е
Кроме того,
— аА ch ах -|- а В sh ах.
Из первого граничного условия следует, что Д = 0, из второго
В = =г-~—г , поэтому
Sasha/ ’ 3
_ . kaa ch ах h al .
x = ku = ~ -r—r =a.~r -T-г ch ax.
Ea sh al • I sh al
42
РАСТЯЖЕНИЕ---СЖАТИЕ
[ГЛ. II
Оказывается, что касательное напряжение в склейке распределено по длине неравномерно.
Рассмотрим два крайних случая. Пусть в первом случае материал полоски будет весьма жестким, а склейка очень податливой, Е велико, тогда как k мало, следовательно, а мало, ch ах =s 1, sh al = а/, т=5=о0-у. Мы получаем равномерное распределение касательных усилий в склейке. Второй случай — это тот, когда клей очень жесткий, а полоска податливая, следовательно, а велико. Наибольшее касательное напряжение будет при х = 1, но при больших al отношение ch al i ~—7=г1, следовательно, sh al ’
Это касательное напряжение не зависит от длины /; таким образом, увеличивать длину приклейки I бесполезно.
§ 21. Стержни переменного сечения. Если сечение стержня переменно, гипотеза о том, что в его поперечных сечениях действуют
весии; для равновесия
только нормальные напряжения; притом равномерно распределенные по сечению, становится неверной. Чтобы доказать это, рассечем стержень (рис. 23) двумя плоскостями тп и pq, перпендикулярными оси. Построим цилиндрическую поверхность с образующими, параллельными оси цилиндра, и основанием — сечением стержня плоскостью pq. Мысленно вырежем из стержня кольцо, ограниченное цилиндрической поверхностью и плоскостью pq. Если предположить, что в сечении pq действуют только нормальные напряжения а, то вырезанное кольцо (на ри-
сунке показано отдельно) не будет в равнонеобходимо, чтобы на цилиндрической поверх-
ности были распределены касательные напряжения т, но по закону
парности им соответствуют равные касательные напряжения в плоскости pq, что противоречит сделанному предположению о существовании в поперечных сечениях одних только нормальных напряжений. Однако если угол между касательной к образующей и осью стержня мал по сравнению с единицей, то можно приблизительно считать и здесь, что в сеченин действуют равномерно распределенные нормальные напряжения, определяемые по формуле
§ 22] ПЕРЕМЕЩЕНИЯ УЗЛОВ СТЕРЖНЕВЫХ СИСТЕМ 43
Здесь F—переменная площадь, W—усилие в сечении. Это усилие может быть постоянным по длине, если действует сила на конце стержня, и переменным, если на стержень действуют массовые силы. Элемент длиной dx, непосредственно примыкающий к тому сечению, в котором напряжение равно о, получает удлинение
. . a dx &dx—-g-.
Отсюда интегрированием находим полное удлинение стержня: i
. , С о dx о
Рассмотрим в качестве примера задачу о так называемом стержне равного сопротивления при сжатии.
Пусть на конце стержня приложена сжимающая сила Р, удельный вес материала есть у- Нужно выбрать закон изменения площади так, чтобы напряжение в каждом Сечении было постоянным.
Сжимающая сила в сечении с координатой х складывается из силы Р и веса верхней части:
X
— F dx.
О
Требуя, чтобы напряжение было постоянно и равно [о], получим.' X
F.
О
Ищем решение для неизвестной функции F(x) в виде F—Fa exp (ах).
Подставляя в уравнение, найдем:
Р-\~Fa [exp (ах) — 1] = [о] Fo exp (ах), а так как это соотношение должно выполняться прн любом х, то у с Р а = А , = гт •
[а] ’ » [а]
Итак,
Поскольку напряжение постоянно, относительное удлинение элементов стержня равного сопротивления тоже постоянно и равно [о]/£, полное удлинение А/ есть [о] l/E.
§ 22. Перемещения узлов стержневых систем. Стержни, работающие на растяжение — сжатие, часто соединяются в стержневые системы более или менее сложного вида.
44
РАСТЯЖЕНИЕ---СЖАТИЕ
{ГЛ. II
Для того чтобы обеспечить возникновение только растягивающих и сжимающих напряжений, необходимо, чтобы соединения стержней в узле допускали свободный взаимный поворот стержней и чтобы силы прикладывались только в узлах. На рис. 16 была приведена схема простейшей фермы. Заклепочное соединение в узлах, строго говоря, не дает возможности свободного поворота концов стержней, поэтому в стержнях, кроме напряжений растяжения — сжатия, возникают напряжения изгиба. Однако эти напряжения невелики, и при расчете ими обычно пренебрегают. Желая рассчитать ферму, изображенную иа рис. 16, мы заменяем действительные узлы идеальными шарнирами. После такой замены определение усилий в стержнях производится по способам статики, если ферма статически определима. Определив усилия в стержнях, мы вычисляем удлинения их, пользуясь формулой
Д/.=Ж.
' EiFf
Здесь I — номер стержня и все величины, относящиеся к данному стержню, отмечены индексом I.
На практике часто возникает вопрос о перемещении какого-нибудь узла фермы. При решении этого вопроса существенно упроща-
I ющим дело обстоятельством является ма-
------------------лость деформаций отдельных стержней, а ------------------------------------i следовательно, и малость перемещений рис 24------------по сравнению с длинами стержней. Пре-
небрегая квадратом отношения перемещения к длине стержня по сравнению с единицей, покажем, что перемещение, перпендикулярное оси стержня, не связано с его удлинением. Действительно, пусть правый конец стержня (рнс. 24) получает перпендикулярное его оси перемещение и, тогда как левый остается на месте. Новая длина стержня:
Разлагая радикал по формуле Ньютона, получим:
Второй и следующий члены в скобке весьма малы по сравнению с единицей. Пренебрегая нми, получим:
1'^1.
Рассмотрим теперь пример, из которого ясен принцип определения перемещений. Кронштейн, схематически изображенный на рис. 25, нагружен на конце А силой Р, направленной вертикально вниз. По правилам статики определяем усилия и N, в стержнях
§ 221
ПЕРЕМЕЩЕНИЯ УЗЛОВ СТЕРЖНЕВЫХ СИСТЕМ
45
и вычисляем удлинения А/, и А/, (А/,<0). Чтобы определить пере» мещение узла А, поступаем следующим образом. Предположим, что шарнир в точке А удален и стержни разъединены. Сохраняя направ-ление стержней, дадим стержню 1 удлиниться на А/,, конец его перейдет в точку а,. Стержню 2 дадим укоротиться на А/,; конец его перейдет в точку а,.
Чтобы найти новое положение узла А, повернем теперь стержни так, чтобы концы их совпали в точке А" пересечения дуг, описанных концами стержней при их вращении около неподвижных шарниров. Отрезок Л Л* есть искомое перемещение. Обычно бывает нужно знать не ЛЛ*, а его проекции на вертикальное и горизонтальное направления. Определение перемещения ЛЛ* или его проекций со
ставляет довольно трудную задачу геометрии, хотя и элементарной. Необходимость решать треугольники, образованные дугами окружности, весьма неприятна. Однако, поскольку удлинение и перемещения малы, вместо того чтобы двигать концы стержней по дугам окружностей, можно перемещать их по перпендикулярам к осям стержней. Соответствующее построение показано на том же чертеже и дает новое положение узла Л'. Такая замена дуг окружностей перпендикулярами означает, что мы как бы дополнительно деформируем стержни, но эта дополнительная деформация имеет порядок и2//*, тогда как порядок величины основной деформации есть и//.
Рис. 25 страдает одной несо
образностью: в нем использованы
разные масштабы для изображения стержней и их перемещений. На чертеже, например, А/, составляет примерно одну пятую от на самом же деле А/,//,— величина порядка 10-’. Поэтому вся картина перемещений узла является грубо искаженной, дуги окружно-
стей на глаз существенно отличаются от перпендикуляров и точки А" и Л' довольно далеки одна от другой. Чтобы избежать этой несообразности и не затемнять основного чертежа, все построения для нахождения точки А' выполняют в другом масштабе отдельно, как показано на том же чертеже внизу. От некоторой точки, изображающей точку Л, в произвольном масштабе, отличном от масштаба основного чертежа, откладываются отрезки А/, и A/t параллельно соответствующим стержням. Из концов этих отрезков
ленных задач,
46 РАСТЯЖЕНИЕ---СЖАТИЕ [ГЛ. II
восставляют к ним перпендикуляры, точка пересечения их есть А'. Если бы к этой диаграмме мы пристроили стержни в том же масштабе, неподвижные шарниры оказались бы очень далеко за пределами страницы книги, и дуги окружностей весьма большого радиуса были бы практически неотличимы от перпендикуляров.
Пример. Рассмотрим систему из двух стержней, составляющих углы а и Р с вертикалью. Пусть под действием нагрузки стержни получают удлинения А/, и А/,. Требуется определить вертикальную и горизонтальную составляющие перемещения точки А (рис. 26). Построим отдельно диаграмму перемещений (черточками отмечены параллельные отрезки). Спроектируем ломаную АВА' на направления стержней. Получим:
А/, = Sr sin а -|- SB cos а, А/, = — Sr sin 0 -|- SB cos р.
Отсюда находим:
» __A/t sin Р 4~ А/, sin а « _А/, cos р — А/, cos а
в sin(a-)-P) ’ г sin(a-)-P)
§ 23. Статически неопределенные задачи на растяжение —сжатие. Теперь мы можем перейти к решению статически неопреде-ie о которых было дано в § 3. Общий план
решения статически неопределенной задачи состоит в следующем:
1. Рассматривая возможные перемещения точек системы, составляем уравнения, связывающие деформации отдельных элементов. Будем называть эти уравнения уравнениями совместности деформаций.
2.. Заменяем в уравнениях совместности деформаций величины деформаций через усилия или напряжения по закону Гука.
3. Составляем уравнения статики.
4. Решаем полученную систему уравнений. Приводимые примеры поясняют эту схему. Пример 1. Абсолютно жесткий брус веса G подвешен на трех параллельных проволоках, как показано на рис. 27. Расстояния между проволоками одинаковы. Сечении проволок тоже одинаковы, но материалы различны. Первая проволока — стальная (£=2-10® кг/см*), вторая — медная (£=1,2-10“ кг1смг) и третья — алюминиевая
(£=0,75-10® кг[смг). Требуется определить усилия, возникающие в проволоках.
§ 23] СТАТИЧЕСКИ НЕОПРЕДЕЛЕННЫЕ ЗАДАЧИ НА РАСТЯЖЕНИЕ---СЖАТИЕ 47
Условие геометрической связи между перемещениями состоит в том, что концы проволок А, В н С остаются на одной прямой.
Отсюда
А/,4-А/, = 2А/Г
нли, заменяя удлинения через усилия, получим:
Й + <23Л)
Условия равновесия дают:
М+4 + ^ = 0. 4 = ^,- (23.2)
Из уравнений (23.1) и (23.2) получаем:
N =-----------^Е,_____'_Q
* 4£.£,+ ’
Рис. 27.
. £,(£, + £,)
;v« —4£1£, + £1£2 + £г£,
G.
вставлен в трубку из
Пример 2. Система из трех одинаковых стержней (рис. 28) нагружена силой Р. Материал и площади сечения стержней одинаковы. Для определения усилий в стержнях строим диаграмму перемещений в порядке, обратном тому, который был принят в предыдущем параграфе.
Дадим узлу А произвольное перемещение АА' и опустим нз точки А’ перпендикуляры на направления стержней. Отсеченные отрезки представляют собою удлинения стержней. Уравнение, связывающее А/,, A/t, А/,, получается точно таким же способом, как в примере предыдущего параграфа. Используя найденный там результат, заметим, что вертикальное перемещение бв, с одной стороны, равно А/,, с другой — выражается через А/, н < по найденной там формуле, в которой р нужно заменить через —р. Уравнение деформации имеет вид:
. . —А/, sin Р Д/, sin а •— sin (а- ₽) ’
Дальнейший ход решения очевиден.
Пример 3. Болт с площадью сечения j
того же материала с площадью сечення Ft, как показано на рнс. 29. Приведя головку болта и шайбу в плотное соприкосновение с трубкой, поворачивают гайку так, что она перемещается по нарезке в направлении оси на величину h. Требуется определить напряжения в болте н трубке.
48
РАСТЯЖЕНИЕ---СЖАТИЕ
|ГЛ. 11
Очевидно, что болт удлинится на величину Д/,, трубка укоротится на Д/2, причем сумма удлинения болта и укорочения трубки будет как раз h.
Имеем:
д/. + д/.^л.
Отсюда
(23-3>
Здесь о.
— растягивающее напряжение, a ct — сжимающее.
Рассекая трубку и болт и составляя уравнение равновесия, получим:
Ojf, =0.
В этом уравнении учтено, что at — сжимающее напряжение. Решая (23.3) н (23.4), найдем:
1 I Л +
О. £А F,
(23.4)
(растяжение),
/ F. + F, втором примере при
(сжатие).
Во У.ДДИнення_.считались положительными, поэтому н в уравнениях статишГ~нуйППГ~считаТь' все усилия поло-Рис. 29. , жд1£льиыми^-В результате~каждое~'усйляе получится со своим знаком, который указывает на то, растянут данный стержень или сжат. В третьем примере мы имеем дело с абсолютными величинами удлинений и абсолютными величинами напряжений. В ответе как о,, так и о, положительны, но мы заранее знаем, что о2— напряжение сжатия. Такой способ во многих случаях имеет преимущество естественности и наглядности.
Желая решить третий пример таким образом, чтобы знаки напряжений получились формально, запишем, что вследствие завинчивания гайки удлинение болта больше, чем удлинение трубки, на величину h. Таким образом,
Д/, —Д/2 = й, о, —о, = ^.
составлении уравнений все.
Заметим, что это условие связывает возможные деформации болта и трубки, поэтому, желая сделать его наглядным, можно рисовать и болт и трубку удлиняющимися. Но тогда и напряжения нужно считать растягивающими и уравнение равновесия следует писать так:
°1Л4-оЛ=0-
Решая эти уравнения, получим тот же результат, что и ранее, но перед о, появится знак минус.
§ 24]
ТЕМПЕРАТУРНЫЕ И МОНТАЖНЫЕ НАПРЯЖЕНИЯ
49
Иногда бывает удобнее видоизменить схему решения статически неопределенной задачи, выделив так называемые лишние неизвестные. Лишними неизвестными мы будем называть реакции тех связей, освобождение которых делает систему статически определимой. При
решении задачи у системы освобождают столько связей, сколько нужно для превращения ее в статически определимую. Прикладывая реакции этих связей, выбирают их величины так, чтобы уничтожить деформации, ставшие возможными благодаря нарушению связей.Эти деформации удобно вычислять по отдельности от действующих сил и от неизвестных реакций, а потом складывать и сумму их приравнивать нулю.
Пример 4. Стержень, концы которого закреплены между не-
подвижными основаниями, нагру- Рис. 30.
жен продольными силами, как пока-
зано на рис. 30. Требуется определить напряжения на всех трех участках стержня.
Освободив верхнюю заделку, мы даем возможность стержню сократиться на величину йр, равную
в Ра Р -2а ЗРа
°p=SS~EF~'EF==i~'EF'
Приложим теперь к верхнему концу неизвестную реакцию X* которая вытягивает стержень на величину йх, равную
. Х-За
Сила X должна быть такой, чтобы в и силы X длина стержня не изменилась,
результате действия сил Р поэтому
Отсюда
ЗРа । ЗХа п
££ + £7=°’
Х=Р.
Теперь легко подсчитать, что иа первом участке усилие Nl=P, на втором Wt==0 и на третьем — — Р.
§ 24. Температурные и монтажные напряжения. Изменение температуры стержней статически неопределимых систем вызывает температурные деформации, которые, как правило, не удовлетворяют условиям совместности деформаций. Поэтому в стержнях возникают
50 РАСТЯЖЕНИЕ--СЖАТИЕ [ГЛ. II
упругие напряжения и соответствующие им упругие деформации. Общие деформации, состоящие из температурных и упругих, должны удовлетворять уравнениям совместности деформации. Рассмотрим простейший пример, когда стержень помещен при температуре /0-между неподвижными стенками, после чего температура его повышается до t. Условие совместности деформации заключается в том, что А/ = 0.
Температурная часть удлинения:
Atl=a(f — l„)l,
здесь а — коэффициент линейного температурного расширения, материала.
Упругая часть:
А , al AJ Е .
Таким образом,
AZ = a(/ —fo)/+^ = O.
Отсюда
о = — aE(t — /0).
Схема решения более сложных статически неопределенных задач о температурных напряжениях ничем не отличается от общей схемы, .zzzzzzzzzzz.zzyzz^zzz^.,,. данной в предыдущем параграфе, только в \ / пункте 2 схемы вместо закона Гука следует
2 / пользоваться формулой
\ у А/,=аЛД^+^-
у Пример. В системе, изображенной на
рис. 31 и собранной при температуре Zo = 2O°, Л средний' стержень нагрет до / = 70°, темпера-
Д1г тура крайних осталась без изменения. Пло-
Рис 31 ЩадИ сечения стержней одинаковы, материал — ' сталь. Требуется найти напряжения.
При построении диаграммы перемещений мы учтем, что система деформируется симметричным образом, поэтому
А/, = AZ, cos ср.
Так как стержень I не нагревается, то А/,-^^-, но
Х = (*-*.)•
Вставив эти значения в уравнение деформаций, получим:
^ = [^ + Ч (* — *»)] cos Ф.
§ 24]
ТЕМПЕРАТУРНЫЕ И МОНТАЖНЫЕ НАПРЯЖЕНИЯ
51
или
<T1 + aE(/-Q = ^.
Отсюда и из уравнения статики
2а! cos ф -|- °s = О находим:
cos’tp _ 2cos’<p ,,
о, =, то аЕ (t — а. =--------------=—г-д—V- «Е (* —
1 14-2 cos’<р ' °'’ * 14-2 cos’ф ' •'
При ф = 30° получим:
о, = 392 кг!см*, о, = — 678 кг 1см*.
При вычислениях принято а=1,2-10_®, Е=2«10® кг/см*.
Если бы нагревался один из боковых стержней, мы должны были
бы рассмотреть более общий случай деформации, сопровождаемый горизонтальным смещением узла, и поступить так, как в примере 2 параграфа 23.
Как видно из решенного примера, температурные напряжения достигают довольно большой величины при сравнительно незначи-
тельных разностях температур. В стержневых системах температурные напряжения сами по себе не представляют опасности, так как наступающая пластичность ограничивает рост напряжений, а температурные деформации остаются во много раз меньше тех деформаций, при которых происходит разрушение (если речь не идет о весьма хрупких материалах). Однако наличие температурных напряжений может существенно повлиять на картину распределения усилий в системе.
Практическое осуществление статически неопределимых стержневых систем требует весьма точного изготовления стержней, чтобы при сборке концы их соединялись в узлах без применения усилия. В противном случае сборка становится возможной только за счет упругой деформации стержней, и в системе воз-
Рис. 32.
никают
напряжения, называемые начальными
или монтажными.
Предположим, например, что в предыдущем примере средний стержень сделан короче крайних на величину А (рис. 32). При решении вопроса о монтажных напряжениях будем предполагать, что
усилия положительны и стержни удлиняются, хотя очевидно, что удлиняется только средний стержень, а крайние укорачиваются.
52 РАСТЯЖЕНИЕ---СЖАТИЕ [ГЛ. 11
Уравнение совместности деформаций будет
Д/j = (Д/, — Д) cos <р.
Отсюда
(У./. ((У./. А \
Д;с°8ф.
Уравнение равновесия:
2а t cos ф а, = 0.
Полученная система уравнений весьма похожа на уравнения для температурных напряжений, только вместо а/(/ — /0) стоит — Д. И действительно, совершенно безразлично, сделать ли стержень короче или сделать его надлежащей длины, но потом укоротить путем охлаждения. Очевидный результат решении задачи следующий:
_________cos* <р £А 2 cos* <р 15=1 1 + 2 cos’ ф = 1-f-2 cos’<р /, *
§ 25. Общие соображения о расчете стержневых систем. Рассмотренные здесь примеры статически неопределимых систем являются простейшими. В технике встречаются значительно более сложные системы, состоящие из растягиваемых и сжимаемых стержней, так называемые фермы. Под фермой мы понимаем стержневую систему, элементы которой соединены шарнирами, обеспечивающими свободный поворот. Внешние силы должны также быть приложены в шарнирах; если же какая-либо сила приложена к стержню, то для того, чтобы не было изгиба, а было только растяжение или сжатие, необходимо, чтобы эта сила была направлена по оси стержня, в противном случае неизбежен изгиб. Простейшая ферма была изображена на рис. 16, причем в соответствующем месте была сделана оговорка о том, что, хотя крепления стержней в узлах и не обеспечивают поворота их концов, при расчете можно считать с достаточной степенью точности, что в узлах устроены шарниры. Точное выяснение этого обстоятельства будет возможно лишь впоследствии.
Ограничение, относящееся к способу приложения внешних нагрузок, наоборот, совершенно обязательно. Если ферма статически определима, усилия в стержнях могут быть найдены по правилам статики, аналитически или графически. , После этого расчет сводится к проверке выполнения условий прочности для каждого стержня.
Если ферма статически неопределима, принципиальная схема расчета остается той же, какая была сформулирована в начале этого параграфа: составляются геометрические уравнения, связывающие возможные удлинения стержней при произвольных перемещениях узлов фермы, после чего мысленно вырезаются узлы и для каждого узла составляются уравнения равновесия. Технически выполнение этого расчета оказывается довольно сложным, основная трудность состоит в составлении уравнений совместности деформаций. Разлнч-
§ 25] ОБЩИЕ СООБРАЖЕНИЯ О РАСЧЕТЕ СТЕРЖНЕВЫХ СИСТЕМ 53
ные приемы для этой цели излагаются в курсах статики сооружений; мы здесь не будем заниматься задачами такого рода, потому что некоторые общие теоремы сопротивления материалов, излагаемые в гл. XII этого курса, позволяют с большой легкостью решать всевозможные статически неопределенные задачи, в том числе и относящиеся к расчету ферм.
Напомним только правило, относящееся к установлению степени статической неопределимости плоской фермы. Пусть число стержней плоской фермы есть п, число узлов есть т;. для каждого вырезанного узла можно составить два уравнения статики, всего 2т уравнений. Но система внешних сил предполагается уравновешенной, значит, три условия равновесия фермы в целом выполняются тождественно. Эти условия равновесия можно получить, исключая из 2т уравнений усилия в стержнях, значит, из 2т уравнений вытекают три тождества; итак, число независимых уравнений есть 2т — 3. Степенью статической неопределимости системы р назовем разность между числом неизвестных и числом уравнений статики.
Таким образом, для плоской фермы р = п — 2т-|-3.
Аналогично для пространственной фермы
р — п — 3m-|-6.
Если р = 0, система статически определима. Если р^>0, система статически неопределима. Так, например, для фермы, изображенной на рис. 16, л = 33, т=18, следовательно, р = 0.
Покажем, что всегда полное число уравнений равно числу неизвестных, то есть число независимых уравнений совместности деформаций равно р.
Предположим, что узлы плоской фермы получили произвольные смещения в ее плоскости. Разлагая перемещения каждого узла на две составляющие по осям координат, найдем, что для задания перемещений всех узлов нужно задать 2m величин. Но не все перемещения узлов связаны с удлинением или укорочением стержней, узлы могут перемещаться вследствие движения фермы как твердого тела. Перемещение твердого тела в плоскости задается тремя величинами, например компонентами поступательного перемещения и углом поворота. Поэтому можно считать, что один узел неподвижен и один из стержней, выходящих из этого узла, не поворачивается. Всего остается 2m — 3 перемещения. Удлинение каждого из п стержней выражается через эти перемещения; исключая их, найдем, что удлинения связаны между собою соотношениями, число которых
Q —— л — 2m 3
равно степени статической неопределимости системы. Если ^<^0, система представляет собою механизм и равновесие возможно только при специально подобранных значениях внешних сил.
54
РАСТЯЖЕНИЕ---СЖАТИЕ
[ГЛ. П
§ 26. Расчет статически неопределимых систем по допускаемым нагрузкам. До недавнего времени расчет статически неопределимых систем на прочность сводился к обеспечению выполнения неравенства
ата„ [о], max L J
При этом в конструкциях, изготовленных из пластического материала, фактический запас прочности оказывался для статически определимых систем, как правило, меньшим, чем для систем, статически неопределимых.
Поясним сказанное примером. В системе из двух стержней при достижении предела текучести точка приложения силы всегда получает значительные перемещения, стержень. Вообще
Рис. 33.
даже если течет только один в статически определимой системе для ее разрушения достаточно, чтобы только один стержень перешел в состояние текучести. Выпадение хотя бы одной связи делает систему изменяемой. В системе из трех стержней, изображенной на рис. 83, расчет, выполненный в предположении упругости стержней, дает следующие величины усилий:
дг _. р —E2S* Ф— дг _ р_______2____,
1 1 4- 2 cos’ ф ’ ’ г 1 4- 2 cos’ ф ’
Видно, что и при увеличении силы
Р в среднем стержне предел текучести будет достигнут раньше, чем в крайних стержнях. Од-означает исчерпания сопротивления всей системы.
нако это не
Крайние стержни, оставаясь упругими, препятствуют пластическим деформациям среднего стержня. Таким образом, можно различать две стадии работы системы: упругую стадию, при которой усилия определяются написанными выше формулами, и упруго-пластическую, наступающую при переходе хотя бы одного стержня в пластическое состояние. Значение силы, при котором происходит переход от первой стадии ко второй, определяется из условия:
— Р1 1 4-2 cos’ ф = °т F
или
Р, = cttF (l-f-2 cos’<р). (26.1)
Во второй стадии, предполагая материал идеально пластичным, имеем:
Nt = aTF.
Таким образом, задача об определении усилия решается с помощью одного только уравнения статики:
Nt + 2Л\ cos ф = Р.
§ 26] РАСЧЕТ ПО ДОПУСКАЕМЫМ НАГРУЗКАМ 55-
Отсюда
(26.2).
1 2 cos ф ' г
При дальнейшем увеличении силы и в наклонных стержнях наступает текучесть. Это уже текучесть всей системы в целом. Соответствующая сила называется несущей способностью системы и. обозначается Рт. Найдем ее из условия
Подставляя это значение в равенство (26.2) н решая его относительно Рт, получим:
PT = aTF(l 4-2cos <р).
Принимая один и тот же коэффициент запаса п, получим следующие выражения для допускаемой нагрузки:
а) при расчете по допускаемым напряжениям
P<^(l + 2cos4),
б) при расчете по допускаемым нагрузкам р^^О+гссжф).
Второй способ расчета приводит к бблыпим допускаемым нагрузкам, нежели первый (при ф = ЗО° на 19°/0). Состояние текучести системы из идеально-пластических элементов называется ее предельным состоянием, и расчет по допускаемым нагрузкам часто называется расчетом по предельному состоянию. Установленный для. рассмотренного примера факт, состоящий в том, что расчет по предельному состоянию дает ббльшую величину нагрузки, чем расчет по допускаемым напряжениям, является следствием общей теоремы,, которая будет доказана в главе XV (§ 164).
Для определения несущей способности нет нужды рассматривать-последовательно упругую и упруго-пластическую стадии работы, конструкции. Нужно просто составить уравнение равновесия, считая,, что в каждом из стержней усилие есть
Рассмотрим теперь совершенно произвольную стержневую систему самого общего вида; пусть степень ее статической неопределимости равна р при числе стержней п. Занумеруем стержни цифрами от единицы до л, пусть длина стержня номер i есть напряжение в нем а,., удлинение Д/,, относительная деформация ez. Уравнения совместности деформаций в случае малых перемещений связывают удлинения стержней линейными соотношениями. Эти соотношения однородны, если не вводятся в рассмотрение натяги или зазоры, то есть не принимаются во внимание монтажные напряжения. Удлинения всегда можно заменить относительными деформациями, поэтому
56
РАСТЯЖЕНИЕ---СЖАТИЕ
[ГЛ. II
самая общая запись уравнений совместности деформаций будет следующей:
auei + «i!e!+---+в|„ев = 0,
аР^ + аР& + • • • + арпьп — °.
Здесь atj — известные постоянные коэффициенты. Уравнения равновесия, из которых исключены реакции внешних связей, числом п — р, также линейны; заменяя усилия через напряжения, можем записать эти уравнения следующим образом:
+---+^во„
bn-p@l “Н b/l-p, ~Н • • • ~\~^п-р^п —Вп-р-
Здесь btj — коэффициенты, зависящие от геометрических характеристик, Вк — некоторые линейные комбинации из внешних сил.
Запишем сокращенно полученную систему таким образом:
2а»8,=0 (i = l, 2, ...,р), (26.3)
= (1 = 1, 2, ..., п — р). (26.4)
Пока внешние нагрузки невелики и вся система находится в упругом состоянии, напряжение и деформация в каждом стержне связаны законом Гука:
ai г‘~Е '
Заменяя в уравнениях (26.3) деформации через напряжения, получим полную систему п уравнений для нахождения п неизвестных напряжений в стержнях.
Предположим, что в стержне номер г напряжение наибольшее. При увеличении внешней нагрузки в этом стержне прежде всего наступает текучесть. Считая пластичность идеальной, рассмотрим следующую стадию работы конструкции. Напряжение в стержне номер г остается постоянным, oz=aT, для этого стержня закон Гука становится несправедлив, так как на пределе текучести деформация может быть произвольной. В уравнениях (26.3) появляется лишняя, неопределенная величина ег. Исключая из этих уравнений ег, получим уже р—1 уравнение совместности для деформаций оставшихся стержней в числе п—1. Так как число уравнений равновесия осталось прежним, система будет содержать всего п — 1 уравнение. Таким образом, переход в пластическое состояние одного из стержней как бы понижает на единицу степень статической неопределимости системы. Среди оставшихся упругими стержней
§ 27] ОСТАТОЧНЫЕ НАПРЯЖЕНИЯ ПОСЛЕ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ 57 один будет напряжен больше остальных, пусть это стержень номер s. При дальнейшем увеличении нагрузки этот стержень перейдет в пластическое состояние; в уравнениях (26.4) мы положим а^=ат, из уравнений (26.3) исключим удлинения ег и es, получим р — 2 уравнения совместности и так далее, до тех пор, пока в пластическое состояние не перейдет р стержней. Появление пластической деформации в следующем стержне определяет предельную нагрузку, так как после этого система становится изменяемой.
§ 27. Остаточные напряжения после пластической деформации. Если удалить внешние силы, стержни, претерпевшие пластические деформации, не вернутся в исходное состояние и не дадут вернуться в исходное состояние тем стержням, которые остались упругими. В системе появятся остаточные напряжения и деформации. Определение остаточных напряжений и деформаций производится на основании теоремы о разгрузке. Для доказательства этой теоремы заметим, что соотношения (26.3) и (26.4) справедливы для любого состояния системы независимо от того, находятся ее элементы в упругом или пластическом состоянии. Изменение нагрузок сказывается лишь на величинах В{. При отсутствии нагрузок мы получаем»
2%е° = 0, (27.1)
2М)=О. (27.2)
Вычтем из уравнений (26.3) уравнения (27.1) и из (26.4) — (27.2). Получим:
aij (е/ 8/)=
/=>
Здесь ък может быть упругой или пластической деформацией; в последнем случае соответствующее оА=ат.
Обращаясь к диаграмме пластичности на рис. 34, убеждаемся, что как в том, так и в другом случае
в/ — 8/=4-(в/ — °’)-
Положим:
Ву —8у = Ву, Оу — Оу = 0у.
58
РАСТЯЖЕНИЕ---СЖАТИЕ
[ГЛ. II
Величины By. и aj связаны следующими уравнениями: п
2 а/уб' = О, i = i
2^^/—
ц0 это — уравнения для решения статически неопределенной задачи в предположении упругости стержней. Решая эти уравнения, найдем в/ и ст,- и вычислим остаточные напряжения и деформации по формулам:
о 'о г
— * 1 8/ —— 8|j ~ (У—~~ О’/.
Таким образом, получаем следующую бг теорему о разгрузке:
Для определения напряжений и деформаций, остающихся
-------------------------- в системе после снятия нагрузки, нужно вычесть из действительных напряжений и деформаций, соответствующих данной нагруз-
ке, те напряжения и деформации, которые получаются при этой нагрузке в предположении упругости всех элементов.
Определим для примера остаточные напряжения в системе из трех стержней, изображенной на рис. 33, если все стержни были выведены за предел текучести. Соответствующая нагрузка есть Рт= = стт/?(1 2 cos<р); фиктивные усилия, вычисленные в предположе-
нии упругости стержней, равны
cos ф
1 т 1 2 cos’ q> ’
Следовательно,
. ,0 г- г. cos’ф
/V1=aTF--PT1+2c^(p,
Д7 ----р
2 т 1 -|- 2 cos’ ф ’
Nt ~ 1 -f- 2 cos’ ф •
Предположим теперь, что разгруженная система нагружается вторично. Усилия, соответствующие нагрузке Р, можно определить так, как если бы никаких остаточных напряжений не было, а потом прибавить к ним остаточные напряжения. Пока материал упруг, получаем:
N, = {Р,-Р) ,+7'соФ,,ф , W, = o,F- (Р, -Р) 1+2'со,.ф •
Из этих формул видно, что при повторной нагрузке система ведет себя совсем иначе, нежели при первой. Теперь предел текучести при увеличении силы Р достигается в обоих стержнях одновременно,
§ 28] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ РАСТЯЖЕНИЯ 59
когда Р=РГ. Обобщая этот результат, можем утверждать следующее:
При повторной нагрузке все элементы остаются упругими до тех пор, пока новая нагрузка не превышает той, от которой произведена разгрузка.
Как это правило, так и теорема о разгрузке справедливы лишь тогда, когда не возникают вторичные пластические деформации. Это значит, что остаточные напряжения при разгрузке, вычисленные в предположении упругой разгрузки, нигде не превышают предела текучести. В рассмотренном примере N®^>0, а Д^<^0. Можно опасаться того, что остаточное сжимающее напряжение во втором стержне окажется по абсолютной величине больше предела текучести. В этом случае говорят о вторичных пластических деформациях; если они появляются, все рассуждения, конечно, становятся неверными. В данном примере легко проверить, что вторичные пластические деформации невозможны.
Заметим, что теорема о разгрузке может быть обобщена на случай вторичных пластических деформаций. Фиктивные напряжения / f
и деформации в(- и а,- при этом нужно вычислять с учетом возможности пластических деформаций, но при удвоенном пределе текучести.
Детальное выяснение обстоятельств последовательного перехода стержней из упругого состояния в пластическое само по себе редко бывает интересно; важно знать несущую способность системы, то есть ту нагрузку, при которой система становится изменяемой. В примере § 26 для определения величины Рт нужно было просто предположить, что в каждом стержне напряжения равны, и из условия равновесия найти эту силу. В сложных стержневых системах далеко не всегда бывает ясно, в каких именно элементах наступает текучесть. Поэтому необходимо или производить полный анализ по вышеописанной схеме, или же пользоваться общими методами, которые будут изложены в главе XV.
§ 28. Потенциальная энергия растяжении. Упругое тело, будучи деформировано, является аккумулятором энергии, затраченной на деформацию. При устранении действующих сил эта энергия отдается упругим телом в том или ином виде. Использование упругого аккумулятора энергии широко распространено и находит применение в конструкции заводного механизма часов, некоторых самопишущих приборов и т. п.
В общем случае внешние силы, прикладываемые к упругому телу, производят работу А, которая идет, с одной стороны, на сообщение скорости частицам тела, то есть переходит в кинетическую энергию Т, с другой — накапливается в виде потенциальной энергии деформации. Уравнение баланса энергии есть
A=T-\-U, (28.1)
60 РАСТЯЖЕНИЕ--СЖАТИЕ (ГЛ. II
Величина U представляет собою ту часть работы, которая тратится на деформирование тела и, если тело упруго, остается в нем до тех пор, пока нагрузка не изменяется. Для подсчета величины U нужно предположить, что внешняя сила прикладывается таким образом, что кинетическая энергия Т равна нулю. Для этого нужно, чтобы сила Р прикладывалась не сразу, а постепенно, а именно возрастала от нуля до максимума так медленно, что можно считать скорость деформации практически отсутствующей и пренебречь силами инерции. В этом и только в этом случае внутренние силы упругости в каждый момент процесса уравновешиваются внешними силами, и поэтому можно приняты
A = U.
Процесс деформации можно представить как последовательность бесконечно малых приращений удлинения rf (Д/), вызываемых ростом силы Р, которая при растяжении — сжатии однозначно связана с удлинением законом Гука:
Р=уГА/. (28.2)
Приращению d(A/) удлинения соответствует элементарная работа: dA-Pd(Al).
Интегрируя от Д/ = 0 до конечного значения Д/, имеем:
ы
U=\Pd(M). (28.3)
О
Заменяя здесь силу Р ее выражением по закону Гука (28.2), получим:
£7=^^. (28.4)
Приводим еще две эквивалентные формы записи выражения потенциальной энергии растяжения:
РЧ
(28.5)
РМ. (28.6)
При пользовании формулами (28.5) и (28.6) нужно помнить, что Р представляет собою внешнюю силу лишь тогда, когда стержень находится в состоянии покоя. В динамических задачах сила, растягивающая стержень, вообще говоря, составляет сумму внешней силы н силы инерции. Эта сумма и фигурирует в формулах (28.5) и (28.6).
§ 29]
НАПРЯЖЕНИЯ ПРИ УДАРЕ
61
Энергию упругой деформации растяжения — сжатия удобно относить к единице объема стержня. Эта величина выражается так:
в
С &В <г ав
*
(28.7)
“’=J о
В стержне, приведенном в пластическое состояние, работа внешней деформирующей силы расходуется также и на пластическое деформирование. Соответствующая часть работы связана с .необратимыми изменениями размеров и переходит в иемеханические виды энергии. Уравнение баланса энергии будет
Здесь W — работа пластической дефор» мации. Повторяя приведенные выше рассуждения, найдем, что
или, обозначив величину W, отнесенную к единице объема, через aM,
Рис. 35.
-пл— J о
(28.8)
Обращаясь к диаграмме растяжения (рис. 35), видим, что сумма ау4“дпл есть площадь фигуры, ограниченной диаграммой растяжения, осью абсцисс и ординатой точки диаграммы, соответствующей достигнутому удлинению. Величина упругой энергии при этом изображается площадью заштрихованного сеткой треугольника, то есть
<теу а* ду= 2 =2г-
§ 29. Напряжения при ударе. Понятие об энергии упругой и пластической деформации оказывается полезным при решении вопроса о напряжениях и деформациях при ударе. В теоретической механике соударение предполагается мгновенным, вследствие чего силы, возникающие при соударении абсолютно твердых тел, бесконечно велики, поэтому в рассмотрение вводятся лишь энергии и импульсы. Если хотя бы одно из тел упруго, то продолжительность удара всегда конечна и величина силы может быть определена. Задача о соударении упругих тел в точной постановке представляет значительные трудности ввиду волнового характера распространения деформации в упругом теле.
Здесь мы дадим приближенное решение вопроса о растягивающем или сжимающем ударе по стержню тела большой массы, которое мы будем условно считать абсолютно твердым. Если масса стержня мала
62
РАСТЯЖЕНИЕ---СЖАТИЕ
[ГЛ. II
по сравнению с массой ударяющего тела, то можно считать первую вообще отсутствующей, а при отсутствии массы деформации в теле распространялись бы мгновенно. Основная гипотеза приближенной теории удара состоит как раз в том, что деформация предполагается
груз — стержень груз до удара:
возникающей мгновенно во всех сечениях стержня, тогда как на самом деле деформация распространяется от конца, на котором происходит удар, со скоростью звука (для стали около 5000 MjceK, как будет показано в § 30). Высказанная гипотеза означает практически, что большая масса ударяется о стержень со max скоростью весьма малой по сравнению со скоростью звука и продолжительность соударения значительно больше времени, необходимого для прохождения упругой волны по стержню.
Предположим, что груз массы М, движущийся со скоростью ударяет о стержень и деформирует его (рис. 36). В течение процесса деформации в каждый момент сумма кинетической и потенциальной энергии системы равна той кинетической энергии, которой обладал
т+и=т„
(29.1)
2 ’
По мере роста деформации скорость груза убывает и становится на мгновение равной нулю в тот момент, когда деформация максимальна. При этом Т=0, и мы имеем:
Пользуясь формулой (28.4), получим:
(Д0шах=(29.2)
Если груз веса Q падает с высоты h (рис. 36), то
Ta = Qh и
А/„„=
Положим:
Й = (ЛЛС1.
Здесь (А/)С1 — деформация от груза Q, приложенного статически. Тогда ______
(A0max = K2A(A/)CT. (29.3)
§ 30] РАСПРОСТРАНЕНИЕ УПРУГИХ ВОЛН В СТЕРЖНЯХ 63
Если груз Q весьма велик и высота h невелика, мы уже не имеем права пренебрегать той дополнительной работой, которую производит груз Q на перемещении Д/. Когда Д/ = (Д/)тах, уравнение работ будет следующим:
Q[A4-(A/)max] = ^(A/)smax.
Отсюда получаем квадратное уравнение:
(ДОтах - 2 ( Д/)ст (Д/)тах - 2Л ( Д/)ст = 0,-
Решение его:
(А/)т„ = (Д0„ 4- /(Д/^ + 2Л(Д/)сГ (29.4)
Мы выбрали знак плюс перед радикалом, чтобы получить наибольшую деформацию. Второе решение, со знаком минус, приобретает реальный смысл тогда, когда груз остается после удара связанным со стержнем и совершает колебания около состояния статического равновесия. В этом случае решение со знаком минус отвечает верхнему положению колеблющегося груза. На самом деле при движении вверх груз отрывается от стержня раньше, чем найденное аналитически положение будет достигнуто.
Важный частный случай формулы (29.4) — это случай внезапного приложения груза, когда Л = 0. Тогда
(Д/)тах = 2(Д/)С1. (29.5)
Наибольшие силы, действующие на систему во время удара и складывающиеся из действующих сил и сил инерции, пропорциональны перемещениям. Поэтому при расчете на ударную нагрузку напряжения, полученные при статическом расчете, следует умножить на динамический коэффициент, равный отношению • Отсюда сле-дует, в частности, что при внезапном приложении тяжелого груза максимальные напряжения вдвое больше, чем статические напряжения.
В заключение заметим, что формулы, выведенные для продольного удара по стержню, сохраняют тот же вид для любой упругой системы, лишь бы перемещение было пропорционально действующей силе.
§ 30. Распространение упругих волн в стержнях. Совершенно иначе будет обстоять дело в том случае, когда по стержню производят удар со значительной скоростью. Для того чтобы выяснить характер деформации стержня в этом случае, предположим сначала, что к концу весьма длинного стержня внезапно приложена сила Р, которой соответствуют напряжение а и упругая деформация е. По истечении времени t после приложения силы картина будет следующая. Участок стержня длины ci будет равномерно сжат или растянут в зависимости от направления силы, остальная часть стержня
64
РАСТЯЖЕНИЕ---СЖАТИЕ
[ГЛ. II
останется еще ненапряженной. Сечение тп (рис. 37), являющееся границей между напряженной и ненапряженной частями стержня, называется фронтом упругой волны. Фронт упругой волны движется со скоростью с, которая зависит только от материала стержня. Возьмем некоторое фиксированное сечение pq, которое в данный момент времени находится на расстоянии ct — х от фронта волны. Участок между сечениями тп и pq равномерно сжат, относительная деформация есть е, следовательно, сечение х ]т_________ РЯ сместилось из первоначального
—| i } I | своего положения на расстояние
' ---------------------
I- —ct------*Н/7 U = &(ct-—х)=—(с/ — х).
Рис’ 37‘ В бесконечно близкий момент
времени t-\-di фронт волны переместился на величину с dt, на эту же величину увеличилось расстояние от фиксированного сечения pq до фронта волны, перемещение этого сечения стало
и du = е (ci — х) —ес di.
Скорость движения сечения pq есть
du dt
= се.
Таким образом, мы установили, что при постоянной сжимающей силе все сечения, находящиеся позади фронта волны, движутся с постоянной скоростью. Отсюда можно сделать и обратное заключение, а именно: если заставить конец стержня двигаться с постоянной скоростью, позади фронта волны напряжения будут всюду и все время постоянными. Представим себе, например, удар по стержню телом весьма большой массы, движущимся со скоростью v. Деформация при этом будет
£______ ( и по закону Гука
/ “ 2 °=ЕТ’ (30.1)
★az
Осталось определить величину скорости рас-
Рис. 38. пределения упругой волны с. Для этого вы-
делим из рассматриваемого стержня участок длины dx между сечениями /—/ и 2—2 (рис. 38). Пусть в момент времени i фронт упругой волны проходит через сечение /—/, в момент t-^-dt— через сечение 2—2. Для этого нужно, чтобы было dx^=cdt.
Применим к выделенной части стержня второй закон Ньютона. В течение времени dt в сечении 1—1 действует сила’ of, сечение 2—2
§ 301
РАСПРОСТРАНЕНИЕ УПРУГИХ ВОЛН В СТЕРЖНЯХ
65
остается ненапряженным, следовательно, импульс силы равен oF dt. В момент времени t вся выделенная часть стержня была в покое, в момент t-\-di вся она движется со скоростью v, следовательно, изменение количества движения есть
vqp dx=vqFc di.
Здесь p — плотность, F—площадь сечения. Приравнивая импульс силы изменению количества движения и используя соотношение между v, е и с, а также закон Гука, найдем: с= У (30.2)
Приводим значения с для некоторых материалов:
сталь алюминий
медь стекло дерево (сосна)
— 4900 м/сек — 5100 м/сек — 3500 м/сек — 5200 м/сек — 4200 м/сек
о)
0
6)
В)
ct Рнс. 39.
Формула (30.1) показывает, что уже при сравнительно небольших скоростях соударения неизбежны пластические деформации. Действительно, для стали, например, если предел текучести равен 3000 и модуль упругости 2,10’ кг/см*, для появления пластических деформаций достаточно выбрать скорость удара превышающей 7,4 м]сек, что соответствует высоте падения всего 2,8 м.
Предположим теперь, что постоянная сила действовала на конец стержня не все время, а в течение определенного отрезка времени т. График зависимости силы Р от времени приведен на рис. 39, а, при t <^0 а = 0, при 0<^/<^т a=const, при а = 0.'
Пока было t т, фронт упругой волны успел распространиться на длину ct, за фронтом всюду
эпюра распространения напряжений изображена на рис. 39, б. При / = т фронт ушел на расстояние ст. При картина меняется, на конце сила уже не действует, значит, напряжение на конце равно нулю; Свободная от напряжений область распространяется по стержню с той же скоростью с, образуется задний фронт волны, эпюра распространения напряжений выглядит так, как показано на рис. 39, в, она движется, сохраняя неизменную форму, со скоростью с. Таким образом, эпюра распределения напряжений по длине стержня воспроизводит график изменения силы, действующей на конце, во времени.
напряжение постоянно и равно а.
3 Ю. Н. Работное
66 РАСТЯЖЕНИЕ--СЖАТИЕ [ГЛ. II
Скорости за задним фронтом волны равны нулю, смещение же остается постоянным.
Сделанный вывод можно распространить и на случай, когда сила Р меняется во времени по произвольному закону.. Пусть этот закон задан некоторым графиком. Заменяя кривую ступенчатой ломаной, мы сведем дело к рассмотрению последовательности волн, посылаемых вдоль стержня весьма кратковременными нагрузками постоянной интенсивности, то есть к рассмотренному случаю, а переходя к пределу, получим перемещающуюся вдоль стержня эпюру распределения напряжений по длине, которая в точности воспроизводит график изменения силы P(t) во времени. Заметим, что если в сечении с координатой х поставить прибор, позволяющий замерить напряжение, зависимость напряжения от времени будет повторять зависимость от времени напряжения на конце, только со сдвигом на время х/с.
Если масса тела, ударяющего о стержень, не бесконечно велика, движение его будет замедленным. Скорость v, с которой происходит соударение, определяет по формуле (30.1) наибольшее напряжение в момент удара, в последующие моменты скорость будет меньше, уменьшится и напряжение. Таким образом, формула (30.1) является совершенно общей, если только стержень достаточно длинен, В коротких стержнях может оказаться, что передний фронт волны дойдет до другого конца стержня, пока еще скорость груза особенно не уменьшилась и напряжение достаточно велико. От второго конца пойдёт отраженная волна в противоположном направлении, и наложение этих волн даст напряжения большие, чем те, которые получаются по формуле (30.1). Последняя формула, строго говоря, верна лишь для стержня бесконечно большой длины, а практически для длинного стержня, по которому производится удар телом малой массы. Если масса ударяющего тела велика по сравнению с массой стержня, расчет нужно производить по формуле (29.2), которую можно преобразовать к следующему виду: __
с=« т/л£.
с Т т
Здесь М — масса груза, т — масса стержня. Как видно, напряжения по этой формуле оказываются значительно большими, чем по формуле (30.1).
. § 31. Концентрации напряжений. Как мы видели, расчет стержней переменного сечения, если изменение сечеиия достаточно плавно, производится принципиально так же, как расчет стержней постоянного сечения. Предполагается, что в поперечных сечениях существуют только нормальные напряжения и распределены они равномерно. Предполагается также, что продольные сечения, параллельные оси
§ 31]
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
67
стержня, свободны от напряжений. При этом для нормального напряжения сохраняет силу обычная формула
Р
a~~F
Мы пользовались этой формулой, например, при нахождении формы бруса равного сопротивления.
В тех случаях, когда сечение стержня меняется резко (около отверстий, выкружек, выточек, галтелей и т. п.) (рйс. 40), сделанные
Рис. 40.
предположения становятся неверными и картина напряженного состояния получается гораздо более сложной, чем при простом растяжении.
Обратимся, например, к случаю, изображенному на рис. 40, в. Растяжение материала в выточке связано с его поперечным сокращением по закону Гука для поперечной деформации. Однако наличие примыкающих утолщенных частей стержня сдерживает эту поперечную деформацию, препятствует ей. Таким образом, простое растяжение стержня в выточке невозможно. Обращаясь к рис. 40, а, рассмотрим равновесие элемента pqr, примыкающего к отверстию. Площадка qr принадлежит поперечному сечению. Если бы в поперечном сечении действовали только нормальные напряжения, то равновесие не было бы возможно. Действительно, эти напряжения уравновешиваются напряжениями на площадке pq, а им по закону парности соответствуют такие же касательные напряжения на площадке qr.
Отступление от распределения напряжений, соответствующего простому растяжению, вблизи мест резкого изменения поперечного сечения называется концентрацией напряжений.
Эффект концентрации напряжений заключается в следующем:
1) нормальные напряжения в поперечных сечениях распределяются неравномерно; около отверстия, выкружки или галтели нормальные напряжения достигают весьма большой величины;
2) напряженное состояние становится не одноосным, а пространственным, в поперечных сечениях возникают касательные напряжения; нормальные и касательные напряжения возникают также в сечениях, параллельных оси.
3*
68
РАСТЯЖЕНИЕ---СЖАТИЕ
[ГЛ. II
Чтобы определить закон распределения напряжений в условиях концентрации, пользуются или методами теории упругости, или же так называемым оптическим методом, позволяющим экспериментально измерить напряжение на модели плоского изделия, изготовленной из прозрачного материала. Нужно отметить, что точных решений задачи о концентрации напряжений известно не так много. Обычно в результате теоретического или экспериментального исследования находят коэффициент концентрации, то есть число, указывающее, ао сколько раз нужно увеличить номинальное напряжение:
чтобы получить величину наибольшего напряжения в сечении:
<*max = a<V
Таблицы и трафики для определения коэффициентов концентрации обычно приводятся в справочной литературе. Так, например, для полосы шириной b с отверстием диаметром d (рис. 41., а) коэффициент
Случай djb = O соответствует отверстию в полосе бесконечно большой ширины. Здесь теоретическое решение сравнительно просто (Кирш, 1898). Для полосы конечной ширины решение становится весьма сложным, и цифры, приведенные в таблице, получены экспериментально, с помощью оптического метода.
Нужно сказать, что знания коэффициента концентрации еще недостаточно для расчета детали на прочность. Изображенное на рис. 41, а распределение нормальных напряжений относится к чисто упругой стадии работы конструкции. Разрушению же, как правило, предшест
§31] КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ 69
вует появление пластических деформаций. Как мы увидим далее, при переменных нагрузках разрушение может происходить и в упругой области, однако для суждения о прочности далеко не достаточно знания одного только нормального напряжения в поперечном сечении, нужно знать все напряженное состояние в целом. Поэтому было бы неправильно принять за расчетное напряжение отах = ао0;. вопрос о расчете на прочность с учетом концентрации требует более подробного исследования и будет нами рассмотрен в главе XVII.
Для пластических материалов вопрос о прочности в условиях концентрации напряжений также далеко не прост. Если разрушению предшествует значительная пластическая деформация в тех местах, где напряжения по расчету особенно велики, то материал перейдет в пластическое состояние, образуются пластические зоны. Напряженное состояние будет пространственным, сложным; для его изучения нужно решать пространственную задачу теории пластичности, что удается лишь в немногих случаях. Экспериментальные' методы определения напряжений в пластической области весьма сложны, и соответствующие измерения крайне немногочисленны. Таким образом, первая трудность состоит в нахождении величин напряжений при переходе за предел упругости. Вторая трудность заключается в установлении критерия прочности при сложном пластическом напряженном состоянии. Мы вернемся к этим вопросам в главе XVII, предварительно рассмотрев общую теорию напряженного состояния и общие законы пластичности, а пока ограничимся грубой трактовкой вопроса на базе элементарных представлений.
Пренебрежем касательными напряжениями, напряжениями в плоскостях, параллельных оси стержня, и будем считать напряженное состояние одноосным. Если в каждой точке сечения действуют лишь нормальные напряжения, то пластическое состояние наступает тогда, когда, это напряжение становится равным пределу текучести от. При идеальной пластичности напряжение не может сделаться больше чем ат, поэтому дальнейший рост силы сопровождается увеличением напряжений в части сечения, оставшейся упругой, а также ростом пластических зон, в которых напряжение постоянно и равно от. Эпюры распределения напряжений по сечению, соответствующие постепенно возрастающим значениям силы, представлены на рис. 41.
На рис. 41, а изображено упругое распределение напряжений, на рис. 41, б и 41, в — упруго-пластическое с разными степенями развития пластической зоны. Наконец, на рис. 41, г представлено распределение напряжений в тот момент, когда все сечение перешло в пластическое состояние. Соответствующая сила является разрушающей, величина ее:
Здесь F—площадь ослабленного сечеиия.
70 РАСТЯЖЕНИЕ-СЖАТИЕ [ГЛ. II
К
Применяя принцип расчета по допускаемым нагрузкам, составим условие прочности следующим образом:
F • п п
Но 2з = Га1, следовательно, П u j»
Это обычная формула расчета на прочность, концентрация напряжений в ней не отражена. Таким образом, при расчете на прочность стержней из пластического материала, находящихся под действием статических нагрузок, концентрацию напряжений во внимание не принимают.
§ 32. Нелинейные задачи на растяжение—сжатие. Принцип малости деформаций, положенный в основу при решении всех рассмотренных задач, используется два раза: 1) при составлении уравнений статики, которые пишутся для недеформированной системы, 2) при построении диаграммы перемещений. Поэтому как уравнения статики, так и те уравнения, которые получаются из условий совместности деформаций, линейны относительно неизвестных усилий или напряжений. Вследствие этого усилия в отдельных стержнях всегда линейно выражаются через внешние силы и перемещения узлов суть также линейные функции внеш-I I j» них сил- Отсюда следует, что
‘ при вычислении перемещений от нескольких сил следует вычислять их от каждой силы отдельно, а затем складывать.
Можно, однако, указать примеры, когда принцип малости деформаций неприменим и задача становится существенно нелинейной. Рассмотрим, например, изображенную на рис. 42 систему из двух стержней, соединенных шарниром и образующих между собой угол, равнйй л. Составить уравнения статики для недеформированной системы нельзя, поэтому мы вынуждены предположить, что узел переместился на величину а, стержни наклонились на угол а, так что tga=-j-. Сравнение статики, составленное для деформированной будет 2Nsl„a_p=0. (32.1)
Перемещение и перпендикулярно оси стержня, однако пренебречь удлинением стержня нельзя; нужно считать, что
—1V
cos a
§ 32] НЕЛИНЕЙНЫЕ ЗАДАЧИ НА РАСТЯЖЕНИЕ----СЖАТИЕ 71
Отсюда по закону Гука
cos а
(32.2)
Исключив из (32.1) и (32.2) усилие N, найдем а как функцию Р. Считая, что угол а мал, хотя и не настолько, чтобы пренебречь его квадратом, положим:
, а2 sin а а, cos а 5= 1 — у.
Тогда из (32.1) и (32.2)
2Ма —Р=0 и N——EF.
Отсюда
(32.3)
Зависимость перемещения от силы оказывается резко нелинейной; при малых перемещениях сопротивление системы, ее жесткость, весьма мала, с увеличением деформации жесткость возрастает.
ГЛАВА III
СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
§ 33. Напряжения на косых площадках при растяжении. В этой главе мы будем изучать общую теорию напряженного состояния и общие зависимости между напряжениями и деформациями в упругих телах, а также введем некоторые понятия, которые понадобятся в дальнейшем при изучении свойств тел пластических. Систематическое изложе
ние этих вопросов дается в курсах теории упругости и пластичности, мы же изберем путь переходаотпростейших типов напряженных состояний к более слож-
Рис. 43.
ным и ограничимся рассмотрением только тех свойств напряженного состояния, которые понадобятся, нам в дальнейшем.
Рассмотрим более подробно напряженное состояние при простом растяжении. Основное предположение здесь состоит в том, что в поперечных сечениях растянутого стержня существуют только равномерно распределенные нормальные напряжения, тогда как в продольных сечениях напряжения отсутствуют. Рассечем стержень плоскостью, наклонной по отношению к его оси (рис. 43). Пусть п — единичный вектор нормали к плоскости се
чения. Обозначим через а угол между вектором я и осью стержня х. Отбросим верхнюю часть стержня и
рассмотрим равновесие нижней, приложив в сечении равномерно распределенные усилия, мерой которых являются нормальное и касательное напряжения а и т. Величины этих напряжений найдутся из условий равновесия оставшейся нижней части стержня. Прежде чем составлять эти условия, нам необходимо установить правило знаков, которое позволило бы фиксировать направления этих напряжений. Для нормальных напряжений такое правило уже было установлено:
нормальное напряжение считается положительным, если оно растягивающее и соответствующий вектор направляется по внешней нор
§ 33] НАПРЯЖЕНИЯ НА КОСЫХ ПЛОЩАДКАХ ПРИ РАСТЯЖЕНИИ 73
мали к рассматриваемой части тела. Для касательных напряжений мы установим совершенно условное правило знаков, а именно будем считать т положительным, если вектор касательного напряжения образует правую систему с вектором внешней по отношению к рассматриваемому объему нормали к площадке. Иначе говоря, положительное направление т устанавливается пр оси т] вспомогательной системы координат £т], ось £ которой направляется по внешней нормали. Если площадь поперечного сечения стержня есть F, то площадь косого сечения
F
п cos а
Составим уравнения равновесия для отрезанной части в проекциях на оси £ и т]. Получим:
onF„ — aFcosa = 0, TnFn-]-or^sin_a = 0.
Отсюда
a„ == a cos* а, а . о хп =— a sin ее cos ее = —<г5|П
На рис. 43 напряжения т„ показаны отрицательными, при составлении уравнений равновесия мы считали их положительными, то есть направленными по оси т], и получили в ответе знак минус.
Отметим некоторые свойства напряженного состояния при растяжении, вытекающие из этих формул:
. 1) На двух взаимно перпендикулярных площадках сумма нормальных напряжений постоянна. Действительно, на площадке с нормалью я', образующей угол у-]~а с осью х,
о„’ = a sin’ а.
Следовательно,
оп + оП' = о. ч
2) На перпендикулярных площадках касательные напряжения равны по величине и противоположны по знаку. Действительно, заме-
. я I
няя а в формуле для тя через y-f-a, получим:
тп, = у sin 2a = — т„.
3) Касательное напряжение достигает максимума в сеченни, составляющем угол 45° с осью. Это напряжение
__а
^шах — ~2 ’
74
СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
[гл. Ill
§ 34. Напряжения при двухосном растяжении. Предположим теперь, что пластинка растягивается по двум взаимно перпендикулярным направлениям, принятым за направления осей х и у (рис. 44, а). На площадке, перпендикулярной оси х, действует нормальное напряжение о,, на площадке, перпендикулярной оси у,— нормальное напряжение os. На косой площадке, нормаль к которой образует
угол а с осью х, имеются напряжения оп и т„ (рис. 44, б), каждое из которых можно представить как состоящее из двух слагаемых, происходящих соответственно от о, и <js. Те части напряжений, которые происходят от о,, определяются по формулам предыдущего параграфа, те, которые соответствуют напряжению о„—по этим же формулам с заменой о, на о, и а на 270°Заметив, что
sin (270° -]- а) = — cos а,
cos (270° а) = sin а, найдем:
а„ = о, cos* а -}- ад sin* а, (34.1)
тя = — °* ~ sin 2а. (34.2)
Формулу для сп удобно писать так:
Zl±£?4-21JZ£«cos 2а.
Отметим для двухосного напряженного состояния те же свойства, которые были отмечены для простого растяжения, а именно:
1) На перпендикулярных площадках сумма нормальных напряжений постоянна:
GB+G»'=oi+°r
2) Касательные напряжения на перпендикулярных площадках равны по величине и противоположны по знаку:
тя— ГП’.
3) Касательное напряжение достигает максимума в сечении, составляющем угол 45° с осями, причем
Tmax =: ~2 I G1 Ga Ь
§ 35. Круговая диаграмма Мора. Определение напряжений в косых площадках по формулам можно заменить простым графическим построением, которое предложил О. Мор (1882). Возьмем
§ 35]
КРУГОВАЯ ДИАГРАММА МОРА
75
две перпендикулярные оси, назовем одну из них осью а, другую осью т (рис. 45)*. Напряженное состояние на любой площадке с нор-малью я, заданное величинами напряжений о„ и т„, изображается точкой в плоскости о — г. Будем обозначать эту точку буквой л, так же как и нормаль к площадке. При переходе от одной площадки
к другой, то есть при изменении угла а, точка, изображающая напряженное состояние в плоскости о — т, перемещается, описывая замкнутую кривую. Формулы
о„ cos 2а,
О'® л =-----~2—1 sin 2а
представляют параметрическое уравнение этой кривой. Легко убедиться, что это окружность. Для построения ее следует отметить
на оси а две точки: точку х с абсциссой а, и точку у с абсциссой о,. На отрезке ху как на диаметре строится окружность. Центр ее о, 4-о,
лежит на оси о, на расстоянии —1 от начала координат, а ра
диус равен q‘ 2 а—, то есть наибольшему касательному напряжению. Чтобы найти точку л на круге Мора, следует провести радиус под углом (—2а) к оси абсцисс, точка пересечения его с окружностью и будет точкой л. Обозначения концов горизонтального диаметра круга Мора буквами х и у не случайны и соответствуют общей системе обозначать точки на круговой диаграмме теми же буквами, что нормали к площадкам. На площадке, перпендикулярной оси х, нормальное напряжение равно а„ а касательное равно нулю, как раз такие координаты имеет точка х на диаграмме Мора. Сравнивая рис. 44, а и рис. 45, мы можем подметить простое правило, позволяющее всегда легко установить соответствие между сечениями рассматриваемого тела и точками круговой диаграммы, а именно: дуговое расстояние между точками, изображающими напряженное состояние, измеряется удвоенным углом между нормалями к соответствующим площадкам, при этом направления отсчета углов между нормалями и на круговой диаграмме противоположны. Площадке, перпендикулярной к данной, соответствует диаметрально противоположная точка на круговой диаграмме, точка л' на рис. 45.
Перечисленные в конце предыдущего параграфа свойства напряженного состояния при двухосном растяжении становятся теперь вполне очевидными. Действительно, точки лил' имеют одинаковые по величине л противоположные по знаку ординаты, полусумма их
76
СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
[ГЛ. Ill
абсцисс равна отрезку ОС, то есть — ф °-, наибольшее касательное &
напряжение равно радиусу круга, то есть —, соответствующая точка находится на конце вертикального диаметра, расстояние ее от точки х составляет 90 дуговых градусов, следовательно, угол между площадками равен 45°.
§ 36. Общий случай плоского напряженного состояния. Общий случай плоского напряженного состояния реализуется тогда, когда все плоскости, параллельные некоторой, свободны от напряжений. Примем одну из этих плоскостей за плоскость хОу, направим оси х и у произвольным образом в этой плоскости. Рассмотрим теперь призму, грани которой параллельны плоскостям уОх и zOx; действующие на эти грани напряжения обозначим так, как показано на
рис. чо, а. для равновесия призмы необходимо, чтобы было т = — т'.
Это следует из уравнения моментов относительно оси г. Если измерения призмы суть а, b и с, то площадь грани, перпендикулярной оси х, есть Ьс, касательная сила (tbc), плечо а, таким образом, момент равен rbca; аналогично момент касательной силы, приложенной к грани, перпендикулярной оси у, есть — x'acb. Приравнивая эти моменты, находим:
т' = — т.
Рассмотренный случай представляет собою самый общий случай плоского напряженного состояния, величины ох, оу и т называются компонентами тензора напряжений.
Напряженное состояние, изображенное иа рис. 46, а, является* однородным напряженным состоянием, если, как это принято, все напряжения распределены равномерно по граням и одинаковы на противоположных гранях. В общем случае компоненты тензора напряжений меняются от точки к точке, то есть являются функциями координат х и у. Следующие ниже выводы относятся Также и к не
§ 36] ОБЩИЙ СЛУЧАЙ ПЛОСКОГО НАПРЯЖЕННОГО состояния 77
однородному напряженному состоянию, если считать размеры а и b бесконечно малыми.
Докажем следующие теоремы:
1. Произвольное плоское напряженное состояние приводится к растяжению — сжатию по двум взаимно перпендикулярным направлениям.
II. Задание компонент тензора напряжений стя, оу и т позволяет найти вектор напряжения на любой площадке, а следовательно, полностью определяет напряженное состояние в точке.
Для доказательства первой теоремы заметим, что если напряженное состояние, изображенное на рис. 46, а, является результатом растяжения — сжатия с напряжениями ст, и ст, на площадках, перпендикулярных некоторым осям 1 и 2, то по формулам, (34.2) и (34.3), отождествляя направление оси х с направлением п и оси у с направлением в', имеем:
CT*=£dp + 2^pcos2a, (36.1)
°y = £4£i-£Li£icos2a’ (36.2)
т = sin 2a. (36.3)
Применяя формулы (34.2), мы заменили в них а через (—а), так как направления отсчета углов на рис. 44 и 46 оказываются противоположными.
Будем считать в этих уравнениях ах, сту, т известными, а ст,, ст„ а — искомыми величинами. Возможность решения написанной системы уравнений относительно ст,, ст, и а доказывает первую теорему. Складывая два первых уравнения, найдем:
ст, + ст, = стя + сту. (36.4)
Вычтем теперь из первого уравнения второе:
стя — Сту = (ст, — ст,) cos 2a. (36.5)
Возведем в квадрат последнее равенство, а также уравнение (36,3) и сложим. Получим:
ст. — ст, = ± /(ст, —CT/4-4T*. (36.6)
Выбор знака в ‘последнем равенстве произволен, поэтому мы условимся принимать за ст, наибольшее напряжение, за ст, — наименьшее. Тогда перед радикалом нужно удержать знак плюс. Из (36.4) и (36.6) следует:
ст.,. = ?^±4/(стя-ст/ + 4т‘. (36.7).
78 СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ [ГЛ. 111
Разделив (36.3) на (36.5), получим:
*е2“... = НЬ-- <36-8>
°х °у
Через а, обозначен угол между осью х и направлением а„ через а,—угол между осью х и направлением at. Уравнение (36.8) дает два решения, разнящиеся. между собою на 90°.
Вывод этих формул может быть заменен графическим построением диаграммы Мора (рис. 46, б). Нанесем в плоскости о —т точку х с координатами оя, т и точку у с координатами оу, —т. Соединяющая их прямая должна быть диаметром круга, следовательно, точка С есть его центр. Координата центра:
Для вычисления радиуса R рассмотрим треугольник, заштрихованный на чертеже. Катеты его: —* 2 и т. Следовательно,
7? = 1/(ал-ау)‘ + 4тг.
Точки 1 и 2 соответствуют площадкам, свободным от касательных напряжений; соответствующие нормальные напряжения суть
ОС -4— Rt
что совпадает с формулой (36.7).
Чтобы найти направление оси 1, воспользуемся правилом предыдущего параграфа. Кратчайший путь от точки х к точке 1 на круге Мора измеряется дугой 2а в направлении по часовой стрелке, поэтому для нахождения оси 1 следует отложить угол а против часовой стрелки от оси х. Это и сделано на рис. 46, а.
Формула (36.8) получается из рассмотрения заштрихованного треугольника. Недостаток ее состоит в том, что, зная решение уравнения (36.8), мы не имеем возможности различить а> и а,. Поэтому удобнее следующие формулы, вытекающие из рассмотрения треугольников 2хМ или х1М:
Нормальные напряжения от, и о, называются главными напряжениями, соответствующие направления 1 и 2 — главными направлениями.
Заметим, что среди нормальных напряжений на всех площадках, параллельных оси г, напряжения от, и о, являются соответственно наибольшим и наименьшим. Наибольшее касательное напряжение действует на площадках, составляющих угол 45° с главными осями, а,— а, и равно —=, или, что то же,
=4 Ж-О/ + 4ТГ- (36-10)
§ 38] ПРОСТРАНСТВЕННОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
79
§ 37. Определение напряжений на произвольной площадке. Доказав существование главных осей, мы тем самым показали, что, зная ох, оу и т, можно вычислить напряжение на любой площадке, нормаль к которой составляет угол 0 с осью х. Действительно, для этого достаточно найти главные оси и главные напряжения, а по ним, пользуясь диаграммой Мора или фор-мулами § 34, определить напряже- _______
ния на заданной площадке.
Удобнее, однако, иметь готовые I *г'С\~-2а.
формулы, выражающие а„ и т„ о I * б
через оя, и т. Для вывода этих Г \ /
формул воспользуемся круговой \
диаграммой (рис. 47). Точка п на \.
диаграмме найдется, если отложить от точки х дугу 20 в направле- Рис. 47.
нии, противоположном отсчету угла0 между осями хил. Опустим из точки л перпендикуляр на радиус Сх; в треугольнике СпК катет пК есть R sin 20, катет СК есть R cos 20. , Абсцисса и ордината точки л суть а„ и т„ соответственно; эти отрезки суть проекции ломаной ОСКп на горизонталь и вертикаль, а именно:
а„ — ОС 4~ СК cos 2а, -]- Кп sin 2а,,
т„ — CTCsin 2а, — Кп cos 2а,, или
<т„ = ОС4~ 7? cos 20 cos 2а, 4~ 7? sin 20 sin 2а,, т„ = R cos 20 sin 2а, — R sin 20 cos 2а,. Так как
— &х “I" — (У.,
ОС=—s— , R cos 2a, = —5? R sin 2a. = t,
то получаем искомые формулы: ex , <зх — o\, o„ = —2”^ 4-----------------------2“^ COS 20 4-T sin 20, (37.1)
t„ =-----—- sin 20 4-1 cos 20. (37.2)
Эти формулы можно использовать как формулы преобразования компонент напряжения к новым осям. Предположим, что новая ось х' направлена по л, тогда ап^=ох>, т„ = т'. Осталось определить оу>, для этого в формуле для о„ вместо 0 нужно положить 04~у •
§ 38. Пространственное напряженное состояние. Плоское напряженное состояние наиболее часто встречается на практике и поэтому представляет наибольший интерес для приложений. Однако
80
СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
[ГЛ. III
это всего лишь частный случай, и нам необходимо рассмотреть общий случай, когда нельзя заранее указать свободные от напряжений плоскости. Исследование общего случая, с другой стороны, дополнит и наши знания о плоском напряженном состоянии, потому что там существуют напряжения на площадках, пересекающих ось z под углом, отличным от прямого. Для нахождения этих напряжений
изложенная выше теория непригодна.
Рассмотрим мысленно вырезанный из напряженного тела парал-
лелепипед, ребра которого ориентированы по координатным осям.
Измерения его могут быть конечны, если напряженное состояние
однородно, и бесконечно малы, если оно неоднородно.
Вектор напряжения, действующий на площадке с нормалью х, представим следующим образом:
г= oxi -|- tXyJ "I-
Аналогично
Составляющие этих трех векторов изображены на рис. 48. Как Рис. 48. видно, Ох, оу и ог суть нормаль-
ные напряжения, тХу, ... — касательные. Первый индекс в обозначении касательного напряжения указывает на ту площадку, к которой оно приложено. Площадка обозначается той же буквой, что и нормаль к площадке. Второй индекс —
это направление касательного напряжения по соответствующей оси
координат. На противоположных гранях, не видных на чертеже,
действуют точно такие же напряжения, но направленные в противоположные стороны. Составляя условия равенства нулю моментов относительно осей координат, найдем, чтотяу = туя, гуг = ггу, ггх = гхг. Это есть следствие закона парности касательных напряжений (§ 10). Совокупность шести величин, образующих симметричную матрицу, называется тензором напряжений:
(®Х> ^Xyt ^хг ^ух, °у’ Two ^zyt &Z
Величины 0Х, ... суть компоненты тензора в осях х, у, г.
Покажем, что задание шести компонент тензора напряжений полностью определяет напряженное состояние, то есть позволяет вычислить вектор напряжения на любой площадке. Пусть площадка задана нормалью п. Рассмотрим тетраэдр, ограниченный площадкой
§ 39]
ГЛАВНЫЕ НАПРЯЖЕНИЯ
81
и тремя координатными плоскостями. Если площадь грани, имеющей нормаль я, есть F (рис. 49), то грань, принадлежащая плоскости yOz, имеет площадь FX = F (ni) = Fnx. Здесь пх — косинус угла между вектором п и осью х. Аналогично
Fy = Fny, Fz = Fnt.
На площадку п действует напряжение
S„ = Xni + YJ+ Znk. /
Сила, действующая на эту площадку, / j
есть SnF. Аналогично на другие грани / \
тетраэдра действуют силы L' \ \
-SXF„ -SyFr — SZFZ. ----------
Приравнивая сумму всех сил нулю и <₽
сокращая F, получим: *
4"fyij,(38.1)
Это векторное равенство эквивалентно трем скалярным:
== °хПх 4“ ХхуПу 4" ХхгПг<
Уп = хухПх + оупу-\-гугпг, (38.2)
^zx^x + "^гуПу 4“ ^г^г'
Таким образом, мы определили вектор напряжения на произвольной площадке, что и доказывает высказанное утверждение.
§ 39. Главные напряжения. Поставим теперь такую задачу: нельзя ли найти площадку, на которую действуют только нормальные напряжения? Предположим, что такая площадка существует, и пусть это будет площадка с нормалью я, причем напряжение на ней а (рис. 49). Так как направление 9 совпадает с направлением л, то
= Уп = <му> Zn = on2.
Подставляя эти выражения в формулы (38.2), получим:
пх (ах — а) 4- пухху 4- nzxxz = О, ПхХух + ПУ^У~ а)4-Лг^г=0. (39.1)
nx^zx 4- ПуХгу 4- пг (°z — 0 = 0.
Это система трех линейных однородных уравнений относительно трех неизвестных направляющих косинусов пх, пу и пг. Нетривиальное решение существует лишь тогда, когда детерминант системы равен нулю. Отсюда получаем кубическое уравнение для а:
0 "^ху
Хух ву~~ &
T-zx xzy
Xxz Xyz а,-а
(39.2)
82
СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
[ГЛ. 111
В алгебре доказывается, что все три корня подобного уравнения всегда действительны, следовательно, существуют три площадки, свободные от касательных напряжений. Мы не будем ссылаться на эту теорему, а пойдем обходным путем. Заметим прежде всего, что уравнение (39.2) имеет, по крайней мере один действительный корень (комплексных корней может быть только пара). Обозначив этот корень через а„ подставим величину а, в уравнении (39.1) и разре-
шим их относительно пх, пу и пг. Система делается определенной вследствие дополнительного условия
и мы находим направление нормали к площадке, на которой действует только нормальное напряжение о,.
Рассмотрим теперь какой-либо прямоугольный параллелепипед, вырезанный из материала
Рнс. 50.
так, что одно из измерений его направлено по оси 3 (рнс. 50). Грани, перпендикулярные осям £ и т], находятся под действием напряжений, параллельных плоскости |т]. Это следует из закона парности
касательных напряжений: поскольку плоскость, перпендикулярная оси 3, свободна от касательных напряжений, параллельные этой оси плоскости не имеют составляющих касательных напряжений по направлению оси 3. Таким образом, получается плоское напряженное состояние с компонентами ог, и т (на чертеже не показаны), на которое накладывается растяжение илн сжатие в направлении оси 3. Ясно, что напряжение 6, не оказывает никакого влияния на напряжения в площадках, параллельных оси 3, поэтому,
применяя теорию плоского напряженного состояния, всегда можно найти такие две взаимно перпендикулярные площадки, на которых касательные напряжения отсутствуют. Нормальные напряжения на них обозначим а, и а,, направления нормалей примем за оси 1 и 2.
Итак, существуют три взаимно перпендикулярные оси, называемые главными осями тензора напряжений, обладающие тем свойством, что на перпендикулярных к ним площадках действуют только нормальные напряжения, так называемые главные напряжения. В тех задачах сопротивления материалов, где речь идет е трехмерном напряженном состоянии, главные оси обычно известны заранее.
Нумерация главных осей и главных напряжений может быть произвольной; в дальнейшем мы условимся для удобства нумеровать
§ 40] ГЛАВНЫЕ КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ 83
их так, чтобы было
1 ж з
Если взять за оси координат главные оси, то формулы для составляющих вектора напряжения иа площадке с нормалью п примут очень простой вид:
*П = °Л. = Л = (39.3)
Здесь п1, пг, nt — направляющие косинусы нормали- к площадке по отношению к главным осям.
Нормальное напряжение на площадке находится проектированием вектора £ на направление нормали:
a==zS» = ainJ-j-at«’-j-atn*. (39.4)
Величина касательного напряжения на той же площадке:
т = ]/$г —ог. (39.5)
Легко убедиться в том, что главные напряжения представляют собою те экстремальные значения, которые принимает нормальное напряжение при всевозможных поворотах площадки. Из формулы (39.4) следует:
osCo, и
Знак равенства при этом возможен только тогда, когда л1=1, nt = nt = 0 либо л1=ла = 0, п, — 1.
§ 40. Главные касательные напряжения. Поставим теперь задачей разыскание тех площадок, на которых касательные напряжения принимают экстремальные значения. По формуле (39.5) получим: тг = а’ (я* — л‘) 4- а’ (л’ — п2) -|- а’ (п3 — пз) —
— 20,0^’п2 — 2ata,n2 п2 — За^л’ я’. (40.1)
Речь идет об отыскании экстремума функции х1 в зависимости от направляющих косинусов л,, л, и nt. Последние связаны известным соотношением:
nlt -j- л, — 1=0.
Таким образом, нужно 'решать задачу отыскания экстремума с дополнительным условием. Напомним, что если требуется найти экстремум функции F(x, у, г) при дополнительном условии Ф(х, у, z) = 0, то составляют уравнения:
«F+l^=0, £+1£=0, dx 1 дх ду ' ду ’ дг • дг
Присоединяя сюда дополнительное условие, получим систему четырех уравнений для нахождения четырех неизвестных х, у, z и Л. В нашем
84 СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ [ГЛ. Ill
случае роль функции F играет т’, тогда как Ф(пп nv п,) = = nJ-J-nJ-J-nJ—1. Дифференцируя т* по и,, получим:
£ = 2atnt [(1 - 2nJ) а, - 2nJ a, - 2nJ a,].
Обращаясь к формуле (39.4), перепишем это выражение так:
Л-г1
g- = 2a1nI(aI-2a).
Продифференцируем теперь дополнительное условие. Получим:
Производные по п2 и п, выразятся совершенно аналогично. В результате мы приходим к такой системе уравнений:
n,[aj— 2ata-j-X] = 0,
n,[aj— 2a,a-j-X] = 0, (40.2)
n, [aj — 2a ,a -f-1] = 0.
Здесь
a = atnj -J- a,nj -J- a,nJ.
Очевидное решение системы (40.2) есть
n, = 1, nt = n, = 0.
При этом a = an из первого уравнения l = aj, два другие удовлетворяются. Точно так же можно принять пх=1 или л,= 1. Эти решения не представляют для нас интереса; найденные площадки суть главные площадки, иа них касательное напряжение равно нулю, а для неотрицательной величины т* нуль есть минимальное значение^
Предположим теперь, что п, и п, отличны от нуля, сократим эти множители в первых двух уравнениях и вычтем одно из другого. Получим:
aj — aj — 2(ax — a1)a=0.
Отсюда
a=a±s.
Следовательно, nJ = nJ =-£- и n, = 0. Третье уравнение при этом выполняется. Соответствующая площадка проходит через ось z и делит угол между плоскостями 13 и 23 пополам. По формуле (40.1) найдем, что при Этом
Совершенно аналогичным образом получаем для т экстремальные значения ± —* и ± -=-=—1 на площадках, делящих пополам углы
Л л
§ 41] ОКТАЭДРИЧЕСКОЕ НАПРЯЖЕНИЕ 85-
между плоскостями 21 и 31, 82 и 12. Назовем экстремальные значения касательного напряжения главными касательными напряжениями^
Очевидно, что т„ является наибольшим касательным напряжением^ если о, о, а,.
§ 41. Октаэдрическое напряжение. В теории пластичности наряду с главными плоскостями и плоскостями главных касательных напряжений существенное значение имеют плоскости, пересекающие главные оси под одинаковыми углами. Таких плоскостей можно провести восемь; для наглядности мы проводим их не через начало координат, а так, как изображено на рис. 51, чтобы они образовали октаэдр. Поэтому и сами плоскости будем называть октаэдрическими. Направляющие косинусы нормали к передней грани октаэдра суть 1 п, ==п. = п. = —=.
1 * ’ уз
Выпишем вектор напряжения на этой грани:
S = 77= [°А + + СТА1-
г &
Здесь elt ег и е, — единичные векторы главных осей. Нормальное напряжение:
а=Sn=у (а, + а, + а,) =р.
(41.1)
Среднее арифметическое из глав- Рис. 51.
ных напряжений р называют гидростатическим напряжением. Мы нашли, что на октаэдрической площадке нормальное напряжение равно гидростатическому. Перейдем к вычислению касательного напряжения на октаэдрической площадке. Воспользуемся формулой (39.5), в которой нужно принять:
S* = у [ст? 4" °»]»
о*[oj 4" 4" °* 4" %aioi 4" 4" 2a»ai]‘
Подставляя в (39.5), получим:
т*=4 [ст? 4- ст? 4- — а, о, — а,а, — ст2а,] ==
=4[(<\ — °.)* + (°. — °.)* 4- (°. —
86 СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ [ГЛ. III
Величина
т0 =-§- у (о, — о,)* + (а, — а,)* + (а, — а,)* (41.2)
называется октаэдрическим касательным напряжением или интенсивностью касательных напряжений. С точностью до множителя это выражение представляет собой среднее квадратичное из трех главных касательных напряжений.
Ввиду той фундаментальной роли, которую играет величина октаэдрического напряжения для теории пластичности, естественно попытаться придать ей некоторую физически более наглядную трактовку. В §49 будет дана энергетическая интерпретация этой величины, сейчас же мы приведем истолкование, принадлежащее В. В. Новожилову.
Вырежем мысленно в напряженном теле сферу бесконечно малого радиуса и вычислим среднее квадратичное значение касательного напряжения на поверхности сферы:
Здесь R— радиус сферы, т — касательное напряжение, определяемое формулой (40.1), da— элемент поверхности сферы; интеграл распространен на эту поверхность. Если х, у, z — координаты точек сферы, то направляющие косинусы нормали к ее поверхности
х у z
При интегрировании по поверхности нам встретятся интегралы двух типов:
п 4^-.у(п:-»:)</«>=4-^р*(/?*-х*)^=2/,
Но J x*zlda = J x'y'da для поверхности сферы, поэтому второй интеграл
По формуле (41.3) получим:
т’р = / [(о, — о,)* + (а, — а,)* + (а, — а,)*].
Отсюда
т ——Ьт °-
Таким образом, октаэдрическое касательное напряжение с точностью до множителя равно среднему квадратичному значению касательного
§ 42]
ЗАКОН ГУКА ДЛЯ ГЛАВНЫХ ОСЕЙ
87
напряжения на поверхности бесконечно малой сферы. Вычислять величину множителя пропорциональности, то есть находить значение интеграла I, не имеет смысла, хотя это просто сделать.
§ 42. Закон Гука для главных осей. Перейдем теперь к установлению тех соотношений, которые связывают напряжения и упругие деформации в сложном напряженном состоянии. Ограничимся рас
смотрением изотропных материалов, как и ранее, для растяжения или сжатия. Рассмотрим элемент, вырезанный из тела и имеющий форму параллелепипеда, ребра которого направлены по главным осям (рнс. 52). Направленное по главной оси 7 ребро, длина которого до приложения нагрузки была а, получает удлинение А«, следовательно, относительная деформация в направлении оси 1 будет Да . Д&
е, = — . Аналогично е, == — , 1 а * о ’
ДС гт
8, = —. Подсчитаем удлинение 8t,
пользуясь законом Гука для продольной и поперечной деформации, а также принципом наложения, состоящим в том, что вследствие линейности закона упругости деформации от действия различных систем сйл можно определять по отдельности и потом складывать. Представим удлинение 8, как сумму трех удлинений:
8j 8i —J— 8] —J— 8] .
Здесь 8t — деформация от напряжения о,, 8t — от о2 и 8t —ото,. Напряжение действует в том же направлении, в каком ищется удлинение, поэтому , а
81=^-
Направление 7 по отношению к а, и а, является поперечным, поэтому при вычислении 8t и 8t мы воспользуемся законом Гука для поперечной деформации:
" va, va.
8. 81 =—7Г-
Складывая, получим:
81=£-[<Ъ — v(o, — а,)],
8. = ^[о* — v(a, — а,)], (42.1)
8,=Jr[a, —v(at —а,)].
38
СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
[ГЛ. Ш
Две последние формулы написаны по аналогии, получают их точно таким же путем, как и первую. Формулы (42.1) представляют собою закон Гука для пространственного напряженного состояния.
§ 43. Изменение объема при упругой деформации. Упругая деформация вообще сопровождается изменением объема. Так, объем изображенного на рис. 52 параллелепипеда до деформации есть
V=abc.
В результате деформации ребра параллелепипеда стали Ъ-\-&Ь, с Ас и новый объем У-j-AV. При этом
V-f- А V— (а Да) (Ь 4~ Д/>) (с 4~ Ас).
Разделим левую и правую части этого уравнения на V=abc и перенесем единицу из левой части в правую. Получим:
^ = (l + 8l)(l + 8,)(l + e,)-l. (43.1)
Это — формула для относительного изменения объема, выражающая указанное изменение через относительные удлинения в направлениях главных осей, так называемые главные деформации. Поскольку деформации малы по сравнению с единицей, то, выполняя перемножение трех скобок в правой части (43.1), мы сохраним только первые степени деформаций, отбросив их произведения, члены второго и третьего порядка малости. Таким образом, для малых деформаций ^ = 8,4-е, 4-е,. (43.2)'
Желая связать относительное изменение объема с напряжениями, сложим три уравнения (42.1).-Получим:
в, + в, 4" в, = (о. 4" °. + °.) (1 — 2У)-
Вспоминая обозначение
°i + °» + °. = 3P.
напишем:
Величина
(43.3) •
называется модулем объемной деформации. Формулу для относительного изменения объема можно переписать так:
ДУ_ р_ V ~к •
(43.4)
чистый сдвиг
8&
§ 44]
Заметим, что если v=X),5, то К=со. Такой материал несжимаем, объем его при деформации не меняется. Величина модуля объемной деформации всегда положительна, поэтому коэффициент Пуассона не может быть больше половины.
Существование материала, для которого v>-^- , противоречило бы закону сохранения энергии. Действительно, представим себе цилиндрический сосуд с поршнем, куда налита несжимаемая жидкость 1 ' и положен кусок материала, для которого v -% и, следовательно, К отрицательно. Прикладывая силу к поршню, мы создаем в теле равномерное сжатие или отрицательные напряжения; по формуле (43.4) изменение объема будет положительно, объем увеличится и поршень поднимется, произведя отрицательную работу.
§ 44. Чистый сдвиг. Прямоугольный параллелепипед, на грани которого действуют касательные напряжения, перекашивается. Первоначально прямые углы между гранями искажаются, как показано на рис. 53. Та величина, на которую изменился первоначально прямой угол между граням^, называется углом сдвига или просто сдвигом и- является мерой деформации, вызванной касательными напряжениями. Величина касательного напряжения связана с соответствующим сдвигом соотношением
Y=^- (44.1)
Формула (44.1) по структуре вполне подобна формуле закона Гука для растяжения; выражаемый этой формулой закон носит название закона Гука при сдвиге. Величина
напряжения, называется модулем сдвига. Как оказывается, закон Гука при сдвиге не является выражением нового экспериментального факта; формула (44.1) вытекает из закона Гука для растяжения, и величина G выражается через ранее введенные упругие постоянные Е и v. Поэтому, если для растяжения, формулы закона Гука были выражением опытной зависимости, для сдвига формулу (44.1) можно вывести.
Чистым сдвигом называется такое плоское напряженное состояние, когда на грани элемента действуют только касательные напряжения (рис. 53). Как мы знаем, всякое напряженное состояние приводится к растяжению — сжатию по взаимно перпендикулярным направлениям. Положим ох = ау = 0, т^О. Тогда по формулам (46.7) и (46.8)
о, = —т, tg2aI2 = oc.
G, имеющая размерность
90
СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
[ГЛ. III
Итак, если осуществить плоское напряженное состояние, в кото-
ром главные напряжения равны по величине и противоположны по знаку, то элемент, стороны которого составляют углы по 45° с глав-
ными осями, будет находиться в условиях чистого сдвига.
Возьмем этот элемент в форме квадрата с диагональю 2а (рис. 54). Вследствие деформации квадрат превратится в ромб, изображенный на той же фигуре. Относительное удлинение вертикальной диагонали:
1 / , 1 + v
(°i —vo«) £ т-
Относительное укорочение горизонтальной диагонали:
(°.— va.) =—Чгт-
В треугольнике А'ОВ' катеты будут:
А'О = а(\-J- в,), ОВ'==а(1-j-в,).
Вычислим гипотенузу:
А’В' = = а]Л2( 1-1-8, H-в,-J-...).
Члены второго порядка малости под радикалом не написаны. Но 8,—[—8, = О, и, таким образом,
A'B’ = aV"2 =АВ
с точностью до величин порядка квадрата деформации. Итак, стороны элемента, находящегося в условиях чистого сдвига, не изменяют длины.
Если изменение первоначально прямого угла есть у, то угол при вершине А’ в треугольнике А'ОВ’ есть 45° -j- —. Тангенс этого угла равен отношению катетов:
tgf 45°-]-^W —
*4 Ч- 2 У АО а (1 -f-e2) *
Воспользуемся формулой для тангенса суммы двух углов. При этом, ввиду малости деформации сдвига, будем считать
й 2 2
§ 45] ДЕФОРМАЦИЯ ЭЛЕМЕНТА ОБЪЕМА В ОБЩЕМ СЛУЧАЕ 91
Получим:
С другой стороны,
Отсюда с точностью
Внесем в (44.2) Получим:
до малых высшего порядка
у-г. — г^ (44.2>
вместо 8, и в, найденные для них значения.
с
, найдем:
Сравнив это с (44.1)
Величина G не может быть отрицательной, так как в противном случае касательные усилия производили бы отрицательную работу. Поэтому J
Вспоминая первую оценку для V, полученную в предыдущем параграфе, имеем:
В действительности неизвестны материалы, для которых v отрицательно.
§ 45. Деформация элемента объема в общем случае. В самом общем случае, выделяя элементарный параллелепипед с ребрами, направленными по координатным осям, мы можем описать его деформацию следующим образом. Представим себе сначала, что ребра элемента получают относительные удлинения (или укорочения). Обозначим их соответственно с направлениями ребер ех, гу и в2. После этого происходят сдвиги, то есть изменение первоначально прямых двугранных углов между каждой парой координатных плоскостей. Изменение угла между плоскостью хОг и плоскостью yOz мы обозначим уху, аналогично определяются еще два сдвига, ууг и угх. В предыдущем параграфе было доказано, что чистый сдвиг не изменяет длин ребер, поэтому сдвиги у ууг и угх не влияют на удлинение ех, гу и е2. Следовательно, относительное изменение объема будет равно
. Др । ।
V^8* + 8J'т8»•
92
СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
[ГЛ. Ш
Совокупность шести величин: ех, еу, тензор деформации. Его записывают
2
1
2 Уф
1
1 2
Ьг, Yxy, Yyi и Y„ —Образует обычно следующим образом:
1 )
2 ^хг I
1 >.
2 Vy* |
ег ’
Порядок индексов в обозначении сдвигов безразличен, поэтому Уху=Уух, ••• Компонентами тензора являются не сами сдвиги, а половины сдвигов, при этом условии теория деформированного -состояния оказывается совершенно подобной теории напряженного состояния. Действительно, в плоском напряженном состоянии наибольшее касательное напряжение на площадке, наклоненной под углом 45* а, — а, к главным осям, равно тогда как сдвиг элемента, поверну-
того по отношению к главным направлениям на 45°, равен et — е, (формула (44.2)). Деформации от нормальных и от касательных напряжений определяются независимо, удлинения находятся по формулам (42.1) так, как если бы ох, оу и ог были главными напряжениями, сдвиги вычисляются по формуле (44.1). Таким образом, уравнения закона Гука для произвольных осей имеют следующий вид:
ex=s-g’[a*~v(o>' + o*)b
V(ax+«9b (45Л)
___1_
Yxy Q ____________________£ Yy* Q Xy» ___________________ 1 ’ Ysx Q ^гх‘
§ 46. Условие пластичности Треска — Сен-Венана. Как указывалось, мягкая сталь в условиях растяжения или сжатия при достижении напряжением величины от деформируется без изменения напряжения, причем величина деформации, если отвлечься от упрочнения, ограничивается только внешними связями. Условие текучести при растяжении или сжатии есть
|а|=ат. (46.1)
Тело, находящееся в сложном напряженном состоянии, тоже может быть переведено в состояние текучести, но в этом случае достиже
§ 46J УСЛОВИЕ ПЛАСТИЧНОСТИ ТРЕСКА---СЕН-ВЕНАНА 93
ние пластического состояния не определяется значением одного только напряжения, а зависит от тензора напряжений в целом. Отнесем тензор напряжений к главным осям и предположим, что существует функция /(а,, о4, о,) такая, что
/(<?» о», о,)<° в упругом состоянии и
/(Оп о». о,) = 0 в пластическом состоянии.
Для растяжения, когда действует только одно главное напряжение, /=о— от. Подобно тому как для идеально пластического материала о не может быть больше, чем от, функция /(ot, <Уа, о,) не может быть больше нуля.
В следующей главе мы рассмотрим более подробно механизм пластической деформации металлов. Основной факт здесь состоит в том, что пластическая деформация каждого кристаллического зерна является сдвиговой, слои атомов скользят один относительно другого. Однако в реальном поликристаллическом металле кристаллические зерна расположены беспорядочно и переход от свойств единичного кристалла к свойствам поликристаллического металла затруднителен. Можно сказать только, что переход металла в пластическое состояние означает, чтр пластические сдвиги происходят во всех зернах или в подавляющем их большинстве. Представим себе теперь, что на то напряженное состояние, которое существует в теле, накладывается всестороннее растяжение или сжатие. Осуществить на опыте всестороннее растяжение, а тем более наложить его на заданное напряженное состояние оказывается невозможным; всестороннее сжатие, наоборот, реализуется довольно просто, для этого нужно нагружать образец в среде жидкости под высоким давлением. При этом все три главных напряжения изменяются на одну и ту же величину. Наибольшие касательные напряжения равны полуразностям главных напряжений, поэтому они не меняются от наложения всестороннего растяжения или сжатия, касательное напряжение на любой площадке также остается неизменным. А так как сдвиговая деформация определяется касательными напряжениями, то естественно ожидать, что условие пластичности не зависит от добавления к тензору напряжений гидростатической составляющей. Это предположение хорошо подтверждается опытами (Карман, Бекер, Бриджмен и другие). При обсуждении этих и подобных им опытов необходимо иметь в виду, что пластическая деформация происходит путем сдвига, но разрушение может происходить путем отрыва. Поэтому обычное деление материалов на хрупкие и пластические оказывается условным. Так, Карйан и Бекер производили опыты над мрамором и песчаником. При обычных условиях испытания мрамор и песчаник хрупки, обладая низким сопротивлением отрыву, они разрушаются, не успев проявить
94 СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ [ГЛ. III
пластических свойств. Но если испытание образца из этих материалов производится в жидкости, находящейся под высоким давлением, они обнаруживают пластические свойства.
Горные породы, хрупкие в обычных условиях, находясь в недрах земли под огромным давлением, медленно текут, получая прн этом весьма большие деформации; эти явления играют существенную роль в процессах горообразования.
Теперь мы можем сделать некоторые заключения о функции f(ot, ст2, ст,); эта функция не должна менять своего вида от того, что ст,, о, и ст, изменяются на одну и ту же величину, поэтому она должна зависеть от разностей главных напряжений, то есть иметь вид:
—<*.)> (о, —о,), (а, —а,)]-
Для доказательства этого утверждения предположим, что ст„ а, и а, получили одинаковые приращения q. Условия пластичности от этого не зависят, следовательно, функция
/(0,4-0, о24-0, 0,4-0)
не зависит от 0 и ее производная по 0 равна нулю. Вычисляя полную производную, получим:
df л df , df _Q da, ' да2 das
Ищем общий интеграл этого дифференциального уравнения с частными производными. По общему правилу составляем обыкновенные дифференциальные уравнения:
do,==do2 = do,.
Интегрируя три возможные комбинации, получим:
°, — о, = с„ ст2 —ст, = с„ ст, — ст2 = с,.
Общий интеграл уравнения с частными производными, как известно, есть произвольная функция от с,, с, и с,.
Достаточно считать, что / зависит не от трех разностей главных напряжений, а от двух, например с, и сг, так как с,=— с, — с2; однако мы сохраним приведенную форму записи вследствие того, что она симметрична.
Простейшее предположение состоит в том, что материал переходит в пластическое состояние тогда, когда наибольшее касательное напряжение достигает предельного значения k. Согласно этому, предположению в пластическом состоянии
= = (46.2)
Условие пластичности (46.2) было предложено Треска и принято Сен-Венаном, который положил его в основу созданной им теории пластичности. Ряд авторов, начиная с Треска, занялись опытной про-
§ 47] УСЛОВИЕ ПЛАСТИЧНОСТИ МИЗЕСА 95
верной этого условия и обнаружили его удовлетворительное соответствие данным опыта.
Применяя формулу (46.2) к растяжению, когда о,=от, о3 = 0, получим:
Поэтому условие (46.2) можно переписать так:
а,—о, = от. . (46.3)
Величина k представляет собою предел текучести при сдвиге. Опыты, произведенные при сверхвысоких давлениях, показали, что k меняется в зависимости от давления, а именно возрастает с повышением давления. Это увеличение пластической постоянной незначительно и становится заметным только при исключительно высоких давлениях; мы не будем принимать его во внимание.
§ 47. Условие пластичности Мизеса. При опытной проверке условия пластичности Сен-Венана были обнаружены систематические отклонения, которые нельзя объяснить случайностью. Вопрос об опытной проверке условий пластичности будет подробно освещен в § 80 гл. VI, поэтому сейчас мы не останавливаемся на технике соответствующих экспериментов. Наиболее простая проверка состоит в том, чтобы сравнить предел текучести при растяжении с пределом текучести при чистом сдвиге. Согласно условию Треска — Сен-Веиана, как мы уже видели, предел текучести при сдвиге, равный fe, представляет собою половину предела текучести при растяжении:
Однако многочисленные опыты показали, что отношение тт/ат больше, чем это отношение колеблется от 0,55 до 0,60.
Согласно условию Треска, среднее главное напряжение никак не влияет на достижение состояния текучести. Для проверки этого факта были предприняты специальные тщательно поставленные и систематические опыты Лоде (1928). Последний установил, что среднее напряжение ст2 влияет на условие текучести.
Помимо этого, условие пластичности Треска — Сен-Венана обладает одним недостатком чисто формального свойства: аналитическая формулировка содержит наибольшее и наименьшее главные напряжения. Часто бывает так, что мы знаем направления главных осей, но не знаем заранее, какое из главных напряжений наибольшее, а какое наименьшее. В этом случае применение условия Треска затруднительно. Особенно трудно бывает в том случае, когда главные оси заранее неизвестны и тензор напряжений задан своими компонентами относительно произвольной системы координат.
96 СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ [ГЛ. III
Поэтому Губер (1904), независимо от него Мизес (1913) и позднее Генки (1921) предложили принять в качестве условия пластичности достижение октаэдрическим касательным напряжением некоторого предельного значения k'. Таким образом, мы приходим к условию пластичности
То = 4^ + (°. — °гУ + — <Л)2 = *'• (47.1)
Соображения Мизеса при этом носили чисто формальный характер, октаэдрическое касательное напряжение представляет собою простейшую симметрическую функцию от главных касательных напряжений. Позднейшая интерпретация В. В. Новожилова (§ 41) делает условие (47.1) более физически наглядным; если в каждом кристаллическом зерне наступление текучести определяется величиной касательного напряжения в определенной плоскости и определенном направлении, то для поликристаллического агрегата, в котором всевозможные ориентации плоскостей скольжения зерен равновероятны, естественно связать наступление текучести во всем материале с величиной, представляющей собою среднее значение касательного напряжения на площадках всех возможных ориентаций. Обращаясь к случаю простого растяжения, когда а, = ат, а, = а, = 0, найдем:
т<, = 1у-ат=*'.
Таким образом, условие Мизеса можно записать в следующей форме:
(<L — 0.)* + (0J — 0»)* + (0, — 0.)* = 20* • (47.2)
Применим условие (47.2) к случаю чистого сдвига. При этом
0, = ^, а, = 0, а, = —тт, следовательно,
rT = -£z 0,557а .
т /3 т
Эта цифра для большинства металлов лучше согласуется с опытом, чем цифра 0,50, даваемая условием Треска — Сен-Венана.
§ 48. Условия пластичности для плоского напряженного состояния. Обозначим главные оси тензора напряжений для плоского напряженного состояния через 5 и Т|. Величины главных напряжений могут быть какими угодно, и в зависимости от этого главные напряжения а. и ач будут отождествляться с а,, а, или а,. Запись условия пластичности Треска — Сен-Венана будет при этом получаться различной. Рассмотрим все возможности, которые могут представиться.
1. а5^>ач^>0. В этом случае наибольшее из трех главных напряжений есть а., примем его за а,. Наименьшим напряжением
§ 48] УСЛОВИЯ ПЛАСТИЧНОСТИ ДЛЯ ПЛОСКОГО НАПРЯЖЕННОГО состояния 97
является равное нулю напряжение на площадках, принадлежащих плоскости ^т]. Таким образом,
= = ст, = 0.
Используя условие (46.2), получим:
- °Е = °т-
II. При этом
= о. = 0.
Условие пластичности:
14- °2 = 0> °> = а71- Условие Треска
принимает следующий вид:
^-°Ч = ат-
IV- <^<^0. Условие пластичности будет тем же, что и
в третьем случае, только ст и меняются местами:
Аналогично предыдущему рассмотрим еще два случая, когда оба напряжения ст и oTj отрицательны:
V- 0^>о^>о1), оч = —от.
VI. 0>ач>а£, ае = — ат.
Выписанные условия легко изобразить графически. Будем откладывать по оси абсцисс ог, а по оси биссектрису координатного угла. Оси координат и эта биссектриса разбивают плоскость на шесть частей, в каждой из которых выполняется одно из вышеприведенных неравенств. В каждой части плоскости условия пластичности изображаются прямой, отрезки этих прямых образуют показанный на рис. 55 шестиугольник. Теперь легко понять, почему условие Треска — Сен-Венана не всегда оказывается удобным в применении. Если напряженное состояние в теле неоднородно, то в различных частях его могут быть осуществлены любые соотношения между ст. и ст^, поэтому того же тела приходится пользоваться различными аналитическими формами условия пластичности. С другой стороны, линейность всех этих условий иногда оказывается чрезвычайно выгодной и удобной.
ординат 0^ (рис. 55). Проведем
для разных областей одного и
4 Ю. Н. Работнов
98 СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ [ГЛ. III
Применяя к случаю плоского напряженного состояния условие Мизеса, мы не должны задумываться о том, какой номер следует присвоить напряжению какой — напряжению ащ, результат всегда будет одинаковым. Примем для определенности, например, 0^ = 0,, оч = а2, 0 = о,. Подставляя в условие (47.2), получим:
а’+ач — <V\ = <4. (48.1)
В координатах а5, оч это — уравнение эллипса. Легко проверить, что эллипс Мизеса проходит через вершины шестиугольника Треска — Сен-Венана, главные оси его направлены по биссектрисам углов между осями координат.
В заключение выпишем условия пластичности по двум теориям для общего случая плоского напряженного состояния, когда известны компоненты тензора напряжений относительно произвольных осей координат х, у. Главные напряжения находятся по формулам (36.7):
<,5=21±й.+|Г(<,х_„^ + 4^>
При этом всегда а?^>ач, поэтому случаи II, IV и VI применения условия пластичности Треска — Сен-Венана отпадают. Если ач^>0, осуществляется случай I и условие пластичности имеет вид:
/(ах— ау)’ + 4т* = ат.
Если о?^>0 и оч^>0, мы получаем случай III, следовательно, — ^)’ + 4т* = стт-
Наконец, если а><^0 и наибольшее напряжение равно нулю, реализуется случай V и мы имеем;
— °п =—+ 4 —°y)* + 4T’ = ат
По теории Мизеса после простых преобразований из формулы (48.1) получается:
j/" ol-J-aJ — Ц-Зт* — стт-
Таким образом, если направления главных осей заранее неизвестны, преимущества линейности условия Треска утрачиваются и условие Мизеса, которое описывается только одним аналитическим выражением, оказывается более простым.
§ 49] потенциальная Энергия упругой деформации 99
§ 49. Потенциальная энергия упругой деформации. Для тела, находящегося в условиях сложного напряженного состояния, можно подсчитать величину накопленной упругой энергии совершенно таким же способом, как это делалось для случая растяжения — сжатия (§ 28). Предположим напряженное состояние однородным и рассмотрим куб, ребра которого ориентированы по главным осям и длина каждого ребра равна единице длины. Тогда площадь каждой грани равна единице площади, а объем — единице объема. Напряжения о,, о, и о, представляют собою действующие на грани силы, эти силы совершают 'работу на перемещениях, равных деформациям е,, е, и в,. Предположим, что напряжения растут постепенно, в каждый момент процесса нагружения действующие напряжения равны Ост,, Ост,, Ост,-. Здесь 0 — параметр, меняющийся от нуля до единицы; когда становится равным единице, процесс нагружения заканчивается. Деформации выражаются через напряжения по закону Гука, то есть линейным образом, поэтому, когда напряжения равны Ост,, 0а,, 0о„ деформации будут 0е,, 08,, Ое,. Пусть параметр 0 получил приращение М, деформации получают при этом приращения d08,, d0e„ dOe,. Действующие на грани силы произведут работу
da = (а,0) (e,d0) + (а,0) (e,dO) -J- (o,0) (e,d0).
Проинтегрируем это выражение от 0 = 0 до 0 = 1. Получим:
а = у(о1е, + а,е,-|-о,е,). (49.1)
Это и есть потенцйальная энергия, накопленная в единице объема. Предполагается, что процесс нагрузки происходит медленно, деформации меняются медленно и, следовательно, в процессе деформаций кинетическая энергия сколь угодно мала.
Заметим, что Для вывода формулы (49.1) нет необходимости изменять все напряжения пропорционально одному параметру. Свойство упругости состоит в том, что конечное состояние тела не зависит от порядка приложения сил, поэтому мы выбрали такой порядок, при котором вычисления получаются наиболее простыми. Внесем в формулу (49.1) выражения деформаций через закон Гука (42.1). Получим:
a = + + — 2*(°Л + О»О.-Н.О1)}- (49.2)
Эта формула дает величину упругой энергии не только в пределах упругости, но и в области пластических деформаций, так как за пределом упругости полная деформация состоит из упругой и пластической частей, причем упругая часть связана с напряжениями по закону Гука.
Уравнения закона Гука (42.1) можно разрешить относительно напряжений и получить из формулы (49.1) выражение потенциальной
4*
100 СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОИНИЕ [ГЛ. Ш
энергии упругой деформации через е„ е, и е,. В настошцем курсе это выражение использовано не будет, мы поэтому его не выписываем.
Применим формулу (49.2) к случаю плоского иаприженного состояния, заданного компонентами тензора наприжений относительно произвольных осей координат. Главные напряжения а, , выражаются через ох, Оу и т по формуле (36.7); о, нужно положить равным нулю. Внося этн выражении в (49.2) и выполняй преобразовании, найдем:
a = 2^{(crx + cry), + 2(1+v)(Tl —0^)}. ’ (49.3)
В частности, дли чистого сдвига отсюда получается:
и «=-£-. (49-4>
Формулу (49.4) можно было бы вывести и непосредственно, подсчитывай работу сил, действующих на грани элемента, находящегося в условиях чистого сдвига.
§ 50. Энергия изменения формы. В конце прошлого столетии было высказано предположение о том, что переход в пластическое состояние связан с достижением предельного значении энергией деформации на единицу объема (Бельтрами). Эта точка зрения была опровергнута опытом. Действительно, подвергая материал всестороннему сжатию, можно накопить в единице объема сколь угодно большую упругую энергию, лишь бы давление было достаточно велико. Однако идея подобного энергетического критерии начала текучести представляется заманчивой, и для ее реализации необходимо суметь отделить энергию изменения объема от энергии сдвиговой деформации, или, как говорят, энергии изменения формы.
Представим себе, что напряженное состояние разложено на две составляющие, которые мы будем называть девиаторной частью тен-вора наприжений и его гидростатической частью.
Девиаторной частью тензора напряжений называют ту его часть, которая не меняется от добавлении всестороннего растяжения или сжатии. Если тензор напряжений отнесен к главным осям, будем обозначать компоненты девиатора oj, о' и а'. Гидростатическая часть — это выделяемое из общего напряженного состояния состояние всестороннего сжатия или растяжения. Компоненты гидростатической части тензора: о” — а" = о"=р. Теперь главные напряжении о,, о, и о, могут быть представлены следующим образом:
<*1 — <*1 = <Т1 ~Ьр> (50.1)
Отсюда компоненты девиатора:
01 = 0, — р, ог = о,—р, аг = а,—р. (50.2)
§ 50]
ЭНЕРГИЯ ИЗМЕНЕНИЯ ФОРМЫ
101
По определению компоненты девиатора не должны меняться от приложения к телу дополнительных напряжений всестороннего растяжения или сжатия. Пусть эти дополнительные напряжения равны q. Каждое из главных напряжений получает приращение, равное q; для того чтобы компоненты девиатора не изменились, необходимо, чтобы величина р также получила приращение, равное q. Для этого нужно принять
P = -3-(°i+°24-°s)- - (50.3)
На рис. 56 показано схематически разложение напряженного состояния на девиаторную и гидростатическую части. Оказывается, что потенциальная энергия упругой деформации может быть представлена
Рис. 56.
как сумма энергий, соответствующих девиаторной и гидростатической частям тензора напряжений. Первая называется энергией изменения формы, вторая—энергией изменения объема. Обозначим энергию изменения формы через ag, энергию изменения объема через аю. Нам нужно доказать, что
а=аг+ао. (50.4)
Следует заметить, что свойство аддитивности вообще на упругую энергию не распространяется, так как энергия является квадратичной функцией от напряжений. Если представить себе напряженное состояние тела как результат последовательного приложения двух систем напряжений, то вычисление конечной энергии можно производить следующим образом.
От приложения первой системы напряжений o', а' и а' в теле накапливается энергия аг Прикладываем теперь вторую систему напряжений, которая вызывает деформации е'', е2 и е"; они вычисляются по формулам закона Гука через напряжения о’, о", о" так, как если бы первая система напряжений отсутствовала. Работа второй системы напряжений на своих перемещениях есть энергия а2. Но на деформациях е", е2, е" производят работу и напряжения cf, о' и а' первой системы, которые были приложены раньше. Обозначим эту работу а,, и запишем:
a = ai-H2 + aI2.
.102 СЛОЖНОЕ НАПРЯЖЕННОЕ СССТОЯНИЕ [ГЛ. Щ
Применяя эти рассуждения к нашему случаю, заметим, что гндро* статическое напряженное состояние вызывает деформации:
Работа напряжений девиаторной части на этих деформациях есть «и = < < + < = « + + <0 р-
Складывая равенства (50.2) и принимая во внимание (50.3), получим:
CTi + <^ + ^==0- (50.5)
Таким образом, а1£ = 0, что и доказывает формулу (50.4). Для вычисления энергии изменения формы ag воспользуемся выражением (49.2) упругой энергии, заменив в нем ст,, ст, и ст, через о', ст; и ст' по формулам (50.2). Получим:
^=2^«2+стг2+<!—2v(ffX+aX+aXH- (50-6)
Для упрощения этого выражения воспользуемся тождеством (50.5). Возведем это тождество в квадрат:
о=+°,+<+2 (<т; ст;+о; о;+ст; о;). (50.7)
С помощью (50.7) можно преобразовывать выражение (50.6) для энергии изменения формы различными способами. Например, исключая попарные произведения компонент девиатора, получим:
Исключая квадраты компонент девиатора, найдем:
- Чг +°Х}-
Однако наиболее удобное выражение а получится, если умно-।_____________2v ®
жить (50.7) на —и результат вычесть из (50.6). Таким образом мы придем к следующему результату:
а*=Чг +а> =
=Чг —°?2+(°;—+(^—о2}-
Из формул (50.2) следует, что попарные разности компонент девиатора равны разности соответствующих компонент исходного
§ 50] ЭНЕРГИЯ ИЗМЕНЕНИЯ ФОРМЫ 103
тензора, поэтому предыдущую формулу на основании (44.3) и (41.2) можно заменить следующей:
1 Зг2
ag = 120 ~ = 4Т • (50,8)
Для нахождения энергии изменения объема ао внесем в формулу (49.2) вместо а1, о, и о, величину р. Получим:
Условие постоянства октаэдрического касательного напряжения тождественно с условием постоянства упругой энергии изменения формы.
Губер в 1904 г. высказал предположение, что разрушение материала происходит тогда, когда достигается предельное значение либо полной упругой энергии, либо энергии изменения формы, в зависимости от того, отрицательно или положительно р. Когда гидростатическая часть тензора напряжений отрицательна, то есть происходит всестороннее сжатие, критерий прочности Губера совпадает с условием постоянства октаэдрического напряжения Мизеса. При всестороннем растяжении начало разрушения определяется, по Губеру, полной удельной энергией.
ГЛАВА IV
НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ
§ 51. Расчеты на прочность изделий сложной формы. Излагая в предыдущей главе теорию сложного напряженного состояния, мы совершенно обошли молчанием вопрос о том, каким образом определить напряженное состояние в телах, подверженных действию сил. Общая задача об определении напряжений и деформаций в упругом теле произвольной формы, подверженном действию произвольных внешних сил, является предметом теории упругости, которая представляет собою раздел механики сплошной среды и развивается в направлении создания и усовершенствования методов решения соответствующих краевых задач для некоторых систем дифференциальных уравнений в частных производных. Несмотря на огромные успехи математической теории упругости, далеко не все задачи, представляющие практический интерес, удается решить; во многих случаях, даже когда точное решение или метод его отыскания известны, практическое использование этого решения для расчета на прочность затруднительно ввиду чрезвычайной сложности и громоздкости вычислений. С другой стороны, знания распределения напряжений в теле в упругой стадии его работы еще недостаточно для суждения о прочности. Как мы убедились на примере статически неопределимых стержневых систем, переход некоторых элементов в состояние текучести еще не означает разрушения системы в целом. Тем более это относится к телу, находящемуся в условиях сложного напряженного состояния. Достижение состояния текучести в одной или нескольких точках само по себе не является опасным: окруженный упругими областями, материал не имеет фактической возможности течь. В то же время, после того как состояние текучести где-то. достигнуто, дальнейшее увеличение нагрузки приводит к образованию пластических зон конечных размеров.
Определение напряжений и деформаций в телах, находящихся в состоянии пластичности, является предметом теории пластичности. Эта теория создана сравнительно недавно; если основные уравнения теории упругости были получены в начале XIX столетия, то теория пластичности как наука сложилась лишь в 20-х—30-х годах этого
§ 52J БЕЗМОМЕНТНЫЕ ОБОЛОЧКИ ВРАЩЕНИЯ 105
столетия (если не говорить о пионерских работах Леви и Сен-Венана, относящихся к 1870 г.). Теория пластичности значительно сложнее, чем теория упругости, особенно трудны так называемые упруго-пластические задачи, когда в теле имеются одновременно и упругие, и пластические зоны.
В инженерной практике к методам теории упругости и теории пластичности прибегают обычно в особо ответственных случаях, подавляющее большинство расчетов производится на основе элементарных приемов. Эти элементарные приемы дают точные или почти точные результаты для стержней и стержневых систем, а определение напряжений и деформаций в стержнях, как уже указывалось, составляет одну из основных задач сопротивления материалов, и этому вопросу посвящена значительная часть настоящего курса. Но уже при изучении напряженного состояния в стержнях при растяжении мы столкнулись с группой задач, выходящих за рамки элементарного рассмотрения. Это задачи о концентрации напряжения. Для пластических материалов качественные рассуждения привели нас к заключению, что при расчете на прочность концентрацию напряжений учитывать не следует и Достаточно вести расчет по формуле
(51.1)
Величина, стоящая в левой части, не является максимальным напряжением, это не есть даже равное пределу текучести напряжение в предельном состоянии, так как в предельном состоянии напряженное состояние не одноосно и условие текучести а = ат неприменимо. В данном случае PjF есть условное напряжение, которое сравнивается с допускаемым. При назначении допускаемого напряжения вводится достаточный запас прочности, величина запаса прочности устанавливается с учетом опыта эксплуатации, данных прямого эксперимента, а также точных решений для аналогичных задач, если такие решения существуют.
Приведенный пример типичен для многих инженерных расчетов, когда вместо подробного и точного рассмотрения истинного напряженного состояния определяют условное напряжение, равное силе, поделенной на площадь, и сравнивают его с допускаемым напряжением, которое выбрано так, чтобы наверняка компенсировать грубость и неточность принятой расчетной схемы. Ряд примеров таких условных расчетов будет рассмотрен в настоящей главе. Однако мы начнем с некоторых задач расчета на прочность в условиях сложного напряженного состояния, когда напряжения удается определить точно.
§ 52. Безмоментные оболочки вращении. Общий случай плоского напряженного состояния почти точно реализуется в тонкостенных оболочках-куполах, резервуарах и т. д. Можно показать, что если оболочка выпукла, то есть полная или гауссова кривизна ее во
106
НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ
[гл. IV
всех точках положительна, то изгиб происходит только вблизи мест закрепления или там, где резко меняется толщина оболочки. В большей части оболочки мы можем считать напряжения равномерно распределенными по толщине. Общая задача о равновесии тонкостенной оболочки является предметом теории упругости, даже в пренебрежении изгибом она довольно сложна. Здесь мы рассмотрим наиболее важный для практики случай, когда оболочка имеет форму поверхности вращения и нагрузка симметрична относительно оси. Введя обозначение S для толщины оболочки, будем искать напряжения в нормальных сечениях оболочки. Вследствие симметрии направления меридианов и параллелей будут в каждой точке направлениями главных осей. Меридиональное сечение {pt на рис. 57, а) есть сечение
оболочки плоскостью, проходящей через ось симметрии. Нормальное сечение, проходящее через параллель, мы будем называть кольцевым сечением (рг на том же рисунке). Это — сечениё оболочки конической поверхностью с вершиной на оси симметрии и образующими, которые являются нормалями к поверхности оболочки вдоль параллели и составляют угол а с осью z. Длина образующей конуса от вершины до поверхности оболочки (внешней или внутренней — безразлично, так как толщина д мала) есть радиус кривизны нормального сечения, то -есть радиус кривизны сечения оболочки плоскостью, проходящей через касательную к параллели и нормаль к поверхности. Это один из главных радиусов кривизны поверхности оболочки. Обозначим его QB. Из чертежа видно, что
__ г
sin а
§ 52] ВЕЗМОМЕНТНЫЕ ОБОЛОЧКИ ВРАЩЕНИЯ 107
Здесь г — расстояние от рассматриваемой точки поверхности до оси вращения. Обозначим также через QM радиус кривизны меридиана. Вследствие симметрии нагрузки в меридиональном сечении действует только нормальное напряжение <тк; будем называть его кольцевым. В кольцевом сечении действует меридиональное напряжение ом. Рассмотрим элемент prst, вырезанный двумя бесконечно близкими меридиональными и двумя кольцевыми сечениями (рис. 57, б). На элемент действуют напряжения <ТМ на гранях рг и is, напряжения ак на гранях pt и rs, кроме того, внешние силы, нормальная составляющая которых, отнесенная к единице площади, есть q.
Составим уравнение равновесия в проекциях на нормаль, проведенную в середине элемента. На грани pt, площадь которой есть 6 dsM, действует напряжение ак; таким образом, сила, действующая по указанной грани, есть
ок6 dsM.
_ „ л . dB
Эта сила составляет с нормалью п угол, равный -угу» поэтому проекция ее на нормаль равна
<тк6 dsK cos (4 + у ) = — у СТк ds« ор-
сила, действующая на грань rs, дает на нормаль в точности такую же проекцию. Рассматривая совершенно аналогичные свлы, действующие на грани рг и st, найдем, что проекция каждой из них на нормаль равна
— у<тмб<*Ма-
Наконец, составляющая внешней силы, направленная по нормали, равна
Находя сумму проекций на нормаль всех действующих на элемент сил и приравнивая эту сумму нулю, получим:
ак5 dsM dp + ам5 dsK da = q ds№ ds*.
Заметим, что
dp=^s., = .
Qk Cm
Окончательный вид уравнения равновесия будет следующим:
(52.1)
При выводе этого уравнения мы пренебрегли тем, что площади граней рг и ts неодинаковы, а также тем, что напряжения на этих гранях, вообще говоря, различны. Это не нарушает правильности уравнения (52.1), так как отброшенные члены имеют более высокий
108 НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ [ГЛ. IV
порядок малости. Учитывая эти члены, можно составить уравнения равновесия в проекциях на оси, лежащие в касательной плоскости к оболочке. В отличие от уравнения (52.1), они будут уже не конечными, а дифференциальными. Мы не будем вставать на этот путь, обычный для теории упругости.
Для нахождения ак и ам к уравнению (52.1) нужно добавить еще одно уравнение. Мы получим его, рассматривая равновесие части оболочки, отрезанной по конической поверхности кольцевого сечения. Площадь конической поверхности сечения есть 2лгб; проектируя все силы иа ось симметрии zz, получим:
2nrS<JMsina — Z — 0. (52,2)
здесь Z— сумма проекций на ось zz внешних сил, приложенных к отрезанной части оболочки.
Рассмотрим два простейших примера приложения этих уравнений: а) Сферическая оболочка под действием внутреннего давления. Вследствие симметрии ам = ак. Так как qm = qk=q, то из уравнения (52.1) получим:
= = (52.3)
б) Цилиндрическая оболочка под действием внутреннего давления. В этом случае Z есть сила, действующая на дио цилиндра:
Z=nrtq.
По уравнению (52.2)
Радиус кривизны меридиана qm = oo, тогда как QK = r. Формула (52.1) сразу дает кольцевое напряжение:
Желая рассчитать на прочность цилиндрическую оболочку, выполненную из пластической стали, мы примем:
_ qr qr л
Если принять за основу условие пластичности Треска, то расчет оболочки производится по следующей формуле:
°! — = f ВН-
ЕСЛИ принять условие Мизеса, то получим:
§ 53] МЕСТНЫЕ НАПРЯЖЕНИЯ В БЕЗМОМЕНТНЫХ ОБОЛОЧКАХ 109
Толщина стенки, рассчитанная по условию Мизеса, при равных запасах прочности оказывается на 14% меньше, чем по условию Треска — Сен-Венана.
§ 53. Местные напряжения в безмоментных оболочках. В местах резкого изменения кривизны уравнения безмоментной теории оболочек перестают быть справедливыми: в оболочке возникают
местные напряжения. Причину появления их можно выяснить на при-
мере цилиндрического котла со сферическим днищем (рис. 58). Напряжения в цилиндрической части:
__qa _______qa
Напряжения в сферической части: „ _ qR ам Стк 2d*
Подсчитаем относительную деформацию окружности цилиндра:
Относительное изменение радиуса цилиндрической части будет также ев, поэтому приращение радиуса:
Д'а = авк.
Сферическая оболочка, напряжения во всех точках которой одинаковы, деформируясь, сохраняет сферическую формация оболочки равна
8 = ^a=g(i-v).
форму.
Рис. 58.
Относительная
де-
Радиус основания сферического днища, равный а до деформации, получает приращение
Д"а = ав.
Деформации, соответствующие тем напряжениям, которые определены по безмоментной теории, не удовлетворяют требованию неразрывности оболочки при переходе от цилиндрической к сферической части. Для обеспечения неразрывности необходимо допустить, что в оболочке появляются напряжения и деформации изгиба в области, примыкающей к месту стыка.
Недостаточность безмоментной теории можно выяснить также с помощью чисто статических соображений. Сделаем два близких кольцевых сечения: одно несколько выше стыка по сферическому
110 НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ [ГЛ. IV
днищу, другое несколько ниже по цилиндрической части. Рассмотрим заключенное между этими сечениями кольцо (рис. 58). Напряжения а в сферической части дают составляющую, направленную к центру кольца. Сила, действующая на единицу длины, есть од sin а.
Кольцо оказывается как бы сжатым этими силами, и если рассмотреть равновесие половины кольца, то мы придем к заключению, что в поперечном сечении кольца возникнут сжимающие напряжения. Но поперечное сечение кольца представляет меридиональное сечение оболочки как в ее цилиндрической части, так и в сферической. По безмоментной теории кольцевые напряжения положительны как в той, так и в другой части оболочки, то есть они являются растягивающими напряжениями. Таким образом, мы пришли к противоречию. Выход из него заключается в том, что в кольцевых сечениях, близких к стыку, нужно допустить существование ие только нормальных сил, но и касательных, вызывающих местный изгиб оболочки. Ширина зоны, в которой напряжения изгиба существенны, имеет порядок У Rd, где R — радиус оболочки, б — ее толщина. Таким образом, если толщина составляет одну сотую радиуса, ширина зоны местных напряжений составляет примерно одну десятую радиуса, или десять толщин.
Тонкие оболочки сопротивляются изгибу значительно хуже, чем растяжению. Поэтому принимают конструктивные меры для усиления оболочки в месте сопряжения, ставят кольцо жесткости. При расчете кольца жесткости обычно пренебрегают изгибной жесткостью оболочки и считают, что кольцо сжимается распределенной по контуру силой об sin а на единицу длины кольца.
§ 54. Большие прогибы мембраны. Мембраной называется тонкая пластинка, в которой напряжения можно считать распределенными по толщине равномерно. Рассмотрим задачу о равновесии круглой мембраны, нагруженной равномерным давлением. Приближенное решение, результаты которого оказываются весьма мало отличающимися от точного, будет основано на предположений о том, что поверхность мембраны после деформации становится сферической. Радиус кривизны сферы р, стрела прогиба f и половина центрального угла меридионального сечения поверхности мембраны связаны очевидными соотношениями (рис. 59):
а __ а sin а а ’
- . а аа
Напряжения сгм и ок равны между собой. Обозначая их общую величину через о, получим из уравнения (52.3):
<?6 qa
26 ~ 26а •
(54-1)
§ 54]
БОЛЬШИЕ ПРОГИБЫ МЕМВРАНЫ
111
Относительное удлинение ем = ек—е представляет собою разность между длиной дуги и длиной хорды, поделенную на длину хорды:
e==Qaz-Q2ina==_a________(54 2)
g sin a sin сс 6 ' '
В упругой области айв связаны между собою законом Гука:
Поэтому
1 — V е==-£-а-
Отсюда находим:
а8___1 — у да
6 Е 2ба‘
Стрела прогиба
„ -1Z о 1 — V да
а=У 3 — у-
Зависимость между так же как в задаче §
получается двух
задач
(54.3)
нелинейной, показывает,
б •
, а 4 / , 1 - V да V 3 ~2 силой и прогибом 32. Сравнение этих
что и методы решения здесь по существу одинаковы.
В пластической области мы ловие
или
Поэтому из уравнения (54.1) ___________________ да а~ 2бат’
или
имеем ус-
(54.4)
(54.5)
Рис. 59.
идеал ь-ста-
J ~~ 4daT ’
Следует отметить, что для ной пластичности задача является тически определенной. Действительно, соотношение (54.5) получено
только из условия статики вместе с условием пластичности.
Когда прогибы мембраны, а следовательно и деформации, велики, формула (54.5) перестает быть верной, так как деформация сопровождается уменьшением толщины мембраны, а это при выводе ие учитывалось. Обозначая по-прежнему толщину через б, мы будем обозначать начальную толщину б0. Объем материала мембраны равен площади поверхности шарового сегмента, умноженной иа толщину. Площадь поверхности выражается следующим образом:
F=n(a‘+n
112 НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ [ГЛ. IV
Условие постоянства объема дает:
бЛ==дЛ
Отсюда
5 = (54.6)
Радиус кривизны связан с радиусом мембраны а и стрелой прогиба следующим соотношением:
е = ^. ' (54.7)
Из уравнения (54.1) следует:
2да
Полагая здесь <т = от и выражая б и g по формулам (54.6) и (54.7), найдем:
' ,54'8)
Представим теперь результаты в безразмерной форме. Положим: f* — L
4 460<тт ’ J а ’
Формула (54.8) примет следующий вид:
?*=(rq55TI- (54,9)
При малых /* приближенно можно считать q* =f*, что совпадает
с формулой (54.8). В упругой области формула (54.3) приводит к следующей зависимости:
= где 0= |/‘-|-gr(l — v).
Начальный участок графика зависимости между /* и q* представлен на рис. 60 отдельно в большом масштабе, кубическая парабола
УСЛОВНЫЕ РАСЧЕТЫ
113
§ 55]
пересекает прямую (54.5) при </*==/* = Р’1. Более точная для области пластических деформаций формула ^54.9) показывает, что нагрузка q* не может превышать величину q^ax =s 0,325; мы убеждаемся в этом, отыскивая максимум правой части в формуле (54.9). При достижении нагрузкой этой величины мембрана прорывается.
§ 55. Условные расчеты. Под общим названием «условные расчеты» объединяют целую группу задач, относящихся к расчету ряда частей машин и сооружений, как-то: заклепок,' болтов, шпонок и т. д. Сюда же относятся расчеты сварных соединений. Перечисленные детали или вообще не являются стержнями, или длина их имеет тот же порядок, что и поперечные размеры. Элементарные соображения показывают, что в этих деталях возникает сложное напряженное срстояние, но теоретическое исследование этого состояния практически невозможно.
В то же время расчет заклепок, болтов, шпонок, сварных швов и т. д. встречается буквально на каждом шагу при конструировании, и для производства этих расчетов необходимо иметь достаточно простые и надежные способы, позволяющие с уверенностью обеспечить прочность конструкции. В основе этих способов лежат крайне упрощенные схемы, при помощи которых находятся некоторые условные напряжения. Расчет состоит в том, что эти условные напряжения сравниваются с условными допускаемыми напряжениями, найденными из опыта, который воспроизводит реальные условия работы детали.
Основные условные схемы, на которых строятся эти расчеты, следующие:
а) разрыв,
б) срез,
в) смятие.
Рассмотрим для примера изображенное на рис. 61 соединение двух полос заклепок. Попытаемся представить себе, как может разрушиться это соединение.
Если ширина полосы b мала и лишь немного превышает диаметр заклепки d, то полоса разорвется, причем разрыв произойдет по сечению с наименьшей площадью, то есть сечению, проходящему через ось заклепки. Площадь его
Fp = (6-d)6.
Здесь б — толщина листа.
На этом же рисунке внизу показаны напряжения, возникающие в сечении с минимальной площадью. Закон распределения этих напряжений неизвестен; можно сказать с уверенностью, что они распределены по сечению неравномерно, так как именно у отверстия площадь сечения резко меняется и, следовательно, наблюдается концентрация напряжений. В § 31 указывалось на сложность вопроса
114
НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ
[ГЛ. IV
о критериях разрушения при наличии концентрации напряжений, а также на смягчение эффекта концентрации вследствие пластической
Рнс. 61.
Поступая обычным способом, будем считать напряжения равно* мерно распределенными по опасному сечению. Тогда
и условие прочности принимает вид:
(55.1) гр
Если диаметр заклепки мал, то сила Р срежет заклепку. Силы давления стенок заклепочного отверстия на цилиндрическую поверхность заклепки вызывают не только срез, но также изгиб заклепки в ее среднем сечении. Мы пренебрегаем напряжениями изгиба и считаем, что сила Р уравновешивается (рис. 62) только касательными напряжениями т, равномерно распределенными по поперечному сечению заклепки.
Предположение о равномерном распределении касательных напряжений по сечению очень грубо. На самом деле напряжения в точках контура сечения по закону парности должны равняться касательным усилиям, действующим на боковой поверхности заклепки. Но часть боковой поверхности соприкасается со стенками отверстия, касатель
§ 55]
УСЛОВНЫЕ РАСЧЕТЫ
115
ное усилие не может превышать величины давления, умноженной на коэффициент трения. Этой величины не могут превышать и
в сечении в соответствующих точках, отверстием образу-части
касательные напряжения
С противоположной стороны между заклепкой и ется зазор, касательные усилия равны нулю, следовательно, и в поперечном сечении на некоторой дуге контура касательное напряжение равно нулю. Таким образом, найденное среднее касательное напряжение
’=А г ср
является условной величиной.
Требуя, чтобы величина условного касательного напряжения не превышала допускаемого
поверхности
некоторой
на
напряжения на срез,
получим:
Г<[4р. (55.2)
Гер
Здесь площадь среза „ nd* г =--------------------------.
ср 4 •
Допускаемое напряжение на срез обозначается так же, как допускаемое напряжение при чистом сдвиге, но эти величины не следует смешивать, при срезе мы имеем по существу сложное напряженное состояние.
Наконец, при малой толщине листа давление между цилиндрическими поверхностями заклепки и заклепочного отверстия может оказаться настолько велико, что материал листа или заклепки начнет пластически деформироваться, отверстие приобретет овальную форму и соединение ослабится.
Для подсчета давления его совершенно условно относят к диаметральному сечению, поскольку не известны ни закон распределения давления по поверхности, ни границы области контакта, и получают следующее условие прочности:
(55.3) г см
Здес(> площадь смятия FCM = firf.
На рис. 63 показана предположительная эпюра распределения давления между заклепкой и стенкой отверстия.
Поскольку расчетные напряжения, найденные выше, являются условными, допускаемые напряжения должны быть найдены из опыта, проведенного в условиях, аналогичных тем, которые реализуются
116 НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ [ГЛ. IV
в рассмотренном заклепочном соединении. Допускаемое напряжение на растяжение при этом выбирают обычным способом, по временному сопротивлению или пределу прочности, найденному путем испытания на растяжение гладкого образца. Обычные запасы прочности оказываются достаточными для того, чтобы учесть неравномерность распределения напряжений. Для
С ' !------------s допускаемого напряжения на
( срез рекомендуется следующее
О\ значение:
J [ Т ] = 0,8 [ ст].
............ Мы видели (§ 47), что предел текучести при сдвиге составляет немного более половины предела текучести при
I растяжении. Рекомендуемое от-
L______ __- ношение допускаемого напря-
жения при срезе к допускае-
• Рис. 63. мому напряжению при растя-
жении не связано с каким-то теоретически обоснованным условием прочности или пластичности,— это чисто эмпирическая величина.
Что касается допускаемого напряжения на смятие, нужно иметь в виду, что частичный переход в пластическое состояние материала вблизи поверхности контакта не является опасным. Поэтому допускаемое напряжение на смятие можно принимать относительно высоким. Обычно рекомендуется
[<Исм = 2[ ст]р.
Для различных материалов и различных условий работы допускаемые напряжения устанавливаются специальными нормами, которые можно найтн в справочных изданиях по строительному проектированию, по деталям машин и т. д.
§ 56. Некоторые дальнейшие примеры условных расчетов. Рассмотрим некоторые типичные примеры условных расчетов.
а) Заклепочные соединения с накладками. Принимая толщину каждой накладки большей, чем половина толщины листа (рис. 64), мы избавляемся от необходимости проверять накладки на прочность. Сила, приходящаяся на каждую заклепку, есть Р]п, где п—число заклепок на одной половине соединения. Изображенное на чертеже соединение называется двухсрезным, потому что срез заклепки может произойти только по двум плоскостям одновременно. При этом площадь среза равна удвоенной площади сечения заклепки.
§ 56] НЕКОТОРЫЕ ДАЛЬНЕЙШИЕ ПРИМЕРЫ УСЛОВНЫХ РАСЧЕТОВ ПТ
Условие прочности на срез:
»-2т
Условие прочности на разрыв:
. |56-2>
Наконец, условие прочности на смятие:
<56-3>
Наивыгоднейший случай будет тот, когда во всех трех условиях прочности соблюдается знак равенства. Для этого между размерами dr би/ должны существовать определенные соотношения. Исключая
величину силы из (56.1) и (56.2), получим:
d = —
л [т]
Если [т] =0,8 [ст], [ст]См = = 2[ст]р, то
d= 1,66.
Исключая Pin из (56.2) и (56.3), найдем:
t == 4,86 3d.
Заклепочное соединение, Рис. 64.
в котором соблюдены найден-
ные выше соотношения размеров, является равнопрочным; обычно при проектировании стремятся к равнопрочности. Однако ицогда сознательна делают какой-то элемент более слабым, чем другие. Если возможность частичного разрушения конструкции вследствие случайной перегрузки неизбежна и это разрушение ие приведет к серьезной аварии, та имеет смысл проектировать конструкцию так, чтобы в первую очередь разрушался элемент, легко поддающийся замене (например, заклепка,, а не листы).
б) Расчет шпонки. Шпонкой называется призматическая деталь, предотвращающая от проворачивания втулку, насаженную на вал (рис. 65). Если момент, передаваемый через шпонку, есть /И, то
118
НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ
[ГЛ. IV
касательные напряжения в сечении тп уравновешиваются силой р_ М 2М * г d '
’Здесь d — диаметр вала.
Площадь среза в этом случае есть Ы, поэтому условие прочности принимает следующий вид:
2М dbl
Площадь смятия является прижимается к стенке шпоночной
той площадью, по которой шпонка канавки. Если, как обыкновенно делают, шпонка утоплена на половину толщины в вал, на другую половину'—во втулку, то
Условие прочности на смятие: 4М г , [ст]см-
Рис. 65. Требуя равнопрочности шпонки
в отношении среза и смятия, получим следующее соотношение между шириной и толщиной ее:
/ = 2rJ^-i>==0,86.
Мем
'§ 57. Расчет сварных соединений. На рис. 66 изображены типичные сварные соединения: впритык, внахлестку фланговым швом и внахлестку торцевым швом. Рассмотрим эти случаи по отдельности:
а) Соединение впритык (рис. 66, а). Шов в этом случае работает на разрыв. Если ширина листа есть Ь, а толщина fi, то можно считать площадь сечения шва равной Ьб, пренебрегая высотой валика наплавленного металла. Условие прочности:
-^-<[<4 (57.1)
Через [ст]р обозначено допускаемое напряжение на растяжение для наплавленного металла, принимаемое обычно меньшим, чем для основного металла конструкции (например, [ст]р = 1000 кг[см* при’ {ст] = 1600 кг}смг).
б) Фланговый шов (рис. 66, б). Считая сечение сварного шва имеющим форму равиокатетного прямоугольного треугольника, найдем, что наименьшая толщина / = ^==5=0,75. Поэтому площадь среза равна 0,7б/ф. Здесь /ф—общая длина всех фланговых швов,
Рис. 66.
§ 57J РАСЧЕТ СВАРНЫХ СОЕДИНЕНИЙ I 19*
воспринимающих силу. Условие прочности имеет вид:
<57-2>'
[т]' — допускаемое напряжение на срез для шва. Оно выбирается равным примерно 0,8 [ст]'. (Если [ст]'=1000 «г/сл!,то [т]'=800«г/сл!.)> в) Условия работы торцевого шва значительно более сложны. Опыты показывают, что разрушение происходит по площадке тп (рис. 66, в). Совершенно условно считают, что по этой площадке происходит срез, и условие прочности пишут так:
® •= W'- ,57-3’
Здесь — длина торцевого шва.
Последняя формула лишена каких-либо теоретических оснований. Мы знаем, что площадка, расположенная под углом к направлению растягивающей силы, находится под действием как нормальных, так
и касательных напряжений, при этом величина касательного напряжения не выражается левой частью формулы (57.3). Но определение этих нормальных и касательных напряжений было бы совершенно бесполезно, на самом деле напряженное состояние — сложное и найти его элементарными методами невозможно. С другой стороны, технология изготовления сварного шва не обеспечивает его идеальной геометрической правильности и свойства материала шва непостоянны, поэтому строгое теоретическое решение задачи, найденное для некоторых идеализированных условий, не имело бы большой практической ценности. Достаточно того, что формула (57.3) подтверждаете» опытом, то есть дает гарантию прочности сварного соединения, может быть, с некоторым излишним запасом прочности. Иногда в правой части условия (57.3) вместо [т]' ставят величину [ст]р. Действительно, с таким же основанием мы могли бы считать, что по площадке тп возможен разрыв. Однако, учитывая незначительность пластических деформаций, которые получает торцевый шов перед, разрушением, будет осторожнее принять для него пониженное допускаемое напряжение, а так как [т]'<^[ст]р, то формула (57.3) и является общепринятой.
Часто в одном соединении комбинируются швы разных типов.. При расчете, например, приварки уголка к листу (рис. 67) условие;
120
НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ
[ГЛ. IV
лрочностн составляют следующим образом: Р= 0,7 [т]' + Ь) б.
(57.4)
Мы предполагаем здесь, что напряжение во всех швах одновременно становится равным допускаемому. Очевидно, что это не так;
желая найти распределение напряжений между швами, мы должны были
бы решать весьма трудную статически неопределенную задачу. Принцип, положенный в основу при. составлении этого условия прочности, получает разъяснение, если встать на точку зрения расчета по допускаемым нагрузкам. Предположим, например, что в торцевом шве раньше достигается предел текучести. При дальнейшем возрастании силы торцевый шов пластически деформируется при постоянном напряжении, приращение нагрузки воспринимается только фланговыми швами. Наконец, момент, когда напряжение во фланговых швах становится равным пределу текучести, нужно принять за момент разрушения всего соединения в целом. Таким образом,
Рт = 0,7гт (/.+/, + *) б. (57.5)
Разделив обе части на запас прочности, получим равенство (57.4)1 В предельном состоянии сила Pt проходящая через центр тяжести поперечного сечения уголка, уравновешивается тремя силами: Pt, Pt и представляющими собою сопротивления трех швов. Уравнение (57.5) дает лишь одно условие равновесия, кроме этого, необходимо, чтобы главный момент системы сил, изображенной на рис. 67, равнялся нулю. Составим это условие:
• p1^_C)4-ps(A_c)_ptC=o.
Но в предельном состоянии
Р=0,7тб/., Л = 0,7ттб/„ Р.=О,7тб7>. Л 'II' * • 1 Z ’ « 1
Подставляя эти выражения в уравнение моментов и сокращая общий множитель 0,7ттб, получим:
/1(£-е)4-^|-С)-|-/гС = 0. (57.6)
Таким образом, длины фланговых швов нужно брать различными. Поскольку b задано, решение уравнений (57.4) и (57.6) определяет Z, и /4 единственным образом.
§ 57] РАСЧЕТ СВАРНЫХ СОЕДИНЕНИЙ 121
Аналогично производится расчет сварных соединений других, типов.
Вышеизложенные соображения являются весьма условными, поэтому практика выработала ряд рекомендаций для проектирования сварных швов, заклепочных соединений и других подобных элементов машин и конструкций. Объяснить эти рекомендации при помощи; представлений и методов механики затруднительно, они приводятся, в специальных руководствах и справочных изданиях.
ГЛАВА V
’ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ
§ 58. Задачи испытания материалов. При изложении первых тлав настоящего курса нам постоянно приходилось ссылаться на данные опытов, в результате которых устанавливались те или иные •свойства материалов. Основные законы упругости и пластичности, полагаемые в основу различных теорий сопротивления материалов, получены путем прямых испытаний образцов, поставленных в специальные условия. Эти законы применимы, строго говоря, лишь в тех пределах, в которых они нашли прямое экспериментальное подтверждение. Так, если сталь проявляет упругие свойства в довольно «большом диапазоне напряжений и закон Гука для стали является весьма точным законом, мягкие металлы, например свинец, обнаруживают пластическую деформацию уже при очень малых нагрузках и вряд ли вообще могут считаться упругими. Поэтому, применяя выводы сопротивления материалов к новым материалам, необходимо подвергать их всестороннему исследованию. Некоторые основные гипотезы сопротивления материалов проверяются лишь для ограниченного числа частных случаев, тогда как теория придает им универ--сальный характер. Так, например, условие пластичности при сложном напряженном состоянии мы считаем справедливым для любых напряженных состояний, хотя имеющийся опытный материал, на основе которого эти условия были сформулированы, относится почти исключительно к двухосному напряженному состоянию, да и то не при всех возможных соотношениях между главными напряжениями. Поэтому •одна из важных задач состоит в принципиальном выяснении на опыте правильности тех или иных механических теорий и установлении траниц их практической применимости.
При решении задач на растяжение — сжатие нам встретилась необходимость в некоторых константах, характеризующих материал. Мы употребляли в расчетах такие величины, как модуль упругости, коэффициент Пуассона, предел текучести. Все эти величины различны для разных материалов, хотя бы и близких по химическому составу. Так, предел текучести различных сталей в зависимости от содержания углерода, наличия легирующих элементов, то есть добавок других
§ 59] СТАТИЧЕСКИЕ ИСПЫТАНИЯ НА РАСТЯЖЕНИЕ 123-
металлов, и термической обработки может быть совершенно различным. Модуль упругости меняется в гораздо более узких пределах, но все же различен для разных марок стали. Поэтому, для того-чтобы использовать материал в сколько-нибудь ответственной конструкции, необходимо определить в лаборатории его механические характеристики. Этим термином мы объединяем всевозможные цифровые показатели, получающиеся в результате опыта, состоящего в деформировании тем или иным способом образца из данного материала. Такие механические характеристики, как модуль упругости и предел упругости или предел текучести, определяются непосредственно и используются при расчетах непосредственно — это некоторые физические константы материалов, имеющие вполне определенный механический смысл.
Наряду с характеристиками, физическое значение которых совершенно определенно, существуют и такие механические характеристики, которые неотделимы от данного частного вида испытаний и хотя характеризуют некоторые свойства материала, но характеризуют их скорее качественно, сравнительно. Как пример приведем такую величину, каю относительное удлинение образца при разрыве. Материал с большим относительным удлинением при разрыве называется вязким в противоположность хрупкому, который рвется при малом относительном удлинении. Кратковременная большая нагрузка, приложенная к детали из вязкого материала, вызовет некоторую пластическую деформацию,, та же нагрузка поломает деталь из хрупкого материала. Действительно, сопротивление ударным нагрузкам определяется главным образом способностью материала поглощать энергию перед разрушением, а величина поглощенной энергии зависит не только от прочности,, нои от вязкости материала. Поэтому вязкость — это положительное свойство материала, и величина относительного удлинения при разрыве является важным показателем качества его. В то же время, если определить относительное удлинение для одного и того же материала на образцах с разным отношением длины к поперечному размеру, результаты будут разными. Чтобы сравнивать степень пластичности разных материалов, нужно определить удлинение на геометрически подобных образцах.
Совокупность механических * характеристик позволяет судить о качестве материала; при составлении технических условий на металл оговариваются те или иные минимальные значения основных механических характеристик.
§ 59. Статические испытания на растяжение. Основным видом-испытаний, дающим наиболее полное представление о материале, является испытание на растяжение цилиндрического образца. Опыт на растяжение — это почти единственная возможность осуществления однородного напряженного состояния, а только при однородном-
124 ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [гл. V
напряженном состоянии в образце достаточных размеров можно произвести необходимые для определения механических характеристик измерения, не прибегая к тем или иным гипотезам.
Для того чтобы условные механические характеристики, полученные при испытаниях, были сравнимы, делают образцы стандартной .формы, например изображенной на рис. 68. Головки служат для захвата образца в зажимах испытательной машины, конические участки
- 320 -Рис. 68.
представляют плавный переход от утолщенной головки к средней цилиндрической части, наконец, средняя часть образца, заключенная между двумя рисками, отступающими от начала конуса примерно на половину диаметра, является его рабочей частью. Отношение длины I рабочей части к диаметру d нормировано, для нормальных образцов оно равно десяти, для укороченных пяти.
При испытании листового материала или прутков некруглого профиля приходится брать образцы некруглого сечения. Для того чтобы -сделать результаты испытаний образцов различного сечения сравнимыми, необходимо обеспечить постоянное отношение длины образца к квадратному корню из площади поперечного сечення. Круглому образцу с отношением l]d = W соответствует некруглый, для которого •
/=11,3 Vf.
Здесь F— площадь поперечного сечения.
Для испытаний на растяжение служат специальные машины, которые делятся на два основных типа: рычажные и гидравлические. Принцип действия рычажной машины показан на рис. 69. Образец захватывается верхним и нижним зажимами а и б; нижний зажим соединен с винтом в. Гайка г не может перемещаться в осевом направлении. При вращении ее вручную нли от электромотора винт опускается и тянет за собою зажим б. Перемещение передается через
§ 59]
СТАТИЧЕСКИЕ ИСПЫТАНИЯ НА РАСТЯЖЕНИЕ
125
образец верхнему зажиму а, рычажная система выходит из равновесия. Перемещая груз е по рычагу, мы добиваемся равновесия рычага, о чем можно судить по указателю ж. Соотношение плеч дает нам нагрузку на образец. Обычно рычаг, по которому движется груз е, градуируется таким образом, чтобы сразу можно было прочесть действующую на образец нагрузку. В настоящее время машины такого
типа строятся сравнительно редко, для больших нагрузок предпочитают гидравлические машины, для малых и средних (до 10 тонн) — машины с маятниковым силоизмерением. Разрывная машина с маятни
ковым силоизмерением является вариантом рычажной машины, схема ее приведена на рис. 69 справа. Здесь также нижний зажим соединен с винтом, который ввинчивается во вращающуюся гайку. Верхний зажим при помощи рычажной или ленточной тяги соединен с маятником. Возникающее в образце усилие отклоняет маятник, по углу отклонения измеряется сила. При такой схеме отпадает необходимость в поддержании горизонтального положения рычага, работать на маятниковой машине удобнее и проще.
На рис. 70 показана схема гидравлической испытательной маши
ны. Нижний 'зажим ее неподвижен, верхний соединен с поршнем, находящимся внутри цилиндра. Насос нагнетает масло в цилиндр, давление масла через поршень передается на образец и создает
126 ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ {ГЛ. V
Рис. 71.
в нем растягивающую силу, о величине этой силы судят по давлению масла, которое измеряется манометром.
Весьма существенное требование, которое предъявляется ко всем без исключения машинам, заключается в надежной центровке образцов, которая должна обеспечивать действительно осевое приложение нагрузки и исключать всякую возможность изгиба. Типичная конструкция самоцентри-рующего захвата изображена на рис. 71. Зажим машины снабжен подушкой со сферической поверхностью, на которую опирается сферический вкладыш. Головка образца удерживается в нем с помощью разрезного кольца. При нагрузке вкладыш поворачивается, устанавливаясь таким образом, что сила проходит через ось образца.
Как видно, любая машина включает в себя силоизмеритель. Для определения деформации в зависимости от задач исследования поль
зуются разными способами. Для снятия диаграммы зависимости между силой и деформацией в области больших пластических деформаций бывает достаточно измерить перемещение зажима машины по масштабной линейке с нониусом, которая всегда имеется на самой машине. Большинство машин снабжается устройством для автоматической записи диаграммы зависимости между силой и перемещением захвата.
§ 60. Исследование металлов в области малых деформаций. Измеряя малые деформации, соответствующие упругой области на диаграмме о — 8, а также началу пластичности, следует заботиться об исключении различных искажающих факторов. Поэтому, например, нельзя изменять малые деформации по перемещению зажимов машины: обмятие головок образца и упругие деформации частей машины совершенно исказят результаты. Основное правило для измерения малых деформаций состоит в том, что измерения должны производиться на рабочей длине и прибор для измерения деформации, экстензометр, должен крепиться непосредственно на образце. На рис. 72 приведена схема зеркального экстензометра Мартенса. Шина а имеет на одном конце жестко с нею скрепленную призму б, лезвие которой прижимается к образцу. На другом конце между образцом и шиной помещается ромбовидная призма в, изготовленная как одно целое со стержнем, как показано на рис. 72 внизу. Этот стержень с одной стороны несет зеркальце г, с другой — противовес. Диагональ ромбовидной призмы есть d. Шина прижимается к образцу струбцинкой. Зеркальце устанавливается так, чтобы через оптическую трубу ж было видно отражение в зеркале рейки е со шкалой, разделенной на миллиметры.
§ 601 ИССЛЕДОВАНИЕ МЕТАЛЛОВ В ОВЛАСТИ МАЛЫХ ДЕФОРМАЦИЙ
127
Пусть начальный отсчет по шкале, то есть цифра, стоящая против нити в поле зрения трубы, есть $. Это значит, что луч, падающий из точки шкалы с пометкой $ на зеркальце и образующий угол ф с нормалью к его поверхности, отражается под тем же углом ф, становясь направленным по оптической оси трубы. Предположим теперь, что образец растянулся, расстояние I между призмами получило приращение Д/. Подвижная призма, а вместе с нею и
л Д*
зеркальце повернулись на угол Дф=у, на этот же угол повернулась нормаль к поверхности зеркальца. Угол между последней и оптической осью трубы стал ф — Дф. Угол между лучом падающим и лучом отраженным вместо 2ф стал 2ф — 2Дф, а так как отраженный луч, направленный по оптической оси трубы, неподвижен, то на угол 2Дф повернулся луч падающий. Отсчет по шкале изменился на Д$; считая шкалу приблизительно перпендикулярной лучу, получим:
. . 2Д/Д
Д« = 2Дф£=—у.
Здесь L — расстояние от зеркальца до шкалы. Отсюда
Д/=~Д5. 2£
Величина у есть увеличение прибора. Оно зависит от диагонали призмы d и фркусного расстояния трубы. Обычно
у=500. а
128
ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [гл. V
Оценивая на глаз 0,2 мм на шкале при расчетной длине /= 100 мм, мы можем мерить относительную деформацию с точностью 4>10-1.
Будем прикладывать нагрузку равными ступенями. После каждой нагрузки будем измерять удлинение. Результаты испытаний для стали
ординат откладывается сила, поделенная на площадь поперечного сечения, то есть напряжение, по оси абсцисс откладывается удлинение, отнесенное к рабочей длине образца (расстоянию между призмами экстензометра). Опытные точки, конечно, никогда не ложатся точно на одну прямую, трение в элементах испытательной машины приводит к ошибкам в измерении сил, экстензометр также вносит случайные погрешности, зависящие от разных причин. Однако отклонение точек от прямой незначительно, и проведенная между ними, прямая представляет собою упругий участок диаграммы. Для стали закон Гука выполняется весьма точно, и' при обычных методах измерения отступления от него незаметны, они меньше, чем случайные отклонения вследствие ошибок измерения. Специальные исследования, произведенные на весьма совершенной аппаратуре, показывают, что иа самом деле существуют систематические отклонения от закона Гука уже при малых напряжениях, но эти отклонения практически никакой роли не играют. Возвращаясь к рис. 73, мы убеждаемся, что, начиная с некоторого напряжения, точки перестают ложиться на прямую, диаграмма о — в заметно искривляется. Однако мы окажемся в большом затруднении, если захотим определить предел пропорциональности, то есть напряжение, начиная с которого закон Гука перестает быть верным. Величина предела пропорциональности является функцией точности измерительных приборов, чем последние, точнее, тем раньше мы заметим отклонение от закона Гука. Поэтому и определение предела пропорциональности можно дать только условное: это напряжение, начиная с которого отступления от закона Гука превышают определенную величину. Чтобы уточнить такое условное
§ 601 ИССЛЕДОВАНИЕ МЕТАЛЛОВ В ОБЛАСТИ МАЛЫХ ДЕФОРМАЦИЙ V2& определение и дать точный способ определения предела пропорциональности, нужно сначала остановиться на нахождении модуля упругости.
Для стали и некоторых других достаточно прочных металлов и сплавов дело обстоит просто: мы проводим прямую, наилучшим образом проходящую через опытные точки и между ними; угловой коэффициент этой прямой принимается за модуль упругости Е. Обычная ошибка при таком определении бывает порядка трех процентов. Но существуют материалы, у которых диаграмма о—е совсем не имеет прямолинейного участка, например чугун. Для таких материалов модуля упругости в обычном смысле не существует, вместо него-вводится понятие о так называемом секущем модуле, который представляет собою угловой коэффициент луча,. проведенного из начала координат в некоторую точку М диаграммы:
Секущий модуль — это переменная величина, ее можно считать функцией напряжения, соответствующего точке М Когда говорят о модуле упругости чугуна, например, и применяют для расчета чугунных изделий закон Гука, имеют в виду некоторое среднее значение секущего модуля, соответствующее диапазону рабочих напряжений.
Наряду с секущим модулем введем касательный модуль, представляющий собою угловой коэффициент касательной к линии о — е:
„ de
Е, = -г-.
* de
Как видно, при а—>-0 Es—► Et, при изменении а касательный модуль Et меняется значительно быстрее, чем Es. Возвращаясь к рис. 73, мы видим, что за пределом пропорциональности секущий модуль изменился мало по сравнению с его значением на прямолинейном участке, тогда как касательный модуль изменился весьма заметно. За предел пропорциональности обычно принимают напряжение, при котором касательный модуль превышает на определенное число процентов (например, на 50%) модуль упругости для прямолинейной части диаграммы.
Описанный опыт не доставляет нам никаких сведений об упругих свойствах материала. Желая найти предел упругости, после каждой нагрузки разгружают образец и следят за появлением остаточной деформации. Более точные приборы, конечно, позволят обнаружить остаточную деформацию раньше, поэтому предел упругости определяют как напряжение, начиная с которого остаточное удлинение превышает некоторую условную величину (от Ь10-1 до 5-10“5 по разным нормам).
5 Ю. Н. Работнов
130 ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [ГЛ. V
§ 61. Диаграмма растяжения мягкой стали. Рассмотрим теперь диаграмму зависимости между силой и деформацией в целом. В качестве наиболее типичного материала выберем мягкую сталь с небольшим содержанием углерода. Будем откладывать по оси ординат силу, поделенную на первоначальную площадь поперечного сечения, по оси абсцисс — удлинение, отнесенное к первоначальной длине. В результате получим диаграмму, изображенную на рис. 74. Горизонтальный участок диаграммы называется участком текучести, а соответствующее напряжение — пределом текучести от. В начале участка текучести на диаграмме часто появляется зуб, напряжение поднимается выше предела текучести, причем деформация приблизительно сле
дует закону Гука, а потом падает до величины от и сохраняет на площадке текучести постоянное значение. После того как достигнута точка В на диаграмме, нагрузка начинает возрастать, материал вновь приобретает способность сопротивляться пластической деформации. Это явление носит название упрочнения. До точки С на диаграмме удлинение' происходит равномерно, первоначально цилиндрический образец сохраняет цилиндрическую форму, утоньшаясь с ростом удлинения. Достижение силой максимального значения в точке С связано с появлением шейки, то есть местного сужения образца. Начиная с этого момента, все растяжение локализируется в области шейки; сечение в середине шейки быстро уменьшается, настолько быстро, что, хотя напряжение продолжает расти, растягивающая сила убывает. Таким образом, падение диаграммы после точки С не означает, что способность материала сопротивляться деформации уменьшается, наоборот, сопротивление продолжает расти, но эффект уменьшения площади сечения оказывается преобладающим. Вне области шейки при уменьшении силы падают и напряжения, поэтому после достижения точки С значительная часть длины образца не подвергается дальнейшей деформации. Наконец, в точке D происходит разрыв образца. Сила, соответствующая точке С, называется разрушающей силой, частное от деления разрушающей силы на первоначальную площадь поперечного сечения называется временным сопротивлением или пределом прочности ств. Нужно заметить, что ств не есть напряжение, при котором происходит разрыв; для определения последнего следовало бы разделить силу, соответствующую точке D, на площадь * сечения шейки в момент разрыва. Эта величина больше, чем временное сопротивление, но и ее нельзя принять за физическую характеристику прочности, так как в шейке напряженное состояние является сложным.
§ 61] ДИАГРАММА РАСТЯЖЕНИЯ МЯГКОЙ СТАЛИ 131
Временное сопротивление вообще не является напряжением, так как оно определяется по первоначальной площади сечения, а к моменту достижения точки С сечение образца успевает существенно уменьшиться. Таким образом, временное сопротивление — это условная характеристика, являющаяся суммарным выражением целого ряда физических свойств. Процесс образования шейки можно трактовать как процесс потери устойчивости равномерного течения металла, малые отклонения от идеальной геометрической формы до достижения точки временного сопротивления мало сказываются на процессе деформирования, тогда как после достижения этой точки эти малые случайные отклонения неизбежно растут и приводят к образованию шейки.
Временное сопротивление чрезвычайно просто определяется на опыте, для этого не нужно измерять деформации, достаточно разорвать образец на машине и отметить при этом максимальное достигнутое значение силы. Поэтому до настоящего времени эта характеристика является основной для суждения о прочности металла и до-недавнего времени величины допускаемых напряжений устанавливались в зависимости от временного сопротивления.
Вторая важная характеристика — это относительное удлинение при разрыве, то есть абсцисса точки D. Важность этой характеристики уже была указана выше, в § 58. Высококачественные легированные стали тем и отличаются от простых углеродистых, что при высоком временном сопротивлении они обнаруживают большое удлинение при разрыве.
Строя диаграмму растяжения, подобную изображенной иа рис. 74, мы не вправе называть величину, откладываемую по оси ординат, напряжением, так как площадь поперечного сечения образца меняется в процессе растяжения. Величина, откладываемая по оси абсцисс, также не может быть названа, строго говоря, относительным удлинением, так как после точки С все удлинение локализируется в области шейки и отнесение его к общей первоначальной длине образца теряет смысл. Истинной диаграммой растяжения, в отличие от приведенной наТ>ис. 74 условной диаграммы, называется диаграмма зависимости между напряжением и относительной деформацией. Для построения такой диаграммы необходимо относить силу каждый раз к фактической площади поперечного сечения. До точки С построение истинной диаграммы не встречает принципиальных затруднений, удлинение определяется обычным способом, наряду с измерением деформации производится измерение поперечных размеров образца и производится соответствующий перерасчет. Истинная диаграмма, показанная на рис. 75, идет всегда выше условной, приведенной на том же чертеже пунктиром. В точке С, соответствующей точке С условной диаграммы, касательная к истинной диаграмме не становится горизонтальной, в соответствии с тем, что было сказано выше. Для дальнейшего построения приходится прибегать к гипотезам,
S*
132 ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [гл. V
относящимся к распределению напряжений и деформаций в шейке; таким образом, часть истинной диаграммы после точки С получается не как результат прямого эксперимента, а на основе некоторого пересчета. Метод подобного пересчета предложил Н. Н. Давиденков.
Другая возможность построения диаграммы растяжения, связывающей не условные, а истинные (с известным приближением) на-.пряжения и деформации, заключается' в том, что по оси абсцисс откладывается не удлинение в направлении действия растягивающей силы, а поперечная деформация. За меру поперечной деформации принимают относительное уменьшение площади разца:
поперечного сечения об-
* о
Fo— первоначальная пло-
Здесь щадь поперечного сечения образца, F—минимальная площадь поперечного сечения деформированного образца.
Пока удлинение равномерно, величины ф и е связаны между собою следующим образом:
Это легко установить, воспользовавшись условием неизмен-^ ности объема (изменение объема происходит только за счет упругой деформации, а ею можно пренебречь, когда удлинение велико).
m Для большинства металлов диаграмма ст — ф от точки С, соответствующей образованию шейки, почти до точки разрыва D (рис. 76) является прямолинейной. Диаграмма ст — ф характеризует зависимость истинного напряжения от истинной деформации при растяжении лучше, чем условная диаграмма, но и она не отражает сложного характера напряженного состояния в шейке.
§ 62. Опыты на сжатие. Пластические металлы, такие, как, например, мягкая сталь, ведут себя при сжатии так же, как при растяжении. Не говоря уж об упругих характеристиках, которые • совершенно одинаковы при растяжении и сжатии, предел текучести оказывается тоже одинаковым, и диаграмма сжатия в пластической области при небольших деформациях повторяет диаграмму растяже-
§ 621
ОПЫТЫ НА СЖАТИЕ
133
ния. При больших деформациях диаграммы оказываются различными, прежде всего из-за того, что сжатие сопровождается увеличением площади поперечного сечения образца, следовательно, нагрузка все время растет. Поэтому для пластических материалов нельзя говорить о пределе прочности при сжатии: если материал очень пластичен, он может быть расплющен и превращен в тонкий лист без разрушения. При проведении и анализе опытов на сжатие нужно считаться с тем, что образец для испытания неизбежно должен быть достаточно коротким. В противном случае происходит так называемый продольный изгиб, то есть боковое выпучивание под действием продольной силы. При сжатии коротких образцов стремлению их расшириться с уменьшением длины препятствуют силы трения на торцах. В результате создается сложное напряженное состояние. Некоторые сорта закаленной стали, алюминиевые и магниевые сплавы ведут себя при растяжении иначе, чем при сжатии, пределы упругости, пропорциональности и текучести при растяжении и сжатии оказываются различными.
Для хрупких материалов, таких, как чугун, бетон, всякого рода камни, испытание на сжатие является основным видом испытаний. У таких материалов, как правило, сопротивление сжатию значительно выше, чем сопротивление растяжению, поэтому в конструкциях их -стремятся использовать так, чтобы заставить работать на сжатие.
Диаграмма сжатия чугуна, как уже указывалось, с самого начала криволинейна (рис. 77), до момента разрушения на ней нельзя указать каких-либо характерных точек, поэтому в качестве основной
Рис. 78.
ВИБЛИ0"Ж* КОЛОШ ОСКОРКА
характеристики принимается величина разрушающей силы, поделенная на площадь сечения образца, то есть предел прочности при сжатии. Испытание бетона проводится обычно на образцах в форме кубиков. На рис. 78 изображены характерные формы разрушения цементных и чугунных образцов. Трение на торцах короткого образца, например цементного кубика, стесняет деформацию и тем самым повышает
ВИ В ЛИО""W а
КОЛОХЗА
ине №33 __ ?
НЕ БОЛЕЕ КНИГИТТ | ОДНИ РУКИ И 2Х В ДВЕ )
134 ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [гл. V прочность. Действительно, если смазать поверхности плит пресса и уменьшить тем самым трение, разрушающая нагрузка существенно уменьшится. При этом меняется и характер разрушения, кубик расслаивается по плоскостям, параллельным направлению силы.
§ 63. Строение и упругая деформация металлических кристаллов. Получив внешнее представление о характере протекания упругой и пластической деформации металлов, естественно задать вопрос: каков же внутренний механизм этих процессов и что происходит в материале при действии на него внешних сил? Металлы в этом отношении изучены наиболее хорошо, в то же время несущие элементы конструкций делаются по преимуществу металлическими, поэтому мы займемся вопросом об упругой и пластической деформации металлов и сплавов.
Металлы имеют кристаллическую структуру. В известных условиях могут образовываться большие единичные металлические кристаллы, так называемые монокристаллы. Существуют способы искусственного выращивания монокристаллов, применяемые в лабораториях для физических исследований. Но при затвердевании металла из расплава возникает .очень много центров кристаллизации, в результате технический металл состоит из большого числа кристаллов неправильной огранки, которые называются кристаллитами или кристаллическими зернами. Расположение зерен носит случайный характер, неправильность их формы вызвана тем, что рост каждого зерна стеснен соседними зернами. Атомы металла в каждом кристалле расположены совершенно определенным образом; соединяя отрезками прямых центры атомов, мы получим то, что называют кристаллической решеткой. Она состоит из повторяющихся совершенно одинаковых элементов. Атомы удерживаются в решетке особого рода связями, которые называются металлическими связями. Природа этих связей состоит в следующем. Каждый атом отдает все свои свободные электроны, они полностью утрачивают связь с индивидуальными атомами и беспорядочно движутся между ними подобно частицам газа. Лишенные части электронов, атомы становятся электрически положительными, и между ними возникают силы электрического отталкивания. Давление электронного газа, наоборот, стремится сблизить атомы, равновесие сил притяжения и отталкивания обеспечивает устойчивость кристаллической решетки. Сила взаимодействия между каждой парой атомов приближенно записывается таким образом:
A R
(63.1)
Здесь г — расстояние между атомами, А, В, т и п — постоянные для данного вещества.
§ 64] ТИПИЧНЫЕ КРИСТАЛЛИЧЕСКИЕ СТРУКТУРЫ МЕТАЛЛОВ 135
Показатель п больше, чем показатель т, поэтому силы отталкивания, преобладающие при малых расстояниях, уменьшаются с увеличением расстояния г значительно быстрее, чем силы притяжения. Примерный график зависимости силы F от расстояния между атомами г изображен на рис. 79. В положении относительного равновесия, когда г = г0, сила F равна нулю. При изме- F нении расстояния возникает сила, отталкивающая при сближении ато- < Го >\ X.
мов и притягивающая при их удале- /
нии. Если это изменение мало, зави- J/__________________________
г г
симость силы от величины г — гв можно /
считать в первом приближении линей- -» /—г,-------*•
ной. Отсюда ясно, что закон Гука / есть лишь приближение, справедли- / вое для малых деформаций.
Если сила такова, что расстоя- Рис. 79.
ние между атомами становится равным то кристаллическая решетка разрушается, так как дальнейшее увеличение расстояния между атомами не требует увеличения силы. Рассмотренная двухатомная модель позволяет судить о свойствах кристаллической решетки Лишь качественно, на самом деле атомы расположены в пространстве и взаимодействие между ними значительно более сложно.
§ 64. Типичные кристаллические структуры металлов. Каждый металл при кристаллизации обнаруживает совершенно определенную кристаллическую структуру, однако некоторые металлы изменяют структуру при изменении внешних условий — температуры и давления. Это явление называется полиморфизмом; модификации, отличающиеся строением решетки, обозначаются обычно греческими буквами. Так, железо при температуре ниже 910° называется «-железом, при более высокой температуре решетка его перестраивается, соответствующая модификация называется ужелезом или аустенитом.
Наиболее распространенными типами кристаллических структур металлов являются следующие три:
1. Гексагональная плотн оу пакованная структура. Представим себе атомы в виде твердых шаров одинакового диаметра. Уложим плотно первый слой этих шаров, как показано на рис. 80 сплошными линиями. Второй слой плотно уложенных шаров показан на том же рисунке пунктиром. На этот слой можно положить третий таким образом, что центры шаров третьего слоя окажутся в точности над центрами шаров первого слоя. Четвертый слой укладывается таким образом, что расположение шаров воспроизводит их расположение во втором слое, и т. д.
136
ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ
[ГЛ. V
На рис. 81 показана основная ячейка гексагональной плотноупа-кованной структуры. Точки изображают центры атомов, буквы устанавливаю! соответствие между рис. 80 и рис. 81, индексы при
о - центры шороб 3- слоя
* - центры шарой слоя
Рис. 80.
буквах указывают на номер слоя. Отрезки, показанные на схеме рис. 81 сплошными линиями, равны между собой и равны диаметру шара. Легко подсчитать, что отношение высоты шестигранной призмы к стороне основания есть 2 — 1,633.
Гексагональную плотноу пакованную структуру имеют магний, цинк, а-никель и другие металлы.
2. Кубическая гранецентрированная структура. Эта структура является также плотноупакованной. Дело в том, что способ плотной укладки шаров, приведенный при рассмотрении гексагональной структуры, не является единственным. После того как первый ряд шаров уложен, соединив центры их отрезками прямых, мы получим чередующиеся ряды треугольников, расположенных вершинами вниз и
§ 64] ТИПИЧНЫЕ КРИСТАЛЛИЧЕСКИЕ СТРУКТУРЫ МЕТАЛЛОВ 137
вершинами вверх. Шары второго слоя мы положили так, что их центры приходятся над центрами треугольников, обращенных верши-слоя имеются две возможности, слоя так, что центры их прихо-
нами вверх, при укладке третьего Если мы помещаем шары третьего дятся под центрами обращенных вниз вершинами треугольников второго слоя, третий слой повторяет первый. Продолжая эту систему укладки, мы получаем гексагональную структуру. Но если мы будем укладывать каждый слой, одинаковым способом, например так, что центры шаров следующего слоя помещаются иад центрами обращенных вершинами вверх треугольников предыдущего слоя, мы получим другую структуру, называемую кубической гранецентрированной (рис. 82). В ней четвертый слой повторяет расположение шаров первого слоя. Основная
бз Сз
Рис. 81.
ячейка гранецентрированиой кубической решетки изображается обычно так, как показано на рис. 83. Плоскостям, в которых укладываются слои шаров, соответствуют октаэдрические плоскости куба, то есть сечения, наклоненные одинаково по отношению к трем ребрам куба. Если вершина соответствует отмеченному той же буквой на рис. 82 центру шара четвертого слоя, атомы, расположенные в плоскости BCD, соответствуют шарам третьего слоя, плоскость EFG соответствует второму слою, атом Н изображается шаром первого ряда. Соответствие между рис. 83 и рис. 82 легко установить, если смотреть на куб по направлению диагонали АН.
Кубическая гранецентрированная решетка характерна для ряда металлов, применяемых в технике, такую структуру имеет у-железо, алюминий, медь, никель, свинец и многие другие металлы и сплавы, в том числе некоторые сплавы на железной основе, так называемые аустенитные стали.
3. Кубическая объемноцентрированная структура. Элементарная ячейка такой структуры изображена на рис. 84. Эту структуру имеют a-железо, большинство сплавов на железной основе, хром, молибден, ванадий и другие металлы. Тип кристаллической решетки для данного металла может быть установлен при помощи рентгенографического исследования. Структура реальных кристаллов никогда не бывает идеально правильной. Помимо местных дефектов, о которых будет сказано ниже, в кристаллах наблюдается так называемая мозаичная, или блочная, структура, кристалл разбивается на блоки
о - центры шороб I- и 4&слоя х - центры шороб 2-слоя □ - центры шороб З^сяоя
Рис. 82
6
Рис. 83. Рис. 84.
§ 65] ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИЯ МОНОКРИСТАЛЛОВ 139
величиной порядка 10-1 см, незначительно отличающиеся ориентировкой кристаллографических плоскостей.
Как мы видели, упругая деформация кристаллов является результатом изменения междуатомных расстояний. Чтобы получить законы упругости, необходимо рассмотреть действительное расположение атомов в кристаллической решетке и учесть, что все атомы взаимодействуют между собой. Простая модель двух атомов, приведенная в § 63, конечно, недостаточна. Такого рода расчеты производились и хорошо подтверждены экспериментами. Существенно заметить, что строение кристаллической решетки сразу указывает, что упругие свойства будут различными для разных направлений; кристаллы не являются изотропными.
§ 65. Пластическая деформация монокристаллов. Механизму пластической деформации монокристаллов посвящено очень большое количество исследований. Это объясняется тем, что в монокристалле, этот механизм проявляется в чистом виде, переход же к реальному поликристаллическому металлу связан с большими дополнительными трудностями. Основной экспериментально обнаруженный факт состоит в том, что пластическая деформация совершается в результате сдвига слоев атомов, причем сдвиг происходит в совершенно определенных кристаллографических плоскостях по определенным направлениям. I
Такими плоскостями являются те, А
в которых атомы упакованы наибо-лее плотно; направления сколь- / \
жения — это опять-таки направле- / I \
ния самого плотного расположения / I \
атомов. Так, например, в кубиче- J J_____\
ской гранецентрированной решетке Г ] \
плоскостями плотной упаковки явля- / \
ются октаэдрические плоскости. / ' \
На рис. 85 стрелками показаны Л/ направления наиболее плотного рас- <s -------------о------—«х.
положения атомов. Совокупность / плоскости возможного скольжения, рис 85.
заданной нормалью я, и направления скольжения, задаваемого вектором s, лежащим в этой плоскости, называется системой скольжения. В гранецентрированной кубической решетке можно провести четыре октаэдрические плоскости, в каждой из них имеется три направления скольжения, таким образом, всего получается 12 возможных систем скольжения.
В гексагональной структуре плоскости плотной упаковки — это плоскости, параллельные основанию шестигранной призмы основной ячейки; таким образом, имеются одна плоскость возможного скольжения и только три системы скольжения.
140 ФИЗИЧЕСКИЕ .ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [гл. V
Поведение монокристалла гексагональной структуры под нагрузкой в очень сильной степени зависит от его ориентировки по отношению к действующей силе. Растягивая монокристаллы цинка в направлении оси шестигранной призмы основной ячейки или в перпендикулярном направлении, мы не получим касательных напряжений в плоскости скольжения; под действием растягивающей силы кристалл разрушается хрупко, без заметной пластической деформации. Для того чтобы вырезанный из монокристалла образец пластически деформировался, нужно, чтобы плоскость возможного скольжения составляла с направлением растяжения некоторый угол, отличный от прямого.
У кубического гранецентрированного кристалла имеется много систем скольжения, и при любой ориентировке его по отношению к растягивающей силе найдутся такие системы, в которых скольжение на самом деле произойдет; такие кристаллы являются высокопластичными.
В кубической объемноцентрированной структуре плоскости плотной упаковки отсутствуют, однако существует направление плотной упаковки, а именно направление диагонали куба. В этом направлении всегда происходит скольжение, тогда как определенных плоскостей скольжения здесь указать нельзя, ибо существует несколько плоскостей, содержащих в себе направления диагонали, по которым скольжение происходит с одинаковой легкостью.
Внешняя картина протекания пластической деформации в монокристалле состоит в следующем. Когда касательные напряжения в одной из систем скольжения достигают критического значения, в соответствующих плоскостях происходят .z------------- \ сдвиги, причем сразу на довольно большую ве-
личину (порядка 1000 междуатомных расстоя-j \ ний), сначала в определенных плоскостях. По
/ меРе увеличения нагрузки вступают в действие
\ другие, близкие плоскости скольжения, обра-
зующие пачку. Расстояние между активными \ плоскостями скольжения в пачке имеет поря-^2 док 100 междуатомных расстояний.
\ Схематически пластическая деформация мо-
\ нокристалла показана на рис. 86. Следы пере-
\ сечения пачкн плоскостей скольжения с на-У ружной поверхностью образуют так называ-V .S' емые линии скольжения. Эти линии можно на-\ блюдать не только под микроскопом, но и не-
вооруженным глазом. Тонкая структура линий Рис. 86. скольжения обнаруживается только под электронным микроскопом. Между линиями скольжения остаются большие области, не принимающие участия в пластической деформации и перемещающиеся на первом этапе деформирования как жесткое целое. С развитием деформации линий
§ 66] ПРОЧНОСТЬ КРИСТАЛЛОВ И СОПРОТИВЛЕНИЕ ДЕФОРМИРОВАНИЮ 14Т
скольжения появляется все больше и больше, части кристалла между пачками плоскостей скольжения дробятся на отдельные блоки, которые в дальнейшем поворачиваются. Течение металла приобретает беспорядочный характер. На рис. 87 приведена микрофотография алюминия, деформированного до 10% (увеличение 650). В поле зрения попала граница двух зерен, разница в их ориентации незначительна, поэтому линии скольжения проходят через границу. Часть
Рис. 87.
снимка оказалась не в фокусе, поскольку поверхность отшлифованного образца искривляется при деформации.
В металлах с гранецентрированной кубической структурой часто наблюдаются пересекающиеся линии скольжения различных направлений. Это указывает на то, что скольжение развивается одновременно в нескольких системах, которые оказываются расположенными примерно одинаково по отношению к направлению действия силы.
§ 66. Прочность кристаллов и сопротивление пластическому деформированию. Разрушение кристаллической решетки возможно в результате преодоления междуатомных сил, величина которых приближенно определяется по формуле (63.1). Разрушающее напряжение, подсчитанное в предположении о том, что решетка является геометрически совершенной, называется теоретической прочностью кристалла. Расчеты дают для теоретической прочности значения, во много раз превышающие фактически наблюдаемые. Низкая прочность реальных кристаллов объясняется тем, что они всегда имеют дефекты строения и разрушения начинаются со слабого места, при этом
142
ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [ГЛ. V
образуются трещины. Край трещины является источником концентрации напряжения, поэтому для продвижения трещины достаточно сравнительно небольшого напряжения. Точно таким же образом для того, чтобы вызвать пластическую деформацию идеального кристалла путем
сдвига на одно междуатомное расстояние в плоскости скольжения, нужно приложить чрезвычайно большое касательное напряжение. Величину его можно приблизительно оценить следующим образом. Рассмотрим упрощенную модель решетки, изображенную на рис. 88. Здесь b — расстояние между атомами в плоскости скольжения, а —
расстояние между плоскостями скольжения. Если сдвинуть ч верхний слой атомов относительно нижнего на вели^ чину а, на каждый атом будет действовать сила F, которая стремится вернуть атом в его первоначальное положение, пока а<^Л/2. При а = />/2 сила равна нулю, но равновесие неустойчиво, при а^>Л/2 верхний ряд атомов стремится занять новое положе-
ние равновесия, повторяющее первоначальное со сдвигом на величину Ь. Таким образом, сила- F есть периодическая функция а с периодом, равным Ь. Разлагая ее в ряд Фурье и удерживая первый член разложения, получим:
F=Fosin?p. (66.1)
При малых смещениях можно принять
F=F„2^-u. (66.2)
Но F—%b*, где т — касательное напряжение в плоскости скольжения. Предположим, что атомы в плоскости скольжения размещены в вершинах квадратов со стороной Ъ. Далее, а = уа, где у — относительный сдвиг. Учитывая это, получаем:
т=50
2па
-ттч-
Сравнивая написанное соотношение с законом Гука т = Оу, найдем:
с Ь’ г Fo~ 2 па а
Здесь Fo — это та максимальная сила, которую нужно чтобы сдвинуть слой атомов на одно междуатомное Соответствующее касательное напряжение
_ £> — 60 ‘
0 Ьг 2ла '
при сдвиге
преодолеть, расстояние.
(66.3)
ДИСЛОКАЦИИ
143
§ 67]
Если считать, что а и b одного порядка, мы получим предел текучести для монокристалла равным примерно одной шестой модуля сдвига. Более точные подсчеты, основанные на учете реального характера сил взаимодействия между атомами, дают для т0 значение около одной тридцатой модуля сдвига. Эта величина в несколько сот раз превышает истинное значение сопротивления сдвигу, которое находится в результате опытоз.
Такое расхождение между теоретическим и действительным сопротивлением сдвигу в кристаллах объясняется тем, что кристаллическая структура никогда не бывает совершенной; уже в процессе кристаллизации возникают неизбежные дефекты. Наличие этих дефектов и делает кристалл значительно более податливым, чем следовало бы ожидать.
§ 67. Дислокации. Основную роль при объяснении механизма пластической деформации кристаллов играют особого вида дефекты кристаллической решетки, называемые дислокациями. Для того, чтобы понять, что такое дислокация, мы будем рассматривать схематизированную модель кристаллической
решетки, а именно простую кубическую сетку, изображенную в од-
себе, что кристалл разрезан между соседними рядами атомов от точки С вверх и в этот разрез вставлен лишний слой атомов. Такая искаженная кристаллическая решетка изображена на рис. 90. Говорят, что в точке С создана краевая дислокация. Принято обозначать краевую дислокацию на чертеже знаком в виде перевернутой буквы Т, вертикальная палочка напоминает о лишнем слое атомов. Такая дислокация считается положительной. Отрицательная дислокация получается тогда, когда разрез делается снизу и в него вводится лишний слой атомов; символом отрицательной дислокации является буква Т уже в нормальном, а не в перевернутом виде. На достаточном расстоянии от центра дислокации Сискажение кристаллической решетки
144
ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [ГЛ. V
незначительно, и нам трудно судить о том, что в кристалле создана дислокация. В окрестности дислокации на чертеже не показано расположение атомов, так как здесь решетка деформирована очень сильно и о ее структуре мало что известно. Область, окружающая дислокацию, в которой искажение решетки значительно, называется ядром дислокации. Краевую дислокацию можно создать не только путем вертикального разреза. На рис. 91 показаны различные способы создания положительной дислокации. Случай а повторяет уже
Рис. 91.
рассмотренную нами схему, в случае в края разреза сдвинуты один относительно другого, в случае г разрез ^ сделан вниз и удален один атомный слой, в случае д * дислокация создана также путем сдвига, но разрез сделан справа от центра дислокации. После того как края разреза соединены, расположение атомов в искаженной решетке будет во всех случаях одним и тем же, так что нет
никакой возможности установить, каким именно способом была создана дислокация.
Образование дислокаций путем сдвига (рис. 91, в и д) не требует удаления материала или добавления лишнего, поэтому такой
путь является наиболее естественным. В кристалле достаточно больших размеров и не содержащем других дефектов дислокация может перемещаться. Действительно, искажение кристаллической решетки, связанное с дислокацией, означает изменение междуатомных сил, а следовательно, изменение энергии кристалла. Чтобы образовать дислокацию, нужно переместить края разреза, при этом придется преодолевать междуатомные силы, то есть совершать работу. Эта работа равна энергии дислокации. Очевидно, что в кристалле неограниченных размеров энергия дислокации не зависит от ее поло-’ жения, следовательно, с энергетической точки зрения дислокация свободна и может перемещаться как угодно. Однако существует кинематическое ограничение возможных движений дислокации. Представим себе, что положительная краевая дислокация переместилась вниз на некоторое расстояние 6. Это значит, что мы должны были сделать дополнительный разрез на длину 6 и вставить туда слой атомов.
§ 68]
ДВИЖЕНИЕ И РАВНОВЕСИЕ ДИСЛОКАЦИЙ
145
Для этого нужно ввести внутрь кристалла дополнительно некоторое количество вещества. Чтобы переместить дислокацию вверх на расстояние 6, нужно из дополнительного разреза удалить один атомный слой. Таким образом, вертикальные движения дислокаций невозможны без сохранения сплошности материала.
На самом деле в кристаллической решетке всегда существуют точечные дефекты, а именно внедренные атомы и вакансии, то есть пустые места в решетке. Внедренные атомы и вакансии мигрируют внутри решетки вследствие теплового движения атомов; движения внедренных атомов и вакансий иосят диффузионный характер и подчиняются законам диффузии. Поэтому вертикальные движения краевых дислокаций возможны, особенно при высоких температурах. Эти движения являются следствием диффузионных движений точечных дефектов и происходят медленно.
Горизонтальное движение дислокаций, наоборот, не связано с нарушением сплошности и поэтому всегда кинематически возможно. Плоскость возможного движения дислокации называется ее плоскостью скольжения; в символе, обозначающем краевую дислокацию, горизонтальная черточка напоминает о плоскости скольжения и, следовательно, о направлении возможного движения.
§ 68. Движение и равновесие дислокаций. В предыдущем параграфе мы упоминали об энергии дислокаций. Мы не сможем, оставаясь в рамках элементарных представлений, вычислить величину энергии, но соображения теории размерностей позволяют нам определить эту энергию с точностью до числового множителя. В неограниченном упругом теле, каким можно считать достаточно большой кристалл, единственным линейным размером, связанным с дислокацией, является величина смещения краев разреза. Будем называть эту величину вектором Бюргерса и обозначать через Ь. Вектор Бюргерса всегда кратен междуатомному расстоянию, но не обязательно равен ему. Действительно, можно представить себе дислокации, образованные путем удаления или добавления не одного только атомного слоя, но любого количества атомных слоев.
Упругие свойства материала характеризуются одной размерной упругой постоянной, например модулем сдвига G. Размерность его—сила на единицу площади. Размерность энергии дислокации W, приходящейся на единицу длины, есть размерность силы. Единственная комбинация из G и Ь, имеющая размерность силы, будет Gb\ Таким образом, W= kGb\
Имеются различные оценки для коэффициента k в этой формуле. По-видимому, достаточно точной оценкой является fe = 0,5. Таким образом,
1F=O,5G6!.
146 ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [ГЛ. V
Полученное выражение для энергии позволяет сделать некоторые заключения о взаимодействии дислокаций. Рассмотрим две положительные дислокации в одной плоскости скольжения (рис. 92). Если эти дислокации достаточно удалены друг от друга, они практически не взаимодействуют между собою и общая энергия двух дислокаций равна сумме их энергий, то есть 2kGb*. При сближении дислокаций появляется энергия взаимодей-____________________________JL_______________________ ствия и общая энергия системы изменяется. Когда расстояние Рис. 92._______________________между дислокациями станет равно
• нулю, они сольются в одну дис-
локацию с удвоенным вектором Бюргерса, энергия которой равна 4feG62. Таким образом, чтобы сблизить две дислокации одного знака, необходимо затратить дополнительную работу. Отсюда можно сделать вывод, что одноименные дислокации в общей плоскости скольжения отталкиваются. Аналогичным образом две разноименные дислокации притягиваются, стремясь слиться и уничтожить друг друга.
Итак, движение дислокаций может являться следствием их взаимодействия между собою. Более сложная картина такого взаимодействия получается в том случае, когда дислокации находятся в разных плоскостях скольжения и оси их непараллельны. /
Дислокации могут двигаться также под действием внешних сил, вызывающих в теле напряженное состояние, что и является причиной пластической деформации. Представим себе, что к блоку, содержащему дислокацию, приложены касательные напряжения, как показано на рис. 93.
Перемещение дислокации в положение С' означает, что на отрезке СС произведен дополнительный разрез и края его сдвинуты
Рис. 93. Рис. 94.
в направлении, указанном стрелками. При этом внешние силы производят положительную работу, следовательно, помогают такому движению. Дойдя до конца блока, дислокация выйдет на поверхность, при этом окажется, что верхняя половина блока сдвинута относительно нижней на величину вектора Бюргерса. В этом состоит элементарный акт пластической деформации. Отрицательная дислокация (рис. 94) в аналогичных условиях будет двигаться влево, результатом выхода ее за пределы блока будет такая же пластическая деформация сдвига.
§ 69]
ИСТОЧНИКИ ДИСЛОКАЦИЙ
147
До сих пор мы считали, что единичная дислокация в ненапряженном кристалле не испытывает никакого сопротивления своему движению. На самом деле кристалл имеет конечные размеры и в свою очередь разбивается на субмикроскопические блоки, границы которых в настоящее время рассматривают как некоторые образования, составленные из дислокаций. В зависимости от расстояния до границы энергия дислокации меняется; таким образом, границы являются препятствиями для движения дислокаций. Движению дислокаций могут мешать другие дислокации в той же или иных плоскостях скольжения, внедренные атомы или вакансии, субмикроскопические выделения разного рода. Наконец, имеется еще одна категория сил, препятствующих движению дислокаций даже в идеальной кристаллической решетке. Центр дислокации С при движении дислокации может совпадать с одним из атомов решетки или может находиться между ними. Оказывается, что энергия дислокации зависит от положения центра. Очевидно, что перемещение дислокации на одно междуатомное расстояние полностью восстанавливает картину, но для того, чтобы произвести такое перемещение, нужно преодолеть некоторый энергетический барьер; дело обстоит так, как есля бы существовали некоторые силы, препятствующие движению дислокаций. Эти силы называются силами Пайерлса, величина их в сильной степени зависит от расположения атомов в кристаллической решетке. Для площадей наиболее плотной упаковки атомов и для направлений, соответствующих наименьшему расстоянию между атомами, силы Пайерлса оказываются наименьшими, для других кристаллических плоскостей и направлений величина их во много раз больше. Этим и объясняется то, что в кристаллах пластические деформации происходят по определенным системам скольжения, как было указано выше.
§ 69. Источники дислокаций. Как мы видели, пластическая деформация кристаллов связана с выходом дислокаций наружу или блокированием их иа границах зерен; таким образом, казалось бы, что после определенной величины пластической деформации кристалл должен освободиться от дислокаций и потерять возможность пластической деформации. На самом деле этого ие наблюдается, наоборот, число дислокаций в результате пластической деформации увеличивается. Следовательно, должен существовать некоторый механизм порождения новых дислокаций в процессе пластической деформации.
Чтобы рассмотреть этот механизм, иам придется сначала ввести понятие о дислокациях более общего вида, чем краевые дислокации. Вообще можно представить себе, что ось дислокации является произвольной пространственной кривой Г, замкнутой или уходящей двумя концами в бесконечность. На рис. 95 изображена замкнутая линия дислокации. Чтобы произвести дислокацию, нужно провести
148 ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [гл. V
Рис. 95.
через контур Г произвольную поверхность 2, сделать по этой поверхности разрез и сместить стороны разреза друг относительно друга на величину вектора Бюргерса Ь. После этого стороны разреза соединяются, причем для восстановления сплошности либо добавляется материал, либо убирается лишний. Приведенному определению удовлетворяет, очевидно, и краевая дислокация; осью ее является бесконечная прямая, замыкающаяся в бесконечно удаленной точке, поэтому поверхностью разреза является бесконечная полуплоскость. Те же соображения, что и в случае краевой дислокации, убеждают нас в том, что дислокация общего вида может перемещаться по ци
линдрической поверхности, образующая которой параллельна вектору Бюргерса.
Представим себе теперь, что в кристалле существует произвольная дислокация с криволинейной осью. В реальной кристаллической структуре такая дислокация имеет очень ограниченную возможность для движения, оно возможно только тогда, когда дислокация лежит в плоскости возможного сдвига для кристалла и вектор Бюргерса параллелен этой плоскости. Но может случиться, что элемент pq линии дислокации (рис. 96) удовлетворяет этим условиям, то есть
Рис. 96.
он лежит в плоскости наиболее плотной упаковки атомов и вектор Бюргерса находится в этой же плоскости. Если в плоскости скольжения действует касательное напряжение, созданное внешними силами, то линия дислокации стремится переместиться. Однако концы ее удерживаются в точках р и q, и поэтому она изгибается по некоторой кривой. Чтобы определить форму этой кривой, мы применим к равновесию дислокации принцип возможных перемещений, справедливый для любой механической системы. Пусть ds — элемент длины линии дислокации, Q— радиус кривизны (рис. 97). Сообщим точкам линии дислокации перемещение би в направлении нормали;, элемент ds займет положение ds'. На заштрихованной площади ds Ьи произошло дополнительное
§ 69]
ИСТОЧНИКИ ДИСЛОКАЦИЙ
14»
смещение сторон разреза на величину вектора Бюргерса Ь, при этом необходимо было преодолеть сопротивление от действующих в плоскости скольжения касательных напряжений, то есть затратить работу xbdsbu. Элемент ds' больше, чем элемент ds, на величину б ds, из чертежа видно, что &ds~^ds. Так как энергия дислокации на единицу длины есть W', энергия элемента ds увеличилась на ds. Приравнивая эту величину работе касательных напряжений, получим:
xbdsbu = — ds hu.
е
Отсюда
Линия дислокации является окружностью, проходящей через точки р и д.
Энергия на единицу длины произвольной дислокации определяется с достаточной степенью той же формулой, что и для краевой дислокации, а именно IT=O,5Z>*G. Поэтому
т==0,5^-. (69.2)
Обращаясь к рис. 96, мы видим, что минимальный радиус окружности, проходящий через точки р и q, равен -у/., где L — рас- -стояние pq, то есть длина источника дислокаций. Отсюда максимальное зиачеиие т равно
ткр=^. (69.3)
Если внешнее напряжение меньше критического, деформация сдвига, являющаяся результатом перемещения линии дислокации,, обратима; оиа исчезнет при снятии нагрузки. Таким образом, наличие источников несколько понижает модуль сдвига материала. Такое понижение упругих постоянных в результате пластической деформации, увеличивающей число дислокаций, наблюдается в действительности.
Но если касательное напряжение достигает критического значения, равновесие дуги дислокации становится неустойчивым, эта дуга неограниченно расширяется, ометая значительную площадь, на которой происходит сдвиг. Макроскопический эффект такого срыва дислокации представляет собою сдвиг на величину вектора Бюргерса.. Заметим, что уравнение равновесия линии дислокации (69.1) имеет тот же вид, что и уравнение равновесия гибкой нити с постоянным натяжением W, нагруженной постоянным давлением, нормальным к нити в каждой точке и равным произведению xb. Как мы уже отметили, после достижения критического напряжения дуга дислокации
150 ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [гл. V i
будет неограниченно расширяться, причем радиус ее кривизны увеличивается. Формула (69.1) показывает, что такое расширение возможно при уменьшающемся напряжении. На самом же деле напряжение остается постоянным, поэтому
расширение дислокации носит динамический характер. Мы не в состоянии точно исследовать этот динамический процесс, но можем высказать некоторые качественные соображения по этому поводу. Естественно предполагать, что движение линии дислокации встречает сопротивление, увеличивающееся с увеличением скорости, поэтому середина дуги дислокации будет двигаться медленнее, а концы — быстрее. Кривая перестанет быть дугой окружности и сплющится. Последовательные формы линии дислокации в процессе ее движения показаны на рис. 98; в конце концов кривая коснется сама себя в точке М. Отрезки тп и т'п' линии дислокации могут рассматриваться как отрезки прямолинейных мент касания они сольются и взаимно
дислокаций разных знаков. В уничтожатся; в результате образуется замкнутое кольцо дислокации и криволинейная дислокация, соединяющая точки р, q, как показано на рис. 98 сплошными линиями. Кольцо под действием «давления» xb немедленно примет круговую формуй будет продолжать неограниченно расширяться, дислокация, соединяющая точки р и q, выпрямится, снова выгнется вправо, и весь процесс будет повторяться неограниченное число раз.
Таким образом, один источник может породить любое количество кольцевых дислокаций; выход каждой из них на поверхность означает сдвиг на величину вектора Бюргерса или одного междуатомного расстояния. Приведенная мбдель носит название модели Франка — Рида. Эта модель описывает неограниченную пластическую деформацию кристалла, не содержащего примесей и имеющего минимальное количество внутренних дефектов.
Формула (69.3) дает величину предела текучести для данного кристалла.
В действительности кольца дислокаций не имеют возможности расширяться неограниченно: в реальном кристалле всегда имеются препятствия для движения дислокаций. Представим себе, что препятствие имеет форму кольца, в центре которого находится источник. Первая дислокация останавливается на препятствии, вторая стремится
§ 70]
ГРАНИЦЫ БЛОКОВ
151
расшириться под действием напряжения г, но она в то же время испытывает силу отталкивания со стороны первой. В результате образуется система кольцевых дислокаций, изображенная на рис. 99. Эти дислокации создают поле напряжений в теле. Касательное напряже-
ние, действующее со стороны отдельных дислокаций на источник, противоположно напряжению т; в результате критическое напряжение источника увеличивается с каждой отделившейся дислокацией и в конце концов становится равным действующему напряжению. Таким образом, если дислокации не имеют возможности свободно выходить на поверхность, а задерживаются препятствиями, при данном касательном напряжении источник может породить лишь определенное число дислокаций,
чему соответствует определенная конеч-
ная пластическая деформация. Для дальнейшей деформации нужно увеличить напряжение. Такого рода поведение характерно для упрочняющихся материалов.
На самом деле очень мало вероятности, чтобы препятствие имело кольцевую форму, притом с центром, совпадающим с источником. Кольца дислокаций при дальней-шем движении сильно деформи- *-----*•
руются, и рассмотреть все мно- ______1_____________
гообразие возможных форм не рис
представляется возможным; поэтому обычно рассматривают самую простую модель группы краевых дислокаций в плоскости скольжения, задержанных препятствием (рис. 100). Условия равновесия такой группы известны совершенно точно; можно указать расстояние между дислокациями в состоянии равновесия под действием напряжения т и сил взаимного отталкивания дислокаций.
§ 70. Границы блоков. Представим себе, что из кристалла вырезана полоса конечной толщины в направлении плоскостей возможного скольжения и на вертикали Оу помещен ряд краевых дислокаций на равных расстояниях d (рис. 101). Чтобы создать первую дислокацию, мы должны сделать разрез от точки С, вверх до границы полосы, раздвинуть края разреза иа одно междуатомное расстояние и ввести туда слой атомов.
Чтобы создать вторую дислокацию, нужно от точки Сг вверх поместить уже два слоя атомов, и так далее. В результате окажется, что две половины полосы, разделенные вертикальным рядом дислокаций,
152 ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [гл. V
‘будут повернуты одна относительно другой на угол, равный отношению bfd. Кристалл окажется разбитым на два блока, слегка отличающихся ориентировкой кристаллографических плоскостей. В реальных кристаллах всегда существует такая блочная структура, обнаруживаемая методами рентгенографического анализа. Границы блоков
являются вертикальными рядами или стенками дислокаций. Причина образования данной структуры состоит в следующем. В результате пластической деформации в параллельных плоскостях скольжения
кристалла всегда образуется большое количество дислокаций, являющихся относительно свободными, то есть удерживаемыми незначительными препятствиями и разного рода силами сопротивления (рис. 102). В результате теплового движения атомов эти дислокации перемещаются, •стремясь сгруппироваться в наиболее устойчивые конфигурации. Такими устойчивыми конфигурациями являются стенки дислокаций. Процесс образования стенок называется полигонизацией. Этот процесс наблюдается, например, при ползучести металлов при высокой температуре (см. гл. XVIII).
§71. Деформация поликристаллических металлов и сплавов. Реальные металлы состоят из большого количества кристаллических зерен, •ориентировка которых случайна. Поэтому микроскопическое поведение •металла изотропно, несмотря на анизотропию отдельных зерен. Применяемые в технике металлы обычно не являются чистыми, а представляют собою сплавы, кристаллы которых содержат атомы различных компонент.
Простейшим типом сплавов являются твердые растворы замещения.
Атомы различных компонент таких сплавов участвуют в создании кристаллической решетки на равных основаниях; они размещаются в узлах кристаллической решетки, причем в каждом узле может оказаться атом любой из компонент. Твердые растворы замещения могут
§ 71] ДЕФОРМАЦИЯ ПОЛИКРИСТ АЛЛИЧЕСКИХ МЕТАЛЛОВ И СПЛАВОВ 153 образовываться в произвольных пропорциях, если атомные радиусы отличаются друг от друга не более чем на 15%. Соотношение атомных радиусов объясняет то, что некоторые металлы образуют твердые растворы замещения, а другие не образуют.
Твердые растворы внедрения получаются тогда, когда растворенные атомы проникают между атомами основной решетки. Для этоп> нужно, чтобы атомные радиусы растворенного элемента были достаточно малы. Примером раствора типа внедрения, служит система железо — углерод. При нормальной температуре растворимость углерода в железе ограничена, она увеличивается с повышением температуры. При охлаждении такого твердого раствора избыточный углерод образует химическое соединение Fe,C, так называемый цементит, отличающийся высокой прочностью. Поэтому в стали зерна железа, содержащего небольшое количество растворенного углерода, оказываются перемешанными с зернами цементита.
Хорошая растворимость углерода при высокой температуре и ограниченная растворимость при низкой связаны с тем, что при высокой температуре железо находится в виде кубической гранецентрированной у-фазы, так называемого аустенита; при охлаждении аустенит превращается в объемноцентрированную a-фазу, называемую ферритом. При быстром охлаждении (закалка) углерод не успевает выделиться из у-фазы, и образуется промежуточная, термодинамически неустойчивая мартенситная структура. Мартенсит очень тверд и хрупок, поэтому после закалки производят отпуск, в результате чего мартенсит частично распадается на устойчивые фазы — феррит и цементит. Относительное содержание названных фаз определяет твердость и прочность термически обработанной стали. Назначая режим термической обработки, можно сообщать стали желаемые свойства.
Многие из сплавов, применяемых в технике, имеют подобного рода сложную, многофазную структуру. Повышение прочности сплава обычно бывает связано с усложнением его внутреннего строения, так как этим затрудняется возможность пластической деформации. В дисперсионно-твердеющих сплавах повышение прочности связано с тем, что упрочняющая фаза в виде субмикроскопических выделений вкрапливается в кристаллическую решетку основного металла и препятствует свободному движению дислокаций.
Кинематическая возможность пластической деформации поликристал-лического металла определяется в первую очередь тем, что произвольная деформация единичного кристалла, как показал Тейлор, может быть получена как результат сдвигов в пяти системах скольжения. Действительно, деформация элемента объема определяется шестью величинами: удлинениями по трем взаимно перпендикулярным направлениям и сдвигами по этим направлениям, но вследствие того, что объем при пластической деформации не меняется, из шести величин независимы только пять. Поэтому, если каждое зерно
154 ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [гл. V
имеет не менее пяти систем скольжения (кубическая гранецентрированная и объемноцентрированная структуры), поликрнсталлический металл может деформироваться без нарушения сплошности. Однако различные зерна ориентированы различным образом по отношению к полю напряжений и поэтому начинают пластически деформироваться в разное время. Начало течения в отдельных, наиболее неблагоприятно ориентированных зернах соответствует пределу упругости. По мере увеличения нагрузки пластичность распространяется на большее количество зерен. Углеродистая сталь отличается от других -материалов тем, что на диаграмме растяжения имеется площадка текучести; для деформации на площадке текучести характерна большая неоднородность степени деформирования на разных участках испытываемого образца, некоторые зерна или группы зерен получают большую деформацию, другие же остаются упругими. В металлах, обнаруживающих значительное упрочнение, зерна деформируются более равномерно.
§ 72. Влияние повышенной температуры на механические свойства. В паровых котлах, двигателях внутреннего сгорания, паровых
и газовых турбинах, а также во многих химических аппаратах металл
работает в условиях высоких температур. Особенно высокие темпе-
ратуры, свыше 1000°, достигаются в авиационных реактивных двигателях. Поэтому представляет интерес изучение механических свойств металлов и сплавов при высоких температурах.
На рис. 103 приведена серия диаграмм растяжения одной и той же углеродистой стали при различных температурах, от 20° до 400°. Интересно отметить, что, начиная с температуры 400°, площадка текучести исчезает и диаграмма становится подобной диаграмме растяжения цветных металлов — меди или алюминия.
При более высоких темпе-
Рис. 103
ратурах прямолинейный участок диаграммы по существу отсутствует и результаты испытаний оказываются в сильной степени зависящими от скорости растяжения. Если подвергнуть образец действию постоянной нагрузки, он будет продолжать деформироваться е некоторой определенной скоростью, зависящей от
§ 72J ВЛИЯНИЕ ПОВЫШЕННОЙ ТЕМПЕРАТУРЫ НА МЕХАНИЧ. СВОЙСТВА 155
действующего напряжения. Медленное течение металла под действием постоянной нагрузки называется ползучестью. Для изделий с более или менее длительным сроком службы ползучесть представляет главную опасность, так как она может привести либо к накоплению недопустимо большой деформации, либо к разрушению. Вопросу о ползучести и прочности при длительном действии нагрузки будет посвящена специальная глава (гл. XVIII), здесь мы ограничимся сделанными замечаниями. Упругие характеристики металлов также меняются с температурой. На рис. 104 представлена зависимость модуля упругости
и модуля сдвига углеродистой стали от температуры. Как видно, при температуре 500° модуль упругости уменьшается примерно на 30%. Коэффициент Пуассона становится при этом весьма близким к одной второй. Следует заметить, что определение модуля упругости при высоких температурах затруднительно вследствие того, что материал ползет. Поэтому его находят или по наклону прямых разгрузки и повторной нагрузки (при этом ползучесть на некоторое время приостанавливается), либо по частоте упругих колебаний стержня из испытываемого материала, которая зависит от размеров стержня, плотности материала и модуля упругости (см. гл. XVI).
Поскольку модуль упругости характеризует силы междуатомной связи, на его зависимость от температуры очень мало влияет наличие в сплаве различных примесей. Для сталей с небольшим содержанием легирующих элементов эта •зависимость мало отличается от представленной на рис. 104. Пластические свойства и прочность при высоких температурах, наоборот, могут быть очень сильно изменены введением в сплав дополнительных элементов и специальной термической обработкой; эти свойства в сильной степени зависят от структуры.
изделия
156 ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [ГЛ. V 3
При выборе материала для работы в условиях высоких температур 1 необходимо считаться с тем, что многие металлы с повышением тем- ' пературы начинают интенсивно окисляться. Способность материала ". сопротивляться окислению при высокой температуре называется жаростойкостью, способность сохранять в этих условиях достаточно высокие механические характеристики — теплоустойчивостью или жаро- ) прочностью. '
Углеродистую сталь не рекомендуется применять при температу- ; рах, превышающих 400°, прочность ее становится низкой, а при . температуре порядка 500° она интенсивно окисляется.
Введением легирующих элементов — хрома, никеля, молибдена— : можно существенно повысить как жаростойкость, так и теплоустой- < чивость; такие стали применяются при тем- ’ пературах до 500°. При большом содер- ; жании хрома и никеля сталь сохраняет 1 структуру аустенита с гранецентрирован- ; ной решеткой при комнатной темпера- j туре. Такие аустенитные стали являются 1 жаропрочными, область их применения до 1 600—650°.
При более высоких температурах при- ч ходится применять сплавы, в которых ос- i новой является не железо, а другие элементы, например, хромоникелевые сплавы, j содержащие небольшие примеси иных ме-таллов (титан, ванадий, ниобий и т. п.). ?
30 3 некоторых из таких сплавов содержится i 5—6 различных металлических компонент.
20 Характерной особенностью углеродистой стали является то, что при темпе- j ® ратурах 200—300° ее прочность увели-
чивается, а пластичность уменьшается. -
7* Это явление называется синеломкостью, потому что в указанном интервале температур на поверхности нагретого сталь-fl синий цвет побежалости. У других метал-ей этого не наблюдается.
На рис. 105 представлены кривые зависимости от температуры предела текучести, предела прочности и удлинения при разрыве для углеродистой стали (сплошные линии) и хромоникелевой стали (пунктир).
«ого лов и
§ 73. Влияние скорости испытания. Вид диаграммы растяжения и ординаты ее характерных точек зависят от скорости, с которой производится растяжение. Для изучения этого эффекта в разных диапазонах скоростей применяются разные методы. Обычные машины для
§ 73]
ВЛИЯНИЕ СКОРОСТИ ИСПЫТАНИЯ
157
испытаний иа растяжение допускают изменение скорости движения элемента в известных пределах. Существуют машины, снабженные дополнительным редуктором, на которых можно производить испытания с весьма малыми скоростями. Для больших скоростей деформации такой путь непригоден, поэтому приходится прибегать к ударным испытаниям на копрах. Для не слишком больших скоростей применяются копры с падающей бабой или маятниковые. Скорость движения захвата в этом случае — это скорость свободного падения груза, масса которого должна- быть достаточно большой для того, чтобы можно было пренебречь потерей энергии на разрушение образца и считать скорость растяжения постоянной. Еще большие скорости по-
лучены на пневматических копрах. Такой копер представляет собою пневматическую пушку, выбрасывающую ударник со скоростью 300м/сек и выше.
Для стали при нормальной температуре зависимость механических свойств от скорости испытания незначительна, ее можно обнаружить, только меняя скорость в тысячи и десятки тысяч раз. /
На рис. 106 схематически показаны статическая и динамическая
диаграммы растяжения углеродистой стали при нормальной температуре; первая получена иа обычной разрывной машине, вторая — на копре с падающей бабой. Сравнение их приводит к следующим выводам:
1. При динамических испытаниях предел текучести и временное
сопротивление повышаются.
2. Площадка текучести исчезает.
3. Максимум диаграммы перемещается ближе к началу.
При высоких температурах зависимость характеристик пластичности от скорости становится более сильной. Проще всего определить из опыта величину временного сопротивления; получение полной диаграммы
растяжения при высоких скоростях связано с серьезными экспериментальными трудностями. На рис. 107 приведены экспериментальные графики зависимости временного сопротивления стали от скорости относительной деформации ё (Надаи и Манджойн). Опыты показали, что при нормальной температуре в диапазоне скоростей от 10~в до 10-1 ощутимой зависимости от скорости не обнаруживается. Заметим, что обычная скорость испытания на стандартной испытательной машине соответствует примерно ё = 10-’. При увеличении скорости до 10’ временное сопротивление возрастает примерно на 45%. При температурах, превышающих 300°, зависимость временного сопротивления
'J
158 ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [гл. V;
от скорости обнаруживается во всем интервале скоростей и стано-_ вится гораздо более сильной.
ческого тела. Считается, что напряжение связано со скоростью деформации следующей зависимостью:
+ 1). (73.1)
Здесь k и v — постоянные при данной температуре характеристики материала. При е«=0 отсюда получается о=от, то есть обычное ' условие идеальной пластичности. ;
Более простая схема — это вязко-пластическое тело с линейной & зависимостью сопротивления от скорости, для которого напряжение » выражается следующим образом:
<г=от-}~т1^- (73.2) "
Уравнение (73.2) довольно плохо согласуется с опытными данными в широком диапазоне скоростей, но в узком диапазоне скоростей всегда можно подобрать константу вязкости t] таким образом, что это уравнение окажется удовлетворительным. Расчеты, основанные на урав- * нении (73.2), обладают преимуществом большей простоты,
ИСПЫТАНИЯ НА ТВЕРДОСТЬ
159
§ 74)
§ 74. Испытании на твердость. Наряду с испытаниями на растяжение или сжатие материалы подвергают и иным видам испытаний с целью выявить те или иные свойства, важные для оценки прочности и технологических свойств. Особенно большое распространение из-за простоты и дешевизны получили испытания на твердость.
Наиболее употребительный метод испытания на твердость — это шариковая проба Бринелля. Шарик из твердой стали вдавливается заданной и точно известной силой в плоскую поверхность металлического образца. По удалении нагрузки на образце остается отпечаток, поверхность которого представляет собою шаровой сегмент. Измеряя диаметр оттиска и зная диаметр шарика, вычисляют поверхность сферического сегмента. Сила давления на шарик в килограммах, поделенная на площадь отпечатка в мм*, называется числом твердости Бринелля.
Число Бринелля зависит от многих механических характеристик, так как процесс образования сферического отпечатка весьма сложен. Существует теория Вдавливания жесткого шарика в идеально пластический, то есть не упрочняющийся, материал (А. Ю. Ишлинский); для реальных же материалов такой теории не существует. Однако многочисленные опытные исследования установили коррелятивную, эмпирическую зависимость между числом Бринелля Нв и временным сопротивлением:
ah 0,35 HR.
Точность этой формулы -4- 10%.
Таким образом, если большая точность не нужна, то сравнительно сложные и дорогостоящие испытания на разрыв, требующие специальной машины, можно заменить простым испытанием на твердость.
Существуют и иные методы определения твердости. Для определения твердости по Роквеллу в металлический образец вдавливается алмазный конус и измеряется глубина отпечатка. Для определения твердости по Виккерсу в образец вдавливается алмазная пирамида и измеряется диагональ ромбоидального отпечатка. Числа твердости по Роквеллу и Виккерсу не имеют размерности и совершенно условны. Однако существуют эмпирические таблицы перевода чисел твердости, поэтому результаты испытаний разными методами сравнимы между собой.
Во многих случаях испытание на твердость можно производить на готовом изделии; небольшая вмятина от шарика, призмы или конуса обычно ничему не вредит. Таким образом, открывается возможность, например, контролировать правильность термической обработки стальных изделий и браковать те, которые отклоняются по твердости от установленной нормы.
160 ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ [ГЛ. V
Испытание на твердость в принципе может быть произведено и „ на очень малом участке поверхности металла. Существуют специальные приборы для измерения микротвердости. Принцип работы боль-? шинства из этих приборов состоит в том, что алмазная пирамида под небольшим давлением оставляет на поверхности чрезвычайно малый . отпечаток, размеры которого измеряются с помощью измерительного микроскопа. Таким способом можно определить, например, твердость • различных структурных составляющих сплавов.
ГЛАВА VI
ТЕОРИИ ПЛАСТИЧНОСТИ, НЕЛИНЕЙНОЙ УПРУГОСТИ И ПОСЛЕДЕЙСТВИЯ
§ 75. Основные принципы построения теории пластичности. Пластические свойства материала при простом растяжении, если отвлечься от таких эффектов, как старение, полностью определяются диаграммой растяжения и законом разгрузки, поэтому для расчета, например, ферм с учетом пластических деформаций можно пользоваться опытными кривыми без каких-либо дополнительных гипотез. В рассмотренных примерах мы заменяли истинную кривую растяжения диаграммой идеальной пластичности, но по существу этого можно было не делать; расчет иа основе истинных кривых не встречает принципиальных затруднений, хотя технически довольно сложен. Если же в теле возникает сложное напряженное состояние и материал переходит за предел текучести, то мы не можем представить зависимость между напряжениями и деформациями при помощи простых эмпирических соотношений; таких соотношений должно быть бесконечное множество в соответствии с неограниченной возможностью варьирования типов напряженного состояния. Поэтому необходимо делать некоторые гипотезы и на основании этих гипотез строить теорию пластичности.
Существующие теории пластичности разделяются на две основные группы:
а) Теория пластического течения
Пластическая деформация металла по теории течения уподобляется течению вязкой жидкости. Считается, что физический закон пластичности связывает напряжения и приращения напряжений с приращениями деформаций или скоростями деформации.
б) Деформационная теория пластичности
Согласно деформационной теории пластичности напряжения и деформации связаны между собою конечными соотношениями, подобно тому как в упругой области напряжения и деформации связаны законом Гука.
Идеально пластический материал характеризуется тем, что в опыте на растяжение, если напряжение равдо пределу текучести, деформация становится неопределенной и может принимать любое
* Ю. Н. Работпов
162 ТЕОРИИ ПЛАСТИЧНОСТИ И НЕЛИНЕЙНОЙ УПРУГОСТИ [гл. VI
1 значение в соответствии с ограничивающими ее внешними связями. ' Величина скорости деформации также неопределенна, тогда как направление деформирования известно: материал течет по направле- < нию растягивающей силы. В сложном напряженном состоянии теку- -? честь наступает тогда, когда некоторая функция от главных напря- Z жений достигает предельного значения. Этой функцией является .* либо наибольшее касательное, либо октаэдрическое напряжение, как ' было выяснено в §§ 45 и 46. По аналогии с одноосным случаем пола- 7 гают, что соотношение между главными напряжениями, соответству-ющее достижению предельного состояния, сохраняется и в процессе { течения. По теории Сен-Венана остается постоянным наибольшее ? касательное напряжение, по теории Мизеса — октаэдрическое каса- < тельное напряжение. s
§ 76. Ассоциированный закон течения. Следующий вопрос, возникающий при рассмотрении идеально пластического тела, в котором достигнуто состояние текучести, состоит в том, чтобы иайти распределение скоростей течения.
Мы будем по-прежнему рассматривать элемент объема отнесенным к. главным осям тензора напряжений. Возьмем этот элемент в в виде кубика (рис. 108), по граням которого
действуют напряжения at, <Tt и <т,. Для изотропного материала первое совершенно естественное предположение, которое мы сделаем, состоит в том, что ребра кубика удлиняются или укорачиваются, но углы оста-ются прямыми и, следовательно, сдвигов не происходит. Таким образом, деформация в каждый момент определяется тремя вели-
Рис. 108. чинами: е„ 8, и 8„ относительными дефор-
мациями в направлении главных осей. Эта первая гипотеза может быть сформулирована следующим образом:
1. Главные оси тензора напряжений и тензора скоростей деформации совпадают.
В приведенной формулировке, сказано несколько больше, чем в предварительных рассуждениях. Дело в том, что напряженное состояние в теле может меняться*и при этом может происходить поворот главных осей. Суммарная деформация элемента состоит из той части, которая вызвана напряжениями <ти и <т„ показанными на рис. 108, и из предварительной деформации, связанной с теми напряженными состояниями, которые возникли в теле ранее. Основная разница между упругостью и пластическим течением состоит в том, что упругая деформация полностью определяется действующими напряжениями, в теории же пластического течения накопленная деформация необратима и задание мгновенного распределения напряжений
§ 76]
АССОЦИИРОВАННЫЙ ЗАКОН ТЕЧЕНИЯ
163
позволяет судить лишь о том, каковы будут приращения деформаций.
Как указывалось, пластическая деформация носит сдвиговой характер и не сопровождается изменением объема. Этот факт подтвержден многочисленными экспериментами (в первом приближении). Сформулируем его в виде второй гипотезы:
2. Пластическая деформация не сопровождается, изменением объема.
Как известно, относительное изменение объема равно сумме главных деформаций (§ 45). Поскольку мы формулировали первую гипотезу в скоростях, удобно записать условие несжимаемости следующим образом:
81+«г+«. = 0-
Для того чтобы сформулировать третью и последнюю гипотезу, будем исходить из обратной постановки задачи. Предположим, что скорости деформации 8„ е2, 8, заданы, требуется определить напряжения <r„ <г2, о,, удовлетворяющие условию пластичности. В общем случае условие пластичности записывается так:
/К, <т2, О.) = 0. (76.1),
Высказанный Мизесом в 1913 г. принцип заключается в следующем:
3. При заданном пластическом течении материала напряжения распределяются таким образом, что мощность пластического формоизменения принимает стационарное значение.
Это и есть третья гипотеза. Мощность — это работа за единицу времени. При,растяжении работа, отнесенная к единице объема и соответствующая изменению относительной деформации 8 на величину ds, . de
равна ads, следовательно, работа за единицу времени равна а-^ =ав. При трехосном напряженном состоянии эта мощность равна
1F = 0,8,
Потребуем, чтобы величина W, рассматриваемая как функция напряжений при заданных скоростях, принимала экстремальное значение. При этом должно быть еще выполнимо условие (76.1). Следуя методу Лагранжа, вводим неопределенный множитель X и составляем
выражение ,
Ф = <г,8, + а282 + <т,82 —А/(о„ <т2, о,).
Приравниваем теперь нулю частные производные от функции Ф по
<т„ <т2 и о,. Получаем:
. df
в2 = X ,
2 да. ’
8, = Л .
• да.
(76.2)
6*
7 У?'
главные два из пластич-
(77.2)
164 ТЕОРИИ ПЛАСТИЧНОСТИ И НЕЛИНЕЙНОЙ УПРУГОСТИ [гл. VI
Эти соотношения выражают закон течения, ассоциированный с условием пластичности /(ст„ ст,, ст,) = 0.
§ 77. Течение при условии пластичиости Сеи-Веиаиа и Мизеса. Рассмотрим сначала условие пластичности Сен-Венана: ’
> /=ст,— ст,— стт = 0.
По формулам (76.2) получаем:
ё, = А, ё, = 0, ё, = —А. (77.1) ।
Уравнения (77.1) показывают, что пластическая деформация при * условии пластичности Сен-Венана и ассоциированном законе течения ~ представляет собою чистый сдвиг в плоскости главных осей 1 и 3. „ В направлении среднего по величине главного напряжения ст, никакой пластической деформации не происходит. Величина указанного сдвига г произвольна, скорости в, и е,, равные по величине и противоположные по знаку, также совершенно неопределенны, но 8,— всегда ско-рость удлинения, а е, — скорость укорочения. Поэтому величина я А положительна.
То, л1то е есть производная по времени от деформации, совер
шенно несущественно. Вместо времени можно взять любую функцию ' от времени, лишь бы она была монотонно возрастающей.
При получении уравнений (77.1) предполагалось, что напряжения все различны: ст, ст, =/= ст,. Если какие-либо главных напряжений равны, например ст, = ст„ то условие ности можно записать в любой из следующих форм:
ст, —ст, = стт, ст, — ст, = стт.
В этом случае считают, что чистый сдвиг происходит менно и независимо в плоскостях 1—3 и 1—2. Воспроизводя вывод * предыдущего параграфа для- каждого из условий (77.2) независимо | и складывая получающиеся скорости течения, получим:
ё, = А-|-р, ё, = —р, е, = — А. (77.3)
Здесь скорости зависят уже от двух неопределенных величин, А и р, но так как три скорости связаны условием несжимаемости, то независимо можно задать только две из них. Итак, при условии, ЧТО СТ, = ст,, скорости могут быть любыми, лишь бы выполнялось условий несжимаемости. Единственное ограничение состоит в том, что Аир в формулах (77.3) положительны. Таким образом, е, и е, всегда отрицательны, а Е„ равная сумме абсолютных величин двух других ' скоростей, всегда положительна.
§ 78)
ЗАКОН УПРОЧНЕНИЯ
165
Принимая условие пластичности Мизеса, мы должны положить:
/= (°i—^)2+(°г—«и2+(<*.—°.)2—2ст1=
-Д = 4а, — 2а. — 2а,, ...
да, 1 2 •*
Внося выражения и в уравнения (76.2) и опуская не-
существенный численный множитель, который включается в неопределенный множитель А, получим следующий закон течения:
8, = А °1 — + »
82 = А , (77.4)
8,= А •
Эти формулы похожи на соотношения закона Гука, только вместо деформаций в них фигурируют скорости деформаций, вместо — неопределенный множитель А, а коэффициент Пуассона принят равным что соответствует несжимаемому материалу. Легко убедиться в том, что условие неизменности объема для законов течения (77.1) и (77.4) выполняется автоматически. Так получается оттого; что условие пластичности ие зависит от гидростатической составляющей тензора напряжений.
§ 78. Закон упрочнения. Реальные материалы не следуют закону идеальной пластичности, площадка текучести характерна только для стали со средним содержанием углерода. Кривая зависимости напряжения а от деформации в при растяжении, которая может быть достаточно точно построена в области не слишком больших деформаций, дает закон упрочнения при растяжении.
В сложном напряженном состоянии понятие закона упрочнения становится неопределенным. Под упрочнением здесь мы будем по-прежнему понимать увеличение пластического сопротивления по мере роста деформации, но выбор количественных характеристик упрочнения в этом случае a priori не ясен.
Обратимся сначала к монокристаллу, находящемуся в условиях сложного напряженного состояния, притом такого, что скольжение происходит в одной только системе. Пусть п — направление нормали к плоскости скольжения, S—направление скольжения. Деформация монокристалла представляет собою чистый сдвиг в плоскости ns, величина этого сдвига yns является функцией касательного напряжения tns, диаграмма зависимости между yns и rns дает закон упрочнения для монокристалла. Вид этой диаграммы не зависит ют типа напряженного состояния. Таким образом, оказывается, что для
166 ТЕОРИИ ПЛАСТИЧНОСТИ И НЕЛИНЕЙНОЙ УПРУГОСТИ [гЛ. VI;
монокристалла при определенных ограничениях (одна система скольже-ния) для того, чтобы охарактеризовать способность материала к упрочнению, нет необходимости вводить в рассмотрение все компоненты • напряжения и деформации. Дело сводится к установлению зависимости , между двумя скалярными величинами, одна из которых (TnJ представляет напряженное состояние, а другая (ynJ — деформированное . состояние.
Чтобы установить закон упрочнения для поликристаллнческого металла, мы выберем в качестве отправного пункта теорию течения Сен-Венана. Согласно этой теории (§ 77) текучесть наступает тогда, ' когда наибольшее касательное напряжение достигает предельного значения. Деформация текучести для неупрочняющегося материала представляет собою чистый сдвиг в системе главных осей 1 и 3. По формуле (44.2), в которой нужно заменить е, через е,, находим, что величина этого сдвига
Ymax---®1
Если построить диаграмму зависимости между Ттах = -1-^ — и утах
для неупрочняющегося материала, то эта диаграмма будет напоминать. диаграмму идеальной пластичности при растяжении (рис. 109). На упругом участке ттах = Оутах, в пластической области ттах = const, тогда как утах может быть любым. Когда материал обладает упроч-
в каждом материальном элементе
нением, естественно предположить, что зависимость между Ттах и утах носит универсальный характер и выражает закон упрочнения, не зависящий от частного вида напря-женнрго состояния. Соответствующая кривая показана на рис. 109 пунктиром.
Это предположение кажется правдоподобным тогда, когда деформация чистого сдвига происходит в одной и той же системе осей объема. Но может случиться, что
в процессе нагружения главные оси поворачиваются по отношению к материалу или меняют свои наименования (например, когда напряжение по оси 2 становится больше, чем по оси 1, мы должны изменить нумерацию осей). В этих случаях нет никаких оснований пред-
полагать, что кривая зависимости ттах от утах сохраняет универсальный характер, теперь она состоит из кусков, соответствующих сдвигам в разных плоскостях и разных осях. Таким образом, можно ожидать справедливости сформулированного закона упрочнения только тогда, когда главные* осн не меняют своей, ориентации и своего
наименования.
§ 79] ДЕФОРМАЦИОННАЯ ТЕОРИЯ ПЛАСТИЧНОСТИ 167
Многочисленные опыты указывают на то, что наступление текучести лучше описывается условием Мизеса, чем условием Сен-Венана. Таким образом, мерой напряженного состояния является октаэдрическое касательное напряжение т0. Естественно принять октаэдрическое напряжение за меру напряженности и в области упрочнения. Мерой деформации при этом является так называемый октаэдрический сдвиг у0, то есть величина, построенная из главных удлинений точно таким же способом, как октаэдрическое напряжение строится из главных напряжений:
Yo =4 Й81 — е»)‘ + (8, — в,)* + (е, — 8J*. (78.1)
Кривая зависимости у0 — То оказывается одной и той же для различных напряженных состояний, если на условия эксперимента наложены некоторые ограничения. Необходимость этих ограничений ясна из тех соображений, которые были высказаны по поводу предыдущей теории, связывающей ттах и утах. Совершенно надежные результаты получаются в случае так называемого простого, или пропорционального, нагружения, то есть тогда, когда в процессе нагружения, все составляющие тензора напряжений меняются пропорционально. Это
Здесь 2 * — постоянный тензор, а X — параметр нагружения; процесс нагружения соответствует монотонному изменению параметра X от нуля до единицы. Строго говоря, приведенные условия пропорционального нагружения являются слишком жесткими. Гидростатическая составляющая тензора напряжений не влияет на пластическую деформацию и может изменяться как угодно. Поэтому достаточно, чтобы изменялись пропорционально не составляющие тензора, а составляющие девиатора, то есть чтобы было
2' = Х2'*. (78.3)
В этих условиях производилось много экспериментов, достаточно надежно подтверждающих закон упрочнения. При нарушении условий пропорционального нагружения закон упрочнения, как правило, не выполняется. Отклонение становится особенно резким тогда, когда в процессе нагружения происходит поворот главных осей.
§ 79. Деформационная теория пластичности. В основу деформационной теории пластичности положено представление о том, что при возрастающих напряжениях поведение материала в области пластических деформаций принципиально ие отличается от его упругого поведения в том смысле, что величины напряжений и деформаций связаны между собою однозначными зависимостями. Простейшее предположение состоит в том, что эти зависимости по форме совершенно совпадают с законом Гука, причем, однако, модуль упругости Е
168 ТЕОРИИ ПЛАСТИЧНОСТИ И НЕЛИНЕЙНОЙ УПРУГОСТИ [гл. VI
и коэффициент Пуассона v уже не являются постоянными величинами, их нужно заменить через Ер и vp— пластический модуль и пластический коэффициент Пуассона, которые зависят от степени деформирования.
Подобная теория для неупрочняющегося материала была предложена Генки и обобщена Надаи на случай материала с упрочнением. Надаи сформулировал основные законы деформационной теорий пластичности, а именно:
1. Закон упрочнения. Октаэдрический сдвиг является функцией октаэдрического касательного напряжения:
Y. =/(*„)• (79.1)
Этот закон был подробно разъяснен в § 78.
2. Закон упругости объемной деформации. Опыты, произведенные при Высоких всесторонних давлениях, показали, что всестороннее сжатие не может привести к переходу в пластическое состояние, поэтому изменение объема всегда упруго и формула (43.4) верна как в упругой, так и в пластической области. Введя обозначение
у(е» + е1 + е») = в> перепишем ее так:
р = ЗКе. (79.2)
3. Закон пропорциональности девиаторов. Как уже было сказано, основные соотношения между напряжениями и деформациями в деформационной теории пластичности записываются так же, как уравнения закона Гука:
82 = £<о2 —v/о, — о,)], (79.3)
е2 = ^[°2 —vp(°i + °2)]-
Величины Ер и vp переменны, но до сих пор не было ясно, от чего они зависят. Теперь, приняв во внимание два первых закона, мы сможем на этот вопрос ответить. Прежде всего сложим уравнения (79.3). Будем иметь:
1 — 2v_ ei + e2 + ei = —Ё---(°i + a» + a»)-
Сравнивая с уравнением (79.2), получим:
1-2V- 1
Ер ~ з№ const
Таким образом, из двух переменных величин Ер и ур независимой является только одна, вторая через нее выражается.
§ 79]
ДЕФОРМАЦИОННАЯ ТЕОРИЯ ПЛАСТИЧНОСТИ
169
Вычтем теперь из левых частей соотношений (79.3) величину е, „ 1 — 2v„
а из правых — равную ей величину —f—- р. После простых преобра-зований придем к следующей системе:
ei —e=53“(°i —Р).
8*-e=2s;(o.-A .. (79-4)
в» —e = U“(o« —Р)-
Здесь р
G = —Ь.
* 2(14-v,)’
Вместо двух переменных параметров Ер и чр мы имеем постоянный объемный модуль упругости К и одну только переменную Gp. Осталось выяснить, от чего зависит Gp. Для этого вычтем уравнения (79.4) одно из другого попарно. Получим;
Bt —в, = 25; (0,-0,),
Подставив’ полученные выражения для разностей относительных деформаций в формулу (78.1) для октаэдрического сдвига, имеем:
~ + (°. — °»)’ + (°. — °i)’-
Вспоминая определение октаэдрического касательного напряжения, найдем отсюда:
= (79-5)
ир
Соотношение (79.5) между у0 и т0 вполне аналогично соотношению между т и у при сдвиге. Именно поэтому при определении у0 по формуле (78.1) перед радикалом был взят множитель */,, а не как в выражении т0. Но в силу первого закона деформационной теории пластичности у0=/(тю), поэтому
Таким образом, пластический модуль сдвига должен рассматриваться как функция либо октаэдрического касательного напряжения, либо октаэдрического сдвига. Третий закон деформационной теории пластичности достаточно надежно подтверждается экспериментами для случая пропорционального нагружения. Для неупрочняющегося материала понятие пропорционального нагружения лишено смысла; при
170 ТЕОРИИ ПЛАСТИЧНОСТИ И НЕЛИНЕЙНОЙ УПРУГОСТИ [гл. VI
соблюдении условия пластичности, связывающего компоненты тензора напряжений, изменение напряженного состояния возможно лишь за счет изменения соотношений между напряжениями. Однако деформационной теорией пользуются и для неупрочняющегося материала (теория Генки) в качестве приближения.
Для суждения о возможности применения деформационной теории нужно знать, в какой мере реализуются условия пропорционального нагружения в каждом элементе объема тела, подвергнутого действию внешних сил. Достаточные условия этого состоят в следующем: 1) внешние силы возрастают пропорционально, 2) упругой сжимаемостью материала можно пренебречь, то есть можно положить е = 0, и 3) функция f (т„) . закона упрочнения (79.1) является степенной функцией (А. А. Ильюшин). Последнее условие мало реально для металлов, поэтому пропорциональное нагружение в действительных изделиях осуществляется редко. Однако, имеются основания полагать, что уравнения теории. пластичности деформационного типа остаются достаточно точными и тогда, когда нагружение несколько отличается от пропорционального; наибольшие расхождения с опытными данными обнаруживаются в тех случаях, когда в процессе нагружения поворачиваются главные оси.
§ 80. Экспериментальная проверка теорий пластичности. Начиная с 1928 г., когда было опубликовано фундаментальное исследование Лоде, посвященное экспериментальной проверке теории пластичности, этому вопросу было посвящено большое количество работ.
Подобные исследования ведутся у нас и за рубежом и в настоящее время, однако центральная проблема сейчас состоит в том, чтобы выяснить закономерности пластической деформации при непропорциональном нагружении. Универсальной теории пластичности, дающей достаточно надежные результаты при произвольном нагружении, пока еще не существует, вопрос находится в стадии накопления опытного материала и проверки разного рода гипотез, зачастую противоречащих друг другу. Вопрос о законах пластичности при пропорциональном нагружении для стали в настоящее время может считаться решенным, и только на этом вопросе мы здесь остановимся.
Единственный надежный способ создания в образце однородного напряженного состояния — это испытание тонкостенных трубок на совместное действие осевого растяжения, внутреннего давления и кручения.
Обозначим средний радиус трубки через R, толщину стенки через б и определим напряжения, возникающие от растягивающей силы Р, внутреннего давления q и крутящего момента М.
1. Растягивающая сила Р. Площадь сечения трубки приближенно равна 2л/?б. Направив ось z по образующей, найдем:
§ 80] ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ТЕОРИЙ ПЛАСТИЧНОСТИ 171
есть 2/S. На этой пло-
£
2. Внутреннее давление q. Внутреннее давление растягивает трубку в поперечном направлении, в продольных сечениях трубки возникают растягивающие напряжения, которые мы обозначим сг^. Для определения этих напряжений обратимся к рис. 110, где изображена половина трубки, рассеченной диаметральной плоскостью. Если длина трубки равна I, то площадь сечения щади действует растягивающее напряжение o,f) направленное параллельно оси у вниз.
Элементарная полоска IRdtp, выделенная вдоль образующей с угловой координатой <р, испытывает действие силы qlRdq.
Проекция ее на вертикальную ось у равна
qlR dq sin<p.
Рис. НО.
Составим уравнение равновесия, проектируя все силы на ось у. Получим: Л
J qlR sin <р dtp = 2/6<j9. О
Отсюда
(80.2)
3. Крутящий момент М. Предположим, что касательные напряжения распределены равномерно по сечению. Будем считать плечо их относительно оси трубки равным среднему радиусу трубки R. Приравняем момент внутренних сил в сечении внешнему моменту М. Получим:
М==2л RStR.
Отсюда
(80.3)
Задавая по произволу Р, М и q, можно осуществить принципиально любое плоское напряженное состояние. Практически же, для того чтобы распределение напряжений по толщине было равномерным, нужно делать трубки достаточно тонкими (S <<: R). Но при наличии сжимающих напряжений тонкая стенка теряет устойчивость, поэтому фактически удается обследовать область, в которой два главных напряжения положительны, а если одно из них отрицательно, то оно невелико по модулю по сравнению со вторым.
172
ТЕОРИИ ПЛАСТИЧНОСТИ И НЕЛИНЕЙНОЙ УПРУГОСТИ
[ГЛ. VI
Пока что не найдено никаких методов изучения пластичности при трехосном напряженном состоянии, поэтому опытное подтверждение теории не может считаться исчерпывающим.
На рис. 111 представлены результаты опытов Девиса, выполненных в 1945 г. над стальными трубчатыми образцами. Образцы подвергались растяжению и внутреннему давлению; отношение поперечного напряжения к продольному равнялось: 0; 0,50; 0,75; 0,762;
Ц0 0J0 0.Z0 ИЗО Ц00 0,50 0,00 0,70 Q80 0730 Ц100
Рис. 111.
0,775; 0,800; 0,975; 1,00; 2,00; оо. В каждом испытании было осуществлено условие пропорционального нагружения. Как видно, точки, соответствующие разным отношениям довольно хорошо ло-
жатся на одну и ту же кривую.
Однако разрыв при различных отношениях о^о2 происходит при различных величинах деформации; буквой R на диаграмме отмечены точки, соответствующие моменту разрыва.
Поскольку опыты проводились в области довольно больших деформаций, по оси абсцисс отложены так называемые логарифмические деформации (§ 81). Пока деформации малы, логарифмическая деформация практически не отличается от обычной.
Если на основании тех же опытных данных построить точки, соответствующие наибольшему касательному напряжению и наибольшему сдвигу, то для каждого отношения получается своя кривая. Таким образом, закон упрочнения для стали нужно брать в виде
Yo=/W-
Для меди Девис в этой же работе получил несколько иные результаты; в плоскости у0 — т0 точки ложатся с разбросом, тогда как в плоскости угаах — Тгаах они укладываются на общую кривую. Поэтому для меди лучше подтверждается закон упрочнения:
Ymax ==f (^тах)"
§ 80] ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ТЕОРИЙ ПЛАСТИЧНОСТИ 173
На рис. 112 представлены результаты аналогичных опытов Института механики АН СССР (А. М. Жуков, 1954 г.). Исследовались образцы из хромоникелевой стали под действием растягивающей силы и внутреннего давления. Отношение напряжений ог/оф было равно 0; 1; 0,3; 0,1 и оо. Одновременно производилась проверка зако-
образца, через 8? окружную и через ег деформацию по направлению толщины образца. Из закона подобия девиаторов следует:
«,-‘ = 2^-"),
8Ф —e = 2G^(a4> —а)>
Вычтем третье уравнение из первого и второго. Получим:
<тг
е' ~ 2Gp ’
S'~~2Gp‘
Отсюда
2G == .
р ег~ег еф - ег
Отношения —-— и —-— измеряются в процессе • опыта. Будем 8^ 8Г 8^ 8Г
откладывать одно из них по оси абсцисс, а другое по оси ординат (рис. ИЗ). Так как они равны, точки должны лечь на биссектрису координатного угла. Были проведены испытания при отношениях равных 0,5 и 1. Как видно, точки ложатся на биссектрису почти
174 ТЕОРИИ ПЛАСТИЧНОСТИ И НЕЛИНЕЙНОЙ УПРУГОСТИ [гл. VI
точно, разница не выходит за пределы обычного случайного разброса. Для некоторых алюминиевых и магниевых сплавов закон упрочнения как й той, так и в другой форме не выполняется (С. И. Ратнер).
Что касается условия пластичности, основная экспериментальная трудность состоит в том, что момент достижения пластического состояния довольно условен и его можно определять по-разному.
Фактический предел текучести, которому соответствует горизонтальный участок диаграммы растяжения, существует только у отожженной углеродистой стали. Для материала с упрочнением -предел текучести определяется как напряжение, при котором пластическая деформация достигает определенной заданной величины (0,2% при растяжении). В сложном напряженном состоянии предел текучести можно определять по достижению условной наперед заданной величины октаэдрического сдвига. На рис. 114 изображены часть эллипса
Мизеса и часть шестиугольника Сен-Венана, соответствующие положительным главным напряжениям, и опытные точки, полученные из экспериментов на растяжение с внутренним давлением.
На рис. 115 приведены данные опытов на совместное действие растяжения и кручения. Для этого случая условие пластичности по Сен-Венану будет
a* -f- 4т2 = о£,
а по Мизесу
а* Зт‘ = <4
(см. § 47).
В координатах а — т и то и другое условие изображается эллипсом, причем опытные точки располагаются ближе к эллипсу Мизеса.
§ 81]
КОНЕЧНАЯ ДЕФОРМАЦИЯ
175
§ 81. Конечная деформация. Пока деформация мала, определение деформации не зависит от того, относить ли ее к начальной длине или к конечной. Действительно, пусть отрезок сначала имел, длину /0, потом его длина стала 1г. Обычное определение относительной деформации будет следующее:
' 4 4 •
Вычислим теперь деформацию, отнесенную к конечной длине:
Но /,е=/о(1-|-s), следовательно, t________________________ В ____ 2
е =^-==6-6 +...
Разница между в' и 8 является малой второго порядка, и ею можно пренебречь, если 8<^1. Для больших деформаций не безразлично, к какой именно длине их относить.
Представим себе процесс удлинения отрезка, имевшего первоначальную длину /0, как последовательность этапов деформирования, на каждом из которых длина получает приращение dl. Относительное удлинение на каждом этапе мы будем относить к той длине, которую имел отрезок в начале соответствующего этапа:
Л а8 = у.
Примем за меру полного удлинения сумму бесконечно малых относительных удлинений de при изменении длины от 1о до /, а именно: i
- Р dl . I
е яв A-j-s=a In . (81.1)
*0
Величина 8 называется логарифмическим удлинением. Она удобна для описания процесса конечной деформации по следующим двум причинам:
1. Представим себе, что деформация производится ступенями. К началу ступени номера k длина была она увеличивается до lk. Соответствующая логарифмическая деформация:
Суммарная деформация после п ступеней:
In lf--в, + . 4-1„.
*0
2. Скорость деформации т| представляет собою отношение скорости абсолютного удлинения к длине. Пока деформация мала, можно
176 ТЕОРИИ ПЛАСТИЧНОСТИ И НЕЛИНЕЙНОЙ УПРУГОСТИ [гл. VI
считать, что е = Т|, но для конечных деформаций это неверно. Действительно, по определению = тогда как г = 111„. Но в = ///, таким образом, скорость деформации равна производной от логарифмической деформации по времени.
Деформация элементарного параллелепипеда, ребра которого направлены по главным осям тензора напряжений, определяется заданием трех удлинений: в, и 8,. Условие несжимаемости Sj-f-Sj-f--|-8, = 0 справедливо лишь для малых деформаций. Обозначим ребра параллелепипеда через а, b и с; в начальном состоянии они равны а0, Ьо и с0. Введем главные логарифмические удлинения:
е, = 1п—, е=1п-£-, в. = 1п—.
1 “o ' V ’ с»
Сумма их:
— I , — , abc , V
е, -4-е, -4-е, = 1п—г—=1птт- .•
11 » ‘ • aoboco V,
Здесь V—объем параллелепипеда, Уо — его первоначальный объем. Таким образом, условие Несжимаемости для логарифмических деформаций такое же, как и для обычных малых деформаций, но является совершенно точным.
Вопрос о выборе меры деформации для конечных деформаций является скорее вопросом удобства, поскольку обычная деформация и логарифмическая деформация связаны между собою однозначной зависимостью. Для материалов с большими упругими деформациями, например каучука, за меру деформации часто принимают так называемую кратность, то есть отношение новой длины к первоначальной. Обозначая ее буквой X, получаем:
1= 1 -|-8.
§ 82. Нелинейно унругое тело. Нелинейно упругим телом называется такое тело, у которого напряжения и деформации связаны нелинейными зависимостями:
=ф1(81, 8„ 8,), аг = ф8(е1, 8,- 8,), <*. = ф.(8„ 8„ 8,).
Однако функции ф,, ф, и ф, fie могут быть вполне произвольными.. Свойство упругости означает, что энергия деформации тела в любом его состоянии определяется только величинами деформаций, соответствующих этому состоянию, и не зависит от того, каким способам производилось деформирование. Обозначим упругую энергию на единицу объема буквой а. Вследствие вышеизложенного это есть функция от в,, е. и в,;
а = а(е,„ 8,, вв).
§ 82]
НЕЛИНЕЙНО УПРУГОЕ ТЕЛО
177
Представим себе, что деформации увеличились, получив приращения de,, de2 и de2. Энергия получила при этом приращение da, причем с точностью до малых высшего порядка
da—^ del-]-^-det + ~de,. (82.1)
ое, 1 1 de2 2 1 дег * ' '
С другой стороны, de„ de2 и d&,— это удлинения ребер единичного кубика (§ 49), на грани которого действовали силы <т,, <т2 и о,, следовательно, da представляет собою работу этих сил:
da — alde,l-{-aldsi-{-atdel. (82.2)
Сравнивая (82.1) и (82.2), найдем:
Таким образом, функции <р,, <р2 и ф2 должны быть производными от одной и той же функции а по е„ е2 и е,.
Дальнейшие ограничения будут вытекать из того, что для изотропного материала энергия должна выражаться симметричным образом через компоненты деформации.
Предположим, что зависимость между гидростатическим напряжением и относительным изменением объема линейна, следовательно, энергия изменения объема выражается формулой (50.9). Вводя объемный модуль упругости и заменяя р через е с помощью закона Гука для обычной деформации (79»2), получим:
Энергию изменения формы будем считать произвольной функцией октаэдрического сдвига у0. Таким образом,
a=^+f(y0). (82.4)
Применим к выражению для энергии (82.4) формулы (82.3). Получим:
Заметим прежде всего, что ЗАе=р. Вычислим теперь производную dyjdit. Возведем в квадрат равенство (78.1):
Yo—4 Ке> ~ 82)‘ + (®2 — е,)2 + — '
Продифференцируем обе части по 8,:
V. Sz=4 f28‘ -82 - 8‘1=т <8‘ -
Таким образом, получается:
о,--р=4Чг)(8‘~е)’ (82‘5)
178 ТЕОРИИ ПЛАСТИЧНОСТИ И НЕЛИНЕЙНОЙ УПРУГОСТИ [гл. VI
и аналогично для <т2 и о,. Сравнивая (82.5) и (79.4), мы убеждаемся, что если принять
°>==Т^. (82.6)
то уравнения нелинейной упругости при частном выборе выражения упругой энергии в форме (82.4) совпадают с уравнениями деформационной теории пластичности. Разница между нелинейной теорией упругости и теорией пластичности состоит в том, что уравнения последней справедливы лишь при продолжающейся пластической деформации, разгрузка происходит по иному закону. Уравнения нелинейной упругости действительны как при нагрузке, так и при разгрузке.
§ 83. Высокоэластические деформации. Каучук и каучукоподоб-иые материалы способны к очень большим упругим деформациям, превышающим во много раз первоначальную длину. Такие деформации принято называть высокоэластическими (термины «эластичность» и «упругость» представляют собой синонимы). Природа упругости каучука и других высокополимерных материалов принципиально отличается от природы упругости металлов. Молекулы высоко-полимеров имеют форму цепей, образованных повторением одной и той же группы атомов, связанной валентными связями. Каждая связь допускает определенную кинематическую свободу, поэтому цепеобразная молекула связывается в клубок. Среднее расстояние между концами молекулы значительно меньше, чем ее длина в растянутом состоянии, если на тело не действуют внешние силы. Под действием силы молекулы вытягиваются, а после снятия нагрузки каждая из них стремится вернуться в исходное состояние, которое является наиболее вероятным.
Упругая энергия высокоэластичного тела может быть определена с большей или меньшей степенью точности на основе теоретических соображений молекулярной физики. Наиболее простое выражение энергии через кратности X,, Х2 и X, (см. § 81) будет следующее (Ривлин):
а«=ус[XJ-]- М4~ М]« (83.1)
Для того чтобы определить напряжения, нам придется несколько ' видоизменить рассуждения предыдущего параграфа, поскольку речь идет о конечных деформациях. Рассмотрим элементарный объем, который до деформации был кубом’ с ребром, равным единице. После деформации ои стал параллелепипедом с ребрами Х„ Х2 и X, (рис. 116). Силы, действующие на его грани, будут:
<х.Х.Х„ а.Х.Х., а.Х.Х..
В • в ’ ход* • ж *
§ 83]
ВЫСОКОЭЛАСТИЧЕСКИЕ ДЕФОРМАЦИИ
179
Работа этих сил на перемещениях dX„ dX, и dX, равна
4Х, Н" 4Х, “I- dkt.
Сравнивая это выражение с полным дифференциалом функции а:
найдем:
da=~ dk. + j£ dX, + dk, OAl 1 1 ОА, ’ 1 GA, 1
_ 1 да 1 да l ~да
>eX,X,3X,’ °«~X,a,1dX,’
Если упругая энергия выражается формулой (83.1), то
а> = сх±> a‘~crf? (83-2>
Большие упругие деформации материалов типа резины носят по преимуществу сдвиговой характер и сопровождаются лишь весьма малым изменением объема. С достаточной степенью точности можно считать, что изменение объема отсутствует. Для несжимаемого материала объем изображенного на рис. 116 параллелепипеда равен объему первоначального куба, то есть единице. Следовательно, 4'
Х,Х,Х, = 1. (83.3)
Если использовать условие не- Рис. 116.
сжимаемости (83.3) для упроще-
ния формул (83.2), то окажется, что три напряжения выражаются через две деформации; исключая их, мы получим некоторое конечное соотношение между а„ о,, о, (а именно <J,cr,cx, = c’), которое лишено физического смысла. Выход из противоречия заключается в том, что к системе напряжений о,, о,, о, можно прибавить произвольное гидростатическое напряженное состояние с интенсивностью р, от этого работа сил, действующих на грани параллелепипеда, не изменяется.
Действительно, заменив в выражении работы напряжения <т„ а, и а, одинаковой величиной р, мы получим:
Р “Ь" “Ь" :==ipd (X,X,X,) e 0
в силу равенства (83.3) для несжимаемого материала. Прибавим величину р к правой части каждого из равенств (83.2) и упростим первый член правой части, умножив в первом уравнении числитель и знаменатель на X,, во втором — на 1, и т. д. Получим:
о, == c%i -J- р, <т, = скг -|- р, <т, = скг -|- р. (83.4)
180 ТЕОРИИ ПЛАСТИЧНОСТИ И НЕЛИНЕЙНОЙ УПРУГОСТИ [гл. VI
I
Напряжения а,, а2 и а, отнесены к фактической площади деформированного сечения. Например, напряжение а, отнесено к площади грани, равной Х2Х2. В некоторых случаях бывает удобно относить напряжения к первоначальной площади поперечного сечения. Будем обозначать напряжения, отнесенные к первоначальной площади, черточкой над буквой. Тогда, очевидно,
о. — Х«Х2о. , '— Х.Х,о., О2" X, Х.о..
Для несжимаемого материала, вследствие условия (83.3), эти соотношения можно переписать следующим образом:
О, = £-<7,, ot===—ot.
Тогда из формул (83.4) следует:
о1 = сХ14-^, <je = cX24-^, <т, = сХ,4-^. (83.5)
Рассмотрим в качестве примера растяжение образца. При этом а2=а2 = 0, Х2 = Х2. Второе из уравнений (83.5) даст:
так как условие несжимаемости принимает вид: Х2Х2 = 1. Внесем найденное для р выражение в первое из уравнений (83.5). Получим:
(83.6)
Это — уравнение кривой растяжения резины, полученное Уоллом. Оно описывает деформацию резины в первом приближении. Для получения более точных результатов необходимо брать вместо (83.1) более сложное выражение для упругой энергии.
§ 84. Упругое последействие. Упомянутый в § 83 механизм упругой деформации резиноподобных материалов состоит в том, что молекулы принимают форму, являющуюся наиболее вероятной для данной нагрузки. Такое равновесное состояние, возникающее в результате внутренней перестройки системы хаотически расположенных молекул, достигается не сразу, а по истечении некоторого времени после приложения или снятия нагрузки. Подобная запаздывающая . упругость характерна для многих материалов органического происхождения и для пластмасс. Изменение со временем деформации при внезапном приложении и снятии нагрузки для данного материала схематически изображено на рис. 117. Если в момент времени / — О к образцу приложено напряжение а, тотчас же возникает мгновенная деформация е,0 = о1Ем. Здесь Ен— мгновенный модуль упругости. Под действием постоянного напряжения образец продолжает удлиняться,
§ 84]
УПРУГОЕ ПОСЛЕДЕЙСТВИЕ
181
кривая АВ изображает изменение удлинения со временем. Эта кривая имеет горизонтальную асимптоту; ордината асимптоты ед представляет собою ту деформацию, которая будет достигнута по истечении бесконечно большого времени. Величина ед пропорциональна приложенному напряжению, ед = . Здесь £д — длительный модуль упругости. Если
в некоторый момент времени (точка В на рис. 117) нагрузка снимается, образец сейчас же укорачивается на величину мгновенной деформации е0. Дальнейшее укорочение следует кривой CD, для которой ось абсцисс является асимптотой; по истечении бесконечно большого времени образец примет, первоначальную длину. Такое
Рис. 118.
поведение материала совершенно аналогично поведению механической системы, изображенной на рис. 118. Здесь с0 и с, —две пружины с соответствующими жесткостями, т] — наполненный маслом цилиндр с поршнем, в котором проделано отверстие. Если двигать поршень со скоростью v, масло будет протекать через отверстие в поршне, сопротивление его движению пропорционально скорости, причем коэффициент пропорционально’сти равен т]. Прикладывая к системе силу Р, мы прежде всего вытянем пружину с0; мгновенное относительное р
перемещение точек А и В будет ii0=>=—. Сопротивление пружины со
пропорционально ее вытяжке, поэтому в первый момент пружина с, не, воспринимает нагрузки, которая вся приходится на цилиндр с поршнем, по мере движения поршня часть силы передается на пружину сж, скорость поршня уменьшается, и в конце концов сопротивление цилиндра с маслом становится равным нулю, вся погрузка воспринимается двумя последовательно соединенными пружинами. Обозначим удлинение пружины с,, равное перемещению поршня, через и,. Скорость поршня есть ut, сила сопротивления его движению равна Т|ит, приходящаяся на пружину с, сила равна u,ct, сумма этих двух сил равна Р'.
P=clul-\- ipi. (84.1)
182 ТЕОРИИ ПЛАСТИЧНОСТИ И НЕЛИНЕЙНОЙ УПРУГОСТИ [гл. VI
Но — и0, где и — полное перемещение системы (изменение Р
расстояния между точками А и В). Как мы видели, и0=—, следовательно, ив = Р/с0. Исключая их из (84.1), получим;
или
\ Ь9 / С0
Перепишем уравнение следующим образом:
Уподобляя поведение растянутого образца поведению рассмотренной механической системы, заменим и через относительную деформацию е, Р через напряжение о. Константе — будет соответствовать новая
По
константа, которую мы обозначим р, жесткости с0 соответствует мгновенный модуль упругости Е , выражение [—соответ-ствует обратной величине длительного модуля 1/Ед.
В результате получается следующее соотношение, связывающее напряжение, деформацию и их первые производные по времени:
= + (84.3)
§ 85. Некоторые свойства вязко-упругого тела. Тело, поведение которого описывается уравнением (84.3), может быть названо вязко-упругим. Действительно, при р = 0 это уравнение переходит в закон Гука, при Ея = оо из него следует:
а = Е.г е. д I р
Первый член в правой части представляет собою упругое сопротивление, второй — вязкое сопротивление, пропорциональное скорости деформации. Если Ел стремится к нулю, а р к бесконечности таким образом, что отношение остается постоянным, мы получим вязкую жидкость, в которой напряжение пропорционально скорости деформации. Мы займемся сейчас исследованием уравнения (84.3) в общем случае.
а) При быстром приложении .нагрузки члены е и а в (84.3) являются преобладающими, остальными членами можно пренебречь, и мы получаем:
1 •
§ 85] НЕКОТОРЫЕ СВОЙСТВА ВЯЗКО-УПРУГОГО ТЕЛА 183
Отсюда
см
б) По истечении достаточно долгого времени после приложения нагрузки 8 и о весьма малы, соответствующие члены в уравнении (84,3) можно отбросить, после чего получается:
а
сд
в) Приложим к стержню мгновенно напряжение а0, которое вызывает немедленную деформацию е0=^-. Предположим, что напряжение остается постоянным, следовательно,• о = 0. Уравнение (84.3) принимает вид:
|iE-|-E=:|.0o, (85.1)
сд
Это —дифференциальное уравнение для функции е, которое нужно интегрировать при начальном условии е(О) = ео —Соответствую-щий интеграл легко находится по общим правилам, а именно:
8 = 80 + (^-6())(1-в-^). (85.2)
При i — 0 отсюда получается при / = оо е = ^.
*^М - *3д
Уравнение (85.2) описывает участок АВ кривой на рис. 117.
г) После того как стержень находился под действием постоянного напряжения а0 в течение времени т, нагрузка снимается. Деформация перед снятием нагрузки была е'; она находится по формуле (85.2) при /=т. Сейчас же после снятия нагрузки восстанавливается деформация е,, после чего происходит постепенное восстановление оставшейся деформации, равной s' — е. Этот процесс описывается уравнением (85.1), в котором нужно положить ао = О. Начальное условие при будет 8 = е'— е0. Решение мы можем получить по формуле (85.2), положив в ней <то = О и заменив е0 через s' — е0 и t через t — т. Таким образом, участок CD приведенной на рис. 117 кривой описывается уравнением
8яс(е' — 80) . (85.3)
д) Представим себе, что образец мгновенно растянут при напряжении <Т0, после чего концы его закрепляются так, что деформация е0 = ств/£м сохраняется неизменной. Нап]ряжение в образце будет изменяться со временем. Действительно, положим в уравнении (84.3) е = 0, 8 = <Тв/£,м. Получим:
184 ТЕОРИИ ПЛАСТИЧНОСТИ И НЕЛИНЕЙНОЙ УПРУГОСТИ [гл. VI
Интеграл этого уравнения при начальном условии a(0) = <Je есть
а=а0{(1-^)ехр(-И|и (*5.4)
Падение напряжения в элементе, длина которого сохраняется постоянной, называется релаксацией напряжения. Кривая релаксации,
построенная по уравнению (85.4), приведена на рис. 119. Напряжение падает до того значения, которое соответствует деформации 80 при длительном модуле упругости.
§ 86. Принцип суммирования Больцмана—Вольтерра. Соотношение (84.3), полученное в результате рассмотрения простейшей ме
ханической модели, далеко не является самым общим из возможных и описывает поведение реальных тел лишь в самом грубом, первом приближении. Более точные результаты можно получить, если
не ограничиться введением первых производных от напряжения и деформации. Естественным обобщением закона (84.3) будет следующее соотношение:
£(е) = М(а).
При этом
£(8) = а08 + а1^+... +ап^,
Af(a) = ft0a4-i>1^4-... +^,~й£.
Здесь a,-, bt— константы материала (при данной температуре). Другой способ описания поведения материалов, для которых зависимость между напряжением и деформацией линейна, состоит в следующем. Пусть в момент времени t действующее напряжение равно о. Деформация в этот момент состоит из двух частей. Первая часть — это мгновенная деформация, зависящая от действующего в данный момент напряжения по закону Гука, то есть г' = а]Е. Вторая часть — это накопленная деформация, зависящая от всех тех нагрузок, которые действовали ранее на тело. Пусть в некоторый момент времени x<^t напряжение было а(т). К моменту времени t от этого напряжения сохранилось «воспоминание» в виде некоторой деформации. Если напряжение действовало в течение времени dx, соответствующая «унаследованная» деформация de" пропорциональна а (т) и времени dx; но это «воспоминание» ослабевает со временем, причем закон его ослабевания выражается некоторой функцией, зависящей от времени,
§ 86] ПРИНЦИП СУММИРОВАНИЯ БОЛЬЦМАНА ВОЛЬТЕРРА 185
протекшего между моментом т и моментом t. Обозначим эту функцию К (i — т) и запишем:
de," — Kit— r)a{r)dr.
Чтобы получить полную деформацию е (t), нужно сложить мгновенную деформацию е' и унаследованную деформацию за все промежутки времени dr до момента t. Получим:
t
е(0=4-<*(0+ j K(t—x}o(x}dx. ' (86.1)
— СО
При o=const = CTe получим:
8=J + ae0(f). (86.2)
Здесь
t
G(/) = $K(t — r)dr.
в
Отсюда следует:
tf(f) = G'(f). (86.3)
За начало отсчета времени мы выбрали момент приложения нагрузки. Функция G(f) в уравнении (86.2) может быть найдена экспериментально, она изображается частью АВ кривой, приведенной на рис. 117. По формуле (86.3) находится функция K(t).
ГЛАВА VII
КРУЧЕНИЕ
§ 87. Кручение стержней круглого сечения. Кручением называют напряженное состояние в стержне, находящемся под действием моментов, направленных по его оси. Общая теория кручения принадлежит математической теории упругости и не может быть построена элементарным путем. Поэтому мы ограничиваемся здесь результатами, относящимися к стержням круглого сечения и тонкостенным стержням. Данные о кручении стержней иного профиля приводятся без доказательств.
В основу теории кручения круглого стержня положим следующие предположения:
1. В поперечных сечениях стержня не возникает иных напряжений, кроме касательных.
2. Поперечные сечения поворачиваются без искривления радиусов,
оставаясь плоскими.
Выделим из стержня трубку с внутренним радиусом р и бесконечно малой толщиной do (рис. 120). Касательные напряжения
элемент mnqp претерпит сдвиг.
в поперечном сечении этой трубки можно считать распределенными равномерно. Возьмем два бесконечно близких сечения на расстоянии dz. Вследствие закручивания они повернутся одно относительно другого на угол ftdz, здесь § — погонный угол закручивания трубки, или угол закручивания на единицу длины. Бесконечно малый причем у == . Но яу? =» dz, рр' =
z=^Q$dz, поэтому
Прибегая величину т:
к формуле Гука для касательных напряжений, найдем
Т== ОФр.
(87.1)
§ 87} КРУЧЕНИЕ СТЕРЖНЕЙ КРУГЛОГО СЕЧЕНИЯ
187
Вследствие второй гипотезы для всех трубок, из которых можно мыслить составленным стержень, величина О является одной и той же. Таким образом, касательные напряжения в сечениях изменяются про
порционально расстоянию от оси.
Рассмотрим теперь равновесие части стержня, мысленно от него отсеченной (рис. 121). На элемент dF, отстоящий на расстояние Q от центра, действует напряжение т, следовательно, элементарный / /
момент в правом сечении будет ^-1/ г
TgdF. Н
Составляя условие равновесия 1 )
моментов относительно оси стержня I J
(М—величина момента, приложен- I у
ного в левом сечении), получим:
М= § TQdF= О& § q* dF. Рис. 121.
F F
Распространенный по площади интеграл от Q*dF носит название полярного момента инерции и обозначается
Jp=^Q\dF.
F
(87.2)
Для вычисления Jp заметим, что в полярных координатах dF=* = qdQd<f, поэтому
0 0
В технике обычно предпочитают иметь дело не с радиусом стержня, а с его диаметром d и записывают формулу для полярного момента инерции так:
4=^. (87.3)
Итак, мы нашли:
Отсюда основная формула для погонного (на единицу длины) угла закручивания:
«==^7-. (87.4)
UJP
Подставляя найденное выражение О в формулу (87.1) для т, получим вторую основную формулу теории кручения круглых стержней:
(87.5)
188
КРУЧЕНИЕ
[ГЛ. VII
Следует отметить, что гипотезы и весь вывод сохраняют силу также для стержня круглого трубчатого сечения. Единственная разница будет состоять в том, что при вычислении полярного момента инерции интеграл придется брать по площади кольца. Если наружный диаметр полого стержня есть d, а внутренний dt, то, очевидно,
л (d* -
JP^ 32
(87.6)
Величина наибольшего касательного напряжения при кручении найдется по формуле (87.5), если принять в ней р = г. Соответствующую формулу пишут обычно так:
__Л£ max-•
(87.7)
Величина Wp называется полярным моментом сопротивления. Для
сплошного цилиндра
w = —; р 16
для полого цилиндра
Расчет на прочность по допускаемым напряжениям при кручении сводится к обеспечению неравенства
М _ г-1 Tmax“ М1
Величина допускаемого напряжения при кручении [т] для пластических материалов должна быть принята согласно гипотезе октаэдрического напряжения равной , а согласно условию Треска рав-у з
ной
§ 88. Упруго-пластическое кручение стержня круглого сечения. Для тонкостенной трубки достижение касательным напряжением величины предела текучести для касательных напряжений тт означает переход всего материала в пластическое состояние и появление больших деформаций. Таким образом, расчет по допускаемым напряжениям такой трубки является одновременно расчетом по допускаемым нагрузкам. Для сплошного круглого стержня или толстостенной трубы появление пластичности в точках, близких к наружному контуру, еще не связано с заметными пластическими деформациями, так как большая часть материала еще упруга. За момент разрушения следует считать момент перехода всего материала в состояние пластичности.
§ 88] УПРУГО-ПЛАСТНЧ. КРУЧЕНИЕ СТЕРЖНЯ КРУГЛОГО СЕЧЕННЯ 189
Таким образом, здесь расчеты по допускаемым напряжениям н допускаемым нагрузкам не совпадают. Ввиду этого представляет интерес более детальное изучение поведения закрученного стержня при переходе за предел текучести. Примем за основу гипотезу идеальной пластичности. Как указывалось в главе VI, диаграмма X— у подобна диаграмме <т — е; на упругом участке справедлив закон Гука т=Оу, прн т=тт рост напряжений прекращается.
По формуле (87.5) стержень находится в упругом состоянии, пока
^лг’ Л1<-2-Тт.
При этом связь между моментом и углом закручивания следующаяр
В упруго-пластическом состоянии внутренняя часть сечення (у < с) остается упругой, внешняя'(q > с)— пластической. В упругой части
х = ОрФ, в пластической ’
х = хт.
Граница между упругой н пластической областями находится из условия
Тт —Gc&.
Отсюда
(88.1)
Вычислим теперь момент. Составляя уравнение равновесия, как и в предыдущем параграфе, получим:
Л4= 2л | j OqOq* dQ J ttq‘ dy } . 0 c
Выполним интегрирование и примем во внимание (88.1). Тогда
Л4=2ятт [-J — -JI , (88.2)
По мере роста угла закручивания & величина радиуса упругого ядра безгранично уменьшается, стремясь к нулю, но никогда его не достигая. Величина момента,М стремится прн этом к предельному значению, равному
- - (88.3)
190
КРУЧЕНИЕ
[ГЛ. VII
_ я Е- 2лг
Это предельное значение момента и следует принять за несущую способность стержня. Как видно, чтобы исчерпать несущую способность стержня сплошного круглого сечения, нужно приложить момент AfT, больший, чем момент, соответствующий появлению текучести, на —у) 100=33%.
Пользуясь формулой (87.4) для упругой области и формулой (88.2) для упруго-пластической, можно построить график зависимости между моментом и углом закручивания (рис. 122).
Заметим, что подробное рассмотрение условий работы стержня в упруго-пластической области нужно лишь для построения графика (рис. 122). Для нахождения несущей способности — а это наиболее важный вопрос.— нет ~ надобности рассматривать процесс перехода к предельному состоянию, достаточно предположить его уже достигнутым. Действительно, считая, что ' всюду т=тт, получим:
Л1Т=
Будучи практически целесообразным, этот способ рассуждения не может быть признан вполне строгим. Предельное состояние, при котором все сечение находится в пластическом состоянии, соответствует бесконечно большому углу закручивания и, следовательно, никогда не реализуется.
§ 89. Гипотеза жесткого контура. Гипотеза о сохранении плоских сечений, принятая за основу теории кручения круглого стержня, неприменима для других сечений. Действительно, если применить выведенные на основе ее формулы (87.4) и (87.5) к стержню, сечение которого отлично от круглого, мы придем к явно неверным выводам. При равной площади круг имеет меньший полярный момент инерции, чем, например, вытянутый прямоугольник, и поэтому в силу формулы (87.4) стержень прямоугольного сечения должен быть более жестким. Повседневный опыт показывает как раз обратное. Сплошная труба и труба, разрезанная вдоль образующей, обладают одинаковыми моментами инерции, и в то же время разрезанная труба имеет гораздо меньшую жесткость. Из гипотезы плоских сечений следует, что вектор касательного напряжения всюду перпендикулярен радиусу, а это противоречит следующей общей теореме:
Вектор касательного напряжения в точках контура направлен по касательной к контуру.
§ 89] ГИПОТЕЗА ЖЕСТКОГО КОНТУРА 191
Выделим бесконечно малую площадку 2 в поперечном сечении и предположим, что вектор касательного напряжения на этой площадке имеет две составляющие: rs по касательной к контуру и т„ по нормали (рис. 123). Напряжению т„ соответствует по закону парности касательное напряжение тя на перпендикулярной площадке 2', притом такой, что линия пересечения площадок перпендикулярна направлению т„. Эта линия есть дуга контура, и площадка принадлежит боковой поверхности стержня. Но боковая поверхность стержня свободна от усилий, *„ = 0, а следователь но, равно нулю напряжение т„.
Из доказанной теоремы вытекает следствие:
В точке контура, образующей выступающий угол, касательное напряжение равно нулю.
Действительно, предположим противное и разложим вектор касательного напряжения на две компоненты, нормальные к пересекающимся дугам. На основании предыдущей теоремы каждая из эт:
Отсюда следует, например, что в вершинах сечения стержня, имеющего форму прямоугольника, напряжения равны нулю. Формула (87.5), наоборот, дает для этих точек, как для наиболее удаленных, самые большие напряжения, чем доказывается ее непригодность.
Для некруглых стержней гипотеза нормальных элементов заменяется гипотезой о жестком контуре.
Согласно этой гипотезе деформация при кручении может быть разбита на две части. Сначала сечение поворачивается как жесткое целое. Потом точки сечения получают перемещения, Направленные вдоль оси стержня. Если смотреть на стержень вдоль его оси, то последние перемещения увидеть нельзя; мы видим только поворот контура как жесткого целого, отсюда и название гипотезы.
Величина перемещения точки вдоль оси зависит только от ее положения в сечении, но не меняется при переходе от одного сечения к другому. В противном случае продольные элементы стержня претерпевали бы изменение длины, а следовательно, кроме напряжений кручения возникали бы нормальные напряжения растяжения и сжатия.
Иначе обстоит дело тогда, когда на стержень наложены связи, препятствующие свободной деформации его поперечных сечений, например, тонкостенный стержень снабжен жесткими диафрагмами. При таком стесненном кручении кроме обычных напряжений кручения возникаю^ другие напряжения. Теория , стесненного кручения будет рассмотрена в главе XI. <
192
КРУЧЕНИЕ
[ГЛ. VII
Следует заметить, что гипотеза жесткого контура принимается для нестесненного кручения и математической теорией упругости, которая доказывает ее правильность.
§ 90. Кручение тонкостенных стержней замкнутого профиля. Рассмотрим тонкостенный стержень, сечение которого ограничено двумя замкнутыми кривыми. Толщина стенок й есть функция дуги средней линии у, отсчитываемой от произвольной точки. При малой толщине стенки нет оснований считать касательные напряжения меняющимися по толщине. Будем считать их зависящими только от коор
динаты s.
Распределение касательных напряжений при кручении такого тонкостенного стержня можно наглядно уподобить течению жидкости между двумя жесткими стенками, причем вектор скорости соответствует вектору напряжения. Условие того, что вектор касательного
напряжения в точке контура направлен по контуру, соответствует
условию обтекания жесткой непроницаемой стенки.
Установленная аналогия пока носит чисто внешний, качественный характер. Она становится точной на основании следующей теоремы:
Произведение касательного напряжения на толщину стенки есть величина постоянная.
Рассмотрим равновесие элемента mnqp, вырезанного из стержня, как показано на рис. 124. По закону парности касательных напряжений в продольном сечении, то есть на грани тр (рис. 124), дейст
вует касательное напряжение т, равное напряжению в поперечном сечении. Сила, действующая на грань трр’т', есть xttdz. Передняя грань nqq'ri отстоит от первой на расстоянии ds по дуге средней линии контура; здесь и т другое, и й отличное. Сила, действующая на эту грань, есть тй dz-\-^ (тй dz) ds. Проектируя на образующую
силы, действующие на элемент, получим:
Отсюда
ТЙ = const.
(90.1)
Если отождествить касательное напряжение со скоростью жидкости, то условие (90.1) выражает тот очевидный факт, что через
§ 90] КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ ЗАМКНУТОГО ПРОФИЛЯ
193
с действующим
ds
Рис. 125.
каждое сечение в одно и то же время протекает одинаковый объем жидкости. Иначе, это есть условие несжимаемости жидкости.
Теперь мы в состоянии связать величину касательных напряжений при кручении тонкостенного замкнутого стержня моментом. Изображая сечение в виде контура, на имеющего толщины (рис. 125), найдем, что на единицу длины действует касательная сила тб, величина которой постоянна. На элемент дуги ds действует сила rfids; она создает момент dM относительно произвольной точки О. Плечо этого момента есть перпендикуляр р, опущенный из точки на касательную к контуру.
Но произведение р ds есть удвоенная Площадь треугольника с основанием ds и вершиной в точке О; обозначим ее 2dF. Тогда
dM=(xb)2dF.
Складывая моменты всех бесконечно малых на все элементы контура, получим:
M=xb2F.
сил, действующих
Здесь F—площадь,>ограниченная контуром сечения. Отсюда
___М
X~2Fd'
(90.2)
Последний вопрос, оставшийся нерешенным,— определение угла закручивания. Для этого докажем теорему, называемую теоремой о циркуляции касательного напряжения. Вследствие гипотезы жесткого контура, как уже отмечалось, деформация стержня может быть представлена состоящей из двух частей: деформации, связанной с поворотом сечения как целого, и деформации, происходящей при перемещении точки сечения вдоль образующей. Рассматривая сдвиг элемента mnqp (рис. 124), будем мыслить его как результат двух последовательных сдвигов:
y=y'+y"-
Определим сначала величину у' — сдвиг вследствие поворота сечения.
Соответствующее построение сделано на рис. 126. Два бесконечно близкие сечения, взятые на расстоянии dz, поворачиваются одно относительно другого на угол $dz. Точка т получает вследствие поворота перемещение тт', равное Oq dz, по дуге окружности с центром в точке О. Отрезок тт вообще составляет с касательной к контуру в точке т угол а. Совершенно то же происходит
7 Ю. Н. Рафотнов
194
КРУЧЕНИЕ
[ГЛ. VII
в точке п. Разложим перемещение тт' на две составляющие: перпендикулярную к контуру и направленную по касательной к контуру. Первая составляющая, не деформирует элемент mnqp, а только
наклоняет его вперед. Вторая составляющая определяет перекашивание прямоугольника mnqp', верхнее основание оказывается сдвинутым относительно нижнего как раз на величину проекции отрезка тт' на касательную, то есть Op dz cos а. Поэтому относительный сдвиг
у' = Qq cos а.
На этом чертеже мы изображали стержень не имеющим толщины, элемент mnqp принадлежит средней поверхности стержня. Выясним теперь, как деформируется эта средняя поверхность от перемещения ее точек вдоль образующей (рис. 127). Обозначим это перемещение и(в). Здесь s — дуга линии контура поперечного сечения, отсчитываемая от произвольной точки. Если та образующая, которая соответствует стороне тр, определяется координатой s, то отрезок тр переместится на величину и (s). Отрезок nq лежит на образующей с координатой s -|- ds, и перемещение его есть а -|- du. Разница du в перемещениях двух сторон прямоугольника
приводит к его перекашиванию, то есть сдвигу. Относительный сдвиг
„ du V = j- • 1 ds
§ 90] КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ ЗАМКНУТОГО ПРОФИЛЯ 195
Таким образом, полная величина сдвига
л । du
у = ъо cos а -4- -j-, ' * 1 ds ’
и поэтому
т = G ( cos а -4-\ * 1 as
(90.3)
Умножим касательное напряжение на ds и проинтегрируем по контуру. В правой части интеграл от , равный разности между значениями и в начальной и конечной точках пути интегрирования, для замкнутого пути обращается в нуль, и мы получаем:
(f) х ds = 00 ф q cos a ds.
Левая часть носит название циркуляции касательного напряжения, правую легко вычислить. Действительно, обращаясь к рис. 125, видим, что о cos а=р, следовательно, Q cos a ds = = 2dF. Поэтому
(fi g cos а ds = 2F, и для угла закручивания получается следующая формула:
(90.4)
(90.5)
В свою очередь величина х находится по формуле (90.2). Поэтому
л М г ds
Пример 1. Тонкостенная труб
ка радиуса R и толщины S. Для
нее F= л/?1, • По формулам (9Q2) и (90.5) находим:
Т==Л_ а= м 2л/?*6’ 2л/?’бО
Эти же результаты получаются, если рассматривать трубку как' круглый полый стержень и применять формулы § 87.
Пример 2. Полый стержень, сечение которого изображено на рис. 128. Средняя линия сечення, показанная штрих-пунктиром, представляет прямоугольник с размерами 9 сл\18 см, следовательно, F= 162 см*.
Л=4+2т=“-
7*
196 КРУЧЕНИЕ [гл. VII
По формулам (90.2) и (90.5) г = а—*_ lmax 324’ v— 7240G ‘
§ 91. Кручение тонкостенных стержней открытого профили. Аналогия между распределением напряжений при кручении и течением жидкости в плоском сосуде, имеющем форму поперечного сечения стержня в плане, позволяет легко составить качественную картину распределения напряжений при кручении тонкостенного стержня открытого профиля (рИС; 129).
Рис. 129.
Траектория жидкой частицы или линия тока в сосуде тако.й формы представляют собою замкнутую кривую, почти параллельную стенке иа большей части длины (части ab и cd на рис. 129). Поворот потока происходит на отрезках линии тока da и Ьс, малых по сравнению. с ab и cd. Пренебрегаем влиянием концов сечения (на рисунке отделены волнистыми линиями) и будем приближенно считать ab cd == I.
Здесь I — длина профиля. По аналогии замкнутую линию, в каждой точке которой вектор касательного напряжения направлен по касательной, будем называть траекторией касательных напряжений.
Теорема о циркуляции, установленная в предыдущем параграфе, может быть применена не только к стержню замкнутого профиля,' но и к любой траектории касательных напряжений. Применим ее к траектории abed. При вычислении интеграла, входящего в формулу (90.4), пренебрегаем частями Ьс и da траектории и будем считать напряжение постоянным на дугах ab и cd. Тогда
J т ds = 2т/.
§ 91] КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ ОТКРЫТОГО ПРОФИЛЯ 197
Площадь F, ограниченная линией тока, с той же степенью точности есть
F=2ly.
Поэтому по формуле (90.4)
2x1 _ т
4Gly~~ 2Gy‘ Отсюда
t = 2G0y. - (91.1)
Здесь у — расстояние точки, в которой ищется касательное напряжение, от средней линии профиля.
Осталось связать погонный угол закручивания й с крутящим моментом М. Возьмем две бесконечно близкие линии тока, отстоящие на dy одна от другой. Заключенная между ними часть сечения может рассматриваться как бесконечно тонкий стержень замкнутого профиля, который принимает на себя бесконечно малую часть крутящего момента dM. Применим к нему формулу (90.5):
Но, как мы уже видели,
У dy~~ dy’
Поэтому
dM = 8Gly*Qdy.
Чтобы подсчитать полный момент, нужно проинтегрировать это л б гт
выражение от у = 0 до у = -%-. Получим:
М = 1GW®. (91.2)
Определяя величину й из (91.2) и подставляя в формулу (91.1), найдем:
г—2Му
о
Наибольшей величины напряжение достигает там, где у = у. Поэтому
^тах=-^-. (91.3)
4-б*/ о
Формулы (91.2) и (91.3) выведены в предположении, что профиль весьма тонкий и д очень мало по сравнению с длиной профиля I.
198
КРУЧЕНИЕ
[ГЛ. VII
Только при этом условии можно пренебречь концами, длина которых имеет порядок б; значит, эта длина зависит только от толщины б, но не от размера I. Поэтому с увеличением I (при постоянном б) роль концов становится все менее значительной. Кроме того, профиль предполагается плавным, радиус кривизны его должен быть велик по сравнению с размером б. В действительности профили обычно составляются из элементов разной длины и ширины, сопрягающихся с образованием углов. В местах сопряжения элементов возникают местные перераспределения напряжений. Природу их можно уяснить, обращаясь к гидродинамической аналогии. При обтекании углов или при резких изменениях сечения распределение скоростей всегда неравномерно. Однако возмущенная зона, или область местных напряжений, простирается на длину порядка б от места сопряжения элементов профиля. Поэтому, если толщина стенки достаточно мала по сравнению с длинами элементов, составляющих профиль, можно пренебречь этими местными напряжениями и считать, что каждый элемент закручивается отдельно. По формуле (91.2) на элемент номер / С ДЛИНОЙ И ТОЛЩИНОЙ б,- ПрИХОДИ^я
2И/==1О/Д’О.
Общий крутящий момент равен сумме таких частных моментов, или
ЛТ=уО2/,б,?й.
Отсюда
0=4-^-------. (91.4)
Теперь можно определить Mk, часть момента, приходящуюся на элемент номер k-.
Наибольшее напряжение в элементе номер k по формуле (91.3)
есть
^*)тах— 1 v
Наибольшее расчетное напряжение получается при этом в стержне, имеющем наибольшую толщину:
(91.5)
§ 92] КРУЧЕНИЕ УПРУГИХ СТЕРЖНЕЙ СПЛОШНОГО ПРОФИЛЯ 199
Формулы (91.4) и (91.5) не являются точными, так как в действительности отношение S/Z всегда конечно. Незначительные поправки, которые нужно вносить в эти формулы при расчете реальных профилей, можно найти в справочной литературе.
§ 92. Кручение упругих стержней сплошного профиля. Выполнение теоремы о циркуляции касательного напряжения представляет тот критерий, который позволяет выделить из бесчисленного множества статически возможных напряженных состояний то, которое реализуется в действительности при кручении упругого стержня.
Так, например, легко видеть, что выражения для касательного напряжения и угла закручивания круглого стержня удовлетворяют требованиям теоремы о циркуляции, поэтому найденное для круглого сечения решение является точным. Теория упругости устанавливает дифференциальные уравнения в частных производных, которым удовлетворяют напряжения при кручении стержня произвольного поперечного сечения. Существуют методы решения этих уравнений, позволяющие исследовать вопрос о кручении стержня эллиптической, секториальной, прямоугольной и многих других форм поперечных сечений. Величины, которые нас практически интересуют,— это угол закручивания в зависимости от крутящего момента и наибольшее касательное напряжение. Для всех случаев, как рассмотренных нами элементарно, так и изученных методами теории упругости, результаты можно представить в следующей форме:
CG ’
где С—так называемая геометрическая жесткость;
т = ^-тах ’
ТГК — момент сопротивления при кручении.
Для круглого стержня диаметра d
C=JP = ^' W*=WP^' (92.1)
Для полого цилиндра с наружным диаметром d и внутренним dx
л (d* — d*\ nJ» г d*\
c=Jp=-Lri-’ »22>
Для тонкостенного стержня замкнутого профиля
4F*
C=^ds' ^=2/An«n- (92-3)
} &
200
КРУЧЕНИЕ
[ГЛ. VII
Для тонкостенного стержня открытого профиля
^=зг-2^.
° ^umax
(92.4)
А
а
В
А
Рис. 130.
Большую практическую важность представляет вопрос о кручении прямоугольного стержня. Рассмотрение этой задачи элементарными средствами невозможно, методы теории упругости позволяют получить выражения для напряжения и углов закручивания в виде бесконечных рядов. Наибольшее напряжение т, как оказывается, получается в серединах длинных сторон (Л и А' на рис. 130). В углах напряжения равны нулю, в серединах коротких сторон (В и Д') отмечается второй максимум напряжения, однако напряжения т' в этих точках меньше, чем о напряжения т в точках А и А .
Такая качественная картина становится понятной, если обратиться к гидродинамической аналогии, то есть представить себе цилиндрический сосуд прямоугольной формы, в котором циркулирует жидкость.
Очевидно, что в углах скорость будет равна нулю. Через сечение ОА в единицу времени протекает то же количество жидкости, что и через сечение ОВ, а так как ОА меньше, чем ОВ, то средние скорости на отрезке ОА больше, чем на ОВ. Поэтому естественно считать и максимальную скорость в точке А большей, чем в точке В. Это, конечно, не доказательство, а довольно правдоподобное рассуждение, основанное на интуиции. Точное представление о характере распределения напряжений можно составить, только имея точное решение задачи теории упругости или данные эксперимента. Последние в части распределения напряжения носят всегда косвенный характер, так как методы непосредственного измерения напряжений отсутствуют. Результаты точного решения можно представить следующим образом:
С=ааЪ*, WK = $ab\
(92.5)
Здесь а — длинная сторона, Ь — короткая сторона прямоугольника. Наконец, напряжение в середине короткой стороны х' связано с максимальным напряжением х соотношением
х' = ух.
Безразмерные коэффициенты а, 0 и у зависят только от одного безразмерного параметра, характеризующего сечение, а именно от отношения а^Ь. Выражения коэффициентов в функции параметра а/Ь не могут быть написаны в конечном виде; они даются бесконечными рядами, приводить которые здесь нет нужды. Эти коэффициенты
§ 93] ОПЫТНОЕ ИССЛЕДОВАНИЕ КРУЧЕНИЯ 201 вычислены для различных значений alb и даются в следующей таблице:
а _ b ~ 1 Г, 5 2 3 4 б 8 10 ОО
а 0,141 0,196 0,229 0,263 0,281 0,299 0,307 0,313 0,333
₽ 0,208 0,231 . 0,246 0,267 0,282 0,299 0,307 0,313, 0,333
Y 1,000 0,858 0,796 0,753 0,745 0,743 0,743 0,743 0,743
Если при расчете встретится какое-либо промежуточное значение отношения а/6, то следует прибегнуть к интерполированию.
Остановимся на последнем столбце этой таблицы. Полагая отношение ajb равным бесконечности, мы считаем ширину сечения весьма малой по сравнению с его длиной. Но как раз в этих предположениях строится теория тонкостенных стержней открытого профиля. Значит, формулы (92.4) применимы и внашем случае. Но они совпадают с (92.5) при а = Р = 1/,. Значение у = 0,743 при а/b — оо получить элементарно не удается. „
§ 93. Опытное исследование кручения. Для опытного изучения
кручения применяют машины рис. 131.Для измерения углов закручивания на образец ставят два зеркала, углы поворота которых определяют с помощью оптических трубок и реек так, как это было разъяснено в § 60.
Испытание на кручение имеет по сравнению с испытанием на растяжение то преимущество, что поперечное сече: ние стержня остается неизменным до самого момента разрушения, следовательно, при испы-
типа схематически изображенной на
Рис. 131.
тании получается истинная диаграмма зависимости между т и у. Однако для получения этой зависимости непосредственно, в чистом виде, испытания следует производить над тонкостенными трубками. Образцы в форме тонкостенных трубок трудно изготовлять, кроме того, при скручивании трубок с очень малой толщиной стенки наблюдается потеря устойчивости. Это значит, что трубка, будучи закрученной, сплющивается. Испытания над тонкостенными трубками производятся весьма редко, в практике обычно испытывают на кручение сплошные
202
КРУЧЕНИЕ
[ГЛ. VII
образцы круглого сечения. Сами испытания могут преследовать различные цели, как-то:
1. Определение модуля сдвига О. Для определения модуля сдвига увеличивают ступенями крутящий момент, измеряя каждый раз угол закручивания стержня. В упругой области угол закручивания и момент связаны зависимостью
а» A1Z
<?=®l = GTp.‘
Здесь /—расстояние между зеркальцами, то есть длина, на'которой измеряется угол закручивания. Применяя эту формулу не к самому углу закручивания и моменту, а к приращениям этих величин на каждой ступени нагружения, получим: г_ /ЛЛ4 и__/рД<р-
(93.1)
Желая компенсировать возможные ошибки измерения, для модуля сдвига принимают среднее значение из ряда величин, получаемых для различных ступеней нагружения.
2. Установление зависимости г— у. Для расчетов-в области пластических деформаций диаграмма т — у является основным и исходным материалом. В результате опыта на кручение мы получаем зависимость между моментом М и углом закручивания <р. Чтобы получить отсюда зависимость г— у, будем предполагать эту зависимость заданной и решим задачу о пластическом кручении стержня. Вследствие гипотезы плоских сечений, как было показано в § 87, у = фр. Следовательно, г = г (йр). Подставив в уравнение равновесия, получим:
Г
М= Jr (Фр) §dF=2n J г (Фр) р* dp. (93.2)
F в
Введем теперь обозначения:
Как т, так и ув непосредственно определяются из опыта, у0 есть сдвиг на поверхности стержня. Вместо диаграммы М — <р можем считать заданной диаграмму т — у0. С другой стороны, из уравнения (93.2) получаем:
То
т = -L I т (у) у* dy. (93.3)
Продифференцируем (93.3) по у0:
То ^=~ip(Y)Y’dY+^T(Yo)’
(93.4)
§ 93] ОПЫТНОЕ ИССЛЕДОВАНИЕ КРУЧЕНИЯ 203
Исключим из уравнений (93.3) и (93.4) интеграл. Получим:
t(y) = Y^4-3/b. (93.5)
Индекс у величины у здесь опущен. Таким образом, для определения зависимости т от у следует взять диаграмму зависимости момента от угла закручивания, изменив масштабы так, чтобы вместо момента был отложен момент, поделенный на постоянную 2лгг, вместо угла закручивания — погонный угол закручивания, умноженный на радиус. После этого строится график производной функции т от у и по формуле (93.5) по точкам — искомая зависимость т от у. Следует заметить, что кривая зависимости т от у более крутая и плавная, чем т от у. Поэтому обнаружить на диаграмме кручения предел пропорциональности или предел текучести труднее, чем на диаграмме растяжения.
Описанный способ обработки диаграммы кручения цилиндрического стержня для нахождения диаграммы т — у был предложен Надаи. Видоизменение этого способа принадлежит Хиллу и состоит в следующем. Имея кривую зависимости т от у, легко построить кривую зависимости у от у. Тогда уравнение (93.5) можно заменить таким:
T(Y) = Y*^(7) + 4/». (93.6)
Графическое дифференцирование кривой зависимости у от у дает более точные результаты, чем дифференцирование кривой зависимости т от у.
3. Нахождение временного сопротивления кручению. При достаточно большом крутящем моменте закрученный образец разрушается. Характер разрушения оказывается различным в зависимости от материала. Образец из пластического материала, как правило, разрушается вследствие среза поперечного сечения, то есть сечения, в котором действуют основные касательные напряжения. Точно такие же по величине касательные напряжения действуют в продольных сечениях стержня вследствие закона парности, поэтому закрученный деревянный стержень расщепляется вдоль волокон. Наконец, при кручении стержней из хрупкого материала, например чугуна, наблюдаются характерные косые изломы. Как известно, чугун обладает низким сопротивлением отрыву, а напряженное состояние чистого сдвига в бесконечно малом элементе закрученного стержня приводится к растяжению — сжатию по двум направлениям, составляющим угол 45° с осью стержня (рис. 132). Поэтому существуют семейства винтовых поверхностей, пересекающих образующую
204
КРУЧЕНИЕ
[ГЛ. VII
под углом 45°, таких, семейству, существуют на площадках другого
- Рис. 132.
что на площадках, принадлежащих одному только сжимающие напряжения, равные — т, семейства — только растягивающие -|- т. По этим винтовым поверхностям и происходит разрушение;
В качестве меры прочности материала при кручении принимают временное сопротивление, то есть величину наибольшего крутящего момента, поделенную на WK. Такое определение является условным; оно основано на предположении о том, что распределение напряжений до самого таким же, как и в упругой области.
момента разрушения остается
Поэтому и величина временного сопротивления кручению является условной характеристикой, имеющей лишь "сравнительное значение.
Рис. 133.
§ 94. Предельное состояние закрученного стержня из идеальир-пластйческого материала. Если стержень изготовлен из идеальнопластического материала, в предельном состоянии касательные напряжения во всех точках сечения равны по величине и меняются только по направлению. Рассмотрим две бесконечно близкие траектории касательных напряжений Г и Г' на рис: 133. Если вырезать из стержня объем, заключенный между двумя цилиндрами с основаниями Г и Г' и образующими, параллельными оси стержня, мы получим тонкостенный стержень замкнутого профиля, боковая поверхность которого свободна от напряжений. Формула (90.1) была получена только при помощи условий статики, и следо-как для упругого состояния, так и для пластиче-к рассматриваемому тонкостенному стержню; по-
вательио, она верна ского. Применим ее . . .
нимая под б расстояние между линиями Г и Г', получим: бт_ = const.
Отсюда
б = const.
Таким образом, траектории касательных напряжений в предельном состоянии -стержня из идеально-пластического материала являются эквидистантными кривыми. Для построения их следует отправляться от контура. Построим семейство прямых, нормальных к контуру, и будем откладывать на этих прямых, начиная от точки контура, отрезки равной длины. Соединяя концы этих отрезков, будем получать
§ 94]
ПРЕДЕЛЬНОЕ СОСТОЯНИЕ ЗАКРУЧЕННОГО СТЕРЖНЯ
205
траектории касательных -напряжений. В случае круга, например, траекториями касательных напряжений являются концентрические круги, что и заранее очевидно.
В случае многоугольного сечения вдоль каждой стороны многоугольника траектории касательного напряжения будут прямыми, параллельными соответствующей стороне. Эти прямые делают излом на биссектрисе угла (рис. 134), только при этом условии расстояние й траектории от многоугольного контура будет постоянным. На биссектрисе вектор касательного напряжения поворачивается. В стержне квадратного поперечного сечения (рис. 135) траектории будут также квадратами, диагонали разбивают квадрат на четыре треугольника, в каждом из которых вектор касательного напряжения имеет по
стоянное направление. Для прямоугольного сечения (рис. 136) траектории являются все более и более вытянутыми прямоугольниками, приближающимися к отрезку тп между точками пересечения биссектрис
углов контура сечения. Отрезок тп представляет собою линию разрыва напряжения, касательные напряжения с двух сторон этого отрезка равны по величине, но противоположны по направлению.
Осталось вычислить крутящий момент в предельном состоянии. Бесконечно близкие линии тока разбивают весь стержень на бесконечно большое число тонкостенных стержней, для каждого из которых крутящий момент ДЛ! найдется по формуле § 90:
Здесь F—площадь, заключенная внутри контура Г.
Просуммируем эти моменты. Для этого построим поверхность, образованную прямыми, проходящими через контур поперечного сечения и составляющими с его плоскостью одинаковый угол, тангенс которого равен тт. Такая поверхность постоянного ската в случае кругового сечения будет конусом, в случае прямоугольника будет состоять из четырех плоскостей, образующих подобие крыши. Назовем эту поверхность Поверхностью напряжений.
206
КРУЧЕНИЕ
(ГЛ. VII
Теперь траектории касательных напряжений можно получить следующим образом: будем рассекать поверхность напряжений плоскостями, параллельными плоскости сечения, и проектировать линии пересечения на эту плоскость. Если условно считать плоскость сечения горизонтальной, то траекториям Г и Г' соответствуют горизонтальные сечения поверхности напряжений, находящиеся одно от другого на расстоянии йтт, так как 6 есть расстояние между линиями Г и Г',
а тг — тангенс угла наклона поверхности напряжений. Объем, заключенный между этой поверхностью и горизонтальными сечениями, равен 6ttF, а сумма таких объемов представляет собою объем V, ограниченный площадью сечения и поверхностью напряжений. Таким образом,
МТ = 2У. (94.1)
В случае кругового сечения V есть объем конуса с радиусом основания г и высотой гтт, следовательно, V=^nr*xT и Л4Т =
2
= у лг*тт, что совпадает с формулой (88.3). Для прямоугольника со сторонами а и Ь дело сводится к определению объема тела, изображенного на рис. 137, причем Л=уТтй. В результате получаем:
М^±хтЬ'\а-±ъ). (94.2)
ГЛАВА VIII
ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
§ 95. Основные определения. Содержание этой главы носит чисто геометрический характер и представляет собою введение к теории изгиба. Моментами плоской фигуры относительно системы координат хОу вообще называются интегралы следующего вида, распространенные по площади:
J= J Р(х, у) dF. (95.1)
F
Здесь Р— однородный полином относительно X и у.
При нахождении центров тяжести плоских фигур встречаются с моментами первого порядка:
Sx = $ ydF, Sy = $ х dF. (95.2)
F F
Очевидно, всякий другой момент первого порядка, то есть интеграл от некоторой однородной линейной функции координат, выражается линейным образом через Sx и Sy. Эти величины носят название статических моментов, потому что нахождением центров тяжести плоских фигур занимается статика. Если представить себе, что фигура вырезана из тонкого листа постоянной толщины и находится в однородном силовом поле, то равнодействующая сил тяжести при любом положении фигуры окажется приложенной в центре тяжести, то есть в точке с координатами хс и ус, которые определяют по формулам:
*с=^, Ус=Т- (95.3)
Три момента второго порядка:
J^y'dF, Jy = \x*dF, JXy = $xydF (95.4)
F F F
достаточны для того, чтобы вычислить любой момент второго порядка, который представится линейной комбинацией вышенаписанных. Два первых называются осевыми моментами инерции относительно осей х и у соответственно^ последний — центробежным моментом
208 ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ [гл. VIII
инерции. Самый термин «момент инерции» заимствован из динамики, где с аналогичными интегралами встречаются, изучая вращение тяжелой однородной фигуры.
Из двух осевых моментов Jx и Jy можно построить полярный момент инерции. Действительно,
Jp = $ г* dF= $ (х‘ +/) dF= Jy + Jx. F F
Определение полярного момента инерции ничем не связано с осями координат, а зависит от положения точки О. Таким образом, мы установили, что сумма осевых моментов инерции относительно любой пары перпендикулярных осей, проходящих через заданную точку, есть величина постоянная.
Аналогичным образом можно строить моменты более высокого порядка— третьего, четвертого и т. д.
§ 96. Общие теоремы о моментах. Остановимся на некоторых основных и очевидных свойствах статических моментов н моментов инерции. При перечислении этих свойств мы будем употреблять просто слово «момент» в тех случаях, когда речь идет о свойстве, общем для всех моментов. В противном случае будет указываться, о каком моменте идет речь.
Теорема 1. Момент составной площади равен сумме моментов ее частей.
Действительно, если фигура состоит из двух частей I и II, то по свойству интегралов
Р(х, у) dF— $ Р[х, у} dF+ J Р(х, у) dF.
Но J Р(х, y)dF есть момент всей площади, интегралы в правой F
части суть моменты того же наименования частей I и II. Следовательно,
Следствие. При вычислении момента площади, ограниченной двумя замкнутыми контурами (двухсвязной), можно вычислить момент площади, ограниченной наружным контуром, и вычесть из него момент площади, ограниченной внутренним контуром (рис. 138). Действительно, момент У, площади, заключенной внутри контура Г,, равен по предыдущему сумме момента Jn площади, ограниченной кривой Г*, и момента J заштрихованной части:
Л =
§ 96]
ОБЩИЕ ТЕОРЕМЫ О МОМЕНТАХ
209
Отсюда
J •—и\ Jlv
Этим замечанием часто пользуются при вычислении моментов инерции.
Теорема 2. Осевые моменты инерции двух равных фигур, симметрично расположенных относительно оси, равны между собою.
Площади фигур I и II (рис. 139) можно разбить на бесконечно малые элементы так, что каждому элементу dFt соответствует
Рис. 138.
равный элемент dFt, причем ординаты их одинаковы, а абсциссы равны и противоположны по знаку:
х, = — Момент инерции первой фигуры относительно оси у: x*dFv
Второй фигуры:
J’1 = 5 x*,dF,. Fn Но xj = xj, dFx = dFt. Поэтому jy—j'y.
Теорема 3. Центробежные моменты двух равных фигур, симметрично расположенных относительно оси, равны по величине и противоположны по знаку.
Обращаясь к рис. 139 и полагая
Х1У1 dFv •^ч/==5 x^y^dF^, Fi Fn
заметим, что xtyt = — xjv dF, = dFt.
210
ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
[ГЛ. VIII
Поэтому
7* —___ 7"
Jxy— Jxy
Следствие. Центробежный момент инерции равен нулю, если одна из осей есть ось симметрии. Пусть, например, осью симметрии является ось у. Она разбивает фигуру на две равные части I и П, симметрично расположенные относительно этой оси. -По первой теореме
Jxy =Jxy-\-Jlxy •
Вследствие третьей теоремы
/ _ _ 7"
Jxy----Jxy
Таким образом,
Jxy = ^
Определение. Оси, для которых центробежный момент равен нулю, называются главными осями инерции. Мы установили, что симметрия фигуры относительно одной из осей является достаточным условием того, что оси главные. Но это условие не необходимо; мы увидим в дальнейшем, что у несимметричных фигур тоже существуют главные оси.
§ 97. Преобразование статических моментов и моментов инерции при параллельном переносе осей. Предположим, что нам известны статические моменты и моменты инерции относительно осей хОу. Требуется определить те же величины для осей х'Оу’, параллельных данным. Обозначим через а и b абсциссу и ординату точки О, то есть координаты старого начала, относительно новых осей. Тогда
х' = х-{-а, у'=у-^-Ь.
Величины
Sx = \ydF, Sy = $xdF. Jx = $y*dF, Jy = ^dF,
F F F F
Jxy=^xydF
F даны. По определению
= J у' dF— (y -J- b) dF= J у dF-\- J b dF.
F F F F
Таким образом,
Sx> = Sx 4- bF, Su. = Sy 4- bF. (97.1)'
Осевой момент инерции относительно оси х':
Jx' = $ (у 4- *)* dF= J (у* 4- 2Ьу 4- b*) dF —
F F
= $ y*dF-\- 2b J ydF 4- b* $ dF.
F F F
§ 98] ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ 211
Все интегралы в правой части известны, поэтому
и аналогично Jx> = Jx-}-2bSx-}-btF, (97.2)
Jy'= Jy a* F, (97.2')
Наконец, найдем центробежный момент для новых осей:
Jx'у' — J (ж л) (у -р- b) dF.
F
Раскрывая скобки и разбивая интеграл на четыре интеграла, получим:
Jx,y, = JXy-\-aSx-^bSy-\-abF. (97.3)
Обычно бывают заданы величины моментов инерции фигуры относительно осей, проходящих через центр тяжести. Будем называть такие оси центральными и обозначать их g и т). Итак, считаем заданными Теперь можно опустить штрихи в обозначениях
новых осей и вместо а, b ввести обозначения х01 у0— координаты центра тяжести. Для центральных осей статические моменты равны нулю, и формулы преобразования моментов инерции приобретают простой вид:
Л = = ^Ху = Лт) + ХаУа^- (97.4)
§ 98. Вычисление моментов инерции. При вычислении момента инерции плоской фигуры, например, относительно оси х в формуле для Jx нужно принять dF=dx dy:
Jx = ^ у* dxdy = ^ у* dy dx.
Интегрируя по х при постоянном у, найдем:
J dx = bx.
Отрезок Ьх есть ширина сечения на расстоянии у по оси х (рис. 140). Вообще, Ьх есть известная функция от у. Для момента инерции получаем формулу у»
J*=\bx(y)y'dy. (98.1)
У1
Аналогично
, Jy = $ by (х) х* dx. (98.2)
Xt
Рассмотрим несколько примеров, относящихся к определению моментов инерции простейших фигур.
212
ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
[ГЛ. VIII
Прямоугольник. Определим момент инерции относительно центральной оси £ (рис. 141). При этом
= ft = const, Л = —А Л =
+4-
Л= J by'dy = b-£. (98.3)
_ Л.
2
Треугольник. Проще всего найти момент инерции треугольника для оси х, проходящей через вершину и параллельной осно-
ванию. При этом (рис. 142) by = b-j , у, —О, yt = h,
h
, С У 1 . bh*
Jx = \b^y dy^^.
О
Желая вычислить момент инерции относительно центральной оси, параллельной основанию, заметим, что по формуле (97.4)
Но
- Отсюда
„ bh 2 .
bh*
(98.4)
Круг. Для любых центральных осей J^=xsJv поэтому
Но полярный момент инерции круга был вычислен в § 87:
. __лг‘__nd4
JP~~~T 32
§ 98] ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ 213
Поэтому
= (98.5)
Эллипс. Эллипс можно рассматривать как проекцию круга радиуса а на плоскость, составляющую с плоскостью круга угол <р, косинус которого есть Ь\а (Ь и а — полуоси).
При вычислении момента инерции относительно большой оси:
Jx=\y'dxdy
заметим, что у и dy представляют собою отрезки, перпендикулярные линии пересечения плоскостей круга и эллипса. Поэтому они равны соответствующим отрезкам для круга, умноженным на cos<p. Следовательно,
Jx=cos2q)J'.
Здесь J' — момент инерции площади круга относительно диаметра.
Аналогично в выражении
Jy = J хг dx dy
х и dx равны соответственным линейным величинам проектируемого круга, a dy есть результат умножения элемента ординаты круга на cos <р. Поэтому
Jy = cos<p J'.
Замечая, что J' = -£-, получим
Jx=^, = 08.6)
h
При определении центробежных моментов инерции заменять двойное интегрирование однократным нельзя. Приведем определение момента инерции прямоугольного треугольника относительно центральных осей, параллельных катетам. Возьмем сначала оси х, у, совпадающие с катетами треугольника (рис. 143).
Центробежный момент прямоугольного треугольника относительно этих осей есть л ьх
Jxy = W хУЛхЛУ-о о
214
ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
[ГЛ. VIII
Пользуясь формулой преобразования центробежного момента инерции при параллельном переносе осей
JXy = J^ + xaytF и полагая в ней
1 . 1 . „ bfL
х» з b, Уа з b, F— 2 > найдем:
= (98.7)
Поперечные сечения балок, для которых приходится находить моменты инерции, обычно представляют сложные фигуры, которые легко разбить на простейшие—прямоугольники и треугольники. Вычисление моментов инерции таких фигур производится путем разбивки на части на основании того свойства, что момент составной фигуры равен сумме моментов ее частей, а также теорем о преобразовании моментов инерции при параллельном переносе.
§ 99. Преобразование моментов инерции при повороте осей. Для вывода формул преобразования моментов инерции при повороте осей воспользуемся комплексным представлением моментов инерции. Обозначив через z = x-\- iy аффикс точки, заметим, что полярный момент инерции
JP= $ dF~= (х* + /) dF= Jy + Jx.
Определим комплексный момент инерции J формулой
J = $ ? dF= $ (х* — у* 4- 2ixy) dF= Jy — Jx + 2iJKy.
Складывая выражения J и Jpt найдем:
^ + 'Лу=у(^ + /). (99.1)
Аналогично
Jx iJ*y==~2 Wp (99.2)
Перейдем от осей х, у к но-рис вым осям х', у’, повернутым-
относительно старых на угол а
(рис. 144). Аффикс точки по отношению к новым осям: г' == ге~'я.
Комплексно-сопряженная величина:
z' = ze/*.
§ 100] ГЛАВНЫЕ ОСИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ 215
Определяя для новых осей Jp и J, получим:
J'P = JP, J' = Je-K*.
По формулам (99.1) и (99.2)
Jy' + ’Jx'y' = у (Jp + е~~ 2,аА
1 - (99.3)
JX' — iJX'y' = -^(Jp—e-^J).
Это и есть формулы преобразования моментов инерции в комплексной форме. Пользуясь выражением J и отделяя действительные части от мнимых, найдем:
Jx> = —cos 2а — JXy sin 2а,
Jv> =^^_4rAcos2a4-JXysin2a, (99.4) JX’W = J* 2 J~ sin 2“+JXy cos 2a-
Как видно, эти формулы почти буквально, с точностью до знака при JXy и Jx>u>, совпадают с формулами для преобразования компонент тензора напряжений (см. § 37). Так же как плоское напряженное состояние, совокупность моментов инерции для множества пар осей, проходящих через точку, так называемый тензор инерции, можно представить с помощью круговой диаграммы Мора (рис. 144).
Будем откладывать осевые моменты инерции по оси абсцисс и центробежный со знаком минус по оси ординат. Аффикс точки х есть Jx—Uxy, таким образом, точка х является изображением осн х. По формуле (99.2) аффикс точки х можно представить как сумму действительного числа -^-Jp (отрезок ОС) и комплексного числа — у — UXy (отрезок Сх).
Вторая из формул (99.3) указывает, что аффикс точки х' получится, если повернуть отрезок Сх на угол 2a по часовой стрелке.
Таким образом, точки, изображающие совокупность осевого и центробежного моментов инерции для разных осей, оказываются точками одной и той же окружности. Правило отсчета углов остается то же, что в теории плоского напряженного состояния, то есть углу а между осями соответствует дуга 2a между точками круговой диаграммы, отсчитываемая в противоположном направлении.
§ 100. Главные оси и главные моменты инерции. Из рассмотрения круговой диаграммы видно, что суи!ествуют две взаимно перпендикулярные оси, для которых центробежный момент равен
216 ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ [гл. VIII
нулю и осевые моменты принимают наибольшее и наименьшее значение, Оси эти называются главными осями инерции, соответствующие осевые моменты — главными моментами инерции. Будем считать, что есть наибольший момент, a J, — наименьший. Формулы для них следующие:
(1оо1) tg2a,,2=j^-.
Jx Jy
Здесь ссж — угол между осями х и 1. Эти формулы мы получили из формул (46.7) и (46.8) для главных напряжений и угла, определяющего направление главной оси, заменив в них ох через Jx, через Jy и Хху через — Jxy. Очевидно, что фигура, для которой круговая диаграмма не вырождается в точку, может иметь только одну пару главных осей. Если из каких-либо соображений известно, что фигура имеет больше одной пары главных осей, то круговая диаграмма вырождается в точку и любая ось является главной осью. Это относится прежде всего к центральным осям всех правильных фигур. Так, момент инерции квадрата относительно любой оси, проходящей через центр тяжести, есть а4/12, если а — сторона.
Действительно, в квадрате можно указать две пары осей симметрии: диагонали и прямые, соединяющие середины сторон. Как показано в § 96, оси являются главными, если хотя бы одна из них есть ось симметрии.
Главные центральные оси и моменты инерции имеют особое значение в теории изгиба. В большинстве случаев фигуру можно разбить на простейшие фигуры — прямоугольники и треугольники.
Схема определения главных центральных моментов при этом следующая:
1. Находится центр тяжести фигуры, и приводятся вспомогательные центральные оси х и у.
2. Через центр тяжести каждой из частей, координаты которого в осях х, у суть xt, yt, проводятся оси £z, т|/, параллельные осям X и у. ~ '
3. Определяются площади Fit моменты инерции j{(, каждой части относительно своих центральных осей и T]z.
4. Находятся моменты инерции всей фигуры относительно осей х и у по формулам:
jx =£<4+Л
' л =S(4+^). <100-2)
Ху = Mil’ll + Х{У •
§ 100]
ГЛАВНЫЕ ОСИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ
217
5. По формулам (100.1) находят главные моменты инерции и угол а(, определяющий направление оси 1. Для уточнения вопроса о том, которая из осей является формулами (36.9), которые применительно к моментам инерции будут иметь вид:
tga,=-гЧ-=-<100-3>
•№"'1 Jxy
Пример. Т ребуется определить главные центральные моменты инерции сечения, изображенного на рис. 145. Фигуру можно считать состоящей из трех частей: прямоугольника с высотой 6 см и шириной 2 см, квадрата со стороной 4 см и крута отрицательной площади диаметра Зсм. Для выполнения первого этапа введем вспомогательные оси и и v (их можно выбирать ложены в следующей таблице:
как угодно). Вычисления распо-Таблица I
Здесь и Vj — координаты центра тяжести каждой части, F[ — площади частей, произведения utFt и ViF{ — статические моменты. Суммируя соответствующие столбцы, находим общую площадь и статические моменты ее относительно осей и и V, после чего определяем координаты центра тяжести:
«о=^7/=Ц=2,62СЛ, t,e==S^=g=3,43^.
Дальнейшие вычисления сведены в таблице П. Здесь х( — и, — и„, yi = v{ — va, моменты инерции прямоугольников вычисляются по
218
ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
[ГЛ. VIII
формуле (98.3):
. __Ыгг _______hb*.
12 ’ Jy 12 ’
ltd*
момент инерции круга равен (98.5); для круга площадь и осевые моменты считаются отрицательными.
Таблица II
yi Л 4 4 У/A *>ysA
I —1,62 — 0,43 12 36 4 0 31,5 2,2 8,3
II 1,38 0,57 16 21,3 21,3 0 30,5 5,2 12,6
III 0,38 0,57 — 7 —4,0 —4,0 0 —1 —2,3 —1,5
53,3 21,3 0 61,0 5,2 19,4
По формулам (100.2) Jx представляет собою результат сложения сумм четвертого и восьмого столбцов: %
Jx = 53,3 + 5,2 = 58,5.
Аналогично
7=21,3 + 61=82,3, J =19,4.
Главные моменты инерции находятся по формулам (100.1):
= 58,5+ 8?.’? (58,5 —82,3)2 + 4.19,4* = 70,4 ± 22,8.
Таким образом,
= 93,2 см*, Jt = 47,5cM*.
По формуле (100.3) находим угол наклона главной оси:
и
а. — 60°40'.
ГЛАВА IX
НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
§ 101. Действие поперечных сил на балку. Рассмотрим стержень, находящийся под действием приложенных к нему поперечных, то есть перпендикулярных его оси, нагрузок. Так как действие системы сил можно рассматривать как результат приложения этих сил поодиночке, то для качественного рассмотрения вопроса мы предположим, что на конце стержня приложена одна-едннственная сосредоточенная сила Р, а другой конец защемлен неподвижно (рис. 146). Предположим, что сечение стержня есть выпуклая фигура, оба измерения которой имеют одинаковый порядок Ь, длина стержня есть I. Очевидно, что если стержень сломается, то это произойдет по сечению, близкому к заделке. Это сечение является наиболее нагруженным, кдк говорят, «опасным». Выясним, какие напряжения возникнут в опасном сечении.
Прежде всего, сила Р стремится срезать балку. Употребляя такое не
точное выражение, мы подразумеваем, что для уравновешения силы Р в сечении необходимо приложить касательные, «срезывающие» напряжения т', направленные вверх (не обязательно параллельно силе, может быть, так, как показано на рис. 146 отдельно). Эти напряжения, закон распределения которых по сечению неизвестен, назовем касательными напряжениями изгиба.
Далее, сила Р, вообще говоря, вызывает кручение балки. Если сечение стержня имеет плоскость симметрии, то, очевидно, напряжения кручения не возникнут в том случае, когда сила Р лежит в этой плоскости. Если сила параллельна этой плоскости, то крутящий момент равен произведению ее величины на расстояние от плоскости симметрии. Для несимметричного профиля всегда существует точка, называемая центром изгиба и обладающая тем свойством, что
220
НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
[гл. IX
кручение не возникает, если линия действия силы проходит через эту точку. Вопрос о ее нахождении пока оставляем открытым.
Напряжения кручения в том случае, когда они существуют, обозначим через г". Если центр изгиба известен, то их определяют по формулам главы VII.
Наконец, для того чтобы уравновесить момент силы относительно оси, лежащей в плоскости сечения, необходимо рассмотреть в сечении нормальные напряжения о. Так как силы, > направленные по оси» стержня, отсутствуют, в сечении должны быть и растягивающие, и сжимающие напряжения, причем в верхней части они будут растягивающими, в нижней — сжимающими.
Дадим грубую оценку величин напряжений т', Xя и о.
Для оценки т' предположим, что сечение есть квадрат со стороной b и напряжения распределены равномерно. Тогда
, Р х —&•
На самом деле напряжения распределены по сечению неравномерно, да и сечение не обязательно является квадратом, это может быть прямоугольник, круг или иная фугура. Поэтому полученная формула неверна. Однако, если определять точно максимальное значение т', результат будет отличаться от полученного лишь числовым множи-в формулу не войдет, т' имеет порядок Pjb*:
произведение силы иа
телем, никаких иных размерных величин Будем говорить, что касательное напряжение
, Р Х Ьг '
Крутящий момент представляет собою
расстояние ее линии действия от центра изгиба. Последнее имеет порядок размера Ь. Момент сопротивления при кручении, как мы видели в § 92, есть величина, отличающаяся от Ь* числовым множителем. Поэтому
х" — х Ь* *
Перейдем к оценке нормальных напряжений. Составляя уравнение моментов относительно горизонтальной оси, проведенной в изучаемом сечении, найдем, что момент внешней силы есть Р1. Момент внутренних сил в сечении зависит только от а и размеров сечения, то есть величины Ь. Соображения размерности убеждают нас в том, что порядок величины этого момента есть ob*. Поэтому
„ Р I
а Ь* Ь '
Если длина балки / велика по сравнению с поперечным равмером Ь, то касательные напряжения т' и Xя малы по сравнению с нормальным а. Это нужно понимать в том смысле, что при увеличении
§ 102] ГИПОТЕЗА ПЛОСКИХ СЕЧЕНИЙ И ПРИНЦИП СЕН-ВЕНАНА 221
длины балки с сохранением ее поперечного сечения касательные напряжения остаются неизменными, а нормальные возрастают пропорционально длине. Таким образом, всегда можно подобрать настолько большое отношение ljb, чтобы максимальные касательные напряжения составляли сколь угодно малую долю от наибольших нормальных. В теории изгиба отношение длины к поперечным размерам принимается достаточно большим и нормальные напряжения считаются наиболее важными. Положение меняется в случае тонкостенных стержней, когда поперечное сечение не определяется одним только характерным размером b (см. гл. XI).
теория изгиоа, построенная л
§ 102. Гипотеза плоских сечеиий и принцип Сен-Венана. Ставя своей задачей определение только нормальных напряжений изгиба, в основу теории достаточно положить гипотезу о том, что плоские до деформации поперечные сечения балки остаются после деформации плоскими и перпендикулярными деформированной оси. Теория изгиба, построенная на гипотезе плоских сеченнй, была в основном завершена уже Л. Эйлером и носит название теории Бернулли — Эйлера или технической теории изгиба. Точная Сен-Венаном для того случая, когда балка загружена сосредоточенными силами, а также немногочисленные строгие решения задачи об изгибе распределенной нагрузкой приводят к заключению, что, хотя гипотеза Бернулли не вполне верна, все же основанные на ней расчеты оказываются весьма точными.
Гипотеза плоских сечений позволяет составить представление о характере деформированного состояния стержня. Рассмотрим два бесконечно близких сечения балки на расстоянии dz одно от другого (рис. 147). Попытаемся определить деформацию элемента тп, параллель
ного оси г и заключенного между двумя сечениями; длина его есть dz. Поместим оси координат х и у в плоскости левого сечения, координаты точки/» суть х, у, 0; точки л — суть х, у, dz. Будем изучать перемещение правого сечения относительно левого, считая последнее неподвижным. Деформация изгиба заключается в' том, что правое сечение, во-первых, перемещается вдоль оси z на величину edz, во-вторых, поворачивается относительно оси х на угол v.xdz и, наконец, поворачивается около оси у на угол ху dz. Вследствие парал-
22/
НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
[ГЛ. IX
дельного перемещения сечения отрезок тп получает удлинение е dz, следовательно, относительное удлинение его есть е.
Вследствие поворота около оси х точка п переместится на длину yixydz, значит, относительное удлинение отрезка тп будет иху. Аналогично находим, что от поворота вокруг оси у удлинение есть (— хух). Полное удлинение отрезка тп есть
e = xxj— иух-\-е. (102.1)
Легко видеть, что v.x и ху суть кривизны проекций изогнутой оси на координатные плоскости.
В теории изгиба употребляют термин «волокно», уподобляя
сплошное вещество, из которого сделан стержень, веществу волокнистой структуры типа дерева. Нужно помнить, что такое уподобление неправильно. Мы будем называть волокном материальную линию, бывшую до деформации прямой, параллельной оси стержня. Координаты х и у точки пересечения волокна с плоскостью любого
поперечного сечения назовем координатами волокна. Таким образом, уравнение (102.1) показывает, что удлинение волокна есть линейная функция его координат.
Для перехода к напряжениям важно отметить, что напряженное состояние волокна является состоянием простого растяжения; в плоскостях, параллельных оси стержня, нормальные напряжения отсутствуют. Последнее нужно понимать только в том смысле, что
эти напряжения весьма малы по сравнению с остальными напряжениями изгиба. Действительно, обратимся к рис. 148, на котором изображена балка квадратного сечения со стороной Ъ и длиной /, загруженная распределенным по верхней плоскости давлением р. Вся сила, действующая на балку, есть
P=plb.
Пользуясь оценкой для а, найдем:
Рассечем балку горизонтальной плоскостью. Очевидно, что в этой плоскости будут действовать нормальные напряжения а' причем если плоскость близка к верхней граничной плоскости, то а' весьма мало отличается от (— р}; если плоскость сечения близка к нижней
§ 103] НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ 223
граничной плоскости, то о' мало отличается от нуля. Поэтому
о'-р.
Сравнивая ст и о', видим, что о' очень мало по сравнению с ст. Если порядок малости касательных напряжений есть Ь[1, то порядок малости ст' есть этим напряжением можно пренебрегать и подавно.
Итак, будем считать, что каждое волокно растягивается в продольном направлении, причем напряжение ст связано с е законом Гука в его простейшей форме:
ст = Ев.
Из формулы (102.1) получаем:
о = Е(иху — (102.2)
Очевидно, рассуждения, приведшие нас к убеждению, что каждое волокно можно считать находящимся в условиях простого растяжения, теряют силу тогда, когда к балке приложена сосредоточенная сила. Части балки, непосредственно примыкающие к месту приложения сосредоточенных сил, не могут рассчитываться по схеме плоских сечений: здесь возникают местные напряжения. Область, в которой отступления от закона плоских сечений существенны, невелика, длина ее имеет порядок поперечного размера. Для изгиба сохраняет силу принцип Сен-Венана, подробно освещенный в § 17 для растяжения-сжатия. Все сказанное там сохраняет силу и для изгиба.
Подчеркнем, что гипотеза плоских сечений и принцип Сен-Венана справедливы лишь для длинных стержней сплошного профиля, то есть имеющих поперечные размеры одного порядка. Для тонкостенных стержней, когда один поперечный размер значительно больше другого, оценки относительных порядков величин нормальных и касательных напряжений перестают быть справедливыми, гипотеза плоских сечений теряет силу и принцип Сен-Венана становится неприменимым.
§ 103. Нормальные напряжения при изгибе. Желая определить нормальные напряжения в сечении тп балки, нагруженной произвольными силами, как показано на рис. 149, поместим в этом сечении начало прямоугольной системы координат xyz таким образом, чтобы плоскость сечения совпала с плоскостью хОу. Мысленно рассечем балку плоскостью хОу, отбросим одну часть балки (на чертеже правую) и рассмотрим равновесие оставшейся части (левой на чертеже). Из шести уравнений статики составим три: условия равенства нулю
224 НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ [ГЛ. IX
к
•Яв
проекций сил на ось z и моментов относительно осей х и у. Получим: -
2^ + $odF=0, F
2/»x+$crydF=0.
F
2«у — J oxdF=0.
F
(103.1)
Индекс «л» вверху обозначает, что суммируются проекции и мо-
менты тех сил, действующих на стержень, которые приложены слева
Рис. 149. Здесь Nt называется продольной
силой в сечении, Мх и Му— изгиба-ющими моментами относительно осей х и у соответственно. Э
Внесем эти обозначения в (103.1) и вычислим интегралы, полагая £
а=Е (xji — ХуХ 4- е). »
Вспоминая определения моментов инерции и статических моментов, 1 найдем:
E(kxSx — KySy-\-eF) — N, = 0, -
£(хЛ-*/^ + ^ + ^ = 0«, (103.2)
ЕtyxJxy ^У^У 4“ е$у> ~ ^у == 0-
До сих пор мы никак не ограничивали выбор, системы координат.
Вид формул (103.2) подсказывает, что начало координат удобнее Я поместить в центре тяжести сечения; тогда статические моменты вы- *
падают и мы получим: £
EFe = Nz, Д [xxJx KyJXyj = Мх, „
EfaxJxy Ху/у]- Му. IS
* «
Две последние формулы становятся еще более простыми, если X принять за оси х, у не любые центральные оси, а главные централь- у ные оси инерции. Тогда Jxy обращается в нуль и мы получаем: ;
хх = -^-, ху= —e=fe. (ЮЗ.З) bj g * EtJу lit1
§ 104] ИЗГИБАЮЩИЕ МОМЕНТЫ И ПЕРЕРЕЗЫВАЮЩИЕ СИЛЫ 225
Формула (102.2) для напряжений приобретает следующий вид:
। (103.4)
J у Г
Это и есть основная формула для нормальных напряжений при изгибе. Здесь хи у — координаты точки сечения относительно главных центральных осей инерции.
Такой выбор осей не является абсолютно необходимым, можно найти е, их и иу из общих уравнений (103.2). Тогда мы получили бы вместо (103.3) значительно более сложные формулы. Практически при расчетах на изгиб всегда пользуются главными осями, поэтому общую формулу мы не выписываем.
§ 104. Изгибающие моменты и перерезывающие силы. Определенные в предыдущем параграфе величины Мх и Му, названные изгибающими моментами, изменяются при переходе от одного сечения к другому, так как по мере движения слева направо изменяются плечи и появляются новые силы, приложенные к левой половине. Поскольку сечение определяется координатой z, то изгибающие моменты суть функции от z.
В § 103 нас интересовали только нормальные напряжения при изгибе, поэтому из шести уравнений равновесия мы фактически составили только три. Составляя оставшиеся уравнения, мы должны были бы включить в них касательные напряжения изгиба и кручения, если бы знали закон распределения их по сечению. При проектировании на оси координат внешних сил поступая, как прежде, мы приходим к выражениям такого вида:
Величины Qx и Qy называются перерезывающими силами по осям х и у соответственно.
Огромное большинство важнейших для практики задач относится к тому случаю, когда внешние силы действуют в одной плоскости, проходящей через ось стержня и пересекающей плоскость каждого сечения по прямой, являющейся главной осью инерции сечения. Так будет, .например, если сечение балки симметрично. Мы будем называть эту плоскость главной плоскостью. Принимая плоскость действия сил з.з плоскость yOz, мы найдем, что /И^ = 0 и Qx=0. Таким образом, остается только изгибающий момент Мх и перерезывающая сила Qy.
Заметим, что все силы, действующие на балку, должны быть уравновешены (в случае движения нужно приложить к действующи» силам силы инерции). Поэтому
£ру=о, 2^=0-
® Ю. Н. Работке I
226
НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
(ГЛ. IX
Но совокупность всех сил, действующих на балку, можно разбить на две части: совокупность сил, приложенных к левой половине балки, и совокупность сил, приложенных к ее правой части. Поэтому
Отсюда
Ограничиваясь случаем стержня, нагруженного силами, действующими в главной плоскости yOz, сформулируем следующие определения:
Перерезывающей силой называется сумма проекций на ось у всех сил, приложенных слева от сечения или приложенных справа, но с обратным знаком.
Изгибающим моментом называется момент относительно оси, параллельной оси х и проходящей через центр тяжести сечения, всех сил, приложенных слева от сечения или приложенных справа, но взятых с обратным знаком.
Определяя таким образом изгибающий момент, мы помещаем начало координат уже не в центре тяжести того сечения, для которого ищется момент, а в некотором фиксированном сечении, например крайнем левом. Это удобно в том отношении, что каждое сечение тп задается координатой z и величины и Мх можно рассматривать как функции координаты z.
§ 105. Дифференциальные соотношения между интенсивностью нагрузки, перерезывающей силой и изгибающим моментом. Эпюры. Рассмотрим стержень, нагруженный силами в плоскости yOz (рис. 150). Разрежем стержень по сечению тп с координатой z и
отбросим левую часть стержня. Рассматривая оставшуюся правую часть, мы должны заменить действие сил, отброшенных вместе с левой частью, их результирующей, равной главному вектору, и парой, момент которой равен главному моменту, приведенными к центру тяжести сечения с координатой z. По определению перерезывающей силы и изгибающего момента главный вектор равен по ве-
личине перерезывающей силе Qy, а главный момент — изгибающему моменту Мх. Рассмотрим бесконечно близкое сечение pq с координатой z-\-dz. Если считать, что Qy и Мх являются функциями от координаты z, то в сечении pq перерезывающая сила есть Qy dQy, изгибающий момент Мх dMx. С другой стороны,
§ 105] ДИФФЕРЕНЦИАЛЬНЫЕ СООТНОШЕНИЯ 227
есть сумма сил, действующих по левую сторону от сечения pq. Если на элемент dz действует сила dP, направленная по оси у и приложенная на расстоянии 6 dz (0=сО=с1) от сечения тп, то
Qy~\~dQy-Qy-\-dP.
Следовательно,
dQy = dP. (105.1)
Точно таким же способом вычисляем изгибающий момент в сечении pq-, он равен
Мх + dMx = МХ+ Qydz + dP (1 — 0) dz.
Отбрасывая малые второго порядка, отсюда пблучаем:
dMx=Qydz. (105.2)
В случае, когда иа балку действует непрерывно распределенная нагрузка qy, dP—qydz; поэтому уравнение (105.1) может быть записано следующим образом:
dQy = qydz.
Для изгиба в плоскости xOz получим аналогичным образом: dMy = — Qxdz, dQx — qxdz.
Чтобы сделать наглядным ход изменения изгибающего момента и перерезывающей силы при переходе от одного сечения к другому, обычно строят графики этих функций — так называемые эпюры перерезывающих сил и изгибающих моментов.
При построении рекомендуется исходить только из определения перерезывающей силы и момента, используя дифференциальное соотношение (105.2) для контроля.
Рассмотрим пример, приведенный на рис. 151. Легко видеть, что в этом случае каждая из реакций равна Р. Точки приложения сосредоточенных сил разбивают балку на три участка.
На первом участке
Qy=-P, Mx——Pz;
на втором
Qy=— Р-\-Р=0, Mx—-Pz-\-P(z — a)=—Pa;
на третьем
Qy=-P+P+P=P,
Мх= —Pz-\-P{z — a)-\-P(z — 2а)= —Р(3а— z).
Эпюры имеют вид, изображенный иа рис. 151.
Во многих случаях построение эпюр возможно и без составления аналитических выражений моментов и перерезывающих сил по
8*
228 НАПРЯЖЕНИЯ ПРИ ИЗГИВЕ [гл. IX
участкам. Достаточно вычислить моменты для некоторых характерных сечений, при построении же следует руководствоваться следующими правилами:
а) Перерезывающая сила претерпевает разрыв только в точке приложения сосредоточенной силы на величину этой силы.
б) На незагруженном участке перерезывающая сила постоянна.
в) На равномерно загруженном участке перерезывающая сила есть линейная функция г, возрастающая, если нагрузка положительна.
г) Изгибающий момент претерпевает разрыв только в точке приложения сосредоточенного момента на величину этого момента.
д) На незагруженных участках эпюра моментов есть прямая, наклон которой пропорционален перерезывающей силе.
е) Эпюра моментов образует изломы только там, где перерезывающая сила разрывна, то есть в точках приложения сосредоточенных снл.
ж) Изгибающий момент принимает экстремальное значение там, где перерезывающая сила равна нулю.
з) На свободном конце или концевой опоре изгибающий момент равен нулю, если там не приложен внешний момент.
и) На равномерно загруженном участке эпюра изгибающих моментов есть парабола, обращенная выпуклостью вверх, если нагрузка положительна (направлена вниз).
Рассмотрим в качестве примера балку, изображенную на рис. 152. Распределенная нагрузка q должна считаться положительной, так как ocbji направлена вниз. Реакции опор суть qa каждая. На участке I по правилу б) перерезывающая сила постоянна, по определению она равна —qa. Проводим прямую с ординатой —qa в пределах первого участка. Совершенно аналогично находим, что на третьем
§ 106]
РАСЧЕТ ПО ДОПУСКАЕМЫМ НАПРЯЖЕНИЯМ
229
участке Qy = -\-qa. При этом, конечно, следует определять перерезывающую силу как сумму сил, приложенных справа от сечения, взятую с обратным знаком. Согласно правилу а) эпюра должна быть непрерывна, так как сосредоточенных сил иет. Поэтому крайние точки эпюр на участках I в соответствии с правилом в). Согласно правилу з) на левом и правом концах изгибающий момент равен нулю, на участках / и II эпюра должна быть прямолинейна вследствие правила д). Вычислим - изгибающий момент иа границе между первым и вторым участками; получим —qa(l—а). Такой же момент будет и на границе между вторым и третьим участками. Отложим соответствующие отрезки и соединим концы их прямыми с концами отрезка, изображающего балку. Средняя часть балки имеет по правилу и); вопрос о выпуклости но можно также руководствоваться
там, где нет сосредоточенных сил, эпюра не может претерпевать излома, то есть параболическая часть сопрягается с прямолинейными. В середине балки изгибающий момент достигает максимума абсолютной величины вследствие правила ж). Это максимальное значение
Л4= — — qa[l—у).
Теперь легко построить параболу, что и выполнено на рис. 152.
§ 106. Расчет иа прочность при изгибе по допускаемым напряжениям. При изгибе поперечной нагрузкой в главной плоскости yOz и при отсутствии продольной силы в формуле (103.4) остается один только член:
параболическую эпюру моментов параболы решается правилом и), правилом е), согласно которому
Из этой формулы видно, что в точках оси х напряжения равны нулю. Поэтому ось х называют нейтральной осью сечения. Геометрическое место нейтральных осей представляет нейтральную поверхность балки.
По одну сторону нейтральной оси напряжения растягивающие, по другую — сжимающие. Желая рассчитать балку на прочность по допускаемым напряжениям, мы должны потребовать, чтобы наибольшее растягивающее напряжение не превышало величины [<г]р, наибольшее сжимающее — величины (<г]сж. Обозначим через и ht расстояния
230
НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
[ГЛ. IX
от центра тяжести сечения до его крайних точек в сжатой и растянутой зонах (рис. 153). В этих точках, как видно из формулы (106.1), напряжения будут наибольшие. Для обеспечения прочности балки необходимо выполнение следующих условий:
_______________ | Наивыгоднейшей формой сечения будет та, для которой запас прочности по растягивающим и сжимающим напряжениям одина-
kjb. Для этого нужно, чтобы ________________________________[р]сж Л, — [01р •
Если допускаемое напряжение на растяжение и сжатие одинаково, то расчет ведется по наибольшей абсолютной величине напряжения, а именно:
|_| __I Яс 11 У Imax
l^lmax— jx
Величина Jx/ymax называется моментом сопротивления изгибу и обозначается Wx. Таким образом, расчетная формула будет следующая:
Ках = ^<[*]р. (Ю6.2)
Иногда вместо [<т]р в этой формуле пользуются величиной Йи — допускаемого напряжения при изгибе. Беря [<т]и больше, чем р, учитывают, что достижение предельного состояния в крайнем волокне при изгибе менее опасно, чем в растянутом или сжатом стержне, где предельное состояние достигается одновременно всеми
волокнами.
Величина момента сопротивления для важнейших фигур: а) круг диаметра d:
W — —: х — 32 ’
ф б) труба с наружным диаметром d и внутренним d,:
—.5^1 ( 1__•
* 32 d* )’
в) прямоугольник с высотой Л и шириной Ь'.
Wx=^,
Последняя формула показывает, что при той же площади сечения, то есть при одинаковой затрате материала, прямоугольное сечение следует делать возможно высоким и узким.
§ 1071
УПРУГО-ПЛАСТИЧЕСКИЙ ИЗГИБ
231
Еще более выгодны такие формы сечений, в которых материал разнесен как можно дальше от центральной оси, перпендикулярной плоскости изгиба, например двутавровое или коробчатое сечения (рис. 154).
Однако, вставая на этот путь, мы имеем дело уже с тонкостен-
ными стержнями, в которых нужно ния изгиба и кручения, если плоскость приложенной нагрузки не является плоскостью симметрии. Для вычисления нормальных напряжений в тонкостенном стержне применяется та же формула (106.1), но расчет на касательные напряжения убеждает в недопустимости уменьшения толщины стенки. Другая причина, препятствующая применению стержней со слишком тонкими стенками, — это возмож-
учитывать 'касательные напряже-
Рис. 154.
ность потери устойчивости — местной, связанной с образованием волн, то есть искривления тонкой стенки, или общей, то есть
скручивания и изгиба в боковом направлении.
§ 107. Упруго-пластический изгиб. Исследование упруго-пластического изгиба при произвольной зависимости а—в ограничим
случаем сечения, имеющего две оси симметрии, за оси х и у. Предполагая, что внешние силы сти уОг, из условий симметрии заключаем, что в этой же плоскости произойдет и изгиб. Зависимость между о и в в растянутой н сжатой областях одна и та же, поэтому, очевидно, ось х является нейтральной осью сечения (ниже это будет проверено).
Сохраняя гипотезу плоских сечений, положим:
е — ку.
Пусть известно, что для материала балки о=<р(е).
Ширина сечения на расстоянии у от нейтральной оси есть Ь.
Будем считать, что b задано как функция отношения у/Л. Элементарный момент сил, дей-
которые мы примем приложены в плоско-
I/
Рис. 155.
ствующих на заштрихованную полосу (рис. 155) ширины b и высоты dy, относительно оси х есть
yabdy = y (xy)b(^}ydy.
232
НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
[ГЛ. IX
Приравнивая сумму моментов внутренних сил в сечении сумме моментов внешних сил, как в § 103, получим:
л
= (107.1)
о
Вследствие симметрии интегрирование от —Л до -\-h заменено интегрированием от нуля до Л, но результат удвоен. Формула (107.1) связывает изгибающий момент с величиной х. Эта формула еще неудобна для практического использования, так как интеграл зависит от двух параметров х и Л.
Преобразуем эту формулу, приняв за переменную.интеграции деформацию ху = е и обозначив деформацию крайнего волокна в.:
J<р (х_у) b ( у dy = j <р (8) b еde = j ф (в)b (J-е de.
о в ° •
Положим
Ф<8о) = -Т f Ф 8 de.
ej J . кв. /
Тогда вместо (107.1) мы получим:
^=Ф(е.). (107.2)
Имея график функции ф (в), можно вычислить функцию Ф(е.) и построить для нее график.
В качестве примера рассмотрим изгиб стержня прямоугольного сечения при условии идеальной пластичности. В этом случае
b =const, ф(8) = £8 ^8< 'От ) -Е )'
Пока в<^ g1, Ф(8)=ОТ ) (е^ ОЗ* II
По формуле ч ф = -£- f Ее* de = •о (107.2) 2МХ в. Ebh*~ 3 ‘ ЬЕъ9 3 • (107.3)
Здесь h — полная высота, а не половина высоты, как в (107.2). Отсюда
___1241^___Мх «
% — Ebh* ~ EJX'
§ 108]
ине №33 __ ?
НЕ БОЛЕЕ 1Й КНИГИ/Т | ОДНИ РУКИ И 2Х В ДВЕ }
КОЛОХЗА
ОСКОР^А
НЕСУЩАЯ СПОСОБНОСТЬ СТЕРЖНЯ ПРИ ИЗГИБЕ
233
что совпадает с ранее найденным решением (103.3), если не обращать внимания на знак.
В области упруго-пластических деформаций ’I «<!
Ф (е0) = -ij £ у Ee*b de -|- J <гтйе dej ==
° о «т
Построим график зависимости величины ев=хЛ от безразмерного 9Л4
момента -етЛ. Пока деформации всюду упруги, зависимость изобра-сои
жается прямой (107.3). Когда напряжение в крайнем волокне стано-2МХ о, вится равным а , то есть т0 состояние становится упру
го-пластическим и вступает в действие формула (107.4). Соответственно
график иа рис. 156 становится криволинейным. При очень больших значениях хЛ безразмерный момент стремится к величине т ==?£. Точка А на
2 2£
графике определяет тот момент, который соответствует началу текучести в крайней точке сечения, то есть признается опасным при расчете по допускаемым напряжениям. Как видно из графика, несущая
способность стержня при этом
еще не исчерпана, он еще сопротивляется изгибу. Полное исчерпа-
ние несущей способности происходит тогда, когда безразмерный момент возрастает до величины от/2Е, то есть становится больше на 33% по сравнению с моментом в точке А.
§ 108. Несущая способность стержня при изгибе. Предельные значения изгибающего момента можно найти иным способом. На рис. 157 изображены графики, так называемые эпюры, распределения напряжений по поперечному сечению стержня для возрастающих значений момента. На рис. 157,а показано распределение напряжений в упругом состоянии, на рис. 157,6 уже образовались
ОСКОРКА
234
НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
[ГЛ. IX
пластические зоны, на рис. 157,в пластические зоны, в которых напряжение постоянно, распространились на большую часть сечения. Наконец, на рис. 157,г изображены эпюры распределения напряжений для предельного состояния, когда весь стержень перешел в пластическое состояние. Скачок напряжений от —а к -|~ст ПРИ переходе через нейтральную ось, конечно, физически невозможен,
о) б) 6) г)
Рис. 157.
и состояние, изображенное на рис. 157,г, никогда не реализуется. Момент внутренних сил, вычисленный для этого состояния, равен величине изгибающего момента, при котором равновесие уже невозможно, тогда как меньшим значениям изгибающего момента соответствуют определенные состояния равновесия с упругой областью вблизи нейтрального слоя. Момент, соответствующий переходу всего стержня в пластическое состояние, называется предельным моментом. Нахождение предельного момента мы произведем для стержня произвольного симметричного сечения, изгибаемого в плоскости симметрии. Нейтральная ось — это прямая пп, параллельная оси х, так как изгиб происходит в плоскости уОг, нО вообще не совпадающая с осью х.
Заметим, что внутренние силы в сечении, уравновешивающие момент внешних сил, должны приводиться к паре; следовательно, главный вектор их равен нулю. Обозначим через и Ft площади частей, на которые делит нейтральная ось сечение. Растягивающая сила в сечении есть oTFlt сжимающая сила <rTFt. По предыдущему
> отЛ-^Л=°-
Отсюда
F —F.
Таким образом, нейтральная ось делит сечение стержня на две равновеликие части. Пусть С, и С2 — центры тяжести этих частей. • Тогда момент внутренних сил относительно нейтральной оси есть
Введем так называемый пластический момент сопротивления:
(108.1)
§ 108] НЕСУЩАЯ СПОСОБНОСТЬ СТЕРЖНЯ ПРИ ИЗГИБЕ 235
Тогда
Л4т=ат1Гт.
Желая рассчитать на прочность по допускаемым нагрузкам стержень, подвергнутый изгибу, мы должны потребовать, чтобы изгибающий момент не превышал величину предельного момента, поделенную на коэффициент запаса л:
* п п т
Но ^ = [о]р. Таким образом,
едр.
При расчете по допускаемым напряжениям формула получается точно такой же, только вместо 1FT будет стоять Wx (см. (106.2)).
Примеры.
а) Круглое сечение. Расстояние центра тяжести полукруга 4 г
от центра окружности равно . По формуле (108.1) о л
тег _9 — —_____— г’___—
* 2 3л~3 6’
jrzP W7 __ П7
= " V'*' 100==70%-
б) Сечение в форме равнобедренного треугольника (рис. 158). В подобных треугольниках площади относятся,
как квадраты сходственных элементов. Поэтому нейтральная ось, делящая пополам площадь треугольника, пройдет на расстоянии h(\f 2 от вершины. Введем вспомогательные оси и и v, проходящие через вершину треугольника. Пусть будет v — координата центра тяжести всего сечения, т/, и vt — коордийаты центров тяжести его частей. По известному свойству статических моментов
F . F
отсюда
vt — 2v — vt.
Расстояние С,С, равно разности vt — »,, таким образом, cici = — ®i = 2 (® — ®i)-
.. 2 , 2 h
Но V = -Z- Л, V. = , поэтому
3 1 3 у 2
С,С, ==-£= (2 — ]Л2) Л^о, 390Л.
236 НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ , [ГЛ. IX
Пластический момент сопротивления
. Гт=х0,0975М*.
Обычный момент сопротивления
1FX= : у Л== °,0417bh*.
Разница между ними составляет 134%.
»
§ 109. Принцип Сен-Веиаиа. При изучении изгиба мы вводим в рассмотрение величину изгибающего момента, поперечной н нормальной силы в сечении, а также крутящего момента, если силы не лежат в плоскости, проходящей через ось центров изгиба. При этом нам совершенно безразлично, каким образом прикладываются внешние силы. Изображая силу в виде вектора, момент — в виде двух стрелок, начала которых соединены прямой, мы отказываемся от конкретного рассмотрения способа осуществления нагрузки, иначе говоря, считаем эквивалентными в отношении изгиба статически эквивалентные между собой нагрузки. В этом и заключается принцип Сен-Венаиа.
В главе I указывалось, что в сопротивлении материалов нельзя заменять систему внешних сил статически ей эквивалентной. Принцип Сен-Венана смягчает это требование. Согласно этому принципу для стержней можно заменять статически эквивалентной такую систему нагрузок, которая приложена в области, имеющей размеры порядка поперечных размеров стержня. На расстоянии от этой области, имеющем тот же порядок величины, напряжения изгиба распределяются по закону плоских сечений, и в расчетных формулах фигурируют лишь величины главного вектора и главного момента приложенных сил. Из принципа Сен-Венана следует, в частности, что уравновешенная система сил, приложенная на торце стержня, вызывает напряжения, весьма быстро затухающие по мере удаления от торца.
Для тонкостенных стержней дело обстоит несколько иначе. Нижеследующий простой пример, принадлежащий В. 3. Власову, убеждает нас в том, что уравновешенная система сил, приложенная к торцу тонкостенного стержня, создает напряжения иа достаточно большом расстоянии от торца.
Представим себе двутавровую балку, нагруженную четырьмя ’ одинаковыми продольными силами Р1»Р1=жР1 = Р4=Р, как показано иа рис. 159. Если стенка очень тонка, то пара PtP, изгибает одну полку в ее плоскости, пара РгР^— другую полку. Напряжения изгиба в полках будут одни и те же в сечениях, достаточно далеких от торца. Так как изгиб полок происходит в разные стороны, стейка закручивается. Однако если стенка очень тонка, то ее
§ ПО]
ВИЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ---СЖАТИЕ
237
крутильная жесткость ие может воспрепятствовать изгибу полок. При конечной толщине стеики силы реакции со стороны закрученной стенки препятствуют изгибу полок, напряжения изгиба, вызванные парами и PJ\, затухают по мере удаления от торца, но зату-
хание происходит гораздо медленнее, чем это следует из принципа Сен-Венана. Поэтому статически уравновешенная четверка сил ^1
является фактором, способным К»
вызвать напряжения, не носящие местного характера. Количественной характеристикой этой четверки служит так называемый бимомент:
B=zPbh.
Желая рассчитать тонкостенный стержень, нагруженный системой сил на торце, мы должны определить не только главный вектор
и главный момент этих сил, ио также и бимомент. Эквивалентными по отношению к изгибу будут такие системы сил, у которых равны главные векторы, главные моменты и бимоменты. Способ определе-
ния бимомента для произвольной системы сил будет дан в главе XI.
§ 110. Виецеитреииое растяжение — сжатие. Возвращаясь
к общему случаю, рассмотренному в§ 103, когда изгибающий момент приложен ие в главной плоскости и существует осевая составляющая внешних сил, применим формулу (103.4) ____________
Or~ Jx ' Jy ' Р к задаче о внецентренном растяжении или сжатии стержня. Пусть линия действия растягивающей силы Р (рис. 160) не совпадает с осью стержня. Точку пересечения ее с плоскостью сечения назовем полюсом', пусть хв и ув суть координаты полюса. Тогда
NZ = P, Мх=-Руа, Му = Рх0.
Подставив это в формулу для напряжений, получим:
238
НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
[ГЛ. IX
Поскольку, например, J есть величина, имеющая размерность длины в четвертой степени, ее можно представить так:
Здесь iy — некоторая лянейная величина, называемая радиусом инерции.
Аналогично
Jx = Fi*.
Окончательная запись формулы для напряжений будет следующая:
<т = —°4-^2 Д-1V (110.1)
Симметрия этой формулы относительно переменных х, у и ха, у0 доказывает следующую теорему:
Теорема 1. Напряжение в точке 1, вызванное силой, параллельной оси стержня, линия действия которой проходит через точку 2, равно напряжению в точке 2 от такой же силы, линия действия которой проходит через точку 1.
Приравнивая нулю левую часть (110.J), получим уравнение прямой, точки которой свободны от напряжений:
— 0. (110.2)
$ %
Эту прямую называют нулевой линией.
Записывая уравнение (110.2) как уравнение прямой в отрезках:
- + т-— 1 =0, а 1 b *
где
а = —1 д = (110.3)
Xq у0
— отрезки, отсекаемые нулевой линией на осях координат, получаем простой способ построения нулевой линии: по заданным координатам полюса находятся отрезки а и b и откладываются по осям координат от начала. Через их концы проводят прямую, которая и будет нулевой линией.
Докажем теперь следующую теорему:
Теорема 2. При перемещении полюса по прямой нулевая-линия вращается около неподвижной точки.
Пусть рр (рис. 161) есть прямая, отсекающая отрезки А и В на осях координат. Примем ее за нулевую линию, тогда по формулам (110.3) координаты соответствующего полюса точки Q суть
§ 111]
ЯДРО СЕЧЕНИЯ
239
Это значит, что если в точке Q находится полюс, то в любой
точке прямой рр, например в точке ЛГ, напряжение равно нулю. Согласно теореме 1, если, наоборот, приложить силу в точке М, то
в точке Q напряжение окажется равным нулю, следовательно, эта точка принадлежит нулевой линии полюса /И. А так как точка М есть произвольная точка прямой рр, то совокупность нулевых линий для всех положений полюса на этой линии есть пучок прямых, проходящих через точку Q.
В частном случае, когда полюс движется по прямой, проходящей через центр тяжести, точка Q уходит в бесконечность, следовательно, нулевая линия перемещается параллельно себе. Это следует из формул (110.3): про-
пропорциональ-
порциональное изменение координат х0 и yt влечет ное же изменение отрезков а и Ь.
§ 111. Ядро сечения. При расчете на внецентренное сжатие стержней из хрупкого материала стремятся к тому, чтобы во всех точках сечения напряжения были сжимающими. Действительно, каменная кладка, например, совершенно не способна воспринять растягивающие силы, при этом неминуемо разойдутся швы. Бетон обладает весьма малой прочностью при растяжении по сравнению с прочностью при сжатии. Чтобы обеспечить постоянство знака напряжения, сжимающую силу следует прикладывать' »
в торцевом сечении внутри некоторой области, называемой ядром сечения. J /р\
Ядром сечения называется геомет- д ' )
рическое место полюсов, для которых I /
напряжения вовсех точках сечения имеют \ /
один и тот же знак. Способ пОстрое- п._________nt
ния ядра сечения очевиден из определения. Если полюс находится на кон- Рис. 162.
туре ядра сечения (рис. 162), то нуле-
вая линия должна касаться контура сечения стержня. Действительно, заставляя полюс двигаться по лучу, выходящему из центра тяжести сечения О, мы перемещаем^ нулевую линию /^л, параллельно себе из бесконечности, если движение полюса начинается из центра тяжести О. Пока полюс находится внутри ядра сечения, нулевая линия не пересекает сечение; она касается контура сечения в тот момент, когда полюс попадает в точку, принадлежащую контуру ядра сечения.
240
НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
[ГЛ. IX
Рассмотрим, например, построение ядра сечения эллипса. Обозначая хг, yt координаты точек эллипса, имеем уравнение его:
*1 У?
_L_L —____1 —о
А1 ‘ В1 *— и-
(111.1)
Уравнение касательной к эллипсу в точке xt, yt:
A* В1
(111.2)
Здесь х, у — текущие координаты точек касательной. *
Отождествляя касательную с нулевой линией, то есть уравнение
(111.2) с уравнением (110.2), получим:
Но для эллипса
Поэтому
Следовательно,
А. = __А. 11- — —^-
А* i* 'в* Рх’
, __it АВ* . ___пА'В
X 4 • Jv 4 >
В* 4 ’
*i 4 ’
F=nAB.
4
4 ’
£1
4 •
*.=
в этой точке соответствует
Рис. 163.
(111.3)
Формулы (111.3) определяют точку ядра сечения такую, что полюсу
нулевая линия, касательная к эллипсу в точке xt, ух. Легко видеть, что геометрическое место таких точек, то есть контур ядра сечения, есть эллипс, подобный данному, но с полуосями в четыре раза меньшими. Отсюда следует, в частности, что для круга радиуса R
1 D ядро сечения есть круг радиуса
Посмотрим теперь, как поступать, если контур имеет угловые точки. Пусть, например, две гладкие кривые, ограничивающие контур, пересекаются в точке Q (рис. 163). При обходе контура Г, касательная непрерывно переходит из положения 1 в положе-" ние 2. Полюс, для которого эта ка-
сательная есть нулевая линия, описывает дугу I—2 контура ядра сечения. Положению 3 касательной соответствует полюс 3, который движется по дуге 3—4 при движении касательной вдоль Г,. Остается соединить точки 2 и 3. Теорема 2 § ПО указывает, что эти точки нужно соединить прямой,
§ 112] НЕСУЩАЯ СПОСОБНОСТЬ ВНЕЦЕНТРЕННО СЖАТОГО СТЕРЖНЯ 241
так как при вращении нулевой линии около точки Q полюс движется по прямой, а точки ее 2 и 3 известны.
Отсюда очевидно, что ядро сечения многоугольника будет также многоугольник, вершины которого суть полюсы, соответствующие
нулевым линиям, совпадающим со сторонами многоугольника..
Для построения ядра сечения многоугольника следует:
1) найти главные центральные оси инерции и соответствующие радиусы инерции;
2) для каждой стороны найти отрезки а и Ь, отсекаемые ее продолжением на осях хну;
3) вычислить координаты вершин ядра сечения по формулам (110.3):
4) соединить вершины ядра прямыми.
Применим эти правила к случаю прямоугольника (рис. 164), для которого
12' ^~12’
Сторона I— I:
а — оо, (>=—, х„ = 0, = — ~ (точка /).
Сторона 2—2:
a = 6==0О> хо==~4'’ -Уо = 0 (точка 2).
Сторона 3—3:
а = оо, Ь — — х„ = 0, Л = 4 (точка 3).
Сторона 4—4:
а = —у, й = оо, х„=-|-, уо = О (точка 4).
Соединим точки 1, 2, 3,. 4 прямыми, получим изображенный на чертеже ромб, который и будет ядром сечения.
§ 112. Несущая способность виецеитреиио сжатого стержня. Ограничимся изучением частного случая, когда полюс находится на оси симметрии сечения. Исследование упруго-пластической задачи может быть выполнено по схеме § 107, однако оно связано с громоздкими и неудобными вычислениями. Мы будем искать предельные значения силы, соответствующие тому моменту, когда все сечение
242 НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ [гл. IX
перешло в пластическое состояние. Пусть Af— полюс, Ft— площадь растянутой части, Ft—площадь сжатой части, С, и С* — центры тяжести этих частей. Имеем два уравнения: 1) условие равенства нулю проекций на ось стержня:
(112.1) 2) условие равенства нулю суммы моментов относительно оси, проходящей через полюс Af:
FJAfC,) — /?1(Л1С1) = 0. (112.2)
Применим эти уравнения к задаче о вне-центренном растяжении стержня прямоугольного сечения (рис. 165). Пусть е — эксцентриситет в приложении нагрузки, s — смещение нейтральной оси в пластическом состоянии.
Уравнение (112.1) дает:
[(Л-|-$)— (Л — $)рпт = Р, или 2t>saT — P.
Введем относительное смещение нейтральной оси
Обозначим, кроме того, »— F 2bh * Получим:
(112.3) ит
Составим теперь уравнение (112.2):
(*+*)(«—Цг) —(*—
Введем кроме ранее принятых обозначений относительный эксцентриситет т] = у. Последнее уравнение приводится к следующему виду:
r + 2f|g-r = 0.
Отсюда
£=/14-П1 —П-
Сравнивая с (112.3), найдем:
(То = стт[И1+111 — П]- (112.4)
Для сравнения решим ту же задачу по способу допускаемых напряжений, предполагая распределение напряжений соответствую-
§ ИЗ] РАСЧЕТ СОСТАВНЫХ ВАЛОК 243 щим упругому состоянию. Наибольшее напряжение в крайней точке сечения со стороны приложения силы:
__________Р . Ре_______р ^tnax f * IF___________F
Но
F—2bh,
О
поэтому
eF Зе „
h “3тЬ
Приравнивая сгтах=<тт и вспоминая, что PjF=ae, найдем:
^2-5)
Если сила приложена центрально, допускаемая величина ее равна
Величина допускаемой внецентренной силы есть p=v.
Таким образом, величина сг0/сгт показывает, какую долю от допускаемой центральной силы составляет величина допустимой силы при заданном относительном эксцентриситете т]. Так, например, если полюс приходится на краю сечения, то т) = 1; по формуле (112.4)
= — 1 = 41’7..
ат г
При расчете по допускаемым напряжениям (формула (112.5))
Как видно, и здесь расчет по допускаемым нагрузкам обнаруживает резерв прочности.
§ ИЗ. Расчет составных балок. В тех случаях, когда размеры сечения по расчету получаются большими и изготовить целую балку с таким сечением невозможно или неудобно, применяют составные балки. Два примера составных балок приведены на рис. 166; это клепаная двутавровая балка и деревянная балка на шпонках. Элемент, скрепляющий части балки (в первом случае заклепка, во втором — шпонка), работает на срез. Для расчета нужно знать силу Т, передаваемую через этот элемент. Определим эту силу для поясной заклепки клепаной балки; полученная формула будет совершенно общей.
244
НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
[ГЛ. IX
Рассечем балку двумя сечениями посередине между соседними заклепками. Расстояние между этими сечениями будет t — шаг заклепок. В левом сечении момент равен Мж, в правом Мх. Так как Мх
Рис. 166.
есть функция z, а приращение z при переходе от левого сечения к правому есть t то по формуле Тейлора
В этом разложении можно ограничиться первыми двумя членами. Действительно, dM, , <РМХ
Но Qy имеет порядок ql, тогда как t мало по сравнению с I. Итак,
^ = ^ + <2/
Рассматривая часть балки длиной t, удалим стенку, оставив два уголка и полку (рис. 167). В левом сечении напряжение а есть
Jx
§ 114]
ИЗГИБ КРИВОГО БРУСА
245
В правом
о'
М'хУ
Проектируя на ось z внутренние в левом и правом сечениях не равны ними и есть сила, действующая на скрепляющий элемент. Обозначив ее через Т, получим:
odF.
Здесь интегрирование распро
страняется на площадь сечения части балки, которая прикреплена той деталью, для которой ищется сила.
Формула для Т преобразуется к следующему виду:
(113.1) Jx
силы, убеждаемся, что силы между собой. Разница между
Здесь/—расстояние между кре- '
пежными деталями, Sx — статиче- ис"
ский момент площади сечения прикрепленной части, Jx — момент
инерции всего сечения.
§ 114. Изгиб кривого бруса. Если ось стержня криволинейна, но размеры поперечного сечения малы по сравнению с радиусом кривизны, то для расчета можно пользоваться теми же формулами, что и для прямого стержня. Когда размеры сечения сравнимы с радиусом кривизны, влияние кривизны существенно сказывается на распределении напряжений. При рассмотрении задачи об изгибе стержня значительной кривизны мы ограничимся тем частным случаем, когда ось является дугой окружности, сечение симметрично относительно плоскости осй и изгибающие силы действуют в этой плоскости. В основу расчета положим две гипотезы:
1. Плоские сечения, перпендикулярные оси стержня, остаются плоскими и перпендикулярными изогнутой оси после деформации.
2. Цилиндрические поверхности, ось которых проходит через центр кривизны и перпендикулярна плоскости оси стержня, свободны от напряжений.
Первая гипотеза выполняется совершенно точно в случае чистого изгиба, то есть изгиба парой сил. Вторая гипотеза означает, что круговые волокна, на которые можно мысленно разделить стержень,
246
НАПРЯЖЕНИЯ ПРИ ИЗГИВЕ
[ГЛ. IX
не взаимодействуют между собой. Это явно невозможно: растянутое криволинейное волокно будет в равновесии только за счет реакции соседних волокон, его можно уподобить изображенной на рис. 168 -веревке, перекинутой через цилиндр. Натягивая концы веревки, мы
вызываем давление ее на цилиндр. -
Точное решение задачи об изгибе кривого бруса с круговой осью прямоугольного поперечного сечения дано Головиным (1880 г.).
Приближенное решение, излагае-
/ТЪкК мое ниже> пригодно для всех форм
поперечных сечений, а для прямо-угольного сечения весьма мало j ’ отличается от решения Головина.
* \ Обращаясь к рис. 169, где и^обра-
рис 1бд жены два бесконечно близких се-
чения до и после деформации, найдем, что удлинение пп' волокна, находящегося на расстоянии q от нейтральной оси, есть q8d<p. Здесь Od<p — угол поворота одного сечения относительно другого. Первоначальная длина этого волокна /ял = (е-4-т])^ф. Поэтому относительное удлинение есть
е==_Л?_# С
нейтральной поверхности, то есть цилинд-являющейся геометрическим местом нейтраль-
Заметим, что Q, радиус рической поверхности, ных осей сечений, заранее неизвестен. Вследствие второй ги-
поэтому
Рис. 169.
потезы волокно испытывает только продольные напряжения, закон Гука дает:
£г]9
Примем за оси х и у центральные оси сечения, направим ось z по
(U4.1)
§ 114]
ИЗГИБ КРИВОГО БРУСА
247
нормали к сечению и составим уравнение проекций всех сил на ось г (рис. 170). В случае чистого изгиба сюда войдут только внутренние силы и мы получим:
J adF=0.
F Отсюда
И* =0.
(114.2}
F
Формула (114.2) послужит в дальнейшем для нахождения положения нейтральной оси. Пока заметим, что если Q велико по сравнению с размерами сечения, то величиной г] можно пренебречь в знаменателе и мы получим:
Следовательно, в этом случае нейтральная ось пройдет через центр тяжести.
Вообще нейтральная ось смещена относительно центра тяжести. Величину этого смещения мы будем обозначать через е. Составим теперь уравнение моментов относительно нейтральной оси. Получим:
М— Jar|df=O. (114.3}
F Но
J 01J ТТГ= а {dF~ °J тта •
Второй интеграл равен нулю вследствие формулы (114.2), первый же интеграл есть статический момент площади сечения относительно нейтральной оси:
or] dF= еР.
Приняв это во внимание, получим из уравнения (114.3)
£8=
М eF‘
Подставляя найденное значение Е9 в формулу (114.Г), получим-
М я
(114.4)
Это и есть основная формула для нахождения нормальных напряжений при чистом изгибе кривого бруса. Если изгиб создается силами, которые растягивают или сжимают сечение, а также вызывают в нем касательные напряжения, то формула (114.4) дает важнейшую
•248
НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
(ГЛ. IX "
часть напряжений. Эпюра распределения напряжений в сечении оказывается уже не прямой, как в стержне с прямолинейной осью, а гиперболой.
Для пользования формулой (114.4) нам не хватает одного: мы пока еще не знаем положения нейтральной оси.
§ 115. Нахождение нейтральной осн в кривом стержне. Как -уже было сказано, для нахождения нейтральной оси используется • уравнение (114.2). Вместо того чтобы отсчитывать координату т] от ; нейтральной оси, мы будем отсчитывать координату у от оси. х, проходящей через центр тяжести. Из рис. 170 видно, что
Обозначив через г радиус кривизны поверхности, являющейся ‘ геометрическим местом осей х, проходящих через центры тяжести сечений, получим также -*
Уравнение (114.2) напишется так:
(45.1) , Положим
= (И5.2) '
Тогда
{ " f '-±1=1 dF=l(F4.»F].
J r + у r J r + y rl T I
F
Из уравнения (115.1) получим;
‘“'Г?*-. J
Весьма простую приближенную формулу для е можно получить t следующим образом. Разложим подынтегральное выражение в формуле (115.2) в ряд и ограничимся' двумя членами разложения. По- .« лучим: >
~-mF^^dF—\^dF^ — ^. -
Jr J * “
* F F
Действительно, первый интеграл обращается в нуль, поскольку ось х проходит через центр тяжести. Отсюда
Jx да ив-А . r*F
С другой стороны, формула (115.3) определяет величину «, малую по сравнению с г. Поэтому т мало по сравнению с единицей
§ 115] НАХОЖДЕНИЕ НЕЙТРАЛЬНОЙ ОСИ В КРИВОМ СТЕРЖНЕ 2491
и е = тт. Окончательно имеем:
* = (115.4)-
При желании решить задачу более точно необходимо вычислить интеграл в формуле (115.2) для заданного поперечного сечения. Иногда этот интеграл удается представить в замкнутой формег в противном случае прибегают к численному интегрированию. Учитывая приближенность всей теории, основанной на ряде допущений,, нужно признать точность формулы (115.4) достаточной для практических приложений.
ГЛАВА X
ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
§ 116. Дифференциальное уравнение изогнутой оси. Будем рассматривать изгиб в главной плоскости, которую примем за плоскость yOz. Вследствие изгиба каждое сечение повернется около оси х на угол nxdz относительно соседнего сечения. Так как сначала сечения были параллельны, то xxdz является углом смежности для искривленной оси стержня и хх есть ее кривизна:
По формуле (103.3)
1 Q Е^х
(116.1)
Искривленная ось изогнутой балки представляет некоторую кривую в плоскости yOz; чтобы задать ее, нужно задать прогиб v
в направлении оси у как функцию координаты сечения z. Формула для кривизны будет следующей:
— =±-------£1— (Ц6.2)
(штрихи обозначают производные по z).
Осталось выбрать знак в формуле (116.2). Если изгибающий момент положителен, как показано на рис. 171, то по формуле (116.1)
кривизна оказывается отрицательной, а вторая производная функции, график которой обращен вогнутостью в сторону положительной оси координат, положительна. Поэтому в формуле (116.2) нужно удержать анак минус. Получим:
у" _МХ
U +EJX
(116.3)
§ 117]
ПРЕДЕЛЫ ПРИМЕНИМОСТИ ПРИБЛИЖЕННОЙ ТЕОРИИ
251
Это и есть точное уравнение изогнутой оси стержня. Его обычно заменяют приближенным уравнением, ограничиваясь теми задачами, в которых прогиб мал по сравнению с длиной балки. Тангенс угла наклона касательной к упругой линии, равный ®', при этом также мал, и квадратом его можно пренебречь по сравнению с единицей. Приближенное уравнение пишется так:
EJxv”'=Mx{z}. (116.4)
Иногда удобно считать заданным не изгибающий момент Мх> а нагрузку q[z). Вспомним, что по формулам § 105 ~~[~—Qy> dQv d*Mx
следовательно, =<7у. Продифференцировав (116.4) два раза, получим:
М (рнс. 172). Изгибающий Пользуясь точным уравне-
§ 117. Пределы применимости приближенной теории. Чтобы выяснить степень точности приближенного уравнения (116.4), сравним результат его решения с результатом решения точного уравнения (116.3) в случае, когда последнее не сложно. Пусть балка длины I нагружена на конце моментом момент всюду постоянен и равен М. нием (116.3) или лучше (116.1), найдем, что радиус кривизны постоянен н прогиб на конце
Рис. 172.
(П7.1)
/ = Ц1 —cos-J.
Разложим косинус в ряд, ограничившись тремя его членами:
I cos — О
Для/получим следующее выражение: 1 Р 1 Р
' 2 q 24q’
или
I ~
Решим теперь ту же задачу с помощью уравнения (116.4) Интегрируя два раза, найдем:
-=2< + ^ + С>-
252
ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
[ГЛ. X
Но C1 = Ct — 0, так как при 2 = 0 v = v' = 0. Поэтому прогиб по приближенной теории есть
А, _ _ 1 Ml
I ~ 2 EJX’
Теперь можно представить точное значение прогиба следующим образом:
т=4~Ит)’- И17'3»
Относительная погрешность вычисления прогиба по приближенной теории: >
LLziAL—_L (ft. у. _ (И7 4)
/о 3 \ I } х
Предположим теперь, что мы при определении прогиба удовлетворяемся точностью в 3%. Большая точность не нужна, так как модуль упругости обычно известен с меньшей точностью. Полагая
3 V I ) ~~ 100 ’ получим:
tj- = 0,3.
Таким образом, уравнение (116.4) дает достаточную точность даже тогда, когда прогиб составляет 30®/о длины. Такие большие прогибы возможны у очень тонких балок. Действительно,
Т=Н- (117.5)
Обозначив через Л расстояние от оси до крайней точки сечения . балки, получим:
___Л
®max Q •
Отсюда
1 __8тах folx
Q - h Eh ’
Подставляя в (117.5), получим:
fa 1 1 Io]g
I Т h E *
Отсюда
2£ 4 Л [ст]и I
Примем для стали
£=2-10’, [o]Hq?=2-10’, -^=0,3.
Тогда
4 = 600. h -
§ 118] ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ИЗГИВА 253
Только если отношение l)h больше шестисот, погрешность приближенного уравнения (116.4) может превысить 3*/,. Как видно, это перекрывает все практические потребности. Исключение, может быть, составляют случай расчета пружин.
§ 118. Интегрирование уравнения изгиба. Интегрированию уравнения (116.4) посвящена весьма большая литература, хотя математически вопрос и представляемая элементарным. Правая часть уравнения обычно не является аналитической функцией координаты z, аналитическое выражение момента меняется от участка к участку. Поэтому задача об определении прогибов может оказаться довольно трудоемкой. На каждом участке появляются свои константы интегрирования, и их приходится определять из условий сопряжения. Излагаемый ниже метод интегрирования по идее восходит к Эйлеру, для более сложных уравнений изгиба балки на упругом основании %колебаний стержня он разработан А. Н. Крыловым; для уравнения (116.4) этот метод использовался многими авторами. Проинтегрировав уравнение (116.4) в пределах от нуля до z, получим:
Z
®'(z) = «'(O)+j^^. (118.1)
Проинтегрируем еще раз от нуля до z уравнение (118.1). Получим;
v (2) = i?(0)4-v'(0)2 4-^^f-dzdz. (118.2)
Эта формула дает общий интеграл уравнения (116.4), зависящий от двух постоянных: v (0) и ®' (0). При вычислении интегралов в формулах (118.1) и (118.2) нам придется иметь дело с особыми функциями ф„(г), определенными следующим образом:
<р„й) = О (г<0), Фв(г)=^ (*>0). (118.3)
Докажем следующую теорему о функциях фп(^):
5<Рп(г —а)^=Ф„+1(г —а). (118.4)
О
Действительно, если то
г
Ф„(я — а)я»0, $Ф„(г — а)^=0 = фп+1(г — а) (г<а), о
если z>a, то
S Ф»(* - а)dz = $ (-^£==Ф„+1 (*- а) (*> а).
• а
254
ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
[гл. X
Изгибающий момент в обычных случаях загружения балки может > быть выражен через функции ф„. Рассмотрим, например, балку, загруженную моментом М в сечении с координатой а, силой Р в сечении с координатой b и равномерно распределенной нагрузкой q, начиная с сечения, имеющего координату с (рис. 173), до сечения z — d.
Изгибающий момент в сечении с координатой z от приложенного момента М равен нулю, если z<^a, и равен М при 2^> а. Это можно написать следующим образом:
Л4х=Л1фв(2 — а).
По определению ф0(2— а) есть прерывная функция, равная нулю при г^а и единице при 2^>о. Рассуждая совершенно так же, найдем, что от силы Р момент равен величине Р, умноженной на ф, (z — b); от нагрузки — величине q, умноженной на ф,(2— с). Последнее верно лишь для загруженного участка при c^z^d.
Если z~>d, можно рассуждать следующим образом. Предположим нагрузку неограниченно простирающейся вправо, но, начиная с сечения d, приложим противоположно направленную нагрузку (—q). Тогда
—с) —Ф» (* — <*)]•
В общем случае, когда на стержень действует несколько моментов, сил и нагрузок,
Мх = 2 {М<ра (г — а) + Рф,(z — b) + q [ф, (z — с) — ф, (z — d)J}.
По формуле (118.1), если EJX= const, получим, принимая во внимание (118.4):
®'(г) = ф'(0)+ ^^{Л4ф1(2-а)4-Рф,(2 — (>) +
-Н 1ф, (* — с) — Ф, (* — <*)]}-
По формуле (118.2)
v (z) = v (0) ®' (0)2’ -{-
+ ^^{А1ф,(2 —О)4-Рф,(2Г —&)4-?[ф4(2—С)—ф4(2 —d)]}.
§ П9]
ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ПРОГИБОВ
255
Последнее выражение и представляет общий интеграл уравнения изгиба. Вспомнив определение функций <р„, запишем формулы для v' и v окончательно следующим образом:
V (z) — V (0) ®' (0) 2
Значок «л» над символом суммы обозначает, что суммируются только те величины, которые относятся к части балки, левой по отношению к рассматриваемому сечению. При переходе от одного участка к другому в формулах прибавляются новые члены.
Эти уравнения легко распространить на нагрузки, распределенные по закону треугольника, трапеции и параболы любой степени. Предоставляем сделать соответствующий вывод читателю.
§ 119. Примеры определения прогибов. Рассмотрим ко примеров, поясняющих применение формул (118.5) и
1. Балка на двух опо-^|
рах, несущая распреде-“1 >
ленную нагрузку (рис.
174). Реакции равны ql\2 каждая, слева от любого сечения приложена сила — <?//2, для которой <>==0, и незакончен
ная равномерно распределенная нагрузка, для которой с = 0. Прогиб в начале координат: ®(0)—0.
По формуле (118.6)
EJ^(2) = 5JX(0)2-^4 + g.
Постоянную ©'(0) найдем из условия, что ®(/)=0:
£Jx«(/) = EJX(0)-^ + g.
несколь-(И8.6).
г —-------
Рис. 174.
Отсюда
^'(0) = g4
Таким образом,
Наибольший прогиб будет при z = //2: _ ( 1 А
®max v 2 ) 384£/х ’
256
ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
, *
[гл. X.
2. Балка на двух 6 посередине (рис. 175). В
юрах, нагруженная силой Р этом случае реакции равны — Р/2. й
На первом участке, то есть при
0^2 ^//2, имеем:
EJxv(z) = EJxv'(0}z —
На втором участке, при II2 z /:
Рис. 175.
EJxv(z) — EJxv' (0)
Для нахождения константы ®'(0) воспользуемся тем, что ®(/)=0: -
EJxv (/) = EJxv’
Отсюда
. рр
v ^~\ЬЁТХ’
Наибольший прогиб будет 4
7 1 \ Р1*
max и I 2 ) 43EJX ’ Г
3. Балка, ващемленная одним концом и несущая *
равномерно распределенную нагрузку и силу на
конце (рис. 176). Обозначая
Рис. 176.
через М момент в заделке, через R—реакцию заделки и замечая, что v (0) = v' (0) — 0, получим:
EJxv=M^R^^.
Если приложена только сила на
конце н нет сплошной нагрузки, то M—Pl, R= — Р и мы имеем:
___ Р [Zz« V~EJX [2 6 J ’
Наибольший прогиб: РР ® (/) = .
Если, наоборот, Существует только нагрузка q,
М=^д~-, R= — ql,
v — JL
EJX L 4 6 ‘ 24j ’
___qP_ — •
। ‘ * *
□m
Рис. 178.
§ 120] ПРОСТЕЙШИЕ. СТАТИЧЕСКИ. НЕОПРЕДЕЛЕННЫЕ ЗАДАЧИ 257
§ 120. Простейшие статически неопределенные задачи. Применение формул (118.5) и (118.6) возможно не только для статически определенных задач,»но и для. задач, статически неопределенных. Рассмотрим, например, балку, лежащую на п опорах (рис. 177). Для неизменяемости системы достаточно двух опор, например крайних. Обозначим их А и В, средние же опоры занумеруем от 1 до Лт—2. Обозначим Rt, Rv . . Rn-t реакции про-, межуточных опор, примем
их за «лишние» неизвестные Рис. 177.
задачи. Уравнение упругой ' линии можно составить, сохранив для этих неизвестных сил буквенные выражения. В результате выражение v(z) будет содержать п неизвестных постоянных: постоянные щ(0) и t>'(0) и п — 2 реакции. Но функция v(z) обращается в нуль на каждой из опор, то есть в п точках; составляя условия равенства нулю прогибов на опорах, найдем все неизвестные.
Таков принципиальный путь решения задачи. Практически он мало удобен, поэтому для сколько-нибудь сложных задач следует употреблять иные методы, излагаемые в главе ХШ. Для простейших задач с одной лишней неизвестной можно применить изложенный способ, а можно вычислцть прогиб от внешних сил и от неизвестной реакции по отдельности, Последний прием, обладающий преимуществом наглядности, поясним на примере.
Решим задачу о балке, лежащей на
ных опорах и несущей по всей длине балки I равномерно распределенную нагрузку q (рис. 178). Представим себе, что сначала балка имела лишь две крайние опоры и нагрузка q вызвала прогиб f в середине, Приложим силу 7? в середине балки и будем ее постепенно увеличивать. Эта сила будет уменьшать прогиб, и при некотором значении силы он обратится в нуль. Поскольку прогибы от различных нагрузок складываются, следует решить задачу о прогибе балки, загруженной силой R посередине. Величина R найдется из условия
(120,1).
Если R такова, что прогиб равен нулю, можно смотреть на эту силу как на реакцию опоры, помещенной в середине балки. В -
9 Ю. Н. Работиов
258
ДЕФОРМАЦИИ•ПРИ ИЗГИБЕ
(ГЛ. X
предыдущем параграфе мы установили, что г Ы* f —SL-'‘rB=3MEJx' JR~48EJX'
Подставив эти выражения в (120.1), найдем:
Реакции крайних опор
А = В = -Д ql. 1о Изгибающий момент
«=-Гб«,2+< (г<4)
Эпюра моментов выглядит так, как показано на рис. 178. ¥
§ 121. Расчет статически неопределимых балок по способу допускаемых нагрузок. Желая рассчитать статически неопределимую балку по допускаемым напряжениям, мы должны найти лишние неизвестные, как показано в § 120, найти наибольший изгибающий момент и подставить величину наибольшего момента в условие прочности
Чтобы составить представление о том, как найти разрушающую нагрузку той же балки, обратимся к примеру последнего параграфа и попытаемся проследить, что произойдет с балкой по мере увеличения нагрузки. Наибольший изгибающий момент появляется над средней опорой. Поэтому именно .здесь ранее всего будет достигнута пластичность. Постепенно пла-
”” стическая зона распространяется
д) .г7б«нУ и в ширину (рис.
' ‘v 179, а). С дальнейшим увеличе-
1 г нием нагрузки верхняя и нижняя
Рис.~179. пластические области сомкнутся
над опорой, образуется так называемый пластический шарнир, то есть полностью пластическое состояние в соответствующем сечении. Изгибающий момент в сече-нци, перешедшем в пластическое состояние, был определен в § 108,
§ 121] РАСЧЕТ ПО СПОСОБУ ДОПУСКАЕМЫХ НАГРУЗОК 259
при дальнейшей деформации он не возрастет. В то же время с увеличением нагрузки растут изгибающие моменты по всей длине балки и возникают пластические зоны в областях, близких к серединам пролетов (рис. 179, б). Эти пластические зоны распространяются в ширину и глубину до тех пор, пока вблизи середин пролетов не возникнут пластические шарниры. Дальнейшее увеличение нагрузки невозможно, изображенное на рис. 179, в состояние балки с тремя пластическими шарнирами является изменяемым состоянием. Схематически балку с тремя пластическими шарнирами можно представить так, как это изображено иа рис. 179, г. Изгибающий момент в каждом из шарниров постоянен, он уже не может возрастать с возрастанием нагрузки. Поэтому всякое увеличение нагрузки остается неуравновешенным.
Проследить весь процесс упруго-пластической деформации балки от упругого состояния до исчерпания несущей способности довольно трудно. С другой стороны, вспоминая результаты § 108, мы видим, что все приведенные выше рассуждения являются схематичными и неточными. Действительно, было показано, что полный переход сечения в пластическое состояние возможен лишь при бесконечно больших деформациях, поэтому, строго говоря, никаких пластических шарниров образоваться не может. Следовательно, определение несущей способности по описанной схеме в значительной мере условно.
Обычный способ расчета по допускаемым нагрузкам заключается в том, что состояние, изображенное на рис. 179, в или схематически на рис. 179, г, считается допустимым. Изгибающие моменты в пластических шарнирах равны Где нужно взять знак плюс, где минус, всегда легко определить.
Обозначив расстояние от левой опоры до первого пластического шарнира через £//2, получим, приравнивая для первого шарнира изгибающий момент предельному моменту Л4Т:
для второго шарнира:
. ,1 2МТ
-----г.
Исключив отсюда реакцию А, получим:
Таким образом, разрушающая нагрузка q оказалась зависящей от величины £, определяющей положение пластического шарнира в пролете. Определить эту величину не так просто, для этого нужно проследить весь процесс перехода от упругого состояния к пластическому. На практике поступают иначе, а именно принимают для £ то значение, которое соответствует минимуму нагрузки. Это правило
9
S60 ДЕФОРМАЦИИ ПРИ ИЗГИБЕ [ГЛ. X
будет строго обосновано в главе XV. Дифференцируя выражение q по £ н приравнивая производную нулю, получим:
6(1-£)-(1-Н)(1-2£) = О.
Отсюда
ГЧ-2&-1=0
£=/2-1.
Подставив это значение в формулу (121.1), найдем:
,121-2р
При расчете по допускаемым напряжениям для определения предельной нагрузки следует приравнять наибольший момент на средней опоре величине момента, соответствующего появлению текучести в крайнем волокне:
5^ = а W
32 г*'
Отсюда
9=32^. (121.3)
Если балка загружена сосредоточенными силами, эпюра моментов всегда состоит из прямолинейных участков и количество пластических шарниров известно заранее, отыскивать минимум нагрузки не приходится.
В статически определимых системах увеличение допускаемой нагрузки при расчете по способу допускаемых нагрузок получается лишь за счет того, что предельный момент в сечении находится из условия перехода сечения целиком в пластическое состояние. Составляя для статически определимой балки уравнения, аналогичные (121.2) и (121.3), мы получили бы одинаковые числовые множители в правых частях. Вся разница состояла бы в том, что в одной формуле фигурирует IFT, в другой Wx.
Статически неопределимая балка, как оказывается, обладает еще дополнительным резервом прочности. Увеличение допускаемой нагрузки 4g 4_________________________________________32
за счет статической неопределимости составляет ——• 100=450/в.
§ 122. Изгиб стержней переменного сечения. Графоаналитический метод. На практике часто приходится рассчитывать на изгиб стержни, сечение которых переменно. За основу при этом примем общий интеграл уравнения изгиба в форме (118.2):
г г
v (х)=v (0)+V* (0) z 4- J J dz dz-
О о
§ 122] ИЗГИБ СТЕРЖНЕЙ ПЕРЕМЕННОГО СЕЧЕНИЯ
261
Обозначим через Jt момент инерции сечения стержня в каком-либо месте, например при z=0. Введем обозначение:
Будем называть функцию q(z) фиктивной нагрузкой. Заметим, что по известной формуле Коши
«г г
0 0 о
Теперь можно написать выражения для прогиба и углового коэффициента касательной к упругой линии следующим образом: g
V(z)=V(0) + ®'(0)^+^-pU)(^-^dL (122.1)
о Z .
*'(*) = *' (O)+-±;p(g)dg. (122.2)
Интегралы в формулах (122.1) и (122.2) допускают^ простую геометрическую интерпретацию. Построим эпюру функции q{z) (рис. 180). Тогда интеграл в формуле (122.2) представляет собою площадь той
части эпюры, которая расположена слева от сечения, в котором ищется прогиб. Интеграл в формуле (122.1) является моментом этой площади относительно точки с координатой z на оси балки. Вспоминая определение перерезывающей силы и изгибающего момента, можем ска-
Рис. 180.
зать, что формулы (122.1) и (122.2) определяют соответственно изгибающий момент и перерезывающую силу в некоторой балке, несущей фиктивную нагрузку q(z) и нагруженной, кроме того, на левом конце силой R=EJov' (0) и моментом Mo=EJov (0). Таким образом, построение упругой линии сводится к построению эпюры изгибающих моментов фиктивной балки. Фиктивные сила и момент R и Мй находятся из граничных условий. Заметив, что формулы (122.1) и (122.2) можно написать так:
где Af и Q—фиктивный изгибающий момент и перерезывающая сила, посмотрим, как нужно закрепить фиктивную балку. Там, где действительная балка имеет концевой шарнир, v = 0, v'^0, следовательно,
262
ДЕФОРМАЦИИ ПРИ ИЗГИВЕ
[гл. я
у фиктивной балки М—0, Qy^O. Но перерезывающая сила на конце при равном нулю моменте существует тогда, когда балка шарнирно оперта. Поэтому концевому шарниру у действительной балки соответствует
Дейстбит?
Фикти&н.
концевой шарнир балки фиктивной. Если конец действительной балки свободен, то прогиб и угол поворота отличны от нуля, следовательно, у фиктивной балки отличны от нуля момент и перерезывающая сила. Это возможно, если конец фиктивной балки считать заделанным. Продолжая подобное рассуждение, получим таблицу соответствия за- ‘ крепленной действительной и фиктивной балок, изображенную на рис. 181.
Сведя задачу интегрирования к вычислению площадей и моментов этих площадей, мы привели нахождение прогибов и . углов наклона оси стержня к построе-
и арифметическим операциям над величинами, находимыми эпюр. Поэтому изложенный метод нахождения прогибов
Рис.
181.
нию эпюр из этих
ры q (z) на треугольники, тяжести и составим момент по частям:
Р11
2 2 1,22
2 3 2 2
Таким образом,
называется графоаналитическим. Поясним его примером,
Определим прогиб на конце балки, изображенной на рис. 182. Пусть = Построим сначала эпюру моментов; примем теперь Jt за j0. Отношение J0]J= 1 на первом участке и равно двум на втором. Поэтому, чтобы получить эпюру д' (z), необходимо ординаты эпюры моментов на втором участке увеличить вдвое. Делая левый конец у фиктивной балки свободным и заделывая правый в соответствии с установленными нами правилами, вычислим фиктивный момент в заделке.
Для этого разобьем площадь эпю-вычислим их площади, найдем центры
Р! — /+1АН— Г3 2П 2
Ар/» 8 1 '
Р
М
У' 8 EJt "
§ 123] О РЕШЕНИИ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 263
§ 123. О решении линейных дифференциальных уравнений с постоянными коэффициентами. Более сложные задачи, относящиеся к изгибу, как-то: продольно-поперечный нзгнб, изгиб балок на упругом основании, поперечные колебания балок — сводятся к решению линейных уравнений с постоянными коэффициентами более сложного вида, чем уравнение (116.4). Трудность интегрирования этих уравнений заключается в том, что правая часть есть функция от z, имеющая разные аналитические выражения на разных участках. Излагаемый ниже метод применялся еще Коши; для нзгнба балок он был детально разработан А. Н. Крыловым.
Пусть дано линейное однородное дифференциальное уравнение порядка п с постоянными коэффициентами
dnu , dn-,« , . т , . „ . ..
+ + - • + = С123-1)
Возьмем произвольную систему линейно независимых частных ре- . шений
и и ... и о’ 1» • • •» п -1
и построим из них новую систему частных решений Uk, обладающих тем свойством, что
t4(0) = U(0)=...-=Un-,)(0) = 0, t4ft)(0)=l. (123.2)
Это всегда возможно. Для этого надо взять линейную комбинацию из частных решений ц(-:
^k = S cki ui-Z=o
Коэффициенты ck6, ckl, ..., cAn_, найдем из уравнений:
О = САоМо (°) + СА1“1 (°) + • • • + Ckn - iUn - ! (°)>
о== сАо“о (°) + с*1ц> (°) + • • • + САп-1Мп-1 (°)- (123.3)
1 — САоМ»Л) (°) + (°) + • • • 4" САп-1М«-1 (°)’
Детерминант этой системы есть детерминант Вронского для системы функций и0, и,, ..., п„_1 при z=Q, он отличен от нуля вследствие линейной независимости функций ц0, ц,, ..., и„_,. Поэтому всегда можно найти коэффициенты ckl и фактически построить функцию Uk (z).
Образуем систему таких частных решений: U9(z), Ц(а’), ..., Un(z). Каждая из этих функций обладает свойством (123.2). Составим
264 ДЕФОРМАЦИИ ПРИ ИЗГИБЕ [ГЛ. X
следующую таблицу, в которой сведены начальные значения функций и их производных:
и 10) W (0) U"(0) U"' (0)
1 0 0 0
иг 0 1 0 0
и» 0 0 1 0
Во всех клетках этой таблицы стоят нули, лишь на главной диагонали— единицы. Поэтому система Uk частных решений уравнения (123.1) называется системой с единичной матрицей. Будем строить общий интеграл уравнения (123.1) именно с помощью этой системы частных решений, линейная независимость которой усматривается из того факта, что ее определитель Вронского при z=0 есть определитель единичной матрицы, следовательно, единица. Таким образом,
«(г)=ед (д) 4-ОД (д) 4-... 4-с„ОД_1 (г).
Займемся теперь решением неоднородного уравнения
£(«)=/(*). (123.4)
Докажем следующую теорему:
Интеграл уравнения (123.4), обращающийся в нуль вместе со своими производными до порядка п — 1 включительно при z = 0, дается формулой g
“^Ц.-Дг-ВШВИВ. (123.5)
О
При этом предполагается, что в уравнении (123.4) коэффициент при старшей производной сделан равным единице. Вычислим последовательные производные функции и (г). Здесь г одновременно является и верхним пределом интеграла, и параметром, поэтому по известной теореме анализа g
«' U) ==»> (0)/(z)4- ${/„-. (г-5)/(В)d$.
о
Но Ц,_1(0)=0 вследствие специального выбора функций (z). Продолжая процесс дифференцирования, найдем:
г
ип и) =-5^. g)/(6)4
§ 123] О РЕШЕНИИ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 265 и так далее, до производной порядка л — 1 включительно. Произ-водная же порядка л
. »
«<и> (z) = ° (0) / (д) + J U™. , (z - g)/(g) dg,
0 причем
Подставим теперь все последовательные производные функции и (г) в уравнение (123.4). Вследствие постоянства коэффициентов под интегралом получится та же комбинация производных функции Un_x (г), что и в операторе £(«). Учитывая же, что коэффициент при и(п> есть единица, получим:
г
$W-,)/(&)^4-/U) ==/(*)• »
Но Un_x есть решение уравнения (123.1), L(Un_l}—Q, поэтому мы получили тождество, что и доказывает теорему.
Формула (123.5) дает не какое-нибудь частное решение уравнения (123.4), а решение, обращающееся в нуль вместе со своими производными до порядка л — 1 включительно при г=0. Это большое преимущество полученного решения, упрощающее определение постоянных из начальных условий.
Общий интеграл уравнения (123.4) может быть представлен следующим образом:
и (Z) = C.Ut (Z) + CXUX U) 4-... + сп_,ип(z) 4-Z о
Постоянные С„ С,, ..., Сп имеют здесь совершенно определенные значения. Действительно, положим д = 0. Получим:
«(0) = С,.
Вычислим производную от и порядка k и положим z — О. В правой части обратятся в нуль все члены, кроме содержащего миожителем Uk, так как U[k) (0) = 1. Получим:
и<*>(0) = СА.
Таким образом, а — 1 2
U(Z) == (0) Uk (z) 4- $ Un_t (z - g)/(g) dt. (123.6)
t=o о
266
ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
[ГЛ. X
Формула (123.6) представляет общий интеграл линейного дифференциального уравнения с правой частью в форме, наиболее удобной для приложений. Постоянные интеграции имеют здесь простой смысл: это начальные (при д = 0) значения искомой функции и ее производных. Поэтому метод интегрирования дифференциальных уравнений, основанный на формуле (123.6) и широко применяемый в сопротивлении материалов и строительной механике, называется методом начальных параметров. Будучи введен А. Н. Крыловым, метод начальных параметров разрабатывался рядом советских авторов не только в применении к балкам, но также к пластинкам и оболочкам.
В качестве примера рассмотрим уже изученное нами уравнение (116.4):
EJX •
Соответствующее однородное уравнение:
©"=0.
Его частные решения, обладающие единичной матрицей, суть
£70=^1, Ux=z.
Действительно, 77О (0) = 1, £70 (0) = О, Ц (0) = О, (0) — 1.
По формуле (123.6)
Z
®(z)=®(O).l+®'(O)z + Ju-^)^^. (123.7)
О
По теореме Коши
Z ZZ
О 0 0
Поэтому формула (123.7) буквально совпадает с непосредственно найденной формулой (118.2).
§ 124. Продольно-поперечный изгиб. Рассмотрим стержень, на который, кроме поперечной нагрузки, действует продольная сжимающая или растягивающая сила. Пока стержень был прямым, эта сила вызывала только растяжение или сжатие стержня; как только стержень изогнулся, сила Р (рис. 183) создает в сечениях изгибающий момент. В случае а) этот момент от силы Р. в сечении с координатой z есть Pv, где v — прогиб. В случае б) момент есть P(v — ®0)== — Ро — М^. Через Мо мы обозначили величину Pv0. Эта величина является неизвестной постоянной, отнесем ее к поперечным нагрузкам, момент от которых в сечении с координатой z есть Мх.
§ 124]
ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ
267
Таким образом, полный изгибающий момент Мх = Pv М'х (2).
Внесем это выражение в уравнение изгиба (116.4). Получим:
v
Р
EJXV~EJ-
(124.1)
Это и есть уравнение продольно-поперечного изгиба. В даль-
нейшем нужно рассматривать
1. -Р^>0, сила растягивает стержень. Положим
Перепишем уравнение (124.1) следующим образом:
V"—(124.2)
X
отдельно два случая.
Применим к нему метод, из- Рис- 183.
ложенный в предыдущем параграфе. Частные решения соответствующего однородного уравнения
4- sh kz, ch kz
R
удовлетворяют условиям, поставленным для функции 77, (z). Действительно, при 2=0 sh&z = 0, производная же этой функции, то есть ch Az, обращается при 2=0 в единицу. Таким образом,
U. = ch kz, U.=^-shkz.
По формуле (123.6)
v (2) = v (0) ch kz v' (0) sh kz
1 e M* (M
+ lJshA(z-S)-f^^- (124.3).
к 0
Это и есть общее решение уравнения продольно-поперечного изгиба. Вычислим входящий в формулу (124.3) интеграл для некоторых видов нагрузок.
а) Момент М в сечении 2 = а.
Л1* = /И<р0 (z—а)
268 ДЕФОРМАЦИИ ПРИ ИЗГИБЕ [ГЛ. X
ИЛИ
Л4* = 0 при z<a, МХ = М при z>crt я г
J sh k (z — I) ф0 (g — a) = $ sh k (z — g) =
= — у ch АЦя — I) £=у [ch A (z — a) — 1 J.
Эта формула пригодна, если z^>a. Если z<^a, то этот интеграл равен нулю.
б) Сосредоточенная сила Q в сечении z = b.
Л£ = ОФ1(* — Ь).
Если z<b,
J shft(z— £)Ф1(£ — b)d^ = O, О
Если z^>b, то этот интеграл равен
Jsh*(2 — g) (g — b)dl. ь
Интегрируя по частям, получим для него следующее выражение:
2
_^chft(^-g)(g-&)|e + |$ch*U-g)dg = ь
= — ^~ — ^shk(z — l) ^=-^shk(z — b) — z~~ .
Таким образом, для балки, загруженной моментами и сосредоточенными силами,
v(z) — v (0) ch kz v' (0) у sh |л! [ch k (z — a)— 1] -|-
4-Q[±shftU-b}-(z —*)] }. (124.4)
Здесь, как и в формуле (118.5), суммирование распространяется иа те силы или моменты, которые приложены слева от рассматриваемого сечения.
2. P<Z 0> сила сжимает стержень. Обозначим теперь через А2 величину— PjEJx. Уравнение продольно-поперечного изгиба принимает вид:
(124.5)
Решение строится буквально так же, как для растягивающей силы, только вместо гиперболических функций будут функции тригономет
§ 124]
ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ
269
рические. Не повторяя выкладок, напишем результат:
v (z) — v (0) cos kz 4“ v' (0) sin kz 4-
1 p Af* (Bl
+ -i-jsinft(* —(124.6) e
Для балки, загруженной моментами и сосредоточенными силами, интеграл принимает следующий вид:
гЦ;г) = ©(0)со8Аг4-©Ч0) ysinA;? —cos k(z — а)] 4~
sinA(s — A)ll. (124.7)
+Q [(*-*) -4
Приведем пример на двух опорах (рйс.
применения этого уравнения. Балка, лежащая 184), сжимается двумя силами, приложенными
Рис. 184.
с эксцентриситетом е. В концевом сечений приложен, таким образом, момент Ре. По формуле (124.7)
v = 4^8inA:.?4~e(l — cos Аг).
Постоянную v'(0) определим из условия v(/)==0:
<0 (/) sin А/4“ е О — cos *0 =
Отсюда
,,лх .и— cos И
° (°> = в*-ет-
Подставляя это в выражение для прогиба, получим:
v = е £1 — cos kz — sin kz 1 ~ос^— j • (124.8)
Если бы сила была растягивающей, в формуле (124.8) следовало бы заменить тригонометрические функции гиперболическими:
v = e[chAz—1—shAzch — 1 . (124.9)
[_ sh kl J
Явления продольно-поперечного изгиба при растяжении и сжатии протекают качественно совершенно по-разному. Предположим, что
270 ДЕФОРМАЦИИ ПРИ ИЗГИБЕ [гл. X
мы увеличиваем растягивающую силу Р. Тогда увеличивается k, гиперболические синус и косинус монотонно возрастают, разница между ними сглаживается, и прогиб v, определяемый формулой (124.9), стремится к нулю. Растягивающая сила как бы повышает жесткость системы, увеличение ее уменьшает прогибы. Совершенно иначе обстоит дело, если сила сжимает стержень. При значениях параметра М, кратных л, обращается в нуль sinfe/ в знаменателе последнего члена формулы (124.8). Таким образом, прогиб обращается в бесконечность при некоторых конечных значениях силы.
Не останавливаясь пока подробно на этом факте, заметим, что он лежит в основе теории устойчивости упругих систем, рассмотренной в главе XII курса.
§ 125. Изгиб балки на упругом основании. Примером балки на упругом основании является железнодорожная шпала, нагруженная двумя силами, передаваемыми через рельсы. Не имея опор, шпала передает эту нагрузку непосредственно грунту, изгибаясь при этом вследствие податливости грунта.
Термин «упругое основание» в применении к грунту является довольно условным, ибо механические свойства грунта не тождественны со свойствами упругого тела в обычном смысле слова, и
«77
*77777777777777777,
Рис. 185.
понимается этот термин в теории упругости и в сопротивлении материалов по-разному. Если поставить задачу о равновесии балки, покоящейся на массивном упругом теле, ограниченном с одной стороны плоскостью, мы получим пример так называемой контактной задачи теории упругости, точное решение которой встречает большие математические трудности. Существо их состоит в том, что деформация тела в одной какой-либо точке зависит не только от давления в этой точке, но и от давлений в соседних точках.
Желая упростить постановку задачи и сделать ее доступной элементарным методам, предполагают, что перемещение упругого основания зависит только от давления в той точке, в которой ищется перемещение. Эта гипотеза, иногда называемая гипотезой Винклера, как бы заменяет реальное упругое тело рядом не связанных между собой пружин или стерженьков (рис. 185). Считая реакцию основания пропорциональной прогибу, найдем, что распределенная непрерывным образом по длине балки реакция есть —kv.
Такая упрощенная модель упругого основания довольно хорошо воспроизводит свойства грунта^ который, собственно, не может счи
§ 125J ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ 271
таться упругим телом: связность между его частицами меньшая» нежели в сплошном упругом теле. Имеются более сложные и более совершенные модели упругого основания. Так, М. М. Филоненко-Бородич предложил модель упругого основания, способную распределять нагрузку и в то же время допускающую применение элементарного математического аппарата.
Для составления дифференциального уравнения изгиба балки, лежащей на упругом, в смысле Винклера, основании, мы будем исходить из дифференциального уравнения изгиба в форме (116.5). В правой части к действующей нагрузке q мы прибавим реакцию основания (—kv} и будем считать жесткость балки при изгибе, то есть произведение EJX, постоянной. Получим;
EJxviy =— kv -f- q (z), или
(4a*=gj-). (125.1)
Уравнение (125.1) встречается не только в задаче о балке на упругом основании, но и в других разделах строительной механики, например в теории цилиндрических оболочек. Займемся сначала интегрированием однородного уравнения
T»IV-|-4a^ = 0. (125.2)
Корни характеристического уравнения суть
а(1-}*г);а(—i-W); ®(—1—г)1 aU—О*
Комбинируя соответствующие частные решения так, чтобы избавиться от мнимостей, получим общий интеграл уравнения (125.2)
v = еаг (Д sin az Bpos аг)-\-е~11г (sin az-j-Z) cos az). (125.3)
Применяя метод § 123, мы должны с помощью общего интеграла (125.3) образовать систему частных решений с.единичной матрицей.
Эти решения суть
Ue (z) = ch az cos az,
Ut (z)=[ch az sin az sh az cos az],
Ut (z) = 2^shazsinaz, (125.4)
Ut (z)=4“« [ch sin az — sh az cos az].
Отметим, что
ut=u>, ux = u't, ut=ui
272
ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
[ГЛ. X
По формуле (123.6)
V U)=V (0) U. (z) + V' (0) Ц (z) 4- V" (0) Ut (z)
-Н"'(0) U.W-t-M*). (125.5) Здесь
vl(z)=^Ut(z-l)^dl. (125.6)
о
Вычислим функцию vr (z) для случая, когда балка загружена сосредоточенной силой в сеЧении с координатой z=b. Заменим сосредоточенную силу равномерно распределенной нагрузкой на участке от b — е до Интенсивность этой нагрузки примем равной Р/2е. По формуле (125.6) t\(z) = 0, если z<^b — е. Если z>b-\-z, то
(^)== У ЦЛ2 ^2еЁТ;^’
Применим к этому интегралу теорему о среднем» Получим:
Vi=^j-xUt(z — b-[-^).
Здесь —1 1-
Будем теперь приближать 8 к пределу, равному нулю. Искомое частное решение представится так:
г»,(г)=0 при z<^b,
v^z^^U^z — b} ПР« z>b-
• Желая получить решение в случае сосредоточенного момента, приложенного в сечении с координатой а, приложим в этом сечении сосредоточенную силу величиной УИ/e, в сечении с координатой a-f-e силу —Af/е. При 8» суммируя найденные решения для двух
сил, получим:
v>(г) =1ГХ(? и»-Т и» а-«)) •
Переходя к пределу при 8=0 и вспоминая, что Ut = Ut, найдем:
С?) == О при z а,
vi(z)—^-^t(z-^a) при z>a.
§ 125] ИЗГИБ ВАЛКИ НА УПРУГОМ ОСНОВАНИИ 273
Рассмотрим, наконец, случай равномерно распределенной нагрузки, начинающейся при z = c. По формуле (125.6)
О
Но, как легко проверить непосредственным вычислением,
Ut(z) = -^U’n{z).
Поэтому
t\(z) = 0 при z<c,
[1 —f/„(z —с)] при z>c.
Если нагрузка заканчивается при z = d, то считаем ее продол" мающейся вправо неограниченно, но прикладываем нагрузку (— q)> начиная с z = d . При z>d получим:
^=1 (1--Ци-с)]—
Окончательная формула для прогибов будет следующей: v (z) = v (0) U, (z) 4- v’ (0) (z) 4- Vя (0) Ц (z) + v(0) Ut (z) 4-
,-4^[Ч(г — *) — Ut(z~ <*)]}. (125.7)
Символ суммы с индексом «л» вверху нужно понимать так же, как в § 118.
Рис. 186.
Рассмотрим в качестве примера задачу об изгибе полубесконеч-ной балки силой и моментом на конце (рис. 186). В формуле (125.5) нужно положить:
’.=0. ’’«>)=£;, *"(0)=^.
Получим:
v=v(0) Ut (z) 4- V1 (0) Ut(z) 4- ~ и, (z) 4- Ut (Z).
Для определения постоянных ®(0) и ®'(0) потребуем, чтобы прогиб на бесконечности был равен нулю. Для этого заметим, что
274 ДЕФОРМАЦИИ ПРИ ИЗГИБЕ [гл. $
при больших значениях аргумента
ch az—>shaz—>-у е”г.
Следовательно, по формулам (125.4)
U (z)—► ~ eaz cos az, U^z)—>---!-ea*(sinaz-l-cosaz),
Ut (z) —► eaz sin az, Us (z) —> eaz (sin az — cos az).
При больших z '
v (z) —>- у eaz (0) cos az i (0) (sin az cos az} -p-
+ 2a’ ЁГх s>n ™ gj- (sin az - cos az)| — °..
Сравнивая коэффициенты при cos az и sin az, найдем:
1 ,,n. , 1 Af 1 P n
2a ' ' 1 * * * V 2a’ EJX 1 4as EJX
Отсюда
, ______M________P
a.EJx 2a-EJx' _ /125 81
_ M , P (125.8)
V 2a*EJx ‘ 2a3E Jx'
Заметим, что прогиб u(z) меняет знак: на некоторых участках балка приподнимается над основанием. Мы предполагаем при решении . задачи, что реакция основания возникает и при отрицательных прогибах.
ГЛАВА XI
ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
§ 126. Нормальные и касательные напряжения при изгибе. Соображения об относительных порядках величин нормальных и касательных напряжений при изгибе, приведенные в § 101, к тонкостенным стержням неприменимы. Касательные напряжения, возникающие вследствие изгиба и кручения^ имеют в такого рода стержнях тот же порядок величины, что и нормальные напряжения, и сбрасывать их со счета нельзя. Касательными напряжениями изгиба мы будем называть напряжения, распределяющиеся приблизительно равномерно по толщине стенки профиля и не связанные с закручиванием стержня.
Очевидно, например, что кручения не будет, если изгибать симметричный стержень, хотя бы двутавр или швеллер, силами, действующими в плоскости его симметрии. Весьма большая жесткость
на кручение замкнутых тонкостенных профилей делает для них вопрос об условиях отсутствия кручения второстепенным. В тех же случаях, когда тонкостенный стержень открытого профиля изгибается в плоскости, даже являющейся главной плоскостью, но не плоскостью симметрии, необходимо принять особые меры для предотвращения кручения. В этом параграфе мы предполагаем, что в силу тех или иных обстоятельств кручение отсутствует, значит, никаких иных
касательных напряжений, кроме как от изгиба, в стержне нет.
Сохранение плоских сечений при наличии касательных напряжений в сечении, очевидно, невозможно. Действительно, касательные
напряжения вызывают сдвиг, то есть изменение первоначально прямого-угла. Таким образом, сечение не может оставаться перпендикулярным изогнутой оси стержня, а так как напряжения в сечении распределяются неравномерно, оно не может оставаться плоским (рис. 187). Однако если стержень загружен сосредоточенными силами, то на каж
дом участке перерезывающая сила постоянна, следовательно, во всех сечениях этого участка распределение касательных напряжений
276 ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. X®
одинаково. Одинаковы и искажения поперечных сечений. Поэтом/ длина элемента тп между двумя сечениями после деформации равн» длине того же элемента, подсчитанной по гипотезе плоских сечений,' то есть т'п', Отсюда следует, что для балки, несущей сосредото% ченные силы, закон распределения нормальных напряжений будет-тем же, что по гипотезе плоских сечений:
ст =
Мху Jx
! МуХ
(126.1)
Более точные подсчеты показывают, что влияние искажений
поперечных сечений вследствие касательных напряжений изгиба
на распределение нормальных напряжений в более общих случаях
нагрузки совершенно незначительно. Поэтому формула (126.1) является общей.
Для нахождения касательных напряжений будем считать, что они распределяются по толщине стенки равномерно (рис. 188). Положение точки на
Рис. 188. Рис. 189.
средней поверхности стержня будем определять двумя координатами: х—расстоянием от фиксированного сечения по образующей и $— дугой, отсчитываемой от какого-либо конца средней линии открытого контура сечения. Всю длину дуги средней линии контура сечения обозначим й, толщину стержня б будем считать функцией s, но не г. Вырежем элемент средней поверхности двумя бесконечно близкими образующими и двумя поперечными сечениями. Силы, действующие на грани объемного элемента, образованного нормальными сечениями, проходящими через стороны элемента средней поверхности, показаны иа рис. 189. Уравнение равновесия элемента примет следующий вид:
д (об) ! d(t6)
~3i—।—эг*—°-
(126.2)-
Заметим, что вследствие закона парности касательных напряжений т = 0 при s=0 и $ = й. Интегрируя (126.2), найдем:
тб=—(126.3)
§127] КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
277
Но по формуле (126.1), учитывая независимость в от г, получим! д(об)_ 6ydMx bxdM, дг Jx дг ' Jу дг "
Вспомнив дифференциальные соотношения между изгибающими моментами и перерезывающими силами, напишем последнее равенство так:
__ Ъу п йх дг ~ }хЧУ~~ТуVx'
Подставив это выражение в формулу (126.3), получим следующую формулу для закона распределения касательных напряжений:
хй ds* (126.4>
о о
Интегралы в формуле (126.4) представляют собою статические моменты части площади сечения, заштрихованной иа рис. 182.
тб = j* уб ds j2
§ 127. Касательные напряжении при изгибе в плоскости симметрии. Если внешние силы действуют в плоскости симметрии сечения, которую мы примем за плоскость уОг, то в формуле (126.4) остается один член:
3
У Рис. 190.
(127.1)
о
Формулу (127.1) применяют иногда Х и для сплошных сечений, предполагая, что вектор т параллелей оси у, и понимая под б ширину сечения иа расстоянии' у от оси х.
Эти гипотезы можно принять с большой. натяжкой, точные решения их ие подтверждают. Неприемлемость предположения о параллельности вектора т оси у усматривается из теоремы § 89 о том, что касательного напряжения касается контура. Одиако для прямоугольного сечения, сплошного или тоикостеииого безразлично, формула (127.1) верна.
Здесь нужно принять
в точке контура вектор
(рис. 190):
б=А Л = ^-, j*>6ds= j ybdy = ~ ,
• л
~Т (127.2)
2 bh L \ h. J J *
278 ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [гл. ХЬ"
Эпюра распределения касательных напряжений по сечению есть парабола (рис. 190); наибольшее напряжение получается на нейтральной оси прн j=0, причем величина его
т _____3 Qy
Tmax 2 bh •
Здесь Qylbh представляет собою перерезывающую силу, поделен- • ную на площадь, то есть среднее напряжение.
Касательные напряжения при Д. И. Журавским (1855 г.)
в
Рис. 191.
изгибе были впервые рассмотрены применении к расчету деревянных балок, у которых сопротивление скалыванию мало и с касательными напряжениями приходится считаться даже для массивных профилей.
Полученное решение убеждает нас в том, что наибольшие касательные напряжения и наибольшие нормальные напряжения получаются в разных точках сечения, причем там, где о максимально, т = 0, и наоборот. В тонкостенных стержнях дело может обстоять иначе, как можно видеть из приводимого ниже примера расчета двутавровой балки.
Будем считать, что размеры b и h значительно больше, чем 6,
и 6t (рис. 191). Определяя касательные напряжения в стенке вычислим статический момент заштрихованной части сечения:
I
Jуд ds=+у — у‘) бх.
По формуле (127.1)
Qy Vhbdt ’ 1 /Л2 \1
Наибольшее касательное напряжение получается в середине стенки, однако в точке А оно еще довольно значительно:
hbbtQy Ха~~ 26, ’
При применении формулы (127.1) для полки нужно найти статический момент части, заштрихованной на рисунке крест-накрест, относительно оси х. Этот момент
§ 128]
ЦЕНТР ИЗГИВА
По формуле (127.1) получим:
Х==~2Ц‘
Наибольшее напряжение в точке В hbQy '
° х
В то же время нормальные напряжения в точках А и В великим в точке В это наибольшее напряжение, в точке А, немного меньше. Поэтому, рассчитывая балку по допускаемым напряжениям, мы должны-считаться с тем, что напряженное состояние является сложным.
§ 128. Центр изгиба. Предположим теперь, что сечение стержня-несимметрично. Покажем, что существует такая ось, параллельная.
оси стержня, что силы, действующие в любой проходящей через эту ось плоскости, ие вызывают кручения. Точку пересечения этой оси с плоскостью сечения называют центром изгиба. Если такая точка С существует, то касательные силы в сечении приводятся к равнодействующей, проходящей через эту точку.
Отсюда следует, что сумма моментов всех касательных сил в сечении относительно точки С равна нулю. На элемент ds с координатами х, у действует сила rbds тельно точки С есть
(рис. 192); момент ее относи-
тб ds р,
где р — длина перпендикуляра, опущенного из точки С на касательную. Если С есть центр изгиба, то
тбр ds = 0.
Но pds—это удвоенная площадь треугольника с основанием ds и вершиной в точке С. Положим pds = da>. Таким образом,
р . dw . п
\ тб -т- ds = 0.
J ds
о
j .
280 ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [гЛ.
I
Применим формулу интегрирования по частям. Получим: л s
тбсо |А — С dffi) © ds = 0. |о J 0s
° i
Но т обращается в нуль при s = 0 и $=й. Воспользуемся, кроме того, для преобразования интеграла уравнением (126.2), вспои- ' нив, что С
д(тд)_ й(об) ।
ds ~ дг J,™ . ;
как показано в § 126. Окончательный результат будет следующий: .
Q А Q А *
у _усоб ds -J- у хаб ds = 0, Х о ? о
а так как Qx и Qy произвольны, положение центра изгиба опреде- “ ляется следующими условиями:
С к
Jmx==\y<s&ds = Q, ?
(128JU
: Л
4y=Jx<o6ds=o. г
J-----------
Совершенно элементарно находится |
Рис’ 193‘ центр изгиба для углового профиля. Если j
принять за полюс вершину, то секто- ' риальная площадь со равна нулю, поэтому условия (128.1) выполняются, и вершина есть центр изгиба (рис. 193). Аналогично для таврового сечения центр изгиба находится в точке пересечения стенки с полкой. Заметим, что в формуле (128.1) к величине ® можно прибавить любую постоянную величину. Действительно,
л л л л j
$ j(«4"C)6ds = ^ j№o6ds-|-c J ybds= J.yco6ds, S
о о 0 О • iX
так как оси x и у предполагаются центральными и статический .? момент площади сечения относительно оси х равен нулю. Вслед- ? ствие этого замечания секториальную площадь ш можно отсчитывать £ не от конца профиля, а от какой-либо его. промежуточной точки, р Для фактического нахождения центра изгиба важно иметь формулу, непосредственно определяющую его координаты. Для этого возьмем -S-некоторую произвольную точку В и примем ее за полюс секториаль- | ной площади ав. Установим связь между шс и ша. Из рис. 194
§ 128J
ЦЕНТР ИЗГИБА
281
видно, что
d<BB=— (хв — х) dy+(у в — у) dx.
Мы считаем, что секториальная площадь возрастает, если обход контура для наблюдателя, находящегося в полюсе, представляется происходящим против часовой стрелки.
Аналогично
dwc=—(xc — x)dy+ + (^с— У>ах-
Поэтому
d<uc =* daB — (хс -xB)dy-}~ +(yc—yB)dx^
. Интегрируя, найдем:
-]~(ус— -Уя)х 4“ const- (128.2)
Аддитивная константа, как мы выяснили, несущественна. Подставляя (128.2) в формулу (128.1), получим:
J ха>вб ds + (ус — ув) Jf = 0. Отсюда
хс — хв
Ус=Ув — Ту^хе>в1>а8-
Применим эти формулы к иа: деиию центра изгиба швеллера ( 195). Примем за точку-В сере; стенки, получим для верхней п< о)=-|-й/2|, для нижней <в=—h для стенки ш = 0. Для соотве венных точек верхней и нижней лок значений х одинаковы, т< как ш одинакова но величине, но различна по знаку. Поэтому
•JxaiBdds = 0, ус = 0.
4
*282 ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. ХГ
я
Для хс получим формулу ь
V V 2 С — — t ___________V I
хс — хв^ГJxz J У 2 — Xb~^~4J\
о
§ 129. Дополнительные напряжения при кручении. Если внешние силы лежат в плоскости, не проходящей через линию центров * изгиба, то в стержне возникают напряжения кручения. Теорией ' кручения тонкостенных стержней открытого профиля мы занимались в § 90 главы VII. Более подробный /^- ........ анализ показывает, что по отношению
V ( • ~7 У/ к тонкостенным стержням задачи об >
изгибе и кручении нельзя рассматривать ,,—.------------ по отдельности, независимо одну от
6) (fe.другой. Специфика работы тонкостен-4-----------------ных стержней в реальных конструкциях
,j_____________ ставит их обычно в такие условия, ’
д) " • ~^п. г когда непосредственное применение г
~результатов § 90 невозможно. Все дело в том, что поперечные сечения тонко- *
Рис. 196. стенных стержней открытого профиля
при кручении значительно искажаются., Возможность свободного искажения поперечного сечения и объясняет малую жесткость таких стержней. Рассмотрим в качестве примера тонкостенную трубу с разрезом. Под действием крутящего момента она деформируется так, как показано на рис. 196,а. Если сварить края разреза (рис. 196,6), то возможность искажения поперечного сечения будет исключена и жесткость трубы значительно j возрастет. В случае а жесткость нужно рассчитывать по формуле для г стержня открытого профиля: „
Са=^2х№. ?
г
В случае б жесткость по формуле для тонкостенной трубы равна Cff=2n/?’6.
Предположим теперь, что левый конец разрезанной трубы заделан, а к правому приложен крутящий момент >(рис. 196,в). Левое сечение при этом не искажается, искажение правого сечения гораздо меньше, чем в случае а, потому что оно связано с продольной деформацией. Действительно, изображенное на рисунке искажение сечений стержня при сохранении одного из них плоским возможно лишь при том условии, что образующая тп укорачивается, a pq удлиняется. Продольные деформации неизбежно связаны с появлением нормальных напряжений в поперечных сечениях. Эти напряже
§ 130] ЗАКОН СЕКТОРИАЛЬНЫХ ПЛОЩАДЕЙ 283-
ния самоуравновешиваются, так как равнодействующая продольных сил в сечении должна быть равна нулю. Жесткость такого стержня, находящегося в условиях стесненного кручения, будет промежуточ<-ной между Са и Сб.
Дополнительные нормальные напряжения при кручении возникают и в других случаях. Предположим, например, что в промежуточном сечении тонкостенного стержня приложен сосредоточенный закручивающий момент. На двух смежных участках стержня-крутящие моменты оказываются различными, под действием этих крутящих моментов сечения стержня на смежных участках стремятся исказиться в различной степени. На рис. 197 показаны две части стержня»
Рис. 197.
разрезанного по плоскости приложения момента. Чтобы выполнить условие неразрывности, необходимо приложить показанные на чертеже продольные силы. Вообще нормальные напряжения получатся во всех тех случаях, когда крутящий момент меняется по длине стержня. Разница в искажениях различных поперечных сечений неминуемо влечет за собой появление этих напряжений.
Обращаясь к примерам разрезанной и неразрезанной трубы, можно понять, какие напряжения в сечении уравновешивают крутящий момент, С одной стороны, это система касательных напряжений, распределенных линейно по толщине и возникающих при обычном кручении тонкостенного стержня открытого профиля. С другой, существование нормальных напряжений, как показано в § 126, связано с существованием касательных напряжений, распределенных по толщине стенки равномерно. Эти касательные напряжения (будем называть их изгибно-крутильными) участвуют в уравновешивании крутящего момента.
§130. Закон секториальных площадей. Нам осталось облечь в аналитическую форму качественные рассуждения предыдущего параграфа. Для этого выясним прежде всего, как искривляется сечение тонкостенного стержня при чистом кручении. В § 90 была получена формула (90.3), выражающая величину касательного напряжения в стержне:
(130.1)
Здесь Q — расстояние от точки сечения до оси вращения его при кручении; а — угол между радиусом-вектором и нормалью
T=o(«'QCosa + ^)
' '..Э
284 ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [гл. хй
-к линии тока, элемент дуги которой есть и— перемещение точки сечення. Так как pcosa=p— расстояние от центра С до каса-тельной (рис. 125), то произведение q cos a ds равно удвоенной ? площади заштрихованного треугольника, то есть </<>. Применим фор* i мулу (130.1) к средней линии контура, которая при кручении сво-. «бодиа от касательных напряжений. Получим:
О d®-|- du = 0. j
Интегрируя, найдем: , ;
«(«)=—0®(s). (130.2) t
Предположим теперь, что угол закручивания меняется по длине. Некоторая точка образующей получает смещение и, бесконечно близкая точка той же образующей — смещение uA-^-dz, Относи- ~ az •
тельное удлинение элемента образующей равно
е = Х=— 0'(-И ® ($). ?
По формуле закона Гука вычислим теперь напряжение: f
о = £е== —£^'(2)®(s). (130.3)
Формула (130.3) показывает, что нормальные напряжения в попе- .? речных -сечениях тонкостенного стержня пря его стесненном кручении ’ распределяются по закону секториальиых площадей.
При применении формулы (130.3) возникает одна неясность. Дело в том, что мы ие знаем центра вращения профиля при кручении, ji который ’ нужно принять за полюс секториальиой площади. <
Из этого затруднения легко выйти, если предусмотреть наряду с кручеинем возможность одновременного растяжения — сжатия Я и изгиба стержня. Прибавим к общей формуле напряжений при Я изгибе член, даваемый формулой (130.3). Получим: Ц
а = Ах + Ву-\-С—Eft'(z)<n (s). (130.4) •>
,
При составлении этой формулы мы ие воспользовались выраже- | ннями для коэффициентов А, В и С через изгибающие моменты, f моменты инерции, продольную силу и площадь сечения, потому что мы не зиаем, является ли самоуравновешеииой система напряжений, распределенных по закону секториальиых площадей. Зато теперь мы- -« можем в формуле (130.4) принимать за полюс для секториальиой ; площади любую точку. Действительно, по формуле (128.2) получается, что изменение полюса изменяет величину секториальиой площади иа линейную функцию от координат. Эту линейную функцию можно объединить с тремя первыми членами уравнения (130.4). Таким образом, изменение полюса ие меняет вида этого уравнения, сказываясь лишь иа величине коэффициентов Л, В и С. Раз так,
ай-i-r'.V
§ 1301
ЗАКОН СЕКТОРИАЛЬНЫХ ПЛОЩАДЕЙ
285
будем руководствоваться при выборе полюса единственно лишь соображениями удобства. Поместим полюс в центре изгиба. Тогда, как известно,
J ушб ds = j хшб ds = 0. (130.5)
Очевидно, что прибавление к функции ш(«) постоянной сказывается лишь на величине С в формуле (130.4), поэтому мы вправе принять за начало отсчета секториальной площади любую точку оси профиля. Выберем эту точку так, чтобы было
Jo)6ds = 0. (130.6)
Секториальную площадь, определенную так, чтобы выполнялись условия (130.5) и (130.6), будем называть главной секториальной площадью.
Составим теперь уравнения статики для части стержня так, как это сделано в § 103.
Подставим выражение о, даваемое формулой (130.4), в уравнения равновесия:
J об d s = Nn J ay б ds= — Мх, J стхб ds — Му.
Вычисляя первый интеграл, получим:
А бх ds В j бу ds С J б ds — ЕЪ' (г) J соб ds = Nt.
Вследствие уравнения (130.6) и того, что оси х и у проходят через центр тяжести, все интегралы, кроме третьего, обратятся в нуль. В то же время
J б d s — F.
Поэтому
Г_Л«
Т‘
Аналогичным образом, принимая во внимание, что оси х и у являются главными, а также условия (130.5), найдем:
Af„ м
А = В= — ^.
J у ** X
Перепишем теперь формулу (130.4) следующим образом:
а=-^4-^4-^-^'(х)ш(5). (130.7)
286
ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[ГЛ. XI
Займемся теперь подсчетом изгибно-крутильных касательных напряжений. Воспользуемся для этого формулой (126.3). Поступая так же, как в § 126, найдем:
3 S J
§ y&ds-]-Qf-§ x&ds-J-E-^-§ a&ds. (130.8)
*0 'о о
§ 131. Уравнение стесненного кручения. Подсчитаем момент касательных сил в сечении, мерой которых служит определенное формулой (130.8) напряжение, относительно центра изгиба. Обозначая этот момент Л4Ш и поступая так, как это делалось при определении центра изгиба, найдем:
л
Л1т = j *6 «?<в. о
Сюда нужно подставить выражение т по формуле (130.8). Дело сведется к вычислению трех интегралов, причем два первых обращаются в нуль. Действительно, первый интеграл будет следующий:
h. s
§ da yfi ds. Оо ,
Интегрируя по частям, получим:
s h
a(s)^y&ds— §ay6ds = 0, о о
так как оси х и у являются главными центральными осями и за полюс при определении секториальной площади выбран центр изгиба. Совершенно аналогично показывается, что и второй интеграл равен нулю. Остается
h
Мт=\хтМа.
О
Здесь
О
Подставляя выражение тш в формулу для момента, получим:
= Eft" da <о6 ds.
О о
§ 131]
УРАВНЕНИЕ СТЕСНЕННОГО КРУЧЕНИЯ
287-
Этот интеграл следует брать по частям:
h s s Л
J da> J сой ds=a J tod ds —Jco’Sds.
0 0 0 * * 0 .
Но при подстановке пределов 0 и Л первый член обращается в нуль вследствие (130.6); Введем обозначение:
ъ. -
О
По внешней аналогии с определением осевых моментов инерции будем называть величину Jw векториальным моментом инерции.
Теперь
(131.1)
Положим
— EJwW = B. (131.2)
Величина В называется бнмоментом. Впоследствии мы покажем, что это та же величина, которая была введена в § 109. Пока что заметим, что нзгнбнв-крутнльный момент связан с .бимоментом так же, как перерезывающая сила с изгибающим моментом:
й = (1Й1.3)
Однако формула (131.3) не позволяет, например, построить эпюру бимоментов. Дело в том, что полный крутящий момент в сечении уравновешивается изгибно-крутнльным моментом лишь частично и величина последнего заранее неизвестна.
Формула (130.7) переписывается теперь в следующей симметричной форме:
МхУ , Му* , IV, , Вю Jx -Г Jy -Г F -Г •
Формула для касательных напряжений (130.8) имеет вид:
т = гг Г У& ds 4- С хб ds — С coS ds.
oJxj"' ' oJyJ
OOo
(131.4)
(131.5)
Мы уже заметили, что полный крутящий момент в сечении уравновешивается лишь частично нзгибно-крутнльным моментом 2ИШ. Кроме нзгнбно-крутнльных касательных напряжений, в сечении существуют еще обычные для тонкостенных профилей касательные напряжения, момент которых Md связан с погонным углом закручивания
288 ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [гл. XI
обычной формулой теории кручения тонкостенных стержней;
Md=bCQ. (131.6)
Здесь С—геометрическая жесткость, вычисляемая так, как указано в § 91. Уравнение моментов относительно оси есть
М» + ^=Мг(4 .
Внося сюда выражения (131.1) и (131.6), получим:
— EJ^" + СО& = Мг (z). (131.7)
Это и есть основное дифференциальное уравнение теории стесненного кручения.
Чтобы составить это уравнение, необходимо уметь вычислять секториальные характеристики сечения, то есть секториальные моменты инерции. Этот вопрос н составит содержание следующего параграфа.
ffs)
Рис. 198.
§ 132. Вычисление секториальных "характеристик. При вычислении секториальных характеристик сечения, то есть величин
. Jxwddy, Jjrtodds, J e>*dds,
для профилей, составленных из прямоугольников, приходится вычислять интегралы от произведений двух функций вида
J ф (у) ф (у) ds.
Если хотя бы одна из функций является линейной, то для нахождения этого интеграла можно приме-нить следующий простой графоаналитический прием. Строим графики, или эпюры, функций <р(у) и ф(у);
пусть ф(у) есть линейная функция (рис. 198). Находим площадь Q эпюры ф (s) и умножаем ее на ординату ф0 линейной эпюры, соответствующую абсциссе центра тяжести эпюры <р. Действительно, выбрав начало отсчета у в точке О, где линейная эпюра ф пересекает ось абсцисс, получим:
$ Ф (у) Ф (у) ds= J ф (у) ks ds.
Здесь k — угловой коэффициент линейной эпюры. Но
J Ф (у) s ds = Qsq, kst — ф„.
О
А . Направление обхода от-
§ 132] ВЫЧИСЛЕНИЕ СЕКТОРИАЛЬИЫХ ХАРАКТЕРИСТИК 289.
Поэтому
йф0.
Это замечание оказывается очень полезным для вычисления сек-ториальных характеристик. Ход выкладок лучше всего пояснить на примерах.
Предварительно сделаем одно замечание. Находя величину для двутаврового профиля, мы встречаемся с особенностью, заключающейся в том, что профиль нельзя обойти от одного конца до другого. В случае таких составных профилей нужно придерживаться i следующих правил;
1. Обход сечения производится от одной и той же точки, принятой за начало отсчета секториальиых площадей.
2. Секториальная площадь растет, если конец вектора, выходящего из полюса и вращающегося против часовой стрелки, движется в направлении обхода.
Примеры.
а) Двутавровое сечение (рис. 199). Для двутаврового сечения центр изгиба будет в центре тяжести. Примем за начало отсчета секториальиых площадей точку
дельных элементов показано стрелками. На левой половине верхней полки конец радиуса-вектора, выходящего из точки С и вращающегося против часовой стрелки, движется по направлению стрелок, причем секториальная площадь, то есть удвоенная площадь заштрихованного треугольника, растет пропорционально расстоянию от точки А. Эпюра секториальиой площади <о изобразится треугольником с наибольшей ординатой На правой стороне полки получим такой же треугольник, только отрицательный. Аналогичную картину получим на нижней полке. Для нахождения нам следует вычислить интеграл
J a* ds
для каждой половины полки и результаты сложить. Применив графоаналитический прием, сообщенный выше, мы должны взять площадь треугольника и умножить ее на величину <о в точке, соответствующей центру тяжести, и результат учетверить:
. _4 1 b Ы hb - _ЬгЬгбг — 2 2 4 ' 3 4 '°*---24~ *
10 Ю. Н. Работвов
290
ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[ГЛ. XI
Рис. 200.
б) Угловое сечение. Как уже отмечалось, центр изгиба такого сечения находится в вершине. Секториальная площадь для полюса, помещенного в центре изгиба, равна нулю, следовательно, Ую = 0. Этот же вывод справедлив для любого профиля, образованного прямолинейными тонкостенными элементами, сходящимися в одной точке, например для тавра. Такие стержни не обладают изгибно-крутильной жесткостью, сечения их при кручении не искажаются.
в) Швеллерное сечение (рис. 200). Центр изгиба для швеллера нахо-. ЫгЬг
дится на расстоянии от стенки
(см. § 128). Примем за начало отсчета секториальиых площадей середину швеллера. Двигаясь от середины вверх, мы вращаем радиус-вектор по часовой стрелке, то есть в отрицательном направлении, секториальная площадь отрицательна; она убывает по линейному закону, достигая значения Щ2 в угловой точке. Движение по полке связано с положительным вращением радиуса-вектора, значит, секториальная площадь растет. Она равна нулю в точке, расстояние которой от угла есть основание треугольника с высотой h\2 и удвоенной площадью' th]2,
следовательно, это расстояние равно t. Максимальное значение о на конце полки есть (д— t)h]2. На нижней половине швеллера картина будет антисимметрична: эпюра та же, что вверху, но противоположных знаков. Условие o>6ds = 0, как видно, выполняется, так как интеграл от со есть общая площадь эпюры. Вычислим теперь Jw. Применяя правило графоаналитического нахождения интегралов, получим:
, — оИ± А 2 (b-t)h | 1 th 2_ №1. ,
7<0 — 2 1)3 2 ' 2 2 3 2J °* ’
! 1 th h 2 th л |
• 2 ’ 2 ‘ 2 * 3 ’ 2 *
Вывод общей формулы для не имеет смысла; следует сразу вести все вычисления в числах.
г) Зетовое сечение. Выберем вспомогательный полюс в центре тяжести и начало отсчета секториальиых площадей в точке пересечении стенки и полки. Получим эпюру, изображенную на рис. 201,а. Для нахождения центра изгиба нам нужно вычислить интегралы
\ ход ds, \ уа>6 ds,
§ 132]
ВЫЧИСЛЕНИЕ СЕКТОРИАЛЬНЫХ ХАРАКТЕРИСТИК
29 Т
где х и у — координаты относительно главных центральных осей сечения, изображенных на рис. 201,5. Для х и у, рассматриваемых как функции s, можно также построить эпюры, они приведены на рис. 201, в, г. Существенно, что эпюры х и у антисимметричны. При нахождении интеграла
\ xcoS ds
нам придется вычислять интеграл от произведения тех же функций
Рис. 201.
с одинаковыми знаками на верхней полке, с разными — на нижней. Поэтому -
^XG>Sds==0. Аналогично ,
yab ds~Q.
Следовательно, по формулам (128.3) центр тяжести зетового сечения является центром изгиба. Для эпюры секториальных площадей не выполняется условие fa>Sds=O. Поэтому нужно изменить
10*
292
ИЗГИВ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[ГЛ. XI
начало отсчета секторнальных площадей. Прибавим к секториальной площади и ($) постоянную величину с таким образом, чтобы было
J (<о— c)6ds=Q
Или
Й'ЛЙ, —c[2Z>S,4-/tSJ=O.
Отсюда
с~ 2&6.4-Л6/
Эпюра главной секториальной площади (со — г) представлена на рис. 201,д.
д) Труба с разрезом (рис. 202). Выбрав вспомогательный , полюс в центре и цачало отсчета секториальной площади при ф = О,
получим:
(0в=ф/?8, x = 7?cosq>,
^ = /?зшф, Jx=nR*i).
Вычисляем интеграл, входящий в первую из формул (128.3):
2х
J yo>BS ds=6R* У <р 51Пф </ф=—2лй/?*.
О
По формуле (128.3)
____
хс~~ nW-
— 2R.
Перенесем полюс в центр изгиба. По формуле (128.2)
<пс = ф₽* 27?у = /?' (ф -|- 2 шп ф).
Осталось выбрать начало отсчета секториальной площади так, чтобы было
\ ad ds = 0.
Очевидно, что это условие будет выполнено, если принять за начало отсчета середину дуги, то есть заменить угол ф углом ф, меняющимся от —л до -|-л:
®=₽*(ф + 2 sin ф).
Вычислим теперь секториальный момент инерции:
С V
Jm = j a>*d ds = /?’d j (ф4-25Шф)'</ф==
— я 9
= У ₽5бл (л* — 6) =5= 8,11/?5б.
§ 133] СТЕРЖЕНЬ, НАГРУЖЕННЫЙ ВИМОМЕНТОМ 293
§ 133. Стержень, нагруженный бнмоментом. Перепишем уравнение (131.7) следующим образом:
V — k*Q = —(133.1)
Здесь
Уравнение (133.1) вполне аналогично изученному в § 124 уравнению изгиба при наличии продольной силы. Общий интеграл его напишется так:
0=0 (0) ch kz + 0' (0) 1 sh kz — у j sh k (z — g) dg. (133.2)
о ш
Чтобы выяснить граничные условия, вспомним, что искажение поперечного сечеиня по формуле (130.2) зависит от О. Поэтому, если сечеиие вынуждено оставаться плоским, для него 0 = 0. Нормальные напряжения зависят от бимомента, который в свою очередь выражается через Ф'. Поэтому если в сеченин нет нормальных сил, то для него Ф' = 0.
Применим уравнение (133.2) к стержню, на который не действуют крутящие моменты и, следовательно, Л1г=0 всюду. Пусть стержень имеет достаточно большую длину. Требуя, чтобы величина стремилась к нулю по мере возрастания г, получим:
fl(0)4-l<F (0) =0.
Поэтому
0 = 0' (0) у [sh kz — ch kz\.
Продифференцируем 0 no z и вспомним определение бимомента (131.2). Умножая О' (г) на EJW, получим:
B=B(0)[chte —shte]-+B(0)e-fa. (133.3)
Мы установили закон затухания бимомента по мере удаления от торца. Если к стержню не приложены изгибающие моменты, то в каждом сечении действуют нормальные напряжения
а=-,_
* ш
затухающие по экспоненциальному закону в зависимости от координаты г. Чтобы создать такое напряженное состояние, к торцу нужно приложить силы, распределенные пЪ закону секториальных площадей:
_В(0)со о, — J (D
294 ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [гл. XI
Фактически внешние силы никогда не бывают распределены по закону секториальиых площадей. Чтобы выяснить, что такое В(0) и каким образом можно приложить бимомеит в торцевом сечении стержня, обратимся к случаю изгиба. Пусть к торцу стержня приложены нормальные силы р (s) иа единицу площади сечения. При изучении изгиба нас не интересует конкретный способ осуществления нагрузки: напряжения на некотором расстоянии от сечения распределяются по закону плоскости. Это можно пояснить следующим образом. Рассмотрим систему трех функций:
1, x(s), y(s).
Поскольку х и у — главные оси, эти три функции ортогональны с весом 6(s). Это значит, что
J1 -х (s) 6 (s) ds — J 1 -у (у) б (s) ds — У х (sj у (s) б (s) ds—0.
Поставим задачу аппроксимировать функцию нагрузки р (s) с помощью линейной комбинации этих трех функций:
p(s)=^-l — ^x(s) + ^y(s) + R(s). (133.4)
Остаток R (s) должен быть ортогональным ко всем трем функциям системы. Поступая, как обычно при определении коэффициентов Фурье, а именно умножая уравнения (133.4) на 1 • б (х), x(s)6(s), у($)б($) и интегрируя от s==0 до s—h, получим:
Nz = J бр ds, — Л4Х = J брх ds, 714^,= ^ Spy ds.
Обычная теория изгиба основывается иа том факте, что часть нагрузки, даваемая первыми тремя членами формулы (133.4), передается как угодно далеко по стержню, не затухая. Статически уравновешенная часть нагрузки /?($) затухает весьма быстро, и с ней на некотором расстоянии от торца можно уже не считаться.
В теории тонкостенных стержней к введенным функциям добав- ’ ляется четвертая, ортогональная к ним функция, а именно- co(s). Ортогональность обеспечивается выполнением условий (130.5), (130.6):
буш ds — § бхш ds= So ds= 0.
Определив некоторую полную систему функций от $, мы можем представить р (s) разложением по этим функциям. В теории изгиба тонкостенных стержней представляют интерес только четыре функции: 1, х (s), y(s), ® (s). Нагрузка p(s) может быть аппроксимирована следующим образом:
. ._Ng . Мх . Му । В । _ . ,
= 7^.у + -/х +т-со + Я! ($)•
§ 133] СТЕРЖЕНЬ, НАГРУЖЕННЫЙ БИМОМЕНТОМ 295
Умножая обе части этого равенства на Seo (у) и интегрируя, получим:
В = J р (у) о (у) б (s) ds. (133.5)
Особо нужно остановиться на том случае, когда к торцу приложены сосредоточенные силы. Интеграл вырождается при этом в конечную сумму:
(133.6)
V
Рассмотрим четверку сил, введенную нами в § 109. Выберем произвольный полюс С (рис. 203) и будем определять бимомент по формуле (133.6). Приняв точку 1 за начало отсчета секториальной площади, обозначим площади заштрихованных треугольников уйр-g- Йх, у Йх. Тогда в точке 1 со, = 0, в точке 2
®х = Йп в точке 3 со, —й, Йх, наконец, в точке 4
—й14-йхйх.
Вспомним, что в точках /, 2, 3, - >>
Р4, причем Рг и Р, равны —Р, а Р2 и Pt равны -J-P. По формуле (133.6) получим:
в=рй,—р (й,+йх)+р (й,+йх+йх)=р (й, 4- йх).
Но, как видно из чертежа,
Й, 4” йх = hd.
Таким образом,
B=dhP. (133.7)
Этот результат совпадает с определением бимомента, данным в § 109. Формула (133.3) решает поставленную там задачу, причем существо дела нужно представить себе следующим образом. В сечении, весьма близком к торцу, решающую роль играют местные напряжения от приложенных сил, но уже на некотором, сравнительно небольшом (порядка поперечного размера) расстояний от торца они становятся распределенными по закону секториальных площадей. В данном случае это то же, что закон плоских сечений для каждой
4 поиложены силы
296 ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XI
полки в отдельности. По мере удаления сечения от торца эти нормальные напряжения затухают по закону (133.3). Помимо этого, в сечениях возникают также касательные напряжения двух родов. С одной стороны, это изгибно-крутильные напряжения, которые можно найти по формуле (130.8). Так как со на каждой полке зависит линейно от координаты у, то легко сообразить, что эти напряжения существуют только в полках и распределяются по закону параболы. Кроме того, в сечении возникают обычные напряжения кручения.
§ 134. Некоторые примеры стесненного кручения. Общее реше-
ние задачи о стесненном кручении тонкостенного стержня дается формулой (133.2). Величина Мг(г} представляет собою крутящий момент в сечении с координатой г, который определяется аналогично
Рис. 204.
изгибающему моменту в теории изгиба: это есть сумма моментов относительно оси z всех сил, действующих слева от сечения с координатой г, или сумма сил, действующих справа от сечения, взятая с обратным знаком. В реальных конструкциях на стержни
действуют или сосредоточенные моменты, или моменты, равномерно распределенные по длине. На рис. 204 схематически показан стержень, загруженный моментом М в сечении с координатой z—а и не-
прерывно распределенным моментом интенсивности т на единицу длины на участке b^z^c. Крутящий момент, создаваемый сосредоточенным моментом М, равен ЛГф0 (z — а). Действительно, этот момент равен нулю при г<^а и равен М при z^>a.
Крутящий момент от распределенного момента т равен нулю при 2<Ь, равен m{z— b) при b^z^c и сохраняет постоянное значение т{с — Ь) при г<^с. Это можно записать следующим образом:
Л«г= Ж [Ф1 (z — Ь) — ф, (г — с)].
Чтобы применить формулу (133.2), нужно вычислить интегралы от функций ф0 и фп умноженных на sh k (z — £). Но эти интегралы вычислялись в § 124. Поэтому при сделанных ограничениях нагрузки формулу (133.2) можно переписать следующим образом:
1 1 л I
6' = 6'(0) chkz-f-(0)~-sh&3 — У, \ Af [chfc (z — a)— 1]-|-
-f-m jysh£(z — b) — (z — b)—-^-sh&(z — c)-{-(z— c)j|. (134.1)
Нам понадобятся еще выражения для бимомента В= —EJm®', для нзгибно-крутильного момента —— EJ^W — B' и для угла
§ 134]
НЕКОТОРЫЕ ПРИМЕРЫ СТЕСНЕННОГО КРУЧЕНИЯ
297
поворота сечения Ф = <р0 + О (z) dz\
О
— j^-=O (0) k sh fez4~O' (0) ch kz — у1 {Affe sh fe(z— a) 4~
4-m[chfe(z — b) — 1] — m[chfe(z — c)— 1]}, (134.2)
— gp- = Oofes ch kz 4- O' (0) A sh fez — сб ch fe (z — a)4~ -|-mfeshfe(z—b)— mkshk(z — c)}, (134.3)
ф = ф (0)4~O (0) -i-sh fez-j-fl' (0) (ch kz—1) —
—[т8Ь*^—а)—a)] +
+m r^chfe(z-ft)-±-^^l-I К К I
-m [lchfe(z-C)-l-(-^^]}. (134 4)
Выражения, заключенные в квадратные скобки в формулах (134.2) и (134.4), должны считаться равными нулю при z<^a, z<^b или z<^e соответственно. Символ «л», поставленный над знаком суммы, указывает, что, например, в формуле (134.2) член chfe(z — b} пишется только тогда, когда z^>Z>; сделанная оговорка заставляет отбрасывать при z<^b и стоящую рядом отрицательную единицу. Более корректная и исключающая всякую, неясность запись была бы следующей:
— (°)k sh fez -j- О' (0) ch fez—у1 {Mkk sh fe (z—а) ф0(г—a)
4-m[chfe(z — Z>)—l]q)0(z — Z>) —
— m[chfe(z — c) — l]<p0 (z — c)}. (134.2')
Здесь фа(г) = 0 при z<^0 и ф0(г)=1 при z>0. Для определения постоянных 0(0) и 0'(0) необходимо помнить, что 0 = 0 в
том сечении, которое не искривляется, а О' = 0 там, где нет нормальных напряжений.
Пример 1. Тонкостенная трубка разрезана вдоль образующей на длине I и закручи-
I
вается приложенными иа концах рис g05
моментами. Требуется определить
угол закручивания (рис. 205). Считаем неразрезанные концы трубки бесконечно жесткими и соответствующие сечения неискривляющимися.
298 ИЗГИВ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [гл. XI
Тогда Ф (0)=$(()=0. По формуле (134.1) получаем:
О = 0'(О)1 shAZ—-1Л1[сЬА/— 1]. к l^(j
Отсюда
А' (ch kl—1)
CG shkl •
Теперь мы можем определить полный угол закручивания по формуле (134.4), подставив в нее найденное значение О' (0), положив Ф (0) = 0 и г=1 и удержав член, соответствующий сосредоточенному моменту М при z=0. Получим:
Ф =
2 chAZ —
k^ sh kl
Если бы трубка была разрезана по всей длине (нестесненное кручение), связь между углом закручивания и моментом была бы следующей:
Ml 4>~CG'
Стеснение кручения повышает жесткость, в полученной формуле как бы фигурирует уменьшенная длина трубки. Величина А = СО/£УШ для разрезанной трубки равна g-L tyR*. Если Z5=£> 1/А, то выражение, заключен-, ное в квадратную скобку в формуле для *ф, мало отличается от Z; если Z мало по сравнению с 1/А, гиперболические функции можно разложить в ряды. Удерживая первые неуничтожающиеся члены, получим:
Рис. 206.
МР
Бимомент достигает наибольшей величины в концевых сечениях трубки:
В(0)=В(П=-Е7.«'(0)=-?£!!Йг.
По формуле (131.4)
о = =у- R* (Ф + 2 sin ф).
J tt> J ш
На рис. 206 построена эпюра нормальных напряжений для концевого сечения. Отложенная по радиусу величина представляет собою sh kl
-Л— —- Наибольшее значение нормального напряжения дости-
М ch kl — I
§ 134] НЕКОТОРЫЕ ПРИМЕРЫ СТЕСНЕННОГО КРУЧЕНИЯ
гается при ф = ±120° (или ф —60°);
299
°тах=1>50
М sh kl М* ch А/ - Г
Аналогичным образом можно подсчитать крутильные и изгибно-крутильные напряжения.
Пример 2. Балка швеллерного сечения равномерно загружена по поверхности верхней полки; эту равномерную нагрузку можно заменить нагрузкой вдоль линии, проходящей по середине полки. Таким образом, линейная нагрузка q приложена в плоскости, проходящей через середины полок (рис. 207). Крутящий момент на единицу длины равен моменту этой нагрузки относительно оси, проходящей через центр изгиба: т—^(<-}-&/2); Здесь t — расстояние от* середины стенки до центра изгиба. Будем считать, что балка имеет длину /, концы ее шарнирно оперты и не могут поворачиваться относительно оси г, но оии могут свободно перемещаться вдоль оси г; нормальные напряжения, а следовательно, и бимоменты равны нулю на концах.
Для нахождения бимомента воспользуемся уравнением (134.2), положив в нем •&' (0) —0. Из условия В(/) = 0 получим:
. ь_ m rchfel-11 “r~CG [ sh kl J
и, следовательно,
shto-ch^+l ].
Рис. 207.
Наибольшее значение бимомента достигается в середине балки при z=//2:
о ____т. / «___1_\
"max кг Ы •
' \ сМ
В этом же сечении будет наибольший изгибающий момент.
Для того чтобы оценить значение секториальных напряжений, укажем, что для швеллера № 20-а при длине балки 2 ли нагрузке 9 = 35 кг/см наибольшее напряжение от Мх равно 982 кг]см\ а от бимомента 140 кг]см\ причем эти напряжения складываются. Секториальные характеристики для стандартных профилей приводятся в литературе (см., например, «Расчеты на прочность в машиностроении», г. 1, Машгиз, 1956).
ГЛАВА XII
УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ
§ 135. Постановка вопроса об устойчивости. Как оказывается, при некоторых определенных значениях внешних сил упругая система может иметь несколько положений равновесия, причем одни из них будут устойчивыми, другие неустойчивыми. Для выяснения этого вопроса обратимся к примеру стержня, сжатого силой Р (рис. 208). Прямолинейная форма стержня в этом случае всегда является формой возможного равновесия. Для суждения об устойчивости ее предположим, что мы приложили к стержню некоторую поперечную силу и деформировали стержень, произведя прогиб v (z). При этом мы затратили работу А. Пра
вый конец стержня сместился на величину Д. Работа А пошла на накопление потенциальной энергии деформации стержня U. В то же время сила Р совершала работу на перемещении А. Эта работа положительна, так как направления силы и перемещения совпадают. Поэтому сила Р как бы помогает прогибу стержня, и уравнение работ будет следующее:
A=U—Р-Ь. (135.1)
Теперь могут представиться два случая. Если сила Р невелика, мы имеем:
У>Р-Д. (135.2)
Величина А положительна, значит, для искривления стержня нужно затратить некоторую работу. В искривленном состоянии запас потенциальной энергии деформации превышает ту величину, которая необходима для преодолении сопротивления силы Р на пути А, то есть для распрямления стержня. Если, наоборот, сила Р велика, то i/<P-A. (135.3)
§ 136] УСТОЙЧИВОСТЬ СЖАТОГО УПРУГОГО СТЕРЖНЯ 301
Величина А отрицательна, значит, стержень сам прогибается от действия силы Р, и поперечная сила представляет собою силу сопротивления; ее нужно приложить, чтобы прогиб происходил не слишком быстро. В искривленном состоянии запас энергии недостаточен для распрямления стержня. Если выполнено неравенство (135.3), то одной и той же силе соответствуют два состояния равновесия, но прямолинейное состояние неустойчиво: если стержень вывести из него, он выпрямиться не сможет. Условие перехода от устойчивого состояния к неустойчивому будет следующее:
t/=PBA. (135.4)
Сила Рк называется критической силой.
К вопросу об устойчивости можно подойти и иначе, не обращаясь к энергетическим соображениям. Составив дифференциальное уравнение изгиба стержня под действием продольной силы, поставим задачу о том, при каких условиях решение этого уравнения не единственно, то есть возможно существование различных форм равновесия. Ход рассуждений лучше всего проследить на примере.
§ 136. Устойчивость сжатого упругого стержня. Решим теперь задачу, поставленную в предыдущем параграфе, с помощью метода, схема которого была дана в конце параграфа. Изгибающий момент в сечении с координатой z есть — Pv(z). Поэтому дифференциальное уравнение изгиба будет
EJxv"-{-Pv=0. (136.1)
Присоединим к нему граничные условия
о(0)=о(/) = 0. (136.2)
Уравнение (136.1) при граничных условиях (136.2) имеет очевидное тривиальное решение о=0, соответствующее прямолинейной форме равновесия. Нас интересуют ненулевые решения. Положим
и перепишем .уравнение (136.1) так:
Его общий интеграл
v(z)=>Asinkz-[-Bcos kz. (136.3)
Из первого граничного условия
В=0,
из второго
Д sinW=0.
(136.4)
302 УСТОЙЧИВОСТЬ УПРУГОГО и пластического равновесия (гл. XII
Если принять Д = 0, то мы получим снова тривиальное решение. Полагая и
sinA/=0, (136.5)
найдем те значения силы, для которых существует ненулевое решение. Из уравнения (136.5)
kl=rm.
Следовательно,
(я=1, 2, ...). (136.6)’
Это так называемая формула Эйлера для критической силы. Если Р=РВ, Ау^О, то прогиб по формуле (136.3) будет
v (z} — A sin у.
Таким образом, мы установили, что если величина силы принимает дискретные значения, даваемые формулой (136.6), то возможны искривленные состояния стержня, имеющие форму синусоид. Очевидно, что Jx должен быть наименьшим из главных моментов инерции.
Результаты произведенного анализа с физической точки зрения не могут нас удовлетворить. Константа А, определяющая величину прогиба, остается совершенно неопределенной, значит, одной и той же силе Рк соответствует произвольный прогиб, равновесие оказывается безразличным. Далее, предположим, что сила больше первой критической силы, соответствующей значению я=1, и меньше второй, получающейся при п = 2. Энергетические соображения § 135 убеждают нас в том, что стержень при этом искривится и прямолинейная форма равновесия существовать не может. Рассуждения же настоящего параграфа в этом случае не обнаруживают никаких иных форм равновесия, кроме прямолинейной, и не позволяют ничего сказать о ее неустойчивости. Причина всех этих несообразностей заключается в том, что уравнение (136.1) представляет собою не точное уравнение изгиба под действием продольной силы, а приближенное.
§ 137. Эластика Эйлера. Рассмотрим задачу, поставленную в предыдущем параграфе, в точной постановке. Напишем дифференциальное уравнение изгиба так:
EJxx=t — Py.
Кривизна х изогнутой оси равна dtyds, где 6 — изображенный на рис. 209 угол между касательной к изогнутой оси стержня и осью, проходящей через его концы.
§ 137)
ЭЛАСТИКА ЭЙЛЕРА
303
У равнение изгиба будет следующим:
-£ = -*>• (137.1)
Здесь k* то же, что и в § 136.
Продифференцируем уравнение (137.1) по $, заметив, что
^==sin6,
aS
Получим:
лгл
^=—fc’sinO. (137.2)
Уравнение (137.2) интегрируется квадратурами обычным спосо
бом. Запишем его так:
______________fe‘sin0 У — 2 35 W А sln0- У
Заметим, что преобразование левой части вполне аналогично преобразованию левой части уравнения движения при выводе теоремы живых сил.
Разделяя переменные и интегрируя, найдем:
(jJY=2А‘ (cos 0 — cos 0О).
Рис. 209.
Мы воспользовались здесь граничным условием: при $ = 0 х = 0 и 0=0..
Перейдем в этом выражении к половинным углам по формуле
0 cosO= 1 —2 sin’ g-.
Получим:
slnsin’у).
Сделаем замену переменной, приняв в 9.
sin-=-== sin ~ sin ф. w л
Это всегда выполнимо, потому что 6^0в.
Дифференцируя (137.4), найдем:
9 л 9 • 90
COS V 3 9-= Sln V C0S Ф d(f‘ 4 Л Л
(137.3)
(137.4)
304 УСТОЙЧИВОСТЬ УПРУГОГО и пластического РАВНОВЕСИЯ [гл. XII
Преобразуем к новой переменной выражение (137.3). Получим, разделяя переменные:
л 1
“37-5>
Положим «о sin у=т.
Заметим, что при у = 0 6 = 6О и ф = л/2. Поэтому, интегрируя левую часть от нуля до s, правую от л/2 до ф, будем иметь:
1 f *Р
k J У1 — тг sin2 <р *
к/г
Знак минус выбран для того, чтобы было s > 0. Это эллиптический интеграл первого рода, то есть табулированная функция. Принимая обычные обозначения эллиптических интегралов:
к/1
Г=( ....
J у 1 — т2 sin2 ф ’ о
г(ф)= C-y=JL=
J У1 — m2 sin2 ф ’ о получим:
ks=— F(q>)-yF.
При s = //2 6 = 0 в силу симметрии, а следовательно, и ф = 0. Поэтому
Р=^. (137.6)
Из этого уравнения определяют неизвестную величину т, связанную с углом наклона касательной на конце стержня. Теперь можуо найти координаты точек изогнутой оси стержня х и у, отправляясь от равенств
dx a du и
j- = sin 6, -/ — cos 6.
ds ’ ds
Перейдем к независимой переменной ф, пользуясь (137.4) и (137.5). Получим:
dx = sin 6 ds —-----£- sm ф t/ф,
d у — cos 6 ds = — у
1
2 p^l — m* sin’ ф
У1 — m2 sin2 Ф .
§ 138] КРИТИЧЕСКИЕ СИЛЫ ПРИ ИНЫХ ВИДАХ ЗАКРЕПЛЕНИЯ СТЕРЖНЯ 305
Интегрируя и принимая во внимание, что х=у = 0 при ф=л/2, получим параметрические уравнения изогнутой оси:
2m
X = -J- COS ф, j (137.7)
y=i [2 (E-E(4Y) - (E- F (ф))].
Здесь
f
E (ф) = J V 1 — nF sin2 ф б/ф 0
—эллиптический интеграл второго рода;
£(f)=£-
Обратимся теперь к исследованию уравнения (137.6).
Полный эллиптический интеграл F не может быть меньше чем л/2; это значение достигается при да=0. Поэтому если А/^>л, то это уравнение не имеет решения; единственно возможная форма равновесия— прямолинейная. Но kl—a, если
р___р — n?EJ
г— к.— р '
Это—первая критическая сила.
Таким образом, искривленная форма равновесия возможна тогда, когда Р>РК. При этом каждому значению Р соответствует совершенно определенное значение т по уравнению (137.6) и определенная кривая прогиба — эластика Эйлера, даваемая уравнениями (137.7). Прогиб растет по мере увеличения нагрузки весьма быстро, как показано на рис. 209.
Теперь понятно, почему мы могли обнаружить криволинейные формы равновесия при Р> Рк только с помощью точных уравнений. Для этих форм прогибы велики, а приближенное линеаризированное уравнение годится лишь для малых прогибов.
§ 138. Критические силы при иных видах закрепления стержня. Сравнение точного решения с приближенным убедило нас в том, что вопрос о критических силах в линейной постановке решается правильно. При этом реальный смысл, конечно, имеет только первая критическая сила. Итак, для стержня с шарнирно закрепленными концами
При потере устойчивости на длине стержня укладывается одна полуволна синусоиды.
806
УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ • [гл. хи
На практике встречаются иные способы закрепления концов. Так,
если стержень жестко защемлен на одном конце, а другой конец
оставлен свободным, то задачу
Рис. 210. Рис. 211.
можно привести к предыдущей, как показано на рис. 210. Подставляя в формулу (138.1) 2/ вместо I, получим:
Р =
* (27^
(138.2)
На длине стержня укладывается половина полуволны синусоиды.
Этими двумя примерами исчерпываются статически определенные задачи об определении критических сил. В качестве примера задачи статически неопределенной рассмотрим следующую. Один конец стержня жестко заделан, другой закреплен шарнирно.
При искривлении стержня в шарнире возникает реакция R, поэто-
му дифференциальное уравнение изгиба принимает вид:
EJif — — Pv—Rz
(см. рис. 211). Это неоднородное уравнение продольно-поперечного изгиба, полученное нами в главе X. Перепишем его так;
if k*v = — COZ-
Интеграл этого уравнения
V (z) — С, sin kz Ct cos kz—j^z. (138.3)
Прогиб v линейно зависит от трех постоянных: Сл, Сг и Со. В то же время прогиб удовлетворяет трем граничным условиям:
v (0) = v (/) = if (/) = 0.
Граничные условия однородны, то есть не содержат свободного члена. Поэтому, подставляя (138.3) в граничные условия, мы получим систему однородных уравнений для трех постоянных Со, С, и Ct. А эта система имеет нетривиальное решение тогда, когда определитель ее равен нулю. Это и есть условие для нахождения критической силы. Составим эти уравнения:
04-Ct = 0, ClSin«4-C±cosW—^ = 0,
CtcosW — Сгsinkl — ~—0, ,
§ 139] ПОТЕРЯ УСТОЙЧИВОСТИ ЗА ПРЕДЕЛОМ УПРУГОСТИ 307
Исключая постоянные, получим: tg kl — kl = 0. Наименьший корень этого уравнения «=4,49. Критическая сила р_(4,49)* к— 1* '
Приводя ее к тому же виду, что формулы (138.1) и (138.2), найдем:
D я*EJ 2nsEJ Z1QQA\
P‘=i0j7j*- = —Р~' (138Л)
Случай стержня, жестко’ заделанного иа двух концах, решается совершенно так же, нужно 1
только ввести в рассмотрение----------------------------------
кроме реакции еще концевой --------------—I*-*'*
момент. Тот же результат можно получить гораздо про- Рис- 212-
ще, если заметить (рис. 212), что упругая линия такого стержня может быть составлена из четырех половинок полуволны синусоиды. Поэтому
= (138-5)* (2 z)
Объединяя все эти формулы, примем p.=-w--
Здесь [л — коэффициент приведения длины.
§ 139. Потеря устойчивости за пределом упругости. Формула Эйлера для критической силы (138.6), очевидно, применима только тогда, когда материал следует закону Гука. Однако может случиться, что сила, определенная по формуле Эйлера, вызывает в материале сжимающие напряжения, превышающие предел пропорциональности. Этим, в частности, объясняется плохое совпадение с опытом, обнаруженное в раниих экспериментах по проверке эйлеровой теории устойчивости. Чтобы судить о пределах применимости формулы Эйлера, придадим ей несколько иной вид. Для этого разделим обе части формулы (138.6) иа площадь поперечного сечения стержня F. Слева мы получим критическое напряжение ак. Величина J\F представляет собою квадрат радиуса инерции I сечения (см. § ПО).
308 УСТОЙЧИВОСТЬ УПРУГОГО и пластического равновесия [гл. хн Введем безразмерную величину А, называемую гибкостью стержня:
х=т-
Формула Эйлера перепишется следующим образом:
= (139.1)
Для длинных и тонких стержней А велико, следовательно, критическое напряжение мало. Предельным для применения формулы (139.1) случаем будет тот, когда ак равно пределу пропорциональности оп. Формула (139.1) справедлива тогда, когда
Так, например, для малоуглеродистой стали при <тп = 2000 кг 1см* предельное значение А равно приблизительно 100.
У более коротких стержней потеря устойчивости происходит при напряжениях, превосходящих предел пропорциональности, то есть в пластической области. Состояние пластического тела, в отличие от состояния упругого тела, зависит не только от мгновенных значений нагрузок, но и от порядка их приложения. Поэтому, если для упругого стержня возможна лишь единственная постановка вопроса устойчивости и сила Эйлера является единственной критической силой, в пластической области возможны различные определения неустойчивости и, следовательно, различные критические силы.
Первые решения задачи об устойчивости сжатого стержня за пределом пропорциональности (Энгессер, Ясинский, Карман) относятся к следующей постановке. Стержень нагружается центральной сжимающей силой, принимаются меры для того, чтобы не произошло выпучивания в процессе нагружения. Когда сила достигает значения Р, она удерживается постоянной и стержню сообщается малый прогиб. Равновесие стержня под действием силы Р устойчиво, если этот прогиб исчезает после устранения вызвавшей его причины, и неустойчиво, если прогиб увеличивается до тех пор, пока не установится новая форма равновесия стержня с искривленной осью. Приближенное исследование, основанное на линеаризированном уравнении изгиба, по существу не позволяет решать вопрос об устойчивости или неустойчивости какой-либо формы равновесия, это исследование дает возможность найти такое значение нагрузки, при котором равновесие является безразличным. Именно этой задачей было фактически заменено исследование устойчивости упругого стержня в § 136.
Итак, предположим, что сжимающее напряжение в стержне есть о. Будем считать, вопреки обыкновению, сжимающие напряжения положительными. Предположим теперь, что стержень изогнулся.
§ 139] ПОТЕРЯ УСТОЙЧИВОСТИ ЗА ПРЕДЕЛОМ УПРУГОСТИ 300
Рассматривая потерю устойчивости по отношению к малым возмущениям, введем в рассмотрение изменение напряжения бо. Так как ве-
личина сжимающей силы при потере устойчивости остается неизмен
ной по предположению, то в одной в другой бо<^0. Там, где бо^>0, мы двигаемся вверх по диаграмме сжатия (рис. 213). Если бо достаточно мало, элемент дуги можно заменить элементом касательной и принять.
6o=Et6e. (139.2)
Здесь Et = da ide— касательный модуль
В области, где бо 0, происходит разгрузка и зависимость между приращением напряжения и при-
части сечения будет бо^>0.
ращением деформации изображается прямой, параллельной начальному, упругому участку диаграммы (рис. 213). Поэтому здесь
бо=Ебе.
(139.3)
, что при потере
Рис. 214.
Будем предполагать сечение симметричным (рис. 214) относительно плоскости наименьшей жесткости, устойчивости справедлив закон плоских сечеиий; поэтому бе = хт], где т] — расстояние точки, принадлежащей сечению, от нейтральной оси лл, положение которой заранее неизвестно.
Так как сжимающая сила при потере устойчивости по предположению остается постоянной, то
j6odF=0. (139.4) F
Ось лл делит сечение на две части, в одной из этих частей справедливо соотношение (139.2), в другой — соотно
шение (139.3) между бо и бе. Разобьем интеграл в условии (139.4) соответственно с этим на два интеграла, заменим в них бо через бе и воспользуемся законом плоских сечений. Получим;
Et J хт] dF-]-Е J хт] dF=0, A /=•>
или
—£S, = 0. (139.5)
310 УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ [гл. XII
Здесь 5, и 5,— статические моменты площадей F, и Ft относительно оси пп (оба считаются положительными).
Вычислим теперь момент относительно оси пп, создаваемый дополнительными напряжениями ба:
б/И == J бегу dF=х [EtJx £/,]. (139.6)
F
Здесь и J, — моменты инерции площадей Fx и Ft относительно оси пп. Формула (139.6) выражает зависимость между изгибающим моментом и кривизной. В упругой области эта зависимость дается следующим соотношением:
&M=EJxn. (139.7)
Здесь Е — модуль упругости, Jx — момент инерции относительно центральной оси х. Перепишем формулу (139.6) таким образом, чтобы
она выглядела анологично вышеприведенной, а именно:
(l-Qh
bM—KJxn. (139.8)
Величина К называется приведенным моментом или модулем Кармана, при этом
K==EtJi+E\ (139.9) Jx
Как видно, приведенный модуль зависит не только от материала, но и от формы поперечного сечения. Теперь можно рассматривать
потерю устойчивости сжатого стержня совершенно так же, как потерю устойчивости в упругой области (§ 136). В дифференциальном уравнении изгиба (136.1), полученном,на основе соотношения (139.7) между моментом и кривизной, в соответствии с (139.8) нужно будет заменить модуль упругости Е модулем Кармана К. В результате для критического напряжения вместо формулы (139.1) получается сле-
дующая:
а“~' X*
(139.10)
Величина Et зависит от положения точки иа диаграмме сжатия, следовательно, от напряжения ок. Таким образом, приведенный модуль К является также функцией <тк; эта величина находится в результате решения уравнения (139.10).
Вычислим приведенный модуль для прямоугольного сечения с высотой h и шириной ft (Л «С ft). Пусть высота зону догрузки будет £Л, высота зоны разгрузки (1—|)Л (рис. 215). Тогда
§ 140] ПОТЕРЯ УСТОЙЧИВОСТИ ЗА ПРЕДЕЛОМ упругости (продолжение) 311
Подставляя эти выражения в уравнение (139.5), получим: r£t-(l—£)*£=0.
Отсюда следует: ?—________________________1 ...
Момент инерции всего сечения относительно оси х равен bh’jW,, моменты инерции частей сечения относительно оси лл
, _Л’А’ з > --з •
По формуле (139.9) модуль Кармана
/С==4 Г(1 — g)’+M Е. | G |
Подставив сюда значение найдем:
„ *EEt -
(139.11)
§ 140. Потеря устойчивости за пределом упругости (продолжение). Исследование устойчивости сжатого стержня приводит к установлению некоторой зависимости между критическим напряжением н гибкостью. Пока напряжение меньше предела упругости, эта зависимость дается формулой (139.1), за пределом упругости — формулой (139.10), если считать справедливой ту постановку задачи,, для которой она была получена.
Будем откладывать критическое напряжение по оси ординат,, гибкость—-по оси абсцисс. Для напряжений, меньших чем предел, упругости, формула (139.1) дает кривую гиперболического типа (рис. 216). Для напряжений, больших чем предел упругости, кривая построена по формуле (139.10). Для построения нужно иметь точную диаграмму сжатия материала, пользуясь этой кривой, можно для данного сечения определить приведенный модуль как функцию сжимающего напряжения. При построении кривой удобно вычислять гибкость А, задаваясь различными значениями сжимающего напряжения.
В первой работе Энгессера (1889 г.) формула для критического, напряжения отличалась от формулы (139.10) тем, что в ней вместо приведенного модуля К фигурировал касательный модуль Et. На возможность образования зон разгрузки при потере устойчивости обратил внимание Ф. С. Ясинский, после чего Энгессер переработал свою теорию и ввел приведенный модуль К. Совсем недавно, в 1947 г., старое решение Энгессера, отброшенное самим автором, получила новое освещение в работе Шенли. Представим себе, что стержень нагружается непрерывно возрастающей силой; когда сила достигает
312
УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ [гл. XII
некоторого значения Ро, стержень начинает искривляться, но одновременно с искривлением происходит дальнейшее сжатие, так как сила продолжает увеличиваться. В результате разгрузка никогда не происходит, напряжения растут во всех точках сечения, быстрее с вогнутой стороны и медленнее с выпуклой. Зависимость между приращениями напряжения и деформации определяется поэтому касательным модулем Et. В результате критическое напряжение находится
из следующего уравнения:
0=2^1
« А,1
(140.1)
На рис. 216 приведена и вторая кривая, нию (140.1). Опытные точки ложатся ближе
рассчитанная по уравне-к этой второй кривой.
Рис. 216.
В постановке Шенли вопрос об устойчивости сводится к вопросу о бифуркации, то есть разветвлении форм движения. Пока сила меньше, чем Ра, прн увеличении силы наблюдается одна-единственная форма движения стержня, а именно его равномерное сжатие. При Р> Ра возможны две формы движения: либо равномерное сжатие, либо непрерывное выпучивание; при этом каждому значению силы Р~^>Ра соответствует вполне определенная величина прогиба. Действительно, хотя при выводе формулы (140.1) мы воспроизводили тот же ход 1рассуждения, который привел нас к формуле Эйлера для упругого состояния стержня, на самом деле малое приращение сжимающей силы делает возможным лишь малые искривления стержня, не сопровождающиеся разгрузкой. При появлении частичной разгрузки сопротивление изгибу возрастает, поэтому равновесие возможно не при любой величине прогиба, а при вполне определенном его значении.
§ 141] ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ЗА ПРЕДЕЛОМ УПРУГОСТИ 313
§ 141. Исследование поведения сжатого стержня при потере устойчивости за пределом упругости. Проследим более детально пове-# дение сжатого стержня при возрастании сжимающей силы. Будем считать материал следующим диаграмме сжатия с линейным упрочнением (рис. 217). Приращения напряжения и деформации при догрузке и
разгрузке соответственно связаны соотношениями (139.2) и (139.3), причем в формуле (139.2) касательный модуль Et постоянен.
Обозначим через Де укорочение оси стержня после бифуркации, то есть при изменении нагрузки от Ро до Р, через х — соответствующую кривизну изогнутой оси стержня. Деформацию волокна с координатой у, происшедшую после бифуркации, обозначим Де. Очевидно, что
Де = Деху. (141.1)
Рис. 217.
На нейтральной оси Дв = 0, сле-
• довательно, эта ось отстает от оси х на расстояние у0 = — Де/х. Внося (141.1) в (139.2) и (139.3), получим:
До=Et (Де4-ху), До = Е (Де ху),
У>У», У<Уа-
В дальнейшем будем считать сечение стержня прямоугольным, с высотой 2Л и шириной Ь. Вычислим ДР=Р—Ро и изгибающий момент Ж:
4~А Л Уо
b.P=b body =.bEt j (Де-[-ху) dy-\-bE ^(Ae-[-xy)dy = -Л у„ -h
=Й^-(Дв-»‘А),+?(Дв+’‘А),Ь (141-2> I £1 I
h h n
M = b j hoy dy = bEt j (Де-[-ху)у dy-\-ЬЕ j (Де-[-ху)у</у = — h ya -h
= (хЛ — Де)’ (2хЛ Дe) 4“"e (хЛ4" д<)* (2хЛ — Де) L (141.3)
Правые части в формулах (141.2) и (141.3) представляют собою однородные функции первой степени относительно Де и х. Поэтому можно перейти к следующим безразмерным параметрам:
« 2Etbh2 - 2Etbh . „ 3 ..
х*=-^х, е*=-^-Де, т* = — М.
314 УСТОЙЧИВОСТЬ УПРУГОГО и пластического равновесия [гл. XII
Уравнения (141.2) и (141.3) примут следующий вид:
_ х*)« _^.(е*-|-х*)1 = 4^х*,
Е 1 Е (141.4)
= е*)*(2х*-Н*) 4-^(х*4-е*)(2х*-е*)].
Ели из системы уравнений (141.4) исключить е*, получится нелинейное соотношение между изгибающим моментом и кривизной. Соответствующие выкладки слишком сложны, для нас достаточно выяснить характер получающейся зависимости. Заметим прежде всего, что соотношения (141.4) справедливы лишь при |у0|<^Л, то
биссектрису координатного
небречь правой частью:
есть когда в сечении существуют зоны догрузки и разгрузки. Вспоминая выражение для у0, найдем, что должно быть хЛ Де и, следовательно, х*> е*. При х*<^е* во всем сечении происходит догрузка, следовательно,
. 2ЕМ1г
М — Е^х х —|—• х.
Переходя к безразмерным величинам, получим:
т* = х* (х*<^е*). (141.5)
» При х* = е* первое из уравнений (141.4) дает х*=1, следовательно, формула (141.5) верна при х*<^1. График зависимости между т* и х* на первом участке представляет собою
угла от начала до точки /л* = х*=1
(рис. 218). Дальше кривую нужно строить с помощью уравнений
(141.4). При больших значениях х в первом уравнении можно пре-
(е* _ м*)« _ (е* х*)1 = 0.
Отсюда следует:
Подставим найденное значение е* во второе уравнение. Получаем:
§ 141J ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ЗА ПРЕДЕЛОМ УПРУГОСТИ 315
Но по формуле (139.11) множитель перед х* в правой части представляет собою отношение приведенного модуля к касательному, следовательно,
т* = А-х*. (141.6)
Таким образом, кривая зависимости между т* и х* имеет асимптотой луч, выходящий из начала координат с наклоном, равным Теперь нам предстоит решить задачу об изгибе сжатого стержня при нелинейной зависимости между моментом и кривизной, установленной графиком на рис. 218. Если прогиб есть v(z), изгибающий момент в сеченни с координатой z М——Pv(z) (см. § 136), кривизна изогнутой оси х=-о'(г), то отсюда следует, что
Х = -1ЛГ.
Перейдем к безразмерным величинам. Получим: ^^m*',4-x*(m*) = 0.
Заметим, что критическая сила Энгессера — Шеили р _____________________n*EtJ_л’ 2Etbh‘
^о— — /1 з >
поэтому предыдущее уравнение можно записать следующим образом:
££л»*'4-н*(л»*)==0. (141.7)
Будем искать приближенное решение уравнения (141.7). Предположим, что стержень, шарнирно закрепленный на двух концах, изгибается по синусоиде, так же как и в случае упругой потери устойчивости. Так как изгибающий момент пропорционален прогибу, можно принять
° I
Подставим т* в уравнение (141.6) и потребуем выполнения этого-уравнения только в одной точке, при х = 1)2, когда sin^y равен единице. Получим:
— x*(m*) = 0. (141.8)
Уравнение (141.8) легко решается графически. Для этого нужно провести из начала координат луч с угловым коэффициентом, равным Р/Ро. Точка пересечения этого луча с кривой х*т-Я1* (рис. 218) имеет своими координатами т* и х* — безразмерный момент и кривизну в среднем сечении стержня. Если Р< Pt, луч ие пересекается
316
УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ [ГЛ. XII
•с кривой, следовательно, прогиб невозможен, стержень остается •прямым. При Р=Р0 значение т* неопределенно, луч совпадает с биссектрисой координатного угла, но ДР=Р—Ро = О, а при переходе от безразмерных параметров к моментам н кривизнам их нужно множить на ДР. Таким образом, прогиб остается равным нулю и при Р = Ро. При Р^> Ро каждому значению силы соответствует -определенное значение прогиба, которое стремится к бесконечности по мере того, как сила стремится к величине Рк. Примерный график зависимости прогиба от силы приведен на рис. 219. При Р=Р0
•области в зоне разгрузки, что большах прогибах.
При испытаниях стержней на
происходит бифуркация, прогиб непрерывно растет, стремясь к бесконечности при Р=Рк, где Рк — критическая сила Кармана, определенная по приведенному модулю. Последний результат является следствием того, что мы воспользовались приближенным выражением для кривизны. Если взять точное выражение кривизны, для*каждого значения силы прогиб будет конечным, как это было показано для упругого стержня в § 137. Заметим, что в приведенном анализе не учтена возможность появления пластической растянутой обязательно будет при достаточно устойчивость обычно реализуются
именно те условия, которые приняты при установлении критерия потери устойчивости Шенли; нагрузка, создаваемая испытательной машиной, непрерывно возрастает. Однако при Р= Рй прогиб первоначально прямого стержня равен нулю, фактически за момент потерн устойчивости принимается момент, когда прогиб достигает некоторой достаточно большой величины, поэтому измеренная критическая сила будет находиться между Ро и Рк, притом ближе к Ро. Для реаль
ных материалов критические напряжения, определенные по приведен-
ному и по касательному модулю, отличаются друг от друга мало, как это видно из графика на рис. 216. В то же время расчет по касательному модулю дает нижнюю границу для критического напряжения, поэтому его и нужно рекомендовать.
§ 142. Расчет иа устойчивость по эмпирическим формулам.
Построение кривой X — ок пб касательному модулю или приведенному модулю предполагает построение точной диаграммы сжатия « требует кропотливой расчетной работы. На практике для' участка АВ кривой просто подбирают какую-либо эмпирическую формулу,
§ 142] РАСЧЕТ НА УСТОЙЧИВОСТЬ ПО ЭМПИРИЧЕСКИМ ФОРМУЛАМ 317 например, заменяют этот участок прямой линией. Одна из таких формул была предложена Ясинским:
ок = а — Ьк. (142.1)
Постоянные а и b различны для разных материалов. Существуют более точные эмпирические формулы, которые мы приводить не будем.
Действующие в СССР Единые нормы строительного проектирования рекомендуют производить расчет на устойчивость по формуле
Здесь [о]С1К — основное допускаемое напряжение на сжатие; <р (А) — так называемый коэффициент уменьшения основного допускаемого напряжения.
Записывая условие устойчивости следующим образом:
п ’
где п — запас устойчивости, найдем, 4to
При составлении приводимой ниже таблицы значений коэффициента ф запас устойчивости взят для разных гибкостей разным, при средних гибкостях он наибольший.
Значение коэффициента ф для стали
X 10 20 30 40 50 60 70 t 80
ф 0,99 0,96 0,94 0,92 0,89 0,86 0,81 0,75
X 90 100 ПО 120 130 140 150 160
Ф 0,69 0,60 0,52 0,45 0,40 0,36 0,32 0,29
ГЛАВА ХШ
ТРУБЫ И ДИСКИ
§ 143. Толстостенные трубы. Дифференциальные уравнения равновесия и совместности. Рассмотрим толстостенную трубу, нагруженную внутренним (или внешним) давлением (рис. 220).
Введем цилиндрические координаты z, г, <р и выделим элемент объема с измерениями dz, dr и rd<p. Этот элемент изображен отдельно на рис. 221. Вследствие симметрии на грани элемента действуют только нормальные напряжения, которые мы обозначим <тг, о„ о^. На рис. 221 показаны силы, действующие на элемент.
Проектируя все силы на направление биссектрисы, угла dtp и приравнивая сумму проекций нулю, составим следующее уравнение равновесия элемента:
(V <*Ф)dr2от dr — °.
Сокращая дифференциалы, получим:
^(гог)_от = 0. (143.1)
§ 143] ТОЛСТОСТЕННЫЕ ТРУБЫ 819
Уравнение (143.1) можно переписать также в следующем виде:
(143.2)
Обратимся к рассмотрению деформаций того же элемента; для которого мы составили уравнение равновесия. Обозначим через и (г) радиальное перемещение точки, находящейся на расстоянии г от оси (точки р и q на рис. 221). Элемент pq займет -положение p’q' (рис. 222); если дуга pq равнялась г dtp, дуга p'q' равна (г-f-и) dtp. Относительное удлинение элемента pq мы обозна- .
чим через 8ф, причем •
8д=рУ . (143.3) Д
<f pq г ' ' \
Точка т после деформации перейдет в поло- \______________ д'
жеиие т', перемещение ее тт' есть u(r-\-dr}==
= и (г) dr. Относительное удлинение отрез- р \ * ка рт мы обозначим ег. Величина его \
8 -Р'Р^ . (из 4\ А
r pm pm dr ' ’ ' \
Главные удлинения ef и гг оказываются вы- \
раженными через одну только функцию а (г). Та- \
ким образом, они не независимы, а связаны соот- рис 222 ношением, которое называется уравнением совместности деформаций. Чтобы получить это уравнение, умножим (143.3) на г, продифференцируем и вычтем (143.4). Получим:
= (143.5)
Другая форма записи уравнения совместности деформаций:
(143.6)
dr 1 г
Сравнивая (143.1) и (143,5) или соответственно (143.2) и (143.6), мы обнаруживаем известную внешнюю аналогию уравнения равновесия и уравнения совместности.
План дальнейшего решевия задачи для упругой трубы состоит в том, чтобы воспользоваться уравнениями закона Гука и выразить либо напряжения через деформации, либо деформации через напряжения. Но здесь мы встречаемся с необходимостью принять во внимание напряжение аг и деформацию вг, которые не вошли ни в уравнение равновесия, ни в уравнение совместности. Если труба достаточно длинная, то плоские сечения трубы, перпендикулярные ее оси, будут оставаться плоскими. Основания для применения в этом случае гипотезы
320
ТРУБЫ И ДИСКИ
[гл. XIII
плоских сечений те же самые, что и для растянутых или сжатых стержней. Для бесконечно длинной трубы все сечения находятся в совершенно одинаковых условиях и нет оснований ожидать, что сечение искривится при деформации в том или ином направлении, так как предпочтительного направления вдоль оси z не существует. Для трубы конечной длины справедлив принцип Сен-Венана. Поэтому осевая деформация 8г для всей трубы, за исключением области, непосредственно примыкающей к ее концам, должна считаться постоянной. Это справедливо как в упругом, так и в пластическом состоянии трубы.
§ 144. Упругое состояние трубы. Формулы Ламе. Задача об упругом состоянии толстостенной трубы — это одна из первых задач теории упругости, которая была решена еще Ламе (1828 г.). Напишем уравнения закона Гука:
8ф=4'1(т?“ va+a)l
8, = 4 А + М-
Из последнего уравнения <тг==£8г4-т(<т,4-<т?). (144.1)
Исключим ог из первого уравнения:
8,=4 А—А ~ “ v4+<М1 =
1 — v* Г v 1
= -£- I5-TTT7. ApJ (144.2)
Аналогично 1 — V2 Г v 1 % = “А- (144.2')
Уравнение равновесия (143.1) будет удовлетворено тождественно, если принять
Функция Д(г) называется функцией напряжений. По формулам (144.2) и (144.2')
1 — V* Г F
r Е Г 1 — V VSz>
1 - V* v F1 (144.3)
ст Е F’ - 1 — V г — VRZ-
§ 144)
УПРУГОЕ СОСТОЯНИЕ ТРУБЫ. ФОРМУЛЫ ЛАМЕ
321
Таким образом, деформации также выражены через функцию напряжений F(r) и неизвестную пока константу 8г. Внесем выражения ъг и по формулам (144.3) в уравнение совместности деформаций (143.6). Получим после сокращений
(144.4)
Для интегрирования этого дифференциалвного уравнения положим F—Crn и подставим это выражение для F в (144.4). После сокращения г”-1 придем к следующему алгебраическому уравнению для показателя л:
л (л— 1)-}-л— 1=0.
Корни этого уравнения л = Ч- 1, поэтому общий интеграл уравнения (144.4) может бытв написан в виде
где А и В—постоянные интегрирования.
Напряжения аг и выразятся следующим образом:
(144.5>
Это н еств формулы Ламе для напряжений в толстостенной трубе. Постоянные интегрирования должны быть определены из граничных условий. Пусть внутренний радиус трубы есть а, наружный радиус Ь. Внутреннее давление равно q, наружное равно нулю. Это значит, что радиальное напряжение аг равно —q при г = а и равно нулю при г = Ь. По первой из формул (144.5)
. t В
А-4- — = °.
Отсюда находим постоянные А и В".
11 Ю. Н. Работнов
322
ТРУБЫ И ДИСКИ [гл. XIII
Окончательные формулы для напряжений получаются следующими:
_ qa* (. Ъ*\
г~~ Ъ* — «Ч1 ~~гЧ *
да2 (. . Ьг А
(144.6)
На рис. 223 показаны графики (эпюры) распределения напряже-
ние. 223.
ний по толщине стенки.
Напряжение аг определится теперь по формуле
ог=58г + ^_. (144.7)
Оказывается, что аг постоянно по толщине стенки. Равнодействующую внутренних сил в поперечном сечении мы обозначим через Р, это сила, растягивающая или сжимающая трубу. Если труба закрыта по концам, растягивающая сила равна
давлению на дно, площадь которого есть ла*. Следовательно, Р—дла2. Площадь поперечного сечения трубы равна л(Ь2— а2). Таким образом,
_ qa2
аг ь2-а'
(144.8)
Сравнивая (144.7) и (144.8), можем найти относительное удлинение 8г. Если материал трубы несжимаем, v=y и ег = 0.
В открытой по концам трубе (например, ствол орудия во время выстрела) ог=0, поэтому
8г=—2v
q а*
Т Ь2 — а2 "
§ 145. Пластическое состояние трубы. Предположим теперь, что материал трубы следует диаграмме идеальной пластичности. При увеличении внутреннего давления пластическое состояние достигается прежде всего на внутренней поверхности. Рассмотрим для определенности закрытую трубу. На внутренней поверхности при г = а по формулам (144.6) и (144.8) получим:
Ь’-ря2 а2
?ьг_а«> — ?ь«_а2-
Отсюда видно, что а. "> о., т г т
§ 145] ПЛАСТИЧЕСКОЕ СОСТОЯНИЕ ТРУБЫ 323
Условие достижения состояния текучести будет следующим;
а) по критерию Треска
ft2 - а2
Ч стт 2b1 ’
б) по критерию Мизеса
62 — а2
9—<Тт Уз7>2 '
Если продолжать увеличивать давление, в трубе образуются две области: внутренняя, где материал находится в пластическом состоянии, и внешняя, упругая. Соответствующую задачу об отыскании упруго-пластического состояния можно решить без особого труда; для оценки прочности это решение нам не понадобится, поэтому мы будем сразу искать предельное значение давления, то есть давление, при котором весь материал переходит в пластическое состояние.
При решении этой задачи можно исходить либо из теории пластичности Сен-Венана, либо из теории пластичности Мизеса. Применим сначала первую теорию. Предположим, что в пластическом состоянии, так же как и в упругом, остаются справедливыми неравенства а^^>аг^>ог. Тогда <7, = ^, о, — аг и условие пластичности примет вид:
crv — ar=aT. (145.1)
Но в уравнение равновесия (143.2) входит как раз комбинация <7^— or. С учетом (145.1) уравнение равновесия принимает вид: dcsr_____________________________<гт
dr г " /
Интегрируем это уравнение. Получаем:
<7г=<7т1пг-|-С. (145.2)
Граничные условия будут следующие: <Jr~—Q при г —а и ог = 0 при г = Ь, тогда как константа интегрирования лишь одна. Значит, полностью пластическое состояние возможно только при определенном значении q = qT. Подставляем граничные в (145.2). Получим:
— 9т=стт1па-|"с> ° = In b С.
Отсюда после исключения С
1 ь ?т = ат1пТ-
Внося значение С=—qT — <7т1па в (145.2), находим помощью условия (145.1) <7?:
— 9т + аг1п^- , а<р——
условия
(145.3) ог, а с
(145.4)
11*
324
ТРУБЫ И ДИСКИ
[гл. Х1П
Величина осевого напряжения аг не может быть определена на основе теории пластичности Сен-Венана. Действительно, нужно только, чтобы было и чтобы равнодействующая напряжений аг
по сечению равнялась силе давления на донья, никаких иных условий для определения az мы не имеем. Положение, совершенно меняется, если допустить, что, как это имеет место в действительности, наряду с пластическими деформациями существуют упругие. Согласно теории Сен-Венана пластической деформации в направлении главного напряжения аг не происходит, значит, труба в предельном состоянии имеет упругую осевую деформацию ег. По закону Гука
V(°r+OT)]-
Отсюда
как и для упругой трубы (см. (144.1)).
Но напряжения ог и оф нужно брать теперь по формулам (145.4). В результате получим:
°г = £,8г + 2'’ [ —?т + ат(4 + 1п’7)]'
Как было показано в § 143, осевую деформацию е2 нужно считать постоянной по сечению. Она определится из условия
ь
2л azrdr = P=q[na*. (145.5)
а
Выражение для аг можно представить следующим образом:
o, = c-l-2voTln — .
< * т а
Здесь с — неизвестная пока константа, определяемая из уравнения равновесия (145.5). Подставляя в это условие выражение для ог и выполняя интегрирование, найдем:
Поэтому
= ~ дГ + 2vgi У + ln J • (145.6)
Особенно простой результат получается тогда, когда материал несжимаем и, следовательно, v=y. В этом случае
<?<=—+ • (145.7)
§ 145]
ПЛАСТИЧЕСКОЕ СОСТОЯНИЕ ТРУВЫ
325
Рис. 224.
На рис. 224 приведены эпюры распределения напряжений о, и <тг, построенные по формулам (145.4)'и (145.7).
Приведенное решение оказалось чрезвычайно простым вследствие того, что в закрытой трубе всегда стф > ог > ог. В открытой трубе в зависимости от отношения b/а может образоваться несколько зон, в которых различные пары из сг^, аг и ог оказываются наибольшими и наименьшими напряжениями. Соответствующий анализ проделан (Кой-тер), результаты его более сложны.
Желая решить ту же задачу с помощью теории Мизеса, мы будем считать материал несжимаемым и пренебрежем упругой деформацией. Предположим, что в трубе осуще
ствляется плоское деформированное состояние, то есть 8г=0. Применяя формулы (77.4), найдем, что
Внесем это значение ог в условие пластичности
(о, — <\)2 + — СТг)‘ = 2от-.
Получим:
Отсюда
|(аг-^), = 2а‘.
2 ст. — 0. — ~т= 0Т. f г /3
Оказывается, что для плоского деформированного состояния условие пластичности по Мизесу имеет тот же вид, что и по Сен-Венану,
только с увеличением от ний о, и получаются
в отношении 2/j/lk Формулы для напряжена формул (145.4) заменой от на
напряжение о2 равно их полусумме:
(145.8)
326
ТРУБЫ И ДИСКИ
[гл. хш
Здесь
2 . b
?’=гт"’ •
Последняя из формул (145.8) отличается от формулы (145.6) только величиной предела текучести, а так как формула (145.6) получена для закрытой трубы, то найденное по теории Мизеса решение для случая плоской деформации соответствует именно закрытой трубе.
Учет упругой деформации в теории Мизеса встречает значительные трудности, и простые замкнутые выражения для- напряжений при этом не получаются. Эта задача может быть решена путем численного интегрирования.
§ 146. Вращающиеся диски. Упругое состояние. Одной из основных деталей паровой или газовой турбины является диск, посаженный на вал и несущий на ободе лопатки. При вращении в диске возникают инерционные напряжения, требование прочности диска ограничивает величину допустимой угловой скорости вращения.
Рис. 225.
Обычно диски имеют толщину, меняющуюся в зависимости от радиуса; задаваясь надлежащим профилем диска, можно добиться его наибольшей прочности. На рис. 225 приведены схемы типичных конструкций дисков. В случае а диск соединен со ступицей, которая сажается на вал, в случае б диск просто имеет центральное отверстие и сажается на вал непосредственно, в случае в диск изготовлен сплошным и крепится к концу вала при помощи фланца. Обозначим толщину диска h (г) и будем считать распределение напряжений постоянным по толщине. Такое предположение совершенно аналогично основному предположению при расчете стержней переменного сечения (§ 21), оно является в такой же мере нестрогим. Вырежем теперь бесконечно малый элемент двумя соседними меридиональными сече
§ 146)
ВРАЩАЮЩИЕСЯ ДИСКИ. УПРУГОЕ СОСТОЯНИЕ
327
ниями и двумя концентрическими цилиндрическими сечениями. Соответствующий чертеж будет Совершенно подобен чертежу, приведенному на рис. 221; разница состоит в том, что размер изображенного
элемента в направлении, перпендикулярном плоскости чертежа, не dz, а Л (г). Соответственно изменяются площади граней элемента и действующие на грани силы. Эти силы показаны на рис. 226. Поскольку диск вращается, нужно рассматривать уже не равновесие элемента, а его движение. Следуя принципу Даламбера, прикладываем к центру тяжести элемента фиктивную силу — центробежную силу, которая равна произведению массы элемента qhrdrdtp на ускорение (о2г. Составляя уравнение равновесия путем проектирования всех сил на биссектрису угла
dtp и сокращая дифференциалы, получим:
(hrar) — hav + = 0.
(146.1)
Уравнение совместности деформации будет точно таким же, как и для трубы, а именно:
Так как осевое напряжение <т2=0, то по закону Гука
8r = -i-(o,— Г р ' г ф/» ф ' ф • '
Не составляет труда и здесь ввести функцию напряжений подобно тому, как это было сделано для трубы. Мы ограничимся здесь лишь простейшими случаями.
Диск постоянной толщины. Сокращаем толщину h в уравнении (146.1) и полагаем
По закону Гука
Еъг = -у--vF' — vqcoV*,
E&v = F’—v~ -f-Qto’r1.
328
ТРУБЫ И ДИСКИ
[гл. ХП1
Внесем эти значения деформаций б уравнение совместности. После упрощения получим:
r + y-^ = -(3 + v)Q®V!. (146.2)
Это уравнение отличается от уравнения (144.4), полученного для трубы, только правой частью. Общее решение однородного уравнения будет то же, что и для трубы (§ 144), частное решение неоднородного есть—Q®*/"1; таким образом, общий интеграл уравнения (146.2)
г=лг+4-Ч2'.е<й!г!-
Напряжения б диске выражаются следующими формулами:
• 1В 3 *4- v 22
0, = / + ^-----j^Qw’r2,
. В 1-4-3V г г
—=t-e®r.
Постоянные А и В определяются из граничных условий. Для сплошного диска радиуса Ь напряжения б центре должны быть конечны, поэтому постоянная В равна нулю. Постоянная А определится из' условия, что радиальное напряжение на периферии диска, то есть при г=Ь, равно нагрузке от центробежных сил обода с лопатками. Пренебрегая массой обода и лопаток, получим ar(Z>) = 0. Следовательно, A = ~-v qco2Z>2. Формулы для напряжений б сплошном вращающемся диске приобретают следующий вид:
<тг=Цре®!(^ —оф = Ц^е®!(*! — • (146.4)
Если диск имеет б центре отверстие радиуса а, постоянные ищутся из граничных условий при г = а и г — Ь. Здесь могут быть заданы напряжения или соотношение между напряжением сг и осевым перемещением, если решается задача о посадке диска на вал или о сопряжении с ободом.
§ 147. Диск равного сопротивления. Посмотрим, нельзя ли подобрать профиль меридионального.сечения диска таким образом, чтобы напряжения во всех точках были постоянны. Положим в уравнении (146.1) ar=.av = a = const. Тогда это уравнение будет дифференциальным уравнением для функции А (г), а именно:
аг 1 (У
§ 148]
ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ ВРАЩАЮЩЕГОСЯ ДИСКА
329
Интеграл этого уравнения
h = h„ exp Г — ^г*
(147.1)
Для того чтобы в диске, профиль которого построен по уравнению (147.1), напряжение было постоянным, необходимо приложить на наружном контуре нагрузку, вызывающую радиальное напряжение, равное а. Практически это условие выполнить довольно трудно, к тому же диск с профилем равного сопротивления, заданным формулой (147.1), сложен в изготовлении. Поэтому в настоящее время диски равного сопротивления на практике почти не применяются.
Мы предоставляем читателю вывести дифференциальное уравнение для функции напряжений диска переменной толщины в общем случае, а также проинтегрировать его при условии, что профиль задан уравнением h = krm (Стодола).
§ 148. Предельное равновесие вращающегося диска. Определение угловой скорости, при которой весь материал диска переходит в пластическое состояние, проще всего про- .
изводится на основе теории пластичности Сен- ШЯ
Венана. В упругом диске, как мы видели, оба напряжения, сг^ и ог, положительны, при /Ц.
этом а?^>аг. Предположим, что это спра- жЦ.
ведливо и для пластического состояния ди-ска. Тогда наибольшее напряжение есть аф, а наименьшее равно нулю, поэтому условие *---------------------г
пластичности Треска принимает вид: I | /
ач,~аг Рис. 227.
Внесем это в уравнение равновесия
(146.1), перенесем второй и третий члены уравнения в правую часть и проинтегрируем по г от г = 0 до г = Ь. Получим:
ь ь
]Ь с р
hra, а =ат J hdr — qco! hr* dr. а а
Найдем отсюда угловую скорость:
^-aha (ar)a] . (148 1)
Здесь Q — площадь половины сечеиия диска (заштрихована на рис. 227), J — момент инерции этой площади относительно оси г.
V
330 ТРУБЫ И ДИСКИ [гл. XIII
Рассмотрим два простых примера.
а) Сплошной диск постоянной толщины h, обод не нагружен.
Q — bh, J = ~, = =
3 ’ Q
Здесь v — окружная скорость.
б) Тонкое кольцо радиуса b с площадью £2; момент инерции Qb*.
/»!<o! = v2=—.
Q
Эти величины интересно сопоставить с найденной в § 20 предельной скоростью конца вращающегося стержня:
Q
а также с предельной окружной скоростью вращающегося диска постоянной толщины, найденной из условия достижения предела текучести в одной точке, а именно в центре диска. Из формулы (146.4) следуете
Интересно отметить, что после того, как появились первые пластические деформации, достаточно очень небольшого увеличения скорости вращения (приблизительно 11%), чтобы весь диск перешел в пластическое состояние.
Нахождение скорости, соответствующей предельному состоянию, по теории Мизеса значительно более сложно.
ГЛАВА XIV
ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
§ 149. Обобщенные силы и обобщенные перемещения. В сопротивлении материалов, говоря о силах, действующих на сооружение, для количественной их оценки часто пользуются некоторыми характеристиками, не являющимися в действительности абсолютными величинами сил. Так, действие изгибающей пары полностью характеризуется равномерно распределенную
ее моментом; говоря, что оалка несет нагрузку q, мы полностью определяем внешние силы, действующие на балку, бимомент является количественным выражением для четырех сил. Вообще часто приходится иметь дело не с одной силой, а с группой их, причем эта группа рассматривается как нечто целое. Необходимость рассмотрения таких групп сил становится особенно очевидной, если обратиться к изуче-. нию статически неопределимых систем.
Так, рассекая изображенную на чертей
Рис. 228.
(рис. 228) статически неопределимую раму, мы должны приложить к краям разреза две равные и противоположные продольные силы N, две поперечные силы Q, два момента М. Поэтому лишними неизвестными являются группы сил, определяемые числами N, Q и М, равными продольной и поперечной силам в сечении и изгибающему моменту. Иногда говорят, что за лишние неизвестные принимаются перерезывающая сила или изгибающий момент. Это неточно, так как Q и Мх представляют собою скалярные величины, которые не являются силой и моментом. Сделав же сечение, мы должны для обеспечения неразрывности тела приложить к краям разреза настоящие силы и пары Q и М.
Будем называть число, определяющее группу сил, обобщенной силой. В этом смысле момент М, бимомент В, распределенная нагрузка q могут рассматриваться как обобщенные силы.
Определим формально обобщенное перемещение как множитель при обобщенной силе в выражении работы. Для момента обобщенным
332 ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ (ГЛ. XIV
перемещением является угол поворота, так как работа момента есть Му. Равномерно распределенная нагрузка, приложенная к балке, прогиб которой есть v(z), производит работу
А= § qv(z) dz — q J vdz==qu>.
Здесь обобщенное перемещение есть <в, то есть площадь, заключенная между первона-_______________ь чальной осью балки и
-— j !-------- "Г ------- изогнутой ее осью.
У В качестве последнего
' ^иг примера возьмем обоб-
Рис. 229. щенную силу, соответст-
вующую двум равным и противоположным силам N, приложенным к концам разрезанного элемента фермы (рис. 229).
Если перемещение левого конца есть перемещение правого иг, то работа двух сил
А = Nu, — = N(ut — иг).
Обобщенное перемещение «, — аг представляет собою относительное расхождение краев разреза.
§ 150. Начало возможных перемещений для деформируемого тела. Если тело под действием системы внешних сил Fh приложенных б точках с радиусами-векторами г,, находится б равновесии, то к телу можно применить начало возможных перемещений. Нужно только иметь б виду, что на возможных перемещениях будут производить работу не только внешние, но и внутренние силы. Запишем условия равенства нулю работы сил на возможных, т. е. согласных со связями, перемещениях точек деформируемого тела следующим образом:
2^6^. = 6 Г. (150.1)
В правой части стоит изменение упругой энергии, соответствующее данной системе возможных перемещений, если тело упруго, или величина рассеянной энергии, если тело пластическое, или, наконец, и то и другое вместе.
Величину 61F, работу внутренних сил в объеме V на возможных перемещениях, можно представить следующим образом:
6U7=j6adV. (150.2)
v
Здесь fia — элементарная работа внутренних сил, приходящаяся на единицу объема. Рассмотрим элемент объема в виде параллелепи-
ВИБЛИО"Ж* колош__
§ 150] НАЧАЛО ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ДЛЯ ДЕФОРМИРУЕМОГО ТЕЛА 333 педа, ребра которого направлены по главным осям тензора напряжений. Пусть действующие напряжения равны о,, о,, приращения деформаций суть бе,, бе2, бе,. Если ребра параллелепипеда равный, Ь, с, на грань с измерениями b и с действует напряжение а,; следовательно, сила, действующая на эту грань, равна bcat. Эта сила производит работу на перемещении, равном удлинению ребра а, то есть на перемещении обе,. Подсчитывая работу сил, действующих на все грани, и относя ее к единице объема, получим:
60 = 0,68, 4-о26е24- о,бе,. (150.3)
В общем случае величина ба не является полным дифференциалом, следовательно, не существует функции а (е„ е2, 8,). Однако для упругого тела такая' функция существует и называется упругим потенциалом. Вспоминая изложенное в § 49, мы убеждаемся, что упругий потенциал есть не что иное, как упругая энергия на единицу объема. Действительно, если о,, о, и о, выражены через 8,, 82 и 8, по закону Гука, то левая часть в формуле (150.3) интегрируется и мы получаем:
а = А { а* +°« +°J ~ 2v (а*°» + + °»°«>
(см. § 49, формула (49.2)).
Существование упругого потенциала было положено в основу определения нелинейно упругого тела (§ 82), поэтому для нелинейно упругого тела выражение (150.3) всегда представляет собою полный дифференциал. Особенно большое значение имеет случай, рассмотренный в § 82, когда упругий потенциал выражается формулой (82.4):
Если воспользоваться еще соотношением (82.6), а именно тем, что
п___2f (у„)
' Зу0 ’
то выражение для упругого потенциала можно переписать следующим образом:
То
« = °/Yo)YodYo+^- (150.4)
О
Мы видели, что уравнения нелинейной теории упругости буквально совпадают с уравнениями деформационной теории пластичности, поэтому выражение (150.4) сохраняет свое значение и б теории пластичности, но должно теперь называться пластическим потенциалом.
ВИВЛИО^ХА
КОЛОХЗА
_иив№33 __ ?
НЕ БОЛЕЕ КНИГИ1Г | ОДНИ РУКИ И 2Х Е ДВЕ }
ОСКОРХА
334
ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
[ГЛ. XIV
§ 151. Теоремы Лагранжа и Кастильяно. Формула (150.2) показывает, что упругая энергия деформации, так же как энергия пластического формоизменения, получающаяся, если определять а формулой (150.4), однозначно определяется заданием деформации. А так как деформированное состояние в свою очередь определяется однозначно заданием внешних сил Р, то W может рассматриваться как функция этих сил или перемещений точек их приложения. Итак, пусть на тело действуют обобщенные силы Plt Рг, ..., Р„, соответствующие обобщенные перемещения суть «г, .... ип. Тогда можно считать, что
1F= Wa (а,, и..... ип) = WP (Л, Pt, ..., Ра).
Сообщим обобщенным координатам а,, аг, ...,ап произвольные изменения 6«t, 6«г, ..., б«„. Элементарная работа внешних сил при этом равна
2^4-
Считая W представленной через обобщенные перемещения, для вариации W будем иметь следующее выражение:
dui ‘
Уравнение (150.1) приводится к следующему:
S(₽i-Kr)s“< = °- OS1.1)
Вследствие произвольности вариаций отсюда следует:
Производная энергии деформации по перемещению равна силе. Это теорема Лагранжа, наиболее общая теорема механики деформируемого тела.
В качестве примера рассмотрим задачу, решенную в § 32 (см. рис. 42). Энергия деформации стержня при растяжении по формуле (28.4)
В рассматриваемом случае
\ cos а
а!/ и*
~2 ~21 '
Следовательно, полная энергия растяжения двух стержней
__EF / и* у__ I \2l )
EFu* 4Р ’
335
§ 151] ТЕОРЕМЫ ЛАГРАНЖА И КАСТИЛЬЯНО
По теореме Лагранжа
p_dW_EFu» г du F *
Отсюда
и
что совпадает с формулой (32.3).
Мы специально выбрали такой пример, в котором зависимость между силой и перемещением нелинейна, чтобы подчеркнуть общность метода.
Представим себе теперь, что потенциальная энергия деформации выражена через внешние силы:
W=W(P„P„ ,..,,Ра}.
Образуем функцию ф = 2рА— (151-3)
Варьируем функцию Ф. Получим:
и>=£ р,ч + s «Рл - S "
Но вследствие теоремы Лагранжа
™_ — р du-t <•
Поэтому
(151.4)
Предположим далее, что функция ф выражена только через внешние силы:
Ф = Ф(Р„Р,.......Р„).
Тогда
Заменяя этим выражением для 6Ф левую часть формулы (151.4) и замечая, что вариации произвольны, получим;
Эта формула выражает ’ теорему Кастильяно.
336 ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. X!V
Функция Ф называется дополнительной работой. Согласно уравнению (151.5) перемещение равно производной от дополнительной работы по силе. Термин «дополнительная работа» легко понять, если обра-
титься к рис. 230. При нелинейной зависимости между Рим
IF = J Pdu.
Таким образом, W равна площади заштрихованной фигуры. Дополнительная работа Ф представляет собою площадь, дополняющую W до прямоугольника.
§ 152. Линейные упругие системы.
Применение общих теорем Лагранжа и Ка-
стильяно к системам, для которых связь между внешними силами и перемещениями точек их приложения нелинейна, будь это вследствие того, что рассматриваются пластические деформации, или, как в примере предыдущего параграфа, вследствие того, что уравнения статики должны’составляться для деформированного состояния, все равно наталкивается, на значительные трудности. В нашем курсе мы ограничимся линейными упругими системами, то есть системами, элементы которых подчиняются закону Гука, сочленения осуществлены без трения и малость деформаций позволяет составлять уравнения статики для недеформированного состояния. При этих условиях, как мы выяснили в § 32, перемещения и силы связаны линейными соотношениями. Легко видеть, что это относится в той же мере к изгибу и кручению, так как везде в этих задачах мы имеем дело с линейными функциями от сил. Исключение представляет случай продольно-поперечного изгиба: там выражение для поперечного изгиба зависит от продольной силы сложным образом, через трансцендентные функции. Легко понять, в чем тут дело. При составлении дифференциального уравнения продольно-поперечного изгиба мы принимаем момент от продольной силы равным произведению силы на прогиб, то есть определяем статический фактор с учетом происшедшей деформации.
Итак, будбм рассматривать линейные системы, для которых
’ Л = (152.1)
или
»/=2¥/- (152.2) ’
Величины бу — коэффициенты влияния я Сц — коэффициенты жесткости связаны очевидными соотношениями:
си
— 1^/1
~ |д| ’
§ 152]
ЛИНЕЙНЫЕ УПРУГИЕ СИСТЕМЫ
337
Здесь |6|—определитель, общий элемент которого есть бу; | by I — алгебраическое дополнение этого элемента. Определители | 6 | и | с | должны быть отличны от нуля. Покажем, что матрицы коэффициентов бу и Су симметричны. По теореме Лагранжа
р_ dW_ ‘ ~~ dUi *
Аналогично
р _
Из факта независимости второй смешанной производной функции от порядка дифференцирования следует;
дРг__дР/ duj ди{
Но по формуле (152.1)
^ = с.
duj
Точно так же
Мы доказали, что Су = Суг, а следовательно, бу = бу.
В линейной системе напряжения выражаются линейным образом через внешние силы, а так как удельная энергия а есть квадратичная функция от напряжений, то Wp представляет собою квадратичную форму от сил Р,, Рг, Рп. Вследствие (152.2) 1FB есть квадратичная форма от перемещений; Для того чтобы написать выражение W в зависимости от сил или перемещений, воспользуемся вариационным уравнением (151.1), приняв в нем
биг = Ли,.
Таким образом, возможные перемещения мы выбираем пропорциональными действительным. Множитель А произволен. Если W есть квадратичная форма от перемещений ир и......... а„, то по известной
теореме Эйлера
i
Воспользуемся уравнением (151.1), внеся в него бг^ = Аиг; по сокращении на А получим:
«’ = 4£рй-
(152.3)
Это теорема Клапейрона.
338 ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XIV
Пользуясь уравнениями (152.1) или (152.2), можем представить потенциальную энергию деформации следующим образом:
(152.4)
ij
ИЛИ
W = ^cUPiPi- 452.5)
§ 153. Теорема о взаимности работ. Условие симметрии коэффициентов бу и можно истолковать следующим образом. Пусть в точке I приложена сила = 1. Прогиб в точке j от этой силы по х формуле (141.2) будет бц. Если теперь приложить силу Ру=1 в точке j, то прогиб в точке I будет по той же формуле д 7. Итак, прогиб в первой точке от силы, приложенной во второй точке, равен прогибу во второй точке от той же силы, приложенной в первой точке.
Более общая формулировка теоремы взаимности будет следующей: Работа сил первой системы на перемещениях точек их приложения от действия сил второй системы равна работе сил второй системы на перемещениях точек их приложения от действия сил первой системы.
Будем отмечать силы первой системы штрихом вверху и занумеруем их от 1 до k'.
Р' Р;..., Р'„. 1’ 2’ ’ К
Силы второй системы будем нумеровать от k 1 до п и отмечать двумя штрихами:
п» р'> р>
Перемещение точки приложения силы номер s первой системы от действия сил второй системы есть
ц'= 2 Pibsi (s=l, 2, ...k).
Аналогично k
Ui = 2 Ps &is (i=fe-|- 1, ...,«). j=i
Работа сил первой системы на перемещениях точек их приложения от действия сил второй системы есть
k k п
А'= 2 />;«;= 2 2 p,p&i'
Аналогично n n n
A"= 2 2 2w&..
I=A4-1 /=*+1 J=1
§ 154] ТЕОРЕМА КАСТИЛЬЯНО ДЛЯ ЛИНЕЙНЫХ УПРУГИХ СИСТЕМ 339
Меняя порядок суммирования и пользуясь симметрией коэффициентов S(J, замечаем, что А' = А'', чем и доказывается теорема.
Рассмотрим примеры применения теоремы о взаимности работ.
1) Известно, что угол поворота <р на конце балки, лежащей на
РР двух опорах, от силы, приложенной посередине, есть - •
Определим прогиб f в середине такой же балки, нагруженной на конце моментом. По доказанной теореме
РР Pf-м^^м^.
Отсюда
. МР
16EJX -
2) При внецентренном растяжении или сжатии стержня силой, полюс которой находится в точке 1, продольное волокно, пересекающее плоскость сечения в точке 2, получит удлинение Д21. Перенесем теперь силу так, чтобы ее полюс был в точке -2. Тогда удлинение волокна, проходящего через точку 1, будет Д21. По теореме о взаимности
а21 = а12.
Но равным удлинениям соответствуют и равные напряжения, поэтому
СТ12= °21-
Теорема, выражаемая этим равенством, была нами положена в основу теории ядра сечения (§ 111).
§ 154. Теорема Кастильяно для линейных упругих систем. Дополнительная работа, определяемая формулой (151.3):
ф=2р,и,—if,
вычисляется весьма просто для линейных упругих систем. Действительно, по теореме Клапейрона
%PiUi = 2W.
Таким образом,
Ф= W.
Теорема Кастильяно для линейных упругих систем формулируется следующим образом:
Производная от энергии деформации по силе равна перемещению'.
dW
ul — др\' (154.1)
340 ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XIV
Иногда удобно сохранять вариационную формулировку этой теоремы:
2“M = Sw7p- (154.2)
Желая применять теорему Кастильяно к тем или иным конкретным задачам, мы должны уметь вычислять потенциальную энергию деформации через внешние силы. Это всегда можно сделать, если воспользоваться. формулой (150.2) и выражением удельной энергии а через напряжения. Во многих случаях это бывает удобнее сделать, переводя внутренние силы в категорию внешних и применяя теорему Клапейрона. Дадим сводку формул упругой энергии для основных видов деформации.
1) Растяжение — сжатие. Как мы уже видели,
В общем случае' стержневой системы
и7 = 2-2^- (154.3)
Суммирование распространяется на все элементы, для которых постоянно выражение под знаком суммы.
2) Кручение. Рассечем стержень двумя бесконечно близкими поперечными сечениями. Приложим к сечениям выделенного элемента два равных и противоположных момента, численно равных Мг. Обобщенное перемещение для такой группы, сил есть угол относительного поворота сечения, то есть 6 dz. По теореме Клапейрона
dW = ±-Mtidz. Z *
Полная энергия кручения стержня
i I
Г I , „ t CM*dz
W' =J 2-/Wt9dz = -g J 2CO ' (154.4)
о о
3) Изгиб. Поступая так же, как в случае кручения, найдем, что энергия элемента стержня длиной dz есть
1 ял
2 dz.
Но
§ 155|
РАСЧЕТ ВИНТОВЫХ ПРУЖИН
341
Поэтому
1
2 J 2EJX ’
О
(154.5>
Аналогичным образом можно вычислить энергию касательных напряжений и дополнительных нормальных напряжений для тонкостенных стержней. Мы этого делать здесь не будем.
§ 155. Расчет винтовых пружин. Простой пример применения теоремы Кастильяно к определению перемещений — это расчет винто-
вой пружины. Приводя направленную по оси силу Р к центру тяжести сечения (рис. 231), получим пару с моментом PR. Разлагая момент этой пары на направление касательной к винтовой линии и перпендикулярное, найдем крутящий момент
Л4г = Р/?соза
и изгибающий момент
Мх = PR sin а.
Здесь а — угол подъема витка.
Так как моменты всюду постоянны, то формулы (154.4) и (154.5) дадут:
if —1 ГС08,« । sin,(Xl г
2 [ CG 1“ EJ J *
Перемещение точки приложения силы, то есть вытяжка пружины:
Р
Рис. 231.
/=" = РИ + . (155.1)
Расчет пружины на прочность в случае, если
сечение круглое, производится так. Наибольшее напряжение изгиба
PR sin а а~
Наибольшее напряжение кручения
__PR cos а__PR cos а
Т— Wp ~ 2WX •
Ha практике обычно применяются пружины с малым углом подъема винта. Для таких пружин можно пренебречь нормальными напряжениями и принять cosa=l. В формуле (155.1) можно также положить
342 ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [гЛ. XIV
а = 0. Получим:
7 CG и
lmax — уу р == Llh
Допускаемое напряжение [т] для пружин берут иногда очень большим, имея в виду высокие механические характеристики применяемой проволоки.
§ 156. Теорема о минимуме энергии. Эта теорема представляет частный случай теоремы Кастильяно применительно к статически неопределимым системам. Пусть мы имеем статически неопределимую систему. Отбрасывая п связей, мы превращаем систему в статически определимую. Введем реакции этих связей Xr, Xt, ..., Хп. Через «лишние» неизвестные Xt можно выразить усилия и моменты во всех элементах системы, таким образом, энергия W будет функцией лишних неизвестных Xt. Теорема состоит в том, что величина W, рассматриваемая как функция лишних неизвестных, имеет минимум для тех значений этих неизвестных, которые получаются в действительности.
Заметим, что обобщенные перемещения, соответствующие лишним неизвестным в статически неопределенных задачах, всегда равны нулю. Если лишняя неизвестная вводится путем отбрасывания внешней связи, то мы требуем, чтобы соответствующее перемещение равнялось нулю. Если неизвестная вводится за счет нарушения внутренних связей, как в примере § 149 (рис. 228), то это есть обобщенная сила, представляющая собою совокупность двух сил или двух моментов, приложенных к краям разреза.
Соответствующее обобщенное перемещение — это или относительное расхождение краев разреза, или угол поворота одного края относительно другого. Так как в действительности стержень должен оставаться цельным, обобщенное перемещение всегда равно нулю. Значит, по теореме Кастильяно
U=0 (i=l, 2, .... п). (156.1)
Уравнения (156.1) представляют условия экстремума функции W. Остается показать, что этот экстремум есть минимум. Для этого вычислим вторую вариацию функции W:
s!r=ly
Но по формуле (156.1)
dlW _
dXjdXy-°'7’
§ 157] ИНТЕГРАЛ ПЕРЕМЕЩЕНИЙ 343-
Поэтому
6*
Итак, S’W' есть потенциальная энергия, соответствующая силам’ бХр Но упругая энергия является положительно определенной квадратичной формой, так как нельзя приложить к системе такие силы, которые сделали бы отрицательной ее энергию. Поэтому S2 О и уравнения (156.1) представляют условия минимума потенциальной, энергии, рассматриваемой как функция лишних неизвестных.
Теорема Кастильяно и следствие ее — теорема о минимуме энергии— позволяют непосредственно находить перемещения стержневых систем и определять лишние неизвестные в стержневых системах. Однако в настоящее время предпочитают пользоваться иными способами практического расчета, которые будут изложены в следующем> параграфе. Эти способы более удобны технически, но они. обладают меньшей общностью, будучи применимыми только для стержней и стержневых систем. Теорема же Кастильяно и начало наименьшей работы — это весьма общие теоремы, верные для всех упругих тел при достаточно широких предположениях; они принадлежат не только сопротивлению материалов, но и теории упругости,, служа основой ряда приближенных методов; принципиальное их значение огромно.
§ 157. Интеграл перемещении. Для определения перемещений в стержневых системах, элементы которых работают на растяжение, изгиб и кручение, можно получить из теоремы Кастильяно очень простую формулу. Воспользуемся для этого вариационной записью-теоремы Кастильяно (154.2):
'£iui6Pi = &Wp. (157.1}
Пусть нам нужно определить перемещение в точке номер s. Предположим, что все силы остаются неизменными, варьируется лишь сила Ps (в частном случае бывшая равной нулю). От изменения силы Ps, которая получает приращение bPs, изменяются усилия в стержнях, крутящие моменты и изгибающие моменты. Очевидно, что изменения усилий и моментов пропорциональны 8Р3, поэтому мы обозначим изменение продольной силы через Nu8Pst изменение крутящегося момента через M2S8PS, изменение изгибающего момента через MxsbPs. Величины S/2i, и Mxs представляют собою продольную силу, крутящий момент и изгибающий момент, вызванные единичной силой, то есть силой, величина которой равна единице,, приложенной в точке s.
В левой части уравнения (157.1) мы получим:
us8Ps.
•344 ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XIV
Первоначальное значение Wp есть
Wp 2CG-d_j2£77‘
Ее приращенное значение
П7 -L-AU7
Wp-\-dWp = ^---------2EF------Г---
Пренебрегая квадратом малой величины 6PS и сокращая ее, по формуле (157.1) получим:
о57-2) *•>Г J wM fj С v %
Формула (157.2) представляет собою так называемый интеграл •перемещений, или интеграл Мора.
Для примера решим задачу об определении перемещения точки А •криволинейного стержня, изображенного на рис. 232. Влиянием продольной силы Nz на * _" £ _ перемещение можно
~~ пренебречь. Изгибаю-
/ \ р / / щий момент от силы Р
/ \ / / есть
•ЯЗЯ 3*2 2Wx = P/?sin ф.
Рис. 232. Обозначим номером
1 вертикальное направление, номером 2 — горизонтальное^ Приложим единичную силу в направлении 1 и в направлении 2. Соответствующие моменты:
Л/г1==7?81пф, 4fZI = /?(l—соэф).
Для перемещений по формуле (157.2) получим:
PR* С . t , лР’Р “*=-ЁТГШ ф</<1,='2£7-’
О
Ut = J sin ф (1 — cos ф) dy .
При решении этой задачи мы пользовались зависимостью между изменением кривизны и изгибающим моментом, следующей из теории прямого бруса, считая размеры сечения малыми по сравнению с радиусом R.
Этот пример очень отчетливо выявляет преимущества энергетических теорем. Желая подсчитать тот же прогиб без этих теорем,
§ 158] ГРАФОАНАЛНТ. СПОСОБ ВЫЧИСЛЕНИЯ ИНТЕГРАЛА ПЕРЕМЕЩЕНИЙ 345"
мы должны были бы составлять дифференциальное уравнение изогнутой оси криволинейного стержня, что требует геометрического рассмотрения. Формула (157.2) дает результат совершенно автоматически. То же относится к расчету винтовой пружины. Чтобы вывести формулу (155.1) без помощи теоремы Кастильяно, нужно прибегнуть-к довольно сложным и малонаглядным геометрическим рассуждениям, тогда как упомянутая теорема дает результат немедленно.
§ 158. Графоаналитический способ вычислений интеграла перемещений. Для систем, состоящих из прямолинейных элементов, функции Mxs(z), Mzs(z), Nzs(z), представляющие собою изгибающий или крутящий момент от сосредоточенной силы или продольную.
4
Рис. 233.
силу, являются на каждом участке линейными функциями. Поэтому для вычисления интеграла (157.2) можно применить графоаналитический прием, изложенный в § 132 применительно к вопросу о вычислении секториальиых характеристик сечения.
Поясним этот способ примером. Пусть для изображенной на рис. 233 рамы требуется определить вертикальное перемещение точки А. Построим эпюру моментов от действующих сил и от единичной силы, приложенной в точке А вертикально вниз. Принимая
346
ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
[ГЛ. XIV
во внимание только изгиб, заметим, что на первом участке, считая •от точки приложения силы, интеграл обращается в нуль. Будем •брать площади с верхней эпюры и ординаты под центрами тяжести •с нижней. Получим:
•1 Гоп о 1 п । ЗРа-п „ . 2Ра-а „ 1 ИРп’ u = Ej |ЗРа-2а.т• 2а-]-- 2а-]----. 2aJ = —.
В этом примере следует обратить внимание на разбивку трапеции
'Рис. 235.
Если ординаты одной то правило сохраняется
на два треугольника. .
Такое графоаналитическое вычисление интеграла перемещений часто называют перемножением эпюр. Не останавливаясь на конкретных примерах, рассмотрим самый способ перемножения для важнейших частных случаев.
1) Две трапеции (рис. 234, а). Произведение эпюр
П=®1л+®.Л-
Здесь
или двух трапеций имеют разные знаки, (рис. 234, б)’.
П=<в1у1 + ®1у1;
al Ы 1 . 2 2,1
—2, 2, у, 3</ 3 с, yt 3d 3 с.
2) Одна из эпюр — параболическая. Такую эпюру представляют как результат наложения симметричной параболы со стрелу
лой на трапецию. Площадь эпюры разбивается на три площади (рис. 235):
al bl qls
®i — 2 ’ — ~2 ’ 12 ‘
Центр тяжести площади параболы приходится посередине.
§ 159. Расчет статически неопределимых систем по методу -сил. Превратим статически неопределимую систему в статически определимую, удалив п лишних связей и введя вместо них обобщенные силы Л,, Xt, .. ., Хп. Обобщенное перемещение, соответ
§ 159] РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ ПО МЕТОДУ СИЛ 347
ствующее силе Xit можно найти как сумму двух перемещений. С одной стороны, внешние силы, совокупность которых мы будем обозначать символом Р, создают обобщенное перемещение Рассматривая теперь систему под действием одних только лишних реактивных сил, определим вызванное ими обобщенное перемещение, равное
Мы выяснили в § 156, что перемещение, соответствующее лишней неизвестной, равно нулю. Поэтому
SV^+Й^О (/=1, 2.............л). (159.1)
Система (159.1). называется канонической .системой метода сил. Будем называть статически определимую систему, полученную из исходной отбрасыванием лишних связей, основной системой. Перемещение, на котором производит работу сила Х{, будем называть перемещением номер i. Выясним, как определяются коэффициенты в уравнениях (159.1). Коэффициенты SZy—это не что иное, как перемещение номер i при условии, что к основной системе приложена сила Ху=1. По правилу, установленному формулой (157,2),. мы должны определить усилия и моменты для сил Л)=1 и Х^=1Г после чего находим S;y-:
S<7 = E^T/+ + J
Точно так же
х __NgiNgp । P Мг1МгР । P MxiMxP •
ЁР Г J CG T"J EJ aZ'
Здесь Л7гР, MxP — продольная сила, изгибающий и крутящий моменты, созданные в основной системе внешними силами.
Рассмотрим в качестве примера раму, изображенную на рис. 236< и имеющую форму квадрата со стороною а. Рассечем ее по оси симметрии, приложим пару продольных сил Хх, пару поперечных сил Xt и пару моментов Xt. Построим эпюры моментов от нагрузки* от сил Л\=1, от сил Хг=\, от пары моментов Х,= \. Применяя правило графоаналитического перемножения эпюр, получим:
„,» Г1 вл’ 2 qa* а 1 л . qcf 3 _4 Е/Sip— [я а 2 3 а 12 2]2Н“а 2 а — 4дй ’
EJo..=-!r-Ta-2-\-a-a-a = -^ а , Z о о
EJ6li=EJ6tt=0,
ЕЛ„ = 4а, EJbtP = 0,
EJblt = 2a\
348 ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XIV
Замечая, что величины btP равны нулю, мы можем вы-
сказать общее правило, что произведение симметричной эпюры
Рис. 236.
«а антисимметричную равно нулю. Величина нам не понадобится, существенно лишь, что
Составим систему уравнений (159.1):
J а’А, + 2агХ, 4- A qa* = О,
2а1 X, 4- 4щ¥, 4- у qa* = 0.
Решение этой системы:
X,=-f, ^ = 0,
Суммарная эпюра изгибающих моментов построена на том же рис. 236.
§ 160. Уравнение трех моментов. Для расчета неразрезной балки, то есть балки, лежащей более чем на двух опорах и не имеющей внутренних шарниров, наиболее удобный выбор основной системы состоит в том, что мы вставляем шарниры в балку над опорами, превращая ее таким образом в ряд однопролетных шарнирно опертых балок. Условимся нумеровать опоры от крайней левой по порядку, пролеты же — по левой опоре. Рассмотрим пролеты i— 1 и I, имеющие общую опору номер i. Пусть 1{ — длина пролета.
Пару моментов, которую нужно, приложить к краям разреза на этой опоре, чтобы обеспечить непрерывность касательной, примем за одну из лишних неизвестных. Величина момента при этом равна величине изгибающего момента в балке неразрезанной. По
§ 160]
УРАВНЕНИЕ ТРЕХ МОМЕНТОВ
349
строим эпюры изгибающих моментов от обобщенной силы М{, считая Л4; = 1, построим также эпюры от Л4/_1 = 1 и Aff+I = l. Применяя правило перемножения эпюр, найдем (рис. 237):
L. 2 , lj 2 J, 2 Т i 2 3 3 ’
Lj_L —Lj 2 3 6 ’
till—Lj 2 3 6 '
6,7 =
6/, ,-i = 6f+1, i==
Обозначая a>i_l и u>{ площади эпюр моментов от внешних сил, построенных для каждого пролета, рассматриваемого как балка на
Ъ-г'...........
двух опорах^ а,-., и bt — расстояния центров тяжестей этих эпюр от соответствующих опор, показанные на рисунке, получим:
350 ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ (ГЛ. XIV
Внося выражение для 8ip в уравнение (159.1), получим:
+ + + • (160.1)
Это и есть так называемое уравнение трех моментов. Если балка имеет л опор, то п — 2 опоры являются лишними и уравнение (160.1) нужно составлять п — 2 раза, полагая последовательно 4 = 2, 3, ... ... ,л—1. В частном случае, когда все пролеты имеют одинаковую длину и загружены одинаково, можно указать общее решение системы (160.1). Положим
/, = /=const,
6 [ (В,- , -4- 4'1 = Al = const.
L 4-1 1 ' 4;J
Уравнение (160.1) примет следующий вид:
(160.2)
Это линейное разностное уравнение. Для таких уравнений применимы те же методы, что и для линейных дифференциальных уравнений. Будем искать частное решение уравнения (160.2) в виде
М{ = const.
Легко видеть, подставляя предполагаемое решение в уравнение, что эта константа равна —Л/6. Теперь будем искать общее решение однородного уравнения. Положим
Подставляя это выражение в уравнение (160.2), полагая Л=0 и сокращая с'-1, придем к следующему уравнению для нахождения с:
1 4с -J- с* = 0.
Отсюда
с1=—24-/’3, с, = —2 —/"З.
Общее решение уравнения (160.2) имеет, таким образом, следующий вид:
А1(. = С, (j/~3 — 2)‘ 4- Ct (-КЗ — 2/ — А . (160.3)
Рассмотрим балку, имеющую очень много пролетов, и нагрузим ее крайний левый конец моментом Мо. Величина опорного момента должна по смыслу задачи убывать от одной опоры к другой. Поэтому в формуле (160.3) нужно принять Ct = 0. Получим:
Л^СДКЗ-2)''.
§ 160]
УРАВНЕНИЕ ТРЕХ МОМЕНТОВ
351
При /=0 2И(- = 2ИО. Поэтому
_C,=Afe>
ч- = Я (/ 3 - 2/ = Мо (- 0,27/.
Подсчитаем несколько опорных моментов:
М,=—0,27ЛЕ, ЛГ = 0,073 Л4., ЛГ=—0,0168 2И„, ...
* ' V' Z * О'в * U’
Если число пролетов конечно и из граничных условий, при i=0 и жны быть заданы. Получаем:
Ч=с1+с.-4’
лтЛ=с.(Кз—2)Л+
+ Ct(-K3-2)A-4.
Решая эти уравнения, находим С. и С..
В качестве следующего приме-
равно k, постоянные найдутся i = k моменты Ма и Mk дол-
Рис. 238.
ра применения уравнения трех мо-
ментов рассмотрим балку с заделанным концом, например изображенную на рис. 238, Вместо заделки продолжим балку влево и закрепим ее на двух опорах, номера которых i = 0 и i=—1, расстояние между ними Сближая эти опоры, то есть приближая к нулю, мы получим заделку. Напишем уравнение трех моментов для i = 0, положив в нем /_, = 0 и Af_j = O. Получим:
2ЛТЛ + Л1Л=-6<»0^. (160.4)
Для следующих пролетов уравнение трех моментов составляется обычным способом.
ГЛАВА XV
ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
§ 161. Жестко-пластическое тело. В предыдущих разделах мы неоднократно рассматривали задачи о предельном равновесии стержней и стержневых систем из идеально-пластического материала. Основная трудность при решении этих задач состоит в том, чтобы правильно определить положение пластического шарнира в балке или установить, какие именно стержни перейдут в пластическое состояние, если мы имеем дело с фермой.
Можно, конечно, как мы иногда делали, рассмотреть сначала упругое состояние системы. Наиболее напряженный элемент первым перейдет в пластическое состояние при возрастании внешних сил. После этого мы должны рассматривать состояние упруго-пластическое, чтобы выяснить, какой элемент перейдет в пластическое состояние во вторую очередь, и продолжать подобным образом до тех пор, пока мы не дойдем до исчерпания несущей способности системы. Такой путь чрезвычайно сложен и громоздок, к тому же он вносит элемент, являющийся для теории предельного равновесия чуждым, а именно представление о переходе от упругого состояния к пластическому. Действительно, в предельном состоянии те элементы, которые не достигли предела текучести, образуют кинематически изменяемую систему и малые упругие деформации этих элементов не играют никакой роли по сравнению со сколь угодно большими деформациями пластических элементов. Поэтому в самом начале при определении предельного состояния мы можем принять за исходный пункт не схему упруго-пластического материала, а схему материала жестко-пластического, который совсем не деформируется при о<^от и получает возможность неограниченной деформации при а=от. Диаграмма зависимости между напряжением и деформацией для такого материала изображена на рис. 239. Если встать на эту точку зрения, то путь нахождения предельного состояния, отправляясь от состояния упругого, представляется’ крайне искусственным.
§ 161]
ЖЕСТКО-ПЛАСТИЧЕСКОЕ ТЕЛО
353
Некоторые общие теоремы, излагаемые в этой главе, позво-лят решить поставленную задачу более прямым и простым путем.
Предварительно нам нужно несколько уточнить представление о жестко-пластическом теле, которое будет лежать в основе дальнейших рассуждений, хотя окончательные результаты применимы и для упруго-пластического тела. Рассматривая изгиб, например, балки из упруго-пластического материала без упрочнения, мы получаем диаграмму зависимости между изгибающим моментом и кривизной, состоящую из трех участков: упругого, упруго-пластического криволинейного и горизонтального участка, соответствующего исчерпанию несущей способности (см. рис. 136, § 107). Переход от упругого со-
стояния к полностью пластическому нас интересовать не будет, поэтому мы заменим эту диаграмму подобной той, которая изображена на рис. 239. Это значит, что мы считаем, как будто балка совсем не деформируется, пока изгибающий момент меньше чем Л4Т, и получает возможность неограниченно изгибаться, когда момент достигает этого предельного значения.
М в
£ эе
В § 76 мы ввели понятие об Рис. 239.
ассоциированном законе течения.
Если, например, о^, о^, о^ — главные напряжения и /(о^, <гч, at)=0 — условие пластичности, то скорости деформации по главным направлениям пропорциональны частным производным функции / по соответствующим направлениям. Условие пластичности может быть истол
ковано как уравнение поверхности в про-
странстве о., <уч, О(.; если элемент иахо-дится в предельном состоянии, этому со-стоянию соответствует точка М на поверх- __________
ности нагружения. Радиус-вектор этой точки
а имеет компоненты <у», Частные рис 940
„ df df df
производные -gy- , и пропорцио-
нальны направляющим косинусам нормали к поверхности нагружения в точке Л4, поэтому, если изображать состояние течения элемента вектором £ с компонентами 8^, еч, ес, этот вектор будет направлен по нормали к поверхности нагружения в точке М (рис. 240). Поверхность нагружения по Мизесу представляет собою круговой цилиндр, равнонаклоненный по всем трем осям, по Сен-Венану______
вписанную в этот цилиндр шестигранную призму. Существенно заметить, что эта поверхность выпукла.
Существуют материалы, для которых условие предельного состояния отлично от условия Мизеса или Сен-Венана, например грунты;
12 Ю. Н. Работнов
354
ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
[ГЛ. XV
излагаемая теория применима и к таким материалам; единственное ограничение состоит в том, чтобы поверхность нагружения была выпуклой.
§ 162. Поверхности нагружения. В сопротивлении материалов, когда рассматриваются стержни и стержневые системы, удобно иметь дело не с напряжениями в каждой точке, а с их интегральными характеристиками, усилиями и моментами в сечении. Вводя понятия обобщенных усилий в сечении, мы не будем делать разницы между усилиями и моментами, обозначая их одинаково через Q{. Соответствующие обобщенные деформации будут qt, а обобщенные скорости деформаций — qt. Если Q, — продольное усилие, a Q. — изгибающий момент, например, то q, будет относительное удлинение стержня, а qt — изменение кривизны. Условие предельного состояния для сечения всегда может быть записано следующим образом:
F(Qit Q„ . ..) = 0.
Поверхность F=0 можно также назвать поверхностью нагружения, оиа всегда будет выпуклой, а обобщенные скорости деформации будут пропорциональны частным производным функции F. Прибегая к геометрической интерпретации, мы можем и здесь изображать
состояние течения вектором q с составляющими qv qt, ...; если состояние сечения стержня изображается точкой М поверхности нагружения, то вектор скорости будет направлен по нормали к этой поверхности в точке М (рис. 240). Фактическое нахождение условия предельного состояния стержня затруднительно и само по себе
представляет сложную задачу теории пластичности, которая может быть решена лишь для частных случаев.
В качестве примера рассмотрим уже разобранную по существу в § 112 задачу о соаместном действии изгиба и
Рис. 241.
растяжения или сжатия на
Стержень прямоугольного сечения; приведенный там анализ мы дополним исследованием скоростей деформации. Обозначим продольную силу через Q,, изгибающий момент через Qt, высота сечения пусть будет к, ширина Ь, смещение нейтральной оси £. Тогда qt представляет собою удлинение средней линии, qt — кривизну. Очевидно, что qt—^qt. Эпюра распределения напряжений показана на рис. 241. Подсчитывая продольную силу и изгибающий момент, найдем:
/А* \
Q1 = 2^aI, Qt=[^—V)ba±.
§ 163] ИСТИННОЕ И ДОПУСТИМЫЕ СОСТОЯНИЯ ЭЛЕМЕНТЕ 355
Исключая отсюда £, получим условие предельного состояния:
i=o,
*т *
м
If
Рис. 242.
Легко проверить справедливость ассоциированного закона течения. Действительно, отсюда По-
скольку мы имеем дело с двумя обобщенными силами в сечении, поверхностью нагружения будет кривая в плоскости Qt, Qt, состоящая из дуг двух парабол (рис.
242). Вектор q направлен по нормали к кривой. В точках А и В направление нормали неопределенно, следовательно, вектор скорости q может принимать любое направление внутри угла, образованного нормалями к каждой из парабол в точке их пересечения. Действительно, если стержень переведен в пластическое состояние путем растяжения, деформация его будет не обязательно деформацией только растяжения, он
может одновременно изгибаться произвольным образом, единственное ограничение состоит в том, чтобы при этом не было разгрузки, следовательно, было Л/2 «с | £ | «с оо.
§ 163. Истинное и доиустимые состояния элемента. Условие предельного состояния F(Q,, Qt, ...) = 0, вообще говоря, выполняется не для всех элементов системы, некоторые элементы остаются в упругом или жестком состоянии, и для них F(Q,, Qt, ...)<^0, тогда как по самому определению идеально-пластического тела такие состояния, для которых F (Qt, Qt, ...)^>0, невозможны. Таким образом, допустимыми состояниями элемента будут такие, для которых
F(Qt, Qt, ...)<0.
Будем говорить, что при этом условие предельного состояния не нарушено. Пусть Q,, Qt, ..., Q„ представляют собою обобщенные усилия некоторого элемента (сечения), находящегося в предельном состоянии. Эти усилия соответствуют точке М на поверхности нагружения (рис. 243), радиус-вектор этой точки есть Q, вектор истинных скоростей деформации направлен по внешней нормали к поверхности в точке М. Наряду с истинным состоянием рассмотрим некоторое допустимое состояние Q*t, ..., Q*, изображаемое
12*
356 ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ [ГЛ. XV
точкой N, находящейся либо на поверхности нагружения, либо внутри нее; радиус-вектор этой точки Q*. Вследствие выпуклости поверхности нагружения вектор Q-Q* всегда составляет острый угол с вектором q, следовательно, скалярное произведение их положительно:
(Q — Q*)q>0. (163.1)
Это неравенство лежит в основе всей дальнейшей теории. В случае, если достижение предельного состояния определяется только одним обобщенным усилием, например при Jr q растяжении — сжатии или изгибе стержня,
N / неравенство (163.1) носит совершенно три-виальный характер. Так, например, при растя-ц*/ жении истинное состояние будет такое, когда
\ N — Nr, следовательно, можно рассматри-4^ вать только такие допустимые состояния, для
р „ которых значит, N—С дру-
гой стороны, направление скорости деформации совпадает с направлением силы, а следовательно, также положительно.
Заметим, что если точка N лежит на поверхности нагружения, а значит, второе состояние также является предельным, то
(Q* — Q)?>o.
Здесь q*— вектор скорости деформации в допустимом состоянии, направленный по нормали к поверхности в точке N.
§ 164. Статический метод определения предельной нагрузки. Будем рассматривать жестко-пластическое тело, находящееся в предельном состоянии под действием внешних снл Pz. При этом обобщенные усилия Qs в некоторых элементах не удовлетворяют условию текучести, в остальных же элементах это условие не нарушено. Соответствующие обобщенные скорости деформации будут qs, а скорости точек приложения внешних сил — Нахождение перечисленных величин и составляет задачу теории пластичности; при этом основная цель состоит в определении внешних сил, то есть несущей способности конструкции. Приближенное решение этой задачи можно всегда получить, если рассмотреть вместо истинного состояния некоторое статически возможное. Под статически возможным состоянием понимается такое состояние, когда выполнены уравнения равновесия и условие предельного состояния нигде не нарушено. Пусть Р*— внешние силы, соответствующие этому статически возможному состоянию, Q* — обобщенные усилия. По условию
/(QJ, Q*t,
§ 164] СТАТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ПРЕДЕЛЬНОЙ НАГРУЗКИ 357
Поскольку силы Р* и Q* находятся в равновесии, к ним можно применить принцип возможных перемещений. Распределение скоростей vi и 4s фактически реализуется в теле, поэтому в качестве системы возможных перемещений можно принять перемещения, пропорциональные этим скоростям. Получим:
2^Ч=2Л- (164.1)
С другой стороны, принцип Лагранжа можно применить и к силам истинного состояния, вследствие этого
2Р^=2<?Л- (164.2)
Вычтем уравнение (164.1) из уравнения (164.2):
2 P^i - 2 ffa=2
Правая часть положительна в силу основного неравенства (163.1), поэтому
2РА>2РХ- (164.3)
Знак равенства возможен только тогда, когда выбранное статически возможное состояние совпадает с истинным. В случае, если на систему действует только одна сила Р, неизвестная скорость v в обеих частях неравенства (164.3) сократится и мы получим:
Р>Р*.
Таким образом, нагрузка, соответствующая произвольному статически возможному состоянию системы, меньше, чем предельная нагрузка. Этот вывод остается справедливым и для системы сил, действующих на тело, если сравниваются нагрузки, отличающиеся пропорциональным изменением всех сил.
Рассматривая различные статически возможные состояния, мы будем находить различные нагрузки, каждая из которых является приближением снизу для истинной предельной нагрузки. Наилучшим приближением согласно доказанной теореме будет то, для которого нагрузка получается наибольшей.
Упругое состояние системы, при котором предел текучести достигнут в одной нли нескольких точках, является по определению статически возможным. Действительно, при решении задачи о нахождении упругого состояния мы должны были позаботиться о выполнении уравнений равновесия; при этом условие текучести нигде не было нарушено и только в отдельных точках это условие достигнуто. Соответствующее значение внешней нагрузки представляет нагрузку, определенную по способу допускаемых напряжений (с запасом прочности, равным единице). Таким образом, мы имеем совершенно
358
ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
I
[гл. XV
строгое доказательство того, что расчет по предельному состоянию приводит к ббльшим значениям допускаемой нагрузки, чем расчет по допустимым напряжениям.
§ 165. Примеры определения предельной нагрузки статическим методом. Метод приближенного определения предельной нагрузки путем подбора статически возможного состояния мы будем называть статическим методом. Этот метод дает для предельной нагрузки всегда приближение снизу. Если нам представляется возможность перебрать все статически возможные состояния и найти такое состояние, которому соответствует наибольшее значение нагрузки, то это значение будет точным.
Рассмотрим в качестве примера неразрезную балку, состоящую из двух равных пролетов и нагруженную по всей ее длине 21 сплошной равномерно распределенной нагрузкой q (рис. 179). Величину этой нагрузки требуется найти. Обозначим через X реакцию крайней опоры. Давая X всевозможные значения, мы переберем все статически возможные состояния балки. Условие того, что наибольший изгибающий момент равен 7ИТ, позволит определить для каждого значения X величину нагрузки q, максимальная нагрузка будет соответствовать предельному состоянию. Изгибающий момент в сечении с координатой х:
Мх= Хх------
Максимальное значение момента, как легко видеть, достигается при X 1 X2
х=х1 — —, (Afx)max = g- —. Требуя, чтобы модуль этого момента не превышал AfT, получим:
Хг 4 2МТ •
С другой стороны, максимальное значение момента может быть
достигнуто на средней опоре при х — 1. Оно равно XI--------
Из условия, что абсолютная величина этого момента не превышает АГТ, найдем:
п « — о/’
Введем безразмерные величины q=-~- и неравенства перепишутся таким образом:
-jj-p . Полученные
(а)
(б)
Ч
ГА
§ 165J ОПРЕДЕЛЕНИЕ ПРЕДЕЛЬНОЙ НАГРУЗКИ СТАТИЧЕСКИМ МЕТОДОМ 359
На рис. 244 штриховкой показана область, в которой выполняются неравенства (а) и (б). .
Наибольшее значение нагрузки соответствует точке А, где пересекаются парабола и прямая g*=2(l-{-А). Абсцисса
этой точки Х=Л1 = 2(1 —J— у/^2), соответствующее значение нагрузки = 6-{-41^2, максимальное значение момента в пролете достигается при х —х1=/-^- = (]/2—1)/. Это решение совпадает с тем, Ч которое было найдено в § 121 без строгого обоснования. Анализ подобного рода становится затруднительным, если система имеет более высокую степень статической неопределенности, когда приходится искать максимальное значение предельной нагрузки как функции нескольких параметров.
Второй пример, который мы здесь рассмотрим, носит несколько менее элементарный характер. Стержень круглого поперечного сечения радиуса г нагружен продольной силой Р и крутящим моментом М; требуется найти распределение напряжений и соотношение м предельном состоянии.
Растягивающая сила вызывает нормальные напряжения о, крутящий момент — касательные напряжения т, как то, так и другое являются функциями от радиуса g. Они удовлетворяют условию пластичности Мизеса
Примем за искомую неизвестную функцию t(g), тогда a(g) = = (oj — 3t(g)!)1''2. Растягивающая сила и крутящий момент выразятся через т (g) следующим образом:
Г
Р= 2л У У'о’ — Зт* g dg, > о
г
АГ=2л У tg’ dg.
8
6
4
а
г
, I_I I ч" i
12 3 4 5 6
Л
Рис. 244.
силой и моментом в
Задаваясь произвольной функцией T(g), мы будем получать различные статически возможные состояния. Одно из этих состояний является истинным; чтобы найти его, нужно найти условие максимума
360
ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
[ГЛ. XV
силы при фиксированном значении момента или наоборот. Получается так называемая задача об условном экстремуме. Следуя общему правилу вариационного исчисления, составляем функционал
Р—А./И = 2л^Ф(Х, r(g))dg.
Здесь
Ф (X, т (q)) _ q — Зтг — Xq’t.
Условие экстремума будет следующее:
В данном случае
Отсюда находим T(g):
<Тт
/3 /3 4-1V ’
Из условия пластичности определяем a (g):
Таким образом, распределение напряжений оказалось зависящим от параметра А, характеризующего соотношение между растягивающей си-
Рис. 245.
лой и крутящим моментом. На рис. 245 построены соответствующие эпюры распределения напряжений (Надаи).
Прием, с помощью которого удалось решить последнюю задачу, приводит к результатам только в одномерном случае, когда искомая функция зависит от одной координаты. Случаи* кручения с изгибом, например, или кручения и растяжения стержней некруглого сечения чрезвычайно трудны для исследования, и точные решения
здесь отсутствуют.
§ 166. Кинематически возможные состояния. Для того чтобы статически возможное состояние жестко-пластической системы было действительным состоянием предельного равновесия, нужно, чтобы это состояние было в то же время кинематически возможным; это значит, что свобода пластической деформации, связанная с переходом
§ 166]
КИНЕМАТИЧЕСКИ ВОЗМОЖНЫЕ СОСТОЯНИЯ
361
отдельных элементов в пластическое состояние, должна иметь возможность реализоваться на самом деле. Обращаясь к первому примеру, рассмотренному в предыдущем параграфе, мы заметим, что состояния, соответствующие внутренности заштрихованной области на рис. 244, отвечают условию того, что система остается жесткой. Кривая а соответствует тому случаю, когда в пролетах образовались пластические шарниры. Этого еще .недостаточно, чтобы балка получила возможность свободно деформироваться (рис. 246, а). Если мы
рассматриваем статически возможное состояние, удовлетворяющее условию (б), пластический шарнир получается над средней опорой, этого опять-таки недостаточно для того, чтобы балка превратилась в изменяемую систему (рис. w w
246, б). Только тогда, когда А * g £
пластические шарниры возник-
нут и в пролетах, и над средней опорой, что соответствуют точке А диаграммы рис. 244, балка получает возможность деформироваться так, как показано на рис. 246, а; такое состояние является кинематически возможным, притом совместным со статическим состоянием. Последнее замечание означает, что ' пластические
усилия должны производить положительную работу на соответствующих перемещениях; грубо говоря, если напряжение в стержне равно 4~”от1 он Должен уДлйййТЬс?, I не укорачиваться. Возвращаясь к Схеме образования пластических шарниров, изображенной на рис. 246, а, следует заметить, что она не исключает возможности деформации по схеме, показанной на рис. 246, а, но при этом в левом шарнире относительный поворот имеет направление, противоположное моменту, работа момента отрицательна, и следова
тельно, кинематически мыслимая схема деформации несовместима
с принятым статически возможным состоянием.
Второй метод определения точного или приближенного значения предельной нагрузки для жестко-пластических систем состоит в том,
что мы рассматриваем различные кинематически возможные схемы перехода системы в состояние текучести и приравниваем работу внешних сил работе внутренних сил перешедших в пластическое состояние элементов. Принятая кинематическая схема дает нам распределение скоростей деформации, это распределение вместе с условием текучести позволяет иайти величины соответствующих усилий. Вопрос об усилиях решается чрезвычайно просто, если в каждом элементе достижение предельного состояния определяется величиной
362
ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
[ГЛ. XV
одного только усилия. Так, в случае фермы, выбирая кинематически возможное состояние, мы допустим, что некоторые стержни могут свободно удлиняться или укорачиваться. Напряжения в соответствующих стержнях будут равны пределу текучести соответственно со знаком плюс или минус. При изгибе балки, пренебрегая влиянием поперечных сил на предельное состояние, нужно считать в пластической части момент равным Мг. Если условие пластичности для элемента содержит несколько обобщенных усилий, то, зная поверхность нагружения и используя ассоциированный закон течения, мы можем найти ту точку на поверхности нагружения, в которой нормаль имеет заданное направление. Коор-y(z)t динаты этой точки дадут величи-
у ны соответствующих усилий.
у тя.
Рис. 247.
Рис. 248.
Условие равенства работы внешних и внутренних сил удобно заменить условием равенства мощностей, то есть работ, произведенных за единицу времени, поскольку мы считаем известным распределение скоростей. Запишем это условие следующим образом;
2^=2 (166.1)
Остановимся несколько подробнее на вычислении мощности внутренних сил. Так, можно предположить, например, что балка изгибается по кривой y — v(x)i, как показано на рис. 247, скорость изменения кривизны в каждом сечении равна if (х), следовательно, работа моментов есть
i
J МУ' dx — Мт [v' (/) — v’ (0)]. о
Величина, заключенная в квадратные скобки, представляет собою разность угловых скоростей поворота касательных к оси балки в начальной и конечной точках. С другой стороны, в качестве кинематически возможного состояния можно взять состояние, соответствующее шарниру текучести (рис. 248). Тогда работа момента в пластическом шарнире за единицу времени будет равна 2Ит<р, где <р — угловая скорость относительного поворота частей балки, разделенных пластическим шарниром. Как видно, эти выражения совершенно совпадают.
§ 167. Кинематический метод определения предельной нагрузки. Выбирая произвольное кинематически возможное состояние, мы можем получить по формуле (166.1) величину внешней нагрузки, которая
§ 168] ОПРЕДЕЛЕНИЕ ПРЕДЕЛЬНОЙ НАГРУЗКИ КИНЕМАТИЧ. МЕТОДОМ 363 представит собою некоторое приближение к истинной предельной нагрузке системы. В отличие от статического метода, кинематический метод дает для определенной нагрузки завышенное значение, то есть оценку сверху.
Обозначим по-прежнему Pt и Qs внешние силы и усилия в пластических элементах для истинного состояния, выберем произвольное кинематически возможное состояние, для которого обобщенные скорости деформации суть qs, а скорости точек приложения внешних сил — Vi. По заданному распределению q3 с помощью условия пластичности находим усилия QJ.
Поле скоростей vt, qs является кинематически возможным полем, поэтому мы можем применить принцип Лагранжа к истинному состоянию, приняв возможные перемещения пропорциональными скоростям Vj, qs. Таким образом, имеем:
2 /^=2 Q&- (i67.i)
Прибавим к правой части этого равенства и вычтем из нее 2 QsQs-Получим
2 Рtv‘ == 2 Qs) У* •
Но вследствие условия (163,1) последняя сумма в правой части положительна. Отсюда следует:
2 2 •
Если иа систему действует только одна сила или если сравниваются системы сил, изменяющиеся пропорционально одному параметру, из полученного неравенства находим:
Р^£о^ = р*.
Таким образом, предельная нагрузка, найденная по кинематическому методу, всегда больше истинной. Знак равенства возможен только тогда, когда кинематический метод дает точное решение, то есть когда кинематически возможное состояние является в то же время статически возможным.
§ 168. Примеры определения предельной нагрузки кинематическим методом. Кинематический метод значительно более прост и удобен для применения, чем статический метод, и поэтому находит гораздо более широкое применение. Рассмотрим два простых примера.
а) Жесткий брус (рис. 249) подвешен на четырех стержнях с различными сечениями или из разных материалов; таким образом,
364
ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
[ГЛ. XV
усилия предела текучести для них равны 5Т1, 5Tt, STt и ST1 соответственно. Сила Р приложена в середине бруса. Для перехода системы в состояние текучести необходимо, чтобы три стержня были в пластическом состоянии, а четвертый оставался жестким. Рассмотрим соответствеиио четыре возможности, когда деформация происходит
в результате поворота относительно точек А, В, С и D. Очевидно, нужно рассматривать только такие состояния, когда сила Р при повороте совершает положительную работу. Соответствующие схемы показаны на рис. 250, а,
б, в и г. Уравнение работ в этом случае тождественно с урав' иением моментов. В случае а мы получаем:
|P*=5T, + 25T,+ 3ST4.
В случае б:
1P*==5T, + 2SI4 + Srl.
В случае в:
4p* = 25t1 + Sm + Si4,
и, наконец, в случае г:
|P* = 3ST1 + 2STS + 5T,.
Таким образом, для четырех кинематически возможных состояний мы получили четыре значения для предельной нагрузки:
p*=|st.+4st,+2st4,
P* = 2St1 + 2St, + 4St4,
P* = 4STl + 2STt + 2ST4,
§ 168] ОПРЕДЕЛЕНИЕ ПРЕДЕЛЬНОЙ НАГРУЗКИ КИНЕМАТИЧ. МЕТОДОМ 865
Теперь остается подставить числовые вначения пределов теку-
чести для стержней и выбрать наименьшее из четырех значений силы Р*, это и будет истинная предельная нагрузка. Остальные три значения силы Р* соответствуют состояниям кинематически возможным,
но невозможным статически, стержне, который предполагался жестким, остается превышающим предел текучести для этого стержня.
б) В качестве второго примера рассмотрим ту же самую двухпролетную неразрезную балку, которая была рассчитана статическим ме-
Дело в том, что при этом усилие в
тодом в § 165. Зададимся координатой пластического шарнира в пролете (рис. 251). Рассматривая половину балки, найдем, что работа внешней нагрузки q* равна произведению этой нагрузки на площадь треугольника ADB, то есть равна у Момент в пролете со-
вершает работу на угловом перемещении «4“Р, момент на опоре — на угловом перемещении 2р, но на каждый пролет приходится лишь половина этой работы. Таким образом,
-lag/‘?* = AfI(a4-2p).
»
Заметим, что p=a сократив на а и введя безразмерную нагрузку так же, как это было сделано в § 165, получим:
-* о/1 । 2
4 =2Н+1-
Условие минимума нагрузки приводит к уравнению для
5’4-25-1=0.
Отсюда
|=/2-1
(второй корень не имеет смысла).
Соответствующее вначение нагрузки
7=64-4/2
совпадает с величиной, найденной при помощи статического метода. Для решения этой задачи в § 121 был применен, по существу, также кинематический метод.
Без строгого обоснования кинематический метод применялся в сопротивлении материалов достаточно давно и довольно широко. Многочисленные приближенные способы расчета, основанные иа
.366
ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
[ГЛ. XV
.гипотезах частного характера, находят обоснование при помощи теоремы, доказанной в предыдущем параграфе. Так, если внимательно посмотреть главу IV, посвященную главным образом условным расчетам, станет очевидно, что эти условные расчеты основываются на допущении определенной кинематической схемы разрушения и, следовательно, дают верхнюю оценку для предельной нагрузки. Вводимый в расчет запас прочности необходим именно потому, что мы получаем верхнюю оценку и не знаем при этом, насколько она превышает истинную величину нагрузки. Положение становится более определенным в том случае, когда для одной, и той же задачи имеются приближенные решения, полученные как статическим, так и кинематическим методом, тогда мы имеем двухстороннюю оценку. Иногда их удается сблизить настолько, что поиски точного решения теряют смысл. Однако нахождение статических решений более трудно, и мы располагаем точными оценками лишь для немногих задач.
§ 169. Предельное равновесие пластинок. Расчет пластинок
в упругой стадии их работы составляет предмет прикладной теории
упругости и выходит за рамки настоящего курса. Нахождение же
верхней оценки несущей способности пластинки из идеально-пластического материала во многих случаях осуществляется достаточно элементарными средствами. Соответствующая теория была первоначально построена применительно к расчету бетонных и железобетонных плит и в настоящее время находит применение главным образом для железобетонных конструкций. Бетонная плита разрушается хрупко,
Рис. 252. с образованием трещин, таким образом,
казалось бы, соображения, развитые для идеально-пластического материала, в этом случае неприменимы. На самом деле при формулировке основных принципов предельного
равновесия и при доказательстве соответствующих теорем, по существу, никакие соображения физического характера ие привлекались, и предельное состояние пластичности может с тем же основанием трактоваться как предельное состояние разрушения. Под ки
нематически допустимым состоянием можно понимать то мгновенное распределение скоростей, которое осуществляется в самый момент разрушения, а что будет делаться с материалом впоследствии, то есть будет ли он течь неограниченно или же разлетится на отдельные куски, это не должно нас интересовать.
Рассмотрим полигональную пластинку, свободно опертую по контуру, и нагруженную сосредоточенной силой Р в точке С (рис. 252),
§ 169]
ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ ПЛАСТИНОК
367
Одной из возможных кинематических схем разрушения (или пластической деформации) такой пластинки будет следующая. По линиям, соединяющим точку приложения силы с вершинами контура, происходят изломы, плоская срединная поверхность переходит в поверхность пирамиды, ребра которой образованы упомянутыми линиями, а грани остаются плоскими. Обозначим прогиб в точке приложения силы S, длины ребер излома ls, двугранные углы между гранями, примыкающими к соответ- г .
ствующим ребрам, а>т. Изгн-бающий момент, приходя-щийся на единицу длины i
линии излома, есть 2ИТ, и уравнение работ приводит к * ' с "
следующему равенству: --------
Рб=s м^- '
Чтобы найти двугранный рис 253
угол (й^, проведем через точ-
ку приложения силы С прямую АВ, перпендикулярную линии ls (рис. 253), и продолжим примыкающие к вершине Cs стороны контура пластинки до пересечения с прямой АВ. Левая часть поворачивается около прямой ACS, правая около прямой BCS, прямая АСВ изламывается, как показано на том же чертеже во второй проекции; на этой проекции виден угол о,. Он равен Но ^C=/,tg<p,,
BC=/itgij?J. Таким образом,
(^ = ^(ctg‘P* + ctg1k)-
Внеся в уравнение работ, получим: /^^(ctgcp. + ctg^). (169.1)
Рассмотрим несколько простых примеров приложения формулы (169.1). а) Пластинка прямоугольного сечения, нагруженная в центре (рис. 254). В этом случае
ctg<P=T, ctgip = —;
по формуле (169.1)
М. \Ъ 1 аj *
б) Пластинка в форме правильного л-у голь ника, нагруженная в центре (рис. 255). При этом
Ф = ф = у^1— -J , Ctg<p=tg-.
368
ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
[ГЛ. XV
Предельная нагрузка дается формулой 2п tg £ 2ИТ.
в) Круглая пластинка, опертая по контуру. Круглую пластинку можно рассматривать как предельный случай плас-
Рис. 254.
тинкн в форме правильного мящемся к бесконечности, дущая формула дает:
многоугольника при числе сторон, стре-При таком предельном переходе преды-
Р=2л<.
Поверхность изогнутой пластинки в предельном состоянии представляет собою конус. Найденное решение является точным; можно
показать, что оно не только кинематически, но и статически допустимо.
Если пластинка несет равномерно распределенную нагрузку, то npif расчете можно поступать точно таким же способом, только для
вычисления работы распределенной нагрузки нужно интенсивность нагрузки множить на объем пирамиды. Пирамидальная форма разрушения при этом не всегда соответствует минимальной нагрузке.
Для пластинки, защемленной по контуру, применяя ту же схему разрушения, мы должны допустить, что изломы образуются не только по линиям,
соединяющим точку С с вершинами, но также вдоль заделанных сторон. Соответствующий угол для стороны at равен б/р, (рис. 256), работа момента на каждую сторону выражается так: MTbaJps.
Внося atlps=cig i|>,4-ctg в уравнение работ, мы найдем, что
в правой части этого уравнения появится еще раз точно такое же выражение, которое было раньше, и уравнение примет следующий вид:
Р== 2МТ V (ctg <р, 4- ctg ф,).
(169.2)
§ 169] ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ ПЛАСТИНОК 369
Для круглой пластинки, защемленной по контуру, получится:
Р=4лЛ4т. (169.3)
Можно показать, что для многоугольника сумма ^](ctg ф, 4~ctg ipj всегда больше, чем 2л, поэтому нагрузка,
вычисленная для круглой пластинки по формуле (169.3), оказывается меньше, чем вычисленная для полигональной пластинки по формуле (169.2). Отсюда следует, что пирамидальная схема разрушения для защемленной по контуру пластинки непригодна, у такой пластинки под действием сосредоточенной силы будет выламываться круг, переходящий в коническую поверхность (рис. 257). Радиус этого круга предельная нагрузка не зависит от радиуса. Рас. 257. неопределенен, так как
ГЛАВА XVI .
ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
§ 170.- Колебания систем с конечным числом степеней свободы. Рассмотрим механическую систему, состоящую из упругого сооружения, которое несет ряд сосредоточенных грузов. Сначала будем представлять себе эти грузы в виде материальных точек, которые мы занумеруем от 1 до п. Массой сооружения будем пренебрегать по сравнению с массой грузов. Обозначим ult ut, ... , ип перемещения грузов, массы которых mt, тг, Связь между
силами, приложенными к грузам, Pr, Pt, ... , Рп, и соответствующими перемещениями устанавливается следующими соотношениями:
«1=в„Л + в1Л+ •••+«>
ип = + • • • + ^ппРп
или, в сокращенной записи,
с170-1)
Единичное перемещение б^ определяется так, как было указано в § 159.
Разрешая (161.1) относительно Pit мы придем к следующим соотношениям:
р.=2с.уИ (i=l, 2, ... ,п). (170.2)
z=i
Коэффициенты влияния б^, как мы видели, находятся просто, вычисление коэффициентов жесткости Сц более затруднительно.
Теперь представим себе, что система пришла в движение. На каждый из грузов действует заданная сила Qz, которая, вообще говоря, является функцией времени; если перемещение груза есть «,• (/), его ускорение равно й,- (/). Чтобы составить уравнение движения, положим в соотношениях (170.1) или (170.2), следуя принципу
§ 170] КОЛЕБАНИЯ СИСТЕМ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ 371
Даламбера,
Pi = Qi — mfli.
Получим:
или
(170.3)
(170.4)
Форма (170.4) для записи уравнений движения механической системы более проста, ио мы будем по большей части пользоваться уравнениями в форме (170.3), именно потому, что коэффициенты влияния Sy определяются проще.
Заметим, что, по существу, нумеровать от единицы до п нужно не грузы, а степени свободы системы. Поэтому, например,
желая решить задачу о колебаниях изображенной на рис. 258 рамы с грузом конечных размеров на конце, мы обозначим цифрами 1, 2 и 3 степени свободы, соответствующие горизонтальному пе
ремещению, вертикаль- J ному перемещению и повороту. Соответственно
m3=mt представляет со-
бою массу груза, тогда как т3 есть его момент инерции, и3 и ut — это линейные перемещения, тогда как ut— угол поворота. Строя эпюры моментов от изображенных единичных сил и единичного момента и применяя графоаналитический способ вычисления интеграла Мора, найдем необходимые для составления уравнений движения коэффициенты влияния Sy.
В технике возмущающие силы бывают известны довольно редко, обычно задана только частота возмущающих сил и задача расчета сводится к определению собственных частот свободных колебаний с целью выявления возможности резонанса. Поэтому мы положим в уравнениях движения Q; —0 и будем искать решение в виде
Uj = sin
(170.5)
В результате подстановки выражения (170.5) в уравнение движения получим:
а,- — со* у Sy mj a.j = 0 (170.6)
j
или
— 2 си aj = 0. (170.7)
372 ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XVI
§ 171. Собственные частоты и главные формы колебание. Будем отправляться для определенности от уравнений (170.6), хотя те же результаты можно получить, если использовать уравнения в форме (170.7).
Рассматриваемая система — это система п линейных однородных уравнений для п неизвестных ах, at, ... ,ап амплитуд свободных колебаний системы. При произвольных значениях со существует лишь тривиальное решение: ax = at= ... = ап = 0. Условие существования нетривиального решения состоит в равенстве нулю определителя системы:
—i + 6u/»i бА -ЛА
6.. m. '—т + б../»,... б,„т„
“ 1 (|Г 1 “ * 2П П __q (171 1)
^nl^i би2/Я± ... •
Уравнение (171.1) представляет собою уравнение степени п относительно со1, которое имеет п корней, каждый из которых определяет собственную частоту системы. Таким образом, упругая система имеет столько собственных частот колебаний, сколько у нее степеней свободы.
Мы будем предполагать, что все корни уравнения (171.1) различны. Действительно, корни могут быть равными только тогда, когда коэффициенты податливости и массы грузов принимают совершенно определенные значения; достаточно немного изменить массу одного из грузов или жесткость какого-либо элемента системы, как корни станут различными. Таким образом, случай равных корней не может представлять каких-либо качественных особенностей, и нам нет необходимости на нем останавливаться.
Перенумеруем корни уравнения в порядке возрастания; соответствующие собственные частоты будут со,, ©t, ...,©я. Если внести в систему (170.6) значение ®, равное ©А, она будет иметь отличные k k k
от нуля решения а1г Совокупность амплитуд, соответ-
ствующих определенной собственной частоте колебаний, называется главной формой колебаний. Главные формы колебаний обладают свойством ортогональности, которое выражается следующими равенствами:
^т{а{а-=0 (171.2)
Для доказательства положим в (170.6) co=coft и перепишем это уравнение следующим образом:
а? =со| 2 ботуау.
§ 171] СОБСТВЕННЫЕ ЧАСТОТЫ И ГЛАВНЫЕ ФОРМЫ КОЛЕБАНИЙ 375
Умножим обе части на и просуммируем по индексу i-Получим:
2 = со* (171.3)-
Но можно было поступить иначе, а именно принять в (170.Gift) =со/ и переписать это уравнение в виде
Умножив на и просуммировав по индексу /, получим: ^miajai—a* (171.4).
В равенствах (171.3) и (171.4) левые части одинаковы, одинаковы и двойные суммы в правых частях, так как (§ 152) бу=бу^ Но соА^сог, поэтому равенства (171.3) и (171.4) могут выполняться, одновременно только тогда, когда двойная сумма равна нулю, а следовательно, справедливо соотношение ортогональности (171.2).
До сих пор мы молчаливо предполагали, что все корни уравнения частот—действительные и положительные числа. Сейчас мы можем это доказать. Действительно, предположим, что <о* — комплексное число. Тогда обязательно найдется второй корень <о*, являющийся комплексным сопряженным числом. Амплитуды главной формы номер fe-будут также комплексными числами вида a*=a1--J~Zpf, амплитуды главной формы номер I будут комплексными сопряженными числами a/=az — Подставляя а* и а* в условие (171.2), мы получим:.
=2 (а? + ₽’) = °-
Но это равенство невозможно, так как в левой части все слагаемые положительные.
С другой стороны, величина со*, полученная в результате решения уравнения (171.1), всегда положительна. Действительно, положим в (171.3) l=k и запишем это равенство следующим образом, опуская* верхние индексы:
2m,a* = co‘2^(m,a,) (»уву)б,7. (171.5>
Сумма, стоящая в левой части, всегда положительна, так как все слагаемые положительны, сумма в правой части представляет собок> удвоенную потенциальную энергию системы, нагруженной силами /»faf (см. формулу (152.5)). Но, каковы бы ни были силы, энергия всегда положительна, поэтому двойная сумма в правой части положительна
374 ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XVI
при любых значениях амплитуд Поэтому ы* также необходимым образом должно быть положительно.
Амплитуды, соответствующие каждой из главных форм колебаний,
определяются в результате
решения системы линейных однородных уравнений, поэтому они известны с точностью до множителя. Чтобы сделать выбор амплитуд главных форм колебаний определенным, подчиним их условию нормирования’
(171.6)
Пример. Балка иа двух опорах длины 4а несет три одинаковые массы, расположенные на равных расстояниях между собою и от опор (рис. 259)'.
Прежде всего строим эпюры моментов от единичных сил и находим коэффициенты влияния по способу Мора:
1 3 2 3,
• 2 • 4 а'а з ‘ 4 аЧ“
. 1 3 „ 2 3 3 ,
+ _._й.3а.у.та=та,
Запишем матрицу коэффициентов влияния следующим образом:
нм =
9 117
И 16 11
7 11 9
X —
А 12EJ'
Обозначим
12EJ та3 ш* г'
§ 171] СОБСТВЕННЫЕ ЧАСТОТЫ И ГЛАВНЫЕ ФОРМЫ КОЛЕБАНИЙ
375-
Уравнение частот (171.1) примет следующий вид:
9 — 2 11 7
11 16 — 2 11 = 0.
7 И 9 — 2
Раскрыв определитель, получим следующее кубическое уравнение: z* — 34Z1 + Пг — 28 = 0.
Корни этого уравнения:
z1 = 31,56, zt=2, zt = 0,444.
Соответствующие частоты:
©,=0,6171/^, ^ = 2,45 1/^-, со, =5,191/^.
1 У та 1 У тег у та*
Уравнения для амплитуд главных форм
колебаний будут такие:
a, (9-z)4-а,114-а37 = 0, at 11 —аа (16 — £)4-a3ll =0,
а, 7 4“ а,114“ at (9 — z) = 0.
Здесь нужно последовательно принимать z = zt, z=z2, z=zt. Фактически всегда приходится рассматривать только два уравнения,
в данном случае можно взять первое и второе. Одна из амплитуд может быть задана по произволу. Примем, например, at= 1 во всех случаях. Получим:
<4 = 1, <4=1,416, аз=\;
а* = — 1, <4 = 0, <4 = 1;
<4 = 1, al = —1,416, al=l.
Выполнение условий ортого- Рис. 260.
нальности легко проверяется.
Амплитуды каждой нз главных форм можно умножить на любое число, подберем в каждом случае это число так, чтобы было выполнено условие нормирования. Нормированные главные формы колебаний будут следующие:
! 0,500 й‘—’ у т г 0,708 1 0,500 ®2 г— > у т
2 0,708 й,= Ут ’ «t = 0, । 2 0,708 ЙЗ=Т^": у т
3 0,500 а'— у т 2 0,708 Й2~ V™ ’ у т 2 0,500 а3=-==-. у т
На рис. 260 изображены найденные главные формы колебаний.
376 ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XVI
§ 172. Представление произвольной конфигурации системы через главные формы. Главные координаты. Рассмотрим произвольную конфигурацию упругой системы с сосредоточенными грузами, имеющей п степеней свободы. Эта конфигурация может соответствовать деформированному состоянию от действия произвольной системы внешних сил, может быть некоторой мгновенной конфигурацией, принимаемой системой в процессе движения, вызванного любыми •силами при произвольных начальных условиях. Задать такую конфигурацию— это значит задать п перемещений ах, а2, ... ,ап. Эти величины мы будем называть координатами системы. По определению п координат системы произвольны и независимы между собой. Но для того, чтобы задать положение системы, существуют и другие возможности, любые п чисел, однозначно определяющих конфигурацию, могут быть приняты за координаты. В частности, за координаты можно принять произвольные линейные комбинации из величин аи, лишь бы они были независимы. Предположим, что главные формы колебаний системы известны. Введем координаты uit соответствующие данной конфигурации, следующим образом:
а, == аХ + a*ut 4~ ... 4~ а”и„, = «Х +
ап = а„и1 -ф- atnut -ф- ... 4“ аХ
или, более коротко,
й. = ^й<4- (172.1)
Для того чтобы показать законность выбора величин uk в качестве координат, нужно убедиться в том, что из уравнений (172.1) величины ик определяются единственным образом. Свойство ортогональности главных форм колебаний позволяет очень просто решить уравнение (172.1) относительно ик.
Для этого умножим уравнение (172.1) на тр* и просуммируем по индексу I. Получим:
трр* = тр* а‘ик.
Переставим в двойной сумме порядок суммирования. В силу условий ортогональности и нормирования те суммы по /, которые относятся к неравным между собой k и $, обратятся в нули, при s = k соответствующая сумма равна единице. В результате из всей двойной суммы останется один только член us и мы получим:
(172.2)
§ 172] ПРЕДСТАВЛЕНИЕ ПРОИЗВОЛЬНОЙ КОНФИГУРАЦИИ СИСТЕМЫ
377
Введенные нами координаты us называются главными координатами системы.
Рассмотрим простой пример, в котором свойство ортогональности
главных форм принимает наглядный смысл и введение главных координат становится естественным. Изображенная на рис. 261 рама несет груз на конце. Матрица коэффициентов влияния в этом случае будет
такой:
Положим
аг 6EJ
_6EJ 1
Z ' та1 а>*'
Уравнение частот дет следующее:
zl— 10*4-7 = 0.
Корни его:
*,=9,24, *t = 0,76. Рис. 261.
Нормированные главные формы колебаний определяются величинами
или
а1, = 0,383 4—. Vm
а? = —0,923 4-.
1 1 а, = —— sin а, Vm
2 1
а. cos а, Ут
al = 0,923 4= I Vm
al = 0,383 4-У т
1 1
= -= cos а, У т
t__1
а2 = -== sin а Ут
(а=22°30').
2 3
3 8
Если через центр груза провести оси координат — горизонтальную ось xt и вертикальную ось xt, величины aj, al и al, al будут компонентами по осям xt и хг двух векторов а, и at (рис. 261).
. Ортогональность главных форм колебаний нужно понимать в этом случае буквально, как ортогональность соответствующих векторов.
Направим оси координат а, и ut по векторам, соответствующим главным формам колебаний. Для рассмотрения динамики системы оси координат и, и «2 более естественны, чем случайно выбранные оси координат х, и хг; по оси и, происходят колебания с частотой cOj, по оси ut — с частотой <о2. Произвольные колебательные движения груза естественно представлять как результат наложения колебаний с двумя разными частотами в двух главных направлениях.
378 ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XVI
По формулам (172.1) в рассматриваемом случае мы получаем:
[a^sin а -|- a2cos а], ut = ]/rm [— axcos а -|- а, sin а].
Это не что иное, как формулы преобразования координат при «переходе от осей х2, х, к осям значит, главные координаты
системы — это составляющие вектора перемещения по осям иг и йж, умноженные на постоянную величину т.
В общем случае произвольной упругой системы главные координаты не находят такого простого и наглядного истолкования, если -не прибегать к геометрической интерпретации'при помощи многомерного пространства. Однако значение их полностью сохраняется.
§ 173. Формула и способ Релея. Определение собственных частот колебаний упругой системы становится чрезвычайно затруднительным тогда, когда число степеней свободы велико и уравнение частот имеет высокий порядок. Уже развертывание определителя требует большого труда, не говоря о нахождении корней уравнения частот. В то же время для приложений достаточно знать наименьшую, первую частоту, так называемую частоту основного тона. Ее можно найти с достаточной для практики точностью, пользуясь приближенным методом Релея.
Выпишем уравнение (170.7):
<B*/»zaz — ^cuaj—°-j
Умножим это уравнение на at и просуммируем по индексу I, после чего найдем со* из получившегося уравнения:
. . (173.1)
Если al=at, то по формуле (173.1) мы получим для со* точное значение со|; если at — произвольное число, то для со2 по этой •формуле получится некоторая величина, вообще говоря не являющаяся частотой каких-либо колебаний системы. Но если az = az, то выполняются п уравнений, следующих из (170.7):
(173.2)
Представим теперь произвольную конфигурацию системы а( размещением ее по главным формам: az==^pzz«ft.
Внесем это выражение в числитель формулы (173.1). Получим:
cijaiaj—2 2 СИ 2 а/ ajukus‘
§ 173] ФОРМУЛА И СПОСОБ РЕЛЕЯ 37£>
Переменим порядок суммирования, выделив сначала сумму Д
По формуле (173.2) эта сумма равна Теперь мы можем выделить сумму которая равна нулю при k^=s и равна
единице при k = s. Таким образом, мы получим:
Преобразуем теперь знаменатель формулы (173.1):
2 т^. = ^т{ Да* а» ukus.
Меняя опять порядок суммирования, найдем:
Таким образом, формула (173.1) может быть переписана так:
Так как со, co, to, ..., то каждый член числителя больше соответствующего члена знаменателя и мы получаем неравенство со2 > <в2 или же
<bJC (173.3)
i
где at — произвольные числа. Знак равенства возможен только тогда, когда ut = а, = ... = ип = 0, то есть конфигурация системы в точности соответствует первой главной форме.
Неравенство, устанавливаемое формулой (173.3), и является содержанием теоремы Релея.
Задаваясь совокупностью амплитуд az, которая, на наш взгляд, близка к первой главной форме колебаний, мы находим по формуле (173.3) приближенное значение квадрата первой собственной частоты. Заметим, что числитель в формуле (173.3) представляет собою удвоенную потенциальную энергию системы при перемещениях а„ знаменатель же представляет удвоенную кинетическую энергию, вычисленную в предположении, что скорости равны перемещениям. Особенно простым становится применение формулы (173.3) тогда, когда совокупность величин а{ представлена как совокупность перемещений от действующих на систему сил Qs. Тогда потенциальную
380
ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XVI
энергию можно вычислить по теореме Клапейрона. Обозначая перемещения от сил Qs через vk, перепишем формулу Релея следующим юбразом:
(173.4)
i
В числителе суммирование идет по тем точкам, где приложены силы, в знаменателе — по точкам, где сосредоточены грузы.
Обратимся к примеру § 171 и вычислим для рассмотренной там •системы первую частоту свободных колебаний приближенно, по формуле Релея. Сначала зададимся формой кривой прогиба, соответствующей одной силе Q, приложенной посередине. При этом
11 Qa> ‘V* 12EJ ’
__16 Qa»
V* 12EJ '
По формуле
(173.4)
FT ==0,386-^-5 таг
_ / FT со, <0,622 1/
* Г та1
Разница с точным решением со, — 0,617 у —i составляет 'всего 0,8%.
Если взять за форму прогиба упругую линию балки, нагруженной тремя одинаковыми силами в точках 1,2, 3, то есть статическую кривую прогиба балки от собственного веса, то три знака приближенного решения совпадают с точным.
§ 174. Нижние оценки для частоты основного тона. При рассмотрении определителя (171.1) коэффициент при неизвестной 1/со* в старшей степени, а именно в степени п, равен (— 1)”. Легко сообразить, чему будет равен следующий коэффициент, при (1/<о*)"— Если раскрыть определитель по элементам первого столбца или •первой строки, то мы обязательно получим член S,,/», (— I)”-1»
но аналогичные члены получаются при раскрытии определителя по элементам любой другой строки или столбца. Поэтому если уравнение частот имеет вид:
\<0г ) 1 / 1
то
=—(su'»i + 4- • • • 4- \птп\
§ 175]
ПРОДОЛЬНЫЕ колебания стержней
381
С другой стороны, коэффициент при втором по старшинству члене в алгебраическом уравнении равен сумме корней его с обратным знаком:
л==__L_
Отсюда
± - б, л,++ • • • + б„„/»„ - ( ± . .4- .
Выражение, заключенное в скобки, всегда положительно, поэтому справедливо неравенство
А- <6»^ + б„/».+ -.. (174.1)
“1
Рассматривая пример в § 170, мы убедились, что собственные частоты довольно сильно разнятся по величине, поэтому формула (174.1) может быть использована для приближенного определения первой собственной частоты. Обращаясь к числовым данным упомянутого примера, получим:
±;<(9+16+9)1g.- =
<.,>0,591/2,.
17 та’ ~6~EJ ’
Полученная нижняя граница отличается от точного значения на 3,74%. Формула (174.1) (со знаком равенства вместо неравенства) была получена из эксперимента Дункерлеем в середине прошлого столетия.
Мы не будем останавливаться на многочисленных методах получения двухсторонних оценок для первой собственной частоты, а также для следующих частот; они излагаются в специальных руководствах по динамике сооружений.
§ 175. Продольные колебания стержней. Перейдем теперь к изучению колебаний систем с непрерывным распределением масс. Простейшим примером здесь может служить задача о продольных колебаниях стержня постоянного поперечного сечения. На рис. 262 показан элемент стержня, который в недеформированной состоянии был заключен между сечениями тп и pq с координатами х и x-\-dx соответственно. Фиксируя некоторый момент времени t, когда сечение тп занимает положение т'п', сечение pq — положение p'q', обозначим перемещение левого сечения, первоначальная координата которого была х, через и. Смещение и является функцией двух
382 ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XVI
переменных — времени t и координаты в недеформированном состоянии х, поэтому смещение сечения с координатой x-\-dx будет и -\-^dx. На том же рис. 262 изображен элемент m'n'q'p' отдельно.
Обозначим напряжение, действующее в сечении т'п', через а, тогда напряжение, действующее в сечении p'q', будет a-{-^dx. Но
Рис. 262.
изображенный элемент находится в д*и движении, его ускорение равно —, * масса qF dx, где q — плотность, F—площадь поперечного сечения. Составим уравнение движения этого элемента:
„ . дги сдо . qF dx-^-t*=F^- dx. 4 dt* дх
уравнение движения и сокращая
Но по закону Гука а=£е, относительная деформация элемента т'р' — тр ди е—-----——- — ; внося это в
тр дх
F dx, получим:
(175.1)
Здесь
д*и 2 ___
д? С дх*
Обращаясь к § 30, заметим, что с есть скорость распространения продольной упругой волны.
Дифференциальное уравнение (175.1) называется волновым уравнением, оно описывает всевозможные динамические процессы в стержне, распространение волн, а также колебания.
В § 30 мы рассмотрели вопрос о распространении волн, не прибегая к дифференциальному уравнению, сейчас мы имеем возможность получить те же результаты иным путем. Действительно, уравнению (175.1) мы удовлетворим, положив u=f(ct — х), где f—совершенно произвольная функция. Но движение, описываемое найденным решением, представляет собою распространение волн со скоростью с. Общее решение уравнения (175.1), принадлежащее Даламберу, имеет следующий вид:
«=/1(с/ —х)+/г(с/-}-х). (175.2)
Два слагаемых представляют собою две волны, бегущие с одинаковою скоростью в противоположных направлениях.
§ 175] ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ 38?
Хотя решение (175.2) является совершенно общим в том смысле, что любые движения стержня могут быть представлены таким образом, при изучении колебаний оно неудобно, так как не позволяет простым способом обнаружить собственные частоты колебаний. Метод, который мы применим для задач о колебаниях, называется методом разделения переменных или методом Фурье. Заметим прежде всего, что уравнение (175.1) является линейным уравнением и его решения обладают следующими очевидными свойствами:
1. Частное решение уравнения (175.1), умноженное на. произвольную постоянную, является опять решением этого уравнения.
2. Сумма двух (а следовательно, любого числа) частных решений является решением.
Будем теперь искать частные решения уравнения (175.1) в виде произведения двух функций T(t) и Х(х):
и = T(t) Х(х). (175.3)
Подставим указанное выражение для и в уравнение (175.1):
ТХ— с*ТХ№ = 0.
Здесь точки обозначают дифференцирование по времени, штрихи — дифференцирование по координате.
Разделение переменных состоит в том, что уравнение это записывают следующим образом:
Первый член представляет собою функцию только времени, второй член — функцию только координаты х, равенство возможно только в том случае, если каждая из этих функций — постоянная. Таким образом, со’—постоянная величина. Для функций T(t)M Х(х) получаются следующие, уже обыкновенные, дифференциальные уравнения:
Т+й>‘Т=0, (175.4)
Х" + ^^=0. (175.5)
Общий интеграл первого уравнения:
Т — A sin at -|- В cos со/.
Отсюда видно, что со представляет собою круговую частоту свободных колебаний. Осталось определить функцию Л"(х). Общий интеграл уравнения (175.5):
A’=Clsin^ + C,cos^. (175.6)
384 ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XVI
При определении констант этого уравнения из граничных условий мы сталкиваемся с тем же положением, что и при решении задачи устойчивости (§ 136). При однородных граничных условиях для определения констант С, и С, получается система однородных уравнений, имеющая тривиальное нулевое решение. Нетривиальное решение существует только при определенных значениях и, кото» рые и являются собственными частотами.
Прежде чем перейти к примеру, выясним возможные виды граничных уравнений:
а) Закрепленный конец, и = 0 при любом t, следовательно, Х=0.
б) Свободный конец. с = 0, следовательно, е=|^=0, а так как T(t) вообще не равно нулю, то X =0.
в) На конце прикреплен груз массы М. Применяя принцип Даламбера, приравняем силу инерции груза внутренней силе в концевом сечении:
— M^tt — Fg — EF^-,
dt* дх *
или
— MTX=EFTX'.
Исключим отсюда Т с помощью уравнения (175.4) и сократим общий множитель ?'(/). Получим:
X — pre*
В качестве примера рассмотрим задачу о колебаниях стержня длины I, один конец которого закреплен, а на другом имеется груз массы М.
Помещая начало координат в точке х = 0, находим сразу, что постоянная Сг в уравнении (175.6) равна нулю. Подставляя значе-
.. . сох ,
ние Х=Сг sin— в граничное условие на конце х=1, где прикреплен груз, находим:
„Г со/ М со . (оЛ п
С. cos------= — sin — = 0.
* L с qF с с J
Если С, — 0, никаких колебаний нет, колебания возникают только тогда, когда обращается в нуль скобка. Обозначим через m массу стержня, m = QFl. Тогда уравнение для нахождения ® примет следующий вид:
to/ tol m
7*7=Й- (175-7>
§ 175]
ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
385
Это трансцендентное уравнение имеет бесчисленное множество корней, число собственных частот системы бесконечно велико. Графическое определение корней производится так, как показано на рис. 263; значения — , удовлетворяющие уравнению (175.7), явля-. с
ются абсциссами точек пересечения кривой и гиперболы:
_____т _ со/ У М ‘ с
При весьма больших значениях — гипербола проходит очень близко к горизонтальной оси и абсциссы точек пересечения гиперболы с тангенсоидой лишь очень немного отличаются от лл. Поэтому для высоких частот получается асимптотическая формула
(175.7) в первом приближении
спи
—
(175.8)
При достаточно большом л собственная частота, определяемая приближенной формулой (175.8), сколь угодно мало отличается от ее точного значения.
Собственную частоту основного тона мы вычислим в предположении, что масса стержня мала по сравнению с массой груза. Тогда со/ ----малая величина и уравнение
можно записать следующим образом:
/ <о/\* т
\ с ) М'
После очевидных преобразований отсюда следует:
Но такое значение собственной частоты мы получили бы, рассматривая колебания системы с одной степенью свободы, а именно стержня, лишенного массы и несущего на конце массу М. Чтобы приближенно учесть массу стержня, удержим в уравнении (175.7) не один, а два члена разложения тангенса, а именно положим:
13 Ю. Н. Работнов
386
ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XVI
Уравнение принимает вид: ш/у । 1 / ш/у т с ) ‘ 3 \ с ) М "
Его приближенное решение:
Отсюда
§ 176. Поперечные колебания стержней. При составлении дифференциального уравнения поперечных колебаний стержня мы будем отправляться от дифференциального уравнения изогнутой оси балки, записанного в форме (116.5):
/ (fit) \
= q(z,t). (176.1)
Единственное различие между уравнениями (116.5) и (176.1) состоит в том, что в последнем уравнении употреблен символ частной производной по координате. Теперь, рассматривая динамические задачи, мы должны считать, что прогиб v является функцией двух переменных — координаты z и временив. Уравнение (176.1) получено для случая равновесия балки, но его можно применить к случаю движения, воспользовавшись принципом Даламбера. Нагрузка q{z, t) должна включать в себя силы инерции. Ускорение элемента балки в сечении с координатой z есть , сила инерции элемента длиной dz
равна — QFdzjp, таким образом, сила инерции на единицу длины
Рассматривая только свободные колебания,балки, когда возмущающая сила отсутствует, мы внесем это выражение q в уравнение движения (176.1) и получим следующее дифференциальное уравнение поперечных колебаний стержня:
5* dV\ । п
дг1 д? °'
Для интегрирования этого уравнения мы применим вновь метод разделения переменных, положив
v (z, t) = T(/) Z {z).
§ 176J ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ 387
Получим:
7'(£JjcZ")"4-qF7’Z = 0.
Здесь точки обозначают дифференцирование по времени, штрихи — дифференцирование по координате. Перепишем это уравнение следующим образом:
t __(EJXZ")"____,
Т qFZ — •
Повторяя рассуждения, проведенные в аналогичном случае применительно к продольным колебаниям, . получим два обыкновенных дифференциальных уравнения:
7'+<в27'=0,
(EJXZ")" — oFqFZ = 0. (176.2)
Первое (незанумерованное) уравнение показывает, что со есть частота свободных колебаний балки. Интегрируя второе уравнение и составляя граничные условия для определения констант, мы убеждаемся, что эти константы не все равны нулю тогда, когда со принимает определенные значения, являющиеся собственными частотами балки. Условимся нумеровать собственные частоты в порядке .возрастания, так что со, со, со, ... Каждому значению собственной частоты сой соответствует главная форма колебаний Zk (z), удовлетворяющая уравнению (176.2) при <в==:сой, а именно:
(EJxZlY — rfkQFZk==O. (176.3)
Конечно, главная форма определена с точностью до постоянного множителя.
Главные формы колебаний обладают свойством ортогональности, которое совершенно аналогично свойству, доказанному в § 171 для систем с конечным числом степеней свободы. Если Zk(z) и Z{(z)— две главные формы колебаний, соответствующие разным собственным частотам и а>1, то
QFZkZtdz=0. (176.4)
О
Для доказательства заметим, что уравнение (176.3) может быть истолковано как уравнение статического изгиба балки распределенной нагрузкой qk, интенсивность которой равна co|QFZft. Точно так же Zz (z) представляет собою статический прогиб балки от распределенной нагрузки —co^qFZj. Применим к этим двум состояниям балки теорему Бетти: i i
$ (-г) Qi U) dz— J Zz (2) qk (z) dz О о
13*
388 ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XVI
или, внося сюда значения qk и qt,
с i
со’ J qFZkZl dz^a^ J QFZtZk dz. 0 0
Так как cofc7^coz, это равенство возможно только при выполнении условия (176.4),
Для определенности будем нормировать главные формы колебаний, выбирая постоянный множитель таким образом, чтобы было
i ^FZ'kdz=\. О
Аналогично тому как произвольная конфигурация системы с конечным числом степеней свободы представляется через главные формы (§ 172), упругая линия балки всегда может быть представлена в виде ряда по главным формам ее колебаний.
Пусть v (z) есть некоторая функция, представляющая собою прогиб балки под действием нагрузки q(z). Функция v(z) удовлетворяет дифференциальному уравнению изгиба
(EJx^)" = q.
Представим v (z) в виде бесконечного ряда:
v(z) = J] Zk(z)uk. (176.5)
ft=l
Внесем этот ряд в дифференциальное уравнение:-2«*(^Л)'=?-
Воспользуемся теперь дифференциальным уравнением (176.3), чтобы исключить производные от функций Zk. Получим:
^uk(i>kQFZk = q.
Умножим обе части этого равенства на Zt и проинтегрируем по длине балки. В силу условия ортогональности от ряда в левой части останется только один член с индексом I, в силу условия нормирования этот член будет . t
и.^'. = qZt dz.
О
Таким образом.
§ 177] КОЛЕБАНИЯ БАЛОК ПОСТОЯННОГО СЕЧЕНИЯ 3§9
Разложение типа (176.5) представляет собою в известном смысле обобщение разложения Фурье по тригонометрическим функциям. Если функция v(z) удовлетворяет тем же граничным условиям, что и функция Zk, и четырежды дифференцируема, то ряд (176.5) сходится абсолютно и равномерно. Но выполнение названных условий автоматически обеспечивается тем, что v(z) является прогибом от действия нагрузки q(z), причем q (z)— интегрируемая функция.
§ 177. Колебания балок постоянного сечения. Если жесткость постоянна, то уравнение (176.2) принимает следующий вид:
EJxZ14 — atQFZ = 0.
Для сокращения записи положим сб2М- = а4. Тогда
Zlv —a4Z = 0. (177.1)
Корни характеристического уравнения будут ±1 и ±1, поэтому общий интеграл уравнения (177.1) имеет вид:
Z= A ch az В sh az 4~ С cos az 4~ D sin az. (177.2)
B§ 123 мы видели, какие преимущества дает использование частных решений с единичной матрицей начальных значений (А. Н. Крылов). Эти решения строятся с помощью общего интеграла (177.2):
Vt (х) = у (ch х -j- cos х),
Vt (х) = у (sh х4- sin х),
Vs(x) = y (chx —cos x),
V4 (*) = у (sh x ~ sin
Легко убедиться в том, что производная по х каждой из последующих функций Pft(x) равна предыдущей функции Р^-Дх), причем функции нужно расположить в круговом порядке так, что за функцией У4 следует функция V\.
Итак, общий интеграл уравнения (177.2) мы будем записывать следующим образом:
z = ct V, (az) 4- CtVt (az) 4- CSVS (az) 4- CtVt (az). (177.3)
Рассмотрим теперь несколько примеров.
а) Балка, лежащая на двух опорах. На каждой опоре равны нулю прогиб н изгибающий момент; Z(0) = 0, Z"(0) = 0, Z(l)~0, Z"(/) = 0. Из граничного условия на левом конце при z=0 сразу
13* Ю. Н. Работное
390 ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XVI
следует, что Ct = Ct = 0. Действительно, при z = 0 все функции Vk равны нулю, кроме V, (0), равной единице. Но при двукратном дифференцировании функция V, переходит в V,, следовательно, коэффициенты при V1 и Va должны обращаться в нуль. Используя остальные граничные условия, мы получим:
'ctvtW)+ctvtW)==o,
WaZ) + WaZ) = 0.
Теперь повторяется обычное рассуждение. Если определитель системы отличен от нуля, то С, = С4==0, следовательно, никаких колебаний не происходит. Если определитель равен нулю, а должно иметь совершенно определенное значение, а зная а, мы находим собственную частоту системы. Условие равенства нулю определителя будет следующим:
Vf (a/) — Vj(a/)=0.
Отсюда
Vs(a/)=±V4(aZ)
и либо sha/ = 0, либо sinaZ = 0. Первый случай исключается, так как гиперболический синус не имеет действительных нулей, кроме как в начале координат. Остается вторая возможность:
ап1 — пл (л=1,2,...).
Вспоминая, что такое а, находим собственные частоты:
п’л* f Е1Х ап— У Qf •
Следует заметить, что собственные частоты растут пропорционально квадрату номера, а не первой его степени, как это было в случае продольных колебаний.
В случае балки, лежащей на двух опорах, использование общего интеграла уравнения колебаний в форме (177.3) не очень оправдано; если обратиться к формуле (177.2), то видно, что граничным условиям задачи удовлетворяет последний член решения, если принять a = ^. Соответствующая главная форма:
Множитель перед синусом выбран так, чтобы было возможно условие нормирования.
б) Балка с одним заделанным и другим свободным концом. Помещая начало координат в заделке, получаем следующие граничные условия:
Z(0) = 0, Z'(0) = 0, Z"(/) = 0, Z"'(/) = 0
§ 178] СПОСОБ РЕЛЕЯ—РИТЦА ДЛЯ ПОПЕРЕЧНЫХ КОЛЕБАНИЙ 391
(в заделке равны нулю прогиб и угол наклона, на свободном конце — изгибающий- момент и перерезывающая сила). Из условий' в заделке следует, что = = 0, из условий на свободном конце:
С,И1(о^) + С4Иг(а/) = 0,
C,V4(aZ) + C4VI(a/) = 0.
Уравнение частот: /
Vl (al) — V2 (al) V4 (aZ) = О
или
cos al ch al—— 1.
Приводим шесть первых корней этого уравнения:
al= 1,875; 4,694; 7,855; 10,996; 14,137; 17,279.
в) Балка с двумя свободными концами (z = 0 и z = l). Граничные условия: Z" (0) = 0, Z"' (0) = 0, Z" (Z) = 0, Z"'(Z) = O. Из двух первых граничных условий следует С, = С4 = 0. Из двух других:
Ciy,(aZ) + CIV4(aZ) = 0,
CIVI(a/) + CIV,(aZ) = 0.
Уравнение частот:
Vl(al) — Vt(al) Vi(al) = 0 или
cos a/ ch а/ = 1;
Первые корни этого уравнения:
aZ = 0; 4,730; 7,853; 10,996; 14,137; 17,279.
§ 178. Способ Релея — Ритца в применении к поперечным колебаниям стержня. Способ Релея, изложенный в применении к системам с конечным числом степеней свободы, находит применение и для приближенного определения частоты основного тона свободных колебаний балки. Пусть V (z) — прогиб балки под действием нагрузки q (г). Составим выражение
i
^v(z) q(z) dz
=—4------------. (178.1)
qFv* (z) dz
о
Правая часть аналогична здесь правой части формулы (173.4), только конечные суммы заменены интегралами. Так как v(z) 13**
392 ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XVI
представляет собою прогиб от нагрузки q, эту функцию можно представить в виде абсолютно и равномерно сходящегося ряда:
k=i
Выпишем числитель выражения (178.1):
г г оо
J v (г) q (z) dz= J uk J Zkqdz= 2 44-0 A=1 0 A=1
Здесь мы воспользовались формулой (176.6). Найдем теперь знаменатель. Нам придется возводить в квадрат ряд для ®(z) и интегрировать либо квадраты, либо попарные произведения функций Zk, умноженные на qF. Принимая во внимание условия ортогональности и нормирования (176.4) и (176.5), получим:
i 00
\ qFv*(z) dz= 2 «*• о k=i
Таким образом,
2 “14
-----• (178.2)
2 4
*=1
Из этого равенства следует, что формула (178.1) определяет частоту свободных колебаний балки тогда, когда функция v (z) совпадает с соответствующей главной формой колебаний. С другой стороны, формулу (178.2) можно переписать следующим образом:
Каждый член числителя, начиная со второго, больше, чем соответствующий член знаменателя, поэтому со* 5s coj, или
i
J о (г) (z) dz
. (178.3)
qFv’ (z) dz
0
При использовании формулы (178.3) для приближенного определения частоты основного тона мы должны постараться угадать пер
§ 178] СПОСОБ РЕЛЕЯ -РИТЦА ДЛЯ ПОПЕРЕЧНЫХ КОЛЕБАНИЙ 393
вую главную форму колебаний. В качестве таковой для балки на двух опорах, например, можно взять кривую прогиба от собственного веса.
Обращаясь к формуле (178.3), заметим, что числитель правой части представляет собою удвоенную потенциальную энергию изгиба балки, прогиб которой выражается функцией v(z), тогда как знаменатель— это удвоенная кинетическая энергия, при вычислении которой скорости заменяются прогибами. Поэтому эту формулу можно переписать в следующем, более общем виде:
Такая более общая трактовка формулы Релея позволяет:
1. Брать в качестве v (z) функцию, выражающую прогиб балок не только от распределенной нагрузки q(z), ио и от сосредоточенных сил Qs в точках rs. Тогда
i
2 W (v) = J v (z) q (г) dz-}- 2 Qs v (zs). « -s
2. Учитывать не только непрерывно распределенную массу балки, но также сосредоточенные массы /»,• в точках z{. Тогда
i
2T(v) = ( qFv* dz-}- 2 («,)•
3. Задаваться функцией v(z), определяя ее не как прогиб от некоторой нагрузки, а просто подбирая непрерывную вместе с первой производной четырежды дифференцируемую функцию, удовлетворяющую граничным условиям задачи.
Воспользуемся формулой (154.5) для упругой энергии изгиба, заменив в ней момент через кривизну при помощи соотношения £/х = УИ*. Получим:
i
2W=^EJx(^dz. (178.5)
, о
Знаменатель в формуле (178.4) сохраняет свое выражение:
i
2T(v) = qFv* dz.
О
Заметим, что при применении метода Релея требование удовлетворения функцией v{z) всех граничных условий является излишним.
394 ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ (ГЛ. XVI
Разрывы вторых производных функции v(z) соответствуют приложенным сосредоточенным моментам, разрывы третьих производных — сосредоточенным силам. Следовательно, если функция v(z) непрерывна вместе с первой производной и удовлетворяет граничным условиям, наложенным на прогиб и угол поворота, она всегда может быть представлена как функция прогиба некоторой балки под действием распределенной нагрузки, сосредоточенных сил и моментов и доказательство теоремы Релея сохраняет силу. Будем называть граничные условия, налагаемые на v(z) и v'(г) кинематическими условиями, а на момент и перерезывающую силу, то есть v" (z) и v"'(z),— дина-' мцческими условиями.
Дальнейшее развитие метода Релея представляет метод Ритца. Выберем п функций каждая из которых непрерывна вместе со-своей производной и удовлетворяет кинематическим граничным условиям. Теми же свойствами обладает линейная комбинация:
® (z) = с,?, (г) + сг<рг (г) -j-... + спф„ (г).
Здесь с„ с2, ..., сп — произвольные постоянные. Выпишем величины W (у) и Т (г/), это будут квадратичные функции коэффициентов с,-; обозначим их 1^(с,, сг,..., сп) и Т(с1г сг, ... , сл). Тогда по формуле (178.4)
Ю1^т7С1’Сг.....N- (178.6)
1 Т (с„ с,....с„) ' г
Формула (178.6) дает верхнюю оценку для <о®, зависящую от коэффициентов cIt ct,..., сп, при этом наилучшей оценкой будет самая меньшая. Вопрос об отыскании наименьшей оценки для со* сводится к нахождению минимума правой части неравенства (178.6), рассматриваемой как функция неопределенных коэффициентов. По общему правилу составляем частные производные этого выражения по с(.(г=1, 2,____, п) и приравниваем их нулю:
± Г*Е т- if—1 =0 Т2 [а, 1 w дс:\
Сократим множитель и обозначим у через ® в соответствии с (178.1). Получим систему п уравнений вида
— — ю2^ = 0. (178.7)
dct oct ' '
Система (178.7) представляет собою систему линейных однородных уравнений относительно с,-; она имеет нетривиальное решение только тогда, когда ее определитель равен нулю. Но условие равенства нулю определителя приводит к уравнению степени п относительно со’, корни этого уравнения дают стационарные значения
§ 178] СПОСОБ РЕЛЕЯ —РИТЦА ДЛЯ ПОПЕРЕЧНЫХ КОЛЕБАНИЙ 395
частот <о, определяемых формулой (178.1). Наименьший корень дает наилучшую при данной аппроксимации прогиба оценку для первой собственной частоты, притом оценку сверху.
Можно показать, что второй корень будет близок к со2 и разница между точным значением со2 и полученным приближением уменьшается с возрастанием числа членов в выражении для v(z). Однако нельзя сказать, будет ли это оценка сверху или снизу.
Пример. Балка постоянного сечения длины / защемлена на одном конце, второй конец свободен. Точное значение собственной частоты основного тона:
_(а/)2 , /~EJX 1,875s , / EJX 3,52 q ГEJX
V qF p . V qF ? V qF •
а) Примем за функцию v(z) кривую прогиба от сосредоточенной силы Q на конце. Уравнение упругой линии:
Q Г/z2 z’l
"6j-
Потенциальная энергия деформации:
Условная кинетическая энергия T(v):
i
Ю1 <
О
По формуле (178.4)
140 EJX
11 PqF
ш
Разница с точным решением обнаруживается, как видно, только в третьем знаке.
б) Применим к рассмотренной уже задаче метод Ритца, положив
v (z) — <\lz* -|- сгг\
При этом
i
W= у EJX J (2cJ + 6csz)2 dz = у EJx(4c‘ + 12c1Cj -|- 12c«) 0
I
№ + ctzy dz=± qFE (| c‘ +1 ctct + у .
396 ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XVI
Уравнения (178.7) получаются следующими:
(8~ у *) с1 + (12~у *)с2 = °.
(12 — А*) с1 + (24—у*)св = О.
Здесь qF/4 ,
Приравнивая нулю определитель, получим квадратное уравнение, наименьший корень его х= 12,46, поэтому
Заметим, что и в том и в другом случае мы выбирали функцию v(z) удовлетворяющей только кинематическим .граничным условиям. Несмотря на это, точность оценки получается довольно высокой. Если взять в качестве v (z) функцию, выражающую прогиб балки от равномерно распределенной нагрузки, будут выполнены и динамические граничные условия. В точном и приближенном решениях при этом совпадают третьи знаки.
§ 179. Действие ударных и импульсивных нагрузок на упругие системы. Ударными или импульсивными мы будем называть нагрузки, действующие в течение весьма короткого времени. Если продолжительность действия нагрузки мала по сравнению с периодом свободных колебаний системы, то за время действия нагрузки не произойдет сколько-нибудь заметных перемещений масс, но эти массы приобретут некоторые конечные скорости. Схематизируя, расчет на действие мгновенных нагрузок можно разбить на два следующих этапа:
1. Определение скоростей, которые мгновенно получают точки системы после удара или импульса.
2. Изучение свободных колебаний системы при заданном распределении начальных скоростей.
Ударное нагружение происходит тогда, когда по упругой системе ударяет некоторая масса, движущаяся с определенной скоростью. Возникающая в момент соударения сила неизвестна, известна скорость удара, а также характер удара (упругий или неупругий).
При импульсивной нагрузке мы обычно знаем величину силы, но деформации системы определяются не величиной силы, а величиной ее импульса. Типичный пример нагрузки импульсивного типа представляет давление взрывной волны. Для простоты мы будем решать эти задачи приближенным методом, основанным на том, что конфи
§ 179] ДЕЙСТВИЕ УДАРНЫХ И ИМПУЛЬСИВНЫХ НАГРУЗОК 397
гурация системы при движении её после удара считается известной заранее и неизменной. Для наглядности мы будем в дальнейшем рассматривать не произвольную упругую систему, а тяжелую балку, несущую на себе п сосредоточенных грузов, все выводы немедленно распространяются на иные системы. Итак, предположим, что конфигурация балки в какой-то момент времени задана прогибом Z (z) и форма кривой прогиба в процессе колебаний неизменна, так что
v(z,
Потенциальная энергия системы:
i
W= 1 ц2 J EJXZ"‘ dz=u‘W (Z).
О
Кинетическая энергия:
i
Т=у й2 j qFZ dz = iiiT (Z).
О
Составим уравнение движения системы в форме уравнения Лагранжа второго рода:
dt \duj ди '
i
Здесь Q= ^qZ dz-\-'^lPlZ(zi}, q— распределенная нагрузка, о
Р( — сосредоточенные силы, приложенные в точках zt.
Если все нагрузки, приложенные к системе, импульсивные, действующие в течение весьма малого времени т, мы можем проинтегрировать уравнение (179.1) по t от / = 0 до i = r. Поскольку второй член ограничен, интеграл от него исчезнет вместе с г и мы получим:
т
g^Q^Q*. (179.2)
О
На втором этапе мы должны интегрировать уравнение (179.1) при Q=0 (действие нагрузки уже закончилось), причем формула (179.2) дает начальное значение > начальные значения перемещений равны нулю. Мы выписали выражение для кинетической энергии, используя его, будем иметь:
a=2»r(Z).
398 ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ [ГЛ. XVI
Следовательно, (й\ =-£-2Т (Z) •
Подставим выражения Т и U в уравнение (179.1), положим в нем Q—0 и разделим иа T(v). Получим:
й-)-со2ц = О. (179.3)
Здесь со2 — частота, найденная по формуле Релея. Интегрируем (179.3) при начальных условиях
О* («)0 = 0, (й0) = •
Найдем:
u==^h. Sjn м
Наибольшее значение прогиба;
«тах = (-7Г. (179.4)
или
“max 2Т (Z) м 2 /Т(2) 179‘5^
Пример. Груз массы М ударяет со скоростью v по середине балки иа двух опорах с массой т, длиной I и жесткостью EJX. Будем считать удар неупругим. Количество движения груза равно количеству движения системы, состоящей из балки и скрепленного с иею груза, движущихся как одно целое. Положим
ZW = 3i_4(f)-,
Это кривая прогиба балки, нагруженной сосредоточенной силой посередине, при этом Z^y)=l, поэтому и есть перемещение груза и й—его линейная скорость. Кинетическая энергия при скорости, равной единице:
i
ги="Й3т— ЧЯР2+4л,=4(л,+®")-О
Потенциальная энергия при ц=1:
i
W(Z)=EJx^^dZ^4-^.
§ 179]
ДЕЙСТВИЕ УДАРНЫХ И ИМПУЛЬСИВНЫХ НАГРУЗОК
399
Отсюда
48EJX
Количество движения системы немедленно после удара:
(S)=2^ T(Z) = Mv.
Отсюда . .. _______________ Mv __ М
'М,« 2742) .. , 17 V‘
М + ^п
Наибольший прогиб:
„ — (“)о _______Mvl''2_____
“max— ш — Г/ .17 \.Q_Z I1/. ’
( М "т" 35 т) 48£7*1
ГЛАВА XVII
ТЕОРИИ ПРОЧНОСТИ
§ 180. Постановка вопроса о прочности. В самом начале курса, формулируя задачи сопротивления материалов, мы употребили термин «прочность» в широком смысле. Во всем последующем изложении речь шла о расчете на прочность тех или иных конструкций из различных материалов, при этом в понятие прочности вкладывался различный смысл. Для пластических материалов под разрушением нужно было понимать возможность появления недопустимо больших деформаций, в этом смысле расчет по теории предельного равновесия (гл. XV) представляет собою расчет на прочность.
Однако даже пластические материалы, будучи поставленными в некоторые специальные условия, могут разрушиться с образованием трещины, без появления заметной пластической деформации. Разрушения такого рода называются разрушениями в результате отрыва или хрупкими разрушениями.
Условное деление материалов на хрупкие и пластические имеет смысл только применительно к стандартным методам испытаний образцов, воспроизводящих некоторые обычные для этих материалов условия эксплуатации. Прежде всего, это относится к виду напряженного состояния. Хрупкий материал, подвергнутый действию высокого всестороннего давления, на которое накладывается растяжение, сжатие или сдвиг, обнаруживает значительные пластические деформации. Такие пластические деформации, например, играют существенную роль в процессах образования рельефа земной коры; граниты и базальты, хрупкие в обычных условиях, текут, находясь под действием колоссального давления в глубинных слоях Земли. Пластическое поведение, казалось бы, хрупких материалов неоднократно обнаруживалось и на опытах; хорошо известны опыты Кармана над мрамором и песчаником (1911 г.), Бекера'над теми же материалами и цинком (1914 г.). В опытах Кармана цилиндрические образцы из мрамора, подвергнутые всестороннему гидростатическому сжатию, сжймались дополнительно в осевом направлении. При отсутствии бокового сжатия разрушение происходило с деформацией, меньшей чем 1’/0, при боковом давлении 1650 кг}см* относительная дефор
§ 181] ХРУПКОЕ И ПЛАСТИЧЕСКОЕ РАЗРУШЕНИЕ 401
мация в момент разрушения составила около 9“/0. С другой стороны, если бы удалось осуществить всестороннее равномерное растяжение, то мы получили бы при достаточно большом напряжении отрыв в чистом виде, без какой бы то ни было пластической деформации. Трехосное напряженное состояние, близкое к состоянию всестороннего растяжения, приводит к хрупкому разрыву даже в том случае, когда материал является пластическим в обычных условиях испытания.
Рассмотренные в предшествующих главах задачи, относящиеся к растяжению — сжатию, изгибу и кручению стержней или напряженному состоянию в трубах, дисках и резервуарах, не давали примеров такого рода напряженных состояний, когда все три главные напряжения положительны, поэтому для материалов типа стали условие прочности сводилось к условию пластичности. Однако можно указать случаи, когда состояния типа всестороннего растяжения реализуются иа самом деле. Сложное напряженное состояние, возникающее в местах концентрации напряжений в растянутом стержне, например, носит характер всестороннего растяжения, и элементарное рассмотрение § 31 далеко не всегда оказывается достаточным для суждения о прочности. Если концентрация вызвана острой и глубокой выточкой так, что коэффициент концентрации (§31) велик, то может оказаться, что материал вовсе не перейдет в пластическое состояние, а уже в упругой области образуется трещина разрушения. В других случаях могут возникнуть пластические зоны и даже все сечеине перейдет в пластическое состояние, ио распределение напряжений и пластических деформаций останется резко неравномерным; в тех местах, где комбинация напряжений окажется наиболее неблагоприятной, может появиться трещина.
§ 181. Хрупкое п пластическое разрушение. Хрупкое разрушение имеет характер отрыва, оно происходит обычно по тем площадкам, на которых действует наибольшее растягивающее напряжение. Поэтому естественно считать, что разрушение наступает тогда, когда наибольшее растягивающее напряжение достигает некоторой предельной величины, называемой сопротивлением отрыву. Обозначив сопротивление отрыву через R, мы получим следующее условие прочности:
(181.1)
С другой стороны, при расчете необходимо предусмотреть возможность появления значительных пластических деформаций, хотя бы и не приводящих к разрушению. Принимая условие пластичности в форме Треска, необходимо потребовать, чтобы наряду с неравенством (181.1) было выполнено следующее неравенство:
а, —а,<ат. (181.2)
402
ТЕОРИИ ПРОЧНОСТИ
[гл. XVII
Для суждения о прочности материала при данном напряженном состоянии можно теперь воспользоваться простым графическим построением. Заметим, что в условия (181.1) и (181.2) напряжение о± не
входит, значит, с точки зрения прочности напряженное состояние характеризуется величинами ot и о,. Построим на этих напряжениях круговую диаграмму (рис. 264). Уравнение 2т = ot— о, = ат определяет в плоскости а — т прямую АВ, параллельную оси о и отстоящую от нее на величину от/2; уравнение a1 = R определяет прямую, параллельную оси г и отстоящую от нее на расстоянии R. Если
жения, нет никакой уверенности в
ния не влияют на прочность г
круговая диаграмма для данного напряженного состояния не пересекает этих прямых и, следовательно, не выходит в заштрихованную область, ни разрушения, ни пластической деформации не произойдет.
Приведенное рассуждение является в достаточной мере схематичным. Хотя физически естественно принимать за меру сопротивления отрыву именно величину наибольшего нормального напря-том, что другие главные напряже-ю отношению к отрыву. Нельзя
утверждать, что величина сопротивления отрыву R является постоянной и не зависит от вида напряженного состояния. Объединение в одной диаграмме на рис. 264 условия пластичности и условия
отрыва основано на довольно грубой схематизации действительного
явления, так как существуют типы разрушения промежуточного характера, а именно отрыв, сопровождаемый пластической деформацией. Возникновение пластической деформации нарушает структуру металла и, очевидно, должно влиять на величину сопротивления
отрыву.
Однако представление о существовании сопротивления сдвигу и сопротивления отрыву, развитое в работах ряда авторов, главным образом Н. Н. Давиденкова, сыграло большую роль для разъяснения физической стороны вопроса о разрушении. Приведенная схема позволяет пояснить чисто феноменологическую теорию прочности, предложенную в свое время Мором (1860 г.) для хрупких материалов.
§ 182. Теория прочности Мора. Согласно этой теории нарушение прочности происходит тогда, когда на некоторой площадке осуществляется наиболее неблагоприятная комбинация нормального и касательного напряжений. В первоначальной формулировке тео
§ 182]
ТЕОРИЯ ПРОЧНОСТИ МОРА
403
рии Мора вопрос о характере разрушения остается открытым; в зависимости от того, какой будет эта неблагоприятная комбинация, речь может идти о наступлении текучести или о разрушении в прямом смысле слова. Запишем условие прочности по Мору следующим образом:
т=/(а). (182.1)
В плоскости а — г это уравнение изображается некоторой кривой (рис. 265). Для суждения о прочности необходимо рассмотреть все-
возможные площадки, проходящие через данную точку, и проверить,
будет ли выполнено равенство (182.1) хотя бы на одной из них.
Каждой площадке соответствует точка с координатами а и т на плоскости чертежа, совокупность этих точек заполняет некоторую фигуру. Покажем, что кривая, ограничивающая снаружи эту фигуру, является кругом Мора, построенным на напряжениях а, и о,. Действительно, точки этого круга изображают напряженные состояния на
площадках, параллельных оси а2, сле-
довательно, принадлежат искомой фигуре. Теперь нам достаточно показать, что точка М, находящаяся вне круга Мора, построенного на напряжениях а, и а,, не может изображать напряженного состояния на какой-либо площадке.
Для доказательства предположим противное. Тогда отрезок МС больше радиуса круга Мора и мы имеем следующее неравенство;
а
Здесь а и т—координаты точки М.
После элементарных преобразований это неравенство примет следующий вид:
^-а(а14-а,)4-а1а,>0. (182.2)
Здесь № = а24~'Гг.
По предположению а и т являются нормальным и касательным напряжениями на некоторой площадке. Пусть направляющие косинусы ее нормали по отношению к главным осям будут nlt nt и nt. Тогда по формулам § 39
404
ТЕОРИИ ПРОЧНОСТИ
[гл. XVII
Внеся эти выражения для s и о в неравенство (181.2), получим: OjO, (1 — п\ — п\) 4- [o’ — а2 (а, а,)] п\ > 0.
Но направляющие косинусы связаны условием п*+п*+п1='-
Поэтому первая скобка равна л*. Сокращая эту величину, придем окончательно к следующему неравенству:
(°i + о.) + > °-
Но это неравенство невозможно. Действительно, левая часть представляет собою квадратный трехчлен относительно о2, корни этого трехчлена о2 = а, и ог = аа. Так как при а2=±оо трехчлен равен -}-оо, то ПРИ и трехчлен положителен, сле-
довательно, при о, <С <С ai он Должен быть отрицателен, а а2 по определению является средним по величине напряжением.
Следовательно, способ проверки же, как в предыдущем параграфе: на
кратно указывалось, опытные данные по
прочности оказывается таким напряжениях о2 и а, строится круг Мора, прочность обеспечена в том случае, когда этот круг не пересекает предельную кривую.
Вид предельной кривой находится из опыта. Для различных напряженных состояний, соответствующих условию разрушения, строятся круги Мора. Предельная кривая будет их огибающей. Как уже неодно-разрушению относятся
главным образом к плоскому напряженному состоянию. Если из-
вестны разрушающие напряжения при растяжении, сжатии и чистом сдвиге, мы можем с достаточной степенью надежности построить участок предельной кривой, позволяющей судить о прочности во всех случаях плоского напряженного состояния. Действительно, при плоском напряженном состоянии, если ^,^>0, то ст8=С0, в противном случае было бы а2 0 и напряженное состояние не было бы плоским; случай же, когда а, 0, невозможен, тогда о2Т^0. Поэтому для плоского напряженного состояния круг Мора, построенный на напряжениях а, и а8, либо заключает в себе начало координат, либо проходит через него.
§ 182j
ТЕОРИЯ ПРОЧНОСТИ МОРА
405
Построим круги Мора, соответствующие предельному состоянию при растяжении, при сжатии и при чистом сдвиге, как показано на рис. 266. Огибающая этих кругов АВ представляет собою часть предельной кривой, которая определяется, таким образом, достаточно надежно. Предельные круги Мора для всех возможных плоских напряженных состояний будут, в соответствии с вышесказанным, касаться предельной кривой на участке АВ. Для того чтобы продолжить предельную кривую влево, необходимо иметь опытные данные испытаний при наложенном всестороннем сжатии..Такие опыты
производились многократно, и соответствующие результаты имеются. Продолжение кривой вправо от точки В носит гипотетический характер, следует ожидать, что она пересекает ось а в точке D. Абсцисса этой точки представляет собою сопротивление отрыву при всестороннем растяжении, то есть при полном отсутствии пластической деформации. Форма кривой вблизи точки D совершенно неизвестна.
У хрупких материалов обычно сопротивление сжатию больше,
чем сопротивление растяжению, соответствующие величины проще всего находятся из опыта. Для расчета на прочность в условиях плоского напряженного состояния в первом приближении можно заменить кривую т=/(а) прямой, касающейся предельных кругов Мора для растяжения и для сжатия. Действительная кривая, как показано на рис. 266, направлена выпуклостью вверх, поэтому сделанное допущение идет в запас прочности.
Рассматривая всевозможные круги Мора, касающиеся прямой АВ (рис. 267), мы найдем, что величины а, и о, для этих кругов связаны линейным соотношением. Действительно, из подобия треугольников ОАВ и КСВ следует:
СК-.АО=СВ-.АВ:
Так как СК—°' 2 g* — радиус круга Мора, СВ=ОВ—ОС=: = ОВ—01 ~ , отрезки АО, ОВ и АВ фиксированы заданием пре-
дельной прямой, то вышеприведенная пропорция принимает следующий вид:
: АО = ( ОВ — V. АВ.
1 \ * /
406
ТЕОРИИ ПРОЧНОСТИ
(гл. XVII
Но это есть линейное соотношение между а, и а,, которое можно записать следующим образом:
01 = а-\-таг. (182.3)
При растяжении а, = 0 и в предельном состоянии о1 = овр (0^,— временное сопротивление при растяжении); поэтому а — 0вр. При сжатии а, = 0 и в предельном состоянии 0,=—0ВС (авс — временное
СУ вр г и /»==—. Условие ^ВС предельного состояния (182.3) запишется следующим
сопротивление при сжатии); поэтому а= та, достижения образом:
°Вр а1——0. = %-ивс
Вводя запас прочности, получим следующее условие прочности:
01—-Г0.<[0]р- (182.4)
ивс
Условие (182.4) справедливо как для хрупких, так и для пластических материалов, так как при 0Вр=овс оно превращается в условие Треска.
Нужно помнить, что применение формулы (182.4) обосновано только для плоского напряженного состояния, так как всякая экстраполяция линейной формулы для уравнения предельной кривой сомнительна.
Недостатком теории Мора является то, что в ней не учитывается роль среднего напряжения 0±. Для пластических материалов условие Мора переходит в условие Треска, а мы видели, что достижение пластического состояния лучше предсказывается условием Мизеса, содержащим все три главных напряжения. Действительно, если построить круги Мора для различных предельных состояний, не ограничиваясь растяжением, сжатием и чистым сдвигом, как это показано на рис. 266, то окажется, что, строго говоря, огибающей провести нельзя.
Развивая ту же идею, которая заставила перейти от условия пластичности' Треска к условию Мизеса, можно предположить, что предельное состояние достигается тогда, когда возникает неблагоприятная комбинация октаэдрического касательного и октаэдрического нормального напряжений. Условие (182.1) при этом заменяется следующим:
т.=/(р). (182.5)
Здесь (см. § 41)
= у /(а. — а.)14- (а, — 0,)‘ -J- (а, — 0J*.
р—у (а14- 0» 4- ао)-
§ 183]
МЕХАНИЗМ ХРУПКОГО РАЗРУШЕНИЯ
407
Соответствующие теории развивались Шлейхером (1926 г.), Ю. И. Ягном (1931 г.), П. П. Баландиным (1937 г.). Для получения расчетных формул целесообразно задаться некоторым аналитическим выражением для функции f(p), что и было сделано упомянутыми авторами. По-видимому, теории такого типа лучше отвечают опытным данным, чем теория *Мора.
§ 183. Механизм хрупкого разрушения. Гриффис в 1921 г. предложил следующее объяснение хрупкого разрушения-. Представим себе пластинку достаточно больших размеров, толщину которой для удобства примем равной единице. Эта пластинка растянута в одном
направлении напряжением о, и края ее неподвижно закреплены, как показано на рис. 268. Потенциальная энергия, приходящаяся на единицу площади пластинки, равна а2/2£, полная потенциальная энергия получается путем умножения этой величины на площадь.
Представим теперь себе, что в пластинке э с возникла трещина в направлении, перпендикулярном направлению растяжения. Эта трещина не изменит существенно распределения напряжений ________________
в большей части пластинки, но в окрестности
трещины общий уровень напряженности пони- Рис. 268.
зится (вблизи концов, наоборот, возникает кон-
центрация напряжений). Потенциальная энергия пластинки в целом уменьшится на величину U; поскольку единственный линейный размер, характеризующий трещину, есть ее длина I, а величина U должна представлять собой произведение удельной энергии на
некоторую площадь, то
п—k — 2Е
Пользуясь решением задачи теории упругости о растяжении полосы с трещиной, Гриффис нашел величину k, она равняется л/2, однако для нас это несущественно. Поскольку рост трещины сопровождается уменьшением потенциальной энергии пластинки, всякая трещина имеет тенденцию к неограниченному росту, так как всякое тело стремится принять состояние с наименьшей потенциальной энергией. Однако образование свободной поверхности связано с появлением энергии поверхностного натяжения. Обозначим величину поверхностного натяжения через S. Представим себе, что трещина длины Z увеличилась на AZ. Потенциальная энергия при этом уменьшится на величину ДCZ, энергия поверхностного натяжения увеличится на 2SAZ. Если окажется, что уменьшение потенциальной энергии больше, чем увеличение поверхностной энергии, трещина будет самопроизвольно
408 ТЕОРИИ ПРОЧНОСТИ [гл. XVII
увеличиваться. Приравняв две эти величины, найдем критическую длину трещины.
Из уравнения k ~^ = 2S следует:
4=^. (183.1)
С точки зрения этой теории прочность материалов по отношению к хрупкому разрушению определяется наличием микротрещин. Внося в формулу (183.1) вместо / длину микротрещины, мы можем определить напряжение а, при котором эта трещина будет расти и приведет к хрупкому разрушению.
Теория Гриффиса дает объяснение так называемому масштабному эффекту, наблюдаемому при хрупком разрушении. Этот эффект заключается в том, что разрушающее напряжение для образцов малого размера выше, чем для больших образцов, и крупные изделия разрушаются при напряжениях значительно меньших, чем те, которые можно было бы счесть допускаемыми на основании лабораторных опытов над образцами из того же материала. Размеры микротрещин, имеющихся внутри материала, различны, распределение их случайно и подчинено законам статистики. Более крупные трещины встречаются редко, тогда как для начала разрушения по теории Гриффиса достаточно, чтобы было очень немного трещин, длина которых превышает критическую. Вероятность нахождения таких трещин в теле значительного объема больше, чем в теле малых размеров. Эти соображения привели к развитию многочисленных статистических теорий прочности, в которых величина разрушающего напряжения и зависимость ее от размеров оцениваются при помощи теории вероятностей.
Теория Гриффиса подвергалась экспериментальной проверке и дала удовлетворительные результаты применительно к стеклу — твердому аморфному материалу, не обнаруживающему заметных пластических свойств. Для металлов теория в ее первоначальном виде вряд ли применима.
В обычных условиях разрушению металла всегда предшествует некоторая пластическая деформация, поэтому возникает вопрос, может ли пластическая деформация привести к появлению и развитию трещин хрупкого разрушения. Одна из возможных схем такого рода была рассмотрена Стро (1954 г.).
Заметим прежде всего, что около краевой дислокации всегда возникает область растягивающих напряжений, причем растягивающие напряжения будут наибольшими иа вертикальной прямой, проходящей через центр дислокации, снизу от нее, если дислокация положительна. Это ясно из схемы образования краевой дислокации, приведенной на рис. 91 (случай г) (§ 67), и иллюстрируется рис. 269.
§ 183J
механизм хрупкого разрушения
409
Как было показано в § 69, группу дислокаций, порожденных источником Франка — Рида и задержанных препятствием, можно представить как группу краевых дислокаций, изображенную на рис. 100 и повторенную на рис. 270. В области, находящейся под препятствием, в которое упирается крайняя дислокация, возникнут растягивающие напряжения. Эти напряжения суммируются от всех дислокаций, следовательно, увеличиваются с увеличением их числа, последнее в свою очередь растет с ростом касательного напряжения т в плоскости скольжения. Наибольшие растягивающие напряжения получаются на
Рис. 269.
t
Рис. 270.
некоторой прямой тп. Может случиться, что эти напряжения окажутся достаточно большими для того, чтобы вызвать образование трещины вдоль тп. Тогда дислокации получат свободу перемещаться и каждая из них, дойдя до края трещины, исчезнет, вызвав дополнительное раскрытие трещины за счет сдвига частей кристалла,, расположенных выше н ниже плоскости скольжения, на величину вектора Бюргерса Ь. В результате возникает положение, изображенное на рис. 270, б, трещина длины L имеет форму клина с основанием nb.
Переход из состояния а в состояние б возможен только тогда, когда энергии этих состояний одинаковы. В состоянии а речь идет об энергии группы дислокаций в плоскости скольжения, удерживаемых напряжением т; в случае б вокруг трещины возникает некоторое напряженное состояние, следовательно, существует энергия упругой деформации, к которой нужно добавить энергию поверхностного натяжения. Энергия трещины, состоящая из упругой энергии и энергии поверхностного натяжения, как оказывается, принимает минимальное значение для некоторой длины трещины L. Приравнивая это минимальное значение энергии трещины энергии группы дислокаций, мы находим условие возникновения трещины. В результате вычислений Стро получил следующие оценки.
-410 ТЕОРИИ ПРОЧНОСТИ [гл. XVII
Касательное напряжение в плоскости скольжения, при котором появляется трещина:
т = (183.2)
Как видно, для образования трещины нужно, чтобы число дислокаций было достаточно большим, для меди, например, получается л = 1000.
Длина трещины при этом
Следует заметить, что эта трещина, в отличие от той, которая рассматривается в схеме Гриффиса, является равновесной, длина ее сохраняется, так как соответствует минимальному значению потенциальной энергии.
Последующее развитие идеи Гриффиса заключается в следующем. Конец трещины является источником концентрации напряжений, которые достигают в упругом теле весьма большой величины. Поэтому вблизи конца трещины образуется область пластических деформаций, при распространении трещины эта область движется, таким образом все новые объемы материала пластически деформируются, а потом разгружаются, возвращаясь в упругое состояние. При этом совершается необратимая работа. Очевидно, что величина этой работы пропорциональна увеличению длины трещины; если последняя возрастает на Д/, то работа пластического деформирования выразится совершенно так же, как и приращение энергии поверхностного натя-окения. Если понимать под 5 не энергию поверхностного натяжения на единицу площади, а эту энергию, сложенную с половиной работы пластической деформации при продвижении трещины на единицу длины, то формулы (181.1), (181.2) и (181.3) сохранят силу (Оро-ван, 1950 г., Ирвин, 1948 г.). Таким образом, величина 5 должна рассматриваться как некоторая константа материала, подлежащая опытному определению; анализ пластического напряженного состояния у конца трещины и теоретический подсчет величины работы пластической деформации затруднительны.
Модифицированная таким образом теория Гриффиса дает более реальные оценки для условия образования микротрещин в соответствии с дислокационным механизмом и для длины равновесной трещины по формуле (183.3). С другой стороны, эта теория позволяет объяснить катастрофическое распространение трещин в конструкциях из •мягкой стали, которое приводит иногда к очень серьезным авариям. Известны и описаны в литературе случаи, когда огромные резервуары для хранения нефтепродуктов разрывались от верха до низа без заметной пластической деформации. По-видимому, разрушение начиналось в месте концентрации напряжений или какого-либо случайного
§ 184] прочность при низких температурах 41Г
дефекта, и появившаяся первая трещина оказывалась неустойчивой. В сороковых годах, во время войны, в американском флоте произошло-несколько аварий, когда корабль буквально ломался пополам.
§ 184. Прочность при низких температурах. Хрупкое разрушение стальных конструкций наблюдается особенно часто при низких температурах. Упомянутые выше случаи разрушения резервуаров и. судов происходили при температурах ниже нуля. В условиях крайнего севера, где металлические конструкции и механизмы работают зачастую при температурах —40° и —50°, хрупкие разрушения, особенно часты, и проектирование сооружений, работающих в этих, условиях, требует особого внимания. Явление хрупкости стали при низких температурах получило название хладноломкости. Схематическое объяснение хладноломкости может быть следующее (А. Ф. Иоффе,. 1924 г.). Пластические свойства металла в сильной степени зависят от температуры, предел текучести с понижением температуры повышается. В то же время сопротивление отрыву практически не зависит от температуры. Поэтому при низких температурах условия перехода от хрупкого разрушения к пластическому меняются и отрыв становится возможным прежде, чем наступит пластическое состояние. В частности, и при растяжении может случиться, что образец разорвется прежде, чем появятся пластические деформации. Не у всех металлов оказывается возможным получить хрупкое разрушение при растяжении за счет понижения температуры; металлы с гранецеитри-рованной решеткой сохраняют пластические свойства при весьма, низких температурах, среднеуглеродистая сталь, весьма пластичная в обычных условиях, становится хрупкой при растяжении лишь при температуре жидкого водорода. При динамическом деформировании, предел текучести оказывается выше, чем при статическом, поэтому критическая температура хладноломкости, то есть температура перехода от вязкого разрушения к хрупкому, повышается. В опытах Давидеикова Н. Н. (1936 г.), который испытывал на ударное растяжение цилиндрические образцы из среднеуглеродистой стали, критическая температура получилась —95° для крупнозернистой структуры и — 160° для мелкозернистой. При сложном напряженном состоянии, например в месте концентрации напряжений, условия перехода от пластического разрушения к хрупкому будут другими и критическая температура, определенная в этих условиях, отличается от критической температуры, найденной путем испытания гладких образцов иа растяжение. В настоящее время не существует теории, которая позволяла бы надежным образом производить расчеты на прочность в условиях низких температур с тем, чтобы предусматривать возможность хрупкого разрушения, однако надлежащий выбор, материалов и соблюдение некоторых конструктивных и технологических предосторожностей позволяют избежать хладноломкости.
412
ТЕОРИИ ПРОЧНОСТИ
[гл. XVII
Для нахождения критической температуры хладноломкости стремятся создать такие условия, при которых склонность к хрупкому разрушению проявляется наиболее сильно. Стандартным методом испытаний для этого в настоящее время является испытание на ударную вязкость. Термин «ударная вязкость» в данном случае не очень удачен, определяемая характеристика не имеет ничего общего с физической вязкостью. Образец для этого испытания изображен на рис. 271, сечение его квадратное, с одной стороны сделай надрез. Образец располагается симметрично на двух опорах так, что на опорах лежит надрезанная сторона, по противоположной стороне, прямо против надреза, производится ятник, падающий с известной торой упал маятник, а также
удар. Копер представляет собою ма-высоты. Отмечается та высота, с кота
Рис. 271.
высота, которую достигнет его центр тяжести после того, как образец разрушен. Разность этих высот, умноженная на вес маятника, представляет собою затраченную на разрушение работу. Ударной вязкостью ~а называется работа разрушения, отнесенная к площади сечения образца в месте надреза. Этой величине трудно приписать какое-то определенное
физическое значение, это есть некоторая условная характеристика, которая, как оказывается, чрезвычайно чувствительна к способности материала к хрупкому разрушению. Пониженная величина ударной вязкости иногда обнаруживается у материалов, для которых обычные механические характеристики — временное сопротивление и удлинение при разрыве — не выходят за пределы нормы. Однако при сложном напряженном состоянии изделия из таких материалов иногда дают хрупкое разрушение. Поэтому испытание на ударную вязкость является обязательным, например, для поковок роторов турбин и турбогенераторов.
Величина ударной вязкости позволяет выявить склонность к хладноломкости раньше, чем другие методы. На рис. 272 приведена типичная кривая зависимости ударной вязкости от температуры (Е. М. Ше-вандин). Как видно, с понижением температуры ударная вязкость снижается, сначала постепенно, а потом внезапно, скачком, достигая чрезвычайно низкой величины. Соответствующая температура Гк называется критической температурой хладноломкости. Описанный метод оценки склонности стали к хладноломкости был детально разработан Н. Н. Давиденковым, Ф. Ф. Витманом и другими. Условия, в которых разрушается образец при испытании иа ударную вязкость, являются настолько тяжелыми, что для реальных металлических конструкций при температурах, превышающих критическую, опасность
§ 185]
ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
413
хрупкого разрушения не возникает. Установлено, что содержание фосфора, серы, кислорода, азота и некоторых других примесей чрезвычайно неблагоприятно влияет на прочность стали при низких температурах. Для крупнозернистой стали критическая температура хладноломкости оказывается выше, чем для мелкозернистой, поэтому отжиг оказывает неблагоприятное действие. Нормализация
или закалка с высоким отпуском повышает хладностой-кость. В конструкциях, предназначенных для службы при низких температурах, следует избегать концентраторов напряжений, а также принимать меры к устранению остаточных напряжений, которые появляются, например, в результате сварки.
§ 185. Прочность при переменных нагрузках. При действии переменных напряжений в металлах наблюдаются типы
Рис. 272.
разрушений, напоминающие по внешнему виду хрупкие разрушения: в пластическом материале развивается трещина, и излом происходит без заметной пластической деформации. Величина наибольшего напряжения при этом может быть значительно ниже предела прочности и ниже предела текучести, лишь бы число циклов изменения напряжения было достаточно большим. Типичным примером изделия, поломка которого происходит вследствие усталости, является вращающийся вал. Представим себе горизонтально расположенный вал, на котором насажен тяжелый маховик. Вес маховика создает в вале напряжения изгиба, нижние волокна оказываются растянутыми, верхние сжатыми. Но вал вращается, в течение каждого оборота одни и те же материальные элементы оказываются то в сжатой зоне, то в растянутой зоне, величина напряжения в каждой точке меняется, как это легко проверить, по синусоидальному закону a = otlsin(o/) где.о^— напряжение изгиба в тот момент, когда точка находится в вертикальной плоскости, проходящей через ось вала, со— угловая скорость вращения.
Рассмотренный пример, когда изгиб создается весом маховика, не является типичным, однако подобных примеров можно привести много. Вал зубчатой передачи, например, будет изгибаться силой давления на зуб шестерни, направление этой силы неизменно в пространстве, поэтому напряжения также будут переменными. В рассмотренных случаях напряжения меняются по симметричному циклу, абсолютная
-414
ТЕОРИИ ПРОЧНОСТИ
[гл. XVII
величина сжимающего напряжения равна величине растягивающего напряжения. Во многих деталях машин цикл изменения напряжений бывает несимметричным, тогда можно считать о — (ат—
среднее напряжение цикла). Переменная часть напряжения не обязательно должна меняться по синусоидальному закону, вместо функ-
ции sin®/ можно ввести любую 2лf®, меняющуюся от — 1 до
периодическую функцию с периодом -[-1, наступление разрушения зависит от величин ат и и от числа циклов, но не от вида этой функции.
Наиболее распространенный метод испытания на усталость — это испытание на знакопеременный изгиб. Соответствующая “4/ методика была создана Вёлером (1870 г.), опубликовавшим пер
вые данные по экспериментальному изучению усталости. С некоторыми видоизменениями эта мето-
дика применяется и в настоящее время.
Образец круглого поперечного сечения зажимается в шпиндель, на другом конце образца помещается подшипник, к которому подвешивается груз. Шпиндель приводится во вращение. Таким образом, образец представляет собою балку, защемленную на одном конце и нагруженную сосредоточенной силой на другом, свободном
конце.
Максимальное напряжение рассчитывается по формулам теории изгиба в соответствии с предположением об упругой работе материала, испытание продолжается до разрушения образца, в момент разрушения автоматически выключается счетчик числа оборотов. Испытание повторяется при различных напряжениях, результаты представляются в виде так называемой кривой Вёлера (рис. 273). По оси ординат откладывается напряжение, по оси абсцисс — число циклов N, при котором происходит разрушение. Эта кривая, как оказывается, имеет горизонтальную асимптоту; при числе циклов порядка 6 — 7-10’ она практически достигает асимптоты. Это значит, что дальнейшее увеличение числа циклов уже не вызовет разрушения. Ордината асимптоты называется пределом выносливости материала <Ту, определение этой величины и является задачей исследования. Особенно отчетливо выявляется предел выносливости при построении диаграммы Вёлера в полулогарифмических координатах. Если перестроить диаграмму рис. 273 так, как показано на рис. 274, откладывая по оси абсцисс логарифм числа циклов N, она будет состоять из двух прямых, причем вторая прямая практически горизонтальна. Ее ордината и есть Оу. Для цветных металлов (например, алюминия) кривая усталостной прочности не имеет асимптоты и, по-видимому, неогра
§ 185] прочность при переменных нагрузках 415>
ниченно приближается к оси абсцисс. В таких случаях предел выносливости определяется как напряжение, при котором материал выдерживает некоторое фиксированное, достаточно большое число циклов.
Описанная схема испытаний на усталость не единственная. Существуют машины для испытания на усталость при изгибе, в которых рабочая часть образца находится в условиях чистого изгиба; образец работает, как балка, опертая с двух концов и нагруженная
двумя симметрично расположенными силами.
При определении предела выносливости необходимо считаться с тем, что опыты обнаруживают значительный разброс, опытные точки не ложатся на кривую, а заполняют некоторую область. Величина предела выно
сливости зависит от раз-
меров образца, на нее влияет масштабный эффект, о котором уже упоминалось выше, в § 183. Так, для образца диаметром 100 мм предел выносливости оказывается примерно на 4О°/0 ниже, чем для стандартного образца диаметром 10 мм. Дальнейшее увеличение диаметра уже слабо влияет на предел выносливости.
Испытание на усталость при знакопеременном изгибе производится в условиях неоднородного напряженного состояния; более чистыми условиями эксперимента являются такие, когда цилиндрический образец подвергается попеременному растяжению и сжатию. Машины для такого рода испытаний существуют; пульсирующая осевая сила создается в них либо механическим путем, либо при помощи электромагнита, возбуждающего продольные колебания. В машинах резонансного типа частота возмущающей силы принимается близкой к собственной частоте колебаний системы, состоящей из образца и присоединенных к нему масс, система автоматического регулирования поддерживает постоянство амплитуды. Основная техническая трудность состоит при этом в центровке образцов; незначительный эксцентриситет приложения нагрузки создает напряжения изгиба, не поддающиеся практически учету. Эти напряжения искажают результаты испытаний. Результаты, полученные на наиболее совершенных современных машинах, показывают, что предел выносливости, определенный при растяжении — сжатии, несколько ниже, чем предел выносливости при изгибе. Это можно объяснить масштабным эффектом: при изгибе максимальные напряжения возникают в зоне образца, примыкающей к поверхности, при растяжении — сжатии во всем объеме напряжения одинаковы.
416
ТЕОРИИ ПРОЧНОСТИ
[гл. XVII
Остановимся еще вкратце на усталости металлов и сплавов при повышенных температурах. Определение предела выносливости для стали по Вёлеру, если температура достаточно велика, оказывается •невозможным: кривая усталостной прочности не стремится к горизонтальной асимптоте и в полулогарифмических координатах излома не обнаруживается; в этом смысле сталь при высокой температуре ведет себя так же, как цветные металлы при нормальной температуре. Поэтому приходится определять условный предел усталости при очень -большом числе циклов и вводить большие запасы прочности.
§ 186. Природа усталостного разрушения. В действительности . усталостное разрушение наблюдается почти всегда при неоднородном напряженном состоянии, при изгибе или при растяжении изделия,
имеющего концентратор напряжения. В том месте, где напряжение является наибольшим, обычно на поверхности, возникает трещина, которая постепенно распространяется вглубь. Несмотря на наличие трещины, изделие еще не теряет несущей способности и может выдержать несколько тысяч и даже миллионов циклов. Когда трещины достигают достаточной глубины и напряжения в неразрушенной части сечения, которая воспринимает всю нагрузку, оказывается
Рис. 275.
Рис. 276.
настолько большим, что материал не может их выдержать, происходит внезапный излом. Сечение образца, поломанного в результате испытания на усталость при изгибе, схематически показано на рис. 275. В кольцевой области А поверхность излома представляется мелкозерни-
стой, блестящей, со сглаженными неровностями. Усталостная трещина раскрывается в растянутой зоне и смыкается в сжатой, результатом этого является обмятие поверхности трещины, иногда эта поверхность кажется как бы заполированной. В области В наблюдается типичная картина хрупкого разрушения, здесь видны относительно крупные зерна, сохранившие острые ребра, поверхность излома матовая. Распространение усталостной трещины обычно начинается от некоторого очага начального разру-
тения; где вследствие тех или иных причин создана большая местная концентрация напряжений или имеется какой-либо дефект материала. При испытании на знакопеременный изгиб первые трещины образуются почти одновременно в нескольких точках иа поверхности образца, распространение их схематически показано на рис. 276; иногда на изломе можно обнаружить несколько отдельных фронтов трещин, идущих от разных точек поверхности.
§ 186] ПРИРОДА УСТАЛОСТНОГО РАЗРУШЕНИЯ 417
Микроскопическое исследование показывает, что усталостная трещина, как правило, проходит сквозь тело кристаллического зерна; по границам зерен она может пройти только случайно, на некоторой части своего пути. Металлографические и рентгенографические исследования показывают, что циклические нагрузки не вызывают в металле каких-либо ст-руктурных изменений, но в отдельных кристаллических зернах наблюдается небольшая пластическая деформация, не отличающаяся принципиально от пластической деформации при статическом нагружении. Наличие пластических сдвигов в металле, подвергнутом действию переменных нагрузок, обнаруживается методами рентгенографии, а также визуально, при помощи оптического микроскопа, когда напряжение и число циклов достаточно велики, и при помощи электронного микроскопа в начальной стадии сдвиго-образования. По-видимому, незначительные пластические деформации в отдельных, наиболее неблагоприятно расположенных зернах существуют и при статических нагрузках тогда, когда напряжения значительно ниже предела текучести или предела упругости. Действительно, предел упругости всегда определяется условно (см. § 60) н нахождение истинной границы, при которой появляются первые пластические деформации, практически невозможно.
При знакопеременных нагрузках группы -дислокаций в плоскостях скольжения движутся то в одном, то в другом направлении, при этом повышается вероятность накопления значительного числа дислокаций на ограниченном участке. Как мы видели в § 183, если число дислокаций, собравшихся около препятствия, достаточно велико, в материале может возникнуть трещина. Накопление дислокаций около препятствия представляет собою локальное упрочнение материала, образование трещины снимает это упрочнение; при следующих циклах в той же плоскости скольжения сдвиг происходит беспрепятственно, новые дислокации как бы стекают в трещину, которая за счет этого растет.
Представление о местном упрочнении материала, способствующем появлению трещины, и о последующем «разрыхлении», сопровождающемся ее ростом, было развито Н. Н. Афанасьевым (1955 г.) без обращения к дислокационной модели.
На рис. 277 приведен график, заимствованный из работы Хантера и Фрике (1954 г.). Авторы подвергали знакопеременной нагрузке алюминиевые образцы и отмечали при каждом напряжении число циклов, которое соответствовало:
1) появлению первых следов скольжения в зернах;
2) появлению первой трещины, обнаруживаемой электронным микроскопом;
3) моменту, когда отдельные микротрещины начинают соединяться;
4) появлению первой видимой трещины;
5) разрушению.
418
ТЕОРИИ ПРОЧНОСТИ
[гл. XVII
Соответствующими цифрами отмечены кривые на графике. Напряжение отнесено к условному пределу выносливости, определенному для числа циклов, равного 2-10’. Интересно отметить, что первые следы
скольжения и первые трещины появляются очень рано, но развитие трещин идет чрезвычайно медленно. Даже при напряжениях меньших, чем предел выносливости, материал после нескольких тысяч циклов оказывается поврежденным.
§ 187. Критерии прочности при переменных нагрузках. Расчет на прочность при знакопеременных напряжениях, меняющихся по симметричному циклу, производится по допускаемому напряжению, определяемому в зависимости от предела выносливости. Условие прочности может быть записано следующим образом:
af
(187.1)
Здесь Оу — предел выносливости, Лу — коэффициент запаса прочности. При выборе коэффициента запаса, кроме N обычных соображений о возможностях перегрузки в условиях эксплуатации, о неточ
ном соответствии расчетной схемы действительным условиям службы изделия, необходимо принимать во внимание также некоторые факторы, специфические именно для усталостной прочности. Прежде всего, нужно иметь в виду, что усталостные испытания дают большой разброс опытных точек. На самом деле опытные точки не ложатся на одну кривую, а заполняют некоторую область, как пока
§ 187] КРИТЕРИИ ПРОЧНОСТИ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ 419
зано на рис. 278. Но даже если принять за кривую Вёлера нижнюю границу области, у нас нет уверенности в том, что следующие образцы не дадут таких точек, которые будут лежать ниже этой кривой. Поэтому существует такая точка зрения, что абсолютной .гарантии прочности вообще никогда быть не может и при расчете нужно задаваться определенной вероятностью разрушения. Прочным считается такое изделие, вероятность разрушения которого достаточно мала. Обрабатывая опытные данные при помощи методов статистики, вместо одной кривой усталостной прочности можно, построить целую серию кривых, каждая из которых соответствует определенной вероятности разрушения в том случае, если напряжение и число циклов изображаются точкой этой кривой. На рис. 278 схематически показаны кривые для вероятности 1°/0 и 99°/0.
г Построение таких кривых требует очень большого количества экспериментов и пока что не получило распространения; фактически разброс опытных данных учитывается выбором повышенного запаса прочности.
Далее, мы уже упоминали о масштабном эффекте; предел выносливости для образцов оказывается выше, чем для изделий больших 'размеров. Существуют теории, дающие объяснение масштабного эффекта и оценивающие его количественно (Вейбулл, Афанасьев, 1955 г.). Однако имеющийся опытный материал пока недостаточен для надежных рекомендаций.
Концентрация напряжений, не играющая существенной роли при оценке статической прочности изделий из пластического материала, сильно влияет на усталостную прочность и обязательно должна учитываться. Этому вопросу ниже будет посвящен специальный раздел, поэтому пока что мы будем считать формулу (187.1) пригодной лишь для одноосных напряженных состояний, как, например, растяжение — сжатие и изгиб.
Предел выносливости определяется при симметричном цикле изменения напряжения, тогда как на практике встречаются и другие циклы. В общем случае, если напряжение колеблется от некоторой величины omIn до <ттах, то можно считать, что на постоянно действующее напряжение накладывается напряжение, изменяющееся по симметричному циклу от — до -|- сто. При этом, очевидно,
_ С^тах & mln п __ Атах Amin
-- 2 ’ 2
Степень, асимметрии цикла принято характеризовать коэффициентом асимметрии, равным отношению наименьшего напряжения цикла к наибольшему:
г_Ат1п =Ат —. (187.2)
A max Ащ Т А®
Для симметричного цикла г =— 1, при постоянно действующем напряжении r= -f-1. Важным случаем является так называемый
420
ТЕОРИИ ПРОЧНОСТИ
[гл. XVII
пульсационный цикл, когда напряжение меняется между нулем и некоторой (положительной или отрицательной) величиной. Для пульсационного цикла г = 0.
Подобно тому как определялся предел выносливости при симметричном цикле изменения напряжения, можно найти предел выносливости и при асимметричном цикле. Принято обозначать предел выносливости символом о/, где г — коэффициент асимметрии. Таким образом, величину, которую мы до сих пор называли Оу, нужно обозначать а_г, предел выносливости при пульсационном цикле будет
а0, а статический предел прочности а+1. Мы не будем останавливаться на методах определения предела выносливости при асимметричном цикле, а перейдем сразу к интерпретации результатов. Один из удобных для этого способов состоит в следующем. Будем откладывать по осям координат ат и 1£ак показано на рис. 279. Пределу выносливости йри каком-либо цикле будет соответ-через эти точки можно провести
ат И @1)’ кривая отсекает на оси ординат отрезок, а на оси абсцисс отрезок, равный пределу прочности ав.
ствовать точка в плоскости кривую. Очевидно, что эта равный о
Часть кривой, изображенная пунктиром, относится к таким разрушениям, которые совершаются при большой пластической деформации и малом числе циклов; определение истинных разрушающих напряжений при этом затруднительно.
Временное сопротивление ав представляет собою условную величину, точки, соответствующие пунктирной части кривой, также могут быть получены только в результате некоторой условной интерпретации данных опыта, поэтому пунктирный участок кривой нельзя считать достоверным. Впрочем, при оценке прочности этот участок никакой роли не-играет. Рассчитывая изделие на прочность, мы также должны потребовать, чтобы не появлялись недопустимо большие пластические деформации, то есть чтобы наибольшее напряжение не превосходило предела текучести. Условие достижения предела текучести будет следующее:
CTmax==CTm+^ = CTT. (187.3)
В координатах ат— уравнение (187. 3) представляет собою уравнение прямой, отсекающей на осях координат -отрезки, равные ат. Эта прямая проведена на графике рис. 279. Теперь все безопасные циклы изменения напряжения, то есть такие циклы, которые не вызывают
§ 187] КРИТЕРИИ ПРОЧНОСТИ ПРИ переменных нагрузках 421
величину [о]=-^
ни большой пластической деформации, ни усталостного разрушения, будут изображаться точками заштрихованной области. Рассуждая подобным образом, мы сочли, что предел текучести при переменных и постоянных нагрузках один и тот же. Это справедливо в первом приближении.
Для расчета на прочность при переменных нагрузках асимметричного цикла необходимо иметь формулу, которая позволяла бы выразить условие того, что данное напряженное состояние является безопасным, а для этого диаграмма рис. 279 должна быть схематизирована. Наиболее простая схематизация, принадлежащая Содербергу, состоит в том, что граница безопасной области заменяется прямой, отсекающей на осях координат отрезки о., и ат соответственно (рис. 280).
Условие достижения предельного состояния запишется так:
^+^-=1. (187.4)
Вводя запас прочности п и принимая за основное допускаемое, напряжение получим следующее условие прочности:
(187.5)
Недостатки изложенного метода состоят в следующем. Во-первых, замена ломаной границы безопасной области прямой представляет собою весьма грубую аппроксимацию действительного положения. Совершаемая при этом ошибка идет в запас прочности, но этот запас оказывается излишним. Во-вторых, величина запаса прочности-, введенная в формулу (187.5), принимается одинаковой независимо от предполагаемого характера разрушения при данном типе напряженного состояния. В крайних случаях — статической нагрузки и переменной нагрузки симметричного цикла — нет оснований принимать запас прочности одинаковым, как это следует из (187.5).
Более точная схематизация границы безопасной области получится в том случае, когда мы заменим ее двумя отрезками прямых, как показано на рис. 281. Прямая /, соответствующая границе области усталостных разрушений, отсекает иа осях координат отрезки о* и <J_p прямая II, определяющая границу текучести, отседает на
422
ТЕОРИИ ПРОЧНОСТИ
[гл. XVII
каждой из осей отрезок стт. Величину о*^можно найти, если известен предел выносливости при каком-либо цикле, отличном от симметрич-
ного, например при пульсирующем цикле, когда напряжение меня-
ется от нуля до максимального значения
о0. Из условия, что точка
= ЛеЖИТ
на прямой = 1
(рис. 282), находим:
= <187’6>
Если предел выносливости при пульсирующем цикле неизвестен, приходится выбирать о* условным способом. В одном из распространенных методов расчета эту вели-
чину няют рис.
принимают равной временному сопротивлению, то есть заме-прямой всю кривую усталостной прочности, показанную на 279. Погрешность такого приема идет в запас прочности, так как кривая усталостной прочности всегда направлена выпуклостью кверху. Условия прочности записываются раздельно, подобно условию (187.4), нос соответствующими запасами прочности:
4- , (187.7)
о 0-1 П}' ' '
«gl. (187.8)
При дельно находят запасы прочности п; и лт,
поверочном расчете от-при определении искомых размеров детали ведут расчет по двум формулам и считают окончательным тот результат, при котором сечение получается большим.
§ 188. Влияние концентрации напряжений на усталостную прочность. Концентрация напряжений оказывает очень существенное влияние на усталостную прочность. Это и понятно: усталостное разрушение происходит без заметной пластической деформации, поэтому напряжения в месте концентрации не выравниваются. Однако знание теоретического коэффициента концентрации а еще не позволяет судить об усталостной прочности. Определяя предел выносливости
§ 188] ВЛИЯНИЕ КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ 423
при симметричном цикле для образца с концентратором напряжений и для гладкого образца, мы найдем, что в первом случае предел выносливости будет меньше в раз. Величина называется эффективным коэффициентом концентрации, при этом всегда’
а.
Это следует, в частности, из того, что напряженное состояние в месте концентрации является сложным, поэтому величина а, представляющая собою увеличение лишь одного из напряжений, не может полностью характеризовать прочность. Далее, при напряжениях меньших, чем предел упругости, все же возникают пластические деформации, и при переменных нагрузках может произойти накопление пластической деформации, изменяющее напряженное состояние. Об-, ласть концентрации напряжений занимает весьма малый объем, поэтому существенную роль играет масштабный эффект. Существуют и другие объяснения того факта, что эффективный коэффициент концентрации меньше теоретического, мы не будем на них останавливаться.
Величины эффективных коэффициентов концентрации для разных материалов и разных концентраторов напряжений приводятся в справочной литературе. Для ориентировочной оценки можно пользоваться следующей формулой:
«/=1+?(«—1)-
Величина q называется коэффициентом чувствительности материала к концентрации напряжений; для конструкционных сталей его следует выбирать в пределах от 0,6 до 0,8.
Заметим, что чугун совершенно нечувствителен к концентрации напряжений, для него q — 0. Это объясняется тем, что чугун прониЗан пластинками графита, которые являются источником чрезвычайно сильной внутренней концентрации напряжений, по сравнению с ней концентрация, вызванная формой изделия, никакой роли не играет.
Зная коэффициент концентрации а,, мы имеем возможность произвести расчет на прочность изделия, работающего при симметричном цикле изменения напряжения. Условие прочности будет следующее:
ct,a .
7 nf
При статической нагрузке коэффициент концентрации совершенно не учитывается. Если напряжение изменяется по несимметричному циклу, весь эффект концентрации напряжений относят к переменной составляющей напряжения оо, умножая ее на а^. Поэтому формула (187.5) заменится следующей:
+ (188.1)
424 теории прочности [гл. xvn
Если расчет ведется по более точным формулам (187.7) и (187.8), то вторая из них остается без изменения, тогда как первая заменяется следующей:-
(188.2) or* 1 or_j tlf
Усталостная прочность в сильной степени зависит от состояния поверхности; обычно образцы для определения предела выносливости полируются. Если образец сохранил на поверхности следы токарной обработки, предел выносливости его будет ниже. Таким образом, шероховатость поверхности играет ту же роль, что и концентрация напряжений. Для количественной оценки этого влияния можно ввести коэффициент, аналогичный коэффициенту концентрации. Для поверхности, обработанной резцом, соответствующий коэффициент может достигать значения 1,25. С другой стороны, упрочнение поверхности путем создания поверхностного наклепа (обкатка, дробеструйная обработка), цианирования и поверхностной закалки повышает предел выносливости.
§ 189. Усталостная прочность при сложном напряженном состоянии. В настоящее время не существует какой-либо теории, позволяющей судить об усталостной прочности при сложном напряженном состоянии. Задача становится особенно трудной, если принять во внимание возможность того, что разные компоненты тензора
напряжений могут меняться с разными частотами или даже с одинаковыми частотами, но несовпадающими фазами. При этом главные оси тензора напряжений, вообще говоря, ие сохраняют своего направления.
Поэтому мы ограничимся простейшим и наиболее важным случаем плоского напряженного состояния, такого, что ая^=0, т^О, но 0^ = 0. Этот случай имеет место, например, для вала при совместном действии изгиба и кручения. На .рис. 283 приведена одна из возможных схем испытания на усталость в таких условиях. Шпиндель соединен с образцом через посредство шарнира Гука (рис. 283), к
§ 189] УСТАЛОСТНАЯ ПРОЧНОСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕН, состоянии 425 шпинделю прикладывается крутящий момент, который разлагается в шарнире на два момента — изгибающий образец и закручивающий его. Соотношение между изгибающим и крутящим моментами зависит от угла ф. Конструкция машины предусматривает установку этого угла по желанию.
Самое простое испытание, дающее основные сведения об усталости при сложном напряженном состоянии, — это испытание гладкого образца при симметричном цикле изгиба и кручения. Изображенная на рис, 283 схема испытания обеспе- z чивает подобие циклов изгиба и кручения, а также синфазное изменение соответст- z вующих напряжений. Так же как и в одно- ---------—
осном случае, испытывается серия образ-
цов при фиксированном отношении изгибающего момента к крутящему, то есть при постоянном отношении амплитуд циклов напряжений оо и то. Строится кривая Вёлера, и определяется предел, выносливо-
Рис. 284.
сти. Значения и то, соответствующие
пределу выносливости, определяют точку в плоскости а — т, совокупность этих точек для различных отношений о„/то определяет кривую (рив. 284). С достаточно хорошей -степенью приближения можно считать, что эта кривая является эллипсом. Уравнение его:
(189.1)
Здесь Of — предел выносливости при изгибе или растяжении — сжатии, xf — предел выносливости при кручении. Величина xf может быть определена в результате специальных опытов на усталость при кру-чёнии, она составляет обычно 0,55 — 0,65 af.
Амплитуды допустимых состояний должны удовлетворять условию, которое получается из (189.1), если заменить знак равенства неравенством и единицу — единицей, поделенной на квадрат запаса прочности:
Соответствующие точки на рис. 284 принадлежат внутренности пунктирного эллипса (на чертеже заштриховано), оси которого в п раз меньше, чем оси предельного эллипса.
Для асимметричных циклов можно рекомендовать следующее условие прочности:
I <*А> V (хт 1 —
' <7-1 ) кт* "Г Т-1 ) п*'
(189.3)
14 Ю. Н. Работное
426
ТЕОРИИ ПРОЧНОСТИ
[гл. XVII
В случае симметричного цикла отсюда получается условие (189.2), при отсутствии касательных напряжений — условие (188.2), при отсутствии нормальных — аналогичное условие усталостной прочности при касательных напряжениях. Необходимо помнить, что коэффициент концентрации для нормальных и касательных напряжений различен.
Если считать т*=тт и о*==от, то условие (189.3) является одновременно условием прочности по отношению к наступлению текучести. Действительно, когда о„=то=0, мы получаем:
\ \ Тт/ ''п1
„ 1
При Тт=-^ат это условие Треска:
Л!
(189. 4)
_ 1
При = отсюда получается условие Мизеса:
G* + 3T’<(£)*.
В общем Случае необходимо отдельно проверить выполнение условия (189.4), приняв в ием
а = + т=тт + т„.
ГЛАВА XVIII
ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
§ 190. Ползучесть металлов. Начальные сведения о ползучести были сообщены в § 72. В настоящее время вопрос о расчете на ползучесть при проектировании изделий, работающих при высоких температурах, приобрел очень большое практическое значение. До недавнего времени с ползучестью сталкивались главным образом в энергомашиностроении при проектировании паровых и газовых турбин. Диск и лопатки турбины находятся под действием больших нагрузок от центробежных сил, и долговечность их определяется в первую очередь ползучестью. Развитие сверхзвуковой авиации И реактивной техники вызвало к жизни и новые задачи, связанные с ползучестью. Обшивка самолета, корпус ракеты испытывают значительный аэродинамический нагрев при скоростях, превышающих скорость звука.
Приведем основные факты, относящиеся к ползучести. Если обра--зец подвергнуть действию растягивающей нагрузки, создающей, постоянное напряжение, он будет медленно деформироваться со временем, кривая зависимости деформации от времени подобна изображенной на рис. 285. Здесь е0 — мгновенная деформация, участок / кривой — участок не-установившейся ползучести, происходящей с уменьшающейся скоростью, участок II—фаза установившейся ползучести, когда скорость приблизительнопостоянна, на участке III происходит ускоренная ползучесть, заканчивающаяся разрушением. В зависимости от
материала, иагрузкй и температуры масштаб кривой и соотношение между величинами соответствующих участков могут быть самыми различными. Мгновенная деформация в0 может быть упругой, пропорциональной напряжению; при больших напряжениях она может быть в основном пластической, то есть зависящей от напряжения существенно нелинейным образом. Деформация в момент разрыва 14*
428
ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
(ГЛ. XVIII
может измеряться долями процента от первоначальной длины при
времени до разрушения порядка сотен тысяч часов, а может составлять десять, двадцать и более лроцентов, причем разрушение проис-
ходит за несколько минут и даже секунд.
В некоторых случаях второй участок вообще выделить невозможно, существует лишь некоторая область вблизи точки перегиба кривой ползучести, где последняя может с известным приближением считаться прямолинейной. Такая кривая ползучести (рис. 286) характерна для высокого уровня напряжений. С другой стороны, многие материалы имеют кривые ползучести, подобные изображенной на рис. 287. Скорость ползучести весьма быстро становится постоянной и сохра-
няет это постоянное значение в течение долгого времени; таким образом, почти вся деформация до момента разрушения может считаться происходящей с постоянной скоростью. Кривые такого рода характерны для длительных испытаний сталей, применяемых в турбостроении, при среднем
Рис. 286.
уровне напряжений порядка рабочих напряжений в дисках и лопатках.
Испытания на ползучесть, о которых более подробно будет рассказано дальше, проводятся в течение некоторого времени, которое в ряде случаев значительно меньше, чем срок службы изделия. Так, например, паровые турбины работают годы и десятки лет, испытания материала в течение такого времени в условиях заводской лаборатории невозможны, обычно длительность таких испытаний не превышает 2000 — 5000 часов. Поэтому очень большое значение имеет вопрос об экстраполяции кривых ползучести, то есть о возможности предсказания ползучести в течение длительного времени на основании сравнительно кратковременных испытаний. Этот вопрос не нашел положительного решения, пригодного для всех материалов и всех условий; разными авторами предлагались эмпирические формулы для кривых ползучести, пригодные для тех или иных случаев. Наиболее простой способ экстраполяции, возможный тогда, когда кривая ползучести имеет вид, изображенный на рис. 287, состоит в том, что первой фазой ползучести пренебрегают и считают всю деформацию происходящей с постоянной скоростью г>(а). Таким образом,
Ba = v (a)i. (190.1)
§ 190]
ПОЛЗУЧЕСТЬ МЕТАЛЛОВ
429
При испытаниях стараются обеспечить длительность достаточную для того, чтобы надежно получить прямолинейный участок и определить его наклон. Зависимость скорости установившейся ползучести от напряжения при постоянной температуре изучена достаточно хорошо. Наиболее употребительные эмпирические формулы для функции v (о) следующие:
ф(о) = Доп, (190.2)
v (а) — k exp %-, (190.3)
v (о) — k sh -у, (190.4)
где А, п, k, s—' постоянные при данной температуре величины. Формулы (190.3) и (190.4) дают практически совпадающие результаты при больших напряжениях, при малых напряжениях формула (190.3) вообще неприменима, так как она дает конечную скорость при о = 0; однако при больших напряжениях эта формула достаточно точна.
Для сравнительной оценки сопротивления материала ползучести вводят так называемый предел ползучести. Это — условная величина, ее определяют как напряжение, при котором за данное время т достигается данная деформация ползучести ет. Величина ет обычно принимается равной одному проценту, а время т в авиационном моторостроении, например, назначается равным 100 часам, а для материалов стационарных паровых турбин его принимают за 100 000 часов.
Для того чтобы определить предел ползучести, нужно провести серию испытаний при разных напряжениях. Если продолжительность испытания не меньше времени т, предел ползучести находится по кривым непосредственно; если длительность испытаний невелика, кривые ползучести используют для нахождения величин постоянных в одной из формул для скорости установившейся ползучести или же просто строят график зависимости t>(o); по этому графику находят напряжение, для которого
®(а) = ^.
Таким образом, приближенно считается, что вся деформация происходит с постоянной скоростью.
Величина предела ползучести используется конструктором для выбора допустимого напряжения при расчете изделия, если нужно гарантировать, чтобы за время службы изделие не получило недопустимо больших деформаций. В настоящее время существуют более точные методы расчета на ползучесть, и величина предела ползучести потеряла свое значение как расчетная характеристика материала, она может служить лишь для сравнительной оценки различных материалов при их предварительном подборе.
430
ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
(гл. XVIII
Для первых участков кривых ползучести достаточно хорошее приближение получается, если описывать их с помощью степенной функции времени
en=S(a)/".
Показатель т для большинства материалов колеблется от « = до m =
§ 191. Процесс ползучести. Механизм пластической деформации при ползучести в основном остается тем же, что и механизм обычной пластической деформации; ползучесть происходит в результате сдвигов по плоскостям наилегчайшего скольжения за счет движения дислокаций. Однако если при кратковременной пласти-\ ческой деформации сдвиги локализованы в пачках пло-
] скостей скольжения, причем блоки значительных раз-
J меров остаются практически иедеформированными, то
21. ползучесть происходит в результате весьма малых сдви-
\ \ \ гов по большому числу плоскостей скольжения; поэто-
) • \ му микроскопическая картина обычно не обнаруживает Js>a следов сдвига, который распределяется более или менее v-\ I равномерно по всему объему кристаллического зерна.
। / Кроме того, длительное действие напряжения при
у , / высокой температуре может вызвать сдвиги в системах 'скольжения, которые в обычных условиях остаются не-\ активными.
1 При объяснении механизма ползучести нужно разли-
J чать начальную стадию и стадию установившейся ползу-
• чести. Если зерно деформировано путем приложения
Рис. 288. касательного напряжения т, большое количество дислокаций оказывается задержанным препятствиями так, что для приведения их в движение достаточно лишь немного увеличить напряжение. Существуют подавленные источники Франка — Рида, для которых критическое напряжение немного превышает действующее. В сплавах, содержащих большое количество более или менее равномерно распределенных субмикроскопических выделений (дисперсионно-твердеющих сплавах), характерно расположение дислокаций, подобное изображенному на рис. 288; под действием приложенного напряжения линия дислокации выгибается между препятствиями. Атомы находятся в состоянии теплового движения, поэтому линии дислокаций никогда не останутся в покое, они колеблются, выгибаясь то больше, то меньше. Поэтому всегда есть вероятность, что два соседних участка примут конфигурацию, изображенную пунктиром и обозначенную буквой а. Тогда соприкасающиеся участки линии дислокации уничтожат друг друга, оставшиеся части сольются и займут положение Ь. Таким образом, препятствие в виде ряда внедренных выделений не
§ 192] ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ 431
является непреодолимым, со временем дислокация полностью или частично пройдет через него. Энергия, которую необходимо сообщить дислокаций, чтобы миновать препятствие, называется энергией акти-вации. В первую очередь будут продвигаться дислокации с низкой энергией активации, для дислокаций с более высокой энергией активации вероятность того, что тепловое движение атомов сообщит необходимую энергию, меньше, поэтому такие дислокации будут двигаться реже. Каждое перемещение дислокации вызывает пластическую деформацию, скорость которой убывает со временем. Так будет продолжаться до тех пор, пока не исчерпается весь запас дислокаций с достаточно низкой энергией активации.
Освободившиеся дислокации задерживаются на препятствиях обычно в виде групп, подобных изображенным на рис. 100, как и при обычной пластической деформации, поэтому ползучесть сопровождается упрочнением материала. Увеличивающееся сопротивление этих групп присоединению новых дислокапий является второй причиной уменьшения скорости ползучести на первом участке кривой.
С другой стороны, вследствие температурных флуктуаций, вызывающих диффузионное движение вакансий и внедренных атомов, задержанные группы дислокаций разрушаются, некоторые дислокации выходят из плоскости скольжения. Как уже отмечалось в § 70, дислокации одного знака, находящиеся в различных плоскостях скольжении, имеют тенденцию расположиться в виде вертикальных рядов, образующих границы блоков. Такая фрагментация зерна, разбивка его на отдельные блоки, слегка отличающиеся своей Ориентацией, действительно наблюдается во второй фазе ползучести.
Данное схематическое описание процесса ползучести является далеко не исчерпывающим. При высоких температурах в сплавах происходят различного рода изменения: выпадение новых фаз, направленная диффузия примесей и т. д. Эти явления влияют на процесс ползучести иногда самым неожиданным образом, именно поэтому экстраполяция кривых ползучести бывает очень ненадежна.
При достаточно высоких температурах в поликристаллическом металле границы зерен становятся более слабыми, чем сами зерна, и значительная часть деформации ползучести происходит за счет скольжения зерен друг относительно друга. Это скольжение носит характер вязкого течения, оно затруднено кинематически, так как зерна имеют неправильную форму и каждое зерно встречает сопротивление со стороны соседних. Это скольжение становится возможным за счет пластической деформации зерен, и иногда оно сопровождается появлением межзеренных трещин, приводящих к разрушению.
§ 192. Длительное разрушение. При расчет» на ползучесть нужно обеспечить либо отсутствие в изделии слишком больших деформаций, нарушающих его конструктивную функцию, либо
432
ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ ' [ГЛ. XVIII
прочность в прямом смысле слова. Для суждения о прочности в условиях ползучести достаточно бывает определить время до разрыва при заданном напряжении. Повторяя испытания при различных напря-
жениях, можно построить кривую длительной прочности (рис. 289).
По оси ординат откладывается напряжение (обычно условное, отнесенное к первоначальной площади сечения образца), по оси абсцисс — время до разрыва. По кривой длительной прочности можно определить так называемый предел длительной прочности от, то есть напряжение, вызывающее разрушение по истечении условно выбранного времени т. Так, в
авиационном моторостроении, как
уже отмечалось, обычно время т принимается равным 100 часам и предел длительной прочности обозначается а100. Кривые длительной прочности бывает удобно строить в логарифмических координатах
(рис. 290), где они достаточно
Рис. 290.
хорошо аппроксимируются прямыми. Типичной является изображенная на этом рисунке диаграмма, состоящая из двух прямых с различным наклоном. Первый, круто падающий участок, соответствует внутризеренному разрушению, второй участок — разрушению по границам зе-,. 1 рен. Для определения предела длительной прочности при больших значениях т необхо-
димо получить достаточно отчетливо второй прямолинейный участок, после чего можно экстраполировать, продолжая прямую так, как показано пунктиром. Переход от одного прямолинейного участка ко второму не всегда бывает выражен ярко, иногда этот переход оказывается более плавным, как показано на чертеже также пунктиром. При высоком уровне напряжений, когда разрыв происходит за несколько минут, разрушение носит пластический характер и время до разрушения можно приблизительно подсчитать следующим образом (Хофф).
Будем рассматривать конечные деформации растягиваемого стержня; тогда за меру деформации естественно принять логарифмическую деформацию
е = 1п — = In ха
§ 192J
ИНВ Ns 33 __ )
HE БОЛЕЕ ИЙ КНШнГ|
ОДНИ РУКИ И 2Х В ДДЕ }
ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ
j ОСКОРЦА
43»
Здесь х0 — начальная длина, х — длина в процессе деформации, | . Скорость деформации
хо
6-т
Обозначая через и истинное напряжение, через о0 — напряжение, отнесенное к первоначальной площади поперечного сечения, заметим, что при постоянной силе
oF=o0F0.
Отсюда
Fo е
-/=o0g.
При этом мы воспользовались условием неизменности объема стержня, а именно тем, что
xF=xtF„.
Будем считать, что скорость деформации зависит от напряжения по степенному закону:
ё —Ао" или
S
Разделим переменные:
• l-l-ndi = A^adt. (192.1)
При t — 0 было £ — 1, за конечное время стержень приобретет бесконечно большое удлинение; это следует из того, что интеграл от левой части в пределах от g = 1 до £ — оо равен конечной величине
го
Выполняя интегрирование, найдем:
_ 1
Т~4по"‘
(192.2)
. Это — уравнение кривой длительной прочности при пластическом разрушении от ползучести. На самом деле разрыв происходит при некотором конечном значении |, но процесс ползучести, описываемый уравнением (192.1), очень сильно ускоряется с ростом деформации, и время, когда деформация достигает 15—20%, что обычно для
ВИ В ЛИО""W 4
КОЛОХЗА
mcnerv £>яе a
434 ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ [гл. XVIII
момента разрушения, мало отличается от времени, при котором деформация стремится к бесконечности.
При малых напряжениях и, следовательно, больших временах до разрушения последнее происходит главным образом за счет разви-е тия внутренних трещин и носит
i хрупкий характер. График зави-
\ симостн удлинения в момент раз-
\ рыва от времени до разрушения
изображен на рис. 291. Пласти-ческий материал, который при
_______ кратковременном разрыве обнаруживает деформацию порядка
—--------1 15—20%, разрушается в усло-
рис 291 виях длительной службы без за-
метной пластической деформации.
С образованием трещин связано ускорение ползучести в третьем периоде.
§ 193. Температурные зависимости ползучести и длительной прочности. К атомам твердого тела, находящимся в состоянии беспорядочного теплового движения, можно применить те же законы, что и к молекулам газа. Распределение энергии между молекулами' газа устанавливается законом Больцмана. Если обозначить dq относительное количество атомов, для который энергия теплового движения находится в пределах от U до U-\-dU, то по формуле Больцмана
<ty==-Lexp(—(193.1)
Здесь К—постоянная Больцмана, Т—абсолютная температура. Для того чтобы атом металла, совершающий тепловые колебания, мог покинуть свой узел и внедриться между соседними атомами, необходимо, чтобы его энергия превысила некоторую величину называемую энергией активации. Формула (193.1) указывает, что всегда существует некоторое количество атомов, имеющих энергию большую, чем энергия активации, и, следовательно, перемещающихся внутри кристаллической решетки. Обозначим относительное количество активированных атомов через q*, очевидно, что
9*=J irехр (- й)du=ехр (- й) ♦ • Uq
Если процесс ползучести определяется в первую очередь освобождением дислокаций, вызванным тепловым движением атомов (вторая фаза ползучести), то естественно предположить, что скорость пол
§ 193] ТЕМПЕРАТУРНЫЕ ЗАВИСИМОСТИ ПОЛЗУЧЕСТИ
433
зучести при одинаковых напряжениях будет пропорциональна величине q*, следовательно,
e = v(a, T) = expf—va(a), (193.2)
Рис. 292.
Энергия активации С70 представляет собою константу материала. Рассматривая механизм ползучести в первой фазе, можно распространить представление об активации на более сложные атомные образования, какими являются петли дислокаций; формула (193.2) сохраняет силу и в этом случае, но энергия активации будет другой. В случае переменной скорости ползучести формула (193.2) позволяет сравнивать скорости при одинаковых степенях упрочнения.
На рис. 292 приведена кривая ползучести чистого алюминия (Дорн, 1954 г.) при температуре, меняющейся в соответст-
вии с помещенным выше трафиком. Пунктиром построена теоретическая кривая, перестроенная из кривой ползучести при постоянной температуре с помощью уравнения (193.2).
Если обратиться к эмпирическим формулам (190.2), (190.3) или (190.4), то окажется, что зависящим от температуры будет лишь один коэффициент, а именно А в формуле (190.2) и k в формулах (190.3) и (190.4). На самом деле температурная зависимость ползу- ' чести технических сплавов имеет более сложный характер, и при обработке опытных данных оказывается, что все постоянные, входящие в формулу, зависят от температуры. Однако, если диапазон изменения температуры невелик (50°—100° для стали), уравнение (193.2) дает достаточно точные предсказания. Нужно только иметь в виду, что энергия активации не постоянна, она меняется в зависимости от температуры и напряжения. Изменение энергии активации свидетельствует о переходе от одного преобладающего механизма ползучести к другому.
Данные по длительной прочности с известной степенью приближения можно бывает представить при помощи так называемого параметра Ларсена— Миллера. Если результаты испытаний на длительную
436 ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ [гл. XVIII
прочность изображаются в координатах, где по одной оси откладывается напряжение (илн, обычно, логарифм напряжения), а по другой— величина T(C-|-logT), то все опытные точки для различных температур и различных напряжений ложатся на одну кривую. Величина С является здесь постоянной материала. При помощи параметра Ларсена — Миллера можно судить о длительной прочности материала при произвольной температуре, если имеются результаты испытаний на длительную прочность при каких-либо двух температурах.
§ 194. Феноменологические теории одномерной ползучести. Кривые ползучести прн растяжении под постоянным напряжением являются основным источником наших сведений о ползучести данного материала, так как подобного рода испытания наиболее просты, проводятся на различных сплавах достаточно широко и ^настоящему времени накоплено много экспериментальных данных. Элементы реальных конструкций находятся обычно в более сложных условиях, нагрузка и температура могут меняться во время эксплуатации, и распределение напряжений часто оказывается неравномерным; нам приходится судить об изгибе стержня, о напряжениях и деформациях в трубе под внутренним давлением, о поведении вращающегося диска на основании кривых ползучести. Для этого необходимы некоторые гипотезы относительно зависимости между напряжением, деформациями и временем, которые должны носить достаточно универсальный характер.
Если большая часть деформации происходит с постоянной скоростью, то приближенно, пренебрегая начальной упругой или пластической деформацией и первой фазой ползучести, можно считать
е = 'п(а). (194.1)
Это уравнение применимо как при постоянных нагрузках, так и при переменных. Скорость ползучести в общем случае зависит не только от напряжения, но й от температуры. Уравнение (194.1) можно применять тогда, когда нас интересует определение деформации при ползучести, притом деформации значительной, во много раз превосходящей начальную деформацию.
В тех случаях, когда кривые ползучести существенно отличаются от прямых или когда нам нужно определить малые деформации, такие, что фазой неустановнвшейся ползучести пренебрегать нельзя, пользуются гипотезой уравнения состояния. Мы видели, что уменьшение скорости ползучести в первой фазе связано с накоплением дислокаций около препятствий, то есть с упрочнением материала. Естественно принять за меру упрочнения величину накопленной деформации ползучести и считать, что скорость этой деформации зависит не только от напряжения и температуры, но и от величины
§ 195] X РЕЛАКСАЦИЯ НАПРЯЖЕНИЙ 437
деформации ползучести. Таким образом, мы получаем следующее уравнение:
ёп = ф(о> У. еп). (194.2]
Это и есть уравнение состояния. Здесь ея'—деформация ползучести. Если начальной пластической деформации не происходит, то еп = а
~ ® Е •
• Уравнение состояния применимо для таких материалов, которые структурно устойчивы в условиях ползучести. Пользоваться уравнением состояния в его общей форме для расчетов затруднительно, поэтому для функции ф(о, Т, еи) обычно подбирают некоторые достаточно простые аналитические выражения. Так, для участков неустановившейся ползучести хорошая аппроксимация будет следующая:
епбп = k ехр £. (194.3)
Здесь а^> 1. Если мы хотим учесть зависимость от температуры, то следует принять в соответствии с вышесказанным
= ехр(—
На самом деле постоянные а и А также зависят от температуры, но слабо.
§ 195. Релаксация напряжений. Одним из проявлений ползучести является релаксация напряжений. Этим термином называется падение
напряжения со временем в напряженной детали. Примером может
служить ослабление натяга болтов во фланцевом соединении, схематически показанном на рис. 293. Крышка сосуда, находящегося под внутренним давлением, привернута болтами. Для того чтобы соединение было плотным, необходимо затянуть гайки достаточно туго, так, чтобы усилие в болтах от затяжки гаек было больше того усилия, которое возникает в них вследствие внутреннего давления. При высокой температуре болтов и фланцев первоначально созданное натяжение будет со временем ослабевать, и наступит няется с рабочим натяжением. Начиная с
момент, когда оно срав-этого момента соедине-
ние перестает быть плотным, и газ или жидкость из сосуда начнет просачиваться через фланец.
В изделиях, имеющих концентраторы напряжений, распределение напряжений в первый момент после приложения нагрузки, как
438
ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ прочность [гл. XVIII
известно, бывает резко неравномерным. Процесс релаксации приводит к тому, что концентрация напряжений со временем ослабевает, распределение напряжений становится более равномерным и максимум напряжений снимается. В этом случае влияние релаксации на прочность благотворно. Части машин, работающие при повышенных температурах, часто оказываются нагретыми неравномерно, а при неравномерном нагреве возникают температурные напряжения. Эти температурные напряжения релаксируют н оказываются вследствие этого не такими опасными, как можно было ожидать.
Для.того чтобы осуществить опыт на релаксацию в чистом виде, необходимо сообщить образцу упругую деформацию е и удерживать
его при этой постоянной деформации, измеряя зависимость напряжения от времени. На рис. 294 приведены кривые релаксации для хромомолибденовой стали.
Для материалов, подчиняющихся уравнению состояния (194.3), кривая релаксации может быть получена из кривых ползучести. Действительно, если из опытов на ползучесть определить, например, константы a, k и А в уравнении (194.3), то вследствие универсального характера этого уравнения оно должно быть пригодно и для случая релаксации. Положим е = -^- = const. Тогда
р=-^— и о = ст0 —Ер.
Внесем а в уравнение (194.3) и разделим переменные. Получим: exp (padp — k exp dt.
k A J А
§ 196] ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ 439
Левая часть интегрируется только тогда, когда а—целое число. Однако для произвольного а это интегрирование всегда можно выполнить численно; таким образом, будет найдена зависимость между временем t и пластической деформацией р или напряжением а. На рис. 294 пунктиром построены кривые релаксации, рассчитанные на основании кривых ползучести для той же стали. Расчет кривых релаксации по кривым ползучести возможен не всегда; для структурно неустойчивых материалов и для больших длительностей уравнение состояния может не выполняться.
§ 196. Длительная прочность при переменных нагрузках. Знание кривой длительной прочности позволяет предсказывать долговечность изделий, находящихся под постоянным напряжением, или назначать величину допускаемого напряжения для заданного срока службы. В действительности многие части машин работают в условиях переменных нагрузок и переменных температур. Возникает вопрос о том, каким образом оценивать в этих случаях их долговечность.
Выше, в § 192, был рассмотрен вопрос об определении времени до разрушения образца из вязкого материала, который разрывается без охрупчивания вследствие ползучести. В основу было положено представление о том, что при постоянном напряжении материал течет с постоянной скоростью. Уменьшение площади образца вызывает при постоянной силе увеличение скорости течения; это увеличение происходит значительно быстрее, чем уменьшение площади сечения. Дифференциальное уравнение (192.1) сохраняет силу и тогда, когда внешняя нагрузка переменна. Если считать, что о, есть заданная функция от времени, то время до разрушения т' найдется из следующего интегрального соотношения:
00 X'
1 о
или
JnX(O# = l. (196.1)
О
Но по формуле (192.2) 1]Апа% есть время до разрушения, соответствующее постоянно действующему напряжению а„. Зная величину а0, можно по диаграмме длительной прочности (рис. 295) найти соответствующее значение времени до разрушения т; если ао(О есть заданная функция времени, то т(/) также представляет собою известную функцию времени. Последнее уравнение перепишется
440
ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
(ГЛ. XVIII
следующим образом:
(196.2)
называемый принцип линейного суммирования повреждаемости. Если нагрузка прикладывается ступенями согласно графику, изображенному на
рис. 296, интеграл в формуле (196.2) заменяется конечной суммой
(196.2')
Здесь т,- — определенное по кривой длительной прочности время до разрушения от действия постоянного напряжения Oj.
Принцип линейного суммирования повреждаемости распространяется и на хрупкое разрушение при ползучести. Для этого мы сделаем некоторые предположения о характере развития трещин. Предположим, что трещины имеют форму кругов, находящихся в плоскости поперечного сечения растянутого стержня (рис. 297). Пусть на единицу площади приходится в данный момент одна трещина, радиус которой Q, а площадь <о. Таким образом, остав-
шаяся площадь, которая воспринимает внешнюю нагрузку, есть 1 — <о. Обозначим номинальное напряжение через о0, фактическое среднее напряжение в сечении через о. Тогда
о0.1=О(1-®), 0=^
Скорость изменения площади трещины (о = лр’ найдется следующим образом:
§ 196] ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
441
Сделаем предположение, что скорость распространения границы трещины есть функция среднего напряжения в сечении, таким образом, 2]/гл^ = ф(ст), следовательно,
^=Уй<р(о), f
или
Если функция ф (ст) — степенная функция, переменные разделяются. Действительно, положим
ф (ст) = аот.
Тогда
^ = |/<1)стстГ(1—<о)~т
или, после разделения переменных,
(о-*/3(1 — a)mda = aa^dt. (196.3)
В начальный момент площадь трещины была чрезвычайно малой по сравнению с единицей, и мы, не делая большой погрешности, можем принять ее равной нулю. Когда <о достигнет значения, равного единице, трещина распространится на всю площадь поперечного сечения и произойдет разрушение. Проинтегрировав уравнение (196.3), получим:
1 Tf
^®_,/’(1—<o)md<o = аст“dt. О о
Интеграл в левой части всегда конечен, это некоторое число, зависящее от т. Нам нет необходимости находить величину этого интеграла, обозначим ее l]k. Тогда условие разрушения запишется следующим образом:
г’
J бастуй =1. (196.4)
о
При постоянной нагрузке
Т =
Эта формула отличается от формулы (192.2), соответствующей вязкому разрушению, только значениями констант, а формула (196.4) имеет ту же структуру, что и формула (196.1) Поэтому совершенно аналогичные рассуждения, снова приводят нас к принципу линейного суммирования повреждаемости, выражаемому формулой (196.2).
442
ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ [ГЛ. XV111
Прямые опыты обнаруживают, что принцип линейного суммирования повреждаемости не вполне точен, наблюдаются некоторые систематические отклонения от предсказаний, даваемых уравнением (196.2), особенно если нагрузки убывают. Однако на практике нм пользуются, так как погрешность невелика, а сами исходные данные
не очень точны; при испытаниях на длительную прочность обычно наблюдается довольно большой разброс экспериментальных точек и всегда бывает необходимо вводить некоторый вапас прочности.
§ 197. Ползучесть при изгибе. Разберем некоторые простые вадачи, решаемые на основе теории установившейся полвучести. Рассмотрим сначала изгиб стержня с сечением, имеющим две оси симметрии (рис. 298). Выбирая оси координат та'к, как показано на чертеже, и считая, что изгибающий момент действует
в плоскости уОг, обозначим через х скорость изменения кривизны нейтрального слоя. Тогда вследствие гипотезы плоских сечений
e = zy.
Примем закон полвучести в виде
Тогда
(197.1)
Изгибающий момент в сечении
dy.
(197.2)
При этом мы сделали допущение о том, что вакон ползучести при сжатии будет тот же, что и при растяжении. Уравнение (197.1) справедливо только для случая растяжения. Если п — целое и нечетное, это уравнение будет действительно и в случае сжатия, тогда отрицательным напряжениям соответствуют отрицательные скорости деформации. Правильная запись, пригодная для любых значений показателя п как при растяжении, так и при сжатии, будет следующая:
ё = Л[а|в“*а.
§ 197]
ПОЛЗУЧЕСТЬ ПРИ ИЗГИБЕ
443
Легко проверить, что при такой записи всегда получаются правиль-ные знаки.
Введем обозначение
’*/* i-1-l
2\by ndy=Jn.
О
При л=1 это момент инерции поперечного сечеиия относительно оси х, при п = оо — удвоенный статический момент верхней половины сечения относительно той же оси. Из уравнения равновесия следует:
к = А
и
J п
(197.3)
В частном случае прямоугольного сечения
Jn 1 + 2n 2 J J
На рис. 299 изображены эпюры распределения напряжений по сече-нию стержня прямоугольного сечения при одинаковых значениях изгибающего момента, но при разных п. Максимальное напряжение
п —4-М 1 -|- 2п (197 4}
Ошах—2п ‘
При п — 1 мы получаем распределение напряжений в упругом стержне, при л = =оо — в сте.ржне из идеально-пластического материала.
На практике нередко значение п оказывается весьма большим, от 8 до 12. Если п = 10, например, наибольшее напряжение отли
чается от напряжения в идеально-пластическом стержне всего на 5°/0. Это замечание будет испольвовано при рассмотрении следующего примера, сейчас же мы остановимся на рассмотрении реального смысла найденного решения.
В первый момент после приложения нагрузки распределение напряжений следует закону упругости, следовательно, изображается прямолинейной эпюрой на рис. 299. Далее начинается процесс
444
ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
[гл. XVIII
перераспределения напряжений вследствие ползучести. Теория установившейся ползучести не позволяет нам ничего сказать об этом процессе; только по истечении достаточно большого времени устанавливается распределение напряжений, даваемое формулой (197.3). Для того чтобы судить о прочности, строго говоря, мы должны знать
тот закон, по которому изменяется максимальное напряжение от начального значения, равного oM/bh1, до того, которое дается формулой (197.4) при соответствующем п. Располагая кривой длительной
прочности материала и применяя принцип линейного суммирования
4------1----------:-----х
f-— а —-4
Рис. 300.
повреждаемости, мы сможем определить долговечность; Многочисленные расчеты, производившиеся на основе более точных и совершенных теорий ползучести, описывающих процесс непрерывного перераспределения напряжений, показали, что, определяя
долговечность но наибольшему напряжению установившейся ползучести, мы не делаем большой ошибки. То эквивалентное напряжение, которое нужно сравнивать с кривой длительной прочности, чтобы учесть большую величину на-
пряжения в первом периоде, превышает напряжение установившейся ползучести всего на 3 — 4°/0, не более.
Выражение для скорости изменения кривизны можно использовать для нахождения прогиба балки. Возьмем, например, балку длины I (рис. 300), загруженную посередине сосредоточенной силой Р. Из-Р
гибающий момент Л4=трх; поскольку момент не зависит от вре-
мени, скорость изменения значит,
кривизны тоже не зависит от времени,
X = 4-5 = X/. дх?
Подставляя сюда значение х через известный момент, получим следующее дифференциальное уравнение изогнутой оси:
дхг
= At
Интегрируя один раз, найдем: до____________________ At f
дх п 4-1 \
Угол наклона изогнутой оси должен равняться нулю в середине балки при х=//2. Отсюда находится функция времени С(?), и вы
§ 198] КРИТИЧЕСКОЕ ВРЕМЯ СЖАТОГО СТЕРЖНЯ 445
ражение для производной от прогиба становится следующим:
dv At ( Р V Г n+i ( I у+Ч дх~п+1 \ L к 2 J J •
Интегрируем еще раз, учитывая начальное условие г>(0) = 0. Получаем:
At ( Р у [ х"+2 / I у+* 1
V~~~n + \\2Jn) |п + 2 k2j XJ •
Определим наибольший прогиб pmav при х = //2. Получим:
______( Р_\п (J_\n+i At ^max \2J„J \ 2 J n-j-2‘
Изогнутая ось балки по мере увеличения п становится все более близкой к ломаной, соответствующей шарниру текучести в том сечении, где приложена сила.
Расчет на ползучесть стержней несимметричного сечения оказывается довольно затруднительным, причем основная трудность состоит в нахождении нейтральной оси сечения. Часто применяемый приближенный прием состоит в том, что нейтральная ось находится так, как если бы материал стержня был идеально-пластическим.
§ 198. Критическое времи сжатого стержня. Сжатый стержень, имеющий начальное искривление, будет выпучиваться вследствие ползучести. Изгибающий момент в сечении пропорционален прогибу стержня, а скорость изменения кривизны зависит от изгибающего момента, как мы видели, нелинейным образом, притом очень сильно. В результате оказывается, что скорость прогиба увеличивается с ростом прогиба настолько быстро, что прогиб достигает бесконечно большого значения за конечное время, называемое критическим временем. Конечно, достижение прогибом бесконечно большого значения нужно понимать в условном смысле, так же как в теории продольнопоперечного изгиба упругих стержней. Мы будем пользоваться упрощенным линеаризированным выражением для кривизны, которое для больших прогибов несправедливо, и стремление к бесконечности решения дифференциального уравнения еще не означает, что прогиб реального стержня ведет себя таким же образом. Приводимый ниже анализ имеет целью не столько определить критическое время для реального стержня из реального материала, сколько убедиться в том, что оно действительно существует, и выяснить, от каких факторов и каким образом может зависеть его величина.
Будем рассматривать стержень идеального двутаврового сечения, изображенного на рис. 301, шарнирно опертый на концах; длина стержня равна I. Площадь каждой полки есть /г/2, размеры полок
момент равен
446 ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ [гл. XVIII
малы по сравнению с h, так что напряжение в каждой полке можно считать равномерно распределенным. Площадь стенки считается весьма малой и не принимается во внимание, функция ее состоит только в том, чтобы воспринять касательные напряжения и тем самым обеспечить работу полок как одного целого. Напряжение равномерного сжатия от силы Р равно Р/F; если прогиб стержня есть г>, то изгибающий ~ этот момент создает в одной из полок дополнительные сжимающие напряжения, в другой — растягивающие. Величина этих напряжений равна 2PvlFh. Таким образом, суммарное напряжение в каждой из полок
Рис. 301.
Введем безразмерный прогиб w = -^, тогда
Р о = ±п>).
Скорость изменения кривизны изогнутой оси есть v", где штрихи обозначают дифференцирование
по х, а точка дифференцирование по t. Скорость деформации каждой полки
* __ * . Й ’ /г
« = «,±-2®. •
Введем безразмерную координату £=у, тогда
• „_ 4 d2v_2
v —hidl~'h dg2' Таким образом,
• • , (Ра>
8—80±^|Г.
Примем зависимость скорости ползучести от напряжения по закону гиперболического синуса:
8 = k sh —. s
Эта формула сохраняет силу для любых значений а, положительных и отрицательных, так как гиперболический синус есть нечетная функция.
Напишем теперь уравнение ползучести для каждой полки в от-, дельности:
8. — = (1—®).
§ 198] КРИТИЧЕСКОЕ ВРЕМЯ СЖАТОГО СТЕРЖНЯ 447
Вычтем из первого уравнения второе. Получим:
d*w , , Р , Pw
3|*d/=ftch . (198.1)
Уравнение (198.1) является нелинейным уравнением в частных производных, точное интегрирование которого невозможно. Для приближенного интегрирования положим
w = a(/)sin^. (198.2)
Предполагаемая форма прогиба является синусоидой, при этом на длине балки укладывается половина волны. Выражение (198.2) ие удовлетворяет дифференциальному уравнению, мы ограничимся тем, что потребуем выполнения этого уравнения в середине балки, при х = //2 и Получим:
л*Л* • , . Р . Ра
— lira==ftchs7shsT.
Заметим, что для идеального двутаврового сечения момент инер-Fh*
ции J=—, поэтому множитель, стоящий перед а в левой части, представляет собою деформацию сжатия от нагрузки, равной эйлеровой критической силе. Обозначим эту деформацию вЕ. Положим Ра Р
— — ==р. Тогда дифференциальное уравнение перепишется следующим образом:
sh$ г
£
Интеграл от левой части есть lnth-|-; интегрируем ее в пределах от £0 до оо, а правую в пределах от нуля до t; Получим:
гв In th
* Р ch р
Это выражение можно немного упростить. Для малых thy=^; для больших р ch Р s* sh р, но k sh р есть скорость ползучести при сжатии силой Р. Обозначим ее е0. Возвращаясь к первоначальным обозначениям, получим следующую формулу для критического времени:
<198-3>
Как видно, критическое время зависит от начального прогиба стержня а0, но зависимость эта не сильная. Принимая в качестве а0
448 ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ [гл. XVIII
предельное значение допуска на непрямолинейность стержня, мы получим всегда нижнюю оценку для критического времени.
Существуют методы определения критического времени сжатых стержней при других законах ползучести и для более реальных форм поперечного сечения; они приводят к тем же качественным результатам, но требуют, как правило, громоздкого численного интегрирования соответствующих уравнений.
§ 199. Ползучесть и длительная прочность при сложном напряженном состоянии. Как мы видели, ползучесть есть одно из проявлений пластичности; механизм ползучести, по существу, не отличается от механизма обычной пластической деформации, поэтому при формулировке законов ползучести в сложном напряженном состоянии мы будем пользоваться теми же идеями и теми же гипотезами, что и для пластичности. Так же, как н для пластичности, существуют различные теории ползучести, которые дают в общем близкие результаты. Та теория, которая будет изложена ниже, является распространением теории пластического течения Сен-Венана с ассоциированным законом распределения скоростей. Согласно теории Сен-Венана пластическое состояние осуществляется тогда, когда наибольшее касательное напряжение достигает предельного значения, это значение сохраняется в процессе пластической деформации постоянным, сама пластическая деформация представляет собою чистый сдвиг. Таким образом, если принять, как обычно, то
о, — о, = const, ё2 = 0, ё, ==— ё„ причем величины скоростей деформации неопределенны. В теории ползучести естественно принять, что деформация является также деформацией чистого сдвига, 8t = 0 по-прежнему, а скорость сдвига 8! — ё2 есть функция наибольшего касательного напряжения или величины ст, — <у„ атак как 8,=—8,, то можно написать
8, = 11(0, —ст,). (199.1)
Функция v здесь та же самая, что в уравнении (194.1); она определяется из опыта на ползучесть при растяжении. Случай, когда два напряжения равны между собою, например о,=ст,, должен быть оговорен особо. В этом случае скорости деформаций ё, и в, неопределенны, но формула (199.1) сохраняет силу. Как раз такой случай представляет растяжение стержня. Растягивающее напряжение есть ст,, напряжения ст, н ст, равны нулю, но скорости деформации в поперечном направлении могут быть любыми, только сумма их ё,-|-ё, равна — 8] вследствие несжимаемости материала.
Были предложены и другие теории ползучести, в некоторых из них отправным пунктом служила теория пластичности типа теории Мизеса, в других использовались уравнения деформационной теории пластичности, куда вводилось как параметр время.
§ 200] ВРАЩАЮЩИЕСЯ ДИСКИ В УСЛОВИЯХ ПОЛЗУЧЕСТИ 449
Что касается условий разрушения, опыты с достаточной точностью показывают, что разрушение в сложном напряженном состоянии определяется величиной наибольшего растягивающего напряжения, которое должно сравниваться с пределом длительной прочности, найденным для образцов при растяжении.
§ 200. Вращающиеся диски в условиях ползучести. В § 146 мы получили дифференциальное уравнение равновесия вращающегося диска переменной толщины:
i(^^h^~S-{-Q(>)rrh== 0. (200.1)
Представим это уравнение в следующем виде:
7^(Aror) = 7’oe'~et°,rA-
Отсюда или
hrar = J Ло6 dr — q<o* J г’Л dr,
hat dr — \ r*h dr
(200.2)
Дальнейший расчет существенным образом зависит от того, какое из напряжений является наибольшим, какое — наименьшим. Для диска
с отверстием мы предположим, что ав >ог^> 0 (это предположение проверяется после того, как построено решение). Тогда нужно считать о6 = о1, 0 = ffs, так ’ ли’ dv
как о, = о„ е, = 0. Но е,=т, где v — ’ ' ' 'аг
радиальная скорость. Следовательно, v = =с , е9 = —. Закон ползучести будет
следующим:
86 = гЦав).
Возьмем функцию v в виде степенной функции ф(о) = Дов. Тогда / С \1'п
Здесь с—^-. Внесем ое в формулу для ог, приняв нижний предел интегрирования равным а (рис. 302). Получим:
ог
hr~,ndr
а
450 ' ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ [гл. XVIII
Напряжение аг обращается в нуль на контуре отверстия при г==а. Если диск не несет лопаточной нагрузки на наружном контуре, при г = Ъ должно быть o', (Z>) = 0. Из этого условия получаем уравнение для нахождения с:
ь ь
ci/n hr-Mn dr—^ rlh dr. (200.3)
a a
Интересно отметить, что распределение тангенциального напряжения не зависит от профиля диска. Случай сплошного диска представляет несколько большую трудность. В центре всегда а7=а6, следовательно, соотношение между скоростями е, и ее неопределенно. С другой стороны, те предположения, которые были сделаны для диска с отверстием, здесь приводят к противоречию. Действительно, скорость в центре должна быть равна нулю, а так как она постоянна, то остается равной нулю всюду. Выход из этого- противоречия состоит в том, что в центральной области диска при 0 г<с принимается o’j = ог, тогда как при г с о8 аг 0, как и в предыдущем случае.
§ 2б1. Расчеты иа ползучесть по теории старении. Допущение о том, что процесс ползучести описывается простейшим уравнением установившейся ползучести:
в=v (а),
во многих случаях означает значительное искажение исходных опытных данных, кривые ползучести могут значительно отличаться от прямых. Гипотеза уравнения состояния действительна далеко не всегда, и применение ее к расчетам наталкивается иа серьезные трудности. Поэтому естественно стремление создать такой способ расчета иа ползучесть, который учитывает все своеобразие действительных кривых ползучести материала и позволяет использовать эти кривые непосредственно без каких-либо искажений, связанных с той или иной аналитической аппроксимацией. Поэтому в расчетной практике конструкторских бюро заводов нашел широкое распространение способ расчета иа ползучесть, основанный на так называемой теории старения. Возьмем серию кривых ползучести материала при дайной температуре (рис. 303). Будем откладывать по оси. ординат полную деформацию 8. Эта серия кривых представляет собою графическое изображение функциональной зависимости трех переменных: напряжения а, деформации 8 и времени t. Зависимость между тремя переменными может' быть представлена и иначе, а именно мы можем строить в координатах а — 8 кривые, соответствующие фиксированным значениям t (рис. 304). Способ перестройки совершенно очевиден. Проводя на рис. 303 вертикальную прямую,
§ 201] РАСЧЕТЫ НА ПОЛЗУЧЕСТЬ ПО ТЕОРИИ СТАРЕНИЯ 451
соответствующую • заданному t, мы отмечаем точки пересечения ее с кривыми ползучести. Ордината каждой точки есть деформация 8, пометка соответствующей кривой дает значение напряжения о. Нанесем соответствующие точки иа графике рис. 304 и соединим их кривой. Это есть кривая зависимости напряжения от деформации для
заданного времени t. Аналогичное построение делается для других значений времени t, в результате получаются изображенные на рис. 304 кривые.
Рис. 303.
Рнс. 304.
При расчете на ползучесть с этими кривыми поступают так же, как и с кривыми напряжение — деформация при расчетах по теории пластичности. Так, например, желая рассчитать стержень на изгиб, мы берем последовательно моменты времени f,, it и т. д. Для каждого момента времени распределение напряжений и деформаций пишется так, как это было показано в § 107, только зависимость о — 8 берется с графика рис. 304 соответствующей данному значению времени. В результате получаем серию эпюр напряжений, каждая из которых строится независимо от предшествующих. По этим эпюрам можно проследить, например, изменение во времени наибольшего напряжения в крайней точке сечения. Конечно, приписывать функциональной зависимости между а, 8 и t, определенной для частного вида испытаний, универсальный физический смысл неправильно, теория старения не является физической теорией ползучести, это лишь приближенный прием, позволяющий весьма простым способом оценить величину напряжений и деформаций при ползучести.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аналогия гидродинамическая при кручении 192, 196, 198, 200
Анизотропия 29
— конструктивная 30
Балка на упругом основании 270
— составная 243
— фиктивная 261
Балки, их расчет 255, 257, 258
Бнмомент 287
Бифуркация 312
Болты, их расчет 47, 113
Брус кривой 24 5
Вектор Бюргерса 145
Вес собственный, его влияние 38
Волны упругие 63
Волокно 222
Время критическое сжатого стержня 445
Выпучивание боковое 133
Вязкость материала 123
— ударная 412
Гибкость стержня 308
Гипотеза Винклера 270
— нормальных элементов 191
— о жестком контуре 191
— плоских сечений 34, 186, 1S0, 221, 245
Движение дислокации 145
Девиатор тензора напряжений 100
Деформация высокоэластическая 178
— изгиба 221, 250
— конечная 175
— логарифмическая 175, 432
— обобщенная 354
— объема 88, 90
— остаточная 2 5, 57
— от собственного веса 38
— пластическая 28, 163
— — вторичная 59
— поперечная 27
— растяжения 24, 34
— сдвига 24
— температурная 49
— унаследованная 184
— упругая 28
Диаграмма Вёлера 414
— идеальная 28
— Мора 74, 215
— пластичности 27
— растяжения 61
— — динамическая 157
— — истинная 131
— — мягкой стали 130
— сжатия 132
--- чугуна 133
Диск вращающийся 326
---в предельном состоянии 329
---в упругом состоянии 326
— — в условиях ползучести 449
— — равного сопротивления 328
Дислокация 143
— кольцевая 150
— краевая 143, 408
Жаропрочность 156
Жаростойкость 156
Жесткость 11
— геометрическая 199
Задача контактная 270
Задачи динамические 370
— — о напряжениях 38
— квазнстатнстнческие о напряжениях 38
— нелинейные на растяжение н сжатие 70
— статически неопределенные 14, 46, 257
Заклепки, их расчет 113
Закон Гука 26, 87, 88, 89, 92
— парности касательных напряжений 24, 80
— пропорциональности девиаторов 168
— секториальных площадей 284
— течения ассоциированный 162, 164, 353
— упрочнения 165, 168
— упругости объемной деформации 168
Замена системы сил статически эквивалент-
ной 17, 18
Запас прочности 37
Изгиб 219, 221
— балки на упругом основании 270
— кривого бруса 24 5
— поперечный 217
— • прОдольно-поперечный 266
— продольный 133
— стержней переменного сечения 260
— тонкостенных стержней 275
— упруго-пластический 231
Изменение объема прн упругой деформации 88
Изотропия 29
Интеграл Мора 344, 345
— перемещений 344, 345
Интенсивность касательных напряжений 86
Испытание материалов, его задачи 122
— на знакопеременный изгиб 414
— на кручение 201
— на ползучесть 428, 429
— на попеременное растяжение и сжатие 415
— на растяжение 123
— на сжатие 1 32
— на твердость 159 /
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Испытание на ударную вязкость 412 — на усталость 414, 424 Источник дислокации 147
Колебания балок постоянного сечення 389
— систем с конечным числом степеней сво-боды 370
— стержней поперечные 386, 391
---- продольные 38!
Кольцо жесткости 110’
Компоненты тензора деформации 92
----напряжений 76
Концентрация напряжений 67, 105, 410, 41 9, 422, 438
— —, ее влияние на усталостную прочность 422
Координаты главные 377
Коэффициент асимметрии цикла 419
— влияния 336, 370
— жесткости 336, 370
— запаса прочности 37
— концентрации напряжений 68
----эффективный 42 3
— поперечного сжатия 27
— Пуассона 27, 89, 122, 155
----пластический 168
— чувствительности материала к концентрации напряжений 42 3
Кратность деформации 176
Кривая длительной прочности 433
— предельная 404
— релаксации 438
Кристаллиты 19, 134
Критерий прочности Губера 103
---- прн переменной нагрузке 418
Круги Мора 75, 215, 403, 404
Кручение 186
— прямоугольных стержней 200
— стержней круглого сечення 186, 188
----сплошного профиля 199
— стесненное 191, 286, 296
— тонкостенных стержней 192, 196
Линин скольжения 140
Линия нулевая 238
Материал вязкий 123
— ндеально-пластнческнй 161
— пластический 93, 400
— хрупкий 93, 123, 400
Машины для испытаний 124, 126
Мембраны, нх расчет 110
Метод начальных параметров 266
— разделения переменных 38 3
— Релея 378
— Релея — Ритца 394
Модель Франка — Рида 150
Модуль Кармана 310
— касательный 129, 3! !
— объемной деформации 88
— пластический 168
— приведенный 310
— сдвига 89, 201
— секущий 129
— упругости 27, 122, 123, 129, 155, 310
----длительный 18!
— ~ мгновенный 182
— Юнга 27
Момент изгибающий 224, 225, 226
— ичгнбно-крутнльный 286, 287
— инерции осевой 207
----полярный 187, 208
----секторнальный 287
----центробежный 207
— предельный 234
453
Момент сопротивления пластический 234
----полярный 188
----прн изгибе 230
---- прн кручении 199
— сосредоточенный 17
— статический 207
Моменты инерции главные 216
Монокристалл 134
Нагружение пропорциональное 167
— простое 167
— ударное 396
Нагрузка импульсивная 396
— переменная 435
— предельная 356, 358, 362; 363
— ударная 63, 396
— фиктивная 26 1
Напряжение 21
— гидростатическое 85
— допускаемое 36
•---иа смятие 116
----иа срез 1! 5'
----прн изгибе 230
— — при крученнн 188
— —. условное ! ! 3
— истинное 22
— касательное 23
— нормальное 23
— октаэдрическое 86, 96
— разрушающее 37
— растягивающее 23
— сжимающее 23
— среднее 22
Напряжения в склейке 40
— во вращающемся стержне 40
— главные 78, 8!, 82
— изгнбио-крутнльные 283, 286
— касательные главные 83, 85
----при изгибе 219, 275, 277
— местные 223
----в безмоментной оболочке 109
— монтажные 5!
— на косых площадках при растяжении 72, 79
— начальные 51 •
— нормальные прн нзгнбе 220, 221, 223, 275
----прн чистом изгибе кривого бруса 247
— остаточные 57
— от собственного веса 38
— прн двухосном растяжении 74
— при изгибе 219
— прн крученнн дополнительные 282
— прн растяжении 34
— прн ударе 61
— температурные 4 9
— условные ! ! 3
Начало возможных перемещений 332
Неизвестные лишние 49, 33!
Область упрочнения 28
Оболочки, нх расчет 105, 109
Осн инерции главные 210, 216
— тензора напряжений главные 82, 162
— — скоростей деформации главные 162
Основание упругое 270
Ось нейтральная 229
— —в кривом стержне 24 8
— стержня 31
Пара сосредоточенная 17
Параметр Ларсена—Миллера 4 35
Парность касательных напряжений 24,80
Перемещение обобщенное 331
— узла фермы 44
454
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Пластинки, их расчет 366
Пластичность 2-5
Плоскость скольжения дислокации 145
Площадь секториальная 279
---- главная 285
Поверхность нагружения 354
— напряжений 205
— нейтральная 229
Ползучесть 155, 427, 430, 434
— одномерная 436
— при изгибе 442
— при сложном напряженном состоянии 448
Полигонизация 152
Полиморфизм 135
Последействие упругое 180
Постоянная пластическая 29
Потенциал пластический 331
— упругий 333
Потеря устойчивости 34
----за пределом упругости 307, 311,313
Предел выносливости 414, 4 15
----при изгибе или растяжении — сжатии 425
— — при кручении 425
длительной прочности 432
— ползучести 429
— пропорциональности 128, 129
— прочности 37, 130, 133
— текучести 29, 95, 122, 123, 130
----прн динамическом испытании 157
— упругости 123, 129
Принцип линейного суммирования повреждаемостей 440, 442
— наложения 87
— отвердения 16
— Сен-Венана 33, 223, 236, 390
— суммирования ВОльцмана — Вольтерра 184
Проба Бринелли 159
Прогибы, их определение 255
Прочность 11, 400
— длительная 434
— — прн переменной нагрузке 439
— кристаллов 14 1 •
— прн длительном напряженном состоянии 448
— при низких температурах 411
— при переменной нагрузке 413
— усталостная 422
----прн сложном напряженном состоянии 424
Пружины винтовые, нх расчет 341
Работа дополнительная 336
Равновесие дислокации 145
— предельное 352
----пластинки 366
Радиус инерции 238
Разрушение 400
— в результате отрыва 400
— длительное 431
—, его вероятность 419
— пластическое 401
— усталостное, его природа 416
— хрупкое 400, 401, 4и7, 411
Растяжение 31
— внецентренное 237
— всестороннее 93, 401
— чистое 23
Расчет на прочность при изгибе по допускаемым напряжениям 229
— на устойчивость по эмпирическим формулам 316
— по допускаемым нагрузкам 188, 189
Расчет по предельному состоянию 55 — составных балок 243 — статически неопределимых балок по допускаемым нагрузкам 258
-------систем по допускаемым нагрузкам 54
— —------по методу сил 346
— условный 113 Релаксация напряжений 184, 437
Свойства механические, влияние на инх скорости испытания 156
-----------температуры 156
Сдвиг 89
— октаэдрический 167
— чистый 24, 89
Сеченне опасное 219
Сжатие 31
— внецентренное 237
— всестороннее 93
Сила внешняя 1 5
— внутренняя 20
— инерции, ее влияние 38
— критическая 301, 305
----Энгессера — Шенли 315
— обобщенная 331
— Пайерлса 147
— перерезывающая 225, 226
— продольная 224
— разрушающая 1 30
— сосредоточенная 15, 16
Синеломкость 156
Система скольжения 139 — стержневая 32, 43, 52 Скорость деформации обобщенная 351 Соединения заклепочные с накладками, их расчет 116
— сварные, нх расчет 113, 118
Сокращение поперечное относительное 24
Сопротивление временное 37, 130, 131 ----, его определение при кручении 203 ----при динамическом испытании 157 — материалов 12
— — н теоретическая механика 13
— — и теория пластичности 26
----н теория упругости 26
Состояние деформированное 24
— допустимое 355
— истинное 355
— кинематически возможное 360
— напряженное 31
----в точке 22
----однородное 23, 76, 123
— — плоское в общем случае 76
— — пространственное 79
----сложное 72
— предельное 55 ----закрученного стержня 204 Способ допускаемых нагрузок 258 — Релея — Ритца 391 Среда сплошная 20
Степень статической неопределимости Фермы 53
Стержень 31 — кривой 24 5, 24 8 —, нагруженный бнмоментом 293 — равного сопротивления при сжатии 43 — тонкостенный 236, 275
Структура металла блочная 138
— —? гексагональная плотноупакованиая 135
---- гранецеитрированная 136
— — кристаллическая 135
— — кубическая объем ноцентрированная 137
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
455
Твердость по Бринеллю 159
— по Виккерсу 1 59
— по Роквеллу 159
Тело анизотропное 29
вязко-упругое 182
— жестко-пластическое 3 52, 353
— идеально-пластическое 162
— изотропное 29
— нелинейно упругое 176
— однородное 1 9
— пластическое 25
— упругое 25
Температура, ее влияние иа механические свойства 154
Тензор деформации 92
— инерции 215
— напряжений 23, 80
— —, его гидростатическая часть 100
— —t его девнаторная часть 100
Теорема Бетти 387
— Кастильяно 335, 339, 342, 343
— Клапейрона 337
— Лагранжа 334
— о взанмиостн работ 338
— о минимуме анергии 342, 343
— о разгрузке 58, 59
— о циркуляции касательных напряжений 193, 196, 199
— Релея 379
Теоремы сопротивления материалов общие 331
Теории прочности 4 00
Теория Гриффиса 407
---модифицированная 410
— изгиба Бернулли — Эйлера 221
— — техническая 221
— — точная 221
— одномерной ползучести феноменологическая 4 36
— пластического течения 161
-------Сен-Веиана 448
— пластичности 26, 104, 161
— — деформационная 161, 167
— —, ее экспериментальная проверка 170
— предельного равновесия 352
— прочности Мора 402
— — статистическая 409
— старения 4 50
— упругости 25
Теплоустойчивость 156
Течение пластическое 161
Траектория касательных напряжений 196
Трещина усталостная 416, 417
Труба толстостенная 318, 320
— — в пластическом состоянии 323
---в упругом состоянии 320
— — в упруго-пластическом состоянии 323
— тонкостенная 195
Угол закручивания 187
— сдвига 89
Удар растягивающий 61
сжимающий 61
— со значительной скоростью 63
Удлинение логарифмическое 175
— относительное 24
— • — при разрыве 123, 131
Упрочнение 130, 165
Упрочнение местное 417
Упругость 25
— нелинейная 178
Уравнение изогнутой оси дифференциальное & 50
— трех моментов 3S0
Уравнения совместности деформаций 46
-------— для толстостенной трубы 319
Усилие обобщенное 354
Условие пластичности Мнзеса 91, 96, 103, 165
---Треска — Сен-Венана 92, 94, 95. 96. 164
— прочности 418
---по Мору 403
Условия динамические 394
— кинематические 394
— пластичности для плоского напряженного состояния 96
Усталость прн повышенной температуре 416
Устойчивость пластического равновесия 300, 307, 311
— сжатого упругого стержня 301
— упругого равновесия 300
Фермы 52
Формоизменение пластическое 163
Формула Релея 379, 380, 393
— Эйлера для критической силы 302. 307. 308
Формулы Ламе 32.1
— эмпирические для расчета на устойчивость 316, 317 .
Формы колебаний главные 372
Фронт ударной волвы 64
Характеристика секториальная 288, 289
Характеристики механические 123
Хладноломкость 411
Центр изгиба 219, 279
Цикл асимметричный 420
— безопасный 420
— пульсационный 4 20
— симметричный 419
Циркуляция касательного напряжения I9S
Частота собственная 372
Число Врннелля 159
Шарнир пластический 259
Швы сварные, их расчет 113
Шпонки, нх расчет 113, 117
Экстензометр зеркальный 126
Эластика Эйлера 302, 305
Энергия активации 434
— деформации 61, 99, 334
— изменения объема 101
---формы 100, 101
— потенциальная растяжения 59
Эпюра изгибающих моментов 227
— перерезывающих снл 227
Эффект масштабный 408, 419
Ядро дислокации 144
— сечения 239
Юрий Николаевич Работное. Сопротивление материалов.
М., Физматгиз. 1962 г., 456 стр. с илл.
Редактор И. А. Маркуаон.
Техн, редактор В. В. Крючкова.
Корректор Т. С. Плетнева.
Сдано в набор 10/V 1962 г. Подписано к печати 16/VIII 1962 г. Бумага 60 X 90*1м. Физ. печ. л. 28,5. Условн. печ. л. 28,5. Уч.-изд. л. 26,06. Тираж 30 000 эка. Т-08570.
Цена книги 88 коп. Заказ № 2992.
Государственное издательство физико-математической литературы. Москва. В-71. Ленинский проспект. 15.
Первая Образцовая типография имени А. А. Жданова Московского городского совнархоза.
Москва. Ж-54, Валовая, 28.