И. А. БИРГЕР, Р. Р. МАВЛЮТОВ
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия
для студентов машиностроительных и авиационных вузов
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ 1986
ББК 30.121 Б 64
УДК 539.3/, 6
Биргер И. А., Мавлютов Р. Р. Сопротивление материалов: Учебное пособие.— М.: Наука. Гл. ред. физ.-мат. лит., 1986.— 560 с.
Изложен курс сопротивления материалов, дополненный элементами теории упругости, пластичности, ползучести и разрушения. Представлены современные методы расчета прочности элементов конструкций, в частности метод конечных элементов. Рассмотрены задачи прочности и устойчивости, колебаний стержней, элементы теории пластинок и оболочек. Даны примеры построения моделей прочностной надежности при разных условиях нагружения.
Для студентов, аспирантов втузов и инженеров, работающих в авиа- и машиностроении.
Табл. 3. Ил. 474.
Рецензенты:
кафедра сопротивления материалов Киевского политехнического института;
доктор технических наук И. И. Трапезин
Исаак Аронович Биргер
Рыфат Рахматуллович Мавлютов
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Редактор Н. П. Ряб'енъкая
Художественный редактор Т. Н. Колъченко
Технический редактор И. III. Аксельрод
Корректоры О. М. Березина, И. Я.. Кришталъ
ИБ М 12812
Сдано в набор 20.06.85. Подписано к печати 09.03.86. Формат 60X90/16. Бумага 3. Гарнитура обыкновенная. Печать высокая. Усл. печ. л. 35. Усл. кр.-от. 35. Уч.-изд. л. 34,58. Тираж 34 000 экз. Заказ М 801. Цена 1 р. 50 к.
Ордена Трудового Красного Знамени издательство «Наука» Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
4-я типография издательства «Наука» 630077 г. Новосибирск-77, Станиславского, 25
Б 2105000000-164 053(02)-86
174-85
(© Издательство «Наука». Главная редакция физико-математической литературы, 1986
ОГЛАВЛЕНИЕ
Предисловие ....................................................... 6
Глава 1. Введение.................................................. 7
1.	Сопротивление материалов — наука о прочности и надежности конструкций....................».............................. 7
2.	Модели прочностной надежности •  ........................... 9
Глава 2. Напряжения .	»	•	.........................23
3.	Нормальные и касательные напряжения.........................23
4.	Напряженное состояние в точке...............................29
5.	Плоское напряженное состояние . ............................32
6.	Объемное напряженное состояние	40
7.	Дифференциальные уравнения равновесия элемента тела и краевые условия «	1	>  ...................................47
Глава 3. Деформации .	• . >..................................  57
8.	Перемещения и деформации ...................................57
9.	Связь перемещений и деформаций...........................	60
10.	Линейная деформация в произвольном направлении. Главные деформации, тензор деформаций  .................................63
И.	Уравнения совместности деформаций ..........................67
Глава 4. Механические свойства конструкционных материалов.	.	.	70
12.	Диаграммы деформирования, пределы текучести и прочности	70
13.	Деформации и характеристики пластичности ......	76
14.	Истинные диаграммы деформирования и их схематизация ...	82
15.	Ползучесть и длительная прочность .........	87
16.	Усталость материала и элементов конструкций.................92
17.	Малоцикловая усталость .	  100
Глава 5. Модели упругости, пластичности и ползучести ....	107
18.	Модели упругости ..........................................107
19.	Модели пластичности .......................................116
20.	Модели ползучести и вязкоупругости.........................130
Глава 6. Растяжение и сжатие стержней.............................141
21.	Растяжение и сжатие стержней сосредоточенными и распределенными силами...............................................  .	141
22.	Статически неопределимые задачи растяжения и сжатия стержней 150
23.	Стержневые системы (фермы) ..........	159

ОГЛАВЛЕНИЕ
24.	Статически неопределимые стержневые системы.............16$
25.	Гибкие нити .	.	.	..................................175
Глава 7. Кручение стержней....................................183
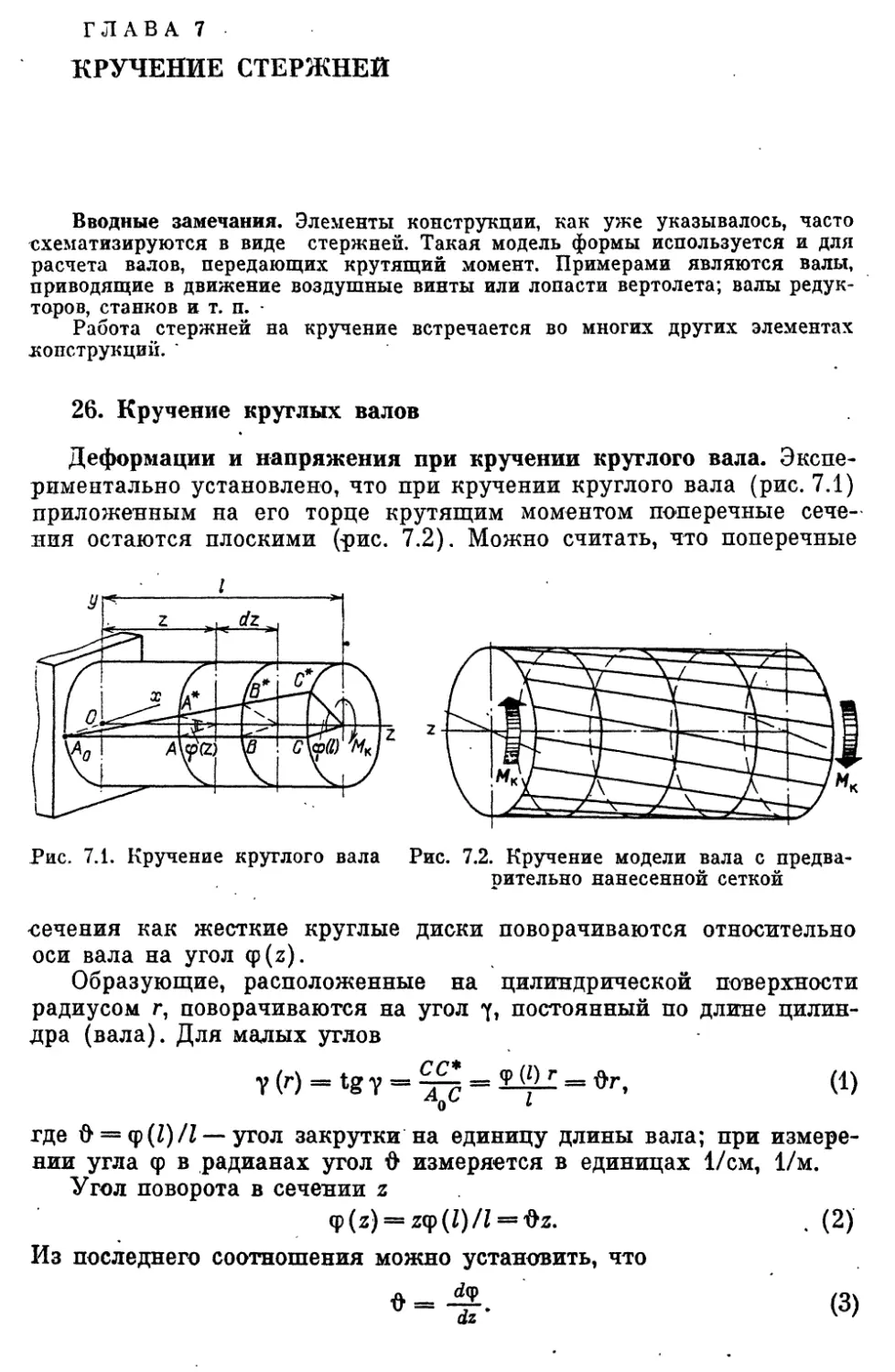
26.	Кручение круглых валов..................................183
27.	Общая задача кручения стержней и концентрация напряжений 19€>
28.	Кручение тонкостенных стержней	210
Глава 8. Изгиб стержней.....................................  220
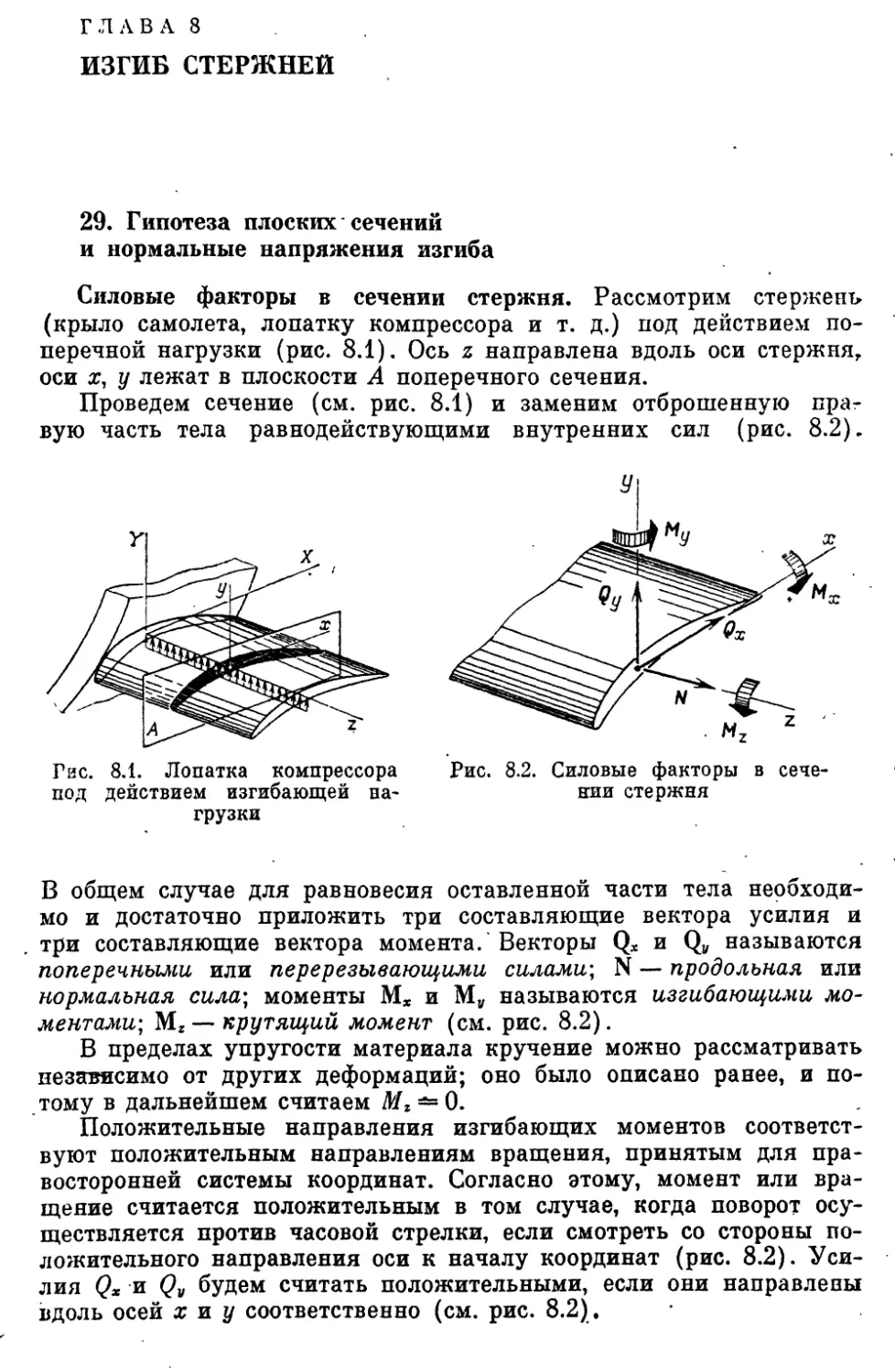
29.	Гипотеза плоских сечений и нормальные напряжения изгиба 220
30.	Упруго-геометрические характеристики сечения стержня при из-
гибе. Главные оси, главные моменты инерции...............231
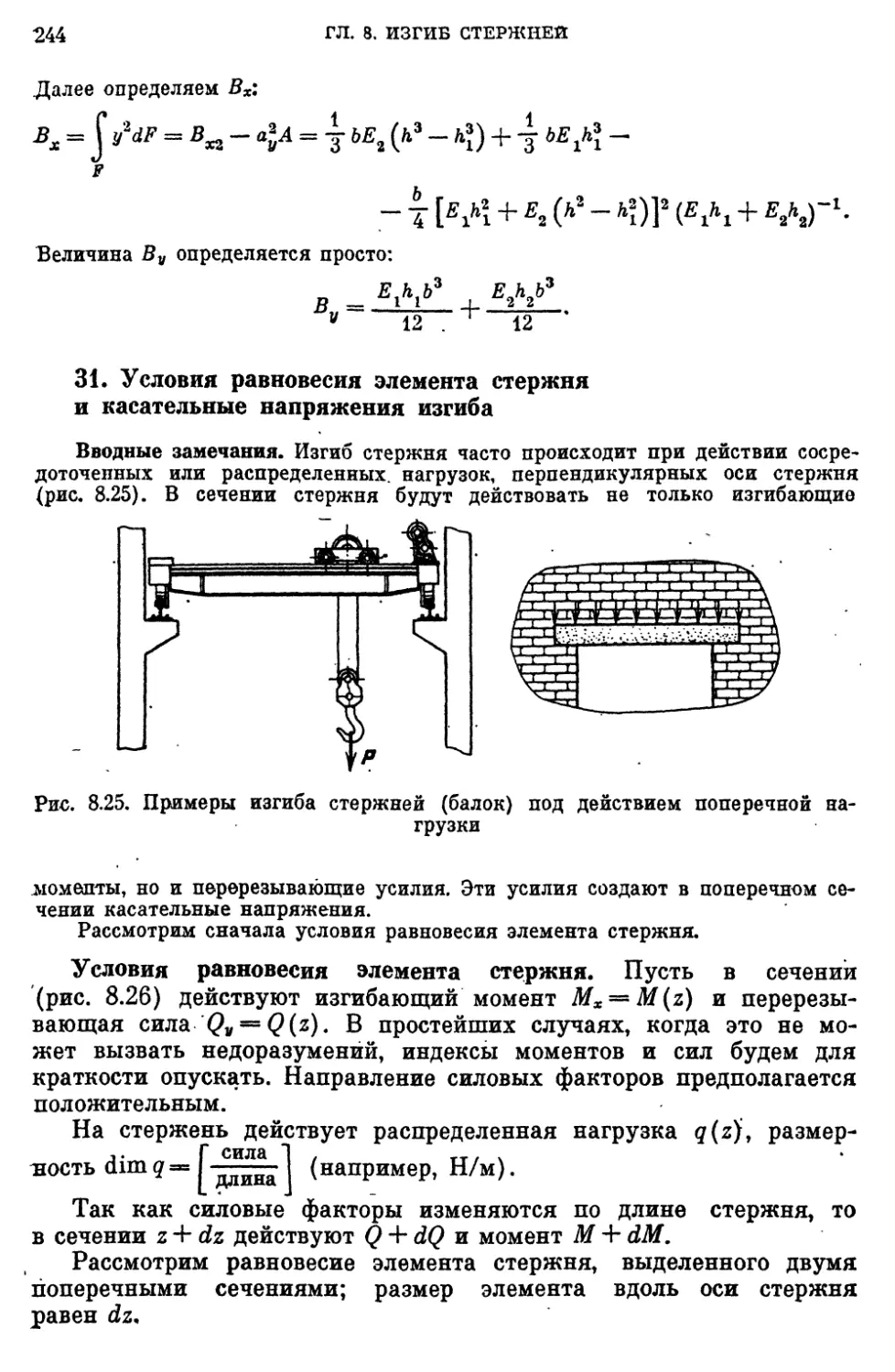
31.	Условия равновесия элемента стержня и касательные напряжения изгиба..................................................244
32.	Изгиб и растяжение стержней с учетом деформации пластичности и ползучести..........................................  259
33.	Прочностные модели надежности при изгибе................274
34.	Прогибы стержней......................................  282
Глава 9. Потенциальная энергия деформации, вариационные методы расчета конструкций, общие свойства упругих систем . . . t	, 305
35.	Потенциальная энергия деформации........................305
36.	Вариационные методы.....................................318
37.	Вариационные методы и общие свойства упругих систем . .	.	334
Глава 10. Сложные модели стержней.............................345
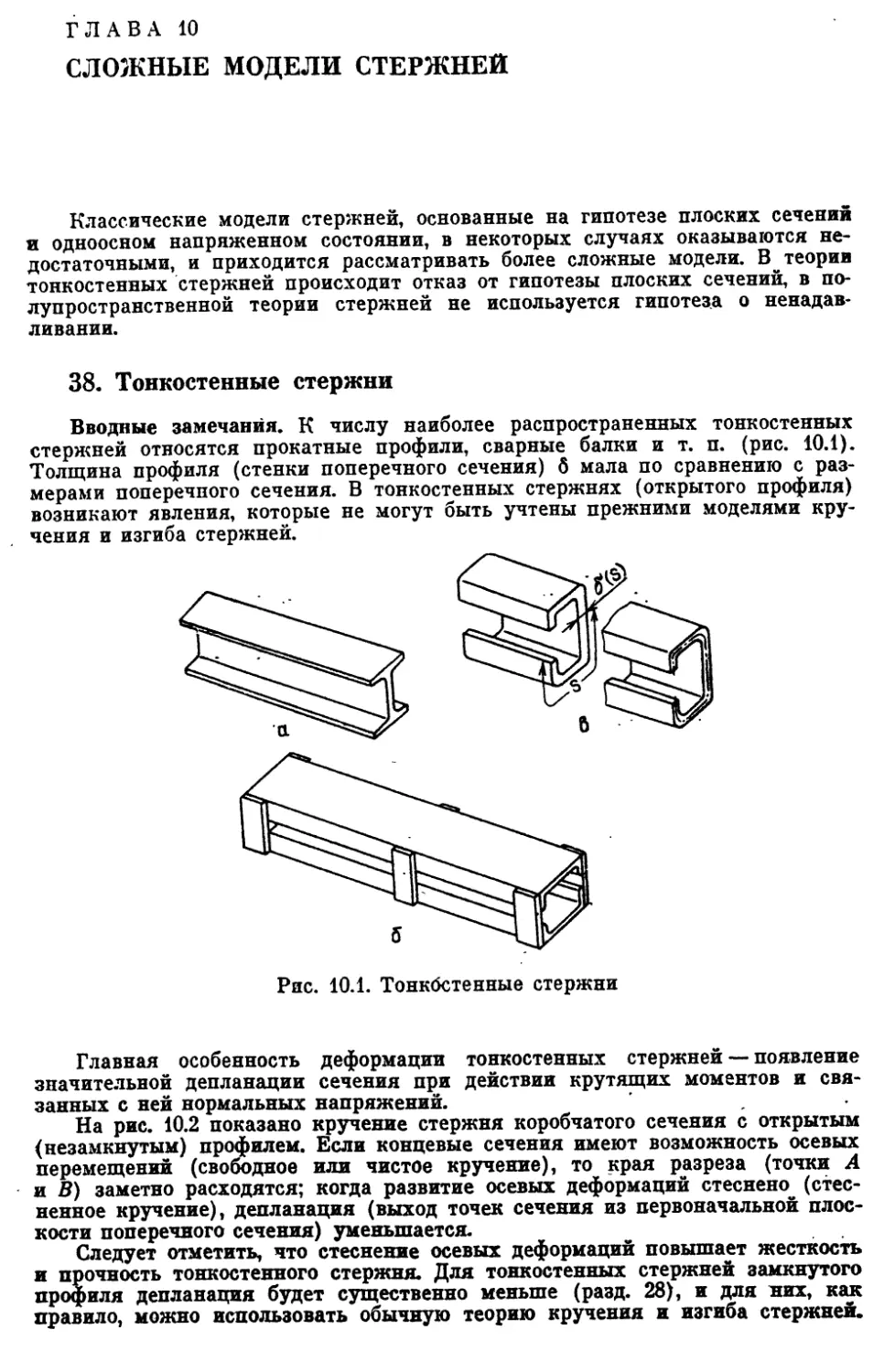
38.	Тонкостенные стержни....................................345
39.	Полупространствепные модели	стержпя.....................376
Глава 11. Кольца .	.	.	.	..............................382
40.	Изгиб колец ............................................382
41.	Осесимметричная деформация	колец........................387
Глава 12. Динамика и устойчивость стержней..................  392
42.	Изгибные и продольные колебания стержней................392
43.	Критические частоты вращения и крутильные колебания валов 413
44.	Устойчивость стержней	425
Глава 13. Модели разрушения . •	.	... . • ...	443
45.	Модели статического и длительного разрушения............443
46.	Модели усталостного и малоциклового разрушения ....	460
Г л а в а 14 Цилиндры и диски ............ 467
47.	Прочностные модели толстостенных труб и цилиндров. Напряжения и деформации..........................................467
48.	Прочностные модели дисков...............................482
ОГЛАВЛЕНИЕ
Глава 15. Балки иа упругом основании, криволинейные стержни и
пружины.......................................................497
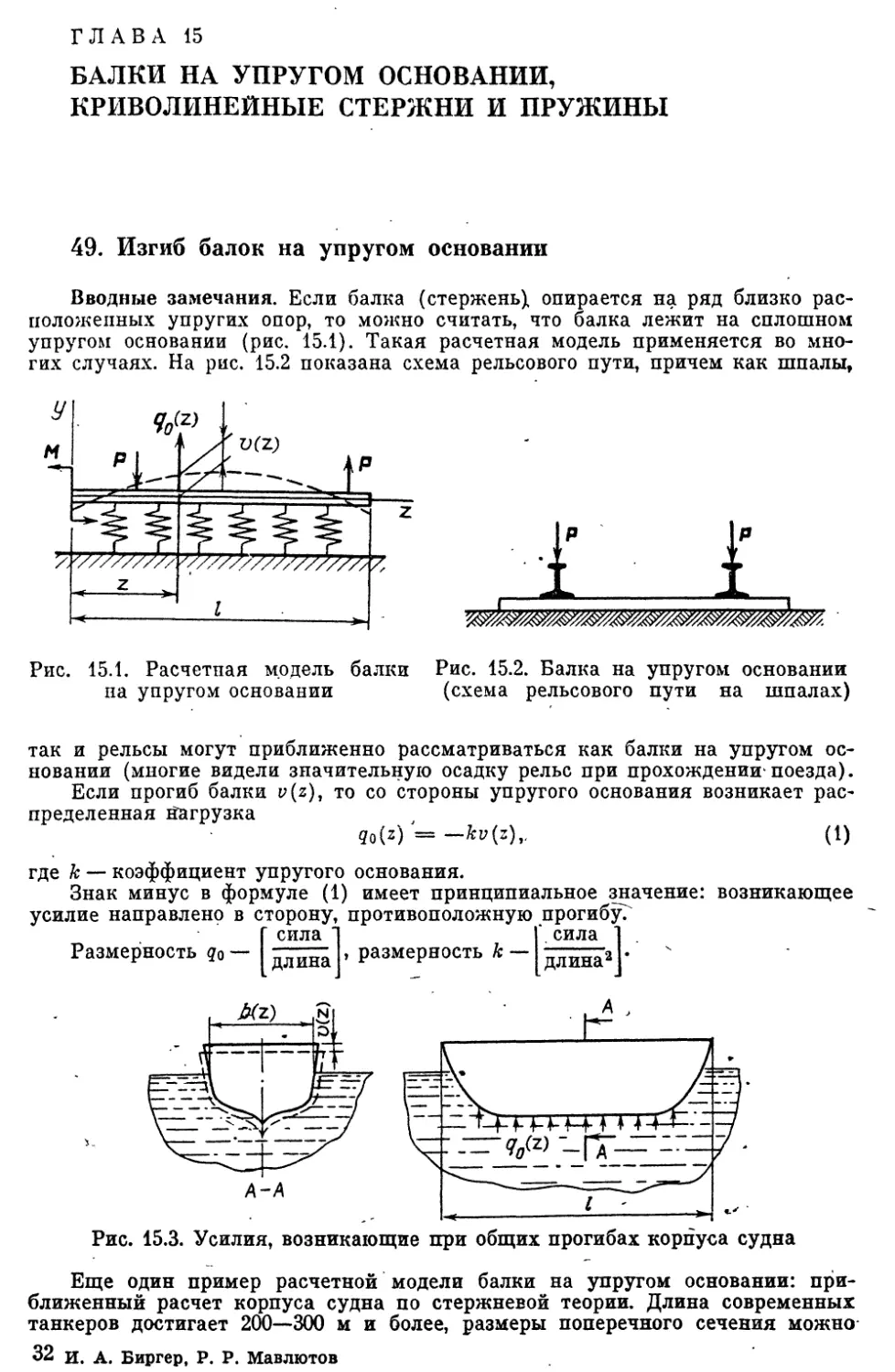
49.	Изгиб балок на упругом основании..........................497
50.	Криволинейные стержни и пружины...........................503
Глава 16. Пластинки и оболочки...................................518
51.	Пластинки.................................................518
52.	Цилиндрические оболочки...................................533
53.	Приближенные методы расчета прочности и устойчивости оболочек вращения при осесимметричном нагружении .....	541
Глава 17. Метод конечных элементов ..............................550
54.	Введение в метод конечных элементов.....................  550
55.	Основные уравнения метода конечных элементов .....	553
ПРЕДИСЛОВИЕ
Сопротивление материалов является одной из основных технических дисциплин, формирующих мышление инженера.
Многие выдающиеся ученые — С. П. Тимошенко, Н. М. Беляев, В. И. Феодосьев и другие посвятили свои усилия созданию курсов сопротивления материалов.
Можно отметить следующие особенности предлагаемого учебного пособия. Более полно изложены основные физические модели сплошной среды — модели упругости, пластичности и ползучести, методы решения упругопластических задач и задач ползучести применительно к стержням и другим элементам конструкций.
Достаточно широко представлены модели разрушения при действии статического, усталостного и малоциклового нагружения. Более обстоятельно описаны вариационные и другие численные способы, матричные и интегральные методы, методы начальных параметров.
Современный этап развития технических наук можно охарактеризовать как переход «от расчета к модели». Создаются математические модели конструкций, машин, отражающие их функциональное назначение, работоспособность, условия надежности.
В книге даны примеры построения прочностных моделей надежности, в которых напряжения и деформации сопоставляются с условиями разрушения при действующих нагрузках. В этом состоит одна из главных особенностей предлагаемого учебного пособия.
Авторы надеются, что книга окажется полезной для студентов, аспирантов и молодых инженеров при изучении проблем прочности и динамики машин и конструкций.
Авторы выражают благодарность Т. Н. Мардимасовой и Ю. А. Кувшинову за помощь при подготовке рукописи к печати.
И. А. Биргер, Р. Р. Мавлютов
ГЛАВА 1
ВВЕДЕНИЕ
1.	Сопротивление материалов — наука о прочности и надежности конструкций
Проблемы прочности и надежности, задачи сопротивления материалов. Современный этап научно-технической революции характеризуется быстрым совершенствованием технических параметров изделий, интенсификацией рабочих процессов, повышением надежности и ресурса. Каждые пять-семь лет создаются новые поколения машин, отражающие достижения научно-технического прогресса. Происходит быстрая смена конструкционных материалов, внедряются новые технологические процессы.
Решающее влияние на инженерную науку и технику оказывает поразительно быстрое развитие и совершенствование ЭВМ. В ближайшие десятилетия проектирование и производство изделий авиационной техники и ряда других областей машиностроения станет автоматизированным с основополагающим участием ЭВМ. При проектировании с помощью ЭВМ создаются математические модели изделий, их машинный образ, которые затем служат основой разработки технологии и производства на станках с программным управлением.
В настоящее время задача состоит не только в разработке конструкции и технологического процесса, но и в оптимизации их параметров.
В современной технике возрастает значение проблем прочности. Это объясняется увеличением сложности технических изделий, необходимостью повышения эффективности, качества, надежности и долговечности.
На рис. 1.1 показана фотография самолета ИЛ-86, перевозящего 350 пассажиров. Понятно, что требования к прочности и надежности конструкции имеют первостепенную важность.
Сопротивление . материалов — наука о прочности и надежности элементов конструкций. В ее задачи входят обобщение инженерного опыта создания машин и сооружений, разработка научных основ проектирования и конструирования надежных изделий, совершенствование методов оценки прочностной надежности и долговечности конструкций.
Основным содержанием сопротивления материалов является разработка моделей прочностной надежности элементов конструкций. С помощью таких моделей инженер может выбрать материал и необходимые размеры элементов конструкции, оценить сопротивление конструкционных материалов внешним воздействиям.
8
ГЛ. 1. ВВЕДЕНИЕ
Для практической деятельности инженеру необходимо выработать навыки создания простых и ясных моделей явлений и реальных объектов, отбрасывая второстепенные факторы.
Сопротивление материалов — инженерная наука, и для нее характерно использование приближенных методов, опирающихся на
Рис. 1.1. Самолет ИЛ-86
опыт и экспериментальные исследования. Содержание курса сопротивления материалов непрерывно изменяется в связи с развитием техники. Если в прежних курсах сопротивления материалов преобладали вопросы прочности строительных конструкций, то в последние десятилетия важное значение получили проблемы прочности, динамики, жесткости и устойчивости объектов машиностроения, турбостроения, авиационной и космической техники и др. г
В последние годы идет быстрый процесс математизации инженерных знаний. В сопротивлении материалов все большее место занимают методы, которые ранее применялись лишь в дисциплинах математического характера. Это стало возможным благодаря все возрастающему влиянию ЭВМ и созданию на основе их применения математических моделей прочностной надежности элементов конструкций.
Связь сопротивления материалов с другими научными дисциплинами. Сопротивление материалов опирается на математические науки, откуда заимствуется математический аппарат исследования, а также на методы теоретической механики (механики абсолютно твердого тела).
Сопротивление материалов примыкает к механике твердого деформируемого тела (теории упругости, пластичности и разрушения). Из этих наук сопротивление материалов черпает общие методы, более полные и точные решения отдельных задач.
2. МОДЕЛИ ПРОЧНОСТНОЙ НАДЕЖНОСТИ
9
Общие методы построения моделей прочностной надежности, разрабатываемые в сопротивлении материалов, получают дальнейшее развитие и уточнение в таких специальных технических дисциплинах, как прочность летательных аппаратов, расчеты на прочность и т. п.
Сопротивление материалов играет выдающуюся роль в инженерном образовании, выполняя связующую роль между теоретическими науками (математикой, механикой и др.) и конкретными техниче-скими дисциплинами.
2.	Модели прочностной надежности
Моделью называется совокупность представлений, зависимостей, условий, ограничений, описывающих процесс, явление. Модель — отображение объективной реальности — может иметь разные природу, структуру, язык и форму представления. Наиболее часто используются математические модели, отображающие реальный процесс, явление с помощью установления зависимостей между параметрами в виде различного рода уравнений, ограничений.
Надежностью называется свойство изделия выполнять заданные функции, сохраняя свои эксплуатационные показатели в определенных пределах в течение требуемого промежутка времени или наработки.
Существенно, что надежность, безотказность изделия (машины; конструкции, детали) связывается с определенным сроком службы, В большинстве случаев под сроком службы понимается время работы изделия под нагрузкой или число циклов нагружений. Например, для самолетных конструкций срок службы определяется числом полетных циклов. Число полетов является важным показателем для оценки работоспособности конструкции, так как наибольшие нагрузки на ряд элементов самолета возникают при посадке.
Допустимый срок службы изделия называется ресурсом. Ресурс указывается в виде общего времени наработки или числа циклов нагружений.
В ряде случаев в связи с возможностью коррозии и старения материала ограничивается календарное время хранения или эксплу-. атации изделия.
Прочностной надежностью называется отсутствие отказов, связанных с разрушением или недопустимыми деформациями элементов конструкции.
Отказом называется нарушение работоспособности изделия.
Критерии прочностной надежности, запасы прочности. Основной количественной характеристикой надежности является вероятность безотказности изделия. Вероятностью события называется число, характеризующее возможность появления события* . Вероятность достоверного события принимают равной единице, вероятность невозможного события — равной нулю<-
10
ГЛ. 1. ВВЕДЕНИЕ
Вероятность события Р можно определить путем проведения достаточно большого числа испытаний, и тогда
Р =	(!)
п Л
где тп —число испытаний, при которых событие наблюдалось; п — общее число испытаний.
Если в технических требованиях на изделие указывается вероятность безотказной работы Р = 0,99, то это означает, что за ресурс (время эксплуатации) может отказать (в среднем) одно изделие из ста.
При оценке прочностной надежности часто определяется вероятность разрушения
F==l-P.	(2)’
Нахождение вероятности разрушения или вероятности безотказной работы на стадии проектирования изделий представляет весьма сложную задачу. В настоящее время основным методом оценки прочностной надежности является определение запасов прочности. Пусть д —параметр работоспособности изделия (например, действующее усилие, напряжение и т. п.).
Запасом прочности называется отношение
(3)-*шах
где дкр — критическое значение параметра, нарушающее работоспособность изделия; gmax — наибольшее значение параметра в рабочих условиях.
Условие прочностной надежности записывается в виде
»>[«].	-	(4)'
где [п] — допустимое значение запаса прочности.
Значение [п] зависит от стабильности условий нагружения, уровня технологии, методов определения запаса прочности и ряда других факторов. Например, при действии постоянных во времени нагрузок часто принимают [п]«1,3—2, при переменных нагрузках случайного .характера [п] = 3—5. Допустимые значения запасов прочности назначают с учетом инженерного опыта создания подобных конструкций.
В некоторых областях техники имеются нормы прочности, регламентирующие допустимые величины запасов прочности. Запасы прочности представляют собой критерии сопоставления прочностной надежности вновь создаваемой конструкции с подобными конструкциями, имеющими положительный опыт эксплуатации.
Модели прочностной надежности. Структура модели прочностной надежности показана на рис. 1.2. Конечной целью, которая должна быть достигнута с помощью модели, является определение запасов
2. МОДЕЛИ ПРОЧНОСТНОЙ НАДЕЖНОСТИ
И
прочности и (или) вероятности разрушения. Для определения критериев прочностной надежности следует разработать или принять четыре вспомогательные модели — материала, формы, нагружения и разрушения. Построение указанных частных моделей является
Рис. 1.2. Структура модели прочностной надежности элемента конструкций
важным этапом, существенно влияющим на достоверность оценки прочностной надежности.
При разработке моделей приходится идти на компромисс между достаточно полным я адекватным описанием материала, формы, условий работы и нагружения элемента и сложностью самой модели. Рассмотрим более подробно построение частных моделей и начнем с моделей материала.
Конструкционные материалы. В качестве материала машиностроительных конструкций используются в основном металлы и их сплавы, а также различные неорганические и органические материалы (полимеры, пластмассы, волокна, керамика и др.). В-последнее время нашли применение композиционные материалы, состоящие из высокопрочных нитей стекла, бора, углерода и связующего (полимеров и металлов). В строительных конструкциях используются бетон (смесь крупных и мелких каменных частиц, скреплен-» ных цементом), железобетон (бетон, усиленный стальными стерж-» нями), кирпич, дерево и другие материалы.
Основными конструкционными материалами в машиностроении являются сплавы черных и цветных металлов.
Рис. 1.3. Схема кристаллической решетки металлов
Металлы имеют кристаллическое строение, представляющее регулярную структуру (рис. 1.3), в которой-в определенном порядке размещены атомы вещества. Многие металлы имеют кубическую объемноцентрированную структуру (железо, хром, молибден), кубическую гранецёнтрированную структуру (алюминий, медь),
12
ГЛ. 1. ВВЕДЕНИЕ
(рис. 1.4). Атомный радиус — половина расстояния между ближайшими атомами в кристаллической структуре — составляет 1—2 А (А— ангстрем — 10~8 см). Реальные металлы и их сплавы имеют обычно поликристаллическое (зернистое) строение (рис. 1.5). Образование кристаллов в процессе охлаждения сплава начинается из очень большого числа центров. Каждое зерно — это кристалл,
Рис. 1.5. Зернистое строение металлов и сплавов
Рис. 1.4. Структура элементов кристаллической решетки: а — кубическая объемноцент-рированная структура; б — кубическая гра-
нецентрированная структура
принявший неправильную форму, так как его дальнейшему росту
помешали соседние кристаллы.
Прочность сплавов определяется не только прочностью зерен, по и прочностью их границ. Например, при работе сплава при высоких температурах разрушение проходит по границам зерен.
Три уровня моделей материала. В настоящее время исследования материала ведутся на различных уровнях с использованием разных моделей материала. Условно можно выделить три уровня моделей материала (рис. 1.6).
а	б	б
Рис. 1.6. Три уровня моделей материала: а — физические модели; б — инженерно-физические модели; в — инженерные модели (модель сплошной среды)
Физические модели изучаются в физике твердого тела. Для описания поведения материалов под действием напряжений и друг гих физических свойств рассматривается. модель в виде кристаллической решетки атомов.
В реальных материалах кристаллические решетки имеют различного рода дефекты, снижающие прочность (теоретическая прочность металлов приблизительно в 10 раз выше практически достигнутой). В решетке могут быть точечные дефекты — вакансии (от
2. МОДЕЛИ ПРОЧНОСТНОЙ НАДЕЖНОСТИ
13
сутствие атома в одном из узлов решетки), внедрения (один из атомов сместился или внедрился в другую ячейку) (рис. 1.6, а).
Встречаются и другие несовершенства кристаллических решеток. В настоящее время с помощью электронных микроскопов и дру-гих приборов можно наблюдать тонкую структуру металлов, что дает возможность изучать на физическом уровне сопротивление материалов внешним воздействиям. На рис. 1.7 показана фотография структуры материала ВТЗ-1 в месте разрушения при увеличении в 6600 раз, полученная на электронном микроскопе. На
Рис. 1.7. Фотография излома материала
фотографии видны следы отдельных нагружений в виде «бороздок» по мере развития трещины.
Физические модели направлены на изучение влияния несовершенств кристаллической решетки на их прочность, на исследования возможностей повышения прочности и пластичности металлов и сплавов, но они не дают оценки механических свойств реальных материалов.
Инженерно-физические модели рассматривают материал как совокупность зерен с . различной ориентированной кристаллической структурой (рис. 1.6, б). Для описания свойств реальных тел учитывается случайный характер размеров зерен и направлений кристаллографических плоскостей. Подобные модели позволяют объяснить ряд важных особенностей поведения материала, но еще не могут служить основой практической оценки прочности материалов. Основное назначение инженерно-физических моделей — выработать научные основы статистического описания механических и других свойств материала.
Инженерные модели сплошной среды рассматривают материал как сплошное и однородное тело. Такие модели осредняют свойства в объемах материала, содержащих достаточно большое число струк
14
ГЛ. 1. ВВЕДЕНИЕ
турных элементов (например, зерен материала). Однородность понимается в том смысле, что все неоднородные дискретные струк-турные элементы заменяются «осредненной» непрерывной средой. Замена материала дискретного, разнородного строения (например, мелкозернистого) однородной средой имеет практический смысл лишь в том случае, если осреднение возможно в пределах объема материала, малого по сравнению с объемом всего элемента конструкции.
Вопрос о допустимости применения модели сплошной среды для конкретного конструкционного материала решается на основании экспериментальных исследований. Проведенные опыты с образцами металлов и других конструкционных материалов показали, что применение модели сплошной однородной среды вполне оправданно. Инженерные модели материала широко применяются в задачах прочностной надежности в сочетании с системой экспериментальных исследований.
Модели материала в общей модели прочностной надежности. При Построении моделей прочностной надежности в сопротивлении материалов используется модель сплошного однородного тела.
Материал рассматривается как сплошное однородное деформируемое тело. Деформируемым называется тело, которое после приложения внешних нагрузок изменяет свою форму и размеры. Учет деформируемости является весьма важным, так как позволяет решить вопрос о распределении силового потока внутри тела.
Обычно в сопротивлении материалов принимают, что изменение формы" тела под действием внешних нагрузок невелико. Это в большинстве случаев соответствует реальной ситуации при работе материала в элементах конструкций.
Модель сплошной среды позволяет рассматривать тело как непрерывную среду и применять при этом методы математического анализа.
Учитывая физические свойства, присущие в той или иной мере. всем конструкционным материалам, модель материала наделяют свойствами упругости, пластичности и ползучести. Упругостью называется свойство тела восстанавливать свою форму после снятия внешних нагрузок. Это свойство материалов знакомо каждому из жизненного опыта (например, прогиб доски или ветки дерева, прогиб моста, железнодорожного полотна и т. п.). Пластичностью называется свойство тела сохранять после прекращения действия нагрузки полностью или частично полученную при нагружении деформацию. Это свойство также хорошо известно (изменения формы тел из глины при давлении, проволоки при большом изгибе и т. п.). Ползучестью называется свойство тела увеличивать деформацию при постоянных внешних нагрузках (осадка фундаментов под действием веса, постепенное удлинение каната, несущего груз, ослабление затяжки болтов вследствие их удлинения со временем и т. д.).
2. МОДЕЛИ ПРОЧНОСТНОЙ НАДЕЖНОСТИ
15
Свойства упругости, пластичности и ползучести и некоторые другие физические свойства будут в дальнейшем рассмотрены более подробно.
Модели формы. Геометрическая форма элементов конструкций часто бывает весьма сложной. На рис. 1.8, а показан вал винта самолета, передающий крутящий момент от двигателя к винту, на рис. 1.8, б приведено зубчатое колесо, сидящее на валу редуктора.
Рис.. 1.8. Геометрическая форма элементов конструкций
Учет всех особенностей геометрической формы часто невозможен или нецелесообразен, так как приводит к сложным моделям.
Для определения напряженного и деформированного состояний применяют упрощенные, схематизированные модели формы элементов конструкций. Основными моделями формы в моделях прочной надежности являются: стержни, пластинки, оболочки, пространственные тела (массивы) (рис. 1.9). Модели формы элемента
Рис. 1.9. Основные модели формы в моделях прочностной надежности
конструкции представляют собой схематизированное описание геометрии элемента с помощью стандартных, типовых элементов. Это позволяет применять для расчета более простые методы, использующие особенности геометрической формьГ типовых элементов. Стержни являются основной геометрической моделью сопротив
16
ГЛ. 1. ВВЕДЕНИЕ
ления материалов. Стержнем называется тело, поперечные размеры которого малы по сравнению с его длиной (рис. 1.10). Образование стержня можно представить как результат движения вдоль пространственной кривой (оси стержня) плоской фигуры (поперечного сечения стержня). Центр тяжести фигуры остается при движении на оси стержня, плоскость фигуры перпендикулярна оси. Поперечное. сечение стержня может быть переменным по длине (рис. 1.11).
Если при движении вдоль оси поперечное сечение поворачивается, то стержень называется закрученным. На рис. 1.12 показана лопатка осевого компрессора, которая может рассматриваться как закрученный стержень переменного сечения. В авиационной и строительной технике часто применяют тонкостенные стержни, у которых один размер сечения мал по отношению к другому и оба они малы по сравнению с длиной стержня (рис. 1.13). Экспериментальные исследования показали возможность применения теории стержней к элементам конструкций, не вполне удовлетворяющим условию малости размеров сечения по сравнению с длиной. Для приближенной оценки общего напряженного состояния крыло самолета, корпус ракеты, зуб шестерни и др. могут рассматриваться на основе теории стержней (рис. 1.14).
Пластинки ограничиваются двумя плоскими или слабоизогнутыми поверхностями. На рис. 1.15 показаны прямоугольная и круглая пластинки. Толщина пластинки много меньше двух других размеров, т. е. h < a, h < Ь, h^iD. Диски компрессоров и турбин авиационных двигателей часто рассматриваются как пластинки переменной толщины.
Рис. 1.11. Пример стержня переменного сечения (телевизионная башня Центрального телевидения)
Рис. 1.10. Схема образования стержня
2. МОДЕЛИ ПРОЧНОСТНОЙ НАДЕЖНОСТИ
17
Рис. 1.12. Лопатка компрессора как закру- Рис. 1.13. Тонкостенные стержни ченный стержень переменного сечения
Рис. 1.14. Стержневые модели конструкций: а — крыло самолета; б — корпус ракеты; в — зуб шестерни
Рис. 1.15. Тонкие пластинки: а — прямоугольные; б —круглые
Рис. 1.16. Оболочки: а — цилиндрическая оболочка (корпус двигателя); б — оболочка сосуда высокого давления
2 И. А. Биргер, Р. Р. Мавлютов
18
ГЛ. 1. ВВЕДЕНИЕ
Оболочки представляют собой тела, ограниченные двумя близкими поверхностями. Расстояние между поверхностями (по нормали)— толщина оболочки — мало по сравнению с радиусами кривизны поверхностей. На рис. 1.16 приведены цилиндрическая оболочка и оболочка сосуда высокого давления.
Пространственное тело (массив) — модель элемента конструкции, в котором все размеры тела соизмеримы. Пространственные
б
б
Рис. 1.17. Пространственные тела как элементы конструкций: а — соединительный элемент в виде проушины; 6 — головка болта (стержня), работающего на растяжение; в — стержень с выточкой
элементы часто вводятся для учета концентрации усилий (напряжений), возникающих в концевых областях простых моделей или в местах резкого изменения сечений (отверстия, выточки и т. п.; рис. 1.17).
Реальные детали машин, элементы конструкций могут быть с достаточной точностью представлены сочетанием более простых
Рис. 1.19. Модель формы фланца: 1 — оболочка; 2 — пространственное тело; 3 — пластинка
Рис. 1.18. Сочетание моделей стержней и пластинок, дающее достаточно полное отображение геометрической формы элементов конструкций: а — подкрепленная панель обшивки самолета; б — вал с фланцем
моделей формы. На рис. 1.18 показаны примеры сочетания моделей стержней и пластинок, приводящие к достаточно полному отображению геометрической формы элементов некоторых конструкций. Часто оказывается целесообразным использовать разные уровни
2. МОДЕЛИ ПРОЧНОСТНОЙ НАДЕЖНОСТИ
19
(степени сложности) моделей. Например, в месте перехода от трубы к фланцу возникает концентрация напряжений, зависящая от радиуса скругления г (рис. 1.19).
Модель формы более высокого уровня можно образовать сочетанием моделей стержня, пластинки и пространственного тела.
Расчет модели более низкого уровня (см. рис. 1.18, б) дает общее напряженное состояние, которое используется для оценки напряжений на сопрягаемых границах пространственного тела. Модели формы и их синтез имеют существенное значение для автоматизированного проектирования и конструирования.-
Модели нагружения. Внешние силы, действующие на элемент конструкции, подразделяют на три группы: 1) сосредоточенные силы, 2) распределенные силы, 3) объемные или массовые силы. , Сосредоточенные силы — силы, действующие на небольших участках поверхности детали (например, давление шарика шарикоподшипника на вал, давление колеса на рельсы и т. п.).
Распределенные силы приложены к значительным участкам поверхности (например, давление воздуха на крыло самолета, давление жидкости или газа на стенки сосуда).
Объемные или массовые силы приложены к каждой частице • материала (например, силы тяжести, инерционные усилия).
При построении модели нагружения внешние нагрузки схематизируются в виде одной из указанных групп, причем принимаемая модель зависит также от задач описания. .Например, для расчета
Рис. 1.20. Различные модели нагружения для расчета вала и шарика шарикоподшипника
вала шестерни реакция усилия на. опоре может рассматриваться как сосредоточенная нагрузка (рис. 1.20, а); для расчета долговечности шарика то же усилие взаимодействия схематизируется в виде распределенного контактного давления (рис. 1.20, б).
Важным моментом при разработке модели нагружения является учет величин внешних нагрузок и характера их изменения по времени. Величины нагрузок определяются в основном параметрами рабочего процесса изделия (например, мощностью, грузоподъемностью, давлением среды, числом оборотов вращающихся деталей 2*
20
ГЛ. 1. ВВЕДЕНИЕ
и т. п.). Для приближенных моделей учитываются только наибольшие, опасные для прочности нагрузки. При построении уточненных моделей принимается во внимание вся «история нагружения».
Довольно часто величины нагрузок имеют случайный характер, и для их оценки применяют вероятностные методы. Нагрузки разделяют на стационарные (постоянные, статические) и нестационарные (переменные).
Статическая нагрузка возрастает от нуля до своей номинальной величины и остается постоянной во всем процессе нагружения. Примеры статической нагрузки — нагружение строительных конструкций (каркаса жилого дома) весом здания, нагружение корпуса ракеты одноразового действия внутренним давлением и т. п. В действительности представление о статической нагрузке дает упрощенную модель нагружения. На реальные конструкции действуют дополнительные силы (например, динамические и др.). Однако модель статического нагружения приводит к простым и полезным методам анализа, широко используемым в моделях прочностной надежности.
Переменное нагружение —• нагружение, изменяющееся во времени. Наиболее важный класс нестационарных нагружений — циклические нагружения. Если циклы образуются за счет запуска и остановки машины, то нагружение обычно не превышает 104—105 циклов и такое нагружение называется малоцикловым. При нагружении, связанном с упругими колебаниями элементов конструкций, число циклов нагружения часто превышает 10s—10е (многоцикловое нагружение). Обычно частота колебаний нагрузки при многоцикловом нагружении составляет 102—104 в секунду.
Нередко многоцикловое нагружение имеет случайный характер. Тогда модель нагружения, должна содержать распределение плотности вероятности нагрузок или другие статистические модели нагружения. Часто встречается динамическое ударное нагружение (соударения элементов конструкций, взрывное нагружение и т. п.). Ударное нагружение характеризуется очень высокой скоростью возрастания нагрузки, что влияет на характеристики деформирования материала.
Модели нагружения должны учитывать воздействие полей и сред. Наиболее часто встречается в современной технике воздействие температурного поля. Это воздействие проявляется двояким образом. Пониженная и повышенная температуры влияют на механическую прочность материала. При неравномерном нагреве тела создаются температурные напряжения, величина которых часто оказывается соизмеримой с напряжениями от внешних сил. В некоторых случаях приходится учитывать влияние нейтронного излучения на свойства материала, влияние электромагнитного поля и др.
Прочностная надежность существенно зависит от воздействия коррозионных сред.
2. МОДЕЛИ ПРОЧНОСТНОЙ НАДЕЖНОСТИ
21
Итак, модели нагружения содержат схематизацию внешних нагрузок по величине, по распределению, во времени, а также по воздействию внешних полей и сред.
Модели разрушения. В соответствии с общей схемой моделей прочностной надежности (см. рис. 1.2) модели разрушения являются завершающими. После обоснованного выбора моделей формы, материала, нагружения переходят к непосредственной оценке надежности с помощью моделей разрушения.
Модели разрушения представляют собой уравнения (условия), связывающие параметры работоспособности изделия (элемента конструкции) в момент разрушения с параметрами, обеспечивающими прочность. Подразумевается начало перехода от состояния прочности к началу разрушения. Эти условия часто называют условиями прочности. Обычно рассматриваются четыре модели разрушения в зависимости от условий нагружения: 1) статического разрушения, 2) длительного статического разрушения, 3) малоциклового разрушения, 4) усталостного разрушения.
На рис. 1.21 показан характер разрушения в зависимости от числа, циклов нагружения. При малом числе циклов (TV < 102) развиваются значительные пластические деформации (рис. 1.21, а.)’
Рис. 1.21. Характер разрушения в зависимости от числа циклов нагружений; « — статическое разрушение; б — малоцикловое разрушение; в — усталостное разрушение
(статическое разрушение), при большом числе циклов (2V> 105) пластические деформации отсутствуют (рис. 1.21, в) (усталостное разрушение). В промежуточной области (102 <N< 105) разрушение носит смешанный характер (рис. 1.21, б) (малоцикловое разрушение).
Если на элемент конструкции действует высокая температура (для алюминиевых сплавов свыше 200°С, для стальных и титановых сплавов свыше 400°С, для жаропрочных сплавов свыше 600°С), то в этом случае рассматривается так называемая длительная прочность материала. Сопротивление материала зависит не только от величины действующего усилия, но и от длительности самого воздействия.
22
ГЛ. 1. ВВЕДЕНИЕ
На структуру моделей разрушения (выбор параметров работоспособности) оказывают влияние свойства материала, из которых очень важным является его пластичность. При недостаточной пластичности возникают хрупкие разрушения, для которых условия разрушения носят особый характер.
Сложность разработки моделей разрушения часто требует проведения дополнительных экспериментальных исследований образцов материала или самих элементов конструкций в условиях, близких к реальным.
Замечание. Конечной целью инженерного проектирования является создание работоспособной и надежной конструкции.
Для оценки надежности детали, элемента конструкции или всего изделия в целом разрабатываются модели прочностной надежности, которые завершаются определением запасов прочности и вероятности разрушения. Конечно, в практических расчетах не все этапы построения модели прочностной надежности прорабатываются достаточно полно. Общая расчетная схема часто выбирается по сложившимся традициям; многое зависит от опыта и интуиции инженера. Однако повышение ответственности технических систем (особенно в авиационной, ракетной и ядерной технике, в химическом и энергетическом машиностроении и других областях техники) требует создания достаточно обоснованных моделей прочностной надежности.
Для сложных элементов конструкции модели прочностной надежности реализуются в виде пакетов программ на ЭВМ.
Условия разработки и создания моделей прочностной надежности, включая необходимый объем экспериментальных исследований, часто регламентируются нормами прочности.
ГЛАВА 2
НАПРЯЖЕНИЯ
Во время работы на элементы конструкции действуют внешние усилия, создающие напряжения и деформации. Рассмотрим общие методы анализа на-пряженного состояния.
3.	Нормальные и касательные напряжения
Метод сечений. Пусть на элемент конструкции, условно изображенный на рис. 2.1, а, действуют внешние силы (сосредоточенные или распределенные на участках поверхности). Считаем, что элемент конструкции под действием указанных сил находится в равновесии. Проведем плоскость П, которая рассечет элемент на две части, и рассмотрим одну из частей, например левую (рис. 2.1, б).
а	б
Рис. 2.1. Напряжения в сечении элемента
Приложим к поверхности сечения П силы взаимодействия между обеими частями элемента. Когда тело находится в равновесии, то и любая часть тела также будет в равновесии, если к поверхности сечения приложить силы взаимодействия между частями. Силы, действующие в сечений, представляют собой силы взаимодействия между частицами материала, вызванные внешней нагрузкой на. элемент. Из условия равновесия рассматриваемой части тела можно определить главный вектор и главный момент внутренних сил, действующих по сечению П. В этом состоит сущность метода сечений — одного из важных методов механики деформируемых сред. Распределение внутренних усилий сечению заранее неизвестно и составляет одну из главных задач дальнейшего изучения.
Понятие напряжения. Оказывается необходимым ввести характеристику интенсивности сил взаимодействия — напряжения, которые в разных точках сечения могут быть, разумеется, различными.
Пусть на малую ’ площадку AF, расположенную в окрестности точки А (рис. 24, б), действует сила ДР.
2k
ГЛ. 2. НАПРЯЖЕНИЯ
Назовем напряжением р в точке А рассматриваемого сечения предел отношения
р = lim	(О
ДГ-*О
при условии, что AF стремится к нулю.
Вектор напряжения совпадает по направлению с вектором уси-
лия ДР. Отметим, что напряжения в сечении элемента не могут
быть определены только из
Рис. 2.2. Напряжения растяжения в сечении болта
дожить, что напряжения стержня болта) направлены
уравнений статики (уравнений равновесия). Для их нахождения, как будет ясно из дальнейшего, необходимо разобраться в характере деформаций элемента. Однако в ряде случаев можно сделать некоторые обоснованные предположения о распределении напряжений, что позволит найти их величину и без рассмотрения деформаций. Использование предположений (гипотез), основанных на результатах ^экспериментальных исследований и дающих достаточную точность при решении инженерных задач, составляет примечательную черту прикладных техниче-
ских дисциплин, в частности сопротивления материалов.
При растяжении болта ч усилием Р (рис. 2.2) есть все основания предпо-в сечении П (поперечное сечение нормально к плоскости сечения и рас-
пределены равномерно. Тогда значение растягивающего напряжения
Р кР
Р Р ,2* г па
(2)
dim р =?=
Из последнего равенства очевидно, что напряжение имеет размерность	х
сила площадь
Размерность обозначается символом dim (начальные буквы слова «dimension» — размерность).
В международной системе единиц СИ' для измерения напряжения (давления) применяется специальная единица — паскаль: 1 Па = 1 Н/м2. Это — очень маленькая величина, и практические расчеты ведут, измеряя напряжения в мегапаскалях (МПа), причем
1 МПа = 10е Па - 10е Н/м2.
В технической литературе напряжения часто измеряют в система
3. НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ
25
Рис. 2.3. Нормальное и касательное напряжения в площадке
МКС. Связь единиц измерения такова: 1 МПа = 0,1 кгс/мм2. В общем случае напряжения в разных точках сечения могут быть различными.
Еще одно важное обстоятельство состоит в том, что напряжение в точке зависит также и от положения плоскости сечения. Поэтому надо всегда указывать не только точку тела, где определяется напряжение, но и ориентацию сечения (площадки), проходящего через рассматриваемую точку.
Нормальные и касательные напряжения. Напряжение р есть вектор и как всякий вектор может быть представлен нормальной (по отношению к площадке) и касательной составляющими (рис. 2.3). Нормальную составляющую вектора напряжений будем обозначать о, касательную т. Экспериментальными исследованиями установлено, что влияние нормальных и касательных
напряжений на прочность материала различно, и потому в дальнейшем . окажется необходимым всегда раздельно рассматривать составляющие вектора напряжений.
Рис. 2.4. Касательное напряжение при срезе болта
При растяжении болта (см. рис. 2.2) в поперечном сечении действует нормальное напряжение
При работе болта на срез (рис. 2.4) в сечении П должно возникать усилие, уравновешивающее усилие Р.
26
ГЛ. 2. НАПРЯЖЕНИЯ
Из условий равновесия следует, что
<2 = Л	(4)
Если приближенно считать, что касательные напряжения во всех точках сечения одинаковы, то они будут равны
Q 4Р
(5)
В действительности последнее соотношение определяет некоторое среднее напряжение по сечению, которым иногда пользуются для приближенных оценок прочности. На рис. 2.4 показан вид болта после воздействия значительных усилий. Началось разрушение болта, и одна его половина сместилась относительно другой: произошла деформация сдвига или среза.
Примеры определения напряжений в элементах конструкций. Разберем простейшие примеры, в которых предположение о равномерном распределении напряжений, можно считать практически приемлемым. В таких случаях величины напряжений определяются с помощью метода сечений из уравнений статики (уравнений равновесия).
Кручение тонкостенного круглого вала. Тонкостенный круглый вал (труба) передает крутящий момент (например, от авиационного двигателя на воздушный винт). Требуется определить напряжения в поперечном сечении вала (рис. 2.5, а). Проведем плоскость сечения П перпендикулярно оси вала и рассмотрим равновесие отсеченной части (рис. 2.5, б).
Рис. 2.5. Кручение тонкостенного круглого вала
Из условия осевой симметрии, учитывая малую толщину стенки, можно принять, что напряжения во всех точках поперечного сечения одинаковы. Строго говоря, такое предположение справедливо только при очень малой толщине стенки, но в практических расчетах
. 3. НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ
27
его используют, если толщина стенки 6
6 0,2 Яор,
где Яср — средний радиус сечения.
Внешние силы, приложенные к отсеченной части вала, сводятся только к крутящему моменту, и потому нормальные напряжения в поперечном сечении должны отсутствовать. Крутящий момент уравновешивается касательными напряжениями, момент которых равен
т-2л7?срб =“
Из последнего соотношения находим касательное напряжение в сечении вала:
Напряжения в тонкостенном цилиндрическом сосуде (трубе).
В тонкостенном цилиндрическом сосуде действует давление р
Рис. 2.6. Напряжения в продольном направлении в стенке цилиндрической трубы
(рис. 2.6, а). Проведем сечение плоскостью П, перпендикулярной оси цилиндрической оболочки,, и рассмотрим равновесие отсеченной части. Давление, действующее на крышку сосуда, создает усилив
#Ор — 4- 6 р « лЯсрР-	' (7)
Это усилие уравновешивается силами, возникающими в поперечном сечении оболочки, и интенсивность -указанных сил — напряжение <^1 ~ будет равна
гг — р	п	/Й\
CT1 ~ 2лЯср5 ~ 2лЯсрб = Р 26 ‘	W
Толщина оболочки & предполагается малой по сравнению со средним радиусом Яср, напряжения щ считаются равномерно распределенными во всех точках поперечного сечения (рис. 2.6, б).
28
ГЛ. 2. НАПРЯЖЕНИЯ
Однако на материал трубы действуют не только напряжения в продольном направлении, но и окружные (или кольцевые) напряжения в перпендикулярном направлении. Для их выявления выделим двумя сечениями кольцо длиной I (рис. 2.7), а затем проведем диаметральное сечение, отделяющее половину кольца.
Рис. 2.7. Напряжения в стенке цилиндрической трубы в окружном направлении
На рис. 2.7, а показаны напряжения на поверхностях сечения. На внутреннюю поверхность трубы радиусом Rt действует давление р.
Рассмотрим теперь равновесие половины кольца (рис. 2.7, б). Найдем сначала равнодействующую силу давления, спроектировав силы на вертикальную ось. К элементу поверхности Z/?4d(p при
Рис. 2.8. Трещина в цилиндрической оболочке при действии разрушающего внутреннего давления
ложено усилие, вертикальная составля-» ющая которого
plRidq sin ф.
Интегрируя по всей поверхности, найдем величину вертикального усилия:
л
N = f plR х sin <fd<f = 2plRt.
о
Из условия равновесия половины коль-
ца получаем
2Z6o2 = N,
что дает следующее равенство:
(9)
В приближенных расчетах полагают Rt ~ Rct, и. тогда
^ср о2==Р—.
(10)
4. НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ
29
Сопоставляя равенства (10) и (8)’, заключаем, что в тонкостенной цилиндрической оболочке окружные напряжения о2 в Два раза больше продольных.
На рис. 2.8 показан общий вид разрушения оболочки (трубы)’ от значительного внутреннего давления. Трещина возникает под действием растягивающих напряжений о2«
4.	Напряженное состояние в точке
тела на параллелепипед заме-
Рис. 2.9. Напряжения, действующие на гранях элемента
Для оценки надежности элемента конструкции следует рассмотреть наиболее напряженные места, а в них наиболее опасные точки. Именно в таких точках при неблагоприятных условиях будет начинаться разрушение. Надо знать напряжения во всех площадках, проходящих через опасную точку, т. е. знать напряженное состояние в точке.
В рассматриваемой точке тела поместим начало системы координат х, у, z (рис. 2.9) и бесконечно близкими параллельными сечениями выделим параллелепипед, размеры ребер которого равны dx, dy и dz. Действие остального ним соответствующими напряжениями.
Обозначение напряжений и правило знаков. На рис. 2.9 показаны нормальные и касательные напряжения по граням параллелепипеда. Нормальные напряжения в площадке обозначаются о, касательные т. Нижний индекс в обозначении нормальных напряжений указывает направление нормали к площадке (ож, ог). В обозначениях касательных напряжений содержится два нижних индекса: первый указывает направление нормали к площадке, второй — направление вектора касательных напряжений.
Нормальные напряжения растяжения считаются положительными. Векторы растягивающих нормальных напряжений направлены в сторону внешней нормали (от внутренних частиц параллелепипеда — наружу). Знак и, следовательно, направление нормальных напряжений весьма существенны — многие материалы значительно лучше сопротивляются напряжениям сжатия, чем напряжениям растяжения. Растягивающие напряжения понижают сопротивление материала действию повторных нагрузок, тогда как сжимающие напряжения повышают его.
30
ГЛ. 2. НАПРЯЖЕНИЯ
Рис. 2.10. Напряжения на гранях элемента тела в цилиндрической системе координат
Условимся о следующем правиле знаков для касательных напряжений: если внешняя нормаль к площадке совпадает с направлением одной из осей координат, то положительное касательное напряжение направлено вдоль соответствующей оси. В противоположном случае (внешняя нормаль к площадке идет по отрицательному направлению оси) положительное касательное напряжение имеет обратное направление.
На рис. 2.9, 2.10 сплошными линиями показаны положительные векторы напряжений на «видимых» гранях прямоугольного элемента. На грани, нормаль к которой идет вдоль оси х, векторы положительных касательных напряжений направлены вдоль осей у и z соответственно. Для передней грани (направление внешней нормали противоположно направлению оси у) положительное касательное напряжение направлено противоположно оси х. Разумеется, векторы напряжений приложены по всем шести граням элемента. Элементарный параллелепипед часто необходимо рассматривать в цилиндрической системе координат (г, 0, z). На рис. 2.10 показаны обозначения напряжений в цилиндрической системе координат. Нормальные напряжения <Ъ называются радиальными, <т0 — окружными напряжениями.
Отметим, что по двум параллельным граням элемента (рис. 2.9, 2.10) действующие напряжения могут различаться только на бесконечно малые величины, так как расстояния между пло
щадками бесконечно малы, а направления площадок одинаковы (см. рис. 2.9).
В силу этого следует считать, что напряжения на гранях элементарного параллелепипеда — это напряжения в площадках, проходящих через рассматриваемую точку.
Если направления площадок, проходящих через одну и ту же точку, различны, то различными (в общем случае) будут и действующие в них напряжения. Например, в тонкостенной оболочке (см. рис. 2.7) нормальные напряжения в двух взаимно перпендикулярных площадках различаются в два раза.
Свойства парности касательных напряжений. Так как элемент тела находится в равновесии, то сумма моментов всех сил относительно любой оси должна обращаться в нуль. Как известно из теоретической механики, для равновесия достаточно выполнения этих условий относительно любых трех осей, не лежащих в одной плоскости (три составляющие вектора главного момента обраща
4. НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ
31
ются в нуль). Рассмотрим условия равновесия моментов. Силы, распределенные по граням параллелепипеда, будем заменять равнодействующими, приложенными в центре грани (см. рис. 2.9). Строго говоря, последнее допущение не обязательно, и можно показать, что учет изменения напряжений в пределах бесконечно малой грани дает добавки более высокого порядка малости. Последнее относится и к массовым распределенным усилиям, которые будем считать приложенными в центре тяжести элемента (составляющие массовой силы обозначаются X, У, Z).
Рассмотрим сумму моментов относительно оси х. Отличные от нуля моменты дают векторы Tzy (верхняя грань) и ryz (задняя грань):
— (xZydxdy) dz -f- (xyzdxdz) dy — (pYdxdydz) • ~ dz 4-
-4-	(pZdxdydz)~dy = 0,	(11)
где p — плотность материала.
Два последних слагаемых в левой части уравнения (И) можно отбросить, так как они имеют более высокий порядок малости.
В результате получим
Xyz == TZy.	(12)
Подобным образом получаем три условия парности касательных напряжений*.
Txv == Тух, Ту3 == TZy, Xzx == TXZ.	(13)
Общий вывод таков: касательные напряжения в точке, действующие по двум взаимно перпендикулярным площадкам, одинаковы. Взаимно перпендикулярные площадки всегда имеют общее ребро. Касательные напряжения в силу свойства парности направлены оба вместе или к ребру, или от ребра. Принятое ранее правило знаков для касательных напряжений (см. рис. 2.9 и 2.10) обеспечивает выполнение указанного условия. Свойство парности касательных напряжений справедливо для взаимно перпендикулярных площадок элементарного объема в любой ортогональной системе координат, например в цилиндрической.
Замечания. 1. При выводе уравнения (И) учитывалось направление векторов напряжений по рис. 2.9 и соответствующим образом определялся знак момента (положительное направление — вращение против часовой стрелки). Выводы уравнений с помощью чертежа (рисунка) будут часто встречаться в дальнейшем.
2.	Вывод одного из трех уравнений (13) позволяет записать два недостающих с помощью правила круговой перестановки индексов. Иллюстрация правила дана на рис. 2.11: при круговой перестановке индекс х замещается индексом у, индекс у замещается z, а последний — снова индексом х. Например, подобным образом из условия (12) могут быть получены все соотношения (13).
х
Рис. 2.11. Иллюстрация правила перестановки ин-
32
ГЛ. 2. НАПРЯЖЕНИЯ
Правило круговой перестановки индексов применяется во многих разделах механики сплошной среды (гидродинамике, теории упругости и др.) во всех случаях, когда векторные соотношения записываются с помощью трех скалярных в прямоугольной (декартовой) системе координат.
5. Плоское напряженное состояние
Определения. Рассмотрим тонкую пластинку под действием сил, лежащих в плоскости пластинки (рис. 2.12). В этой плоскости расположим систему координат (х, у). Торцевые (фасадные) по-
Рис. 2.12. Плоское напряженное состояние
верхности пластинки свободны от напряжений, и потому
ог = 0, т2Х = 0, t2v==0.	(14)
Так как пластинка тонкая, то допустимо считать справедливыми условия (14) для всех площадок, нормальных к оси z (лежащих в плоскости пластинки)*).
Векторы напряжений ох, оу и х*у лежат в одной плоскости, и напряженное состояние называется плоским. Отметим, что все точки пластинки находятся в плоском напряженном состоянии. В общем случае понятие «плоское напряжен-
ное состояние» относится к рассматриваемой точке элемента конструкции.
Если в данной точке А существует
мальное
и касательное)
площадка, в которой отсутствуют (норнапряжения, то напряженное состояние
в точке является плоским. Например, в точках свободной поверхности детали (рис. 2.13) напряженное состояние будет плоским (ось z в точке А направлена по нормали к поверхности).
Особая важность плоского напряженного состояния связана с тем, что оно реализуется в точках поверхности элементов конструкции, которые часто являются «опасными точками». (точками с наибольшими напряжениями в поверхностном слое).
Напряжения в косых площадках при плоском напряженном состоянии. Изучим напряжения в
косых площадках, перпендикулярных плоскости пластинки (рис. 2.14).
Рис. 2.13. Плоское напряженное состояние в точках свободной поверхности детали
♦) Строгое доказательство вытекает из того, что на малом участке функция обращается в нуль по концам участка, а производная функции ограничена.
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
33
Условный термин «косая» или «наклонная» площадка означает, что нормаль к площадке не совпадает ни с одной из осей выбранной системы координат.
В площадке ВС, нормаль к которой v составляет угол а с осью х, действуют нормальное ov и касательное tv напряжения. Напря-
жения распределены равномерно по толщине пластинки h, торцевые грани элемента АВС не загружены. Ближайшая задача состоит в определении величин Qv и Tv из условий равнове-сия элемента АВС. Проектируя все усилия на направление нормали v, найдем
(j^ds  h = Oxdy cos a • h + <judx sin a • h + + Xxv(dy sin a + dr cos а) Л. (15) Массовые силы, действующие на элемент, 1 1 pX--^dxdy-h, pY-^dxdy-h,
Рис. 2.14. Напряжения в косой площадке при плоском напряженном состоянии
составляют усилия второго порядка малости, и в уравнении (15) они отсутствуют. Учитывая, что из рис. 2.14 следует
— = sin a, — = cos a,	(16)
ds	'ds	'	v '
получим из соотношения (15)
tfv == cos2 a + ay sin2 a + x*y sin 2a.	(17)
Проектируя все усилия на направление вектора tv, найдем
x„ds • h = Oydx cos a • h — a^dy sin a • h + x*y (dy cos a — dx sin a) h, (18) или
tv = (<jy — ox) sin 2a + Txy cos 2a.	(19)
Формулы (17) и (19) дают значение нормальных и касательных напряжений в косой площадке.
Замечания. 1. Следует строго уяснить, что при выводе уравнений (15) и (18) рассматриваются условия равновесия не напряжений (таких условий не существует!), а действующих усилий по граням элемента.
2. Напряжения по граням элементарного объема (рис. 2.14) распределяются равномерно. Косую площадку можно рассматривать как косое сечение в элементарном параллелепипеде (рис. 2.15), и те же результаты (равенства (17) и (19)) вытекают из условий равновесия заштрихованной части параллелепипеда.
3. Неизвестные векторные величины, для которых принято определенное правило знаков, при выводе следует принимать положительно направленными. Например, av на рис. 2.14 направлено как растягивающее напряжение.
3 И. А; Биргер, Р. Р. Мавлютов
34
ГЛ. 2. НАПРЯЖЕНИЯ
Направление tv выбрано таким, чтобы при а — 0 (рис. 2.16) оно совпадало с направлением для Тху (см. рис. 2.9). Впрочем, знак касательного напряжения в отличие от нормального обычно несуществен.
4. Кроме рассмотренных
Рис. 2.15. Косая площадка как сечение в элементарном параллелепипеде
косых площадок, можно с помощью дополнительных сечений образовать и другие косые площадки.
Метод определения напряжений в косых площадках остается всегда одним и основывается на условиях равновесия малого элемента.
Рис. 2.16. Косая площадка при а = О
Главные площадки при плоском напряженном состоянии. Главными площадками называются площадки, в которых отсутствуют касательные напряжения; нормальные напряжения в таких площадках называются главными напряжениями.
При плоском напряженном состоянии одну из главных площадок в точке тела можно указать сразу — это площадка, нормаль к которой направлена по оси z (см. рис. 2.12) (площадка, лежащая на свободной торцевой поверхности). В такой площадке отсутствуют и касательное, и нормальное напряжения (главное напряжение равно нулю). Найдем главные площадки в точке А среди серии площадок, перпендикулярных основной плоскости.
Как уже указывалось,, грани треугольного элемента на рис. 2.14 как раз представляют такие площадки.
Из условия т = 0 получим с помощью соотношения (19)
2т
tg2a* = —(20) UX У
где а* — угол, который составляет нормаль v главной площадки с осью х.
Так как tga — периодическая функция с периодом л, то уравнению (20) будут удовлетворять углы
2а^ = 2а* + пл (п = 0,1, 2,3, ...).
Таким образом,
= a*, а* = а* + л/2, а% = a* + л, a^ = a* + Зл/2,
<х« = a* + 2л, ... (21)
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
35
Из рис. 2.17 видно, что существуют всего два взаимно перпендикулярных направления, которые составляют с осью х углы а* и а* + л/2. Эти направления называются главными.
Проведенный анализ показывает: среди рассматриваемых площадок (нормали к площадкам лежали в плоскости действия напряжений Ох» оу, Txv) имеются две главные площадки; касательные напряжения в таких площадках отсутствуют. Если учесть еще главную площадку, перпендикулярную оси z, то имеются всего три
Рис. 2.18. Главные площадки при плоском напряженном СОСТОЯНИЙ
Рис. 2.17. Главные направления ари плоском напряженном состоянии
главные площадки (рис. 248). Нормальные напряжения в главных площадках (главные напряжения) обозначаются а2? 0з. При плоском напряженном состоянии о3 « 0.
В дальнейшем будет показано, что в любой точке тела при действии произвольной системы внешних сил в общем случае имеются всего три главные площадки, или, что то же самое, три взаимно перпендикулярных главных направления.
Замечание. При анализе уравнения (20) исключался из рассмотрения случай, когда
(Уж = Хху == 0.	(22)
Такое напряженное состояние создается в пластине, равномерно растягиваемой одинаковыми усилиями в двух взаимно перпендикулярных направлениях.
При условии (22) из уравнения (19) вытекает, что в любой косой площадке касательные напряжения отсутствуют и главных площадок бесчисленное множество. Поэтому более строгое утверждение таково: или существуют три главные площадки, или (в отдельных частных случаях) их может быть бесчисленно много.
Случай, когда главных направлений бесконечно много, встречается, конечно, редко (например, всестороннее сжатие или растяжение) и не содержит каких-либо трудностей для анализа напряженного состояния. Важно, что не может быть одного, двух, четырех, пяти и т. п. главных направлений: их или три, или бесконечно много.
3’
36
ГЛ. 2. НАПРЯЖЕНИЯ
Главные напряжения при плоском напряженном состоянии. Главные напряжения могут быть определены из уравнения (17) при а = а*:
ov = ох cos2 a* 4- о,7 sin2 a* + тху sin 2a* =
= у (Ox + ay) + у (ax — aw) cos 2a* + Txj, sin 2a*.	(23)
Учитывая равенства
cos 2a* — ± —y?- * ------y sin 2a* = Hz ~y=========.	(24)
V 1 + tg2 2a*	V 1 + tg2 2a*
и соотношение (20), получим после нескольких громоздких, но простых выкладок выражение
av = у (a* + °v) ± V V — °у)2 +	(25)
Последнее равенство дает два значения главных напряжений:
Oj =y(ax + av) + И(ОХ — (Jy)2 + 4тзд,	(26)
°2 = у (°* + °г/) — у К(°х — сту)2 +	(27)
Третье главное напряжение при плоском напряженном состоянии а3 = 0.	(28)
Рис. 2.19. Определение главных напряжений из равновесия элементарной треугольной призмы» одной из граней которой является главная площадка
Так как корень в равенствах (26) и (27) имеет арифметическое (положительное) значение, то ot> > о2 (в алгебраическом смысле с учетом знака напряжения).
Приведем теперь другой способ нахождения главных напряжений, который будет использоваться в дальнейшем и для объемного (неплоского) напряженного состояния.
Рассмотрим равновесие элементарной треугольной призмы (рис. 2.19), одной из граней которой является главная площадка. На главной площадке действует нормальное напряжение (Jv; касательное напряжение отсутствует.
Нормаль к главной площадке составляет с осями х, у углы соответственно а* и л/2 ~ а*. Косинусы углов нормали (они называются
направляющими косинусами) обозначаются I и т:
Z = cos a*, Tn = cos(n/2—a*) = sina*.	(29)
Площадь косой площадки равна dsh, площади прямых площадок
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
37
составляют
dsx == ds hl » ds h cos a*,	_
dsv = ds hm = ds h cos (л/2— a*) = ds h sin a*.
Проектируя все силы на направления осей х и у1 найдем
ая ds I ds т « ov ds I,	..
Хху ds 14- сгу ds т = ov ds m.	'
Из уравнений (31) получаем однородную систему линейных алгебраических уравнений относительно неизвестных величин I и т:
($Х Hv) I 4" Xxyffl “ 0,	/32 Y
Xxyl + (ov — Ov)^ = 0.	' *
При любом значении av (оно заранее тоже неизвестно) система (32) не может иметь нулевых решений относительно I и т, так как I2 4- т2 = cos2 a* + sin2 a* = 1.
По известной теореме линейной алгебры детерминант системы (32)
Х X а I ~	(<7у — CFv) — хху == 0.	(33)
1XI/ иу av I
Записав уравнение (33) в виде
а? (о* 4- оу) Оу 4- охоу — хху == 0,	(34)
находим два корня уравнения, выражаемые равенствами (26)' и (27).
Уравнения (32) позволяют достаточно просто указать расположение площадок, в которых действуют напряжения щ и о2.
Для того чтобы найти направляющие косинусы нормали площадки, в которой действует напряжение оъ достаточно внести значение о, в любое из двух уравнений (32), например в первое. Тогда получим
(35)
Аналогично для напряжения о2
^==tga(‘3) = ^z^.	(36)
В последних соотношениях ai и углы с осью х площадок, где действуют напряжения Qi и о2 соответственно. Величины а< й о2 определяются равенствами (26) и (27).
Если направления линий, соответствующих углам ах и а2, взаимно перпендикулярны, то
*	* sina,*n sin fctzV + л/2)
tga<i)-tga(2)------------->9; = -1.	(37)
cosa(2) cos (a(1) 4-л/2)
38
ГЛ. 2. НАПРЯЖЕНИЯ
Учитывая зависимости (35), (36), (26) и (27), находим
О. — OL. (К — О
I х . 2 х     л
Т	Т	’
xj/	ху
(38)
что доказывает взаимную перпендикулярность главных площадок.
Замечания. 1. Были найдены значения главных напряжений, но не было указано, какое именно главное направление соответствует большему напряжению Oi и какое — меньшему о2. Это будет сделано чуть позже.
2.	Были даны два различных вывода главных напряжений и два доказательства ортогональности главных напряжений.
Различные параллельные способы вывода характерны для технического анализа, в котором прежде всего необходима достоверность. Никогда не следует жалеть времени на то, чтобы получить дополнительное подтверждение результата!
Разберем вопрос о наибольших нормальных напряжениях в рассматриваемых площадках. Нормальное напряжение, как следует из формулы (17), зависит от угла наклона площадки а. Для отыскания максимума или минимума функции приравняем нулю производную:
d(Jv
—- = — 2ах cos a sin а + 2ov sin а cos а + 2тху cos 2а = 0. (39)
Теперь получим значение угла, при котором достигается экстремум (максимум или минимум функции).
Из равенства (39) находим 2т
tg2a = T-2L-.	(40)
vx uy
Сопоставляя формулу (40) с формулой (20), заключаем: нормальные напряжения' достигают наибольшего или наименьшего значения в главных площадках.
Для различения’ максимума или минимума функции составим выражение второй производной:
d2ov
—=х — 2 [(ах — (jy) cos 2а 4- 2txv sin 2а].	(41)
da.
Последнее равенство представим так:
—г = — 2 соз 2а [<уж — <tv -Ь 2T3CVtg 2а] =»
в_1с^[к_а# + 4т^ (42)
Условие существования максимума
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
39
реализуется в двух случаях:
cos 2а >0, Ох > оу, cos 2а <0, Ох < Оу.
В первом случае (ох > оу) нормаль к площадке, где действует напряжение 01, составляет с осью х угол 0< 12а| <л/2 или — л/4< <а*<л/4. Во втором случае (ох<Оу) угол лежит в пределах л/4 < 1а*1 < Зл/4. В перпендикулярной главной площадке напряжение равно о2.
Наибольшие касательные напряжения. Выясним вопрос о максимальных касательных напряжениях в косых площадках. С помощью зависимости (19) находим
== (<*у — <*х) cos 2а — 2txv sin 2а.
Приравнивая нулю производную, получаем
(43)
где а< — угол нормали к площадке с осью х.
Внося зависимость (43) в равенство (19) и учитывая формулы (24), приходим к следующей величине экстремальных касательных напряжений:
Tv = ± у V\<3X — Ov)2 + 4тхУ-	(44)
Максимальное и минимальное значения касательного напряжения равны по величине и различаются только знаком, что, как указывалось ранее, несущественно для обычных конструкционных материалов.
Вспоминая формулы (26) и (27) для_главных напряжении, находим
Tmax = |Tv(aT)| = ylCT! —<т2|.	(45)
Максимальная величина касательных напряжений равна абсолютному значению полуразности главных напряжений.
Подобно проведенному анализу для главных напряжений, можно установить, что площадки с наибольшими (по абсолютной величине) касательными напряжениями взаимно перпендикулярны. Такой вывод следует также из свойства парности касательных напряжений:
Как же расположены площадки с максимальными касательными напряжениями по отношению к главным площадкам?
Сопоставляя равенства (20) й (43), находим
tg 2a, • tg 2a* = —1.	(46)’
Из этого условия следует, .что стороны углов 2a, и 2a*— взаимно. перпендикулярны: 2a, = 2a* + л/2, и потому а, = а* + л/4.
40
ГЛ. 2. НАПРЯЖЕНИЯ
Плоскость площадок с наибольшими (максимальными) касательными напряжениями делит пополам прямой угол между плоскостями главных площадок. Этот вывод оказывается справедливым и для любого (не только плоского) напряженного состояния.
Рис. 2.20. Главные направления | и т] и площадки с максимальными касательными напряжениями
На рис. 2.20 показаны главные направления | и т|, которые можно рассматривать как оси координат, повернутые на угол а* к основной системе координат.
По граням элементарного параллелепипеда, построенного на осях
Я» будут действовать только нормальные напряжения as = Оц ®= @2 •
Рассмотрим теперь напряжения в площадке, составляющей угол л/4==45° с главными осями (рис. 2.20, б). В_ этой площадке должны действовать максимальные касательные напряжения. Из условия равновесия треугольной призмы аналогично выводам уравнений (27) и (19) находим
ал/4 — *2* (ai +
1 / \ ТЛ/4------у (<?!	а2).
(47)
(48)
Равенство (48)' подтверждает сделанный ранее вывод о величине максимального касательного напряжения. Примечательно, что в площадках, где действует ттах, имеются и нормальные напряжения.
6. Объемное напряженное состояние
Определения. Ранее указывалось, что в любой точке нагружаемого тела существуют три главные площадки, в которых действуют главные (нормальные) напряжения, а касательные напряжения отсутствуют.
Если все три главных напряжения отличны от нуля, то напряженное состояние в точке называется объемным или трехмерным. При условии равенства нулю одного из главных напряжений напряженное состояние считается плос-
6. ОБЪЕМНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
41
ним или двумерным. Наконец, при отличии от нуля только одного главного напряжения напряженное состояние будет линейным или одномерным.
Для анализа объемного напряженного состояния необходимо рассмотреть площадки произвольной ориентации, проходящие через данную точку тела.
Произвольная наклонная площадка. Ранее при исследовании напряжений в наклонных (косых) площадках рассматривались пло-
щадки определенного вида — нормаль к ним лежала в плоскости
х, у. Для плоского напряженного состояния статочно, но в общем случае требуется знание напряжений в произвольной наклонной площадке, заданной в выбранной системе координат.
Рассмотрим теперь элементарный четырехгранник (тетраэдр), построенный на осях прямоугольной системы координат с центром в точке А (рис. 2.21).
Произвольная косая площадка BCD характеризуется единичным вектором нормали v. Составляющие вектора по осям х, у и z равны Z, тп, п:
v = (/, тп, п).	(49)
Рис. 2.21. Произвольная косая площадка
По физическому смыслу величины Z, т и п являются косинусами углов вектора нормали v с осями координат:
I ~ cos а, т = cos п = cos у.
(50)
чай равновесия тетраэдра: по всем граням действует одинаковое давление р
Величины Z, т и п часто называются направляющими косинусами. Если обозначить площадь наклонной грани dS, то площадь грани ABD
dSx^ldS.	(51)
Для граней АВС и ACD dS^mdS, dS^ndS.	(52)
Подобные соотношения в. частном случае использовались ранее (уравнения (30)), а сейчас установим их с помощью наглядных физических представлений.
Из повседневного опыта ясно, что если поместить в жидкость тетраэдр из материала с тем же удельным весом, to он будет находиться в равновесии при любом давлении столба жидкости.
Так как размеры тетраэдра бесконечно малы, можно считать, что давление по всем его граням одинаково (рис< 2.22).
Проектируя все силы на направление х, находим
р dSx —pldS = 0, dSx = ldS.	(531
42
ГЛ. 2. НАПРЯЖЕНИЯ
Аналогично по другим осям
р dSv — pm dS = 0, dSv = т dSt р dSz~ pndS = 0, dSz — ndS.
Конечно, последние соотношения можно было установить из чисто геометрических соображений, но проведенный анализ дает дополнительную информацию.
Если по трем взаимно перпендикулярным площадкам действуют одинаковые нормальные напряжения, а касательные напряжения отсутствуют, то в любой наклонной площадке действует то же нормальное напряжение и так же отсутствует касательное напряжение. Это пример, когда главных площадок оказывается бесконечно много.
Напряжения в произвольной косой площадке. В наклонной площадке, нормаль к которой v (рис. 2.23), действуют нормальное ом
(Tv и касатель-
и касательное rv напряжения, подлежащие определению. По грани АВС приложены известные напряжения оу, tv3C, tvx; по двум другим граням — соответственно Ох, Тхж и Ог, Tzx, Тзу. ТГак как размеры элементарного тетраэдра бесконечно малы, то напряжения по граням представляют, в сущности, напряжения в различных площадках, проходящих через точку А (или какую-либо другую точку тетраэдра,—разницы нет). Бесконечно малые размеры четырехгранника (тетраэдра) дают
ное tv напряжения в косой площад- так же возможность пренебречь ке; pv —вектор полного напряже- массовыми силами по сравнению ния в площадке « <х* + т*); с поверхностными, приложенными Р», Руч Р* — проекции полного напря- по его граням.
жения на оси я, р, z	Для определения напряжений
в наклонной площадке проще всего найти сначала составляющие полного напряжения по осям. Проектируя силы (а не напряжения!), действующие по граням тетраэдра, на направления осей, находим
(JxdSx *4“ Xy^dSy 4* XtxdSt —1 pxdS) XxydSx + GydSy 4- XzydSx = pydS Xxz&Sx ! XyzdSy I ““ p%dS»
(54)
6. ОБЪЕМНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
43
Учитывая зависимости (51), (53), получаем важные соотношения р*z=z Gxl "Ь 4" т2Жд,	(55)
Pv ~ Vxyl + <7уТП 4- хгуп.	(56)
Рг = хХ214“ Ху2Л1 4- Qzn.	(57)
Напомним, что в силу парности касательных напряжений
Тху == ХуХ1 Ху2 я XZy, тгж == тжх.	(58)
Для того чтобы найти величину нормального напряжения, надо спроектировать каждую из составляющих вектора pv на направление v и образовать их сумму
Gv = рх14- рут 4- р2п.
Ссылаясь на соотношения (55) — (57), можно утверждать
Ov == ож/2 4- аут2 4- огп2 + 2хху1т 4- 2xyzmn 4- 2т2Жп/.	(59)
В частном случае плоского напряженного состояния, когда рассматривается наклонная площадка, параллельная оси 2, будем иметь « = 0} и тогда
Ov = gJ? 4- Gym2 -4- 2x^1™,.	'	(60)
Так как в разбираемом случае
I = cos а, т = cos & = cos (л/2 — а) == sin а,
то формула (60) совпадает с аналогичной формулой (17). Касательное напряжение в косой площадке равно
Tv = Pv — ffv = [рх + Ру + р? — (рх1 + Рут + ргп)2}1/2. (61)
Направление tv можно определить из условия, что линия действия касательного напряжения является линией пересечения плоскости, содержащей векторы pv и ov. Однако направление т* для дальнейшего несущественно, и детализацию вопроса опустим.
Замечания. 1. Знание напряжений (нормальных и касательных) по трем взаимно перпендикулярным площадкам, проходящим через данную точку тела, дает возможность определить напряжения в любой другой площадке, также проходящей через эту точку.
2. После получения общей формулы для нормальных напряжений в косой площадке она была применена для уже известного частного случая (плоского напряженного состояния). Такая процедура всегда желательна, а при исследовании новых вопросов просто необходимо проверять результат на известных ранее случаях,
Главные площадки и главные напряжения при объемном напряженном состоянии. Пусть косая площадка (рис* 2.24) является главной. Тогда полное напряжение в площадке совпадает с нормальным напряжением, касательное напряжение отсутствует. Для главной площадки
; Рх	Ру “ (Jv/7Z, р2 == ОуЛ,	(62)(
где I« cos а, т =» cos {J, п cos у.
44
ГЛ. 2. НАПРЯЖЕНИЯ
Теперь из (55) — (57) получаем систему линейных однородных уравнений:
(Ох — Ov) I + ХухГП + тгжп = О,
TxvZ + (оу — Оу) т + хгуп = 0,	(63)
+ xyzm + (ог ~ ov)n = 0.
Основными неизвестными в этой системе являются величины I, т,
Рис. 2.24. Определение главных площадок и главных напряжений
нант системы обращается в
лху Txz
п, характеризующие положение главной площадки. Они связаны соотношением
Р + тЧв’»!,	(64)
так как являются проекциями на оси х, у, z единичного вектора нормали v (Iv’l = 1).
В силу равенства (64) величины Ц т и п не могут все одновременно быть равными нулю.
Из линейной алгебры известно, что однородная система уравнений может обладать ненулевым решением только в том случае, когда детермину ль:
(65)
Развертывая сщределитель и учитывая свойства парности касательных напряжений, находим
(Ох Оу) (<Уу — Оу) ((Jj Оу) 4- ^X^yXyzXzx fax Оу) XyZ ~~
— (а„ — CTV) Тгх — (аг — Ov) Хху = 0.	(66)
Последнее уравнение представляет уравнение третьей степени от
носительно о., которое запишем в виде
Ov 0v*7 j_	Ov*72Jз —* 01
(67)
(68)
Jt = —0«0v — GyOz ~ Wz + Txy + Туг + T*x,	(69)

Tzx
<*z
— (Jx&'ijGz + 2TxyTyzTzx Ox^yz Qy^zx ®z^xy* (70)

Уравнение (67) называется характеристическим уравнением напряженного состояния. Корни характеристического уравнения (знамения Ov) представляют величины главных напряжений. В частном
6. ОБЪЕМНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
45
случае плоского напряженного состояния ог = 0, тгх = 0, хуг = 0 оно соответствует уравнению (34). Для плоского напряженного состояния коэффициент J3 = 0 и один из корней характеристического уравнения равен нулю, т. е. одно из главных напряжений обращается в нуль.
В случае линейного напряженного состояния два главных напряжения равны нулю, и, следовательно, в уравнении (67) должно быть Л = Л == 0.
В общем случае характеристическое уравнение (67) имеет три действительных корня: оь о2, вз — три главных напряжения.
Внося значения (Ь в любые два уравнения (63) и присоединяя уравнение (64), получаем систему уравнений для определения значений Z(n, и п(1), определяющих положение главной площадки с напряжением оь Подобным образом находятся направляющие косинусы двух других главных площадок.
Корни уравнения (67) могут быть найдены по точным формулам для решения кубических уравнений (формулам Кардано). Во многих случаях удобно воспользоваться численным методом Ньютона, представив уравнение (67) в виде
/ (CTv) — Оу — OyJi — OyJ2 — «7з = 0.	(71)
Если ov(i} — i-e приближение для значения корня, то следующее приближение
== o’v(i)—(i = 0,1, 2, ...);	(72)
dov (av(i))
производная
(cTv(i)) ==3	— 2crV(i)/1 — J2-
Схема численного решения показана на рис. 2.25. Для выбора исход-
ного приближения полезно предварительно определить приближенно области перемены знака функции /(ov). Расчет по формуле (72) заканчивается, когда исходное и последующее приближения достаточны близки.
Инварианты напряженного состояния в точке. Рас
Рис. 2.25. Схема численного решения характеристического уравнения /(<Jv) = 0 методом Ньютона
положение главных площадок и значения главных напряжений в точке зависят от гео
метрии детали, действующих
на нее нагрузок и других факторов. Например, при растяжении трубы одна из главных площадок в точке поперечного сечения будет лежать в плоскости сечения; при кручении трубы такая пло
46
ГЛ. 2. НАПРЯЖЕНИЯ
щадка не будет главной, так как в ней будут действовать касательные напряжения.
Понятно, что расположение главных площадок и значения главных напряжений не могут зависеть от того или иного выбора системы координат или принятого направления осей. Тогда коэффициенты характеристического уравнения напряженного состояния (уравнения (67)) не должны зависеть от выбора системы координат, т. е. быть инвариантными при изменении системы координат (например, при повороте системы координат). Коэффициенты характеристического уравнения называются инвариантами напряженного состояния. Величина называется линейным, А — квадратичным и Л — кубичным инвариантами (по отношению к компонентам напряжений).
Понятие о тензоре напряженного состояния. В механике много фундаментальных понятий связано с векторными величинами (сила, скорость, ускорение и т. п.). Вектор в обычной (трехмерной) системе координат можно представить в виде столбца
Рис. 2.26. Обозначения напряжений при тензорном описании напря-
женного состояния
а
(73)
где aXt ау и az — три скалярные величины — проекции вектора на оси координат. Для векторных величин определены аналитические операции: сложение, вычитание, умножение. Например, сумма двух векторов а и о равна
Однако существуют физические величины более сложной природы, например напряженное состоя-
ние в точке нагруженного тела, которое нельзя описать с помощью какои-ли-бо векторной величины. Тогда вводится понятие «тензор», который образуется из трех векторных величин подобно тому, как сам вектор образуется из трех скалярных величин. Таким образом, тензор характеризуется девятью
скалярными величинами — компонентами тензора, которые записываются в виде таблицы. Например, тензор напряжений записывается в следующем виде:
т ху
т
zy
(75)

Понятно, что тензор напряжений может полностью характеризовать напряженное состояние, так как его таблица включает компоненты напряжений по трем взаимно перпендикулярным площадкам. Из предыдущего нам известно, что этих данных достаточно, чтобы выяснить напряжения в произвольной площадке.	“
Тензор напряжений является" симметричным, так как таблица (матрица) -тензора симметричная. Симметрия тензора напряжений является следствием
7. УРАВНЕНИЯ РАВНОВЕСИЯ
47
парности касательных напряжений. Симметричный тензор характеризуется не девятью, а шестью скалярными величинами. К более компактной записи векторов и тензоров ведет несколько иной способ обозначения осей, если вместо х, у, z обозначить оси хь х2, х3. Компоненты напряженного состояния в осях xi, х2, (рис. 2.26) обозначаются О|2, ...
Тензор напряжений в компактной записи будет таким:

Q12	а13
а22	а23 ’
а32	а33
= {%}’ = 2’ 3-
(76)
Тензор, к сожалению, не имеет геометрического образа, однако по отношению к тензорным величинам определен ряд операций. Напрнмер, сумма двух тензорных величин и Т^есть тензор, причем
Го = та> + Т<2)= (а(1) + сг(2)}.	(77)
Действия над тензорами во многих случаях совпадают с действиями над матрицами.
Тензор напряжений имеет компоненты с двумя индексами, пробегающими значения от 1 до 3. В силу этого он называется тензором второго ранга. Существуют тензоры более высоких рангов; с другой стороны, вектор можно назвать тензором первого ранга.
При повороте системы координат компоненты тензора изменяются, так как по физическому смыслу они представляют собой напряжения в координатных площадках. Однако величины J h /2 и Л (см. формулы (68)— (70)) являются инвариантами тензора напряжений.
7. Дифференциальные уравнения равновесия элемента тела и краевые условия
Вводные замечания. Ранее при анализе напряженного состояния рассматривались условия равновесия элементов тела для определения напряжений в различных площадках. Изменение напряжений по граням элементов в связи
с приращением координат не учитывалось.
Учет указанных изменений приводил к бесконечно малым более высокого порядка малости, т. е. был несущественным. По этой же причине исчезли из уравнений и массовые силы (силы тяжести, силы инерции и др.). '
При анализе напряжений в косых площадках достаточно было считать, что на параллельных гранях основного параллелепипеда (рис. 2.27) с точностью до бесконечно малых первого порядка напряжения одинаковы. Сейчас приступаем к дальнейшим уточнениям, необходимым для анализа распределения напряжений в различных точках тела.
Рис. 2.27. К выводу дифференциального уравнения равновесия элемента в случае одноосного напряженного состояния — растяжения вдоль оси
Уравнение равновесия элемента тела в случае одноосного растяжения. В точке (Xj у, z) выделен элементарный параллелепипед (см. рис. 2.27) с размерами ребер dx, dy, dz, Будем считать, что
48
ГЛ. 2. НАПРЯЖЕНИЯ
на грани, проходящей через точку А, действует нормальное напряжение Ох.
Так как рассматривается только растяжение (сжатие) вдоль оси х, то по другим граням нормальных напряжений нет, а касательные напряжения по всем координатным граням отсутствуют.
В элементарных площадках, перпендикулярных оси х, но проходящих через различные точки тела, напряжения ох будут в общем случае также различными, т. е.
Ох = /(^, У, Z).
Тогда следует заключить, что на грани, проходящей через точку Z?, действует нормальное напряжение
д(У„
(78>
где дОх/дх = 5/(х, у, z)/dx — частная производная функции ох = = /(х, у, z) (дифференцирование ведется по переменной х; переменные у и z условно считаются постоянными величинами).
Например, если напряжение ох является линейной функцией координат
Ох = Со + С.х + С2у + C3z,	(79)
то
<80>
На тело действует массовая сила (на единицу массы) X (центробежная сила, сила тяжести и т. п.). Массовая сила, приложенная к элементарному объему,
pXdxdydz,	(81)
где р — плотность материала.
Из условия равновесия элемента получаем
— Q^dydz + ^ах + dxjdydz + pXdxdydz = 0,	82)
или в окончательной форме
да
^г + рХ = 0.	(83)
Замечание. При выводе условия равновесия напряжение ох в пределах грани считалось постоянным. Можно показать, ссылаясь на бесконечно малые размеры граней, что учет изменения напряжений в различных точках грани дал бы слагаемые более высокого (четвертого) порядка малости.
Пример 1. Определить распределение растягивающих напряжений в бурильной штанге под действием собственного веса. Схема бурильной установки показана на рис. 2.28. Штанга рассматривается как стержень постоянного сечения. Распределение растягивающих напряжений по поперечному сечению предполагается постоянным. Ось х направляем вдоль оси стержня. Па штангу действует усилие веса.
7, УРАВНЕНИЯ РАВНОВЕСИЯ
49
(, Г вес материала 1 dim т = [объем материала]’ например Н/см3 j, то на единицу массы приходится усилие
Х =	(84)
Из условия равновесия (83) следует выражение
* +рХ=^ + ? = О.	(85)
ОХ	ох
Из последнего уравнения получаем ах(х) = — ух + С.
Рис. 2.28. Расчетная схема бурильной штанги: а —общая схема; б —элемент штанги; в —эпюра распределения растягивающих напряжений по длине штанги
Произвольная постоянная С находится из краевого условия: при х = I Ох(0 == — + С = 0.
Определяя С, находим
ох(х) «Л (* — *)•	(86)
Наибольшее напряжение получается в сечении х = 0:
Ox max s yk	(87)
Из формулы (87) вытекает, что длина штанги не может быть беспредельной: она ограничивается прочностью материала на растяжение.
Если допустимое напряжение на растяжение
[а]р = А,	(88)
п
где Oft —предел прочности, л —запас прочности (обычно л = 1,5—2,5), то 4 И. А. Биргер, Р. Р. Мавлютов
50
ГЛ. 2. НАПРЯЖЕНИЯ
предельная длина штанги постоянного сечения по равенству (87)
I - 1СТЬ _ 1 0Ь ‘пр - — - —• —
(89)
Из последней формулы вытекает, что для штанги наиболее подходящими будут материалы, обладающие высоким пределом прочности и малым удельным весом. Отношение

У
(90)
иногда называют удельным пределом прочности (dim (оь/'Т) » [длина]). Эта характеристика чрезвычайно важна для авиационных материалов, так как вес авиационной конструкции является одним из ее основных показателей; обычно вь = 15—40 км.
Пример 2. Определить распределение растягивающих напряжений по длине вращающегося стержня. На рис. 2.29 показана расчетная схема. Направим
Рис. 2.29. Растяжение быстровра-щающегося стержня (лопатки)
ось у по оси вращения, ось х — по оси стержня. В точке А (л, у, z), находящейся от оси вращения на расстоянии г, на элемент материала действует центробежная сила
dC = pco2r-dx dy dzt
жения распределены равномерно по действия центробежных сил
где p — плотность материала d im р =
[масса 1
например кг/см3); <в —уг-ловая скорость вращения ^dim со = [рад]
=[-г]-с )•
Размеры поперечного сечения считаем малыми по сравнению с продольными размерами, полагая г « ж. Предполагается, что растягивающие напря-поперечному сечению. Массовая сила от
X = со2*.
Из условия равновесия получаем
dOL. а + рЛ = о, дх
откуда
ах (х) = — у (А?2 4-С.
Определяя произвольную постоянную из условия
ах (/?) = — у рсо2Я2 +С = 0, находим распределение растягивающих напряжений:
ах (ж) = 4 Р®2	•	(91)
7. УРАВНЕНИЯ РАВНОВЕСИЯ
51
Если радиус корневого (заделанного) сечения равен Яо, то наибольшее напряжение
1	/	/?2\	«
ахшах — — Pw	И
где uR = ©Я —• окружная скорость на внешнем радиусе стержня; | = RQ/R — относительный радиус корневого сечения.
Из формулы (92) видно, что окружные скорости вращающегося стержня ограничены прочностью материала. Предельная допустимая окружная скорость при малом радиусе втулки (§ = 0) соответствует условию
ab 1	2
ахш'ах -------2 VйR*
откуда
(93) н г лр f пу
В равенстве (93) g — ускорение силы тяжести (g = 981 см/с2); оь, п, 7 — предел прочности, запас прочности и удельный вес. Для стали с <j& = 90 000 Н/см2, 1 = 0,08 Н/см3, п = 2
, _ 1/2-981-9-104
Ur~ У “нй---------
= 340-102 — = 340—• с с
Дифференциальные уравнения равновесия элемента тела. Рассмотрим равновесие элемента тела, примыкающего к точке А(х, у, z) (рис. 2.30); размеры ребер dx.dy.dz. На гранях элемента, содержащих точку А. напряжения имеют следующие значения:
ADEF: Ох» Тх^, тжг;
ABCF). Оу, ABGF: ог, Tzx, Xzy.
Рис. 2.30. Условия равновесия элемента тела
На рис. 2.30 показаны или обозначены не все напряжения, чтобы излишне не загромождать чертеж. На других гранях будем иметь:
HGBC :ох+ ~-dx, ^ + -SLdz, T„ + -^-dx; u^c	их.	vX
HGFE:ov + ^- dy, zyx+^-dy, + ^-dy,
HCDE+ dz, тгх + dz, t2V + dzr.
52
ГЛ. 2. НАПРЯЖЕНИЯ
Приращение напряжений по отношению к другой параллельной грани связано с приращением одной из координат. Кроме напряжений на гранях элемента, на него действует массовая сила, компоненты которой обычно обозначают X, У, Z.
Составим суммы проекций всех сил на оси координат. Удобно сразу рассматривать две параллельные грани, так как напряжения на них направлены в разные стороны. Рассмотрим проекцию сил на ось х. На гранях ADEF и BCHG составляющие по оси х имеют только нормальные напряжения:
7	7	(	9^Х	1	\	1
—	axdydz + I ох + dx I dydz.
Среди сил, действующих по граням ADCB и FEHG, проекцию на ось х дают касательные напряжения
—	'lyx dx dz + ^ХуХ 4—dy^ dx dz.
Силы на гранях ABGF и DCHE составляют проекцию на ось х
(дх \ т2Х + dz 1 dx dy.
Сумма проекций всех сил с учетом массовой силы дает следующее условие:
_^+^£ + _^L + pX = 0, дх	ду	dz 1 г	’	(94)
и аналогично для других осей: дх	до,.	• -Т1 + ^- + Чг- + рк = 0, дх	ду	dz	‘	’	(95)
дх	dxvz	d(Jz -Ч- + -Ч- + -Ч + pz = о. дх	ду	dz	v	(96)
Уравнения (94) — (96) представляют собой три дифференциальных уравнения равновесия элемента тела в прямоугольных (декартовых) координатах.
Из механики известно, что в общем случае для любого тела, находящегося в равновесии, должны выполняться шесть условий равновесия (три — относительно составляющих усилия и три — для составляющих момента). Три условия для моментов были рассмотрены ранее, и они не изменяются при учете приращения напряжений по граням элемента. Эти три условия представляют свойства парности касательных напряжений
Тху = Тух, Тух === Тху, Tzx 383 Txz.	(97)
Пример. Покажем, что для случая плоского напряженного состояния, когда
Ох » 0, Тхх = 0, Tzy = 0	(98)
и массовые силы отсутствуют (Х = У = 2 = 0), условия равновесия будут
7. УРАВНЕНИЯ РАВНОВЕСИЯ
53
удовлетворены, если положить д2Ф	д2Ф	д2Ф
°х = ду2 ’	= "дх2"1 Х*У = ~ дх ду'
Ф(я, у) — произвольная непрерывная функция координат. Действительно, надо позаботиться только об условиях (94) и (95), так как уравнение (96) удовлетворяется в силу равенства (98). Подстановка соотношений (90) в уравнения (94) и (95) приводит к тождествам
д3Ф д3Ф дх дуг ~ дудхду~ ' з	з	(100)
д3Ф	53Ф
“ дх2ду + ^5? “ °’
так как частные производные непрерывных функций не зависят от порядка дифференцирования.
Замечание. Не следует думать, что равенства (99) дают полное решение плоской задачи. Используя соотношения (99), удается удовлетворить только уравнения равновесия, однако, как будет ясно из дальнейшего, для полного решения задачи функция Ф(ж, у) должна еще удовлетворить условия совместности деформаций всех элементов.
Дифференциальное уравнение равновесия элемента в тензорной форме. Вспоминая тензорные обозначения и учитывая свойство парности касательных напряжений вц == о^, можно записать уравнения равновесия в следующем виде: .
dxt -J-^21 _	^22	+ dx о .£^3	+ pxx-o, 1		 A
dx*	‘ dxa	1 dx_	* РЛ2 —• 0,
1	2	3	
g<T31 ,	do32	5ff33 dx3	+ px3 = o.
dx^ ‘	dx%		
(101)
Числовая индексация осей позволяет применить приемы сокращенной записи. Три уравнения (101) запишем в виде
j +	= 0 (i == 1, 2, 3).	(102)
В уравнении (102) запятая в индексе означает дифференцирование по координате, указываемой следующим за запятой индексом. Далее в тензорной записи используется правило Эйнштейна: по двум одинаковым индексам проводится суммирование от 1 до 3. В уравнении (102) такое суммирование проводится по индексу /. Давая индексу i значения 1, 2, 3, получаем каждый раз одно из уравнений (101).
Краевые условия для напряжений. Уравнения равновесия (94) — (96) справедливы для всех внутренних элементов. Равновесие элементов, примыкающих к поверхности тела, обеспечивается выпол-нением краевых условии (рис. 2.31, а, б).
Допустим, что на поверхности тела заданы внешние распределенные нагрузки (напряжения на поверхности). Вектор напряжения
pv(p«, pz)
54
ГЛ. 2. НАПРЯЖЕНИЯ
Рис. 2.31. Краевые условия для напряжений: а —общий случай действия распределенной по поверхности нагрузки; б — поверхностные нагрузки, действующие на хвостовик лопатки компрессора газотур-. бинного двигателя
имеет составляющие по осям х, у и z соответственно рх, ру, рг. Элемент поверхности dS, нормаль к которому v, можно рассматривать как косую площадку и записать аналогично соотношениям
(55) —(57):
Ох^ “Ь Xyxm 4“ Т2х72 = рх,
Тху2 + (5уШ + ХгуП = ру, (103} TxzZ + Хугт + вгП = рг,
где Z, ш, п~ составляющие единичного вектора нормали (направляющие косинусы нормали) ; ах, ..хух, .;компоненты напряженного состояния в точках поверхности.
Если часть поверхности свободна от действия внешней нагрузки, то для точек этой части поверхности
Рх = 0, ру = 0, рг = 0. (104)
Действие сосредоточенных сил. В конструкциях встре-
чаются внешние нагрузки, приложенные к небольшим участкам поверхности (рис. 2.32). В таких случаях удобно ввести понятие (модель) «сосредоточенное воздействие» или «сосредоточенная сила».
Рис. 2.32. Пример действия со- Рис. z.33. Сосредоточенная сила как ре-средоточенных сил (взаимодейст- зультат предельного перехода: а — повив вала и. шарикоподшипника) верхностная распределенная нагрузка; б —замена распределенной нагрузки сосредоточенной силой
Пусть на участке поверхности 50 (рис. 2.33) приложены внешние распределенные нагрузки, интенсивность которых (напряжение) равна р. Если площадь 50 мала, а напряжения р велики, то их действие можно заменить сосредоточенным усилием
Р =	(105)
7. УРАВНЕНИЯ РАВНОВЕСИЯ
55
На достаточном удалении от малой площадки 50 в двух схемах действия внешней нагрузки напряжения будут практически одинаковыми, что дает основания для использования представления о сосредоточенном воздействии внешней нагрузки. Точнее, под сосредоточенным усилием понимается предел
lim (pS0) = Р.	(106)
р-*оо so->o
В местах приложения сосредоточенных усилий интенсивность поверхностной нагрузки стремится к бесконечности. Это заключение в соответствии с равенствами (103) относится и к компонентам напряженного состояния в точке приложения силы (в некоторой малой области).
Следует всегда иметь в виду, что модель сосредоточенного воздействия является расчетной схемой, дающей достоверные результаты на некотором удалении от точки приложения силы. Однако представление о сосредоточенном воздействии часто очень удобно, и оно широко применяется в технических расчетах.
Принцип Сен-Венана для краевых условий. Рассмотрим тело, которое нагружается на одном из небольших участков распределенными усилиями. В одном случае (рис. 2.34, а) нагрузка рас-
Рис. 2.34. Принцип Сен-Венана
пределена в пределах участка равномерно, в другом (рис. 2.34, б) — неравномерно. Равнодействующие двух распределенных нагрузок P=§pdSQ	(107)
so
одинаковы.
Отметим, что системы внешних сил на участке, й^еющие оди- ' наковые значения равнодействующего усилия, называются статически эквивалентными. В двух случаях нагружения напряженные состояния в детали в пределах участка нагружения будут, конечно, различными, но на некотором удалении от рассматриваемого участка окажутся практически одинаковыми.
Сущность принципа Сен-Венана состоит в следующем. На удалении от нагруженного участка поверхности, порядка наибольшего
56
ГЛ. 2. НАПРЯЖЕНИЯ
линейного размера участка особенности распределения нагрузки и пределах участка несущественны, важна только величина равнодействующего усилия. Для нагружения, показанного на рис. 2.34г при г > rQ напряжения и деформации в точке В будут практически одинаковыми. Принцип Сен-Венана имеет большое практическое значение, так как часто позволяет упростить краевые условия, если основной интерес представляют напряжения и деформации на некотором удалении от места приложения нагрузки.
Замечания. 1. Принцип Сен-Венана не доказан в общем случае, но во всех полученных точных решениях он соблюдался. Принципы, справедливые для широкого класса задач, но не доказанные в общем виде, называются эвристическими. Принцип Сен-Венана принадлежит к числу эвристических.
2. Принцип Сен-Венана не указывает конкретно то расстояние, на котором уже не сказываются отличия в распределении внешней нагрузки. В нем утверждается, что такие расстояния имеют порядок наибольшего размера участка приложения нагрузки.
Напомним, что в физике принято называть величинами одного порядка величины, различающиеся не более чем в десять раз.
Несмотря на некоторую неопределенность в количественном отношении, физическая сущность принципа Сен-Венана важна для инженерного анализа конструкций.
3. Принцип Сен-Венана распространяется на статически эквивалентные системы внешних нагрузок, приложенных на малых участках поверхности тела.
ГЛАВА 3
ДЕФОРМАЦИИ
Из опыта известно, что под действием внешних усйлий элементы машин и конструкций изменяют свои первоначальные размеры и форму (удлинение болта, прогиб лопастей вертолета под действием собственного веса, прогиб труб и балок и т. п.).
В большинстве случаев изменения размеров и формы после приложения нагрузки невелики, но в ряде случаев могут препятствовать нормальной работе. Умение определять деформации, установление их допустимых значений имеют важное значение при проектировании и расчете конструкций. Рассмотрение деформаций необходимо также для. выяснения закона распределения напряжений в элементах конструкций, для оценки работоспособности по условиям прочности.
В теории деформаций сопоставляются начальное и деформированное состояния тела. Время деформирования, траектории точек тела в процессе деформации, физические свойства тела оставляются в стороне. Изучается геометрическая задача — изменение длины и взаимных углов поворота линейных элементов тела.
8.	Перемещения и деформации
Перемещения и деформации в случае простого растяжения.
Если к стержню, закрепленному в корневом приложить на другом торце осевое усилие, то ние стержня — точка А перейдет в точку А*.
Перемещение точки А в процессе деформации (отрезок АА*) обозначается на рис. 3.1 величиной и. Чем длиннее будет стержень, тем больше перемещение его конца под действием нагрузки. Деформацию материала стержня характеризует отношение перемещения к первоначальной длине:
сечении (рис. 3.1), произойдет удлине-
Величина е является безразмерной и называется линейной деформацией или, более кратко, деформацией. При сжатии стержня и < 0) деформация становится отрицательной (е<0). Деформация в материале конструкции в рабочих условиях составляет сотые, редко десятые доли процента. При разрушении
Рис. 3.1. Удлинение — деформация стержня при растяжении
деформация конструкционных материалов до-
стигает десятков процентов (обычно до 30%). Равенство (1) используют для определения малых деформаций (е<0,1). При больших деформациях следует рассмотреть весь процесс деформи-
рования. Пусть в данный момент нагружения перемещение конца
58
ГЛ. 3. ДЕФОРМАЦИИ
стержня составляет и и происходит приращение перемещения du. Тогда приращение деформации
j du
dt— -т-г Zo + “
Деформация стержня при изменении его длины от 19 до I составит
1~1о f du
о
'о
(2>
Величина еи, определяемая из последнего равенства, называется истинной деформацией (или логарифмической деформацией). Разлагая в ряд выражение (2), находим
т / j । \ U	1 / U \	1 о . 1 «
еи = In (1 + е) = - — у j + ... = е — у8- + у е3 — .,.
При малых е формулы (1) и (2) совпадают, при s > 1% расхождение может быть заметным, при е > 10% — существенным. Причина расхождения очевидна: удлинение и в равенстве (1) относится к первоначальной длине 10. Если относить удлинение к «средней длине», в процессе деформации полагая
еи «---« е — у еа,	(3)
-.+4“
то совпадение с истинной деформацией будет вплоть до квадратичных членов. В дальнейшем основное значение имеет случай малых
деформаций, что позволяет использовать наиболее простую зависимость (1).
Погрешность равенства (1)
Д= -Ц2-" <у|8|.	(4)
Например, если, как обычно, деформация в рабочих условиях меньше 0,5%, то погрешность формулы (1) меньше 0,25%; такая погрешность вполне допустима в техниче-
Рис. 3.2. Определение линейной деформации в точке А в задан-
ном направлении	ских расчетах, так как она меньше
погрешности самих измерений.
Определение линейной деформации. Рассмотрим определение линейной деформации в точке А деформируемого тела (рис. 3.2). Линейная деформация, в различных направлениях будет различна, и следует указать не только точку, в которой определяется деформация, но и ее направление. Пусть деформация определяется в направлении, задаваемом единичным вектором s (см. рис. 3.2).
8. ПЕРЕМЕЩЕНИЯ И ДЕФОРМАЦИИ
59
На указанной прямо!! рассматривается вторая, бесконечно близкая точка В и прослеживается изменение отрезка АВ =*ds в результате деформации. После общей деформации тела точка А перешла в точку А*, точка В — в точку В*.
Будем называть линейной деформацией в точке А в направлении 5 следующую величину:
— АВ ds* — ds
е3-----ЗВ—=
где А* В* — ds* — длина отрезка ds после деформации.
В дальнейшем будет показано, каким образом вычисляется линейная деформация, если известны перемещения точек в деформи
рованном теле.
Определение угловой деформации. Линейная деформация не мо
жет полностью охарактеризовать изменение элемента тела при его
деформировании, так как возможно не только изменение линейных размеров, но и скос граней. На рис. 3.3 показан общий случай деформации
Рис. 3.4. Определение угловой деформации в точке между двумя взаимно перпендикулярными направлениями
Рис. 3.3. Общая деформация элемента как сумма линейной и угловой деформаций
плоского элемента. Переход от начального состояния ABCD в конечное A*B*C*D* (точки А и А* условно совмещены) осуществляется за счет изменения длины (без изменения углов) и за счет изменения углов (без изменения длины).
Изменение угла между двумя взаимно перпендикулярными до деформации направлениями называется деформацией сдвига. В общем случае для определения деформации сдвига в точке А между направлениями 5 и г рассматриваются два бесконечно малых отрезка АВ и АС вдоль указанных направлений (рис. 3.4). Деформация сдвига
== У1лг +	(6)
где 714г, 7г*г “ углы поворота отрезков в плоскости sr относительно первоначальных направлений.
60
ГЛ. 3. ДЕФОРМАЦИИ
9.	Связь перемещений и деформаций
Перемещения, составляющие перемещений. Допустим, что имеется система координат х, у, z (рис. 3.5), неподвижная в пространстве (например, жестко связанная с точками закрепления тела). Произвольная точка тела до деформации обладает координатами X, у, Z.
После деформации точка А перейдет в точку Л*. Вектор А*А представляет собой перемещение точки А. Перемещения точек тела
Рис. 3.5. Определение деформации 8Х
в результате деформации обычно считаются малыми относительно линейных размеров конструкции.
Замечание. Следует-подчеркнуть, что порядок малости всегда предполагает наличие «эталонных» величин, относительно которых определяется порядок малости. Например, перемещения точек поверхности Земли в результате температурных напряжений могут составлять-50—100 км, однако эти перемещения являются малыми по сравнению с радиусом Земли R ~ 6400 км.
Составляющие перемещения точки А по осям х, у, z обозначим и, и, w. Рассмотрим отрезок АВ, параллельный оси х. Длина отрезка равна dx. Составляющие перемещения точки В будут отличаться от составляющих в точке А, так как функции и, v, w получат приращения (координата вдоль оси х в точке В имеет значение x + dx). Составляющие перемещения в точке В будут такими:
u+^dx» Р + w+^dx'
В результате деформирования точки А и В перейдут в точки Л* и В*. Координаты указанных точек Л, В, Л*, В*:
Л(х, у, 2), B(x + dx, у, 2),
Л*(х + и, y + v, z + w),
\	С/«ь	W	UJb
9. СВЯЗЬ ПЕРЕМЕЩЕНИЙ И ДЕФОРМАЦИЙ
6t
Формулы Коши для линейных деформаций. Линейная деформация в точке А (х, у, z) в направлении оси х будет равна
Из аналитической геометрии известно, что расстояние I между двумя точками с координатами (х2, у2, z2) и (xb yh z4) равно
1 = 1/ (х2-Х1У + (у2 - у{}2 + (z2 - Zt)2.
Применяя эту формулу для определения длины отрезка получим
A*B* = dx	+
у \ дх J \дх / \дх J
Учитывая, что АВ — dx, находим из равенства (7)
ех = 1/1+2^+(?-)2 + (гГ+(?)2 - 1.	(8)
у дх \дх ] \дх] \дх J	х '
Рассмотрим теперь случай малой деформации, когда
. (9)
дх ’ дх' дх	4 '
Вспоминая, что при а < 1
(1 + а)п = 1 + па + ...,
из соотношения (8) находим
„ ди , 1 Г/йА2 . (dv\2 , ZduA2]
8» = di +	+ W + tej ]•	<10>
Членами, стоящими в квадратных скобках, при малых деформациях (условие (9)) допустимо
пренебречь, и тогда
(И)
Соотношение (И),которое представляет первую формулу Коши можно получить сразу, если воспользоваться правилом, справедливым при малых деформациях: для определения линейной деформации в заданном направлении достаточно рас-
Рис. 3.6. Определение малой деформации ех
смотреть проекции перемеще-
ния точек на заданное направление. Иными словами, для определения малой деформации вдоль оси х достаточно принять во вни-
мание только составляющие перемещения по оси х.
62
ГЛ. 3. ДЕФОРМАЦИИ
На рис. 3.6 показаны проекции точек 4* и В* на направление АВ, параллельное оси х. Отрезок Ах А равен и, а В*В = и, + —dx. Малая деформация в точке А в направлении оси х равна ди
_ А* В* - АВ
8х	АВ	дх дх'
Аналогичным образом можно найти следующие зависимости:
ди
J ду
ди>
ег = т-. dz
(12)
(13)
Соотношения (11) —(13) составляют
Рис. 3.7. Определение деформации сдвига в точке А в плоскости уОх
перемещений на плоскость . хОу
Проекции отрезка 4*5* на оси х Далее, находим
три первые формулы Коши.
Формулы Коши для угловых деформарий. Рассмотрим определение деформации сдвига в точке 4 (рис. 3.7) в плоскости, параллельной плоскости уОх. Для этого проследим за изменением угла между отрезками 45 и АС, составляющими первоначально прямой угол. Длина отрезков до деформации составляет 45 =» = dx, АС = dy. Предполагая деформации малыми, достаточно рассмотреть проекции (условно считая w ~ 0). И у будут dx + ^dx, ^dx.

dxdx
dv
dx'
<41+
\ ”x /
так как ди/дх < 1.
Проекции отрезка 4*С* на оси х и у соответственно равны ди ду	ди
' —	~ Угол сдвига
JZdy>dy + j^dy и tgT2==»-V2= f , v \ dy) , du du W=V1 + Y2 = - + -
(14)
10. ГЛАВНЫЕ ДЕФОРМАЦИИ
6?
Аналогичным образом можно получить
Tzx
ди dw
dw ди
дх ’ dz*
(15)
(16)
Формулы (14)— (16) представляют формулы Коши дЛД малых деформаций сдвига.
Сводка результатов. При малых деформациях, когда производные перемещений по координатам значительно меньше единицы, связь перемещений и деформаций выражается формулами Коши
ди	до	dw
* .	дх ’ у ду'	dz
ди ди	до	dw	dw	ди
^ху ду + дх1 ^yz dz	ду ’ ^zx дх	dz*
(17)
10.	Линейная деформация в произвольном направлении. Главные деформации, тензор деформаций
Линейная деформация в произвольном направлении. Часто при исследовании деформаций, например с помощью проволочных тензометров (тензорезисторов), необходимо определять линейную де-формацию в направлении, составляющем произвольный угол а с осью х. .
Рассмотрим случай плоской деформации, когда перемещение вдоль оси z отсутствует (рис. 3.8).
Рис. 3.8. Линейная деформация в произвольном направлении (при плоской де* формации, w = 0)
Перейдем к определению линейной деформации вдоль прямой, проходящей через точку А. Прямая лежит в плоскости, параллельной плоскости уОх, и направлена под углом а к оси х. Направление характеризуется единичным вектором s. Рассмотрим отрезок AB^ds (см. рис. 3.8), лежащий на указанном направлении. ✓
64
ГЛ. 3. ДЕФОРМАЦИИ
Компоненты перемещения точки А в результате деформирования составляют и, и, компоненты перемещения точки В
, ди j , ди . t ди j , ди j и + ^r-dx + ^-dy, и + — dx 4- dy.
дх ду 17 ’ дх ду J
Так как теперь обе координаты точки В отличаются от координат точки 4, то составляющие и и и получили приращения. Малая линейная деформация в направлении s будет равна
Л*В* — АВ	А* В* —ds
8* = АВ = S :
(18)
отрезок
А* В* = ds + (и + 5^- dx + dp) I + (и + dx + dp) т — ul—vn— \ дх ду v j	\ дх ду j
-ds+(^dx + ^dy)l + [rxdx + Wdy)m' <19)
где I = cos а, т = cos (л/2 — а) — sin а — направляющие косинусы направления s (проекции единичного вектора s на оси координат).
Из соотношений (18) —(19) получаем
(ди dx	,	ди dy\	(ди dx . ди dy\
е«= т--г	+	т-/ Н +	(г-~г + т- т-1т-	(20)
\дх ds	ду ds)	\дх ds ду ds J	v 7
Так как ds2 = dx2 + dy2,	(21)
то
=	'	(22)
ds 1 ds	47
С учетом последних соотношений находим выражение для линейной деформации в направлении s: ди , ди 9 , / ди , ди \ т е$ ==: — I * + — щ* +	—F	\1т
дх ду уду дх J
или в силу зависимостей (11) ев = ехР + еутп2 + \ху1т.	(23)
В другой форме имеем
8, = 8« cos2 а + eg sin2 а + sin а cos а.	(24)’
Замечание. Последняя зависимость по своей структуре аналогична формуле для нормальных напряжений в направлении, составляющем угол а с осью х (формула (17) гл. 2).
Если заменить ох на е«, оу на ev и на ^/2, то выражения для линейной деформации или нормальных напряжений в заданном направлении будут одинаковыми.
Рассмотрим теперь общий случай/ когда направление s характеризуется направляющими косинусами Z, тп и п и точка В имеет
10. ГЛАВНЫЕ ДЕФОРМАЦИИ
65
координаты (x + dx, y + dy, z + dz). Повторяя вывод уравнения (24) для пространственного случая, найдем
(ди dx , ди dy . ди dz\ . , _ ------__
дх аз ду ds dz ds J
(dvdx do-du du dz\	(div dx	dw du div dz \
' ds dy ds dz ds) Ш	ds dy ds dz ds J
Учитывая равенства
получим
8« » гх12 + еутп2 + 8zn2 +	+ ^гтп + ^гхп1. (25)
Главные направления и главные деформации. При определении главных направлений напряженного состояния в точке было показано, что в указанных направлениях нормальные напряжения* обладают экстремальными свойствами (имеют наибольшие значения по отношению к напряжениям в других направлениях). Воспользуемся этими свойствами для нахождения главных направлений деформации. Ограничимся практически наиболее важным случаем плоской деформации (деформация в плоскостях, параллельных плоскости хОу; перемещение ш = О).
Найдем экстремальное значение 8в в зависимости от угла а, характеризующего направление деформации. Приравнивая нулю производную, получим
d&
— 2ех cos a sin а + 28^ sin а cos а + уХ2/ (cos2 а — sin2 а) == О,
что дает
2gxy
tg 2ае =
8х Qy 8х еу
(26)
Величина
8 -Iv
(27)
называется тензорной компонентой сдвига.
Как уже указывалось, по аналогии между напряженным и деформированным состоянием величина 8^ соответствует Тху.
Соотношение (26) определяет два главных направления при плоской деформации (третье направление к ним перпендикулярно, соответствует деформации 83 ~ 0).
Представляя соотношение (24) в виде
е3 == у(ех + ev) + у (8х — ej cos 2а + ~ sin 2а (28)
5 И. А. Биргер, Р. Р. Мавлютов
66
ГЛ. 3. ДЕФОРМАЦИИ
и учитывая зависимости (26) и (27) гл. 2, найдем с помощью равенства (26) главные деформации
81 = 4	+ ev) + Т К(8* — 8«)2 + Yw>
= "jT (®х "Ь ®у)	~2	(®х	®У)2 Yaw
(29)
Тензор деформаций.	Тензор деформаций		имеет структуру,	, полностью	ана-
логичную тензору напряжении (с; 8х 8ху 8xz		и. разд. 6): 8Х	1	1	1 2 7ху 2 4		
^8	8ух kezx	& со со со со	| ~2 Yyx iTYzx	л -со N СО -гч |СМ	•	(30)
По аналогии с инвариантами напряженного состояния запишем инварианты деформированного состояния:
Ле = еж 4-	+ 8Z;	(31)
1 1 1
^28 ~ 8х8у “Ь 8y8z “Ь 8z8x Уху ~4* Ууг ~1± ?zx» (32)
Лв —
A L 8х 2 ^ху 2 7xz
1 , 1
Т у их еУ 2 Yyz
1	1
2	Угх 2 ^zv ez
(33)
Рис. 3.9. Изменение объема элемента при деформации
Напомним, что инвариантами деформированного (или напряженного) состояния называются величины, не зависящие от выбора системы координат. Разберем физический смысл первого инварианта дефор^ мируемого состояния. Найдем изменение объема элемента тела (рис. 3.9) при деформации. Первоначальный объем элемента
dV = dx dy dz. (34) После деформации ребра получили деформации 8Ж, ev, 82. Новый объем можно вычислить, пренебрегая деформациями сдвига: № (1 + 8х)(1 + 8у) х
X (i + ez)dxdydz. (35)
Объемная деформация составит dV — dVn
«У = —Зй—* - (1 + М (1 + »„) (1 + Ъ) - 1 о
или в пределах малых деформаций 8? = ех +
(36).
(37)
И. УРАВНЕНИЯ СОВМЕСТНОСТИ ДЕФОРМАЦИЙ
67
Первый инвариант Л8 представляет объемную деформацию, т. е. относительное изменение объема частицы материала. Это изменение зависит от свойств материала и напряженного состояния и не может зависеть от выбора осей системы координат.
Отметим, что тензор деформаций является симметричным, так как по определению
= Ту* в ТгУ’ ^zx == Yxz*	(38)
Если применяются для осей х, у, z обозначения xb z2, х3, то тензор деформации имеет следующий вид:
	е11	612	813?	
Т = * е	S21	822	823	= {8у},	(39)
	631	832	8зз	
где е-п = 8Х, 8^2 = еху = у е13 = еХ2 = у ух2. Компоненты перемещения обозначаются «2, »з-
Преимущества тензорных обозначений легко видеть на примере тензорной записи уравнений Коши для компонентов тензора деформаций:
eU = y(«ij+ttj,i) (г,/ = 1,2,3),	(40)
где запятая в нижнем индексе обозначает дифференцирование по координате, указываемой следующим за запятой индексом. Например,
е11=~дх^>	е12	И Т-Д*
11.	Уравнения совместности деформаций
Первая группа уравнений. Деформация в окрестности точки деформированного тела описывается шестью скалярными величинами: линейными деформациями 8у и 8z по трем взаимно перпендикулярным направлениям и угловыми деформациями ^.zx. Например, линейная деформация в произвольном направлении, характеризуемом направляющими косинусами Z, т и п (формула (26)), может быть определена, если известны шесть указанных величин.
Вместе с тем из формул Коши следует, что шесть величин €х, Sy,	Чух, 7 zx выражаются через производные трех функций
и, v и w. Следовательно, между компонентами деформаций должны существовать зависимости, вытекающие из условия, что для непрерывных дифференцируемых функций порядок дифференцирования не оказывает влияния на окончательный результат; например,
___________9_ fdf\ _	_ д2/ дх \ ду j ду \ дх J дхду дудх*
Возьмем для сопоставления следующие -формулы Коши:
Л ди	ди	ди . ди
х ~ ~дх '	— ~ду'	~ду ~дх*
5*
68
ГЛ, 3. ДЕФОРМАЦИИ
= g3“ . дх дУ дх ду'
Дифференцируя величину по х и по у, найдем _________________________________д\ { д\ дх2 ду ду" дх2.
Подобным образом или способом круговой перестановки индексов можно получить
(41)
д2у и «г/z		
ду dz	~ +	ду~
	-А.	
dz дх	- дх1	dz2
(42)
 (43)
Уравнения (41) — (43) образуют первую группу уравнений совместности деформаций.
Вторая группа уравнений. Существуют еще три тождества, которые получаются несколько более громоздким путем.
Выпишем выражения для деформаций сдвигов:
Уху	ди ди ду + дх 1	(44)
	ди dw dz + ду ’	(45)
Тгх	dw ди дх + dz *	(46)
Для того чтобы связать производные деформаций сдвигов с производной от ех, попытаемся исключить из правых частей уравнений (44) функции и и и?.-Так как следует сохранить в правой части одну производную от и, то нужно продифференцировать уравнение (44) по z, а уравнение (46) — по у. Тогда получим дУху _ д2и , д2 и ду dz дх dz' д2 w । дх ду ‘ ду dz
(47)
(48)
dz
дУ Из (47) и (48) найдем
дУху  дЪх _ 9 д2и , д2у , д2и> dz ду ду dz дх dz дх ду Сумма двух последних членов в правой части равенства в силу зависимости (45) равна д2у , д2и> _ дх dz дх ду дх ’ и тогда можно записать
&Уху __ дУуг .	__ 2 д2ц
dz дх ду ду dz
(49) -
(50)
Теперь, чтобы получить в правой части равенства производную от 8Х достаточно продифференцировать соотношение (50) по х:
д ( ^ху ___ ^yz |	\ _ 9 gx	/зд
.	дх \ dz дх ду ) ду dz
И. УРАВНЕНИЯ СОВМЕСТНОСТИ ДЕФОРМАЦИЙ
69
д
ду I дх
д [ aVzx
dz \ ду
(52)
(53)
С помощью круговой перестановки индексов получаем еще два тождества: ду ду \ ггх 1 <ху | __ 2_________________________________L
ду	dz /	dz дх'
Э?ху 	- 9
dz	дх )	дх ду
Уравнения (51) —(53) составляют вторую группу уравнений совместности деформаций.
Замечание. Шесть уравнений совместности деформаций (уравнения (41) — (43), (51) —(53)) были установлены французским инженером Б. Сед-Венаном, одним из создателей современной теории упруго-сти. Уравнения совместности часто называют тождествами Сен-Венана.
Физический смысл уравнений совместности деформаций. Компоненты деформации однозначно описывают деформацию элемента тела. В деформированном состоянии все элементы должны . образовывать единое тело. Если условия совместности деформаций нарушаются, то из отдельных элементов нель- _ зя составить тело без разрывов и пустот (рис. 3.10). В том случае, когда уравнения совместности удовлетворяются в каждой точке тела, перемещения и, и и w будут непрерывными функциями координат, что гарантирует непрерывное преобразование начальной формы тела в конечную (деформированную).
Если решение задачи о напряженном и стояниях сводится к отысканию перемещений и, у, w й последние выбираются среди класса непрерывных функций с непрерывными частными производными до третьего порядка, то уравнения совместности деформаций удовлетворяются тождественно.
Ml
Рис. 3.10. Деформированное состояние тела при нарушении условий совместности деформаций
деформированном со-
ГЛАВА 4
МЕХАНИЧЕСКИЕ СВОЙСТВА
КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ
Рис. 4.1. Схема испытания круглых образцов па растяжение
Вводные замечания. Для оценки прочностной надежности конструкций необходимо изучить поведение материала в служебных условиях при действии внешних нагрузок, температур и т. п.
В соответствии с принятой моделью материала — моделью сплошной среды— мы отказываемся от изучения внутренней микроструктуры материала (поведения кристаллической решетки, развития дислокаций и т. д.) и будем использовать феноменологический (описательный) подход. Такой подход означает, что, не вдаваясь в сущность внутренних процессов, явление (феномен) изучается по его внешним проявлениям при различных внешних воздействиях.
Не обсуждая общности подобного метода, используемого во многих областях науки и техники, укажем, что феноменологический подход предопределяет необходимость экспериментального изучения механических свойств материалов. Эти свойства изучаются в системе опытов с образцами материалов простой формы, при воспроизведении основных особенностей нагружения.
12.	Диаграммы деформирования, пределы текучести и прочности
Испытания на растяжение образцов материала. Основным опытом для определения механических свойств материала является получение зависимости между напряжениями и деформациями при растяжении. На рис. 4.1 показана схема испытания образцов в специальных испытательных машинах. Головки образца размещаются в захватах машины, к которым прикладывается внешнее усилие Р. В процессе испытания измеряется величина усилия и средняя деформация на определенной длине образца Zo. В результате строится зависимость между напряжениями и деформациями в образце материала:
Q = /(e),	(1)
которая называется диаграммой деформирования.
Напряжение в цилиндрической испытуемой части образца
g — P/F,	(2)
где Р — внешнее усилие, F — площадь поперечного сечения образца (F = nd2/4, d — диаметр образца).
Деформация
где Z —длина контрольного участка образца после деформации.
12. ПРЕДЕЛЫ ТЕКУЧЕСТИ И ПРОЧНОСТИ
71
Упругость, модуль упругости, пластичность, закон разгрузки и
закон упрочнения. При проведении опытов с растяжением образцов выявляются общие свойства конструкционных материалов — свой-
ства упругости и пластичности. На рис. 4.2 показаны типичные результаты опытов на растяжение. Если напряжение о не превышает определенной величины — предела упругости оу, то зависимость между напряжением о и деформацией е оказывается линейной:
а = Ее.	(4)
В этой зависимости Е — модуль упругости материала. Величина Е является важной характеристикой материала. Так как деформация 8 является безразмерной
Рис. 4.2. Свойства упругости и пластичности мате-
риала при испытании на растяжение
величиной, то размерность модуля упругости совпадает с размерностью на-
пряжения.
В системе единиц СИ dim Е = [сила/площадь] (например Н/мм2, МПа — мегапаскаль).
В технической системе единиц величина Е измеряется обычно в кгс/см2.
Значение Е для некоторых конструкционных материалов (Н/мм2, МПа) таково: для сплавов на основе железа Е = 2 • 105, для титановых сплавов Е = 1 • 105, для алюминиевых сплавов Е = 0,78 • 105.
Значение Е на кривой деформирования при определенных масштабах для о и 8 численно равно тангенсу угла наклона линейного
участка.
(5)
Е = tg р.
Линейная зависимость между напряжениями и деформациями является важным проявлением упругости материала. Однако основное проявление упругости материала состоит в следующем.
Если в точке А (а < оу) прекратить нагружение материала и снятье внешнюю нагрузку, деформация материала исчезнет (точка; изображающая состояние материала, вернется в начало координат) .
Напомним, что свойство упругости материала как раз и заключается в том, что после снятия внешнего воздействия все размеры детали (элемента конструкции) восстанавливаются. Для подавляющего большинства конструкционных материалов, как показывает опыт, свойство упругости сохраняется до определенного значения действующего напряжения.
При возрастании напряжений свыше предела упругости (о>ау) зависимость о от 8 перестает быть линейной.
Если в некоторый момент нагружения А прекратить нагружение и снять нагрузку, то разгрузка пойдет по прямой ЛЛ*, приблизь-
72
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
тельно параллельной начальному участку (закон разгрузки). Точка А перейдет в точку 4*, и в материале сохранится остаточная деформация которая представляет собой пластическую деформацию в материале, образовавшуюся при его нагружении. Полная деформация е в момент нагружения А
б = ев4-8р,	(6)
где упругая деформация
8е = О/Е.	(7)
Уравнение (6) справедливо для любого момента деформации. Упругая составляющая деформации не исчезает при появлении пластических деформаций, поэтому следует говорить об упругопластических деформациях материала. Однако если упругая деформация для металлов достигает значения примерно 0,2—0,8%, то пластическая деформация может быть 20—40%. В тех случаях, когда пластическая деформация значительно больше упругой (пластическое деформирование при технологических процессах и т. п.), упругими деформациями пренебрегают (модели жесткопластического тела).
Значение модуля упругости Е в формуле (7) принимается в большинстве расчетов не зависящим от пластической деформации. Опыты показывают, что некоторое влияние пластических деформаций на значение Е имеется: при еР>1% возможно снижение Е на 5—10%.
При повторном нагружении из точки 4* процесс нагружения пойдет по прямой 4*4, т. е. зона упругой деформации (по уровню напряжений) возрастет. После предварительной пластической деформации происходит упрочнение материала (закон упрочнения), при дальнейшем нагружении (переход от точки 4 к точке В) деформирование идет так же, как в случае однократного нагружения.
Замечание. Закон упрочнения прогнозирует повышение сопротивления материалов возникновению пластических деформаций при повторном нагружении — повышение предела упругости после предварительной пластической деформации. Существенно, что повторное деформирование идет в том же направлении. Если после пластической деформации растяжения провести деформирование в противоположном направлении (на сжатие), то упрочнение не наблюдается.
Предел текучести и предел прочности. На зависимость между условным напряжением о Условное напряжение вычисляется по формуле
_ 4Р 0 “ FO ~ ndo'
где — первоначальный диаметр образца.
При значительных деформациях (е>1%)
между условными и истинными напряжениями ( см. стр. 82 )
Р __ 4Р
Ои- Р ~ nd2'
рис. 4.3 показана и деформацией 8.
(8)
(9)
заметна разность
12. ПРЕДЕЛЫ ТЕКУЧЕСТИ И ПРОЧНОСТИ
73
где d — диаметр образца в процессе нагружения (деформирования). Значение ои на диаграмме деформирования показано штриховой линией.
Наиболее важными характеристическими сопротивлениями материала внешним нагрузкам являются пределы текучести и прочности. Предел текучести характеризует сопротивление материала
возникновению пластических деформаций. Так как переход от участка упругости к зоне появления пластических деформаций для большинства материалов носит плавный характер, то условились назначить определенную границу, после которой пластические деформации признаются существенными. Такой границей выбрано значение остаточной деформации 0,2%.
Пределом текучести о0,2 называется напряжение, которому соответствует остаточная (пластическая) деформация 0,2%. Часто предел
Рис. 4.3. Определение пределов пластичности и прочности на диаграмме деформирования
г текучести называется пределом пластичности; в технической литературе предел текучести о0.2 обозначается также От, ов. Важнейшей характеристикой прочности является предел прочности. Он определяется как отношение
оь =
Р max
(10)
где Ртах — наибольшее растягивающее усилие в процессе испытания до разрушения; Ро — первоначальная площадь поперечного сечения образца (для круглого образца Fo в л^о/^)-
На последнем этапе растяжения образца в его цилиндрической части образуется местное сужение («шейка», см. рис. 4.3) и процесс разрушения идет при уменьшающемся внешнем усилии Р. В точке В происходит потеря устойчивости равномерного пластического деформирования (пластическая деформация в этой точке е&), и на последнем этапе деформация происходит лишь в зоне шейки.
Наибольшее усилие при разрыве образца Ртах (оно действует в точке В) легко определяется измерительным устройством, так как нарастание усилия идет плавно.
Поскольку величины Ртах и Ро определяются просто, учитывая, что истинное сопротивление в момент отрыва ожр>а& (см. рис. 4.3), условились определять предел прочности по равенству (10).
74
Г-1!. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
Пределом прочности аь называется напряжение, соответствующее наибольшему усилию при разрушении образца, отнесенному к первоначальной площади поперечного сечения. Значения пределов текучести и пределов прочности для некоторых конструкционных материалов приведены в табл. 1.
Таблица I
Значения пределов прочности, текучести и удлинения при растяжении
Материал	а,, Н/мм2 О	%.2’ Н/Мм2	д, %
Низкоуглеродистые стали	300—400	180—250	20—40
Среднеуглеродистые стали	500—700	300-500	10-20
Легированные стали	800-1200	600—900	8-16
Титановые сплавы	900—1100	800-900	8-20
Алюминиевые сплавы	200-450	180-300	8—20
Обычно пределы текучести составляют а0,2 = (0,5—0,9) оь, причем большие значения относятся к пределу прочности для легированных сталей и титановых сплавов.
Пределы текучести и прочности при сжатии. Построение диа-
граммы деформирования при
сжатии связано с рядом трудностей. Первая из них состоит в том, что при сжатии стержня может наступить потеря устойчивости (искривление оси стержня). Проблема устойчивости стержней будет изучаться в дальнейшем, а сейчас отметим, что для устранения потери устойчивости надо применять образцы с малым отношением l/d. Однако по мере уменьшения этого отношения возрастает влияние на результаты опытов сил трения, возникающих меж-
Рис. 4.4. Образцы материалов ДУ опорными поверхностями.
для испытания на сжатие	На рис. 4.4, а показаны образ-
цы для испытаний на сжатие. Наиболее простой способ — передача усилия через плоские торцы. Образец должен быть обработан достаточно точно, с тем чтобы получить равномерное распределение напряжений сжатия по торцам. Для уменьшения влияния сил трения торцы смазываются консистентными смазками (вазелином, парафином и т. п.). Другой способ компенсации сил трения состоит в применении полбгих конических поверхностей на торцах (рис. 4.4, б).
Для проведения последовательных испытаний на растяжение и сжатие используются трубчатые образцы (рис. 4.4, в), причем усилие на тело образца передается с помощью резьбы. Основная об-
12. ПРЕДЕЛЫ ТЕКУЧЕСТИ И ПРОЧНОСТИ
75
применяется для исследования
Рис. 4.5. Разрушение хрупких строительных материалов при сжатии: а — торцы образца не смазаны; б — торцы смазаны парафином
ласть применения испытаний на" сжатие — исследование прочности и деформации хрупких материалов, так как они используются в первую очередь для элементов конструкций, работающих на сжатие. Испытание на сжатие широк строительных материалов (бетона, кирпича, камня и т. п.). В качестве образцов обычно применяют кубики размером ребра 30—40 мм.
Для хрупких материалов разрушение происходит при деформации всего несколько процентов, и основное значение имеет предел .прочности на сжатие. На рис. 4.5 приведены два типа разрушения строительных материалов при сжатии. В нервом случае
(рис. 4.5, а) (на торцах образца действуют силы трения) разрушение связано с действием касательных напряжений. Во втором случае (рис. 4.5, б) (силы трения по торцам малы) образуются продольные трещины, вызываемые деформацией растяжения в поперечном направлении. Следует отметить, что для
Рис. 4.6. Расплющивание пластичных материалов при сжатии
хрупких материалов прочность на сжатие во много раз больше прочности на растяжение.
При испытании на сжатие пластичных материалов происходит увеличение поперечных сечений («расплющивание») образца (рис. 4.6). Четко определяется предел текучести, который для большинства пластичных конструкционных материалов оказывается таким же, как и при растяжении. Последнее объясняется тем, что ответственными за появление пластических деформаций являются касательные напряжения, которые
при действии растягивающих и сжимающих усилий различаются только знаком.
Предел прочности при сжатии пластичных материалов при одноосном сжатии не выявляется. При всестороннем сжатии материалы выдер-
живают очень высокие давления, причем обычно хрупкие материалы (мрамор и др.) становятся пластичными.
Можно считать, что пластичные материалы выдерживают очень большие сжимающие напряжения, а разрушение может наступить
в результате наличия в наклонных площадках ' касательных напряжений.
Определение предела прочности материала с помощью испытания твердости. В заводских условиях часто требуется определить прочность материала детали, например для проверки правильности
76
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
проведенной термообработки. Вырезка образца из окончательно изготовленной детали невозможна, и для косвенного определения
прочности материала применяют испытания на твердость.
Наиболее распространенными являются пробы твердости по
Бринелю и Роквеллу (рис. 4.7). Твердость по Бринелю, обозначав-
Рис. 4.7. Испытания на твердость по Роквеллу и по Бринелю
мая НВ, определяется диаметром отпечатка при вдавливании в материал твердого шарика диаметром 10 мм под нагрузкой 30 000 Н. Твердость по Бринелю принимается равной напряжению сжатия на поверхности полученного отпечатка
______2Р______ 4Р
лО(/)- /я2—d2) ~ ж? ’
где D — диаметр вдавливаемого шарика, d — диаметр отпечатка. Чем выше твердость (прочность), тем меньше диаметр отпечатка. Например, для
хромоникелевой стали с <ь = 1600 МПа d = 2,71 мм, для той же стали при Оь = 1100 МПа d = 3,42 мм. Диаметр отпечатка измеряется с помощью лупы. Твердость по Роквеллу (шкала С), обозначаемая HRc, определяется как разность глубин проникновения
алмазного конуса основной нагрузки (1500 Н) и предварительной (100 Н). Твердость по Роквеллу используют для контроля закаленных деталей (поверхности зубьев шестерен и т. п.).
<4.
. О
13.	Деформации и характеристики пластичности
Продольная деформация при растяжении образцов. Продольная деформация образца при растяжении, как уже указывалось, определяется по формуле (3)	_
Деформация измеряется тензометрами или оптическим методом (рис. 4.8).
Поперечная деформация, коэффициент Пуассона. Измерения показывают, что при растяжении происходит не только увеличение длины образца, но и уменьшение его поперечных размеров.
Деформация в поперечном направлении
где d —диаметр цилиндрической части образца после растяжения. Экспериментально установлено, что при упругих деформациях
е± = —це,	(12)
где ц — коэффициент Пуассона (постоянная материала).
13. ДЕФОРМАЦИИ И ХАРАКТЕРИСТИКИ ПЛАСТИЧНОСТИ
77
Для большинства конструктивных материалов р.«0,3. Объемная деформация при растяжении
еу =	= (Fl ~ FM ЧП",	(13)
К	О	0*0
где первоначальный объем материала шения (И) —(13), найдем при упругих деформациях
е„=(1-це)2(1 + е)-1.	(14)
Пренебрегая малыми членами, получим следующее значение объемной деформации при растяжении:
Рис. 4.8. Измерение деформаций с помощью тензометров или оптическим методом
ег«в(1-2|л).	(15)
Из физических соображений очевидно, что при растяжении объем материала не
должен уменьшаться, и потому ц < 0,5.
Для изотропного материала коэффициент Пуассона должен лежать в пределах — 1 < р, < 0,5.
Отрицательная нижняя граница связана с энергетическими соображениями, рассмотрение которых опускаем.
Практически отсутствуют материалы, имеющие отрицательное значение коэффициента Пуассона, и потому следует считать
0<ц^0,5.	’	(16)
Замечание. В принципе отрицательные значения р, т. е. увеличение поперечных размеров при растяжении, могут иметь место, если процесс деформирования сопровождается обратимыми физико-химическими изменениями.
Коэффициент Пуассона в упругопластической стадии. Соотношение (12) справедливо и при появлении пластических деформаций, но при этом значение ц становится зависящим от величины деформации: е± = —ц(е)е.
При возрастании деформации и появлении значительных пластических деформаций ц(е)->0,5.
Экспериментально установлено, что пластическая деформация протекает без изменения объема материала. Последнее обстоятельство становится физически понятным, если учесть, что деформация пластичности образуется за счет сдвига слоев материала.
Относительное удлинение при разрыве. Важной характеристикой пластичности материала является остаточное’ (относительное) удлинение при разрыве. На рис. 4.9 показан образец до и после разрушения. Для простого измерения удлинения на образец предварительно наносят две риски на расстоянии Zo; после деформации
78
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
определяют расстояние между рисками Ц складывая вместе две половинки образца;
б = ЗцЛ.юо%, '	(17)
"О остаточное удлинение принято измерять в процентах.
Так как после образования шейки удлинение материала происходит только в этом районе, то величина б зависит от соотношения длины и диаметра образца. Для стандартных образцов применяют Щ = 5 и Zo/do==10 и соответственно обозначают удлинение при разрыве б5 и бю.
Расположение сечения разрыва на образце в его цилиндрической части может быть случайным, связанным с некоторыми нарушениями однородности свойств материала по длине.
Рис. 4.9. Измерение удлинения образца и диаметра шейки при обрыве
Рис. 4.10. Диаграммы деформирования для пластичного (а) и хрупкого (б) материалов
Если обрыв произошел в сечении, близком к головке, то развитие пластической деформации в шейке было затруднено и значение б получилось заниженным. В подобных случаях либо повторяют испытание, либо используют для оценки б ту часть образца, в которой пластическая деформация не была стеснена.
Пластичные и хрупкие материалы при испытаниях на растяжение. На рис. 4.10 показаны диаграммы деформирования для пластичных и хрупких материалов.
Материалы, обладающие к моменту разрушения значительной величиной б (б >10%), называются пластичными. Значения б для некоторых конструкционных материалов приведены в табл. 1. Материалы, для которых-остаточное удлинение б меньше 3%, относят к хрупким материалам. Для элементов конструкций в подавляющем большинстве случаев необходимо применять достаточно пластичные материалы.
Пластичные материалы обладают способностью повышенного сопротивления в условиях концентрации напряжений, ударных и
13. ДЕФОРМАЦИИ И ХАРАКТЕРИСТИКИ ПЛАСТИЧНОСТИ	79
тепловых воздействий, при наличии трещин и поверхностных повреждений и т. п. Материалы с высокими характеристиками прочности часто не могут использоваться в конструкциях, если они являются хрупкими. Малейший поверхностный дефект в виде риски, царапины приводит к значительной потере прочности (достаточно привести пример резки стекла). Часто хрупкие материалы очень сложны в производстве, так как не позволяют использовать сварку, клепку, рихтовку, правку, не выдерживают перенапряжения при монтаже и т. п.
Замечание. Не следует считать, что в современной технике невозможно применение малопластичных материалов. Широкое использование жаропрочных литых материалов для лопаток турбин опровергает такое мнение. При правильном проектировании (в первую очередь, если исключены концентраторы напряжений и работа на растяжение) могут оказаться работоспособными конструкционные материалы с удлинением при разрыве в пределах 0,5—3%.
Относительное сужение поперечного сечения при разрыве. Второй важной характеристикой пластичности материала является сужение поперечного сечения образца при разрыве:
F — F
Ф = V.....->100%,	(18)
о
где Fq — первоначальная площадь поперечного сечения образца, FK — конечная площадь сечения в шейке образ-
ца после разрушения:
Fq = я^/4, FK = л4/4,	(19)
где dm — диаметр шейки образца.
Обычно величину ф, которую называют по-
перечным сужением, измеряют в процентах. Величина ф как характеристика пластичности имеет преимущество по сравнению с величиной б — удлинением при разрыве, так как не зависит от геометрической формы цилиндрического образца (отношения lQ/dQ).
Естественно, что поперечное сужение свя- , зано с максимальной деформацией растяжения в шейке образца. Эту связь можно установить, принимая, что пластическая деформация протекает без изменения объема.
Рис. 4.11. Деформация материалов в зоне шейки
Рассмотрим слой материала образца толщиной До (рис. 4.11), который в момент разрушения оказался в зоне шейки. Из условия постоянства объема находим

FKAK — FoAo.	(20)
«J/читывая равенства ад»1-ф,	(21)
Дк/До = 1 + ек,	(22)
80
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
где ек = (Дк — До)/До — относительное удлинение материала образца в зоне шейки, ф — поперечное сужение, получим
1- + -ГТ77-	(23)
Из последнего соотношения вытекает
8к = Г±ф-	С25)
Следует отметить, что ек существенно больше S, так как выражает местную, а не среднюю деформацию на длине /0.
Для большинства материалов
6 < ф < 8К.	(26)
Дополнительные характеристики хрупкости и пластичности материала. Ранее отмечалась необходимость оценки хрупкости и пластичности для правильного выбора материала детали (элемента конструкции). Важное значение для этих целей имеет испытание на удар — определение ударной вязкости. Принципиальные схемы испытания на удар даны на рис. 4.12. Груз падает и ударяет по образцу; разность энергии груза до и после удара должна быть равна работе, поглощенной в процессе деформации образца, если пренебречь имеющим место небольшим рассеиванием энергии.
Если первоначальная длина образца Zo, то работа деформации может быть определена по формуле
ик	__
л= JP(u)du,	(27)
О
где и — перемещение головки образца, ик — перемещение в момент, предшествующий разрушении^ Если известны диаграмма деформирования
o = P/Fe = /(e) ,	(28)
и деформация е «u/Z0, найдем из соотношений (27) и (28)
(29)
О
б
где 6 — предельная деформация при растяжении, Лх = ]/(е)йе — о
площадь диаграммы деформирования (работа деформации на единицу объема материала). Из соотношения (29) следует, что спо
13. ДЕФОРМАЦИИ И ХАРАКТЕРИСТИКИ ПЛАСТИЧНОСТИ
81
собность поглощать энергию удара за счет деформации зависит от площади диаграммы деформирования (рис. 4.13), т. е. от способности материала получать пластические деформации. Обычно при испытании на удар для выявления хрупкости материала образцы
Рис. 4.12. Принципиальные схемы испытания на удар: а — испытание на ударное растяжение; б — испытание на ударный изгиб
Рис. 4.13. Работа деформации при разрушении материалов
снабжают концентраторами напряжений. Тогда энергия удара поглощается в сравнительно небольшой области, и ее относят к поперечному сечению стандартного образца.
Ударной вязкостью называют величину
ав = A/F,	(30)
где А — работа, -идущая на разрушение образца, и F — площадь поперечного сечения.
Рис. 4.14. Испытания образцов с концентрацией напряжений: а —образец с выточкой; б — образец с трещиной
Для сталей ударная вязкость лежит в пределах ан =« 50— 100 Н • м/см2. Материалы с ударной вязкостью аа < 30 Н • м/смх относятся к числу хрупких.
6 и. А. Биргер, Р. Р. мавлютов
82
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
Еще одной важной характеристикой хрупкости материала является чувствительность к концентрации напряжений. Для исследования применяются образцы с выточкой стандартного профиля (рис. 4.14) и образцы с предварительно нанесенной трещиной (до испытаний образец подвергается действию переменных напряжений для образования предварительной трещины). Если диаметр выточки стержня d, то предел прочности образца с концентрацией напряжений
Материал может быть отнесен к числу хрупких, если
Обк 6b)
где оь — предел прочности гладкого образца.
14.	Истинные диаграммы деформирования и их схематизация
Обычная кривая деформирования (диаграмма деформирования) строится как зависимость условного напряжения а = Р/Ро от условной деформации е =(Z — Zo)/Zo, устанавливаемая в процессе испытания на растяжение. Истинная диаграмма деформирования
представляет зависимость между величинами ои = P/F, 8И = In (Z/Zo). При относительно небольших деформациях (е<5%) различие между обычной и истинной диаграммами деформирования несущественно. Истинное удлинение при равномерной деформации меньше условного, так как приращения деформации
йеи = dill < cZZ/Zo =cZe.
На рис. 4.15 сопоставлены истинная и обычная (условная) диаграммы деформирования. Моменту дей-точка Во на обычной
ствия максимального усилия соответствуют кривой деформирования и точка В на истинной кривой.
Усилие, растягивающее образец,
Р = oaF.
(31)
В момент достижения максимума усилия
dP = doHF + o.dF = 0.	(32)
Применяя условие постоянства объема, найдем d (Fl) = dF I + F dl = О,
14. ИСТИННЫЕ ДИАГРАММЫ ДЕФОРМИРОВАНИЯ
83
или
4-=-4=-^и;	<33>
теперь из соотношений (32) и (33) вытекает, что в точке В d<\
Точка В характеризует потерю устойчивости равномерной по длине образца пластической деформации и начало образования шейки. Равенство (34) показывает, что кривая истинных напряжений в точке В должна иметь определенный тангенс угла наклона касательной оиВ. Приближенно, исходя из условия постоянства объема, получим
аив = 00(1 + 64),	(35)
где е6 — относительное удлинение материала, соответствующее пределу прочности (обычно 8& «(0,1—0,4)6).
Истинное сопротивление отрыву SK определяется как напряжение в момент разрушения:
SK = (Ои)разр =	= к А	(36)
где к = Р^азр/Лпах — коэффициент разрушающей нагрузки (обычно 0,6 < А<1).
Истинная деформация в момент разрушения определяется из условия постоянства объема материала при его пластической деформации:
kF	1
ек = In = In / = In СТ.	(37)
Замечание. Величина истинного сопротивления отрыву должна использоваться с осторожностью и только в тех случаях, когда в процессе разрушения не происходит потери устойчивости пластической деформации. Усилие, надежно воспринимаемое стержнем при его растяжении, определяется обычным пределом прочности материала и первоначальным сечением стержня. При использовании величины SK необходимо знать истинные размеры сечения с учетом пластической деформации.
Истинная кривая деформирования и ее характерные параметры (5К, е« и др.) имеют практическое значение для расчета пластических деформаций, для оценки прочности в местах концентрации напряжений, для оценки сопротивления отрыву.
Особенности кривых деформирования. В тех случаях, когда диаграмма деформирования используется как зависимость о = /(е), она чаще называется кривой деформирования.
Для расчета работы элементов конструкции в упругопластической стадии применяют истинные кривые деформирования. Так как обычно расчет относится к деформациям до 10%, то в дальнейшем
(см. стр. 86) +
84
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
опустим специальные обозначения для истинных напряжений и деформаций, подразумевая, что в общем случае имеются в виду их истинные значения. Начальный (упругий) участок кривой деформирования (или диаграммы деформирования) имеет в соответствующем масштабе угол' наклона (рис. 4.16)
[} = arctg Е, (38) где Е — модуль упругости материала.
Важной характеристикой протекания кривых мирования является тельный модуль
~~ dz '
дефор-каса-
(39)
Рис. 4.16. Кривая деформирования По фЕзическому смыслу
Ек = tg рк, (40) где — угол наклона касательной кривой деформирования к оси абсцисс (оси в).
Приращение растягивающего усилия (см. соотношения (32) и (33))
dP = doF + adF = F(da — ade) = (— —
о I F dz.
(41)
В момент начала образования шейки величина dP = 0 и касательный модуль в точке В
. ^KB=tg₽b = -g|gb = Ob.	(42)
Касательная к кривой деформирования в точке В параллельна линии OBt. Обычно до точки В, соответствующей Ртах> усилие возрастает (dP > 0) и
£к=5>а-	(43)
После-, точки В dP <0 и
do dz

(44)
Равенства (43) и (44) могут использоваться для оценки значений касательного модуля.
Для некоторых материалов (например, малоуглеродистых сталей, широко используемых для профильных балок в строительных конструкциях) при напряжениях, близких к пределу текучести ог, наблюдается «площадка» текучести (рис. 4.17). Происходит ^увеличение пластической деформации до 2—3% при постоянном или даже понижающемся внешнем усилии. Обычно считается, что это
14. ИСТИННЫЕ ДИАГРАММЫ ДЕФОРМИРОВАНИЯ
85
явление связано только со структурными изменениями в материале (разрушением карбидной сетки в случае сталей). Отметим, что на истинной кривой деформирования характерного для условной кривой начального «цикла» на площадке текучести часто не получается.
Рис. 4.17. Кривые деформирования при наличии «площадки текучести». Условная (а) и истинная (б) кривые
Если считать, что пластические деформации растут при постоянном напряжении о = от, то из равенства (41) следует
dP = —gtF d&,
т. е. нагрузка на образец должна уменьшаться, что и поясняет наличие «пика» на условной диаграмме деформирования.
Схематизация кривых деформирования. Для построения приближенных моделей материала часто используются схематизированные кривые деформирования.
Рис. 4.18. Схематизация кривой деформирования по характерным точкам: а — линейное упрочнение по пределам прочности и текучести; б — линейное упрочнение по пределу текучести и истинному сопротивлению отрыва
Простая схематизация состоит в том, что до о < от принимается упругий участок, при о > от — участок с линейным упрочнением (рис. 4.18, а).
86
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
(см. стр.83)ф
В качестве приближенного значения можно принять
Ек = 0ь(1 + е6).	(45)
Если известна пластическая деформация е6, соответствующая пределу прочности щ (обычно е6 =(0,2—0,8)6), то допустимо считать, что линия упрочнения проходит через точки предела прочности и предела текучести (см. рис. 4.18,а); тогда
Е = °ь ~ °т еь ет
(46)
где ет — пластическая деформация, соответствующая точке Т (обычно ет = 0,002 = 0,2%).
Принимая, что линия упрочнения проходит через точку предела текучести и точку разрушения (рис. 4.18,6), найдем
. аб
£к ~ ек - 6Т ~ ,	1
1ПГ=^-6Т
(47)
Линейная схематизация является простой и удобной, но не достаточно точно описывает начальный участок пластических деформаций. Для расчетов иногда используется аппроксимация следующего вида:
е==Еу + 8р = — +	—	,	(48)
где постоянные А и п определяются из условия, что в некоторых точках приближенная и действительная кривые деформирования совпадают. Например, из условия совпадения в точке предела текучести От = Со,2 получаем А = 0,002. Показатель определяется из условия прохождения через точку В и обычно составляет п = 6—10.
Рис. 4.19. Схематизированные кривые деформации без учета упрочнения материала
в
Наконец, для анализа поведения конструкции при развитых пластических деформациях используется степенная аппроксимация:
8 = er f-21V=5an.	(49)
к J
15. ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
87
Для построения приближенных решений широко используются схематизированные кривые деформации, в которых упрочнение материала не учитывается (рис. 4.19). Пластичность без упрочнения называется иногда идеальной пластичностью (рис. 4.19, а). Применяются и схемы жесткопластического тела (рис. 4.19,6), в которых упругими деформациями пренебрегают. Последние схемы используются для построения моделей предельного состояния. Следует отметить, что упрочнение материала можно приближенно учесть в приведенных схемах соответствующим изменением величины Отметим, что степенная аппроксимация (49) выражает диаграмму деформирования жесткопластического тела при п -► <».
15.	Ползучесть и длительная прочность
Влияние повышенных температур. В современных условиях работа конструкций часто бывает сопряжена с высокими температурами. Элементы конструкций сверхзвуковых самолетов нагреваются в полете до 200°С и выше, детали газовых турбин авиационных двигателей работают при температуре 600—1000°С. С действием высоких температур приходится считаться в энергетическом и химическом машиностроении и т. д.
При повышенных температурах конструкционные материалы обнаруживают два новых свойства — ползучести и длительной прочности. Ползучестью называется возрастание пластической (остаточной) деформации при постоянных нагрузках; длительной прочностью называется зависимость разрушающих напряжений (пределов прочности) от длительности работы.
Свойства ползучести и длительной прочности проявляются у углеродистых сталей при Т > 300°С, для легированных сталей при Т > 350°С, для алюминиевых сплавов при Т > 100°С. Для некоторых материалов (полимеров, бетонов и др.) указанные свойства наблюдаются и при нормальных температурах.
В условиях повышенных температур происходит снижение обычных пределов прочности и текучести, определяемых при кратковременных испытаниях. На рис. 4.20 даны зависимости пределов прочности различных конструкционных материалов от температуры. Наиболее резкое снижение о6 наблюдается на алюминиевых сплавах. Углеродистые стали в области 200—300°С обнаруживают некоторое повышение пределов прочности, а затем монотонное снижение. Наибольшие значения оь при высокой температуре показывают литые жаропрочные сплавы, содержащие 70—80% никеля.
Снижение пределов текучести при повышении температуры происходит примерно так же, как и снижение о&. При высоких температурах снижается значение модуля упругости на 30—40% (в предельной области температур, при которых используются материалы). При высоких температурах происходит интенсивное окисление поверхности и часто оказывается необходимым защищать поверхность специальными покрытиями.
88
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
Наиболее существенной особенностью прочности при высоких температурах является сильное влияние времени нагружения. Это объясняется тем, что, начиная с определенного диапазона температур, в материалах происходят структурные и фазовые превращения, развивающиеся во времени.
Рис. 4.20. Снижение пределов прочности при увеличении температуры (кратковременные испытания): 1 — алюминиевые сплавы (АК4-1, ВД-17); 2—углеродистые стали (сталь 20, сталь 45); 5 —титановые сплавы ВТЗ; 4 — хромоникелевые стали; 5 — деформируемые жаропрочные сплавы на никелевой основе; 6 — литые жаропрочные сплавы на никелевой основе
При исследовании прочности элементов конструкций, работающих при высоких температурах, необходимо проводить не только кратковременные, но и длительные испытания материалов (полу
Рис. 4.21. Кривая ползучести: / — стадия неу становившейся ползучести; II — стадия установившейся, ползучести;
III — стадия разрушения
чение кривых ползучести и определение длительной прочности).
Кривые ползучести. Пределы ползучести. Графическое изображение зависимости остаточной деформации от времени испытаний при постоянных напряжении и температуре называют кривой ползучести (рис. 4.21). При испытаниях образец находится внутри электронагревательного устройства,
удлинение измеряется механическим или оптическим методом. Начальная деформация образца (она может быть упругой или упругопластической) не учитывается. Остаточная (пластическая) деформация, увеличивающаяся
во времени при постоянном напряжении, называется деформацией ползучести и обозначается 8в (индекс с — начальная буква слова «creep» — ползучесть). Скорость деформации ползучести, или
15. ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
89
короче скорость ползучести,
Эксперименты показывают, что на кривых ползучести
ес==/(0
наблюдаются три характерные стадии. Первая стадия (участок О А) — стадия не установившейся ползучести. Скорость ползучести, наибольшая в начальный ’ момент, постепенно уменьшается. Вторая стадия (участок АВ) характеризуется постоянной (минимальной) скоростью ползучести. Наконец, третья стадия (участок ВС) представляет собой стадию разрушения; на образце образуется сетка трещин, стадия заканчивается хрупким изломом или при высоких уровнях напряжений вязким изломом с местным утонением. Ползучесть материала в элементах конструкций допустима до определенной величины. Например, при ползучести ротора турбины может произойти касание рабочих лопаток о корпус.
Для оценки ползучести материала используется специальная характеристика — предел ползучести. Пределом ползучести называ-; ется напряжение, при котором деформация ползучести за определенный промежуток времени достигает заданной величины. Например, для никелевого жаропрочного сплава ХН77ТЮР (нимо-ник-80) при температуре 700°С за время 100 ч и деформации ползучести 0,2% предел ползучести составляет 400 Н/мм2:
По.гцоо (700) = 400 Н/мм2.
При обозначении предела ползучести указываются величина деформации, время и температура испытаний.
Скорость ползучести. Основное время развития ползучести приходится обычно на установившуюся стадию с постоянной скоростью ползучести.
Результаты экспериментального определения скорости ползучести на установившейся стадии представляют в виде степенной зависимости
V = 5art,	(51)
где В, п~ параметры материала, зависящие от температуры.
В логарифмических координатах уравнение (51) соответствует линейной зависимости lg V от 1g о.
Параметр п является безразмерным и обычно лежит в пределах 3—6, т. е. зависимость скорости ползучести от напряжения весьма существенна. Размерность параметра В зависит от выбранной размерности V, о и значения п.
Влияние ползучести на напряженное состояние в элементах конструкций. Как уже указывалось, ползучесть материала приводит к росту деформаций, что может быть нежелательным или недопустимым по конструктивным соображениям. Однако наибольшее
90
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
влияние ползучесть материала оказывает на перераспределение напряжений в элементах конструкций, так как деформации ползу-чести сопоставимы, а часто и превышают упругие деформации. Указанное явление приводит, например, к релаксации (падению) напряжений затяжки в болтах, к релаксации благоприятных остаточных напряжений после применения упрочняющей технологии и т. д.
Длительная прочность, предел длительной прочности. Свойство длительной прочности материала при повышенных температурах ограничивает ресурс изделий и приводит к необходимости учета времени нагружения в моделях прочностной надежности. Прочность материала при повышенных температурах характеризуется пределом длительной прочности.
Пределом длительной прочности называется напряжение, при котором материал разрушается не ранее заданного времени. Например, для никелевого жаропрочного сплава ХН77ТЮР (нимоник-80) при температуре 700°С и времени 1000 ч предел длительной прочности составляет 330 Н/мм2
оДл1000 (700) = 330 Н/мм2.
При обозначении предела длительной прочности указываются длительность нагружения и температура испытания. Для сравнения укажем, что для того же сплава при температуре 700°С пределы прочности и текучести (при кратковременных испытаниях)
о& = 830 Н/мм2, о0>2 == 560 Н/мм2.
Во многих случаях пределы длительной прочности ниже пределов
Рис. 4.22. Кривые длительной прочности в логарифмических координатах
текучести при кратковрем*енных испытаниях.
Зависимость пределов длительной прочности от времени нагружения. Эта зависимость получается при испытаниях в условиях постоянной температуры (рис. 4.22).
Кривые длительной прочности выражают зависимость пределов длительной прочности от времени испытаний. Эта зависимость применяется в .виде
= С	(52}
где /и = m(Т), С = С(Т)— параметры материала, зависящие от температуры, tv — время до разрушения. В логарифмических координатах уравнение (52) изображается прямой линией, причем угол наклона зависит от параметра пг
tg- а = 1/тп.
15. ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
91
Параметр т обычно лежит в пределах т = 4—16, что показывает резкую зависимость времени до разрушения tp от уровня действующих напряжений. При повышении температуры параметр т уменьшается.
Испытания на двух уровнях напряжений щ и о2 и определение времени до разрушения позволяют определить параметры т и С
+	г**
а1 *Р1 в а2 *Р2>
в *8 (*Р2/*Р1) (°1/а2) '
С = О^р1.
(53)
(54)
Рассеяние долговечности при испытаниях длительной прочности. Эксперименты .показывают, что время работы образца без разрушения (долговечность) при заданном уровне напряжений и температуры имеет существенное рассеяние. На рис. 4.23 показан
разброс значений логарифма долговечности. Зависимость (52) определяется для среднего времени до разрушения £р.
Долговечность (время до разрушения) целесообразно рассматривать как случайную величину, имеющую статистическое распределение. Экспериментально доказано, что для логарифма долговечности можно использовать нормальное распределение, плотность которого

W/i г
сп ^•7______________________—
х
Рис. 4.23. Рассеяние логарифма долговечности при испытаниях длительной прочности
где х — среднее значение случайной величины, $х — среднеквадратичное отклонение. Плотность вероятности («вероятность на единицу длины») показана на рис. 4.23; по мере удаления от среднего значения плотность вероятности падает.
Замечаниие. При любом повторении опыта наблюдается рассеяние результатов вследствие влияния множества второстепенных факторов.
Стабильность опыта можно охарактеризовать коэффициентом вариации и ~ sx/x.
Разброс данных наблюдается при определении обычных пределов прочности, текучести и других характеристик, но с относительно низким коэффициентом вариаций (0,01—0,05). При испытаниях долговечности коэффициент вариации достигает значений 0,2—0,3 и статистическое описание результатов эксперимента становится необходимым.
Зависимость пределов длительной прочности от температуры. С увеличением температуры пределы длительной прочности падают. На рис. 4.24 показана зависимость предела сточасовой прочности от температуры для литого жаропрочного сплава на никелевой основе ЖС6-К. Отметим, что при 1000 °C предел кратковременной
92
ГЛ. £ МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
прочности составляет 540 МПа, тогда как предел сточасовой прочности 150 МПа.
Длительная пластичность и особенности разрушения при длительной прочности. После работы материала при высокой температуре происходит снижение начальных показателей пластичности (б и ф) часто на 30—50%. Разрушение жаропрочных материалов
Рис. 4.24. Зависимость предела длительной прочности для жаропрочного сплава ЖС6-К от температуры
Рис. 4.25. Разрушение при длительной прочности, идущее по границам зерен
при длительной прочности носит хрупкий характер. Разрушение идет по границам зерен (рис. 4.25), начальный участок трещины обычно сильно окислен.
16.	Усталость материалов и элементов конструкций
Явление усталости. Усталостные поломки составляют основной вид разрушения деталей машин и нередко приводят к тяжелым последствиям, так как возникают внезапно. Разрушение происходит
Рис. 4.26. Следы микропластической деформации при повторном нагружении (увеличение на электронном микроскопе)
без заметной пластической деформации, как правило, в зоне концентрации напряжений. Источником усталостного разрушения является действие переменных (во времени) напряжений.
Риск 4.27. Усталостный излом лопатки: 1 — место зарождения трещины; 2 — зона развития трещины; 3 — вона окончательного излома
16. УСТАЛОСТЬ МАТЕРИАЛОВ
93
При повторном циклическом деформировании в неблагоприятно расположенных зернах материала происходит накопление микро-пластических деформаций. На рис. 4.26 при увеличении 500 видны следы остаточных сдвигов.
Процесс постепенного накопления микропластических деформаций приводит к образованию микротрещины, которая начинает расти при повторных приложениях нагрузки в результате концентрации напряжений у ее краев. Усталостное разрушение — разрушение в результате постепенного развития трещины при повторных нагружениях.
При усталостном разрушении на поверхности излома всегда обнаруживаются две зоны: зона зарождения и развития трещины и зона окончательного излома. Зона развития трещины (рис. 4.27) обычно имеет гладкую поверхность, так как микронеровности «стираются» при повторном сближении краев трещины. Излом происходит в результате ослабления сечения, когда статическая прочность оказывается недостаточной. Если статическая нагрузка невелика,, усталостная зона излома может составлять 50—70% общей по- <*' верхности излома.
Начало усталостного излома возникает в местах действия наибольших переменных напряжений, обычно на поверхности детали.
При высоком уровне переменных напряжений - может возникнуть несколько очагов развития Рис/4.28. Цикл переменных на-усталостной трещины.	пряжений
Усталостное разрушение часто
начинается от забоин, рисок, в местах концентрации напряжений. Особое значение для усталостной прочности имеют поверхностные* слои элемента конструкции. Усталостное разрушение в отличие от статического имеет резко выраженный локальный характер.
Циклы переменных напряжений. Рассмотрим циклически изменяющиеся напряжения (рис. 4.28) и обозначим ^тах, Фт1п наибольшее и наименьшее напряжения цикла.
Действие цикла напряжений можно представить как сумму постоянной составляющей
<Ут = ~2~ famax 4" Шп1п)	(56)?
и периодически изменяющихся напряжений с амплитудой z
Оа==“2~(птах — tfmin)*	(57^
Величина dm называется средним напряжением цикла, величина оа — амплитудой переменных напряжений или переменным напряжением.
34
ГЛ. 4’. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
Переменное напряжение изменяется во времени: / 2jx \
Oa(t) =Ga COSI —f | = Оа COS , \ 4Ц /
(58)
где £ц — период колебаний, с; f = 1/t^ — частота колебаний, Гц (1 герц = 1 колебание/с).
Если среднее напряжение от«0, цикл напряжений называют симметричным, при от 0 — асимметричным.
Для характеристики цикла используется коэффициент асим
метрии
amin ^max
(59)
Для симметричного цикла г = —1; для отнулевого, или пульсирующего, цикла г = 0; при действии постоянных напряжений г = 1.
Испытания на усталость. Испытания усталостной прочности
проводятся на специальных испытательных машинах обычно при
К усилителю
Рис. 4.29. Электродинамический' стенд для испытаний лопаток компрессоров и турбин
на усталость
симметричном цикле нагружения. В процессе испытания, как правило, задается величина амплитуды переменного напряжения и находится число циклов нагружения, при которых образуется трещина определенной величины или происходит поломка. Испытание усталостной прочности материала проводят на образцах диаметра 7—10 мм. Часто проводятся испытания
на усталость натурных
деталей.
На рис. 4.29 показан электродинамический стенд для испытания лопаток компрессоров и турбин на усталость. С помощью генератора частоты возбуждаются колебания, близкие к частоте собственных колебаний лопатки; амплитуда колебаний поддерживается автоматически; напряжения определяются с помощью, проволоч-
ных тензометров, наклеенных на лопатку. .
Влияние числа циклов нагружения на усталостную прочность, кривые выносливости, пределы выносливости. Зависимости среднего 'числа циклов до разрушения от величины амплитуды переменных напряжений цикла называются кривыми выносливости (рис. 4.30). В логарифмических координатах кривые выносливости представлены полигональными кривыми (отрезками прямых линий).
16. УСТАЛОСТЬ МАТЕРИАЛОВ
95
Кривая первого типа (рис. 4.30, а), свойственная углеродистым сталям, при N = Nq имеет точку перелома и выходит на горизонтальный участок. Обычно точка перелома соответствует N = 10е— 107 циклам; ордината точки перелома обозначается tf-i и называется пределом выносливости. При амплитуде переменных напряжений ба < 0-1 усталостное повреждение невозможно.
Когда экспериментальные исследования относились главным образом к углеродистым сталям, считалось, что предел выносливости
Рис. 4.30. Три типа кривых выносливости (в логарифмических координатах) г а — кривые первого типа; б — кривые второго типа; в — кривые третьего типа
существует для всех конструкционных материалов. Исследования последних десятилетий показали, что для многих материалов после-точки перелома снижение усталостной прочности продолжается.
Кривая второго типа (рис. 4.30, б) после точки перелома имеет замедление усталостного разрушения (легированные стали, титановые сплавы). Для кривых третьего типа (рис. 4.30, в) точки перелома при большом числе циклов не существует (алюминиевые-сплавы, жаропрочные сплавы в определенном интервале температур) и темп снижения усталостной прочности остаётся неизменным до момента разрушения.
Замечание. При малом числе циклов == 102 — 103) кривые усталости имеют перелом, связанный ,с переходом в малоцикловую область. Проблема малоцикловой усталости будет рассматриваться в следующем разделе.
Условные пределы выносливости. Для кривых выносливости второго и третьего типов находится условный предел выносливости для определенного числа циклов (N6 — база испытаний); обычно-принимают = 2 • 10е—5 • 107 циклов. Условным пределом выносливости называется значение амплитуды переменного напряжения^ при котором происходит разрушение при базовом числе циклов.
Условные пределы текучести обозначаются (а~4)я или
Уравнение кривых выносливости. Кривые выносливости в ’логарифмических координатах в общем случае состоят из двух участков. В интервале числа_ циклов Nt< N < NQ уравнение кривой выносливости имеет вид
amN = С (A\ < N < No),	(60>
96
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
где т и С — параметры материала. Тангенс угла наклона равен tga = l/m.	(61).
Обычно значения т лежат в пределах 4—12, для деталей с концентрацией напряжений т => 4—8. Параметры т и С определяются по формулам, аналогичным соотношениям (53) и (54).
На втором участке (N > АГ0) уравнение кривой выносливости om°iV = C0	(62)
Параметр mQ обычно значительно больше т (т9 ==(5—10) тп). При возрастании тп0 направление линии второго участка приближается к направлению оси абсцисс.
Так как в точке Ао (см. рис. 4.30, б) обе прямые пересекаются, то параметры уравнений (60) и (62) связаны соотношением
С^Сщ^т.	(63)
Замечания. 1. Испытаниям на усталость при постоянной амплитуде переменных напряжений свойствен большой разброс значений числа циклов до разрушения. В уравнениях кривых выносливости под N понимается среднее число циклов до разрушения.
2. Для моделей второго и третьего типов происходит монотонное снижение пределов выносливости при увеличении числа циклов нагружения. Не означает ли это неизбежное разрушение деталей машин, испытывающих переменные напряжения (например, в лопатках турбомашин, в коленчатых валах двигателей и др. всегда имеется «фон» переменных напряжений около 10—20 Н/мм2) ?
Простой подсчет показывает, что при сравнительно высокой частоте нагружения (103 Гц) за 100 лет непрерывной работы деталь должна выдержать
2V = 1(Я.З,6Л0М,7-10М02 « 3-1012 циклов.
Принимая для точки перелома No = 107, находим амплитуду разрушающих напряжений при N == 1014, mQ == 20:
aio1-10w=a®o-107,
а_г • 10u « ae- 10“7/20 « 0,44 а0.
Амплитуда переменных напряжений порядка 1
у (a-i) практически не может привести к усталостному разрушению за неопределенно Долгий срок.
Влияние постоянных напряжений на усталостную прочность. Эксперименты показывают, что наличие средних растягивающих напряжений снижает предел
выносливости. Здесь и далее не будет оговариваться особо, что речь идет об условных пределах выносливости для материалов второго или третьего типа или о пределе выносливости для первого чипа материала (см. рис. 4.30).
На рис. 4.31 дана схематическая зависимость предела выносливости от величины среднего напряжения. Существенно, что придей-
Рис. 4.31. Зависимость пределов выносливости от среднего цикла
16. УСТАЛОСТЬ МАТЕРИАЛОВ
07
ствии постоянных сжимающих напряжений усталостная прочность возрастает. Это дает основание для применения упрочняющей технологии (обдувка дробью, шариками и т. п.), создающей в наиболее напряженных поверхностных слоях остаточные напряжения сжатия.
Наибольшее практическое применение получила линейная зависимость предельной амплитуды переменного напряжения от величины ат:
оа = o-i — ipoOm.	(64)
Коэффициент равен
=	•	(65)
°ь
где о» — предел прочности материала. Кроме линейных можно использовать зависимости более сложного вида:
/ а \т /а V
21. = 1 _ р» .	(66)
Для углеродистых и легированных сталей зультаты получают при т = 2, п = 1. В этом случае
В уравнениях (64) и (67) растягивающее напряжение ат > 0, сжимающее От < 0.
Влияние концентрации напряжении. Концентрация напряжений . оказывает очень сильное влияние на усталостную прочность, так как усталостное разрушение носит локальный характер. Максимальное напряжение в месте концентрации напряжений для упругого материала определяется с помощью теоретического коэффициента концентрации напряжений а0
х	^тах О^аОд,
удовлетворительные ре-
Рис. 4.32. Пример элемента конструкции с концентрацией напряжений
(68)
где оя — номинальные напряжения, определяемые без учета концентрации напряжений. Например, для концентрации напряжений в пластинке с отверстием (рис. 4.32) принимается
<>ь = а—.	(69)
Замечание. Способ определения номинального напряжения, для которого дано значение аа, должен быть всегда четко указан.
7 и. А. Биргер, Р. Р^ Мавлютов
98
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
Если считать, что в момент усталостного разрушения в точке максимального напряжения достигается предел выносливости материала, то предел выносливости детали с концентрацией напряжений должен быть равен
О-1к = -г—*	(/0)
В действительности, как показывают опыты,
a-хи =	(71)
где Ко — эффективный коэффициент концентрации напряжений, причем
Ко^ао.	(72)
*
Равенство достигается только для деталей больших размеров, выполненных из материалов с высокой чувствительностью к концентрации. В практических расчетах эффективный коэффициент концентрации оценивают согласно зависимости
Z<a=l + g(aa-l),	(73)
где q — коэффициент чувствительности к концентрации напряжений.
В приближенных расчетах принимают: для литых материалов q = 0,1—0,2; для малоуглеродистых сталей и жаропрочных деформируемых сплавов q = 0,2—0,4; для алюминиевых сплавов q — = 0,3—0,5; для легированных сталей q = 0,6—0,8; для титановых сплавов q = 0,8—0,9.
Замечание. Литые материалы менее чувствительны к концентрации напряжений, так как они имеют «внутренние» источники концентрации, понижающие их усталостную прочность.
Влияние поверхностного слоя. Это влияние оказывается весьма существенным и зависит от трех основных факторов: качества поверхности (шероховатость), коррозионного воздействиями поверхностного упрочнения.
Если 0-1 — предел выносливости образца, поверхностный слой которого признается эталонным, то предел выносливости материала с фактически имеющимся поверхностным слоем
(о-Оп = Ро-ь	(74)
где р — коэффициент влияния поверхностного слоя.
Коэффициент р может быть представлен в виде произведения частных коэффициентов:
Р ~ РшРкорРуп»	(75)
Коэффициент рш, учитывающий шероховатость поверхности, обычно принимают равным: для полированной поверхности рш — 1; шлифованной (без наличия прижогов) рш » 0,8—0,9; тонкого точения рш = 0,7—0,9; грубого точения, фрезерования Рш == 0,6—0,7. Меньшие значения относятся к стали и сплавам повышенной прочности (о& > 1000 Н/мм2). Чем более прочным является материал, тем большие требования предъявляются к качеству поверхности для реализации потенциальных возможностей материала.
Коэффициент Ркор, показывающий влияние коррозии, принимается: при нормальной атмосфере Ркор = 1; при следах коррозийного повреждения Ркор = 0,8—0,9; при наличии морской воды или агрессивных сред рКор » 0,5—0,8.
16. УСТАЛОСТЬ МАТЕРИАЛОВ
99
Коэффициент рун, учитывающий технологическое упрочнение, при пластическом деформировании (наклепе) обдувкой дробью 1,1—1,4; при химико-термической обработке 1,1—1,3. При наличии концентрации напряжений значение рул должно быть увеличено па 30—50%.
Влияние абсолютных размеров деталей. С увеличением размеров деталей машин, элементов конструкций предел выносливости уменьшается (масштабный эффект). Это объясняется статистической теорией, в соответствии с которой увеличивается вероятность пребывания «слабых зерен» в зонах повышенных напряжений. Следует также учитывать, что при увеличении размеров усложняются технологические процессы, ухудшается однородность и т. п.
Предел выносливости детали с характерным диаметром d
(a-Od « eoa«b	(76)
где 80 — коэффициент масштабного фактора; a-q — предел выносливости материала, определяемого па образцах диаметром 7 — 10 мм.
Коэффициент е0 может быть представлен в виде
80 = 8оо + (1 — Еоо)^М.	(77)
В приближенных расчетах принимают е«» =0,5 для деформируемых материалов, 8е» = 0,4 для литых материалов. В первом приближении X = 0,01— 0,03 1/мм, значение d принимается в мм.
Оценка пределов выносливости элементов конструкций. Для ответственных деталей машин, элементов конструкций предел выносливости определяется путем натурных испытаний. В тех случаях, когда требуется предварительная оценка усталостной прочности, используется следующая приближенная формула:
Ре
где О-1 — предел выносливости материала при симметричном цикле переменных напряжений; р, е и Кв — коэффициенты влияния поверхностного слоя, масштабного эффекта и эффективный коэффициент концентрации напряжений.
Предел выносливости a_i связан с величиной о& следующей приближенной зависимостью:
о_1	(0,55—0,0001 оь) Об,
где (Зь, Н/мм2 — предел прочности.
Равенство (78) оценивает значение предела выносливости детали при симметричном цикле.
При действии постоянных получим
а-1д
Формула (79) служит для детали. Влияние концентрации
ных напряжений цикла; предел выносливости a-i определяется для базового числа циклов нагружения.
Приведенные ранее соотношения для приближенной оценки усталостной прочности справедливы и для случая переменных касательных напряжений. Естественно, что во всех формулах-индексы нормальных напряжений а замещаются на т; в некоторых случаях изменяются также числовые коэффициенты. Значение предела выносливости при кручении определяется по формуле
Т-t a? 0,6o-i.
Рассеяние усталостной долговечности. При экспериментальных исследованиях, как уже отмечалось, наблюдается разброс значе-?♦
напряжений am, принимая зависимость
(79)
к сть приближенной оценки предела выносливости напряжений учитывается только для перемел-
100
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
ний числа циклов до разрушения при одинаковом значении амплитуды переменных напряжений. При обработке опытных данных число циклов до разрушения рассматривается как случайная величина.
Доказано, что для логарифма числа циклов до разрушения можно использовать нормальное распределение. Плотность распределения определяется формулой (55), в которой х = lg N.
При сравнительно невысоком уровне амплитуд переменных напряжений оказывается целесообразным ввести «пороговое значение» числа циклов до разрушения N*. Предполагается, что при N < Nn усталостное разрушение не происходит. При наличии порога нормальное распределение относится к величине
* = lg(Ar-JVa). ,
Пороговое значение числа циклов до разрушения Nn оказывается дополнительным параметром распределения.
17. Малоцикловая усталость
Циклическое деформирование. Кривая деформирования при растяжении и сжатии показана на рис. 4.33. Предел текучести при растяжении обозначен Ор, при сжатии о?. Для большинства кон
структивных металлических сплавов (углеродистых и легированных сталей, титановых и алюминиевых сплавов и др.) пределы текучести при растяжении и сжатии приблизительно одинаковы:
&т ~ в?.	(80)
Рассмотрим деформирова ние «растяжение — сжатие» при циклическом изменении внешних
Рис. 4.33. Кривая деформирования при растяжении и сжатии (of — предел текучести при растяжении, Оу — предел текучести * при сжатии)
напряжении от о до —о, причем о > От (рис. 4.34, а). При первом нагружении точка,- изображающая состояние материала, в плоскости о, е, движется по кривой ОАВ. Далее, напряжения умень-
шаются и точка продолжает движение по участку BBiAt. После достижения минимального напряжения в точке Ai снова начинается нагружение по кривой. На рис. 4.34, б показан цикл деформаций, сопровождающий цикл изменения внешней нагрузки.
Размах упрутопластических деформаций
Ав ~~ Вшах ^minj
(81).
17. МАЛОЦИКЛОВАЯ УСТАЛОСТЬ
101
где emaXl emin — наибольшая и наименьшая (в алгебраическом смысле!) деформации за цикл.
Размах пластической деформации
Двр = 8р max mln?	(82)
где 8? max, £р mm — наибольшая и наименьшая пластические деформации при циклическом изменении деформаций.
Изотропное и анизотропное упрочнения при пластических деформациях. Пластическая деформация приводит к повышению «мгновенного» предела текучести. Если в точке В (см. рис. 4.33) снизить нагрузку до нуля, а затем опять произвести нагружение,
Рис. 4.34. Циклическое деформирование: а — изменение действующих напряжений во времени; б — цикл деформаций
то переход к пластическому деформированию начнется при о > ><у(8р) и процесс нагружения пройдет по начальной кривой деформирования (см. разд. 12).
Предел текучести при повторном нагружении называется мгновенным пределом текучести. В первом приближении можно считать, что значение мгновенного предела текучести зависит от значения пластической деформации в данный момент нагружения.
В наиболее простой модели поведения материала (в модели изотропного упрочнения) предполагается, что кривые деформирования при повторном нагружении (кривые OJ3C и OJ^A^ рис. 4.35) зависят только от величины достигнутой пластической деформации и не зависят от ее знака.
Кривые деформирования после предварительной пластической деформации ър (кривая AiBtOJBC) или после — гр представляют собой одинаковые кривые, но «сдвинутые» по оси абсцисс.
В модели изотропного упрочнения мгновенные пределы текучести на растяжение и сжатие одинаковы не только при начальном, но и при повторных деформированиях (рис. 4.35, а). Экспери
102
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
ментально установлено, что у многих конструкционных материалов наблюдается понижение мгновенного предела текучести при изменении знака деформирования. Такой эффект, называемый эф-» фектом Баушингера, связан с анизотропным упрочнением материала (т. е. упрочнением, зависящим от направления нагружения).
Рис. 4.35. Изотропное (а) и анизотропное (б) упрочнения при пластических деформациях
После разгрузки в точке В мгновенный предел текучести понижается:
(Ут <Z (Ут •
При изменении знака пластической деформации мгновенный предел текучести на сжатие будет меньше, чем при растяжении.
Простая модель анизотропного упрочнения показана на рис. 4.36, б. Предполагается, что в любой момент нагружения
<Ут + (Ут = -&т	(83)
(принцип Мазинга).
Кривые деформирования в различные моменты деформирования имеют участки упрочнения, лежащие на линиях упрочнения при первоначальном деформировании.
Замечание. Модели поведения материала при циклическом деформировании являются приближенными. В ответственных случаях связь напряжений и деформаций при цйклическом деформировании должна устанавливаться на основании экспериментальных данных.
Явление малоцикловой усталости. Малоцикловой усталостью на- -зываются разрушения при повторных упругопластических деформациях. Обычно разрушения малоцикловой усталости происходят при числе циклов повторения нагрузки N < 105.
Малоцикловая усталость имеет много общего с обычной усталостью, но отличается от нее наличием макропластических деформаций в зоне излома. Как и при обычной (многоцикловой) усталости, разрушение начинается в местах концентрации напряжений в результате развития первоначально образовавшейся трещины.
17. МАЛОЦИКЛОВАЯ УСТАЛОСТЬ
103
Однако механизм малоцпклового разрушения значительно отличается от механизма усталостного разрушения, так как пластические деформации возникают в значительно больших объемах материала.
В частности, различие сказывается в том, что сопротивление материалов малоцикловой усталости существенно зависит от их пластичности, тогда как подобная зависимость для обычной усталости проявляется слабо.
В машиностроении малоцпкловая усталость часто определяет ресурс (долговечность) изделий в связи с повторением циклов «запуск — работа — останов». Характерный пример — диски авиационных двигателей, испытывающих (5—10) * 103 выходов на максимальные обороты, при которых напряжения приближаются к пределу текучести материала.
Характеристики нагруженности при малоцикловой усталости. Прп обычной усталости в качестве характеристики нагруженности используются переменные напряжения цикла (амплитуда переменных напряжений оа). Переменные деформации, возникающие при действии переменных напряжений, однозначно определяются соотношением
8а = J Оа,	(84)
где Е — модуль упругости, еа — амплитуда переменных деформаций.
При малоцикловой усталости, протекающей в упругопластической области при процессах нагружения и разгрузки, зависимость ев = /(о«)	(85)
имеет значительно более сложный характер, а для материалов с
Рис. 4.36. Циклы напряжений и деформаций на диаграммах деформирования
отсутствующим или очень малым упрочнением практически не является однозначной. На ряс. 4.36 показаны два цикла деформаций с переменным напряжением
Gal Ga2 *” От^
где от предел текучести материала.
104
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
При отсутствии упрочнения, что свойственно малоуглеродистым сталям при ер<2%, цикл переменных напряжений не определяет реальных условий деформирования. Условию (85) может соответствовать цикл ABBiAi или АСС{А{ в зависимости от деформаций на границах упругопластической области.
Для материала с пластическим упрочнением (см. рис. 4.35, а) наибольшие изменения амплитуды переменных напряжений (от Gai ДО оа2) приводят к значительным изменениям амплитуды переменных деформаций. Указанные соотношения обосновывают целесообразность использования при анализе малоцикловой усталости переменных деформаций в качестве характеристик нагруженности. Для пластически упрочняющихся материалов возможно описание малоцикловой усталости с помощью переменных напряжений.
При экспериментальном определении малоцикловой прочности используются режимы «жесткого» и «мягкого» нагружений. При жестком нагружении задается амплитуда переменных деформаций еа или размах деформаций
'	Де Стах 6min = 2ба.	(86)
Жесткое нагружение встречается в элементах конструкций при «принудительной» л деформации (например, циклический нагрев стержня при жесткой заделке его концов). Жесткое нагружение характерно для работы материала в зонах концентрации напряжений, где приближенно можно считать, что деформация задается смещением границ упругой области.
При испытаниях в условиях жесткого нагружения измеряется деформация образца. При мягком нагружении происходит циклическое изменение внешнего усилия, действующего на образец.
Условия нагружения при малоцикловой усталости. При испыта- , ниях с постоянной амплитудой переменных деформаций (жесткое нагружение) установлена следующая зависимость:
е™%,==СР,	(87)
где еар — амплитуда пластических деформаций; Np — среднее число циклов до малоциклового разрушения; Ср, тр — параметры материала.
Условие (87) представляет модель малоциклового разрушения, предложенную Коффином. Он определяет величину Ср, используя уравнение (87) для случая однократного (статического) разрушения, принимая условно N = 1/4 (в первой четверти цикла происходит нагружение до максимального значения) и полагая тр = 2, вер » 8к/2. Тогда
.	(88)
где ек=1п истинная деформация в момент разрушения (см.
17. МАЛОЦИКЛОВАЯ УСТАЛОСТЬ
105
разд. 13); ip — поперечное сужение материала. Условие малоциклового разрушения будет таким:
=	(89)
Из последнего соотношения следует, что малоцикловая прочность зависит от пластичности материала. Чем больше относительное сужение в шейке при разрыве образца ф, тем выше прочность при повторных пластических деформациях.
Условие (89) не включает упругую деформацию цикла и пригодно для случаев, когда пластическая часть переменной деформации существенно превышает упругую. При таких условиях число циклов N до разрушения обычно меньше 103. В общем случае условие малоцикловой прочности должно учитывать и обычную усталость в области больших переменных напряжений.
В практических расчетах часто используется экспериментально установленная формула Менсона, связывающая амплитуду полных деформаций цикла (пластических и упругих) с числом циклов до разрушения NP:
= у (in j^)0’8 N;°'s +	,	(90)
где о6, Е — предел прочности и модуль упругости материала. Первое слагаемое в правой части уравнения (90) выражает сопротивление материала повторным пластическим деформациям, второе — переменным упругим деформациям. При малом числе циклов до разрушения основное значение имеет первое слагаемое, при Np > > 103 — второе.
Недостатком формулы Менсона, получившей широкое распространение, является приближенный учет сопротивления повторным упругим деформациям.
Используя закономерности усталости при высоких напряжениях (см. разд. 16)
(£N «	(91)
где o-i — предел выносливости для базового числа циклов 7V0 (точки перелома); т — показатель кривой усталости (тп== 6—20), можно найти амплитуду переменных деформаций
(92)
Условие разрушениям при малоцикловой усталости можно записать в виде модифицированного уравнения Менсона:
=4 (1п гМ°’в 0,8+N*m N?'m-	<93>
« \ А — у/
106
ГЛ. 4. МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
Влияние постоянного напряжения цикла. Постоянные напряжения оказывают влияние па малоцикловую прочность, причем главным образом па сопротивление повторным упругим деформациям. Учитывая значения предела выносливости при действии постоянных напряжении по формуле (64):
(П-1) т = 0-1 ( 1 - От/Об) ,	(94)
получПлМ из (93) следующее условие разрушения при наличии постоянных напряжений:
е“ = 4 (1п гМ°’6 yV₽0,6 +	g-1(1~qm/gt>)	(95)
Для формулы Менсона учет соотношения (94) приводит к равенству
еа = y(ln рЦг)0’6 А70’6 + 1,75	(96)
Средние напряжения растяжения понижают прочность при малоцикловом нагружении, средние напряжения сжатия — повышают. Часто в практических расчетах повышение «в запас прочности» не учитывается.
ГЛАВА 5
МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
Вводные замечания. Ранее изучалась картина напряжений и деформаций в твердом деформируемом теле. Связь напряжений в различных площадках, проходящих через рассматриваемую точку тела, условия равновесия элемента тела устанавливались с помощью уравнений статики и не зависели от физических свойств материала.
Связь перемещений и деформаций, условия совместности деформаций выводились из геометрических соображений и также не зависели от физических свойств материала. При изучении напряжений (статическая задача) и деформаций (геометрическая задача) материал рассматривался как сплошная однородная среда, и знания конкретных свойств материала не требовалось Теперь необходимо выяснить общие связи между деформациями и напряжениями, что представляет собой физическую задачу, так как должно учитываться поведение реальных тел.
В предыдущей главе мы познакомились с результатами экспериментальных исследований, проводимых главным образом при растяжении образцов материала. Наша ближайшая задача — обобщение экспериментальных данных для общего случая нагружения при многоосном напряженном состоянии. Всякое обобщение представляет собой модель явления, и нам предстоит рассмотреть модели упругости, пластичности и ползучести.
Замечание. Ранее неоднократно упоминалось о моделях надежности материала п т. п. Установление зависимостей между параметрами, описывающими явление, в сущности, и есть построение модели. Можно говорить о модели идеального газа, жидкости и т. д. Каждая модель, отражая объективную реальность, имеет область существования, в которой она дает необходимую точность. Наиболее универсальные, практически проверенные модели называются законами.
18. Модели упругости
Связь относительных линейных деформаций и нормальных напряжений. При экспериментальном исследовании растяжения образца были установлены в пределах упругих деформаций зависимости для продольной и поперечной деформаций соответственно
8 = 4-0,	О)
ех= —ре,	(2)
где Е — модуль упругости материала, Н/мм2; р — коэффициент Пуассона. Форма образца (цилиндрическая или призматическая} несущественна для приведенных зависимостей.
' Если на .призматический образец (рис, 5.1, а)' наклеить на боковые грани тензометры для измерения линейных деформаций, то при действии напряжения о, вдоль оси образца получим ' следующие значения деформаций:
1	И	Р	/04
=	82 =-H8i = —	83 = — ре, = —	(3)
108	ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
Зависимости (1) — (3) следует считать экспериментально установ-
ленными для изотропного материала, т. е. материала, упругие
Рис. 5.1. Напряжения и линейные деформации при одноосном (а) и трехосном (6) напряженных состояниях
свойства которого во всех направлениях одинаковы. В случае трехосного (объемного) напряженного состояния (рис. 5.1, б) следует учесть действие всех трех напряжений: о4, о2, о3.
Принимая в пределах малых упругих деформаций постулат независимости действия сил, представим линейную деформацию в направлении 1 в. виде
Ci = ei (оО + 6t (о2) + ei (а3).	(4)
Деформация в направлении 1 от действия напряжения равна ei(0t)= aJE.
Направление 1 является поперечным для направлений 2 и 5, и потому
61 (О2)---
е2(а3) =---|<т3.
Окончательно
8i = ^[ai —Н(а2 + 0з)]-	(5)
Подобным образом устанавливаем зависимости для линейных деформаций в направлении осей 2 и 5. В результате будем иметь следующие важные соотношения, которые называются законом Гука для линейных деформаций:
8i = g- [<Ti — Н (а2 + <ъ)Г,
' е2 = -^[а2 —ц(оз + °1)1.	(6)
е3 = -£[о3 —ц(<У1 + а2)].
18. МОДЕЛИ УПРУГОСТИ
109
Z
Уравнения (6) неоднократно подтверждались с помощью экспериментальных исследований при двухосном напряженном состоянии й другими способами. Соотношения упругости для линейных деформаций были установлены для главных направлений (в перпендикулярных площадках действовали только нормальные напряжения).
Используя приведенные в разд. 4 и 10 соотношения для нормальных напряжений и линейных деформаций в косых площадках, можно показать, что соотношения (6) будут справедливы для любых трех взаимно перпендикулярных направлений (осей х, у, z, рис. 5.2):
еж =	—	+ Ог)1,
е» =	— ц(ог + ах)],.
ег = ^[аг — ц(ах + ау)], где ех? 8У, ez — относительные линейные деформации вдоль соответствующих осей; ох, оу, о2 — нормальные напряжения в площадках, перпендикулярных осям х, у, z соответственно.
Соотношения (7) справедливы и при наличии касательных напряжений в соответствующих площадках. Последнее понятно, так как при малых деформациях, вызываемый касательными напряжениями скос (сдвиг) не влияет на изменение длины отрезков.
Связь деформаций сдвига и касательных напряжений. Экспериментальное определение, зависимости деформаций сдвига от величины касательных напряжений можно провести, наблюдая скручивание тонкостенной трубы (рис. 5.3). В результате деформации точки А и В на образующей цилиндра перейдут в точки Х*иВ*. Эксперименты показывают, что деформация сдвига при упругих деформациях пропорциональна действующим касательным напряжениям:
1
(7)
У '
Рис. 5.2. Общий случай трехосного напряженного состояния
определение завися-
ное л .
мости деформации сдвига от величины действующих касательных напряжений
(8)
где G — модуль сдвига, Н/мм2. Модуль сдвига G представляет параметр материала, который, как будет показано ниже, зависит от модуля упругости и коэффициента Пуассона. В общем случае де
но
ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
формация сдвига (изменение прямого угла) между направлениями х и у (см. рис. 5.2) вызывается касательными напряжениями и можно написать
Уху = o' ^ху-	(9)
Подобным образом для трехосного напряженного состояния будем иметь три уравнения, выражающие закон Гука для деформации сдвига в изотропном материале:
_ 1
Уху
=	(10)
1
У*х — o’
Существенно, что деформация сдвига в изотропном материале не зависит от нормальных напряженш! в тех же площадках. Дей-
а	б
Рис. 5.4. Деформация сдвига между направлениями,	составляющими
угол л/4 с направлением растяжения
ствие нормальных напряжении приводит к удлинениям вдоль направлений осей х, у, z, но не изменяет угол между указанными направлениями.
Связь модуля сдвига с модулем упругости и коэффициентом Пуассона. Эту связь установим на проком примере одноосного растяжения (рис. 5.4).
Найдем деформацию сдвига между направлениями, составляющими угол л/4 с направлением
одноосного растяжения пластинки. Рассмотрим деформацию квадрата ABCD, диагонали которого равны 21 (АС == BD = 21). Размеры квадрата при рассмотрении деформаций следует считать бе-
сконечно малыми, но так как на-
пряжения во всех точках пластинки одинаковы, то вывод сиравед-лив и для квадрата конечных размеров. После деформации вершины квадрата будут в точках 4*, В*, ..и произойдет деформация сдвига (изменение угла) между направлениями АВ и ВС:
у = 2(л/4 — ^).
(И)
Деформация растяжения в продольном направлении равна еъ в поперечном она составляет и потому
+ <12>
18. МОДЕЛИ УПРУГОСТИ
11.1
В последнем равенстве учтено, что величина мала по сравнению с единицей и тогда
_1_ — 1 _ ег _ O(ei) « 1 — ev	(13)
Символ О (е*) означает члены, порядок малости которых не ниже ef. Из соотношения (11) получаем
8 = tff- 2) = Jg#*~£W2. = LrVg = 1 - v	(14)
cgp	2/ l+tgn/4tgv/2 l + T/2	1 V’	{l'
так как деформация сдвига мала по сравнению с единицей ^tg 2 « «2? Y<Clj. Сопоставляя зависимости (12) и (14), находим
1 ==(1 + Н)еь	(15)
Пе граням действуют касательное напряжение
=	(16)
и такой же величины нормальное напряжение (на рис. 5.4, а оно не показано). Равенство (16) вытекает из результатов разд. 5, не его легко получить непосредственно, рассматривая напряжения в площадке под углом 45° (рис. 5.4, б).
Используя равенство (8) и учитывая, что
= Oi/E,
находим из соотношения (15)
Ссылаясь на зависимость (16), получаем важный вывод:
С . Е
U ~ 2 (1 + |х) •
(17)
Температурная деформация. Многие элементы конструкций в современной технике работают при высокой температуре. При анализе деформаций должно быть учтено тепловое расширение, что свойственно всем физическим телам.
Линейная деформация при наличии нагрева состоит из двух частей
8 = 8сил “Ь ^темп»	(1®)
здесь ес«л — деформация, вызванная силовым воздействием элементов; етемп — температурная деформация, вызванная тепловым расширением,
бтемп	О&Т*,
112
ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
где а — коэффициент линейного расширения, Т — изменение температуры при нагреве. В технических расчетах температура измеряется в градусах Цельсия (°C) или в кельвинах (К).
Коэффициент линейного расширения а составляет для сталей (11—12) • 10“в для алюминиевых сплавов (20—25) • 10“в для жаропрочных сплавов на никелевой основе (12—20)-10~в для титановых сплавов (8—10) • 10“8 К”1.
Для липейпой упругой деформации
б = с/£ + аГ.	(19)
В изотропном материале температурная деформация не изменяет угол между направлениями, а приводит в данной точке к одинаковым удлинениям во всех направлениях. При неравномерном нагреве или при стеснении границ тела с равномерным распределением температуры могут возникнуть не только температурные деформации, но и температурные напряжения.
Замечание. Учет температурных деформаций обычно проводится при предположении, что распределение температур не зависит от напряженного, состояния тела. Для большинства конструкционных материалов это вполне оправданно (так называемые несвязанные задачи термоупругости).
Общая форма закона упругости. Уравнения упругости для ли-- иейных и угловых деформаций с учетом температурных деформаций получаются из соотношений (7), (10) и (19).
Для произвольной ортогональной системы координат
Sx == j [ах — ц + аг)] + аГ,
— 4 1°!/ — Н (а* + а*)1 + а?1>	(20)
ег =	_ Н (°х + °у)1 +
_ 1 _ 1 _ 1
Уху — Q ^ху, Ууг — o' Чух, Угх — ~q ^гх»
Уравнения (20) выражают общую форму закона упругости (закона Гука). Они содержат два независимых параметра упругости, в качестве которых обычно принимают модуль упругости Е и коэффициент Пуассона ц.
Уравнения упругости можно записать в более краткой форме: е« =-g~И(°У + Oz)l + аЛ •••, Vxy = 4Txv..---	(21)
Символ (я, у, z) означает, что недостающие уравнения выписываются по правилу круговой перестановки индексов.
Частный случай закона упругости — соотношение упругости для объемной деформации. Рассмотрим элемент тела (рис. 5.5), который до деформации имел объем
Vo = abc.
18. МСДЕЛИ УПРУГОСТИ
113
В результате деформации ребра элемента достигли размеров а(1+ех), 6(1+ ev), с(1 + ег), и, следовательно, объемная деформация равна
V — 7
еу =г —-—2 = (1 + еж) (1 + ev) (1 + ez) — 1. ко
Деформации сдвига не изменяют объема тела и потому не влияют на величину объемной деформации. Пренебрегая квадратами дефор-
маций как малыми величинами, получим 8у == 8Х !" Sy !' 8Х —* Зе,
где величина е = j (ех + еу + е2) называется
средней деформацией. Складывая три первых равенства закона
Гука (уравнения (20)), находим (проверьте!) 8 =	+ «Л	(22)
где величина о = у (ох + ау + о2) называется средним(яля гидростатическим)напряжением.
объема элемента при упругих деформациях
Замечание. Название «гидростатическое напряжение» связано со следующими обстоятельствами. Для идеальной жидкости ах = оу = ах = —р, где р — давление в жидкости и о = —р. Для вязкой жидкости величина а рассматривается как среднее давление в точке.
Другие формы закона упругости. Ввиду обширных и разнообразных применений соотношений упругости приведем другие формы зависимостей (20). Вычитая из уравнения для ех величину средней деформации е (уравнение (20)), получим
'	2 (1 + р.) Г 1 ,	, Ч1 1 + Н7 ч
ех — е =	— у (Оу + аг) j = —(ах — о).
В результате приходим к девиаторной форме закона Гука:
ех — е = \ОХ о), ..., у уху » Хху, ... (х, у, z).	(23)
Для полной эквивалентности уравнений (20) и (23) к последним следует добавить условие (22), связывающее 8 и а.
Во многих задачах оказывается необходимым выразить зависимость напряжений от деформаций, вытекающую из закона упругости. Это проще всего получить из соотношений (23) и (22):
е» + а -	~ 2Свх + 8 (г^-аТ.
Подобные соотношения можно найти для <зу и oz.
8 И. А. Биргер, Р. Р. Мавлютов .
114
ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
В результате получим
ох = 2Ge,x + 31е —
= 2Gey + 318 - аТ,	(24)
ог = 2Gez + 318 — - £ л -аТ,
1 -
^ху =я ^Yxyj Пуг &Чуг1 ^zx = ^Yzr,
r Е	\iE
W G = 2(1+7Г -модуль сдвига> Ь = (1 + и) (1 _ 2И) — постоянная Ламе.
Величина 8 представляет среднюю деформацию:
е = у (ех + 8У + ег).
Замечание. Соотношения упругости для изотропного материала содержат два физических параметра. В сопротивлении материалов в качестве основных параметров принимаются Е и ц. Можно выбрать и другие параметры, например G и X, или любую другую комбинацию двух параметров.
Матричная запись закона упругости. Линейные зависимости (21) удобно записать в матричной форме:
{е) — [а]{о) + {аТ},	(25)
где векторы деформаций, напряжений и температурных деформаций
				(У			
		X		X		аТ	
		еУ		°У		аТ	
-	{8} =	Уху	. {<*} =	1 Тх» '		\ аТ 1 0	(26)
		Ууг		Tj«		0 А	
				,Та> .			
матрица упругих коэффициентов
	i/E -р/Е	-ME ЦЕ	— МЕ — ME	0 0	0 0	0 0	
(а] -	-р/Е 0	0	-i/E 0	0 i/G	0 0	0 0	(27)
	0	0	0	0	i/G	0	
	0	0	0	0	0	i/G-	
Матрица упругих коэффициентов симметрична.
Замечание. Представление совокупности скалярных величин в виде мно-» томерного вектора — удобный прием современной вычислительной математики, позволяющий использовать аппарат матричной алгебры.
Следует, однако, помнить, что такое представление не имеет физического обоснования и справедливо при неизменной системе координат. Шесть ком-
18. МОДЕЛИ УПРУГОСТИ
115
понептов напряженного и деформированного состояний образуют тензоры (см. разд. 6 и 10). Тем не менее векторные представления наглядны и удобны, в ими широко пользуются в современной механике.
Модель упругости для анизотропного тела. В современной технике используются анизотропные материалы. В частности, к таким
Рис. 5.6. Композиционный материал с волокнахми в двух взаимно перпендикулярных направлениях
материалам относятся композиционные материалы, состоящие из набора прочных волокон (нитей стекла, углерода, бора и т. п.) и наполнителя (связующего) в виде смолы, мягких материалов и т. п. На рис. 5.6 показан композиционный материал, имеющий волокна в двух взаимно перпендикулярных направлениях. Для такого материала оси х, у, z являются осями упругой симметрии. Материал, обладающий тремя взаимно перпендикулярными осями упругой симметрии, называется ортотропным. Уравнения упругости для ортотропного
материала к гих коэффш [<*] =		южно представить щентов 1/^д:	Рху/^у Рух/^х	УЕу -Pzx/^x -PzylEy 0	0 0	0 0	0	в виде (25), причем - ижг/я2	0	0 0	0 1/EZ	0	0 0	1/G^	0 0	0	HGyz 0	0	0	матриц* о - 0 0 0 0 1№гх__	1 упру- , (28)
где	ЕХ1 Еу, . .	Pzy	Ег — модули упругости в направлении — коэффициенты Пуассона; G^, Gy2.		осей х, у, z; , Gzx — модули	
сдвиуа. Матрица (28) содержит 12 параметров упругости, но независимых всего 9, так как в силу симметрии матрицы существуют следующие зависимости:
Рух __ Рху	Ргу ___ №yz	Pxz __ Pzx
Ех	Еу ’	Еу	Ez	Ez	Ея
Для ортотропного тела ахТ 1
{аТ} =	.
-	1	0
0 о ,
(29)
(3U)
В общем случае для анизотропного тела модель упругости представляет линейные зависимости деформаций от шести компонентов 8*
116
ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
напряжений
= ЛцОх +	+ <*1302 + «14Тху + а15туг + а16тгх +	...	(х, у, z).
(31)
Матрица упругих коэффициентов является квадратной матрицей шестого порядка, содержащей 36 упругих параметров. Из условия симметрии матрица содержит 21 независимый параметр (6 — на главной диагонали и 15 — на боковых). Температурные деформации образуют тензор.
В уравнениях упругости (25) вектор температурных деформаций
ауТ
(«п-
%zT
(32)
В анизотропном теле в общем случае температурная деформация приводит не только к дополнительным удлинениям, но и сдвигам.
19. Модели пластичности
Стремление к наименьшим весу и габаритам изделий приводит к необходимости - увеличения напряжений в элементах конструкций и наиболее полному использованию прочностных возможностей материала. Во многих деталях машин, особенно в местах концентрации напряжений, в рабочих условиях возникают пластические деформации.
Оценка надежности подобных конструкций требует знания распределения напряжений и деформаций в упругопластической области. Модели пластичности необходимы для определения несущей способности элементов конструкций, т. е. величины внешних усилий, при которых происходит потеря работоспособности изделия. Изучение пластичности весьма важно для теории многих технологических процессов.
В настоящее время существует несколько моделей поведения материала при упругопластических деформациях. Наиболее простая модель пластичности строится на основе деформационной теории Генки — Ильюшина.
Основные уравнения деформационной теории пластичности. В основу деформационной теории пластичности положены следующие основные допущения.
1. Объемная деформация материала является упругой.
По уравнению (22) для упругих деформаций
8 =	+	(33)
19. МОДЕЛИ ПЛАСТИЧНОСТИ
117
где
1	1
8 = -т-еу = -х-(ех + 8.. + 8г) — средняя деформация, (34) и	о
а == -у (ах + оу + о2) — среднее напряжение;	(35)
Е, ц и аТ — модуль упругости, коэффициент Пуассона и температурная деформация.
Опыты, проводимые при всестороннем давлении до 20 000 атм, подтверждают, что средняя деформация остается упругой.
Уравнение (33) справедливо для состояния всестороннего равномерного растяжения или сжатия. При таком напряженном состоянии касательные напряжения (в любой площадке) отсутствуют. При отсутствии касательных напряжений деформации упруги. Исследования деформаций показывают, что пластические деформации связаны с деформациями сдвига. Ответственными за появление пластических деформаций являются касательные напряжения.
Замечание. Средняя деформация 8 пропорциональна объемной деформации бу. Более удобно для сопоставления с обычными деформациями рассматривать величины е, что, конечно, не меняет физической сущности допущения.
2. Второе допущение деформационной теории пластичности сводится к утверждению, что тензор-девиатор деформаций пропорционален тензору-девиатору напряжений.
Ранее приводились тензоры деформаций и напряжений (см. разд. 6 и 10):
	8Х	1_ 2 ?ху	1 2 ^XZ
	i-L v 2 *vx	ey	1 2
	1	1	
	2	2	8Z
°х
Хух
Tzx
Хху Txz ®у Tyz Xzy \
(36)
Напомним, что в тензор деформаций входят у уху, -yTi/z, -y?zx, так как исключается поворот элемента, вызванный деформацией сдвига (см. рис. 3.7).
Тензором-девиатором называется тензор, первый инвариант которого (сумма элементов главной диагонали) равен нулю.
Тензоры-девиаторы деформаций и напряжений будут такими:
	8x““8	1 2 ^xy	1 2 7xz
	1		1
Dq 		2 Vy*	Zy~*	2
	1	1	
	2 7zx	2 7zy	8z~*8
	Gx	a	Txy	Txz Xyx	ay ~~	Q	xyz Tzx	Xzy	az	a	; (37)
118
ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
где 8 и о— средние деформации и напряжения. Для Dt и Da суммы компонентов главной диагонали равны нулю (проверьте!):
еж + + ez — Зе = 0, Ох + бу + ог — Зо == 0.
Понятно, что для описания пластичности используются именно девиаторы напряжений и деформаций.
Девиаторы Р8 и Da получаются из Те и Та после «вычитания» деформаций и напряжений, соответствующих всестороннему растяжению или сжатию. На рис. 5.7 показан переход от основного
Рис. 5.7. Переход от основного напряженного состояния (а) к девиаторному 1
(б, в). Нормальные напряжения даны в Н/м2,о = у (Gx + бу + crz). Касательные напряжения при переходе не изменяются
напряженного состояния к соответствующему девиаторному состоянию. Касательные напряжения для обоих состояний остались неизменными, Термин «девиатор» происходит от слова «девиация» — отклонение. Девиатор напряжений характеризует отклонение данного напряженного состояния от состояния всестороннего растяжения или сжатия. Такие «отклонения» и вызывают деформации сдвига и связанные с ними пластические деформации.
Условие пропорциональности девиаторов деформаций и напряжений записывается в виде
•	£>8 = &£>.,	\ (38)
где к — коэффициент пропорциональности, который удобно представить в следующем виде:
.	'	(39)
В равенстве (39)’ ф — безразмерный коэффициент, называемый параметром пластичности. Если материал находится в упругом состоянии, то ф = 1 и уравнение (28) соответствует уравнениям (23).
Из тензорного равенства (38) вытекают девять скалярных равенств, из которых в силу симметрии тензоров (ух?в Тух, Тху == Тух),
19. МОДЕЛИ ПЛАСТИЧНОСТИ
119
различными будут только шесть:
. 1 4- ц .	.
ех — е = -ф —(аж — о),
, 1 4- и /1 ч е» - е = ф (сту — а),
ег — е = ф —р- (аг — а),
1	, 1+Н 1	, 1 + .ч 1 u 1 “г И
~ V*!/ — Ф	"2 Yv* — Ф £ Tyz> У** — Ф Ё Тгх‘
Уравнения (40) называются уравнениями Генки — Ильюшина. Они аналогичны закону Гука для упругого материала, если присоединить к ним условие (33).
Уравнения пластичности в векторной форме. В девиаторы деформаций и напряжений входят девять скалярных величин, которые можно представить как составляющие девятимерных векторов:
- ( х f	111111V
V/ — |ех 8j ez 2	”2*Уух1 "% Yzy? ~2 ^yZl Т^zx' ~2 Ухг\ *
(41)
{5} == {(Ух (У, Оу О, (У2 СУ, ТХу, ^ух, У'уг, ^zxi ^xz} •	(42)
Верхний индекс т означает операцию транспонирования, при которой столбец заменяется строкой. Конечно, в равенствах (41) и (42) выписаны по три «лишние» составляющие, так как Тхуs тух, уху = = Ьх, ... Это сделано из физических соображений, с тем чтобы «размерности» вектора и тензора совпадали.
Уравнения пластичности в векторной форме будут такими:
{е} = 1|)Ц^{5}.	(43)
Вектор-девиатор деформаций {е} коллинеарен (пропорционален) вектору-девиатору напряжений {5}.
Из уравнения (43) следует, что и модули векторов (их длины) связаны тем же соотношением:
|е| = фЦ^14	(44)
Модули векторов характеризуют интенсивность напряжений и деформированного состояния в точке:
|$| = ]/"(ах —а)2 4- (сту —а)2 4- (ог — о)2 4- 2тД, 4- 2т^ 4- 2т^, (45)
I е | = ]/(ех — е)2 4- (8V — е)2 4- (ег — е)2 4- j + у	+ 7 т=с’
(46)
120
ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ .
Для случая одноосного растяжения отличны от нуля следующие величины:
0х = Оо,	8У==—ц*е0, ez = —|i*e0,	(47)
где ц* — коэффициент Пуассона при упругопластических деформациях (ц < ц* < 0,5). Из равенства (45) находим для одноосного растяжения (проверьте!)
<48>
Для более удобного и наглядного сопоставления с результатами экспериментальных исследований при простом растяжении определим интенсивность напряжений о» следующим образом:
=	.	(49)
Тогда для случая одноосного растяжения будем иметь
о< = Оо.	(50)
Интенсивность напряжений при одноосном растяжении совпадает с растягивающим напряжением.
Значение let при простом растяжении в соответствии с равенствами (46) и (47) будет таким:
1Н“/4(1 + И*)в0.	(51)
Приближенное значение для упругопластических деформаций: р*« 1/2. Целесообразно определить интенсивность деформаций 8j следующим образом:	.	-
(52)
Тогда для одноосного растяжения
8{=2<1 + иЧео.	(53)
При коэффициенте Пуассона ц* = 0,5 интенсивность деформации при одноосном растяжении совпадает с деформацией растяжения.
Учитывая равенства (49), (52) и (44), получим важную зависимость:	.	.	•	'
.	8{ =	(54)
Замечание. Зависимость (54) можно получить непосредственно из уравнений пластичности (40), если каждое из шести равенств возвести в квадрат, сложить их, предварительно удвоив последние три равенства, и извлечь из суммы квадратный корень.
Интенсивность напряжений и деформаций. Понятия интенсивно-* сти напряжений и деформаций занимают центральное место в де
19. МОДЕЛИ ПЛАСТИЧНОСТИ
121
формационной теории пластичности, так как позволяют установить эквивалентность между сложным напряженно-деформированным состоянием и простым растяжением.
Интенсивности напряжений и деформаций были определены следующими зависимостями:
щ == ]/у У(ах — а)2 + (ау — а)2 + (аг — а)2 + 2txy + 2туг + 2т^,
 _ ______________________________________________________(55)
6i = ]/у У (fix — е)2 + (еу —е)2 + (ez — е)2 + у у2у + у + у yzx.
Приведем другие выражения для о, и е<, более удобные для практических расчетов. Учитывая, что
(ах — а)2 + (fiy — о)2 + (аг — а)2 = а! + Оу + а2 — За2 ==
— у (оя *Ь Оу + Ог	СГхОу Oyfiz OzOx} я
= у К°х — Оу)2 + (ау — аг)2 + (ог — Ох)2], (56)
получим из равенства (56) часто применяемую формулу для интенсивности напряжений
Ci =	]/"(Пх — Пу)2 + (Оу — ог)2 + (ог — Ох)2 + 6 (тД, -ь Туг + Т^х).
(57)
С помощью аналогичных преобразований находим
е» =	]/(ех — бу)2 + (fiy — ez)2 + (ег — ех)2 + у (у2у +	+ у«).
(58)
Отметим, что для любого напряженного и деформированного состояния величины о< и положительны (модули векторов!). Интенсивности напряжений и деформаций могут быть выражены через вторые инварианты тензоров-девиаторов (их первые инварианты равны нулю!).
Напомним, что вдррой инвариант тензора напряжений (см. уравнение (69) гл. 2) равен
2 (Та) “	®у£у	(JzQx + ^ху "Ь ^yz 4“ ^zx*
В девиаторе компоненты ох, ov, oz заменены на ож —о, оу — о, о, — о, и потому второй (квадратичный) инвариант тензора-девиатора имеет вид
Ц (Dg) == — (Jx — a) (cjy — а) — (оу — а) (а2 — а) — (а2 — а) (ах — а) + .
+ ^ху “Ь Hyz + ^ZX* (59)
122
ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
Сопоставляя равенства (59) и (57), устанавливаем: квадрат интенсивности напряжений пропорционален квадратичному инварианту тензора-девпатора напряжений. Подобный вывод справедлив для £» и /2(/)е).
Наконец, отметим, что интенсивность напряжений пропорциональна касательному напряжению в октаэдрической площадке.
Рис. 5.8. Нормальное и касательное напряжения в октаэдрической площадке: а — напряжения в октаэдрической площадке; б — правильный октаэдр
Октаэдрической площадкой (рис. 5.8) называется площадка, нормаль к которой наклонена одинаково по отношению к главным направлениям. Октаэдрическая площадка является гранью правильного восьмигранника (октаэдра, рис. 5.8, б); направляющие косинусы нормали
I2 + пг2 + п2 = 1, I = ш — м = 1/УЗ.
Нормальное напряжение в октаэдрической площадке по формуле (59) гл. 2
<*окт = у fax + °У + Qz) =	(60)
Касательное напряжение
Токт == Р* --- Фонт*	(61)
В силу равенств (55) —(57) гл. 2
в рх + Ру + Pt == у- (<*!.+ 0*2 + °з)«	(62)
Из последних соотношений вытекает
-Гокт= (°* +	+ °») — J (°1 + °2 + °з)2 =
= 7 /(О1 — °2)2 + (<Т2 — Оз)2 + (<Ъ — <h)2-	(63)
19. МОДЕЛИ ПЛАСТИЧНОСТИ
123
Учитывая выражение о» для главных напряжений (ох = av»<уъ Oz = Оз7 тХ1/ = 0, Ту2 = 0, тгх « 0), получим
Рис. 5.9. Кривая деформирования при растяжении

Существует еще одна трактовка интенсивности напряжений. Как показал В. В. Новожилов, величина Oi пропорциональна среднеквадратичному значению касательных напряжений на поверхности сферы единичного радиуса.
Замечание. Величина сг< отражает не общий уровень напряжений, а интенсивность касательных напряжений, что вытекает из равенства = 0 для всестороннего растяжения или сжатия.
Общепринятый термин «интенсивность напряжений» не вполне точен. Лучше говорить о «приведенной интенсивности касательных напряжений, выраженной через эквивалентное нормальное напряжение при простом растяжении», или. короче, об «эквивалентном напряжении растяжения».
Интенсивность упругих и пластических деформаций. Как известно, общая деформация материала в состоит из упругой й пластической частей (рис. 5.9). При простом растяжении
8о = 8Г+ 8о-	(65)
Здесь и в дальнейшем верхние индексы р и е означают соответственно пластичность и упругость.
Уравнения пластичности (40) относятся к общим деформациям, но их можно записать отдельно для упругих
и пластических деформаций. Полагая ф == 1, получим для упругих деформаций
е е 1 Ц .	1 е 1 4~ И
_ех 8 ~ Е .(ах О’),...,	2 Уху ~ Е	(66)
В разделе 18 эти соотношения были получены из уравнений упругости. Вычитая равенства (66) из (40), получим значения пластических деформаций:
_	14- ц	14- и
6р = (1|>-1)—£-(<тя-а), ...2у	=	... (*,?.«)• (67)
При выводе последних равенств было учтено, что пластические деформации протекают без изменения объема материала:
8₽ = Т(8£+8£ + 80=°’	(68)
и потому
8 я= 8е.
Из уравнений (67) находим
®х “ е£= (» - 1) (<тя - ау), .у WЧп• • • <*’ У’ z>.
(69)
Возводя каждое равенство в квадрат, складывая все шесть равенств, предва*
124
ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
рителыю умножив три последние па 6 и извлекая квадратный корень из суммы, найдем
= (-Ф - 1)	°i-	(™)
Интенсивность упругих деформаций в силу зависимостей (66) или равенства (54) при ф = 1 равна
Последние соотношения приводят к важному результату:
8i = ei +	•
(72)
Интенсивность деформаций равна сумме интенсивностей упругих и пластических деформаций (равенство Генки — Беляева).
Обобщенная кривая деформирования. Ранее было установлено соотношение (54), содержащее пока неизвестный параметр пластичности ф. Соотношение (54) показывает, что между интенсивностью деформаций и интенсивностью напряжений о< должна существовать зависимость
0г=/(еО,	(73У
которая называется обобщенной кривой деформирования.
Зависимость (73) в рамках деформационной теории пластичности следует считать справедливой для любого напряженного состояния.
Для несжимаемого материала (ц = ц* = 0,5) по уравнениям (50) и (53) находим 8г-== е0, Ог = о0, и обобщенная кривая деформи-
Рис. 5.10. Обобщенная кривая деформирования
рования совпадает с обычной кривой деформирования при растяжении образцов.
В общем случае, используя уравнения/50) и (53) :
= <j0, е4 = 2 (1	е0, (74)
можно построить зависимость (73)' (рис. 5.10) по значениям е0, (Jo, взятым из опытов на растяжение, и по экспериментальному или расчетному значению коэффициента Пуассона ц* при упругопластических деформациях.
С помощью обобщенной кривой деформирования выясняются
значение и физический смысл параметра пластичности нение (54) и рис. 5.10):
ЗЕ «г о*
2(1 + И) о, ’
(см. урав-
(75)
где а* — значение интенсивности напряжений в идеально упругом
19. МОДЕЛИ ПЛАСТИЧНОСТИ
125
теле, соответствующее интенсивности деформаций 8< в упругопластическом теле.
Однако построение обобщенной диаграммы деформирования о,- не обязательно для расчета упругопластического деформирования. Можно и гораздо удобнее в качестве обобщенной кривой деформирования принять обычную кривую деформирования е0, о0 при растяжении, понимая под е0 и о0 эквивалентные деформации и напряжения.
При простом растяжении интенсивность пластической деформации .
е? = V2 - 8£)2 + (е? - 8Г)2 + (е? - е£)2 - 8*. (76)
так как
₽р_₽р pp__JL₽p рр___________1₽р
с-х — иь —	2 °®’	°2 —	2
где 8q — пластическая деформация при растяжении (см. рис. 5.9). Интенсивность упругой деформации по (71)
е_2(1Ч-Ц) е«	£	Q0>
и потому интенсивность деформации при простом растяжении
е. _ еР . 2d+н)	_	_% . 2(1 + ц)
е» — е0 +	3£	о0 — 8о .£ + з£	°о«
или
Рис; 5.11. Кривая деформирования при растяжении стержня как обобщенная кривая деформирования (£в = Оо/е0 — секущий модуль)
е. _ ₽	1 - 2|х ао
Интенсивность напряжений последних соотношений получаем эквивалентные деформации и напряжения*. *
, 1 — 2|Л аг
(78)
Кривая деформирования при растяжении может рассматриваться как обобщенная кривая деформирования (рис. 5.11), если эквивалентные деформации и напряжения определяются по формулам (78).
Еще одна форма уравнений Генки — Ильюшина. После того как выяснена связь величин е< и о<, можно указать еще одну форму уравнений Генки — Ильюшина. Внося значения ф из уравнения
0	3	v '
в опытах на растяжение = Из
126
ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
(75) в соотношения (40), найдем
ех —е = -^-(ах —а),	| уху =	тХ(/, ... (x,y,z)	(79)
и далее
3 8i	1	3 ei
8* - 8 = Т/^0 (<Тж “ О)..Т = ТГ(^Тжу’ • • ’ (х’у'гЬ
Коэффициент Пуассона при упругопластических деформациях. Деформационная теория пластичности позволяет определить величину коэффициента Пуассона при упругопластических деформациях. Из соотношений (74) и (77) находим
2(1 + ц*)	1-2ц %
Ьг ~	3 ео - ео — Е ,
(80)
или
..ж	<	1-2ц £с
И ~ 2	2	Е ’
Рис. 5.12. Сопоставление экспериментального (точки) и теоретического (кривая) значений коэффициента Пуассона в упругопластической области
где Ес = о0/е0 — секущий модуль на кривой деформирования (см. рис. 5.11).
На рис. 5.12 показано сопоставление экспериментального значения ц* и значений, определяемых по уравнению (80). Соотношение (80) дает удовлетворительное совпадение с данными опытов. Отметим, что если в упругой области ц = 0,5 (упруго несжимаемый материал), то и в упругопластической области по равенству (80) р* = 0,5.	'
Интенсивность деформаций при растяжении в соответствии с равенством (77)
8< « 1 —
Метод переменных параметров упругости. Уравнения пластичности, связывающие деформации и напряжения, при о<> >ат нелинейны. Если в пределах упругих деформаций (о< < от) увеличение напряжений в к раз вызывает такое же увеличение деформаций, то при появлении пластических деформаций пропорциональность нарушается. Нелинейность уравнений Генки — Ильюшина отчетливо проявляется в их записи в форме (79). Нелинейность физических уравнений теории пластичности создает большие трудности при решении практических задач (нарушается принцип независимости действия отдельных нагрузок и т. п.) .
19. МОДЕЛИ ПЛАСТИЧНОСТИ
127
Метод переменных параметров упругости сводит решение задач деформационной теории пластичности к решению последовательности обычных задач упругости, что существенно облегчает расчеты.
Уравнения пластичности Генки — Ильюшина (зависимости (40)) сначала запишем формально в виде уравнений упругости. Например, соотношение
8Х — е = (ах — о)
с учетом зависимости (33) будет таким:
— о) + е = ф (аж — а) + -^--о + аТ.
Продолжая преобразования, представим уравнения пластичности в виде
8х =	—+ °г)]+аТ, ..?хг/=	... (x,y,z).
Здесь переменные параметры упругости £* и ц* равны
(81)
(82)
(83)
2(14-И)<ф + 1 —2|л * (1 + Ц) — (1 — 2ц) И ф(1+ц) + (1—2ц) ’ где Е — модуль упругости, ц — коэффициент Пуассона (в упругой области), ф — параметр пластичности.
Параметры Е* и ц* называются переменными параметрами упругости, так как они зависят от напряженного состояния в точке (параметра пластичности -ф). В упругой области ф = 1 и Е* = ЕГ - р*==ц.
Для несжимаемого тела (коэффициент Пуассона ц = 0,5)
£* = 4 = — = т2- =	(84)
Ф. Ч «о
ц* = 0,5.	(85)
Принимая в качестве обобщенной кривой деформирования кривую деформирования при растяжении, получим для параметра пластичности из соотношений (75) и (77) следующее выражение:
ЗЕ _ з / е 1-2ц\
'Р 2(l-f-p) at 2(1 + р) ^£с	3 J’
(86)
где Ее = <J0/e0 — секущий модуль.
Теперь из соотношений (82), (83) и (86) вытекают основные формулы метода переменных параметров упругости:
Е* = Ес,.
,_1 l-2ggc
2	2 Е'
(87)
(88)
128
ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ. ПОЛЗУЧЕСТИ
Уравнения деформационной теории пластичности можно представить как уравнения теории упругости, если модуль упругости в них заменить секущим модулем (рис. 5.13). Менее существенной
Ряс. 5.13. Схема расчета по методу переменных параметров упругости
является поправка значения коэффициента Пуассона по формуле (88).
Замечание. Влияние коэффициента Пуассона на распределение напряжений обычно невелико, и часто проводят расчеты при ц » 0,5, т. е. для несжимаемого материала.
Использование простых равенств (87) и (88) пе требует каких-либо предположений относительно величины коэффициента Пуассона.
Соотношения (87) и (88) можно получить более простым путем, если представить уравнения (79) в виде зависимости
1 + н*
ех —в—	(^х”^),	(89)
что соответствует одной из форм закона Гука (см. уравнение (23)). Будем иметь
1 + ц* Зе{
Используя эквивалентные значения е0 и а0, находим
,	1 - 2ц Ес
1 + ц« 3	3	Е
Е* ~ 2	Ес
(90)
В силу соотношения (80) приходим к равенствам (87), (88).
Запись уравнений пластичности в форме уравнений упругости еще не продвигает дело, так как значения секущего модуля и коэффициента Пуассона заранее неизвестны. Решение задачи находят методом последовательных приближений.
В первом приближении (см. рис. 5.13) материал считается упругим	Е. |1(i) == |i) и решается обычная задача упругости.
В результате определяются интенсивность напряжений о1(1)-в упругом теле и соответствующее значение эквивалентной деформации е0(1) e ai(l)/^«
По величине 80(d, определяются по кривой деформирования величина а<(1) и секущий модуль
ЯС(1) = 0<(1)/во(1)«
Во втором приближении полагают г* — р	♦	1	1 — 2ц *С(1)
£(2)~ Ес (1)’	Ц(2)= у--2----Ё~
19. МОДЕЛИ ПЛАСТИЧНОСТИ
129
и снова решают задачу упругости при полученных значениях параметров упругости. В результате получают значения вцъ), £0(2) и новое значение секущего модуля
^С(2)~ Ф(2)/бо(2И
Процесс считается законченным, если для n-го приближения
| О’г(п) — Ф(п—1) | < А1> | CFj(n) ^i(n) | < А2,	(*Ю
Рис. 5.14. Определение деформации растяжения при заданном напряжении по методу переменных пара-
где А < — принятая точность сходимости приближений, Д2 — принятая точность расчета.
В плоскости эквивалентных напряжений и деформаций о0, 8в (см. рис. 5.13) точки «упругого расчета» стремятся к кривой деформирования. Не останавливаясь на доказательстве сходимости процесса, отметим, что обычно необходимая точность достигается после нескольких приближений. Условия (91) гарантируют сходимость и точность решения.
На рис. 5.14 дана иллюстрация метода переменных параметров для простейшей задачи — определить деформацию при растяжении с заданным напряжением	Од. Решение	задачи
соответствует пересечению	линии
Од == const с кривой деформирования. Последовательные приближения пока-
заны точками 1,2,...	метР°в У*РУ™ти
Замечание. Метод последовательных приближений является одним из наиболее общих математических методов. Для решения задачи разрабатывается процедура (алгоритм), при которой в каждом последующем шаге учитываются результаты предыдущего шага (предыдущего приближения). Метод является строгим, если доказаны сходимость последовательных приближений к точному решению и независимость результата от выбора исходного приближения.
В технических задачах доказательство сходимости, как правило, несущественно — ее наличие или отсутствие видно уже после первых шагов. Важно иметь возможность проверки правильности полученного результата.
Ограничения при использовании модели пластичности на основе деформационной теории. Эксперименты показали, что лежащие в основе модели пластичности уравнения Генки —• Ильюшина достаточно хорошо описывают процесс монотонного нагружения. При таком процессе на всех этапах нагружения (внешними силами, температурами и т. п.) интенсивность напряжений щ все время возрастает.
Монотонное нагружение обычно реализуется при простом нагружении, когда все внешние силовые факторы изменяются пропорционально одному возрастающему параметру. При простом нагружении соотношение между внешними нагрузками в процессе нагружения остается неизменным. Если наступает процесс разгрузки, когда во всех точках тела интенсивность напряжений убывает (например, при снятии внешних усилий), то приращение (уменьшение) напряжений и деформаций на этапе разгрузки определяется на основе уравнений упругости (закон разгрузки; см. рис. 5.15). Основные ограничения рассматриваемой модели пластичности связаны с тем, что уравнения пластич-9 И. А. Биргер, Р. Р. Мавлютов
130
ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
ности относятся к конечной точке процесса и потому не учитывают историю нагружения. Если из физических соотношений ясно, что имеет место монотонное нагружение, то указанный недостаток несуществен.
В рамках применяемой модели пластичности можно учесть действитель-
ную историю нагружения,
Рис. 5.15. Процесс разгрузки при упругопластическом деформировании
если рассматривать нагружение как совокупность нескольких этапов. Если на каком-либо промежуточном этапе происходит разгрузка, то расчет ведут с использованием уравнений упругости.
Другие модели пластичности. Более совершенной, но и значительно более сложной является модель пластичности, основанная на теории пластического течения Сен-Венана, Мизеса, Прандтля и Рейса. В Соответствии с этой теорией рассматриваются раздельно приращения деформаций упругости и пластичности:
rfes = dex + de’, .... dy^ = dy^ + dy*y, ...
(92)
Приращение пластической деформации принимается пропорциональным составляющим девиатора напряжений:
1
deP=F(Oi) dcri(ax-a), .... у = F(о<) do^, ...	(93>
где dot — приращение интенсивности напряжений. Функция F(a,) определяется на основании экспериментальных данных при растяжении образцов.
Изложение теории пластического течения и других моделей пластичности можно найти в специальной литературе.
20. Модели ползучести и вязкоупругости
Как уже указывалось в разд. 15, ползучестью материала называется возрастание деформаций с течением времени при постоянном нагружении. Ползучесть металлов возникает главным образом в теплонапряженных элементах конструкций, при работе в условиях повышенных температур. Для полимерных и композиционных материалов, бетонов и др. ползучесть проявляется и при нормальной температуре. Для подобных материалов обычно используются модели вязкоупругости.
Практическая важность проблемы приводит к необходимости оценки влияния ползучести на работоспособность конструкции. Ползучесть влияет на перераспределение напряжений в элементах конструкций, а в ряде случаев приводит к недопустимому возрастанию деформаций. Разберем сначала модели ползучести металлических конструкционных материалов.
Основы моделей ползучести. Модели ползучести основаны на следующих допущениях.
Общие деформации, вызываемые действующими напряжениями и нагревом, представляют сумму деформаций упругости, пластичности, ползучести и температурной деформации:
ех в 4 +	+ аТ + ...	(я, у, z).	(94)
20. МОДЕЛИ ПОЛЗУЧЕСТИ И ВЯЗКОУПРУГОСТИ
131
Верхние индексы указывают природу деформации (е — упругость, р — пластичность, с — ползучесть); а — коэффициент линейного расширения; Т — температура.
На рис. 5.16 дана схематическая модель материала, соответствующая равенству (94).
Материал рассматривается как последовательное соединение элементов. Тепловое воздействие вызывает тепловое расширение,
Рис. 5.16. Схематическая модель материала
а также влияет на параметры всех элементов (уменьшение модуля упругости в результате нагрева и т. п.).
Часто деформацию упругости и пластичности объединяют (деформационная теория пластичности), относя к ним и температурную деформацию. Равенство (94) справедливо и в дифференциальной форме:
dex = d&x + d&x + d&x + d (аТ) + ,. ♦ (я, у, z).	(95)
В практических расчетах под de«, ..« понимают приращение деформации Дех за малый промежуток времени At
Второе допущение, используемое при построении моделей ползучести, состоит в том, что скорости деформаций ползучести или суммарные деформации пропорциональны составляющим девиатора напряжений.
Модели ползучести переносят результаты простых экспериментов (растяжение стержня при постоянных температуре и напряжении) на общий случай деформирования.
Модели ползучести, основанные на теории старения. Изохронные кривые ползучести. Наиболее простой теорией ползучести является теория старения. В соответствии с этой теорией должна существовать зависимость
F(e0, Go, t П = 0,	(96?
где во и о0 — суммарная деформация и напряжение при простом растяжении, t и Т — время и температура нагружения. В соответствии с равенством (94) суммарная деформация
®о =“ ео + 8$ + е0 + а?1.	(97)
Для сложного напряженного состояния зависимость (96) относится к интенсивностям деформаций и напряжений:
t ?) = 0,	<	(98)'
9*
132	ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
или в другой форме
et=8i(Oi, t, Г).	(99)
Интенсивность суммарной деформации (упругости, пластичности и ползучести) определяется интенсивностью напряжений, временем и температурой нагружения.
Для стационарного режима нагружения (о0 = const, Т = const) зависимость
во = е0(оо, Т)	(100)
может быть определена из эксперимента (кривых ползучести). Основная гипотеза теории старения состоит в том, что зависимость (99) справедлива при нестационарном нагружении (o = var, Т == = var).
Расчет ползучести основывается на кривых ползучести (см. разд. 15), построенных при постоянных температурах для различного уровня напряжений. На рис. 5.17 показана сетка кривых ползучести при напряжениях
01 < Оо Оз 04»
По оси абсцисс откладывается время, по оси ординат — деформация при растяжении стержня (образца) при постоянном напряжении. В момент £ = 0 (начало отсчета) начальная деформация
Рис. 5.17. Построение изохронных кривых ползучести (6) по сетке кривых ползучести (а)
соответствует мгновенной деформации (упругой или упругопластической) в результате действия приложенного напряжения. Температурная деформация
ет==аГ
при построении кривых ползучести так же, как и кривых деформирования, не учитывается.
Если провести сечение t = const, например t « tu то прямая t = ti пересечет кривые ползучести в точках Аь 42, 43, Л4, которым соответствуют деформации ползучести 82, 83, 84. В каждой точке
20. МОДЕЛИ ПОЛЗУЧЕСТИ И ВЯЗКОУПРУГОСТИ
133
Л2, ... известно значение действующего напряжения щ, ..< Эти данные позволяют построить зависимость
о
Рис. 5.18. Поверхность суммарных деформаций при ползучести F(t, «о, ио) = 0
ео = ф(<*о) |!=<г = <р(^о^1)-	(10П
На рис. 5.17 кривая (101) проходит через точки О, Alt Л2, А3, Л4. Зависимость (101) выражает изохронную кривую ползучести для времени t.
Для начального значения времени t = 0 изохронная кривая совпадает с обычной кривой деформирования при растяжении стержня. Сетку кривых деформирования можно представить в виде поверхности суммарных деформаций при ползучести (рис. 5.18) в координатах Л €0 и По. Плоскости t = const (на рис. 5.18 они заштрихованы) при пересечении с поверхностью образуют изохронные кривые ползучести.
По теории старения, которая излагается в трактовке Ю. Н. Работно-ва, ползучесть приводит к уменьшению упругопластического сопротивления материалов — с увеличением времени условные кривые деформирования понижаются, материал «со-старивается».
Отметим, что деформации ползучести возникают и при напряжениях, меньших предела текучести, и потому «понижение» происходит и на упругом участке условных кривых деформирования.
После нахождения изохронных кривых ползучести задача сводится к расчету упругопластического тела по деформационной теории пластичности (разд. 19). Для начального момента времени (£ — 0) расчет полностью совпадает с определением напряжений и деформаций по деформационной теории пластичности.
Для момента времени t проводится точно такой же расчет, но в качестве кривой деформирования принимается изохронная кривая ползучести для соответствующего момента времени.
Модели ползучести, основанные на теории старения, пригодны для описания монотонного, или стационарного, нагружения, процессов релаксации (падения) напряжений при неизменной деформации.
Основным недостатком теории старения является отрицание влияния истории нагружения. Из уравнения (98) следует, что в момент времени t данному напряжению соответствует определенная деформация ползучести. Следовательно, если напряжение мгновенно возрастет, то должна мгновенно увеличиться и деформация ползучести, что, конечно, произойти не может. Более правильно считать, как это делается в других теориях ползучести, что при мгно-
134
ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
венном возрастании напряжений подобным образом увеличивается
скорость ползучести.
Модели ползучести, основанные на теории течения и теории
упрочнения. На рис. 5.19 показана кривая чистой ползучести при одноосном растяжении — зависимость деформации ползучести ej от времени нагружения. Мгновенная
деформация в начальный момент, связанная с упругостью и пластичностью материала, не учитывается. В теориях течения и упрочнения деформация ползучести рассматривается отдельно от деформации упругости и пластичности. Скорость деформации ползучести
Рис. 5.19. Кривая чистой ползучести при о = const, Т =» const; деформации упругости, пластичности и температурное расширение (деформация в начальный момент времени (t =s 0) не учитывается)
Г. - е; -	<’02>
Для кривых ползучести VQ представляет (в определенном масштабе) тангенс утла наклона касательной (рис. 5.19).
Проводя испытания при различных напряжениях и температурах, по кри-
вым ползучести можно установить зависимость
t, Г).
(ЮЗ)
В теории течения для общего случая напряженного состояния в уравнении (103) величина Vo заменяется интенсивностью скоростей деформации
(Уя-У^+ ... +	(Ю4)
..	•	ТГ	* dBV	„	’
где Vx —	ех —	Vv —	е„ — —,	..., Vxy = уху =	... —
скорости компонентов деформации; величина о, заменяется интенсивностью напряжений
<Ti = ХД Y (°х —• °v)a + • • • + 6t*v + «• • •	(Ю5)
По теории течения предполагается, что должна существовать зави
симость
W, о,, t, Г) = 0,	(106)
или в другой форме
7<-V<(0<, t, Т).	(107)
Интенсивность скоростей деформации ползучести определяется интенсивностью напряжений, временем и температурой нагружения.
20. МОДЕЛИ ПОЛЗУЧЕСТИ И ВЯЗКОУПРУГОСТИ
135
Основная гипотеза теории течения состоит в том, что зависимости (103) и (107) остаются справедливыми не только для стационарного режима нагружения (Oi = const, Т = const), но и при нестационарном нагружении (o<==var, Г = уаг).
Деформация ползучести, как и всякая остаточная деформация, происходит без увеличения объема:
4	+ 8сг = 0.	(108)
Из последнего соотношения после дифференцирования по времени вытекает равенство нулю скорости объемной деформации:
V ~ + еу + е® = Vx + Vy + Vz ~ 0,	.	(109)
где V — скорость средней деформации.
В соответствии с общими принципами построения моделей ползучести девиатор скоростей деформации ползучести принимается пропорциональным девиатору напряжений:
rs = бх = к(ах — о), у Vxy = у уху = ктху, ... (x,y,z). (НО)
В левые части зависимости (110) не входит скорость средней деформации, так как F = 0. Равенства (110) можно записать в эквивалентной форме:
— Vy ssss к (рх Gy), • • •, "2* Vху = ктху, • •.	(х, у, z). (Ill)
Символ (х, у, z), как и раньше, означает, что недостающие соотношения выписываются с помощью круговой перестановки индексов. Возводя каждое из шести равенств (111) в квадрат, складывая все шесть равенств, предварительно умножив последние три соотношения на 6, и извлекая квадратный корень, получим
У(Ух-уу)*+ ... + ^v2xy + ... =
« к V(°х — Oj/)2 + ... + 6-rjy + ... .
С учетом зависимостей (104) и (105) находим
= к = ^.	(112)
Для случая одноосного растяжения
Vi = Vo “ '•о.	= СГ0	(113)
и
136
ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
В общем случае для двухосного (плоского) или трехосного (объемного) напряженного состояния
где Уо — скорость деформации ползучести в момент времени t в опытах на растяжение, проводимых при напряжении о0 = о, и температуре Т.
Модель ползучести по теории течения характеризуется следующими соотношениями:
_ 	ЗУ0(а,...Г)	±	_± .	_
г х — ьх —	2д.	\и»	’ 2 F ху-2	—
37 (<т{, t, Т\	'
=-----2^----- т>ху, ••• {х, у, z).	(116)
Обращает на себя внимание аналогия с уравнениями деформационной теории пластичности, если вместо деформаций рассматривать скорости деформации.
Подобные, зависимости справедливы и для модели ползучести по теории упрочнения, в которой принимается
^о = ^о(ао,еос,П	(117)
Зависимость (117) отличается от (103) тем, что величина скорости характеризуется не временем нагружения, а достигнутой величиной деформации ползучести.
Установившаяся ползучесть. Процесс ползучести, протекающий при постоянных, не изменяющихся во времени напряжениях, называется установившейся ползучестью. Очевидно, установившаяся ползучесть может иметь место только при неизменных во времени внешних усилиях и нагреве. При постоянных напряжениях приращения деформации упругости и пластичности должны отсутствовать, и из уравнения (95) при постоянной температуре следует dex = dex, ... (*,*м).	(118)
Разделив обе части равенства на dt, находим
(119)
При установившейся ползучести скорость изменения деформации - равна скорости ползучести.
Для ползучести при одноосном напряженном состоянии (растяжении) по сетке кривых ползучести (см. рис. 5.19) для различных напряжений можно найти скорость VQ на участках с постоянной скоростью ползучести:
Уо = ф(ао, Т).	(120)
20. МОДЕЛИ ПОЛЗУЧЕСТИ И ВЯЗКОУПРУГОСТИ
137
Для аналитического описания часто используется степенная зависимость
V0 — B(T)<$m.	(121)
При одноосном напряженном состоянии для наступления стадии установившейся ползучести достаточного того времени, при котором скорость ползучести во всех точках тела не будет зависеть от времени.
При указанном времени соответствующие кривые ползучести «выходят» на прямолинейный участок. Более строго, установившаяся ползучесть наступает с того момента времени, когда скорости ползучести становятся подобными по времени, т. е. могут быть выражены соотношением
Го = ф(о0, ТШО,	(122)
где £(£) —функция времени,. одинаковая для различных значений о0 и Т (в частном случае £(£)=!).
При действии значительных напряжений порядка предела текучести развивается ползучесть за небольшие промежутки времени (порядка секунд и минут). На рис. 5.20 показаны кривые ползучести при кратковремен- *о ной ползучести, которые практически мож- / s 3 но считать прямыми линиями. Для таких	//
кривых ползучести справедливо соотноше-ние (120), и кратковременную ползучесть	______
мыкав рассматривать как установившуюся 0	t
ползучесть; ее можно представить как пре- Рис 520 Кривые пол. дельное состояние, которое устанавливается зучести при высоком при большом времени нагружения при уровне напряжений постоянных внешних нагрузках и темпера- (кратковременная пол-турном поле. При установившейся ползучее- зучесть, . ти деформации упругости оказываются малыми по сравнению с деформациями ползучести.
Расчет стадии установившейся ползучести более прост, чем расчет общего случая ползучести. Для расчета установившейся стадии могут быть использованы соотношения (116) при условии (120):
(о.-а)............................   (w),
(123) Часто используется зависимость (121), и тогда основные уравнения для модели установившейся ползучести имеют вид
Уя = 45-а),	1^ =
= |В(Т)а?<Г)-1тЖ!,1 ... (x.y.z). (124)
Сопоставляя уравнения (124) и соотношения (79) для деформа.-
138
ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
ционной теории пластичности, приходим к следующему выводу. Распределение напряжений в установившейся стадии ползучести совпадает с распределением напряжений при упругопластических деформациях, если кривая деформирования имеет степенной вид:
е< = 5(Т)ст?(Г>.	(125)
Предполагается также, что при упругопластических деформациях материал является несжимаемым (ц = 0,5, 8=0). Вместо деформаций рассматриваются их скорости, что не изменяет решения задачи, так как все уравнения сохраняют прежний вид после соответствующей замены обозначений.
Модели вязкоупругости. В классической механике со времен Ньютона используется модель вязкой жесткости, в которой касательные напряжения пропорциональны скорости деформации сдвига
d
тхУ==П^(Тху), ...	(*,У,*),	(126)
где л — коэффициент вязкости.
Если рассмотреть сплошную среду, обладающую свойствами вязкой жидкости и упругости, то получим модели вязкоупругости, которые были предложены Максвеллом, Фойгтом и Кельвином д	" Пз—L	О в связи с изучением свойств густых раство-
Ё—ров» суспензий и упругих тел. В дальнейшем А	_S..Г В оказалось, что модели вязкоупругости приго-
_	_	дны для описания полимерных материалов,
Рис. 5.21. Модель Максвелла имеющих широкое распространение в современной технике.
Модель Максвелла представляет последовательное соединение элемента упругости и элемента вязкости (последний иллюстрируется в виде движения -поршня с зазором внутри цилиндра с вязкой жидкостью (рис. 5.21)). Относительное перемещение точек А я. В
S = 6* + 6C,	(127)
где упругая часть перемещения пропорциональна действующему усилию:
6е = KQ.	(128)
Для вязкого элемента усилие Q пропорционально скорости движения поршня относительно цилиндра:
<? = п5-	(129>
at
Дифференцируя равенство (127) по времени и учитывая соотношения (128) и (129), находим
d& dQ 1	'
= (130)
Для элемента тела при одноосном напряженном состояний аналогично последнему уравнению получаем
de 1 da , <т
dt ~ Е dt + t) ’	(131)
где о, е — напряжение и деформация растяжения; Е — модуль упругости; ц —
20. МОДЕЛИ ПОЛЗУЧЕСТИ И ВЯЗКОУПРУГОСТИ
139
постоянная вязкости, определяемая из экспериментальных данных. Величины е и ц зависят от температуры Г.
Модель Максвелла совпадает с основной моделью тела при упругих деформациях и деформациях ползучести, для которого скорость ползучести линейно зависит от напряжения (см. рис. 5.16).
Модель Максвелла с нелинейной вязкостью
de __ 1	1 n
dt~ E dt ‘ Ц a
(132)
может быть использована для приближенного описания деформации не только полимерных материалов, но и металлов.
‘Модель Фойгта (рис. 5.22) содержит параллельное соединение элементов упругости и вязкости, для которого общее усилие
= + = +
(133)
где б = 6е = 6е — относительное перемещение точек А и В. Для элемента тела при одноосном напряженном состоянии, подобно равенству (133), получаем
de а = £е + г]^.
(134)
Модель Фойгта не дает правильной картины поведения конструкционных материалов под нагрузкой, но она-может быть использована для описания микропроцессов в материале, в частности внутреннего трения при переменных напряжениях.
Рис. 5.22: Модель Фойгта
Модель Кельвина (рис. 5.23) представляет обобщение моделей Максвелла и Фойгта.
Для модели Кельвина относительное перемещение точек А и В ' б == б ас + без,
(135)
где б ас ~ XiQ “ перемещение звена АС.
Дифференцируя соотношение (135), находим
d& _ dQ t ?дСв dT^^lt^'^dF*
(136)
С помощью равенства (133) для модели Фойгта находим d6CB _Q_	_Q_ J_/A , их
dt ~ t] “ X2n °св - г] - х2г) (° _
(137)
140	ГЛ. 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ, ПОЛЗУЧЕСТИ
Из соотношений (136) и (137) вытекает равенство
= + <138>
df	у ^2/
В последнем равенстве М я %2 — коэффициенты податливости упругих элементов. Переходя на основании модели Кельвина к элементу тела при одноосном растяжении, будем иметь
de e2q 1 da 1
dt + г) — Ex it + T)	°-	<139>
Если E{ = E, E2 = 0, то уравнение (139) совпадает с уравнением (131) для модели Максвелла; при Ei->oo, Е2 = Е получается соотношение (134) для модели Фойгта.
ГЛABA 6
РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
Вводные замечания. В настоящей главе рассматриваются приближенные модели растяжения и сжатия стержней. В инженерной практике широко применяются приближенные модели надежности, когда оценки прочности проводятся по средним напряжениям в сечении стержня без учета концентрации напряжений, влияния условий закрепления концов стержня и других факторов. Приближенные модели часто используются для начального этапа проектирования при предварительном выборе размеров. Они позволяют оценить силовые потоки в элементах конструкций, взаимодействие элементов между собой и опорными узлами, выбрать оптимальные конструктивные схемы.
Общие перемещения в стержнях, влияющие на распределение усилий, достаточно точно определяются средними напряжениями.
Модели надежности, основанные на приближенных схемах, часто позволяют более четко выяснить физический смысл различных методов оценки надежности конструкций, определения запасов прочности. В свете этих посылок ниже рассматриваются деформации растяжения и сжатия стержней.
Работа стержней на сжатие имеет свои особенности. Тонкие и длинные стержни при действии сжимающих усилий теряют устойчивость прямолинейной формы равновесия, получают дополнительные прогибы. С этими проблемами мы познакомимся далее, а пока будем считать, что при рассматриваемых напряжениях сжатия потери устойчивости стержней не происходит.
21. Растяжение и сжатие стержней сосредоточенными и распределенными силами
Пример точного решения. Рассмотрим растяжение призматического стержня усилиями на его торцах (рис. 6.1). Допустим, что внешние силы распределены равномерно по площади сечения и
Рис. 6.1. Растяжение стержня усилиями на его торцах
создают растягивающие напряжения а. Материал стержня предполагается упругим.
Найдем распределение напряжений и деформаций в стержне, не прибегая к каким-либо допущениям. Решение построим так называемым обратным методом: сначала предположим, что существует' некоторое решение, а затем проверим, выполняются ли все необходимые условия.
142
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
Допустим, что напряженное состояние в произвольной точке стержня (точке А) таково:
а« = 0, ov = 0, о2 = о, Txv =	= т2Х = 0.	(1)
Единственная, отличная от нуля компонента напряженного состояния предполагается постоянной во всех точках тела.
Проверим справедливость уравнений равновесия (уравнений разд. 7). Они удовлетворяются, так как производные обращаются в нуль, а массовая сила отсутствует.
Далее проверяем выполнение краевых условий. Составляющие вектора напряжения на поверхности (см. уравнения (103) гл. 2) равны
Рх =	+ Хух771 4“
Ру = Хху1 +	(2)
Pz ==	+ xyzm + огп,
где Z, тп, п — направляющие косинусы нормали к поверхности. На боковых поверхностях стержня рх = ру = рг == 0 — внешние напряжения на боковой поверхности отсутствуют. Условия (2) выполняются, так как п = 0.
На торцевых поверхностях
Рх = 0, ру = 0, р2 == о,
что не противоречит решению (1). Для завершения проверки следует определить деформации по закону Гука и убедиться, что уравнения совместности выполняются.
Из уравнений упругости (уравнений (20) гл. 5) следует ц	и	а
—	£y — — -prQ,
Чху~ ^yz^ 0.	(3)
Уравнения совместности (уравнения (41) —(43) гл. 3) удовлетворяются, так как производные деформаций обращаются в нуль. Следовательно, напряжения (1) и деформации (3) составляют точное решение задачи. Определим перемещения точек стержня. Так как ди ц . ди u	dw a	//v
8* “ дх ~~	Е°'	— ду 11°' Ъг="дг~ Е'
то, интегрируя, находим х f u j ,	ца	иа	. а
и = — J ^(jdx+ u0=»u0 — jr*, v^Vq — ^у, iv = iv0 + о
(5)
где Uo, i?o, Wo — смещения точки стержня, совпадающей с началом координат.
21. СОСРЕДОТОЧЕННЫЕ И РАСПРЕДЕЛЕННЫЕ СИЛЫ
143
Наличие в решении постоянных u0, показывает, что перемещения определяются с точностью до смещения стержня как твердого тела.
Из- равенства (5) следует, что точки плоскости поперечного сечения (г =« const) в результате деформирования получают одинаковое смещение w, т. е. сечения стержня остаются плоскими. Далее
отметим, что напряженное состояние является одноосным. Волокна стержня испытывают лишь растяжение вдоль оси z. Точки стержня получают также смещения в плоскости сечения. Если конец стержня закреплен в массивной детали, то указанные смещения стеснены и в районе закрепления (рис. 6.2) возникает искажение одноосного напряженного состояния. По принципу Сен-Венана (см. разд. 7) эти искажения должны иметь местный характер и распространяться на длину порядка диаметра стержня.
Определим равнодействующую внешних усилий, приложенных к торцам стержня (рис. 6.3). В качестве точки приведения выберем центр тяжести сечения, где и поместим
начало местной системы координат yt. Сумма всех сил приводит к усилию
Рис. 6.3. - Растяжение стержня сосредоточенными усилиями
P = j‘adP = aF,	(6) ’
F
где F — площадь поперечного сечения. Моменты относительно осей и yi равны соответственно
МХ1 = J cy^dF =« a J yxdF » 0, MV1 == — J <3xtdF ==—aj xxdF =0, F	F	F	F
144
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
так как начало координат лежит моменты площади
[ y±dF = О,
F
в центре тяжести. Статические
j‘x1dF = O	(7)
F
относительно осей, проходящих через центр тяжести сечения, равны нулю. Система равномерно распределенных по площади напряжений статически эквивалентна растягивающей силе Р = о/7, приложенной в центре тяжести сечения.
Правильно и обратное утверждение: растягивающая сила, действующая вдоль оси стержня, вызывает в сечениях стержня равномерно распределенные нормальные напряжения. Отличия имеют место только возле торцов стержня. Системы внешних сил (распределенные или сосредоточенные усилия) статически эквивалентны, и указанные отличия по принципу Сен-Венана распространяются вдоль оси стержня на расстояние порядка размеров поперечного сечения.
На рис. 6.2 показаны различные условия закрепления конца стержня при его растяжении. Во всех случаях в концевой зоне стержня создаются статически эквивалентные системы внешних усилий, влияние которых сказывается в концевой области. Вне
Рис. 6.4. Нарушение допущений приближенной модели
пределов краевого эффекта можно принимать равномерное распределение напряжений.
Приближенные модели растяжения и сжатия стержней. В приближенных моделях растяжения и сжатия стержней используются два основных допущения:
1) поперечцые сечения стержня остаются плоскими (напряжения распределяются равномерно по поперечному сечению);
2) напряженное состояние в стержне является одноосным.
Как было показано для идеального случая растяжения (стержень постоянного сечения при равномерно распределенных по тор
21. СОСРЕДОТОЧЕННЫЕ И РАСПРЕДЕЛЕННЫЕ СИЛЫ
145
цам внешних усилиях), принятые допущения вполне оправданны. Однако эти допущения и принцип Сен-Венана применяются и в тех случаях, когда существуют зоны резких отклонений небольшой протяженности (рис. 6.4, а) или небольшие отклонения, но распространяющиеся на весь стержень (рис. 6.4, 6).
Для решения задач на основе сделанных допущений нет необходимости рассматривать условия равновесия и деформации бесконечно малых элементов. Появляется возможность сразу учесть равновесие и деформирование участков стержней или всего стержня в целом.
Растяжение стержня с учетом действия собственного веса. Рассмотрим длинную трубу, опущенную в шахту (рис. 6.5). На конце
Рис. 6.5. Распределение напряжений и перемещений (а) при растяжении стержня (трубы) с учетом собственного веса: б — эпюра нормальных напряжений и эпюра упругих перемещений
трубы действует вес G. В сечении z приложено растягивающее усилие
2V(z) = G + ^(Z-z),	(8)
где F — площадь поперечного сечения стержня; «» pg — удельный вес материала (Н/см3); р — массовая плотность материала (кг/см3); g = 981 см/с2 — ускорение силы тяжести. Напряжение растяжения
a (z) = N(z) IF == Oi + 7 (Z — z),	(9)
где Of = G/F—напряжение от усилия на конце трубы. Деформация удлинения в сечении z для упругого материала с модулем упругости Е составит
e(2)=2«. = ^ + 2.(Z_2),	<1()>
10 и. А. Биргер, Р. Р. Мавлютов
146
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
Упругое перемещение сечения z (при z = 0 перемещение отсутствует)
С a(zi) ^(z) = j-^-dzv	(И)
О
В равенстве (11) величина zt является переменной интегрирования О < z4 < z.
Учитывая (10), найдем перемещение в сечении z:
Z
u? (z) = J + -g (I zi)^ dzT — — z U zi)2 Io =® о
= T'2 + isz(2Z-z)- <12>
На рис. 6.5 показаны эпюры распределения напряжений и перемещений по длине стержня.
Растяжение стержня в поле центробежных сил. Рассмотрим растяжение лопатки осевого компрессора или турбины, лопасти воздушного винта или вертолета в поле центробежных сил. Лопатка рассматривается как стержень переменного поперечного сечения.
Рис. 6.6. Растяжение лопатки осевого компрессора или турбины от действия центробежных сил
Ось лопатки (геометрическое место центров тяжести поперечных сечений) совпадает с осью z (рис. 6.6).
Начало системы координат помещено в центре тяжести корневого сечения, на расстоянии Ri от оси вращения. Внешний радиус лопатки равен /?2. Найдем напряжение растяжения в поперечном сечении лопатки.
Центробежная сила, действующая на элемент стержня, dN « о2 (Я, + z1)pF(z1)dz1,	(13)
где ®, рад/с —угловая скорость; р, кг/см3 — плотность; Р(^),смг — площадь поперечного сечения.
21. СОСРЕДОТОЧЕННЫЕ И РАСПРЕДЕЛЕННЫЕ СИЛЫ
147
При определении центробежной силы элемент стержня рассматривается как точечная масса, сосредоточенная в центре тяжести сечения. Растягивающее усилие в сечении z
N (z) = рш2 J (Rx + zj F (zx) rfz1. z
Напряжение растяжения
a (z) = Fw = p“2 fir f(/?1 + Z1) pF dZ1' Г \Z)	г \Z) J
z
Для стержня (лопатки) постоянного сечения
. a (z) = -у prfRz
Величина
®Я2 = и
(14)
(15)
(16)
(17)
Л1 + 2Г|
*2 /.
представляет окружную скорость на внешнем радиусе лопатки 2?2-Формулу (16) представим в виде
Наибольшее напряжение получается в корневом сечении при 2 = 0
Стах = О (0) « Р“2 ^1 — j-	(18)
Выражение ри2 = ок ,	(19)
составляет напряжение растяжения во вращающемся тонком кольце. Значения ок даны в табл. 2.
Таблица 2
Значения а к (Н/мм2) и типичные значения предела прочности материала
Материал	р,	кг/см3	и, м/с					а&, Н/мм2
		100 |	I 2.00 1	300 |	400 |	500	
Алюминиевые сплавы	2,75	28	112	252	448	700	150—450
Титановые сплавы	4,5	46	184	415	735	1150	700-1100
Стали	у	7,85	80	320	720	1280	2000	500—1200
Из формулы (15) следует, что напряжения не зависят от абсолютного размера площади поперечного сечения.
При изменении площади F(z) на всех радиусах в к раз напряжения растяжения остаются прежними. Для уменьшения напря-!()♦
148
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
жений растяжения сечения лопатки на больших радиусах уменьшают (рис. 6.7).
Приближенная модель прочностной надежности лопатки газовой турбины. Приближенная модель оценивает надежность лопатки по
Рис. 6.7. Лопатка газовой турбины авиационного двигателя
запасу длительной прочности. Условие надежности имеет вид
пШ|П--^Ур>1п],	(20)
где nmIn — минимальное значение запаса прочности в различных сечениях лопатки; одл (z) — предел длительной прочности (см. разд. 16) материала при температуре в рассматриваемом сечении стержня (лопатки), о(z) —напряжения растяжения; [м] — допустимое значение запаса прочности. Для лопаток газовых турбин обычно принимают [п] = 2—2,5.
Рис. 6.8. Распределение напряжений растяжения о, температуры Г, длительной прочности Одл за время 1000 ч и запаса прочности п
Значение запаса прочности зависит от температуры сечения и длительности работы.	у
На рис. 6.8 для одной из лопаток газовой турбины показаны распределения растягивающих напряжений, температуры, длительной прочности при длительности работы 1000 ч и запаса длитель
21. СОСРЕДОТОЧЕННЫЕ И РАСПРЕДЕЛЕННЫЕ СИЛЫ
149
ной прочности. Минимальный запас имеет место в средней части лопатки, для которой характерен более высокий уровень температуры.
Замечание. В неравномерно нагретых стержнях опасное сечение — сечение с минимальным запасом прочности — не всегда совпадает с сечением, где имеется максимальное напряжение.
Связь запаса прочности по напряжениям и запаса прочности по долговечности. В моделях прочностной надежности, связанных с длительной прочностью материала, используется запас прочности по напряжениям (формула (20)) при требуемой длительности работы t
T=GOnst.
t«const
Lgt
Рис. 6.9. Связь запаса прочности по напряжениям и запаса прочности по долговечности
Для определения запаса прочности по долговечности воспользуемся связью значений пределов длительной прочности и времени работы:
Пдл (0 t == const.	'	(21)
На рис. 6.9 показана точка Л, характеризующая работу материала лопатки (стержня) — напряжение о и длительность работы t.
Запас прочности по напряжениям
по = аДл(0^	(22)
запас прочности по длительности работы (долговечности)
=	(23)
где £р — время работы до разрушения при напряжении а. Так как точки At и Ла находятся на одной прямой, то *	\
и потому
адл(0/ат==^
или
(24)
Так как обычно тп = 6—20, то запас по долговечности существенно выше запаса прочности по напряжениям.
150
ГЛ. в. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
22. Статически неопределимые задачи растяжения и сжатия стержней
Понятие статической неопределимости. Рассмотрим задачу, показанную на рис. 6.10.
На стержень, оба конца которого приварены к двум недеформи-рующимся и неподвижным плитам, действует усилие Р, Требуется найти распределение усилий и напряжений в стержне.
Система, показанная на рис. 6.10, а, статически неопределима
в том смысле, что усилие в произвольном сечении z неизвестно и
Рис. 6.10. Стержень, жестко заделанный в неподвижной плоскости: а — статически неопределимая система; б — эквивалентная статически определимая система; в — распределение усилий; г — распределение напряжений
из уравнений статики не может быть определено. Метод сечений (например, сечение стержня плоскостью z == const) не приводит к результату, так как неизвестны усилия, приложенные к отсеченной части.
Задачи сопротивлеия материалов, в которых уравнений статики недостаточно для определения усилий в стержнях, называются статически неопределимыми.
Один из общих методов решения статически неопределимых задач. Метод
заключается в последовательном проведении двух процедур.
1. Система освобождения от лишних связей, взамен- которых прикладываются неизвестные силовые факторы, т. е. система превращается в статически определимую (формально).
2. Составляются уравнения, допол
нительные к статическим, учитывающие действительные условия деформирования элементов системы.
В задаче, показанной на рис. 6.10, на первом этапе отсекаем
одну из заделок стержня, например верхнюю, заменяем ее действие неизвестным усилием X. Полученная система (рис. 6Л0, б) является статически определимой.
Второй этап решения состоит в учете уравнения
Wb =» 0,
(25)
что выражает невозможность перемещения точки В в статически неопределимой системе (рис. 6.10,а).
Перемещение точки В равно
Х1г (Р-Х)12
(26)
22. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ
151
так как на первом участке постоянная деформация ai X
81 “El
а на втором участке
(27)
(28)
В последних равенствах Л, F2, Еъ Е2 — площади поперечного сечения и модули упругости участков. Из уравнения (25) получаем х-^р’ (29) где Xi = IJ (EJFi), Х2 = 12/ (E2F2) — коэффициенты податливости, мм/Н. Величины EtFt и E2F2 называются жесткостями сечений стержня на растяжение.
На первом участке действует растягивающее усилие х
=	(30)
на втором участке — усилие .
y2=s_p + x = _T2i_p.	(31)
Усилие, растягивающее стержень, будем считать положительным, сжимающее — отрицательным (в соответствии с правилом знаком для нормальных напряжений). Распределение усилий и напряжений по длине стержня показано на рис. 6.10, в и 6.10, г.
Величина X по формуле (29) получилась положительной. Это означает, что предварительно выбранное направление неизвестного усилия X (рис. 6.10, б) оказалось правильным. Можно было, предварительно принять усилие X направленным в другую сторону. Легко проверить, что это не повлияло бы на решение.
Замечание. Рассмотренный метод является общим, применимым для любых статически неопределимых систем. Он называется методом сил, так как в качестве неизвестных принимаются усилия. Однако метод отнюдь не является единственным. Существуют и другие, достаточно общие методы, например метод перемещений, которые в некоторых случаях приводят к более простым расчетным схемам.
Прочностная модель болтового соединения» Конструктивная схема болтового соединения — очень важного разъемного соединения во многих конструкциях — показана на рис. 6.11. Промежуточные детали I, 2 соединения стягиваются болтом.
Промежуточные детали моделируются эквивалентными по жесткости втулками, имеющими площади поперечных сечений Fu Fu модули упругости Еи Е2.
Болтовые соединения всегда предварительно затягиваются, что, как будет ясно из дальнейшего, уменьшает дополнительную нагруз
152
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
ку на болт. Если усилие затяжки Qq, то болт растягивается силой а промежуточные детали (втулки) сжимаются той же силой.
Теперь допустим, что на соединение начинает действовать основная нагрузка — внешнее растягивающее усилие Р, которое при
Рис. 6.11. Прочностная модель болтового соединения: а — конструктивная схема; б — расчетная модель по методу спаянного стыка; I, 2 — промежуточные детали соединения; 0 — болт
кладывается в опорных сечениях. Ясно, что болт должен получить дополнительную вытяжку, а напряжения сжатия во втулках, созданные при затяжке, должны уменьшиться.
Будем считать, как это всегда делается на практике, что усилие затяжки превышает основную нагрузку (Qq>P) и стык деталей не «раскрывается». Тогда при рассмотрении действия внешнего усилия плоскости стыка можно считать «спаянными». Предполагая детали соединения работающими в упругой области, разберем по принципу независимости действия сил отдельно действие внешнего усилия Р. Для раскрытия статической неопределимости (неизвестно, какая часть усилия
Р воспринимается болтом и какая — втулками) проводим сечение на стыке гайки и втулки (не перерезая болт). Обозначая неизвестное усилие X, запишем равенство удлинения болта и втулок в виде

Х12
(32),
где It, Et, Fi — длины, модули упругости и площади сечений.
В правую часть равенства (32) входят величины со знаком минус, так как усилие X по рис. 6.11, б предполагалось направленным на сжатие втулок. Из равенства (32) находим


(33)
где
Ъ~М(Е,Г(), г = 0,1,2~ '	(34)
— коэффициенты податливости болта и промежуточных деталей.
Знак минус в равенстве (33) означает, что действительное направление X противоположно предварительно выбранному. Допол
22. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ
153
нительное усилие на болт в результате действия усилия Р
^i + ч х0 + Ч + Ч
тде х==
— коэффициент основной нагрузки.
Общее растягивающее усилие, действующее на болт,
Q = Q* + rf.
(36)
Усилие сжатия, приложенное к промежуточным деталям (усилие на стыке),
2с = -(?0+(1-х)Я
(37)
Коэффициент основной нагрузки % зависит от соотношения между податливостью промежуточных деталей и податливостью стержня болта. Для того чтобы усилие на болт при приложении внешней (основной) нагрузки возрастало незначительно, т. е. для уменьшения коэффициента основной нагрузки, надо делать «жесткие фланцы— податливые болты». Это — правило конструирования болтовых соединений, особенно для работающих при переменной нагрузке. При возрастании Р может наступить раскрытие стыка (<2с>0).
Из равенства (37) находим условие потери плотности стыка:
После раскрытия на болт:
Р(1-Х)><2о.	(38)
стыка внешняя нагрузка полностью передается
Q-Qq + P.	(39)
Вот почему во всех динамически нагруженных конструкциях принимают специальные меры, предотвращающие отворот гаек (специальные контровки, шайбы и т. п.).
Модель прочностной надежности болта при действии статической нагрузки (нагрузки, постоянной по времени)
n = z^->[n],	(40)
umax
где Съ ~ предел прочности материала, отах — максимальное напряжение в стержне болта.
Допустимый запас прочности при статических нагрузках .принимается наибольшим [п] == 1,3—1,5.
Учитывая соотношение (36), находим условие надежности
4(<?0 + XP)^[nj’
где dmin — минимальный диаметр стержня болта.
154
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
Модель прочностной надежности болта при действии переменных нагрузок. Допустим, что внешняя нагрузка на болт периодически изменяется от 0 до Р. Тогда на болт будет действовать переменная нагрузка, имеющая максимальное и минимальное значения
Q max	Qo + %Р, ^?mla Qq*
(42)
При переменной нагрузке опасными являются места концентрации напряжений. В болте (рис. 6.12) типичными являются три таких места: резьба, выточка и радиус перехода
Рис. 6.12. Места концентрации напряжений в болте: 1 — резьба; 2 — выточка;
3 — галтель
от головки болта к стержню. Особенно опасным является концентрация напряжений в резьбе, для которой (теоретический) коэффициент концентрации а0» 5. Цикл переменных напряжений в резьбовой части болта
• ^(Зтах	4@niin	//Q\
Стах —----Cmin ---------(4о)
ла*	ла*
где di — внутренний диаметр резьбы.
В резьбовой части болта действует переменное напряжение (см. разд. 16)
Са = "у (Стах — Cmin) = —Т Х^	(44)
Л	ла.
и постоянное напряжение
4<?0
где о0 == —— напряжение затяжки, лс^
Отметим, что переменное напряжение в болте пропорционально коэффициенту основной нагрузки. Модель прочностной надежности болта при действии переменных напряжений (модель усталостной прочности) имеет вид
Па > [Па],
(46)
где [па] —допустимое значение запаса прочности по. переменным напряжениям.
Так как значение коэффициента основной нагрузки определяется приближенно и вследствие значительного рассеяния усталостной прочности при наличии технологических отклонений, принимается [па]>4. Запас прочности поч переменным напряжениям равен
"а=~,	(47)
22. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ
155
где о-1Д —предел выносливости детали (болта). По равенству (79) гл. 4
П-1Д = у- сг__ ь	(48)
а
где и 8 — коэффициенты, учитывающие состояние поверхности и масштабный характер.
Эффективный коэффициент концентрации напряжений
К,==1 + ?(аа-1),	(49)
где q — коэффициент чувствительности материала'
Модель усталостной надежности болтового соединения имеет вид
------2КДР-------<50'
Повышению усталостной надежности способствует уменьшение коэффициента концентрации напряжений, коэффициента основной нагрузки, увеличение предела выносливости материала.
Приближенные модели термоциклической прочности элемента конструкции. Детали теплонапряженных конструкций часто подвергаются циклам нагревов, причем деформации элемента стеснены
Г
Рис. 6.13. Напряжение и деформации в стержне, закрепленном между двумя жесткими плитами при циклическом нагреве
^2
Рис. 6.14. Изменение температуры и температурных напряжений по времени
другими частями конструкции. В таких условиях работают поверхностные слои материала при нестационарных тепловых воздействиях. В качестве типичной модели термоциклической прочности элемента конструкции рассмотрим стержень, закрепленный между двумя жесткими неподвижными и холодными плитами и подвергающийся циклам нагрева до температуры Т (рис. 6.13).
Рассмотрим сначала случай, когда температурные напряжения при нагреве не превышают предела текучести материала. Определим напряжение в стержне при нагреве до температуры Т.
156
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
Для решения задачи отсекаем верхнюю заделку и заменяем ее действие усилием X. Перемещение точки В с учетом температурных деформаций при нагреве
wB=-jp + aTl^0,	(51)
где Е — модуль упругости материала; а — коэффициент линейного расширения.
Из соотношения (51) находим температурные напряжения в стержне:
о « -ЕаТ.	(52)
Температурные напряжения пропорциональны модулю упругости материала и коэффициенту линейного расширения. Такое заключение, вытекающее из формулы (52), справедливо и в других, более общих случаях.
Изменение температуры во времени показано на рис. 6.14. Напряжение в стержне изменяется от нуля в точке Ci до ~ЕаТ в точке С2, далее сохраняется на участке С2С3 (ползучесть материала не учитывается) и снова обращается в нуль в конце цикла на участке CiCi.
Так как наибольшая (по величине) деформация материала отрицательна, то следует считать
Emax == 0, Emin == (З/Е == ОсТ*
Амплитуда цикла деформации
1 1
Sa = “j* (етах — emin) = "ту (XT.	(53)
При повторении циклов термических напряжений обычно наиболее опасной является малоцикловая усталость.
Приближенная модель термоциклической прочности элемента конструкции выражается в виде уу*
пп = “дГ* 1пд] 1	(54)
где — запас по числу циклов, — среднее число циклов до разрушения, Nn — число циклов^ за ресурс изделия. Необходимый запас по числу циклов
[О 5.	(55)
Высокие значения [лц] принимаются главным образом для учета рассеяния малоцикловой прочности и сильного влияния параметров нагружения на долговечность.
Величина определяется из уравнения Менсона
|аТ«|(1пг±-)в,’л70’в + 1,75^ЛГрв’12.	(56)
22. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ
157
При упругих деформациях первым слагаемым можно пренебречь, полагая
аГ = 3^ь ДГр0-12.
Тогда число циклов до разрушения
/3,5ак\1/о,12 “ \£а7г )
(57)
Модель термоциклической прочности при повторных нагревах (соотношения (54) и (57)) имеет вид
1 /3,5оЛ8>3
= N~\~EaTj .	(58)
Влияние параметров модели термоциклической прочности на запас по числу циклов. Запас по числу циклов нагревов (формула (58)) зависит от ряда параметров:
пц = F(N* аь, Е, а, Г),	(59)
каждый из которых известен при разработке конструкции с определенной точностью.
Оценим относительное влияние параметров. Рассмотрим сначала вопрос в общем виде, предполагая, что имеется функция параметров х и у щего вида:
F = Схтуп.
Тогда по правилу дифференцирования функции многих переменных dF дЕ
~ дх^ dx ~ду ~ Стхт 1yndx + Спх™уп rdy.
Разделив обе части равенства на Е, найдем dF dx dy Т==т—+п-
Для малых относительных приращений
ДЕ Sx Sy — =mT + n—.
Последнее соотношение имеет четкий физический смысл: 1% отклонения параметра х дает т % отклонения величины Е; 1% отклонения параметра у дает п% указанного отклонения.	___
Применяя этот прием для анализа зависимости (58), находим
^==_^3 + 8,3|/—(63> «ц	\ В а.Т )
Знак минус перед отдельными слагаемыми означает, что приращение параметра вызывает уменьшение запаса числа циклов пц.
С помощью зависимости (63) устанавливаем, например, что погрешность в определении температуры нагрева на 1% вызывает погрешность 8,3% запаса по долговечности.
Учет ползучести материала при определении температурных напряжений. На рис. 6.14 показано изменение температурных напряжений при циклическом изменении температуры без учета ползу
следую-
- (60)
--(61)__
(62)
158
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
чести материала. Рассмотрим теперь влияние ползучести на температурные напряжения в стержне с заделанными концевыми сечениями (см. рис. 6.13).
Будем считать в начальный момент времени
о(0)--£аТ.	(64)
Далее следует учесть, что в любой момент времени сумма упругой деформации е»(£), деформации ползучести 8С(£) и температурной деформации справедливо уравнение
ев (0 +ес(О + аТ = 0,	(65)
гак как расстояние между заделками и температура не изменяются. Упругая деформация
М*) = ^.	(66)
Дифференцируя по времени зависимость (65)’ и учитывая, что температура после нагрева остается постоянной, находим
Пренебрегая неустановившейся стадией ползучести, примем для скорости ползучести степенную зависимость (см. разд. 20)
= V = Во1,	(68)
где В, п — параметры материала.
Теперь из соотношения (67) получаем
= <69>
Zu сы	Du
Интегрируя в пределах от 0_до t, найдем
(п -W [gl"n V ~ °1-П (°)1 = к ™
Учитывая, что в практических случаях п > 1, запишем"'последнее равенство так:
»('>-—•, 1 ..............-	ТО
ИЛИ	*
____	(72)
V i+at
где а = (я—1)В£о**_,(0)’. Значение о(0) определяется равенством (64)«
23. СТЕРЖНЕВЫЕ СИСТЕМЫ (ФЕРМЫ)	159
С увеличением времени t абсолютная величина температурного напряжения в результате влияния ползучести падает. Этот процесс называется релаксацией температурных напряжений.
Деформация ползучести представляет собой остаточную деформацию. Из уравнения (65) можно получить
ec(t)e-^-aT.
. Если в момент времени t снять нагрев, то в стержне возникает остаточное напряжение растяжения
оост =-Еес(0,	(73)
так как длина стержня должна оставаться неизменной, а материал стержня в результате ползучести получил остаточную деформацию сжатия ec(i). В силу образования остаточных деформаций ползучести температурные напряжения сжатия в момент нагрева все время падают, а в период останова в стержне появляются растягивающие остаточные напряжения.
23. Стержневые системы (фермы)
Вводные замечания. В различного рода конструкциях (подмо-торных' рамах двигателей, пространственных конструкциях крепления корпусов, отсеков и т. п.), в подъемно-транспортных сооружениях (кранах, подъемниках), в строительных конструкциях (мостах,
Рис. 6.15. Системы стержней
перекрытиях, каркасах, и т. д.) часто используются стержневые системы (фермы), в которых стержни работают на растяжение или сжатие. На рис. 6.15 представлены некоторые типы стержневых систем. Наклонные стержни фермы часто называют раскосами, подкосами, тягами; вертикальные стержни — стойками; горизонтальные стержни — поперечинами (траверсами).
160
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
Фермы бывают плоскими и пространственными. В дальнейшем ограничимся рассмотрением плоских ферм.
Для того чтобы стержни передавали усилия, направленные вдоль оси, соединения стержней должны быть шарнирными, т. е. допускать относительный поворот. На рис. 6.16 приведена конструктивная схема шарнирного соединения. Предполагается, что трение в
Рис. 6.16. Конструктивная схема шарнирного соединения стержней
шарнире пренебрежимо мало. Если стержень имеет два шарнирных конца и поперечная нагрузка на стержень отсутствует, то из условия его равновесия немедленно следует, что усилие на стержень
Рис. 6.17. Схемы опорных узлов фермы и их условное обозначение: а —• опорный узел; не допускающий смещений; б, в — опорный узел, допускающий смещение в одном (горизонтальном) направлении
действует вдоль его оси. Внешние силы, действующие на фермы, приложены в узлах. Узлами называются точки соединения стержней. Собственный вес стержней обычно значительно меньше внешних нагрузок и при расчете не учитывается. Фермы в большинстве
23. СТЕРЖНЕВЫЕ СИСТЕМЫ (ФЕРМЫ)
161
случаев имеют несколько узлов, опирающихся на другие элементы конструкции или на фундамент.
Опорные узлы предполагаются шарнирными, причем закрепление опорных узлов должно допускать свободное температурное расширение стержней фермы. Схемы опорных узлов и их условные обозначения приведены на рис. 6.17.
Замечание. Узлы фермы часто выполняют с помощью сварки (рис. 6.18). Определение усилий в стержнях в предположении шарнирного соединения узлов является в таком случае приближенным. Для длинных стержней погрешность приближения невелика.
Статически определимые фермы. В статически определимых фермах усилия в стержнях полностью определяются условиями равновесия. На рис. 6.15 такими ферма^ми являются фермы а, б, г; фермы в, д на рис. 6.15 статически неопределимые. В дальнейшем будет указано правило, позволяющее сразу определить статическую определимость или неопределимость фермы.
Расчет статически определимых ферм проводится методом сечений, сущность которого
Рис. 6.18. Схема сварного узла
поясним несколькими примерами.
Пример 1. Двухраскосная ферма (рис. 6.19) с одинаковыми стержнями. Проводим сечение, вырезающее узел Л, заменяем внутренние силы усилия-.
Рис. 6.19. Определение усилий в двухраскосной'ферме: а —расчетная схема; б — равновесие узла; в — определение перемещений
ми N в стержнях и рассматриваем условие равновесия узла А 2/Vcosa = P,	(74)
откуда усилие в стержнях
ЛГ = 2^-	'	(75)
Заметим, что при a л/2 N оо. Знак плюс в формуле (75) означает, что предварительно выбранное направление усилий оказалось правильным.
11 И. А. Биргер, Р. Р. Мавлютов
162
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ.
В некоторых случаях может понадобиться значение перемещения точки А Удлинение стержня составит
Nl Р1
= »«=« = ЕР = 2 cos aEF ’
(76)
где EF — жесткость сечения стержня на растяжение.
Положение точки А после нагружения можно найти, если провести две дуги радиусом I + и, приняв в качестве центров опорные узлы. Так как деформации малы, то достаточно отложить отрезки на оси стержня и восставить перпендикуляры из точек
Л| и А2 (см. рис. 6.19). Это правило можно сформулировать так: удлинение (или укорочение) стержня равно проекции перемещения конца стержня на первоначальное направление оси. В общем случае следует составить разность проекций перемещений концов стержня (если оба конца подвижны). Такпм образом, перемещение точки А равно
Р1
Рис. 6.20. Явление «распор» в стержнях
6 = и = cos а 2 cos2 aEF
Замечание. На рис. 6.20 показана двухраскосная ферма, работающая в «распор». Усилия в стер- • жнях очень велики, если угол а близок л/2.
Избегайте в конструкциях стержней, работающих в «распор»!
Пример 2. Треугольная ферма (рис. 6.21). Расчет фермы начнем с опреде7 ления реакций опор.
Рис. 6.21. Треугольная ферма: а— расчетная схема; б—.равновесие узла 4; в — определение перемещений точки А
В точке В действует реакция опоры RB, в точке С — реактивные усилия Н и Rc. По отношению к ферме реактивные усилия следует рассматривать как внешние нагрузки.
Проектируя все силы на горизонтальное и вертикальное направления, находим*	'
Rc Ц- RB Р sin 9 =0, Н — Р cos 9=0,	(77)
Из условия равенства нулю момента относительно какой-либо точки, например точки С, получаем
RBa + Ph, cos 9 + sin 9 = 0.	(78)
23. СТЕРЖНЕВЫЕ СИСТЕМЫ (ФЕРМЫ)
163
Из приведенных общих уравнений равновесия фермы (77) и (78) следует
=— Р ( — cos 0 + — sin 0 ), Rr = Г — cos \ a	a J G [a
Методом сечения выделим узел А и рассмотрим условия его равновесия. Приравнивая пулю сумму проекций сил на горизонтальное и вертикальное направления, приходим к системе уравнений
—2V1 cos «1 — N2 cos a2 + P sin 0 = 0,
sin 9 Р.
—A’i sin at 4- N2 sin a2 — P cos 0 = 0.
Из последних соотношений находим
cos(ao + 0)	cos (a,— 0)
/V • — — P--—------— N — P-------—-----—
1 sin(a1 + a2)’	2 sin(a1 + a2)’
Соотношения (80) можно получить и проще, спроектировав усилия, ные к 4, па направления, перпендикулярные N\ и /У2. Проекции полного смещения точ'ки 4 на направления стержней (удлинения стержней)
ui~E1Fx' u2~E2F2’
где Zt, EiFi — длины и жесткости стержней.
Восставив перпендикуляры из точек и 42, найдем на их пересечении точку
в которой окажется узел 4 после приложения нагрузки.
На рис. 6.22 дана картина перемещения точки 4. Проекция полного перемещения 6 на ось первого стержня показана с учетом его действительного знака по равенству (81). Отрезки Л [Л* = и 424* = и2 легко определяются, ' если спроектировать отрезок 44* = 6 на
щ == — и2 cos (a! +a2) + v2 sin (ai + a2),
(81)
4*
(79)
(80)
пр и ложе н-
а
А
Рис. 6.22.
П
2
az+a2


Картина перемещений точки А
направления
стержней:
(82)
и2 == — щ cos (ан- a2) + pi sin (a! + a2).
то становятся известными значения vi и p2 и величина
Так как значения щ и и2 известны,
,2
v*-	(83)
Пример 3. Ферма составлена из равнобедренных треугольников (рис. 6.23). При большом числе узлов и стержней полезно установить общее правило для их обозначения. Будем обозначать узлы 41, 42, ... в порядке обхода коп-тура по часовой стрелке.
Обозначения усилий в стержнях составим из номеров узлов, которые они соединяют: Nit2t N2,5 номера узлов разделяются запятой, так как возможны многоразрядные номера.
усилий в опорных узлах. Они составля-
Рис. 6.23. Ферма из равнобедренных треугольников
Расчет начинается с определения ___________г__— ______ ___. _______
ют Р/2 (рис. 6.23). Далее удобно рассмотреть условия равновесия узла, к которому подходят не более двух стержней (например, узла 41). 11*
164
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
(84)
= 0.
(85)
Из условия равновесия узла (неизвестные усилия считаем направленными на растяжение стержней) получаем
1
N. 9 sin а + -у Р = О, JV, 9 cos а + /V. . = О, Лум	и*	1уО
откуда 1	cos а
^1.2	2 sin а *	1.5	2 sin а
Условия равновесия узла А 2 дают
—iVi, 2 sin а — 1^2,5 sin а = О, (N2,5 — Nit 2) cos а 4- N2, з
Учитывая соотношения (84), получаем
1	cos а
^2.5 = 2 sin аР’ N1,3 = ~ sin а Р'
Окончательные результаты имеют вид
Л'1,2 = 'V3,4 — ~ 2 sin а Р’ cos а
Л 2,3 = ~ sin а Р'
. cos а ~ Л1.5 = 2 sin а Р'
= ^3,5 — 2 sin а Р‘
Объясните, почему стержень 2, 3 оказался сжатым!
Общие замечания о статически определимых фермах и сопоставление со статически неопределимыми. В статически определимых системах стержней (фермах) усилие, приходящееся на стержень, не зависит от размеров его поперечного сечения и физических свойств материала. Следовательно, усилия будут одинаковыми при упругих и пластических деформациях материала, при его ползучести и т. п.
При разрушении одного из стержней -разрушается сразу вся статически определимая система, которая превращается после этого в механизм. Вместе с тем в таких фермах получаются вполне определенные значения усилий в стержнях; отсутствуют начальные (монтажные) и температурные напряжения.
В статически неопределимых системах размеры сечения и свойства материала стержней влияют не только на деформации и перемещения, но и на величину усилий в стержнях. В таких системах имеется резервирование*, при выходе из строя Одного из стержней нагрузка передается, как правило, на другие.
Распределение усилий в стержнях статически неопределимой фермы зависит от целого ряда факторов (точности изготовления, начальных и температурных напряжений и т. д.). Оптимальный выбор силовой схемы системы стержней зависит от особенностей конструкции и условий работы. В машиностроении чаще используются статически определимые системы стержней.
23. СТЕРЖНЕВЫЕ СИСТЕМЫ (ФЕРМЫ)
165
Определение статической определимости или неопределимости ферм. В простых случаях удается сразу сделать вывод о характере системы. Например, для системы на рис. 6.15, а ясна ее статическая определимость, для системы на рис. 6.15, в — неопределимость. Для ферм на рис. 6.15, б, г и д решение подобного вопроса требует спе-
циального анализа.
Остановимся сначала па условиях закрепления.
Если реакции- (усилия) в опорах фермы быть определены из условий равновесия, то ся статически определимым. Так как опоры являются шарнирными, то они могут воспринимать только силы и не могут воспринимать моменты (отсутствуют «плечи» для уравновешивания) .
В зависимости от структуры опора уравновешивает силу произвольного направления (см. рис. 6.17, а) или только одного направления (рис. 6.17, б). В первом случае опора обладает двумя связями (двумя «стерженьками» ), во втором — одной связью (одним «стерженьком»).
Как известно, плоская система сил может быть уравновешена силами в двух точках плоскости. Одна из точек должна иметь возможность воспринять силу произвольного
от внешних сил могут закрепление называет-
Рис. 6.24. Статическая определимость закрепления фермы
направления, вторая —- силу, создающую момент относительно другой точки. Следовательно, статически определимое закрепление фермы при плоской системе сил осуществля-
ется двумя опорами, одна из которых воспринимает силу произволь-
ного направления.
На рис. 6.24, а показана ферма со статически определимыми опорами. Она имеет три опорные связи (три опорных стержня). На рис. 6.24, б имеются в опорных узлах две дополнительные связи (система два раза статически неопределима по опорным узлам). Ферма на рис. 6.24, в по условиям закрепления 5 раз статически неопределима (имеет 5 «лишних» опорных стержней) <
Замечание. Статическая определимость закрепления определяется числом связей в опорах. Для плоской фермы оно должно быть равно трем, так как имеются три условия равновесия плоской системы сил (равенство нулю двух проекций равнодействующей внешней системы сил и равенство нулю момента относительно произвольной точки). Однако имеется один исключительный случай, когда при .трех связях (в двух точках) уравнения равновесия не могут быть удовлетворены. Такое закрепление называется мгновенно изменяемым. Оно характеризуется тем, что в точке закрепления с одной связью направление связи проходит через другую точку закрепления, и поэтому опоры ле могут воспринимать момент от внешних сил. Такая конструкция неработоспособна! Закрепление называется мгновенно изменяемым, так как после
1G6
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
некоторого довольно значительного поворота включится в работу имеющаяся связь и движение фермы остановится.
Установление степени статической неопределимости ферм. В основе конструкции всякой фермы лежит ячейка в виде треугольника как геометрически неизменяемой конфигурации с шарнирными узлами. Каждый новый узел в статически определимой форме присоединяется двумя стержнями.
При статически определимом закреплении число стержней с и число узлов п в статически определимой ферме связаны соотношением
с = 2п — 3.	(86)
В число узлов п входят и опорные узлы. Например, ферма на рис. 6.23 имеет 5 узлов и 7 стержней и условие статической определимости (86) соблюдается: 7 = 2 • 5 — 3. При с > 2п — 3 система шарнирно связанных стержней статически неопределима, при с < < 2п — 3 система превращается в механизм (имеет свободное движение).
Для фермы со статически неопределимым закреплением опорных узлов условие статической определимости всей конструкции
с = 2п - 3 - г,	(87)
где г— число статической неопределимости или число «лишних» связей в опорном закреплении. Например, для системы стержней на рис. 6.15, а г=1, с = 2, п = 3. Условие (87) удовлетворяется:
2 = 2-3 —3 — 1.
Будем условно называть степенью статической неопределимости системы стержней число «лишних» связей (стержней) в системе. Обозначая степень статической неопределимости /?, получим с помощью равенства (87)
. 7? = с-2п + 3 + г.	•	(88)
Для системы, показанной на рис. 6.15, в.
д == 3 _. 2 • 4 +3 +3 = 1. ,	(89)
Степень статической неопределимости R показывает, что удаление R стержней из системы делает ее статически определимой.
24. Статически неопределимые стержневые системы
Вводные замечания. Всякое деформируемое тело при определении в нем напряжений и деформаций представляет собой в общем случае статически неопределимую систему, так как уравнений статики недостаточно для решения задачи.
Статически неопределимые стержневые системы являются простейшими моделями общих задач механики деформируемого тела.
24. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
167
Они позволяют выявить закономерности поведения элементов конструкции в рабочих условиях при работе материала в упругой области при возникновении пластичности и ползучести, температурных напряжений и т. д. Однако не только методические соображения делают полезным изучение статически неопределимых стержневых систем — они встречаются на практике в различного рода машинах и сооружениях.
Особенности поведения статически неопределимых систем разберем на примере трехстержневой системы.
Трехстержневая система. Работа в упругой области. Модель надежности по допускаемым напряжениям. Система показана на рис. 6.25. Усилие Р воспринимается тремя стержнями, причем крайние стержни одинаковые. Требуется определить при работе материала в упругой области усилия и напряжения в стержнях и
а	б . б
Рис. 6.25. Трехстержневая система
построить модель уравнения задачи (рис. 6.25, б):
прочностной надежности системы. Статические представляют собой условие равновесия узла А
^ + 2^coSp = P,
(90)
где Nu N2 — усилия в стержнях. Геометрические уравнения связывают перемещение точки А и удлинение стержней:
ui = 6,	(91)
и2 = 6 cos Р,	(92)
где б — перемещение, точки А в результате действия усилия Р. Из последних уравнений вытекает равенство
и2 = Ui cos р.	(93)’
Условие (93) представляет собой условие совместности перемещений стержней в узле А.
Деформации в стержнях связаны соотношением
е2 == cos2 р,	(94)
168
ГЛ. G. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
так как
Zi = /2cosp.	(95)
Физические уравнения выражают работу материала стержней в упругой области (см. гл. 5):
81 =0!/^,	(96)
62 = 02/^	(97)
где 81, Oi, Et (г = 1, 2) —деформация, напряжение, модуль упругости.
Так как
81 == Ut/Zi, 82 = u2/l2,	(h^Ni/Fz, (98)'
находим перемещения концов стержней:
“х -	(")
V I
(100) 2 2
Соотношения (90) — (92), (94) и (98) образуют систему линейных уравнений, которая легко решается относительно перемещений щ и и2 или усилий (напряжений).
При решении задачи «в перемещениях» усилия и N2 в уравнении равновесия выражают через удлинения стержней. Из уравнений (99) и (100) получаем
Е F
-JrLu1,	(101)
*1
N2 = -^-u2.	(102)
Внося значения Nt и N2 в соотношение (90) и учитывая зависимость (93), получаем
иг + 2 cos РU1 cos р == А	(ЮЗ)
*1	‘2
Из последнего соотношения находим
Внося значение в равенство (101) и учитывая (95), находим

Р.__________ р
1 + 2XCOS3P
l + 2cos руу
(105)
24. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
169
Из условия (90) следует, что
N2 = (Р -	(106)
2 COS р 1 + 2Л cos3£	'	'
В последних соотношениях коэффициент
Е F
представляет отношение жесткостей сечений стержня. Удлинение
центрального стержня
1
ц. = б = —1------------—-.
Я? 11 + 2Х Cds3p
(108)
Если модули упругости материала и площади поперечных сечений стержней одинаковы, то X = 1.
Для-решения задачи «в напряжениях или усилиях» используем уравнение совместности (93), куда вносятся значения щ и и2 из соотношений упругости
_ Nlll а cos₽
или
== VVX cos2p.
(109)
Используя уравнение равновесия (90), получим соотношения (105) и (106). В рассматриваемом случае решение задачи в усилиях проще, чем в перемещениях.
Модель надежности по допускаемым напряжениям исходит из условия
%
(110)
где Отах — наибольшее напряжение растяжения; [о] — допускаемое напряжение; — предел прочности материала; пь — запас прочности по пределу прочности.
Так как материалы стержней разные, то допускаемое значение для внешней нагрузки Р определяется по условиям прочности отдельных стержней.
Из условия прочности для центрального стержнй
Отах = Oi = NJFi OM/n6j,	{111)
где Ом — предел прочности материала центрального стержня. Для боковых стержней условие прочности имеет вид
Отах =* 02 === N2/F2 (5ьг/пЬу	(112)
где ой2 — предел прочности материала боковых стержней.
170
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
Модель надежности системы будет содержать два условия:
Р	(1 + 21 cos2₽),	(ИЗ)
пь
р <	1 + 2Х cos3p	(114)
пь X cos2p ‘	'
Неравенства (113) и (114) вытекают из (111) и (112), если учесть соотношения (105) и (106).
По условиям надежности ограничение величины усилия Р определяется наиболее слабым звеном системы, т. е. минимальным значением Р.
Если площади сечений и материалы стержней одинаковы (F{ = = F2 = F, Et= Е2= Е), надежность лимитируется центральным стержнем:
(1 + 2cos3p).	(115)
пь
В некоторых случаях запас прочности определяют относительно предела текучести ог. Тогда модель надежности приобретает следующий вид:
Р .ZllL. (1 + 21 cos3 ₽),	(116)
Пу
jD < ^Т2^2 (1 + 2Х COS р)	(117)
пт X cos2p ’	V '
где пт — запас прочности по пределу текучести.
Анализ работы конструкции в упругой области проведем для случая стержней с одинаковой площадью поперечного сечения и выполненных из одного материала (Х = 1). Из формулы (109) сразу следует
N2 = Ni cos2 р.
Центральный стержень под действием усилия Р (см. рис. 6.26) загружен существенно больше боковых. Например, при р »45°
Это объясняется тем, что удлинение центрального стержня больше удлинений боковых (П1>п2), а деформация еще больше, так как l2 > При Р = л/4 центральный стержень воспринимает больше половины всей нагрузки:
Л',------------------- 0.59Р.
1 + 20O3-i 1+Х1
С точки зрения оптимального проектирования целесообразно принять р = 0 (рис. 6.26), и тогда Nl = Ni — Ni — P/3. Такое решение
Ы. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
171
является оптимальным, если на систему не могут действовать случайные (нерасчетные) усилия, имеющие составляющие, перпендикулярные оси стержней.
Замечание. При создании инженерных конструкций необходимо учесть все возможные внешние силы не только в рабочих условиях, но и при транспортировке, монтаже и т. п.
Здравый смысл, жизненный опыт крайне необходимы при проектировании!
Работа статически неопределимой системы после возникновения пластических деформаций. Продолжим рассмотрение трехстержневой системы (см. рис. 6.25). Напряжение в центральном стержне в упругой области
Р 1
+2Xcos3p’
ст1=7"
(И8)
В боковых стержнях ^2 °2 = У-2
Рис. 6.26. Трехстержневая система при
р = о
(119)
___Р X cos2p
~ F2 1 + 2Х cos3p ‘
Примем для материалов стержней схематизированные диаграммы деформирования, показанные на рис. 6.27.
Если при возрастании нагрузки Р напряжение Oi превысит предел текучести оТ1, то в центральном стержне возникнут пластические деформации; то же самое можно сказать о боковых стержнях, если Ог Фуг»
Рассмотрим приближенное решение, когда упрочнение материала не учитывается (рис. 6.27, б). Такое решение пригодно для материалов, у которых значения пределов текучести и прочности
Рис. 6.27. Схематизированные диаграммы деформирования материалов стержней: а — диаграмма с учетом упрочнения; 6 — диаграмма без учета упрочнения
близки между собой. Оно применяется и в тех случаях, когда возникновение больших пластических деформаций недопустимо, а материалы имеют незначительное упрочнение на начальном участке
172
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
пластического деформирования (типа «площадок» текучести). Предельное значение усилия в центральном стержне
Л\т =
aTiF! = PiT
1
1 4- 2% cosV
(120)
где PiT — значение внешней нагрузки, при которой возникает пластичность в центральном стержне (предполагается Оп^Отг). При дальнейшем увеличении нагрузки при Р>Р[Т усилие в стержне 1 остается неизменным, а усилия в боковых стержнях будут возрастать до предельного значения
Л^2Т — ОтъР 2»
(121)
Внешнее усилие Р при возникновении пластических деформаций во всех стержнях достигает для принятых кривых деформирования (см. рис. 6.27, б) предельного значения Р==РРазр.
Так как в предельном состоянии усилия в стержнях известны, то из условия равновесия имеем
Р = ЛГ1Т + 22V2T cos 0 = OtiFz + 2ат2Р2 cos 0.	(122)
Построим зависимость перемещения точки приложения силы (точки 4, см. рис. 6.25) от величины Р.
На первом этапе деформирования (Р С Р1Т) перемещение определяется соотношениями упругости (формула (104)). Максимальное смещение на первом этапе — точка Ci на рис. 6.28, а.
Рис. 6.28. Зависимости усилие ~ перемещение (а) и напряжение — деформация (б) для трехстержневой системы
На втором этапе (Pit < Р Рра8р) наибольшее смещение будет в точке С2, когда наступает текучесть в боковых стержнях:
Л = “2 == -hi. =
2 cos 0 = cos 0 cos 0£2*
В этот момент исчерпывается несущая способность системы. Даже
24. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
173
при небольшом повышении нагрузки сверх Рразр перемещение точки А резко возрастает (б <»).
В точке Ci деформация центрального стержня (см. рис. 6.28, 6)
gl(D =	1	е2( 1) “ е1(1) COS“P.
В точке С2	.
Какой из стержней разрушится раньше при возрастании нагрузки? Это зависит от свойств материалов стержней.
Соотношение между деформациями стержней (94) справедливо в любой момент нагружения.
Если (рис. 6.28, б)
ем < 1 еь2 cos2{3 ’
то первым разрушится центральный стержень.
Модель надежности по несущей способности. Несущая способность трехстержневой системы (см. рис. 6.25) исчерпывается, когда нагрузка достигает величины Рразр.
Модель надежности по предельной нагрузке имеет вид
(123)
лн
i
где пя — запас прочности по несущей способности. Для принятых кривых деформирования (без упрочнения) допускаемая нагрузка
р (аТ1Р1 + 2 cos ₽от2^2)-	(124)
/1«г
Сопоставление двух моделей надежности. Сопоставим допускаемую нагрузку в моделях надежности по напряжениям и по несущей способности.
Для этого сравним значение Р из уравнений (116), (117) и (124) при одинаковой величине запаса прочности (пг=па). Предполагая, как и раньше, ^t = £2, получим из условий (116) и (117)
+ 2соз3₽от1Л),	(125)
р <------Цт- (<*Г2Л + 2 cos’PonFa).	(126)
ТЬг£ COS р
При аГ1<От2 определяющим будет условие (125).
Сопоставляя значения Р по формулам (124) и (125), при равенстве пределов текучести материалов стержней ((jT1 = <yT2) и
174
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
равенстве запасов прочности получим
^нес ,сп _	+ 2 cos PF2 >
^доп.напр /г1 + 2 cos3(3F2
Допускаемое усилие по несущей способности больше, чем по допускаемым напряжениям. Это понятно, так как модель надежности по допускаемым напряжениям считает опасной нагрузку Р, при которой в каком-либо одном элементе системы возникает напряжение, равное пределу текучести. В модели надежности по несущей способности допускаемое усилие определяется при условии, что пластичность охватывает все элементы системы.
Замечание. Не следует думать, что во всех случаях надо применять модель по несущей способности: она эффективна для оценки прочности при действии однократной статической нагрузки.
При циклических нагрузках разрушение наступает в наиболее напряженном элементе конструкции задолго до того, как исчерпывается несущая способность всей конструкции.
Для расчета инженер должен выбирать подходящую модель надежности!
Расчет в упругопластической стадии методом переменных параметров упругости. Метод переменных параметров упругости (см. разд. 19) является общим методом определения напряжений и деформаций при работе конструкции в упругопластической стадии. Покажем применение метода для рассматриваемо^ трехстержневой
Рис. 6.29. Зависимости усилие'—перемещение (а) и напряжение — деформация (б). Решение методом переменных параметров упругости
системы (см. рис. 6.25) и построим зависимость «усилие — перемещение» при произвольных кривых деформирования (рис. 6.29, а).
Пусть задано действующее усилие Р и требуется найти напряжения в стержнях и перемещение точки приложения силы. Расчег ведется методом последовательных приближений. В первом приближении материал считается упругим. Из равенств (28) и (29)
25. ГИБКИЕ НИТИ
175
находим напряжения первого приближения:
* ________________1
1(1)	1 + 2Х(1) cos3p ’
ф Р ^*(i) Р
°2(1) ~ К 1 + 2%(1) cos3₽ ’
(127)
(128)
где
><ц -
тт	Y	*	*
На кривых деформирования напряжениям Okd и o2(D соответствуют деформации е1(1) и е2(1) (см. рис. 6.29, б) и напряжения Oi(1) и о2(1). Во втором приближении рассматривается снова упругая конструкция, имеющая параметры упругости
Г &	^1(1) Z7 77	_ ^2(1)
= ^2С(1) — ------•
81(1)	s(l)
Напряжения в стержнях во втором приближении равны ♦	р	1
01(2) -	! + 2Х(2) cos3p >
♦   р	cos р
 °2(2) -^14-2Х(2) cos3p ’
(129)
(130)
где
%(2) =
^2С(1)^*2
Процесс продолжается до n-го приближения, когда Щ(п) ~ Щ(п) и а*(п) ~ сг2(п). Обычно это достигается после трех-четырех приближений. После определения et « е1(п) находят б =» еЛ и получается точка (Р, б) (см. рис. 6.29, а).
25. Гибкие нити
В современных конструкциях часто используются в. качестве несущих элементов гибкие нити (мосты, перекрытия, подвесные дороги, расчалки, детали из композиционных материалов и т. п.). Это связано с тем, что в гибких нитях осуществляется наиболее полное использование механических свойств материала. Модели гибких нитей служат для расчета тросов, цепей, струн, ремней, проводов и т. п.
Основные свойства гибких нитей и условия равновесия? Основное свойство гибких нитей — нить работает только на растяжение. Сечение нити не может передавать изгибающий момент (два звена
176
, ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
цепи не сопротивляются взаимному повороту); участок нити не может выдержать сжатие — он будет искривляться. Вместе с тем нить может воспринимать поперечную нагрузку — за счет изменения направления нити (рис. 6.30). Усилие, растягивающее нить,
Рис. 6.30. Усилия, действующие
в сечении нити
Рис. 6.31. Условия равновесия
элемента нити
всегда направлено по касательной к ней (см. рис. 6.30). Это вытекает из того, что сечение нити не может уравновешивать изгибающий момент (каждое сечение нити является шарниром!).
Полное усилие
N=1Q2 + H\	(131)
где Q — поперечная сила (вертикальная составляющая натяжения нити 2V), Н — горизонтальное натяжение (горизонтальная составляющая натяжения нити ZV).
Из условия равновесия нити сила Q равна алгебраической сумме всех вертикальных сил, приложенных к отсеченной (левой) части нити. Обычно значения силы Q в сечениях нити можно считать известными.
Так как усилие N направлено по касательной к нити, то
tga =*dy/dx = Q/H.	(132)
Рассмотрим условие равновесия элемента нити (рис. 6.31). Если q й h — составляющие распределенной внешней нагрузки, приложенной к нити, то из условия равновесия участка найдем
dQ/dx^q,	(133)
dH/dx~h.	(134)
Если внешние нагрузки на нить направлены вертикально (Л = 0), то горизонтальное натяжение Н постоянно по длине нити (Н ~ == const).
Из уравнений (132) и (133) получается основное уравнение равновесия нити:
' <135>
25. ГИБКИЕ НИТИ
177
По физическому смыслу q — нагрузка, приходящаяся на единицу длины оси х. Размерность q — |^^д а’ j (единицы измерения, например, Н/м, Н/см и т. п.).
Гибкая нить под действием сосредоточенных усилий (рис. 6.32). Предполагается, что собственный вес нити мал по сравнению с приложенными усилиями. На практике встречаются две постановки задачи:
1. Заданы внешние нагрузки и горизонтальное натяжение нити; требуется определить натяжение нити и ее длину.
Рис. 6.32. Нить под действием сосредоточенных сил
2. Заданы внешние нагрузки и длина нити L	требуется найти
натяжение нити.
Рассмотрим сначала первый вариант и определим реакции RA ilRb из общих уравнений равновесия (суммы моментов относительно точек А п В рав-
ны нулю)	лд-	-Я ‘ -	(,36). 1	if	1
-	Rb = -^- + ^- + h£-.	(137)
Теперь можно определить перерезывающую силу Q(x) в сечении нити (см. рис. 6.30). Будем иметь
0<x<ar ()(х) = — RA1
Л1<^<а2, Q(x)==-Ra + Pv	(138)
a2<z<Z,	^(х) = -ЯА + Рх + Ра.
По равенству (132) находим  to а = -£1 а> —		Р1 1~а1	- Р2 1~а2	
		Н 1	Н 1	1 ' 1~а2	।	(139)
tg“i Н 1 • Р. «л tor a' = —1	i- -4- 82 И I 12 и. А. Биргер, Р. Р. Мавлютов	Н рг н	1	+ 1 ’ g2 , с 1- Г -	
178
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
Натяжение нити составит
О х < ah N = Hyi 4- tg2 а0,
^1	х < а2,	N = II}' 1 -J- tg2 аь
а2	х < Z,	N = ЯУ1 4- tg2 а2.
Прогибы нити определяются равенством X
У {х) = у (0) + J dx. О
Учитывая равенства .(139), получим
у (а Л = tg аа1 = — —13-1Z L- — 13____4
к 17	8 0 1	Hl	III
,(a) = __p4~^)gi________рЛ1~а^ + „аг
1 2)	Hl	Hl	I
(140)
(141)
а, С —i
I
Если обе опоры находятся на одном уровне (с = 0), то прогибы нити обратно пропорциональны величине горизонтального натяжения (распора). При подъеме опоры В на высоту с получается дополнительный прогиб
х
не зависящий от Н.
Длина нити (деформацией растяжения нити пренебрегаем) равна
L = f Z1 +	= f 1/1 + -J-dx-	(142)
0	0 F
В рассматриваемом случае
L = atyi 4- tg2 ao 4- (<*2 — «1)У1 4* tg2 at 4- (Z — а2)У1 + tg2 «2,	(143)
где значения tga0, tgab tga2 определяются равенствами (139).
При решении задачи по второму варианту, когда задана длина нити L и требуется найти Я, решение строится методом последовательных приближе-
Рис. 6.33. Модель надежности для нити под действием сосредоточенной силы
Из уравнений (139) при P2 «
ний. Сначала задаются произвольным значением Н == Я(1) и находят соответствующую этому значению L(i). Если £и) < L, то выбирают второе приближение: Я(2> < < Я(1), и расчет повторяется. Задачу можно решить графическим способом, построив зависимость £(Я) и определив значе* ние Я для заданной величины L.
В простейших случаях зависимость £(Я) может быть найдена аналитически. :	Пример построения модели надежно-
сти. Требуется разработать модель надежности для конструкции в виде гибкой нити при действии сосредоточенной силы (рис. 6.33).
0 и с = 0 находим
Р(1—а)	Ра
’«“о----HI ’ ^а1~ НГ
25. ГИБКИЕ НИТИ
179
Наибольший прогиб пити составит
у (а) = tg аоа =
Р (Z — а) а
~ Ш '
(144)
Натяжение нити будет равно
,УМ = Л-О_Я|/' 1 +
при 0 < х < а,
при а х < Z,
(145}
Длина нити по формуле (143) Составляет
Г	£1 4
(146)
Проведем анализ для наиболее неблагоприятного случая, когда сила приложена в середине пролета. При а = Z/2 получаем
. f 1 Р2
L = J |/	+ 4 др.
(147)
Из последнего равенства получаем зависимость горизонтального натяжения от длины нити н==р__________________________________1
2 / L2/!2 — 1 ’
Натяжение нити при а = 1/2 будет таким:
(148)
(149)
(150)
Модель надежности принимаем по допускаемому напряжению Стах = N/F [с], где F — площадь сечения нити.
Наибольшая допустимая нагрузка на нить Р [o]F-2Vl- /2/L2.
Из модели надежности следует, что при L-+1 допустимое значение Р->0. Это-становится понятным,- если учесть равенство (148). При L . = I в нити возникают бесконечно большие напряжения.
Замечание. Следует учесть, что модель относится к нерастяжимой нити. С учетом упругости нити напряжения в рассматриваемом случае (L = I) будут определены в дальнейшем. Они окажутся не бесконечно большими, но весьма значительными.
При анализе надежности всегда необходимо составить отчетливое представление о тех допущениях, которые были приняты, для упрощения модели.
Гибкая нить под действием распределенной нагрузки. Распределенные нагрузки создаются внешними усилиями и собственным весом нити. Для гибких нитей в строительных конструкциях следует учитывать возможность обледенения, ветровую нагрузку, изменение .температурных условий и т. д. 12*
180
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
Если Н/см — вес единицы длины нити, то на единицу длины вдоль оси х (рис. 6.34) приходится нагрузка

(152)
При малых прогибах (отклонениях от оси х) у’ < 1 я q М = q0. Из нения равновесия (135) при Я = const d2y __ q (х} dx2 Н
Интегрируя находим
действием распределенной (вертикальной) нагрузки
обе части равенства от 0
dy
p(*i)	(°>-
о
урав-
(153)
до а
(154)
Переменная интегрирования обозначена xt, так как под х понимается верхний предел интегрирования. Напомним, что величина интеграла не зависит от обозначения переменной интегрирования. Снова интегрируя от 0 до х, получаем
X Х1
. У (*) = -Jf J J g (®2) <&г dxy + у (0) 4- у' (0) X.
(155)
о о
Обозначения переменных указывают порядок проведения интегрирования. По условиям закрепления
Н0)=0, у(1) = с	(156)
получаем’ (хх1	IХ1	\
J J g (хг) dx2 dxt — У J q (z2) dx~t j + c (157) 0 0	0 0	/
Длина нити определяется из уравнения I _________________________________________
Z, =J /1 + y’^dx.	'	 (158)
О
Нить при малых провисаниях Назовем провисанием нити f(x) (см. рис. 6.34) разность между точками прямой, соединяющей опоры нити, и точками нити.
При малых провисаниях величину q(x) можно считать постоянной:
+ • (159)
Из уравнения (157), полагая q(x) = q, находим	,
у (х)= — 2я х	с "7" <	(1^)
25. ГИБКИЕ НИТИ
181
Провисание нити составит
/ (г) = с -у — у (х) = уц (lx — X2) .	(161)
Провисание нити f(x) представляет собой параболу, проходящую через точки подвески нити. .
Длина нити определяется по формуле (158):
L = J j/^1+	+ 'й’х+т]
Используя равенство
1 -f-CC 1 -J- ОС, справедливое при (а|	1, находим
1-П, + т[-А + -в-' + тГ)'"' о
После интегрирования получаем
(162)
Из последнего соотношения вытекает равенство я___^_______________________________________
.. 21/6 L 1 ? •
I -1“ 2 га
Наибольшее провисание нити определяется из условия
W __1_п У-А-П dx - 2Я (г -
что дает х = 1/2. Наибольшее провисание нити получается в середине пролета и равно по формуле (161)
f -q— 'max~ 8Я»
(163)
(164)
или
Anax ql
I = 8Я*.
(165)
В практических задачах натяжение нити больше суммарной нагрузки на нить:
Н > ql.	(166)
и	'	.
Аиах Л л — <0,1.
Случай малого провисания является основным для практических расчетов нитей.
Учет упругой и температурной деформации при малых провисаниях нити. Если £о — первоначальная длина нити (при монтаже), то в рабочем состоянии
L == £о(1 + 8+ет),	(167)
где 8 и 8т — упругая и температурная деформации.
182
ГЛ. 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
При малых провисаниях можно считать усилие, растягивающее нить, постоянным' xV = II ]/* 1 4- у'2 = Н У1 + c2!l2, и тогда
О N Н V1 + c2/Z2
s —	— EF~ HF ’	(168>
где Е — модуль упругости, F — площадь сечения нити, о — напряжение растяжения нити.
Температурная деформация
£т = ат(Г-Г0),	(169}
где ат — коэффициент линейного расширения, (Т — TQ) — разность температур в рабочих условиях и условиях монтажа.
Из уравнений (162) и (167) получаем
1	Q2/3	?
С1 + 8 + 8т) — 1 + "24	+ 22 ’	(170>
При малых провисаниях можно считать, что
£0 « /о,	(171)
где 10 — расстояние между точками подвеса нити. Так как == у/2 + с1 ~ I + 4- c2/(2Z), то равенство (170) можно представить в следующем виде:
1 q2l3
д + дн + дг = 14ть	(172>
п где
д = £0 —Zo	(173)
— разность длины нити и расстояния между точками подвеса;
hi V1 + с2//2	hi*
дн = EF ~ EFl	(174>
— упругое удлинение нити;
Ат = аНГ-ТоИо	(175)
— температурное удлинение (или укорочение) нити.
Из уравнения (172) следует, что учет упругой деформации и температурного удлинения существен только в тех случаях, когда величины Дн и Дт одного порядка с разностью первоначальной длины нити и расстояния между опорами.
Замечание. Последнее обстоятельство весьма существенно при инженерных расчетах.
Прежде чем учитывать или отбрасывать какие-либо факторы, надо оценить их значение по сравнению с другими подобными факторами, действующими на конструкцию.
Модель надежности гибкой нити. Из условий статической прочности найдем напряжение в нити:
о аь/п = [а],	(176)
где Оь — предел прочности материала, п — запас прочности (обычно п = 2—3). Часто ставится условие
/шах<[/]»	(177)
где [/] — допускаемая величина провисания в связи с габаритными условиями. Основными для расчета являются, уравнения (172) и (165).
ГЛАВА 7
КРУЧЕНИЕ СТЕРЖНЕЙ
Вводные замечания. Элементы конструкции, как уже указывалось, часто схематизируются в виде стержней. Такая модель формы используется и для расчета валов, передающих крутящий момент. Примерами являются валы, приводящие в движение воздушные винты или лопасти вертолета; валы редукторов, станков и т. п. 
Работа стержней на кручение встречается во многих других элементах конструкций. *
26. Кручение круглых валов
Деформации и напряжения при кручении круглого вала. Экспериментально установлено, что при кручении круглого вала (рис. 7.1) приложенным на его торце крутящим моментом поперечные сечения остаются плоскими (рис. 7.2). Можно считать, что поперечные
Рис. 7.2. Кручение модели вала с предварительно нанесенной сеткой
Рис. 7.1. Кручение круглого вала
сечения как жесткие круглые диски поворачиваются относительно оси вала на угол ф (z).
Образующие, расположенные на цилиндрической поверхности радиусом г, поворачиваются на угол постоянный по длине цилиндра (вала). Для малых углов
Y(r) = tgV = ^ =	=	(1)
где О'= ф (Z)/Z — угол закрутки на единицу длины вала; при измерении угла ф в радианах угол 6* измеряется в единицах 1/см, 1/м.
Угол поворота в сечении г
ф(г) = ^ф (Z)/Z ==. (2)
Из последнего соотношения можно установить, что
$=4е-	(3)
dz	х '
184
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
Рассмотрим перемещения и деформации в произвольной точке поперечного сечения А, лежащей на расстоянии г от оси вала (рис. 7.3). Перемещение точки At равно АГА{ и направлено перпендикулярно радиусу. В кольцевом слое толщиной dr возникает деформация сдвига (рис. 7.4)
?(г) = ^Г = «г.	(4>
По закону упругости углу сдвига соответствует касательное напряжение (разд. 18)
т = Gf,
где G — модуль сдвига, G =
Учитывая (4), находим важную зависимость:
т(г)= G^(r) = ^Gr.
(5)
Касательное напряжение т(г) направлено по касательной к окружности радиусом г. Величина касательного напряжения пропорциональна радиусу (рис. 7.5).
Рис. 7.4 Деформация сдвига в кольцевом слое
Рис. 7.5. Распределение касательных напряжений при кручении
Рис. 7.3. Картина перемещений точек вала при кручении
Из общих условий равновесия следует, что касательные усилия т (г) dF должны создавать крутящий момент
Мк = J тгdF = OG J г2 dF. ~ $GJV,	(6)
F	F
где J9 == J г2 dF — полярный момент инерции сечения вала. Вели-г	'
чину полярного момента легко вычислить, приняв
dF = 2лг dr,
26. КРУЧЕНИЕ КРУГЛЫХ ВАЛОВ
185
тогда к
Т С О 3 л л/f4 л^4	п\
Jp = J 2лг3 аг == — = -gp	(7)
о
Из соотношения (6) получаем формулу для относительного угла
закрутки
А МК ft = —
Величина GJP называется жесткостью (сечения) вала на кручение.
Угол поворота сечения вала
А/к2 ф (z) = Oz = gy-.
Взаимный поворот сечений на участке вяла длиной L МК1 ф(0 = 4.
Внося значение О в формулу (5), находим важную висимость:
(8)
(9)
расчетную за-
Мк
’'р
Наибольшее касательное напряжение радиусе
_ d _____ Mr
Ттах-^-- 2 “ nd3/16-
Величина
(Ю)
называется кручению;
1Ук.= ^«0,2й3 [ моментом сопротивления таким образом,
Tmax«MK/WK.	(13)
решения методами теории Полученное решение о рас-
получается
У
(И)
(12)
на внешнем
Рис. 7.6. Кручение круглого вала. Расчет методом теории упругости


Анализ упругости, пределении напряжений и деформаций при кручении вала основывалось на экспериментальных наблюдениях. Попробуем подвергнуть его анализу с позиции общих уравнении механики деформируемого тела. В соответствии с принятой моделью деформации вала перемещение точки Ai(x, у), равное Л*4х(рис. 7.6), . имеет составляющие по осям
и = —— пр (z) sin 9 я» — гф (z) — « — ф (z) у,
V == пр (z) COS 0 =» Гф (z)
<р (z) х.
(14)
186
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
Перемещение вдоль оси z отсутствует (и? = 0). Составляющие касательного напряжения равны
TM = GVac= -G-g-y = -G(h/,
Tz2z = GV2!/ = G-g-x = G&x
(15)
Полное касательное напряжение
т = ]/"тхх 4-	= GOr,
что совпадает с равенством (5).
Можно показать, что при Мк = const удовлетворяются уравнения равновесия и краевые условия на боковых поверхностях вала. Принятую модель деформации круглого вала следует признать точной.
Замечания. 1. Предполагается, что в концевых сечениях вала внешний крутящий момент реализуется в виде линейно распределенных касательных напряжений (см. рис. 7.5). В действительности момент обычно прикладывается по-другому (например, с помощью шлицевого соединения (рис. 7.7)), и
Рис. 7.7. Передача крутящего момента на вал с помощью шлицевого соединения
поэтому по принципу Сен-Венана решение будет справедливым на некотором удалении от торцов.
Более строго следовало бы сказать, что решение является точным для неконцевых областей вала.
2. Граница между понятиями «точного» и «приближенного» решения я применении к практическим задачам часто носит условный характер. Например, можно получить точное решение для весьма приближенной модели (расчетной схемы) или приближенное решение для более точной модели. Что-лучше для практических целей? Однозначного ответа на этот вопрос не существует.
На основании практического опыта вырабатываются модели различных уровней, используемые на разных этапах проектирования (предварительный выбор размеров на стадии технического предложения, более точные модели на этапах эскизного и рабочего проектирования).
Кручение полого вала. Полые круглые валы (трубы) часто используются для передачи крутящего момента, так как приводят к конструкции с наименьшей массой по сравнению со сплошным ва
26. КРУЧЕНИЕ КРУГЛЫХ ВАЛОВ
187
лом. Кинематическая картина деформации остается такой же, как при кручении сплошного круглого вала. Распределение касательных напряжений определяется соотношением (10). Полярный момент инерции сечения будет таким:
где do — внутренний диаметр вала (рис. 7.8). Наибольшее касатель-
ное напряжение
d
^тах — Л "V" — ~	7 i
/₽ 2	•_±Лз_ 1 Л
16 \ d 0
(16)
Рпс. 7.8. Распределение напряжений при кручении полого вала
Кручение вала с переменными параметрами упругости по радиусу. Такая модель описывает кручение вала с покрытиями из другого материала, биметаллического вала и т. п. Модель используется для расчета упругопластической деформации вала. Кинематическая картина деформации остается прежней, что можно показать с помощью точного решения. Касательное напряжение в соответствии с равенством (5) составит
т(г) = йС(г)г,	(17)
где С? (г)—модуль сдвига материала в слое на расстоянии г.
Из условия равновесия (6) имеем
= f тг dF == » [ G (г) г2 dF.	(18
F	F
Относительный угол закручивания
е = 7—«—.	>	(19)
j G (г) dF F
Теперь для касательного напряжения получаем (17) и (19)
из соотношении
j —- р--------/•
| G (г) г2 dF
F
При G(r)= const = G равенства (20) и (10) совпадают.
Замечание. Структура формулы (20) представляет интерес. Кольцевой слой воспринимает касательное напряжение пропорционально модулю сдвига (модулю упругости) слоя. Это означает, что слой из непрочного материала может работать на поверхности высокопрочного вала, если слой имеет малый модуль упругости.
Кручение вала переменного сечения при переменных по длине крутящих моментах. Полученные ранее расчетные зависимости установлены для круглого вала постоянного сечения при действии постоянного крутящего момента по длине. В этом случав решение
188
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
удовлетворяет уравнениям теории упругости. На концевых сечениях краевые условия соответствуют действующему крутящему моменту, т. е. удовлетворяются в смысле Сен-Венана. Если крутящий момент изменяется по длине или диаметр вала различен на разных участках, то в инженерных расчетах используется приближенное решение.
Касательное напряжение в сечении вала определяется по* формуле
MK(z) Т = -7-7-7 Г.
Угол закрутки на единицу длины вала
dq (z) = Мк Ф dz G7p(z)‘
(21)
(22)
Таким образом, основные расчетные зависимости (21) и (22) используются для параметров рассматриваемого сечения вала.
Замечание. Приближенный метод, несколько расширяющий область применения расчетных зависимостей за пределы принятых допущений, является типичным для инженерных расчетов прикладных моделей надежности. Уравнения (21) и (22) строго справедливы только для вала постоянного сечения при действии крутящего момента по концам вала.
В приближенном решении предполагается, что каждый малый участок вала «ведет себя» так, как будто весь вал имеет такое же сечение и закручен тем же моментом. Влияние соседних участков признается второстепенным.
Справедливость приближенных методов обосновывается практическим опытом и экспериментальными исследованиями. Часто весьма убедительным оказывается сопоставление с примерами более точных решений, полученных численными или аналитическими методами.
Кручение вала в упругопластической стадии. Если напряжения при кручении
т>тг,	(23)
где Тт — предел текучести при сдвиге (кручении), то в материале вала возникнут пластические деформации.
На рис. 7.9 показаны кривые деформирования при кручении (зависимости т—-7). Они могут быть получены при кручении тонкостенных труб, для которых можно считать известным значение касательных напряжений при заданной величине крутящего момента:
где До, 6 — средний радиус и толщина трубы. Приближенно кривые
26. КРУЧЕНИЕ КРУГЛЫХ ВАЛОВ
189
деформирования при кручении могут быть найдены из обычных кривых деформирования, если положить
Т =	^=/Зе0,
где Go, 80 — напряжение и деформация при растяжении образцов. Часто для упрощенных оценок принимается кривая деформирования без участка упрочнения (рис. 7.9,6).
Рис. 7.9. Кривые деформирования при кручении (тг —предел текучести на срез, — предел прочности на срез): а — экспериментальная кривая деформирования; б — кривая деформирования без упрочнения; в — кривая деформирования с линейным упрочнением
Рассмотрим кручение сплошного вала при наличии пластических деформаций. При крутящем моменте
=	(25)
впервые появляется пластическая деформация на наружной поверхности вала.
Эксперименты показывают, что при возникновении пластичности кинематическая картина деформаций вала остается неизменной — сечения остаются плоскими, радиальные направления до деформации остаются радиальными и после деформации.
Рассмотрим упрощенную диаграмму деформирования без упрочнения. При	в сечении возникают две зоны (рис. 7.10).
При г < п (зона упругих деформаций)
т==тт~. •	(26)
При г > п (зона пластических деформаций)'
т = тг.	(27)
Из условия равновесия имеем
Ч	я
Мк = ^urdF =х £л Jтг ~dr + 2л^xTr2dra
190
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
ИЛИ
Л7к = тт.2л(|/?а-^г?).
Из последнего соотношения получим з / 6ЛГ
^ = 1/4^-^.	(28)
г/	Л tgn
Зависимость (28) показывает, что при возрастании крутящего момента зона упругих деформаций в центре вала уменьшается. При
Рис. 7.10. Распределение касательных напряжений при кручении вала (материал не обладает упрочнением)а — предельное значение крутящего момента б — распределение напряжений при действии предельного момента
Л = 0 наступает предельное состояние — наибольшее (предельное) значение крутящего момента
.Мкт = 4лЛ3тг = тт^.	(29)
О	1^4
Сопоставляя равенства (25) и (29), получаем
МкГ = |м°кГ.	(30)
Развитие пластических деформаций увеличивает приблизительно на 30% сопротивление вала. Угол закрутки вала на единицу длины (см. (4))
^ = ^2 = dz г ‘
Применяя это равенство при r = rt (т = хт), находим
_ тт’ _ тт 1	/ЧП
dz “ Gr “ G '3 f--------ем"*
1/ 4Л3- — JTTj»
При приближении Л/к к Ж-r величина dqp/dz-><» и деформация вала резко возрастает.
26. КРУЧЕНИЕ КРУГЛЫХ ВАЛОВ
191
г2 dr.
Более полное описание свойств материала дает схематизация в виде кривой деформирования с линейным упрочнением (рис. 7.9, в). Распределение касательных напряжений при действии предельного момента показано на рис. 7.11; имеем
<Г = ТГ + X (Ть — тт),	(32)
где т6 — предел прочности на срез (сдвиг).
Из условия равновесия
в
Мкразр = J гт dF = 2л J |тт + у (ть — тт) F	О
После интегрирования получаем ./Г	ЛЛ$ л/?3	2л rj. I л7? я — \	/qqv
Мкра3р = —Tb + -g-Tr = -y/?3TT + —(ть —тт).	(33)
Из- сравнения равенств (29) и (33) устанавливаем влияние учета упрочнения материала. Например, если
4
Ть = уТт,	#
то
М к. разр	l,25J/Kr.
В общем случае для расчета применяется метод переменных
Рис. 7.11. Определение предельного момен-	Рис. 7.12. Применение метода
та при кручении вала из материала с ли-	переменных параметров упру-
нейным упрочнением	гости
параметров упругости (рис. 7.12). В первом приближении рассматривается вал из упругого материала.
Из соотношения (21) находим
♦
9
192
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
затем
А, — Т(* ) Г — Т(П
Далее по равенству (20) находим второе приближение:
* G(i) (г)
Т(2) = р------------,
j G(1) (г) г2 dF
и, следовательно,
л, — <2) Г	<2>
Y(2) =	<Л2) = ~
^(1)	?(2)
и т. д. Обычно достаточную точность дает второе-третье приближение. В рассматриваемом случае можно найти замкнутое решение, если учесть линейное распределение деформации сдвига по радиусу. Однако в более сложных случаях (например, при действии крутящего момента и осевой силы) решение приходится выполнять методом переменных параметров упругости.
Кручение вала в стадии установившейся ползучести. В этой стадии скорость возрастания деформации сдвига зависит только от величины касательного напряжения. Применяя уравнение (124) гл. 5 для случая кручения (т^ = т, уху—Т, остальные компоненты напряжений и деформаций равны нулю), находим
= g = 3B<fi~\	(34)
где В и п — параметры экспериментальных кривых ползучести (гл. 5, формула (121)).
Так как	_
ch = УЗт,
то получаем
3(п+т)/2 Вхп= 5ктп.	(35)
at
Кинематическая картина деформации остается такой же, как в упругой стадии, и поэтому
7 == Or.	(36)
Из последних соотношений находим
При ползучести касательные напряжения кручения паспределяют-ся по закону г1/п.
26. КРУЧЕНИЕ КРУГЛЫХ ВАЛОВ
193
Из условия равновесия
R
Мк = j тг dF « 2л f тг2 drT	(38)
F	О
учитывая соотношение (37), находим
Мк = 2л (^^-У/”-7^тгЯ3+1/п.	(39)
\dt Вк] 3 + 1/л	•'
Теперь по равенству (37) получаем
т = (з + -) ...^-7- г1/п.	(40)
\ п ) 2лЯ3+1/п
При п = 1 касательные напряжения распределяются по линейному закону, и формулы (40) и (10) совпадают.
Замечание. Интересно отметить, что распределение касательных напряжений кручения (40) при установившейся ползучести совпадает с распределением напряжений в упругопластической стадии, если принять уравнение кривой деформирования в виде
7 = Вктп.
Действительно, в силу равенства (36) получаем
T=s(^K)!/«rl/«
и далее соотношение (39), в котором вместо Mjdt стоит О, Иу наконец, формулу (40). При одинаковом распределении напряжений в стадии ползучести и пластичности есть существенная разница в поведении вала: при ползучести все время увеличивается угол закрутки вала, тогда как при пластичности он не изменяется во времени.
Деформации или скорости деформаций часто играют одну и ту же роль в механике твердого деформируемого тела — они отражают геометрическую картину деформации.
Модели прочностной надежности вала при кручении. При построении модели прочностной надежности (разд. 2) следует прежде всего рассмотреть характер напряженного состояния, условия работы вала в составе всего изделия, особенности нагружения и возможных разрушений.
, На площадках, лежащих в плоскости поперечного сечения скручиваемого вала, действуют только касательные напряжения. Для анализа рассмотрим точку Л, находящуюся *на поверхности вала, и расположим оси х, у так, как показано на рис. 7.13. Напряженное состояние характеризуется следующими значениями компонентов:
Ох = 0, Gv = 0, Txv = ~Т, Ож = 0, Tyz = 0,. Tzx = 0.
Напряженное состояние в каждой точке вала является плоским, так как в площадках, нормаль к которым совпадает с осью z (радиальное направление), напряжения отсутствуют. Главные 13 И. А. Биргер, Р, Р, Мавлютов
194
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
напряжения вычислим по формулам (26) и (27) гл. 2:
= 4 (<ТЖ + <3у) + 4 1/ (оя — оу)2 + 4-Схз, = т, / ' f ____________________________ (41)
о2 = -j- (°х + aj — у V (°* — °»)3 +	= — т.
Далее устанавливаем
*2а*- 5^ = 00, 2а* = 4, а* = ±
Площадки главных напряжений направлены под углом 45° к оси вала. По формулам (35) и (36) гл. 2 находим
♦ ai ~ ах т	.	.	♦ а2 — аг — т .
tg«(D = —;----==—=—1, tga(a)--2-------------- -- = 1.
ТХ|/	т	ТХ1/	т
Растягивающее главное напряжение щ направлено вдоль винтовой
Рис. 7.13. Площадки главных напряжений при кручении вала: а — схема напряженного состояния; б — тлаъъое напряжение
линии; при взаимном повороте поперечных сечений такие волокна растягиваются (направление а*). Для волокон, идущих по ортогональным винтовым линиям (направление а*), при действии момента Мк (см. рис. 7.13) происходит укорочение.
Замечание. Анализ напряженного состояния очень важен, например, для правильного конструирования деталей из композиционных материалов. Если труба из материала, усиленного волокнами, должна работать на кручение, то волокна следует располагать по винтовым линиям, составляющим угол 45° с осью вала.
При построении модели статической прочности исходят из условия прочности для пластичного материала
тш»х<ть/пь,	(42)
где пь — запас по напряжениям, т» — предел прочности материала на срез (сдвиг).
Используя равенство (И), найдем допускаемое значение крутящего момента;
26. КРУЧЕНИЕ КРУГЛЫХ ВАЛОВ
195
Модель статической прочности по несущей способности использует условие
—А^кразр»	(44)
лн.с
где пя.с — коэффициент запаса по несущей способности. С учетом равенства (33) получаем допускаемую величину крутящего момента
»/Г	1 /nd3 , nd3/ ч\ 1 ( nd3 , nd3\	//сч
+ 16 (Ti> — Tr) / ~ n“	IT + TT IS-/*
При одинаковых значениях пь и пНЛ5 условие (45) дает значение Л/к, на 15—30% большее. Однако это увеличение может быть использовано только при действии однократной статической нагрузки, например для оценки величины крутящего момента, разрушающего вал.
Если вал выполнен из хрупкого материала (удлинение при разрыве меньше 3%), то условие статической прочности следует принять, исходя из величины наибольшего растягивающего напряжения:
Oimax < Оь/л&?
(46)
где бь — предел прочности материала на растяжение. Так как
01 max	Tmaxi
т
то допускаемое значение крутящего момента

ab nd3 nb 16 *
(48)
Значение тг6 для хрупких материалов обычно принимается в 1,5— 2 раза больше, чем для пластичных материалов. Значение 7ИК по условию (47) одновременно характеризует и несущую способность вала, так как у хрупких материалов перераспределение напряжений не происходит — они работают в упругой области практически до разрушения. При построении моделей статической прочности вопросы концентрации напряжений не являются главными, так как у пластичных материалов происходит выравнивание напряжений.
Для моделей прочностной надежности, связанных с усталостью (вал при действии переменных напряжений), прочность в местах концентрации напряжений обычно является определяющей.
В некоторых случаях при построении моделей прочностной надежности используют ограничения по углу поворота (на единицу длины вала)
<49>
13»
196
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
или по полному углу поворота

(50)
Наконец, дополнительные ограничения могут быть связаны с динамическими явлениями (например, с необходимостью устранения крутильных колебаний). Эти вопросы частично рассматриваются в дальнейшем. Перейдем к изучению работы на кручение стержней некруглого сечения.
27. Общая задача кручения стержней и концентрация напряжений
Перемещения и деформации. Рассмотрим кручение упругого стержня постоянного сечения под действием крутящего момента. Сечение стержня показано на рис. 7.14.
Допустим сначала, что общая картина перемещений остается . такой же, как при кручении круглого вала: сечение стержня как
Рис. 7.14. Картина перемещении точек при кручении стержня
жесткая пластинка поворачивается вокруг оси стержня, причем относительный угол закрутки остается постоянным по длине. Тогда точка сечения А на расстоянии г от оси переходит в точку Л*, а сечение поворачивается на угол
Ф = dz,	(51)
где d — угол поворота на единицу длины I dim d =	, напри-
рад\
мер -— — постоянная величина, м. /
Составляющие перемещения по
осям х и у равны
и = — ЛЛ* sin 0 == — гф sin 0 = — гф ~ == — dz#, (52)
v == ЛЛ* cos0 = гф cos 0 = гфу = ftzx.	(53)
Далее допустим, что перемещение вдоль оси z (оси стержня)
w = ш(х, у)	(54)
не зависит от координаты z.
При кручении круглого вала принималось ^ = 0;'в общей задаче кручения существует перемещение, перпендикулярное плоскости поперечного сечения ш, которое называется депланацией.
27. ОБЩАЯ ЗАДАЧА КРУЧЕНИЯ СТЕРЖНЕЙ
197
С помощью формул Коши (разд. 9) находим следующие значения деформаций:
п ди Л	да л	div
£х == ЗТ = 0,	8„ = т- = 0, £г = - = 0,
дх	у ду	dz ’
да , ди ~	div , da div ,
= 17 + 17 = °> bz = 17 + 37 =
div , du div a
V- = 17 + 17 = 77-^
Напряжения, условия равновесия. Так как линейные деформации равны нулю, то по уравнениялм упругости (разд. 18) обращаются в нуль и нормальные напряжения:
(jx = 0, оу = 0, ох = 0.	(56)
Касательное напряжение x*y также равно нулю. Отличными от нуля будут только касательные напряжения, действующие в плоскости поперечного сечения:
TZx — Gyzx ~ G ^У^ i	(5/)
=» Gyzy == G	,	(58)
где G — модуль сдвига.
Перейдем к рассмотрению уравнений равновесия (разд. 7)'. .
Первые два уравнения удовлетворяются тождественно (массовые силы считаем отсутствующими), а из третьего уравнения вытекает
Учитывая соотношения (57) и (58), получаем
2	2
д tv д IV л	/ог\\
—г- Н-----г = 0.	'	(60)
ду
Из последнего уравнения следует важный чтобы удовлетворились уравнения равновесия, может быть произвольной функцией — оно должно удовлетворять уравнению Лапласа (уравнению (60)).
Замечание. Дифференциальное уравнение для функции двух переменных
У)
результат: для того осевое смещение не
d2F	d2F	/ О2 , д2 \ 2п Л
1 о •>	I о 4- о I F —— v F == 0
дх2 т ду2. 1дх2 ду2 j	-
называется уравнением Лапласа.
Уравнена^ Лапласа часто встречается в технических науках, в гидродинамике, теории теплопроводности и др. Функции, удовлетворяющие уравнению Лапласа, называются гармоническими.
198
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
Рис. 7.15. Краевые условия на боковой поверхности стержня
Краевые условия. Рассмотрим теперь краевые условия для напряжений. Нормаль к боковой поверхности (рис. 7.15) образует с осями х, у, z углы соответственно а, л/2 — а, я/2. Направляющие косинусы указанных углов
I = cos а, т = sin а, п = 0.
Считая боковую поверхность стержня свободной от распределенных усилий, получим из краевых условий (формула (103) гл. 2)
+ тгуШ = 0,	(61)’
или
тгх cos а + Tzy sin а = 0.	(62)
Последнее условие имеет следующий физический смысл. Величины тгх и тгу представляют собой составляющие касательного напряжения в точке поперечного сечения по осям х и у. В точке Л, лежащей на контуре поперечного сечения, составляющая полного касательного напряжения по направлению нормали
Tv Tzx cos а + Tzy sin ос = 0.	(63)
Краевое условие на боковой поверхности (условие (62)) означает, что в точках контура касательное напряжение направлено вдоль касательной к контуру, составляющая по нормали равна нулю. Соотношение (63) можно было написать сразу из условия парности касательных напряжений, так как на боковой поверхности касательные напряжения отсутствуют. Из равенства (62) возникают краевые условия для w(x, у). Внося в (62) соотношения (57) и (58), получаем
G (— — Фу) cos а + G f + б’х) sin а = 0»	(64)
I дх	\ду )
~ cos а + ~~ sin а == Ф (у cos а — х sin а).	(65)
Рассмотрим теперь краевые условия на торцах.стержня, где приложен крутящий момент. Точное распределение внешних касательных условий неизвестно — оно зависит от конструктивных особенностей конкретных способов передачи крутящего момента. Но при любом способе задания внешних распределенных усилий на торцах стержня они должны быть статически эквивалентными крутящему моменту Мк.
Краевые условия на торцевых поверхностях будем выполнять не в отдельных точках, а для всего сечения в целом:
j (TzvX — W) dF = Мк.	(66)
F
27. ОБЩАЯ ЗАДАЧА КРУЧЕНИЯ СТЕРЖНЕЙ
199'
называются краевыми у слов и-
Рис. 7.16. Краевые условия на торцевой поверхности стержня
Последнее условие можно также рассматривать как условие равновесия участка стержня (рис. 7.16).
Замечание. Краевые условия, которые выполняются интегрально для главного вектора или главного момента внешних сил, ям и Сен-Венана, по имени знаменитого французского ученого и инженера, впервые решившего задачи о кручении и изгибе стержней.
Отйаз от строгого, пунктуального выполнения краевых условий во всех точках поверхности тела, использование интегрального краевого условия составили новый этап развития механики деформируемого тела. Существенно, что искажения напряженного состояния, вызванные различными способами передачи крутящего момента, при условии (66) распространяются только на области вблизи торцов стержня (принцип Сен-Венана).
Математическая постановка задачи. Функция кручения. Математическая постановка задачи означает сведение
задачи к разрешающей системе уравнений и условиям однозначного их решения.
Полученные ранее основные уравнения достаточны для математической постановки задачи, но часто оказывается целесообразным преобразование уравнений, переход к другим переменным и т. п; Для решения задачи введем функцию кручения Ф(я, у), положив осевое смещение
w{x, у) = ЪФ(х, у);	(67)
тогда из уравнения (60) следует, что
<?2ф	<?2Ф	.
+ = (68)
дх	ду
Для точек контура сечения находим из условия (65)
дФ	, дФ .	.	znnx
cosa + -я— sin а = у cosa — zsina.	(69)
дх	ду	у	' 7
Отметим, что для всех контурных точек можно считать известными их координаты и значение угла нормали контура с осью х (утла а).
Отыскание функции Ф(х, у), удовлетворяющей для всех точек области (поперечного сечения) уравнению Лапласа, а на внешнем контуре условию для производных, называется задачей Неймана. В математической физике доказывается существование и однозначность решения.
Замечания. Если составлять разрешающее уравнение для функции w(x, у), то краевое условие содержало бы неизвестную постоянную О. Функция кручения Ф(х, у) определяется только сечением стержня и не зависит от величины приложенного крутящего момента, разумеется, в пределах упругих деформаций.
По физическому смыслу она численно равна осевому смещению при
200
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
Краевое условие (69) можно записать в виде
зф
—— = у cosa — я sin а,
Av *	1
(70)
где дФ/dv — производная функции Ф(х, у) вдоль направления нормали. Из общего правила определения производной вдоль направления имеем
Рис. 7.17. Определение производной вдоль направления v для функции Ф(л\ у)
дФ dv
дФ dy ду dv ’
du
= sin а, dv	’
дФ dx дх dv
Так как (рис. 7.17)
dx
— == cosa, dv	1
то получаем условия (69) или (70). Если функция Ф(я, у) определена, то
( дФ \ Tzx — Gb дх	У),
+ х)-
(71) .
(72)
Для полного решения задачи требуется определить величину 6*, что можно сделать по условию (66). Внося в это условие уравнения (71) и (72), находим
+z)*-(^~y\y]dF-MK.	(73)
Примем обозначение
+	(^-y\y\dF~j*	<74>
F L -	7 Х	7 J
и будем называть JK геометрической жесткостью стержня на кручение. Для круглого стержня поперечное сечение при кручении остается плоским,
и? =-&ф(д:, у)= 0,	(75)
и тогда
/к-J т2 + у2)^ = /р. F
(76)
Из равенства (73) получаем величину относительного угла закрутки
<77)
Теперь ясно, что значение функции кручения Ф(х, у) полностью решает, задачу, т-. е. позволяет найти напряжения и деформации при кручении упругого стержня произвольного сечения заданным
27. ОБЩАЯ ЗАДАЧА КРУЧЕНИЯ СТЕРЖНЕЙ
201
крутящим моментом. Тем не менее решение с помощью функции кручения является одним из возможных способов решения. Другой способ (в некоторых случаях более удобный) связан с функцией напряжения.
Функция напряжения. Предположим, что касательные напряжения при кручении можно представить в следующем виде:
Tae = G^,	(78)
(79)
где F(x, у) — подлежащая определению функция напряжения, G — модуль сдвига, 0* — относительный угол закручивания. Такая форма представления позволяет сразу удовлетворить уравнениям равновесия (59). Из соотношений (71) и (72) находим связь функций напряжения и кручения:
dF	/ 5Ф. ,
__ = _.  -----р х
дх	I ду
(81)
Дифференцируя равенство (80) по у, а равенство (81) по х и скла* дывая, найдем
d2F d2F = __ < дх2 + ду2
(82)
Это уравнение называется уравнением Пуассона, Оно отличается от уравнения Лапласа наличием заданной функции в правой части уравнения.
Для точек контура из условия (62) получаем
dF	•	A	/QQ\
-з— cos а г— sin а == 0.	(83)
Пи	Пт	х '
Далее следует учесть соотношения для элемента дуги контура cos а = -уЧ sin а = — ~	(84)
ds г	ds ’	v '
и тогда из равенства (83) с необходимостью следует
dF dy	dF dx   dF
dy ds	dx ds	ds
В точках контура производная функции F(x, у) вдоль дуги равна нулю. Следовательно, для точек контура
F(x, t/) = C,	(86)’
где С — постоянная.
202
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
Замечание. Условие (86) можно получить несколько другим путем. Умножая уравнение (85) на ds, получаем для точек контура dF dF
-^dx+-^-dy = dF = G,
и, следовательно, справедливо условие (86).
Для односвязной области, т. е. для поперечного сечения без внутренних полостей, постоянную С можно принять равной нулю, и тогда для точек контура
F(x, у) = 0.	(87)
Итак, задача кручения сводится к нахождению функции напряжения как решению уравнения Пуассона при постоянном значении функции на контуре.
Перейдем к определению величины '0. Из условия (66) находим
+ (88> го
где Fo — площадь поперечного сечения. Учитывая очевидные соотношения
х = -%- (Fx) - F, dx	dx ' '	*
dF	& i р \	р
-^y = j-(Fy}-F, находим
Мк = 2Gb J FdFQ,	(89)
так как в силу условия (87)
(90>
F0
Доказательство условия (90) можно провести различными путями: преобразуя интеграл по площади в интеграл по контуру или проводя интегрирование по dx и dy с учетом условия (87). Геометрическая жесткость стержня на кручение (для односвязного сечения)
JK = 2fFdF0.	(91)
Мембранная аналогия для функции напряжения. Рассмотрим мембрану, например тонкую резиновую пленку, закрепленную по контуру Г (рис. 7.18) . Мембрана предварительно растянута в двух направлениях с напряжением а на плоском диске, имеющем отверстие, по форме сечения стержня, и затем изнутри дается давление
27. ОБЩАЯ ЗАДАЧА. КРУЧЕНИЯ СТЕРЖНЕЙ
203
р. В результате мембрана получит прогибы /(х, у), но на контуре сечения прогиб / = 0. Предполагается, что прогибы мембраны невелики и предварительные напряжения о не изменятся в процессе прогиба. В каждом из направлений мембрана ведет себя как гибкая нить (разд. 25).
Условие равновесия мембраны составляется как равенство нулю сил, действующих в вертикальном направлении. В результате
Рис. 7.18. Мембранная аналогия для функции кручения: а — прогиб мембраны; б к выводу уравнения мембраны
изменения прогибов / вдоль оси х составляющая от растяжения мембраны будет равна
об—~ dxdy, дх
где б — толщина мембраны.
С учетом изменения прогибов вдоль оси у получим
дх	ду	°
где р — давление на мембрану.
Принимая р/о = 2 и сопоставляя уравнения (82) и (92), на-» ходим
F = /S,	(93)
так как функции F и /б удовлетворяют одинаковым уравнениям и краевым условиям. Прогиб мембраны под действием внутреннего давления пропорционален функции напряжения. В этом и состоит мембранная аналогия, позволяющая экспериментально решать задачу кручения при соответствующем выборе давления, натяжения и толщины мембраны.
Отметим, что опорный контур мембраны может соответствовать контуру сечения стержня и в некотором масштабе, что приведет только к изменению множителя.
204
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
Достоинство мембранной аналогии заключается также и в том, что она позволяет представить поведение функции напряжения F(x, у), так как характер прогибов (провисания) мембраны можно предвидеть из физических соображений. Например, для контура сечения в виде вытянутого прямоугольника (рис. 7.19) прогибы
Рис. 7.19. Прогибы мембраны (функция напряжений) для сеченпя стержня в виде вытянутого прямоугольника: а — прогибы мембраны; б — распределение касательных напряжений
мембраны вдоль длинной стороны будут практически постоянными (за исключением областей, примыкающих к малым сторонам).
Касательные напряжения пропорциональны углу наклона поверхности мембраны:
Хгх=‘^'^у' ХгУ = — * д7’
где к — коэффициент пропорциональности. Примерное распределе-
Рис. 7.20. Кручение стержня эллиптического сечения
ние касательных напряжений показано на рис. 7.19, б. В углах прямоугольника напряжения равны нулю.
Примеры точных решении. Стержень эллиптического сечения. Рассмотрим кручение стержня эллиптического сечения (рис. 7.20), контур которого описывается уравнением
2	2
£_ + 2_==1,	(95)
а о
где а, Ъ — полуоси эллипса. Решим задачу с помощью функции напряжения. Так как функция F(x, у) обращается в нуль на контуре, то примем
(2	2	\
^- + 4-1.	(96)
а Ъ /
Постоянную С определяем из уравнения (82).
27. ОБЩАЯ ЗАДАЧА КРУЧЕНИЯ СТЕРЖНЕЙ
205
Учитывая соотношения
d2F __ 2С	d2F = 2С
дх2	а2 '	ду2 Ъ2 ’
получаем
^ + ^=-2, а- Ь"
откуда 2,2 с = __£2_ а +Ь2
По формулам (78) и (79) находим напряжения
^y = G&^-jX. a -f- о	a -f о
В точках А (а, 0) и 5(0, Ь) напряжения равны ,t-	П	_ /пгд, ^6 Л
TzxA — 0, TzyA — CrV 2 - ,2’ Л "4” 0
X.A 2Л	n
TzxB---2 ( 75, ^zyB.— V.
a -j— 6
Положительные направления для касательных напряжений показаны на рис. 7.20. В точке В величина касательных напряжений (по модулю) больше, чем в точке А при а > Ь.
Геометрическая жесткость стержня на кручение по формуле (91)
С / 2	2	\	2,2	/	4	4 X
Л = 2 С 4 + 4-1 ^0-24Ц
Jia2 b2 /	a2 + 62\ a2 b2
F	,	1	4	'
где Fo, Jy, Jx — площадь и моменты инерции сечения стержня. Вычисления дают
-ЗгЗ*
/к = л4£-2.	(99)
a —b
Для случая а = b — R
Jк — ~2	Jр>
что совпадает с решением для круглого стержня. Взаимный угол поворота сечений вала на участке длиной Z
(юо) к
(97)
(98)
206
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
Учитывая равенства (98), найдем расчетные зависимости для. определения напряжений:
2а" = — j 2	2 У
J к а 4- о
Я 3
Г*6
МКх та ь
(101)
Если а>Ь (эллипс вытянут вдоль оси х), то наибольшее ное напряжение будет в точках В{ и В и равно
Ттах “
где момент сопротивления
WK = ^-ad2.
Представляет интерес определить осевое перемещение цию) при кручении. Как известно (уравнение (67)), w(x, у) = ЪФ(х, у).
С помощью равенств (80) и (81) находим дф dF , 2С ,	а2-Ьг
дФ	dF	2С	-2
=.---_----х =--------х — х ~ — X
ду	дх
Из последних равенств устанавливаем
2___ 7 2
Ф (х, у) =----г—? ху.
ъ к2 а — о
1
Далее находим "
Мк(а2-Ь2)
U>(*, у) -------г-з7з---ХУ-
Ьтса о
касатель-
(102)
(деплана-
(ЮЗ)
На рис. 7.21 показаны линии равных значений осевого перемещения. В первой и третьей четверти w < 0, во второй и четвертой w > 0.
Для круглого сечения (а = Ь) осевое смещение w(x, у)==0.
Стержень прямоугольного сечения. В этом случае (рис. 7.22)' решение получается более сложным. Оно представляется в виде ряда Фурье
>	Л*Л) = 2/И!/)со8-^,	(104)
ft
где fk(y)— функции, подлежащие определению.
Так как функция F(x, у) (прогибы мембраны) должна обращаться в нуль на контуре, то в (104) используются только нечет-
27. ОБЩАЯ ЗАДАЧА КРУЧЕНИЯ СТЕРЖНЕЙ
207
пые значения к (к = 1, 3, 5, ...). Внося выражение (104) в уравнение (82), находим
2	=	(105)
й=1,3,... \ аУ	Ь	/
Для решения разложим правую часть уравнения в следующий ряд: — 2= А.соз^,	(106)
/<=1,3,...
где коэффициенты Ak могут быть найдены общим способом (умножением обеих частей равенства (106) на cos(кях/b) и интегриро
Рис. 7.21. Линии равных значений осевого перемещения при кручении стержня (гиперболы со = — кху); вдоль линий х = 0» у = 0 смещения отсутствуют
Рис. 7.22. Кручение стержня прямоугольного сечения — распределение касательных напряжений в точках контура
ванием по х в пределах от -6/2 до 6/2). Тогда из (85) следует, что функции Д(у) должны удовлетворять уравнениям
^2/а(у)	f кп,\\ ( х	л	7	л о е	,лг^х
—71-------ГУ /Иу) =	Л,	* =	1,3,5,	...	(107)
ay \ и J
Две постоянные при решении уравнений (107) определяются из условия
А(Л/2)=0, Д(-Л/2)=0<
Опуская подробности решения, приведем конечные результаты: геометрическая жесткость на кручение (6 > h)
J^K.bh3;	(108)
момент сопротивления кручению (6 > Л)
Жк = Яа6Л2;	(109)
208
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
максимальное касательное напряжение (оно действует в точках В и в середине длинной стороны прямоугольника)
т
Тщах ~ w • к
Значения коэффициентов и К2 даны в таблице 3 в зависимости от отношения b/h.
Таблица 3
Коэффициенты для геометрической жесткости и моментов сопротивления при кручении стержня прямоугольного сечения
b/h	1,0	2,0	3,0	4,0	10,0	оо
Ki	0,141	0,229	0,263	0,281	0,312	0,333
Кг	0,208	0,246	0,267	0,282	0,312	0,333
Примерная эпюра распределения касательных напряжений вдоль контура сечения показана на рис. 7.22. В середине малой стороны
Та ~ &Ттахэ	(110)
причем значение к изменяется от к == 1 при b/h = l до к = 0,743 при b/h == °©.
Для коэффициентов Кх и К2 можно использовать приближенные формулы (Ь>й):
iz _______________1__________
1 ~ 3 + 2 (Л/6 + /г2/+) '

1
3 + 1,8Т
(111)
(112)
Для сильно вытянутого прямоугольника (b > Л)
2^ = /^ = А «0,333.
Концентрация напряжений при кручении. При кручении вала, имеющего шпоночные канавки, шлицы и т. п., возможно появление мест, в которых наблюдается резкое повышение напряжений — концентрация напряжений. При кручении стержней возрастание напряжений происходит возле острых углов, направленных внутрь сечения (точки А на рис. 723). Если во внутренних углах, скругление отсутствует (г->0), то касательные напряжения кручения в этих точках теоретически^ становятся бесконечно большими. Противоположное наблюдается во внешних углах (точка В нд рис. 7.23).
27. ОБЩАЯ ЗАДАЧА КРУЧЕНИЯ СТЕРЖНЕЙ
209
В вершинах внешних углов касательные напряжения отсутствуют. Эти важные выводы можно получить из точных решений соответствующих задач о кручении, но они вытекают из мембранной аналогии (в вершинах внутренних углов прогиб мембраны резко изменяется) .
в
Рис. 7.23. Распределение касательных напряжений при кручении стержня
Укажем на существование физически наглядной гидродинамической аналогии. Касательное напряжение численно равно скорости жидкости, вращающейся внутри цилиндрического сосуда, стенки
Рис. 7.24. Концентрация напряжений при кручении вала со шпоночной канавкой: а — сечение вала; б — линии тока (гидродинамическая аналогия) или линии постоянного прогиба мембраны (мембранная аналогия) возле шпоночной канавки
которого совпадают с боковой поверхностью вала. На рис. 7.23 показаны линии-тока: во внутренних углах жидкость «обтекает» препятствие и скорости (касательные напряжения) резко возрастают. Вдоль линии тока значения функции напряжений (или прогиба мембраны) остаются постоянными.
Рассмотрим кручение вала со шпоночной канавкой (рис. 7.24). Максимальное касательное напряжение действует в точках А и 14 и. А. Биргер. Р. Р. Мавлютов
210
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
может быть выражено следующим равенством:
Ттах 5=1	(113)
где та — номинальное напряжение, ах — коэффициент концентрации напряжений (безразмерная величина). В качестве номинального напряжения обычно принимается напряжение в вале, определяемое без учета концентрации напряжений.
Для круглого вала со шпоночной канавкой принимают
16
Тн = nd3
(114)
т. е. максимальное напряжение, которое действовало бы в вале при отсутствии шпоночной канавки.
Коэффициент концентрации напряжений должен зависеть от относительных величин, характеризующих геометрию канавки:
ах = f(r/t, t/d, t/b).
Из физических аналогий вытекает, что ах должно возрастать при
Рис. 7.25. Концентрация напряжений при кручении шлицевого вала: а —- сечение шлицевого вала; б —линии тока или постоянного прогиба мембраны
уменьшении радиуса скругления. При действии переменных напряжений малая величина радиуса скруглений часто является причиной усталостных поломок. На рис. 7.25 показана концентрация напряжений в шлицевом валу.
28. Кручение тонкостенных стержней
Тонкостенные стержни замкнутых и открытых профилей. Стержень называется тонкостенным, если один из размеров поперечного сечения существенно меньше другого. Поперечное сечение тонкостенного стержня часто называется профилем. На рис. 7.26 показаны замкнутые и открытые профили тонкостенных стержней. Наиболее частое применение имеют стержни открытого профиля (рис. 7.27).
28. КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
211
Распределение касательных напряжений при кручении в стержнях замкнутого и незамкнутого сечений принципиально различно. Это понятно из гидродинамической аналогии, если представить касательные напряжения как скорости циркулирующей внутри сечения жидкости. В замкнутом тонкостенном сечении касательные
Рис. 7.26. Стержни замкнутого и открытого профилей поперечного сечения
Рис. 7.27. Стержни открытого профиля
напряжения распределяются по толщине почти равномерно; в незамкнутом сечении распределение происходит по линейному закону, причем на средней линии профиля касательные напряжения обращаются в нуль (рис. 7.28).
Примером распределения касательных напряжений в замкнутом профиле может служить распределение в тонкостенном кольце, в
Рис. 7.28. Схема потоков касательных напряжений в замкнутом и открытом • (разомкнутом) профилях поперечного сечения
открытом профиле — распределение в вытянутом прямоугольнике.
Легко понять, что стержень с замкнутым сечением значительно лучше сопротивляется кручению, чем стержень открытого профиля. Общая теория стержней, изложенная в предыдущем разделе, позволяет полностью решить задачу о кручении стержня произвольного сечения с помощью решения уравнений Лапласа или Пуассона при соответствующих краевых условиях. Однако условие тонкостенно-сти сечения стержня позволяет использовать простые приближенные решения, что представляет практический интерес в инженерном деле.
14*
212
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
Кручение стержня замкнутого профиля. Рассмотрим приближенное решение задачи о кручении трубчатого тонкостенного стержня (рис. 7.29). Предположим, что касательные напряжения распределены равномерно по толщине стенки и направлены по касательной к средней линии профиля. Составим условие равновесия части
d’fS) ds.
Рис. 7.29. Кручение трубчатого стержня (тонкостенного замкнутого профиля): а — сечение стержня; б — условия равновесия элемента стержня
стержня (рис. 7.29, б). Так как сумма всех сил в направлении осй стержня равна нулю, то
Т161 =а ^2^2»
ИЛИ
т (5) б (5) = const =» С,	(115)
где т($)—касательное напряжение, б($)—толщина стенки в точке А средней линии контура (положение точки А характеризуется длиной дуги 5, отсчитываемой от некоторой точки 08).
Замечание. Исходя из гидродинамической аналогии, условие (115) означает, что «расход жидкости» одинаков во всех сечениях.
Момент касательных усилий относительно оси, проходящей через точку О, выражается следующим образом4 (рис. 7.29, а). На участке ds создается момент P(s)t(s)6(s) ds, где p(s)—плечо силы (длина перпендикуляра, опущенного из точки О на касательную к средней линии контура); полный момент равен
L
J р ($) т (5) б (5) ds — Мк.
о
Интеграл берется по всему контуру L. Учитывая равенство (115), находим L
% (s) б (5) J р (s) ds = мк.	(116)
о
Так как у р (s) ds == do, где do — площадь сектора, соответствующего дуге ds, то
г,
j р (s) ds = 2®,	(117)
О
тде о —площадь, ограниченная средней линией контура (рис. 7.30).
28. КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
213
Из соотношений (116) и (117) вытекает
26 ($)<о*
(118)
При кручении трубы замкнутого сечения максимальное касательное напряжение возникает в наиболее тонком месте.
Рис. 7.30. Площадь, ограниченная средней линией контура
Рис. 7.31. Два сечения стержня замкнутого профиля
Пример. Рассмотрим сначала определение напряжений в тонкостенной круглой трубе для сопоставления приближенного и точного решения (рис. 7.31).
По формуле (118) находим величину касательного напряжения
т = Мк = 2Мк	(119)
26	П8(%’ '
где 6 = у (^2 ~ ^1) толщина трубы, dc == у d2) — средний диаметр.
Из точного решения для полого вала (разд. 1) получаем следующее значение для максимального напряжения при кручении:
2 d2
Tmax = J Р

(120)
Учитывая соотношения
d2 = de 4~ б, d\ = dG — б
и полагая б dc, находим, что равенства (119) и (120) совпадают.
Для трубы прямоугольного сечения с толщиной стенки б (рис. 7.31) касательное напряжение при кручении'
т
• .'мк
28аЬ
(121)
26
214
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
Замечания. 1. Приближенное решение для кручения трубчатых стержней достаточно точно описывает распределение напряжений на основе гипотезы равномерного распределения по толщине.
Деформационная картина оказывается сложнее, так как при кручении некруглой трубы возникает депланация (перемещение вдоль оси грубы). В связи с этим вопрос об угле закручивания рассмотрим после того, как по* знакомимся с энергетическими методами.
2. При кручении тонкостенных труб может возникнуть потеря устойчиво* сти (образование складок по винтовым линиям). Это обстоятельство надо иметь в виду в практических расчетах.
Кручение тонкостенных стержней открытых профилей. Пологие профили. Особенность кручения открытых (незамкнутых) профилей состоит в том, что касательное напряжение не может быть постоянным по толщине стенки (см. рис. 7.28), так как «поток касательных усилий» должен циркулировать внутри сечения.
Рассмотрим сначала кручение стержня с пологим тонкостенным профилем (рис. 7.32). Профиль ограничен двумя пологими кривыми fx(x) и /г(^). Так как
Рис. 7.32. Кручение стержня с пологим тонкостенным профилем: а —профиль стержня; б — распределение касательных напряжений по сечению
функция напряжений при кручении должна обращаться в нуль на контуре профиля, то примем для нее следующее выражение:
у) ==~(y~/IW)(y-/2(x)).	(122>
Функция напряжений должна удовлетворять уравнению Пуассона
д2р д*р
дх2 + ду2-------2'
(123)
Если пренебречь производными пологих функций fi(x) и /2(я) по сравнению с единицей, то принятое выражение для F(z, у) удовлетворяет уравнению (123). Геометрическая жесткость на кручейие ь/2
Л)	° h.
0 = 2 С ^F(x,y)dydx9	(124>
Учитывая, что /а	^2
Jf(x,y)^ = -J[/-y(71 + /2) + /1/2]^ = 4(4-/i)3«
fi	it		.
28. КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
215
найдем L
/K = yJe3W^,	(125)
о
где 6(х) = /2(х) — f\[x) — толщина профиля.
Крутящий момент выражается через функцию напряжений следующим образом:
MK = dG/K = G/Kg,	(126)
где Ф = dqjdz — угол закрутки на единицу длины, G — модуль сдвига. Касательные напряжения
dF Г 1	1
/« = -00^=206 ^-у(/1 + /2)} dF
(127)
Из равенств (127) вытекает, что касательные напряжения распределяются линейно по толщине профиля, причем обращаются в нуль на средней линии профиля (рис. 7.32, б). Напряжения на контуре профиля
Мк
т (z) = $G (/2 - fj = j- б (х).	(128)
Наибольшие напряжения кручения будут в местах наибольшей толщины..
Приближенные формулы для кручения стержней тонкостенного открытого профиля. В основе приближенного метода лежит замена участка профиля участком сечения в виде вытянутого прямоугольника. Для стержня прямоугольного сечения (6 X £/), когда толщина б значительно меньше длины L, было получено ранее (см. разд. 27): геометрическая жесткость на кручение
7к = уб3£;	(129)
максимальная величина касательного напряжения
т = «//к.	(130)
Распределение касательных напряжений (за исключением концевых областей) является линейным по толщине стенки. Предполагая, что каждый участок работает как часть прямоугольного сечения, представим приближенно геометрическую жесткость на кручение в следующем виде:
L
= 83(s)ds’ (131)
о
где интегрирование ведется вдоль средней линии профиля (рис. 7.33). Для пологого профиля эта формула была обоснована приближенным представлением функции напряжения. Кривизна профиля несущественно влияет на распределение касательных напряжений, за исключением концевых областей. Продолжая обобщение, представим касательные напряжения в точках контура равенством
t(»)«-j-«W.	(132)
•'к
216
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
Кручение прокатных балок. В металлических конструкциях часто используются стержни (балки) прокатных профилей — двутаврового, швеллерного, уголкового и других сечений (рис. 7.34). Для расчета кручения тонкостенных
Рис. 7.33. К выводу при-ближенных формул для тонкостенного открытого профиля
Рис. 7.34. К определению жесткости на кручение и касательных напряжений в прокатных профилях
балок, как показали эксперименты, можно использовать приближенные формулы (131) и (132). Заменяя интегрирование приближенным суммированием, получим для швеллерного профиля
з
4 =	(133)
1=1
где If, Si — длина и средняя толщина i-ro участка. Аналогично для балки двутаврового сечения
J
к
(134)
Касательные напряжения кручения на i-м участке Мк
(135)
В действительности жесткость на кручение балок несколько выше даваемой формулами (133) и (134), что объясняется влиянием радиусов скругления в углах профиля и другими факторами (поправочный коэффициент составляет обычно 1,1—1,2).
Замечание. Приведенные формулы определяют кручение стержней открытого профиля при условии, что торцы стержня имеют возможность смещения вдоль оси стержня (возможность депланации). Если торец стержня заделан в массивную жесткую плиту, то в заданном сечении возникает другое напряженное состояние, в частности появляются нормальные напряжения. Стесненное кручение тонкостенных стержней рассматривается ниже. Отметим, что возникающие дополнительные эффекты существенны для непологих открытых профилей.
Пример. Сравним жесткость на кручение и касательные напряжения тонкостенной трубы замкнутого сечения и при наличии продольного разреза (рис. 7.35).
28. КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
217
Для сплошного сечения геометрическая жесткость на кручение (см. разд. 27)
7к = = I [4 - 4] = й + б)4 - (<*с - б)4] = б.
Для сечения с тонким продольным разрезом
L
JK = L^3ds = ^63xdc=*dct>3. О
Отношение жесткостей на кручение 7	о Id \а
J кспл_2. ( _£ ]
•^кпр	4 \ -6 /
Касательные напряжения в сплошной трубе (формула (119))
Т = —
в трубе с продольным разрезом
т = л62<*с'
Отношение максимальных касательных напряжений тспл 2 6 тпр 3
(136)
(137)
Из соотношений (136) и (137)' вытекает, что разрез трубы вдоль образующей существенно понижает сопротивление трубы крутящим нагрузкам.
Кручение тонкостенных стержней открытого профиля с переменными параметрами упругости. Рассмотрим сначала стержни пологих профилей (см. рис. 7.32) с переменным модулем сдвига. Учитывая дальнейшее использование решения применительно к упругопластическим задачам по методу переменных параметров упругости (разд. 19), будем считать, что модуль сдвига изменяется по толщине сечения (координате у).. Считая для пологих профилей изменение функции напряжения вдоль координаты х пренебрежимо малым, представим уравнение для функции напряжений в таком виде (см. разд. 27):
д ( 1 Oy\G[y\
Из уравнения (138) вытекает, что
1 dF
7Цу)ду = ~ 2у +	(139)
где Л1(х) — произвольная функция х,
Рис. 7.35. Кручение тонкостенной круглой трубы: а— сплошня труба и б — с продольным разрезом.
£^= — 2.	(138)
ду }	_	.
218
ГЛ. 7. КРУЧЕНИЕ СТЕРЖНЕЙ
Умножая обе части равенства (139) на G(y) и интегрируя в пределах от /( до у, находим
у	у
(140)
функция
F (*, У) = — 2 J G (yj y1dy1 + A± (x) J G (yj dyv
В последнем равенстве учтено, что в точках контура у — t\ (х) F(x, /j) = 0. Так как при у = f2 (см. рис. 7.32)
^2
F(X^2)=:-2\G (У1) У 1^1 + А1 & J G 04)	= °>
то, определяя Ai(x), будем иметь
Л
F (*, у) = 2 т------- f G (у Л dy-^G (у,)	dy .
(141)
J G (yj dV1 fi	4
'i
Если модуль сдвига постоянен (G(y) = G), то из последнего равенства получаем соотношение (122).
Касательные напряжения
dF
=	(у)
р(5\) У^У1 h__________
^2	#
н
В другом виде
ТхЯ = -25ГС(1')(У-Уср). тг» = -^№=°-
(142)
(143)
В этих равенствах ^2
j/Cp =	(144)
р(У1)^ 'х
— среднее значение ординаты профиля. При постоянном модуле сдвига
1
уср ~ 2 (Л +
28. КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
219
Жесткость стержня на кручение
L
С = 2 J F (х, у) dy dx ~ J C^dx^	(145)
F	О
ГДе / / /
J2	J2 f У	У	\
сх = J F (*, у) dy = 4 J I уср G (yj dyt — J G (yj y1 dy± I dy.
' jji	'
По физическому смыслу Ci — жесткость на кручение единицы длины средней линии профиля.
При постоянном по толщине модуле сдвига
сх = 4G фср {У -	1 - /!)] = у G (/2 - /1)3 = у G 63 (^).
h
(146)
где 6 (х) = f2 — /1 —- толщина профиля в сечении ж.
Г Л А В A 8
ИЗГИБ СТЕРЖНЕЙ
29. Гипотеза плоских сечений
и нормальные напряжения изгиба
Силовые факторы в сечении стержня. Рассмотрим стержень (крыло самолета, лопатку компрессора и т. д.) под действием поперечной нагрузки (рис. 8.1). Ось z направлена вдоль оси стержня, оси х, у лежат в плоскости А поперечного сечения.
Проведем сечение (см. рис. 8.1) и заменим отброшенную праг вую часть тела равнодействующими внутренних сил (рис. 8.2).
Гис. 8.1. Лопатка компрессора под действием изгибающей на' грузки
В общем случае для равновесия оставленной части тела необходимо и достаточно приложить три составляющие вектора усилия и три составляющие вектора момента. Векторы Qx и Qy называются поперечными или перерезывающими силами-, N — продольная или нормальная сила; моменты Мх и Му называются изгибающими моментами; Мг — крутящий момент (см. рис. 8.2).
В пределах упругости материала кручение можно рассматривать независимо от других деформаций; оно было описано ранее, и потому в дальнейшем считаем Mz = 0.
Положительные направления изгибающих моментов соответствуют положительным направлениям вращения, принятым для правосторонней системы координат. Согласно этому, момент или вращение считается положительным в том случае, когда поворот осуществляется против часовой стрелки, если смотреть со стороны положительного направления оси к началу координат (рис. 8.2). Усилия Qx и Qy будем считать положительными, если они направлены вдоль осей х л у соответственно (см. рис. 8.2) .
29. ГИПОТЕЗА ПЛОСКИХ СЕЧЕНИЙ
221
Замечание. В приведенном соглашении о знаках силовых факторов существенно, что рассматриваются усилия, действующие на левую часть стержня (нормаль к сечению идет в положительном направлении оси z). В силу равенства действия и противодействия в таком же сечении, но принадлежащем правой части стержня (рис. 8.3), силы и моменты будут точно такими же, но противоположно направленными. Естественно, что для правой части стержня (внешняя нормаль к сечению направлена вдоль отрицательного направления
Рис. 8.3. Силовые факторы, приложенные к левой и правой частям стержня: а — положительные силовые факторы в сечении стержня; б — правило знаков для перерезывающей силы и изгибающего момента
оси z) положительные направления будут противоположными. Подобное обстоятельство встречалось, ранее (разд. 3) при установлении знаков напряжений.
Таким образом, правило знаков зависит от направления внешней нормали к сечению и принятой системы координат. На рис. 8.3 показаны положительные силовые факторы в сечении стержня.
Гипотеза плоских сечений. Точное решение задачи о распреде
лении нормальных и касательных представляет большие трудности. В инженерной практике нашло широкое признание приближенное решение, основанное на знаменитой «гипотезе плоских сече-пий», впервые использованной (в простейших случаях) еще в работах Бернулли и Эйлера.
Гипотеза плоских сечений состоит в следующем: точки плоскости поперечного сечения после деформации лежат в одной плоскости. Физически это означает, что сечение стержня можно пред-
напряжений при изгибе стержня
Рис. 8.4. Распределение упругого смещения в поперечном сечении стержня при изгибе
ставить как тонкую, абсолютно жесткую пластинку, получающую в результате деформации стержня
линейное смещение и углы пово-
рота. Перемещение точки А поперечного сечения (рис. 8.4) вдоль оси jz по гипотезе плоских сечений будет таким:
Ш +фху — ФЛ
(1)
где фхИфл- углы поворота сечения относительно осей х и у соот
222
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
ветственно, — смещение вдоль оси z точек оси стержня. Величины фх, фу одинаковы для всех точек сечения, но в общем случае зависят от z. Углы упругого поворота сечения в формуле (1) считаются малыми, так что
sin фх ~ фх, sin фу « фу.
Замечание. Гипотеза плоских сечений является важнейшим приближенным методом описания деформации изгиба и растяжения стержней. Исследования показывают, что основой гипотезы плоских сечений является предположение о малости углов сдвига элементов по сравнению с углами их поворотов.
При изгибе’стержней из анизотропных материалов, у которых модуль сдвига может быть на порядок величины меньше модуля упругости при растяжении, деформации сдвига возрастают и область применения гипотезы плоских сечений становится ограниченной.
Распределение нормальных напряжений изгиба. Относительная деформация в точке поперечного сечения в направлении продольной оси стержня z
где Во == dwo/dz — деформация в точках, лежащих на оси стержня.
Таким образом, из гипотезы плоских сечений вытекает линейное распределение деформации 8г по плоскости поперечного сечения. При определении напряжений oz, действующих перпендикулярно плоскости сечения, примем, что два других нормальных, напряжения о, и Оу отсутствуют (гипотеза одномерного напряженного состояния, или гипотеза о ненадавливании).
Для деформаций в области упругости материала справедлив закон Гука, согласно которому между напряжениями и деформациями существует линейная зависимость
8, = <h/E + атТ,	(3)
где Е — модуль упругости материала, ат — коэффициент теплового линейного расширения, Т — изменение температуры материала.
В дальнейшем для простоты индексы в выражении (3) опускаем, так как будут рассматриваться деформации и напряжения только вдоль оси z.
Из уравнения (3) следует, что
о =» Ее — ЕатТ,	(4)
или с учетом равенства (2) получим
о = я(е0 + y^.-xd^\-EaTT.	(5)
Величина напряжений о будет известной в том случае, когда известны параметры деформации е«, dqjdz, d^y/dz.
Замечание. Величина е0 представляет собой деформацию волокна, совпадающего с осью стержня (геометрическим местом центров тяжести сечения).
29. ГИПОТЕЗА ПЛОСКИХ СЕЧЕНИЙ
223
Физический смысл параметров dyjdz и dyv!dz будет разъяснен в дальнейшем — они выражают составляющие векторы кривизны оси стержня после деформации.
Для определения параметров деформации воспользуемся общими условиями равновесия (рис. 8.5). Изгибающие моменты и нор-
мальная сила в сечении стержня, которые определяются условиями
равновесия отсеченной (правой) части стержня, одновременно являются равнодействующими внутренних сил в сечении, т. е. усилий о dF (см. рис. 8.5):
^adF = N, F
\vydF = Мх, F
^oxdF ~— Му.
Рис. 8.5. Общие условия рав-Знак минус в последнем равенстве свя- новесия при изгибе стержня
зан с тем, что момент относительно
оси у, создаваемый вектором edF, противоположен моменту Му.
Замечание. При согласовании знаков в составляемых уравнениях надо всегда руководствоваться рисунком, на котором все участвующие в уравнении величины принимаются положительными!
Например, на рис. 8.5 нормальное напряжение показано растягивающим, величины х и у в точке А положительны, момент Му принят положительным.
Система уравнений для определения нормальных напряжений изгиба и растяжения стержня и ее упрощение. Эта система получается путем подстановки значения о из соотношения (5) в уравнения равновесия (6) —(8). Для общности будем считать, что модуль упругости Е и температура Т не одинаковы в различных точках сечения.
Внося (5) в равенства (6) —(8), получим следующую систему уравнений, записанную в матричной форме:
[С0]{Х} =	+ {Мт}>
О)
где
—вектор параметров деформации,
—вектор внешних нагрузок,
224
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
{Мт} =
л/хТ МуТ.
J Еат Т dF F
J ЕуатТ dF F
— J ЕхатТ dF
F	I
—вектор температурного нагружения.
Р F	(10).
dF, С33 = x2EdF.
Симметричная матрица (3 X 3) коэффициентов жесткости имеет следующие элементы:
-	С12 = С21 = f уЕ dF, С13 = С31 = — \xEdF,
F	F
У2Е dF, С23=С32 = — J хуЕ
F	F	F
Основное уравнение гипотезы плоских сечений (уравнение (1)) справедливо для произвольных осей х, у.
Покажем, что с помощью рационального выбора осей координат можно существенно упростить матрицу жесткости приведя ее к диагональному виду. Выберем начало координат в приведенном центре тяжести сечения.
Если представить себе сечение как очень тонкую пластинку с равномерно распределенной массой, то центр тяжести сечения, как известно из теоретической механики, характеризуется тем, что ста-, тические моменты относительно любой проходящей через него оси обращаются в нуль:
f xdF = 0, JydF = O.	(11)
F '	F
Для приведенного центра тяжести ^xEdF = Q, \yEdF = 0.	(12)
F	F
При определении обычного центра тяжести все элементы dF обладают одинаковой массой. При нахождении приведенного центра тяжести элементу dF приписывается масса, пропорциональная модулю упругости Е. Для стержня с постоянным модулем упругости (Е e const) приведенный центр тяжести совпадает с обычным. В следующем разделе будут указаны способы нахождения центров тяжести поперечных сечений стержня; При условии (12) обращаются в нуль элементы С12, Сги Cis и С31 мат-
рицы жесткости. Начало координат еще не полностью определяет положение всей системы. На рис. 8.6 показаны две центральные системы координат, т. е. системы, имеющие начало в центре тяжести или в приведенном центре тяжести сечения.
Рис. 8.6. Главные оси сечения
29. ГИПОТЕЗА ПЛОСКИХ СЕЧЕНИЙ
225
Положение системы х, у будем характеризовать углом а, на который она повернута относительно заранее выбранной системы координат Xi, У1. Угол а принят таким, чтобы
\xyEdF =0.	(13)
F
Последнее условие вместе с условиями (12) определяет главную систему координат, оси которой называются главными осями сечения. В следующем разделе будут даны способы нахождения главных осей сечения.
При условии (13)
С*23 ~ С32 “ 0.
Итак, если оси х, у являются главными центральными осями сечения, то матрица жесткости становится диагональной, т. е. отличные от нуля элементы расположены на главной диагонали; тог-
да получаем f ЕатТ dF
, N + NT *	, F_______
° Cu J E dF j* E dF *
F	F
f Eya,T T dF = Mx + MxT = Ms j.___________________
di CM J y*E dF j* y2E dF ’ F	F
C ExuTT dF d^y __ MyT__________My p_________________
dz C33 §x2EdF ^x*EdF
F	F
(14)
(15)
(16)
В правых частях равенств (14)—(16) первое слагаемое выражает действие внешних усилий, второе — влияние изменения температуры.
Замечание. Задачу изгиба и растяжения стержня можно решать, конечно, в произвольной системе координат, но тогда простых соотношений (14)—(16) не получается.
В общем случае из системы (9) вытекает, что
<Х}«[С«Г4({М} + ШТ}),
где [CJ-1 — матрица, обратная матрице жесткости [CJ.
Если оси х, у являются главными осями, то матрица жесткости и обратная матрица имеют вид
	Сц	0	0 ~		Г^н	0	0 ’
[Су] -	0	С99 АА	0	, (СуГ1 =	0	1/С22	0
	0	0	^33-		0	0	^33
226
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Гипотеза плоских сечений и, следовательно, соотношения (14) — (16), полученные на основании гипотезы плоских сечений, справедливы и для стержней переменного сечения, если сечения достаточно «плавно» изменяются по длине стержня. В местах резкого (ступенчатого) изменения сечений может возникнуть концентрация напряжений, которая рассматривается в дальнейшем.
Напряжения растяжения и изгиба в стержне от действия внешних сил. Предположим, что температура тела во время работы не изменяется. Тогда, полагая в соотношении (5) атТ = 0, получим
d4y\ и = Е\^о + у-^-— x-—j.
Учитывая равенства (14) —(16), найдем общую формулу для нормальных напряжений в стержне при действии внешних силовых факторов;
_ ту	М	М
0==Е -р-----+	----х Г V ' ’
 Е dF \ у* EdF	J x*E dF '
F	F	F t
ИЛИ
{пт	М,,\
4 +	<17>
где А == J Е dF — жесткость при растяжении; 2?х = j у2Е dF^ Ву =* F	F
„J х2Е dF — жесткости при изгибе.
F
Для стержня с постоянным модулем упругости (основной расчетный случай)
о ==
(18)
где F = j dF — площадь поперечного сечения;
F
Jx=\y2dF, Jv=^x2dF F	F
(19)
— моменты инерции сечения относительно осей х и у соответственно.
Первый член в правой части равенства (18) выражает напряжения от растяжения или сжатия, два последующих члена — напряжения изгиба.
Замечания. 1. Формула (18) является одной из основных во всем сопротивлении материалов. Она показывает, что для анализа напряжений за начало координат надо принять центр тяжести сечения и к этой точке сечения (точнее, к системе координат) привести внешние силы. Нормальное усилие, действую
29. ГИПОТЕЗА ПЛОСКИХ СЕЧЕНИЙ
227
щее в центре тяжести, вызывает напряжения растяжения или сжатия, одинаковые во всех точках сечения. Напряжения изгиба зависят от величины изгибающих моментов, геометрических характеристик сечения (моментов инерции) и координат точки.
2. Нормальные напряжения от внешних силовых факторов не зависят от абсолютной величины модуля упругости материала, а только от его распределения в точках сечения. Из равенства (17) следует, что при изменении модуля упругости во всех точках сечения одновременно в к раз напряжения остаются прежними.
Если модуль упругости одинаков во всех точках сечения (формула (18)), то напряжения в стержне не зависят от Е. В стальном или дюралевом стержне при одинаковых геометрических размерах и действующих нагрузках напряжения не различаются. Упругие перемещения стержней будут, разумеется, разными. Для закона распределения напряжений (формула (18)) решающим было предположение об упругости материала. Подобный результат имеет общее значение в задачах теории упругости.
3. Формулы (17) и (18) применимы и для стержней переменного сечения, когда упруго-геометрические характеристики сечения изменяются по длине стержня достаточно плавно.
Пример и некоторые дополнительные понятия. Определим напряжения при изгибе стержня прямоугольного сечения под действием сосредоточенной
•У
Рис. 8.7. Изгиб стержня прямоугольного сечения: а — стержень; б — поперечное сечение стержня
силы Р (рис. 8.7). Рассмотрим сечение на расстоянии z от заделки. Начало координат поместим в центре тяжести сечения.
Изгибающий момент возрастает по мере удаления от точки приложения силы. Напряжения изгиба определим по формуле (18), считая модуль упругости материала стержня постоянным.
Учитывая, что осевое усилие N и изгибающий момент Mv отсутствуют, получим
Остается определить момент инерции поперечного сечения: л/з	3
=	= & j* y*dy = ^,
F	-h/2
и окончательно bh3
(20)
15»
228
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Опасным будет сечение, в котором действует наибольшее напряжение. Если стержень призматический, то опасным будет сечение, где изгибающий момент наибольший. В рассматриваемом примере оно расположено в заделке стержня.
Как следует из равенства (20), напряжения изгиба распределяются линейно по высоте сечения. В точках сечения, лежащих на линии у = 0, напряжения изгиба отсутствуют. Линия, в точках которой напряжения изгиба отсутствуют, называется нейтральной линией сечения. В рассматриваемом примере нейтральной линией является ось х. По мере удаления от нейтральной линии напряжения изгиба возрастают. В опасном сечении (z = 0) точки с наибольшими напряжениями изгиба называются опасными точками.
Максимальное напряжение изгиба будет при у = h/2:
Pl Pl М
аи max ~ 1	_ — jy ~ W *
Tbh
где М — действующий в рассматриваемом сечении изгибающий момент.
_	тт.	. 1 2 _
Величина ку—“тт-о/г —;---- называется моментом сопротивления сече-
° Углах
ния изгибу. В точке В (у = —h/2) напряжение изгиба будет таким же по ве-Р1
личине, но противоположным по знаку: ов= — -т-.
Расчетные формулы (17) и (18) для нормальных напряжений в стержне по своей структуре достаточно просты, затруднения могут возникнуть при определении главных осей и упруго-геометрических характеристик сечения, что будет разобрано в следующем разделе, а сейчас рассмотрим вкратце расчет температурных напряжений.
Температурные напряжения. В пределах упругости материала напряжения от внешних сил и нагрева можно находить независимо. Рассмотрим определение температурных напряжений в стержне, считая, что внешние нагрузки отсутствуют. Внося равенства (14) — (16) в соотношение (15), получим формулу для температурных напряжений
(J ЕатТ dF J ЕуатТ dF J ЕхатТ dF \
Р F у—я— --------------Ь® Р ~ сс^Т 1. (22)
\Е dF	/Е dF	zE dF	I
F	f	F	J
Покажем, что в равномерно нагретом стержне, когда атТ = const = С,	(23)
температурные напряжения отсутствуют. Подставляя значение атТ из (23), находим o«m = 0, так как оси х, у проходят через приведенный центр тяжести. Результат справедлив при статически определимых условиях закрепления, когда температурные деформации стержня не стеснены (например, один из торцов стержня свободен от закрепления).
Если нагрев (однородного стержня) осуществляется до температур, при которых изменением модуля упругости можно прене
29. ГИПОТЕЗА ПЛОСКИХ СЕЧЕНИЙ
22$
бречь (Е = const), то из соотношения (22) получаем более простую зависимость:
(I атТ dF (* уатТ dF f хатТ dF \
F	,	F	I F	Г/ Т Г	(^4)
----Р— + У------J----+ X------7-------атТ /
•'х	•'у	/
Рассмотрим в качестве примера определение температурных напряжений в стержне прямоугольного сечения (рис. 8.8, а), основание которого Ь, высота Л. Температура изменяется по степенному закону (рис. 8.8, б):
у) ’	(25)
причем показатель степени п является четным и температура имеет симметричное распределение; по координате у температура не изменяется.
Рис. 8.8. Определение температурных напряжений в стержне: а — неравномерный нагрев стержня; б—распределение температур и температурных напряжений
а
Предполагается для простоты, что влиянием нагрева на величину модуля упругости можно пренебречь.
Отметим, что
J уатТ dF = О, J хатТ dF = 0	(26)
F	F
как статические моменты площади сечения с симметрично распределенным «весом»; это вытекает из физических предпосылок, так как принятое распределение температур не вызывает изгиба стержня, сечение стержня как жесткое тело может получить только поступательное движение, оставаясь параллельным своему положению до нагрева. Наконец, равенство (26) доказывается строго с помощью интегрирования по площади сечения. Далее находим
hb3
F = bh,
f	п ъ /ffaK аТТтя-№
J aTT dF — 2arTmaxA J b ) dx — n . f	о
230
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Из формулы (24) вытекает
атем
Г 1 fzfV]
Ь + 1~ U j ]•
(27)

Распределение температурных напряжений по координате х показано на рис. 8.8, б.
В более нагретых частях стержня возникают сжимающие температурные напряжения. Физически это объясняется тем, что крайние волокна стержня получают большую температурную деформацию и при отсутствии поперечных
У
Рис. 8.9. Картина температурных деформаций в стержне: а — поперечные связи отсутствуют; 6 — в конце стержня имеется жесткая пластинка
связей стержня деформируются так, как показано на рис. 8.9, а. Поперечные связи удерживают крайние волокна (рис. 8.9, б), создавая в них напряжения сжатия, а в менее нагретых частях стержня — растяжения.
Замечания. 1. При выводе формулы для температурных напряжений (22) или (24) предполагалась справедливость гипотезы плоских сечений. При определении температурных напряжений она нарушается вблизи свободного торца стержня.
Действительно, по равенству (22) температурные напряжения одинаковы по всей длине стержня, вместе с тем свободный торец стержня свободен от каких-либо напряжений. Если же на торце стержня имеется жесткая пластинка, то температурные напряжения будут во всем стержне одинаковыми по длине и строго соответствовать формуле (22). При свободном торце в концевой области должны возникнуть касательные напряжения (поперечные связи), которые на некотором удалении от свободного торца (порядка размера сечения) сделают все-таки поперечные сечения плоскими и, следовательно, формулы (22) и (24) справедливыми.
2. Напряжения от неравномерного нагрева (температурные напряжения) в статически определимом стержне (илц свободном от закрепления) всегда самоуравновешены. Это означает, что
J атем^ =	J хсгтем^ = f ^атем	=
F	F	F
В сущности, эти условия были использованы при выводе уравнений (6) — (8); уравнения (22) и (24) удовлетворяют этим условиям при любом распределении температуры.
Свойством самоуравновешенности обладают и остаточные напряжения, существующие в элементах конструкции после их изготовления. Температурные и остаточные напряжения имеют, в сущности, одну причину возникновения — неравномерные первоначальные деформации (в результате нагрева или в процессе изготовления).
Обоснование гипотезы плоских сечений. Пусть имеется стержень постоянного сечения с постоянными силовыми факторами по
30. УПРУГО-ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЕЧЕНИЯ
231
длине (рис. 8.10). Предполагается, что температура материала стержня одинакова по всей длине, но может быть различной в точках поперечного сечения. Если внешние факторы нагружения постоянны по длине стержня, то, за исключением концевых областей, напряжения и деформации не будут зависеть от координаты z.
В этом случае в уравнениях совместности деформаций (разд. 11) производные по z обращаются и тогда
Ц-0, дх2
нуль,
<Ге2 Л д2е_
——г==0.
ду2 ' дх ду
Из последних соотношений при
^-0
(28)
(29)
Рис. 8.10. Стержень с постоянными силовыми факторами по длине
следует
Cz== Cq 4“ С ,х С'ъУч где Со, Ci, С2 — постоянные величины. Условие (30) совпадает с равенством (2) плоских сечений.
(30)
и выражает гипотезу
в
Замечание. В основе доказательства гипотезы плоских сечений лежит предположение о постоянстве силовых факторов по длине стержня. Это справедливо, когда стержень загружен по торцам изгибающими моментами и осевыми усилиями, но не соблюдается при наличии поперечной нагрузки. При изгибе от поперечной нагрузки для стержней переменного сечения расчет по гипотезе плоских сечений является приближенным методом.
Часто в инженерных расчетах решения, строго доказанные при определенных ограничениях, успешно используются за пределами таких ограничений, если, разумеется, возникающие погрешности оказываются второстепенными.
30. Упруго-геометрические характеристики сечения
стержня при изгибе. Главные оси, главные моменты инерции
Упруго-геометрические характеристики. При определении напряжений изгиба и растяжения (по формуле (17)), температурных напряжений (по формуле (22)) необходимо знать упруго-геометрические характеристики сечения стержня: жесткость при растяжении A=^EdF-,	(31)
F
жесткость при изгибе относительно главной оси х
Bx — §y2EdF;	(32)
F жесткость при изгибе относительно главной оси у
By^^EdF.	(33)
F
232
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Главные оси сечения проходят через приведенный центр тяжести сечения, и для главных осей координат выполняются условия j‘x£dF = O, Jy£dF = O, ^xyEdF = 0;	(34)
Г	F	F
жесткости Л, Вх и Ву называются упруго-геометрическими характеристиками сечения при изгибе.
При постоянном (в точках сечения) модуле упругости
A=EF, BX^EJX, By=*EJv,	(35)
где F — площадь поперечного сечения; /х, Jv — осевые (экваториальные) моменты инерции сечения относительно осей х и у соот-
ветственно. Величины г, Jx и Jy называются геометрическими характеристиками сечения, так как они определяются только геометрической конфигурацией сечения. Упруго-геометрические характеристики зависят также от распределения модуля упругости по сечению.
Определение приведенного центра тяжести сечения. Для определения приведенного центра тяжести сечения выберем произвольным обра-координат х2, у2 (рис. 8.11).
зом вспомогательную систему
Пусть точка Ot — приведенный центр тяжести. Во вспомогательной системе его координатами будут ах, ау.
Если оси Xi, уь параллельные осям х2, у2, проходят через приведенный центр тяжести, то статические моменты сечения относительно указанных осей обращаются в нуль:
Sxl^^ytEdF = 0, S^-^EdF = 0.	(36)
F	F
В последних равенствах Е — модуль упругости в данной точке сечения (Е > 0). Отметим, что dF всегда считается положительным (dF > 0).'Из рис. 8.11 следует, что
it =	у, — Уг — а».	(37)’’
Теперь из равенств (35) находим
j (у2 - ay) Е dF ~ 0, J (ха - ах) EdF — Q.	(38)
F	- F •
Координаты приведенного центра тяжести определяются зависимостями
J хгЕ dF	J у^Е dF
-----, ай = ^-------.	(39)
£ dF	\EdF
F	~ F
30. УПРУГО-ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЕЧЕНИЯ
233
При постоянном модуле упругости получаем значения координат центра тяжести, известные из курса теоретической механики:
— '~р' J #2 dF?	аУ — р j Уч dF•
F	F
(40)
Отметим, что если какая-либо чения, то центр тяжести сечения
ось является осью симметрии се-обязательно лежит на этой оси.
Для приведенного центра тяжести это справедливо, если распределение модуля упругости симметрично относительно указанной оси. При двух осях симметрии центр тяжести сечения лежит на их пересечении.
Замечание. Если статический момент относительно какой-либо оси равен нулю, то ось проходит через центр тяжести сечения. Доказательство основано на том, что по определению центр тяжести удовлетворяет условиям (36). Но если статический момент обращается в нуль для двух осей, то он равен нулю и для любой оси, проходящей через точку пересечения этих осей (докажите!).
Пример определения приведенного центра тяжести. Рассмотрим биметаллический стержень прямоугольного сечения (рис. 8.12) и выберем начало вспомогательной системы координат в левом нижнем углу. Так как сечение имеет ось симметрии, то ах = 6/2.
Величину ау определяем по формуле (39). Предварительно вычислим жесткость при растяжении и
Рис. 8.12. Определение приведенного центра тяжести для биметаллического стержня прямоугольного сечения
жесткость при изгибе
J Е dF = £16А1 + £26Л2, F
р	Г	Г	1 п
J угЕ dF = bEt J у2 dy2 4- ЪЕг j ,у2 dy^^bE^-^- ЪЕ2 (Л2 - А2). F	.	О
Далее находим
аи- 2(Е1&1 + ЕаА2) •
При одинаковых значениях модулей упругости (Ех = Е2) получаем ау === Л/2.
Геометрические характеристики сечения стержня. Рассмотрим сначала наиболее часто встречающийся случай однородного стержня, когда все точки сечения имеют одинаковый модуль упругости (2? = const). В этом случае сопротивление стержня изгибу и растяжению зависит от геометрических характеристик сечения (моментов инерции относительно главных осей и т. д.)« В ближайших разделах рассматривается крут вопросов, связанных с определением геометрических свойств сечений. Затем полученные результаты легко распространяются на определение упруго-геометрических характеристик сечения.
234
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
В рассматриваемом случае (Е = const) требуется найти оси х9 у, проходящие через центр тяжести сечения и удовлетворяющие условию
$xydF = 0.	(41)
F
Пусть имеются произвольные центральные оси х. у (рис. 8.13); начало координат расположено в центре тяжести сечения.
Осевым. или экваториальным, моментом инерции относительно оси Хх называется интеграл
Рис. 8.13. Определение центральных моментов инерции сечения
(42)
J хх = J Ух'йЕ*
F
По определению момент инерции — величина положительная; размерность dim Jx == [L4] (обычно в см4 или мм4).
Для оси ух осевой момент J ух= J хх dF. F
В расчетных соотношениях часто встречается величина^
(43)
У xlyi — j
F
(44)
которая называется центробежным моментом инерции сечения относительно системы координат xiy Несколько странное название момента связано с тем, что он ранее встречался в механике при учете момента центробежных сил. '
Отметим еще полярный момент инерции сечения
Jn = J г2 dF = J (^ + И) dF,	(45)
* F	F
где г — расстояние от ния (см. рис. 8.13).
Очевидно, что
элемента площади до центра тяжести сече-
Jpi	JуХ 4“ Jxl*
(46)
Полярный момент инерции сечения рассматривался ранее в задачах кручения круглых стержней (валов).
Для главных4 осей сечения центробежный момент инерции равен нулю:
Jxy e J ху dF = 0.	(47)
30. УПРУГО-ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЕЧЕНИЯ
235
Напомним, что оси имеют произвольное, заранее выбранное направление. Пусть главные оси х, у повернуты на угол а по отношению к осям xt1 yt. Прежде всего нам понадобится известная из математики формула для координат точки в новой, повернутой системе координат. Проектируя отрезок ОА (рис. 8.14) на ось х и рассматривая его как сумму векторов ОБ и ВЛ, получим &
х = Xi cos а + yt sin а. (48)
Подобным образом
у = —X! sin а + yi cos а.	(49)
Замечание. Формулы (48) и (49) часто ветре- рис. 344 Изменение коор-чаются в различных технических задачах, и их динат точки Л при поворо-вывод надо обязательно усвоить и повторить са- - системы координат настоятельно!
Угол поворота главных осей найдем из равенства (41) после учета соотношений (48) и (49);
Jxy = J xydF = J (ях cos а + Ух sin а) (— хх sin а + уг cos а) dF == О, F	F
или
4
Jху=== —9- («7*х1	*7"щ) sin 2о& *4“ J«ил cos 2ос10.	(50)
Из последнего равенства получаем важную зависимость tg2cx0-24?7-.	<51>
J У1
где «о — значение угла а, удовлетворяющее условию (50). Полученная формула определяет углы, на которые должна быть повернута система координат х, у по отношению к системе координат х^ yt. Так как тангенс угла — функция периодическая с периодом л, то уравнение (51) справедливо и при углах
2а0 ± Тел == 2аЛ (к == 1, 2, 3,...) ,
или
аЛ = а0 ± к А.	(52)
Различные положения системы координат х, у \к = 0, 1, 2, 3, 4) показаны на рис. 8.15. Однако все они соответствуют одним и тем же главным направлениям 1 и 2. В связи с этим условимся об определенном выборе угла а, характеризующего положение главных осей.
Для положительных значений tg 2а0 имеем 0 < 2а0 < л/2 и будем считать О^ао<я/4. Для отрицательных значений tg2a0 пот
236
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
лучим —л/2 < 2а0 < 0 и — л/4	а0 С 0. Таким образом, достаточно
рассматривать поворот главной системы координат в пределах
—л/4<а0<л/4.	(53)
Положение главных осей х, у относительно вспомогательных хи yi показано на рис. 8.16. Во многих случаях главные оси сечения могут быть названы без предварительного расчета. Например,
Рис. 8.15. Различные положения системы координат, соответствующие одним и тем же главным направлениям 1 и 2
если какая-либо. ось является осью симметрии сечения, то она и любая ей перпендикулярная образуют главные оси сечения ! (рис. 8.17). В самом деле, элементу площади dF всегда соответ-. ствует «нормальный» элемент, у которого изменился знак одной
из координат, и поэтому для указанных на рис. 8.17 осей
JxV == J ху dF=0. F
Замечание. Сколько главных (центральных) осей имеет сечение? Только две (оси х, у) или бесчисленное множество. Последний случай встречается не так часто; к нему относятся сечения, имеющие бесконечно много осей симметрии (например, круглые), или сечения с полной циклической симметрией (например, квадратные).
30. УПРУГО-ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЕЧЕНИЯ
237
Главные моменты инерции сечения. Осевые моменты инерции относительно главных осей х, у называются главными моментами инерции.
Если ось х составляет угол ас осью хи то осевой момент инерции
Jx e j* У2 dF = j* (— хг sin а + у х cos а)2 dF. F	F
Из последнего соотношения получаем
Л = hi cos2 а + Jvi sin2 а — Jxl vi sin 2a.	(54)
Так как
1 1
cos2 a = у (1 4- cos 2a), sin2 a == у (1 — cos 2a),
то зависимость (54) представим в виде
Jx = Т Х1 "Ь у^ 2* Jcos 2a Jxiyi sin 2a.	(55)
Равенство (55) справедливо для любой оси х, составляющей угол a
осей ж, у относительно вспо- • могательных yi
Рис. 8.17. Симметричное сечение (ось симметрии всегда является одной из главных осей сечения)
с осью х^ Для главной оси a = a0 и в силу условия (51) можно написать
J* ~ ~2 (Jxi Jyi) “2" ^у1 cos 2a0 *
Учитывая тождество
cos2a0= , 1	,	(57)
Уц-tgX
справедливое при. условии (53),. и формулу (51)', находим для
238
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
главной оси х
Л = 4 (Л1 + /„) - у (^vi - Лг) V1 + 77^Н- (58> *	\Jyi JX1)
Ось х составляет с осью угол а0, причем
(59>
Jyi Jxi	*	*
Величина Jx представляет один из главных моментов инерции сечения. Второй главный момент соответствует осевому моменту инерции относительно оси у. При повороте осей координат на угол а
Jy = J x2dF = J cos а + у± sin а)2 dF = F	F
= Jyl cos2 а + JX1 sin2 а + Jxlyl sin 2а. (60)
Если а = а0, то для главного момента инерции получим равент ство, аналогичное (56):
л-4-(л. + /и) + 4(л1-л1)=^-,	(во
или
Jy = у (Л1 + Jyi) + у (Л1 - /«) У 1 +	(62)
Г	V VI Jxl)
Формулы (57) и (60) дают значения осевых моментов инерции относительно главных осей х, у (главные моменты инерции сечения).
Свойство экстремальности главных моментов инерции. Осевой момент Jx относительно оси, повернутой на произвольный угол» определяется равенством (55). Найдем значение угла а, при котором Jx получает экстремальное (наибольшее или наименьшее) значение. Для этого приравняем нулю производную:
dJ
== —. 2 JX1 cos a sin a + 2 Jyl sin a cos a — 2 cos 2a = 0, dctt
что дает для угла a *
Так как значения, а*? и а0 совпадают, то, следовательно, момент инерции относительно главной оси х обладает свойством экстремальности — он или наименьший, или наибольший для осей, проходящих через начало координат. Сумма моментов инерции отно
30. УПРУГО-ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЕЧЕНИЯ
239
сительно любых двух взаимно перпендикулярных осей с общим началом постоянна:
J* + =	=
Следовательно, если Jx имеет минимальное значение, то Jy — максимальное, и наоборот.
При Jyi > JX1 значение Jx по формуле (58) соответствует минимальному значению. Из среднего значения (/* + Jwi)/2 вычитается положительная величина.
При Jyl > Jxi получим из равенства (58)
J min = “2" («^xi + Jyi)-V1 — Jxi)2 +	•	(63)
При Jyi < Jxi момент относительно оси x будет иметь максимальное значение
Jx ~ J max = ~2 (Jxi + Jyl) + “Tf (Jyl — J xl)2 + 4J xlyl •	(64)
Последнее соотношение вытекает из (58), если учесть, что при Jyi < Jxi
1/1 + У»» ~	„А.	/(/ _ А1)2 + 4/3 . (б5)
'	'«I
Замечания. 1. В обоих случаях (Jvi > hi и hi < hi) расчет, разумеется, можно вести по формуле (58) без дополнительных преобразований, но равенства (63) и (64) обладают большей наглядностью. Как уже отмечалось, при
Рис. 8.18. Положения главных осей сечения относительно вспомогательной системы координат х^ yi
h ~ min имеем Jy = max и при Jx ® max будет h == Положение главных осей х, у при различной ориентации сечения стержня относительно вспомогательной системы координат xi, yi показано на рис. 8.18.
2. Ось с минимальным моментом инерции (рис. 8.19) направлена так, чтобы среднеквадратичное отклонение элементов площади относительно оси было бы минимальным ( Д = ^- J у2 dF == -у Уж == min Y Так как для всех осей F =
\ F /
«« const, ТО Д == min €= Лт1а.
240
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Моменты инерции относительно произвольных осей, выраженные через главные моменты. Будем характеризовать произвольную (центральную) систему координат углом а, который она образует
Рис. 8.19. Ось х — ось с минимальным моментом инерции (Л == Лиш). Ось расположена так, что дает минимум среднеквадратичного отклонения элементов площади от оси
с главной системой координат х, у. В связи с этим изменим обозначения и будем теперь считать, что оси у^ повернуты на угол а. Тогда после простого изменения обозначений получим из равенств (50), (54), (60)
Jxlyi = “2" (*^ж — у) S*n	(66)
Jxl = Jx cos2 а 4- Jу sin2 а,	(67)
J vi == Jx sin2 а + J у cos2 а.	(68)
Из последних соотношений вытекают интересные выводы. Если главные моменты инерции равны (Л = 4), то все оси сечения
Рис. 8.20. Сечения, имеющие одинаковые главные моменты. Для них любые центральные оси являются главными, а все осевые моменты инерции одинаковы
являются главными, так как = 0 для любого значения а. При одинаковых главных моментах инерции Jx Jy моменты инерции относительно любой центральной оси имеют одинаковые значения. На рис. 8.20 показаны некоторые сечения с одинаковыми главными моментами.
Расчет геометрических характеристик сечения. Для простейших сечений стержня геометрические характеристики показаны на рис, 8.21.
30. УПРУГО-ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЕЧЕНИЯ
241
Для расчета сложных сечений полезными являются соотношения между моментами инерции для параллельных осей (рис. 8.22) (оси xh yi являются центральными):
= [ У* dF = J (У1 + а/ dF = JX1 + a’F,	(69>
^2 = p2^ = ^l + axf.	(70>
F
^х2у2 = J (^1 “Ь ау) + ах) ~ ^xlyl “Ь axayF'	(70
F
Момент инерции полых сечений (рис. 8.23) можно рассматривать как разность
•	= pl J у1 dPi ~ J у1 dF2’	<72>
F	Ft	Ft
где Fi, F2 —площади, ограниченные наружным и внутренним Г2 контурами»
Рис. 8.21. Моменты инерции простейших сечений: а — прямоугольник, » ® bh3/i2> Jy = Лд3/12; б — круг, Л = 4 == nd4/64; в — треугольник, Jx = =» дЛ3/36, Jv
Рис. 8.22. Соотношение между моментами инерции для параллельных осей, оси Xi, у{ — центральные
Рис. 8.23. Момент инерции полых (нео дно связных) сечений
Для сложных сечений геометрические характеристики находят с помощью численного расчета на ЭВМ. Координаты профиля задаются во вспомогатель-* пой системе координату, у 2 в виде значений (рис. 8.24) ординат у верх == /2 (*2)1 16 и. А. .Биргер, Р. Р. Мавлютов
242
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Упиж = /1 (xi). Площадь сечения
Х2В
F = ,f (М*2)-М*2))^	ПЗ)
К2А
координаты центра тяжести находятся по формуле (40):
х2в
= 7 J х2 14 (Х2) ~ fl (*2) 1 dx2' Х2Л
Х2В
av ~ 2F J ~ (гг)] dZ2‘
Х2А
(74)
Моменты инерции относительно осей х2, у2 могут быть вычислены по следующим формулам:
*2 В
7Х2 = У j [^(гг) ~^l(x2)] dz2’
Х2А
Х2В
А/з ~ J *2 [4 (*2) ~ (хг) 1 ^2*
Х2А
Х2В
^Х2у2 ~ ~2 J Х2 [^2 (Хг) fo) ] dX2*
Х2А
(75)
При выводе равенств (75)
у2
4
А<
fz(z) dF
ff(x)
использовались соотношения для элементарного „ прямоугольника с размерами [/2(^2) —/1(^2)] и dx2. Моменты относительно осей ух оп- * г ределяются формулами (69), (70), угол —равенством (51).
Главные моменты инерции находятся с помощью зависимостей (58) и (62). Для дополнительной проверки могут использоваться формулы ДЛЯ 7min И Утах.
Для расчета напряжений изгиба необходимо знать координаты точек профиля в главной системе координат. С помощью соот-
Х2
Х2В
главной системе координат. С помощью ношений (48) и (49) находим
Х= (х2— Лх)С08<Хо+ (у2 — Ду) sin «о»
(76)
Рис. 8.24. Численный расчет геометрических сечений (ж, у — главные центральные оси)
(см.



у = —. (я2 — ах) sin (Хо + (Уг — ву)соз Оо, где координаты точек х2, у2 заданы рис. 8.24).
Упруго-геометрические характеристики сечения стержня. Из сопоставления упруго-
геометрических характеристик с чисто геометрическими характеристиками (соотношения (42)—(47)) следует практически важный вывод: упруго-геометри-ческйе характеристики сечения получаются из геометрических, если каждому элементу площади приписать множитель («вес»), численно равный величине модуля упругости в данной точке сечения.
30. УПРУГО-ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЕЧЕНИЯ
243
Приведенный центр тяжести определяется соотношениями (12). Положение главных приведенных осей находится с помощью зависимости
2 J х^Е dF
tg 2а. =	-----т—-----.	(77)
0 j х^Е dF — dF
F	F
При E = const соотношения (77) и (51) совпадают. Жесткость сечения на из-гиб относительно главной оси х (равенство (32)) представляет приведенный момент инерции относительно этой оси;
вх = J* = J угЕ dF.	(78)
F
Аналогично формулам (56) и (61) будем иметь
1 1 1
Вх = “2 (^«1 + Bvi) ““ ~2 (Byi ~ Bxi) cos 2а0 ’
Ву = ~2 (^*1 + Byi) Т (Byi Bxi} cos 2а0 ?
ВХ1 =	= J № dF, BV1 =	= J х[Е dF.
F	F
Соответствующим образом переносятся и другие результаты, полученные для однородных сечений. В частности, формулы для параллельных осей (69)— (71) будут иметь следующий вид:
ВХ2 = Вх1	Ву2 = Byl ахА> Вх2у2 = Вх1у1 + ахауА* (80)
где А = J Е dF — жесткость сечения при растяжении, ах, ау — координаты е
приведенного центра тяжести.
Пример определения упруго-геометрических характеристик Рассмотрим биметаллический стержень прямоугольного сечения (см. рис. 8.12). Оси проходящие через приведенный центр тяжести, будут одновременно и главны* ми (центральными) осями х, жесткость при растяжении
А = J Е dF = £1йЛ1 + EJh*.
Координаты приведенного центра тяжести сечения были определены ранее:
а	_ Erf + E^-h*)
х' 2 ’	"	2(£Л + £Л) •’
Для определения жесткости сечения на изгиб относительно главной оси xt = х найдем сначала жесткость относительно вспомогательной оси Х2*
• \ = f AEb dy2 ~ у ЬЕ2 (Л3 - Л3) 4- у ЪЕ&
244
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Далее определяем Вх:
В* - J№	ЪЕг (л3 - Л?) + 4	-
F
- т [^хЛ1+е2 № - "D]2 (*Л+W"1-
Величина Ву определяется просто:
__ E^b*	E2h2b*
у ~ 12 .	12
31. Условия равновесия элемента стержня и касательные напряжения изгиба
Вводные замечания. Изгиб стержня часто происходит при действии сосредоточенных или распределенных, нагрузок, перпендикулярных оси стержня (рис. 8.25). В сечении стержня будут действовать не только изгибающие
Рис. 8.25. Примеры изгиба стержней (балок) под действием поперечной нагрузки
моменты, но и перерезывающие усилия. Эти усилия создают в поперечном сечении касательные напряжения.
Рассмотрим сначала условия равновесия элемента стержня.
Условия равновесия элемента стержня. Пусть в сечений (рис. 8.26) действуют изгибающий момент Mx = M(z) и перерезывающая сила (?у = ()(г). В простейших случаях, когда это не может вызвать недоразумений, индексы моментов и сил будем для краткости опускать. Направление силовых факторов предполагается положительным.
На стержень действует распределенная нагрузка g(z), размерность dimg =	(например, Н/м).
Так как силовые факторы изменяются по длине стержня, то в сечении z + dz действуют Q + dQ и момент М + dM.
Рассмотрим равновесие элемента стержня, выделенного двумя поперечными сечениями; размер элемента вдоль оси стержня равен dz.
31. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ИЗГИБА
245
Проектируя все силы на вертикальное направление, находим d(? + gdz = O, или dQ/dz~—q.	(81)
Составим сумму моментов относительно оси х, лежащей в сече-
нии z + dz\
— М — Qdz + qdz2 + М +
+ dM = О?
Отбрасывая qdz*/2 как бесконечно малую второго порядка, получим
dM/dz = Q. (82)’
Производная изгибающего Рис. §26. Условия равновесия элемен-момента равна перерезываю-	та стержня
щей силе. Уравнения (81) и
(82) образуют условия равновесия элемента стержня при изгибе.
Замечание. Полученные условия равновесия справедливы для стержня постоянного или переменного сечений; при любых свойствах материала стержня они являются прямым следствием состояния равновесия.
При движении с ускорением элемента стержня к распределенным усилиям следует добавить по принципу Даламбера инерционные усилия.
Скачки перерезывающей силы и изгибающего момента. Допустим теперь, что в пределах элемента dz на стержень действует внешняя сосредоточенная сила Р (рис. 8.27, а).
qJP-rfb+dz).
dz •
9(2)
Me №+dQ
Рис. 8.27. Действие на элемент сосредоточенных силовых факторов
ИИНИ1

Тогда из условия равновесия сил получаем
-Q(z)+qdz + P + Q(z + dz) = O, или
Q(z + dz) = Q(z)-P.	(83)’
В результате действия внешней сосредоточенной силы перерезывающая сила в сечении получает конечное приращение на
246
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
участке dz — скачок, равный величине силы:
Д<? = Q (z + dz) - Q (z) = -Р.	(84)
В зависимости от направления действия силы Р скачок может быть положительным (Q(z + dz) < Q(z)) или отрицательным. Если в пределах участка dz к стержню приложен сосредоточенный момент (рис* 8.27, б), то из условия равновесия моментов
— М (z) — Q dz + — q dz2 + Ma + M (z + dz) = О,
или, отбрасывая бесконечно малые слагаемые,
M(z + dz)~M(z)--MB,	(85)
где Мв —внешний изгибающий момент. При действии внешнего изгибающего момента общий изгибающий момент получает конечное приращение на участке dz, т. е. скачок, равный по величине приложенному моменту:
A2lf==Jf(z + dz)~M(z) = -JfB.	(86)
Знак скачка зависит от направления момента М3.
Замечание. Как уже отмечалось ранее (разд. 2), представление о сосредоточенном воздействии силы является идеализацией. На рис. 8.28, а, б показаны
Рис. 8.29. Условия равенства. элемента стержня при наличии распределенных изгибающих моментов
Рцс. 8.28. Сосредоточенная сила и момент, приложенные к стержню
реальные случаи передачи силы и момента на стержень. Для расчетной схе* мы удобно представить, что участок является малым, в пределе — бесконечно малым.
Условие равновесия элемента стержня при наличии распределенных изгибающих моментов. В некоторых случаях (рис. 8.29) на стержень могут действовать распределенные моменты (например, от продольных сил, приложенных с эксцентриситетом относительно оси стержня). Условие равновесия для сил (уравнение (81)) остается без изменений, а для равновесия моментов получим
— М — Qdz + ~qdz2 — mdz + М + dM = 0.
6л
31. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ИЗГИБА
247
Пренебрегая членами второго порядка малости, найдем dM/dz = (? + m,
(87)
где т — интенсивность распределенных моментов; величина т имеет размерность силы.
Касательные напряжения изгиба. При изгибе от поперечных нагрузок в стержне возникают касательные напряжения, уравновешивающие перерезывающую силу. Рассмотрим плоский изгиб стержня (рис. 8.30), происходящий в плоскости у, z; пусть ось у является осью симметрии сечения. Основное допущение при определении касательных напряжений состоит в следующем: касательные
Рис. 8.30. Определение касательных напряжений изгиба
напряжения направлены параллельно плоскости изгиба и распределены равномерно по прямой у =» const (т. е. постоянны по ширине сечения Ь (у)).
Рассмотрим два близких поперечных сечения на расстоянии dz (см. рис. 8.30). Оси х, у проходят через центр тяжести сечения, ось х является нейтральной линией (в точках этой линии о = 0). Проведем сечение у ® const и рассмотрим равновесие отсеченной' части элемента стержня (части ABAJD^CD). Вдоль линии DD^ действуют касательные напряжения т. Такие же по величине напряжения в силу парности касательных напряжений должны действовать в площадке AAJDJ), размеры которой dz и Ь(у)\
248
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
(88>
Нормальные напряжения в сечении
Мх (z)
В общем случае изгибающий момент и момент инерции сечения могут зависеть от z. Нормальное усилие, действующее на рассматриваемую заштрихованную часть сечения, площадь которой составляет /, будет равно

1>
Nf = J a df == J / v
где 1/1 — переменная интегрирования (у	Внося значение-
напряжения из соотношения (88), находим
Л1
дг	С А/
N/ = ~7Ж J У1Ь {yi)dyi ~ V
(89>
(90>
где
5/= ^yib(y1)dy1
V — статический момент части сечения.
В общем случае Sf = Sf(y, z), так как величина &2==&2(z).
Выражения (88) и (90) справедливы для стержня с постоянным по сечению модулем упругости. Для стержня с переменным модулем упругости, симметрично распределенным относительна плоскости yz,
(91)
£(3)Mx(z) °- вх(2)
где жесткость сечения стержня на изгиб
(92)
(93)
F
Нормальное усилие, приложенное к части сечения /,
у	х 5 '
где
8=8 J yF dF f
— упруго-статический момент части сечения^
(94)
(95)
31. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ИЗГИБА
249
Рассмотрим теперь условие равновесия отсеченной части элемента стержня. Проектируя все силы на направление оси z, получим
— Nf — ibdz + Nt + ^-dz = 0.
Приращение Nt выражено с помощью частной производной, так как величина Nf зависит также от у.
Далее получаем
Из последнего равенства вытекает важная формула
b dz
(96)
(97)
Замечания. 1. Физический смысл соотношений (96) и (97) состоит в следующем: касательные напряжения образуются вследствие необходимости уравновесить изменение осевых сил по длине стержня. Если в стержне постоянного сечения нормальные напряжения постоянны по длине, то никаких касательных напряжений не возникает.
2. В соответствии с равенствами (88) или (89) рассматриваются нормальные напряжения изгиба от действия внешних сил. В более общем случае, изучение которого опустим, нормальные напряжения могут быть связаны с действием продольных сил и (или) неравномерного нагрева. Если продольное усилие постоянно по длине, то оно не вызывает касательных напряжений.
Распределение касательных напряжений в стержне постоянного сечения. Если модуль упругости постоянен по сечению стержня, то усилие, приложенное к части сечения, определяется по равенству (90). Теперь из соотношений (90) и (97) получаем
1 д/	\
ь \
(98)
Так как сечения стержня по длине одинаковы, то от z зависит лишь величина Mx(z) и
dMx Sf QSf ~dz bTx ~ bJx'
(99)
где по соотношению (82)
dM dz
Важная для дальнейшего формула (99) называется формулой Журавского, по имени выдающегося русского инженера — специалиста в области мостостроения.
Покажем, что перерезывающая сила в сечении является равнодействующей касательных напряжений. Интегрируя равенство (99J
250
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
по у, находим
^2	^2
J тЬ dy = -j- J Stdy = Q
-л1 х ~л1
(с помощью интегрирования по частям устанавливаем
Л2 У Sfdy = -Л1	^2 /^2	\	^2 = yi У b(y1)y1dy1 jdy= У ь (у) у2 dy =JX). /	-h>i
(100)
Для стержня с переменным модулем упругости
ЬВХ- -
Примеры. Рассмотрим распределение касательных напряжений в стержне прямоугольного сечения (рис. 8.31). Статический момент отсеченной части
Л/2	/24
С	1	( h 2^
5/=]	-у ).
V
Перерезывающая сила в сечении стержня в соответствии с принятым правилом знаков
? = -Р.
Учитывая значение момента инерции сечения Jx == М3/12,
по формуле (99) находим
Т-----bh I 2. ~ 6 h2 Г
(101)
Знак минус означает, что касательные напряжения направляем противоположно положительному вектору поперечного усилия Q (см. рис. 8.31).
Рис. 8.31. Распределение касательных напряжений в стержне прямоугольного сечения
Максимальное касательное напряжение (по величине) получается в точках оси х (у =» 0) и равно
ЗР 3 Tmax — 2bh ~ 2 Тср>
гд§ тСр = Pl(bh) — среднее касательное напряжение.
31. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ИЗГИБА
251
Рассмотрим теперь распределение касательных напряжений в стержне круглого сечения (рис. 8.32).
Статический момент отсеченной части
S/ = 2 j ]/"г2 — У2 dy^ v
После замены переменных
У1	= гсоз9, djh =» —г sin 0 d0 получаем
sf = 4 г3 sin’ е=4 (
По формуле (99) находим при
Jx	= ^T’ Му) =2 />-у2 следующую зависимость для касательного напряжения:
* = -—J*--4)-	(юз)
Злг2 \ г2 /
Максимальное касательное напряжение будет при у == 0:
4 Q 4 ттах~ 3 пга= 3 Тср>
где Тер = Q/i^cr2) —среднее касательное напряжение. Распределение касательных напряжений вдоль оси у показано на рис. 8.32.
Рис. 8.32. Распределение касательных напряжений в стержне круглого 4	сечения
Замечание. В рассматриваемом примере допущение о том, что касательные напряжения параллельны оси у, строго не выполняется. В крайних точках (точки D и Di) вектор касательного напряжения должен быть направлен по касательной к контуру в силу свойства парности касательных напряжений (иначе должно действовать на-свободной боковой поверхности стержня касательное напряжение!). Поэтому допущение о постоянстве касательных напряжений по прямой можно заменить более общим условием: постоянство составляющих касательных напряжений вдоль оси у. Более строго следовало бы назвать величину т по формуле Журавского осредненным значением касательного напряжения по прямой, параллельной оси х.
252
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Распределение касательных напряжений в стержнях переменного сече* ния. В этом случае основной расчетной зависимостью является соотношение (98). В качестве примера разберем изгиб клина под действием сосредоточенной силы (рис. 8.33, а). Расчетная модель представляет собой клин прямоугольного сечения с углом а при вершине.
Нормальные напряжения в сечении z
М (z)
Так как /	„ \з
b \2z tg \	2 /	2 сс
Л/ (z) = Pz.	Jх (z) =	|2	= bz tg3"*)"»
то напряжение
ЗР а= ---------у.
2bz2^T
(Ю5)
При z->0 о->оо, и поэтому у конца стержня сделано подкрепление (местное утолщение) (рис. 8.34).
Рис. 8.33. Касательные напряжения в стержне переменного сечения
Для расчета по формуле (98) определяем статический момент отсеченной части
1	( о о Ot
3= “у b I z tg у — у
Далее, находим
Соотношения (105) и (106) применимы при z > а. Распределение касательных напряжений показано на рис. 8.33, б. Максимальное касательное напряжение будет в крайних точках и равно
3 Р ттах = “2* ~ s Зтср,	(107)
bz у
Р где тср =------— —	среднее касательное напряжение,
26z tg у
31. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ИЗГИБА
25а
Рис. 8.34. Особенности распределения нормальных и касательных напряжений в клинообразном стержне
О А, как это следует из точного
Замечания. 1. Наличие касательных напряжений, перпендикулярных контуру сечения, для стержня переменного сечения не нарушает свойства пар- . пости касательных напряжений, так как перпендикулярная площадка не лежит на поверхности стержня.
2. Распределение касательных напряжений по поперечному сечению может существенным образом изменяться в стержнях переменного сечения.
Точное решение задачи об изгибе клина, полученное методами теории упругости, показывает (см. рис. 8.34), что в цилиндрическом сечении АВС действуют только нормальные напряжения. В поперечном сечении АВХС в соответствии с приближенным решением имеются нормальные и касательные напря-(а \ у == z tg — ] из равенства (105) и (106) получаем f т а а = tg Т’
т. е. главное напряжение идет вдоль волокна
решения. При достаточно малых углах а (а < л/3) точное решение и решение, основанное на гипотезе плоских сечений, совпадают.
Касательные напряжения изгиба в тонкостенных стержнях. При анализе касательных напряжений изгиба в стержнях с массивным (компактным) поперечным сечением (см. рис. 8.30) было сделано t допущение об их равномерном распределении вдоль прямой у =* — const. Было показано на примере круглого сечения (см. рис. 8.32), что в ряде случаев такое допущение носит приближенный характер, так как вектор касательного напряжения в точках контура не направлен по касательной к контуру. Для стержней с тонкостенным сечением касательные напряжения изгиба можно определить более точно, так как их направление практически известно заранее. Они должны быть направлены вдоль средней линии тонкостенного профиля (см. рис. 8.35). Так как толщина профиля б мала, то касательные напряжения изгиба можно считать постоянными по толщине.
Таким образом, предполагается, что касательные напряжения направлены вдоль средней линии тонкостенного профиля и постоянны по толщине.
Рассматривается изгиб в плоскости у, z (рис. 8.35). Для определения величины касательного напряжения вдоль нормали к средней линии AAi отсекается часть элемента стержня, показанная на рис. 8.35. Равнодействующая нормальных усилий, приложенных к площади отсеченной части /г обозначается, как и раньше, Nf, Из условия равновесия отсеченной части находим
Ldh 6 dz ‘
Т =
(Ю8)
Для стержня постоянного сечения с постоянными модулями
254
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
упругости

Мх & sf ^х
(109)
и тогда получаем формулу Журавского — Власова для тонкостенных стержней
QSf
(110)
Замечание. ТЪо структуре формула (ПО) не отличается от формулы Журавского (99), но, в сущности, здесь речь идет о решении иной задачи.
Рис. 8.35. Касательные напряжения изгиба в тонкостенных стержнях
Примеры определения касательных напряжений изгиба в тонкостенном стержне. Рассмотрим стержень, имеющий сечение швеллерного типа, причем толщина стенки 6 мала по сравнению с высотой Д и шириной b (рис. 8.35, б).
Момент инерции поперечного сечения
, 1 . 2	6Л2
= 12 + ~2 b6h = 12 <h + 6Ь)'
Для определения касательных напряжений в верхней полке (участок К\К2) проведем сечение на4 расстоянии s (рис. 8.35); площадь отсеченной части / ss $6, статический момент = -j- sdh. Касательное напряжение в верхней полке
Qh. 6<?»
т “ 2JX * = h (fe + 66)	(Ш)
пропорционально величине $.
В вертикальной стенке на расстоянии у статический момент отсеченной части
+	“S'2)-
Первый член правой части выражает статический момент верхней полки, вто
31. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ИЗГИБА
255
рой — участка вертикальной стенки от у до h/2. Наибольшее касательное напряжение будет при у = 0:
3 Q h + 46
ттах= 2 66 /14-66’	<112>
Распределение касательных напряжений показано на рис. 8.35, б. Вертикальная стенка воспринимает существенную часть касательных напряжений, она полностью воспринимает перерезывающее усилие Q,
Замечание. Внимательный читатель, по-видимому, обратил внимание на то, что поток касательных напряжений изгиба (см. рис. 8.35) не только уравновешивает усилие Q, но и создает крутящий момент. Это означает, что при
Рис. 8.36. Касательные напряжения при изгибе в тонкостенной трубе
приложении внешней нагрузки в центр тяжести сечения стержень будет закручиваться.
Рассмотрим теперь касательные напряжения при изгибе тонкостенной трубы (рис. 8.36, а). Толщина стенки б считается малой по отношению к радиусу средней линии г.
Момент инерции сечения
= y = J 2лгбгг = лг3б.
Отсеченную часть примем в виде части кольцевой области (см. рис. 8.36), соответствующей центральному углу 20; касательное напряжение
QS<
. ^(0) = irs: .	<113>
статический момент 5/, считая б < г,
о
Sj = 2 J г соз 0х6г = 2бг2 sin 6;	(114)
о
касательное напряжение
л (J*26r2sin0 Q л	..._ч
Х(0)= 26«?s“=^Sin0-	Щ5)
Максимальное касательное напряжение (рис. 8.36, б) будет при 0 ® л/2 (У==0):
Tmax s лгб=	(116)
где Тер » @/(2лгб) — среднее касательное напряжение.
256
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Обоснования приближенного метода расчета касательных напряжений изгиба. В изложенном методе касательные напряжения находились из уравнений равновесия элемента стержня, причем нормальные напряжения считались заданными. Предполагалось, что в свою очередь касательные напряжения не влияют на распределение нормальных напряжений. Естественно, что такой подход является приближенным, так как при строгой постановке задачи нормальные и касательные напряжения в силу соотношений упругости связаны между собой не только уравнениями равновесия, но и уравнениями совместности деформаций (гл. 2, 3). Однако в некоторых простейших случаях приближенное решение совпадает с точным.
Рассмотрим снова задачу изгиба прямоугольного сечения (рис. 8.37),
начало координат в центре тяжести корневого сечения.
На основании приближенного решения имеем следующие значения компонентов напряженного состояния:
Рис. 8.37. Решение задачи об изгибе стержня как задачи теории упругости
стержня поместив
<JX = O,
12Р (Z — Z) а„ = °, а2 = —у.
'ху ~ О»
.____р (3 _R № \ _ _0
Проверим, удовлетворяются ли уравнения равновесия и совместности деформаций и можно ли считать полученное решение достаточно строгим.
Уравнения равновесия рассматриваются при отсутствии массовых сил: dxxz	d°z n
dx ‘ dy ‘ dz
Таким образом, дифференциальное уравнение равновесия удовлетворяется.
Проверим теперь выполнение условий совместности деформаций (гл. 3, уравнения (11)—(13))., Определим сначала деформации в соответствии с законом упругости: _	/
p-12P(Z—z)	'	12P(Z—z)
es = 8v = -^- = -....£6А3..........8г=т=-
Р / 3	\
Yxy==0,	~~~~Gbh
Все уравнения совместности удовлетворяются тождественно, кроме уравнения (И) гл. 3, относящегося к деформации еж. Если считать, что размер Ь значительно меньше Л, то перемещениями в направлении оси х (см. рис. 8.37) можно пренебречь. Этот случай соответствует задаче о плоском напряженном состоянии. Можно считать, что уравнения совместности выполняются. Наконец, следует отметить, что краевые условия по торцам стержня (z === О и z = Z) выполняются в интегральном смысле. Таким образом, при изгибе стержня прямоугольного сечения (Ь < h) приближенное решение совпадает с точным. Решения, полученные методами теории упругости, и экспериментальные исследования показывают, что приближенная теория изгиба стержней применима для инженерных расчетов.
31. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ИЗГИБА
257
Замечание. В ряде случаев приближенный анализ должен дополняться исследованием местных напряжений при резком изменении поперечного сечения — в зонах закрепления стержня и передачи внешних усилий, в коротких стержнях и т. д., о чем будет сказано в дальнейшем.
Роль касательных напряжений при изгибе стержня. Обычно для достаточно длинных стержней касательные напряжения малы по сравнению с нормальными напряжениями изгиба.
Например, для консольного стержня постоянного сечения (см. рис. 8.37) наибольшие нормальные и касательные напряжения равны
__6Я	ЗР
атах ~ ^2» Tmax “ 2bh,'
Отношение
Tmax 1 ^тах t
уменьшается по мере увеличения длины стержня I.
Влияние касательных напряжений па прочность сказывается для балок из обычных конструкционных, материалов только в коротких стержнях (l^.2h). Для композиционных материалов влияние касательных напряжений изгиба оказывается более существенным, так как их сопротивление сдвигу обычно значительно меньше, чем растяжению и сжатию. Однако основное значение касательных напряжений состоит в том, что они обеспечивают совместную деформацию всех частей стержня при его изгибе.
На рис. 8.38 рассматривается изгцб консольного стержня в двух случаях. -В первом случае (рис. 8.38, а) связь обеих половин нарушена и стержень
Рис. 8.38. Касательные напряжения изгиба (обеспечивают совместную деформацию частей — плоское сечение всего стержня при изгибе)
изгибается так, что каждая часть воспринимает половину нагрузки. Во втором случае (рис. 8.38, б) обе части стержня спаяны и сечение остается при изгибе плоским.
Для двух параллельно работающих стержней максимальное. напряжение
изгиба	_ 6 Pl _12рг aimax - 2 Ь (А/2)2 ~ bh2 '
Во втором случае	п	1 rf • °2max ~ ^2	aimax<
При отсутствии касательных напряжений изгиба на поверхности контакта нормальные напряжения изгиба в рассматриваемом случае возрастают в два раза!
17 и. А. Биргер, Р. Р. Мавлютов
258
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
В еще большей степени падает жесткость стержня на изгиб. Для первого случая суммарный момент инерции
Ъ (Л/2)3	№3
Л ~ 2	12 ~ 48’
(117)
(И8) '
при совместном деформировании
Ы?
= 12
что превышает Ц в четыре раза!
Отмстим, что при изгибе стержня моментами (так называемый чистый изгиб стержня) касательные напряжения не возникают (рис. 8.39). Совместная деформация всех частей стержня обеспечивается наличием жестких пластинок по торцам стержня или линейным распределением внешних нагрузок в концевых сечениях в соответствии с гипотезой плоских сечений. В этом
случае можно считать, что продольные волокна стержня работают независимо. Учет касательных напряжений в изгибе важен при расчете стержней (балок)
Рис. 8.40. Касательные напряжения при изгибе составных балок
Рис. 8.39. Изгиб стержня моментами, при которых касательные напряжения не возникают
составного сечения. На рис. 8.40 показана балка, состоящая из стенки, к которой прикреплены стержни уголкового профиля. -
Сечение работает на изгиб совместно, так как через заклепки передается касательное усилие 53:
QSf
S3 = Nf (z) - Nf (z + t) = t,	(119)
-	* X
где t — шаг заклепок (расстояние между заклепками); Sf — статический мо-мент инерции уголка; Jx — момент инерции всего сечения стержня относительно оси х.
Напряжение среза в заклепке
QStt ^-F3-FaJx
(120)
где F3 — площадь сечения заклепки.
Распределение касательных напряжений изгиба имеет важное значение при армировании (укреплении) материала прочными волокнами (композиционные материалы, армированный бетон и др.). Прочные волокна должны располагаться по линиям действия главных напряжений.
32. УЧЕТ ДЕФОРМАЦИИ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
259
32. Изгиб и растяжение стержней с учетом деформации пластичности и ползучести
Применение гипотезы плоских сечений. Деформации пластичности и ползучести могут достигать сравнительно больших величин (примерно 5—10% и более), возникает вопрос о возможности использования гипотезы плоских сечений.
Опыты по пластическому деформированию полосы свидетель-
ствуют, что гипотеза практически пригодна при деформациях по-
рядка десятков процентов. На рис. 8.41 показаны полосы (риски), нанесенные на боковой поверхности стержня при изгибе на круглой оправке; после значительного изгиба риски остаются прямыми. Гипотеза плоских сечений связана с кинематической картиной деформации при изгибе изотропных материалов. Практически установлено, что она применима при работе материала в стадии пластичности и ползучести.
Схематизация кривой деформирования.
Если при изгибе и растяжении в упругой области использовалась линейная зависимость напряжений и деформаций, то нову принимается кривая деформирования
Рис. 8.41. Экспериментальное подтверждение гипотезы плоских сечений при больших деформациях
при пластичности в ос-(гл. 4) (рис. 8.42, а)
o = f(e).
(121)
В общем случае зависимость (121) может быть различной при растяжении и сжатии. Для расчета часто принимаются схематизи-
Рис. 8.42. Кривые деформирования и их схематизации
рованные кривые деформирования (рис. 8.42, 6, в), причем одинаковые в области растяжения и сжатия.
Кривая, имеющая при о = от (ог — предел текучести)1 горизонтальный участок, описывает пластичность без упрочнения (см. 17*
260
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
рис. 8.42,6); используется кривая деформирования с линейным упрочнением (рис. 8.42, в). Учет пластичности материала, если исключить процессы разгрузки, может быть использован для описания изгиба стержней из нелинейно-упругого материала. Для упрощенного описания конструкционных материалов иногда используется степенной закон деформирования
о = /се",	(122)’
где Л, п — постоянные материала.
Так как кривая деформирования должна проходить через точку, соответствующую пределу текучести от, то
от = к (ат/Е + 0,002)п == Ле?,
и тогда
о = От(е/ет)п.
Обычно 0,1 < п < 0,5.
Замечание. В тех случаях, когда учитываются касательные напряжения изгиба и соответствующие деформации сдвига, под о и 8 в уравнении (121) понимаются интенсивности напряжений и деформаций. Это обстоятельство имеет обычно второстепенный характер, а при ц == 0,5 им можно пренебречь.
Изгиб стержней при пластичности без упрочнения. Предельный изгибающий момент. Рассмотрим сначала стержень прямоугольного сечения. Это наиболее простой случай, который помогает* выяснить основные особенности задачи (рис. 8.43, а).
Рис. 8.43. Упругопластическая деформация стержня прямоугольного сечения (пластичность без упрочнения)
Пусть на стержень действует изгибающий момент М. Если наибольшее значение напряжения изгиба
6Л/ tfmax “ТГ bh
(123)
ИЛИ

OTbh2
то стержень работает при упругих деформациях.
32. УЧЕТ ДЕФОРМАЦИИ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
261
При возрастании М в наиболее удаленных от нейтральной линии (у = h/2) точках возникает пластическая деформация и напряжение изгиба станет равным ог (рис. 8.43, б, пластичность без упрочнения). Пусть при данном значении момента пластические
1	1	।	।	Лт
деформации занимают область у hr < | у | < у	При ] у | в об-
ласти упругости напряжения изменяются по линейному закону:
0 = От^.	(124)
Из условия равновесия
[ оу dF = М F
находим
Л/2	ЛГ/2
2b j aTy.dy+2b у2dy =	(й2 — hr) + стЬ= М.
hj>/2	О
Из последнего равенства получаем
Ьа »т» п btiTh2
=	----М,	(125)
ИЛИ
АТ = ^Ж1/±-aTbh2-M.	(126)
у vTb f 4
Так как hT > 0, то предельное значение изгибающего момента равно
Мах> = ±oTbh2.	(127)
Легко проверить, что такое значение М получается при распределении напряжений изгиба по рис. 8.43, г.
Сечение стержня из материала без упрочнения в стадии пластичности не может воспринять момент М>Мпр: в сечении образуется пластический шарнир (точнее, сечение представляет собой шарнир, в котором действует «момент трения», равный Мпр). В общем случае плоского изгиба предельный момент находится следующим образом (рис. 8.44), Условие отсутствия продольного усилия имеет вид
J о dF =	— OtF1 « 0f	(128)
F •
где F2, Ft — площади частей сечения стержня, в которых действуют растягивающие или сжимающие напряжения. Ссылаясь на условие (128), можно утверждать, что нейтральная линия аа делит
262
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
площадь F па две равновеликие части: = Fz = F/2. Предельный
момент равен
Мар — GtF С,
(129)
где с — расстояние от центра тяжести какой-либо половины сечения до центра тяжести всего сечения (рис. 8.44, б).
Рис. 8.44. Предельный изгибающий момент при пластичности без упрочнения
Остаточные напряжения. Определим остаточные напряжения в стержне после снятия момента, вызвавшего пластическую деформацию. Если материал стержня идеально упругий, то ^момент М приведет к напряжениям
По такой зависимости будут убывать напряжения при снятии момента, так как при разгрузке деформации становятся упругими.
Остаточные напряжения (рис. 8.43, в)
оОст = а —а*,	(130)'
где о — напряжения при упругопластических деформациях. Значения о и а* соответствуют одному и тому же изгибающему моменту, причем о* — напряжение в идеально упругом теле (такое тело деформируется по законам упругости при любом уровне напряжений) .
Замечание. Условие (130) для определения остаточных напряжений после возникновения (в прямом нагружении) пластических деформаций является следствием теоремы Генки.
Плоский изгиб и растяжение стержня с учетом деформации пластичности. На стержень действуют изгибающий момент М и растягивающее усилие N (рис. 8.45). Изгиб стержйя происходит в плоскости у, х.
По гипотезе плоских сечений деформация
8 = ео + ^=8о + М'	<131>
Задача состоит в определении параметров деформации е0 и X = dfyjdz*
32. УЧЕТ ДЕФОРМАЦИИ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
263
Из условий равновесия вытекает, что
лз
J a dF = J а (у) Ь (у) dy = N,	(132)
F
h2
У ау dF = у о (у) yb (у) dy =	-	(133)
F	-hl
Перейдем к новой переменной е, и тогда с учетом зависимости (131) равенства (132) и (133) будут такими: ' 82 / \
У/(е)И ^2)* = ХЛ>	(134)
' у
82	/ \ / \
. Г / (8) ( --— ] 6 ( j de =	(*35)
J	\ *У /	\ *У /
81
где е2, 61 — величины деформации при у = /г2 и у = —hit
62 = So + Х1/^2,
Si = £о — Х1Л1*
Задача существенно упрощается при отсутствии растягивающего (сжимающего) усилия 2V и для сечений с двумя осями симметрии (рис. 8.46). Помещая начало координат в центре тяжести сечения и считая зависимость (121)
Рис. 8.45. Общий случай плоского	Рис. 8.46. Изгиб стержня с по-
изгиба при упругопластических	перечным сечением, обладаю-
деформациях	щим двумя осями симметрии
одинаковой *при растяжении и сжатии, получим е0 » 0, так как ось х оказывается нейтральной линией сечения. Из условия (135) находим
етах
2 f Це) eb de = J	\ kyJ
0
(136)
264'
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
где emax = е2 = —в! — наибольшая деформация в крайних волокнах сечения. В рассматриваемом случае
1 , етах 2 *^уг'
и из равенства (136) получаем
етах
F (8тах) = f / (8) eb f 2гЧ de = М.	(137)
2smax J	V max/
о
При заданном значении h строится функция F ( бтах) и находятся значения 6m ах» А/, удовлетворяющие условию (137). Вычисление Е(ет ах) начинается с определения значений вшах, соответствующих работе материала в упругой области:
(1) __ М h
smax ~~ EJX 2 *
В упругопластической стадии р	р(1>
°тах стах*
При совместном действии изгиба и растяжения, используя условия равновесия (132) и (133) и зависимость (131), приходим к системе уравнений
f f(8e + Xvy)^ = ^
/	(138)
J / (% + 1уУ} У dF = М
F
относительно параметров деформации е0 и Обозначив
Fl	(е0>М = J/(8o+M)rff>
	5	(139) (е0’Ху) =] F
решим систему уравнений	(138) методом Ньютона — Раффсона. Выбирая ис-
ходное приближение	и	и раскладывая функции Fi и F2 в ряд в
окрестности указанных приближений, получим
где производные относятся к точке \ Отметим следующие равенства:
где Ек = df/dz — касательный модуль.
32. УЧЕТ ДЕФОРМАЦИИ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
265
Из уравнения (140) находим значения е0 и Ху» которые принимаются в качестве второго приближения. Первое приближение может быть принято по формулам для упругого материала.
Расчет заканчивается при достаточной близости двух соседних приближений.
Замечание. Процедура расчета по равенству (140) близка к методу переменных параметров упругости, но является менее общей. Она пригодна в тех случаях, когда деформация определяется на основе гипотез кинематического характера.	4
Общий случай расчета стержня в упругопластпческой стадии. Метод переменных параметров упругости. Расчет проводится по формуле (17) с помощью последовательных приближений (рис. 8.47) .
Рис. 8.47. Общий случай изгиба в упругопластической стадии: а —сечение стержня; б — схема расчета
В первом приближении материал считается (идеально) упругим = Е} и нахъдйтся напряжение (рис. 8.47, а)
_5L + и — а* F + У /я
Му
J У
(142)
Звездочка в индексе означает, что напряжения относятся к упругому материалу. Далее по кривой деформирования находим (рис. 8.47, б)
= №/Е	(143)
и соответствующее значение о(1).
Во втором приближении принимаем в каждой точке сечения £<2> = о<Ч/8(1).	(144);
Теперь заново находим положение приведенного центра тяжести и главных осей сечения. Напряжение второго приближения
266
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
где
4(2) = J Ew dF, В™ = J у2Е™ dF, В,2) = J х2Е(2) dF,
F	F	F
Далее находим
и значение «модуля упругости» для следующего приближения
£(3)=О(2)/е(2)в	(!46)
Расчет заканчивается при достаточной близости двух соседних приближений:
|а(«)_а(п-1)|<Д1	(147)
и при условии, что изображающая точка (см. рис. 8.47, б) лежит на кривой деформирования:
|а^_о(п)|<д2.	(148)
Величины Д4 и Д2, имеющие размерность напряжений, характеризуют необходимую точность расчета (обычно Д4 = Дг = (5—10) МПа).
Стержни из нелинейного или разномодульного материала. Зависимость напряжение — деформация для нелинейного материала показана на рис. 8.48, а. Она может быть неодинаковой в области растяжения и сжатия, так как ряд материалов (композиционные и пористые материалы, чугуны и т. п.) имеют
Рис. 8.48. Зависимости а — е для нелинейного (а) и разномодульного (б) материалов
различные свойства в указанных областях. Пористые материалы лучше сопротивляются напряжениям сжатия, армированные материалы с мягким наполнением — растяжению. Частный случай нелинейного материала составляет билинейный или разномодульный материал, обладающий разными модулями упругости в области растяжения и сжатия. Задачи растяжения и изгиба стержней из нелинейного или разномодульного материалов решаются методом переменных параметров упругости. В первом приближении применяется посто*
32. УЧЕТ ДЕФОРМАЦИИ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
267
янный модуль упругости одинаковый для растяжения и сжатия. Напряжения не зависят от величины выбранного модуля и определяются по формуле (18). Далее в каждой точке сечения находятся значения деформации
Е{1)
и затем (см. рис. 8.48) значения модуля упругости Е(2) в зависимости от значения и1 знака е(1). Выбор первоначального модуля упругости не имеет существенного значения: процесс сходится при произвольном значении Можно принять
£(1)=.т(£+ + £-)>
где Е+, Е_ — модули упругости при растяжении и сжатии. Процедура заканчивается при выполнении условий (147) и (148),
Рис. 8.49. Изгиб стержня из разномодульного материала
В простых случаях можно получить решение в замкнутой форме. Рассмотрим изгиб стержня прямоугольного сечения из разномодульного материала (рис. 8.49, а).
Для такого материала
Е = £р при о > О,
£ = £сж при а<0.
Направим ось вдоль нейтральной линии; тогда деформация выражается следующим равенством:
8 = ЧуУу	(150)
Так как в сечении суммарное усилие равно нулю, то лр	о
J О dF = J Е^ТуУ-fi dyt + J Е^уУуЬ dyt = Qt F	о
что дает
(151)
p p u/t4 uxtt
268
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Из условия равновесия
(hp	о	\
J ЕрУ1с1У1+ J	= М
о 	-ЛСЖ	/
(152)
получаем ______________________________ЗМ________ ~ b (E.hl + Е^3ст) '
Наибольшие напряжения растяжения и сжатия (рис. 8.49, б) равны Ср = ХуЬр> Осж = Ху^сж.
Жесткость стержня на изгиб
Учитывая, что
Й-сж/^р	V^p/V&сж,	4“ ^СЖ = Ь,
найдем из равенства (153) приведенный модуль упругости: ________________________________________ Е°*-уутг9+уЁ^
Замечание. Величина ЕПр называется модулем Кармана по имени го, впервые получившего решение рассматриваемой задачи в связи с проблемой устойчивости стержней.
Касательные напряжения при изгибе стержней в упругопластической стадии. В приближенной теории стержней касательные напряжения изгиба определяются из условий равновесия.
(153)
(154)
Рис. 8.50. Касательные напряжения при упругопластическом изгибе стержня (материал не обладает упрочнением в пластической области)
Рассмотрим изгиб стержня прямоугольного сечения под действием момента М и поперечной силы Р (рис. 8.50). Напряжения изгиба для материала без упрочнения (сМ. зависимости (124), (125)
32. УЧЕТ ДЕФОРМАЦИИ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
269
И (126)).
2у I I 1 и
(155)
Величина hT, характеризующая размер упругой зоны, определяется соотношениями (125) и (126). Она зависит от z, так как изгибающий момент в сечении изменяется по длине стержня. На рис. 8.50, а показана зона пластических деформаций, которая увеличивается при возрастании изгибающего момента в сечении. Касательное напряжение на расстоянии у от оси
1 b dz ’
(156)
где усилие, действующее на отсеченную часть сечения стержня,
/1 \ 1 1 •
Ьат (у h — у}, у hT < | у К у А,
bijT±-(h — hT) + От г4-^т — 4- ], 0<|г/|<-уЛт. &	I Tt	ll/jy /	м
(157)
В зоне пластических деформаций
dNf dz
d Г, / 1 , V
= 0,
и в этой зоне касательные напряжения отсутствуют.
В зоне упругих деформаций
д Г 1	/, z, \ ,	/ 1 ,	№ \1	„ (1	у2 \ dhT
'с = 77|тат(/1“/гг) +	i;)]------°т
(158)
Дифференцируя равенство (125) по z, находим bOj’hjt dh?	эм  р
6 dz	dz ’
(159)
так как
M(z) = P(Z-z) + M.
Окончательно получаем
0,

1

,4' 4
у2 6Р
(160)
1
270
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Распределение касательных напряжений по сечению приведено на рис. 8.50, б. По мере увеличения изгибающего момента до предельного значения (127) величина hT уменьшается и касательное напряжение возрастает.
Замечание. Изложенное решение является, конечно, приближенным, так как не учитывает влияние величины касательных напряжений на возникновение пластических деформаций. Его достоинство состоит в том, что оно позволяет выявить своеобразную концентрацию касательных напряжений в упругом ядре сечения.
Расчет стержней в упругопластической области с учетом нормальных и касательных напряжений изгиба. Рассмотрим плоский изгиб стержня (рис. 8.51, а) при действии изгибающего момента,
Рис. 8.51. Упругопластическая деформация стержня при учете нормальных и касательных напряжений и обобщенная кривая деформирования
нормального и перерезывающего усилий. Расчет проводится методом переменных параметров упругости. Предполагается, что кривая деформирования одинакова в области растяжения и сжатия.
В первом приближении материал предполагается упругим, нор-
мальные	и касательные напряжения определяются так: <4х) = у + у^-,	(161) Г	J х - §•,	(162)
где нижний индекс * указывает, что напряжения соответствуют упругому материалу. Далее определяем эквивалентное напряжение: о£ = /<41)2 + з<1>2 -	(163)
и соответствующее значение эквивалентной деформации:
82. УЧЕТ ДЕФОРМАЦИИ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
271
Значению е(01^ по кривой деформирования (рис. 8.51, б) соответствуют напряжение OqX) и модуль упругости
р(2) _Дг)/ (D Я —	/ ь0« •
(164)
Во втором приближении, принимая в каждой точке модуль упругости равным Ew, получаем по формулам (17) и (100) гл. 8
(2) _ р(2) ( N М г °* ~Е
(2) __
6В(2) ’
(165)
(166)
где
= J у2^(2) dF^ 5(2) = J Е^у dFf Л(2) = [ £(2) dF.
F	f	F
В равенствах (165) и (166) главные оси координат расположены в приведенном центре тяжести сечения, соответствующем модулю упругости E(2)j усилие N считается постоянным по длине стержня.
Далее по формуле (163) после замены верхних индексов с (1) на (2) находим значение Со*, затем	и новые значения
модуля упругости Е(3) и т. д. Расчет заканчивается при соблюдении условий (147) и (148).
Учет деформации ползучести при изгибе стержня. Сведения о ползучести материала получаются из сетки кривых ползучести при различных напряжениях и температурах. Расчет на ползучесть по теории старения сводится к построению изохронных кривых ползучести, которые рассматриваются как условные кривые деформирования. Дальнейший ход расчета такой же, как при учете упругопластических деформаций.
Если нагрузки на стержень остаются неизменными во времени, то после обычно непродолжительного первоначального периода наступает установившаяся ползучесть. При установившейся ползучести скорость ползучести при растяжении выражается следующей зависимостью!
70=.'4т = В(Т)^т\	(167)
где положительные параметры Вии зависят от температуры. Рассматривая материалы, у которых свойства ползучести при растяжении и сжатии одинаковы, представим зависимость (167) в таком виде:
е «Bl(j|ft signer,	(168)
«
тде 8 = de/df; зависимость параметров В и п от температуры для
272
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
краткости не указывается. Напомним, что «знаковая» . функция
sign о =
при о>0,
при о<0.
Из соотношения (168) следует, что
8
в
а =
1/п
sign е
(169)
Вначале рассмотрим чистый изгиб стержня с двумя осями симметрии (см. рис. 8.46). В этом случае нейтральной линией будет ось х, а деформации определим по гипотезе плоских сечений:
е = ХуУ-Скорость деформации
de/dt = е = ЪУ-
Из условия равновесия получаем
J aydF = Мх.
F
(170)
Внося сюда значение о из равенства (169) п учитывая зависимость (170), получим-
li (1/л С
(171)
Так как
sign (ъу) = sign %, • sign у,
то
у sign г/= |у|, '
111/'*	л
lvngnXV
F
Обозначая геометрическую характеристику сечения
Л(П)= [|у|1+1/п<*Л F
находим из соотношения (172)
у	М	п .	,,
" -4-= —SlgnMx, В	Jxtn)
JLf
a =-r^-\y\Vn sign У-Jx(n)
(172)
(173)
(174)
(175)
32. УЧЕТ ДЕФОРМАЦИИ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
273
На рис. 8.52 показано распределение напряжений, соответствующее формуле (175). При п=1 оно соответствует упругому материалу.
Общий случай расчета стержней на изгиб при учете ползучести материала. Рассматривается общий случай, когда на неравномерно нагретый стержень действует переменная по времени нагрузка.
Ограничимся для простоты изучением изгиба стержней, сечения которых обладают осью симметрии. Нагружение разбивается по времени на этапы (Д^, Д2£, ..., AJ)-
Пусть за время от £< до изгибающий момент в сечении стержня и растягивающая сила получили приращения ДгМх и ДД.
Приращение- деформации на i-м этапе нагружения д-о
A,s == —g- + Aj (аГ) + AiS .	(176)
Первый член правой части соответствует приращению упругой деформации, второй — температурной, третий — приращению деформации ползучести.
Используя гипотезу плоских сечений и как при выводе формул (17), получим
уравнения равновесия,
	Г &.N	Д4МХ 1	_4_ >>	1 х	+ ДгОтемп +	(177)
AiO — Е.	J Е dF .	j у2Е dF F	F ’	
где приращение температурных напряжении
kpTdF
Д10темп — Е
Рис. 8.52. Распределение напряжений изгиба при установившейся ползучести (стержень имеет прямоугольное или другое двусимметричное сечение)
(178)
F
Аналогично определяется приращение напряжений, вызванное деформацией ползучести:
Дг^пол — Е
J b^dF	J* уД{8с dF
-7--------------------~“Aie'
£ dF	J у2Е dF
F	F
(179)
Суммарные напряжения и деформации в стержне после Z-ro этапа нагружения в момент времени ti+i равны соответственно
о (£<+1) = о (k) + Д,о, е = е (£<) + Д,е«
18 и. А. Биргер, Р. Р. Мавлютов
274
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Остается конкретизировать приращение деформации ползучести. Оно определяется по напряжениям, деформациям и температурам в начале этапа нагружения, так как сами этапы считаются достаточно малыми:
Alec = 7o[a(Q’, T(tj, 8С(^)]ДЛ	(180);
где Уо — скорость ползучести, соответствующая начальному этапу нагружения и определяемая по кривым ползучести. Расчет проводится последовательно, начиная с первого этапа.
33. Прочностные модели надежности при изгибе
Назначение и структура прочностных моделей. Прочностные модели надежности предназначены для выбора материала и размеров конструкции, технологии изготовления, обеспечивающих отсутствие отказов (разрушений) при определенных условиях эксплуатации в течение заданного времени. Общая структура прочностных моделей приведена на рис. 1.2.
Рассматривается частный случай прочностных моделей для элементов конструкций, которые могут схематизироваться в виде стержней при деформации изгиба. Основным для построения моделей прочностной надежности является тип (модель) нагружения.
Прочностная модель надежности при статической нагрузке по разрушающим усилиям. Статическое нагружение означает постепенное возрастание нагрузки до максимального значения. Модель статического нагружения является идеализированной, так как в чистом виде практически встречается редко. Наиболее близким к условиям статических нагружений являются несущие стержни (балки) в строительных сооружениях (зданиях) при воздействии силы тяжести. В машиностроении модель статического нагружения (статической прочности) используется главным образом для определения статических разрушающих нагрузок или для сравнительных оценок напряженности.
Детерминированные модели прочностной надежности состоят в определении запасов прочности по разрушающим усилиям и сопоставлении их с рекомендуемыми значениями. Для пластичных материалов запас по разрушающей нагрузке
(181) ш max
где Л/разР — изгибающий момент в сечении, вызывающий разрушение стержня; Л/тах— наибольший изгибающий момент в рассматриваемом сечении стержня при наиболее неблагоприятном сочетании внешних нагрузок; [пр] — допустимое значение запаса прочности по разрушающим усилиям (обычно [пр] = 1,4—2).
Величина Мра3р определяется из условия, что при распределении напряжений с учетом пластических деформаций (гл. 8, разд. 7)
33. ПРОЧНОСТНЫЕ МОДЕЛИ НАДЕЖНОСТИ
275
напряжение изгиба достигает предела прочности материала (рис. 8.53).
Для материала, обладающего площадкой текучести или слабым упрочнением (алюминиевые сплавы и некоторые высоколегирован-* ные стали), принимают (прямоугольное сечение, формула (127))
МразР = От ± bh? = От^т,	(182)
где WT = -^bh2 —пластический момент сопротивления прямоугольного сечения.
При наличии упрочнения в пластической области разрушающий момент изгиба определяется по схематизированной диаграмме де-формирования. В крайней точке прямоугольного сечения (у = у М возникает напряжение, равное пределу прочности о6 (рис. 8.54),
Рис. 8.53. Схематизированная диаграмма деформирования при наличии больших пластических деформаций (жесткопластическое тело)
Рис. 8.54. Распределение напряжений при действии разрушающего момента
Распределение напряжений при действии разрушающего момента имеет вид
о = вт + (Оь — От) -у-.	(183)
Из условия
Л/2
j ®yb dy == Л/разр	(184)
-Л/2 находим
Л/2
м разр = 2 J Гот + (<Ъ — От) -у-1 yb. dy,
о L	J
ИЛИ
Мразр = OtWt + (а» - От) W,	(185)
18*
276
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
где W — bh2/Q — момент сопротивления стержня прямоугольного сечения в упругой области.
Отметим, что при выводе формулы (185)’ для разрушающего момента изгиба изменением сечения стержня в процессе деформации пренебрегали. Основная область применения прочностных моделей по разрушающим усилиям — однократное статическое нагружение достаточно пластичных материалов. Это связано с тем, что при определении запаса прочности предполагается перераспределение напряжений с учетом пластических деформаций.
Прочностная модель надежности при статической нагрузке по напряжениям. Рассматриваемый выше запас по разрушающим усилиям является интегральной характеристикой предельного опасного состояния материала бруса по всему сечению. Вместе с тем для малопластичных материалов или для всех конструкционных материалов, но при повторном статическом нагружении разрушение носит локальный характер и начинается в наиболее напряженных точках сечения. Детерминированная модель прочностной надежности содержит условие для запасов прочности
п = -^->[Пс],	•	(186)
ишах
где — предел прочности материала, атах — наибольшее напряже- . ние (изгиба), [пс] — допускаемое значение запаса статической прочности по напряжениям (обычно пс == 1,3—2,5).
Величина. запаса по напряжениям часто используется как критерий сравнения надежности конструкций. При таком сопоставлении под Отах обычно понимаются наибольшие номинальные напряжения. Это объясняется тем, что при небольшом числе повторных статических нагружений (N < 103) для пластичных материалов влияние концентрации напряжений сказывается незначительно, i Для хрупких материалов при определении <Jmax концентрацию на- i пряжений необходимо учитывать.
В общем случае при действии нормальных и касательных на- -пряжений изгиба модель прочностной надежности имеет вид
п=-Л-<[Пс1.	'	(187)
°тах	,	. ;
Наибольшее эквивалентное напряжение принимается в виде-
Сметах = ^гтах»	(188)
где	_______.	/ ,
Ci == ]/а2 + Зт2	(189)
— интенсивность напряжений.
Замечание. Интенсивность напряжений применяется в качестве критерия наступления пластических деформаций (условие о< От) и частб^ используется как критерий прочности (условие Oi o&). При длительно действующей
33. ПРОЧНОСТНЫЕ МОДЕЛИ НАДЕЖНОСТИ
277
статической нагрузке и повышенных температурах модель прочностной надежности имеет вид
п =
адл (^> О ^етах
[Пд]>
(190)
где Одл(7\ 0 — предел длительной прочности при температуре Т и времени нагружения t; [пд]'— допускаемое значение коэффициента запаса по длительной прочности.
Прочностная модель надежности при переменной нагрузке. На рис. 8.55 показан элемент конструкции, на который действует переменное усилие:
P(t) = Pa cos tot, (191) где со — круговая частота нагружения (число колебаний нагрузки в секунду), £ —время, /==со/(2л)	(192)’
Рис. 8.55. Прочностная модель надежности при переменном изгибе
— частота нагружения.
Опасным сечением в рассматриваемом элементе является сечение AAif где начинается переход к более прочному участку. Напряжения изгиба в точках А и At в момент времени t
P(t)l Ра1
a (t) = —= -ppr COS tot = Ga cos tot,
где Oa — амплитудное значение переменного напряжения:
Оа = Л//РК	* (193)
Момент сопротивления прямоугольного сечения W = 6^76. . '
Величина оа представляет собой номинальное (условное) значение амплитуды переменных напряжений (разд. 16), так как в точках перехода А и At возникает концентрация напряжений. Наибольшее амплитудное значение переменного напряжения изгиба
Oa шах = С&оОа»	(194)
где а0 — коэффициент концентрации напряжений. Значение определяется методами теории упругости аналитически или численными методами.
В инженерных расчетах часто используется зависимость
aa « 1 + к у-,
(195).
278
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
где г—радиус скругления. Коэффициент к обычно принимают равным 0,15—0,20.
Рассмотрим прочностную модель надежности при большом числе нагружений (число циклов нагружения zV> 10е), что соответствует длительности нагружения (в часах)
106 = 101
> 3,6-103/ ~ W
Иными словами, рассмотрим модель надежности при усталостном разрушении. Детерминированная модель прочностной надежности состоит в условии
па —	[лу],
иа
(196)
где а_1д — предел выносливости детали, определяемый для базового числа циклов iV0 (обычно 7V0 ~ 2 • 107); аа — наибольшее (номинальное) напряжение (амплитудное значение переменного напряжения в опасной точке); [пу] — допустимый запас усталостной прочности (обычно [пу] = 2—4).
Величина О-1Д определяется с помощью натурных испытаний элемента конструкции на усталость. При невозможности или нецелесообразности подобных испытаний величина о-1д оценивается расчетным путем по формуле (см. разд. 16)
а_1д = -^а_1,	(197)
О
где О-1 — предел выносливости материала, определяемый на гладких образцах, изготовленных по стандартной технологии; fj и е — коэффициенты, характеризующие поверхностный слой и влияние абсолютных размеров; К9 — эффективный коэффициент концентрации напряжений (разд. 16).
Запас усталостной прочности можно представить в другом виде:
=	(198)
где оеа — эквивалентное переменное напряжение:
Oea— •
(199)
Эквивалентное напряжение аев сопоставляет действующее напряжение с прочностью материала.
Детерминированная и статистическая модели усталостной прочности лопатки компрессора или турбины, вероятность разрушения. Основная причина разрушения лопаток компрессора или турбин в эксплуатации — изгибные колебания, возникающие в результат©
33. ПРОЧНОСТНЫЕ МОДЕЛИ НАДЕЖНОСТИ
279
неравномерности потока воздуха или газа (рис. 8.56). Детерминированная модель усталостной прочности состоит в условны
= О-1д/Оа > [™а],	(200)
где О-1д — экспериментально определенный предел выносливости лопатки па базе 2 • 107 циклов; оа — экспериментально замеренное
с помощью проволочных тензометров (тензорези-сторов) наибольшее переменное напряжение при изгибных колебаниях. Так как величины предела выносливости и амплитуды действующих напряжений имеют рассеяние, то обычно указываются условия их определения. В «запас прочности» величина о-1Д принимается наименьшей по техническим условиям или по нескольким испытаниям, тогда как значение оа принимается наибольшим среди измеренных. Более полно рассеяние результатов экспериментальных исследований учитывается в статистической модели надежности, целью которой является определение вероятности разрушения.
На рис. 8.57 даны плотности распределения
Рис. 8.56. Статистическая модель усталостной проч-
пределов выносливости и амплитуды переменных пости лопатки ком-напряжений в лопатках определенного типа тур- прессора или тур--	-	бины при изгио-
бомашин. Величины о_1д и оа выражают средние Ных колебаниях значения для всей совокупности лопаток.
Рассеяние о_1д связано с неизбежными отклонениями свойств материала и технологии изготовления; разброс оа вызывается различными условиями возбуждения и демпфирования колебаний. Все
Рис. 8.57. Плотности распределения предела выносливости и амплитуды переменных напряжений в лопатках
это дает основание рассматривать для каждой конкретной лопатки величины о_1д и ао как случайные.
Разность случайных величин
£ = б_1д —(201)
есть также величина случайная. Вероятность разрушения Ppa3P = P(S<0) = F(0) (202)
равна вероятности того, что случайная величина £ окажется отрицательной; F(Z) — функция распределения случайной величины Предполагая, что О-1Д и ов имеют нормальное распределение, найдем
^(о=4+ф
(203)
280
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
где Ф (х) — функция Лапласа:
Ф (х) — —= I
(204)
Среднее значение и среднеквадратичное отклонение равны соответственно
С = а-1Д —	(205)
Ч= V «о_1д + Ч,	(206)
где $а_1д, $(уа — среднеквадратичные отклонения случайных величин о_1д и Оа. При определении случайные величины о_1д и оа предполагались независимыми.
Вероятность разрушения
= 4 +	(207)
Статистическая модель усталостной прочности представляет собой условие
Рразр	Р%азр],	(208)
где [Рразр] — допустимое значение вероятности разрушения (обычно [Рразр] = IO'6 ~ IO'3) .
Значение Рра3р определяется величиной
/<1Д + Ч К“Х_1Д + < ’
где па = о-1Д/Оа — запас прочности по средним значениям; «=* == 5а-1д/о-1д, v<ja == S<ja/Qa ~ коэффициенты вариации случайных величин О-1д и ов. Связь вероятности разрушения и запаса прочности (по средним значениям) выражается равенством
-4-ф(,,-д(209)
Для лопаток компрессоров и турбин коэффициенты вариации обычно составляют
гла_1Д«ОД — 0,2;	= 0,1 - 0,3.
Прочностная модель надежности валов. Валы являются ответственными высоконагруженными элементами машин. При построении моделей прочностной надёжности, рассматривается «опасное се
33. ПРОЧНОСТНЫЕ МОДЕЛИ НАДЕЖНОСТИ
281
чение» вала, в котором имеется точка с наибольшими напряжениями (точка А на рис. 8.58).
Обычно наиболее важным оказывается обеспечение надежности при переменных напряжениях с асимметричным циклом. В опасной точке действуют нормальное и касательное напряжения. Рас-
смотрим сначала случаи, когда эти напряжения изменяются по симметричному циклу (т. е. не имеют постоянных составляющих).
Условие усталостной прочности для гладкого участка вала (при отсутствии концентрации напряжений) имеет вид
Gia = VО*2 + ЗТЯ*2 = (Т_1( (210)
♦ *
где оа, — значения амплитуд переменных напряжений в момент разрушения.
Если Оа и Та — амплитуды действующих переменных напряжений, то в момент разрушения
О* = naOa, Т* = Пата. (211 )
У
I/ а	• 5
Рис. 8.58. Модель прочностной надежности вала: а — опасное сечение вала; б —• нормальное a и касательное т напряжения в опасной точке вала
Запас усталостной прочности из соотношений (210) и (211) будет таким;
a-i '  Па= .....== —.
K°a + 3Ta	ia’
Прочностная модель надежности имеет вид па [п0].
(212)
(213)
При наличии концентрации напряжений и с учетом влияния других факторов в условие усталостной прочности следует подставлять эквивалентные напряжения, и тогда в момент разрушения имеем
/ *Кг V
« a-ir
(214)
где Ка, Кх — эффективные коэффициенты концентрации при изгибе и кручении; ро, 8а, рт, — коэффициенты состояния поверхности и учета масштабного фактора. Значения Ка, sa указаны в разд. 16; в первом приближении можно принимать
Рт — Ра» 6т —Sq.
282
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Прочностпая модель надежности по зависимости (212) будет такой:
При асимметричном цикле нагружения эквивалентные нормальные и касательные напряжения будут следующими:
К_
(Уеа == (У а <Г”Т Ь	(216)
Раьа
Кх
^еа =	Ь 'фтТти,	(21/)
Ртьт
где *фа, фт •—коэффициенты влияния постоянных напряжений (обычно принимают фа = О-1/о6, фг = Т-1/т&).
Прочностная модель надежности при усталостных разрушениях, связанных с асимметричными циклами нагружения, имеет вид
Замечание. При одновременном действии переменных нормальных и касательных напряжений условие усталостного разрушения принимают в виде
aia = (J-v	(219)
т. е. в момент разрушения интенсивность напряжения равна пределу вынос-ливости. Условие (219) подтверждено экспериментально для пластичных конструкционных материалов.	— _ _ -	- —
Для хрупких материалов условие усталостной прочности будет таким: =	(220)
где о*а — наибольшее главное напряжение в момент разрушения*
34. Прогибы стержней
Вводные замечания. Во многих случаях важно обеспечить не только прочность стержней, но и отсутствие значительных прогибов под нагрузкой. Прогибы вала, несущего шестерню, могут нарушить правильность зацепления. Прогибы вала турбины могут привести к недопустимому касанию лопаток о корпус и т. п.
Рассмотрение прогибов стержня весьма важно в задачах устойчивости колебания и в ряде других задач. Наконец, расчет прогибов необходим для решения статически неопредилимых задач, когда изгибающий момент в сечении заранее неизвестен. Оставляя пока в стороне статически неопределимые условия закрепления, изучим сначала прогибы стержня, считая силовые факторы в сечении стержня известными.
Параметры деформации и их физический смысл. Рассмотрим изгиб стержня в главной плоскости yOz (рис. 8.59). По гипотезе
34. ПРОГИБЫ СТЕРЖНЕЙ
283
плоских сечений (см. уравнение (2) гл. 2) деформация в точках поперечного сечения стержня
ег = ео+^-	(221)
Для параметров деформации 80 и dq>x/dz были установлены следующие зависимости для равномерно нагретого стержня (уравнения (14) гл. 2): N N N °~\EdF~ А F d<fx _ Мх _ Мх _ dz J i/EdF В* EJX F
(222)
(223)
где F, Jx — соответственно площадь и момент инерции поперечного сечения стержня.
Рис. 8.59. Связь прогибов оси стержня v(z) и углов поворотов q>(z) сечений (положительное направление поворота сечения показано на рис. 8.4)
Как известно, гипотеза плоских сечений предполагает, что сечение стержня остается после деформации плоским. Второе важное допущение — будем пренебрегать деформациями сдвига. Тогда плоскость поперечного сечения останется перпендикулярной изогнутой оси стержня после деформации.
Ось стержня —геометрическое место центров тяжестей сечения — в деформированном состоянии показана на рис. 8.59. Прогибы стержня в плоскости yOz обозначены v(z). Ось стержня в деформированном состоянии часто называют упругой линией стержня.
Физический смысл параметра деформации 80 hcqh; его величина представляет удлинение оси стержня. Сечение стержня как жесткая пластинка составляет угол л/2 с касательной к оси стержня. Учитывая положительное направление отсчета, принятое для угла <рх, следует записать
<рх = — arctg	(224)
Если углы поворота малы, то
(225)
284
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Угол поворота сечения равен (по величине) производной от функции прогиба стержня.
Дифференцируя равенство (255), находим
dz . dzr
(226)
Рис. 8.60. Геометрическая интерпретация изгибной
Параметр пзгпбной деформации при малых углах поворота сечения равен (по величине) второй производной прогиба.
Замечание. Допущение об отсутствии сдвига существенно упрощает картину деформации стержня при изгибе. Стержень можно представить в виде проволоки (ось стержня), к которой припаяны жесткие пластинки (поперечные сечения). Прогибы оси стержня и ее растяжение полностью определяют изменение расстояний, а следовательно, и деформации во всех точках стержня.
Геометрическая картина изгибной деформации. Рассмотрим чисто изгибную деформацию, когда удлинение оси стержня отсутствует (ео = О). Картина деформации приведена на рис. 8.60. Угол поворота сечения стержня фх показан в положительном направлении.
Отрезок АВ на расстоянии у .после деформации приобретает длину А* В*. Отрезок AqBq на оси стержня после деформации сохраняет свою длину (ео==О):
Л050 = Л5 = А*50* = ds. (227)
Деформация растяжения волокна на расстоянии у от оси стержня
__ Я*В* — АВ d<Px (Ry + y) — ds ez~~ АВ —	ds
<228>
здесь использовано очевидное соотношение
ds — Rydq)x.	(229)
Величина Ry выражает радиус кривизны упругой линии. Кривизна кривой — величина, обратная радиусу кривизны:
= 1 _ d<p* ,Ry ds *
Деформация удлинения оси стержня может быть добавлена к чисто изгибной деформации, и тогда
— 80 +	(231)
34. ПРОГИБЫ СТЕРЖНЕЙ
285
При малых поворотах сечений соотношения (231) и (221) совпадают, так как
. d s = dz
(232)
и при
dv V dz J
(233)
получим
ds = dz.
(234)
Применение условия (233) практически возможно при углах поворота до 20—30°.
Замечание. Переход от уравнения (224) к (225) связан с использованием условия (233). В общем случае из соотношения
dv t8<Px = -’d7
после дифференцирования по z получаем d /зшфх\ t d<px /у dz-^cos фху	С032фж dz ~ ~ ^2-
(235)
Так как
d2v(dz2
(236)
1	2	(dv \2
- ; = 1 + tg ф = 1 + I — j , COS фх	Л \az I
находим из соотношения (235)
fox 1
~ Ry~ [l+{dvldz)2\3lr
Если углы поворота сечения малы и условие (233) выполняется, то формулы (221) и (231) совпадают.
Уравнение упругой линии стержня. Продолжим рассмотрение изгиба в одной из главных плоскостей (в плоскости yOz) и будем считать, что нормальные усилия N в сечениях стержня отсутствуют.. Тогда из уравнений (223) и (226) находим * d2v (z) _	Мх W
dz2 -	EJx(zY
(237)
Полученное соотношение представляет уравнение упругой линии в дифференциальной форме.
Проинтегрируем обе части уравнения (237) от 0 до z; получим
dv z ч ( d7(z) = -J
О
+ £ (0).
‘ (238)
286
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
где zt — переменная интегрирования	В последнем ра-
венстве (0) — угол поворота (точнее, угол поворота в сечении стержня г-0).
Проинтегрировав обе части равенства (238)’ в тех же пределах, найдем
Z Z1
р (г) = - И dz*dz* + v (°) + (°)г- <239)
о Одинаковое обозначение
где р(0) — прогиб стержня в сечении z = 0.
Уравнение (239) представляет собой уравнение упругой линии. Входящие в него значения прогиба и угла поворота сечения при 2 = 0 определяются из условия закрепления стержня и граничных условий.
Замечание. Напомним, что величина интеграла не зависит от обозначения переменной интегрирования. Например,
XXX
J г2 dx = g2 d% = J «1	== 4"
0	0
именной интегрирования и переменного предела интегрирования может приводить к недоразумениям, поэтому в равенствах (238) и (239) вводятся обозначения zi и z2.
Примеры, поясняющие применение уравнения упругой линии.	ъ
1.	Прогибы консольного стержня постоянно-* го сечения под действием сосредоточенной силы Р (рис. 8.61). Стержень называется консольным, если одно из концевых сечений жестко закреплено, а другое свободно. Жесткое закрепление в сечении z = 0 (заделка) означает, что
dv
*(0)=0,	d7(°) = 0»
т.	е. смещение и угол поворота в заделке отсутствуют.. Изгибающий момент в сечении z
Mx(z) = P(l — z)>
Рис. 8.61. Прогиб консольного стержня под действием сосредоточенной силы
Из уравнения (239) получаем
Z Z1	Z
V W = — etJ J (1 ~ za) d22 dzi = ~ ЁГХ J “ Т Z1) dz 0 0	о
или
^(z) - — EjJ^ 2 lz*~ б z3)-
34. ПРОГИБЫ СТЕРЖНЕЙ
.287
Наибольший прогиб будет при z = I'.
Pl3
V^—3EJX-
2.	Прогибы консольного стержня постоянного сечения под действием распределенной нагрузки (рис. 8.62). Решение начинаем с определения изгибающего момента в сечении. Равнодействующая сил, приложенных к отсеченной
Рис. 8.62. Прогиб консольного стержня под действием распределенной нагрузки; а — расчетная схема; б —эпюра изгибающих моментов
Рис. 8.63. Прогиб двухопорного стержня (балки) под действием распределенной нагрузки: а — расчетная схема; б — эпюра изгибающих моментов
части, равна q(l — z); плечо равнодействующей (J —z)/2, следовательно, Mx(z) = -q(l-z)2-^. 	.
Из уравнения (239) находим
z Z1	-	-	--- 2
i’ (г) = — 2ЁТХ J J (г ~ za)2 dz2 dzi = — У ~ Zzi + T zi) = 0 0	0
_	_1_ (Zz3 , z4 \
-	2EJx\-2	Т +
Прогиб конца стержня (z == I)
ql* V^~~8EJX
3.	Прогиб двухопорного стержня постоянного сечения под действием распределенной нагрузки (рис. 8.63). В опорах стержня возникают реакции
Яд ==	= — gZ.
Изгибающий момент в сечении z 1 1 ЛГЖ (z) = — -у qlz + gz2.
В рассматриваемом случае условия закрепления таковы: г>(0) = 0,	v(0= 0,
288
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Из уравнения упругой линии (239) находим zzl
.v w = ~ih'x J j* (ч - zi) dz2 dzi+(°)z-о 0
Проведя интегрирование, получим q f «	1 >\ dv
v ~ i2EJx \JZ ~~2Z J	z'
Из краевого условия при z = I определяем dv (0) ql3 "dT =~2АЁТХ
Производная от функции прогибов в начале координат отрицательна (рис. 8.63).
Подставляя значение (0) в уравнение упругой линии, получаем а / 1	1	\
v (2\ = — 1257^. \ Т ^z ~~1г3 + ~2 2 * )*
Наибольший прогиб будет при z = J/2: И А _	5
Д 2 /-----384 EJX
Замечание. В технической литературе стержень, работающий на изгиб, часто называют балкой. Особенно распространено такое наименование в строительной технике, судостроении и в других об-

Рис. 8.64. Стержень (балка) на двух опорах под действием сосредоточенной силы: а — расчетная схема; б — распределение, изгибающего момента
ластях. Так как «стержень» дает описание геометрической формы элемента конструкции, то в дальнейшем он будет иметь преимущественное применение. В старой технической литературе вместо термина «стержень» использовался- тер- — мин «брус», который сейчас практически вышел из употребления.
Уравнение упругой линии при изгибе стержней постоянного сечения. Приведенные примеры определения деформирования оси стержня были относительно просты тем, что изгибающий момент Мх имел одно аналитическое выражение для всего стержня. Но уже для балки, показанной на рис. 8.64, изгибающий момент имеет два выражения:

»/,й-
при
при	Z,
с*
что делает более громоздким процесс интегрирования в уравнении (239). Можно, однако, существенно упростить использование уравнения (239) для нескольких типичных нагрузок, приведя уравне-
34. ПРОГИБЫ СТЕРЖНЕЙ
289
пие упругой линии к «стандартной форме». Разумеется, такая форма возможна только для стержней постоянного сечения. Для приведения уравнения упругой линии 'к стандартной форме, естественно, потребуется определенная формализация. Начало координат будем всегда помещать в левом конце стержня; направлениям внешних нагрузок в принятой системе координат припишем определенные знаки. На рис. 8.65 показаны положительные направления внешних нагрузок.
Рис. 8.65. Положительные направления внешних нагрузок для уравнения упругой линии в стандартной форме
Рис. 8.66. Единичная разрывная функция (функция Хевисайда)

К числу внешних сил относятся усилия и моменты в опорах стержня, и потому опоры стержня не показаны. Уравнение упругой линии (239) представим в следующей стандартной форме:
Р(2)^А-ф(2) + у(0) +J(0)Zj	(240)
где функция нагрузки
Ф (Z) =
J J Мх (z2) dz2 dz19 о о
(241)
При действии внешнего момента в сечении z = а выражение для изгибающего момента принимает вид ,
Mx(z) = P при	(242)
(— М при z>a.	4	'
Последнее равенство можно записать более кратко, если ввести единичную разрывную функцию (функцию'Хевисайда):
ЯМ-1? ПРИ	(243)
(1 при z>a.	'	'
График функции Хевисайда приведен на рис.,8.66. Если /(z)— произвольная (интегрируемая) функция, то
z	z
^^1,a)f(z1)dz1 = H(z,a)y(z1)dz1.	(244)
О	'	. а
. 19 И. А. Биргер, Р. Р. Мавлютов
290
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Последнее равенство очевидно, так как функция II(z, а) «уничтожает» все значения /(z) при z<a, Повторное интегрирование дает (проверьте!)	*
ZZl	Z *1
J j Н (z2, a) f (z2) dz2 dzx = H(z,a)§ J f (z2) dz2 dzv	(245)
0 0	a a
Равенство (242) представим в виде
Mx(z)=-II(z, а)М.	(246)
Функция нагрузки для внешнего момента па основании формулы (245) будет такой:
Ф (z) = Н (z, a) J j М dz2 dzr - Н (z, а) М	(247)
а а
Для внешней силы в сечении Ь
Мх (z)«< D.	, ч -	,	(248)
' P(z — д) • при z>b,	7
или
JMz)=-tf(z, b)P(z-b).
Функция нагрузки для внешней силы в сечении z имеет вид г2! Ъ	.
Ф (z) - Н (z, b) J j Р (z2 - b) dz2 dzx = Н (z, b) Р	(249)
ь ъ
Па участке	(рис. 8.65) к стержню приложена равномер-
но распределенная нагрузка с постоянной интенсивностью <?. Допустим сначала, что распределенная нагрузка приложена на всем протяжении (до-конца стержня) при с. Тогда изгибающий момент в сечении
Mx(z}-
0	при zс
L— с)2 ПРИ 2>с,
или
Функция нагрузки для распределенной нагрузки при z>c имеет вид
«zi	2
Ф (2) = J J я (z, С)	dzt = Н (z, с) q
*0 о
34. ПРОГИБЫ СТЕРЖНЕЙ
291
Представим теперь, что на участке при z > d приложена такая же нагрузка, по в противоположном направлении. Тогда для нее функция нагрузки представляется в виде
Ф(2) = -Я(г,^)?^=^.
Функция нагрузки для распределенной нагрузки на участке с z d будет такой:
Ф(2) = Я(2,С)?Ц^-Я(2,Й)(7Ц1^.	(250)
Рассмотрим теперь общий случай, когда на стержень в сечениях аь а2. ... приложены моменты Мь М2,	; в сечениях bt, b2, ...—
усилия Р2, •. и па участках с», распределена нагрузка qi. Всего таких сечений п (1 i С п).
В соответствии с принципом независимости действия сил, справедливым для упругих систем, при одновременном воздействии всех „ нагрузок уравнение упругой линии будет таким:
4	/	(z — аЛ2	(z —
^) = я (z’ а^м —2Г~ + H(z,bi)P L—1L +
X i=] \
+ Я(2,С{)7Ц^-Я(г,^/-Ц^-4) +P(O) + g(O)Z. (251)
Это и есть уравнение упругой линии в стандартной форме (или универсальное уравнение упругой линии). Его, можно дополнить учетом распределенной нагрузки с линейным и квадратным законом изменения по z, но в этом нет необходимости, так как нагрузку g(z) всегда можно аппроксимировать участками постоянной интенсивности. '
Пример использования уравнения упругой линии стержня в стандартной форме. Определим уравнение упругой линии стержня на двух шарнирных опо-. рах при действии сосредоточенной силы в середине пролета (см. рис. 8.64)'.
К стержню приложены три внешние силы в сечении z == 0 (Pi = Р/2), в сечении z = 1/2 (Р2 =="— Р) ив сечении z — Z (Р3 = Р/2).
По формулам (240) и (249) находим
P(z) = £y[tf (*,<))• ТРС-Я(г’Тг)Р^^^:г^-) + Т(0)г-
" * х \	“ о	6	/ dz
Сила Р3 (реакция в опоре В) в явном виде не участвует, так как приложена в правом конце стержня (Я(г, I) = 0). Из краевого условия и(1) = 0 получаем
dv	Pl*
dz (0) - “ 16£VX:
тогда уравнение упругой линии стержня примет вид
t9*
292
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Наибольший прогиб получается при z — 1/2\
( 1 \ PL3 и \ 2 / ~
Основная форма дифференциального уравнения плоского изгиба стержня. Ранее было установлено дифференциальное уравнение изгиба (уравнение (237)), которое запишем в следующей форме: £jx(2)^£l = _Mx(z).	(252)
dz
После интегрирования уравнения (237) или (252) были получены значения прогиба v(z) и угла поворота dv/dz (соотношения (238) и (239)). Однако во многих случаях более удобно определить в результате интегрирования все основные параметры задачи: прогибы, углы поворота, изгибающие моменты и перерезывающие силы. Для этого следует перейти к другой, эквивалентной форме дифференциального уравнения изгиба.
Дифференцируя равенство (252) по z и используя уравнение равновесия (82), получим
az \	dz ]
(253)
Снова повторяя дифференцирование и ссылаясь на соотношение
Рис. 8.67. Виды закрепления конца стержня: д—заделка; б —шарнирное закрепление; в — свободный конец; г — загруженный конец
(81), приходим к следующему дифференциальному уравнению: 2 /	2	\
A EJS(Z)£^ =9„(2)-	.(254)
az \	. dz /
Это и есть основная форма дифференциального уравнения плоского изгиба стержня.
Для стержня постоянного сечения (7x(z) = const) уравнение (254) будет таким:	,
d4v (z) Qy (z)
dz4
Дифференциальное уравнение определяет широкий класс функций.
34. ПРОГИБЫ СТЕРЖНЕЙ
293
Из него должна’ быть выбрана функция, удовлетворяющая краевым условиям задачи (т. е. условиям закрепления концов стержня). Разберем эти условия при 2 = 0 (рис. 8.67); при 2 = 2 они имеют точно такой же вид.
Конец заделан: и (0) = 0,	(0) = 0.
и
Шарнирное закрепление: v (0) = 0, —^(0)=0.
dz
Свободный конец:	(0) = 0,	\ EJX )	=0.
dz"	az \ dz" / |z=o
о	2
Загруженный конец: jt(0) =— „г-- EJ^	= — Р.
dz	L az J z==o
Если производная dlx/dz ограничена при 2 = 0, то второе условие для свободного конца может быть принято в более простом
виде:
(0) = 0.
dz3 7
Условия на загруженном конце согласованы с правилами знаков для Мх и Qx и условиями (252) и (253) (рис. 8.3).
Уравнение (254) представляет дифференциальное уравнение четвертого порядка, и для однозначности решения должны быть заданы четыре краевых условия (по два'на каждом конце). При наличии сосредоточенных моментов и сил должны быть заданы скачки производных в соответствующих сечениях.
Замечание. Уравнение (254) называется основным, так как объединяет основные уравнения изгиба: геометрические, физические и статические. Уравнение (252) включает уравнения равновесия только косвенно (при определении изгибающего момента).
В форме (254) уравнение изгиба используется в задачах колебания и устойчивости стержней и других задачах, где требуется более полный анализ. Уравнение изгиба в основной форме является разрешающим, т. е. позволяет по заданной функции g(z) найти основные параметры задачи без предварительного определения изгибающего момента в сечении.
Дифференциальное уравнение плоского изгиба в матричной форме. Уравнения изгиба (254) можно представить в виде совокупности четырех уравнений первого порядка. Введем следующие функции у, (.2) (г = 1, 2, 3» 4), подлежащие определению:
y1(z) = i?(z), t/2(z) = ^, y3(z)==Ms(z), y4(z) = <?y(z).
Тогда из уравнений (252) —(254) получим
J/'i(z) = y2(z)t j4(z) = —g-^y3(z), Уз(з) = у4(г), ^(z) = gv(z),
'(256)
где штрих означает производную по 2.
294
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Систему уравнений (256) запишем в матричной форме:
=	+	(257)
где вектор состояния			
(г/}т = (г/1, Уг	, Уз, yj =	v', м*, ел		(258)’
матрица MJ =	-0 1 о о- 0 0 -i/(EJx) 0 0 0	0	1 .00	0	 0-	>	
вектор внешней нагрузки {FY	= {0, 0, 0, 9„(z)}.		(259)
Уравнения в матричной форме хорошо приспособлены для-численного интегрирования на ЭВМ. Обычно для этих целей используются метод Рунге — Кутта и его различные модификации. Но весьма эффективным для решения уравнения (257) является метод последовательных приближений.


Рис. 8.68. Замена сосредоточенных воздействий распределенными
При наличии сосредоточенных силовых факторов их следует заменить эквивалентными распределенными нагрузками, действующими на малых участках (рис. 8.68)/При действии силы Р на участке 6 прикладывается распределенная нагрузка
=	(260)
момент М заменяется «парой» распределенных нагрузок и интенсивностью
qM = M/82.	(261)'
Величина б. в равенствах (260) и '(261) может быть задана произвольно, но она должна отражать реальные условия нагружения и особенности передачи сосредоточенных усилий на конструкцию (ширину накладок, местные утолщения и т, п.).
34. ПРОГИБЫ СТЕРЖНЕЙ
295
Замечание. Следует отметить, что понятие сосредоточенного воздействия является идеализированным. В действительности такие воздействия осуществляются в виде распределенных нагрузок на малых участках (см. рис. 8.28).
Нормальные фундаментальные функции дифференциального уравнения изгиба и начальные параметры. Если имеется линейное дифференциальное уравнение n-го порядка
(262)
то его общее решение может быть представлено в виде
^(2) = C1?/1(z)4-... . + Cnyrt(z) +{/*(z),	•	(263).
где yi(z) (f = l, п) —-линейно независимые частные решения, однородного уравнения
£(р) = 0;	(264)
г/* (z) — какое-либо частное решение; С\, ..., Сп — произвольные постоянные, определяемые из краевых условий.
Функции yi(z) (г=1, п) образуют систему фундаментальных функций уравнения (262) или (264). Так как любые линейные комбинации частных решений однородного уравнения также являются его решениями, то можно выбрать в качестве частных решений функции, удовлетворяющие следующему условию для производной /-го порядка в начале координат:
и) ™	(0) _ 1° при	р’ = 0,1,2,3;\
° —	— (1 ПРИ j = i —1 (i = 1,2,3,4 )• (265)
Верхний индекс в круглых скобках означает порядок производной-.производной нулевого порядка является сама функция (y(i0) = Vi)*. Например, функция yz{z) должна иметь при z = 0
г/2(0) = 0, ^(0) = !, ^2)(0)“0, j43)(0) = 0.	(266)
Частные решения однородного уравнения yf(z), удовлетворяющие при г = 0 условию (265), называются нормальными фундаментальными функциями. Выберем частное решение y*(z) таким, что при z = 0 само решение и его п — 1 первых производных обращаются в нуль:
у*(0) = 0, у*(1)(0)==0, ..., у*(Л-1)(0) = 0.	(267J
Непосредственным дифференцированием можно показать, что для дифференциального уравнения с постоянными коэффициентами условию (267) и уравнению (262) будет удовлетворять функция
y*(z) ==]«/„ (z-zJHzJdz,.	(268)
о
Если y,(z) являются нормальными фундаментальными функциями
296
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
и частное решение #*(z) соответствует условиям (267), то постоянные Ci. С2 получают ясный физический смысл.
D результате общее решение дифференциального уравнения (262) можно записать в следующей форме:
• L'(z) = v(Q)yt(z) + vw(0)y2(z) + ... + w(n-1)(0)y„(z) + y*(z). (269)'
Совокупность значений y(0), г/1>(0), ... называют начальными параметрами краевой задачи.
Особыми преимуществами обладают нормальные фундаментальные функции для дифференциальных уравнений с постоянными коэффициентами, весьма распространенными при решении технических задач. Для таких уравнений удается сразу записать решения, имеющие скачки производных. Пусть в сечении а3 заданы скачки производных
Д,у (z) = Д'°>, Д5у' (Z) = Д'1’, ..., Д'"-1’ (z) = Д'"-1’.	(270)
Общий интеграл уравнения (262) при наличии скачков пройзвод-ных в сечении z == а8 будет таким:
v (z) = v (0) г/1 (zj + ... 4- v(n-1) (0) уп (z) +
+ Ё Я (z, as) Д«%+1 (z — as) + у* (z). (271) 2=0
При скачках в других сечениях (a1? а2, ...) добавляются аналогичные суммы.
Рассмотрим теперь дифференциальное уравнение изгиба стержня постоянного сечения (уравнение (255)):
L(p;=$. = ^l.	.	(272)
dz. nJ х
Частными решениями однородного уравнения
= о	(273)
~	dz
могут быть любые линейно независимые полиномы не выше третьей степени. Легко проверить (проверьте!), что нормальными фундаментальными функциями для уравнения (272) будут следующие:	г .
Ъ	z3
У1(г) = 1, У2(г) = z,-y3(z) = -^-, y4 (z) = -^-.	(274)
Уравнение упругой линии стержня теперь получим как частный случай решения (271):
v(z)- у(0) + £(0)z + -$-(0)4 + $-(0)4 +
34, ПРОГИБЫ СТЕРЖНЕЙ
297
+ 2 Я (2, а8) [	+ Д<1’ (г - as) +' Д?’	+ Д?>	+
\	О:	/
о
Формула (275) представляет _ наиболее общее выражение для прогиба стержня. '
В практических задачах скачок прогиба почти не встречается, и можно положить
Д?* = V (а, + 0) - V (а, - 0) = 0.
Скачок первой производной (угла поворота двух смежных сечений) может быть при наличии внутренних шарниров. Скачки второй и третьей производных происходят в сечениях, где приложены сосредоточенные моменты и силы (см. рис. 8.65):
Z	д(2) _ М Л(3) _ Р
3 EJX' 1X3 ~ EJX'
В качестве начальных параметров в задаче об изгибе стержня обычно принимают следующие величины:
у(0), -^(0), Л/х(0) = -^-(0)£/х, <?«(0) = --7|(0)£Jx. az	dz	dz
Статически неопределимые задачи изгиба стержней* Если силовые факторы в сечении стержня (изгибающий момент, перерезывающая сила) не могут быть определены из условий равновесия (отсеченной части), то такие задачи относят к числу статически неопределимых. Рассмотрим несколько примеров решения подобных задач.
Пример 1. Стержень под действием распределенных усилий. Одно из концевых сечений заделано, другое шарнирно оперто (рис. 8.69, а). В системе имеется «лишнее закрепление» — шарнирное закрепление в точке А. Отбросим лишнее закрепление, заменив его неизвестным усилием Х\ (рис. 8.69, б).
Тогда получим статически определимую систему, которая называется «основной». По условиям задачи
р(0 =^61р + Х161г= 0,	(276)
где б ip —прогиб точки А от заданной нагрузки Р в направлении усилия Хь 6ц — прогиб от единичной силы, приложенной в точке 4, в направлении усилия Хь
Направление неизвестного усилия всегда предполагается заранее. Если в результате решения неизвестная величина Xi получается со знаком минус, то, следовательно, она направлена в противоположную сторону. Значение бц> может быть взято из решения задачи на рис. 8.62:
’ip - 8Е j;
298
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Величина 6ц определяется из решения задачи па рис. 8.61: о	1*
°11 “ 3EJ •
Теперь из уравнения (276) находим
~	8
Эпюры изгибающих моментов показаны на рис. 8.69, в.
Пример 2. Стержень на трех шарнирных опорах под действием распределенной нагрузки (рис. 8.70). Первый этап расчета — превращение системы
Рис. 8.69. Решение статически неопределимой задачи изгиба: а — расчетная схема; б — основная (эквивалентная) система; в — эпюры изгибающих моментов
Рис. 8.70. Расчет балки на трех опорах: а — расчетная схема; б — основная (эквивалентная) схема; в — эпюры изгибающих моментов
в статически определимую путем отсечения «лишних связей» и замены их действия неизвестными усилиями (рис. 8.70, б). Выберем основную систему в виде балки с двумя шарнирными опорами. Прогиб в точке А отсутствует, и потому
6[р + Xi6(I = 0.	(277)
Прогиб от внешней нагрузки в основной системе 6ip может быть определен из ранее решенной задачи (рис. 8.63). Учитывая, что общая длина балки 2/, найдем^
_	5 q(2lf 5 gZ4
°iP 384 EJX _ “ 24 EJX •
34. ПРОГИБЫ СТЕРЖНЕЙ
299
Величину бц —прогиб в направлении от единичной силы того же направления — принимаем из решения приведенного выше примера (рис. 8.64)
1-(2Z)3	№
дп~ 43и7х ~<iEJx'
Теперь из уравнения (277) находим
5
Эпюры изгибающих моментов (от нагрузки д, реакции в средней опоре п суммарная) приведены на рис. 8.70, в.
Замечание. Общин прием решения статически неопределимых задач изгиба (отбрасывание лишних связей, замена их неизвестными усилиями и определение последних из условий закрепления) составляет метод сил.
Учет деформации сдвига при изгибе стержня. Как уже указывалось, для коротких стержней и для стержней из материалов с небольшим сопротивлением сдвигу (композиционные материалы) перемещения, вызванные деформацией сдвига, оказываются соизмеримыми с перемещениями при деформации изгиба. Экспериментальные исследования и анализ точных решений показали, чго деформации сдвига можно рассматривать независимо от деформации изгиба. На рис. 8.71 показана деформация сдвига консольного
Рис. 8.72. Перемещение и деформация сдвига элемента стержня при
Деформации сдвига
Рис. 8.71. Деформация сдвига при поперечной нагрузке консольного стержня
стержня под действием поперечной нагрузки Р. Сечения стержня получают перемещения вдоль оси у, взаимный поворот сечений отсутствует.
Деформацию сдвига на оси стержня между направлениями у, z при работе материала в упругой области можно принять следующей:
(278)
где G —модуль сдвига; F(z)—площадь поперечного сечения;* Qv(z) —- перерезывающая сила в сечении; Ky(z) — безразмерный коэффициент, учитывающий неравномерное распределение каса
300
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
тельных напряжений при поперечном изгибе (рекомендации по определению величины Kv будут даны ниже).
Перемещение и деформация сдвига элемента стержня показаны на рис. 8.72.
Кроме поступательного смещенпя на усд(*) элемент может повернуться как жесткое целое на угол <р0, одинаковый для всех элементов стержня, так как взаимный поворот сечений отсутствует. Приращение прогиба, вызванное деформацией сдвига на участке dz
dvca (г) = Ку dz + <р0 dz,	(279)
откуда
dvnri (z) Q„
-^1 = Ку^ + фо.	(280)
Проинтегрировав обе части равенства в пределах от 0 до z, находим
z
Усд (z) = J Kv^ dz + 1>сд (0) + <Poz>	(281)
О
где рсд(0) и фо — соответственно прогиб, угол поворота сечения z = 0. Уравнение (281)—основное уравнение для определения прогиба стержней в результате деформации сдвига.
Пример 1. Определить прогиб сдвига для консольного стержня под действием усилия Р (см. рис. 8.71). Перерезывающая сила в сечении стержня Qy = Р. По формуле (281) находим прогиб на конце (угол поворота сечения и прогиб при z = 0 отсутствуют):
Р1 рсд — ку GF'
Прогиб конца стержня в результате изгиба, как было получено выше, равен
Р13
РИ (0 - 3EJX'
Отношение прогибов
Для прямоугольного сечения b X h (h — высота сечения)
F = bh, Jx = ЬЛ3/12.
Касательное напряжение при изгибе стержня прямоугольного сечения на оси
т — 3 vmax —
34. ПРОГИБЫ СТЕРЖНЕЙ
301
деформация сдвига
_ ттах _ 3 Qy G 2 GF'
Принимая = 3/2, получим для прямоугольного сечения
Х ~ 8 G f
Для обычного конструкционного материала
£/G = 2(l + |x), где р. — коэффициент Пуассона. Отношение прогибов сдвига и изгиба
3 Д2
_ Х=Т(1 + ц)-^.
При высоте сечения h = I прогибы приблизительно одинаковы. При расчете на прочность зубьев шестерни, витков резьбы деформация сдвига должна обязательно учитываться.
Пример 2. Определить прогиб двухопорного стержня в результате деформации сдвига (рис. 8.73).
Реакции в опорах равны
1
Яд —	— 2
У
*АМ
Я
ШШНМИМИ1
в
А
Перерезывающая сила в сечении равна-1
Qy ^)= — ~2Ql + qz.
По формуле (281) находим прогиб двухопорного стержня z
гсд <z> =	(“4 + ?2i) dzi + V-
_ Рис. 8.73. Определение прогиба сдвига двухопорной балки
Для стержня постоянного сечения
К
"ед (z> = - ор- у <Zz - z2) + Фо2-
Из условия г>сд(О = 0 находим фо = 0.
Последний результат можно установить сразу, так как сечение z == 1/2 не поворачивается вследствие, симметрии.
Окончательно получим	-
к
Рсд(г) = _2^’з(/г“г2)‘
Замечание. Нельзя сделать вывод, что сечения стержня вообще не поворачиваются при деформации сдвига. Если, например, в задаче на рис. 8.73 половина балки имела бы другие размеры сечения, то фо ф 0. При наличии заделки или плоскости симметрии фо == 0.
Уравнение упругой линии стержня при изгибе в двух главных плоскостях. 'Как уже указывалось, если нагрузки действуют в плоскости, совпадающей с одной из главных,, то стержень йены-
302
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
тывает плоский изгиб. В этом случае упругая линия стержня является плоской кривой.
Однако часто нагрузки действуют не в главной плоскости пли даже не в одной плоскости либо стержень обладает начальной закруткой (воздушные винты и др.) — все это приводит к задачам пространственного изгиба стержня.
На рис. 8.74 рассматриваются изгиб и растяжение лопатки турбины. Главные оси сечения х, у повернуты относительно осей конструкции х0, Уо на угол а (ось х0 направлена вдоль осп вращения, ось z— вдоль оси лопатки в радиальном направлении).
Рис. 8.74. Изгиб стержня в двух главных плоскостях (yOz и xOz): а —- изгиб лопатки компрессора (изгибающие моменты изображаются векторами); б — правило изображения
В сечении z действуют растягивающее усилие # и изгибающие моменты MXq и MyQ. На рис. 8.74 они изображены векторами, причем момент стремится осуществить поворот против часовой стрелки, если смотреть от конца вектора момента к его началу (правая система координат). Наиболее важное правило при исследовании пространственного изгиба-состоит в следующем: изгибы в главных плоскостях можно рассматривать независимо друг от друга.
Изгибающий момент,- действующий в главной плоскости yOz (рис. 8.75),
Мх = MXq cos а + MyQ sin а.	(283)
По уравнению (237)
Л/ '	4
(Мх0cos а + sin “)•	(284>
Изгибающий момент, осуществляющий изгиб в главной плоскости xOz,
Му = MVq cos а — MXq sin а.	(285)
Из уравнения (16). при отсутствии температурной деформации и
34. ПРОГИБЫ СТЕРЖНЕЙ
303
при постоянном модуле упругости получаем dVy == Му dz	EJ у ’
(286)
где Jу — ) я2 dF — момент F
инерции сечения относительно оси у.
Рис. 8.75. Определение изгибающего момента относительно главных осей
Рис. 8.76. Пространственная упругая линия стержня
Будем обозначать компоненты смещения центра тяжести сечения но осям х и у соответственно u(z) и v(z). Учитывая принятое правило знаков для углов поворота сечения (рис. 8.76) и считая их малыми, будем иметь
dv (z)
<ря = ——
du (z)
^ = 7^—
(287)
(288)
(Дайте объяснение, почему формулы (287) и (288) имеют в правых частях разные.знаки!)
Из соотношений (285), (286) и (288) находим ч
(289>
ttZ	у	у
В общем случае изгиба упругая линия является пространственной кривой — точки оси стержня получают смещения по направлениям х. и у. Уравнения (284) и (289) определяют прогибы стержня в общем случае изгиба:
Напряжения в точках поперечного сечения стержня находятся по формуле (18):	~	_
N	Мх	Му
° = Т + у — ' Л	X	у
(290).
Замечание. Приведенные уравнения пространственной упругой линии относятся к призматическим стержням. Если главные оси сечений имеют в начальном состоянии взаимный поворот (стержни с первоначальной закруткой: воздушные винты> лопатки и т. п.), то уравнения (284) -и (289) дают компоненты вектора кривизны, которые следует проектировать на общие оси хо, уъ
304
ГЛ. 8. ИЗГИБ СТЕРЖНЕЙ
Пример. Стержень прямоугольного сечения изгибается силой Р и растягивается усилием N (рис. 8.77). Требуется найти напряжения в точках стержня и перемещения точки приложения сил. Главные оси сечении — оси х, у.
Рис. 8.77. Пространственный изгиб стержня
Изгибающие моменты в опасном сечении (т. е. в сечении, где имеются точки с наибольшими напряжениями) определим двумя способами. Сначала определим общий момент, модуль которого Мр = Р/, а проекции момента на оси х и у
"Мх = — Pl sin а, Му == Pl cos а.
Более просто в рассматриваемом примере разложить усилие Р на составляющие Рх и Ру и найти значения Мх и Ми. Напряжения в поперечном сечении
2V	Му
а =	4- аи = — -у у —у— 4. х —j--,
где аР — напряжение растяжения, распределенное равномерно по площади поперечного сечения; напряжения изгиба
*'х
аи — У j х у *	(291)
Jx
В поперечном сечении существует линия, которая называется нейтральной* в точках которой напряжение изгиба равно нулю. Уравнение этой линии, проходящей через центр тяжести сечения, имеет вид
у	^у
х х J у
В рассматриваемом примере
У х
cos а / Ь \2 sin а 1 Л /
Если b = h, то нейтральная линия перпендикулярна плоскости действия нагрузки/
ГЛАВА 9
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ, ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ, ОБЩИЕ СВОЙСТВА УПРУГИХ СИСТЕМ
Ранее для анализа распределения напряжений и деформаций применялись дифференциальные методы, основанные на геометрических, статических и физических соотношениях, описывающих поведение частицы материала или элемента конструкции. В результате получались дифференциальные уравнения, характеризующие «условия жизни» малого элемента. Интегрирование указанных уравнений давало описание работы всей конструкции, т. е. учитывало совместную работу всех сопряженных элементов. Краевые условия при интегрировании дифференциальных уравнений отражали особенности поведения элементов, примыкающих к границам тела. Однако существуют и другие методы анализа, которые могут быть названы вариационными. Эти методы основаны на изучении общих количественных характеристик конструкции (функционалов), таких как энергия деформации, работа внешних сил при деформации конструкции и т. п. Условие того, что функционал для всей конструкции должен приобретать минимальное значение, накладывает определенные ограничения па поведение каждого элемента. Эти ограничения или условия оказываются как раз теми дифференциальными уравнениями, которые изучались ранее. Таким образом, дифференциальные и вариационные методы не противоречат, а взаимно дополняют друг друга. Общность анализа, возможность использования приближенных методов, удобных для численной реализации на ЭВМ, делают вариационные или энергетические методы весьма важными для прочностного анализа конструкции.
Вариационные методы связаны с понятием функционала. Функционалом называется скалярная величина (число), зависящая от поведения функции или нескольких функций в определенной области. Например, длина кривой, соединяющей две заданные точки пространства, является функционалом; он имеет минимальные значения для линейной функции (прямой).
Вариационные методы приложимы для различных моделей материала, но в дальнейшем ограничимся рассмотрением работы конструкций в упругой области.
35. Потенциальная энергия деформации
Предварительное замечание. При деформации упругое тело накапливает энергию деформации за счет работы внешних сил. Сжатая пружина может возвратить затраченную на ее сжатие работу, так как обладает потенциальной энергией деформации. Это явление используется в ряде технических устройств (заводные пружины часов, пружины воздушных тормозов железнодорожных вагонов и т. п.). Ближайшая задача состоит в получении общих формул для определения потенциальной энергии деформации, но начнем с рассмотрения простейшего случая — растяжения стержня.
Потенциальная энергия деформации при растяжении и сжатии стержней. Рассмотрим растяжение стержня усилием N (рис. 9.1,а). Усилие возрастает медленно от 0 до А и по закону упругости: пропорционально силе увеличивается удлинение стержня. Пренебрегая кинетической энергией частиц стержня и изменением их тепловой энергии в процессе нагружения, считаем по закону сохранения энергии, что потенциальная энергия деформации U 20 и. А. Биргер, Р. Р. Мавлютов
306
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
равна работе внешней силы: ы
(1)
о
где Nt и AZi — значения усилия и удлинения в промежуточный момент нагружения.
По физическому смыслу интеграл (1) равен площади па рис. 9.1, б:
U = ±-NM.	(2)
При растяжении стержней
А 7 т
^1 = -Ге'
(3)
упругости; F — площадь поперечного сечения (из-
Рис. 9.1. Зависимость N и удлинения Д/ при растяжении стержня: а _ этапы нагружения; б — изменение усилия и удлинения в процессе нагружения
N
5
менением F в процессе деформации пренебрегают как малой величиной); I — первоначальная длина стержня.
Множитель 1/2 в формуле (2) появился потому, что в процессе нагружения усилие было переменным (от 0 до 2V). Из равенств (2) и (3) получаем два эквивалентных выражения:
77= 1	= 1 EF^ (Л\
U 2 EF 2 I
Введем понятие удельной потенциальной энергии деформации Ut или Потенциальной
энергии деформации, приходящейся на единицу объема. Тогда

(5)
где V — объем тела.
При растяжении стержня силой N величина Ut одинакова для всех элементов стержня, и потому
где IF = V —- объем стержня.
Из соотношения (4) находим
тт 1	- 1 а2 1^2
U г — 2 08 — 2 Е — у £е ,
(6)
35. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
307
где e — N/F и е = &1/1 — напряжения и деформации в стержне. Важное для дальнейшего рассмотрения равенство (6) можно получить непосредственно из уравнения (1).
Введем замену переменных, обозначая
где 81 = Д/t/Z — деформация в данный момент нагружения (новая переменная). Тогда из равенства (1) получаем
х	U == IF J Й8г
о
и удельная энергия деформации равна
е
=	(7)
о
Принимая соотношение упругости
01 == Ееъ найдем
С71 = 1Ее2, что совпадает с равенством (6).
Другой вывод формулы для потенциальной энергии деформации при растяжении и сжатии стержней. При действии внешней (растягивающей) нагрузки в сечениях стержня возникают внутренние силы упругости. Так как стержень деформируется, то внутренние силы упругости совершают работу.
Рис. 9.2. Вычисление потенциальной энергии деформации как работы внутренних сил упругости: а — работа внутренних сил упругости с учетом перемещений сечений стержня; б — работа внутренних сил упругости как работа при деформации элемента
Рассмотрим элемент стержня (рис. 9.2, а). В сечении стержня действуют напряжения о, которые прикладывались статически. Работа внутренних сил упругости при деформации элемента стержня может быть вычислена так: 1	1	/ du \	1	‘ ,
= — "2 Раи + ”2* PQ ( и + "fa ~ ”2*
20*
308	ГЛ. 9- ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
где u(z) — перемещение сечения стержня, е = du/dz — деформация материала стержня.
Работа внутренних сил упругости во всем объеме стержпя
I	I
Ав =	= f Mdz = V™	(8)
J	«J	£
о	0
где V = IF — объем стержня.
По закону сохранения энергии работа внутренних сил равна работе внешних сил и одновременно потенциальной энергии деформации:
Удельная потенциальная энергия равна
U 1
= V =~2 а8>
что совпадает с равенством (6).
Наконец, равенство (9) можно получить еще одним способом, рассматривая работу при деформации элемента (рис. 9.2, б).
Сечения элемента при деформации получат относительное смещение е dz. Работа сил упругости при деформации элемента
1 1
= у 08 dz F = ~2 ое dV', удельная потенциальная энергия деформации
Z7=±L = Aa6)	(10)
1 dV 2	’
что снова приводит к прежним результатам.
Удельная потенциальная энергия деформации. Рассмотрим теперь общий ^случай определения потенциальной энергии деформации произвольно нагруженного упругого тела. Сначала будем считать, что на элемент тела действуют только нормальные напряжения (рис. 9.3). По граням элемента цриложены напряжения ох, ог. Изменения этих величин, вызванные приращением координат в пределах элемента, можно не учитывать, так как соблюдаются уравнения равновесия.
Работа внутренних сил упругости в результате деформации будет такой:
1 1
dU — -yOxdy dz-e.xdx + у avdzdx-zvdy +
1 1
+ yQzdxdy• ezdz =	(axex + vy&y + а2ег) dV,
где dV = dx dy dz.
Потенциальная энергия деформации равна
V
((Мх + VySy + Сге2) dr,
35. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
309
а удельная потенциальная энергия деформации — ^1=4 (°хе*++ga)-	си)
В частном случае одноосного растяжения получаются прежние зависимости.
Перейдем к определению удельной потенциальной энергии при деформациях сдвига. На рис. 9.4 изображен элемент тела, испытывающий дефомацию сдвига в плоскости ху.
Рис. 9.3. Определение потенциальной энергии деформации* при трехосном растяжении (сжатии)
. тенциальной энергии деформации при сдвиге
Первоначально прямой угол между осями х и у после деформации изменяется на величину
Ixv = Tfixv + 72X1/.	(12)'
Работа внутренних сил упругости, характеризующихся касательными усилиями на гранях элемента, можег быть выражена таким образом:
1 •
dU = (Тху dy dz-y1Xy dx Хух dx dz • у%ху dy)*.
Множитель 1/2, как и раньше, связан со статическим приложением усилий от нуля до максимальной величины к упругому телу, Вследствие свойства парности касательных напряжений
Тзеу — Тух, и с помощью соотношения (12); находим dU — -g- ХхуУху
Удельная потенциальная энергия, деформации при сдвиге в плоско-» сти ху равна
в у ХхуУху:	(^)
310
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
Существенно, что удлинение ребер элемента не влияет на энергию; деформации сдвига, гак как касательные напряжения не производят работы при деформациях 8Х и 8^. Соотношения, подобные (13), справедливы при сдвиге в других плоскостях.
Объединяя результаты для растяжения и сдвига, получим общую формулу для удельной потенциальной энергии деформации:
U 1 = ~ (^Х^Х 4" ®У&У 4"	4“ ^ХуУху 4" 'tyz4yz 4" ^ZxYzx) •	(14J
В более кратком виде формулу (14) можно записать так: ^ = jHN = |{e}TM	(15)
где {о} и {е) — векторы напряжений и деформаций; т — знак транспонирования.
Другие формулы, для удельной потенциальной энергии деформации получаются из основной зависимости (14) при учете соотношений упругости (разд. 18).
Если не принимать во внимание температурную деформацию, то для изотропного тела.
1 1
 бх = j fax — Н (^ + <ъ)], •• Уху = Q Ъу, •  • (х, у, г).	(16)
Внося соотношения (16) в формулы (14), получим после песлож-ных преобразований
U, = oV [о? 4- <Jy + Gz — 2|Л (OxOj, + ОуСг + ozax) +
4- 2 (1 4- p) (тхт/ 4: t?/z 4- TzX)]. (17)
При выводе была учтена зависимость между модулем упругости Е и модулем сдвига G:
г = _А_ 2(1 + р)‘
Формулу (17) можно записать в более кратком виде, если представить соотношения упругости в матричной форме (разд. 18):
{е} = [Л]{о}.	*	(18)
Тогда получим следующий результат:
£71 = |{о}тЦ]{о}.,	(19)
Последняя зависимость справедлива и для анизотропного тела, что отражается только в структуре матрицы.
Представим теперь удельную потенциальную энергию деформации как квадратичную функцию деформаций. Ддя изотропного уп
35. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
311
ругого тела, пренебрегая температурными деформациями, будем иметь (разд. 18)
°x = 2G8x + (T+W^)8- •	W
где 8=(ех + еу4-8г)/3 — средняя деформация.
Из соотношения (14) получаем
иi = 2 (1 ц) Г8* + £У + £z + ! __2ц	+ V (Уху + Ууг + Yzx)l, (21)
* Ц I Р? L	*	“Г*	~	J
или в другой форме
U 1 = 2 (i'T7t~ /—"2р	+	+	+ 1 — 2|л' ^хЕу + £уЁг + e*8x) +
+ У (тху + Ууг + Yzx)]- (22)
Дадим матричную запись уравнений (21) и (22). Так как
{о) = [С] {е),	(23)
где [С] = [А]-1 — матрица коэффициентов жесткости, то из соотношения (А5) получаем
U, = |{8}тА{е).	(24)
Последнее равенство справедливо и для анизотропного тела, если соответствующим образом выбрать матрицу коэффициентов жесткости.	.
Отметим еще две группы соотношений, представляющие интерес в теоретическом плане. Они получаются непосредственным дифференцированием равенств (17) и (22):
= 4 (ff* — Н (°у +	= 2 (1 + Тж;/ _	(25)
^=2Сех + йТШГ^ад8 = Ох’ 2"1'Тй)Тху==Тху- (26)
Потенциальная энергия деформации стержней при растяжении и изгибе. Ранее была установлена формула для'потенциальной энергии' при растяжении стержня постоянного сечения двумя усилиями по концам:	*	'
(27)
Получим теперь более общую формулу с помощью выражения (17).
При растяжении стержня отличным от нуля является нормальнее напряжение ог = о (ось z направлена вдоль, оси стержня).
Из соотношения (17) следует, что
312
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
Потенциальная энергия стержня будет равна
и =	= J(j^dF|dz.	(28)
V	О	J
Здесь предполагается, что ось стержня прямолинейна и совпадает с осью
В общем случае стержень может состоять из отдельных участков, оси которых направлены под углом друг к другу, или быть криволинейным; тогда
i .
= - (29>
о \г /
где ds — элемент длины стержня, I — полная длина стержня. Для стержня с постоянными параметрами упругости
(30)
J & 2ЕГ‘ (i) J 2EF Ы f	if
Потенциальная энергия стержня при растяжении равна i
О
В частном случае при постоянных значениях 2V(z)' и F(z\ получав гея равенство (27).
Для стержня с переменными параметрами упругости (разд. 4)
EN .
Е dF,' F
Теперь из равенства (28) находим
(31) •
о
где A (z) = J Е dF — жест&ъсть сечения стержня на растяжение. •
F	а’
Рассмотрим теперь потенциальную энергию деформации при плоском изгибе стержня с постоянными параметрами упругости (рис. 9.5). Пренебрегая сначала касательными напряжениями изгиба,
35. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
813
воспользуемся равенством (28), полагая
Мх
° = —у-
* X
Так как
Со2 М*
I U 7 Г»______X
J 2£	~ 2£V_’
F	*
то получаем значение энергии деформации:
U =
X
(32)
О
Аналогичное соотношение
имеет
место
при
изгибе
плоско-
сти
£dz.
у
о
Рис. 9.5. Определение потенциальной энергии деформации при изгибе стержня
Рис. 9.6. Определение потенциальной энергии деформации, связанной с касательными напряжениями изгиба
в
Потенциальная энергия деформации при одновременном растяжении и изгибе стержня равна
и = <зз>
Z J Ег	4 J LJX	£ J tLJ	'	'
о	о	О
Для стержня с переменными параметрами упругости получаем
314
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
подобную зависимость:
ООО
где А = J Е (IF, Вх = J Еу2 dF, Ви = j* Ex2 dF — жесткости сечения F	F	F
стержня па растяжение и изгиб.
Замечание. Равенства (33) и (34) не учитывают касательных напряжений изгиба. Как уже указывалось, их влияние может быть значительным для коротких стержней и для стержней из материалов с малым сопротивлением сдвигу.
Потенциальная энергия деформации, связанная с касательными напряжениями изгиба. При изгибе стержней поперечной нагрузкой возникают касательные напряжения (разд. 31).
Для плоского изгиба (рис. 9.6) касательное напряжение
где Qy — перерезывающая сила в сечении, SXf = J у dF — статиче-/
ский момент части сечения.
Потенциальная энергия деформации по формуле (17) будет равна
1 /
и = f IJ Ul dV = J (J ё dF Idz' (36) V	о	/
так как учитывается только касательное напряжение туг = т.
Далее найдем с помощью равенства (35)
=	=	(37)
F	х F
где безразмерный коэффициент
(М)
учитывает неравномерное распределение по поперечному сечению касательных напряжений изгиба.
Потенциальная энергия деформации, связанная с касательными напряжениями изгиба, равна
<39>
о
35. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
315
Если касательное напряжение распределяется равномерно по сечению:
т —- F (z) ’
то из уравнений (37) и (38)	—
Зависимость, подобная (39), существует и для изгиба в другой главной плоскости:
. <«> о
Для стержня с переменными параметрами упругости касательное напряжение изгиба
где SExf == j* уЕ dF; Вх = J Еу2 dF. f	F
Выражение для потенциальной энергии деформации можег быть принято в такой форме:
' <42>
О	"
где
 - -	Д/== [ GdF	-	(43)
F
— жесткость сечения на сдвиг, • к	(44)
Для использования приведенных зависимостей необходимо знать величины К* и Kv. Их определение покажем на следующем примере.	\	.
Пример определения коэффициентов касательных напряжении. Рассмотрим стержень прямоугольного сечения (рис. 9.7). Для такого сечения
р_.. т ' bh\ *	_ 1 Jh?
F = bh’ ^ = ^2’	=	J"
Расчет проводим по формуле (38). Находим
316
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИИ
Далее получаем
Ку
F CS2xf bh-122 bh5
~J2A b2 F~ bW 12-10- 5 -1-X F
Замечание. Коэффициент Ky определяется в результате осреднения энергии деформации сдвига. При учете влияния сдви-
Рис. 9.7. Расчет коэффициента касательных
га на прогибы стержня (разд. 34) принималось для прямоугольного сечения Ку = 3/2 по максимальному значению касательных напряжений.
Величину Ку — 1,2, выражающую «среднеквадратичное касательное напряжение», следует считать более точной.
В общем случае в сечении стержня действуют растягивающее усилие N(z), перерезывающие усилия Qx и Qv, изгибающие моменты Мх и Му.
Потенциальная энергия деформации вы-
напряжений ражается следующим равенством:
1 И^2 , = i +
'О
Г И’
Ы.*+ о
СО2 СО2]' \Kx£ds +	. (45)
J Crr J Стг I О	0	. >
Формула (45) объединяет ранее рассмотренные составляющие энергии деформации.
Возможность простого суммирования энергии растяжения и из-.гиба вытекает из того, что оси х и у являются главными осями сечения. Элемент длины вдоль оси стержня обозначен ds (см. формулу (29)), так что имеется возможность использования равенства (45) для стержней ^ непрямой осью.
Для стержней с переменными параметрами упругости имеем
О ~ у
где Л, Вх, Бу и Лт — жесткости сечения на растяжение, изгиб и сдвиг; коэффициенты Кх и Ку вычисляются по формулам типа (44). " Потенциальная энергия деформации стержней может быть представлена по-другому.
Из соотношений (14)— (16) гл. 8, пренебрегая температурными деформациями, получим
Мх dz	EJX ~~ Вх*
dz	EJy В*
35. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
317
Деформации сдвига для точек оси стержня „ Qu „ Qy
Уух -	- Ку-^,
v — К ®х — К $х
Ухг -	ХЛ7’
(47)
В формулах для деформаций отмечается и общий случай, когда параметры упругости переменны по сечению и длине.
На основании равенства (45) и последних зависимостей получим
{I	I	I	I	I	ч
J 7Ve0 ds + У Мх	ds + J Mv ds + J ds+^Qyyyz ds •
0	0	0	0	0
(48)
Равенство (48) имеет ясный физический смысл: потенциальная энергия деформации равна работе внутренних силовых факторов.
Рис. 9.8. Работа силовых факторов при деформации элемента стержня
На рис. 9.8 показана деформация элемента стержня при плоском изгибе.
Работа внутренних силовых факторов при деформации элемента стержня равна .
dU= N&0 ds + -i- Мх dtp» + -у Qy^xy ds.	(49)
< Наконец, можно выразить потенциальную энергию деформации стержня через параметры деформации:
r;“i J 'О
о
о
О
I	' <
С JT- Ау (Ууг)I 2 ds .	(50)
v
о
318
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
Замечание. В большинстве практических задач при вычислении потенциальной энергии деформации слагаемыми, связанными с учетом касательных напряжении изгиба, можно пренебречь.
36. Вариационные методы
Введение. После приложения внешней нагрузки произойдет деформация конструкции (тела) и установится равновесие. Состояние равновесия можно проверить по выполнению условий равновесия каждого элемента тела, по можно использовать и другой путь: проанализировать поведение системы при малых возможных отклонениях (вариациях). Именно этим путем в теоретической механике (механике твердого, недеформируемого тела) были получены общие уравнения равновесия Лагранжа (начало возможных перемещений). Состояние упругой деформированной системы может быть однозначно описано перемещениями ее точек в процессе деформации — функциями u, v и w. Полная потенциальная энергия, как будет показано в дальнейшем, может рассматриваться как функционал
J = J(zz, у, w).	(51)
При вариациях функций u, v, w (малых отклонениях, согласовап-обозначаются би, би и 8w, изменяется величина функционала. Считая отклонения достаточно малыми, можно записать
6J = J(u + 6u, р + би, zz; + 6zz?)’~
— 7(u, u, zp). (52) Состояние равновесия системы характеризуется условием
67 = 0.
Прежде чем перейти к дальнейшему изложению, остановимся вкратце па математической стороне вопроса.
Пусть имеется функционал, зависящий от функции f(x): b'
/(/) = Р (/,/', Г,	(53)
а
где F — некоторая функция, зависящая от функции /, ее первых производных и независимого переменного х. Например, если /(х) представляет кривую, проходящую через две заданные точки- А и В (рис. 9.9), то функционал
ь
. /(/)’ J + а
равен длине кривой Lr
пых со связями), которые
Рис. 9.9. Понятие вариации функции
36. ВАРИАЦИОННЫЕ МЕТОДЫ
319
Рассмотрим другую функцию /t (х) — функцию сравнения, которая проходит через те же точки, и назовем вариацией функции
б/(^)= Л(о;)— /(хг).	(54)
Вариацию функции можно дифференцировать, причем
<55>
Операции варьирования и дифференцирования переставимы; 6/' (х) означает вариацию функции /' (х). Вариация функционала (53) равна приращению функционала в результате вариации функции / и ее производных:
ь	ъ
67 (/)= р(/ + б/, Г + 6/', f + 6f, x)dx- f F(f, f, Г. x}dx~ а	а
Ъ
= j (7 + б/,/'+ 6/',/"+6f", х) — F x)J dr. (56) а
Считая вариации функции малыми величинами и рассматривая /, /' и f" как независимые аргументы функции F, запишем
Л/ + б/, Г + б/',Л+бГ,х)==
= F и, Г, f\ *)+ % У + W 4- 6f + О (6/, 6/', 67"), (57)
где O(5f,	6f") — величина более высокой степени малости отно-
сительно б/, б/', 6/".
Теперь, используя соотношение (57) и пренебрегая 0(6/,б/',б/"), находим нз равенства (56)	_	____
о
б/ (/) = J б/ +	67' +	6/j dx.	(58)
а 4
Замечание. Поясняя равенство (57), папомним, что функция многих переменных Ф(х, у, z) может быть разложена в ряд в окрестности точки х^ уъ, zo по формуле
дФ дФ дФ
Ф(х, у, г) = Ф(х0, у0, 20) + ^-.Дх + ^-Ду + -^-Дг + О(Дл:, Ду, Дг),
где Дх = х — х0, Ду — у —- у0, Дг = z — z0.
Равенство (57), в сущности, совпадает с приведенной формулой. Напри-• мер, если
Г, Г» == //' +/^4-/'2, то dF , dF , dF df — ’ df —	• df“
В равенстве (57) отсутствует частная’ производная по х, так как величина х'не варьируется.
320
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
Условия экстремума функционала, уравнение Эйлера — Пуассона, метод Рэлея — Ритца. Поставим задачу — отыскать функцию /(х),для которой первая вариация функционала обращается в пуль:
6J(/) = 0.	(59)
Функция /(х) а этом случае называется экстремалью, а значение J(j) — экстремумом функционала.
Равенство (58) не дает сразу ответа для поставленной задачи, так как подынтегральные члены разнородны. Преборазуем правую часть уравнения (58) с помощью интегрирования по частям. Предварительно отметим ь*	ь	ь
а	а	а
Подобные преобразования дают b	ь	’	ь
J д± 6Г dx = J£ (6П dx=d± 6Г Га - J £ (57) 6/' dx. (61) а	а	а
Повторяя интегрирование по частям в последнем члене равенства (61), находим Ь	ь
JУ W	- Яй - В (Я	J(’Я «	<62>
а	а
Теперь условие (59) можно записать так: ъ ИдР	d (дР\ , d2 !дР\\^ , ,
df dx [df'} +	(d/")] W dx +
+ p7“ s(5?)]e/K + ^S/'ii-0- (S3) Равенство (63) должно быть справедливым для произвольной вариации б/. В частности, если рассматривать вариации б/ и б^\ обращающиеся в нуль на концах интервала, а в промежуточных точках произвольные, то интеграл будет равен нулю только при условии дР d !дР\ , d\(dF\ А	,а/ч
Это и есть дифференциальное уравнение Эйлера — Пуассона для функции /(я). Опять же в силу произвольности вариации б/ должны выполняться краевые условия
<65>
^8/'Й-0-	(66)
3G. ВАРИАЦИОННЫЕ МЕТОДЫ
321
Итак, для решения вариационного уравнения (59) следует найти решение уравнения (64) при краевых условиях (65) и (66)'.
Построение точных решений дифференциальных уравнений часто оказывается затруднительным, и для решения уравнения (59) применяют приближенные методы, в частности метод Рэлея — Ритца.
Метод Рэлея — Ритца состоит в следующем. Допустим, что функция /(х) может быть представлена рядом
/W = ici/i(x),	(67)
i=l
где /<(х)—заранее выбранные функции, удовлетворяющие наложенным на систему связям; с* — коэффициенты, подлежащие определению.
Соответственно
/' (х) = S Ci/i (*),	(68)
i=l
Г(х)= Sci/Цх).	(69)
Внося значения /(х), f (х) и /" (х) в равенство (59) и проведя интегрирование, находим
J(/) = J(C1, с2, ..., сп).	(70)
Вариация функционала теперь определяется так:
Учитывая условия (59) и считая вариации совершенно произвольными, получаем п уравнений
а/ А . Л—
^ = °>	(71)
из которых определяем п неизвестных: си .., сп.
Примеры использования уравнения Эйлера — Пуассона и метода Рэлея — Ритца будут приведены в дальнейшем.
Точное решение вариационного уравнения
W(/)-o
должно обеспечивать его выполнение при произвольных вариациях f, разумеется, согласованных со связями системы. В методе Рэлея—Ритца вариация.
6/=S&i/i(x).'
Класс вариаций функций ограничен выбором и числом функции, что означает наложение дополнительных связей на систему» 21 И. А. Биргер. Р. Р. Мавлютов
322
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
повышающих ее «жесткость». Очевидно, если система функций обладает достаточной полнотой, приближенное решение будет ближе к точному.
Применение начала возможных перемещений, вариационное уравнение Лагранжа. Пусть имеется твердое деформируемое тело (рис. 9.10), к поверхности которого приложены распределенные нагрузки р, а на элементы тела действуют массовые (объемные) силы F.
Допустим, что упругие смещения точек тела и, у, w получили вариации (возможные перемещения) би, би, би?, совместимые с геометрическими связями. Поэтому на части поверхности где смещения являются заданными (например, поверхность заделки), вариации смещений отсутствуют. В результате вариации смещений изменится потенциальная энер
гия деформации и произойдет работа внешних сил
6Ж = J J (рхби + руби + р2би?) dS + J J J (Гхби + Губи + Ггби?) dV,
Sjp
(72) где Sp ~ часть поверхности тела с заданными внешними усилиями. Начало возможных перемещений применительно к деформируемому телу формулируется следующим образом: в состоянии равновесия возможная работа внешних сил равна приращению потенциальной энергии деформаций:
bU~6W.	(73)
Начало возможных перемещений (73) можно записать в виде вариационного уравнения Лагранжа
бП = б(С7- JF) = O, '	(74)
где U — потенциальная энергия деформации;
+ Pvv + P*w) dS + J J J (Гхи + FyV + r2u?) dV (75) Sp .	v
— возможная работа внешних сил.
При определении возможной работы значения и направления внешних нагрузок считаются неизменными (множитель 1/2 отсутствует).
Вариация функции W (уравнение (72)) получается в результате варьирования перемещений при постоянных^ внешних силах. Легко видеть, что W равно удвоенной работе внешних сил, приложенных статически к упругому телу:
W = 2А.	(76)
36. ВАРИАЦИОННЫЕ МЕТОДЫ
323
Величина
П = U-W
(11)
называется полной потенциальной энергией системы.
Величину П можно представить в матричной форме (см. уравнение (15)):
п=т Ш нт <е>dv - И{р}Т	ds - Ш{F}r {и} dv> <78)
V	Sp	V
где
— векторы перемещений, поверхностной нагрузки и массовых сил.
При решении задач теории упругости с помощью вариационного уравнения Лагранжа обычно в качестве основных неизвестных принимаются смещения и, и, w, что обеспечивает выполнение условий совместности деформаций.
Вариационное уравнение
6П == 0	(79}
гарантирует выполнение уравнений равновесия и краевых условий, т. е. приводит к точному решению задачи.
Замечания. 1. При выводе формулы для полной потенциальной энергии системы (функционала Лагранжа) не требовалось выражение для вариации энергии деформации. Оно имеет следующий вид:
6С7 = J J J{<7}T{6e}dF.	(80)
v J
В правой части равенства (72) стоит возможная работа внутренних силовых факторов, которые при вариации деформаций считаются постоянными. В связи с этим начало возможных перемещений для деформируемого тела можно представить в более общей форме:
f J J {а}т {бе} dV = f f (р}т {6u} dS + J J J {ЛT (6u) dV, (81) V	Sp	V
пригодной и для неупругих систем.
В состоянии равновесия возможная работа внешних сил равна возможной работе внутренних силовых факторов.
2. Вариация полной потенциальной энергии происходит в результате вариации перемещений. Последние должны удовлетворять наложенным на Систему связям, (внешним—условиям закрепления и т. п. и внутренним — условиям непрерывности деформаций).
Полная потенциальная энергия деформации выражается через перемещения и их производные. Методы, основанные на начале возможных перемещений, часто называют методами вариации перемещений.
Вариационное уравнение изгиба стержня. Применим общее вариационное уравнение (79) к плоскому изгибу стержня переменно-21*
324
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИИ
го сечения (рис. 9.11). Стержень подвергается действию распределенной нагрузки q(z), усилия Р и момента М.
Потенциальная энергия деформации стержня
= <82>
о	о	7
В равенстве (82) i?(z) представляет прогиб оси стержня. Возможная работа внешних сил
онного уравнения изгиба стержня
И7 = ^q(z)v(z)dz + Pv(l) —	(83)
е/ о
Полная потенциальная энергия системы П=г7- Ж=

Вариационное уравнение изгиба стержня i
6П = 6 J -у EJ* И® - 9р] dz - P8v (z) +	=0.	(84)
О
Можно считать
i	i
J EJX (if)2 — gvj dz = J F (v, v', Vя, z) dz, о	o.
где F — Eh\v"yi2 — qv. Далее находим
<№_____'	<№ ___л &F ____ t? г гр	/or\
dv ~~ dv' “ 0» £7' EJx v •
Пользуясь формулой (63), полагая /=» v, x~z, получим
-г(£М?Н+г/'$5Н ’(86>
Вариационное уравнение изгиба стержня (82) можно записать.
36. ВАРИАЦИОННЫЕ МЕТОДЫ
325:
в такой форме:
dz —

л
+	8v'(l)=0, (87>
dz	I
так как 8v = 6z/ = О при z = 0 (заделка).
Уравнение (87) должно быть справедливо для произвольной . вариации, и потому оно эквивалентно уравнению
d2 dz2
=4
и краевым условиям при х = I
,2
£jx£i = -M, dz*
d (pt d2v
* \	 dz*
-P.
(88)
(89)
(90).
Уравнение (88) является дифференциальным уравнением изгиба стержня, условия (89), (90)—силовые краевые условия при х = 1.
Краевые условия при х = 0 должны выполняться для функции y(z) по построению
*(0)-0, ^(0) = 0.	(91)
Таким образом, вариационное уравнение эквивалентно дифференциальному уравне-
нию и краевым условиям.	•
Применение метода Рэлея —Ритца к рис. 942. Применение задаче изгиба стержня. Метод Рэлея — Рит- метода Рэлея — Ритца ж ца применяется для решения многих задач задаче изгиба стержня определения напряжений и деформаций в твердых деформируемых телах. Покажем алгоритм метода на простом примере изгиба стержня постоянного сечения под действием равномерной нагрузки (рис. 9.12).
Полная потенциальная энергия деформации
п = A J EJX (г/)2 dz -J qv dz.	(92).
0	О	-
В соответствии с равенством (67) примем прогиб стержня равным
h
*>(*) = 2^А(г).
(93)
826
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
где fi(z) — возможные функции для прогиба стержня. В рассматриваемом примере они должны удовлетворять наложенным (геометрическим) связям
А(0)~0, /'i(0)=0.	(94)
Можно принять
Решим сначала задачу с одним параметром, положив / z \2	2с,
). y’(z) = y.
Внося значения v a v" в равенство (92), находим
„ EJxf4c2	f (	, 2EJX 2 Чс ?
n“TJ i*dz	z“ i3 C1 I2 3 *
о	0
Из условия
dct p С1 з u находим
-1"" 12£JX’
Наибольший прогиб составит
(95)
что отличается от точного значения (см. разд. 34)'
p(Z)
8£JX
Для уточнения решения примем
/ 2 \2	/ 2	6с* т
v (z) =® j + с2 , v (z) =	4	,
и далее
Дифференцируя последнее соотношение по ct и с2, получаем систему
36. ВАРИАЦИОННЫЕ МЕТОДЫ
327
уравнений
Й; - EJj (2 ? + т? т) 7 -9 f (т)’й - »• 1	о	о
J“ = £7xf (271 + Тт)'?'4/г_?1 (т) dz = 0 *	о '	о
или ,3	1 ql4 . „	1 ql4
С1 + 2 С* ~ 12 EJ х C1 + 2<?2 ~ 24 £/х ’
Из последних уравнений находим _ 5 ql4	ql4
C1 2iEJx> С*~ 12EJX’ и далее
. >	5 gZ2? gZz3
Наибольшее значение прогиба равно
V ® “ зЪ/
(96)
что совпадает с точным решением.
Как видно, добавление одного параметра в ряде (93) сущест-
венно повысило точность расчета.
Применение начала возможных перемещений для определения прогибов стержней. Интеграл Мора. Этот метод имеет- широкое распространение при решении практических задач. Пусть имеется стержень, загруженный произвольными силами (основная система, рис. 9.13, а), и в сечении а возник прогиб р(а). Для его определения поступим следующим образом.
Рассмотрим тот же стержень под действием единичного усилия Р = 1 (единичная система, рис. 9.13, б).
Стержень получит прогиб щ(г), в Рнс 913 Вывод интеГрала Мора сечениях стержня под действием из начала возможных перемеще-единичной силы возникнут изгиба- ний: д —основная система; б — ющий момент Afu(z) и перерезыва-	единичная система
ющая сила Qiv(z)-
Допустим теперь,' что единичной системе (рис. 9.13, б) сообщили возможные смещения, равные действительным прогибам стержня в основной системе:
6vt(z) = v(z_).
(97)
328
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИИ
Равенство (97) вполне закономерно — прогибы v(z) являются малыми величинами, удовлетворяющими связям системы.
Так как возможная работа внешних сил равна возможной работе внутренних силовых факторов (начало возможных перемещении), то i	i
1 • v (а) = j Mt (z) dtp (z) + J Qlv (z) yvz (z) dz = о	0
I	I
~ У ix(z)	& + «J Q\y (z) yVz (z) dz, (98)
о	0
где dqtjdz и ?fvt соответствуют прогибам v(z) в основной системе.
Далее имеем с учетом температурных деформаций (см. уравнение (15) гл. 8}
.	=	(99)
dz
где Вх=* j у2Е dF — жесткость сечения на изгиб, МХт = ] Eya^T dF— F	F
температурный момент.
Деформация, сдвига (см. разд. 35) равна
=	(100)
Таким образом, прогиб
С М1Х(2)МЯ(Х) у (а) = -------5------
в сечении а будет
dz.
(101)
Это и есть интеграл Мора для вычисления прогиба стержня.
Для того чтобы найти прогиб в заданном сечении, нужно приложить единичную силу в этом сечении, определить изгибающий момент и перерезывающую силу от единичной силы и вычислить интеграл Мора (101). Если величина и (а), получается положительной, то прогиб совпадает по направлению с единичной силой.
Во многих практических задачах интеграл, связанный с действием перерезывающей силы, может быть опущен.
Для стержня с постоянными параметрами упругости, пренебрегая перерезывающими усилиями и неравномерным нагревом, будем иметь
’W-J—
(W2)
36. ВАРИАЦИОННЫЕ МЕТОДЫ
329.
Замечание. Следует отметить, что Mix(z) имеет размерность длины, а Qw(z) — безразмерная величина, так как в равенстве (98) была сокращена размерная единица силы (см. примеры).
Пример. Пусть требуется определить прогиб конца консольного стержня прямоугольного сечения, загруженного силой Р (рис. 9.14), с учетом деформации сдвига.
Воспользуемся формулой (101), считая параметры упругости постоянными, материал стержня равномерно нагретым (Мхт = 0),
V {1} = — f U ~ г) р ~ г) dz —
J о
№dF =_f-P±+6.fL) =
•J FG \№J* 5 GF I 0	'
___/4Р13 , 6 Pl \
\Ebhr 5 Gbh j
Рис. 9.14. Определение прогиба стержня с помощью интеграла Мора: а — основная система; б — единичная система
Знак минус означает, что прогиб направлен в сторону, противоположную приложенной единичной силе.
Решение совпадает с прежними результатами (см. разд. 34).
Общий случай определения прогибов с помощью интеграла Мора, в том, коорди-заранее
Одно из основных преимуществ интеграла Мора состоит что он, в сущности, не связан с какой-либо общей системой нат. Правило знаков для силовых факторов выбрано
Рис. 9.15. Правило знаков для изгибающих моментов и сил (показаны положительные направления)
Рис. 9.16. Физический смысл интеграла Мора (проекция перемещения точки на направление приложенной единичной силы)
в местной системе координат (рис. 9.15), которая может быть ориентирована произвольным образом в пространстве. Ось s в каждом сечении направлена по касательной к оси стержня.
330
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИИ
• Важно только, что для силовых факторов от внешней нагрузки и единичного силового фактора применяется единое правило знаков. Перемещение точки стержня в направлении единичной силы определяется следующим равенством:
1	1	1 С N N , ё М.ХМХ , С М. „М„ ‘-иЧ х. *+J в, 0	0	0	, , f „ QlxQx , , L QiyQy , ds -|- J Кх ' д ds J Ky  a о	7	о	7 (103)
Напомним, что оси х, у являются главными приведенными осями сечения; А, Вх, Ву, Лт —жесткости сечений на растяжение, изгиб и сдвиг; Nh Mlx, Miy, Qlx, Qiv — силовые факторы в сечении стерж-
ня от действия единичной силы. Подчеркнем, что по смыслу вывода
величина 6 не является полным перемещением точки оси стержня, а является проекцией на направление действия единичной силы. Например, для стержня, показанного на рис. 9.16, полное перемещение точки А равно иА, а интеграл Мора дает величину 6.
Для неравномерно нагретых стержней к величине 6 добавляется
i	i	i
X С N1NT 1	С MlxMxT ,о , f М1 уМуТ ,
о	о	о *
(104)

ругопластических деформациях. В
У
мо-
Рис. 9.17. Работа единичного мента
где в соответствии с равенствами * (14) — (16) гл. 8 температурные усилия равны
7Vth= J ЕатТ dFy МхТ = J уЕатТ dF, МуТ = — ^xEaTTdFt F	'	F	F
(105) Замечание. Интеграл Мора применим для определения прогибов при уп-этом случае характеристики жесткости Л, Вх, Ву и Лт определяются методом пере^ менных параметров упругости.
Определение угла поворота с помощью интеграла Мора. Для этого в сечении (рис. 9.17), где требуется определить угол поворота, прикладывается единичный момент (М =* = 1). В стержне под действием единичного момента М =* 1 возникнут силовые факторы Jflx(z), Qlv(z) и т. д.
Считая прогибы стержня под действием внешней нагрузки возможными перемещениями для единичной системы, получим, подобно f MlX W (z)
равенству (102), 1-<р(а)«1----r-gj-----az, где Mx(z) — изгибаю*
о	х
щий момент от внешней нагрузки.
36. ВАРИАЦИОННЫЕ МЕТОДЫ
331
В общем случае справедлива формула (ЮЗ), в которой S заменяется на ф, а силовые факторы М1Х, Л/1У, ... определяются от единичного изгибающего момента.
Замечание. Возможны дальнейшие обобщения интеграла Мора, когда прикладывается не единичный силовой фактор, а единичная система сил. Физи
ческий смысл интеграла Мора вытекает из того, что он представляет возможную работу единичной системы сил на перемещениях
основной системы.
Вычисление интеграла Мора по правилу Верещагина. В общем случае (стержень переменного сечения, сложная система нагрузок) интеграл Мора определяется путем численного интегрирования. Во многих практически важных случаях, когда жесткость сечения постоянна по длине стержня, интеграл Мора может быть вычислен по правилу Верещагина. Рассмотрим определение интеграла Мора на участке от а до b (рис. 9.18).
Эпюры момента от единичного силового фактора состоят из отрезков прямых. Не нарушая общности, предположим, что в пределах участка
Mix(z) = Az + B,	(106)
Рис. 9.18. Правило Верещагина для вычисления интеграла Мора
где А и В — параметры прямой;
Интеграл Мора на рассматриваемом
участке постоянного сече
ния имеет вид
а	ь
а	а
(Ь	Ъ	%
A f zMx (z) dz + В (* Mx (z) dz j; (107) J	J	/
a	a	/
при ЭТОМ b
jM,(z)dz = F,	(108)
a
где F — площадь под кривой Mx(z) (площадь эпюры изгибающих • моментов от внешних сил на участке z).
Далее следует учесть, что статический момент площади эпюры моментов равен
ь
J zMx (z) dz = zuF,	(109)
a
где z4 — абсцисса центра тяжести площади
.332
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
Равенство (109) справедливо, когда Mx(z) в пределах участка не изменяет знак и Mx(z) dz = dF может рассматриваться как элемент площади эпюры. Теперь из соотношений (107) —(109) по
Рис. 9.19. Площади и положение центров тяжести эпюр моментов
ры Mx(z), соответствующую центру
лучаем ь
f	dz^ (ИО)
х а
где
Mlu = Azn + B
— момент от единичной нагрузки в сечении z = иц.
Вспомогательная таблица для использования правила Верещагина дана на рис. 9.19.
Замечания. 1. Если эпюра от действия внешних сил на участке линейна (например, при действии сосредоточенных сил и моментов), то правило можно применять в обращенном виде: площадь эпюры от единичного силового фактора F] умножить на ординату эпю-тяжести площади Е\. Это вытекает из
приведенного доказательства.
2. Правило Верещагина может быть распространено на интеграл Мора в общем виде (уравнение (103).). Основное требование при этом состоит в сле-
Рис. 9.20. Примеры определения прогиба и углов поворота по правилу Вере
щагина
дующем: в пределах участка внутренние силовые факторы от единичной нагрузки (2Vh Mu, М\у, Q\x, Qw) должны быть линейными функциями вдоль оси стержня (линейность эпюр!).
36. ВАРИАЦИОННЫЕ МЕТОДЫ
133
Примеры. 1. Определить прогиб в точке А консольного стержня при действии сосредоточенного момента М (рис. 9.20, а).
Прогиб в точке А определяем по формуле (для краткости индекс опускается)
0
dz = - A fm., = — — mi-L i
EJ 1ц EJ 2
__ Ml2
2EJ'
Знак минус связан с тем, что М\ и М имеют разные знаки.
2. Определить прогиб в точке А в консольном стержне под действием распределенной нагрузки.
Прогиб определяем по формуле
£ М М	Г QQ
sa = J-T7-* + Js^*'
О	о
Эпюры изгибающего момента М и перерезывающей силы Q от внешней нагрузки показаны на рис. 9.20, б, ниже на этом рисунке приведены эпюры и Q\ при действии единичной силы. Далее находим
6. = -L._L2^.bA-Z + A.-Lgbz-i	+
А EJ 3 2	4 GF 2 4 8EJ 2GF
3. Определить прогиб в точке А и угол поворота в точке В для двухопор-пой балки, загруженной сосредоточенным моментом (рис. 9.20, в).
Прогиб определяем по формуле (деформацией сдвига пренебрегаем)
I смм о
Так как эпюра момента от единичной силы не изображается одной линией, то интеграл разбиваем на два участка:
_ 1 1 1	2 17 . JL 1 L mL L 17
° А ““ — EJ’ 2 * 2 М 2 ’ 3 ’ 4 1 + EJ’ 2 ’ 2 М 2 ’ 3 ’ 4 1 “"°*
Угол поворота в точке В равен
Ф =A.1.1m1A.i-А.1.1м1(1+1Ъ = --1.^
Е J 2 2	2 6	Е J 2 2	2 \ 2	6 / Е J 24
Замечание. Из приведенных примеров видно, что способ Верещагина в простых случаях позволяет быстро определить прогибы и углы поворота. Важно только применять единое правило знаков для M(z) и Mi(z). Если условиться при изгибе стержня строить эпюры изгибающих моментов на «растянутом волокне» (см. рис. 9.20), то сразу легко видеть положительные и отрицательные значения моментов.
Особое преимущество правила Верещагина состоит в том, что оно может быть использовано не только для стержней, но и для рам (разд. 17).
Ограничения для применения правила Верещагина. Эти ограничения вытекают из вывода формулы (НО), но обратим на них внимание еще раз.
1. Эпюра изгибающего момента от единичной нагрузки должна быть в виде одной прямой линии. На рис. 9.21, а показан случай, когда это условие не соблюдается. Интеграл Мора необходимо вычислять отдельно для участков I и II.
334
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИИ
2. Изгибающий момент от внешней нагрузки в пределах участка должен иметь один знак. На рис. 9.21, б показан случай, когда правило Верещагина следует применять для каждого участка в отдельности. Это ограничение не относится к моменту от единичной нагрузки.
Рис. 9.21. Ограничения при использовании правила Верещагина: а — эпюра имеет излом; б — эпюра имеет разные знаки; в — стержень имеет разные сечения
3. Жесткость стержня в пределах участка должна быть постоянна, иначе интегрирование следует распространять отдельно на участки с постоянной жесткостью. Ограничения по постоянной жесткости можно избежать, если строить эпюры
37. Вариационные методы
и общие свойства упругих систем
Два основных вариационных метода. Ранее рассматривался вариационный метод, основанный на начале возможных перемещений (метод вариации перемещений). Перемещения предполагались достаточно непрерывными функциями, с тем чтобы выполнялись условия совместности (непрерывности) деформаций. Условия равновесия и краевые условия для напряжений удовлетворялись с помощью вариационного уравнения Лагранжа.
Другой вариационный метод — метод вариации напряжений — основан на сравнении двух близких напряженных состояний, каждое из которых удовлетворяет условиям равновесия и краевым условиям. Вариационное уравнение метода эквивалентно условиям совместности деформаций.
В некотором смысле методы противоположны: при вариации перемещений условия совместности удовлетворяются заранее и находится решение, соответствующее уравнениям равновесия. В качестве основных неизвестных принимаются перемещения. В методе вариации напряжений заранее выполняются уравнения равновесия и краевые условия и строится решение, удовлетворяющее условиям совместности; основными неизвестными являются напряжения.
Рассмотрим теперь основные уравнения метода вариации напряжений сначала на простом "примере растяжения стержня.
Метод вариации напряжений. Стержень переменного сечения (лопатка турбины) растягивается в поле центробежных сил (рис. 9.22). В концевом сечении z = i приложена распределенная поверх-
37. ОБЩИЕ СВОЙСТВА УПРУГИХ СИСТЕМ
335
постпая нагрузка, интенсивность которой равна
где 5 (Z) —- площадь поперечного сечения стержня при 2 = ?. На стержень действуют массовые силы, причем интенсивность на единицу объема
Гг = рй)2(А + 2),	(112)
где р — плотность материала, о — угловая скорость, — радиус корневого сечения.
Растягивающее усилие в сечении z
- JV(z) = 7VI + J^(21)5(z1)dz1,	 (ИЗ)
где 5(zt) — площадь поперечного сечения стержня.
Рис. 9.22. Растяжение стержня: а — расчетная схема; б — равновесие элемента стержня
Напряжение растяжения в поперечном сечении
’ И -	'	(114)
Условие равновесия элемента стержня имеет вид
^ = -Fz5(z).	(115)
Теперь рассмотрим вариации напряженного состояния при вариации внешних нагрузок (усилия на конце стержня Nt и объемных распределенных усилий Fz). Геометрические размеры стержня не варьируются.
Будем считать, что вариации напряжений, вызываемые вариациями внешних нагрузок, согласованы с условиями равновесия и краевыми условиями.
На торце стержня (z = I) вариация внешнего усилия
8Nt = S(l) 6pt.	(1161
Следовательно, вариация растягивающего напряжения в сечении
336
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИИ
z = I должна быть
diV
® °° Т(1) = 8pz'
(117)
где бр, — вариация поверхностной нагрузки на торце стержня.
Вариация растягивающего усилия
6/V(z) = 6o,(z) S(z)	(118)’
^.должна удовлетворять уравнению равновесия (115):
^(6a,(z)5(z)) = -6F,5(Z),	(119)
где 6F, — вариация объемного усилия.
Причина, вызывающая вариацию объемного усилия, для дальнейшего несущественна; это может быть изменение угловой скорости вращения или плотности материала.
Рассмотрим вариацию (изменение) потенциальной энергии стержня, считая материал упругим:
i
6/7-
Так как вариация усилий предполагается малой, правой части равенства можно пренебречь:
то вторым членом'
dz.
(120)
Учитывая, что
N Т ~ Gz’
запишем равенство (120) в таком i
6U - J 8, mz = J J J e, ба, dV. о	v V
виде:
(121)
(122)
.2
I
I
о
о
о
о
О
Е ~ Бг’
Так как
6N = J J бс, dS = ба, S,
(123) .
то величина
е, ба, = 8Ut представляет вариацию удельной потенциальной дни. Преобразуем формулу для вариации потенциальной энергии
(124) энергии деформа-
37. ОБЩИЕ СВОЙСТВА УПРУГИХ СИСТЕМ
337
стержня с помощью интегрирования по частям:
i	i	it
= Je26ax5dz =	=	— Jw^(6az5)dz, (125)
О	0	0	0
где w(z) — перемещение сечения стержня вдоль оси 2, одинаковое во всех точках сечения; ш(0) = 0 при z = 0. Учитывая условие равновесия (119), находим
i 6U=w(l)6az(l)S(l) + $w6FtSdz О или I
(Z) &Nt + J w 8FtS dz.	(126)
0
Последнее равенство устанавливает связь между вариацией потенциальной энергии стержня и работой вариаций внешних сил. Соотношение (126) представляет частный случай вариационного уравнения метода вариаций напряжений.
Замечание. Равенство (126) можно записать так: i	I
J е, 6аг S dz = w (I) SNt + J w 5FZ S dz.	(127)
0	0
Величина i
J 82 6crz S dz = [ J J ez 6az dV = 6Я	(128)
о	‘ v


ъ
® ffH-e ffs
о

называется вариацией потенциальной функции напряжений. Для упругих деформаций потенциальная функция напряжений равна потенциальной энергии стержня (энергии деформации):
H=>U.	(129)
На рис. 9.23 показана кривая деформирования (о, в). Площадь под кривой деформирования равна удельной энергии деформации. Величина В представляет площадь, дополняющую U до площади прямоугольника а X е:
В «= as — U. >	(130)
Величину В иногда называют дополнительной энергией деформации. Если зависимость (о, е) выражается прямой линией (упругие деформации), то справедливо равенство (129).
В дальнейшем ограничимся применением
метода вариации напряжений для линейно упругого материала. Ограничения могут быть сняты, если вместо U подразумевать J7.
e
Л.
e
Рис. 9.23. Связь энергии деформации и потенциальной функции напряжений
Вариационное уравнение метода вариации напряжении. В разобранном частном случае было получено вариационное уравнение 22 и. А. Биргер, Р. Р. Мавлютов
338
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
(126), которое запишем теперь в более общей форме:
8U = J J J ег 8oz dV = J J w 8pz dS + J f J u> &FZ dV,
V	8	J VJ
(131)
так как
w (Z) 6Ni == w (I) 6pzS = J J w 6pz dz.	(132)
Интеграл распространяется на поверхность тела 5Р, на которой заданы внешние усилия (торец стержня z==Z); величина w(l)6pt одинакова во всех точках Концевого сечения стержня.
В общем случае вариационное уравнение метода вариации напряжений имеет следующий вид:
8U == j J J (ех 6ох + 8у 6оу + . • • + ТгхбТгх) dV == v
= J J(u ^Рх + и $Pv + w ^Р^ + J J J(u ^Fx + v SFy + w 8FZ) dV. (133) sp	v
Вариация потенциальной энергии деформации равна работе вариаций внешних сил на действительных перемещениях.
Действительные перемещения — это перемещения в упругой системе от действия внешних нагрузок.
Вариация энергии деформации всего тела равна
8U = J J ^U^V,	(134)
V J
где Ut — удельная потенциальная энергия,
6Z7i = ex бох+еу бОу + ... + Yzx бт».	(135)
Удельная потенциальная энергия деформации в методе вариации напряжений выражается через основные неизвестные — напряжения
U = Ui (о,, оу, ..т2х).	(136)
Вариация потенциальной энергии деформации может быть представлена в такой форме:
ди. л	dU.	ди.
=	+	+ ... +	(137)
х	v у	v,,zx
Из формулы для потенциальной энергии упругого тела (соотношение (17)) получаем
5CZi _ ах
дах Е Е Е ~Ъхч1
что подтверждает идентичность зависимостей (135) и (137), а также и то обстоятельство, что левая часть уравнения (133) содержит вариацию потенциальной энергии деформации.
37. ОБЩИЕ СВОЙСТВА УПРУГИХ СИСТЕМ
339
Вариационное уравнение (133) можно представить в матричной форме:
Ш dV=J f {«г {wds+Ш dV- (139) V	sp	. V
При упругих деформациях JJJ{e}T{6o}dV = 6Z7.	(140)
V
Замечание. В уравнении (133) или (139) вариация внешних сил может быть произвольной! Некоторые нагрузки могут рассматриваться как постоянные, другая часть сил или даже одна сила могут варьироваться. Вариации напряжение связаны с вариациями внешних сил условиями равновесия и краевыми условиями.
Следствия вариационного уравнения. Теорема Кастильяно. Пусть на малом участке поверхности Д5 приложена сила Р, вектор кото-
рой составляет утлы а, с осями координат (рис. 9.24). Косинусы углов (направляющие косинусы):
cos а = I, cos £ = тп, cos 7 ® п.
(141)
Рассматривая сосредоточенную силу как распределенную нагрузку на малом участке, будем иметь следующие компоненты поверхностной на-
гРУзки:	Рис. 9.24. К доказательству те-
PAS = IP, Pv&S = тР, p,AS = пР.	оремы Кастильяно
(142)
Проводя вариацию этих компонент нагрузки, получим
бр«Д5 = /бР, бр,Д5 = тбР, брхД5 = пбР. (143).
Предполагая, что варьируется только сила Р, получим из вариационного уравнения (139)
б U = (иА1 + vAm + wAn) 6Р — бР бР,	(144)
где б₽ = uAl + vAm + wAn — проекция полного перемещения точки приложения силы на направление ее действия.
Приращение потенциальной энергии деформации вызвано приращением усилия 6Р, и потому
6t/ = ^6P.	(145)
Теперь из равенств (144) и (145) получаем g = 6p.	(146)
Равенство *(146) составляет теорему Кастильяно. 22*	.
3'10
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
Частная производная потенциальной энергии деформации по силе равна проекции полного перемещения точки приложения силы на направление ее действия.
Замечания. 1. Вполне естественно, что по теореме Кастильяно определяется только проекция перемещения точки приложения силы на направление силы, а не полное перемещение. Это вытекает из того, что вариационное уравнение содержит работу вариации силы (скалярное произведение перемещения и силы).
По условиям (143) вариация силы происходит в направлении ее действия.
2. Величина бр определяется не только усилием Р, величина которого варьировалась, а всеми приложенными к телу нагрузками (проекция действительного перемещения точки А на направление усилия Р). Все другие нагрузки влияют на величину потенциальной энергии деформации и ее частной производной по Р,
3. Теорема Кастильяно при наличии пластических деформаций выражается следующим образом:
др — °р-
' Элементарные доказательства теоремы Кастильяно. Рассмотрим в качестве примера упругой системы балку, нагруженную силами
Р-1	₽=/ ч
, Рис. 9.25. К доказательству теоремы Кастильяно элементарным способом
Р и Q (рис. 9.25). Прогибы в точках приложения сил Р и Q обозначены бр и 6q. Считая для упругих систем действие сил независимым, можно записать
6p==6ppP+6pq(?,	(147)
где брр — перемещение в точке А от единичной силы в точке Л, 6pq — перемещение в точке А от единичной силы в точке В.
Будем считать, что потенциальная энергия деформации не зависит от порядка приложения нагрузок и определяется работой внешних сил.
Пусть к балке сначала приложена только сила Р. Она совершит работу
А^-^РЬррР-^ЬррР3.
Во втором нагружении статически прикладывается сила Q, причем сила Р в процессе второго нагружения остается постоянной. Работа внешних сил при втором нагружении
л - 4	+р =4-	+6pqP/?-
37. ОБЩИЕ СВОЙСТВА УПРУГИХ СИСТЕМ
341
Потенциальная анергия системы после двух нагружений U ~	+ Л2 = -у дррР1 + -у 8qqQ2 + SpqPQ.
Дифференцируя по Р, находим
» ЬррР + SpqQ = бр,
(148)
что и составляет теорему Кастильяно. Существенно, что перемещения от единичных сил зависят только от геометрических размеров системы и модуля упругости и не зависят от внешних усилий (в пределах упругости материала) — при дифференцировании они должны рассматриваться как постоянные.
Замечание. Можно привести несколько других элементарных доказательств теоремы Кастильяно, но всегда используется прием двух нагружений: независимость результата от порядка приложения нагрузок. Во всех доказательствах не рассматриваются другие порядки нагружения, так как они требуют привлечения теоремы взаимности. Однако элементарные доказатель-
ства всегда привлекательны — в них более четко выступает физическая сущность вопроса.
Примеры применения теоремы Кастильяно. 1. Прогиб консольного стержня при действии силы на конце стержня (рис. 9.26).
Рис. 9.27. Определение прогиба в произвольной точке стержня по теореме Кастильяно (способ фиктивной силы)
Рис. 9.26. Определение прогиба стержня с помощью теоремы Кастильяно
Для определения прогиба в . точке А составляем выражение потенциальной энергии деформации:
2 oJ
р213
По теореме Кастильяно имеем
о
, ди Р13
°Р- др- 3>EJX'
что соответствует ранее полученным результатам.
2. Определение прогиба в произвольной точке стержня (рис. 9.27). К стержню приложен момент Л/, и требуется определить прогиб в точке А. Для этого приложим в этой точке А силу Ф, применим теорему Кастильяно, но в окончательном результате положим Ф = 0.	-
342
ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
Потенциальная энергия деформации стержня (по участкам) равна
	M2l	МФ12	ф213
V 2 J	EJX	*S + 2 J ' EJ dz2	~ AE J x	8EJX	
O	1/2			
Далее находим
QU	ЗМ12 Ф13
дФ	8£JS + 35
Прогиб в точке А получаем при Ф = 0:
_W|	_ зм;3
6А-5Ф|Ф=0-------85/я"
В рассматриваемом случае результат можно получить проще, если провести дифференцирование под знаком интеграла и положить Ф = 0. Тогда получаем
dU I Г М W дФ dz ____________Г* М (I — z) 3MZ2
бА = дФ|ф=0 = J EJX	J EJX dz~~8EJx’
о	о
Знак минус показывает, что прогиб направлен противоположно силе Ф.
3. Определение перемещения фермы в точке приложения нагрузки (рис.
9.28)	. Определяем усилия в стержнях по условиям хм	равновесия
Ni cos р = W2 cos a, 2Vi sin p + N2 sin a = P,
---Из этих равенств получаем яг ~ cos а	cos Р
/ \fp	i ~ sin (а + ₽)’ ;v2~r sin(a+P)‘
SSL/*/
Потенциальная энергия деформации системы
Рис. 9.28. Определение перемещений фермы с помощью теории Кастильяно
и “ 2 EF + 2 EF =
e 2EF (Г1 со®2 “ + 1г со®2 0)3in2 (a + Р)’
Перемещение точки А в направлении действия силы Р по теореме Кастильяно равно с ди р /,	2	'	2	1
6Р- дР~ EFyiC0S a + *2cos ^)sin2(a + P)‘
Замечание. В рассматриваемом примере очевидна эффективность метода вариации напряжений (усилий) при определении перемещений в сложных системах. Решение задачи на основании геометрических соображений значительно труднее.
Общие свойства упругих систем. Рассмотрим два важных свойства линейных упругих систем произвольной структуры, которые называются принципом независимости действия сил и принципом взаимности.
Принцип независимости действия сил утверждает, что в упругой' системе напряжения и деформации от действия одной нагрузки не
37. ОБЩИЕ СВОЙСТВА УПРУГИХ СИСТЕМ
343
зависят от наличия или отсутствия других нагрузок. Более строгая формулировка требует указания о линейности системы; напряжения и деформации должны быть пропорциональны действующей нагрузке.
Например, при контактной деформации упругих шаров принцип независимости действия сил несправедлив, так как зависимость перемещения от силы оказывается нелинейной. По этой же причине принцип независимости действия сил не может использоваться при наличии пластических деформаций или деформаций ползучести. Из принципа независимости действия сил вытекает, что действие суммы сил равно сумме действий каждой силы в отдельности.
Важным следствием принципа является утверждение, что результат действия суммы сил не зависит от порядка их приложения.
Принцип независимости действия сил подтверждается экспериментально и хорошо проверен на практике. Его теоретическое доказательство основывается на том, что линейные упругие системы описываются линейными дифференциальными уравнениями, для которых справедлив принцип суперпозиций.
Замечания. 1. Важным условием, сопутствующим применению принципа независимости действия сил, является принцип начальных размеров, в соответствии с которым условия равновесия рассматриваются для начального, не-деформированного состояния. Если принцип начальных размеров в рассматриваемой задаче не может быть использован, то, как правило, неприменим и принцип независимости действия сил.
2.	Для справедливости принципа независимости действия сил требуется одинаковая линейная зависимость усилий и перемещений при нагружении и разгрузке.
3.	Разномодульные упругие конструкции, у которых параметры упругости зависят от знака действующих напряжений, не относятся к числу линейных систем, и для них, следовательно, принцип независимости действия сил неприменим.
Принцип взаимности. Этот принцип основан на принципе независимости действия сил и является его
следствием.
Рассмотрим произвольное упругое тело (рис. 9.29), к которому приложены единичные силы Л = 1 и Р2 = 1. Пусть 51 — перемещение точки At при действии только одного усилия Pt и би — проекция этого перемещения на направление Pt. В точке А2 от единичного усилия возникает перемещение в направлении усилия Р2, равное 62i. Если к телу приложена единичная сила Р2 « 1, то она
Рис. 9.29. Принцип взаимности для упругих систем
вызывает перемещение точки Л2, обозначенное б22, и в точке At — перемещение 6i2.
В соответствии с принципом независимости действия сил результат воздействия и, в частности потенциальная энергия деформации, не должен зависеть от порядка приложения нагрузки. Пусть

ГЛ. 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИИ
к упругой системе статически приложена сначала сила Pi = 1. Тогда потенциальная энергия деформации, равная работе внешних сил, составит-~2 б1х-1. Если затем статически приложено усилие Р2 = 1» то произойдет увеличение потенциальной энергии деформации за счет работы внешних сил. Усилие Р3 совершит работу — б22-1> но, что самое важное, произведет работу усилие Р{ = 1, которое в процессе возрастания усилия Р2 оставалось постоянным (работа равна 1-б„-1). При указанном порядке нагружения (сначала Рь затем Р2) потенциальная энергия деформации равна
+	+	(149)
£ &
Если изменить порядок нагружения (сначала Р2, затем Pi), получим
+ убц-И-би-!- •	(150)
Приравнивая значения U{ и Uz, находим
«12 = 821.	(151)
Перемещения 6i2 и 62i от единичных сил в других точках называются коэффициентами влияния.
Принцип взаимности утверждает: коэффициенты влияния являются симметричными, т. е. не изменяются при перестановке их индексов.
_ В общем случае
А=8Я.	(152)
Замечание. В общем случае принцип взаимности утверждает: работа сил первой системы на перемещениях от второй системы сил равна работе сил второй системы на перемещениях от первой системы. В частном случае, ког^ да первая система представляет единичную силу Pi, а вторая — единичную силу Р2, получается равенство (151).
' Доказательство в общем случае полностью повторяет приведенный вывод.
ГЛАВА 10
СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
Классические модели стержней, основанные на гипотезе плоских сечений и одноосном напряженном состоянии, в некоторых случаях оказываются недостаточными, и приходится рассматривать более сложные модели. В теории тонкостенных стержней происходит отказ от гипотезы плоских сечений, в по-лупространственной теории стержней не используется гипотеза о ненадав-ливании.
38. Тонкостенные стержни
Вводные замечания. К числу наиболее распространенных тонкостенных стержней относятся прокатные профили, сварные балки и т. п. (рис. 10.1). Толщина профиля (стенки поперечного сечения) б мала по сравнению с размерами поперечного сечения. В тонкостенных стержнях (открытого профиля) возникают явления, которые не могут быть учтены прежними моделями кручения и изгиба стержней.
Рис. 10.1. Тонкостенные стержни
Главная особенность деформации тонкостенных стержней — появление значительной депланации сечения при действии крутящих моментов и связанных с ней нормальных напряжений.
На рис. 10.2 показано кручение стержня коробчатого сечения с открытым (незамкнутым) профилем. Если концевые сечения имеют возможность осевых перемещений (свободное или чистое кручение), то края разреза (точки А и В) заметно расходятся; когда развитие осевых деформаций стеснено (стесненное кручение), депланация (выход точек сечения из первоначальной плоскости поперечного сечения) уменьшается.
Следует отметить, что стеснение осевых деформаций повышает жесткость и прочность тонкостенного стержня. Для тонкостенных стержней замкнутого профиля депланация будет существенно меньше (разд. 28), и для них, как правило, можно использовать обычную теорию кручения и изгиба стержней.
346
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
Определяющим для учета влияния «тонкостенности» профиля является параметр
V =* Jmln/Ло
где 7min — минимальный момент инерции сечения на изгиб, 7К — геометрическая жесткость сечения стержня на кручение.
При малых v (v < 3) следует использовать обычную теорию изгиба и кручения, при больших v — учитывать дополнительные эффекты, связанные с
Рис. 10.2. Депланация при кручении тонкостенного стержня открытого профиля: а — схема нагружения; б — чистое кручение; в — стесненное кручение
«тонкостенностыо» стержня. Например, для стержня (рис. 10.3, а) с коробчатым сечением при наличии разреза (открытый профиль)
„ /6а8 , 6а3\	2	-	4,	1а2
Anin — 2 V 12	4 / — 3 &* ’ А — з Ь, V - 2
Для замкнутого сечения (рис. 10.3, б) т____________________________% С з Г Зо
Anin — 3 ба , /к — а 6, v — £ .
Таким образом, для стержня замкнутого сечения использование рассматри-
Рис. 10.3. Определение параметра тонкостенности для стержня коробчатого сечения с открытым (а) и замкнутым (б) профилями
ваемых ниже моделей не принесет новых результатов, тогда как для коробчатого сечения открытого профиля учет «тонкостенности» необходим уже при д 0,25 а. Дальнейшее рассмотрение относится к тонкостенным стержням открытого профиля.
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
347
Замечание. Не следует полагать, что для тонкостенных стержней замкнутого сечения всегда можно использовать обычные модели стержней. Во многих случаях оказывается необходимым учет деформации поперечного сечения, особенно для криволинейных труб (эффект Кармана).
Чистое кручение тонкостенных стержней открытого профиля. Кручение стержня моментами, приложенными по торцам стержня при отсутствии стеснения осевых перемещений, называется чистым (свободным) кручением.
При чистом кручении сечение стержня не деформируется (в плоскости поперечного сечения) (рис. 10.4), оно поворачивается как
Рис. 10.4. Чистое кручение тонкостенного стержня
Рис. 10.5. Распределение касательных напряжений при чистом кручении
жесткое на угол 0(z) (разд. 28). Крутящий момент чистого кручения равен	. _
(1)
здесь С — жесткость стержня на кручение:
L
С= С x(s)ds,	'	(2)
О
где С/($) — жесткость единицы длины средней линии профиля, £ —длина средней линии (разд. 28). При постоянных параметрах упругости
Cx(s)^-Lg^(s),
где G — модуль сдвига, S ($) — толщина профиля. Жесткость стержня на кручение при G « const равна
где
C = GJM
ь
О J О
(3)
348
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
Касательные напряжения чистого кручения при G = const распределяются линейно по толщине профиля (рис. 10.5)
2МК т(«, «) = —«,
(4)
где п — расстояние по нормали до средней линии профиля.
В крайних точках сечения
( б \	(	6 \
В точках средней линии профиля (zi = 0) касательные напряжения и, следовательно, деформации сдвига отсутствуют.
Замечание. В задаче о чистом кручении в качестве оси поворота сечения (оси кручения) может рассматриваться любая ось, параллельная оси стержня. Расчетные соотношения (значения напряжений, жесткость на кручение и др.) не зависят от выбора центра поворота сечений (разд. 26); перемещения определяются с точностью до движения стержня как твердого тела. В задачах стесненного кручения, когда, стержень закреплен, такой произвол отсутствует — ось кручения, как будет показано в дальнейшем, становится вполне определенной.
Стесненное кручение тонкостенных стержней. Основные гипотезы. Рассмотрим
</
dz
'z
z
кручение стержня, оп-
Рис. 10.6. Стесненное ре деление сдвига в срединной поверхности стержня
au)

теперь стесненное кручение, при котором какое-либо сечение стержня лишено возможности осевого смещения (депланации) (рис. 10.6). Примем две основные гипотезы, предложенные В. 3. Власовым:
1. Сечение стержня не искажается в своей плоскости.
2. В срединной поверхности стержня отсутствует деформация сдвига.
Эти гипотезы полностью справедливы для чистого кручения; в ус
ловиях стесненного кручения они носят приближенный характер. Произвольную точку срединной поверхности А характеризуют две координаты: z — расстояние вдоль оси z, s — расстояние вдоль дуги средней линии, отсчитываемое от начальной точки А9 (положение начальной точки будет указано в дальнейшем). В соответствии с первой гипотезой сечение стержня при кручении поворачивается как жесткое целое. Если Oi — центр поворота, то смещение точки А (рис. 10.7) равно
иА = r0(z), где г —расстояние от точки А до оси поворота, 0(z) — угол пово
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
349
рота сечения в своей плоскости. Составляющая перемещения и точки А вдоль касательной к контуру равна
u = pO(z),	(5)
где р — длина перпендикуляра, опущенного из точки Oi на направление касательной к средней линии контура в точке А, Положение
оси поворота определяется после рассмотрения условий равновесия. Угол сдвига в срединной поверхности стержня (разд. 8) равен
Эи , ди)
V = +	(6)
где ш— составляющая перемещения точки А вдоль оси z.
На основании второй основной гипотезы у =т 0, и потому
ди) ди	dQ (z)	/Г7\
_ = — _ == — р	(7)
ds dz	dz	' <
Рис. 10.7. Касательное перемещение точки средней линии профиля при кручении
Интегрируя равенство (7) по переменной 5, находим (рис. 10.8) .8
«’ = —	+	(8)
О
где wQ — осевое смещение в точке Ло (в точке начала отсчета дуги). Величина
р ds — da)	(9)
равна удвоенной площади сектора, основание которого ds,^вершина 01; р — перпендикуляр, опущенный на
основание. Имеем 8 J р ds =« J Ло == со (5),	(Ю)
о
где (o(s)— удвоенная площадь сектора
AoOtA с вершиной в центре поворота (точке О4) (рис. 10.8)1 Величину <о($) называют секгориалъной площадью, и эта
Рис. 10.8. Секториальная геометрическая характеристика играет площадь как функция центральную роль в теории тонкостен-средней Ъинии профиля ных стержней. В дальнейшем будут ука-
заны примеры определения секториаль-ных площадей. Равенство (8) представим так:
•^®(S) + U7O.
(Н)
Депланация сечения (w — пропорциональна векториальной площади.
350
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
Нормальные напряжения стесненного кручения. Из равенства (И) получаем для деформации в направлении оси z следующую зависимость:
где е0 ~ dwo/dz — осевая деформация в точке 5 = 0 (точке Ло) . Нор* мальные напряжения при упругих деформациях равны
о = £е,	(13):
где Е —модуль упругости.
Равенство (13) предполагает, что «поперечные» нормальные напряжения отсутствуют (гипотеза ненадавливания) и стержень равномерно нагрет.
При кручении стержня (в том числе при стесненном) внешние силы (см. рис. 10.6) сводятся только к крутящему моменту, и потому должно быть
Ja^==O,	(14)
F
J от dF = 0,	(15)
F
§ yvdF = 0.	(16)
F
Из уравнений равновесия (14) — (16) и соотношений (12) и (13) находим
— f(oEdF + eo <\EdF	= 0,	(17)
dz J	J
F	F
^xaEdF^Q,	(18)
F
^ya>EdF	= 0,	(19)
F
так как оси x, у являются главными приведенными осями сечения. Для главных осей имеем
f хЕ dF = 0, f уЕ dF - 0, • f xyEdF = 0.	(20)
F	F	F
Из уравнения (17) следует, что
С dF
„ _________
° ^^EdP'
(21)
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
35!
Далее находим
(22)
О
/ i d)E dF \
/о ,	<?е р I f |
—2 о) + е0 = — —,j £ о) — -------- .
dz	/ dz I	i £ dp I
\	F	J
Начало отсчета дуги з (точку Ло) выберем таким образом, чтобы выполнялось условие
(23)
J <дЕ dF == О, F
Условие (23) означает, что точку Ао надо выбирать так, чтобы среднее значение секториальной площади (для всего сечения) обращалось в нуль.
Теперь вернемся к условиям (18) и (19) для секториальной площади. Как будет показано в дальнейшем, они определяют точку Oi —центр поворота сечения (центр кручения).
Как только при кручении появляются нормальные напряжения, ось поворота сечений становится определенной в силу необходимости удовлетворения условиям равновесия (15) и (16).
Секториальная площадь, для которой равенствами (15) и (16) установлен полюс (точка GJ, а соотношением (23) — начало отсчета дуги, называется главной секториальной площадью. Полюс секториальной площади помещается в центре кручения.
Из равенства (22) вытекает
а_-Л£в. dz*
(24)
Нормальные напряжения стесненного кручения пропорциональны главной секториальной площади. Эти напряжения при постоянном модуле упругости распределены равномерно по толщине стенки, так как осевая деформация принимается одинаковой по толщине профиля.
Касательные напряжения стесненного кручения. Внешний крутящий момент передается от сечения к сечению с помощью касательных напряжений чистого и стесненного кручения.
Будем предполагать, что момент касательных напряжений чистого кручения, распределенных линейно по толщине стенки, определяется прежним соотношением:
(25)
где С — жесткость стержня на кручение (см. разд. 28). При постоянном модуле сдвига имеем
(26)
352
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
При передаче крутящего момента следует принять во внимание касательные напряжения, вызываемые нормальными напряжениями стесненного кручения.
Рассмотрим равновесие элемента стержня, показанного па рис. 10.9.
Обозначим Nf нормальную силу, действующую на часть сечения с площадью /. Учитывая зависимость, (24), находим
N; =	= \E^dF.
1	dzf
Из условия равновесия элемента стержня получим dNf r(s)6(s) = -^. -
(27)
(28)
Предполагается, что кромки профиля свободны от касательных усилий.
На основании равенства (27) получаем
Т (s) = - -L f EotdF. '	(29)
' ' dz3 6 (s) J	' '
Величина
(30)
/
называется приведенным секториальным статическим моментом от
сеченной части сечения.
Рис. 10.9. Определение касательных напряжений стесненного кручения
Рис. 10.10. Определение крутящего момента касательных напряжений стесненного кручения
Крутящий момент касательных напряжений стесненного кручения (рис. 10.10) определяется так:
У = — J т($)6($)р($)с&=—- J т ($) 6 (s) d(d. F	F
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
353
Подставляя значение т($) «из равенства (29), находим
F \/	/
С помощью интегрирования по частям устанавливаем /==г
f ( \ E<adF\dG> = (i) f I — f EardF. (31)
F V	/	f	/==0 F
Первый член правой части равенства обращается в нуль в силу условия (23).
Величину
=	(32)
F
будем называть векториальной жесткостью сечения.
При постоянном модуле упругости имеем
.	= EJ„,	(33)
где Уш =	—секториальный момент инерции.
F
Момент касательных . напряжений стесненного кручения (Е = const)	*
=	(34)-
. dz
В общем случае
dz	•
Замечание. Момент касательных напряжений стесненного кручения называют иногда изгибно-крутильным моментом М&:
Ч2) = ^
так как он появляется в результате стеснения осевых деформаций и возникновения нормальных напряжений в поперечных сечениях стержня.
Дифференциальное уравнение стесненного кручения. Внешний крутящий момент уравновешивается касательными напряжениями чистого и стесненного кручения:
Мк = М1) + М(к(35)
Моменты определяются относительно оси, проходящей через центры'кручения (ось zK на рис. 10.11).
Принимая во внимание соотношения (1) и (34), находим
'	GJKg—	(36)
dz
23 и, А. Биргер, Р. Р. Мавлютов
354
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
В общем случае на стержень могут действовать распределенные крутящие моменты (см. рис. 10.11) mK(z).
В сечении z крутящий момент
i
мк (z) = Мк + J тк (zj dzlt	(37)
z
где thk(zi) — крутящий момент на единицу длины стержня.
Из соотношения (37) следует равенство
что можно установить также
Рис. 10.11. Кручение тонкостенного стержня распределенными моментами. Ось zH — ось, проходящая через центры кручения (центры поворота) сечений
из условия равновесия элемента стержня между сечениями z и z + dz.
Дифференцируя равенство (36) по z, приходим к основному уравнению стесненного кручения: d ( j? г	d /г г <&\	/\
\EJe> ) ~Tz [GJ*Tzj ~ m* (39)
Для стержня с переменными параметрами упругости уравнение стесненного кручения будет таким:
(40)
Для стержня постоянного сечения с постоянными характеристиками жесткости по длине
_ В2 — =	(z}
dz1 dz2	EJ& ’
(41)
где
nJto
(42)
Решение уравнения стесненного кручения тонкостенных стержней и краевые условия. Рассмотрим решение уравнения (40) для стержня с постоянными параметрами. Предполагая частные решения однородного уравнения в виде
0 = ce*\
найдем характеристическое уравнение r-g2r = 0,
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
355
корни которого
А-i “О, А»2 ~ 0, Хз — Р, Х4 == —р.
Решение уравнения (40) можно записать так:
9 — Ci + c2z + с3 ch $z + с4 sh $z + 0*,	(43)
где Ci, c2, ..произвольные постоянные, 0* — частное решение неоднородного уравнения.
Более удобно представить решение с помощью нормальных фундаментальных функций:
в = 9 (0) Ф1 (z) + §-(0)Ф2 (z) +	(0) Ф3 (Z) +	(0) Ф4 (z) +Ф* (Z),
az	р dz	р dz*
(44) где
Ф1(г)=1, Ф2(г)=г, Ф3(г) = ch $z — 1, Ф4(г) = sh [Jz — 0z. Частное решение,имеет вид
Z
®*(z) =£7^f<I)4(z-zi),n(zi)dzr	(45)
шо
В равенстве (44) величины 9 (0),^ (0),	(0),	(0) представ-
dz dz
ляют собой начальные параметры. При отсутствии распределенной нагрузки
Ф*(2>0.
Для практического использования решение (44) вместе с производными фуйкции 0(z) целесообразно записать в матричной форме:
{0(z)} = [Ф] • {0(0)},	(46)
где
(£1 / \1Т /л / \	^0 )
(0(z)} = 0(Z),-	—
(	az az )
— фундаментальная матрица;
	1	Z	4 (ch pz — 1) Р	4 (sh ₽z — pz) P	
[ф] =	0	1	IshPz	7г ($h Pz 1) P	(47)
	0	0	ch (Jz	1 , _ jshpz	
	_0	0	Pshfk	ch pz	. _	
В решении (46) предполагается, что распределенные моменты отсутствуют.	_
Рассмотрим теперь краевые условия.
23*
358
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
Жесткая заделка торца стержня (рис. 10.12, а) „ В этом случае 0 (0) = 0,	(48)
f(0)=0.	.	(49)
Последнее, соотношение справедливо в силу равенства (И), так. как осевое смещение w = 0 во всех точках заделанного сечения.
Рис. 10.12. Краевые условия при стесненном кручении: а — жесткая заделка; б — свободный торец; в — скользящая заделка
Из условия (49) вытекает важный вывод: в жесткой заделке касательные напряжения чистого кручения отсутствуют (см. равенство (1)); крутящий момент передается касательными напряжениями стесненного кручения.
Торец стержня свободен. Предполагается, что на торце стержня (рис. 10.12, б) нормальные напряжения отсутствуют. Из формулы (24) получаем
7?(0)-0.	(50)
az
Крутящий момент на торце стержня является заданным, и в силу соотношения (36)
(51)
Если крутящий момент на торце отсутствует, то
' GJRg(0)-£J^(0) = 0.	(52)
az	dz	-
Торец стержня свободно оперт, но поворот сечения невозможен. (рис. 10.12, в). При наличии скользящей заделки торец стержня имеет возможность осевого перемещения, нормальные напряжения на торце отсутствуют
7?(0)-0.	(53)
az
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
357
Угол поворота сечения равен
0(0) = 0.	*	(54)
Замечание. Краевые условия в сечении z = I составляются точно таким же образом, как и при z = 0.
Рассмотрим кручение стержня при жесткой заделке одного из торцов сечения будем считать извест-
(55)
(рис. 10.13, а). Геометрические лыми (их определение рассматривается ниже). В сечении z — 0 имеется жесткая заделка, и по условиям (48) и (49) начальные параметры равны
0(0) = 0,	(0) =0.
Краевые условия при z = I будут такими (условия (50) и (51)): d20
T2-W=°> az
d6	d3B
(56)
С помощью решения (46), используя строчки матрицы.(47), находим из условий (55) и (56) в" (0) ch pz + 9" (0) 4sh pz = 0,
(57)
Р2 k(0) 4sh pZ + В"' (0) 4 X L p	p
характеристики
Рис. 10.13. Кручение стержня при жесткой заделке корневого сечения: а — схема стержня; б, в, г— эпюры крутящих моментов чистого и ' стесненного кручения и нормальные напряжения а
X(ch₽Z-l) - [0" (0) ₽ sh PZ+
М
+ e"'(01ch₽/] = .£j^- (58)
Уравнение (58) после очевидных сокращений дает Мк
r(0) = _^,	-
что можно было установить сразу в силу равенства (36), Из соотношения (57) находим
. (59)
(60)
sh BZ
Используя решение (46), находим момент касательных напряжений чистого кручения:
= GJK = GjJe'(0) 1 Sh Pz+0”’(°) 4 (eh р2-1)1.	
dz. ц P	P	J
358
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
Внося значения 0"(О) и 0"'(0), получаем
М<к1} = Мк 1
_ ch 3 (Z — z)l ch pi J
Момент касательных напряжений стесненного кручения
М(к2) = - EJa —i = -EJa [6" (0) Р sh pz + 0"' (0) ch pz],
ИЛИ
М(2) _ м ch Р ~_£ Ch рг
Легко видеть, что условие
Мк ’ + Мк ’ = Мк
выполняется.
Нормальные напряжения стесненного кручения
о = - £©—г = - Еш 0" (0) ch Pz + 0"' (0) 4- sh pz az	L	P
или
мк sh P (i — z) CT = -pjo“ ch PZ •
Примерное распределение крутящих моментов Мк и нормальных напряжений о по длине стержня показано на рис. 10.13, б — г.
Изгиб и кручение тонкостенных стержней. Нормальные напряжения. Разберем теперь общий случай нагружения стержня, когда внешние силы дают в поперечном сечении не только крутящий
У
Рис. 10.14. Изгиб и кручение тонкостенного стержня: О — центр тяжести сечения; 01 — центр кручения, или центр жесткости сечения; еж, еу — координаты центра кручения; ж, у — главные оси
момент, как это предполагалось ранее, но также изгибающие моменты и усилия (рис. 10.14).
Внешние силы приводятся к главным осям сечения х, у в виде перерезывающих усилий Qx и QV1 осевого усилия N, изгибающих
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
359
моментов Мх, Му и момента Мг относительно оси z, проходящей через центр тяжести сечения. Будем считать, что сечение стержня не деформируется в своей плоскости и к обычным деформациям стержня на основе гипотезы плоских сечений добавляются деформации, связанные с депланацией сечения при кручении.
Тогда перемещения точки А сечения стержня могут быть представлены так (см. разд. 27):
IV = iv0 +	— <рух —	<0,	(61)
где <Pv — углы поворота сечения относительно осей х, у. Последний член правой части равенства (61) выражает осевое смещение (депланацию) при кручении. Угол поворота сечения 0 определяется относительно оси, перпендикулярной плоскости поперечного сечения (он одинаков для осей z и zK, проходящих через центр тяжести О или через центр кручения Ot).
Величина ш в равенстве (61) представляет секториальную площадь и зависит от дуги s, характеризующей положение точки А (см. рис. 10.14), и полюса, который принимается в центре кручения 01.
Здесь и в дальнейшем под со понимается главная векториальная площадь, удовлетворяющая условиям
Ею dF = 0, [ Ex® dF = 0, j* Еуы dF = 0.	(62)
F	F	F
Оси х, у являются главными осями сечения, и для них
J Ex dF = 0, f Еу dF = 0. J Еху dF = 0.	(63)
F	F	F
Деформация в точке А в направлении оси z равна
dw	, d<Px	d^v	d2$	
e’~dz =	e»+ dz У'	dz		 dz2	(64)
Для упругого, равномерно нагретого материала, используя гипотезу одноосного напряженного состояния, находим, что деформациям 8 отвечают напряжения

d<Py dz
d20
X------5®
dz2 ,
(65)
Теперь из условий равновесия
[ о dF = N, оу dF = Мх, \ oxdF = — Му, (66) F	F	F
учитывая равенства (62) и (63), получим
Л d<fx_Mx d<fv_My
е«“4’ ‘й7-'в7’ dz ~ Ву'	W
3G0
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
где жесткости стержня на растяжение и изгиб равны A=^EdF, Bx=*\y~EdF, Bu = ^,3~EdF.	(68)
F	F	F
Нормальные напряжения в стержне с учетом соотношений (67) и (65) будут такими:
„(У , Мх Му d4 ) о = £	+г/-------х	и.	(69)
И	я?/ dz J
Формуле для нормальных напряжений в тонкостенном стержне можно придать более удобный вид, если ввести понятие бимомента
Мв = f wtidF.	(70)
F
Умножая обе части равенства (69) на о и интегрируя по всей площади сечения, находим в силу условий (62)
Мв^-^В^,	(71)
az *	х
где == J Ею2 dF —секторпальная жесткость сечения.
Подставляя значение d20/dz2 в соотношение (69), получаем (у	М „	М
a =	+	+ <о^}.	(72)
(73)
Для стержня с постоянными параметрами упругости имеем N  Мх	М	Мв
о = у +у—-х—w + ® — Г	JX	J у	J (д
Замечания. 1. Как видно из -соотношения (73), в теории* тонкостенных . стержней распределение деформаций и напряжений при изгибе не подчиняется гипотезе плоских сечений. Гипотеза дополняется, законом секториаль-' ной площади.
2. Величина бимомента Мв имеет размерность [сила X длина2], т. е. отличается от размерности обычных моментов.
Другое отличие состоит в том, что значение Мв в поперечном сечении стержня в противоположность изгибающим моментам Мх и Mv не может быть найдено из условий равновесия. Это объясняется тем, что, величина М3 определяется самоуравновешенной системой сил. Значения Мв определяются в самом процессе решения. Если в концевых сечениях стержня внешние усилия заданы, то становится известной и величина бимомента.
Условие (71) показывает, что осевые силы, приложенные к торцу стержня, могут вызвать закручивание тонкостенного стержня при
Мв Ф 0.
3. Формулу для нормальных напряжений (69) можно представить в виде суммы
с = Си 4* Сек,	(74)
где
/У мх м\
аи = £(л
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
361
— обычные напряжения изгиба;
сГ9
— нормальные напряжения стесненного кручения (соотношение (24)).
Такое «разделение» произошло потому, что координаты ж, у и секториаль-ная площадь удовлетворяют условиям (62) и (63).
Касательные напряжения изгиба. Центр жесткости сечения. При кручении и изгибе тонкостенного стержня возникают касательные напряжения чистого и стесненного кручения и касательные напряжения изгиба. Все эти группы касательных напряжений могут рассматриваться отдельно. Ранее были изучены касательные напряжения чистого и стесненного кручения, и потому займемся касательными напряжениями изгиба. Вкратце они рассматривались в разд. 31, где был разобран соответствующий пример.
Исходным для расчета является условие равновесия (28), причем выражение для Nf будет таким:
Nf = §odF = % Е dF + t	/
МО м с
B^JEydF — -g^ExdF.

Интегралы распространяются на отсеченную часть сечения, площадь которой /. Из равенства (28), считая осевое усилие N постоянным, находим касательные напряжения поперечного изгиба
4	( 4 dM„	4 dM,t ]
(76)
где Se/x = f EydF, Se/у = J ExdF — упруго-статические моменты . /	f	•	-
отсеченной части сечения.
Из условий равновесия элемента стержня (рис. 10.15) получаем
dMx А й^--о dz ~	^х'	(77) (78)
и тогда формула для касательных напряжений изгиба имеет вид
При постоянном модуле упругости
•	-	(ОД
где S/x, Slv — статические моменты части'площади сечения f. Ка-
362
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
сательные напряжения изгиба в поперечном сечении образуют систему сил (разд. 30), которая, если ее приводить к центру тяжести сечения, эквивалентна не только перерезывающему усилию, но и крутящему моменту Мх (рис. 10.16, а).
Точка поперечного сечения/ относительно которой касательные напряжения изгиба не дают момента, называется центром жесткости
Рис. 10.15. Условия равновесия элемента стержня
Рис. 10.16. Понятие о центре жесткости поперечного сечения (О — центр тяжести, О\ — центр жесткости). Система касательных усилий приводится к центру тяжести (а) или к центру жесткости (б)
сечения или центром изгиба. Покажем сначала, что центр жесткости совпадает с центром кручения (точкой OJ. _
Определим момент касательных усилий изгиба относительно точки 01, в которой помещается полюс главной секториальной площади. Момент будет равен (см; рис. 10.10 и (30))
ЛГти —
= — J t(s)5(s)p(5)c?5=— J т (5) 3 (5) da « — J SEfx da — J SEfy da.
р	F	XF	yF
(81)
Учитывая (62), (63) и интегрируя по частям, находим*
\ /==F
EydF j = со J EydF | —^2Jy(odF==0, /	/	>	(82)
Ex dFA da — со J ExdF | — J Exa dF « 0. /	/	/=0 F
Следовательно, момент касательных усилий, вызванных касательными напряжениями изгиба, обращается в нуль относительно центра кручения (точки поворота сечения при кручении). Центр жесткости совпадает с центром кручения.
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
363
Этот же результат можно получить другим путем. Равенство (81) справедливо, конечно, при произвольном выборе точки Ol9 Нетрудно заметить, что
Мти = О, если всегда выполняются условия
J Efx d<o == О, J Se/у do) = 0.	(83)
k	F
Для главных осей сечения х, у условия (83) и равенства (82) приводят к зависимостям
J Eyco dF = 0, j* Ехю dF = 0,	(84)
f	f
определяющим положение центра жесткости (центра изгиба).
Но соотношения (84) ранее были установлены для центра кручения (уравнения (62) и (63)), что и доказывает их совпадение.
Замечания. 1. Тождественность центра жесткости и центра кручения при упругих деформациях можно рассматривать как следствие теоремы взаимности. Для этого достаточно рассмотреть две системы сил, приложенных к свободному торцу консольного стержня: поперечную силу и крутящий момент.
2. Равенства (84), определяющие положение центра жесткости тонкостенного профиля, получаются из обычного рассмотрения касательных напряжений изгиба.' Они не связаны непосредственно с проблемой стесненного кручения.
Пример. Изгиб стержня швеллерного сечения поперечной силой (рис. 10.17).
Рис. 10.17. Изгиб тонкостенного стержня поперечным усилием
Определим касательные напряжения при изгибе стержня, пользуясь формулой (80).
Найдем положение центра жесткости сечения по распределению касательных напряжений изгиба.
Крутящий момент касательных усилий при изгибе относительно точки 01 — центра жесткости, отстоящего от средней линии стенки ВС на расстояние а, должен быть равен нулю:	.	.
Л/о = Qa — 4-	bSh —	- (85)
2 ОП (П -f- 00)	v '
364*
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
Первый член выражает момент от касательных усилий в стенке ВС (их равнодействующая равна Q)\ второй член — момент от касательных усилий в полках (множитель 1/2 появляется в силу линейного распределения напряжений вдоль полки; толщина профиля 6 считается малой). Из равенства (85) получаем
e=_aL
/г + 66
Расстояние между центром жесткости и центром тяжести сечения
362	, Ъ2 _	462 (А + 36)
h + 66 h + 26 (h + 66) (А + 2b)
(86)
Этот результат можно получить из общих формул (84) для координат центра жесткости, что будет сделано в дальнейшем. Относительно оси стержня касательные напряя«ения изгиба (точнее, касательные усилия) создают момент
Л/q — Мхп —— —Q&*
Так как внешние силы, приложенные к стержню, сводятся к силе Q, то полный крутящий момент в сечении (относительно оси стержня) должен обращаться в нуль. Следовательно, в сечении должны образоваться касательные усилия, дающие крутящий момент, равный но противоположно направленный. Он возникает за счет крутильной деформации стержня, вызываемой моментом
MK = Qe.
Если осевое стеснение в заделке отсутствует, то крутящий момент Мк вызывает касательные напряжения чистого кручения, распределенные линейно по толщине стенки (рис. 10.18).
При несовпадении центра тяжести и центра жесткости сечения поперечная нагрузка, приложенная в центре тяжести (рис. 10.17), вызывает не только
Рис. 10.18. Касательные напряжения изгиба тя и чистового кручения тк в поперечном сечении стержня
изгиб, но и кручение стержня. Величина крутящего момента равна моменту силы относительно центра жесткости сечения.
Оценим величины касательных напряжений изгиба и кручения для стержня швеллерного профиля -(рис. 10.18). Касательное напряжение чистого кручения по формуле (4)
т - м*8 -	-	3<?е
К	у (А+26) 6*	62(Л+2й)
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
365
Наибольшее касательное напряжение изгиба
3(> (Л 4- 46) ти max — 26Л (А 4- 66)'
При h — Ъ
тк _ 32 k_ х» max “ 45 6 ’
Для тонких профилей (h » 6) касательные напряжения кручения, вызванные поперечной силой Q (см. рис. 10.18), значительно превосходят касательные напряжения изгиба.
Угол поворота концевого сечения
om M«l W
W “ GJK ~ G (/»4* 26) 63"
При малых б угол поворота возрастает, так как е не зависит от б.
У равнения изгибно-крутильных деформаций тонкостенного стержня. При деформации изгиба сечение стержня получает поступательное смещение вдоль осей х и у (см. рис. 10.14). Деформация кручения приводит к повороту на угол 9 вокруг оси, проходящей через центры жесткости сечения. Связь упругих перемещений (u, v) центров тяжести (точек оси стержня) и центров жесткости (ut, pj выражается следующими простыми соотношениями:
и = Ut + еу0, р ==
где еж, ev — координаты центра жесткости.
Поступательное движение профиля характеризуется упругими перемещениями центра жесткости; остальные точки сечения получают дополнительные смещения в результате поворота.
Параметры изгибной деформации (соотношения (67))
d<fx	«га
dz	dz* ' dz	'°''
выражаются через вторые производные компоненты смещения центра жесткости. С помощью соотношений (67) находим
d2v	d2u.
Вх-± = -Мх,	(88)
az	az
dz Vx»
(89)
Учитывая условия равновесия элемента стержня (см. рис. 10.15) dz	dz	dz
получаем уравнения изгибных перемещений
d* (р	(р d*“l |_„
U \Вх~^~ / ~' 9х’	7? \ Ву ~
az \ ал /	az \ az /
Зависимости (89) полностью совпадают с обычными уравнениями
3G6
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
изгиба стержня (см. разд. 34), но относятся к смещениям центра жесткости.
Перейдем к рассмотрению крутильных деформаций. Крутящие моменты относительно оси центров жесткости (оси zK, см. рис. 10.14) дают касательные напряжения (точнее, касательные усилия) чистого кручения
и стесненного кручения
М(2) ==__В
к	w dz* ’
Момент касательных усилий поперечного изгиба относительно оси центров жесткости равен нулю.
Из условия равновесия имеем
(«О)
где Л/к — крутящий момент относительно оси zK:
Мк == Мг + eyQx — exQy,	(91)
Мг — момент внешних сил относительно оси z.
Дифференцируя равенство (90) по z и учитывая завпсимость (91), находим
d / D \ d ( г с?0 \	~
"dz ( В(Л "d?	+ e“qx ~~ €xqy' (92)
где, как и раньше, qx и qy — распределенные нагрузки на единицу длины оси стержня (оси z), тг — распределенный (на единицу длины) момент относительно оси z..
Обозначая распределенный момент относительно оси zK в виде тпк == тг + eyqx — exqy.	(93)
получим
d / п	d3$ \ d	i\	/0/\
T-	t —7-	\ C —	== mK.	(94)
dz \	dz3 I dz	\ dz J	K	4 '
Уравнение для угла закрутки 0 при действии изгибающих и крутящих нагрузок совпадает с уравнением (40) для стесненного кручения.
Уравнения (89) и (94) описывают изгибные и крутильные деформации тонкостенного стержня. Краевые условия для уравнения (94) аналогичны краевым условиям уравнения (40) и были разобраны ранее-(соотношения (48)—(54)).
Поскольку теперь среди внешних нагрузок рассматриваются и нормальные усилия на торцах стержня, то следует указать краевое
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
367
усилие при действии внешнего бимомента. Если в сечении z = I известна величина бимомента, то (см. уравнение (71))
dz2 W В„
(95)
Для стержня с постоянным модулем упругости
(I) ____
Замечание. Для упругих перемещений ub и 9 уравнения (89) и (94) оказались независимыми, но связь между изгибной и крутильной деформациями проникает обычно через краевые условия. Такая связь не возникает, если центры тяжести и жесткости сечений совпадают.
Пример. Крутильные деформации тонкостенного стержня при действии продольных сил.
Рис. 10.19. Действие продольных самоуравновешенных усилий на тонкостенный стержень: а — расчетная схема; б — действие осевых сил на торец стержня; в — определение главной секториальной площади; г — картина деформаций
Пусть на торец стержня двутаврового сечения действуют четыре силы Р, образующие самоуравновешенную систему сил.
Краевые условия при z = О имеют вид
0(0) =0,	5Г(0)=0,
368
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
а при z = 2
d20	мв
.2 (0 — EJ » dz	о
где Мв = J crco dF— бимомент внешних осевых сил.
F
Так как касательные усилия па торце z = I отсутствуют, то по условиям (52)
d0	d30
Г(0=0.
Перейдем к определению векториальных характеристик. На рис. 10.19, в показано определение главной секториальной площади со для двутаврового сечения. Центр жесткости (полюс секториальной площади) совпадает с центром тяжести, так как сечение обладает двумя осями симметрии. Принимая начало отсчета площади в точке 40, получаем для точки А значение со а, равное удвоенной площади треугольника OAqA:
bh
<°А = -—•
Знак минус появился потому, что радиус-вектор движется вдоль отрезка АоА по часовой стрелке (более подробно определение секториальных характеристик сечения рассматривается ниже), векториальный момент инерции
Л/
F
.можно вычислить по правилу Верещагина, умножая эпюру со «саму на себя»:
1 bh Ъ 2 bh 1 ~ 2л
7«> — 4' 2 4 2’3 4 6 = 24 Ь h 5‘
Значение бимомента в сечении z — Z по равенству (70) будет таким:
Мв(1) == (ОаР — <овР + (ИсР— coDP == —Pbh.
d0
С помощью решения (46), учитывая равенства 0(0) = 0 и-^- (0) =0,находим
е (2) = 0" (0) 4- (ch fk -1) + 0да (0) ± (sh pz - ₽2), .	р	р
0' (z) = 0* (0) 4 sh Pz + 0* (0)4- (ch pz - 1), p	p	’
0* (3) - 0" (0) ch Pz + 0" (0) j sh Pz, (z) = 0" (0) p sh Pz + 0да (0) ch pz.
Из краевых условий при z = I получаем .
1
0" (0) ch Р/ + 0'" (0) j sh.pZ - — ej^~, P2 J©* (0) sh pit + 0" (0) (ch pZ - 1)] - [0* (0) p sh PZ + 0да (0) ch PZ] = 0.. Из последнего условия следует
0"'(О) = 0,
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
360
и тогда
MB(Z) 1 6" (0) = -	----Г-77Т .
£> Jо) Сц р/
Нормальные напряжения находим из формулы (69): о = — £0"(z)co или
ch $z	Pbh ch Pz
a	° = “7Г “chpT °*
Учитывая значение Л>, находим
24Р ch pz a~~ b2h&. ch|JZ “•
Напряжения изгиба в-точке А при z = l равны
-	24jP bh ёР
aA — bafcS 4 ~ bb • Этот результат может быть получен, если считать, что момент РЬ действует на верхнюю полку:
6Р6 6Р °А~ Ь28 ~ Ъ6 •
Картина деформаций представлена на рис. 10.19, г. Каждая из полок двутаврового сечения испытывает деформацию изгиба.
Замечание. В корневом сечении z = 0 нормальные напряжения а(0)=п(0-^.
Происходит «затухание» напряжений по мере удаления от сечения z '== lt что вполне естественно, так как внешняя нагрузка самоуравновешенная.
Скорость затухания зависит от величины
Жесткость стержня на кручение
GJK^=G-~ б3 (Л4-26), и тогда
й,_ . / ~i	1	2463 (6 4-26) I2	_ 251 1/ i 6	4-26
Р V 2(14-р)	3	63636 м V 1 + н ь	•
При 6 = 6
₽/“ 63	1+Р*
При малой толщине б затухание невелико, и принцип Сен-Венана о быстром затухании действия самоуравновешенной нагрузки в тонкостенных стержнях нарушается.
24 и. А. Биргер, Р. Р. Мавлютрв
370
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
Определение секториальных упруго-геометрических характеристик сечения и координат центра жесткости. Ранее было установлено, что главная секториальная площадь должна удовлетворять следующим условиям:
^EwdF = 0,	(96)
F
\ExadF = (),	(97)
F
^Eya>dF — Ot	(98)
k
где x, у — координаты денных главных осей
элемента площади dF относительно приве-сечения; Е — модуль упругости материала
стержня;
3
J Р («1) dst, о
(99)
<0 — секториальная площадь, соответствующая дуге s (удвоенная площадь сектора AqAOi). Секториальная площадь представляет криволинейный интеграл, и при его вычислении следует учитывать
Рис. 10.20. Зависимость величины секториальной .площади от изменения начала отсчета
направление обхода (рис. 10.20). В правой системе координат приращение da положительно, если радиус-вектор г получает дополнительный поворот против часовой стрелки (по направлению положительного крутящего момента). Если начало отсчета секториальной площади переносится из точки Л о в точку Л*, то новая секториальная площадь, соответствующая точке Л, равна
со* == со+со0,	(100)
где — секториальная площадь (соответствующая точке Ло) при начале отсчета в точке Л*. При изменении начала отсчета секто-риалъной площади ее значение изменяется на постоянную величину. Для выполнения условия (96) можно выбрать произвольную точку средней линии профиля в качестве начала отсчета секториальной площади.
Подставляя соотношение
<о = 0* — со0‘
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
371
в равенство (96), находим
Е(л) dF= J Е (со* — со0) dF = О, F	F
или
J £oj,dF
F
(101)
Значение соо определяет положение точки
главной секториальной площади. Выражение для со при произвольном начале отсчета имеет вид
J E®*dF
<о = о* - F .	(102)
w
F
Формула (102) справедлива при любом полюсе секториальной площади.
Определение координат центра жесткости. Пусть имеется система координат я*, у* (рис. 10.21), оси которой соответственно параллельны главным осям сечения х, у(х*\\х, У* В у), и для точки О^~ рассматриваемой как полюс, определена секториальная
Aq — начала отсчета
Рис. 10.21. Определение координат центра жесткости (точки 01) в системе координат, оси которой соответственно
площадь (о* при начале отсчета в точ- параллельны главным осям ке Л*. Найдем связь между сектори-
альной площадью со, имеющей полюс в центре жесткости (точ-
ке 01), и величиной со*. Начало отсчета (точка Л*) остается
неизменным.
Будем иметь
= p*ds, dco == pds.	(ЮЗ)
Если а — угол между касательной к средней линии профиля и осью у, то (см. рис. 10.21)
р* == Р + cos а + ау s*n а,	(104)
где
ах, dy — координаты центра жесткости в системе
у*. Так как cosa ==
координат
dy* __ dy ds ds ’
sin a =
dx*   dx ds	ds r
то из соотношений (103) находим
dca == f p*	dx dy —J == dxdy dy dx*
24*
372
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
Интегрируя это выражение вдоль дуги $, получим о = ю* — аху + аух + С,
(105)
где х, у ~ координаты точки средней линии профиля (в главной системе координат), для которой определяется секториальная площадь; С — настоянная интегрирования. В силу условий (97) и (98)
j Ех(д dF = ) Ex (со* — аху + аух +C}dF = 0,
;	'с	(106)
) Еуы dF = ) Еу (cd* — аху + аух + С) dF = 0. F	F
Так как оси х, у являются главными, то, ссылаясь на равенства (63), получим из соотношений (106)
ах = I Eya* dF, ау = —~\ Еха* dF.	(107)
xf	»f
Для стержня с постоянными параметрами упругости
= -г У®* dF, J xj F
ay =------ I xcd* dF,
(108)
(109)
где Jx, Jv — моменты инерции сечения относительно главных осей. Координаты центра жесткости относительно главных осей равны вх = ах+6х, еу = ау+Ьу,	(110)
где Ьх, Ьу — координаты произвольного полюса О*.
Отметим, что формулы для координат центра жесткости справедливы при любом выборе начала отсчета секториальной. площади.
Рис. 10.22. Расположение центра жесткости О\ и центра тяжести О некоторых ,	профилей
Общие свойства расположения центра жесткости. Равенства (97) и (98), определяющие положение центра жесткости, позволяют указать некоторые общие правила его нахождения.
1.	Если сечение стержня имеет ось симметрии, то центр жесткости так же, как и центр тяжести, лежит на этой оси (рис. 10.22, а).
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
373
Напомним, что для таких сечений ось симметрии является одной из главных осей. Считая ось х совпадающей с осью симметрии, заметим, что равенство (97) будет удовлетворено, так как значения со в двух симметрично расположенных точках средней линии одинаковы по величине, но противоположны по знаку.
Предполагается, что модуль упругости Е постоянен или удовлетворяет, как и элементы площади, условиям симметрии.
2.	Если сечение имеет две оси симметрии, то центр жесткости так же, как и центр тяжести, лежит на пересечении указанных осей (рис. 10.22,6).
3.	Если сечение имеет радиальную точку, то центр жесткости совпадает с ней (рис. 10.22, в). Радиальной точкой сечения назовем точку, по отношению к которой средние линии частей сечения имеют радиальное направление. Очевидно, все средние линии должны быть прямыми.
В связи с этим для любой точки средней линии главная секто-риальная площадь равна со ’=»0, так как ее полюс находится в точке Oi. Сечения, обладающие радиальной точкой, не имеют депланации при кручении; в тонкостенных стержнях с такими сечениями (типа тавра, уголка) стесненное кручение не возникает. Отметим, что при ю = 0 условия (96) — (98) выполняются тождественно.
Примеры определения координат центра жесткости. 1. Рассмотрим сечение швеллерного типа (рис. 10.23) и выберем начало местной системы координат я*, у* в центре тяжести стенки профиля. Центр тяжести всего сечения отстоит
Начало примем
от средней линии стенки
Ъ2
bx — ~h + 2b-
отсчета секториальной площади в точке (9*. Вдоль линии В А радиус-вектор вращается по часовой стрелке и потому со * < 0. В точке А секториальная площадь равна удвоенной площади треугольника О* В А:
bh
^♦А =	2 ‘
Рис. 10.23. Определение центра жесткости. сечения швеллерного типа
Момент инерции сечения равен
dh3 b8h2
Jx= 1-2 + 2 *
Положение центра жесткости (координату ах) находим по формуле (108). Предварительно вычисляем
с „	1 bh h b2h38
Sa>x — J V®* dF ~ — 2- 2 2 66 2 — — 4 ' F
Значения у. для верхней полки у = Л/2, для нижней у = —Л/2. Далее находим Ь2Л23 ЗЛ2
Ох=— ых Л + В6-
374
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
Расстояние между центром жесткости и центром тяжести равно 362 Ь2	46 2 (/» 4- 3b)
ex=ax+bx==— л 4-66“ Л4-26 =	(Л4- 66) (h + 2by
Этот результат был получен ранее (формула (86)) путем непосредственного определения момента касательных напряжений изгиба. —
2. Определить центр жесткости сечения . стержня в виде дуги окружности радиуса Я. Площадь сечения F = 2Яаб (рис. 10.24). Центральный угол 2а, толщина 6.
Выберем начало местной системы координат в центре окружности. Центр тяжести сечения отстоит на расстояние
Рис. 10.24. Определение центра жесткости сечения стержня в виде дуги окружности
Знак минус связан с поворотом секториальная площадь должна
а
Начало отсчета секториальной площади примем на оси у* (точка .4*). .Секториальная площадь в точке А (удвоенная площадь сектора О*А*А) равна
со* Я2ф.
радиуса-вектора по часовой стрелке. Главная удовлетворять условию
j* ало dF = б j Я sin ф (a,yR sin ф — Т?2ф) R dq> = 0,
F	—а
что дает значение а J sin ф-ф <2ф -а	л sin а — а cos а
ау = ——------------= 2---------------R.
~Jsin2<pd<p а-Т sin 2а —а
При а = л (сечение в виде кольца с разрезом)
ау = 2R.
При малых а, считая
1 з	1
sin а == а — -g- а -|- ..., cos а = 1 —	а2+ • • м
получаем
•27? = Я,
т. е. центр жесткости приближается к центру тяжести.
38. ТОНКОСТЕННЫЕ СТЕРЖНИ
375
Расчет секториальных характеристик сечений. Для определения напряжений и деформаций в тонкостенных стержнях, кроме обычных геометрических характеристик (координат точек, моментов инерции), требуются значения секториальной площади и ее моментов. Секториальная площадь, соответствующая точке средней линии профиля, может рассматриваться как обобщенная координата точки наряду с другими ее координатами (х, у и т. д.). Определение секториальных характеристик для Сечений стержней с постоянным модулем упругости покажем на примерах.
Пример 1. Определить главную векториальную площадь и ее моменты для сечения швеллерного типа. Толщина профиля 6 (рис. 10.25). Ранее было определено расстояние от центра жесткости О\ до стенки — величина ах (рис. 10.23):
_ 362 ах - h + 66-
Полюс главной секториальной площади находится в точке О|, начало отсчета (нулевая точка секториальной площади) лежит па оси х (точка До).
Рис. 10.25. Эпюры главной секториальной площади и секториального момента отсеченной части
Секториальная площадь в точке В равна удвоенной площади треугольника Q\A.qBz
1 '
®В~~ 2
Значение е>в > 0, так как радиус-вектор точки средней линии, исходящий из центра жесткости, на рути AqB поворачивается против часовой стрелки. На участке В А поворот радиуса-вектора получается по часовой стрелке; приращение секториальной площади, равное удвоенной площади треугольника 0^4, оказывается отрицательным:
111
“а = Т a*h ~ Т bh = Т (вх - 6)h'
376
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
Значение (о = 0 на верхней полке соответствует расстоянию ах от точки В, Отметим, что распределение со характеризует распределение нормальных напряжений стесненного кручения.
Рассмотрим теперь секториальный статический момент отсеченной части:
5Ш= J (adF,
F воспроизводящий распределение касательных напряжений стесненного кручения. ,
Величина представляет площадь эпюры (о, если начинать обход с точки А. Наибольшая величина получается после прохождения дуги b — ах, так как на этом участке знак со не изменяется:
сотах ~	"4" (& ах)2
В точке В значение представляет разность площадей треугольников с основаниями b — ах и ах:
1 1
5<оВ = - — (Ь - ах)2 4- — фб.
Эпюра S& показана на рис. 10.25, б.
Определим секториальный момент инерции:
Je, = J(O2d/’.
F
Для его аналитического определения удобно воспользоваться правилом Верещагина, умножая эпюру аг«на себя». Будем иметь
f 1 axh h 2 axh 1 aji 2	,
J<a — 2{ 2 2 2'3 2 5 + 2 2 “x* 3 2 S’r
'11	2	ф’б a®h26 (b — ax)shx&
+ 2'2 (ax-6)ft(6~ax)- 3	2 J ~ 12 +	6 + tj
Замечание. В современных расчетах геометрические характеристики се--чений определяют путем численного интегрирования на ЭВМ. Для стандартных прокатных профилей секториальные характеристики указываются в справочниках.
39. Полупространственные модели стержня
Вводные замечания. В обычной теории стержней нормальные напряжения направлены вдоль оси стержня; нормальные напряжения, действующие «в плоскости сечения», т. е. перпендикулярно оси стержня, считаются отсутствующими (гипотеза о_яенадавливании волокон стержня).
В некоторых случаях, например при неравномерном нагреве стержней с массивным поперечным сечением, пренебрегать указанными напряжениями нельзя.
39. ПОЛУПРОСТРАНСТВЕННЫЕ МОДЕЛИ СТЕРЖНЯ
377
Основные уравнения. Нормальные напряжения в поперечном сечении. Рассмотрим сначала стержень постоянного сечения, за-
груженный по торцам моментами п осевым усилием (рис. 10.26). Температурное поле по длине стержня не изменяется. В этих условиях можно считать напряжения и, следовательно, деформации постоянными по длине стержня.
Из уравнений совместности деформаций (см. разд. 11) после приравнивания нулю производных по z находим
с постоянными
Рис. 10.26. Стержень напряжениями по длине
-2	п2
д	л 0 8, л <7 8_
—^ = о, -4 = о, ^«0.
дх2	ду*	дх ду
(111)
При постоянных по длине стержня напряжениях и деформациях осевая деформация 8г распределяется по поперечному сечению по линейному закону относительно координат х и у:
е2 = Со + CiX + С2у.	(112)
Соотношение (112) удовлетворяет условиям (111). В соответствии с принципом независимости действия сил кручение стержня можно рассматривать в пределах упругих деформаций отдельно, и в дальнейшем будем считать Мг = 0. При действии изгибающих моментов и осевой силы линейное распределение 82 эквивалентно гипотезе плоских сечений.
В соответствии с гипотезой плоских сечений (см. разд. 29) , ^Фх ^Фу Б* = ео + -^--йГж’
(ИЗ)
где параметры деформации 80, dcp^dz, dqy/dz в рассматриваемом случае — постоянные величины.
На основании обобщенного закона Гука имеем
8г = А- [ог — р, (ах + 0^)] + аТ.	(114)
Используя соотношение (ИЗ), находим
ог = Е (е0 + у — х^\ — ЕаТ + ц (ох + ау). (115) \	az az у
Условия равновесия отсеченной части стержня
fodF-JV, \cydF = Mx, C\oxdF = -My (116)
F	F	F
378
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
приводят к системе трех уравнений относительно параметров деформации 80, dyjdz и dcpv/dz.
Для главных осей сечения л, у, удовлетворяющих условиям
= j£ydF = O, J^dF = O, (117)'
F	F	F
указанные уравнения существенно упрощаются.
После нахождения параметров деформации из равенства (115) получаем
йх Ои “Ь От ем	Пдоп?
(118)
где изгибные напряжения ои и температурные напряжения отем определяются прежними формулами (разд. 29), а дополнительные напряжения
/ Jp(ox+ay)dF
СГдоп = — I —------j---------^°х +	+
\	х F
+ /- J Н (Ох + av) dF - -%- (ах + о,) • (И9) У F	/
Нормальные напряжения в поперечном сечении стержня зависят от напряжений о« и оу, действующих «в плоскости поперечного
сечения».
Напряжения в плоскости поперечного сечения. На рис. 10.27 показан элемент стержня, выделенный двумя поперечными сечениями на расстоянии, dz друг от друга.
Рис. 10.27. Напряжения в плоскости поперечного сечения стержня
Рис. 10.28. Краевые условия для функции напряжений
Напряжения о», оу и будем для краткости называть напряжениями в плоскости поперечного сечения (точнее, напряжениями, векторы которых лежат в указанной плоскости). Так как напряжения не зависят от z и составляющие массовых сил отсут
39 . ПОЛУПРОСТРАНСТВЕННЫЕ МОДЕЛИ СТЕРЖНЯ
379
ствуют, то первые два уравнения равновесия будут удовлетворены, если положить
d2F	d2F
Тху~ дхду'	<1J)>
где F = F(x, у) — функция напряжений.
Третье уравнение равновесия будет удовлетворено, так как напряжение ог постоянно по длине, а касательные напряжения тгх и т2у отсутствуют (кручение стержня не рассматривается). Из соотношений упругости следует, что
у [ffx — И (ау + <т2)] + аТ =
d2F ду2
d2F
+аТ-
ОХ
1 * 1
' 6У = -£-	— и (а* + ст*)1 + аТ = у
d2F дх2
д2Р
Нтт ду
1
----G- Xxv
И Е , (121)
+ аГ-ц
(122)
(123)
2 (1 + р.) д2Р
Е	дх ду*
ех
Рассмотрим теперь уравнения совместности деформаций (см. разд. И). Из первого уравнения и зависимостей (121) —(123) получаем	.
— (
дх2 \
1	4- — f 1 —
Е дх2 / ду2 \ Е ду2 )
-2 д2 fi + jld2F\ . дхду\ Е дхду)
g2 / р. _ — ( JL дх2 \ Е ду2 / ду2 v & дх2 /
= —V3(a7’) + V2(|iy),
(124)
где V2 — двумерный оператор Лапласа:
а2	п2
V2 -	+ —г.
дх2	ду2
Все остальные уравнения совместности деформаций будут выполняться. Уравнение (124) представляет уравнение плоской задачи с дополнительным членом, зависящим от напряжения ох.
Краевые условия для функции напряжений вытекают из условий равновесия элемента, примыкающего к контуру стержня (рис. 10.28):
Ox cos (v, х) -и тху cos(v,
Ow COS (v; ^)+TxyCOS(v, ж) — Ру, ‘	(125)
где v — вектор нормали к контуру; рх, ру — распределенная нагрузка на поверхности (в мегапаскалях); cos(v, х), cos(v, у) — косинусы углов между направлением v и осями х и у. Нагрузки рх и ру должны быть постоянными по длине и самоуравновешенными. Ис
380
ГЛ. 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
пользуя зависимости (120), получаем краевые условия (в точках контура) для функции напряжений
—Г cos (V, х) - cos (V, у) = рх,
d2F .	. d2F .	.
COS (V, у) - cos (v, х) = Pv.
(126)
Расчет стержней по полупространственпой теории. Напряжения в стержнях описываются связанной системой уравнений (118) и (124) (в уравнение (118) входят ц(ох4-ау), в уравнение (124) — величина цог/Е).
Для случая постоянного коэффициента ц уравнение плоской задачи (124) может быть решено независимо от уравнения (118). В большинстве практических задач допущение ц = const не вызывает существенной погрешности.
При постоянном ц из соотношения (118) получаем
(4)=v2(аГ)+(г+1441 (127) 
\ & /	дх & ду ]
Простой вид равенства (127) связан с тем, что формулы (118) содержат линейные члены относительно х и у, которые после двукратного дефференцирования исчезают. Внося значение (127) в уравнение (124), получаем
g2 / 1. g2?\ + —	-и 2 d2 f 1 а2/? \
дх2 J + ду2 ду2 / + 1 — И дх ду хЕ дх ду)
д2 /1 52?\ дх2 ду2 /
4- — ( 1 d2F • P/U дх2
(128)
И
1 — р
1 —р
Наконец, при постоянном модуле упругости Е из уравнения (128)
находим
V4 = (V2)2 =
W = - -L_V2(aT),	(129)
где д2 <?2 \ / д2 \ -21 х ?	. 21
дх2 ду2) ^fo:2 ду2) дх* дх2ду2 ду*
— бигармонический оператор.
Уравнения (128) или (129) являются уравнениями плоской задачи теории упругости (задачи о плоской деформации) для области,, представляющей собой поперечное сечение стержня.
После решения плоской задачи становятся известными значения ох и av, которые подставляются затем в равенство (119). Получен
39. ПОЛУПРОСТРАПСТВЕННЫЕ МОДЕЛИ СТЕРЖНЯ	38f
ные результаты распространяются на приближенный расчет стержней переменного сечения при наличии поперечных нагрузок. Уравнения (118) и (128) используются для каждого сечения независимо от других, как это принято в обычной теории стержней.
Касательные напряжения изгиба определяются из уравнений равновесия.
Замечания. 1. Из приведенного решения следует, что напряжения в плоскости сечения связаны главным образом с действием неравномерного нагрева. Если коэффициент Пуассона постоянный и распределенные усилия на боковой поверхности отсутствуют, то в равномерно нагретом стержне ох = О, ау = о, Txi, = 0 (однородное уравнение (128) при однородных краевых условиях имеет только нулевое решение).
2. Возникновение указанных напряжений при. изменении коэффициента Пуассона в точках поперечного сечения не имеет практического значения ввиду их малости. Сказанное подтверждает используемую в обычной теории стержней гипотезу об одноосном напряженном состоянии, за исключением случаев неравномерного нагрева сечения стержня и (или) значительной (са-моуравновешенной) поперечной нагрузки.
ГЛАВА 11
КОЛЬЦА
40. Изгиб колец
Вводные замечания. В технике часто используются кольца как силовые .элементы конструкций (рис. 11.1). Они служат для подкрепления оболочек (силовые кольца, шпангоуты), особенно при передаче сосредоточенных усилий. и нередко представляют самостоятельные конструктивные элементы.
Рассмотрим замкнутые круговые кольца, у которых одна из главных осей поперечного сечения лежит в плоскости кольца. Будем считать, что нагрузки совпадают с главной осью и действуют в плоскости кольца и что размеры сечения малы по сравнению кольца.
Основные уравнения. \	замкнутом кольце под
Рис. 11.1. Кольца как элементы произвольной нагрузки (в конструкции	кольца) является статически неоп-
ределимой задачей.
Разрезав кольцо .в произвольном месте (рис. 11.2), получим статически определимую систему, в которой действуют три неизвестных силовых фактора: нормальное усилие перерезывающее усилие Х2 и изгибающий момент Х3.
Замкнутое кольцо является. три раза статически неопределимой системой.
При определении перемещений будем использовать интеграл Мора
Кольцо '
поперечного с радиусом
Задача о действием плоскости
~ЁЁ~ ds +
KQpQi л ~Gp ds* (1)
ы(в)
,хз
х2
*3
7
Рис. 11.2. Основная система при расчете колец
где МР, Np, Qp — изгибающий момент, перерезывающая и нормальная силы •от внешних нагрузок; Nb Qi — то же от единичных силовых факторов;
_£7Х, EF, GF — жесткости на изгиб, растяжение и сдвиг; К — коэффициент, зависящий от формы сечения.
Анализ показывает, что влиянием перерезывающих и нормальных сил для колец в большинстве случаев можно пренебречь.
В качестве основной системы принимаем кольцо, «разрезанное» и сечении А (рис. 11.2).
40. ИЗГИБ КОЛЕЦ
383
Составим канонические уравнения метода сил, считая относительные смещения точек А и А* равными нулю:
6цХх + 612Х2 + 613X3 4- Д1р = 0,	(2)
621^1 + 622Х2 4- 623Х3 4- Дгр ~ О,	(3)
631X1 4- 632X2 4- 633X3 + Дзр = 0-	(4)
Уравнение (2) выражает отсутствие относительного смещения разреза (в основной системе) в направлении силы Хь уравнение (3) обращает в нуль взаимное смещение разреза в направлении силы Х2, наконец, уравнение (4) свидетельствует об отсутствии взаимного поворота разреза.
Для определения коэффициентов канонических уравнений (2) — (4) построим эпюры изгибающих моментов (рис. 11.3). Используя
Рис. 11.3. Эпюры изгибающих моментов от единичных силовых факторов
свойства произведения симметричных и кососимметричных эпюр,, находим
612 == 621 = 0, 623 == 652 === 0.
Из уравнения (3) находим
Х2 == —Дгр/бгг*	(5)‘
Уравнения (2) и (4) принимают вид
6uXi + 613X3 + Д 12> == 0,	6з1Х1 + 633X3 + Д3р = 0
и приводят к следующим значениям неизвестных силовых факторов:
X = Азр^13Д^зз у __ AiAi ~ A3p6n .	,g
6ц633	6!з	*	6П633 613
Перейдем к вычислению коэффициентов влияния. Изгибающий^ момент в сечении под углом 0 в эпюре Mi (рис. 11.3, а)
2Ии(0)=1 • R(1 - cos 0).
Изгибающие моменты будем считать положительными, если они уменьшают кривизну стержня (положительное направление показано на рис. 11.2).
384
ГЛ. И. КОЛЬЦА
Изгибающие моменты в эпюрах 2 и 3 от единичных силовых факторов (рис. 11.3, а, б) равны
М12(0)=1 .flsinO, М13(0)=1.
Далее вычисляем 2Л	2Л
«и - тт; J «г.™ " еИ - “s«)! л -	
О	о
2Л	2Л
613 - irx f 13Rde = J (1 - cos 9) de =
X 0	X 0
2Л	2Л
622 = jj- j M2l2R de = ~\^ sin2 9d9 =
X 0	X 0	*	X
2Л	2Л
633 = £77 f Mi3^ d® = Z77 J dQ “ ЁЦ' 0	0
Перемещения от внешних нагрузок составляют 2Л	2Л
Д = A- f MpMirR de = £- f Мр (1 - cos 9) de, X J	x J
0	0
2Л	2Л
Д2Р = gy- J MpM'l2R = J Mp sin 9d9, X 0	X 0.
2Л	2Л
Д13 = £?; f MPM137? de = Д- J Mpde, x 0	x 0
тде Л/Р(0) —изгибающий момент в сечении под углом 0 в разрезанном кольце от внешних нагрузок.
Подставляя вычисленные значения в формулы (6), найдем после несложных преобразований
2Л
Х1 = -4( Mp(9)cos0d9,	(7)
о 2Л
Хй = - J Мр (9) sin 9 de,	(8)
О 2Л	‘	2Л
Х3 = —Tji-f Mp(9)d9 —-V Mp(9)cos9d9.	(9) '
«Л J	2T J
0	0
Изгибающий момент в сечении 9 в замкнутом кольце
М(9) = Jf,(0) + Х^(1 - cos 9)+ X2R sin 9.+ Х3.	(10)
40. ИЗГИБ КОЛЕЦ
385
Учитывая равенства (7) — (9), получим основную формулу
2Л	2Л
М (0) = Мр (9) - 2^- ) Мр (9) </9 - J Мр (6) cos 0 dd -о	о
2Л
J Mp(0)sin0d0. (И)
О
Изгибающий момент в сечении замкнутого кольца равен изгибающему моменту в разрезанном кольце за вычетом трех первых членов разложения этого момента в ряд Фурье.. При вычислении интегралов можно пользоваться приближенными численными методами.
В равенстве (11) угол 9 отсчитывается от сечения разреза, которое можно выбрать произвольным. Если внешние нагрузки имеют ось симметрии или ось асимметрии, то разрез целесообразно проводить по этим осям.
Для нагрузки, симметричной относительно линии разреза,
л	л
м (0) = Мр (0) - У Мр (0) dQ - У Мр (0) cos 0 Од. (12) о	о '
Для нагрузки, кососимметричной относительно линии разреза,
-	л
М(0) = МР(0)-^^ j” 3/p (0) sin 0 ей). _ (13)
О
Замечание. При раскрытии статической неопределимости_кольца учитывались только изгибающие моменты. В некоторых случаях, например при действии на кольцо большого числа одинаковых радиальных сил, существенное значение , приобретают нормальные усилия, и их следует учесть в равенстве (1). Это понятно, потому что при равномерном давлении на кольцо изгибающие моменты в нем отсутствуют и вся деформация происходит за счет усилий N. •
Пример 1. Определить изгибающие моменты в кольце под действием сосредоточенных сил (рис. 11.4, а). Проведем разрез по оси симметрии и распределим нагрузку поровну по краям разреза (рис. 11.4, б).
Изгибающий момент в сечении под углом 0
1
Мр (0)	— у PR sin 0.
Применяя формулу (12), находим л	л	~~
У Мр (0) dQ = - Lpr у Sin 0 de = — PR,
О	о
л	х л
J Мр (0) cos 0 d0 = — -TfPR J Sin 0 cos 0 dQ = 0, о	о
25 и. А. Биргер, P. P. Мавлютов
386
ГЛ. 11. КОЛЬЦА
и окончательно
М = Pr(L — J_sin 0). \л 2	/
При 0 = 0 и 9 = л/2
М (0) == _L PR = 0,318РЯ, м (	= | — — -I) PR = — 0,182/»/?.
л	\2/ \л 2/
Распределение изгибающих моментов показано на рис. 11.4, в.
Рис. 11.4. Кольцо под действием сосредоточенных сил
Пример 2. Определить изгибающие моменты в кольце, загруженном двумя сосредоточенными моментами М (рис. 11.5, а). Проведем разрез по оси
Рис. 11.5.. Кольцо под действием сосредоточенных моментов
симметрии (рис. 11.5, б). Изгибающий момент в основной системе в сечении под углом 0
9 I— М, а<0<л.
Определяем
л	л
J Мр (0)d0 = — J М = — М (п — а),
о	а
л	л
J Му (0) cos 0 dO = —. М j cos 0 г/0 = М sin а.
о	а
41. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КОЛЕЦ
387
Далее по формуле (12) находим
М (0) =	(0) + М (1 — 2.) — 2cos9Msin а.
р	\ Л / л
При 0	0 а
М (0) = М (1 — - )— 2cos9 sin а. \ л / л
При а < 0 л
М(0)=.— М (—2cos - sin а). \л Л	J
Эпюра изгибающих моментов показана на рис. 11.5, в.
41. Осесимметричная деформация колец
Во многих конструкциях встречаются кольца, работающие при осесимметричном нагружении (рис. 11.6, а). Пусть на кольцо (рис. 11.6, б) действуют осевые и равномерно распределенные ра-
диальные нагрузки: q2, qr.
Центр тяжести поперечного сечения кольца расположен на ок-
ружности радиусом г0; ось х
Рис. 11.6. а — осесимметричная деформация колец; б — нагрузки, приложенные к кольцу
направлена в радиальном направлении. Рассмотрим равновесие половины кольца (рис. 11,7).
Осевое усилие из условия равновесия равно
N = ?гЛ3,
Рис. 11.7. Определение силовых факторов в сечении кольца
по которой равномерно распределены усилия qr [сила/длина] (рис. 11,6,6).
Изгибающие моменты относительно оси х составляют Л/2	Л/2	Л/2
М = [ a2sin P-g2a2dp —	J axsin р.^А^Р —	eqT J	cosP-a3dp,	(14)
о	о	л	0
где	e — эксцентриситет	приложения	радиальжТго	усилия	gr.	Пер
25*
388
ГЛ. 11. КОЛЬЦА
У1*—
Рис. 11.8. Сечение кольца после деформации
вые два слагаемых правой части уравнения (14) в пояснениях не нуждаются; последнее слагаемое получается в результате проектирования момента, распределенного на дуге a3d^ на ось х. После интегрирования находим:
М = 4^2 — «171 — «з^7г-	(15)
Осесимметричное нагружение приводит к появлению в поперечном сечении кольца осевого усилия и изгибающего момента.
Рассмотрим теперь деформации кольца. В приближенном решении будем пренебрегать деформацией сечения в своей гГлоскости, считая, что кольцо состоит из жестких шайб, связанных кольцевыми упругими нитями. В результате деформации центр тяжести кольца смещается на и0, а сечение поворачивается на угол 0 (рис. 11.8). Смещение точки А в радиальном направлении
U = Uo“"70.	"	(16)
Деформация в кольцевом направлении
2л (г + и) — 2лг и ио 9
‘ . ее==-----------2^Гг---(17>
где г—радиус окружности, проходящей через точку А. Размеры сечения кольца будем считать малыми по сравнению с радиусом окружности центров тяжести г = г0,	-	(18)
и тогда
=	(19)
О о
Предполагая напряженное состояние одноосным, получим в пределах упругих деформаций окружное напряжение (рис. 11.9)
а = £(е9-аТ)=»£(^-у^-а7’1,	(20)
Vo го /
где аТ — температурная: деформация (а — коэффициент линейного расширения, Г —температура).
Из условия равновесия следует, что
=	(21)
F
^aydF = -M. '	(22)
Рис. 11.9. Напряжения в поперечном сечении кольца
41. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КОЛЕЦ
389
Подставляя в уравнения (21) и (22) величину о из соотношения (20), получим при 2? = const
Е f dF - Е f аТ dF = N, °F	F
^Е j ij-dF + E\yaTdF = М,
так как
( У dF = 0
F
(ось х проходит через центр тяжести сечения) * Из уравнений (23) и (24) находим
Г .Л? Г J °	F
0	М if /р
(23)
(24)
(25)
(26)
(27)
Подставляя эти значения в равенство (20), получаем формулу для напряжений в кольце
N М I 1 С	1 dF 1
а==7“^Г + £ Jr]a7W + yi—---аТ L (28)
РисГ 11.10. Кольцевая пружина
Первая группа членов представляет напряжение в кольце от внешних сил, вторая — температурные напряжения.
Пример 1. Определить напряжение в элементах кольцевой пружины при действии осевой нагрузки (рис. 11.10).^Распределенные усилия q\, qz и осевая сила Р связаны соотношением
Р =	= 2ла2^2«	(29) /
Изгибающий момент в сечении кольца находим по формуле (15):
- M = ^(a2-a!):	С30)
Напряжения в элементах кольцевой
Р (а2 ~ а1)	6Р (°2 ~ а1)
°- у 2nJx ~ у nbh3-
будут такими:
Наибольшие напряжения при у = ± h/2:
,	ЗР(а2~а1)
атах“ лдЛ2- '
(31)
390
ГЛ. И. КОЛЬЦА
Растягивающие напряжения действуют при у — — h/2, сжимающие — при у = 4- Д/2. Осадка кольца пружины
61 = 0(й2 — «1).
Угол поворота кольца
„ Мг0 6Р (а2 ~ а1) ГВ
EJX~ nEbk* '
Осадка всей пружины
6 = z6x = z
&Р (а2~а1)Ч лЕ&Л3
(32)
Для расчетного анализа и выбора размеров удобно использовать связь между осадкой пружины и максимальными напряжениями (формулы (31) и (32)):
6 — 2zcrmax
(Я2 ~ а1) ГВ h
(33)
Для увеличения осадкй пружины (при одинаковом уровне напряжений) надо увеличивать число колец z, уменьшить толщину кольца h.
Замечание. 1Рри сильном уменьшении толщины кольца h (h<Z 0,2(а2 — at)) приближенное решение может оказаться не справедливым, так как предположение о жестком поперечном сечении кольца будет приводить к погрешностям. В таких случаях кольца следует рассчитывать по теории пластинок.
Рис. 11.11. Кольцо под действием радиальной нагрузки
Рис. 11.12. Различные случаи закрепления кольца
Пример 2. Определить напряжения и перемещения в кольце прямоугольного сечения под действием радиальной нагрузки (рис. 11.11).
Силовые факторы в поперечном сечении кольца равны
r'_	N = aqr,	М = —aeqr»
Напряжения в кольце находим по формуле (28):
aqr aeq aqr 12aeqr
a=- + !/-J-= — + y—r...	(34)
Радиальное смещение центра тяжести сечения кольца
и - jVr° - аЧтГ«
0 EF Ehb '
41. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КОЛЕЦ
391
Угол поворота поперечного сечения
i2aeqr
0 = -------з
Ebh3
Замечание о пределах применимости приближенного решения. Рассмотрим два различных случая закрепления кольца (рис. 11.12). В первом случае (рис. 11.12, а) кольцо приварено к массивной детали. Применение приближенного решения неоправдано — сечение кольца должно деформироваться. В этом случае окружными (кольцевыми) напряжениями можно пренебречь и рассматривать кольцо как ряд независимо изгибающихся стерженьков единичной толщины с высотой сечения h. Во втором случае (11.12, б) кольцо получает угол поворота; основные напряжения — окружные. В общем случае для расчета осесимметричной деформации колец используется теория круглых пластин.
ГЛАВА 12
ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Динамические явления играют важнейшую роль в современной технике. Колебания элементов конструкций часто являются причиной разрушений и катастроф. При проектировании технической системы необходимо знать ее частотные характеристики и избегать динамического усиления внешних воз-буждений. Основы теории колебаний излагаются в курсе теоретической механики. Однако колебания упругих систем, особенно систем с распределенными параметрами, имеют ряд особенностей, с которыми необходимо познакомиться.
42. Изгибные и продольные колебания стержней
Колебания груза, закрепленного на стержне (балке). Такая динамическая схема встречается при расчете фундаментных балок и стержней, крепящих тяжелые агрегаты (дизели, турбины и т. п.), и в ряде других случаев. Будем считать массу стержня малой по отношению к массе груза.
Рассмотрим сначала свободные колебания балки с грузом (рис. 12.1), вызванные случайным первоначальным отклонением.
Рис. 12.1. Свободные колебания груза, закрепленного на стержне
В отклоненном положении, которое характеризуется смещением v(i), зависящим от времени t, на груз действуют сила тяжести Q и сила упругости
F = J-v(i),	(1)
и11
где 6ц — прогиб балки в месте приложения груза (массы) от единичной силы.
Уравнение движения груза имеет вид
2
<2>
где m — Q/g — масса груза.
42. ИЗГИБПЫЕ И ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
393
Обозначая
получим дифференциальное уравнение
+ AG) =-—•	(4)
dt* г > т	v ’
Общий интеграл этого уравнения можно представить так:
v (t) = и (0) cos pt + -—• (0)у sin pt + уСт (1 — cos pt), (5) где уст = —@бц— прогиб балки под действием силы веса; у(0), •—(О) — начальное отклонение и скорость (при t = 0).
Пусть в начальный момент времени груз получил отклонение
У ( 0) == Уст + ^о.	(6)
Тогда из соотношения (5), считая начальную скорость равной нулю, получим
у (0 = Уст + Уо cos pt.	(7)
После начального отклонения система начинает совершать колебания с круговой частотой р, амплитудой у относительно положения статического ^равновесия (прогиба уст). В дальнейшем постоянные во времени силы не будут рассматриваться, следует только считать, что система совершает колебания относительно положения равновесия.
Замечание. Для дифференциального уравнения колебаний
нормальными фундаментальными функциями (разд. 31) являются следующие:
1
v1(t) = cos pt, v2(t) sin pt,	(9)
и общее решение уравнения (8) примет вид t dv 1	i Г
v (f) = р (0) cos pt + yy (0) у sin pt + у j sin p(t — tj f (t^dt^ (10) о
При f(t) = —Qlm получаем решение (5).
Собственные колебания груза. Как известно, колебания условно разделяют на свободные, при которых внешние возбуждающие силы отсутствуют, и вынужденные, происходящие под действием переменных по времени внешних нагрузках. Силы трения в материале (внутреннее трение), в узлах сочленений (конструкционное демпфирование) и другие виды трения считаются всегда присутствующими. В силу этого свободные колебания — всегда затухающие.
394
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Силы демпфирования обычно невелики и не сказываются на частоте и форме колебании системы.
При анализе частот и форм колебаний рассматриваются свободные колебания без учета сил демпфирования. Такие колебания называются собственными. В расчетную модель собственных колебаний входят лишь силы инерции и силы упругости. Уравнение собственных колебаний груза (рис. 12.1) имеет вид
+ ^y{z)==0. (11)
dt °11
Частное решение этого уравнения можно принять в виде p(^)=pcospi,	(12)
где v — амплитуда колебания, р — круговая частота. Внося равенство (12) в уравнение (И), получаем
Частота колебаний измеряется в герцах:
/ = ^.	(14)
Период колебаний равен
r=V=f-	(15)
Частота колебаний в соответствии с равенством (13) тем меньше, чем больше масса груза и упругая податливость системы.
Отметим важную для дальнейшего статическую аналогию упругих колебаний. Решение (12) приводит к тому, что уравнение (11) превращается в уравнение для амплитудных прогибов
— p2mv + и = 0.	(16)
°ii
Его можно было написать сразу, если считать, что усилие, с которым колеблющаяся масса действует на балку, равно
Fn = pzmv	(17)
и направлено в сторону прогиба.
Условие равновесия дает
р2ти — -Д~ v = О, 6П
т. е. уравнение (16).
Замечание. Величина и в решении (12) цри собственных колебаниях остается неопределенной; она равна величине произвольного начального отклонения. Но частота колебаний не зависит от амплитуды (свойство изохронности малых колебаний). В нелинейных системах проявляется зависимость частоты колебаний от величины первоначального отклонения.
42. ИЗГИБНЫЕ II ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
395
Вынужденные колебания груза. Пусть на сосредоточенную массу действует внешняя возбуждающая сила P(t) (рис. 12.2): P(t) — Р cos (i)t,	(18)
где со — круговая частота возбуждающей силы.
Например, если масса представляет турбину с частотой вращения ротора п (об/мин), то при наличии неуравновешенности ротора воз-
никнет возбуждающая сила с частотой
0 = ^=2^,	(19)
где — число оборотов в секунду.
Уравнение движения груза будет таким:
т d v == — -L v (t) 4- P cos (oL (20) dr
Рис. 12.2. Вынужденные колебания груза, закрепленного на стержне
В системе возникнут собственные колебания, связанные с начальными условиями движения, которые вскоре затухают вследствие неизбежных сил трения. Вынужденные колебания соответствуют частному решению неоднородного уравнения (20), которое можно искать в виде
г(£) = v coscot
(21)
Внося решение (21) в равенство (20), получаем
1 — 0?//	1 —со2//’
(22)
где р = 1/V6uzn — круговая частота собственных колебаний, vQ =» = Рби — отклонение системы под дейст-
вие. 12.3. Зависимость коэффициента динамического усиления от частоты возбуждающей силы
вием амплитудного дающей силы при ее жении. Отношение
значения возбуж-
статическом прило-
1
i 1 - CD2// |
(23)
сутствуют силы трения,
называется коэффициентом динамического усиления.
При совпадении частоты возбуждающей силы и частоты собственных колебаний наступает резонанс: прогиб балки v -*• -* оо, коэффициент динамического усиления кД -> °°. В действительных условиях амплитуда колебаний остается конечной, так как в системе неизбежно при-однако резонансные колебания могут пред-
ставлять серьезную опасность для конструкции.
/Сд ---
896
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
На рис. 12.3 показана зависимость коэффициента динамического усиления от частоты. Обычно рекомендуется исключать из зоны рабочих режимов частоту возбуждения 0,7р < со < 1,3р.
Отметим, что очень высокие частоты колебаний не опасны для конструкции с низкой собственной частотой (А?д-*• О при со -*•<»).
Замечание. Ёсли на конструкцию действует возбуждающая сила с часто-той со, то конструкция испытывает стационарные колебания с этой же частотой. Вынужденные колебания конструкции происходят с частотой возбуждающей силы.
Собственные колебания стержня с несколькими сосредоточенными массами. Рассмотрим сначала колебания балки с двумя сосредоточенными массами (рис. 12.4). Воспользуемся статической аналогией и будем считать, что в отклоненном положении на массы действуют усилия
Рис. 12.5. Формы колебаний, соответствующие двум частотам колебаний двухмассовой системы
Рис. 12.4. Колебание упругой системы с двумя сосредоточенными массами
закрепления масс. Прогибы стержня под действием усилий F\ и Fz (рис. 12.5) равны
Vi ===	। “F" &iZFZ == 5цР 171 iVi “I”	77lrZVZl
(24)
VZ — &izF£ “F" §22^2 — biZp^l7l>iVi *1” 622Р Zn2P2,
где Sij — коэффициенты влияния (прогиб в сечении i от единичной силы в сечении /; они определяются с помощью интеграла Мора).
Напомним, что коэффициенты влияния удовлетворяют условиям взаимности
6ij = 6j{.	(25)
Равенства (24) приводят к системе однородных уравнений относительно Vi и vz:
(panini — 1) Vi + р2б127П2У2 в О,
(26)
Р2б 12^1^1 + (р2622^2 ~ 1) Vz = 0.
Эту же систему можно получить другим путем, считая, что на стержень действуют силы инерции масс

$
42. ИЗГИБНЫЕ И ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
397
Предполагая далее
рt (t) = i?! cos pt, v2 (t) = v2 cos pt, получаем соотношения (24).
Однородная система уравнений (26) будет иметь отличное от нуля решение в том случае, если определитель системы равен пулю:
Al"1!"1 л12т3	=0.	(27)
₽2б12т1	^б22т2 “ 1
Из условия (27) получаем характеристическое уравнение для определения частот колебаний
р4т1т2 (бпб22 — б{2) — р2 (бцТ^ + б22тп2) + 1=0.	(28)
Из этого уравнения относительно р находим два значения круговой частоты:
2 =	+	~	+ б22та2)2 -	~ б12)	(29v
2та1та2(б11б22-б12)_______________ ’
2 _ «„Wj + 622w2 + V(61Л + 622m2)2 - 4ТО1тг (6U622 - 622)
Pi • (0)
Низшей частоте Pi соответствует обе массы двигаются в одну сторону; частоте р2 отвечает движение грузов в разные стороны (вторая форма колебаний, рис. 12.5).
Если определитель системы уравнений равен нулю, то соотношение между прогибами i2i и и2 при данной частоте можно получить из любого (одного) уравнения системы (26). Например, ]
первая форма колебания, когда
Рис. 12.6. Колебание многомассовой системы
первого уравнения находим
У2П	1 ’	Г22)	Al"1!-1
Величина отклонений при данной частоте колебаний остается неопределенной, но соотношение амплитудных прогибов масс — форма колебаний — строго определено равенствами (31).
Рассмотрим теперь колебания упругой системы с п сосредоточенными массами (рис. 12.6).
Амплитудный прогиб t-й массы
Vi = р26цт^1 + p28i2m2v2 +... + р2ЬцТП,р} +... + p2§inmn vn. (32)
Составляя выражения прогиба для всех масс (i — i, 2, 3,	п),
придем к системе однородных уравнений, которую представим в
398
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
матричной форме:
(33) где
'10 0 ..."
1 J 0 0 1 ...
— единичная матрица порядка и, {i;}T = v2t ..., pj — вектор амплитудных прогибов.
Частотное уравнение получается после приравнивания нулю определителя системы:
lpW^]~[£]l=0.	(34)
Уравнение (34) дает значения п собственных частот колебаний РьРг, и каждой частоте соответствует своя форма колебаний. Если в определителе уравнения (34) сохранить только члены» стоящие на главной диагонали, симость для первой частоты
1
то получается приближенная зави-
2 4-,	(35)
где Р(г) « 1/(6н7П:) — частота колебания системы (балки) при наличии только одной массы т{. Формула (35) дает обычно хорошее приближение для первой частоты, меньшее действительного значения. Отметим, что Pi < р(<}, ъ = 1, п.
Дифференциальное уравнение изгибных колебаний стержней. Рассмотрим теперь непрерывное распределение массы; пусть
т = pF	(36)
— масса, приходящаяся на единицу длины стержня (р — плотность материала, F —площадь поперечного сечения стержня).
При изгибных колебаниях на единицу длины стержня действует распределенная нагрузка д:
й2	а2
О V	п О V
(37>
Уравнение изгибных колебаний можно получить из основного уравнения изгиба стержней (см. разд. 31)
*^\=qv(z),	(38)
dz \	dz j
где qv — интенсивность распределенной нагрузки (рис. 12.7). При-
42. ИЗГИБНЫЕ И ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
399
менительно к колебаниям величина qy определяется равенством (37). Прогиб оси стержня v(z, t) зависит теперь не только от z, но и от времени t, и потому в уравнение (38) должны входить частные производные
д* /ч d2y(z, t) \	р d2v(z, t)
^\EJx (2) J*	= - pF —i-2-.	(39)
az k	az 1	at	4
При анализе собственных колебаний предположим
v(z, £)== z?(z)cos pty	(40)
где p — круговая частота колебаний, v{z)— амплитудное значение
прогиба при колебаниях. С помощью соотношения (40) получаем обыкновенное дифференциальное уравнение:
4 ( EJX (z)	) - p°-pF (z) v (z) = 0. (41)
dz \	dz
Этот результат можно было сразу получить из статической аналогии, положив
Рис. 12.7. К выводу уравнения колебаний стержня
q — p^pFv.	(42)
Изгибные колебания стержней постоянного сечения. Для стержней постоянного
сечения при колебании в главной плоскости
yOz (рис. 12.8) уравнение изгибных колебаний (41) будет таким:
d*v (z)	2 pF , v А
—H--p2^-v(z) = °.
dz
(43)
Рассмотрим в качестве примера балку, закрепленную по концам на двух шарнирных опорах (см. рис. 12.8),
Рис. 12.8. Колебания стержня постоянного сечения: а —расчетная схема; б — две первые формы колебаний
Краевые условия для амплитудного прогиба таковы: ,2	j2
p(0) = i/(Z)eO, 4±.(O)=4^(Z)=O,	(44)
dz	dz
т. e. прогибы и изгибающие моменты на концах балки отсутствуют.
400
ГЛ. 12. ДИНАМИКА II УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Уравнению (43) и условиям (44) соответствует функция
v (z) = v sin у (к = 1, 2, 3, ...).	(45)
Внося выражение (45) в уравнение (43), находим
Р
значению к соответствует определенная частота колебаний
№ }/EJx
Ph Z2 ' $Е
(46)
Наименьшая круговая частота колебаний получается при к = 1:
„2 Г F Г
(«>
Первая частота колебаний (в герцах) равна
i =	— 2L Л/ EJ *	(4(q\
71 2л - 2/2 V
Из формул (45) и (46) вытекают выводы, справедливые и при других условиях закрепления стержня. Система с непрерывным распределением масс имеет бесчисленное количество частот и форм колебаний. Каждой собственной частоте рк соответствует своя форма колебаний vk. Спектр собственных частот упругой системы — дискретный, как это следует из равенства (46). Разберем общее решение уравнения (43), которое запишем в виде
-^-X4v(z) = 0, Х4=Р3^.	(49)
dz	x
Непосредственным дифференцированием можно проверить, что функции
Vi = cos Az, v2 == sin Az, v3 = ch Az, v4 = sh Az
являются частными решениями уравнения (49). Из них можно составить нормальные фундаментальные функции (функции Крылова)
Vr (z) = V (ch	+ cos V2 (z) =~ 4“ (sb Az + sin Az),
i <5°>
y3 (z) = — (ch Xz — cos Xz), V\ (z) = —5 (sh Xz — sin Xz),
удовлетворяющие условию
dz3 [Ъ 7 — 1
(51)
42. ИЗГИБНЫЕ И ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
401
Например, dV	d^V	d3V.
^(0) = 1, -йг(°) = 0. -г?-(0) = 0, —зЧ0) = 0; az	dz	dz0
dV	d3V„
^(0) = 0, -^(0) = l, -^-(0) = 0, _^(0) = 0.
Общее решение уравнения (49) будет таким:
» (2) = V (0) Ух (2) +	(0) Уа (2) +	(0) V3 (2) +	(0) 74 (2). (52)
az	dz	dz
Начальные параметры р(0), i/(0), ... определяются из краевых условий. Для определения частоты получается определитель второго порядка; два из четырех краевых факторов известны заранее.
Изгибные колебания балки переменного сечения. Решение с помощью интегральных уравнений. Уравнение изгибных колебаний запишем в виде
4 (EJX (2) 4^1 = Рг?Р (*) V (2).	(53)
dz у	dz j
Из соотношений (29) и (30) разд. 31 следует
.A [ejx (2)	= -Qy (2),	(54)
EJX (2)	_ мх (z),	(55)
dz
где <?y(z), Mx(z)— амплитудные значения перерезывающей силы и изгибающего момента при колебаниях балки (рис. 12.9).
Рис. 12.9. Изгибные колебания стержней переменного сечения
Уравнение (53) может быть приведено к форме интегрального уравнения, что дает ряд преимуществ для приближенного решения. Проинтегрируем уравнение (53) в пределах от z до I. Учтем, что
402
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
перерезывающая сила при z = I отсутствует. Получим
-~[eJx (2) ~p^pF (zj V (zx) dzx. (56) '	' z
Повторим операцию с учетом условия Мх(1) = 0: i i
Ejx (2)	=pi Л pf v dz*dzi-
z *1
Теперь, перенося EJx{z) в правую часть равенства и дважды интегрируя от 0 до z, с учетом условий
*(0) = 0, $(0) = 0	(57)
получаем интегральное уравнение колебаний консольного стержня
z Z1	II
v (z) =. р2 J J  J J pF (zt) V (z4) dz4 dz3 dz2 dzt. (58) 0 0	* 2 z2z3
Это — однородное краевое интегральное уравнение, эквивалентное дифференциальному уравнению и соответствующим краевым условиям. Оно называется интегральным потому, что неизвестная функция входит под знак интеграла (в дифференциальном уравнении неизвестная функция подчиняется операциям дифференцирования). В кратком виде уравнение (58) записывается так:
v = pzKv,	(59)
где Ко — интегральный оператор, входящий в правую часть уравнения (58).
Легко видеть, что если v(z) является решением уравнения, то функция Cv(z), где С — произвольное число, также представляет его решение (амплитудные прогибы при собственных колебаниях задаются с точностью до множителя).
Уравнение (59) имеет решение которое называется три-9	2	2
виальным, но при некоторых значениях P =Pi,p2, ••• оно имеет отличные от нуля решения. Каждому значению р?, pl, ...» которые называются собственными значениями уравнения (оператора), соответствуют решения vi9 и2, ...— формы колебаний стержня (собственные функции).
Для отыскания первой собственной частоты применяется метод последовательных приближений. Задаемся произвольно первым приближением для формы колебаний, например
p(1)=(z/Z)2.	(60)
Следующее приближение находим из уравнения (59) по схеме
^(2) = Ph)Kvw.	(61)
42. ИЗГИБНЫЕ И ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
403
Если бы р(1) было точным решением, то функции v(i} и v{2} совпадали бы во всех сечениях. Найдем величину p(i} из условия, что значения v(l} и и(2} совпадают на конце стержня, где прогибы наибольшие.
Из условия i?(2)(Z) = yd)(0= 1 получаем
------1-----74-------------------------<02>
оо Z2Z3
Обычно уже первое приближение дает погрешность не более 2—5%.
Можно показать, что процесс последовательных приближений всегда сходится к первой собственной частоте. Получение таким способом последующих частот и форм колебаний требует проведения процесса ортогонализации.
Решение с помощью матричного уравнения. Примем в качестве основных переменных следующие функции (см. разд. 31):
Y^) = v(z), Y^z)-^, Y3(z) = Mx(z), Y^z) = Qy(z) (63)
и представим уравнение (53) в виде системы четырех уравнений первого порядка, учитывая, конечно, соотношения (54) и (55): yl(Z) = y2(2), уД^^-^у,^.	(64)
Уз (2) = У4 (2), У* (2) = - Р2рР (2) Ух (2),
где штрих, как и раньше, означает дифференцирование по z.
В матричной форме уравнения будут такими:
{Fr-pqm,	(65)
где вектор состояния
	{nT = {y1yIysy4} = {v, и',	Мх, Qv}-,	(66)
матрица	“0	10	0 ~	
	0	0 —ёП"	0	
	л=	EJ*		(67)
	ООО	1	
	p2pf 0	0	0_	
Расчет частот и форм колебаний покажем		на примере	колебаний
консольного	стержня. Задаемся сначала	некоторым	значением
частоты р; тогда все элементы матрицы А становятся известными.
Учитывая условия (57), найдем два частных решения ({Ф3(г)> и {Ф4(z)}) уравнения (65) при начальных условиях
о о
1
о
Ф<(0) =
о о о
1
(68)
Ф3(0) =
404
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Интегрирование уравнения (65) проводим одним из численных методов, например методом Рунге — Кутта. Общее решение уравнения (65) можно представить в виде
{У (г)} =	|М У2 ^3	= С3{Ф3(2)} + С4{Ф4(2)} = С3	ф 31 ф 32 Ф 33	 + С4 •	[ф 1 41 Ф 42 Ф 43	, (69)
	И		Ф 1 34,		Ф 44 J	
поскольку краевые условия при z = 0 удовлетворены выбором начальных условий (68).
Так как в концевом сечении У3(0 и У4(^) обращаются в нуль,
У,(0“С3Ф,3(г; p2) + G<D43(Z; р2) = 0,
(70) y4(W?M; р2)+с4Ф14(г; /) = о.
В записи уравнений (70) подчеркивается зависимость от р2, так как эта величина входит в матрицу [Л]. Из условия существования решения (70) получим
F(/) =
ф330;р2) фз4(^2)
ф4з0;р2) ф440;р2)
(71)
Так как выбранное заранее значение р2 не удовлетворяет условию (71), то расчет проводят заново и находят значения РьРъ •••— корни уравнения (71). Это и будут частоты колебаний стержня.
Применение вариационного метода для определения частот и форм изгибных колебаний стержня. Ранее было получено вариационное уравнение изгиба стержня в виде (разд. 36)
6П = О,	(72)
где 1 , * 4	С	/j2	\2	С
п == и - W ~ 4- \EJX Р4 dz-\qvvdz.	(73)
J	\dz	]	J
о	4	о
Возможная работа внешних сил при вариации прогиба равна i
6Ж = J qyf>v dz, о
Для задачи о колебаниях стержня
?в = />2РА’у,
вариация возможной работы
i
SW = р2 J pFvftvdz.
о
42. ИЗГИБНЫЕ И ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
405
Возможная работа внешних сил
i
о
По физическому смыслу величина W представляет амплитудное значение кинетической энергии при колебаниях стержня. Полная потенциальная энергия системы равна
1	/ 2 V	1
п = U — W = Ijzvjin dz-^p^pFv2dz. (75) о	Х 7	о
Величина П равна разности между потенциальной энергией деформации и ее кинетической энергией. Наиболее простое решение по методу Рэлея — Ритца получается для одного параметра, когда предполагается
^^(z),	(76)
где /i(z) —заранее выбранная функция из числа допустимых.
Например, для консольного стержня можно принять
А(2) = ж	(77)
Более точные результаты, но несколько более сложные вычисления получаются, если принять /4(z) пропорциональной прогибу консольного стержня постоянной толщины при действии равномерной статической нагрузки:
z2 2 z3 1 z4
+ (78)
В этом случае выполняются не только необходимые (кинематические) условия при z = 0:
/1(0)»= о, Х(0)=0,
но и (силовые) краевые условия при z = Z:
А (0 = 0, /Г (0 = 0.
В соответствии с методом Рэлея — Ритца частота колебаний находится из уравнения
дП __ дс± дс± 2 отсюда	cl У EJX (A)2 dz - С*рг J pF/2 dz = 0,	(79) >	0	0 рЛ(А)2* p2 = 2j	.	(80) J pFfl * 0
406
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Метод Рэлея— Ритца всегда дает несколько завышенное значение частоты колебаний, так как он накладывает дополнительные связи на систему. Наиболее точное решение по формуле (80) дает функция, обеспечивающая минимум р. Формулу (80) часто называют формулой Рэлея. Высокую точность расчета дает использование нескольких параметров при аппроксимации прогиба функцией
V = 2 Cjfj (z). ;=i
Полная потенциальная энергия деформации равна
{*	/ п	\2	L / п	\ 2	'
j	j dz — p2 Jр/Ч 2(z)) dz
o \j=i J	0 \j=l J
Из вариационного уравнения
следует
ягт дП «	дП я п
6П = ^-	+ ... + — &п = о
— = О, I == 1, 2, ..., п. дс. ’	’ ’	’ ’
(81)
(82)
(83)
что и образует систему п линейных однородных уравнений для определения с2, ..сп.
Частная производная полной потенциальной энергии имеет вид
дП дс.
*	/ П
о	\;==1
dz —
р2 JpF (S Cj/j(z)']fi(z)dz, \j=l /
i == 1.
, n.
В матричной форме имеем
([««] -/[₽«]) W = 0,	(84)
где элементы матрицы для i-й строки и у-го столбца равны
i	i
= J EJxfifj	Pi; = J	_
О	o	(bo)
{cl === (ci, c»}•
Из условия равенства нулю определителя системы:
(86) находим значения частоты ...
42. ИЗГИБНЫЕ И ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
407
Например, при двух членах ряда (81) уравнение (86) будет таким:

“11 ~-р2₽11 а21~Р%1
“12	Р ^12
®22	Р ^22
(87)
Отметим, что коэффициенты а0- и обладают свойством сим
метрии:
С&17 = CLjii =
что вытекает из равенств (85).
Динамическая модель лопатки осевого компрессора при изгибных колебаниях. Резонансные колебания лопаток являются одной из главных причин разрушения компрессоров. Динамическая модель лопатки должна обеспечить отсутствие резонанса при колебаниях по первой форме на максимальных оборотах. Сначала требуется найти частоту изгибных колебаний лопатки. Лопатка осевого компрессора жестко закрепляется в ободе диска замком типа «ласточкин хвост» (рис. 12.10).
В качестве динамической модели принимаем
Рис. 12.10. Определение частоты изгибных колебаний лопатки компрессора
консольный стержень переменного сечения. Для
построения приближенной модели сечение лопатки можно считать постоянным. Для определения первой частоты изгибных колебаний будем использо-
вать метод интегральных уравнений. По формуле (61) вычислим
2 __J_____________________1_____________
Р(1) -	- 1Ч I t
О О zaz3
что соответствует первому приближению
Последовательно находим
z I I
KvW — gj* F f J J J dz* dZl ~ о о гагз
pF i
о 0
или
KvW~ EJx?
1	+ X
8	18	360
408
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Значение £v(i) при z == I составляет
к„ I ~ 180 EJX * Первое приближение для круговой частоты изгибпых колебаний равно = 13,85^—, р ,=3,72 13 pF	pF р F1
Для дальнейшего уточнения вычисляем
2 „—1^2 Г1 М2 1 М3 и второе приближение
р<2) = ^ = 12,32 Sv* ^> = 3’51?]/
Для третьего приближения
6
Р(з) — 3,5199
что совпадает с точным решением.
Величину Ки{2) удобнее вычислить численным интегрированием, разбив длину лопатки на 10—20 участков.
Применим
Рэлея при
теперь для определения частоты изгибных колебаний формулу /1(2) = 2*ц\
Тогда
о
2 Р
dz
= 20^1, р = 4,47 pF
о
Результат первого приближения получился довольно грубым. В рассматриваемом примере (стержень постоянного сечения) точное значение получается с помощью решения (52):
Р
Результат расчета по формуле Рэлея можно улучшить, определяя /i (z) по формуле (78), что дает
р = 3,530 -Г
После определения собственной частоты колебания лопатки по первой форме перейдем к определению резонансной частоты вращения для лопатки компрессора. Частота возбуждающих сил /воаб в компрессорах, турбинах и других турбомашинах оказывается кратной числу оборотов:
/воз б ==
(89)
42. ИЗГИБНЫЕ И ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ	409
Рис. 12.11. Диаграмма возбуждения для определения резонансной частоты вращения для лопатки компрессора (1, 2, 3, 4 — гармоники возбуждения)
где п\ — число оооротов ротора в секунду; к — целое (положительное) число, характеризующее кратность возбуждения (гармоника). Если перед лопаткой имеются три стойки опоры, то опасное возбуждение может иметь третью кратность (к = 3). В общем случае в машинах имеются все гармоники возбуждения (к = 1, 2, 3, ...), так как неравномерность газового потока, температуры и т. п. представляется рядом Фурье с достаточно большим числом членов. Условие резонанса для изгибных колебаний лопаток состоит в следующем:
/ == knh	(90)
где / — частота изгибных колебаний лопатки (в герцах).
Динамическую модель лопатки часто представляют в виде диаграммы возбуждения (рис. 12.11). На рис. 12.11 штриховой полосой обозначены частоты колебаний лопаток в колесе. Они имеют разброс 5—10% в результате технологических отклонений геометрии сечения лопаток (частоты лежат в пределах 330 < / < 360 Гц). Максимальная частота вращения ротора компрессора равна 8000 об/мин. Из диаграммы видно, что при максимальной частоте резонанс отсутствует, что и составляло возможны на меньших частотах; уровень переменных напряжений при резонансных режимах проверяется экспериментально с помощью тензометри-рования.
условие проектирования. Резонансы
Продольные колебания стержня. В некоторых случаях в стержнях возникают продольные колебания, при которых сечения стерж-
Рис. 12.12. К выводу уравнения продольных колебаний стержня
ня, оставаясь плоскими, перемещаются вдоль оси стержня (передача ультразвукового возбуждения, удар по торцу стержня и др.). Дифференциальное уравнение продольных колебаний получается из уравнений движения элемента стержня (рис. 12.12):
pF^-dz^^dz, (91)
5t2	dz '	'	’
где pF dz — ыэлсл элемента (р —плот-
ность, F — площадь поперечного сечения) ; 2V (я) — усилие в сечении стержня; w — перемещение точек оси стержня. Для упругих колебаний
N(z) — qF = eEF = EF
(92)
Из соотношения (91) получаем ±.(ef^}-pF^4^q. dz \ dz j r
Это и есть уравнение продольных колебаний стержня.
(93)
410
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Для определения частот и форм собственных колебаний считаем w = n?(z)cos pt,	(94)
где р — круговая частота продольных колебаний. Тогда для амплитудных смещений получаем следующее уравнение (соотношение (93) подставляется в уравнение (94)):
^EF^ + p2pFiv{z) = Q.	(95)
Для стержня постоянного сечения (рис. 12.13)
^ + Vw(z) = 0,	(96)
где
w = p2-^.
(97)
Решения уравнения (96) с помощью нормальных фундаменталь-
ных функций записывается так: w(z) = ir(0)cos%z + у (0) sin Xz.
(98) Рассмотрим некоторые примеры.
t
Рис. 12.14. Смещение сечения стержня как функция расстояния и вре-
мени
Рис. 12.13. Продольные колебания стержня постоян-
ного сечения
Пример. Рассмотрим колебания стержня постоянного сечения, свободного от закрепления. Так как усилия в сечениях z == 0 и z = I отсутствуют, то краевые условия таковы:
dw dw
(99)
Из решения (98) и условий (99) получаем
w (z) = w (0) cos to, (Z) = —	(0) sin X/ = 0,	(100)
откуда следует, что
XZ = кл (к = 1, 2, 3, ...).
42. ИЗГИБНЫЕ И ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
411
Частота продольных колебаний с учетом соотношения (97) равна
V V (* = 1,2,3, ...).	(101)
На основании соотношений (94) и (100) при к = 1 имеем
(л \	/2л \
— z j cos I -jT t j,	(102)
где T = 2л/p — 1// —период колебаний (время полного колебания).
На рис. 12.14 даны значения u?(z, t) в различные моменты времени. В момент времени t = 0 смещение при z = 0 равно wifi). Через промежуток времени t = Т/2 это перемещение достигнет конца z = I. Можно считать «скорость распространения деформации» равной
21 _ 2р1 __ /ТГ
V~ Т ~ 2л “ У р ’ Величина
7ё7р = а	(юз)
представляет скорость распространения звука (упругих колебаний). Она определяется характеристиками материала: модулем упругости Е и плотностью р. Для многих конструкционных материалов (стали, титана, алюминия) она практически одинакова и составляет а ж 5000 м/с.
Продольные колебания стержней (рис. 12.15). Перейдем к интегральным проинтегрируем сначала уравнение (95) от 0 до 2. Получим z
EF (2)	— — Р2 J pF (21) w (Z1) dzx + N (0),
О
(104) тде
tf(O) = p£F(O)g(O) (105)
— величина амплитудного усилия при 2 = 0. Разделив обе части уравнения
(104) на EF(z) и снова интегрируя от 0 до 2, находим
Z	21	Z
(*	4	(*	С dzA
w(z)~ — р* J J pF (z2) w (z2) dz2 dzt + w($) + N (0) J
0	'	o' 17
(106)
Это и есть интегральное уравнение продольных колебаний стержня переменного сечения. Начальные параметры ш(0) и N(0) определяются из краевых условий.
Рассмотрим колебания консольного стержня. Краевые условия будут такими:
№(0) = 0, Л’ (l)=EF(l) g(D=O.
переменного сечения
уравнениям, для чего
Рис. 12.15. Продольные колебания консольного стержня
412
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Из соотношения (104) и условия для N(l) находим i
N (0) = р2 J pF (21) w (zj dzv о
и уравнение (106) можно представить в виде однородного краевого интегрального уравнения
w = p2Kw,	(107)
где интегральный оператор равен z	I	z	zi
Kw = f	J	(zi) w (b) dzl - J ЁР7Г) J pF (Z2) W (Z2) dZl- (108)
О ' 1 0	0	' 1jo
Уравнение (107) решается методом последовательных приближений по схеме
где ш({), u?(i+i) — исходное и последующее приближения. Из условия
W(i + l)(Z) « M>(t)(Z) находим (0
$) = Kur(i) (I)'	(109)
Простая приближенная формула для низшей частоты продольных колебаний получается, если принять z z^
(НО)
Функция удовлетворяет краевым условиям
*w(o)=o, -dTW = 0-
Переходя к безразмерной переменной § = z/Z, получим из формулы (109) при постоянных Е и р
Для стержня постоянного сечения 2 _Е^__________________________________1____________________=
J2p 1	1
О	0 0
или
Точное решение дает
Погрешность приближенной формулы невелика.
43. КРИТИЧЕСКИЕ ЧАСТОТЫ, КРУТИЛЬНЫЕ КОЛЕБАНИЯ
413
Замечание. Применение исходного приближения, удовлетворяющего краевым условиям в методе интегральных уравнений, совсем необязательно. При программировании на ЭВМ в качестве исходной функции можно принять любое выражение, например ip(d = 1, так как уже следующее приближение будет удовлетворять всем краевым условиям.
43. Критические частоты вращения и крутильные колебания валов
Валы (роторы) являются одним из наиболее распространенных элементов машин. При расчете вал рассматривается как стержень. Такая модель пригодна для большинства валов. Исключение могут составить тонкостенные полые валы (роторы), для которых оказываются существенными оболочечные эффекты, и очень короткие валы, где следует учитывать пространственное напряженное состояние.
При построении динамических моделей валов следует учитывать критические частоты вращения и возможность крутильных колебаний.
Понятие о критической частоте вращения. Рассмотрим вращение двухопорного вала с диском посредине (рис. 12.16). Для того чтобы выяснить, является ли вращение
вала с прямолинейной осью устойчивым, дадим ему некоторое отклонение и. Центр тяжести диска будет двигаться по окружности радиусом v, и возникнет центробежная сила
(Ill)
где со — частота вращения вала (рад/с), т — масса диска. Отклонение вала приведет к появлению силы упругости, стремящейся вернуть вал в не деформированное состояние:
(112)
где — прогиб сечения вала от единичной силы в том же сечении.
Для вала постоянного сечения (см. разд. 42)
z3
611 = 4857’
Рис. 12.16. Критическая частота вращения двухопорного вала с диском посредине: а — идеально уравновешенный диск; б — диск с начальным эксцентриситетом
где 7 —момент инерции поперечного сечения (индекс х опускается, так как сечение вала предполагается круглым). Пренебрегая весом диска, можно заключить, что при С <F вращение вала будет устойчивым, так как после отклонения вал вернется в первоначальное положение. В момент равновесия, когда С прогибы вала могут неограниченно возрастать: в любом отклоненном положении центро
414
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
бежные силы и восстанавливающие силы упругости равны. Частота вращения вала, при которой наступает равенство центробежных сил и сил упругости при отклоненном положении вала, называется критической. Приравнивая значения С и F. находим
&*inv = 7Г~и.
(114)
ИЛИ
(Or — —г_______ —»
Критическая частота вращения (в оборотах в минуту) равна
60	30	1
__	(ок —		.	.
Л
(115)
(116)
Можно представить, что при критической частоте вращения вал совершенно теряет жесткость на изгиб — даже малая внешняя сила может вызвать опасные прогибы.
Замечание. Из равенства (115) и формулы (14) получается, что критическая частота вращения вала равна круговой частоте собственных изгибных колебаний. Этот вывод справедлив и в более общих случаях (вал с распределенными массами и т. п.), если детали, закрепленные на валу, рассматриваются как точечные массы, т. е. когда пренебрегают инерцией поворота.
Учет начального эксцентриситета центра тяжести диска. В практических задачах центр тяжести диска имеет некоторый эксцентриситет (смещение) е по отношению к оси вращения (геометрической оси вала). Для быстроходных машин обязательно применяется предварительная балансировка роторов с целью уменьшения сок-Точность балансировки характеризуется величиной неустранимого (остаточного) дисбаланса
D = Ge,	(117)
где G—-масса диска, и составляет обычно от 2—10 г-см (для роторов с G = 5—10 кг) до 100—1000 г-см (при массе ротора 100— 500 кг). Следует учесть, что в рабочих условиях вследствие нагрева, остаточных деформаций дисбаланс возрастает.
При наличии эксцентриситета е центробежная сила (см. рис. 12.16) будет равна
С = й)2тп(у + е).	(118)
Сила упругости определяется, как и раньше, равенством (112), Наличие эксцентриситета делает возможным состояние устойчивого статического равновесия, когда С = F:
со2 m (у + е) = ~-и.	(119)
43. КРИТИЧЕСКИЕ ЧАСТОТЫ, КРУТИЛЬНЫЕ КОЛЕБАНИЯ
415
Из равенства (119) находим
2 ей) т	е
1/61г — o)2zn й)£/й)2 — 1
(120)
вращения
Зависимость абсолютной величины прогиба вала от частоты вращения показана на рис. 12.17.
При наличии эксцентриситета е прогиб вала возникает при любой частоте вращения вала со, так как на вал действует неуравновешенная центробежная сила. Если < < сок, то прогиб направлен в сторону эксцентриситета. Когда со достигает критической частоты вращения (со (дк), то прогиб v -*• 00. Анализ поведения вала при наличии начального эксцентриситета подтверждает сделанный ранее вывод об опасности критического режима вращения.
В реальных динамических системах при наличии значительного демпфирования в опорах, тщательной и надежной балансировки удается работать на критических режимах, но опасная ситуация сохраняется.
При со > (ок (закритический режим) v<0, что означает противоположность направлений и и е. В закритической области центр тяжести диска расположен ближе к оси вращения, чем точка крепления диска к валу. При очень большой частоте вращения v = —е, т. е. центр тяжести диска оказывается на оси вращения. Такое явление называется самоустановлением диска в закритической области.
Замечание. Проведенный анализ основывался на формуле (120), выражающей условие равновесия. Однако вопрос об устойчивости положения равновесия не обсуждался. Из физических соображений ясно, что равновесие вала будет (о < <ок устойчивым (при отклонении силы упругости больше центробежных сил). Анализ показывает, что в закритической области движение ротора оказывается неустойчивым. Для создания устойчивости движения и успокоения колебаний требуется введение дополнительного демпфирования (упру-годемпфирующих опор и др.). Во всех случаях желательно работать с жесткими роторами.
Работа с гибкими роторами (a>max > <ок) возможна, но требует применения специальных опор или других средств демпфирования.
Учет упругости опор. В действительных условиях опоры роторов (подшипники, узлы крепления) не являются абсолютно жесткими. На рис. 12.18 приведена схема ротора на упругих опорах. Податливость (одинаковых) опор характеризуется коэффициентом податливости бо (см/кг). Смещение в опоре
₽о = боЯ,	(121)
где R — реакция в опоре. Центр тяжести диска (начальный эксцентриситет отсутствует) двигается по окружности радиусом у, центры
41G
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
опор — по окружности радиусом z>0. Центробежная сила диска С = СОк/ЛР.
Сила упругости вала
_ 1
Так как
то из равенства C — F
1
/?=4С-следует, что 1 1
где Ок» = 1/Уби^ —- критическая частота вращения ротора
(122)
(123)
(124)
жест-
на
ких опорах.
Из формулы (124) вытекает, что поправка, связанная с учетом податливости опор, зависит от податливости вала. Чем более жестким является вал, тем важнее для
Рис. 12.18. Расчетная схема вала на упругих опорах
диска dm в точке А действует
него учет податливости опор.
Силы, действующие на вращающийся диск при прогибах вала. В предыдущем изложении диски представлялись точечными массами. Рассмотрим теперь силы, приложенные к диску, при вращении относительно оси z (рис. 12.19). Ось диска (ось Zi) составляет угол ср с направлением оси вращения; v — прогиб вала в месте крепления диска и одновременно смещение центра тяжести диска (точки ОЦ. На элемент массы центробежная сила
dC = tifrdm,
(125)
где г—расстояние от точки А до оси вращения. Центробежная сила dC может быть разложена на две составляющие dCy и dCx (см. рис. 12.19). Усилия dCx вследствие симметрии образуют взаимно уравновешенную систему сил и для дальнейшего не существенны. Сила
dCv == со2 (yt cos ф + v)dm.	(126)
Величина г^созфЧ- v — АА{ представляет проекцию радиуса г на ось у (см. рис. 12.19).
Приведем центробежные силы элементов диска к равнодействующим силе и моменту, приложенным в центре тяжести диска. Тогда
С =» Су = J dCy = со2 J (у + у± cos ф) р dV,	(127)
V	V
43. КРИТИЧЕСКИЕ ЧАСТОТЫ, КРУТИЛЬНЫЕ КОЛЕБАНИЯ
М7
где интеграл распространяется на весь объем диска V; pd7 = dm — масса элемента диска. Так как величины v (смещение центра тяжести) и <р (угол поворота плоскости диска) одинаковы для всех точек диска, то
С = со2у J pdV + со2 cos ф J i/ip dV.	(128)
V	V
Интеграл
У yYp dV = У yYdm^ О
v	v
как статический момент отпосительпо прямой, проходящей через
Рис. 12.19. Силы, действующие на вращающийся диск
центр тяжести диска. Из равенства (128) получаем важный результат:
C = <b2vm.	(129)
Равнодействующая центробежных сил такова, как если бы вся масса диска была сосредоточена в его центре тяжести. Но центробежные силы создают момент
М = со2 У (и + cos ф) yt sin фр dVf
или
М = cousin ф У z/jLp dV + со2 cos Ф sin фУ у2р dV. (130) у	v
Первый интеграл в правой части равенства (130) обращается в нуль, как статический момент, и тогда
М = ш2 cos ф sin ф Jm,	(131)
где Jm == У у[р dV — осевой момент инерции массы диска. Для v
418
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
ТОНКИХ ДИСКОВ
- _ 1
2
ртп,
(132)
где Jpm — полярный момент инерции массы диска. Например, для диска постоянной толщины Ъ и радиусом R (рис. 12.20)
R
Jpm = И г2р- 2лг dr = 4- рблТ?4 = 4"(133) J	Z	&
о
где т =» рл7?2& — масса диска.
Так как рассматриваются малые прогибы вала, то следует
принять
sin ф ~ ф, cos ф — 1.
Угол поворота плоскости диска dv (z)
<Р~-2Г’
(134)
где v(z)—прогиб вала. Из равенства (131) получаем важную формулу
М =	%	(135)
(LZ
Рис. 12.20. Определение по- Если при прогибах вала плоскость дис-лярного момента инерции ка отклоняется от первоначального по-з&ассы диска	и
ложения, то на диск действует момент, препятствующий повороту плоскости диска. Такой момент называется гироскопическим, так как впервые был изучен в связи с движением гироскопов (простейший пример гироскопа — «волчок»; гироскопы — важнейшие приборы для управления самолетами и ракетами). Гироскопический момент пропорционален углу поворота плоскости диска.
Замечание. Рассматриваемое движение вала и диска (диск неподвижен относительно плоскости, содержащей изогнутую ось вала) называется прямой синхронной прецессией. Возможны и другие, более сложные движения вала, напоминающие движения гибкого валика в изогнутой и вращающейся трубчатой обойме. Такого рода движения (несинхронные прецессии) на практике встречаются очень редко и в дальнейшем не рассматриваются.
Критическая частота вращения вала с дисками. Будем пренебрегать массой вала по сравнению с массами дисков. На рис. 12.21 даны конструктивная и расчетная схемы (динамическая модель) ротора газовой турбины. Рассмотрим движение ротора при наличии прогиба вала. При вращении вала в изогнутом состоянии диск действует на вал с усилием и моментом соответственно
С = (о2тпр, Л/==со2Утф.	(136)
Для определения деформации вала рассмотрим единичные силы и
43. КРИТИЧЕСКИЕ ЧАСТОТЫ, КРУТИЛЬНЫЕ КОЛЕБАНИЯ
419
момент (рис. 12.21,6), приложенные в точке крепления диска. Обозначим би прогиб от единичной силы (первого силового фактора) в направлении силы, б22 угол поворота от единичного момента (второго силового фактора) в направлении действия единичного
Рис. 12.21. Критическая частота вращения вала с диском ротора газовой турбины
момента, 6i2 угол поворота от единичной силы в направлении второго силового фактора, 62i — прогиб от единичного момента в направлении первого силового фактора. По условиям взаимности получим
6i2 = 62f.
Прогиб вала и угол поворота в месте крепления диска равны
v = 6iiC-62Jlf,	(137)
Ф = 612С — 622Л/.	(138)
Знак минус в этих равенствах согласован с разным направлением М и Учитывая зависимости (136), получаем систему однородных уравнений относительно v и ф
V (^ — 1) — фй)2621= о, 1?(02612тп — ф ((02622 Jm + 1) = 0.
Отличные от нуля значения и и ф получаются в том случае, когда детерминант системы обращается в нуль:
А^"1 А/ш
Аг™ А2/т+1
или
(вцб22 — fin)	+ (В2 (6nm — &227т) — 1 = 0.	(139)
Из последнего уравнения получаем величину критической частоты
420
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
вращения
““ _ '
|/ Т(«п”-УЯ)±У T(6n/n-62/m)2 + mJm(6u622 -6!2)
(140)
Как будет показано в дальнейшем, для всех упругих систем
М22-б?2>0,	(141)
и потому формула содержит только одно действительное значение критической частоты вращения (знак минус в формуле (140) должен быть отброшен). При /т==0 из формулы (140) получаем известный результат
(ок = 1/Убит.
Гироскопический момент дисков повышает критические частоты вращения, так как препятствует повороту плоскости диска. Разберем предельный случай	Разделив в равенстве (139) все
члены па /т и сохраняя те, которые не содержат в знаменателе /т, найдем
-------1--------- J_	(142)
здесь бц=6п — 612/^22—прогиб от единичной силы при отсутствии поворота сечения, где закреплен диск. Получим этот результат другим путем, считая заранее, что поворот диска отсутствует (рис. 12.22). При смещении диска на величину и возникают сила С и реактивный момент Л/3.
Из условия ф¥=0 (уравнение (138)) находим
б22
Прогиб вала в месте крепления диска равен
v = 5UC - 621М3 - (бц -	) С = -1- С&хЛ-л-би) С. (143)
\	°22/	°22
Из физических соображений ясно, что прогиб v должен быть направлен в сторону действия силы (объясните, почему!), что и доказывает условие (141). Соотношения (143) и (136) приводят к равенству (142).
При Jm 00 плоскость сечения диска при деформации вала не поворачивается. Влияние гироскопического момента диска сказывается сильно, если диск закреплен вблизи от опоры. Если вал имеет опоры в концевых сечениях и несет несколько дисков, влияние гироскопического момента обычно оказывается небольшим. Если пренебречь влиянием гироскопического эффекта дисков, то, как
43. КРИТИЧЕСКИЕ ЧАСТОТЫ, КРУТИЛЬНЫЕ КОЛЕБАНИЯ
421
указывалось, критическая частота вращения совпадает с круговой частотой собственных изгибных колебаний балок. Следовательно, для расчета могут быть использованы формулы разд. 42.
Критическая частота вращения вала переменного сечения с непрерывно распределенными массами. Роторы осевых компрессоров, паровых турбин часто могут быть представлены динамической моделью в виде стержня переменного сечения с непрерывным
распределением масс. Будем пренебрегать гироскопическим эффектом дисков, ограничиваясь нижней оценкой критической частоты вращения. Отдельные диски также могут быть заменены в пределах участка распределенной массой. В изогнутом положении на вал действует распределенная нагрузка (рис. 12.23)
q(z) = o2Tn(z)p(z), (144)
Рис. 12.22. Схема деформации вала при защемленном конце ротора (плоскость диска не имеет возможности поворота)
где m(z)— масса, приходящаяся на единицу длины вала. Перерезывающая сила в сечении z равна
Z	-
Qy = — Ri — .( ч (zi) dzi-	(145>
0
Учитывая, что
находим
z Z1
Mx (z) = — Rxz — J j q (z2) dz2 dzt.	(146)''
0 0
Из условия
Mx(l) = 0 следует ’	i zi
R1=------- J J q (zj dz2 dzx,
о b
Подставляя значение Ri в равенство (146), получаем z zi	‘	« i Z1
Мх (z) = — J J ?,(z2) d4 dzt + -7 J J ? (z2) dz2 dzi-	(147)
0.0	00
422
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Выражение (147) определяет изгибающий момент в сечении стержня (рис. 12.23) при произвольной распределенной нагрузке q(z). Учитывая равенство (144), можно записать
,	/	12i	z 2i	\
Мх (z) = <о2 I -у-J J ш (Z2) v (z^ dz2 dz1 — ^m (z2) v (z2) dz2dzt j =
\	0 0		0 0	/
= coMv(z), (148)
где оператор
(149)
Если задана величина v(z), то по
I
формуле (149) может быть вычислено значение Av(z) в каждом сечении z. Будем использовать уравнение упругой линии (разд. 31)

. V (z) = —
00"'"'
+ p(0) + z^-' (150)
Рис. 12.23. Вал с непрерывно распреде-	az .
ленными массами (ротор компрессора) n
В рассматриваемом случае
-v(0)==0, а из условия y(Z)==O находим значение v'(0), что дает
v (z)=И dz*dzi ~ dZi dzi" (151>
Выражение (151) определяет прогиб вала при произвольном распределении изгибающего момента. Внося в равенство (151) величину. Mx(z)1 из соотношения (148) получаем интегральное уравнение для критической частоты вращения
v-rfKv,	(152)
где интегральный оператор равен
111 ,	2 21
  <153>
, О О	0 0.	'
Интегральное уравнение (153) может быть решено методом последовательных приближений по схеме	z
43. КРИТИЧЕСКИЕ ЧАСТОТЫ, КРУТИЛЬНЫЕ КОЛЕБАНИЯ
423
В качестве исходного приближения принимается

4z (I — z)
Частота находится из равенства прогибов
(^/2) — P(t) (Z/2).
Расчет проводится точно таким же методом, как и в разд. 39.
Крутильные колебания валов. В валах поршневых машин (в двигателях внутреннего сгорания, поршневых компрессорах и т, п.)
часто возникают крутильные колебания, связанные с неравномерностью (по времени) вращающего момента или момента , сопротивления. Крутильные колебания могут возникать и в других машинах, если крутящий момент, передаваемый валом, не является постоянным. В качестве динамической модели при крутильных колебаниях обычно используется вал с дисками. Моменты инерции масс дисков Jlt А, ..., Jn рассматриваются как приведенные моменты инерции. Например, в поршневых машинах инерционные массы связаны с движением поршней, шатунов и других элементов и приводятся к дискам с эквивалентными моментами инерции. Жесткость участков валов, соединяющих дискщ принимается как эквивалентная для участков с непрямой осью (коленчатые валы и др.), при шлицевых соединениях и т. п. На рис. 12.24 показаны конструктивная схема коленчатого вала двигателя внутреннего сгорания и динамическая * модель крутильных колебаний. Существуют более сложные модели крутильных колебаний
Рис. 12.24. Конструктивная схема коленчатого вала . двигателя внутреннего сгорания .(автомобильные и тракторные двигатели, дизели и т. п.) и динамическая мо де ль крутильных- колебаний
с несколькими ветвями,' что определяется конструктивными особенностями машин; остановимся на схеме «цепочной системы» (рис. 12.25).
Выведем уравнение/крутильных колебаний к для системы из п дисков. Рассмотрим уравнение движения i-ro диска (рис. 12.26), Обозначая угол поворота i-го диска (f)/получим
/е4 (о d?
= Mi — Mi-i,
(154)
424	ГЛ. 12- ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
где Miy Mi-i — крутящие моменты, действующие на диск со стороны валов правого г-го и левого (£— 1)-го участков. Угол поворота диска зависит от времени.
Если обозначить жесткость i-ro участка то
Мх = Сг(0,+1(^)-0{(^));	(155)
здесь 0t+b О»-—углы поворота конечных сечений i-ro участка;
Рис. 12.25. Динамическая модель	Рис. 12.26. К выводу
крутильных колебаний в маши-	уравнений крутильных
нах	колебаний
— б» — упругий угол поворота вала на i-м участке
~	GJ .
Ci =	.	(156).
где Ц — длина участка» Jpi — эквивалентная жесткость вала" на кручение, G — модуль сдвига.
Подобным образом получаем
= Cw(Si (0-6<-1 (0)‘	.
Теперь из уравнения (155) находим
J‘--^ ’=Ci<0i+i(O -0i(O) -Ci-iCMO-ei-xW). (157) at
Пренебрегая моментами инерции участков вала, можем считать, уравнение (157) при 4 = 1, ..., п дифференциальным уравнением крутильных колебаний цепочной системы. Полагая
0,(4) = Ojcospf,	(158)’
где 0, — амплитудное значение угла поворота, р — круговая частота крутильных колебаний, из уравнения (157) получим
+ [р2Л-(С^ + С.)]0, + С<0,+1 = О (1 = 1,..., п; .
•_	. Со = О,' С„+1 = 0). (159)
44. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
425
Это и есть уравнение амплитудных углов поворота при крутильных колебаниях цепочной системы.
Пример. Рассмотрим крутильные колебания -динамической модели, состоящей из двух дисков, соединенных валом (рис. 12.27), Применяя уравнение (159) при i = 1 и i == 2, находим
(р2Л -	) 0! + С^2 = 0, СлО! + (р2У2 - Cj) 02 == 0.
Приравнивая нулю детерминант системы:
= (₽Ч-с1)(₽Ч-с1)-^=о,
находим
Р4Л72 - С1Р2(Л +/2) = р.
Из этого уравнения получим
(160)
Замечание. Нулевая частота характерна для любой незакрепленной системы, 'которая может двигаться как недеформируемое.
твердое тело. Поскольку «возвращающие» силы упруго-' сти отсутствуют, частота системы равна нулю.	T_J ~	2 и
, Уравнение крутильных колебаний в матрич- s Ы ной форме. Систему п уравнений (159) предста- 1227 к вим в матричной форме:	’ .	тильные’ колеба-
ния системы из (161) двух дисковд вала
' [с]{е} = о,
где вектор состояния {0}т = {01, 02, .
0П} и динамическая матрица
	Vj1-c1	сх	о
	- ci ' A-(ci+Q с. о	0	0
Частотное уравнение получается из условия	" *
det[C]==l[C]l==O.
Система с п дисками имеет п частот, среди* которых одйа нулевая..
44. Устойчивость стержней	4
Непосредственный жизненный опыт приводит к понятию об’устойчивости и неустойчивости системы. На рис. 12.28 показаны три формы равновесия механической системы, из которых первая является устойчивой, вторая — безразличной и третья — неустойчивой. Равновесное положение системы считается устойчивым, если после случайного отклонения система стремится к своему первоначальному положению. Естественно,^ что оценка устойчивости может
426
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
зависеть от величины случайного отклонения. На рис. 12.29 приведена система, «устойчивая в малом» и «неустойчивая в большом».
В теоретической механике рассматриваются проблемы устойчивости движения и даются строгие критерии устойчивости на основе теории Пуанкаре — Ляпунова. В механике деформированного твердого тела оценка устойчивости основывается обычно на анализе статического поведения конструкции.
Рис. 12.28. Три формы равновесия механической системы: а — устойчивое; б — безразличное (критическое); в — неустойчивое.
Рис. 12.29. Система, устойчивая при малых отклонениях и неустойчивая при больших
На рис. 12.30 показаны результаты простейшего эксперимента. При некотором усилии стержень (линейка) начнет изгибаться. Явление резкого увеличения прогибов стержня при сжимающем осевом усилии называется потерей устойчивости.
Для нормальной работы конструкций потеря устойчивости недопустима.
Перейдем к анализу устойчивости стержней.
Критическая нагрузка для стержня с шарнирно закрепленными концами. Формула Эйлера. Рассмотрим двухопорный стержень (рис/12.31), сжатый осевыми силами 2V, и предположим, что стержень получил.прогиб в плоскости yOz. Если в сечении стержня.
Рис. 12.30., Потеря устойчивости - Рис. 12.31. Потеря устойчивости стержня при сжатии	двухопорного стержня
возникнут изгибающие моменты, способные удержать стержень в изогнутом состоянии, то первоначальная прямолинейная форма Зравновесия стержня окажется неустойчивой.
Уравнение изгиба стержня имеет вид
j2
EJX2£—MX. .	.	(163)
dz
Изгибающий момент в сечении равен .	_ .
'	Jfx = ^(z).	(164);
44. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
427
Из уравнений (163) и (164) получаем дифференциальное уравнение изгиба стержня
-^- + l2y(z)=0,	(165)
dz
где
Решение уравнения (165) можно записать в виде
v{z} — Ci cos Xz + C2 sin Xz,	(167)
где Ct и Сг — произвольные постоянные.
При z = 0 прогиб v(0) =0, поэтому получаем (Ct = O)
p(z) = C2sinXz.	(168)
Прогиб снова обращается в нуль при z = Z, и потому
C2sinXZ = 0.	(169)
Здесь С2*0, так как при С2 = 0 прогиб стержня вообще отсутствует, а рассматривается изогнутое состояние стержня. При С2 ¥= О
sin XI = О, и, следовательно,
XI —кп,	(170)
где к —0, 1, 2, ... Значение fc = 0 не представляет интереса, так как соответствует прямолинейному состоянию стержня.
Равенства (166) и (170) приводят к формуле Эйлера i^^EJ
N^--------(к = 1,2,3,...).	(171)
Из соотношения (171) вытекает, что имеются бесчисленные значения N, при которых могут существовать изогнутые формы равновесия стержня.
Наименьшее значение осевой силы (первое критическое значение) получается при к — 1:
(172)
При > 2VKp уже возможна потеря устойчивости стержня, и поэтому значение осевой силы, найденное по формуле (172), называется критическим.
При рассмотрении изогнутого состояния предполагалось, что изгиб происходит в плоскости yOz. Точно такой же вывод справедлив и для изгиба в другой главной плоскости, что дает
^кр = ^.	(173)
428
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Очевидно, выпучивание при действии усилия N = /VKp произойдет раньше в той плоскости, где жесткость сечения меньше. Поэтому формулу для определения критической силы записывают в таком виде:
Л/’кр =
я ^Anin
Z2
(174)
Замечания. 1. Уравнение (165) имеет решение v s О, что соответствует прямолинейной форме равновесия. Ври N > ;VKp возможны две формы равновесия: первоначальная прямолинейная форма и = 0 и изогнутая форма равновесия
и = С sin nz.	(175)
Прямолинейная форма равновесия оказывается устойчивой при N < УКр и неустойчивой при N > 2VKP. Изогнутая форма равновесия (174). наоборот, будет устойчивой при N >» iVKp. Существование новой устойчивости форм равновесия отдельного элемента при N 2> #кр и неустойчивость прежней прямолинейной формы делают конструкцию в целом неустойчивой: при возрастании силы N может произойти выпучивание — система (стержень) внезапно перейдет к другой форме равновесия, прогибы стержня и напряжения в нем резко возрастают.
2.	Более детальный анализ показывает, что при всех высоких значениях критической силы (при к = 2, 3, 4, ...) равновесие оказывается неустойчивым; практическое значение имеет только первая критическая сила, или просто критическая сила (формула (172)).
3.	Существенным моментом вывода уравнения (165) явилось составление условия равновесия (164) для стержня (системы) в деформированном состоянии. В этом уже содержится отказ от линейной постановки задачи, при которой перемещения считаются настолько малыми, что деформированное и не-деформироваппое состояния при составлении условий равновесия не различаются (принцип начальных размеров).
4.	Рассматриваемая модель устойчивости стержня (уравнение (165) и рис. 12.32) является приближенной. Она позволяет найти критическое значение силы из условия существования нетривиального (ненулевого) решения
Рис. 12.32. К составлению уравнения Рис. 12.33. Сближение конусов устойчивости при отрицательном про- стержня при его изгибе гибе
однородного линейного дифференциального уравнения. Это — задача о собственных значениях, которая была основной при изучении собственных колебаний (разд. 39). Величина прогибов определяется решением (168) с точностью до масштаба величины С. Модель не дает возможности описать состояние системы при N NK?.
Более точная модель основана на строгой нелинейной постановке задачи, Сделав один шаг по учету деформированного состояния — приняв во вни-
44. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
429
манне изгибающий момент от осевой силы, следовало бы сделать и второй шаг — уточнить краевые условия при z = /, так как вследствие изгиба стержня происходит смещение опоры на величину А (рис. 12.33).
Пренебрегая деформацией сжатия стержня, можем представить, что элемент стержня ds проектируется на ось z как отрезок dz, и в результате
Д = J(<*- *) = J( И 1 +	* - Л)= т J (£•/ dz- (176)
0	0	о
Краевое условие на втором конце стержня будет таким:
у(/_Д)=0.	(177)
Далее следует использовать точное выражение для кривизны стержня, и тогда дифференциальное уравнение изгиба становится следующим:
cTvl dz*
EJ* ?--------аТТл, + Nv (z) = 0.	(178)
Уравнение (178) и краевое условие (15) позволяют получить точное решение. Не рассматривая самого решения, укажем простую зависимость, вытекающую из него;
ртах __ 2	_ ^кр
I	V N ’
Например, если усилие N превысит критическое значение на 1,5%, стержень длиной 1 м получит прогиб 11 см.
Для практики важно установить усилие, при котором конструкция перестает быть работоспособной. Рассматриваемая приближенная модель позволяет это сделать.
5.	Вид дифференциального уравнения (165), разумеется, не зависит от того, в какую сторону предполагался изгиб стержня. На рис. 12.32 показан стержень с отрицательными прогибами. Это вполне согласуется с решением (168), где величина G может быть произвольной, в том числе отрицательной.
Изгибающий момент (см. рис. 12.32)
Мх = —Лг(—v(z)) = Nv(z), что приводит к уравнению (165).
Общее дифференциальное уравнение устойчивости стержня и краевые условия. Рассмотрим более общий случай, когда на стержень действуют осевая сила N, приложенная на конце стержня, распределенная осевая нагрузка qt (рис. 12.34) и поперечные нагрузки Р. Изгибающий момент в сечении z
i
Мх (z) = Мх (z) — N [V (О — v (z)] — J q (z,) [w (zj — v (z)] dzlt (179) z
где Slx(z) —изгибающий момент от поперечной нагрузки.
Подставляем (179) в уравнение (163):
i
EJX^ = - Мх (г) + ЛГ [v (I) - v (z)J + [& (zj [v (zj - v (z)] dzt. dz	v
z
(180)
430
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Дифференцируя это равенство по z, получаем
(181>
х	'	Z
где = dffljdz — перерезывающая сила от поперечных нагрузок.
Рис. 12.34. Определение изгибающего момента в сечении стержня
Повторяя операцию дифференцирования, находим
d2 d?
EJX~ dz1
Л . V « У + TV — -dz
dv (z) dz
= 0.
(182)
Предполагается, что поперечная распределенная нагрузка qy от-2	*	сутствует. Уравнение (182) представляет
/vl v(l)	общее дифференциальное уравнение ус-
у '	\ l\xfz тойчивости стержня.
Г|-----г \ I Ч Рассмотрим краевые условия для урав-
\	нения устойчивости на примере консоль-
\	ного стержня. При г = 0 стержень имеет
\	заделку, и потому
1	W	v(0) = 0, -g(0)=0.
б
На конце z = I изгибающий момент отсут
ствует:
,2
-^(Z) = 0.
dz2
Рис. 12.35. краевые уело- Для перерезывающей силы из уравнения вия в задачах устойчиво- (lol) получаем при z I
сти стержней: а — расчетная схема; б — условная
перерезывающая сила
4 (£/-	--"-£(« (183)
Условная перерезывающая сила на конце стержня появляется за счет проекции усилия N (рис. 12.35).
Отметим, что уравнение (182) является дифференциальным уравнением четвертого порядка, и для его однозначного решения
44. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
431
должны быть указаны четыре краевых условия (обычно по два при з = О и z = I).
Замечания. 1. Напомним правило дифференцирования определенного интеграла по параметру:
/B(z)	ч B(z)
Л. [ F{z,z)dz )= f ^(z^dz + -^.F(z,B)-l±F(z,A).	(184)
dz I J \	1/ i I J dz v 17 1 dz	dz
' A(z)	/ A(z)
Это правило легко установить, рассматривая приращение
В(г>+57й	ад
dJ = J F (z -J- dz, z^j dz± — j* F (z, zj dz±.
л. . , dA .	A(z)
A&)+—dz
dz
Соотношение (184) применялось при дифференцировании уравнения (180).
2. Следует обратить внимание, что при выводе краевого условия (183) направление усилия N оставалось неизменным. Если усилие N считать направленным по касательной к оси стержня («следящая» нагрузка), то решение задачи усложняется.
Решение дифференциального уравнения устойчивости для стержня постоянного сечения. Уравнение устойчивости при отсутствии распределенной осевой нагрузки qz будет таким;
л4	л2
+	(185)
dz	dz
Предполагая частные решения в виде
v = Се*1, получим характеристическое уравнение р2(рг + гг) = 0, которое имеет четыре корня:
р.1 = 0, р2 = 0, р.3 = i%, р.4 = — il.
Решение уравнения (185) можно записать так:
p = Ci + Gz + C3Coslz + C4sin%z.	(186)
Построим теперь решение по методу начальных параметров, основываясь на применении нормальных фундаментальных функций:
v (z) = v (0) V, (z)4- v' (0) V2 (z) + v" (0) V, (z) + vm (0) (z). (187) Функции V{(z) являются частными решениями уравнения (185) и удовлетворяют условию
0-0,1,2,3).	(188)
432
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Для нахождения нормальных фундаментальных функций воспользуемся общим решением (186). Допустим, требуется определить функцию Vi(z). Полагая
Vj = Ci + C2z + С3 cos Xz + C4 sin Xz, будем иметь при z = 0 в соответствии с условиями (188) 71(0) ==	+ С3 = 1, V[ (0) = С2 + ХС4 = 0,
71(0) = -ГС3 = 0, РГ (0) = - Х3С4 = 0.
Из последних соотношений получаем
Pi(z)=l.
Подобным образом находим всю систему решений:
^i(z) = l, y2(z) = z. уз(г) = тт(1 —cosb), r4(z) = 4j-(Xz —sinXz). A	К
(189)
С помощью равенства (187) и формулы (189) получаем следующие важные для дальнейшего соотношения:
v (z) = v (0)• 1 + v' (0) z + v" (0) -Ь.(1 — cos Xz) + v'" (0) -b (Xz—sin Xz), Л	X
v' (z) = 0 + v' (0) + v" (0) -y- sin Xz + v'" (0) -7- (1 — cosXz),
X	(190)
v" (z) = 0 + 0 + v" (0) cos Xz + vw (0) A-sin Xz,
v"' (Z) = 0 + 0 — v" (0) X sin Xz + vM (0) cos Xz.
Последние соотношения можно записать в матричной форме:
U(z)} = [V]{y(0)},	(191)
где столбец-решение имеет вид
{p(z)}T = {у, у', и", ₽"'}	(192)
и столбец начальных параметров —
Ь(0)}т = Ь(0), и'(0), р"(0), v'"(0)k	(193)
Элементы нормальной фундаментальной матрицы легко установить из уравнений (190). Решение (191) называется решением дифференциального уравнения (185) в матричной форме.
Влияние условий закрепления концов стержня на величину критической силы. Ранее была определена критическая сила для стержня с двумя шарнирными опорами по концам (формула Эйлера). Рассмотрим на нескольких примерах другие случаи закрепления.
Пример 1. Устойчивость консольного стержня под действием сжимающей силы.
44. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
433
же длины, но с
Рис. 12.36.
Сравнение значений критической силы при консольном и шарнирном закреплении
Краевые условия задачи таковы:
N	2
i?(0)=0, и'(0) = О, i/'(0 = 0,	(0 = — JJ- и' (Z) = - Л2р' (Z).
Из решения (190) для краевых условий находим
1
v" (0) cos К1 + i/" (0) -г- sin XZ = 0,	(194)
л
— V" (0) 1 sin и + vm (0) cos и = — 12(у" (0)4 sin М + vm (0) 4- (1 — cos W)).
Л	Л
(195)
Из уравнения (195) получаем г/"(0) = 0, и уравнение (194) дает
v"(0)cos KI = 0.
Так как и"(0) У= 0, то из условия cos KI = 0 находим KI = кл/2 (к = 1,2, 3, »,.)«. Критическое значение (к == 1)
*КР==^Г	(196)
получилось в четыре раза меньшим, чем для стержня той шарнирными опорами. Этот результат вполне естествен, так как консольный стержень работает в тех же условиях, что и шарнирно опертый стержень двойной длины (рис. 12.36). Полученное решение дает не только величины критического усилия (196), но и форму прогиба. Из формулы (187) находим
v(z) = v"(0)V3(z) ==С(1 —cos Az),	(197)
где С — произвольная постоянная.
Ввиду практического значения рассматриваемой задачи приведем обычное элементарное решение. Будем использовать уравнение (163):
EJX—г = - Мх (z) = N (v (Z) - v (z)), dz или о	о
—r + K2v = Kv(l).	(198)
dz
Общее решение этого уравнения можно представить так: p(z) = Сх cos Kz + С2 sin Kz + v(Z).	(199)
Из краевых условий при z = 0 находим
у(0) = Ci + v(Z) = 0,	v'(Q) = — КС2 == 0.
Таким образом, решение (199) приобретает вид
v(z) = v(l) (1 — cos Az).	(200)
В равенстве (200) v(l) — неопределенный прогиб в koi
рис. 12.35). При z~l равенство (200) сохраняется, если cosXZ = 0~ что приводит к формуле (196).
В рассматриваемом частном случае решение получилось простым, но менее общим, так как краевые условия использовались в неявной форме.
434
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
заделанными
сечениями
Пример 2. Устойчивость стержня с двумя (рис. 12.37). Краевые условия будут такими:
у(0)=0, у'(0) = 0,	y(Z)=O,
y'(Z) = 0.
Из последних краевых условий с учетом равенств (190) получаем
1	1 /	1	\
у" (0) “2 (1 — cos XZ) + уw (0) ~21Z — -г sin М) = 0, X	X \	л	/
1	1
и" (0) Тsin М + vm (0) — (1 — cos XZ) =0. л	X
уравнений должен обращаться
в нуль, что дает
чивость стержня с двумя заделанными сечениями
Рис. 12.38. Схема решения уравнения
(1 — cos XZ)2 + sin2 XZ — XZ sin XZ = 0, или
v 0^ у
Рис. 12.39. Устойчивость стержня с одним заделанным и другим шарнирным концами
2 xz xz xz 2(1— cos XZ) — XZ sin XZ = 4 sin — 2XZ sin -j- cos = 0,
Из последнего уравнения находим
sin у = 0,	(201)
„ XI XI tg 2 “ 2 ’
(202)
Наименьшие корни этих уравнений имеют вид
XZ у = л,	(203)
у = 4,493	(204)
Наименьшее значение критической силы соответствует значению (203) 2VkP = WEJJIK	(205)
Замечание. Схема решения уравнения tg z « z показана на рис. 12.38. Так как при малых z ъмьыи tg z > z, то пересечение прямой /(z) = z и тан-
U. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
435
генсоиды получается при значении z*, несколько меньшем Зл/2 = 4,71. Точное значение корня z* = 4,493.
Пример 3. Устойчивость стержня с одним заделанным и другим шарнирным концами (рис. 12.39).
Краевые условия имеют вид
у(0) = 0,	у'(0) = 0, v (Z) = 0,	у" (Z) = 0.
Из решения (190) находим 1	1 /	1	\
и" (0) — (1 — cos XZ) + у"'(0) — IZ — — sin XZl =0, X	X \»	X	J
1 Vя (0) cos XZ 4- v"' (0) V sin XZ = 0.
Из равенства нулю определителя уравнения получаем sin XZ — XZ cos XZ = 0, или
tg XZ = XZ.
Наименьший корень этого уравнения (см. рис. 12.38) равен
XZ = 4,493 « л/0,7. Критическая сила составит
N
КР (0.7Z)2
(206)
Приведенная длина стержня. Обобщенная формула Эйлера. Разобранные примеры показывают, что критическое значение сжимающего осевого усилия на стержень можно выразить по формуле
дт ______
К₽ -	(VZ)2
(207)
где vl — приведенная длина стержня. Коэффициенты приведения: v == 1 — шарнирное закрепление обоих концов, № 2 — консольный стержень, №0,5— стержень с двумя заделками, № 0,7 — стержень с заделкой и шарнирной опорой.
Формула (207) называется обобщенной формулой Эйлера. Напомним, что она справедлива, если напряжения и деформации в стержне в момент потери устойчивости находятся в упругой области:
<?кр —
^кр___ п ^Anin
Р ~ F(vl)2
(208)
где аПц — предел пропорциональности материала. Величина
Zmin —
(209)
называется минимальным радиусом инерции поперечного сечения.
436
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Введем еще одно важное понятие — гибкость стержня
Х =	(210)
lmin
Тогда обобщенную формулу Эйлера можно представить в простой форме:
а«Р — ТТ •	(211)
А
Условие (208) ограничивает область применения формулы Эйлера.
Минимальное значение гибкости, ниже которой формула Эйлера перестает быть пригодной, равно
Xmin = Л
(212)
Например, для малоуглеродистой стали при Е = 2 • 105 МПа и От = 200 МПа
Xmin — ЛС
/2-105
2-102
«99.
Формулу Эйлера можно применять, если X > Xmln.
Замечание. Критическое напряжение, конечно, является сжимающим. В задачах устойчивости по традиции, чтобы устранить знак «минус» в расчетных формулах, критические сжимающие напряжения считаются положительными.
Интегральное уравнение устойчивости стержня. Рассмотрим
z
Рис. 12.40. Устойчивость стержня переменного сечения
стержень переменного сечения под действием распределенных и сосредоточенных усилий (рис. 12.40).
Изгибающий момент в сечении z
Mx(z) = — 2 [1 — i=l
I
— V (z)) — J qz (z1)(p (zj — v(z))dzlt (213) z
где функция Хевисайда
Я(г, zj =
О при
1 при Z> Zi.
К стержню в п сечениях г» z2, .... zn приложены сжимающие усилия Nu N2, .... Nn. Изгибающий момент от силы Ni в сечении z — = z{ появляется при z<2i, что и учитывается с помощью функции Хевисайда.
44. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
437
Интегрируя дважды в пределах от 0 до z уравнение (163) и учитывая краевые условия и (0) == 0, — (0) = 0, находим
z г1
(2м>
0 0
Подставляя значение v(z) в уравнение (213), получаем однородное интегральное уравнение относительно изгибающего момента Mx(z)\ Mx(z) = KMXl	(215).
где оператор равен
п	zi Z1
=	^rdz2dz1 +
1=1	J J ^Jx\z2/
z 0
Z	zi 22
+ 1 M2i) j I*e'j dz3 dz2 dzx.
(216)
Уравнение устойчивости (215) позволяет определить значения усилий Ni и распределенной нагрузки qz(z), приводящие к потере устойчивости. Будем считать, что относительные значения нагрузок известны, например, по отношению к
i
Nt =	j Чг (Z) dz =	(217)
0
Тогда в критическом состоянии (Wi==2VKp) получим
MX = N^KMX,	(218).
где оператор равен
КМХ = 2 [ 1 — Н (z, г)] Xi J J ЁТ^) dz2 dzi + г~	Z о
+ Xq ( У qz (z) dz\ У qz (2i) J J 7~c dz3 dz2 dz1<t (219) '0	' 0	z 0	x ' 3
где значения и известны. Уравнение (219) пригодно и для случая, когда некоторые усилия Nj являются растягивающими. Они вводятся в уравнение со знаком минус (К) < 0).
Уравнение (218) решается методом последовательных прибли-» жений. В первом приближении полагают
Mx(1) = l~z2/Z2.	(220)
438
ГЛ. 12. ДИНАМИКА II УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Приравнивая последующее и исходное приближения при г = 0, па-
ходим
1
-^кр(1)	I
ЛЛ2Х(1) |z=0
(221)
И т. д.
Пример. Рассмотрим устойчивость консольного стержня постоянного сечения под действием усилия (см. рис. 12.35).
Оператор КМХ (уравнение (219)) для рассматриваемого случая (zi = I, Nt = N, H(z, I) = 0) равен
izi
x Z 0
Значение при условии (220) равно
O/I(1) =
или
ХМх(1) = £7^ [т	~ 2^]'
Первое приближение дает
.. 1 12 EJ*
N^~ KMxW\z^~ 5 f -2’40 P
Точное значение равно
„	n2EJx	EJX
Nur. = т---о- — 2,47 —г •
кр	4 i2	i2
Устойчивость стержней при Модуль Кармана. Рассмотрим
упругопластических деформациях, случай, когда окр от и дефор-
мация стержня происходит в пластической области.
После предварительного сжатия напряжениями о = — акр. начинается изгиб стержня иг на стороне растяжения (рис. 12.41) возникает разгрузка, а на стороне сжатия продолжается нагружение. Состояние материала стержня после пред-
Рис. 12.41. Точки разгрузки и нагрузки при боковом прогибе стержня после предварительного сжатия
варительного сжатия характеризуется точкой (рис. 12.42). При изгибе получается приращение напряжений, причем в силу закона разгрузки (разд. 19)
Ле = у	(разгрузка),
Л Ла t '	(222)
Де = —	(нагрузка),
где Е и Ек — модуль упругости и касательный модуль.
44. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
439
При нагружении изгибом предварительно сжатого (или' растя-
нутого) в. пластической области стержня материал стержня ведет
разномодульный. Уравнение изгиба стержня (см.
себя как
рис. 12.41) имеет вид
5Х.^ = — Nv, (223) dz
где Вх — жесткость стержня на изгиб.
Для диаграммы деформирования с линейным упрочнением имеем
Вх~ Eka^Jx, (224) где ^кар — модуль Кармана.
Для прямоугольного сечения стержня
₽ -
Дкар“(Уё+/^'
Рис. 12.42. Зависимость напряжение-деформация при анализе устойчивости сжатого стержня
Для двутаврового сечения,
если пренебречь моментом инерции
стенки,
г ______
кар — Е + £к •
Существенно отметить, что всегда
Ек < ЕКь$ < Е.
(225)
Из уравнения (223) точно так же, как и для упругого стержня,
Рис. 12.43. Изгиб в условиях продолжающегося нагружения осевыми силами (распределение напряжений в разные моменты нагружения)
получаем
NK» = n2E^Jx/l\ (226)
что меньше критического значения по формуле Эйлера.
Появление пластических деформаций снижает устойчивость конструкций, делает их более податливыми.
Устойчивость стержней в условиях продолжающегося нагружения в пластической области. Наиболее неблагоприятный случай для устойчивости — потеря устойчивости при таком возрастании нагрузки, когда, несмотря на изгиб, напряжения сжатия возрастают
во всех точках сечения (рис. 12.43).
_ Тогда в условиях пластической области
Де = Да.
(227)
440
ГЛ. 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Для материалов с линейным упрочнением (£к = const) можно считать при анализе дополнительного изгиба, что материал имеет «модуль упругости» Ек. Выражение для критической нагрузки будет таким:
/VHp=n2£KJmin/Z2.	(228)
Эта формула, полученная Энгессером — Шенли, совпадает с формулой Эйлера, где модуль упругости Е заменяется на касательный модуль Ек.
В другой форме
гг - ^Ек
Пкр — —Г2~-л
Формулы (228) и (229) справедливы при условии
^кр От.
Если
л2£к
— . ~ П'Г.
(229)
(230)
(231)
то принимается окр = от.
Таким образом, в упругопластическод области
^кр —
(232)
Значение окр принимается наибольшим из двух указанных формулой (232) при условии, что любое из выбранных значений меньше критического напряжения по формуле Эйлера.
Замечание. Любопытна история вывода формулы Энгессера — Шенли. Работы Эйлера по устойчивости стержней были выполнены еще в 1744 г. и долгое время не находили практического применения. К ним обратились во второй половине XIX века, когда началось возведение железных конструкции особенно железнодорожных мостов. Тогда выяснилось, что для коротких стержней формула Эйлера дает завышенные и, следовательно, опасные для практики значения напряжений. Причина явления — работа стержня в неупругой области — была установлена русским инженером Ф. С. Ясинским. Вскоре была опубликована первая статья Энгессера (1889 г.), в которой была предложена формула (228). Эта работа подвергалась критике, так как не принималось во внимание явление разгрузки. Задача устойчивости стержня с учетом разгрузки была решена Карманом. Энгессер признал правильными критические замечания и отказался от формулы (228). В 1947 г. Шенли вновь вернулся к ней, считая ее справедливой в условиях продолжающегося нагружения.
Следует отметить, что в упругопластической области в отличие от упругой задача становится физически нелинейной и прогиб стержня не может быть неопределенной величиной, как в задачах о собственных значениях.
Формула Энгессера — Шенли справедлива как нижняя граница начала выпучивания (изгиба) стержня, но не описывает его дальнейшее поведение.
44. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
441
Обобщенные кривые устойчивости связывают значения критического напряжения окр и гибкости в упругой и упругопластической областях. Параллельно кривой акр = /(Х) строится кривая деформирования (о, е). На рис. 12.44 дана схематизированная кривая деформирования с линейным упрочнением. При акр < ог
(X > Хпред) справедлива гипербола Эйлера (зависимость между (5г{р и X гиперболического типа)
оКР = п2Е/№.
При напряжениях окр > пспользуется гипербола Энгессера — Шенли
Рис. 12.44. Обобщенные кривые устой-
Значение окр = От соответствует горизонтальному участку кривой изменения X.
Практические расчеты на устойчивость. При действии на стержень сжимающей силы N запас устойчивости определяется следу-
ющим равенством:
ny =
(233)
где ЛкР — усилие, вызывающее потерю устойчивости стержня (появление новой формы равновесия стержня в изогнутом состоянии).
Еще задолго до' приближения N к 2VKp в стержне -могу г возникнуть большие прогибы в результате эксцентричного приложения усилия, наличия первоначального искривления и т. и.
'Запас устойчивости обычно назначают для различных материалов в пределах пу = 1,6—5, причем для стержней с большой гибкостью значение пу принимают большим, так как для таких стержней влияние начальных отклонений сказывается сильнее.
Запас устойчивости можно представить в виде
^у = окр(Х)/о,	(234)
где oKp = A^Kp/F, о -=N/F — критическое напряжение и предельное напряжение^на сжатие в стержне (в задачах устойчивости по традиции напряжения сжатия считаются положительными).
Значение окр(Х) определяется по зависимости типа рис. 12.44 или по экспериментальным данным. При проектировочном расчете, когда требуется выбрать тип сечения (трубчатое, коробчатое и т.п.) и его размеры или определить их в процессе расчета, используется метод- последовательных приближений.
Расчетные уравнения имеют вид
£крМ 12 =
F	1	Anin
(235)
442
ГЛ. 12. ДИНАМИКА II УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Сначала задаются типом и размерами сечения (величинами F(1) и Jmln(1)) и находят
„ _ N „	М X	12
а(1) — Т » акр(1) — 0кр (А(1)), А(1) — -7	.
г(1)	*/min(i)
Если Нкр(1)/п(1) < пу, то повторяют расчет, выбирая большие размеры. При оКр(1А(1) > пу во втором приближении размеры сечения уменьшают или расчет заканчивается, если превышение невелико.
Захмечание. В строительной технике распространен расчет на устойчивость с помощью «коэффициента ослабления» <р, при котором допускаемое напряжение на устойчивость равно
[а]у= ф[о_] = <р -ZL,
где [о~] = От/п — допускаемое напряжение на сжатие.
Значения коэффициента <р в зависимости от X рекомендуются специальными таблицами. Техника расчета приводится во всех курсах сопротивления материалов. Метод обладает принципиальным недостатком — он не дает отчетливого представления о действительном запасе устойчивости стержня, и его рассмотрение опускаем.
Напомним, что цель расчета не число, а понимание.
ГЛАВА 13
МОДЕЛИ РАЗРУШЕНИЯ
При. построении моделей прочностной надежности необходимо ’знать условия разрушения материала конструкции» Соотношения, связывающие параметры работоспособности в момент разрушения с характеристиками материала, называются моделями разрушения.
Они называются моделями, так как на определенном уровне схематизируют сложный процесс разрушения, зависящий от действующих напряжений и свойств материала, характера нагружения и целого ряда других факторов. Модели разрушения различаются в зависимости от условий нагружения, в первую очередь от числа циклов нагружения, от свойств материала (пластичности или хрупкости) и, наконец, могут быть представлены в детерминированной или статистической формах. В детерминированных моделях (основной вид моделей разрушения при практическом использовании) действующие напряжения и характеристики материала имеют вполне определенные (детерминированные) значения. Обычно рассматриваются наиболее опасные расчетные случаи, когда действующие напряжения имеют максимальные значения, а характеристики материала соответствуют нижним границам технических условий.
В статистических моделях напряжения и (или) параметры материала считаются величинами случайными, представленными средними значениями и среднеквадратичными отклонениями. В дальнейшем основное внимание уделяется детерминированным моделям разрушения.
45. Модели статического и длительного разрушения
Вводные замечания. Статическое нагружение — медленное возрастание нагрузки от нуля до максимальной величины. Предполагается, что нагружение осуществляется однократно. Примерами статического нагружения могут служить нагружение металлического каркаса зданий, сосуда при гидравлическом испытании, болта при его затяжке. Практически к числу статического нагружения относят случай, когда нагружение повторяется несколько раз, однако встречается и заметное понижение прочности даже после малого числа циклов нагружений (N <*10).
В ряде случаев разрушение происходит в результате продолжительного действия нагрузки — длительное разрушение (см. разд. 15). Модели статического и длительного разрушения можно представить в следующем виде:
Оэкв =/(Оь о2, Оз; Хо, Xi, ...) = оКр(7\ t),	fl)
где Оэкв — эквивалентное напряжение; (ц, о2, Оз — главные напряжения, причем <71 > а2 > Оз; Ко» 1ь ... — параметры, зависящие от механических свойств материала. Величина оКр представляет критическое напряжение, зависящее в общем случае от температуры Т и времени нагружения t. Для статической прочности принимается окр = о&, где — предел прочности материала при растяжении; для длительной прочности аКр = одл, где адл — предел длительной прочности.
Если во всех точках материала конструкции
Оэкв	Окр,	(2^
условия прочности считаются выполненными; при
Оэкв	Окр	(3)
в опасной точке наступает разрушение. Величина аЭкв в равенстве (1) назы
444
ГЛ. 13. МОДЕЛИ РАЗРУШЕНИЯ
вается критерием прочности. Эквивалентное напряжение приводит сложное напряженное состояние к эквивалентному по опасности разрушения одноосному растяжению. Прочность при одноосном растяжении считается известном по экспериментальным данным.
Модели статического разрушения пластичных материалов. У пластичных материалов разрушение связано с появлением значительной деформации сдвига. Для таких материалов, как показали экспериментальные исследования, в качестве критерия разрушения могут быть приняты интенсивность напряжений или максимальные касательные напряжения.
Критерий интенсивности напряжений. В соответствии с этим критерием
0экв ==	(4)
где	___________________________________________________
V(ax — ау)2 + (Сту — Oz)2 + (аг — Ох)2 + 6 (т2у + т2г + Tzx)
(5).
— интенсивность напряжений. Модель статического разрушения имеет вид
= о6.	(6)
Если оси х, ’ у, z являются главными осями напряженного состояния, то
CTi = ~ + ~ + ~ °^2'
В частном случае плоского напряженного состояния (oz = 0)
Рис. 13.1. Критерии статической прочности для пластичных материалов в плоскости главных напряжений Ох и оу
ст, =	(8)
изображается в плоскости главных напряжений в виде эллипса (рис. 13.1), оси которого повернуты на 45° к осям х и у. Точка А соответствует одноосному растяжению по оси х, точка С — одноосному растяжению по оси у. Наибольшее «превышение» ординаты эллипса над прямой оу = оь получается при ох = ov/2 и составляет 0,115об. Если точка (ох, оу), изображающая напряженное состояние, находится внутри эллипса — материал остается прочным, при выходе этой точки за границы эллиптической области происходит разрушение.
Критерий интенсивности напряжений
предписывает одинаковую прочность при растяжении и сжатии, так как интенсивность напряжений в обоих , случаях одинакова.
45. МОДЕЛИ СТАТИЧЕСКОГО РАЗРУШЕНИЯ
445-
Замечания. 1. Критерии прочности в курсах сопротивления материалов было принято называть теориями прочности. Такое название нельзя признать-удачным, так как теоретические обоснования критериев прочности невелики. Их следует считать разумными обобщениями экспериментальных данных.
2.	Критерий интенсивности напряжений был предложен Губером (1902 г.) и независимо Мизесом (1913 г.) на основании совершенно различных исходных предположений. При постоянном значении о» оказываются постоянными:
а)	касательное напряжение в октаэдрической площадке;
б)	удельная потенциальная энергия изменения формы;
в)	среднее значение касательного напряжения по всем площадкам, проходящим через точку.
3.	Критерий прочности для пластичных материалов часто используется как критерий появления пластических деформаций
Of == or,	(9)
где От — предел текучести при одноосном растяжении. Значение о<, так же как и максимальное значение касательного напряжения Ттах, отражает интенсивность сдвига в рассматриваемой точке тела.
Критерий максимальных касательных напряжений. Ответственными за разрушение признаются касательные напряжения. Разрушение наступает, если значение максимального касательного напряжения равно
'Ттах = Ть,	(Ю)
где тд— предел прочности материала при действии касательных, напряжений. Применяя условие (10) для растяжения стержня и учитывая, что при растяжении стержня
1 Т==уО, получим
1
Тщах 2	(11)
Величина ттах при сложном напряженном состоянии равна
Ттах — "2" 0*1 — аз)?	(12)
где Of и о3 — наибольшее (в алгебраическом смысле) и наименьшее главные напряжения. Из соотношений .(И) и (12) получаем модель разрушения
Of — Оз — Об
или
Оэнв Of — Оз ОЬ.	(13)
Если главные напряжения ох, оу, о2 не упорядочены по величине, то оЭкв равно наибольшей по модулю разности
Оэкв —
max
= ОЬ.
(14)
Рассмотрим двухосное напряженное состояние (с2 = 0), и пусть
446
ГЛ. 13. МОДЕЛИ РАЗРУШЕНИЯ
ох и оу — главные напряжения. Если ож > 0 и оу > 0 (первая четверть на рис. 13.1), то при ож>оу имеем Oi = ож, Оз = 0, и условия (13) и (14) дают ож = о6 (прямую АВ на рис. 13.1) при тех же условиях (Ох > 0, оу > 0), но при Оу > Ох получаем оу = оь (прямую СВ), Если Ох<0, оу>0 (вторая четверть), то сч = оу, о3 = ох, и тогда по условию (13) имеем	•
Оу —Ох==о&.	(15)
Уравнение (15) изображается прямой DC, Подобным образом находим, что условие (13) при плоском напряженном состоянии изображается шестиугольником ABCDEF,
Как видно из рис. 13.1, модели разрушения для пластичных материалов по критерию интенсивности напряжений или по критерию максимальных касательных напряжений дают довольно близкие результаты.
Замечания. 1. Критерий максимальных касательных напряжений был впервые указан Треска на основании экспериментальных исследований и использован Сен-Венаном как критерий пластичности.
2. Экспериментальные данные свидетельствуют, что критерий максимальных касательных напряжений уступает по точности критерию интенсивности напряжений, однако он иногда оказывается проще для анализа предельных состояний конструкции, и его использование «идет в- запас прочности».
Предельные поверхности по критериям интенсивности напряжений и максимальных касательных напряжений. Для двухосного
^z
М
О
Рйс. 13.2. Пространство главных напряжений. Точка ЛТ(Ох, оу, Oz) характеризует напряженное состояние в соответствующей точке материала; £ — гидростатическая ось (а =
= ₽ = Y)
напряженного состояния (ог = 0) на рис. 13.1 были указаны предельные кривые по критериям интенсивности напряжений (эллипс) и максимальных касательных напряжений (шестиугольник, вписанный в эллипс). Для точек предельных кривых выполняются условия (6) или (14). При объемном напряженном состоянии критерии прочности характеризуются предельными поверхностями, в точках которых зна
чение критерия постоянно и равно предельному значению.
Рассмотрим сначала критерий интенсивности напряжений. Пусть ож, оу и ог представляют главные напряжения (рис. 13.2). В пространстве главных напряжений напряженное состояние характеризуется точкой М. Ось g оди-
наково наклонена к осям х, у и 2, а ее направляющие косинусы равны
cos а = cos Р = cos у =
1
Уз’
45. МОДЕЛИ СТАТИЧЕСКОГО РАЗРУШЕНИЯ
447
Ось g называется гидростатической осью, гак как величина
£ ==	(<*х + <Jy + <Tz)
пропорциональна среднему (гидростатическому) напряжению. Проведем плоскость D, содержащую точку М и перпендикулярную оси g; эта плоскость называется девиаторной. Расстояние г от точки М rq qwl g найдем по формуле
г2 = (Jx + OTz-------з" (<?х ~Ь (Jy + Qz)2
“ -д' (о’х + (Jy + (Jz (J%(Jy (Jy(Jz Wx) =
ИЛИ
г=]/уа{.	(16)
Модель статического разрушения по критерию интенсивности напряжений соответствует постоянному значению
i/T ,/”2'
r=|/yOi«y уСГ& . .	__	(17)
и, следовательно, изображается круговым цилиндром,, ось которого совпадает с гидростатической осью /рис. 13.3). При пересечении
Рис. 13.3. Предельные поверхности по критерию интенсивности напряжений (а) и максимальных касательных напряжении (б)
цилиндра с плоскостью ог = О получается эллипс, изображенный на рис. 13.1. Для критерия максимальных касательных напряжений предельная поверхность представляет правильную шестигранную призму, вписанную в цилиндр (см. .рис. 13.3). При объемном напряженном состоянии возможен случай равномерного (гидростатического) ^растяжения	i
Ох = оу = о2 = о.
В этом случае оба критерия прогнозируют бесконечную прочность, что не соответствует физическому смыслу понятия прочности. При
448
ГЛ. 13. МОДЕЛИ РАЗРУШЕНИЯ
объемном напряженном состоянии в тех случаях, когда все три главных напряжения растягивающие (но не обязательно одинаковые), модель статического нагружения пластичных материалов должна быть дополнена ограниченпем по наибольшим растягивающим напряжениям*
Замечание. Интенсивность напряжений обращается в нуль и при всестороннем равномерном сжатии. Опыты показывают, что при таком напряженном состоянии применяющиеся в технике материалы обладают практически неограниченной прочностью. В связи с этим не имеет места ограничение по наибольшим сжимающим напряжениям.
Модель статического разрушения пластичных материалов, дополненная условием отрыва. Условие отрыва состоит в ограничении -значения наибольшего растягивающего напряжения:
<5К,	(18)
max
где SK — истинное сопротивление отрыву (разд. 12). В технических расчетах можно принять
8К~
где гь — удлинение материала
Рис. 13.4. Предельная поверхность по критерию интенсивности напряжений при ограничении растягивающих напряжений (щ < 5К)
о6(1 + е6),	(19)
при разрушении (в опытах на растяжение образцов). Предельная поверхность по критерию интенсивности напряжений, дополненная условием (18), показана на рис. 13.4. Модель статического разрушения пластических материалов выражается следующими условиями:
Oi>a6Vot>5K, (20)
где V — знак логического суммирования — осуществление одного из событий или обоих вместе.
Условие статической прочности пластических материалов имеет вид
щ < Об А 01 <
где Д — знак логического умножения — одновременного осуществления событий.
Модели статического разрушения хрупких материалов. Хрупкие материалы отличаются малым удлинением при разрыве (6 < 3%) и малой ударной вязкостью (ап<30 Н/мм2). Разрушение хрупких материалов происходит путем отрыва без значительных
45. МОДЕЛИ СТАТИЧЕСКОГО РАЗРУШЕНИЯ
449
следов пластических деформаций. Ответственными за хрупкие разрушения являются нормальные напряжения. Наиболее простая и часто применяемая модель статического разрушения хрупких материалов имеет следующий вид (рис. 13.5):
(21)
где Ci — наибольшее растягивающее напряжение, оь — предел проч
ности материала при растяжении.
Условие (21) для плоского напряженного состояния выражается линиями СгС^СВ и ВААхА2. Критерием прочности по условию (21) является наибольшее нормальное напряжение (в алгебраическом смысле)
оэкв — 01.	(22)
В соответствии с условием (21) при действии сжимающих напряжений даже при одноосном сжатии разрушение невозможно. Опыты с хрупкими материалами показывают, что при сжатии они
разрушаются по площадкам с максимальными касательными напряжениями при значении
= *2* О'сж,	(23)
где оСж — предел прочности материала при сжатии.
Условию (23) соответствуют линии
Ох — оу = осж	(линия FAi),
Оу —- Ох = Осж	(линия DCl )
и линии FE и ED,
Модель статического разрушения хрупких материалов имеет вид
Рис. 13.5. Критерий наибольших растягивающих напряжений для хрупких материалов
Ох Ofe V Ттах “2" ^сж*
(24)
На рис. 13:5 условиям (21) и (23) соответствует внешняя область для кривой DjCiCBAA^FED.
Внутренняя область указанной кривой представляет условие прочности
0*1 А Тщах < “2 ^сж*
Более общие модели статического разрушения. При построении моделей разрушения пластичных и хрупких материалов учитывались возможности разрушения путем среза или путем отрыва. Первый вид разрушения характерен для пластичных материалов, второй— для хрупких. Разделение материалов на пластичные и хрупкие по опытам на простое растяжение не является исчерпывающим. При всестороннем растяжении пластичный материал ведет себя как 29 и. А. Биргер, Р. Р. Мавлютов
450
ГЛ. 13. МОДЕЛИ РАЗРУШЕНИЯ
хрупкий; при всестороннем сжатии хрупкий материал проявляет пластические свойства.
Более общие модели статической прочности учитывают взаимное влияние двух механизмов разрушения (среза и отрыва) и потому справедливы как для пластичных, так и для хрупких материалов.
Критерий Мора является дальнейшим развитием критерия максимальных касательных напряжений. Предполагается, что в момент разрушения в опасной площадке величина касательного напряжения зависит от величины и знака действующего в этой площадке нормального напряжения
т* = /(а*).	(25)
В качестве опасной площадки принимается площадка с макси-
Рис. 13.6. Кривая предельных напряжений в плоскости (ат , * Y)
*	>	111 а Ль, 111а Л /
по гипотезе Мора •
мальными касательными напряжениями
тогда Т*= Ттах;	(26)
а* “ а*тах
— нормальное напряжение в площадке максимальных касательных напряжений.
В общем случае напряженного состояния
Тчпах == “J" (<Ч	^з)?	_ (27)
= 4 (°1 + °’) ’ (28>
где 01, Оз — наибольшее и наименьшее (в алгебраическом смысле) главные напряжения.
По гипотезе Мора прочность не* зависит от промежуточного главного напряжения о2.
На рис. 13.6 представлена кривая предельных напряжений в плоскости (тщах, <*ттах) по гипотезе Мора. Точка А соответствует одноосному растяжению, точка D — одноосному сжатию, точка К — кручению. В первом приближении предельная кривая заменяется прямой
Типах == 0iOrmax4“	(29)
• где а0, 01 — параметры прямой.
Наиболее полная аппроксимация получается в том случае, когда прямая проводится через точки А и D. Тогда для точек Л и О имеем
1	1	1	У1 .
— 01 2	• 0(ь	“2* Фсж — 0j “2" ^сж 4" 0q?
45. МОДЕЛИ СТАТИЧЕСКОГО РАЗРУШЕНИЯ
451
где о& — предел прочности, осж — предел прочности при сжатии (абсолютная величина сжимающих напряжений при разрушении). Далее находим
^0
°Ч°сж асж “Ь °Ь’
асж асж
(30)
Уравнение (29) с учетом соотношений (27), (28) и (30) будет таким:
ai аз —
-----:--- (01 + Ог) + 2 ------;---.
°СЖ «Ь	°СЖ "Ь
или, после простых преобразований,
аь
а1 — 7Г~ аз = Qb‘ исж
(31)
Предельное сопротивление отрыву So (при ттах = 0) будет по (29) равно
g __ __ ар '_ ^сж________аЪ
о ~ т; ~ асж - аь “ 1 - аь/оС№1-
Если аСж считается известным, го предел прочности на срез составит
т»-ао- 1 + аь/Осж-
Эквивалентное напряжение (критерий Мора) в соответствии с условием (31) равно
Оэкв =	" Оз*	(32)
исж
Если оСж — о6, то критерий Мора совпадает с критерием максимальных касательных напряжений. При оСж -*•00 критерий Мора переходит в критерий наибольших растягивающих напряжений для хрупких материалов.
Предельную прямую можно провести через точку К (кручение, сдвиг) и А (растяжение), если известно экспериментальное значение т6. Тогда
fl’o " Tft,
at = — (2т6/Об—.1),
и критерий Мора будет таким:
Сакв = 01 — 03 (Оа/т6 — 1) = Об.	(33)
Предел прочности на сжатие и сопротивление отрыву прогнозируются 29*
452
ГЛ. 13. МОДЕЛИ РАЗРУШЕНИЯ
следующими в еличинами:
Псж = а /т 1 1	(34)
Замечания. 1. Щри традиционном изложении теории прочности Мора (1902 г.) исходят из геометрической интерпретации с помощью кругов Мора. Предельная кривая представляется как огибающая предельных кругов Мора для различных напряженных состояний. Однако геометрическая интерпретация напряженного состояния с помощью кругов Мора не связана с механической трактовкой процесса разрушения и потому необязательна.
2. Критерий Мора принадлежит к числу двухпараметрических критериев— требуется знание двух экспериментальных характеристик материала (аг> и аСж или аь и Ть). При задании о& и хь (см. рис. 13.6) получается более точная аппроксимация, но в более узком диапазоне напряженных состояний при 01 > 0.
Предельная поверхность в пространстве главных напряжении по критерию Мора. Для плоского напряженного состояния (ог = 0)
предельная поверхность переходит в предельную линию (неправильный шестиугольник), показанную на рис. 13.7. В первой четверти (ох>0, оу>0) величина о3 = 0 и критерий Мора совпадает с критерием максимальных касательных напряжений. Во второй четверти (Ох<0, Ov > 0) 01 = 02/, о3 = ох и по равенству (32)
Оу — ох = оь.	(36)
,	исж
Уравнение (36) выражается прямой DC. В третьей четверти (ох<0, оу<0) 01 = 0, тогда по условию (32) имеем
Оз = 0Сж,
что соответствует прямым DE (при loxl > lovl) или EF (при loj>loxl). в пространстве главных напряжений
Рис. 13.7. Критерий Мора (шестиугольник) и критерий Писаренко — Лебедева (неправильный эллипс) для плоского напряженного состояния
Предельная поверхность
представлена на рис. 13.8. В сечении плоскостью ог = 0 получается шестиугольник (см. рис. 13.7); вершина поверхности (точка So) лежит на гидростатической оси. При осж = о6 точка So уходит в бесконечность и поверхность на рис. 13.8, а совпадает с поверхностью на рис. 13.3, б.
Критерий Писаренко — Лебедева основан на существовании зависимости
а< = /(о4),	(37)
связывающей интенсивность напряжений щ и наибольшее нормальное напряжение щ в момент разрушения (рис. 13.9). Заменяя в
45. МОДЕЛИ СТАТИЧЕСКОГО РАЗРУШЕНИЯ
453
первом приближении зависимость (37) прямой • ot == a^i + а0,	(38)'
находим параметры и ай из условия, что прямая проходит через.
Рис. 13.8. Предельные поверхности в пространстве главных напряжений по критерию Мора (а) и по критерию Писаренко — Лебедева (б)
Рис. 13.9. Кривая предельных напряжений в плоскости (a,-, ai) по гипотезе Писаренко — Лебедева
точки А и D (точки одноосного растяжения и сжатия)» Получаем =	(о^сж/Оъ — 1) , Ло ~ ОСж, _
так как в точке D €4 = 0,	= осж, где оСж — предел прочности на
сжатие.
Из условия (38) следует
о» + (1 —	= аь.	(39)
исж \ мсж/
Эквивалентное напряжение по гипотезе Писаренко — Лебедева (критерий прочности) равно
Оэкв = (Ji +, (1 — aV исж \ исж/
Предельная поверхность в пространстве главных напряжений по критерию Писаренко — Лебедева. Для плоского напряженного состояния (oz = 0) уравнение (39) представляет неправильный эллипс, описанный вокруг шестиугольника Мора (см. рис. 13.7). Предельная поверхность в пространстве главных напряжений представляет круговой конус, вершина которого лежит на оси, одинаково наклоненной к направлениям глав
ных напряжений (см. рис. 13.8). Сопротивление отрыву по соотношению (39) равно
°	1 аь/асж
454
ГЛ. 13. МОДЕЛИ РАЗРУШЕНИЯ
r=const
bgtp/ tgtp
Рас. 13.10. Зависимость предела длительной прочности от времени нагружения (в логарифмических координатах)
Модели длительного разрушения. В современной технике часто встречаются конструкции, элементы которых работают при повышенных температурах (900°С и более). В этих условиях прочность конструкционных материалов, особенно металлов и их сплавов, существенно зависит от температуры и длительности нагружения.
Разрушение, наступающее вследствие длительного действия нагрузки, называется длительным разрушением. Связь между пределом длительной прочности оял и временем до разрушения устанавливается зависимостью
фдл^р ~ С,	(41)
где nz = /n(T), С = С(Т)~~ константы материала, зависящие от температуры.
В логарифмических координатах зависимость (41) выражается прямой линией. В
некоторых случаях наблюдается перелом после времени нагружения £Р1 (рис. 13.10), и более общая зависимость имеет следующий вид:
фдл^р == С При	*
тп-	(42)
Пдл^р — С 1 При tp £р1«
Константы материала связаны зависимостью, вытекающей из того, что точка Ai принадлежит одновременно двум участкам:
. 4-(lgC-lg«pl) = A-(lgC1-lgipl).	(43)
Модель длительного разрушения при стационарном (постоянном по времени) нагружении имеет вид
^ЭКВ==ОДЛ(^, Г),	(44)
где оДл(^ Z)—Предел длительной прочности при растяжении, t и Т — длительность и температура нагружения. Эквивалентное напряжение можно принимать по критерию Мора (31):
Оэкв = <^1 — ——“—	(45)
°дл.сж
где Одл. сж ~ предел длительной прочности на сжатие.
По экспериментальным данным получается
Одл. СЖ >2одЛ.	-	(46)
Принимая
Идя. СЖ = 2ОдЛ,	(47)
получим
Пэкв = Oi —(48)
45. МОДЕЛИ СТАТИЧЕСКОГО РАЗРУШЕНИЯ
455
В качестве критерия длительной прочности используется критерий Сдобырева
Оэкв = -у (°* +	(49)
который можно рассматривать как критерий Писаренко — Лебедева при условии (47).
Модель длительного разрушения при нестационарном нагружении. Принципы линейного суммирования повреждений. Часто элементы конструкций работают на различных режимах нагружения.
Рис. 13.11. Изменение напряжений и температур при нестационарг ном нагружении
Рис. 13.12/ Нестационарное нагружение при неправильном изменении режимов
Например, авиационный двигатель пассажирского самолета работает 2—4% своего ресурса на наиболее тяжелом (взлетном) режиме, 20—30% на номинальном режиме, остальное время на более легких режимах.
Допустим, что нагружение состоит из к режимов (рис. 13.11), причем на г-м режиме (в опасной точке) действуют температура Ti и напряжение длительность /-го режима равна Л; суммарное время работы обозначим £2. Пусть tp< составляет время до разрушения при непрерывной работе в условиях i-ro режима, (т. е. при температуре Л и напряжении о,). Назовем повреждением, полученным материалом в результате работы на i-м режиме, величину
(50)
Очевидно, что	’
При £< = 0 повреждение отсутствует, при =	(г< = 1) материал
разрушается полностью за счет работы на /-м режиме.
При работе на нескольких, режимах в соответствии с принципом линейного суммирования повреждений разрушение наступает при
Ь- = У = 4 et *₽i
2i_
*pi	*р2
(51)
456
ГЛ. 13. МОДЕЛИ РАЗРУШЕНИЯ
Условие (51) представляет модель длительного разрушения при нестационарном нагружении. При непрерывном изменении режимов нагружения повреждение за время dt равно
где £р(о, Т) — время до разрушения при напряжении о и температуре Т (в данное время t) (рис. 13.12).
Модель длительного разрушения при непрерывном изменении режимов имеет вид
f________1______
= 1.
(53)
Замечание. Принцип линейного суммирования повреждений был впервые выдвинут Пальгреном (1924 г.) при оценке долговечности шарикоподшипников. Для длительной прочности этот принцип был применен Робинсоном (1952 г.). Принцип получен как обобщение экспериментальных данных. Он может быть обоснован, если принять скорость развития повреждений равной
dr
(54)
где /(а, Т) — функция произвольной структуры, зависящая от напряжения и температуры.
Существенно, что время t не входит в явном виде в правую часть равенства (54), т. е. процессы старения, (диффузии, коррозии и др.) исключаются из рассмотрения. Они считаются второстепенными по сравнению с влиянием напряжения и температуры.
Эквивалентные напряжения и запасы прочности при нестационарном нагружении. Рассмотрим длительную прочность на г-м ре-
*  жиме (рис. 13.13). Точка Л(ф, ti) ха-
1g
| r^const) - рактеризует напряжения о< и длитель-
ность работы ti. на j-m режиме. Запас длительной прочности по напряжениям на i-м режиме
— Орг/^г«
lg t
Запас длительной прочности на i-м режиме по времени нагружения
Рис. 13.13. Длительная прочность при работе на i-м режиме
— tpilti.	(55)
Уравнение длительной прочности (41) позволяет установить важное со--отношение между величинами n0i и nti.
Учитывая, что точки Лра и Лр< удовлетворяют уравнению длительной прочности
<2 *S
О	о



a t = Cif
(56)
45. МОДЕЛИ СТАТИЧЕСКОГО РАЗРУШЕНИЯ
457
запишем
или
t j =S Q| fpj
(57)
В другой форме имеем
= (и0{) 
(58)
(59)
Запас по долговечности равен запасу по напряжениям в степени mit Так как показатель длительной прочности т лежит в пределах т — 4, ..., 16, то запас по долговечности значительно превышает запас по напряжениям. Условие линейного суммирования повреждений с учетом зависимости (58) представим в таком виде:
ai Г1
pfe/
к
С») лод *-1 %
Допустим, что все режимы приводятся к условиям первого режима, но при действии эквивалентного напряжения оЭКв. При наличии только одного (первого) режима условие прочности (60) будет следующим:
(61)
Запишем равенство (60) так:
JL= 1.
П т1 аэкв
(62)
Приравнивая выражения (61) и (62), находим \
, Ч	Ч I
1 +	+ * • ’ + I’
Ч /
. (63)
Эквивалентное напряжение приведено к первому режиму, в каче-* стве которого обычно принимают наиболее тяжедый (режим с минимальным запасом прочности). Из уравнений. (60} и (61)’ получаем формулу для эквивалентного запаса прочности:
к
1 х 1
Ля*	’
п°экв	П°1
(64)
458
ГЛ. 13. МОДЕЛИ РАЗРУШЕНИЯ
Соотношения (63) и (64) показывают, чго основное значение для повреждаемости имеют режимы с наименьшими запасами прочности. Это обстоятельство используется для проведения ускоренных испытаний на надежность.
Прочность при наличии трещин. Линейная механика разрушения. В ряде случаев оказывается необходимым оценить прочность элементов конструкции при наличии трещин.
Трещины могут оказаться в результате пропуска при контроле технологических дефектов (литейных, ковочных и сварочных трещин) или возникнуть под действием внешних нагрузок. Влияние трещин па работоспособность конструкции зависит прежде всего от вида нагружения. При переменных нагрузках почти все конструкционные материалы резко снижают прочность при наличии трещин (в два-три раза и более), так как в вершине трещины образуется высокая концентрация напряжений. При статических нагрузках существенное влияние трещин проявляется у хрупких материалов (высокопрочных сталей и сплавов с удлинением при разрыве 6 < 3%).
Практика показывает, что возникновение трещины часто не означает окончания безопасного периода работы конструкции. До некоторого критического размера повреждение оказывается безопасным.- Если имеется возможность обнаружения и слежения за дефектом, то это дает обоснование эксплуатации дорогостоящей конструкции по «техническому состоянию».
Анализ распределения напряжений возле трещин и других линейных дефектов, изучение условий роста трещин и их влияния на прочность составляют теперь специальный раздел механики твердого деформируемого тела — линейную механику разрушения.
Распределение напряжений возле вершины трещины. Рассмотрим узкую трещину длиною 21 в тонком листе (рис. 13.14). В окрестности вершины трещины напряжения определяются следующими равенствами:
1
C0S "Г 0 /	1 Q \
'	= yg7k1 + sinT0sinT9/-'
1 л
COS 96/	J	о Д
ах = Kt—-?==- ( 1 — sin-i-Ssin -к-0 ),	(65)
у 2лг \	*	* /
1
COS 9 0	2
== Ку	sin у 0 COS у 0’
где йГ1 = оУл/; г, 0 —полярные координаты точки; о — напряжение растяжения в листе.
Величина
=	(66)
называется коэффициентом интенсивности напряжений.
Формулы (65) получены из решения Инглиса для эллиптического отверстия в тонкой пластинке. При щели в толевом листе (случай плоской деформации) формулы (65) остаются справедливыми, но возникает дополнительно напряжение
o»==|x(ox + av),	(67)
45. МОДЕЛИ СТАТИЧЕСКОГО РАЗРУШЕНИЯ
45а
где ц— коэффициент Пуассона. Из соотношений (65) вытекает, что по мере приближения к вершине трещины напряжения стремятся к бесконечности, как 1/]/г при г 0.
Критическая длина трещины. Формула Гриффитса. При образовании трещины длиной 21 (см. рис. 13.14) освобождается упругая
Рис. 13.14. Распределение напряжений возле вершины трещины
энергия, так как берега трещины и область, к ним примыкающая, освобождаются от действия напряжений. Вертикальное перемещение точек берега трещины из решения Инглиса имеет вид ]/> —я2.	(68)
Изменение упругой энергии деформации можно считать равным работе, которую совершает’напряжение о при «закрытии» трещины: (I	X
|<тЛ f =	(69)
Z	J	/	Zi
— I	'
где h — толщина листа.
При росте трещины на величину Д/ освобождается упругая энергия.
дуу __ л U + Д/)2 аЧ-_~ 2ло2/А
Е	Е Е —
с другой стороны, должна быть затрачена работа на продвижение трещины
ДЛ = 2/2ДгЛ7, . .
где 7 — плотность поверхностной энергии разрушения.
Критическая длина трещины Z* находится из условия
ДИ^ДЛ,
что дает	,
О VHQ = V2Ey. • .	(70)
460
ГЛ. 13. МОДЕЛИ РАЗРУШЕНИЯ
Формула (70) была впервые установлена Гриффитсом. Величина
/2^ = Я1е .
получила название вязкости разрушения^ она считается постоянной материала. Условие начала быстрого роста трещины состоит в следующем:
Kt^Klc.
В момент начала лавинного разрушения коэффициент интенсивно-
сти напряжений в вершине трещины равен критическому значению вязкости разрушения. Размерность вязкости разрушения и коэффициента интенсивности напряжений равна
dim 2£1с = dim = Н • мм“3/2.
Для конструкционных сталей, титановых сплавов Лдс = (1 — 3) * 103 Н • мм~3/2.
Образцы для определения вязкости разрушения. Для определения Kie используются образцы с надрезом (рис. 13.15). В вершине надреза с помощью специальных испытательных
Рис. 13.15. Схема образцов для определения А:1С (по ГОСТ 90215—76)
машин (пульсаторов) получают усталостную трещину длиной не менее 1,5 мм.
Далее осуществляется статическое нагружение образца усилиями Р и расчет Kic проводится по максимальному значению растягивающего усилия, предшествующего разрушению образца.
46. Модели усталостного й малоциклового разрушения
Вводные замечания. Ранее были изложены основные сведения об усталостных разрушениях элементов конструкций (разд. 16).
Усталостные разрушения возникают при действии переменных нагрузок при числе циклов N > 105 и характеризуются резким влиянием концентрации напряжений и качества поверхности.
Усталостные разрушения не имеют следов пластической деформации в очагах зарождения трещин. При числе циклов* нагружения N < 105 наблюдаются разрушения малоцикловой усталости. Закономерности малоциклового разрушения занимают «промежуточное положение» между статической и усталостной прочностью. В частности, локальный характер усталостной прочности, зависимость от состояния поверхности проявляются при малоцикловой усталости в меньшей степени.
Рассмотрим сначала модели усталостного разрушения.
46. МОДЕЛИ УСТАЛОСТНОГО РАЗРУШЕНИЯ
461
Модели усталостного разрушения’ при одноосном напряженном состоянии. Модель усталостного разрушения принимается в виде условия
*
Оэкв
(71)
где Ка — эффективный коэффициент концентрации (нормальных) напряжений; [} и е — коэффициенты влияния поверхности и масштабного эффекта; 1|)0 — коэффициент постоянных (нормальных) напряжений (их значения указаны в разд. 16).
В равенстве (71) оа и — переменное и постоянное напряжения в момент разрушения; u-t — предел выносливости стандартного гладкого образца.
Если в рабочих условиях в опасной точке детали действуют переменное и постоянное (номинальные) напряжения аа и ото и к моменту разрушения происходит их пропорциональное возрастание, то
(За = П(За, Um = nUw,	(72)
где п— запас усталостной прочности по подобному циклу (разрушающий и рабочий циклы подобны).
Из соотношений (71) и (72) находим запас по подобному циклу:
П =	.	(73)
Запас по подобному циклу применяется для прочностной модели зубьев шестерен и в других случаях. Чрезвычайно широко распространено нагружение, при котором. происходит возрастание только переменных напряжений (резонансные конструкции иг т. д.). Тогда в момент разрушения
Ua — Паба,
(74)
где па — запас усталостной прочности по переменным напряжениям. Из модели-усталостного разрушения (71) находим
_a_1-ipCTam К,
режимы работы
Рис. 13.16. Определение запасов усталостной прочности (геометрическая иллюстрация)
(75)
Геометрическая иллюстрация модели усталостной прочности при одноосном напряженном состоянии дана на рис. 13.16 для постоянного
462
ГЛ. 13. МОДЕЛИ РАЗРУШЕНИЯ
значения
“фа — 0-1/Obf
(76)
где Оь — предел прочности материала.
При От = 0 получаем величину предела выносливости детали при симметричном цикле:
о-1д = а-1ре/£а,	(77)
при От — Оь (точка В) материал не может сопротивляться переменным напряжениям. При подобном цикле точка А перемещается вдоль луча ОА*- при возрастании переменной составляющей — по направлению ААа.
Рассматриваемая модель усталостного разрушения справедлива при действии касательных напряжений
Кх *	*
Та + фттт = T-i,	(78)
где т*, Тт — переменное и постоянное касательные напряжения; т-! — предел выносливости при кручении.
Замечание. Величина запаса прочности по подобному циклу всегда меньше, чем по переменным напряжениям:
п <Z па.
Однако не следует считать, что можно ограничиться определейием величины п как наименьшей. Дело в том, что допускаемые значения для п и па различны! Часто принимают
[л] = 1,5—2, [па] =.2,5—4.
Модели усталостного разрушения при многоосном (многокомпонентном) напряженном состоянии. Рассмотрим многоосное напря-

Z
Рис. 13.17. Многокомпонентное нагруженное состояние при действии переменных и постоянных нагружений
женно-е состояние, при котором составляющие тензора напряжений имеют переменные и постоянные части (рис. 13.17):
Ох 0Ха "Ь Oxrrij Оу === Оуа
“Р ОутП] • .т zx 4>zxa "Ь 'Tzxm*
Составим интенсивность переменных напряжений
+ 6т22Ха.
\ (79) Модель усталостного разрушения
стоянии и при симметричном
принять в виде
при сложном напряженном со-цикле изменения напряжений можно
Оэкв	О {а — 0—1.
(80)
46. МОДЕЛИ УСТАЛОСТНОГО РАЗРУШЕНИЯ
463
Например, для случая действия переменных напряжений изгиба бха = На и кручения тх1/а = то (другие компоненты напряженного состояния отсутствуют) получим из условия (80)
/ ol + Зт; = а-ь	(81)
При действии одних касательных напряжений (переменное кручение) из соотношения (81) находим
что является хорошим приближением для пластичных конструкционных материалов. Для хрупких материалов (легированных сталей, сплавов повышенной твердости) модель усталостного разрушения при многоосном напряженном состоянии можно принять такой:
0экв Хо0<д Xi0ia О—(82)
где aia — наибольшее переменное напряжение. Применяя условие (.82) для испытаний на переменный изгиб или растяжение — сжатие, получим
,	'	XqO—t “Ь Х10—1 == О-i, Xq У Xi == 1.
Для испытаний на переменное кручение
Хо /З Т_J + XfC-i == 0—1, Хо /3 + %i = ~.
-1
Из приведенных уравнений находим
1   *	(Szl X = f V3~ ZzjA
^-уз-iU-r Г \ 1/3--Д
Условие усталостной прочности (82) приобретает следующий видг
<*экв = Т7=-'	ITT-i	0ia = 0-1. (83)
уз — 1 v-1	/ уз—1\	т-1/
При 0-1/т-! = уЗ получаем условие (80), при 0-1/т-! = 1 (хрупкие материалы) соотношение (82) дает
01a = 0-1.	(84)
Модель усталостного разрушения при многокомпонентном напряженном состоянии и асимметричном цикле действующих напряжений является обобщением условия (80) и может быть представлена в виде	„	.
0экв == 0ia У ^P<J01m == 0—1,	(S3)
где alm — наибольшее- постоянное нормальное напряжение. При наличии концентрации напряжений при сложном напряженном со-.
464
ГЛ. 13. МОДЕЛИ РАЗРУШЕНИЯ
стоянии величина oia относится к истинным максимальным переменным напряже ниям:
Gia ==	Y(KxGxa — Ky(Jya)2 + . . . + 6/<zxTzx = K^ia, (86)
где Кх, Ку, ..., Kzx — коэффициенты концентрации напряжений Пх, Оу, ..т«; Ki — коэффициент концентрации интенсивности напряжений.
Модели усталостного разрушения при стационарном нагружении с учетом числа циклов нагружений. При одноосном напряженном состоянии такие модели рассматривались в разд. 16:
ога-У==С)	> (а_i)w ,
т	(87)
оа °7V = CQ, ва (о_1)2’у0,
где оа — переменное напряжение; т, С, mQ, CQ — постоянные материала, связанные соотношением непрерывности кривой
С(а.Д'т = Со,
(a_i)jv0 — предел выносливости при числе циклов 2V0, соответствующем точке прогиба.
При многоосном состоянии и асимметричном цикле напряжений в равенствах (87) следует положить (рис. 13.18)
Оа Оэкв 0<а	*ф01т,'	(88)
где Ога — интенсивность переменных напряжений, alm — наибольшее
постоянное напряжение.
Рис. 13.18. Модель ч устало-
стного разрушения при стационарном нагружении
Модели усталостного разрушения при нестационарном нагружении. Уровень переменных напряжений, действующих в элементах
конструкции, зависит от режима работы, т. е. является нестационарным. Пусть" на j-м режиме амплитуда переменных напряжений равна Oj (индекс а для краткости опускается). Число циклов нагружений на ;-м режиме обозначено Nji суммарное число циклов составляет N2:
k
ДГ2 = ЛГ1+ДГ2+ ...+ TVfe = 2 Nj.
j=l
Обозначим относительную длительность (по числу циклов) /-го режима в виде

(89)
Во многих случаях нестационарного нагружения относительная длительность режимов остается постоянной. Модель усталостного разрушения основывается на принципе линейного суммирования
46. МОДЕЛИ УСТАЛОСТНОГО РАЗРУШЕНИЯ
465
повреждений, в соответствии с которым к моменту разрушения
^Р1
п it'1’
Nk = у ^_= 1
(90)
где JV* — число циклов, накопленных к моменту разрушения на 7-м режиме (при нестационарном нагружении); Nvi — число циклов до разрушения приу работе только на ;-м режиме.
Условие усталостного разрушения (90) можно выразить через суммарное число циклов до разрушения 2Vp2, так как
и тогда
N* = ?Лрх,	(91)
=	(92>
7=1 ы
Если при нестационарном нагружении элемент конструкции имел суммарное число нагружений (на всех режимах) то запас долговечности (по числу циклов)
n^N^/Nt.	(93)
Из условия (92) находим
nN = I IT" j \ j==i vpj/
(94)
где" Nj = Nxqj — число циклов нагружения на ;-м режиме в условиях эксплуатации. Так как
NJN^njN	(95)
— запас по долговечности при работе только на /-м режиме, то суммарный запас по долговечности составит
/ k \ -1
nN =	У—	1	(96)
	к		
1 nN	-2--Я"»		(97)
или
(98)
Запас по долговечности и запас по напряжениям при работе на 7-м режиме связаны следующим соотношением:
mj ftjN ==	»
что вытекает из равенства
(99)
где opJ — переменное напряжение, при котором происходит разрушение за Nj циклов.
*30 И. А. Биргер, Р. Р. Мавлютов
466
ГЛ. 13. МОДЕЛИ РАЗРУШЕНИЯ
Запас по напряжениям па ;-м режиме равен
(100)
Запас по долговечности равен
•^=вд.	. (ion:
Из соотношений (99) — (101) вытекает равенство (98).
Модели малоциклового разрушения при одноосном и сложном напряженных состояниях. В разд. 16 была приведена модель ма-лоцпклового разрушения при одноосном напряженном состоянии (условие разрушения Мэнсона):
еа = у (In гЧУ’8 77-0,6 + V5 F 77"°’12’	(102)
где 8а — амплитуда изменения деформаций; ф — коэффициент поперечного сужения при разрыве; оь — предел прочности материала; Е — модуль упругости; N — число циклов до разрушения. Величина 8а включает пластическую и упругую части циклической деформации. При сложном напряженном состоянии величина 8а в уравнении (92) заменяется эквивалентной деформацией
8а Сэкв	(103)
где 8ia — интенсивность амплитудных значений деформаций:
eia ==	— Sya)2 + . . . + J Vzxa •	(104)
Величины 8Xa, 8i/a, ..., Yzxa являются амплитудными значениями, циклически изменяющихся компонент деформации.
При асимметричном цикле изменений деформаций, когда имеются переменные и постоянные составляющие цикла, эквивалентная деформация
8экв == 8<а “Ь февцтц	(105)
где 81m — наибольшая постоянная линейная деформация.
Модели малоциклового разрушения при нестационарном нагру^ женин. При работе элемента конструкции на разных режимах с циклическими деформациями sai, 8a2, . • •» бал условие разрушения может быть принято в виде
где №* и — число циклов нагружения на у-м режиме, накопленное к моменту разрушения при нестационарном режиме нагружения; —число циклов до разрушения при работе только на одном 7-м режиме. Условие (106) выражает принцип линейного суммирования повреждений при малоцикловой усталости.
Запас долговечности выражается равенством (94) <
ГЛАВА 14
ЦИЛИНДРЫ и диски
Многие ответственные элементы машин и сооружений могут рассматриваться как полые цилиндры, работающие при действии внутреннего или внешнего давления (толстостенные трубы, цилиндрические сосуды высокого давления, валы и втулки при наличии прессовых посадок и т. д.). Часто применяются высоконагруженные, быстровращающиеся диски (турбины, осевые компрессоры), шлифовальные круги и т. д.
47. Прочностные модели толстостенных труб и цилиндров. Напряжения и деформации
Рассмотрим круговой цилиндр при осесимметричном, постоянном по длине нагружении. На рис. 14.1 представлен участок толстостенной трубы под внутренним давлением. Внешний радиус цилиндра обозначим Ь, внутренний а. Предположим, что по длине

Рис. 14.2. Напряжения по граням элемента цилиндра
Рис. 14.1. Круговой цилиндр при осесимметричном, постоянном по длине нагружении
цилиндра (по оси z) нагрузка N и температурное поле не изменяются. Длина цилиндра I существенно больше его радиуса, и при указанных условиях поперечные сечения цилиндра остаются плоскими. Искажения, которые могут возникнуть только возле торцов, занимают по принципу Сен-Венана небольшие области, и ими в рассматриваемой модели пренебрегаем.
Выделим элемент цилиндра двумя поперечными сечениями, отстоящими друг от друга на расстояние dz, двумя цилиндрическими поверхностями радиусами г и г + dr и, наконец, двумя меридиональными плоскостями, составляющими угол d0 (рис. 14.2, а). По 30*
468
ГЛ. 14. ЦИЛИНДРЫ и диски
граням этого элемента будут действовать: радиальное ог, окружное
о9 и осевое о2 напряжения (рис. 14.2,6).
В силу осевой симметрии и постоянства нагружения по осп
указанные напряжения будут главными: по граням элемента
Рис. 14.3. Перемещение и деформации в цилиндре при осесимметричном нагружении
(рис. 14.2, б) касательные напряжения отсутствуют. Точка А цилиндра (рис. 14.3) получает радиальное смещение и (г).
Для определения деформации в радиальном направлении в соответствии с общей теорией деформации (разд. 9) рассматриваем дв.е точки А и В, отстоящие на расстояние dr. Так как перемещение и зависит от радиуса, то радиальное перемещение в точке В будет равно u + dr. Деформация в
радиальном направлении равна
А*В*-АВ “ + dr+dr~u-dr_du.
£r	АВ	dr	dr ‘
(1)
Для определения деформации в окружном направлении надо проследить за изменением длины отрезка А С. Тогда
4*С* — АС (г 4- и) dQ — г dQ и -g9 _	—	—	(2)
Формулы (1) и (2) выражают деформации в полярной системе координат (г, 0) при осесимметричном нагружении.
Выражение для осевой деформации имеет такой же вид, как и в декартовой системе координат (разд. 9):
дш dz ’
где w — перемещение в направлении оси z. При плоской деформации величина е2 постоянна:
е2 == const = е.	(3)
Уравнения равновесия элемента цилиндра. На рис. 14.4, а представлены элемент цилиндра и действующие ла него усилия. По граням элемента приложены напряжения: ог, о в и а2, зависящие о г радиуса г; по 0 и z напряжения постоянны. К элементу цилиндра может быть приложена распределенная массовая сила (на единицу массы), которая при вращении цилиндра равна
F, = со2 г,	(4)
где со — угловая частота вращения.
Окружное напряжение о9 одинаково на двух противоположных гранях, составляющих угол d0, так как оно не зависит от угла 0.
47. ПРОЧНОСТНЫЕ МОДЕЛИ ТОЛСТОСТЕННЫХ ТРУБ
469
Постоянным на гранях элемента оказывается и напряжение ог, так как напряжения не изменяются по координате z. Разными будут радиальные напряжения в силу возрастания радиуса соответствующих граней (г и г4-dr). Рассмотрим равновесие сил в радиальном направлении. На рис. 14.4, б показана проекция элемента на
Рис. 14.4. Условия равновесия элемента цилиндра
плоскость, перпендикулярную оси цилиндра (оси z). Проектируя все силы на ось г, проходящую через центр тяжести элемента, получаем
/ d(Tr \
— огг dO dz 4- I (jr 4-	dr j (г + dr) dO dz —
—2uesin(d0/2) dr dz 4- $Frr dO dr dz = 0, (5)
где p — плотность материала.
В уравнении (5) учитывается, что усилия на боковых гранях дают составляющие на направление г (рис. 14.4, б).
Полагая, что
sin = 4-d0,
и пренебрегая величинами высшего' порядка, получим
d<S
аг dr dOdz 4- r dr dO dz — a0 dr dO dz 4- pco2r2 dr dO dz == 0.
Так как dr d0 dz ¥* 0, to
d(Jr
r ——I- ar — ae + pco2r2 = 0.
ar
(6)
Уравнение (6) представляет условие равновесия для элемента цилиндра. Два других условия (проекции на направление, перпендикулярное г, и на ось z) выполняются -по условиям задачи.
470
ГЛ. 14. ЦИЛИНДРЫ и диски
Уравнения упругости. Рассматривая изотропное упругое . тело, будем иметь следующие соотношения упругости (разд. 18):
= 4 ~~ И (ае + а*)1 +
Л/
ее = [ав — р (аг + ог)] + аТ,	(8)
ег = е = -g- [ог — р (аг + ае)1 + аТ.	(9)
В дальнейшем потребуется выразить напряжение через деформации.
В рассматриваемой задаче, учитывая условие (3), удобно исключить величину о2 из соотношений (7) и (8) с помощью равенства (9):	'
аг~ Ее +	+ ЕаТ.	(10)
Подставляя последнее соотношение в уравнения (7) и (8), представим их так:
ег = у- (аг — ро0е) + сс0Т — Це,	(11)
о
ее = (се — ро0г)- +	— ре,	(12)
^0
где параметры упругости для плоской деформации имеют вид
Е° = 1 —и2’ .	=
* г*
и коэффициент линейного расширения равен
а0 = а(1 + ц).	(14)
Из уравнений (11) и (12) легко находим
Е /	ЕаааТ Е<№
+ + <15>
л rQ•	г V	' О
Е /	к Е^аТ	En^
09 ~ 4—7Г <80 +	— ттгтг + е- (16)
1 — Н	1 Но 1 Но
В тех случаях, когда напряжение аг в цилиндре отсутствует, соотношения (7) и (8) приводят к более простым зависимостям:
Е z	. EaT
Or = (er + pee) -	,	(17)
°9 = 4 72 (E0 + И8г) “ 1^7?	<18)
"	1 — P	x Г*
которые также будут использованы в дальнейшем.
Основное дифференциальное уравнение. Это уравнение составляем относительно радиального перемещения и (г). Если восполь-
47. ПРОЧНОСТНЫЕ МОДЕЛИ ТОЛСТОСТЕННЫХ ТРУБ
471
зеваться уравнением равновесия (6) d<Ir ,
__ + _(Ог — Од) = -р«2Г
(19)
и внести значения аг и а0 из соотношений (15) и (16), то, учитывая формулы (1) и (2), получим
d #0	/ du
dr 1 - Но \dr
1	/ du и
r 1 + Р'б
о , d = - P® r +
^oao^* \   d
1 —Ho j	dr
e.
(20)

Уравнение (20)\ представляет неоднородное дифференциальное уравнение второго порядка относительно функции и (г).
Если параметры упругости Е и pi постоянны вдоль радиуса, то из уравнения (20) находим
d2 и	1 du
dr2	г "dr*

(21)
где функция
/(г) ^г + (1 + н.)^-(«.л--	Prfr +
+	<22>
С помощью небольших преобразований уравнение (21) можно представить в более удобном для последую- * "
щего интегрирования виде:
- -т-(-^1=7(0-	(23)
dr \ г dr J J 4 7	х/
Толстостенная труба под действием внутреннего и внешнего давлений. Рассмотрим равномерно нагретый цилиндр с постоянными параметрами упругости вдоль радиуса, нагруженный давлением (рис. 14.5); вращение отсутствует («=.0), и торцы цилиндра свободны от напряжений. Для указанного случая /(г) = 0, и дифференциальное уравнение (21) будет
Рис. 14.5. Цилиндр под действием внутреннего и внешнего давлений
таким:
d2u	1 du г	и   d f 1 d(ur)\  ~
dr2	r dr	r2	dr \r dr J
(24)
Решение уравнения (24) можно искать в следующем виде:
и =	(25)
472
ГЛ. 14. ЦИЛИНДРЫ И диски
После подстановки в уравнение (24)
C[/c(/c-l)+/c-l]rft-2 = 0
приходим к характеристическому уравнению к2 — 1 = 0, корни которого равны ki = 1, к2 = —1.
Решение уравнения (24) будет таким:
u^Gr + G/r,	(26)
где Ct и С2 — произвольные постоянные. Этот же результат можно получить другим путем. Из уравнения (24) имеем
1 d (itr)	П	/О*7\.
---з— == const = 2С,.	(27)
г dr	1	'	'
Перенося г в правую часть равенства и интегрируя» получаем
ur = Gr2 + С2,	(28)
что совпадает с решением (26). Так как на торцах цилиндра внешние усилия отсутствуют, то можно положить ог = 0 и воспользоваться соотношениями (17) и (18), пренебрегая температурными членами. Тогда
Е [ du , и \
+ M	<29>
Г* V	/
Е / u , du\
00 = 7^?	7 + ^ -	<30>
Подставляя и из уравнения	(26),	находим
=	+	ЮС1-^С2], .	(31)
°0 = 7^7	+ Н) Ц	(32)
Постоянные Ci и С2 следует определять из краевых условий (для радиальных напряжений)
вг(а)=~ ра	при г = а,
От(Ь)=—рь	при г=д.
Будем иметь
(1 + >и)с1_1^с2 = _Ц^ Ра,	(зз)
(1 + И)	с2 = -	(34)
Из последних соотношений находим
2	>2
_1_p,apa-ipb
С1~ Е	’
2 2	(33)
r _ 1 + ц « b (pa - pb)
47. ПРОЧНОСТНЫЕ МОДЕЛИ ТОЛСТОСТЕННЫХ ТРУБ
473
Внося значения С\ и лы Ламе
С2 в равенства (31) и (32), получаем форму-
Or =
°	2
Ра~ b Ръ
2 °
1 а Ь" (Ра ~Рь)
ае =
г 2  2
о — а
2	,2
а Ра —b РЬ
Ь2-а2
1 (Ра — Рь)
2
(36)
Ь2 — а2
.2
,2	!
Ь — а
(37)
Для радиального перемещения из соотношений (26) и (35)’ устанавливаем следующую зависимость:
и (Г) =	1 + ц aV (Ра - Рь) 1
(38)
Е. b2_at	Е
Замечания. 1. Обоснованность предположения, что о2 = 0, сделанного построении решения, доказывается следующим образом. Из уравнений и (32) (или (36) и (37)) вытекает, что на всех радиусах
<Jr + о а = const.
Так как в рассматриваемых задачах е = const, то из соотношения (10) аТ = 0 получаем, что напряжение о2 также должно быть постоянным. Внешнее усилие вдоль оси цилиндра отсутствует, и потому напряжение а2 должно обращаться в нуль (иначе условия равновесия не удовлетворяются).
(26) следует положить г~>0. Из условия на
при (31)
при '
2.	Для сплошного цилиндра в общем решении С2 = 0, так как при С2 =£ 0 перемещение и оо при внешнем контуре (34) получим
1 —и
Е р»
и тогда из соотношений (29) и (30)
аг = Ов = —рь.
Интересный результат!
3.	Напряжение в цилиндре не зависит от природы упругого материала, формулы (36) и (37) не содержат модуля упругости и коэффициента Пуассона.
4.	Формулы для напряжений в цилиндре были впервые получены Ламе (1795—1870) — французским ученым, долгое время работавшим в России.
Действие осевого усилия. Если на цилиндр (рис. 14.6) действует осевое усилие 7V, то при постоянных параметрах упругости решение задачи будет таким:
С
(39)
14.6. Цилиндр под
Рис. действием осевого усилия.
N
— о, О0 — 0, Oz------------772	2\">
л(Ь —а )
—	=	, ег —е —
(40)
(41)
Очевидно; что уравнения равновесия и совместности деформаций удовлетворяются. Эти уравнения дифференциальные, а напряжения и деформации по равенствам (40) и (41) — постоянные ве->
474
ГЛ. 14. ЦИЛИНДРЫ И диски
личины. На торпах цилиндра краевое условие выполняется в интегральном смысле:
j OzdF = N.	(42)
F
Точное решение требует приложения на торцах цилиндра постоянных напряжений.
При действии давлений по цилиндрическим поверхностям и осевого усилия в пределах упругих деформаций напряжения и деформации суммируются.
Прочностная модель цилиндрической части сосуда высокого давления. Рассмотрим напряженное состояние в цилиндрической части сосуда высокого давления (рис. 14.7) при действии внутреннего давления р, Внешнее давление считаем отсутствующим. Осевое усилие равно
N = ла^р. (ау~~ цилиндрическая?)
Напряжение в пределах упругости материала опеределяем по формулам (36), (37) и (40):
4	4	г.
a	I а о р
0Г9==Т^7/’ + ’77^’	(44)
Л
=	<45)
о — а
Распределение напряжений по толщине
показано на рис. 14.7, б. Наиболее
б
Рис. 14.7. Прочностная модель цилиндрической части сосуда высокого давления
напряженными являются точки внутренней поверхности (точки А), в которых (при ау а) полагая ау = а?
Ъ2 + а2	а2р
Ог---Р, o6~b2_a2Pi bz_ar
(46)
47. ПРОЧНОСТНЫЕ МОДЕЛИ ТОЛСТОСТЕННЫХ ТРУБ
475
Модель статической прочности примем в виде условия прочности Мора Оэкв == 01 — х Оз = 06,	(47)
где % — Oblo^, оь — предел прочности материала.
В рассматриваемом случае Oi == ое, о3 = Or. Модель статической прочности имеет вид (,2 ,	2	\
b —I— л	\
72----5 + X Р =	(48)
Ь — а	I
В запас прочности можно-считать х = 1-
Модель малоцикловоп прочности используется при повторении циклов нагружений.
На основании условия Мэнсона (разд. 17) имеем е = L fin -JL- Г’в№°’в4- 1,75 ^ь~ q?n) jV-0’12, °	2 k 1 —ф/	Е
где еа — амплитуда переменных деформаций, -ф — поперечное сужение материала, от — среднее напряжение, N — число циклов до разрушения.
Цикл нагружения соответствует возрастанию давления от 0 до р. При сложном деформированном состоянии под 8* понимается амплитуда эквивалентной деформации
1 еэква — 2	(49)
где 8i —• интенсивность деформаций в опасной'точке при действии давления р: множитель 1/2 связан с тем, что нагружение от 0 до р можно представить в виде постоянного нагружения давлением р/2 и переменного нагружения давлением с амплитудой р/2.
Интенсивность напряжений
CTi =	“ °е)2 + <сте “ ст02 +	- ffr)2
с учетом соотношений (46) равна
где для краткости обозначено п == а/Ь.
В окончательном виде имеем Ь2
<Ti = V3-2----jp.	(50)
о — а
Интенсивность деформаций в упругой области равна 2(1+и) 2 (1 + И) Ь2 Р
8i- ЗЕ ai “ уз Ь2_аг Е’	<51>
Модель малоцикловой прочности с учетом соотношений (49) — (51) принимает следующий вид:
-L. 1 + и У . р _ 1 f Щ -1-)О,Уо,в  ! 75 fo ~	дг-O.U
УЗ Е ?-агР~ 2V 1-ф/ N +1,75 Е	N . ’
ГДе	о	,
1	1 »2+«
~ 2 ^9	2 ъ2 — а2 Р'
476
ГЛ. 14. ЦИЛИНДРЫ И диски
Условие (52) связывает размеры цилиндра, величину циклически действующего давления, характеристики материала с числом циклов до разрушения. Допускаемое число циклов нагружения в рабочих условиях
[N] = N/п», где п*г — запас по числу циклов.
Учитывая рассеяние результатов в силу отклонений по свойствам материала, технологическим и другим факторам, принимают
п х — 3—5.
Прочностная модель прессового соединения. Прессовое соединение (рис. 14.8) получается за счет сборки с натягом двух сопрягаемых деталей (например, кольца шарикоподшипника и йала). За счет сил упругости па поверхности сопряжения создается давление ра.
Рис. 14.8. Прочностная модель прессового соединения
При построении прочностной модели требуется найти условия, при которых в соединении не возникнут пластические деформации. Давление ра вызовет радиальное перемещение охватывающей детали, которое может быть определено по формуле (38). ПЬлагая ра == р и ръ = 0, получим
м = ((• -	+ (‘ + ».) jAr) т - (^7 + ) Т- (53)
\	о —а	о —а / ^2 \о —а /	2
Радиальное перемещение внутреннего сплошного цилиндра (ръ = р) . равно
1	(1- Ml)
“1 = Ё~ (ffe - ’Ч0’-)а = - —Ё--ар'	(54>
так как ое == <5г = — р (формула (39)).
• Разность радиальных перемещений должна быть равна радиальному натягу (по условиям, неразрывности деформаций натяг «компенсируется» перемещениями) :
(а) — и± (а) = -75г Д.	(55)
Учитывая равенства (53) и (54), находим
1__Д ____________1__________.
2 а ( 1 b2 + a*^ \ , 1 ~ Рч
(56)
47. ПРОЧНОСТНЫЕ МОДЕЛИ ТОЛСТОСТЕННЫХ ТРУБ
477
Если наружный диаметр втулки очень велик (отверстие в листе), то при 1 А 1
Р~ 2 а 1 + ц2 1-И1	(57>
Е2 + Е1 наибольшее напряжение по втулке будет на поверхности радиусом а
»2 ।	2
о а ог2г (а) = — р, а20 (а) = а2 Р-
Интенсивность напряжений равна
ai2 у а2г а2га20 4" а2б Р у 1 4“ “о 4~ I 2 1 Р 72	2 *
» Ь—а \Ъ —а ) Ь—а
Напряжения в цилиндре (валике) равны
(Jir ~ Ою == рч 6ц~Р>
Модель прочностной надежности прессового соединения имеет вид
Д/Зд4 + <г4	1	Д агТ
b2-a2 ilf + J \
е2 + е2
__________1____:_____z59\
1 ft2 j_ а2	1-И12а^пг’	(&9)
Г ,2	2 4-Н24- £
Ь — a z
где air, Пгт — пределы текучести материала втулки и валика; пт — запас п(/ пределу текучести (обычно пт 1,3).
Условие (58) обеспечивает отсутствие пластических деформаций во втулке, условие (59) — в валике. Предполагается, что величина Д соответствует «эффективному» натягу, учитывающему «сминание» гребешков на поверхности (обычно Д = 0,6—О,9До, где До — номинальный натяг).
Температурные напряжения и, напряжения от центробежных сил. Рассматривается цилиндр с постоянными параметрами упругости. При неравномерном нагреве и вращении дифференциальное уравнение для радиального смещения будет неоднородным (уравнение (23)).
Интегрируя уравнение (23) от а до г, получим
г
Х^г) = р(Г1)^1 + 2С1>	(60}
о
где 2Ci — произвольная постоянная (множитель 2 взят для удобства дальнейших записей). Перенося г в правую часть равенства; повторяя операцию интегрирования, находим
г ri
“=	+ Cj + -^.	(61}
а о
478
ГЛ. 14. ЦИЛИНДРЫ И диски
Формула (61) выражает общее решение уравнения (23) при произвольной правой части. Далее составляются выражения для ог и <j0 и находятся постоянные С{ и С2 из краевых условий для радиального напряжения:
oz(a) = 0, ог(&) = 0.	(62)
Решения для случая, когда на цилиндрических поверхностях действуют давления, были получены ранее.
Покажем более подробно последовательность решения для температурных напряжений, при которых
/(г) = (1 + Ио)4(аоЛ-	(63)
В этом случае из равенства (61) получаем
U = (1 + ц0) -у J гга.0Т drx + С хг + -у-,	(64)
причем значения, соответствующие нижнему пределу интегрирования, включаются в' произвольные постоянные.
Дифференцируя равенство (64), получаем г
= — (1 + Но)А ^r\a.0Tdi\ + (1 + |л0)а0Г + Сх— (65) а
Подставляя значения du	и
£о = — dr ’	и г
в равенства	(15) и (16), находим
п -	(1 + ,и0) Сх -	С2 - (1 - но) F (г) 1 +	lie, (66) Г	J	F0
Е “	1 ~ U	Е* Щ —	2 (1 + Но) +	2 ^2 + (1 Но) (F (г) ао?) +	це, 1-HoL	r	J 1 И0	
	• (67)
где	——
F = Z У Г1а°т dr^ а
е — деформация вдоль оси z, постоянная для всех точек сечения. Определяя произвольные постоянные из условия (62), получаем
,2	г	2,2
Сх =.{1 - Но) F (Ъ)	2 - (Хе, С2 = (1 + Но) F (Ь).-р-2,	(69)
о — а	о — а
ь
где F(b) = ь
J r^T drx.
47. ПРОЧНОСТНЫЕ МОДЕЛИ ТОЛСТОСТЕННЫХ ТРУБ
479
Учитывая полученные значения Ci и С2, приходим к следующим формулам для радиального и окружного температурных на-
пряжений:
ог = Eq
пе = £0
2	/	*> \
1-4	>
о — а \ г f ,2	/	2 \
1 + А- +F(r)-a0T’ о — а \	• г /
(70)
(71)
Для определения осевого напряжения oz имеется формула (10)\ которую запишем так:
о2 = Ее + ц(ог + ое) — (1 — у^Е^Т.	(72)
Неизвестную величину е определяем из условия
L
j* (3zdF = 2л J ozr dr = 0.	(73)
F	a
В результате находим
ах = Ео(т(&)_^_2_аоА	(74)
\ о —ча	/
При использовании формул (70), (71) и (74) следует помнить, что
^0 = :	2» сс0 = а (1 + jx).
1 ~ Н
Подобным образом, полагая / (г) = — pft)2r,
можно получить формулы для напряжений в быстровращающемся цилиндре.	-
Анализ распределения температурных напряжений. Сначала установим, что в равномерно нагретом, свободном от закрепления цилиндре температурные напряжения отсутствуют. В рассматриваемом случае
a0(r)T(r) = const = А,
г
р w=4- f raoy *=4-а G - 4Y
г J	\ г /
а
Подставляя значение F(r) в равенства (70), (71) и (74), находим
°г = £0
ае = £0
°г = £о
что и требовалось доказать.
480
ГЛ. 14. ЦИЛИНДРЫ И диски
Получим из соотношений (70), (71) и (74) формулы для температурных напряжений па внутренней (г = а) и на внешней (г = Ь) поверхностях ци-линдра: при г = а
(ni2	\
F(b)———_—a. (а) Г (а) ;	(75)
о — а	/
при г = Ь
Or(b) = Q, а0(Ь) = аг(6)=Яо[/’(г>)_2^_-ао(&)Т(Ь)|.	(76)
*\ b — а*	)
Отметим, что окружные и осевые температурные напряжения на граничных цилиндрических поверхностях одинаковы. Для выяснения «физического смысла» формул (75) и (76) определим «среднюю» температуру, точнее, температурную деформацию цилиндра
Т(Ь)
Т(а)
Рис. 14.9. Распределение, температурных напряжений в цилиндре .
. j aQT dF = F
ь
С учетом последнего соотношения формулы (75) и (76) представим так: <т9(а) = аг(«) = Ео[(аоТуе9 — а0(а)Г(а)], а,(&) = Ol(6) =£0[(а0Г)ор-а0(&)Г(&)].
Если периферия диска нагрета больше (температура возрастает вместе с радиусом) (рис. 14.9, а), то во внешних "областях температурные напряжения будут сжимающими.
Типичное распределение температурных напряжений показано на рис. 14.9, б. Отметим, что температурные напряжения пропорциональны модулю упругости и коэффициенту линейного расширения. **
I
а	. б 
Рис. 14.10. Распределение.температурных напряжений по длине цилиндра: а — цилиндр с абсолютно жесткими шайбами; б — цилиндр со свободными торцами
Замечания. 1. Температурные напряжения определяются температурной деформацией:
8Т — аТ.
Так как коэффициент линейного расширения а заметно зависит от температуры, то более правильно говорить не о распределении температур, а о распределении температурных деформаций.
47. ПРОЧНОСТНЫЕ МОДЕЛИ ТОЛСТОСТЕННЫХ ТРУБ
481
2. Полученное решение предполагает равномерное распределение температурных напряжений по длине цилиндра. Это осуществляется, если к торцам цилиндра (рис. 14.10) припаяны абсолютно жесткие шайбы. При свободных торцах ог = 0 и полученное решение справедливо па некотором удалении от торцов.
Цилиндр с переменными параметрами упругости. Необходимость рассмотрения подобной задачи связана с рядом ее приложений: учетом влияния температуры на величину модуля упругости, расчетом слоистых цилиндров, расчетом в упругопластической области методом переменных параметров упругости.
Составим систему дифференциальных уравнений первого порядка относительно двух неизвестных функций ог(г) и и (г). Первое уравнение получается из соотношения (15):
4г = -тт2 - V и + (1 + <аГ - н*).	(77)
Второе уравнение возникает в силу зависимости (19):
^ar	i Е (d,u и\ 2	/7О.
_	........... __-----— р(о2г.	(78)
dr г 1 4-	\ dr г j k	4 '
Используя соотношение (77), представим уравнение (78) в таком виде:
5 = — 1—«г + и — (а0Т — це) — р<о2г. (79)
В матричной форме система уравнений (79) и (77) имеет вид {П' = [А] {П + {fT} + {fe} + {/J,	(80)
где	.
Элементы матрицы [А] равны
Векторы нагрузки
( Е^т '
{fr} =
Ч(1 + н0)аГ
е} = е j г
{м=<4т}-
Краевые условия при интегрировании уравнений . (80j имеют вид Ог(а)=огв, 0г(6) = 0гь,
где 0га и Ort —• заданные радиальные напряжения (в частности, нулевые) при г = а и г = &.
31 и. А. Биргер, Р. Р. Мавлютов
482
ГЛ. 14. ЦИЛИНДРЫ и диски
Величина е определяется из условия
ъ
[ о2 dF = 2л j* огг dr = /V,
F	а
где N — заданное осевое усилие, действующее на цилиндр.
48. Прочностные модели дисков
Вводные замечания, основные предположения. На рис. 14.11 приведен ротор авиационного газотурбинного двигателя, наиболее ответственными элементами которого являются диски. Окружная скорость составляет 400 м/с и более. Разрушение дисков несет катастрофические последствия. Обеспечение надежности дисков составляет одну из основных проблем проектирования, производства и эксплуатации газотурбинных двигателей, паровых и газовых турбин, ультрацентрифуг и т. д. Наибольшее практическое применение получило
Рис. 1411. Ротор авиационного газотурбинного двигателя (макет с разрезом)
представление диска как тонкой круглой пластинки переменной толщины (рис. 1412). При инженерной оценке надежности диска используются два основных предположения.
1. Напряженное состояние в диске двухосное. В диске действуют радиальные и окружные напряжения; напряжение а2 считается отсутствующим, т. е. напряженное состояние предполагается плоским.
2. Напряжения постоянны по толщине диска h(г).
Оба эти предположения оправдываются для тонких дисков, обладающих -плоскостью симметрии. Предполагается, что центробежные силы и температурное поле симметричны относительно оси вращения; рассматривается растяжение диска в его срединной плоскости.
48. ПРОЧНОСТНЫЕ МОДЕЛИ ДИСКОВ
483
Замечание. В реальных дисках действуют поперечные нагрузки вследствие разности давления среды, неравномерный нагрев по толщине и другие факторы, вызывающие деформацию изгиба. Они рассматриваются в следующей главе. В большинстве случаев надежность диска связана с его растяжением центробежными усилиями и неравномерным нагревом по радиусу.
Рпс. 14.12. Конструктивная схема диска (а), радиальные ог и окружные Ое напряжения (б)
Напряжения, условия равновесия. В диске возникают (рис. 14.12) радиальные ог(г) и окружные о9(г) напряжения и соответствующие усилия
Nr = orh(r),	(81):
NQ = aQh(r).	(82)
Рассмотрим равновесие элемента диска, образованного двумя ци-
линдрическими сечениями радиусами г и г + dr и двумя меридиональными сечениями, образующими угол-^dQ (рис. 14.1*3). Касательные напряжения на гранях элемента отсутствуют. Если на грани элемента, лежащей на цилиндрической поверхности ра- / диуса г, действует (на единицу длины) радиальное усилие 2Vr, то на противоположной грани его величина будет zVr + Н- dNr. Усилие NQ одинаково по двум меридиональным граням элемента диска. Составим проекцию внешних сил, приложенных к элементу диска, на радиальное направление:
Рис. 14.13. _ Равновесие элемента диска
—Nrr dQ+ ^Nr + dr] (г + dr) dQ — 2Nq sin ~ dr + ptfrhr dQ.dr = 0.
Члены первого порядка малости взаимно уничтожаются. Пре-< небрегая членами высшего порядка малости, находим
dN
Nr drdQ + dr г dQ — Nq dQ dr + рщ2г2Л dQ dr = 0,
31*
484
ГЛ. 14. ЦИЛИНДРЫ и диски
или
— + 4	- АГе) + (М = 0.	(83)
Уравнение (83) представляет уравнение равновесия элемента диска.
Деформации и соотношения упругости. Вследствие осевой симметрии точки диска получают радиальные смещения и (г), одинаковые по толщине диска. Радиальная и окружная деформации {см. разд. 47) равны
^ = -57-	<84>
= ' <85)
Соотношения упругости представим так:
ег = 4“ (рг — цое) +	+ «г,	(86)
е0 = -тг (од — |.iar) + аТ + Ё0>,'	(87)'
где Е, ц —модуль упругости и коэффициент Пуассона; аТ — температурная деформация; е°, Eq— дополнительная деформация, которая может рассматриваться как остаточная деформация, деформация ползучести или деформация другой природы, не связанной с упругостью материала.
Из уравнений (86) и (87) получаем
Or = -^-2 (8г + Н80) —	— 0г,	(88)
1 — р	1 — р,	'	'
ое= ~~2(ев + |Л8г) —	— 4,	(89)
’	1 — р	1 — р	4	7
где «дополнительные напряжения»
О? = 4—3(8г° + н4),	'	(90)
1 — И
о°е = -Ц(е9в + И8°г)	(91)
1 |А
представляют условные напряжения, которые соответствуют дополнительным деформациям в упругом теле.
Краевые условия. Краевые условия в большинстве случаев задаются для радиальных напряжений. На внешнем конгуре диска
Ог(Ь) = ог6,	(92):
где Огъ — напряжения от центробежных сил лопаток и замковых частей диска. На внутреннем контуре диска чаще всего
Ога = 0.	(93)
48. ПРОЧНОСТНЫЕ МОДЕЛИ ДИСКОВ
485
В случаях, когда применяется прессовая посадка диска па вал, аг(^)= —Р»	(94)
где р — давление на поверхности г = а в рабочих условиях.
Дифференциальное уравнение для диска постоянной толщины с постоянными параметрами упругости. Для диска постоянной толщины h = const уравнение равновесия (83) будет таким:
cfo- i
77 + -у (о-- - °о) + Р«г = 0.	(95)
Из соотношений упругости (88) и (89) при отсутствии дополнительных напряжений находим
Е (du . и \ ЕаТ
Q = ---------Ц --- — ----- (96)
1 — р2 \	Г у 1 — р г	'	'
Е (и , du\ ЕаТ
=----------Ь ц — | — ---.	(97)
°	1 __ р2 \ г *ar )	1 — р	'	'
Внося зависимости (96) и (97) в уравнение (95), получим
2 + = (98)
9 UI
где
/ (Г) = - Р<о2г + (1 + и) 4 <аТ)‘	(")
Уравнение (98) совпадает с уравнением для цилиндра (соотношение (21)), если значения Ео, Цо, а0 заменить на £, ц, а.
Замечание. Полученный результат не является случайным, так как задачи об осесимметричном напряженном состоянии цилиндра (плоская деформация) и диска (плоское напряженное состояние) являются вариантами одной и той же плоской задачи.
Напряжения в диске постоянной толщины. Как было показано ранее (разд. 47), общий интеграл уравнения (98) можно записать так:
Г г1
u(r) = C1r + C2-|- +(100)
а а
Учитывая равенство (99), находим
J / (r2) dr3 = - L-/ pa? А (г* - а*) + (1 + н) (аТ (гх) - ааТа), (101)
486
ГЛ. 14. ЦИЛИНДРЫ и диски
if f\z ч л	А г3 , а4 а2г\ ,
— J rij/(r2)dr2 =----~	+	+
а а г
1 С	( 1 а2 \
+ (1 + Н) Т )r,aT (rx) dr, - (1 + р) ааТа [A r _ ±_J.	(101)
а
Подставляя (101) в равенство (100) и включая постоянные величины, относящиеся к г = а, в произвольные постоянные, получим г
и (г) = С* г + С*± - ро?г3 + (1 + р) A J r,aT (rx) dr„ (102) а
где С*, С* — новые значения произвольных постоянных, что для дальнейшего несущественно. Дифференцируя равенство (102), находим
а. (г) = с; - с; а _ рО2Г2 _ а+а f Г1аГ (Г1) dri + и>Г	у*	у </
+ (1 + р)аГ. (ЮЗ)
Внося значения и и du/dr в соотношения упругости, будем иметь Стг = _А_ (1 + и) С* - АА с*\ - р<02г2 АА.) _ EF (г),	(104)
а0 =	[(1 + И) СГ +	^‘] - Р<А2 (-ЦА + Е (F (г) - аТ),
(105) где
Г
F (г) = A J г,аТ (г,) dr,.	(106)
а
Из краевых условий для радиальных ^напряжений Or (^) Ога» 6г (Ь) Orb
находим значения произвольных постоянных: c*i = f 1 а2 (агЬ&2 — агаа2) +
2	2а2
+	(3 + н) (1 - Р) (Ь2 + а2) + (1 - и) АА_2 F (6), (107)
ол	b — а
2 2	2
С2* ==Ц^АА(аг6-ага) + А.(3 + р)(1 + р)а2&2 + 2 2
+ (1 + Н)/\^(Ь). (108) о — а
48. ПРОЧНОСТНЫЕ МОДЕЛИ ДИСКОВ
487
Если теперь подставить значения С* и С* в равенства (104) и (105), получим следующие важные формулы:
,2	/	2 \	2	/	>2 \
О [л	I	®	| л С? I .	.	/<
Or = Orb ---------5 1------- — (Уга~--------г, 1-------- + Ог» + ОгТ, (109)
Ь" — а \ tj b" — (Г \ г" /
,2	/	2\	2	/	, 2 \
О | л , CL I	(I I A t О \	.	•	/АЛ ГХ\
Оу = Orb “2-------7 1 4-----7 — 0>а ----------7 I 1 4--Г I +	+ ^97» (ИО)
b — а \ г /	6“ — а\ г /
где напряжения от центробежных сил равны
'о .	/	'	2,2	\
О -f- Ц о/то. •>	& О	о I
Оги =	р<0“ \Ъ- + а--т,-HI,
°	\	rJ /
3 + И <> (о .	1 4“ 31Х
Ote = par \b* + а- + — - Н
Температурные напряжения составляют
СТгГ = £р(&)-^-3(1-4]-Лг) , Z? — а \	7 /	_	.
,2	/	2 \
(JOT = Е F (b)	1 + М + F (г) -аТ
(111)
(112)
(ИЗ)
(114)
где F(r) определяется соотношением (106).
Первые группы членов в равенствах (109) и (110) дают напряжения от контурных нагрузок. Сопоставление с формулами (36) и (37) показывает, что напряжения от контурных нагрузок в диске постоянной толщины и цилиндре одинаковы. При сравнении температурных напряжений следует учесть различие в зависимостях (65) и (106) (а0 = а(1 4-ц.)). Тогда приходим к выводу, что при одинаковом распределении температурной деформации вдоль радиуса в цилиндре температурные напряжения в 1 / (1 — р,) раз больше, чем в диске; кроме того, в цилиндре имеются температурные напряжения Пгт, которые в диске отсутствуют.
Перемещения в диске находятся из соотношения
и = ~(о0—fiar) + гаТ,	(115)
где значения Ое и ог определяются из формул (109) и (110) .
Рассмотрим теперь диск без центрального отверстия (сплошной диск). В центре диска г = 0 содержится особая точка, в которой в силу осевой симметрии
Иго = Иво.	(116)
Дифференциальное уравнение (102) остается справедливым, но в его решении (100) следует считать <72 = 0/так как иначе в центре
488
ГЛ. 14. ЦИЛИНДРЫ и диски
диска перемещение не обращается в нуль. Решение уравнения (98) следует принять таким:
г Г1
u(r) = cir+ yjri	(117)
О о
Несмотря на наличие множителя 1/г, второй член равен нулю при г = 0. Учитывая значение /(г), получим
г
и (г) = с{г — pco2r3 + (1 + Ji) I. J гуО-Т (rj drv.
О
Продолжая выкладки, найдем напряжения в сплошном диске:
Vr = о% +	Р®2 (Ь2 - Г2) + Е (F (b) - F (г)),	(118)
а0 = агЬ + Ц^р®26>2-ШМ + E(F{b) + F{r)-aT), (119) где
т
F{r) = ^r&T^drv	(120)
о
В центре сплошного диска
аг (0) = а0 (0) = ог6 + рсо262 + Е (f (b) -1 аТ (0)), (121) так как г	г
F (0) = lim 4 f rjaT (г,) dr1 = aT (0) lim ~ f rx di\ = -i- aT (0). r-»o r 0	r^orJ
Распределение напряжений в диске постоянной толщины. Распределение напряжений при действии контурной нагрузки и центробежных сил представлено на рис. 14.14 и 14.15; значения напряжений на внешнем и внутреннем контурах вытекают из формул (109), (110) и (118), (119).
Из рис. 14.14 видно, что возле отверстия окружные напряжения существенно повышаются. При малом центральном отверстии величина окружного напряжения становится приблизительно в 2 раза больше, чем. в сплошном диске. В циклически нагруженных дисках отверстия нежелательны, так как концентрация напряжений возле отверстий снижает циклическую долговечность.
Определим температурные напряжения в сплошном диске, считая температуру возрастающей по степенному закону (п > 0):
Г(г) = Г(0) + ДТ(г/Ь)я,	(122)
где ДТ ® Т(Ъ) —Т(0) — перепад температуры между ободом и центром диска; коэффициент линейного расширения а предполагаем постоянным.
Из соотношения (120) находим
1	аДТ г71
/(г)=-2 аГ(0) + ^г2-.
48. ПРОЧНОСТНЫЕ МОДЕЛИ ДИСКОВ
489
Z| ___________д
Рис. 14.14. Распределение напряжений в диске с отверстием от контурной нагрузки и центробежных сил
Рис. 14.15. Распределение напряжений в сплошном диске от кон- -турной нагрузки и центробежных сил
Рис. 14.16. Распределение температурных напряжений в сплошном диске
490
ГЛ. 14. ЦИЛИНДРЫ И диски
Формулы (118) и (119) дают следующие значения температурных напряжений:
агТ —
Еа\Т п 4“ 2
ает =
ЕаЛТ д 4"
1 —(« + !).£_ Ьп
Как и следовало ожидать, постоянная температура не вызывает в диске температурных напряжений. ГРри возрастании температуры по радиусу в ободе возникает сжимающее напряжение
п а9Г (0) = ЕаЛТ п 2’
Распределение температурных напряжений в сплошном диске показано на рис. 14.16.
Напряжения в диске переменной толщины с переменными параметрами упругости. В общем случае расчет дисков на растяжение проводится приближенными методами. Важность проблемы прочности дисков вызвала большое число исследований, и в настоящее время известно свыше сорока различных методов расчета. Основные методы можно подразделить на следующие группы:
1)	методы разбиения на участки с последующим их сопряжением:
2)	методы конечных разностей;
3)	методы интегральных уравнений:
4)	методы численного интегрирования.
Указанные методы типичны и для других сложных задач инженерного дела. В первой группе диск разбивается на участки более простых профилей, для которых могут быть использованы точные решения (например, на участки дисков постоянной толщины и т. п.). Во второй группе дифференциальные уравнения заменяются конечно-разностными. Методы интегральных уравнений основывались на иххчисленном решении с помощью последовательных приближений. Наконец, численные методы используют прямое интегрирование системы дифференциальных или интегральных уравнений первого порядка. Эти методы, получившие широкое применение в связи с расчетами на ЭВМ, излагаются ниже. Рассматривается диск с переменными параметрами упругости и дополнительными деформациями, что дает возможность учета деформаций пластичности и ползучести. Составим систему дифференциальных уравнений первого порядка относительно радиального усилия Nr(r) и радиального перемещения и (г). Эти переменные не претерпевают разрывов даже при скачкообразном изменении параметров диска (толщины, модуля упругости, температуры и т. п.).
Одно из уравнений непосредственно следует из соотношения упругости (88), которое представим в виде
1-Н
। .. и \	EhaT дт°
dr + Н-1  ------2Vr
1 —ц
где Nr — orh. Nr — <Jrh — радиальные усилия.
(123)
48. ПРОЧНОСТНЫЕ МОДЕЛИ ДИСКОВ
491
Из равенства (123) вытекает d И 1 II n г	i / A t \ ГП I 1 М* л ГО	/ А П / v
^ = -ёГ-^-^7 + <1 + .ц)а? + -ЁГ-уУ-	<124>
Далее используем уравнение равновесия (83): d.Vr 1
= - у Wr - МО - P<o2rft.	(125)
Из соотношений упругости (88) и (89) имеем
дгг_ yV9 = -А-,(1 - И) № -	- №г +• П
1 — р	\йг г J
и потому
7 = - -Г—(1 - и) & - - ) - №r +	- раН.
dr	г [j__р/ г 7 dr г J	j *
Внося значение du/dr из уравнения (124), получаем
Л = — i-^Nr + ^u — — аТ — рМ + — Nr — -№в. (126) dr	г	г2 г * k	г	г v '
Зависимости (126) и (124) образуют систему дифференциальных уравнений
{У}' = [Л ] {У} + {/J + {/т} + {/0},	(127)
где	.
Z ДГ \	Z	2 Л •	(	m 1
{П= Л {Ы = Т - {М = Г“ •	<128)
1 “ J - I и J	1(1 + И) аТ)
Вектор дополнительной нагрузки
р^о__1л7 г г г н
{/о}	) 4  п 2
1
< Eh г
(129)
Элементы матрицы равны
д_____1 — Ц j ______Eh j _ 1 И д _____________
"11	г »	"12	^2’ . ^21	»	"22	г •
Уравнение (127) решают по методу начальных параметров, представляя решение в виде
{П = NratYj + ua{Y2} + {У*}, где {У J — решение однородного уравнения
{yj^HKyj при начальном значении
(130)
492
ГЛ. 14. ЦИЛИНДРЫ и диски
Вектор {У2} соответствует решению однородного уравнения при начальных условиях
{У2(а)) = {5}-
Вектор {У*} представляет решение неоднородного уравнения (127) при начальном значении
Неизвестные значения начальных параметров определяются из краевых условий. Для дисков с отверстием величина Nra обычно известна, и тогда векторы {УД п {У*} объединяются: решение принимается в форме
{У} = {У1‘} + иа{У2},	(131)
где {У*} является решением уравнения (127) при начальном условии
{V 1
О Р
Для сплошных дисков для устранения числовых погрешностей краевое условие удобно ставить на некотором малом радиусе а (обычно а = (0,05—0,1) Ь).
Тогда, полагая для сплошного диска
^r(a) = /Ve(a),	(132)
получим из соотношений упругости
Nra + ааТа + 4,	(133)
где нижний индекс а указывает, что значение параметра относится к радиусу а. Зависимости между 2Vre и иа возникают и при упругом закреплении дисков.
Модели общей статической и длительной прочности диска. Модель общей статической и длительной прочности содержит условие
КЬ^^2^[КЬ],	(134)
"max
где Лразр — частота вращения, при которой произойдет разрушение диска с учетом. температуры и длительности работы; птлх — максимальная частота вращения диска в рабочих условиях; Кь — запас прочности по разрушающей частоте вращения (разрушающим оборотам); — допустимое значение запаса.
Разрушение может произойти по диаметральному (меридиональному) или по цилиндрическому сечениям, и соответственно различают запасы.
48. ПРОЧНОСТНЫЕ МОДЕЛИ ДИСКОВ
493
При определении запаса по диаметральному сечению исходят из предположения, что в момент разрушения окружное напряжение
Ое(г) = 0дл(г),	(135)
где Одл (г) — предел длительной прочности, соответствующий температуре на радиусе г и заданной длительности работы.
Рассмотрим равновесие диска непосредственно в момент разрушения. Радиальное напряжение на внешнем радиусе диска будет равно
Orb == Orb'-;-1	Цоо)
^max
где Orb ” радиальное напряжение на ободе диска при максимальной угловой скорости (или частоте вращенпя). Определим равнодействующую центробежных сил, приложенных к массе диска. На элемент диска действует центробежная сила
* dC = рсоразрг h г dB dr = р(0разрГ2 dF dQ, где dF = h dr — элемент площади диаметрального сечения. Равнодействующая центробежных сил, приложенных к половине диска, равна ЛЬ	Ь	Л
С = J j dC sin 0 = р®разр J г2 dF • J sin 0 d0, О a	a	о
ИЛИ
С = 2p^a3p J r2 dF = 2pa>V,	(137)
F b
где J = J r2h dr — момент инерции половины диаметрального Ce-fl
чения диска относительно оси вращения. Проектируя все силы на вертикальное направление, получим	-ч
со2	С
2огъ bhb +. 2р<4азР/ == 2 аялЛ dr.	(138)
^max	> а
Напряжениями на внутреннем, контуре г —а пренебрегают (свободное отверстие). Если даже в рабочих условиях по внутреннему контуру была запрессовка, то к моменту разрушения давление запрессовки исчезает.
Из равенства (138) находим запас по разрушающей частоте вращения по диаметральному сечению (рис. 14.17):

Юразр ютах
Ъ
J amhdr а_________
arbbhb + РЫ2/
(139)
495
48. ПРОЧНОСТНЫЕ МОДЕЛИ ДИСКОВ
Из условия (140) получаем
/С	( zd \
~	1/	] адлл dr + адл (гц) гц\ ( 1 ~ 2лги )
Ч =	|/ i_______________________ <141>
“аХ Г	агЛ + р^ц
Расчет проводят для различных радиусов гц и для оценки прочности учитывается минимальное значение К^. Обычно это значение соответствует подободной части диска. В удовлетворительно работающих дисках
[Л^] = 1,4; ..1,5.
Замечания. 1. Допускаемое значение	так как диаметраль-
ное разрушение диска более опасно по своим последствиям.
2. Запас Къ определяют для гц > а, иначе отверстие предполагается «несущим», что неправильно. При г = а следует считать Кь% =
3. В общей модели статической прочности температурные напряжения не учитываются. Предполагается, что к моменту разрушения идут процессы пластичности и ползучести, приводящие к релаксации температурных напряжений. Влияние температуры сказывается на значениях адл(г).
Эквивалентный запас по разрушающей частоте вращения. Если диск работает на различных режимах с температурами Т{ с длительностью то определяется эквивалентный запас по разрушающей частоте вращения по принципу линейного суммирования повреждений (гл. 13):
(142)
где 7пэкв = если, как обычно, режим 1 относится к режиму наименьшего запаса прочности. В равенстве (142) входят во второй степени, так как запас по частоте вращения соответствует квадрату запаса по напряжениям.
Модели локальной статической и длительной прочности диска» Эти модели служат дополнительными критериями прочностной надежности диска, оценивая местные запасы прочности гг адл 0 m а и экв max
(143)
где Сдл(7\ i)’—предел длительной прочности при температуре Т и длительности нагружения i; оЭКв max — наибольшее эквивалентное напряжение.
В практических расчетах часто принимают
Цэкв max = O'max,
494
ГЛ. 14. ЦИЛИНДРЫ и диски
При кратковременном разрушении или при работе в условиях нормальной температуры величина длительной прочности оял заменяет
Рис. 14.17. Определение запаса по диа-
ся пределом прочности о6. Из формулы (139) следует, что для увеличения прочности диска надо увеличивать толщину ближе к центру диска (в области ступицы), так как при этом момент инерции возрастает медленнее, чем площадь сечения. В достаточно надежных дисках
Кы = 1,5;	1,6.
Перейдем к определению запаса по цилиндрическому сечению. В этом случае разрушение происходит по цилиндрической поверхности ра-
метральному сечению
14.18). Считаем для общности, что стий диаметром d.
диусОхМ Гц и по участкам диаметрального сечения (рис. на радиусе гц имеется z отвер-
гло. 14.18. Определение запаса по цилиндрическому сечению
Рассматривая равновесие сил в вертикальном направлении, находим
о2	С
2&гъ ”7—' bhb + 2р(Оразр«^ ц == 2 j a^hdr + одл (г ц) гцЛц fl	2лг~ / ’ (^0)
^тах	г	\	ц /
b
где /ц = J r2h dr.
ru 
49G
ГЛ. 14. ЦИЛИНДРЫ И диски
где Стах—наибольшее напряжение (радиальное или окружное) па данном радиусе.
Значение Кт определяется для сечения, в котором Кт минимально. При работе диска па различных режимах определяется эквивалентный запас прочности. Обычно принимают
[А\]>1Д
Модели малоцикловой прочности диска. Модель малоцикловой прочности диска содержит условие
(144)
где ТУрдзр — число циклов нагружения до разрушения диска, N — число циклов нагружения в процессе эксплуатации, KN — запас по циклической долговечности.
Для удовлетворительно работающих дисков расчетный запас долговечности равен [/G] == 5. При экспериментальном определении запаса долговечности в составе изделия = 3. Минимальные значения KN получаются в местах концентрации напряжений.
ГЛАВА 15
БАЛКИ НА УПРУГОМ ОСНОВАНИИ, КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
49. Изгиб балок на упругом основании
Вводные замечания. Если балка (стержень} опирается на ряд близко расположенных упругих опор, то можно считать, что балка лежит на сплошном упругом основании (рис. 15.1). Такая расчетная модель применяется во многих случаях. На рис. 15.2 показана схема рельсового пути, причем как шпалы,
Рис. 15.1. Расчетная модель балки на упругом основании
Рис. 15.2. Балка на упругом основании (схема рельсового пути на шпалах)
так и рельсы могут приближенно рассматриваться как балки на упругом основании (многие видели значительную осадку рельс при прохождении поезда). Если прогиб балки v (z), то со стороны упругого основания возникает распределенная йагрузка
go(2) = —fcZ7(z),,	(1)
где к — коэффициент упругого основания.
Знак минус в формуле (1) имеет принципиальное значение: возникающее усилие направлено в сторону, противоположную прогибу.
Г сила 1	I* сила
Размерность ?о~	. размерность
Рис. 15.3. Усилия, возникающие при общих прогибах корпуса судна
Еще один пример расчетной модели балки на упругом основании: приближенный расчет корпуса судна по стержневой теории. Длина современных танкеров достигает 200—300 м и более, размеры поперечного сечения можно 32 и. А. Биргер, Р. Р. Мавлютов
498
ГЛ. 15. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
считать малыми по сравнению с длиной. Это дает основания для применения модели стержня.
При прогибе v(z) (рис. 15.3) возникает дополнительное усилие (на единицу длины)
?o(z) = — '(b(z)v(z) = — k(z)v(z),	(2)
где у _ удельный вес жидкости, b(z) — поперечный размер по ватерлинии. Коэффициент упругого основания может изменяться по длине балки.
Дифференциальное уравнение изгиба балки на упругом основании. На элемент балки длиной dz (рис. 15.4) кроме распределенной нагрузки от внешних сил действует
распределенная нагрузка от упругого основания qQ.
Уравнение изгиба балки на упругом основании отличается от основного
уравнения изгиба стержня (разд. 34) только наличием дополнительного члена в правой части
Рис. 15.4. Условие равновесия элемента балки на
EJA^
упругом основании
d\ dz"
= Qy Wo =
= qy — к (z) v (z), (3)
— ( dz1 I
или в окончательной форме ]+k(z)v(z)^qy(z).	(4)
dz j
Для изгибающего момента и перерезывающей силы справедливы по
лученные ранее зависимости:
=	(5)
az
^CEJx[z)^\^-Qv(z).	(6)
az. \	dz 1
Замечания. 1. Распределенная нагрузка от упругого основания принимается равной
qQ(z) = — k(z)v(z)
и соответствует физической модели, -когда пружины (рис. 15.1) припаяны к балке. При положительном прогибе (v(z) > 0) усилие основания направлено вниз. Такие связи балки и основания называются двусторонними.
Во многих случаях упругая среда оказывает сопротивление, когда прогиб направлен в глубь среды (см. рис. 15.1) при и < 0, и не действует на балку при противоположном направлении прогиба (у > 0) (балка положена да пружины, балка на грунте и т. п.); тогда следует считать
, , ч (0,	v>°,
A(z’p)~pt(z), v<0.	'	№
Для односторонних связей (условие (7)) уравнение (4) оказывается нелинейным и решается методом последовательных приближений. В первом
49. ИЗГИБ БАЛОК ПА УПРУГОМ ОСНОВАНИИ
499
Рис. 15.5. Балка, лежащая на упругом полупространстве
приближении связи считаются двусторонними и определяются области, где v > 0. Во втором приближении в указанных областях полагают qQ — 0 и находят новые границы областей и т. д.
2. Упругое полупространство (упругая среда) лишь приближенно можно рассматривать как упругое основание (рис. 15.5). В равенстве (1) предполагается, что прогиб v(z) определяется усилием 7о(з) в том же сечении.
В упругом полупространстве прогиб v(z) зависит от распределений нагрузки во всех других сечениях
i о где 6(з, Z() —прогиб в сечении z от единичной силы в сечении Z| (функция влияния).
В рассматриваемом случае решение получается значительно более сложным и относится к контактным задачам.
3. Интересно отметить, что задача об изгибе балки на упругом основании имеет много общего с задачей осесимметричной деформации оболочек вращения. Роль «упругого основания».в оболочках играет реакция кольцевых слоев па радиальное перемещение.
Уравнения изгиба для балки постоянного сечения на упругом основании. Структура решения. В случае, когда EJx(z) = EJX и коэффициент упругого основания постоянен (fc(z) = &), уравнение изгиба (4) становится таким:
Решение уравнения (8) можно получить общими методами решения дифференциальных уравнений с постоянными коэффициентами, и оно имеет следующую структуру:
v(z) = CiVt (z) 4- C2vz (z) + C3vs (z) + C4v4 (z) + v* (z),	(9)
где Vi(z)—частные, линейно независимые решения однородного уравнения (8) при ^ = 0; v*(z) — частное решение неоднородного уравнения; С,произвольные постоянные. Однородное уравнение удобно записать в следующем виде:
^±l + 4^(z) = 0,	(10)
az
где '
(11)
Частное решение предполагается в виде
v(z) = Ce\	(12)
Подставляя его в уравнение (10), найдем
л4 + 4[}4 = 0.	'	(13).
32*
500
ГЛ. 15. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
Используя формулу Муавра для корней из комплексных чисел, найдем четыре корня уравнения (13):
X1 = ^(i + i),	=	X4 = -p(i + Q. (14)
Решение будет таким:
4 I г v(z) = Sc/i + y*(z).	(15)
i=l
Учитывая формулы Эйлера для тригонометрических и гиперболических функций
e±i₽z cos $z ± i sin [}z, e±₽z = ch $z ± sh pz,	(16)
можно представить решения (15) в различных формах, приспособленных для конкретных условий.
Длинные балки. Запишем решение (15) в следующем виде: v(z) = е~*г((\ cos pz + С2 sin pz) + e₽z(C3 cos $z + C4 sin pz) + p* (z). (17) Если балка является длинной (например, рельсовый путь), то величина еЭг может быть очень большой, и по условиям ограниченности прогиба следует положить С3 = 0, С4 = 0.
Решение для длинных балок будет таким:
z?(z) = Cie-^cos $z + C2e^z sin $z+ u* (z).	(18)
Непосредственным дифференцированием получаем полезные для дальнейшего формулы:
v’ (2) = — (cos Pz + sin Pz) + C$e~^z (cos Pz — sin Pz) + v*' (z), y"(z) = Cr2P2e_₽zsin₽z-C2.2p2e_pzcospz + v*" (z),	(19)
v'" (z) = C1-2P3e~₽z(cosPz—sin pz) + C2-2P3e“₽z(cos pz+sin |Jz) + y*w (z).
Рассмотрим действие сосредоточенного усилия на бесконечно длинную балку (рис. 15.6). Поместим начало коор-
У	динат в сечении, где приложена сила.
р	Краевые условия при z = 0 будут
такими:
Рис. 15.6. Действие сосредоточен- Таьскак перерезывающая сила ной силы на длинную балку на уп- у	р
ругом основании	Qy (0) = -у,
(20)
(21) в сече-
внешняя распределенная нагрузка qy(z) отсутствует, и потому v*(z) =0. Из соотношений (18) — (21) находим
-с1+с2 = о, 2р3(с1+с2) = -г£;
49. ИЗГИБ БАЛОК НА УПРУГОМ ОСНОВАНИИ
501
или
(\ = С, = - -JL-^3EJX
Теперь из соотношений (18) и (19) находим значение прогиба и изгибающего момента:
V = — /й2'с, e~^Z <C0S ₽2 + Sin PZ)»
4Р
2 Р
Мх (z) = — EJX = 2(j- е~^г (sin ₽z — cos pz).
Из решения видно, что наибольшие значения прогиба и изгибающего момента получаются в сечении z — 0, где приложено усилие.
По мере удаления от сечения z = 0 прогибы затухают, так как они содержат множитель (рассматривается половина балки при г > 0; во второй половине распределение симметрично).
На расстоянии I можно практически пренебречь прогибами и моментами, если
> 3,	(23)
при этом е~&1 < 1/20. Условие (23) позволяет отнести рассматриваемую балку, к числу длинных балок. Дальнейшее увеличение длины практически не оказывает влияния на максимальный прогиб и изгибающий момент.
Короткие балки на упругом основании. Функции Крылова. Зна
чительно более сложным оказывается решение для коротких балок,
когда требуется учесть условия на обоих концах балки (рис. 15.7). Для решения удобно воспользоваться нормальными фундаментальными функциями (функциями Крылова) уравнения (8). Эти функции (УДз), y2(z), y3(z), У4(я)) являются решениями однородного уравнения (8),
У
о
Рис. 15.7. Короткие балки
удовлетворяющими специальному условию на упругом основании в начале координат z = 0. Например,
функция У2 (z) должна при z = 0 удовлетворять следующим условиям:
dyrt	d2yrt	d3yrt
У2(0) = 0, -^(0) = 1,	—/(0) = 0, —JL(0) = 0.	(24)
dz	dz
В порядке упражнения напишите аналогичные условия для остальных функций!
Как известно (разд. 34), функции Крылова могут быть образованы из частных решений однородного уравнения (8) путем надлежащего выбора произвольных постоянных:
Ya(z)=W‘;
i=l
502
ГЛ. 15. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
надо найти постоянные Ci из систем линейных уравнений
у2 (0) = 2 Ci = о, г=1
у; (0) = 2	= о,
1=1
у;<о) = 2 ха = 1, 1=1
у; (0) = 2	= о,
1=1
где Xi определяются равенствами (14). Не останавливаясь на алгебраической стороне вопроса, приведем окончательные результаты (функции Крылова):
У1 (z) = ch cos Pz, y3(z) = ^2sh pzsinpz,
У2 (z) = (ch Pz sin pz + sh Pz cos Pz), У4 (z) = -1_ (ch p2 sin pz — ch Pz cos Pz).
40
(25)
Решение дифференциального уравнения балки па упругом основании с помощью функций Крылова имеет следующий вид:
p(z) = i;(0) Pi(3)W(0)y2(z) + L/'(0) Y3(z) + и" (0) Y4(z) + Y* (z),
(26)
где частное решение (см. разд. 34)
X
у* (2)= J у4 (2 _ 21) Л_ q (21)	(27)
о	EJ*
Как уже указывалось, одно из главных преимуществ применения нормальных фундаментальных функций состоит в том, что произвольные постоянные приобретают конкретный физический смысл.
Метод начальных параметров и решение уравнения изгиба балки на упругом основании в матричной форме. Представим решение (26) для прогиба и его производных в матричной форме:
{t?(z)}т = [У (z)]{^(0)) + {У* (z)},	(28)
где {l?(z)}t= {u(z), y'(z), v" (z), vf" (z)} — вектор состояния, {l>(0)}вектор начальных параметров, {У* (z)} —вектор частного решения.
Нормальная фундаментальная матрица имеет следующую структуру;
	Г У1	У2			
[У (*)]==	-40% -40%	А -40%	У2 А	% % О	(29)
	--40%	-40%	-40%		
где У»= y,(z) — функция Крылова.
Интересно отметить, что производные функции Крылова по z выражаются снова через те же функции.
50. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
503
Матричная форма (28) удобна для конкретных расчетов, в которых требуется определить не только значение прогибов, но и производных прогибов. Примеры применения функций Крылова и решения (28) будут даны в разделе о цилиндрических оболочках.
Замечание. Решение (28) справедливо, разумеется, для балки па упругом основании произвольной длины, как общее решение уравнения (8). Но для длинных балок преимущества функции Крылова теряются, так как с ростом рз функции возрастают, и происходит потеря -точности (результат оказывается зависящим от малых разностей больших чисел). Для балок с параметром $1 > 5 применение функций Крылова не рекомендуется; большую точность можно получить с помощью решения (18).
Из этого замечания следует, что во многих случаях целесообразно изменять форму решения, приспосабливая ее к условиям задачи.
50. Криволинейные стержни и пружины
Рис. 15.8. Стержень с криволинейной осью
Вводные замечания. В ряде случаев элементы конструкций могут рассматриваться как стержни с криволинейной осью (кольца, пружины и т. п.). Ось стержня — геометрическое место центров тяжести сечений — представляет пространственную кривую (рис. 15.8).
В дальнейшехМ основное, внимание уделяется стержням с криволинейной осью, лежащей в одной плоскости, т. е. когда ось стержня является плоской кривой.
В центре тяжести поперечного сечения помещается местная система координат; ось 31 направлена вдоль касательной к оси стержня, оси zi, у\ — главные оси сечения.
Внешние силы приводятся к главному вектору Q и главному моменту М:
Q = Qxi{ + О + TVk, = {&, Qy, N],
M = Л/Ui + A/Ji + AGlq = {Mx, My, Mz},
(30) где ii, jt, ki — единичные векторы по осям z\, у\, В равенствах (30) Qx, Qu, N — перерезывающие и нормальные усилия; Мх, МУ1 Мг — изгибающие в крутящий моменты.
Важным параметром, характеризующим криволинейный стержень, является радиус кривизны оси стержня (рис. 15.8). 3 зависимости от отношения
. v=fc/tfo,	(31)
где Rq — радиус кривизны оси стержня, & —наибольший размер сечения вдоль радиуса кривизны, криволинейные стержни разделяются на стержни малой кривизны (v < 1/5) и стержни большой кривизны (v > 1/5).
Для стержней малой кривизны при определении напряжений и параметров деформации могут использоваться формулы для прямолинейных стержней (разд. 31).
Для стержней большой кривизны требуется учесть дополнительные факторы, которые будут рассмотрены в дальнейшем. ’ -
Винтовые пружины. Наибольшее распространение в различных областях техники имеют винтовые пружины, которые обычно могут рассматриватьсякак стержни малой кривизны; винтовые пружины изготавливаются чаще всего путем навивки ifa цилиндрическую
504
ГЛ. 15. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
оправку проволоки диаметром от 0,2 до 50 мм и выше (рис. 15.9). Диаметр цилиндрической поверхности, содержащей центры тяжести сечений (средний диаметр), обозначен D9 (рис. 15.9), диаметр проволоки d, шаг навивки t, ось стержня является винтовой линией с углом подъема а:
а « tg а = 2р.	(32)
Рис. 15.9. Расчетная схема витой пружины: а — конструктивная схема; б — силовые факторы в сечении пружины
В большинстве случаев угол а — малая величина (tg а С 0,2, а < 12°). Наибольшее распространение получили пружины, работающие на сжатие (рис. 15.9) (клапанные пружины, пружинные рессоры и т. п.); через тарелки или торцевые плоскости передается усилие Р, действующее вдоль оси пружины.
В поперечном сечении создается крутящий момент
л
Мк = Mcosa « у PDQ1
(33)
так как cosa~l. Изгибающим моментом в сечении при малых углах а можно пренебречь.
Важным геометрическим параметром витой пружины является ее индекс с:	•
c = DQ/d,	(34)
где Do — средний диаметр пружины, d — диаметр проволоки.
Для пружин большого индекса (с > 8) распределение касательных напряжений при действии крутящего момента такое- же, как при кручении прямого вала (рис. 15.10, а):
16МК 8PDn
W.	_	К	V
Ч'ктах ,з ?з nd nd
(35)
Перерезывающая сила в сечении Q — P дает касательные напряжения среза, приближенно равные (рис. 15.10, б)
тср = —(Зб)
Максимальное касательное напряжение находится в точке попереч
50. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
505
ного сечения, ближайшей к оси пружины (точка А на рис. 15.10) S
^тах — 'Гктах + Тср —
— ^ктах | 1 +
Тср
Тктах
nd3
(37)
Разрушение пружин обычно начинается в точке А, где напряжения наибольшие.
В общем случае максимальное касательное напряжение равно
^max —
nd
(38)
где = ат( с) —коэффициент концентрации напряжений на внутреннем волокне пружины (в точке А). Приближенно можно принять,
Рис. 15.10. Касательные напряжения кручения тк и среза тср в сечении пру-» жины
что при кручении касательные напряжения на внутреннем волокне возрастают пропорционально отношению радиусов винтовых линий:
а ~ ______________________
До ““ 2 d
Такое предположение основано на том, что при кручении сечение стержня остается неизменным, а углы сдвига и касательные напряжения изменяются обратно пропорционально длинам винтовых линий. Коэффициент концентрации касательных напряжений равен
' И
При уменьшении индекса с величина at возрастает.
Для определения осадки пружины (сближения точек приложения усилий Р) найдем величину потенциальной энергии деформации:
1 С М* ds 1 Г Х(?2 ds /
cz = tJ-^- + tJ-gf--	<4°)
О	о
В качестве длины стержня принимают	;
l==nDn,	(41)
где п — число рабочих витков.
506
ГЛ. 15. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ II ПРУЖИНЫ
Для передачи осевого усилия на пружину витки иа концах пружины поджимаются при навивке и сошлпфовываются для получения опорной плоскости (рис. 15.9). Обычно принимается число рабочих витков
лг = л?о — А, где Д = 1, ..2 — число концевых витков.
Учитывая, что
Л = JP == лб/‘732, F = лбР/4, и принимая К ~ 1, получаем из соотношения (40)
тт 1 (ZP'D^Dn 4P-D?in\ i (8P2D*n	^D(n\
J^J _ I	J j	I x I	I ’’ I
~ 2 \ GW Gnd2 I \ Gd* Gd2 J
Потенциальная энергия деформации равна работе внешней (закон сохранения энергии)
и = 1 Рб,
где б — осадка пружины. Из уравнений (43) и (44) находим
Gd4- Gd4 Gd4 (	2 ро /'
Вторым слагаемым практически можно пренебречь; тогда
(42)
(43)
силы
(44)
(45)
(46)
(47)
жины б и действующего усилия Р
где
Gd* — осадка одного витка.
Формулы (38) и (46) являются основными для расчета пружин. Связь осадки пружины б и действующего усилия Р показана на рис. 15.11. Усилие предварительной затяжки (осадки) Pi принимается в зависимости от назначения пружины в пределах
Pt = (0,l-0,5)P2,	(48)
где Р2 — максимальная нагрузка на пружину. Величина Р2 представляет наибольшую допустимую нагрузку по условиям статической прочности. При осадке пружины бпос происходит соприкосновение витков и удар. Необходи
мо выполнение очевидного условия
б<бцюс.	(49)
Из этого условия назначается шаг пружины (в свободном
50. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
507
состоянии)

(50)
где бз —осадка при допустимой (статической) нагрузке; п — число рабочих витков; к =1,1;	1,3 — коэффициент, гарантирующий
зазор между витками при наибольшей нагрузке.
Модели прочностной надежности пружин. В качестве материала пружин используются высокоуглеродистые и легированные сталн, термообработанные па высокий предел прочности (щ = 1200—3000 МПа). Они характеризуются сравнительно малой пластичностью. В качестве критерия разрушения можно принять максимальные растягивающие напряжения щ; при напряженном состоянии типа кручения илп сдвига
Hi — Ттах»
(51)
ВПД
Модель прочностной надежности пружин при статических нагрузках имеет
"ст ’
(52)
где оь — предел прочности материала, пст — запас статической прочности. Обычно при расчете пружип принимают
Пст = 1,7 - 3,5.	(53)
Величина предела прочности щ зависит от диаметра проволоки; при уменьшении диаметра проволоки о& возрастает.
Модель прочностной надежности пружин при циклических нагрузках. Прй числе циклов нагружений N 106 опасным становится усталостное разрушение. Условие усталостной прочности имеет вид
=	'	(54)
Рь
где т*, т* — амплитуда переменных напряжений и постоянное напряжение в момент разрушения; т-i — предел выносливости для касательных напряжений; Кх, р, s — эффективный коэффициент концентрации напряжений, коэффициент поверхности и масштабный фактор; — коэффициент влияния постоянных напряжений.. При подобии рабочего и предельного' циклов имеем
Та = "пдТа» тт = лпдт?п»	(55)
где та, хт — наибольшие переменные и постоянные напряжения в рабочих условиях, «пд — запас по подобному циклу. Из соотношений (54) и (55) находим
^—1
ЛПД =----JT----------•	(56)
При возрастании только переменной части напряжений:
та = паха, хт = хт	(57)
получаем пз соотношений (54) и (57)

508
ГЛ. 15. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
Запас по переменным напряжениям па применяется в тех случаях, когда имеется опасность усталостных разрушений пружин вследствие резонансных явлений. Если внешняя нагрузка циклически изменяется от Ртах = Рг до Рmin — Р1» ТО
Т°-ат nd3 ’ Тп»_а* nd3 ’	(59)
где
1 1
?а~ 2 (^max	~ ~2 (^тах "t” ^min)* '	(60)
Так как «концентрация- напряжений» отражена в величинах ха и Тт, то ее дополнительный учет не требуется — можно принять в равенствах (56) и (58) Кх & 1. Величина £ при наличии упрочняющей обработки (например, обдувки
микрошариками) принимается равной 1,3—1,4. Влияние чистоты поверхности, коррозии и других факторов на величину £ указывалось в разд. 16.
Масштабный фактор е принимается по формулам разд. 16,	« 0,1. Запас прочности по по-
добному циклу пПд = 1,4—2,5; запас по переменным напряжениям па = 2—3.
Замечание. Возрастание касательных напряжений на внутренних волокнах (в окрестности точки А) носит плавный характер и только условно относится к концентрации напряжений. В сущности, коэффициент ат вводится скорее как приближенная поправка к простым формулам для прямого бруса, позволяющего избегать более точного, но громоздкого расчета.
Рис. 15.12. Ударное нагружение пружины
Модель прочностной надежности пружин при ударном нагружении. Рассмотрим действие на . пружину груза весом Q, падающего с начальной 'скоростью Ко* (рис. 15.12).
Для определения наибольшей динамической нагрузки используется приближенное решение, основанное на том, что энергия падающего груза С7гр переходит в потенциальную энергию сжатия пружины ип$. Будем сначала пренебрегать массой пружины и покрывающей тарелки по сравнению с массой груза. Статическая осадка пружины под действием усилия Q равна
бет — 6ц(?,
(61)
где 611 —осадка пружины при единичной (статической) силе. После удара груза в пружине возникают динамическая осадка бд и потенциальная энергия пружины
=	VW	(62)
Изменение энергии груза равно разности энергии груза в момент соприкосновения и после полной осадки пружины:
10	10
= ^гр - ^2ГР = 2 f + <?Я - $	- бд)• = 2 д К+ <?бд, (63)
где QH — потенциальная энергия груза в поле силы тяжести (Я — высота)« Предполагается, что груз останавливается при полном сжатии пружины. Пре-* небрегая рассеянием энергии и приравнивая С7Пр и С7гр, найдем
1 1	tn
50. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
509
что дает
(65)
где коэффициент динамического усилия
(66)

Коэффициент динамического усилия показывает, во сколько раз возрастает осадка (прогиб) упругой системы при динамическом приложении внешней нагрузки по сравнению со статическим (медленно возрастающим ее приложением).
Если нагрузка прикладывается мгновенно, но с нулевой скоростью (Уо si = 0), из формулы (66) получ'аем
£д - 2.	.	(67)
При наличии начальной скорости Кд > 2. Для уменьшения Кл следует увеличивать податливость системы (величину бн).
Максимальное напряжение в пружине при ударе равно
8Уо
ттах — ат Я(/з -атб11Л</3-
(68)
Рассмотрим теперь удар падающего груза при наличии на торце пружины массы т\ (буфера).
Считая удар неупругим, получим, что после соударения массы т и mi начнут двигаться с общей скоростью которую можно определить из равенства количества движения:	'
т/  тг т	1
”	1	0 т + тг “ Уо 1 + mjm'
Повторяя предыдущий вывод, найдем для рассматриваемого случая
|то)
Наличие массы т{ перед пружиной понижает динамические напряжения в пружине. Ранее считалось, что масса пружины пренебрежимо мала по сравнению с массой груза. Для приближенного учета массы пружины считаем, что к mi должна быть добавлена приведенная масса (приведенная к сечению пружины, воспринимающему удар). Если скорость начального сечения Ртах, то кинетическую энергию приведенной массы и всей конструкции (пружины) получим в виде
2 wшротах
(71)
где Ki — кинетическая энергия, которую приобретает пружина после удара.
При статическом приложении усилия осадка витков линейно изменяется по длине:
б (5) = 6max у,	(72)
где 5 — длина вдоль проволоки пружины, Z — общая длина пружины, б — мак* симальная осадка (при s = Z).
510
ГЛ. 15. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
В пижнем сечении ($ == 0) осадка (перемещение) отсутствует. Предполагая приближенно, что распределение динамического прогиба (осадка) остается подобным статическому распределению, получим, дифференцируя равенство (72) по времени,
s
V (s) = р тах —.
Кинетическая энергия пружины
I
о
где ц — масса единицы длины пружины, ц/ — тпПр — масса всей пружипы. Из равенства (71) находим приведенную массу пружины
1 о 1 1
“2* ^lnp^max “ "2* ‘"З шах’	(73)
или
1
7721 пр ~ з 772 пр*
Коэффициент динамического усилия с учетом массы пружины равен
(74)
Замечание. Приближенная модель ударного воздействия, рассмотренная на примере пружины, используется для общего случая ударного нагружения
а	б
Рис. 15.13. Ударное нагружение конструкций
конструкций (рис. 15.13). Формула .для коэффициента динамического усилия (74) остается прежней, но изменяются 6Ст — прогиб оси статического воздействия груза — и значение приведенной массы тпр.
Для стержня (рис. 15.13) приведенная масса
для балки
_ 1
т inp	3 ^стержень’
__ 17
т1пр	35771 балка*
Стержни большой кривизны. Нормальные напряжения. Рассмотрим стержень с плоской криволинейной осью, причем плоскость симметрии поперечного сечения лежит в той же плоскости (рис. 15.14). Начало местной системы координат помещается в приведенном центре тяжести сечения, отстоящем на расстояние е от центра тяжести сечения; величина е определяется в дальнейшем. Ось стержня представляет геометрическое. место приведенных центров тяжести сечений; радиус кривизны оси стержня обозначен г, элемент дуги dsQ.
50. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
511
Приближенная теория стержней большой кривизны основана па гипотезе плоских сечений.
Перемещения точек поперечного сечения вдоль оси стержня to =	+ г/фх,	(75)
где wQ — перемещение точки Ос, лежащей на оси стержня; срх —
Рис. 15.14. Стержни большой кривизны. Перемещения по гипотезе плоских сечений
угол поворота сечения. Приращение перемещения dui ,	,
d” ^d^dSt> + y^dS0'
Относя величину div к первоначальной длине отрезка, найдем е = —=	+ г/ — —
dsy dso dsv У dsa dsv где dsv — длина дуги на расстоянии г + у.
dSy = dS()r-^-.
Учитывая соотношение (78), получим е —dW(> г । Уг d^x & ~ dsQ г + у ~г+ у dsQ'
Считая напряженное состояние одноосным (гипотеза ненадавли-вания), получим при упругих деформациях о = £’(е — аТ), или
V + У dSQ Г + У dSQ где аТ — температурная деформация. Из условий равновесия имеем §<jdF = N, F
(76)
(77)
(78)
(79)
(80)
(81)
(82)
512
ГЛ. 15. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
Учитывая соотношения (80), (81) и (82), получим систему двух уравнений относительно параметров деформации:
-^-dF + Е -^-dF - [EaTydF^N, (83)
ds J	г + у dsJ	г + у J	у	'
° F	° F	F
^F-^-rdF +	^E-^-dF-\EaTydF = Mx. (84)
dsQ J Г + у dsa J r + у J y	x ' ’
Определим положение начала координат (центра сопротивления) из условия
f E—^—dF = 0.	(85)
J г У	.	' 7
F
Из соотношений (83) и (84) находим параметры деформации dwJdsQ и dyJdsQ и по равенству (80) получаем
(( С EaT dF	f EaTy dF \
V	J	I
г F	, ry F
~+у	А + г+у ~ВХ---------аТ)>
. ,	(86)
где жесткости сечений на растяжение и изгиб равны соответственно
A=§E—^—dF, Bx=^E-^-dF.	(87)
J г+ у ’	J r + у	4 '
F •	' F
Учитывая соотношение (52), запишем
A = f E^-^-~-v-dF = ^\EdF,	(88)
J	r + у J	’	' '
F	F
B* = r$^ydF + r$^ydF = r$EydF-	(89)
F	F	F
Первая группа членов в формуле (86) выражает напряжения в криволинейном стержне от внешних сил.
Обычное (линейное) распределение напряжений в прямом стержне содержит множитель г/(г + у), приводящий к увеличению напряжений при у<0 (на более близких к центру кривизны волокнах). Вторая группа членов дает температурные напряжения.
Замечание. Характерной чертой, преобразований в теории криволинейного стержня является использование равенства (85). В частности, при выводе формулы (89) к исходному интегралу был добавлен нулевой член.
Определение приведенного центра тяжести сечения криволинейного стержня. Примеры. Центр кривизны К обычной оси стержня (геометрического места центров тяжести сечений) считаем извест-
50. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
513
ным, и требуется определить величину г — расстояние от приведенного центра тяжести до центра кривизны.
Из условия (85) находим
E^£~r dF = \ EdF —	=	(90)
J г+ у J г + у	J	J r + y »	' '
F	F	F	F
что дает
f E dF f E dF
~ fEdF_ {EdFJ	' 7
J r + У J ri F	F
где n = r + у — расстояние от элемента dF до центра кривизны (известная величина).
Можно установить приближенную формулу для величины
е == г0 — г.	(92)
Учитывая, что
у^у-е
— расстояние до главной оси сечения, J EyrdF = 0, получим из F
равенства (90)
+ у г° ₽ \ г° / р	р	*	'
или
e^EdF — L^EyldF «0.
F	Q F
Из последнего соотношения находим
g ^ХПр го~ г*А'
где Вх пр — жесткость сечения на изгиб для прямолинейного стержня.
При постоянном модуле упругости имеем
где А = J yfaF — г
главный момент инерции сечения.
Пример. Рассмотрим стержень с прямоугольным поперечным сечением (рис. 15.15, а). Модуль упругости Е считаем постоянным.
514
ГЛ. 15. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
По формуле (91) находим
F F
{ dF ~	т0+К1‘
h
r0 + h/2’ 1пг0-/</2
F 1
'о
Смещение центра тяжести сечения жести равно
относительно приведенного центра тя-
h
в — Г - ---------.
°	, го + Ь/2
nr0-W2
Учитывая разложение натурального логарифма в ряд, получим е го~12< что соответствует формуле (93).
Для круглого сечения (рис. 15.15, б) укажем окончательный результат, опуская промежуточные довольно громоздкие преобразования:
r0 7  16 го’
-=4р-
Г0 2 \
(94)
(95)
(96)
Где d — 2R — диаметр круглого сечения.
Приближенное значение e/rQ вытекает из соотношения (93).
а	б
Рис. 15.15. Криволинейный стержень с прямоугольным (а) и круглым (б) поперечными сечениями
Замечание. Ось х проходит через приведенный центр тяжести, отстоящий на расстояние е от центра тяжести сечения; поэтому
^Еу dF = Е (ух +e)dF = е^Е dF,	(97)
F	F	F •
так как	‘	-
[ Eyx dF = 0
F как обобщенный статический момент относительно главной оси.
50. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
515
Касательные напряжения при изгибе криволинейного стержня* Касательные напряжения, как и в прямолинейном стержне (разд. 31), определяются из условия равновесия отсеченной части
элемента стержня (рис. 15.16). Предполагая касательные напряжения распределенными равномерно по хорде Ь и проектируя все силы па горизонтальное направление, находим
^_т^+±2/==0,
К
Рис. 15.16. Касательные напряжения при изгибе криволинейного бруса
(98)
где /V/, Qt — нормальное
и касательное усилия,
действующие на отсеченную часть с площадью сечения / (общая площадь поперечного сечения F):
Nf = ^adF, Qf — ^-xdF.
Опуская вывод, приведем окончательный результат для криволинейного стержня с постоянными параметрами упругости:
rQ I sj_ _ f_ 'j b (r + y)2 \$f F
(99)
где S/= ] ydF, Sf = j у dF— статические моменты относительно /	F
но оси х, проходящей через приведенный центр тяжести; f, F — площади отсеченной части и всего поперечного сечения.
Перемещения на изгибе криволинейного стержня. Для нахождения перемещений составим сначала выражение потенциальной энергии деформации равномерно нагретого криволинейного стержня. В результате деформации сечение стержня получает поступательное смещение иь и угол поворота фх (рис. 15.17).
Работа, совершаемая при деформации элемента стержня, равна

(100)
где параметры деформации имеют вид
^Фх _ мх fto = # ds В*' ds А ’
(101)
В равенстве (67) пренебрегается работой перерезывающих сил.
516
ГЛ. 15. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
Потенциальная энергия деформации всего стержня
Рис. 15.18. Определение перемещений в криволинейном стержне
Рис. 15.17. Определение потенциальной энергии элемента стержня
Если к стержню (рис. 15.18) приложена сила Р, то перемещение точки приложения силы по направлению ее действия по теореме Кастилиано составит
6p = g-	(103)
Этот же результат можно получить с помощью интеграла Мора
(104)
Рис. 15.19. Изменение радиуса кривизны при деформации криволинейного стержня
где Mlx, Ni — единичный изгибающий момент и осевая сила. Формула (104), как и в случае прямолинейного стержня, справедлива для определения прогиба в точке приложения единичной силы вдоль линии ее действия.
Замечания. 1. Обычно при нахождении энергии деформации криволинейного стержня большой кривизны интегрирование ведется вдоль оси центров тяжести и внешние нагрузки приводятся к обычным главным* осям сечения. Тогда появляется необходимость учитывать работу момента от перемещений, вы-
званных усилием. При интегрировании вдоль оси приведенных центров тяжести формулы для криволинейного и прямолинейного брусьев совпадают.
50. КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ	5(7
2. Параметр изгибной деформации dfyjds связан с изменением радиуса кривизны оси приведенных центров тяжести сечений. Если г — первоначальный радиус кривизны (рис. 15.19):
ds = гЖро,	(105)
то после деформации его величина будет г* и угол между гранями элемента становится равным d<px + d<po. Пренебрегая удлинением оси при рассмотрении изгибной деформации, получим
r*(dq?x+ &?о) =
Из последнего соотношения находим
_ _L JL_ м* ds г* г Вх *
Параметр dfyjds выражает изменение кривизны стержня*
(106)
(107)
ГЛАВА 16
ПЛАСТИНКИ И ОБОЛОЧКИ
В современной технике многие элементы конструкций могут рассматриваться как тела, у которых один размер (толщина) мал по сравнению с двумя другими.
Если срединная поверхность таких тел плоская, то они называются пластинками, если искривленная — оболочками.
51. Пластинки
По форме срединной поверхности в плане различают круглые и прямоугольные пластинки (рис. 16.1). Значительно реже используются расчетные модели в виде эллиптических, треугольных и других пластинок.
Рис. 16.1. Круглые и прямоугольные пластинки
В зависимости от относительной толщины пластинки (h/R, h/a) различают тонкие (h/R < 0,1) и толстые пластинки (плиты) (h/R > 0,4). Расчетные модели для указанных пластинок различны.
В дальнейшем ограничимся изучением прочностных моделей тонких пластинок.
Основные гипотезы при * построении прочностных моделей пластинок. В инженерной практике применяются две основные гипотезы при построении прочностных моделей тонких пластинок.
Обе они используют то обстоятельство, что толщина пластинки мала по сравнению с её размерами в плане.
Первая гипотеза, принадлежащая Кирхгофу, утверждает, что нормаль к срединной поверхности (плоскости) оболочки остается нормалью к ней после деформации. Эта гипотеза, вполне аналогичная гипотезе плоских сечений при изгибе и растяжении стержней, называется гипотезой жесткой нормали.
Вторая гипотеза утверждает, что напряженное состояние в точках пластинки является двуосным; нормальными и касательными напряжениями в площадках, перпендикулярных оси z, можно пренебречь.
Уравнения равновесия для осесимметричного изгиба и растяжения круглых пластинок. Осесимметричная деформация круглых
51. ПЛАСТИНКИ
519
пластинок возникает, когда нагружение и условия закрепления являются осесимметричными. В общем случае к элементу пластинки (рис. 16.2) приложены распределенные (па единицу площади срединной поверхности) нагрузки qr и qz. По граням элемента действуют (на единицу длины) изгибающие моменты Mr, MQl усилия Nr, Nq и перерезывающее усилие В силу симметрии имеем <?е = 0.
Измененное значение силового фактора в связи с приращением
координаты г отмечено верхним индексом (звездочкой).
Составим проекцию всех сил на радиальное направление (см. уравнение (83) разд. 48):
— NrrdQ + ( Nr + — dr j(r + dr) dQ— — Nq dQ dr + qrr dQ dr = 0,
или
^+l0Vr--/Vu) + ?r = O. (1)
Рис. 16.2. Усилия и моменты, приложенные к элементу пластинки
При действии центробежных сил получим .
g(r) = p<o2rft.	(2)
Уравнение (1) было выведено ранее (в разделе о растяжении дисков). Равновесие сил в вертикальном направлении приводит к следующему равенству:
Qrr dQ — (фг + dr\ (г + dr) dQ — qzr dQ dr = 0,
или
^(<2гг) = -дгг.
(3)
Теперь составим уравнение моментов относительно касательной к окружности радиусом г (рис. 16.2):
— МrrdQ + (мг +	dr^ (г -J- dr) dQ —M^drdQ —
/ dQ„ \	4
— I(?r + -j- dr I (r + dr) dQdr — qzrdBdr--^- dr = 0. (4) \	• dr /
Моменты MQ вошли в уравнение, так как имеют составляющие 2Ме sin(d0/2) относительно рассматриваемой оси. В уравнении (4) должны быть сохранены члены второго порядка малости, так как -
520
ГЛ. 16. ПЛАСТИНКИ И ОБОЛОЧКИ
члены первого порядка взаимно уничтожаются, члены третьего порядка, и среди них момент от поперечной распределенной нагрузки, должны быть отброшены.
В результате получим. dM । -^ + ±(Mr-Me)-QT = 0.	(5)
Деформация круглых пластинок. Точка лежащая в срединной плоскости пластинки, при осесимметричной деформации получает смещение и0 вдоль радиального направления (рис. 16.3) и смещение (прогиб) w вдоль оси z. Положи-
Рпс 16.3. Деформация при осесимметричном нагружении круглых пластинок
Внося в последние раве
тельное направление прогиба w примем противоположным направлению оси z. Перемещение в радиальном направлении точки А, отстоящей на расстояние z от точки А о, будет равно
. u = u0 + z<p(r)\	(6)
где ф(г)—угол поворота нормали (отрезка АоА) в результате деформации.
Соотношение (6) является выражением гипотезы жесткой нормали.
При осесимметричной деформации имеем
&r = du/dr,	(7)
8e==u/r.	.	(8)
тва соотношение (6), находим
8Г = 8ГО + z	(9)
ее = е0о + z %.,	(Ю)
где 8ro = du0/dr, £QQ = Uo/r — деформации срединной поверхности. Из равенств (9) и (10) вытекает, что деформации в пластинке рас* пределяются по толщине стенки линейно.
Соотношения упругости для круглых пластинок. При двуосном напряженном состоянии (вторая гипотеза)
1 8г = у (Or — цае) + аГ,	(И)
1 ее = £- (се — Ц0г) + аТ,	(12)
или, в другой форме,	
2(ег+ре0)—	аТ, 1 — р	1 и	(13)
О0 = 1_|х2(е0 + В8г) —	(14)
51. ПЛАСТИНКИ
521
Температура в точках пластинки
T = T(r,z)
(15)
изменяется по радиусу и толщине.
Учитывая соотношения (9) и (10)’, запишем уравнения (13) и (14) в такой форме (при отсутствии нагрева)
Or === Ого "1" Оги,	( 16)
Ое=О90 + а9и,	(17)
где напряжения в плоскости пластинки (напряжения растяжения) равны
Е	.	ч
Ого — “-----2 \er0 +
Е	/	ч
°бо = _------- (е0о + p,er0),j
1 — а напряжения изгиба —
Е Zd© ,	©\
aru==z М?+р 1 А г* \	/
oeu = z——(-2 +
1 — Ц \ r dr )
(18)
(19)
(20)
(21)
Отметим, что напряжения изгиба линейно изменяются по . толщине
стенки. Для точек срединной плоскости они обращаются в нуль. Усилия и моменты (на единицу длины), действующие в пластинке, связаны с напряжениями следующими простыми соотношениями (рис. 16.4):
Л/2	Л/2
Nr = j <yrdz-i, Ne=> [ aedz-1, (22) -Л/2	-Л/2
Л/2	Л/2
Мг =— f Orzdz-i, Mq = — J a^zdz-i. —Л/2	—Л/2
Рис. 16.4. Связь напряжений и силовых факторов
Подставляя в последние равенства зависимости (13), (14) и считая параметры упругости постоянными, получаем важные соотношения:
+	(23)
- гОг + >4”) - "р .	<24>
г* '	*	•
. л/2
Mr = -Z)f^+U-2-1+j-5- f a/Tzdz.	(25)
\dr r r J 1 — u J	’	'
—Л/2 .
522
ГЛ. 16. ПЛАСТИНКИ И ОБОЛОЧКИ
Л/2
м6 = - D (% +	+ T^-l f aT’z dz,	(26)
—Л/2
где
Л/2	/г/2
= f aTdz>	f E2^	^3	(27)
1 M/2	_{/2	12(1-h)
— жесткость па изгиб единицы длины сечения (множитель (1 —ц2) в знаменателе связан с плоским напряженным состоянием). Из уравнений (23) — (26) и уравнений равновесия вытекает существенный результат: напряженные состояния в плоскости пластинки определяются независимо от ее изгиба.
Усилия Nr и Nq определяются из условия равновесия (1) и соотношений (23), (24). Они соответствуют уравнениям, полученным в разд. 48 для растяжения пластинки.
Для определения изгибных напряжений в пластинке используются уравнения равновесия (3), (5) и соотношения (25), (26).
Круглая пластинка постоянной толщины с постоянными параметрами упругости. Подставляя в уравнение равновесия (5) величины изгибающих моментов из соотношений (25) и (26), приходим к дифференциальному уравнению
Й2Ф . 1 dtp 1	Qr . 1 dMT
+ т	= ~ D + р—>
где
Л/2 г* р
Мт = -л--- ] a Tz dz
1-Н J
-Л/2
(28)
(29)
— температурный изгибающий момент.
Уравнение изгиба пластинки (28), составленное относительно угла поворота нормали q?(r), оказалось точно таким же, как уравнение для радиального перемещения и (г) при растяжении пластинки (см. разд. 48).
В соответствии с решением (10) разд. 48 можно записать
Г Г1	г
Ф (г) = Cf + С2 у —	j rx J Qr (r2) dr2 drt + 75 f r\MT (rx) drx.	(30)
a a	a
Внося значение <p(r) в равенства (25) и (26), получим г
Mr(r) = -D(l + H)Ci + D^C2+ а r ri	с
— f ri f Qr (гг) dr2 dr2 + 1=^ J rxMT (r x) dr-L, (31)
Г i i	r a
51. ПЛАСТИНКИ
523
Me = - D (1 + ц)	C2 + p J Qr (rx) drr +
a r ri	r
4-	f Г! ( Qr (r2) c?r2dr1 — 1-=-^ f drt + (1 — p) MT. (32)
r~ J J	r“ j
a a	a
После интегрирования по частям второго интеграла представим равенства (31) и (32) в таком виде:
Mr = - D (1 + и) С2 + Р(1-^ С2 - Ft (г) + F2 (г) +F (г),	(33)
М6 = - D (1 + р) С\ - -Д(17и) С2 + Ft (г) - F2 (r)—F (г) + (1-р)Мт, (34) где функции нагрузки
Г
Л(г) = Ц^1[<2г(г1)^1,	(35)
а г
FA^^^QrQ-Jdr,	(36)
2г </ а
и температурная функция
Г
F(r)^i-^^r1MT(r1)drl.	(37)
г J а
Произвольные постоянные определяются из краевых условий Л/г(а) = Л/га, Mr(b) = Mrb,	(38)
где МГа9 Мгъ — заданные (распределенные) изгибающие моменты на внутреннем и внешнем контурах пластинки.
Из соотношений (33) — (37) имеем
D (1 + р) Сг = -j-Ц- [а*Мга - &Мгь - F. (Ь) - F2 (b) - F (&)], о — а
D (1 - И) С2 -[Мга - Мгъ +	(*>) + F2 (&) + F (&)].
о — а
Подставляя значения произвольных постоянных, в равенства (33)
524
ГЛ. 16. ПЛАСТИНКИ И ОБОЛОЧКИ
и (34), получим следующие формулы: »2	/	2 \	2	/	7 2 \
М __ ъ/ b | 1_______L. __м а 11___________ __
тт — Л1гЪ ,2	2 1	2 1 шга , 2	2 1	2 /
b — а \ г )	b — а \ г /
,2	/	2 \
-	(Л (Ъ) + Рг (b))	1 -	+ Ft (г) + F2 (г) -
о — а \ г /
А2	/	„2 \
-^тгЧг 1-Л- +F (г), (39)
Ъ — а \	г /
а2 /	2 \	2	/ а2 \
М& = Мгь-^-г I + 4	1 + -4- -
Ъ — а \ г /	Ь — а \ г /
А2 /	2 \
-	(^1 (Ь) + F2 (Ь)) -А_ 1 + ^ + Л (г) - F2 (г) -
о — а \ г / а2 /	2 \
-Р(Ъ)-^- 1 + ^- -F(r) + (l-n)Mr. (40) b — а \ г /
Для сплошной пластинки (пластинки без центрального отверстия) следует считать С2 = 0 из условия ограниченности решения при г->0. Полагая в равенствах (39) и (40) а = 0, находим
Мг = Мг6-Л(Ь)-Л(&)+^(г) + Л(г)-7г(6) + /г(г),	(41)
Me-Mrb-F^b)-F2(b) + Fdr)-F2(r)-F(b)-F(r) + (l^iJL)MT.
(42)
Функции Fifr), F2(r) и F(r) вычисляются при а = 0. В центре
пластинки:
Fi=(0)=0, Л(0)=0, F(0) = ^^-Мт.
Соотношения (39) и (40) позволяют определить изгибающие моменты в пластинке, если известно значение перерезывающего усилия Qr(r). Величина Qr(r) может быть определена из условия равновесия при наличии закрепления только на одном контуре
Рис. 16.5. Определение пере- (статически определимое закрепление резывающей силы пластинки).
Рассматривая равновесие части пластинки радиусом г (рис. 16.5),
получаем
ИЛИ
г
2naQra — (rx) drx — 2nrQr (r) — 0, a
(r	\
aQra — J Г2дх (rj dr-L j.	(43)
51. ПЛАСТИНКИ
525
При наличии двух опорных контуров необходимо сначала найти неизвестные силовые факторы, действующие на одном из контуров закрепления, из условия отсутствия прогибов или- углов поворота. Во многих случаях удобно функции ^(r), F2 (г) и F(r) находить путем численного интегрирования.
Напряжения изгиба в круглой пластинке. Если учесть зависимости (25) и (26), то получим следующие формулы для напряжений:
Е Cfr '*	~ Z ,	Л\
(i-g2)^
Е________
(1 - g) (1 - и2) D
Л/2
J a/Tz dz
h/2
EaT
h/2
a9 = — z -—— M0 + z--------------5-— | aTzdz —
0	(l-g2)z>	(l-g)(l-g2)^ J2
EaT
1 —g
(44)
(45)
Так как
12(1- g2)
то формулы для изгибных напряжений
TWy -f- 2
приобретают следующий вид:
(h/2
z-12- f a.Tzdz — a.T h J/2
(h/2
z 12. f aTzdz— aT h
(46)
Вторые слагаемые связаны с неравномерным нагревом по толщине пластинки.
Определение прогибов круглой пластинки. Из соотношений (25) и (26) вытекает, что
+ dr г г г г dr
Мг Мт
D D *
Mq Мт D D ’
(47)
где, как и раньше,
h/2
Мт — т—— { aTz dz.
1 —g J
-Л/2
Из равенства (47) следует важная формула:
7- - (Г=да~	+ йТюр^-
(48)
526
ГЛ. 16. ПЛАСТИНКИ II ОБОЛОЧКИ
Угол поворота ср (г) п прогиб ш(г) связаны соотношением ^ = ф(г).	(49)
Если при г = с прогиб обращается в пуль, то
W (г) = W (с) + J <р (rx) drv	(50)
С
Прогибы часто оказывается удобным определить численным методом, так как аналитическое выражение обычно весьма громоздко.
Пример определения напряжений и прогибов круглой пластинки. Рассмотрим сплошную, шарнирно опертую пластинку (рис. 16.6) под действием распределенной нагрузки q и с линейным распределением температуры по толщине ДТ = kz.
Значение Qr(r) находим по формуле (43):
б
Рис. 16.6. Пример определения напряжений п прогибов пластинки
Qr (г) = — у-J Г±дг di\ = — ^ qr. О
Далее вычисляем h/2
Мт = , J aATzdz =
..	-Л/2
Л = f Qrdrx = -(1 + 'lt^r2, J	о
о
S3»
\ о
n / \	1 — ц ( д Г j Eakh*
Р (И = —J r±MT dr = —
о
По формулам (41) и (42) определяем
Mr =	_ Г2), .
Me = -1±±. q (Ъг — 1 ~*~ 3ц г2
U0	16 ч\а з _|_ р, .
51. ПЛАСТИНКИ
527
Отметим, что выражения для Мг и MQ нс содержат температурных членов. Напряжения в пластинке находим по формулам (46):
12М. °'--2—
л3
Е
1 -Р'
-Е
1-р.
12	7 h3 1
z—^ak-rr — akz
h3 14
12 . h3 7
z — ak — — akz
h3 14
12Mr li3 ’
12J7ft
= — z
+
+
При линейном распределении температуры по толщине стенки и шарнирном опирании на контуре температурные напряжения отсутствуют. Напряжения растяжения возникают при z < 0 и достигают наибольшей величины:
/ И
М — Т в —т-i
А
2
h*
Угол поворота нормали по формуле (48) равен
Р (1-/)О	18 [Ь	-1*^ г >] + (! + Ц) О :‘"
- - (ГПоо -ЙГК3 + ь' - + и.)Mr.
Прогиб определяем по формуле (50>, полагая с = &: ь
W {г) = — J ф (г о drt.
Прогиб в центре пластинки (г — 0) Ъ	л
С	а Ь4	МТЬ
W (0) = — J ф (rj drr = (1 + ^D — (5 + и) — 2 (1 + J1) •
О	'	'
Прогиб/ вызванный температурной деформацией,
-	МТЬ2	ЕМ3Ь2 '	_ акъ2
WT^)~	2(1 + И)Р -	-i2Eh3	2 '	.
Линейное изменение температуры не вызывает напряжений в пластинке, но приводит к прогибу.	.
Изгиб прямоугольных пластинок. Деформации. Рассмотрим прямоугольную пластинку (рис. 16.7), отнесенную к системе координат х, у, z. Элемент поверхности после деформации показан на рис. 16.8; точка Ло до деформации лежит в срединной плоскости, после деформации она получает смещения u0, ^о, Wo Точка Л, отстоящая на расстояние z от точки До, после деформации переходит в точку Л*. Угол поворота «жесткости нормали» (гипотеза Кирхгофа) имеет составляющие фх й в координатных плоскостях*
528
ГЛ. 16. ПЛАСТИНКИ И ОБОЛОЧКИ
Перемещения произвольной точки пластинки (точка Л) равны u = u04-zq:x, v = + ш==шОэ	(51)
где уо, — смещения точки Ло, лежащей в срединной плоскости.
Деформацией в направлении нормали пренебрегаем. В соответ-
где
Рис. 16.7. Изгиб прямо-	ди^	dvQ	дип dvQ
угольной пластинки ех0 = eyo = -J^",	= “дТ” + “дГ
•—деформации в.срединной плоскости пластинки.
Рис. 16.8. Деформации изгиба прямоугольной пластинки
Учитывая, что дм?	ди?
фх------Фу— -jp	(53)
получим следующие зависимости: д2м?	’	д2м?	’ п д2м? /с/ч
— £хо	— £?/0 z	— Yxyo	(54)
Уравнение упругости. Предполагается, что напряженное состоя^ ние является плоским. Пренебрегая для простоты температурной деформацией, будем иметь
Е	Е	' Е
= 1_ft2 (е* +	°" = i—ц2 +	Тху = 2(1 + |Х)
.(55) f •
51. ПЛАСТИНКИ
529
Внося в (55) равенства (54), получим
д2 iv )
Нтт » ду J д2и>
Е ( д"и> дх2
~ д2ю
°У — &У0 Z “	2 I “Т"! I* Н я 2 I«
1 — р \ ду"	дх /
/л \ Е д2ю
^ху — Тхуо — Z (1 — р.)	_ 3 дхд ,
1 1л
&х — <?хо	:
1-|Х
Е
(56)
где Охо, оу0, Тхуо — нормальные и касательное напряжения в срединной плоскости пластинки. Они определяются по равенствам (55) для значений ехо, еу0, Чхуо.
Силовые факторы в сечениях прямоугольной пластинки. В слое dz (рис. 16.9) действуют нормальные (ох, оу) и касательное (тху)
Рис. 16.9. Силовые факторы в сечении пластинок
напряжения, которые создают усилия длины):
и моменты (на единицу
Л/2
Nx = - j Ox dz,
-Л/2 •
л/2
Мх = — J gxz dz,
-h/2
Л/2
Ny= J ву dz, —h/2 h/2
My = — J GyZ dz, —h/2
Л/2
Nху ~ J хху dz,
—h/2
л/2
Мху = — J XxyZ dz.
'	—h/2
(57)
Подставляя значения о*, Gy и Тху из формул (56), найдем для усилий в срединной плоскости
Nx	== Nхо, Nу==: Gy oh==s NyQ, Nxy == Xxy^h = N
Для изгибающих и крутящих моментов получим
(*\2	о2	\
<58>
ох	оу	/
(2	2	\
+	(59)
оу	ох	/.
л2
(60)
34 и. А. Биргер, Р. Р. Мавлютов
530
ГЛ. 16. ПЛАСТИНКИ И ОБОЛОЧКИ
где

Е
1 — и?
Л/2
J z2dz =
—Л/2
Eh3
12 (1 - (л2) ’
(61)
Величина D называется жесткостью (единицы длины)’ пластинки.
Замечание. Отметим очевидное свойство парности касательных напряжений:
Try - Тух
и вытекающие из пего условия для касательных усилий и крутящих моментов: Л'ху = N ух, Мху = Мух»
Условия равновесия элемента прямоугольной пластинки. На рис. 16.9 показаны усилия и моменты, действующие на грани элемента пластинки.
Рассматривая равновесие сил по осям х и у, приходим к следующим уравнениям:
dNv dN		
dx	dy	= о,	(62)
dN„, dN.,		
xy |	у dx	dy	= 0.	(63)
Условие равновесия сил по оси z дает		
dx	dy	= ?•	(64)
Условие	равновесия для моментов приводит к двум уравнениям: + + = <65> ^+^ + ^ = 0.	' (66>
Пять условий равновесия (62) —(66) характеризуют равновесие элемента пластинки.
Замечание. Шестое уравнение равновесия относительно оси z приводит к уже известному результату
Nxy == N ух»
Разрешающие уравнения. Ранее были рассмотрены три группы уравнений: геометрические уравнения (51) — (54), описывающие геометрию деформации пластинки; физические уравнения (55) , (56), устанавливающие связь деформаций и напряжений; статические уравнения равновесия (62) —(66).
Первая группа параметров: u0, еж0, еу0, Мео, NyQ, — характеризует усилия и деформации в плоскости пластинки. Уравнения равновесия будут удовлетворены, если положить
N -fL N N
51. ПЛАСТИНКИ
531
Используя уравнение совместности деформаций
d gxQ ,	6?/0 _ У.хт/О
ду2 "И дх2 ~~ дхду 1
приходим к бигармоническому уравнению для функции усилий F. Легко заметить, что для определения усилий в плоскости пластинки получается плоская задача, разобранная в гл. 2.
Усилия, напряжения и деформации в плоскости пластинки определяются независимо от деформации изгиба.
__	d2w d2w d2w n/r	~
Вторая группа параметров:	~дП& Мху Mxy' $х'
характеризует изгиб пластинки.
Разрешающее уравнение (уравнение, решение которого позволяет определить неизвестные параметры задачи) получается следующим образом. Дифференцируя уравнение (65) по ж, уравнение (66) по у, затем складывая их, получим с учетом соотношения (64)
д2Мя дх2
2д2Мх„
-----j--------1	_ а дхду - q/
(67)
С помощью зависимостей (58) —(60) находим для пластинок постоянной толщины
д*ю . л d*w d*w ___________
дх± да? ду2 ду^ &
(68)
Это * и есть разрешающее уравнение изгиба * пластинки постоянной толщины. В более краткой форме оно записывается так:

(69)
где	•
-4^,0	9*	, д*
дх* дх2 ду* ду*
— бигармонический оператор.
Определение прогибов и напряжений в пластинке вариационным методом. Будем использовать вариационный метод Галёрки-на, в соответствии с которым примем следующее выражение прогиба:
m w (х, у) = S Ci<Pi (х, у), г==1
где ф<(я, у)'—заранее выбранные функции, удовлетворяющие краевым условиям задачи; с, — коэффициенты, подлежащие определению, 34*
532
ГЛ. 16. ПЛАСТИНКИ И ОБОЛОЧКИ
Коэффициенты Ci найдем из системы уравнений
а Ь
И(^ + о о
Система уравнений (70) может быть форме:
а b
[Ац] W = {А}, АН = f J(<PiV4)dx dy, о о
<7 \
27 I q^dx dy = О
(i = 1, .т).
представлена в матричной
а Ъ
А = —i^Widxdy' <7°) О о
Точность решения возрастает при увеличении числа членов ряда.
Пример. Определить прогиб пластинки, шарнирно опертой по четырем сторонам (рис. 16.10), при действии равномерно распределенного давления.
пластинка, шарнирно опертая по четырем сторонам, под действием постоянного давления
Краевые условия состоят в отсутствии прогибов и изгибающих моментов по краям пластинки. Этим условиям удовлетворяет . функция
лх	лу
w ~ с sin — sin -г-, la	о
При одном параметре из уравнений (70) находим
с1 =
а Ь
J
о о_______________
а Ъ
J J <P1V4<P1 dx dy о о
Вычисления дают
а Ъ	’a b	а	Ъ
И. лх лу	С лх Г . лу 4аЬ
sin— sin-y dx dy = I sin— dx I sin-y dy =
oo	oo	о	о
Окончательно получаем
la =
16да4Ь4	Пу
лЧ^ + Ь^й sinTsinT’
что дает погрешность порядка 10%. Знак минус означает, что прогиб направлен противоположно оси z.
Замечание. В круглых и прямоугольных пластинках применялось различное правило знаков для положительного значения прогиба. Разумеется, окончательные результаты не зависят от правила знаков, но следует выработать умение делать вывод, сопоставляя его с расчетной схемой »и принятыми в ней положительными направлениями.
52. ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
533
52.	Цилиндрические оболочки
Гипотеза жесткой нормали, деформации. При осесимметричной деформации цилиндрической оболочки (рис. 16.11) точка срединной поверхности Ао (рис. 16.12) получает смещения по оси оболочки uQ и вдоль радиуса wQ. Точка 4, отстоящая от срединной поверхности на расстояние z, будет иметь перемещения и0,
Рис. 16.11. Цилиндрическая оболочка
Рис. 16.12. Схема деформации оболочки
нормаль к срединной поверхности повернется на угол <р. По гипотезе жесткой нормали получим
u==u0 — zq).	(71),
Если пренебречь деформацией материала тонкостенной оболочки в радиальном направлении, то
w ==»	(72)
Деформации в слое z
8эс = dT = 8x0““2Jh
где ъхо~дий/дх~- деформация в точках срединной поверхности. По гипотезе жесткой нормали имеем
(75)
Полагая для тонкостенной оболочки г + z « г, получим
d2u> еж — ех0 z —%, ах
80 = 1Р/Г.
(76)
534
ГЛ. 16. ПЛАСТИНКИ И ОБОЛОЧКИ
Рис. 16.13. Усилие и моменты на единицу длины сечении оболочки
Напряжения и силовые факторы. В слое на расстоянии z от срединной поверхности действуют напряжения о« и Ое (рис. 16.13), создающие усилия и моменты (па единицу длины сечения):
Л/2	Л/2
Nx= ) oxdz,	J	aedz,
—h/2 ,	—h/2	/IQX
h/2	(Z°)
JV7x ===	j Ox^ dz j
—h/2 h/2
M Q = — j* oez dz.
-h/2
Уравнения упругости. Напряжения и деформации связаны следую
щими соотношениями упругости:
8х = у (Ох — ро9] + «л	(79)'
8е = y [о0 — НОг] + «Т,	(80)
где Е, pt — модуль упругости и коэффициент Пуассона, а — коэффи-» циент линейного расширения, Т — температура.
Из уравнений (79) и (80) следует, что
Ох = ^3^2 (8х + P8e) ~ аТ'	(81)
<т0 ~ -^-2 (е9 + М8х)-	«Т.	(82)
В дальнейшем для упрощения будем пренебрегать температурной деформацией, полагая аТ ~ 0.
Учитывая соотношения (76) и (77), находим
,2	\
d w , w \	'	/оо\
exo — z—г + Ц- ,	(83)
dx г I
Е (	d2w , w \	/о/х
с0 = ------2 рех0 — pz —г + т .	(84)
1 — р \	dz г /.
Подставляя величины вх и а0 из соотношений (81) и (82) в (78), получим
лг Eh I , W \	/ОСГ\
----2 ( ®ХО "Ь Н *7 Ь	(85)
^в = 7^(г + ^4	<86>
г* \	7
Е
^Х — “	2
1-К
52. ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
535
где
dx
r dx-
h/2
D = —. f z2 dz = 1-H 4, — h/2
Eh3
12 (1 - Ц2) ‘
(871
(88)
(89)
Величина D называется цилиндрической жесткостью. По физическому смыслу она представляет жесткость на изгиб полоски, ширина которой единица, а высота h (множитель 1/(1 — ц2) связан с плоской деформацией).
Равенства (85) и (86) позволяют выразить деформации срединной 'поверхности через усилия
6x0 "lx — Eh Т	(90)
еео = 7 = Ж^-^-	<91>
Рис. 16.14. Условие равновесия элемента оболочки
Уравнения равновесия. Рассмотрим равновесие элемента оболочки (рис. 16.14). Будем считать, что к срединной поверхности приложены внешние распределенные нагрузки (на единицу площа
ди) qx и qz. Проектируя силы на направление осей жиг, находим
dNx
dQ 1 N7 .	Л
_^__Лгв + дг = о.
(92)
(93)
Условие равновесия для моментов приводит к соотношению, которое встречается при изгибе стержней:
7Г+<? = °-	(94)
'Дифференцируя уравнение (94) по х и принимая во внимание зависимость (93), находим
<f2M_.	1
7^ + 7^ = ^	(95)
ах г
Замечание. Следует помнить, что усилия и моменты в уравнениях равновесия относятся к единице длины соответствующих сечений.
536
ГЛ. 16. ПЛАСТИНКИ И ОБОЛОЧКИ
Разрешающее дифференциальное уравнение. Оно получается из уравнения равновесия (95), если выразить силовые факторы через прогиб срединной поверхности Замечая, что из соотношения (91) следует
Ne = y-w + ^Nx,	(96)
и используя зависимость (87), находим из уравнения (95j разрешающее уравнение
d ( r\ d ip \ Eh	р»	/Л'тч
72 Р—Т + — =	(97)
dx I dx Jr	r
Для оболочки постоянной толщины с постоянными параметрами
Рис. 16.15. Изгиб балки-полоски единичной ширины, выделенной из цилиндрической оболочки
упругости разрешающее уравнение будет
таким:
+	=	(Q8)
dx	и \ r J
где
=	(99)
ИЛИ
R^tZ3(l-H2) ~\/ rh
При обычном значении коэффициента Пуассона ц = 0,3 имеем .
Р =	(100)
у гп
Уравнение осесимметричной деформации цилиндрической оболочки (102) совпадает с уравнением изгиба балки на упругом основании '(разд. 49). Такое совпадение имеет физическую основу. Рассматривая изгиб полоски единичной толщины, выделенной из оболочки (рис. 16.15), замечаем, что окружные усилия Ne дают составляющую в плоскости изгиба (уравнение (95)). Эта составляющая оказывается связанной с величиной прогиба (соотношение (96)), и ее действие эквивалентно упругому основанию.
Напряжения в сечениях оболочки. Если известно значение прогиба оболочки ш(ж), то силовые факторы определяются равенствами (87), (88)' и (96). Осевое усилие (на единицу длины) равно
JVx ~ 2яг’
(101)
52. ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
537
где N — осевое усилие, действующее на оболочку. Перерезывающее усилие Q (на единицу длины), находится из соотношений (94) и (87)/.
,3
=	(102)
dx
В поперечном сечении оболочки нормальные напряжения распределяются по толщине стенки линейно (рис. 16.16) ;
Ox = &XQ 4" &ХИ я	“з	(ЮЗ)
В продольном (меридиональном) сечении
V	4? /if
а9 = аео + аеи = -/---(104)
Отметим (см. соотношения (87) и (88)), что
М9==цМх.	(105),
Касательные напряжения существуют только в поперечном сечении
Рис, 16.16/Силовые факторы и напряжения в сечениях оболочки
и распределяются, так же, как в стержне прямоугольного сечения;
(106)
Длинные оболочки. Цилиндрическая оболочка называется длинной, если
Q ( 3	6?
* ~ h ( 2	h*
где I — длина оболочки.
Решение уравнения (98) для длинной оболочки следует принять в виде w (х) == cos fte + sin рх + ip* (х),	(108)
где Ci и С2 — произвольные постоянные, определяемые из условий закрепле-» ним оболочки, ip* (я) — частное решение уравнения (98),
538
ГЛ. 16. ПЛАСТИНКИ И ОБОЛОЧКИ
Дифференцируя равенство (108), получаем следующие зависимости (штрих означает производную по х):
и/ (х) = —	(cos fix + sin рх) + С2Ре“^х (cos рх — sin Рх) 4“ w* (х), (109)
w" (х) = 2С^е~^ sin ₽х - 2С2Р2е~®г cos рх + ш’ (х),	(110)
w" (х) = 2С1Р3е~®“ (cos Рх — sin Рх) + 2С2Р3е~^ж (cos Рх -J- sin рх) + w* (х). (111)
Из структуры решения (108) видно, что первая часть, зависящая от условий закрепления при х = 0, имеет множитель и по мере возрастания х затухает (при рх > 3 ею можно пренебречь).
Рис. 16.17. Длинная оболочка под действием внутреннего давления; Z, II — зоны краевого эффекта
Таким образом, в зоне закрепления оболочки имеется краевой эффект. Решение (108) описывает прогибы оболочки возле края х = 0. Для определения . прогибов возле края оболочки х = I используется то же решение, но для координаты
xI==Z-x.	(112)
Рассмотрим в качестве примера цилиндрическую оболочку под действием внутреннего давления q (рис. 16.17). Края оболочки приварены к жестким диафрагмам. Считая радиус внутренней поверхности оболочки г приближенно равным радиусу срединной поверхности, получим
= д;	(ИЗ)
осевое усилие N = nr2q и
N qr
Частное решение уравнения (98) будет постоянной величиной!
или
1 ( И А 4р w* — 2) I g — 2 к’
г2 (1-ун) ш* =----Eh----q‘
(115)
Легко понять физический смысл частного решения. В оболочке, свободной от закрепления, под действием внутреннего давления q создаются окружные напряжения
аео = Т*
При действии осевого усилия напряжения в поперечном сечении
°хо — h — 2 q h’
Деформация, в окружном направлении
Л 1 \ .	г 1— Т и J
8ео = г — Е (сте — >*ах) = Eh q‘
52. ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
539
Следовательно, частное решение (115) представляет прогиб (перемещение) срединной поверхности оболочки, свободной от закрепления, под действием внешней нагрузки. Произвольные постоянные Ci и С 2 найдем из условий при х = 0:
u>(0)==0, м/(0) = 0.	(116)
Из уравнения (108) и (109) получаем
Г2 fl— у!1)
С1 = — и>* (0) =	q, С2 = Су
Для прогиба оболоч1ш приходим к следующему равенству:
г2(1-4»х)
ш(х) =-----рГГ----q [1 — е (cos + sin |3я)].	(117)
Изгибающий момент Мх (на единицу длины) найдем из соотношений (110): д(1 — у PJ
(118)
— sm
2₽2 в °
Осевое усилие постоянно по длине:
лх=49Гф 
Окружное усилие определяется по формуле (96):
jV0(x)==gr 1 —	(cos + sin fte) j.
При > 3 (e~0x < 1/20) можно считать, что
7»
X
(119)
и? (я) = w* (х) =
(120)
/Ve(z)=gr,
т. е. влияние закрепления оболочки не сказывается. Расчетные соотношения справедливы и для края х = Z, если расстояние х отсчитывать от этого края (замена х на х\). Модель прочности оболочки содержит раздельную оценку общих и местных напряжений (напряжений в зоне краевого эффекта).
Условие прочности по-общим напряжениям имеет вид
]/а»о + аео-°хоа0о ^l0J’
где Ово == Oxo = Nxlh, о& — предел прочности материала, [п0] — допускаемое значение запаса по общим напряжениям. Условие прочности для местных напряжений (в сечениях х = 0 и х = I)
--7=^==^>Ы,	(122)
V ах + ае - ах°е
где [пм] допускаемое значение запаса по местным напряжениям; а», Не — наибольшие напряжения в оболочке при z — ±Л/2 (см. уравнения (103) и
540
ГЛ. 16. ПЛАСТИНКИ И ОБОЛОЧКИ
(104)); обычно принимается
1«м] « ^[П0]‘
Меньшее значение допускается потому, что за счет появления пластических деформаций изгибные напряжения уменьшаются.
Замечания. 1. Для оболочек из хрупких материалов следует принимать [пм] » [По].
2. Модель прочности учитывает однократное статическое нагружение. При повторных (циклических) нагружениях роль местных напряжений возрастает.
Краевой эффект и безмоментное напряженное состояние в длинных цилиндрических оболочках. Для длинной оболочки прогиб можно представить в виде
w = w* +	(123)
здесь и?* — прогиб оболочки при безмоментном напряженном состоянии, -
== C^^cos + C2e~₽xsin	;	(124)
w2 = С*е~$х cos ₽ (Z - х) + С*е~р(1~х) sin ₽ (Z - x),	(125)
где произвольные постоянные Ci и C2 определяются из условия закрепления при «г = 0; Сг и С2 — из краевых условий при ж = ?. Предполагается, что влияние условий закрепления при х = 0 и х»I не сказывается друг на друге. Решения и w2 выражают краевой эффект. Для примера на рис. 16.17 имеем
гг(1-ун)
Возможность представления (123) вытекает из того, что дифференциальное уравнение (97) содержит малый параметр при старшей производной (изгибная жесткость D для тонких оболочек является малой величиной). Если q2 и Nx —- достаточно плавные функции и их производными можно пренебречь по сравнению с малыми функциями, то частное решение можно принять в виде
=	— —• Nx) =	~ Nx). (126)
Прогиб выражает безмоментное напряженное состояние, при котором Мх«0, М»»0, Q«0. Решение (123) представляет приближенное решение уравнения цилиндрической оболочки. Это решение называется асимптотическим, так как его точность возрастает при h -* 0. Приближенное решение позволяет проводить раздельное определение произвольных постоянных для краевых условий и дает общую приближенную формулу для частного решения (формула (126)).
53. ПРОЧНОСТЬ И УСТОЙЧИВОСТЬ ОБОЛОЧЕК ВРАЩЕНИЯ
541
Замечания. 1. Зоны возмущения возникают не только в зонах закрепления оболочки, но и в збнах, где приложены сосредоточенные воздействия.
2. Уравнение с малым параметром при старшей производной и краевой эффект для таких уравнений встречаются и в других задачах математической физики (например, в задачах теплопроводности).
Короткие оболочки. Для коротких оболочек (^<3) решение уравнения (98) удобно представить с помощью нормальных фундаментальных функций (функций Крылова). Решение уравнения (98) запишем в виде
w (х) =х w (0) Yх (х) + и/ (0) У2 (х) + w" (0) У3 (х) + иГ (0) У4 (х) + У ^х),
(127)
где функции Крылова равны
У х (х) = ch fta cos fta,
У2 {%) = ozr (ch ftasin fte + ch pa: cos pa:), y3(x) = ^jshpxsinpo:,
I
У4 (a:) == —з (ch Pa: sin Pa: — sh Pa: cos Pa:);
4p
функция
(128)
*
77 \	(<^i) Nx (^1) /
(129)
О
выражает частное решение уравнения (98). Для коротких оболочек приближенное решение (123) непригодно, так как зоны краевого эффекта занимают всю длину оболочки. Модели прочности коротких оболочек основываются на решении (127).
При оценке прочности учитывается различная опасность равномерно распределенных напряжений по толщине стенки (напряжений от усилий) и изгибных напряжений, которые уменьшаются при появлении пластических деформаций.. .
53. Приближенные методы расчета прочности и устойчивости оболочек вращения
' при осесимметричном нагружении
Вводные замечания. Срединная поверхность оболочек вращения может быть образована путем вращения отрезка кривой вокруг оси (рис. 16.18). Оболочки вращения (цилиндрические, конические, сферические, тороидальные и др.) имеют широкие технические применения (корпуса двигателей, летательных аппаратов, сосуды и т. п.). Элемент оболочки вращения показан на рис. 16.19 (п — вектор, нормальный к срединной поверхности). Плоскость, проходящая через точку А и ось вращения, называется меридиональной плоскостью; A A j — элемент кривой меридионального сечения; Ri — радиус кривизны в точ-
542
ГЛ.’ 16. ПЛАСТИНКИ И ОБОЛОЧКИ
ке 4; О\ — центр кривизны дуги меридионального сечения. Через нормаль к поверхности можно провести множество плоских сечений (среди них — два главных). Одним из главных сечений является меридиональное.
Рис. 16.18. Оболочки вращения и отрезки кривых, вращением которых она образуются
Рис. 16.19. Радиусы кривизны срединной поверхности оболочки вращения
Второе главное сечение проходит через нормаль п и перпендикулярно меридиональной плоскости. Радиус кривизны плоской кривой в указанном сечении равен Яг, центр кривизны лежит на оси вращения в точке О2.
Безмоментное напряженное состояние и условие равновесия элемента оболочки. В общем случае осесимметричного нагружения в оболочке действуют нормальные усилия 2Vt и N2, перерезывающее усилие Q, изгибающие моменты и М2 (рис. 16.20). На некотором удалении от края и других зон возмущения в оболочке возникает безмоментное напряженное состояние, при котором изгибающими моментами и перерезывающей силой можно пренебречь. Ранее это было показано для цилиндрической оболочки, но такое явление происходит и в других оболочках вращения.
Рассмотрим условие равновесия элемента оболочки при безмо-ментном напряженном состоянии (рис. 16.21) .
53. ПРОЧНОСТЬ И УСТОЙЧИВОСТЬ ОБОЛОЧЕК ВРАЩЕНИЯ
543
По граням элемента действуют и 2V2; на срединной (на единицу площади) qn. В большинстве практических задач qn — давление среды в мегапаскалях. Составим проекцию сил,
(на единицу длины) усилия Ni
поверхности распределены нормальные усилия
Рис. 16.20. Силовые факторы в сечениях оболочки вращения
Рис. 16.21. Условие равновесия элемента оболочки при безмоментном напряженном состоянии: а — элемент оболочки; б — сечение в меридиональной плоскости
приложенных к элементу оболочки, на направление нормали п: qn dSi ds2 = 2Л\ ds2 sin dqpi + 22V2 dst sin d<p2.	(130)
Так как
sin dqh « dqh, sin dq>2 ~ dcp2	(131)
и
dq>i = dsJRb	dqp2 = dsjR2,	(132)
то из условия (130) находим важное соотношение
NJR1 +NJR2=* qn.	(133)
Считая нормальные , напряжения о4 и о2 равномерно распределенными по толщине оболочки Л, получим oji « o2fe«N2, Теперь из соотношения (132) следует, что
aJRi + п2/Т?2 = qjh.	(134)
Уравнение (134) часто называют уравнением Лапласа.
Замечания. 1. Уравнение (134) и рис. 16.21 показывают, что при безмоментном напряженном состоянии оболочка противостоит внешнему давлению за счет кривизны элемента.
544
ГЛ. 16. ПЛАСТИНКИ И ОБОЛОЧКИ .
2. Напряжение Ct называется меридиональным, напряжение Ог — кольцевым или окружным. При осесимметричной деформации оболочек вращения напряжения Ot и 02 являются главными. Однако не следует считать, как это часто делается при анализе напряженного состояния, что Oi является наибольшим напряжением. Здесь индексы 1 и 2 присваиваются направлениям действия напряжений.
Общее условие равновесия произвольной части оболочки. Для
определения действующих в оболочке усилий и напряжений необ
Рис. 16.22. Условие равновесия части оболочки
ходимо рассмотреть равновесие части оболочки (рис. 16.22). Допустим, рассматривается часть оболочки, заполненной жидкостью, выделенная сечением А В соответствии с методом сечения в каждой точке поверхности должны быть приложены действующие усилия. При сечении «по металлу» прикладываются напряжения щ, при сечении «по жидкости»—давление р. Условие равновесия всех сил в направлении оси оболочки имеет вид
оЛ cos а • 2лг » рлг2 +	+ G06, (135)’
где Gjk—-вес жидкости, G06 —вес оболочки. Из уравнения (135)[
находим
рт_____, ^ж 4" go6
2/icosa 2nr/icosa *
(136)
При составлении условия равновесия радиусы внутренней и средней поверхностей оболочки считались приблизительно одинаковыми.
Примеры. 1. Цилиндрический сосуд под действием газообразной среды с давлением р. Радиус цилиндрической оболочки равен г, толщина стенки h
(рис. 16.23). В рассматриваемом случае главные радиусы кривизны равны == oo, R2 = г. Из уравнения (134) получаем кольцевое напряжение
=	(137)
53. прочность и устойчивость оболочек вращения 545
Меридиональное напряжение находим из уравнения (136), пренебрегая весом среды и весом оболочки (а = 0);
1 г
(138)
В цилиндрической оболочке при действии внутреннего давления окружные напряжения в два раза больше, чем продольные (меридиональные). Этим, кстати» объясняется, почему в трубах при избыточном давлении трещины идут вдоль образующих.
2. Сферический сосуд под действием газообразной среды с давлением р* Радиус сферической оболочки равен г, толщина стенки h (рис. 16.24),
= R2 == г, Ot = о2 =
По формуле (134) получаем
а =“2* р	(139)
Сопоставляя равенства (137) и (139), находим, что наибольшие напряжения в стенке сферического сосуда в два раза меньше, чем в сосуде цилиндрическом. Этим объясняется, что часто сосуды для хранения газообразной среды под давлением делают сферическими.
3. Сосуд с тяжелой жидкостью (рис. 16.25). Сосуд имеет цилиндрический и конический участки, заполнен тяжелой жидкостью с удельным весом
Рис. 16.25. Определение напряжений в стенках сосуда с тяжелой жидкостью
Рассмотрим сначала напряжения в цилиндрической части сосуда. Кольцевые напряжения по формуле (134) равны
го го
°2(г1) = ₽(Х1)Т = ^1Т’
(140)
где p(^i) =	— давление жидкости на расстоянии xi от свободной поверхно-
сти. Продольное напряжение определим из уравнения (136). Пренебрегая весом оболочки, получим
/ ч 1 Го л
2^~h [яг2о (а “ *1) ? + 4 пго ~ л) ?]•
35 и. А. Биргер, Р. Р. Мавлютов
546
ГЛ. 16. ПЛАСТИНКИ И ОБОЛОЧКИ
ИЛИ
а1 (х1) = 7 Т + 7 ? ~ а) 1*	(141)
цилиндрической части в конической части
Продольные (меридиональные) напряжения в постоянны по длине. Определим напряжения (х2 > а). Из условия равновесия (136) имеем
а1 (хг) = Т	aS + ^(•xJfeTosa'-T пг* (*г) (6 “ *2) V-
сосуда сосуда
Так как
то
т(х2} = (& —х2) tga,
1 (Ь “ хг) sin« • sin a	,
», И - Т Т», —hcos.a	+ р - *,)!Т.
Для конической части сосуда главные радиусы кривизны равны
Й1(Х2)=°°-	Я2(г2)=Г(г2)^ =(Ь-Х2)^^-
Из уравнения (134) находим
, ч , ХД2(Х2)	V*2	• .sin a
a2 (Ж2) = Р (*2) —Г = “ (Ь - Х2> ^77’
В сечении х{ = 0 будем иметь
ai(0) = ya?f+ -|(b-a)Y-^, a2 (0) = 0.
В сечении х2 = а
ст1(а) = 4а^т+4a2<a)=avi-
(142)
(143)
Примерное протекание напряжений Ci(^) и а2(х) показано на рис. 16.25, б, в. В месте перехода от цилиндрической части сосуда к конической имеется скачок напряжений. Кроме того, в месте перехода возникает моментное напряженное состояние, и потому переходные зоны в оболочках подкрепляются кольцевыми поясами.
Приближенная модель прочности оболочки вращения при осесимметричном нагружении. При построении приближенной модели принимается, что основное напряженное состояние оболочки является безмоментным. Краевой эффект учитывается приближенно с помощью расчета «эквивалентной цилиндрической оболочки» (рис. 16.26). Напряжения в оболочке при безмоментном напряженном состоянии определяются на основе зависимостей (134) и (136).
Местные изгибные напряжения возникают в зонах крепления оболочки. Для определения моментного напряженного состояния возле сечения я = 0 оболочка вращения замещается полубесконеч-ной цилиндрической оболочкой с радиусом
г = Я2(0).	(144)'
53. ПРОЧНОСТЬ И УСТОЙЧИВОСТЬ ОБОЛОЧЕК ВРАЩЕНИЯ
547
Для расчета используется решение (124)
w == Схе Р°х cos (30я + С2е sin	(145)
где при |i = 0,3
g _	^285
Ро /я2 (0) МО) ’
jR2(O), h (0) — второй главный радиус кривизны оболочки и толщина оболочки в сечении х = 0. Произвольные постоянные С\ и Cz
a	ff
Рис. 16.26. Приближенная модель прочности оболочки вращения: а — схема оболочки; б — напряжения при безмоментном напряженном состоянии
определяются из условий закреплений края я=*0. Например, при: заделке края эквивалентной цилиндрической оболочки
= с2 = - М- (Ух (0) - рЛ2 (0)). jLjlb
Для края при х — I моментное напряженное состояние определяется из решения
w.— С*е ₽i(i Х) cos рг (Z — х) + С2е X>sin 0, (I — х),	(146>
где при р, = 0,3
В =	I»285
Р/ /Я2 (l)h(l) ’
Модель прочности при статическом нагружении по общим (безмо-ментным) напряжениям
(147}
V СТ10 + СТ20 “ а10СТ20
где вь— предел прочности материала, [п0] — допускаемое значение запаса по общим напряжениям — обычно принимается равным:
.[п0] = 1,3-2,5.
35*
548
ГЛ. 16. ПЛАСТИНКИ И ОБОЛОЧКИ
Модель прочности по местным напряжениям имеет вид
°ь
V + S -
а!а2
(148)
где а2 — напряжения, учитывающие изгибную деформацию оболочки, [пм] — допускаемое значение запаса по местным напряже-
ниям.
Приближенные модели устойчивости оболочки. Потеря устойчивости (внезапный рост прогибов и деформаций) может возникнуть
Рис. 16.27. Оболочка, потерявшая устойчивость при действии внешнего давления
в оболочках (рис. 16.27), если в них имеются значительные зоны, в которых действуют (общие) сжимающие напряжения. При внешнем давлении q в цилиндрической оболочке возникают сжимающие окружные напряжения и, следовательно, при
g>gKP (149)
в оболочке может возникнуть потеря устойчивости (дкр— величина внешнего давления, соответствующая потере устойчивости оболочки). По приближенной формуле Папковича (вывод формулы опускается)
дкр = 0,92^/1	(150)
где Е —модуль упругости; г, Л, 1~ радиус, толщина и длина оболочки (расстояние между закрепленными контурами). Приближенная модель устойчивости цилиндрической оболочки при внешнем давлении имеет вид
9<-Ц-0,92^- V-, (151)
[Лу] Zr F г т v '
[га,] — допускаемое значение запаса устойчивости оболочки; Хяо'М-1,5-2,5.
53. ПРОЧНОСТЬ И УСТОЙЧИВОСТЬ ОБОЛОЧЕК ВРАЩЕНИЯ	549
При недостаточном запасе устойчивости проводится подкрепление оболочки кольцевыми и продольными стержнями.
Стенки оболочки могут потерять устойчивость при сжимающих продольных напряжениях
а1кр = 0,6£у.	(152)
Эта величина может служить оценкой для опасных (в смысле устойчивости) напряжений сжатия при изгибе тонкостенных оболочек.
ГЛАВА 17
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
Современные ЭВМ дают возможность широкого использования численных методов определения напряжений и деформаций в элементах конструкции сложной формы. Среди таких методов наибольшее практическое значение имеет метод конечных элементов, разработанный и усовершенствованный в последние годы.
54. Введение в метод конечных элементов
Связь вариационных методов и метода конечных элементов» В вариационных методах упругие смещения, возникающие в теле под нагрузкой, представлялись в виде
п	П	п
u=S aifi(x,y,z), V = 2 bi(pi{x, у, z), w = 5 с^(а:, у, z), (1).
1=1	1=1	i=l
где Д, фо ф»—заранее выбранные функции; аг, —неизвестные
Рис. 17.1. Разбиение области на конечные элементы
коэффициенты, определяемые из условия минимума полной потенциальной энергии системы.
Основные трудности при использовании вариационных методов состоят в выборе аппроксимирующих функций //, фг, ф<. Разумеется, что с помощью увеличения числа таких функций точность решения может быть повышена, однако учет местных, особенностей напряженного состояния (концентрации напряжений) остается весьма трудным.
В методе конечных элементов тело разбивается на малые,, но конечные элементы. Аппроксимация функций u, о, jp про
водится в каждом элементе отдельно. В качестве основных неиз-
вестных принимаются смещения в узловых точках, сопрягающих отдельные конечные элементы (рис. 17.1).
Аппроксимация смещения внутри малой области позволяет использовать простейшие функции (линейные и квадратичные функции координат). Как и в вариационных методах, для получения разрешающей системы уравнений относительно неизвестных
54. Введение в метод конечных элементов
551
смещений узлов используется начало возможных перемещений:
{bu}T{p}dS
(2)
{бе}
где {F}, {р} — векторы объемной и поверхностной нагрузки;
{би} — вариации (малые отклонения)'векторов деформаций и смещений; верхний индекс т означает транспонирование.
Основные этапы решения в методе конечных элементов^
1.	Разбиение конструкцш! на элементы.
2.	Выражение перемещений и деформаций в элементе через смещения граничных точек (узлов) элемента.
3.	Составление разрешающих уравнений с помощью начала возможных перемещений.
4.	Определение узловых смещений,. деформаций и напряжений.
В качестве конечных элементов могут использоваться не обязательно малые элементы. Важно только, чтобы поведение элемента (части конструкции) достаточно точно описывалось смещениями его узлов. Например, в качестве конечного элемента можно использовать стержень и т. п.
Рассмотрим несколько примеров.
Пример 1. Статически неопределимая ферма (рис. 17.2). Считаем конечными элементами стержни; узлами' элементов являются шарниры. Отличным от нуля будет узловое смещение Деформация в элементе 2 равна
Деформация в элементах 1 и 3 равна
чески неопределимой фермы методом конеч-
и..
Напряжения в элементах
Начало возможных
перемещений (2) запишем для системы в следующем виде:
объему тела рассматривается как сумма интег-»
В этом равенстве интеграл по ралов по объему каждого элемента. Так как
552
га. 17. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
ТО
COS- а
cos а
Где р — площадь сечения стержней. По
du
uAF
изическому смыслу
{6u}T {р} dS =
усилие, которое следует приложить
По физическому'смыслу К и представляет усилие, которое следует приложить в узле 1 для единичного смещения узла (и{ = 1). Be* личина К\\ называется коэффициентом жесткости.
Пример 2» Статически неопределимая ферма под действием произвольной нагрузки (рис. 17.3). Смеще* ние узла 1 имеет составляющие и\ и щ. Для определения деформаций в стержнях находим проекцию» полного смещения узла 1 на направления стержней и. . относим эту величину к его длине Z:
sin а cos а
Расчет неопре-
Напряжения в стержне di = Eeit <т2
статически
делимой фермы под действием произ-. вольной силы мето-дом конечных элементов
Используя начало возможных перемещений (уравнение (3)), получим
55. ОСНОВНЫЕ УРАВНЕНИЯ
553
где
и —	01X1	XV -- х
Собирая члены прп одинаковых вариациях, найдем
о [ f 2 cos3 aEF ou, < -----------

V

(6)
где матрица жесткости
1*1
EF
(А’]
V
силу произвольности вариации
из уравнения
(8) получаем
14
U
(Ю)
DI
Зависимости (10) позволяют определить смещение и затем деформации п па пряжения в стержнях.
55. Основные уравнения метода конечных элементов
элемента. Ограничимся (например, растяжение листа с от-
Аппроксимация перемещений внутри рассмотрением плоской задачи верстием и т. п.).
Область тела разбивается на малые, в частности треугольного типа (рис. 17.4). Упругие перемещения в пределах n-го элемента будем счи-функциями Koop*
но конечные элементы
тать линеиными линат
«1
а4
а2х + а3у, (11J а5я + а6у. (12)'
ис. 17.4. Конечный элемент прп решении плоской задачи
Неизвестные параметры аъ а2, ... ..ав выразим через смещения узлов.
Применяя равенство (И)
а2Яг
для
узлов
получаем
«1
«зУ<



0С23?тп

В матричной форме имеем
(14)
ГЛ. 17. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
Определяя из этого уравнения а2, а3? представим равенство (11) в таком виде:
коэффициенты равны
1	4	Л
ai = (XjDm хтУг) зд, bi = (у j— Ут)?^, Cj = (хт—^j)^. (1®)
Остальные коэффициенты ah .ст получаются из равенств (16) с помощью круговой перестановки индексов i, j, т. Например, а} = — (ХтУг — Xiym)/(2Д) и т. д. Для смещений вдоль оси у будем иметь
(17)
Формула для v аналогична (15):
v (х, У) = (а< + Ьх + с{у) + Ь^х + с,у) Vi + (am + bmx + cmy) vm. (18)
Равенства (15) и (18) выражают смещения точек треугольного ко печного элемента через смещения его вершин (узлов).
В матричной форме уравнения (15) и (18) представим так:
= {(ФП, [ФД
(19)
(20)
(21)
По физическому смыслу матрица формы [Ф,] выражает перемещения точек элемента в случае, когда компоненты смещения узла i равны единице (u-< 1, р, = 1), а смещения других узлов отсутствуют» В соотношении (19) вектор-строка и вектор-столбец имеют блочную структуру; в более компактной форме зависимость (19) можно записать следующим образом:
Ч2Х2 2X1
» 1Фп] {Un}.
1X3 3X1
(22>
55. ОСНОВНЫЕ УРАВНЕНИЯ
555
где
(23)
В равенстве (22) п в некоторых числа строк и столбцов в блоках и столбцов в самой матрице или векторе (нижние цифры).
Замечание. Главное преимущество при разбиении матрицы на блоки состоит в следующем: в дальнейшем блоки могут рассматриваться как обычные элементы матрицы. При умножении матриц (вектор также рассматрива-. ется как матрица) «внутренние» числа, указывающие размерности матриц и их блоков (попарно одинаковые), пропадают! Например, в равенстве (22) такими числами являются 3 в нижней казывают числа строк и столбцов в чаются в результате перемножения.
Деформации и напряжения связь деформаций и перемещен известными соотношениями (см. разд. 9): ди	ди	ди
случаях в дальнейшем указаны (верхние цифры) и числа строк
строке и 2 в верхней. Крайние числа по той матрице и ее блоках, которые полу
внутри элемента. В плоской задаче 1Й в тг-м элементе устанавливается

ду дх*
Запишем эти равенства в векторной форме:
(25)
тде вектор деформаций в п-м элементе
(26)
v z
и матрица-дифференцирования
дх
[D]
(27)
Если учесть соотношение (22), то
<е„) = [Р][Фп]{£/
(28)
где матрица
[В„] = Р][Фп).	(29)
* «
Получим теперь равенство (29) непосредственно из соотношений
(15) и (18). Дифференцируя, находим
Уху
(30)
556*
ГЛ. 17. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
В матричной форме имеем
О
причем матрица
(31)
(32)
дальнейшем матрицу [Вп] удобно представить в блочной форме з
3X2
(33)
Каждый блок матрицы относится к определенному узлу. Соотношения упругости для плоской задачи:
1 1
Бх = у (ох — fxoy) + аТ, == — (а?/ — р,ах) + аТ, у =
и)
или
аТ
“ 2 (14- |Л) УхУ
Последние уравнения представим в матричной форме:
{а}
[Л]({8}-{аП)
(351
где матрица
Ml
Вектор температурной деформации
{аТ} = аТ 1 .
Учитывая формулу (28), получим
3X2
3X1 зхз
[Вп] {tfn}-{aT}l;
3X1
ху
(36)
(37)
(38)


m
О
О
m
а.Т, а
р

1X1	1X1 \ 1X3 8X1	1X1 /
в последнем равенстве снова указана блочная приспособленная к принятой структуре матрицы
структура матриц,
55. ОСНОВНЫЕ УРАВНЕНИЯ
557
Вариационное уравнение метода конечных элементов. Применяя начало возможных перемещений для всего тела, запишем
У J J {бе}- {о} dV - j f j {8и?{Р} dV - J J {6иГ {?} dS = 0, (39)
V	V	S
V и S — объем и поверхность тела. Векторы объемной и поверхностной нагрузки
{р} =
(40)
Интеграл по всему объему равен сумме интегралов по объемам элементов.
{беп}- {an} dV - У (У {6un}T {F} dV -vn
(41)
где
э — число элементов.
Последний интеграл распространяется только на участки поверхности элементов, принадлежащие внешней поверхности тела (Sn^S). Из равенства (28) вытекает
{6en}==[Bn]{6i7n}
(42)
и для транспонированного вектора
{en}T==Wn}T[5n]T.
(43)
Уравнение (46) представляет вариационное уравнение метода ко вечных элементов для плоской задачи.
Матрица жесткости элемента. В основном вариационном урав нении (46) элемент представлен матрицей жесткости
558
ГЛ. 17. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
Отметим, что при транспонировании матрицы числа строк и столб цов меняются местами.
В развернутой форме
получим
(48)
где квадратные подматрицы — блоки n-го элемента (индекс краткости опускается):
(49)
Матрица [К^ содержит компоненты усилий в г-м узле при единич ных смещениях J-го узла при условии, что остальные узлы смеще ний не имеют.
Узловые нагрузки. В уравнении (46) внешние воздействия водятся к эквивалентным нагрузкам, приложенным к узлам мента. Если элемент примыкает к внешней поверхности (SneS), то распределенная нагрузка дает следующий вектор тически эквивалентных узловых усилий:
при-эле-
тела ста-
(50)
границ элементов {^рП)} = 0. Вклад массовых сил и температурных воздействий в узловые составляет
Для внутренних
f f f [5П]т [А] {aT}dV.
Рис. 17.5. Формиро ванне матрицы же сткости для дву: элементов
(51)
Отметим, что узловые нагрузки не зависят от искомых смещений и могут считаться заданными.
Разрешающая система линейных алгебраических уравнений метода конечных элементов (МКЭ). Уравнение (46) представим в следующей записи:
{6C7’](k(n)]{C7n}-{^n)})
(53)
где суммарный вектор узловых усилии равен
{<?”} = {<?(т >} + {&п)1 +	(54)
Рассмотрим в качестве простейшего примера плоское тело, разбитое на два конечных элемента (рис. 17.5). Для указанного тела
55. ОСНОВНЫЕ УРАВНЕНИЯ
559
{Ui} содержит компоненты смещения
В уравнении (55) вектор Vi узла i (i»l, 2, 3, 4) Теперь запишем уравнение (55) в другой форме, суммируя все
члены, содержащие
вариацию
смещения данного узла:
Вариации смещения узлов могут быть совершенно произвольными, и равенство (56) возможно только в том случае, когда выражения при вариациях обращаются в нул нейных алгебраических уравнений вых смещений:
. Отсюда получаем систему ли-относительно неизвестных узло-
ЖЧ {uj + да] {и2} + да] {ил} = о, МЧ {UJ + (кЙЧ + [^Ч) Ш + (Ж] + Ж ]) {U3} + + да] {^} - {&} = о, да] {ил + (да] +	+ (ЖЧ + да]Ж) +
+ МЧ {£/<}-{<2з} = О, да] {и2} + даж>+да] ш - «?4}=о,
вектор усили
действующий на узел i со стороны всех
примыкающих к узлу элементов. Например,
Уравнения (57) представим в
матричной форме:
[£]{Ш «{<?},
(58]
560
ГЛ. 17. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
где векторы узловых смещении и усилии равны 1X2
1X2
{0
{0
(59)
N
1XN
где N — общее число узлов.
Записанное в общей форме уравнение (58) является основным разрешающим уравнением метода конечных элементов. Матрица [Я] называется матрицей жесткости конструкции.
Матрица [/£] является квадратной матрицей N X N, элементы которой квадратные матрицы. Каждая строчка матрицы соответствует узлу и содержит кроме смещения соответствующего и смещения других узлов элементов, примыкающих му узлу.
Строчка матрицы для плоской задачи содержит два уравнения относительно компонентов смещений.
В общем случае можно записать для i-й строчки уравнения (58) следующее выражение, вытекающее из (53):
узла еще к данно-
линейных
основного уравнения
2 ([Мп)]{£Ч-К>(п)1) = о.
Символ п е г означает, что в уравнение входят только элементы, примыкающие к i-му узлу; матрица [КVе] содержит только одну строчку матрицы [&(я)], относящуюся к узлу с номером мер, для второго уравнения (57) получим из равенства i== 2. 72 — 1.
(60)
i. Напри-(60) при
уравнением (57).
система уравнений метода конечных элементов определенной симметричной матрицей ленточной структуры. Для численного решения часто используется метод блочного исключения Гаусса, метод Холецкого и др.
2. Описанный вариант метода является простейшим. Применяются более сложные элементы с большим числом узлов и обобщенных узловых смещений. В качестве конечного элемента можно использовать участки пластинок, оболо-
что совпадает со вторым
Замечания. 1. Основная (58) обладает положительно