Дисперсия числа выбросов в реализациях нормального шума конечной длительности - Тихонов В.И.

Автор: Тихонов В.И.
Теги: электроника радиотехника электротехника радиосвязь
Год: 1964
Похожие
Статистическая радиотехника
Радиотехнические цепи и сигналы
Колебательные системы (Основы радиотехники и радиолокации)
Антенны и устройства СВЧ. Расчет и проектирование антенных решеток и их излучающих элементов
Текст
                    17.	Т н х о н о в В. И. Дисперсия числа выбросов в реализациях нор-
мального J шума конечной длительности. «Радиотехника и электроника»,
1964, № 1.
18.	Т и х о н о в В. И., Горяйнов В. Т. и др. Исследование
выбросов случайных процессов. Отчет № 9161. ВВИА им. проф Н. Е. Жу-
ковского, 1961.
19.	Кузнецов П. И, Стратонович Р. Л., Тихо-
нов В. И. О длительности выбросов случайной функции. ЖТФ, 1954, № 1.
20.	Cartwright D. Е., Longuet—Higgins М. S. The
statistical distribution of the maxima of random function. Proc. Roy, Soc., A,
1956, № 1209.
21.	Тихонов В. И Флуктуационные процессы. ВВИА им.
проф. Н. Е. Жуковского, 1961.
22.	Т и х о н о в В. И. Распределение максимумов огибающей квази-
гармонического шума. «Известия вузов», Радиотехника, 1963, № 5.
23	Тихонов В. И. О распределении наибольших значений в реа-
лизациях флуктуаций конечной длительности. «Известия вузов», Радиотех-
ника, 1961, № 5.
24.	Тихонов В. И., Куликов Е. И. Распределение выбро-
сов и максимумов флуктуаций. «Радиотехника», 1962, № 2.
Раздел III
ОПТИМАЛЬНЫЕ МЕТОДЫ
РАДИОПРИЕМА

Глава 19
АПОСТЕРИОРНЫЕ ВЕРОЯТНОСТИ
§ 1. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ
В радиосвязи, радиолокации и других системах передачи инфор-
мации сигнал, предназначенный для передачи сообщений, в процессе
передачи маскируется помехами и подвергается искажениям. Поэто-
му даже п ри самом тщательном конструктивном выполнении радио-
технических устройств с целью свести к минимуму влияние помех,
на выходе радиоприемного устройства не удается точно воспроиз-
вести переданное сообщение.
Предположим, что в отсутствие помех и искажений сигнала на
выходе приемника точно воспроизводится переданное сообщение.
Тогда при наличии помех и искажений сигнала сообщение на
выходе того же приемника будет воспроизводиться неточно, а
с искажениями. Приемник, обеспечивающий минимальные искаже-
ния сообщения, называется оптимальным или идеальным (наилуч-
шим). В зависимости от назначения приемника критерии или
количественные характеристики искажений могут быть разными
(см. ниже). При выбранном критерии и заданных условиях приема
оптимальный приемник определяет минимальные искажения сооб-
щения. Этот минимальный уровень искажений часто называют по-
тенциальной помехоустойчивостью.
При заданных условиях радиоприема потенциальная помехоус-
тойчивость не может быть превзойдена реальным радиоприемником
и можно лишь стремиться к ее достижению. Сравнивая помехоустой-
чивость реальных приемников с потенциальной помехоустойчи-
востью, можно выяснить степень технического совершенства реаль-
ных приемников и возможные резервы повышения их помехоустой-
чивости.
Теория оптимального радиоприема позволяет также определить
наилучшие виды передаваемых сигналов. Для этого следует срав-
нить значения потенциальной помехоустойчивости при различных
393
видах сигналов. Сигнал, для которого при заданных условиях
радиоприема получается наибольшая потенциальная помехоустой-
чивость, является наилучшим.
Следует заметить, что теория оптимальных методов радиоприема,
давая руководящие принципы при конструировании радиоаппара-
туры и количественные характеристики оптимальных устройств,
не исключает творческую инициативу конструктора. Достаточно
указать, что иногда оптимальные устройства оказываются прак-
тически трудно реализуемыми. Конструктор также должен стремить-
ся свести к минимуму аппаратурные ошибки и учесть ряд факторов,
не принимавшихся во внимание при теоретическом рассмот-
рении.
Решение основных задач теории оптимального радиоприема
базируется на хорошо разработанных методах математической ста-
тистики. Непосредственное применение математической статистики
к решению прикладных задач радиотехники и автоматики было на-
чато А. Н. Колмогоровым, В. А. Котельниковым, Н. Винером и др.
в 50-х годах. В последующие годы и, особенно, в последнее десяти-
летие как у нас, так и за границей было выполнено много важных
исследований в этой области. Научно-прикладное содержание этих
исследований состоит в решении новых сложных задач, направлен-
ных на совершенствование радиотехнической аппаратуры.
В зависимости от целевого назначения разные системы передачи
информации работают в различных условиях и к ним предъявляются
разные требования. Исходя из этих требований, а также из методи-
ческих соображений, для типовых систем условно можно сформу-
лировать пять частных задач, рассматриваемых в теории. Ниже
приведен простой пример, позволяющий составить представление
о характере этих задач и, тем самым, о содержании настоящего раз-
дела. Конкретные условия, при которых в дальнейшем рассматри-
ваются аналогичные задачи, указаны в § 2.
Пусть на конечном временном интервале Т принимается колеба-
ние представляющее собой сумму полезного сигнала s(t) и
шума п(0:
£(/) = $(/) +«(0, 0</<Т.	(10.1.1)
Будем, например, считать, что сигналом является прямоугольный
радиоимпульс длительностью ти, который полностью укладывается
на интервале Т:
s(t}= Исоэ^ + ф), т<г<т + тй<Т, /1012)
U I 0	/<т, t>T,	\	)
где т — момент появления импульса.
В данном случае сигнал зависит от пяти параметров: ампли-
туды А, частоты со, начальной фазы ф, момента появления т и дли-
тельности ти. В значениях этих параметров может содержаться по-
394
лезная информация, которая должна быть извлечена из принятого
колебания ь результате приема.
Заметим, что если бы мы не располагали никакими предваритель-
ными сведениями о сигнале (т. е. о его параметрах), то его нельзя
было бы принять, так как было бы невозможно отличить сигнал от
любой помехи. Наоборот, прием сигнала с заранее известными пара-
метрами не дает никакой информации. Действительно, если заранее
известны все параметры сигнала, то его можно точно воспроизвести
па приемной стороне. Поэтому носителями полезной информации
могут являться только неизвестные параметры сигнала.
В дальнейшем интересующий нас параметр сигнала предпола-
laeTCH всегда неизвестным, а остальные параметры, все или частич-
но — известными. При решении конкретных задач наибольшие труд-
ности возникают тогда, когда имеется мало предварительных (апри-
орных) сведений о принятом сигнале.
После этих общих замечаний сформулируем основные задачи
[еории помехоустойчивости для принимаемого колебания
g (/) = A cos (o>i -ф ф) -ф и (О, 0<Д<Т.	(10.1.3)
1.	Обнаружение сигнала. Различение двух сигналов. Предпо-
ложим пока, что все параметры сигнала (10.1.2) не зависят от вре-
мени, причем частота, фаза и длительность импульса известны,
а амплитуда может принимать два значения: А = 0 (сигнал отсутст-
вует) с вероятностью рг и Л = Л0 0 (сигнал присутствует)
е вероятносгью р2 = 1—Pi- Требуется по принятой конкретной реа-
лизации £(0 на интервале Т оптимальным образом определить,
отсутствует или присутствует сигнал. (Основные критерии опти-
мальности указаны в § 1 гл. 11). Это — типичная формулировка
юдачи обнаружения сигнала на фоне шума, которая весьма характер-
на для радиолокации.
Задача обнаружения сигнала является частным случаем задачи
различения двух сигналов. Пусть в колебании (10.1.3) амплитуда
(.игнала А может принимать два значения: А = Д1 с вероятностью
piuA = Л з с вероятностью pa =1—рг. Нужно по принятой реали-
<ации колебания £(/) установить оптимальным образом, присутствует
ли сигнал с амплитудой Ai или с амплитудой Да. При Аг = 0 задача
различения двух сигналов переходит в задачу обнаружения сигнала.
Задачу различения двух сигналов можно сформулировать не
юлько относительно амплитуды, но и для любого другого пара-
метра сигнала, принимающего два значения (например, частоты,
фазы и т. д.). Эта задача характерна для различных систем передачи
бинарных символов и, в частности, для телеграфии.
2.	Различение нескольких сигналов. Пусть амплитуда сигнала
(10.1.2) может принимать только одно из п возможных значений Аъ
1з.	.. Ап, п>2, разделенных, например, интервалами квантова-
395
ния ЛА* = Ak+\ — Ak, причем известны априорные вероятности от-
дельных значений plt рг, рп. Требуется по принятой реализа-
ции g(^) решить оптимальным образом (т.е. с минимальной вероят-
ностью ошибки), какое именно из п возможных значений имеет ам-
плитуда. Результаты решения этой задачи могут быть использова-
ны, например, для целесообразного выбора интервалов квантова-
ния ДА*. Аналогично формулируется данная задача для других
параметров сигнала, принимающих несколько дискретных значе-
ний.
Задача различения нескольких сигналов является более общей
и сложной, чем задача обнаружения и различения двух сигналов.
С подобными задачами приходится сталкиваться в радиосвязи и те-
леуправлении.
3.	Оценка параметров сигнала. Пусть амплитуда А является
случайной величиной с плотностью вероятности И7(А). По принятой
реализации £(/) необходимо с минимальной погрешностью опреде-
лить значение амплитуды. Это простейшая, но типичная задача одно-
го из важных разделов теории помехоустойчивости — теории оцен-
ки параметров.
Если полезный сигнал зависит от нескольких случайных пара-
метров, то может быть поставлена задача о совместной оценке двух
и большего числа параметров. Например, применительно к сигналу
(10.1.2) можно говорить о совместной оценке времени появления
сигнала т и частоты со.
Задача оценки параметров характерна для измерительной
техники, радиолокации и радионавигации. Результаты решения
этой задачи характеризуют предельную точность измерения пара-
метров сигнала и позволяют составить структурные схемы соот-
ветствующих оптимальных измерительных устройств.
4.	Фильтрация сигналов. Пусть «амплитуда» А зависит от вре-
мени и представляет собой случайный процесс A (t) с известными ста-
тистическими характеристиками. Зная характер шума n(t), нужно
по конкретной реализации £(/), содержащей случайный процесс А(/),
решить оптимальным образом, какая именно реализация случайного
процесса А(/) присутствует в принятом колебании |(/). Задачи по-
добного типа рассматриваются в общей теории фильтрации.
Задача фильтрации переходит в задачу оценки параметра сигна-
ла, если оцениваемый параметр за время наблюдения Т не успевает
существенно измениться. Задача фильтрации является более общей
и сложной, чем задача оценки параметров.
Задачи фильтрации возникают в радиосвязи (выделение речевого
сообщения из шума), в телевидении (выделение телевизионного
сообщения из шума), в радиолокации (непрерывное определение
дальности и допплеровского смещения частоты) и т. д.
5.	Разрешение сигналов. Пусть принятое колебание g(^) пред-
ставляет сумму шума n(t) и двух сигналов s^t, Х2, Х3) и
s2( t, Zi,XaA3), зависящих от трех параметров Х2, Х3:
396
£(/) — sl G» ^1»	^s) + S2 (Л ^1, ^2, X8) H“ П (/),
/о<7<7о+Г.	(10.1.4)
Априорные вероятности появления каждого из сигналов считаются
известными. Предположим, что параметр Хх является случайным и
статистические характеристики остальных параметров Хг, Хз из-
вестны.
Задачу разрешения двух сигналов можно сформулировать сле-
дующим образом. При возможности одновременного наличия двух
i игналов необходимо по принятой реализации £(/) разрешить опти-
мальным образом два сигнала по параметру Хх. В понятие «разре-
шить» можно вкладывать различный смысл. Можно, например,
иметь в виду только раздельное обнаружение сигналов или же как
раздельное обнаружение, так и определение значений парамет-
ров Хх в двух сигналах.
Задача разрешения может быть обобщена на случай нескольких
параметров и многих, а не двух сигналов. Необходимая разрешаю-
щая способкость, как правило, обеспечивается подбором наилучших
видов сигналов и оптимальной обработкой принятого колебания.
Выше условно указаны пять основных задач, тесно связанных
между собой. В дальнейшем не все эти задачи будут рассмотрены
одинаково додробно. Однако будут приведены соображения, касаю-
щиеся всех перечисленных задач.
§ 2. ОБЩАЯ ХАРАКТЕРИСТИКА СИГНАЛОВ И ПОМЕХ
Пусть сигнал, излучаемый передающей антенной, является ква-
зигармоническим:
s„ (0 = f (Qcos [®/ + ф (t)].	(10.2.1)
Это означает, что функции /(/) и ф(/), отображающие законы ампли-
тудной и частотной модуляции, медленно изменяются по сравнению
с колебанием несущей частоты cos®/. Поэтому сигнал яи(/) будет уз-
кополосным: ширина А® его спектра много меньше несущей часто-
ты ®, т. е jA®|<^®.
При выбранной форме передаваемого сигнала (10.2.1) вид полез-
ного сигнала в месте приема существенно зависит от параметров ли-
нии, по которой он передается. Например, при одном и том же пере-
даваемом сигнале sH (/) принимаемый сигнал в радиолокации и в раз-
личных системах радиосвязи (наземной, ионосферной, тропосферной,
метеорной, космической и др.) будет несколько разным.
Не касаясь детального рассмотрения различных линий связи [1],
укажем, что при распространении электромагнитных колебаний
через турбулентную среду и вследствие изрезанности диаграмм на-
правленности антенн, полезный сигнал в месте приема $(/) во мно-
397
гих случаях можно представить в виде суммы двух составляю-
щих: детерминированной и случайной, т. е.
s (t) = af (t — т) cos [со/ Ц-ф (/ — т)—6] +
4~Р (/)cos [со/4-ф (/ — т) — е (/)].	(10.2.2)
Здесь а и 6 представляют собой амплитудный коэффициент и фазо-
вый сдвиг детерминированной составляющей сигнала (а и 6 — пос-
тоянные величины), а Р и 8 — амплитудный множитель и фазовый
Рис. 10.1. Соотношение между
а, 0, а, М и е.
сдвиг случайной составляющей. Ве-
личина т характеризует время за-
паздывания принимаемого сигнала.
Сигнал (10.2.2) можно записать
иначе в виде квазигармонического
колебания:
s (/) = а (/) f (/ — т) cos [со/ 4-
+ Ф(/ —т) —0(/)],	(10.2.3)
где
a cos 0 = a cos б р cos 8,
а sin 0 = а sin 6 4- р sine.
Соотношение между а, 0,а, 6, р и 8 показано на рис. 10.1. Множитель
а(/) характеризует замирания (фединги) радиосигнала и 0 — фазо-
вый сдвиг по несущей частоте.
Будем считать, что Р и е представляют собой независимые слу-
чайные величины, причем Р распределена по закону Релея, а
е — равномерно на интервале (—л, л):
BMP, s)
В	/ R2 \
•н^-g-exp —, Р > 0, — л<е<л,
2л:а2 г 2з2) г >	’ 00 2.4)
0	при других Р, 8.
В § 4 гл. 7 было показано, что при сделанных предположе-
ниях совместная плотность вероятности случайных величин а и
6 определяется формулой вида (7.4.7):
№2(а, 0) =
а (	а2-^а2—2aacos(0—Ь))	. n si
₽ехр{-16-б|<л, (Ш 2 5)
0	при других а, 0.
Интегрируя (10.2.5) по 0 и а, получим одномерные плотно-
сти вероятности для случайных величин а и 6:
398
lt7H = ^expU^2^l/0^) а>0,	(10.2,6)
F (0) = ~ е~т + tCO5(6_~^ Ф [у cos (6 — 6)]	1‘5in2(<1~5))
(10.2.7)
| 0 —б|С Л, Т =-J-.
Так как формулы (10.2.6) и (10.2.7) совпадают соответственно с фор-
мулами (7.5.1) и (7.6.1), то для W(a) и 117(0) будут справедливы гра-
фики, прш еденные на рис. 7.9 и 7.11.
Оказывается, выбранная модель принимаемого сигнала (10.2.5)
удовлетворительно описывает флуктуации отраженного сигнала
в радиолокации и фединги во многих системах радиосвязи. В радио-
локации часто полагают а = 0 и ограничиваются рассмотрением
случая, коща амплитуда отраженного сигнала флуктуирует по реле-
евскому закону. Результаты экспериментальных исследований мед-
ленных замираний сигналов в радиолиниях, использующих ионо-
сферное ши тропосферное рассеяние, показывают, что фединги
is таких системах описываются также законом Релея и имеют квази-
стационаркый характер на временных интервалах порядка несколь-
ких минут Для систем радиосвязи, использующих отражение от
ионосферы, в (10.2.5) величины а и о должны определяться экспе-
рииенталыо и, как правило, имеют конечные значения, так как
в таких системах принимаемый сигнал содержит как регулярную
(зеркальную), так и случайную (рассеянную) составляющие.
В выбранной модели принимаемого сигнала (10.2.3) некоторые
параметрымогут быть заранее (до приема) известными или неизвест-
ными. Предварительно известные статистические характеристики
части параметров сигнала составляют априорные сведения отно-
сительно сигнала. Априорные сведения о сигнале могут быть пол-
ными (полностью известна статистика сигнала), неполными (изве-
стна статистика лишь части параметров сигнала) или отсутство-
вать совсем (полностью неизвестна статистика сигнала). Чем боль-
шими априорными сведениями мы располагаем, тем проще и точ-
нее решаюгся задачи. Поэтому всегда следует стремиться к тому,
чтобы разумно и в полной мере использовать всю априорную ин-
формацию о сигнале и шуме.
Априорное знание статистики сигнала может быть получено на
основе предварительного статистического анализа как самих сооб-
щений, так и радиосигналов, если, конечно, в прошлом существовал
ансамбль ситуаций, аналогичных условиям данного приема.
В радиосвязи, телевидении и телеуправлении, как правило, апри-
орная статдстика сигнала известна в большей мере, чем в радиолока-
ции, радионавигации и измерительной технике.
В радюсвязи сообщения передаются при помощи русского
1екста (радиотелефония) или заранее известного кода (радиотеле-
399
графия). На основании анализа русского текста можно подсчитать
вероятность появления отдельных букв или соответствующих сим-
волов кода, а также вероятности появления различных двубуквен-
ных, трехбуквенных и т. д. сочетаний. В настоящее время такие
данные уже известны (см. § 6 гл. 15).
Аналогичное положение имеет место в телеуправлении, где в ка-
честве сообщений обычно используется набор конечного числа типо-
вых символов, а также при передаче изображений в телевидении
(например, при помощи квантованных сигналов).
В радиолокации, радионавигации и измерительной технике мы
часто располагаем меньшими априорными сведениями как о вероят-
ности появления сигналов, так и о статистике отдельных параметров
сигнала. Так, например, применительно к измерению задержки т
(дальности до цели) в отраженном радиолокационном сигнале за-
труднительно заранее указать соответствующую плотность вероят-
ности.
С учетом априорных сведений о сигнале в дальнейшем при реше-
нии отдельных задач теории оптимального радиоприема будут рас-
смотрены следующие частные виды радиосигналов.
1.	Сигнал с полностью известными параметрами*
5(/) = ) (/ —т0)со.8[о)а/+ф(/— т0) —90], /0</<4+ти.	(10.2.8)
В данном случае все параметры сигнала считаются известными.
В задаче обнаружения остается неизвестным лишь факт наличия
сигнала.	И
2.	Сигнал со случайной начальной фазой
— т0)cos [ю0 ^+ф (t — т0) — 0], /0 < t < ^0+ти.	(10.2.9)
Все параметры сигнала предполагаются известными, за исключением
начальной фазы 0, которая считается случайной величиной, равно-
мерно'граспределенной на интервале (—л, л).
3.	Сигнал со случайными амплитудой и начальной фазой
s(/)=a/(Z — t)cos [со^+ф (t— т) — 6], t0 < t < £0-|-Ти.	(10.2.10)
Будем предполагать, что а и 0 являются независимыми случайными
величинами, причем а распределена по закону Релея, а 0 — равно-
мерно’на интервале (—л, л).
4.	Если сигнал s(t) представляет ’ собой последовательность
(пачку ) из нескольких радиоимпульсов, то следует различать коге-
рентную и некогерентную пачки импульсов. Пачка, в которой на-
чальная фаза первого импульса случайная, а изменение фазы от им-
пульса к импульсу является закономерным (детерминированным),
называется когерентной. Если же фазы отдельных импульсов слу-
чайны и независимы, то пачка называется некогерентной. Амплиту-
* В дальнейшем известные параметры сигнала, как правило, отмечены
нулевым индексом.
400
чы импульсов в пачке могут изменяться по детерминированному или
случайному законам.
Определив основные виды сигналов, укажем некоторые характе-
ристики рассматриваемых помех. В различных радиотехнических
устройствах приходится сталкиваться с различными видами помех.
Однако во всех случаях является общим и характерным наличие
нормального флуктуационного шума, обусловленного естественны-
ми причинами, которые не могут быть устранены (тепловые и другие
шумы окружающего пространства и собственные шумы радиоприем-
ных устройств). Тепловые шумы пространства, окружающего при-
емную антенну, принимаются антенной вместе с полезным сигна-
лом и складываются с собственным шумом радиоприемного
устройства.
Напомним, что без учета потерь между антенной и приемником
величина мощности шумов на входе радиоприемного устройства Рп
выражается через коэффициент шума kn формулой [21:
Pn=kTobfa(kn + tA-V),	(10.2.11)
где k = 1,38 -10~23 дж/град — постоянная Больцмана;
То = 290° К — стандартная (комнатная) температура в граду-
сах Кельвина (kT(1 = 4-10~21 вт/гц);
— энергетическая полоса пропускания линейной
части приемника до детектора (см. табл. 3.14.1).
tA — Т\/То — относительная шумовая температура приемной
антенны, имеющей абсолютную шумовую тем-
пературу излучения ТА.
Собственный шум радиоприемника и тепловые шумы окружаю-
щего пространства складываются линейно с полезным сигналом на
входе приемника. Помехи, которые складываются (суммируются)
с сигналом линейно, называются аддитивными помехами.
Так как часто только аддитивный нормальный шум является
случайной помехой, то значительное внимание было уделено реше-
нию задач теории помехоустойчивости для случая, когда приня-
тым колебанием является сумма (аддитивная смесь) полезного сиг-
нала и нормального шума. Наличие других случайных помех, от-
личных от нормального шума, существенно усложняет задачу.
К настоящему времени многие конкретные задачи получили за-
конченное решение для случая приема сигналов на фоне нормаль-
ного шума. В дальнейшем будут рассмотрены некоторые из этих
.адач, причем для простоты будем считать нормальный шум белым.
)то предположение упрощает математические вычисления.
Итак, в дальнейшем будем предполагать, что полезный сигнал
s(Z) принимается на фоне аддитивного нормального белого шума
n(f) с нулевым средним значением, т. е. колебание |(^), принятое на
конечном интервале времени Т, представляет собой случайный
процесс
£(O = s(Z) + «(fy	(102.12)
401
Здесь белый шум n(f) имеет следующие основные характеристики:
<п(ф=0,	(10.2.13)
где Ао — физически измеряемая спектральная плотность шума;
6 (г) — дельта-функция.
§ 3. АПОСТЕРИОРНАЯ ВЕРОЯТНОСТЬ
При решении задач теории помехоустойчивости ответ должен
быть получен на основе предварительных (априорных) сведений и
анализа принятых данных.
По сравнению лишь с некоторыми априорными сведениями
о принятом колебании, знания наблюдателя об исследуемой ситуа-
ции в результате анализа принятого колебания увеличиваются.
Вновь сформированное знание называется апостериорным.
Анализ и обработка принятого колебания %(t) с целью принятия
определенного решения могут осуществляться двумя методами;
дискретным и непрерывным.
Если наблюдение производится в отдельные моменты времени
(дискретное наблюдение), то информация о принятых данных будет
заключена в случайных величинах = ё(^1), ,	= пред-
ставляющих выборочные значения принятого колебания l(t) в Мо-
менты времени А> •••, tm Из интервала наблюдения Т:	+
+ Т, i = 1, 2, m. Чаще всего дискретные значения берутся
через равноотстоящие моменты времени, т. е. h — tt~i ~ Д = const.
Выборочные значения принятого колебания £(/) описываются сов-
местной плотностью вероятности U7m(Si, £2. |m),	а соответствую-
щие выборочные значения шума n(t) —плотностью вероятности
Щт(п1; П.2, ..., п„).
Предположим, что производится дискретное наблюдение, и
сигнал
s(t) = s(t, %)	(10.3.1)
зависит от одного неизвестного параметра Л, имеющего априорную
плотность вероятности W (X).
Все то, что можно узнать о параметре Л после приема колеба-
ния g(t) заключено в условной вероятности
ГРЛХ) = Г(Х|^,...,^),	(10.3.2)
называемой апостериорной вероятностью.
Согласно известной теореме об умножении вероятностей (1.5.1)
имеем
Г (X; ёр ..., U) =	UWi..........и =
^=^Г(Х)Г(^, ...,^х),	(10.3.3)
402
Отбрасывая левую часть равенства и учитывая, что	•
не зависит от интересующего нас параметра Л, на основании фор-
мул (10.3.2) и (10.3.3) можем написать
Wps(K) = kWpr(K)W(^....U4	(10.3.4)
। де коэффициент k определяется из условия нормировки.
Рассматриваемая как функция от X, условная вероятность
1У(^, ...,gm|X) называется функцией правдоподобия. (Иногда функ-
цию правдоподобия определяют как In 1(7). При фиксированных зна-
чениях £i...она показывает, насколько одно возможное значе-
ние параметра Л «более правдоподобно», чем другое. Обозначим
функцию правдоподобия через Л(Х):
(Ю.3.5)
1огда формулу (10.3.4) можно записать в окончательном виде
Wps^)=-kWpr^)L^),	(10.3.6)
। де
fe = [J^r(X)£(l)dx]"'.	(10.3.7)
Формула (10.3.6), по существу, аналогична формуле (1.7.1)
и представляет математическую запись теоремы Байеса. Напомним,
чго теореьса Байеса показывает, каким образом из априорных данных
н результатов анализа принятого колебания формируется апосте-
риорное знание.
Формула (10.3.6) может быть обобщена. Если параметр Л может
принимать только одно из нескольких дискретных значений Л,г,
...... то можем написать
Wps^S^kWpT(^)L(K), i = 1, 2, .... v, (10.3.8)
। Де
k = 2 wPr<ML (Ч)Г'-	(Ю.з.9)
. «=1
Если сигнал зависит от р параметров Xj, Ч, Ч> т. е.
sit) = s(t, Ч, ..., Ч),	(10.3.10)
io формула принимает вид:
.................. Ч) = kWpr(Klt ЧН(Ч.........Ч). (Ю.3.11)
I де
k = [Г ... f^r(4,	Ч)£(Ч, .... ЧИЧ ...	(10.3.12)
Из формул (10.3.6), (10.3.8) и (10.3.11) видно, что при известных
шриорных плотностях вероятностей нахождение апостериорных
иероятностей сводится к вычислению функций правдоподобия.
403
В том случае, когда принятое колебание представляет аддитивную
смесь сигнала и шума, т. е.
g(Z) = s(0 + «(0>	(10.3.13)
и многомерные плотности вероятности шума wm(nlt ..., пт) известны,
функции правдоподобия вычисляются сравнительно просто. В дру-
гих же случаях их вычисление представляет весьма сложную зада-
чу.
В дальнейшем мы ограничимся рассмотрением того важного, но
частного случая, когда принятое колебание представляет собой
аддитивную смесь (10.2.12) полезного сигнала s(t) и нормального
белого шума n(t). При этом значение спектральной плотности шума
No будем предполагать известным.
Рассмотрим простейший метод дискретного наблюдения, когда
отсчеты берутся через равноотстоящие моменты времени. Разобьем
интервал времени (t0, to + Т) равноотстоящими точками ..., tm,
где tt — ti-i = Д = const, i— 1, 2, .... т. Обозначим средние за
элементарный интервал времени значения колебания Ш). сигнала
s(Z, X) и шума n(t) соответственно через
ъ = Г st(X) = 4- ( sw
'А
h	(10.3.14) ‘
Очевидно, что
(10.3.15)
Будем считать, что в выражении для функции правдоподобия
(10.3.5) фигурируют указанные средние значения^/. При этом имеет-
ся ввиду, что в дальнейшем нас будет интересовать предельный слу-
чай Д -> 0.
Вычислим сначала совместную плотность вероятности для слу-
чайных величин nt, i = 1, 2, ..., т. Случайные величины n-t яв-
ляются нормально распределенными и согласно (10.2.13) имеют
следующие характеристики:
<«£>=0,	=	=	<«,^>=0 при i4=j.
Поэтому совместная плотность вероятности имеет вид

404
Подставляя значения щ из (10.3.15) в формулу (10.3.5) и учи-
тывая, что якобиан преобразования от переменных к переменным
h равен единице, получаем формулу для функции правдоподобия
параметра X:
=	.... UP9 =^(?i-Si(X), ..., ^m-sm(X)). (10.3.17)
Таким образом, при дискретном наблюдении формула (10.3.6)
принимает следующий окончательный вид:
Wp^) = kWpr(K)L(K),
(10.3.18)
где
.	...____т_
L (X) = fit -дЛ 2 ехр
т
(О-5(^Л)]2А
i=l
(10.3.19)
Если параметр X может принимать несколько значений Xi, Х2.
X», то в формулу (10 3.8) нужно подставлять функцию правдоподо-
бия при соответствующем значении параметра X.
Путем аналогичных рассуждений нетрудно убедиться, что для
сигнала (10.3.10), зависящего от нескольких параметров, функция
правдоподобия, входящая в формулу (10.3.11), имеет вид:
L (Х1( .... Хи) = (к 2 ехр - -1- £ [£(Q -S(^,Xb..., ХР)]2Д ..
»=i
(10.3.20)
Рассмотрим теперь случай непрерывного наблюдения. Чтобы пе-
рейти к случаю непрерывного наблюдения, нужно в формулах
(10.3.16), (10.3.19) и (10.3.20) перейти к пределу при А 0. При этом
информация о случайном процессе £(£) будет заключена в форме реа-
лизации, т. е. в том, какой конкретный вид имеет функция £(Z)
на интервале (/0, £0~Ь Т). Разумеется, что при непрерывном наблю-
дении получаются более точные результаты, чем при дискретном,
так как в случае непрерывного наблюдения используется информа-
ция, содержащаяся во всей реализации £(£), а не только в отдельных
выборочных значениях ..., ^т. При А ->0 плотности вероятности
Wm и перейдут в соответствующие функционалы вероятности,
а функция правдоподобия — в функционал правдоподобия [3].
Введем для них следующие обозначения:
W [п (01 = lim /гд wm (пъ ..., пт),	(10.3.21)
Д-о
zn->oo
F (X) - lim L (X),	(10.3.22)
д-о
m-fco
405
где множитель k±, зависящий только от А, подбирается так, чтобы
предел имел смысл.
Осуществляя предельный переход при соответствующем подбо-
ре £д, получим
W7 [п (/)] = ехр
<о+Т
-i ] n2(t)di
i*e
f	^о"ЬТ
f(X) = exp-^_
' К
(10.3.23)
(10.3.24)
Таким образом, при непрерывном наблюдении формула (10.3.6)
принимает следующий окончательный вид:
Wpi(K)--=kWpr(K)F(K),
(10.3.25)
где FCk) — функционал правдоподобия (10.3.24).
В аналогичном виде можно записать формулу (10.3.11)
Wps(\, ..., М = kWpr^, ..., KJFfa, ХД (10.3.26)
где
F(Xx,
При решении некоторых задач приходится оперировать не с са-
мими функционалами, а с их отношением, в частности, с отношением
правдоподобия. Отношение правдоподобия представляет собой от-
ношение функционалов (функций) правдоподобия при наличии и
отсутствии сигнала и определяется формулой вида
ехр
/ /П - FW - _
4 1 ~ W [5(0]
t, нт
— s(t,
(10.3 28)
/Vo J
	^0_______
/о+Г
ехр
Если в формулы (10.3.25) и (10.3.26) вместо функций правдопо-
добия подставить отношение правдоподобия, то получим
Wps(M — k0Wpr(k) I (К),	(10.3.29)
Wp,(Kh ..., X,) = koW^, ..., X11)Z(X1, ..., ХД (Ю.3.,30)
где k0 — некоторый постоянный коэффициент.
406
Имея в виду, что в дальнейшем окончательное решение задач
истся на основании отношения правдоподобия, для сокращения
математических записей мы будем пользоваться на промежуточных
папах функционалами. Конечно, можно поступить иначе: сначала
оперировать с многомерными плотностями вероятностей и функция-
ми правдоподобия, а затем в конечных результатах (где входит их
отношение) переходить к пределу при Л - > 0.
Продуктивность использования функционалов в теории опти-
мального радиоприема была убедительно показана в монографии
II Н Амиантова [3], являющейся одной из первых
§ 4. СТРУКТУРА АПОСТЕРИОРНОЙ ВЕРОЯТНОСТИ В ЧАСТНОМ
СЛУЧАЕ
Рассмотрим на простейшем примере использование апостериорной
pi роятности и методику формирования ее, а также выясним качест-
ва ппо влияние на апостериорную вероятность отдельных фак-
|<>рОВ.
Пусть осуществляется радиолокационное измерение расстояния
ю одной неподвижной цели по запаздыванию отраженного импульс-
ною сигнала. Обозначим излученный радиоимпульс через sH(^),
। отраженный от цели сигнал, принимаемый приемником, — через
U — т). Длительность сигнала s(t— т) равна тн<7\ где Т —
интервал наблюдения. В случае импульсной радиолокации под Т
нжно понимать интервал времени между соседними излученными
импульсами периодической последовательности. Будем считать,
•но все параметры сигнала, за исключением временного запаздыва-
нии т, известны. Возможные значения параметра т заключены внутри
инюрвала (0, Г) с известной априорной плотностью вероятности
11 \ г (т).
В данном случае назначение приемника-измерителя состоит
и юм, чтобы на основе анализа принятого колебания
£ (/) = s (/ — т) + п (0, о < t < Т,
определить с минимальной погрешностью величину т.
Согласно § 3 вся доступная информация о параметре т дается
н нремой Байеса (10.3.25), которая применительно к рассматривае-
и му случаю принимает вид:
= kWpr(T} ехр
s (/ — т)]М/
(10.4.1)
407
Упростим это выражение. Для этого распишем показатель
экспоненты:
т	т
О	о
т
+ <10-4-2>
о
где через Е обозначена энергия (интеграл от квадрата) принятого
сигнала
т
Е = J s\t — r)dt.	(10.4.3)
о
Если сигнал представляет напряжение, то величина Е равна энергии,
выделяемой на сопротивлении потерь 1 ом в течение времени Т.
В правой части равенства (10.4.2) первое слагаемое, равное отно-
шению энергии принятого колебания к спектральной плотности
шума, не содержит информации об интересующем нас параметре
т, так как оно не зависит от т. Поэтому в формуле (10.4.1) множитель
т
ехр J можно включить в постоянную k. Таким об-
о
разом, можем написать
^(т) = kWpr (т) ехр (- ехр [<? (т)],	(10.4.4)
где
т
О
Во многих случаях множитель ехр (—E/No) можно также вклю-
чить в постоянную k. В данном случае это оправдано тем, что энер-
гия сигнала предполагается независящей от его запаздывания т;
в других случаях обычно ограничиваются рассмотрением (сравне-
нием характеристик) сигналов, обладающих одинаковой энергией.
Следовательно, формулу (10.4.4) можно записать так:
= ^^г(т)ехр[д(т)].	(10 4.6)
Экспоненциальная функция изменяется монотонно в зависимости
от значений своего показателя. Поэтому функция q(r) с определен-
ной деформацией воспроизводит характер изменения апостериорной
вероятности. Отсюда следует, что при известной априорной ве-
408
роятности определение апостериорной вероятности эквивалентно
вычисление функции q(x).
Таким образом, первый и главный этап при обработке принятого
колебания е целью получения апостериорной вероятности параметра
। состоит в вычислении функции <?(т) согласно формуле (10.4.5).
-)та функция определяет ту существенную операцию, которую нужно
выполнить над принятым колебанием, чтобы извлечь всю доступ-
ную информацию о параметре т, содержащуюся в реализации 5(0.
Как следует из формулы (10.4.5), для получения <?(т) необходимо
располагать копией сигнала s(0 на приемной стороне. На рис. 10.2
приведена функциональная схема устройства, позволяющего полу-
чить функцию q(x).
Рис. 10.2. Упрощенная схема кор-
реляционного приемника.
Правая часть формулы (10.4.5) с точностью до постоянного мно-
,кителя напоминает выражение для функции взаимной корреляции
между 5(0 и s(t — т). Поэтому можно сказать, что функция q(x)
характеризует меру «взаимной корреляции» между принятым коле-
банием 5(^ и полезным сигналом s(t — т). Соответственно этому
хегройство, изображенное на рис. 10.2, можно условно назвать
корреляционным приемником.
Функцию взаимной корреляции q(x) можно получить не только
при помощи корреляционного приемника, но также и при помощи
(оответств^ющим образом подобранных фильтров, которые назы-
ваются согласованными (см. § 6).
Пусть истинное значение параметра т в принятой реализации
5(0 равно т0, т. е.
g(0 = s(t-x0) + n(t).	(10.4.7)
11одставивэто выражение 5(0 в (10.4 5), функцию q(x) можно пред-
ъявить в виде суммы двух слагаемых:
Я Й) = qДт) -ф qn (т),	(10.4.8)
। ле
о Г
qs Д) = v; I s ~ то) S (/ — т) dt,	(10.4.9)
о
т
9 С*
= n(t)s(t — x)dt.	(10.4.10)
о
409
Функция <7s(t), получаемая на выходе корреляционного прием-
ника, представляет собой «автокорреляционную функцию» входного
полезного сигнала, и ее можно назвать сигнальной функцией. Функ-
ция <7„(т), воспроизводимая на выходе приемника и обусловленная
шумом, есть «функция взаимной корреляции» между шумом и вход-
ным полезным сигналом; ее можно назвать шумовой функцией.
Существенное различие между сигнальной и шумовой функциями
состоит в том, что первая при каждом фиксированном значении т
является детерминированной, а вторая — случайной. Говоря
о случайном характере шумовой’ функции qn (т), имеют ввиду,
что даже при детерминированном сигнале. s(t— те) конкретный вид
этой функции из-за шума n(t) будет различным для разных реали-
заций (10.4.7).
Рассмотрим характер сигнальной и шумовой функций. Покажем,
что сигнальная функция имеет максимум при т = т0, равный
Ь™Ит«)=“=<г-	(10.4.11)
Действительно, из очевидного неравенства [s (t — т0) — s (t — т)]2>0
имеем	s2 (t — т0) -f- s2 (/ — т) > 2s (t — т0) s(t — т).
Правая .часть этого ^соотношения при любых т и т0 не может превы-
шать значение левой части. Однако при т = т0 имеет место знак
равенства. Следовательно, произведение 2s(/ — t0)s(/ — т) мак'
симально при т = т0 и равно 2s2(t—т0). Полагая в формуле
(10.4.9) т = т0, получим (10.4.11)
В качестве примера вычислим сигнальную функцию для прямо-
угольного видеоимпульса длительностью ти:
5(|_то)=|л I‘I<т"/2,
(0 при \t— т01 > ти/2.
Под т0 понимается момент времени, соответствующий средине им-
пульса. Рассматривая раздельно случай т<т0 (рис. 10.3, а) и слу-
чай т>т0 (рис. 10.3, б), интегрируя в обоих случаях по заштрихо-
ванным участкам, где подынтегральное выражение в (10.4.9) отлич-
но от нуля, получим
<МТ)= ^0(l — -T~Toi) при |т —т0|<ти. (10.4.12)
Сигнальная функция изображена на рис. 10.3, в. Она представляет
собой равнобедренный треугольник с основанием 2ти и высотой
7.-=тм(то) = 2E/No, где Е = Л2ти.
Выясним теперь структуру шумовой функции qn (т). Формула
(10.4.10) показывает, что функция </д(т) получается ^з нормального
410
| лого шума путем линейного преобразования. Поэтому шумовая
рункция при каждом фиксированном значении т имеет нормальную
। i пность вероятности. Согласно (10.2.13) среднее значение шумовой
Пункции равно нулю
г
9 Р
«7л(т)>=-^ <« (0>	= 0,	(10.4.13)
b
। для дисперсии получим формулу
т т
-- <?nW> = ^2 J J <«(^i)«(^)> s(^i — T)s(/2 — t)dttdt2 =	.
° 0 0
(10.4.14)
a)
S)
S(t r) S(t-T-0)
Рис 10.3. Сигнальная функция для прямоуголь-
ного импульса.
Обращает на себя внимание тот факт, что как максимальное зна-
чение сигнальной функции, так и дисперсия шумовой функции рав-
ны одной и той же величине
<2-^.	(10.4.15)
Назовем величину Q, равную отношению удвоенной энергии
 и,нала к спектральной плотности шума, отношением сигнал/шум
по мощности на входе приемника. В дальнейшем мы убедимся, что
величина Q входит во многие соотношения и играет фундаменталь-
ную роль.
411
Если учитывать мощность шумов радиоприемника по формуле
(10.2.11) и вместо энергии Е ввести импульсную мощность сигнала
на входе приемника Ps = Е/тъ, то для Q получим следующую фор-
мулу:
1,  <10А16>
Это отношение сигнал/шум практически получается на выходе согла-
сованного УПЧ (см. § 6).
Для выяснения характера изменения шумовой функции в зави-
симости от т найдем «функцию корреляции» для qn(x). Воспользо-
вавшись формулами (10.4.10) и (10.2.13), получим
т т
<.Яп Си) Яп (т2)> = J J	(f х) п (t2)y s (/х — тх) S (/2 — т2) dti dt2 =
° о о
т
= -^JS(/-Tx)S(/-T2)Jt	(10.4.17)
о
Сравнивая подынтегральные выражения в формулах (10.4.9)
и (10.4.17), замечаем, что они по характеру одинаковы. Следова-
тельно, корреляционная функция для дДт) по форме подобна сиг-
нальной функции дДт), т. е. автокорреляционной функции сигнала
на входе. Но функция корреляции случайного процесса дает неко-
торое представление о характере изменения его во времени. Поэтому
можно сказать, что операция образования функции взаимной корре-
ляции (10.4.5) сопровождается «выравниванием» временных струк-
тур сигнальной и шумовой функций.
В то время как в принятом колебании £(0 сигнал s(/) и белый
шум n(t) существенно различаются по характеру изменения во
времени, «сигнал» qs и «шум» qn на выходе корреляционного прием-
ника или согласованного фильтра становятся подобными друг
другу. Иначе говоря, корреляционный приемник или согласован-
ный фильтр устраняют существенное различие во временном пове-
дении сигнала и шума.
Не следует думать, что «выравнивание» временных структур
сигнальной и шумовой функций затрудняет определение истинного
значения интересующего нас параметра т. Наоборот, операция обра-
зования функции взаимной корреляции (10.4.5) обеспечивает наилуч-
шую фильтрацию сигнала из шума, давая по сравнению с другими
возможными операциями максимальное отношение сигнал/шум.
Таким образом, «выравнивание» временных структур сопровож-
дается улучшением амплитудных различий сигнала и шума или,
иначе, существенным понижением шумового фона qn, на котором
наблюдается сигнал qs. В этом и состоит сущность образования
функции взаимной корреляции (10.4.5).
412
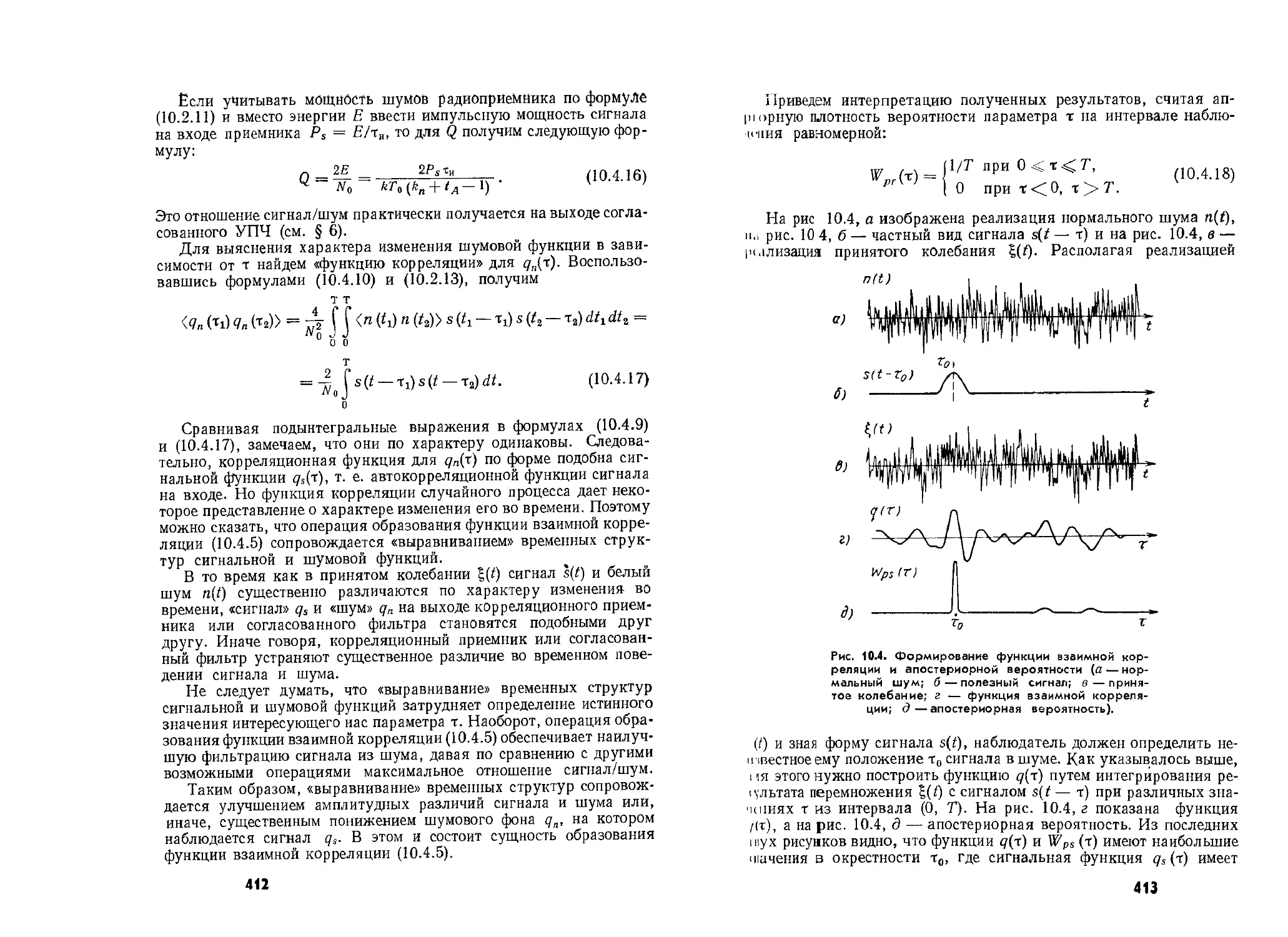
Приведем интерпретацию полученных результатов, считая ап-
рюрную плотность вероятности параметра т на интервале наблю-
вния равномерной:
”|)И	(10.4.18)
( 0 при т < 0, т > Т.
На рис 10.4, а изображена реализация нормального шума n(t),
।i.i рис. 10 4, б — частный вид сигнала а(/ — т) и на рис. 10.4, в —
рылизация принятого колебания £(/). Располагая реализацией
Рис. 10.4. Формирование функции взаимной кор-
реляции и апостериорной вероятности (а — нор-
мальный шум; б — полезный сигнал; в — приня-
тое колебание; г — функция взаимной корреля-
ции; д—апостериорная вероятность).
(О и зная форму сигнала s(t), наблюдатель должен определить не-
известное ему положение т0 сигнала в шуме. Как указывалось выше,
। ш этого нужно построить функцию д(т) путем интегрирования ре-
цльтата перемножения с сигналом з(/ — т) при различных зна-
кпиях т из интервала (0, Т). На рис. 10.4, г показана функция
/(т), а на рис. 10.4, д — апостериорная вероятность. Из последних
। пух рисунков видно, что функции q(t) и Wps (т) имеют наибольшие
шачения в окрестности т0, где сигнальная функция qs (т) имеет
413
максимум. Поэтому в качестве оценки истинного значения т0 пара-
метра т можно принять то значение т = т*, при котором апостериор-
ная вероятность имеет максимум максиморум. Погрешность измере-
ния можно характеризовать шириной (на определенном уровне) апо-
стериорной вероятности в окрестности максимума максиморума.
Подробное рассмотрение вопросов, связанных с выбором критериев
оценки параметров, будет приведено в § 1 гл. 12.
Q-0
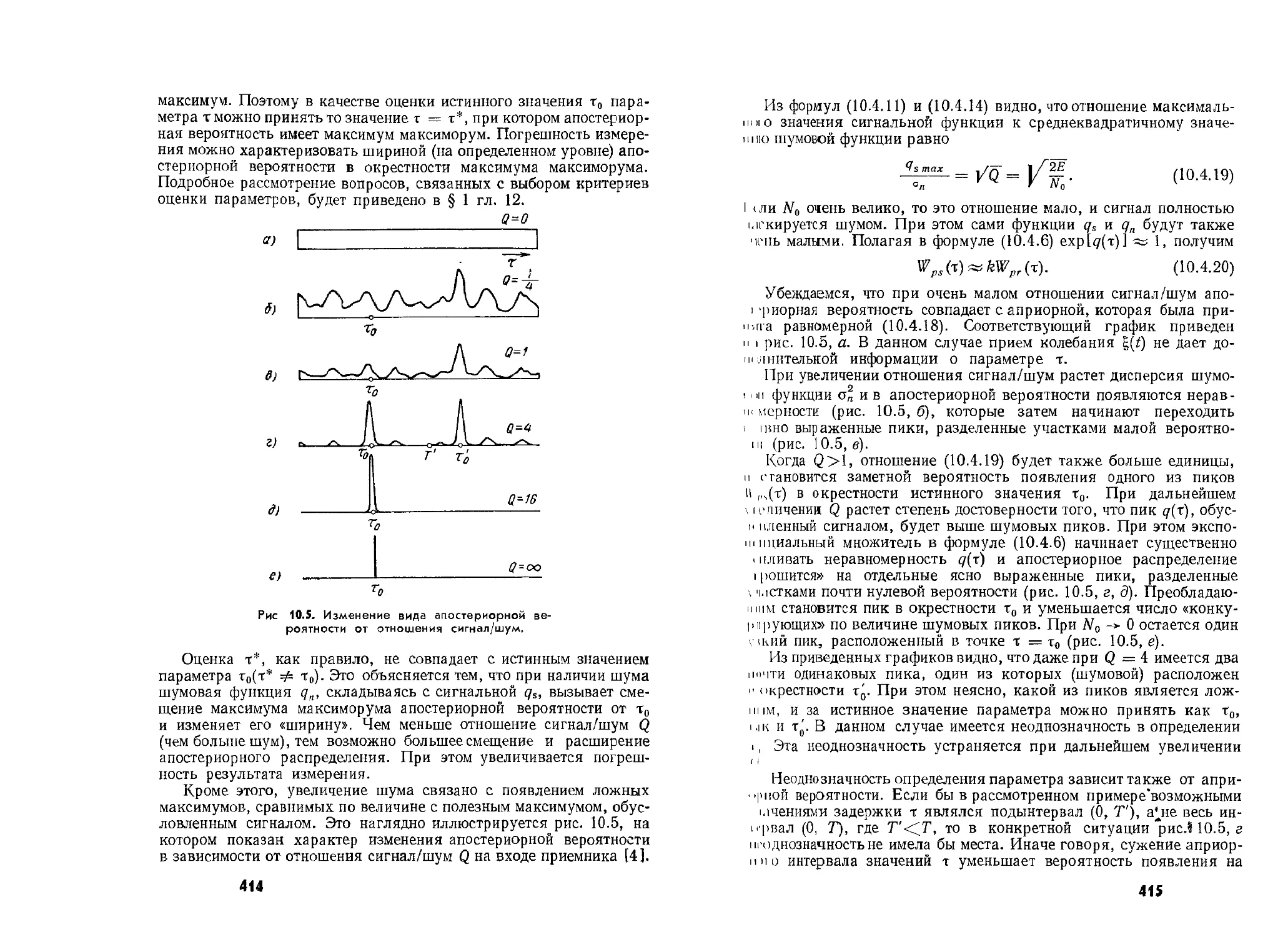
Рис 10.5. Изменение вида апостериорной ве-
роятности от отношения сигнал/шум.
Оценка т*. как правило, не совпадает с истинным значением
параметра т0(г* =# т0). Это объясняется тем, что при наличии шума
шумовая функция qn, складываясь с сигнальной qs, вызывает сме-
щение максимума максиморума апостериорной вероятности от т0
и изменяет его «ширину». Чем меньше отношение сигнал/шум Q
(чем больше шум), тем возможно большее смещение и расширение
апостериорного распределения. При этом увеличивается погреш-
ность результата измерения.
Кроме этого, увеличение шума связано с появлением ложных
максимумов, сравнимых по величине с полезным максимумом, обус-
ловленным сигналом. Это наглядно иллюстрируется рис. 10.5, на
котором показан характер изменения апостериорной вероятности
в зависимости от отношения сигнал/шум Q на входе приемника [4].
414
Из формул (10.4.11) и (10.4.14) видно, что отношение максималь-
ною значения сигнальной функции к среднеквадратичному значе-
нию шумовой функции равно
= j/q =	.	(10.4.19)
I <ли No очень велико, то это отношение мало, и сигнал полностью
(локируется шумом. При этом сами функции qs и qn будут также
чепь малыми. Полагая в формуле (10.4.6) ехр[<у(т) ] ш 1, получим
Wps(^kWpr(x).	(10.4.20)
Убеждаемся, что при очень малом отношении сигнал/шум апо-
। 'риорная вероятность совпадает с априорной, которая была при-
нята равномерной (10.4.18). Соответствующий график приведен
н । рис. 10.5, а. В данном случае прием колебания £(/) не дает до-
||| лнителькой информации о параметре т.
При увеличении отношения сигнал/шум растет дисперсия шумо-
। mi функции о„ и в апостериорной вероятности появляются нерав-
||| мерности (рис. 10.5, б), которые затем начинают переходить
1 тио выраженные пики, разделенные участками малой вероятно-
||| (рис. 10.5, в).
Когда Q>1, отношение (10.4.19) будет также больше единицы,
и становится заметной вероятность появления одного из пиков
II Дт) в окрестности истинного значения т0. При дальнейшем
\ । сличении Q растет степень достоверности того, что пик q(x), обус-
к пленный сигналом, будет выше шумовых пиков. При этом экспо-
||| пциальный множитель в формуле (10.4.6) начинает существенно
«пливать неравномерность д(т) и апостериорное распределение
। решится» на отдельные ясно выраженные пики, разделенные
\ 'метками почти нулевой вероятности (рис. 10.5, г, 5). Преобладаю-
щим становится пик в окрестности т0 и уменьшается число «конку-
рирующих» по величине шумовых пиков. При No -> 0 остается один
\ жий пик, расположенный в точке т = т0 (рис. 10.5, е).
Из приведенных графиков видно, что даже при Q — 4 имеется два
почти одинаковых пика, один из которых (шумовой) расположен
о окрестности т0. При этом неясно, какой из пиков является лож-
||| iM, и за истинное значение параметра можно принять как т0,
и к и Тц. В данном случае имеется неоднозначность в определении
।, Эта неоднозначность устраняется при дальнейшем увеличении
I I
Неоднозначность определения параметра зависит также от апри-
орной вероятности. Если бы в рассмотренном примере’возможными
ычениями задержки т являлся подынтервал (0, Т'), а^не весь ин-
к-рвал (0, 71), где Т’<^Т, то в конкретной ситуации рисЛ 10.5, г
।п'однозначность не имела бы места. Иначе говоря, сужение априор-
н но интервала значений т уменьшает вероятность появления на
415
этом интервале больших шумовых выбросов. Тем самым обеспечи-
вается возможность более надежного определения параметра при
меньших значениях Q.
На частном примере оценки задержки сигнала мы рассмотрели
операции, позволяющие получить апостериорную вероятность, и
выяснили влияние на апостериорную вероятность отдельных факто-
ров (в частности, отношения сигнал/шум и априорной вероятности).
§ 5.	КОРРЕЛЯЦИОННЫЙ ПРИЕМ
В §4 указывалось, что наиболее существенная операция, которую
необходимо выполнить над принятым колебанием £(/) для получе-
ния апостериорной вероятности, состоит в вычислении функции
взаимной корреляции (10.4.5)
т
9
<7(t) = ^ |	(10.5.1)
о
По функции взаимной корреляции можно однозначно найти апосте-
риорные вероятности без дополнительного обращения к принятому
колебанию Но апостериорные вероятности содержат все сведения,
которые можно извлечь из принятой реализации сигнала В этом
смысле можно сказать, что взаимокорреляционный приемник явля-
ется оптимальным.
Заметим, что если бы в формуле (10 5.1) перед интегралом стоял
множитель 1/Г, то она была бы подобна формуле (3.9.3), и функция
д(т) представляла бы выражение кратковременной функции взаим-
ной корреляции (т. е. функции взаимной корреляции, когда время
усреднения конечно) Однако наличие постоянного множителя
1/Т сказывается лишь на характере работы интеграторов. Отвле-
каясь от этих подробностей, можно говорить, что (?(т) есть функция
взаимной корреляции между принятым колебанием и полезным сиг-
налом, а устройство рис. 10.2, осуществляющее операции (10.5.1),
можно назвать взаимокорреляционным приемником.
Рассмотрим подробнее работу взаимокорреляционного приемни-
ка. Практически функцию взаимной корреляции q(i) для нескольких
фиксированных значений т можно получить при помощи устрой-
ства, функциональная схема которого изображена на рис. 10.6.
Линия задержки имеет общую задержку, равную априорному ин-
тервалу? ожидаемых значений г. От линии задержки сделаны равно-
мерно отводы; разность в задержках между соседними отводами рав-
на постоянной величине А. При этом схема рис. 10.6 позволяет
получить на выходе интеграторов, следующих за перемножителями,
значения функции взаимной корреляции, соответствующие задерж-
кам т,- — t’A, I =0, 1,2, ..., v; vA =?,
41$
Если дополнить корреляционный приемник схемой сравнения,
। ( юрая выдавала бы на выходе номер т того подынтервала Д,
। котором функция </(тт) имеет наибольший максимум, то все
тройство можно использовать для определения неизвестного мо-
ннта появления т0 импульсного сигнала. При этом точность изме-
рения будет характеризоваться величиной Д. Для импульсных ра-
июлокационных станций величину Д берут приближенно равной
длительности импульса.
Применительно к конкретному случаю измерения времени за-
паздывания сигнала схема сравнения может состоять из обычного
Рис 10.6, Функциональная схема взаимокорреляционного приемника
для определения временного положения импульсного сигнала
> сциллографа с линейной разверткой вдоль оси т и устройства, фик-
< ирующего номер т задержки, при которой появляется наибольший
I ыброс.
Корреляционные методы приема оказались особенно полезными
। ри приеме повторяющихся (радиолокационных) сигналов на фоне
ы\ма 15] Пусть полезный сигнал s(t—т) представляет пачку из п
юротких прямоугольных видеоимпульсов с амплитудой А, длитель-
кктью тн и известным периодом следования 7\ (рис. 10.7, а).
I! каждом периоде время запаздывания т0 одинаково и может при-
। пмать значения в интервале То, т. е. в i-м периоде время запазды-
। шия равно гт0, причем (г— l)^ < ixQ^iTQ, где i = 1, 2.......п.
Нетрудно показать, что сигнальная функция
пт,
2 Г
= У? J т°) S^~ x}di	(10.5.2)
° о
417
имеет вид равнобедренных треугольников (рис. 10.7, б), отстоящих
друг от друга на расстоянии То с основанием 2ти и высотой
Qsfj'v-') — И)> Тр. = т0 i Р- =t0, 1, 2, ..., п.
Здесь Е — энергия одного импульса.
Наибольший пик при т = т0 имеет высоту
qS maX(to) = п2~ .	(10.5.3)
s(t-ro)
Рис. 10.7. Пачка прямоугольных импульсов и ее функция ав-
токорреляции.
Высота пиков, расположенных симметрично относительно этою
главного пика, постепенно уменьшается, причем разность высот двух
соседних пиков одинакова и равна Ь-q = 2E/N0.
Шумовая функция
пТя
=	(10.5.4)
о
имеет нулевое среднее значение. Дисперсия ее равна
rtT" Q tlT Q
О» = (<7«(т:)> = 4- f f <n(/On(f2)>s(11 —r)s(^ — 1)61^2=
nT„	n iTa
= J s4/-T)^ = ^2 J S2(/-r)JT = n^.	(10.5.5)
° о	° <=i (i— i)T0
418
Из формул (10.5.3) и (10.5.5) получаем отношение максималь-
ного пика сигнальной функции к среднеквадратичному значению
ш/мовой функции
?SCTa*(To).	(10.5.6)
Таким образом, если отношение сигнал/шум по напряжению на
походе взаимокорреляционного приемника для одного импульса
р; вно y2E/N0, то при приеме п таких же периодически следующих
импульсов это отношение увеличивается в У п раз. Поэтому в слу-
ч.-ie пачки импульсов полезный пик в окрестности т0 как у функции
<;(т), так и у апостериорной вероятности будет более отчетливо выде-
1я-1ься на фоне шумовых выбросов, чем для одного импульса.
4 За счет увеличения числа'импульсов можно добиться требуемого
опюшения сигнал/шум (10.5.6) на выходе взаимокорреляционного
приемника. Можно сказать, что увеличение времени наблюдения
(интегрирования) в п раз сопровождается улучшением отношения
। игнал/шум в|//граз. Этот результат можно практически использо-
вать как для обнаружения периодических импульсных сигналов на
фоне сильных помех, так и при оценке неизвестных параметров. При
> юм в отличие от одиночного импульса здесь решение принимается
। запаздыванием во времени в п раз болыйим.
Именно в подобных случаях, когда требуется большое время
ипегрирования, практически применяются взаимокорреляционные
приемники, а несогласованные фильтры. Как правило, оптимальные
фильтры имеют весьма ограниченное время интегрирования (на-
юпления).
Укажем, что результат (10.5.6) справедлив не только для видео-
импульсов, но и для пачки из п когерентных радиоимпульсов. Если
ье пачка составлена из некогерентных радиоимпульсов, то отноше-
ние сигнал/шум будет меньше 16]. При этом радиоимпульсы, после
фильтрации соответствующим оптимальным фильтром, должны
предварительно детектироваться и лишь затем суммироваться.
Ьогда отношение сигнал/шум в каждом импульсе мало (энергия
импульса того же порядка или меньше, чем спектральная плот-
ность шума), то оптимальная характеристика детектора близка
к квадратичной. При больших отношениях сигнал/шум оптимальная
характеристика детектора близка к линейной. В случае флуктуи-
рующих импульсов оптимальной всегда является квадратичная
характеристика детектора.
Как следует из формулы (10.5.1), для получения функции взаим-
ной корреляции необходимо на приемной стороне знать форму
полезного сигнала s(/). Однако это не всегда просто достигается, что
< I раничивает возможность практического применения взаимокор-
|еляционного приема.
419
В том случае, когда приемное и передающее устройства располо-
жены в одном месте (радиолокация), в качестве местного (опорного)
сигнала s(t) на приемной стороне можно взять колебания местного
гетеродина или импульсы передатчика, задержанные соответствую-
щей линией задержки (рис. 10 8). Интенсивность колебаний гете-
родина или импульсов передатчика настолько велика, что мешаю-
щими напряжениями на входе приемника, сопровождающими эти
импульсы, всегда можно пренебречь. Без учета искажений прини-
маемого сигнала опорное напряжение будет совпадать по форме
с принимаемым сигналом. В данном случае является важным требо-
Рис. 10.8. Взаимокорреляционный прием.
вание высокой стабильности частоты колебаний гетеродина (за вре-
мя обработки интересующей нас пачки импульсов фаза колебаний
гетеродина не должна существенно изменяться).
Сложнее обстоит дело с формированием опорного сигнала s(t)
в радиосвязи, когда передающее и приемное устройства простран-
ственно разнесены. Считая фазовые флуктуации радиосигнала из-за
распространения радиоволн через ^турбулентную атмосферу или
ионосферу медленными, здесь для формирования опорного сиг-
нала обычно применяют несколько видов устройств.
Если колебания передатчика имеют высокую стабильность по
частоте, то на приемной стороне можно использовать высокостабийь-
ный гетеродин, работа которого предварительно и периодически
синхронизируется колебаниями передатчика. Иногда применяют ав-
токорреляционный прием. При автокорреляционном приеме опор-
ным напряжением служит принятое колебание. Работа автокорреля-
ционного приемника описывается формулой
ц+г
I	(Ю.5.7)
Автокорреляционный прием является менее помехоустойчивым,
чем взаимокорреляционный прием, так как при одинаковых услови-
ях приема отношение сигнал/шум на выходе автокорреляционного
приемника будет меньше, чем на выходе взаимокорреляционного
приемника. Это объясняется тем, что при взаимокорреляционном
420
1|>иоме опорное напряжение по форме точно совпадает с полезным
шпалом, а при автокорреляционном приеме опорное напряжение,
। роме полезного сигнала, содержит также шум.
В тех случаях, когда фаза колебаний передатчика сравнительно
кдленно и не очень сильно изменяется за время наблюдения сиг-
|| । ia Т, опорное напряжение можно формировать из принятого ко-
пбания £(t) при помощи специальных устройств синхронизации
/рис. 10,9), предложенных А. А. Пистолькорсом, В. И. Сифоровым,
Ь П. Костасом и др. [7, 8]. Назовем условно такой метод приема
. nixpoHHHM или квазикогерентным. Из-за наличия шума в канале
Рис. 10.9. Синхронный (квазикогерентный) прием.
। ннхронизации параметры опорного сигнала s0(f) будут случайны-
ми, что обусловливает меньшую помехоустойчивость такого метода
п| иема по сравнению с взаимокорреляционным. Степень пониже-
III я помехоустойчивости определяется отношением сигнал/шум
п канале синхронизации (см. § 5 гл. 11).
Если не предъявлять особых требований к стабильности частоты
передатчика, то для получения опорного сигнала следует применять
< амостоятельный канал синхронизации с использованием различных
и.риантов фазовой автоподстройки частоты (см. § 4 гл. 13).
§ 6. СОГЛАСОВАННЫЕ ЛИНЕЙНЫЕ ФИЛЬТРЫ
В § 4 отмечалось, что функцию взаимной корреляции </(т) между
колебанием |(£), принятым на интервале (0, 71), и полезным сигна-
лом s(t) можно получить на выходе согласованного фильтра. Рас-
смотрим этот вопрос подробнее с привлечением спектрального ана-
лиза. Приведем сначала определение согласованного фильтра, а
ытем рассмотрим свойства этих фильтров и некоторые практи-
ческие рекомендации по их реализации.
Если s(f) есть некоторое физическое колебание, принимаемое
на фоне белого шума, то согласованным фильтром для этого колеба-
ния является фильтр, имеющий импульсную характеристику:
G(t) = ks(t0 — t),	(10.6.1)
421
где k — постоянная, равная максимальному усилению фильтра;
t0 — фиксированное время, при котором наблюдается выходной
сигнал (см. ниже).
Чтобы представить себе функцию G(t), обратимся к рис. 10.10.
На рисунке изображен импульсный сигнал s(/). Очевидно, что функ-
ция s(t0 + /), изображенная пунктиром, появляется на время t0
раньше, чем сигнал s(i). Функция же s(t0 — f) является зеркаль-
ным отображением функции s(f0 + t) относительно оси ординат.
Умножив функцию s(t0 — t) на коэффициент k, получаем импульс-
ную характеристику согласованного фильтра (10.6.1).
Рис. 10.10. Сигнал и импульсная характеристика O[t) согла-
сованного фильтра (^=1).
Передаточная функция согласованного фильтра по формуле
(6.1.3) равна
/С (/to) = J G(t)e~imtdt = J s(t')
—co	—do
Учитывая выражение для спектра сигнала
S(/co)= J s(Z) e~i di,
— co
получим
К (/to) = ke-W° S(— /to) = kS* (/to)	(10.6.2)
где — функция, комплексно-сопряженная спектру сигна-
ла S (/to).
Таким образом, если прием сигнала осуществляется на фоне бе-
лого шума, то с точностью до амплитудного множителя и постоянной
задержки (определяемых множителем йе-^») передаточная функ-
ция согласованногофильтра представляет собой функцию, комплекс-
но-сопряженную со спектром полезного сигнала. Следовательно,
частотная характеристика согласованного фильтра целиком опре-
деляется спектром сигнала, а импульсная характеристика фильтра—
формой сигнала («согласована» с сигналом).
422
Согласованные фильтры обладают следующими свойствами:
1. Среди всех линейных фильтров согласованный фильтр дает
и । выходе максимальное отношение пикового значения сигнала
। <реднеквадратичному значению шума, равное Y2E/N0. Это замеча-
ильное свойство часто принимается за определение согласованных
| II11| ьтров.
2. Сигнал на выходе согласованного фильтра по форме совпадает
< «функцией автокорреляции» входного полезного сигнала, и функ-
и и I корреляции выходного шума имеет вид функции автокорреляции
входного полезного сигнала.
Докажем эти свойства, начав со второго. Обозначим полезный
। шиал на выходе согласованного фильтра через хв(/) и шум на вы-
ходе через tiB (/). Используя формулу интеграла Дюамеля, можем на-
писать
sB(t)- j G(x)s(t— x)dx = k J s(t0— x)s(t— x)dx, (10.6.3)
—00	— 00
nB(?) = f G(x)n(t— x)dx~k J s(ta— x)n(t — x)dx. (10.6.4)
—00	—00
Из формулы (10.6.3) ввдно, что сигнал на выходе согласованного
|>ильтра с точностью до постоянного множителя представляет собой
функцию автокорреляции входного полезного сигнала, причем мак-
। ииальное значение выходного сигнала имеет место при t = t0 и
Р >вно
SBmax (to) = kE,	(10.6.5)
। це E — энергия входного сигнала.
Функция корреляции выходного шума легко вычисляется:
оо
tB(tl, ^)= <МЛ)"в(М> = k2^- J s(t0 — x)s(t0 — x+ti—t2)dx —
— oo
oo
= j s(t)s(t + t1 — ta)dt.	(10.6.6)
—co
<ia формула подтверждает, что функция корреляции выходного
шума имеет вид автокорреляционной функции входного сигнала.
Полагая в формуле (10.6.6) гф = 12, получаем дисперсию выходного
hi /ма
а2 = йаЦ£.	(10.6.7)
423
Из формул (10.6.5) и (10.6.7) находим отношение максимального
значения выходного полезного сигнала к среднеквадратичному зна-
чению выходного шума:
SBmax(^	лшсоч
---------ИлГ0’	(106 8>
что, как и следовало ожидать, совпадает с результатом (10.4.19).
Характерно, что отношение сигнал/шум на выходе согласован-
ного фильтра определяется только отношением энергии сигнала
к спектральной плотности шума и не зависит от формы сигнала.
Отношение сигнал/шум на выходе согласованного фильтра можно
пересчитать к его входу. Пусть А/э — энергетическая (шумовая)
полоса сигнала или согласованного фильтра (3.10.4). Тогда мощность
шумов на входе в энергетической полосе согласованного фильтра
равна Рп = Af0A/3, а мощность сигнала на входе фильтра равна
Ps — Е!%и, где ти — эффективная длительность сигнала. Подста-
вив отдельные величины в формулу (10.6.8), получим
1/2А/эти^.
ав	*	“п
(10.6.9)
Произведение А/Эти часто называют базой сигнала. При заданной
энергии сигнала Е и равномерной спектральной плотности шума
No увеличение ти или А/э порознь не оказывает непосредственного
влияния на отношение сигнал/шум на выходе согласованного
фильтра; это отношение можно увеличить за счет увеличения
базы сигнала.
Убедимся теперь в выполнимости первого свойства. Пусть
K(/<d) есть передаточная функция некоторого линейного фильтра.
При воздействии на такой фильтр сигнала s(t) спектр сигнала на
выходе будет определяться произведением S(/co)/<(/o)), а сам выход-
ной сигнал — равенством
оо
J	(ю.6.10)
— QO
При воздействии белого шума со спектральной плотностью Л/о/2
(имеется ввиду двусторонняя спектральная плотность), дисперсия
шума на выходе фильтра равна
СО
J lK(/®)|2dco.
— со
(10.6.11)
424
Из (10.5.10) и (10.6.11) получаем формулу для отношения мгно-
венного значения сигнала на выходе фильтра некоторый момент
времени к среднеквадратичному значению выходного шума
,	J S(;M)K (/<->)
С ИЛ	d
I ~-N0 j | К (/“) I2 do>\
\ —co	/
Найдем такую передаточную функцию при которой отно-
шение (10.6.12) в момент времени /0 достигает максимума. Для этого
в< спользуемся неравенством Шварца — Буняковского. Неравенст-
ве Шварца — Буняковского гласит, что если имеются две комплекс-
на функции F(x) и Г(х), то выполняется соотношение
| р*(х)Г(х)бД|< ( J|F(x)|26?x ||Г(х)|2(Д)г,	(106.13)
причем знак равенства имеет место в том и только в том случае,
когда
Г (х) — kF (х),	(10.6.14)
। де k — постоянная.
Положив Г (со) = К (/®), F* (ю) = S (/(о)е^* и применив неравен-
 ню (10.6.13) к числителю выражения (10.6.12), получим
।
I I . (JIS I2 М 1 * I2 2	1/2Ё Z1 9 R 1
-	“Г— V N-.'	(1ЛЬЛ5)
J |Д(/а>)|
। <и< как энергия входного полезного сигнала равна
со	со
£ = f s2(t)dt = ~ j \S(ja)\2d&.	(10.6.16)
— со	—оо
Таким образом, отношение максимального значения сигнала на
выходе любого линейного фильтра к среднеквадратичному значению
выходного шума не может превышать величину уl2E/N0. Это мак-
। нмально возможное значение, как показывает равенство (10.6.14),
достигается при выполнении условия
К (/cd) = kS* е~ fai>.	(10.6.17)
I Io фильтр, имеющий такую передаточную функцию, является согла-
< ованным фильтром. Следовательно, согласованный фильтр яв-
иется единственным линейным фильтром, дающим максимально
425
возможное отношение сигнал/шум на выходе. Никакой другой
фильтр не может дать отношение сигнал/шум больше, чем согла-
сованный.
Запишем спектр входного сигнала и передаточную функцию
фильтра в виде
5 (/(о)-= | S (/о)) | e/?i (,), К(>) = |/<(/®)|е'?<ш>. (10.6.18)
Для согласованного фильтра из (10.6.17) получим
Юсо)| =£|S(/co)|, <р (<>)) = —[ф5(и)+ со/о]. (10.6.19)
Видно, что амплитудно-частотная характеристика согласован-
ного фильтра пропорциональна амплитудно-частотному спектру ожи-
даемого сигнала, а фазовая характеристика равна сумме фазового
спектра сигнала, взятого с обратным знаком, и задержки (—и/0).
Совпадение формы амплитудно-частотной характеристики филь-
тра с амплитудным спектром сигнала обеспечивает наилучшее вы-
деление наиболее интенсивных участков спектра сигнала. Слабые
участки спектра сигнала фильтр ослабляет; в противном случае,
наряду с ними проходили бы интенсивные шумы. При этом форма
сигнала на выходе фильтра искажается. Однако это не имеет зна-
чения, так как задача фильтра в данном случае состоит не в точном
воспроизведении входного сигнала, а в наилучшем выделении пика
сигнала на фоне шума. Существенную роль в этом отношении играет
фазовая характеристика фильтра <р(со).
» Подставив в (10.6.10) функцию передачи (10.6.17), получаем вы-
ражение сигнала на выходе согласованного фильтра
«в (0
2 e/Mf-U da>
= ~ J |S (/со) |2 cos и (/ — t0)d(i>.
(10.6.20)
Отсюда видно, что сигнал на выходе фильтра определяется толь-
ко амплитудно-частотным спектром входного сигнала и не зависит
от его фазового спектра. Последнее объясняется тем, что взаимные
фазовые сдвиги спектральных составляющих входного сигнала
(ps(co) компенсируются фазо-частотной характеристикой фильтра.
Поэтому все гармонические составляющие одновременно достигают
амплитудных значений в момент времени t = /0, и, складываясь,
дают пик выходного сигнала:
00
Sb maX(t0) ~= ~ j | S (]ш) | 2 d(l> kE.
- OQ
426
и бы фазо-частотная характеристика фильтра не компенсировала
1ч>|1ых сдвигов спектральных составляющих входного сигнала,
 максимумы гармонических составляющих не совпадали бы по
I" мени, что привело бы к уменьшению или раздроблению пика вы-
' того сигнала.
11ри практическом конструировании согласованных фильтров,
> |и>ме основных формул (10.6.1) и (10.6.2), следует также иметь
> виду условия физической осуществимости линейных фильтров
G(/) = 0 при t < 0,
оо
С log I К (/«>) I
J 1 -I
— оо
2
- da
(10.6.21)
। м ювия практической реализуемости фильтров. Условия физиче-
... осуществимости определяют принципиальные возможности
• । роения фильтров, а условия практической реализуемости —
। и шческие возможности создания
;и п.тров.
Когда импульсная характеристика
। hi 6.1) или функция передачи (10.6.2)
иргделяют физически осуществимый
инейный фильтр, задачу отыскания
। цсованного фильтра в принципе
। । кпо считать решенной.
I ели сигнал, с которым должен
10.11. Сигнал s(0 конеч-
длительности и импульс-
характеристика согласо-
ванного фильтра
входного сигнала для
111 ь согласован фильтр, начинается Рис
। момент времени I = 0 и полностью Ной
 Г* кращается при ^>ти (рис. 10.11), "ая
। । первое из условий (10.6.21) выпол-
и н"ся при ?0>ти. Только при этом
ювии будет использована вся энергия
| приирования сигнального пика на выходе фильтра в момент t0.
ноличение t0 сверх ти, не влияя на величину пика, сдвигает его
। сторону большего запаздывания, что нежелательно. Поэтому
кдует брать t0 = ти.
Иногда для аппроксимации реальных импульсных сигналов ис-
|| hi ьзуют бес конечно длинные импульсы (гауссов, экспоненциальный
и др ). В подобных случаях приходится искусственно брать конечное
hiачение длительности аппроксимирующего импульса, содержащей
и повную долю энергии сигнала.
Если даже согласованный фильтр является физически осутцест-
। пмым, то эго не означает, что данный фильтр можно реализовать
фактически. Может оказаться, что для построения такого фильтра
। ребуется слишком много элементов, или же эти элементы должны
обладать практически трудновыполнимыми характеристиками и
' д-
В тех случаях, когда для сигнала получаются практически не-
реализуемые фильтры, можно предложить два пути.
427
Для многих применений целесообразно заранее подбирать такие
сигналы, для которых получаются сравнительно легко реализуемые
фильтры. Иначе говоря, чтобы обеспечить наилучший общий
результат, нужно одновременно заниматься как построением согла-
сованных фильтров, так и подбором желательных форм сигналов [9].
Если желательная форма сигнала выбрана и для него согласо-
ванный фильтр все же не реализуем, то следует использовать тот из
практически осуществимых фильтров, который обеспечивает мак-
симальное отношение сигнал/шум на выходе. (Во избежание недора-
Рис. 10.12. Согласованный фильтр для прямоугольного видео-
импульса (а) и напряжения на выходе отдельных каскадов
согласованного фильтра (б)
зумений отметим, что здесь имеются в виду импульсные сигналы
без внутриимпульсной модуляции. При использовании сигналов
с внутриимпульсной модуляцией часто специально применяюй
несогласованные фильтры для подавления боковых «лепестков»!
допуская некоторое уменьшение отношения сигнал/шум.)
Оказывается, отклонение характеристик фильтров от формуя
(10.6.1) и (10.6.2) во многих случаях не сопровождается значителья
ным уменьшением отношения сигнал/шум. Поэтому без существен
ного ухудшения характеристик систем можно применять вмеся|
строго согласованных фильтров практически легко реализуемой
фильтры, дающие примерно те же результаты (см. § 7).	“ч
В качестве примера рассмотрим согласованный фильтр для пря«^
моугольного видеоимпульса [10]. Пусть импульс появляется в м<$
мент времени t = 0, имеет амплитуду Л и длительность
(рис. 10.12, б), т. е.
5(0 =
А при 0 < t < ти,
0 при t < 0, ти.
428
 к р такого сигнала равен
S(/а) = A Jе~А>'di = — (1 — е~/шти).
о
i мд to—Xs, по формуле (10.6.2) находим передаточную фужк-
। ’ согласованного фильтра
~ е-/
I! соответствии с формулой (10.6.1) импульсная характеристика
1кованвогс фильтра равна
[kA при 0 < t < тн,
W ~ | 0 при t > tu.
i । ।ином частном случае импульсная характеристика фильтра по
1'ме совпадает с сигналом.
। )диа из возможных функциональных схем этого согласованного
и и.гра представлена на рис. 10.12, а. Он состоит из идеального
> ь оугилителя с коэффициентом усиления kA, интегратора, лн-
 и задержки на ти и вычитающего устройства. Напряжение
выхода интегратора подается на вычитающее устройство по двум
и 1лаи: непосредственно и через линию задержки. Характер
। палов на выходе отдельных элементов схемы показан к а
। । 10 12, б. На выходе вычитающего устройства получается треу-
п ный импульс с высотой kE — kA^t., и длительностью 2ти;
sB (t} =
kA? t при о < t ти,
kA? (2ти — t) при ти < t < 2ти,
О при Z'j>2th.
7. ОПТИМАЛЬНЫЕ И КВАЗИОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ
>|>ИЛЬТГЫ
Характерным свойством согласованных фильтров является то,
и) их характеристики (10.6.1) и (10.6.2) полностью определяются
и.ко полезный сигналом. Этот результат является следствием:
। ипятого ранее предположения, что шум «(/) является нормаль-
in бедым шумом.
Рассмотрим >олее общий случай нормального стационарного
,ма н(/). Назовем оптимальным фильтром линейный фильтр,
шщий на выходе максимальное отношение сигнал/помеха, когда
меха /;(/) является произвольной. В том частном случае, когда
429
помехой n(t) является нормальный стационарный, но не белый
шум, передаточная функция оптимального фильтра определяется
формулой
где S*(/©) — функция, комплексно-сопряженная спектру сиг-
нала S (/©);
Л/(©) — спектральная плотность шума n(t).
В справедливости этой формулы можно убедиться путем сле-
дующих формальных рассуждений [11].. Пусть принятое колебание
представляет сумму полезного сигнала s(t) и нормального стацио-
нарного шума n(t) со спектральной плотностью N(m).
Рис <0.13. Оптимальный линейный фильтр для приема
на фоне нормального коррелированного шума.
Представим оптимальный линейный фильтр в виде двух после-’
довательно соединенных линейных четырехполюсников, как пО-
казано на рис. 10.13. Предположим, что первый четырехполюсник
имеет передаточную функцию /Сф/со) — V	где Nq — по*
стоянный коэффициент?
Спектральная плотность нормального шума пг(/) на выходу
первого четырехполюсника будет равна N(a)N0 /N(a) = No, т. е.(
шум на выходе становится белым.
Сигнал на выходе первого четырехполюсника искажается и бу-
дет иметь спектр
> / No
S1(/©)=S(/©)|/
Согласованный фильтр (второй четырехполюсник) для приема такогй
сигнала на фоне нормального белого шума согласно формул®
(10.6.2) должен иметь передаточную функцию
К2 (/со) -= k2 5* (/со) |/ —у
Следовательно, передаточная функция оптимального фильтра,
состоящего из двух четырехполюсников, равна
К (/©) = Ki (/©) К2 (/©) = k е- k = k2N'o,
что совпадает с приведенной формулой (10.7.1).
430
Отношение пика сигнала на
। среднеквадратичному значению
выходе оптимального фильтра
выходного шума равно:
ОО
= l С	(10-7.2)
ав тс J N (о>)	v 7
— СО
>1,1 формула является обобщением формулы (10.6.8) на случай
||><>извольюго нормального стационарного шума.
Заметим, что для белого шума n(f) со спектральной плотностью
1 (<») — Moi2 — const формула (10.7.1) дает передаточную фуккцию
и.засованного фильтра (10.6.2). Когда же амплитудно-частотный
цистр сигнала совпадает по форме со спектральной интенсивностью
ц|\ма, т. е S*(/<d)	A'(o))e -THs('"Ji то из формулы (10.7.1) лолу-
। им, что амплитудно-частотная характеристика оптима.гьного
|>и 1ьтра должна быть равномерной: |K(jco)| — k = const.
Из этихдвух частных случаев следует, что максимизация отно-
1К-11ИЯ сигнал/шум на выходе оптимального и согласованного фильт-
। <>» достигается только за счет спектральных различий сигнала и
|\ма. 7ак»й результат можно было ожидать заранее. Все стат-
ические мрактеристики шума (который предполагается нормаль-
ный, стационарным с нулевым средним значением) определяются
|-\ пкцией юрреляции или спектральной плотностью. Поэтому при
и местном спектре сигнала вся информация, которую можжо ис-
...ьзовать для выделения сигнала на фоне шума, сосредогочена
। гнектрах сигнала и шума. Для ненормального входного шума
in .1ьзя утверждать, что операция образования функции взаимной
<иреляци1 (10.4.5) является оптимальной. Здесь можно исполь-
инать различия в других характеристиках сигнала и шума. Как
н|)1вило, в этом случае должны применяться более сложные нели-
|н иные устройства.
В ряде случаев оптимальные и согласованные фильтры »казы-
|| потея практически трудно реализуемыми. Убедимся на конкрет-
но примерах, что вместо оптимальных (согласованных) фильтров
нжио пргменять другие надлежащим образом подобранные
|>|гп>тры, та выходе которых получается незначительное уменыпе-
HII отношения сигнал/шум по сравнению с оптимальными (согла-
 пминьми) фильтрами. Назовем такие фильтры квазиоптжмаль-
III.ми [12]
Обозначим через р отношение максимального значении сиг-
iiOiuyn по напряжению на выходе произвольного линейного
|'П1ьтра к отношению сигнал/шум на выходе согласованного фильт-
I’ । Воспользовавшись формулами (10.6,8) и (10.6.12) и учитывая
 ннцошеШе (10.6.16), получим
431
J S (ia>) к (/«) do
~ 00_______________________________
1
co	oo	' —
J |S(/o>)|2d<o J | К (io) I 2 do 2
— co	— oo
(10.7.3)
Здесь под t0 понимается момент времени, когда сигнал на выходе
фильтра с передаточной функцией K(j®) достигает наибольшего зна-
чения.
Пользуясь формулой (10.7.3), можно вычислить, насколько
ухудшается отношение сигнал/шум, если для прямоугольного ра-
диоимпульса
Де^ при |/|<ти/2,
О при 111 > ти/2
(10.7.4)
вместо согласованного фильтра используются более простые и прак-
тически легко реализуемые фильтры. Рассмотрим три таких
фильтра: идеальный прямоугольный фильтр, колебательный контур
и гауссов фильтр.
1)	Идеальный прямоугольный фильтр. Передаточная функция
такого фильтра имеет вид прямоугольника:
I	w0	9	--% “I у ,
% при	2
’	®о----g	+ ~2'
О при других о.
В данном случае
где
(10.7.5)
(10.7.6)
Z
Si (г) = J dx — интегральный синус,
о
Результаты вычислений по формуле (10.7.6) представлены на
рис. 10.14 (кривая 1). Величина р имеет максимум
?тах = 0,91, р^-0,82 при Д/ = Ж (10.7.7)
ти
Следовательно, если идеальный фильтр имеет полосу пропускания
Д/ = ^,	(10.7.8)
432
ю ухудшеие отношения сигнал/шум по сравнению с согласован-
ный фильтюм по напряжению равно примерно 10%, а по мощности—
примерно 17%. В окресгности максимума кривая изменяется очень
медленно. Гак, например, при изменении Д/ти/2 от 0,4 до 1,0 ве-
1И1Ина р вменяется от 0,82 до 0,84.
Условится в дальнейшем называть реальный фильтр с полосой
пр шу сканы А/ (на уровне 0,5 по мощности), при которой величи-
на р ииееттмаксимум, фильтром, согласованным с сигналом по по-
носе. Приенительно к рассмотренному примеру можно сказать,
что идеальный фильтр с полосой пропускания (10.7.8) согласован
i чрямоупльным радиоимпульсом по полосе.
Рис. 10.14. Уменьшение отношения сигнал/шум на
выходе квазиоптимальных фильтров.
Такая терминология оправдана тем, что, если согласованный
фильтр «согласуется» со всем спектром сигнала, то в фильтре, со-
। тасованшм по полосе, подбирается только оптимальная ширина
полосы пр>пускания, при которой получается максимальное отно-
шение синал/шум. Рассмотрением таких фильтров занимались
'(.О. Нор, В. И. Сифоров и др. [10, 13, 14, 15].
2)	Одиючный резонансный колебательный контур
К (М = Ко ,	------ -	(10.7.9)
Вкчислен1я по формуле (10.7.3) дают следующий результат:
Р = /-^	а=лА/. (10.7.10)
1’сзультатг расчетов по этой фюрмуле приведены на рис. 10.14
(юивая 2 При Д/ти = 0,4 величина р имеет максимум ртах = 0,9,
и] ичем максимум является пологим.
3)	Фил»тр с гауссовой резонансной кривой
К (» = К9 ехр
— 1,4
— /®Й)
(10.7.11)
433
В данном случае на основании формулы (10.7 3) получим
\г'2,8/	[ ( /2,8/	2
(10.7.12)
Результаты вычислений по формуле (10.7.12) показаны на рис. 10.14
(кривая <?). При Afrtl = 0,72 величина р имеет максимальное зна-
чение ртах = 0,94.
Фильтр с гауссовой передаточной функцией (10.7.11) является
согласованным для радиоимпульса гауссовой формы
Г / t 2
s(/) = Xexp — 2,8(—) +/(.)/ •
(10.7.13)
Величина р равна

Характер изменения р в зависимости от А/Чи показан на рис. 10.14
(кривая 4). Максимальное значение ртах = 1 при А/ти = 0,63.
Из рассмотренных частных примеров, относящихся к прямо-
угольному радиоимпульсу, вытекает следующий общий вывод.
Вместо согласованных фильтров можно применять квазиопти-
мальные фильтры. При этом получается несущественное уменьше-
ние отношения сигнал/шум, если фильтры будут согласованы с сиг-
налом по полосе, хотя само такое согласование оказывается не
очень критичным.
В табл. 10.7.1 для нескольких пар радиоимпульс—фильтр ука-
заны значения ртахи приведены оптимальные значения А/ти, при
которых достигается р.иаА-.
Таблица 10.7.1
Основные характеристики квазиоптимальных фильтров
Радиоимпульс	Фильтр	ДГ-и	Ртах
Прямоугольный	Идеально прямоугольный .	1,37	0,91
Прямоугольный	Гауссов .	....	0,72	0,94
Гауссов	Идеально прямоугольный	0,72	0,94
Гауссов	Гауссов	.	.	...	0,63	1,0
Прямоугольный	Одиночный резонансный контур . .	0,40	0,90
Прямоугольный	Двухкаскадный резонансный усили-		
	тель	...	0,61	0,93
Прямоугольный	Пятикаскадный резонансный усили-		
	тель	.	.	...	0,67	0,94
В радиоприемных устройствах супергетеродинного типа переда-
точная функция усилителя промежуточной частоты в принципе долж-
на совпадать с передаточной функцией соответствующего, оптимцлц-
434
ii< io или (ъазиоптимального фильтра. Однако на практике полосу
щопусканая усилителя промежуточной частоты выбирают в 1,5—
’ раза больше оптимальной. Главная причина этого — нестабиль-
1н >'ть частоты гетеродина.
Принципиальную целесообразность расширения полосы про-
никания фильтра (практически УПЧ) при наличии расстройки
—fp между частотой радиоимпульса fo и центральной час-
1ПГОЙ филггра /р можно уяснить на следующем частном примере.
he. 10.15. Уменьшение отношения сигнал/шум в зави-
симости от постоянной расстройки.
Пусть прямоугольный радиоимпульс (10.7.4) воздействует на со-
। 11сованннй фильтр, расстроенный относительно частоты радио-
импульса па величину Af. В данном случае отношение (10.7.3) равно
sin TtAf ти
тгД/Ти
Р =
(10.7.15)
11. рис. 1015 приведена зависимость величины р от А^ (кривая 1).
Л1ожно показать, что при воздействии прямоугольного радио-
импульса на расстроенный колебательный контур справедлива
[><»чмула
а	1 — 2е аТи cos 2-Д/ ти - г е 2а и
(^р+т^д^Р
I
2
а = лА/. (10.7.16)
н С1гсутствле расстройки (Aj = 0) эта формула переходит в (10.7.10).

Результаты расчетов по формуле (10.7.16) для двух полос про-
пускания контура: А/ = А/Опт = 0,4/ти (кривая 2) и А/ = 2A/onT
(кривая <?), представлены на рис. 10.15.
Из графиков видно, что при значениях А,ли > 0,6 отношение
сигнал/шум на выходе фильтра с полосой пропускания А/ = 2А/ОПГ
больше, чем в двух других случаях, имеющих оптимальные полосы
пропускания.
Рис. 10.16. Уменьшение отношения
сигнал/шум при случайных нор-
мальных вариациях расстройки Др
Если расстройка Ау медленно и случайным образом изменяется
во времени по нормальному закону
1 i д? \
Оу у х7С	у	у
то естественно интересоваться средним значением (р) или (р2),
которые находятся на основании (10.7.15)—(10.7.17) по формулам
<р>- f puy(A/)dA/, <р2>= J	(10.7.18)
-СО	—- 00
Результаты численных расчетов величины <ф2) для колебатель-
ного контура при нескодрких значениях ОуТн приведена 98
436
pie 10 16м 10.17*. Из графиков рис. 10.17 видно, что приэадан-
н( и величине оутн существует свое оптимальное значение Д/т и, при
Phi. 10.17. Влияние полосы пропускания на отношение
сигнал/шум при случайной расстройке.
i.iriopoN <о2) имеет максимум. С увеличением сг^т,, оптимальное
чачение Д/ти медленно возрастает, а максимальное значение < р2 >
1111 ко уменьшается.
Q 8. АПОСТЕРИОРНЫЕ ВЕРОЯТНОСТИ ПАРАМЕТРОВ
РАДИОИМПУЛЬСА
Вычислим апостериорные вероятности некоторых параметров
р.циоимпульсов, указанных в § 2. Для этого применим формулу
11 1.3.26), жапример, к сигналу вида (10.2.10). Если вид фтнкций
/( ) и <р(/) известен,'то сигнал (10.2.10) зависит от четырех парамет-
ры! а, г, о, 9. Будем считать эти параметры постоянными (неиз-
'.нпяющшмися за время наблюдения Т) и независимыми, имеощими
и честные априорные плотности вероятности. Тогда
_ Wpr(a,x, <о, Q) =Wpr(a)Wpr^)Wpr(m)Wpr(Q). (10.8.1)
' Графики рис 10 15—10 17 рассчитаны В Т. Горяйновым
437
На основании формулы (10.3.26) для апостериорной вероят-
ности можем написать
Wps (а, т, со, 6) = kWpr (a) Wpr (т) Wpr (<о) Wpr (0) х
X ехр
— 4	[1(0 — af (t — т) cos (со^-рф (/— т)—0)|М/
io
.(10.8.2)
Среди параметров а, т, со, 0 некоторые могут быть заранее из-
вестными, а остальные неизвестными (информационными). Рассмот-
рим здесь три случая:
1)	все параметры, кроме одного, заранее точно известны;
2)	фаза 0 является случайной величиной, равномерно распре-
деленной на интервале (—л, л), а все остальные параметры, кроме
одного, точно известны;
3)	величины а и 0 являются случайными и независимыми, при-
чем величина а распределена по закону Релея, а 0 — равномерно
на интервале (—л, л).
В дальнейшем будем предполагать выполняющимися два усло-
вия:
Т > ти, ыТ > 1.	(10.8.3)
Если интервал наблюдения много больше длительности импуль-
са ти, то можно считать, что практически все принимаемые сигналы,
независимо от конкретных значений отдельных параметров, пол-
ностью расположены в пределах интервала наблюдения. При этом
интеграл J ^(t)dt не зависит от интересующих нас параметров
t0	t„+T
и в формуле (10.8.2) множитель ехр[—I
\ N 0 J
^0
включить в постоянную k. При выполнении обоих условий (10.8шЗ)
и медленно изменяющихся функциях f(t) и <p(Z) справедливо прибли-
женное равенство
tv+T	t'+T
^s2(t)dt-^ J a?f2(t— t)cos2((oZ+<p (t — t) — O)dt =
io	i&
io+T
=4 I p(/-t)^ = 4>	(io-8-4)
^0
где
t.+T
a= J /2(/ — i)dt.	(10.8.5)
всегда можно
438
I Пусть неизвестным является лишь амплитудный множитель а,
и. е остальные параметры точно известны: т -= т0, ы = ю0, 0= 0О.
I. I.in пом случае нужно положить
" (т) =б(-т —т0), Fpr((0) = 6(0)-t00), №pr(6)=6(6-e0). (10.8.6)
Гели подставить выражения (10.8.6) в (10.8.2) и проингегри-
। и,its правую часть по известным параметрам, для чего следует
> ниользовгться соотношением (П.4), то получим окончательную
!<>>мулу дхя апостериорной вероятности параметра а
Wp, (а) = kWpr (а) ехр
^о+Г
j [В (0 —	— т0) х
X cos (pet + ф(/-т0) — 0О)]2 dt 1 — kWpr(a) ехр
аа2 .
2ЛГО +
Со+Т
+	£ (И f (z — То) COS (ffi01 + <p (/ — To) — 0O) dt
io
(10.8.7)
Аналогичным путем находятся апостериорные вероятности для
н< бого другого параметра при известных остальных Например,
(t)=kWpr (т)ехр
J [ь(0 — «of (t — т) х
> cos(co0/-X Ф(£—т) — 0o)]2d/ = kWpr(x) <
X ехр
<.+Т
J4 f cos (“о т)~ео) dt
i о
(10.8.8)
Грд®) = Wpr(®) х
I	1
exp — J- | [g(0 — aof(t— t0) cos (<oZ+-<p (/ — t0) — 0o)]2c/( =
| л 0 J
kWp (<п)ехр | g(Of(/-T0)cos(m/ + <p(Z — То)-еоМП. (10 8 9)
2. Предположим, что фаза 0 является случайной и нас кнтере-
\’|'т апостериорная вероятность какого-либо другого неизвестного
и фаметра (например, т). В данном случае имеется два неизвестных
। фаметра т и 6, причем интерес представляет лишь информация,
439
содержащаяся в т, безотносительно к истинному значению 0. Чтобы
подчеркнуть это различие, параметр т можно назвать существен-
ным (информационным), а параметр 0 — несущественным. При на-
хождении апостериорной вероятности существенных параметров
несущественные параметры исключаются путем статистического
усреднения апостериорной вероятности по несущественным пара-
метрам.
Подставим в формулу (10.8.2) априорную плотность вероят-
ности для фазы
Wpr(Q) = ^-' -я<0<л,	(10.8.10)
и проинтегрируем правую часть по всем возможным значениям
фазы:
Wps (а, т, <о) = kWpr (a) Wp, (т) Wpr (<в) х
j 1^(0 — af (t — T) cos (®Н-ф (^ — T) — ty]2dt dQ.
В силу условий (10.8,3) это выражение приводится к виду:
f OLtl^ \
Wps (а, т, (В)=const Wpr (a) Wpr (т) Wpr (а) ехр ( — X
и	^оЧ-т
f ехр [ %(t)f(t~ т) cos (<в/+ <р (Z — т) — Q)dt dQ.
ж J по J
Обозначим
t„+T	)
X (т,	ы)	=	J	^(t)f(t—	т) COS (at + ф (t—т))Л,	I
to	I
г'оН-Г	(
Y (т,	<b)	=	j*	l(t)f(t —	t)	sin (<в/-фф (Z — r))dt,	]
h	!
Z(t, <b) = VX* + У2 > 0.
Нетрудно показать, что
л f
g (t) fft — n) cos (at ф (t — r) — 0) dt\dQ =
(10.8.14)
(10.8.12)
1
2п
Г2а
~~ Z (т, <в) cos (0 + хЯ <*0 = /о Hr Z (Ч «Л
/V Q	'*0
(10.8.13)
где /0(z)— функция Бесселя от мнимого аргумента.
440
I h отому можем окончательно написать
аа2
(I f [а, т, со) = const Wpr (d) Wpr (т) Wpr (co) exp (— gj-j Zo ~ Z (t, co)
(10.8.14)
Из этой общей формулы можно получить разные частные ре-
\.1ьтаты. Например, если параметр а точно известен, т. е. а=а0,
и /г(а) = 6(а — а0), то
(10.8.15)
Г9<т	*1
(т, со) = const W/?r(T) WpT (со) 1й Z (т, со) .
I < 1И также известно запаздывание сигнала т = то, то из (10.8.15)
io |учим апостериорную вероятность для частоты
Wpr (со) = const Wpr (со) 10 Z (т0,со)’ .
3. Пусть в апостериорной вероятности (10.8.2) величина 9 рас-
1><делена равномерно (10.8.10), а величина а имеет релеевскую
и । ггность вероятности со средним квадратом (а2) = 2о2:
(10.8.16)
^л«) = 5ехр(-й
(10.8.17)
Подставив (10.8.17) в (10.8.14) и интегрируя по всем значениям
можем написать
ОО
и)=const IF (т) W (со) f W (а) ехр f —
с	J	с	\	ZlV о
О	4
о
><)lпользовавшись известным интегралом
ОО
J л'е~рх2 40(рх) dx
о
1	/ 32\
-н- ехр 4- »
2р r Up ’
О, (10.8.18)
11 <» |у чим
Wp,(г, ш) =const V„ (»)ехр Г	1, (10.8.19)
I I
/о+Г ta+T
Z2(t, со) = № + У2= J J
^0 to
t)cos[®H q>(^ — т) — at'— ср(Г — T)]dtdt'. (19.8.20)
441
При известном параметре г=т0 из (10.8.19) находим апосте-
риорную вероятность для частоты
Wps (®) = const Wpr (®) ехр	•	(10.8.21)
Когда отношение сигнал/шум велико (осп2 No), формула (10.8.21)
несколько упрощается:
Wps (<в) = const Wpr (со) ехр Г-^^-1.	(10.8.22)
Предположим, что сигналом s (/) является отрезок квазигар-
монического шума вида (7.1.4):
s (/) - А (/) cos [св/— ф (/)], 0</<Т,	(10.8.23)
с функцией корреляции
ks (т) = <s (/) s (/ + т)> = о2 е—(1 т > cos сот. (10.8.24)
Можно показать [16], что в данном случае при Т^>1/у апо-
стериорная вероятность для частоты определяется формулой
Wps (со) = const Wpr (со) ехр
2-р2
2г (<о)
(10.8.25)
где
т т
e—iAt-t'] cosco(/—
(10.8.26)
11 ,	2c2
Полученные выше формулы будут использованы в гл. 12 Для
определения предельной точности измерения параметров радио-
импульса, принимаемого на фоне белого шума.
ЛИТЕРАТУРА
1	Вопросы дальней связи на ультракоротких волнах Сборник пере-
водов под ред. В. И. Сифорова. Изд-во «Советское радио», 1957.
2	Сифоров В И Радиоприемные устройства Воениздат, 1951.
3	. А м и а н т о в И. Н. Применение теории решений к задачам обнару-
жения сигналов и выделения сигналов из шумов. ВВИА им. проф. Н. Е. Жу-
ковского, 1958
4	. В у двор д Ф. М. Теория вероятностей и теория информации
с применениями в радиолокации. Пер. с англ. Изд-во «Советское радио»,
1955.
5	Вайнштейн Л А, Зубаков В. Д. Выделение сигналов
на фоне случайных помех Изд-во «Советское радио», 1960.
442
G Marcum J. 1. A statistical theory of target detection by pulsed
hi Trans IRE, 1960, IT-6, № 2.
7	Петрович H. T. Передача дискретной информации в каналах
|>1з:>вой манипуляцией. Изд-во «Советское радио», 1965.
8	Тихонов В. И. Основные статистические характеристики кана-
> ннхрэнизации. «Электросвязь», 1966, № 4.
9	Турин Г. Л. Согласованные фильтры. Пер. с англ. «Зарубежная
ыоэлектроника», 1961, № 3.
10	. Лезин Ю. С. Оптимальные фильтры и накопители импульсных
। алов Изд-во «Советское радио», 1963.
11	. Фалькович С. Е. Прием радиолокационных сигналов на фоне
I । чктуационных помех. Изд-во «Советское радио», 1961.
12	Тихонов В. И, Левиков А. А. О квазиоптимальных ли-
и ihx фильтрах для импульсных сигналов. «Радиотехника», 1965, № 1.
13	. Норс Д. О. Анализ факторов, определяющих обнаружение сиг-
|| на фэне шумов в системах с импульсной модуляцией несущей. Пер.
| .1Л. «Труды института инженеров по электронике и радиотехнике», 1963,
?.
14	. С и ф о р о в В. И. О влиянии помех на прием импульсных радио-
। hi лов. ^Радиотехника», 1946, № 1.
15	Белоусов А. П. О наивысшей реальной чувствительности
। и-мника «Радиотехника», 1946, № 5.
15	Стратоиович Р. Л. Оптимальный прием узкополосного сиг-
। и с неизвестной частотой на фоне шумов. «Радиотехника и электроника»,
। и,	№ 7
Глава 11
ОПТИМАЛЬНЫЕ УСТРОЙСТВА ДЛЯ ОБНАРУЖЕНИЯ
СИГНАЛОВ И РАЗЛИЧЕНИЯ ДВУХ СИГНАЛОВ
§ 1. КРИТЕРИИ ОПТИМАЛЬНОГО ОБНАРУЖЕНИЯ СИГНАЛОВ
Пусть принятое колебание представляет сумму
£(/)	+	0<U<r,	(11.1.1)
где «(/) — белый нормальный шум, s(/) — полезный сигнал из-
вестной формы (детерминированный сигнал), полностью располо-
женный на интервале наблюдения (О, Т). Параметр к является не-
известным и может принимать только одно из двух значений: X = 1
(в принятом колебании присутствует сигнал) и Х = 0 (в принятом
колебании сигнал отсутствует).
Что касается априорных сведений о параметре X, то возможны
два случая: 1) априорные вероятности Wpr (1) и 1Грг(0) наличия и от-
сутствия сигнала известны; 2) эти априорные вероятности неиз-
вестны. Первый случай характерен для радиосвязи, второй — для
радиолокации, (см. стр. 399).
По принятой конкретной реализации £(/) необходимо решать
оптимальным (в некотором смысле наилучшим) образом, какое
именно значение имеет параметр X, т. е. присутствует или отсут-
ствует сигнал. Иначе говоря, нужно найти такой метод обработки
принятого колебания £(/), который бы позволял наилучшим обра-
зом обнаруживать наличие сигнала на фоне шума.
Практическая необходимость строгого решения подобных задач
возникла в последнее десятилетие в связи с широким применением
в радиотехнических системах электронных вычислительных машин,
обладающих большим быстродействием и высокой надежностью.
Раньше решение предоставлялось оператору. Например, наблюдая
визуально картину на экране индикатора радиолокационной стан-
ции, оператор на основе своего опыта и интуиции принимал реше-
ние о наличии или отсутствии цели. Замена оператора автомати-
ческими вычислительными устройствами позволяет исключить эле-
444
и iii субъективности и составить оптимальный алгоритм (правило),
к дуя которому вычислительное устройство принимает в опре-
к'нном смысле наилучшее решение о наличии или отсутствии
 ли.
Ниже будут кратко рассмотрены три метода (критерия) обна-
। \ жения сигнала на фоне шума: критерий идеального наблюдателя
ритерий Котельникова — Зигерта), критерий Неймана — Пир-
ин и критерий последовательного анализа. Каждый из этих кри-
п рпев имеет дело с оптимальностью в своем смысле (см. ниже),
и, (есообраэность применения того или иного критерия опреде-
шся характером задачи, а также зависит от того, известны или
, твестныаприорныевероятности Wpr (1) и Wpr (0) = 1 — Wpr (1).
1. Идеальный наблюдатель [1,2]. Критерий идеального наблю-
। юля применяется в системах радиосвязи, когда априорные ве-
и-,|гности Wpr (1) и Wpr (0) известны.
Гак как апостериорные вероятности содержат всю доступную
шсюрмацию о принятом колебании, то можно прийти к заключе-
н1|), что решение о наличии или отсутствии сигнала в принятой
। шзации должно приниматься на основе апостериорных вероят-
и‘ итей.
При непрерывной обработке принятой реализации апостериор-
। । -I вероятность наличия детерминированного сигнала (Л = 1)
инея формулой (10.3.25);
^(1) = ^г(1)ехр
т
-J-Jo)-s(/)p^
о
(11.1.2)
\и>стериорная вероятность отсутствия сигнала (%=0), очевидно,
। । па
Fpi(0) = Wp,(0)exp
т
лИ
о
(11.1.3)
i|i ,чем
Грг(0) + Грг(1) = 1.	(11.1.4)
Хотя апостериорные вероятности содержат максимум сведений
иосителыо наличия или отсутствия сигнала, однако практически
। приемника-обнаружителя требуется просто один из двух ответов:
> п> сигнал или нет. Естественно считать, что решение о наличии
। । отсутствии сигнала должно приниматься путем сравнения апо-
н риорных вероятностей по определенному правилу.
Для выяснения этого правила обратимся к рис. 11.1. На рисунке
р шедены четыре реализации случайного колебания: первые две
«пражаюг шум на выходе согласованного фильтра qn, а две дру-
к - сумму сигнала и шума q = <у(1). Пусть установлен неко-
|'>|1ый порог Н. Для конкретных реализаций, приведенных на ри-
445
Рис. 11.1. Четыре возможных слу-
чая при обнаружении сигнала на
фоне шума.
сунке, замечаем, что шум в первой реализации не превышает по-
рога. Во второй реализации хотя сигнала и нет, однако выброс
шума превышает порог. В третьей реализации сумма сигнала и шума
превышает,, порог, а четвертая реализация, несмотря на наличие
сигнала, не достигает порога._Из рассмотренных четырех случаев
* в двух случаях (первом и третьем)
будет принято правильное реше-
ние, а в двух (втором и четвер-
том) — неправильное. Если взять
другой порог Н, то описанная си-
туация может измениться.
Из такого качественного рас-
смотрения приходим к выводу, что
при конечном значении энергии
сигнала и наличии случайного
шума принятие решения о нали-
чии или отсутствии сигнала всегда
сопровождается ошибками двух
видов;
1) несмотря на отсутствие сиг-
нала, шум превосходит порог и
принимается неправильное реше-
ние о наличии сигнала (ошибка
первого рода),
2) хотя сигнал присутствует,
но пороговый уровень не превы-
шен и принимается ошибочное
решение об отсутствии сигнала
(ошибка второго рода).
Обозначим вероятность ошибки первого рода через Ро = Р(110)
и вероятность ошибки второго рода через Pi = Р(0|1). Для этих
вероятностей можем написать формулы:
сю	Н
= $ Wps(qn\0)dqn, P^W^q^dq. (11.1.5)
н	о
Средняя вероятность общей (суммарной) ошибки равна
сю	Н
Pe^P0 + Pi^\ Wps(qn\O)dqn+\wps(q\l)dq, (11.1.6)
н	о
а вероятность правильного обнаружения сигнала равна;
D = l— Pi.	(11.1.7)
Согласно критерию идеального наблюдателя пороговый уро-
вень Н устанавливается таким, чтобы вероятность общей ошибки Ре
была минимальной и, соответственно, вероятность правильного
446
р тения максимальной. Таким образом, оптимальный характер
и ;еального наблюдателя состоит в том, что он минимизирует вероят-
п )сть суммарной ошибки или, иначе, максимизирует общую jse-
1>)ятность правильного решения.
Чтобы правая часть равенства (11.1.6) имела минимум, нужно
п)иравнять производную по Н нулю. В результате получим, что
। <ли для принятой реализации окажется
^(//|1)/^рД//|0)>1,	(11.1.8)
к; следует констатировать факт наличия сигнала, и наоборот.
Рис. 11.2. Оптимальная схема для обнаружения детерминированного
сигнала на фоне шума.
Подставив в (11.1.8) выражения апостериорных вероятностей
in (11.1.2) и (11.1.3), получим, что решение о наличии сигнала
принимается при выполнении неравенства
т
9 С
 ° о
ехр
wpr (0)	/ Е \
ЗДеХР(^}
.Считывая монотонный характер логарифмической функции и лога-
рифмируя обе части этого неравенства, содержащего положитель-
11ые величины, получим
т
9 С -	F	№Пг(0)
(11.1.9)
о
Из этой формулы видно, что для вынесения решения о наличии
или отсутствии детерминированного сигнала, принимаемого на
<]юне белого шума, нужно принятую реализацию £(() перемножить
( сигналом s(/), проинтегрировать произведение в течение интер-
। ала времени Т, где известна реализация, и результат интегриро-
вания сравнить с порогом h, определяемым правой частью формулы
(11.1.9). Если этот пороговый уровень превышен, то принимается
|ешениео наличии сигнала. Если же порог не превышен, то кон-
i гатируется отсутствие сигнала. Функциональная схема приемного
устройства, осуществляющего указанные операции, приведена
на рис. 11.2.
447
Область применимости критерия идеального наблюдателя огра-
ничивается следующими физическими и формальными соображе-
ниями.
В этом критерии не делается существенных различий между
вероятностями ошибок Рп и Рх. Такое положение является оправ-
данным для радиосвязи, где пропуск какого-либо символа из-за
помех или ошибочная регистрация помехи в качестве переданного
символа примерно равнозначны. Наоборот, в радиолокации ве-
роятности ошибок Ро и Рх существенно не равнозначны и ведут
к разным последствиям. Так, например, при ложном обнаружении
цели, характеризуемом вероятностью Р<г, должен проводиться це-
лый ряд мероприятий системы обороны, в то время как пропуск цели
(вероятность Рг) не является сигналом к какому-либо действию.
Кроме этого, в § 2 гл. 10 указывалось, что иногда невозможно
достаточно обоснованно задать априорные вероятности, и задача
обнаружения должна решаться без использования их.
2. Наблюдатель Неймана — Пирсона [3, 4]. Этот критерий
применяется в радиолокации, когда априорные вероятности 1Грг(1)
и Wpr(0) неизвестны.
Если априорные вероятности неизвестны, то задача обнаружения
сигнала решается на основе отношения правдоподобия. Для рас-
сматриваемого случая детерминированного сигнала отношение
правдоподобия (10.3.28) можно записать так:
(11.1.10)
Решение о наличии или отсутствии сигнала принимается путем
сравнения отношения правдоподобия с некоторым порогом h0.
Если отношение правдоподобия превышает порог h0, т. е. »
/(1)>й0,	(11.1.11)
то принимается решение о наличии сигнала в обратном случае при-
нимается решение об отсутствии сигнала.
Вероятность Ро того, что хотя сигнала 'нет, но выполняется
неравенство (11.1.11), и принимается решение о наличии сигнала,
в радиолокации называется вероятностью ложной тревоги и обозна-
чается через F. Такое название вполне оправдано, так как величина
F характеризует вероятность такого события, когда сигнала (цели)
нет, однако принимается ложное решение (делается ложная тре-
вога) о наличии сигнала (цели).
Вероятность правильного обнаружения по-прежнему опреде-
ляется формулой (11.1.7), причем теперь величину Pi можно наз-
вать вероятностью пропуска цеди.
449
। огласно критерию Неймана — Пирсона пороговый уровень h0
। прмуле (11.1.11) определяется из условия, чтобы при заданной
[оятносги ложной тревоги Р вероятность правильного обнару-
• ।ия D была максимальной. Следовательно, оптимальный харак-
I критерия Неймана — Пирсона состоит в том, что он максими-
iipycT вероятность правильного обнаружения при фиксированной
|п>ятностк ложной тревоги.
Отметим, что если в формулу (11.1.11) подставить выражение
I 1 I 10) при Л = 1 и положить порог Ло = Wpr(0)/Wpr( 1), то при-
'I к соотношению вида (11.1.9). Поэтому можно сказать, что как
1> перий Неймана — Пирсона, так и критерий идеального наблю-
। сля базируется на отношении правдоподобия и отличается толь-
, правилом выбора порога h.
1 Последовательный наблюдатель [5, 6]. В двух рассмотренных
|.|не критериях предполагалось, что решение принимается за
I пксированный интервал времени Т. Однако может оказаться, что
I' ntпие можно принять за интервал времени, меньший Т. Этот
| и । учитывает последовательный наблюдатель.
11ри последовательном наблюдении производится непрерывный
hi шз отношения правдоподобия и сравнение его с двумя порогами
,	(1 —О)/(1 — Р) и й2 = DIP. Если отношение правдоподобия
, ныне Aj, то принимается решение о наличии только шума. Если
। । отношение правдоподобия больше /г2, то принимается решение
мличии сигнала. В том случае, когда отношение правдоподобия
। годится между нижним уровнем h± и верхним h2, имеющихся
распоряжении данных недостаточно для принятия решения и
। |ытание продолжается.* Такая процедура повторяется до тех
। >р, пока не будет принято определенное решение. Последователь-
H.и анализ был разработан А. Вальдом [5].
I [реимущество последовательного наблюдателя состоит в том,
। । можно независимо задавать вероятности Р и D, и он дает опре-
н иную экономию в энергии сигнала или во времени за счет сравни-
। и,по быстрого принятия решения об отсутствии цели. Поэтому
- ледовательный наблюдатель или его модификации применяются
радиолокации, особенно когда предполагается наличие малого
। ила целей и радиолокатор имеет небольшое число каналов по даль-
н '-ти. Последовательные испытания часто применяются так же при
•ледовании надежности и при отбраковке деталей.
Однако применение последовательного анализа предполагает
чее сложную работу аппаратуры (например, переменную ско-
|. > ль обзора пространства в радиолокации) и его труднее осуще-
। нить практически.
1 При использовании последовательных испытаний можно продуктивно
||).п>зовать тот факт, что для детерминированных сигналов q(y), рассмат-
1..1смая как функция интервала наблюдения Т, является марковским про-
сом [16, 17]
449
В следующих параграфах будут рассмотрены конкретные при-
менения наблюдателя Неймана — Пирсона и идеального наблюда-
теля. Ввиду того, что ряд расчетов требует громоздких выкладок,
для иллюстрации методики анализа подробно рассматриваются
лишь простейшие случаи, а для более сложных случаев приводятся
окончательные результаты.
Отметим также, что хотя мы рассматриваем обнаружение сиг-
нала и оценку его параметров раздельно, на практике эти две задачи
часто решаются совместно.
§ 2. ОБНАРУЖЕНИЕ СИГНАЛА ПО КРИТЕРИЮ
НЕЙМАНА — ПИРСОНА
Рассмотрим задачу обнаружения сигнала на фоне шума по кри-
терию Неймана — Пирсона раздельно для трех видов сигналов:
детерминированных, со случайной начальной фазой и со случай-
ными амплитудой и фазой (см. § 2 гл. 10).
1.	Обнаружение детерминированного сигнала. Как следует из
формул (11.1.10) и (11.1.11), решение о наличии или отсутствии сиг-
нала должно приниматься на основании сравнения с порогом отно-
шения правдоподобия:
т
о
S/Zo-
Учитывая монотонный характер показательной функции и лога-
рифмируя обе части, получим, что решение о наличии или отсут-
ствии сигнала можно принимать на основании сравнения с некото-
рым порогом /г величины
г
0 о
(11.2.1)
Структурные схемы оптимального обнаружителя с использо-
ванием согласованного фильтра и корреляционного приемника при-
ведены на рис. 11.3.
Пусть присутствует детерминированный сигнал, т. е. £(/) =
= s(t) + n(t). Тогда замечаем, что случайная величина
т
° о
45Q
получается в результате линейного преобразования белого нормаль-
ного шума. Поэтому она будет иметь нормальную плотность вероят-
ности w^q) со средним значением и дисперсией, равными:
_	, . 2Е 2	,,	2Е
«i = <4i> = ^>	= <(4i~-/«i)2> = ууу
6)
Рис. 11.3. Схемы оптимальных обнаружителей детермини-
рованного сигнала с использованием корреляционного
приемника (а) и согласованного фильтра (б).
В отсутствие сигнала g(z‘)=n(z£) и случайная величина
Рис. 11.4. Нормальные плотности вероятности te>i(?) и
ш2(?) при наличии и отсутствии сигнала (? — вероят-
ность ложной тревоги; D — вероятность правильного
обнаружения)
имеет также нормальную плотность вероятности ш2(4), причем
т2 = <42^ — о, 02 = <42> = ТГ'-
Ло
Плотности вероятности шх(4) и и»2(4) изображены на рис. 11.4.
451
Согласно критерию Неймана — Пирсона должна задаваться
вероятность ложной тревоги F, т. е. вероятность превышения шумом
порогового уровня h:
СО
F а>2 (q) dq
h
^2E/N0)
(11.2.2)
где Ф(г) — интеграл вероятности (см. приложение IV). .
При этом вероятность правильного обнаружения будет равна:
ОО
D = f w1(q)dq = 1-ф(—1/^-Y (11.2.3)
J W	V2£/W0 'AW V '
На рис. 11.4 площади, соответствующие вероятностям F и D, за-
штрихованы.
Формулы (11.2.2) и (11.2.3) показывают, что вероятность лож-
ной тревоги F, как и вероятность правильного обнаружения D,
Рис. 11.5. Кривые обнаружения де-
терминированного сигнала
однозначно определяются отно-
шением порогового уровня /г к
величине сигнал/шум. Поэтому
по заданной вероятности лож-
ной тревоги F однозначно опре-
деляется уровень h, а зная его,
находим вероятность правиль-
ного обнаружения D.
Таким образом можно рас-
считать кривые обнаружения
сигнала (рис. 11.5). Кривые
обнаружения представляют за-
висимость вероятности правиль-
ного обнаружения D от отно-
шения сигнал/шум при фикси-
рованной вероятности ложнбй
тревоги F.
Пользуясь кривыми обнаружения, можно определить пороговый
сигнал. Пороговым называется сигнал, который при заданной ве-
роятности ложной тревоги F можно обнаружить с требуемой ве-
роятностью правильного обнаружения D. Пороговый сигнал ха-
рактеризуется его энергией (или мощностью).
На основании полученных результатов можно сделать следую-
щий фундаментальный вывод. Возможность обнаружения сигнала
при оптимальном приеме с заданными вероятностями D и F не за-
висит от формы сигнала и определяется только отношением энер-
гии сигнала к спектральной плотности шума, т. е. отношением сиг-
нал/шум на выходе согласованного УПЧ.
В формулах (11.2.2) и (11.2.3) вероятности F и D выражены че-
рез безразмерные величины. На практике порог устанавливают по
452
и к'персии шума на выходе приемника. Чтобы ввести дисперсию
in ма (10.5.7) на выходе рассматриваемого приемника, запишем
]и рмулу (11.2.2) иначе:
Е = 1 — ф(“),	(11.2.4)
।	= Ж/1/2.
Пользуясь таблицами интеграла вероятности, по заданной ве-
роятности ложной тревоги F находим значение аргумента Я/ов и,
v	2	Г Т
• сдовательно, при известной дисперсии oD определяем порог п.
2.	Обнаружение радиосигнала со случайной начальной фазой.
[ I )вторив рассуждения, которые привели к формуле (10.8.14), мож-
но показать, что отношение правдоподобия для радиосигнала
110.2.10) имеет вид
, , ч	( о а2 \ , /2aZ\	„ г,
I (п) = ехр	(j?)	1-2-5)
|де положительная величина Z определена формулой (10.8.12) и
физически представляет огибающую принятого колебания. При
обнаружении нефедингующего сигнала, содержащего лишь неиз-
вестную начальную фазу, безразмерный коэффициент а считается
постоянным.
Как видно из (10.8.4),* величина а/2 равна энергии сигнала
пзи а = 1, т. е. Ех = а/2. Полная энергия сигнала равна
Е = а2Е1.	(11.2.6)
При a—const отношение правдоподобия (11.2.5) можно записать
гик:
I (а) - ехр (-	= const,,	(] 1.2.7)
Так как функция Бесселя /0(z) является монотонной, то реше-
ние о наличии или отсутствии сигнала можно принимать на основа-
нии сравнения с некоторым порогом любой монотонной функции
<зт огибающей Z. Если сравнивать с порогом h саму огибающую Z
(линейный: детектор огибающей), то получим следующее правило.
Решение о наличии или отсутствии сигнала принимается в зависи-
мости от выполнения неравенств
Z^h.	(11.2.8)
Структурная схема оптимального приемника приведена на
рис. 11.6. Она состоит из согласованного фильтра, линейного детек-
тора огибающей и порогового устройства.
Предположим, что в принятой реализации |(/) присутствует
сигнал (10.2.10), т. е.
£ (/) = п (/) + af (t — т) cos (со/ + ф (t — т) — 6).	(11.2.9)
453
Будем считать пока фазу 9 постоянной. Ниже мы убедимся, *1Тб
в окончательные формулы она не входит. Подставив выражение
(11.2.9) для %,(f) в формулы (10.8.11), получим, что при выполнении
условий (10.8.3) случайные величины X и Y являются нормально
распределенными с одинаковыми дисперсиями
= ±N0Elt	(11.2.10)
а условные средние значения их соответственно равны
тх = <Х|0> = aEi cos 0, ту = <У]0> = aE-L sin 0.
Рис. 11.6. Оптимальная схема для обнаружения радиосигнала
со случайной начальной фазой.
Заметим, что величины X и Y можно считать практически неза-
висимыми, так как функция корреляции между ними приближенно
равна нулю:
k^X, Y) = ^-p2(* —r)sin2[<^ — <р(г —т)]^«0.
Поэтому плотность вероятности U7X(Z1 а) случайной величины
Z = }ЛХ2 + Г2 при а = const согласно формуле (5.2.21) опреде-
ляется законом Райса:
П7 /-7, \ 2Z (	Zi-\-a2E1\ Т !2aZ\ n Л ,1ч
=ад;«р(--------( -2- 11
Рассмотрим теперь случай, когда сигнал отсутствует, т. е.
= n(t). Подставив в формулы (10.8.11) n(i) вместо £(0, полу-
чим, что независимые нормальные случайные величины X и Y имеют
нулевое среднее значение и одинаковую дисперсию (11.2.10). На
основании формулы (5.2.26) плотность вероятности W2(Z)- случай-
ной величины Z в данном случае будет релеевской:
^(2) = «7<Гет1>(-«5г)-	(11.2.12)
Заметим, что для сигнала со случайной начальной фазой без-
размерный коэффициент а = const можно считать включенным
в функцию Это соответствует тому, что в формулах (11.2.11)
454
ii (11.2.12) нужно положить а = 1, Е = Ev Тогда можем окойЧй-
п пьно напасать
2Z / Z2 + Е \ , [2Z
^i(z) — NoE ехР ( NoE )Io[no
2Z [ Z2 \
^2(Z) — ^0EeXP ( Noe}'
(11.2.13)
(11.2.14)
В соответствии с критерием Неймана — Пирсона по заданной
ш роятности ложной тревоги
ОО	OO	1	19
г*	р	— —- d2	— ha	h
I = j42(Z)dZ=J ue 2 du = e 2 °, Ао=	(Ц.2.15)
Л	na
шределяется пороговый уровень ho, а затем вычисляется вероят-
ность правильного обнаружения
оо	оо	/	пр \
р	р	I 7,2	\	_____
/) = i ^x{Z)dZ= и ехр у--------------------I/0	du. (11.2.16)
h	ha
Вероятность D является частным значением табулированной функ-
ции [7,8]
00
Q (и, и) = J z ехр
и
—Io (ZV) dz.
(11.2.17)
Результаты расчетов по формулам (11.2.15) и (11.2.16) представ-
юпы на рис. 11.7.
3.	Обнаружение федингующего радиосигнала. Пусть в радио-
< игнале (10 2.10) является случайной не только фаза 0,но и ампли-
|удный множитель а, причем плотность вероятности для безразмер-
ной случайной величины а является релеевской:
Wpr(a) = 4 ехр	а>0.	(11.2.18)
Оа	2со /
Отношение правдоподобия для рассматриваемого сигнала можно
получить путем усреднения выражения (11.2.5) по а. Воспользо-
втвшись интегралом (10.8.18), получим
</ (а)> = J I (a) Wpr (a) da =
«
Wo
-——ехр
Nо (аОд 4- Wo)
(11.2.19)
455
Как следует из (11.2.6) и (10.8.17), величина аоа равна сред-
ней энергии сигнала:
Е = <Е> = <а2> Ег = Ех J a2 Wpr(a)da=2o2a Ei- (11.2.20)
о
Поскольку показательная функция является монотонной, то
можно принять прежнее правило (11.2.8) решения вопроса о на-
личии или отсутствии сигнала в принятой реализации.
Рис. 11.7. Кривые обнаружения для детерминированного сигнала (сплошные
линии), сигнала со случайной начальной фазой (пунктир) и сигнала со
случайными амплитудой и начальной фазой (штрих-пунктир).
Усреднив выражение (11.2.11) по флуктуирующему амплитуд-
ному множителю а с плотностью вероятности (11.2.18), получим
релеевскую плотность вероятности огибающей Z при наличии сиг-
нала:
W\(Z) =-----22 о--о ехр/----------22 д- 2 Y (11.2.21)
W0E1 + 2o2£2	,v0£i + 2c2e2 у V	7
Плотность вероятности огибающей Z при наличии одного шума по-
прежнему дается формулой (11.2.12).
Кривые обнаружения по критерию Неймана — Пирсона строят-
ся так. По заданной вероятности ложной тревоги
ОО	!	2
Т-С 1Г2 (Z) rfZ=e h„ = 	*.,	(11.2.22)
J	у Л о Е1/2
456
||>еделяется пороговый уровень h0 и затем вычисляется вероят-
। >-и, правильного обнаружения
(11.2.23)
D — 1 iTi (Z) dZ = exp
Если нужно сравнивать характеристики обнаружения федин-
\ ощих и нефедингующих радиосигналов, то естественно произ-
iriTb такое сравнение для случая, когда средняя энергия федин-
' \ опдего сигнала равна энергии нефедингующего сигнала. Для
мио, как видно из формулы (11.2.20), нужно положить
<у2а = 1/2.	(11.2.24)
I' 1 да формулу (11.2.23) можно записать в таком виде:
D=Fi,('l+^.	(11.2.25)
На рис 11.7 приведены рассчитанные по формулам (11.2.3),
11 I 2.16) и (11.2.25) кривые обнаружения для трех видов сигналов:
I) детерминированного (сплошные линии); 2) сигнала со случайной
и 1шльной фазой (пунктир) и 3) сигнала со случайными амплитудой
и начальной фазой (штрих-пунктир) [9].
Видно, что при увеличении отношения сигнал/шум все кривые
начала растут медленно, а затем быстрее. При больших вероятно-
' гях правильного обнаружения кривые для сигнала со случайной
и 11альпой фазой и особенно для сигнала со случайными амплитудой
и фазой смещены в сторону больших отношений сигнал/шум. На-
порот, при малых вероятностях правильного обнаружения
|/><0,2) кривые обнаружения для федингующего сигнала идут
। ыше соответствующих кривых для других двух сигналов. Это объ-
н ияется тем, что при равенстве энергий (11.2.24) амплитуда федин-
। \ ощего сигнала с вероятностью
1 1
j Wpr(a) da= J 2ae~a’dax 0,74
о	о
пудет превышать амплитуду нефедингующих сигналов.
§ 3. РАЗЛИЧЕНИЕ ДВУХ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
Задача обнаружения сигнала на фоне шума является частным
> лучаем задачи различения двух сигналов. Рассмотрим здесь задачу
различения двух детерминированных сигналов.
Пусть принятое колебание представляет сумму
^(/) =ZS1(/) +(1 — X)s2(0+«(0, 0</<Т, (11.3.1)
457
где n(0 — белый шум, sx(/) и s2(i) — полностью детерминиройанйые
сигналы. Неизвестный параметр Л может принимать одно из двух
значений: X - 1 (присутствует только сигнал s,) и А = 0 (присут-
ствует сигнал s2). Априорные вероятности ITpr(s1) присутствия сиг-
нала sx и Wpr(s2) присутствия сигнала s2 предполагаются извест-
ными.
По принятой реализации £(7) нужно решить, какое именно зна-
чение имеет параметр А, т. е. какой из сигналов s^t) или s2(t) при-
сутствует в реализации.
Для апостериорных вероятностей наличия сигналов s^t) и
$2(/) нетрудно получить следующие выражения:
rpi(Sl) = ^r(S1)exp
(11.3.2)
где
г	т
Et = j S| (/) dt, Ег = J S2 (0 dt.
о	о
(11.3.4)
В соответствии с критерием идеального наблюдателя будем
считать, что присутствует сигнал s4(A = 1), если выполняется соот-
ношение
т
WpS($i)	Ех—Е2. 2 (\... . ...	...... . ,
ехрГAvT~ +	J 6(0 [S‘< Н'
I	о
(11.3.5)
Отсюда получим
т
<7 = ЛД-J в (О [S1 (0 — s2 (01 dt > In	= h. (11.3.6)
о	r
Назовем систему передачи двоичных сигналов симметричной,
если для нее выполняются равенства:
^z(S1) = ^(s2)= 1, Е1 = Е^Е. (11.3.7)
Для симметричной системы формула (11.3.6) упрощается:
т
Q =	h(01s1(0-s2(01^>/i = 0.	(11.3.8)
О
458
Таким образом, на основании сравнения апостериорных ве-
роятностей получаем следующее правило различения двух детер-
птированных сигналов. Принимается решение о наличии сигнала
>(/), если <? (> 0; при q <" 0 принимается решение о наличии сиг-
н 1ла s2(t).
На рис. L1.8 приведены две схемы оптимального приемника для
различения двух детерминированных сигналов: с использованием
। оррелометра и согласованных фильтров. Второй из них состоит
Рис. 11.8. Оптимальные схемы для различения двух детерминированных
сигналов с использованием корреляционного приема (а) и согласован-
ных фильтров (6).
и । двух линейных фильтров, согласованных с сигналами s^t) и
.(/) соответственно, вычитающего устройства и порогового устрой-
 гва (например, типа электронного реле). В первом принятое коле-
ь nine £(£) раздельно перемножается с известными сигналами s^t)
и s_(0, интегрируется и разностное напряжение подается на поро-
ииое устройство.
'Предположим, что выполняются условия (11.3.7). Вычислим
11 роятность общей ошибки. Пусть присутствует сигнал s^f), т. е.
|(0 = 81(0 + «(0.
1<пда случайная величина
г
q = qi - J [Si (0 + п (OJ [sx (0 - s2 (Z)] dt
о
(11.3.9)
459
будет иметь нормальную плотность вероятности w1(q) со сле-
дующими характеристиками:
=	=	(П.З.Ю)
Здесь
т
(и.з.п)
о
— коэффициент взаимной корреляции между сигналами st (()
и s2(().
Рис. 11.9. Нормальные плотности вероятности при
наличии одного из двух сигналов и вероятности
ошибок.
Если присутствует сигнал s2(/), т. е.
£(0 = М0 + «(0>
то случайная величина
т
7 - 7г- J 1«2 (0 + «(01 (si (0 - «2 (01 dt (11.3.12)
о
имеет нормальную плотность вероятности w2{q) с характеристи-
ками
Щ2 = <?2> = -^-(1 -Rs), d = <722>-m^ =^-(1 ~RS).
(11.3.13)
Плотности вероятности w^q) и w2(q) изображены на рис. 11.9;
Обозначим через P(sx | s2) условную вероятность принять реше-
ние о наличии сигнала s1; когда в действительности присутствует
сигнал s2, и через P(s21 sx) — условную вероятность принять реше-
ние о наличии сигнала s2, когда в действительности присутствует
сигнал Sj. Очевидно, что вероятность общей ошибки равна
Ре = ^рЛь2) Р (S1|S2) + Wpr (S1) Р (S2|S1),	(1 1.3.14)
460
oo	h
P(sL|s2) = J w2(q) dq, P(s2Si) = J Wi(q)dq. (11.3.15)
h	—oo
Подставив в (11.3.14) значения априорных вероятностей из
ill 3.7), находим вероятность суммарной ошибки
Ре
’ оо	h
J + J Wikqjdq
_h	—00
(11.3.16)
= 2
1 1олагая, как это следует из (11.3.8), h = 0 и выполнив вычисления,
н >лучим
p.=i- М-
(11.3.17)
Следовательно, при известном отношении сигнал/шум 2E/N<j,
। । шисление вероятности суммарной ошибки для детерминированных
иг налов сводится к определению коэффициента взаимной корре-
ыпии между сигналами. Так как интеграл вероятности Ф(с) яв-
1яегся монотонно возрастающей функцией аргумента, то при одина-
|<)|юм отношении сигнал/шум наибольшей помехоустойчивостью
। меньшей вероятностью ошибки Ре) обладают сигналы, для которых
! огффициенг взаимной корреляции минимален.
Если сигналы обладают одинаковой энергией, то коэффициент
и мимной корреляции Rs может изменяться от — 1 (при st(/) =
— s2(i)) до + 1 (когда sx(/) = s2(/)). В том случае, когда Rs — О,
творят, что сигналы ортогональны. Очевидно, что одинаковые
сигналы (Z?, = 1) невозможно различить и поэтому Ре =
I —Ф (0) = 6,5. Наоборот, если сигналы одинаковы по форме и про-
швоположны по знаку (Rs = — 1), то их различить легче, чем лю-
пые другие два сигнала (например, ортогональные). Сказанное ил-
нострируется рис. 11.10, на котором представлены результаты рас-
четов по (формуле (11.3.17) [10].
Кривые, характеризующие зависимость вероятности суммарной
ошибки Ре от отношения сигнал/шум при оптимальных методах
приема, в радиосвязи часто называют кривыми потенциальной по-
мехоустойчивости. Получим такие кривые для некоторых видов
манипулированных сигналов, применяемых в радиотелеграфии.
Амплитудная манипуляция (AM). При амплитудной манипу-
1ЯЦИИ
Si (/)=А/И cos (о/+ qp), s2(0 = 0, 0<£<7\ (11.3.18)
14 данном случае на основе критерия идеального наблюдателя нуж-
но решить задачу обнаружения сигнала s^f) на фоне шума.
Положив в выражениях (11.3.9) и (11.3.12) s2(/) = 0, получим,
ЧТО плотности вероятности &i(q) и w^(q) величин и q2 являются
401
нормальными со следующими средними значениями и диспер-
сиями:
Рис. 11.10. Зависимость вероятности
общей ошибки Ре от коэффициента
взаимной корреляции Rs между де-
терминированными сигналами.
Рис. 11.11. Зависимость вероятно-
сти ошибки от отношения сиг-
нал/шум для детерминированных
сигналов при AM, ЧМ и ФМ.
Пусть априорные вероятности наличия и отсутствия сигнала
st(f) одинаковы и равны 0,5. По формуле (11.3.16) записываем
выражение для вероятности суммарной ошибки:
00
1	1 I / Я2 \ Л г
2	4Е/М0)^ +
h
h
+ / 4-£/Л^=_ J еХр
— 00
Значение оптимального порога h находим по формуле (11.3.6):
h = E/No = (mJ — m2)/2. Отсюда следует, что порог определяет?^

"< циссой точки пересечения плотностей вероятностей w^q) и
(</) При таком пороге вероятность ошибки минимальна и равна
(11.3.19)
। |> и|)ик этой функции представлен на рис. 11.11.
Частотная манипуляция (ЧМ). При ЧМ используются два гар-
। 'нических сигнала одинаковой амплитуды и длительности, имею-
 111' различные несущие частоты:
«г (0 = Ат cos (Wi t — фО, I о <П Г. (11.3.20)
s2(t) = Ат cos (со21 — ф2), I
Согласно (11.3.11) в данном случае имеем
п _ sin(to2 —о>1) Т
s~ К-М1)7 •
II практике обычно выполняется неравенство (со2—
I битому можно положить Rs = 0, и для вероятности ошибки из
I |>рмулы (11.3.17) получим
Р, = 1-ф(/А).	<11.3.21)
Зависимость вероятности ошибки от отношения сигнал/шум
и поражена на рис. 11.11.
Фазовая манипуляция (ФМ). При фазовой манипуляции ис-
। > п.зуются сигналы
S1 (0 = Ат cos (О/, | 0</<7\	(11.3.22)
S2 (0 = — Ат COS G)/, J
I ы таких сигналов Ks = — 1 и вероятность ошибки согласно
113 17) равна
Ре = 1-ф(р^).	(11.3.23)
। г фик этой функции представлен на рис. 11.11.
Сравнивая графики рис. 11.11 для AM, ЧМ и ФМ, видим, что
||П1 одной ж той же энергии из трех рассмотренных видов манипу-
и1!и наибольшей помехоустойчивостью обладает фазовая мани-
1яция и наименьшей — амплитудная.
13ыше был рассмотрен один из простейших примеров теории
। । шчения двух сигналов на фоне помех. Конечно, практические
\'|<1И оказываются более сложными. Так, например, в радиосвязи
। I щиолокации не приходится оперировать с полностью известны-
||| (детерминированными) сигналами. Обычно бывают заранее не-
46?
прихода) сигнала, его амплиту-
известными начальная фаза (время
да и другие параметры.
Сигналы с полностью известными параметрами можно исполь*
зовать в качестве своеобразных теоретических «эталонов», позво
ляющих получить максимальную информацию. Результаты опти<
мальной обработки сигналов с различными неизвестными пара"
метрами целесообразно сравнивать с соответствующими результат
тами, получающимися для аналогичных сигналов с известными
параметрами.
§ 4. РАЗЛИЧЕНИЕ ДВУХ РАДИОСИГНАЛОВ СО СЛУЧАЙНОЙ
НАЧАЛЬНОЙ ФАЗОЙ
Пусть в выражении (11.3.1) сигналы s^t) и s2(f) имеют виД
si(t) T)cos(®J+ ф» (0i^l, 2, (11.4.1)
где ю( — несущие частоты, ft(t— т) и qp,(O — функции, отобра-
жающие законы амплитудной и фазовой (частотной) модуляции,
0( — начальные фазы, представляющие собой независимые слу-
чайные величины, распределенные равномерно на интерн
вале (— л, л). Предполагается, что ширина спектров сигналов
Si(0 и s2(0 много меньше их несущих частот и, кроме этого^
|®2— ।
По критерию идеального наблюдателя нужно решить задачу
различения двух таких радиосигналов со случайными начальными
фазами [11].
Апостериорные вероятности наличия сигналов si(0 и s2(0 cd
случайными начальными фазами получаются путем усреднений
правых частей выражений (11.3.2) и (11.3.3) по начальным фазам
как несущественным параметрам, т. е. можно написать

1
2л
7t
4Jexp
—«
Т
J S(OfiG— т)cos (®1^+ф1(0— °i) dt
о
^s(S2) = ^r(S2)e-Wx
т
J £(0М“ т) cos (®з^+ф2(0— 62) dt
° о
(11.4.2|
(11.4.35

1’сли ввести обозначения
т
X, = J g (t) f, (t — r) cos t 4- q>i (/)] dt,
о
т
Y, = J g (t) f, (t — r) sin [од t + qpt (7)] dt,
о
(11.4.4)
Zz=/xf+y?(	(11.4.5)
’ из (11.4.2) и (11.4.3) для апостериорных вероятностей полу-
\i следующие выражения:

(11.4.6)
(11.4.7)
11 ^о(г)—функция Бесселя нулевого порядка от мнимого аргу-
। ига.
Согласно критерию идеального наблюдателя решение о нали-
III сигнала s^t) или сигнала s2(f) принимается в зависимости от
и волнения неравенств
ГС7И31) = Wpr (sx)	]д ^iNp) <
^pi(s2) Wpr (sz)	^o(2Z3/?Zo) '=~
и
Ei— E* Wnr (s2)
In /о (2Z!/2VO) - In Io (2Z2/NO) ==-V-^- + In =	(11.4.8)
Положительная величина Zi, определенная равенством (11.4.5),
> 11 па корню квадратному из суммы квадратов двух нормально
к пределенных случайных переменных X, и У,. Физически вели-
|Цна Z, представляет собой огибающую суммы сигнала st(Z) и
пума n(t) на выходе согласованного фильтра, имеющего импуль-
II мо характеристику
Gt (/) =
Si(T-t)
О
при
при
0<7
^<0, t>T.
(11.4.9)
।  шчину ln/0(2Zj/jV0) можно получить в явном виде на выходе
к'ктора огибающей с законом 1п70(г). 1 J
Структурная схема оптимального приемника для различения
. .\ радиосигналов с неизвестной начальной фазой представлена
। рис. 11.12. Принятое колебание g(f) = s((Z) + n(f) воздействует
। два согласованных фильтра с импульсными характеристиками
11 I 4.9). На выходе каждого из фильтров стоят детекторы огибаю-
465
щей, напряжения детекторов вычитаются, и эта разность возденет*
вует на пороговое устройство с порогом h. Если напряжение пре-|
вышает порог h, то принимается решение о наличии сигнала s^);!
если же порог не превышен, то констатируется наличие сигнала)
Отметим, что при выполнении условий (11.3.7), когда система
является симметричной, пороговый уровень h — 0, и решение о на-
личии сигналов s1(zI) и s2(/) принимается в зависимости от выполне-
ния неравенств
in/0(2Z1M)^in/a(2Z2/2V0).	(н.4.10)
Рис. 11.12. Оптимальная схема для различения двух радиосигналов со слу-
чайными начальными фазами.
Функция Бесселя /0(г) является монотонной функцией аргумента».
Поэтому закон детектирования не имеет существенного значения
при различении двух сигналов. Важно лишь, чтобы выходное на:
пряжение детектора было монотонной функцией огибающей Zt,
Если, например, в оптимальном приемнике (рис. 11.12) применить
линейный детектор огибающей, то различение двух сигналов нужно
производить путем сравнения значений самих огибающих Zr и Z2,
При Zp^ принимается решение о наличии сигнала s^t), и на-
оборот.
Ограничимся в дальнейшем рассмотрением симметричных ка^
налов и примем, что различение сигналов производится путем срав-,
нения огибающих и Z2. Для симметричных каналов условные
вероятности ошибок равны друг другу:	'
Р («1|5з) = Р (S2|S1)-
Для вычисления этих вероятностей нужно предварительно найти
совместную плотность вероятности огибающих IF2(Z4, Z2), ноль’
зуясь выражениями (11.4.4) и (11.4.5). Тогда
Р (st|s3) = pZx J W2 (Zlt Zs) dZs
0 Zi
466
Г in вероятности общей ошибки согласно (11.3.14) получим фор-
0
СО	00
Ре-\ dZ^ W2(Zlt Z2)dZ2.	(11.4.11)
О	Zt
Весьма громоздкие расчеты приводят к следующему оконча-
।иному результату:
И'
Ps-f,	0<р,<1,
т
J f А (0Л»(0 cos[(<o2—<щ)/+<р2(/) —	... . 1O.
o	(*1 *4-13)
т
bs = i J sin K®2- z+ *Р2(0— Ti(01dt'
0
• Н'сь Q (?, и) табулированная функция (11.2.17).
На рис. 11.13 приведены вычисленные по формуле (11.4.12)
рпвые, характеризующие зависимость вероятности ошибки от
ыффициента взаимной кор-
1> тяции сигналов ps при не-
кольких значениях отноше-
ния сигнал/шум. Из кривых
видно, что при заданном от-
пмнении сигнал/шум вероят-
11 )сть ошибки минимальна
ия ортогональных сигналов
। р._ = 0). Наоборот, для двух
• in налов, совпадающих по
|орме с точностью до началь-
и>й фазы (ps = 1), вероят-
ие ть ошибки всегда макси-
ольна и равна Ре = 0,5.
к 11.1). Зависимость вероятно-
и общей ошибки Ре от коэф-
[иииента взаимной корреляции
между сигналами со случай-
ными начальными фазами,
467
По формулам (11.3.17) и (11.4.12) были выполнены расчеты кри-
вых потенциальной помехоустойчивости для различных сигналов,
применяемых в радиотелеграфии. Ниже кратко указаны основные
результаты вычислений.
Амплитудная манипуляция (AM). Если в (11.3.18) начальная
фаза ф случайна и равномерно распределена, то вероятность
ошибки равна
Ре = 1-[1+ехр(-1	/г)],	(11.4.14)
где оптимальный порог h находится из уравнения

Частотная манипуляция (ЧМ). Считая в
<р2 случайными, получим
(11.3.20) фазы (ft и
sin у (<1>2 — cui) Г
ТУ (й2 — (Dj) Т
О при ^((о2 — ®i)T> 1.
В данном случае формула (11.4.12) упрощается:
d	1/Т~2Ё\	1	( 1 2Е\
?е	И 2 Л/о '	2 еХр \ 4 JVo/’
Учитывая, что Q(0, н)—ехр у п2 окончательно получим
Pe=|exp(-~у	(11.4.16)
Тональная манипуляция АМ-АМ. В данном случае имеем
«1(0 = Ап(1+miCosQOcos(o^--e1), 1	о</<Т	(11417)
s2 (t) = Am (1 + m2 cos ^0 cos — 62), Г "
Можно показать, что для таких сигналов формула (11.3.17) при-
нимает вид
р __ 1	(Т) / , / 1 2^1 (от1 тг)2 ) р _ 1 д2 р /1 ,	1	2\
*	+ 2тф
(11.4.18)
При фиксированном значении 2EjN0 эта вероятность будет ми-
нимальной, когда «!=! и т3=0. При этом
Р.= 1-ф(/те^- )	(11.4.19)
468
Тональная манипуляция ЧМ-АМ, При тональной манипуля-
ции ЧМ-АМ используются сигналы
+mcosQ1Z)cos(wZ— Oj), 1	0<t<T, (11 4 20)
s2 (1) = Am(l 4- m cos Q21) cos {at— 62), J
июргии которых равны
Е,	= Е2 = ^А^Т
В случае детерминированных сигналов полагаем 6,=0 и поль-
ыемся формулой (11.3.11):
т
Rs =	=
и
г
А2 Г
— I (1 ф- ni cosQi t) (1 + tn cos П2 0 cos^tdt.
о
Па практике обычно выполняются соотношения Т = Л,2я/Йг,
<" Нг, где Лг—большие целые положительные числа (#,^1). С уче-
ны этих условий после несложных преобразований получим
Rs = 2/(2 + иг2).
Подстановка этого значения Rs в формулу (11.3.17) дает
(11.4.21)
При т — 1 сигналы ЧМ-АМ различаются с минимальной ве-
роятностью ошибки:
(11.4.22)
Для сигналов (11.4.20) со случайными начальными фазами 0,
вычисления по формулам (11.4.13) приводят к прежнему резуль-
мгу:
Ps = Rs = 2/(2 + т2).
Ьсроятносгь ошибки при т=1 согласно (11.4.12) равна
Р. = « (““) - 4 «Р (- т /» (4 24). (Ч -4-23)
। |е
- 1 / 1 2Е 3~	/ 1 ЧЕ 3+Г5~
|/	4 Wo 3	’	“	4 Я, 3
469
Тональная манипуляция ФМ-АМ. Ё данном случае исполй*
зуются сигналы:
Si(0 = +mcosQ0cos((oZ —9J | Q<t<T (114 24)
s2 (() = Ат (1—т cos QZ) cos (о/—б2)) ’
Энергии сигналов равны
Е^Ег=^А2тт(\Д-^т^ = Е.
Коэффициенты взаимной корреляции /?s и р5, вычисленные по
формулам (11.3.11) и (11.4.13), одинаковы:
Es = ps (2 — m2)/(2 + m2).
Обычно берут т = 1. При этом // = рд. = 1/3.
Подставляя Rs=l/3 в формулу (11.3.17), получаем выражение
для Ре при приеме детерминированных сигналов ФМ-АМ:
(11.4.25)
Вероятность ошибки Ре при приеме сигналов ФМ-АМ (tn = 1)
с неизвестной начальной фазой вычисляется по формуле
А — Q (у> и) — ~2 ехР 4“ А ^Т2	( .4.26)
где
, / 1 2Е 3 —2/2	, / 1 2Е 3 + 2/Г
°=|/	“=|/ ТГ.АА’
которая получается из (11.4.12) путем подстановки р5 = 1/3.
Тональная манипуляция АМ-ЧМ. При тональной манипуляции
АМ-ЧМ используются следующие сигналы:
S1 (0 = cos (о>/ + ₽1 cos £11 ~ 61), 1 Q<rt<T (Ц.4.27)
S2(t) = Amcos(®i? +02 cos — 62), J "
Энергии сигналов одинаковы:
Ej. = E2 = T = E.
При вычислении коэффициентов взаимной корреляции нужно вос-
пользоваться известным разложением:
ОО
cos (х cos ф) ~ Jo (х)4-2 2 (—1)" Ап (х)cos 2жр
470
П'сть обычно выполняющиеся соотношения: Т = 2nk/£l, со
 /. —большое целое положительное число (&>1). Получим сле-
ищие результаты:
^ = Л(₽а-Pi). P.s-1Л(р2“(Ш
. /„(г) — функция Бесселя нулевого порядка.
11ри достаточно большой разности индексов модуляции
|’>.—можно приближенно принять
Ps ~ р4 = 0.
11 pi этом вероятности ошибок Ре для разных случаев приема сиг-
> । юв АМ-ЧМ будут определяться соответствующими формулами,
и ученными ранее для сигналов ЧМ.
I опальная телеграфия ЧМ-ЧМ. При тональной минипуляции
। пда ЧМ-ЧМ используются сигналы
Sj(O = Awcos((oZ + pcosiV — 6i), ] o<t<T (11.4.28)
s2 (t) = Am cos (со/ + P cos Q21 — 62), I ’	>
и рги и которых равны
Ei = Е2 = 1 A2m Т = Е.
Воспользовавшись разложениями
ОО
cos (х cos <р) = Jo (х) + 2 S (-1)" J2n(*)cos 2шр,
гг = 1
00
Sin (х COS ф) = 2 2 (—l)n Ла+1 (x)cos(2«+ 1)<р,
п == 0	)
11жно получить следующие выражения для коэффициентов /Д и р5:
Л(Р).
Для достаточно больших значений р (практически Р>3) можно
и, южить Ps = ps = 0. При этом вероятности ошибок Ре будут
иределяться соответствующими формулами, полученными выше
। in сигналов ЧМ.
471
Тональная телеграфия ФМ-ЧМ. При тональной телеграфии
ФМ-ЧМ применяют радиосигналы
Sj (/) =- Ат cos (at 4~ 6 cos Qt — 04, ]
' л / r п/ о > 0 </ <7. (11.4.29)
s2 (0 = Ат cos (at — р cos Qf — 02), J	v '
Энергии сигналов равны
е1 = е2 = 4л-г = £-
Коэффициенты Rs и ps вычисляются по формулам (11.3.11) и (11.4.13)
аналогично тому, как это делалось в двух предыдущих случаях;
они равны
^ = J0(2₽), Pi = |J0(2p)l.
Для достаточно больших |3, когда Rs = ps = 0, вероятности
ошибок при приеме сигналов ФМ-ЧМ определяются формулами
для соответствующих сигналов ЧМ.
По формулам (11.3.19), (11.3.21), (11.3.23), (11.4.14), (11.4.16),
(11.4.19), (11.4.22), (11.4.23), (11.4.25) и (11.4.26) были выполнены
расчеты кривых потенциальной помехоустойчивости для указанных
выше сигналов, применяемых в радиотелеграфии. Результаты этих
расчетов представлены на рис. 11.14, причем сплошные кривые
относятся к детерминированным сигналам, а пунктирные — к со-
ответствующим сигналам со случайной начальной фазой, г;./
Эти кривые позволяют количественно сравнить различные сис-
темы радиотелеграфии по помехоустойчивости, указать значения
отношения сигнал/шум, при которых получается заданная вероят-
ность ошибки, а также оценить проигрыш в помехоустойчивости,
получающийся из-за незнания начальной фазы.
Из графиков рис. 11.14 видно, что наименее помехоустойчивой
является система с тональной манипуляцией вида АМ-АМ. При
приеме детерминированных сигналов наибольшей помехоустой-
чивостью обладает фазовая манипуляция. Несмотря на это, на
практике часто применяются также системы с частотной манипуля-
цией ввиду более простой их технической реализации.
Если задаться моделью принимаемого сигнала в виде (10.2.3),
то для всех перечисленных примеров можно определить оптималь-
ные схемы приемников и вычислить кривые помехоустойчивости
с учетом не только случайных начальных фаз, но и амплитудных
замираний (федингов) [10]. При рассмотрении амплитудных федин-
гов следует различать два предельных случая: быстрые и медлен-
ные замирания.
Под быстрыми замираниями понимаются такие, когда амплитуда
сигнала в течение длительности элементарной посылки испытывает
472
Рис. 11.14. Вероятность общей ошибки для различных систем радио-
телеграфии при приеме на фоне шума детерминированных сигна-
лов (сплошные линии) и сигналов со случайной начальной фазой
(пунктир).
473
Рис. 11.15. Зависимость вероятности
ошибки от отношения сигнал/шум для
радиоимпульса с полностью известными
параметрами (сплошная линия), с неиз-
вестной начальной фазой (пунктир) и со
случайными амплитудой и фазой (штрих-
пунктир).
заметные флуктуации. Медленные замирания характеризуются тем,
что амплитуды двух соседних посылок практически постоянны, но
эти амплитуды изменяются случайным образом от одной пары посы-
лок к другой.
Учет быстрых замираний требует специального математического
рассмотрения. Это объясняется тем, что при случайной начальной
фазе и быстро федингующей
амплитуде сами сигналы
представляют собой отрезки
квазигармонического шума.
В данном случае оценка по-
мехоустойчивости сводится к
решению специфической за-
дачи различения двух реали-
заций квазигармонического
шума конечной длительности
на фоне белого шума [12,
13, 14].
Для иллюстрации влия-
ния медленных флуктуаций
амплитуды сигнала на ве-
роятность общей ошибки на
рис. 11.15 приведены кривые,
дающие зависимость вероят-
ности ошибки от отношения
сигнал/шум при приеме пря-
моугольного радиоимпульса
(11.3.18) на фоне шума для
трех случаев: 1) все пара-
метры сигнала известны
(сплошная линия); 2) началь-
ная фаза случайная'(пунктир)
и 3) при случайной началь-
ной фазе амплитуда сигнала
изменяется по закону Релея
(11.2.18) при (Те = 1/2 (штрих-пунктир). Из рисунка видно, что
при наличии амплитудного фединга помехоустойчивость сущест-
венно понижается.
§ 5. О КВАЗИКОГЕРЕНТНОМ ПРИЕМЕ
ФАЗОМАНИПУЛИРОВАННЫХ СИГНАЛОВ
В §3для помехоустойчивости оптимального приема детерминиро-
ванных сигналов фазовой манипуляции была получена формула
(11.3.23). Как следует из соотношения (11.3.8), такая помехоустой-
чивость может быть реализована лишь при условии, если опорные
474
iii палы si(/) и sa(/) известны на приемной стороне с точностью до
мыльных фаз. На практике опорные сигналы часто формируют из
i| и пятого колебания £(/) и поэтому они могут отличаться от истин-
ах сигналов si(t) и Такое отличие приводит к понижению
и мехоустойчивости приема сигналов фазовой манипуляции. Вы-
н< лим степень этого понижения для двух конкретных методов
J нема, которые можно назвать квазикогерентными или квазисинх-
р иными 115].
Пороговое
устройство —--------о
h=U v<0^-i2
Рис. 11.16. Схема оптимального приемника для различения двух фазо-
манипулированных сигналов.
На основании (11.3.22) замечаем, что при фазовой манипуляции
и/) = — 5г(/). Поэтому формула (11.3.8) несколько упрощается:
т
о
(11.5.1)
Следовательно, оптимальное приемное устройство для разли-
чная двух фазоманипулированных сигналов должно формировать
I" 1ИЧИНу
г
и = J £ (/) Si (/) dt
о
(11.5.2)
н сравнивать ее с нулевым порогом h = 0 (рис. 11.16). При «>0
принимается решение о наличии сигнала s^t); при u<'Q принимает-
। решение о наличии сигнала s2(f).
Предположим, что на один вход перемножителя приемника
11 >ис. 11.16) воздействует принятое колебание (11.3.1), а на второй —
норный сигнал
s0 (0 = kAm cos (со/ + 0),
(11.5.3)
пинающийся от сигнала si(/) постоянным амплитудным множи-
н icM k и начальной фазой 0.
475
Тогда для напряжения на выходе перемножителя можем напи-
сать
т
и — kAm J | (t) cos (cof 4- 0) dt =
0
T
= kA2m J cos [cof 4- (i 4- 1) я] cos (at 4- 6) dt 4-
0
T
4- kAm J n (t) cos (at 4- 6) dt.
0
Здесь i = 1 при наличии в принятой реализации g(7) сигнала Sj/Z)
и i = 2 при наличии в ^(t) сигнала s3(Z).
После несложных преобразований получим
г
и = (—1)‘ + 1 kE cos 6 4- kAm j n(f) cos (at 4- b')dt. (11.5.4)
0
Величина и нормально распределена со средним значением
<и> =(—l)z + 1 kEcosQ и дисперсией од = k2EN0/2. Следовательно,
плотность вероятности случайной величины « при условии нали-
чия в колебании £(/) полезного сигнала sf(£), i = 1, 2, равна
/ । \	1	( Iй 4 (—1)‘ kE cost)]2 )	/1 } к
w(u\s.) =—7= exp 1— -------------,24------—L (11.5.5)
v 1 kV^ENQ F( /г2ЕЛ» j v !
Условные вероятности P (St | s2) и P (s21 Si), входящие в (11.3.14)
в данном случае определяются равенствами
00	О
4>(Si|s2)=J w(u\s2)du, P(s2|si)= J w(u\si)du. (11.5.6)
0	—00	•
В результате несложных вычислений получим формулу
РД0) = 1-ф(]/^со50).	(11.5.7)
При s0(t) = Si(t), т. е. 0 = 0, эта формула переходит в (11.3.23).
Предположим, что фаза 9 случайно и медленно изменяется с из-
вестной плотностью вероятности 1У(0) на интервале (— л, л).
В данном случае помехоустойчивость системы можно характери-
зовать средним значением вероятности общей ошибки
7Г	Я
<РД9)> = Г Р (0) W (0) dQ = 1 —	COS 0W(0) J0. (11.5.8).
J	J	\ ' N 0	/
—-Л	—rt
476
।  1меним эту формулу к двум случаям, представляющим практи-
iiii интерес.
I Пусть опорное напряжение s0(/) формируется из принятой
 (и £(/) последовательности фазоманипулированных радиоим-
|,сов и белого шума схемой, состоящей из устройства снятия
опой манипуляции и высокодобротного колебательного контура
и1. 11.17), который осуществляет фильтрацию немодулирован-
। о гармонического колебания частоты о.
ис. 11 17. Схема
формирования опорного сигнала при помощи
колебательного контура.
В данном случае опорное напряжение s0(f) представляет собой
нпгармокический случайный процесс, плотность вероятности
ччайной фазы которого определяется формулой (7.6.1):
V(0) = ^eH“-x
I Ч- У 2яа cos 0Ф(а cos 6) е2
— л 9 С л. (11.5.9)
1нь а = Ъ]/2.Е/Л4 —отношение сигнал/шум на выходе контура;
Ai — коэффициент, зависящий от фильтрующих свойств
контура.
Подставив выражение (11.5.9) в формулу (11.5.8), получим
/Р,(0)> = 1 -iej®(]/^coso)x
---	+ az cos2 &
X 1 + 1 2л a cos 0Ф (a cos 0) e 2
de. (11.5.10)
Интеграл, входящий в (11.5.10), элементарно вычисляется
in при й — }/2E/.V0. В этом случае найдем
1	/	F \
(6)> = "2 ехР ( Jv"oy •
(11.5.11)
\ .штаты численного интегрирования (11.5.10) для нескольких
нений коэффициента фильтрации ki приведены на рис. 11.18.
«сличением коэффициента фильтрации ki помехоустойчивость
। ышается, однако при этом увеличивается длительность процесса
I пювления.
477
2. Предположим, что опорный сигнал формируется фазовой
автоподстройкой частоты. В данном случае
«о (0 = Um cos (ti)t + 0),
где 9 — случайная разность фаз.
Рис. 11.18. Зависимость вероятности ошибки от отноше-
ния сигнал/шум при формировании опорного сигнала
колебательным контуром.
В § 3 гл. 8 показано, что в отсутствие начальной расстройки
плотность вероятности для 0 имеет вид
Г (9)	eDcos8, —л<9<л,	(11.5.12)
где D — параметр, зависящий от отношения сигнал/шум на входе
фазовой автоподстройки частоты.
478
Подставке (11.5.12) в формулу (11.5.8), получим
<РД6)> = 1
-2ЯЛ5) J®(/^cose)eO — de.	(11.5.13)
•—Л
Рис. 11.19. Зависимость вероятности ошибки от от-
ношения сигнал/шум при формировании опорного
сигнала фазовой автоподстройкой частоты.
Результаты численного интегрирования (11.5.13) представлены
nt рис. 11.19. При расчетах принималось
D = k
2Е
2 No’
(11.5.14)
479
где kz — коэффициент, характеризующий фильтрующие свойства
фазовой автоподстройки.
Как и в предыдущем случае, помехоустойчивость повышается
с увеличением коэффициента фильтрации Лг.
ЛИТЕРАТУРА
1	Котельников В А Теория потенциальной помехоустойчи-
вости. Госэнергоиздат, 1956
2	Пороговые сигналы. Пер с англ под ред. А. П. Сиверса. Изд-во
«Советское радио», 1952
3	Крамер Г. Математические методы'статистики Изд-во иностран-
ной литературы, 1948
4	. Питерсон В, Бердсал Т., Фокс В. Теория обнаруже-
ния сигналов Пер. с англ Теория информации и ее приложения Сборник
переводов под ред А. А. Харкевича Физматгиз, 1959.
5	. В а л ь д А. Последовательный анализ. Пер с англ. Физматгиз,
1960.
6	Башарннов А Е, Флейшман Б С Методы статисти-
ческого последовательного анализа и их приложения Изд-во «Советское
радио», 1962
7	. Marcum J I A statistical theory of target detection by pulsed
radar Trans IRE, 1960, IГ-6, №2
8	Барк Л С, Большее Л. H, Кузнецов П. И, Че-
ренков А. П. Таблицы распределения Релея — Райса. ВЦ АН СССР,
1964
9	ШирманЯ- Д.ГоликовВ Н Основы теории обнаружения
радиолокационных сигналов и измерения их параметров Изд-во «Советское
радио», 1963
10	. Т и г 1 п G. L. Error probabilities for binary symmetric ideal recep-
tion through nonselective slow fading and noise. Proc IRE, 1958, № 9.
11	. Helstrom C. W. The resolution of signals in white gaussian
noise Proc IRE, 1955, № 9
12	Хе л стром К Статистическая теория обнаружения сигналов.
Пер с англ Изд-во иностранной литературы, 1963.
13	Миддлтон Д Введение в статистическую теорию радиосвязи.
Пер. с англ , т 2 Изд-во «Советское радио», 1962
14	. В е 1 1 о Р. Some results on the problem of discriminating between
two gaussian processes Trans IRE, 1961, IT-7, №4	‘
15	. Горяйнов В T Помехоустойчивость систем фазовой радио-
телеграфии с учетом флуктуаций фазы опорного колебания Сборник докла-
дов XXII всесоюзной научной сессии НТОРиЭ им. А С. Попова, 1966.
16	Selin I The sequential estimation and detection of signals in nor-
mal noise. Information and control, 1964, № 4, 1965, № 1
17	. V i t e r b i A J The effect of sequential decision feedback on com-
piunication over gaussian channel Information and control, 1965, № 1.
Глава 12
ПРЕДЕЛЬНЫЕ ТОЧНОСТИ ИЗМЕРЕНИЯ ПАРАМЕТРОВ
РАДИОСИГНАЛА
§ 1 ХАРАКТЕРИСТИКИ ОЦЕНКИ И МЕТОДЫ ОЦЕНКИ
ПАРАМЕТРА
В простейшем случае, когда оценивается один параметр сиг-
нала заданной формы, задача ставится следующим образом. Пусть
принятое на интервале (О, Т) колебание £(/) представляет сумму
< игнала s(/,X), зависящего от одного неизвестного параметра Л,
и белого шума n(t):
1(0 = s(/,X) + n(f),	(12.1.1)
11редп слагаете я, что параметр X является постоянным на интервале
наблюдения (0, Т), т. е. не изменяется во времени, и известна априор-
1114 плотность вероятности этого параметра WPr(k). По принятому
। олебанию £(/) нужно решить наилучшим образом, какое именно
качение из интервала возможных значений имеет параметр X.
Из-за наличия шума n(f) и случайного характера параметра X
I» ллизация £(/) представляет собой случайный процесс. Поэтому
hi льзя получить точное значение параметра X, а можно лишь ука-
। гь приближенную оценку.
Указать оценку — это значит каждой возможной реализации
। /) на входе приемного устройства — измерителя поставить в со-
। нетствие некоторое значение X* из интервала возможных значений
т е. формировать некоторый функционал X* = [[Щ) ], назы-
। । мый оценкой.
Пусть в принятой реализации параметр X имеет значение Хо.
11 за случайного характера оценку характеризуют условной плот-
। н>ю вероятности Р(Х‘,:|Хо). Вид плотности вероятности Р(Х1 |Хо),
। исящий от функции /Ч£(01, определяет качество построенной
и пки. Естественно стремиться подобрать такую функцию f,
н <>ы плотность вероятности Р(Х*|Хо) была как можно теснее сгруп-
481
пирована около значения Хо. Если плотность вероятности имеет
достаточно «хороший» вид, а именно, имеет одну вершину и почти
симметрична, то в качестве количественных характеристик оценки
целесообразно использовать величины
от(Х*|Х0) = J (Ло — X*) Р (Х*|Х0) dX*, (12.1.2)
—00
оз(Х*|Л0)= j (Хо —V)2P(X*|X0)dX*.	(12.1.3)
— ОО
Величина т(Х*|Хо) характеризует разность между оценкой Л*
и истинным значением параметра Хо, и поэтому ее можно назвать
смещением. Величина о3(Х*|Хо) определяет степень разброса (рас-
сеяния) значений оценки X* относительно Хо Конечно, всегда жела-
тельно построить оценку с нулевым смещением и минимальным
рассеянием.
Величины т(Х*|Хо) и о2(Х*|Хо) не могут быть использованы как
полные характеристики качества оценки. При определении таких
характеристик нужно учесть, что в соответствии с априорным рас-
пределением й^рг(Х) одни значения параметра X встречаются чаще,
чем другие; для редко встречающихся значений можно допустить
большие смещения и рассеяния, чем для часто встречающихся
значений.
В связи с этим можно ввести средние (по априорной вероятности)
смещение и рассеяние:
<Х*> = J m(X*|X0)№pr(X0)dX0,	(12.1.4)
—СО
(Т2х = j°o2(X*lX0)^pr(X0)dX0.	(12.L.5)
—оо
Среднее смещение < X* > характеризует величину систематической
погрешности результата измерения параметра, а среднеквадратич-t
ное значение — величину случайной погрешности.
Приведем теперь несколько определений. Оценка называется
несмещенной, если среднее смещение равно нулю «X*) = 0), и
смещенной — в противоположном случае. Оценка называется эф-
фективной, если дисперсия of для данной оценки меньше, чем для
любой другой возможной оценки.
Один из методов нахождения оценки, т. е. выбора функции
/[£(/)] — состоит в том, что в качестве критерия оптимальности
оценки используется требование получения эффективной оценки.
При этом функция /[£(/)] подбирается из условия минимума выра-
жения (12.1.5).
482
В § 4 гл. 10 отмечалось, что вся информация об интересующем
 к параметре содержится в апостериорной плотности вероятности
и (X). На основании анализа аспостериорного распределения при-
знается то или иное решение об оцениваемом параметре. В мате-
1нической статистике известно несколько правил (критериев), на
 иове которых делается оценка параметра. Укажем здесь сущность
методов оценки параметра [1,2]:
1) оценка по минимуму среднеквадратичной погрешности;
2) оценка по максимуму аспостериорной вероятности;
1) оценка по максимуму функции (функционала) правдоподобия.
1.	В соответствии с критерием минимума среднеквадратичной
нибки минимизируется по Л* выражение
J(X — V)3№ps(X)dX = min.	(12.1.6)
Л
11| правнивая производную дисперсии оценки по Л* нулю 1^ = 0
/о2
при	>Оу, получаем, что в качестве оценки необходимо взять
|нднее значение (центр тяжести) апостериорного распределения
X* = f XWps (X) dl.	(12.1.7)
Л
2.	В дальнейшем нас в основном будет интересовать случай
 ныпих отношений сигнал/шум. Напомним (см. § 4 гл. 10), что
при больших отношениях сигнал/шум апостериорная плотность
11 1>оятности имеет наибольший максимум в окрестности истинного
и тения параметра с вероятностью, близкой к единице. Это об-
 । >ятельство указывает, что в качестве оценки целесообразно взять
|" значение %* = Хт, которое обращает в максимум апостериорное
р кшределение 1Гр4(Л). Такой метод построения оценки называется
и годом максимальной апостериорной вероятности.
Важный достоинством метода максимальной апостериорной ве-
Р< ятности (так же, как и рассматриваемого дальше метода макси-
има функции правдоподобия) является то, что точка максимума не
и меняется при произвольном взаимно однозначном преобразовании
। постер норного распределения. Поэтому в качестве оценки часто
|обно брать тот корень уравнения
In Wps (X) = 0,	(12.1.8)
। шорый явным образом зависит от £(/).
3.	Во многих практических случаях априорная плотность вероят-
на ти Wp,(X) оказывается неизвестной и ее полагают достаточно
1> ншомерно распределенной на некотором интервале (c,rf). При
ним координата максимума апостериорной вероятности будет
483
совпадать с соответствующей координатой функции (функционала)
правдоподобия. В этом случае метод максимума апостериорной ве-
роятности переходит в метод максимального правдоподобия. Здесь
в качестве оценки берется тот корень уравнения

(12.1.9)
который явно зависит от £,(f).
Можно показать, что оценка любого параметра сигнала, прини-
маемого на фоне нормального шума, по методу максимального прав-
доподобия асимптотически эффективна, т. е. при большом отноше-
нии сигнал/шум оценка имеет минимально возможную дисперсию.
Кроме этого, при большом отношении сигнал/шум все три метода
оценки асимптотически эквивалентны [3].
Укажем, что параметры сигнала можно разделить на энергети-
ческие (например, амплитуда) и неэнергетические (время запазды-
вания, частота, фаза). Энергетическими называются те параметры
сигнала X, от которых зависит энергия сигнала Е — Е(Е). В даль-
нейшем раздельно рассмотрим оценку амплитуды радиоимпульса,
как наиболее интересного для практических приложений энергети-
ческого параметра, и оценку неэнергетических параметров.
§ 2. ОЦЕНКА АМПЛИТУДЫ СИГНАЛА
Пусть на вход приемного устройства поступает сумма полезного
сигнала s(t,a) с неизвестной амплитудой а, которая подлежит
оценке, и белого шума n(t)
l(t) = s(t,a) + n(f).
(12.2.1)
В общем случае полезный сигнал s(t,a) может представлять собой
радиоимпульс вида
asT (t) = s (/, а) = й/ (t) cos [ю/ Ц- ф (/)—0], 0 < t < Т, (12.2.8)
где f(f) и ф(/)—законы амплитудной и фазовой модуляции;
со — несущая частота;
0 —- начальная фаза.
Рассмотрим оценку амплитуды X = а сигнала по максимуму
функции правдоподобия раздельно для известного сигнала и для
сигнала со случайной начальной фазой, равномерно распределен-
ной на интервале (— л, л).
1.	Оценка амплитуды детерминированного сигнала. Согласно
(10.3.24) функционал правдоподобия параметра а в данном случае
равен
/(й)-ехр — ~ J[^(0~ as^ttfdt
(12.2.3)
494
Поэтому уравнение Правдоподобия (12.1.9) принимает вид
т
~ In F (а) = Д J [£ (0 - as, (/)] S1 (/) dt = 0.	(12.2.4)
о
Это уравнение имеет решение
т	т
а* - J t,(t)s,(t)dt I ^s2i(t)dt,	(12.2.5)
о	' о
шисящее от £(£), которое и является оценкой по максимуму функ-
ции правдоподобия.
Формула (12.2.5) вскрывает структуру оптимального приемного
। решающего устройств дл§ оценки неизвестной амплитуды. Ос-
новной операцией является линейная операция интегрирования
меси сигнала и шума (12.2.1) с весом si(Z). Эту операцию можно
|.ыполнить при помощи соответствующего линейного фильтра или
। оррелометра.
Найдем смещение оценки амплитуды, считая, что истинное зна-
и1ше амплитуды равно ао. Имеем
т
f [«оМО + <«(О>]$1 (t)dt
-------f---------------= а0,	(12.2.6)
о
। с. оценка, несмещенная.
Дисперсия оценки определяется выражением
т т
f J <n (rt) п (/2)> St (i,) sA (G) dt, dtt
Подставив сюда функцию
I > |учим
Т	р	. х-----/
J
. о
корреляции белого шума из (10.2.13),
-----= ^,	(12.2.8)
2 J (t)dl
к согласно (10.8.4)
т
a-?Jsi(0dt	(12.2.9)
о
485
Таким образом, дисперсия оценки амплитуды полностью изве-
стного сигнала прямо пропорциональна мощности шума на единицу
полосы частот и обратно пропорциональна удвоенной энергии сиг-
нала при единичной амплитуде.
В качестве характеристики оценки амплитуды часто рассматри-
вают относительную дисперсию оценки амплитуды
где
т
E0=G2j s2^dt	(12.2.11)
о
— энергия принятого сигнала.
Из (12.2.10) видно, что относительная дисперсия оценки ампли-
туды детерминированного сигнала обратно пропорциональна уд-
военному отношению энергии сигнала к спектральной плотности
шума.
2.	Оценка амплитуды радиосигнала со случайной начальной
фазой В соответствии с (10.8.14) функционал правдоподобия ампли-
туды при приеме сигнала со случайной начальной фазой имеет
вид
F (а) = const e-“flS/2Wo l0 .	(12.2.12^
Подставив это выражение в формулу (12.1.9), для оценки а* по-
лучим уравнение
ад* , /2а* Z\ 2Z j (2а* Z V -
Л'о /о ( tfo J +Л'оУЦ /Уо /]е
па*г
= 0,
(12.2.13)
так как /0 (л) = (х). Отсюда находим
2Z h(2a*Z/N^
a IQ(2a*ZIN0) ’
(12.2.14)
Множитель /1(х)//0(х) нелинейно зависит от аргумента и изме-
няется от 0 до 1 при изменении х от 0 до оо, причем при х>Л
Л(*)//о(х)~1. Поэтому для больших отношений сигнал/шум
(2tzZ/N0^>l) справедливо равенство
(12.2.15)
Следовательно, при больших отношениях сигнал/шум оценка
амплитуды радиоимпульса со случайной начальной фазой линейно
зависит от огибающей. Эта зависимость нарушается при малых
отношениях сигнал/шум.
486
Если воспользоваться асимптотическим представлением (7.5.5),
к» для больших отношений сигнал/шум апостериорную вероятность
Шри равномерном априорном распределении амплитуды в интервале
и пок) можно представить в виде
_ 1	_ /аа_! __ 2aZ \	— (—
\Vps(a) = const(^) 2 е	2°а, (12.2.16)
\"о/	V 2™а	v
1 и' Од— дисперсия оценки, равная
оа = ^-	(12.2.17)
Из сравнения формулы (12.2.17) с формулой (12.2.8) можно
клать вывод, что дисперсии оценок амплитуды полностью извест-
ною радиоимпульса и радиоимпульса со случайной начальной
| ной при большом отношении сигнал/шум (2£/Лго>1) одинаковы.
Для прямоугольного радиоимпульса длительностью ти, когда
<12-2Л8)
I 0,	/<0, />ти,
hi основании формулы (12.2.17) получим
о„=—°.	(12.2.19)
Дисперсия оценки амплитуды прямоугольного радиоимпульса
прямо пропорциональна спектральной плотности шума и обратно
нрипорциокальна длительности импульса.
Если радиоимпульс имеет гауссову форму, т. е.
/ (/) = ехр
(12.2.20)
। и ти — длительность импульса на уровне 0,5 от максимального
иичения, то из формулы (12.2.17) получим
(12.2.21)
Lji Г «J , и
i. ОЦЕНКА НЕЭНЕРГЕТИЧЕСКИХ ПАРАМЕТРОВ
РАДИОИМПУЛЬСА
Рассмотрим более подробно методику оценки одного неэнерге-
ni'iecKOro параметра сигнала х(/Д) по методу максимума функции
I । > шдоподобия. Сначала исследуем оценку параметра полностью
и местного сигнала за исключением оцениваемого параметра Л, а за-
ь л полученные результаты обобщим на оценку параметра радио-
III пала со случайной начальной фазой.
487
1. Оценка параметра известного сигнала. Воспользовавшись
формулой (10.3.24) и повторив рассуждения, приведшие к формуле
(10.4.4), для функционала правдоподобия параметра А можем
написать выражение
ГР
F (А) = const ехр — ^ + <7 (Л) -= const ехр [<у (X)],
где
т
9 Г
<7W = ^J ^)dt
о
(12.3.1)
(12.3.2)
— логарифм функционала правдоподобия, зависящий от оценки.
На основании формулы (12.3.2) нетрудно получить общую струк-
турную схему оптимального измерителя одного параметра сигнала
по методу максимума функционала (функции) правдоподобия.
5(Мг>
Рис 12.1. Общая структурная схема оптимального из-
мерителя одного параметра сигнала известной формы.
Структурная схема устройства, позволяющего получить функцию i
q(k) для нескольких фиксированных значений параметра Х(, i =j
= 1, 2, 3, ..., п, приведена на рис. 12.1.	।
Поступающая на вход измерителя аддитивная смесь сигнала*!
шума £(t) перемножается с сигналом s(t,X) при всевозможны!
значениях оцениваемого параметра из априорного интервала (с,
и затем интегрируется в течение времени Т. Результаты интегрир^
вания в отдельных каналах подаются на решающее устройство
которое сравнивает значения <7(XZ) в отдельных каналах и выдаем
на выходе номер канала, в котором значение д(Х() максимально
Число каналов п зависит от требуемой точности измерения паря*
метра. Применительно к конкретным частным случаям общая схем|
рис. 12.1 может быть уточнена (см. § 7).
Введем параметр
(12
488
юрагно пропорциональный корню квадратному из отношения
игпал/шум.
Тогда функцию q (X) можно представить в следующем виде:
<7(M = £t[S(X-X0)+еЛ^(Х)],	(12.3.4)
। Щ
/ т 1 т
S(X — X0)=(j s2(/,X)p I' s(t,XC)s(Z, %)dt,
\o	/6
/ т	i/2 T
N (X) = J sz(t,k)di}	J n(t)s(t,%)dt.	(12.3.5)
\	0	/	0
Введенные функции S(X— Хо) и N(X) являются преобразован-
ными «сигналом» и «шумом» на выходе оптимального корреляцион-
ного приемника. Эти функции обладают важными свойствами.
l.S(X)=S(X— Хо) — нормированная автокорреляционная
Дикция входного полезного сигнала s(/,X) по оцениваемому пара-
метру %-, она симметрична относительно X = Хо и зависит только от
юсолютногозначения разности ] X — Хо|, причем S(X—Хо) = 1 при
' ~ Хо.
2. А/(X) — нормированный случайный процесс, зависящий от
и щаметра X. Поскольку <«(0) = О, то
<А/(Х)> =
т
J <п (ty> s (I, /) dt
о
7
фр (М)<И
О
(12.3.6)
1’ункция корреляции случайного процесса N (X) равна
т т
J f <п (6)« Us)> «(Д >i)s(G. Whdti
Wi) W> = Д --------------------------------— =
| s2 (t, л) dt
6
f т	i т
= s2 (^X)^j p(^Xx)s(^X2)^ =S(X!—Х2). (12.3.7)
Хо	/о
Таким образом, шум на выходе оптимального приемника имеет
нфмальное распределение с нулевым средним значением и функ-
цией корреляции, совпадающей по форме с нормированной авто-
।' ^реляционной функцией полезного сигнала. Этот шум 7V(X)
 । щионарен, гак как его функция корреляции зависит лишь от
нчолютного значения разности Xi — Хг.
489
Определим ошибки оценки параметра А по максимуму
При этом ограничимся рассмотрением случая, когда отношение сиг-
нал/шум велико:
(12.3.8)
В данном случае максимум функции q(X) или функционала правдо-
подобия (а при равномерном априорном распределении и апостериор-
ной вероятности) будет расположен вблизи истинного значенияi
параметра А.
Из свойств логарифма функции правдоподобия q(ty следует, -
что при е-> 0 (отсутствие шума) положение максимума функции,
7(A) совпадает с положением максимума функции $(А— Ао), т. е.:
с истинным значением оцениваемого параметра А = Ао. Это озна-
чает, что в отсутствие шума оценка по максимуму функции правдо-
подобия всегда совпадает с истинным значением параметра Ао.
В реальных задачах е=^0. Однако при малых значениях е<1
(е — малый параметр) оценку Ат можно представить в виде ряда
по степеням малого параметра е:
Ат = Ао -|- еАю -J- е2А20 е3Азо + ...,	(12.3.9)
где в качестве нулевого приближения выбирается Ао, а поправки
к следующим приближениям (Аю, А20, А30 и т. д.) необходимо опре-
делить. Ради простоты ограничимся первым приближением, -т. е.
положим
Am = A0+eA10.	(12.3.Ю)
Для нахождения А10 разложим правую часть уравнения (12.3.4)
в ряд Тейлора в окрестности А = Ао и учтем, что в точке максимуму
А — А„ должно выполняться равенство
[^1	+	=°-	(12.3.11)
dk х г2 \ dk 1 dk2 х	'	*
L	L	J m
Так как e=/=0, то, ограничиваясь двумя первыми членами раз
ложения, имеем
dS(A) , „О())1	, [d2S(A) , Ж
dK е d\ х + dK2 е di2
JAo L	J
eA1o=0. (12-3.12!
Приравнивая члены сев первой степени, получим
Аю —
г
d2 ,
у//.2*5!)
(12 3.11
Статистические характеристики величины А1о определяют оши^
ки оценки
АА= Ат — Ао-= еА10.	(12.3.1J
490
' in как согласно (12.3.6) </V (1)> -О, тс)
<ДА> =е<Х10> = ~
d
db <N W>
d2Sp)
(12.3.15)
Следовательно, оценка параметра к по максимуму функции
। р шдоподобия при больших отношениях сигнал/шум несме-
< । тая.
Дисперсия оценки параметра % определяется выражением
О2 = <ДЛ2>=еЧЧо> =
дг
2Е	d2S (л)	2
/Vol	d/.2	
(12.3.16)
о
итывая соотношение (12.3.7), формула (12.3.16) преобразуется
1.НДУ
Ол
1
2f/A’o
д\1д\2
S"2O)
_ 1
(2£/,Vo)S"po) ‘
(12.3.17)
1аким образом, дисперсия оценки параметра обратно пропор-
.и, пыльна отношению сигнал/шум и кривизне нормированной авто-
Р реляционной функции полезного сигнала по оцениваемому пара-
1 PV в ее максимуме.
Ih первого равенства (12.3.5) и формулы (12.3.2) следует, что
т
ър	9 I
^S(A) = qs(K) = ±\ s(t,le)s(t,X)dt. (12.3.18)
О
ii дому формулу (12.3.17) можно записать иначе
ст? = — 1/<?Ж)-	(12.3.19)
1 .ледовательно, дисперсия оценки параметра % обратно пропор-
чшльна кривизне функции автокорреляции сигнала на выходе
। । мпика в ее максимуме.
1’> качестве примера определим дисперсию оценки фазы радио-
i\ 1ьса (12.2.2). По формуле (12.3.18) функция qs(&) равна
т
7s (9) = J Р (О COS [(О/ + ф (0—9о1 cos	+ ф (0 — Q]dt»
О
»^cos(0 — 0О).	(12.3.20)
491
Отсюда находим <у5(Оо) ——2E/N0. Поэтому
ае - N0/2E.	(12.3.21)
Дисперсия оценки фазы обратно пропорциональна отношению
сигнал/шум и не зависит от вида амплитудной и фазовой моду-
ляции.
2. Оценка параметра радиосигнала со случайной начально^
фазой. При приеме на фоне белого шума n{i) радиосигнала s(/,X)
со случайной начальной фазой, равномерно распределенной на
интервале (— л, л), функционал правдоподобия параметра Л
согласно (10.8.14) может быть представлен в виде
F (X) == const Io [q (Л.)],
где
2
т
J K)dt
о
(12.3.22)
(12.3.23)
— огибающая (модуль) напряжения на выходе согласованного
линейного фильтра.
Уравнение правдоподобия в соответствии с (12.1.9) определяется
выражением
__ ( Л [<?0)1 dq (X))
[it [<7(М1 ' rfA Jx
m 4	' m.
(12.3.241
Так как ^(Zm)=^0 и функции Бесселя /0 [<? (X.m)] и Л [q (Zffl)] таю
же не равны нулю, то уравнение правдоподобия упрощаете^
и принимает вид
dg (У)'
d'K )
= 0.
(12.3.25)
m
Из последнего выражения видно, что для оценки параметра сигнал!
со случайной начальной фазой оптимальной операцией являете!
образование функции </(%) согласно (12.3.23) или любой монотон
ной от нее функции.
Итак, при приеме радиосигнала со случайной начальной фазой
равномерно распределенной на интервале (— л, л), в дополненИ
к структурной схеме для оценки параметра полностью известног
сигнала (рис. 12.1), в каждом из параллельных каналов долже.
стоять амплитудный детектор огибающей с произвольной монетой
ной характеристикой.
Так же, как и при оценке параметра полностью известного сигна
ла, для больших отношений сигнал/шум, оценку можно искать в вид
соответствующих приближений по малому параметру. Можно по
казать [4], что и в данном случае оценка параметра несмещенная^
492
। щсперсия оценки по-прежнему определяется формулой (12.3.19),
н‘ теперь функция qs (А.) должна вычисляться по формуле
т

= Д f s(t, b)dt
(12.3.26)
о
Укажем, что если интересоваться вторым приближением оценки,
। > дисперсия оценки параметра сигнала оказывается равной [4].
1	?‘V
" /1 \	*	*2
s(?o)	qs Oo)
(12.3.27)
(. второе приближение имеет поправку по отношению к первому
।'сближению, зависящую от отношения четвертой производной
 квадрату второй производной автокорреляционной функции по-
шого сигнала в точке ее максимума.
Если вместо функции qs(ty рассматривать нормированную функ-
। ню S(A), то поправка к первому приближению обратно пропорцио-
. । шна отношению сигнал/шум и зависит также от четвертой и
Kipoii производных нормированных автокорреляционных функций
юзеого сигнала в точке ее максимума.
I [вложенный выше метод нахождения оценок при помощи малого
ip 1иетра можно обобщить на случай совместных оценок двух пара-
। 1 ров радиосигнала [5].
4. ДИСПЕРСИЯ ОЦЕНКИ ВРЕМЕННОГО ПОЛОЖЕНИЯ
РАДИОИМПУЛЬСА СО СЛУЧАЙНОЙ НАЧАЛЬНОЙ ФАЗОЙ
Обычно применяемые на практике радиосигналы (12.2.2) яв-
। нс гея узкополосными, т. е. их несущая частота (оо значительно
"I । восходит ширину спектра. Для таких сигналов удобно исполь-
н нь условное комплексное представление
s(/, Л) = aU(t, X)e/f“«'+?>,	(12.4.1)
— комплексная функция, медленно изменяющаяся по
сравнению с высокочастотным гармоническим колеба-
нием частоты <в0;
Ф—результирующая начальная фаза.
1> этом случае модуль автокорреляционной функции сигнала на
' <»де фильтра можно записать в виде
। /1
Ло) s (t, Л) dt
т
= £j U*(t, K0)U(t, K)dt. (12.4.2)
2
493
До сих пор оцениваемый неэнергетический параметр X (за исклю-
чением оценки фазы) был лишен конкретного физического смысла,
Между тем, конкретизация физического смысла параметра А по-
зволяет значительно упростить выражение (12.3.19) для диспер*
СИИ Од.
Рассмотрим случай, когда оцениваемым параметром является
временное положение т радиоимпульса
s(t — т) = af(t — т) cos [<о0 (t — т) + ф (t — т) — 0],	0 < t — т Т
(12.4.3J
Под т будем понимать момент времени, соответствующий средин^
радиоимпульса, и под 9 — начальную фазу в этот момент времен!
(рис. 12.2).
Комплексной огибающей сигнала (12.4.3)
U (t—(12.4.^|
соответствует комплексный спектр
ОО
F (j(d)= § U	(12.4.4
—оо
Согласно (12.4.2) автокорреляционная функция сигнала
определяется выражением
т
qsW = U*(t—x0)U (t— r)dt, (12.4.0
О
а вторая производная ее в точке т = т0 равна
т
gs(r0) = — J t/*(^ — т0) f/(Z —т)| dt. (12.q
494
Выразим qs (т0) через параметры комплексного спектра oi ибак>
null. Для этого воспользуемся преобразованием Фурье, обратным
। 12 4.5),
СО
U(t — т) = ± J F (до) dt	(12.4.8)
—СО
11 у чтем, что
оо
U*(t — То) =27 J	(12.4.9)
—ОО
I пфференцируя дважды равенство (12.4.8) по т, получим
^U(t — т)=— Т- f <o2F(/(o)e'“('-^.	(12.4.10)
—оо
1 учетом равенств (12.4.9) и (12.4.10) выражение (12.4.7) преоб-
। । дуется к виду
оо оо	Т
(т0) = ~4п2/у0 j J co2F (/io) F*(/Q) е~/(«-а)’о d<£>d^l J e/(“~'-)z dt.
—ос — оо	о
(12.4.11)
Так как по предположению радиоимпульс полностью располо-
<п на интервале (О, Т), то значение внутреннего интеграла опре-
i-ляется формулой (П. 9). В результате интегрирования с дельта-
Ьнкцией получим
ОО
^ = ~2^Га I ®2]^(/<о)|2^<о.	(12.4.12)
— 00
1 ’пределим ширину спектра огибающей радиоимпульса формулой
J “2 I F (J«)|2 da>
Р2 = ^---------------..	(12.4.13)
J I F (/со) |2 da
— ОО
И । основании равенства Релея — Парсеваля имеем
ОО	Г
2~ а3 У |F(/<o)|2d® = У s2(t)dt = Е, (12.4.14)
— оо	О
। к Е — энергия сигнала.
495
(12.4.15)
С учетом последних Двух соотношений можем написать
ч'. W = -“₽’•
Подставив это выражение в (12.3.19), получаем окончательную
формулу для дисперсии оценки временного положения радио-
импульса
2	1
” R2£/No) 
(12.4.16)
Вычислим для радиоимпульсов прямоугольной и гауссовой
форм без внутренней частотной модуляции (ф(/) = 0). Напомним,
что основная формула (12.3.19) справедлива в тех случаях, когда
Рис. 12.3. Спектр прямоугольного радиоимпульса, ограниченного полосой
А<й (а), и огибающая соответствующего радиоимпульса (б).
сигнальная функция qs(r) является аналитической в окрестности
то. Однако для прямоугольного радиоимпульса функция qs(x)
при т = то имеет излом (см. рис. 10.3). Поэтому к ней неприменимо
разложение (12.3.12) и нельзя пользоваться формулой (12.3.19).
На практике импульсы не являются идеально прямоугольными,
так как нулевое время нарастания и спада импульса требует бес-
конечно широкой полосы пропускания. Чтобы вычислить ошибку
в определении времени запаздывания, которая получается для ре-
ального «прямоугольного» импульса, можно рассуждать там [6].
Будем считать спектр прямоугольного видеоимпульса
Г(/<о) = ти5ш^Д^	(12.4.17)
отличным от нуля только внутри полосы шириной Aw. Это эквива-
лентно тому, что прямоугольный импульс пропускается через иде-
альный фильтр с прямоугольной амплитудно-частотной характери-
стикой шириной До). Если Д®ти^>1, то на выходе фильтра появится
«сглаженный» импульс длительностью приблизительно равной ти,
но с конечным наклоном переднего и заднего фронтов, и спектром,
ограниченным полосой частот Дсо. Такой прямоугольный импульс
с ограниченным спектром показан на рис. 12.3. Для этого сглажен-
ного импульса функция gs(r) оказывается непрерывной и можно
496
пользоваться формулой (12.3.19), только интегрирование в (12.4.13)
нужно выполнять в пределах от — Дсо/2 до Д®/2.
Подставив (12.4.171 в (12.4.13) и выполнив интегрирование,
получим
= J___________(Асоти/2)_ sjn(Aa>xH/2)	,	2 4 J
Н г2 Si (Дюти/2)-|-[со5 (Дшти/2)—1] / (До>ти/2) ’	‘ ‘ 7
। де Si(z)—интегральный синус; Si (z -* сс)=л/2.
При Дитц>1 из формулы (12.4.18) получаем
Р2 ж Д(1)/лтн = 2Д//ти-	(12.4.19)
Р.(Счеты, выполненные по формуле (12.4.18), показывают, что равен-
। гво (12.4.19) является достаточно хорошим приближением при
шачениях Л<йти, встречающихся в практических задачах.
Следовательно, дисперсия оценки времени запаздывания для
прямоугольного импульса длительностью ти> ограниченного по
> иеитру полосой Д/, приближенно равна
2Af (2Е/Л/0) '	(12,4-
1 овладение этой формулы с результатом (9.2.10) показывает, что
предельная точность измерения времени запаздывания радиоим-
пульса практически может быть реализована способом, рассмотрен-
ным в § 2 гл. 9.
Формально величину о? для идеально прямоугольного радио-
импульса можно вычислить другим способом 17]. В пренебрежении
шумовой функцией <?п(т) апостериорная плотность вероятности па-
ртметра т на основании формул (10.4.6) и (10.4.12) равна
^ps(t) = const ехр [<75(т) ] = const ехр
2Е
No
1
2Е
N о
1 т т0| ти,
= k ехр
(12.4.21)
1 н' lz— Е/ NqTи .
При выполнении условия (12.3.8) можно положить
• |>(-—2E/Nо) «0. Тогда получим
"о+ти
о2х= J (т — т0)2№Р5(т)Лт = 2г1((2Е/Л/0)2.	(12.4.22)
1о--и
Вычисления по формуле (12.4.13) для радиоимпульса гауссо-
! и формы (12.2.20) дают следующий результат:
Р2-2,8/т2 = (лД/)2/1,4,	(12.4.23)
497
(12.4.24)
где Af— ширина энергетического спектра импульса на уровне
0,5. Поэтому
„2	'и	1,4
2,8(2Е/Л/0)	(лД/)Д2Е/Л?0)
Видно, что при фиксированной энергии точность измерения вре-
мени запаздывания радиоимпульса повышается с уменьшением
длительности импульса.
§ 5. ДИСПЕРСИЯ ОЦЕНКИ СМЕЩЕНИЯ ЧАСТОТЫ
РАДИОИМПУЛЬСА
Принимаемый полезный сигнал запишем в виде
s(t, Q)~af (^)cos [(<о0 — й)/+ф(/) — 9],-
где оцениваемый параметр Q обычно представляет собой смещений
несущей частоты из-за эффекта Допплера.
Комплексная огибающая радиосигнала (12.5.1) равна
[/(/, Q)=/(/)e-/-^+/HO	(12.5.2)
Подставляя выражение (12.5.2) в формулу (12.4.2), имеем
д5(Й)=^- f fW^-^dt.	(12.5.3)
°— Т/2
Отсюда находим вторую производную
g"(Q0)= —(* t2f2(t)dt.	(12.5.4)
"°-Т/2
Подставив в это выражение значение а2 из соотношения
Т/2
Е —~~ a2 f Г (Г) Л,
— Т/2
по формуле (12.3.19) получаем дисперсию оценки частоты f=fi/2fl|
Здесь параметр а равен
Т/2
J t2f2(i)dt
а2 = (2л)3^72	(12.5.^|
f P(t)dt
^Т/2
498
I ели применить формулу (12.5.6) к прямоугольному радио-
шульсу длительностью тн, то получим
/ ти/2
аi 2 —- (2л.)2 У t2dt J Л=л2т„/3.
ти/2 / ти/2
I I и ИОМу
° f = (пти)2 (2E/N0) 	(12.5.7)
Для радиоимпульса гауссовой формы (12.2.20), практически
шестью расположенного внутри интервала (— Т/2, Т/2), по-
лним
тсти)а (12.5.8)
«2 = (2я)2^------
ехр
—ОО
1 (довательно, дисперсия оценки частоты гауссова радиоимпуль-
1 равна
о2.=______(12 5 91
f (-ти)2(2Е/А'о)	1,4(2E/WO)’	'
i । последнее равенство написано на основании (12.4.23).
Формула (12.5.5) получена при условии, что полезный сигнал
и '5.1) не флуктуирует по амплитуде и фазе. Однако на практике
। счет фединга полезный сигнал на входе приемника подвержен
 шлитудным и фазовым флуктуациям. При этом, естественно,
। 11яние фединга будет сказываться и на измерении смещения час-
и> 1,1 сигнала, причем это влияние будет тем больше, чем больше
ip шеходит расширение спектра федингующего сигнала по сравне-
нии со спектром нефедингующего сигнала.
Рассмотрим измерение допплеровского смещения частоты федин-
। \ пщего по амплитуде a(t) и фазе 0(/) узкополосного радиосигнала
s(f,fi)=a(f)cos[(tt>o-|-aK — 9(0], —(12.5.10)
io 1см считать, что сигнал (12.5.10) является отрезком стационар-
.... нормального узкополосного шума с функцией корреляции
и ил
< s (t) s (^+т)> =&(т)= Оо р (т) cos((o0-|-Q)r.	(12.Б.11)
и <>5—средняя мощность полезною ситнала.
499
При произвольном соотношении времени наблюдения Т и вре-
мени корреляции полезного сигнала тк аналитически затрудни-
тельно получить выражение для дисперсии оценки частоты. Задача
существенно облегчается, если время корреляции сигнала s(t)
много меньше времени наблюдения Т (Т>тк). Так как этот случай
Рис. 12.4. Зависимость нормированной средне-
квадратичной ошибки измерения смещения
частоты узкополосного шума от отношения
сигнал/шум (Тк — время корреляции, Т — ин-
тервал наблюдения).
представляет практический интерес, то приведем относящиеся
к нему результаты. При этом ограничимся рассмотрением достаточ<»|
но больших отношений сигнал/шум
2Е __ 2ао т
No ~~ Л'о
(12.5.121
Можно показать [8], что при приеме федингующего полезного
сигнала с функцией корреляции вида
/г(т)—Оое~тi‘l cos (®0+Q)t, тк=т~> (12.5.13|
дисперсия оценки смещения частоты Q определяется формулой
т2
2 _	41
2 2Е/ЛГ0
(12.5.14
500
1Д(2Е/Д0)^.	(12.5.15)
1 la рис. 12.4 приведена зависимость нормированной среднеквад-
। яичной ошибки измерения смещения частоты оатк от отношения
hi нал/шум (12.5.12) для четырех отношений времени корреляции
. 'мового сигнала к интервалу наблюдения (тк/Т). Из кривых
тио, что при фиксированных 2Е /No и Т с уменьшением времени
। рреляции тк среднеквадратичная ошибка увеличивается.
1П формул (12.4.20) и (12.4.24) видно, что при заданном отно-
ПЧ1ИИ сигнал/шум погрешность измерения временного положения
к'ньшается при расширении спектра сигнала. Погрешность из-
|< рения смещения частоты £2, как следует из формул (12.5.7) и
11 ’ 5.9), всегда уменьшается при увеличении длительности радио-
||\ пульса.
Если интересоваться совместной или раздельной оценкой пара-
к । ров т и £2, то возникает вопрос о выборе такой формы сигнала,
। горый обеспечивал бы высокую точность определения как т,
। 1к и £2. Предельные возможности подобных измерений и некото-
ine соображения о выборе рациональных видов сигналов приво-
н ся в следующем параграфе.
Ь. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТИ И ВЫБОР ФОРМЫ
< ИГНАЛА
Для простоты рассмотрим случай, когда оценка временного
ч< 'южения и смещения частоты радиоимпульса производится не
। пместно, а раздельно и независимо, причем радиоимпульс не
имеет внутренней частотной модуляции (ф(/) = 0), т. е.
(/, т, £2) = <Д(/—т) cos [(<оо — £2) t — 6],-(12.6.1)
। к' f(t — т) — действительная функция аргумента.
Огибающая (12.4.4) такого импульса является также действи-
н 1ьной функцией времени U(t — т) = f(t — т). Поэтому фор-
।' ну (12.4 7) в данном случае можно записать так:
2 Т’2
<h(t0) = -^ J	(12.6.2)
' г штрихом обозначена производная по т при т = то.
Покажем, что при независимых измерениях среднеквадратичные
। шбки измерения временного положения т и смещения частоты £2
> । нала s(f,x,£2) удовлетворяют следующему неравенству:
< л(2Е/У0) ‘	2-6,3)
501
Действительно, из формул (12.4.16) и (12.5.5) следует, что
= 'а ₽ (2£/N0f •	(12.6.4)
Но произведение величина и Р, определенных соответственно фор-
мулами (12.5.6) и (12.4.13), удовлетворяет неравенству
оф Д л,	(12.6.5)
известному под названием «соотношения неопределенности».
Таким образом, для доказательства неравенства (12.6.3) необ-
ходимо лишь убедиться в справедливости соотношения неопределен-
ности (12.6.5). Из (12.4.13) и (12.5.6) Имеем
00	Т/2
J ®2|F(/o)|2dM J t2P(i)di
(а₽)2=(2л)2=^-------------------------- •	(12.6.6)
J |£(/W)|2dM f f*(t)dt
— OO	—772
Приравнивая правые части выражений (12.4.12) и (12.6.2),
находим
00	Т/2	Т/2
J 1F (До) |2 tfo = ~ 2л j f"(t — t0)f (t~ r0)di = 2л J
-co	-Г/2	—7/2
(12.6.7)
Последнее равенство получено путем интегрирования по частям,
при этом предполагается, что функция f(t — то) исчезает на концах
интервала наблюдения.
Запишем также известное равенство Релея — Парсеваля
Т/2	со
j f2(<)dt = ~ j |F(/«)|2d«.	<12.6.8)
—Т/2	‘ —со
Подставив (12.6.7) и (12.6.8) в (12.6.6), получим
Т/2	Т/2
J f’*(t)di j t^p(t)dt
И)2-(2л)2-~<^-	— Т/2 Т/2 -1/2	1	.	(12.6.9)
Применим к числителю выражения (12.6.9) неравенство Швар-
ца—Буняковского (10.6.13), положив	=
Т/2	Т/2	(Т/2	12
f P(t)dt J Z2/2(/)d/> I tpf)p)dt\
—Т/2	—Т/2	I—Т/2	J
Т/2	42Г Т/2	2
=4-=-4-	.
— Т/2	L-Т/2
(12.6.10)
502
। * i. знак равенства имеет место только в том случае, когда
I/) constr(Z), т. е. когда
f'(t) =const	(12.6.11)
। l щ гавив (12.6.10) в (12.6.9), убеждаемся в справедливости соот-
 нения неопределенности.
Неравенство (12.6.3) показывает, что время запаздывания и
и । ота в принципе могут быть измерены с заведомо гарантирован-
  । погрешностью лишь за счет увеличения отношения сигнал/шум.
' iii.iKO при фиксированном отношении сигнал/шум погрешность
• кно уменьшить за счет выбора формы сигнала.
11олная энергия импульсного сигнала Е при разработке системы
। «и обычно определяется из уравнения дальности системы. Тем
мим для известных условий приема величина 2EIN0 будет фикси-
, панной. Поэтому для достижения высокой точности измерения
• 1|>аметров сигнала нужно применять такие виды сигналов, для
 орых величина оф имеет большое значение. Так как а растет
нечичением длительности сигнала, ар — с увеличением ширины
<мра сигнала, то для получения высокой точности определения
г'мени запаздывания и частоты необходимо использовать длин-
। сигналы, обладающие широким спектром (узкой функцией
и и корреляции).
Нетрудно убедиться, что для гауссова радиоимпульса (12.2.20)
। шолняется равенство (12.6.11) и ар = л. Следовательно, точность
 п'рения т и f в гауссовом радиоимпульсе ниже, чем в любом
р>гом радиоимпульсе.
11риведенные соображения о выборе формы сигнала важны не
। ' и>ко с течки зрения получения высокой точности измерения, но
। i/ке и с точки зрения устранения неоднозначности определения
и ।|>.1метров и требования высокого разрешения сигналов. Под раз-
। ионием понимается свойство системы различать два или несколь-
, > сигналов.
Как следует из пояснений, приведенных в § 4 гл. 10, для устра-
..ня неоднозначности (ненадежности) желательно использовать
и палы, для которых сигнальная функция имеет лишь один узкий
null в окрестности истинного значения оцениваемого параметра,
и ' требование согласуется с требованием получения высокой точ-
.1 > нт оценки параметра.
11роблема разрешения является весьма сложной. Мы ограничим-
। «десь лишь элементарными пояснениями. Необходимость разре-
. < ния в радиолокации возникает при наличии нескольких целей,
> и радиосвязи — при многолучевом распространении радиоволн.
। жность хорошего разрешения целей в радиолокации очевидна;
пеним важность разрешения в радиосвязи. Обычно многолучевое
। и пространение радиоволн приводит к замираниям сигнала в месте
||и1ема вследствие интерференции радиосигналов, приходящих
503
по различным лучам. Это считается вредным явлением. Однако
если сигналы, распространяющиеся по разным путям, можно раз-
решить (принять раздельно), то затем их можно сложить, и тем
самым использовать многолучевое распространение с выгодой для
повышения отношения сигнал/шум.
Пусть требуется разрешить два сигнала: Sj(/) = s(/,ti) и s2(/) =i
— s (/.та), отличающихся только временами запаздывания. На
рис. 12. 5 изображены сигнальные функции сигналов и их апосте-
риорные вероятности. По-видимому, возможность различения двух
Wps (rt)
Рис. 12.5. Сигнальные функции и апостериор-
ные вероятности для двух сигналов.
целей при малых значениях разности т = т2 — Tj будет опреде-
ляться тем, насколько узки главные максимумы апостериорных
вероятностей и как сильно они выделяются среди побочных боко-
вых лепестков; чем выше и уже максимумы и чем меньше боковые
лепестки, тем при меньших значениях т можно раздельно зафиксиро-
вать два сигнала. Но вид апостериорной вероятности при больших
отношениях сигнал/шум определяется сигнальной функцией. Сле-
довательно, для получения хорошего разрешения нужно применят»
такие сигналы, автокорреляционные функции которых имеют iwj
возможности один высокий и узкий пик (широкий спектр). Добиты^
этого за счет уменьшения лишь длительности импульса (например^
прямоугольного) практически не удается.
Для обеспечения большой дальности действия обычно требуются)
высокие значения энергии, а следовательно, при малой длителы!
ности и большие мощности Е/г„. Во многих случаях радиотехник
ческие устройства не могут нормально работать при очень больших
мощностях (пробой волноводов и т. д.). Чтобы, несмотря на наличи^
этих «пиковых ограничений», можно было независимо выбират^
дальность и разрешающую способность, применяют импульсных
504
। налы специальной формы — сигналы с внутриимпульсной моду-
iiiiieft (частотной, фазовой и др.).
(о сих пор речь шла о точности и разрешающей способности по
, пени запаздывания. Итог приведенных рассуждений состоит
। >м, что для получения высокой точности и разрешающей способ-
||| нужно применять сигналы с узкими автокорреляционными
нкциями (широким спектром) без боковых лепестков. Если инте-
।  зваться точностью и разрешающей способностью одновременно
времени запаздывания и частоте, то можно показать [9, 10],
• вид сигнала должен определяться на основе анализа модуля
^мерной функции корреляции
|Я(г, й)1 =
т
J U (t~ т) U:f (/) е/ ' dt
о
(12.6.12)
1кция |R (т, Q) | называется функцией неопределенности,
вопросы, указанные в данном параграфе, более подробно рас-
ириваются в гл. 14.
>, г ОПТИМАЛЬНАЯ СХЕМА ЧАСТОТНОЙ АВТОПОДСТРОЙКИ
I [окажем на частном примере, что общую структурную схему
ипмального измерителя (рис. 12.1) можно конкретизировать и
и| остить.
Пусть в принятом колебании (12.1.1) полезным сигналом s(Z)
1 яется отрезок квазигармонического шума (10.8.23) с функцией
I реляции (10.8.24). Частота полезного сигнала со считается по-
। Инной на интервале наблюдения (0, Т), но заранее точно неиз-
. < той. Предполагается известным априорное распределение час-
। и и; будем: считать его равномерным на некотором интервале
!•", со2), т. е. положим
Wpr (<о) =
1/(со2 —(0j)
0
при
при
со^ со со2,
CO<^COj, С0^>6)2.
(12.7.1)
Нужно яайти оптимальную схему измерителя, определяющего
 нсвестную частоту сигнала. В качестве критерия оптимальности
н пользуем критерий максимального правдоподобия, согласно ко-
। 1>ому оптимальный приемник-измеритель частоты должен следить
। наиболее правдоподобным значением частоты.
После приема колебания на интервале (0,Т) нужно указать
 и ночное значение частоты, соответствующее виду колебания
о) Обозначим это оценочное значение, зависящее от Т, через
(Г). С течением времени Т оценочное значение частоты со0 уточ-
к । ся, поскольку увеличивается объем апостериорных сведений.
11тобы получить уравнения оптимальной схемы в дифференциаль-
 г форме, исследуем изменение апостериорного распределения
505
(10.8.25) при увеличении времени наблюдения Т. С этой целью
прологарифмируем обе части равенства (10.8.25):
2 а2
lnIFps(®)=-^Zr(®)+lnC, О| = ^а2.	(12.7.2)
1*0	о
Здесь C=const— нормировочная постоянная.
Беря производную по Т и обозначив ее точкой сверху, получим
Wps=[F(T, со) -X] Wps,	(12.7.3)
где
2 а? dZPM
(12:7.4)
Через коэффициент X здесь обозначена величина	In С.
Коэффициент X всегда можно определить, пользуясь тем, что по
условию нормировки
J rps(®)dw=^ J rps(co)d®=0.
— СО	—00
Поэтому в результате интегрирования (12.7.3) по со получим
Х = J F(T, co)IFps(co)dco = (F(T, со)>.	(12.7/5)
— ОО
В дальнейшем будем предполагать, что отношение сигнал/шум
велико. Естественно ожидать, что при больших отношениях сиг»
нал/шум оценка будет достаточно точной, т. е. апостериорная плот»
ность вероятности частоты, будет тесно сконцентрирована в неболь»;
шой окрестности около оценки. При этом функцию F (Т, со) можно
разложить в ряд Тейлора в окрестности со0 и ограничиться .учето^
лишь первых трех членов разложения:
п ,гг ч г. д F(T, ш0) ,	.	1 a2F(T,<o0)	.
F (Т, со)	F (Т, со0) 4~	(со со0/+ %	(со сод)
(12.7.6j
Следствием принятого упрощения (12.7.6), справедливого прЦ
большом отношении сигнал/шум, как следует из уравнения (12.7.3)1
является тот результат, что апостериорная плотность вероятности
считается при этом нормальной (гауссово приближение). Запишем
ее в обычном виде:
Wps (со) = ехр
|/
2 о.2
(12.7.7J
506
 । оценка coo и ее дисперсия о2, зависят от Т, т. е. соо — ю0 (Т),
।	Из (12.7.7) имеем
2
[W _	1	I —ыо) | (о — "о)2 2 w>
IVps—-------~2----1------2---------.71----- ™ ps-
z %	°;	2i J
(12.7.8)
Подставив (12.7.8) в левую часть и (12.7.6) в правую часть
(нвнения (12.7.3), получим равенство
2
— 1	% । (ю —G)o) • _| ((и'"<,)о)2гт2_/7/т	\
2	2 '	2	^0 । п 4	^о>	’ ®о)
Со>	° СО
/	\\ । dF(T,w0)z	\ f 1	(Т, о>о)	„
— (F(T, CD0)>+ —(co — ®0) + -2-------------(» - ®o)2.
(12.7.9)
нем соотношение
<F (Г, co0)> - F(T, coo) = 4 °-	>	(12.7.10)
оюрое получается в результате подстановки (12.7.6) и (12.7.7)
. (12,7.3).
Приравнивая члены при одинаковых степенях (св — ®0) в ле-
|'И и правой частях равенства (12.7.9), получаем
• _ 2а?	2 дЧ2гЫ о?	_ 2с?	<?з£2(а)о)
N2 дшдТ	’ а4 д,2	д^дТ	’
11 >с л ед нее соотношение можно записать иначе
_2^ 2с? a2z?(®0)
а“ “7^	•
Таким образом, окончательные уравнения, определяющие
".(Г) и о? (Г), имеют вид:
. __ 2а?	2^Z2(o,o)
Wo ~	Э<»дТ '
,	,	(12.7.11)
_2_ 2с? д22?(ш0)
1 II 1ема, моделирующая эти уравнения, дает на выходе оптималь-
ц\1о оценку интересующей нас частоты сигнала.
507
Преобразуем первое из уравнений (12.7.11), для чего восполь-
зуемся известной формулой дифференцирования интеграла по пара-
метру. Если
₽<у>
J(y)= ^f(x, y)dx,
“(У)
то
?(У)
J fy(x> У)^+₽'(У)/(Р(У).У) —«'	(12.7.12)
а(У)
Из выражения (10.8.26) с учетом (12.7.12) получим
т
(Xi)	с
-	2g (Г) J е -г.I (/) cos о0(Т - A) dt=2? (Г) Хо (Т).
о
(12.7.13)
Применяя формулу (12.7.12) к выражению
т
Х0(Л= [	l{t) cos со0 (Т — t) dt, (12.7.14)
о
нетрудно убедиться, что Л0(Г) удовлетворяет дифференциально-
му уравнению
Л'о+2УЛ + («о - Y?)	= £ (Г) + Yi % (Г).
Считая, что (оо^ у и учитывая выполняющееся при этом нера-
венство £ (Т) > Yi & (Т), имеем
Л+2тЛ+^Х0=иТ).	(12.7.15)
Таким уравнением определяется напряжение на колебательном
контуре с резонансной частотой со0 и затуханием когда на кон-
тур воздействует случайный ток £(Т). Следовательно, Х0(Т) пред-
ставляет собой напряжение на колебательном контуре при воздей-
ствии на него принятого колебания %(t).
С учетом соотношения (12.7.13) первое уравнение (12.7.11)
можно записать
дш
2 £ /т,ч дХ0 (Г)
®0 = 77Г S (?)--------------
N о
или, иначе,
2<т2
«о = Хт	[В (П Х1(Т) - £ (Т) Х2 (Г)].	(12.7.16)
/v0&
508
। < । АДГ) соответствует частоте (о1=(оо-[—~ А, ЛДТ)— частоте
1л *
<»□ —£- А и Л — небольшая разность резонансных частот
нуров (А <у1).
< )птимальный приемник-измеритель частоты можно моделиро-
। и. при помощи блок-схемы, представленной на рис. 12.6. На вход
параллельных резонансных контуров с одинаковыми затуха-
...ми но расстроенных друг относительно друга на малую
1 'пчину А, воздействует принятое колебание Выходные
। । пряжения контуров перемножаются порознь с принятым колеба-
Рис, 12.6. Функциональная схема оптимальной частотной авто-
подстройки частоты.
пнем и затем вычитаются. Полученная разность усиливается и
подается на интегратор. Напряжение на выходе интегратора, даю-
1111-е оценочное значение частоты ю0 (Г), посредством обратной связи
и дампы реактивного сопротивления регулирует резонансную час-
III iy контуров.
Из формулы (12.7.16) видно, что коэффициент усиления уси-
III еля
п_ 2
(12.7.17)
ло
। оптимальной схеме должен быть переменным вследствие того, что
шспереия апостериорного распределения о,7, в общем случае за-
। исит от времени.
Общеизвестная система частотной автоподстройки [11] отличается
и схемы рис. 12.6 тем, что вместо «автокорреляционных детекто-
ре ь-пер емно жителей» в ней применяются обычные детекторы оги-
".нощей, вместо идеального интегратора — интегрирующие цепочки
1'(2 и, наконец, вместо перестройки контуров дискриминатора ис-
иользуется изменение собственной частоты гетеродина. Существен-
509
ное отличие состоит в том, что параметры оптимальной схемы, как
следует из формулы (12.7.17), должны изменяться в зависимости от
значения отношения сигнал/шум на входе (см. ниже).
Точно вычислить ст2 из второго уравнения (12.7.11) весьма слож-
но. Поэтому ограничимся рассмотрением стационарного состояния,
когда выполняется условие
(У-4-У1) т = У?(1 + |/1 + ^)»1.	(12.7.18)
Противоположный случай (уТ 1) является более простым: сигнал
s(t) можно рассматривать как отрезок -не квазигармонического,
а чисто гармонического колебания.
При выполнении условия (12.7.18) и при больших отношениях
сигнал/шум флуктуации дисперсии о2 будут малыми и с некоторым
приближением во втором уравнении (12.7.11) можно заменить слу-
чайную величину
т т
Z2T (со) = J J е-Ы'-''1 cos со (^ — Г) l(t) ЦГ) dt dt’ (12.7.19)
О о
ее средним значением <Zr(co)>.
Пусть истинное неизвестное значение частоты сигнала в при-
нятом колебании равно со*. Учитывая, что случайные процессы
As (/)=Л (/) sin q> (/), ЛС(/')=Л (/') cos ф (/') и /?(/") взаимно незави-
симы, причем
<4(/)ЛД/')> = <Лс(/)Л(/')> = о2е-т1/-<'1,
получим
<£ (0 £ (О> = ст2 е~11z”r I cos ю* (/ — /') +	— /'). (12.7.20)
На основании выражений (12.7.19) и (12.7.20) можем написать
т т
<Z^((D)>= 4-У0Т+ f fe-C'+n)!/-/'! X
Z	Z	t v
о 0
X [cos (co* —co) (t — /')+ cos (co*-ф co) (/ •— t')] dt dt'.
Разность частот co* — co имеет порядок сгш и при указанных выше
условиях будет малой величиной. При этом интеграл от второго
слагаемого, содержащего cos (со* + со) (/ — /') cos2co* (t — t')
будет значительно меньше интеграла от первого слагаемою.
Воспользовавшись формулой
т т
Ce-(T+n)l^^iCos(co*—со) (/—’/') dt dt’ =
о о
т
= 2 J (Г— т) е~( i+ti) 1 cos (со* — со) т dr
о
510
11ПЮЛНИВ вычисления, получим
<Z| (®)> = -L А^оГ+o2 [(Y+Yj)2 - (со* - со)2]-2 х
- {e-CM-ri)7" [((y+Yi)2—(®* —со)2) cos (со* — со) Т — 2(y+Yi)X
Х(й* — со) sin (со* —со) Т]— [(Y+Yi)2 — (®* — ®)21}-
11|>и выполнении условия (12.7.18) это выражение упрощается:
<z?(m)> -	(12.7.21)
1 'I пода находим
I2 Z2 (<>))	6с2	(1 + 2р — р*) (\—2p — pS) , р = СО* — О.
дв>2 ~~(7 + h)1	(Ч Р2)4	’	7 + 71
(12.7.22)
I < in в этом выражении положить со=со0 и затем подставить во
। трое уравнение (12.7.11), то получим
_2	12а2а2	(1-|-2р0 - /J2) (1	2р0 Рр)	м* — й,0
°" “«’(, + „)• (T+7IP  л“ТнГ-
(12.7.23)
Но физическому смыслу дисперсия не может быть отрица-
н плюй величиной. Поэтому следует предположить, что оптималь-
ны схема (рис. 12.6) может нормально работать лишь при одно-
|'Р менном выполнении двух неравенств
I 4-2р0 — ро < 0) 1	2р0 ро 0.
1'ипая совместно эти два неравенства, находим
i Pol <1/(1 + /2~) = 0,41.	(12.7.24)
Подставив в (12.7.24) выражение р0 из (12.7.23), определяем
и» максимальное значение разности — соо, при которой система
11 тотной автоподстройки работает еще нормально. Эту максималь-
ные) расстройку в автоматике принято называть полосой схваты-
н шия:
Дсосх = | ы*т - со 0| = 1+н = _ 7_ (1 + 1/1 + <1/
1	01	1 + Y 2	1 + Y 2 \	'	1 7< '
(12.7.25)
Если задан равномерный априорный интервал возможных час-
и |', (coi, спз), то начальная частота сигнала со* может находиться
г побой точке этого интервала. Целесообразно принять начальное
511
оценочное значение частоты и0 равным центральной частоте априор-
ного интервала, т. е. положить
юй = (кц 4- со2) при Т — 0.	(12.7.26)
Тогда оптимальная схема будет выполнять свое назначение лишь
при выполнении неравенства
|(и2-со1)<Аисх.	(12.7.27)
При этом колебательные контуры схемы рис. 12.6 в начальный мо-
мент времени должны быть настроены соответственно на частоты
и со2.
В тех случаях, когда неравенство (12.7.27) не выполняется, нуж-
но априорный интервал возможных частот разбить на
(а>2—со1)/2Ао>сх примыкающих подынтервалов, и в каждом из них
осуществлять точное определение частоты при помощи самостоя-
тельной схемы указанного вида.
Возвращаясь к условию (12.7.18), заметим, что оно гарантирует
получение достаточно точной оценки, соответствующей |ро| Cl-
Пренебрегая ро по сравнению с единицей, из формулы (12.7.23)
получим следующее значение дисперсии оценки частоты:
2	_ Л'о И + 11)*	П1 Л , 71\4 / 2а2 \-2	/19 7 904
а<“-“2(^)2	+ (jvJ •	(12-7.28)
Подставив это выражение для в (12.7.17), находим оптимальное
значение коэффициента усиления
k = ±г +jiV = Г (1 + т/1 +	.	(12.7 29)
ба2 6з2 \ Г fA?o /
Заметим, что ширина энергетического спектра стохастического
сигнала s(t), имеющего функцию корреляции (10.8.24), равна
А/э — у/2. Поэтому yNo/2 = есть энергия белого шума
в полосе сигнала и, следовательно,величину 2о2/yN0 условно мож--
но назвать отношением сигнал/шум на входе.
Формула (12.7.29) показывает, что коэффициент усиления в оп-
тимальной схеме зависит от дисперсии о2 и времени корреляции
тх~1/у сигнала, а также от отношения сигнал/шум на входе. Ве-
личина апостериорной дисперсии оценки частоты о,7, определяется
только отношением сигнал/шум на входе и временем корреляции
сигнала.
$12
ИИТЕРАТУРА
I.	Крамер Г. Математические методы статистики Изд-во иностран*
поп литературы, 1948.
2.	S 1 е р I а п D. Estimation of signals parameters in the presence of noi-
। Trans. IRE, 1954, IT-3, March.
3.	Фалькович С E. Прием радиолокационных сигналов на фоне
Ф i уктуационных помех. Изд-во «Советское радио», 1961.
4.	Куликов Е. И. Предельная точность оценки параметра сигнала
пр । приеме в нормальном шуме. «Радиотехника», 1962, №7.
5.	К у л и к о в Е. И. Предельная точность совместной оценки двух
параметров сигнала при приеме в нормальном шуме. «Радиотехника»,
1963, № 1.
6.	SkolnikM I. Introduction to radar systems. McGraw-Hill, 1962.
7.	Шир ма н Я. Д-, Голиков В. H. Основы теории обнаруже-
нии радиолокационных сигналов и измерения их параметров. Изд-во «Совет-
• кое радио», 1963.
8.	Куликов Е. И. Предельная точность измерения центральной
ысготы узкополосного нормального случайного процесса на фоне белого
шума. «Радиотехника и электроника», 1964, № 10.
9.	3 и б е р т В. Общие закономерности обнаружения целей при по-
ищи радиолокации. «Вопросы радиолокационной техники», 1957, № 4 (41).
10.	Бакман Д. Е. Сложные сигналы и принцип неопределенности
। радиолокации. Изд-во «Советское радио» 1965.	_
11.	Крив ицкий Б. X. Автоматические системы^ радиотехниче-
к их устройств. Госэнергоиздат, 1962.
Глава 13
ФИЛЬТРАЦИЯ СЛУЧАЙНЫХ СИГНАЛОВ ИЗ ШУМОВ
§ 1. ФОРМУЛИРОВКА ЗАДАЧИ ФИЛЬТРАЦИИ
Рассмотрим общую постановку задачи фильтрации сигнала из
шумов и затем конкретизируем ее применительно к двум частным
случаям, которые будут подробно рассмотрены в дальнейшем.
Пусть колебание £(/), принятое на некотором интервале вре-
мени, является функцией от сигнала	и шума ц(^):
Г](0).	(13.1.1)
Сигнал s(C^(0) в общем случае может зависеть не от одного, а от
нескольких «параметров» причем сам сигнал s(t, А.(£)) или инте-
ресующий нас параметр — случайный процесс. Шум т](/)
может быть произвольным; сигнал и шум не обязательно представ-
ляют аддитивную смесь.
Предполагаются априорно известными вид функции F (т. е.
способ комбинирования сигнала и шума) и некоторые статисти-
ческие характеристики случайного сигнала и шума. Располагая
этими априорными данными, нужно решить оптимальным образом,
какая реализация самого сигнала з(^,Л) или его «параметра»
содержится в принятом колебании |(Z).
Из-за наличия шума и вследствие случайного характера сигнала
оценка реализации сигнала или его параметра, вообще говоря,
не будет совпадать с истинной реализацией, что приводит к ошиб-
кам фильтрации. Для количественной характеристики качества
фильтрации можно использовать несколько критериев. Укажем два
таких критерия: критерий минимума среднеквадратичной погреш-
ности и критерий максимума апостериорной вероятности.
1. Обозначим оценку истинной реализации сигнала s(/,A(/))
в принятом колебании |(£) через 5*(1,к (Z)). В некоторых задачах
качество фильтрации целесообразно характеризовать величиной
средней квадратичной погрешности е2 = <([s* (t, Л (^)) — s(t, Ц/))13),
$14
мреднение производится по всем априорным сведениям. При
। '.и.зовагии критерия минимума среднеквадратичной погреш-
||| структура оптимального фильтрующего устройства опреде-
ли я из условия получения минимума величины е2 (см. § 2).
'. В ряде задач фильтрации более просто находится решение
критерию максимума апостериорной вероятности. В данном
1 >чае оптимальное фильтрующее устройство должно следить за
шимумом апостериорной вероятности; точность этого слежения
’ кпо характеризовать дисперсией апостериорной вероятности
। । § 3).
В дальнейшем ограничимся в основном рассмотрением того прак-
||  юски важного, но частного случая, когда сигнал и шум являются
। щионарными случайными процессами и взаимодействуют ад-
। ШВН0, т. е. просто складываются:
g(O = s(Z, X(0) + n(0, 0<J<T.	(13.1.2)
В зависимости от дополнительных предположений о характере
и шала и шума ниже раздельно рассмотрены два вида фильтрации:
н юйная и нелинейная.
ч 7 ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ
Предположим, что сигнал s(/) и шум r|(Q в (13.1.2) являются
 .1висимыми стационарными нормальными случайными процес-
>"1Н с известными корреляционными функциями £s(t) и ^(т)
и равными нулю средними значениями. Требуется определить сис-
MV, которая с минимальной средней квадратичной погрешностью
। । целяет из шума не информационное сообщение, а сам полезный
и шал, т. е. минимизирует величину
с2 -<ls,:(0-s(/ + A)]2>,	(13.2.1)
и нычислигь значение
1десь для общности введен временной сдвиг на А. При Д>-0
и пка s*(fj должна предсказывать значение входного сигнала
и I на А вперед; если А<4), то оценка информирует нас о том, какое
и пение входного сигнала было до момента времени t — А. На-
> >ец, при А -- 0 задача сводится только к выделению сигнала
। шума.
Строгое математическое решение сформулированной задачи было
ню А. IL Колмогоровым [1] и Н. Винером [2]. Оптимальное
1111ьтрующее устройство является линейным и для полубесконеч-
। о интервала наблюдения ( — оо, Т) может быть рассчитано по
"рии Колмогорова — Винера. В ряде последующих работ эта
<’рия была обобщена для конечного интервала наблюдения (О, Г)
нестационарных процессов [3, 4, 5].
515
Не приводя здесь всех математических доказательств, ограни-
чимся простыми физическими рассуждениями.
Если сигнал и шум являются независимыми нормальными ста-
ционарными случайными процессами с нулевыми средними зна-
чениями, то они могут отличаться только корреляционными функ-
циями или, иначе, спектральными плотностями. Этот факт исполь-
зуется при осуществлении фильтрации. По-видимому, нужно стре-
миться К ТОМу, ЧТОбы ПО В03М0Ж-
s(th^(t)
G0(t)	S*(t)
Рис. 13.1. К определению опти-
мального линейного фильтра.
ности с наименьшими искажениями
воспроизвести спектр сигнала и
как можно сильнее подавить спект-
ральные' компоненты мешающего
шума. Как известно, задача частот*,
ной селекции успешно решается
Надлежащим образом подобран-
ными линейными фильтрами.
Итак, будем искать оптимальное фильтрующее устройство среди
линейных фильтров. В качестве оценки входного сигнала берется
выходной сигнал фильтра (рис. 13.1), т. е. если G(t) — импульсная
характеристика искомого фильтра, то
t
b
(13.2.2)
При этом выражение для средней квадратичной погрешности
(13.2.1) принимает вид
। t
е2 — / ) J [S (/ ----------т) 4- Y] (t — т)] G (т) dr — s (t + Л)
х 1о
= о* +
t	[ I
+ J G (т2) dr2 f (т2 — Tj) + (т2— тх)] G (тх) dxx — 2ks (т24- A)
о	lb
(13.2.3)
Для того чтобы определить импульсную характеристику G0(t)
оптимального фильтра, обеспечивающего минимум средней квад-
ратичной погрешности, воспользуемся известным приемом вариа*
ционного исчисления. Пусть G(t) = G0(f) + ря(0> где Н — паРЭ’
метр, не зависящий от t, a g(t) — произвольная функция.
Условие минимума средней квадратичной погрешности теперь
можно записать в виде
гйа I
I р.=0
= 0.
(13.2.4)
516
»к1 условие приводит к соотношению
i	t
J g (*а) J [&s (t2 — tx) + kri (т2 — т i)] X
x Go (Ti) — ks (т2+A) = 0.
(13.2.5)
I ^скольку это соотношение должно выполняться при произвольной
фикции g(0, то отсюда следует, что импульсная характеристика
h i имальното фильтра Gg(t) должна удовлетворять интегральному
равнению Фредгольма первого рода
j [йДт—х) + ^(т—х)] G0(x)dx = £Дтф-А). (13.2.6)
Это интегральное уравнение является основным уравнением
нории линейной фильтрации и называется уравнением линейной
|ц'| рессии или уравнением Винера — Хопфа [61. Найдя из него
'..,(>) и подставив ее вместо G(t) в (13.2.3), получим значение е«(Л-
Следует заметить, что оптимальные линейные фильтры, опреде*
। юные уравнением (13.2.6), отличны от согласованных и оптималь-
||| is фильтров, рассмотренных в § 6, 7 гл. 10; их функции и назначе-
ние различно. Если основное назначение рассматриваемых здесь
рнпьтров состоит в наилучшем воспроизведении формы полезного
hi пала из аддитивной смеси его с шумом, то задача согласованных
||цпьтров заключается не в воспроизведении формы сигнала,
। и формировании максимально возможного пика сигнала на шу-
। том фоне.
Теория оптимальной линейной фильтрации (по критерию мини-
цма средней квадратичной погрешности) имеет ряд недостатков:
I) она охватывает мало практически интересных случаев;
2) интегральное уравнение регрессии не всегда решается;
1) даже в тех случаях, когда удается решить это уравнение, опти-
11пьные фильтры оказываются практически трудно реализуемыми.
Первый недостаток очевиден из исходных предпосылок, на кото-
। н> базируется теория линейной фильтрации. Линейные фильтры
1.1ЯЮТСЯ оптимальными лишь для выделения не сообщения, а са-
। ч о сигнала в виде нормального случайного процесса. Однако
п р; диотехннке обычно используются модулированные радиосигналы
। щечной длительности, не являющиеся нормальными процессами,
и । явится задача оптимальной фильтрации какого-либо параметра
in пала*. Поэтому значительно больший практический интерес
и pi вставляет рассмотрение теории нелинейной фильтрации, когда
11 к дположение о нормальном характере сигнала не требуется.
* Примеры применения линейной фильтрации к когерентному приему
। штудно-модулированных сигналов рассмотрены в [22].
517
Для иллюстрации двух остальных недостатков, наиболее суще-
ственным из которых является третий, приведем один простой
конкретный пример. Пусть требуется с минимальной средней квад-
ратичной погрешностью отфильтровать сигнал в виде нормального
стационарного шума с нулевым средним значением и экспоненциаль-
ной функцией корреляции
(т) = ст2 е~“111	(13.2.7)
от аддитивного белого ш>ма т](/) = п(£) с характеристиками
(10.2.13).
Учтем, что согласно выражению (13-2.5) переменная т в урав-
нении (13.2.6) является положительной (0<т</). Полагая далее
А — 0, после подстановки выражений для корреляционных функ-
ций в (13.2.6) получим
t
ст2 Jе_о |Т -Л]	= O2S е-“- — 2 No G0(t).	(13.2.8)
о
Разобьем интервал интегрирования (0, t) на два интервала
(0, т) и (т, t), в каждом из которых показательную функцию можно
записать без модуля:
т	t
е-ат e«G0(x)dx -|-е7Т е~ах Go (х) dt е~а’ — Go (т). (13.2.9)
о	-	2з«
Умножим левую и правую части на еят и затем дважды продиф-
ференцируем по т. В результате придем к следующему дифферен-
циальному уравнению второго порядка:
/	4т2 \
G” (т) — у2 G(, (т) —0,	(13.2.10)
Общее решение этого уравнения имеет вид:
G0(T) = cLe-iT + c2er,	(13.2.11)
где произвольные постоянные сг и <?2 определяются путем подста-
новки решения (13.2.11) в уравнение (13 2.9) и приравнивания
коэффициентов при е~“т и
Выполнив вычисления, найдем уравнения для определения коэф-
фициентов и с2:
—-—С] 4----с2 — — 1,	—!—e~Gc, -]----1—erzc2 —0.
а ~ 7 1 1 « 1 [ 2	« Н	7 “ 7
Отсюда получим
С (а-И)^-7)е2|/
1	(’-г 7)2 е2т/— G — V2’
(а 4 7) (а - 7)з
(х + 7)2е2-П_ («-7)3-
(13.2.12)
518
1 !екоторые простые решения интегрального уравнения линейной
|>пльтрации (13.2.6) для других случаев приведены в приложении
HI 171.
Для рассмотренного простейшего примера (экспоненциальной
РМ1кции корреляции полезного сигнала и дельтокоррелированного
। цитивного шума) уравнение решается сравнительно просто.
1 цпако импульсную характеристику оптимального фильтра из-за
и. линия в ней функций ей и е2й реализовать нелегко.
», 3. НЕЛИНЕЙНАЯ ФИЛЬТРАЦИЯ
Хотя общая теория нелинейной фильтрации охватывает разно-
разные и весьма сложные задачи, для разъяснения применяемых
кгодов рассмотрим простейший частный случай, для которого
• । |юрмулируем исходные предпосылки.
Пусть принимаемое колебание £(^) представляет собой сумму
nt пала s{t, Х(/)), зависящего от одного «параметра» Х(/), и ста-
ционарного белого шума n(ty.
=	+ Q<t^T. (13.3.1)
I 1редполагается, что характеристики шума n(t) известны и опреде-
। иотся формулой (10.2.13), а закон изменения параметра Х(1) на
интервале (0, Т) задан известным стохастическим дифференциаль-
ным уравнением, например, вида
g + aX=ttl(0.	(13.3.2)
Чесь n^t)—другой белый шум с известными характеристиками
и а — заданный коэффициент.
Располагая этими априорными данными, нужно найти устрой-
11во, которое бы с наилучшей точностью воспроизводило изменяю-
щийся во времени случайный параметр Л(£). Иначе говоря, опти-
мальное устройство должно с наименьшей ошибкой следить за
। iyчайный процессом k(t).
Тот факт, что полезный сигнал	как правило, зависит
' >| интересующего нас параметра k(t) нелинейно, определяет не-
ынейный характер устройства оптимальной фильтрации.
В качестве критерия оптимальности будем применять критерий
мпссимума апостериорной вероятности. Тогда, естественно, пер-
вый этап в решении данного примера состоит в вычислении апосте-
риорной вероятности параметра Х(0. С принципиальной точки зре-
ния эту апостериорную вероятность можно найти в двух случаях:
11 когда параметр представляет собой марковский процесс и
’I когда параметр А(£) является нормальным случайным процессом.
519
По этим двум направлениям и развивалась теория нелинейной
фильтрации.
Второе направление, развитое в работе [8], основано на ис-
пользовании того, что случайный процесс k(f) является нормальным.
При этом ответ дается интегральным уравнением, результат реше-
ния которою часто моделируется фильтрами с переменными пара-
метрами. Ряд решенных практических примеров приведен в [9].
Первое направление было разработано Р. Л. СтратоновичеМ
[10, 11]. Ввиду того, что соответствующие результаты будут ис-
пользованы в дальнейшем, остановимся на этом направлении под-
робнее, изложив его применительно к .сформулированному част-
ному случаю [12].
Итак, предположим, что параметр 7(0 на интервале (0, Т)
является марковским процессом. Обозначим значения параметра
в два близкоотстоящих момента времени: t и t + т, т>0,
соответственно через А, и А.х, а вероятность перехода — через
рг(Лт, Z) = р(Х,х,тЛ).
Будем интересоваться изменением вероятности перехода в зави-
симости от т, считая t фиксированным. Возьмем очевидное началь-
ное условие
limpT(AT, Л) = б(Хг —Л),	(13.3.3)
т-.О	V	'
где б(г) — дельта-функция.
Как указывалось на стр. 125, вероятность перехода определяется
уравнением Фоккера — Планка (3.19.7):
= ~5Г	| [Ка(М д]. (13.3.4)
Коэффициенты Ki(^t) и Ка(?ч) находятся из дифференциального
уравнения, описывающего поведение параметра Х(£), ло известным
формулам (3.19.5):
<Х — Х\	((\ т— Х)2\
/ММ-lim^----------К2(М = Ит —------------. (13.3.5)
Т-.0 Т	'^0
Для малых временных интервалов т справедливо равенство
dpjdx = Арт/т, где Ар- — приращение вероятности перехода
за малое время т. Поэтому соотношение (13.3.4) можно записать
иначе:
Арх = - т А [Кх (Хт) б (Хт- л)] + | т [К2 (М б (Хт - Л)] + т2 ...
520
Очевидно, что при малом т вероятность перехода для момента
времени t + т равна начальной вероятности б(Х,х— X) в момент
времени t плюс ее приращение Ар- за время т:
рс (К, А) = б (Xt — Л) — т [/<! (Хх) б (к. — X)] +
+ | т [К2(М б (Хт — 1)] -ф т2...	(13.3.6)
1гэ соотношение будет использовано несколько позже.
Перейдем теперь к вычислению апостериорной вероятности па-
p. метра A(f). Разобьем весь интервал наблюдения Т на m элемен-
।ирных интервалов одинаковой длительности А = Tim, причем
выберем А настолько малым, чтобы выполнялось неравенство
А«тАл,	(13.3.7)
। де Ш — время корреляции случайного процесса Х(£).
При выполнении условия (13.3.7) параметр X, на каждом из эле-
ментарных интервалов можно считать практически постоянным и
равным, например, его значению в конце рассматриваемого эле-
ментарного интервала.
При таком рассмотрении вся априорная информация о пара-
метре к дается совместной плотностью вероятности lFm(A15 Z2,..., Xm),
। де —значение параметра к в конце i-ro элементарного интер-
н. на, т. е. = kftt), i = 1, 2...tn. Согласно формуле (3.18.6)
шриорная вероятность 1Гт(Хд, кг, ..., Хт) выражается через на-
чальную вероятность \F(X,i) и вероятность перехода:
W m (^1> ^2, •••, ^/п) = Рд (^m>	1) X
X P&(ktn— 1, km — 2) ••  Рд (кг, ki) W (A»i).	(13.3.8)
Запишем выражения совместных апостериорных плотностей
। <.роятностей последовательно для значений параметра в конце
I ю интервала, в конце 1-го и 2-го интервалов, в конце 1-го, 2-го
и 1-го интервалов и т. д. Обозначим эти апостериорные вероятности
 «ответственно через W'ps(^i), Wps(ki, кг), irps(ta, кг, к3) и т. д.
Очевидно, что апостериорная вероятность значения парамет-
1>. к в конце 1-го элементарного интервала определяется формулой
(11.3.25) и равна:
(XO^WOexp
। е — несущественная произвольная постоянная, не зависящая
к к.
J [g (0 —s(£, k^dt
521
При записи совместной апостериорной вероятности для Xi и
Хг нужно учесть два обстоятельства. Во-первых, апостериорные
сведения, полученные на первом элементарном интервале, целесо-
образно использовать в качестве априорных для второго интервала.
Во-вторых, необходимо также учесть априорно известный факт,
что параметр X изменяется с значения Xi до Х2, причем из условия
(13.3.7) видно, что Xi и Хг коррелированы. Дополнительные априор-
ные сведения о параметрах Xi даются условной вероятностью
1Г(Хг|Х1), которая согласно (3.18.2) совпадает с вероятностью
перехода UZ(X2|Xi) = рд(Х2,Х1).
С учетом сказанного можем написать
Х2) — k2Wps('k1) Xj) х
2	,	,
х П ехР —	(0~s (Л
/=1	(4- 1)А
Аналогично поступаем при вычислении апостериорной вероят-
ности Wps (Xi, Хг, Хз). Следует лишь иметь в виду, что для простого
марковского процесса условное распределение Х/+j зависит только
от Х(- и не зависит от Xx-_i, Х(-_2, ••• Поэтому все дополнительные
априорные сведения, которые необходимо учесть, будут опреде-
ляться вероятностью перехода рд(Хз, Хг). Таким образом, можем на-
писать
X ехр
Wps(\i, Х3) — k.. Wps (Х1( Х2) Рд (Х3, Х2) х
зд	!
± С £(/)- s(t, Х3)Р^ =^№/2(Х1,Х2)рд(Х3, Х2) х
° А	!
3	1 ‘р
хЦехр -1- J [g(O-s(Z, Х()]2^ .
г=1	(г-i) А
Здесь при написании последнего равенства была использована фор-
мула (13.3.8).
Если продолжить эти рассуждения, то для апостериорной ве-
роятности первых (v + l)«^m значений Хх получим формулу
Wps (Хъ ..., Х„ Х,+.) = Д+, Wp (Хь ..., Х„_,, ХЗрд(Х,+1, Х0 х
X ехр
М-D А
± J	Xv+I)]2^l.
vA
(13.3.9)
522
Будем интересоваться лишь финальной апостериорной вероят-
иостью, т. е. апостериорной вероятностью только последнего зна-
к иля A-v-i-i. Обозначим ее через (X,+ i) =	Финаль-
н in апостериорная вероятность	(X^i) характеризует инфор-
|.|цию о последнем значении параметра Vp после обработки
1"’ализации 5(0 на всех (v + 1) первых интервалах.
Для этого нужно проинтегрировать (усреднить) апостериорную
и ютность вероятности (13.3.9) по всем v первым значениям Xi,
, ..., Л,, рассматривая их как несущественные. На основании
\< товия согласованности (3.2.5) имеем
(Z„_|_i) =	i (Х,+ ,) = J ... J pS (^i,	i-i)
—oo —co
(13.3.10)
Подставив сюда выражение (13.3.9), получим последовательную
u< почку преобразований одномерных апостериорных вероятностей:
(X,+i) = k,+ \ ехр
OO
х J №,(^)рд(^+1,
—oo
(13 3.11)
I ю
F{t, x,)--^ol5(0-s(^ MP- (13.3.12)
Заметим, что, как и при оценке параметров (см. стр. 484),
к дует различать энергетические и неэнергетические параметры.
I । ли параметр K(t) является неэнергетическим и сигнал s(t, X)
|.щионарен, то в формуле (13.3.11) множитель
ехр
± f №(t) + s4t,V]dt
v*A
н»кно включить в постоянную k,+i и соответственно функцию
I (I, X,) определить равенством
О
F(t, =	%).
(13.3.13)
523
Если в формуле (13.3.6) положить Ат= 1 — Av, т = А, Тб
для малых Д-э-0 можем написать
Рд (АЧ4-1, Ач) = 6 (Av-[-i — А,) — А
д
d/:+i
[A"i 1) 6 (Av-h — Av)] +
+ А [К8 (Av+I) б (Av+I - Ач)] + А2...
Z	С"..-LI
(13.3.14)
Подставив выражение вероятности перехода из (13 3.14]
в (13.3.11) и выполнив интегрирование-с дельта-функцией, полуи
чим
W\+I (Av+i) = А\,+| ехр
(’4-1) А
X
х [^(Ah-OUMAv-h)] +4 А^-[К2(А,+1)^’(^.4-1)] +д2-
(13.3.15)
Кроме этого, при А-> 0 экспоненциальный множитель в пра«
вой части (13.3.15) близок к единице и, следовательно,
lim Av-f-i = limlFv+i (Av+l)/Wrv(A,+i) = l.
д.о д-.о
Поэтому при достаточно малых А можно положить
^’4-i — 1 — уА,
ехр
А
J F(t,K+i)dt
= ехр [F (t, А,+1) А] = 1 + F (t, Av+i) A. (13.3.16]
Во избежание недоразумений отметим, что при написании послед
него соотношения использована симметризованная форма запися
стохастических интегралов, предложенная Р. Л. Стратоновичея
[131.
Подстановка соотношений (13.3.16) в (13.3.15) дает
(Av+I) = [1 + (F - у) А + у РА2] Г, (Av+,)- А^А_ х
X [Ki(Av+I) W, (Av-h)] + I А [К2 (A,+l) №v (А,+ |)] + А2...
524
пли иначе
Г,+1(^.)—Гдл,+1) = 4 Adr~ w,(X,+l)] -
z dx>+i
- A di~ [Ki(M^(*4-i)] + A (F- T) w. (Z,+l)+ A2... (13.3.17)
Разделив обе части этого равенства на А и переходя к пределу
при А-> 0, получим, что одномерная апостериорная вероятность
должна удовлетворять уравнению
^Цг21 = I да [К. (М «*] - g 1X1(Ч «1 + [F (/, X)—Т1 Г.
(13.3.18)
Чтобы определить не зависящую от X, постоянную у, нужно
проинтегрировать выражение (13.3.18) по всем значениям 1 и
учесть, что lim W (t, Х)=0, и по условию нормировки
^->±оо
J "м.= * J ®-((,х)л = о.
—оо	—со
Тогда получим
y = <F(^,X)> = J F (t, 1) W (/, Z) dK. (13.3.19)
—co
Следовательно, финальная апостериорная вероятность опреде-
щется следующим дифференциальным уравнением в частных
производных:
= уда	[*1(Ч	+
+ [F(/, М—<F(C MW.	(13.3.20)
Таким образом, если принятая реализация представляет собой
। дативную смесь сигнала и белого шума (13.3.1), причем интере-
< ующий нас случайный параметр сигнала является простым
марковским стационарным процессом, то оптимальное фильтрующее
\стройство определяется уравнением (13.3.20). Это уравнение
юлжно формировать апостериорную вероятность W(t, 1) и опреде-
ыгь значение соответствующее, например, максимуму апо-
криорной вероятности. Это значение hm(t) принимается за истин-
ное мгновенное значение параметра Х(/), а дисперсия апостериор-
ного распределения сгх(/) будет характеризовать погрешность сле-
1ЛПИЯ за параметром Хц).
52$
Однако практическое осуществление этих операций оказывается
весьма сложным. Поэтому ограничимся решением задачи в гаус-
совом приближении. Оно базируется на предположении, что апо-
стериорная плотность вероятности является нормальной:
“Р	' 03 3-21>
V 2.4-f (/)	| 2стх (О J
Рассмотрение задачи в гауссовом приближении существенно
упрощается, так как апостериорная плотность вероятности (13.3.21)
определяется всего двумя параметрами; средним значением Хо(0,
максимизирующим апостериорную вероятность, и дисперсией
d(t), характеризующей ширину апостериорного распределения.
Поэтому вместо формирования и анализа апостериорной вероятно-,
сти оптимальное фильтрующее устройство может определять только
эти два параметра.	;
Как следует из рассуждений, приведенных в § 2 гл. 12, предпо-i
ложение о том, что апостериорная плотность вероятности является!
нормальной, в известной мере оказывается оправданным при боль-’
ших отношениях сигнал/шум и нормальном шуме. Вследствие нор-:
мальности шума в рассматриваемом случае должно выполняться
подобное условие. В общем виде гауссово приближение справед-
ливо при условии ох<^АХ, где АХ дь s(/,X)/ ds^ — некоторый
масштаб по X.
В пределах малой «ширины» апостериорной вероятности ст>(/)
коэффициенты A\(X), /С2(Х) и F(t, X) будут мало изменяться и их
можно представить первыми членами разложения в ряд Тейлора
в окрестности точки Хо:
= Л’1(Х0) + К,(Х0)(Х-Х0), /С2(Х) = К2(ХО),
1 „	(13.3.22)
F (/, Х) = Е (/, Xo)+F' (/, Хо) (X - Хо)+ F" (/, Хо) (X - Хо)2.
Здесь и ниже штрихами обозначены производные по параметру X.
Число учтенных членов ряда здесь выбрано исходя из того,
что используемые разложения (13.3.22) должны находиться в сог-*
ласии с нормальной плотностью вероятности (13.3.21), а не проти-
воречить ей.
Отметим, кстати, что приведенные выражения для 7С1(Х) и ^2(X)
означают, что априорно сам параметр X в окрестности Хо изменяет*’
ся по нормальному закону [см. выражение (3.19.19) ].
Получим дифференциальные уравнения, определяющие Хо(/)
и ofc). Если подставить выражения (13.3.21) и (13.3.22) в исходное
уравнение (13.3.20), то после несложных преобразований получим
526
^ + 2(X-X0)^ +
C - X»)2 d* _
$ dt
- ]_2a? Kx (Xo) + K2 (Xo) + 2a? <F (/, X)> - 2a? F (t, Xo)] +
+ 2 (X - Xo) [Лх (4 + a? F’ (t, Xo)] +
+ G— M2
2/G (M + 4-^2 (M-И/ F" (t, Xo)
ax
(13.3.23)
(13.3.24)
Заметим, что первое слагаемое в квадратных скобках в правой
। нти равенства (13.3.23) можно несколько упростить, если учесть
и< гношение
<F (f, К)> - F ((, Ч) = 4 a? F" (t, U
। оюрое получается в результате подстановки выражений (13.3.21)
и (13.3.22) в формулу (13.3.19).
Приравняв члены при одинаковых степенях (Л — Хо) в левой и
правой частях выражения (13.3.23), получим окончательные диф-
ференциальные уравнения, определяющие Хо(() и о\(/):
^ = JG(X0) + a? (t)F'(t, Хо),
= 2а? К, (Ьо) + К2 (Ч) + at F (t, Хо).
Если Хо(/) принимается за оптимальную оценку параметра, то
> щача оптимальной нелинейной фильтрации состоит в совместном
ранении уравнений (13.3.24). Система, моделирующая эти уравне-
ние, будет воспроизводить на выходе интересующий нас параметр
/(/), отфильтрованный от помех оптимальным образом.
Основные уравнения нелинейной фильтрации (13.3.20) и (13.3.24)
ю/кно обобщить на случай другого шума и когда параметр Л(/) яв-
। потея многомерным марковским процессом, т. е. сигнал зависит
и нескольких параметров:	... [111.
Пусть, например, сигнал s(t, Xi, Х2) зависит от двух параметров:
' i(/) и Х,2((). В данном случае уравнение (13.3.4) имеет вид:
Х2г> G.G) у, д ..	. .	. .
f=l 1
2
+ 4 2	1*‘'(Хь’X2xW (13Л25)
527
Теперь вместо (13.3.21) нужно использовать двумерную нормаль-
ную апостериорную плотность вероятности
W (t,	Л2)=-----z. 1 - ехр
°2
2(ф1-^)
Оч — W
где k (t) — функция взаимной корреляции между параметрами.
Введем обозначение:
F(;,	Л2) =	[Ut)-,s(t, Klt М2.	(13.3.26)
Тогда можно получить уравнения оптимальной нелинейной филь-
трации следующего вида:
%- ,„2dF .hdF
-rfT = K1 + G' ^ + feaT2>
d^-zo tz ।	2 dF . . dF
T = *2+<^ + *^
d° I _ K , пп2 дКг 4 d2 F	F
I	d2F , dKi
+2feo,i;^ + 2k ax?’
Л2 Г I 9^2	!	4 F f fe2 d2 F f
^ = ^22+20^ + 0^+^^ +
OAj (7Л2
dk S' I hld^l I дК*\ I	d2F 2d2F\ I
dT =K* +	+ яг) + *V"TiF + ’’ ®i)+
1 Z^-2 2 . h«\ d2 F .	2 dKi 1 „2 ЭК1
4-(oiff2 + k) aX1ax2 + ff| dXr + °2lxr-
(13.3.27)
В дальнейшем мы ограничимся рассмотрением частного случая,1
когда параметр Х(?) представляет собой нормальный марковский
процесс, т. е. описывается уравнением (13.3.2), в котором пх(0 —
нормальный шум с нулевым средним значением и функцией кор?
реляции
+	(13.3.28)
$28
K<ik следует из (3.19.24), в данном случае /<1(Х,)=— аК,	=
V i/2. Поэтому уравнения (13.3.24) принимают вид:
^ = -aX0 + of (t)F’(t, U
~ = - 2асгх + | Л/i + ox F" (t, Хо).
(13.3.29)
Ниже эти уравнения будут применены к частным примерам.
При этом основная цель состоит не в решении сложных практи-
> i ких задач, а в том, чтобы проиллюстрировать применение теории
 линейной фильтрации на простейших примерах. Будет показано,
 и в этих примерах теория позволяет получить устройства, кото-
। । и известны и широко используются на практике. Несмотря на
 н , рассмотрение примеров оказывается полезным в трех отно-
। п-ииях: 1) оно в некоторой мере демонстрирует принципиальные
। о 1можности теории и трудности строгого решения задач; 2) по-
। нывает, насколько те или иные устройства приближаются к оп-
। цмальным, 3) позволяет установить оптимальные характеристики
i ройств и их отдельных элементов.
§ 4. ФИЛЬТРАЦИЯ СЛУЧАЙНОЙ ФАЗЫ УЗКОПОЛОСНОГО
СИГНАЛА И ФАЗОВАЯ АВТОПОДСТРОЙКА ЧАСТОТЫ
Применим уравнения оптимальной нелинейной фильтрации
(13.3.20) и (13.3.24) к следующему практически важному случаю.
Пусть параметром А,(/) является блуждающая фаза q>(t) узкополос-
ного радиосигнала
s (/, ф) = Ао cos [соо t ф- ф (£)].	(13.4.1)
Хмплитуда радиосигнала Ао и его частота соо считаются известны-
мп, а фаза ф(/) — случайной (блуждающей):
Ф=^ = М0>	(13.4.2)
|де n^t) — белый шум с функцией корреляции
<«i (М «1 О = 4	6 (G - М-	(13-4.3)
Если не учитывать амплитудные флуктуации, то радиосигнал
(13.4.1) описывает автоколебания генератора томсоновского типа,
причем под П1(1) нужно понимать собственные флуктуации генера-
। ора.
529
Нетрудно убедиться, что применительно к данному случаю
отдельные коэффициенты, входящие в уравнение (13.3.20), согласив
(13.3.5), (13.3.13) и (13 3 19) равны:
К1(ф) = 0, Ка(ф) = |Л1-
ф)) =- J s(t, фПф,
F(t, ф) =	Ф) = ^чюх
X [cos (ф — фо) COS (й)0 i + фо) —
— sin (Ф — ф0) sin (®01 + фо)].
Поэтому уравнение (13.3.20) принимает вид:
(13.4.4)
1 дг1	+ [F (t, ф) - <F (t, ф)>] W (t, ф). (13.4.5)
Покажем, что оптимальным устройством для выделения блуж-
дающей фазы радиосигнала, принимаемого на фоне аддитивного
белого шума, является фазовая автоподстройка частоты (ФАПЧ).
При этом не будем заранее пользоваться гауссовым приближе-
нием, а, базируясь на предварительном знании статистической дина-
мики ФАПЧ [141, решим данную задачу при несколько более об-
щих исходных предпосылках. Они физически адекватны характеру
рассматриваемой задачи и в принципе охватывают нестационарный
режим работы; в стационарном режиме получаются результаты
работы [151. Рассматривая переход от нестационарного режима
к стационарному, можно высказать определенные соображения
о пределах применимости гауссового приближения в теории нели-
нейной фильтрации.
Приведем некоторые предварительные сведения о работе ФАПЧ
при наличии флуктуационных помех. Поскольку частота <во при-
нимаемого сигнала я(/,ф) предполагается заранее известной, то
частоту колебаний синхронизируемого генератора можно предва-
рительно установить равной ю0. Поэтому в дальнейшем будем
считать, что начальная расстройка по частоте равна нулю. Обозна-
чим фазу колебаний синхронизируемого генератора через ф0 =
•= фо(О-
Пусть в момент времени t = 0 на схему ФАПЧ начинает действо-
вать принятое колебание £(?Г). Если бы шум n(t) отсутствовал и
фаза сигнала была бы постоянной ф(/) = ф(0) = const, то после
включения синхронизирующего сигнала фаза ф0 стремилась бы
к стационарному синхронному значению ф(0). Так как начальная
фаза сигнала ф(0) хотя и постоянна, но заранее неизвестна, то
в ходе установления плотность вероятности разности фаз Аф0 —
— ф(0) — ф0 изменяется от равномерной 1Г(Аф0, 0) = 1/2л при
530
i 0 до дельтообразной 1Г(Аф0,со) — б(Аф0) в пределе при t 00.
1 1.1личие флуктуационного шума «(/) приводит к тому, что стацио-
н 1рная плотность вероятности из дельтообразной превращается
|. фугую, а именно [16]:
11/ (ф — <Ро> °°) = 9 е°соь (v—ч>о), — л < ф — фо < л, (13.4.6)
4-7^/о xJJ)
1 де I0(z) — функция Бесселя, а коэффициент D определяется от-
ношением сигнал/шум на входе и параметрами схемы ФАПЧ.
Рис. 13.2. Характер изменения плотности вероятности разно-
сти фаз во времени.
Таким образом, в процессе установления распределение раз-
ности фаз И7(ф — ф0, /) проходит все этапы эволюции от начального
равномерного до конечного стационарного (13 4.6). Характер из-
менения плотности вероятности разности фаз во времени иллюстри-
руется на рис. 13.2, на котором приведен вид плотностей вероятно-
стей для пяти моментов времени:	— 0.
Примем, что плотность вероятности вида (13.4.6) с изменяющим-
ся коэффициентом D описывает финальную апостериорную вероят-
ность на всех этапах слежения за фазой ф(/) принимаемою сигнала,
начиная с момента включения до установления стационарного
рс'жима, причем оценочное значение фазы ф0 и параметр D изме-
няются во времени, т. е. ф0 ф0(() и D — £>(/). Следовательно,
полагаем, что применительно к рассматриваемому конкретному
531
случаю финальная апостериорная вероятность, входящая в основ-
ное уравнение (13 4.5), имеет вид:
W, о = ср0,0 =
= ^WeD-COS(tp_'io)’ —п с ф — <р0 < п. (13.4.7)
Основанием для такого предположения является то, что фор-
мула (13 4.7) находится в согласии с кривыми рис. 13.2 Действи-
тельно, если при t>0 параметр D очень мал (D<1), то, используя
приближенные равенства expLDcos(cp — <р0)]	1, /0(£>)	1 при
D<^\, из (13.4.7) получим равномерное распределение разности
фаз. В тех случаях, когда при достаточно больших t параметр L)
оказывается большим (D> 1) и обеспечивается хорошее слежение
за фазой (ср — фо<1), на основании известных соотношений
cos (ф — ф0) « 1 — 1 (ф — ф0)з,	[0 (D) =
из (13.4.7) получим нормальную плотность вероятности
,) = ^|7а ехр
(? —?<>)2
2а2
(13.4.8)
Финальная апостериорная вероятность (13.4.7) определяется
двумя параметрами ф0 и D. Получим дифференциальные уравнения
для определения этих параметров.
Рассмотрим вспомогательную функцию
z (t, ф) = In W (t, ф) = D cos (ф — фо) — In [2tcZ0 (I?)]. (13.4.9)
Нетрудно убедиться, что основное уравнение (13.4.5) для функ-
ции z (7, ф) имеет вид:
= ^Ni [Z>2 sin2 (ф—фо)—Рсоз(ф—ф0)]-|-Г((, ф) —<F((, ф)>.
(13.4.10)
Функция 2 зависит от t через параметры ф0 = ср0 (0 и В =
= D(t). Поэтому из (13.4.9) получим
57 =- В cos (ф — ф0) — ф0 D sin (ф — ф„) — Р —Цу-, (13.4.11)
так как для модифицированных функций Бесселя нулевого и пер-
вого порядков выполняется равенство I0(x) = Л(х). В правой
части (13.4.11) точкой сверху обозначены производные по времени.
532
Воспользовавшись плотностью вероятности (13.4.7) и двумя
последними выражениями (13.4.4), получим
В (0 cos (со°1 + фо)’	(l ЗЛ12)
ик как
те
(COS (ф — ф0)> = j cos (ф — ф0) W (t, ф) г/ф =
— тс
=	f cosipeD cos 4-d/ty =	,
2jt/o (u) J	/о (и)
—
•n
(sin(<p — ф0)> = J sin (ф — ф0)^(/, ф)й!ф =
—те
те
= 2к /о (О) f 81п^созф^ = 0.
Приравнивая правые части соотношений (13.4.10) и (13.4.11)
н подставив выражения для F (t, ф) и {F (t, ф)> из (13.4.4) и
(13.4.12), получим
D cos (ф — фо) — фо D sin (ф — фо) — D =
=	Л<1 D [D — D cos 2(ф — ф0) — 2cos (ф — ф0)] +
2А
-д-’ I (t) [COS (ф — фо) COS ((00 i + Фо) — 81П(ф—фо) sin («о t 4 фо)1 —
л о
-	£ (0cos (“»1 + Фо)-	(13-4.13)
zv о 20 \ы)
Производная от оценки ф0 (0 входит в это равенство лишь
I качестве множителя при эт(ф— ф0). Приравнивая коэффици-
енты при з1п(ф — фо) в обеих частях равенства (13.4.13), полу-
чим дифференциальное уравнение для определения фо(0:
	9 4
fo +	’ № sin (“°1 + <р°) = °-	(13.4.14)
Так как равенство (13.4.13) должно выполняться при всех воз-
пожных значениях оценки ф0, то оно, в частности, должно выпол-
533
няться и при ф - ср0. Полагая ср = фв, из (13.4,13) получим сле-
дующее дифференциальное уравнение для параметра D:
D+^NJ^D) =^Шсо5(®0г + ф0),	(13.4.15)
где
Типовая схема <РАПЧ
Рис. 13.3. Оптимальная схема ФАПЧ.
Введем в рассмотрение мгновенную ошибку слежения за фа-
зой сигнала
М0 = Фо (0- Ф (0-	(13.4.17)
Тогда уравнение (13.4.14) с учетом (13.4.2) принимает вид
ef + 1$) % sin + Фо) = — «1 (0-
Это уравнение можно записать в форме, характерной для обыч-
ной фазовой автоподстройки частоты [17]:
в» + Ai \tsk | (0 sin (сй0 t 4- ф0) = —	(0, k =	— •
(13.4.18)
Если бы в уравнении (13.4.18) параметр D был постоянным,
то оно моделировалось бы типовой схемой ФАПЧ, представленной
в верхней части рис. 13 3 Она состоит из умножителя с коэффициен-
том пересчета р, усилителя с коэффициентом усиления k, фильтра
низкой частоты (ФНЧ), лампы реактивного сопротивления с кру-
534
к >н преобразования s и гетеродина, вырабатывающего гармони-
ке колебание /IjSin + <р0).
) 1нако s общем случае параметр D, зависящий от отношения
ыл/шум, изменяется во времени. Поэтому для полного модели-
1-1НИЯ уравнений (13.4.14) и (13.4.15) типовую схему ФАПЧ
по дополнить усилителем с переменным коэффициентом усиле-
и /е~ - \!D. В соответствии с урав-
ипем (13.4.15) коэффициент усиления
U1O регулировать схемой АРУ, при-
i иной в нижней части рис. 13 3.
hi.। состоит из фазовращателя на 90°,
 । смножителя, усилителя и нелиней-
10 фильтра (НФ), характеристика
юрою определяется выражением
d -4.16) и представлена на рис. 13.4
1Н|.
11а основании асимптотических пред-
। тлений функций Бесселя (7.5.4) и
। й 5) имеем 1 при , f(D~)^.2D
||>и О^>1. Поэтому для малых и боль-
ше D уравнение (13.4.15) можно не-
। < лько упростить. В частности, для
>|’1ьших D оно примет вид:
П |-|л\£)2=^Ч(Осоз(<оД + фп),
D>1.	(13.4.19)
Если в уравнениях (13.4.14) и (13.4.19) перейти от параметра D
июстериорной дисперсии o2(f) = 1 /Z>(Z), то получим следующие
1>. внения нелинейной фильтрации:
ф о +	(0 £ (0 sin (®01 + Фо) = О,
Ор + ~ с* %, (/) cos;(w0 ft+ ф0) = J Л\,
D^l. (13.4.20)
Путем подстановки значений коэффициентов ЛДф) и /С2(ф) из
1144.4) в (13.3.24) нетрудно проверить, что уравнения (13.4.20)
н)чпо совпадают с уравнениями нелинейной фильтрации в гаус-
сом приближении.
В стационарном режиме работы при больших отношениях сиг-
ii.i.i/шум типовую схему ФАПЧ (рис. 13.5) можно рассматривать
। н квазиоптимальное приближение к наилучшему устройству,
ндящемуза случайной фазой радиосигнала.
Действительно, в стационарном состоянии при слабом шуме пара-
u-ip £>(/) будет флуктуировать около некоторого постоянного сред-
535
него значения Do = const. Если принять D(f) = Do, то отпадает
необходимость в дополнительном усилителе (/г~) и схеме АРУ.
При этом коэффициент усиления в типовой схеме следует взять
равным
ka = 2A0/Ai No Do sji.	(13.4.21)
Некоторая погрешность, связанная с заменой D на Do, окупается
упрощением оптимальной схемы.
Для определения величины Do нужно обратиться ко второму
уравнению (13.4.20), которое является нелинейным стохастическим
дифференциальным уравнением. Хотя при малом шуме можно пред*
Рис. 13.5. Квазиоптимальная схема ФАПЧ (О^>1).
ложить стройную процедуру последовательных приближений с ис-
пользованием малого параметра [151, оценим Do = l/ао путем
следующих нестрогих упрощений. Так как в стационарном состоя-
нии дисперсия не должна зависеть от времени, то = о0 = 0.
Учитывая малость шума n(t), положим cos(<p — <Ро)~1 и отбросим
вибрационный член с двойной частотой 2®0. Последнее оправды-
вается тем, что в цепи обратной связи ФАПЧ в качестве фильтра
применяют низкочастотные фильтры, не пропускающие колебания,
с частотой 2ы0. После этих упрощений из второго уравнения (13.4.20)'
получим
= i =	(,3-4'22)
Подставив это значение Do в (13.4.21), определяем коэффициент
усиления
(13.4.23J
Формула (13.4.23) показывает, что оптимальное значение коэфя
фициента усиления /г(1 при других фиксированных параметрах пряма
пропорционально корню квадратному из отношения интенсивности^
блуждания фазы сигнала к интенсивности аддитивного шума и нН
зависит от амплитуды сигнала.
536
Иметиы, что основные уравнения нелинейной фильтрации
1 I 14) и (13.4.15) выше были получены в предположении, что на-
I п>ная расстройка между частотой полезного сигнала и колеба-
и,|ми гетеродина равна нулю. Реализовать практически этот слу-
। I можно лишь тогда, когда частота сигнала сй0 постоянна и ап-
и>рно известна, что, как правило, не имеет места в реальных ус-
ипях. Наличие случайной начальной расстройки учитывается
> 5.
। 5. ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ ЧАСТОТЫ УЗКОПОЛОСНЫХ
( ИГНАЛОВ
Рассмотрим задачу оптимального приема узкополосных сигналов
iHCTOTHoa модуляцией. Предположим, что радиосигнал
s — (/, ф) = Ао cos [а>а t + ср (/)]	(13.5.1)
имеет постоянные амплитуду До и частоту со0, а фаза ф(/) пред-
। являет собой компоненту двумерного марковского процесса:
ф = Q, Q = —aQ-f-ziifi).	(13.5.2)
: iecb n^t)— нормальный белый шум с дельта-функцией корреля-
ции (13.4 3). Полезным сообщением является процесс изменения
11 тоты Q(f), причем согласно второму уравнению (13.5.2) Q есть
нормальный марковский процесс В данном случае П(0 не входит
непосредственно в выражение для сигнала (13 5.1).
Решим задачу оптимальною выделения сообщения ££(/) при
приеме сигнала 5(^,ф) на фоне аддитивного нормального белого
шума n(t)
По практическому содержанию указанная задача наиболее
и шзко подходит к проблеме измерения допплеровского смещения
|.итоты узкополосных сигналов. При этом а есть ширина спектра
ижплеровских флуктуаций, а (АТ/4а)‘/2—среднее квадратичное
нклонение частоты. Точно так же ставится задача приема частот-
in > модулированных радиосигналов при .условии, что сообщение
п| едставляет собой экспоненциально-коррелированный случайный
процесс. В этом случае а есть ширина спектра сообщения, а
| Л\/4а'а — индекс модуляции.
Ограничимся решением задачи в гауссовом приближении. При
ч ом структура оптимального приемника будет определяться пер-
шми двумя уравнениями (13.3.27), а его параметры — тремя по-
 чедними. Тот факт, что решения этих трех уравнений в общем
* учае зависят от времени, означает, что оптимальный приемник
клжен иметь переменные параметры. Для упрощения результатов
и реализации оптимального приемника произведем усреднение
537
коэффициентов в уравнениях для щ, о2, k [15], и будем интересе»
ваться только их стационарными значениями.
Применительно к рассматриваемой задаче имеем
О
£(0 = 3 0, ф) + п(0. F(t,y) = y^(t)A0cos(<AQt + ф),
Ki = Й, К2 = - ай, Кп - K1Z = о, = 4 /Vb (13.5.3)
/W\ = __^о
\dX2 / No '
После усреднения последние три уравнения системы (13.3.27)
можно записать в таком виде:
2k — of Д’= О,
/Vi— 2аог —	= О,
о2 —afc — ka\ K = £>.
Эти уравнения имеют следующее решение
= -4 (/TT2Q - 1),
о* = £(1 + Q -/T+2Q) /F+2Q-
k = ~ (! + Q - 1/V+2Q).
(13.5.4)
(13.5.5)
Здесь величина Q характеризует отношение сигнал/шум и равна
« =j7	<136-6)
Перейдем к выяснению структуры оптимального приемника.
С учетом соотношений (13,5.3) запишем первые два уравнения
(13.3.27):
^--=Q0-o^B(Osin(^ + To),
jq	Ы	(13.5.7)
— аЙ0 — й £ (/) sin (тоо t + ф0).
Учитывая, что перемножение принятого колебания £(0 с сигна-
лом Ло sin((o0/ + Фо) может быть выполнено при помощи фазового
детектора, уравнения (13.5.7) можно трактовать как уравнения
системы фазовой автоподстройки частоты.
538
 ответствуюЩая схема привёдена на рис 13.6. В ее состав
i n. местный генератор (Г), вырабатывающий напряжение
hi (соо/ + <р0), перемножитель (фазовый детектор) с коэффициен-
। ередачи р, два усилителя с коэффициентами усиления ky и
инерционное звено и сумматор, образующие параллельный
и. ip (на рисунке он обведен пунктиром) и, наконец, управитель
।________________________________________________________________________________________________________________________________________________________J
Рис 13.6. Оптимальная схема ФАПЧ.
। ), который изменяет частоту местного генератора пропорциональ-
। напряжению на выходе
। 1чение сообщения Qo(^)
uia (интегрирующей це-
। 1ки RC).
Параллельный фильтр
и юны может быть заме-
.. последовательным,
hi.i варианта такого
I и п>тра, называемого про-
< рционально-.и нтегри-
। кицим, показаны на
। in 13.7. Последователь-
фильтра. Согласно (13.5.7) оценочное
реализуется на выходе инерционного
ц| с ним должен быть
। । печен усилитель с коэф-
|нциентом передачи
а)	б)
Рис 13.7. Две схемы пропорционально-ин-
тегрирующего фильтра.
ii \-k/\isN0 Отношение
противлений Ri^R-^Ri) в схеме рис. 13.7,с или отношение емко-
н и ^/(C+CJ в схеме рис. 13.7, б должно равнятьсяаод/(£-|-асп).
Можно показать, что в гауссовом приближении рассматриваемая
1ма остается оптимальной и в том случае, когда амплитуда сиг-
и । ш Ао не постоянна, а изменяется во времени. Однако теперь
<му нужно дополнить автоматической регулировкой уровня
in нала, поступающего на фазовый детектор [19,20]. Параметры
|’\11Ч и величины о? и сохраняются прежними, а величи-
। Д' в формулах (13 5.4) и (13.5.5) следует определять иначе:
'	<A2o>W0
539
§ 6. синхронный приемами литудно-модулиров а ином
РАДИОСИГНАЛА
Выясним схему оптимального приемника для фильтрации
белого шума сообщения ш(/), когда принимаемый радиосигнв
имеет вид:
s (t, tn) = A (t) cos (®01 + qp0) = [Ло + tn (/)] cos (®0 t + фо)- (13.6Л
Здесь До, ®o и Фо предполагаются известными постоянными веЛ|
чинами, а сообщение m(t) представляет собой случайный марко!
ский процесс, описываемый уравнением вида (13.3.2):
т -ф ат =- пг (t),	(t) nr (t -ф т)) = у S (т).	(13.6.1
В данном случае параметр m(t) является энергетическим
функция F(t,m) определяется формулой (13.3.12):
F(t, m)^-±[^t)-s(t, m)]2—
= —	15 (0 — (До + т) cos (а>01 4- ф0)]2.
Если в функции F(t,tri) отбросить вибрационный член с двойн^
частотой (что практически легко реализуется при помощи линв!
ного фильтра), то
F(t,m) = — -у g2(/) — 2(Д0+/п)?(Осо8(®о^ + фо) + у(Д°+/?г)1|
(13'1
Подставив в (13.3.29) значения производных функции Е(/,|
при т = т0, получим уравнения оптимальной фильтрации:]
, /	,	1	2 \	2	2
^0 ”f“ ( а ”(
И- 2(ХО,^ -р- у От= у A/j.
£(0 cos (соо ^Д-фо)— Я I
1 >(13.61
I
Решая второе уравнение (13.6.4), получим следующее выраЯД
ние для апостериорной дисперсии [21]:
a2m(t) = M)(e2V — I)-1 [(? + “) + (? — а)е2'Ч, у = а
2аа ЛЯ
(13.6Я
Полагая	из (13.6.5) находим стационарное значение д^
Персии
2
СТО
JV1_ 1
2а^0
540
I iK следует из (13.6.5), в первом уравнении (13.6.4) диспер-
(/) в общем случае зависит от времени. Однако если за-
। н ь Оо;(/) на Oo = const, то первое уравнение (13.6.4) прини-
। вид:
tn0 4 Ро -=
2
No
cos (и0t -|- фо) — у А О
(13.6.7)
4 В (О
\ равнение (13.6.7) моделируется синхронным приемником
>i и 13.8). Он содержит умножитель, на который воздействует
снятое колебание и гармоническое колебание /t0cos (<»(/+Фо)
синхронного гетеродина (СГ). Напряжение с выхода
Рис. 13.8. Синхронный радиоприемник.
ш «жителя, смещенное на постоянную величину 0,54о подается на
и литель и интегрирующую цепочку RC с постоянной времени
1/7?С. Усилитель имеет коэффициент усиления
& = 2 сго/у2У0-	(13.6.8)
ж ценность коэффициента усиления k от постоянной у объясняет -
। 1ем, что в правую часть дифференциального уравнения, опреде-
пчцего напряжение на емкости цепочки RC, входит не просто
। действующее напряжение r](i), а величина ут](О 1см., например,
ю 1 1)1.
Напряжение на выходе цепочки RC дает оценку величины m(t).
Рассмотренные примеры дают представление о круге задач,
 ’юрые позволяет решать теория нелинейной фильтрации, и
1	рактической ценности получаемых результатов. Можно ска-
нь, что теория нелинейной фильтрации позволяет составить
। рхктурные схемы оптимальных систем передачи непрерывной
 ||||х)рмации для многих практически интересных систем радио-
। пи и оценить минимально достижимые погрешности.
1ИГЕРДТУРА
I Колмогоров А Н. Интерполирование и экстраполирование
 । попарных случайных последовательностей. «Известия АН СССР», сер
нематическая, 1941, № 5.
541
2	W i e n e r N Extrapolation, interpolation and smoothing of stall*
nary time series. John Wiley, 1949
3	ЯгломА M Введение в теорию стационарных случайных фунКЙ
ций УМН, 1952, вып 5 (51).	j
4	Пугачев В. С. Теория случайных функций и ее применен!
к задачам автоматического управления. Физматгиз, 1960.
5.	Л э н и н г Дж. X, Бэттин Р. Г. Случайные процессы в 31
дачах автоматического управления. Пер. с англ. Изд-во иностранной Л1
тературы, 1958
6	Солодовников В. В. Статистическая динамика линейны
систем автоматического управления Физматгиз, 1960.
7.	А м и а н т о в И. Н. Применение теории решений к задачам общ
ружения сигналов и выделения сигналов из шумов. ВВИА им. проф. Н. I
Жуковского, 1958.
8.	Большаков И. А, Репин В. Г. Вопросы нелинейной
фильтрации. «Автоматика и телемеханика», 1961, № 4.
9.	Бакут П. А, Большаков И. А, Герасимов Б. М.
Курикша А А., Репин В. Г, Тартаковский Г. П«
Широков В. В. Вопросы статистической теории радиолокации, т. II
Изд-во «Советское радио», 1964.
10.	Стратонович Р. Л. К теории оптимальной нелинейной филе
трации случайных функций. «Теория вероятностей и ее применения», 1959
№ 2.
11.	Стратонович Р. Л. Применение теории процессов Марков!
для оптимальной фильтрации сигналов. «Радиотехника и электроника!
1960, № 11.
12.	Т и х о н о в В. И. Нелинейная фильтрация и квазиоптимальны:
характер фазовой автоподстройки частоты. «Техническая кибернетика!
1965, № 2.
13.	С т р а т о н о в и ч Р. Л. Новая форма стохастических интегр|
лов и уравнений. «Вестник Московского университета», сер математ,, механ,
1964, № 1.
14.	Тихонов В.
устройств синхронизации
15.	К у л ь м а н Н.
И. Влияние флуктуаций на точность работ,
УФН, 1964, в. 4.
К., Стратонович Р. Л. Фазовая автс
подстройка частоты и оптимальное измерение параметров узкополосной
сигнала с непостоянной частотой в шуме. «Радиотехника и электроника,
1964, № 1
16	Тихонов В И. Работа фазовой автоподстройки частоты при н!
личии шумов. «Автоматика и телемеханика», 1960, № 3.
17	Тихонов В. И Влияние шумов на работу схемы фазовой авт|
подстройки частоты. «Автоматика и телемеханика», 1959, № 9.
18.	Т и х о н о в В. И. Основные статистические характеристики К(
нала синхронизации. «Электросвязь», 1966, №4.
19.	V a n Trees Н. L. Analog communication over randomly—time-
varying channels «Wescon—64», pt.4.
20.	Бакаев Ю. H., Гуж А. А. Оптимальный прием сигнале
частотной модуляции в условиях эффекта Допплера «Радиотехника и эле!
тропика», 1965, № 1.
21.	К у л ь м а н Н. К- Оптимальное выделение амплитудно-модуль
рованного сигнала из шумов при помощи синхронного детектирования «Р1
диотехника и электроника», 1964, № 5
22.	Lindsey W С. Optimal coherent linear demodulation. Trans. IEEE
1965, COM—13, № 2.
глава 14
ФОРМИРОВАНИЕ И ПРИЕМ СИГНАЛОВ
С ВНУТРИИМПУЛЬСНОЙ МОДУЛЯЦИЕЙ
§ 1.	ХАРАКТЕРИСТИКИ ЗОНДИРУЮЩИХ СИГНАЛОВ
Конкретизируем некоторые общие положения, изложенные
и предыдущих главах, применительно к радиолокации. В частно-
< ги, рассмотрим подробнее теорию зондирующих сигналов.
Наиболее важными являются следующие характеристики зон-
дирующего сигнала.
1.	Ширина спектра А/, определяющая разрешающую способ-
ность по дальности. При правильно выбранной форме спектра зон-
дирующего сигнала временная длительность сигнала на выходе
радиотракта приближенно равна 1/А/, причем максимальное отно-
шение сигнал/шум в пике равно 2ElN0.
2.	Длительность сигнала Т, которая определяет разрешающую
i нособность по скорости. При правильно выбранной форме огибаю-
щей «протяженность» сигнала в зависимости от допплеровского
•двига частоты равна 1/Д.
3.	Энергия сигнала Е, определяющая максимально достижимое
ощошение сигнал/шум на выходе радиотракта РЛС, равное 2E/N0.
Напомним основные результаты теории, относящиеся к зонди-
рующим радиолокационным сигналам [1].
Теория оптимального приема устанавливает, что при оценке
неизвестных параметров сигнала, отраженного от цели, таких,
к ж временная задержка т и сдвиг Q несущей круговой частоты юо,
приемное устройство должно произвести операцию взвешивания
принимаемых данных с весом s(t, т, Q), где s(t) — зондирующий
щдиосигнал. Указанная операция может быть выполнена с помощью
। огласованных фильтров или многоканальных корреляторов, либо
с тройств смешанного типа. Сигнал на выходе оптимального устрой-
। та, нормированный так, чтобы его максимальное значение равня-
лось единице, имеет вид:
$43
Iй)|
J s(/)s+(/— r) e/2/dt
(14.1.1)
и называйся функцией неопределенности зондирующею сигнала.
При оптимальном приеме отношение сигнал/шум в максимуме
выходною сигнала равно 2Е/Л/0; отношение сшнала к шуму при
любом другом способе приема меньше чем 2EINO.
Зондирующий сигнал s (t) можно представить в виде
s(t) — A (t)eJ'JJ« *,
где Л(0 — комплексная огибающая зондирующего сигнала;
<оо — его несущая частота.
С учетом этого, (14.1.1) можно записать в следующей форме:

J A(t) A*(t~ x^dt
(14.1.2)
Если положить здесь й = 0, то получим
0)| = i
— ОО
A (t) A* (t — т) dt
(14.1.3)
В соответствии с этим сечение функции неопределенности (14.1.1),.
плоскостью й = О иногда называют модулем корреляционной,
функции огибающей A(t) сигнала s(/).
Функция неопределенности позволяет узнать все характеристи-
ки сигнала, определяющие его выбор. Совместная разрешающая
способность по задержке т и сдвигу й несущей со0 определяется
формой поверхности | R (т, й)|, конкретнее, формой главного
максимума (в окрестности точки т = О, Й = 0), величиной и рас-
положением побочных максимумов (так называемых боковых лепе-
стков). Неоднозначность измерений определяется количеством и
расположением побочных максимумов, сравнимых с главным.
Обнаруживаемость сигнала зависит главным образом от величины
отношения сигнал/шум и в меньшей степени от вида функции неоп-
ределенности. Точность измерений зависит от скорости спадания
главного лепестка функции неопределенности и отношения
сигнал/шум.
В настоящей главе содержится краткий качественный обзор
функций неопределенности некоторых зондирующих сигналов, ис-
пользуемых в радиолокации. Более подробно рассмотрены два
вида сигналов- импульсы с линейной частотной модуляцией (ЛЧМ
импульсы) и импульсы с фазовой манипуляцией (ФМ импульсы).
Перечисленные выше характеристики зондирующих сигналов
не определены количественно; используется только интуитивное
544
pi цтавление, базирующееся в основном на следующих поло-
<пнях:
1)	разрешающая способность увеличивается, если протяжеи-
> 1Ь функции неопределенности по соответствующей координате
н'ньшается;
2)	разрешающая способность увеличивается, если боковые ле-
। тки функции неопределенности по соответствующей координате
\ еньшаются;
3)	точность измерения координаты возрастает, если протяжен-
пкть основного лепестка функции неопределенности уменьшается;
4)	неоднозначность измерений уменьшается, если растет расстоя-
ние по соответствующей координате между конкурирующими выбро-
1\!И функции неопределенности;
5)	ширина главного максимума функции неопределенности вдоль
«и задержек имеет порядок l/Af;
6)	ширина главного максимума функции неопределенности вдоль
"сп частотных сдвигов имеет порядок 1/Т.
Функция неопределенности, как это видно из приведенных выше
 < обращений, играет в радиолокации фундаментальную роль. Сле-
зет, однако, заметить, что область применений функции неопре-
ютенности ограничена. Среди ограничений особо важными являют-
 и следующие.
1.	Время Т когерентного накопления сигнала должно быть зна-
и цельно меньше, чем время корреляции фединга цели В противном
< I учае части сигнала, расположенные друг от друга на временных
интервалах, превышающих это время корреляции, будут суммиро-
ваться в произвольной фазе и выходной сигнал оптимального
\<гройства существенно исказится.
2.	Спектр сигнала значительно меньше его несущей центральной
ыстоты, вследствие чего можно считать, что все составляющие спект-
1> .1 имеют одинаковый сдвиг частот за счет эффекта Допплера. Дру-
। ими словами, ширина главного лепестка функции неопределен-
ности по оси задержек должна быть такой, чтобы за время накоп-
к'ния Т задержка принимаемого сигнала за счет движения цели
была бы значительно меньше, чем временная протяженность вы-
ходного сигнала.
3.	Движение цели за время Т является равномерным и не учиты-
в >ется радиальное ускорение цели.
Необходимо различать функции неопределенности, построенные
и следующих двух случаях. Функции неопределенности импульсных
 in налов, называемые в дальнейшем «импульсными» функциями
неопределенности, получаются в том случае, когда огибающая
Д) радиосигнала з(7) занимает во времени конечный отрезок; это
может быть, например, одиночный импульс или серия импульсов,
< юдующих с определенным периодом (так называемая «пачка»
импульсов), или серия «случайно» расположенных импульсов раз-
Н1ЧН0Й Стормы. При этом бесконечные пределы интегрирования
545
в (14.1.1) имеют символическое значение; фактически интегриро-
вание распространяется только на области, где произведение
A(t) Л*(/ — т) отлично от нуля. Соответственно приемное устрой-
ство имеет «память», равную длительности Т огибающей А(/).
Другой частный случай имеет место, если используется периоди-
ческий сигнал с периодом Та и выбрано время усреднения, равное
периоду То. Функция неопределенности, построенная в этих усло-
виях, называется далее «непрерывной» функцией неопределенности.
Конкретные примеры импульсных и непрерывных функций неоп-
ределенности приведены ниже.
Общее ограничение, накладываемое на функцию неопределен-
ности зондирующего сигнала, известно под названием «принцип
неопределенности»: объем под квадратом функции неопределен-
ности равен единице. Таким образом, при любом преобразовании
зондирующего сигнала «тело неопределенности» деформируется
так, что
J J | Я (т, й) [2 dt dQ = const.	(14.1.4)
— ОО
§ 2. ФУНКЦИИ НЕОПРЕДЕЛЕННОСТИ ПОСЛЕДОВАТЕЛЬНОСТИ
ИМПУЛЬСОВ
Рассмотрим функции неопределенности некоторых видов конеч-
ных импульсных последовательностей, т. е. имеющих начало и конец
последовательностей одинаковых импульсов, расположенных друг
относительно друга различным образом [2].
Равномерная импульсная последовательность. Предположим,
что высокочастотное заполнение импульсов получается «вырубкой»
из одного колебания и импульсы расположены на одинаковых
расстояниях друг от друга (рис. 14.1, а). При условии, что длитель-
ность ти отдельного импульса меньше половины периода повторе-
ния То, функция неопределенности в сечении по оси т при v ~
£1 „
=	= 0 состоит из неперекрывающихся треугольников, высота
которых линейно уменьшается по закону 1 —(рис. 14.1, б),
где N — число импульсов, | m | — целое число периодов повторе-
ния импульсов, укладывающихся на величине запаздывания т.
За единицу принята высота центрального пика при т = 0. Высоты
остальных пиков уменьшаются вследствие того, что при увеличе-
нии г все меньшее число импульсов входит в произведение /1(f)
4*(f — т).
Рассмотрим теперь сечение поверхности неопределенности плос-
костью т = 0. Очевидно, что функция | /?(0, v)| представляет собой
546
<нейтральное преобразование произведения A(f)A*(t), являюще-
еся последовательностью прямоугольных видеоимпульсов.
Спектр последовательности N прямоугольных видеоимпульсов
'при условии, что суммарная площадь N импульсов равна единице)
имеет вид
sin ~>ти sin mNTa I
sinirvTo )
(14.2.1)

। де ти — длительность одного импульса;
То—период повторения импульсов.
Вид функции 17?(0, v) | представлен на рис. 14.2.
Рис. 14.1. Равномерная последовательность импульсов (а) и сечение
ее функции неопределенности плоскостью Q —0 (б).
В сечении поверхности неопределенности плоскостью т = тТ0
получается кривая, определяемая выражением
|/?(/ггТ0, v)| =
sin луси sin эту (Л< — | /п Уо / j
itvtH ' sinn7’0 I
Размеры пунктирной кривой (или «огибающей») по оси ординат
с ростом т сокращаются и по оси абсцисс остаются неизменными,
ширина же внутренних пиков увеличивается и становится равной
[(/V — |/zz DT’o]~1. Это происходит из-за того, что произведение
A(t) A*{i— т) представляется не /V прямоугольными импульсами,
как при т = 0, a N — \т\ импульсами, т. е. длительность последо-
вательности прямоугольных импульсов A(t) A*(t — тТц) сокра-
щается на | т | импульсов.
Теперь рассмотрим сечение поверхности неопределенности плос-
костью т = тТ0 А, где | А|<(ти. В этом случае произведение
A(t) A*(t— т) представляет собой последовательность N— | т |
547
прямоугольных импульсов, каждый из которых имеет длительность
т„ — А. В данном случае «огибающая» как бы расплывается по
оси абсцисс. Ширина первого лепестка «огибающей» становится
равной 1/т„ — А, а амплитуда «огибающей» уменьшается вследствие
уменьшения площадки каждою импульса произведения. При ти<;
< | А К То произведение	— т) = 0 и его спектр ра-
вен нулю.
Таким образом, функция неопределенности равномерной после-
довательности импульсов, заполненных одной несущей частотой,
имеет несколько выбросов, величина которых конкурирует с глав-
Рис. 14.2. Сечение функции неопределенности равномерной последова-
тельности импульсов плоскостью т = 0.
ным максимумом (т = 0, v = 0), причем эти выбросы расположены
в точках с координатами т - р То lf v - q/То, где р, q — целые
числа Происхождение этих побочных максимумов легко понять,
если рассмотреть поведение такой последовательности в приемном
устройстве (рис. 14.3).
Описываемое приемное устройство состоит из набора линий
задержек с отводами, сделанными через период последовательности
Т9. На каждом отводе расположен фазовращатель, поворачиваю-
щий фазу несущей на некоторый угол. Каждый канал устройства
настроен на прием последовательности, несущая которой сдвинута
на определенную величину Q. При большой скважности допплеров-
ское смещение частоты проявляется как сдвиг начальной фазы вы-
сокочастотного заполнения у первого импульса на величину = 0,
у второго импульса на ср2 = QTa, у третьего импульса на <р3 =
= 2&Та, у четвертого импульса на ф4 = ЗЙГ0, у пятого импуль-
са на величину <р5 = 4QT0
Если вся последовательность вошла в линию задержки первого
канала, настроенную на данный сдвиг частоты Q, то все дополни-
548
ильные сдвиги фаз компенсируются и пять импульсов суммируются
в фазе. При этом па выходе канала появляется главный максимум
функции неопределенности. Если последовательность с допплеров-
ским сдвигом попадает в канал, настроенный на другой допплеров-
i кий сдвиг, то фазовращатели не компенсируют фазовых сдвигов
полностью, импульсы складываются не в фазе и максимума не
получается. Этот случай соответствует одному из небольших лепе-
стков (рис. 14.2), расположенных между большими боковыми лепе-
A(t) )
Рис. 14 3. Устройство для приема последовательности когерентных
импульсов.
стками. При некоторых допплеровских сдвигах может оказаться,
что приращения фаз несущих за период находятся в соотношении
2nv17’o—2jtv2То= Qj То— й2 То = 2nk, v,—v3 = Д, & = 1, 2, ...
о
При этом условии на выходе каналов приемника, настроенных на
сдвиги Qi и Й2, будут почти одинаковые максимумы сигнала в мо-
мент, когда последовательность с фактическим сдвигом, например
Q], полностью войдет в линии задержки. Это будут главный мак-
симум I большой ложный максимум. Величина сигнала на выходе
канала в момент полного входа сигнала в линию, изображенная
как функция допплеровского сдвига (или номера канала), пред-
ставляет сечение функции неопределенности при т = 0.
Формирование сечения функции неопределенности при Q = 0
можно проследить таким же образом. Большие боковые лепестки
соответствуют случаям, когда в линию задержки вошла только
часть последовательности, состоящая из одного, двух, трех и че-
тырех импульсов соответственно.
Наличие конкурирующих максимумов приводит к потере разре-
шающей способности в соответствующих точках (т, Q), и к неод-
нозначности измерения координат. В ряде случаев, однако, рабо-
549
чий диапазон сдвигов r,nat < Тй и vma, < поэтому равномерную
‘ о’
последовательность импульсов можно использовать без всяких
шраничений характеристик радиолокатора.
Последовательность с линейно нарастающими расстояниями
между импульсами (рис. 14.4). При правильно выбранных парамет-
рах такой последовательности можно обеспечить следующее важное
свойство, при любом временном сдвиге сигнала s(t) по времени
произойдет не более, чем одно совпадение импульсов основной и
Рис. 14.4. Последовательность с линейно нарастающими
расстояниями между импульсами (а) и сечение ее
функции неопределенности плоскостью £2 = 0 (б).
сдвинутой последовательности. Это свойство обеспечивает получе-
ние небольших боковых лепестков при сечении функции неопре-
деленности плоскостью Q = 0. На рис. 14.4 представлена также
корреляционная функция рассматриваемой последовательности.
Отношение главного максимума к максимальному боковому лепе-
стку здесь равно 1 IN, где N — число импульсов последователь-
ности. Аналогичным образом, в сечении т = 0 будут отсутствовать
ярко выраженные максимумы, характерные для периодической по-
следовательности импульсов. Действительно, функция 17?(0, Q) |
пропорциональна спектру F(/Q) последовательности A(Q, причем
ЛГ-1	п
Г(/Й)~ Го(/Й) ехр{/£Д„}, tn •= 2 т 1Л I (w — 1) АТ»],
п=0	т~\
(14.2.3)
где Ao(/Q) — спектр одиночного прямоугольного импульса дли-
тельностью ти, \Т0 — приращение периода по сравнению с преды-
дущим периодом.
Графическая интерпретация этого соотношения приведена на
рис. 14.5. Здесь угол а = 2nvT0 — поворот вектора за счет периода
повторения импульсов, угол (J = 2nvAT0— поворот за счет при-
550
щения к перйоду повторения. Таким образом, углы а и 0 завися’!
1 величины допплеровского смещения. Модуль каждого вектора
। ределяе-ся величиной спектральной составляющей отдельного
импульса Fo(/T2) при данном £2. Спектральная составляющая всей
последовательности импульсов определяется как сумма всех век-
коров.
Рис. 14.5. Графическая интерпретация спектра F(/Q) по-
(ледовательности с линейно нарастающим расстоянием
между импульсами
Нетрудно убедиться, что там, где для периодической последова-
кльности были максимумы (АД, = 0,	= 2nk, k — целое
число), теперь за счет дополнительных приращений фаз не проис-
ходит синфазного сложения импульсов. Сечение функции неопре-
деленности плоскостью т = О, полученное непосредственным расче-
том для госледовательности рис. 14.4, представлено на рис. 14.6.
Последовательность импульсов с минимальным числом совпа-
дений. Последовательность с линейно нарастающим расстоянием
между импульсами является частным случаем последовательности
с минимагьным числом совпадений. Другой частный случай полу-
чается, если потребовать сохранения свойства «не более чем одного
i овладения» и ограничиться последовательностями с минимально
возможно» длиной (при заданном числе импульсов N). Такие по-
c.аедоватеньности, рассмотренные Шерманом [3], подробно об-
суждаютс! в дальнейшем. Здесь отметим лишь некоторые харак-
। орные свойства их функций неопределенности. Требование не более
551

08
0,8
0,0
ОЛ
О
Юги
2
'Оти
Рис. 14.6. Сечение функции неопределенности последователь-
ности с линейно нарастающим расстоянием между импульса-
ми плоскостью Т = 0.
fi)
Рис. 14.7. Последовательность Шермана (а) и се-
чение ее функции неопределенности плоскостью
й=0 (б).
552
। ri одного совпадения импульсов при сдвиге на любое т означает,
но все боювые лепестки автокорреляционной функции не превы-
и. нот уровгя UN. На рис. 14.7, а представлена последовательность
ПНрмана для М = 4, а на рис. 14.7, б — ее автокорреляционная
функция. Е этом примере боковые лепестки образуют «однородный
|и»н боковпх лепестков», в общем случае имеющий вид ломаной
пиши. Указанная особенность позволяет достаточно просто рас-
чптать селение функции неопределенности при т = 0. Результаты
। । i\oro расчета для указанного примера приведены на рис. 14.8.
Р«с. 14.8. Сечение функции неопределенности последо-
вательности Шермана плоскостью т = 0.
«Псевдсхаотическая» расстановка импульсов позволяет значи-
к'льно уменьшить боковые лепестки в сечении т = 0 по сравнению
«регуляршм случаем.
В сечении т = тти, где т — целое число, функция неопределен-
ности представляет собой спектр прямоугольного импульса (свой-
» гво одного совпадения!) длительностью ти и высотой 1/Ути (с уче-
1см нормировки центрального пика к единице). Поэтому высота
боковых лепестков в этих сечениях меньше MN. Это тем более
шраведливо для сдвигов, не кратных ти, но больших, чем ти.
следовательно, во всех точках плоскости (т, Й), за исключением
\ зкой подосы — т„ С ти, — оо<^Й<)оо, функция неопре-
1<ленност! меньше, чем MN. Внутри указанной полосы боковые
испестки 1не области — l/T^v^l/T, где Т = Л4ти — общая дли-
тельность последовательности, также достаточно малы.
§ 3. ОПТИМАЛЬНЫЙ ПРИЕМ СИГНАЛОВ С ВНУТРИИМПУЛЬСНОЙ
МОДУЛЯЦИЕЙ
Среди сигналов, имеющих функции неопределенности подходя-
щего вида, наибольшее распространение на практике получили
сигналы с линейным изменением частоты внутри импульса (лчм
импульсы) и сигналы с фазовой манипуляцией внутри импульса
(ФМ импульсы). В последнем случае производится специальное
впутриимпульсное кодирование (изменение фазы колебаний в за-
висимости от времени по определенному закону), причем закон
подбирается так, чтобы получить желаемый вид функции неопре-
деленности.
Am Am Ami
Первая Вторая Третья	Т	Пятая
позиция пози позиция	I	позиция
ция	Am f
Четвертая
позиция
Рис. 14.9. Векторная диаграмма фазо-манипу-
лированного зондирующего сигнала. Длитель-
ность каждой позиции А.
В большинстве случаев длительность импульса такова, что за
время импульса изменение фазы несущей вследствие движения
цели (эффект Допплера) незначительно. При этом вид функции
неопределенности на всей плоскости (т, Q) уже несуществен,
важен лишь вид корреляционной функции (14.1.3) сигнала.
Корреляционная функция сигнала обычно имеет протяженность
порядка 1/А/, где А/ — полоса сигнала. Таким образом, исход-
ный сигнал длительностью Т преобразуется в приемном устройстве
в сигнал, имеющий длительность 1/Af. При А/Т>1 выходной сиг-
нал значительно короче входного.
Основная цель внутриимпульсного кодирования состоит в том,
чтобы получить на выходе радиотракта РЛС сигнал, длительность
которого меньше длительности огибающей 4(/) исходного импульса
$(/). Желательно, чтобы при таком «укорочении» не происходило
уменьшения отношения сигнал/шум в пике выходного сигнала по
сравнению со случаем использования немодулированного по фазе
зондирующего импульса. Рассмотрим кратко физику укорочения.
Предположим, что зондирующий импульс длительностью Т
разделен на пять одинаковых частей (позиций), причем фаза коле-
баний, посылаемых на каждой позиции, может иметь два значения:
О или л (рис. 14.9). В качестве приемника используем устройство
(рис. 14.10), состоящее из широкополосной линии задержки с от-
554
нит, фазовращателя на втором отводе линии, сумматора колеба-
и филыра, согласованного с элементарным прямоугольным
ншмпульсом длительностью А = 775. Все устройство реали-
кя на высокой или промежуточной частоте.
I Годной шум, задерживаясь в линии, складывается в сумматоре,
приводит к увеличению мощности на единицу полосы частот
। । гь раз. Входной сигнал, проходя через устройство, претерпе-
। более существенные изменения. Сначала колебание первой по-
|Цin по первому отводу линии передается на вход сумматора. Вы-
|| те колебание при этом имеет амплитуду Лт и длится А сек. Да-
Рис 14.10. Устройство для приема фазо-манипулиро-
ванного зондирующего импульса.
। 1 в сумматоре складываются колебания двух позиций (первой и
in] ой), причем первое колебание, будучи повернуто по фазе на л,
шленсируегвторое и в течение следующих А сек выход сумматора
шеи нулю. В дальнейшем в сумматоре будут складываться три
11ебания (хва в фазе и одно в противофазе, так что выход имеет
in литу ду Аот) и четыре колебания (два синфазных и два проти-
।'фазных, тчк что выход равен нулю). Наконец, когда колебание
н ])вой позиции достигнет последнего отвода, на выходе будут
। ладыватьс! пять колебаний, при этом все пять составляющих
। взываются синфазными, поскольку единственное противофазное
। ибание в зондирующем импульсе как раз проходит через фазо-
p.нцатель и восстанавливает фазу 0. По мере «выхода» сигнала из
ними задеркки описанный процесс повторяется в обратном поряд-
। Таким образом, огибающая U(t) сигнала u(t) на выходе сумма-
цы имеет вид, показанный на рис. 14.11, а.
Фильтр, стоящий после сумматора, должен быть согласован
прямоугольным импульсом длительностью А. Все прямоугольные
шпульсы в этом случае растягиваются по длительности в два раза,
гн< что огибающая У(/) сигнала v(f) на выходе фильтра имеет вид,
и юбраженный на рис. 14.11, б.
Характерные особенности выходного сигнала v(t) состоят в сле-
ц ющем.
1.	Максимальное значение отношения сигнал/шум по мощности
равно 2£/Vo.
555
2.	Главный максимум сигнала по амплитуде в пять раз превы*
шает максимальный боковой лепесток.
3.	Боковые лепестки занимают вместе с главным максимумом
время, равное удвоенной длительности Т зондирующего импульса.
Описанный способ приема фазо-манипулированного зондирую*
щего импульса не является единственным. Рассмотрим работу усТч
ройства, изображенного на рис. 14.12.
U(t)
Рис. 14.11. Огибающие сигналов на выходе сумматора
(а) и выходе фильтра (б) приемника фазо-манипулиро-
ванного импульса.
Принимаемый сигнал поступает на вход пяти каналов. Каждый
канал состоит из смесителя (См), фильтра на промежуточной час*
тоте (Ф), детектора (Д) и селектора (С). Опорные напряжения, по*
даваемые на смесители в каналах, отличаются сдвигом по времен^
на одну позицию и по форме повторяют зондирующий сигнал, от*5
личаясь только несущей частотой. Символически опорные сигналь^
можно записать в следующем виде:
иг = 1;	1;	1;	—1;	1;
ы2 =	1;	1;	1;	—1;	1;
w3 =	1;	1;	1;	—1;	1;
«4=	1;	1;	1;	—I; 1;
иь =	1;	1;	1; —1; 1.
Здесь через «1» обозначен элементарный радиоимпульс с фазой 0,,|
а через « — 1» — с фазой л.	1
Предположим, что принимаемый сигнал совпадает, например,
с опорным напряжением п5(1). Фаза колебаний на выходе пятого
смесителя на всех позициях остается постоянной, поскольку фазы
входного и опорного сигналов меняются все время одинаково. Н1
556
ходе пятою смесителя получается, таким образом, немодули-
п г1ный пс фазе прямоугольный радиоимпульс длительностью
5Д. Проходя через согласованный фильтр, этот импульс рас-
пвается пс длительности в два раза, причем амплитуда импульса
 гпгает максимума в момент окончания входного сигнала. В этот
' 'мечт и должна осуществляться выборка напряжения с выхода
к'нтора.
Принимая коэффициент передачи фильтра равным единице,
11учим, что и в этом случае отношение сигнал/шум по мощности
, максимуме равно ЧЕ/No.
₽ис. 14.12. Многоканальный коррелятор для приема фазо-манипу-
лированного импульса
Следует обратить внимание, что сущность получения одного и
। ч о же отнопения сигнал/шум в рассмотренных устройствах раз-
шчна. В перюм приемном устройстве (рис. 14.10) полоса пропуска-
। пя согласованного фильтра в пять раз больше, чем полоса пропу-
। шля согласованного фильтра во втором приемнике (рис. 14.12)
। кроме этою, с отводом линии задержки складываются пять не-
1Г.ПСИМЫХ шумов. Поэтому дисперсия шума на выходе фильтра
. нервом случае в двадцать пять раз больше, чем дисперсия шума
• втором случае. Однако в первом приемнике имеет место когерент-
суммирование колебаний элементарных радиоимпульсов дли-
ншостью Д, в результате чего пиковое значение сигнала в пять
। 11 превышает пиковое значение сигнала во втором случае.
Сигнал, совпадающий с опорным напряжением проходя
I входы друшх каналов, дает на их выходах мешающие колебания.
I । ко видеть, что на выходе фильтра четвертого канала склады-
по гея два синфазных и два противофазных колебания; в результате
моиент стробирования (которое производится в конце импуль-
i'ii o сигнала «4(0)> на выходе четвертого канала сигнал отсутствует.
। целом, амплитуды выходных сигналов каналов (расположенные
557
в порядке от 5-го к 1-му каналу) находятся в соотношениях 5; 0; U
0; 1, что соответствует импульсной автокорреляционной функц1И
зондирующего сигнала.
Описанное выше устройство является примером корреляцией
ного приемника (§ 5 гл. 10). Исследуемый интервал дальносЛ
разбивается здесь на несколько отрезков, причем каждый каД
коррелятора обеспечивает наилучший прием сигнала, отражение
от цели, находящейся в середине определенного отрезка рабочД
интервала дальности. Задержка между серединами соседних Л
резкое в данном примере равна длительности позиции Д. КаждИ
канал коррелятора оптимален, если импульсный отклик его филЫЯ
согласован с огибающей зондирующего импульса (в рассматривав
мом примере импульсный отклик каждого канала должен быть nd
моугольным с длительностью Т). В этом случае, если дискретД
выходы каналов линейно интерполировать, приняв задержку меяД
дискретами равной задержке между опорными сигналами, вых<Я
ной сигнал коррелятора при дискретном зондирующем сигнаЯ
совпадает с импульсной автокорреляционной функцией сигнал!
Если задержка принимаемого сигнала находится между задержкали
на которые настроены соседние каналы коррелятора, то амплитуд
сигнала на выходе соответствующего канала уменьшается в соотвя
ствии с главным лепестком корреляционной функции.	I
Для того чтобы перекрыть дискретными каналами интервал За
держек, равный длительности импульса, необходимо иметь чисЛ
каналов, равное числу позиций в импульсе. Задержки, лежащЯ
вне этого интервала, можно перекрыть теми же физическими каД
лами. С этой целью опорные сигналы коррелятора делаются nepd
дическими с сохранением сдвига между ними. Стробирующие d
пульсы также повторяются периодически с сохранением задержв
между ними. Импульсные отклики в каждом канале являкия
прямоугольными.	В
Такая система позволяет измерять задержки в единицах длЯ
тельности импульса по номеру периода селектирующего строба (rd
бая шкала), а в единицах позиций — по номеру канала (точнЯ
шкала).	» Я
Для подсчета корреляционной функции ФМ сигнала, т. е. cd
нала на выходе оптимального приемника, можно воспользоватЛ
представлением зондирующего сигнала в виде Af-мерного вект(Д
1 = (S1, s2,..., sN),	(14.3.1
где s( Л£ ехр Л; и — амплитуда и фаза колебания |Ц
i-й позиции.
В рассмотренном примере при At -= 1
— ехр{/-0) = 1; s2 — ехр {/-О} - 1, s3 = ехр {/-0} - 1;
s4 = ехр {/. л} = — 1; $5 -= ехр {/-0} = 1.
558
11мпулыный отклик оптимального приемника также удобно
- ставит! в виде //-компонентного вектора
H--(sN,	S1).	(14.3.2)
। । 1'1исляя теперь корреляцию векторов s и Н при различных сдви-
। \ между 1ими, можно найти значения гг выходного сигнала в точ-
। т = О т = ±Д, т = ± 2Д, ..., используя следующие
к гношения:
si SN
=/?(— (N— 1)Д) =Я((М-1) Д),
«1	+ s2 sN	= R (- (N-2) Д) =R ((У-2) Д),
1 — S1S2- • •• + SA/_ J SN —	0)>
^S2 4 4 + ... + S2,=/?(0).
(14.3.3)
I
Рис 14.13. Типовая схема РЛС, использую-
щей зондирующие сигналы с внутриим-
пульсной модуляцией.
• н<1чения сигнала в промежуточных точках получаются линейной
и и герполяцией.
Типовая схема РЛС, использующей импульсы с внутриимпуль-
нсй модуляцией, приведена на рис. 14.13. В ее состав входят
) одирующес устройство (КУ), формирующее код для внутриимпуль-
п(й модуляции; устройство, формирующее радиочастотный сиг-
и гл на низком уровне мощ-
1ОСТИ (УС>); усилитель
юцности (КМ), усиливаю-
ni.ifl входной модулирован-
ный импульс низкого
\ рсвня до нужной пиковой
юцности; переключатель
прием — передача (П); уси-
III гель высокой частоты
। V ВЧ); преобразователь
। icroTbi и усилитель про-
южуточной частоты
illp-УПЧ); декодирующее
(.тройство (ДУ).
Декодирующее устройство может быть выполнено в виде согла-
||'ванного фильтра. В этом случае на его выходе от каждой цели
появляется отраженный укороченный импульс длительностью no-
li щка 1/Д/. Если декодирующее устройство выполнено в виде кор-
релятора, то оно имеет много выходов, причем на любом из них
|<>гут появиться отраженные сигналы, имеющие длительности
порядка Т. Каждый канал «настроен» на определенную дальность
и расстоянье между каналами по задержке равно 1/А/.
559
В кодирующем устройстве для формирования ЛЧМ импульсов
можно использовать линейное видеонапряжение, а для формиро«
вания ФМ импульсов — набор видеоимпульсов, соответствующий
используемому коду. Формирование ЛЧМ импульсов может быТв'
выполнено так называемым «пассивным» или «активным» способом^
В первом варианте для формирования ЛЧМ импульсов исполи
зуется основное свойство согласованного фильтра: импульсные
отклик согласованного фильтра является зеркальным отражением
формы сигнала, с которым этот фильтр согласован. Поэтому пре
подаче на вход согласованного с ЛЧМ импульсом фильтра достатОв
но короткого импульса на выходе фильтра получается ЛЧМ И|М
пульс с законом изменения частоты от начала к концу импульсм
противоположным нужному. Для формирования нужного законе
с помощью преобразователя частоты вычитают частоту выходя
согласованного фильтра из постоянной частоты гетеродина. 1
При «активном» способе формирования ЛЧМ импульсов испольч
зуется задающий генератор, частота которого зависит от величина
управляющего напряжения на одном из электродов. Подборой
формы управляющего напряжения можно добиться изменения час*
тоты задающего генератора с нужной крутизной. Для обеспечений1
требуемой точности формирования импульсов в «активном» способе
иногда используется автоподстройка частоты.
Формирование ФМ импульсов имеет специфические особенности
и часто основано на использовании специальных генераторов посла
довательностей символов, подробнее описываемых далее.
§ 4. ИМПУЛЬСЫ С ЛИНЕЙНОЙ ЧАСТОТНОЙ МОДУЛЯЦИЕЙ
Импульсные сигналы с линейным изменением частоты внутри
импульса используются в радиолокации чаще всего. Это объясняем
ся тем, что функция неопределенности ЛЧМ импульсов имеет ДОЯ
таточно хорошие свойства и прием ЛЧМ импульсов может произвЯ
диться с помощью компактных согласованных фильтров.
Зондирующий импульс с ЛЧМ имеет постоянную амплитуду Л1
(рис. 14.14), а его мгновенная частота меняется по линейному эЯ
кону с наклоном к. [Мгц/мксек]-.
f-f0 = kt,	(14.4.И
где /о — центральная частота. Соответственно круговая частоте
св — ш0 — 2nkt,
а фаза внутри импульса изменяется по параболическому закон/
Ф — nkt2 4- <в01 Д ф0.	(14.4.2/
560
(снмальиая девиация частоты от начала до конца импульса
к ia:
F = kT.
1риращение фазы за время длительности импульса обычно зна-
игльно превышает число л. Так, например, если Т7 = 10 Мгц,
10 мксек, то «квадратичная часть» приращения фазы за время
шульса составляет 100 л.
№)
Ат
-V2 0 Т/г
Рис 14.14. Параметры зондирующего импульса с линейной частотной
модуляцией.
Возможности импульсных ЛЧМ сигналов достаточно хорошо
и 1люстрируются их функцией неопределенности, аналитическое
। ыражение которой имеет вид
sin
(тгч-ртгАт) ( 1
IЯ (т, М | =
(тг, -j- nkz) 7'
— Т Ст СТ,
0 при других т.
(14.4.3)
1 ечение этой функции неопределенности плоскостью задержка —
। ютотный сдвиг (т, v) на уровне 3 дб от максимального значения
приведено на рис. 14.15.
Особенность функции неопределенности ЛЧМ импульса со-
. юит в том, что в направлении v — кт функция неопределенности
шпянута, а в перпендикулярном к нему направлении сжата.
В тех частных случаях, когда значение центральной частоты
принимаемого сигнала отличается от частоты гетеродина приемника
н>чао на промежуточную частоту (v = 0), или когда стробирование
ыдодов приемников производится в момент, соответствующий
приходу отраженного сигнала (т = 0), на выходе приемного устрой-
 1ва получаются сечения функции неопределенности, представлен-
ные на рис. 14.16. Как следует из (14.4.3), сечение функции неопре-
561
деленности ЛЧМ импульса плоскостью т = 0 представляет собой
спектр прямоугольного видеоимпульса (рис. 14.16, а):
| R (0, v) | =
Sin тТ
тТ
(14.4.4)
а сечение ее плоскостью v = 0 имеет вид:
I R (т, 0)| =
TtktT
(14.4.8J
Таким образом, длительность корреляционной функции вдоль ОСЯ
задержек, совпадающая с временной протяженностью выходного
сигнала, имеет порядок 1/F и, например, при F = 10 Мгц составляем
Рис. 14.15. Топографическая проекция функции неопреде-
ленности ЛЧМ импульса.
0,1 мксек. Эта величина не зависит от длительности огибающей!
импульса Т и определяется только максимальной девиацией чаМ
тоты F. Форма сигнала на выходе оптимального приемника для|
случая F7"^A определяется выражением (рис. 14.16, б)
sin TtFt
|/?(т, 0)| = | £(т)| =
(14.4.6Й
tzFz
Таким образом, входной сигнал длительностью Т, в оптимальной
приемнике укорачивается; выходной сигнал имеет длительности
порядка 1/F. Коэффициент FT называется иногда коэффициентом!
укорочения.
Вытянутость функции неопределенности вдоль оси v = Af
приводит к тому, что разрешающая способность, например, дл®
двух целей, координаты которых (допплеровский сдвиг и задержи!
по времени) неизвестны, значительно ухудшается. Если, однако,
т = 0 или v — 0, то, как показано выше, разрешающая способ»
ность по другой координате достаточно высока.
562
В случае одиночной цели, движущейся с неизвестной радиаль-
|| скоростью, возникает неизвестный сдвиг максимума выходного
hi нала во времени относительно истинного положения. Если ско-
i' 1сть цели известна, то указанный сдвиг можно учесть в дальней-
. и м. Этот эффект является в некоторых случаях неприятной осо-
. иностью ЛЧМ импульсов. Однако вытянутость функции неопре-
.тенности может играть и положительную роль. Например, на
11 поде согласованного фильтра (подробнее согласованные фильтры
। in ЛЧМ импульсов описаны ниже), настроенного на v = 0, при
и «явлении допплеровского сдвига в пределах — !/7<^vC\/Т вид
Рис. 14.16. Сечения функции неопределенности ЛЧМ импульса плоскостя-
ми т=0 (а) и v=0 (б).
। игнала на выходе фильтра меняется мало и отношение сигнал/шум
|| пике почти не уменьшается. Это обстоятельство выгодно для
работы систем обнаружения. Сдвиг v можно рассматривать и как
результат различных частотных нестабильностей, поэтому РЛС,
использующие ЛЧМ импульсы, оказываются малочувствительными
। нестабильностям частоты, если они не превышают указанных
нише пределов.
В ряде технических приложений самостоятельное значение
имеет амплитудно-фазовый спектр £(/©) ЛЧМ импульса. Точное
выражение для такого спектра достаточно сложно [4]. Однако при
/ 7»1 его амплитудный спектр |5(/<в) | приближается к прямоуголь-
ному (рис. 14.17, а) с протяженностью по оси частот от fo— FI1
io fo + F/1, где fo — несущая частота. Фазовый спектр Ф(ш)
имеет параболический характер и определяется соотношением
ipfic. 14.17, б)
Ф (®) = Фо +-^=^-2.	(14.4.7)
I 1ытересно отметить, что амплитудно-фазовый спектр ЛЧМ импульса
но форме повторяет зависимости амплитуды и фазы от времени,
причем переход от временных соотношений к частотным совершает-
। умножением времени на коэффициент к наклона «ЧМ пилы».
>ю обстоятельство часто используется в теории устройств, работаю-
щих с ЛЧМ импульсами.
$63
Рассмотрим некоторые схемы приема ЛЧМ импульсов.
Применительно к импульсным ЛЧМ сигналам кор реляционны!
приемник может иметь специфические особенности. Рассмотрим!
в частности, приемник, позволяющий обрабатывать сигналы, прИ«
Рис. 14.17. Амплитудный и фазовый спектры ЛЧМ импульса.
ходящие лишь с некоторого участка дальности (рис. 14.18). Такого
рода устройства используются в радиолокационных станцияХ'
сопровождения целей [5].
Отраженные от целей сигналы после усиления широкополосны^
усилителем высокой частоты (УВЧ) поступают на вход смесителе
Стробирующие
импульсы
Рис. 14.18. Многоканальный коррелятор для приема ЛЧМ
импульса
(См.). Сигнал гетеродина является также ЛЧМ импульсом, причМЙ
крутизна изменения его частоты во времени совпадает с крутизной
зондирующего импульса, а длительность 0 превышает длительности
Т зондирующего импульса на величину интервала возможных}
задержек т отраженных импульсов.
564
На рис 14.19 представлены временные зависимости частоты и
। нбающей для зондирующего импульса и импульса гетеродина,
редина импульса гетеродина соответствует моменту to, являю-
|«муся серединой интервала возможных задержек отраженных
ишалов относительно зондирующего. Очевидно, что полный ин-
рвал возможных задержек равен 0 — Т и лежит в области
(14.4.8)
Если отраженный сигнал находится в середине этого интервала,
и> на выходе смесителя имеет место импульсный сигнал длитель-
нктью Т, заполненный номинальной промежуточной частотой
Зондирующий
ин нуль с
A(t)
ftthfo
Ттат
И
Г to
J—i——H-
III	I	* 1
; Отраженные импульсы I
Wt)i I	IA (t)	I	I
I i I
I
О
t
О
Ar(t)
|	I*— т—^1
I	3
Импульс гетеродина
ftthfr
to
в-
*1
t
Рис. 14.19. Зондирующий и отраженные от цели сигналы и им-
пульс гетеродина при гетеродинном способе приема ЛЧМ
импульсов.
/иг = f° —fr- Отраженным импульсам, имеющим минимальную
г^1П и максимальную ттах задержки, на выходе смесителя соответст-
0__________________________________________у1	0__р
вуют импульсы с частотами заполнения /пр---и/пР + —•
Промежуточная частота произвольно расположенного импульса,
имеющего задержку т, будет равна /пр(т) = /пр + (т — /о) k.
Таким образом, ЧМ гетеродин превращает различия в задерж-
ках т отраженных сигналов в различия в промежуточных частотах
/,,р(т).
Частота, заполнения fnp(r) импульсов на выходе смесителя опре-
щляется с помощью гребенки согласованных с ними фильтров (Ф),
настроенных на различные центральные частоты и перекрывающих
весь диапазон (0 — Т) к возможных изменений /1|р(т).
565
Поскольку определенная частота соответствует Определенной
задержке, продегектированные детекторами (Д) выходы фильтров
должны стробироваться в селекторах (С) в различные моменты вре»
мени, принадлежащие области (14.4.6), сдвинутой на Т/2. Так, к при»
меру, фильтр, настроенный на частоту Д = ДР(Т1), стробируется
т
в момент t — Ti + -g. Отметим, что работа устройства слабо зави»
сит от ширины стробирующих импульсов.
Таким образом, каждый выход устройства (рис. 14.18) соответ»
ствует определенной дальности. В этом смысле устройство подобно
многоканальному коррелятору. Отличие состоит в том, что различу
ные опорные сигналы объединены здесь в один сигнал импульсного
ЧМ гетеродина, вследствие чего каждый канал по необходимости
настроен на свою промежуточную частоту. Так же, как в много-
канальном корреляторе отношение сигнал/шум, равное 2E!N^t
достигается здесь за счет фильтрации шума в фильтре, согласован-
ном с импульсом на выходе смесителя.
Частотный масштаб на выходе рассматриваемого приемника легко
пересчитывается в задержку или дальность. Два фильтра, отстоя-
щие по центральным частотам на Д/пр, анализируют точки, отстоя-
щие по оси задержек на Ат= АД,р/&. Так, например, для ЛЧМ им-
пульса с параметрами Т = 10 мксек, F = 10 Мгц величине А/пр=«
= 100 кгц соответствует интервал Ат = 0,1 мксек, равный поло-
вине ширины (по нулям) центрального пика автокорреляционной
функции. Если фильтры расставлены на \/Т Мгц, то это означает,
что временные отсчеты берутся через \/F мксек и корреляционная
функция передается этими дискретными отсчетами. Расстановка
фильтров определяется многими обстоятельствами.
Рассматриваемая схема может быть легко получена при радио-
технических интерпретациях оптимальных операций над входным^
данными, которые предписываются выражением логарифма функ^
ции правдоподобия задержки, измеряемой в белом шуме с помощью
зондирующего ЛЧМ импульса.
На примере многоканального коррелятора легко понять роль
неизвестного частотного сдвига в формировании выходного сигналя
приемника.
В том случае, если принимаемый сигнал сдвинут по несущей
частоте на v из-за движения цели в радиальном направлении и если
этот сдвиг заранее нескомпенсирован в гетеродинном напряжении,
промежуточная частота отличается от своего значения на величину
Afnp = v и, следовательно, максимум сигнала будет зарегистриро-
ван в фильтре, соответствующем другой задержке; ошибка в опре-
делении задержки составит v/k.
Как отмечалось ранее (§ 6 гл. 10), согласованным фильтром
называется линейное устройство, импульсный отклик G(f) которого
является зеркальным отражением (относительно произвольного
момента времени) сигнала s(f), с которым фильтр согласован. При
566
। )M начальная фаза высокочастотного заполнения импульснб?о
। \'1ика произвольна. Для ЛЧМ импульсов примерный вид сигна-
। и отклика фильтра представлен на рис. 14.20.
Зеркальное отображение импульсного отклика согласованного
pi льтра по сравнению с формой зондирующего сигнала означает,
и ) амплитудно-частотная характеристика фильтра совпадает с ам-
итудным спектром сигнала, а его фазо-частотная характеристика
йратна по знаку фазовому спектру сигнала; таким образом, согла-
। манный с ЛЧМ импульсом фильтр имеет прямоугольную в полосе
/ амплитудно-частотную характеристику и параболическую фазо-
। статную характеристику.
1*ис 14.20. ЛЧМ импульс (а) и импульсный отклик (б)
согласованного с ним фильтра.
Можно предложить много различных способов построения
фильтров, согласованных с ЛЧМ импульсами. Некоторые из них
могут быть реализованы.
Изготовление согласованных фильтров для ЧМ сигнала является
грудной задачей, поскольку необходимо обеспечить своеобразный
импульсный отклик (или частотную характеристику). Как правило,
для синтеза требуемого импульсного отклика ЧМ импульса с за-
коном модуляции, обратным исходному сигналу, используются
схемы, содержащие линии задержки (ЛЗ). Поскольку реальный
фильтр всегда отличается от идеально согласованного, более пра-
вильно такие схемы называть укорачивающими устройствами
(или фильтрами).
Рассмотрим несколько типовых схем построения укорачиваю-
цих устройств и покажем формирование требуемого импульсного
отклика или частотной характеристики.
ЛЗ с дискретными отводами (рис. 14.21). Сигналы с отводов ЛЗ
после прохождения делителей с заданным коэффициентом ослабле-
ния складываются. При подаче на вход 6-функции на выходе поя-
вится набор сдвинутых во времени 6-функций с амплитудами, опре-
567
деляемыми ослаблением в соответствующих отводах. Правильны^
подбором коэффициентов ослабления можно добиться, чтобы огМ
бающая этих 6-функций давала требуемый отклик. Дискретное®
устраняется фильтром с полосой 1/Д, где А — задержка меж®
соседними отводами.
Рис. 14.21. Реализация согласованного с ЛЧМ импульсом
фильтра в виде линии задержки с отводами.
ЛЗ с непрерывным съемом (рис. 14.22). Принцип работьДана-
логичен предыдущему случаю, но вместо дискретных отводов при»
меняется непрерывный съем, например, в виде куска фольги, на,
ложенной на линию. Связь осуществляется через емкость «ЛЗ —
Рис 14.22. Реализация согласованного с ЛЧМ им-
пульсом фильтра а виде линии задержки с непре-
рывным съемом.
съем», фигурная форма последнего обеспечивает изменение этой
связи в зависимости от времени задержки и соответственно требуе-
мую форму отклика.
Диспергирующая ЛЗ. Этот вид укорачивающих устройств ис-
пользует элементы, имеющие равномерную амплитудно-частотную
характеристику и существенно нелинейную фазо-частотную харак-
теристику, аналогичную приведенной на рис. 14.23. Конструктивно
ЛЗ такого типа состоит из последовательно соединенных мостико-
вых фильтров, количество и параметры которых подбираются так,
568
• ил получить максимальное приближение к требуемой параболй-
оп фазовой характеристике в заданной полосе частот.
I (оследнее время большое распространение получили ультразву-
। i.k дисперсионные ЛЗ, использующие в качестве звукопровода
11 1лическую ленту. Для
। ичего участка выби-
||ггся области частот, в
 юрых наиболее сильно
11 ражена нелинейность фа-
 ной характеристики (1-я
। 2-я зоны на рис. 14.23).
।' 1<;очую полосу такого
• фойства можно значи-
ьно расширить, делая
Рис. 14.23. Фазо-частотная характеристика
диспергирующей линии задержки.
глкопровод с переменной
I' 1.11ЦИН0Й.
При приеме очень ши-
ЩПОПОЛОСНЫХ ЛЧМ ИМ-
11 у 1ьсов с большим произведением FT применяются комбинированные
ичоды приема. В этих случаях оптимальная обработка (полная
вертка) сигнала с помощью согласованного фильтра становится
Рис. 14.24. Схема комбинированной обработки ЛЧМ импульса.
ытруднительной из-за отсутствия линий задержки с соответствую-
щими свойствами. С другой стороны, для перекрытия заданного
интервала дальности пришлось бы использовать коррелятор с очень
большим числом каналов. Одна из схем комбинированной обра-
ботки, описанная Тором [6], приведена на рис. 14.24. Схема со-
стоит из У идентичных каналов, образованных входными смесите-
лями (Cmi) и гетеродинами (Г1) фильтрами (Ф), линиями задержки
569
(ЛЗ), диспергирующими линиями задержки (ДЛЗ) и выходными
смесителями (См 2) и гетеродинами (Га). Выходы всех каналов
подключены к сумматору.
С помощью входных преобразователей и фильтров спектр ВХОД*
ного широкополосного ЛЧМ импульса разбивается на N примыкаюч
щих друг к другу подспектров. На выходе каждого фильтра пмеЦ
место ЧМ колебание, соответствующее выделенному фильтром ПОД^
спектру. Поскольку для входного ЛЧМ импульса каждому подспек*
тру соответствует определенный временной интервал, ЧМ колеб|^
ния на выходе фильтров оказываются сдвинутыми во времени,
временные сдвиги выравниваются канальными линиями задержки^
Следующие за ними диспергирующие ЛЗ осуществляют свертку ЧЛ|
колебаний с данным подспектром, а выходные преобразователи един*
гают несущие частоты и фазируют колебания укороченных ЧМ коле»
баний. При сложении этих колебаний в сумматоре происходит окои«1
чательное укорочение входного ЛЧМ импульса до величины !//<•
Таким образом, основная идея рассматриваемой схемы обработки
широкополосных ЛЧМ импульсов состоит в том, что здесь дисперч
гирующие ЛЗ каналов обеспечивают свертку лишь в части частот»
ного диапазона, в N раз более узкой, чем спектр входного сигнала.
Недостатком такой схемы является необходимость жесткой фазы»
ровки колебаний входных и выходных гетеродинов.
Как отмечалось выше, фильтр, согласованный с ЛЧМ импульсом,
при FT^>1 дает на выходе сигнал
боковые лепестки которого весьма велики (максимальное значение
первого и бокового лепестков составляет 21%, а второго — 13% от
максимального значения главного лепестка). Уже упоминалось о том,
что боковые лепестки сигнала по дальности оказывают вредное
влияние, снижая возможности РЛС. В частности, ухудшается раз-
решающая способность по дальности в режимах^обнаружения И
сопровождения целей в многоцелевых РЛС. Желательно поэтому
по возможности уменьшить уровень боковых лепестков.
Форма выходного сигнала, в частности ширина главного лепестка
и уровень боковых лепестков, чувствительна к изменению частот-
ной характеристики укорачивающего фильтра. Согласованный
с ЛЧМ импульсом фильтр имеет параболическую фазо-частотную
и прямоугольную амплитудную характеристики. Если, 'однако,
сгладить амплитудно-частотную характеристику 1 /("(/со) | фильтра,
допустив спадание к краям спектра сигнала, то боковые лепестки
существенно уменьшаются; главный лепесток при этом расширяет-
ся. Одновременно несколько уменьшается отношение сигнал/шум
на выходе фильтра. Можно показать, что существует оптимальная,
но физически нереализуемая амплитудно-частотная характеристика
570
юльфа—Чебышева, обеспечивающая минимальные боковые лё-
сгки при заданном расширении главного лепестка. Реализуемой
пнроксимацией характеристики Дольфа — Чебышева является
ip актер истина Тейлора,
। римерный вид которой
щедставлен на рис. 14.25.
Хорошие результаты
получаются также в слу-
ые, когда амплитудно-ча-
 iотчая характеристика
|>ильтра аппроксимируется
|>унхцией
Р) cosg ,
Рис. 14.25. Амплитудно-частотная характе-
ристика Тейлора.
Р
(14.4.9)
(де р и q имеют различ-
пые значения.
Приведем табл. 14.4.1, содержащую данные по подавлению боко-
вых лепестков с помощью различных фильтров, имеющих амплитуд-
но-частотные характеристики вида (14.4.9).
Таблица 14.4.1
Подавление боковых лепестков
р	Q	Уровень максималь- ного бокового лепес г- ка относительно главного, дб	Расширение глав- ного лепестка	Потери в отноше- нии сигяал/шум, дб
0,08	2	—42,8	1,47	— 1,34
0	2	—32,2	1,62	— 1,76
0	3	—39,1	1,87	—2,38
0,04	1	—23,0	1,31	—0,82
0,16	2	—34,0	1,41	—1,01
0,02	3	—40,8	1,79	—2,23
Вид сигнала на выходе фильтра для случая р = 0,08, q = 2
(фильтр с характеристикой Хэмминга) представлен на рис.
14.26 [7].
Таким образом, с помощью подходящей амплитудно-частотной
характеристики приемного устройства можно значительно умень-
шить боковые лепестки выходного сигнала по сравнению с уровнем
на выходе согласованных фильтров. Подавление боковых лепестков
сопровождается расширением главного лепестка и уменьшением
отношения сигнал/шум в максимуме.
Другие сюсобы уменьшения боковых лепестков состоят в спе-
циальном подборе отклонений от линейного закона изменения
частоты или формы огибающей импульса с тем, чтобы автокорре-
19В*
571
ляционная функция получающегося сигнала имела бы желаемый
вид. Так, например, нереализуемая идеальная гауссова форма ИМ»*
пульса при линейной частотной модуляции приводит к гауссовому
укороченному импульсу. Вообще при достаточно большом коэффй*
Рис. 14.26. Сигнал на выходе фильтра Хэмминга.
циенте укорочения справедливо следующее приближение для корре»
ляционных функций ЛЧМ импульсов различной ’формы:
|Я(т)1
00
Л2(х)ехр {j2nkxx} dx
— 00
(14.4.10)
и, следовательно, подбором формы импульса A(f) всегда можно биН>
тезировать нужный сигнал R(x). Этот путь, однако, трудно осуще-
ствить на практике.
§ 5. ИСКАЖЕНИЯ ЛЧМ ИМПУЛЬСОВ В РАДИОТРАКТЕ РЛС
Применение описанных выше принципов формирования и прием®
ЛЧМ импульсов ограничивается искажениями сигнала, которые
возникают в различных элементах радиотракта РЛС. Существует
много источников искажений. Основные из них следующие.
Даже при идеальном модулирующем импульсе частотные харак*
теристики усилителя мощности не являются идеальными. АмпЛИ»
572
ио-частотная характеристика в пределах рабочей полосы имеет
• ' юбания» и «скосы» и может выглядеть так, как это представлено
рис. 14 27. Соответственно и реальная фазо-частотная характе-
|Ика отличается от линейной.
Модулирующий импульс, подаваемый на усилитель мощности,
- является: идеальным и имеет фронты, скос и осцилляции на вер-
। не. Этим амплитудно-временным искажениям из-за электронного
। щения фазы в приборе соответствуют также фазо-временные
шжения
Искажения ЛЧМ импульсов сильно зависят и от дисперсионных
। HI1CTB волноводного тракта. Фазо-частотная характеристика волно-
г.ода нелигейна и может быть разложена в окрестности центральной
Рис. 14.27, Амплитудно-частотная характеристика
усилителя мощности.
'ыстоты /о в ряд Тейлора, коэффициенты которого зависят от отно-
шения несущей к критической частоте. Линейный член обусловли-
вает постоянную задержку выходного сигнала, квадратичный —
изменение наклона ЧМ в импульсе, а кубический — несимметрич-
ное искажение формы укороченного импульса и увеличение боко-
впх лепестков. (Если изменение наклона не будет компенсировано,
к это приведет к увеличению боковых лепестков.)
Несогласованные неоднородности в волноводном тракте за счет
щойного отражения сигнала (сначала в направлении, противопо-
ложном основному, а затем при отражении обратной волны от дру-
1ой неоднородности в прямом направлении) также приводят к уве-
шчению боковых лепестков.
Специфические искажения типа отклонения от линейности изме-
нения частоты в зависимости от времени возникают при формирова-
нии «частотной пилы». В реальных устройствах на идеальную «пилу»
накладываются гармонические и полиномиальные составляющие
различной скорости.
Наконец, частотные характеристики приемного устройства,
включая укорачивающий фильтр, также отличаются от идеальных,
что приводит к появлению дополнительных лепестков.
573
Перечисленные выше основные искажения могут иногда в зНЯ»
чительной степени изменить укороченный импульс, расширяя его
главный лепесток и увеличивая боковые лепестки.
Рассмотрим кратко некоторые типичные искажения и их влип»
ние на форму выходного сигнала. Как уже упоминалось, амплитуд*
ный и фазовый спектры ЛЧМ импульса по форме повторяют зав№
симость амплитуды и фазы от времени. Поэтому одинаковые п4
Рис 14.28. Периодические искажения ЛЧМ импульса.
форме и величине искажения частотной характеристики радиотрак-
та и временные отклонения самого сигнала будут приводить к оди-
наковым результатам. Этот принцип эквивалентности частоты И
времени часто используется в теории искажений. Поэтому в част-
ности, на рис. 14.28—14.30 и 14.32 ось абсцисс, соответствующая
о
° S	г
I ч	'
5 а о
< г»
Рис. 14.29. Искажения типа «скос».
оси времени для временных искажений, для частотных искажений?
соответствует оси частот. Вследствие этого на этих рисунках точка г1
на временной оси совпадает с точкой F на частотной оси.
Рассмотрим влияние наиболее типичных искажений на форму*
укороченного импульса.	1
Периодические искажения амплитуды величиной а и фазы велИ*
чиной Дер вызывают появление пары ложных импульсов для каждой
«гармоники» с амплитудами, равными соответственно а/2 и \ф/2,
Эти ложные импульсы симметрично сдвинуты относительно основ-
ного лепестка на величину, зависящую от числа периодов искаже-
ний, укладывающихся на длительности импульса (или на ширине
574
нектра). Указанный сдвиг равен т/F для временных и т/Т для
11СТ0ТНЫХ искажений, где m — число периодов, укладывающихся
г । длительности Т или на ширине спектра F соответственно.
На рис. 14.28 изображена идеальная форма огибающей импульса
и in амплитудный спектр ЛЧМ импульса, возможные периодиче-
кие^искажения амплитуды и фазы и форма выходного сигнала.
Рис. 14.30. Параболические искажения фазы ЛЧМ импульса.
Если принять высоту неискаженного импульса равной единице,
। о скос зондирующего сигнала величиной ас приводит к уменьше-
нию амплитуды на величину ос/2 и симметричному расширению
укороченного импульса на уровне 0,7 на величину ss 0,02 а2
(рис 14.2^). Уменьшение амплитуды символизирует уменьшение сиг-
нал/шум в пике сигнала.
Выходной Укороченный
Рис 14.31. Частотный сдвиг закона модуляции ЛЧМ импульса.
Параболические искажения фазовой характеристики (допол-
нительное приращение А<р фазы на краю спектра сигнала относи-
тельно определяемого соотношением (14.4.7) значения) также приво-
дят к уменьшению амплитуды укороченного импульса на величину
0,02(А<р)2, что ухудшает отношение сигнал/шум, и обусловливает
расширение импульса на 0,05 (А<р)2. (рис. 14.30).
Вследствие допплеровского сдвига и неточности привязки зако-
на модуляции частоты может возникнуть частотный сдвиг на вели-
чину АД это приводит к сдвигу укороченного импульса во времени
на Af = AfM (рис. 14.31).
575
Во многих случаях точный вид искажений неизвестен. Тогда
удобно считать их случайной функцией с нулевым средним значе-
нием, дисперсией о2 и временем корреляции тк. Такие искажения
Случайные
искажения
Выходной
Рис. 14.32. Случайные искажения ЛЧМ импульса.
приводят к появлению случайных боковых лепестков со средне-
квадратичным значением o'oJT, расположенных во временном ин-
тервале 1/Атк около основного импульса (рис. 14.32).
Теория искажений развита в нескольких работах, в том числе
в 18, 9].
§ 6. ДИСКРЕТНЫЕ СИГНАЛЫ
Наряду с ЛЧМ импульсами в современной радиолокации ши-
роко используются дискретные сигналы, которые строятся сле-
дующим образом. Отрезок времени Т (длительность импульса)
разбивается на N временных позиций длительностью Д = T/N каж-
дая. На Ай позиции формируется колебание А, ехр {;<р,}, где At
и ф, — заранее выбранные амплитуда и фаза колебаний высокой
частоты. Наборы А1Г ...,АмИфг....образуют коды, которые
выбираются так, чтобы обеспечить функцию неопределенности
с нужными свойствами.
В зависимости от ограничений, наложенных на А, и ф,, полу-
чаются разные классы сигналов. Например, если все AL = const,
а <р, могут принимать лишь два значения (обычно 0 и л), то полу-
чается класс сигналов, называемый обычно классом ФМ импульсов.
Сравнительная простота реализации фазового кодирования и выго-
ды, связанные с постоянством амплитуды при усилении по мощ-
ности, обеспечили ФМ импульсам широкое применение.
Функция неопределенности дискретных сигналов при достаточно
большом числе позиций М имеет почти идеальнй вид, представлен-
ный на рис. 14.33. На этом рисунке около нуля расположен гда^-
57ф
пли максимум функции неопределенности, сосредоточенный в об-
। 1сти
—Д < т < Д, — 1/7 < v <г 1/7.
(14.6.1)
Рис 14.33. Топографическая проек-
ция функции неопределенности.
1 '>пе этой области расположены боковые лепестки, ^имеющие значи-
1ельно меньший уровень. За исключением сечения т == О уровень
। оковых лепестков зависит от
числа позиций N и обычно со-
. гавляет Примерный вид
.ечений функции неопределен-
ности ФМ импульсов при v = О
и т= 0 представлен на рис. 14.34.
()тметим, что уровень боковых
юпестков зависит от вида ис-
пользуемою кода. Приведенные
рисунки относятся к случаю
ык назыв1емых «псевдослучай-
ных» кодов.
Спектр ФМ импульса также
<ависит от вида используемого
кода. Некоторую общую ориен-
и-фовку дает рис. 14.35, где
представлены амплитудный |S(jco)| и фазовый Ф(со) спектры три-
надцатипозиционного сигнала Баркера.
Используя введенную ранее символическую запись (+1 —
колебание с единичной амплитудой и фазой 0 и —1—колебание с еди-
Рис 14.34. Сечение функции неопределенности ФМ импульса плоскостя-
ми v=0 (а) и т = 0 (б).
пичной амплитудой и фазой л), тринадцатипозиционный сигнал
Баркера можно представить в виде следующей последовательности
(пмволов:
1, 1, 1, 1, 1,-1, —1, 1, 1, -1, 1, —1, 1.
577
Рис. 14.35. Амплитудный (а) и фазовый (б) спектры три-
надцатипозиционного сигнала Баркера.
Рис. 14.36. Тринадцатипозиционный сигнал Баркера (а)
и его корреляционная функция (б).
57?
Корреляционная функция 7?(т) сигнала Баркера имеет специфиче-
. кий регулярный характер (рис, 14.36), причем уровень ее боковых
шестков не превышает величины UN. Характерная особенность
ншлитудного спектра рассматриваемого сигнала Баркера со-
< гоит в появлении на определенных частотах выбросов. Для других
i игналов Баркера появляются провалы, иногда доходящие почти
io нуля. Фазовый спектр сигнала имеет регулярный характер.
В дальнейшем рассмотрим некоторые классы кодов для дискрет-
ных сигналов, причем основное внимание уделим получению сигна-
1ов с хорошими корреляционными функциями Д(т). Как уже ука-
зывалось ранее, корреляционная функция Д(т) является определяю-
щей характеристикой зондирующего сигнала в случае, если макси-
мальный сдвиг частоты, независимо от того, какую природу он имеет
(допплеровский сдвиг или нестабильности гетеродинов), удовлет-
воряет условию
Утах « VT.	(14.6.2)
§ 7. ДИСКРЕТНЫЕ СИГНАЛЫ, СВЯЗАННЫЕ С ЛИНЕЙНЫМИ
РЕКУРРЕНТНЫМИ ПОСЛЕДОВАТЕЛЬНОСТЯМИ
Обширный класс дискретных сигналов строится на основе ли-
нейных рекуррентных последовательностей (ЛРП) [10]. Исполь-
зование ЛРП целесообразно по следующим основным причинам.
Импульсные ФМ сигналы, использующие ЛРП, имеют хорошие
корреляционные свойства, а именно, отношение главного макси-
мума к максимальному боковому лепестку автокорреляционной
функции растет приближенно как VN, где N — число позиций
в импульсе длительностью Т. Кроме того, рекуррентный характер
последовательностей и некоторые их свойства позволяют построить
компактные формирователи сигналов и приемники корреляцион-
ного типа И, наконец, непрерывные ФМ сигналы, построенные на
основе ЛРП, могут иметь идеальные автокорреляционные функции.
Структура сигнала рассматриваемого вида имеет случайный
характер, хотя способ его формирования вполне регулярен. Шумо-
подобный характер сигнала при манипуляции фазы на два положе-
ния (0 или л) проявляется, в частности, в том, что общее число
позиций, содержащих колебания с фазой 0 и с фазой л, почти оди-
наково, общее число пар соседних позиций, содержащих фазы
(С, 0), (0, л), (л, 0) (л, л), также почти одинаково и т. д.
Линейной рекуррентной последовательностью называется перио-
дическая последовательность символов
... , sb s2, s3, ..., st.	(14.7.1)
каждый из которых может принимать значения из области G (0, 1,
. , р — 1), удовлетворяющая рекуррентному правилу
cz0S; a b«iVi+...+a„s<-n,	(14.7.2)
579
причем a, at Q G и операции сложения и умножения производятся
по модулю р*. Предполагается, что модуль р является простым
числом. Соотношение (14.7.2) называется правилом кодирования,
число р — основанием последовательности, число п — памятью
последовательности.
ЛРП удобно строить, задав произвольную «начальную комби-
нацию» из п символов Sj, 5ls ..., sn и применяя далее правило коди-
рования (14.7.2).
Пример 1. Пусть р = 5, п = 2, s? = s(-_i + 3s,-2 — пра-
вило кодирования и начальная комбинация (0, 1). Тогда ЛРП имеет
вид: 0, 1, 1, 4, 2, 4, 0, 2, 2, 3, 4, 3, 0, 4, 4, 1, 3, 1, 0, 3, 3, 2, 1,
2, 0, 1, ...
Далее основное внимание уделяется частному случаю а = 0.
При этом рекуррентное соотношение (14.7.2) может быть записано
в следующем матричном виде. Пусть sk = [s*+n—1» •••, s*]+ —
вектор-столбец и определена производящая матрица:
Пд Пд ... (1ц—1
1	0	0	...	0	0
0	1	0	...	0	0
0	0	1	...	0	0
(14.7.3)
0 0 0 ... 1	0
Тогда
з*+1 = Да* = Ak Sj.	(14.7.4)
Вектор sk характеризует состояние, в котором находится после-
довательность на k-м шаге.
Ниже перечислены некоторые свойства ЛРП.
ЛРП является периодической последовательностью с периодом
=	1.	(14.7.5)
•
Действительно, имеется всего рп различных состояний после-
довательности. Состояние 0 = [0, ..., 01+ является особым, так как
Ak0 — 0. За исключением этого состояния имеется всего рп— 1
возможностей. Если при построении последовательности пробе-
гаются все возможные состояния, то последовательность имеет
* Операция сложения двух чисел а и Ь по модулю т определяется пра-
вилом:
а + b , а + b < т,
а -Г Ь — т, а-$- Ь > т
Например, 2	3 = 1 (/п = 4).
$80
а + b =
шксимаЛьный период, в противном случае — период, Меньший
шксимального. В примере 1 максимальный период Ртах равен
\ = 5а — 1 = 24. Последовательности максимального периода
(МЛРП) имеют для радиолокации особое значение.
Период МЛРП содержит по рп — 1 символов вида 1, 2,...,
ji — 1 и рп~1 —1 нулей и распадается на р—1 «цугов» длительностью
17 = N/(p~ 1) = (рп— — 1) каждый, причем в матрице
$1 s2 ... SM
SM+i	SM + 2 •" S2M
(14.7.6)
c
_M (p-2) + \
... sN __
I) — 1 строка, M столбцов и все строки пропорциональны. Коэф-
фициент пропорциональности k является первообразным корнем
единицы модуля р*. Значения первообразных корней для некото-
рых значений модуля р приведены в табл. 14.7.1.
Таблица 14.7.1
Первообразные корни k единицы модуля р					
р	3	5	7	11	13
k	2	2; 3	3; 5	2; 6; 7; 8	2; 6; 7; 11
Отыскание МЛРП или, точнее говоря, правил кодирования, фор-
мирующих МЛРП, производится с помощью ограниченного пере-
бора возможностей. В настоящее время составлены таблицы правил
кодирования, формирующих МЛРП. Показано также, что при лю-
бых заданных р и п число Q различных МЛРП равно
Q=±q>(pn~l),	(14.7.7)
где ф(/г) — функция Эйлера в теории чисел**.
В результате исследования МЛРП в различное время было по-
строено несколько специальных классов сигналов.
* Первообразным корнем единицы модуля р называется число k, удов-
цетворяющее условию;
М = 1 только для q = р — 1,
=£ 1 для любого другого q<p— 1.
** Функция Эйлера ср (Д) равна количеству целых чисел, включая еди-
ницу, меньших числа h и взаимно простых с /г. Например, если h равно про-
стому чисту р, то <р(р) = р — 1.
$81
Сигналы Хаффмена [111. Ёсли р = 2, то получаются двоичные
последовательности, состоящие из единиц и нулей. Значения числа
различных МЛРП при заданных п приведены в табл. 14.7.2.
В качестве примера ниже приведены правила кодирования
МЛРП для n С 5:
выписанных правил.
Сигнал Хаффмена строится на основе рассмотренных МЛРП
с р = 2 в соответствии со следующим правилом: нулю последова-
тельности соответствует колебание единичной амплитуды и нулевой
фазы, единице последовательности соответствует колебание еди-
ничной амплитуды и фазы л. Символически это правило можно пред-
ставить следующим образом:
О ->	1 = ехр {/0},
1	— 1 — ехр {/л}.
Пример 2. Пусть правило кодирования определяется соот-
ношением st = s(-i -j- S{_3, начальная комбинация представляет
собой последовательность (0; 0; 1). При этих условиях МЛРП имеет
вид:
0, 0, 1, 1, 1, 0, 1, 0, 0, 1, ..., N - 23 — 1 = 7,
а соответствующий ей сигнал Хаффмена предствляет собой следую-
щую последовательность символов:
1, 1, —1, —1, —1, 1, —1, 1, 1,-1, ...
582
В непрерывной радиолокации используется бесконечный пе-
риодический сигнал Хаффмена; в импульсной локации может быть
использован любой период МЛРП, т. е. период, начинающийся
i любой фазы, что соответствует заданию произвольной начальной
комбинации при построении МЛРП.
Корреляционные свойства сигналов Хаффмена в настоящее
время достаточно хорошо изучены. Легко показать, что в непрерыв-
ном режиме работы автокорреляционная функция имеет главный
максимум, равный 1, и одинаковые по величине боковые лепестки,
равные — 1IN. Это фундаментальное свойство сигналов, связанных
с МЛРП. К сожалению, «непрерывные» корреляционные функции
юндирующих сигналов обычно важны лишь в тех случаях, когда
нельзя пренебрегать сдви-
юм Допплера и, следо-
вательно, важен полный
вид функции неопреде-
ленности, а не только ее
сечения вдоль оси задер-
жек при нулевом частот-
ном сдвиге. Однако хоро-
шие свойства «непрерыв-
ной» автокорреляционной
функции отражаются и
па «импульсной» автокор-
реляции. Если обозначить
«импульсную» автокорре-
Рис. 14.37. Автокорреляционная функция
сигнала Хаффмена.
ляцию как
N • ' N—1 > '
|де гдг — значение главного лепестка, а п..... гя-\—значе-
ния боковых лепестков автокорреляционной функции, то для сиг-
налов Хаффмена справедливо равенство
rq + rN_^-\, q~\, Ч......... tt-1.	(14.7.8)
Это соотношение накладывает ограничения на боковые лепестки,
примыкающие к главному. Общий характер боковых лепестков
автокорреляционной функции соответствует рис. 14.37, причем
вровень боковых лепестков не превышает величины 1/]/ф/.
Уровень 1/]/дГобъясняется псевдослучайным характером сиг-
нала. Боковой лепесток корреляционной функции является суммой
произведений компонент сигнала. В силу случайного характера
( игнала в указанной сумме содержится приблизительно одинаковое
число 4-1 и —1. Таким образом, среднее значение бокового лепестка
равно нулю, а дисперсия равна N. Разделив среднеквадратичное
шачение бокового лепестка на максимальное значение глав-
ного лепестка, равное N, получим уровень \J\rN.
583
Как отмечалось выше, при заданных Рип существует опреде-
ляемое формулой (14.7.7) число Q различных МЛРП. Любой период
каждой из этих МЛРП, отличающийся начальной комбинацией
символов, может быть использован для формирования сигнала.
Соответствующие этим МЛРП сигналы Хаффмена отличаются как
порядком чередования символов 4-1 и —1, так и максимальными
значениями г боковых лепестков. В каждом из возможных при за-
данных р = 2 и п сигналов Хаффмена можно указать боковой ле-
песток, имеющий наибольшее по сравнению с остальными лепест-
ками максимальное значение, равное гтал. Путем перебора возмож-
ных (при сформулированных выше условиях) сигналов Хаффмена
можно отыскать среди них сигнал, у которого наибольшее макси-
мальное значение гтаХ боковых лепестков будет наименьшим среди
рассматриваемых сигналов. В дальнейшем это «минимаксное» зна-
чение бокового лепестка' обозначается через гт1пта., а соответ-
ствующий ему сигнал называется минимаксным сигналом Хаф-
фмена. Некоторые характеристики минимаксных сигналов Хаф-
фмена приведены в табл. 14.7.3. Из таблицы, в частности, следует,
что минимаксное значение гт1П тах несколько меньше ]/N, однако
по мере увеличения N оно все больше приближается к этой вели»
чине.
Таблица 14.7.3
Некоторые характеристики минимаксных сигналов
Хаффмена
п	N	rmin max	V N	i/Vn
3	7	1	2,6	0,39 п .
4	15	3	3,9	0,26 1 
5	31	4	5,6	0,17 ,
6	63	6	7,9	0,13 ,
7	127	8	11,3	0,09	,
8	255	13	16,0	0,06 ’
В качестве примера ниже приведен минимаксный сигнал Хаф-
фмена для п = 5:
_1,—1,1,—1,—1,—1,—1,1;_1(1;—1,1, 1, 1,-1, 1, 1,-1,
—1, —1, 1, 1, 1, 1, 1, —1, —1, 1,1, 1,1.
Модуль его ненормированной автокорреляционной функции име-
ет следующий вид:
1, 0, 1, 4, 1, 2, 3, 2, 3, 2, 3, 0, 1, 2, 3, 2, 1, 0, 1, 2, 3, 2, 1, 2, 3,
2, 3, 2, 1, 0, 31.
584
Сигналы Цирлера 110]. Эти сигналы получаются из МЛРП при
к бом р и п заменой символов МЛРП на колебания по правилу:
0	-> ехр{/-0-2п/р},
1	-> ехр (/-1 -2л/р},	(14.7.9)
р— 1 -> ехр {/ (р — 1) 2л/р}.
Корреляционные свойства сигналов Цирлера аналогичны свой-
। гвам сигналов Хаффмена как в непрерывном, так и в импульсном
режиме работы.
Следующие классы сигналов связаны с заменой элементов МЛРП
на символы Лежандра.
Сигналы Пэли-Плоткина [12, 13]. Частным случаем МЛРП
авляется последовательность единичной памяти, имеющая следую-
щее правило кодирования:
=	(14.7.10)
и представляющая при р, = 1 натуральный ряд чисел
0, 1, 2, ..., р— 1, 0, 1, 2, ...
Предположим, что р - 4k — 1, k = 1, 2, 3, ..., и сигнал стро-
ится в соответствии с правилом
(14.7.11)
|де — символ Лежандра числа s(- по модулю р*, причем
= ±1- Получающаяся при этом последовательность символов
Лежандра обладает хорошими корреляционными свойствами. В част-
ности, в непрерывном режиме боковые лепестки автокорреляцион-
ной функции равны —1, а главный лепесток равен р.
Пример 3. Пусть р = 7, $, = 2 Н s(_|. Тогда МЛРП имеет
вид: ..., 0, 2, 4, 6, 1, 3, 5, ...,
* Символ Лежандра V = (—j числа s равен -f- 1, если s является квад-
ратичным вычетом модуля р, и равен— 1, если s является квадратичным
невычетом модуля р. Число является квадратичным вычетом, если оно пред-
ставляет квадрат по модулю р какого-либо целого числа и невычетом— в про-
тивном случае. Например, при р — 5 имеем
12 = 1; 22 = 4 - 32 = 4. 42 = 1
и поэтому 1,4— квадратичные вычеты, а 2,3 — квадратичные невычеты моду-
ля 5 Таким образом,
= - 1; (?) = - 1; (Й = + 1
\5/	\5/
585
а Соответствующая ей последовательность символов Лежандра
равна
±1, 1, 1, L, 1, -1, -1, ±1, 1, ...
Легко установить, что непрерывная автокорреляционная функция
такого сигнала имеет следующий вид:
7, —1, —1, —1, —1, —1, —1, 7, ...
Импульсные автокорреляционные функции сигналов Пэли-
Плоткина аналогичны автокорреляционным функциям псевдослу-
чайных сигналов. Уровень их боковых лепестков приблизительно
равен 1/]Лр. Кроме того, боковые лепестки таких сигналов подчи-
няются условию rQ + ГК-\ == —1.
Последовательности символов Лежандра МЛРП общего вида.
Предположим, что построена последовательность максимального
периода при произвольных р и п в соответствии с правилом
Si^Vi=={^\	(14.7.12)
причем символ Лежандра нуля считается равным нулю.
В результате такой замены получается периодический сигнал
с периодом j-, равным удвоенной длительности цуга. Полу-
периоды сигнала отличаются только знаком.
Построенные таким способом сигналы имеют примечательные
корреляционные свойства. Непрерывная функция корреляции имеет
нулевые боковые лепестки и главный максимум, равный ±рп~'.
Следует, однако, оговориться, что непрерывная функция корреля-
ции подсчитывается при интегрировании за полпериода последо-
вательности, в соответствии с чем ее главные максимумы следуют
через полпериода.
1 В импульсном режиме могут использоваться полупериоды по-
следовательности символов Лежандра, начинающиеся с любой
фазы. Эти сигналы содержат нулевые провалы по огибающей и ко-
дирование по фазе производится на два состояния: Ойл. Сигналы
имеют псевдослучайные свойства и их ненормированные автокорре-
ляционные функции обладают боковыми лепестками с уровнем
/рП |
р—1" '
Пример 4. Пусть р — 29, п = 2 и правило кодирования
выбрано в виде s, = 16s,-~i + lls,-2- Если начальной комбинацией
является (0, 1), то сигнал имеет вид:
О, 1,-1, 1, 1,-1,— 1, 1,-1, —1, 1,-1, 1, —1, С —1. —1- - 1.
— 1, — 1, — 1, —1, 1, 1, 1, —1, -1, 1, 1, 1.
586
1 in нал содержит = 30 символов, но так как единственный
нулевой символ стоит первым, фактически имеется 29-позицион-
пый фазо-манипулированный сигнал.
Азтокорреляционная функция такого сигнала имеет вид:
о,1, 0,1, 0, 1, 0, —3, 0, 1, 0, —3, 0, —3, 0, —3, 0, —3, 0, 1, 0,
3,0, 1,0, 1,0, 1, 0, 29, причем максимальный боковой лепесток ее
равен 3.
Класс сигналов, построенный на основе МЛРП при п = 2,
нобопытен тем, что здесь на полупериоде последовательности имеет-
1Я только один нуль.
§ 8. ДРУГИЕ КЛАССЫ ДИСКРЕТНЫХ СИГНАЛОВ
Сигналы Баркера [14]. Особое место занимают сигналы, имею-
щие минимально возможный при данном N уровень боковых лепест-
ков, равный 1. Такие сигналы существуют только для определенных
шачений N — 2, 3, 4, 5, 7, 11, 13 и называются сигналами Баркера.
Вид таких сигналов при различных N и соответствующие им авто-
корреляционные функции приведены в табл. 14.8.1.
Таблица 14.8.1
Сигналы Баркера
Сигналы Баркера
Автокорреляционная функция
Сигналы Баркера являются уникальными сигналами, имеющими
регулярные автокорреляционные функции.
Некоторые усложненные сигналы. Усложнение дискретного
сигнала (например, фазовая манипуляция на несколько уровней,
дополнительная амплитудная манипуляция и др.) приводит к улуч-
шению его корреляционных свойств. Проиллюстрируем это поло-
жение несколькими примерами.
Предположим, что боковые лепестки автокорреляционной функ-
ции должны удовлетворять условию
]Г1 ) = 1, Г2 =Гз = =^rN-i = °-
587
Можно показать, что сигналы с корреляционными функциями,
удовлетворяющими этому требованию, могут быть найдены в классе
сигналов, дискреты s( которых являются действительными числами.
Формирование таких сигналов возможно при произвольной ампли-
тудной манипуляции и манипуляции фазы на два положения (О
или л). Легко убедиться, что при JV = 5 требуемую функцию
корреляции имеет сигнал вида 1; </; <72/г; —<7; 1. Например, при
<7 = 2 такой сигнал представляет собой последовательность 1, 2, 2,
—2, 1, а его корреляционная функция имеет вид 1, 0, 0, 0, 14.
В некоторых случаях можно отказаться от требования нулевых
боковых лепестков. Имеющиеся здесь возможности можно показать
на примере следующего сигнала с дополнительной амплитудной
манипуляцией:
1; 1; 0,5; —3; —3; —3; +3; —3; —0,5; 1; —1.
Нетрудно убедиться, что автокорреляционная функция такого сиг-
нала имеет вид:
—1, 0, 0, 0, 0, 0, 0, 0, 0,1, 0, 50.
Хорошей иллюстрацией возможности дополнительной амплитудной
манипуляции на два уровня (0 или 1) является сигнал, представ-
ляющий собой последовательность
1, 1, -1, —1, 1, 1, 1, 1. 1, —1, 1, -1, 0, 0, —1,
автокорреляционная функция которого имеет следующий вид:
— 1, —1, 1, 0, —1, 0, —1, 0, 1, 0, —1, 0, 0, 1, 13.
Сигналы Шермана [3]. Сигналы Шермана могут принимать на
позициях два дискретных значения 0 или 1, что соответствует при-
менению только амплитудной манипуляции. Как отмечалось в §2,
сигналы Шермана удовлетворяют требованию не более чем одного
совпадения при сдвиге на любое т. Вследствие этого импульсные
корреляционные функции этих сигналов имеют боковые лепестки,
принимающие лишь два значения: 0 или 1. Так, например, сигнал
Шермана для У = 8 имеет вид 1, 1,0, 1, 0, 0, 0, 1, а его автокорре-
ляционная функция —1, 1, 0, 1, 1, 1, 1, 4.
С точки зрения обработки желательно иметь наименьшую длину
сигнала, сохраняя при этом заданное число единиц. Такие «опти-
мальные» сигналы найдены для случаев М = 3, 4, ..., 10 (44
число единиц в сигнале) и представлены в табл. 14 8.2.
Зависимость log N от М имеет вид прямой линии. Экстраполируя
значения М, можно найти, что для М = 30 ожидается N ж 1000.
Таким образом, сигналы Шермана при значительной длительности
Т обеспечивают сравнительно небольшую энергию в импульсе.
588
Таблица 14.8.2
Сигналы Шермана
N
Расстояние между единицами
4
7
12
18
26
35
46
62
3
4
5
6
7
8
9
10
1, 2
1,	3,	2
1,	3,	5,	2
1,	3,	6,	2,	5
1,	3,	6,	8,	5,	2
1,	3,	5,	6,	7,	10, 2
1, 3, 9, 11, 6, 8, 2, 5
1, 6, 4, 15, 13, 8, 9, 3, 2
Многофазовые коды Фрэнка [15]. Естественный путь построения
фазо-манищлированного импульсного сигнала с фазовой манипу-
ляцией на несколько уровней состоит в передаче дискретными уров-
нями параболической зависимости фазы от времени, что соответ-
ствует в непрерывном случае ЛЧМ импульсу. Подобного рода коды,
построенные Фрэнком, имеют хорошие непрерывные свойства.
Пусть р и N — целые взаимно простые числа, а единица фа-
ювого сдвига равна ф = 2np/N. Значения фаз на позициях, изме-
ренные в единицах ф фазового сдвига, удобно изобразить в виде
матрицы:
ООО	о	о
0	1	2 (N — 2)	(N— 1)
0	2	4	2 (У— 2)	2(У —1)
0 (V —2) 2(У — 2)... (У — 2) (У — 2) (У —2)(У—1)
_0 (V—1) 2(2V — 1)... (2V — 1)— 2) (N — 1)(У — 1)_
(mod N).
При этом временная кодовая последовательность Фрэнка форми-
руется последовательным выписыванием строки за строкой. Вслед-
ствие того, что матрица С содержит У строк и N столбцов, период
такой последовательности равен №.
Пр имер 1. Пусть N = 4. Тогда матрица С принимает вид
“0 0 0 0“
с 0 12 3
~ 0 2 0 2 ’
0 3 2 1_
что соответствует следующей последовательности Фрэнка:
0, 0, 0,0,0, 1, 1,3, 0, 2,0,2, 0, 3, 2, 1, ...
589
Автокорреляционная функция непрерывного сигнала Фрэнка
имеет нулевые боковые лепестки и главные максимумы, равные №,
следующие с периодом №.
Рис. 14.38. Уровень боковых ле-
пестков корреляционных функций
сигналов Фрэнка.
Кроме того, структура кодов
В качестве кода для импульсного
сигнала Фрэнка может быть ис-
пользована любая циклическая
перестановка периода. Лучшие
результаты, однако, получаются
при использовании основного пе-
риода.
На рис. 14.38 приведена зави-
симость уровня боковых лепестков
от длины кода, заимствованная из
работы Фрэнка. Здесь черезр
обозначено отношение главного
максимума к уровню максималь-
ного бокового лепестка. Эти ре-
зультаты показывают, что много-
фазное сигналы Фрэнка имеют
существенно лучшие корреляцион-
ные свойства, чем, например,
двухфазные сигналы Хаффмена.
Фрэнка позволяет построить ком-
пактные схемы генераторов кодов.
В заключение отметим, что функция неопределенности сигналов
Фрэнка на плоскости «частота — задержка» имеет много общего
с функцией неопределенности ЛЧМ импульсов.
§ 9. ПОДАВЛЕНИЕ БОКОВЫХ ЛЕПЕСТКОВ
ПРИ НЕОПТИМДЛЬНОМ ПРИЕМЕ
Дискретные сигналы, в особенности при сравнительно неболь-
шом коэффициенте укорочения и достаточно простой форме (на-
пример, прямоугольная огибающая и фазовая манипуляция на два
уровня: 0 и л), имеют автокорреляционные импульсные функция
с большими боковыми лепестками. Для подавления боковых ле-
пестков следует использовать не согласованные фильтры, а фильт-
ры, специально подобранные таким образом, чтобы выходной сиг-
нал имел требуемые боковые лепестки.
Подавление боковых лепестков сопровождается проигрышем
в отношении сигнал/шум в максимуме выходного сигнала по сравне-
нию с оптимальной величиной 2EIN0. В отличие от импульсов с ли-
нейной частотной модуляцией подавление боковых лепестков кор-
реляционных функций ФМ импульсов не сопровождается расши-
рением главного максимума. Вместо этого расширяется область
боковых лепестков выходного сигнала.
$90
Приемное устройство в данном случае удобно представить в виде
и реальной линии задержки (с максимальной задержкой 6 ~^> Т)
। отводами, отстоящими друг от друга на длительность позиции А
(рис. 14.39). На выходе каждого отвода помещен фазовращатель
(ФВ), который может изменить фазу на л, и аттенюатор (А), изме-
няющий амплитуду сигнала в нужное число раз. Выходные сигналы
1ттенюаторов суммируются, и результат суммирования фильтрует-
(Я в полосе 1/А. Результат совместного действия фазовращателя
и аттенюатора сводится к умножению сигнала с каждого входа от-
вода на действительный вес hi, где i — номер отвода.
Рис 14.J9. Приемное устройство, подавляющее боковые ле-
пестки ФКМ импульсов.
Выходной сигнал фильтра в зависимости от конкретного вида
весов hi имеет различный характер. Для получения желаемого эф-
фекта веса подбирают так, чтобы выходной сигнал имел большой
главный лепесток (шириной по основанию 2А) и маленькие боковые
лепестки.
При теоретическом синтезе устройства удобно пользоваться од-
ним из двух критериев. Пусть величина р. равна отношению глав-
ного максимума к максимальному боковому лепестку выходного
сигнала, а величина v — отношению главного максимума к корню
квадратному из суммы квадратов боковых лепестков.
Если веса hi выбраны из условия максимизации величины р при
заданной форме входного сигнала, то соответствующий фильтр
называется далее ц-фильтром. Если значения весов максимизируют
параметр v, то фильтр называется v-фильтром. Оба вида фильтров
могут быть использованы в радиолокации.
Для отыскания весов по ц-критерию используются модернизи-
рованные алгоритмы линейного программирования. Для отыскания
весов по v-критерию используется обычная методика отыскания
условного экстремума функции многих переменных и различные
специальные приемы решения систем линейных уравнений. Теоре-
тически дело сводится к отысканию экстремума квадратичной формы
591
при некоторых дополнительных ограничениях линейного вида.
Техника решения таких задач разработана сравнительно хорошо.
Поэтому практически пользоваться v-критерием легче, чем р-кри-
терием.
Ниже приведены результаты построения р- и v-фильтров, по-
давляющих боковые лепестки сигналов Баркера с N = 5, 7, 13.
Рис. 14.40. Подавление боковых лепестков сигна-
ла Баркера с ^=5.
На рис. 14.40 — 14.42 представлены зависимости параметров |4,
v и р2 (где р2 — отношение сигнал/шум по мощности в максимуме
выходного сигнала, поделенное на 2E/No) от максимальной задержки
линии, измеренной в единицах длительности позиции: k = 0/А + 1,
Для сигналов Баркера с N = 5 и 7.приводятся сравнительные ре-
зультаты по ц- и -v-фильтрам. Для сигналов Баркера с А?= 13
приводятся результаты по v-фильтрам.
Эффективность подавления боковых лепестков увеличивается
с возрастанием параметра k приблизительно экспоненциально.
592
к
Рис. 14.41. Подавление боковых лепестков
сигнала Баркера с N=7.
Рис. 14.42. Подавление боковых лепестков по
v-критерию для сигнала Баркера с N=13.
593
При достаточно большом k может быть достигнут любой наперед
заданный уровень боковых лепестков. При этом проигрыш в отно-
шении сигнал/шум по мощности

'Ъ
с
05
*
13
3
к
6 6996'0
- тио
~~сбъэг'1
(6891'0
шоо'о
661(6 ‘о
61(99'0
9 6(8 ('О
(9(0 6‘l
(8160'0
coioe's
2бб66 'L
~6(96l 9
10(96'8
11(86'9
0(696k
99(066
0(696 '(
11(86 9
'19(96'8
8(961 ‘9
(66(6 L
(8198'9
(8160'0
(9Z06'l
96(8(0
61(99'0
661(6’0
66(00'0
A^'-L669('i
(76996'0
Б
«3
X
5
по сравнению с оптимальной
фильтрацией незначителен. По-
следнее объясняется тем, что
импульсный отклик ц- и V-
фильтров, в основном, имеет
следующую структуру; цен-
тральная часть импульсного
отклика почти согласована с
используемым сигналом; начало
?? и конец импульсного отклика
7 хотя и могут быть довольно
длинными, по амплитуде значи-
2 тельно меньше центральной
II части. Таким образом, начало
и конец импульсного отклика,
а выполняя корректирующую
£• роль в смысле подавления бо-
о. ковых лепестков, мало влияют
>3 на отношение сигнал/шум. Ска-
g занное иллюстрируется следую-
х щим примером.
5 Для пятипозиционного сиг-
ik нала Баркера 1, —1, 1, 1,
ч: 1 веса отводов линии задерж-
ку ки, используемые в ц-фильтре
с при k = 19, равны 1,2, 1, —3,
е- —8, —8, 1, 21, 37, 23, —37, 21,
i —1, —8, 8, —3, —1,2, —1, при-
« чем ц = 139, v = 49, р2 = 0,88.
2 Импульсный отклик этого
d фильтра, снятый на выходе сум-
£ матора, будет состоять из серии
6-функций, коэффициенты при
которых равны выписанным
весам.
На рис. 14.43 представлен
ц-фильтр с числом отводов
k = 33, построенный для сигна-
ла Баркера с N — 13. Характе-
ристики fi и р2 такого фильтра
соответственно равны ц — 96
и р2 = 0,96.
Среди большого разнообразия различных дискретных сигналов
имеются сигналы, хорошо «поддающиеся» неоптимальной обра-
594
пике, и сигналы, для которых «несогласованный» прием неэффек-
। ивен. В частности, сигналы Баркера с числом позиций 5 и 13 в этом
• мысле более эффективны, чем с числом позиций 7 и 11.
Интересно отметить также, что ц- и v-фильтры дают не очень
сличающиеся результаты. Это, в частности, следует из сравнения
рис. 14.40 и 14.41.
§ 10. ВОПРОСЫ «СВЕРХУКОРОЧЕНИЯ»
При помощи специальных фильтров можно укоротить входной
< игнал таким образом, что длительность сигнала на выходе фильтра
будет значительно меньше величины 1 /А/, где Af — полоса исход-
ного сигнала. Такое укорочение сопровождается, конечно, значи-
шльными потерями в отношении сигнал/шум. Однако в некоторых
случаях (например, как мера борьбы с пассивными помехами мас-
сового типа) сверхукорочение является целесообразным.
Ниже представлены результаты построения укорачивающих
|i- и v-фильтров для прямоугольного импульса без фазовой внутри-
импульсной модуляции. С помощью комбинаций дифференцирую-
щих устройств можно, конечно, добиться разнообразных форм вы-
ходного сигнала. Однако фильтры, построенные по ц- и v-крите-
риям, являются в этом отношении оптимальными.
Пусть необходимо укоротить исходный прямоугольный импульс
в L раз. Импульсный отклик ц-фильтра имеет следующий харак-
герный вид (приводятся веса отводов);
— 1, 2, 0,... , 0, нуля 1 з®ено	—3, 4, 0,..., 0, —5, 6, 0,..., 0,.. Л —2	L—2 нуля	нуля 2 звено	3 звено
-(27 — 1), 27, 0. О,	27, —(27 — 1),
	А —2 нуля
Импульсный отклик симметричен относительно середины, прохо-
дящей между звеньями, содержащими веса —(27 — 1), 27 и 27,
—(27— 1). Ходули весов отводов образуют натуральный ряд чи-
сел, причем знаки весов чередуются.
Фильтр, состоящий из пяти звеньев и укорачивающий в L = 5
раз, представлен на рис. 14.44. Там же представлены входной и вы-
ходной сигналы фильтра.
Физика риботы этого фильтра достаточно проста. Входной им-
пульс всегда действует только на пару соседних отводов, веса ко-
595
торых противоположны по знаку и отличаются по величине на еди-
ницу. Поэтому на выходе сумматора будет появляться сигнал
—1, 1, 1, 1, —1, 1, 1, 1, —1, 1, 1, 1, 12, 1, 1, ...
Максимум, равный 12, появляется в случае, когда импульс занял
в линии задержки среднее положение. За счет наращивания звеньев
линии можно получить теоретически любые отношения главного
максимума к боковому лепестку.
Рис. 14.44. Укорачивающий р-фильтр.
Сигнал на выходе р-фильтра имеет следующие параметры:
Л Т	Л 1	9	2	3
р _ 4J; v — 4 у -j- ; Р — (2/ + ц . Р — JL •
Последнее равенство справедливо при достаточно большом J.
Для того, чтобы получить достаточно большое подавление бо«
ковых лепестков (например, р »50), необходимо выбрать число
звеньев порядка 10. При этом p2«bl/3L, т. е. отношение сигнал/шум
по мощности в пике выходного сигнала примерно в три ]Лз<
меньше отношения сигнал/шум по мощности для РЛС, работающей
с зондирующим импульсом в L раз более коротким, чем исходный.
Определенный ранее v-фильтр, укорачивающий прямоугольный
импульс, имеет структуру, подобную р-фильтру. Ниже приведены
сведения, относящиеся к v-фильтру.
Импульсный отклик такого фильтра имеет вид:
— 2, 24--, 0,..., 0, — 4 — — , 4 + -, 0,..., 0,
L — 2	L — 2
нуля	нуля
1 звено
2 звено
596
6--, 6-I--3 0,..., 0,..., — 2J — -—\ 2J + -, 0,..., 0,
L—2	L — 2
нуля	нуля
3 звено
ii далее симметрично относительно середины отклика. Параметры
। hi нала на выходе такого фильтра равны
^„27 + 1; y = yiJ + ?L-
। де L = 2е -ф 1 — число раз, в которое укорачивается исходный
импульс. Последнее равенство справедливо при больших J и е.
§ 11. ФОРМИРОВАНИЕ ДИСКРЕТНЫХ СИГНАЛОВ
Формирсвание дискретных сигналов имеет специфические особен-
ности.
К. числу их, в частности, относится наличие правила кодирова-
ния у дискретных сигналов, основанных на ЛРП.
Пусть [sz] представляет собой ЛРП с правилом кодирования
S; = Я1 S, _ 1 4 ... 4" ап si—n,
\д.еат, Si—двоичные числа, и сложение производится по модулю 2
Последовательность двоичных символов [s, ] может быть сформи
рована с помощью устрой-
ства, изображенного на
рис. 14.45.
Устройство состоит из
сдвигающего регистра, имею-
щего п разрядов, причем
каждый разряд может нахо-
диться в одном из двух со-
стояний (0 или 1), умножи-
телей на коэффициент ат
(в двоичном случае это озна-
чает просто наличие или от-
Рис. 14.45. Генератор двоичной последо-
вательности символов.
сутствие связи с суммато-
ром), сумматора по модулю 2
и цепи обратной связи. Уст-
ройство работает от внешних
запускающих импульсов, следующих с периодом, равным дли-
тельности позиции А. В каждом такте в разрядах регистра хра-
нятся двоичные числа: se-_i хранится в первом разряде, ..., s,_n—
в n-м разряде. При этом на выходе сумматора формируется
597
число st, определяемое правилом кодирования. В случае появления
очередного запускающего импульса происходит сдвиг содержимого
регистра на один разряд в направлении, указанном на рис. 14.45.
При этом в первый разряд записывается число se, хранившееся
в предыдущем такте на выходе сумматора, во второй разряд записы-
вается число s;_i, хранившееся в первом разряде предыдущего такта
и т. д. Начиная с первого такта, в регистре хранится последова-
тельность состояний:
[Si, S„], [S2, ... , Sn+l], ...
Прямое решение задачи формирования последовательности сим-
волов с периодом N = 2п — i потребовало бы применения устрой-
ства, имеющего «память» N, например, линии задержки с макси-
мальной задержкой, равной Т = NA. Сдвигающие регистры, охва-
ченные петлей обратной связи, имеют «память» п » log2AZ, что поз-
воляет упростить устройство в целом.
В некоторых случаях двоичные сигналы псевдослучайного ха-
рактера не имеют столь простого правила кодирования. Однако
выбором подходящей памяти и применением нелинейной логики
можно всегда сформировать генератор, подобный описанному.
После того, как последовательность видеоимпульсов, соответ-
ствующая коду, получена, формирование радиочастотного сигнала
может быть выполнено при помощи быстродействующего комму-
татора, пропускающего на вход усилителя мощности один из сигна-
лов (например, cos или —cos <oQi) в зависимости от величины
коммутирующего напряжения.
Вторая особенность применения дискретных сигналов заклю-
чается в возможности получения кодовых последовательностей,
задержанных относительно исходной, с помощью логических опе-
раций над разрядами сдвигающего регистра. В качестве примера
рассмотрим эти операции применительно к сигналам Хаффмена.
Предположим, что, кроме основной цепи обратной связи, над
разрядами сдвигающего регистра осуществляется линейная опера-
ция вида
И; = Cj se—1	+ сп Si—n,
где cm — двоичные числа и сложение производятся по модулю 2.
Можно показать, что каждой комбинации коэффициентов ci,
..., сп (т. е. каждому виду связи разрядов с дополнительным сумма-
тором) соответствует последовательность [sj, задержанная отно-
сительно исходной на некоторое число символов, т. е.
[wj = [s,u], 1	— 1.
Общее число комбинаций из п символов с(, с2, ..., гп, за исключе-
нием нулевой, равно 2"— 1 = N.
598
На рис. 14.46 представлены генератор последовательности и фор-
трователи сдвинутых последовательностей ЛРП класса р = 2,
I = 3 с периодом N — 7.
В случае использования сигналов Хаффмена логика получения
двинутых последовательностей является линейной. В других слу-
чаях можно воспользоваться нелинейной
Рис. 14.46. Генератор опорных сигналов для многоканаль-
ного коррелятора.
10 0 10
0 0 10 1
0 10 11
10 111
0 1110
1110 0
110 0 1
Описанный генератор может быть использован и в многоканаль-
ном корреляторе в качестве задающего устройства для формирова-
ния опорных сигналов в каналах коррелятора.
§ 12. ИСКАЖЕНИЯ ФМ ИМПУЛЬСОВ В РАДИОТРАКТЕ РЛС
Дискретные сигналы, проходя по тракту РЛС, претерпевают
искажения, ограничивающие практическое использование таких
сигналов. Некоторые искажения ФМ импульсов и ЛЧМ импульсов
имеют общую природу. К их числу следует отнести, в частности,
перечисленные в § 5 искажения, вызываемые неидеальностью ам-
плитудно частотной характеристики усилителя мощности и укора-
чивающего фильтра; дисперсионными свойствами волноводов антен-
но-фидерного тракта; отличием формы модулирующего импульса,
подаваемого на усилитель мощности, от прямоугольной; наличием
несогласованных неоднородностей в антенно-фидерном тракте
в т. п.
599
Кроме того, имеются искажения, связанные с дискретной струк-
турой зондирующего сигнала и соответственно с дискретностью
формирователя и дискретностью в приемном устройстве. Эти иска-
жения можно разделить на две группы:
1) искажения, связанные с неточностями установки фазы мани-
пуляции сигнала и с неточностями весов отводов линии задержки
по амплитуде и фазе (амплитудно-фазовые неточности);
2) искажения, связанные с неточностями временной структуры
сигнала и фильтра, в частности, с неточностями моментов манипу-
ляции фазы сигнала и неточностями в расположении отводов на лит
нии задержки (временные неточности).
Рассмотрим влияние некоторых видов искажений на форму вы-
ходного сигнала. Характер этого влияния в определенной степени
зависит от конкретного вида дискретного сигнала. Хорошие оценки
можно получить, если воспользоваться процедурой усреднения по
значениям сигнала, считая, что значения сигнала от позиции к по-
зиции независимы и значения фазы на позиции (например, Ойл
при р = 2) равновероятны. Оценки, полученные таким способом,
очевидно, соответствуют случаю использования псевдослучайного
сигнала с большим числом позиций А/)^>1.
Влияние искажений сказывается не только на уровне боковых
лепестков выходного сигнала, но также и на форме главного ле-
пестка и на отношении сигнал/шум в главном лепестке. Проигрыш
в отношении сигнал/шум удобно оценивать параметром р2, который
равен фактическому отношению сигнал/шум по мощности при на-
личии искажений, отнесенному к отношению сигнал/шум на выходе
согласованного фильтра.
Амплитудно-фазовые неточности. Пусть щ — дисперсия фазо-
о	2
вых неточностей сигнала, аа — дисперсия амплитудных неточно-
стен весов отводов ЛЗ, — дисперсия фазовых неточностей весов
отводов ЛЗ. Сами неточности предполагаются нормальными слу-
чайными величинами с нулевым средним значением. Тогда диспер-
сия значений выходного сигнала имеет вид рис. 14.47. Здесь Z2 —
дисперсия дополнительных боковых лепестков, отнесенная к квад-
рату центрального пика, равная при t — О
(14.12.1)
Характерные особенности этих искажений заключаются в том,
что наибольшие дополнительные лепестки возникают в окрестности
главного максимума и линейно уменьшаются к краям корреляцион-
ной функции. Величина дополнительных боковых лепестков обратно
пропорциональна числу позиций N. Таким образом, эти искажения
можно уменьшить, выбрав псевдослучайный код с большим числом
позиций.
X,2=-J- <4(1 —-) + <4 + (4
/V \ Г /
600
Отношение сигнал/шум при наличии такого рода искажений
и ределяется формулой
Р2= 1 - о2(1~	- а2 - а2 = 1 - W.
(14.12.2)
Неточности момента манипуляции фазы сигнала. Пусть о? —
щеперсия неточности момента коммутации фазы, причем сама не-
юхность распределена по равномерному закону в пределах дли-
Рчс 14.47. Относительная дисперсия боковых лепест-
ков, возникающих из-за амплитудно-фазовых неточ-
ностей.
дельности позиции с нулевым средним значением. Относительная
дисперсия боковых лепестков имеет вид рис. 14.47, причем величина
дисперсии в районе главного максимума равна:
1,25 / сД2
~ А/ (л ) ’
(14.12.3)
Проигрыш в отношении сигнал/шум по мощности при наличии иска-
жений такого вида определяется формулой
(14.12.4)
Таким образом, этот вид искажений также зависит от числа пози-
ций N.
Неточности установки отводов ЛЗ по задержке. Пусть о? —
дисперсия неточности установки отводов ЛЗ по задержке. Пред-
полагается, что приращение фазы, возникающей из-за указанной
неточности, выбрано при настройке фазовращателей в отводах ли-
нии. Сама неточность распределена равномерно на интервале А
с нулевым средним значением. Относительная дисперсия боковых
601
лепестков имеет вид рис 14.47, причем в этом случае Справедливы
соотношения
№ =
0,9 МЛ2
/V \ д/ ’
(14.12.5)
(14.12.6)
Данные искажения также могут быть ослаблены выбором большо-
го /V.
Помимо появления дополнительных лепестков и уменьшения
отношения сигнал/шум временные неточности приводят также к ис-
кажению формы главного максимума. Средний главный максимум
Рис. 14.48. Среднее значение главного лепестка при
временных искажениях.
отличается от треугольника и имеет вид, изображенный на рис.
14.48. Здесь о может быть ct или от в зависимости от того, какая
неточность рассматривается. Средний главный максимум расши-
ряется и уменьшается по амплитуде. Последнее символизирует про-
игрыш в отношении сигнал/шум по напряжению.
Рассмотрим теперь сигнальные искажения непрерывного ха-
рактера, такие, как непрерывная модуляция сигнала по фазе и по
амплитуде. Анализ этих искажений приводит к следующим резуль-
татам.
Синусоидальная фазовая или амплитудная модуляция. Этот
тип искажений представлен на рис. 14.49. Количественно искаже-
ния выходного сигнала характеризуются дисперсией, причем усред-
нение производится по ансамблю зондирующих сигналов так же,
как и при анализе дискретных искажений. Относительная диспер-
сия имеет вид рис. 14.47, причем максимальное значение для фазо-
вых искажений равно Аф2 /2JV, а для амплитудных искажений —
602
' 2/V. При больших > 1 и ma» 1 проигрыш в отношении сиг-
и<1л/шум не зависит от гщ и та и равен
Р2=1-	(14.12.7)
иля амплитудных и фазовых искажений соответственно.
Искажения типа «скос». Наличие скоса у огибающей импульса
(рис. 14.29) приводит к появлению несимметричных относительно
in ля дополнительных боковых лепестков. Наибольшее значение
1аких лепестков достигается при t = А и равно а2с /ЗА.
Рис. 14.49. Непрерывные амплитудно-фазовые искажения ФМ
импульса.
Приведенные результаты по регулярным искажениям ФМ сиг-
налов показывают, что их влияние на выходной сигнал ослабляется
в зависимости от числа позиций N. Формально это является след-
ствием усреднения по сигналу, который считается случайным. По
существу уменьшение искажений объясняется тем, что регулярные
искажения, проходя по отводам ЛЗ согласованного фильтра, при-
обретают случайный характер и затем суммируются уже как слу-
чайные величины.
Важным видом искажений является частотный сдвиг несущей
частоты относительно центральной, на которую настроен согласо-
ванный фильтр. Анализ влияния этого сдвига на боковые лепестки
и форму главного лепестка для случайных сигналов показывает,
что уровень боковых лепестков не зависит от частотного сдвига,
вто время как отношение сигнал/шум по мощности в главном пике
уменьшается в соответствии с квадратом |/?(0, Q)j2 функции не-
определенности.
Сравнивая результаты влияния однотипных искажений ЧМ
импульсов и ФМ импульсов на форму выходного сигнала, можно
заметить, что псевдослучайные ФМ сигналы проявляют значительно
большую устойчивость к большинству типовых искажений, чем
ЛЧМ импульсы. Относительная дисперсия боковых лепестков ФМ
603
сигналов в этих случаях обратно пропорциональна числу позиций,
что позволяет эффективно подавлять «технические» боковые ле-
пестки.
ЛИТЕРАТУРА
1	Вудворд Ф. М. Теория вероятностей и теория информации
с применениями в радиолокации. Пер. с англ. Изд-во «Советское радио»,
1955
2.	Рихачек А. В Разрешающие свойства импульсных последо-
вательностей. Пер. с англ Труды института инженеров по электротехнике ц
радиоэлектронике, 1964, № 2.
3.	Sherman Н. Some optimal signals for time measurement. Trans.
IRE, 1956, IT-2, № 1.
4.	С о о k С. E. Pulse compression key to more efficient radar transmis-
sion. Proc. IRE, 1960, № 3.
5.	T и м и с Ц. Л., Сайтрин А., Л э в и о л а М. А. Блок
сжатия импульсов для РЛС сопровождения. «Зарубежная радиоэлектро-
ника», 1964, № 11.
6.	Т о р Р. К- Техника сжатия импульса с большим произведением
длительности на ширину спектра, «Зарубежная радиоэлектроника», 1963,
№ 12.
7.	Т е m е s С. L. Sidelobe suppression in a range channel pulse —
compression radar. Trans. IRE, 1962, MiL-6, № 2.
8.	К л а у д e p Д. P. и др. Теория и расчет импульсных радиолока-
ционных станций с частотной модуляцией. «Зарубежная радиоэлектроника»,
1961, № 1.
9.	Дифраико Ж- В., Рубин В. Л. Анализ искажений при об-
работке радиолокационного сигнала. «Зарубежная радиоэлектроника»,
1963, № 9.
10.	II и р л е р Н. Линейные рекуррентные последовательности. «Ки-
бернетический сборник», 1963, вып. 6.
11.	X а фф м е и Д. Синтез линейных цепей последовательного коди-
рования. Сб. ст.: «Теория передачи сообщений». Изд-во иностранной литера-
туры, 1957.
12.	Плоткин М. Двоичные коды с заданным минимальным расстоя-
нием. «Кибернетический сборник», 1963, вып. 7.
13.	Д ж о ш и. О верхних границах для кодов с минимальным расстоя-
нием «Кибернетический сборник», 1960, вып. 1.
14.	Burker R. Н. Group synchronizing of binary digital systems.
Communication theory. Academic Press, 1953.
15.	Фрэнк P. Многофазовые коды с хорошими непериодическими
корреляционными свойствами. «Зарубежная радиоэлектроника», 1963, №12.
Раздел IV
ТЕОРИЯ ИНФОРМАЦИИ