Ф. ДРАЗИН
ВВЕДЕНИЕ В ТЕОРИЮ
ГИДРОДИНАМИЧЕСКОЙ
УСТОЙЧИВОСТИ
МОСКВА
ФИЗМАТЛИТ
2005

УДК 532.59	-j.	Издание осуществлено при поддержке
ББК 22.253	-^ТТ 32L Российского фонда фундаментальных
д 72	**	исследований по проекту 04-01-14057д
Дразин Ф. Введение в теорию гидродинамической устойчивости /
Пер. с англ. Г.Г. Цыпкина; Под ред. А.Т. Ильичева. — М.: ФИЗМАТЛИТ,
2005. - 288 с. - ISBN 5-9221-0629-5.
Данная книга посвящена неустойчивости течений и их переходу к турбу-
турбулентности, которые являются распространенными явлениями в природе и тех-
технике. Задачи об устойчивости течений часто возникают в таких областях
естественных наук, как прикладная математика, астрофизика, биология, гео-
геофизика, метеорология, океанография и физика. В книге приводятся математи-
математические модели движения жидкости, в которых проявляется гидродинамическая
неустойчивость, дается их теоретический анализ и описываются лабораторные
эксперименты. Примеры неустойчивости представлены при помощи многочис-
многочисленных рисунков. Обсуждается взаимоотношение понятий хаоса и перехода
к турбулентности. Идеи, изложенные в книге, иллюстрируются большим чис-
числом примеров и упражнений.
Для выпускников и аспирантов механико-математических и физических
факультетов университетов, ученых других специальностей.
ISBN 5-9221-0629-5 (русск.)	@ Cambridge University Press, 2002
ISBN 0-521-80427-2 (англ.)	© ФИЗМАТЛИТ, 2005 (русск.)

Содержание
Предисловие редактора перевода		7
Предисловие автора		9
1.	Общее введение		11
1.1.	Вступление		11
1.2.	Методы теории гидродинамической устойчивости		17
1.3.	Что читать и смотреть далее		19
2.	Введение в теорию стационарных течений, их бифуркации
и неустойчивость		21
2.1.	Бифуркация		21
2.2.	Неустойчивость		30
2.3.	Устойчивость и линеаризованная задача		39
3.	Неустойчивость Кельвина-Гельмгольца		59
3.1.	Основное течение		59
3.2.	Физическое описание неустойчивости		60
3.3.	Основные уравнения для возмущений		61
3.4.	Линеаризованная задача		63
3.5.	Поверхностные гравитационные волны		65
3.6.	Внутренние гравитационные волны 		65
3.7.	Неустойчивость Релея-Тейлора		66
3.8.	Сдвиговая неустойчивость		67
4.	Капиллярная неустойчивость струи		77
4.1. Теория Релея капиллярной неустойчивости струи жидкости .	77
5-	Развитие неустойчивости во времени и в пространстве . .	83
5.1.	* Эволюция возмущений в пространстве и во времени		83
5.2.	Слабонелинейная теория		90
5.3.	Уравнение для возмущений энергии		97
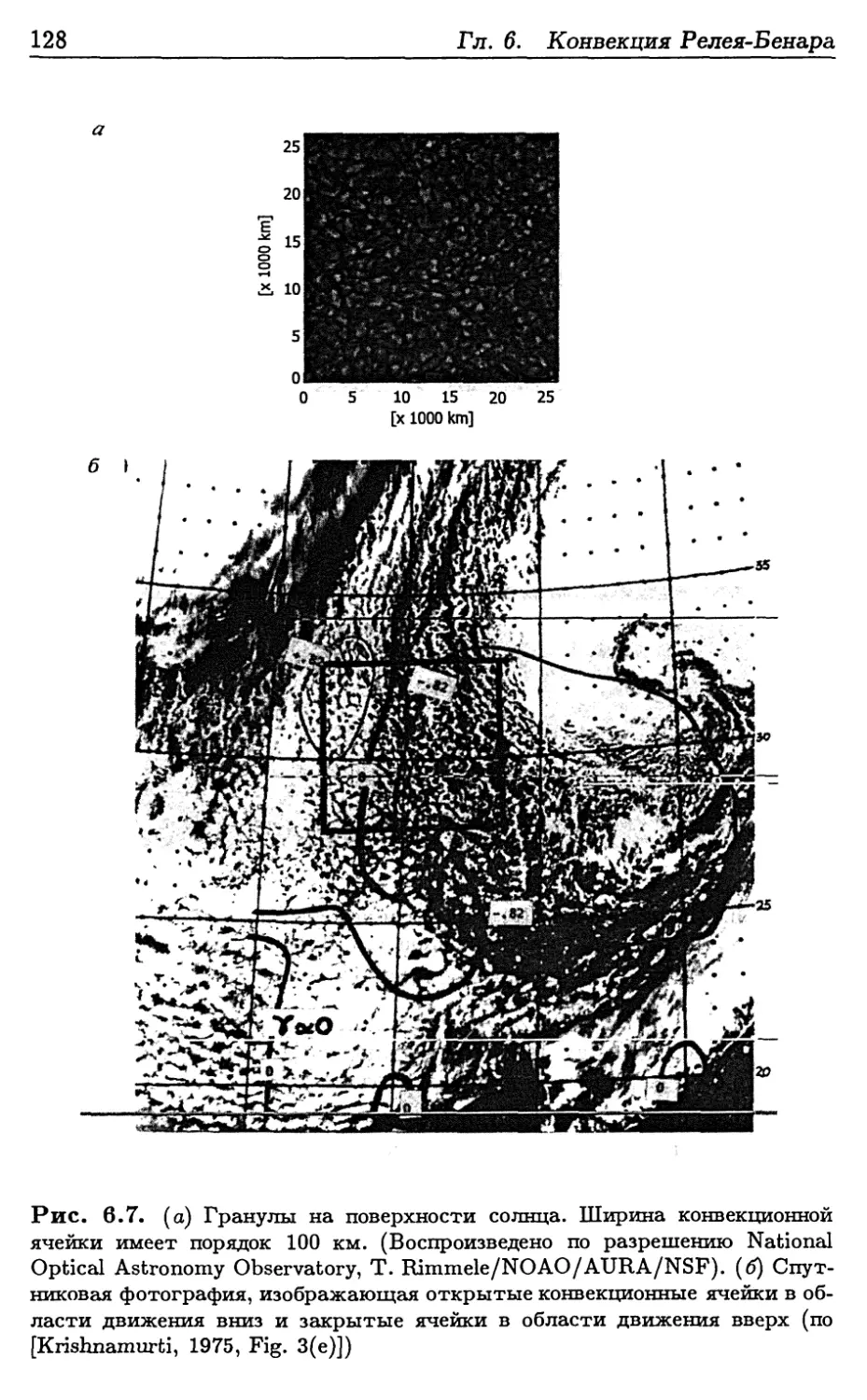
6-	Конвекция Релея-Бенара		109
6.1. Тепловая ^онт^тгпуя1 - • » • 		109
6.1. ({Ьздвгя^ироьйщщш задача		112
устойчивости 		113

6 Содержание
6.4. Нелинейная конвекция	117
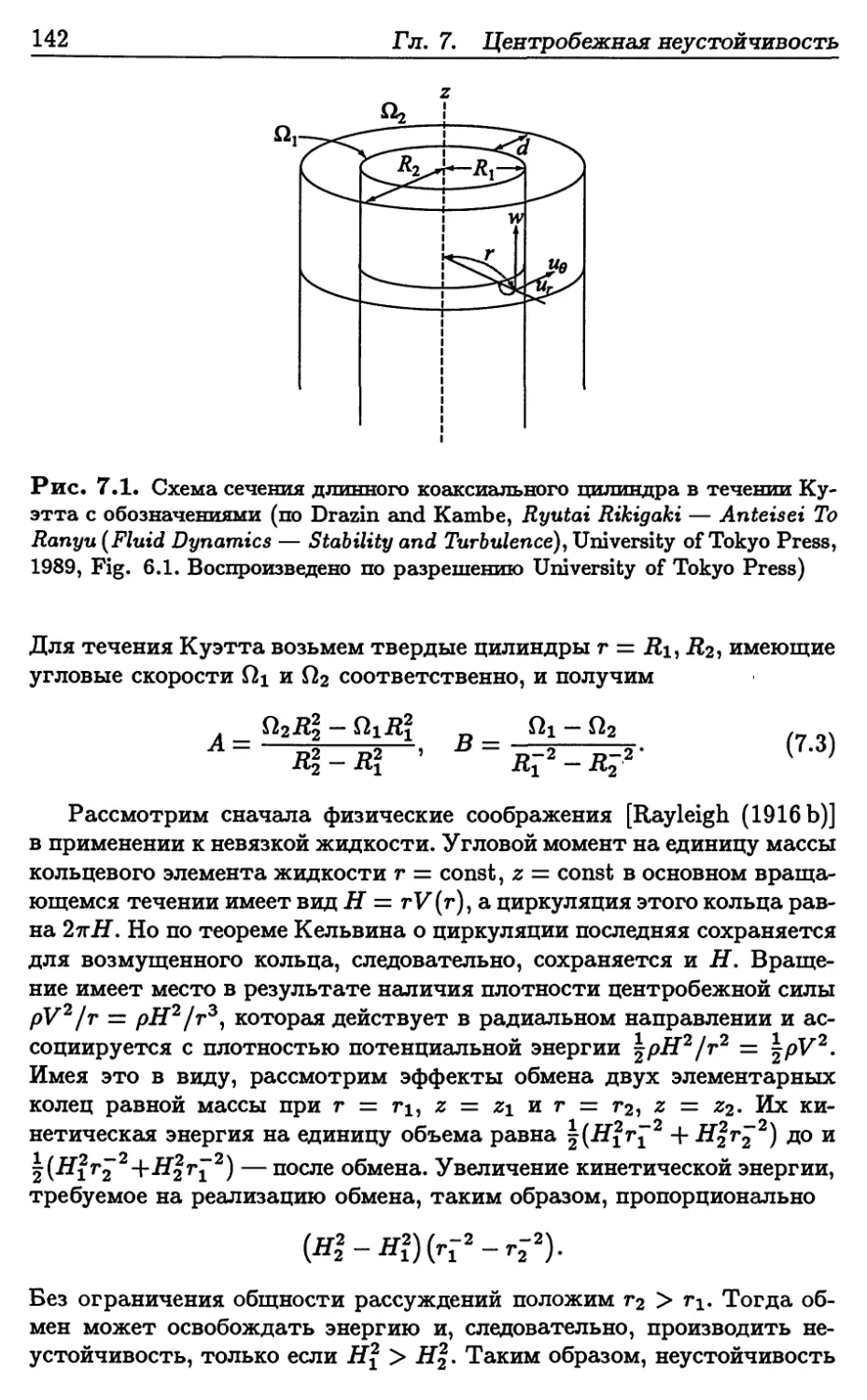
7.	Центробежная неустойчивость	141
7.1.	Вращающиеся течения	141
7.2.	Неустойчивость течения Куэтта	143
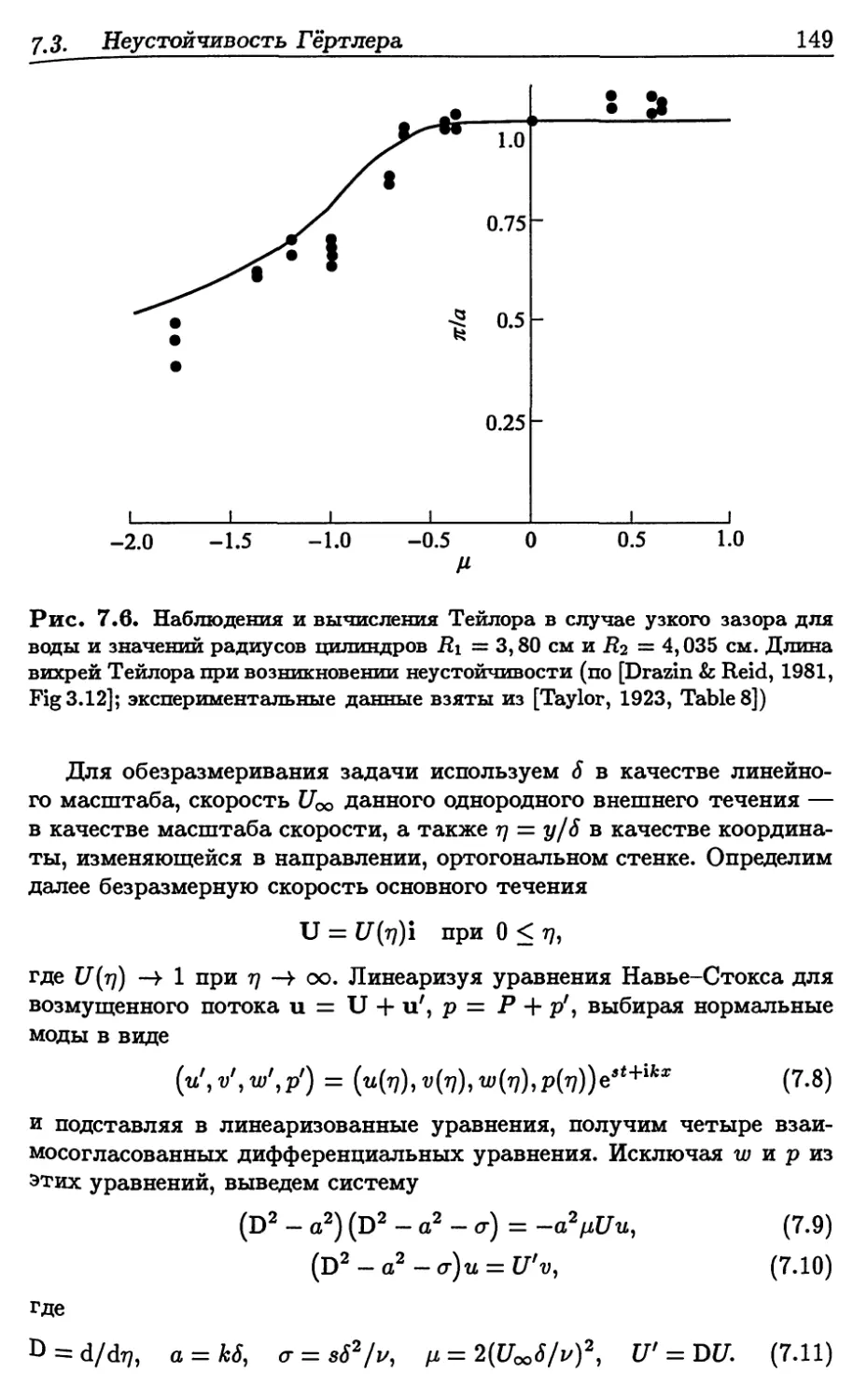
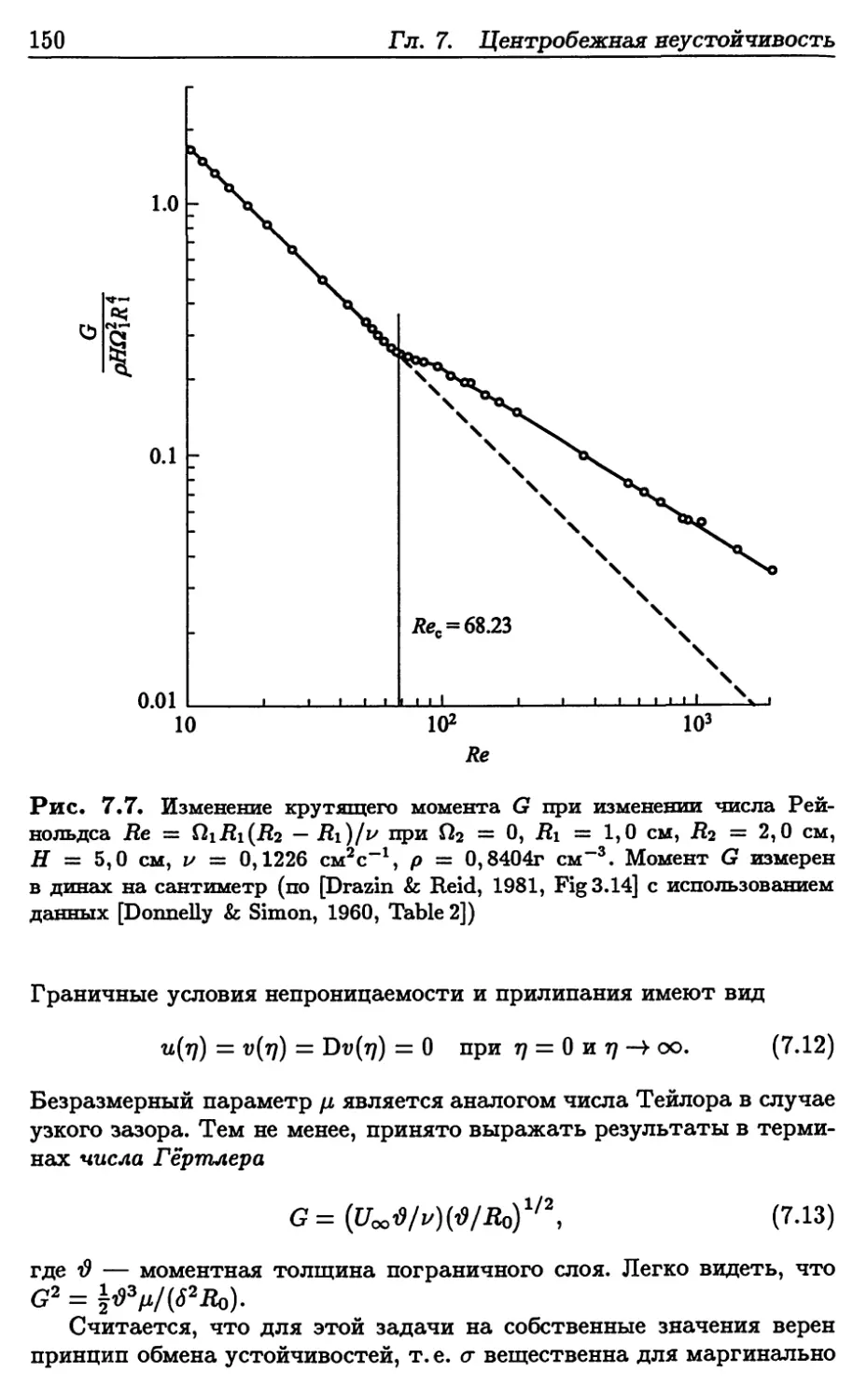
7.3.	Неустойчивость Гёртлера	148
8.	Устойчивость параллельных течений	157
8.1.	Устойчивость плоско-параллельных течений идеальной жид-
жидкости 	157
8.2.	Общие свойства задачи устойчивости Релея	163
8.3.	Характеристики устойчивости некоторых течений идеальной
жидкости	169
8.4.	Нелинейные возмущения параллельного течения идеальной
жидкости	174
8.5.	Устойчивость плоско-параллельных течений вязкой жидкости 176
8.6.	Некоторые общие свойства задачи Орра-Зоммерфельда .... 181
8.6.1.	Энергия	182
8.6.2.	Неустойчивость в невязком пределе 	184
8.7.	Характеристики устойчивости некоторых течений вязкой
жидкости	188
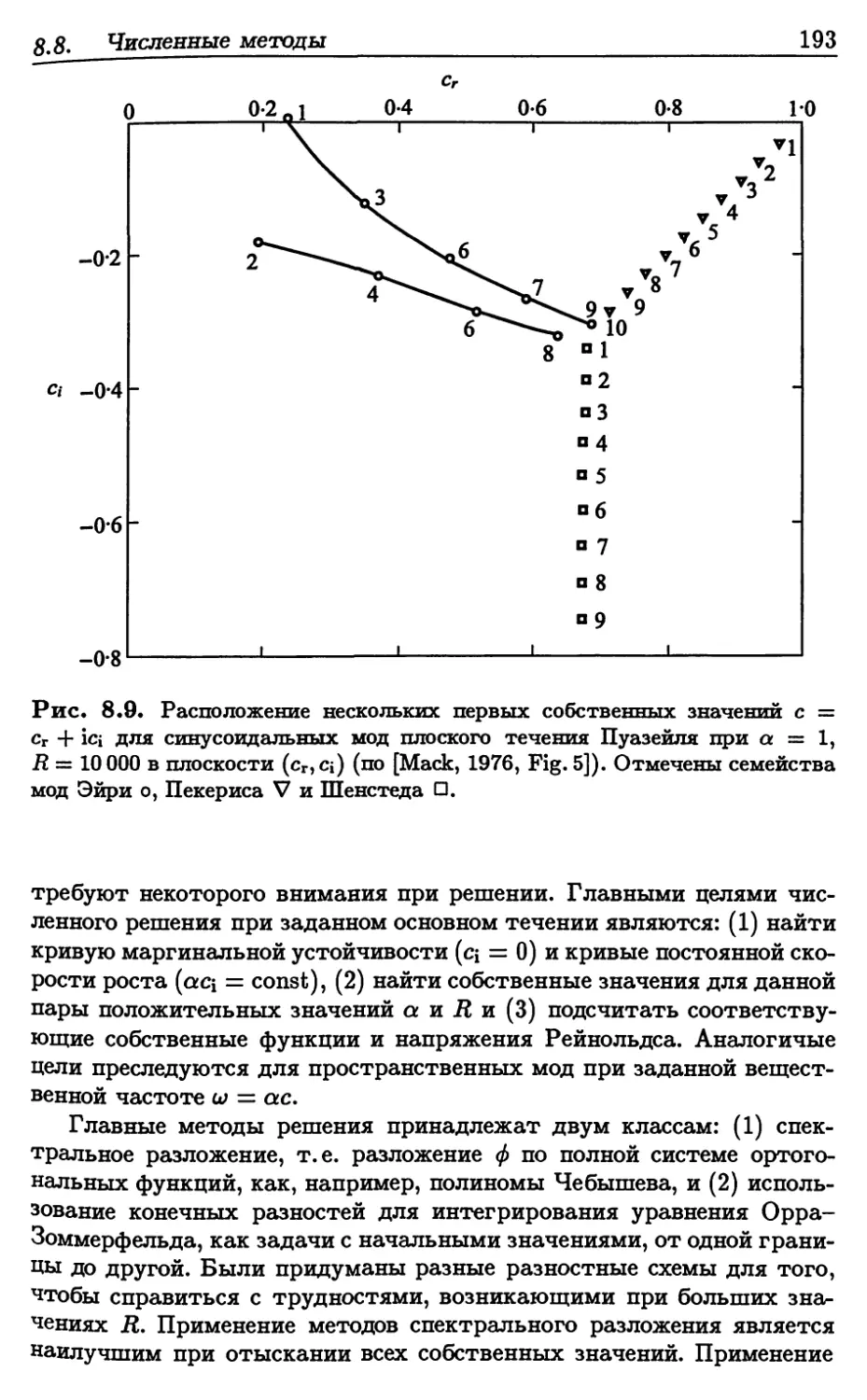
8.8.	*Численные методы решения задачи Орра-Зоммерфельда . . 192
8.9.	Экспериментальные результаты и нелинейная неустойчивость 194
8.10.	Устойчивость осесимметричных параллельных течений .... 200
9.	Пути к хаосу и турбулентность	233
9.1.	Эволюция течений при увеличении числа Рейнольдса	233
9.2.	Пути к хаосу и турбулентность	237
10.	Случаи перехода к турбулентности	241
10.1.	Синтез 	241
10.1.1.	Введение	 241
10.1.2.	Неустойчивость течения за плоской пластиной при ну-
нулевом угле атаки	243
10.2.	Переход течения с однородным потоком за телом плохо обте-
обтекаемой формы	246
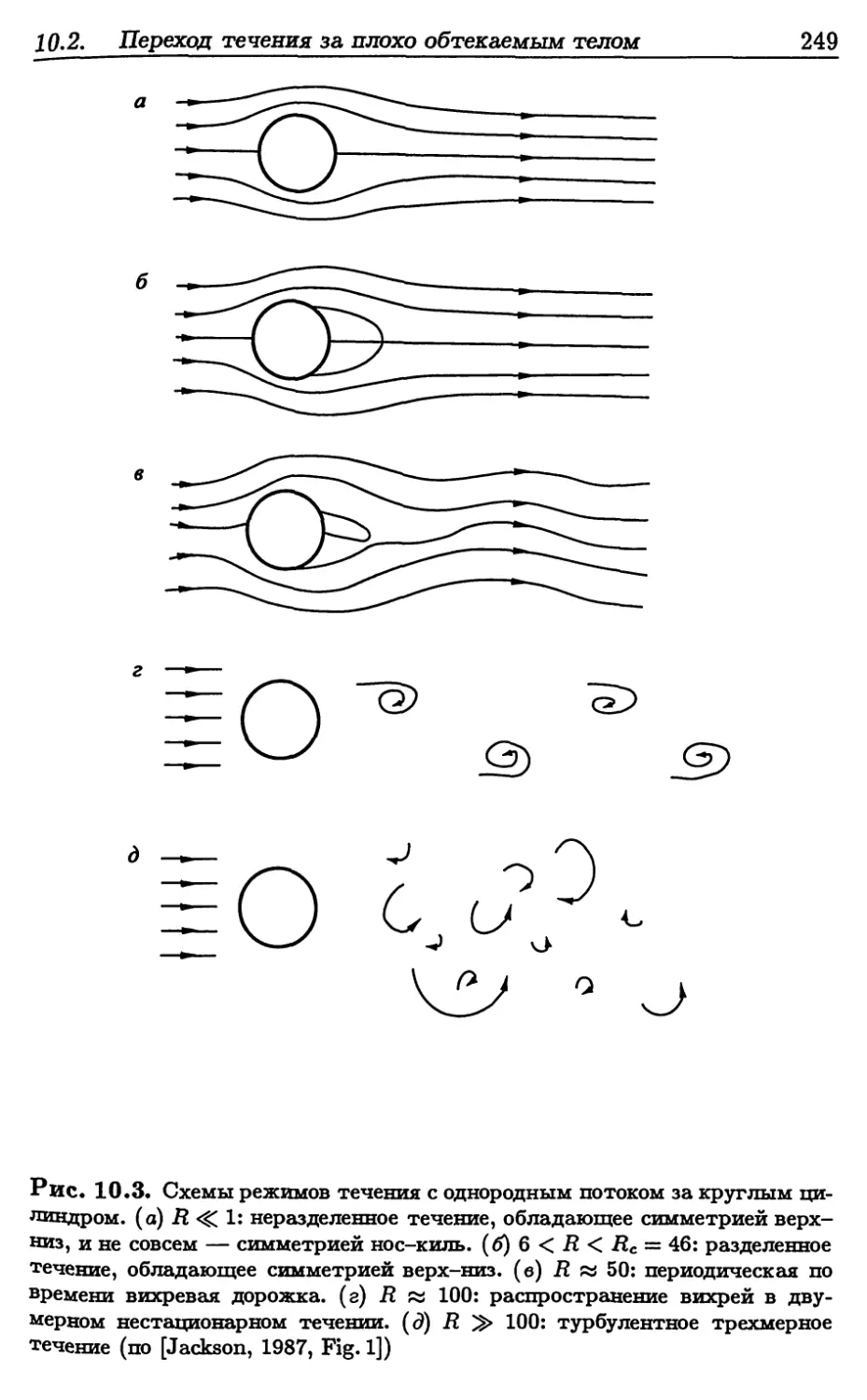
10.2.1.	Течение за круглым цилиндром	246
10.2.2.	Течение за сферой	251
10.3.	Переход течений в расходящемся канале	253
10.3.1.	Введение		253
10.3.2.	Асимптотические методы		254
10.3.3.	Некоторые парадоксы		259
10.3.4.	Нелинейные волны		260
10.3.5.	Выводы		261
Список литературы	264
Указатели 	279

Предисловие редактора перевода
Название книги недавно умершего известного английского ученого Фили-
Филипа Дразина вполне соответствует идее автора-создать учебник по теории
гидродинамической устойчивости. Написание такого учебника является до-
довольно непростой задачей и это связано с высокой степенью академичности
данной науки и вытекающими отсюда объективными трудностями доступ-
доступного изложения относящихся к ней фактов математического и физического
характеров. Все это оказало влияние на книгу, которая представляет собой
скорее монографию без изложения ряда деталей, необходимых для подробно-
подробного знакомства с положением дел в современной теории гидродинамической
устойчивости, чем стандартный учебник по методически освоенной облас-
области классической науки. С учебным пособием книгу явно сближают справоч-
справочный характер, а также приведенные в конце каждой главы многочисленные
упражнения, от самых легких до очень трудных, которые позволят терпе-
терпеливому читателю активным образом освоить теорию гидродинамической
устойчивости. Написанное выше ни в коей мере не умаляет ценности книги
как учебного пособия, тем более, что до сих пор такого пособия не было и
само по себе появление подобной книги вне всякого сомнения свидетельству-
свидетельствует о полноценном формировании теории гидродинамической устойчивости
в самостоятельный раздел гидромеханики, которому вполне может быть
придан классический статус.
К несомненным достоинствам книги можно отнести четкую формули-
формулировку и последующее изложение методов и задач теории гидродинамической
устойчивости. Так, в главе 2 книги излагается, по сути дела, метод нор-
нормальных мод, представляющий собой один из основных математических
инструментов линейной теории устойчивости, причем пристальное внима-
внимание уделяется очень важному обстоятельству непосредственной связи по-
потери устойчивости и возникновения бифуркации, приводящей к ответвле-
ответвлению вторичного режима от потерявшего устойчивость течения. В главе 5
вводятся фундаментальные понятия конвективной и абсолютной неустой-
неустойчивости, кратко дается представление о пространственном развитии воз-
возмущений, а также рассматриваются основные положения слабонелинейной
теории, которая учитывает влияние ведущих нелинейных эффектов малых
возмущений на экспоненциальный рост возмущений в результате этапа ли-
линейной неустойчивости. В главах 9 и 10 дается краткий обзор методов тео-
теории развитой неустойчивости, описывающих допустимые и типичные пути
к хаосу и турбулентности, с привлечением классических примеров обтека-
обтекания. В главах 3, 4, 6-8 на примерах классических задач о неустойчивости

8	Предисловие редактора перевода
Кельвина-Гельмгольца и струи с учетом капиллярных эффектов, конвек-
конвекции Релея-Бенара, центробежной неустойчивости, теории устойчивости па-
параллельных и почти параллельных течений иллюстририруется приложение
методов гидродинамической устойчивости. При изложении этого материала
автор не злоупотребляет абстрактными теориями, более того, у читателя
формируется вполне устойчивое (и совершенно справедливое) впечатление,
что высокая математика играет далеко не ведущую роль в данной области.
Трудности при качественном анализе возникают для неоднородных течений
уже на первом этапе неустойчивости — линейном, когда приходится решать
линейные уравнения с переменными коэффициентами, и в общем случае это
решение может быть выполнено до конца только численными методами.
Тем более на этапах развитой неустойчивости и перехода к турбулентнос-
турбулентности, наличие которых представляет собой интригующую особенность теории
гидродинамической устойчивости, численные методы представляют собой
основной инструмент теоретического изучения этих явлений. Едва ли не
самую важную роль в исследованиях на этапах развитой неустойчивости
играют эксперименты и натурные наблюдения, более того, даже типы пер-
первичных бифуркаций в сложных течениях могут быть идентифицированы
только экспериментально. Очень полезным для изучения развития неустой-
неустойчивости было бы знакомство с цитированными в книге фильмами, иллюст-
иллюстрирующими это явление. К сожалению, доступ к библиотеке этих фильмов
затруднен для отечественного читателя.
За пределами изложения остался ряд современных аналитических мето-
методов теории устойчивости, таких, например, как метод исследования пере-
перехода к неустойчивости при помощи функции Эванса и модификация мето-
метода Ляпунова для бесконечномерных гамильтоновых систем с симметриями.
Эффективность этих методов, однако, ограничена задачами устойчивости
весьма частного вида, и их использование актуально лишь для специалис-
специалистов, активно работающих в данной области.
В книге представлена довольно полная библиография, иллюстрирующая
историческое развитие и современное состояние теории гидродинамической
устойчивости и содержащая ссылки как на теоретические, так и на экспе-
экспериментальные работы.
А. Т. Ильичев

Посвящается Юдифь
Предисловие автора
Данный текст появился из записей лекций, прочитанных студентам Бри-
Бристольского университета в восьмидесятых годах. Эти записи были пере-
переработаны и напечатаны для курса лекций, прочитанных аспирантам То-
Токийского университета в 1995 г., который способствовал сотрудничеству
с профессором Цутому Камбе (Tsutomu Kambe) при написании книги на
японском языке "Динамика жидкости — устойчивость и турбулентность",
опубликованной издательством Токийского университета в 1998 г. Насто-
Настоящая книга является расширенным английским вариантом первой части
книги, изданной на японском языке. Доработанная версия была написана
для лекционного курса, прочитанного студентам и аспирантам Оксфорд-
Оксфордского университета в 2001 г. Я благодарен многим студентам Бристоля,
Токио и Оксфорда, которые стимулировали меня яснее выражать мои идеи,
а также за их желание узнать больше. Я особенно благодарен профессору
Камбе за те факты, что узнал от него и включил в текст.
В результате получился скорее учебник, чем исследовательская моно-
монография. Хотя, несомненно, многие вопросы текущих исследований были
включены в текст, но не было предпринято попыток подвести читателя
к переднему фронту этих исследований. Так, математическая теория пред-
представлена по возможности просто и кратко с привлечением многочисленных
примеров и доступных упражнений, разработанных специально для студен-
студентов. Я процитировал много публикаций, возможно в силу глубоко укоренив-
укоренившейся привычки, и уж, конечно, не потому, что когда-либо мог подумать о
большом числе студентов, заботящихся о ссылках — пусть хотя бы обратят
внимание на них. Явное намерение включения ссылок состоит в стимулиро-
стимулировании преподавателей следить за различными деталями и, что более важно,
использовать иллюстрации и фильмы, которые дополняют книгу в процессе
обучения.
Конечно, там где только представляется целесообразным, в тексте дает-
дается описание соответствующих гидромеханических экспериментов. Это до-
достигается прежде всего включением иллюстраций. Однако практические
ограничения объема привели к дополнению иллюстративного материала
в этой книге цитированием других источников, в особенности прекрас-
***** книг: Albom of fluid motion, ed. Van Dyke A982) и Visualized Flow, ed.
JNakayma A988). Гидродинамическая неустойчивость, однако, является су-
существенно динамическим явлением, поэтому фильмы могут передать мно-
многие вещи, которые иллюстрации отразить не в состоянии. В соответствии

Предисловие автора
с этим, часто делаются ссылки на ряд прекрасных классических фильмов
Национального Центра Образования. Эти фильмы являются старыми и бо-
более не поступают в продажу. Они были переизданы в качестве видеофиль-
видеофильмов корпорацией Британская Энциклопедия. Более того, недавно был вы-
выпущен компактный диск Homsy et al. (CD2000) Multi-media fluid mechanics.
Его раздел Video Library содержит ряд коротких видеофильмов, которые
имеют отношение к предмету этой книги и цитируются в тексте. Надеюсь,
что новые видеофильмы будут в будущем занесены на этот диск, и уверен,
что скоро достижения в компьютерных технологиях приведут к улучшению
иллюстративного материала настоящей книги.
Предполагается, что читатели этой книги знакомы с элементами тео-
теории и экспериментальным материалом гидродинамики в объеме, который
обычно содержится в стандартных курсах по динамике идеальной и вязкой
жидкостей. Так, теория уравнений движения Эйлера, потенциальных те-
течений, теория вихрей, уравнения Навье-Стокса, теория пограничного слоя
и отрыва пограничного слоя и так далее, будут использоваться с небольши-
небольшими объяснениями в тексте по мере надобности. Это касается также элемен-
элементарной теории линейной алгебры, комплексных переменных, обыкновенных
уравнений и уравнений в частных производных. Разделы, абзацы и упраж-
упражнения, которые требуют более глубоких знаний или относятся к более спе-
специальным вопросам, помечены звездочками.
Я благодарен профессору Уильяму Риду (William H. Reid) за его вели-
великодушие, позволившее мне воспроизвести с небольшими изменениями гла-
главы 1, 4 и 5 нашей книги Hydrodynamic stability, в качестве раздела 1.1,
глав 3 и 4 настоящей книги, а также некоторые упражнения. Я благода-
благодарен ему за огромное количество информации о том, как писать книги, и о
теории гидродинамической устойчивости, которую я получил от него за
многие десятилетия. Я благодарен профессору Герберту Гапперту (Herbert
Е. Huppert), доктору Ричарду Керсуэллу (Richard R. Kerswell) и профес-
профессору Стефану Моббсу (Stephen D. Mobbs) за идеи, которые легли в основу
упражнений, приведенных в книге. Я благодарен доктору Алану МакАль-
пину (Alan Me Alpine) за материалы для рисунка 8.10. Я благодарен док-
доктору Альваро Месеге (Alvaro Meseguer) и профессору Николасу Трефете-
ну (L. Nicholas Trefethen) за их конструктивные комментарии, относящие-
относящиеся к содержанию отдельных частей рукописи и за копии рис. 8.14 и 8.15.
Я благодарен профессору Уильяму Сэрику (William Saric) за дискуссию,
проливающую свет на задачу о течении за плоской пластиной. Я благода-
благодарен владельцам прав за их великодушное разрешение на воспроизведение
многих рисунков в этой книге и тем авторам, которые выразили согласие
на публикацию их оригинальных рисунков.
Филип Дразин
Университет Бата
Июль, 2001

Глава 1
Общее введение
Кто любит наставление, тот любит знание...
Притч. 12, 1
В этой главе изложение начинается с неформального определения по-
понятия устойчивости и объяснения природы неустойчивости конкрет-
конкретного течения — течения в трубе, в качестве базовой модели. Эта мо-
модель иллюстрирует важность неустойчивости как предварительной
стадии перехода к турбулентности. Кратко представлены основные
методы изучения неустойчивости течений.
1.1. Вступление
Предметом изучения теории гидродинамической устойчивости явля-
являются устойчивость и неустойчивость движения жидкостей.
Понятие устойчивости состояния физической или математической
системы было осознано в восемнадцатом веке, а в девятнадцатом веке
Клерк Максвелл (см. [Campbell & Garnett, 1882, p. 440]) ясно выразил
качественную идею:
Когда ... бесконечно малое возмущение данного состояния будет изменять-
изменяться только на бесконечно малое количество в некоторый будущий момент
времени, положение системы, является ли оно покоем или движением, назо-
назовем устойчивым; но когда бесконечно малое изменение в данном состоянии
может принести к конечному отклонению системы за конечное время, поло-
положение системы назовем неустойчивым.
Таким образом, теория гидродинамической устойчивости есть
важная часть гидромеханики, в силу того обстоятельства, что не-
неустойчивое течение ненаблюдаемо и в реальности быстро разрушает-
разрушается какими-либо "малыми изменениями". С другой стороны, неустой-

12
Гл. 1. Общее введение
Рис. 1.1. Эксперимент Рейнольдса по исследованию течения в трубе
[Reynolds, 1883, Fig. 13]
чивые течения часто эволюционируют в важное состояние движения,
называемое турбулентностью, с хаотическими трехмерными вихре-
вихревыми полями, которые обладают широким спектром временных и про-
пространственных масштабов.
Важные проблемы гидродинамической устойчивости были опре-
определены и сформулированы в девятнадцатом веке преимущественно
Гельмгольцем, Кельвином, Релеем и Рейнольдсом. Трудно обозначить
эти проблемы проще, чем это сделал Осборн Рейнольде в 1883 г., опи-
описав ряд своих классических экспериментов по неустойчивости течения
в трубе (рис. 1 с безымянным человеком викторианской эпохи, кото-
который изображен для сравнения масштабов).
Эксперименты были проведены на трех трубах... . Диаметр труб был около
1 дюйма, 1/2 дюйма, 1/4 дюйма. Все они были ... соединены с соплами, так
что вода могла втекать в них без возмущений. Вода прокачивалась через
трубы извне большого стеклянного резервуара, в котором были заключены

1,1. Вступление	 13
Рис. 1.2. Схемы (а) ламинарного течения в трубе, показанного окрашен-
окрашенной полоской; F) перехода к турбулентному течению в трубе; и (б) перехода
к турбулентному течению, видимого при освещении вспышкой [Reynolds,
1883, Figs. 3, 4 и 5]
трубы, струя или струйки окрашенной жидкости втекали в трубы вместе
с чистой водой.
Общие результаты были следующими:
A)	Когда скорости были достаточно малыми, слой окрашенной жидкос-
жидкости растягивался в красивую прямую линию через всю трубу, рис. 1.2 (а).
B)	Если вода в резервуаре не была приведена в состояние покоя, то
при достаточно малых скоростях слой смещался относительно трубы, но
волнистости не проявлялось.
C)	По мере того как скорость понемногу увеличивалась, в некоторой
точке трубы, всегда на значительном расстоянии от раструба сопла или
водозаборника, окрашенная полоска перемешивалась с окружающей водой,
так что часть трубы ниже по течению заполнялась окрашенной водой, как
^то изображено на рис. 1.2 (б).
Всякое увеличение скорости приближало точку разрушения струи к рас-
TPJf6y, но она его не достигала ни при каких скоростях.
Наблюдение за трубой при освещении светом электрической вспышки
показало, что окрашенная масса трасформируется в массу более или менее
отчетливых завитков, отвечающих вихрям, как показано на рис. 1.2 (в).
* Рейнольде пошел дальше, чтобы показать, что ламинарное тече-
течение — гладкое течение, описанное им в абзаце A), — разрушается,
когда отношение Va/v превосходит определенное критическое значе-
значение, где V является наибольшей скоростью жидкости в трубе, а —
радиус трубы, a v — кинематическая вязкость воды при соответству-
соответствующей температуре. Безразмерное число Vajv, названное числом Рей-
«ойд, определяет класс динамически подобных течений в трубе;

14	Гл. 1. Общее введение
Рис, 1«3« Схема турбулентных пятен в трубе [Reynolds, 1883, Fig. 16]
будем обозначать это число буквой R. Ряд экспериментов определил
величину критического число Рейнольдса Rc в окрестности 13000.
Однако,
критическая скорость была очень чувствительна к возмущениям в жидкос-
жидкости перед входом в трубы ....
Это обстоятельство сразу подсказало идею, что данное условие могло бы
быть условием неустойчивости для возмущений определенной амплитуды
и [устойчивости] для возмущений меньшей амплитуды.
Сразу за критическим значением скорости наблюдалось
Другое явление ... состояло в том, что возмущения носили прерывистый ха-
характер. Возмущение вдруг внезапно возникало через определенное растоя-
ние вдоль трубы и пропадало, а затем возникало снова, вызывая "вспышки",
которые часто появлялись последовательно в некоторой точке трубы. Ситу-
Ситуация, когда вспышки быстро следуют друг за другом, проиллюстрирована
на рис. 1.3.
Такие "вспышки" получили название турбулентных пятен или тур-
турбулентных вспышек. При значениях числа Рейнольдса ниже крити-
критического имело место ламинарное течение Пуазейля в трубе с парабо-
параболическим профилем скорости, при этом сила сопротивления со сто-
стороны трубы,- была пропорциональна средней скорости. Рейнольде об-
обнаружил, что по мере того, как скорость возрастала выше этого кри-
критического значения, течение становится турбулентным с хаотическим
трехмерным движением, которое сильно перемешивает краситель при
движении жидкости по трубе. Сопротивление турбулентному потоку
растет пропорционально квадрату средней скорости.
Оригинальная установка Рейнольдса находится в Манчестере
в Англии и была использована в 1970 г. для повторения его экспери-
экспериментов. Именно поэтому фотографии течения" в этой установке [Van
Dyke, 1982, Fig. 103] предлагаются вниманию читателя. Позднее экспе-
экспериментаторы вводили возмущения конечной амплитуды на входе или
использовали трубы с шероховатыми стенками, чтобы снизить число
Рейнольдса Rc до 2000 и, наоборот, создавали такие регулярные те-
течения в трубах с настолько гладкими стенками, что Rc достигало 105
или даже более. Описание, данное Рейнольдсом, иллюстрирует цели

1.1. Вступление	15
изучения гидродинамической устойчивости: определить, является ли
данный ламинарный поток неустойчивым и если это так, то как он
разрушается и переходит в турбулентность или в какое-нибудь другое
ламинарное течение.
Методы исследования устойчивости течений появились еще во вре-
времена Рейнольдса. Метод нормальных мод для изучения колебаний и
неустойчивости динамических систем частиц и твердых тел был уже
хорошо разработан. Известное решение уравнений движения Ньютона
или Лагранжа для рассматриваемой системы подвергалось возмуще-
возмущению. Уравнения сводились к линейным при пренебрежении произве-
произведениями возмущений. Далее предполагалось, что возмущения каждой
искомой функции могут быть разложены по независимым компонен-
компонентам или модам, изменяющимся со временем t как est с некоторой по-
постоянной s — в общем случае комплексной величиной. Значения s для
мод вычислялись из линеаризованных уравнений. Если оказывалось,
что действительная часть s положительна для какой-либо моды, то
система считалась неустойчивой, потому что начальное малое возму-
возмущение системы росло экспоненциально со временем вплоть до того
момента, когда оно уже переставало быть малым. Стоке, Кельвин и
Релей адаптировали метод нормальных мод к задачам гидродинами-
гидродинамики. Существенное математическое различие между гидродинамикой и
динамикой частиц заключается в том, что в первом случае уравнения
движения являются уравнениями в частных производных, а во-втором
— обыкновенными дифференциальными уравнениями. Это различие
приводит ко многим техническим трудностям в задачах гидродина-
гидродинамической устойчивости, которые до настоящего времени были пол-
полностью преодолены только для некоторых классов течений, имеющих
простую конфигурацию.
Конечно, эксперименты Рейнольдса сами по себе еще не до конца
поняты [Eliahou et a/., 1998]. Однако мы можем объяснить качественно
переход от ламинарного течения к турбулентному с некоторой долей
уверенности. Течение Пуазейля в трубе с параболическим профилем
является устойчивым по отношению к бесконечно малым возмуще-
возмущениям при всех числах Рейнольдса. Для существенно малых значений
числа Рейнольдса, скажем, для R < Rg, все возмущения параболи-
параболического течения, как большие так и малые, затухают со временем;
наблюдения показывают, что Rg га 2000. Несколько ниже наблюдае-
наблюдаемого критического числа Рейнольдса возмущения могут расти, если
они не очень малы. Выше значения критического числа Рейнольд-
Рейнольдса довольно малые возмущения, возможно возникающие на входе или
порожденные неровностями на стенках трубы, растут быстро, имея
колебательный характер. Вскоре возмущения вырастают до таких
Размеров, что влияние нелинейности становится сильным и формиру-
формируется крупномасштабные вихри (рис. 1.2 (в)) или турбулентные пятна
(рис. 1.3). (Такой механизм, посредством которого течение, устойчи-

16	Гл. 1. Общее введение
вое по отношению ко всем бесконечно малым возмущениям, внезапно
меняется на турбулентное или около турбулентное течение из-за дей-
действия возмущений конечной амплитуды, часто называется побочным
переходом (bypass transition). По мере того, как возрастает число Рей-
нольдса, порог для амплитуды возмущений, вызывающих неустойчи-
неустойчивость, уменьшается. Для больших чисел Рейнольдса турбулентность
возникает немедленно как результат неизбежного присутствия возму-
возмущений малой амплитуды и поток становится случайным, существенно
трехмерным (т.е. существенно не осесимметрическим) и везде силь-
сильно нелинейным1. Характер неустойчивости течения Пуазейля в трубе
отличается от характера неустойчивости плоского течения Пуазейля,
которое является неустойчивым по отношению к бесконечно малым
возмущениям при достаточно больших значениях числа Рейнольдса.
Объяснение этого различия дает теория линейной устойчивости тече-
течения Пуазейля в трубе, изложенная в параграфе 8.10. Однако на прак-
практике неустойчивость плоского течения Пуазейля обнаруживает сход-
сходство с неустойчивостью течения Пуазейля в трубе, по крайней мере
на первый взгляд (см. рис. 1.4).
Физические эффекты экспериментов Рейнольдса по исследованию
неустойчивости течения Пуазейля в трубе ярко проиллюстрированы
в фильме [Stewart, FL1968], сделанным для Центра развития обра-
образования. Этот ролик состоит из отредактированных отрывков более
протяженного фильма о турбулентности [Stewart, F1968]. Детали об
этих и других фильмах о гидродинамической устойчивости могут
быть найдены в конце этой книги после списка литературы. Видео-
Видеофильмы эксперимента можно увидеть на компакт-диске [Homsy et al.,
CD2000]; этот диск является более доступным, чем сам ролик филь-
фильма или его видео-версии, хотя видеофильмы на компакт диске коро-
короче. В собрании фильмов Видео-библиотека в подразделах "Reynolds
Transition Apparatus" и "Reynolds Transition Experiment", демонст-
демонстрируются некоторые короткие видеофильмы недавних эксперимен-
экспериментов на оригинальной установке Рейнольдса; дальнейшие эксперимен-
эксперименты могут быть найдены в подразделах "Pipe Flow", "Tube Flow"
и "Turbulent Pipe Flow". В разделе Boundary Layers и подразделах
"Instability, Transition and Turbulence" и "Instability and Transition in
Pipe and Duct Flow" доступны и другие короткие видеофильмы.
1 Множество черт перехода от ламинарного течения к турбулентному можно
легко увидеть, наблюдая дым от сигареты. Зажгите сигарету, поднимите заж-
зажженный конец вверх и наблюдайте за дымом, как он поднимается. См. также [Van
Dyke,1982, Fig. 107].

1.2. Методы теории гидродинамической устойчивости	17
Рис. 1.4. Турбулентное пятно, вызванное струями, бьющими из стен-
стенки, для плоского течения Пуазейля при R = 1000, где R = Vd/v, V -
максимальная скорость течения; стенки находятся на расстоянии 2d друг
от друга [Carlson et a/., 1982, Fig. 4]
1.2. Методы теории гидродинамической
устойчивости
Прежде всего полезно заметить, что гидродинамическая устойчивость
имеет много общего с устойчивостью в многих других областях, та-
таких как магнитная гидродинамика, физика плазмы, теория упругости,
реология, теория горения и общая теория относительности. Физика
явлений может сильно отличаться, но математические методы иссле-
исследования аналогичны. Математическое существо вопроса заключается
ватом, что физические явления моделируются уравнениями в част-
частных производных и исследуется устойчивость известных стационар-
стационарных и нестационарных решений. Гидродинамика является достаточно
зрелой наукой (уравнения Навье-Стокса были выведены в первой по-
половине девятнадцатого века), а заданное движение жидкости часто
н?трудно воспроизвести и наблюдать в лаборатории, так что гидро-
гидродинамическая устойчивость может служить прототипом аналогичных
свойств в нелинейной физике в более широком контексте.
Неустойчивость течений и переход к турблентности изучается раз-
разными способами в рамках следующих пяти более или менее различных
направлений.

18	Гл. 1. Общее введение
A)	Природные явления и лабораторные эксперименты. Очевидно,
не потребовалась бы теория, описывающая гидродинамическую
неустойчивость, если бы последняя не проявлялась в природ-
природных явлениях, процессах, связанных с человеческой деятельнос-
деятельностью, и лабораторных экспериментах. Наблюдения природных
явлений и экспериментов, таким образом, преставляют собой
предварительный этап изучения. Все теоретические исследова-
исследования должны быть связаны прямо или косвенно с объяснениями
этих наблюдений. Наоборот, теоретические представления явля-
являются необходимыми для описания и интерпретации наблюдений.
B)	Численные эксперименты. Вычислительная гидродинамика ста-
стала играть все большую роль в исследовании гидродинамической
устойчивости с 1980 г., с тех самых пор, как возможности чис-
численного моделирования возросли, а компьютеры увеличили свое
быстродействие и стали обладать большей памятью, в резуль-
результате чего уравнения Навье-Стокса могут быть решены для все
большего числа течений. Действительно, вычислительная гид-
гидродинамика находится сейчас на такой стадии развития, что мо-
может конкурировать с лабораторными исследованиями гидроди-
гидродинамической устойчивости, моделируя контрольные эксперимен-
эксперименты.
C)	Линейная и слабо нелинейная теория. Линеаризация методом
малых возмущений заданного основного течения является са-
самым первым методом, который следует применять в теории гид-
гидродинамической устойчивости, и этот метод использовался го-
гораздо чаще, чем другие вплоть до шестидесятых годов XX века.
Он остается основным в теории и до сих пор. В то же время,
слабо нелинейная теория, которая строится на основе линейной
теории при помощи рассмотрения главных нелинейных эффек-
эффектов для малых возмущений, берет начало в девятнадцатом веке
и интенсивно развивалась, начиная с 1960 г.
D)	Качественная теория бифуркаций и хаоса. Математическая те-
теория дифференциальных уравнений показывает, что течения мо-
могут развиваться по мере того, как безразмерные параметры, на-
например, число Рейнольдса, возрастают. Последовательность би-
бифуркаций от одного режима течения к другому при возрастании
параметра не может быть предсказана количественно без акку-
аккуратных численных расчетов, но допустимые и типичные пути
к хаосу и, следовательно, к турбулентности могут быть уста-
установлены математической теорией на качественном уровне. Та-
Таким образом, качественная теория динамических систем, также
как и слабо нелинейный анализ, очерчивают полезные концеп-

1.3. Что читать и далее	19
туальные рамки для интерпретации лабораторных и численных
экспериментов.
E) Сильно нелинейная теория. Имеются различные математичес-
математически точные методы, особенно теорема Серрина (Serrin) и прямой
метод Ляпунова, которые дают детальные результаты в случае
произвольно больших возмущений для конкретных течений. Эти
результаты являются обычно ограничениями, дающими доста-
достаточные условия для устойчивости течения, или ограничениями
на величины, характеризующие течение.
В книге планируется подробно развить основные идеи и методы
теории и затем применить их к исследованию неустойчивости неко-
некоторых течений, устанавливая связь между теоретическими и экспери-
экспериментальными результатами. Этот план подробно отражен в оглавле-
оглавлении. Во-первых, в этой и в следующей главах многие идеи и методы
будут описаны и проиллюстрированы на простых примерах. Затем,
раз за разом, эти методы и идеи, вместе с некоторыми другими, будут
использоваться в последующих главах для того, чтобы установить
условия устойчивости некоторых важных классов течений. Теория
гидродинамической устойчивости была применена к такому множес-
множеству различных классов течений, что невозможно, да и нежелательно,
дать исчерпывающую трактовку приложений данной теории в этой
книге. Выбор приложений является произвольным и, возможно, чрез-
чрезмерно продиктован традицией. Тем не менее этот выбор покрывает
многие полезные и важные классы течений и хорошо иллюстрирует
пять классов основных методов, кратко изложенных выше.
1.3. Что читать и смотреть далее
Для того чтобы найти более полное изложение некоторых аспектов,
затронутых в этой книге, возможно будет полезным обратиться к сле-
следующим книгам, хотя многие из них устарели, будучи написанными
до того, как пришествие компьютеров оказало сильное воздействие на
теорию гидродинамической устойчивости. (Возможно, вычислитель-
вычислительная гидродинамика привела к наиболее важным достижениям в недав-
недавние годы, а теория динамических систем или приложения этой теории
привели к расширению круга новых физических задач). Тем не ме-
менее, предмет исследований является старым, важность большинства
результатов выдержало испытание временем, поэтому эти книги все
еЩе представляют научную ценность.
Монография [Betchov & Criminale, 1967] заключает в себе, главным
образом, теорию устойчивости плоско-параллельных течений, особен-
особенно хорошо отражая вычислительные аспекты проблемы. Внушитель-
Внушительный трактат [Chandrasekhar, 1961] является сокровищницей ислледо-

20	Гл. 2. Общее введение
вательских результатов как в теоретической, так и в эксперименталь-
экспериментальной областях. В книге сделан акцент на задачи линейной устойчивости
течений, отличных от плоско-параллельных, с учетом влияния внеш-
внешних магнитных полей, плавучести и сил Кориолиса. Освещение лите-
литературы является необычным, информативным и представляет боль-
большой интерес. В монографии [Drazin & Reid, 1981] предмет изложен
с высокой степенью подробности. Монография содержит отдельные за-
задачи для студентов, некоторые из этих задач довольно просты. Книга
[Huerre & Rossi, 1998] представляет собой набор лекций, хотя заметно
более высокого уровня, чем настоящая книга. Это обзор, относящийся,
главным образом, к линейной устойчивости плоско-параллельных те-
течений, с хорошим современным освещением численных, эксперимен-
экспериментальных и теоретических результатов. В монографии [Joseph, 1976]
сделан упор на нелинейные аспекты, особенно на энергетический ме-
метод, в то же время большой материал посвящен основным (базовым)
течениям. Книга [Landau & Lifshitz, 1987] является прекрасным трак-
трактатом, замаскированным под учебник, где физические особенности
гидродинамической устойчивости изложены с мастерством и краткос-
краткостью. Монография [Lin, 1955], дополняющая трактат Чандрасекхара,
является классической и посвящена, главным образом, вопросам ли-
линейной устойчивости плоско-параллельных течений вязкой жидкости.
Монография [Schmid & Henningson, 2001] представляет собой совре-
современное и всеобъемлющее исследование по устойчивости и переходам
к неустойчивости плоско-параллельных течений.
Мы уже обращались к иллюстративному материалу, чтобы обога-
обогатить понимание эксперимента Рейнольдса. Такие иллюстрации, без
сомнения, представляют ценность и для понимания многих других
типов гидродинамической неустойчивости. Книга [Van Dyke, 1982] яв-
является прекрасным собранием фотографий течений, в том числе и
гидродинамически неустойчивых. Накаяма [Nakayama, 1988] собрал
другую замечательную коллекцию фотографий течений, некоторые
из них также подвержены гидродинамической неустойчивости. Обра-
Обратите внимание на эффекты гидродинамической устойчивости, изобра-
изображенные на этих фотографиях, обдумайте их и соотнесите их с теорией,
излагаемой в этой книге.
Гидродинамическая неустойчивость, тем не менее, представляет
собой динамическое явление, которое лучше всего воспринимается
в фильмах. Множество соответствующих фильмов, роликов, видео-
видеофильмов и компакт-диск [Homsy et aZ., CD2000], перечислены в переч-
перечне фильмов, представленном в конце списка литературы. Представ-
Представляется уместным добавить здесь несколько слов в предостережение.
Результаты визуализации нестационарных течений весьма легко не-
неправильно интерпретировать. Будьте осторожны. В частности, про-
проверьте, правильно ли вы понимаете различие между линиями тока,
струйками и траекториями, прежде чем сделать какие-либо выводы.

Глава 2
Введение в теорию стационарных
течений, их бифуркации и неустойчивость
... кто слушает слова Мои сии и исполняет их,
уподоблю мужу благоразумному, который построил
дом свой на камне; и пошел дождь, и разошлись реки,
и подули ветры, и устремились на дом тот, и он
не упал, потому что основан был на камне.
Мф. 7, 24-25
В настоящей главе при помощи простых иллюстративных примеров
обыкновенных дифференциальных уравнений описаны общие типы
бифуркации, т. е. общие типы смены режимов течения. Показано, что
бифуркации возникают, когда возникает неустойчивость. В заключе-
заключение с математической строгостью определяется понятие устойчивости
течения и описываются методы линеаризации и нормальных мод.
2.1. Бифуркация
Рассмотрим течения несжимаемой вязкой жидкости в заданной об-
области V. Обозначим: р — плотность жидкости, v — кинематическая
вязкость, и*, р* — скорость и давление в данной точке х* в момент
времени t*. Течение описывается уравнениями Навье-Стокса
Уравнением неразрывности
V* • и* = О

22	Гл. 2. Введение в теорию стационарных течений
в области V, а также некоторыми граничными условиями на границе
dV области V, например,
и* = Uo* на части 9V, и* периодична на другой части dV.
Здесь А* — оператор Лапласа и Uo* — заданная скорость жидкости
на границе.
Предположим, что данные уравнения имеют решение (приближен-
(приближенное или точное), удовлетворяющее приведенным граничным условиям
и описывающее стационарное течение, устойчивость которого подле-
подлежит изучению. Пусть этому основному течению соответствует поле
скоростей U* и давление Р*. В дальнейшем часто будет удобно вво-
вводить безразмерные переменные и определять соответствующее число
Рейнольдса Д. Выберем некоторый характерный масштаб длины L
основного течения, например, диаметр области V, а также некоторый
характерный масштаб скорости V, например, максимальное значение
|U*| в V. Для обтекания сферы однородным потоком, например, в ка-
качестве V можно выбрать скорость потока на бесконечности, а в ка-
качестве L — радиус или диаметр самой сферы. Далее, определим без-
безразмерные переменные х = х*/?, t = Vt+/L, u = u*/V, p = p*/pV2
и т.д., а также число Рейнольдса R = VL/v. Безразмерные поля ско-
скорости U(x, Д) и давления Р(х, Д) основного течения удовлетворяют
уравнениям Навье-Стокса
U . VU = -VP + Д^Ди,	B.1)
V • U = 0	B.2)
в области V и граничным условиям
U = Uo на части 5V; U периодична на другой части 9V. B.3)
В общем случае U, Р зависят от Д, и может существовать более одно-
одного стационарного решения U, Р для одного и того же значения Д и тех
же граничных условий. Мы увидим, что бифуркация, т. е. изменение
числа или качественных свойств возможных стационарных течений
(или нестационарных течений в состоянии динамического равнове-
равновесия), при изменении Д часто связана с переходом к неустойчивости.
Важная физическая идея, относящаяся к чередованию неустойчи-
востей и смены режимов течения на "пути к турбулентности" при
увеличении числа Рейнольдса, будет представлена далее на примере
ряда очень простых модельных задач о бифуркации. Может показать-
показаться на первый взгляд, что модельные алгебраические и обыкновенные
дифференциальные уравнения, относящиеся к этим задачам, являют-
являются слишком простыми для того, чтобы служить описанием каких-либо

2.1. Бифуркация
23
Рис. 2.1. Бифуркационная диаграмма в плоскости (Д, G) для точки пово-
поворота при I > О
задач гидродинамики. Тем не менее, мы покажем, что эти уравне-
уравнения не только иллюстрируют многие важные идеи устойчивости, но
также асимптотически описывают локальные свойства большого чис-
числа неустойчивостей и бифуркаций. Это происходит по той причине,
что хотя уравнения Навье-Стокса и являются уравнениями в частных
производных и их решения принадлежат бесконечномерному функцио-
функциональному пространству, решение может быть приближено элементом
пространства низкой размерности. На практике решение представля-
представляется в виде спектрального разложения, например, в виде ряда Фурье
по пространству и асимптотически приближается только небольшим
числом компонент разложения. Амплитуды этих компонент удовле-
удовлетворяют системам обыкновенных дифференциальных уравнений низ-
низкого порядка. Мы вернемся к этому вопросу в следующих главах
и проиллюстрируем его на примере ряда течений.
Пример 2.1: Точка поворота. В качестве простой модельной задачи
рассмотрим для иллюстративных целей вспомогательную задачу:
а - 1{U - UoJ = О,

24	Гл. 2. Введение в теорию стационарных течений
где a = k(R — Rc) и к > О, / ф О, Uq и Rc — некоторые постоян-
постоянные. Вспомогательная задача может оказаться полезной при изучении
сложного свойства движения жидкости, если она описывает именно
изучаемое свойство, даже не имея отношения к большинству других
свойств движения. Величина U может рассматриваться в качестве
компоненты скорости жидкости в некоторой заданной точке стацио-
стационарного течения в зависимости от числа Рейнольдса. Тогда
U = U0±[k(R-Rc)/l]1/2.
Имеем два решения, когда k(R — Rc)/l > О, одно, когда R = Rc, и ни
одного, когда k(R — Rc)/l < 0. Удобно изобразить решение на бифур-
бифуркационной диаграмме, где дана зависимость некоторых переменных,
описывающих состояние специальных течений от некоторого пара-
параметра, характеризующего жидкость или форму течения, и т.д. На
рис. 2.1 изображен график зависимости U от R для случая Ы > 0. Бу-
Будем говорить, что имеет место простая точка поворота, складка или
бифуркация седло-узел при R = Лс, U = Uq. Эта точка называется
точкой бифуркации, так как число (и свойства) решений меняются
в ней.	D
Пример 2.2: Транскритическая бифуркация. В качестве другой очень
простой модели бифуркации стационарных течений уравнений Навье-
Стокса рассмотрим следующее квадратное уравнение:
aU-lU2 = 0.
Таким образом,
U = 0 или U = а/1 = k(R - Rc)/l,
так что имеют место два решения при R ф Rc. Бифуркация при
R = Дс, U = 0 дает пример транскритической точки (рис. 2.2). D
Пример 2.3: Вилообразная бифуркация [pitchfork bifurcation). Рассмот-
Рассмотрим далее модельное уравнение
aU - IU3 = 0,
которое является типичным для первой бифуркации течений с сим-
симметрией ±U. Тогда
U = 0, mmU = ±[k{R-Rc)/l]1/2, если k(R - Rc) > 0.
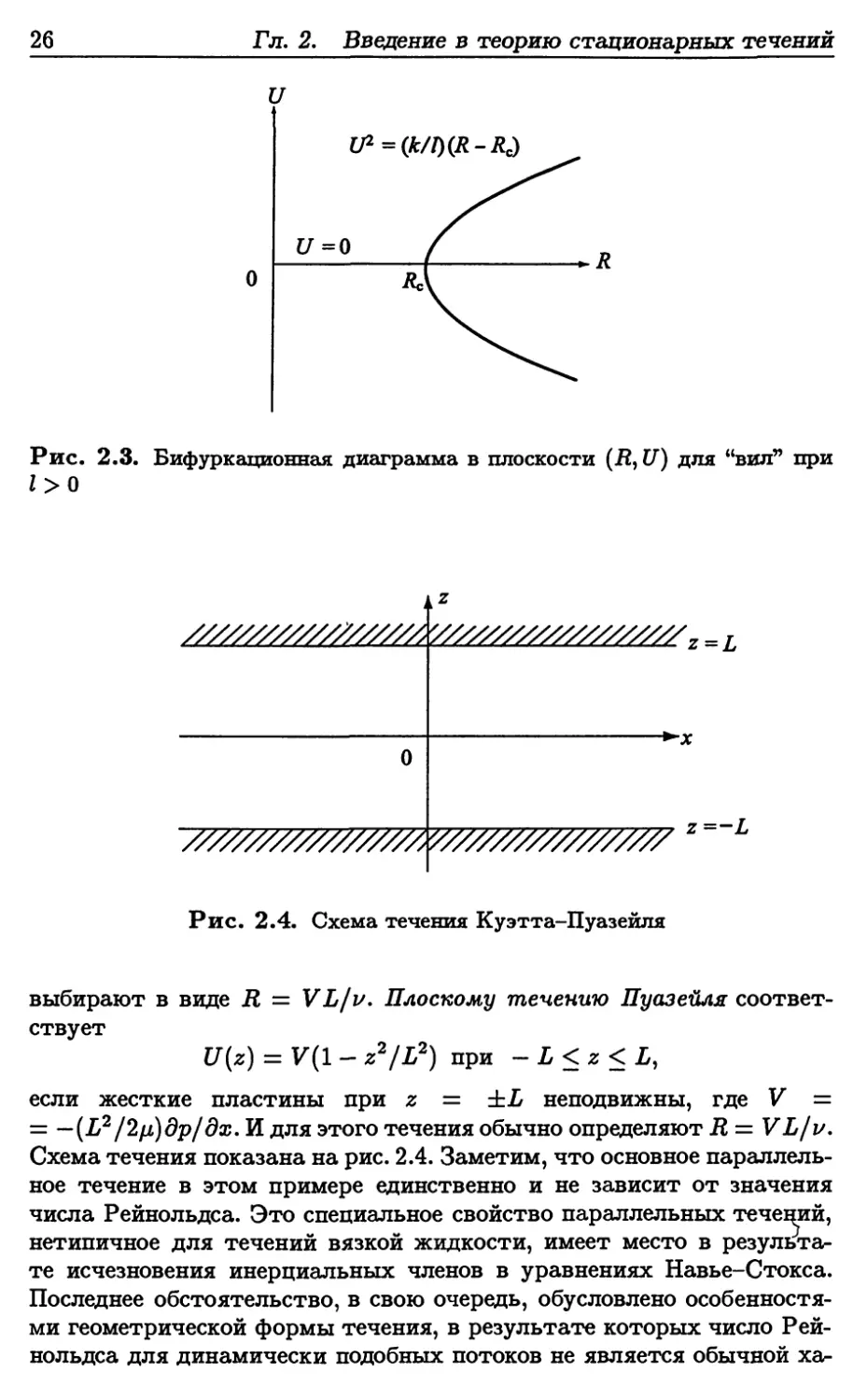
Говорят, что имеет место вилообразная бифуркация при R = Rc,
U = 0. Легко видеть, что в результате этой бифуркации происходит
нарушение симметрии при R = Rc в том смысле, что если М > 0, то

2.1. Бифуркация
25
U
(*//) (Я-
Рис. 2.2. Бифуркационная диаграмма в плоскости (i?, U) для транскри-
транскритической точки при I > О
имеет место единственное симметричное решение при R < Дс, а так-
также и пара несимметричных решений при Л > Rc (см. рис. 2.3). О
Пример 2.4» Плоское течение Куэтта-Пуазейля. Для того чтобы
определить плоско-параллельное течение несжимаемой вязкой жид-
жидкости, будем искать вектор скорости, например, в виде U = U(z)i.
Подставим это выражение для скорости в размерное уравнение за-
завихренности двумерного течения в плоскости (ж, z) (которое является
удобной формой записи уравнений Навье-Стокса для настоящего рас-
рассмотрения):
dt dx
где rj = ди/dz — dw/дх. Имеем
d3i7
dz
= 0.
Следовательно,
U(z) = Az2 + Bz + С,
где постоянные A, jB, С определяются градиентом давления и гра-
граничными условиями. Для того чтобы последнее выражение было ре-
решением, градиент давления должен быть постоянен вдоль трубы.
На стенках должно выполняться условие прилипания. Имеем А =
= B/г)~19р/9ж, где /л — динамическая вязкость жидкости. В част-
частности, для плоского течения Куэтта
U{z) = Vz/L при - L < z < L,
если др/дх = 0, и жесткие пластины при z = ±L двигаются со ско-
скоростями ±V соответственно. В этом случае число Рейнольдса часто

26
Гл. 2. Введение в теорию стационарных течений
Рис. 2.3. Бифуркационная диаграмма в плоскости (i2, U) для "вил" при
z=L
/У/////////////////////////////////////
Рис. 2.4. Схема течения Куэтта-Пуазейля
z=-L
выбирают в виде R = VL/u. Плоскому течению Пуазейля соответ-
соответствует
U{z) = V(l - z2/L2) при -L<z<L,
если жесткие пластины при z = ±L неподвижны, где V =
= —(L2/2/j,)dp/dx. И для этого течения обычно определяют R = VL/u.
Схема течения показана на рис. 2.4. Заметим, что основное параллель-
параллельное течение в этом примере единственно и не зависит от значения
числа Рейнольдса. Это специальное свойство параллельных течений,
нетипичное для течений вязкой жидкости, имеет место в результа-
результате исчезновения инерциальных членов в уравнениях Навье-Стокса.
Последнее обстоятельство, в свою очередь, обусловлено особенностя-
особенностями геометрической формы течения, в результате которых число Рей-
Рейнольдса для динамически подобных потоков не является обычной ха-

2.1. Бифуркация
27
0 = 0
Рис, 2,5. Схема течений Джеффри-Гамеля и обозначения
рактеристикой отношения инерционных и вязких сил. Обычно стацио-
стационарное основное течение меняется при увеличении числа Рейнольдса
и не является единственным при данных обстоятельствах.	D
* Пример 2.5: Течения Джеффри-Гомеля. В качестве следующего при-
примера выберем некоторые стационарные течения, которые меняются
при увеличении числа Рейнольдса и не являются единственными (см.,
например, [Batchelor, 1967, параграф 5.6]).
Рассмотрим двумерное течение несжимаемой вязкой жидкости
между двумя твердыми плоскостями, заданными уравнениями в =
= ±а. Течение возбуждается стационарным линейным источником
(или стоком) с объемным расходом Q на единицу расстояния по норма-
нормали к плоскости течения. Источник (сток) расположен на пересечении
т** = 0 двух плоскостей, где (г*,в) — полярные координаты. Схема
течения изображена на рис. 2.5. Граничные условия имеют вид
V>* = ±-Q, дф*/дв = 0 при в = ±а,
где ф+ — функция тока, так что радиальная и касательная компо-
компоненты
скорости даются соответственно формулами иг* = дф*/г*дв и и$ =
ak/ft

28
Гл. 2. Введение в теорию стационарных течений
Рис. 2.6. Формы профилей скорости для наиболее важных течений
Джеффри-Гамеля (по P. Drazin & Т. Kambe, Ryitai Rikigaku — Anteisei To
Ranyi (Fluid Dynamics — Stability and Turbulence), University of Tokyo Press,
1989, Fig. 2.4. Воспроизведено по разрешению University of Tokyo Press)
Будем искать стационарные течения, для которых функция тока
зависит только от 0, т.е. -0* = Ф*@)- В результате имеем чисто ради-
радиальное течение со скоростью ur = ?/* = d^/r^dfl и завихренностью
222
C	V	/
Определим далее безразмерные переменные ф = V>*/§Q и т.д.
и число Рейнольдса R = Q/2i/. Тогда безразмерная форма уравнения
для завихренности имеет вид
m г д(г,в)
B.4)
Это уравнение для *ф = Ф@) превращается в обыкновенное дифферен-
дифференциальное уравнение
B.5)
Граничные условия принимают вид
Ф = ±1, d$/d0 = 0, при в = ±а.
B.6)
Решение задачи может быть выражено в явном виде через эллипти-
эллиптические функции Якоби, однако во многих отношениях его проще полу-
получить численно. Имеют место разнообразные решения, принадлежащие

2.1. Бифуркация
29
10
Рис. 2.7, Области возникновения наиболее важных типов течения
Джеффри-Гамеля на плоскости (i2, a). Здесь R > 0 отвечает линейному
источнику (с расходящимся течением для Q > 0, a R < 0 соответствует ли-
линейному стоку (со сходящимся течением) в точке г = 0 (по [Fraenkel, 1962,
Fig. 5]; воспроизведено по разрешению Королевского общества)
типам I, IIn, IIIn, IVn и Vn в обозначениях Френкеля [Fraenkel, 1962,
р. 124]; форма некоторых профилей скорости представлена на рис. 2.6.
(Для настоящей цели демонстрации иллюстративного примера нет
необходимости знать подробности о перечисленных типах решений).
С риском чрезмерного упрощения, в общих чертах свойства тече-
течений Джеффри-Гамеля можно суммировать следующим образом. Для
любой заданной пары (iJ, а) существует бесконечное число стацио-
стационарных течений. Наиболее важные из них (включая все устойчивые)
изображены как на плоскости (Д, а) (рис. 2.7), так и на бифуркаци-
бифуркационной диаграмме (рис, 2,8) в плоскости (а, Ф'@)) для заданного "ти-
"типичного" значения R. Главным для нас в этих диаграммах являют-
являются не количественные детали, но то обстоятельство, что имеет место
сложная структура, содержащая большое число точек поворота и вил.
Отметим также, что входящее течение более устойчиво, чем исходя-

30
Гл. 2. Введение в теорию стационарных течений
/_*г
IV?
a
-1.0
-0.5
Ду,
/v.
0.5
1.0
Рис. 2.8. Бифуркационная диаграмма течений Джеффри-Гамеля на плос-
плоскости (a,[d*/d^]e=0) для R = 20 (по [Sobey & Drazin, 1986, Fig.3]). Эту
диаграмму можно рассматривать как результат проекции на плоскость
пространственной кривой, каждая ветвь которой представляет собой реше-
решение Джеффри-Гамеля. Здесь a > О отвечает линейному источнику и, как
обычно, a < 0 — стоку. Заметим, что два решения типа 1Ь могут возник-
возникнуть между вилообразной бифуркацией Вг (вид "сбоку") и точкой поворота
Вз. Устойчивое решение обозначено сплошной кривой, а неустойчивое —
пунктирной
шее; другие свойства одинаковы для обоих типов течений. Наводя-
Наводящие соображения для того, чтобы показать, какие решения устойчи-
устойчивы, а какие нет, приведены в параграфе 10.3.3.
(На плоскости (а, [с12Ф/с102]0=о) лучше видно, что Вг соответству-
соответствует вилообразной бифуркации с Щ в качестве "ручки", Иг в качестве
среднего "зубца" и IVi, Vi в качестве боковых "зубцов" в силу то-
того обстоятельства, что IV i и Vi имеют одну и ту же скорость ur на
центральной линии в = 0; симметричные течения I, Ип, Шп, однако,
удовлетворяют условиям d2\?/d02 = 0 при в = 0).	?
2.2. Неустойчивость
Сложность течений вязкой жидкости и соответствущих им решений
уравнений Навье-Стокса послужила основанием для того, чтобы ра-
разобрать в данном параграфе ряд модельных задач с простыми обык-
обыкновенными дифференциальными уравнениями для объяснения фунда-
фундаментальных идей теории устойчивости. В предыдущем параграфе уже
были представлены некоторые стационарные решения и их бифурка-
бифуркации; далее будет обсуждаться неустойчивость этих решений, а также
других решений, стационарных или нестационарных, в которые эти
решения могут переходить под действием малых возмущений. Для

2.2. Неустойчивость
31
Рис. 2.9. Бифуркационная диаграмма в плоскости (Я, и) для примера
точки поворота с I > 0. Устойчивое стационарное решение 17+ обозначено
сплошной кривой^ а неустойчивое U- — пунктирной кривой. Вертикальные
линии со стрелками обозначают изменение зависящего от времени решения
и при увеличении t и фиксированном R
введения в предмет в предыдущем параграфе рассмотрены лишь не-
немногие из простейших бифуркаций. Более общие системы обыкновен-
обыкновенных дифференциальных уравнений имеют как бифуркации, которые
сходны с этими простейшими бифуркациями локально (так же как
гладкая кривая с вертикальной касательной в данной точке имеет
сходство с параболой той же кривизны с той же касательной в этой
точке), так и обладают более сложными формами бифуркаций. Кроме
того, более общие системы часто имеют последовательности бифурка-
бифуркаций при увеличении параметра, числа Рейнольдса, например; важный
пример эволюции решений при увеличении параметра дается в при-
примере 2.5 и в упражнении 6.И и будет подробно разобран в главе 9.
Реальные гидродинамические задачи обычно требуют большого
численного счета и поэтому являются менее поучительными, чем
простые модельные задачи; некоторые задачи об устойчивости те-
течений, обладающих сильной симметрией (например, плоскопарал-
плоскопараллельные течения обладают симметрией относительно группы сдви-
сдвигов в направлении течения) могут быть решены при помощи сведения
к обыкновенным дифференциальным уравнениям, решения некоторых
из этих уравнений записываются в явном виде. Эти простые (и нети-
нетипичные) решения часто приводятся в учебниках и лекционных курсах.

32
Гл. 2. Введение в теорию стационарных течений
/
Рис. 2.10. Эскиз бифуркационной диаграммы в плоскости («R, и) для
транскритической бифуркации в случае I > 0
Пример 2.6: Снова точка поворота. Рассмотрим модельное уравне-
уравнение
l-.-K.-D»",
B.7)
где снова а — k(R — Rc), k > 0. Используя легко получаемое в яв-
явном виде аналитическое выражение точного решения этого диффе-
дифференциального уравнения, либо производя качественный анализ знака
du/dt (и, следовательно, свойств монотонности и с увеличением ?),
можно показать, что любое малое возмущение стационарного решения
и — J7+ = С/о + (а/0^2 будет убывать при t —>• оо и, следовательно, это
решение устойчиво. Аналогично, некоторые малые возмущения реше-
решения и — J7_ = Е/о — (а//I/2' будут расти, так что в результате они не
будут более малыми и, следовательно, это решение неустойчиво. Для
/ > 0 и Л > Дс малое начальное возмущение J7_ приводит к асимп-
асимптотике u(t) —> J7+ при t —> оо или u(t) —> —оо, если t —)¦ к конечному
пределу, в зависимости от знака возмущений. Малое начальное воз-
возмущение [/+ дает u(t) —>• [/+ при t —>• оо (рис. 2.9).	О
Пример 2.7: Снова транскритическая бифуркация. Рассмотрим да-
далее уравнение
-
B.8)
где а= fc(iu — Rc), k > 0. Снова при помощи точного решения или
качественных методов можно показать, что решения обладают пове-
поведением, как представлено на рис. 2.10.	D-

2.2. Неустойчивость
33
Рис. 2.11. (а) Надкритическая устойчивость при 0 < R — RC<&1 и.1 > 0:
зависимость решения it уравнения Ландау B.9) от времени для некоторых
начальных данных но. (б) Докритическая устойчивость при 0 < Rc — R ^ 1
и I < 0: зависимость решения и уравнения Ландау B.9) от времени для не-
некоторых начальных данных uq. На каждой диаграмме ие = [k(R — Rc)/I]1 f2.
(По [Drazin & Reid, 1981, Figs7.1(a), 7.2(a)])
Пример 2.8: Снова вилообразная бифуркация. Рассмотрим уравнение
B.9)
du	з
- = au-lu,
где а = k(R—Rc), к > 0. Это уравнение Ландау, которое, по-существу,
является уравнением, впервые предложенным в 1944 г. Ландау в ка-
качестве модели гидродинамической устойчивости. Форма уравнения не
меняется при изменениии знака щ так что оно часто' возникает как
слабонелинейное уравнение, управляющее амплитудой наиболее не-
неустойчивых (или наименее устойчивых) собственных функций для те-
течений с подобной симметрией (это может быть зеркальная симметрия
течения относительно некоторой плоскости или трансляционная сим-
симметрия, когда амплитуда волны в точке равна амплитуде с обратным
знаком при сдвиге этой точки на половину длины волны). Будем рас-
рассматривать это уравнения, которое является классическим прототи-
прототипом нарушения симметрии, при помощи тех же методов, что и ранее,
различая два случая соответствующих знаков постоянной Ландау I.
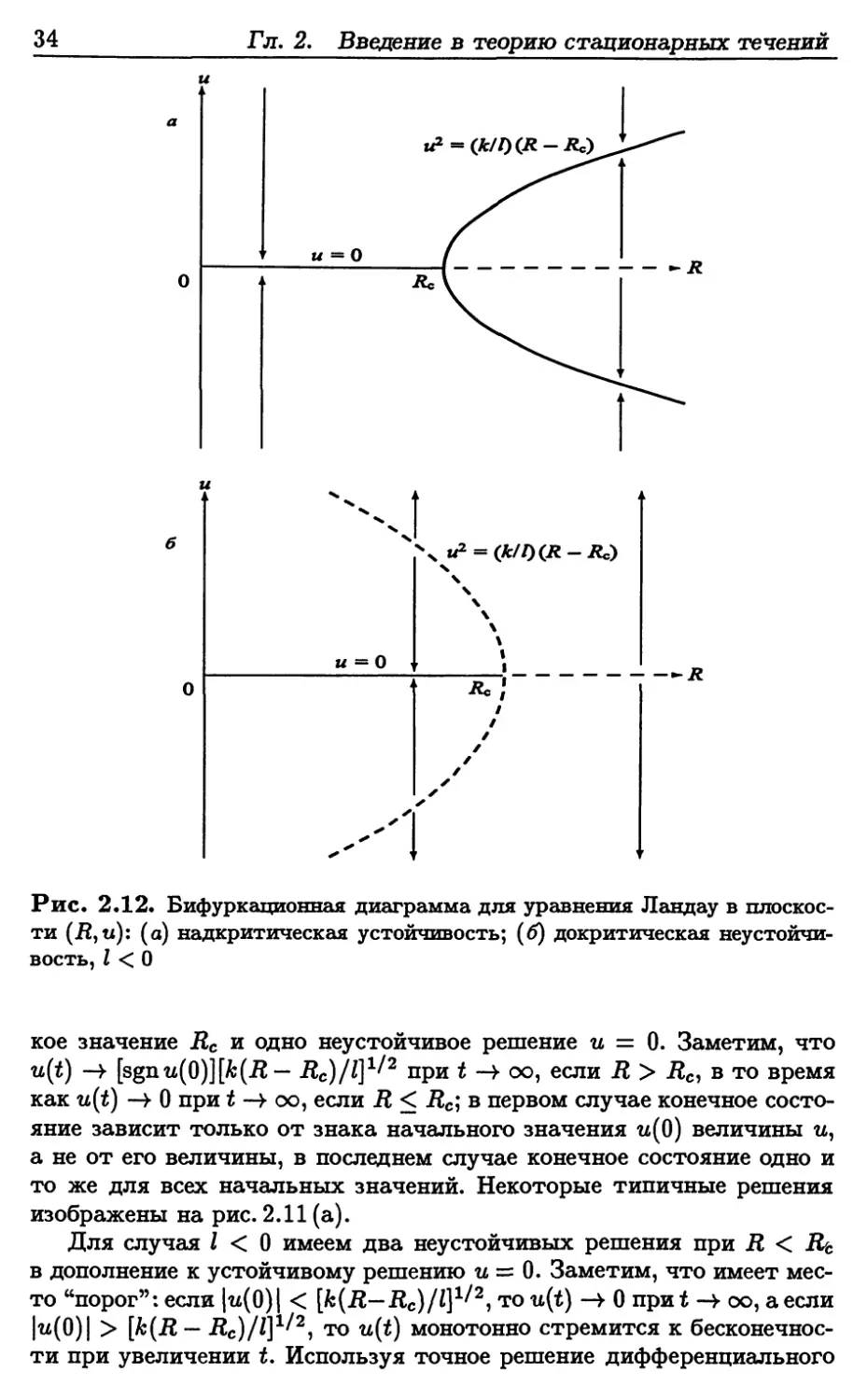
Для случая / > 0 имеем надкритическую устойчивость, т.е.
Два линейно устойчивых решения для R больших, чем критичес-

34
Гл. 2. Введение в теорию стационарных течений
и =0
Рис. 2.12. Бифуркационная диаграмма для уравнения Ландау в плоскос-
плоскости (Л,и): (а) надкритическая устойчивость; (б) докритическая неустойчи-
неустойчивость, I < О
кое значение Дс и одно неустойчивое решение и = 0. Заметим, что
u(tf) -> [sgnu@)][k(R- Лс)//]1/2 при 2 -> оо, если Л > Лс, в то время
как u(tf) -> 0 при ^ -> оо, если Л < Лс; в первом случае конечное состо-
состояние зависит только от знака начального значения и@) величины щ
а не от его величины, в последнем случае конечное состояние одно и
то же для всех начальных значений. Некоторые типичные решения
изображены на рис. 2.11 (а).
Для случая / < 0 имеем два неустойчивых решения при Л < Rt
в дополнение к устойчивому решению и = 0. Заметим, что имеет мес-
место "порог": если \и{й)\ < [k(R-Rc)/l]1/2, то u(t) -> 0 npnt -* оо, а если
Щ0)| > [k(R - Лс)//]1/2, то u(t) монотонно стремится к бесконечнос-
бесконечности при увеличении t. Используя точное решение дифференциального

2.2. Неустойчивость	35
уравнения можно показать, что u(t) —> [sgnii@)]oo при t стремящем-
стремящемся к конечному числу (во всяком случае, в рамках данной модели),
которое зависит как от и@), так и от &, Л, I. Некоторые типичные
решения изображены на рис 2.11 (б).
Можно подтвердить некоторые из этих результатов при помощи
изучения поведения малых возмущений стационарных решений. Опре-
Определим возмущение U для данного решения и как
u'(t) = u{t) - U,
где U — одно из решений уравнения all = IU3. Тогда
du' du	. о
-=- = au-lu> =
= aU- IU3 + (a - 3lU2)u' + O(u'2) при и' -»• О
= {a-ZlU2)u' + O(u'2),
так как U — одно из стационарных решений. При изучении устой-
устойчивости изучается поведение решений вблизи данного решения 17,
т.е. производится линеаризация, которая в данном случае приводит
к уравнению
С
Для нулевого решения U = 0 имеем
du' ,
—- = аи .
dt
Следовательно,
uf{t)=u{0)est,
где показатель экспоненты s = а = k(R — Rc) для к > 0 (в реалисти-
реалистических приложениях). Таким образом, имеет место линейная устойчи-
устойчивость с экспоненциальным убыванием возмущений при R < Rc и ли-
линейная неустойчивость с экспоненциальным ростом возмущений при
R > Rc. Экспоненциально растущее со временем решение линеаризо-
линеаризованного уравнения дает пример нормальной моды.
Если U = ±[k(R - Rc)/l]1/2 при I > О, R > Дс, тогда аналогично
находим u'(t) = u@)est, но теперь
s = а - ЗИ72 = -2k(R - Rc) < 0
и» таким образом, имеем надкритическую устойчивость, как указано
на Рис. 2.12 (а).

36	Гл. 2. Введение в теорию стационарных течений
Все эти результаты могут быть подтверждены при помощи ана-
анализа точного решения уравнения Ландау.	?
Пример 2.9: Бифуркация Хопфа. Рассмотрим уравнения
¦^ = -2/ + (а - ж2 - у2)ж, -| = х + (а - х2 -
где а = k(R — Ес), к > 0. Единственным стационарным решением
этой системы уравнений является нулевое решение х = у = 0. Для
исследования его устойчивости линеаризуем систему по отношению
к малым возмущениям этого решения:
dec	dy
= y + ax =
Будем решать эту систему линеаризованных уравнений, снова исполь-
используя метод нормальных мод, т. е. полагая ж, у а е** и замечая, что
о«?/ — Cv«?/ ^^ €/* g(j — «(/ I С« С/*
откуда следует, что 5 должно быть собственным значением матрицы
[1 о
Таким образом,
О = det(J - Л) = (а - «J + 1.
Отсюда
s = a±i= k(R- Rc)±i.
Следовательно,
x(t) = l(AJ* + Л*е-?*)ев*, y(t) = -h(Ae{t - Л*е-?*)ев*,
где А — некоторая комплексная постоянная, которая определяется из
начальных условий, а знак * означает комплексное сопряжение. В ре-
результате имеем устойчивость с экспоненциальным затуханием воз-
возмущений, если Re(s) < 0 для обоих собственных значений, т.е. при
R < Rc и, аналогично, — неустойчивость при R > Лс«
Удобно перейти к полярным координатам г, в, г > 0, х = г cos в,
у — г sin в, в которых система распадается на два независимых урав-
уравнения:
Точное решение уравнений имеет асимптотику r(t) -» 0 при t -> оо
для всех г@), если R < Дс, и г(*) ->> a1/2 = [k(R - Дс)]1/2 при t -* оо

2.2. Неустойчивость
37
Рис. 2.13. Две орбиты системы уравнений dx/dt = — у + (а — х2 — у2)х,
dy/dt = х + (а — х2 — у2)у из примера 2.9 в плоскости (ж,у) при R> Rc (no
P.Drazin & T.Kambe [i2yw?ai Rikigaku — Anteisei To Ranyu (Fluid Dynamics
— Stability and Turbulence), University of Tokyo Press, 1989, Fig. 2.10]. Вос-
Воспроизведено по разрешению University Tokyo Press)
для всех r@) при R > Rc (см. пример). Имеем также 0(i) = во +1,
где 0@) =0о — любое число. В результате для всех R> Rc получаем
нелинейное решение х = rcos0, у = rsin0 периода 2тг при t -> оо.
Такое периодическое решение дифференциального уравнения, к кото-
которому приближаются соседние решения при увеличении времени на-
называется предельным циклом. Две типичные орбиты изображены на
фазовой плоскости (ж, у) для R > Rc на рис. 2.13. На рисунке видно,
как предельный цикл притягивает соседние орбиты.
Это типичный пример бифуркации Хопфа, когда вещественная
часть Re(s) комплексно сопряженной пары собственных значений пос-
после прохождения через ноль увеличивается при увеличении или умень-
уменьшении параметра по отношению к критическому значению. Здесь при
прохождении Л через Rc и дальнейшем увеличении возникает осцил-
осциллирующее решение из постоянного, причем последнее становится не-
неустойчивым. Конечно, не является случайностью, что реальные сис-
системы часто имеют пару комплексно сопряженных собственных зна-
значений, так что бифуркации Хопфа для уравнений в частных произ-
производных, описывающих течения жидкости, встречаются так же как
и в этом простом примере с обыкновенными дифференциальными
уравнениями. Таким образом, важно определить из линейной задачи,
является ли показатель экспоненты s нулем или чисто мнимым на гра-
границе устойчивости; в первом случае типичными являются бифурка-
бифуркации точки поворота, транскритическая или вилообразная, а в послед-
последнем — бифуркация Хопфа. В гидродинамическом контексте иногда
говорят, что справедлив принцип обмена устойчив остей (exchange

38	Гл. 2. Введение в теорию стационарных течений
of stabilities ), если показатель экспоненты наименее устойчивой нор-
нормальной моды равен нулю на границе устойчивости.	?
Перед тем, как двигаться дальше, заметим, что в примере 2.9 было
использовано комплексное представление вещественного решения ве-
вещественной задачи. Возможность такого представления, которое бу-
будет часто использоваться далее, основана на следующем свойстве: ес-
если комплексная функция удовлетворяет вещественному однородному
уравнению, то вещественная и мнимая части функции удовлетворяют
этому уравнению по отдельности. Будем записывать комплексное ре-
решение вещественного линеаризованного уравнения или системы урав-
уравнений, неявно подразумевая, что его вещественная часть представля-
представляет собой соответствующую физическую величину, как-то: возмуще-
возмущение компоненты скорости или давления; можем написать, например,
x(t) = Ae(a+1)f, где А — некоторая комплексная постоянная, имея в ви-
виду вещественную часть \(Azlt + A*e~{t)eat = \A\eat cos(t + a,igA). Это
и есть традиционный путь использования метода нормальных мод.
Изложенные примеры представлены скорее из соображения их
простоты, нежели для иллюстрации всех аспектов гидродинамичес-
гидродинамической устойчивости. Они не описывают общее явление неустойчивости
надкритично устойчивого потока, возникшего в результате вилооб-
вилообразной бифуркации или бифуркации Хопфа, когда число Рейнольдса
продолжает увеличиваться, значительно превосходя критическое зна-
значение. Будем называть начальное течение первичным течением, его
неустойчивость — первичной неустойчивостью, надкритично устой-
устойчивое течение — вторичным течением и его неустойчивость — вто-
вторичной неустойчивостью. Эти следующие одна за другой неустойчи-
неустойчивости обсуждаются далее в параграфе 9.1.
В целом, этот параграф предназначен для знакомства с некоторы-
некоторыми важными понятиями (основное решение, устойчивость, бифурка-
бифуркация) и методами (линеаризации, нормальных мод) теории гидроди-
гидродинамической устойчивости на примере обыкновенных дифференциаль-
дифференциальных уравнений. Обыкновенные дифференциальные уравнения будут
использоваться и в дальнейшем для иллюстрациии других важных
понятий (таких, как квазипериодические решения и хаос) и методов
(слабонелинейных возмущений) теории гидродинамической устойчи-
устойчивости. Тем не менее, не следует забывать, что движение жидкости
происходит не только во времени, но и в пространстве и моделиру-
моделируется дифференциальными уравнениями в частных производных. Это
обстоятельство ограничивает использование моделей с обыкновенны-
обыкновенными дифференциальными уравнениями, которое, тем не менее, пред-
представляется целесообразным с педагогической точки зрения. Более ре-
реалистичные модели с уравнениями гидродинамики в частных произ-
производных рассматриваются в следующем параграфе, в котором также
представлены некоторые фундаментальные понятия и методы теории
гидродинамической устойчивости, в особенности линейной теории.

2.3» Устойчивость и линеаризованная задача	39
2.3. Устойчивость и линеаризованная задача
Сначала выбирается интересующее нас основное течение — решение
уравнений движения, устойчивость которого подлежит исследованию.
Это решение может быть просто или непросто найти, оно может быть
получено в явной форме или только численно. Например, в качестве
характеристик потока в несжимаемой вязкой жидкости можно искать
поле скоростей U(x, t) и давлений Р(х, t) в заданной области V с гра-
границей 9V. Течение определяется из уравнений Навье-Стокса, которые
в безразмерном виде записываются в форме
^ + U. VU = - VP + й AU	B.10)
V-U = O	B.11)
в области V; U = Uo на части границы dV и периодична на другой
ее части. Здесь R — число Рейнольдса.
Для общих начальных данных скорости и(х, 0) и давления р(х, 0)
существует полное течение, которому отвечает скорость u(x, i) и дав-
давление р(х,2), при t > 0 удовлетворяющие уравнениям
-^ + и • Vu = - Vp + R Аи,	B.12)
V.u = 0	B.13)
в области V и
и = uo и т. д. на dV.	B«14)
Определим величины возмущений и' = и — \]ир'=р—Р. Вычитая
соответствующие уравнения друг из друга, получим, не накладывая
ограничений на величину возмущений:
^ + и' - VU + U - Vu' + и' • Vu' = -Vj/ + Д-^Ди',	B.15)
V.u' = 0	B.16)
в области V и
и' = 0 на части dV и и' периодична на другой ее части.	B.17)

40	Гл. 2. Введение в теорию стационарных течений
Пример 2.10: Течение Пуазейля в трубе. Точным решением уравне-
уравнений Навье-Стокса (записанным в размерной форме), является
U, = V(l - r2ja2)\, P*=po*-4/w/Fs,/a2,
где течение занимает область
V = {х* : 0 < гф < а, 0 < в < 2тг, -оо < ж* < оо}
в цилиндрических координатах (ж*,г*,0). Это решение представляет
собой изученное Рейнольдсом [Reynolds, 1883] стационарное течение
в трубе радиуса а, поддерживаемое градиентом давления 4pV/a2. В
безразмерных переменных г = r*/a, x = я*/a, U = U*/F, p = p*/pV2
имеем
U = (l-r2)i, P = po-4x/R,
где R = Va/v. В качестве граничных значений возьмем
и = 0 при г = 1, и —> U при х —>¦ ±оо,
где У = {х:0<г<1}в безразмерной форме. В качестве других
граничных условий можем взять
и = 0 при г = 1, и имеет период L по ж,
где
V = {х : 0 < г < 1, 0 < в < 2тг, 0 < х < L}
и
dv
= {х : г = 1 при 0 < х < L, или х = 0, L при 0 < г < 1}
для данного L > 0. Без ограничения общности будем полагать, что и
имеет период 2тг по в.	D
Будем говорить, что данное основное течение устойчиво, если все
малые начальные возмущения остаются малыми в течение всего вре-
времени и неустойчиво, если по крайней мере одно изначально малое воз-
возмущение растет и перестает быть малым по прошествии некоторо-
некоторого времени. Для того чтобы строго математически определить, что
такое устойчивость, необходимо ввести некоторую метрику для при-
придания смысла понятию малости. Это может быть сделано многими
эквивалентными способами. Определим устойчивость в смысле Ляпу-
Ляпунова следующим образом.
Основное течение устойчиво, если для всех е > 0 существует 8(е)
такое, что если
0)||<«5,	B.18)

2.3. Устойчивость и линеаризованная задача	41
то
||и'(х,*||, ||р'(х,*)||<€ для всех t > 0.	B.19)
Здесь норма || • || может быть выбрана различными способами (и, тем
самым, определения устойчивости будут несколько различаться); на-
например, можем выбрать ||u;(x,t)|| = supxey|u;(x,i)\ или [/vu2dx]2
в каждый момент. Устойчивость с ||и;|| ос [Jvu'2dx]5 называется
устойчивостью в среднем.
Течение называется асимптотически устойчивым, если оно
устойчиво и, более того,
||u'(x,t||, |Ь/(х,*)||-Ю прн*-юо.	B.20)
В теории динамических систем асимптотически устойчивое реше-
решение, стационарное или нестационарное, называется аттрактором,
так, в примере 2.9 нулевое решение является атрактором для Л < Дс,
а предельный цикл является атрактором для Л > Дс. Система может
иметь более одного аттрактора, как в примере для R > Лс и I > 0.
Существенным в определении устойчивости является свойство ма-
малости возмущений, подвергающихся эволюции, и это свойство мо-
может служить основанием для пренебрежения в процессе исследования
устойчивости произведениями возмущений искомых функций, входя-
входящих в уравнения движения и граничные условия. Эта процедура при-
приводит к линеаризованной задаче. Из приведенных выше уравнений
получаем
u; + U • Vu; + и' • VU = - Vp' + Л^Ди',	B.21)
V • и; = 0	B.22)
в V, а также
и; = 0 или является периодическим на dV.	B.23)
Если основное течение стационарно, т.е. если U не зависит от t, то
коэффициенты линеаризованной задачи также не зависят от t. Отсю-
Отсюда следует, что можно разделить переменные так, что общее решение
задачи с начальными данными является линейной суперпозицией нор-
нормальных мод, которые имеют вид
и'(х, *) = е"й(х), р'(х, <) = е"р(х),	B.24)
где собственное значение s и соответствующие собственные функции
u, p могут быть в принципе определены из решения результирующих
уравнений и граничных условий, а именно:
зй + U • Vu + и • VU = - Vp + Л Аи,	B.25)

42	Гл. 2. Введение в теорию стационарных течений
V.u = O	B.26)
в V и
и = 0 или является периодическим на 6V.	B.27)
(Выделение переменной t может быть мотивировано и во многих слу-
случаях обосновано при помощи преобразования Лапласа). Собственные
значения s этой вещественной задачи являются действительными чис-
числами или парами комплексно сопряженных чисел. Если область V
ограничена, то имеется счетное число собственных значений. Основ-
Основное течение устойчиво, если Re(s) < 0 для всех собственных значе-
значений з, и неустойчиво, если Re(s) > 0 для по крайней мере одного
собственного значения з, потому что эта мода растет со временем как
(В случае нейтральной устойчивости по линейной теории, когда
Re(s) = 0, учет нелинейных членов может привести к неустойчивости
течения). Для одной нормальной моды пространственная структура
возмущения не изменяется по мере того, как мода распространяется,
растет или затухает со временем, хотя, конечно, структура суперпо-
суперпозиции более чем одной моды может изменяться по пространству.
Следует заметить, что для некоторых основных течений общее ре-
решение задачи с начальными данными не может быть выражено в виде
суперпозиции экспоненциально растущих или затухающих нормаль-
нормальных мод. Упражнение 2.8 (i) иллюстрирует суть этого утверждения.
Заметим также, что если собственное значение s является комп-
комплексным числом, то представление B.24) решения вещественной зада-
задачи должно интерпетироваться как неявное обозначение его действи-
действительной части. Это допустимо, потому что комплексные собственные
значения вещественной системы встречаются в виде комплексно со-
сопряженных пар, а действительные и мнимые части решения вещест-
вещественной линеаризованной системы удовлетворяют этой системе по от-
отдельности.
Определим критическое число Рейнолъдса Лс, например, следую-
следующим образом: если R < Дс, то Re(s) < 0 для всех собственных значе-
значений и Re(s) > 0 для, по крайней мере, одной моды и для, по крайней
мере, одного значения R в любой окрестности Rc. При R = Rc назо-
назовем основное течение маргинально устойчивым2 в силу того обстоя-
обстоятельства, что это течение устойчиво при R < Rc и неустойчиво для
всех достаточно малых положительных значений R — Rc\ на практике,
течения обычно становятся более неустойчивыми, по мере того, как
они ускоряются, таким образом следует ожидать неустойчивости для
2От английского слова margin — край, грань. (Прим. ред. перев.)

2.3. Устойчивость и линеаризованная задача	43
всех R > Rc. Маргинальная устойчивость подразумевает нейтраль-
нейтральную устойчивость. Понятия нейтральной и маргинальной устойчи-
устойчивости почти всегда совпадают, когда жидкость является вязкой, но
для идеальных жидкостей это обычно не так и часто приходится раз-
различать две эти устойчивости.
*Если имеется счетная полная система нормальных мод, состоящее
из собственных функций йп, рп, отвечающих собственным значениям
sn для п = 0,1, 2..., тогда любое начальное возмущение может быть
выражено как суперпозиция мод
u'(x,0) = f>nun(x), p'(x,O) = f>npn(x),	B.28)
1 = 1	t=l
с некоторыми коэффициентами ап,6п. Теперь задача на собственные
значения является вещественной, так что каждая собственная функ-
функция или действительна или представлена в паре со своей комплекс-
комплексно сопряженной функцией. Поэтому каждый коэффициент а„,6п яв-
является действительным или представлен вместе со своим комплекс-
комплексно сопряженным. Моды могут быть упорядочены таким образом, что
> Re($2) > ... . Тогда имеем
i=i	t=i
B.29)
а значит,
и'(х,2) ~ aiui(x) exp(sitf), p'fat) ~ &iPi(x) exp(sitf) при t -> оо,
B.30)
если имеется единственная наиболее быстро растущая или наиболее
медленно затухающая мода, т.е. Re(si) > Re($2) > Re(ss) > ..., или
u'(x^) - aiui(x) expEi^) + ajuj(x) exp(s^),
p'(x, 0) - biPi(x) expEi^) + Ь1р1(х) ехр(ф) при t -> oo, B.31)
если имеется комплексно сопряженная пара мод, растущая наибо-
наиболее быстро или затухающая наиболее медленно Re(si) = Re($2) >
> Re E3) > ... . Если система собственных функций являются пол-
полной, но их несчетное число, тогда суперпозиция может выражаться
интегралом, например, интегралом Фурье вместо суммы и могут при-
присутствовать моды, растущие только бесконечно мало медленнее, чем
наиболее быстро растущая мода.

44	Гл. 2. Введение в теорию стационарных течений
¦Классический метод нормальных мод, который был описан, и при-
примеры применения этого метода, которые будут приведены в последу-
последующих главах, могут дать преувеличенное представление о важности
наиболее быстрорастущих неустойчивых мод. Считается, что экспо-
экспоненциально растущие моды столь эфемерны, что они редко наблюда-
наблюдаются в природных процессах и лабораторных экспериментах. Одна из
причин недостаточной наблюдаемости экспоненциального роста воз-
возмущений состоит в том, что неустойчивое основное течение на прак-
практике не устанавливается мгновенно; скорее, устойчивое основное тече-
течение медленно изменяется, пока не станет неустойчивым, а затем быст-
быстро разрушается под воздействием естественных возмущений. Другая
причина состоит в том, что в общем случае возмущение не представ-
представляет собой наиболее быстро растущую моду, а является суперпозици-
суперпозицией всех мод, как устойчивых, так и неустойчивых, каждая из них или
растет или затухает экспоненциально с различными скоростями, так
что возмущение не растет экспоненциально со временем. Несомненно
также, что суперпозиция экспоненциально затухающих мод может вы-
вырастать на несколько порядков на некоторое время. (Упражнение (ii)
иллюстрирует это обстоятельство). Согласно линейной теории возму-
возмущение растет экспоненциально B.30) только после прошествия боль-
большого промежутка времени, когда быстро растущая мода доминирует
над другими, однако на практике возмущения не являются малыми
и обычно влияние нелинейности становится значительным до дости-
достижения стадии экспоненциального роста. Почти все возмущения, кото-
которые наблюдаются на практике для неустойчивых стационарных или
периодических по времени основных потоков, являются нелинейными.
Однако, критерий устойчивости основного течения, который дает ли-
линейная теория нормальных мод, выполняется на практике (за исклю-
исключением случаев, когда имеет место докритическая неустойчивость).
Также и экспоненциальный рост контролируемых возмущений можно
наблюдать при численном моделировании течений.
*Мы вполне можем забыть определение B.18), B.19) для практи-
практических задач, потому что для того, чтобы установить устойчивость
основного течения достаточно только найти собственные значения ли-
линеаризованной задачи. При этом течение считается устойчивым, если
не существует собственных значений с положительной действитель-
действительной частью. Такой образ действий оправдывается соответственными
ответами на два математических вопроса, которые могут побудить
к размышлениям читателя, более склонного к теории, и быть спо-
спокойно проигнорированы читателем, имеющим практические наклон-
наклонности; последнему рекомендуется перейти сразу к следующему абза-
абзацу. Первый вопрос: является ли основное течение устойчивым в том
и только в том случае, если нулевое решение линеаризованной сис-
системы устойчиво, иными словами управляется ли устойчивость нели-
нелинейной задачи устойчивостью линеаризованной или нет. Существуют

2.3. Устойчивость и линеаризованная задача	45
простые контрпримеры, показывающие, что основное течение может
быть неустойчивым в то время, когда линеаризованная система яв-
является нейтрально устойчивой. Второй вопрос состоит в том, управ-
управляется ли устойчивость нулевого решения линеаризованной системы
спектром нормальных мод. Далеко не очевидно, что всегда <тт = и)т,
где
<гт = sup{Re(s) : s есть собственное значение},
и верхняя грань берется по решениям линеаризованной задачи при
всех гладких начальных условиях. Об этих вопросах было написано
много и найдено много контрпримеров, опровергающих наивную веру
в то обстоятельство, что собственные значения определяют устойчи-
устойчивость как линеаризованной, так и первоначальной задач для систем
нелинейных уравнений в частных производных. Тем не менее, эта на-
наивная вера, по-видимому, вполне оправдана при решении задач об
устойчивости течения ньютоновских жидкостей, когда принимается,
что если нулевое решение линеаризованной системы является асимп-
асимптотически устойчивым, то основное течение устойчиво, хотя при этом
допускается, что основное течение может быть неустойчивым, когда
линеаризованная система является нейтрально устойчивой. Принима-
Принимается также, что линеаризованная система устойчива, если <тт < 0. Ис-
Исходя из этого, будем рассматривать устойчивость течения, определяя
ее, главным образом, при помощи собственных значений линеаризо-
линеаризованной задачи.
*Эти вопросы не являются надуманными в математической тео-
теории устойчивости идеальной жидкости по той причине, что подобные
теории являются структурно неустойчивыми, т.е. небольшое изме-
изменение в модельных уравнениях может привести к существенному из-
изменению результатов. Например, если основное параллельное течение
идеальной несжимаемой жидкости в бета-плоскости Россби не имеет
нормальной моды, растущей со временем (и поэтому могло бы быть
сразу объявлено устойчивым), то волновое возмущение малой ампли-
амплитуды € генерирует возмущение с амплитудой порядка б" в тонком
критическом слое ширины б по прошествию большого интервала вре-
времени порядка б, как можно показать с помощью слабо нелинейной
теории [Warn & Warn, 1978; Brown & Stewartson, 1979], и, тем самым,
делают течение неустойчивым (по крайней мере, согласно определе-
определению неустойчивости в терминах некоторых норм).
Для типичных основных течений единственным способом найти
множество характеристик устойчивости, т.е. свойств собственных
значений и собственных функций для всех значений числа Рейнольд-
са, является использование численных методов. В связи с этим пред-

46	Гл. 2. Введение в теорию стационарных течений
ставляется уместным ограничиться в учебнике только представлени-
представлением некоторых результатов вычислений и сопоставлением их с наблю-
наблюдениями. Тем не менее, для конкретных простых течений большая
часть теории может быть развита аналитически. Если U, Р являют-
являются независимыми от одной или более пространственных переменных,
например, когда основное течение инвариантно относительно сдвига
или вращения, тогда возможно разделение пространственных пере-
переменных. (Разделение переменных может быть обосновано при помощи
преобразования Фурье или обобщенного преобразования Фурье). Так,
например, если U не зависит от х и 2, то можно представить нор-
нормальные моды в виде u'(x,tf) = e8t+lkxu(y, г), где к является волно-
волновым числом в направлении оси х; если U зависит только от полярной
координаты г, тогда и; = е5*+1(*х+пв)й(г), где п — (целое) азимуталь-
азимутальное волновое число, а в — азимутальный угол вокруг оси х. (Понят-
(Понятно, что каждая физическая величина является действительной частью
ее комплексного представления, которое допустимо ввиду линейности
и однородности задачи). Разделение переменных может привести к за-
задаче на собственные значения для обыкновенных дифференциальных
уравнений, а не для уравнений в частных производных, и таким обра-
образом, к более легко решаемой математической задаче нахождения ха-
характеристик устойчивости для основного течения. Именно по причине
математического, а не физического характера, так часто рассматрива-
рассматриваются простые симметричные стационарные течения в курсах лекций,
книгах и статьях по гидродинамической устойчивости.
Пример 2.11: Устойчивость течения Пуазейля в трубе. Если U =
= A - r2)i, Р = ро - 4ж/Д и и',р' ос е**+'1(кх+пв\ то линеаризованная
задача об устойчивости B.25)-B.27) имеет вид (см. упражнение 2.17)
dp	Jd2 Id Д 2 l + n2\"l	2тл
+ -~
2 t ar
Л.2 ,
- {* +
.+ ^+^ ,
r ar r
где
йх = йг = ив = 0 при г = 1
и
й, р не имеют особенностей при г = 0.

Упражнения	47
Здесь U(г) = 1 — г2, и = (йх,йу,йе) в цилиндрических координатах.
Это сложная, хотя и линейная, задача на собственные значения для
определения s и структуры моды. Многочисленные вычисления (см.
[Salwen et a/., 1980]) показывают, что, как ни странно, Re(s) < 0 для
всех мод, всех R и всех волновых чисел &,п. Отсюда следует, что
течение Пуазейля в трубе является устойчивым, что находится в оче-
очевидном противоречии с экспериментами Рейнольдса [Reynolds, 1883];
считается, что хотя в рамках данной теории течение устойчиво по от-
отношению к бесконечно малым возмущениям, на практике оно неустой-
неустойчиво по отношению к возмущениям малой, но конечной амплитуды
из-за проявления некоторой формы докритической неустойчивости. ?
В качестве послесловия к этой главе напомним содержание пара-
параграфа 1.1, где было замечено, что течение в трубе устойчиво для
всех достаточно малых возмущений для любого числа Рейнольдса
Л, но устойчиво ко всем возмущениям любой амплитуды только при
R < Rg, где Rg га 2000. Математически это выражается определени-
определением основного течения как глобально асимптотически устойчивого:
любое возмущение исчезает после прошествия достаточно большого
времени и соотношение B.20) оказывается справедливым для любо-
любого начального возмущения, а также определением Rg как наибольше-
наибольшего числа, для которого течение является глобально асимптотически
устойчивым при всех R < Rg.
Упражнения
2.1,	Точка поворота и транскритическая бифуркация, (а) Найди-
Найдите точное общее решение и уравнения B.7) для примере 2.6
и воспроизведите схему бифуркационной диаграммы, данной на
рис. 2.9 для I > 0.
(Ь) Найдите точное решение и уравнения () для примера 2.7
и воспроизведите бифуркационную диаграмму, изображенную
на рис. 2.10 для I > 0.
2.2,	Уравнение Ландау. Покажите, что если и удовлетворяет уравне-
уравнению
для k, R, Rc > 0 и действительных I, то
k(R-Rc)ul
U2(t) =
[k(R - Rc) - lul] exp[-2Jfe(i? - Rc)t]'
пока и остается конечным. Докажите, что нулевое решение
U(t) = 0 является устойчивым, если R < Rc, и неустойчивым,

48	Гл. 2. Введение в теорию стационарных течений
если R > Rc* Воспроизведите схему бифуркационной диаграммы
в плоскости (iE, u) для случаев I > О, / < 0.
2.3. Инвариантность комплексного уравнения Ландау, (i) Покажи-
Покажите, что если комплексная амплитуда А удовлетворяет уравнению
Ландау
для комплексных постоянных з, I и если В(Т) = eie-A(t), T =
= 2 + to, для действительных постоянных 0, tо, то
Докажите, что если ЛB) является решением уравнения (Е2.1),
то e1$A(t — to) также является решением.
(ii) Покажите, что если
для Т = t — to, X = х — хо и комплексных постоянных о, 6, то
и уравнение инвариантно относительно сдвига по времени и про-
пространству. Докажите, что если u(x,t) = A(t)elkx является ре-
решением уравнения (Е2.2) для действительных &, то u(x,t) =
= A(t — toje1^"*"^), где 0 = — fexo, также является решением.
Покажите, в частности, что если to = 0, хо = тг/fc, то знак Л
изменяется при этом преобразовании.
2.4. .Бифуркация из бесконечности. Дано
для Я > 0. Покажите, что U = 0 является устойчивым стацио-
стационарным решением для всех R. Имеются ли другие стационарные
решения? Для каких значений R они устойчивы? Нарисуйте схе-
схему бифуркационной диаграммы.
Если и = А при t = 0, для каких значений А верно, что u(t) -» 0
при t —> оо? Прокомментируйте ваши выводы для случая боль-
больших Д.

Упражнения	49
2.5. Вторичная неустойчивость. Дано
Покажите, что первичное решение U = О подвергается вило-
вилообразной бифуркации при R = 1, а вторичное решение U =
= (Д — II/2 имеет вторичную неустойчивость в точке транс-
транскритической бифуркации при Л = 2, и = 1.
2.6. Различные определения устойчивости. Рассмотрим простую ди-
динамическую систему:
Вначале покажите, что общее решение имеет вид
х = a cos(at + с), у = a sin(at + с)
для произвольных постоянных а > 0, с. Далее, покажите, что
из этих решений устойчивым по норме ||(ж,у)\\ = (ж2 + у2I^2
является только решение ж = у = 0.
Определяя новые координаты г = (ж2 + у2I/2 и ^ так, что
ж = г cos(r? -f ф),	у = rsin(rt + ф),
покажите, что данная система эквивалентна системе уравнений
Покажите, что общим решением этой системы являются г = а,
ф = с и что все эти решения являются устойчивыми по норме
3 3/а
Что означает то обстоятельство, что одно и то же решение
устойчиво в одной системе координат и неустойчиво в другой
[Cesari, 1959, параграф 1.9]?
2.7. Математическая и физическая концепции устойчивости —
пусть математика будет твоим слугой, а не твоим хозяином.
Рассмотрим вспомогательную математическую систему
ди ди

50	Гл. 2. Введение в теорию стационарных течений
где гл(ж, t) -» 0 экспоненциально при х -» dzoo для всех t > 0.
Покажите, что u = U является стационарным решением систе-
системы, где U(x) = 0 для всех х.
Покажите, что если и(ж,0) = ф(х), где ф не равно нулю, беско-
бесконечно дифференцируемо и затухает экспоненциально на беско-
бесконечности, то u(x,t) = ф(хе*) для всех t > 0.
Сформулируйте аксиоматические свойства нормы. Пусть
1/р
для р > 0. Проверьте, что это — норма в соответствующем
векторном пространстве. (Подсказка: используйте неравенство
Минковского).
Покажите, что для вышеприведенного решения
Г /юо	-|
1/Р
при t -> оо.
Докажите, что решение U является асимптотически устойчи-
устойчивым, если р < 1, и экспоненциально неустойчивым, если'р > 1.
Означает ли это, что заданное решение некоторой гидродинами-
гидродинамической задачи может быть и устойчивым и неустойчивым одно-
одновременно? Обсудите [Yudovich, 1989, р. 101].
2.8. Неполное и полное множества нормальных мод. (i) Предполо-
Предположим, что
-j = Ax,	х@) =	Т
где
Во-первых покажите, что
Является ли нулевое решение устойчивым?
Во-вторых, решите задачу, используя метод нормальных мод;
полагая х(?) ос е**, найти собственные значения s^ и ассоцииро-
ассоциированные собственные векторы щ матрицы А. Сколько существу-
существует собственных значений и собственных векторов? Может этот

Упражнения	51
метод быть использован для решения задачи с начальными зна-
значениями для всех жо, 2/о?
(ii) Используйте метод нормальных мод для решения возмущен-
возмущенной задачи, а именно:
где
B=f"o6-t]' 0<c«L
Покажите, что
x(t) = («о " Уо/
где ui = [1,0]т, U2 = [1,е]т. (Заметим, что собственные век-
векторы почти параллельны). Сколько здесь собственных значений
и собственных векторов? Можно ли использовать этот метод для
решения задачи с начальными данными для всех жо, 2/о?
Докажите, что |х(?)| —> 0 при t —у оо для всех фиксированных
х0ч 2/о и €- Устойчиво ли нулевое решение?
С другой стороны, покажите, что тах*>0|х(?)| —>• ||2/о|Д при
е —> 0 для всех фиксированных жо, у о ф 0. Устойчиво ли ну-
нулевое решение? (Подсказка: может оказаться полезным ввес-
ввести величину E(t) = A — exo/yo)e~€t и найти точки поворота
|x(t)|2 = [yo/e(l-exo/yo)]2E(tJ{[l-E{t)]2 + e2}. Чтобы понять,
как все это относится к теории гидродинамической устойчивос-
устойчивости см. упражнение 8.44, [Ttefethen et aZ., 1993] и [Waleffe, 1995]).
2.9. * Градиент давления в течениях Джеффри-Гомеля. Покажите,
что в задаче Джеффри-Гамеля градиент радиального давления
выражается в виде
где p — плотность жидкости.
Докажите, что градиент давления противоположно направлен
на стенке, если там d2U/d92 < 0. Покажите, что [dU/de]$=a ме-
меняет знак с отрицательного на положительный для решений ти-
типа Их, П2, когда R возрастает и становится больше В,2-

52	Гл. 2. Введение в теорию стационарных течений
2.10.*Точное общее решение задачи Джеффри-Гомеля. Покажите,
что интегралом уравнения Джеффри-Гамеля B.5)
является
Ф'" + 4Ф' + Д(Ф'J = А,
где Ф' = dty/dO и А — постоянная интегрирования. Получите
выражение
2 + 1д(ф'K = А9' + В,
2i	о
и установите таким образом, что решение Ф уравнения B.5)
с граничными условиями B.6)
Ф@) = ±1,	Ф'@) =0 при в = ±а,
может быть выражено в терминах эллиптических функций Яко-
би [Jeffrey, 1915; Hamel, 1916; Abramowitz & Stegun, 1964, пара-
параграф 17.4.61]; см. также [Fraenkel, 1962; Batchelor, 1967, пара-
параграф 5.6].
2.11.*Профили скоростей типов I, Пп и Шп для течения Стокса.
Покажите, что если R = 0, то задача Джеффри-Гамеля B.5),
B.6) имеет решение
_ sin 20-20 cos 2а
sin 2а — 2а cos 2а *
2.12.*Плоское течение Пуазейля. Покажите, что если а -> 0 для
фиксированного в /а, то задача Джеффри-Гамеля B.5), B.6)
имеет предельное решение Ф@) = 30/2а — 03/2а3, то есть
§22
2.13. *Линеаризация уравнения завихренности. Линеаризуя уравнение
завихренности B.4) для малых возмущений решения уравнений
B.5): ф = Ф + ф', покажите, что
ее , 1 а* д? 2 а2Ф дф' 1 d3* w t ,
¦аГ + гаё^ + ^-^Ж+^ар-аГ-21 АС' (Е2'3)
где С = —Афг. Для стационарные нормальных мод фг =

Упражнения	53
вывести уравнение Дина (Dean)
Ф1У + [Л2 + (А-2) 2]<?" + Л2(Л - 2Jф =
= Д[(А-2)Ф'(<?" + >?Ф) - 2Ф"<?' - №'ф], (Б2.4)
где
ф(в) = ф'(в) = О при в = ±а.	(Е2.5)
Эти соотношения представляют собой задачу Дина определения
собственных значений А и собственных функций ф при заданных
Ф, R и а.
Почему переменные ?, г не разделяются? [Dean, 1934; Banks
et aln 1988].
2.14. *3адача Орра-Зоммерфельда для стационарных возмущений
плоского течения Пуазейля. Покажите, что rA ~ const х elkx
при а —> 0 и фиксированных к = —iaA, aro, и х = (г — го)/аго.
Докажите, что уравнения (Е2.4), (Е2.5) принимают вид
<?iv - 2к2ф" + fcV = ikR [и{ф" - к2ф) - и"ф],
Ф(У) = Ф'{У) =0 при у = ±1,
если a —)• 0 для фиксированных у = О/а; штрих здесь обозначает
дифференцирование по у, и Ф'@) —> U(y) = |A — у2).
2.15. *Четыре точные собственные функции. Проверьте равенство
(*iv + 4Ф" + гДФ'Ф")' = Фу + 4Ф//; + гДФ'Ф'" + 2Д(Ф"J.
Докажите, что собственные функции задачи (Е2.4), (Е2.5) имеют
вид: (i) А = 0, ф = Ф;, (И) А = 2, ф = Ф;, (III) А = -1, ф = cos в Ф;,
и (iv) А = —1, ф = sin^ Ф', если Ф" = 0 при в = ±а.
(Дин [Dean, 1934] нашел решения (i), (ii). Фактически уравнение
завихренности B.4) инвариантно относительно действия группы
вращений г *-? г, в *-+ в + 6, ip *-> ф для всех действительных J,
поэтому 9@+6) = 9{0)+69'@)+О{62) при 6 ->• 0 также является
решением этого уравнения, в результате имеем фг = Ф', т. е. А =
= 0, ф = Ф'. Уравнение также инвариантно при преобразова-
преобразованиях х \-? х + Jcos/3, у *-? у + Jsin/З, ф и-)- -0, для которых
( Jr-^in^ - )9)) = Ф(в) - бг-'-вшф - )9)Ф; + О{62) при
¦ 0, поэтому А = -1, ф = sin@ - /3)9'@)).

54	Гл. 2. Введение в теорию стационарных течений
2.16.*Собственные функции для течения Стокса. Покажите, что ес-
если R = О, то четной собственной функцией задачи (Е2.4), (Е2.5)
является
cos(A - 2H
где А — ноль функции У(-А), а У определяется выражением
V(p) = (р + 1) sin 2a + sin 2a(p -f 1).
Докажите, что 2 — А также является собственным числом.
Аналогичным образом найдите нечетные собственные функции.
2.17.Задача об устойчивости течения Пуазейля в трубе. Запишите
уравнения Навье-Стокса в цилиндрической системе координат
(ж, г, 0), используя безразмерные переменные и число Рейнольд-
са R.
Линеаризуйте эти уравнения относительно основного течения
несжимаемой вязкой жидкости со скоростью U = U(r)i и дав-
давлением Р = Р(ж), где U(r) = 1 - г2, Р(х) = Ро- 4ж/Д для
О < г < 1, полагая u = U + и', р= Р + р' (см. пример 2.11).
2.18.Неустойчивость вследствие линейного резонанса. Положим
dx	Ay
— = -iuxx + epi</,	— = ep2x -
где 0J = wi + be цдя действительных u>i, e, b. Покажите, что
подстановка нормалы
онному соотношению
подстановка нормальных мод ж, у ос е lu)t приводит к дисперси-
и = иг + -be ± e(b2 -
Докажите, что нулевое решение х — у = 0 является устойчивым,
если € = 0, и неустойчивым для малых е, когда 4piP2 > b2.
(Физики, работающие в области физики твердого тела, называ-
называют этот резонанс "avoided crossing. Посредством него слабая
линейная связь двух нейтрально устойчивых волн приводит к не-
неустойчивости основного состояния. Дразин [Drazin, 1989] пока-
показал, что при помощи этого механизма плову честь, обычно счита-
считающаяся стабилизирующим фактором, может дестабилизировать
3Буквально переводится как "перекресток, который избежали". (Прим. ред.
перев.)

Упражнения	55
короткие волны для устойчивого основного параллельного те-
течения; см., например, [Drazin & Reid, 1981, уравнение D4.36)]).
2.19.	Нормальные моды, которые являются точными решениями не-
нелинейных уравнений. Пусть u = U(x,tf), p = Р(х,2) являются
решениеми уравнений Навье-Стокса
ди	1
—+ u- Vu= —Vp+z/Au,	Vu = 0,
at	p
которые описывают течение однородной несжимаемой вязкой
жидкости в неограниченной области. Считая это течение основ-
основным и полагая u = U + и', р = Р + р', где и' = /(х,2)йB), для
некоторых функций /, и таких, что V • и' = 0, покажите, что
соотношение
и' • Vu' = О
удовлетворяется тождественно. Докажите, что если линеари-
линеаризованная задача имеет решение в виде нормальной моды, где
/(х, t) = p(k • х — u)t) и й ос е** для действительных k, cj, <t, то
это возмущение также является точным решением нелинейной
задачи.
Возвращаясь к рассмотрению основного течения покажите, что
если U(x,tf) = S(tf)x + UoB) —неустойчивое линейное сдвиговое
течение с некоторой матричной функцией S, то
—- = S2 = М,	trace(S) = О,
где М(?) — симметрическая матричная функция [Craik &
Criminale, 1986].
2.20.	Неустойчивость эллиптического течения. Рассмотрим ста-
стационарное основное течение однородной несжимаемой вязкой
жидкости с функциями
~~ а2 + Ь2	'	(а2 Л-Ь2J
где а, 6, р, Г2 — положительные постоянные. Покажите, что
вектор вихря V х U = 2Qk постоянен. Проверьте, что это тече-
течение удовлетворяет уравнениям Навье-Стокса и что U • п = 0 на
эллипсоиде, заданном уравнением
d2 + ? + 'с2 =1'

56	Гл. 2. Введение в теорию стационарных течений
где п — вектор нормали к эллипсоиду (хотя течение и не удов-
удовлетворяет условию прилипания на эллипсоиде).
Рассмотрим возмущение скорости в форме
u' = (aqz/c — ary/b, brx/a — bpz/c, cpy/b — cqx/a)
для некоторых функций p, q, г, зависящих только от t. Покажите,
что вектор вихря имеет вид
V х и' = ((Ь2 + с2)р/Ьс, (с2 + a2)q/ca(a2 + Ъ2)т/аЪ),
являясь вектором, постоянным в каждый момент времени,
и с учетом этого приведите линеаризованные уравнения для за-
завихренности в вязкой несжимаемой жидкости к виду
;-а2)Р)
—-О
Подставив нормальные моды р, q <х е**, покажите, что
2_ 4п2а2Ь2(с2-Ь2){а2-с2)
откуда следует, что течение является неустойчивым, если а <
< с < 6 или 6 < с < а, и устойчивым (по отношению к этим
возмущениям) в противном случае [Lamb, 1932, параграф 384].
(Заметим, что найденная выше устойчивость для случая b = a
согласуется с устойчивостью основного течения при вращении
твердого тела (см. упражнение 5.12), хотя и имеет место не-
неустойчивость при 0<Ь-а<1 при условии а < с <Ь. Заметим
также, что значение вязкости не влияет на результаты, потому
что члены с вязкостью обращаются в ноль для рассмотренных
возмущений специального вида).
2.21. Принцип минимума энергии Кельвина и устойчивость потен-
потенциальных течений. Докажите, что из всех течений идеальной
несжимаемой жидкости в односвязной области с заданным нор-
нормальным потоком на поверхности, безвихревое течение имеет
наименьшую энергию.
Объясните, рассматривая двумерные возмущения однородного
течения U = Ui в квадрате — L < х,у < 1/, почему основ-
основное безвихревое течение, хотя и представляет собой течение

Упражнения	57
с минимальной кинетической энергией, не является с необходи-
необходимостью устойчивым. Покажите, что линеаризованное уравнение
для возмущений завихренности удовлетворяется при С {xi Уч t) =
= /(ж — Ш, у) для любой дифференцируемой функции / и, следо-
следовательно, задача для возмущений скорости u.'(x,y,t) не являет-
является корректной, если граничные условия таковы, что нормальная
компонента и7 обращается в ноль на сторонах квадрата. Кроме
того, если С'О^ЗЛО) = д(х,у) в квадрате и ?'(-?,у,*) = h(y,t)
при t > О, где U > О, а д и h являются заданными функциями,
найдите ?' внутри квадрата для t > 0. Докажите, что С не обя-
обязана быть малой при t —>• оо, даже если д(х, у) = 0 для всех ж, у.
(По [Drazin & Reid, 1981, Problem 1.1]. См. [Lamb, 1932, параграф
45]. Подсказка: dC/dt + UdC'/dx = 0, С'(*. У,*) = д{* - ^*. У)
для 0 < t < {х + L)/U и С; = Л(у, * - ж/17) для (я? + ?)/17 < <).
2.22. Неустойчивость Джинса для самогравитирующего газа. Ди-
Динамика самогравитирующего межгалактического газа модели-
моделируется уравнением Пуассона
Д<? = 4тг(?/>,
уравнениями Эйлера, уравнением неразрывности
а также уравнением состояния р = р(р) для баротропной иде-
идеальной жидкости, где ф — гравитационный потенциал, a G —
постоянная гравитации.
Рассматривая малые возмущения основного состояния покоя
с ф = Ф(х), р = Д(х), и = 0 обозначая их штрихами:
линеаризуя уравнения движения и пренебрегая произведениями
возмущений, получите
Аф' = 4irGp',
= °2V/>/ р/УФ ЛУ^'	Ж + V " (Ли/) = 0>
где с = ^(iij/dii]1/2 — скорость звука для основного течения.
Предполагая, что основное состояние является однородным
с й = const, Ф = const (хотя последнее соотношение влечет

58	Гл. 2. Введение в теорию стационарных течений
за собой равенство R = 0 не имеющее физического смысла, и
в дальнейшем будем предпологать, что R > 0), используя нор-
нормальные моды и', //, ф* ос eik#x+e*, покажите, что
Докажите, что однородный газ является гравитационно неустой-
неустойчивым по отношению к длинным волнам [Jeans, 1902].

Глава 3
Неустойчивость Кельвина-Гельмгольца
Отправляющиеся на кораблях в море,
производящие дела на больших водах,
видят дела Господа и чудеса Его в пучине:
Он речет, — и восстает бурный ветер
и высоко поднимает волны его...
Пс.106, 23-25
Для лучшего понимания механизмов и концепций линейной теории
устойчивости, изложенной во второй главе, полезно рассмотреть не-
несколько простых примеров. Во всех этих примерах можно усмотреть
общие этапы изучения устойчивости: A) идентификация физического
механизма неустойчивости данного течения и моделирование неустой-
неустойчивости выбором соответствующей системы уравнений и граничных
условий; B) выбор решения, удовлетворяющего системе уравнений,
для описания основного течения; C) линеаризация системы методом
малых возмущений на фоне основного течения; D) использование ме-
метода нормальных мод; и E) приложение результатов для понимания
характера наблюдаемой неустойчивости или контроля за ней. Для
начала будет рассмотрена классическая задача, которая не требует
много математики. Эта задача относится к описанию важного фи-
физического механизма, посредством которого градиент завихренности
основного течения стремится дестабилизировать течение.
3.1. Основное течение
Рассмотрим основное течение в двух горизонтальных параллельных
бесконечных и расположенных один над другим слоях несжимаемых
идеальных жидкостей, имеющих различные скорости и плотности.
Основное течение задается, соответственно, распределениями скорое-

60	Гл. 3. Неустойчивость Кельвина-Гельмгольца
ти плотности и давления
>°' C.1)
P0-9PiZ лляЖО, V ;
где ?/i, C/2 — скорости течений в двух слоях, pu P2 — плотности
слоев, ро — постоянное давление, z — вертикальная координата и д
— ускорение свободного падения.
3.2. Физическое описание неустойчивости
Гельмгольц [Helmholtz, 1868] отметил, что "каждая геометрически
идеальная острая кромка, обтекаемая жидкостью, должна разрезать
ее на две части, формируя поверхность раздела при медленном дви-
движении жидкости", тем самым неявно признавая существование пред-
представленного выше основного течения; математическая задача о не-
неустойчивости, однако, была впервые поставлена и решена Кельвином
[Kelvin, 1871], а эта неустойчивость получила название неустойчи-
неустойчивости Кельвина-Гельмгольца. Мотивы, в соответствии с которыми
Кельвин выбрал указанное основное течение, ясны не до конца, но он
был другом Гельмгольца и, как увидим, применил эту модель с целью
попытаться понять механизм генерации ветром океанических волн.
Физический механизм неустойчивости Кельвина-Гельмгольца был
описан Бэтчелором [Batchelor, 1967, р. 515-516] в терминах динами-
динамики вихревых движений. Для простоты описания положим на некото-
некоторое время, что U\ = — V, Е/2 = V > 0 и р2 = pi, т.е. рассмотрим
специальный случай вихревго слоя в однородной жидкости, пренебре-
пренебрегая эффектом плавучести. Далее, рассмотрим начальное возмущение,
которое слегка смещает слой, так что его отклонение становится си-
синусоидальным. Вновь для простоты полагаем, что течение является
двухмерным в плоскости (e,z), так что отклонение слоя в последу-
последующие моменты времени описывается соотношением z = ?(ж,?). Бэт-
челор проследил динамику вихрей, используя их следующие фунда-
фундаментальные свойства: каждая вихревая линия в идеальной жидкости
переносится вместе с жидкостью и вызывает вращательное течение
с циркуляцией, равной интенсивности вихревой линии. Завихренность
du/dz — dw/dx в слое положительна для V > 0. Положительная за-
завихренность сносится из точек типа А (рис. 3.1), где С = 0, д?/дх > 0,
по направлению к точкам типа С, где С = 0, дС/дх < 0, потому что
завихренность в части слоя, смещенной вверх (или вниз) индуциру-
индуцирует скорость с положительной (или отрицательной) компонентой по
оси х в любой части полосы, где z > 0 (или < 0). В частности, ин-
индуцированная скорость в точках типа В в каждой части смещенной
вихревой полосы имеет положительную компоненту по оси х. Положи-

3.3. Основные уравнения для возмущений	61
Рис. 3.1. Рост синусоидального возмущения вихревого слоя с положитель-
положительной завихренностью, направленной по нормали к плоскости рисунка. Вели-
Величина локальной интенсивности слоя соответствует его толщине. Стрелки
указывают направления самоиндуцированного движения завихренности в
слое и показывают (а) накопление завихренности в точках типа А и (б)
общее вращение вокруг точек типа С, что все вместе ведет экспоненциаль-
экспоненциальному росту возмущения (по [Batchelor, 1967, Fig. 7.1.3])
тельная скорость, накапливающаяся в точках типа С, будет генериро-
генерировать направленные по часовой стрелке скорости вокруг таких точек
и тем самым усиливать синусоидальное смещение вихревой полосы.
Совместное действие процессов накопления завихренности в точках
типа С и вращения близлежащих точек слоя будут приводить к экспо-
экспоненциальному росту возмущения без изменения его пространственной
формы до тех пор, пока возмущение остается достаточно малым для
того, чтобы значительно изменить основное состояние. В дальнейшем
справедливость этого физического описания будет обоснована при по-
помощи некоторых математических деталей.
3.3. Основные уравнения для возмущений
Кельвин предположил, что возмущенное течение является безвихре-
безвихревым с каждой стороны вихревого слоя. Так будет, если начальное
возмущение являлось безвихревым, потому что безвихревое течение
в невязкой жидкости остается таковым всегда. Тем не менее, также
возможны начальные возмущения с завихренностью. Для упрощения
используемого математического аппарата примем это ограничитель-
ограничительное предположение Кельвина, имея в виду, что оно позволяет дока-
доказать неустойчивость, но не позволяет судить об условиях устойчивос-
устойчивости потому, что это предположение не содержит информации о вихре-
вихревых возмущениях. Фактически, как будет видно из упражнения 3.4 и
главы 8, вихревые возмущения не являются неустойчивыми, так что
Кельвин нашел как необходимое, так и достаточное условие неустой-
неустойчивости. Таким образом, предполагается существование потенциала
скорости ф с каждой стороны поверхности раздела между двумя по-

62	Гл. 3. Неустойчивость Кельвина-Гельмгольца
токами с U = V^, где
(ф2 для*>С,
Y \</>! ДЛЯ Z < С,
поверхность раздела имеет форму
когда течение является возмущенным. Уравнения неразрывности и
несжимаемости дают V • и = 0 и поэтому лапласианы потенциалов
обращаются в ноль, т. е.
Аф2 = О для z > С, A<^i = 0 для z < ?.	C.4)
Заметим, что уравнения движения Эйлера были использованы только
неявно, обеспечивая сохранение безвихревого движения.
Граничные условия определяются следующим образом:
(а)	предполагается, что начальное возмущение возникает в конеч-
конечной области, так что для любого момента времени
Уф -+ U при z -> ±оо;	C.5)
(б)	жидкая частица на поверхности раздела двух жидкостей долж-
должна двигаться вместе с этой поверхностью, движение происходит без
образования полости между жидкостями. Поэтому вертикальная ско-
скорость определяется при помощи субстанциональной производной от
возвышения поверхности (см. [Lamb, 1932, р. 7]):
Это кинематическое условие совпадает с соответствующим условием
для поверхностно-гравитационных волн, которые, как будет показано,
могут являться продуктом рассматриваемой неустойчивости. Разрыв
касательной скорости на поверхности раздела приводит к двум урав-
уравнениям:
(в) нормальное напряжение в жидкости является непрерывным на
поверхности раздела. Для идеальной жидкости это дает динамическое
условие непрерывности давления:
Pi [Ci - j(V*iJ - дфг/dt - gz^ =
= Р2 [Сз " \ (V^2J - дф2/д1 - gz] при z = <:, C.8)

ЗА. Линеаризованная задача	63
которое следует из теоремы Бернулли для безвихревого течения, спра-
справедливой с каждой стороны вихревого слоя z = ?. Для того чтобы
основное течение удовлетворяло этому условию, постоянные Ci,C2
должны быть связаны соотношением
= Р2 (с* - \ut} .	C.9)
Рг
Уравнения C.2)~C.9) представляют собой полную нелинейную
систему уравнений для возмущений основного течения C.1).
3.4. Линеаризованная задача
Для исследования линейной устойчивости запишем
z > С, ^i = E7isc + ^i для z < С, C.10)
а для эффективного определения малых возмущений искомых функ-
функций пренебрежем произведениями ф\, ф'2, С- В силу того, что отсут-
отсутствует характерный масштаб длины для скорости основного течения,
не совсем ясно, насколько малой должна быть величина ? Для то-
того, чтобы процедура линеаризации была справедливой. Однако можно
достаточно убедительно оправдать линеаризацию, если смещение по-
поверхности и ее наклон являются малыми в безразмерной форме, т.е.
ЗС/Зж, dC/ду <С 1 и </? <С U\, Щ. Если эти неравенства выполняют-
выполняются, а также признается, что точное положение поверхности при z = ?
может быть заменено положением z = 0 в основном состоянии при
разложении в ряд Тейлора
то линеаризация уравнений C.4)-C.8) является оправданной, приводя
к следующим уравнениям и граничным условиям:
Аф'2 = 0 для z > 0, Аф[ = 0 для z < 0;	C.11)
>¦ 0 при z —>¦ =роо для & = 1,2 соответственно; C.12)
^ЙГ = S" + ^ё при * = 0 для * = 1,2,	C.13)
C.14)

64	Гл. 3. Неустойчивость Кельвина-Гельмгольца
Легко заметить, что все коэффициенты этой системы линейных
уравнений в частных производных являются постоянными величина-
величинами, а все границы — горизонтальны. Далее используем метод нор-
нормальных мод, предполагая, что произвольное возмущение может быть
выражено при помощи независимых мод в виде
(С, Ф[, Ф'2) = (С, Ш, Ш) ei(**+'»>+".	C.15)
Эта процедура сводит задачу к системе обыкновенных дифференци-
альных уравнений, где z — независимая переменная, ^i, ф2 — функ-
/ч
ции только переменной я, а ? является постоянной величиной.
Из уравнений C.11) следует
fo(z)=A2e-iez+B2eicz,	C.16)
где А2 и В2 являются произвольными постоянными и к = (к2 +Z2I/2
— полное волновое число. Из граничного условия C.12) на плюс бес-
бесконечности следует, что В2 = 0 и поэтому
h(*)=A2e-fez.	C.17)
Аналогично получаем
*.	C.18)
Уравнения C.13)^ C.14) приводят к трем однородным линей-
линейным алгебраическим уравнениям для трех неизвестных постоянных
С, ill, il2- Уравнения C.13) дают
А2 = -(« + УЫ72)С/*, ill = (в + iW7i)C/*,	C.19)
и, следовательно, определяют собственные функции C.15) с точнос-
точностью до произвольных постоянных сомножителей. Тогда уравнение
C.14) приводит к уравнению для собственных значений
Pi [kg + {s + ад2] = />2 [kg - (s + ikU2J] .	C.20)
Решение этого квадратного уравнения дает две моды, для которых
11/2
C.21)
., PiUi+p2U2
О — —1Л* •	'	 ZH
/>1+/>2
	kgjpi -/>гI
(Pi + Р2J	Р1+Р2 J '
Обе моды являются нейтрально устойчивыми, если
1 - Pi) > k2piP2{Ui - U2J.	C.22)

3.5. Поверхностные гравитационные волны	65
В случае равенства имеет место маргинальная устойчивость. Одна
мода является асимптотически устойчивой, но другая неустойчива,
если
ЫА - А) < к2Р1Р2(иг - U2J.	C.23)
Это и есть необходимое и достаточное условия устойчивости мод
с волновыми числами fc, l. Таким образом, течение всегда неустойчиво
(по отношению к модам с достаточно большими fc, т. е. по отношению
к коротким волнам), если U\ ф U2.
3.5.	Поверхностные гравитационные волны
В качестве приложения полученного результата рассмотрим отдельно
специальный случай. Условия р2 = 0 и Ui = U2 = 0 соответствуют
модели поверхностных гравитационных волн на глубокой воде. Эти
волны являются устойчивыми и имеют фазовую скорость
с = ie/jfe = ±(g'/kI'\	C.24)
как это хорошо известно. Данный случай иллюстрирует идентичность
волн и колебательно устойчивых нормальных мод. Часто оказывается
полезным рассматривать волны как специальный случай гидродина-
гидродинамической устойчивости.
3.6.	Внутренние гравитационные волны
Когда основное течение является состоянием покоя (Ui = U2 = 0),
имеем
1/2
s = ± \кд{р2 - Л)/(Л + Р2Ц .	C.25)
Состояние неустойчиво в том и только в том случае, когда р± < р2,
т.е. когда тяжелая жидкость находится над легкой. Однако если
Pi > />2» то состояние устойчиво, а нормальная мода представлят со-
собой волну, распространяющуюся с фазовой скоростью
1/2
Г	-	I1/2
= ± [д{р2 - pi)/*(pi + р2)\ .	C.26)
Собственные функции C.15) для потенциала скорости затухают экс-
экспоненциально с расстоянием при удалении от поверхности раздела,
как во всех случаях неустойчивости Кельвина-Гельмгольца, и, та-
таким образом, движение является ограниченным в окрестности по-
поверхности раздела двух жидкостей. Эти волны представляют собой

66
Гл. 3. Неустойчивость Кельвина-Гельмгольца
Рис. 3.2. Результат ранней стадии неустойчивости Релея-Тейлора Кра-
бовидной туманности, наблюдаемой через большое время после расшире-
расширения газа в пространство (воспроизведено с разрешения Chandra X-Ray
Observatory)
специальный случай внутренних гравитационных волк, которые мо-
могут распространяться внутри стратифицированной жидкости вдали
от какой-либо границы. Они могут наблюдаться в слоях между прес-
пресной и соленой водой, которые появляются в устьях рек; верхняя грани-
граница пресной воды может быть очень гладкой, в то время как сильные4
внутренние гравитационные волны возникают метром или двумя ни-
ниже, потому что для пресной и соленой воды (pi — p2)/{pi + Р2) &
« 10~2 < 1 и уравнения C.23) дают относительно малые скорости
для заданной амплитуды смещения поверхности раздела.
3.7. Неустойчивость Релея-Тейлора
Собственные числа C.25) могут интерпретироваться иначе, если жид-
жидкая система в целом имеет направленное вверх вертикальное ускоре-
ускорение величины /. Тогда, используя принцип эквивалентности в дина-
динамике или решая задачу с нормальными модами, имеем
-*[¦
¦Р2)]
1/2
C.27)
4 Величина амплитуды внутренней волны получается из нелинейной теории и
оказывается пропорциональной (р\ — рг). (Прим. ред. перев.)

3.S. Сдвиговая неустойчивость	67
где g' = f+д — кажущееся гравитационное или результирующее вер-
вертикальное ускорение системы. Отсюда следует, что неустойчивость
имеет место в том и только в том случае, если д' < 0, т. е. результи-
результирующее ускорение направлено от легкой жидкости к тяжелой. Эта не-
неустойчивость была названа неустойчивостью Релея-Тейлора в честь
теории Релея [Rayleigh, 1883] устойчивости стратифицированной жид-
жидкости, находящейся в состоянии покоя под воздействием гравитаци-
гравитационных сил, и наблюдения Тейлора [Taylor, 1950] о важной роли уско-
ускорений, отличных от гравитационных (см. упражнение 8.20).
Неустойчивость Релея-Тейлора можно легко наблюдать при быст-
быстром ускорении стакана воды вниз (если он прозрачный!). Количест-
Количественные наблюдения были сделаны Льюисом с соавторами [Lewis et
al.j 1950]. Существует большое количество приложений данной тео-
теории. Одно из них относится к наблюдению молодых сверхновых звезд,
в которых газ концентрируется в тонких оболочках позади поверхнос-
поверхности раздела, теряющей ускорение после взрыва, в результате которо-
которого более плотный газ оказывается лежащим внутри менее плотного,
по мере того, как расширяющаяся сфера распространяется в область
межзвездного газа [Gull, 1975]. После этого долгое время наблюдает-
наблюдается последовательное нарушение симметрии с формированием волокон
(см. рис. 3.2).
3.8. Сдвиговая неустойчивость
Естественный механизм сдвиговой неустойчивости в отсутствии пла-
плавучести имеет всеобъемлющую важность. Лундгрен [Lundgren, 1982]
выдвинул гипотезу, что именно эта неустойчивость является основной
при возникновении турбулентности при больших числах Рейнольдса,
разрушая сдвиговые слои.
В присутствии вихревого слоя в однородной жидкости (pi = />2>
?Г1 ф С/г) уравнение C.21) дает
8 = -^ВД + U2) ± ^к(иг - U2).	C.28)
Одна из этих мод растет экспоненциально, так что течение всегда
неустойчиво; моды являются растущими и затухающими волнами,
имеющими фазовую скорость, по величине равную средней скорости
основного течения с — §fc(?/i + С/г) Д» спроецированной на направле-
направление (к/к, 1/1) распространения. Неустойчивыми являются волны всех
Длин из-за отсутствия масштаба длины для основного течения. Ско-
Скорость роста возмущений пропорциональна &, так что короткие волны
растут быстрее, однако не существует наиболее быстрорастущей вол-
волны. Фактически, линеаризованная задача с начальными значениями

68
Гл. 3. Неустойчивость Кельвина-Гельмгольца
Рис. 3.3. Схема сворачивания вихревого слоя вследствие сильно-
сильнонелинейного роста двумерного возмущения. Форма поверхности посчитана
для различных временных интервалов по [Krasny, 1986, Fig. 2]; воспроизве-
воспроизведено с разрешения Academic Press)
для этого течения является плохо поставленной и особенность в про-
профиле вихревой полосы может развиваться за конечное время, даже
если начальные данные являются аналитическими. Также можно ви-
видеть, что среди всех волн заданной длины А = 2тгД наиболее быстро
растут волны, которые распространяются в направлении основного
течения (т.е. к = к). Таким образом, через некоторое время волны
в направлении течения становятся доминирующими.
Можно было бы ожидать, что не будет границ устойчивости вихре-
вихревого слоя в идеальной жидкости, потому что не существует безразмер-
безразмерной комбинации физических параметров С/г — C/i? Pi, определяющих
рост возмущений в этой модели. (Существенной является только раз-
разность скоростей, поскольку возможно, без потери общности, придать
любое значение средней скорости \{U\ + С/г)? применив преобразова-
преобразование Галилея). Взяв в качестве характерного масштаба длины L дли-
длину волны Л, а характерной скорости — половину разности компонент
скорости основного течения V = \{U\ — С/г)> находим характерный
масштаб времени L/V = 4tt/Aj(C/i — U2), в течении которого ампли-
амплитуда волны вырастает в exp(kc{L/V) = ехрBтгк/к) га ехрBтг) га 536
раз. На практике неустойчивость не растет так быстро, из-за идеал и-

3.8. Сдвиговая неустойчивость	69
заций в модели Кельвина: хотя уравнение C.28) и хорошо описывает
очень быстрый рост длинных волн малой амплитуды в сдвиговом слое
слабо-вязкой жидкости, модель является сильно упрощенной для опи-
описания неустойчивости реальной жидкости. Тем не менее, амплитуда
растет быстро и нелинейность искажает профиль волны в направле-
направлении основного течения и скручивает поверхность раздела, как пока-
показано на рис. 3.3. Для реального сдвигового слоя конечной толщины,
называемого свободным сдвиговым слоем или слоем смешения, будет
показано (в главе 8), что короткие волны являются устойчивыми. Ной
[Neu, 1984] дал более реалистичное описание сворачивания вихревой
полосы и развития вторичной неустойчивости в слабо-вязкой жидкос-
жидкости. Тем не менее, полученный здесь результат с несомненностью де-
демонстрирует неустойчивость сдвигового слоя по отношению к волнам
с длинами много большими толщины слоя. Кельвин [Kelvin, 1871] (см.
также упражнение 3.2 этой главы) включил в модель также поверх-
поверхностное натяжение и плавучесть и нашел границы устойчивости вих-
вихревого слоя, определив соответстветствующее критическое значение
безразмерного параметра.
Общее условие C.23) неустойчивости Кельвина-Гельмгольца вы-
выражает нарушение балланса между дестабилизирующим влиянием
инерции и стабилизирующим влиянием плавучести, когда более тя-
тяжелая жидкость расположена под более легкой. Кельвин [Kelvin, 1871]
использовал эту теорию в качестве модели генерации океанских ветро-
ветровых волн. Гельмгольц [Helmholtz, 1890] применил эту теорию к вол-
волнистым облакам, возникновение которых в виде регулярных после-
последовательностей свидетельствует о неустойчивости ветров с сильным
сдвигом. Замечательная фотография волнистых облаков показана на
рис. 3.4 (а), где фотографу посчастливилось запечатлеть регулярную
форму облаков в направлении, перпендикулярном к направлению рас-
распространения волны. Волнистые облака, видимые под углом, часто
называют "небом макрели" ("mackerel sky") вследствие аналогии с
полосатым узором на коже этой североатлантической рыбы. Рассмат-
Рассматриваемая неустойчивость приводит к тому, что называется турбу-
турбулентностью чистого воздуха {clear-air turbulence), когда не имеется
достаточного количества водяного пара для того, чтобы сформиро-
сформировать облака, и тем самым сделать неустойчивость видимой.
В статье [Reynolds, 1883] о течении в трубе также описываются
некоторые эксперименты по неустойчивости Кельвина-Гельмгольца,
хотя он и не идентифицировал ее как таковую. Рейнольде заполнил
трубу водой (сверху) и дисульфидом углерода (снизу) и наклонил ее.
Результирующее относительное движение двух жидкостей привело
к неустойчивости границы раздела между ними. Торп [Thorpe, 1969]
позднее усовершенствовал этот эксперимент и явно идентифицировал
неустойчивость Кельвина-Гельмгольца. Один из его результатов по-
показан на на рис. 3.4F) и (в).

70
Гл. 3. Неустойчивость Кельвина-Гельмгольца
Рис. 3.4. Неустойчивость Кельвина-Гельмгольца. (а) Волнистые облака
около Денвера, Колорадо; фотография Поля Бранстайна (Paul E. Branstine).
О метерологических деталях, см. [Colson, 1954]
Следует подчеркнуть, что эта грубая модель Кельвина, являясь
ценной первой попыткой осознать неустойчивость, тем не менее не
описывает многих важных черт наблюдаемой неустойчивости, таких
как ненулевая толщина сдвигового слоя, влияние вязкости и нели-
нелинейности возмущений. Кельвин также не исследовал конечную ста-
стадию эволюции неустойчивости. Как видно из рис. 3.4, в реальности
вихревая полоса укручается, а затем и скручивается; Клаасен и Пел-
тье [Klaasen & Peltier, 1985] показали теоретически, а Тори [Thorpe,
1985] — экспериментально, что трехмерная вторичная неустойчивость
Релея-Тейлора в ядрах волнистости развивается на поздних стадиях,
после чего происходит окончательный распад сдвигового слоя и пере-
переход в турбулентность. Об этом сложном явлении может быть написано
гораздо больше, чем здесь.
Поверхностные волны иллюстрируются в фильме [Bryson, FL1967,
содержащем отрывки из F1967] и внутренние гравитационные волны
в фильме [Long F1968], содержащем лишь несколько эпизодов о них.
Неустойчивость Кельвина-Гельмгольца модифицированная на слу-
случай присутствия вязкости, показана в одном эпизоде фильма [Mollo-
Christensen & Wille, FL1968], а неустойчивость Релея-Тейлора, моди-
модифицированная введением поверхностного натяжения — в другом.

Упражнения
71
Рис. 3.4. (продолжение), (б) Развитие неустойчивости на границе двух
жидкостей равной глубины, имеющих разные ускрения вследствие наклона
канала [Thorpe, 1968]. (в) Момент эксперимента Торпа секундой позже
Упражнения
3.1. Закон поверхностного натяжения Лапласа. Пусть 5 — огра-
ограниченная односвязная гладкая поверхность с гладким замкну-
замкнутым периметром С, принадлежащая поверхности раздела между
жидкостью и газом. Предполагая, что поверхностное натяжение
7 приводит к возникновению силы *у Jc n x dx на, С и что эта
сила находится в равновесии с результирующей силой, возника-
возникающей вследствие разности давлений Ар в направлении поперек
поверхности раздела, покажите что
7 /n x dx = jj (Ap)ndS.
Докажите, что
Ар = 7V • п.
(Е3.1)
Ослабление неустойчивости Кельвина-Гельмгольца поверх-
поверхностным натяжением. Покажите, что если имеется поверхност-
поверхностное натяжение 7 между двумя жидкостями (параграф 3.3), то

72	Гл. 3. Неустойчивость Кельвина-Гельмгольца
уравнение C.21) замененяется соотношением:
с = \k PlUl
± [
Р1 + Р2	I	(Pi + P2j2
(E3>2)
P1 + P2
Докажите, что течение является устойчивым в том и только том
случае, если
(?/i - U2J < 2(Р1 + ЯШ* ~ Р2)]1/2/Р1Р2,	(ЕЗ.З)
при длине волны наименее устойчивой волны на границе устой-
устойчивости А = 2тг/Л = 2n[y/g(pi - рг)]1/2.
Используя модель Кельвина, покажите, что ветер генерирует
волны на море, если разница скоростей основных течений для
воздуха и воды такая, что
\U!-U2\> 6.6 м/с,
а наименее устойчивые волны имеют длину Л =0,017 м и ско-
скорость 0,008 м/с [Drazin & Reid, 1981, Problem 1.4; Kelvin, 1871].
(Подсказка: используйте уравнение (Е3.1) упражнения 3.1, что-
чтобы учесть поверхностное натяжение в динамических условиях
на поверхности раздела. Используйте значения />i = 1020 кг-м",
р2 = 125 кг-м, д = 9,8 м-с", у = 0,074 Н-м).
3*3. Задача с начальными значениями для возмущений вихревой по-
полосы. Предположим, что основное течение представляет собой
вихревой слой в однородной идеальной несжимаемой жидкости
и используем уравнения C.2)-C.9) с {72 = V > 0, Ui = —V, Р2 =
= р\. Рассмотрим безвихревое двумерное возмущение для кото-
которого начальное возмущение, поверхности раздела имеет вид
Находя ф'х, ф'2) докажите, что
С(ж, t) = Яехр [(V2t2 - ж2) /2L2] cos (V xi/L2) для t > 0,
[Drazin & Reid, 1981, Problem 1.5]. (Подсказка:
/+OO	/ -I
expf-i

Упргхяевжя	73
Следовательно,
С(М) = B*)-1/2Н if °° exp (~\h2L2 + \кЛ ch(fcVt) dfc,
так как в ± kV и #?/#? при ? = 0. Поэтому
f °°ехр (-ifc2?2 + ikz\
х (sin fcz ch(kVt) + соз А;ж eh(ibV^)) dfc,
с аналогичным выражением для ф^ отличающимся только зна-
знаками в некоторых местах. Заметим, что V^i, V<^ Ф 0 при
)
3.4. Влияние возмущений с ненулевой завихренностью на неустой-
неустойчивость Кельвина-Гельмгольца. Покажите, что в задаче пара-
параграфа 3.3 линеаризованные уравнения движения Эйлера имеют
вид
ди' ди'	л ,
Ж + и2!)х~ = ~р2 р
Докажите, что Ар' = 0 и возмущение вектора вихря удовлетво-
удовлетворяет уравнению
u/(x,*) = w'(x - U2t,y,z) для z > С-
Отсюда заключите, что присутствие вихря в начальных возму-
возмущениях не влияет на критерий неустойчивости C.23) [Drazin &
Reid, 1981, Problem 1.6].
3.5. Устойчивость Релея-Тейлора жидкостей заключенных в вер-
вертикальный цилиндр и расположенных одна над другой. Рассмот-
Рассмотрим несжимаемую идеальную жидкость плотности р±, располо-
расположенную под аналогичной жидкостью плотности />2, обе жидкос-
жидкости находятся в состоянии покоя и заключены в длинный верти-
вертикальный твердый цилиндр радиуса г = а. На горизонтальной по-
поверхности раздела z = 0 действует поверхностное натяжение 7-
Воспользуемся цилиндрическими координатами г, 0, z, где ко-
координатная ось Oz направлена вверх. Покажите, что так же, как
и в упражнении 3.2, малые безвихревые возмущения состояния
покоя могут быть найдены как суперпозиция нормальных мод
вида
ф' ос Jn{kr)cosn0e-fc|z|+" и Сое Jn{kr)cosn0e",

74	Гл. 3. Неустойчивость Кельвина-Гельмгольца
п = О,1,..., где
- Pi)k - -yk3
Р1 + Р2
ика = fnTn — положительный ноль под номером m производной
J'n Функции Бесселя n-го порядка, га = 1,2,... . Докажите, что
устойчивость имеет место, если
а2д{р2 - Pi) < 7iiV
[Drazin & Reid, 1981, Problem 1.12]. Этот результат показывает,
что стабилизация длинных волн присутствием границы, а ко-
коротких волн — поверхностным натяжением, может иметь место
для всех возмущений и в случае, когда тяжелая жидкость нахо-
находится над легкой жидкостью. Данное физическое явление можно
наблюдать в эксперименте [Mollo-Christensen, F1968] для реаль-
реальных (и поэтому вязких) жидкостей, короткие волны в которых
стабилизируются влиянием вязкости [Maxwell, 1876].
3.6. * Неустойчивость Релея-Тейлора в^ присутствии вязкости и
поверхностного натяжения. Рассмотрим две несжимаемые
жидкости, находящиеся в состоянии покоя и разделенные гори-
горизонтальной границей z = 0. Пусть р\ — плотность нижней жид-
жидкости, а р2 — верхней. Предположим, что обе жидкости имеют
ту же самую кинематическую вязкость i/ина поверхности разде-
раздела действует сила поверхностного натяжения с коэффициентом
поверхностного натяжения 7- При помощи метода малых воз-
возмущений покажите, что нормальные моды, пропорциональные
e*t+i(kx+iy) ^ подчиняются соотношению на собственные значения
(/>1 + Л) [дЦрг - Р ~ 2) + *37] (г - 1) + 4*2м/(Л - Р2J{г - 1)+
+4s2PlP2 =
где к2 = к2 + /2, г = A + в/к2»I'2 и Re(r) > 0. (Подсказ-
(Подсказки: Линеаризуйте уравнения движения, а затем положите w' =
= Wj(z)est+1(kx+ly\ где j = 1 под поверхностью раздела и j = 2
над ней; докажите, что уравнения движения и граничные усло-
условия на бесконечности удовлетворяются выбором wi(z) = Aiekz +
+Biekrz, г&2 = A2e~kz -f B2e~krz. Покажите, что непрерывность
нормальной и касательной компонент скоростей на возмущенной
поверхности означают непрерывность г&, Dw при z = 0 соответ-
соответственно. Покажите, что непрерывность нормальной и касатель-
касательной компонент напряжений на возмущенной поверхности дает
при z = 0
2 P

Упражнения	75
- k2)]Dw2 - pi[l - us~1(D2 - k2)]Dw2 =
- px) - k2j]w - 2k2i/s~1(p2 - pi)Dw
соответственно [Harrison, 1908); Bellman & Pennington, 1954].
См. также [Chandrasekhar, 1961, параграф 94]).
3.7.	Неустойчивость Релея-Тейлора и критерий Шварцшильда для
атмосферной устойчивости. Можно показать, что'идеальная
несжимаемая жидкость плотности p(z) будет устойчива, если
p(z) < 0 для всех 2, при помощи следующего эвристическо-
эвристического "физического" довода. "Положим, что частица жидкости на
уровне zo немного поднимается (или опускается, если Sz < 0) на
высоту zo -\-Sz. Тогда ее плотность остается p(zo) (потому что в
несжимаемой жидкости плотность не рассеивается, но окружа-
окружающая жидкость имеет плотность p(zo + Sz) = p(zo) + Szpf(zo) +
0[(<fcJ] при Sz —> 0. Поэтому, если частица плотнее, чем окру-
окружающая жидкость (легче, если Sz < 0), то p(zo) > p(zo+Sz), т.е.
p'(zo) < 0, и силы плавучести тянут частицу назад к ее началь-
начальному уровню. Наоборот, если p'(zo) > 0, то частица продолжает
удаляться от ее первоначального уровня. Отсюда следует, что
жидкость является устойчивой, если pf(z) < 0 для всех 2, и не-
неустойчивой, если p'(z) > 0 для некоторых z". (Релей [Rayleigh,
1883] произвел линеаризацию уравнений Эйлера, чтобы проде-
продемонстрировать этот результат более убедительно. См. упраж-
упражнение 8.19).
Известно, что атмосфера, состоящая из совершенного газа, на-
находящегося в состоянии покоя, является устойчивой по отноше-
отношению к малым возмущениям, если Г < Га, и неустойчивой, ес-
ли Г > Га, Г = — dQ/dz — скорость падения температуры
(lapse rate) атмосферы, представляет собой вертикальный гра-
градиент температуры, взятый с обратным знаком, Га называет-
называется адиабатической скоростью падения температуры^ т.е. Га
— скорость падения температуры атмосферы в состоянии адиа-
адиабатического равновесия. Придумайте или найдите "физическое"
обоснование этого критерия устойчивости для атмосферы (пла-
(планеты или звезды).
(Подсказка: Р = Лр0, R = ср — cv, 7 = cp/cv для совершенного
газа, а Р/р1 не зависит от высоты в состоянии адиабатического
равновесия).
3.8.	Неустойчивость Кельвина-Гельмгольца трехмерного основно-
основного течения. Задано основное течение, скорость, плотность и дав-
давление для которого имеют вид
¦ _ JP0-9P2Z при z > 0,
при z < 0.

76	Гл. 3. Неустойчивость Кельвина-Гельмгольца
Покажите, что нормальным модам, пропорциональным
ei(kx+iy)+st ^ соответствует дисперсионное соотношение
JJHpiUi +P2U2) + l(piVi + P2V2)] ^
s —	—	±
Докажите, что течение устойчиво, если
(Pi + P2)(pi г- Р2)д > PiP2{AUJ{k2 + Z2I/2,
где AU = [k(U2 - иг) +l(V2 - Vi)]/(fc2 + Z2I/2 — разность скорос-
скоростей основного потока в направлении вектора волновых чисел.
3.9. Неустойчивость Саффмана-Тейлора или неустойчивость Ре-
лея-Тейлора в пористой среде. Рассмотрим неустойчивость ос-
основного течения, для которого две несжимаемые вязкие жидкос-
жидкости двигаются с горизонтальной поверхностью раздела и одно-
однородной вертикальной скоростью в пористой среде. Известно, что
движение жидкости в пористой среде подчиняется закону Дарси
u = V^, где ф =¦ — k(p + gpz)/ii, р — плотность жидкости, /х —
динамическая вязкость, а к — постоянная величина, называемая
проницаемостью пористой среды по отношению к жидкости.
Пусть жидкость, расположенная снизу, имеет плотность pi и
ВЯЗКОСТЬ /Xi, а ВерХНЯЯ ЖИДКОСТЬ 	 ПЛОТНОСТЬ />2 И ВЯЗКОСТЬ /Х2
соответственно; пусть среда имеет проницаемость ti по отно-
отношению к нижней жидкости и проницаемость &2 по отношению
к верхней, а скорость основного течения жидкостей равна Wk.
Покажите, что течение устойчиво в том и только том случае,
когда
[Drazin & Reid, 1981, Problem 1.11; Saffman & Taylor, 1958]. (Под-
(Подсказка: используйте для мгновенного положения средней поверх-
поверхности раздела уравнение z = 0, а для возмущенной поверхности
— уравнение z = С- Докажите, что Аф = 0 при z ф С» Используя
непрерывность нормальной скорости и давления, линеаризуйте
задачу. Полагая для нормальных мод С ос exp(s? + iau), покажи-
покажите, что

Глава 4
Капиллярная неустойчивость струи
Польется как дождь учение мое...
Втор. 32, 2
Еще одна классическая проблема, не требующая применения слож-
сложных математических методов, формулируется и решается в этой гла-
главе. Это опять идеализированная модель важного физического явления,
на сей раз — распада круглой струи жидкости под действием сил по-
поверхностного натяжения.
4.1. Теория Ре лея капиллярной неустойчивости
струи жидкости
Для иллюстрации идей и методов главы 2 рассмотрим другой пример
классической задачи, впервые решенной Релеем в 1879 г. Взгляните
на рис. 4.1, где изображена струя воды, распадающаяся на капли. Про-
Процесс распада выглядит как проявление неустойчивости. Будем описы-
описывать струю жидкости в воздухе (например, падение воды из приот-
приоткрытого крана) как цилиндрический объем несжимаемой идеальной
жидкости, движущейся с постоянной скоростью параллельно оси ци-
цилиндра. Положим далее, что присутствует сила поверхностного натя-
натяжения, а объемлющая жидкость вне цилиндра имеет нулевую плот-
плотность. Теперь уже наиболее трудная часть нашего задания, а именно,
моделирование явления с помощью поддающейся анализу математи-
математической задачи, преодолена!
Удобно использовать цилиндрические координаты (ж, г, в). Тогда
размерные уравнения, описывающие струю в возмущенном состоянии,

78
Гл. 4. Капиллярная неустойчивость струи
"-¦*-%-i;H^r^'.i-4-'y"*:'~ ~;''-:i:%;;^^4i^5^^^*.Wt*;**«^Cft' Ц'-S-V.."•¦•" V '•- .-'л*':^'-^*
fi3^^
Рис. 4.1. Распад струи воды, по мере возбуждения различных длин волн
[Van Dyke, 1982, Fig. 122]
— это уравнения движения Эйлера идеальной жидкости
(дм	„ \
р I	(- и • Vu 1 = — Vp,
D.1)
а также уравнение неразрывности для несжимаемой жидкости
V • и = 0.	D.2)
Результат Лапласа (см. упражнение 3.1) о том, что скачок давления
в направлении, поперечном к поверхности струи жидкости, равен про-
произведению коэффициента поверхностного натяжения 7 и суммы глав-
главных кривизн дает
-n при г = С,
D.3)
где г = С(ж, 0, t) — уравнение возмущенной поверхности, р^ — внеш-
внешнее давление и единичный вектор внешней нормали от поверхности
равен
п =
[(дС/дхJ+1+(дС/гдвJ]
2-11/2*
D.4)
Необходимо также использовать кинематическое условие, что каждая
частица, принадлежащая поверхности, остается на этой поверхности:
D.5)

4.1. Теория Релея капиллярной неустойчивости струи	79
Для того чтобы описать основное состояние, воспользуемся, без
потери общности, преобразованием Галлилея, применение которого
приводит основное состояние к состоянию покоя. Получаем
U = О,	Р = роо + у/а при 0 < г < а,	D.6)
где а — радиус струи, 7 — коэффициет поверхностного натяжения
и роо — давление окружающей жидкости, так как V • п = дпх/дх +
+д(гпг)/гдг + дщ/гО = 1/г, когда п = @,1, 0).
Для определения характеристик устойчивости линеаризуем урав-
уравнения относительно малых возмущений и' = и, р' = р — Р, С' = С — а-
Находим, таким образом,
p^ = -VP',	D.7)
V•и' = 0,	D.8)
так как V • п = 1/г — д2С'/дх2 — д2С'/г2д92 плюс квадратичные члены
относительно С' и производных ?'• Заметим, что эти уравнения дают
1 = 0,	D.10)
где оператор Лапласа в цилиндрических координатах определяется
выражением
а = о2/дх2 + д2/дг2 + д/гдг + д2/г2зе2.
Переходя к нормальным модам
сразу получаем из уравнения D.10)
fP+lff^+ *)fi = 0.	D.11)
dr2 r dr \ r2)
Уравнение D.11) представляет собой модифицированное уравнение
Бесселя тг-го порядка для функций /п(/гг), Kn(kr); можно взять п > 0
без потери общности. Из условия ограниченности р(г) при г —> 0,
получим
p(r) = AIn(kr)	D.12)

80	Гл. 4. Капиллярная неустойчивость струи
для некоторой постоянной А. Из у равнение D.7) тогда имеем
u = -Aips)-1 (ikln(kr), kl'n(kr),тг-х7п(Лг)) .	D.13)
Наконец, линеаризованные граничные условия дают
AIn(a) = -7A - а2 - п2)С7<*2, -Л(о/»)-1аГя(а) = <, D.14)
где а = ак. Исключая А, получаем соотношение на собственные зна-
значения
,» = 4-^A-а*-»*).	D.15)
а3р I(a) v	y
В силу свойств функций Бесселя имеем аГп(а)/ 1п(а) > 0 для всех
афО. Поэтому s2 < 0 для всех а, если п ^ 0, но з2 > 0 для —1 < а < 1
и з2 < 0 для а > 1 или а < —1, если п = 0. Следовательно, струя яв-
является устойчивой Re(s) = 0 по отношению ко всем возмущениям,
которые не являются осесимметрическими, и неустойчивой — по от-
отношению к осесимметрическим возмущениям, длина волны которых
А = 2тг/& больше, чем длина окружности струи 2тга. Если мы опреде-
определим кт как значение fc, для которого Re(s) является наибольшим, то
в результате несложных вычислений получим кт « 0,7/а.
Что представляет собой нелинейная стадия развития этой неустой-
неустойчивости? Бифуркации отсутствуют (в этой модели, потому что струи
всех радиусов являются неустойчивыми: неустойчивость нарастает
быстрее для более тонких струй). Безразмерной комбинации физичес-
физических параметров а, 7? А определяющих модель, нет, в связи с чем не-
невозможно определить критическое значение параметра, отвечающее
границе устойчивости. Ожидается, что малое начальное возмущение
струи возбуждает моды всех волновых чисел кип. Экспоненциально
растут только моды сп = 0и0<а&<1ипо прошествии небольшого
промежутка времени эти моды будут доминировать, содержа наиболее
быстро растущую моду, скорость роста которой опережает скорость
роста всех остальных мод. Экспоненциальный рост, предсказанный
данной линейной теорией, не может длиться долго, потому что по
мере роста возмущения становится существенной нелинейность. Без
численных расчетов стадии сильно нелинейного развития возмуще-
возмущения возможно только ориентироваться на результаты экспериментов
или рискнуть предсказать, что струя жидкости будет разрушаться
с длиной волны равной 2ir/km га 9а. Отправляйтесь на кухню, от-
откройте кран и проверьте для себя это утверждение! Можно также
взглянуть на фотографии аккуратного лабораторного эксперимента
(рис. 4.1). Бще лучше посмотреть анимацию [Trefethen FL1965, отре-
отредактированный F1965], где используется высокоскоростная фотогра-
фотография с тщательно контролируемым освещением. Рисунок 4.2 показы-
показывает некоторое количественное подтверждение теории Релея.

Упражнения
81
0.4г-
0.2
0.5
1.0
1.2
a=ak
Рис. 4.2. График безразмерной скорости роста (агр/чI128 как функ-
функции безразмерного волнового числа а для осесимметрических капилляр-
капиллярных мод (п = 0). Кривая соответствует теоретическим результатам Релея,
а точки — экспериментальным результатам, представленным в [Donnely &
Glaberson, 1966]
Эта задача была выбрана здесь как простая иллюстрация ме-
методов линейной теории гидродинамической устойчивости, которая
может быть непосредственно связана с физическим наблюдением. Од-
Однако, кроме того, она является фундаментальной для понимания яв-
явления атомизации с формированием капли и брызг. Эти более общие
аспекты проблемы, а также более современные результаты по распаду
струй содержатся в обзоре [Lin & Reitz, 1998].
Упражнения
4.1. Капиллярная неустойчивость струи газа. Для струи газа
в жидкости, которая находится в состоянии покоя в области
г у а вне газа, покажите, что соотношение на собственные зна-
значения D.15) заменяется на
'а3
т. е. что неустойчивость имеет место только для варикозной мо-
моды (п = 0) с — 1 <а< 1и что безразмерная относительная
скорость роста [cPp/iY^s достигает своего наибольшего значе-
значения 0,820 при а =0,484 [Drazin & Reid, 1981, Problem 1.8].

82	Глава 4. Капиллярная неустойчивость струи
4.2.	Роль завихренности при капиллярной неустойчивости. Из урав-
уравнения D.7) следует, что вектор вихря w' = V х и' не зависит от
времени. Докажите, что
ы'(х,«) =«'(*, 0).
Обсудите значение этого факта для решения линеаризованной
задачи о капиллярной неустойчивости с начальными данными,
замечая, что безвихревые и вихревые компоненты возмущения
удовлетворяют принципу суперпозиции [Drazin & Reid, 1981,
Problem 1.9].
4.3.	Капиллярная устойчивость плоской струи. Идеальная несжи-
несжимаемая жидкость с плотностью р и коэффициентом поверхност-
поверхностного натяжения j находится в состоянии покоя между свобод-
свободными плоскими поверхностями z = dba. Покажите, что устойчи-
устойчивость жидкости определяется уравнением
Ар' = 0 для — оо < ж, у < оо, — а< z < a
и граничными условиями
=±r[+) при •
Полагая р1 ос exp[st + i(kx + ly)], покажите, что
3 2
—-— = —a3tha или — a3ctha,
7
где a = a(k2 + Z2I/2. Докажите, что такая плоская струя яв-
является устойчивой, в отличие от круглой струи, которая не-
неустойчива по отношению к осесимметрическим возмущениям.
[Drazin & Reid, 1981, Problem 1.10]. (Подсказка: pdu!/dt =
= _Vp', V - u' = 0, n = ±(-дС'/дх, -дС'/ду, 1), p' = -7V • n,
w1 = —d?'/dt при z = dba. Заметим, что s2 ~ —*ya3/a3p при
a —У оо для коротких капиллярных волн на свободной поверх-
поверхности как и в случае с круглой струей).

Глава 5
Развитие неустойчивости во времени
и в пространстве
И настанут устойчивые времена твои,
изобилие спасения, мудрости и ведения...
Ис. 33, 6
Более сложные свойства неустойчивостей будут описаны и объяснены
в этой главе: эволюция нормальных мод как в пространстве, так и по
времени, эффект малой нелинейности и балланс энергии.
5.1. *Эволюция возмущений в пространстве
и во времени
Для уравнений в частных производных, описывающих движение жид-
жидкости, полезно более детально проанализировать природу устойчи-
устойчивости.
Во-первых, заметим, что если течение ограничено (а на практике,
разумеется, все течения ограничены), то имеет место счетное множес-
множество нормальных мод; если течение неограничено, то нормальных мод
несчетное число. Для течения Пуазейля в примере 2.11, которое не-
неограничено в направлении ж, существует континуум мод с непрерывно
изменяющимся волновым числом к наряду с дискретными волновыми
числами в направлениях в и г, в то же время для течения в кубе име-
имеют место три дискретных волновых числа, отвечающих каждой нор-
нормальной моде. Таким образом, для неограниченного течения наиболее
неустойчивой модой может быть только первая среди»равных, а для
ограниченных течений скорость роста наиболее неустойчивой моды
в общем случае будет значительно больше, чем у второй из наиболее
неустойчивых мод. Для ограниченных течений с большим отношени-

84	Гл. 5. Развитие неустойчивости
ем масштабов (или большим числом Рейнольдса) наиболее неустой-
неустойчивые моды обычно близки друг к другу, тем самым аппроксимируя
континуум.
Полезно также делать различия между течениями, которые часто
называются закрытыми и открытыми. На этот счет не принято стро-
строгих определений и закрытым обычно называется такое течение, в ко-
которым все жидкие частицы, проходящие через каждую точку, не поки-
покидают области течения. Течение, в котором жидкие частицы покидают
область течения или входят в нее через границы или бесконечность
называется открытым. Например, состояние покоя жидкости в не-
непроницаемом ящике или течение Куэтта между двумя коаксиальными
цилиндрами являются закрытыми. Течение Пуазейля вдоль бесконеч-
бесконечно длинной круглой трубы представляет собой открытое течение, так
же как и течения в каналах, пограничный слой Блазиуса на плоской
пластине, струя, след, вихревая дорожка и свободный сдвиговый слой
(слой смешения). Открытое течение часто имеет естественное начало,
например, край пластины, на которой расположен пограничный слой,
сопло струи или движущийся край разрезающей пластины, которая
производит свободный сдвиговый слой; в этих явлениях открытое те-
течение не обладает галилеевой инвариантностью.
Неограниченное течение допускает физически различные типы не-
неустойчивости. Оно абсолютно неустойчиво, если достаточно ма-
малое возмущение вырастает больше заданного порога в фиксированной
точке течения. То же самое может быть выражено в математической
форме определением абсолютно неустойчивого течения как течения,
в котором существует малое начальное возмущение, удовлетворяю-
удовлетворяющее линеаризованной задаче, такое, что
|и'(х,?)| —> оо при t —> оо
для всех фиксированных х. Течение конвективно неустойчиво, ес-
если, аналогично, достаточно малое возмущение не вырастает больше
заданного порогового значения ни в какой фиксированной точке, но
растет в движущейся точке; в этом случае возмущение может рас-
расти экспоненциально в процессе распространения вниз по потоку (и за
пределы лаборатороной сточной трубы). Отсюда имеем
для всех фиксированных х, но существует V такое, что
|и;(х + V*, t) | ->• оо при t -> оо.
Заметим, что это различие не является галилеево инвариантным.
Конвективная и абсолютная неустойчивости проиллюстрированы на
рис. 5.1.

5.1. Эволюция возмущений
85
Рис. 5.1. Схема развития (а) абсолютной и^б) конвективной неустойчи-
неустойчивости в плоскости (ж,*) (по [Schmid & Henningson, 2001, Fig. 7.6]; воспроиз-
воспроизведено по разрешению Springer-Verlag GmbH & Co. KG)
Пример 5.1: Дисперсия. Для представления понятия дисперсии и неко-
некоторых обозначений расмотрим линейное уравнение, имеющее только
вспомогательное значение:
ди'
ди' д2и'
E.1)
где W — постоянная. Это уравнение можно рассматривать как лине-
линеаризованное уравнение для задачи об устойчивости некоторого основ-
основного "течения" U. Подстановка нормальных мод
u'(x,t) = Ве[Ае11кх-ы*>]	E.2)
дает дисперсионное соотношение частоты и волнового числа:
V{k,w;R) = 0,	E.3)
где2}(&,с*;; R) = —iw+iWfc + fc2—(Д—Дс) для уравнения E.1). Отсюда
« = /(*), где f(k) = Wk-ik2+i(R-Rc) nW = /'@), Д-Дс = -i/@).
Уравнение E.1) может быть записано также в символическом виде
V{-id/dz,id/9t]R)v,' = 0.
"Течение" асимптотически устойчиво, если R < Лс, потому что
все моды экспоненциально убывают. "Течение" конвективно неустой-
чиво, если R > Rc и W ф 0, потому что экспоненцивльно рас-
растущие моды также и распространяются. "Течение" обсолютно не-
неустойчиво, если R > Rc и W = 0. Групповая скорость волн E.2)
ся =
= W - 2ift.
//
Другая важная идея, пришедшая из физики плазмы, оказывается
полезной при рассмотрении возмущений, генерируемых вибрирующи-
вибрирующими лентами или маленькими громкоговорителями, которые помеща-
помещается экспериментаторами в течения в каналах или пограничные слои

86	Гл. 5. Развитие неустойчивости
в качестве малоразмерного источника колебаний фиксированной час-
частоты. Если течение абсолютно неустойчиво, то внесение источника
сразу приведет к появлению возмущений, которые растут по линей-
линейной теории в его окрестности, там где можно ожидать скорого возник-
возникновения нелинейных эффектов и, может быть, турбулентности. Бели
течение устойчиво или конвективно неустойчиво, то возмущения мо-
могут иметь ту же частоту, что и источник в его окрестности, где они
затухают или растут по пространству. Эти возмущения называют-
называются пространственными модами. Если источник имеет частоту о;, то
возмущения могут затухать или расти по пространству как elfcx, где
к — корень V(k, w; R) = 0.
Можно предвидеть, что в общем случае будет бесконечный спектр
таких комплексных корней к и что наиболее быстрорастущая из нор-
нормальных мод будет преобладать в возмущении вскоре после включе-
включения источника, располагаясь вниз или вверх по потоку от источника
в соответствии со знаком групповой скорости.
Для простого обоснования этих идей, рассмотрим другую вспо-
вспомогательную одномерную задачу, например, основное "течение" U с
возмущением u'(x,t) is. некоторой дисперсионной функцией 2>(fc,u>), по
которой можно восстановить линеаризованное уравнение
V(-\d/dx,id/dt)uf{x,t) = 0.	E.4)
Для изучения развития возмущений от различных источников рас-
рассмотрим функцию Грина G мгновенного локализованного единичного
источника при t = 0, х = 0. Она удовлетворяет неоднородному урав-
уравнению
V(-id/dz,id/dt)G{x,t) = 6{tN{x)	E.5)
и исчезает при t < 0 и при х —> ±оо для фиксированных t > 0. Поучи-
Поучительно отметить, например, поведение G при t —> оо и фиксированных
x/t = V. Если основное течение асимптотически устойчиво, то
G{x,t) -» 0 при t -» оо VV.	E.6)
Если основное течение экспоненциально неустойчиво, то
G(x,t) -» оо при t -» оо	E.7)
для, по крайней мере, одного значения V. Если, более того, основное
течение конвективно неустойчиво, то
G{x,t) -+ 0 при t "->¦ оо для V = 0;	E.8)
и если основное течение абсолютно неустойчиво, то
G(x,t) -+ оо при t -+ оо для V = 0.	E.9)

5.1. Эволюция возмущений	87
Такому рассмотрению линеаризованной задачи с начальными зна-
значениями и изучению решения по прошествии большого времени
было положено начало Ландау [Landau, 1946] и дано всеобъемлю-
всеобъемлющее развитие Бриггсом [Briggs, 1964] для физики плазмы. Аналогич-
Аналогичные идеи были впоследствии применены в теории гидродинамичес-
гидродинамической устойчивости, в значительной степени Хуэрром и Монкевитцем
[Huerre & Monkewitz, 1990]. Разумеется, в этих теориях поведение воз-
возмущений по прошествии большого времени является важным и с физи-
физической точки зрения. В зависимости от природы дисперсионной функ-
функции V возникают дополнительные сложности, поэтому остановимся
только на основных правилах. Используя преобразования Лапласа и
Фурье, выразим функцию Грина:
С eKkx-vt)
E10)
где F — контур в комплексной плоскости &, подходящий для обраще-
обращения преобразования Фурье по fc, a L — контур в комплексной плоскос-
плоскости и, подходящий для обращения преобразования Лапласа. Располо-
Расположение контуров F и ?, а также действия с ними, представляют собой
тонкий технический вопрос, решение которого зависит от расположе-
расположения особенностей интегралов, т.е. нулей дисперсионной функции V.
Поведение G{x,i) при t —>• оо может быть определено методом наи-
наибыстрейшего спуска. Седловые точки находятся там, где групповая
скорость удовлетворяет соотношению
- - —(к)
t ~ difeW'
а ветвь функции и [к) определяется из равенства !D(fc,u>(fc)) = 0. Во
многих задачах может быть найден комплексный корень ко, удовле-
удовлетворяющий уравнению
jj-iko) = 0,
и может быть показано, что если Im(a;(A;o)) > 0, то течение абсолютно
неустойчиво, а если Im(a;(fco)) < 0, то течение конвективно неустой-
неустойчиво.
Аналогично, линейное возмущение от локализованного элементар-
элементарного источника в точке х = 0, имеющее вещественную частоту и воз-
возникающее в момент t = 0, может быть выражено в виде интеграла
с ^пользованием преобразований Фурье и Лапласа, и можно получить
асимптотическую оценку этого интеграла при t —у оо и фиксирован-
фиксированных ж. Это даст пространственные моды частоты ш вниз или вверх
по потоку от источника в зависимости от знака групповой скорости,
если течение не является абсолютно неустойчивым.

88	Гл. 5. Развитие неустойчивости
Линеаризованные задачи с начальными данными в трех измерени-
измерениях имеют гораздо более сложную структуру, чем вспомогательные од-
одномерные задачи, тем не менее оба типа задач подчиняются сходным
закономерностям. Часто оказывается, что для течений вязкой жидкос-
жидкости все моды устойчивы при Л < Лс, некоторые из них конвективно
неустойчивы при Лс < Л < Ла, а некоторые абсолютно неустойчи-
неустойчивы только при R > Ла, где Ra — значение числа Рейнольдса R или
какого-либо другого безразмерного параметра.
Совершенно другой подход к развитию возмущений в пространст-
пространстве и по времени был применен в случае эволюции волновых пакетов,
состоящих из слабо неустойчивых мод. Этот подход может быть схе-
схематически представлен на интуитивном уровне снова в случае одного
измерения, так что независимыми переменными являются только х
и t. Многие из идей могут быть достаточно легко обобщены на слу-
случай более высоких размерностей. В теории гидродинамической устой-
устойчивости имеет место множество задач, которые инвариантны отно-
относительно обращения оси х и однородны по пространству, так что
будем предполагать эти свойства выполненными. Пусть линеаризо-
линеаризованная задача допускает решение в виде нормальных мод
u'{x,t) = Re(Aeikx+8t),	E.11)
с вещественными волновыми числами к и дисперсионным соотноше-
соотношением s = <т + \т = /(&, Д), где R является параметром задачи, на-
например, числом Рейнольдса. Основная идея заключается в том, чтобы
алгебраически аппроксимировать дисперсионную функцию V(k, s; R)
для 0 < Л - Лс < 1 с целью описания узкой полосы слабо неустой-
неустойчивых мод, а затем восстановить приближенное дифференциальное
уравнение, которому подчиняется и'.
Из инвариантности относительно отражения следует, что выраже-
выражение Ae~lkx+8t также представляет из себя решение линеаризованной
задачи и, следовательно, /(—fc, R) = /(&, Л). Предположим далее, что
существует наиболее неустойчивая или наименее устойчивая мода, от-
отвечающая волновому числу kc(R) ^Ои что функция / аналитична по
к в точке &с, тогда <т = Re (/) имеет простой максимум при к = kc(R).
Таким образом,
= a - b(k2 - klf + О[(к2 - fcc2K] при к
где а ~ 7(# - Rc), 0 < Ь -> Ьс при Л -» Лс и к > 0. Маргинальная
кривая <r(fc, Л) = 0, характерная для многих задач гидродинамичес-
гидродинамической устойчивости, схематически изображена на рис. 5.2 (а). График a
как функции от к при фиксированном Л в малой окрестности Лс тог-
тогда имеет форму, изображенную на рис. 5.2F). Заметим, что ширина
полосы неустойчивых волн имеет порядок величины е при е -> 0, где
A/2

5.1. Эволюция возмущений
89
О
б
а
О
-0(в)	1
\
Рис. 5.2. (а) Вид типичной критической кривой а = О в плоскости
(б) Вид графика <r(fc, i?) при фиксированных R, 0 < е2 = R — Rc <?1
Положим и = — Im[/(fcc, Rc)]. Задача при 0 < R—Rc <^C 1 допускает
приближенные моды вида
тф, t) = Re{A(X, T) exp[i{kcx - erf)]},	E.12)
где X, Т — "медленные" координата и время соответственно. Имеем
X = €2ж, Т = е2?, а функция А удовлетворяет эволюционному уравне-
уравнению, члены которого соответствуют членам в уравнении E.3). Пере-
Переходя при помощи преобразования Галилея к системе отсчета, движу-
движущейся с групповой скоростью наиболее неустойчивой моды на грани-
границе устойчивости cg = — [dr/dk]R=Rcik=koi можно устранить слагаемое
дА/дХ. Здесь введено обозначение ко = kc(Rc)' Модуляции наиболее
неустойчивой моды, таким образом, подчиняются уравнению
дА
—
E.13)
^To уравнение в частных производных приближенно описывает моду-
модуляцию растущего пакета слабо неустойчивых волн по пространству
и во времени при распространении пакета с групповой скоростью и
перестает быть верным, как только нелинейность становится сущест-
существенной.

90	Гл. 5. Развитие неустойчивости
5.2. Слабонелинейная теория
Другим важным методом теории гидродинамической устойчивости
является слабонелинейная теория, по-существу представляющая со-
собой метод возмущения характеристик линейной теории устойчивости
для возмущений малой амплитуды. Этот метод также включает в
себя локальную теорию бифуркаций режимов течения. В параграфе
1.1 упоминалось о том, что Рейнольде [Reynolds, 1883] осознал физи-
физическую важность нелинейных возмущений течения Пуазейля в тру-
трубе. Первые шаги в нелинейной теории были сделаны Стоксом [Stokes,
1880] для поверхностных гравитационных волн в глубокой жидкости,
Бором [Bohr, 1909] для капиллярной неустойчивости и Нётер [Noether,
1921], а также Гейзенбергом [Heisenberg, 1924] для неустойчивости
плоско-параллельных течений вязкой жидкости, однако первые общие
результаты по неустойчивости были получены Ландау [Landau, 1944].
Он имел свое видение слабонелинейной теории, которое позволило ему
выписать уравнение, называемое ныне уравнением Ландау, но он не
выводил его непосредственно для неустойчивости конкретных тече-
течений. Стационарная форма этого уравнения впервые была выведена
из одной задачи механики жидкости независимо Горьковым [Gor'kov,
1957], а также Малкусом и Веронисом [Malkus & Veronis, 1958], ко-
которые решили слабонелинейную задачу о конвекции Релея-Бенара со
свободно-свободными условиями на границе. Стюарт [Stuart, 1960] и
Ватсон [Watson, 1960 b] первыми асимптотически вывели полное урав-
уравнение Ландау для слабонеустойчивых возмущений плоскопараллель-
плоскопараллельных течений.
Из общих соображений можно описать генерацию слабонеустой-
слабонеустойчивым возмущением слабонелинейных взаимодействий и посредст-
посредством этого подавление собственной неустойчивости. В линейной тео-
теории устойчивости стационарного основного течения имеющего ско-
скорость U, например, рассматривается возмущенное течение u = U+u',
уравнение движения линеаризуется для малых возмущений и' и воз-
возмущения выражаются в виде суперпозиции нормальных мод вида
u' = e[A(t)u + A*(t)u*] с некоторым малым параметром е и комп-
комплексной амплитудой A(t) = Aoe5*, имеющей порядок единицу для уме-
умеренных значений времени t.
Эта аппроксимация обычно обоснована при рассмотрении эволю-
эволюции наиболее неустойчивой моды, когда игнорируется влияние дру-
других мод, а течение только-только становится неустойчивым, так что
имеет место либо одна неустойчивая мода, либо узкая полоса неустой-
неустойчивых мод в волновом пакете. Между тем, уравнения Навье-Стокса
квадратично нелинейны и нелинейная часть и' • Vu' их нелинейно-
нелинейного члена и • Vu будет генерировать члены, пропорциональные |А2|,
А2 и А*2 при порядке б2. Сначала эти члены будут расти экспонен-

5.2. Слабонелинейная теория	91
циально вместе с А. Затем вскоре они генерируют каскад дальней-
дальнейших нелинейных взаимодействий друг с другом и нормальной модой.
В некотором порядке по б, в общем случае квадратичном, имеет место
резонансное взаимодействие с нормальной модой, которое изменит ско-
скорость ее роста. Тогда главным эффектом слабой нелинейности долж-
должно быть изменение медленной экспоненциальной скорости неустойчи-
неустойчивой линейной моды, но не изменение ее венного характера.
Можно более полно описать каскад нелинейных взаимодействий,
когда нормальная мода является плоской волной вида
u' = e[A(t)el"xu(y, z) + A*(t)e-l"xu*(y, *)],
например. Тогда образующиеся квадратичные члены будут пропор-
пропорциональны \А\2 и A2e2lQX, А*2е~2шх. Назовем волновую моду ос-
основной, а вклад в течение, представленный членами e±2iax первой
гармоникой. Таким образом, основная мода как генерирует первую
гармонику, которая имеет половину ее длины волны и растет в два
раза быстрее, так и изменяет средний поток (при помощи члена,
пропорционального \А\2 и не зависящего от х). Первая гармоника
и изменение среднего потока через квадратичные члены в уравне-
уравнениях Навье-Стокса в свою очередь генерируют члены порядка б3,
пропорциональные \A\2Aeiax, |A|2A*e~ia*, а также A3e3iax, А*3ешх.
(Трансляционная симметрия течения приводит к тому, что старшая
нелинейность имеет не квадратичный, а кубичный порядок по б). По-
Последняя пара членов представляет собой генерацию второй гармо-
гармоники, длина волны которой составляет треть от длины волны основ-
основной моды. Первая пара членов резонансно взаимодействует с основной
модой и может увеличивать или уменьшать скорость экспоненциаль-
экспоненциального роста; в частности, это взаимодействие может уравновешивать
основную моду, в результате чего образуется стационарная нелиней-
нелинейная волна. В соответствии с этим механизмом слабо неустойчивая
нормальная мода малой величины может расти экпоненциально в те-
течение длительного времени и, в конце-концов, генерировать слабую,
но важную нелинейность, которая подавляет рост основной моды.
Технические детали слабонелинейной теории для задач гидродина-
гидродинамики сложны и их изложение не очень уместно для первого знакомства
с предметом. Поэтому для иллюстрации основных идей теории обра-
обратимся здесь к простой модельной задаче [Matkowsky, 1970].
Пример 5.2: Модельная задача для нелинейного уравнения диффузии.
Рассмотрим уравнение
ди .	1 д2и
EЛ4)
вместе с граничными условиями
и = 0 при z = 0,тг.	E.15)

92	Гл. 5. Развитие неустойчивости
Эту задачу можно рассматривать как модельную для течения жидкос-
жидкости со скоростью u(z, t) вдоль канала между параллельными стенками
z = 0 и z = тг, где R — число "Рейнольдса".
Сначала рассмотрим основое "течение" u = U, где U — нулевое
решение: U(z) = 0 для всех z. Затем предположим, что основное те-
течение возмущается следующим образом: и = U + ей' + о(б), и' = 0A)
при е —у 0, а постоянная в может рассматриваться как малая ампли-
амплитуда возмущения. Подставим решение в этом виде в уравнение E.14),
учтем граничные условия E.15) и, приравняв коэффициенты при е,
т. е, линеаризовав систему, получим
W-U=R-W>	EЛ6)
и1 = 0 при2 = 0,тг	E.17)
Решение этой линеаризованной задачи может быть представлено в ви-
виде ряда Фурье
оо
v!(z,t) = ^2 An(t) sin nz.	E.18)
n=l
Подставляя E.18) в E.16) и интегрируя по z от 0 до тг с использова-
использованием граничных условий E.17), получим
Решением является нормальная мода вида
Am{t)=Am{0) exp(sm*), *та = 1 - т2/Д.
Отсюда следует, что мода с номером m устойчива, если R < т2.
Основное "течение" устойчиво, если все моды устойчивы, т. е. если
R < Rc = minm2 = 1.
m>l
Аналогично, "течение" неустойчиво по отношению хотя бы к одной
моде, если R > 1.
Эти результаты линейной теории могут быть получены проще,
хотя и более примитивным способом: (i) используя сразу нормальную
моду uf(z,t) — u(z)est, (ii) выводя из уравнений E.16), E.17):
_

5.2. Слабонелинейная теория	93
и = О при z = О, тг;
а также (III) заключая, что
u(z) = sin гая, s = 1 — m2/R,
как и прежде.
Рассмотрим далее слабо нелинейную стадию развития неустойчи-
неустойчивых возмущений, когда 0 < R — Rc <^[ 1 так, что основное "течение"
является слабо неустойчивым. Можно взглянуть на проблему эврис-
эвристически следующим образом. Все моды с m > 2 сильно затухают, ког-
когда значение R близко к Дс, таким образом, все компоненты начально-
начального малого возмущения, за исключением первой компоненты «Ах, будут
быстро исчезать. Если А\ @) достаточно мало, то А будет сначала рас-
расти экспоненциально по линейной теории, приближенно удовлетворяя
уравнению
а по прошествии длительного времени порядка 1/si га 1/(Д — Rc),
амплитуда Ai(t) не будет более малой, а нелинейность начнет влиять
на эволюцию. Можно ожидать, что нелинейные по А\ члены долж-
должны будут добавляться к вышеуказанному линейному амплитудному
уравнению в целях описания эволюции А\ для таких больших вре-
времен. Заметим, что изначальная нелинейная задача E.14), E.15) инва-
инвариантна по отношению к сдвигам координаты z на тг и что указанный
сдвиг меняет знак sin2, а это влечет за собой смену знака у А\. За-
Замечая, что амплитудное уравнение для А\ должно быть инвариантно
относительно смены знака у А\, получим, что нелинейный член мини-
минимальной степени по А\ должен быть кубическим, а не квадратичным,
и уравнение для амплитуд слабонелинейных возмущений, таким об-
образом, представляет собой уравнение Ландау
где / — некоторая постоянная Ландау. Для описания эволюции А\ на
больших временах необходимо, чтобы эти члены были одного поряд-
порядка малости при € —У 0, т. е. при переходе к замечательному пределу
при е —)¦ 0. Таким образом, необходимо потребовать si = О(е2) и,
следовательно, R-Rc=z О(е2) при е -> 0.
Интуитивный подход, описанный в последнем абзаце, предполага-
предполагает формальное введение медленного времени
Т = е\
а также разложения
u{z, t) = U{z) + €ui(z, T) + €2u2{z, T) + • • •	E.20)

94	Гл. 5. Развитие неустойчивости
при € —> О при фиксированных z, Т, где е = [(R — Rcj/R^2 и R2
не зависит от R. Можно взять R2 = ±1, чтобы фиксировать положи-
положительную функцию € от Л в зависимости от того, больше или меньше
Д, чем Rc. Такое разложение мотивировано соображениями, приве-
приведенными в последнем абзаце, однако обоснование будет дано позже,
когда будет проверена его непротиворечивость (вопрос о доказатель-
доказательстве сходимости такого асимптотического решения слишком сложен,
чтобы его ставить для подобных задач).
Используем далее разложение E.20) для решения задачи и для про-
проверки того, что она всегда разрешима. Перепишем в терминах Т пол-
полную задачу, расположив меньшие члены в правой стороне уравнения:
д2и	дч
•5-=г + Rcu = Д -57 + Rciu - sin u) — (Л — Rc) sin it =
oz*	at
= e2ii-^ + Rc(u - sinu) - €2R2sinu	E.21)
01
и учтем граничные условия E.15). Остается только приравнять ко-
коэффициенты при соответствующих степенях е и решить возникшую
в результате последовательность линейных задач, определяя С/, RC1
iti, U2, ... по очереди. Полагая 6 = 0, что эквивалентно приравнива-
приравниванию коэффициентов при 6°, получим, что равная нулю функция U
является решением задачи.
Приравнивая коэффициенты при ?, находим
где u\ удовлетворяет условиям E.15). Для наиболее неустойчивой мо-
моды имеем
Rc = 1, tii(z, T) = А(Т) sin 2,
как и ранее в линейной задаче. Произвольная функция А подлежит
определению в дальнейшем.
Приравнивая коэффициенты при б2, находим
д2и2
где U2 удовлетворяет условиям E.15). Отсюда U2{z) = 0 для всех z (u2
пропорционально u\\ без ограничения общности рассуждений констан-
константу пропорциональности можно положить равной нулю; это не повли-
повлияет на окончательное решение, а только на способ его нахождения).
Приравнивая коэффициенты при €3, получим

5.2. Слабонелинейная теория	95
dA .	1, . . ч о
= — sinz -f -(Asmz) —
i A») sin г - 1а3 sin 3z,
подчиняется условиям E.15). Согласно альтернативе Фредгольма
(см. упражнение 5.8) эта линейная неоднородная двухточечная гра-
граничная задача имеет либо (i) единственное решение, если соответ-
соответствующая однородная задача не имеет решения, либо (ii) не имеет
решения или имеет бесконечное множество решений, если однород-
однородная задача имеет решение. Следовательно, эта задача не может иметь
единственного решения, так как было показано, что и\ — решение од-
однородной задачи. Таким образом, для существования из и справедли-
справедливости разложения в ряд по степеням необходимо выполнение условия
разрешимости. Условие разрешимости находится следующим обра-
образом. Какой бы ни была неизвестная функция w3, граничные условия
E.15) дают
= Уо
= / sin z I —- sin z + -A3 sin3 z — R2A sin z) dz =
Jo	\dT	6	/
1 AL4
= 24dT
Следовательно,
АЛ	1
^ = R2A-tA3.	E.22)
Это — уравнение Ландау, в котором Д2 — il в зависимости от то-
того, сверхкритично или докритично "число Рейнольдса"Д. Изменение
значения i?2 меняет не решение, а только способ выражения для него,
меняя масштаб е или делая его комплексным, так как на самом деле
вышеприведенное уравнение Ландау имеет вид
eA.
Можно продолжать дальше с целью нахождения бесконечного числа
решений из и воспроизвести единственное из, используя нормировоч-
нормировочное условие, найти условие совместности для существования и4, за-
затем найти само w4 и так далее, однако асимптотическое поведение

96	Гл. 5. Развитие неустойчивости
решения и уравнения Ландау в гЛавном порядке для малых R — Rc
уже найдено и этим следует ограничиться. Читатель может проделать
итерацию самостоятельно и убедиться в непротиворечивости проце-
процедуры.
Главной особенностью поведения решения E.20) при R —У Rc явля-
является то, что пространственный характер неустойчивости определяет-
определяется собственной функцией (а именно, sin z) для наиболее неустойчивой
моды линейной задачи, а временной характер — решениями А нели-
нелинейного амплитудного уравнения E.22).
В качестве комментария к данному примеру рассмотрите снова,
как было получено условие разрешимости. Как вы думаете, каково бы-
было основание начинать с равенства 0 = [sin zdu^/dz — из d sin z/dz] J?
Если осталась непонятным мотивация выбора этого равенства, поста-
постарайтесь решить упражнение 5.7.	?
Напомним, что в параграфе 5.1 было показано, почему слабоне-
слабонеустойчивый волновой пакет часто описывается амплитудным уравне-
уравнением E.13). Делая те же самые предположения о дисперсионном со-
соотношении для линеаризованной задачи гидродинамической устойчи-
устойчивости, рассмотрим слабонелинейную задачу для слабонеустойчивых
мод так, что \А\ и R — Rc малы. Снова положим
u{z, t) = Re[A(JC, T) exp(iacz - Ы)],	E.23)
где X = б2ж, Т = €2t. Тогда А удовлетворяет нелинейному эволю-
эволюционному уравнению, линейные члены в котором те же самые, что и
в уравнении E.13). Предположение о пространственной однородности
теперь означает, что задача также инвариантна относительно сдвигов
х \-ь х -\-1 для всех Z, при этом А \-? Aexp(iacZ). Следовательно, веду-
ведущие слабонелинейные члены в амплитудном эволюционном уравнении
6y^YT кубическими и будут включать в себя только |А|2А, потому что
уравнение инвариантно относительно отражений и всех сдвигов по х.
Пример 5.2 также показывает, что А имеет порядок б. Отсюда сле-
следует, что слабонелинейные модуляции наиболее неустойчивой моды
удовлетворяют уравнению Гинзбурга-Ландау, а именно,
^ = kA- l\A\2A + 4iagbc|^,	E.24)
где I — некоторая комплексная постоянная. Это уравнение примени-
применимо для описания возмущений многих типов течений (и, разумеется,
ко многим нелинейным явлениям, которые не касаются жидкостей),
хотя вычисления значений постоянных очень длинны и сложны.
Формы амплитудных уравнений, отличные от уравнения Ландау
B.9), могут возникать в других задачах в рамках слабонелинейного
приближения.

5.3. Уравнение для возмущений энергии	97
Как мы видели в параграфе 2.2, могут возникать алгебраические
члены, отличные от тех, что содержатся в правой части B.9); сис-
системы обыкновенных дифференциальных уравнений могут иметь по-
порядок выше первого и содержать более одной амплитуды; система
уравнений может быть интегро-дифференциальной.
Далее, для возмущений открытых течений в общем случае имеет
место слабонелинейная модуляция амплитуды как в пространстве, так
и во времени, как показано в параграфе 5.1 для линеаризованнной
задачи. Крейк [Craik, 1985] рассмотрел эти вопросы подробно.
Тем не менее, используя симметрии задач слабонелинейной гид-
гидродинамической неустойчивости, может оказаться возможным пре-
преодолеть длинные и подробные вычисления и найти значения коэф-
коэффициентов в амплитудном уравнении и определить форму амплитуд-
амплитудного уравнения с относительной легкостью. Такая форма, например,
совпадающая с формой уравнения Ландау, называется нормальной
формой. Качественные свойства слабонелинейных возмущений могут
быть определены из нормальной формы, так же как они определялись
из уравнения Ландау в параграфе 2.2.
5.3. Уравнение для возмущений энергии
В настоящем параграфе изучаются важные физические вопросы, от-
относящиеся к баллансу энергии возмущения основного течения общего
вида. Используя точное уравнение B.15) для и', р', запишем в тензор-
тензорных обозначениях
Э(A/2)и'2) _ ;<Ц_
at ~щ dt ~
Следовательно,
a((i/2)u'2) а /1 ,2г \ „ , , /ч а (\ ,2 л
(А)	(В)	(С)
8
(E)	(F)

98	Гл. 5. Развитие неустойчивости
так как V-u' = OhV-U = O;
представляет собой тензор скоростей деформаций основного течения.
Уравнение E.25) описывает скорость изменения энергии возмущения.
Каждый из входящих в него шести членов может быть интерпрети-
интерпретирован следующим образом: (А) представляет собой скорость увели-
увеличения плотности кинетической энергии (напомним, что используются
безразмерные переменные с р = 1); (В) представляет перенос кинети-
кинетической энергии возмущения основным течением, (С) — энергию пе-
передаваемую возмущению основным течением, (D) — перенос энергии
возмущения возмущением основного течения; (Е) представляет собой
скорость работы возмущения давления, a. F — вязкую диссипацию
энергии.
Это можно увидеть более ясно, проинтегрировав уравнение энер-
энергии по области, занятой течением. Определим полную кинетическую
энергию возмущения:
K=f1-ui2
Jv z
dx.	E.27)
Тогда, если V не меняется со временем t, используя уравнение E.25)
теорему Гаусса о дивергенции5 и граничные условия, получим
E'28)
Это знаменитое уравнение энергии Рейнольдса-Орра [Reynolds, 1895;
Огг, 1907b, Art. 28]. Среднее от —ри[и^ часто называют тензором на-
напряжений Рейнольдса, потому что свертка этой величины с тензором
скоростей деформаций основного течения равна локальной скорости
передачи энергии от основного течения к возмущению.
Заметим, что -Л J^du'JdxjJ dx < 0 для всех возмущений, так
как вязкость всегда рассеивает энергию. Кубичные члены исчезают
при интегрировании, потому что нелинейные члены в исходном урав-
уравнении Навье-Стокса, дающие здесь кубические слагаемые, описыва-
описывают только конвекцию энергии, а не ее возникновение или исчезнове-
исчезновение; в результате уравнение энергии оказывается таким же, каким
оно было бы, если бы задача была линеаризована (так как энергия
5Формулу Гаусса-Остроградского. {Прим. ред. перевода.)

5-3. Уравнение для возмущений энергии
не поступает в V через границу 0V). Величина K~1dK/dt зависит от
пространственной структуры возмущений скорости, а не непосред-
непосредственно от их величины, однако сама пространственная структура
зависит от величины возмущения.
Энергетический метод представляет собой способ строгого вы-
вывода условий устойчивости, часто имеющих определенную общность.
Основная идея этого метода заключается в том, чтобы показать, что
если R достаточно мало, например, R < R, то вязкая диссипация на-
настолько велика, что
dx<0.
- ' "	\OXjJ j
Отсюда следует, что
?<»¦
Следовательно, K(t) < К@) для всех t > 0, т.е. основное течение
устойчиво в среднем. Это может означать, что u'(x, t) —> 0 при t —> оо
для всех х G V. Тем не менее, вполне вероятно, что K(t) —> О при
t —У оо, но u'(xo,t) в одной единственной точке хо Е V не остает-
остается малым при t —> оо, так что течение может быть устойчивым или
неустойчивым в зависимости от выбора нормы в определении устой-
устойчивости.
На этом пути может оказаться возможным доказать достаточное
условие для устойчивости (в среднем) по отношению к возмущениям
всех величин и Д< Д, определяя R как
1	Г JyDijKu'jdK 1
]	E-29)
для всех и', таких что V-u' = 0bVhu' = O или периодичной на
0V (см. упражнение 5.13). Заметим, что эти аргументы составляют
содержание прямого метода Ляпунова с функционалом Ляпунова К.
Основное течение устойчиво в среднем (с нормой ||u|| = B.K"I/2), если
R < R и, следовательно, Rc > R.
Часто оказывается полезным знать, что основное течение является
единственным стационарным решением, когда R < R. Если, напри-
например, R ~ Rc, то докритическая неустойчивость не имеет места.
Со времени оригинальной работы Рейнольдса в 1895 г. было много
исследований, посвященных энергетическому методу, с использовани-
использованием вариационных принципов. Джозеф [Joseph, 1976] применил энерге-
энергетический метод ко многим задачам гидродинамической устойчивости.
Строган [Straughan, 1982] дает обзор метода и его приложений в меха-
нике сплошных сред в общем и в теории гидродинамической устойчи-
вости в частности. Не имея возможности подробно излагать здесь этот

100	Гл. 5. Развитие неустойчивости
подход, заметим, что если R может быть найдено, то R < Rc, хотя воз-
возможно, что R настолько меньше Rc, что это неравенство не представ-
представляет никакой практической ценности при определении, какое течение
устойчиво, а какое нет. Теорема Серрина, однако, является одним из
подобных результатов, которые имеют большую теоретическую цен-
ценность: все стационарные основные течения U* (х) несжимаемой вязкой
жидкости в ограниченной области V устойчивы, если R < 5,71, где
R = LV/v, L — максимальный диаметр V и V = supx6V |U*(x)|. Cep-
рин [Serrin, 1959] получил этот результат при помощи прямого приме-
применения неравенств, устанавливающих, что основное течение является
устойчивым, если число Рейнольдса достаточно мало. Сюда попадает
хорошо известный результат, что стационарное течение Стокса, т. е.
течение, для которого R = 0, единственно и устойчиво.
Энергетический метод является дополнительным к линейной тео-
теории устойчивости в том смысле, что в рамках линейной теории можно
показать, что данное течение неустойчиво для некоторых возмуще-
возмущений, но нельзя показать, что течение устойчиво для всех возмущений,
в то время как в рамках энергетического метода можно показать, что
течение устойчиво для всех возмущений, но нельзя показать, что те-
течение неустойчиво по отношению к некоторым из них.
Упражнения
5.1.	Дисперсионные соотношения. Покажите, что (i) для дисперси-
дисперсионной функции V(k,u) = и2 — о>о ~ у2к2 с постоянными о>о?
v > 0, соответствующее "течение" является устойчивым, а ес-
если (ii) V(k,u) = ш2 -f Wq — v2k2, то соответствующее течение
абсолютно неустойчиво.
5.2.	Абсолютная и конвективная неустойчивость. Рассмотрите ли-
линейное модельное уравнение
ди ггди
— + V— = au, -оо<ж<оо,
ОТ	ОХ
с вещественным а и V > 0, заметив, что и = 17, где U(x,t) = 0,
для всех х и t является решением, описывающим основное со-
состояние покоя. Взяв нормальные моды в виде и = Re [e1*^*)],
найдите дисперсионное соотношение, определяющее комплекс-
комплексную скорость с как функцию волнового числа к и получите кри-
критерий для устойчивости каждой моды.
Покажите, что если и(х, 0) = /(ж), где / дифференцируема везде
и / = 0 при |ж| > X для некоторого X > 0, то

Упражнения	101
при t > 0. Покажите, что нулевое решение U = 0 устойчиво,
если a < 0, и конвективно неустойчиво, если <т > 0.
Покажите, тем не менее, что если f(x) = C/bsech2^ B области
—оо < х < оо, то u(x,t) —> 0 при t —)• оо для фиксированного ж
только если сг < 2V.
5.3. Конвективная и абсолютная неустойчивость. Дано линейное
модельное уравнение
<9и ди	д2и
для V, v > 0 и вещественных ст. Покажите, что дисперсионное
соотношение V(k,w) = 0 для нормальных мод с и ос е1(кх~ш*)
имеет вид
V(w, к) = -i(u> -kV)-a + vk2.
Покажите, что нулевое решение устойчиво, если а < 0, и кон-
конвективно неустойчиво, если а > 0.
5.4. Пространственные моды уравнения Бюргерса. Положив
ди ди д2и
dt дх
с некоторой вещественной постоянной С/, линеаризуйте это урав-
уравнение
моду
нение для малых и' и, подставив пространственную нормальную
для данной частоты ш > 0, выведите равенство
а = Ыи/и) [-1 ± A - Aivw/U2I'2] =
/	/U3 + O(u2u3/U5) или
-H7/i/ - w/Cf + О (vu2/U3) при г/а;/С/2 -> 0.
Найдите групповые скорости cg = дш/да этих мод для малых
vu/U2.
Взаимодействие мод вследствие нелинейности. Покажите, что
если и = и\ + u2, где
Uj(x, t) = Re[uj(t) exp(iajx)], щ = \uj\ exp(i^) для j = 1, 2,

102	Гл. 5. Развитие неустойчивости
ah ^i 00 — соответственно вещественные постоянная и функция,
то
ф2)
и
u— = -- { ai|ui|2sin2(aiE + <?i) + a2\u2\2sin2(a2x + Ф2)
=
+(ai + a2)|ui||u2| sin[(ai + a2)x + (фг + ^г)]' +
+(ai - a2)|ui||u2|sin[(ai - a2)x + (фг - ф2)]}.
Аналогично выразите udu/дх, когда
Uj (x, t) = Re[uj (t) exp(iai - x)], uj = \uj | exp(i^),
гдео,- = (otjiPjiij), x= {x,y,z).
Какие моды кроме первых двух гармоник п\ и и2 могут быть воз-
возбуждены нелинейными взаимодействиями в механике жидкости?
5.6. Рост волнового пакета в пространстве и во времени. Дана опе-
операторная форма линеаризованного уравнения в частных произ-
производных
Покажите, что подстановка комплексных волновых решений
u(x,t) = е1(кх~ш*) дает дисперсионное соотношение ш = f(k).
Рассмотрите решение типа волнового пакета, описываемое как
u(x,t) = A(X)t)U(x,t), где комплексная амплитуда А является
медленно меняющейся функцией пространства и времени, а "не-
"несущая волна" U(x,t) = е1(Кх~п>*) имеет частоту п = f(K) для
данного волнового числа К •=/=¦ 0. Выведите приближенное урав-
уравнение
если /" непрерывна.
Далее, дано, что слабонелинейное приближение для веществен-
вещественных волн u(x,t) = Re[A(x,t)U(X)t)] приводит к уравнению
где I — некоторая комплексная постоянная Ландау. Устраните
слагаемое с дА/дх преобразованием Галилея (замечая, что груп-
групповая скорость cg = f (К)) и перенормируйте х и t так, чтобы

Упражнения	103
получить нелинейное уравнение Шрёдингера в виде
(Слагаемое Z|A|2A, описывает главное приближение самодейст-
самодействия слабонелинейной волны в однородной среде в общем случае;
однородность влечет инвариантность по отношению к сдвигам,
см. упражнение 2.3).
5.7. Некоторые условия разрешимости. Определите скалярное про-
произведение как
(щу) = I u(z)v(z) dz
Jo
для всех щу ? С2[0, тг] и линейный оператор L : С2[0, тг] —>¦ С[0, тг]
как
d2v dv
для данных гладких функций р, q. При помощи интегрирования
по частям покажите, что
d« du	I к
u — -v — +puv\ ,
O.Z	Q.Z	JQ
где оператор LT, называемый сопряженным к L, определен как
Vu=
d?u
dz2 dz
Это равенство иногда называеся тождеством Лагранжа. По-
Покажите, что если, к тому же, и = 0, v = 0 при z = 0, тг, то
{щ Lv) = AДи, v).
(ii) Рассмотрите задачу
Ъип = К, ип = 0 при z = 0, тг,
для данных непрерывных функций Лп, если известно, что су-
существует ненулевая функция и[ такая, что
L*u[ = 0, и[ = 0 при z = 0, тг.

104	Гл. 5. Развитие неустойчивости
Полагая и = гг[, v = un, докажите, что необходимое условие для
существования ип есть
или, эквивалентно,
/*
/о
5.8. Альтернатива Фредголъма. Даны вещественная п х п матрица
А и вектор-столбец Ь ? Мп. Будем искать решения х Е iRn
уравнения
Ах = Ъ.	(Е5.1)
Покажите, что
х = А-1!*,	(Е5.2)
если А обратима.
Предположим далее, что матрица А необратима. Покажите, что
если у G Мп — собственный вектор транспонированной матри-
матрицы Ат, отвечающий нулевому собственному значению, т.е. если
Ату = 0 и у ф О,
то
утЬ = 0.	(Е5.3)
Условие (Е5.3), таким образом, является необходимым для су-
существования решения уравнения (Е5.1).
Докажите альтернативу Фредгольма: либо решение уравнения
(Е5.1) единственно, либо существует решение z ф О уравнения
Az = 0, которое показывает, что в первом случае А обратима
и ноль не является собственным значением А, а в последнем —
А необратима и х существует, только если b ортогонально всем
собственным векторам Ат с нулевым собственным значением,
и если х существует, то оно неединственно. (В самом деле х
существует тогда и только тогда, когда b ортогонально всем
собственным векторам с нулевым собственным значением).
Обсудите обобщение этих результатов на случай линейного опе-
оператора А : Н —> if, где Н — некоторое бесконечномерное ве-
вещественное векторное пространство со скалярным произведени-
произведением (•••,•••), заменяя транспонированную матрицу А сопряжен-
сопряженным оператором А», определяемым из равенства
(v, Аи) = (щ А Т v)

Упражнения	105
для всех u,v 6 Н. (Конечно, для матричного оператора мож-
можно отождествить AT и Ат, выбрав Н = Мп и определив ска-
скалярное произведение (щ v) = uTv. Оператор А, для которого
выполняется альтернатива Фредгольма называется фредгольмо-
вым оператором; не все линейные операторы являются фред-
гольмовыми. В качестве контрпримера можно заметить, что
оператор рождения С, определенный равенством C[xi, Ж2, ...]т =
[0, xi, Ж2, ...]т, не является фредгольмовым, потому что Сх = О
влечет за собой х = 0, хотя Сх = [1, 0,0, ...]т не имеет решения).
5.9.	Сопряженные операторы и биортогональность в линейной ал-
алгебре конечномерных пространств. Определив скалярное про-
произведение равенством
(u,v) = v*Tu
для всех n-векторов u, v E (Сп, покажите, что
(и, и> > 0, А(и, v> = (Аи, v> = (и, A*v>, (и, v) = (и, v>*
для всех А Е <Е
Для данной комплексной пхп матрицы А определите сопряжен-
сопряженную А * так, что
(Аи, v) = (и, А'-у)
для всех и, v E <Fn. Покажите, что А' = А*т.
Покажите, что если Аи = Ли для некоторого комплексного соб-
собственного вектора и/Ои собственного значения А, то сущест-
существует такой собственный вектор v ф 0 сопряженной матрицы,
что A'v = A*v.
Покажите, далее, что если
Аи = Аи и AW = /xv
для и, v ф 0, то либо /х = А*, либо
(u,v> = 0.
(Это свойство собственных векторов оператора А и его со-
сопряженного называется биортогональностью; часто использу-
используют нормировку (u, v) = 1, если /х = А*).
5.10.	Нелинейные моды для уравнения Бюргерса. Преположим, что
для заданных v > 0 и вещественной функции /
ди ди д2и

106	Гл, 5. Развитие неустойчивости
и(х, 0) = f{x) для 0 < х < 2тг,
uBir,t) = u{O,t), uxBw,t) = ux(O,t) при t > 0.
Положив uf = u — U для некоторой вещественной постоянной
"основной скорости" J7, покажите, что
дч' TTdu' t ,дч' д2и'	,„ .,
-w+ui;+vfi; = ''w (E5-4)
Используя разложение Фурье
где гг_п = гг*, чтобы гг' было вещественным, покажите что
для m = ±1, ±2,.... Что такое г^о@)? Умножая уравнение (Е5.4)
на e"lwa: и интегрируя от х = 0 до 2тг, покажите, что
• гг	2	1-
= -imUum - vmrum - -ira
Докажите, что uo(tf) = uq{Q) и что, если v велико, то
[-i(?7 + uo)t - i^].
5.11. Устойчивость однородного течения. Проверьте, что однород-
однородное основное течение несжимаемой вязкой жидкости с постоян-
постоянной скоростью U и давлением Р дает точное решение уравнений
движения Навье-Стокса и уравнения неразрывности. Представ-
Представляя u(x,i?) = U + u'(x, t) и полагая, что и' исчезает на границе
dV области течения V (но не считая и' малым), покажите, что
d Г 1 ,2_	Г (дч'
Докажите, что течение устойчиво (в среднем). Обсудите соот-
соответствие этого результата теореме Серрина об устойчивости ос-
основного течения при малых числах Рейнольдса (см., например,
[Drazin & Reid, 1981, параграф 53.1]).

Упражнения	107
5.12.	Устойчивость равномерно вращающейся жидкости. Будет
расматриваться устойчивость равномерномерного вращения не-
несжимаемой вязкой жидкости внутри твердого контейнера. Пока-
Покажите, что уравнения Навье-Стокса в системе отсчета, вращаю-
вращающейся с постоянной угловой скоростью ft, принимают вид
ди	\v I	ol
— + и • Vu +2Йхи = -V -+-ЙХХГ+ z/Au, V • и = 0.
at	ip 2	J
(Подсказка: см., например, [Batchelor, 1967, параграф 3.2 и урав-
уравнение G.6.1)]).
Покажите, что основным течением может быть, например, вы-
выбрано течение с нулевой относительной скоростью U = 0 и
давлением Р = — |p(ft x xJ внутри области V покоящегося в
подвижной система отсчета контейнера dV. Используя теорему
о дивергенции Гаусса и граничное условие и = 0 на V, докажите,
что
d Г 1 2 ,	[ (дщ\2 л
— / -щ dx = -v \ -— ) dx.
dtjv2 '	Jv \dxjj
Покажите, что течение устойчиво (по [Drazin & Reid, 1981,
Problem 1.2; Sorokin, 1961]).
5.13.	Уравнение энергии Рейнольдса-Орра. Пусть
где S множество гладких векторных полей и\ в V таких, что
V • и' = 0 в V и и' = 0 на dV.	(E5.6)
Покажите, что
где К = Jv \u^ dx, а также, что
^ < (Л-1 - Я) / (I^-V dx < 0, если R < R.
dt - v	J Jv \dxj/
Покажите, что вариационный принцип, выведенный из уравне-
уравнения E.29), дает уравнения Эйлера-Лагранжа
ЗА'

108	Гл. 5. Развитие неустойчивости
где — 2Л', р — множители Лагранжа, связанные с соответству-
соответствующими ограничениями, что дивергенция скорости равна нулю
и диссипативный интеграл нормирован. Покажите, что если R
меньше, чем минимальное собственное значение р линейной за-
задачи (Е5.7), (Е5.6), то основное течение глобально асимптоти-
асимптотически устойчиво, т.е. асимптотически устойчиво относительно
всех возмущений независимо от их величины.

Глава 6
Конвекция Релея-Бенара
... когда вы видите облако, поднимающееся с запада,
тотчас говорите: дождь будет, и бывает так...
Лк. 12, 54
В данной главе рассмотрены частные задачи о неустойчивости тече-
течений. Неустойчивость, когда жидкость нагревается снизу, обнаружи-
обнаруживает себя как тепловая конвекция. Это явление моделируется имею-
имеющей отношение к наблюдениям классической задачей, которая решена
математически и представляет важность в качестве базовой модели
тепловой конвекции и перехода к турбулентности.
6.1. Тепловая конвекция
В 1900 г. Бенар произвел ряд количественных экспериментов по теп-
тепловой конвекции. Он растопил некоторое количество воска в метал-
металлической посуде, нагревая ее основание, на котором находился слой
воска толщиной 1 мм. Когда основание не было еще достаточно го-
горячим, чтобы растопить весь воск, движение жидкого воска вначале
отсутствовало. Однако когда основание было нагрето выше некоторой
критической температуры, Бенар увидел шестиугольную структуру,
образующиеся на поверхности воска, и сделал вывод о наличии ячеек
конвекции под поверхностью. Посмотрите на рис. 6.1 для того, чтобы
понять, что он увидел.
Рэлей смоделировал эту задачу в 1916 г. и исследовал ее, применяя
теорию гидродинамической устойчивости. Он рассмотрел бесконеч-
бесконечный слой жидкости, ограниченный неподвижными горизонтальными
плоскостями 2* = 0 и z+ = d, температура которых поддерживается
постоянной и равной во и в\ соответственно. Геометрия задачи и обо-
обозначения изображены на рис. 6.2. В основном состоянии покоя темпе-

по
Гл. 6. Конвекция Релея-Бенара
Рис. 6.1. Вид сверху поверхности слоя спермацета, нагретого снизу (по
[Benard, 1900])
в. -*,
0. =
z.
Рис. 6.2. Геометрия задачи о конвекции Релея-Бенара
ратура распределяется за счет теплопроводности, а давление является
гидростатическим. Скорость, температура и давление, соответству-
соответствующие основному течению, имеют, таким образом, вид
U* = 0, 0* = в0 - 0Z; Р* = ро - 9Р0 (** + 2
соответственно, для 0 < z* < d, где /3 = (во — 0i)/d — величина,
противоположная градиенту температуры основного течения, /?о —
средняя плотность и a — коэффициент кубического расширения жид-
жидкости. Можно предвидеть, что если /3 достаточно мало, то вязкость и
тепловая диффузия будут стабилизировать течение, даже если /3 > 0
(т. е. горячая жидкость располагается ниже более холодной и, следо-
следовательно, более плотной жидкости), но если /3 превосходит некоторое
критическое значение, то возникает "опрокидывающая" неустойчи-
неустойчивость.

б. 1. Тепловая конвекция	111
Буссинеск [Boussinesq, 1903, vol. II, p. 172], и, фактически, Обербек
[Oberbeck, 1879] еще до него поняли, что когда изменения температу-
температуры малы, изменение таких термодинамических параметров жидкости
как вязкость, тепловая диффузия, плотность и удельная теплота так-
также малы и жидкость приближенно можно считать несжимаемой, хотя
пловучесть жидкости значительна. Это происходит вследствие того,
что ускорение жидкости много меньше, чем ускорение свободного па-
падения и может оказаться, что произведением д и малой разности плот-
плотностей не всегда можно пренебречь по сравнению с другими членами
в уравнениях вертикального движения. Они предполагали также, что
в уравнении состояния плотность линейно зависит от температуры и
не зависит от давления. Вскоре Релей предложил моделировать кон-
конвекцию в тонком слое при помощи уравнений движения, энергии и
состояния для жидкости Буссинеска:
-^ + и* • V*u* = -V* (р*/р0 + gz*) + ag{9* - 90)k + z/A*u*, F.2)
V, • u, = 0,	F.3)
89
^ + u»-V*0, = /cA*0*,	F.4)
ОТ»
p. =ро[1-а{0,-во)].	F.5)
Звездочки в качестве нижних индексов используются для обозначения
размерных зависимых и независимых переменных. Эти уравнения на-
называются уравнениями Буссинеска.
На неподвижной твердой поверхности, z* = const, нет проскальзы-
проскальзывания и проникновения жидкости, так что
и* = 0.
Это условие соответствует наличию твердой плоской горизонталь-
горизонтальной пластины. Релей считал свободную поверхность горизонтальной
и стационарной с нулевым сдвиговъьм напряжением, т.е.
ди* dw* dw* dv*
w* = 	1" "a— = "л	1" л— = 0
oz* ox* oy* oz*
на свободной поверхности, задаваемой уравнением z* = const. Если,
более того, поверхность является идеальным проводником тепла, то
0* = const.
Рассматривались также другие граничные условия, например, описы-
описывающие идеальные изоляторы, когда градиент температур в основном
течении возникает за счет внутреннего источника тепла.
Можно проверить, что основное состояние покоя является решени-
решением вышеприведенных уравнений.

112	Гл. 6. Конвекция Релея-Бенара
6.2. Линеаризованная задача
Записав
линеаризуем уравнения Буссинеска F.2)—F.5) для малых возмуще-
возмущений. В безразмерных переменных х = x*/d, t = K.t+/d2, u = dul/к, в =
= 0^/Cd, p = сРр'/рок2 эти уравнения примут вид
^ =-Vp + ДРг 0k+ PrДи,	. F.6)
СП
V • и = 0,	F.7)
Яй
%-w = Ae,	F.8)
где R = a/3gd4/Ku — число Релея и Рг = и/к — число Прандтля.
Безразмерное число Релея характеризует отношение дестабилизиру-
дестабилизирующего эффекта пловучести (для /3 > 0) к стабилизирующим эффек-
эффектам молекулярной диффузии и пловучести; число Рг характеризует
свойства жидкости (а не форму слоя).
Применение оператора ротора к обеим частям уравнения F.6) дает
пи)
^- = R PrV6 x k + PrAU	F.9)
at
где w = Vxu — завихренность. Применение оператора ротора к обе-
обеим частям уравнения F.9) и использование уравнения неразрывности
F.7) дает
I)
= RPr [ Д0к - V^ I + РгД2и.
at
Компонентой z этого уравнения является
F.10)
где Дх = д2/дх2 + д2 /ду2 — оператор Лапласа по горизонтальным
переменным. Исключая 0 из F.8) и F.10), окончательно получим

6.3. Характеристики устойчивости	113
Граничные условия, которые уже линейны, и уравнение неразрывнос-
неразрывности F.7) дают
на твердой плоскости z = const и
-=??-=•
на свободной поверхности z = const.
Релей использовал нормальные моды вида
в = T{z)f{x, уУ\ w = J7(*)/(s, у)е".	F.12)
При таких условиях разделения переменных уравнение F.8) приводит
к уравнению Гельмгольца для /:
Ai/ + a2/ = 0,	F.13)
где а2 — постоянная разделения; будем отождествлять а с горизон-
горизонтальным волновым числом моды. Уравнения F.8), F.10) принимают
соответственно вид
-W,	F.14)
(D2 - a2) (D2 - a2 - s/Pr)W = a2RT,	F.15)
уравнение F.11):
(D2 - a2) (D2 - a2 - a) (D2 - a2 - s/Pr)W = -a2RW, F.16)
а граничные условия на идеальном проводнике:
W = DW = Т = 0 (твердый) \
2	/
= T = 0 (свободный)/ =P"* = 0.1i I6'17)
где D = d/dz иТ= (а2Л)-1(Б2 - a2)(D2 - а2 - з/Рг)Т7. Уравнения
F.16), F.17) представляют собой задачу на собственные значения для
определения характеристик линейной устойчивости.
6.3, Характеристики устойчивости
Можно доказать с достаточной степенью общности (см. упражне-
ние 6.2), что для рассматриваемых задач справедлив принцип обмена

114	Гл. 6. Конвекция Релея-Бенара
устойчивостей, т.е. если R < 0, то Re(s) < 0 и, таким образом, тече-
течение устойчиво, а если R > О, то Im(s) = 0. Первый результат физи-
физически правдоподобен: если нижняя пластина охлаждена @о < #i)? то
тогда имеет место устойчивость. Второй результат влечет за собой
равенство s = 0 везде на границе устойчивости.
Релей [Rayleigh, 1916 a] решил задачу точно в специальном слу-
случае двух свободных границ (которые иногда называются свободно-
свободными границами) при z = 0,1 (пример 6.1 далее). Он выбрал
две границы свободными с целью удобства математического характе-
характера; хотя свободная граница на дне и может показаться искусственной,
ее можно представлять себе, заменив нижнюю пластину слоем жид-
жидкости много меньшей вязкости [Goldstein & Graham, 1969]. Точное
решение является также полезным для объяснения структуры реше-
решений задачи с другими граничными условиями.
Пример 6.1: Параметры устойчивости для свободно-свободных иде-
идеально проводящих границ. Здесь необходимо решить уравнение F.16)
с свободно-свободными граничными условиями F.17). Можно усмот-
усмотреть, что
W = Wn, s = sn для п= 1,2,...,	F.18)
где
Wn(z) =sinmrz	F.19)
и
(п2тг2 + а2) (п2тг2 + а2 + sn) (nV + a2 + sn/Pr) = a2R. F.20)
Отсюда
1/2
± 1(
Можно проверить в этом случае, что если R < 0, то Re(sn) < 0, и
sn = 0 на границе устойчивости при R > 0. Положив sn = 0 в квад-
квадратном уравнении для sn, найдем зависимость R, соответствующую
маргинальной устойчивости моды с номером п, от волнового числа а:
Rn(a)=(n27r2 + a2K/a2.	F.21)
График кривой Ri(a) изображен на рис. 6.3. Она назывется марги-
маргинальной кривой, задающей границу между растущими и убывающими

6.3. Характеристики устойчивости
115
8000 г
Рис. 6.3. Маргинальная кривая — график зависимости критического чис-
числа Релея Ri от безразмерного волнового числа а. Минимум Ri находится в
точке a = ac [Drazin & Reid, 1981, Fig. 2.2(а)], обработано
модами в плоскости, где изменяются число Релея и волновое число;
минимум числа Релея на кривой дает его критическое значение.
Для определения границы устойчивости течения находим мини-
минимум Rn для всех п, полагая п = 1 (для наименее устойчивой вер-
вертикальной моды), и затем берем минимум по всем горизонтальным
волновым числам а. В результате получаем
Rc = min JSi (a2) = 27тг4/4 = 657,5,
-оо<а<оо ч '
минимум достигается при а = ас = (тг/2I/2 = 2,221. Отсюда следует,
что при R < Rc имеет место устойчивость, а при R > Rc — неустой-
неустойчивость. Если R лишь немного превосходит Лс, то следует ожидать,
что только мода с п = 1 при а & ас, и никакая другая, растет экспо-
экспоненциально.	?
Этот тип неустойчивости иногда называют конвективной не-
неустойчивостью, иногда неустойчивостью Релея-Бенара, а иногда
конвекцией Релея-Бенара. Необходимы численные расчеты для на-
нахождения Rc и ас для конвекции в случае двух твердых границ, назы-
называемых иногда твердо-твердыми, а также твердой нижней границы
и свободной верхней границы, которые иногда называют свободно-
твердыми (см. табл. 6.1). Форма кривых R = Лп(«) в каждом случае
качественно подобна форме кривой R = Ri(a) на рис. б.З.
Размер ячеек определяется через горизонтальное волновое число
ас а их форма — через решение / уравнения Гельмгольца F.13), ко-
которое является неопределенным в настоящей модели. Моделируя тон-
тонкий слой жидкости неограниченным слоем, ищем решение уравнений

116
Гл. 6. Конвекция Релея-Бенара
Таблица 6.1. Критические значения числа Релея и волнового числа
для конвекции Релея-Бенара между идеально проводящими горизон-
горизонтальными плоскостями с различными граничными условиями
R
ас
Свободно-свободная
657,5
2,211
Свободно-твердая
1101
2,682
Твердо-твердая
1708
3,117
Гельмгольца, которые имеют вид мозаики на плоскости, состоящей из
периодических ячеек, например, треугольных, прямоугольных, имею-
имеющих форму параллелограмма или шестиугольника. Для большего реа-
реализма необходимо учитывать влияние боковых стенок (которое делает
волновое число а дискретным) или нелинейности (которое может сде-
сделать некоторые формы ячеек неустойчивыми) для того, чтобы найти
формы ячеек по функции /. Так, например, если стенки имеют круго-
круговое сечение, то можно ожидать возникновения кольцеобразных ячеек
(см. [Van Dyke, 1982, Fig. 140]).
Самым простым является случай длинных роликов. Можно усмот-
усмотреть, что /(ж, у) = cos ах является решением уравнения F.13) и имеет
период 2тг/а по х. Также при помощи уравнения неразрывности F.7)
можно показать, что в этом случае
и = -a'1 smaxDWest, v = 0, w = cos ax Wes\
и, следовательно, и = 0 при х = kir/a для к = 0,±1,±2,... . Это
решение описывает ячейки в форме длинных роликов, параллельных
оси у.
В теории Релея, которая здесь описана, слой жидкости бесконе-
бесконечен, поэтому волновое число а является непрерывным параметром.
Любой реальный слой жидкости, однако, является ограниченным —
должны быть боковые стенки, ограничивающие жидкость, и беско-
бесконечный слой рассматривается только как приближение слоя больших
горизонтальных размеров. Так что лучше учитывать боковые стенки
(см. упражнение 6.7), волновое число при этом становится собствен-
собственным значением и, следовательно, дискретной переменной, для данных
числа Релея и области течения. Для слоя, глубина которого сравни-
сравнима с его шириной, дискретность собственых значений и собственных
функций является физически важной.

6.4. Нелинейная конвекция
117
Юг
Nu
X	+
д. ОД
1	4	10	40	100
R • Ю-3
Рис. 6.4. Некоторые экспериментальные результаты, относящиеся к пе-
переносу тепла в различных жидкостях в различных контейнерах. Изображен
график изменения числа Нуссельта в зависимости от числа Релея: о — вода
(Рг = 7,02); Н	гептан (Рг = 7,05); х — этилен гликоль; • — силиконо-
силиконовое масло АК 3 (Рг = 4,20); ^ — силиконовое масло АК 350 (Рг = 44,0);
Л — воздух (Рг = 0,62); D — меркурий (Рг = 0,025) (по [Drazin & Reid
1981, Fig. 2.6; Silveston, 1958; Rossby, 1969])
Обратимся к конвекции снова. Для начала ознакомьтесь с книгой
[Van-Dyke, 1982, Figs. 139-142]. Взгляните на рис. 6.4, где представ-
представлены измеренные значения переноса тепла (см. упражнение 6.8) как
функция от числа Релея для жидкостей с различными значениями
числа Прандтля. Изображена зависимость от числа Релея числа Нус-
Нуссельта, которое представляет собой отношение актуального переноса
тепла к тому переносу тепла, который присутствовал бы в случае
чистой теплопроводности без конвекции. Число Нуссельта, таким об-
образом, равно единице в случае отсутствия конвекции. Обратите вни-
внимание на то, как было обнаружено, что число Релея в начале неустой-
неустойчивости почти не зависит от жидкости и, значит, от числа Пран-
Прандтля тоже. Можно с успехом произвести собственный эксперимент
(см. упражнение 6.18).
6.4. Нелинейная конвекция
Итак, линейная теория устойчивости дает наиболее неустойчивую мо-
ДУ в виде
0{x,t)=A{t)f{x,y,a)T1{z),
F.22)
где

118	Гл. 6. Конвекция Релея-Бенара
dt
И
«i ~ k(R - Rc) при R-+Rc
для некоторого А; > 0. Для свободно-свободной конвекции T±(z) =
= sin7T2. Представляется правдоподобным, что если R > Rc и R — Rc
достаточно мало, то имеет место только одна неустойчивая мода
(строго говоря, для обоснования этого необходимо учитывать боко-
боковые стенки с целью превращения горизонтального волнового числа в
дискретное). Тогда все другие моды будут экспоненциально убывать
и их влиянием, таким образом, можно пренебречь. Неустойчивая мода,
имея малую амплитуду А@) вначале, медленно растет с экспоненци-
экспоненциальной скоростью s ~ k(R — Rc). В конце концов нелинейность станет
значительной и умерит экспоненциальный рост (чем меньше R — Дс,
тем позже это произойдет).
Слабонелинейная теория по существу показывает, что для неустой-
неустойчивой моды трансляционно инвариантной задачи
(Эта специальная форма амплитудного уравнения возникает для мод,
которые не зависят от фазы комплексной амплитуды; если волна
с Af = lAle^1**"*) инвариантна относительно сдвигов в направлении
оси ж, то эволюционное уравнение для амплитуды должно не зави-
зависеть от изменений ту, которые соответствуют изменениям кх). В слу-
случае конвекции Релея-Бенара были найдены вещественные s и можно
установить, что нет нужды в комплексных числах, по крайней мере,
для роликовых ячеек, так что можно взять А, /, l±, fa, ... веществен-
вещественными. Таким образом,
В общем случае 1г может быть как положительным, так и отри-
отрицательным. Но фактически, для конвекции Релея-Бенара вычисле-
вычисления с применением теории возмущений по аналогии с упражнением
5.3 дают 1\ > 0. Это означает, что имеет место уравновешивание
и можно вполне обоснованно пренебрегать fa -А5,..., если А@) мала
и 0 < Л- Rc <^ 1. Тем самым установлено каноническое уравнение
для надкритической вилообразной бифуркации, такое же, как в пара-
параграфе 5.2:
^ = k{R - RC)A - hA3.	F.23)

6.4. Нелинейная конвекция	119
"Ручка" и "средний зубец" вил отвечают решению А = О, которое
представляет собой основное состояние покоя. Два остальных "зуб-
"зубца" отвечают решениям А = ±[k(R — Rj/li]1/2, которые описывают
ячеистое движение, "+" для течения в одном направлении и "—" для
течения в противоположном направлении. Можно подсчитать вели-
величину полей скорости и температуры при помощи этого решения, в то
время как линейная теория дает только пространственную структуру
ячеистого движения и скорость (мгновенную) его роста. Заметим, что
нелинейная теория дает ячеистое движение независимо от начального
возмущения, которое в конце концов определяет только направление
движения.
Характер первичной бифуркации при увеличении числа Релея из
состояния покоя тонкого слоя жидкости, нагретой снизу, слабо зави-
зависит от числа Прандтля. После первой бифуркации происходит много
дальнейших бифуркаций при увеличении числа Прандтля в зависи-
зависимости от его величины (и ряда других обстоятельств). Структура
бифуркаций сложна и, хотя и с некоторым риском чрезмерного упро-
упрощения, полезное впечатление о ней может быть получено из рис. 6.5,
который в компактной форме описывает результаты многих лабора-
лабораторных экспериментов. Часто, однако, имеет место гистерезис, когда
число Релея сначала медленно увеличивается, а затем уменьшается.
Для больших значений числа Релея наблюдалось множество различ-
различных форм ячеек (см. рис. 6.6).
Большинство ранних экспериментов было предпринято с мелкими
жидкостями для того, чтобы согласовать эксперимент с моделью Ре-
Релея. Трелфолл [Threlfall, 1975] начал эксперименты с жидком гелием
в контейнерах, которые не были мелкими. Жидкий гелий позволяет
с меньшими трудностями производить аккуратные измерения. Нали-
Наличие не малой глубины ячейки уменьшает скорость наступления после-
последовательных бифуркаций и они легче поддаются изучению, а также
изменяет природу бифуркаций. Используя эти преимущества Алерс
(Ahlers) и Либхабер (Libchaber) с коллегами сделали много интерес-
интересных экспериментов по переходу конвекции к турбулентности в кон-
конце семидесятых и в восьмидесятых годах XX века. Фактом особой
важности является наблюдение Либхабером и Маурером [Libchaber &
Maurer, 1978] бифуркаций удвоения периода и начала хаоса при кон-
конвекции в ячейке в глубоком слое жидкости, а также теоретическая
интерпретация их результатов Фейгенбаумом [Feigenbaum, 1980].
К настоящему моменту написано гораздо больше, чем здесь, о
формах ячеек, боковых стенках, небуссинесковых жидкостях, пере-
переходе к турбулентности при увеличении R далеко за значение Rc и
об экспериментальных результатах. Конвекция Релея-Бенара может
быть обобщена, если принять во внимание эффект Марангони, ког-
когда поверхностное натяжение свободной поверхности меняется вмес-
вместе с температурой (см. упражнение 6.17), наличие пористой среды,

120
Гл. 6. Конвекция Релея-Бенара
юб
gio5
о
1 Нестационарное
I * трехмерное течение
+* !
рр
-\j-	| 1
:Стационарное Ш ¦
CQ.
Стационарное
двумерное течение
, Покои
ю-2
ю-1
10 102
Число Прандтля
103
104
Рис. 6.5. Режимная диаграмма наблюдавшихся форм конвекции Релея-
Бенара в тонком слое жидкости между твердыми горизонтальными плас-
пластинами для заданных значений чисел Релея и Прандтля. Горизонтальная
линия Nu = 1 отмечает начало первичной неустойчивости состояния по-
покоя при увеличении числа Релея. Кривая II отмечает появление вторичной
неустойчивости, так что стационарные длинные ролики (с осями, парал-
параллельными более коротким сторонам прямоугольного контейнера) обычно
располагаются преимущественно ниже кривой, а трехмерные стационарные
ячейки — над ней. Выше кривой III течение становится нестационарным.
На кривой IV наклон графика зависимости числа Нуссельта от числа Релея
увеличивается (достаточно внезапно) снова. В области V над кривой IV час-
частоты нестационарных течений увеличиваются в процессе того, как течение
становится хаотическим, о — стационарные течения; • — нестационар-
нестационарные течения; * — точки перехода с наблюдаемым изменением наклона; ?
— результаты Россби наблюдений нестационарного течения [Rossby, 1969];
? — результаты Уиллиса и Деадорфа наблюдений турбулентного течения
[Willis & Deadorff, 1967]; Л — точка Силверстона [Silverston, 1958] перехода
к нестационарному течению (по [Krishnamurti, 1973, Fig.4])
такой, как песок или горная порода (см. упражнение 6.13), двойную
диффузионную конвекцию, когда изменения плотности, так же как и
температуры, обусловлены присутствием раствора (см. упражнение
6.16), вращение основной системы отсчета, излучение тепла, эффек-
эффекты Сорета и Гиббса-Томсона при росте кристаллов и другие эф-
эффекты, возникающие в приложениях. Фактически, эффект Марангони
был важен в оригинальных экспериментах Бенара. Также изучались
различные геометрические конфигурации, например, слой жидкости
на нагретой сфере, вращающейся и невращающейся, в присутствии
и отсутствии силы тяжести. Книга [Koschmieder, 1993] предоставляет
большое число деталей этих и других вопросов, относящихся к линей-
линейной и нелинейной теориям и лабораторным наблюдениям. Неустойчи-

6.4. Нелинейная конвекция
121
Рис. 6.6. Фотографии различных типов ячеек, стационарных и неста-
нестационарных, которые наблюдались при различных значениях чисел Релея
и Прандтля. (а) Вид сверху роликовых ячеек (стационарных) (по [Srulijes,
1979]; см. [Koschmieder, 1993, Fig. 5.3])
вость Релея-Бенара имеет отношение к большому числу разновид-
разновидностей конвекции, происходящей в природе, даже несмотря на то, что
модель не учитывает деталей этих процессов достаточно верно; это
относится, например, к грануляции на поверхности солнца и облаков,
показанных на рис. 6.7. Кроме того, большинство положений теории
неустойчивости Релея-Бенара представляет интерес в связи с ши-
широким применением в нелинейной физике; многие другие проблемы
эволюции в слоях, например, электрически возбужденное движение
в^жидком кристалле, имеют те же симметрии и, таким образом, де-
демонстрируют множество сходных типов неустойчивости и образова-
образования структур. Возможно, конвекция Релея-Бернара была предметом
большего теоретического исследования, чем это было обосновано ее
физической важностью, но она может рассматриваться как базовая
Модель для многих типов образования структур и неустойчивостей,
так же как и конвекции.

122
Гл. 6. Конвекция Релея-Бенара
Рис. 6*6 (продолжение), (б) Вид сбоку роликовых ячеек (стационарных)
в силиконовом масле (по [Oetrtel & Kirchartz, 1979]; см. [Van Dyke, 1982, Fig.
139]; воспроизведено по разрешению Springer-Verlag GmbH & Co. KG)
Упражнения
6.1. Линейное обыкновенное дифференциолньное уравнение, которое
грубо моделирует конвекцию Релея-Бенара. Дано в качестве
вспомогательной задачи:
-^ = -vdT2w + адв, — = -квГ2в + Cw.
at	at
Покажите, что имеют место нормальные моды ги, в ос e**, где
a = ~(v+ K)d~2 ± 1 [{v - KJd~4 + 4аCд]1/2.
Докажите, что нелевое решение w = 0, в = 0 устойчиво, если
R > 1, где R = aCgdA/K,v.
Покажите, что если отсутствует диссипация, т.е. v — к = 0, то
d2w
N2w = 0,
где N2 = —аCд определяет частоту "пловучести"N.
6.2. Принцип обмена устойчив остей для конвекции Релея-Бенара.
Умножая уравнение F.14) на комплексно сопряженное Т* к Т,
интегрируя от z = 0 до 1 и используя любое из условий F.17) при
z = 0,1 для идеально проводящих или идеально изолированных
неподвижных границ, покажите, что
в/о +
Г1
= / WT*dz,
Jo

Упражнения
123
Рис. 6.6 (продолжение), (в) Перекрестно-роликовая неустойчивость (ста-
(стационарный случай, взаимодействие двух роликов одинаковой длины) при
R = 3000, Рг = 100, силиконовое масло Dow Corning 200 (по [Busse &
Whitehead, 1971, Fig. 10])
где /о = /о1 \Т\2 dz, h = /o(|DT|2 + а2|Т|2) dz. Умножая уравне-
уравнение F.15) на W*, аналогично покажите, что
J2
Г1
= a2R /
Jo
W*Tdz,
где Л = /o
+ a?\W\2) dz и
Г1
= /
Jo
Отсюда покажите, что для a = Re(s), и = Im(s) выполняются
равенства
a(a2RI0 - Ji/Pr) + a2Rh - J2 = 0, a;(a2RI0 +
= 0.
Докажите, что если R < 0, то a < 0 и имеет место устойчивость,
а если R > 0, то и = 0 и, следовательно, справедлив принцип
обмена устойчивостей [Pellew & Southwell, 1940].
6.3. Конвекция Релея-Бенара в необычной жидкости, (i) Жидкость
под названием "Hupnol", имеющая плотность ро при темпера-
температуре 0о, обладает необычным свойством, которое заключается

124
Гл. 6. Конвекция Релея-Бенара
Рис. 6.6 (продолжение), (г) Зигзаговая неустойчивость (стационарный
случай) при R = 3600, Рг = 100 (по [Busse & Whitehead, 1971, Fig. 11])
Рис. 6.6 (продолжение), (д) Пинчевая (pinching) неустойчивость, R = 18х
103, Рг = 100 (по [Busse & Whitehead, 1971, Fig. 15])
в том, что возмущения ее плотности р0 изменяются как куб воз-
возмущений температуры во и меньшая плотность соответствует
большей температуре, т.е. р = ро[1 — а(в — #оK]> где а — поло-
положительная постоянная.
В лабораторном эксперименте некоторое количество жидкости
Hupnol заключается между двумя горизонтальными плоскостя-
плоскостями, которые обеспечивают, с хорошей степенью аппроксимации,
свободные от напряжений граничные условия для Hupnol. Тем-
Температура на нижней плоскости равна во, а на верхней z = d
равна $i. Расстояние d между плоскостями много меньше, чем
их горизонтальная протяженность.
Пренебрегая эффектами сжатия, изменения плотности вследст-
вследствие инерции и полагая коэфициенты вязкости, теплопроводности
и т.д. постоянными, покажите, что устойчивость состояния по-

Упражнения
125
Рис. 6.6 (продолжение), (е) Бимодальная неустойчивость (стационарное
взаимодействие роликов различной длины) при R « 20 х 103 — 65 х 103,
Рг = 100 (по [Busse & Whitehead, 1971, Fig. 14])
коя определяется решением линеаризованной задачи
в' = АО' = Д V = 0 при z = 0, d,
где 0; — возмущение температуры, Ai — оператор Лапласа по
горизонтальным координатам, g — ускорение свободного паде-
падения, к — коэффициент тепловой диффузии и v — кинематичес-
кинематическая вязкость жидкости Hupnol.
(ii) Выведите обыкновенное дифференциальное уравнение, пред-
представляющее собой задачу на собственные значения для нормаль-
нормальных мод.
(iii) Докажите, что принцип обмена устойчивостей справедлив
для настоящей задачи на собственные значения. (Подсказка:
Представьте /0 z2 \T\2 dz как квадратный полином от 5 с коэффи-
коэффициентами, выражающимися через положительно определенные
интегралы).
(iv) Придумайте метод для нахождения приближенного значе-
значения критического числа "Релея" А = ga@o — 0iKd3//c/i/, ни-

126
Гл. 6. Конвекция Релея-Бенара
Рис. 6.6 (продолжение), (ж) Косая варикозная неустойчивость (неста-
(нестационарная) для R и 104, Рг = 3, 7 (по [Busse & Clever, 1979, Fig. 7])
же которого никакое возмущение не будет расти. Не предприни-
предпринимая точных вычислений, кратко опишите, каким образом может
быть получена наиболее аккуратная оценка критического значе-
значения. Как вы думаете, будет ли это критическое значение мень-
меньше, больше или равно критическому значению числа Релея, если
жидкость Hupnol заменить водой в эксперименте? [Н. Е. Huppert,
частное сообщение].
6.4. Горизонтальное движение нормальной моды в конвекции Релея-
Бенара. Используйте уравнение F.9) для вывода уравнения диф-
диффузии
(Е6.1)

Упражнения
127
Рис, 6,6, (продолжение), (з) Узловая неустойчивость (нестационарная)
для R и 5 х 104, Рг = 7,1 метил алкоголь (по [Busse & Clever, 1979, Fig. 8])
где ? = dv/dx — ди/ду — вертикальная компонента завихрен-
завихренности возмущения. Покажите (правдоподобно, по крайней мере),
что С —>¦ 0 при ? —)- оо при фиксированном х.
Далее, предполагая, что dv/dx = ди/ду и используя уравнение
неразрывности F.7), покажите, что
d2w
Докажите, что для нормальной моды
4^
а2 ду
(Е6.2)
(Е6.3)

128
Гл. 6. Конвекция Релея-Бенара
О 5 10 15 20 25
[X1000 km]
Рис. 6.7. (а) Гранулы на поверхности солнца. Ширина конвекционной
ячейки имеет порядок 100 км. (Воспроизведено по разрешению National
Optical Astronomy Observatory, T. Rimmele/NOAO/AURA/NSF). (<5) Спут-
Спутниковая фотография, изображающая открытые конвекционные ячейки в об-
области движения вниз и закрытые ячейки в области движения вверх (по
[Krishnamurti, 1975, Fig. 3(e)])

Упражнения	129
6.5. Прямоугольные ячейки. Проверьте, что
/(ж, у) = cosaiz cosc^y
является решением уравнения Гельмгольца F.13), если a\-\-a\ =
= а2. Покажите, что / имеет период 2ir/ai по ж и период 2тг/а2
по у. Покажите, что и = О при ж = 0, тг/ai и v = 0 при 2/ = 0, тг/аг.
Покажите, что функция / описывает движение внутри перио-
периодических ячеек с вертикальными границами и прямоугольным
сечением, каждый прямоугольник имеет стороны длины 2?r/ai,
6.6. Шестиугольные ячейки. Проверьте, что
/(ж, у) = cos -a (У/2ж + у) + cos -a (з1/2ж - 2/) + cos ay
является решением уравнения Гельмгольца F.13). Покажите,
что / инвариантно относительно поворотов на угол 60° отно-
относительно оси z и что и = 0 при х = |3X/2L, — \L < у < |L, где
L = 4тг/3а.
Покажите, что функция / описывает движение внутри регуляр-
регулярных шестиугольных ячеек, каждая сторона шестиугольника, при
этом, имеет длину L [Christopherson, 1940].
6.7. Роликовые ячейки при наличии боковых стенок. Из примера
6.1 следует, что для маргинальной устойчивости первой моды
свободно-свободной конвекции
покажите, что это уравнение имеет три корня: а2(Л), а2,(
а|(Л), где а\ > а\ > 0 > а§, если R > Rc = 27тг4/4.
Покажите, что если имеет место стационарная двумерная линей-
линейная конвекция с идеально проводящими стенками, расположен-
расположенными при х = ±?, то некоторые собственные функции имеют
вид
ч fAicosaix Агсоэагж А3сЬ|аз|ж\ .
W(X, Z) = 	г— + 	— + ——.	ту- ) 81П 7TZ,
\ cos a\L	соэагЬ	ch a3\L )
где

130	Гл. 6. Конвекция Релея-Бенара
а дискретные значения R, отвечающие маргинальной устойчи-
устойчивости, удовлетворяют соотношению
а\ + 7Г2 \>3| a2) a| + 7T2Vai \o>z\
и
Здесь использованы обозначения [Drazin, 1975]:
rj, T2 = tga2L, T3 = tg|a3|?.
6.8. Передача тепла в слабонелинейной конвекции Релея-Бенара.
Покажите, что число Нуссельта
где Н — фактический перенос тепла в жидкость на единицу
площади пластины, к = срк, — теплопроводность и с — тепло-
теплоемкость жидкости.
Используя уравнение F.22), покажите, что
когда R га Лс, где 6 — некоторая безразмерная постоянная, ко-
которая зависит от формы ячейки, а А удовлетворяет уравнению
Ландау F.23). Выразите число Нуссельта в виде функции числа
Релея. Сравните ваш результат с экспериментальными измере-
измерениями на рис. 6.4.
6.9. Энергетический метод для конвекции Релея-Бенара. Дано, что
безразмерные нелинейные уравнения, которым подчиняются воз-
возмущения основного состояния покоя с тепловой проводимостью,
а именно, U = 0 и 0 = — 2, описывающие конвекцию Релея-
Бенара, имеют вид
ди
— + и • Vu = -Vp + RPrOk + Pr Au,
at
V-u = 0,
at

Упражнения	131
Предположив, что течение удовлетворяет свободно-свободным
граничным условиям при z = 0,1 и имеет период 2тг/ах по х
и период 2тг/ау по у, вывести уравнение "энергии" для возмуще-
возмущений:
1	/Лц V 1Д/W\*|
2	VftBi/ 2 \dxjj J
(
(Е6.4)
где
а областью интегрирования является кубоид
V = {х : 0 < х < 27г/ах, О < у < 2тг/ау, 0 < z < 1}.
Используя связь дщ/dxi = 0 с лагранжевым множителем р,
покажите, что вариационный принцип минимизации интегра-
интеграла в правой части уравнения "энергии" (Е6.4) дает уравнения
Эйлера-Лагранжа
0 = -Vp + R6k + Аи
-w = Д0,
т.е. линеаризованные уравнения F.6), F.8) для стационарных
возмущений. Далее покажите, что все возмущения, малые или
большие, убывают (иными словами, течение является асимпто-
асимптотически устойчивым), если R < Лс, где Rc критическое значение
числа Релея, которое определяется при помощи линейной теории
со свободно-свободными граничными условиями при z = 0,1 (по
[Drazin & Reid, 1981, Problem 7.13; Joseph, 1965]).
6.10. Вывод системы Лоренца как модели тепловой конвекции. Из-
Известно, что возмущения и и 0, соответственно полей скорос-
скорости и температуры в жидкости, подогретой снизу, подчиняются
уравнениям Буссинеска, а именно,
ди
— + и • Vu = - Vp + <t9\l + о-Аи,
at
V • и = 0,
-5- + и • V6 = Rw + Д0,
at

132	Гл. 6. Конвекция Релея-Бенара
при —оо < х < оо, 0 < z < тг, где <т = i///c — число Прандтля для
жидкости, R = agd3AT/K,v — число Релея; используются безраз-
безразмерные переменные, обезразмеренные при помощи масштабов d
длины, d2/K времени и AT/R температуры. Здесь ird — глубина
слоя жидкости, AT — разница температур поперек слоя, a —
коэффициент теплового расширения, к, — тепловая диффузия и
v — кинематическая вязкость жидкости. "Свободные" идеально
проводящие границы расположены при z = 0, тг и
ди
— = w = в = 0 при z = 0, тг.
az
Далее дано, что имеют место слабонелинейные роликовые ячей-
ячейки, форма которых приближенно описывается выражениями
u{x,z;t) = 21<2(k2 + l
w{x,z;t) = -242{k2-
a(T ~. f\ _ _(u2 I I \3jl-
1/1*1/, /6, Uj —	I ft \^ II Л»
где 5X = sin fcx, C2 = cos z, Cx = cos fcx, S2 = sinz и 5г2 = sii
(i) Проверьте, что удовлетворяется уравнение неразрывности,
(ii) Проверьте, что удовлетворяются граничные условия.
(III) Покажите, что каждый нелинейный член в уравнении мо-
моментов пропорционален sin 2kx или 5г2 • Отсюда или иным спосо-
способом покажите, что двукратное применение ротора к уравнению
моментов приводит к уравнению
^=(т(У-Х),	(Е6.5)
dr
где г = (А:2+1J, если соответствующие компоненты можно опус-
опустить. (Подсказка: Покажите, что
du/dz - dw/dx = -2?(к2 + +l)AT1XSa;S2).
(iv) Аналогично покажите, что
-^- = rX -Y- ZX,	(Еб.б)
dr
-^ = -ЬХ + ХУ,	(Е6.7)
где г = k2R/(k2 + IK, b = 4/(k2 + 1). (Подсказка: Покажите, что
и - V0 = (Jt2 + lL-2(XYS2z + 23/2ZXCxS2C22 [Lorenz, 1963]).

Упражнения	133
6.11.	Решения системы Лоренца. Используйте систему Лоренца
(Е6.5)-(Е6.7) из предыдущего упражнения в качестве модельной
задачи для устойчивости, бифуркации, нарушения симметрии,
начала хаоса и восстановления симметрии следующим образом.
Выясните, когда нулевое решение системы Лоренца устойчиво и
объясните физическое значение результата с точки зрения кон-
конвекции Релея-Бенара.
Найдите все другие стационарные решения системы Лоренца.
Обсудите физическое значение этих решений с точки зрения кон-
конвекции Релея-Бенара.
*Обсудите устойчивость этих других стационарных решений и
изменения множества аттракторов при увеличении г от нуля до
бесконечности при фиксированных а и 6. (Подсказка: Для то-
того чтобы сделать это, вам, вероятно, придется почитать книгу,
например, [Drazin, 1992, параграф 8.1]).
Предполагалось, что система Лоренца моделирует определенные
свойства турбулентной конвекции. Обсудите достоинства и не-
недостатки этой системы в качестве модели.
6.12.	Модель нелинейной тепловой конвекции Свифта-Хоэнберга.
Дано, что возмущения w некоторой скорости подчиняются урав-
уравнению
при —оо < ж < оо и t > 0, где R — параметр, моделирую-
моделирующий число Релея. Найдите характеристики линейной устойчи-
устойчивости методом нормальных мод ос elkx+st. Изобразите марги-
маргинальную кривую на плоскости (Л, к). Чему равно критическое
значение Ш
Найдите другие решения, которые независимы от ж, t и укажите
вилообразную бифуркацию.
Предполагая, что w имеет период 2тг по х и выражая решение
уравнения в виде комплексного ряда Фурье
покажите, что iu_n = iu*. Найдите бесконечную систему обык-
обыкновенных дифференциальных уравнений для {wn}. Проверьте
устойчивость нулевого решения и определите, когда устойчивы
остальные решения.

134	Гл. 6. Конвекция Релея-Бенара
Предполагая, что
^(x1t)=(il-ilcI/2[W1(t)eb+^_i(t)eb]+O(il-ilc) при Д-^ДС+,
выведите уравнение Ландау для надкритической бифуркации:
где T={R- Rc)t [Swift & Hohenberg, 1977].
6.13. Конвекция Релея-Дарси в пористой среде. Дано, что двумерная
конвекция в бесконечном слое жидкости Буссинеска в пористой
среде описывается следующими безразмерными уравнениями и
граничными условиями
дв
Аф = —R— (результат применения ротора к закону Дарси),
дв , дфдв дфдв Ап ,	,
— + -г-	-^--^- = Ав (уравнение теплопроводности),
at oz ox ox oz
^=0, 0= — 1 при z=l (твердая идеально проводящая
верхняя крышка),
^=0, 9=0 при z=0 (твердая идеально проводящая
нижняя крышка),
где R — модифицированное число Релея. Покажите, что Ф = 0,
0 = — z описывают основное состояние покоя, представляющее
собой однородное распределение тепла за счет теплопроводности
от дна до вершины слоя.
Линеаризуйте систему для возмущений ф = ^ + ф^в = & + 0г.
Покажите, что спектральное соотношение для нормальных мод
вида ф' = е*г+{кхф^), в1 = e8t+ikx§{z) принимает вид
s= u2kIR2 2-(k2+n2) Дляп=1,2,....
к2 + п2тг2 V	/
Докажите, что течение неустойчиво, если R > Rc = 4тг2, а наи-
наиболее неустойчивая мода имеет длину волны 2 в направлении
оси х [Horton & Rogers, 1945; Lapwood, 1948].
6.14. Слабонелинейная конвекция Релея-Дарси в пористой среде.
(i) Покажите, что из уравнений в предыдущем упражнении 6.13

Упражнения	135
без дальнейших приближений следуют сильно нелинейные урав-
уравнения для возмущений
2	дУ>' дв' дф' дв'
€
дв>
-W-- 2— дУ дв дф дв
дх ~€ дТ dz дх дх dz'
ф1 = 0' = 0 при z = О,1,
гдев = (Л-ReI12 и Т = еН.
(ii) Предполагая, что в', ф* имеют период 2 по ж (так как по ли-
линейной теории наиболее неустойчивая мода имеет волновое число
к = тг), определяя амплитуду
Г1 Г2
А(Т) = 2€~г / Ф' cos тгж sin irz dx dz
Jo Jo
(для нормировки функции тока); налагая фазовое условие (без
ограничения общности рассуждений, так как оно эквивалентно
просто сдвигу по ж)
I / ^'si
Уо Jo
sin 7гж sin nz dx dz = 0,
Jo Jo
и полагая
0' = €01 + €202 + • • •, ф1 = €^1 + €2V>2 + ' ' ' При € -* 0,
покажите, что
сЫи	90i
- -?^ = 0, AV>i + лс-^- = 0 при 0 < х < 2, 0 < г < 1,
^1 = 01 = 0 при z = 0,1,
Г1 л2
Л(Т) = 2 /	фхсоя пх sin 7Г2 eta dz,
Jo Jo
фг sir
Jo Jo
I sin 7гж sin 7Г2; da; dz = 0.
Выведите выражения: Лс = 4тт2 и

136 	Гл. 6. Конвекция Релея-Бенара
(iii) Покажите, что если
Аи дфп - F
Авп- — - Fn,
&Фп + Rc-z^ = Gn при 0 < х < 2, 0 < z < 1,
ох
и
фп = вп = 0 при z = 0,1
для некоторых регулярных функций Fn(E, г), Gn(aj, z), то
Интегрируя повторно по частям, покажите, что
Отсюда выведите условие разрешимости для существования 0п,
(iv) Покажите, что
(v) Покажите, что
Tr7r'-A2sin27rz, V2 = 0.
16
дф2 двг дфг дв2 дф2
дфз__дв± дф^дв^ дф2 двг дфг дв2 дф2 двг
3" дх ~ дТ + dz дх + dz дх дх dz " дх dz'
+ Дс?^- = -?^ при 0<»<2,
ох	ох
и
ф3 = вз = 0 при z = 0,1;
а также выведите уравнение Ландау
dA1A
для надкритической вилообразной бифуркации [Palm et a/.,
1972].

Упражнения	137
6.15. Простая линейная система обыкновенных дифференциальных
уравнений, которая моделирует некоторый аспект двойной
диффузионной конвекции. Дано
dw	d6
— = -Aw -кв- 4ew, — = 20 + kw- ев.
at	at
Покажите, что у нормальных мод ги, в ос e8t
Докажите, что для к2 > 8 нулевое решение устойчиво, если е = О
и € —> оо для фиксированного А;, и неустойчиво при 8 < к2 < 9
и Bе — IJ < 9 — fc2. (Можно увидеть, что состояние (при
8 < к2 < 9) устойчиво при € = 0 и для больших €, но неустойчиво
для некоторых положительных значений е; таким образом, так
называемая "стабилизирующая сила" может дестабилизировать
течение [Hinch, 1973]).
Обсудите это явление как модель двойной диффузионной конвек-
конвекции — явления, когда два количества (например, тепло и рас-
раствор или два раствора) диффундируют с различными скоростя-
скоростями.
6.16. Неограниченная стационарная двойная диффузионная нелиней-
нелинейная волна. Известно, что возмущения основного состояния покоя
в жидкости Бусссинеска с постоянными градиентами темпера-
температуры и концентрации раствора подчиняются уравнениям
д{Аф')
dt
где и1 = дф'/dz, wf = —дф'/дх, якобиан J определяется из ра-
равенства
АФ,Ф) = {дф/дг){дф/дх) - {дф/дх){дф/дг)
для любых дифференцируемых функций ф и ф, Pr = vjк —
число Прандтля, 5 = /с*//с — число Шмидта, R = а/ЗдсР/кг/
— число Релея, Rs = lg(Ac)d3/K,v —число Релея для раствора,
а к3 — коэффициент диффузии в растворе концентрации с.

138	Гл. 6. Конвекция Релея-Бенара
Проверьте, что существует точное стационарное нелинейное ре-
решение вида
c'=csinx
при —оо < ж, z < оо и условии, что Rs = 5(jR+1), где постоянные
W, 0, с удовлетворяют уравнениям [Stern, I960]
W = Д0 - Д,с, 0 = - W\ с = -W/S.
6Л7. Неустойчивость и конвекция под влиянием изменения поверх-
поверхностного натяжения с изменением температуры. Рассмотрим
линейную устойчивость слоя однородной несжимаемой тепло-
теплопроводной вязкой жидкости с пренебрежимо малой плову честью,
ограниченной твердой пластиной при 2*=0и свободной поверх-
поверхностью z* — d.
Предположим, что пластина является идеальным проводником
тепла и имеет постоянную температуру 0О, а свободная поверх-
поверхность — идеальный изолятор с температурой 0i в основном со-
состоянии и поверхностным натяжением у = 70 — ?#* ? где с > 0 —
некоторая постоянная.
Покажите, что условия на касательные напряжения на поверх-
поверхности дают
— = -с-— при z* = d для г = 1,2,
x	ctx
oz*
а остальные уравнения и граничные условия те же, что в пара-
параграфе 6.2 для R = 0 и свободно-твердых граничных условий.
Рассматривая нормальные моды с волновым числом а и предпо-
предполагая выполнение принципа обмена устойчивостей, покажите,
что на границе устойчивости
W ос sh az Ч- (a cth а — l)z sh az — az chaz
M = 8a2(ch ash a — a)cha/(sh3a — a3cha) = /(a),
где М — число Марангони, М = /3cd2/K,p. Докажите, что
устойчивость имеет место тогда и только тогда, когда М <
< minima) = 79,607, который достигается при а — 1,993 (по
[Drazin fe Reid, 1981, Problem2.13; Pearson, 1958]).

Упражнения
139
Чистая вода
Воронка
езиновая
трубка
Зажим
Стеклянная
трубка
Стеклянный
сосуц
Горячий
окрашенный
рассол
Чистая вода
Белая бумага ~6
Стол
Рис. 6.8. Схема аппарата для простого эксперимента по термохалинной
конвекции. См. упражнение 6.19 (по [Drazin & Reid, 1981, Fig 2.7])
6.18. Домашний эксперимент по тепловой неустойчивости. Налей-
Налейте легкое масло (кукурузное масло хорошо подходит) в чистую
глубокую сковородку, чтобы образовался слой масла имеющий
глубину около 2 мм. Осторожно и равномерно прогрейте дно
сковородки. Для того чтобы наблюдать неустойчивость, осто-
осторожно бросьте немного порошка (хорошо подходит порошок ка-
какао). Небольшое количество порошка, распространенное по по-
поверхности, обнаруживает стационарные шестиугольные ячейки.
Можно увидеть движение индивидуальных частиц порошка, ко-
которые восходят вблизи центра ячейки и нисходят вблизи ее гра-
границ. Слегка наклоните сковородку для того, чтобы установить
критическую глубину, при которой возникает конвекция. Про-
Проверьте, что размер ячеек и критическое число Релея имеют по-
порядок величины, предсказываемый теорией Релея (по [Drazin &
Reid, 1981, Problem2.5]).

140	Гл. 6. Конвекция Релея-Бенара
6.19. Простой эксперимент по термохалинной конвекции. Наполни-
Наполните наполовину большую стеклянную чашку горячим окрашен-
окрашенным рассолом (несколько граммов соли и очень мало голубых
чернил или метилена на пол-литра воды в литровую чашку).
Налейте холодной свежей воды в рассол. Для того чтобы огра-
ограничить перемешивание воды и рассола, наливайте воду медлен-
медленно через трубку близко ко дну чаши как, например, показано
на рис. 6.8. Поместите чашку на белую бумагу (чтобы отчетли-
отчетливо видеть последующую конвекцию), сохраняйте ее неподвижной
(для того, чтобы избежать появления внутренних гравитацион-
гравитационных волн) и убедитесь, что отсутствует вращение (для того,
чтобы избежать закручивания конвекционных ячеек). Плотность
горячего рассола долна быть меньше, чем плотность холодной
воды, так что жидкости должны находиться в гидростатичес-
гидростатическом равновесии. Тем не менее, вследствие различных скоростей
диффузии тепла и соли, так как диффузия соли является очень
медленной, вскоре возникнет термохалинная неустойчивость.
Сделайте наблюдения роста пальцеобразных ячеек со скоростью
порядка 10" мм/с с горизонтальным масштабом порядка 3 мм.
Обсудите это явление в качестве примера двойной диффузион-
диффузионной конвекции, когда два количества (тепло и один раствор, как
здесь, например, или два раствора) диффундируют с различны-
различными скоростями (по [Drazin & Reid, 1981, Problem 2.6; Stem, 1960;
Baines & Gill, 1969]).

Глава 7
Центробежная неустойчивость
Идет ветер к югу, и переходит к северу,
кружится на ходу своем, и возвращается
ветер на круги свои.
Еккл. 1, 6
Центробежная сила, аналогичная пловучести с точки зрения создания
или подавления неустойчивости течений, изучается в этой главе так
же как пловучесть изучалась в предыдущей главе. В качестве модель-
модельной задачи рассматривается (но не во всех деталях) задача о неустой-
неустойчивости течения Куэтта между двумя вращающимися коаксиальны-
коаксиальными цилиндрами.
7.1. Вращающиеся течения
Другой важный тип гидродинамической неустойчивости представ-
представляет собой неустойчивость осесимметричных вращающихся тече-
течений. Они аналогичны тепловой конвекции, и аналогом центробежной
силы служит пловучесть. Под вращающимися течениями имеются
в виду основные течения, скорость и давление для которых имеют
вид: u = U(r), р = Р(г), где
{/r = 0, U$ = V(r), U2=0 при -oo<z<oo	G.1)
в цилиндрических координатах (г, 0, z) (см. рис. 7.1, где представлена
геометрия и обозначения). Эти выражения с произвольной функци-
функцией V являются точными решениями уравнений Эйлера движения не-
несжимаемой идеальной жидкости. Для уравнений Навье-Стокса вязкой
жидкости потребуем
V{r) = Ar + B/r.	G.2)

142
Гл. 7. Центробежная неустойчивость
Рис. 7.1. Схема сечения длинного коаксиального цилиндра в течении Ку-
этта с обозначениями (по Drazin and Kambe, Ryutai Rikigaki — Anteisei To
Ranyu (Fluid Dynamics — Stability and Turbulence), University of Tokyo Press,
1989, Fig. 6.1. Воспроизведено по разрешению University of Tokyo Press)
Для течения Куэтта возьмем твердые цилиндры г = Hi, jR2, имеющие
угловые скорости Qi и fi2 соответственно, и получим
А =
_ U2R2 -
R\ - R\
в =
G.3)
Рассмотрим сначала физические соображения [Rayleigh A916 b)]
в применении к невязкой жидкости. Угловой момент на единицу массы
кольцевого элемента жидкости г = const, z = const в основном враща-
вращающемся течении имеет вид Н = rV(r), а циркуляция этого кольца рав-
равна 2тгН. Но по теореме Кельвина о циркуляции последняя сохраняется
для возмущенного кольца, следовательно, сохраняется и Н. Враще-
Вращение имеет место в результате наличия плотности центробежной силы
pV2/r = рН2/г3, которая действует в радиальном направлении и ас-
ассоциируется с плотностью потенциальной энергии \рН2 /г2 = \pV2.
Имея это в виду, рассмотрим эффекты обмена двух элементарных
колец равной массы при г = ri, z = z\ и г = гг, z = z2. Их ки-
кинетическая энергия на единицу объема равна \{Н2г^2 + Н^г^2) до и
\{Н2Г22 Л-Н2г^2) — после обмена. Увеличение кинетической энергии,
требуемое на реализацию обмена, таким образом, пропорционально
Без ограничения общности рассуждений положим г2 > т\. Тогда об-
обмен может освобождать энергию и, следовательно, производить не-
неустойчивость, только если Н2 > Я|. Таким образом, неустойчивость

7.2. Неустойчивость течения Куэтта	143
может иметь место только если Н^ > Н\ для т\ < Г2, т.е. только если
d(r2V2)
dr
< 0	G.4)
где либо в области течения. Это неравенство называется критерием
Релея неустойчивости. Наоборот, если
-4_1 > о	G.5)
везде в течении, то течение является устойчивым по отношению ко
всем осесимметричным возмущениям. Можно показать математичес-
математически строго [Synge, 1933], что это условие является необходимым и до-
достаточным условием для устойчивости вращающегося течения несжи-
несжимаемой невязкой жидкости по отношению к осесимметричным возму-
возмущениям. Тем не менее, течение может оказаться неустойчивым по от-
отношению к неосесимметричным возмущениям (которые не рассматри-
рассматривались в рассуждении Релея), даже если d(r2V2)/dr > 0 везде. Можно
видеть, что по отношению к коротковолновым возмущениям могла
бы иметь место неустойчивость Кельвина-Гельмгольца (как описа-
описано в параграфе 3.8), если V было бы разрывным, независимо от того
выполняется ли критерий Релея или нет, также весьма правдоподоб-
правдоподобным выглядит заключение о возможности неустойчивости, когда V
меняется очень резко, хотя и гладким образом.
7.2. Неустойчивость течения Куэтта
В своей выдающейся в истории гидродинамики работе Тейлор [Taylor,
1923] проанализировал неустойчивость течения Куэтта между вра-
вращающимися коаксиальными цилиндрами и проверил свою теорию на
эксперименте. Для начала посмотрим на рис. 7.2 (а) для визуального
знакомства с неустойчивостью, а затем объясним теорию и экспери-
эксперимент. Достаточно просто
A)	выбрать основное течение Куэтта G.2);
B)	линеаризовать уравнения Навье-Стокса и граничные условия для
малых возмущений вокруг основного течения;
C)	выбрать безразмерные переменные и параметры;
D)	использовать нормальные моды вида
E) вывести задачу на собственные значения в форме обыкновенных
Дифференциальных уравнений для определения s, u для данного ве-
вещественного волнового числа к и целого волнового числа п.

144
Гл. 7. Центробежная неустойчивость
Рис. 7.2. (а) Фотография вихрей Тейлора, когда внешний цилиндр по-
покоится, а внутренний цилиндр вращается, (б) Фотография волновых вих-
вихрей Тейлора, которые возникают вначале вторичной неустойчивости, когда
внутренний цилиндр вращается быстрее (по [Koschmieder, 1993, Figs. Il, 12])
Возникающая в результате численная задача была слишком труд-
трудна для решения во времена Тейлора. Поэтому он сделал ряд упро-
упрощающих предположений, основанных на экспериментальных наблю-
наблюдениях:
A)	Он предположил, что наиболее неустойчивые возмущения являют-
являются осесимметричными, и поэтому положил п = 0.
B)	Он предположил, что справедлив принцип обмена устойчивостей,
т. е. Im(s) = 0 при возникновении неустойчивости и поэтому, положив
s = 0 искал параметры, соответствующие границе устойчивости.
C)	Он предположил, что зазор между цилиндрами является узким,
т.е. R2- Ri < R2.
Эти три предположения дали ему возможность выразить решение ос-
основной задачи на собственные значения в явном виде через функции
Бесселя и подсчитать характеристики устойчивости численно. Впо-
Впоследствии теоретики получили характеристики устойчивости общей

Ji2. Неустойчивость течения Куэтта	145
задачи, находя s не только при п = О, но и при n/Ои для большего
диапазона значений Лх, Д2> Пх> ^2> г/, а также А:.
Для представления результатов удобно использовать безразмер-
безразмерные переменные. Определим
H = n2/toi и rj = R1/R2.	G.6)
В качестве меры квадрата отношения величин, характеризующих си-
силы инерции и вязкие силы, будем использовать величину, называемую
сейчас числом Тейлора:
_ 4ABRJ _ 4П;Д} A П2/П!)A П2Д|/П!Д;)
i/2 ~ v2	AД2/Д2J	* ( ]
Можно видеть, что это не что иное, как квадрат числа Рейнольд-
са, построенного по вращательной линейной скорости. Иногда вместо
G.7) используются числа Рейнольдса, построенные по вращательным
скоростям двух цилиндров. Критерий вращения Релея предполагает
наличие устойчивости по отношению к осесимметричным возмуще-
возмущениям в пределе при v —У О в том и только том случае, когда
в)'=	+
r	ч	J
dr	dr
т. е. тогда и только тогда, когда
(U2R22 ~ ftiflx)V(r) > 0 при Дх < г < R2
или тогда и только тогда, когда внешний цилиндр имеет большую
циркуляцию, чем внутренний цилиндр, и цилиндры вращаются в од-
одном направлении. Таким образом, неустойчивость вязкой жидкости
при не очень большом значении вязкости ожидается, если внутренний
цилиндр имеет большую циркуляцию, чем внешний, или цилиндры
вращаются в противоположных направлениях, т.е. если Т превосхо-
превосходит некоторое критическое значение.
Маргинальная кривая s = 0 в плоскости (а,Т) для фиксирован-
фиксированных значений других безразмерных параметров и для осесимметрич-
ных возмущений (п = 0), где а — (R2 — R\)k — безразмерное волно-
волновое число, имеет форму, сходную с кривой на рис. 6.3 для конвекции
Релея-Бенара. Однако и другие параметры являются здесь важны-
важными. Свойства характеристик устойчивости, определенные численно и
подтвержденные наблюдениями, наилучшим образом иллюстрируют-
иллюстрируются на рис. 7.3-7.6.
Эти характеристики линейной устойчивости предполагают воз-
возникновение стационарных (потому, что Im(s) = 0, когда Re(s) = 0),
осесимметричных (потому, что линейные возмущения обычно наибо-
наиболее неустойчивы, когда п = 0) тороидальных вихрей с осевым волно-
волновым числом 2ir(R2 — Ri)/ac при переходе Т через значение Тс в сторону

146
Гл. 7. Центробежная неустойчивость
3500
-3389.9
1178.6
1000
Рис. 7.3. Критическое число Тейлора как функция от /l* = ^2/^1 в пределе
узкого зазора R2/Ri -)¦ 1 (по [Harris & Reid, 1964, Fig. 2] и [Drazin & Reid,
1981, Fig 3.8])
увеличения. Так и происходит! Смотрите фотографии на рис. 7.2 (а), а
также [Van Dyke, 1982, Figs. 127-128] и два великолепных ролика Coles
(FL1963a,b). Поинтересуйтесь также Video Library в [Homsy et al.,
CD2000], просмотрите видео с подзаголовком "Steady Taylor Cells" и
"Taylor Instability". Вычисления Тейлора [Taylor, 1923] и наблюдения
согласуются изумительным образом с точностью от 1 до 5 процентов,
как показано на рис. 7.5.
Он наблюдал стационарные тороидальные вихри, которые раз-
развивались при возникновении неустойчивости, как и предсказывалось
теоретически формой собственных функций. Эти вихри называются
вихрями Тейлора. (Течение является более сложным, если знаки Ог и
Qi отличаются).
Начиная с 1923 г. появились сотни, а может быть, и тысячи работ,
где было изложено множество взглядов на переход к турбулентности
в течении Куэтта. В частности, слабонелинейная теория [Davey, 1962]
дает вилообразную бифуркацию с положительной постоянной Лан-
Ландау для первичной неустойчивости. Эта бифуркация приводит к воз-
возникновению вихрей Тейлора, когда внешний цилиндр покоится. При
увеличении числа Тейлора сами вихри становятся неустойчивыми и
развиваются азимутальные (не осесимметричные) волны в результате
вторичной неустойчивости (см. рис. 7.2 (б), где изображены волнистые

7.2. Неустойчивость течения Куэтта
147
г 3.127
3.0
Рис. 7.4. Критическое безразмерное волновое число ас = ас/A — ц) как
функция от [х = ^2/^1 в пределе узкого зазора R2/R1 —? 1 (по [Harris &
Reid, 1964, Fig. 1] и [Drazin & Reid, 1981, Fig 3.9])
вихри Тейлора). Просмотрите также фотографии в [Van Dyke, 1982,
Figs. 127, 128, 130] и соотнесите их с результатами теории. Проделай-
Проделайте то же для крутящего момента, график зависимости которого от
числа Тейлора показан на рис. 7.7.
При дальнейшем увеличении числа Тейлора возникает последова-
последовательность бифуркаций с хаосом при сложном переходе к турбулент-
турбулентности (см. [Fenstermacher et aZ., 1979]). Особенно интересным является
то обстоятельство, что иногда может возникнуть хаос, пропасть, а за-
затем возникнуть опять в результате последовательности бифуркаций
при увеличении числа Тейлора. Путь к турбулентности зависит от
R2/R1, ^г/^1 и длины цилиндров. Влияние некоторых из этих фак-
факторов можно наблюдать при различных значениях чисел Рейнольдса
Rei = R\Q.\/v и Лег = R\Q.2/v в случае двух цилиндров, изображен-
изображенном на рис. 7.8. Для того чтобы познакомиться с большим числом экс-
экспериментальных результатов и их связью с теоретическими резуль-
результатами как в линейной, так и в слабонелинейной теориях, читайте
монографию [Koschmieder, 1993].
Бифуркации в случае коротких цилидров, который отличается
от случая длинных цилиндров в идеализированной модели Тейло-
Тейлора, также были изучены (см. [Benjamin & Mullin, 1982]). Критичес-
Критические значения числа Тейлора, отвечающие возникновению бифурка-
бифуркаций сильнее различаются, чем для длинных цилиндров, а некоторые
из этих бифуркаций проще наблюдать в эксперименте. Особенно ин-
интересным представляется то обстоятельство, что Бенджамин и Мул-
лин [Benjamin & Mullin, 1982] наблюдали до 20 сосуществующих раз-

148
Гл. 7. Центробежная неустойчивость
• Данные экспериментов
о Данные расчетов
50
200
Неустойчивость
150
100
Устойчивость/
/
J/
1.292
I
-250 -200 -150 -100 -50
0
50
100 150 200
Q2lv (cm-2)
Рис. 7.5. Схема (по [Taylor, 1923]) маргинальной кривой в плоскости
(Cli/iS) Пг/^) для его пары цилиндров, т. е. для jRi = 3,55 см и i?2 = 4,035 см
(по [Drazin & Reid, 1981, Fig 3.13])
личных устойчивых стационарных течений (с различным числом или
направлением вращения вихрей, располагающихся между концами па-
пары цилиндров), а также констатировали существование еще 19 не-
неустойчивых стационарных течений для одной и той же стационарной
экспериментальной конфигурации. Подробности приводятся в книге
[Koschmieder, 1993].
7.3. Неустойчивость Гёртлера
В дополнение к неустойчивости, приводящей к образованию вихрей
Тейлора существует еще один важный тип центробежной неустой-
неустойчивости, открытый Гёртлером в 1940 г. Гёртлер рассматривал не-
неустойчивость пограничного слоя на вогнутой стенке, изображенной
на рис 7.9. Неустойчивость, называемая неустойчивостью Гёртлера,
проявляется в возникновении вихрей Гёртлера. Он сделал следующие
три допущения при моделировании. Толщина S пограничного слоя
предполагалась малой по сравнению с радиусом Ro кривизны стенки.
Основное течение, таким образом, считалось близким к параллель-
параллельному стенке и центробежная сила не учитывалась при определении
основного течения, хотя и сохранялась в линеаризованных уравнени-
уравнениях для возмущений. Далее, предполагалось, что основное течение за-
зависит только от поперечной координаты у в рамках используемого
квазипараллельного приближения.

Неустойчивость Гёртлера
149
/
1 1 1
4У^т 1.0
0.75
1 0.5
0.25
i
-
-
-
1 1
-2.0
-1.5
-1.0
-0.5
0.5
1.0
Рис. 7.6. Наблюдения и вычисления Тейлора в случае узкого зазора для
воды и значений радиусов цилиндров R\ = 3,80 см и ife = 4,035 см. Длина
вихрей Тейлора при возникновении неустойчивости (по [Drazin & Reid, 1981,
Fig 3.12]; экспериментальные данные взяты из [Taylor, 1923, Table 8])
Для обезразмеривания задачи используем 8 в качестве линейно-
линейного масштаба, скорость Е/оо данного однородного внешнего течения —
в качестве масштаба скорости, а также г) = у/8 в качестве координа-
координаты, изменяющейся в направлении, ортогональном стенке. Определим
далее безразмерную скорость основного течения
U = U(rj)\ при 0 < ?7,
где U(t}) -> 1 при 7} -)¦ оо. Линеаризуя уравнения Навье-Стокса для
возмущенного потока u = U + u',p= Р + р', выбирая нормальные
моды в виде
(u',v',w\P') = (u(r,),v(v)Mv)Mv)h't+ikx
G.8)
и подставляя в линеаризованные уравнения, получим четыре взаи-
взаимосогласованных дифференциальных уравнения. Исключая w и р из
этих уравнений, выведем систему
G.9)
G.10)
где
(D2 - a2) (D2 -a2-a) = -a2fiUu,
(D2-a2-a)u = U'v,
U' = T>U. G.11)

150
Гл. 7. Центробежная неустойчивость
1.0
0.1
0.01
-
-
1 1 1 1 1
Rec = 68.23 Ч^ч
	i \ .
10
102
103
Re
Рис. 7.7. Изменение крутящего момента G при изменении числа Рей-
нольдса Re = Qii2i(i?2 — Ri)/v при tyj = 0, Ri = 1,0 см, i?2 =2,0 см,
H = 5,0 см, v = 0,1226 см^", р = 0,8404г см". Момент G измерен
в динах на сантиметр (по [Drazin & Reid, 1981, Fig 3.14] с использованием
данных [Donnelly & Simon, I960, Table 2])
Граничные условия непроницаемости и прилипания имеют вид
u(tj) = v(tj) = Dv(tj) = 0 при т) = 0 и г) -+ оо.	G.12)
Безразмерный параметр /х является аналогом числа Тейлора в случае
узкого зазора. Тем не менее, принято выражать результаты в терми-
терминах числа Гёртлера
1/2
G.13)
где 'в — моментная толщина пограничного слоя. Легко видеть, что
G2 = \&n/{6*Ro).
Считается, что для этой задачи на собственные значения верен
принцип обмена устойчивостей, т. е. а вещественна для маргинально

7.3. Неустойчивость Гёртлера
151
2000
Rex
1000
-4000
-3000
-2000
Re,
-1000
1000
Рис. 7.8. Режимы течений наблюдаемых для случая двух длинных вра-
вращающихся коаксиальных твердых цилиндров с числами Рейнольдса Re\ =
R\ui/u и Re2 = F&Slilv (по [Andereck et a/., 1986, Fig 1])
устойчивых мод. Таким образом, для выявления маргинальной устой-
устойчивости, положим G = 0. Уравнения при этом примут вид
(D2 - a2) (D2 - a2) v = -a2
(D2 - а2) = U'v. G.14)
В течении 40 лет, прошедших после публикации статьи Гёртлера бы-
было предпринято много исследований этой задачи на собственные зна-
значения с вычислениями для различных профилей U. Холл [Hall, 1983],
однако, показал, что предположение о локально параллельном течении
несправеливо, за исключением случаев невязкой жидкости (G = 0)
или коротких волн (а ^> 1), потому что все члены линеаризованной
системы должны быть сохранены во всех случаях, кроме коротковол-
коротковолнового предела для того, чтобы правильно учесть пространственное
развитие пограничного слоя. Отсюда следует, что маргинальная кри-
кривая или скорость роста в данной точке не имеет смысла, а параболи-
параболическая система уравнений в частных производных должна решаться
как граничная задача. Сарик [Saric, 1994] предпринял обзор экспери-
экспериментальных результатов и их связь с теорией.

152
Гл. 7. Центробежная неустойчивость
500 (mm)	6Ю	700	800	900	1000
Рис. 7.9. (а) Схема основного течения и некоторые обозначения, (б) Схема
вторичного течения, которое возникает в начале неустойчивости в погра-
пограничном слое вдоль вогнутой стенки (по [Gortler, 1940] и [Drazin & Reid,
1981, Fig. 3.20]). (в) Фотография неустойчивости Гёртлера (по [Nakayama,
1988, Fig. 30], воспроизведено по разрешению профессора Акиры Ито (Akira
Но))

Упражнения	153
Упражнения
7.1. Задача устойчивости слоя основного вращающегося течения
несжимаемой невязкой жидкости. Полагая
где
U = @,F(r),0), P = P(r), и' = (и'г,и'в,и'2)
в цилиндрических координатах (г, 0, z) и линеаризуя уравнения
Эйлера, которые описывают движение несжимаемой невязкой
жидкости, покажите, что
д< ди'г	1др'
_ + П__2(Ъ<,---—,
&V
ft	flff p dz'
dr + r +r дв + dz "u>
где локальная угловая скорость основного течения определяется
равенством п = V/r.
Покажите, что если течение ограничено жесткими цилиндрами
при г = Ri, Л2, то
и'Т = 0 при г = Ri, Л2.
7.2. Осесшшетпричные возмущения вращающихся течений. Покажи-
Покажите, что если д/д9 = 0, то из линеаризованных уравнений упраж-
упражнения 7.1 следует уравнение
д2 [д2и'г 1<ч и'г д*и>Л
т2 \дг2 + г dr r2+ dz2 )
где
Ф = r~3d{rVJ/dr
представляет собой дискриминант Релея (являющийся аналогом
N2 — квадрата частоты плову чести, определенной в упражне-
упражнении 8.21).

154	Гл. 7. Центробежная неустойчивость
Выбирая нормальные моды в виде
(u'r,u'e,u'z,p') = (u(r),Q,w(r),v*(r))exp(st + ikz),
покажите, что
(DD, - к2)ч - ^Фи = О,
где
D = d/dr, D* = d/dr + 1/r.
Покажите также, что
и = О при г = iii, Лг-
Используя теорию задачи Штурма-Лиувилля, покажите, что все
собственные значения к2/s2 — отрицательны, если Ф > 0 внут-
внутри интервала Ri < г < R2 и положительны, если Ф < 0 внутри
этого интервала; если же Ф меняет знак, то имеют место как по-
положительные, так и отрицательные собственные значения к2 /s2
с предельными точками на ±оо [Synge, 1933].
Покажите, что если Ф <. О где-либо, то течение неустойчиво
в соответствии с вращательным критерием Релея.
7.3. Двумерные возмущения вращающегося течения. Основываясь на
упражнении 7.1, покажите, что если
ti,, d/dz = 0, и'г = дф'/гдв, и'в = -дф'/дг,
то линеаризованные уравнения приводятся к виду
где завихренность основного течения Z = г 1D(rV) = D*V,
а лапласиан имеет вид
А-— -— — —
Зг2 + тдт + г2 дв2 '
(Возможно, легче вывести это уравнение, линеаризуя уравнение
завихренности B.4) с R = оо).
Выбирая нормальные моды в виде
ф'(г, в, t) = ф{г) exp{st + infl),

Упражнения	155
покажите, что
(s + inO)(D*D - п2/г2)ф- тг-1{^г)ф = О,
ф = О При Г = ill, -Й2-
Покажите, что необходимым условием неустойчивости относи-
относительно двумерных возмущений является смена знака градиента
завихренности DZ основного течения где-либо внутри интервала
течения [Rayleigh, 1880]. (Подсказка: Используйте доказательст-
доказательство из параграфа 8.2 для аналогичной задачи о неустойчивости
параллельного течения).
7.4. Аппроксимация узкого зазора. Рассмотрев основное течение Ку-
этта со скоростью V(r) = Ar+B/r и угловой скоростью ft = V/r
в обычных обозначениях, докажите, что
ft (г) -+ Oi[l - A - /м)С] при ту -> 1
для фиксированных ? = (г — Ri)/(R2 — Л1), где r\ = Ri/R2,
/
Покажите, что дискриминант Релея
Ф(г) ~ -2^i^[l _ A _
7.5. Неустойчивость течения Куэтта невязкой жидкости. Пока-
Покажите, что если
как в упражнении 7.4, то устойчивость относительно осесиммет-
ричных возмущений (упражнение 7.2) определяется при помощи
следующей задачи на собственные значения
(D2 - а2)и = -а2а~2[1 - A - /i)<]«,
и = 0 при С = 0,1,
где
<т = «/(-4АП1I'2 ~ «[2A - г,) 1A - /i)]1/2/2Oi, a = k(R2 - Rt).
Докажите, что
-7—2 = х«, u = 0 при х =
о. ж

156	Гл. 7. Центробежная неустойчивость
где
х = [а<т2/A - МJ/3{1 - [1 - A -
и что соотношение на собственные значения имеет вид
Ai(si) _ Ai(g0)
где Ai, Bi — функции Эйри. (Численные расчеты подтвержда-
подтверждают устойчивость при /л > 1 и неустойчивость при /л < 1, что
соответствует критерию Релея [Reid, I960]; см. [Drazin & Reid,
1981, параграф 16]).

Глава 8
Устойчивость параллельных течений
Так как они сеяли ветер, то и пожнут бурю...
Ос. 8, 7
В настоящей главе рассматриваются неустойчивости многих важных
течений: течений в канале, таких как течение Куэтта и плоское те-
течение Пуазейля, пограничного слоя Блазиуса на плоской пластине,
двумерных струй, следов и свободых сдвиговых слоев, а также тече-
течений в трубе и осесимметричных струй. Глава начинается с обсужде-
обсуждения неустойчивости плоско-параллельных течений несжимаемой иде-
идеальной жидкости и продолжается рассмотрением аналогичных вопро-
вопросов в вязкой жидкости. Будет видно, что для одних течений модель
идеальной жидкости дает хорошее приближение для характеристик
устойчивости вязкой жидкости при больших числах Рейнольдса, а для
других это не так. Мы также увидим, что несмотря на то, что вяз-
вязкость приводит к диссипации энергии, ее наличие может дестабили-
дестабилизировать течение, которое устойчиво для идеальной жидкости. Итак,
начнем с относительно простой теории несжимаемой идеальной жид-
жидкости.
Часть 1: Идеальная жидкость
8.1. Устойчивость плоско-параллельных течений
идеальной жидкости
Для заданного плоско-параллельного течения возьмем величину V
в качестве характерной скорости, а величину L — в качестве ха-
характерной длины. Для течения в канале или для струи, например,

158	Гл. 8. Устойчивость параллельных течений
за величину V можно было бы принять скорость в центре течения,
а для свободного сдвигового слоя или пограничного слоя на пластине
— взять скорость свободного потока; за величину L можно было бы
принять полуширину канала, в котором течет жидкость, или шири-
ширину струи, сдвигового слоя или пограничного слоя на пластине. Опре-
Определим затем безразмерные переменные х = х*/?, t = Vt*/L, u =
= u*/V, p = p*/pV2. Тогда уравнения Эйлера для идеальной жидкос-
жидкости могут быть записаны в безразмерной форме следующим образом:
^	-Vp,	(8Л)
уравнение неразрывности для несжимаемой жидкости в виде
V.u = 0,	(8.2)
а граничные условия непроницаемости твердых стенок при z = z\, zi
в виде
w = О при z = 2i, 22-	(8-3)
Можно взять или z\ = —оо или 22 = оо, если течение является по-
полуограниченным или использовать оба эти равенства, если течение
неограниченно. Используем далее выражения
U = U(z)i, Р = const при zi < z < Z2	(8.4)
для задания основного течения в канале (см. рис. 8.1). Можно прове-
проверить, что это течение удовлетворяет основным уравнениям и гранич-
граничным условиям для любой функции U.
Для того чтобы найти характеристики линейной устойчивости ли-
линеаризуем уравнения и граничные условия относительно малых воз-
возмущений и, как обычно, используем метод нормальных мод. Так, по-
положим,
u(x, t) = V(z) + u'(x, *), р(х, t) = Р + р'(х, *),	(8.5)
и линеаризуем уравнения (8.1)—(8.3), пренебрегая произведениями воз-
возмущений (обозначенных штрихами). Отсюда следует, что
-ы v-u'=0' (8-6)
•и/(х, t) = 0 при z = 2i, 22.	(8.7)
Беря дивергенцию от обеих частей уравнения (8.6), получаем

Плоско-параллельные течения идеальной жидкости	159
z
/У//////////////////////////////////////
Рис. 8.1. Геометрия основного течения
Др' = -2——.	(8.8)
dz dx	v '
Отсюда можно вывести, что применение оператора Лапласа к урав-
уравнению (8.6) для 2-й компоненты приводит к уравнению
(8'9)
Коэффициенты в этих уравнениях не зависят от ж, у, ?, но зависят
от 2, следовательно, можно разделить переменные, выразив независи-
независимые нормальные моды в форме
u'(x,t) = u{z)e^ax+^'QCt\ j/(x,t) = p(z)ei(a*+/3y-act), (8.10)
при этом, как обычно понимается, что каждая физическая величина
представляется действительной частью комплексного выражения, так
что ги;, например, отвечает физической величине
[Re(t3) cos(ax + (Зу — acTt) — lm(w) sin(a:c 4- (Зу — acTt)] exp(acit),
где сг = Re (с), с\ = Im(c). Эта мода представляет собой бегущую
в направлении (а,/3,0) волну с фазовой скоростью acr/(a2 + /З2I/2,
которая затухает или растет со временем как exp(acit). Говорят, что
она будет соответственно линейно устойчивой, если <хс\ < 0, и не-
неустойчивой при <хс{ > 0. (Можно было бы записать —iac = 5, так что
u'?p' ос е**, но общепринятым является использование комплексной
скорости с для тех задач, в которых обычно возникают моды типа
бегущей волны).
Таким образом, из уравнений (8.6) следует
dU.
ia(U — c)u+ —w + iap = 0,
(8.11)

160	Гл. 8. Устойчивость параллельных течений
0,	(8.12)
<^ = 0,	(8.13)
Q.Z
^ = 0.	(8.14)
dz
Из граничных условий (8.7) также следует
ги(х, t) = 0 при z = zb z2.	(8.15)
Уравнения (8.11)—(8.14) и граничные условия (8.15) представляют со-
собой формулировку задачи на собственные значения для определения
всех собственных функций й, р, принадлежащих собственным значе-
значениям с для заданных ?/, zi, 22,a? )9. Течение является линейно устойчи-
устойчивым, если ас\ < 0 для всех действительных значений а, /?. Наоборот,
течение является неустойчивым, если ас\ > 0 для по крайней мере
одной пары действительных волновых чисел а,/3. Идея здесь состоит
в том, что любое начальное возмущение может быть выражено в виде
суперпозиции собственных функций для всех значений волновых чи-
чисел, по крайней мере, если множество собственных функций является
полным, и что течение является устойчивым, если нет моды, расту-
растущей неограниченно.
Для того чтобы решить задачу на собственные значения (8.11)-
(8.15), полезно определить величины
a = (a2+/32I/2, u= {au + /3v)/a, p = ар/а. (8.16)
Уравнения (8.16) являются невязким аналогом преобразования Сквай-
Сквайра, которое Сквайр [Squire, 1933] впервые использовал для вязкой жид-
жидкости. Возьмем далее сумму произведений а и уравнения (8.11) и /3 и
уравнения (8.12), и, деля эту сумму на а, получим уравнение
dU
ia(U-c)u+ — t3 + iap = 0,	(8.17)
которое, по-существу, является компонентой линеаризованных урав-
уравнений Эйлера в направлении волнового вектора a = ai+/3j, для а = \а\
ий = §-и, где ^ = а/а. Уравнения (8.13), (8.14) могут быть также
записаны в виде
ia(U - c)w + Щ = 0,	(8.18)
dz
-^- = 0,	(8.19)
dz

8.1. Плоско-параллельные течения идеальной жидкости
161
У
0
а
Я
ОЛ
U соава
U
tf sin0Cxk)
Ux
Рис. 8.2. Волновой вектор и компоненты скорости основного течения
в плоскости z = const, (а) а = ai + /Ч« (б) U = ?f(cos 0а + sin 0а" x k)/a
соответственно. Теперь можно увидеть, что преобразованная задача
на собственные значения (8.17)—(8.19), (8.15) имеет тот же самый вид,
что и первоначальная задача на собственные значения (8.11)—(8.15)
в специальном случае двумерных волновых мод, когда /3 = v = 0;
отсюда следует, что соотношение на собственные значения для за-
заданного основного течения имеет вид
с, S) = 0
(8.20)
для некоторой функции Т, собственные значения с зависят от вол-
волновых чисел только через сумму их квадратов. Таким образом, от-
относительная скорость роста ас\ является наибольшей для заданного
волнового числа S, когда /9 = 0, так как равенство в выражении а < а
достигается только при /3 = 0.
Существенный физический результат состоит в том, что трехмер-
трехмерная мода представляет собой волну, распространяющуюся наклонно
к плоскости основного течения, и только компонента основного тече-
течения в направлении движения волны влияет на рост волны, так что
скорость роста пропорциональна этой компоненте. Это означает, что
каждой неустойчивой трехмерной моде соответствует более неустой-
неустойчивая двумерная мода. Этот факт становится более прозрачным, ес-
если определить в как угол между волновым вектором а = (а, /3, 0)
и направлением скорости основного течения, именно, направлением
оси ж. Тогда в = arctan(/3/a) и компонента скорости основного тече-
течения в направлении волнового вектора равна U cos в, как изображено
на рис. 8.2. Уравнения показывают, что компонента вектора скорости
основного течения, перпендикулярная волновому вектору, не влияет
на рост волны.
Из изложенного ясно, что задача на собственные значения для
трехмерной моды может быть преобразована в задачу для двумер-
двумерной моды и поэтому можно ограничиться решением задачи на собст-
собственные значения только для двумерных мод. В рассмотренной выше

162	Гл. 8. Устойчивость параллельных течений
задаче на собственные значения удобнее начать заново, подставляя
функцию тока ф' для возмущения в линеаризованные уравнения, чем
полагать /3 = v = О в вышеприведенной задаче на собственные значе-
значения и исключать 2, р, выделяя w. Итак, положим
и используем нормальные моды вида
^(*,М) = *(*)еИ-«*>.	(8.22)
Следовательно,
u=^-, w = -ia<f>,	(8.23)
и уравнение (8.11) дает
Поставляя это выражение для рв уравнение (8.13), получаем уравне-
уравнение устойчивости Релея,
{U - с){ф" - а2ф) - J7'V = 0,	(8.25)
которое вместе с граничными условиями (8.15), записанными в виде
ф(г) = О при z = *i, я2,	(8.26)
определяет задачу на собственные значения в простейшей форме, где
штрихи теперь используются для обозначения дифференцирования
по z (не следует путать со штрихами, которые ранее обозначали воз-
возмущения физических величин). Данную задачу, впервые поставлен-
поставленную Релеем в 1880 г., иногда называют задачей устойчивости Релея.
Заметим, что в задачу на собственные значения (8.25), (8.26) а вхо-
входит только во второй степени. Таким образом, если величины ф, с яв-
являются решением задачи, т.е. собственной функцией и соответству-
соответствующим собственным значением, для данного значения а, то они также
являются решением и для отрицательного значения —а. Это свойст-
свойство связано с обратимостью задачи по времени и пространству. В свя-
связи с этим, без потери общности, будем рассматривать далее только
случай а > 0. Тогда критерием для неустойчивости моды являются
условия с\ > 0 и а > 0. Далее заметим, что комплексно-сопряженное
собственное решение ф*, с* = cr — ici является также собственным ре-
решением для того же самого волнового числа а, потому что задача на

8.2. Общие свойства задачи устойчивости Релея	163
собственные значения является действительной. Поэтому для каждой
затухающей устойчивой моды существует соответствующая расту-
растущая неустойчивая мода и наоборот. Этот факт объясняется обрати-
обратимостью задачи по времени, которая включает периодические движе-
движения идеальной жидкости со стационарными граничными условиями.
Полученный результат может казаться парадоксальным в том смыс-
смысле, что если существует экспоненциально затухающая мода, также
существует экспоненциально растущая мода и поэтому течение явля-
является неустойчивым. Это означает, что течение может быть устойчиво
только в том случае, когда все моды являются нейтрально устойчи-
устойчивыми с действительными собственными значениями с; но это неуди-
неудивительно для недиссипативных систем: хорошо известно, что для га-
мильтоновой системы с одной степенью свободы все устойчивые состо-
состояния равновесия являются центрами, а все неустойчивые равновесия
являются седлами на фазовой плоскости.
Можно заметить, что уравнение устойчивости Релея (8.25) имеет
сингулярность в точке или точках zc в области течения, где U(zc) = с,
если Um < с < Um ? где Um — минимум U(z) в интервале z\ < z < Z2
течения, a Um — максимум. Плоскость, где z = zc, называется кри-
критическим слоем моды. Заметим, что критические слои могут возник-
возникнуть только, если с вещественна, т. е. только если мода нейтрально
устойчива, более того, критические слои обязательно возникают для
маргинально устойчивых мод. Будет показано, что критические слои
важны при решении задач с начальными условиями для идеальной
жидкости и для обобщения задачи устойчивости Релея на случай вяз-
вязкой жидкости, т. е. для задачи Орра-Зоммерфельда.
Фактически собственные решения с, ф для заданных гладких U
и ?i,?2, а могут быть двух видов (моды для кусочно-линейных про-
профилей U несколько отличаются). Существует непрерывный спектр
собственных значений с для всех с в интервале [C/"m, Um]-> каждая со-
соответствующая собственная функция имеет разрывную производную
в точке zc. Также может иметь место дискретный спектр комплексно-
сопряженных пар собственных значений; число пар больше или равно
нулю и меньше или равно числу точек перегиба профиля скорости U.
8.2. Общие свойства задачи устойчивости Релея
Содержание предыдущего параграфа главным образом следует рабо-
работе [Rayleigh, 1880]. Релей также нашел некоторые общие свойства ре-
решения и несколько точных решений задач на собственные значения
Для кусочно-линейных профилей скорости основного течения. Данный
параграф представляет собой обзор некоторых общих результатов,
полученных Релеем и другими исследователями. Некоторые детали
специфических решений приводятся в следующем параграфе.

164	Гл. 8. Устойчивость параллельных течений
Возможно, наиболее известным и наиболее полезным общим ре-
результатом, полученым Релеем, является результат о том, что необхо-
необходимым условием для неустойчивости является наличие точки переги-
перегиба в профиле основного течения. Его доказательство проводится сле-
следующим образом. Во-первых, запишем уравнение устойчивости Релея
(8.25) в виде
Ф"-«2ф-1^ГсФ = О	(8.27)
и предпожим, что течение является неустойчивым для этой моды,
так что с\ > 0. Теперь умножим уравнение (8.27) на ф*, комплексно-
сопряженное к ф, проинтегрируем от z\ до zi по частям и используем
граничные условия (8.26). Получим
ф\2)йг+ ['2-Е!!-\ф\*<Ь = о.	(8.28)
Jzi и с
Мнимая часть уравнения (8.28) имеет вид
Ci Г W~7v \Ф\2** = 0.	(8.29)
Jzi \и ~~ С1
Имеем q > 0. Поэтому U" должна изменять знак по крайней мере
один раз в открытом интервале (^i,^). Это условие, будучи только
необходимым условием, не может быть использовано для того, чтобы
показать, что какое-либо заданное течение является неустойчивым,
но может быть использовано, чтобы показать, что некоторые течения
являются устойчивыми.
Тейлор [Taylor, 1915, р. 23-26] дал физическое объяснение для усло-
условия неустойчивости, рассматривая перенос х-й компоненты импульса
посредством возмущения. Он показал, что если возмущение является
неустойчивым и U" > 0 всюду в жидкости, то ж-компонента импульса
каждого слоя жидкости должна возрастать. Но поток импульса через
стенку равен нулю, потому что идеальная жидкость там проскальзы-
проскальзывает, что приводит к противоречию.
Тейлор заключил, что если поток является неустойчивым, то U" не
является величиной, положительной всюду в жидкости, и, аналогич-
аналогично, U" не является величиной отрицательной, придя, таким образом,
к результату Релея. Интересно, что Тейлор пророчески добавил, что
наличие бесконечно малой вязкости может привести к неустойчивос-
неустойчивости, когда U" имеет один и тот же знак везде в жидкости, допустив
перенос импульса вследствии трения на стенке. Лин [Lin, 1955, пара-
параграф 4.4] объяснил физический механизм неустойчивости в терминах
динамики вихрей, идентифицируя точку перегиба с плоскостью, где
градиент завихренности основного течения становится равным нулю;

2. Общие свойства задачи устойчивости Релея	165
//////////////Л
у/////////////
7 **	**\ ////////
//////////////л
У/////////////
//////////////У/////////////// z_Zi /////////////Л///////////////
УУУУУУУУУ/УУУУУ/УУУУУУУУ/УУУ/У
в
-и
1/////////УУУУУ/s
У/////////////
Рис. 8.3. Некоторые примеры течений, удовлетворяющие необходимому
условию неустойчивости Релея-Фьёртофта. (а) Устойчиво, потому что вез-
везде U" < 0. (б) Устойчиво, потому что U" > 0 в каждой точке, (в) Устой-
Устойчиво, потому что U"(za) = 0, но U"(U — Ua) > 0. (г) Течение возможно
неустойчиво, так как U"(za) = 0 и U"(U - Ua) < 0
Бейнс и Мицудера [Baines & Mitsudera, 1994] сделали то же в терми-
терминах линейного резонансного механизма. Мы вскоре вернемся к друго-
другому физическому объяснению условия Релея в терминах напряжений
Рейнольдса. Однако этот механизм является довольно сложным и не
может быть легко объясним при помощи простых физических поня-
понятий.
Более сильная форма условия Релея была получена Фьёртофтом
[Fj0rtoft, 1950] семидесятью годами позднее: необходимым условием
неустойчивости является условие Un{U — Us)<0 где-либо в поле те-
течения, где z8 является точкой, в которой U"(zs) = 0 и U8 = U(zs). При-
Применение условий Релея и Фьёртофта проиллюстрировано на рис. 8.3.
На практике, условия Релея-Фьёртофта часто являются необходи-
необходимыми и достаточными для неустойчивости. Толлмин [Tollmien, 1935]
правдоподобно показал, что условие Релея является необходимым и до-
достаточным для неустойчивости симметричных течений в канале. Его

166	Гл. 8. Устойчивость параллельных течений
довод основан на демонстрации существования нейтрально устойчи-
устойчивого решения вида
c = Us, а = а, >0, Ф = Ф,	(8.30)
и дальнейшем возмущении его, чтобы показать, что оно маргинально
устойчиво, т. е. имеются как устойчивые, так и неустойчивые моды,
соответствующие значениям а в каждой окрестности а8. Далее, Лин
[Lin, 1955, р. 123] показал асимптотически, что
при а —>¦ а8—, где Р обозначает главное по Коши значение интег-
интеграла. Фактически, существуют неустойчивые моды этого класса для
0 < а < а,, но не для а > а8.
Пример 8.1: Контрпример достаточности условий Релея-Фъёртоф-
та для неустойчивости. Толлмин [Tollmien, 1935] рассмотрел про-
профиль скорости основного течения в виде
U(z) = Sin2 При Z\ < 2 < 22-
Имеем U" = — J7, откуда U8 = 0, если целое кратное тг лежит в интер-
интервале [zi, 22] течения, z8 кратно тг и U"(U — U8) = — sin2 z < 0. Поэтому
существует маргинально устойчивое собственное решение
с = U. = 0, а = а, = [1 - n27T2/(z2 - 2ХJ]1/2,
ф = ф8= sin[n7rB - z1)/(z2 - zi)]
для каждого положительного целого п < (z2 — 2i)/tt. Отсюда можно
показать, что если 22 — 2Х < тг, то течение яляется устойчивым, да-
даже при условии существования точки перегиба при z = 0 в области
течения и выполнении необходимого условия неустойчивости Фьёр-
тофта. .	?
Ховард [Howard, 1961] изящно показал, что если мода является
неустойчивой, т. е. С{ > 0, то
\(U + DijJ + с\
г - \(Um + DifjJ + с\ < \±{UM - %.)] ,	(8.32)
где Um является минимумом функции U(z) на интервале z\ < z < z2
внутри течения, a Um — максимум, так что с лежит в полуокруж-
полуокружности в верхней комплексной полуплоскости с центром ^(Um + Um) и

8 2. Общие свойства задачи устойчивости Релея	167
радиусом \{Um — Um). Это неравенство называется теоремой полу-
полукруга Ховарда. Оно полезно для того, чтобы легко получить оценку
скоростей роста и фазовых скоростей нормальных мод, хотя формаль-
формально это не есть оценка, а только ограничение. Эта теорема также по-
показывает, что Um <cT< Um в пределе при с\ —у 0+ для маргинально
устойчивой моды.
Было замечено, что уравнение устойчивости Релея имеет сингу-
сингулярность в точке или точках zc в области течения, где U(zc) = с,
т. е. в критических слоях моды. Вид линий тока около критического
слоя был получен Кельвином [Kelvin, 1880]. Переходя в систему отче-
отчета, движущуюся со скоростью с, т. е. примененяя преобразование Га-
Галилея, приведем движение к установившемуся течению относительно
преобразованной системы. Тогда линии тока совпадут с траекториями
частиц. Физическая функция тока для этого установившегося течения
имеет вид
где
= [l[U(y)-c]dy
представляет собой функцию тока основного течения в преобразован-
преобразованной системе, г. А — вещественная постоянная пропорциональная ам-
амплитуде волновой моды. моды. Около критического слоя z = zc при-
приближенное уравнение линий тока имеет вид
-U'(zc)(z - zcJ + A<t>(zc) cosaz = const,	(8.33)
где <f>(zc) выбрана действительной при помощи нормировки. Теперь
линии тока, как это можно увидеть на рис. 8.4, имеют известную фор-
форму кошачьего глаза.
Напряжения Рейнольдса в уравнении энергии Рейнольдса-Орра
E.28) представляют собой среднее по х:
т = ?- / (-w'uf)dx = -^	Re(wE)Re(uE)ds,
2тг Jo	2тг Jo
где Е = eia(x~ct) = Fexp(acit) и F = exp[ia(z - cvt)}. Поэтому
r = ~ f Ке[{-1аф)Е] Ке(ф'Е)] dx = \ш(фф'* - ф*ф') expBaCi*),
^тг JQ	4
так как Ке{ф'Е) = \{ф'Е + фГ*ЕГ) = \{&F + ф'+F-1) exp(aCi*) и так
Далее. Используя уравнение устойчивости Релея (8.25), далее получим
^ = \\а{фф"* - ф*ф") expBaci*) =
Q.Z 4

168
Гл. 8. Устойчивость параллельных течений
Рис. 8.4. Форма "кошачьего глаза" Кельвина для линий тока около кри-
критического слоя с точки зрения наблюдателя, движущегося вместе с ней-
нейтрально устойчивой волновой модой (по [Drazin & Reid, 1981, Fig. 4.3])
= -aaU"\U - c|-2|<?|2expBacit).	(8.34)
Рассматривая сингулярность в критическом слое, где U(z) = с, мож-
можно показать (см. упражнение 8.4), что "скачок" напряжений дается
выражением
(8.35)
в пределе при с\ —у 0+; это выражение определяет разрыв напряжений
Рейнольдса для маргинально устойчивой моды. Скачок функции г на
разрыве zc определяется здесь как Лг = r(zc -f 0) — r(zc — 0).
Эти формулы имеют некоторые важные физические следствия.
Уравнение энергии Рейнольдса-Орра E.28) показывает, что возму-
возмущение получает (или отдает) энергию из основного потока с помо-
помощью напряжений Рейнольдса, так что волновая мода забирает энер-
энергию там, где функция |т?7' положительна. Уравнение (8.34) пока-
показывает, что для нейтрально устойчивой моды dr/dz = 0 везде, где
U(z) ф с; поэтому напряжение Рейнольдса является постоянной вели-
величиной между критическими слоями. Заметим также, что г исчезает
на каждой стенке, потому что, как следует из граничных условий, w
там обращается в ноль. Этот факт показывает, что сумма скачков на-
напряжения Рейнольдса для нейтрально устойчивой моды равна нулю.
Отсюда следует, что если имеется самое большее один критический
слой, как это должно быть, если профиль основной скорости представ-
представляет собой монотонную функцию, то напряжение Рейнольдса должно
быть равно нулю во всем потоке. Поэтому для нейтрально устойчивой
моды не только U" = 0 там, где U = с, но также и!7 = с, где U" = 0.

g j. Характеристики устойчивости некоторых течений	169
8.3. Характеристики устойчивости некоторых тече-
течений идеальной жидкости
Для плоского течения Пуазейля и многих других течений в канале U"
не обращается в ноль в области течения, поэтому эти течения иде-
идеальной жидкости являются устойчивыми по отношению к двумерным
бесконечно малым возмущениям. Однако некоторые течения в кана-
канале, все неограниченные струйные течения и свободные сдвиговые слои
являются неустойчивыми. Чтобы решить задачу на собственные зна-
значения и, следовательно, найти характеристики устойчивости для кон-
конкретного основного течения, в общем случае необходимо использовать
численные методы. Тем не менее, известны некоторые аналитические
результаты, которые полезны с педагогической точки зрения в качест-
качестве примеров.
Большинство известных аналитических результатов получены
для кусочно-линейных профилей скорости основного течения. При по-
получении этих результатов использовались условия, выведенные и ис-
использованные Релеем [Rayleigh, 1880], которым удовлетворяет возму-
возмущение на разрыве функции U или С/7. Предположим, что U или Uf
разрывна, скажем, при z = zq. Тогда, как следует из уравнения (8.24),
условие непрерывности давления дает
A[{U - с)ф' - и'ф] = 0 при г = zq.	(8.36)
Здесь опять используется символ А для обозначения скачка физичес-
физической величины, так что условие (8.36) означает, что (U — с)ф' — и'ф
непрерывна при zq. Также может быть показано, что условие сплош-
сплошности жидкости на возмущенной поверхности z = zq + C{x>t) Дает
DC/Ш = w при z = zq + ? и, следовательно, после линеаризации
= 0 при z = zq.	(8.37)
U-c
Теперь, вооруженные условиями (8.36) и (8.37), мы уже готовы ре-
решить любую задачу с кусочно-линейным профилем скорости С/, пото-
потому что в слое, где U" = 0, уравнение устойчивости Релея (8.25) имеет
общее решение в явном виде
Ф№ = Аеа*+Ве-а\	(8.38)
где А и В — произвольные постоянные.
Пример 8.2: Устойчивость плоского течения Куэтта. См.
Рис. 8.5 (а). Если
U{z) =z при - 1 < z < 1,

170
Гл. 8. Устойчивость параллельных течений
-1
-1
О 1
Z
1-
О
-1 +
-1
-1 ¦¦
-1
-1
Рис. 8.5. Схематическое изображение некоторых основных профилей ско-
скорости, (а) Плоское течение Куэтта: U(z) = z. (б) Неограниченная вихревая
полоса: U(z) = sgn(^). (в) Неограниченный сдвиговый слой, (г) Треугольная
струя
тогда уравнение устойчивости Релея принимает вид
(г-с)(ф"-а2ф) = 0,
и поэтому
там, где z ф с. Не существует решения этого уравнения, которое
удовлетворяет обоим граничным условиям (8.26), так что дискрет-
дискретный спектр представляет собой пустое множество и плоское течение
Куэтта идеальной жидкости является устойчивым. Однако условия
задачи могут удовлетворяться на кусках при помощи непрерывной
функции ф с разрывной производной на критическом слое z = с для
всех с таких, что — 1 < с < 1 и для всех а. Собственная функция, как
легко можно увидеть, будет пропорциональна 0, где
х( \ — / 8ЬаA + 2)/sha(l + с) для - 1 < z < с,
Ф(г) ~ \ sha(l - *)/sha(l - с) для с < z < 1.
Это дает непрерывный спектр [Case, 1960].

8.3. Характеристики устойчивости некоторых течений	171
Пример 8.3: Неустойчивость Кельвина-Гельмгольца. Гельмгольц
[Helmholtz, 1868] описал физическую природу неустойчивости вихре-
вихревой полосы в нескольких словах, а Кельвин [Kelvin, 1871] проанали-
проанализировал полностью эту линейную неустойчивость, выбрав в качестве
скорости основного течения
—1 для z < О,
как изображено на рис. 8.5 (б) и описано в главе 3. Кельвин, по-
существу, нашел кусочно-гладкое решение уравнения устойчивости
Релея, используя граничные условия на бесконечности, и получил
м9\- JAe-QZ дляг>0,
nZ)~ \BeQZ для*<0
и некоторых постоянных А, В. (Вспомним, что по соглашению, а > 0).
Условие (8.36) в точке z = 0 дает
а из условия (8.37) получаем
-а(-1 - с)В = -аA - с)А.
Исключая А, В из этих двух линейных однородных уравнений, полу-
получаем, что
с2 = -1
в соответствии с уравнением C.28). Поэтому с = ±i и относительная
скорость роста ас\ = ±а дает одну экспоненциально затухающую и
одну возрастающую моду для каждого значения волнового числа. Сле-
Следовательно, течение является неустойчивым для волн с любой длиной
волны.
Заметим, что скорость роста стремится к бесконечности при
стремлении к нулю длины волны, так что тонкая структура начально-
начального возмущения быстро растет. Для того чтобы рассмотреть эффекты
быстрого роста коротких волн, в качестве примера предположим (см.
[Saffman, 1992, Chap. 8]), что начальные условия таковы, что профиль
поверхности раздела С имеет период 2тг/а и возбуждаются только рас-
растущие моды, так что
оо
С(М) = ^4n(*)sinnaz,
n=l
где An(t) = Лп@)епа*. Предположим далее, что
Лп@) = exp(-n1/2 -

172
Гл. 8. Устойчивость параллельных течений
для некоторого to > 0. Отсюда следует, что ? является гладкой функ-
функцией для 0 < t < to, но не для t > to- Таким образом, сингулярность
кривизны вихревой полосы может развиться за конечное время, по
крайней мере, согласно линейной теории.	П
Пример 8.4-' Неограниченный непрерывный кусочно-линейный сдвиго-
сдвиговый слой. Возьмем
при	z > 1,
при — 1 < z < 1,
при	z < —1,
(8.39)
как показано на рис. 8.5 (в). Решая уравнение устойчивости Релея на
кусках и используя граничные условия на бесконечности, получаем
Be-a(z-l) + Cea(z+1)
DeaB+1)
при
при
z > 1,
z < 1,
z < -1
(8.40)
для некоторых постоянных А, Б, С, D. Выберем множитель еа про-
произвольным, а также, как и прежде, а > 0, чтобы немного упростить
вычисления. Тогда условия (8.36), (8.37) при z = ±1 дают
А = В + Се2а, -A - с)аА = A - с)а (-В + Се2а) - (В + Се2а) ,
Ве
2а
C=D, (-1 - с)а (-Ве
2а
- (Ве2а + С) = а(-1 -
соответственно. Исключим далее A,B,C,D из этих четырех линей-
линейных однородных уравнений, находя, что
0 =
11	е2а	О
-A-с)а A-с)а(-1)-1 [A-с)а-1]е2а О
О	е2а	11
О -[(-1-с)а+1]е2а (-l-c)a-l a(-l-c)
откуда получаем соотношение на собственные значения
c2 = Da2)[(l-2aJ-e-4a].
(8.41)
Это соотношение описывает пару нейтрально устойчивых волн, рас-
распространяющихся в противоположных направлениях, если с2 > 0,
и пару стационарных мод, одну растущую и одну затухающую, если
с2 < 0. Единственный положительный ноль выражения 1 — 2а + е~2а
as » 0,64, откуда делаем вывод, что мода неустойчива, в том и толь-
только в том случае, когда 0 < a < a8. Отсюда следует, что сдвиговый
слой является неустойчивым.	?.

8.3. Характеристики устойчивости некоторых течений
	z=l
173
Рис. 8.6. Символическое изображение мод неустойчивости симметричной
струи. Они представляют собой линии тока в движущейся системе отсче-
отсчета в данный момент времени. (Вспомним, что моды движутся с постоян-
постоянной скоростью, по мере того как они растут экспоненциально, являются
произвольно нормированными и развиваются на фоне основного течения),
(а) Синусоидальная мода, (б) Варикозная мода
Пример 8.5: Треугольная струя. Возьмем профиль скорости основного
течения в виде
О
U[z)={l-\z\
О
при	z > 1,
при — 1 < z < 1,
при	z < —1,
(8.42)
как изображено на рис. 8.5 (г). Вновь будем решать уравнение устой-
устойчивости Релея на кусках, используя граничные условия на бесконеч-
бесконечности. Можно показать, что если U является четной функцией и гра-
граничные условия симметричны в точках ±z, как в этой задаче, то
каждая собственная функция ф является либо четной, либо нечетной,
так что достаточно отдельно рассмотреть случаи четных и нечетных
функций (см. упражнение 8.13). Возмущение с четной функцией ф на-
называется синусоидальной модой или антисимметричной модой, по-
потому что струя колеблется синусоидально и линии тока являются ан-
антисимметричными относительно линии z = О, возмущение с нечет-
нечетной функцией ф называется варикозной модой или симметрической
модой, потому что струя выглядит вздувшейся и линии тока сим-
симметричны относительно z = О (см. рис. 8.6). Рассматривая сначала
случай четной собственной функции, положим, что
при
при
1*1 > 1.
ф(г) =
^ cha ' "~ sha
Для некоторых постоянных А, Б, D. Условия (8.36), (8.37) при z = ±1
Дают
А = В + D, саА = -са (В tha + Dctha) + (В + D),

174	Гл. 8. Устойчивость параллельных течений
а при z = 0 имеем
A — c)aD cosech a + В sech a = — A — c)aD cosech a — B sech a.
Исключая А, В, D из этих трех линейных однородных уравнений,
окончательно получаем соотношение на собственные значения
2а2с2 + а A - 2а - е-2а) с - [l - а - A + а)еа] = 0. (8.43)
Решая это квадратное относительно с уравнение с целью установить,
когда существует пара комплексно-сопряженных корней, легко пока-
показать, что as = 1,833 и U8 = 0,367. Таким образом, струя является
неустойчивой по отношению к распространяющимся растущим сину-
синусоидальным волнам, которые не являются короткими.
Аналогично, для варикозных мод можно показать, что
с = Bа)-1 A - е-2а) ,	(8.44)
предполагая, что собственная функция является нечетной. Отсюда
следует, что варикозная мода является устойчивой для всех волновых
чисел а. Заметим, что синусоидальная мода является более неустой-
неустойчивой, чем варикозная мода, для данного симметрического течения.
Фактически этот результат имеет гораздо большую общность. D
8.4. Нелинейные возмущения параллельного тече-
течения идеальной жидкости
Слабо нелинейная теория неустойчивости параллельного течения иде-
идеальной жидкости все еще нуждается в солидном обосновании в си-
силу того обстоятельства, что заданное основное течение является или
устойчивым или неустойчивым и не является слабо неустойчивым,
когда параметр, аналогичный разности между значением числа Рей-
нольдса и его критическим значением, мал. Кроме того, следует ска-
сказать еще о многом.
Задача о нелинейной неустойчивости Кельвина-Гельмгольца
представляет собой задачу о свертывании вихревой полосы между
полу-пространствами безвихревых течений, которая является класси-
классической проблемой гидродинамики. Сингулярность кривизны поверх-
поверхности раздела на конечном отрезке времени, предсказанная линейной
теорией двумерного движения, фактически не имеет места в сильно
нелинейной теории (см. [Saffman, 1992, Chap. 8]). Бил с соавторами
[Beale et a/., 1984] доказали для двухмерного движения идеальной не-
несжимаемой жидкости, что если начальные условия являются гладки-
гладкими, то поле скоростей яляется также гладким для любого момента
времени.

8.4. Нелинейные возмущения	175
Хорошо известно, что для двумерного движения несжимаемой иде-
идеальной жидкости вихрь движется вместе с частицами жидкости, так
что интеграл по области течения от любой заданной гладкой функции
вихря является постоянной величиной, если вихри не входят в данную
область и не покидают ее. Кинетическая энергия движения является
также постоянной величиной. Отсюда следует, что, неустойчивости
двумерного течения, в общем случае, порождают все меньшие и мень-
меньшие масштабы движения.
При помощи преобразования Сквайра линейная задача была све-
сведена к двумерной задаче динамики вихрей. Хорошо известно [Herivel,
1955], что такие течения могут быть описаны бесконечномерной га-
мильтоновой системой, а также что гамильтонова система не имеет
притягивающего множества (аттрактора). (Эта система отличается
от гамильтоновой системы, которая описывает двумерное движение
жидкой частицы вдоль линиии тока). Также, с точки зрения теории
динамических систем, любое стационарное течение может рассматри-
рассматриваться либо как обобщенный центр в случае устойчивости, либо как
обобщенное седло в случае неустойчивости. С этой точки зрения яв-
является естественным тот факт, что стационарное течение имеет как
растущие, так и затухающие возмущения в случае неустойчивости и
только нейтрально устойчивые возмущения для устойчивого случая.
Такое рассмотрение позволяет нам глубже понять на качественном
уровне аспекты, связанные с сильно нелинейным распространением
возмущений для параллельного течения идеальной жидкости. Если
существует единственная неустойчивая мода, тогда малое начальное
возмущение общего вида будет расти вблизи от неустойчивого од-
одномерного многообразия основного течения; для периодических гра-
граничных условий обычно находится единственная неустойчивая мода
неустойчивого параллельного течения, но для неограниченной облас-
области существует волновая полоса неустойчивых мод.
Однако следует помнить, что модель сдельной жидкости не яв-
является структурно устойчивой, так что ожидается слабое затухание
с устойчивыми фокусами, а не центрами, когда жидкость слегка вяз-
вязкая, или даже когда имеется слабая диссипация из-за ошибок прибли-
приближения в вычислительной гидродинамике; тогда устойчивые течения
являются аттракторами. Для реальной жидкости малые масштабы
движения в конце концов будут диффундировать под влиянием вязкос-
вязкости, так что будет происходить некоторым образом локальное осред-
осреднение этих малых масштабов.
Из лабораторных и численных экспериментов видно, что двумер-
двумерные неустойчивости некоторых параллельных течений развивают-
развиваются таким образом, что данное течение в конце-концов превращается
в Другое двумерное стационарное течение, периодичное по горизон-
горизонтальной координате х. Также были найдены некоторые вихри (см.
упражнение 8.17), описываемые простым точным решением двумер-

176	Гл. 8. Устойчивость параллельных течений
ного уравнения завихренности, которое представляет собой сильно не-
нелинейное обобщение линейно устойчивого неограниченного сдвигово-
сдвигового слоя, однако смысл этих вихрей еще предстоит осознать.
Как видно из лабораторных и численных экспериментов, началь-
начальное возмущение основного параллельного течения в маловязкой жид-
жидкости растет в соответствии с теорией идеальной жидкости, так что
по прошествии некоторого времени формируется течение, почти пери-
периодичное по пространству с характерной длиной, равной длине наибо-
наиболее неустойчивой моды. Затем, через большой промежуток времени,
вязкость "размазывает" правильную структуру возмущения так, что
стационарное двумерное течение данной периодичности формируется
только приближенно. Это стационарное волновое течение оказывает-
оказывается существенно независимым от того, каким было начальное возмуще-
возмущение параллельного течения. Оно является устойчивым к двумерным
возмущениям и определяется при помощи максимизации некоторой
общей формы энтропии методами статистической механики, предло-
предложенными Онзагером [Onsager, 1949]. После прошествия еще большего
времени трехмерные неустойчивости разрушают это равновесное вол-
волновое течение, и в конце концов возникает турбулентность.
Часть 2: Вязкая жидкость
8.5. Устойчивость плоско-параллельных течений
вязкой жидкости
Возьмем снова
U = U{z)\, P=:po-Gx при z1 < z < z2,	(8.45)
для основного течения в канале с некоторым постоянным градиентом
давления с обратным знаком G. Для вязкой жидкости можно прове-
проверить (как в примере 2.4), что это течение удовлетворяет уравнениям
Навье-Стокса только при d3U/dz3 = 0, т. е. только если оно являет-
является плоским течением Куэтта-Пуазейля с параболическим профилем
скоростей.
Как и прежде, выберем безразмерные переменные, определим чис-
число Рейнольдса R = VL/v при помощи некоторых масштабов дли-
длины L и скорости V основного течения, рассмотрим малые возмуще-
возмущения (8.5) основного течения, линеаризуем уравнения Навье-Стокса,
возьмем нормальные моды (8.10) и поставим задачу на собственные
значения, определяющую с через С/, zi, Z2, (а2 +/32I/2, аR. Все это
снова приводит к преобразованию Сквайра с модифицированным чис-
числом Рейнольдса R = aR/a < R, где равенство достигается только для

8.5. Плоско-параллельные течения вязкой жидкости	177
двумерной волны. В результате получим важный результат, носящий
название теоремы Сквайра, о том, что для получения минимально-
минимального критического значения числа Рейнольдса достаточно рассмотреть
только двумерные возмущения.
На этом основании рассмотрим только двумерные возмущения
и используем существование функции тока для двумерного течения,
а также возможность записать уравнение для завихренности в терми-
терминах функции тока. Следует помнить, однако, что трехмерные возму-
возмущения необходимо рассматривать при решении некоторых задач, так
как они являются физически важными для некоторых задач с началь-
начальными значениями и при некоторых нелинейных взаимодействиях.
Рассмотрим далее уравнения завихренности в форме
и граничные условия непроникания и непроскальзывания на твердых
стенках при z = z\, z2:
ф(х, z,t) = const, -—(aj,z,t) = O при z = zi,Z2.	(8.47)
Oz
Представим далее функцию тока в виде ф = Ф + фг, где Ф = / U(z) dz
— функция тока основного течения, а ф' — возмущение функции тока,
и, линеаризовав уравнение завихренности, получим
Подставив сюда нормальные моды (8.22), получим
ф1У - 2а2ф" + а*ф = iaR[{U - с){ф" - а2ф) - и"ф], (8.49)
где штрих снова используется для обозначения дифференцирования
по z. Это уравнение называется уравнением Орра-Зоммерфелъда. Гра-
Граничные условия (8.47) дают
ф{г) = ф'{г) = 0 при z = zu z2.	(8.50)
Задачи на собственные значения (8.49), (8.50) называется задачей
Орра-Зоммерфелъда. Ее решение для собственных значений может
быть записано в форме
F(c,a*aR)=Q.	(8.51)
Эта задача рассматривалась независимо Орром [Огг, 1907 b, Art. 25] и
Зоммерфельдом [Sommerfeld, 1908], хотя фактически эти авторы сфор-
сформулировали ее для плоского течения Куэтта.

178	Гл. 8. Устойчивость параллельных течений
Несмотря на то, что уравнение Орра-Зоммерфельда имеет осо-
особенность на каждом критическом слое в пределе R —У оо, оно несин-
несингулярно при каждом заданном Д, так что Т — целая функция своих
аргументов, если течение происходит на ограниченном интервале и U
аналитична; Шенстед [Schensted, I960] доказал, что тогда имеет мес-
место счетное множество собственных значений и соответствующее мно-
множество собственных функций полно, так что начальное возмущение
может быть выражено как линейная комбинация дискретных нормаль-
нормальных мод. Если течение происходит на неограниченом интервале, то в
дополнение к дискретному спектру имеет место непрерывный спектр
с нейтрально устойчивыми собственными модами (см. [Неггоп, 1987]).
Для заданных С/", a, R обычно оказывается, что либо не существу-
существует неустойчивых собственных мод, либо существуют только одна или
две. Полезно строить кривые маргинальной устойчивости неустойчи-
неустойчивых мод в плоскости (а, Л), т.е. решать соотношение на собственные
значения и находить функции с(а, R) для каждой неустойчивой моды и
строить графики зависимости Ci(a, Д) = 0. Минимальным значением
R вдоль кривых является критическое значение Rc числа Рейнольдса,
такое, что если R < Rc то все моды устойчивы, а если R > Лс, то по
крайней мере одна мода неустойчива.
Заметим, что уравнение Орра-Зоммерфельда было выведено
в предположении, что основное течение представляет собой как плос-
плоско параллельное течение, так и точное решение уравнений Навье-
Стокса, так что строго говоря, задача Орра-Зоммерфельда имеет при-
приложение только к неустойчивости плоского течения Куэтта-Пуазейля.
Тем не менее, Толлмин [Tollmien, 1929] рассмотрел задачу Орра-
Зоммерфельда для z\ = 0, Z2 = оо, где U — скорость в пограничном
слое Блазиуса на плоской пластине. Это рассмотрение было в конеч-
конечном счете оправдано подтверждением полученных результатов акку-
аккуратными лабораторными экспериментами Шубауером и Скрамшта-
дом [Schubauer & Skramstad, 1947], а также может быть обосновано
следующим образом.
Отвлечемся на некоторое время и рассмотрим автомодельное ре-
решение Блазиуса уравнений пограничного слоя, описывающее течение
в однородном потоке, набегающем на плоскую полубесконечную плас-
пластину под нулевым углом. Как сообщается во многих учебниках (на-
(например [Batchelor, 1967, параграф 5.8]), функция тока для решение
Блазиуса имеет вид
Ф* = Bi/V*.I/2/(C),
где V — скорость окружающего однородного потока, параллельного
плоской пластине z+ = 0, / — решение нелинейных обыкновенных
дифференциальных уравнений с граничными условиями, отвечающи-
отвечающими задаче Блазиуса, и ? = (V/2vx+I/2z* — автомодельная перемен-

8.5. Плоско-параллельные течения вязкой жидкости	179
ная, которая в окрестности пластины имеет смысл расстояния в на-
направлении нормали к пластине. Таким образом, толщина погранич-
пограничного слоя S = B1/X+/VI/2 увеличивается по параболическому закону
с увеличением расстояния ж* вниз по потоку. Скорость основного те-
течения имеет вид
U, = VTK). V* = 0. W* = (vV/2x*)V2[Cf'(Q - /(С)]-
Это решение представляет собой хорошую аппроксимацию далеко от
передней кромки ж* = 0 пластины, где глобальное число Рейнольдса
Vx*/v велико. Вдалеке от передней кромки линии тока почти парал-
параллельны, немного расходясь при увеличении ж* на толщину 8 погра-
пограничного слоя. Вблизи передней кромки вязкие эффекты существенны
и линии тока расходятся существенно при увеличении х* на S. Оче-
Очевидно, что это течение почти параллельно далеко вниз по потоку, но
не вблизи передней кромки, и что толщина слоя безгранично увели-
увеличивается при ж* -> оо. Там, где пограничный слой почти параллелен,
можно использовать S как масштаб поперечного расстояния, V — как
масштаб скорости, а также определить локальное число Рейнольдса
R = VS/i/ = BVX+/VI!2, которое пропорционально квадратному кор-
корню глобального числа Рейнольдса и расстоянию ж* вниз по потоку.
В соответствии с [Tollmien, 1929], традиционный метод рассмот-
рассмотрения устойчивости пограничного слоя состоит в фиксации данного
значения ж*, нахождении локальной продольной скорости ?/*(#*, 2*)
в этой точке, представлением скорости ?/*(С) = W(z)i гДе z = z*/$i
пренебрежением поперечной скоростью W*, так как она меньше ?/* в
Вт1!2 раз, а затем решением задачи Орра-Зоммерфельда для профиля
скорости ?/. Эта процедура является правдоподобной при условии, что
(i) результирующее решение задачи Орра-Зоммерфельда дает боль-
большое критическое значение Rc числа Рейнольдса Л, что свидетельст-
свидетельствует о том, что основное течение и в самом деле почти параллельно
и что поперечным течением можно пренебречь в момент возникнове-
возникновении неустойчивости и (ii) наиболее неустойчивые волны не являются
слишком длинными, что свидетельствует о том, что профиль скорос-
скорости не изменяется достаточно сильно на расстояниях порядка одной
длины каждой из этих мод. (Далее увидим, что эти условия факти-
фактически удовлетворяются в теории пограничного слоя Блазиуса на плас-
пластине). Тем не менее, данная процедура подверглась критике Тэйлором
в 1938 г., несмотря на то, что данные экспериментов по неустойчивос-
неустойчивости, сделанных со времени критики Тейлора, в основном подтвердили
теоретические реультаты Толлмина. Может быть, следовало бы кон-
констатировать, что метод Толлмина приводит к определению того, где
неустойчивость пограничного слоя начинается, а не того, начинает-
начинается ли она или нет, так как равенство R = Rc определяет положение
^	где начинается неустойчивость, и пограничный слой

180	Гл. 8. Устойчивость параллельных течений
неустойчив вниз по потоку, где R > Rc. Также приближение погра-
пограничного слоя для больших JR, для которого давление не зависит от
поперечной координаты z, радикально отличается от линеаризации,
которая приводит к уравнению Орра-Зоммерфельда. Могло бы пока-
показаться, что линеаризованные уравнения в частных производных явля-
являются параболическими с коэффициентами, зависящими от ж*, и, та-
таким образом, переменная ж* не может быть отделена, что позволило
бы использовать нормальные моды вида (8.22). Эта идея была исполь-
использована при выводе параболизированных уравнений устойчивости, ко-
которые учитывают слабый непараллелизм и кривизну в основном тече-
течении наряду с влиянием области вверх по потоку [Bertolotti et a/., 1992];
эти уравнения представляют собой параболическую систему, которая
может быть легко проинтегрирована вниз по потоку, хотя уравнения
Навье-Стокса, которые эта система уравнений приближает, являются
эллиптическими.
*На основании вышеприведенных соображений, развитие про-
пространственной моды данной размерной частоты и* по пространству
может быть найдено при помощи ВКБ-приблйжения [Bouthier, 1973;
Gaster, 1974]. Пусть А*(ж*) — комплексная амплитуда моды, напри-
например, возбужденная в аэродинамической трубе вибрирующей мембра-
мембраной или громкоговорителем:
* (ж* )
в размерной форме, и приближенно выполняется уравнение
где а* — размерное комплексное волновое число и ф — собственная
функция, отвечающая наиболее неустойчивой (или наименее устойчи-
устойчивой) моде локально параллельного течения в положении ж*, которая
находится из решения задачи Орра-Зоммерфельда в этом положении.
Такая мода называется локальной модой, так как она определяется
приближением почти параллельного течения локально в данном по-
положении.
Гораздо больше может быть сказано и написано по вопросу о не-
непараллелизме, тем не менее, этот вопрос является сложным и не до
конца разрешенным и не будет далее рассматриваться здесь; будем
использовать задачу Орра-Зоммерфельда для множества почти па-
параллельных течений и решать ее, памятуя об ограниченности этого
приближения.

8.6. Свойства задачи Орра-Зоммерфельда	181
8.6. Некоторые общие свойства задачи Орра-
Зоммерфельда
Сейчас возможно при помощи современных компьютеров и числен-
численных методов довольно просто подсчитать собственные решения для
любого заданного значения волнового числа и, следовательно, постро-
построить маргинальную кривую для любого заданного основного течения.
В следующем параграфе будут представлены некоторые численные
результаты для некоторых типичных основных течений. Тем не ме-
менее, в первую очередь следует обратить больше внимания на физичес-
физические механизмы неустойчивости, различные аналитические результа-
результаты, тонкую асимптотическую структуру решений при больших чис-
числах Рейнольдса, а также на трудности численного решения задачи.
Общеизвестно, что явление неустойчивости параллельных тече-
течений вязкой жидкости представляет собой весьма сложное явление, фи-
физические механизмы которого, тем не менее, возможно удовлетвори-
удовлетворительным образом описать довольно грубо. Если скорость основного
течения имеет точки перегиба и профиль неустойчив для идеальной
жидкости, то действие вязкости является в основном стабилизирую-
стабилизирующим. Сдвиговая неустойчивость, проявляющаяся в задаче Релея, по-
подавляется при достаточно малых числах Рейнольдса Л, когда дейст-
действие вязких эффектов, рассеивающих энергию, преобладает над дейст-
действием напряжений Рейнольдса, генерирующего ее. Тем не менее, при
больших значениях R вязкость может дестабилизировать узкую поло-
полосу волн, которая устойчива, когда R бесконечно. Конечно, часто ос-
основное течение неустойчиво при больших и умеренных значениях Л,
хотя и устойчиво для невязкой жидкости; тогда каждая волна данной
длины устойчива при достаточно больших Л, потому что только ис-
исчезающая полоса длинных волн неустойчива, когда R увеличивается
до бесконечности (это можно более ясно видеть, если посмотреть на
верхний рис. 8.8 (а)). Таким образом, вязкость играет двоякую роль:
стабилизирующую вследствие рассеяния энергии и более тонкую —
дестабилизирующую. Тейлор [Taylor, 1915], как указано в парагра-
параграфе 8.2, предположил, что противодействие вязкости проскальзыва-
проскальзыванию на стенках может вызвать появление момента возмущения в на-
направлении оси х и, тем самым, привести к неустойчивости. Прандтль
[Prandtl, 1921; 1935, параграф 28] предположил, что вязкость может
приводить к передаче энергии от основного течения к возмущению
вблизи критического слоя при помощи напряжения Рейнольдса, пото-
потому что оно может менять фазу компонент скорости г/, w' и тем самым
среднее значение их произведения на длине волны. Таким образом,
наличие вязкости изменяет результаты параграфа 8.2, касающиеся
напряжения Рейнольдса маргинально устойчивых или неустойчивых
мод, сглаживая скачки напряжения Рейнольдса вблизи критических

182	Гл. 8. Устойчивость параллельных течений
слоев и делая напряжение Рейнольдса ненулевым, когда имеет место
только один критический слой. Знак результирующего напряжения
Рейнольдса обычно такой, чтобы обеспечить передачу энергии от ос-
основного течения к возмущению, что часто приводит к возникновению
неустойчивости, но иногда — от возмущения к основному течению.
Достаточно недавно Линдзен и Рамбальди [Lindzen & Rambaldi, 1986]
объяснили механизм неустойчивости физически при помощи явления,
которое называется сверхотражением, а Бейнс [Baines et а/., 1996] —
при помощи линейного резонанса (см. упражнение 2.18).
Исследуем далее балланс энергии и структуру критического слоя
более подробно, с целью освещения механизма Прандтля и других
вопросов.
8.6.1. Энергия
Для нахождения уравнения энергии для возмущений умножим снача-
сначала уравнение Орра-Зоммерфельда (8.49) на комплексно сопряженное
ф* величины ф, затем, проинтегрировав по частям от Z\ до z% с ис-
использованием граничных условий (8.50), получим
-шПс{1\ + a2ll) = -(if + 2а21{ + a*I2)-iaR Г[Щф'\2 +
+ (U" + а2) \ф\2 + 1Гф'ф*] cb,	(8.52)
где
%= [ 2\Ф(П)\2^ при п = 0,1,2.	(8.53)
Jzi
Беря вещественную часть уравнения (8.52), получим уравнение
Wll)-\mR Г и'(ф'ф*-ф*'ф) d*,
(8.54)
которое и является уравнением энергии E.28) для возмущений ос-
основного параллельного течения. Члены в левой части представляют
собой скорость увеличения кинетической энергии возмущения, пер-
первая группа членов в правой части уравнения представляет собой ско-
скорость диссипации возмущений вследствие вязкости, а последний член
— энергию передачи от основного течения к возмущению посредством
напряжения Рейнольдса (см. упражнение 8.26).
Далее оставим на время уравнение Орра-Зоммерфельда и рассмот-
рассмотрим множество 5 гладких функций ф, которые удовлетворяют гранич-
граничным условиям (8.50) и уравнению энергии (8.54). Множество S вклю-

8.6. Свойства задачи Орра-Зоммерфельда	183
чает в себя собственные функции уравнения Орра-Зоммерфельда сре-
среди бесконечного множества других функций. Это обстоятельство поз-
позволяет доказать достаточные условия для устойчивости при помощи
демонстрации, что осс\ < 0 для всех функций множества S при доста-
достаточно малых значениях числа Рейнольдса R. Физическим основанием
этого метода является то, что если R достаточно мало, то вязкость
рассеивает энергию быстрее, чем энергия создается напряжением Рей-
Рейнольдса для любого геометрически возможного течения, в котором
сохраняется масса и которое удовлетворяет граничным условиям и,
таким образом, течение является устойчивым. Это пример энергети-
энергетического метода, который является естественным приложением пря-
прямого метода устойчивости Ляпунова с функционалом, а не функцией
Ляпунова.
Для доказательства потребуем
О > aRa (I2 + а2/2) = - (If + 2а2/2 + а4/4) -
-\iaR f 21Г'(ф'ф* - ф*'ф) dz
2	Jxi
для всех ф ? S. Определим q = max|{7'| и заметим, что
I Г и'{ф'ф* - ф*'ф) dz < 2q Г \ф'\\ф\ dz < 2qloh (8.55)
\Jzi	Jzi
вследствие неравенства Коши-Шварца. Таким образом, остается до-
доказать, что
/| + 2а2/2 + а4/2 > aRqloh
для всех ф Е S.
Синг [Synge, 1938] получил и использовал этот результат для вы-
вывода специфических достаточных условий для устойчивости ограни-
ограниченных течений (с z\ = —1, 22 = 1). Он показал, что одно из доста-
достаточных условий имеет вид
(rj2qaRJ < 4 B<*У + ft - ?2 + 2rj) (<*У + ? - l)
для любой вещественной пары ?, ту, таких что
2аУ +?г) - ?2 + 2г) > 0, аУ + ? - 1 > 0.
(Для неограниченных течений необходимо брать ? = 0, в результате
чего условия сильно ослабляются). Полагая ? = rj = 1/а, получим
и, полагая ? = 0, rj = 3/а2, получим
{qRJ < 25ба4/27.

184	Гл. 8. Устойчивость параллельных течений
Эти условия устойчивости являются довольно слабыми. Джозеф
[Joseph, 1968; 1969] усилил неравенство, но даже после этого условия
оказались недостаточно полезными, потому что энергетический ме-
метод не принимает в расчет механизм неустойчивости, обусловленный
наличием критического слоя, вследствие чего этот метод не может
привести к точным ограничениям на значение Rc.
8.6.2. Неустойчивость в невязком пределе
Асимптотики сыграли важную роль в историческом развитии тео-
теории задачи Орра-Зоммерфельда; с их помощью была сформулирована
сложная математическая задача и их использование оказалось сущест-
существенным для правильного понимания различных физических механиз-
механизмах в задаче Орра-Зоммерфельда и сходных задачах даже, несмотря
на то, что задача Орра-Зоммерфельда может быть сегодня решена
численно без существенных трудностей. В настоящей книге, одна-
однако, не совсем уместно приводить асимтотическую теорию в деталях
и строго, так что ограничимся только ее схематическим изложением.
Для того чтобы соотнести задачу Орра-Зоммерфельда с задачей
Релея, естественно перейти к пределу R —> оо в уравнениии Орра-
Зоммерфельда и получить уравнение Релея. Сразу заметим, что урав-
уравнение Орра-Зоммерфельда является уравнением четвертого порядка
и несингулярно для всех значений R, в то время как уравнение Ре-
Релея представляет собой уравнение второго порядка и имеет сингуляр-
сингулярность, когда U(z) =св комплексной плоскости z. Переходя к пределу
при R -> оо, можно найти два независимых асимптотических решения
Ф\ и <f>2 уравнения Орра-Зоммерфельда, называемых невязкими реше-
решениями, которые удовлетворяют уравнению Релея (8.25) везде, кроме
может быть, критического слоя.
Уравнение же Орра-Зоммерфельда имеет не два, а четыре незави-
независимых решения, так что его общее решение имеет вид
Ф = Агфг + А2ф2 + Аъфъ + А4ф4	(8.56)
для некоторых постоянных А\, А2, -Аз, А±. Гейзенберг работал над
этой задачей перед тем, как его внимание было привлечено к более
важным проблемам физики; в статье 1924 г., основанной на его док-
докторской диссертации, он нашел два других решения асимптотически.
Он нашел при помощи метода, который впоследствии был назван ме-
методом ВКБ, вязкие решения, такие, что
ф3(г), ф4{г) ~ Щг) - c]-^4exp[^{aR)^2Q{z)] при <xR -> оо (8.57)
для фиксированных z ф zc, где
Q{z) = е"/4 Г [U{z') - с]1'2 dz'.	(8.58)

g 0. Свойства задачи Орра-Зоммерфельда	185
Вязкие решения представляют собой возмущения пограничного слоя
на стенках толщины порядка Я/2. Гейзенберг использовал эти при-
приближенные решения для того, чтобы показать эвристически, что на-
наличие вязкости может дестабилизировать данное основное течение
при больших значениях Я, так же как и стабилизировать его при ма-
малых значениях Л, рассеивая энергию; более точно, он показал, что если
основное течение ограничено при a = a8 > О, то существует неустой-
неустойчивая мода с этим волновым числом для достаточно больших значе-
значений R- Тем не менее, по-крайней мере одно из невязких решений и оба
вязких решения сингулярны на критическом слое и, таким образом, не
могут быть использованы там в качестве правильного приближения
точных решений несингулярного уравнения Орра-Зоммерфельда.
Толлмин [Tollmien, 1929] осознал эти ограничения на решения
Гейзенберга и исследовал другое приближение решений уравнения
Орра-Зоммерфельда, где и z близко к 2С, и R велико. Заметим, что
U(z) - с ~ U'(zc)(z - zc) при z ->• zc. Два члена <?iv, \aR(U - с)ф"
в уравнении Орра-Зоммерфельда могут доминировать над осталь-
остальными и баллансировать друг друга вблизи критического слоя при
R —у оо. Интуитивные соображения наводят на мысль, что решение
обрезанного уравнения
хорошо аппроксимирует решение уравнения Орра-Зоммерфельда око-
около критического слоя при больших значениях aR. Можно показать
формально, что уравнение Орра-Зоммерфельда принимает вид
в пределе при aR —у оо для фиксированных ?, определяя
S = (z-zc)/e, e=[iaRU'(zc)]-1/3,
подставляя переменную ? вместо z и параметр е вместо aR в урав-
уравнение Орра-Зоммерфельда и затем переходя к пределу. Можете про-
проверить, что это действительно так. Следовательно, d2<^/d?2 — функ-
функция Эйри (см. упражнение 8.36). Это дает четыре независимых ре-
решения, которые могут быть выражены в простой явной форме через
Функции Эйри и их интегралы. Решения локально осциллируют как
Функция Эйри. Толлмин использовал эти асимптотики решений сов-
совместно с численными методами, для первого успешного решения зада-
задачи Орра-Зоммерфельда, хотя его методы и представляются доволь-
довольно грубыми с точки зрения современных стандартов. Можно легко
усмотреть, что толщина критического слоя, имеющая порядок €, т. е.

186	Гл. 8. Устойчивость параллельных течений
Д/3, гораздо больше, чем толщина пограничного слоя на стенке, ко-
которая имеет порядок Л/2. Толлмин также показал, что правильная
ветвь сингулярного невязкого решения в пределе aR -» оо может быть
найдена при помощи неустойчивого решения уравнения устойчивости
Релея в пределе с\ —¦>• 0+.
Таким образом, из этих асимптотических теорий выясняется, что
для больших значений числа Рейнольдса поведение волнового возму-
возмущения сильно различается в четырех разных областях, каждая из ко-
которых может присутствовать или отсутствовать в соответствии с ви-
видом данного основного течения:
A)	Если основное течение однородно на бесконечности, то возмущение
является там невращательным, т. е. если U(z) —> Uqo при z —> оо, то
ф(г) ~ Aie~az приг-юо.
B)	Возмущение является вращательным, как в невязкой жидкости,
везде, кроме бесконечности, критического слоя, или пограничного слоя
вблизи стенки, т. е.
ф(г)=А1ф1{г)+А2ф2{г).
C)	В критическом слое толщины (^[(аЛ)^3] около zc, где U(zc) = с,
возмущения подвержены существенному влиянию вязкости, тем не ме-
менее, aR велико.
D)	В пограничном слое толщины O[(aR)~x^2] около z\ или z2 возму-
возмущения подвержены существенному влиянию вязкости, тем не менее,
R велико.
Возникновение этих областей дает примеры того, что называет-
называется палубами в трехпалубной теории и зависит от основного течения
и значений числа Рейнольдса и волнового числа. Для пограничного
слоя Блазиуса, например, на верхней ветви маргинальной кривой воз-
возмущение имеет пять палуб (невращательное "невязкое" течение на
бесконечности, критический слой, две области вращательного "невяз-
кого" течения на каждой стороне и пограничный слой около стенки. На
нижней ветви маргинальной кривой возмущение имеет три палубы,
потому что там с настолько мало, что критический слой достигает
стенки при z = О и поглощает более тонкую область пограничного
слоя; см. схему палуб на рис. 8.7 и рис. 8.8 (а), где изображены вет-
ветви маргинальной кривой. В настоящем контексте трехпалубная тео-
теория обеспечивает только другой способ вывода классических асимп-
асимптотических результатов для задачи Орра-Зоммерфельда, но кроме
этого, она также обеспечивает и способ нахождения асимптотических
свойств медленно меняющегося основного течения и слабонелинейных
возмущений для больших значений R [Smith, 1979 a,b].

8.6. Свойства задачи Орра-Зоммерфельда
187
z2..
z2..
s§ °««f/3>
O{(aR)-m} б
Рис. 8.7. Схема областей для волновых возмущений пограничного слоя
Блазиуса. Слой невращательного течения на бесконечности не изображен,
(а) Пятикратная палуба для верхней ветви маргинальной кривой при aR ->
оо. (б) Тройная палуба для нижней ветви маргинальной кривой (по [Drazin
&Reid, 1981, Fig. 4.5])
Из написанного следует, что главные эффекты вязкости для боль-
больших значений R обуславливаются критическим слоем, если он есть,
а не пограничным слоем на стенке. Внутри критического слоя реше-
решение Орра-Зоммерфельда сильно отличается от любого решения урав-
уравнения Релея, и именно вблизи критического слоя фазы и' и w* настоль-
настолько изменяются, что напряжение Рейнольдса может передавать энер-
энергию от основного течения к возмущению. В некоторых случаях значе-
значение с таково, что критический слой достигает стенки и "поглощает"
более тонкий пограничный слой, а в других случаях критический слой
находится внутри почти невязкой области течения, отделяющей его
от каждого из пограничных слоев.
Гораздо в большей степени, чем эвристические идеи этого пара-
параграфа, должны быть осознаны тонкости асимптотической теории ре-
решения уравнения Орра-Зоммерфельда и соотвествующей ему задачи
на собственные значения при больших числах Рейнольдса. Вышепри-
Вышеприведенные результаты об асимптотических решениях уравнения Орра-
Зоммерфельда для фиксированных с становятся более сложными, ког-
когда граничные условия, которые также определяют с, рассматривают-
рассматриваются вместе с асимптотическими решениями. Для этого рекомендуем
читателю читать главы 4 и 5 книги [Drazin & Reid, 1981].

188	Гл. 8. Устойчивость параллельных течений
8.7. Характеристики устойчивости некоторых тече-
течений вязкой жидкости
Сложные свойства задачи на собственные значения, изложение кото-
которых находится за рамками материала данной книги, с некоторым рис-
риском чрезмерного упрощения могут быть просуммированы следующим
образом. Если для данного профиля скоростей основного течения, A)
некоторая мода неустойчива и собственное значение равно Cqo для иде-
идеальной жидкости (R = оо), то собственное значение с для вязкой жид-
жидкости стремится к Соо при R -> оо, но B) если эта мода устойчива для
идеальной жидкости, то с^ может не быть пределом какого-либо соб-
собственного значения для маловязкой жидкости. Если данное течение
устойчиво при R = оо (т. е. устойчиво для всех мод, когда жидкость
является идеальной), то оно может оказаться неустойчивым, имея по
крайней мере одну моду с с\ = O^R^3) при R -> оо. Таким об-
образом, наличие вязкости может привести к неустойчивости течения,
которое было устойчиво в идеальной жидкости; также вязкость может
сделать более неустойчивым течение, которое неустойчиво и в идеаль-
идеальной жидкости. Тем не менее, любое течение, кроме неограниченного
сдвигового слоя, устойчиво, когда число Рейнольдса достаточно ма-
мало. Заметим, что при больших значениях числа Рейнольдса, скорость
роста при неустойчивости Толлмина-Шлихтинга, обусловленная ме-
механизмом критического слоя, много меньше чем скорость роста не-
неустойчивости Релея, обусловленной вихревой динамикой в идеальной
жидкости. Некоторые детали, обосновывающие это заключение, бу-
будут объяснены в следующем параграфе.
Задача Орра-Зоммерфельда не является легко решаемой, поэтому
лишь немногие решения удается найти аналитически. Могло бы пока-
показаться, что для вязкой жидкости скорость основного течения должна
быть непрерывной и соответствующие ей напряжения должны быть
также непрерывны (т. е. непрерывны градиенты скорости в жидкости
однородной вязкости). Это так, тем не менее, имеет некоторый смысл
рассмотреть задачу Орра-Зоммерфельда, когда U или U' разрывны,
в качестве приближения решения для длинных волн (малых а). Это
сделано в упражнении 8.39, а ниже разберем простейший пример, от-
относящийся ко всему изложенному здесь.
Пример 8.6: Постоянная скорость основного течения. Предположим,
что U постоянна в канале. Тогда без ограничения общности можно
положить
U{z) = О при - 1 < z < 1.
Уравнение Орра-Зоммерфельда (8.49) в этом случае приобретает вид
ф™ - 2а2ф" + о*ф = -1аВс{ф" - а2ф).

#.7. Характеристики устойчивости	189
Общее решение этого уравнения может быть записано в виде
., ч л chaz _ sh az . cos pz
0B;) A+ #	+ A+
0B;) = Ai—— + #1 —— + A2	— + В2-г-^-
v '	en a	sna	cosp	sinp
с произвольными постоянными Ai, jBi, A2, B2, где р = (iaRc — a2)
И снова синусоидальная и варикозная моды могут быть разделены.
Так для синусоидальной моды (четное ф) имеем
спая	cos pz
ф(г) = Ai-г— + А2	.
en a	cosp
Граничные условия (8.50) дают
/спая cospjA
^(z) = Ai —	,
\ cha cosp /
где
+ ptgp= 0.
Можно показать [Rayleigh, 1892], что это уравнение на собствен-
собственные значения имеет счетное число вещественных корней р и ас =
= — \(а2 + p2)/R имеет отрицательную вещественную часть, а, зна-
значит, все синусоидальные моды устойчивы. Аналогично можно пока-
показать (см. упражнение 8.31), что все варикозные моды (с нечетными
собственными функциями) также устойчивы, так что данное основ-
основное состояние покоя устойчиво. Это едва ли удивительно, потому
что в уравнении Орра-Зоммерфельда (8.54) отсутствуют напряжения
Рейнольдса, генерирующие неустойчивость.	?
В шестидесятых годах 20 века, результаты численных расчетов
для плоского течения Куэтта позволили предположить, что оно устой-
устойчиво по отношению к волнам любой длины и при всех значениях числа
Рейнольдса. Это было доказано Романовым [Romanov, 1973]. Первые
решения задачи Орра-Зоммерфельда, описывающие неустойчивость,
были численно найдены Толлмином [Tollmien, 1929] и Шлихтингом
[Schlichting, 1933], фактически для неустойчивости пограничного слоя
Блазиуса на плоской пластине. Они использовали метод, комбини-
комбинирующий некоторые асимптотические и численные приемы, который
в настоящее время представляет чисто исторический интерес. Тем
не менее, неустойчивые моды, возникающие в результате механизма
критического слоя (в отличие от невязкого механизма Релея) до сих
пор называются волнами Толлмина-Шлихтпинга в их честь. Уравне-
Уравнение Орра-Зоммерфельда является трудно исследуемым при больших
значениях чисел Рейнольдса (а такие значения обычно и представ-
представляют физический интерес), поэтому его нелегко решать численно в
этом случае, трудности такого решения были преодолены только при

190
Гл. 8. Устойчивость параллельных течений
О Re
Рис. 8.8. Изображения некоторых типичных маргинальных кривых не-
неустойчивости a = 0 в плоскости (jR, а) для различных классов основных
течений, (а) Основное течение устойчиво, когда жидкость идеальна, (б)
Ограниченное течение с точкой перегиба, (б) Неограниченный сдвиговый
слой, (г) Неограниченная струя или след. (Одна мода является синусоидаль-
синусоидальной, а другая — варикозной тогда и только тогда, когда струя симметрич-
симметрична)
помощи использования электронных компьютеров. Первое решение
задачи Орра-Зоммерфельда при помощи электронного компьютера
было предпринято в 1953 г., когда Томас (Thomas) по предложению
фон Неймана решил задачу для плоского течения Пуазейля прямым
численным интегрированием и нашел неустойчивость при несколь-
нескольких значениях пар a, R. Теперь уже стало рутинным решать задачу
Орра-Зоммерфельда одним из множества надежных численных мето-
методов (см. [Drazin & Reid, 1981, параграф 30]), хотя и сложность урав-
уравнения по прежнему требует некоторого внимания при решении.
Приведем некоторые детали результатов для частных основных
течений, суммируя главные свойства многих численных решений из-
известных в настоящее время. Маргинальные кривые, изображенные на
рис. 8.8 и численные результаты в таблице 8.1 делают это весьма эф-
эффективно, хотя и кратко. Сначала посмотрите на рис. 8.8 (а), где из-
изображена маргинальная кривая, типичная для основного течения, ко-
которое устойчиво в идеальной жидкости, такого как плоское течение
Пуазейля и пограничный слой Блазиуса (но не плоское течение Куэт-
та, потому что оно казывается устойчивым для всех значений числа
Рейнольдса К). Для этих течений существует единственная неустой-
неустойчивая мода (синусоидальная мода для плоского течения Пуазейля).
Можно видеть, что неустойчивость не имеет места для любого задан-

g#7. Характеристики устойчивости
191
Таблица 8.1. Сводка численных результатов для четырех важных
первообразов основных параллельных течений
Основное
течение
Однородное
Плоское
Куэтта
Плоское
Пуазейля
Погранслой
Блазиуса
Сдвиговый
слой
Струя или
след
Профиль
U = const
U = z:
-1<z<1
U=l-z2:
-l<z<l
U=f'(z):
z>0
U = thz:
—00<2<00
17=sech2 z:
— 00<2<00
Устойчивый?
Да
Да
Нет
Нет
Нет
Нет
Re
оо
оо
5772
520
0
4,02
—
—
1,02
0,30
0
0,17
Маргинальная
кривая на рис.
—
—
8.8 (а)
8.8 (а)
8.8 (в)
8.8 (г)
ного волнового числа а при R —> оо. Тем не менее, неустойчивость
имеет место для по крайней мере одного значения а при все R боль-
больших Лс, потому что вязкость дестабилизирует течение. Тем не менее,
когда R достаточно мало, вязкое рассеяние энергии преобладает над
дестабилизирующим эффектом и течение остается устойчивым для
всех инфинитезимальных возмущений, если R < Rc. Рис. 8.8 (б) отно-
относится к основному течению в канале, которое имеет одну маргиналь-
маргинально устойчивую моду Us, ф$ в идеальной жидкости, а, значит, имеет
одну точку перегиба. Можно видеть, что результаты для идеальной
жидкости получаются при R —> оо и достаточно большая вязкость
стабилизирует течение.
Рис. 8.8 (в) относится к основному неограниченному сдвиговому
слою, U(z) = thz, который имеет одну маргинально устойчивую моду
U*, Фз в идеальной жидкости, а значит также имеет одну точку пе-
перегиба. Читателя может удивить, что критическое число Рейнольдса
равно нулю, так что как бы ни велика была вязкость, всегда имеют-
имеются неустойчивые моды, что очевидно противоречит теореме Серрина;
тем не менее этот парадоксальный результат не имеет физического
смысла, потому что сдвиговые слои далеки от параллельных тече-
течений, когда число Рейнольдса мало. Рис. 8.8 (г) отвечает неограничен-
неограниченной струе или следу, например струе Бикли (Bickley) с U(z) = sech2 z;

192	Гл. 8. Устойчивость параллельных течений
такое основное течение имеет две точки перегиба и две маргинально
устойчивые моды Us, ф8 в идеальной жидкости. И снова, собственные
числа для малых чисел Рейнольдса не отвечает действительности ко-
количественно, потому что тогда струя или след не являются почти
параллельными.
Асимптотическая теория соотношения на собственные значения,
когда Д стремится к бесконечности является математически интри-
интригующей и находится вне рамок начального курса настоящего пред-
предмета, так что перечислим только некоторые результаты. Для сим-
симметричных течений в каналах, таких как течение Пуазейля, а ~
~ const х Д/7, с ~ const х R~2I7 при R —у оо вдоль нижней вет-
ветви маргинальной кривой иа^ const x Д/11, с ~ const x Д~2'n при
R —У оо вдоль верхней ветви маргинальной кривой. Для полуограни-
полуограниченных течений типа пограничного слоя, однако, a ~ const x Д'4,
с ~ const х Д/4 при Д —> оо вдоль нижней ветви. Нормировка на
верхней ветви зависит от градиента давления. При наличии гради-
градиента давления a ~ const х Д/6, с ~ const x Д/6, в то время
как для пограничного слоя Блазиуса с нулевым градиентом давления
а ~ const х Д/10, с ~ const х Д/10 при Д -^ оо.
Образец расположения всех собственных значений изображен на
рис. 8.9. Различаются пристеночные моды, которые иногда называ-
называют модами Эйри (Airy) или А-модами, для которых сг —>• 1, с\ =
= О[(аД)/3] (критические слои которых расположены около стенок)
и центральные моды, иногда называемые модами Пекериса (Pekeris)
или Р-модамщ для которых сг —у 0, сх = О[(аД)/2] при aR -У оо.
В дополнение, имеют место моды Шенстеда (Shensted) или S-моды,
для которых сг -у |, ci ~ -i[7r(n + 2)]2а/4Д при аД/п -+ 0; они
возникают для всех значений числа Рейнольдса, даже для больших,
если номер п моды достаточно велик, потому что тогда скорость мо-
моды изменяется настолько быстро с изменением z, что локальное число
Рейнольдса моды мало (см. пример 8.6).
Интересно также знать вид собственных функций и, следователь-
следовательно, характер возмущений для различных профилей скорости при раз-
различных значениях пары числа Рейнольдса и волнового числа. Соб-
Собственная функция для маргинально устойчивой моды пограничного
слоя Блазиуса показана на рис. 8.10. Обратите внимание на структу-
структуру моды и на то, где располагается критический слой.
8.8. ^Численные методы решения задачи Орра—
Зоммерфельда
Уже отмечалось, что вопрос о численном решении уравнения Орра-
Зоммерфельда любым из множества существующих надежных чис-
численных методов является рутинным, хотя сложности этого уравнения

g.g. Численные методы
193
(
-02
Ci -0-4
-0-6
л.о
) 02 i
2 ^
-
i
0-4
ч
i
0-6
8
i
рЗ
пб
п 7
р8
d9
0-8
i
1-
-
Рис. 8.9. Расположение нескольких первых собственных значений с =
ст + ici для синусоидальных мод плоского течения Пуазейля при а = 1,
R = 10000 в плоскости (cr,Ci) (no [Mack, 1976, Fig. 5]). Отмечены семейства
мод Эйри о, Пекериса V и Шенстеда D.
требуют некоторого внимания при решении. Главными целями чис-
численного решения при заданном основном течении являются: A) найти
кривую маргинальной устойчивости (ci = 0) и кривые постоянной ско-
скорости роста (aci = const), B) найти собственные значения для данной
пары положительных значений а и Л и C) подсчитать соответству-
соответствующие собственные функции и напряжения Рейнольдса. Аналогичые
цели преследуются для пространственных мод при заданной вещест-
вещественной частоте и) =¦ ас.
Главные методы решения принадлежат двум классам: A) спек-
спектральное разложение, т.е. разложение ф по полной системе ортого-
ортогональных функций, как, например, полиномы Чебышева, и B) исполь-
использование конечных разностей для интегрирования уравнения Орра-
Зоммерфельда, как задачи с начальными значениями, от одной грани-
границы до другой. Были придуманы разные разностные схемы для того,
чтобы справиться с трудностями, возникающими при больших зна-
значениях R. Применение методов спектрального разложения является
наилучшим при отыскании всех собственных значений. Применение

194
Гл. 8. Устойчивость параллельных течений
8п
0.0 0.2
0.4
Рис. 8.10. Формы собственной функций ф = фт-\-1ф{ для пограничного слоя
Блазиуса на верхней ветви, R = 1000, a = 0,23, сг = 0,25, zc = 0,40. (а) За-
Зависимость фт от z. (б) Зависимость |<?'(г)| и S(z) = фг(г)Ф{(г) — Ф'т^)Ф^)
от z. Отметим, что напряжение Рейнольдса пропорционально 5
конечно-разностных методов с использованием предиктора и коррек-
корректора является наилучшим для эффективного нахождения маргиналь-
маргинальной кривой (которая включает только наиболее неустойчивое собст-
собственное значение).
Дразин и Рид [Drazin & Reid, 1981, параграф 20] суммируют тех-
технические детали многих из этих численных методов и отсылают чита-
читателя к многим оригинальным статьям. Шмид и Хенингсон [Schmid &
Henningson, 2001, Appendix] не только дают современный обзор, но и
приводят программы MATLAB для простого подсчета характеристик
устойчивости течения Куэтта и плоского течения Пуазейля. Это про-
программы обеспечивают полезный задел, на основе которого студенты
могут начинать проектную работу.
8.9. Экспериментальные результаты и нелинейная
неустойчивость
Перед второй мировой войной численные решения уравнения Орра-
Зоммерфельда для пограничного слоя Блазиуса, предпринятые Тол-
лмином [Tollmien, 1929; 1935] и [Schlichting, 1933], Шлихтингом
повсеместно не вызвали доверия. Основное течение не было парарал-
лельным, их асимптотика носила эвристических характер, вычисле-
вычисления были трудоемкими и сложными, а результаты не согласовались
с экспериментами (и даже между собой с высокой степенью точнос-
точности). Тем не менее, во время войны Шубауэр (Schubauer) и Скрамш-
тад (Skramstad), спроектировав аэродинамическую трубу с беспре-
цендентно низким уровнем турбулентности вверх по потоку для плас-

g дл Экспериментальные результаты	195
тины, введя контролируемые колебания вибрирующей мембраны с
заданными частотами и амплитудами и разработав чувствительные
проволочные анемометры для измерения роста и убывания вынужден-
вынужденных колебаний, смогли подтвердить теоретические результаты о "но-
"носике" маргинальной кривой вполне убедительно. Они опубликовали
свои результаты после войны [Schubauer & Skramstad, 1947].
Клебанов с соавторами [Klebanoff et aZ., 1962] повысили качество
этих экспериментов и усовершенствовали их. Они нашли, что пер-
первые двумерные волны Толлмина-Шлихтинга растут по амплитуде
вниз по потоку, но когда их. амплитуда достигает конкретного кри-
критического значения, они подвергаются трехмерным возмущениям и
в результате явно случайных вспышек возникают турбулентные пят-
пятна. Пространственная эволюция схематично проиллюстрирована на
рис. 8.11 и приведена на фотографии на рис. 8.12. Эти авторы также
использовали контролируемые колебания, которые изменялись попе-
поперек течения, для изучения трехмерных эффектов и интерпретировали
их рост как вторичную неустойчивость исходной волны Толлмина-
Шлихтинга. Мгновенное поле скоростей демонстрирует наличие боль-
больших градиентов в профиле средней скорости в поперечных положени-
положениях (называемых пиками), где вторичное течение направлено от плас-
пластины и малых градиентов в промежуточных поперечных положениях
(долинах); такое поле скоростей отвечает структурам, показанным на
рис. 8.13, которые называются А-вихрями.
Было бы полезным посмотреть соответствующие картинки в кни-
книгах [Van Dyke, 1982, Figs. 29, 30, 104-106, 109-111] и [Nakayama,
1988, Figs. 20, 21, 23, 34, 27]. Фильмы [Brown, FL1964] и [Lippisch,
FL1964] показывают волны Толлмина-Шлихтинга, развивающиеся
в пространстве и во времени. Также и фильмы из Video Library [Homsy
et at., CD2000] с подзаголовками "Transition of Boundary Layers" и
"Visualization of Flow on a Flat Plate" и из их же Boundary Layers
с подзаголовками "Instabiliy, Transition, and Turbulence" имеют много
кадров о неустойчивости и переходу к турбулентности.
Пограничный слой Блазиуса на пластине был здесь использован
в качестве первообраза неустойчивости параллельных течений, но
имеется также множество экспериментов по неустойчивости других
параллельных течений. Было установлено обнадеживающее соответ-
соответствие между линейной теорией и наблюдениями тщательно контрол-
лируемых возмущений в в аэро и гидродинамических трубах с низким
уровнем турбулентности вверх по потоку, наблюдения докритических
неустойчивостей и неустойчивостей, вызванных турбулентностью бо-
более высокого уровня, однако, труднее интерпретировать. И снова экс-
экспериментальное соответствие с результатами линейной и слабо нели-
нелинейной теорий неустойчивости плоского течения Пуазейля [Nishioka
et at., 1980] не оставляет никаких сомнений по поводу применимостии

196
Гл. 8. Устойчивость параллельных течений
Псрсходн&я
Рис. 8.11. Схема, в общих чертах описывающая области развития не-
неустойчивости в пограничном слое Блазиуса на пластине при нулевом угле
падения набегающего слабо-турбулентного потока, вид сверху. А — лами-
ламинарное течение; Б — волны (двумерные, малоамплитудные) Толлмина-
Шлихтинга; В — трехмерно развившиеся волны; Г — нелинейное развитие
типа пик-долина с вихрями вдоль по потоку; Д — опрокидывание с форми-
формированием и ростом турбулентных пятен; Е — полное развитие турбулент-
турбулентности (по [Young, 1989, Fig. 5.13]; воспроизведено по разрешению Blackwell
Science Ltd.)
этих теоретических моделей для описания аккуратных экспериментов
в низко-турбулентных аэродинамических трубах и водных каналах.
Переход к турбулентности до сих пор не очень хорошо понят. Дву-
Двумерная неустойчивость по линейной теории с последующим примене-
применением преобразования Сквайра контрастирует с наблюдаемой трехмер-
трехмерностью турбулентности, а также с локальной природой турбулентных
пятен. Имеется фактически два класса теорий для объяснения тур-
турбулентных пятен. В теориях первого класса слабонелинейные волны
Толлмина-Шлихтинга дают развития вторичным неустойчивостям,
которые уже трехмерны. Происходит короткая последовательность
бифуркаций с последовательностью режимов течения вниз по пото-
потоку, которая быстро ведет к трехмерности, хаосу и турбулентности.
В теориях второго класса имеет место некий "побочный" механизм,
посредством которого докритическое возмущение конечной амплиту-
амплитуды вызывает турбулентность непосредственно.
Слабонелинейные теории волн Толлмина-Шлихтинга могут быть
далее разделены на два класса, в первом из них рассматривают-
рассматриваются развитие и неустойчивость единственной волны, а во втором —
взаимодействие двух или более волн. Следуя пионерским работам

Экспериментальные результаты
197
Рис. 8.12. Фотографии развития неустойчивости пограничного слоя на
пластине при нулевом угле набегания слабо-турбулентного потока: течение
происходит слева направо. На верхней фотографии представлено ламинар-
ламинарное течение при низких числах Рейнольдса; волны Толлмина-Шлихтинга
[на нижней фотографиии) появляются при в пять раз больших значениях
числа Рейнольдса (по [Van Dyke, 1982, Fig. 104]; воспроизведено по разре-
разрешению ONERA)
[Heisenberg, 1924], [Landau, 1944] и [Meksyn & Stuart, 1951], Стюарт
[Stuart, 1960] и Ватсон [Watson, 1960 b] поставили слабонелинейную
теорию на количественную основу, когда они показали, как найти
уравнение Ландау, описывающее эволюцию слабо-неустойчивого воз-
возмущения параллельного течения для малых положительных значе-
значений R — Дс. Постоянная Ландау в общем случае является комплекс-
комплексным числом, так что параллельные течения подвергаются бифурка-
бифуркации Хопфа. Течения в каналах в общем случае подвержены докри-
тлческой неустойчивости, а струи и неограниченные сдвиговые слои
— надкритической неустойчивости. Было установлено, однако, что
вещественная часть постоянной Ландау для многих течений меняет
знак на маргинальной кривой в линейной теории. Это обстоятельство
было подтверждено аккуратными экспериментами Нишиока с соавто-
соавторами [Nishioka et al., 1975] с плоским течением Пуазейля. Вторичная
неустойчивость волн Толлмина-Шлихтинга приводит к трехмернос-
трехмерности в различных слабонелинейных теориях, часто с точками перегиба
в профилях средних скоростей в некоторых точках поперек течения,
так что последующая неустойчивость (при пренебрежимом влиянии
вязкости) развивается очень быстро. Орзаг и Патера [Orzag & Patera,
1983] установили при помощи численных расчетов, что двумерная
волна Толлмина-Шлихтинга, наложенная на пограничный слой Бла-

198
Гл. 8. Устойчивость параллельных течений
I Л ...
Рис, 8.13. Фотография Л-вихрей в неустойчивости в пограничном слое
на пластине при нулевом угле набегания слабо-турбулентного потока:
вид сверху, обтекание происходит слева направо (по Сарику (Saric);
см. [Herbert, 1988, Fig.3])
зиуса на пластине, сама неустойчива. Эта вторичная неустойчивость
трехмерна с областями, занятыми вращающимися течениями, имею-
имеющими форму, похожую на эллипс. Считается [Bayly et aZ., 1988], что
эта эллиптическая неустойчивость является важным механизмом пе-
перехода к турбулентности для многих течений.
Рац [Raetz, 1959] рассмотрел резонансное взаимодействие трех ней-
нейтрально устойчивых двумерных волновых возмущений погранично-
пограничного слоя. Келли [Kelly, 1967] изучал субгармоническую параметричес-
параметрическую неустойчивость сдвигового слоя. Крейк [Craik, 1971] рассмотрел
общий случай слабонелинейного резонансного взаимодействия трех-
волновых возмущений, двух- или трехмерных, параллельного основ-
основного течения. Он показал, как эти возмущения могут привести к
субгармонической неустойчивости пограничных слоев. Его теория не

$jge Экспериментальные результаты	199
описывала экспериментальных результатов Клебанова с соавторами
KlebanofF et а/., 1962], которые возбуждали сильные возмущения вы-
выбранной частоты. Сарик и Томас [Saric & Thomas, 1984], а также Ка-
чанов и Левченко с сотрудниками (см. [Kachanov, 1994]) обнаружили
предсказанный субгармонический резонанс, возбуждая очень малень-
маленькие возмущения в пограничном слое.
С 1980 г. существенно возросло количество прямых численных рас-
расчетов нелинейной эволюции неустойчивостей параллельных течений.
Некоторая часть этой работы и ее достижения описаны Дразином и
Ридом [Drazin & Reid, 1981], гораздо в большей степени — Шмидом и
Хенингсоном [Schmid & Hennigson, 2001].
Обзор взаимоотношения современных экспериментальных резуль-
результатов и слабонелинейной теории дан Качановым [Kachanov, 1994];
можно сказать, что имеется хорошее согласие теории с аккуратно
произведенными экспериментами при низком уровне турбулентности
вверх по потоку, но природа перехода на практике ясна меньше.
Решающим фактором является то, что на практике переход в па-
параллельном или почти параллельном течении происходит в резуль-
результате значительных возмущений вверх по потоку и нерегулярностей
поверхности канала и т.д., а не в результате аккуратно контроли-
контролируемых вынужденных синусоидальных возмущений течения с очень
низким уровнем турбулентности. Одной из попыток осознать это яв-
явление явилось недавнее предложение Батлером и Фареллом [Butler
febFarrell, 1992] и Редди и Хенингсоном [Reddy & Henningson, 1993]
побочного механизма сильного мгновенного роста (возможно, в 105
раз или более при больших числах Рейнольдса) слабо неустойчивого
или даже устойчивого возмущения по причине несамосопряженнос-
несамосопряженности задачи Орра-Зоммерфельда в соответствии с линейной теорией.
Упражнение 8.44 дает намек на этот механизм при помощи некоторой
аналогии, однако чтобы правильно его понять, необходимо обратить-
обратиться к цитированной литературе. Этому механизму внутренне присущ
учет трехмерных эффектов, а также возможность возникновения не-
нелинейности после периода сильного роста в соответствии с линейной
теорией.
Многие инженеры, работающие в области аэродинамики, остав-
оставляют в стороне эти сложные вопросы нелинейной неустойчивости,
предпочитая eN -метод, предложенный независимо ван Ингеном (Van
Ingen) и Смитом и Гамберони (Smith & Gamberoni) в 1956 г. Этот эм-
эмпирический метод состоит в предсказании возникновения турбулент-
турбулентности в пограничном слое там, где возмущение, распростаняющееся
вниз по потоку, выросло по линейной теории в eN раз, где N = 9 или
около того. Ясно, что этот метод имеет концептуальный изъян, так
как величина возмущения в данном месте пропорциональна, по край-
крайней мере по линейной теории, начальной величине этого возмущения
и, следовательно, величина N должна зависеть от уровня турбулент-

200	Гл. 8. Устойчивость параллельных течении
ности далеко вверх по потоку в атмосфере или в аэродинамической
трубе. Также не учитывается и нелинейное взаимодействие и резонан-
сы. Тем не менее, в качестве подходящего правила этот метод широко
и успешно используется.
Данное обсуждение касалось неустойчивости и перехода к турбу-
турбулентности в пограничном слое на плоской пластине при нулевом угле
набегания однородного потока. Однако эти явления для других парал-
параллельных и почти параллельных течений без точки перегиба, напри-
например, течений в каналах и пограничном слое на поверхности, располо-
расположенной под углом к однородному потоку, качественно одинаковы.
Течения, подобные течению Куэтта, которое устойчиво по отно-
отношению ко всем инфинитезимальным возмущениям при всех значениях
числа Рейнольдса, радикальным образом отличаются от рассмотрен-
рассмотренных. Однако и для них переход к турбулентности под действием ма-
малых, хотя и конечноамплитудных возмущений, в чем-то похож на это
явление в пограничном слое Блазиуса, по-крайней мере в некотором
конкретном смысле, который еще до конца не осознан.
Течения с точкой перегиба или скорее течения, которые неустойчи-
неустойчивы при всех больших значениях числа Рейнольдса, например, погра-
пограничный слой с обратным течением, струи, спутные следы и свободные
сдвиговые слои, также радикально отличаются от рассмотренных в
данном параграфе. Механизмом их неустойчивости является не меха-
механизм Толлмина-Шлихтинга, а невязкий механизм Релея при больших
значениях чисел Рейнольдса и иногда вязкий механизм при меньших
значениях, соответствующих возникновению неустойчивости.
Шмид и Хеннигсон [Schmid & Henningson, 2001] подробно описа-
описали множество тонкостей перехода к турбулентности в параллельных
течениях и процитировали большое количество современной литера-
литературы.
8.10. Устойчивость осесимметричных параллель-
параллельных течений
В настоящем параграфе будет сделан краткий обзор устойчивости
осесимметричных параллельных течений, в значительной мере это
касается течения Пуазейля в трубе и неограниченных струй как для
идеальной, так и для вязкой жидкостей. Как будет видно, теория и
результаты являются до некоторой степени похожими на теорию и
результаты для плоско-параллельных течений.
*Будет уместно заметить вначале, что задача Орра-Зоммерфель-
да имеет очень специальный вид, потому что основное течение явля-
является не только стационарным и инвариантным по отношению к про-
продольным сдвигам, но также и двумерным. Инвариантность парал-
параллельного течения по отношению к продольному сдвигу приводит как

Устойчивость осесимметричных течений	201
к отделению продольной переменнной х в задаче об устойчивости, так
и к независимости основного течения от числа Рейнольдса. Тем не ме-
менее, задача линейной устойчивости данного основного стационарного
течения в однородной вязкой жидкости в общем случае представляет
собой систему уравнений в частных производных, в которой перемен-
переменные не разделяются, а если и разделяются — то систему обыкновен-
обыкновенных дифференциальных уравнений, которая обычно имеет шестой по-
порядок (в специальном случае плоско-параллельного течения система
уравнений шестого порядка распадается на две независимых системы
— задачу Орра-Зоммерфельда четвертого порядка и задачу Сквайра
второго порядка — см. упражнение 8.43). Эти идеи иллюстрируются
ниже на примере задачи для осесимметричного параллельного тече-
течения.
Предположим, что имеется стационарное основное течение вида
XJ(x) = U(r)i, P{x)=po-Gx, для гг<г<г2, (8.59)
между твердыми цилиндрами при г = гх,гг в цилиндрических ко-
координатах (ж, г, 0), где G — градиент давления вдоль оси. Цилинд-
Цилиндры могут находиться в состоянии покоя или равномерного движения
с осью симметрии, и при ri = 0 внутренний цилиндр отсутствует,
а при Г2 = оо имеем неограничные течения такие, как струи. Можно
проверить, что это решение удовлетворяет уравнениям Навье-Стокса,
только если
Gr2
U{r) = A + B\nr-^j,	(8.60)
где постоянные А и В определяются из условий непроскальзывания
на обоих цилиндрах. Можно, однако, использовать другие функции
U для приближения характеристик устойчивости почти параллель-
параллельных течений вязкой жидкости и любые функции U для того, чтобы
получить точное решения уравнений Эйлера идеальной жидкости.
Сформулируем далее задачу об устойчивости в соответствии
с [Sexl, 1927 a,b] и [Batchelor & Gill, 1962]. Рассмотрим возмущения
основного течения:
u = U + u', p = P + p',	(8.61)
и линеаризуем уравнения Навье-Стокса. Переменные разделяются, ес-
если взять нормальные моды в виде
u'(x, t)=(us(r), 8, (г), ue(r)h4a*+ne-act), p'(*, i)=p(r)eM
(8.62)
с постоянными вещественным аксиальным волновым числом а и це-
целым азимутальным волновым числом п. Зметим, что характеристики

202	Гл. 8. Устойчивость параллельных течений
устойчивости остаются теми же, если поменять знак п на противопо-
противоположный, так как задача обладает осевой симметрией, поэтому можно
рассматривать случай п > 0 без ограничения общности. Определяя
безразмерные переменные обычным образом, получим
Й? + iff, - К + а2 + iaR{U - сЛ % - RU'ur - iaRp= 0, (8.63)
^- + ее2 + 1аД(С/ - сЛ ur - ^щ - Rjf = 0, (8.64)
"«% - Г^т^ + «2 + ЬЛ(^ - сI % + ^Ч - — р = 0, (8.65)
% + -ur + i (aux + -цд) = 0,	(8.66)
r	\	г /
где R = VL/i/ — число Рейнольдса и штрих обозначает дифференци-
дифференцирование по г. Граничные условия непроникновения и непроскальзы-
непроскальзывания для возмущений на поверхности цилиндров дают
ux(r) = ur(r) = йя(г) = 0 при г = 7-1, г2	(8.67)
если ri^O; если же г± = 0, то условие при г = ri заменяется усло-
условиями
2, (г) = ur(r) = ti^(r) = p(r) = 0 при г = 0 для n ^ 1, (8.68)
ux(r) = p(r) = 0, 2r(r) + i2fl(r) = 0 при г = 0 для п = 1. (8.69)
Определяя пременные
fc2 = a2 + n2/r2, ф = -irur, П = (аг2в - nux)/k2r2 (8.70)
и линейные операторы
исключив ux,UrtUe,p, получим
SJ2 + Ban/fc4r2) T<^ = iaR [(U - c)U - (nU'/ak2r3) ф], (8.72)
Т2ф - 2апТП = ia [(U - с)Тф - k2r (U'/k2r)' ф] , (8.73)

8.10. Устойчивость осесимметричвых течений	203
где
ф(г) = ф'(г) = Щг) = 0 при г = п, г2,	(8.74)
или, если гг = 0 и п ф 0,
<?(г) = г2-п^'(г) = П(г) = 0 при г = 0.	(8.75)
Легко видеть, что если п = 0, то уравнения (8.72), (8.73) распада-
распадаются на систему второго порядка для п и систему четвертого порядка
для ф, но если п ф 0, то они представляют согласованную систему
шестого порядка. Для невязкой жидкости аналогично находим
(U - с)Тф - fc2r (U'/k2r)' ф = 0,	(8.76)
или, если п = 0,
{U - сI^ - г{и'/г)'ф = 0,	(8.77)
где L = d2/dr2 — r^d/dr — а2. Граничные условия в этом случае
принимают вид
ф(г) = 0 при г = п, г2.	(8.78)
Теория в этом случае вполне аналогична теории для задач Релея и
Орра-Зоммерфельда для случае плоско-параллельных течений; нача-
начало этих теорий для идеальной жидкости восходит, вне всяких сомне-
сомнений, к работе Релея [Rayleigh, 1880]. Среди осесимметричных течений
основной физический интерес представляют течение Пуазейля в трубе
и неограниченная струя.
Результаты численных расчетов [Salwen et a/, 1980] указывают на
то обстоятельство, что течение Пуазейля в трубе с U(г) = 1 — г2
при 0 < г < 1 является устойчивым по отношению ко всем инфини-
тезимальным возмущениям при всех числах Рейнольдса. Спектр осе-
осесимметричных мод в некоторой степени аналогичен спектру плоского
течения Пуазейля (см. рис. 8.9), хотя и нет ни одной неустойчивой мо-
Ды. Не осесимметричные моды отличаются в большей степени (см.
рис. 8.14 и 8.15). Фактически, переход к турбулентности эксперимен-
экспериментально наблюдается при значениях числа Рейнольдса порядка 2000
пРи уменьшении амлитуды возмущений на входе трубы [Reynolds,
1883].
Автомодельное решение Ландау-Сквайра уравнений Навье-
Стокса для круглой струи локально имеет вид U(r) = 1/A + г2J при
0 < г (см. например [Batchelor, 1967, р. 206]). Рассматривая струю
как неограниченное параллельное течение, Барридж [Burridge, 1970]
нашел численно, что оно неустойчиво для мод при п = 1 и R > Rc,

204
Гл. 8. Устойчивость параллельных течений
Рис. 8.14. Центральная мода (наимение устойчивая мода) течения Пуа-
зейля при R = 3000, n = I, fc = 1. (а) Сечения функции тока при постоян-
постоянном z. (б) Векторное поле возмущений скорости (по [Meseguer & Trefefchen,
2000, Fig. 4])
где Rc « 37,5 иас« 0,43. Этот и другие расчеты указывают на то,
что моды с п = 1 обычно являются наиболее неустойчивыми возму-
возмущениями осесимметричных параллельных течений.
Имеется множество расчетов характеристик неустойчивости осе-
осесимметричных течений идеальной жидкости, от [Rayleigh, 1880] до
[Batchelor & Gill, 1962] и настоящего времени. В частности, удобно
использовать разрывные профили скорости с условиями на "скачке"
в местах разрывов, аналогичные таким профилям для случая плоско-
плоскопараллельных течений.
Упражнения
8.1. Вывод уравнения устойчивости Релея. Пусть скорость основно-
основного течения несжимаемой идеальной жидкости имеет вид U{z) =
= U(z)\. Используя безразмерные переменные, линеаризуйте
уравнение завихренности двумерного течения
где т) = du/dz — dw/dx. Покажите, что
дт,' ft/ d2U<W__
~dt+dx ~ d*2 дх ~и>
где г]' — Аф'. Полагг1Я i>'(x, z, t) = <j>(z)eia(x~ci\ выведите урав-
уравнение устойчивости Релея.

Упражнения
205
Рис. 8.15. Пристеночная мода течения Пуазейля при R = 3000, п = 1,
к = 1. (а) Сечения функции тока при постоянном z. (б) Векторное поле
возмущений скорости (по [Meseguer & Trefethen, 2000, Fig. 8])
8.2. Возвышение материальной поверхности. Покажите, что если
? — возвышение жидкой частицы над своим основным поло-
положением, скажем, (a3o?2/o?^o) при возмущении основного течения
U(z)i идеальной несжимаемой жидкости, то w = D?/Dt при
х = х0, у = у0 , z = zq + С
Выведите из задачи устойчивости Релея, что моды имеют вид
С(«, г, t) = F(z)eia(*-Ct), где F = -<?/(*/ - с) и
(Е8.1)
8.3. Некоторые свойства собственных решений задачи устойчивос-
устойчивости Релея. Определим скалярное произведение
в пространстве C2[zi,z2], а также линейный оператор
C2[][]
Ъф=(и- с){ф" - а2ф) - и"ф.
Покажите, что уравнение (Е8.1), поделенное на U — с, представ-
представляет собой уравнение, сопряженное уравнению устойчивости Ре-
Релея в форме (8.25), где F также удовлетворяет граничным усло-
условиям (8.26).

206		Гл. 8. Устойчивость параллельных течений
Умножая уравнение (Е8.1) на F*, комплексно сопряженное к F,
интегрируя от z\ до 22 и используя граничные условия, покажи-
покажите, что
Г\и - сJ (|*"|2 + a2\F\2) dz = 0.
Jzi
Беря мнимую часть последнего уравнения, покажите, что ес-
если течение неустойчиво по отношению к моде сг, то сг лежит
внутри области значений U (т.е. Um < сг < Um, где Um =
= max2l<2<22 U(z), a.Um= minZl<2<22 U(z)) [Rayleigh, 1880].
8.4. Скачок сдвигового напряжения на критическом слое идеальной
жидкости. Покажите, что
если U(zc) = cr, U'c ф 0, [f"//|^|2]jr=z ф 0. Правдоподобно пока-
покажите, что
Выведите отсюда, что уравнение (8.35) следует из (8.34).
8.5. "Подъемный" механизм Орра. Рассмотрите плоское течение Ку-
этта с основной скоростью U = z\. Покажите, что линеаризован-
линеаризованное уравнение завихренности для двумерных возмущений имеет
вид
т + дх
в обычных обозначениях, где т/ = Аф'. Покажите, что
Аф' = F{x - zt, z)
для произвольной дифференцируемой функции F.
Обсудите отношение задачи устойчивости Релея для плоского
течений Куэтта к вышеприведенному подходу к решению задачи
с начальными значениями.
Обсудите вышеприведенное представление переноса завихрен-
завихренности возмущения основным течением, которая иногда назы-
называется подъемным механизмом, а иногда механизмом жалюзи
[Огг, 1907 а, Art. 13].

Упражнения-	207
8*Q* Устойчивость или неустойчивость плоского течения Куэтта.
Рассмотрите упражнение 8.5 как задачу с начальными значе-
значениями для определения rf в полосе
V = {(ж, z) : -оо < х < оо, -1 < z < 1}
плоскости (ж, z) следующим образом (считайте, что F и dF/dz
ограничены и непрерывны в V).
(i) Определив норму \\rj\\ = supxGy \т)(х, я)|, покажите, что нуле-
нулевое решение rf = 0 устойчиво.
(ii) Покажите, однако, что нулевое решение rf = 0 неустойчиво
по норме \\г)\\ = snpxei/{(df)(x,z)/dzJ + [ф,z)]2}1'2 [Yudovich,
1989, р.101].
8.7. * Задача на собственные значения для двумерных возмущений
плоского течения Куэтта идеальной жидкости. Рассмотрим
основное течение идеальной несжимаемой жидкости со скорос-
скоростью U = z\ между твердыми плоскостями, при z ± 1 движущи-
движущимися с вместе течением. Проверьте, что точное решение, нели-
нелинейных уравнений Эйлера дается следующим выражением для
возмущения функции тока:
odz)
при —оо <ж<оо, —1<z<1th всех вещественных а, а, 7-
Покажите, что плотность кинетической энергии на единицу мас-
массы и длины волны имеет вид
Покажите, что если волновые фронты в начальный момент были
наклонены так же, как и профиль скорости (т. е. 7 имеет тот же
знак, что и а), то К монотонно убывает до нуля при возраста-
возрастании t. Покажите, что в противном случае G имеет противопо-
противоположный знак) К возрастает до момента t = 7/&, а затем убывает
до нуля; покажите, что ее максимум велик для короткой волны,
распространяющейся в направлении основного течения.
Покажите далее, что если
'{х, z, 0) = bsin \^nn{z + 1I

208	Гл. 8. Устойчивость параллельных течений
где п — положительное целое, то линеаризованная задача имеет
решение вида
Tf>'(x,z,t) = - |ib (a2 + IiAr2) eiQ* x
e-in7r(z+l)/2-icr*z
! a2 + (A/2)птг - atJ ~~ a2 + (A/2)птг + atJ
kchaz
cha	sha J
где А, В могут выбраны так, что тр' удовлетворяет граничным
и начальным условиям. Покажите, что
1) __ chaz
[	а2+п2тг2 ~ cha
и, следовательно,
/J,	1 \1
\a2 а2 + п2тг2Я
ф'{х, г, птг/2а) - -^in2w2W(ex+flir/2) (l - z2) при а -^ оо
при фиксированных z, n. Покажите далее, что в рамках линейной
теории для идеальной жидкости начальное возмущение может
стать произвольно большим по прошествии большого времени,
хотя и в конечном итоге убывает как t~2 при t —у оо. Устойчиво
ли течение в смысле Ляпунова? Как вы думаете, что произойдет
при учете нелинейности? [Kelvin, 1887, параграфы 32-34; Огг,
1907 а; Craik & Criminale, 1986, p. 18].
8.8. Алгебраическая неустойчивость плоско-параллельного течения
Куэтта идеальной жидкости относительно двумерных воз-
мущений. Покажите, что двумерные возмущения основного те-
течения несжимаемой идеальной жидкости, имеющего скорость
U = U(z)i, удовлетворяют линеаризованным уравнениям
+0	+ 0	°
где предполагается, что и;, р1 не зависят от ж, а ?' =
= dwf/dy - dv'/dz. Покажите, что v!{y,z,t) = u'(y,z,0) -
-tU'(z)w'(y,z,0), v'{y,z,t) = v1 (у,z,0), ™'(y,z,t)	'{0)
[Ellingsen & Palm, 1975], (см. упражнение 8.25).

Упражнения
209
S.9. Неустойчивость параллельных течений идеальной жидкости.
Проверьте, что
u = U{y)i + W{x - Я7(у))к, р = const,
удовлетворяет уравнениям Эйлера движения и уравнению не-
неразрывности несжимаемой идеальной жидкости. Покажите, что
вектор вихря имеет вид
w = Vxu= -tU'{y)W'{x - tU{y))i - W'{x - tU{y))j - U'{y)k.
Рассмотрите устойчивость основного течения U = U(y)i при
—oo < у < oo по отношению к возмущениям с периодом 2тг по х
и z. Определяя норму возмущения и;, р1 с периодом 2тг по х и z
как
/»27Г	V^
dx
покажите, что существуют начально малые возмущения основ-
основного решения такие, что ||u'|| ~ const х t при t —} oo при условии,
что С/7 квадратично интегрируема и J7 не равна постоянной. Та-
Таким образом, основное течение неустойчиво вне зависимости от
того, имеет ли оно точку перегиба или нет.
Что это говорит о нашем выборе определения устойчивости, о не-
нелинейных возмущениях и течении? [Yudovich, 1989, р. 101].
8.10. Неустойчивость ломаной плоской струи невязкой жидкости.
Рассмотрим ломаную струю из несжимаемой идеальной жидкос-
жидкости в неограниченном параллельном течении с профилем скорос-
скорости
{0, если	z > 1,
1, если - 1< z < 1,
0, если	z < —1.
(Иногда это течение называют струей "цилиндр" (шляпа) по
форме графика U). Покажите, что волновой моде отвечает сле-
следующее соотношение на собственные величины:
(c+lJth|a| + c2 = 0.
Докажите, что струя неустойчива по отношению к волнам всех
длин.
Найдите соотношение на собственные числа для варикозных мод
[Rayleigh, 1894, р. 380-381].

210	Гл. 8. Устойчивость параллельных течений
8.11. Неустойчивости плоского течения Куэтта между двух сво-
свободных поверхностей. Рассмотрим основное течение несжимае-
несжимаемой идеальной жидкости со скоростью U(z) = z при — 1 < z < 1,
где поверхности с основными положениями при z = ±1 являются
свободными.
Покажите, что ф удовлетворяет уравнению устойчивости Релея
при — 1 < z < 1 и (U — с)ф' — и'ф = 0 при z = ±1. Докажите, что
2_ (atha-l)(a-tha)
С	^^
откуда следует, что течение неустойчиво при а < ас, где
ас « 1,2 определяется как положительный корень уравнения
atha = 1.
8.12 Неустойчивость свободного сдвигового слоя. Покажите, что
если U(z) = thz при —оо < z < оо, то U9 — 0. Проверьте,
что соответствующее маргинально устойчивое решение задачи
устойчивости Релея имеет вид
с = 0, a = 1, ф — sech z.
Покажите, что
|"dc j	_ _2i
Выведите, что нормальная мода неустойчива, когда 0 < a < 1.
8.13. Симметрия: синусоидальная .« варикозная моды. Пусть
S : С2[—?, L] —> С[—L, L] таким образом, что S/e — четная функ-
функция для всех четных fe G C2[—L, L], а S/o — нечетная для всех
нечетных функций fo G С2[—X, L]. Покажите, что если
(S/)(*) = 0 Vze[-L,L] и f(±L) = 0,
ТО
= 0 Vz €[-?,?],
() = 0 V* €[-?,?],
где
(Заметим, что fe или /о могут быть тождественными нулями).

Упражнения	2U
Покажите, что если действие оператора Т определено как Т/ =
= d2f/dz2+\f для всех / € С2[—тг, тг], то Т сохраняет указанные
выше свойства симметрии. Покажите далее, что задача
-0 = А*, ф{±к) = О,
имеет собственные решения Л = Ап, ф = фп для п = 0,1,..., где
Лп = -(п+1J, ф2т{г) = cos(m+-)z, ^2m+i(^) = sin(m+l);z.
8.14.	Неустойчивость струи Бикли (Bickley). Покажите, что если
U(z) = sech2z при —оо < z < oo, то U8 = |. Проверьте, что со-
соответствующие маргинально устойчивые решения задачи устой-
устойчивости Релея представляют собой синусоидальные моды
с = -, а = 2, ф = sech2z,
и варикозные моды
2
с = -, а = 1, ф = sechzthz.
о
Выведите, что струя устойчива по отношению ко всем корот-
коротким волнам с a > 2 и неустойчива по отношению к некоторым
длинным волнам с а < 2.
8.15.	Стабилизирующий эффект наличия границ в сдвиговом слое
и струе идеальной жидкости. Рассмотрим имеющее скорость
U(z) основное параллельное течение несжимаемой идеальной
жидкости между твердыми границами z = ±L. Дано, что это те-
течение неустойчиво по отношению к некоторым растущим по вре-
времени инфинитезимальным возмущениям, если L = оо, и устой-
устойчиво в пределе L —у 0. Покажите, что для того чтобы подсчи-
подсчитать значение Lc такое, что течение неустойчиво при L > Lc
и устойчиво при L < ?с, достаточно положить а8 = 0 и решить
следующую задачу с граничными условиями:
фв = 0 при z = ±LC.
Проверьте, что ф8 = U — U8 представляет собой одно из решений
уравнения
уравнения.

212	Гл. 8. Устойчивость параллельных течений
(i) Сначала положите U(z) = thz. В каком диапазоне волновых
чисел неустойчив сдвиговый слой, когда L = оо? Почему тече-
течение устойчиво в пределе L -> 0? (Подсказки: упражнение 8.12,
упражнение 8.37, пример 8.2).
Далее, подсчитайте Lc. (Замечание: Lc — корень простого транс-
трансцендентного уравнения, которое не требуется решать точно,
достаточно построить чертеж, показывающий, что существует
единственный положительный корень, и оценить ?с, ограничи-
ограничиваясь одной значащей цифрой после запятой).
(ii) Подсчитайте соответствующее значение Lc, когда U(z) =
= sech2z при —L < z < L. Укажите, почему при вычислении
можно предположить, что ф8 — четная функция. Покажите, что
симметричная струя с симметричными граничными условиями
остается неустойчивой до тех пор, пока точки перегиба остаются
внутри области течения (Н. Е. Hupert — частное сообщение,
[Howard, 1964]; подсказка: упражнение 8.14).
8,16, Маргинально устойчивые моды неограниченной струи. Числен-
Численно исследуйте задачу устойчивости Релея для струи с U(z) =
= sech z при —оо < z < оо.
(i) Покажите, что
</>(z) ~ const х eaz при z -> —оо.
Правдоподобно покажите, что граничное условие ф(г) -> 0 при
z —> — оо хорошо приближается, если вместо него использовать
условие ф1 — аф = 0 при z •= —L, где L — велико; приближение
будет тем лучше, чем больше L.
(ii) Покажите, что U" = A - 2U2)U, U8 = 2/2 и, отсюда,
ф8{г)-±0 при z -> ±оо.
Покажите, что ^@) = 0 для синусоидальной моды и ф8@) = 0
для варикозной моды.
(iii) Маргинальная синусоидальная мода может быть посчита-
посчитана при помощи метода пристрелки. Ваш расчет, от начала до
конца, займет менее часа, если вы уже знакомы с компьютер-
компьютерной системой, имеющей пакет для интегрирования обыкновен-
обыкновенных дифференциальных уравнений.
Для определения а8 укажите какое-нибудь начальное значение
а5, возьмите систему уравнений

Упражнения	213
с начальными условиями
ф,(-Ь) = e-aL, v(-L) = аф,(-Ь),
и проинтегрируйте ее от z = — L до z = 0 для того, чтобы
оценить ^@). Затем, методом проб и ошибок или коррекцией
(с линейной экстраполяцией, например) повторите процесс до
тех пор, пока будет найдено значение а,, для которого ^@) бу-
будет достаточно малым. Покажите, что а3 = 1,465 при "больших"
значениях L.
(iv) Аналогично покажите, что для варикозной моды а3 = 0,646.
8.17. Нелинейное решение для "кошачьего глаза". Проверьте, что
ф(х, z) = In [(I + А2I/2 ch z + a cos ж]
является решением уравнения Лиувилля
для всех А. Выведите, что это решение описывает функцию тока,
соответствующую точному решению уравнения завихренности
стационарного двумерного течения неограниченной несжимае-
несжимаемой идеальной жидкости.
Изобразите линии тока для "типичного" значения -А, например,
для А = 1. Докажите, что
ф(х, z) = ln(chz) + Asechzcosx + О(А2) при А —у 0.
Соотнесите вышеприведенное решение с нейтральной устойчи-
устойчивостью параллельного течения с U(z) = thz при —оо < z < оо.
Докажите также, что в пределе А —У оо решение представляет
собой течение, генерируемое бесконечным множеством равных
линейных вихрей, имеющих циркуляцию —4тг, расположенных
на расстоянии 2тг от оси х и параллельных оси у [Schmid-Burgk,
1965; Stuart, 1967, параграф 6; Lamb, 1932, p. 224].
8.18. Нелинейные волновые моды для параллельных течений несжи-
несжимаемой идеальной жидкости. Дано уравнение завихренности
для двумерного течения идеальной несжимаемой жидкости:
д(х,у)

214	Гл. 8. Устойчивость параллельных течений
где ф — функция тока, ? = Аф — завихренность и компоненты
скорости есть и = —дф/ду, v = дф/дх.
Показать, что если решение имеет вид
ф{х,у,1) = F{X,y), X = x-ct,
где с — некоторая постоянная, то F удовлетворяет нелинейному
уравнению Пуассона
(E8.3)
Q — некоторая функция интегрирования.
Покажите, что если F = Ф(у) — одно из решений уравнения
()
(Е8.3) и Q дифференцируема, то
Q'{F + cy) = -K,	(E8.4)
где К определяется из равенства К (у) = —Uff(y)/ [U(y) — с].
Покажите далее, что если Q — однозначная функция, то спра-
справедливо одно из следующих свойств.
(a) U постоянна;
(Ъ)и строго монотонна и
с = ?%.),	(Е8.5)
где у8 — единственная точка, такая что U"(y8) = 0 внутри об-
области, занятой течением;
(c)	уравнение (Е8.5) удовлетворяется во всех точках у8, где
U11 [ув) в области течения; или
(d)	с лежит вне области значений U внутри области течения.
Проверьте, что:
(a)	если U(у) = siny при -|тг < у < |тг, то с = 0;
(b)	если U(y) = 1—у2 при — 1 < у < 1, то не существует волновых
решений;
(c)	если U(у) = sech2y при —оо < у < оо, то с = |; и
(d)	если U{у) = th у при —оо < у < оо, то с = 0, если только с
не лежит вне области значений U.
Найдите функцию Q в явном виде в каждом из вышеприведен-
вышеприведенных случаев, для которых существует волновое решение с за-
заданным с.
Рассмотрите далее периодичные по X волновые решения F урав-
уравнения (Е8.3) с функцией Q для данного параллельного течения
U [Barcilon & Drazin, 2001].

Упражнения	215
8.19.	Неустойчивость поперечного течения или неустойчивость
спирального течения. Рассмотрим основное течение несжима-
несжимаемой идеальной жидкости, ограниченное твердыми плоскостями
при z = zi, Z2, имеющее скорость U(z) = U(z)\ + V(z)j, где ?/, V
— заданные функции. Линеаризуя уравнения движения Эйлера
и полагая нормальные моды пропорциональными е1(ах+^~ас*),
покажите, что устойчивость течения определяется из задачи на
собственные значения
(и - с) (D2w - a2w) - U"w = О,
W = О При Z = j&i, 22,
где D = d/dz, U = {aU + CV)/a, с = ac/2, a = (a2 +/32I/2 ф 0.
Докажите, что устойчивость течения определяется бесконечным
числом задач устойчивости Релея для всех вещественных значе-
значений а и /3, так что некоторое трехмерное возмущение может
быть неустойчивым, когда все двумерные возмущения устойчи-
устойчивы (см. [Gregory et a/., 1955]).
8.20.	Неустойчивость Релея-Тейлора стратифицированной жид-
жидкости и внутренние гравитационные волны. Дано, что дви-
движение несжимаемой идеальной жидкости переменной плотности
под действием силы тяжести подчиняется уравнениям Эйлера,
уравнению состояния и уравнению неразрывности, а именно:
(дм	^ \ „
р I — + и • Vu 1 = -Vp - gpk,
^ + u.V/>=0 и V-u =
at
где g — ускорение свободного падения, к — единичный вектор
в вертикальном направлении; диффузией жидкости пренебрега-
ется.
Покажите, что основное состояние покоя, заданное функциями
для р непрерывно дифференцируемой представляет собой реше-
решение уравнений движения, если p(z) = р0 — g Jz p(Q dC, где р0 —
произвольная постоянная.
Полагая и = (и', г/, г//), /> = р + />', р — р + р', линеаризуя урав-
уравнения движения для малых возмущений и выбирая нормальные
моды с w' = w(z)ei(kx+ly~'u;t) и т.д., покажите, что

216	Гл. 8. Устойчивость параллельных течений
D(pDw) - (А:2 + l2)pQ - iS^^l^m = О,	(Б8.6)
где D = d/dz.
Покажите далее, что если течение ограничено твердыми гори-
горизонтальными пластинами при z = z\, #2, то
w(z) — О при z = zi,Z2.	(E8.7)
Осознав, что (Е8.6), (Е8.7) представляют собой регулярную за-
задачу Штурма-Лиувилля, покажите, что имеет место неустойчи-
неустойчивость тогда и только тогда, когда dp/dz > 0 где-либо в облас-
области, занятой течением. (Релей [Rayleigh, 1883] открыл результа-
результаты этого упражнения, вследствие чего его имя было присвоено
неустойчивости Релея-Тейлора после появления работы [Taylor,
1950], описанной в параграфе 3.7).
Покажите, что если плотность приближается постоянной, кроме
члена, описывающего пловучесть, в соответствии с аппроксима-
аппроксимацией Буссинеска, то
Dw-(k2+ I2)w-av ' '210 = 0.	(Б8.8)
U) О	(JLZ
Покажите, что если p = poe~&z при />o,/3 > 0 и z\ = —оо, ^2 = оо,
то собственные решения имеют вид
w(z) = const х е0*/2+1т*^ w2 = _.
для всех вещественных к, I, т, представляющих собой спектр
внутренних гравитационных волн. Получите, что в аппрокси-
аппроксимации Буссинеска
w = const х eimz, и = ±[дC(к2 + /2)/(&2 + I2 + m2)]1/2.
(Релей [Rayleigh, 1883, р. 174] заметил, что "в противополож-
противоположность тому, что мы встречаем в большинстве колебательных
систем, имеет место предел (в случае устойчивости) со стороны
быстроты колебаний и нет его со стороны медленности").
8.21. Неустойчивость параллельного течения стратифицированной
жидкости. Покажите, что основное течение
и(ж, t) = U(z), />(x, t) = p(z), p(x, t) = p{z)

Упражнения	217
является решением уравнений движения несжимаемой идеаль-
идеальной жидкости переменной недиффузионной плотности при нали-
наличии гравитации, если
при произвольных постоянной ро и гладких функциях 17, р.
Рассматривая только двумерное движение, заданное функциями
u(x, t) = U(z)i + и'(ж, z,t), u = v!\ + гу'к,
p(x, t) = p{z) + //(*, z, *), p(x, t) = p(z) + p'{x, z, t),
линеаризуя уравнения движения для малых возмущений и вы-
выбирая нормальные моды в виде
w'{x,z,t) = w(z)eikl*-et\
покажите, что
{U-cJ[D{pDw)-k2pw]-{U-c)[D{pDU)]w-^pN2w = О, (Е8.9)
где D = d/cb, а частота пловучести N (иногда называе-
называемая частотой Брянта-Вяйсяля) основного течения определя-
определяется равенством N2{z) = —gp'(z)/p(z).
Покажите далее, что если течение ограничено жесткими гори-
горизонтальными пластинами при z = z\, 22, то
w = 0 при z = zu z2.	(E8.10)
Докажите, что если плотность приближается постоянной за ис-
исключением члена, описывающего пловучесть в соответствии
с аппроксимацией Буссинеска, то
{U - с) (w" - k2w) - U"w + r^—w = 0.	(E8.ll)
Это уравнение называется уравнением Тейлора-Голдстейна.
(Название уравнения (E8.ll) не учитывает того обстоятельства,
что оно было получено независимо от Тейлора [Taylor, 1931] и
Голдстейна [Goldstein, 1931] также и Гурвицем [Haurwitz, 1931]).
8.22. Достаточные условия устойчивости Майлса-Ховарда. Пола-
Полагая, что имеется задача Тейлора-Голдстейна (E8.ll), (Е8.10),
определите
Н = w/(U- сI/2

218	Гл. 8. Устойчивость параллельных течений
и покажите, что
?
Беря мнимую часть этого уравнения, получите, что если сг ф О,
то
iI ~c|2dz=о>
и что условие
N2(z) > hi'2[г) при zi < z < z2
является достаточным для устойчивости основного течения
[Miles, 1961; Howard, 1961; Drazin & Reid, 1981, параграф 44.3].
8.23. Уравнение Тейлора-Голдсшейна для трехмерного основного
течения. Покажите, что если основное течение стратифици-
стратифицированной идеальной несжимаемой жидкости имеет скорость
U(z) = U(z)i + V(z)j и плотность />(z), то нормальные моды,
пропорциональные e*(b*+iy-kct)^ B приближении Буссинеска под-
подчиняются уравнению
(k+l) N2
(Ш+lV-kc) [D2w-(k2+l2)w] - (kU"+lV")ffi^
(E8.12)
где используется обычное обозначение D = d/dz.
Покажите, что обобщением достаточного условия Майлса-
Ховарда является следующее: если
(k2 +l2) N2 > hkU' + IV'J
при z\ < z < Z2, то течение устойчиво по отношению к данной
моде.
8.24. Неустойчивость вращающихся и стратифицированных сдвиго-
сдвиговых течений. Рассмотрим устойчивость осесимметричной вра-
вращающейся струи идеальной несжимаемой жидкости с компонен-
компонентами скорости основного течения

Упражнения	219
в цилиндрических координатах (г, 0, z) и давлением и плотнос-
плотностью Р(г) и р(г). Течение ограничено твердыми цилиндрами при
г = ri, гг. Линеаризуйте уравнения движения для осесимметрич-
ных возмущений, выберите нормальные моды пропорциональ-
пропорциональными произведению elklz-ct) и векторной функции от г и пока-
покажите, что
D [p(W - cJD*F] - pk2{W - cJF + $F = О,	(Е8.13)
где D=d/dr, D^r-^Dr, $=r-3D(pr2V2), F = u/ik{W-c)
и u'r = u(r)elk(z~ct) — возмущение радиальной компоненты ско-
скорости.
* Прокомментируйте аналогию между уравнением (Е8.13)
и уравнением Тейлора-Голдстейна (Е8.9). Докажите, что вра-
вращающееся течение устойчиво, если
везде в области занятой течением [Leibovich, 1969; 1979].
8.25. Трехмерная устойчивость неограниченного течения Куэт-
та вязкой жидкости. Предположим, что u(x,t) = rj(t)z —
—CWSA и(х,?) = ~|?WZ» wfat) = ^(t)y для некоторых функ-
функций ?, т/, ?. Покажите, что V • и = 0 и вектор вихря & = (?, т/, ?).
Докажите, что вихревое поле является точным решением урав-
уравнения завихренности для вязкой несжимаемой жидкости при
условии, что
Почему вязкость не влияет на динамику?
Определяя возмущения ?' = ?, rjf = tj — сг, С = С Для некоторого
постоянного сдвига а основного течения и линеаризуя, покажи-
покажите, что
d*'_0 V_o dC l ,
Докажите, что?'(<) = ('@), tf(t) = i/@), C'(*) = C@) + |^'@)<,
так что возмущения растут линейно not и основное течение
U = crzi оказывается неустойчивым (хотя начальные возмуще-
возмущения скорости не ограничены по пространству).

220
Гл. 8. Устойчивость параллельных течений
Покажите далее без линеаризации, что
т=т,
T)(t) = 77@) COS
C(*)=C@)cos
+ C@) sin
—17@) sin
и, следовательно, основное состояние ? = 0, tj = a, C = 0 не-
несомненно неустойчиво, хотя возмущение и ограничено для всех
времен [Waleffe, 1995]. (См. упражнение 8.8).
8.26. Уравнение энергии. Покажите, что если U = U(z)i при z\ < z <
< 2:2, то уравнение Рейнольдса-Орра E.28) для двумерного воз-
возмущения, имеющего период 2тг/а по ж, в безразмерных перемен-
переменных принимает вид
где
Г2к/а
rz2 Г2к/а 1
К=	^ {и12 + W12) dx dz,
Jzx Jo 2
Л) ^
Отсюда выведите уравнение (8.54). Интерпретируйте физичес-
физический смысл К, М и N.
8.27. Задача устойчивости для асимптотически подсасываемого
пограничного слоя. Проверьте, что уравнение завихренности для
двумерного течения несжимаемой вязкой жидкости
at	o(x,z)
удовлетворяется функцией ф = Ф при z > 0, где
*(s, z) = Wo»
для произвольных Uo,Wo,i/. Покажите, что соответствующая
скорость основного течения имеет вид U = (Е/, V, W), где
Щг) = 17о[1 -
= 0,
= -Wo.

Упражнения
221
Полагая ip = Ф + -0', линеаризуя и выбирая нормальную моду
в виде il>'(x, z,t) = </>(z) exp[ia(x — ct)}, покажите, что
v (^iv-2aV+aV) =ia [(U-c) {ф"-а2ф) -и"ф] -Wo {фт-а2ф')
где
ф(г) = ф'(г) = 0 при z = О, ф(г), ф\г) -* 0 при z -> оо
[Hughes & Reid, 1965] (фактически, с = 0,150 при Лс = 54 370,
ас = 0,1555, если выбрать масштаб длины L = vjW§, так что
число Рейнольдса определяется как R = Uq/Wq [Hocking, 1975]).
8.28. Преобразование Сквайра. Обратите внимание, что для данного
неустойчивосго параллельного течения преобразование Сквай-
Сквайра показывает, что относительная скорость роста моды с вол-
волновыми числами (а,/?) есть сг(а,Р,R) = aci(a,aR/a), где а =
= (а2+/32I/2.
Определяя
<г2(Д) = тах<г(а, 0, Л), cr3(R) = max cr(a,C, R)
а>0	а/3>0
сгм = max а-(а,/3,Д)
арл>0
и полагая, что
покажите, что сгм — 0*2 (Дм") и максимум достигается для неко-
некоторой двумерной моды с волновым числом ам при числе Рей-
Рейнольдса Rm > Re- Предполагая, что сг2(Л) возрастает монотонно
от нуля до сгм > когда R возрастает от Rc до Rm , покажите, что
если Rc < R < Rm, to a2(R) > o-z(R), т.е. наиболее быстро
растущая мода является двумерной, но если R > Rm , то наибо-
наиболее быстро растущая мода могла бы быть трехмерной [Watson,
1960 а]. (Все проведенные расчеты не указывают на то, что име-
имеется значение R и основное течение, для которых наиболее быст-
быстро растущая мода является трехмерной. В любом случае значе-
значение RM является настолько большим, что течение уже является
турбулентным и теоретическая возможность того, что наиболее
быстро растущая мода может оказаться трехмерной, не имеет
никакого практического значения. Фактически, для плоского те-
течения Пуазейля ам « 0, б при ам » 0,8, Rm fc* 50 000).

222	Гл. 8. Устойчивость параллельных течений
8.29. Простое точное решение уравнения Орра-Зоммерфелъда. По-
Покажите, что уравнения Навье-Стокса инвариантны относитель-
относительно непрерывной группы сдвигов z н* z + S для всех веществен-
вещественных S. Покажите, что непрерывно дифференцируемая скорость
основного течения U(z)i t-» U{z + S)i = U(z)i + 6U'(z)i + O(S2)
при S —у 0. Отсюда выведите, что решение уравнения Орра-
Зоммерфельда дается значениями а = /? = 0, ф = U при всех с,
R при условии, что основное течение описывается точным реше-
решением уравнений Навье-Стокса. Дает ли это собственное реше-
решение?
8.30. Другое простое решение уравнений Орра-Зоммерфелъда для од-
однородного течения. Покажите, что если U = const, то общим
решением уравнения Орра-Зоммерфельда является
ф{х) = Агеа* + A2e-
где Ах, Аг, Аз,.А4 — произвольные постоянные и 72 = а2 +
+iaR(U — с). (Фактически, решение *ф' = е±72ас*, когда а = О,
ас ф 0, отвечает волнам Стокса, генерируемым колеблющейся
плоской стенкой (см., например, [Batchelor, 1967, параграф 4.3]).
8.31. Устойчивость однородного течения несжимаемой вязкой
жидкости. Предположим, что несжимаемая жидкость с кине-
кинематической вязкостью v имеет скорость U* = Vi и ограничена
твердыми стенками (двигающимися со скоростью основного те-
течения Vi при z* = ±L. Покажите, что двумерные нормальные
моды, пропорциональные eia(*"c*), подчиняются безразмерным
уравнениям на собственные значения:
c
=l-i(a2 +pl) /ai?,l-i(a2 + q2n) /aR,
где Л = VL/u и рп(а) — положительные корни уравнения
ptgp= —atha,
при n = 0,2,4,..., а дп(а) — уравнения
gctgg = actha,
при n = 1,3,5,... . Докажите, что течение устойчиво [Rayleigh,
1892].

Упражнения	223
8.32. Моды Шенстеда (Schensted). Полагая, что собственные реше-
решения задачи Орра-Зоммерфельда при — 1 < z < 1 могут быть
выражены как
j=0	j=0
для достаточно малых aR и фиксированных а, и что почленное
дифференцирование допустимо, покажите, что
= 0 при z = ±1.
Используя результат упражнения 8.6 для волновых мод, поло-
положите
cha cospn
для п = 0,2,4,..., где рп(а) — положительный корень уравнения
ава + ptgp = О
с номером |(п + 2). Покажите, что рп@) = \{п + 2)тг и отсюда
найдите с(°) и ^@), когда a = 0.
Покажите, что
(D2-a2 + с<°>) (D2 - а2) ф^= [(u-CW) (D2-a2) -U"} ф<°\
= 0 при*±1.
Не решая эту задачу для ф^, выведите условие разрешимости
Г ф1°)(г) [{U - cW) (D2 - a2) - U"] ф^ dz = 0
для определения с^.
Покажите, что если U(z) = 1 — z2 и а = 0, то
при п = 0,2,4,... [Pekeris, 1936]. (Подсказка: J1cospnzdz =
= 0, J^ctxPpnzdz = 1, J^1z2cospnzdz = 4cospn/p?,

224	Гл. 8. Устойчивость параллельных течений
8.33. Маргинальная кривая. Предположим, что дисперсионное уравне-
уравнение для нормальной моды, пропорциональной е1аа?+**, имеет вид
^(а, з, R) = 0 в некоторой вспомогательной задаче, где R > О —-
"число Рейнольдса" и
Т{а, з, R) = Rs + {a8R2 - a3R + 1) + iaiJ.
Постройте маргинальную кривую в плоскости (Д, а) и покажи-
покажите, что Rc = ff (fI/2 « 14.1.
8.34. Преобразование Гастера (Gaster). Предположим, что диспер-
дисперсионное соотношение для нормальной моды, пропорциональной
eiaa?+**, имеет вид
Т(а, s, R) = О,
где R — число Рейнольдса, а Т — комплексная функция. Пока-
Покажите, что для временной моды нейтральная кривая в плоскости
(U, а) определяется корнями пары вещественных уравнений
Re [^(a, -iw, R)] = 0, Im [^(a, -iw, R)] = 0,
считая и = is вещественным параметром вдоль кривой. Покажи-
Покажите, что для пространственной моды нейтральная кривая в плос-
плоскости (U, и) определяется той же парой уравнений, где парамет-
параметром вдоль кривой является а.
Полагая s = а — iw, a = ar + iai, и считая s аналитической
функцией от а, используйте условия Коши-Римана, и для про-
пространственной моды выведите уравнение
= -cg,	(E8.14)
где cg = дш/даТ — групповая скорость. (Эта формула полезна,
после нахожения да/да\ при а\ = 0, для определения относитель-
относительной скорости ai роста пространственных мод через временную
относительную скорость роста а около маргинальной кривой пу-
путем оценки групповой (не фазовой) скорости и, следовательно,
для определения, с какой стороны от кривой находится область
неустойчивости).
Предположим, что для частной модельной задачи
ди ТТди	д3и ту_1д2и
dt дх	д3	д2

Упражнения	225
где a > 0. Покажите, что дисперсионная функция имеет вид
F{a,s, Д) = s - 1 +a2/R + iaU- iaa3.
Изобразите нейтральную кривую в плоскостях (Д, а) и (-R,w)
и проверьте преобразование Гастера (Е8.14) [Gaster, 1962].
8.35.	Убывание пространственных мод. Покажите, что рост или убы-
убывание по пространству стационарных возмущений основного па-
параллельного течения вязкой несжимаемой жидкости со скорос-
скоростью U(z)i при — 1 < z < 1 описывается задачей на собственный
значения
ф{у - 2а2ф" + а*ф = iaR [U (ф" - аф) - и"ф],
где ф = ф1 = 0 при z = ±1.
Покажите, что если R = 0, то либо
,, ч cosaz zsinaz	. _
ф(г) =	:	, sin 2a = —2а,
cos a sin а
либо
,, ч sinaz zcosaz	. _
ф[г) = —:	, sin 2а = 2а.
sin a cos a
Докажите, что a = an, a* при п = 0,1,2,..., где
an ~ тBп + 3)тг + -iln[Bn + 3)тг] при п —у оо.
[Wilson,
1969]. (Фактически а0 « 2,10620 + l,12536i, ai « 3,74884+
+ l,38434i, a2 « 5,35627 + l,55158i).
8.36.	*Менее простое точное решение уравнения Орра-Зоммерфелъ-
да для плоского течения Куэтта. Покажите, что если U(z) =
= z, то общее решение уравнения Орра-Зоммерфельда имеет
вид
ф(г) = Агеа2 + A2e-QZ + i f sinh[% - z)]u{y) dy,
где
ft (у) = 43Ai(w) + ^4Bi(iy),
А1,Л2,-Лз,-Л4 — произвольные постоянные, Ai, Bi — функции
Эйри и w = ei7r/6(ailI/3B/ - с - ia/Я).

226	Гл. 8. Устойчивость параллельных течений
8.37. Стабилизирующий эффект наличия границ. Является ли плос-
плоское течение Куэтта несжимаемой вязкой жидкости устойчивым
или неустойчивым? Для каких чисел Рейнольдса?
Рассмотрим некоторое заданное гладкое параллельное течение
U вязкой несжимаемой жидкости между твердыми плоскостями
при z = 2i, 22 и предел z2 -> z\ при фиксированных U и числе
Рейнольдса; как называется хорошо известное течение, которое
приближает U асимптотически внутри области течения? Дока-
Докажите эвристически, что все гладкие течения устойчивы в ука-
указанном пределе (ср. упражнение 8.15).
8.38.	Усточивостъ по отношению к коротким волнам. Рассмотри-
Рассмотрите следующий довод. "Малое локализованное возмущение основ-
основного сдвигового слоя, составленное из коротковолновых компо-
компонент, восприимчиво только к локальным свойствам основного
течения, так как влияние этого возмущения убывает экспонен-
экспоненциально быстро с увеличением расстояния от места его локали-
локализации. Следовательно, возмущение локально устойчиво, так же
как и плоское течение Куэтта, которое локально приближает-
приближается основным течением". Если вы верите этому грубому доводу,
обоснуйте его как можете, если же нет — опровергните его.
8.39.	*Граничные условия в задаче Орра-3оммерфелъда} когда про-
профиль скорости основного течения является разрывным. Пока-
Покажите, что если U или Uf разрывны при z = zq, to решение ф
уравнения Орра-Зоммерфельда удовлетворяет граничным усло-
условиям на "скачке"
А[ф] = 0, А[Т>ф] = О, Д [В2ф + iaR{U - с)ф] = 0,
Д [В3ф - iaR{{U - с)Вф - и'ф}] = 0
при z = zq, где D = d/cb (здесь Д обозначает скачок величины,
заключенной в скобки, а не оператор Лапласа).
(Подсказка: проинтегрируйте уравнение Орра-Зоммерфельда
поперек разрыва четыре раза. Можно показать, что несмотря
на то, что разрывный профиль скоростей несовместим с урав-
уравнениями движения вязкой жидкости, использование разрывно-
разрывного профиля при решении уравнения Орра-Зоммерфельда может
быть оправдано тем обстоятельством, что он дает приближен-
приближенное решение для длинноволновых мод струи или сдвигового слоя
[Drazin, 1961]).

Упражнения	227
Отсюда выведите, что если взять основное течение в виде вих-
вихревой полосы (слоя) при
1 при z < О,
то
Д[$=0, А\рф]=О, A [(D2+/?2) ф] =0, A [(D2-^
при z = 0, где )82 = а2 + iail({7 — с). Докажите, что
сг = 0,
откуда сразу следует, что маргинальная кривая задается урав-
уравнением
Д = 4х31/2а,
а также, что
с	4ia/3ii при R/a -* 0
[Tatsumi & Gotoh, 1960].
8.40. Сопряженная задача Орра-Зоммерфелъда. Определим оператор
Lc следующим образом:
Ьсф = (D2 - а2J ф - iaR [{U - с) (D2 - а2) ф - и"ф] ^
для комплексных с, всех ф Е 5 и данных С/", Л > 0, z\ < 22, а > 0,
где, как обычно, D = d/dz и 5 — множество комплекснозначных
функций на интервале [zi, Z2] с непрерывной четвертой произ-
производной. Покажите при помощи интегрирования по частям, что
[ \ьсф)ф* dz = Г ф (Lj^*) dz + [ф*ф'" - ф*'ф" + ф*"ф'-
Jzi	Jz1
-ф*'"ф-2а2 (ф*ф'-11>*'ф) -iaR{{U-c) (ф'ф*-фф*') -и'фф*}]]]
для всех ф, ф G 5, где сопряженный оператор Lj определяется
следующим образом:
Lty = (D2 - а2J ф* + 1аЛ [(D2 - a2) (U - с*) ф* - 1/"ф*].
Предположим далее, что
Ьсф = 0 и ф(г) = Т>ф(г) = 0 при z = zi, 22

228
Гл. 8. Устойчивость параллельных течений
определяет собственное решение с, ф задачи Орра-Зоммерфель-
Орра-Зоммерфельда и
Ь\ф* =0 и ф*(*) = DV>* (*) = 0 ПРИ z = zx,z2
определяет собственное решение d, ф сопряженной задачи Орра-
Зоммерфельда. Покажите, что либо d = с*, либо
' ф (D2 - a2) <0*dz = 0.
(Заметьте, что
(D2 - а2) ф = iaR [(D2 - а) (С/ - д)ф - t/"V>] ,
V>(^) = Т)ф(г) = 0 при z = z\, Z2,
и что
^ (D2 - а2) <0*dz = - / [{Вф){Щ*) + а2фф*] dz
J
после интегрирования по частям и использования граничных
условий. Было обнаружено, что множество {d} собственных зна-
значений Lj комплексно сопряжено множеству {с} собственных зна-
значений Lc, хотя собственные функции связаны не просто. Подсказ-
Подсказка: Как это упражнение соотносится с упражнением 5.9?).
8,41, Численный метод решения задачи Орра-Зоммерфельда для про-
пространственных мод. Рассмотрим задачу Орра-Зоммерфельда
для пространственной моды, а именно,
ф{у - 2а2ф" + а*ф = LR [{all - и) {ф" - а2ф) - а1/"ф] ,
где ш = ас — вещественная частота моды.
Покажите, что уравнение Орра-Зоммерфельда эквивалентно
системе
dz
из
а2и± -f U3
.-laRWux + iR(aU - w)u3 + a2n3.
(Подсказка: положите и\ = 0, U3 = ф" — a2 ф).

Упражнения
229
Дано, что при помощи специального разложения собственной
функции эта задача приближенно приводится к алгебраической
задаче на собственные значения
Ах = аВх + а2Сх,
где А, В, С — некоторые n x n матрицы (зависящие от 17, 17",
и и R), а х — столбец размерности п (представляющий собой
собственную функцию и{). Определяя
у = ах
и 2п-столбец
•¦I;
покажите, что алгебраическая задача приводится к блочно-мат-
ричным уравнениям
А01	ГВ С
0I|Z = O: I 0|Z
А-В]	ГО С,
о i\z = a io|z-
8.42. Задача Орра-Зоммерфельда с поперечным течением. Рассмот-
Рассмотрев основное течение со скоростью U = U(z)i, представив нор-
нормальные моды в виде
и т.д., где а = а\ + /?j, покажите, что уравнение Орра-
Зоммерфельда может быть переписано как
(D2 - a2J w = iR [(а ¦ U - ш) (D2 - а2) w - а ¦ (d2U/dz2) w].
Покажите, что если скорость основного течения имеет вид U =
= U(z)i + V(z)j, то линеаризованное уравнение не изменяется.
8.43. Вывод задач Сквайра и Орра-Зоммерфелъда. Рассмотрим ос-
основное течение вязкой несжимаемой жидкости со скоростью
U == U(z)i между фиксированными твердыми плоскостями при
z = zi,z2. Полагая, как обычно, u= U + u',p = P+p', линеа-
линеаризуйте уравнения Навье-Стокса и покажите, что

230	Гл. 8. Устойчивость параллельных течений
где U" = d2U/dz2 и z-компонента возмущения вектора вихря
имеет вид С = dv'/dx - ди'/ду.
Покажите, что решение является суперпозицией
(a)	мод, которые пропорциональны el{<**+Py-<*ct)y для кото-
которых с = сE2,аД) — собственное значение задачи Орра-
Зоммерфельда
(D2 - a2) w' - iaR [{U - с) (D - а2) - U"] w' = 0,
к/(х,^) = Diy;(x,t) = 0 при z = zi, Z2,
где D = d/dz; и для которых
[D2 - й2 - iaii(^ - с)] С' = i/M/V,
Cr(x, *) = 0 при z = zi, z2;
а также
(b)	мод, которые пропорциональны el(ax+Py-adt) и для которых
d = d(a2, a Л) — собственное значение однородной задачи Сквай-
Сквайра
[22]
Сг(х,^) = 0 при z = zi,z2.
Покажите, что если С = ^z)e^ax+^y~adt^ для моды Сквайра, то
Докажите, что все моды Сквайра устойчивы.
8.44. Устойчивое равновесие, несмотря на большие возмущения.
Найдите общее решение системы уравнений
at	at
(i) Положив далее с = 2Л", d = R при R > 0, покажите, что
= (RAo + B0J/AR\A0\ - ^R\A0\ R->oo
и при фиксированных Ло, Во. Изобразите фазовый портрет.

Упражнения	231
(Эта система грубо моделирует линейное взаимодействие моды
Орра-Зоммерфельда амплитуды А и моды Сквайра амплитуды
В> Обратите внимание, как начальное возмущение асимптоти-
асимптотически устойчивой точки равновесия может очень значительно
усиливаться, когда R велико; см. упражнение 2.8 и [Trefethen et
al, 1993]).
(ii) Решите далее задачу с начальными значениями для системы
дифференциальных уравнений в специальном случае, когда d =
= с. Как выглядит тах*>о |.В(^)|» когда с = В,~г и R — велико.
(Это — модель исключительного случая резонанса между устой-
устойчивыми модами Сквайра и Орра-Зоммерфельда).
8.45. Матери и дочери. Рассмотрите следующую простую линейную
систему обыкновенных дифференциальных уравнений в качест-
качестве вспомогательной модели эволюции двух мод с амплитудами
Аи А2:
dA
где
[Al	\i-cr-€ in
О iuj-
для заданных вещественных постоянных <т>0, €>0,о>, п. По-
Покажите, что общее решение этой системы может быть записано
в виде
A(t) = а ГJl e(-'+e+i")< +p L/J e<-"+iw>'
для некоторых комплексных постоянных а и /3.
Определим векторы
¦И-
и условно назовем их матерью и дочерью соответственно. Далее
рассмотрим задачи с начальными значениями А@) = d и А@) =
= т. Покажите, что соответствующие решения этих двух задач
имеют вид
A{t) = ine-MCe6* - l)e<-"+iw>' + me'-^)' ~>
in*de("<r+iw)* + me'"'+lw|< при е^Ои фиксированных t.

232	Гл. 8. Устойчивость параллельных течений
Основываясь на этих результатах, объясните заключение Бобер-
га и Броза:
A) дочь-сирота увядает; B) мать должна родить дочь; C) дочь
растет, пока ее мать жива.
* Примените эту аналогию к быстрому росту мод в устойчивом
течении, таком, например, как течение Куэтта или течение Пу-
азейля в трубе [Boberg & Brosa, 1988].

Глава 9
Пути к хаосу и турбулентность
Снова наступает хаос.
Отелло, III, 3
В этой главе будут сведены воедино некоторые общие свойства воз-
возникновения хаоса и турбулентности. Теория динамических систем
и, в частности, теория бифуркаций и хаоса дает математическое опи-
описание, при помощи которого можно качественно интерпретировать
переход к турбулентности, не загромождая свой ум множеством под-
подробностей. Это описание вместе с физическими соображениями, отно-
относящимися к механике перехода, могут быть использованы для пони-
понимания сущности неустойчивости течений, геометрия которых может
быть настолько сложна, что соответствующее решение нельзя най-
найти иначе, как численными методами. Динамика жидкостей, однако,
сильно различается и детали перехода к турбулентности зависят от
свойств предыдущих переходов, которым подвергалось течение и, по-
поэтому, подобные детали могут быть определены только при помощи
аккуратных экспериментов и методов вычислительной гидродинами-
гидродинамики отдельно в каждом случае.
9.1. Эволюция течений при увеличении числа Рей-
нольдса
Детали перехода к неустойчивости являются не только очень сложны-
сложными, но и сильно меняются от течения к течению, так что нет никакой
возможности представить краткую сводку всех возможных переходов.
Тем не менее, имеется ряд единообразных фактов в теории, а неко-
некоторые пути к турбулентности естественным образом характерны для

234	Гл. 9. Пути к хаосу и турбулентность
многих течений, даже если физические механизмы одного и того же
пути могут различаться от течения к течению.
Одним из главных фактов является то, что при увеличении числа
Рейнольдса (числа Релея, числа Тейлора или любого другого пара-
параметра, измеряющего скорость класса динамически подобных течений
данной стационарной конфигурации), временная и пространственная
сложность наблюдаемых течений часто увеличивается в результате
последовательности бифуркаций вплоть до возникновения турбулент-
турбулентности. Каждая бифуркация знаменуется возникновением неустойчи-
неустойчивости одного течения и приводит к формированию другого устой-
устойчивого течения, стационарного или нестационарного. Эта идея, вос-
восходящая к теории Ландау [Landau, 1944] и экспериментам Малкуса
[Malkus, 1954], который интерпретировал таким образом свои измере-
измерения для нелинейной конвекции Релея-Бенара при увеличении числа
Релея, впоследствии развивалась и совершенствовалась многими дру-
другими авторами.
Проследим эволюцию устойчивых течений данной стационарной
ограниченной конфигурации, когда число Рейнольдса Л увеличивает-
увеличивается квазистатически. При Д = О имеем течение Стокса, которое ста-
стационарно и единственно. Теорема Серрина^ утверждает, что когда Л
достаточно мало, стационарное течение устойчиво и единственно. При
увеличении R могут возникнуть другие устойчивые течения. Бенджа-
Бенджамин [Benjamin, 1976] показал (при помощи теории степени отображе-
отображения Лере-Шаудера (Leray-Shauder)), что в случае общего положения
(по-крайней мере для тех значений Л, где не происходит бифурка-
бифуркации) имеет место нечетное количество стационарных течений. Таким
образом, могут возникать точки поворота, транскритические бифур-
бифуркации и вилообразные бифуркации, в результате которых рождаются
множества стационарных течений при некоторых значениях Д. Не-
Некоторые, все или никакие из этих стационарных течений являются
устойчивыми. Бенджамин и Муллин [Benjamin & Mullin, 1982], напри-
например, наблюдали 20 различных устойчивых стационарных множеств
вихрей Тейлора в различных экспериментах при вращении пары ци-
цилиндров с довольно малым зазором и одинаковыми угловыми скорос-
скоростями, а также выявили 19 сосуществующих неустойчивых стационар-
стационарных решений. Множество устойчивых вихрей Тейлора, наблюдаемых
в данном эксперименте, зависит от того, как эксперимент поставлен,
т. е. от того, каковы начальные условия и каким образом достигаются
предписанные значения угловых скоростей цилиндров.
Если при увеличении Л стационарное решение становится не-
неустойчивым и Re(s) = 0 и Im(s) = 0, то ожидается точка поворота в
случае общего положения. В исключительном случае может оказаться
транскритическая или вилообразная бифуркации; если течение обла-
обладает отражательной симметрией, то следует ожидать вилообразную
бифуркацию. Если, однако, там, где стационарное решение теряет

9.1. Эвлюция течений при увеличении числа Рейнольдса	235
устойчивость Re(s) = 0 и Im(s) ф О, то ожидается бифуркация Хоп-
фа и ответвление либо надкритического устойчивого периодичного
по времени решения при R > Лс, либо докритического неустойчивого
периодического по времени решения при R < Rc. Например, надкри-
надкритическая бифуркация Хопфа возникает, когда спутный след за тупым
телом становится неустойчивым и образуется вихревая дорожка; дру-
другая бифуркация возникает, когда вихри Тейлора становятся волнис-
волнистыми. Это показывает практическую важность справедливости или
нарушения принципа обмена устойчивостей, несмотря на то, что этот
принцип может казаться не важным в контексте только линейной те-
теории. Исчезновение или наличие Im(s) при маргинальной устойчивос-
устойчивости определяет факт происхождения бифуркации к стационарному или
периодичному по времени течению; вид слабой нелинейности на гра-
границе устойчивости далее определяет тип бифуркации, является ли эта
бифуркация надкритической или докритической и т.д.
После надкритической бифуркации Хопфа развивается устойчивое
периодическое по времени течение, когда R возрастает далее, и это
течение может в конце концов стать также неустойчивым. Неустой-
Неустойчивость может быть определена математически при помощи линеа-
линеаризации для малых возмущений периодического по времени решения
с использованием теории Флоке (Floquet), которая играет такую же
роль для неустойчивости периодических решений дифференциальных
уравнений, какую играет метод нормальных мод для устойчивости
стационарных течений. Периодические решения дифференциальных
уравнений подвергаются параметрической неустойчивости, так же
как в методе нормальных мод, параметрически неустойчивые моды
могут иметь новый период любой величины. Но общий тип парамет-
параметрической неустойчивости возникает в результате субгармонического
резонанса, который ведет к возникновению неустойчивых мод, име-
имеющих удвоенный период периодического по времени течения. Если
эта неустойчивость приводит к надкритической бифуркации, то при
дальнейшем увеличении R развивается устойчивое квазипериодичес-
квазипериодическое течение (у которого имеются два или более главных периодов).
Такое происходит, например, когда волнистые вихри Тейлора стано-
становятся неустойчивыми. (Иногда в результате субгармонического ре-
резонанса может развиваться устойчивое течение с периодом, равным
удвоенному периоду исходного периодического течения. Такое может
произойти в случае конвекции Релея-Бенара в высоких ячейках). При
дальнейшем увеличении R могут возникнуть неустойчивости и би-
бифуркации, в результате которых появляется устойчивое течение с тре-
тремя главными частотами. В качестве альтернативы или при дальней-
дальнейшем увеличении R может развиваться хаотическое течение; в спектре
Фурье хаотического течения отсутствуют острые пики при фундамен-
фундаментальных частотах, вместо этого имеет место широкая полоса частот,
а корреляция между скоростями в данной точке в разные моменты вре-

236	Гл. 9. Пути к хаосу и турбулентность
мени быстро убывает при увеличении разности времен. (Для спектра
Фурье берется временной ряд данной характеристики течения, на-
например, компоненты скорости в данной точке при больших временах,
и далее производится преобразование Фурье для нахождения величи-
величины компоненты каждой частоты).
Устойчивое течение, образующееся в результате первой бифур-
бифуркации основного течения при увеличении числа Рейнольдса в фи-
физической литературе часто называется вторичным течением, а его
неустойчивость при второй бифуркации с увеличением числа Рей-
Рейнольдса — вторичной неустойчивостью. Тогда основное течение до
первой бифуркации следовало бы называть первичным течением, а об-
образовавшееся после первичной неустойчивости течение — вторичным
течением. Например, если первая неустойчивость ведет к возникно-
возникновению стоячей или бегущей волны, а сама эта волна становится не-
неустойчивой к краеполосным (side bandN или каким-либо другим ре-
резонансным волновым взаимодействиям, то это — вторичная неустой-
неустойчивость. Часто первичная неустойчивость двумерного течения при-
приводит к возникновению стационарной устойчивой двумерной волны
(на практике чаще квазистационарной), а трехмерность возникает в
результате вторичной неустойчивости, когда нарушается двумерная
симметрия. Возникновение квазипериодического течения, следующего
за периодическим течением, возникшим в качестве вторичного тече-
течения в результате бифуркации Хопфа основного течения, есть другая
общая форма вторичной неустойчивости, снова дающей пример обра-
образования вихрей Тейлора.
Последовательные бифуркации обычно следуют одна за другой при
уменьшающихся приращениях числа Рейнольдса, так что на практике
эти бифуркации уже не удается различить. Нелинейные самовоздей-
самовоздействия неустойчивых мод генерируют гармоники, а нелинейные вза-
взаимодействия мод — субгармоники. Таким образом, при увеличении
временной сложности течения при этой последовательности бифур-
бифуркаций с увеличением R пространственная сложность обычно увели-
увеличивается также. Возникают движения на меньших масштабах дли-
длины и на более широких диапазонах этих масштабов. Представляется
правдоподобным, что для любых данных динамически подобных тече-
течений, характеризуемых числом Рейнольдса, при достаточно больших R
существует единственное статистически стационарное турбулентное
течение, независимое от начальных условий; это было бы так, если
бы существовал единственный аттрактор для больших значений R.
Если течение обладает некоторыми симметриями, то обычно они
сначала нарушаются одна за другой при бифуркациях с увеличени-
увеличением R, а в конце концов "восстанавливаются" в момент возникновения
6См., например, Ekhaus, W. A965) Studies in nonlinear stability theory, N.-Y.:
Springer-Verlag. (Прим. ред. перевода.)

9.2. Пути к хаосу и турбулентность	237
турбулентности, так что среднее турбулентное течение имеет все эти
симметрии [King & Stewart, 1991]; примером сужит нарушение сим-
симметрии вращения и сдвига в течении Куэтта между длинными коакси-
коаксиальными цилиндрами. В действительности течение Куэтта является
прекрасным прототипом течений с последовательностями бифурка-
бифуркаций в направлении перехода к турбулентности при увеличении числа
Рейнольдса; Коулс [Coles, 1965] и Фенстермахер и др. [Fenstermacher et
а/., 1979] предприняли классическое экспериментальное исследование
этого явления.
Описание перехода с точки зрения теории динамических систем
дает полезное представление, но и доставляет риск чрезмерного упро-
упрощения, поэтому дополнительное описание перехода с физической точ-
точки зрения чрезвычайно важно. Однако физические механизмы сильно
меняются от класса к классу основных течений. Механизмы перехо-
перехода для некоторых основных течений, особенно параллельных и почти
параллельных течений, также являются тонкими, а практическая ре-
реализация течения часто гораздо более сложна, чем его модель, идеали-
идеализированная теоретиками. Так что переход необходимо описывать фи-
физически для каждого из различных классов основных течений, и у всех
этих переходов совсем немного общего.
Переход, особенно для параллельных и почти параллельных тече-
течений, происходящий при помощи отличного от экспоненциального рос-
роста нормальных мод, называется "побочным переходом", его концепция
и название были придуманы Морковиным [Morkovin, 1969]. Побочный
переход может возникать вследствие докритической неустойчивости,
когда отсутствует устойчивое течение, смежное основному течению
в фазовом пространстве в окрестности пограничного значения числа
Рейнольдса. Этот переход может иметь место в результате неустой-
неустойчивости по отношению к возмущениям конечной амплитуды, когда ос-
основное течение устойчиво по отношению ко всем возмущениям беско-
бесконечно малой амплитуды; например, когда сильный мгновенный рост
малых возмущений пограничного слоя ведет к полосатому возмуще-
возмущению, удлиняющемуся вниз по потоку, которое вызывает сильное не-
нелинейное усиление.
9.2. Пути к хаосу и турбулентность
Выше было упомянуто о том, что переход к турбулентности происхо-
происходит вначале как последовательность бифуркаций. При завершающих
стадиях гидродинамической неустойчивости имеет место возникнове-
возникновение хаотического течения с малым числом степеней свободы как, на-
например, в явлении тепловой конвекции в ящике, нагретом снизу. Пред-
Представляется возможным грубо охарактеризовать различные типы тур-
турбулентности. "Фазовая турбулентность" с большим числом степеней

238	Гл. 9. Пути к хаосу и турбулентность
свободы, содержащая целый диапазон пространственных масштабов
и являющаяся хаотичной по времени, имеет место, например, в явле-
явлении тепловой конвекции в сильно подогретом снизу тонком слое. Клас-
Классическая "турбулентность сдвигового течения" (shear-flow turbulence),
включающая широкий спектр волновых чисел, но содержащая коге-
когерентные пространственные структуры, имеет место, например, в ка-
канале или в трубе при довольно больших числах Рейнольдса. И на-
наконец, приходится сталкиваться с турбулентностью при очень боль-
больших числах Рейнольдса, которая хаотична по времени и пространст-
пространству с очень широким спектром волновых чисел, таким, что на малых
масштабах течение изотропно с инерционной областью и вязким обре-
обрезанием, как, например, турбулентность вниз по потоку для быстрого
обтекания решетки в большой аэродинамической трубе. Гидродина-
Гидродинамическая устойчивость, однако, представляет собой явление, относя-
относящееся к развитию неустойчивости вплоть до возникновения фазовой
турбулентности, так что не мы будем рассматривать далее последние
стадии перехода.
Итак, мы обсудили некоторые пути к турбулентности при уве-
увеличении числа Рейнольдса R. Можно усмотреть некоторый порядок
в беспорядочном наборе бифуркаций, и, по всей видимости, имеют
место только несколько главных типов путей к турбулентности или,
по крайней мере, к хаотическому течению. Представляется полезным
привести краткое резюме, дополненное некотороми деталями.
A)	Докритпическая неустойчивость. На этом пути устойчивое те-
течение, стационарное, периодическое или квазипериодическое,
становится неустойчивым при медленном увеличении и переходе
R через критическое значение. Течение при этом быстро "пере-
"перескакивает" в турбулентное, которое не является непрерывным
продолжением устойчивого течения для меньших значений R.
Подобное происходит, например, при вилообразной бифуркации
с отрицательной постоянной Ландау; при этом течению некуда
перейти в малой окрестности самого себя, так что оно долж-
должно измениться существенно и может быстро развиться в турбу-
турбулентное течение (либо может перепрыгнуть в другое устойчи-
устойчивое стационарное течение с гистерезисом, если R увеличивает-
увеличивается, а затем уменьшается). Такое развитие турбулентности было
по-другому названо "внезапным", "быстрым" и "диким". Для
течения Пуазейля в трубе, плоского течения Пуазейля, плоского
течения Куэтта и других течений в канале оказывается харак-
характерным такое внезапное возникновение турбулентности. Для та-
таких течений это явление часто называется побочным переходом.
B)	Путь Рюэля-Такенса-Ньюхауза. Этот путь сначала был обо-
обозначен Рюэлем и Таккенсом [Ruelle & Takens, 1971], а затем пе-

9.2. Пути к хаосу и турбулентность	239
ресмотрен Ньюхаузом и др. [Newhouse et а/., 1978] при помощи
использования теории динамических систем. Вдоль этого пути
происходит последовательность бифуркаций при увеличени i?,
в результате которых некоторое стационарное течение может не-
непосредственно или через другие стационарные течения стать пе-
периодическим по времени, затем квазипериодичным с двумя, а за-
затем, может быть, тремя или даже четырьмя частотами, вплоть
до появления хаотического течения, которое можно рассматри-
рассматривать как упорядоченное, если не как полностью развитое тур-
турбулентное. По-видимому, квазипериодические решения с пятью
или большим числом главных частот неустойчивы, и поэтому
подобные течения не наблюдаются. При увеличении R главные
частоты, скажем, wi, o^, могут изменяться и становиться рацио-
рационально зависимыми, так что u2/vi есть отношение двух целых
чисел; в этом случае частоты "запираются" и течение обращает-
обращается в периодическое и остается периодическим при увеличении R
до тех пор пока оно не станет неустойчивым и возникнет новое
квазипериодическое течение. Таким образом o^/^i может уве-
увеличиваться вместе с R "урывками" до тех пор, пока, в конце
концов, не возникнет хаос.
Этот путь является достаточно общим для течений с положи-
положительной постоянной Ландау, например, для течения Куэтта меж-
между вращающихся цилиндров и конвекции Релея-Бенара. Переход
является "медленным" по эволюции спектра: одна бифуркации
следует за другой до тех пор, пока, в конце концов, не возникает
турбулентность или, по крайней мере, хаос. Иногда при увели-
увеличении числа Тейлора возникает хаос, который затем заменяет-
заменяется квазипериодическим течением перед тем как, окончательно
устанавливается турбулентность.
C)	Удвоение периода. Иногда турбулентность или скорее хаос воз-
возникают после последовательности бифуркаций удвоения перио-
периода при увеличени R. Здесь в результате бифуркаций возника-
возникает последовательность периодичных по времени течений, когда
период течения равен удвоенному периоду предыдущего тече-
течения. Подобное наблюдалось Либхабером и Маурером [Libhaber
& Maurer, 1978] при конвекции Релея-Бенара в высоком ящи-
ящике и было теоретически предсказано Фейгенбаумом [Feigenbaum,
1980] в достаточно общем случае.
D)	Скачкообразный переход. На этом пути, который впервые
был намечен математически Помо и Маневиллем [Pomeau &
Manneville, 1980], периодическое течение становится неустойчи-
неустойчивым при переходе R через критическое значение в сторону рос-
роста, при этом устойчивое периодическое течение сначала стано-

240	Гл. 9. Пути к хаосу и турбулентность
вится неустойчивым по отношению к возмущениям все мень-
меньшей и меньшей конечной амплитуды. При критическом значе-
значении Rc величины R устойчивое периодическое течение объеди-
объединяется с неустойчивым периодическим движением (конечно, не
наблюдаемым). Для малых положительных значений R — Rc это
периодическое решение оказывается сохраняющимся большую
часть времени (хотя оно более не является точным решением
основных уравнений), но изредка прерывается "вспышками",
интенсивность которых не мала. При дальнейшем увеличении
it — Rc вспышки возникают чаще, но сильно не изменяются по
величине. Среднее время между вспышками стремится к беско-
бесконечности как (Л — Rc)'1!2 при R -» Дс+. Эта теоретическая
идея, по-видимому, объясняет турбулентные пятна и нарушение
ламинарности.
Упражнения
9.1. Что определяет критическое значение безразмерного парамет-
параметра для возникновения неустойчивости? Рассмотрим следую-
следующий физический довод, который можно бы было использовать
перед подсчетом характеристик устойчивости. "Безразмерный
параметр, такой как число Рейнольдса или Релея, выделяющий
класс динамически подобных течений, обычно предсталяет собой
характеристическое отношение дестабилизирующих и стабили-
стабилизирующих сил. Поэтому критическое значение параметра при
возникновении неустойчивости основного течения, которое этот
параметр определяет, могло бы предполагаться имеющим поря-
порядок величины 1". Конечно, нет причин ожидать, что критичес-
критическое значение параметра в точности равно единице, потому что
определение безразмерного параметра обычно в некоторой степе-
степени произвольно. Тем не менее, в задачах, обсуждаемых в данной
книге, критические значения изменяются от нуля до бесконеч-
бесконечности, и многие из них имеют порядок величины тысяча. Почему
так часто возникают такие большие критические значения?
(Этот вопрос задан скорее с целью вызвать размышления по
данному поводу, чем для того, чтобы получить конкретный пра-
правильный ответ. Может оказаться полезным рассмотреть изме-
изменение критических значений числа Релея при перемещении го-
горизонтальных плоскостей из положений z* = 0, d в положения
z* = 0, 7Г<2 в главе 6 о конвекции Релея-Бенара).

Глава 10
Случаи перехода к турбулентности
Ибо Я дал вам пример, чтобы и вы делали то же, что Я сделал вам.
Ин. 13, 15
10.1. Синтез
10.1.1. Введение
В данной книге планировалось описать важные общие понятия и мето-
методы теории гидродинамической устойчивости в первых главах, а в по-
последних — применить эти понятия и методы к некоторым конкретным
течениям. Рассматриваемые течения выбирались отчасти из-за прос-
простоты их математического описания, а отчасти — из-за их важности
с точки зрения истории предмета (эти две причины связаны между
собой) и их физической значимости. Многие из рассматриваемых за-
задач являются сильно идеализированными; тем не менее, все эти зада-
задачи имеют гораздо более широкую область применения, чем на первый
взгляд можно было бы допустить, исходя из их точной формулировки.
Теория конвекции Релея-Бенара, например, может быть использована
не только для интерпретации неустойчивости бесконечно тонкого го-
горизонтального слоя нагреваемой снизу жидкости, но и многих конвек-
конвективных неустойчивостей течений, которые имеют локальное сходство
с тонким слоем нагретой снизу жидкости. Теория вихрей Тейлора мо-
может быть использована для интерпретации неустойчивостей течений
с кривыми линиями тока, как будто под действием локальной центро-
центробежной силы. Теория вихрей Гёртлера может использоваться при ин-
интерпретации локальных неустойчивостей течений с выпуклыми вих-
вихревыми линиями, так что этот механизм является дополнительным к
механизму вихрей Тейлора и может быть применен, когда линии тока

242	Гл. 10. Случаи перехода к турбулентности
или стенка "искривлены по-другому". Теория неустойчивости парал-
параллельных течений с теоремой Релея о точке перегиба и задачей Орра-
Зоммерфельда может быть использована для интерпретации неустой-
чивостей течений, которые являются близкими к параллельным, по
крайней мере, локально; в действительности эта теория уже была
использована для интерпретации неустойчивых пограничных слоев,
струй и свободных сдвиговых слоев. Использование перечисленных
идеализированных задач для интерпретации неустойчивостей более
сложных течений является важным, но нелегким делом, до тех пор
пока не будет накоплен опыт в изучении гидродинамической неустой-
неустойчивости.
Классические задачи теории гидродинамической устойчивости бы-
были поставлены и решены частично в силу их простоты, и частично
из-за их физической важности. Простота этих задач была обусловлена
временной и пространственной симметриями, которые приводят к воз-
возможности рассматривать задачи линейной устойчивости, сводящиеся
к задачам на собственные значения для обыкновенных дифференци-
дифференциальных уравнений, а не для уравнений в частных производных. Без
этого сведения к обыкновенным дифференциальным уравнениям за-
задачи гидродинамической устойчивости не могли бы быть решены до
появления суперкомпьютеров в восьмидесятых годах прошлого века.
Простота этих линейных задач, в свою очередь, позволяет предприни-
предпринимать слабонелинейный анализ неустойчивости. Тем не менее, на пу-
пути перехода к турбулентности при возрастании от нулевого значения
числа Рейнольдса, числа Релея, или какого-либо другого параметра,
возникающие задачи могут быть решены только при помощи мето-
методов вычислительной гидродинамики. Таким образом, компьютер был
"двигателем" многих недавних продвижений в этой области. В то же
самое время, понимание многих механических концепций и более прос-
простых задач является весьма полезным для интерпретации результатов
лабораторных и вычислительных экспериментов.
Без умения использовать простые задачи, приводящие к обыкно-
обыкновенным дифференциальным уравнениям в качестве моделей, волей-
неволей приходится полагаться на лабораторные и вычислительные
эксперименты вместе с качественной теорией динамических систем
и разнообразными физическими аргументами. Эти аргументы могут
быть основаны на более простых задачах гидродинамической устой-
устойчивости, для которых в качестве локальных приближений допустимо
использование обыкновенных дифференциальных уравнений.
Изложив эти общие замечания, адресуемся к неустойчивостям
двух важных течений, для которых задачи линейной устойчивости
могут быть легко поставлены, но допускают решения только метода-
методами вычислительной гидродинамики. Соответствующий анализ будет
предпринят с использованием всех доступных методов исследований,
для лучшего понимания неустойчивостей и пути к турбулентности.

ЮЛ. Синтез	243
10.1.2. Неустойчивость течения за плоской пластиной при
нулевом угле атаки
Использование физических аргументов и общих соображений труд-
трудно переоценить, тем не менее оно может привести к неправильным
выводам при рассмотрении достаточно глубоких вопросов. Для ил-
иллюстрации вернемся к неустойчивости пограничного слоя Блазиуса
на плоской пластине, рассматривая пограничный слой в потоке как
единое целое (см. рис. 10.1). Заглянем для начала в [Van Dyke, 1982,
Figs. 29-30] и [Homsy et al, CD2000, Video Library, "Flow Past a Flat
Plate"].
Рассмотрим далее идеализированный мысленный эксперимент по
неустойчивости стационарного двумерного течения бесконечного од-
однородного потока несжимаемой жидкости, имеющей кинематическую
вязкость v и скорость V за длинной тонкой пластиной длины L с ну-
нулевым углом атаки. Из динамического подобия следует, что такие
течения характеризуются единственным безразмерным параметром,
например, глобальным числом Рейнольдса Re = VL/v. Разумеется,
могут быть скрытые переменные в реальном эксперименте вследствие
дефектов, таких как ненулевая толщина пластины, форма передней
и задней кромки, ее кривизна, легкий наклон пластины к набегаю-
набегающему потоку, входные и выходные условия в аэродинамической тру-
трубе конечной длины, сжимаемость воздуха, уровень турбулентности
в набегающем потоке или даже нарушение справедливости уравнений
Навье-Стокса на масштабе длины, соизмеримом с размером молекул.
Однако из обсуждений, приведенных в этой книге, ясно, что в идеаль-
идеальном эксперименте будет возникать последовательность бифуркаций
при возрастании числа Рейнольдса Re от нулевого значения до бес-
бесконечности, начинающаяся с симметричного двумерного течения как
глобально устойчивого аттрактора, ведущая к начальной неустойчи-
неустойчивости (как в главе 2) и заканчивающаяся хаотической завихренностью
и существенно трехмерной турбулентностью. Представляется очевид-
очевидным, что первая бифуркация является надкритической бифуркацией
Хопфа. Возмущения в спутном следе и в пограничном слое на плас-
пластине, как было обнаружено, распространяются вниз по течению, так
что кажется вполне правдоподобным рассматривать неустойчивости в
следе и в пограничном слое независимо во многих случаях, по крайней
мере как хорошее приближение. Указанная глобальная точка зрения,
противоречит точке зрения, представленной в главе 8 и опирающейся
на построение теории неустойчивости параллельных и близких к па-
параллельным течений. Локальные аргументы, основанные на теории
пограничного слоя (справедливой, конечно, только если глобальное
число Рейнольдса Re велико) использовались там для того, чтобы
обосновать применение задачи Орра-Зоммерфельда, не принимая во
внимание длину пластины вообще.

244
Гл. 10. Случаи перехода к турбулентности
Рис, 10.1. Вид сбоку течения в постоянном потоке за плоской пластиной
при нулевом угле атаки, когда Re = 10 000: пограничный слой и спутный
след (по [Van & Dyke, 1982, Fig. 29]; воспроизведено по разрешению ONERA)
В параграфе 8.5 было использовано локальное число Рейнольдса
R = B1Лс*/1/I/2, построенное по толщине S = {2VX+/VI!2 погранич-
пограничного слоя для выбранного положения ж*, и было найдено критическое
число Rc « 520. Каким образом это значение определяет критическое
значение глобального числа Рейнольдса Re? Следует предположить,
что неустойчивость возникает, когда локальное число Рейнольдса на
задней кромке ж* = L приблизительно равно 520 и, таким образом,
критическое значение Re имеет порядок величины 5202/2 « 135 000.
Для скорости потока V = 1 м/с при комнатной температуре и давле-
давлении это дает маргинальную устойчивость для пластины длины L «
« 0.14 м, если пластина обтекается водой, и L ъ 2 м, если пласти-
пластина обтекается воздухом. Все это подробно изложено во многих учеб-
учебниках по теории пограничного слоя (см., например, [Batchelor, 1967,
параграф 5.8]).
Общепризнано, что такая аргументация является грубой и ее сле-
следует использовать для получения оценок по порядку величины и для
анализа качественных механизмов. Такое рассмотрение не принима-
принимает во внимание ни сложной стуктуры пограничного слоя на задней
кромке, ни, что более важно, следа за пластиной. Полутолщина следа
может быть отождествлена с толщиной пограничного слоя на зад-
задней кромке и, таким образом, имеет порядок величины (VL/2VI/2,
а критическое значение числа Рейнольдса спутного следа приблизи-
приблизительно равно 4 и наиболее неустойчивые моды являются длинными

10.1. Синтез	245
синусоидальными волнами (см. параграф 8.7). Тогда след становится
неустойчивым по отношению к синусоидальным возмущениям, ког-
когда V{2vL/VI/2/u га 4, т.е. Re га 8, что значительно меньше, чем
135 000. Это наводит на мысль о том, что неустойчивость течения
рколо пластины возникает из-за локальной неустойчивости течения
в следе с критическим числом Re га 8, а не в результате появле-
появления золн Толлмина-Шлихтинга на пластине, и что волны Толлмина-
Шлихтинга возникают при гораздо больших значениях Re как чисто
локальная неустойчивость. Визуальные наблюдения неустойчивости
течения около пластины [Taneda, 1959] дают синусоидальные возму-
возмущения в кормовой части пластины при критических значениях Re на
три или четыре порядка меньших, чем 135 000, что позволяет предпо-
предположить, что неустойчивость спутной струи является механизмом пер-
первой бифуркации Хопфа течения при увеличении Re от значения, рав-
равного нулю. Этот факт согласуется с интуитивными доводами главы 8,
состоящими во том, что невязкий механизм неустойчивости течений
с точками перегиба оказывается существенно более сильным, чем вяз-
вязкий механизм неустойчивости Толлмина-Шлихтинга без них. Однако
эксперимент, приближенный к идеализированному, нелегко реализо-
реализовать в лабораторных условиях, и, кажется, окончательное критичес-
критическое число Рейнольдса Re еще не найдено до сих пор. Из экспериментов
в аэродинамической трубе [Schubauer & Skramstad, 1947; Klebanoff et.
ai, 1962]; Kachanov et a/, 1975] и многих других, становится ясным,
что локальное приближение задачи Орра-Зоммерфельда действитель-
действительно xoponio представляет возникновение неустойчивости течения для
потока с низким уровнем турбулентности за пластиной. Для боль-
большинства этих экспериментов R ^> ite, а теория Орра-Зоммерфельда
используется не столько для того, чтобы найти, устойчиво течение
или нет, сколько для того, чтобы определить, где, почему и как те-
течение стало локально неустойчивым. Около передней кромки течение
близко к установившемуся (вследствие условий прилипания на плас-
пластине), так что локальное число Рейнольдса мало и локально тече-
течение хорошо аппроксимируется течением Стокса; отсюда следует, что
течение является локально устойчивым (хотя не является близким
к параллельному) на некотором расстоянии вниз по течению от пе-
передней кромки. Но по мере того, как пограничный слой становится
толще вниз по потоку, течение приближается к почти параллельно-
параллельному и в некотором положении локальное число Рейнольдса согласно
теории Орра-Зоммерфельда достигает своего критического значения,
и следует ожидать, что неустойчивость будет расти вниз по потоку
от этого положения или в его окрестности. Частично этот вопрос об-
обсуждался в параграфе 8.5, но детали сложны и до сих пор являются
предметом исследования.
* Явный парадокс, состоящий в том, каким образом существова-
существование континуума локальных неустойчивых мод, например, в спутном

246	Гл. 10. Случаи перехода к турбулентности
следе или пограничном слое, соотносится с дискретными глобальны-
глобальными модами течения как целого был объяснен в работах [Stone, 1969] и
[Drazin, 1974] для некоторых простых задач. Авторы этих работ свя-
связали локальные моды медленно меняющегося течения с глобальной за-
задачей, используя приближение ВКБ. Гент и Лич [Gent & Leach, 1976]
удачно применили эту идею к бароклинной неустойчивости течения
в различным образом нагреваемых вращающихся кольцах, предпо-
предполагая, что течение почти параллельно. Впоследствии, Хуэрр и Мон-
кевитц [Huerre & Monkewitz, 1990] развили этот подход и успешно
применили его ко многим почти параллельным течениям.
10.2. Переход течения с однородным потоком за те-
телом плохо обтекаемой формы
Неустойчивость течения с однородным потоком за плохо обтекаемым
телом в чем-то качественно подобна неустойчивости за тонким телом,
но разделение течения грубым телом ведет к развитию "правильно-
"правильного" спутного следа, поперечное сечение которого подобно поперечному
сечению тела перпендикулярно потоку. В аэродинамике пограничный
слой на плохо обтекаемом теле и его неустойчивость особенно важны,
потому что положение точки разделения влияет на размер спутного
следа и, следовательно, на сопротивление тела. В действительности
неустойчивость часто инициируется, скажем, при проходе проволо-
проволоки, когда создаются возмущения значительных амплитуд, для того
чтобы сделать пограничный слой турбулентным как можно дальше
вверх по потоку и, тем самым, уменьшить неблагоприятный гради-
градиент давления в пограничном слое, задерживая разделение, и, следо-
следовательно, уменьшая лобовое сопротивление. Рассмотрим два примера
однородного установившегося течения несжимаемой вязкой жидкости
за телами плохо обтекаемой формы.
10,2Л, Течение за круглым цилиндром
Сначала изучим неустойчивость течения с однородным потоком не-
несжимаемой вязкой жидкости около круглого цилиндра. Нет лучше-
лучшего способа начать исследование, нежели взглянуть на последователь-
последовательность картинок течения при возрастании числа Рейнольдса от нулево-
нулевого значения. Вы могли бы начать с рассмотрения картинок в вашем
любимом учебнике (например, в книге [Batchelor, 1967, Figs. 4.12.1,
4.12.6, 5.11.4] и рис. 10.2 в настоящей книге. См. также [Van Dyke,
1982, pp. 4-5, Figs. 6, 24, 40-48, 94-98; Nakayama, 1988, p. iii, x в цве-
цвете, Figs. 1-9] и [Homsy et a/., CD2000, Video Library, "Flow Past a
Cylinder"].

-10.2. Переход течения за. плохо обтекаемым телом	247
Рис. 10.2. Течение с однородным потоком за круглым цилиндром при
R = 140. Течение направлено справа налево; показана вихревая дорожка
в спутном следе цилиндра (по [Van Dyke, 1982, Fig. 94]; воспроизведено с
разрешения профессора Садатоши Танеда (Sadatoshi Taneda))
Можно заметить, что для очень маленьких значений числа Рей-
нольдса течение является симметричным в носовой и кормовой частях
цилиндра, также как вверх и вниз в перпендикулярном направлени-
направлениях. Картина течения выглядит не только стационарной, но и очень
устойчивой. Когда число Рейнольдса, например, R — VD/v, где V —
скорость свободного потока, a D — диаметр цилиндра, увеличивается
до приблизительно 1, симметрия перед носом и за кормой цилиндра
визуально нарушается. Когда R возрастает до приблизительно 10, те-
течение визуально разделяется на пару рециркуляционых вихрей с под-
подветренной стороны цилиндра. При дальнейшем росте R линии раздела
движутся вверх по течению и растут в длину как спутный след, но
течение остается стационарным и сохраняет свою симметрию меж-
между верхней и нижней частями. Однако когда R возрастает до Лс, где
Rc & 45, течение становится нестационарным и вихри начинают ос-
осциллировать. Для потока со скоростью V = 1 м/с при комнатных
температуре и давлении реализуется маргинальная устойчивость для
Цилиндра диаметром длины L « 0,045 мм, если в качестве жидкости
берется вода, и длины L « 0,7 мм, если в качестве жидкости берет-
берется воздух. Возникновение периодического по времени течения свиде-
свидетельствует о надкритической бифуркации Хопфа. По мере того, как
R растет, вихри срываются попеременно с разделяющих линий тока,
расположенных выше и ниже цилиндра, формируя в спутном следе то,
что фон Карман [Кагтап, 1911] назвал вихревой дорожкой. Вихревая
Дорожка обладает симметрией бегущей синусоидальной моды. Все это

248	Гл. 10. Случаи перехода, к турбулентности
подробно описано во многих учебниках по теории пограничного слоя
(см. например, [Batchelor, 1967, параграфы 4.12, 5.11], и рис. 10.3).
Когда R возрастает до приблизительно 200, развивается вторичная
неустойчивость, по мере того как нарушается двумерность течения
и вихревая дорожка начинает распадаться. Когда R становится при-
приблизительно равной 1000, течение на цилиндре и вверх по потоку от
передней части цилиндра выглядит ламинарным, являясь гладким и
вполне установившимся с различаемым пограничным слоем на ци-
цилиндре, но течение в спутной струе является турбулентным, буду-
будучи хаотическим, существенно трехмерным и сильно диффузионным.
Можно видеть, что на больших масштабах течение все еще сохраняет
характер вихревой дорожки, не становясь полностью нерегулярным,
представляя собой еще один пример когерентной структуры. По мере
дальнейшего увеличения R структура турбулентного течения стано-
становится более мелкой.
Конечно, свойства такого сложного пространственного течения не
могут быть описаны просто несколькими обыкновенными дифферен-
дифференциальными уравнениями и для получения количественных результа-
результатов необходимо проводить лабораторные и численные эксперименты.
Тем не менее, можно использовать расчеты неустойчивости погранич-
пограничного слоя на цилиндре и аппарат качественной теории бифуркаций,
чтобы получить некоторое* представление об экспериментальных ре-
результатах. Следует понимать, что не существует лабораторных экс-
экспериментов, которые являются точно двумерными и даже численный
эксперимент не может быть предпринят для бесконечной области те-
течения, так что результаты аккуратных экспериментов могут немного
отклоняться от идеала и немного изменяться от эксперимента к экс-
эксперименту в зависимости от соотношения масштабов канала, условий
вдали от цилиндра и т. д. Имея все это в виду, вернемся снова к сце-
сценарию, когда число Рейнольдса возрастает от нулевого значения, и
дадим более детальное его описание.
При R = 0 реализуется течение Стокса, которое единственно, и по-
поэтому имеет все типы симметрии — стационарность, двумерность и
симметрию верх-низ; это течение также обратимо по времени и таким
образом имеет симметрию нос-корма. Теорема Серрина показывает,
что это течение устойчиво (хотя теорема строго применима только
к ограниченным течениям) для малых значений Рейнольдса R > 0.
Для 0 < R < Rc имеется устойчивое ламинарное двумерное тече-
течение с симметрией верх-низ. Симметрия между носовой и кормовой
частями разрушается при Л, отличном от нуля, и формируется спут-
ный след, который удлиняется по мере увеличения R. При R = Rc
начальное течение становится неустойчивым при бифуркации Хопфа,
когда теряется стационарность. Симметрия верх-низ в любой данный
момент нарушена, но течение в некоторый момент времени является
зеркальным отражением течения на пол-периода раньше в централь-

Ю.2. Переход течения за плохо обтекаемым телом
249
G)
=о с
г
,г
э
Рис. 10.3. Схемы режимов течения с однородным потоком за круглым ци-
цилиндром, (а) Л < 1: неразделенное течение, обладающее симметрией верх-
низ, и не совсем — симметрией нос-киль. FN<jR</?c = 46: разделенное
течение, обладающее симметрией верх-низ, (в) R и 50: периодическая по
времени вихревая дорожка, (г) R « 100: распространение вихрей в дву-
двумерном нестационарном течении, (d) R > 100: турбулентное трехмерное
течение (по [Jackson, 1987, Fig. 1])

250	Гл. 10. Случаи перехода к турбулентности
ной плоскости. Численный расчет Джексона [Jackson, 1987] линейных
характеристик устойчивости дает R га 46, в.то время как лаборатор-
лабораторные эксперименты [Provansal et а/., 1987] дали диапазон значений Rc
от 47 до 123 в зависимости от соотношения масштабов цилиндра; оба
исследования подтвердили количественно некоторые детали бифурка-
бифуркации Хопфа для комплексного уравнения Ландау. Вычисления линий
тока в различные моменты времени в течение одного периода тече-
течения для малых R — Rc > 0 [Jakson, 1987] показаны на рис. 10.4. Для
-Rc < R < #2» например, существует устойчивое ламинарное перио-
периодическое по времени течение с распространяющимися вихрями, при-
присоединенные вихри формируют вихревую дорожку в спутном следе за
цилиндром. Период течения может быть вычислен с помощью числа
Струхаля (Strouhal), St = fD/V, где / — частота вихревой дорожки.
По мере того, как R растет, St растет медленно от примерно 0,13.
При R = R2 вторичное течение само становится неустойчивым, с воз-
возникновением третьего измерения в вихревой дорожки. Эксперименты
показывают, что R2 га 200. Вильямсон [Williamson, 1996] установил
последующие режимы в диапазоне больших чисел Рейнольдса.
При R га 260 возникает другая трехмерная мода неустойчивости
в спутном следе. По мере роста R трехмерное течение в следе ста-
становится все больше неупорядоченным и развивается мелкомасштаб-
мелкомасштабная структура. При R га 1000 отдельные сдвиговые слои за цилинд-
цилиндром, где течение отделяется от цилиндра, порождают неустойчивость
Кельвина-Гельмгольца, которая принципиально двумерна. Спутный
след цилиндра остается турбулентным, но когерентная структура
вихревой дорожки продолжает существовать. Вильямсон также об-
обнаружил начало локальной неустойчивости пограничных слоев на
цилиндре, когда R га 200 000. Можно видеть, что даже для такого
казалось бы простого течения имеет место очень сложный сценарий
неустойчивостей и перехода к турбулентности при возрастании числа
Рейнольдса. Результаты численных и лабораторных экспериментов
не описываются какой-либо теорией настолько хорошо, как этого хо-
хотелось бы математику, но путь к турбулентности, по-видимому, опи-
описывается моделью Рюэля-Такенса-Ньюхауза.
Возмущения распространяются главным образом вниз по потоку,
так что имеет смысл говорить о неустойчивости пограничного слоя
на цилиндре отдельно от неустойчивости спутного следа. Действи-
Действительно, в целом проблема неустойчивостей течений около плохо обте-
обтекаемого тела не может быть изучена методами, отличными от чис-
численных и лабораторных экспериментов, поэтому очень хотелось бы
рассогласовать неустойчивости в спутном следе и пограничных сло-
слоях, чтобы получить некоторое понимание процесса перехода. Погра-
Пограничный слой на искривленном теле, таком как цилиндр, является бо-
более сложным, чем пограничный слой Блазиуса на плоской пластине,
потому что градиент давления изменяется вниз по течению, но при

10.2. Переход течения за плохо обтекаемым телом	25J.
помощи наблюдений и теоретически было найдено, что при больших
значениях числа Рейнольдса сход линий тока на цилиндре происходит
при углах ±0 от передней точки торможения, где 0 « 80°. Согласно
теории безвихревого течения около цилиндра внешнее течение по от-
отношению к пограничному слою на цилиндре имеет скорость 2Fsin0
при угле 0, отсчитываемом от передней точки торможения. Отсюда
получаем грубую оценку для порядка толщины пограничного слоя
S = (vDO/VI/2. Поэтому локальное число Рейнольдса достигает кри-
критического значения 520 в двух точках схода, когда R « 135 000, что
опять грубо согласуется с наблюдениями.
10.2.2. Течение за сферой
Далее изучим неустойчивости течения с однородным потоком за
сферой. Можно было бы начать изучение с рассмотрения картинок
в вашем любимом учебнике по гидродинамике (например, [Batchelor,
1967, Figs. 4.12.8, 5.11.7]). Затем взглянуть на картинки в [Van Dyke,
1982, Figs. 7, 8, 26-28, 49-58] и [Homsy et al., CD2000, Video Library,
"Flow Past a Sphere" и Boundary Layers, "Instability, Transition, and
Turbulence" с подзаголовками "Flow over spheres: effect of Re" и
"Tripping the boundary layer"]. Сценарий развития неустойчивостей
при возрастании числа Рейнольдса от нулевого значения напомина-
напоминает сценарий для течения за цилиндром. Но при интерпретации этих
картинок следует помнить, что конфигурация течения за сферой яв-
является осесимметрической, а не двумерной. Таким образом, имеется
установившееся вторичное течение, и не вихревая дорожка, а перио-
периодически распространяющиеся кольцевые вихри являются третичным
течением.
Определим снова R = VL/u, где L — диаметр сферы. При R = 0
существует единственное устойчивое стационарное течение Стокса,
с симметрией нос-корма, а также осевой симметрией. Для 0 < R <С 1
снова имеет место единственное устойчивое стационарное осесиммет-
рическое течение, но без симметрии нос-корма. Визуальные наблюде-
наблюдения Накамуры [Nakamura, 1976] наводят на мысль, что реализуется
разделение с обратным течением за сферой, которое возникает при
R « 7, я надкритическая устойчивость при возникновении первич-
первичной неустойчивости при Re « 190, выше которого формируется вто-
вторичное нестационарное течение. Ким и Перлстайн [Kim & Pearlstein,
1990] посчитали основное стационарное течение, линеаризовали урав-
уравнения Навье-Стокса и определили характеристики устойчивости; они
нашли первичную неустойчивость при Re « 175 с наиболее неустойчи-
неустойчивой колебательной модой, которая имеет азимутальное волновое чис-
число п = 1. Однако Натарьян и Акривос [Natarajan & Acrivos, 1993],
аналогичным образом вычислив характеристики устойчивости, на-
нашли первичную неустойчивость, удовлетворяющую принципу обмена

252
Гл. 10. Случал перехода к турбулентности
ж
Рис. 10.4. Периодическое по времени течение за круглым цилиндром.
Линии тока через интервалы, равные J- периода, когда R немного больше
чем Rc (по результатам численных расчетов [Jackson 1987, Fig. 13])
устойчивостей, при Re га 210, с наиболее неустойчивой стационарной
модой, сосредоточеной в тороидальной области разделенного течения
непосредственно за сферой, и имеющей азимутальное волновое число
п = 1. Следующая наиболее неустойчивая мода имеет колебательный
характер и становится неустойчивой, когда Re га 277, что, как пред-
предположили Натарьян и Акривос, может быть связано с началом от-
отделения вихрей при вторичной неустойчивости. Танеда [Taneda, 1978]
представил визуальные наблюдения течения при больших числах Рей-
нольдса.

IQ.3. Переход течений в расходящемся канале	253
10.3. Переход течений в расходящемся канале
10.3.1. Введение
Течение несжимаемой вязкой жидкости, движущейся стационарно
в канале, представляет собой классическую задачу гидромеханики,
изучение которой восходит к работе Леонардо да Винчи в пятнадца-
пятнадцатом веке. Мы рассмотрим задачу или скорее круг задач и их приложе-
приложений, используя результаты современных лабораторных эксперимен-
экспериментов, численного моделирования и математических методов. Для пони-
понимания явления неустойчивости всех течений в расходящихся каналах
важно иметь общий подход, а не только детальные и лабораторные и
численные результаты для нескольких частных течений, которые го-
говорят только о свойствах этих частных течений. Математические и
физические идеи формируют этот подход для интерпретации лабора-
лабораторных и численных экспериментов, а также для мотивации постанов-
постановки новых экспериментов. Соби [Sobey, 2000, гл. 10] описал основные
стационарные течения в расходящихся каналах, используя интерак-
интерактивную теорию пограничного слоя и численное моделирование, а так-
также дал описание бифуркаций этих течений; нарушение их симметрии
дает пример того, что называется эффектом Коанда (Coanda).
Теория динамических систем наводит на мысль, что полезно рас-
рассмотреть ансамбль динамически подобных течений при возрастании
числа Рейнольдса от нуля до бесконечности. Теорема Серрина [Serrin,
1959] показывает, что имеет место единственное стационарное ре-
решение, когда R существенно мало и это решение представляет собой
глобальный аттрактор. С возрастанием числа Рейнольдса происходит
последовательность бифуркаций, ведущих к хаосу. Не идентифицируя
хаос с турбулентностью, ожидаем, что хаотический аттрактор будет
представлять собой турбулентность, когда R существенно велико.
Если канал имеет зеркальную симметрию (а, значит, инвариан-
инвариантен относительно группы преобразований Z2) в одной или двух плос-
плоскостях, то можно будет наблюдать сначала нарушение симметрии,
а затем ее востановление при бифуркациях с ростом R. Из теоремы
Серрина следует, что течение при малых значениях числа R облада-
обладает всеми симметриями канала и вполне правдоподобно, что среднее
тУРбулентное течение для любого достаточно большого значения R
также обладает всеми этими симметриями.
Качественные методы являются действенными для интерпретации
лабораторных и численных экспериментов (см. рис. 10.5, 10.6 и 10.7).
Эти эксперименты ясно показывают возникновение надкритической
вилообразной бифуркации и нарушение симметрии. В лабораторных
экспериментах Соби и Дразина [Sobey & Drazin, 1986, Fig. 12] имеет-
имеется очевидность последующей вилообразной бифуркации с нарушени-

254	Гл. 10. Случаи перехода к турбулентности
ем симметрии в поперечном направлении и возникновения развитого
трехмерного течения.
10.3.2. Асимптотические методы
Асимптотические методы можно использовать, если канал имеет либо
почти параллельные стенки, либо почти плоские стенки (т. е. стенки
малой кривизны), хотя ни один из этих случаев не покрывает прак-
практически важного резкого расширения канала с плоскопараллельными
стенками. В первом случае течение локально подобно плоскому тече-
течению Пуазейля и при помощи задачи Орра-Зоммерфельда могут быть
найдены характеристики устойчивости относительно малых возмуще-
возмущений с точностью до членов ведущего порядка асимптотики. Это есть
классическая аппроксимация устойчивости почти параллельных те-
течений, таких как пограничный слой Блазиуса, который был рассмот-
рассмотрен в параграфе 8.5. В последнем случае течение локально подобно
течению Джеффри-Гамеля (см. пример 2.5) и аналогичный асимпто-
асимптотический подход может быть применен к исследованию течения в рас-
расходящимся или сходящимся канале [Fraenkel, 1962, 1963] и его устой-
устойчивости [Sobey & Drazin, 1986]. Использование предположения о том,
что кривизна стенок канала мала, могло бы казаться очень ограничи-
ограничительным. Тем не менее, качественные результаты асимптотической
теории применимы даже когда кривизна стенок не очень мала, таким
образом теория течений Джеффри-Гамеля является более важной, чем
представляется на первый взгляд.
Напомним (см. пример 2.5) классическую теорию Джеффри-
Гамеля точных решений уравнений Навье-Стокса, которые описыва-
описывают стационарное двумерное радиальное течение несжимаемой вязкой
жидкости между твердыми плоскими стенками. Существует беско-
бесконечное количество таких течений для каждой пары значений основ-
основных безразмерных параметров — половинного угла а между двумя
наклонными стенками и числа Рейнольдса
R = Q/2i/,
где Q — величина потока на единицу длины от линейного источни-
источника, расположенного в точке пересечения стенок. Было показано, что
первичное течение Джеффри-Гамеля, которое симметрично и пере-
переходит в плоское течение Пуазейля при a = О, для фиксированного
а ф О обладает докритической вилообразной бифуркацией с наруше-
нарушением симметрии при увеличении Л, когда R переходит через крити-
критическое значение, обозначаемое R2{a).
Существуют серьезные технические трудности в задаче устойчи-
устойчивости течений Джеффри-Гамеля, так как оказывается невозможным
разделить время и все пространственные переменные и, тем самым,

10.3. Переход течений в расходящемся канале
255
Рис. 10.5. Результаты численного моделирования трех стационарных
двумерных течений через резкое расширение слева направо при большом
значении числа Рейнольде а (настолько большом, что следовало бы ожи-
ожидать неустойчивость как асимметричных так и симметричных течений).
(а) Симметричное течение (неустойчивое), (б) Асимметричное течение, (б)
Другое асимметричное течение (по [AUeborn et а/., 1997, Fig 8])
свести задачу о линейной устойчивости к системе обыкновенных диф-
дифференциальных уравнений. Игле [Eagles, 1966] использовал прибли-
приближение (упомянутое в начале этого параграфа) для почти параллель-
параллельного течения, чтобы исследовать устойчивость течения Джеффри-
Гамеля по отношению к временным нормальным модам в пределе при
а ->• 0. Предполагая течение локально-параллельным в любом данном
положении, он нашел, решая задачу Орра-Зоммерфельда, что рост
а от нуля (когда течения Джеффри-Гамеля является просто плос-
плоским течением Пуазейля) до малого положительного значения являет-
является сильным дестабилизирующим фактором. Эта дестабилизация це-
целиком обусловлена изменением профиля скорости основного течения,
потому что Игле пренебрег расходимостью линий тока. Однако Бенкс
с соавторами [Banks et a/., 1988, параграф 5] подвергли сомнению кон-
концептуальную основу использования стандартного метода нормальных
мод в секторе без исключения областей, соответствующих г = 0, оо.
Дин [Dean, 1934] обнаружил, что существует также расщепляемая
задача на собственные значения в виде линейных обыкновенных урав-
уравнений для стационарных двумерных пространственных мод, взяв мо-
ДУ возмущения функции тока в виде
A0.1)

256	Гл. 10. Случал перехода к турбулентности
Рис. 10«в. Течение в расходящимся канале. Установившееся течение во-
воды, преимущественно слева направо, визуализировано с помощью малень-
маленьких частиц, (а) Низкое значение R. (б) Число R увеличено в пять раз (по
[Nakayama, 1988, Fig. 112, 113]; воспроизведено с разрешения профессора
Масанобу Ямамушу (Masanobu Yamamusu))
Здесь г, в являются полярными координатами, а Л, ф должны быть
определены как собственные решения. Отсюда следует, что мода рас-
растет или затухает в пространстве как exp [Re(A)lnr], осциллируя как
exp[i Im(A)lnr]. Задача на собственные значения, как можно теперь
показать, полагая ф = Ф + ф' и линеаризуя вихревое уравнение B.4)
для малых возмущений фг, имеет вид
ф™ + [Л2 + (А - 2J] ф" + Л2(Л - 2Jф =
= R [(Л - 2)Ф' (ф" + Х2ф) - 2Ъ"ф - \Ъ'"ф] ,	A0.2)
ф(в) = ф'(в)=О при 0 = ±а,	A0.3)
где Ф — функция тока основного течения, а штрих здесь обозначает
дифференцирование по в. Назовем эту задачу задачей Дина (Dean).
Имеют место два счетных семейства собственных значений Л с соот-
соответствующими собственными функциями ф. Действительная часть Л
дает алгебраическую скорость роста или затухания моды как функ-
функции г. Представляется, что условием пространственной устойчивос-
устойчивости [Banks et a/., 1988] будет отсутствие роста возмущений вниз и
вверх по потоку, так что Re (А) < 0 для всех мод одного семейства и
Re(A) > 2 для всех мод другого семейства для данных Ф, Л, а. (Хотя
устойчивость и была определена в терминах временного роста малых
возмущений, иногда говорят, что течение является пространственно
устойчивым, если все стационарные малые возмущения затухают по
пространству). Это дает критерий для неустойчивости по отношению
к стационарным двумерным возмущениям, но, конечно, ничего не го-
говорит об осциллирующих по времени возмущениях, т.е. о нормаль-
нормальных модах, которые не подчиняются принципу обмена устойчивостя-
ми, а также и о трехмерных возмущениях. Бэнкс с соавторами [Banks

10.3. Переход течений в расходящемся канале
257
Рис. 10.7. Течение в расходящимся канале с плоскими стенками и полу-
полууглом a = 10° при R = 300. Установившееся течение воды преимущест-
преимущественно слева направо, главным образом, визуализируется с помощью линии
пузырьков кислорода, которые производились через восемь секундных ин-
интервалов в каждом из четырех положений (по [Nakayama, 1988, Fig. 105];
воспроизведено с разрешения профессора Ясуки (Yasuki) Накаяма)
et a/., 1988] нашел таким способом, что расходимость течения явля-
является сильным дестабилизирующим фактором, а сходимость — сильно
стабилизирующим. Сравните две фотографии на рис. 10.8.
МакАльпин и Дразин [McAlpine & Drazin, 1998] удовлетворили ли-
линеаризованному уравнению завихренности нестационарного двумер-
двумерного течения асимптотически при больших г, выбрав моды в виде
ф'(г, 0, t) = Re {exp [ifc (a lnr - ct/a2r2)] f(y)} ,	A0.4)
где у = в/a. Мотивом для их предположения послужило то обсто-
обстоятельство, что экспонента, обратно пропорциональная квадрату г и
пропорциональная 2, нужна для баланса членов d('/dt и А(' в возму-
возмущенном вихревом уравнении (где ?' — возмущение завихренности).
Заметим, что удобна нормировка с на а2, для того чтобы впоследст-
впоследствии получить уравнение Орра-Зоммерфельда, гладким образом пере-
переходя к пределу при a —)• 0. Это решение с разделенными переменными
не удовлетворяет точно линеаризованному вихревому уравнению, но
удовлетворяет ему асимптотически при г^оои фиксированных 2, у.
Отсюда следует, что
- [Л-2 + (fc
+ 2iaJ] /"
2ia)U - кс]
+ Aiakc{k
к2(к + 2iaJ/ =
(/" - k2f) - kU"f+
ia)f} ,
A0.5)

258
Гл. 10. Случая перехода к турбулентности
Рис. 10.8. (а) Течение при резком сжатии, (б) Течение при резком рас-
расширении (по [Nakayama, 1988, Figs. 114, 115]; воспроизведено с разрешения
профессора Масанобу Ямамушу)
где штрих обозначает дифференцирование по у и U определена как
СУ (у) = ac№@)/d0. Граничные условия дают
/(У) = /*(») = 0 при у = ±1.
A0.6)
Заметим, что при с = 0 и обозначении А = ik/a уравнение A0.5)
становится эквивалентным уравнению Дина A0.2), а когда a = 0 оно
сводится уравнению Орра-Зоммерфельда:
/v _ 2k2f" + k4f = ikR {(U - с) (/" - k2f) - U"f] . A0.7)
Заметим далее, что уравнение A0.4) дает классическую моду Орра-
Зоммерфельда в виде
в пределе при a —у 0 для фиксированных безразмерного расстояния
вниз по потоку х = (г — ro)/aro и локальной полуширины аго канала
в положении г = го- Таким образом, получено обобщение задач устой-
устойчивости Орра-Зоммерфельда и Дина для каналов с почти плоскими
стенками.
МакАльпин и Дразин [McAlpine & Drazin, 1998] численно решили
задачу на собственные значения A0.5), A0.6) для нескольких случа-
случаев и подтвердили сделанные ранее выводы о сильном стабилизиру-
стабилизирующем влиянии сходимости и сильном дестабилизирующем влиянии
расходимости в канале. В этой задаче волны Толлмина-Шлихтинга
задачи Орра-Зоммерфельда преобразуются непрерывно в моды Ди-
Дина с уменьшением волнового числа возмущения и являются, таким
образом, связанными с вилообразной бифуркацией течений Джеффри-
Гамеля. Эти результаты также проливают свет на значительное изме-
изменение механизма неустойчивости вследствии даже легкого отклонения
от параллельности стенок канала.

10.3. Переход течений в расходящемся канале	259
10.3.3. Некоторые парадоксы
Применяя теорию течений Джеффри-Гамеля к каналу с почти парал-
параллельными плоскими стенками, Соби и Дразин [Sobey & Drazin, 1986]
предположили, что первая бифуркация с потерей симметрии происхо-
происходит когда R = Яс, где
Rc к R2 Q
Параметры а, /3 определяются как углы между касательными плос-
плоскостями к стенкам канала и плоскостью (ж, z) в положении ж; ось
х направлена вдоль канала, вниз по течению, а ось z — в попереч-
поперечном направлении. (Напомним, что R2 представляет собой значение Л,
где симметричное течение впервые становится неустойчивым, при ви-
вилообразной бифуркации течений Джеффри-Гамеля). Представляется,
что этот критерий находит подтверждение в некоторых численных
экспериментах, хотя и не было специально предпринято эксперимен-
эксперимента для проверки этого критерия, когда он должен был бы выполняться
(для каналов со стенками очень малой кривизны). Теория простран-
пространственной устойчивости [Banks et aZ., 1988] показывает, что, когда
R > Дс, нарушается принцип Сен-Венана и малые стационарные воз-
возмущения течения на входе или на выходе могут существенно влиять
на течение во всем канале. Этот вывод подтверждается численными
результатами [Dennis et aZ., 1997]. Отсюда следует, что эксперимен-
экспериментаторы должны жестко контролировать условия на входе и выходе,
так как эти условия могут существенно влиять на их наблюдения и
поэтому должны быть известны для того, чтобы повторить экспери-
эксперименты.
Тем не менее при R > Rc не существует симметричного или
асимметричного течения Джеффри-Гамеля, представляющего наблю-
наблюдаемые установившиеся течения в канале (см. рис. 10.5 (б)). Далее,
течения Джеффри-Гамеля демонстрируют первую неустойчивость и
нарушение симметрии при докритической вилообразной бифуркации,
тогда как лабораторные и численные эксперименты дают первую не-
неустойчивость и нарушение симметрии для надкритической вилооб-
вилообразной бифуркации, хотя эти эксперименты и не производились для
малых полууглов а между стенками канала. Хамадиш с соавторами
[Hamadiche et al., 1994] провел специальные численные исследования
этой неустойчивости течения Джеффри-Гамеля в канале, который яв-
являлся сектором, ограниченным дугами малого и большого радиусов, и
нашел неустойчивость при сверхкритической бифуркации Хопфа для
некоторого диапазона значений угла а. Эти замечания указывают на
то, что течения Джеффри-Гамеля не описывают течение в канале,
если R > Rc.

260	Гл. 10. Случал перехода к турбулентности
Плоское течение Пуазейля, как хорошо известно из решения зада-
задачи Орра-Зоммерфельда, обладает докритической бифуркацией Хопфа
при числе Рейнольдса Rc « 3848. (Заметим, что определенное здесь
число Рейнольдса составляет две третих от числа Рейнольдса, опре-
определенного в параграфе 8.7: § х 5772 = 3848). Однако соответству-
соответствующее приближающее течение Джеффри-Гамеля, как было показано
в результате решения задачи Дина, обладает докритической вилооб-
вилообразной бифуркацией, когда R = 3848, если полуугол а составляет 0,07
градусов. Это очень маленький угол, который мало отличается от от-
отклонения, которое допускается в промышленности при изготовлении
каналов с параллельными стенками. МакАльпин и Дразин [McAlpine
& Drazin, 1998] воспроизвели две различные моды неустойчивости,
связанные с задачами Орра-Зоммерфельда и Дина, но не объяснили,
почему докритическая вилообразная бифуркация происходит в расхо-
расходящимся канале. Можно было бы добавить, что весьма правдоподоб-
правдоподобно, что если стенки канала приблизительно параллельны, т.е. если
тах.х[<х(х) +/3(ж)] <С 1, то реализуется бифуркация Хопфа, а не вило-
вилообразная бифуркация, но в настоящее время не существует ни теории,
ни эксперимента, чтобы описать это качественное изменение в пове-
поведении системы, когда таха:[а(ж) +/3(ж)] стремится к нулю.
10.3.4. Нелинейные волны
Татти [Tutty, 1996] при численном изучении установившихся двумер-
двумерных течений в канале обнаружил некоторые замечательные волны,
сочетающиеся в основной части с плоскими стенками (как в тече-
течении Джеффри-Гамеля), но более сложные на входе и выходе. Для не-
нескольких пар значений полуугла а между плоскими стенками и числа
Рейнольдса R он нашел течения, которые, по-видимому, приближенно
периодичны по In r для больших значений г расстояния вниз по тече-
течению [Tatty, 1996, Figs. 7-10]. Такая стационарная волна описывается
функцией тока, которая зависит как от г, так и от в, и сосуществу-
сосуществует с некоторыми течениями Джеффри-Гамеля, функции тока которых
зависят только от в. Можно было бы предположить, опираясь на ре-
результаты численных экспериментов Татти, что эти волны являются
устойчивыми, по крайней мере по отношению к двумерным стацио-
стационарным возмущениям при соответствующих значениях a, R.
Керсуэлл с соавторами [Kerswell et aZ., 2002] пролили свет на свой-
свойства этих стационарных сильно нелинейных двумерных волновых воз-
возмущений течений Джеффри-Гамеля при помощи численных расчетов.
Эти авторы обнаружили сложную структуру бифуркаций этих возму-
возмущений, используя метод интегрирования вдоль траекторий. Заметим,
что в соответствии с наблюдениями, при увеличении числа Рейнольд-
Рейнольдса за критическое значение после первой бифуркации, нарушающей
симметрию, короткий пакет подобных волн (см. рис. 10.5 (б)) развива-

Упражнения
ется вниз по течению в расширяющихся частях каналов, и в других
упомянутых здесь экспериментах. Таким образом, волны Татти пред-
представляют собой интересное продвижение по сравнению с течениями
Джеффри-Гамеля и их неустойчивостями на пути к хаосу и переходу
к турбулентности в теории течения в расходящимся канале.
10.3.5. Выводы
Суммируя, можно сказать, что был описан существенный прогресс
в понимании ранних стадий перехода к турбулентности для течений
в каналах, сделанный за последние два десятилетия, однако понима-
понимание последующих стадий перехода еще слабое. Упомянутый прогресс
дает практическую возможность качественно интерпретировать ос-
основные свойства течения в большом множестве каналов, при условии,
что число Рейнольдса невелико. Изложенные идеи иллюстрируют бо-
более общо необходимость понимания устойчивости непараллельных те-
течений. Представляется несомненным, что данные задачи о бифурка-
бифуркации и неустойчивости течений в каналах заключают в себе поучи-
поучительный случай изучения гидродинамической устойчивости.
Упражнения
10.1. Неустойчивость спутного следа и образование вихревой до-
дорожки. Дано, что установившееся двумерное течение вокруг те-
тела плохо обтекаемой формы с однородным потоком вязкой не-
несжимаемой жидкости формирует спутный след, который стано-
становится неустойчивым при бифуркации Хопфа и возрастании чис-
числа Рейнольдса выше критического значения. Течение, образо-
образовавшееся в результате бифуркации, выглядит при умеренных
значениях числа Рейнольдса как вихревая дорожка, распростра-
распространяющаяся от задней части тела в виде зигзагообразных рядов
вихрей (с одинаковым и противоположным направлениями вра-
вращения, когда тело симметрично относительно плоскости, парал-
параллельной однородному потоку), которая стационарно распростра-
распространяется вниз по течению.
Фон Карман [Karman, 1911] моделировал вихревую дорожку в
спутном следе от симметричного тела как безвихревое течение
невязкой жидкости около линии вихрей с циркуляцией к в точках
(та + Vty |Ь) и —к — в точках ((п + \)а + Vt, — |b) в плоскости
(ж, у) при га, n = 0, ±1, ±2,... и заданных постоянных расстояних
а, Ь > 0 и некоторой постоянной скорости V.
Используя теорию плоского безвихревого течения, покажите, что
скорость вихревой дорожки Кармана определяется выражением
V = Gr/c/a)thGr6/a).

262	Гл. 10. Случаи перехода к турбулентности
Докажите,	что	нестационарное	течение
имеет период a2/irKth(nb/a) по времени, а также период а по
х. Изобразите линии тока при t = 0 [Lamb, 1932, параграф 156].
10.2. Неустойчивость вихревой дорожки. Выбирая вихревую поло-
полосу из упражнения 10.1 в качестве основного течения, сместим
вихри следующим образом: (ma -f Vt + жт, |б + Ут), {{п + \)а +
+Vt + ajJj,—|6+yjj). Покажите (используя теорию Флоке для не-
устойчивостей периодических решений, если вы ее знаете), что
выглядит вполне правдоподобным, если каждое линейное возму-
возмущение является суперпозицией мод
хт = ае , ут '•
где 0 < ф < 2тг без ограничения общности, и а, а', /3, /3' —
некоторые функции t. (Если ф = 0, то мода обладает той же
самой длиной волны а по ж как и основное течение; если ф = тг,
мода является субгармонической, но изменение фазы ф моды на
длине волны а может составлять любой угол).
Предполагая, что имеется двумерное безвихревое течение около
линии вихрей и линеаризуя бесконечную систему обыкновенных
дифференциальных уравнений, которые описывают координаты
каждого вихря в двух рядах вихрей по отношению к малым сме-
смещениям, покажите, что
к at	к at
где
А = -ф{2тг -ф)~ 7r2sech2(for),
В = i [Tr^sh &(тг - ф) sech (kit) + 7r2sh(fc^)sech2(br)] ,
С = тг2сЦкф) sech2(fc7r) - тг^сЬ &(тг - ^)sech(for)
и к = b/a.
Докажите, что приведенная выше мода может быть выражена в
виде суммы двух типов независимых мод: симметричной моды
с а1 = а, /3' = —C и антисимметричной моды са'= —а, /3' = /3.
Полагая а, C ос е**, покажите, что
а2з/к = В±(А2-С2I/2
для антисимметричной моды и что подобная формула (с заме-
заменой В на —В) описывает симметричную моду. Докажите, что

Упражнения	263
вихревая дорожка является экспоненциально неустойчивой, ес-
если только равенство Ь = кса не выполняетя в точности, где
кс = тг^-1^-1/2) = 0,2806 [Lamb, 1932, параграф 156].
10.3. *Эволюция малых возмущений течения Джеффри-Гамеля во
времени и по пространству. Уравнение завихренности для дву-
двумерного движения вязкой несжимаемой жидкости имет вид
ac + ia^
at rd{r,9) ц'
где ф — функция тока, С = —&Ф — завихренность, а лапласиан
имеет вид А = д2 /дг2 + д/гдг + д2 /г2дв2 в полярных коор-
координатах (г, в). Взяв малые двумерные возмущения радиального
течения, положите
где Ф@) — решение задачи Джеффри-Гамеля (см. пример 2.5),
линеаризуйте уравнение завихренности и граничные условия на
фиксированных твердых стенках в = -±а и покажите, что
d9d? ,Rd4d^ 2i?d*<ty
~w~fr + ^ аё5"^+й~ !р-дб' (Е10'2)
1>'(г, в, t) = ^(r, в, t) = 0 при в = ±а,	(Е10.3)
где С = —Аф' — возмущение завихренности, число Рейнольдса
определяется как R = Q/2u и используются безразмерные пере-
переменные (см. упражнение 2.13).
Положив для мод
i>(r,9,t) = Re {exp [ifc (огЧпг - rf/aV)] f(y)} , (E10.4)
где у = в/а, к — действительное волновое число, ас — комп-
комплексная скорость, покажите, что
= iR{ [(к + 2\a)U - кс] (/" - k2f) - kU"f+
+2iaU'f + 4iakc{k + ia)/}	(E10.5)
в пределе при г —У со для фиксированного t и, что
f(y) = f'(y) = 0 при у = ±1,	(Е10.6)
где U(у) = ac№@)/d0 и штрих обозначает дифференцирова-
дифференцирование по у. Проверьте, что отсюда следует уравнение Орра-
Зоммерфельда, если a = 0 и уравнение Дина (Е2.4), если с = 0
[MeAlpine & Drazin, 1998].

Список литературы
Abramowitz, M. & Stegun, LA. (Editors) A964) Handbook of Mathematical
Functions, Appl. Math. Ser. No. 55 (Govt. Printing Office, Washington,
D.C.; also Dover, New York, 1965). Рус. пер.: Справочник по специаль-
специальным функциям с формулами, графиками и математическими табли-
таблицами/Под ред. М. Абрамовица, И. Стиган. - М.: Наука, 1979.
AUeborn, N., Nandakumar, К., Raszillier, & Durst, F. A997) Further contri-
contributions on the two-dimensional flow in a sudden expansion, J. Fluid Mech.
330, 169-188.
Andereck, CD., Liu, S. & Swinney, H. A986) Flow regimes in a circular Cou-
ette system with independently rotating cylinders, J. Fluid Mech. 164,
155-183.
Baines, P.G. & Gill, A. E. A969) On thermohaline convection with linear gra-
gradients, J. Fluid Mech. 37, 289-306.
Baines, P.G., & Mitsudera, H. A994) On the mechanism of shear flow instabi-
instabilities, J. Fluid Mech. 276, 327-342.
Baines, P.G., Majumdar, S. & Mitsudera, H. A996) The mechanics of the Toll-
mien-Schlichting wave, J. Fluid Mech. 312, 107-124.
Banks, W.H.H., Drazin, P.G. & Zaturska, M.B. A988) On perturbation of Jef-
frey-Hamel flow, J. Fluid Mech. 186, 559-581.
Barcilon, A. & Drazin, P.G. B001) Nonlinear waves of vorticity, Studies Appl.
Math. 106, 437-479.
Batchelor, G.K. A967) An Introduction to Fluid Dynamics (Cambridge Uni-
University press). Рус. пер.: Бэтчелор Дж. Введение в динамику жидкос-
жидкости. - М.: Мир, 1970.
Batchelor, G.K. & Gill, A.E. A962) Analysis of the stability of axisymmetric
jets, J. Fluid mech. 14, 529-551.
Bayly, B.J., Orszag, S.A. & Herbert, T. A988) Instability mechanisms in she-
shear-flow transition, Ann. Rev. Fluid Mech. 20, 359-391.
Beale, J.T., Kato, T. & Majda, A. A984) Remarks on the breakdown of
smooth solutions for the 3-dimensional Euler equations, Commun. Math.
Phys. 94, 61-66.

Список литературы	265
Bellman, R. & Pennington, R.H. A954) Effects of surface tension and viscosity
on Taylor instability, Quart Appl. Math. 12, 151-162.
Benard, H. A900) Les tourbillons cellulaires dans une nappe liquide, Revue
Gen. Sci. Pure Appl 11, 1261-1271, 1309-1328.
Benjamin, T.B. A976) Application of Leray-Schauder degree theory to pro-
problems of hydrodynamic stability, Math. Proc. Camb. Phil. Soc. 79, 373-
392.
Benjamin, T.B. & Mullin, T. A982) Notes on the multiplicity of flows in the
Taylor experiment, J. Fluid Mech. 121, 219-230.
Bertolotti, F.P., Herbert, T. & Spalart, P.R. A992) Linear and nonlinear sta-
stability of the Blasius boundary layer, J. Fluid Mech. 242, 441-474.
Betchov, R. & Criminale, W.O. A967) Stability of Parallel Flows (Academic
Press, New York). Рус. пер.: Бетчов Р. Вопросы гидродинамической
устойчивости. - М.: Мир, 1971.
Boberg, L. & Brosa, U. A988) Onset of turbulence in a pipe, Z. Naturforsch.
439, 697-726.
Bohr, N. A909) Determination of the surface-tension of water by the method
of jet vibration, Phil. Trans. Roy. Soc. bond. A 209, 281-317. Also in
Collected Works 1, 29-65. Рус. пер.: Бор Н. Определение коэффициента
поверхностного натяжения методом колебания струи// В кн.: Бор Н.
Избранные научные труды: Т. 1: Статьи A909-1925). - М.: Наука,
1970.
Boussinesq, J. A903) Theorie Analytique de la Chaleur (Gautheir-Villars, Pa-
Paris).
Bouthier, M. A973) Stabilite line air e des ecoulements presque paralleles. Partie
II. La couche limite de Blasius, /. Mec. 12, 75-95.
Briggs, R. J. A964) Electron-Stream Interactions in Plasmas (M.I.T. Press,
Cambridge, MA).
Brown, S. N. & Stewartson, K. A979) On the secular stability of a regular
Rossby neutral mode, Geophys. Astrophys. Fluid Dyn. 14, 1-18.
Burridge, D. M. A970) The instability of round jets, Tech. Rep., No. 29,
Geophys. Fluid Dynamics Lost., Florida State University.
Busse, F. H. & Clever, R. M. A979) Instability of convection rolls in a fluid of
moderate Prandtl number, J. Fluid Mech. 91, 319-335.
Busse, F. H. & Whitehead, J. A. A971) Instabilities of convection rolls in a
high Prandtl number fluid, J. Fluid Mech. 47, 305-320.
Butler, K. M. & Farrell, B. F. A992) Three-dimensional optimal perturbations
in viscous shear flow, Phys. Fluids A 4, 1637-1650.
Campbell, L. & Garnett, W. A882) Life of James Clerk Maxwell (Macmillan,
London).
Carlson, D. E., Widnall, S. E. & Peeters, M. F. A982) A flow-visualization
study of transition in plane Poiseuille flow, J. Fluid Mech. 121, 487-505.

266	Список литературы
Case, К. М. A960) Stability of inviscid plane Coutte flow, Phys. Fluids 3, 143-
148.
Cesari, L. A959) Asymptotic Behaviour and Stability Problems in Ordinary
Differential Equations (Springer, Berlin). Рус. пер.: Чезари Л. Асимп-
Асимптотическое поведение и устойчивосить решений обыкновенных диф-
дифференциальных уравнений. - М.: Мир, 1964.
Chandrasekhar, S. A961) Hydrodynamic and Hydromagnetic Stability (Oxford
University Press).
Christopherson, D. G. A940) Note on the vibration of membranes, Quart.
J. Math. 11, 63-65.
Coles, D. A965) Transition in circular Couette flow, J. Fluid Mech. 21, 385-
425.
Colson, D. A954) Wave-cloud formation at Denver, Weatherwise 7, 34-35.
Craik, A. D. D. A971) Non-linear resonant instability in boundary layers,
J. Fluid Mech. 50, 393-413.
Craik, A. D. D. A985) Wave Interactions and Fluid Flows (Cambridge
University Press).
Craik, A. D. D. & Criminale, W. O. A986) Evolution of wavelike disturbances
in shear flows: a class of exact solutions of the Navier-Stokes equations,
Proc. Roy. Soc. Lond. A 406, 13-26.
Davey, A. A962) The growth of Taylor vortices in flow between rotating cy-
cylinders, J. Fluid Mech. 14, 336-368.
Dean,W. R. A934) Note on the divergent flow of fluid, Phil. Mag. 18G), 759-
777.
Dennis, S. С R., Banks, W. H. H., Drazin, P. G. & Zaturska, M. B. A997)
Flow along a diverging channel, /. Fluid Mech. 336, 183-202.
Donnelly, R. J. & Glaberson, W. A966) Experiments on the capillary instabi-
instability of a liquid jet, Proc. Roy. Soc. Lond. A 290, 547-556.
Donnelly, R. J. & Simon, N. J. A960) An empirical torque relation for super-
supercritical flow between rotating cylinders, /. Fluid Mech. 7, 401-418.
Drazin, P. G. A961) Discontinuous velocity profiles for the Orr-Sommerfeld
equation, J. Fluid Mech. 10, 571-583.
Drazin, P. G. A974) On instability of slowly-varying flow, Quart. J. Mech.
Appl. Math. 27, 69-86.
Drazin, P. G. A975) On the effect of side walls on Benard convection, Zeit.
angew. Math. Phys. 26, 239-243.
Drazin, P. G. A989) Internal gravity waves and shear instability, pp. 61-73 of
Waves and Stability in Continuous Media, eds. A. Donato & S. Giambo
(Editel, Italy).
Drazin, P. G. A992) Nonlinear Systems (Cambridge University Press).
Drazin. P. G. & Reid, W. H. A981) Hydrodynamic Stability (Cambridge Uni-
University Press).

Список литературы	267
Eagles, P. M. A966) The stability of a family of Jeffery-Hamel solutions for
divergent channel flow, J. Fluid Mech. 24, 191-207.
BHahou, S., Tumin, A. & Wygnanski, I. A998) Laminar-turbulent transition
in Poiseuille pipe flow subjected to periodic perturbation emanating from
the wall, J. Fluid Mech. 361, 333-349.
Ellingsen, T.& Palm, E. A975) Stability of linear flow, Phys. Fluids 18, 487-
488.
Feigenbaum, M. J. A980) The transition to aperiodic behaviour in turbulent
systems, Commun. Math. Phys. 77, 65-86.
Fenstermacher, P.R., Swinney, H. L. & Gollub, J. P. A979) Dynamical insta-
instabilities and the transition to chaotic Taylor vortex flow, J. Fluid Mech.
94, 103-123.
FJ0rtoft, R. A950) Application of integral theorems in deriving criteria of
instability for laminar flows and for the baroclinic circular vortex, Geofys.
Publ.} oslo 17F), 1-52.
Fraenkel, L . E. A962) Laminar flow in symmetrical channels with slightly cur-
curved walls. I. On the Jeftrey-Hamel solutions for flow between plane walls,
Proc. Roy. Soc. Lond. A 267, 119-138.
EVaenkel, L .E. A963) Laminar flow in symmetrical channels with slightly
curves walls. II. An asymptotic series for the stream function, Proc. Roy.
Soc. Lond. A 272, 406-428.
Gaster, M. A962) A note on the relation between temporally-increasing and
spatially-increasing disturbances in hydrodynamic stability, J. Fluid
Mech.14, 222-224.
Gaster, M. A974) On the effects of boundary-layer growth on flow stability,
J. Fluid Mech. 66, 465-480.
Gent, P.R. & Leach, H. A976) Baroclinic instability in an eccentric annulus,
J. Fluid Mech. 77, 769-788.
Goldstein, R. J. & Graham, D. L. A969) Stability of a horizontal fluid layer
with zero shear boundaries, Phys. Fluids 12, 1133-1137.
Goldstein, S. A931) On the stability of superposed streams of fluids of different
densities, Proc. Roy. Soc. Lond. A 132, 524-548.
Gor'kov, L.P. A957) Stationary convection in a plane liquid layer near the
critical heat transfer point, Sov. Phys. JETP 6, 311-315; пер. на англ.
ст.: Горькое Л. П. Стационарная конвекция в плоском слое жидкос-
жидкости вблизи критического режима теплопередачи, ЖЭТФ. - 1957, 33,
402-407.
Gortler, Н. A940) Uber eine dreidimensionale Instabilitat laminarer Grenz-
schichten an konkaven Wanden, Nachr. Ges. Wiss. Gottingen N.F. 1,
No. 1, 1-26. Translated as "On the three-dimensional instability of
laminar boundary layers on concave walls", Tech. Memor. Nat. Adv.
Comm. Aero., Wash. No. 1375 A954).
Gregory, N., Stuart, J. T. & Walker, W. S. A955) On the stability of three-
dimensional boundary layers with application to the flow due to a rotating
disc, Phil. Trans. Roy. Soc. Lond. A 248, 155-199.

268	Список литературы
Gull, S. F. A975) The X-ray, optical and radio properties of young supernova
remnants, Mon. Not. Roy. Astr. Soc. 171, 263-278.
Hall, P. A983) The linear development of Gortler vortices in growing boundary
layers, J. Fluid Mech. 130, 41-58.
Hamadiche, M., Scott, J. & Jeandel, t>. A994) Temporal stability of Jeffery-
Hamel flow, J. Fluid Mech. 268, 71-88.
Hamel, G. A916) Spiralformige Bewegungen zaher Flussigkeiten, Jber. dtsch.
Math.-Ver. 25, 34-60.
Harris, D. L. & Reid, W. H. A964) On the stability of flow between rotating
cylinders. Part 2. Numerical*analysis. J. Fluid Mech. 20, 95-101.
Harrison, W. J. A908) The influence of viscosity on the oscillations of
superposed fluids, Proc. bond. Math. Soc. 6B), 396-405.
Haurwitz, B. A931) Zur Theorie der Wellenbewegungen in Luffc und Wasser,
Veroff. Geofys. Inst. Univ. Leipzig 6, No. 1.
Heisenberg, W. A924) Uber Stabilitat und Turbulenz von Flussigkeitsstromen,
Ann. Phys., Leipzig 74D), 577-627. Translated as "On stability and
turbulence of fluid flows", Tech. Memor. Nat. Adv. Comm. Aero., Wash.
No. 1291 A951).
Helmholtz, H. von A868) Uber discontinuirliche Flussigkeitsbewegungen,
Monats. Konigl. Preuss. Akad. Wiss., Berlin 23, 215-228. Also in
Wissenschaftliche Abhandlungen 1 A882), 146-157. Translated as "On
discontinuous movements of fluids", Phil. Mag. 36D) A868), 337-346.
Рус. пер.: Гелъмголъц Г. О прерывном движении жидкости// В кн.:
Гелъмголъц Г. Основы вихревой теории. - Москва-Ижевск: ИКИ,
2002, 41-51.
Helmholtz, H. von A890) Die Energie der Wogen und des Windes, Ann.
Phys. 41, 641-662. Also in Sitz. Akad. Wiss., Berlin 23, 853-872, and
Wissenschaftliche Abhandlungen 3 A895), 333-355. Translated as "The
energy of the billows and the wind" by Cleveland Abbe, pp. 112-129
of The Mechanics of the Earthys Atmosphere (Smithsonian Institute,
Washington, D.C., 1891).
Herbert, T. A988) Secondary instability of boundary layers, Ann. Rev. Fluid
Mech. 20, 487-526.
Herivel, J. W. A955) The derivation of the equations of motion of an ideal fluid
by Hamilton's principle, Proc. Camb. Phil. Soc. 51, 344-349.
Herron, I.H. A987) The Огг-Sommerfeld equation of infinite intervals, SI AM
Rev. 29, 597-620.
Hinch, E.J. A973) Instabilities due to dissipation, Eureka 36, 17-18.
Hocking, L. M. A975) Non-linear instability of the asymptotic suction velocity
profile, Quart. J. Mech. Appl. Math. 28, 341-353.
Horton, C. W. & Rogers, F. T. A945) Convection currents in a porous
medium, J. Appl. Phys. 16, 367-370.
Howard, L. N. A961) Note on a paper of John W. Miles, J. Fluid Mech. 10,
509-512.

Список литературы	269
Howard, L. N. A964) The number of unstable modes in hydrodynamic stability
problems, J. Mec. 3, 433-443.
Huerre, P. & Monkewitz, P. A. A990) Local and global instabilities in spatially
developing flows, Ann. Rev. Fluid Mech. 22, 473-537.
Huerre, P. & Rossi, M. A998) Hydrodynamic instabilities: open flows, Chapter
2, pp. 81-294, of Hydrodynamics and Nonlinear Instabilities, eds. C.
Godreche & P. Manneville (Oxford University Press).
Hughes, T. H. & Reid, W. H. A965) On the stability of asymptotic suction bo-
boundary-layer profile, J. Fluid Mech. 23, 715-735.
Jakson, C. P. A987) A finite-element study of the onset of vortex shedding in
flow past variously shaped bodies, J. Fluid Mech. 182, 23-45.
Jeans,, J. H. A902) Stability of a spherical nebula, Phil Trans. Roy. Soc. bond.
A 199, 1-53.
Jeffery, G. B. A915) The two-dimensional steady motion of a viscous fluid,
Phil. Mag. 29F), 455-465.
Joseph, D. D. A965) On the stability of the Boussinesq equations, Arch. Rat.
Mech. Anal. 20, 59-71.
Joseph, D. D. A968) Eigenvalue bounds for the Orr-Sommerfeld equation, J.
Fluid Mech. 33, 617-621.
Joseph, D. D. A969) Eigenvalue bounds for the Огг-Sommerfeld equation. Part
2, J. Fluid Mech. 36, 721-734.
Joseph, D. D. A976) Stability of Fluid Motions (Springer-Verlag, Berlin). Рус.
пер.: Джозеф Д. Устойчивость движений жидкости. - М.: Мир, 1981.
Kachanov, Y. S. A994) Physical mechanisms of laminar-boundary-layer tran-
transition, Ann. Rev. Fluid Mech. 26, 411-482.
Kachanov, Y. S., Kozlov, V. V. & Levchenko, V. Y. A975) The development
of small-amplitude oscillations in a laminar boundary layer, Fluid Mech.
Sov. Res. 8 A979), 152-256. Рус: Качанов Ю. С, Козлов В. В., Лев-
Левченко В. Я. Развитие колебаний малой амплитуды в ламинарном по-
пограничном слое, Учен. зап. ЦАГИ. - 1975, 6E), 137-140.
Кагтап, Т. von A911) Uber den Mechanismus des Widerstandes, den ein
bewegter Korper in einer Flussigkeit erfahrt, Nachr. Ges. Wiss.
Gottingen, Math.-phys. Klasse, 509-517. Also in Collected Works 1
A956), 324-330.
Kelly, R. E. A967) On the stability of an inviscid shear layer which is periodic
in space and time, J. Fluid Mech. 27, 657-689.
Kelvin, W. A871) Hydrokmetic solutions and observations, Phil. Mag. 42D),
362-377. Also in Math. Phys. Papers, IV A910), 69-85.
Kelvin, W. A880) On a disturbing infinity in Lord Rayleigh's solution for waves
in a plane vortex stratum, Nature 23, 45-46. Also in Math. Phys. Papers,
IV A910), 186-187.
Kelvin, W. A887) Stability of fluid motion - rectilineal motion of viscous fluid
between two parallel planes, Phil. Mag. 24E), 188-196. Also in Math.
Phys. Papers, IV A910), 321-330.

270	Список литературы
Kerswell, R. R., Tutty, О. R. & Drazin, P. G. B002) Spatially periodic steady
flows of a viscous fluid between two inclined planes (to be pubished).
Kim, I. & Pearlstein, A. J. A990) Linear stability of the flow past a sphere, J.
Fluid Mech. 211, 73-93.
King, G. P. & Stewart, I. N. A991) Symmetric and chaos, pp. 257-315 in
Nonlinear Equations in the Applied Science, eds. W. F. Ames & C. F.
Rogers (Academic Press, New York).
Klaasen, G. P. & Peltier, W. R. A985) The onset of turbulence in finite-ampli-
finite-amplitude Kelvin-Helmholtz billows, J. Fluid Mech. 155, 1-35.
Klebanoff, P. S., Tidstrom, K. D. & Sargent, L. M. A962) The three-dimen-
three-dimensional nature of boundary-layer transition, J. Fluid Mech. 12, 1-34.
Koschmieder, E. L. A993) Benard Cells and Taylor Vortices (Cambridge Uni-
University press).
Krasny, R. A986) Desingularization of periodic vortex sheet roll-up, J. Com-
putat. Phys. 65, 292-313.
Krishnamurti, R. A973) Some further studies on the transition to turbulent
convection, J. Fluid Mech. 60, 285-303.
Krishnamurti, R. A975) On cellular cloud pattern. Part 3.: Applicability of the
mathematical and laboratory models. J. Atmos. Sci. 32, 1373-1383.
Lamb, H. A932) Hydrodynamics, 6th edn. (Cambridge University Press). Рус.
пер.: Ламб X. Гидродинамика. - М.-Л.: Гостехиздат, 1947.
Landau, L. D. A944) On the problem of turbulence, Dokl. Akad. Nauk SSSR
44, 311-314. Also in Collected Papers, ed. D. ter Haar (Pergamon,
Oxford), 387-391; пер. на англ. ст.: Ландау Л. К проблеме турбулент-
турбулентности, ДАН СССР. -1944, 44, 339-342.
Landau, L. D. A946) On the vibrations of the electronic plasma, J. Phys. USSR
10, 23-34. Also in Collected Papers, ed. D. ter Haar (Pergamon, Oxford),
445-460; пер. на англ. ст.: Ландау Л. О колебаниях электронной плаз-
плазмы, ЖЭТФ. РАН. - 1946, 16, 574-586.
Landau, L. D. & Lifshitz, Е. М. A987) Fluid Mechanics, 2nd edn. (Addison-
Wesley, New York); пер. на англ.: Ландау Л. Д., Лифшиц Е. М. Гид-
Гидродинамика. - М.: Наука. Физмат лит, 1986.
Lapwood, E. R. A948) Convection of a fluid in a porous medium, Proc. Carrib.
Phil. Soc 44, 508-521.
Leibovich, S. A969) Stability of density stratified rotating flow, AIAA J. 7,
177-178.
Leibovich. S. A979) Waves in parallel or swirling stratified shear flows, J. Fluid
Mech. 93, 401-412.
Lewis, D. J. A950) The instability of liquid surface when accelerated in a di-
direction perpendicular to their planes, II, Proc. Roy. Soc. bond. A 202,
81-96.
Libchaber, A. & Maurer, L. A978) Local probe in a Rayleigh-Benard experi-
experiment in liquid helium, J. Physique Lett. 39, L369-372.

Список литературы	271.
Lin, C.C. A955) The Theory of Hydrodynamic Stability (Cambridge University
Press). Рус. пер.: Линь Цзя-цзяо Теория гидродинамической устойчи-
устойчивости. - М.: Изд-во иностр. лит., 1958.
Lin, S. Р. & Reitz, R. D. A998) Drop and spray formation from a liquid jet,
Ann. Rev. Fluid Mech. 30, 85-105.
Lindzen, R. S. & Rambaldi, J. S. A986) A study of over-reflection in viscous
Poiseulle flow, J. Fluid Mech. 165, 355-372.
Lorenz, Б. N. A963) Deterministic nonperiodic flow, J. Atmos. Sci. 20, 130-
141.
Lundgren, T. S. A982) Strained spiral vortex model for turbulent fine
structure, Phys. Fluids 25, 2193-2241.
Mack, L. M. A976) A numerical study of the eigenvalue spectrum of the Blasius
boundary layer, J. Fluid Mech. 73, 497-570.
Malkus, W. V. R. A954) Discrete transitions in turbulent convection, Proc.
Roy. Soc. bond. A 225, 185-195.
Malkus, W. V. R. & Veronis, G. A958) Finite amplitude cellular convection,
J. Fluid Mech. 4, 225-260.
Matkowsky, B. J. A970) A simple nonlinear dynamic stability problem, Bull.
Amer. Math. Soc. 76, 620-625.
Maxwell, J. C. A876) Capillary action, Encyclopedia Britannica, 9th edn, 5,
59. Also in Sci. Papers 2 A890), 587.
McAlpine, A. & Drazin, P. G. A998) On the spatio-temporal development of
small perturbations of Jeffery-Hamel flows, Fluid Dyn. Res. 22, 123-138.
Meksyn, D. & Stuart, J. T. A951) Stability of viscous motion between parallel
planes for finite disturbances, Proc. Roy. Soc. Lond. A 208, 517-526.
Meseguer, A. & Trefethen, L. N. B000) A spectral Petrov-Galerkin formulati-
formulation for pipe flow. I. Linear stability and transient growth. Technical Report
NA 00/18, Oxford University Computing Laboratiry.
Miles, J. W. A961) On the stability of heterogeneous shear flows, Part 2,
J. Fluid Mech. 16, 209-227.
Morkovin, M. V. A969) The many faces of transition, in Viscous Drag, ed.
С S. Wells (Plenum Press, New York).
Nakamura, I. A976) Steady wake behind a sphere, Phys. Fluids 19, 5-8.
Nakayama, Y. (ed.) A988) Visualized Flow (Pergamon, Oxford).
Natarajan, R. & Acrivos, A. A993) The instability of the steady flow past
spheres and disks, J. Fluid Mech. 154, 323-344.
Neu, J. С A984) The dynamics of stretched vortices, J. Fluid Mech. 143, 253-
276.
Newhouse, S., Ruelle, D. & Takens, F. A978) Occurence of strange axiom A
attractors near quasi-periodic flows on Tm, m > 3, Commun. Math. Phys.
64, 35-40.

272	Список литературы
Nishioka, М., Iida, S. & Ichikawa, Y. A975) An experimental study of the sta-
stability of plane Poiseuille flow, J. Fluid Mech. 72, 731-751.
Nishioka, M., Asai, M. & Eda, S. A980) An experimental investigation of se-
secondary instability, pp. 37-46 in Laminar-Turbulent Transition, eds. R.
Eppler & H. Fasel (Springer-Verlag, Berlin).
Noether, F. A921) Das Turbulenz problem, Z. angew. Math. Mech. 1,125-138,
218-219.
Oberbeck, A. A879) Ueber die Warmleitung der Flussigkeiten bei Berucksich-
tigung der Stromungen infolge von TemperaturdifFerenzen, Ann. Phys.
Chem. 7, 271-292.
Oertel, H. & Kirchartz, K. R. A979) pp. 355-366 In Recent Developments in
Theoretical and Experimental Fluid Mechanics, eds. U. Muller, K. G.
Roesnet & B. Schmidt (Springer-Verlag, Berlin).
Onsager, L. A949) Statistical hydrodynamics, Nuovo Cimento 6B), 279-287,
suppl. ser. IX.
Orr, W. M'F. A907a) Stability or instability of the steady motions of a perfect
liquid, Proc. Roy. Irish Acad. A 27, 9-69.
Orr, W. M'F. A907b) The stability or instability of the steady motions of a
liquid, Proc. Roy. Irish Acad. A 27, 69-138.
Orszag, S. A. & Patera, A. T. A983) Secondary instability of wall-bounded
shear flows, J. Fluid Mech. 128, 347-385.
Palm, E., Weber, J. E. & Kvernold, O. A972) On steady convection in a poro-
porous medium, J. Fluid Mech. 54, 153-161.
Pearson, J. R. A. A958) On convection cells induced by surface tension, J. Flu-
Fluid Mech. 4, 489-500.
Pekeris, C. L. A936) On the stability problem in hydrodynamics, Proc. Camb.
Phil. Soc. 32, 55-66.
Pellew, A. & Southwell, R. V. A940) On maintained convective motion in a
fluid heated from below, Proc. Roy. Soc. bond. A 176, 312-343.
Pomeau, Y. & Manneville, P. A980) Intermittent transition to turbulence in
dissipative dynamical systems, Commun. Math. Phys. 74, 189-197.
Prandtl, L. A921) Bemerkungen uber die Enstehung der Turbulenz, Z. angew.
Math. Mech. 1, 431-436. Also in Phys. Z. 23 A922), 19-25, and
Gesammelte Abhandlungen2, 687-696.
Prandtl, L. A935) The mechanics of viscous fluids, in Aerodynamic Theory,
ed. W. F. Durand (Springer, Berlin) 3, Division G, 34-208. Рус. пер. с
нем.: Прандтлъ JI. Движение вязких жидкостей// В кн. Прандтлъ JI.
Гидроаэромеханика. - М. - Ижевск: РХД, 2000, 142-347.
Provansal, М., Mathis, С. & Воуег, L. A987) Benard-Karman instability:
transient and forced regimes, J. Fluid Mech. 182, 1-22.
Raetz, G. S. A959) A new theory of the cause of transition in fluid flows, Norair
Rep. NOR-59-383, Hawthorne, CA.

Список литературы	273
Rayleigh, J. W. S. A879) On the instability of jets, Proc. bond. Math. Soc. 10,
4-13. Also in Sci. Papers 1, 361-371.
Rayleigh, J. W. S. A880) On the stability, or instability, of certain fluid moti-
motions, Proc. Lond. Math. Soc. 11, 57-70. Also in Set. Papers 1, 474-487.
Rayleigh, J. W. S. A883) Investigation of the character of the equilibrium of
an incompressible heavy fluid of variable debsity, Proc. Lond. Math. Soc.
14, 170-177. Also in Sci. Papers 2, 200-207.
Rayleigh, J. W. S. A892) On the question of the stability of the flow fluids,
Phil Mag. 34E), 59-70. Also in Sci. Papers 3, 575-584.
Rayleigh, J. W. S. A894) The Theory of Sound, 2nd edn. (MacmiUan, London).
Рус. пер.: Стрэтт Дою. В. (лорд Рэлей) Теория звука, т. 1-2. - М.-Л.:
Гостехиздат, 1944.
Rayleigh, J. W. S. A916a) On convection currents in a horizontal layer of fluid,
when the higher temperature is on the under side, Phil. Mag. 32F), 529-
546. Also in Sci. Papers 6, 432-446.
Rayleigh, J. W. S. A916b) On the dynamics of revolving fluids, Proc. Roy. Soc.
Lond. A 93, 148-154. Also in 5c*. Papers 6, 447-453.
Reddy, S. C. & Henningson, D. S. A993) Energy growth in viscous channel
flows, J. Fluid Mech. 252, 209-238.
Reid, W. H. A960) Inviscid modes of instability in Couette flow, J. Math. Anal.
Applies. 1, 411-422.
Reynolds, O. A883) An experimental investigation of the circumstances which
determine whether the motion of water shall be direct or sinuous, and of
the law of resistence in parallel channels, Phil. Trans. Roy. Soc. Lond. A
174, 935-982. Also in Sci. Papers 2 A901), 51-105.
Reynolds, O. A895) On the dynamical theory of incompressible viscous fluids
and the determination of the criterion, Phil. Trans. Roy. Soc. Lond. A
186, 123-164. Also in 5c*. Papers 2 A901), 535-577.
Romanov, V. A. A973) Stability of plane-parallel Couette flow, Func. Anal.
Appl. 7, 137-146; пер. на англ. ст.: Романов В. А. Устойчивость плос-
плоскопараллельного течения Куэтта, Функц. анал. и его прил.. - 1973, 7,
62-73.
Rossby, Н. Т. A969) A study of Benard convection with and without rotation,
J. Fluid Mech. 36, 309-335.
Ruelle, D. & Takens, F. A971) On the nature of turbulence, Commun. Math.
Phys. 20, 167-192.
Saffman, P. G. A992) Vortex Dynamics (Cambridge University Press). Рус.
пер.: Сэффмэн Ф. Дою. Динамика вихрей. - М.: Науч. мир, 2000.
Saffman, P. G. & Taylor, G. I. A958) The penetration of a fluid into a porous
medium or Hele-Shaw cell containing a more viscous liquid, Proc. Roy.
Soc. Lond. A 245, 312-329.
Salwen, H., Cotton, F. W. & Grosch, С E. A980) Linear stability of Poiseuille
flow in a circular pipe, J. Fluid Mech. 98, 273-284.

274	Список литературы
Saric, W. S. A994) Gortler vortices, Ann. Rev. Fluid Mech. 26, 379-409.
Saric, W. S. & Thomas, A. S. W. A984) Experiments on the subharmonic
route to turbulence in boundary layers, pp. 117-22 of Turbulenve
and Chaotic Phenomena in Fluids, ed. T. Tatsumi (North-Holland,
Amsterdam).
Schensted, I. V. A960) Contributions to the theory of hydrodynamic stability,
Ph.D. thesis, University of Michigan.
Schlichting, H. A933) Zur Entstehung der Turbulenz bei der Plattenstromung,
Nachr. Ges. Wiss. Gottingen, Math.-phys. Klasse 181-208.
Schmid, P. J. & Henningson, D. S. B001) Stability and Transition in Shear
Flows (Springer, New York).
Schmid-Burgk, J. A965) Zweidimensionale selbstkonsisten Losungen stationa-
ren Wlassovgleichung fur Zweikomponentenplasmeri, Diplomarbeit,
Ludwig-Maximilians-Universitat, Munchen.
Schubauer, G. B. & Skramstad, H. A947) Laminar boundary-layer oscillations
and transition on a flat plate, J. Nat. Bur. Standards 38, 251-292. Also
in Rep. Nat. Adv. Comm. Aero., Wash. No. 909 A948).
Serrin, J. A959) On the stability of viscous fluid motions, Arch. Rat. Mech.
Anal. 3, 1-13.
Sexl, T. A927a) Zur Stabilitatsfrage der Poiseuilleschen und Couetteschen
Stromung Ann. Phys., Leipzig 83D), 835-848.
Sexl, T. A927b) Uber dreidimensionale Stoning der Poiseuilleschen Stromung,
Ann. Phys., Leipzig 84D), 807-822.
Silverston, P. L. A958) Warmedurchgang in waagerechten Flussigkeitsschich-
ten, Forsch. Gebiete Ingenieurwes. 24, 29-32.
Smith, A. M. O. & Gamberoni, N. A956) Transition, pressure gradient, and
stability theory, Douglas Aircraft Co., Inc., Rep. No. ES 26388.
Smith, F. T. A979a) On the non-parallel flow stability of the Blasius boundary
layer, Proc. Roy. Soc. Lond. A 366, 91-109.
Smith, F. T. A979b) Nonlinear stability of boundary layers for disturbances of
various sizes, Proc. Roy. Soc. Lond. A 368, 573-589.
Sobey, I. J. B000) Introduction to Interacting Boundary Layer Theory (Oxford
University Press).
Sobey, I. J. & Drazin, P. G. A986) Bifurcation of two-dimensional channel
flows, J. Fluid Mech. 17, 263-287.
Sommerfeld, A. A908) Ein Beitrag zur hydrodynamische Erklaerung der tur-
turbulent en Fluessigkeitsbewegungen, Proc. 4th Intl Congr. Math., Rome,
vol. Ill, pp. 116-124.
Sorokin, V. S. A961) Nonlinear phenomena in closed flows near critical Rey-
Reynolds number, J. Appl. Math. Mech. 25, 366-381; пер. на англ. ст.: Со-
Сорокин В. С. Нелинейные явления в замкнутых потоках вблизи крити-
критических чисел Рейнольдса, ПММ. - 1961, 25, 248-258.

Список литературы	275
Squire, H. В. A933) On the stability of three-dimensional disturbances of
viscous flow between parallel walls, Proc. Roy. Soc. bond. A 142, 621-628.
Srulijes, J. A. A979) Zellularkonvektion in Behalten mit horizontalen Tem-
peraturgradienten, Dissertation, Universitat Karlsruhe.
Stern, M. E. A960) The "salt fountain" and thennohaline convection, Tellus
12, 172-175.
Stokes, G. G. A880) Supplement to a paper on the theory of oscillatory waves,
Math. Phys. Papers I A880), 314-326.
Stone, P. H. A969) The meridional structure of baroclinic waves, J. Atmos.
Sci., 26, 376-389.
Straughan, B. A982) Instability, Nonexistence and Weighted Energy Methods
in Fluid Dynamics and Related Theories (Pitman, London).
Stuart, J.T. A960) On the non-linear mechanics of wave disturbances in stable
and unstable parallel flows. Part 1. The basic behaviour in plane Poiseuille
flow, J. Fluid Mech. 9, 353-370.
Stuart, J. T. A967) On finite amplitude oscillations in laminar mixing layers,
J. Fluid Mech. 29, 417-440.
Swift, J. & Hohenberg, P. C. A977) Hydrodynamic fluctuations at the convec-
tive instability, Phys. Rev. A 15, 319-328.
Synge, J. L. A933) The stability of heterogeneous fluids, Trans. Roy. Soc, Ca-
Canada 27C), 1-18.
Synge, J. L. A938) Hydrodynamic stability, Semi-centenn. Publ. Amer. Math.
Soc. 2, 227-269.
Taneda, S. A959) Downstream development of wakes behind cylinders, J. Phys.
Soc. Japan 14, 843-848.
Taneda, S. A978) Visual observations of the flow past a sphere at Reynolds
numbers between 104 and 106, J. Fluid Mech. 85, 187-192.
Tatsumi, T. & Gotoh, K. A960) The stability of free boundary layers between
two uniform streams, J. Fluid Mech. 7, 433-441.
Taylor, G. I. A915) Eddy motion in the atmosphere, Phil. Trans. Roy. Soc.
bond. A 215, 1-26. Also in Sci. Papers 2, 1-23.
Taylor, G. I. A923) Stability of a viscous liquid contained between two rotating
cylinders, Phil. Trans. Roy. Soc. Lond. A 223, 289-343. Also in Sci.
Papers 4, 34-85.
Taylor, G. I. A931) Effect of variation of density on the stability of superposed
streams of fluid, Proc. Roy. Soc. Lond. A 132, 499-523. Also in Sci.
Papers 4, 34-85.
Taylor, G. I. A938) Some recent development in the study of turbulence, Proc.
5th Intern. Congr. Appl. Mech., 294-310. (Wiley, New York).
Taylor, G. I. A950) The instability of liquid surfaces when accelerated in a
direction perpendicular to their planes, I, Proc. Roy. Soc. Lond. A 201,
192-196. Also in Sci. Papers 3, 532-536.

276	Список литературы
Thomas, L. H. A953) The stability of plane Poiseuille flow, Phys. Rev. 91B),
780-783.
Thorpe, S. A. A968) A method of producing a shear flow in a stratified fluid,
Fluid Mech. 32, 693-704.
Thorpe, S. A. A969) Experiments on the instability stratified shear flows: im-
immiscible fluids, /. Fluid Mech. 39, 25-48.
Thorpe, S. A. A985) Laboratory observations of secondary structures in Kel-
vin-Helmholtz billows and consequences for ocean mixing, Geophys.
Astrophys. Fluid Dyn. 34, 175-190.
Threlfall, D. C. A975) Free convection in low-temperature gaseous helium, Flu-
Fluid Mech., 67, 17-28.
Tollmien, W. A929) Uber die Entstehung der Turbulenz, Nachr. Ges. Wiss,
Gottingen, Math.-phys. Klasse, 21-44. Translated as "The production
of turbulence", Tech. Memor. Nat. Adv. Comm. Aero., Wash. No. 609
A931).
Tollmien, W. A935) Ein allgemeines Kriterium der Instabilitat laminarer Ge-
schwindigkeitsverteilungen, Nachr. Wiss. Fachgruppe, Gottingen, Math.-
phys. Klasse 1, 79-114. Translated as "General instability criterion of
laminar velocity distributions", Tech. Memor. Nat. Adv. Comm. Aero.,
Wash. No. 792 A936).
Trefethen, L. N., Trefethen, A. N., Reddy, S. С & Driscoll, T. A. A993) Hy-
drodynamic stability without eigenvalues, Science, 261, 578-584.
Tutty, O. R. A996) Nonlinear development of flow in channels with non-parallel
walls, /. Fluid Mech. 326, 265-284.
Van Dyke, M. A982) An Album of Fluid Motion (Parabolic Press, Stanford).
Рус. пер.: Ван-Дайк М. Альбом течений жидкости и газа. - М.: Мир,
1986.
van Ingen, J. L. A956) A suggested semi-empirical method for the calculation
of the boundary layer transition region, Dept Aeronaut. Engng, Tech.
Univ., Delft, Reps. Nos. VTH 71, 74.
Waleffe, F. A995) Hydrodynamic stability and turbulence: beyond transients
to a self-sustaining process, Studies Appl. Math. 95, 319-343.
Warn, T. & Warn, H. A978) The evolution of a nonlinear critical level, Studies
Appl. Math. 59, 37-71.
Watson, J. A960a) Three-dimensional disturbances in flow between parallel
planes, Proc. Roy. Soc. bond. A 254, 562-569.
Watson, J. A960b) On the non-linear mechanics of wave disturbances in stable
and unstable parallel flows. Part 2. The development of a solution for
plane Poiseuille flow and for plane Coutte flow, J. Fluid Mech. 9, 353-
370.
Williamson, С. Н. К. A996) Vortex dynamics in the cylinder wake, Ann. Rev.
Fluid Mech. 28, 477-539.
Willis, G. E. & Deardorff, J. W. A967) Development of short-period tempera-
temperature fluctuations in thermal convection, Phys. Fluids 10, 931-937.

Список литературы	277
Wilson, S. A969) The development of plane Poiseuille flow, /. Fluid Mech. 38,
793-806.
Young, A. D. A989) Boundary Layers (BSP Professional Books, Oxford).
Yudovich, V. I. A989) The Linearization Method in Hydrodynamic Stability
Theory, Translation Math. Monographs, vol. 74 (American Mathematical
Society, Providence, RI); пер. на англ.: Юдович В. И. Метод лине-
линеаризации в гидравлической теории устойчивости. - Ростов: Изд-во
Ростовск. ун-та, 1984.
Указатель фильмов
В шестидесятых годах XX века Центр развития образования (Education De-
Development Center) выпустил несколько фильмов для Национального коми-
комитета по фильмам о гидромеханике (National Committee for Fluid Mechanics
Films). Были произведены 16 миллиметровые звуковые пленки, каждая дли-
длительностью 30 минут, а также 8 миллимитровые ролики фильмов, каждый
длительностью примерно 4 минуты. Большинство роликов содержит из-
извлечения из длинных фильмов. Многие из фильмов посвящены демонстра-
демонстрации экспериментов по гидромеханической неустойчивости и большинство
из них по-прежнему остаются превосходными. Эти фильмы впоследствии
были конвертированы в видео-фильмы, которые все еще находятся в про-
продаже. Они распространяются в Соединенных Штатах Америки и во мно-
многих других странах Образовательной корпорацией Энциклопедии Брита-
ника (Encyclopaedia Britannica Educational Corporation), расположенной по
адресу: 310 South Michigan Avenue, Chicago, Illinois 60604, а также по всему
миру некоторыми другими специальными распространителями.
Первый компакт диск с движущимися картинками из механики жид-
жидкости был издан в 2000 г. издательством Cambridge University Press. Он
воспроизводит некоторые короткие извлечения из фильмов Центра разви-
развития образования (Education Development Center) и из многих других филь-
фильмов и видео-фильмов о лабораторных экспериментах и природных явлени-
явлениях. Большинство из этих видео-фильмов высокого качества и многие из них
посвящены гидродинамической неустойчивости.
Многие из этих движущихся картинок были цитированы в тексте и их
указатель приведен ниже. Обозначения CD используются для компакт дис-
дисков, F — для фильмов, a FL — для роликов фильмов.
Brown, F. N. М. (FL1964) Stages of boundary-layer instabiity and transition.
B/W-No. S-FM092.
Bryson, A. E. (F1967) Waves in fluids. B/W-No. 21611.
Bryson, A. E. (FL1967) Small-amplitude gravity waves in an open channel.
B/W-No. S-FM139.
Coles, D. (FLl963a) Instabilities in circular Couette flow. B/W-No. S-FM031.

278	Список литературы
Coles, D. (FL1963b) Examples of turbulent flow between concentric rotating
cylinders. B/W-No. S-FM032.
Homsy, G. M., Aref, H., Breuer, K. S., Hochgreb, S., Koseff, J. R., Munson, B.
R., Powell, K. G., Robertson, C. R. & Thoroddsen, S. T. (CD2000) Multi-
Multimedia Fluid Mechanics (Cambridge University Press).
Lippisch, A. M. (FL1964) Tollmien-Schlichting waves. B/W-No. S-FM023.
Long, R. R. (F1968) Stratified flow. Color-No. 21618.
MoUo-Christensen, E. L. (F1968) Flow instabilities. Color-No. 21619.
MoUo-Christensen, E. L. & Wille, R. (FL1968) Experimentsl study of a flow
instability. B/W-No. S-FM147.
Stewart, R. W. (F1968) Turbulence. Color-No. 21626.
Stewart, R. W. (FL1968) Laminar and turbulent pipe flow. Color-No. S-FM134.
Trefethen, L. M. (F1965) Surface tension in fluid mechanics. Color-No. 21610.
Trefethen, L. M. (FL1965) Breakup of liquid into drops. Color-No. S-FM076.

Указатели
1868 Helmholtz, 60, 171
1871 Kelvin, 60, 69, 72
1876 Maxwell, 74
1879 Oberbeck, 111
1879	Rayleigh, 77
1880	Kelvin, 167
1880 Rayleigh, 155, 163, 169, 203,
204, 206
1880 Stokes, 90
1882	Campbell & Garnett, 11
1883	Rayleigh, 67, 75, 216
1883 Reynolds, 12-14, 40, 47, 69,
90, 203
1887 Kelvin, 208
1890 Helmholtz, 69
1892 Rayleigh, 189, 222
1894	Rayleigh, 209
1895	Reynolds, 98
1900 Benard, 110
1902	Jeans, 58
1903	Boussinesq, 111
1907 a Orr, 206, 208
1907	b Orr, 98, 177
1908	Harrison, 75
1908	Sommerfeld, 177
1909	Bohr, 90
1911 Karman, 247, 261
1915 Jeffrey, 52
1915	Taylor, 164, 181
1916	Hamel, 52
1916 a Rayleigh, 114
1916 b Rayleigh, 142
1921 Noether, 90
1921 Prandtl, 181
1923	Taylor, 143, 146, 148, 149
1924	Heisenberg, 90, 197
1927 a Sexl, 201
1927 b Sexl, 201
1929 Tollmien, 178, 179, 185, 189,
194
1931 Goldstein, 217
1931 Haurwitz, 217
1931	Taylor, 217
1932	Lamb, 56, 57, 62, 213, 262, 263
1933	Schlichting, 189, 194
1933 Squire, 160
1933	Synge, 143, 154
1934	Dean, 53, 255
1935	Prandtl, 181
1935	Tollmien, 166, 194
1936	Pekeris, 223
1938 Synge, 183
1938 Taylor, 179
1940 Christopherson, 129
1940 Gortler, 152
1940 Pellew & Southwell, 123
1944 Landau, 90, 197, 234
1944	Landay, 33
1945	Horton & Rogers, 134
1946	Landau, 87
1947	Schubauer & Skramstad, 178,
195, 245
1948	Lapwood, 134
1949	Onsager, 176
1950	Fj0rtoft, 165
1950 Lewis et a/., 67
1950	Taylor, 67, 216
1951	Meksyn & Stuart, 197
1953	Thomas, 190
1954	Bellman & Pennington, 75
1954 Colson, 70
1954	Malkus, 234
1955	Gregory et a/., 215
1955 Herivel, 175
1955	Lin, 20, 164, 166
1956	Smith & Gamberoni, 199
1956 van Ingen, 199

280
Авторский указатель
1957	Gor'kov, 90
1958	Malkus & Veronis, 90
1958 Pearson, 138
1958 Saffman & Taylor, 76
1958	Silverston, 117, 120
1959	Cesari, 49
1959 Raetz, 198
1959 Serrin, 100, 253
1959	Taneda, 245
1960	Case, 170
1960 Donnelly & Simon, 150
1960 Reid, 156
1960 Schensted, 178
1960 Stern, 138, 140
1960 Stuart, 90, 197
1960 Tatsumi & Gotoh, 227
1960 a Watson, 221
1960	b Watson, 90, 197
1961	Chandrasekhar, 19, 75
1961 Drazin, 226
1961 Howard, 166, 218
1961 Miles, 218
1961	Sorokin, 107
1962	Batchelor & Gill, 201, 204
1962 Davey, 146
1962 Fraenkel, 29, 52, 254
1962 Gaster, 225
1962	Klebanoff et a/., 195, 199, 245
1963	Fraenkel, 254
1963 Lorenz, 132
1963 a FL Coles, 146
1963	b FL Coles, 146
1964	Abramowitz & Stegun, 52
1964 Briggs, 87
1964 FL Brown, 195
1964 FL Lippich, 195
1964 Harris & Reid, 146, 147
1964	Howard, 212
1965	Coles, 237
1965 F Trefethen, 80
1965 FL Trefethen, 80
1965 Hughes & Reid, 221
1965 Joseph, 131
1965	Schmid-Burgk, 213
1966	Donnely & Glaberson, 81
1966	Eagles, 255
1967	Batchelor, 27, 52, 60, 61, 107,
178, 203, 222, 244, 246,
248, 251
1967 Betchov & Criminale, 19
1967 F Bryson, 70
1967 FL Bryson, 70
1967 KeUy, 198
1967 Stuart, 213
1967	Willis & Deadorf, 120
1968	F Long, 70
1968 F Mollo-Christensen, 74
1968 F Stewart, 16
1968 FL Stewart, 16
1968 FL MoUo-Christensen& WiUe,
70
1968 Joseph, 184
1968	Thorpe, 71
1969	Baines & GiU, 140
1969 Goldstein & Graham, 114
1969 Joseph, 184
1969 Leibovich, 219
1969 Morkovin, 237
1969 Rossby, 117, 120
1969 Stone, 246
1969 Thorpe, 69
1969	Wilson, 225
1970	Burridge, 203
1970	Matkowsky, 91
1971	Busse & Whitehead, 123-125
1971 Craik, 198
1971	Ruelle & Takkens, 238
1972	Palm et a/., 136
1973	Bouthier, 180
1973 Hindi, 137
1973 Krishnamurti, 120
1973	Romanov, 189
1974	Drazin, 246
1974	Gaster, 180
1975	Drazin, 130
1975 Ellingsen & Palm, 208
1975 Gull, 67
1975 Hocking, 221
1975 Kachanov et a/., 245
1975 Krishnamurti, 128
1975 Nishioka et a/., 197
1975	Threlfall, 119
1976	Benjamin, 234
1976 Gent & Leach, 246
1976 Joseph, 20, 99
1976 Mack, 193
1976	Nakamura, 251
1977	Swift & Hohenberg, 134

Авторский указатель
281
1978 Libhaber & Maurer, 119, 239
1978 Newhouse et a/., 239
1978 Taneda, 252
1978	Warn & Warn, 45
1979	Brown & Stewarson, 45
1979 Busse & Clever, 126, 127
1979 Fenstennacher et a/., 147, 237
1979 Leibovich, 219
1979 Oertel & Kirchartz, 122
1979 Srulijes, 121
1979 a Smith, 186
1979	b Smith, 186
1980	Feigenbaum, 119, 239
1980 Nishioka et a/., 1980, 195
1980 Pomeau & Manneville, 239
1980	Salwen et a/., 47, 203
1981	Drazin & Reid, 20, 33, 55,
57, 72-74, 76, 81, 82, 106,
107, 115, 117, 131, 138-
140, 146-150, 152, 156,
168, 187, 190, 194, 199,
218
1982	Benjamin & Mullin, 147, 234
1982 Carbon et a/., 17
1982 Lundgren, 67
1982 Straughan, 99
1982	Van Dyke, 14, 16, 20, 78, 116,
117, 122, 146, 147, 195,
197, 243, 244, 246, 247,
251
1983	Hall, 151
1983	Orzag & Patera, 197
1984	Beale et a/., 174
1984 Neu, 69
1984	Saric & Thomas, 199
1985	Craik, 97
1985 Klaasen & Peltier, 70
1985	Thorpe, 70
1986	Andereck et a/., 151
1986 Craik & Criminale, 55, 208
1986 Krasny, 68
1986 Lindzen & Rambaldi, 182
1986	Sobey & Drazin, 30, 253, 254,
259
1987	Herron, 178
1987 Jakson, 249, 250, 252
1987 Landau & Lifshitz, 20
1987	Provansal et a/., 250
1988	Banks et a/., 53, 255-257, 259
1988 Bayly et a/., 198
1988 Boberg & Brosa, 232
1988 Herbert, 198
1988	Nakayama, 20, 152, 195, 246,
256-258
1989	Drazin, 54
1989 Young, 196
1989	Yudovich, 50, 207, 209
1990	Huerre & Monkewitz, 87, 246
1990	Kim & Pearlstein, 251
1991	King & Stewart, 237
1992	Bertolotti et a/., 180
1992 Buttler & Farell, 199
1992 Drazin, 133
1992	Saffman, 171, 174
1993	Koschmieder, 120, 121, 144,
147, 148
1993 Natarajan & Acrivos, 251
1993 Reddy & Henningson, 199
1993	Trefethen et a/., 51, 231
1994	Baines & Mitsudera, 165
1994 Hamadiche et a/., 259
1994 Kachanov, 199
1994	Saric, 151
1995	Waleffe, 51, 220
1996	Baines et a/., 182
1996 Tutty, 260
1996	Williamson, 250
1997	Alleborn et a/., 255
1997	Dennis et a/., 259
1998	Eliahou et a/., 15
1998 Huerre & Rossi, 20
1998 Lin & Reitz, 81
1998 McAlpine & Drazin, 257, 258,
260, 263
2000 CD Homsy, 16, 20, 146, 195,
243, 246, 251
2000 Meseguer & Trefethen, 204,
205
2000	Sobey, 253
2001	Barcilon & Drazin, 214
2001	Schmid & Henningson, 20, 85,
194, 199, 200
2002	Kerswell et a/., 260

282
Предметный указатель
Адиабатическая скорость паде-
падения температуры, 75
альтернатива Фредгольма, 95,
104
аналогия между вращающимися
и стратифицированны-
стратифицированными течениями, 141, 153,
218
аппроксимация
Буссинеска, 111, 216
ВКБ, 180, 184, 246
узкого зазора, 144, 146, 147,
149, 155
аттрактор, 41
Биортогональность, 105
бифуркационная диаграмма, 24
бифуркация, 18, 21, 22
Хопфа, 37, 236, 248, 260
вилообразная, 24, 30, 33, 118,
133, 136, 234
из бесконечности, 48
седло-узел, 24
складка, 24
точка поворота, 24, 32, 47
транскритическая, 24, 32, 47,
234
Вариационное исчисление, 131
вихревая дорожка, 247, 250, 261,
262
Кармана, 261
вихри
Гёртлера, 148
Тейлора, 146
возмущение, 14, 35, 39
волн ветровых генерация, 72
волна
Толлмина-Шлихтинга, 189,
195, 196
внутренняя гравитационная,
66, 215
двойная диффузионная нели-
нелинейная, 137
поверхностная гравитацион-
гравитационная, 65
волновой пакет, 90, 102
Гармоника, 236
вторая, 91
первая, 91
Дискриминант Релея, 153, 155
диффузия, 126
Жидкость Буссинеска, 111, 134
Задача
Дина, 53, 256
Орра-Зоммерфельда, 53, 226
Сквайра, 229
Штурма-Лиувилля, 154, 216
вспомогательная, 23
линеаризованная, 41
устойчивости Релея, 162, 205
закон
Дарси, 76, 134
Лапласа поверхностного на-
натяжения, 71, 78
Конвекция
Лапвуда, 134
Марангони, 138
Релея-Бенара, 116
Релея-Дарси, 134
в пористой среде, 134
двойная дифузионная, 137,
140
нелинейная тепловая, 133
при изменении поверхност-
поверхностного натяжения с из-
изменением температуры,
138
кривая
маргинальная, 114, 224
для плоского течения Пуа-
зейля, 190
для плоской струи, 192
для спутного следа, 191
для струи, 191
для струи Бикли, 192
для пограничного слоя
Блазиуса, 190
неограниченного сдвиго-
сдвигового слоя, 191
нейтральная, 224

Предметный указатель
283
критерий
Шварцшильда, 75
неустойчивости вращающе-
вращающегося течения Релея, 143,
154, 156
критическое число
Рейнольдса, 14, 42, 174, 240
течения Пуазейля в трубе,
14
Релея, 115, 240
Ламбда-вихри, 195
Маргинальной кривой
верхняя ветвь, 187, 192
нижняя ветвь, 187, 192
мембрана вибрирующая, 180, 195
метод
е*, 199
Ляпунова прямой, 19, 99, 183
нормальных мод, 15, 36, 38,
44
пристрелки, 212
численный, 192, 194, 228
энергетический, 99, 130, 183
механизм
жалюзи, 206
неустойчивости Орра подъ-
подъемный, 206
мод взаимодействие нелинейное,
91, 101
мода
Орра-Зоммерфельда, 231
Пекериса (Р-мода), 192
Сквайра, 230
Шенстеда (S-мода), 192
Эйри (А-мода), 192
антисимметричная, 173, 212
варикозная, 81, 173, 189, 209-
212
временная, 224
глобальная, 246
локальная, 180, 246
нелинейная, 105
нормальная, 15, 35, 38, 41, 44,
101
точное решение нелиней-
нелинейных уравнений, 55
основная, 91
мода
пристеночная, 192, 205
пространственная, 86, 87,
101, 180, 193, 224, 225,
228, 255
для уравнения Бюргерса,
101
симметрическая, 173, 212
синусоидальная, 173, 189,
190, 193, 210, 245, 247
центральная, 192, 204
модель Свифта-Хоэнберга, 133
моды нелинейные уравнения
Бюргерса, 105
Напряжения Рейнольдса, 98, 165,
168, 181
небо макрели, 69
неустойчивость, 11
Гёртлера, 148
Джинса, 57
Кельвина-Гельмгольца, 60,
71, 73, 75, 143, 171, 250
Релея-Бенара, 115
Релея-Тейлора, 66, 67, 70,
74-76, 215, 216
Саффмана-Тейлора, 76
абсолютная, 84, 101
асимптотически отсасывае-
отсасываемого пограничного слоя,
220
вихревого слоя, 61, 171
вследствие линейного резо-
резонанса, 54
вторичная, 38, 49, 236
двойная диффузионная, 140
докритическая, 238
конвективная, 84, 101, 115
ломаной струи, 209
параллельного течения стра-
стратифицированной жид-
жидкости, 216
параметрическая, 235
первичная, 38, 236
плоского течения Куэтта,
190, 207, 210
плоского течения Пуазейля,
12, 191, 192
пограничного слоя, 189, 245

284
Предметный указатель
неустойчивость
пограничного слоя Блазиуса,
178, 187, 189, 190
пограничного слоя на плас-
пластине, 178, 187, 189
поперечного течения, 215,
229
самогравитирующего газа,
57
сдвигового слоя, 67, 210
th, 191
неограниченного, 191
следа, 190, 246
струи, 190, 203
sech, 211
sech2, 192, 211
Бикли, 211
Ландау-Сквайра, 203
в форме цилиндра, 209
газа капиллярная, 81
плоской капиллярная, 82
термохалинная, 140
течения за плоской пласти-
пластиной, 243
течения за сферой, 251
течения за цилиндром, 246
треугольной струи, 173
эллиптическая, 55, 198
эллиптического течения, 55
нормальная форма, 97
нормальных мод
неполнота, 50
полнота, 43, 50
Облака, 121
оператор
Фредгольма, 105
сопряженный, 103, 104, 227
для задачи Орра-Зоммер-
фельда, 227
Переход
к турбулентности, 146, 200,
233, 237
побочный, 16, 196, 199, 237,
238
скачкообразный, 239
пики и долины, 195
гоювучесть, 54
поверхности отклонение, 62, 205
поверхностное натяжение, 71, 74,
78
зависящее от температуры,
138
постоянная
Ландау, 33, 93
Ландау комплексная, 102
предел замечательный, 93
преобразование
Галилея, 68, 89, 102, 167
Гастера, 224
Сквайра, 160, 175, 221
принцип
Кельвина минимума энер-
энергии, 56
вариационный, 107, 131
обмена устойчивостей, 38,
114, 122, 138, 144, 150,
235
эквивалентности, 66
проницаемость пористой среды,
76
путь
к турбулентности, 18, 22, 238
к хаосу, 18, 238
Рюэля-Такенса, 238, 250
Решение
вторичное, 49
нелинейное для структуры в
форме кошачьего глаза,
213
первичное, 49
уравнения Орра-Зоммерфе-
льда, 222, 225, 228
вязкое, 185
невязкое, 186
решения
Гейзенберга уравнения Ор-
ра-Зоммерфельда, 185
Толлмина уравнения Орра-
Зоммерфельда, 185
рост кристаллов, 120
Сверхновая, 67
сверхотражение, 182
симметрии нарушение, 24, 33, 67,
236, 237, 247, 253, 259

Предметный указатель
285
система Лоренца, 131, 133
скорость
групповая, 86, 87, 89, 101,
102, 224
падения температуры, 75
фазовая, 65
слабонелинейная теория вихрей
Тейлора, 146
слой
вихревой, 227
критический, 163, 167, 168,
178, 181, 182, 184-187,
189, 192, 206
свободный сдвиговый, 69, 84,
210
смешения, 69
совершенный газ, 75
солевые пальцы, 140
солнечная грануляция, 121
соотношение дисперсионное, 85,
88, 100, 224
структур образование, 121
структура
в форме кошачьего глаза,
167, 213
когерентная, 248
струя
sech, 211
sech2, 192, 211
Бикли, 192, 211
Ландау-Сквайра, 203
субгармоника, 236
Теорема
Серрина, 19, 100, 106, 234,
248, 253
Сквайра, 177
полукруга Ховарда, 167
теория
Флоке, 235, 262
степени отображения Лере-
Шаудера, 234
течение
Джеффри-Гамеля, 27, 51,
254, 263
Куэтта, 155
Куэтта плоское, 25, 207, 208
Куэтта-Пуазейля плоское,
25
течение
Пуазейля в трубе, 14, 40, 46
Пуазейля плоское, 16, 26, 52
Стокса, 52, 100, 234, 245, 248,
251
в пористой среде, 76
вторичное, 38
закрытое, 84
квазипериодическое, 235
ламинарное, 13
однородное, 106
осесимметричное параллель-
параллельное, 200
основное, 22
открытое, 84
первичное, 38
равномерно вращающееся,
107
тождество Лагранжа, 103
точка
бифуркации, 24
поворота, 23, 32, 47, 234
трехпалубная теория, 186
турбулентность, 11, 12, 119
сдвигового течения, 238
фазовая, 237
чистого воздуха, 69
турбулентные вспышки, 14
турбулентные пятна, 14
Удвоение периода, 119, 235, 239
в случае конвекции Релея-
Бенара, 239
уравнение (я)
Буссинеска, 111, 131
Бюргерса, 101, 105
Гельмгольца, 113, 115, 129
Гинзбурга-Ландау, 96
Дина, 53
Ландау, 33, 47, 48, 90, 93, 95-
97, 130, 134, 136
комплексное, 48
Лиувилля, 213
Навье-Стокса, 17, 21, 22, 40,
54, 55, 222
Орра-Зоммерфельда, 177,
222, 225
Пуассона, 57

286
Предметный указатель
уравнение(я)
Тейлора-Голдстейна, 217,
218
Шрёдингера нелинейное, 103
Эйлера, 57,141,153, 158, 201,
207, 215
Эйлера-Лагранжа, 107, 131
диффузии, 126
нелинейное, 91
нелинейное Пуассона, 214
сопряженное
Орра-Зоммерфельда, 227
Релея, 205
устойчивости Релея, 162
вывод, 204
сопряженное, 205
энергии, 107, 182, 220
Рейнольдса-Орра, 98, 107,
167, 168, 220
условие
Майлса-Ховарда устойчи-
устойчивости, 217, 218
неустойчивости Релея необ-
необходимое, 164, 165
неустойчивости Фьёртофта
необходимое, 165, 166
разрешимости, 95, 103, 136,
223
фазовое, 135
условия
граничные, 22, 111
свободно-свободные, 114,
116
свободно-твердые, 116
твердо-твердые, 116
на разрыве основного тече-
течения, 169
на скачке, 169, 204, 226
устойчивости
уравнения параболизирован-
ные, 180
характеристики, 45
устойчивость, 11, 40
абсолютная, 84
асимптотическая, 41
атмосферы, 75
безвихревого течения, 56
в смысле Ляпунова, 40
в среднем, 41, 99, 106
устойчивость
глобальная асимптотичес-
асимптотическая, 47, 108
докритическая, 33
конвективная, 84
маргинальная, 42, 43
надкритическая, 33
нейтральная, 42
нелинейная, 90
непараллельных течений,
261
однородного течения, 106,
222
в канале, 188
плоского течения Куэтта,
170, 190, 207, 226
по отношению к коротким
волнам, 226
потенциального течения, 56
почти параллельных тече-
течений, 148, 179, 242, 246,
254, 255
пространственная, 100, 256
равномерно вращающейся
жидкости, 107
слабонелинейная, 90
статическая атмосферы, 75
структурная, 45
течения Пуазейля в трубе,
15, 46, 54
Функционал Ляпунова, 99, 183
функция Эйри, 156, 185, 225
Хаос, 18, 38, 119, 147, 239
Цикл предельный, 37
Частота
Брянта-Вяйсяля, 217
пловучести, 122, 153, 217
число
Гёртлера, 150
Марангони, 138
Нуссельта, 117, 130
Прандтля, 112, 132, 137
Рейнольдса, 13, 22, 25, 28
Релея, 112, 132, 137
Струхаля, 250

Предметный указатель	287
число
Тейлора, 145
Шмидта, 137
Эксперимент Рейнольдса, 12, 15
энергии
балланс, 97
диссипация, 98
конвекция, 98
перенос, 98
энергия
возмущения, 98
кинетическая, 57, 98
эффект
Гиббса-Томсона, 120
Марангони, 120, 138
Сорета, 120
Ячейки конвекционные
прямоугольные, 129
роликовые, 118, 129, 132
шестиугольные, 129

Научное издание
ДРАЗИН Филипп
ВВЕДЕНИЕ В ТЕОРИЮ ГИДРОДИНАМИЧЕСКОЙ
УСТОЙЧИВОСТИ
Редактор И.Л. Лееостаева
Оригинал-макет: А.Т, Ильичев
Оформление переплета: А.Ю. Алехина
Л? №071930 от 06.07.99. Подписано в печать 23.06.05.
Формат 60x90/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 18. Уч.-изд. л. 19,8. Тираж 300 экз. Заказ № 3332.
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru;
http://www.fml.ru
Отпечатано с готовых диапозитивов
в ОАО «Ивановская областная типография»
153008, г. Иваново, ул. Типографская, 6
E-mail: 091 -018@adminet.ivanovo.ru