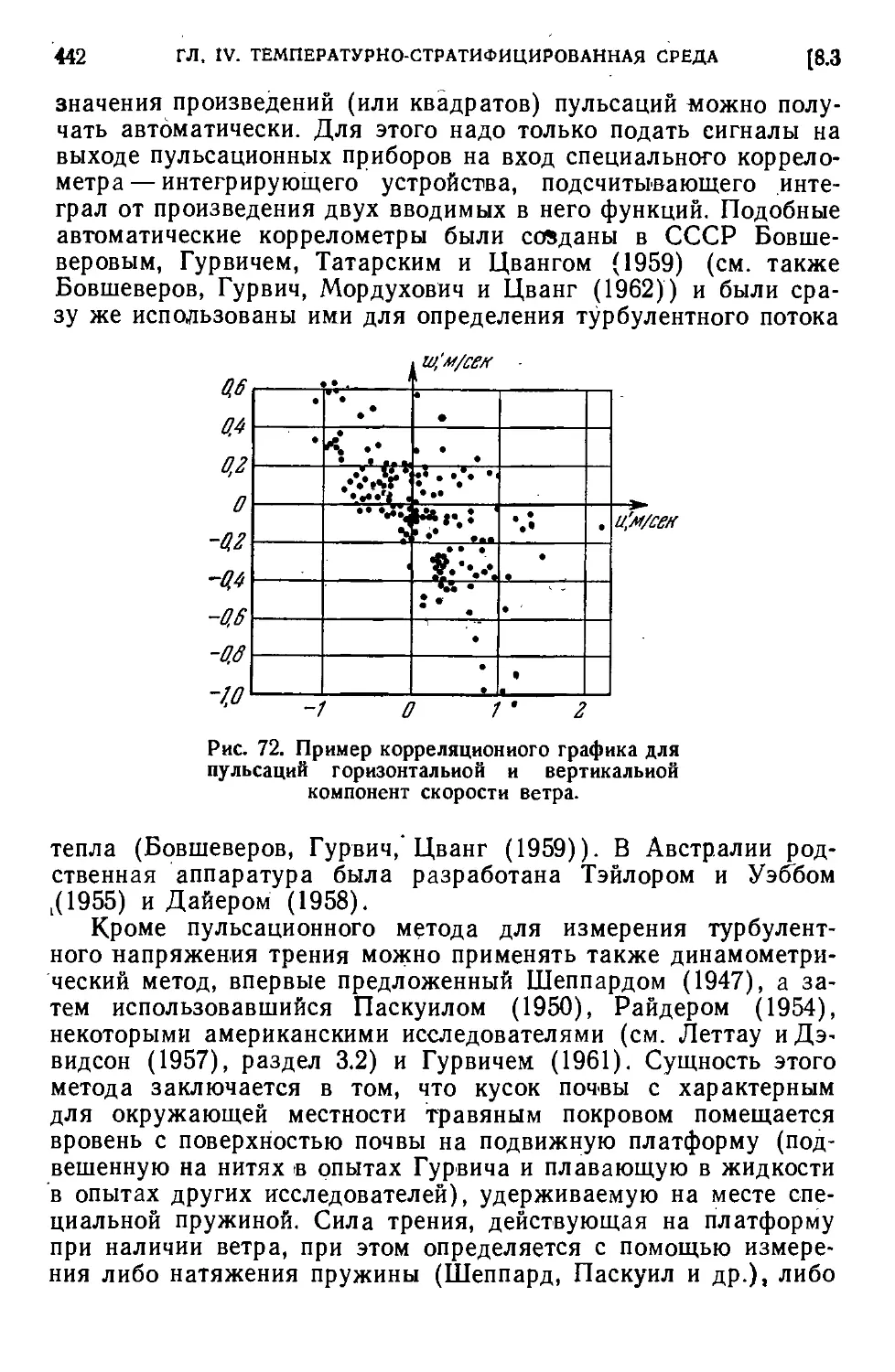
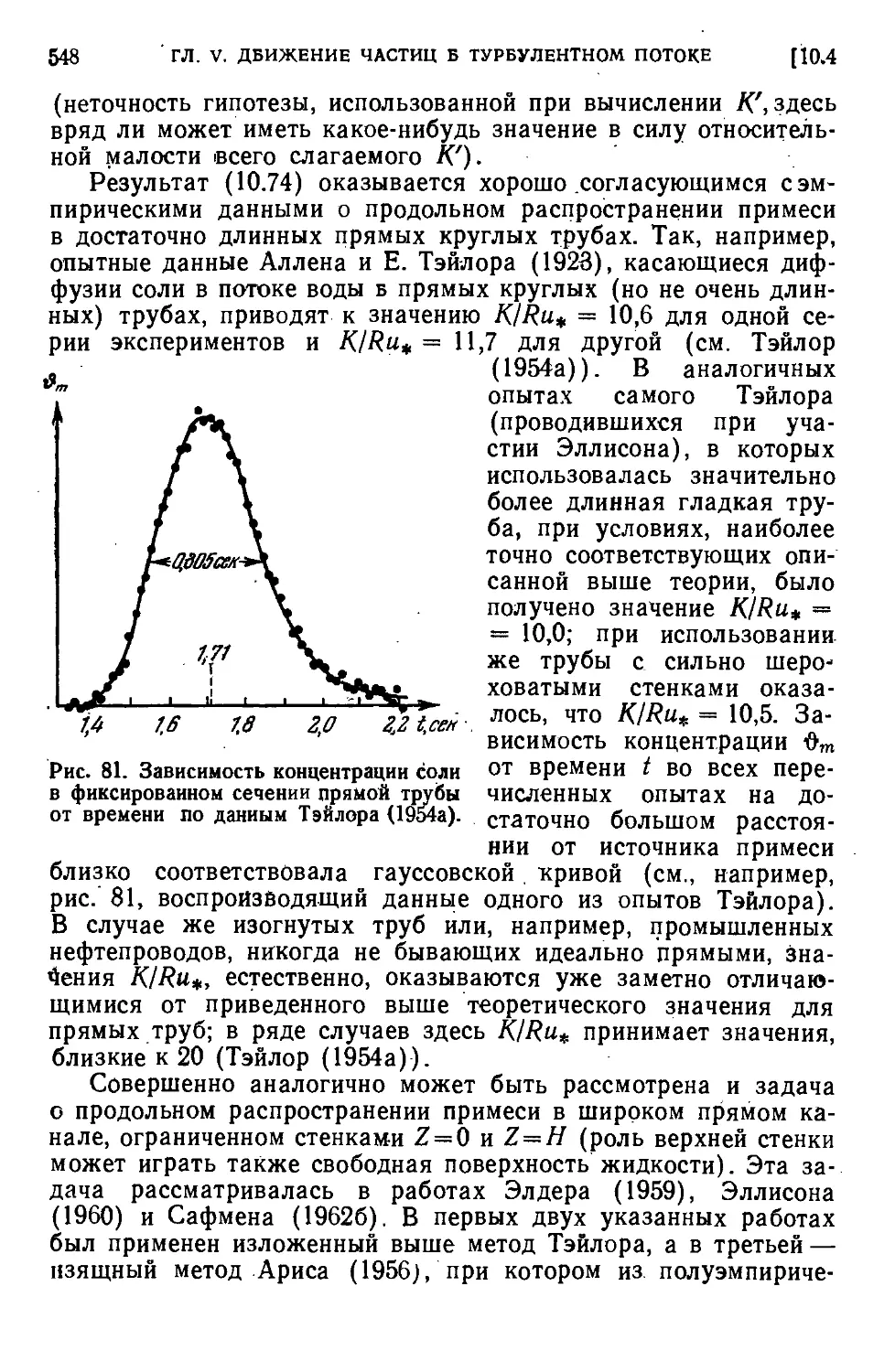
Статическая Гидромеханика. Часть 1. Механика турбулентности - Яглом А.М., Монин А.С.

Автор: Яглом А.М. Монин А.С.

Теги: движение жидкостей гидродинамика гидромеханика турбулентность

Год: 1965

Похожие

Динамика пограничного слоя атмосферы

Вычислительная гидромеханика и теплообмен. В 2-х томах. Том 2

Теория пограничного слоя.

Вычислительные методы в задачах механики жидкости

Текст

А.С:МОНИН,А.М.ЯГЛОМ
СТАТИСТИЧЕСКАЯ
ГИДРОМЕХАНИКА

А. С. МОНИН, А. М. ЯГЛОМ
СТАТИСТИЧЕСКАЯ
ГИДРОМЕХАНИКА
МЕХАНИКА ТУРБУЛЕНТНОСТИ
ЧАСТЬ I
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1965

M 77
УДК 532.507

ОГЛАВЛЕНИЕ
Предисловие . 7
Введение . 9
ГЛАВА I
ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
§ 1. Уравнения динамики жидкости них основные следствия ... 35
1.1. Система уравнений динамики несжимаемой жидкости C5).
1.2. Простейшие течения несжимаемой жидкости C9). 1.3. Число
Рейнольдса и критерий подобия D5). 1.4. Теяеиия с большими
числами Рейиольдса;. пограничный слой D8). 1.51 Общее уравне-
уравнение притока тепла и уравнение теплопроводности; вынужденная
и свободная конвекция E8). 1.6. Критерии подобия для темпера-
турно-неоднородной жидкости; температурный пограничный
сдой F5), 1.7. Малые колебания сжимаемой жидкости G0).
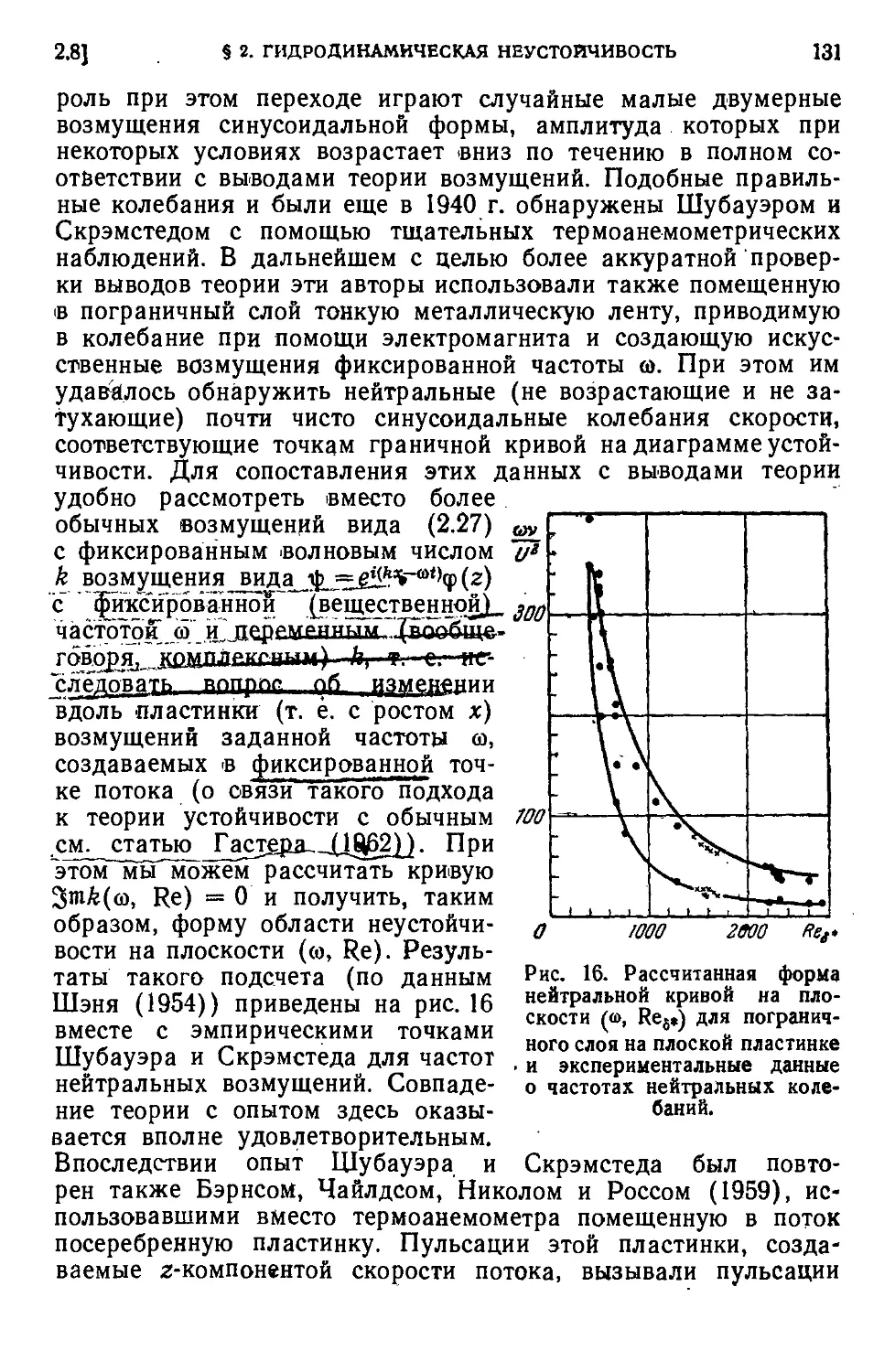
§ 2. Гидродинамическая неустойчивость и возиикиовеиие турбу-
турбулентности ,.....' 77
2.1, Понятие о турбулентности; эмпирические данные о возникно-
возникновении турбулентности в трубах и в пограничном слое G7).
2.2. Данные о турбулентном обтекании: отрыв пограничного слоя,
кризис сопротивления и механизм туроулизации пограничного
слоя (85). 2.3. Гидродинамическая неустойчивость (91). 2.4. Про-
Простейшие примеры абсолютно неустойчивых потоков жидкости (95).
2.5. Математическая формулировка вопроса об устойчивости от-
относительно малых возмущений (98). 2.6. Устойчивость течения
между двумя вращающимися цилиндрами A02). 2.7. Устойчивость
слоя жидкости, подогреваемой снизу A09). 2.8. Устойчивость
плоскопараллельиых течений и течений в трубе и в пограничном
слое A13). 2.9. Устойчивость по отношению к конечным возму-
возмущениям; возрастание возмущений и переход к турбулеитиости A36).
ГЛАВА II
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ.
СРЕДНИЕ ЗНАЧЕНИЯ И КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
§ 3. Методы осреднения. Поля гидродинамических характеристик
как случайнее поля 162
3.1. Практические методы осреднения и условия Рейиольдса A62).
3.2. Случайные поля гидродинамических величии и вероятностное

ОГЛАВЛЕНИЕ
осреднение A66). 3.3. Понятие об эргодичности. Статистическая
формулировка основной задачи теории турбулентности A72).
3.4. Характеристические функции и характеристический функцио-
функционал A75).
§ 4. Моменты гидродинамических полей . 180
4.1. Моменты и семиинварианты случайных величин A80). 4.2. Мо-
Моменты и семиинварианты случайных полей A83). 4.3. Случайные
поля с нормальными распределениями вероятности (гауссовские
поля) A89). 4.4. Определение моментов ц семиинвариантов слу-
случайного поля по его характеристическому функционалу A95).
4.5. Стационарные случайные функции B01). 4.6. Однородные слу-
случайные поля B04). 4.7. Эргодическая теорема B08).
ГЛАВА 111
УРАВНЕНИЯ РЕЙНОЛЬДСА И ПОЛУЭМПИРИЧЕСКИЕ ТЕОРИИ
ТУРБУЛЕНТНОСТИ
§ 5. Турбулентные течения в трубах и в пограничном слое . . . 215
5.1. Уравнения Рейнольдса B15). 5.2. Общий вид профиля средней
скорости течения около стенки B22). 5.3. Течение около гладкой
стенки; вязкий подслой и логарифмический пограничный слой B27).
5.4. Влияние неровностей стеики; параметр шероховатости и вы-
высота вытеснения B39). 5.5. Турбулентные течения в каналах и
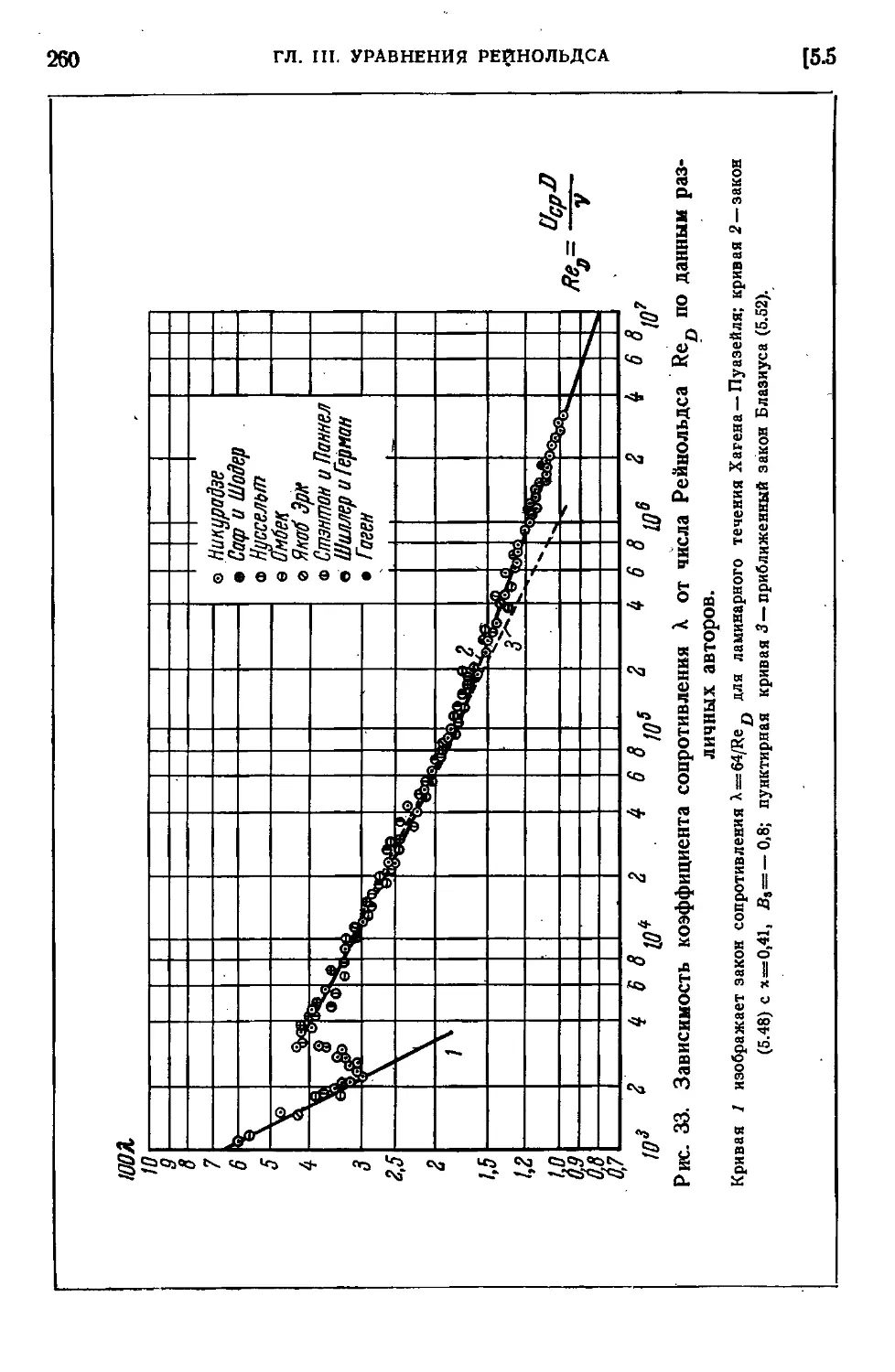
круглых трубах; законы сопротивления B50). 5.6. Турбулентный
пограничный слой на плоской пластинке B63). 5.7. Профиль кон*
центрации пассивной примеси около стенки; диффузия и теплопе-
теплопередача в турбулентном пограничном слое B79). 5.8. Полуэмпири-
Полуэмпирические теории турбулентности B91). 5.9. Свободная турбулент-
турбулентность C04).
§ 6. Уравнение баланса турбулентной энергии и его следствия . . 318
6.1. Уравнение для тензора напряжений Рейнольдса C18). 6.2. Урав-
Уравнение баланса турбулентной энергии C25). 6.3. Общее понятие
о коэффициентах турбулентной вязкости и теплопроводности C31).
6.4. Баланс турбулентной энергии в сжимаемой жидкости C37);
6.5. Число Ричардсона и коэффициент турбулентной вязкости в тем-
пературно-стратифицированной среде C42). 6.6. Турбулентность
в планетарном пограничном слое атмосферы C47). 6.7. Распреде-
Распределение взвешенных частиц в турбулентном потоке C54).
ГЛАВА IV
ТУРБУЛЕНТНОСТЬ В ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННОЙ
СРЕДЕ
§ 7. Обобщение теории логарифмического пограничного слоя на
случай температурно-стратифицированной среды 358
7.1. Турбулентный пограничный слой в температурно-стратифици-
рованной среде как модель приземного слоя атмосферы C58).
7.2. Применение соображений размерности к турбулентности
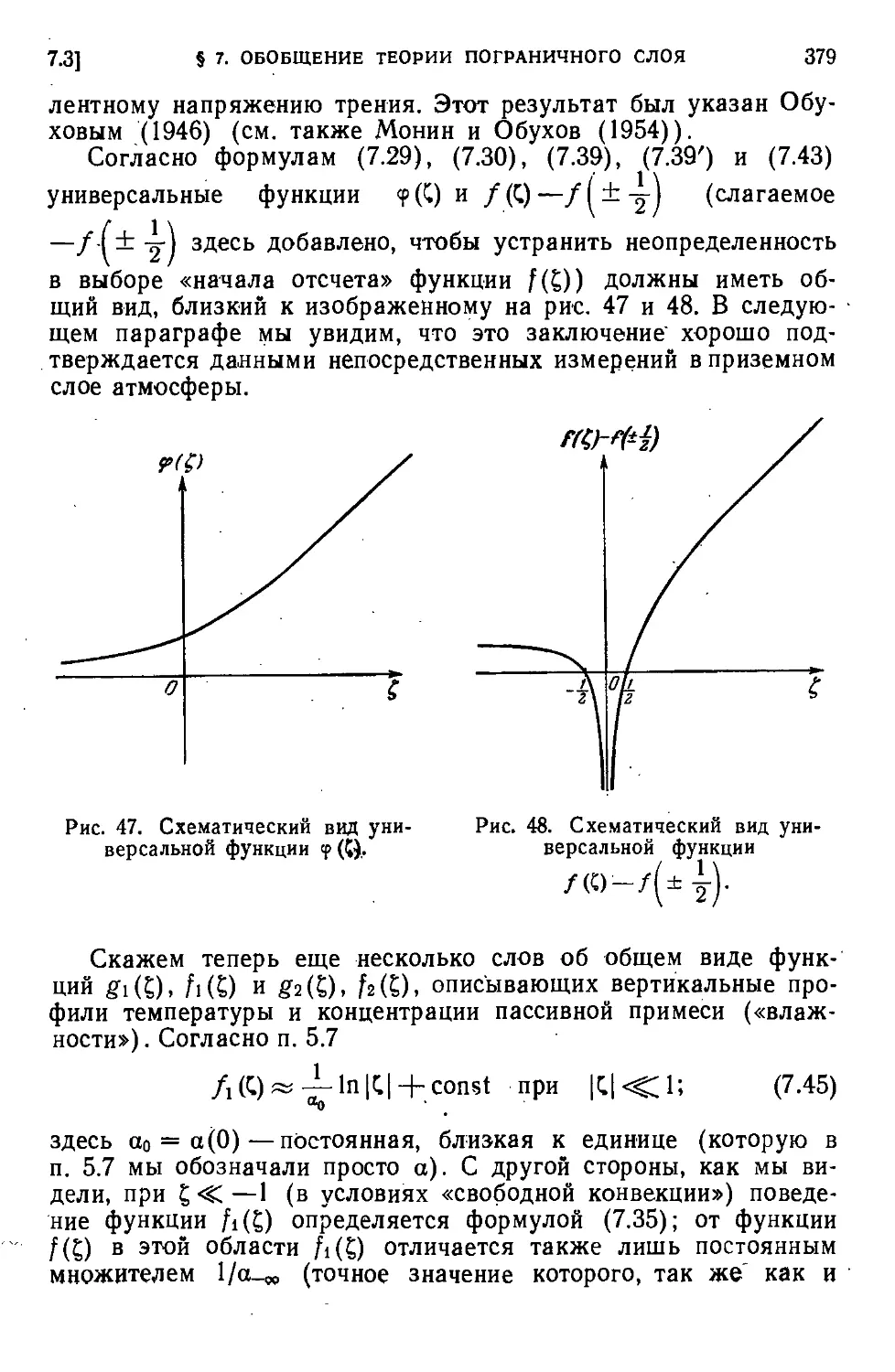
в стратифицированной среде C66). 7.3. Общий вид универсальных
функций, описывающих турбулентный режим в стратифицирован-

ОГЛАВЛЕНИЕ О
ной среде C71). 7.4. Дальнейшие соображения о виде универсаль-
универсальных функций; интерполяционные и полуэмпирические формулы C83).
7.5. Общая формулировка гипотезы подобия для турбулентного
режима в приземном слое атмосферы и ее применение к исследо-
исследованию пульсаций метеорологических полей C97).
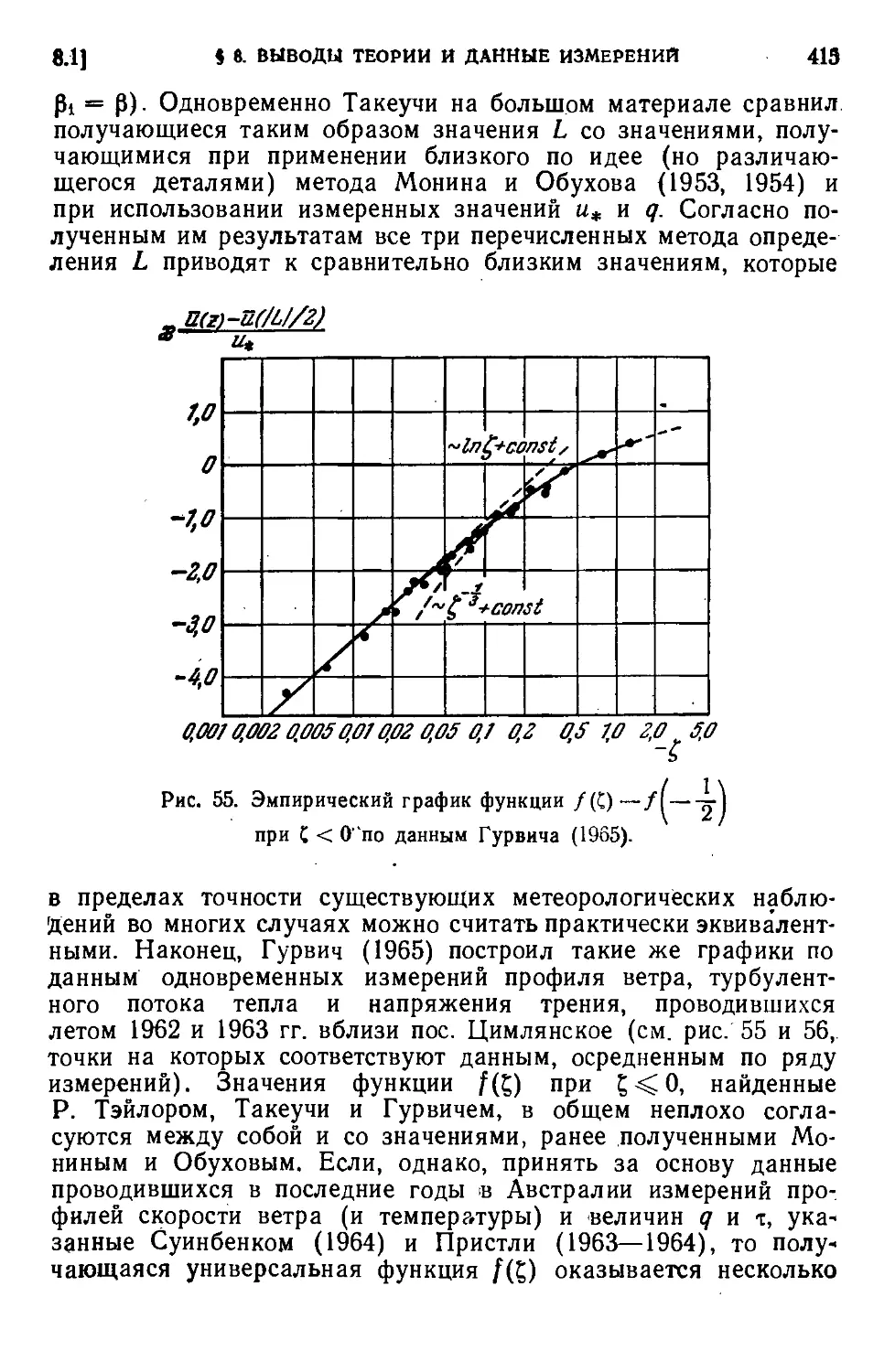
§ 8. Сопоставление выводов теории с данными измерений в при-
приземном слое атмосферы 408
8.1. Профили скорости ветра в приземном слое атмосферы D08).
8.2. Данные о профилях температуры и влажности D23). 8.3. Ме-
Методы измерения турбулентных потоков импульса, тепла и влаги D37).
8.4. Определение турбулентных потоков по данным о профилях
метеорологических величин D44). 8.5. Пульсации скорости ветра
и температуры в приземном слое D54).
ГЛАВА V
ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ
§ 9. Лагранжево описание турбулентности . 460
9.1. Уравнения гидродинамики несжимаемой вязкой жидкости
в переменных Лагранжа D60). 9.2. Лагранжевы статистические
характеристики турбулентности D66). 9.3. Характеристики смеще-
смещения фиксированной жидкой частицы; случай однородной турбу-
турбулентности D71). 9.4. Смещение жидких частиц в турбулентности
за' решеткой и в турбулентных потоках с градиентом средней
скорости D78). 9.5. Лагранжева корреляционная функция скорости
и её связь с эйлеровыми статистическими характеристиками D97).
§ 1#. Турбулентная диффузия 505
10.1. Постановка задачи об описании турбулентной диффузии E05).
10.2. Взаимодействие между молекулярной и турбулентной диф-
диффузией E16). 10.3. Полуэмпирическое уравнение турбулентной
диффузии E29). 10.4. Диффузия в поле однородной турбулентности
и в поле простейших течений с градиентом скорости E37).
10.5. Диффузия в приземном слое воздуха E59). 10.6. Диффузия
с конечной скоростью E88).
Библиография 603

ПРЕДИСЛОВИЕ
Теория турбулентности, рассматриваемая в этой книге, исхо-
исходит из макроскопического описания течений жидкостей и газов,
как непрерывных сред, на основе классических уравнений гидро-
гидромеханики. Но в отличие от обычной гидромеханики теория тур-
турбулентности изучает не индивидуальные особенности течений,
а статистические свойства ансамблей течений при макроскопи-
макроскопически одинаковых внешних условиях. Поэтому мы и озаглавили
эту книгу «Статистическая гидромеханика». Однако следует
иметь в виду, что такие, вопросы, как вывод макроскопических
уравнений гидромеханики из статистических законов кинетиче-
кинетической теории газов,' к которым^-иногда также относят это назва-
название, в наШей книге излагаться не будут.
Основные понятия и^»идеи, касающиеся турбулентности, и
подход к изложению теории турбулентности, который' мы из-
избрали в этой книге, обрисованы во введении, где дан также крат-
краткий исторический очерк и приведен план как настоящей первой
части книги, так и последующей второй части. Введение при-
призвано дать читателю самое общее представление о проблематике
и методах современной теории турбулентности и об ее приклад-
прикладном значении; при этом, конечно, приходится использовать ряд
понятий, детальная расшифровка которых дается лишь в после-
последующих разделах книги.
Книга разбита на главы, параграфы и пункты. Главы и
параграфы имеют сплошную нумерацию, а пункты нумеруются
внутри каждого параграфа, причем отдельно указываются
номер параграфа и номер пункта (например, четвертый пункт
второго параграфа обозначается как пункт 2.4). Аналогично ну-
нумеруются и формулы: например, формула B.15)—это пятна-
пятнадцатая формула во втором параграфе. При ссылках на литера-
литературу, приведенную в библиографических списках в конце каждой
части, в тексте указывается фамилия автора и в скобках — год
появления работы. В тех случаях, когда упоминается несколько
работ данного автора, вышедших в одном и том же году, эти
работы дополнительно нумеруются русскими буквами, Кроме

8 предисловие
введения, инициалы авторов в тексте указываются только
в тех случаях, когда это необходимо для различения однофа-
однофамильцев.
Мы старались по мере возможности использовать в книге
общепринятые обозначения. В тех же многочисленных случаях,
когда для встречающихся в теории турбулентности величин раз-
разными авторами используются различные символы, мы предпо-
предпочитали, как правило, избирать одно из них, а не вводить какие-
то новые обозначения. В некоторых случаях это привело к тому,
что пришлось в разных частях книги использовать один и тот
же символ для различных величин. Кое-где по ряду причин ока-
оказалось также удобным одну и ту же величину в разных разделах
обозначать по-разному. Во всех таких случаях используемые
обозначения специально оговариваются в тексте.
Наша книга представляет собой совместный труд обоих ав-
авторов. Мы считаем также необходимым отметить, что на ее на-
написание, как и на наши собственные исследования, глубокое
влияние оказали беседы с нашим учителем Андреем Николаеви-
Николаевичем Колмогоровым, многие идеи которого мы постарались отра--
зить в настоящей книге.
Мы многим обязаны и А. М. Обухову, который был одним
из инициаторов написания этой книги и оказал нам большую
помощь своими советами по отбору материала и изложению
ряда вопросов. Отдельные части рукописи были прочитаны
Л. А. Диким, Е. А. Новиковым и В. И. Татарским, высказав-
высказавшими ряд полезных замечаний. В обсуждении эксперименталь-
экспериментальных данных об атмосферной турбулентности активно участво-
участвовали А. С. Гурвич и Л. Р. Цванг. Большую помощьчг подготовке
и редактировании книги оказал Г. С. Голицын. Всем этим лицам
мы выражаем свою глубокую благодарность.
А. С. Монин
А. М. Яглом

ВВЕДЕНИЕ
Настоящая книга посвящена теории турбулентных течений
жидкостей и газов. Она начинается с напоминания основных
уравнений, описывающих движения жидкой и газообразной
среды, и от читателя, вообще говоря, не требуется, чтобы он за-
заранее знал, что такое турбулентность. Поэтому нам кажется,
что в начале введения небесполезно хотя бы вкратце объяснить,
о чем же, собственно, будет идти речь в этой книге.
Известно, что все течения жидкостей и газов делятся на два
резко различные типа: спокойные и плавные течения, называе-
называемые ламинарными, и их противоположность — так называемые
турбулентные течения, щзд. которых скорость, давление, темпе-
температура и другие гидродинамические величины беспорядочно
пульсируют, крайне нерегулярно изменяясь в пространстве и во
времени. В качестве типичного примера мы приводим на рис. 1
запись колебаний во времени скорости ветра, вертикальной ком-
компоненты скорости и температуры в атмосфере вблизи земли, по-
полученную при измерении скорости и температуры с помощью
специальных малоинерционных приборов. Сложный характер
этих кривых сразу показывает, что соответствующее движение
воздуха было турбулентным. Множество пульсаций различных
периодов и амплитуд, наблюдающееся на представленных на
рис. 1 записях, иллюстрирует сложную внутреннюю структуру,
турбулентных течений, резко отличающихся в этом отношении
от ламинарных течений. Эта сложная структура сказывается на
многих свойствах течения, оказывающихся весьма различными
в ламинарном и турбулентном случаях. Так, турбулентные тече-
течения обладают гораздо большей способностью к передаче коли-
количества движения (образно говоря, турбулентная среда имеет ог-
огромную эффективную вязкость) и потому во многих случаях
оказывают гораздо большее силовое воздействие на обтекаемые
жидкостью или газом твердые тела. Аналогичным образом тур-
турбулентные потоки обладают повышенной способностью к пере-
передаче тепла и пассивных примесей, к распространению химиче-
химических реакций (в частности, горения), к переносу взвешенных

10
ВВЕДЕНИЕ
частиц. Благодаря наличию внутренних неоднородностей турбу-
турбулентные течения способны рассеивать проходящие сквозь жид-
жидкость или газ звуковые и электромагнитные волны и вызывать
флюктуации их амплитуд и фаз и т. п.
Ясно, что перечисленные свойства турбулентных течений мо-
могут быть весьма существенными для многих задач естествозна-
естествознания и техники. Поэтому вопрос о том, часто ли встречаются
Вертикальная компонента
скорости ветра
Рис. 1. Типичный пример записи пульсаций температуры, скорости
ветра и вертикальной компоненты скорости ветра.
турбулентные течения, представляет несомненный интерес.
Оказывается, что подавляющее большинство реально встречаю-
встречающихся в природе и технике течений является именно турбулент-
турбулентным; ламинарные же течения, подробно изучающиеся в гидро-
гидромеханике, представляют собой лишь довольно редкое исклю-
исключение.
Турбулентными, в частности, являются разнообразные дви-
движения воздуха в земной атмосфере, начиная от слабого ветра
вблизи поверхности земли (к которому относятся измерения,
воспроизведенные на рис. 1) и кончая движениями общей цир-
циркуляции, имеющими масштабы планеты в целом. Атмосферная
турбулентность играет основную роль в процессах переноса теп-
тепла и влаги воздушными массами, в испарении влаги с поверх-
поверхности земли и водоемов и в тепловом и динамическом взаимо-
взаимодействии между атмосферой и подстилающей поверхностью,
существенно влияющем на изменения погоды; она определяет
распространение примесей в воздушной среде, зарождение ве-

ВВЕДЕНИЕ И
гровых волн на поверхности моря и образование ветровых тече-
™й в океане, болтанку самолетов и других летательных аппара*
гов и вибрации многих наземных сооружений; наконец, турбу*
аентные флюктуации показателя преломления обусловливают
многие важные особенности распространения света и радиоволн
от наземных и космических источников. Турбулентными оказы«
ваются и течения воды в реках, морях и океанах, а также колос-
колоссальные по сравнению с масштабами земли движения газов в
межзвездных газовых туманностях. Наконец, турбулентными яв-
являются практически все имеющие прикладное значение течения
в трубах — в водопроводах, газопроводах, нефтепроводах, соп-
соплах реактивных двигателей и т. д.; движения в пограничных
слоях, образующихся около поверхности движущихся летатель-
летательных аппаратов; в струях жидкости или газа, вырывающихся с
большой скоростью из сопла; в следах за быстро перемещающи-
перемещающимися твердыми телами — лопастями пропеллера, лопатками
турбины, пулями, снарядами, ракетами. Таким образом, турбу-
турбулентность буквально окружает нас и в природе и в технических
устройствах, связанных с течениями жидкостей и газов; поэтому
ее изучение безусловно является очень важной практической
задачей.
Большой интерес представляют турбулентные течения и с
чисто теоретической точки зрения как примеры нелинейных
механических систем с очень большим числом степеней сво-
свободы. В самом деле, движения любой непрерывной среды, строго
говоря, описываются бесконечным числом обобщенных коорди-
координат (в качестве которых можно принять, например, коэффи-
коэффициенты разложения поля скорости по какой-либо полной системе
функций от пространственных координат). Однако в случае ла-
ламинарных движений эти координаты обычно можно выбрать та-
таким образом, что лишь небольшое число отвечающих им степе-
степеней свободы будет возбуждено, т. е. будет реально участвовать
в движении. В случае же турбулентного движения возбужден-
возбужденным всегда оказывается огромное число степеней свободы, в
результате чего изменение во времени любой физической вели-
величины здесь описывается функциями, содержащими громадное
число компонент Фурье, т. е. имеющими очень сложный харак-
характер (см. опять рис. 1). По этой причине здесь уже практически
безнадежно пытаться описать индивидуальные изменения во
времени всех обобщенных координат, соответствующих возбуж-
возбужденным степеням свободы (т. е. математически выразить зави-
зависимость от времени полей скорости, давления и т. д. одного от-
отдельного течения). Единственно возможным в теории турбулент-
турбулентности представляется статистическое описание, опирающееся
на изучение специфических статистических закономерностей^

12 ВВЕДЕНИЕ
присущих большим совокупностям однотипных объектов. Таким
образом, теорией турбулентности может быть лишь статистиче-
статистическая гидромеханика, изучающая статистические свойства ан*
самблей течений жидкостей или газов, находящихся в макро-
макроскопически одинаковых внешних условиях.
Теория турбулентности по самому своему существу не может
не быть статистической — индивидуальное описание полей ско-
скорости, давления, температуры и других характеристик турбу-
турбулентного течения принципиально невозможно и было бы даже
бесполезным, так как крайне запутанный и нерегулярный ха-
характер этих полей исключает возможность использования точ-
точных данных о них в каких бы то ни было практических задачах.
Поэтому не имеет смысла иногда встречающееся в литературе
противопоставление так называемой полуэмпирической и стати-
статистической теорий турбулентности. Полуэмпирическая теория, ра-
разумеется, также является статистической и выделяется из дру-
других теорий турбулентности вовсе не отказом от использования
статистических характеристик, а лишь приемами, используе-
используемыми для их определения.
Говоря о статистическом характере теории турбулентности,1
е& часто сравнивают с кинетической теорией газов, изучающей
системы из очень большого числа взаимодействующих между
собой молекул. Это сравнение оправдано в том смысле, что в
обеих указанных теориях точное описание эволюции исследуе-
исследуемой механической системы теоретически безнадежно, а практи-
практически было бы бесплодным. Однако надо иметь в виду, что ме-
между статистической механикой молекулярных ансамблей, изу-
изучавшейся Гиббсом, Больцманом и другими исследователями, и
статистической гидромеханикой вязкой жидкости-} существует и
большое принципиальное различие. Оно связано, '^ первую оче-
очередь, с тем, что суммарная кинетическая энергия совокупности
движущихся молекул не меняется во времени (во всяком случае
при простейших предположениях о молекулярных взаимодей-
взаимодействиях, обычно принимаемых в кинетической Теории тазов), то-
тогда как при движениях реальной жидкости ее кинетическая
энергия всегда диссипируется в теплоту под действием вязкости.
Менее существенным, но также не безразличным оказывается
то, что молекулярные ансамбли дискретны по своей природе
и их временная эволюция описывается системами обыкновен-
обыкновенных дифференциальных уравнений, в то время как в гидро*
механике речь идет о движениях непрерывной среды, описывае-
описываемых уравнениями в частных производных. В результате всего
этого аналогия с кинетической теорией газов сравнительно мало
помогает построению теории турбулентности, облегчая лишь са-

ВВЕДЕНИЕ 13
мое первоначальное понимание идеи о статистическом подходе
к физической теории.
Может быть, даже более плодотворной окажется аналогия
между теорией турбулентности и квантовой теорией поля, свя-
связанная с тем, что система взаимодействующих между собой по-
полей— это также нелинейная система с теоретически бесконеч-
бесконечным числом степеней свободы. Отсюда проистекает близость
математического аппарата, используемого в обеих теориях, поз-
позволяющая надеяться, что существенные сдвиги в одной из них
могут оказать решающее влияние и на развитие второй. В на-
настоящее время, однако, квантовая теория поля сталкивается с
большими затруднениями принципиального характера, а в тео-
теории турбулентности также имеются лишь частные успехи; по-
поэтому глубокое воздействие одной из этих теорий на другую
пока еще остается делом будущего.
Несмотря на то, что течения жидкостей и газов, встречаю-
встречающиеся в природе и технических устройствах, как правило, яв-
являются турбулентными, во всех существующих общих курсах
гидромеханики теории турбулентности посвящены в лучшем слу-
случае лишь небольшие разделы, содержащие кое-какие отрывоч-
отрывочные сведения о методах статистического описания неупорядо-
неупорядоченных течений жидкости и газа и о некоторых статистических
характеристиках таких течений. Монографическая литература,
пЬевященная турбулентности, также очень бедна и насчитывает
вси*о несколько названий (почти все они могут быть найдены в
списке литературы, приложенном к настоящей книге); при этом
большая часть из них относится к книгам сравнительно узкого
содержания. Нетрудно понять, почему сложилось такое поло-
положение. Турбулентные течения являются значительно более слож-
сложным объектом, чем ламинарные, и требуют для своего изучения
Существенно новых методов, отличных от классических методов
математической физики, в течение почти двух столетий считав-
считавшихся единственно годными для количественного изучения зако-
законов природы. Математический аппарат, нужный для логически
аккуратного построения статистической механики непрерывных
сред —теория случайных полей, — был создан лишь за послед-
последние 25—30 лет и до сих пор еще мало известен за пределами
узкого круга специалистов по теории вероятностей. В эти же
годы сформировалась и современная теория турбулентности, ко-
которая до сих пор еще далека от завершения. Нам кажется, од-
однако, что уже имеющиеся в этой области достижения безуслов-
безусловно заслуживают того, чтобы занять заметное место в обязатель*
ном объеме знаний каждого образованного гидромеханика и
физика-теоретика, и если этого еще не произошло, то лишь
ввиду относительной молодости теории турбулентности. Можно

U ВВЕДЕНИЕ
выразить уверенность, что в дальнейшем удельный вес этой тео
рии в учебных руководствах и программах по гидромеханике
для высших учебных заведений, в обязательном объеме знаний
специалистов по гидромеханике и по теоретической физике и в
планах научно-исследовательских работ будет быстро возра-
возрастать. Мы будем рады, если наша книга будет в какой-то мере
способствовать этому процессу.
Перейдем теперь к краткому историческому очерку развития
науки о турбулентности. При этом мы перечислим те подходы и
результаты, развернутое изложение которых составит основное
содержание книги, и постараемся объяснить, почему нам кажется,
что такую книгу целесообразно написать именно сейчас — на со-
современном этапе развития статистической гидромеханики.
Существование двух резко различающихся типов течений,
называемых в настоящее время ламинарными и турбулентными,
было замечено еще в первой половине XIX в., но теория турбу-
турбулентности появилась только вместе с замечательными работами
Осборна Рейнольдса A883, 1895). В этих работах Рейнольде
уделил основное внимание условиям, при которых ламинарное
течение жидкости в трубах превращается в турбулентное тече-
течение, и установил общий критерий динамического подобия те-
течений вязкой несжимаемой жидкости. В отсутствие внешних сил
таким критерием является, кроме геометрического подобия, сов-
совпадение значений так называемого числа Рейнольдса Re=UL/v,
где U и L — характерные- масштабы скорости и длины в рас-
рассматриваемом течении, a v — кинематический коэффициент вяз-
вязкости жидкости. С динамической точки зрения числолЯе может
быть интерпретировано как отношение типичных значений сил
инерции и сил вязкости, действующих внутри жидкости. Силы
инерции.вызывающие перемешивание различных объ&мпв,жип-
кости. движущихся «пЪ инерции» с разными скоростями, осуще-
осуществляют п^ед?Ч2_энерхии,.ох..к^п|юЩЩтабньГхТкомпвнент дви-
жения^к^мелком^Г'ЧТ?бннм и.те» самым способствуют образо-
ванию~~в потоке. резкии^-лзджомасшшбньхх.неоднородностей. ха-
рактерных для турбулентного течения. Силы вязкости, наоборот,
приводят к сглаживанию мелкомасштабных неоднородностей.
Поэтому следует ожидать, что течения с достаточно малыми
значениями Re будут ламинарными, а с достаточно большими
Re — турбулентными. Этот основной результат и был четко
сформулирован Рейнольдсом.
Рейнольде сделал еще один очень важный для теории тур-
турбулентности шаг. Он предложил представлять значения всех

ВВЕДЕНИЕ }5
гидродинамических величин в турбулентном течении в виде сум-
суммы осредненных (регулярных) и пульсационных (нерегулярных)
составляющих и изучать лишь осредненные величины, сравни-
сравнительно плавно меняющиеся в пространстве и во времени, отка-
отказавшись от практически безнадежных попыток описания всех
деталей индивидуальных реализаций гидродинамических полей.
Для определения средних значений Рейнольде предложил при-
применять обычное осреднение по некоторому интервалу времени
или некоторой пространственной области, но фактически он
пользовался лишь определенными алгебраическими свойствами
вводимой операции осреднения, позволяющими существенно
упростить ее применение к уравнениям гидромеханики. Поэтому
в настоящее время, когда при исследовании турбулентности
принято понимать осреднение иначе, чем во времена Рейнольд-
са, все его выводы тем не менее полностью сохраняют силу,
поскольку, как оказывается, использованные им свойства
осреднения оказываются совсем очевидными именно при совре-
современном понимании этой операции.
Для дальнейшего нам будет удобно сразу же указать, как
теперь понимается осреднение в теории турбулентности. В со-
современной статистической гидромеханике всегда подразуме-
подразумевается, что гидродинамические поля турбулентного течения
представляют собой случайные поля в смысле, принятом в тео-
теории вероятностей. Иначе говоря, каждая конкретная реализа-
реализация такого поля рассматривается как некий «представитель»,
извлеченный из «статистического ансамбля всевозможных по-
полей», характеризуемого определенной.вероятностной мерой на
множестве функций от пространственных координат и времени,
удовлетворяющих необходимым кинематическим и динамиче-
динамическим условиям (вытекающим из законов гидромеханики). При
этом осреднение любых гидродинамических величин можно по-
понимать как теоретико-вероятностное осреднение по соответ-
соответствующему статистическому ансамблю, и все свойства операции
осреднения, наличия которых требовал Рейнольде, оказываются
вытекающими из обычных свойств вероятностного среднего зна-
значения (математического ожидания), излагаемых в учебниках по
теории вероятностей. Тем самым сразу устраняются многие
трудности, неизбежные при применении временного или про-
пространственного осреднения (но, правда, реальная интерпретация
результатов формальной теории оказывается требующей исполь-
использования некоторых предположений об эргодичности, обычных,
впрочем, для статистической физики).
В предыдущем абзаце мы отступили от хронологического
принципа изложения основных этапов формирования теории
турбулентности. Однако, прежде чем вернуться к историческому.

16 ВВЕДЕНИЕ
обзору, мы еще несколько разовьем допущенное отступление и
дадим современную формулировку общей проблемы статисти-
статистического описания турбулентных течений (или, коротко, пробле-
проблемы турбулентности). Ограничимся при этом для простоты слу-
случаем несжимаемой жидкости, в котором течение полностью
определяется соленоидальным (т. е. бездиеергентным) полем ско-
скорости и(х, t) = {«1 (х, t), u2(x, t), «з (х, t)}, где ии и2, «з— компо-
компоненты скорости, X — точка .пространства, t — время (поле дав-
давления с помощью уравнений гидродинамики может быть выра-
выражено через поле скорости в тот же момент времени). В этом
случае проблема турбулентности сводится к нахождению рас-
распределения вероятностей P{da>) на фазовом пространстве тур-
турбулентного потока Q = {со}, точками <о которого являются всевоз-
всевозможные соленоидальные векторные поля и(Х, t), удовлетворяю-
удовлетворяющие уравнениям гидродинамики и надлежащим краевым условиям
на границах потока. Во многих случаях полезной оказывается
также более узкая (т. е. менее полная) формулировка проблемы
турбулентности, при которой рассматриваются лишь синхрон-
синхронные (отвечающие одному и тому же моменту времени) значения
гидродинамических величин. При таком подходе проблема тур-
турбулентности заключается в нахождении однопараметрического
семейства распределений вероятностей Pt{da>) на фазовых про-
пространствах Qt = {со}, точками со которых являются всевозмож-
всевозможные соленоидальные векторные поля и(х), удовлетворяющие со-
соответствующим граничным условиям (могущим, вообще говоря,
зависеть от времени — именно поэтому мы ввели индекс t в обо-
обозначение Qt фазового пространства). Зависимость распределе-
распределений Pt(d(u) от времени отражает эволюцию поля скорости в со-
соответствии с уравнениями гидродинамики. В самом деле, если
записать решение этих уравнений символически в виде и(х, t) =
= Ttu(x, 0), где Tt — соответствующий нелинейный оператор, то,
очевидно, для любого измеримого множества А пространства Q*
будет иметь1 место равенство Pt(A) = P0(T-tA), где T_tA — при-
принадлежащее Qo множество всех тех начальных полей скорости
и{х, 0), которые под действием оператора Tt переходят в поля
и(х, t), принадлежащие к множеству А. Отсюда видно, что се-
семейство распределений вероятностей Pt(da) в принципе одно-
однозначно определяется заданным начальным распределением
Po(d(d), так что в излагаемой формулировке проблема турбу-
турбулентности— это задача с начальными условиями об эволюции
вероятностной меры в функциональном пространстве.
Полное определение распределений вероятностей P(da>) или
хотя бы Pt(du>) является задачей исключительной трудности, в
настоящее время еще далекой от решения. Однако для многих

ВВЕДЕНИЕ 17
задач практики вовсе не требуется, чтобы проблема турбулент-
турбулентности была решена полностью. В большинстве практических за-
задач достаточно определить лишь некоторые простейшие харак-
характеристики распределений вероятностей для значений гидроди-
гидродинамических полей турбулентного потока — такие, как средние
значения скорости и давления в различных точках пространства
или времени, вторые моменты пульсаций гидродинамических
полей в заданной точке (например, дисперсии пульсаций скоро-
скорости, характеризующие интенсивность турбулентности, или сме-
смешанные вторые моменты пульсаций скорости и температуры, че-
через которые выражаются компоненты турбулентных потоков
импульса и тепла) и коэффициенты корреляции между пульса-
пульсациями гидродинамических полей в двух точках пространства —
времени (характеризующие пространственно-временную стати-
статистическую связанность или структуру гидродинамических полей
турбулентного потока). Поэтому естественно, что большинство
исследований по теории турбулентности посвящалось не проб-
проблеме турбулентности в целом, а попыткам определения (хотя бы
приближенного) некоторых простейших характеристик распреде-
распределений вероятностей для значений гидродинамических полей тур-
турбулентных течений. Такие исследования позволили получить ряд
ценных сведений о физической природе и свойствах турбулент-
турбулентности и удовлетворительно ответить на ряд важных практиче-
практических аопросов.
Возвращаясь теперь к историческому изложению основных
этапов развития теории турбулентности, упомянем прежде всего
интересную работу Джеффри Тэйлора A921) о турбулентной
диффузии, в которой впервые выявилась важная роль корре-
корреляционных функций (т. е. смешанных вторых моментов) поля
скорости (правда, не для обычной эйлеровой скорости тече-
течения в фиксированной точке, а для более сложной лагранжевой
скорости фиксированной жидкой частицы). Однако в общем
виде идея о том, что корреляционные функции и другие стати-
статистические моменты гидродинамических полей должны быть
признаны основными характеристиками турбулентного дви-
движения, была впервые высказана Л. В. Келлером и А. А. Фрид-
Фридманом A924), предложившими общий метод построения
(с помощью уравнений движения реальной жидкости) диффе-
дифференциальных уравнений для моментов произвольного порядка
гидродинамических полей турбулентных течений. Определение
всех таких моментов при некоторых общих предположе-
предположениях эквивалентно определению соответствующего распреде-
распределения вероятности в функциональном пространстве P(da) или
Pt(doi), т. е. решению проблемы турбулентности. Поэтому
полная бесконечная система уравнений Фридмана — Келлера

18 ВВЕДЕНИЕ
для всевозможных моментов дает аналитическую форму-
формулировку проблемы турбулентности. Но эта система уравнений
оказывается весьма сложной: любая конечная подсистема этой
системы уравнений всегда незамкнута, т. е. содержит боль-
больше неизвестных, чем имеется уравнений в данной подсистеме
(невозможность получить замкнутую систему уравнений для ко-
конечного числа моментов является прямым следствием н е л и -
ней ноет и уравнений гидродинамики). Таким образом, при
использовании метода Фридмана — Келлера в применении к
конечному числу моментов возникает проблема замыкания урав-
уравнений для моментов, во многом аналогичная проблеме замыка-
замыкания цепочки уравнений для многочастичных функций распре-
распределения в кинетической теории газов.
Можно сказать, что большинство теоретических работ по ди-
динамике турбулентных течений посвящалось (и посвящается)
способам преодоления трудностей, связанных с проблемой за-
замыкания. Полностью преодолеть эти трудности до сих пор еще
не удалось. Тем не менее, в теории турбулентности получено
много важных и практически ценных результатов на двух об-
обходных направлениях, одно из которых посвящено описанию
крупномасштабных компонент турбулентности (масштабы кото-
которых сравнимы с масштабами течения в целом), а другое — опи-
описанию мелкомасштабных компонент. Основное различие в
поведении этих двух типов компонент заключается в том, что
крупномасштабные характеристики турбулентности существен-
существенно зависят от геометрии границ потока и характера внешних
воздействий и поэтому оказываются весьма различными для
разных типов течений, тогда как мелкомасштабные характери-
характеристики оказываются имеющими в значительной мере универсаль-
универсальный характер.
Крупномасштабные компоненты вносят основной вклад в
передачу через турбулентную среду импульса и тепла, и вслед-
вследствие этого их описание необходимо для таких важнейших проб-
проблем техники, как расчеты сопротивления и теплообмена при об-
обтекании твердых тел жидкостью или газом. Поэтому естествен-
естественно, что при развитии теории турбулентности разработке методов
описания крупномасштабных компонент было уделено самое
первоочередное внимание. Неотложные нужды практики потре-
потребовали проведения большого числа экспериментальных исследо-
исследований свойств крупномасштабных компонент турбулентности
при течениях в трубах, каналах, пограничных слоях и в свобод-
свободных турбулентных течениях (струи, следы за обтекаемыми жид-
жидкостью телами и т. п.). На базе этих исследований и были
построены так называемые полуэмпиричёские теории турбулент-
турбулентности, позволяющие систематизировать получаемые эксперямен-

ВВЕДЕНИЙ 19
тальные данные и использовать их для предсказания результа-
результатов последующих аналогичных экспериментов.
Создание полуэмпирических теорий турбулентности явилось
"важным этапом в развитии статистической гидродинамики. Этот
этап начался еще в середине 10-х годов текущего столетия, но
расцвет его приходится на последующие два десятилетия B0-е
и 30-е годы); впрочем, возможности полуэмпирического метода
до сих пор еще отнюдь не исчерпаны, и содержательные работы
такого направления продолжают появляться и в наши дни. Ре-
Решающие шаги в развитии полуэмпирического подхода к теории
турбулентности были сделаны Джеффри Тэйлором A915, 1932),
Людвигом Прандтлем A925) и Теодором фон Карманом A930).
Полуэмпирические теории турбулентности строятся на осно-
основе аналогии между турбулентностью и молекулярным хаосом.
В них основную роль играют такие понятия, как путь перемеши-
перемешивания (аналог средней длины свободного пробега молекул), ин-
интенсивность турбулентности (аналог средней скорости движения
молекул), коэффициенты турбулентной вязкости, теплопровод-
теплопроводности и диффузии. На основе той же аналогии делается пред-
предположение о существовании линейной зависимости между тензо-
тензором турбулентных напряжений и тензором средних скоростей
деформации, а также турбулентным потоком тепла (или пассив-
пассивной примеси) и средним градиентом температуры (или концен-
концентрации примеси). Эти предполагаемые зависимости дополняются
затем еще некоторыми гипотетическими закономерностями, об-
общий вид которых устанавливается с помощью качественных фи-
физических рассуждений или же просто подбирается «наудачу»
из соображений простоты. Далее принятые предположения (или
какие-либо простые следствия из них) проверяются на эмпири-
эмпирическом материале, и при этом попутно находятся значения не-
неопределенных постоянных, входящих в используемые полуэмпи-
рические соотношения. Если результаты проверки оказываются
удовлетворительными, то полученные выводы распространяются
на целый класс турбулентных течений, родственный тем, к
которым относились выбранные для проверки теории эмпири-
эмпирические данные.
Полуэмпирические теории 20-х и 30-х годов обычно рассмат-
рассматривали только простейшие статистические характеристики тур-
турбулентных течений. Как правило, принимаемые в этих теориях
гипотезы позволяют замкнуть уже самые первые уравнения си-
системы Фридмана — Келлера, содержащие только одноточечные
первые и вторые моменты гидродинамических полей — так назы-
называемые уравнения Рейнольдса турбулентного движения. Замет-
Заметную роль в полуэмпирических теориях играет также использо-
использование свойств симметрии турбулентности в потоках того или

20 ВВЕДЕНИЕ
иного вида и некоторых простейших гипотез подобия (являю-
(являющихся, в частности, обязательной частью всех полуэмпирических
теорий турбулентных струй и следов за обтекаемыми телами).
Однако гипотезы подобия, опирающиеся на конкретные физиче-
физические представления о механизме турбулентности, не были един-
единственной основой этих теорий и всегда дополнялись (иногда
даже и без настоящей надобности) предположениями более спе-
специального характера. Так, например, одним из важнейших вы-
выводов полуэмпирических теорий явилось установление универ-
универсального (т. е. справедливого при всех не слишком малых
числах Рейнольдса) логарифмического закона для профиля
осредненной скорости в трубах, каналах и пограничных слоях
на плоской пластинке. В настоящее время известно, что этот
закон можно вывести из одной только естественной гипотезы
подобия, касающейся распределений вероятностей гидродина-
гидродинамических полей турбулентности в полупространстве, или из со-
соображений размерности, опирающихся на простейшие предпо-
предположения о физических величинах, определяющих в этом случае
турбулентный режим. Тем не менее, в полуэмпирических теориях
и этот результат всегда обосновывался с помощью некоторых
специальных гипотез, причем, к сожалению» подобные его вы*
воды до сих пор остаются господствующими в учебной литера-
литературе по гидромеханике.
Полуэмпирические теории турбулентности оказались очень
ценным оружием для решения ряда важных практических за-
задач; однако принимаемые в этих теориях гипотезы часто не
имеют надежного физического обоснования и мало что дают
для понимания физического механизма турбулентности. Совсем
иной характер имеет теория универсального стационарного ста-
статистического режима мелкомасштабных компонент турбулент-
турбулентности при очень больших числах Рейнольдса. Эта теория непо-
непосредственно вытекает из новых гипотез подобия для мелкомас-
мелкомасштабных компонент, предложенных А. Н. Колмогоровым
A941а, б) (к тем же выводам пришел и А. М. Обухов A941),
рассмотревший специальную модель физических процессов, обу-
обусловливающих эволюцию этих компонент). Ее создание яви-
явилось новым большим этапом в развитии статистической гидро-
гидромеханики.
Прежде чем приступить к описанию вклада в теорию тур-
турбулентности, внесенного Колмогоровым и Обуховым, нам ка-
кажется необходимым,, однако, соблюдая исторический принцип
изложения, назвать двух их предшественников. Одним из них
явился английский ученый Льюис Ричардсон A922, 1926), авто-
рым— уже дважды упоминавшийся выше Дж. Тэйлор A935а).
Ричардсон в книге, опубликованной в 1922 г., высказал глубо-

ВВЕДЕНИЕ 21
кие соображения (мало замеченные в то время) о физическом
механизме турбулентного перемешивания при большом числе
Рейнольдса. Согласно его представлениям, развитая турбулент-
турбулентность представляет собой иерархию «вихрей» (т. е. возмущений
или неоднородностей) разных порядков, в которой «вихри»
данного порядка возникают за счет потери устойчивости более
крупных «вихрей» предыдущего порядка, заимствуют у них
энергию и, в свою очередь, теряя устойчивость, порождают бо-
более мелкие «вихри» следующего порядка, которым они пере-
передают свою энергию. Таким образом возникает своеобразный
«каскадный процесс», при котором энергия осредненного тече-'
ния последовательно передается движениям все более и более
мелких масштабов, вплоть до движений минимального мас-
масштаба, оказывающихся уже устойчивыми. Для того чтобы быть
устойчивыми, эти наиболее мелкомасштабные движения должны
характеризоваться достаточно малым числом Рейнольдса; от-
отсюда вытекает, что в них вязкость уже играет существенную
роль И; следовательно, происходит заметная диссипация кине-
кинетической энергии, переходящей непосредственно в теплоту. Со-
Соответствующая физическая картина развитой турбулентности
хорошо передается английскими рифмованными строчками, по-
видимому, также принадлежащими Ричардсону:
Big whorls have little whorls,
Which feed on their velocity;
Little whorls have smaller whorls,
And so on unto viscosity l).
Ричардсон высказал эти общие соображения лишь в каче-
качественной форме и не сделал из них никаких выводов, формули-
формулируемых на точном языке математики. Но сила его интуиции
была столь велика, что в работе 1926 г. он сумел тем не менее
чисто эмпирическим путем установить один из общих количе-
количественных законов мелкомасштабных турбулентных движений,
вытекающих из математической теории, основанной на представ-
представлениях о каскадном процессе передачи энергии по совокупности
турбулентных движений разных масштабов. Этот закон заклю-
заключается в том, что эффективный коэффициент диффузии облака
примеси в среде с развитой турбулентностью пропорционален
размеру облака в степени четыре трети. В 1941 г., когда Колмо-
Колмогоров и Обухов сформулировали основные положения количе-
количественной теории мелкомасштабных компонент турбулентности.
') Крупные завихрения рождают мелкие завихрения, питающиеся за счет
их скорости; мелкие завихрения рождают еще меньше завихрения, н так да-
далее До начала действия вязкости.

22 ВВЕДЕНИЕ
«закон четырех третей» Ричардсона был фактически единствен-
единственным эмпирическим результатом, указывавшим на существова-
существование каких-то простых общих закономерностей, управляющих
мелкомасштабной структурой турбулентности.
Большую роль в создании современной теории мелкомас-
мелкомасштабных турбулентных движений сыграла также работа Тэй-
лора A935а), в которой было введено понятие об однородной
и изотропной турбулейтности. Такая турбулентность опреде-
определяется тем условием, что для нее все конечномерные распреде-
распределения вероятностей значений гидродинамических полей в конеч-
конечном числе точек пространства — времени инвариантны относи-
относительно любых ортогональных преобразований (параллельных
переносов, вращений и отражений) системы пространственных
координат. Однородная и изотропная турбулентность является
тем частным случаем турбулентных .течений, для которого струк-
структура статистических моментов гидродинамических полей и вид
соответствующих уравнений Фридмана—Келлера оказываются
наиболее простыми. Правда, и в этом простейшем случае все
принципиальные трудности, связанные с проблемой замыкания
уравнений Фридмана — Келлера, остаются в силе. Однако соот-
соответствующие уравнения оказались все же гораздо более доступ-
доступными для математического анализа, чем общие уравнения, отве-
отвечающие произвольной турбулентности, и с их помощью удалось
получить целый ряд результатов, разъясняющих отдельные за-
закономерности турбулентных течений.
Сама по себе модель однородной и изотропной турбулентно-
турбулентности непригодна для описания каких-либо реальных турбулентных
течений, поскольку для таких течений предположения об одно-
однородности и изотропности никогда не выполняются (хотя бы по-
потому, что пространственная однородность предполагает, в част-
частности, отсутствие у потока каких-либо границ и строгое постоян-
постоянство его средней скорости). Но математический аппарат теории
однородной и изотропной турбулентности после некоторого его
обобщения оказался весьма ценным для описания свойств мел-
мелкомасштабных компонент реальных турбулентных течений, так
как статистический режим этих компонент, как мы, следуя Кол-
Колмогорову, поясним чуть ниже, уже естественно предполагать
однородным и изотропным. Иначе говоря, любую развитую тур-
турбулентность с достаточно большим числом Рейнольдса можно
считать локально однородной и локально изотропной, что сразу
резко упрощает.ее математическое исследование.
Остановимся теперь на основных идеях принадлежащей Кол-
Колмогорову теории локально изотропной турбулентности (или тео-
теории локального строения турбулентности при больших числах
Рейнольдса) — ниже нам будет удобно использовать это срав-

ВВЕДЕНИЕ 23
нительно короткое название вместо того, которое употреблялось
на стр. 20. Прежде всего Колмогоров существенно дополнил
представление о каскадном процессе передачи энергии от круп-
крупномасштабных компонент (получающих энергию непосредствен-
непосредственно от осредненного течения) ко все более и более мелкомас-
мелкомасштабным компонентам, заметив, что вследствие хаотичности
такой передачи энергии ориентирующее влияние среднего тече-
течения должно ослабляться при каждом переходе к более мелким
возмущениям. Поэтому на свойствах компонент турбулентности
с достаточно малым масштабом (т. е. достаточно большим по-
порядковым «номером») вовсе не должно сказываться это ориен-
ориентирующее влияние. Другими словами, несмотря на то, что сред-
среднее течение и наиболее крупномасштабные неоднородности лю-
любого реального турбулентного движения, вообще говоря,
неоднородны и анизотропны, статистический режим достаточно
мелкомасштабных пульсаций в любой турбулентности с очень
большим числом Рейнольдса можно считать однородным и изо-
изотропным. Кроме того, естественно ожидать, что характерные пе-
периоды, пульсаций разных порядков будут тем меньше, чем боль-
больше их порядок, и в случае пульсаций достаточно высокого по-
порядка (т. е. достаточно малых пространственных масштабов)
будут много меньше времени заметного изменения среднего те-
течения. Следовательно, режим таких пульсаций будет квазиста-
квазистационарным — практически стационарным в течение промежут-
промежутков времени, содержащих много характерных периодов.
Итак, мы видим, что в области возмущений достаточно ма-
малых масштабов, по-видимому, должен господствовать однород-
однородный, изотропный и практически стационарный статистический
режим, характеризуемый наличием определенного среднего
притока энергии е к наиболее крупным из рассматриваемых
возмущений и равной ему диссипацией энергии в теплоту под
действием вязкости, сосредоточенной в основном в области
возмущений минимального масштаба. Исходя отсюда, Колмо-
Колмогоров сформулировал гипотезу о том, что статистический режим
достаточно мелкомасштабных компонент любой турбулентности
с большим числом Рейнольдса является универсальным и опре-
определяется лишь двумя размерными параметрами — средней ско-
скоростью диссипации энергии (на единицу массы жидкости) е и
коэффициентом вязкости v. Отсюда уже с помощью простых
соображений размерности можно вывести, что масштаб наи-
наибольших пульсаций, на которые вязкость еще оказывает суще-
существенное влияние, должен иметь порядок т\ = v*'*/?'4. Следова-
Следовательно, естественно предположить, что в случае, когда область
масштабов возмущений, подчиняющихся указанному универ-

24 ВВЕДЕНИЕ
сальному статистическому режиму, простирается вплоть до
штабов, много больших г\, должен существовать так называе-
называемый инерционный интервал масштабов (много меньших типич-
типичного масштаба течения в целом L, но много больших г\), в
котором вязкость уже не будет играть роли, т. е. статистический
режим будет определяться единственным параметром е. Это
предположение представляет собой вторую основную гипотезу
Колмогорова.
Изложенные гипотезы Колмогорова позволяют сформули-
сформулировать ряд конкретных выводов о статистических характери-
характеристиках мелкомасштабных компонент турбулентности. Наиболее
важным из них является выведенный Колмогоровым «закон
двух третей», согласно которому средний квадрат разности
скоростей турбулентного течения в двух точках на расстоянии
г друг от друга при г, принадлежащем инерционному интерва-
интервалу масштабов, равен С(егJ/3, где С — универсальная числовая
постоянная. Другой формой этого утверждения (впервые ука-
указанной Обуховым A941)) является так называемый «закон
пяти третей», согласно которому плотность распределения
кинетической энергии по спектру волновых чисел k турбулент-
турбулентных неоднородностей в инерционном интервале имеет вид
Ci€2/3&~5'3, где С\ — новая числовая постоянная (просто связан-
связанная с С). Имеется также много других следствий из рассматри-
рассматриваемых гипотез, на которых мы здесь уже не будем задержи-
вгться.
Работы Колмогорова послужили основой всего последующего
развития теории локальной структуры турбулентности и ее при-
приложений в 40-х и 50-х годах текущего столетия. За этот период
была изучена локальная структура не только поля скорости, но
и полей концентрации пассивных примесей и температуры
(включая случай- температурно-стратифицированной тяжелой
жидкости, в котором, благодаря появлению архимедовых сил,
температуру уже нельзя считать «пассивной примесью»), дав-
давления и турбулентного ускорения. Полученные сведения о
статистических свойствах мелкомасштабных компонент турбу-
турбулентности нашли приложение к задачам об относительном рас-
рассеянии частиц и дроблении капель в турбулентной среде, об
образовании ветровых волн на поверхности моря, генерации
магнитного поля в турбулентном потоке проводящей ток жид-
жидкости и распределении неоднородностей электронной плотности
в ионосфере, о пульсациях коэффициента преломления в атмо-
атмосфере и создаваемых ими рассеянии и флюктуациях парамет-
параметров распространяющихся электромагнитных волн и к ряду дру-
других интересных задач,

ВВЕДЕНИЕ 25
Следствия теории Колмогорова, в первую очередь сформу-
сформулированные выше «закон двух третей» и «закон пяти третей»,
в 40-х и 50-х годах неоднократно проверялись на материалах
измерений статистических характеристик конкретных турбу-
турбулентных течений. При этом, однако, в конце концов выяснилось,
что в лабораторных экспериментах (производившихся обычно в
аэродинамических трубах) числа Рейнольдса недостаточно ве-
велики для существования заметного инерционного интервала в
спектре турбулентности и, следовательно, результаты таких из-
измерений в аэродинамических трубах, собранные за 20 лет,
не годятся для проверки указанных законов. Измерения же в
природе, где числа Рейнольдса, как правило, имеют гораздо
большие значения, чем,в лабораторных течениях, до последнего
времени давали результаты со значительным статистическим
разбросом; поэтому, хотя общая совокупность эксперименталь-
экспериментальных данных несомненно свидетельствовала в пользу теории,
ее подтверждение все же оказывалось не совсем непосредствен-
непосредственным и не позволяло надежно оценить входящие в теорию чис-
числовые параметры. Лишь в самые последние несколько лет по-
положение в этом отношении кардинально изменилось — за этот
период несколькими экспериментаторами были проведены
очень точные измерения характеристик турбулентности в раз-
различных природных и искусственных турбулентных течениях с
очень большим числом Рейнольдса, результаты которых пре-
прекрасно совпали друг с другом, окончательно подтвердили спра-
справедливость теории и позволили, наконец, с достаточной точно-
точностью определить постоянные С и Сх.
В настоящее время есть веские основания считать, что тео-
теоретическая разработка и экспериментальная проверка идей об
универсальном статистическом режиме мелкомасштабных ком-
компонент турбулентности в основном уже завершены, и для даль-
дальнейшего развития теории турбулентности требуются какие-то
существенно новые идеи, о поисках которых мы скажем немного
.ниже. Поэтому нам кажется, что именно сейчас уместно под-
подвести итоги всего того значительного периода развития теории
турбулентности, который был связан с разработкой указанной
идеи. Попытка в какой-то мере выполнить эту задачу и яв-
является одной из целей настоящей книги.
Назовем теперь несколько работ, посвященных поискам
новых путей в развитии статистической гидродинамики. В ра-
работах А. Н. Колмогорова A962) и А. М. Обухова A962), доло-
доложенных на двух примыкающих друг к другу международных
конференциях по теории турбулентности, состоявшихся в Мар-
Марселе в начале осени 1961 года, предложен путь дальнейшего
уточнения основных представлений о локальной структуре

26 ВВЕДЕНИЕ
турбулентности при больших числах Рейнольдса. А именно, в
изложенной выше теории статистические характеристики мел-
мелкомасштабной турбулентности, как мы видели, предполагаются
зависящими лишь от среднего значения е скорости диссипации
энергии. Но на самом деле поле диссипации энергии е (х, t)
также беспорядочно пульсирует, причем есть основания (и тео-
теоретические и чисто эмпирические) думать, что его изменчивость
должна быть весьма велика. Статистические характеристики
этого поля, очевидно, могут зависеть от особенностей крупно-
крупномасштабного течения; в частности, следует ожидать, что дис-
дисперсия поля е будет расти с ростом Re. Поэтому статистические
характеристики мелкомасштабных турбулентных движений,
определенные по одному только значению е, следует интерпрети-
интерпретировать лишь как условные средние значения, по-
получаемые при условии, что значение е строго фиксировано (и
равно е). Безусловные же средние значения, полу-
получаемые с помощью осреднения результатов расчета при фикси-
фиксированном е по флюктуирующим значениям этого параметра,
будут, вообще говоря, отличаться от условных средних значе-
значений (и могут оказаться уже не универсальными, т. е. различ-
различными для разных типов, крупномасштабных течений и, в ча-
частности, зависящими от Re). Методам оценки влияния этого
обстоятельства и были посвящены работы Колмогорова и Обу-
Обухова. Получение на этом пути конкретных количественных ре-
результатов требует в первую очередь выяснения статистических
свойств поля диссипации энергии е (х, /), т. е., иначе говоря,
более детального изучения механизма диссипации энергии в
турбулентном потоке. Предварительные оценки показывают,
что поправки к законам «двух третей» и «пяти третей», получае-
получаемые при учете изменчивости диссипации энергии, по-видимому,
имеют порядок, близкий к степени точности лучших из имею-
имеющихся в настоящее время экспериментальных данных.
Упомянем также своеобразный вариант теории возмущений
для уравнений гидродинамики, развитый Р. Крейчнаном
A959, 19626) и основанный на предположении, что прямые
динамические взаимодействия между тройками пространствен-
пространственных компонент Фурье поля скорости играют значительно боль-
большую роль, чем их непрямые взаимодействия (через все
остальные компоненты Фурье). Укажем еще метод описания
крупномасштабных компонент турбулентности, предложенный
У. Малкусом A9546) (см. также Таунсенд A9626) и Спигел
A962)) и опирающийся на использование гипотетического ва-
вариационного принципа максимума диссипации и представление
гидродинамических полей в виде суперпозиций конечного

ВВЕДЕНИЕ 27
числа соответствующих собственных функций (где мини*
мальный масштаб учитываемых компонент турбулентности со-
соответствует пределу гидродинамической устойчивости осред-
ненного поля). Оба эти подхода вызывают в последнее время
много споров — они приводят к некоторым интересным и прав-
правдоподобным результатам, но опираются на непроверенные
гипотезы и встречаются с рядом трудностей. Так, например,
первое приближение теории возмущений Крейчнана приводит
к формулам для спектра турбулентности в области малых мас-
масштабов, не согласующимся с прекрасно оправдавшимися пред-
предсказаниями теории Колмогорова и указывающим на необъяс-
необъяснимую зависимость статистических характеристик мелкомас-
мелкомасштабных компонент от режима крупномасштабных компонент.
Теория Малкуса в случае свободной конвекции приводит к ре-
результатам, не согласующимся с выводами из простейших пред-
предположений о подобии характеристик турбулентности в страти-
стратифицированной среде (и указывающим на существенную
зависимость крупномасштабных компонент конвективного те-
течения от молекулярной теплопроводности жидкости). Та
же теория, примененная к течению между параллельными
стенками, приводит к очень спорному выводу о зависимости
крупномасштабных характеристик от молекулярной вязко-
вязкости при сколь угодно больших числах Рейнольдса и к расхож-
расхождению с общепринятым (и хорошо подтверждающимся на
опыте) универсальным логарифмическим законом для профиля
средней скорости. Поэтому в настоящее время еще невозможно
сказать, окажутся ли эти подходы (или какие-либо простые
их модификации) плодотворными для развития теории турбу-
турбулентности или нет.
Укажем, наконец, на перспективы решения общей проблемы
турбулентности, связанные с использованием аппарата харак-
характеристических функционалов, гидродинамических полей. Эти
характеристические функционалы однозначно определяют рас-
распределения вероятностей P(dco) или Pt(da>) на фазовом про-
пространстве турбулентного потока, и потому их нахождение
явилось бы полным решением проблемы турбулентности. В ра-
работе Эбергарда Хопфа A952) для характеристического функцио-
функционала турбулентного поля скорости в несжимаемой жидкости
было выведено уравнение в вариационных производных, заме-
замечательной особенностью которого является его линейность.
Таким образом, хотя "динамика жидкости нелинейна, основная
проблема статистической гидромеханики, сформулированная в
терминах характеристических функционалов, оказывается линей-
линейной задачей. Отметим также, что уравнение Хопфа оказалось
формально близким к так называемым уравнениям Швингера

28 ВВЕДЕНИЕ
квантовой теории поля — уравнениям в вариационных производ-
производных для функции Ррина взаимодействующих квантованных по-
полей (на имеющуюся аналогию между теорией турбулентности и
квантовой теорией поля мы уже указывали выше).
Решение уравнения Хопфа встречается со значительными
трудностями как из-за того, что пока еще не ясно, какие именно
конкретные задачи для этого уравнения должны быть рассмот-
рассмотрены в первую очередь, так и по причине отсутствия до сих пор
каких-либо общих методов решения уравнений в вариационных
производных (и даже общих результатов о существовании и
единственности таких решений). В самые последние годы боль-
большое внимание в этой связи привлекает новый математический
аппарат континуальных интегралов — интегралов от функцио-
функционалов, распространенных по некоторому функциональному
пространству. Уже сегодня формально удается записать реше-
решение уравнения Хопфа в виде континуального интеграла по не-
некоторой «обобщенной мере» в функциональном пространстве
(не обладающей некоторыми обычными свойствами мер, исполь-
используемых в математическом анализе, и тем, напоминающей пре-
пресловутую «меру Фейнмана», возникающую в квантовой меха-
механике и квантовой теории поля). Однако пока такая запись
решения все еще остается лишь чисто формальным приемом,
мало облегчающим эффективное построение и изучение иско-
искомых решений.
Заканчивая введение, мы хотели бы сказать несколько слов
о содержании настоящей книги. Разумеется, совершенно невоз-
невозможно в одном или двух томах исчерпать весь круг вопросов,
связанных с проблемой турбулентности1). Мы и не пытались
это сделать, а отобрали лишь тот материал, который, как нам
кажется, может помочь выяснению физической природы турбу-
турбулентности. Поэтому мы почти не останавливались на конкрет-
конкретных приложениях инженерного характера и на математических
тонкостях, связанных с расчетом статистических характеристик.
С этим связано и то, что мы всюду ограничивались рассмотре-
рассмотрением лишь простейших течений и простейших задач. Так, на-
например, в книге говорится только о течении в прямых круг-
круглых трубах; пограничный слой рассматривается только на
плоской пластинке и при отсутствии градиента
давления в обтекающем потоке; диффундирующие
') Заметим в этой связи, что книга Чандрасекара A961), посвященная
фактически лишь материалу наших пп. 2.6 и 2.7 и некоторым его обобщениям,
содержит около 700 стр. текста!

ВВЕДЕНИЕ 29
частицы предполагаются практически точечными и
имеющими тот же удельный вес, что и окру-
окружающая среда, и т. д. Далее, мы ничего не говорим о тур-
турбулентных течениях проводящей жидкости в магнитном поле,
а учету сжимаемости уделяем лишь совсем немного места в
главе об изотропной турбулентности для того, чтобы иметь воз-
возможность объяснить связанные с этим новые физические эф-
эффекты. Однако мы включили в книгу главу, посвященную тур-
турбулентности в среде, вертикально стратифицированной по плот-
плотности (для простейшего случая плоскопараллельного течения
в полупространстве z>0), так как влияние стратификации на
турбулентность имеет отчетливый физический характер и может
исследоваться с помощью простых общих методов, широко ис-
использовавшихся в других частях книги.
Стремление сделать книгу как можно более «физической»
диктовало также и выбор предпочтительных методов исследова-
исследования. Уравнения турбулентного движения всегда оказываются
незамкнутыми (содержащими больше неизвестных, чем урав-
уравнений), и поэтому задачи теории турбулентности обычно не мо-
могут быть непосредственно сведены к нахождению единственного
решения некоторого дифференциального уравнения (или урав-
уравнений), определяемого известными начальными и граничными
значениями. В этих условиях неизбежно приходится привлекать
помимо уравнений движения какие-то дополнительные сообра-
соображения. Нам представляется, что среди таких дополнительных
соображений наиболее отчетливый физический смысл имеют
соображения подобия (опирающиеся на инвариант-
инвариантность условий задачи относительно некоторых групп преобразо-
преобразований) и соображения размерности (основанные на
выделении физических параметров, влияющих на исследуемое
турбулентное течение). Поэтому мы старались наиболее по-
подробно осветить именно выводы из соображений размерности и
подобия, которые могут применяться в теории турбулентности
значительно шире, чем это обычно предполагается. Соответ-
Соответственно полуэмпирическим теориям турбулентности, использую-
использующим более специальные гипотезы, в книге уделено сравнительно
немного места; особенно кратко здесь изложены «классические»
применения полуэмпирических теорий к течениям в трубах, ка-
каналах и пограничных слоях, подробно изложенные в известных
монографиях С. Гольдштейна A938), Л. Г. Лойцянского A941)
и Г. Шлихтинга A951) (вместе с полуэмпирическими теориями
«свободной турбулентности», вовсе опущенными в нашей книге).
Однако мы включили все же некоторые сравнительно новые и
менее известные применения полуэмпирических теорий и рассмо-
рассмотрели ряд применений полуэмпирической теории турбулентной

30 ВВЕДЕНИЕ
диффузии (которой чаще всего вообще только и ограничивают»
ся при обсуждении проблемы распространения примесей в тур»
булентном потоке). Кроме того, мы детально проанализировали
также различные гипотезы о переносе энергии по спектру изо-
изотропной турбулентности, близкие по характеру к полуэмпири-
полуэмпирическим гипотезам, но проливающие некоторый свет на физиче-
физический механизм турбулентного перемешивания и ранее не изла-
излагавшиеся во всей полноте.
Большое внимание, уделенное в книге методам подобия и
размерностей, обусловило также то, что изложению принад-
принадлежащей А. Н. Колмогорову теории локально-изотропной
турбулентности (целиком построенной на применении этих мето-
методов) здесь отведено много места. Мы уже отмечали, что стрем-
стремление подвести определенные итоги развитию идеи об универ-
универсальном локальном строении любого турбулентного течения с
очень большим числом Рейнольдса было одним из основных
стимулов к написанию этой книги. Мы рассмотрели также
предложенные в 1961 г. А. Н. Колмогоровым и А. М. Обуховым
уточнения этой идеи вместе с дополнительными данными по
этому вопросу, полученными в более позднее время. Но вызы-
вызывающие много разногласий теории Р. Крейчнана и У. Малкуса,
приводящие к результатам, противоречащим выводам из сооб-
соображений размерности, мы почти не упоминаем после историче-
исторического очерка, помещенного в настоящем введении.
Желая систематически изложить теоретические основы ста-
статистической гидромеханики, мы в то же время отнюдь не хоте-
хотели придать нашей книге формально-математический характер,
а стремились все время подкреплять теоретические выводы
анализом эмпирических данных. Сочетание теоретического и
экспериментального подходов, крайне плодотворное во всех
естественно-научных исследованиях, особенно необходимо в
статистической гидромеханике, в которой теория часто еще
имеет лишь предварительный характер и почти всегда бази-
базируется на ряде гипотез, нуждающихся в экспериментальной
проверке. Однако мы избегали привлекать данные эксперимен-
экспериментальных исследований турбулентности, не имеющие теоретиче-
теоретического объяснения и не служащие базой для определенных
теоретических выводов, даже если эти данные сами по себе каза-
казались весьма интересными или практически важными. В каче-
качестве источника экспериментальных данных о турбулентности
особенно часто в этой книге используется атмосферная турбу-
турбулентность. В какой-то мере это связано с тем, что оба автора
в течение многих лет работают в Институте физики атмосферы
и значительно лучше знакомы с атмосферной турбулентностью,
чем с другими турбулентными течениями. Но и помимо этого

ВВЕДЕНИЕ 31
имеются веские причины, оправдывающие специальное внима-
внимание авторов к такой турбулентности. Дело в том, что атмосфера,
которую еще Карман A935) назвал гигантской природной ла-
лабораторией для изучения турбулентности, обладает очень цен-
ценными свойствами, делающими ее особенно подходящей для
проверки выводов современной статистической теории. Мы уже
отмечали, что атмосферные движения обычно характеризуются
гораздо большими числами Рейнольдса, чем течения, осуще-
осуществляемые в лаборатории, и, следовательно, гораздо более
удобны для исследования специфических закономерностей, от-
относящихся к случаю очень больших Re. Кроме того, и геоме-
геометрические условия атмосферной турбулентности (а именно, от-
отвечающие ветру в приземном слое условия плоскопараллельно-
плоскопараллельного течения в полупространстве, ограниченном твердой стенкой,
которую в ряде случаев можно считать к тому же плоской и
однородной, или хорошо описывающие движения воздуха в
свободной атмосфере условия течения в безграничном про-
пространстве) оказываются более простыми, чем в большинстве
лабораторных экспериментов. Единственным дополнительным
осложнением, возникающим при переходе из лаборатории в
атмосферу, является необходимость учета влияния термической
стратификации, но, как мы уже отмечали, это осложнение при-
приводит к дополнительным интересным теоретическим рассмотре-
рассмотрениям и расширяет число наблюдаемых на опыте закономерно-
закономерностей, допускающих физически обоснованное объяснение.
Широкая распространенность турбулентных течений, их
большое значение для множества разнообразных практических
задач и интерес к ним теоретиков привели к тому, что литера-
литература, касающаяся турбулентности, колоссальна — она насчиты-
насчитывает много десятков тысяч статей, разбросанных по громадному
числу физических, механических, математических, химических,
метеорологических и технических журналов. К сожалению,
однако, теория турбулентности оказалась крайне трудной
и до сих пор она продвинута «е очень далеко; поэтому многие
относящиеся сюда работы являются чисто эмпирическими,
содержат лишь самые начатки теории или даже являются оши-
ошибочными. Эти обстоятельства, разумеется, очень осложняют об-
обзор литературы по статистической гидромеханике. В нашей
книге мы первоначально предполагали ограничиться лишь ми-
минимальным количеством необходимых ссылок; но, потратив
очень много времени на изучение литературы (а без этого
нельзя было выяснить, что же является необходимым), мы ре-
решили, что более целесообразно не скупиться на ссылки, осо-
особенно относящиеся к работам последних лет. Мы сделали это,
рассчитывая дать читателю достаточно полное представление

32 ВВЕДЕНИЕ
о современном состоянии исследований в теории турбулентно-
турбулентности, облегчить ему нахождение необходимых справок и как-то
.помочь ориентироваться в безграничном море книг и статей.
В ряде мест книги мы включили даже небольшие обзйры лите-
литературы (чаще всего напечатанные мелким шрифтом), в кото-
которых старались по возможности кратко изложить содержание
значительного числа типичных работ, относящихся к соответ-
соответствующему разделу теории. Мы, разумеется, понимаем, что
большое количество библиографических ссылок несколько за-
громождает текст книги, а также (в силу полной невозможно-
невозможности охватить хотя бы большую часть имеющихся.работ) значи-
значительно увеличивает число авторов, могущих почувствовать себя
несправедливо обойденными в столь обширном списке литера-
литературы. Мы заранее просим извинения у всех этих авторов и спе-
спешим- предупредить читателя, что вовсе .не считаем включенные
в наш список работы самыми лучшими или наиболее важными,
никак не претендуем на его полноту и сознаем, что в вопросе
об авторском приоритете (которым мы специально не зани-
занимались) у нас вполне может встретиться ряд неточностей.
Разумеется, на отбор материала для книги оказали извест-
известное влияние и наши личные научные вкусы. В частности; в.
книгу включен ряд результатов наших собственных работ.
Большая часть этих результатов изложена здесь в' перерабо-
переработанном и дополненном виде, представляющемся нам сегодня
наилучшим; также и результаты других авторов часто изла-
излагаются нами по-новому, с учетом более поздних данных, а так-
также общего подхода к проблеме, терминологии и обозначений,
принятых в настоящей книге. Естественно поэтому, что приве-
приведенные ссылки во многих случаях содержат лишь какой-то эк-
эквивалент вывода или формулы, в связи с которыми они указаны.
Отступление от изложения, принятого в оригинальной рабо-
работе, часто бывает также обусловлено нашим стремлением во всех
случаях как можно более четко указывать все предположения,
используемые в ходе того или иного вывода. В частности, мы
старались всегда отмечать, какие результаты непосредственно
вытекают из основных уравнений движения (т. е. из общих за-
законов физики), какие следуют из соображений размерности7
(т. е. из определенных представлений о том, какие физические
величины являются существенными, а какие несущественными
для данного явления), какие требуют привлечения специаль-
специальных полуэмпирических гипотез (и каких именно), а какие
являются просто эмпирическими фактами.
Статистическая гидромеханика широко использует резуль-
результаты и методы классической гидромеханики и теории вероят~
ностей. Поэтому знание указанных двух дисциплин сильно

ВВЕДЕНИЙ 33
облегчит знакомство с настоящей книгой. Тем не менее, мы на-
надеемся, что наша книга будет доступной и для лиц, имеющих
лишь общую математическую и физическую подготовку. Имея
ё виду таких читателей, мы включили в первые две главы
основные необходимые сведения из классической гидромеха-
гидромеханики (начиная е уравнений неразрывности и движения) и из
теории вероятностей (начиная с самого понятия вероятности).
Уже в этих главах, как и во всех дальнейших, мы старались
уделять основное внимание принципиальным вопросам* не за-
задерживаясь на технических деталях. С этим стремлением свя-
связано то, что мы нигде, не излагаем методов решения встретив-
встретившихся дифференциальных уравнений или других стандартных
математических задач, а ср-азу приводим ответ (который ино-
иногда совсем не легко найти). В то же время мы сравнительно
подробно останавливаемся на некоторых недостаточно широко
известных, но важных математических вопросах, традиционно
©пускаемых во всех книгах и статьях, предназначенных для ме-
механиков или физиков (типа, например, вопроса об эргодических
теоремах или спектральных разложениях случайных полей);
этим объясняется то, что целых две главы книги оказались по-
посвящены математической теории случайных полей.
По техническим причинам книгу оказалось удобным издать
в виде двух частей. В первую из них включены вопросы, изложе-
изложение которых не требует использования никаких спектральных
представлений (вероятно, многих наших коллег удивит, что та-
таких вопросов набралось на толстую книгу). Здесь излагаются
общие сведения об уравнениях гидромеханики и их простейших
следствиях (кончающихся несколько более специальной теорией
малых колебаний сжимаемого газа); рассматривается вопрос
о возникновении турбулентности и гидродинамической неустой-
неустойчивости (включая элементы нелинейной теории неустойчивости);
приводятся элементарные сведения из теории вероятностей и тео-
теории случайных полей (в том числе некоторые сведения об усло-
условиях эргодичности); подробно разбирается применение сообра-
соображений размерности и подобия к турбулентным течениям в тру-
трубах, каналах, пограничных слоях и к свободным турбулентным
течениям (струям, следам за обтекаемыми телами и т. д.) и
кратко перечисляются основные идеи и результаты полуэмпири-
полуэмпирических теорий турбулентности (с конкретными примерами); де-
детально исследуется теория подобия для турбулентности в вер-
вертикально стратифицированной по плотности среде, и полученные
при этом результаты сопоставляются с обширным эмпирическим
материалом наблюдений над ветром и температурой в призем-
приземном слое воздуха; изучаются лагранжевы характеристики турбу*
лентности и теория турбулентной диффузии.

34" ВВЕДЕНИЕ
Вторая часть начинается с математической главы, посвящен-
посвященной спектральной теории случайных полей (в том числе и полей,
являющихся не однородными, а только локально однородными);
далее подробно излагается теория изотропной турбулентности
(основное внимание здесь уделено различным методам замыка-
замыкания уравнений для моментов гидродинамических полей изотроп-,
ной турбулентности в несжимаемой жидкости, но приводятся
также и некоторые выводы, относящиеся к сжимаемому случаю);
рассматриваются общие представления об универсальном ло-
локальном строении турбулентности при больших числах Рей-
нольдса и их следствия (включая и вопрос об относительной диф-
диффузии, т. е. увеличении размера облака примеси, переносимого
турбулентным потоком) и исследуются спектральные характе-
характеристики турбулентности в расслоенной жидкости; приводятся
основные сведения о распространении электромагнитных и зву-
звуковых волн в турбулентной среде и, наконец, рассматривается
общая формулировка проблемы турбулентности, опирающаяся
на изучение характеристических функционалов гидродинамиче-
гидродинамических полей.

ГЛАВА Г
ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
§ 1. УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ И ИХ ОСНОВНЫЕ
СЛЕДСТВИЯ
1.1. Система уравнений динамики несжимаемой жидкости
Турбулентность представляет собой сложное физическое явле-
явление, теоретическое изучение которого должно опираться на ос-
основные законы физики, находящие свое выражение в уравнениях
гидро- и термодинамики. Поэтому мы начнем с того, что кратко
напомним здесь эти уравнения и некоторые важнейшие вытекаю-
вытекающие из них следствия, ограничившись, естественно, лишь теми
формулами и фактами, которые нам понадобятся в дальнейшем
(более подробное изложение см., например, в книгах Гольдштей-
на A938), Кочина, Кибеля и Розе A963), Ламба A932) и Лан-
Ландау и Лифшица A953)). Поток жидкости ') мы, как обычно, бу
дем характеризовать полем скорости и(х, t)—{ui{xu x2, x3, t),
«2(*ь Х2, *з, t), «з(*ь *2, *з, 0} и полями двух каких-либо термо-
динамических характеристик среды — например, полем давления
р(х, t) и полем плотности р(х, t) или температуры Т(х, t) —
всего пятью функциями от четырех переменных. Кроме того, нам
будут нужны также значения молекулярных коэффициентов
переноса, определяющих физические свойства жидкости, — коэф-,
фициента вязкости ц (или кинематической вязкости v = —J и
второго коэффициента вязкости ?, а в дальнейшем также и коэф-
коэффициента теплопроводности и (или температуропроводности
у = ——» где ср — теплоемкость жидкости при постоянном дав-
ср?
лении).
') Словом «жидкость» мы здесь и ниже будем обозначать любую жид-
жидкую или газообразную среду.

36 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [1.1
Простейшим уравнением механики жидкости, выражающим
физический закон сохранения вещества, является уравнение не-
неразрывности
ИЛИ -
(здесь и ниже мы всегда будем предполагать, что по дважды по-
повторяющемуся в одночленном выражении индексу производится
суммирование от единицы до трех, так что ^ ¦ например,
з \
имеет тот же смысл, что. и Zt a I1)- Основные динамические
¦*¦ "¦*« /
уравнения, выражающие второй закон Ньютона, примененный к
малому объему жидкости, т. е. представляющие собой уравнения
баланса количества движения (импульса), имеют следующий
вид:
^Ь2,з, A.3)
где pXi*=pXi(x, t) —это i-я компонента плотности внешних сил
в точке х в момент t. Из уравнения (Г. 1) следует, что плотность
р можно вынести за знак производной -^ в первом члене левой
части A.3), одновременно вынеся также и риа за знак произ-
производной -д—¦ во втором члене. Что же касается до коэффициентов
вяз.кости ц. и ?, то изменение их значений в пространстве (обу-
(обусловленное зависимостью этих коэффициентов от температуры,
меняющейся от точки к точке) на практике чаще всего оказы-
оказывается весьма незначительным, так что членами, содержащими
производные этих коэффициентов, обычно вполне можно пре-
иебречь. Но это значит, что величины ц. и ? в уравнениях A.3)
также могут быть вынесены за знак производной, после чего эти
') Чтобы иметь возможность как можно шире пользоваться этим согла-
соглашением, при выводе общих уравнений мы всегда будем обозначать оси коор-
координат через Охи i = 1, 2, 3. В конкретных же примерах, в которых направле-
направления трех осей определяются специальным образом, мы иногда будем обозна-
обозначать координаты также и буквами х, у н г.

1.1] § 1. уравнения динамики жидкости 37
уравнения принимают вид
Четыре уравнения A.2) и A:4) содержат пять неизвестных
функций и поэтому еще не образуют замкнутой системы. На
практике, однако, изменения плотности р движущейся жидкой,
частицы в очень многих случаях оказываются столь малыми, что
ими также можно пренебречь. Такое пренебрежение, в част-
частности, всегда будет законным в случае так называемых «капель-
«капельных жидкостей», т. е. сред, являющихся жидкостями в обычном
смысле этого слова. В случае же газообразных сред при стапио-
иарном движении (со скоростью и (х), не зависящей от Q изме-
изменениями плотности, обусловленными изменениями давления
вполне можно пренебречь, если только абсолютная енорость
движения и=\и\ во всгх точках потока мала по сравнению
со скоростью распространения звука а. В общем случае не-
нестационарного дрижения газа изменения плотности р будут пре-
пренебрежимо малы, если кроме условия и <а будет выполняться
еще и условие T^s>L/a, где Т и L — характерные время и рас-
расстояние, на которых скорость жидкости и (х, t) претерпевает за-
заметное изменение (Ы. Ландау и Лифшиц A953), ч. 1, § 10). Во
всех перечисленных случаях плотность р обычно вообще оудет
принимать постоянное значение во всем пространстве, заполнен*
ном жидкостью. При этом р будет уже представлять собой зара-
заранее заданную постоянную величину (характеризующую свойства
среды), и четырех уравнений A.2) и A.4) здесь будет доста-
достаточно для определения четырех неизвестных функций щ{х, t),
i = 1, 2, 3, и р(х, t) (npji заданных начальных и граничных ус-
условиях)..
'_ Сами эти уравнения в рассматриваемом, теперь случае не
сжимаемой жидкости приобретают более простой вид, так
как в них можно опустить ряд членов, содержащих производные
от р (или выражающихся через такие производные). Так, в урав-
уравнении неразрывности A.2) мы можем в этом случае опустить
все слагаемые в левой части, после чего оно приобретает вид
?-а A.5)
В силу A,5) в уравнениях движения A.4) последний член в
правой части тождественно обращается в нуль, после чего эти
уравнения переходят в известные уравнения Навье— Стокса

38 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [1.1
Уравнения A.6) представляют собой основные уравнения дина-
динамики вязкой несжимаемой жидкости. Мы видим, что они содер-
содержат уже~ единственный коэффициент вязкости, так что вторая
вязкость оказывается существенной лишь при учете сжимае-
сжимаемости. ; :."..¦...
Легко видеть, что давление р может быть с самого начала
исключено из уравнений; A.6). В самом деле, для этого надо
только применить к обеим сторонам A.6) операцию взятия ро-
ротора, которая в тензорных обозначениях записывается как опе-
операция гьы~дх~' где BkQ*— полностью антисимметричный тензор
третьего ранга (т. е. е*р,=О, если индексы k, p и i не все раз-
различны, и 6ftp< = +1 или =—1, если тройка (k, p, i) получается
из тройки A, 2, 3) при помощи четной или соответственно нечет-
нечетной подстановки). Предполагая для простоты, что внешние силы
отсутствуют, мы придем при этом к системе трех уравнений
где
— компоненты вектора вихря. В принципе из уравнений A.7) и
A.8) могут быть определены три функции щ{х, t); после этого
для нахождения поля давления надо только решить уравнение
Пуассона
получаемое с помощью применения к уравнениям A.6)
(с Х4=0) операции -^- (т. е. с помощью составления диверген-
дивергенции векторного уравнения Навье — Стокса).
Из уравнения A.9) следует, что с точностью до слагаемого,
являющегося гармонической функцией хг
Р Гд>1ив(х')и?(х')] dx*
-^J dx'.dx't \x-x'\' (L9)
где интегрирование распространяется на весь объем, заполнен-
заполненный жидкостью. В частности, если течение жидкости происходит
во всем безхраничном пространстве, то соответствующей гармо-
гармонической функцией может быть лишь постоянная. Но поскольку
в. уравнениях движения фигурируют лишь производные от дав-
давления, то постоянное слагаемое в выражении для давления

\й] § 1. УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ 39
вообще не играет никакой роли; поэтому здесь допустимо счи-
считать, что уравнение A-9') является точным без всяких добавлен
ний. Для течений в ограниченных областях гармоническую до-
добавку к правой части'A.9') следует определять из граничных
условий для Давления; в ряде случаев и здесь она также оказы-
оказывается постоянной и поэтому может не учитываться.
1.2. Простейшие течения несжимаемой
жидкости
Для получения однозначного решения системы уравнений
A.5) — A.6) надо задать начальные значения полей щ{х, t)
и учесть, что скорость должна обращаться в нуль на поверхно-
поверхностях всех погруженных в поток твердых тел. Так как, однако, эта
система нелинейна, нахождение ее точных решений в явном ана-
аналитическом виде, вообще говоря, является очень трудным делом.
Лишь для некоторых специальных потоков нелинейные члены
уравнении A.6) тождественно обращаются в нуль; при этом сйс-
тема уравнений гидродинамики сразу очень упрощается, и в та-
таких случаях ее точное решение обычно находится без большого
труда. Ниже мы перечислим некоторые точные решения такого
рода; примеры более сложных точных решений уравнений
A. 5) — A.6) можно найти, например, в книгах Ландау и Лиф-
шица {1953) и Кочина, Кибеля и Розе A963). Во всех рассмат-
рассматриваемых ниже примерах будет предполагаться, что объемные
внешние силы ^отсутствуют1); кроме того, в этих примерах'
потоки будут всегда предполагаться стационарными, t. e. не за-
зависящими от t. - • ¦-'.'¦¦ -г
Отметим предварительно,, что в случае стационарного течения
полный импульс жидкости в фиксированной части пространства
не меняется со^временем, т, е. потери импульса, связанные с со-
сопротивлением погруженных в жидкость твердых тел, баланси-
балансируются с прцтоком импульса благодаря действию сил, вызываю?
щих движение жидкости (при ^=0^-благодаря действию яйлы
перепада давления). Иначе говоря, при/установившемся режиме
вызывающая движение сила перепада давления,^действующая
на всю жидкость, уравновешивается действующей на жидкость
силой, торможения . (отличающейся .лишь знаком от суммарной
силы воздействия потока на погруженное в него тело).'Формула,
выражающая это равновесие, позволяет установить связь между
1) Заметим, что всегда присутствующую объемную силу тяжести
ЛС«ч (О,.О, —pg) _П?И .отсутствии свободной-поверхности жидкости, можно
легко исключить, заменив истинное давление р его отклонением от таквазы*
баемого гидростатического . давления .р0 = -^pg*s + const,

40 ГЛ. Г. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ A.2
характерной скоростью течения и перепадо** давления, называе-
называемую обычно законом сопротивления.
Сила W воздействия потока на тело равняется интегралу по
новерхиоети тела 2 от потока импульса по нормали к этой по-
поверхности. Поток *-й компоненты импульса через единичную
площадку, перпендикулярную оси. О*ь,- имеет вид pUiUk+p'6ik—
— аь, где б«—единичный тензор Fjfc=l при i=k и б<*=0 при
1фЩ, a Oik — вязкий тензор напряжений, в несжимаемой жид-
жидкости равный {*(-^"~Ь -j^) (СР- ниже формулу A.61)). По-
Поскольку скорость движенюг жидкости на поверхности тела равна
нулю, для i-й компоненты силы W получаем
A.10)
где iti — компонента единичного вектора внешней нормали к по-
поверхности, a Fi — интеграл по поверхности тела от Oikik- Первое
Слагаемое в правой части A.10) связано с передачей телу им-
импульса силами давления и не зависит от вязкости жидкости. Это
слагаемое в ряде случаев (например, в случае обтекания плос-
плоской пластинки или при течениях в прямых трубах) оказывается
равным нулю. Второе слагаемое F< представляет собой сопротив-
сопротивление трения, которое в вязкой жидкости всегда отлично от нуля.
В случае геометрически подобных тел за характерную величину
силы W можно принять выражение -% pU2S, где U — характер-
характерная скорость, a S — некоторая характерная площадь, например
площадь поверхности тела или его миделево сечение. Безразмер-
Безразмерная величина
называется коэффициентом сопротивления тела. Если сопротив-
сопротивление связано только с трением (Wt=>Ft), то коэффициент сопро-
сопротивления обозначается С/ и называется коэффициентом сопро-
сопротивления трения.
Примеры точных решений уравнений гидромеханики
1) Начнем с простейшего плоского стационарного течения
вязкой жидкости, заключенной между двумя ^параллельными
плоскостями, одна из которых неподвижна, а вторая движется
с постоянной скоростью U. Обозначим через Н расстояние ме-
между плоскостями и выберем систему координат, в которой урав-

1,2] 5 1. УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ 41
нения этих плоскостей будут иметь вид z^O (неподвижная
плоскость) и 2 = Я (подвижная), а ось Оде направлена вдоль
вектора (/• В таком случае все гидродинамические величины
будут зависеть только от г, а скорость движения жидкости,всю-
жидкости,всюду будет направлена вдоль оси Ох. Поэтому уравнение A.5) и
второе уравнение A.6) ¦ здесь будут удовлетворяться тожде-
тождественно, а первое и третье уравнения A.6) приобретают вид
где и{г) = Щ(г) —единственная отличная от нуля компонента
скорости потока. Следовательно, здесь р = const и и = аг + Ь;
учитывая еще граничные условия (и = 0 при г = 0ии = {/ при
г = Я), получаем
и(г) = ^г. A.13)
Итак, рассматриваемый поток характеризуется линейным про-
профилем скорости, причем средняя скорость Ucp равна -у. Сила
трения, действующая на каждую единиду площади стенок г = О
и г = Я, равна
I du I u-U I, , .v
причем эта сила на плоскости г = 0 направлена вдоль оси Ох,
а на плоскости z = H имеет противоположное направление.
Если лоложить
r = ±PU2cp;Cf, A.15)
где Cf — коэффициент сопротивления трения, то
С^0 = г*е Re = (Ы6)
Стационарное плоское течение жидкости между двумя без-
безграничными параллельными плоскостями, описываемое форму-
формулами A.13) и A.16), очевидно, представляет собой математичеч
скую идеализацию, которая, однако, в некоторых случаях может
оказаться полезной. В руководствах по гидродинамике это иде-
идеализированное течение иногда называется течением Куэтта.
2) Рассмотрим теперь стационарное двумерное течение ме-
между двумя неподвижными параллельными плоскостями г = 0 и
г = Н под действием приложенной на бесконечности внешней
силы, создающей градиент давления по направлению оси Ох.
Легко видеть, что в этом случае скорость потока также будет
во всех точках направлена вдоль оси Ох и будет зависеть лишь
от г, так что и (г) = щ (г) опять будет единственной ненулевой

42 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [1.1
компонентой поля и. Поэтому уравнение A.5) и второе урав-
уравнение A.6) здесь также будут удовлетврряться тождественно;
первое же и.третье уравнения A.6) будут иметь вид
др - d*u dp п /1 it\
Отсюда видно, что давление здесь не будет зависеть от г, т. е.
будет постоянным по всей толщине слоя жидкости, и, следова-
следовательно, первое уравнение A.17) будет выполняться лишь при
|1 = const ^ if, «(«) —?-^.*Ч-«Ч-Ь A-18)
где Дгр — перепад давления между плоскостями х = х6 и
х = Xq + /. Учитывая еще граничные условия (и = О при z — Q
z — H), получаем
так что профиль скорости в этом случае будет иметь форму па-
параболы. Сила трения т на обеих стенках здесь будет равна
du_
dz
поэтому безразмерный коэффициент сопротивления С/ формулы
A.15) будет равен
ср ¦ "¦"
Н
0-21)
< г г 1 /* , ч - Я2 Д/р 2
ибо в нашем случае t/cp = jj / u(z)dz — ^—j = 3"
Точное решение A.19), разумеется, также описывает идеали-
идеализированное течение жидкости, которое, иногда называется тече-
течением Пуазейля между параллельными плоскостями.
3) Перейдем к случаю стационарного течения жидкости в
прямой бесконечной круглой трубе данного диаметра D. На-
Направим ось Ох вдоль оси трубы; тогда отличной от нуля будет
только компонента поля скорости ид(У, z) = u(y, z). Поэтому
уравнение A.5) ив этом случае будет удовлетворяться тожде-
тождественно; кроме того, из второго и третьего уравнений A.6)
Дудет следовать, что -? = -? = 0, т. е. что давление здесь по-
постоянно по сечению трубы и зависит только от х. Введем те-
теперь в плоскости Oyz полярные координаты (г, (jp). Тогда в рилу

1,23 s 1- уравнения динамики жидкости . ^43
симметрии трубы и(у, г) —и(г) и, следовательно, в этих коор-
дицатах первое уравнение A.6) будет лметь вид : :
iAfri
г dr У dr
Так как правая часть здесь зависит только ot'jc, а левая от г,
то должно быть -3j = const = ~ (где Aip — перепад давле-
давления на участке трубы длины /). Учитывая теперь граничное ус-
условие u(D/2) =0 и ограниченность функции и (г) при всех г,
получаем
'• (г)-ig-<*"-'') (где /?=|-). A.23)
Таким образом, и в этом случае профиль скорости (вдоль лю-
любого диаметра) оказывается параболическим. Средняя скорость
¦течения, определяемая формулой >
2я R
здесь оказывается равной ~щ-№= *2* > поэтому расход
жидкости (т. е. объем жидкости, протекающей через сечение
трубы за единицу времени) равен
Т0Т Же
Сила трения о стенку равна т = |
зультат можно получить и иначе, сообразив, что полная сила
трения nDl-x на участке трубы длины /должна уравновеши-
уравновешиваться силой перепада давления Aip, действующей на сечение
трубы nR2. Следовательно, коэффициент сопрртивления_, Cj
здесь равен '
8v .16 UCDD
где Re = -—, A.26)
Решение A.23) уравнений гидродинамики также
к идеализированному потоку, так как труба здесь предполагает-
предполагается бесконечно длинной, а течение — строго стационарным. Ока-
Оказывается, однако, что в случае реальных конечных труб проте-
протекание по нцм жидкости в случае постоянного напора Д(р^до-
Д(р^довольно часто очень быстро становится практически стационар-
ным, причем на расстояниях от входа трубы порядка (по

44 ГЛ. t. ЛАМИНАРНЫЕ Й ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ {1.2
теоретическим расчетам Шиллера A934), приведенным также
и в книге Гольдштейна A938), т. 1, § 139, уже при х>
> 0,115—^?-1 влияние конечной длины трубы также перестает
ощущаться, и течение хорошо описывается формулой A.23).
Таким образом, закономерности A.23), A.25) и A.26) могут
быть проверены на опыте; исторически дело обстояло так, что
они впервые были обнаружены именно на опыте (Г. Хагеном в
1839 г.) и Ж. Пуазейлем в 1840—1841 гг.) и лишь затем объяс-
объяснены теоретически (Дж. Стоксом в 1845 г.). В исследованиях
Хагена было обнаружено также, что эти закономерности справед-
справедливы только в случае достаточно большой вязкости v и при
достаточно малой скорости ?/Ср — обстоятельство, о котором мы
еще будем подробно говорить, в § 2, Течение несжимаемой
жидкости, описываемое формулами A.23) и A.25), часто на-
называется течением Пуазейля ^илн Хагена — Пуазейля) в круг-
круглой трубе или (в тех случаях, когда нет опасений спутать его
стечением A.19)) просто течением Пуазейля.
' 4) В качестве последнего примера мы рассмотрим стацио-
стационарное движение жидкости,, заключенной между двумя коакси-
коаксиальными бесконечными цилиндрами радиусов RA и Rz> Ru вра-
вращающимися вокруг своих осей с угловыми скоростями Qi и й2;
перепад давления вдоль оси цилиндров мы примем равным
нулю. В таком случае все гидродинамические величины не будут
зависеть от координаты х, отсчитываемой вдоль оси цилиндров.
Кроме того, если в плоскости Оуг, перпендикулярной оси ци-
цилиндров, ввести цилиндрические координаты (г, ф), то из сооб;
ражений симметрии ясно, что отличной от нуля будет лишь ком-
компонента скорости и = ич и что скорость и и давление *р будут
Зависеть только от г. Отсюда следует, что уравнение неразрыв-
неразрывности A.5) и первое уравнение A.6) здесь будут удовлетрорять-
ся тождественно; что же касается до второго и третьего урав-
уравнений A.6), то они после перехода к цилиндрическим коорди-
координатам примут вид
Общее решение второго из уравнений A.27) имеет вид и (г) =
s=ar-f —; так как к тому же и (г) должно равняться QiRi
при г = Ri и QiRz при г = Яг, то искомая функция и (г) будет
определяться формулой

Щ § 1. УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ 45
С помощью первого уравнения A.27) теперь очень легко найти
и р(г), но мы на этом не будем останавливаться. Течение
жидкости, задаваемое формулой A.28), в ряде отношений, род-
родственно течению примера 1), но оно значительно проще может
быть сравнительно точно воспроизведено в лаборатории. Это
течение иногда называется течением Куэтта между цилиндрами.
1.3. Число Рейнольдса и критерий подобия
Все перечисленные выше точные решения уравнений гидро-
гидродинамики относились к крайне простым идеализированным те-
течениям. В более сложных случаях нахождение точного реше-
решения обычно оказывается невозможным, и приходится прибегать
к численному решению уравнений A.5) — A.6) с помощью тех
или иных приближенных методов. При этом очень важно уметь
оценить порядок величины различных членов наших уравнений,
чтобы знать, в каких случаях можно пренебречь некоторыми
из этих членов и ограничиться рассмотрением упрощенных урав-
уравнений, легче поддающихся интегрированию.
Будем пока' считать, что речь идет о стационарном течении
вязкой несжимаемой жидкости при отсутствии внешних сил.
С помощью соотношения A.9) нетрудно показать, что члены
уравнений A.6), содержащие давление, вообще говоря, будут
иметь тот же порядок величины, что и нелинейные члены
дш diii
ца -j?*-. так что сравнивать надо лишь порядки членов аа -*?¦
и \Ащ, описывающих влияние на поток ?ил инерции и сил вну-
внутреннего трения Обозначим через U характерный масштаб
скоростей нашего течения (за U можно принять, например, мак-
максимальную скорость потока или как-то определенную среднюю
скорость), а через L — характерный масштаб длин (например,
средний размер тел, обтекаемых потоком, или типичное расстоя-
расстояние между твердыми стенками, или вообще расстояние, на ко-
котором скорость потока претерпевает заметное изменение AU,
имеющее порядок U). В таком случае порядок первой произвол*
ной поля скорости будет определяться отношением U/L, а
вторых производных — отношением U/L2, так что члены, опи-
описывающие силы инерции, будут иметь порядок U2/L, а члены,
описывающие силы трения:—порядок \U/L2. Отношение этих
величин
называется числом Рейнольдса потока; оно является очень
важной характеристикой течения, определяющей относительную

4§ ГЛ. !. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
роль сил инерции и сил трения в динамике потока (выше это
число нам уже встречалось в формулах A.16), A.21) и A,26)).
При.малых числах Рейнольдса вязкость оказывает существен-
существенное влияние на весь поток в целом, сглаживая возникающие в
потоке мелкие неоднородности; поэтому изменения характери-
характеристик течения от точки к точке при малых Re оказываются обыч-
обычно весьма плавными. При больших числах Рейнольдса домини-
доминирующую роль в потоке играют силы инерции, действие которых
приводит к передаче энергии от крупномасштабных компонент
движения к мелкомасштабным и, следовательно, к образованию
резких локальных неоднородностей течения; этот тип течений
нас и будет интересовать в дальнейшем. ,
Понятие о числе Рейнольдса очень упрощает исследование
геометрически подобных течений жидкости, таких, как. напри-
например, течения жидкости в трубах с сечением заданной формы или
обтекание безграничным потоком жидкости твердого тела за-
заданной формы. Поскольку в этих случаях речь идет о совокуп-
совокупности потоков с геометрически подобными границами, то свой-
свойства границ здесь могут быть охарактеризованы одним-един-
ственным масштабом L размерности длины (в наших примерах
за L можно принять средний диаметр сечения рассматриваемой
трубы или средний диаметр обтекаемого потоком тела). Кроме
того, сама течение будет характеризоваться еще некоторой ти-
типичной, скоростью U (например, максимальной скоростью в фи-
фиксированном сечении трубы или скоростью набегающего на .тело
потока). Наконец, единственный входящий в уравнения A.6) и
A.6) размерный^ параметр — это коэффициент кинематической
вязкости v, характеризующий физические свойства текущей
жидкости. Таким образом, в случае установившегося течения
при отсутствии внешних сил геометрически подобные потоки
будут зависеть лишь от длины L и от размерных.параметров
U и v, имеющих размерности
[U\ = LT\ Н = 12Г'\ A.30)
-где через L и Т в правых частях равенств, как обычно, обозна-
обозначены размерности длины и времени. Ясно, что из параметров
L, U и v можно составить единственную безразмерную комби-
комбинацию — число Рейнольдса Re = -^—. Поэтому, если мы будем
измерять длины в единицах L, скорости — в единицах U, а да-
давление— в единицах pU2, то уравнение A.5) и граничные усло-
условия для всех геометрически подобных потоков будут иметь один
и тот же вид, а уравнения A.6) будут отличаться самое боль-
большее значениями безразмерного параметра Re, -могущего- войти
в эти уравнения после перехода к безразмерной форме, Сле-

1.3] § 1. УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ 47
довательно, для геометрически подобных потоков скорость, из-
измеренная масштабом U, будет зависеть только от координат,
измеренных масштабом L, и от числа Re. Иначе говоря,
ul(x) = U9i(f, Re), A.31)
где ф,E, Re)—некоторые универсальные функции, описываю-
описывающие сразу всю рассматриваемую совокупность течений (заме-
(заметим, что в примерах 1)—4) предыдущего пункта функции щ
"по некоторым специальным причинам оказываются вовсе не за:
висящими от Re). Точно так же p{x) = pLJ2t?0(-^-, Rej, где
Фо — новая универсальная функция. Далее, если W—сила
воздействия потока на какое-то обтекаемое потоком твердое
тело, то коэффициент сопротивления Cw = ~, ^— будет зави-
сеть уже только от числа РейнольДса Re, причем L2 в опреде^
лении Cw можно заменить также площадью S всей обтекаемой
поверхности тела (как мы и поступали выше, полагая, что
Cf=—лт-где т — средняя сила, приходящаяся на единицу по-
поверхности) или площадью So миделева сечения тела. Иначе го-
говоря, геометрически подобные течения в случае равенства от-
отвечающих им чисел Рейнольдса (но, вообще говоря, только в
этом случае) будут также и механически подобными, т. е. будут
обладать геометрически подобными конфигурациями линий тока
й будут описываться одними и теми же функциями от безраз-
. мерных координат (так называемый закон подобия Рей-
Рейнольдса). Этот закон, естественно, имеет важное значение для
теоретического изучения течений, имеющих место в аналогич-
аналогичных условиях, для унификации обработки наблюдений над та-
такими течениями и для моделирования течений, встречающихся
в практических задачах. Кроме того, он показывает, что всевоз-
всевозможные геометрически подобные течения будут описываться
лишь однопараметрическим семейством решений уравнений
A.5) — A.6) —это, разумеется, сильно упрощает задачу числен-
численного интегрирования этих уравнений.
Подчеркнем еще раз, что закон подобия Рейнольдса спра-
справедлив лишь для установившихся течений несжимаемой жидко-
жидкости, на которые не оказывают существенного влияния внешние
силы. В случае же движений, существенно зависящих от внешних
,сил (например, от силы тяжести), а также нестационарных дви-
движений, характеризующихся некоторым типичным периодом Т,
отличным от L/U, закон подобия оказывается более сложным:
здесь для механического подобия необходимо, чтобы кроме чисел

48 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [1.4
Рейнольдса Re равные значения принимали также и еще не-
некоторые дополнительные безразмерные «критерии подобия».
В случае течений сжимаемой жидкости число критериев подо-
подобия также увеличивается; на этом мы еще остановимся в п. 1,6.
Заметим еще, что в некоторых случаях весьма небольшие
нарушения геометрического подобия могут приводить к очень
резкому нарушению механического подобия. Так* например, не-
небольшие изменения условий у входного сечения круглой трубы,
вносящие в поток небольшие возмущения, могут совершенно из-
изменить характер течения в трубе (см. по этому поводу § 2).
1.4. Течения1 с большими числами Рейнольдса;
пограничный слой
Будем теперь считать, что число Рейнольдса Re потока очень
велико. В таком случае нелинейные инерционные члены урав-
уравнений A.6) будут существенно превосходить по величине чле-
члены, содержащие коэффициент вязкости, так что на первый
взгляд может показаться, что влиянием вязкости здесь можно
попросту пренебречь. На самом деле, однако, дело будет об-
обстоять не совсем так: отбрасывая члены с v в уравнениях /1.6),'
мы тем самым понижаем порядок этих дифференциальных урав-
уравнений, и решения получающихся упрощенных уравнений идеаль-
идеальной жидкости не могут уже удовлетворить граничным «усло-
«условиям прилипания», требующим обращения в нуль скорости на
всех твердых поверхностях, ограничивающих поток. В то же
время хорошо известно, что для вязкой жидкости (со сколь
угодно малым коэффициентом вязкости) «прилипание» обяза-
обязательно должно иметь место. Поэтому при движениях вязкой
жидкости, характеризующихся большим числом Рейнольдса,
только вдали от твердых стенок течение будет близким к тому,
которое могло бы иметь место в случае идеальной жидкости (с
нулевой вязкостью); вблизи же от стенок образуется тонкий
слой, в котором скорость течения очень быстро изменяется от
нулевого значения на стеике до значения иа внешней границе
слоя, весьма близкого к тому, которое получилось бы при те«
чении идеальной жидкости. Быстрое изменение скорости вну-
внутри этого так называемого пограничного слоя приводит к тому,
что в его пределах влияние сил треиия на деле оказывается^
вовсе не малым, а _ршюлшм. тот..же„.порядок, что и_влдяние сил
инерции. •¦-¦-_-
Таким образом, при больших числах Рейнольдса вязкость
жидкости сказывается лишь вблизи от ограничивающих поток
твердых стенок. В этой области течения члены, содержащие v,
никак не могут быть отброшены, но зато уравнения гидродина-

(.4] » 1- УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ 40
цщш здесь могут быть заметно упрощены, исходя из специфи-
специфических особенностей движения тонкой пленки жидкости,, обво-
Да кивающей твердое тело. В свободном же пространстве тече-
течение будет определяться уравнениями гидродинамики идеальной
жидкости, причем за граничные условия здесь уже надо при-
принять условия на верхней границе соответствующего погранич-
пограничного слоя (или слоев).
Рассмотрим теперь простейшую задачу о пограничном слое
на плоской пластинке длины L и бесконечной ширины, располо-
расположенной в плоскости Оху (так что она заполняет область
0-<дг<1 этой плоскости) и обтекаемой потоком жидкости,
движущейся с данной скоростью U по направлению оси Ох.
Прежде чем переходить к математическому решению этой за-
задачи, изложим некоторые предварительные соображения каче-
качественного характера. Поскольку в нашем случае характерным
масштабом длины будет L, а скорости — U, то нелинейные чле-
члены уравнений A.6) (точнее говоря, первого из этих уравнений)
в области пограничного слоя будут иметь порядок IP/L. С дру-
другой стороны, продольная скорость и — щ здесь будет меняться
от значения и — 0 на поверхности пластинки до значения по-
порядка U на внешней границе пограничного слоя. Поэтому, если
мы обозначим через б толщину пограничного слоя1), то-^р- бу-
дет иметь порядок Ufa2, и главный член у-§р- описывающий
силу трения, будет иметь порядок v?//62. Но внутри погранич-
пограничного слоя сила хр.ения должна иметь тот же порядок, что и сила
инерции. Следовательно, lfl\L ~ vf//82, и, значит,
Таким образом, толщина пограничного слоя зависит от числа
Рейнольдса потока — чем больше это число (т. е. чем меньше
рязкость жидкости и чем больше скорость набегающего потока),
тем тоньше оказывается пограничный слой.
') Разумеется, толщина 6 пограничного слоя является условным поня-
понятиен, так как пограничный слон не имеет четкой границы, и скорость и лишь
асимптотически стремится к U при удалении от пластинки по направле-
направлению Ог. Поэтому под б следует понимать расстояние от пластинки по на-
направлению Ог, на котором скорость и достигает определенной, достаточно
большой доли от U, например становится равной 0,99 и (такое определение 6
часто используется в гидромеханике). Существуют также и другие опреде-
определения толщины пограничного слоя, имеющие несколько менее формальный
характер (но приводящие практически к эквивалентным результатам); оО
этом ем. ниже, стр. 56—58.

50 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [1.4
Для определения толщины пограничного слоя над заданной
точкой пластинки на расстоянии х от ее передней кромки мы
должны заменить в этом расчете полную длину пластинки L
величиной х. Следовательно,
ь~\/^ в точке х, A.33)
т. е. толщина пограничного слоя при увеличении расстояния х
от передней кромки возрастает пропорционально У~х. Что же
касается напряжения трения т, на стенке (равного силе трения,
действующей на единицу площади пластинки), то т = (*.-^р(где
надо взять при z-— 0). Поскольку ~а~~~т~* т0 Л^"^Т~'
или, в силу A.32),
у^ A.34)
Таким образом, напряжение трения здесь пропорциональна ско-
скорости в степени 3/2; соответствующий коэффициент сопротивле-
сопротивления трения
естественно., зависит только от числа Рейнольдса и убывает
е возрастанием этого числа. : -'
Перейдем к выводу уравнений, определяющих поле скорости
внутри пограничного слоя. Поскольку в рассматриваемом нами
случае движение, очевидно., будет строго двумерным (в плос-
плоскости Охг), и все его характеристики не будут зависеть от у, то
общие уравнения A.6) и A.5) здесь-принимают вид
да . да ( да 1 др
-w+u-w+'w-dT—j-?
dw . dw . dw 1 dp
где и = «i, w — из. Постараемся теперь оценить порядок от<-
дельных членов этих уравнений. Напомним, что и внутри по-
пограничного слоя, вообще говоря, равно конечной доле скорости
*» г. да да
U, т. е. имеет тот же порядок, что и U, а производные -g- и -g-
имеют порядок JJ/L и, соответственно, U/6. Интегрируя третье
уравнение A.36) по г рт О до некоторого г = сб, 0^l

X4] § I; уравнения- -динамики жидкости 51
вляющего конечную часть полной толщины б пограничного
слоя, получим
«5
о
Отсюда видно, что w примерно в— = ^== раз меньше и. Учи-
L у Re
тывая еще соотношение A.32), убеждаемся, что в первом урав-
уравнении A.36) члены й-? , 'sy-gj- и ч-gp- имеют один и тот же
порядок U2/L, а член v-^-—много меньший порядок -j--^-;
поэтому этот последний член мы можем опустить. Далее, из
второго уравнения A.36) видно, что член —-^ будет иметь
ич ?/* 8 . ¦
порядок не выше чем —^- = -j- • -j- (так как ни один член этого
второго уравнения не имеет более высокого порядка); поэтому
с точностью до членов относительного порядка -?- мы можем
пренебречь поперечными изменениями давления и считать, что
^ 0, т. е. р = р(лс).'Но.в таком случае давление р(х) внутри
пограничного слоя можно заменить давлением на его верхней
границе. Следовательно, член -^ в первом уравнении
A.36) можно независимо определить из уравнений гидродина-
.мики идеальной жидкости, описывающих течение вне погра-
пограничного слоя: полагая v = 0 в первом из уравнений A.6), мы
1 до ди , т т ди /
найдем, что Т^=="аГ~г"^'5~1 или же (в стационарном
случае) ~W = U~дх~= ~2 ~дх~' ^аким образом, для нахож-
нахождения и и w мы получаем систему двух уравнений
Эта система вместе с граничными условиями
u = w = 0 при 2 = 0, 0<jc<X; u->U(x, t) при z->oo. A.40)
позволяет однозначно определить функции u(x,z,t) и w(x,z,t)
по начальным значениям одной из этих функций.
Уравнения "A.38) и A.39) представляют собой знаменитую
систему -уравнений пограничного слоя, впервые полученную

52 ГЛ, !. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ {1.4
Л. Прандтлем в 1904 г. В дальнейшем и сами-м Прандтлем и
другими авторами было предложено несколько разлнчных вы-
выводов этой системы уравнений. При этом, в частности, было
установлено, что уравнений Прандтля справедливы ив случае
двумерного обтеканий искривленной поверхности (с не слишком
большой кривизной) и что они могут быть формально.получены
из общих уравнений гидромеханики в качестве первого прибли-
приближения при помощи разложения'всех членов в ряды по степеням
— (см. Кочин, Кибель, Розе A963), ч. 2, гл. II, § 29; Гольд-
штейн A938), т. I, гл. IV; ср. также монографии Лойцянокого •
A941, 19626) и Шлихтянга A951)). В общем случае под г,'
естественно, надо понимать координату, отсчитываемую по нор-
нормали к обтекаемой поверхности, а под х — продольную коорди-
координату в касательной плоскости.
Рассмотрим теперь подробнее простейший случай устано-
установившегося обтеканий плоской пластинки стационарным потоком,
имеющим постоянную скорость U по направлению . оси Ох.
В этом случае в уравнении A.38) выпадут члены -^- и —-gj>
так что это уравнение здесь принимает особенно простой вид
ди , да д*и ., ..•.
Условимся считать длину пластинки L бесконечной. Так как
естественно думать, что при рассматриваемом нами обтекании
скорости в каждом сечении х=const пограничного слой не
будут существенно зависеть от скоростей в последующих сече-
сечениях вниз по течению, то можно ожидать, что предположение
о бесконечной длине не будет заметно влиять на решение нигде,
кроме узкой окрестности задней кромки и области *>-L, распо-
расположенной за пластинкой, которых мы здесь не будем касаться.
При L= 6о граничные условия A40) будут иметь вид
u = w = O при 2 = 0, x^>0; a-*-U при z-*-oo. A.42)
Таким образом, нам надо лишь найти решение уравнений
A.39) и A.41), удовлетворяющее условиям A.42).
Чтобы избавиться от параметров v и U, перейдем к безраз-
безразмерным величинам
A.43)
задаваемым в соответствии с соотношениями A.32) и A.37);

1.4] I t. УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ 53
длину L в A.43) мы теперь можем выбрать произвольно (так
как условия задачи не содержат никаких характерных длин).
Подставив A.43) в A.41), A.39) и A.42), получаем
дхг дгг dz{ dxt дгг
щ — wi — О при 2j = 0, х\ !> 0; щ -*- 1 при гх ¦-*• со. - A.45)
Но поскольку длина L была выбрана произвольно, то смысл
может иметь только решение, не зависящее от L. Отсюда ясно,
что «i = TT может зависеть только от комбинации •») = —т^=- =
= гу — переменных z\ и х\, не содержащей L. От этой же
комбинации должна зависеть и функция Yxi w1 = wy -4jt . так-
также выражающаяся лишь через да, х, v и U. Итак, мы видим, что
где jf и /i — две универсальные функции одного переменного (не
зависящие от U и у). Из A.46), в частности, следует, что про-
профили скоростей и и да над всеми точками любых пластинок,
обтекаемых потоком постоянной скорости, должны быть подоб-
подобны друг другу. Если мы обозначим
/О1) = <Р'М. A.47)
то уравнение A.39) обратится в равенство /i (ц) = у (щг — <р);
после этого уравнение A.41) и условия A.42) легко приво-
приводятся к виду
<р'@) = 0( ?'(оо)=1. A.48)
Таким образом, наша система уравнений свелась к одному
нелинейному обыкновенному уравнению третьего порядка
с тремя граничными условиями. Это уравнение может быть
проинтегрировано численно, например, при помощи разложения
функции ф(т]) в степенной ряд вблизи i\—Q и в асимптотический
ряд при г\ -у оо (такой метод решения был использован в
1908 г. Блазиусом, впервые исследовавшим рассматриваемую
здесь задачу); некоторые другие численные методы применили
к решению уравнения A.48) в последующие годы Тепфер, Бер-
стоу, Гольдштейн, Хоуарт и др.' (см. ссылки в книгах Гольд-
штейна A938), Шлихтинга A951) иЛойцянского A941,19626».
Полученные в результате этих расчетов профили продольной и

ГЛ. I/ ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
11,4
вертикальной скоростей в пограничном слое над плоской пла-
пластинкой приведены на рис. 2 и 3. Толщина 8 пограничного слоя
(определяемая как. то значение г, при котором u(z) =0,99G)
здесь оказалась имеющей значение
¦ 1 / v-*:
Щ. -A.49)
(ср. формулу A.33)). Напряжение трения в точке пластинки,
as
U6
и
0,2
/
/
f\
J
¦
/
J
V
xaf*
+ 7,08-70s
• 1,62-JO5
o'W'tO5
• 5,46-705
• 7,26-fO5
¦
-
10 2.0
40
4,0
6,0 7.0
Рис. 2. Профиль продольной скорости в пограничном слое на плос-
- кой пластинке.
Экспериментальные данные —по измерению! Никурадзе (см. Шлттинп A951)).
удаленной на расстояние^*_от передней кромки, дается форму-
'дойт(д:) = ш-Д) = i*-l/ ~—<р"@); поскольку результаты числен-
; \ 0Z /Z=O ¦ V ЧХ
ного интегрирования показывают, что-q>"(G) =0,332, то, следова-
следовательно,
,—, сЛх) = -^ = -==-, Re, = -—. (L.50)
пластинки длины L, смачиваемой с обеих сторон, полная
сила трения (на единицу ширины пластинки) будет равна
F = 2 J i (x)dx = 1,328 р Y^JPL, A.51)
о

1.4] § i. уравнения динамики жидкости 53
т. е. она будет пропорциональна скорости в степени 3/г и корню
квадратному из длины пластинки (сравнительно медленное воа-
растание F с ростом L естественно объясняется тем, что трение
ч(х) убывает с удалением от передней кромки в связи с увелит
чением толщины пограничного слоя). Вместо F обычно исполъ*
зуют безразмерный коэффициент сопротивления Cf,- который
UJ
пУ
0,8
/Ш
V
0,4
у
-
-. ¦
„ -
о
Рис. 3. Профиль вертикальной скорости в пограничном слое на
плоской пластинке.
для плоской, пластинки длины L и ширины В будет определят^
ся из равенства
Экспериментальная проверка изложенной здесь теории об-
обтекания плоской пластинки производилась, в частности,
И. М. Бюргерсом и Б. Г. Ван дёр Хегге Цийненом в 1924г., М. Хан-
зеном в 1928 г. и И. Никурадзе в 1942 г. (ссылки на оригиналь-
оригинальные работы см., например, в книге Шлихтинга A951)). При
этом было обнаружено, что при не слишком больших числах
Re = —^- эмпирические значения коэффициента сопротивления
достаточно точно описываются формулой A.52). Точно так же
и измеренные значения толщины пограничного слоя 8, и форма
профиля продольной скорости u(z) внутри этого слоя при не
слишком большом, но и не слишком MaflOMRex = -^-(T. e. всю*
ду кроме узкой полоски, примыкающей к переднему ребру
I d2» I „I дЧ |
пластинки, где не выполняется условие -дтг <С!\-^t >и еще,
быть может, задней части пластинки в случае, когда —^- очень
велико) оказались весьма хорошо соответствующими теорети-

ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
{1.4
ческим .предсказаниям. Небольшие расхождения теории с
опытом, наблюдавшиеся в ранних измерениях, вполне могут
объясняться влиянием конечной толщины пластинки и формы
заострения на передаем ребре, а также наличием небольших
продольных градиентов давления в обтекающем потоке; эти об-
обстоятельства были специально учтены в опытах Никурадзе,
сумевшего получить почти идеальное совпадение с вычислен-
вычисленным профилем и(г) (см. рис. 2, на котором нанесены эмпири-
эмпирические данные Никурадзе). Однако при больших значениях
скорости U и длины пластинки L, начиная с некоторого значе-
U х
ния х, для которого Re*= -g- имеет порядок 3-Ю5 —3-Ю6, все
выведенные выше закономерности оказались реако искаженны-
искаженными (см., например, рис. 4, на котором приведены результаты
измерении толщины погранич-
пограничного слоя 8, произведенных
Ханзеном, показывающие, что
начиная примерно с Re*=3,2X
X 10s эта толщина начинает
возрастать гораздо быстрее,
чем следовало бы сЪгласно
формуле A.49)). О причинах,
вызывающих эти искажения,
мы еще будем подробно гово-
1в
t6
и
12
""*¦¦*#¦
•
у
¦ +
¦
рить в § 2.
До сих пор толщину погранично-
пограничного слоя б мы определяли чисто ус-
условно как то значение координаты г,
при котором продольная скорость и(ж)
принимает значение, равное какой-то
определенной достаточно близкой
к единице доле от U (например,
равное 99% рт U). Такое не очень
четкое определение мы вынуждены
были принять из-за того, что и(г)
лишь асимптотически приближается
к U при z-хх>, нигде не достигэя
этого последнего значения; поэтому,
строго говоря, надо считать, что
пограничный слой не имеет резкой
границы. Тем не менее, поперечный
масштаб пограничного слоя можно характеризовать и с помощью некото-
некоторых величин, имеющих отчетливый физический смысл. Одной из таких ве-
величин является так называемая толщина вытеснения б*, определяемая
формулой
10 1Z
Рис. 4. Зависимость толщины погра-
кнчного слоя 8 на плоской пластинке
от расстояния х от передней кромки
пластимкиГпо данным Ханзена f I928U
пластинки (по данным ланзена ^яд») J.
A.53)

L4l
§ 1. УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ
Смысл этой величины заключается в том, что б* равно расстоянию, на ко-
которое оттесняется наружу обтекающий поток из-за вызванного трением умень-
уменьшения продольной скорости в пограничном слое. В самом деле, рассмотрим
некоторую линию тока, отстоящую от пластинки у переднего ее края на рас-
расстояние г0 (см. рис. 5). Так как расход жидкости через любое сеченне труб-
трубки тока, заключенной между этой линией тока и поверхностью пластинки,
должен быть одним и тем же, а продольная скорость и убывает вниз йо
течению вследствие трения а пластинку, то сечение трубки тока должно ра-
расти с ростом х. На расстоянии х от переднего края пластинки линия тока
отойдет от пластинки на расстояние зц, т. е. как бы «вытесннтся» на рас-
расстояние Zt — Zo, которое можно
определить из условия постоян-
постоянства расхода жидкости через
начальное сечение трубки тока
и через сечеиие с абсциссой х:
Uz.
откуда
= )и{х,
z)dz,
Рис. 5. Схематический вид линии тока
A.54) в пограничном слое на плоской пластинке.
gH_zj->oo разность z\ — Zo как раз и стремится к толщине вытеснения 6*.
ля случая ттационариого обтекания плоской пластинки
8* =
-»' <Ч>1
Ч-><»
jt, A.55)
откуда можно получить формулу
8* « 1,73
V
A45)
Заметим, что ранее вычислявшаяся толщина пограничного слоя б (опреде-
(определяемая соотношением U(i)=0,99 V) оказывается в этом случае примерно в
трн раза больше толщины вытеспения б*. Из-за «вытеснения* лини* тока
вертикальная компонента скорости w не стремится к нулю прн ?->оо (см.
рис. 3), а приближается к некоторому асимптотическому значению, оказы-
оказывающемуся равным
w (со) = 0,895 U
X ТЛ'
A.57)
Таким образом, вытеснение приводит к тому, что поток оказывается искажен-
искаженным даже и вне пограничного слоя (как бы ни определялась его толщина),
т. е. пограничный слой оказывает влияние иа внешний поток, с чем иногда
приходится считаться при расчетах.
Другой величиной, характеризующей поперечный масштаб пограничного
слоя, является так называемая толщина потери импульса, определяемая

58 гл. !.' Ламинарные и турбулентные движений \t&
формулой
Наименование этой величины связано с тем, что импульс, передаваемый си-
силами трення за единицу времени части пластинки, имеющей единичную ши-
ширину и простирающейся от передней кромки дс=О до сечёння " пластинки' с
заданным х (т. е. теряемый за единицу времени столбом жидкости, распо-
расположенным над этой частью пластинки), как можно показать, равен рЧ/2б**,
т. е. характеризуется длиной б**. В случае стационарного обтекания пла-
пластинки потоком, постоянной скорости U эта длина в силу A.46), A.47) и
A.48) будет равна
со '
' О - ?') *i =. 2<Р" @) |/^ = 0,664 |/ 2L; A.59)
о : .•¦¦¦¦
таким образом, здесь б** оказывается еще почти в три раза меныые, чем б*.
Отметим еще, что теория пограничного слоя, позволяет также объяснить,
почему течение-Пуазейля, представляющее собой точное решение уравнений
гидродинамики, устанавливается лишь на расстояниях порядка-—-от входа
-грубы* (см. стр, 43—44). В самом деле вблизи входного отверстия трубы тор-
тормозящее действие стеиок будет сказываться лишь в пределах тонкого погра-
пограничного слоя, а, в центральной' части трубы жидкость будет двигаться с по-
постоянной скоростью, ие испытывая действия вязкости. По мере продвижения
в глубь трубы толщниа пограничного слоя на стенках будет возрастать про«
6К,1Р
порциональнег \/ -уу, где х — расстояние от входа. Наконец, иа расстоянии
R2U
х~ от входа *пограиичный слой заполнит все сечеине трубы, и вязкость
начнет сказываться иа всем потоке в целом. Только после этого, разумеется,
и может установиться теоретическое параболическое распределение скорости,
задаваемое формулой A23) (ср. Шиллер A932, 1934) или Гольдштейи
X1938I, т. I, гл. VII, § 139).
1.5. Общее уравнение^дитока тепла и уравнение
теплопроводности; вынужденная и свободная конвекция
В дальнейшем больше всего внимания будет уделено тече-
течениям несжимаемой жидкости, описываемым уравнениями
Навье — Стокса A.6) и условием _несжимаемости A.5). По-
Поскольку, однако, гл. IV будет посвящена изучению более общего
случая температур но-неоднородной жидкости, а во второй части
книги вкратце будет рассмотрен также и Случай"турбулентно-
Случай"турбулентности в, сжимаемой среде, та целесообразно остановиться здесь н?
вопросе о замыкании общей системы уравнений гидродинамики)
Полученные при этом результаты помимо всего прочего позво-
позволят нам выписать уравнение для поля температуры несжимае-

1,5] § i- уравнения динамики жидкости 59
мой температурно-неоднородной среды, которое будет играть
важную роль в последующем изложении.
В сжимаемой среде уравнение неразрывности (т. е. баланса
массы) и уравнения динамики (т. е. баланса трех компонент
импульса) имеют вид A.2) и соответственно A.4). Поскольку
эти четыре уравнения содержат пять неизвестных функций, то
для получения замкнутой системы к ним надо добавить еще
пятое уравнение — уравнение притока тепла, выражающее фи-
физический закон сохранения энергии. В самом общем виде
уравнение может быть записано в виде '
где е — внутренняя энергия единицы массы жидкости (так что1
сумма р(ц2/2+е) представляет собой полную энергию единицы
массы движущейся жидкости), w — e-\- —— так называемая
тепловая функция '), к — коэффициент теплопроводности, Т —
температура, а
ди, 2 йи.
— вязкий тензор вапряжещцй, 'входящий поя;зна~ком производной
-s— в правую часть уравнения баланса импульса A.3) (см.,
например, Ландау, и Лнфшиц A953), ч. 1, § 49). Из уравнения
баланса энергии A.60) может быть выведено также уравнение
баланса энтропии; в самом деле, воспользовавшись термодина-
термодинамическими соотношениями, позволяющими выразить de и dw
через dp, dp и ds, где s — энтропия единицы массы жидкости, и
учитывая также и уравнения A.2) и A.4), "мы можем преобра-
преобразовать уравнение A.60) к виду
') Вообще говоря, использование здесь и ниже термодинамических ве-
величии и термодинамических соотношений требует известных оговорок, так
как движущаяся жидкость при наличии градиентов скорости и температуры
ие является термодинамически равновесной системой. Можно, однако, пока-
, зать, что при не слишком больших градиентах, характеризующих реально
встречающиеся гидродинамические потоки, основные термодинамические ве-
величины все же могут быть определены так, чтобы для них удовлетворялись
обычные формулы термодинамики равновесных сред; см., например, Ландау и
Лифшиц A953), ч. 1, § 49, а также Толмен и Файн A948) и специальные
руководства по кинетической теории газов (Чепмен и Каулйнг A952), Гирш-
фельдер, Кертисс, Берд A9&4)). • '

60 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [1.5
(ср. Ландау и Лифшнц A953)). Таким образом, в случае спра-
справедливости уравнений A.2) и A.4) уравнения A.60) и A.62)
оказываются эквивалентными друг другу, в любое из них с оди-
одинаковым правом может быть положено в основу вывода замкнут
той системы уравнений, описывающей движения сжимаемой
жидкости. ,
Для Получения такой замкнутой системы надо только выра-
выразить термодинамические величины е н w или s через давление р.
н плотность р (или температуру Т) при домощи общих уравнений
термодинамики и уравнения состояния рассматриваемой среды
(связывающегр р, р и Т). Мы ограничимся здесь простейшим
случаем, когда это уравнение состояния совпадает с уравнением
состояния идеального газа, т. е. имеет вид
P = R?T, , A.63)
где Т — температура в градусах Кельвина, а постоянная R рав-
равна разности удельных теплоемкостей среды при постоянном дав-
давлении ср и при постоянном объеме с„:
R = cp-cv. . A.64)
Кроме того, в соответствии с выводами кинетической тео-
теории газов и с данными многих экспериментов мы будем считать,
что теплоемкости ср и сс по отдельности являются постоян-
постоянными (т. е. не зависят от температуры). В таком случае нетруд-
нетрудно показать, что е = cvT + во, w = е + ¦?• = срТ + е0 и s =
== — R In p + с„ In Т + const = — R In p + ср In T + const (см.,
например, Ландау и Лифшиц A951), § 43). Подставляяэти вы*
ражения для е и до в уравнение A.60) и применяя A.2) и A.41.
или же подставляя одно из выражении для s в уравнение A.62),
можно без труда преобразовать общее уравнение притока тепла
к виду
Т д ( дТ \ ; ,, ес.
или, что экдивалентно, к

L5] * I. УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ 61
Величина е представляет собой умноженный на рГ приоост эн-
энтропии s за единицу времени, связанный с переходом части ки-
кинетической анерпш в теплоту в результате внутреннего трения
жидкости: инзче гороря, е совпадает с количеством тепла, выде-
выделяющимся в результате действия вязкости за единицу времени
в единице объема жидкости. При наличии ещпгпритока тепла,
вызванного лучистой теплопроводностью, химическими реакция-
реакциями, фазовыми превращениями, или какими-то другими причи-
причинами, к правым частям A.60), A.62), A.65) и A.65') должно
быть добавлено еще слагаемое pQ, где Q — дополнительный
приток тепла на единицу массы за единицу эремени. Уравнения
A.2), (J.4) и A.65) или A650 вместе с равенствами A.63) и
A.66) дают иам общую систему пяти уравнений для определе-
определения пяти неизвестных функций щ(х,г), /¦* 1, 2, 3; p(x.t)u
р(х. t) или Т(х, t).
Уравнение типа A.65') может быть получено и для неодно-
неоднородно нагретых «капельных жидкостей», т. е. сред, являющихся
жидкими в обычном смысле этого слова. Здесь роль уравнения
состояния будет играть закон теплового расширения жидкости
Р-Ро = -РРоG"-Го), A.67)
где р и ро — плотности при температурах Т и соответственно То,
а (И—коэффициент теплового расширения-.Можно показать, что
при этом условии уравнение A.62) примет следующий вид:
причем в выражении для s в случае жидкости можно считать,
д
что "gj~ = O, так что
т
A-69)
(см., например, Хоуарт A953), т. II, гл. 14). Коэффициент р
для обычных жидкостей очень мал (например, для воды
р ж 1,5-10~4 град~1 при температуре 15°С); поэтому в уравне-
уравнении A.68) можно пренебречь членом, содержащим этот коэф-
коэффициент. В результате получается уравнение
где Х^т?—-коэффициент температуропроводности нашей
среды, который здесь и всюду ниже предполагается принимаю-
принимающим постоянное значение (ср. переход от A.3) к A.4) на

62 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [1.5
стр. 36). Член ¦?- в уравнении A.70) описывает общее прогре-
прогревание среды, вызываемое внутренним трением жидкости; это.
прогревание в реальных условиях обычно играет совершенно
незначительную, роль и им вполне можно также пренебречь;.
При этом уравнение A-70) еще более упростится и перейдет
в'.обычно"е уравнение теплопроводности в движущейся среде '
?4-«.?:-хАГ. A.71)
которым мы и будем широко пользоваться в дальнейшем.
Весьма существенно, что уравнение A.71) применимо не
только к капельным жидкостям, но и к газам, если только ско-
скорость движения этих газов много меньше соответствующей ско-
рости звука а = |/ т —, "{ — ~!г- Можно показать, что при
таких скоростях изменения давления будут играть вjуравне-
вjуравнении A.65') гораздо меньшую роль, чем изменения температуры,
так что членами с р в правой части A.65') можно пренебречь;
после этого мы немедлтгннб приходим к уравнению*, A.70) или,
пренебрегая также и прогреванием среды из-за внутреннего
трения, к уравнению A.71). Заметим, что сопоставление A.70)
с A.65) показывает, что в уравнении A.65) в отличие от A.65')
да*
нельзя пренебречь членом —Р~дх~'' локальные сжатия и рас-
расширения, вызываемые изменениями плотности при нагревания
и охлаждении, в уравнении притока тепла должны учитываться
даже и при малых скоростях движения. Однако в динамических
уравнениях при движениях со скоростью, много меньшей ско-
скорости звука, поле скорости вполне можно считать «несжимае-
«несжимаемым», если только изменения плотности, вызванные неоднород-
неоднородностью поля температуры, будут малыми по абсолютной вели-
величине, т. е. если имеющиеся в потоке абсолютные разности
температур будут малы по сравнению со средней абсолютной тем-
температурой Го. При этом условии и в выражении для е можно
также считать, что dujdxa= 0,.т. е. е снова можно считать
пред ставимым в виде_П.69). Так как к тому же в не-
несжимаемой среде [Tds ==¦ с&\ то в несжимаемой жидкости вели-'
чина е будет точно равна приросту внутренней энергии единицы
массы за единицу времени, т. е. количеству кинетической энер-
энергии, диссипирующейся (переходящей в тепло) за единицу вре-
времени в единице массы жидкости (ср. Ландау и Лифщиц
A953), ч. I, § 16). Хотя при расчете поля температуры этой ве-
величиной обычно можно пренебречь, она тем не менее является
отень важной физической характеристикой движения; для

1,5] § 1. Уравнения Дййамйкй жидкости- 63
краткости в дальнейшем мы ее будем называть просто
пацией энергии.
Подчеркнем еще, что по своему виду уравнение A.71) точно
совпадает с уравнением диффузии
вписывающим изменение концентрации О(лг. t) некоторой пас-
пассивной {т. ,е.-не оказывающей влияния на динамику потока)
примеси в среде; только коэффициент % в этом~последнем слу"
чае надо интерпретировать не как коэффициент температуро-
температуропроводности, а как молекулярный коэффициент диффузии. Так
как уравнения A.71) и A.72) имеют один и тот же вид, tq в
дальнейшем, рассматривая уравнение A.72), мы всегда будем
иметь в виду, что величина О здесь может ?ыть как концентра-
концентрацией некоторой пассивной примеси, так и температурой. Учиты-
Учитывая особую важность для приложений исследования поля темпе-
температуры, мы для краткости часто будем даже называть -в просто
температурой; однако следует запомнить, что фактически бук-
буквой О всегда будет обозначаться концентрация некоторой пас<
сивяой примеси и чта в тех случаях, когда .температура у нас
будет рассматриваться не как пассивная, примесь, мы ее будем
обозначать не буквой ,~Ф„ а" буквой Т.. .J ......
Предположение о пассивности примеси означает, что.поле
скорости ut(x,t) может .быть определено независимо от иссле^
дованйя поля О из'обычной системы уравнений гидродинамики
несжимаемой жидкости и затем подставлено в уравнение A.72).
Если под О понимать температуру, то для этого разности тем-
дыми. чтоРн яиапвимш» "ии йя"М?ненйя физических Двойств
жидкости не оказывали никакого влияния на двцжРИие, но в. ю
Же время постцт$чрг>--Лппмпинп* для тпгп HTnfifj пр
с. ними можно было пренебречь нятрриянием,
¦ЛДД тепла п рр!>улптпто. ппуФр^эдн^ра-^рения, R таком слу*
чаё температурные неоднородности будут просто перемещаться
вместе с потоками жидкос!И»_сгдажи.ваясь попутно под влия-
влиянием fмaiie>(y^яpн^й^2|плo?PJg?OJЩOJШц) возникающее при этом
Движение масс неоднородно нагретой жидкости называется
обычно^вынужденной конаекиией
-"-¦¦¦ Важный класс потоков, ^которых температура уже не мо-*
жет рассматриваться как пассивная примесь, представляют со-
собой- потоки неоднородно нагретой жидкости в поле тяжести;
возникающие под влияни^^^^™рйо^^С3^1 вызывающих
всплывание наверх более теплых и опускание вниз более холод-
холодных-объемов жидкости. Такие движения гемпературно-неод-

64 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [1.5
нородной жидкости носят название свободной конвекции. Выяс-
Выясним, как будут выглядеть в этом случае уравнения: движения.
Будем считать, что скорости нашего движения настолько неве-
ЛИКИ," чтгёГизменениями плотйбеУйГ
н леУйГ ^ щн
во не температуры!^, можно пренебречь. Отсюда сле-
Цуи мы можем пользоваться обычными уравнениями не-
несжимаемости A.5) и Навье — Стокса A.6), но только в A.6)
надо учесть внешнюю силу X ¦« —ge, (где es — единичный век-
вектор бей О*з=Ог), и плотность р считать зависящей от темпера-
температуры. Предположим теперь, что (абсолютная) температуре
7{Х\ х%, х3, t) **T(x, у, г, t) может быть представлена в виде
Т =* Т« + 3"ь где Г»— некоторое постоянное среднее значение,
a ft — небольшие отклонении от Г». В таком случае, очевидно,
р ш ре + jst, где ро — постоявши* плотность, отвечающая темпе-
температуре То, a pi = р— ро 0п|»еделяется из уравнения A.67):
P, = -ft>07\ A.78)
(коэффициент теплового расширения р =—Т"(^) ДЛя газа?
уловлетворяющеге 0-63^, очевидно, будет равен у-\. Заметим,
что при Т = То = const и р = ро .= cotist давление ро «все равно
не будет постоянным, а будет убывать с высотой вместе с убы-
убыванием веса столба жидкости, расположенного выше заданной
точки:
Ро = — Ро?*з-г-const. A.74)
Полагая р = ро + pi. с точностыо до малых величин первого по*
рядка будем иметь:
Р «**з Ро дхз Ро **з Ро ^з Ро дхз
Отсюда видно, что третье ураввеоде Навье—Стокса в вашем
еяучае будет записываться в виде
(наличие в этом уравнения слагаемого, содержащего Ти как
раз н показывает, что температура здесь не может считаться
пассивной примесью). Первое же и второе уравне»ня Навье —
Стокса в нашем случае будут иметь обычный вид A.6), при-
причем р в них с самого начала можно заменить постоянным зна-
ченнем р0, а под р .понимать отклонение Р\ давления от среднего
давления ре, зависящего от 2=»жв. Наконец, уравнение для тем-
температуры» как всегда, когда среду можно считать несжимае-
несжимаемой, будет иметь вид обычного уравнения теплопроводности в

1.6] §!. УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ 65
движущейся жидкости
(членом сев уравнении для температуры мы, как обычно, пре-
пренебрегаем). Пгутученная приближенная система пяти уравнений
A.5), A.6) с i = 1, 2, A.75) и A.76) относительно пяти неизве-
неизвестных функций tti {x, t),i = 1, 2, 3, pi(x, t) и Ti(x, t) и описы-
описывает свободную конвекцию жидкости^ поэтому она называется
системой уравнений свободной конвекции.
1.6. Критерии подобия для температурно-неоднороднои
- жидкости; температурный пограничный слой
Выше мы видели, что два геометрически подобных течения
несжимаемой жидкости будут также и механически подобными,
если только числа Рейнольдса этих двух течений совпадают
между собой. В случае температурно-неоднороднои или сжи-
сжимаемой жидкости это утверждение уже оказывается неверным.
Здесь для наличия механического и теплового подобия двух
геометрически подобных течений требуется совпадение сразу
нескольких безразмерных характеристик («критериев подо-
подобия»),^ рассмотрению которых мы сейчас и перейдем.
Начнем с простейшего случая таких течений неравномерно
нагретой жидкости, при которых температура может рассматри-
рассматриваться как пассивная примесь. В этом случае течение будет
описываться обычными уравнениями A.5) —A.6) гидродинами-
гидродинамики несжимаемой жидкости (с постоянным р), к которым только
надо будет добавить еще уравнение теплопроводности A.72),
описывающее изменение поля температуры. Будем для просто-
простоты рассматривать только стационарные движения, т. е. счи-
считать, что все поля щ, р и О не зависят от времени. В наши
уравнения входят два постоянных коэффициента v и % (оба
имеющие одинаковую размерность L2T~l, где L и Т символизи-
символизируют размерности длины и времени). Кроме того, краевые ус-
условия задачи при сохранении геометрического подобия будут
характеризоваться некоторой длиной L, характерной скоро-
скоростью U, а также еще и характерной разностью температур
¦&i — Оо (например, типичной разностью температур между
твердыми границами и потоком). Поскольку, однако, темпера-
температура у нас рассматривается как пассивная примесь, не оказы-
оказывающая влияния на динамику, то единица температуры может
быть выбрана произвольным образом; поэтому мы должны счи-
тать, что

66 ГЛ. 1. ЛАМИНАРНЫЕ И ТУРЁУЛЁНТНЫЁ ДЙйЖеМЙЯ [1Л
где в — новая независимая от L и Т размерность (например,
«градусы Цельсия»). Но в таком случае из v, х> L, U и 6i— Go
можно составить всего две независимые безразмерные комби-
комбинации, в качестве которых можно принять, например, число
Рейнольдса Re = —— и так называемое число Прандтля
В случае, когда ф—это концентрация пассивной примеси, а не
температура, отношение v/x иногда называется также числом
Шмидта и обозначается символом Sc.
Иногда вместо Рг удобно использовать число Пекле
Pe = -^ = Re-Pr, A.78)
определяющее порядок отношения адвективных членов и„-^г-
и члена хДФ в уравнении A.72) и играющее при исследовании
поля температуры роль, аналогичную роди числа Рейнольдса
в динамических задачах. Однако число Прандтля имеет перед'
числом Пекле то преимущество, что оно зависит лишь от при-
природы движущейся жидкости (т. е. является характеристикой
среды), но не от особенностей движения. Для воздуха (и дру-
других двухатомных газов) Рг « 0,7 и почти не зависит от темпе-
температуры; вообще для большинства газов Рг имеет порядок еди-
сницы. Для жидкостей (за исключением жидких металлов) число
Прандтля обычно превышает/ единицу и заметно убывает с ро-
ростом температуры; например, для воды (при атмосферном да-
давлении) Рг « 7 при температуре 20°С и Рг ~ 2 при 80°С. Для
очень вязких технических масел число Рг оказывается, есте-
естественно, много большим, чем для воды, достигая значений по-
порядка нескольких сотен или даже тысяч. Наоборот, для жидких
металлов, отличающихся очень большой теплопроводностью,
число Прандтля принимает значения, много меньшие единицы;
например, для ртути Рг «* 0,023 при 20° С, а для других рас-
расплавленных металлов это число часто оказывается даже еще
меньшим (порядка 10~3). В случае, когда % — это коэффициент
диффузии пассивной примеси, числе! Прандтля (или, что то же
самое, число Шмидта) также имеет существенно разный поря-
порядок для газов и для жидкостей: в газообразных средах коэффи-
коэффициенты диффузии и вязкости имеют одинаковый порядок, так что
v/x~ 1» в ю время как для жидкостей типа воды v/x—Ю3, а
для очень вязких жидкостей это отношение оказывается еще
много большим и может достигать значения порядка 106 и бо-
более того.

1,6] $ 1. УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ 67
Для подобия полей температуры в двух геометрически по-
подобных течениях у этих течений должны совпадать и числа Рей-
нольдса Re и числа ГГрандтля Рг (или Re и Ре). В общем же
случае только геометрически подобных течений поля темпера-
температуры будут определяться формулой
& (х) - &0 = (», - &0) <р (?. Re, Pr). A.79)
отличающейся от аналогичной формулы A.31), относящейся к
полю скорости, тем, что функция ф здесь зависит уже от двух
безразмерных параметров.
Точно так же, если мы обозначим через q плотность потока
тепла через поверхность тела, погруженного в жидкость (т. е.
d» ¦
положим q ——/7ш где п — внешняя нормаль к поверхности
тела), то
Иначе говоря, в каждой точке границы тела безразмерное от-
отношение Nu = .„- „ . будет зависеть лишь от чисел Рей-
нольдса и Прандтля. Если же мы заменим здесь поток тепла
в точке средним потоком тепла qCp через единицу площади по-
поверхности тела, характеризующим полный теплообмен тела и
жидкости, то-в формуле
^ Pr) A.80)
функция ф будет уже универсальной функцией двух переменных,
определяющей зависимость теплообмена от физических свойств
жидкости и масштабов длины, скорости и перепада температуры
для всей совокупности геометрически подобных потоков. Вели-
Величина Nu в теплотехнике называется числом Нуссельта. Можно
также вместо него для характеристики теплообмена использо-
использовать так называемый коэффициент теплопередачи (иначе —
число Стэнтона)
г — q — Nu _ Nu /1 Я.(\'\
А — cpPt/ (9, — 90) — RePr — W V V)
Перейдем теперь к случаю свободной конвекции. Здесь диф-
дифференциальные уравнения задачи содержат три размерных ко-
коэффициента v, х и ё$,. (где для идеального газаР = у-). гра-
граничные же условия теперь будут характеризоваться типичной
длиной L и типичной разностью температур Тщ— fg (заметим

68 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [1.6
что никакой типичной скорости в этом случае не будет). Из этих-
величин, очевидно, можно составить две безразмерные комбина-
комбинации. В качестве таких комбинаций можно принять, например,
число Прандтля Рг и так называемое число Грассхофа
Можно также вместо числа Грассхофа использовать родствен-
родственное ему число Рэлея
^3G7V)=Gr.pr. ' A-81')
Ra=
Таким образом, в случае свободной конвекции в геометрически
подобных потоках поля скорости и температуры будут подобны
друг другу только в случае совпадения критериев подобия Pi
и Gr (или Рг и Ra); вообще же говоря, из геометрическогр по-
подобия здесь будут вытекать лишь соотношения вида
' Рг'
где fu i= 1, 2, 3, <р и ф — новые универсальные функции. В об-
общем случае течений сжимаемой жидкости, описываемых полной
системой уравнений A.2), A.4), A.63), A.65) и A.66), число
критериев подобия оказывается еще значительно большим; на
этом, однако, мы не будем задерживаться.
UL
Для течений с очень большим числом Ре= (т.е. ijph числе Прандтля,
меньшем или порядка единицы, для течений с очень большим Re) член
Х&Ф в уравнении теплопроводности будет гораздо меньше нелинейных чле-
ОЬ ' '
нов иа -5— ; поэтому в первом приближении влиянием молекулярной тепло-
оха
проводностн здесь можно пренебречь. Однако, как и в случае учета вязкости
в уравнениях движения, пренебрежение это будет законным лишь вдали от
погруженных в поток твердых тел. Вблизи же поверхности таких тел может
образоваться тонкий температурный пограничный слой, в котором темпера:
ту"ра быстро изменяется от температуры тела fy до температуры, близкой к
температуре Фо, которая наблюдалась бы в свободном потоке, если бы ника-
никакого твердого тела не было. В этом слое влияние теплопроводности будет
уже иметь тот же порядок, что и влияние адвекции температуры, опнсывае-
дЬ _ ,
мой членами и„-з—. Отсюда можно вывести (аналогично выводу соотноше-
ння A.32)), что толщина Ь\ температурного пограничного слоя будет иметь
порядок »— = - ¦¦-. Иначе говоря, она также будет обратно пропор-
У Ре у Re ¦ Рг
T
циональна KTfc и при числах Прандтля порядка единицы будет совпадать

1.6] $ 1. УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ
по порядку с О. Учитывая еще, что q = — * -5— ~* ¦ .
что при больших числах Рейнольдса
дп
-. легко найдем.
Внутри температурного пограничного слоя уравнение теплопроводности
может быть упрощено аналогично тому, как упрощаются уравнения движе-
движения внутри обычного пограничного слоя. В частности, при стационарном об-
теканнн потоком жидкости данной температуры 0О плоской пластинки, под-
поддерживаемой прн некоторой другой температуре blt уравнение теплопровод-
теплопроводности в пределах пограничного слоя будет записываться в виде
дЬ . дЬ дЧ
аналогичном A.41). Что же касается граничных условий, то они, очевидно,
в этом случае будут иметь вид Ь =* bt _прн_ г — 0 н Ь-*-Ь„ прн z-> со. Пола-
Полагая здесь
Ь(х, г)=&1—(&i—90)в ( 1/ fr=\ и подставляя эту формулу
\ г v у х I
1,00 г-
0,75
0.50
0,25
i
14
W
t/Pr .
t,lA
Ж
*Оп7
1,0 2,0
3,0
4,0
Рнс. 6, Профиль температуры в пограничном слое на плоской
пластинке прн различных числах Прандтля.
вместе с формулами A.46) и A.47), определяющими поле скорости в преде-
пределах пограничного слоя, в уравнение A.83), мы немедленно получаем
e»-f-y fS' = 0; в @) - 0. в (оо) = 1. A.84)
где (р — решение уравнения A.48). Таким образом, для в(т)) получается про-
простое линейное уравнение, решение которого в явном виде впервые было вы-
выписано Польгаузеном § 1ЭД г. (см. Гольдштейн A938), т. 2, § 268; Х

70 ГЛ, I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ . [1.7
'A953), т. 2, гл. 14, § 13; Шлихтннг A951), гл. 14, § 7). В частности, прн
Р'Г *= 1 сопоставление уравнений A.84) и A.48) показывает, что'решение
в(г\) имеет внд в(г\) -»<р'(*))- Таким образом, в этом случае профиль Тем-
Температуры оказывается в точности подобным профилю скорости. Прн других
же значениях Рг функция в(т)) легко может быть найдена численно по- из-
известной нз рнс. 2 функции ф'(т)) (см. рис. 6).
1.7. Малые колебания сжимаемой жидкости
. Течения сжимаемой жидкости, описываемые общей системой уравнений
A.2), A.4), A.63)', A.65) н A.66), обычно имеют очень сложный Характер,
н их теоретическое изучение наталкивается на значительные трудности. Мы
здесь ограничимся лишь простейшим случаем малых колебаний относительно
состояния покоя (нлн движения с постоянной скоростью), прн исследовании
которого может быть использован метод линеаризации уравнений. Как было
показано Карьером и Карлсоном A946), Ягломом A948) и Коважным A953),
всевозможные движений среды прн этом распадаются на колебания трех ти-
типов, отчетливо различающихся по своему характеру. Это/ распадение будет
нграть важную роль прн расемртреНнн изотропной турбу'лентндстн в сжнмае-.
мом газе и процессов распространения волн в турбулентной среде во второй
части настоящей книги..
Итак,, пусть мы имеем неподвижную* массу идеального газа постоянной
плотности ро и при постоянном давлении р0 (случай газа, движущегося с по-
постоянной скоростью, в. может быть, очевидно, сведен к случаю неподвиж-
неподвижного газа прн помощи перехода к новой ннерцнальной системе координат).
Предположим теперь, что в начальный момент времени в газе возникли ма-
малые возмущения, характеризуемые полями пульсаций гидродинамических ве-
величин щ (х, t), р' (х. t) = р (х, t) — р, н р' (х, t) = p (х. i) — ро. где
• Ре
¦Li— <^ 1 и -^- <^ 1 (здесь а0 = 1/ ^ — — скорость звука в невозму-
Рв ¦ «о \ г Ро
ср \
щенной среде, 7 = ~^" I • В таком случае изменение во времени полей щ (х. t).
cv I .
р' (х, t) и р' (х. t) в первом прнблнженнн можно будет определнть нз снстемы
уравнений A.2), A.4), A.63), A.65) и A^6), линеаризованной Относительно
компонент скорости ui н относительно отклонений давления, плотности н тем-
температуры от соответствующих невозмущенных значений Ро. Ро н Л» = „ •
"Ро '
Прн этом уравнение состояния A.63) позволяет с самого начала исключить
температуру нз числа неизвестных н получить замкнутую систему уравне-
уравнений относительно пяти неизвестных, в качестве которых можно принять,
например, три компоненты скорости н какие-либо две однозначные функции
давления н плотности. Следуя работам Коважного A953) н Чжу и Коваж-
ирго A958), примем з качестве этих двух функций безразмерное давление
•Р=—— и поделенную на с„ энтропию S= — =*\п— f- const. Тогда
[Ро ср р
с точностью до малых высшего порядка

1.7] * 1- УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ 71
Линеаризованная система уравнений гидродинамики в переменных u<, P и
S будет иметь вид
= 0. A.87)
Преобразуем уравнения A.85) н A.86), введя вместо компонент и< поля ско-
ди*
ростн в качестве неизвестных компоненты внхря <oj = е*ав -т~ и дивергенцию
v охл
?>=,'*. При этом трн уравнения A.86) сведутся к равенствам
оха
~- — vA<oft = 0. k = 1.2,3, A.88)
а A.85) в силу A.87) перепишется в виде
i? O. A.90)
Отметим прежде всего, что компоненты внхря ю* входят только в ура-
уравнения A.88), совпадающие с линеаризованными уравнениями для поля
вихря в несжимаемой среде. Напомним в этой связи, что в случае несжи-
несжимаемой жидкости По полю вихря (о» и соответствующим граничным условиям
всегда можно' однозначно восстановить и поле скорости и,-; в сжимаемой
же среде поле Скорости можно представить в виде суммы несжимаемой (со-
ленондальной) и безвихревой (потенциальной) компонент, последняя из ко-
которых уже не зависит от поля вихря. Таким образом, в случае движений,
представляющих собой лишь слабое возмущение состояния покоя, система
уравнений гидродинамики в первом приближении распадается на замкну-
замкнутую систему уравнений относительно компонент поля внхря «в», описываю-
описывающую несжимаемое течение; н на систему уравнений относительно переменных
D, Р и 5, описывающую безвихревой сжимаемый поток. При этом пульсации
давления и энтропии в том же приближении будут связаны лишь со сжимае-
сжимаемым безвихревым потоком, т. е. в несжимаемой (вихревой) компоненте те-
течения они будут отсутствовать. В следующем приближении теории возмуще-
возмущений эти две компоненты будут уже взаимодействовать друг с другом, созда-
создавая дополнительные изменения давления н энтропии (на этом мы вкратце
остановимся в самом конце настоящего пункта).
Чтобы подробнее разобраться в характере движений, описываемых лине-
линеаризованной системой A.87) —A.90) и, в частности, показать, .что уравнения
относительно D, Р я S на самом деле описывают два разных типа колебаний,
воспользуемся обычным методом Фурье. С этой целью предположим, что все
поля щ (X, t), D(x,l), P(x,t) и S(x,tl являются периодическими функциями
пространственных координат с заданным волновым вектором k и, кроме того,
замешм. обычное вреыя t безразмерным временем т - a^kt, где А = J к\,

72 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ {I-7
а дивергенцию — безразмерной дивергенцией —-г'.
Я (х, 0 = Р (t) ****. 5 (х. 0 = 5 (т) ****.
Тогда уравнения A.88) примут вид
da>i (т) vfe
а остальные уравнения преобразуются в следующую систему обыкновенных
линейных уравнений:
A.92)
Отсюда следует, что амплитуды coj(f) компонент поля внхря будут затухать
во времени по закону
-'*\ A.93)
а амплитуды ?>(<). ^О и 5@ дивергенции скорости н полей давления и
энтропии будут представляться в виде
где A.I, А« и Хз—три корня характеристического уравнения системы A.92J:
«о
Дальнейшее упрощение полученных результатов может быть достигнуто,
если мы заметим, что формулы A.91)—A.94) содержат безразмерные по-
постоянные, имеющие очень разный порядок величины. В самом деле, все коэф-
коэффициенты системы A.92) н уравнения A.94) могут быть выражены через сле-
следующие три безразмерные величины:
Vife Vi с„
»!--?-¦ *<=Т« 7==Т-;
«О X LV
в равенствах же A.91J фигурирует безразмерная постоянная * = —» отли-
4°
чающаяся от 6i лишь заменой коэффициента вязкости ^ =» -^ v -j-1) =¦
¦» -к- ( 1 определяющего внутреннее трение в потенциальном потоке,
« Ро Ро
на обычную кинематическую вязкость v. Но Hi является аналогом
V
обычного числа Прандтля Рг = — и имеет тот же порядок величины, так
что в газообразной среде «i <¦•» V, точно так же и у ~ 1 (для воздуха у *» 1,4).

1.7] i 1- УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ 73
, Ik
В то же время величина о а= — имеет тот же порядок, что и отношение
-г длины свободного пробега газа / к длине волны возмущения Л = т-г-
(поскольку v ~ о/, где о — средняя скорость теплового движения молекул,
a~v, а А~1/Л). Поэтому во всех случаях, когда движения газа могут
быть описаны с помощью обычных гидродинамических уравнений, Ь <^ 1;
в частности, для воздуха при нормальных условиях — «0,5-10 см, т. е.
"в
даже если Л« 1 мм, то б < 1СИ. Тот же порядок величины имеет
8,=-iR; поэтому н 6i<^l.
Пренебрегая теперь в основных уравнениях A.91)—A.92) членами, имею-
имеющими порядок малости о (или б|), мы придем к упрощенной системе
Согласно первым двум уравнениям A.96), поле внхря ш,(л, t) и ноле энтро-
энтропии S(x, t) в рассматриваемом приближении будут неподвижны в простран-
пространстве (илн в случае, когда основное состояние — это состояние движения с по-
постоянной скоростью в, будут переноситься без всякого изменения этим дви-
движением) -^ малость числа 6 как раз н означает, что влияние вязкости (и
теплопроводности) на малые возмущения будет гораздо меньше влияния
инерционного переноса. Последние же два уравнения A.96) показывают, что
или,/переходя снова от одной компоненты Фурье к полным полям D(x, t) и
Р(х, t), что
3? 4? A.97)
Таким .образом, для поля давления Р(х, t) и поля дивергенции скорости
В (х, t) здесь получаются одинаковые волновые уравнения, описывающие со*
вокупность волн, распространяющихся со скоростью звука по-
Мы видим, что в нулевом приближении (по параметру малости 6) поля
малых возмущений гидродинамических элементов потока распадаются уже
на три не взаимодействующих между собой компоненты. Этими компонентами
являются вихревая несжимаемая компонента, описываемая полем внхря
4>j(x), не меняющимся во времени (нлн переносящимся без изменений невоз-
невозмущенной скоростью и), энтропийная компонента, описываемая также непо-
неподвижным (нлн перемещающимся со скоростью в) полем энтропии S(x), соз-
созданным первоначальными иеоднородностямн поля температуры, и потенциаль-
потенциальная (нлн акустическая) компонента, связанная с пульсациями потенциальной
части поля скорости н пульсациями давления н представляющая собой со-
совокупность волн, распространяющихся с невозмущенной скоростью звука а0.
Если мы учтем еще и эффекты порядка малости 6, то прежде всего убг-
димся, что поле скорости вихревой компоненты будет медленно затухать под
действием вязкости в соответствии с формулой A.93). Чтобы описать с точ-
точностью до членов порядка 6 также н энтропийную и акустическую компонен-
компоненты, удобно прежде всего переписать уравнение A.94) в виде

74 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [1.7
содержащем лишь величины A.95). После этого трр корня уравнения A.94')
легко определите с точностью до членов порядка б4 включительно с помощью
обычного метода степенных рядов. В результате получаются формулы
2*. ""
.»• 1
»i. A.98)
Х|--/- »,.
2*.
Эти формулы показывают, что если ограничиться членами порядка ие выше
6i и исключить из рассмотрения вихревую компоненту, то в сжимаемой сре-
среде будут существовать три различных волны с одинаковым волновым векто-
вектором к. Две волны из этих трех будут затухающими с одинаковым декре--
ментом затухания ' "Т.—:— 8iaofe= ' 9 * * и "УДУТ распростра-
распространяться с невозмущенной скоростью звука ао в направлениях векторов к и
— *, а третья из них будет неподвижной относительно невозмущениого по-
потока с декрементом затухания -&— aaft = x*J )• Предполагая далее, что за-
висимость функций D(x), P(x) и S(x) от т будет определяться множителем
е I, / = 1, 2, 3, и подставляя соответствующие частные решения в систе-
систему A.92), легко убедиться, что общее решение этой системы с точностью до
членов порядка oi включительно можно представить в виде суммы следую-
следующих двух решений:
S{z)=,Suex^, Я(т)=0. D(T) = —ii-So<?^ A.99)
и
D (т) = ?>j,V'x + 0gV", S(t) = - I=i J, [4V + D[2)^],
"' (uo°)
Отсюда видно, что в рассматриваемом приближении энтропийная компонента
нашего возмущения будет соответствовать произвольному начальному рас-
распределению энтропии (или температуры), не перемещающемуся в простран-
пространстве, но медленно выравнивающемуся под действием теплопроводности.'С-этой
компонентой будет связано также и очень слабое (порядка 6i) распределение
по объему газа потенциальной компоненты скорости и величины D=-~^-,
ах,
создаваемое тепловым расширением и сжатием элементарных объемов тем-
пературно-неоднородной среды. Акустическая же компонента будет состоять
из волн давления и величины D(X,i) вида Doe * рас-
распространяющихся со скоростью ад, слегка затухающих под влиянием вяз-
вязкости и теплопроводности и создающих весьма слабый (порядка 6i) перенос
энтропии.
') Нетрудно проверить, что учет еще и членов порядка fij изменит лишь
мнимые части корней fa и Хг, т. е. приведет к появлению слабой зависимости
скорости распространения акустических волн от коэффициентов вязкости и
температуропроводности (см. Яглом A948) J,

1.7] $ 1. УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ 75
¦ Описанное разбиение произвольных возмущений гидродинамических по-
полей на вихревую, энтропийную и акустическую компоненты легко может быть
прослежено во всех порядках малости по б и 6i; практически, однако, во
всех случаях достаточно ограничиться членами, которые были выписаны
выше. Несколько .большее значение представляет вопрос о влиянии на от-
отдельные компоненты возмущений нелинейных членов уравнений гидродина-
гидродинамики, к которому мы сейчас и перейдем. Чтобы учесть это влияние, надо
перейти к следующему приближению теории возмущений, состоящему в том,
что в уравнениях A.87.)—A.90) сохраняются также и билинейные по гндро-
, динамическим полям члены, в которых эти поля определяются по формулам
первого приближения, т. е. считаются совпадающими с выписанными выше
решениями линеаризованных уравнении. Таким образом, уравнения A.87)—
A.90) в следующем приближении будут содержать еще небольшие добавоч-
добавочные слагаемые известного функционального вида, которые естественно пере-
перенести в правые части этих уравнений и рассматрнвать как объемные «источ-
«источники» соответствующих гидродинамических полей. При этом решения урав-
уравнений будут отличаться от рассмотренных выше решеннй однородных урав-
уравнений A.87)—A.90) дополнительными членами, порожденными соответствую-
соответствующими источниками, т. е. билинейными комбинациями или «взаимодействиями»
отдельных членов решеннй лннеарнзованных уравнений друг с другом. Пред-
Представив снова решения линеаризованных уравнений в виде суммы вихревой,
энтропийной и акустической компонент, мы получим шесть различных парных
билинейных (и квадратичных) комбинаций этих трех компонент, т. е. шесть
различных «взаимодействий», каждое из которых, в свою очередь, может со-
создавать определенные добавки к решениям, описывающим любую из трех ком-
компонент, т. е. «порождать» эту компоненту.
Существенно, однако, что многие из возникающих таким образом 18 эф-
эффектов второго порядка будут выражаться билинейными относительно воз-
возмущений членами, содержащими еще множитель б или бь и поэтому будут
играть очень малую роль. Так, например, нз того, что с точностью до членов
порядка Si энтропийная компонента содержит только пульсации энтропии,
можно вывести, что в нулевом по 6 приближении эта компонента вовсе не
будет взаимодействовать сама с собой, а ее взаимодействие с вихревой ком-
компонентой будет вносить определенный вклад (связанный, очевидно, с кон-
ds
вектнвнымн членами иа-з—• уравнения A.62)) только в энтропийную же ком-
оха
поненту поля возмущений. Полный анализ с этой точки зрения всех возмож-
возможных «взаимодействий» может быть найден в работе Чжу и Козажного A958).
Основные результаты итого анализа иллюстрируются таблицей на стр. 76,
в которой указан порядок по 6i всех упомянутых 18 эффектов второго поряд-
порядка, « для эффектов нулевого порядка кратко объяснен нх фнзнческнй смысл.
Помимо того Чжу и Коважный для всех эффектов нулевого порядка по Si при-
велн явные выражения соответствующих объемных источников, которые сле-
следует добавить к правым частям лннеарнзованных уравнений. Мы здесь, од-
однако, не будем детально изучать все эффекты нулевого порядка, значитель-
значительная часть которых, как видно нз таблицы, сводится к простому переносу
гидродинамических неоднородностей полем скорости нз одного элемента объ-
объема жидкости в другой. Более подробно мы остановимся лишь на наиболее
важном взаимодействии вихревой компоненты с самой собой (напомним, что
в обычной слабо сжимаемой среде вихревая компонента, как правило, замет-
заметно превосходит другие по интенсивности).
Так1 как вихревая компонента связана лишь с возмущением поля скоро-
скорости, то ее взаимодействие с собой будет вызываться только билинейными по
скоростям членами уравнений гидродинамики. В уравнении баланса энтро-
энтропии (т. е. притока тепла); такие билинейные члены содержатся (в слагаемом
ре) лишь вместе с коэффициентом вязкости, откуда ясно, что эффект

76
ГЛ. 1. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
[1.7
Взаимодействие
акустической
компоненты с
акустической
вихревой ком-
компоненты с вихре-
вихревой
энтропийной
компоненты с
г энтропийной
акустической
компоненты с
вихревой
акустической
компоненты с
энтропийной
вихревой ком-
компоненты с энтро-
энтропийной
Порождение
акустической
компоненты
0A)
«рассеяние зву-
звука на звуке» и
«нелинейное ис-
искажение акусти-
акустических волн»
0A)
«порождение
звука вихревым
движением»
0(*,)
0A)
«рассеяние
звука на внхре-
вых неоднород-
иостях поля ско-
скорости»
0A)
«рассеяние
звука на неодно-
родностях поля
температуры»
0(8.)
вихревой
компоненты
0(8.)
0A)
«растяжение
вихревых тру-
трубок», или иначе
«инерционный
перенос завнх-
реиностн внхре-
вым полем ско-
скорости»
0(8?)
0A)
«перенос за-
завихренности аку-
акустическими вол-
волнами»
0A)
«порождение
завихренности
взаимодействием
градиентов эн-
энтропии н давле-
давления» (эффект
Бьеркнеса)
0 (8.)
энтропийной
компоненты
0(8^
0(8.)
0(8.)
0(8.)
0 A)
«перенос тепла
акустическими
волнами»
0A)
«перенос тепла
вихревым, дви-
движением»
порождения энтропийной компоненты указанным здесь взаимодействием будет
иметь порядок не выше б. Заметно более существенную роль будут играть
билинейные по скоростям члены "> -пг Уравнений движения; именно они и
будут определять все «значимые» эффекты второго порядка, связанные со
взаимодействием вихревой компоненты с самой собой.

2.1] § 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 77
Сохранив в уравнениях движения члены иа -^-=- и перейдя затем к урав-
охл
нению для вихря, мы придем к уравнению A.7)
д<лк , ди>к дик
dt ~ * ' дха~ " дх„
отличающемуся от A.88) правой частью, описывающей процесс порождения
завнхренностн за счет растяження внхревых трубок. Считая в этой правой ча-
части поле и„ несжимаемым и удовлетворяющим A.88), мы получим первый
значимый «эффект второго порядка» — порождение вихревой компоненты
поля скорости за счет взаимодействия этой компоненты с самой собой. Что
же касается до влияния этого же взаимодействия на акустическую компонен-
компоненту, то в нулевом приближении по б его можно определить, опустив в уравне-
уравнениях гидродинамики все члены, содержащие коэффициенты вязкости и тем-
пературопроводностн, и все нелинейные члены, кроме членов «,-хг в урав-
уравнениях движения. Но в таком случае легко видеть, что вместо последнего
уравнения A.97) мы получим уравнение
, д див
Правая часть здесь, очевидно, описывает дополнительные пульсации давле-
давления, возникающие из пульсаций поля скорости в соответствии с уравнением
д I диЛ
A.9), имеющим вид А/»= — р-т—\и*~л~ }• Подставляя в правую часть
A.101) в качестве щ(х, t) несжимаемое поле скорости, удовлетворяющее
«уравнению вихря» A.88) или (если не предполагать, что пульсации скоро-
скорости являются малыми) уравнению A.7), мы можем найти звуковые колеба-
колебания, создаваемые взаимодействием несжимаемого поля скорости с самим со-
собой; правую часть A.101) в этом случае, очевидно, можно также записать
дих да, д1 (и„ие)
как —~Лх~~Лх~ нлн как дх~дх -Порождение звука вихревыми гидроди-
гидродинамическими потоками, описываемое уравнением A.101), изучалось в работах
Лайтхнлла A952, 1954); оно как раз и представляет второй «значимый
эффект второго порядка», связанный с взаимодействием вихревой компоненты
поля скорости с самой собой.
S 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ И ВОЗНИКНОВЕНИЕ
ТУРБУЛЕНТНОСТИ')
2.1. Понятие о турбулентности; эмпирические данные
о возникновении турбулентности в трубах
и в пограничном слое
В предыдущем параграфе были приведены уравнения, опи-
описывающие движения жидкости, и указаны некоторые их про-
простейшие решения. При этом мы отмечали, что полученные реше-
ния далеко не всегда хорошо соответствуют каким-либо реально
') В основу настоящего параграфа положена обзорная статья Моннна и
Яглома A962),

78 ГЛ, I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [ЙЛ
наблюдаемым течениям. Так, например, на стр. 44 было ска-
сказано, что течение в трубе описывается формулами A.23) — A.26)
лишь в случае достаточно большой вязкости или 'достаточно ма-
малой средней скорости, а на стр. 56 мы подчеркнули, что найден-
найденное Блазиусом решение уравнений пограничного слоя на плос-
плоской пластинке только при не слишком большом значении Ux/v
хорошо соответствует эмпирическим данным. Сказывается, что
так же обстоит дело и в громадном большинстве других слу-
случаев. Как правило, найденные теоретически решения уравне-
уравнений гидродинамики, точные или приближенные, лишь при неко-
некоторых специальных условиях удовлетворительно описывают
реально наблюдаемые потоки. Если же эти условия не соблю-
соблюдаются, то характер течения резко меняется, и вместо законо-
закономерного плавного изменения значений гидродинамических по-
полей, соответствующего теоретическим решениям, наблюдаются
беспорядочные пульсации всех гидродинамических полей во вре-
времени и пространстве, имеющие сложный характер — типа тех,
которые изображены на рис. 1. Таким образом, течения жид-
жидкости распадаются на два резко различающихся класса: плав-
плавные и спокойные течения, меняющиеся во времени лишь в связи
с изменением действующих сил или внешних условий, назы-
называются ламинарными, а течения, сопровождающиеся бестюря-»
дочными пульсациями всех гидродинамических полей как во
¦времени, так и в пространстве, — турбулентными.
Различие между ламинарным и турбулентным режимами те-
течения жидкостей проявляется в ряде явлений, имеющих большое
значение для многих технических задач. Например, воздействие
потока на твердые стенки (т. е. трение о стенки) при
турбулентном режиме оказывается значительно большим, чем
при ламинарном режиме (так как передача импульса в турбу-
турбулентной среде происходит много интенсивнее). Наличие беспо-
беспорядочных пульсаций поля скорости приводит также к резкому
возрастанию перемешивания жидкости; в этой связи
крайне интенсивное перемешивание часто даже рассматривается
как наиболее характерная черта турбулентного движения. С воз-
возрастанием перемешивания резко увеличивается также и теп-
теплопроводность жидкости и т. д. По всем этим причи-
причинам установление условий перехода ламинарного режима тече-
течения в турбулентный режим является весьма актуальной задачей.
Кроме того, выяснение механизма возникновения турбулентно-
турбулентности должно помочь пониманию ее природы и тем самым способ-
способствовать изучению важных для практики закономерностей тур-
турбулентных потоков.
Подробный обзор экспериментальных данных, касающихся
перехода ламинарного течения в турбулентное, содержится в

2.1] $ 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 79
статьях Шлихтинга A959) и Драйдена A959). Теории этого во-
вопроса посвящены многие обзорные статьи (одна из наиболее
полных среди которых принадлежит Дж. Стюарту A963)) и спе-
специальные монографии Линя A955) и Чандрасекара A961).
В нашей монографии мы ограничимся рассмотрением лишь
важнейших (и наиболее простых) течений и основное внимание
уделим принципиальной стороне дела. За деталями математи-
математических расчетов и подробным описанием экспериментов, а так-
также за сведениями, относящимися к более сложным потокам, чи-
читатель должен обратиться к перечислейным выше источникам и
к специальным статьям.
Первые результаты об условиях возникновения турбулент-
турбулентности были получены Хагеном A839). Хагён изучал течения
воды в прямых круглых трубах небольших радиусов и устано-
установил, что при постепенном уменьшении вязкости воды (что дости-
достигалось повышением ее температуры) скорость течения при од-
одном и том же напоре сначала возрастает до некоторого предела,
а затем начинает уменьшаться. Вытекающая из трубы струя
воды до указанного предела имеет гладкую форму, а после пе-
перехода через этот предел испытывает резкие колебания. Хаген
объяснял эти явления тем, что при достаточно малом значении
вязкости в потоке образуются внутренние движения и вихри,
которые приводят к повышению сопротивления и, следователь-
следовательно, к уменьшению скорости течения. Хаген обнаружил, что изме-
изменения характера течения можно добиться, меняя напор воды
(т. е. среднюю скорость) или радиус трубы; однако никакого
общего критерия для перехода ламинарного течения в турбу-
турбулентное ему установить не удалось.
Общий критерий возникновения турбулентности был уста-
установлен Рейнольдсом A883) при помощи соображений о механи-
механическом подобии течений вязкой жидкости. Этот критерий заклю-
заключается в том, что поток остается ламинарным, пока число
Re = f/L/v не превосходит некоторого критического значения
Recr, а при Re > Recr он становится турбулентным. Как было
объяснено в п. 1.3, число Рейнольдса имеет смысл отношения
характерных величин сил инерции и сил вязкости. Силы инер-
инерции' приводят к сближению первоначально удаленных друг от
друга объемов жидкости и тем самым способствуют образова-
образованию резких неоднородностей течения. Силы вязкости, наоборот,
приводят к выравниванию скоростей в близких точках, т. е к
сглаживанию мелких неоднородностей. Поэтому при малых Re,
когда силы вязкости доминируют над силами инерции, в потоке
не может быть резких неоднородностей, т. е. гидродинамические
поля изменяются весьма плавно, и течение имеет ламинарный
характер. При больших Re, наоборот, сглаживающее дейстрие

Ш ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.1
сил вязкости оказывается слабым и в потоке возникают беспо-
беспорядочные пульсации — резкие мелкомасштабные неоднородно-
неоднородности, т. е. течение становится турбулентным. Этими соображе-
соображениями и объясняется критерий Рейнольдса.
Для экспериментальной проверки указанного критерия и для
измерения Recr Рейнольде провел серию опытов с течениями
воды в стеклянных круглых трубах. В этих опытах на оси трубы
у ее входи помещался источник красящего вещества. Окрашен-
Окрашенная вода при малых Re принимала форму тонкой четко очер-
очерченной струйки, что указывало на ламинарный режим течения.
При возрастании Re в момент перехода через критическое зна-
значение форма окрашенной струйки резко изменялась: уже неда-
недалеко от входа в трубу струйка расширялась и на ней появля-
появлялись волны, затем появлялись отдельные вихри и к концу трубы
окрашенной оказывалась вся жидкость. Если в таком опыте
осветить поток электрической искрой, то можно видеть, что окра^
щенная масса состоит из более или менее отчетливых завитков,
указывающих на наличие завихренности. При докритических
числах Re, близких к Recr, в ламинарном потоке наблюдаются
переходные явления, заключающиеся в появлении впервые на-
наблюдавшихся еще Рейнольдсом кратковременных вспышек пуль-
пульсаций высокой частоты, в форме своеобразных «турбулентных
пробок», заполняющих все сечение трубы, но на небольших от-
отрезках ее длины (появление таких «вспышек» позже Щиллер
A934) связал с чередующимся образованием й разрушением
крупных вихрей на внутренней стенке трубы у ее передней
кромки). Аналогичный характер имеет течение в начальном
участке трубы и при Re > Recr, причем с увеличением Re длина
этого начального участка, на протяжении которого течение еще
оказывается не полностью турбулентным, быстро уменьшается.
Согласно измерениям Ротта A956), при таком промежуточном
режиме средняя доля времени, в течение которого в данной
точке трубы наблюдается турбулентный режим («коэффициент,
перемежаемости»), монотонно возрастает с увеличением рас-
расстояния х от входа в трубу. Имеющиеся экспериментальные дан-
данные (наиболее детальные из которых принадлежат Линдгрену
A957, 1959)) позволяют объяснить это возрастание тем, что
местная скорость на переднем крае «турбулентной пробки» пре-
превосходит местную скорость на ее заднем крае, и поэтому
«пробки» растягиваются при своем передвижении по трубе
(и некоторые из них иногда «догоняют» друг друга и сли-
сливаются, образуя одну большую пробку).
Опыты Рейнольдса производились с трубами различных диа-
диаметров с плавным входом, соединяющимся с резервуаром. Изме-
Изменения числа Re= UCj>D/\ (где t/Cp — средняя скорость течения)

J^Jj « 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 81
в*-этйх опытах достигались как переходом к новой трубе (с дру-
другим диаметром D), так и варьированием скорости течения и ййз*
кости воды (путем изменения ее температуры). Значение Recr
в указанных опытах оказалось равным в среднем 12830 с отно-
относительно небольшим разбросом по данным отдельных опытов..
Дальнейшие исследования показали, однако, что значение Recr,
соответствующее переходу от ламинарного течения к турбулент-
турбулентному, в различных опытах может оказаться очень разным, так
как оно сильно зависит от степени-возмушенности ламинарного
течения (или, как говорят, от «начальной турбулентности», ко-
^горгш~опред,еляется главным образом условиями на входе в
трубу).( АбсолютШдстационарного ламинарного течения _в_1$>у-
бах осуществить неудается__и^в потокр
мущения,^ характеризующиеся сравнительно редкими пульса-
пульсациями скорости, происхождение которых частично связано свих-*'
рями, отрывающимися от передней кромки трубы. ТТнтёнсив-
ность этю^вшмущений4 (которую можно охарактеризовать пар4»
метром Д/7^ср./где V — типичная величина пульсаций х-компо-
ненты скорости) может быть довольно большой, но вследствие
своей малой повторяемости эти возмущения не меняют лами-
ламинарного характера течения и не сказываются существенно на
профиле скорости, величине сопротивления и других средних
^еадактеристиках потока. При достаточно малых числах Рей-
Рейнольдса возникшие возмущения, перемещаясь вниз по течению,
затухают. Но при возрастании числа Рейнольдса в момент до-
достижения его критического значения Recr (зависящего от ин-
интенсивности возмущений, а также, возможно, от их масштаба и
частоты) возмущения скачкообразно порождают турбулент-
турбулентность. Установлено, что значение Recr, соответствующее пере-
переходу ламинарного течения в турбулентное, оказывается тем
меньше, чем больше интенсивность возмущений. Так, например,
в случае трубки с острыми краями, вставленной в сосуд с плос-'
кой стенкой, края трубки создают значительные возмущения и
Recr оказывается равным уже, примерно, 2800. Уменьшая же С
помощью тех или иных приемов степень возмущенности тече-
течения у входа в трубу, можно задержать переход ламинарного
течения в турбулентное до весьма больших чисел Рейнольдса
(это явление называется затягиванием ламинарного режима).
Так, Барнесу и Кокеру A905) удалось задержать возникновение
турбулентности в трубах до значения Recr» 20 000, а Экману
A911) — даже до Recr » 50'000.
Эти результаты показывают, что число Рейнольдса само по
себе еще не является однозначным критерием возникновения
турбулентности: для течения в трубе, по-видимому, вообще
нельзя указать такого универсального критического значения

82 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.1-
Recr, чтобы при Re > Recr режим течения обязательно был тур-
турбулентным. Чтобы установить значение Re, являющееся верхней
границей для чисел Рейнольдса ламинарного течения, нужно
иметь сведения о степени возмущенности ламинарного течения,
и указанная верхняя граница чисел Re будет функцией от пара-
параметра U'lUcv (монотонно возрастающей при убывании'этого па-
параметра).
Без сведений о степени возмущенности ламинарного потока
можно установить лишь более слабый критерий, указывающий
условия, при которых возможен только ламинарный режим те-
течения. Для этого нужно определить критическое число Рей-
Рейнольдса В&хдуп, соответствующее переходу от ламинарного
режима к турбулентному при наибольшей возможной степени
возмущенности ламинарного течения у входа в трубу. При
Re<Recrmin поток будет всегда оставаться ламинарным, т. е.
любые возмущения, как бы интенсивны они ни были, будут за-
затухать. .
Опыты для измерения Recrmin были поставлены еще самим
Рейнольдсом. Поскольку в таких опытах необходимо вводить
в трубу возможно более возмущенную жидкость, то ясно, что
для обнаружения перехода от ламинарного режима к турбулент-
турбулентному метод окрашенных струек здесь непригоден. Поэтому пере,
ход к турбулентности здесь приходится определять иначе (на-
(например, по изменению закона сопротивления, определяющего
зависимость средней скорости от перепада давления). В опы-
опытах Рейнольдса минимальное критическое значение числа
Re = UcvDh оказалось равным Recr min «* 2300. Близкие значе-
значения (лежащие в пределах от 1900 до 2320) были получены и
всеми последующими исследователями.
Сходные во многих отношениях результаты об условиях воз-
возникновения турбулентности получаются и при изучении течений
в пограничных слоях, образующихся при обтекании тел вязкой
жидкостью. Рассмотрим, например, пограничный слой, образую-
образующийся при обтекании плоской пластинки потоком с постоянной
скоростью U, направленной параллельно пластинке. Число Рей-
Рейнольдса пограничного слоя можно определить, например, фор-
формулой Re8 = (Л/у, где 8 — толщина пограничного слоя. Можно
также вместо этого использовать легче измеряемое число
Re,; = Ux/v, где х— расстояние вдоль потока от переднего края
пластинки. Числа Re5 и Re* связаны функциональной зависи-
зависимостью; например, при ламинарном течении согласно результа-
результатам п. 1.4 Re5 «* 5 "jARe^. (см. формулу A.49) на стр. 544^Вниз^
по течению оба числа Rej и Re* растут, и в некоторой[точке~х^г.
они достигают «критического значения», при котором течение
резко изменяет характер и становится турбулентным. Таким об-

2,1] ¦ i- ГИДРОДИНАМИЧЕСКАЯ НЁУСТОЙЧИбОСТЬ 63
разом, при х < хС1 (точнее говоря, при Re6 < Re8Cr и ReK<ReK Cr)
течение в пограничном слое является ламинарным, а при х > хст
(т. е. Re6 > Re5Cr и Re* > Re* сг) турбулентным. Непосредствен-
Непосредственно вблизи х = хст образуется «переходная область», где наблю-
наблюдаются лишь отдельные «вспышки» турбулентности, возникаю-
возникающие в виде небольших «турбулентных пятен», увеличивающихся в
размере и сливающихся друг с другом по мере своего продви-
продвижения вниз по течению (см., например, Шлихтинг A959), § 14,
а также Элдер (I960)). Появление «турбулентных пятен» приво-
приводит к тому, что в точках переходной области имеет место пере-
перемежающееся чередование'во времени ламинарного и турбулент-
турбулентного режимов, причем в начале этой области и частота появле-
появления и продолжительность существования турбулентного режима
незначительны, а у ее конца ламинарный режим возникает уже
лишь очень редко и на весьма короткие промежутки времени.
Первые измерения критического числа Рейнольдса погра-
пограничного слоя были выполнены в 1924 г. Бюргерсом и Ван дер
Хегге Цийненом, изучившими в аэродинамической трубе обте-
обтекание воздушным потоком плоской стеклянной пластинки. Не-
Несколько позже аналогичные измерения были произведены также
Ханзеном A928) (см., в частности, рис. 4 на стр. 56). Согласно
данным этих авторов,
что, очевидно, соответствует значениям
cr = (—) —2750-5-3500,
\ v /
сг
имеющим тот же порядок величины, что и значения Recr для
течения в трубе. В дальнейшем выяснилось, что, как и в случае
течений в трубах, критическое число-Рейнольдса пограничного
слоя существенно зависит от степени возмущенности основного
потока — в зависимости от которой число Rex сг может меняться
в пределах от 1 • 105 почти до 3* 10е (см. рис. 7, иллюстрирую-
иллюстрирующий зависимость Re*cr от И'IV, где 3U'2 принимается равным
среднему _квадр_ату абсолютной величины пульсаций скорости
|^§1ё^. заметим^ однако7~что~~рттс. 7~"оставляет
б '\U
^§цх)р
впечатление, что при неограниченном убывании \J'\U значение
Re* сг не возрастает неограниченно, а стремится к определен-
определенному пределу (порядка 3« 106), выше которого пограничный слой
будет турбулентным при сколь угодно малой степени возмущен-
возмущенности набегающего потока. С другой стороны, в случае течения
jjcgyr^ofl_TEy_6e_ эксперимент не показывает резкого замедления
ростаДёсг при приближении U'\U к нулю; поэтому представ-
представляется правдоподобным, что здесь Десг-коо при U'IU-4-O (т. е.

84
ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
[2.1
что при любом значении Re течение в трубе может оставаться
ламинарным, если только удастся обеспечить достаточно низ-
низкий уровень возмущенности потока у входа в трубу). Об этом
важном различии течений в пограничном слое и в трубе мы еще
будем подробнее говорить в п. 2.§.
С турбулизир'ующим влиянием возмущений в обтекающем
потоке связано также то, что критическое число Рейнольдса
n-B
г —
1
к
ч
Yi
-л.
и ш
Рнс. 7. Зависимость критического числа Рейнольдса для погра-
пограничного слоя на плоской пластинке от степени возмущенностн
набегающего потока (по Драйдену A959)).
Разными значками на рнсуаке отмечены данные разных экспериментаторов.
оказывается заметно меньшим при обтекании шероховатых пла-
пластинок, содержащих естественные или искусственные неровно-
неровности, создающие дополнительные возмущения. Согласно дан-
данным многочисленных измерении, даже одна-единственная не-
неровность может вызвать переход ламинарного пограничного
слоя в турбулентный, если только .высота /^ этой неровности
имеет тот же порядок, что и «толщина вытеснения» 8* « 0,38
пограничного слоя в ее окрестности. Еще более значительное
влияние оказывает наличие множества неровностей, разбросан-
разбросанных по всей плоскости (см., например, Шлихтинг A959), гл. X,
или Драйден A959), § 5). Оыень существенно меняет значение
Re* cr также наличие хотя бы небольших продольных традирн-
тов давления в обтекающем потоке. На этом, однако, мы не бу-
будем здесь задерживаться, а ограничимся лишь рассмотрением
одного специального эффекта, связанного с наличием отрица-
отрицательного продольного градиента давления, к которому мы сей-
сейчас и перейдем.

12]
$ 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ
2.2. Данные о турбулентном обтекании: отрыв пограничного
слоя, кризис сопротивления и механизм турбулизации
пограничного слоя
Возникновение турбулентности при обтекании тел вязкой
жидкостью может проявляться не только в виде турбулизации
пограничного слоя, но и в виде образования турбулентного следа
за телом в результате отрыва от его поверхности макроскопиче-
макроскопических вихрей.
Образование турбулентного следа обычно бывает связано
с тормозящим действием отрицательного продольного градиента
давления в обтекающем
потоке. Рассмотрим, на- \и
пример, обтекание прямо-
прямого круглого цилиндра по-
потоком Яез циркуляции
перпендикулярным к оси
цилиндра (см. рис. 8, на
котором изображено об-
обтекание верхней части ци-
лийдра). Вне погранич-
пограничного слоя жидкость моЖ:
но считать идеальной, а
ее движение — безвихре-
безвихревым. Линии тока этого
потенциального движения
более всего.сгущаются над верхней точкой цилиндра (точка С),
где, следовательно, касательная скорость и достигает максиму^
ма. Вследствие известного уравнения Бернулли
-g- + pip = const
(вытекающего из равенства а -? = -Д, приведенного на
стр. 51 перед уравнением A.38)) давление над точкой С во
внешнем потоке достигает минимума^ так что на участке АС
оно падает, а на участке СЕ возрастает. Такие же изменения
давления вдоль поверхности тела имеют место к в пограничном
слое (так как поперек пограничного слоя давление почти не
меняется). Следовательно, на участке СЕ жидкость в погранич-
пограничном слое должна двигаться по направлению возрастания давле-
давления, что приводит к ее торможению. Наиболее сильно это тор-
торможение сказывается, конечно, на частицах жидкости, движу-
движущихся около самой поверхности цилиндра, т. е. обладающих
Рис. 8. Схематическая форма линий тока
(пунктир) и профилей скорости (сплошные
линии) иад различными точками при обте-
обтекании прямого цилиндра.

86 ГЛ, I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.2
наименьшей скоростью. В некоторой точке D вниз по потоку от
точки С эти частицы останавливаются, а за точкой D даже дви-
двигаются вспять по сравнению с более удаленными от поверхности
цилиндра и поэтому еще не заторможенными частицами. Обра-
Образующийся у поверхности тела за точкой D возвратный поток
оттесняет внешнее течение от поверхности цилиндра — происхо-
происходит, как говорят, отрыв пограничного слоя от обтекаемой по-
поверхности с образованием в жидкости поверхности раздела DF.
Ясно, что если только скорость U внешнего потока достаточно
быстро убывает за точкой С, то такой отрыв пограничного слоя
обязательно будет иметь место. Если даже пограничный слой до
отрыва был ламинарным, то после отрыва он ведет себя как
свободная струя в затопленном пространстве и быстро стано-
становится турбулентным (при заметно меньших Re, чем не отры-
отрывавшийся пограничный слой, так как наличие стенки действует
на течение стабилизирующим образом). Поверхность раздела
DF, являющаяся поверхностью тангенциального разрыва скоро-
скорости, весьма неустойчива (см. ниже) и быстро свертывается в
один или несколько вихрей. В области FDE за поверхностью
раздела около цилиндра образуется крупный вихрь; второй та-
такой же вихрь образуется в нижней части цилиндра. Эти вихри
попеременно отрываются от поверхности цилиндра, уносятся
вниз по течению и постепенно рассеиваются; на их месте об-
образуются новые вихри.
В результате за телом образуется турбулентный след, в ко-
котором движение является завихренным, в то время как вне это-
этого следа и вне пограничного слоя движение является безвихре-
безвихревым (т. е. потенциальным). В самом деле, жидкость вне погра-
пограничного слоя можно считать идеальной; отсюда вытекает, что
при ее движениях циркуляция скорости вдоль любого замкну-
замкнутого жидкого контура сохраняется и, следовательно, при уста-
установившемся движении имеет место постоянство вихря скорости
вдоль линий тока. Поэтому ясно, что область завихренного тур-
турбулентного движения вдали от поверхности тела может воз-
возникнуть только при выходе линий тока из пограничного слоя
(в котором движение становится завихренным вследствие дей-
действия вязкости) н'аружу, т. е. лишь в связи с непосредственным
перемещением жидкости из пограничного слоя в удаленные
части пространства.
Ясно также, что линии тока не могут выходить из области
течения, в которой вихрь скорости отличен от нуля, т. е. из об-
области турбулентного следа (но они могут входить в след из об-
области потенциального течения). Другими словами, жидкость мо-
может втекать в турбулентный след из области потенциального
течения, но не может вытекать из турбулентного следа. В то же

22\ § '• гидродинамическая неустойчивость 87
время турбулентные пульсации скорости могут проникать из
следа в область потенциального движения, но со значительным
ослаблением. Действительно, легко видеть, что в случае потен-
потенциального движения несжимаемой жидкости уравнения движе-
движения в форме A.7) будут удовлетворяться тождественно. По-
Поэтому течение здесь будет описываться одним лишь условием не-
несжимаемости A.5), эквивалентным уравнению Лапласа А<р = О
относительно потенциала скорости ср, определяющего поле ско-
скорости по формуле щ = dy/dxi. Пусть z обозначает координату
поперек следа; тогда поле <р(х, у, z), описывающее турбулент-
турбулентные пульсации окорости, удобно разложить на периодические по~
х, у компоненты вида <р — фо(г)еЧ*'лг+*»у). Из уравнения А<р = О
следует, что -^| = &2ср0, где k=Vk\-\-kl — волновое число, об-
обратно пропорциональное горизонтальному (в плоскости Оху)
масштабу рассматриваемых периодических пульсаций. Отбрасы-
Отбрасывая физически бессмысленное решение для <p0, возрастающее вме-
вместе с z, убеждаемся, что затухание амплитуды пульсаций при
удалении от следа в области z>0 описывается множителем e~hz,
так что пульсации затухают тем быстрее, чем меньше их мас-
масштаб. Следовательно, достаточно далеко в глубь потенциального
движения проникают лишь сравнительно плавные крупномас-
крупномасштабные пульсации. Для таких пульсаций диссипация энергии
в тепло не играет большой роли; поэтому почти вся осуще-
осуществляющаяся в потоке диссипация энергии происходит внутри
вихревого турбулентного следа ').
Наличие значительной диссипации энергии во всем объеме
турбулентного следа, а также образование поверхности раз-
раздела при отрыве пограничного слоя приводят к тому, что тела,
при обтекании которых возникает отрыв пограничного слоя,
оказывают большое сопротивление набегающему потоку. При
этом сопротивление, вообще говоря, будет тем меньше, чем уже
турбулентный след, т. е. чем дальше на поверхности тела рас-
расположена точка отрыва. При достаточно больших числах Рей-
нольдса, при которых, однако, пограничный слой до точки от-
отрыва остается ламинарным, коэффициент сопротивления
(V (где W — полная сила сопротивления, S — пло-
щадь обтекаемого тела или его сечения) оказывается не зави-
зависящим от Re, так как положение точки отрыва не зависит от Re
') Изложенное рассуждение принадлежит Ландау и Лифшицу A953); оио
лежит Также в основе детальных исследований поля скорости потока вие об-
области турбулентного следа или турбулентной струи, выполненных филлид«
сом A955) и Стюартом A956).

88
ГЛ. I, ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
[2J2
(абсцисса точки отрыва находится из уравнения
г=0
0,
в которое, как можно показать, число Рейнольдса не входит).
Однако при достижении чисел Рейнольдса, при которых погра-
пограничный слой турбулизируется до точки отрыва ламинарного по-
пограничного слоя, точка отрыва пограничного слоя перемещается
вниз по течению; при этом турбулентный след заметно сужается,
и сопротивление тела резко (в несколько раз) уменьшается. Это
явление, называемое кризисом сопротивления, объясняется тем,
что перенос импульса внутри пограничного слоя при его туцбу-
лизации резко возрастает; следовательно, увлечение жидкости
в пределах пограничного слоя внешним потоком существенно
усиливается, и жидкие частицы в пограничном слое продви-
продвигаются в направлении роста давления дальше, чем в случае
ламинарного пограничного слоя.
Кризис сопротивления при обтекании шара впервые наблю-
наблюдался Эйфелем A912). Переход от больших сопротивлений к
малым происходит в этом
300t—1—i—i—-1—i—i i—i случае при значениях чис-
числа Рейнольдса Re = UD/v
(где D — диаметр шара),
близких к 5,0-105; коэффици-
коэффициент сопротивления Cw при
этом падает, примерно, от
0,5 при Re = 10? до 0,15 при
Re = 10е. Прн тщательном
проведении эксперимента
удается даже зафиксиро-
зафиксировать минимальное значение'
WO
30
10
О.З
0.7
\\
\
\
\
Цилиндр
Шар
ч
•-
<»——
Si,
1
1
1 /
Cw, меньшее 0,1. Аналогич-
O,J 7 70 7О2 103 70* 10s 70е W7 но ведет себя коэффициент
Re
Рис. 9. Зависимость коэффициентов со-
сопротивления шара и круглого цилиндра
от qHCJja Рейнольдса.
Cw н для круглого цилинд-
цилиндра. Зависимость коэффици-
коэффициентов сопротивления для ша-
шара и круглого цилиндра от
числа Рейнольдса изобра-
изображена на рис. 9. Из сказанного выше ясно, что кризис сопро-
сопротивления наступает тем раньше, чем выше степень возмущен-
ности набегающего потока, т. е. чем меньше критическое число
Рейнольдса для перехода к турбулентному режиму в погра-
пограничном слое. Это наглядно подтверждается известным опы-
опытом Прандтля A914), который добивался перехода через кри-
кризис сопротивления при .обтекании шара, надевая на шар прово-
проволочное кольцо, т. е. создавая в потоке дополнительные возму-
возмущения, турбулизирующие пограничный слой,

V2] $ 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 89
Необходимым условием для отрыва пограничного слоя яв-
является рост давления по направлению течения на каком-то уча-
участке поверхности тела. Это условие выполняется не только при
обтекании выпуклых поверхностей, но и в других случаях, как,
например, при течении в расширяющейся конической трубе
(диффузоре) или в резко изогнутой трубе. В этих случаях также
может возникнуть отрыв пограничного слоя.
Явление отрыва пограничного слоя под действием отрицательного про-
продольного градиента давления может в известной мере объяснить также и
влияние возмущений в набегающем потоке на значение ReXcr. В самом деле,
можно предполагать, что это влияние в значительной степени связано как раз
с тем, что такие возмущения создают пульсации продольного градиента да-
давления, приводящие к турбулизирующему пограничный слой образованию" на
непродолжительное время в отдельных его местах неустойчивых S-образиых
профилей скорости (типа профиля в точке Е иа рис. 8) и отрывов погранич-
пограничного слоя. Основываясь иа этой гипотезе, Тэйлор A936а) попытался теоретиче-
теоретически иайти характер зависимости критического числа Рейиольдса ReICr погра-
пограничного слоя от интенсивности начальной турбулентности набегающего пото-
потока (позже Вигхардт A940) дал более короткий вывод результатов Тэйлора).
В своей работе Тэйлор исходил из приближенной теории Кармана —
Польгаузеиа ламинарного пограничного слоя при наличии продольного гра-
градиента давления др/дх, согласно которой форма профиля скорости в различ-
различных сечениях пограничного слоя зависит лишь от едииствеииого безразмер-
Ьг до
иого параметра А = 7Г~'~Зх пограничном слоена плоской пластинке
др/дх*=О, ио могут существовать пульсации давления, и Тэйлор предположил,
что характер движения в фиксированном сечении здесь определяется пара-
параметром А = jj- ——¦ (где р' — пульсация давления, а о/бх означает со-
соответственно определенное типичное значение производной д/дх). Иначе гово-
говоря, согласно Тэйлору точка перехода ламинарного пограничного слоя в турбу-
турбулентный определяется тем, что параметр Л достигает некоторой «критической»
1 ЬР'
величины. Но в силу уравнении движения величина ^—- должна иметь
, Ъи' 1 Ъи'*
тот же порядок, что и и -т—- = -н- ¦ .. • где и — пульсация продольной ско-
Ъи'г U'2
рости в набегающем потоке. Далее можно положить -г— -^ —^— • где V —
ОХ А
типичное значение пульсации скорости, а X — так называемый тэйлоров мик-
< < 'я (Ьи' \2 U'* ,
ромасштаб турбулентности, определяемый из условия I -t—I = -jtj— (этот мас-
масштаб еще будет неоднократно использоваться нами в дальнейшем). Масштаб
А, можно связать с внешним (интегральным) масштабом турбулентности L
(определяющим порядок величины наибольшего расстояния, на котором еще
проявляется связь между мгновенными значениями пульсации скорости) при
помощи следующего рассуждения: средняя удельная диссипация энергии
- /6«'\2 я 4U'2
а <** v I -j^- I , с одной стороны, пропорциональна —-^— , а с другой сторо-
стороны, при больших U'L/v оиа пропорциональна также и U's/L (об этом факте
мы еще будем подробно говорить во второй части настоящей каиги).

90 fл, i. ламинарные и турбулентные движения
Следовательно,
U'Ly-'b 1 Ър' U'* fUrt\4*
[2.2
Учитывая еще, что для ламинарного пограничного слоя на плоской пластин-
пластинке б ~ (vJf/1/J1'1, получим
82 »¦/>' ( и'\Ч>( x\4i( Ux\4i
Таким образом, если считать, что Re«r = <р(Лсг), то
В качестве длины L, входящей в эту формулу, можно принять характерный
размер устройства, порождающего турбулентность (например, если турбулент-
турбулентность создается помещенной в поток решеткой, то L приближенно совпадает,
с расстоянием между прутьями решетки).
QT2
0,08
0,04
Ц8 Г,2 1,6 2,0 2,4 20
RecrW5
Рис 10. Зависимость Recr при обтекании
(
w -
к
°D=72Jcm
>-&
°2t?
u.
шара от величины — | —
Результат B.1), согласно которому Recr зависит только от величины
•jj- I -у- J *, выведен здесь для случая обтекания плоской пластинки. Однако
его можно обобщить и на случаи обтекания других тел, заменяя координа-
координату * расстоянием s от точки набегания потока на тело до точки перехода ла-
ламинарного пограничного слоя в турбулентный, отсчитываемым вдоль контура
тела, или же характерным размером тела D и используя вместо Re« =¦ Ux/v
число Re.= i/s/v или Re=t/D/v. При этом оказалось, что этот результат,
несмотря на всю нестрогость его вывода, находится в весьма хорошем соот-
соответствии с экспериментальными данными (см., например, рис. 10, на котором
приведены эмпирические данные Драйдена, Шубауэра, Мока и Скрэмстада
A937), измерявших значения^еСг для пограничного слоя на шарах различ-
различного радиуса при различных значениях интенсивности и масштаба начальной
турбулентности свободного потока).

23] § 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 91
2.3. Гидродинамическая неустойчивость
При теоретическом анализе вопроса о возникновении турбу-
турбулентности следует исходить из того, что функции, описывающие
поля скорости и давления в любом потоке жидкости, как лами-
ламинарном, так и турбулентном, являются решениями уравнений
гидродинамики при надлежащих начальных и краевых условиях.
Установившееся ламинарное течение, в частности, описывается
стационарными решениями этих уравнений; в случае же турбу-
турбулентного течения каждой индивидуальной реализации потока
соответствует некоторое, вообще говоря, весьма сложное неста-
нестационарное решение уравнений гидродинамики. Невозможность
осуществления, ламинарного течения при достаточно больших
числах Рейнольдса, несмотря на то, что уравнения гидроди-
гидродинамики имеют стационарное решение при любом Re, ясно пока-
показывает, что не всякому решению соответствует движение жид-
жидкости, реально существующее в природе. Естественно связать
это обстоятельство с хорошо известным положением, согласно
которому реальные движения должны не только удовлетворять
уравнениям гидродинамики, но и быть устойчивыми в том
смысле, что неизбежно возникающие в реальных условиях ма-
малые возмущения этих движений должны затухать со временем,
не меняя общей картины движения. Если же, наоборот, возни-
возникающие возмущения будут разрастаться со временем, то это
приведет к существенному искажению исхбдного движения и,
следовательно, такое движение не сможет существовать сколько-
нибудь длительное время.
Исходя отсюда, можно ожидать, что значение Recr соответ-
соответствует как раз потере устойчивости: при Re < Recr ламинарное
течение устойчиво, но при Re > Recr оно становится неустойчи-
неустойчивым и под влиянием всегда имеющихся малых возмущений пре-
превращается в турбулентное движение. Но в таком случае, иссле-
исследуя математически вопрос об устойчивости решения уравнений
гидродинамики, соответствующего ламинарному течению, можно
(по крайней мере в принципе) теоретически определить соот-
соответствующее критическое число Рейнольдса.
Турбулентность характеризуется наличием весьма сложных
колебаний поля Скорости и других характеристик течения. Ме-
Механизм возникновения этих колебаний можно уяснить с обще-
общемеханической точки зрения, рассматривая текущую жидкость
как динамическую систему с очень большим числом степеней
свободы, в которой в результате притока энергии извне возни-,
кают автоколебания.
Применение понятия о степенях .свободы к потоку жидкости
требует прежде эсего введения каких-то, «обобщенных, коорди,-

92 гл. i. ламинарные и турбулентные движения 12.3
нат», однозначно характеризующих конфигурацию течения. При
определении таких обобщенных координат можно исходить из
разложения движения на элементарные компоненты,
й
р р у р
гийкоторых равняется энергии потока в целом и состояние каж-
дой~"из которых характеризуется небольшим числом параметров.
Параметры всех таких элементарных компонент движения и бу-
будут тогда обобщенными координатами потока жидкости, а число
тдкдх^коорд)щатдмо?увд|хменя1ься при заданных внешних ус-
ловдюсГ~Т)у11ётшвпадатьсТолнь1м числом степеней свободы
потока. С математической точки зрения разложение движения
на элементарные компоненты сводится к разложению поля ско-
скорости по рртргпнядь^пй системе функций; каждая из этих функ-
функций будет описывать поле скорости соответствующей элемен-
элементарной компоненты движения, а коэффициенты разложения бу-
будут обобщенными координатами потока. Выбор той или мной
ортогональной системы функций диктуется формой границ по-
потока. Для потоков, занимающих в пространстве ограниченный
объем,-ортогональная система функций всегда оказывается счет-
счетной, так что такие потоки имеют не более чем счетное множе-
множество обобщенных координат *).
При установившемся ламинарном течении значения обобщен-
обобщенных координат однозначно определяются заданными внешними
условиями, так что число степеней свободы ламинарного потока
равно нулю. Число степеней свободы турбулентного потока,
занимающего в пространстве ограниченный объем, весьма ве-
велико, но практически является конечным. Действительно, при
разложении поля скорости в ряд по ортогональным функциям
различные слагаемые описывают элементарные движения раз-
разных масштабов, и неограниченное увеличение номера слагае-
слагаемого соответствует неограниченному уменьшению масштаба
соответствующего элементарного движения. Однако из-за нали-
наличия вязкости колебания слишком малых, масштабой существо-
существовать не могут. Поэтому при стационарных внешних условиях
коэффициенты разложения поля скорости по ортогональным
функциям, имеющие достаточно большие номера, не зависят от
') Представление о потоке жидкости, занимающем неограниченный объем
пространства, всегда является идеализацией. При этой идеализации вместо
разложения поля скорости в ряд по ортогональной системе функций прихо-
приходится прибегать к разложению в интеграл Фурье — Стилтьеса (которым мы
будем швроко пользоваться во второй части настоящей книгиI и допускать
в ряде случаев • существование непрерывной компоненты спектра. Поэтому
неограниченный поток жидкости может, вообще говоря, обладать коитииуу-
jioj*_56ii6j!iejjHjbix_K0OEflBHaT. Однако в ограниченных областях пространства
и времени колебания с ТсйЯтинуальиым набором волновых чисел, разумеет-
разумеется, снова могут быть аппроксимированы счетньщ числом гармонических ко-
колебаний,

'^3J S 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 93
времени, что и означает, что число степеней свободы потока яв-
является конечным. Ясно также, что число степеней свободы
должно расти при убывании коэффициента вязкости, т. е., иначе
говоря, при возрастании числа Re. Согласно оценке Ландау и
Лифшица A953), число степеней свободы турбулентного потока,
занимающего в пространстве ограниченный объем, вообще го-
жу^дропорционально Reg/«, где Re — число Рейнольдса потока
(bjSjjiom) (этот результат будет подробнее обсуждаться во второй
части книги). Отсюда видно, что с ростом числа Рейнольдса
число степеней свободы быстро растет, и для развитой турбу-
турбулентности при больших числах Рейнольдса оно достигает гро-
громадных значений.
Чтобы охарактеризовать в заданный момент времени не
только конфигурацию системы, но и состояние ее движения,
нужно кроме значений ее обобщенных координат указать так-
также значения соответствующих обобщенных скоростей. Набор
значений всех обобщенных координат и обобщенных скоростей
определяет некоторую точку в фазовом пространстве системы,
полностью характеризующую ее мгновенное состояние. Процесс
изменения состояния системы изображается в фазовом про-
пространстве определенной линией — фазовой траекторией системы.
Указание фазовой траектории является удобным способом опи-
описания эволюции системы.
Рассмотрим эволюцию потока жидкости при фиксированных
стационарных внешних условиях (в частности, при постоянном
притоке энергии извне), но при различных начальных условиях.
Каждому из этих начальных условий соответствует некоторая
фазовая траектория, выходящая из соответствующей начальной
фазовой точки, и представляет интерес выяснить поведение ука-
указанных фазовых траекторий для больших промежутков времени.
Из статистической механики известно, что динамические си-
системы с большим числом степеней свободы при стационарных
внешних условиях имеют тенденцию стремиться к некоторому
предельному равновесному режиму, при котором в среднем по
времени внешний приток энергии уравновешивается диссипа-
диссипацией полной энергии системы, а полная энергия имеет фиксиро-
фиксированное значение и определенным образом распределяется по
степеням свободы. Можно высказать гипотезу, что для широкого
класса Потоков жидкости существуют два возможных предель-
предельных режима — ламинарный и турбулентный, так что каждая
фазовая траектория потока жидкости с течением времени либо
асимптотически приближается к точке, соответствующей лами^
нарному течению, либо накручивается на некоторый «предель'
ный цикл», соответствующий установившемуся турбулентному
режиму. Критерий возникновения турбулентности должен

94
ГЛ, I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
[2.3
позволить по начальной точке фазовой траектории предсказать,
какой из этих двух предельных режимов будет иметь место.
Возможность разложения движения жидкости на элемен-
элементарные компоненты означает, что поток жидкости можно рас-
рассматривать как совокупность взаимодействующие друг г пругом
элементарных нелинейных осцилляторов. В каждом из этих ос-
осцилляторов за счет поступления энергии извне могут возникать
автоколебания. Возможность возникновения колебаний опреде-
определяется соотношением между получаемой осциллятором энергией
Е+ и теряемой им энергией Е~ при различных амплитудах коле-
колебаний а (см. рис. 11). Если при всех амплитудах Е~>Е+
(рис. 11, а), то колебания, очевидно, будут затухать при любой
о
а)
Рис. П. Различи е варианты зависимости получаемой и теряемой осцилля-
осциллятором энергии от амплитуды колебаний.
их начальной амплитуде, и система будет устойчивой по отноше-
отношению к любому возмущению. Если Е~ < Е+ при ai < а < а„, но
Е- > Е+ при а < ai и а > а0 (рис. 11,6), то колебания с началь-
начальной амплитудой а<а\ будут затухать, но при начальной ампли-
амплитуде a>ui они будут возрастать, пока их амплитуда не достиг-
достигнет равновесного значения по. При этом система будет устойчи-
устойчивой по отношению к малым возмущениям, но неустойчивой по
отношению к возмущениям ^5О^таточно_большои амплитуды (та-
(такая система называется системой с жестким самовозбуждением).
Наконец, если Е+ > Е~ при сколь угодно малых амплитудах
(рис. 11,в), то система будет неустойчивой по отношению к бес-
бесконечно малым возмущениям, т. е. абсолютно неустойчивой и
практически всегда будет находиться в автоколебательном ре-
режиме с амплитудой колебаний а0 (такая система называется
•системой с мягким возбуждением). Как будет видно из даль
нейшего, есть все основания предполагать, что в потоках жидко-
жидкости, вообще говоря, могут иметь место все три ситуации, изо
браженные на рис. 1,1; однако точные условия, позволяющие
во всех случаях выяснить, какая именно из них реализуется s
конкретном течении, до си.х пор_оотаются

14]
i. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ
2.4. Простейшие примеры абсолютно неустойчивых потоков
жидкости
Приведенные выше экспериментальные данные о зависимо-
зависимости Recr для течений в трубах и пограничных слоях от интен-
интенсивности начальных возмущений и о затягивании ламинарного
режима определенно показывают, что при числе Re, немного
превосходящем Recrmin. указанные течения представляют собой
автоколебательные системы с жестким возбуждением (неко-
(некоторое представление о возможном механизме возбуждения ко-
колебаний в этих системах дает изложенная в п. 2.2 теория Тэй-
лора). Сейчас мы покажем, что нетрудно указать также при-
примеры движений жидкости, неустойчивых уже и по отношению к
бесконечно-малым возмущениям, т. е. с точки зрения теории
^солабаний, представляющих собой системы с мягким возбуж-
возбуждением, .
Один из простейших примеров абсолютно неустойчивого по-
потока жидкости представляет собой течение около поверхности
тангенциального разрыва скорости, о котором уже упоминалось
выше. Качественно возникновение здесь абсолютной неустойчи-
неустойчивости может быть объяснено с помощью совсем простых физи-
физических соображений. В самом деле, рассмотрим идеальную жид-
жидкость с нулевой вязкостью, два слоя которой скользят один по
другому с противоположными скоростями U и —U, образуя
поверхность разрыва скорости. Допустим, что в результате не-
некоторого возмущения на поверхности раарыва образовалась
волна малой амплитуды (см. рис. 12). Предположим для про-
простоты, что эта волна остается не-
неподвижной. В таком случае над
гребнями волны линии тока будут
сгущаться, т. е. скорость повысится,
а в ложбинах линии тока станут
реже и скорость уменьшится. Вслед-
Вследствие уравнения Бернулли и2/2 +
+ р/р - const, над гребнями волн Рис 1?_ схематическая форма
давление будет понижено, а в лож- линий тока и распределения
бинах — повышено (на рис. 12 это давления вблизи возмущенной
обозначено знаками -(-и —). Та-
Таким образом, в жидкости возник-
возникнут поперечные градиенты давле-
давления, которые будут стремиться увеличить амплитуду волны.
В дальнейшем это увеличение амплитуды приведет к тому, что
волна распадется на отдельные вихри, положив начало турбу-.
лизованной зоне.
поверхности тангенциального
разрыва скорости.

96 ГЛ. t. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ {2.4
В реальной жидкости возникающие волны, разумеется, не
неподвижны, но аналогичные процессы и здесь приводят к их
распаду. Этот процесс можно реально наблюдать, например,
при турбулизации струи, бьющей из какого-то отверстия и рас-
распространяющейся затем в пространстве, заполненном той же
(но неподвижной) жидкостью (границу такой струи, очевидно,
можно рассматривать как поверхность тангенциального разры-
разрыва скорости). Аккуратный количественный анализ неустойчи-
неустойчивости поверхности тангенциального разрыва скорости был вы-
выполнен Гельмгольцем A868) (ср. Ламб A932), § 232 или Лан-
Ландау и Лифшиц A953), § 30). При наличии вязкости скольжение
двух слоев жидкости друг по другу, разумеется, будет невоз-
невозможным, и вместо поверхности разрыва мы будем иметь между
двумя течениями узкий переходной слой, в котором профиль
скорости будет иметь S-образную форму. Вопрос об устойчиво-
устойчивости такого слоя является более сложным; однако и Здесь удает^
ся показать (и теоретически и экспериментально), что он яв-
является весьма мало устойчивым (см. ниже.п. 2.8). Заметим
еще, что абсолютна^ неустойчивость поверхности тангенциаль-
тангенциального разрыва скорости представляет собой лишь простейший
случай так называемой неустойчивости Гельмгольца — абсо-
абсолютной неустойчивости специального типа поверхностей раз-
раздела, отделяющих друг от друга области течения, заполненные
одной и той же или разными жидкостями, движущимися с раз-
разной скоростью. Обзор основных относящихся сюда результатов
и ссылки на дальнейшую литературу можно найти в статье
"Бйркгоф a JYQ6%)TJ
Другим простейшим примером абсолютной неустойчивости
является равновесие в поле тяжести жидкости с переменной по
оси 2 плотностью в случае возрастания плотности с высотой.
Легко понять, что лри любом законе изменения с высотой плот-
плотности р = p(z) несжимаемой жидкости уравнения движения
будут допускать решение и (х, у, z, t) = 0, соответствующее
состоянию покоя; при этом только при наличии поля тяжести
давление должно меняться с высотой по закону
оо
ТЪГ^-Ь т' е' P(z) = gfp(z')dz' +const B.2)
Пусть теперь вследствие какого-то возмущения некоторый эле-
элемент жидкости переместится с уровня z на новый уровень
z' = 2 + h. Если плотность р убывает с высотой, то при h > 0
иаш элемент будет под действием силы тяжести стремиться опу-
егиться «низ, а при h < 0 под действием архимедовой силы он
будет стремиться подняться наверх, так что равновесие будет

2.4] § 2- ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 97
устойчивым. Однако если плотность возрастает с высотой, то
при любом знаке h переместившийся элемент жидкости будет
стремиться еще дальше удалиться от своего первоначального
положения, и состояние равновесия будет абсолютно неустойчи-
неустойчивым. Заметим еще, что в случае идеальной жидкости (не обла-
обладающей трением) уравнения движения будут при любом
р = p(z) допускать также стационарное решение с произволь-
произвольным вертикальным профилем х-компоненты скорости и = u(z)
(и нулевыми, компонентами скорости по двум другим осям),
причем в. силу тех же соображений и это течение будет абсо-
абсолютно неустойчиво при dp/dz > 0. В случае dp/dz < 0 вопрос
об устойчивости такого течения заметно более сложен; заранее
можно лишь .сказать, что в силу соображений подобия критерий
устойчивости здесь должен выражаться через значение так на-
называемого числа Ричардсона — безразмерного параметра
Л JEP.
Случай расслоенной по оси г жидкости представляет большой интерес
для метеорологических задач, в которых такое расслоение вызывается нали-
наличием определенного, профиля температуры Т = Т(г). В этом случае, однако,
мы не можем просто считать жидкость несжимаемой, а должны привлечь к
ее рассмотрению уравнение состояния й элементарные термодинамические то-
тождества (ьм^ например, Ландад_иi _Лифшиц A953), ч. 1, §4). При этом оказы-
оказывается, что элемент жидкости, переместившийся' с уровня г на уровень г + ft,
будет при h > 0 более легким, чем окружающий его воздух, а при ft < 0 бо-
более тяжелым, чем окружающий его воздух, тогда и только тогда, когда
йг < сру\дТ)р'
где под Т теперь понимается абсолютная температура, а V — удельный объем.
Условие B.4) и будет условием абсолютной неустойчивости состояния покоя
при наличии профиля T=T(z) поля температуры. В случае, когда среду мож-
ldV\ R V
но считать идеальным газом, 1-^jH ~~^~'f' так что критерий неустой-
неустойчивости будет иметь вид
dz
(в таком виде это условие можно иайти во всех курсах динамической метео-
метеорологии) . Величина Ga = ~ в метеорологии называется адиабатиче-
7 "
ашм гР9оиентом температуры (Для воздуха этот_градиент равен приблизи-
приблизительно 1 С/100 м). [Термическое расслояние воздуха^) при котором —(dT/dz)
больше, равно или меньше ТТ^Гназывается соответственно устойчивой, безраз»
личной или неустойчивой стратификацией.

98 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [15
Еще один способ представления условия неустойчивости B.4) или B.5),
также часто использующийся в метеорологии, связан с введением вместо,
обычной температуры Т так называемой потенциальной температуры
О = Т(М Т , B-6)
где ро — некоторое стандартное давление (обычно принимаемое равным нор-
нормальному давлению иа уровне моря). В силу выражения для энтропии иде-
идеального газа, приведенного иа стр. 70, сР In 0—s + const. Отсюда ясно, что
при адиабатических пррцессах потенциальная температура не меняется, так
что 6 равно температуре, которую будет иметь воздух, если его адиабатиче-
' . db dT „
ски привести к стандартному давлению ро- Легко видеть, что -т— ~ —: Ga,
поэтому с помощью понятия о потенциальной температуре критерий неустой-
чивости B.4) может быть сформулирован следующим образом: состояние по-
покоя будет неустойчивым, если -dv/dz^CO (т. е. если потенциальная температу-
температура убывает с высотой), и будет устойчивым, если dQJdz> 0 (т. е; если по-
потенциальная температура возрастает с высотой).
При наличии произвольного профиля скорости ветра движение в слу-
случае неустойчивой стратификации всё равно будет иеустойчивым; в случае же
устойчивой стратификации устойчивость или неустойчивость движения дол-
должна как-то определяться значением числа Ричардсона
?-(L_a\ ?-.
T\dz Ua) _ 6 dz
R1 тжъ Т*л2' ( }
тжъ Т*л2'
\dz) [IF)
2.5. Математическая формулировка вопроса об устойчивости
относительно малых возмущений
Условия возникновения турбулентности далеко не всегда
удается выяснить столь простыми средствами, как это имело
место в изложенных выше примерах. В общем случае эффектив-
эффективным средством исследования устойчивости является так называе-
называемый метод малых возмущений, идею которого мы сейчас изложим
в применении к движениям несжимаемой жидкости постоянной
плотности р.
Метод малых возмущений состоит в том, что поля скорости
ut(x,t) и давления p(x,t), удовлетворяющие уравнениям гидро-
гидродинамики, пишутся в B»js,eul = Ul -\-u'r р = Р + р',гце U{(x,t)
и Р(х, t) представляют собой частное решение тех же уравне-
уравнений, устойчивость которого исследуется, а и'г р' — малое воз-
возмущение.: Учитывая, что поля Ui и Р сами удовлетворяют урав-
уравнениям гидродинамики, и пренебрегая квадратичными выраже-
выражениями относительно возмущений, удается для m и рг получить

2J}J J J. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 99
линейные уравнения вида
Продифференцировав уравнение B.7), содержащее du'Jdt,
по *<, лросуймировав результат по i и использовав последнее
уравнение B.7), можно выразить р' через и\ с помощью фор-
формулы, аналогичной формуле A.9'). Поэтому общее решение
системы B.7) будет определяться заданием одних лишь на-
начальных значений и. \(х, 0) функций и\(х, t). При этом можно
(по крайней мере в принципе) попытаться установить условия,
при которых не, все решения соответствующей задачи с началь-
начальными условиями будут затухать во времени; эти условия и бу-
будут условиями абсолютной неустойчивости1) решения 1/<, Р.
Разумеется, если даже соответствующие условия и не будут вы-
выполняться, так что решение Uu P будет абсолютно устойчиво
(относительно малых возмущений), остается еще возможность,
что относительно конечных возмущений и[ ^р' (описываемых
существенно нелинейными уравнениями) это решение все же
будет неустойчиво, т. е. что течение, описываемое этим реше-
решением, будет представлять собой систему с жестким возбужде-
возбуждением. Однако для того, чтобы опровернуть и эту возможность,
требуются уже существенно иные методы исследования (см.
ниже п. 2.9).
В случае, когда решение Ui'— Ui{x), P = Р(х) описывает
стационарное ламинарное течение жидкости, коэффициенты си-
системы уравнений B.7), очевидно, не будут зависеть от времени.
В таком случае эта система будет допускать частные решения
¦вида
а'(х,1) = е'^/ш(х), p'(x,t) = e-^gu>(x), B.8)
зависимость которых от времени задается экспоненциальным
множителем еш с, вообще говоря, комплексной «частотой» со.
^Допустимые значения «собственных частот» со и отвечающие им
') Отметим, что терминология здесь не является вполне установившейся.
Часто под условиями абсолютной неустойчивости понимают условия, при ко-
Т(фЫх уравнения B.7) будут иметь возрастающие по абсолютной величине
решения, т. е. случаи наличия только затухающих и ограниченных решений
Причисляют к устойчивым. Нам здесь, однако, будет более удобно считать
неустойчивыми также и течения, для которых существуют ограниченные (но
незатухающие) возмущения,

100 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.§
«амплитуды» fa{x), g,o(x) при этом будут определяться из не-
некоторой задачи на собственные значения для линейной системы
уравнений с частными производными. В тех случаях, когда ко-
коэффициенты этой системы не зависят от каких-то простран-
пространственных координат, число независимых переменных,- входящих
в полученную систему, можно уменьшить, предположив заранее,
что зависимость амплитуд /ш и g№ от соответствующих коорди-
координат будет также экспоненциальной с фиксированным «волновым
числом» (т. е. зафиксировав заранее, пространственный мас-
масштаб возмущения >в направлении осей координат, по которым
невозмущенное течение является однородным). Так, например,
если невозмущенное течение зависит только от координаты х3,
то можно положить
ш;,„ка(х3), gm(х) = *c»*+**fc4tuкг(х3); B.9)
при этом собственные частоты со = ш k &2) и амплитуды
faikuk и ?»;*„*,будут уже определяться из задачи на собствен-
собственные значения для системы обыкновенных дифференциальных
уравнений, содержащей параметры ?4 и /г2. Аналогичные фор-
формулы, в которых лишь ехр [/(Л^-т-Л^г)] заменяется на
СХр (/Vl> а Л; *,. ft, (*з) И 8«; ft,, ft, Ы - Н3 Л; ft, (*2- Хз) "
gm.k(x2, x3) будут иметь место для течения, существенно зави-
зависящего лишь от х% и хз.
Существенно, что весьма часто собственные функции fu>(x)
оказываются образующими полную систему функций в про-
пространстве всех векторных функций f = (fu /2, /з), удовлетворяю-
удовлетворяющих уравнению неразрывности dfjdxi и соответствующим крае-1
вым условиям (если /ш (х) = el**fa. к> (х2, х3) или /ш (х) =
==0'.(*1-*1+*1*»)у?(в_Л *,(-^з)' то для этого, разумеется, достаточно, что-
чтобы функции /ш. ft|(x2, х3} или /m. kukl(x3) при любом фиксиро-
фиксированном h или фиксированных klt kz образовывали полную си-
систему функций в пространстве соответствующих векторных
функций от двух или одного переменного) !). В таком случае
любое начальное поле и(х, 0) можно разложить в ряд (или ин-
интеграл) по этим собственным функциям. Поэтому общее реше-
') С математической точки зрения возникающие здесь задачи на соб-
собственные значения являются задачами о собственных значениях некоторого
линейного несамосопряженного оператора в функциональном пространствг.
Для установления полноты системы собственных функций (или хотя бы соб-
собственных н родственных' им присоединенных функций) такого оператора в
ряде случаев можно воспользоваться теоремой Келдыша A951) (см. также
Келдыш и Лидский A963)),

2J5J i 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 101
ние задачи с начальными условиями для системы уравнений
B.7) здесь может быть представлено в виде суперпозиции эле-
элементарных решений, экспоненциально зависящих от времени,
так что общая задача об устойчивости может быть сведена к
изучению лишь соответствующей задачи на собственные значе-
значения. А именно, здесь для устойчивости рассматриваемого лами-
ламинарного течения по отношению к малым возмущениям необхо-
необходимо и достаточно, чтобы у всех возможных «собственных ча-
частое ю мнимая часть Зт<о была отрицательной. При наличии
Пространственной однородности по каким-то координатам раз-
различные собстйенные частоты и будут, вообще говоря, зависеть
от ".прЬЙтраяСгвенных «масштабов> возмущений (т. е. от волно-
¦Цщ чисел k\ или ki и k2) и от числа Re. Ясно, что при Re-*-0
мнимые части всех частот <о будут стремиться к отрицательным,
значениям (так как при р = const состояние покоя всегда устой-
устойчиво). Однако при возрастании Re мнимые части некоторых час-
частот могут возрастать и, в конце концов, становиться положитель-
положительными. Предположим, что задача на собственные значения, отве-
отвечающая, фиксированному масштабу возмущений (т. е. фиксиро-
фиксированным k\ или ki и k%), имеет дискретный спектр -собственных
частот а>} (это предположение выполняется для многих важных
течений). В таком случае критическое число Re, соответствующее
границе устойчивости ламинарного течения по отношению к ма-
малым возмущениям данного масштаба, будет определяться из
уравнения max Sittoj = 0, где Snuo означает мнимую часть чис-
числа <о. Наименьшее из таких критических значений Re для воз-
возмущений различных масштабов будет критическим числом Recr
'Потока в целом, т. е. при Re>-Recr рассматриваемое ламинар-
ламинарное течение будет абсолютно неустойчивым, а при Re < Recr — •
устойчивым. Заметим еще только, что введенное здесь число Recr,
характеризующее абсолютную неустойчивость, очевидно, долж-
должно быть не меньше, чем критическое число Рейнольдса, характе-
характеризующее устойчивость потока относительно возмущений конеч-
конечной амплитуды. Поэтому, следуя обозначениям, использованным
на стр. 82, его можно было бы обозначить как Recrmax. С дру-
другой стороны, однако, наличие неустойчивости при Re > Recr mas
означает только, что при таких числах Рейнольдса соответ-
соответствующее ламинарное течение не может существовать, но со-
совсем не означает еще, что оно обязательно перейдет в турбу-
турбулентное течение. В самом деле, вообще говоря, возможно, что
щя нарушении устойчивости данное ламинарное течение пре-
рратится в новое ламинарное течение, являющееся уже устой-
igttMK s переход к турбулентности осуществится лишь при на-
ш усто.й.чи.вости и этого цорохо ламинарного, течения при

102 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.6
числах Рейнольдса, значительно превосходящих Re»max (см.
примеры в пп. 2.6—2.7).
В заключение подчеркнем еще раз, что возможность разло-
разложения произвольного решения системы B.7) в ряд по специаль-
специальным решениям вида B.8) будет иметь место часто, но все же
не всегда — это обстоятельство часто забывается при рассмо-
рассмотрении задач гидродинамической теории устойчивости. В част-
частности, более сложная ситуация возникает, если система B.7)
оказывается сингулярной (т. е., например, если какой-то коэф-
коэффициент при старшей производной у этой системы где-то обра-.
щается в нуль). В таком случае полнота системы.собственных
функций не может быть просто доказана, и даже само понятие
собственной функции должно определяться с осторожностью.
Дело в том, что здесь часто и при фиксированном масштабе
возмущения возникает непрерывный спектр собственных значе-
значений, которому отвечают собственные функции, удовлетворяю-
удовлетворяющие более сложным, чем обычно, граничным условиям или
имеющие более сложную структуру (например, не убывающие
на бесконечности или имеющие разрывы производных в особой
точке). В приложениях такие более сложные «собственные
функции» часто просто упускаются из виду, в результате чего
система «элементарных решений» вида B.8) оказывается заве-
заведомо неполной (ср. Кэйз A962), Линь A961), Линь и Бенни
A962)). В тех случаях, когда система функций по каким-то
причинам оказывается неполной, исследование одной лишь со-
соответствующей задачи на собственные значения недостаточно
для_ решения задачи об устойчивости, и для полного выяснения
вопроса приходится исследовать поведение общего решения со-
соответствующей задачи с начальными условиями. Такое исследо-
исследование весьма сложно; однако в частном случае идеальной
жидкости с v = 0 оно тем не менее позволило получить ряд
вполне окончательных результатов (см. работы Дикого A960а, б)
и Кэйза A960а, б), о которых подробнее ещё будет гово-
говориться ниже).
2.6. Устойчивость течения между двумя вращающимися
цилиндрами
Одним из важных примеров абсолютной неустойчивости, до-
допускающей полный математический анализ, является неустойчи-
неустойчивость движения Куэтта между цилиндрами — плоского стацио-
стационарного течения жидкости между двумя вращающимися
цилиндрами. Пусть /fy и Qi^ радиус и угловая скорость вра-
вращения внутреннего цилиндра, a R2 и ^ — внешнего. В цилин-
цилиндрических координатах г, <р, г с осью Ог по оси цилиндров поле

2.6) * 2- ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 103
скорости стационарного течения определяется формулами
М1 BЛ0)
/?2 — /?! Щ — /?i
вывод которых был приведен выше (см. формулу A.28) на
стр. 44).
Пренебрегая сперва действием вязкости, можно определить
критерий неустойчивости из следующих элементарных физиче-
физических соображений. При стационарном ламинарном течении дей-
действующая на элементы жидкости центробежная сила уравнове-
уравновешивается радиальным градиентом давления. Пусть теперь
элемент массы т сместился под действием возмущения из поло-
положения с координатой го в положение с координатой г > го.
Тогда в силу закона сохранения момента количества движения
Vf в. новом положении его скорость будет равна
и, следовательно, на него будет действовать центро-
: г2
бежная сила т Л U\ (r0). Равновесие будет неустойчивым, если
ща, сила окажется больше ее равновесного значения на рас-
стоянии г 6т оси, равного по величине градиенту давления на
расстоянии г. Следовательно, условие неустойчивости (которое
ддя рассматриваемого здесь.течения невязкой жидкости было
установлено Рэлеем A916а)) будет иметь аид
или, иначе,
0. B.11)
С помощью формулы. B.10) критерий неустойчивости Рэлея
приводится к виду (Q2R2 — 2i/?i)?fp <()• Если цилиндры вра-
вращаются в разные стороны, то U где-то между цилиндрами ме-
меняет знак; таким образом, в этом случае течение наверное будет
неустойчивым. При одинаковом направлении вращения цилинд-
цилиндров можно положить fii > 0, й2 > 0, и тогда всюду будет Uf>0;
при этом рэлеевский критерий неустойчивости принимает вид
Аккуратный математический вывод этого результата с помощью
применения к движению невязкой жидкости методов теории

104 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ B-6
возмущений был дан Сингом A933) для случая осесимметричных
(т. е. не зависящих от <р) возмущений поля скорости и Чандрасе-
каром A960) для случая произвольных возмущений этого поля.
Более полный анализ (учитывающий также влияние вязко-
вязкости) может быть осуществлен только с помощью метода малых
возмущений, впервые примененного к данной задаче Тэйлором
A923). Так как невозмущенное поле скорости B.10) здесь за-
зависит только от координаты г, то, следуя B.8) и B.9), возму-
возмущение скорости и давления здесь можно искать в виде
и'г (х, t) = е1 с**+»*-о/о (r)> ц; (Х; t) = е1 <**+»*--0/W (г)>
где 2n/fe — длина волны возмущения в направлении оси Ог,
tir— целое неотрицательное число, определяющее зависимость
возмущения от угла ср, а /(г)^/ш.к>п(г) = (/г)(г),/м(г),/2)(г))
и g(r) = gm. k п (г) —зависящие от г «амплитуды» возмущения
с заданной длиной волны, заданным значением п и собственной
частотой со. Подставляя формулы B.10) и B.13) в общую си-
систему уравнений B.7) и учитывая граничные условия
и'(г, ф, z, t) =0 при г = /?i и г = Rj, мы придем к задаче на
собственные значения, определяющей спектр частот со, допусти-
допустимых при данных k и п. Можно показать (см., например, Ди При-
Прима A961)), что эта задача после некоторых преобразований
(включающих, в частности, исключение из полученной системы
функций f<z) и g) может быть сведена к следующей системе диф-
дифференциальных уравиений относительно двух неизвестных функ-
функций /И и f№>:
VJ- BЛ4>
где А и В определяются из BЛ0), а N — это дифференциальный
оператор
B.15)

2.61 § 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 105
Граничные условия, при которых должна решаться система ше-
шестого порядка B.14), имеют вид
f\r)=/M(r)=^ = 0 при >=/?, и г = /?2. B.16)
По-видимому, нетрудно показать, что задача B.14) — B.16)
всегда имеет дискретное множество собственных значений
©j = (Hj{k, n, Q1( Й2, #i, Rz), причем соответствующие собствен-
собственные функции /??*>я(г), f$)ktn(r) образуют полную систему в
пространстве пар функций (/(г), /?)), удовлетворяющих гранич-
граничным условиям B.16). Отсюда уже вытекает, что определяемые
6 помощью B.13) начальные поля а? (ху 0), отвечающие соб-
собственным функциям со всевозможными к и целыми небтрица-
тельными п, будут образовывать полную систему функций в про-
пространстве векторных функций oix= (r, <р, г), удовлетворяющих
условию со'леноидалыюсти и обращающихся в нуль при г = R\
и г = R2. Таким образом, исследование задачи на собственные
значения B.14) — B.16) полностью исчерпывает исследование
устойчивости течения Куэтта между цилиндрами. Однако сама
эта задача на собственные значения столь сложна, что она до
сих пор остается неизученной1).
Вместо того, чтобы рассматривать общую систему уравнений
B.14), почти Все исследователи, занимавшиеся вопросом об ус-
устойчивости течения Куэтта между цилиндрами, заранее пред-
предполагали, что п = 0, т. е. ограничивались лишь осесимметрич-
ными возмущениями поля скорости основного течения. В таком
случае эта система заметно упрощается и, как нетрудно видеть,
может" быть переписана в виде
где
') Кажется, единственным исключением в этом отношении является ра-
работа Ди Прима A961), в которой при ряде упрощающих предположений
(включающих, в частности, предположение о малости зазора между цилин-
цилиндрами d=R2 — R\ по сравнению со средним радиусом R0=(R\+R2)/2 для
некоторых значений R2/R1 и п = 0, 1, 2 или 3) приближенно (и притом до-
вольво грубо) оцениваются численно те наименьшие значения Re = rf2Qi/v,
при которых впервые хоть одно собственное значение системы B.14)—B.16);
будет иметь неотрицательную мнимую часть Полученные при этом результа-
результаты полностью согласуются с гипотезой о том, что раньше всего неотрицатель-
неотрицательна)! МЯИЦая часть всегда появляется у собственного значения с ц = 0.

106 ГЛ. Г. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.6
Краевая задача B.17) — B.16) при фиксированном k имеет
счетное число собственных значении ©j = ©j(fe, йь йг, Ri, Rz) и
собственных функций /;(г) — /]*\к{г). Однако соответствующие
функции eikzfa . k (г) теперь уже, разумеется, не будут образо-
образовывать полную систему в пространстве допустимых начальных
полей и'(х, 0) =и'(г, ф, г) (хотя бы потому, что все эти функ-
функции не зависят от .<р). Тем не менее, обычно область пар
(йь Q2), которым отвечают неустойчивые возмущения вида
exp[i(kz — ©03/ (г) (т- е- возмущения такого, вида с З^0» !>()),
просто отождествляются со всей областью неустойчивости (см.,
например, Линь A955), Чандрасекар A961), Дж. Стюарт
A963)). Иначе говоря, обычно предполагается (хотя это и не
всегда специально оговаривается), что при всех значениях Ri,R2,
Qi и й2, при которых имеется хоть одно собственное значение
©j(fe, л, Qit Q2, Ru R2) с пФО и Зт<^>0, будет иметься
также и значение ©j(fe, fii, Q2, Ru Rz) (отвечающее л = 0) с
Зш^^-О (т. е. что при возрастании числа Рейнольдса неотри-
неотрицательная мнимая часть у ©j(fe, и, fii, й2, Ru R2) всегда рань-
раньше всего появляется при п = 0). Так как данные экспериментов,
как будет видно из дальнейшего, прекрасно подтверждают сов-
совпадение области неустойчивости, определяемой из рассмотрения
одних лишь осесимметричных возмущений, со всей областью
неустойчивости течения между вращающимися цилиндрами, то
они подтверждают тем самым и это последнее предположение
(см. также сноску на стр. 105).
Будем теперь считать радиусы Ri и R2 фиксированными.
Нетрудно видеть, что при достаточно малых fij и йг все соб-
собственные значения щ(к, Qit fi2) и ©j(fe, n,' Qu fi2) будут иметь
отрицательную мнимую часть (так как состояние покоя всегда
устойчиво). Если же мы будем увеличивать угловые скорости
fii и fi2, не меняя отношения Q2/fii (что в данном случае соот-
соответствует увеличению числа Рейнольдса без нарушения геомет-
геометрического подобия), то при некоторых Qz/Qi нулевая мнимая
часть ни у одного щ(к, fib fi2) так и не появится (т. е. движе-
движение все время останется устойчивым), в то время как при дру-
других значениях Йг/Й! при некотором Recr = 22^2/v впервые по-
появится значение kcr такое, что какое-то юД^сг. йь йг) будет
уже иметь нулевую мнимую часть (т. е. движение станет не-
неустойчивым).
Любопытно, что в этой задаче при всех fia/fii потеря устой-
устойчивости имеет место в связи с появлением собственного значе-
значения fflj такого, что не Только 3m ©j= 0, но и вообще ©j = 0 (точ-
(точное математическое доказательство этого факта, по-видимому,

2.6) 4 4. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 107
было дано лишь для случая, когда R2— R^(Ri + Rz)/% в ра-
работах Пэлью и Саусвелла A940) и Мексина A946); однако
и данные экспериментов и результаты численных расчетов под-
подтверждают, что на самом деле он имеет общий характер). Это
значит, что при потере устойчивости течения Куэтта между ци-
цилиндрами появляется новое стационарное движение с полем
скорости я = U-\-u', где и' = exp(ikz) f(r) (такое движение
имеет характер ряда вихрей, расположенных в меридиональных
плоскостях). То, что переход от устойчивого состояния к неус-
неустойчивому происходит через стационарное состояние, которому
отвечает чисто нулевое собственное значение© = 0, в работах
по. гидродинамической теории устойчивости иногда называется
принципом смены устойчивости. В свое время этому принципу
придавалось большое значение, но в настоящее время известно,
что он выполняется лишь в некоторых специальных случаях и
нарушается" для многих простых течений (например, для плос-
плоского течения Пуазейля). При дальнейшем возрастании числа Re
появляется целый интервал значений k, для которых имеются
собственные значения ©j c3ma);^0- Опыт показывает, однако,
что при этом возмущенное движение довольно долго еще имеет
характер совокупности стационарных периодических вихрей,
но уже с периодом, который не может быть определен из ли-
линейной теории (ср. ниже п. 2.9). При дальнейшем значительном
возрастании Re и это периодическое движение в конце концов
становится неустойчивым и переходит в неупорядоченное тур-,
булентное движение.
Хотя краевая задача B.17) — B.16) значительно проще, чем
B.14) — B.16) '), вычисление соответствующих собственных
значений a>](k, Qu й2) все равно наталкивается на значитель-
значительные трудности. Поэтому первоначально это вычисление было
осуществлено Тэйлором A923) лишь в предположении очень
узкого зазора между цилиндрами (т.е. при R2—#i<C!(#i + #2)/2),
позволяющем еще значительно упростить исходные уравнения.
Метод Тэйлора основан на разложении решений системы урав-
уравнений {2.17) по некоторой специальной ортонормированной си-
системе, функций; при этом рассматриваемые дифференциальные
уравнения, очевидно, сводятся к бесконечной системе линейных
алгебраических уравнений. Позже этот метод был несколько
усовершенствован Сингом (Ш38); другие численные методы
(в частности, метод, опирающийся на сведение рассматривае-
¦ ' ') Отметим, в частности, что в силу справедливости для задачи B.17)—
B.16) принципа смены устойчивости при определении границы области устой-
устойчивости здесь можно считать, что ю=0. В случае же задачи B.14)—B.16)
с it ф 0 этот принцип ие выполняется, и поэтому в расчетах участвует до-
дополнительный параметр Ще

108
ГЛ. t. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
f2.fr
мой краевой задачи к некоторой вариационной задаче, и метод
Галеркина), также применимые только в случае узкого зазора
между цилиндрами, были развиты Пэлью и Саусвеллом A940),
Мексином A946), Чандрасекаром A954, 1961), Ди Прима
A955), Стайнмен A956), Дьюти и Ридом A964) и другими
авторами. Лишь сравнительно недавно Виттинг A958) предло-
предложил более общий подход, использующий разложение решений
по степеням параметра d/R0 (где d = R2-~Ru Ro= (Ri + #2O2),
а в работах Чандрасекара A958),ЧандрасекараиЭлберт A962),
Кирхгеснера A961) и Спэрроу, Мунро и Джонсона A964)
были разработаны еще более общие методы численного ре-
решения задачи о собственных значениях B.17) — B.16) при про-
произвольных R^ и /?2- Заметим еще, что сам факт неустойчи-
неустойчивости течения вязкой жидкости между вращающимися цилинд-
цилиндрами при некоторых значениях fii и Q2 был. строго доказан
Крыловым A963) без всякого использования численных мето-
методов, но такое доказательство не дает возможности определить
границу области неустойчивости. Численные же методы позво-
позволяют иайти эту границу с большой степенью точности и пока-
показывают, что она во всех случаях имеет примерно одинаковую
форму.
-200 400
о
а)
100 200
-6-4-2
Рис. 13. Расположение области неустойчивости на плоскости (Q,, Q2) для
течения Куэтта между цилиндрами при двух значениях отношения Hi/Ri.
Область неустойчивости на рисунке заштрихована. Пунктиром нанесена граница области
неустойчивости для соответствующего течения невязкой жидкости (по Рэлею).
Для примера мы воспроизводим на рис. 13, а расположение
области плоскости (Qi, Q2), в которбй возможны неустойчи-
неустойчивые возмущения, не зависящие от <р, при fo/tfi = 1,13 (по
расчетам Тэйлора, прекрасно согласующимся и со всеми после-

2.7J $ 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 109
дующими расчетами), а на рис. 13,6 — расположение той же
области при Ri/Ri = 2 (по расчетам Чандрасекара). В обоих
случаях (а также и при всех других Яг/Я*) в области Q^fii >
>(Я\/Я2J ни при каких Re не возникает неустойчивости, так
что вязкость здесь может иметь лишь стабилизирующее значе-
значение. В области же Q2/Qi < (Яг/ЯгJ согласно данным рис. 13
при достаточно большом Re обязательно возникает абсолютная
неустойчивость. В незаштрихованной на рис. 13 области дви-
движение оказывается устойчивым по отношению к бесконечно ма-
малым возмущениям, но, как показывает опыт, при достаточно
больших Re оно все же неустойчиво по отношению к возмуще-
возмущениям конечной величины, причем в этом случае потеря устойчи-
устойчивости приводит к спонтанному образованию развитой турбу-
турбулентности. Граница области устойчивости, рассчитанная Тэйло-
ром, прекрасно совпала, с опытными данными, найденными и
им самим, и рядом других исследователей, и это явилось пер-
первым большим успехом гидродинамической теории возмущений
(см. рис. 13, а, на котором точками указаны эмпирические значе-
значения ряда'пар (Oi, Я2), при которых впервые возникает потеря
устойчивости). Расчеты для случая Я2/Я\ — 2 также прекрасно
подкрепляются имеющимися опытными данными Доннели и
Фультца A960) (точки на рис. 13,6; ср. также Доннели A962)).
2.7. Устойчивость слоя жидкости, подогреваемой снизу
# При наличии в жидкости вертикального градиента темпера-
температуры, направленного сверху вниз, архимедовы силы, очевидно,
действуют на поток дестабилизирующим образом, аналогич-
аналогичным действию сил инерции при криволинейном движении
жидкости, при котором скорость вращения жидкости убывает при
удалении от центра кривизны. Наоборот, градиент температуры,
направленный снизу вверх, действует на течение стабилизирую-
стабилизирующим образом, т. е. так же, как действует при криволинейном
движении возрастание.скорости при удалении от центра кри-
кривизны. Поэтому неудивительно, что задача об устойчивости
тонкого слоя жидкости между двумя бесконечными плоскостя-
плоскостями, имеющими разные температуры, оказывается математически
весьма близкой к задаче об устойчив.ости течения несжимаемой
жидкости между двумя вращающимися цилиндрами1). При ре-
решении указанной задачи, очевидно, надо исходить из системы
') Джефрис A928) показал, что первая из этих задач фактически экви-
эквивалентна частному случаю второй (ср. Линь A955), § 7.3). См. также работу,
Гертлера A959), в основе которой лежит аналогия между учетом центро-'
f бежаых сил и архимедовых сил при исследовании устойчивости сравнительно
широкого класса гидродинамических течений.

110 ГЛ. t. ЛАМИНАРНЫЕ И тУтЛЁНТШЕ ДВИЖЕНИЯ f2.7
уравнений свободной конвекции, рассмотренной в конце п. 1.5.
Если принять, что жидкость ограничена плоскостями х% = 0 и
х$ = Я, поддерживаемыми при постоянных температурах То и
7*1, то к этим уравнениям надо еще добавить граничные усло-
условия щ = О, Т = То при х3 = 0; щ = 0, Т =Ti при- Х3 = Н\ в слу-
случае же свободной поверхности жидкости постоянной темпе-
температуры граничное условие для поля скорости изменяется так,
чтобы оно обеспечивало постоянство давления на этой поверх-
поверхности. Стационарным состоянием, устойчивость которого нас
интересует, здесь будет состояние__покоя, при котором 1)
0 + ^x3,
Полагая Т = Т(хз) + Т.г, р = р(Хз) + р' и линеаризуя уравне-
уравнения свободной конвекции относительно возмущений щ, Т' и р',
мы придем к системе пяти уравнений с пятью неизвестными, из
которой нетрудно исключить все переменные, кроме Т. Если
теперь перейти к безразмерным переменным и затем, следуя
B.8) и B.9), искать T'(X,t) в виде произведения
Т'(х, 0=exp[/(^ + *f--^]e(C), С—§. B.19)
то можно прийти к следующей задаче на собственные значения:
, Pr /X, R ,
с граничными условиями на твердых поверхностях фиксирован*
ной температуры "
6=5- - ж {w - *2 + "'•Рг)е = ° B-20/)
и на свободных поверхностях фиксированной температуры.
') В соответствии с предположениями приближенной теории свободной
конвекции мы считаем изменения плотности р с высотой столь малыми, что
их можно не учитывать в уравнениях для возмущений. Поэтому излагаемые
здесь результаты применимы лишь в случае сравнительно тонких слоев с не-
небольшими Н. Заметим, впрочем, что в случае слишком тонких слоев жидко-
жидкости (при Я'порядка нескольких миллиметров) эти результаты опять же ока^
зываются неприменимыми из-за иарушеиия условия линейности профиля тем-
температуры и некоторых других условии, принимаемых в рассматриваемой тео-
теории (см. Саттои A950), Снджел и Дж. Стюарт A962)),

2,7] S 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ Ш
(см., например, Чандрасекар A961), Дж. Стюарт A963), Линь
{1955)). Близкие граничные условия получаются также дЛя
случаев, когда на поверхностях ? = 0 и ? = 1 фиксируется не
температура, а поток тепла или связь между потоком тепла и
температурой (ср., например, Спэрроу, Голдстайн и Джонсон
(•1964)). Во всех случаях мы приходим к задаче, которая при
фиксированном числе Прандтля Рг содержит всего два пара-
параметра: волновое число k и число Рэлея Ra. Следовательно, лю-
любым заданным значениям k и Ra здесь будет отвечать свой
набор собственных чисел a>j(k, Ra). Оказывается, что при отри-
отрицательных или малых положительных значениях Ra (т. е. в слу-
случае, когда нижняя плоскость имеет более низкую температуру,
или же когда нижняя плоскость подогрета относительно верх-
верхней, но не слишком сильно) все числа a>j(k, Ra) при всех зна-
значениях k будут иметь отрицательную мнимую часть; начиная же
с некоторого «критического значения» Racr (т. е. с некоторой
критической разности температур То—Tlt зависящей также и
от расстояния Н между плоскостями) появляется значение
fe = feCr, при котором одно из собственных значений tOj(feCr, RaCr)
имеет нулевую мнимую часть. При этом, так же как и в задаче
об устойчивости, движения жидкости между вращающимися
цилиндрами, здесь выполняется принцип смены устойчивости,
т. е. первое собственное значение a>j(k, Ra) с SntWj = 0 оказы-
оказывается нулевым (строго математически этот факт был доказан
Пэлью и Саусвеллом A940)). Поэтому потеря устойчивости
состояния покоя при достижении критической разности темпе-
температур То — 7\ приводит к возникновению стационарного конвек-
конвективного движения, периодического по Х\ и" !ie2.
Качественно все основные черты процесса потери устойчи-
устойчивости в подогреваемой снизу жидкости были выяснены еще
Рэлеем A9166), разобравшим математически заметно более
простую {но нереальную физически) задачу о конвекции в слое
жидкости между двумя свободными поверхностями фиксиро-
фиксированной температуры. Математически эта задача сводится к ис-
исследованию дифференциального уравнения B.20) при краевых
условиях B.20") при ? = 0 и ? = 1. Для определения значений
Racr и fecrj достаточно рассмотреть уравнение B.20) с <в = 0,
Пение
(|^K2Ra0 = O. B.21)
решения этого уравнения, удовлетворяющие условиям B.20")
Ц№ ? == 0 и ? = 1, все имеют вид Э = sin яя?, п = 1, 2, ... По-
9?Ому при достаточно больших значениях Ra мы будем иметь
различных нейтральных возмущений (с <в = 0)А волновые

112 ГЛ. Г ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.7
числа которых будут удовлетворять соотношению
B.22)
где л— целое число. Минимальное число Рэлея при каждом
заданном k будет отвечать возмущению с- п = 1; следователь-
но, RaCr здесь определяются из условия RaCr = min-—Т2
Отсюда получаем: Racr = 27^/4 « 657,5, kcr = * Y~U/2 « 2,2.
Для реального случая конвекции в слое между твердыми
поверхносТяШПТ^шксированной температуры аналогичный рас-
расчет в связи с большей сложностью граничных условий требует
уже применения численных методов. Такой расчет был выпол-
выполнен Джефрисом A926) и Пэлью и Саусвеллом A940) (см. так-
также Линь A955) и Чандрасекар A961)); он показал, что в этом
случае Racr « 1708 и kCT « 3,13. Заметим еще, что значение k
определяет лишь периодичность возникающего течения в пло-
плоскости (ХиХг), но не его. форму; в самом деле, нетрудно видеть,
что функцию exp[i(kiXi/H + k2X2/H)] в формуле B.19) можно
без изменения всех последующих ©ыводов заменить произволь-
произвольной функцией <р(хьXi), удовлетворяющей уравнению
Явный вид функции <р определяет форму ячеек, на которые рас-
распадается конвективное движение, но он не может быть одно-
однозначно определен исходя из линейной теории возмущений. Од-
Однако данные многочисленных экспериментов (описанных, напри-
например, в книге Чандрасекара A961); см. также Дж. Стюарт
A963) и цитированную там литературу.) определенно показы-
показывают, что возникающее течение обычно распадается на сово-
совокупность ячеек (так называемые ячейки Бенара) в виде ше-
шестигранных призм, в середине которых жидкость движется
вверх, а по краям вниз или наоборот. Таким ячейкам соответ-
соответствует вполне определенная форма функции ф, которая была
указана Кристоферсоном A940). Сопоставление отвечающих
этой функции ф значений скорости с данными наблюдений ячеек
Бенара можно найти в книге Чандрасекара A961) и' в статье
Дж. Стюарта A964) (использовавшего также результаты не-
нелинейной теории конвекции, о которой будет речь в п. 2.9); оно
приводит к хорошему согласию теории и эксперимента.
Аналогично обстоит дело и в случае, когда верхняя поверх-
поверхность жидкости является свободной поверхностью фиксирован-
фиксированной температуры; в этом случае только граничное условие
B.20') при ?= 1 должно быть заменено на B.20"). В резуль-

2.8] § 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ ИЗ
тате мы приходим к нойой задаче на собственные значения, для
которой численный расчет показывает, что здесь потеря устой-
устойчивости происходит при Racr ~ 1100 (Пэлью и Саусвелл A940),
Чандрасекар A961)). Это значение Racr, так же как и значение
Racr для конвекции между твердыми поверхностями, прекрасно
подтверждается на опыте (см., например, Чандрасекар A961),
Саттон A950)). Значения Racr, отвечающие некоторым другим
граничным условиям для температуры, можно найти в статье
Спэрроу, Голдстайна и Джонсона A964).
При дальнейшем повышении То — 7"i (т. е. при увеличении
Ra) после достижения значения Racr стационарная «ячеистая»
конвекция сперва сохраняет свой характер, а затем_ и она ста-
становится неустойчивой и при Ra ~ 500000 возникает неупорядо-
неупорядоченное турбулентное движениё"ГПо5бпытно, что переход к тур-
турбулентному режиму здесь, по-видимому, происходит постепен-
постепенно— в виде ряда дискретных «скачков», в результате каждого
из которых устанавливается новый режим конвекции, менее
упорядоченный, чем предыдущий (см. Малкус A954а)).
2.8. Устойчивость плоскопараллельных течении
и течений в трубе и в пограничном слое
Выше мы рассмотрели два примера применения метода
возмущений к исследованию гидродинамической устойчивости.
Однако с точки зрения экспериментатора или инженера оба
эти примера являются довольно, специальными. Значительно
более удобными для экспериментальной проверки и важными
для приложений являются случаи течения в круглой трубе и
обтекания плоской пластинки (которым именно поэтому и было
уделено основное внимание в начале настоящего параграфа).
И если тем не менее в качестве иллюстрации метода возмуще-
возмущений прежде всего были рассмотрены течение между вращающи-
вращающимися цилиндрами и свободная конвекция в слое между двумя
плоскостями постоянной температуры, то это объясняется тем,
что в указанных двух случаях (по-видимому, из-за наличия до-
дополнительных сил — центробежной в первом случае и архиме-
архимедовой во втором) метод возмущений приводит к относительно
простым задачам на собственные значения, позволяющим полу-
получить вполне законченные результаты. Что же касается до тече-
течений в трубах и в пограничном слое, то здесь применение метода
возмущений наталкивается на очень значительные трудности,
которые до сих пор никак еще нельзя считать полностью прео-
преодоленными.
В связи со сложностью математического анализа в случае
течении в трубе и в пограничном слое громадное большинство

114 ГЛ, I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.8
имеющих сюда отношение исследований посвящено рассмотре-
рассмотрению лишь простейших плоскопараллельных двумерных течений,
которые в какой-то степени можно считать моделями упомяну-
упомянутых выше реальных течений. Поэтому мы здесь также начнем с
рассмотрения вопроса об устойчивости плоскопараллельных те-
течений и лишь затем укажем, что известно о возможности пере-
перенесения получаемых при этом результатов на течения в трубе и
в пограничном слое. Заметим еще, что в силу уравнений гидро-
гидродинамики A.6) стационарное .плоскопараллельное течение
жидкости с отличной от нуля вязкостью, при котором отлична от
нуля лишь одна компонента поля скорости ,U = щ, зависящая
только от координаты х3 = г, возможно только при условии, что
профиль U(г) зависит от г квадратично. Иначе говоря, такое
течение всегда представляет собой комбинацию течения Куэтта
с линейным профилем скорости и течения Пуазейля с парабо-
параболическим профилем (см. примеры 1 и 2 на стр. 40—42). Учиты-
Учитывая, однако, что плоскопараллельные течения нас интересуют
как возможные модели более сложных реальных течений, мы
будем здесь рассматривать также и более сложные профили
U (г) в надежде на то, что получаемые при этом результаты
можно будет затем применить и к потокам, не являющимся
строго плоскопараллельными.
Итак, будем считать, что ось Oxi = Ох направлена вдоль
потока и что скорость основного течения не зависит от jc2 = у
и задается произвольной функцией U(x3) = U(z). Существенно
отметить, что при нахождении критерия неустойчивости такого
плоскопараллельного течения можно ограничиться рассмотрени-
рассмотрением лишь двумещшцвозмущений вида и' = {и'(х, z, t), w'(x, z, t)},
гак как более общие трехмерные возмущения теряют устойчи-
устойчивость позже (при больших числах Рейнольдса), чем двумерные
возмущения. Это утверждение, доказанное Сквайром A933)
(см. также Линь A955), § 3.1), можно пояснить, представив
возмущение в виде суперпозиции элементарных компонент,
имеющих вид плоских волн. Двумерным возмущениям будут
соответствовать волны, распространяющиеся вдоль основного
потока, а трехмерным — волны, направление распространения
которых не совпадает с направлением основного течения. Но
нетрудно показать, что на волновую компоненту возмущения с
заданным волновым вектором к влияет только компонента ско-
скорости основного течения по направлению указанного волнового
вектора, равная Ukjk, где kt — это ^-компонента вектора к, а
k — его модуль. Математически это проявляется в том, что в
случае плоскопараллёльного течения со скоростью U = U(z)
подстановка формул B.8) й B.9) с хх = х, х% = у, *, = г в о&-

2,8] 4 4. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 115
щую систему B.7) после некоторых преобразований (и исклю-
исключения из системы всех неизвестных функций, кроме функции
/(г) =flw)(z), задающей компоненту U3(x, t) = w'(x, t) возму-
щения и'(х, t)) приводит к уравнению
B.24)
которое вместе с соответствующими граничными условиями
определяет частоты задачи со = coj, /. = 1, 2, ..-. Если мы рас-
рассмотрим теперь двумерное возмущение с тем же модулем вол-
волнового вектора k (т. е. возмущение вида B.8) — B.9) с ki = k
и &2 = 0), то новое уравнение B.24) будет отличаться от ста-
старого лишь заменой kiU на Ш, т. е. будет совпадать с написан-
написанным выше уравнением, в котором только скорость U(z) уве-
личена в k/ki разг Таким образом, для волновых возмущений,
распространяющихся под некоторым углом к основному тече-
течению, эффективное число Рейнольдса оказывается меньшим, чем
для возмущений с той же длиной волны, распространяющихся
вдоль, основного потока, и следовательно, критическое число
Рейнольдса для двумерных возмущений будет докритическим
для трехмерных возмущений. Поэтому при нахождении грани-
границы устойчивости для плоскопараллельных течений всегда мож-
можно считать, что &2=0, т. е. что возмущение не зависит от у. При
этом допустимо считать также, что и'2(х, f) = v'(x, t) = 0, так
как пульсации v' никак не будут сказываться на системе урав-
уравнений относительно переменных и', до' (и будут затухать во
времени) ').
•¦) Разумеется, отсюда еще не следует, что и при Re > Recr существен-
' ными будут только ие зависящие от у двумерные возмущения. Поскольку
имеющиеся в настоящее время эмпирические даииые определенно показы-
показывают, что при турбулизации двумерного пограничного слоя трехмерные воз-1
мущения играют большую роль (см., например, Клебанов, Тидстром и Сард-
жент A962)), то исследование поведения таких возмущений при сверхкриги-
ческих числах Рейнольдса также представляет интерес. Такое исследование
было проведено Уотсоном A9606) и Майклом A961). Эти авторы показали,
что в рамках линейной теории возмущений для любого плоскопараллельного
течения всегда имеется такой интервал ReCr<Re<Ret значений Re, в пре-
пределах которого среди всех неустойчивых волновых возмущений наиболее бы-
быстро возрастающим (т. е. имеющим наибольшее значение 3П1.а>) будет неко-
некоторое двумерное возмущение (хотя среди возмущений с фиксированным вол-
волновым числом k при некоторых к наиболее неустойчивыми могут оказаться и
трехмерные возмущения). По-видимому, однако, трехмерные возмущения ча-
часто начинают играть основную роль уже при Re, лишь слегка превышающем
ReCr, в результате возникновения существенно нелинейных эффектов (см. ни-
ниже п. 2.9),

116 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ B.8
Уравнения B.7) в применении к двумерным возмущениям
плоскопараллельного течения имеют вид
B.25)
дх р дг
д2 д1
где Д = -j-j + -0р—двумерный оператор Лапласа. Краевые
условия для этих уравнений заключаются в обращении в
ноль обоих компонент скорости и' и до' на ограничивающих по-
поток стенках (или, в случае неограниченного потока, на беско-
бесконечности, т. е. при 2-»-оо, или при 2-*-— оо, или при 2-V±oo,
в зависимости от характера неограниченности). Пользуясь ура-
уравнением неразрывности, перейдем в первых двух уравнениях
B^25) от компонент скорости «' и до' к функции тока г(), полагая
У=—яг- <" = <?•
Тогда после исключения давления для функции тока получает"
ся. уравнение в частных производных
Для нахождения критерия неустойчивости надо найти решение
ty(x, z,t) этого уравнения при указанных выше краевых усло-
условиях и при заданном начальном значении $(х,г,0) = tyo(x, z),
где урв(х, z) —произвольная функция, отличная от нуля в огра-
ограниченной области пространства (и удовлетворяющая краевым
условиям и условию малости возмущения |V\f>0|<c?/). Харак-
хер изменения со временем величины max |V<j>(.k, z, ^)| будет за-
U )
)
висеть от числа Рейнольдса основного течения: при достаточ-
достаточно малых Re эта величина всегда будет затухать, а при доста-
достаточно больших Re может оказаться иногда и возрастающей со
временем. Граница между указанными областями значений Re
.(если она существует) и будет определять критическое число
Рейнольдса.
Решение сформулированной задачи с начальными условия-
условиями обычно очень сложно. Поскольку, однако, коэффициенты ура-
уравнения B.26) не зависят от / и х, to это уравнение может иметь

§ 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧЙЙОСТЬ 11?
частные решения вида
Ф (х, z, t) = е1 (**-•<Хр B) = etk <*-«<Хр (г), B.27)
где с = a>/k. Если таких «волновых решений» окажется доста-
достаточно много, так что решение ty(x,z;t) задачи с начальными
условиями всегда можно будет разложить в ряд по решениям
вида E^) со всевозможными (вещественными) волновыми
числами k, то общая задача нахождения значения Recr сведет-
сведется к определению лишь допустимых значений с. С этой целью
надо подставить формулу B.27) в уравнение B.26), после чего
мы получим следующее обыкновенное дифференциальное ура-
уравнение для' определения функции ф(г):
\и — с) (ср" — k\) — U\ = — ? (cpi v _ 2k\"+k*r) B.28)
(штрихи здесь означают производные по г). Уравнение B.28)
часто называют уравнением Орра — Зоммерфельда. Краевые ус-
условия для этого уравнения заключаются в обращении в ноль зна-
значений <р и <р' на границах потока (которые могут находиться и
на бесконечности). Однородное уравнение B.28) с указанными
однородными краевыми^словиями будет иметь нетривиальные,
решения лишь при неко_тор_ы?^?ВДЦиальных_ зд?чениях^_парамет-
ра с. Эти""собственные значения з-адачи будут~~вооб"ще говоря,
комплексными числами с =± Ci + icz, зависящими от волнового
числа & и от вязкости v (т. е. от числа Рейнольдса Re). Дей-
Действительная часть d будет иметь смысл скорости распростра-
распространения волны, а мнимая часть с2 будет определять изменения
амплитуды волны со временем, которые описываются множите-.
лем ekCl: при с2 < 0 амплитуда будет затухать, при с2=0—
оставаться постоянной (волна в этом случае называется ней-
нейтральной), а при с2 > 0 — расти со временем. Таким образом,
значение Recr здесь определяется как то Re, при котором впер-
впервые Cz(k, Re) = 0 хотя бы при одном к.
Итак, в рассматриваемом случае для нахождения критерия
неустойчивости надо только определить величину с2 как функ-
функцию от & и Re. Заметим еще, что при значении Re = Recr, при
котором с2(&, Re) впервые обращается в нуль, вещественная
часть С{ собственного числа с(&, Re) с Зга с = °г = 0 не будет,
вообще говоря, равна нулю (в нарушение «принципа смены
устойчивости»). Это значит, что собственному числу с, вообще
говоря* отвечает распространяющаяся вдоль оси Ох волна
B.27). При значениях Re, немного превосходящих Recr, най-
найдется уже небольшой интервал значений k, при которых сг
будет положительным (a ct — отличным от нуля). Волны со

Ill ГЛ. t. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДёИЖёНИД B.8
значениями k из этого интервала образуют волновой пакет, ко-
который будет усиливаться со временем, перемещаясь одновремен-
одновременно вниз по течению. Действительно, значение kez будет наи-
наибольшим где-то около центра указанного интервала значений
k\ поэтому вблизи этого центра ¦^¦(^с2) = 01и групповая ско-
рость -^ (kc)«^- (fcCj) нашего волнового пакета будет вещест-
вещественной, т. е. будет представлять собой истинную скорость пере-
перемещения пакета (ср. Ландау и Лифшиц A953)^ § 29). В этом
отношении рассматриваемая здесь неустойчивость, очевидно,
отличается от неустойчивости течений, рассмотренных в пп. 2.6
•и 2.7, в которых неустойчивые возмущения были неподвиж-
неподвижными и в каждой фиксированной точке возрастали до конечной
величины.
Устойчивость плоскопараллельных течений идеальной- жидкости
Подставляя в уравнение B.28) какой-либо конкретный про-
профиль скорости U\z), мы придем к весьма сложной задаче на
собственные значения, решение которой требует выполнения
громоздких расчетов. В целях упрощения этих расчетов есте-
естественно начать с попытки воспользоваться экспериментальными
данными, согласно которым критическое число Рейнольдса для
большинства плоскопар.аллельных потоков очень велико. Следо-
Следовательно, можно ожидать, что при числах Рейнольдса, близких
к критическому, слагаемые в правой части уравнения Орра —
Зоммерфельда B.28), описывающие действие сил вязкости на
малое возмущение, будут малы по сравнению со слагаемыми в
левой части. Поэтому можно попробовать сперва считать^ид-
кость идеальной, т.е. пренебречь правой частью уравнения B.28),
и рассмотреть укороченное уравнение
(U—с) (ср" — №у) — U"<? = 0, B.29)
подробно изученное еще Рэлеем A880, 1887, 1895, 1913). По-
Поскольку это уравнение уже не четвертого, а только второго
порядка, то мы -не можем здесь требовать выполнения четырех
краевых условий и должны ограничиться обычным для тече-
течений идеальной жидкости требованием, чтобы на ограничиваю-
ограничивающих поток стенках обращалась в нуль лишь нормальная ком-
компонента скорости. Вспоминая определение функции тока ¦$ и
формулу B.27), заключаем, что на стенках должно выполнять-
выполняться равенство <р = 0.
Однако полное пренебрежение вязкостью и использование
укороченного уравнения B.29) наталкиваются на ряд трудно-

2JS\ t 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ Ш
стей. Эти трудности связаны в первую очередь с тем, что при
вещественных собственных значениях с (отвечающих нейтраль-
нейтральным волнам, представляющим наибольший интерес для нахо-
нахождения критерия неустойчивости) может найтись такое значе-
значение 2 (скажем, 2 = Zo), при котором соответствующее значение
скорости основного потока U(Zo) = Uo окажется равным с, так
что точка 20 будет особой точкой уравнения B.29). Более того,
еще Рэлей, а затем при более общих условиях Толмин и Преч
A946) доказали, что при плоскопараллельном течении идеаль-
идеальной жидкости скорость с распространения нейтральных волн все-
всегда оказывается меньше максимальной скорости основного пото-
потока, так что внутри течения обязательно возникает особая точка Zo
(ср. также Линь A955), § 8.2). Если U'(z0) Ф0-, то в окрестности
этой точки можно положить U(г) — с « U'(z0) (z — z0), и при
z -*¦ At функция <р//- будет стремиться к бесконечности как
it i Ч/ \ • Поэтому ^-компонента скорости . нейтрального
возмущения в окрестности особой точки будет иметь вид
* T U' (г„)
Таким образом, в случае нейтральной волны одна из двух ли-
линейно независимых решений укороченного уравнения B.29)
оказывается разрывным и многозначным, и возникает вопрос,
какую ветвь получаемой многозначной функции следует вы-
выбрать. Кроме того, имеется еще одно затруднение, заключаю-
заключающееся в том, что при наличии у уравнения B.29) комплексного
собственного значения с (отвечающего собственной функции
<р(г)) комплексно-сопряженное число с* также, очевидно, бу-
будет собственным значением этого уравнения (отвечающим соб-
собственной функции <р*(г)). Следовательно, наряду с затухающей
волной уравнение для функции тока всегда будет иметь также
и решение в виде возрастающей волны. Поэтому для невязкой
жидкости не имеет смысла характеризовать устойчивый случай
как случай наличия одних лишь затухающих колебаний, т.' е.
само определение устойчивости, опирающееся на рассмотрение
элементарных волновых решений, здесь должно быть как-то из-
изменено.
Наиболее обычный способ преодоления всех этих трудно-
трудностей состои.т в том, что возвращаются, обратно к полному ура-
уравнению Орра — Зоммерфельда B.28) и нужную ветвь решения
укороченного-уравнения B.29), описывающего нейтральные ко-
колебания, так же как и имеющие физический смысл волновые
решения этого уравнения с Зтс=?0( отбирают при помощи
тщательного исследования асимптотического поведения решения

120 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.8
уравнения четвертого порядка B.26) при v-»-0 (т. е. при
Re-^-ooI). При этом, в частности, оказывается, что имеющие
физический смысл возрастающие и затухающие волновые ре-
решения уравнения B.29) вовсе не являются сопряженными друг
к другу и что в некоторых случаях такие решения следует кон-
конструировать при помощи «склеивания» различных выражений в
различных областях изменения переменного г (см., например,
Линь A955), гл. 8). Естественно, что такой подход к исследо-
исследованию устойчивости невязкой жидкости оказывается довольно
громоздким и что преимущества, заключающиеся в относитель-
относительной простоте уравнения B.29), при этом фактически теряются.
Существует, однако, и другой подход к той же задаче, поз-во-.
ляющии использовать относительную простоту уравнений гидро-
гидромеханики невязкой жидкости; он будет указан немного ниже.
Перечислим теперь основные результаты, полученные при
исследовании устойчивости плоскопараллельных течений невяз-
невязкой жидкости. Началом этих исследований послужили^ указан-
указанные выше важные работы Рэлея, который, в частности, еще в
1880 г. доказал, что если U"(z) нигде в пределах течения не
обращается в нуль, то укороченное уравнение B.29) не может
иметь собственных значений таких, что Зга^>0 (а, следова-
следовательно, и вообще комплексных собственных значений). В са-
самом деле, переписав уравнение B.29) в виде
а затем умножив его на комплексно-сопряженную функцию <р*
и проинтегрировав в пределах от z = zt -до z = гг (где 2t и
22 — границы течения, на которых «р(г) обращается в нуль),
получим
\fvc+^J^dz^ B.зо)
При с2 Ф 0 обращение <в нуль мнимой части последнего равен-
равенства, очевидно, может иметь место, лишь если U"(z) где-то ме-
между Zt И; 22 меняет знак, откуда и вытекает выделенный курси-
курсивом, результат. В течение многих лет всеми принималось, что
эта теорема Рэлея дает полное доказательство устойчивости (в
смысле отсутствия возрастающих возмущений) плоскопарал-
') Заметим, что в случаях, когда речь идет о нейтральных волнах (с ве-
вещественным с), вязкость приходится учитывать лишь в окрестности особой
точки г = Zq, где, таким образом, вводится дополнительный «внутренний по-
граничньф слой»,

2.8J § 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 121
лельных течений идеальной жидкости, профиль скорости кото-
которых не имеет точки перегиба (заметим, что для идеальной
жидкости с v = 0 любой профиль p(z) является допустимым
с точки зрения уравнений движения, в отличие от положения,
имеющегося в случае вязкой жидкрсти). На самом деле, од-
однако, дело здесь обстоит вовсе не тек просто. Оказывается, что
из-за наличия особенности, связанной с обращением в нуль
коэффициента при старшей производной, уравнение B.29)
обычно имеет непрерывный спектр ^собственных значений; при
этом собственные функции, отвечающие точкам непрерывного
спектра, не удовлетворяют обычным; условиям, накладываемым
на собственные функции, и чаще всего просто упускаются из
виду (в частности, и доказательству теоремы Рэлея относится
лишь к простейшим дискретным собственным значениям). Но
если ограничиться лишь дискретны^ спектром, то краевая за-
задача для укороченного уравнения {2.29) вообще, как правило,
при каждом фиксированном k будеу иметь лишь конечное чис-
число собственных функций, так что ни о какой полноте системы
этих функций не может быть и речи (а в частном случае те-
течения Куэтта, где ?/" = 0, собственные функции, обращающиеся
в нуль на двух границах течения, даже вообще отсутствуют).
Если же добавить еще и собственные функции непрерывного
спектра, то. прежде (Всего надо точно определить, что под этим
понижается, и исследовать поведение всех соответствующих
функций при t-+-<x>; в дальнейшем требуется еще доказать пол-
полноту полученной системы функций, что также представляется
не простым делом. Таким образом, на самом деле доказатель-
доказательство устойчивости течений невязкой жидкости не вытекает из
одной только теоремы Рэлея, а требует привлечения еще каких-
то дополнительных тонких рассмотрений.
В этой связи Кэйз A960а, б) и Дикий A960а, б) указали не-
независимо друг qt друга, что при исследовании устойчивости те-
течений идеальной жидкости целесообразно вообще отказаться от
рассмотрения элементарных волновых решений вида B.27). Вме-
Вместо этого следует с самого начала решать задачу е начальным
условием т!р(х, г, 0) — ^0(x, г) для дифференциального уравне-
уравнения в частных производных B.26) с нулевой правой частью
(т. е. с v — 0; это и есть тот второй подход к задаче об устой-
устойчивости течений идеальной жидкости, о котором говорилось на
стр. 120). Оказывается, что общее решение этой задачи с на-
начальным условием может быть представлено в виде некоторого
интеграла Лапласа, асимптотическое поведение которого при
^-»-оо может быть изучено с помощью обычных методов тео*
рии функций комплексного переменного. При этом подынте-
подынтегральное выражение в соответствующем интеграле Лапласа

122 ГЛ. I. ЛАМИНАРНЫЕ Й ТУРБУЛЕНТНЫЙ ДВИЖЕНИЙ . [2.8
может быть также использовано и для аккуратного определе-
определения набора собственных функций (относящихся как к непре-
непрерывному, так и к дискретному спектру) уравнения .B.29); тог-
тогда полнота этого набора функций получается уже автоматиче-
автоматически (так как по ним разлагается решение произвольной задачи
с начальным условием). Однако, как мы уже отмечали; с
точки зрения теории устойчивости рассмотрение элементарных
волновых решений, удовлетворяющих B.29), вовсе не нужно,
так как поведение при t-*-oo общего решения задачи с на-
начальным условием сразу определяет, будет ли течение.устойчи-
течение.устойчивым или нет. Кэйзом A960а) и Диким A9606) было независимо
показано, что во всех случаях возрастающие решения задачи с
начальными условиями для уравнения B.26) могут существо-
существовать лишь тогда, когда соответствующее уравнение B.29) имеет
дискретные собственные значения с, у которых Зт с > 0 (или
кратные собственные значения с, у которых Зтс = 0), Тем са-
самым они впервые строго оправдали вывод, который обытао де-
делался из теоремы Рэлея (заметим, что более детальное иссле-
исследование уравнения B.29) показывает, что изменение знака
i/"(z) внутри потока необходимо также и для существования
чисто вещественных собственных чисел с; см. Линь, A955),
§ 8.2). Любопытно, что для частного случая плоского течения
Куэтта в идеальной жидкости описанный здесь подход был
применен еще Орром {1906—1907), выписавшим решение зада-
задачи с начальным условием для малого возмущения в таком те-
течении и показавшим, что оно будет затухать; позже, однако,
этот результат Орра был забыт. Дикий и Кэйз показали так-
также (см., особенно, Кэйз A961)), что решение задачи с началь-
начальным условием ty(x, z, 0) = \f>o(*, z) для полного уравнения
B.26) при v-»-0 всегда стремится к решению той же задачи
для укороченного уравнения. Таким образом, и в этом отноше-
отношении задача с начальным условием имеет заметное преимуще-
преимущество перед краевой задачей для уравнения B.28), в которой нет
никакой простой связи между собственными значениями и функ-
функциями полного и укороченного уравнений (ср. Линь A961),
Линь и Бенни A962)).
Предположим теперь, что профиль скорости U(z) имеет
точку перегиба, т. е. что U"(z) в какой-то точке обращается в
нуль. Толмином A935) было доказано (см. также Линь A955),
§ 8.2), что при некоторых дополнительных условиях (выпол-
(выполняющихся во многих практически интересных случаях) отсюда
уже следует, что соответствующее' уравнение B.29) будет
иметь собственные значения с такие, что Зт с > 0. В случаях,
к которым применим результат Толмина, течение невязкой
жидкости, очевидно, будет неустойчивым. Другие точные уело-

' I 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 123
вия неустойчивости плоскопараллельных течений идеальной
жидкости можно найти у Розенблюта и Саймона A964).
Заметим еще, что трудности, возникающие при исследова-
исследовании неустойчивости плоскопараллельных течений идеальной
жидкости, в случае жидкости с переменной по «высоте» (т. е.
координате г) плотностью сохраняются и при наличии отличной
от нуля вязкости, т. к. здесь соответствующее обобщенное ура-
уравнение Орра — Зоммерфельда даже и при хф 0 будет иметь осо-
особенность в точке, в. которой U(z) — с (см., например, Дикий
A960а).) 1). Поэтому механическое перенесение на этот случай
правил выбора ветви многозначных решений, разработанных
для случая течений жидкости постоянной плотности, произве-
произведенное в работе Шлихтинга A9356), нельзя считать обоснован-
обоснованным. Также и непосредственное сведение задачи об определен,
нии критерия неустойчивости к задаче на собственные значе-
значения без привлечения непрерывного спектра здесь оказывается
несостоятельным из-за неполноты соответствующей системы
собственных функций. Отсюда вытекает, что в случае течений
жидкости переменной по высоте плотности и при v = 0 и при
v Ф 0 строгий анализ устойчивости течения требует изучения
асимптотического поведения при t-+oo решения соответствую-
соответствующей общей задачи с начальным условием. Возникающая при
этом задана анализа является весьма трудной, и некоторые
успехи здесь были' достигнуты лишь сравнительно недавно и
притом лишь в предположении, что v = 0 (т. е. для идеальной
жидкости).
А именно, Элиассен, Хойланд и Риис A953), а затем, более
аккуратно, Дикий A960а) и Кэйз\ A9606) исследовали асим-
асимптотическое поведение решения задачи с начальным условием
для функции тока возмущения в случае двумерного потока не-
неоднородной тяжелой жидкости с экспоненциально убывающей
плотностью, заполняющего неограниченное полупространство и
имеющего линейный профиль скорости. Они показали при этом,
что, как и в случае плоскопараллельных течений идеальной од-
однородной жидкости, неустойчивость (в смысле наличия возра-
возрастающих возмущений) здесь может возникнуть лишь при су-
существовании волновых возмущений вида B.27) с возрастаю-
возрастающими амплитудами (т. е. с 3mc>0). В силу результатов ис-
исследования волновых возмущений в таком потоке, произведен-
произведенного еще в 1915 г. Дж. Тэйлором (но опубликованного много
') Правда, если кроме отличной от нуля вязкости учесть еще и отлич-
отличную от нуля теплопроводность, то мы снова придем к обычной задаче на соб-
собственные значения (на этот раз уже шестого порядка), не содержащей осо-
особенности в коэффициенте при старшем члене (см. Коппел A964)).

124 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.8
позже, см. Тэйлор A931)), дополненного недавно более стро-
строгим математическим анализом поведения нулей гипергеометри-
гипергеометрических функций Уиттекёра, независимо выполненным Диким
A960в) и Дайсоном (I960), отсюда вытекает, что рассматри-
рассматриваемый поток неоднородной жидкости будет устойчивым (в ука-
указанном смысле) при всех значениях Ri > 0 (а не только при
Ri > 1/4, как утверждается в известных монографиях Прандт-
ля A949) и Шлихтинга A951, 1959). Позже аналогичный же
метод исследования был применен Майлсом A961) к общему
случаю плоскопараллельного потока невязкой неоднородной
тяжелой жидкости с практически произвольным профилем плот-
плотности p(z) (таким, что p'(z) <0 при всех г, так что плотность
монотонно убывает по высоте) и любым монотонным профилем
скорости U(г). При этом им было показано, что и здесь из су-
существования неустойчивых возмущений вытекает также суще-
существование неустойчивых волн с функцией тока вида B.27). Да-
Далее Майлс детально исследовал возможные в таком потоке вол-
волновые возмущения; в результате ему удалось доказать, что рас-
рассматриваемый поток наверное будет устойчивым, если во всех
его точках Ri > 1/4 (частные случаи этого последнего резуль-
результата фактически содержатся также в работах Гольдштейна
A931) и Дразина A958), посвященных рассмотрению волно-
волновых возмущений в некоторых специальных потоках идеальной
жидкости переменной плотности). Общий результат Майлса
был доказан также значительно более просто (с помощью не-
некоторых интегральных неравенств, аналогичных использовав-
использовавшимся в свое время Рэлеем) и. при более общих условиях (без
всяких ограничений на профили скорости и плотности) Хоу-
ардом A961). Кроме того, Кэйз A960в) проанализировал так-
также и поведение решения задачи с начальным условием для воз-
возмущения в неподвижной идеальной жидкости в полуплоскости
z >0 с экспоненциально возрастающей плотностью; при этом
он, естественно, нашел решения, неограниченно возрастающие
с течением времени (ср. выше стр. 97), и оценил максимальную
достижимую скорость их роста. Некоторые другие примеры
анализа поведения решений задачи с начальным условием для
возмущений в жидкости с возрастающей с ростом г плотно-
плотностью (но уже отличным от нуля градиентом скорости) можно
найти в работе Элиассена, Хойланда и Рииса A953). Подроб-
Подробное исследование возможных волновых возмущений в некото-
некоторых конкретных плоскопараллельных течениях расслоенной по
плотности идеальной жидкости (с убывающей с высотой плот-
плотностью) было произведено Майлсом A963) и Хоуардом A963).
При этом выяснилось, что «принцип смены устойчивости» (см.

2.8J $ 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 125
стр. 107) здесь выполняется лишь при некоторых специальных
условиях, а область неустойчивости на плоскости (?>Щ) мо-
может состоять из нескольких кусков.
Теория неустойчивости для плоскопараллельных течений
вязкой жидкости
Вернемся теперь снова к более сложному случаю течений
вязкой жидкости; плотность, как обычно, будет считаться по-
постоянной. В этом случае уравнение Орра — Зоммерфельда B.28)
имеет чисто дискретный спектр, и, по-видимому, нет оснований
для сомнений в том, что любое решение уравнения B.26) может
быть представлено в виде суперпозиции «плоских волн» вида
B.27). Поэтому здесь вполне можно ограничиться изучением
обычной задачи на собственные значения для уравнения Орра —
Зоммерфельда B.28). Первые попытки такого изучения, пред-
предпринятые (с помощью не очень строгих математических мето-
методов) около 1910 г. рядом авторов (В. Орр, А. Зоммерфельд,
Р. Мизес, Л. Хопф и др.) в применении к плоскому течению
Куэтта с линейным профилем скорости, привели к выводу, что
это течение является устойчивым при всех числах Рейнольдса.
Этот вывод казался, с одной стороны, довольно естественным
(так как Орром A906—1907) было доказано, что при отсут-
отсутствии вязкости течение Куэтта устойчиво, а действие вязкости,
естественно, предполагалось стабилизирующим); но, с другой
стороны, он явно противоречил эмпирическим фактам о тур-
булизации всех известных течений при достаточно больших чис-
числах Рейнольдса. В начале 20-х годов Прандтль A921) и Тить-
енс A925) рассмотрели вопрос об "устойчивости течений с про-
профилем скорости, составленным из отрезков прямых, и пришли
к совсем неожиданному выводу, что при наличии вязкости та-
такие течения будут неустойчивыми при любых (в том числе и
сколь угодно малых) числах Рейнольдса. В те же годы появи-
появилась большая работа Гейзенберга A924), посвященная иссле-
исследованию с помощью метода малых колебаний устойчивости
плоского течения Пуазейля. В этой работе с помощью тонкого
исследования .асимптотического поведения решения соответ-
соответствующего уравнения Орра -~ Зоммерфельда при большом Re
(т. е. малом v) был получен казавшийся в то время парадоксаль-
парадоксальным (но оказавшийся тем не менее правильным) результат о
том, что течение Пуазейля, которое при отсутствии вязкости бу-
будет устойчивым по отношению к малым возмущениям, в случае
вязкой жидкости при достаточно больших числах Рейнольдса
становится неустойчивым. Результат Гейзенберга, однако, долго
вызывал серьезные, сомнения, и доказательства устойчивос.ти,

126 ГЛ, I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ B.8
плоского течения Пуазейля продолжали' публиковаться еще
много лет (по-видимому, последнее такое «доказательство» бы?
ло дано Пекерисом в 1948 п).
В работе Толмина A929) методом малых возмущений иссле-
исследовалось течение в пограничном слое, которое он рассматривал
как плоскопараллельное и имеющее профиль скорости, состав-
составленный из отрезков прямых и парабол; при этом впервые удалось
получить форму «кривой нейтралвных возмущений» на плоско-
плоскости (k, Re), отделяющую область устойчивых возмущений от
неустойчивых возмущений. В дальнейшем Толмин A930, 1947) и
Шлихтинг A933а, б; 1935а) перенесли эти результаты также
и на случай произвольных профилей скорости. В 1944—1945 гг.
вся теория устойчивости плоскопараллельных потоков была кри-
критически пересмотрена Линем A945), пересчитавшим заново
основные примеры и уточнившим численные результаты
Толмина и Шлихтинга. Тем не менее, сложность используемых
при этом методов анализа асимптотического поведения реше-
решений уравнения B.28) приводит к тому, что еще до сих пор по-
лучейные результаты в некоторых отношениях нельзя считать
окончательными. Дело в том, что используемые асимптотиче-
асимптотические ряды обычно имеют особенность в точке г, в которой
U(г) —с — 0, в то время как исходное уравнение регулярно в
этой точке. Поэтому большой интерес представляет нахожде-
нахождение равномерно сходящихся асимптотических разложений, но
построение таких разложений пока наталкивается на большие
трудности (см., например, Линь и Бенни-A962)).
Выше мы уже отмечали, что, строго говоря, плоскопарал-
плоскопараллельный поток вязкой жидкости может быть лишь комбина-
комбинацией течений Куэтта и Пуазейля. В настоящее время мало кто
сомневается в том, что плоское течение Куэтта яв-
является устойчивым по отношению к любым бесконечно малым
возмущениям; но строго этот факт, по-видимому, до сих пор
никем не был доказан. Большинство относящихся сюда иссле-
исследований использует некоторые асимптотические соотношения
для рассмотрения предельных случаев (обычно случаев очень
большого числа Рейнольдса), в то время как для не слишком
больших значений параметров применяется прямой численный
расчет собственных значений соответствующего уравнения
B.28). Такой подход был систематически развит еще Саусвел-
лом и Читти A930) (ограничившимися, впрочем, лишь чисто
мнимыми собственными значениями в соответствии с «принци-
«принципом смены устойчивости»). В последние годы он достиг очень
большого развития в связи со значительным усовершенствова-
усовершенствованием техники.асимптотических оценок и применением для чис-
численных расчетов быстродействующих электронных вычисли-

Щ $ 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ Й7
тельных машин (см., например, Вазов A953), Троне A954),
Риис A962) •), Галлахер и Мерсер A962, 1964), Дирдорф
X1963)). Во всех перечисленных работах были обнаружены
лишь устойчивые . волновые возмущения плоского течения
Куэтта. Это делает очень правдоподобным, что неустойчивых
возмущений здесь вообще не существует, но не позволяет все
же считать проблему окончательно решенной, так как вся об-
область значений параметров, к которой не приложимы асимпто-
асимптотические оценки, еще не исчерпана. По-видимому, единствен-
единственный точный математический результат, относящийся к собст-
собственным значениям уравнения B.28) с U(z) = Az при произ-
произвольных числах Рейнольдса, принадлежит Дикому A964), до-
доказавшему (без применения численных расчетов), что чисто
мнимые собственные значения с этого уравнения все удовлет-
удовлетворяют неравенству %тс <—k/Re (где Re — число Рейнольдса,
построенное по значению #i = Я/2 полуширины канала и мак-
максимальной скорости течения U = 2AHi). Этот результат, в част-
частности, показывает, что переход к неустойчивости здесь никак
не Может происходить с соблюдением «принципа смены устой-
устойчивости», но и он не гарантирует, что неустойчивость вообще
невозможна.
Значительно более, удовлетворительным представляется по-
положение в отношении плоского течения Пуазейля.
Здесь, после того как тщательные расчеты Линя, основанные
на асимптотических разложениях специального типа, примени-
применимых при больших Re, подтвердили основной вывод Гейзенбер-
га о неустойчивости этого течения и позволили найти форму
кривой нейтральных возмущений- %тс(k, Re) =0, эти резуль-
результаты были еще раз проверены Томасом A953) с помощью чис-
численного решения соответствующей задачи на собственные зна-
значения, а затем частично также и Локком A955), использовав-
использовавшим усовершенствованную форму асимптотических разложе-
разложений. Результаты всех этих расчетов оказались вполне удовле-
удовлетворительно совпадающими друг с другом (см., например,
рис. 14). В дальнейшем Шэнь (.1954) рассчитал по методу Линя
для этой задачи также и форму кривых %m.c(k, Re) = const, оп-
определяющих совокупность возмущений с заданной быстротой
возрастания. Форма «нейтральной кривой» ^mc(k, Re) = 0, где
Re = UHJv, U — максимальная скорость невозмущенного те-
течения, найденная Линем и Локком, показана на рис. 14. Крити-
Критическое число Рейнольдса (отвечающее самой левой точке этой
кривой) оказалось равным примерно 6000 по данным Локка и
') В этой работе исследуются также и волновые возмущения в потоке
вязкой жидкости переменной плотности с линейным профилем скорости.

128
ГЛ. 1. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
[2.8
примерно 5300 по данным Линя, причем ему у обоих исследо-
исследователей отвечает значение k~'\/Hi (близкие значения Recr »
«5780 и k ~ 1,02/Н+ были получены также Томасом). При
Re-»-oo обе ветви нейтральной кривой (и верхняя и нижняя)
стремятся к нулю (верх-
kHi . Расчет Линя
Pscven?
1.0
о,в
0,6
20
Рис. 14. Форма нейтральной кривой на
(* R)
няя ветвь асимптоти-
асимптотически пропорционально
Re-'/", а нижняя — про-
пропорционально Re-'/'). Та-
Таким образом, при увели-
увеличении Re возмущения с
фиксированным (но не
слишком большим) к сна-
сначала оказываются в об-
области устойчивости (т. е.
затухают), затем попа-
попадают в область неустой-
неустойчивости, а в конце кон-
р р р
плоскости (*, Re) для плоского течения
Пуазейля по расчетам Лння A945) и НОВ-снова оказываются в
Локка A955). области устойчивости.
Отсюда понятно, почему
в пределе при Re-»-oo (т. е. v-»-0) течение оказывается устой-
устойчивым относительно любых возмущений.
Устойчивость течений в трубе и в пограничном слое
Результаты, относящиеся к плоскопараллельным течениям,
разумеется, не могут быть непосредственно применены к те-
течению Пуазейля в трубе. Можно, однако, попытаться
и к этому течению применить теорию возмущений. Ограничив-
Ограничившись лишь простейшими волновыми возмущениями вида
и'(х, t) =/ (r)ei(ftx+n<P-@(), Тйы, как обычно, придем к некоторой
задаче на собственные значения. Исследования различных част-
частных случаев этой задачи, проводившиеся разными авторами
(см., например, Преч A9416), Белякова A950), Сексл и Шпиль-
берг A958), Коркос и Селларс A959) и Кропик A964), где
можно найти также дальнейшие ссылки), не привели к об-
обнаружению каких-либо возрастающих волновых возмущений.
Поэтому в настоящее время большинство специалистов пред-
предполагает, что течение-Пуазейля в трубе (так же, как и плоское
течение Куэтта) при всех числах Рейнольдса устойчиво по от-
отношению к любым бесконечно малым возмущениям! Однако ни
одна из_имекццихся работ не содержит строгого доказательства
этого фактаТПрежде всего, большинство авторов 'вообще рас-
рассматривало только самые простые не зависящие от <р осесим-

2.8] 8 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 129
метричные волновые возмущения с п = 0 (для которых возни-
возникающая задача на собственные значения оказывается родствен-
родственной задаче, определяющей устойчивость или неустойчивость
плоскопараллельных течений типа плоского течения Куэтта);
для общих же волновых возмущений с пФ 0 устойчивость пока
доказана лишь в некоторых очень специальных случаях (на-
(например, в случае не зависящих от х возмущений с k = О или
таких возмущений, что. tir(x, ?)=0). Таким образом, пока
нельзя исключить возможности существования каких-либо бо-
более сложных не осесимметричных волновых возмущений,
являющихся неустойчивыми. Кроме того, даже и для осесимме-
осесимметричных возмущений дело обстоит не так просто, как это обыч-
обычно предполагается. В связи г. наличием в уравнении для осе-
осесимметричных возмущений течения Пуязейля особой точки при
г = О общее решение задачи с начальными условиями здесь
"опять не'может быть разложено по простейшим «волновым воз-
возмущениям», отвечающим дискретному спектру; поэтому общее
исследование устойчивости таких возмущений не оводится к
задаче на собственные значения. Отсюда вытекает, что вопрос
об устойчивости течения Пуазейля в трубе даже и для простей-
простейших осесимметричных возмущений (для которых строго дока-
доказано отсутствие возрастающих волновых решений) пока нельзя
считать выясненным до конца.
Перейдем теперь к рассмотрению случая течения в погра-
пограничном слое на плоской пластинке. Так как со-
согласно результатам а. 1.4 толщина пограничного слоя возра-
возрастает сравнительно медленно ji вертикальная ^корпгть здесь
^НЯЧИТРЛЬНО МРНЫН<* тризпитпттьяпй тп ррть m4jm»QU»fl ряОГЧГ'
ТЫвать, ЧТО И К ?Т"МУ трчрниш г нрплпуои точности" можно
приложить теорию yr™ft4iinntvrn длтт пгсппгорзраллельных тече-
ний (некоторые оценки влияния поправочных членов в уравне-
уравнении Орра — Зоммерфельда B.28), возникающих при рассмотре-
рассмотрении почти, но не точно плоскопараллельных течений, позволяю-
позволяющие в известной мере оправдать это предположение, были
выполнены Пречем A941а)). Поэтому Толмин и Шлихтинг в сво-
своих расчетах много внимания уделили устойчивости плоскопа-
плоскопараллельного течения с профилем скорости, совпадающим или
близким к профилю Блазиуса (изображенному на рис. 2
на стр. 54). В результате они сумели построить кривую
%mc(k, Re) = 0, т. е. определить границу области неустойчиво-
неустойчивости в плоскости (k, Re), имеющую по их данным примерно ту же
форму, что и кривая %mc(k,Re) =0 на рис. 14. Критическое
число Рейнольдса Res» « = (—7") • гДе 6* — толщина вытесне-
вытеснения пограничного слоя, определяемая формулой A.53), по Тол-

1.50
ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЙ
[2.8
мину оказалось равным 420, а по Шлихтингу—575. Согласно
формуле A.56) это означает, что Re*Cr = {Ux/\)CT = 0,6- 105 по
Толмину и Re*cr= 1,1 • 105 по Шлихтингу. Тот факт, что эти
значения Reacr несколько ниже указанных в п. 2.1, может быть
естественно объяснен тем, что потеря устойчивости вовсе не дол-
должна сопровождаться мгновенным переходом к турбулентному
режиму. В точке потери устойчивости лишь возникают некото-
некоторые нарастающие колебания, которые усиливаются, сносясь
вниз по течению, и при каком-то большем х вызывают пе-
переход к развитой турбулентности. С другой стороны, однако,
полученные значения Recr сами по себе никак не могут рассма-
рассматриваться и как подтверждающие теорию Толмина — Шлихтин-
га, и поэтому неудивительно, что еще Тэйлор A938) высказы-
высказывал сомнение в законности применения этой теории к реаль-
реальному течению в пограничном слое, не являющемуся на самом
деле плоскопараллельным. Однако непосредственная экспери-
экспериментальная проверка теории Толмина — Шлнхтинга, произве-
произведенная Шубауэром и Скрэмстедом A947) как раз на примере
течения в пограничном слое, подтвердила в основных чертах
все ее выводы и тем самым показала, что сомнения в правиль-
правильности этой теории не являются основательными. После этого
Линь A945) и Шэнь A954) еще раз повторили расчеты Тол-
Толмина и Шлихтйнга и получили снова значение Res««r = 420, но
несколько отличающуюся от прежних форму границы области
неустойчивости, показанную на рис. 15.
Упоминавшиеся выше опыты Шубауэра и Скрэмстеда про-
производились в аэродинамической трубе Национального ^бюро
0,4t—i/T^taLj—i—i—i—т—i—i стандартов США в Вашинг-
Вашингтоне, обладающей особенно
малой начальной турбулент-
турбулентностью; параметр U'/U в
этой трубе нри соблюдении
некоторых специальных мер
предосторожности может
быть доведен до значе-
значений порядка 0,0003—0;0002.
Это обстоятельство ока*
залось очень. важным,
так как некоторые -имею-
-имеющиеся в настоящее время результаты показывают, что при
значениях U'/U, превышающих 0,002 (т. е., в частности, при
значениях, имевшихся во всех более старых опытах) переход
к турбулентности, по-видимому, вызывается влиянием конеч-
конечных возмущений во внешнем потоке в соответствии с описанной
в п. 2.2 схемой Тэйлора, Однако при U'/U < 0,002 основную
Рис. 15. Форма нейтральной кривой на
плоскости (*, Re5.) для пограничного
слоя над плоской пластинкой.

2.8]
§ 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ
131
роль при этом переходе играют случайные малые двумерные
возмущения синусоидальной формы, амплитуда которых при
некоторых условиях возрастает вниз по течению в полном со-
соответствии с выводами теории возмущений. Подобные правиль-
правильные колебания и были еще в 1940 г. обнаружены Шубауэром и
Скрэмстедом с помощью тщательных термоанемометрических
наблюдений. В дальнейшем с целью более аккуратной провер-
проверки выводов теории эти авторы использовали также помещенную
в пограничный слой тонкую металлическую ленту, приводимую
в колебание при помощи электромагнита и создающую искус-
искусственные возмущения фиксированной частоты а. При этом им
удавилось обнаружить нейтральные (не возрастающие и не за-
затухающие) почти чисто синусоидальные колебания скорости,
соответствующие точкам граничной кривой на диаграмме устой-
устойчивости. Для сопоставления этих данных с выводами теории
удобно рассмотреть вместо более
обычных возмущений вида B.27)
с фиксированным волновым числом и*
к возмущения_вида_^_=^ЦИ~<й')фB)
с "фиксированной .(вещественной^. 301)'_
гтУпгм^„дшпдпгппдм) h\ т г ггг
"следовать fi
700
р
вдоль пластинки (т. ё. с ростом х)
возмущений заданной частоты <а,
создаваемых в фиксированной точ-
точке потока (о связи такого подхода
к теории устойчивости с обычным
c^i:^jcjra™o__racTe4ia--Xl§g2}j. При
"этом мы можем рассчитать кривую
Зт&(<й, Re) = 0 и получить, таким
образом, форму области неустойчи-
неустойчивости на плоскости (со, Re). Резуль-
Результаты такого подсчета (по данным
Шэня A954)) приведены на рис. 16
вместе с эмпирическими точками
Шубауэра и Скрэмстеда для частот
нейтральных возмущений. Совпаде-
Совпадение теории с опытом здесь оказы-
оказывается вполне удовлетворительным.
Впоследствии опыт Щубауэра и Скрэмстеда был повто-
повторен также Бэрнсом, Чайлдсом, Николом и Россом A959), ис-
использовавшими вместо термоанемометра помещенную в поток
посеребренную пластинку. Пульсации этой пластинки, созда-
создаваемые z-компонентой скорости потока, вызывали пульсации
1000
Рис. 16. Рассчитанная форма
нейтральной кривой на пло-
плоскости (ш, Re5») для погранич-
пограничного слоя на плоской пластинке
и экспериментальные данные
о частотах нейтральных коле-
колебаний.

132
ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
[2.8
отражения направленного на нее пучка света, которые легко
поддавались измерению. Результаты, полученные этими авто-
авторами, указаны на рис. 16 крестиками; они также хорошо сов-
совпадают с выводами теории1). На рис. 17 приведены эмпириче-
эмпирические данные Шубауэра и Скрэмстеда, касающиеся на этот раз
0,4
0,2
•
¦**—
—¦—,
•
¦•¦—
*
— —
¦——
— —
2М0
3200
Рис. 17. Эмпирические данные о волновых числах ней-
нейтральных возмущений в пограничном слое иад плоской
пластинкой по данным Шубауэра и Скрэмстеда.
волновых чисел нейтральных возмущений; эти данные тоже не-
неплохо укладываются на теоретическую кривую. Дальнейшие
данные, касающиеся сравнения эмпирических данных Шубауэ-
Шубауэра и Скрэмстеда с выводами теории, можно найти в книгах
Линя A955) и Шлихтинга A951, 1959) и в обзорных статьях
Драйдена A959) и Стюарта A963).
Аналогично проводятся также расчеты нейтральной кривой
и в случае более сложных профилей скорости, соответствую-
соответствующих, например, пограничному слою при обтекании искривлен-
искривленных поверхностей и при течениях с градиентом скорости во
внешнем потоке. Любопытно, что форма получаемой при этом
кривой существенно зависит от того, имеет ли профиль скоро-
сти точку перегиба (т. е. обращается ли -^ в нуль при неко-
некотором z) или нет. В последнем случае граница области устой-
устойчивости имеет то же характер, что и в случаях течения Пуазей-
'} В работе Бэрнса и др. отмечается, впрочем, что полученные экспери-
экспериментальные результаты со старой нейтральной кривой Шлихтинга согласуются
даже немного лучше, чем с кривой, рассчитанной Линем и Шэнем. Однако
эти результаты все относятся к той части нейтральной кривой, относительно
которой результаты Шлихтиига и результаты Линя н Шэня очень мало рас-
расходятся друг с другом; поэтому их никак нельзя считать решающими при
сравнении соответствующих теоретических кривых.

2.8]
§ 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ
133
ля между двумя плоскостями и ллоскопараллельного течения в
полупространстве г>0с профилем Блаузиуса (см. рис. 14 и
15), т. е. при Re-ххэ обе ее ветви стягиваются к оси абсцисс.
Таким образом, при отсутствии у
профиля скорости точки перегиба
любые возмущения фиксированной
длины волны (или фиксированной
частоты) при возрастании числа
Рейнольдса в конце концов стано-
становятся устойчивыми. В случае же
наличия у профиля скорости точки
(или точек) перегиба верхняя гра-
граница области устойчивости при
Re -*¦ оо имеет конечную асимпто-
асимптоту (см. рис. 18); иначе говоря, здесь
существует интервал длин волн
(или частот) таких, что соответст-
соответствующие возмущения неустойчивы
при сколь угодно больших числах
Рейнольдса. Это обстоятельство,
очевидно, непосредственно связано
с определяющей ролью наличия точки перегиба у профиля ско-
скорости для неустойчивости течений идеальной жидкости.
Устойчивость некоторых плоскопараллельных течений
в безграничном пространстве
В качестве конкретного примера течения с профилем, имею-
имеющим точку перегиба, рассмотрим плоскопараллельное течение
в безграничном пространстве —с» < z < с», имеющее профиль
вида
"* ШГ B.31)
Re
Рис. 18. Схематическая форма
нейтральной кривой в плоско-
плоскости (k. Re) для течения с про-
профилем скорости, имеющим
точку перегиба (например, для
пограничного слоя при наличии
замедляющего градиента да-
давления).
(см. рис. 19, а). Согласно расчетам Шлихтинга и Бикли (см.,
например, Шлихтинг A951), гл. IX, § 6, или Цольдштейн
A938), т. I, § 57) формулой такого вида будет задаваться про-
профиль продольной скорости «1 = U в ламинарной плоской
струе (бьющей из бесконечного тонкого линейного отверстия,
расположенного йдоль прямой х = 0, z = 0, в пространство, за-
заполненное той же жидкостью) на большом расстоянии от этого
отверстия. При этом параметры ?/о и Н здесь будут лишь сра-
сравнительно слабо зависеть от х, а поперечная скорость us= w
будет мала по сравнению с продольной. Таким образом, плоско-
плоскопараллельное течение с профилем B.31) можно рассматривать

134
ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
[2.8
как модель плоской струи на большом расстоянии от выход-
выходного отверстия; именно в этой связи его устойчивость и изуча-
изучалась рядом авторов (в частности, Керлом A956), Тацуми и
Какутани A958), Хоуардом A959) и Кленшоу и Эллиоттом
(I960)).
Определение нейтральной кривой на плоскости (k, Re) для
течения с профилем B.31), как всегда, сводится к исследова-
исследованию задачи на собственные значения для соответствующего
уравнения Орра — Зоммерфельда B.28), причем неограничен-
неограниченность этого течения позволяет даже немного упростить расчеты
z/V
z/H
-и„
г/Я
-ио
Рис. 19. Схематические формы профилей скорости для некоторых плоско-
параллельных течений в безграничном пространстве. N
а) Плоская струя; 6) течение с поверхностью тангенциального разрыва скорости; в) и г) зоне
смешения двух плоских потоков разной скорости.
по сравнению со случаем течения между твердыми стенками
(так как здесь надо рассматривать^только решения уравнения
B.28), затухающие на бесконечности). Кроме того, в силу сим-
симметричности профиля B.31) все собственные функции <p(z)
здесь распадаются на четные и нечетные по г. Так как и экс-
эксперименты и предварительные расчеты показывают, что наи-
наиболее неустойчивыми всегда оказываются возмущения с чет-
четным <p(z), то при детальных вычислениях можно ограничиться
лишь областью 0<г<оо и граничными условиями <р(оо) =
= ф'(оо) =0 и ф'@) = <р"'@) = 0. Результаты таких вычисле-
вычислений, проведенных двумя различными методами Керлом A956)
и Тацуми и Какутани A958), представлены на рис. 20. Мы ви-
видим, что они в общем неплохо согласуются друг с другом (кро-
(кроме области малых значений к, где метод Керла является недо-
недостаточно точным). Согласно рис. 20, при Re-voo все возмуще-
возмущения с k < 2/# оказываются неустойчивыми; кроме того, с ростом
R? область неустойчивых волновых чисел монотонно расши-

2.8]
§. 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ
135
ряется, так что увеличение вязкости может оказывать лишь
стабилизирующее действие на возмущения (в отличие от ситуа-
ситуации в случае течений с профилем скорости без точки перегиба).
Критическое число Рейнольдса здесь принимает очень неболь-
небольшое значение (что также типично для течений с профилем скоро-
скорости, имеющим точку перегиба): согласно тщательным численным
расчетам Кленшоу и Эллиотта A960), для профиля B.31)
(^) «3,7 и &сг « 0,25/Я (заметим, что в реальных
Расчет
Тацулш и h'акутами
Расчет Нерла
Рис. 20. Форма нейтральной кривой на плоскости
(Л, Re) для плоской струи по расчетам Керла A956)
и Тацуми и Какутани A958).
струях значение Re « 4 обычно достигается в области течения,
в которой струю никак нельзя считать плоскопараллельной).
Другой важный тип течений в безграничном пространстве
с профилем скорости U(z) с точкой перегиба представляют
собой течения, для которых U(z) -*¦ Uo при z->- + се и
U(г)-*-—Uo при Z-+-—оо. Простейшим течением такого типа
является идеализированное течение с ломаным профилем ско-
скорости, изображенным на рис. 19, б; это течение описывает пло-
плоскую поверхность тангенциального разрыва
скорости. Более реальные профили того же типа изобра-
изображены на рис. 19, в и 19, г; они качественно соответствуют ла-
ламинарной зоне смешения двух плоскопараллельных по-
потоков, текущих с разными скоростями один над другим. Как
мы уже говорили в п. 2.4, в пренебрежении вязкостью неустой-
неустойчивость течения с профилем, изображенным на рис. 19, б, была
строго доказана еще Гельмгольцем. Позже Рэлей подробно

136 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.9
исследовал вопрос об устойчивости течения невязкой жидкости
с профилем, изображенным на рие. .19, в (а также и с некото-
некоторыми другими ломаными профилями, приближенно описываю-
описывающими плоские струи; см. Рэлей A894), т. 2, гл. 21); его резуль-
результаты также указывают на неустойчивость всех рассматривае-
рассматриваемых течений (в последние годы эти исследования Рэлея были
продолжены Дразиным и Хоуардом A962) и Михалке A964)).
С учетом вязкости устойчивость течения с профилем типа
рис, 19, г была изучена Лессеном A950); однако результаты
Лессена относились только к случаю достаточно больших
чисел Рейнольдса и фактически показали лишь, что здесь
Recr < 20 (в книге Линя A955), исходя отсюда, было ошибочно
предположено, что в этом случае Recr по порядку близко к чис-
числу 20). Позже Эш A957) исследовал численно задачу на соб-
собственные значения для уравнения Орра — Зоммерфельда B.28)
с функцией U(z), изображен-
изображенной на рис. 19, в, уже дл$ всех
значений Re и впервые нашел,
что течение с таким профилем
скорости на самом деле при
всех Re является неустойчив
0 jq 20 30 40 рГ вым (как показали Тацуми и
Гото A960), этот результат
Рис 21. Расположение нейтральной не связан со специальной фор-
кривой и области неустойчивости (на й пппЛиля пяггмятпивяв-
рисунке заштрихована) на плоскости мо» профиля, рассматривав-
(A, Re) для зоны смешения двух шеися Эшем, а относится к
плоскопараллельиых потоков по дан- широкому классу профилей,
иым Бетчова и Шевчика A963). соответствующих плоской зоне
смешения двух потоков). Об
общем характере нейтральной кривой на плоскости (k, Re) для
случая плоской зоны смешения дает представление рис. 21, на
котором изображены результатыг полученные Бетчовым и Шев-
чиком A963) (с помощью численного интегрирования соответ-
соответствующего уравнения Орра — Зоммерфельда) для профиля
U(z) = f/oth(z/H) (типа рис. 19,г).
2.9. Устойчивость по отношению к конечным возмущениям;
возрастание возмущений и переход к турбулентности
.Рассмотренная выше теория возмущения позволяет во мно-
многих случаях теоретически определить условия потери устойчи-
устойчивости ламинарных течений и тем самым выяснить, некоторые
важные обстоятельства, связанные. С переходом к турбулентно»
сти. Совершенно ясно, однако, что.сама по тебе потеря устойчи-
устойчивости еще не является таким переходом и что линейная теория,

2.9] § 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 137
о которой шла речь >в пп. 2.5—2.8, в лучшем случае может опи-
описать лишь самое начало процесса возникновения турбулентности,
но не дать полную картину этого процесса. Кроме того, в случае
некоторых важных течений, таких как, например, течение Куэтта
между двумя плоскостями или течение Пуазейля а трубе, теория,
возмущений в принципе не может помочь объяснению наблю-
наблюдаемого на опыте возникновения турбулентности, так как эти
течения, по-видимому, устойчивы относительно любых бесконеч-
бесконечно малых возмущений. С другой стороны, в случае, например,
течения Пуазейля между двумя плоскостями (близкого к реаль-
реальному течению в плоском канале) теория устойчивости хоть и
приводит к" выводу о возможности потери устойчивости, но ука-
указывает на значительно более высокое значение Recr, чем значе-
значения чисел Рейнольдса, при которых на самом деле происходит
турбулизация потока (эмпирические данные Дэвиса и Уайта
A928) показывают, что турбулизация плоского течения Пуазей-
Пуазейля, по-видимому, реально происходит уже при Re = UHJv »
«5 1000, в то время как согласно линейной теории Recr«* 6000).
Наконец, принципиальное различие между движениями, возни-
возникающими после потери устойчивости течения между вращаю-
вращающимися цилиндрами или состояния покоя подогретой снизу
жидкости, с одной стороны, и плоского течения Пуазейля или
течения в пограничном слое, с другой стороны, также никак не
может быть объяснено с точки зрения линейной теории возму-
возмущений. Все эти обстоятельства заставляют придавать большое
значение разработке более полной нелинейной теории возник-
возникновения турбулентности, находящейся пока что еще в началь-
начальной стадии своего развития.
Баланс энергии конечного возмущения
Простейший подход, позволяющий исследовать вопрос об
устойчивости потока по отношению к возмущениям конечной
амплитуды, связан с применением так называемого «энергети-
«энергетического метода», использовавшегося еще Рейнольдсом A894)
(и являющегося, таким образом, даже более старым, чем метод
теорий возмущений). Сущность этого метода состоит в опреде-
определении баланса энергии возмущения в заданном течении с целью
выяснения условии, при которых энергия такого возмущения
будет возрастать, (или, наоборот, убывать) во времени.
Пусть Ui(x, t) и Р(х, t) —поля скорости и давления основ-
основного течения, a u't (х, t) и р' (х, t) — поля скорости и давления
возмущения. В таком случае оба поля ut = Ut -j- u\ и Ut должны
удовлетворять уравнениям Навье—Стокса A.6) и неразрывности

138 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.9
A.5) (как обычно, жидкость предполагается несжимаемой).
Вычтя уравнения для щ и для ?/< одно из другого, мы получим
следующие уравнения для скорости a'e^aj, u'v а'аУ-
ди\ ди\ dUt ди, \ др'
(от уравнений B.7) они отличаются лишь наличием в первом
из них нелинейного по и' слагаемого, опускаемого в линейной
теории возмущений). Умножив, далее, первое из уравнений
B.32) на Uj/2, просуммировав по i и проинтегрировав получен-
полученную сумму по всей области течения, мы придем к уравнению
баланса энергии, определяющему изменение во времени полной
энергии возмущения. В частности, если течение жидкости про-
происходит в конечном объеме, ограниченном твердыми стенками
(неподвижными или движущимися), на которых ы^ = 0, то урав-
уравнение баланса энергии возмущения можно записать в виде
B.33)
рде dy — элемент объема (в таком виде оно фактически исполь-
использовалось еще Рейнольдсом A894) и Орром A906—1907)). Тот
же результат будет верен и для многих неограниченных тече-
течений; например, он будет справедлив, если возмущение допусти-
допустимо считать периодическим по тем^ координатам, по которым
течение является неограниченным (в этом случае следует счи-
считать, что интегрирование в равенстве B.33) в направлении та-
таких осей распространяется лишь на один период возмущения).
В уравнении B.33) первый член справа ^описывает обмен
энергией между основным течением и полем возмущений и, как
правило, оказывается положительным (перенос энергии ©бычдао
происходит от основного течения к возмущениям). Второй же
член справа описывает вызываемую вязкостью диссипацию
энергии возмущений и всегда является отрицательным. Относи-
Относительная величина двух членов в правой части B.33) и опреде-
определяет, будет ли энергия возмущения убывать или возрастать.
Если мы перейдем в равенстве B.33) к безразмерным вели-
величинам, измеряя расстояния в единицах характерной длины L,
скорости — в единицах характерной скорости U, а время—.в

2.9) § 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 139
единицах L/U, то размерный коэффициент v при втором члене
правой части перейдет в безразмерный коэффициент I/Re. Отсю-
Отсюда ясно, что если число Рейнольдса достаточно мало, то отри-
отрицательный второй член справа будет перевешивать положитель-
положительный первый член и энергия любого возмущения будет затухать,
т. е. течение будет устойчивым по отношению к возмущениям
произвольной величины. Исходя из равенства B.33), можно
получить некоторые оценки снизу значения Recrmin. ограничи-
ограничивающего диапазон «достаточно малых», чисел Рейнольдса, в
пределах которого энергия любого возмущения может только
убывать. Так, например, Серрин A959) показал, что для любой
пары соленоидальных векторных полей и' (X) и U(x) в произ-
произвольной ограниченной области с диаметром D, таких, что W об-
обращается в нуль на границе области, имеют место неравенства
''3 B.34)
где С/щах — максимум модуля поля U(x). Подставляя эти нера-
неравенства в B.33), найдем, что в случае течения в области диа-
диаметра D энергия E(t) возмущения заведомо удовлетворяет
неравенству
так 4ToReCrmin = (———)• >-1^3 я я» 5,44. Аналогичные не-
равенства Серрин вывел и для полей и' (х) и U(x), отвечающих
течениям в прямой трубе произвольного сечения с макси-
максимальным диаметром D или в канале максимальной тол-
толщины D. При этом только ему пришлось постоянную Зтс2 во
втором неравенстве B.34) в первом из указанных случаев заме-
заменить на 2т?, а во вторим — на тс2; тем самым он показал, что
Recr mm !> V^ iv «* 4,43 для течения в прямой трубе (произволь-
(произвольного сечения) и Recr min^- я « 3,14 для течения в плоском канале.
Позже Вельте A962) еще немного улучшил значения постоян-
постоянных коэффициентов во втором неравенстве B.34) и показал,
что Recr Ш|п >• У~6 тс « 7,7 для течения в ограниченной области
диаметра D, Recr mm^> ^4,7 iv ж 6,8 для течения в прямой трубе
диаметра D и Recr шт > V^J iv «* 6,0 для течения в канале

140
ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
[2.9
ширины D; одновременно он показал, что найденные им число-
числовые значения Recr mm очень близки к наибольшим,- могущим
быть полученными с помощью общих неравенств типа B.34).
Заметим еще, что неравенства того же типа существуют и для
полей и' (х) и U(x) в кольце между концентрическими цилинд*
рами радиусов Ri и Rz; с их помощью Серрин получил следую-
следующее достаточное условие устойчивости относительно произволь-
произвольных возмущений течения Куэтта между цилиндрами:
-It О tt
^г/v
На рис. 22 область B.35) на плоскости (Qi, йг) (для -исследо-
-исследовавшегося экспериментально Тэйлором случая /?i —3,55, /?2—4,03)
нанесена вместе с перенесенной
с рис. 13, а областью неустойчи-
неустойчивости соответствующего течения
относительно бесконечно малых
возмущений.
Результаты Серрина и Вель-
те довольна просто выводятся и
являются очень общими, но они
дают очень грубую оценку Recr mm,
заниженную по сравнению с дан-
данными экспериментов на не-
несколько порядков .(напомним,
что, например, эмпирическое зна-
значение Recrmin для прямой круг*
лой трубы близко к 2000). Не-
Несколько лучшие результаты по-
получаются, если вместо исполь*
зования общих (но грубых) не-
неравенств типа B.34) искать те
возмущения и'(х), для которых
отношение притока энергии от
заданного основного течения к
диссипации энергии под действи-
действием вязкости будет наибольшим
возможным. Рассмотрим, напри-
например, плоскопараллельное течение
между плоскостями г = 0 и z = ff с профилем скорости ?Д =
= U(z)', Uz = 0 и будем для простоты считать возмущение »'
также двумерным: и' = (u'(x,z, t), w'(x,z,t)). Измеряя рас-
расстояния в единицах Н, скорости — в единицах Umax = maxf/ (z)
и время — в единицах #/C/maxi < мы можем переписать общее
Рнс 22. Расположение области
неустойчивости относительно бес-
бесконечно
области
тельно любых конечных возмуще-
возмущений для изученного Тэйлором
течения Куэтта между цилиндрами.
Верхняя заштрихованная область соот-
соответствует неустойчивости относительно
бесконечно палых возмущений, а течения,
отвечающие точкам заштрихованной по-
полоски, определенно являются устойчивыми
относительно любых конечных возмуще-
возмущений. Сплошная прямая на рисунке —гра-
—граница, области неустойчивости мя случая
невязкой жидкости (ср. рис. 13, ау

2.9] 12. гидродинамическая неустойчивость t4I
уравнение баланса энергии B.33) в виде
dB _ d Г Г u'2+w'2 . . _
~dt~~~dlJ J 2 axdz —
Я4Ц i Г ГI du' dw' \2 or.»
и w —j— dx dz —g— / / I —x з— I dx dz, B.33)
Re = ^/тахЯ/у.
В силу уравнения неразрывности (второго уравнения B.32))
можно далее ввести функцию тока 1р, положив и' = —д^/дг,
w' = д^/дх. Тогда условие неустойчивости dE/dt >• 0 будет за-
записываться в виде
dU
ox
-,- -dxdz
oz dz еглЛ ^23g^
j j (Щ2 dx dz
Максимум функционала F Щ на множестве всевозможных функ-
функций tf>, удовлетворяющих заданным граничным условиям, и
будет при этом иметь смысл 1/Recrmin( поскольку при числах
Рейнольдса, меньших обратной величины этого максимума,
энергия возмущения наверное будет убывать). Можно надеять-
надеяться, что получаемые таким образом значения ReCrmin будут уже
больше тех, которые следуют из неравенств B.34). Ясно, одна-
однако, что и они вполне могут оказаться сильно заниженными, так
как от поля скорости возмущения здесь требуется только, что-
чтобы оно удовлетворяло уравнению неразрывности и краевым
условиям, но вовсе не учитывается, что сумма этого поля и
поля скорости основного движения должна удовлетворять си-
системе динамических уравнений. И действительно, попытки опре-
определения критерия неустойчивости энергетическим методом с
помощью подсчета значений .F[i|>] для каких-то специальных
функций 1р (приводящих к относительно низкому значению
этого функционала) или с помощью решения соответствующей
вариационной задачи, предпринимавшиеся Лоренцом A907),
Орром A906—1907), Гамелем A911), Карманом A924) и дру-
другими исследователями, все также привели к чрезмерно малым
значениям ReCrmin (примерно на порядок меньшим реально
наблюдавшихся значений этого числа). Анализируя это обстоя-
обстоятельство, Петров A938) пришел к выводу, что экстремали 1р,
обращающие F[ty] <в максимум, по-видимому, во всех случаях не
описывают никакого динамически возможного движения. Та-
Таким образом, энергетический метод никогда не может дать
точного значения ReCrmin, а годится лишь для получения весьма
предварительных грубых оценок этой величины.

142 ГЛ, 1. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.9
Теорий Ландау
Значительно более перспективным (но и гораздо более труд-
трудным) представляется подход к исследованию поведения конеч-
конечных возмущений основанный на рассмотрении полной системы
нелинейных уравнений гидродинамики B.32). При этом интерес
представляет как исследование возмущений в потоке с числом
Рейнольдса, меньшим определяемого из линейной теории воз-
возмущений числа Recr = Recrmax (с целью определения крити-
критического числа Рейнольдса по отношению к конечным возмуще-
возмущениям), так и исследование возмущений при Re > Recr (с целью
изучения дальнейшей эволюции слабых возмущений, экспонен-
экспоненциально возрастающих с ростом t согласно линейной теории).
В настоящее время, однако, в отношении обеих указанных
здесь задач имеются только отдельные изолированные резуль-
результаты, причем почти все они относятся лишь ;к случаю чисел
Рейнольдса, мало отличающихся от Recr (по поводу более точ-
точной оценки области допустимых значений Re см. работу Дж.
Стюарта (I960)).
Наиболее общие закономерности поведения конечных воз-
возмущений при Re, близком к Recr, не зависящие даже от кон-
конкретного вида уравнений гидродинамики, были указаны Лан-
Ландау A944) (см. также Ландау и Лифшиц A953), § 27). Будем
сперва считать, что Re > Recr, но Re — Recr мало. Так как при
Re = Recr впервые появляется малое возмущение с «часто-
«частотой» о, имеющей нулевую мнимую часть, то при малом положи-
положительном Re — Recr будет существовать инфинитезимальное воз-
возмущение с полем скорости вида
а (л, t) = A(t)f{x), B.37)
где А @ = е~ш *> «?'-*«•', T=3m<»>0 и ?->() при Re^Recr
(так что у *С |o)il при достаточно малом Re — Recr). Отсюда
ясно, что АA) удовлетворяет уравнению
^- = i-[\Af. B.38)
Однако формула B.38) верна лишь в рамках линейной тео-
теории возмущений. При возрастании же A (t) неизбежно наступает
момент, когда эта теория перестает действовать и должна быть
заменена более полной теорией, учитывающей нелинейные по
возмущениям члены уравнений гидродинамики. Правую часть
уравнения B.38) при этом можно рассматривать как первый
член разложения —-^— в ряд по степеням Л и Л* (где звез-
звездочкой обозначена комплексно-сопряженная величина). В сле-
следующем приближении (действующем при больших t) необходи-

2.9] § 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 143
мо учесть еще и следующие по порядку члены этого ряда. Сле-
Следующие члены — это члены третьего порядка; однако надо
учесть, что движение B.37) сопровождается быстрыми (по
сравнению с характерным временем 1/у возрастания амплиту-
амплитуды) периодическими колебаниями, описываемыми множителем
егХтЛ в выражении для A (t). Эти периодические колебания нам
неинтересны; поэтому для их исключения имеет смысл осред-
нить выражение d\A\2/dt по периоду времени, большому по срав-
сравнению с 2л/а»1 (но малому по сравнению с 1/у). Так как члены
третьего порядка по Л и А*, очевидно, все будут содержать
периодический множитель, то они выпадут при таком осредне-
осреднении. Что же касается членов четвертого порядка, то из них
после осреднения сохранится лишь слагаемое, пропорциональ-
пропорциональное \А\4. Таким образом, сохраняя слагаемые не выше четвер-
четвертого порядка, мы будем иметь уравнение вида
^Ш1 2Т1Л|2 — 8|Л|4 B.39)
^Ш1 = 2Т1Л| — 8|Л|
(так как период осреднения много меньше 1/^, то величины
\А\2 и |Л|4 при осреднении практически не изменятся, так что
B.39) можно считать точным уравнением для амплитуды
осредненного возмущения). При этом о знаке коэффициента 8
ничего сказать нельзя: вообще говоря, следует ожидать, что
он может быть как положительным, так и отрицательным.
Общее решение уравнения B.39) может быть записано в
виде
где С — неопределенная постоянная интегрирования. Из фор-
мулы B.40) следует, что если о>0 и ] А@)|2 = y+сщ- доста-
достаточно мало, то амплитуда A (t) сначала возрастает экспоненци-
экспоненциально (в соответствии с линейной теорией), но затем скорость
этого возрастания убывает, и при f-voo амплитуда стремится
к конечному значению Л (се) = B^/6)|/2, не зависящему от Л@).
Заметим теперь, что i—эт0 функция от числа Рейнольдса,
которая обращается « нуль при Re = Recr и может быть разло-
разложена в ряд по степеням Re — Recr (последнее обстоятельство
может быть выведено из теории возмущений), в то время как
8 Ф 0 при Re = Recr. Поэтому i ~ (Re — Recr) и, следователь-
следовательно, Л(оо) = H|max~(Re — Recr)'/* при малых Re — Recr.
Если же о < 0, то решение B.40) формально обращается
в бесконечность при t = [In Bу/С|о|)]/2у; следовательно, еще

144 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.9
значительно раньше оно достигает столь больших значений, что
Далее уже приходится отказаться от использования уравнения
B.39), полученного с помощью сохранения лишь двух первых
членов в разложении d\A\2/dt по степеням \А\2. В этом случае,
однако, уравнение B.39) может быть применено для исследова-
исследования поведения конечных возмущений при Re < Recr. В самом
деле, при Re < Recr коэффициент 7, очевидно, будет отрицатель-
отрицательным, т. е. малое возмущение вида B.37) будет затухать. Так как/
второй член в правой части B.39) (равный —8|/4|4) положителен^
при fl < 0, то при достаточно большом \А\2 производная d\A\z/dt
(осредненная по соответственно выбранному периоду времени)
может стать положительной, т. е. по отношению к конечному
возмущению движение будет неустойчивым уже при Re < Recr.
При не слишком больших амплитудах, при которых можно
пользоваться уравнением B.39), амплитуда \А\ будет возра-
возрастать, если \А\ > B|-[|/|6|)'А. Учитывая, что |f| ~ (Recr — Re), мы
найдем, что относительно возмущений заданной амплитуды \А\
поток будет неустойчив при Re > ReA сг = Reer — а\А\2, где а>0.
Отсюда ясно, что в этом случае Reormin будет меньше значения
Recr, даваемого линейной теорией. Точный подсчет Recr ты,
однако, не может быть сделан на основе приближенного урав-
уравнения B.39), применимого лишь при малых И|, так как он тре-
требует определения числа ReA сг для сколь угодно больших зна-
значений \А\.
Перейдем теперь снова к случаю fl > О, Re < Recr, рассма-
рассматривавшемуся нами выше. Мы видим, что здесь разрастание
возмущения B.37) при .Re, немного превосходящем Recr, можно
описать как мягкое самовозбуждение элементарного осцилля-
осциллятора, приводящее в конце концов к появлению установившегося
периодического колебания с определенной конечной амплиту-
амплитудой. При этом существенно, что уравнение B.39) определяет
только амплитуду этого колебания; фаза же" его не определяется
однозначно внешними условиями, а зависит от случайных на-
начальных значений фазы возмущения, т. е. фактически может
быть произвольной. Таким образом, предельный режим устано-
установившихся колебаний рассматриваемого осциллятора характери-
характеризуется наличием одной степени свободы (в отличие от ста-
стационарного ламинарного течения, однозначно определяемого
граничными условиями и поэтому вовсе не обладающего степе-
степенями свободы-).. •
¦> При дальнейшем возрастании Re это установившееся перио-
периодическое движение само может стать неустойчивым по отноше-
отношению к малому возмущению Щ(jc, ^.Исследование такой неустой-
неустойчивости потока с полем скорости ?/(jc)-f-»j(jc, t) (где щ —
установившееся значение возмущения B.37)) в принципе можно

2.9] S 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 145
произвести с помощью обычного метода возмущений. Для этого
надо только исследовать частные решения линейного уравнения
относительно Щ(х4) вида»2=ехр(—/юО/С** /) (где /—перио-
/—периодическая функция t периода 2ic/o)i) и определить частоту о) = оJ,
у которой при возрастании Re прежде всего (при Re=Re2 Сг)
появляется положительная мнимая часть. Тогда можно ожи-
ожидать, что при Re, немного большем Re2 Cr. колебание с этой часто-
частотой будет возрастать до некоторого конечного предела, так что
при t-*-oo возникает квазипериодическое колебание с двумя
периодами 2ic/a>i и 2it/oJ, обладающее уже двумя степенями сво-
свободы (фазами колебаний). При дальнейшем возрастании Re
все новые и новые осцилляторы приходят в колебательный ре-
режим, причем естественно думать, что интервалы между соот-
соответствующими «критическими» числами Рейнольдса будут все
уменьшаться, а возникающие колебания будут становиться все
более высокочастотными и мелкомасштабными. В результате
при достаточно большом Re движение оказывается имеющим
очень много степеней свободы и очень сложным и запутанным.
Этому движению соответствует «предельный цикл» фазовых
траекторий, в котором некоторые обобщенные координаты пото-
потока принимают фиксированные значения, а изменяются со вре-
временем (по формулам вида <p(t)=(ut+a) лишь координаты, отве-
отвечающие фазам соответствующих осцилляторов.
Траектория, образующая «предельный цикл», занимает в
фазовом пространстве область, соответствующую всевозможным
наборам начальных фаз колебаний осцилляторов, и с течением
времени проходит практически через все точки этой области.
Действительно, в моменты времени tn = 2пп/щ, п = 0, 1,2,..., в
которые , фаза q>i(/) =омй-а принимает значение аь фаза
(fz(t)=o>zt+a2 любого другого колебания будет принимать
значения 2imoJ/o)i +аг, «=0,1,2,... В силу того, что отдельные
частоты ©1 и ©2 будут, вообще говоря, несоизмеримыми (за
исключением очень специальных случаев, представляющихся
совершенно неправдоподобными), последняя совокупность бу-
будет содержать значения, которые после приведения к интер-
интервалу [0, 2я] оказываются сколь угодно близкими к любому на-
наперед заданному числу из этого интервала. Отсюда вытекает,
что возникающее таким образом развитое турбулентное дви-
движение будет обладать определенной «эргодичностью», прояв-
проявляющейся в том, что с течением времени жидкость проходит
через состояния, сколь угодно близкие к любым ее возможным
состояниям движения.
Приведенные общие соображения и составляют суть предло-
предложенной Ландау теории возникновения турбулентности. Они пред-
представляются очень наглядными и физически убедительными;

146 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.9
надо, однако, иметь в ©иду, что пока еще они ни в одном кон-
конкретном случае не были подтверждены непосредственными
расчетами, и что описываемый ими механизм перехода к турбу-
турбулентности заведомо не является универсальным. Так, напри-
например, в случае течения Пуазейля в трубе число Recr = Recr max,
определяемое из линейной теории возмущений, по-видимому,
равно бесконечности (т. е. уравнение B.38) не имеет смысла);
следовательно, турбулентное движение здесь должно возникать
в результате неустойчивости по отношению к конечным возму-
возмущениям '), причем оно с самого начала, вероятно, обладает
очень большим числом степеней свободы. При возникновении
турбулентности в пограничном слое на плоской пластинке суще-
существенную роль, возможно, играет то обстоятельство, что воз-
возникающие при некотором числе Рейнольдса неустойчивые воз-
возмущения здесь переносятся вниз по течению в область с боль-
большим значением числа Рейнольдса. Во всяком случае, имеющие-
имеющиеся эмпирические данные о турбулизации пограничного слоя
(о которых еще будет речь, ниже) та"кже не укладываются в
рамки развитых выше соображений. Значительно более напо-
напоминает описанный механизм возникновения турбулентности
процесс появления турбулентного следа при обтекании конеч-
конечных тел (см. выше стр. 85—86). По-видимому, относящиеся к
этому процессу эмпирические данные могут быть объяснены
исходя из теории Ландау, если предположить, что в потоке,
обтекающем тело, б > 0, а критические числа Рейнольдса для
неустойчивостей различного порядка близки друг к другу. К со-
сожалению, расчет критического числа Рейнольдса для обтекания
конечного тела даже в рамках линейной теории представляет
собой очень сложную задачу, не поддающуюся точному мате-
математическому решению. Поэтому количественное сопоставление
развитой выше теории с имеющимися эмпирическими дан-
данными о турбулизации следа пока еще не представляется воз-
возможным.
Значительно более изученными являются случаи течения
Куэтта между вращающимися цилиндрами, свободной конвек-
конвекции между параллельными плоскостями и течения Пуазейля
между параллельными плоскостями, для которых линейная тео-
теория возмущений может быть доведена до вполне окончатель-
окончательных результатов (см. выше пп. 2.6—2.8). Поэтому на вопросе
о применении к указанным трем течениям теории Ландау (или,
') Заметим, впрочем, Что в работе Тацуми A952) была предпринята по-
попытка объяснить возникновение турбулентного течения в круглой трубе на
основе линейной теории возмущений, прилагаемой к области течения у вхо-
входа в трубу, где еще не успед образоваться параболический профиль Х
нз — Пуазейля,

2,9] § 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ I4t
точнее говоря, уравнения Ландау B.39)) мы остановимся не-
немного более подробно.
. В первых двух из перечисленных трех случаев движение,
возникающее при Re = Rcr (или Ra = Racr), является ста-
стационарным (т. е. для него ©i = 0). Тем не менее, развитые
выше соображения вполне могут быть применены и к этим
случаям, так как неустойчивое возмущение здесь зато оказы-
оказывается периодическим относительно некоторых координат (ко-
(координаты z в первом случае и координат х и у во ©тором);
поэтому вместо осреднения по времени здесь можно воспользо-
воспользоваться осреднением по этим координатам. Другое, более суще-
существенное осложнение возникает в этих случаях в связи с тем,
что неустойчивые возмущения здесь относятся к непрерывному
спектру (они зависят от непрерывно меняющегося волнового
числа k); поэтому, строго говоря, при Re > Recr (или Ra >
> Racr) здесь всегда существует непрерывное множество раз*
личных неустойчивых возмущений. Тем не менее, и это об-
обстоятельство в конце концов оказывается непринципиальным,
так как эмпирические данные явно показывают, что при малом
Re—Recr (или Ra—Racr) всегда «выживает» (и достигает ко-
конечного значения) только одно неустойчивое возмущение со
строго определенным волновым числом. О возможной причине
такого положения мы еще скажем ниже; пока же примем за
основу, что в обоих указанных случаях допустимо ограничиться
исследованием отдельных возмущений вида B.37) с фиксиро-
фиксированным волновым числом k и фиксированным значением о = q,
определяемым из линейной теории.
Как эмпирические данные, так и теоретический анализ не-
нелинейных уравнений (типа {2.32)), описывающих поведение
конечных возмущений в течении Куэтта между цилиндрами и
в подогретом снизу слое жидкости, показывают, что при
Re < Recr (или Ra < Racr) здесь не существует стационарных
возмущений с d\A\2/dt = 0 (см., например, работы Сорокина
A954) и Уховского и Юдовича A963) об уравнениях свободной
конвекции). В то же время при Re = Recr (или Ra = Racr) в
обоих случаях происходит «разветвление» стационарных реше-
решений соответствующих нелинейных уравнений. А именно, в этой
точке наряду с обычными ламинарными решениями появляются
дополнительные стационарные решения, отличающиеся от
обычных периодическими относительно координаты z (или ко«
ординат х и у) членами, амплитуда которых при малых значе*
ниях Re—Recr (или Ra—Racr) пропорциональна (Re—RecrI/!l
(или (Ra—Racr)'/«). Такие дополнительные решения нелиней-
нелинейных уравнений свободной конвекции были изучены в работах
Сорокина A954), Горькова A957) и Малкуса и Верониса

148 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЙ [2.9
,A958); для течения Куэтта между цилиндрами они могут быть
определены исходя из излагаемых ниже результатов Дж. Стю-
Стюарта A958) и Дэви A962). Поэтому есть все основания пред-
предполагать, что в случаях вихревого движения в потоке жидкости
между вращающимися цилиндрами при Re > Recr и свободной
конвекции между плоскостями при Ra > Racr мы сталкиваемся
как раз с мягким самовозбуждением колебаний (только про-
пространственных, а не временных) по схеме Ландау с о > 0.
Имеющиеся эмпирические данные показывают также, что воз-
возникающее здесь стационарное движение оказывается устойчи-
устойчивым в большом интервале значений Re (или Raj, так что кри-
критические числа Re (или Ra) первого и второго порядков здесь
широко раздвинуты относительно друг друга (см., в частности,
ниже рис. 23). Напомним также, что согласно данным Малкуса
A954а), о которых шла речь на стр. 113, в случае термической
конвекции можно экспериментально определить даже несколько
критических значений Racr разных порядков.
Представляет несомненный интерес получение для рассма-
рассматриваемых двух случаев уравнений типа B.39), описывающих
эволюцию во времени неустойчивых согласно линейной теории
возмущений, непосредственно из динамических уравнений
B.32). В применении к течению Куэтта: между цилиндрами
именно этому и были посвящены упоминавшиеся выше работы
Дж. Стюарта A958) и Дэви A962). В первой из этих работ
предполагалось, что d = R2 — Ri < (Ri + Rz)/2 = Ro и. что вра-
вращается (с угловой скоростью Qi) только внутренний цилиндр.
В этом случае вместо числа Рейнольдса удобно рассматривать
так называемое число Тэйлдра Та = Q^RiC^/ч2; течение Куэтта
становится неустойчивым при Та > Тасг « 1708. Стюарт предпо-
предположил далее, что разность Та — Тасг мала (но положительна)
и что в момент t = 0 в рассматриваемом течении возникло не-
неустойчивое согласно линейной теории малое возмущение. Счи-
Считая, что форма этого возмущения мало меняется во времени
(так что применима формула B.37)), можно определить зави-
зависимость соответствующей амплитуды A(t) от времени с по-
помощью уравнения баланса энергии возмущения B.33) (яв-
(являющегося следствием уравнений движения). При этом для
\А\2 получилось уравнение вида B.39) с коэффициентами |и J,
явно выражающимися через число Тэйлора Та, число Рейнольд-
Рейнольдса Re = QiRid/v, волновое число k = kCT и собственную функцию
соответствующей задачи на собственные значения B.16) — B.17),
подсчитанную Чандрасекаром A953). В результате расчета вы-
выяснилось, что действительно о > 0 и, значит, существует ко-
конечное значение |Л|тах, причем |Л|тах ~ A — ТаСг/Та)'/>~
у (Та — ТасгI/2 при малом Та — Тасг. Зная |ЛЦах и форму воз-

2.9] i S. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 149
никающего возмущения (приближенно даваемую линейной
теорией возмущений), Стюарт смог рассчитать также и
момент сил трения, действующих на поверхность цилиндров.
Полученные им значения этого момента оказались вплоть до
чисел Та, почти в десять раз превышающих Тасг, весьма близ-
близкими к данным непосредственных измерений Тэйлора A9366).
Более аккуратно уравнение для амплитуды возмущения в
течении Куэтта между цилиндрами было выведено в работе
Дэви A962). В этой работе было учтено, что начальное осесим-
метричное возмущение вида и' (Jc) = Af(r)eihz в силу нелиней-
нелинейности уравнений гидромеханики будет порождать также и выс-
высшие гармоники (пропорциональные einhz, п = 2, 3, ...) и что
зависимость от г формы этого возмущения также будет слегка
меняться со временем. Поэтому поле скорости возмущения
здесь записывалось в виде
*(*,*) = «о(г, *) + а,(г, Це"*+щ(г, t)e™* + ... B.41)
(где член чо(г, t) описывает искажение формы ламинарного те-
течения Куэтта, вызванное возмущением). Далее предполага-
предполагалось, что при <->-0в правой части B.41) сохраняется лишь сла-
слагаемое, содержащее ю,(г, t), причем в пределе это слагаемое
переходит в решение я'==/(г}ет<+/*г, определяемое из линей-
линейной теории возмущений. Тогда и при небольшом положитель-
положительном t указанное слагаемое также остается главным, причем
ю,(г, t) при таком t можно представить в виде
»i(r, t) = A (t)f(r)-\- члены высшего порядка малости. B.42)
Подставляя B.41) и B.42) в нелинейные уравнения B.32),
можно снова получить для A(t) уравнение вида B.39), где ?
определяется из линейной теории возмущений и
8 = 8,4-82 + 83. B.43)
Здесь 6i > 0 определяется притоком энергии от течения Куэт-
Куэтта (искаженного слагаемым щ(г, t)) к основному возмущению
Щ (г, t) eihz (только это«слагаемое фактически и учитывалось
в работе Стюарта), ог описывает порождение основным возму-
возмущением высших гармоник, а бз — искажение его формы. Для
всех трех слагаемых в правой части B.43) Дэви получил гро-
громоздкие формулы (содержащие решения соответствующей за-
задачи на собственные значения линейной теории возмущений);
после этого для случаев a) d>c/?o, Q2 = 0> б) d^.Ro, Й2/Й1 «* 1
н в) /?2 = 2#i, ?2г = 0 он подсчитал численно значения этих сла-
слагаемых. При этом коэффициент б во всех случаях оказался
положительным; в случае а) его значения близко совпали с ре-
результатами менее точных вычислений Стюарта, а в случаях б)

150 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ B.0
и в) они также привели к значениям момента сил трения при
сверхкритических условиях, хорошо совпадающим с имеющи-
имеющимися экспериментальными данными.
Совпадение вычисленных и наблюденных значений момента
сил трения убедительно свидетельствует, что полученное Стюар-
Стюартом и Дэви уравнение Ландау" B.39) с о > 0 правильно описы-
описывает процесс возрастания неустойчивого по линейной теории
осесимметричного возмущения. Однако свидетельство это все
же является косвенным, так как с экспериментом здесь срав-
сравнивается не само значение амплитуды Л, а подсчитанная по
этой амплитуде интегральная характеристика течения — сум-
суммарный момент сил трения. Более непосредственную проверку
применимости теории Ландау к течению между цилиндрами
осуществил Доннелли A963). Он наполнил зазор между ци-
цилиндрами (радиусов Ri = 1,9 см и /?2 = 2,0 см) электролитом
ССЦ и измерил силу проходящего через электролит тока, по-
поступающего на коллектор — небольшую площадку на непо-
неподвижном внешнем цилиндре, перемещающуюся с постоянной
скоростью в направлении оси Oz. При Та >- Тасг в электролите
между цилиндрами возникает правильная совокупность ста-
стационарных тороидальных вихрей-, поле скорости которых имеет
вид и'(х) = A/ (r)eihz, где коэффициент А — это Л (се) =
= Лтах теории Ландау. Появившиеся вихри разрушают слои
электрически заряженной жидкости около электродов и поэто-
поэтому влияют на силу проходящего через электролит тока. Расчет
этого явления показывает, что появлелию вихрей должно соот-
соответствовать появление в выражении для силы тока / добавоч-
добавочного слагаемого вида А/ = СА cos kz, где С — вполне опреде-
определенный постоянный коэффициент. Результаты измерений под-
подтверждают, что при Qi >-QCr = (v^Tacr/Rid3)'1* такая компонента
действительно появляется, причем квадрат ее амплитуды Л2
оказывается пропорциональным 22 — Q^^—-Та — Тасг (в полном
соответствии с теоретическим выводом Ландау) вплоть до зна-
значения Qi = Ягсп такого, что^гсг —2?г)/2сг«*0,15 (см. рис. 23).
Исходя из общих представлений теории Ландау, можно пред-
предположить, что резкое изменение закона Лтах~(Та—Тасг)'/*при
fii = Огсг связано с достижением «второго критического значе-
значения» Та2сг числа Тэйлора, при котором тороидальные вихри
становятся неустойчивыми и распадаются на более сложные
возмущения (по-видимому, уже не осесимметричные).
Более сложно обстоит дело с применением нелинейной тео-
теории возмущений к течению Пуазейля между двумя плоскостя-
плоскостями. Первая попытка в этом направлении была предпринята
Мексиным и Дж. Стюартом A951), получившими при ряде

2.9]
§ 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ
151
упрощающих предположений, что для плоского течения Пуа-
зейля критическое число Рейнольдса ReAcr для конечных дву-
двумерных возмущений амплитуды \А\ убывает при возрастании
\А\. Этот результат заставляет предполагать, что здесь б < 0.
С другой стороны, в более поздней работе Дж. Стюарта A958)
для получения уравнения вида B.39) для амплитуды такого
возмущения было использовано уравнение баланса энергии
B.33'); здесь уже при некоторых других упрощающих предпо-
предположениях было найдено, что б > .0. В этой связи Дж. Стюарт
Рис. 23. Зависимость квадрата амплитуды добавочного
тока (AyJ в электролите между вращающимися цилин-
цилиндрами от угловой скорости внутреннего цилиндра (по
Доннелли A963)).
(I960) и Уотсон A960а) произвели более полный анализ пове-
поведения двумерных конечных возмущений в плоском течении
Пуазейля при Re, близком к Recr, основанный на использовании
полных уравнений движения и формул типа B.41) и B.42)
(этот анализ и был затем принят за образец в работе Дэви
A962)) В результате они снова получили уравнение вида
;() для амплитуды возмущений, но коэффициент б на этот
раз оказался суммой трех слагаемых (имеющих тот же смысл,
что и .слагаемые в равенстве B.43)), не все из которых были
правильно учтены и в работе Мексика и Дж. Стюарта A951)
и IB работе Дж. Стюарта A960). Оказалось также, что для всех
этих слагаемых могут быть даны явные выражения, сложным
образом содержащие собственные функции и собственные зна-
значения соответствующего лилейного уравнения Орра — Зоммер-

152 гл, т, ламинарные и турбулентные движения [2.9
фельда. Однако численный подсчет этих слагаемых и нахожде-
нахождение по ним точного значения коэффициента б, позволяющее
окончательно решить вопрос о его знаке, представляет собой
очень сложную, задачу численного анализа, решение которой
пока еще никем не было получено. Поэтому и на вопрос о по-
поведении конечных возмущений в плоском течении Пуазейля по-
пока нельзя дать окончательного ответа.
В случае плоскопараллельных течений, неустойчивых при
v = 0, уравнение Ландау B.39), разумеется, может иметь смысл
и в применении к слегка неустойчивым возмущениям в идеаль-
идеальной жидкости. Естественно, что пренебрежение вязкостью при-
приводит здесь к упрощению всех вычислений. Поэтому неудиви-
неудивительно, что для течения идеальной жидкости в безграничном
пространстве с профилем скорости U(z) = Uoth {z/H) Шаде
A964), предположив, что форма возмущения близка к форме
однозначно определяемой в этом случае «нейтральной волны»,
сумел аналитически определить значение коэффициента б (ока-
(оказавшегося положительным). Приняв затем для i значение, от-
отвечающее наиболее неустойчивому возмущению, он смог при-
приближенно оценить также порядок амплитуды возмущения в
«плоской зоне смешения», начиная с которой становится не-
неприменимой линейная теория возмущений.
Выше мы уже отмечали, что уравнение Ландау B.39) при
б > 0 приводит к интересным физическим результатам только
в применении к возмущениям в течении с Re > Recr, а при
б < 0 — только в применении к конечным возмущениям в по-
потоке с Re < Reor. В случае же б > 0 и Re < Recr или же
б>0, Re>Reor и -j>0 это уравнение быстро оказывается не-
неприменимым и должно быть дополнено следующими членами
разложения по степеням \А\2. Общее уравнение для d\A\2/dt,
учитывающее все члены такого разложения, очевидно, будет
иметь вид
B.44)
т=0
(уравнение Ландау получается отсюда, если учесть только два
первых члена правой части). Уравнение вида B.44) для ам-
амплитуды двумерного возмущения в плоскопараллельном тече-
течении также было формально получено Уотсоном A960а) исходя
из уравнений движения. При этом, однако, выражения для ко-
коэффициентов Ощ с т > 1 оказались еще гораздо более слож-
сложными, чем для коэффициента Ci = —б, так что их определение
пока представляется совсем уже мало реальным. В последую-
последующей работе Уотсона A962) аналогичный анализ был проияче-

2.9] § 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 153
ден для плоского, течения Пуазейля, исходя из представления
возмущения и'(х, t) в виде A(x)f(z, t), где амплитуда А(х)
в линейном приближении равна е^н-гад*. в этом случае для
А(х) получаются уравнения, отличающиеся от B.39) и B.44)
лишь заменой / йа х, причем определение коэффициентов этих
уравнений, естественно, упирается в те же трудности, что и
определение коэффициентов уравнений для зависящей от вре-
времени амплитуды A(t).
Взаимодействие конечных возмущений. Роль трехмерных
возмущений в плоскопараллельном течении
Изложенная выше теория Ландау касалась эволюции од-
ного конечного возмущения в ламинарном течении. Поскольку,
однако, эта эволюция определяется нелинейными дифферен-
дифференциальными уравнениями, то решение, отвечающее наличию в
заданном течении нескольких различных начальных возмуще-
возмущений, уже не будет простой суммой решений, описывающих эво-
эволюцию каждого из них по отдельности. Поэтому в теории ко-
конечных возмущений недостаточно исследовать лишь процесс
развития простейших «элементарных возмущений», по которым
можно" разложить любое начальное поле и(х, 0), а требуется
описать также и взаимодействие возмущений, т. е. влияние
каждого из них на развитие всех остальных.
Вообще говоря, вопрос о взаимодействии конечных возму-
возмущений относится к числу наименее изученных в гидромеханике.
Тем не менее, кое-какие частные результаты, касающиеся та-
такого взаимодействия, могут быть все же указаны и заслужи-
заслуживают того, чтобы на них остановиться немного подробнее.
Начнем с хорошо изученного экспериментаторами случая
термической конвекции в слое подогреваемой снизу жидкости
при числе Р^элея Ra > Racr. Как мы знаем из" п. 2.7, линейная
теория возмущений приводит к выводу, что при таком значении
Ra должно иметься бесконечное множество неустойчивых ин-<
финитезимальных возмущений (с экспоненциально возрастаю-
возрастающими амплитудами), соответствующих некоторому интервалу
значений волнового вектора k, окружающему значение k = kCI,
при котором впервые проявляется неустойчивость. Наиболее не-
неустойчивыми (т. е. быстрее всего возрастающими) будут воз-
возмущения с одним определенным k, но и таких возмущений бу-
будет бесконечное множество (так как при заданном k горизон-
горизонтальная форма возмущения может описываться произвольной
функцией q>(*i, x2), удовлетворяющей уравнению B.23)). Экс-
Эксперимент же показывает, что на самом деле всегда возникает

154 Гл. i. Ламинарные И турбулентные движений B.9
лишь возмущение с одним определенным значением k, имеющее
строго определенную форму (соответствующую разбиению го-
горизонтальной плоскости (дсь дсг) на совокупность правильных
шестиугольных ячеек) и строго определенную конечную ампли-
амплитуду. Теория Ландау позволяет лишь найти эту установившую-
установившуюся амплитуду (с помощью соответствующего уравнения B.39),
получающегося из нелинейных уравнений конвекции в пред-
предположении, что функция (fixuXz) заранее задана; ср. Горькое
A957)). Но эта теория ничего не говорит о том, почему в жид-
жидкости никогда не возникают возмущения с несколькими разны-
разными значениями k и почему среди наиболее неустойчивых воз-
возмущений реально наблюдаются лишь возмущения с одной опре-
определенной функцией ф(*1, х2).
Исследованию этого последнего вопроса посвящены работы
Палма (I960), Сиджела и Дж. Стюарта A962) и Палма и
Зйянна A964). Палм, в частности, впервые указал на то, что
обычные уравнения свободной конвекции A.5), A.6), A.75) и
A.76) в принципе не могут удовлетворительно объяснить основ-
основные особенности ячеистой конвекции, так как эксперименты Тии-
пельскирха A956) показывают, что характер циркуляции в
ячейках определяется формой зависимости коэффициента вяз-
вязкости v от температуры Т (при d\)dT < 0 жидкость поднимается
в середине ячейки и опускается по краям, а при d\/dT > 0 —
поднимается по краям и опускается в середине). Поэтому он
принял за основу более сложные уравнения, учитывающие так-
также и возможную зависимость v от Т (и оценил влияние этой за-
зависимости на значение Racr). Далее, Палм предположил, что в
начальный момент времени в жидкости возникло, некоторое
«основное возмущение» в форме плоской волны (например,
пропорциональное cos{kxi]H) = cosfcr), где ц = xJH, H — тол-
толщина слоя жидкости, и не зависящее от %=xjH), на которое
накладывается еще слабый «фон» различных других возмуще»
ний малой амплитуды с тем же самым (наиболее неустойчи*
вым) значением волнового вектора k. В таком случае естествен»
но допустить, что основную роль здесь будут играть «парные
взаимодействия» основного возмущения с прочими и в соответ*
ствии с этим ограничиться лишь рассмотрением эволюции воз»
мущений с полем Ub(X,t) = ы(|, т|, ?,/), гДе 1~Хз/Н, вида
%(?, % С, 0 = [А @ cos кщ-\- Aj(t) cos k? cos ^J/(C),
_p B-45)
Но при этом особенно тесно связанными с основным возмуще*
нием будут те возмущения сk\-^l^ = k2, квадратичные комби»

2.9] § 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 155
нации которых (входящие в уравнения гидромеханики) могут
снова порождать члены того же вида, что и основное возмуще-
возмущение. Можно даже думать, что взаимодействие таких возмуще-
возмущений с основным может при определенных условиях приводить
к взаимному усилению обоих возмущений, в результате кото-
которого только эти возмущения и будут в конце концов играть су-
существенную роль. Исходя из таких соображений, Палм пред-
предложил прежде всего рассмотреть специальный случай, когда
и3 F, % С, 0=[А @ cos fcij+Ла (t) cos (\ГЗ Щ2) cos (ВД]/(С) B.46)
(так как здесь два слагаемых являются как раз сильно связан-
связанными друг с другом). Ограничившись для простоты граничных
условий лишь физически нереальным случаем конвекции в слое
между двумя свободными поверхностями (это упрощение
принималось затем и в работах Сиджела и Дж. Стюарта
A962), Сиджела A962) и Палма и Эйянна A964)) и приняв
для определённости, что /(?)=sinA,?, Палм вывел систему
дифференциальных уравнений для амплитуд Ai(t) и A2(t). Эта
система после отбрасывания членов выше третьего порядка и
некоторых других второстепенных членов может быть пред-
представлена в виде
*?±- = ТД -1 е Al - М? - B82 - 8,/2) Д4,
B 47)
8,) .AM2,
где 7, e, fli и бг — постоянные коэффициенты, 7~Ra—Racr и
е ~ \dv/dT\ (ср. Сиджел и Дж. Стюарт A962)). Существенно,
что система B.47) имеет стационарные решения вида
А=±2Д, B.48)
отвечающие как раз шестигранным призматическим ячейкам.
Кроме того, согласно результатам Палма при е Ф 0 (т. е. при
dv/dT Ф 0, но не при dv/dt = 0) только такие решения и будут
устойчивыми относительно малых возмущений амплитуд А\. и
Лг, так что именно они будут реализоваться « пределе при
t-+oo. Так как к тому же устойчивым решениям при разных
знаках dv/dT соответствует, как оказалось, именно то напра-
направление циркуляции жидкости в ячейках, которое наблюдается
на опыте, то Палм заключил, что эти результаты полностью
объясняют основные экспериментальные факты.

156 ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ [2.9
В дальнейшем теория Палма была критически пересмотрена
Сиджелом и Дж. Стюартом A962) и Палмом и Эйянном
A964) (также исходившими из третьего приближения теории
возмущений). При этом выяснилось, что некоторые заключения
работы Палма A960) не совсем точны. В частности, оказалось,
что решения B.48) системы B.47) на самом деле устойчивы
лишь при не слишком малом \d\jdT\ (превосходящем некоторую
постоянную / > 0, зависящую от значений коэффициентов си-
системы). Кроме того, при \dv/dT\ > f решения вида B.48)—не
единственные устойчивые решения системы B.47); однако все
остальные ее стационарные решения становятся неустойчивыми,
если немного расширить класс допустимых возмущений: В то
же время отвечающее B.48) стационарное движение в виде
совокупности шестигранных ячеек (с зависящим от знака
dv/dT направлением циркуляции жидкости в ячейках) оказа-
оказалось устойчивым относительно сравнительно широкого класса
возмущений и совпадающим с пределом при /-*-оо произволь-
ного возмущения вида
Ах (t)cos Jbi+AC) соб(/3 кф) cos (??]/2)+А,(*) cos /
(а также, по-видимому, и любой другой комбинации конечного
числа неустойчивых волн с фиксированным волновым чис-
числом k). В предположении, что при реальных граничных уело-,
виях значение f будет достаточно мало, эти факты хорошо
согласуются с эмпирическими данными об исключительной роли
шестигранных ячеек, хотя, разумеется, нельзя ручаться, что в
реальных экспериментах не оказываются существенными еще
какие-нибудь обстоятельства, не учтенные в рассматриваемой
здесь приближенной теории.
То, что в ряде случаев нелинейные взаимодействия могут
привести к разрастанию возмущений одной определенной фор-
формы за счет подавления всех остальных, подтверждают и расчеты
Сиджела A962), относящиеся к случаю возмущений с различ-
различными волновыми числами в слое подогретой снизу жидкости.
Этот автор рассмотрел простейшее «парное взаимодействие»
двух «одномерных волн», не зависящих от координаты ц
(т. е. Хг). Иначе говоря, исследовалась эволюция возмущения,
для которого поле и3(х, t) = ua(g, ч, ?. *) имеет вид
«з (•*» *) =¦ А С)cos #/i W + Aj @ COS /S/2 (Q + малая добавка. B.49)
Применив затем метод работ Дж. Стюарта A960) и Уотсона
A960а), Сиджел получил в первом нелинейном приближении

2.9] § 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 157
для коэффициентов Ai и А2 систему уравнений вида
B-50)
обращающуюся при Л2 = О или /li = 0 в уравнение, равносиль-
равносильное уравнению Ландау B.39) для амплитуды одного возму-
возмущения (зависимостью v от Т, учтенной в уравнениях B.47),
здесь пренебрегается). Система B.50), очевидно, имеет следую-
следующие стационарные решения:
A)А=А=о,
(И) д = о, л = (ТА)*.
(III) 4, = М»,)*. 42 = 0,
(IV) д=(ГА - ъЫ1'1 (»А - PiW*.
Устойчивость этих решений может быть проверена с помощью
обычных методов качественной теории дифференциальных
уравнений (cMi, например, Андронов, Витт и Хайкин A959)).
При этом оказывается, что в наиболее важном случае, когда
7t > О, 72 > 0, fit > 0, вг > 0, из устойчивости хотя бы одного
из решений (II) и (III) уже следует, что не может существовать
устойчивое решение (IV). Отсюда видно, что существует широ-
широкий класс ситуаций, в которых окончательное состояние всегда
будет содержать лишь одно возмущение (с волновым числом
k или /), но не смесь их обоих. С другой стороны, при некоторых
значениях коэффициентов из системы уравнений B.50) выте-
вытекает, что взаимодействие одного устойчивого и одного неус-
неустойчивого возмущения (например, возмущений с 71 > 0 и с
7г < 0) может привести к тому, что неустойчивое возмущение
начнет расти, и в конце концов установится «смешанное состоя-
состояние», отвечающее решению типа (IV). Правдоподобно, что такая
ситуация также может иногда встретиться в гидромеханике
(например, в случае плоскопараллельных течений). Но для урав-
уравнений B.50), отвечающих случаю термической конвекции при
числе Ra, лишь слегка превышающем Racr, и неустойчивости
обоих исходных возмущений (т. е. 71 > 0. 7г >¦ 0) устойчивым
относительно всех двумерных возмущений вида B.49) всегда
оказывается только решение (II) или (III). Это обстоятельство
в какой-то мере поясняет, каким образом наличие взаимодей-
взаимодействий между возмущениями приводит к тому, что при малых
Ra — Racr из всего интервала неустойчивых волновых чисел

158
ГЛ. I. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ
[2.9
всегда реально наблюдается только одно значение k. Однако
при большой разности Ra—Raer исследование системы B.50)
сильно затрудняется, причем кажется правдоподобным, что при
малом числе Прандтля здесь могут встретиться и случаи, когда
устойчивым окажется как раз решение типа (IV), соответствую-
соответствующее смеси двух исходных возмущений.
Аналогичный анализ возможен и для других течений, к ко-
которым выше применялась обычная линейная теория возмуще-
возмущений. В частности, очень большой интерес представляет случай
практически плоскопарал-
плоскопараллельного течения в погра-
пограничном слое на плоской
пластинке, которому было
уделено много внимания в
п: 2.8. Мы уже отмечали,
что согласно экспериментам
Шубауэра и Скрэмстеда
первоначальное развитие
неустойчивых возмущений в
таком течении полностью
согласуется с выводами ли-
линейной теории Толмина —
Шлихтинга — Линя. Одна-
Однако последующие наблюде-
наблюдения целого ряда авторов
(например, Шубауэра и
Клебанова A956), »Хама,
Лонга и Хегарти A957),
Клебанова и Тидстрома
A959) и, особенно, Клеба-
Клебанова, Тидстрома и Сарджен-
та A962)) убедительно по-
показали, что так дело обстоит
лишь на первой стадии раз-
развития возмущений; затем
положение заметно изме-
изменяется. Непосредственно
О—Для х=7,6см, А — для х=15,2 см, X— для
Q.O7 0.02 0,03 0.04 0.05 0.06 0,07
U'/U
Рис. 24. Зависимость относительной
величины типичной пульсации продоль-
продольной скорости U' от «боковой» коорди-
координаты у в пограничном слое над плоской
пластинкой на различных расстояниях х
от колеблющейся металлической ленты,
создающей возмущения.
x=i9см. вслед за этой первой ста-
стадией следует стадия, в тече-
течение которой ранее двумерное возмущение приобретает явно вы-
выраженный трехмерный характер за счет появления продольных
вихрей с осями, направленными вдоль основного течения, при-
приводящих к резкому перераспределению интенсивности пульса-
пульсаций в «боковом» направлении Ох2 = Оу (см. рис. 24). Вслед за
этой второй стадией следует третья стадия, в течение которой

2.9] § 2. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ 159
в отдельных точках потока возникают резко очерченные «тур-
«турбулентные пятна» (в результате процесса почти взрывного ха-
характера); в дальнейшем эти пятна все сливаются друг с дру-
другом, порождая полностью турбулентное течение.
При теоретическом изучении упомянутой второй стадии тур-
булизации пограничного слоя, очевидно, необходимо учесть, что
при сверхкритических числах Рейнольдса в плоскопараллель-
плоскопараллельном течении будут существовать также и трехмерные (завися-
(зависящие от у) неустойчивые волны, которые при достаточно боль-
большом Re—Recr могут даже оказаться наиболее быстро возра-
возрастающими (т. е. самыми неустойчивыми). Исходя отсюда,
Дж. Стюарт A962) рассмотрел поведение в плоскопараллель-
плоскопараллельном течении возмущения с полем скорости вида
и(х, y,z,J) =
= Д (t) cos kxfx (г) -j- Aj (t) cos kx cos /y/2 (z) + малая добавка. B.51)
С помощью метода работ Дж. Стюарта A960) и Уотсона A960а)
он получил при этом для амплитуд А\ и Л2 систему уравнений
вида B.50). Таким образом, здесь также могут существовать
стационарные решения четырех типов (I) — (IV) и основную роль
будет играть степень устойчивости этих стационарных решений
относительно тех или иных возмущений. К сожалению, количе-
количественное исследование устойчивости даже относительно одних
только возмущений вида B.51) требует определения значений
коэффициентов соответствующей системы уравнений B.50), что
наталкивается на очень большие трудности (как мы уже отме-
отмечали на стр. 151 —152, даже знак коэффициента fli, совпадаю-
совпадающего с коэффициентом 26 соответствующего уравнения B.39)
для одной амплитуды Ai, до сих пор не подсчитан ни для одного
плоскопараллельного течения). Однако эмпирические данные
рис. 24 создают впечатление, что при некоторых k и / устой-
устойчивым может оказаться именно смешанное стационарное реше-
решение типа (IV), причем устойчивость здесь будет иметь место не
только по отношению к возмущениям вида B.51), но и по отно-
отношению ко многим другим обычным типам возмущений.
Аналогичный вывод можно сделать и исходя из результатов
Бенни A961, 1964) и Линя и Бенни A962), подошедших к той
же задаче с другой стороны. Эти авторы представили решение
уравнений гидромеханики в виде ряда теорий возмущений
o(jc, 0 = «@)(-*)-г-явA>(лг, t)+a?uV(x, *) + ••, B.52)
где а <; 1 — безразмерный коэффициент, определяющий отноше-
отношение амплитуды возмущения к амплитуде основного течения
ю(°>(лг). При конкретных расчетах в качестве основного течения

160 ГЛ, 1. ЛАМИНАРНЫЕ И ТУРБУЛЕНТНЫЕ ДВИЖЕНИЯ {2.9
в работах Бенни A961) и Линя и Бенни A962) было выбрано
плоскопараллельное течение в безграничном пространстве с
профилем скорости U0(z) = UQthz, изображенным на рис. 19,г,
а в работе Бенни A964)—течение в полупространстве z>-0
с профилем U0(z), линейно возрастающим до некоторого зна-
значения z = Н, а затем принимающим постоянное значение V0(H).
Первичное возмущение ФЦх, t) в обоих случаях полагалось
имеющим вид
ф)(х, t) = [цtf, B) + Хя, (*) е«у] elk <*-">. B.53)
Здесь Ui(z) = (Ui(z),. V{z))\ k и с находились из обычной
(«двумерной») линейной теории (и соответствовали слегка не-
неустойчивому возмущению при Re, немного превосходящем
Recr), *i(z) = (iii{z), Vi(z), W\(z)) определялось из линейной
теории, описывающей поведение трехмерных возмущений, а от-
отношение ц/Х характеризовало относительную роль двумерного
и трехмерного возмущений. Расчеты производились с точно-
точностью до вторичных возмущений (порядку а2); они показали,
что даже при цД^>1 взаимодействие двумерного и трехмерного
возмущений приводит к возникновению вторичных продольных
вихрей и заметному перераспределению энергии возмущений
в направлении оси Оу. В результате суммарное движение (опи-
(описываемое тремя членами правой части B.52)) оказывается
очень близким к тому, которое реально наблюдается в погра-
пограничном слое (имеющем совсем другой профиль скорости Uo(г)).
Выяснение важной роли трехмерных возмущений в процессе
турбулизации пограничного слоя побудило Мексина A964)
снова вернуться к задаче об устойчивости плоского течения
Пуазейля по отношению к конечным возмущениям. Приняв
предположения, близкие к использовавшимся раньше в работе
Мексина и Стюарта A951), Мексин произвел аналогичные рас-
расчеты уже в применении к конечным трехмерным возмущениям
(с полем скорости вида и(х, t)= 2 е'1я'(*"<г"ш0+Я2'у!Ия1,в,B)' где
tti и Пг — произвольные целые числа). В результате очень гро*
моздких вычислений он нашел, что, по-видимому, для некоторых
конечных трехмерных возмущений критическое число Рейнольд-
са Recr вполне может оказаться довольно близким к значению
1000, даваемому экспериментами в качестве значения Recrmia
для рассматриваемого течения.
Теоретическое исследование третьей стадии турбулизации
пограничного слоя, характеризуемой возникновением турбулент-
турбулентных пятен, является еще значительно более трудным, чем иссле-
исследование второй стадии, и пока очень мало продвинуто. Возмож-
Возможно, что появление такого «пятна» связано с тем, что в некоторый

2.9] $ 2. гидродинамическая Неустойчивость 161
момент времени в определенной точке сразу становятся неустой-
неустойчивыми многие элементарные возмущения и в результате уста-
устанавливается сложный «смешанный» режим, обладающий боль-
большим числом степеней свободы. Весьма правдоподобно, что зна-
значительную роль при этом играет возникновение вдутри течения
(в результате наложения на среднее течение развившихся во
время второй стадии конечных трехмерных возмущений) край-
крайне неустойчивых слоев с профилем скорости, имеющим точку
перегиба (ср. Бетчов (I960)). Такие слои, вообще говоря, бу-
будут нестационарными; их толщина и отвечающий им перепад
средней скорости могут быстро изменяться во времени, при-
приводя к возникновению непосредственно перед появлением пят-
пятна областей течения, характеризуемых резко повышенной не-
неустойчивостью. Несложные расчеты," проведенные Гринспаном
и Бенни A963) (в рамках линейной теории возмущений) в при-
применении к простой модели с профилем скорости того типа, ко-
который изображен на рис. 19, в, но с зависящими от времени
перепадом скоростей 2U0 и толщиной слоя 2#, показали, что
развитие такого слоя вполне может привести к очень бурному
порождению мелкомасштабных возмущений, энергия которых
достигает больших значений в течение ничтожно малого про-
промежутка времени. Эти результаты находятся в хорошем каче-
качественном соответствии с имеющимися эмпирическими данны-
данными, касающимися перехода пограничного слоя к режиму раз-
развитой турбулентности (см., в частности, Миллер и Фейер
A964)).
Что же касается теоретического исследования развитой
турбулентности, возникающей после полного завершения npoj
цесса турбулизации течения, то ему будут посвящены все после-
последующие главы настоящей книги. При этом, однако, нам пона-
понадобится ряд сведений из теории вероятностей и теории случай-
случайных функций, к краткому изложению которых мы теперь и
перейдем.

ГЛАВА II
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ
ТУРБУЛЕНТНОСТИ. СРЕДНИЕ ЗНАЧЕНИЯ
И КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
§ 3. МЕТОДЫ ОСРЕДНЕНИЯ. ПОЛЯ ГИДРОДИНАМИЧЕСКИХ
ХАРАКТЕРИСТИК КАК СЛУЧАЙНЫЕ ПОЛЯ
3.1. Практические методы осреднения и условия Рейнольдса
Как мы уже говорили выше, характерной особенностью тех
движений жидкости (или газа), которые называются турбу-
турбулентными, является наличие беспорядочных флюктуации гидро-
гидродинамических характеристик потока, В результате как зависи-
зависимость мгновенных значений гидродинамических полей от про-
пространственных координат, так и временной ход этих значений
приобретают очень сложный и запутанный характер, причем
при многократном осуществлении потока в одинаковых усло-
условиях точные значения всех полей каждый раз оказываются
иными. Вернемся снова к рис. 1, на котором представлены
образцы кривых, выражающих зависимость некоторых гидро-
гидродинамических величин в турбулентном потоке от времени. Мы
видим, что все эти кривые состоят из совокупности пульсаций
разнообразных периодов и амплитуд, налагающихся друг на
друга без какой-либо заметной закономерности. Аналогично вы-
выглядят и распределения мгновенных значений гидродинамиче-
гидродинамических элементов в пространстве: они представляют собой бес-
беспорядочную совокупность трехмерных пульсаций различной
амплитуды, длины волны и ориентации. В силу крайней неупо-
неупорядоченности и резкой изменчивости во времени и в простран-
пространстве полей всех гидродинамических величин при изучении тур-
турбулентности необходимо использовать какие-либо методы
осреднения, позволяющие перейти от исходных гидродинамиче-
гидродинамических полей к более плавным и регулярным средним значениям
характеристик потока, которые можно исследовать с помощью
обычных методов математического анализа.

3.1] § 3. МЕТОДЫ ОСРЕДНЕНИЯ 163
Вопрос о правилах вычисления средних значений является
тонким вопросом теории турбулентности, имеющим большую
историю. На практике при определении среднего значения чаще
всего пользуются временным или пространственным осредне-
осреднением по какому-либо промежутку времени или области про-
пространства. Можно также рассматривать более общее простран-
пространственно-временное осреднение функций f(xit x2, x3, t) = f(x, t),
задаваемое формулой
i, Х2, Х3, t) —
•*! ~S1' *2—&2' -*3 — %г, t — х) 0) (Si, Sjj, S3, X)
C-1)
где черта сверху служит символом осреднения, а (о(§, т)—не-
т)—некоторая весовая функция (чаще всего неотрицательная), удо-
удовлетворяющая условию нормировки
оо
Если функция ей равна нулю вне некоторой четырехмерной
области и принимает постоянное значение внутри нее, то C.1)
обращается в простое осреднение по заданной пространственно-
временной области. Полагая же ю (|, т) = ю (|) 6 (т) или
1и(|,т) = (о(тNA), где буквой б обозначена 6-функция Дирака,
а <оA) и (о(т)—функции, имеющие постоянное значение на не-
некотором параллелепипеде или отрезке и равные нулю вне его,
мы придем к пространственному или соответственно временному
осреднению. Ясно, однако, что среднее значение C.1), вообще
говоря, будет зависеть от вида весовой функции о (в частности,
при использовании осреднения по некоторому интервалу време-
времени или области пространства оно будет зависеть от длины ин-
интервала или формы и объема области). Таким образом, фор-
формула C.1) приводит к множеству различных «средних значе-
значений», и надо еще выяснить, какое из них является «наилучшим».
При выборе какого-либо определенного «правила осредне-
осреднения» прежде всего следует четко сформулировать общие тре-
требования, которые целесообразно предъявлять к этому правилу.
С точки зрения теории турбулентности важнейшим из таких
общих требований, очевидно, является требование, чтобы при-
применение рассматриваемого осреднения к дифференциальным
уравнениям гидродинамики позволяло получить достаточно
простые уравнения относительно средних значений гидродина-

164 ГЛ. II. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [3.1
мических полей. Это хорошо понимал уже основоположник
теории турбулентности О. Рейнольде, который сам использовал
лишь простейшее осреднение по некоторому временному ин-
интервалу, но одновременно указал и естественные общие условия,
которым должно удовлетворять любое осреднение, применяемое
в гидродинамике. На самом деле, правда, не все нужные общие
условия были аккуратно выписаны Рейнольдсом A894); но,
слегка уточнив его рассуждения, легко прийти к выврду, что
следует требовать выполнения следующих пяти соотношений:
а/=а/, если а = const, C.4)
а = а, если а = const, C.5)
•% = -^-> где 5 —это хи х2, хъ или t, C.6)
7g=fl C-7)
В настоящее время условия C.3)—C.7) обычно называются
условиями Рейнольдса.
Условие C.6) можно также заменить более общим условием
перестановочности операций осреднения и предельного перехода
C.6')
Я-^оо П->со
Полагая в C.7) последовательно g — 1, g — Ъ и g = h' = h — Ъ
(штрихом у нас всегда будет обозначаться пульсация соответ-
соответствующей величины, т. е. ее отклонение от-своего среднего зна-
значения) и используя также C.5) и C.3), мы получаем следую-
следующие важные следствия из условий Рейнольдса:
f=l f'=f-f=O, fh=fh, fh'=fh' = O. C.7')
Ясно, что условия C.3), C.4), C.5) и C.6) или C.6') будут
выполняться при любом осреднении C.1) с произвольной весо-
весовой функцией ю, удовлетворяющей C.2). Иначе обстоит дело
с наиболее сложным условием C.7). Так, например, если поль-
пользоваться временным или пространственным осреднением по не-
некоторому интервалу, то можно показать, что, строго говоря,
ни при каком выборе интервала осреднения это условие не бу-
будет точно выполняться. Нетрудно, однако, привести соображе-
соображения в пользу того, что интервал осреднения можно выбрать
так, чтобы это условие приближенно выполнялось со сравнитель-

3.1] S3. МЕТОДЫ ОСРЕДНЕНИЯ 165
но большой степенью точности: для этого надо только, чтобы
интервал осреднения был велик по сравнению с характерными
периодами пульсационного поля f — f — f, но был мал по срав-
сравнению с периодами осредненного поля / (ср., например, Кочин,
Кибель, Розе A963), ч. 2, стр. 689—690). Подобного рода сооб«
ражениями и ограничился в свое время Рейнольде; в настоящее
время, однако, эти качественные соображения вряд ли могут
быть признаны вполне убедительными.
Возможность выбора интервала осреднения, промежуточного между пе-
периодами пульсационного и осредненного движения, предполагает заранее, что
турбулентное движение может быть разбито на сравнительно плавное и
медленно меняющееся «среднее движение» н налагающееся на него крайне
нерегулярное «пульсационное движение», причем между областями частот,
характерных для того и другого движения, имеется заметный разрыв.
Иначе говоря, здесь предполагается, что преобразование Фурье (по вре-
времени или по координатам) функции f отлично от нуля в некоторой области
вблизи нуля и в некоторой далекой от нее области больших частот (или
волновых чисел) и равно нулю в промежутке между этими областями. Та-
Такая картина более или менее соответствует действительности в случае мно-
многих искусственных турбулентных потоков, создаваемых в лаборатории. Од-
Однако в случае, например, естественных турбулентных движений в зем-
земной атмосфере и океане она вряд ли может быть всегда принята, поскольку
атмосферная и морская турбулентность часто имеет широкий непрерывный
спектр.
Наиболее последовательное использование представления о том, что
среднее значение / и пульсация f функции / отличаются в первую очередь
характерными периодами (или длинами волн) состоит в определении сред-
среднего значения f как части разложения функции f в интеграл Фурье, отвечаю-
щей интегрированию по области значений соответствующей переменной (ча-
(частоты или волнового числа), меньших по абсолютной величине некоторого
фиксированного числа ро. Легко понять, что в этом случае условия C.3), C.4),
C.5) и C.6) будут выполняться'); будут выполняться также и первые два
из условий C.7'), следующих из C.7). Однако общее условие C.7) здесь, во-
вообще говоря, ие будет иметь места; для его выполнения необходимо нало-
наложить на рассматриваемые функции f и g некоторые весьма специальные ус-
условия, несовместимые с предположением о том, что их преобразования Фурье
всюду отличны от нуля (см. по этому поводу подробное исследование Изак-
сона A929), а также заметку Кампе де Ферье A951)).
Отметим еще, что Г. Биркгоф, Кампе де Ферье, Рота и некоторые другие
авторы опубликовали ряд работ (ссылки на которые можно найти, например,
в обзорной статье Кампе де Ферье A956) и в статье Рота (I960)), посвя-
посвященных исследованию общих «операций осреднения», точно удовлетворяющих
условиям Рейнольдса C.3)—C.7) (или некоторым родственным условиям
того же типа) и определенных на различных классах функциональных про-
пространств (т. е. иа совокупностях функций, удовлетворяющих тем или иным
специальным условиям)-. Полученные в этих работах результаты позволяют
в некоторых случаях дать полное описание (в абстрактных алгебраических
терминах) всех таких операций осреднения. Однако все эти исследования
имеют формально-математический характер и их результаты не нашли
|) Это следует и из того, что такое осреднение, как легко видеть, являет-
является частным случаем осреднения C.1).

166 ГЛ. П. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [3.2
непосредственного применения в теории турбулентности. Впрочем, это оказы-
оказывается и ненужным, так как в современной теории 1урбулентности вопрос о
смысле операции осреднения решается соверщеннр иначе и притом так, что
все условия Рейнольдса очевидным образом оказываются точно выполняющи-
выполняющимися (но зато возникает совсем новый вопрос'о выполнении так называемого
условия эргодичности, о котором еще будет речь ниже).
3.2. Случайные поля гидродинамических величин
и вероятностное осреднение
Использование временного, пространственного или простран-
пространственно-временного осреднения, задаваемого какой-либо фор-
формулой вида C.1), очень удобно с практической точки зрения,
но неизбежно приводит к большим аналитическим трудностям
при теоретических расчетах. Кроме того, такое осреднение обла-
обладает тем существенным недостатком, что при его использовании
каждый раз приходится специально решать вопрос о форме
функции (о(|, т), наиболее удобной для данной задачи. По всем
этим причинам представляется желательным в теории турбу-
турбулентности вовсе не использовать осреднения такого типа, а
принять вместо него какое-нибудь другое определение среднего
значения, обладающее более простыми свойствами и более уни-
универсальное по своей природе. Такое более удобное определение,
которым мы и будем все время пользоваться в настоящей книге,
возникает при теоретико-вероятностной трактовке полей гидро-
гидродинамических величин в турбулентном потоке как случайных
полей.
Основой теоретико-вероятностного (или, как чаще говорят,
Статистического) подхода к теории турбулентности является
переход от рассмотрения одного-единственного турбулентного
потока к рассмотрению статистической совокупности аналогич-
аналогичных потоков, задаваемых некоторой совокупностью фиксиро-
фиксированных внешних условий. Чтобы понять, что это означает, рас-
рассмотрим какой-либо конкретный класс гидродинамических
потоков, например класс потоков, возникающих в аэродинами-
аэродинамической трубе при обтекании прямого кругового цилиндра. Основ-
Основное различие между случаями ламинарного и турбулентного
рбтекания состоит в следующем. При ламинарном обтекании,
Поместив одинаковым образом два равных цилиндра в две
идентичные трубы (или, что то же самое, повторив дважды наш
рпыт с одним и тем же цилиндром в одной и той же трубе), мы
через заданное время t после включения мотора в заданной
точке х рабочей части трубы будем иметь одно и то же значе-
значение Ui (х, t) компоненты скорости вдоль оси Oxi и других гидро-
гидродинамических характеристик потока (которые можно, во вся-
КОМ случае в принципе, найти с помощью решения некоторой

3.2] 3. МЕТОДЫ "ОСРЕДНЕНИЯ ' 167
Задачи с краевыми и^ачальными условиями для системы ур
нений Навье — Стокса). В случае же турбулентного обтекания
влияние малых неконтролируемых возмущений в потоке и в на-
чальных условиях приводит к тому, что, проведя два раза один
и тот же опыт в практически одинаковых условиях, мы получим
два различных значения величины Ut(x,t) и других характе-
ристик. Но в таком случае можно ввести в рассмотрение «мно-
«множество всех значений величины Ui(x,t), получающихся во все-
всевозможных опытах по турбулентному обтеканию цилиндра при
заданных внешних условиях», и значение щ(х, t), полученное
в каком-то конкретном опыте, считать одним «представителем»,
выбранным наудачу из этого множества1). Если теперь мы за-
зафиксируем внешние условия и при этих условиях будем много
'?аз повторять наш опыт, каждый раз записывая получающееся
значение ut(x, t), то среднее арифметическое всех полученных
значений величины Ui(x,t) на практике обычно оказывается
довольно устойчивым; иначе говоря, начиная с некоторого до-
достаточно большого числа опытов, оно при дальнейшем возра-
возрастании этого числа обычно уже мало меняется, колеблясь все
время около некоторого постоянного значения (наличие такой
устойчивости средних и означает, что наш набор аналогичных
опытов представляет собой статистический ансамбль). В таком
случае значение, около которого все время колеблется среднее
арифметическое значений щ(х, t), наблюдавшихся в совокуп-
совокупности аналогичных опытов, мы будем называть теоретико-вероят'
постным средним значением скорости щ{х, t) и обозначать сим-
символом щ(х, t), в дальнейшем черта сверху у нас всегда будет
обозначать именно такое теоретико-вероятностное осреднение).
Подобным же образом и эмпирические средние значения
всех других гидродинамических характеристик потока, взятые
по совокупности аналогичных опытов, оказываются устойчивы'
ми и при достаточно большом числе опытов обычно лишь слабо
отклоняются от некоторых постоянных чисел. Особый интерес
для нас будет представлять характеристика Хи,(х,ц(и'> и")> и" >
') Заметим, что в случае природной турбулентности (например, атмо-
атмосферной) выбор множества аналогичных опытов представляет большие труд-
трудности, так как здесь «внешние условия» (сводящиеся в первую очередь
к метеорологическим условиям) не могут быть повторно воспроизведены по
нашему желанию. Однако и здесь обычно удается подобрать ряд ситуаций,
в которых все условия, существенно влияющие на измеряемую величину
(например, при измерении скорости ветра на высоте 2 м — значение средней
скорости ветра, градиентов ветра и температуры и направление ветра), ока-
оказываются практически одинаковыми. В таком случае совокупность этих
ситуаций и будет представлять собой «статистический ансамбль аналогичных
опытов», не отличающийся от ансамбля всевозможных обтеканий равных
цилиндров в идентичных аэродинамических трубах.

168 ГЛ. И. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [3.2
>и', равная нулю, если значение величины щ(х, t) оказывается
большим, чем и", или меньшим, чем и', и равная единице в
противоположном случае. Число р(и',и"), около которого ко-
колеблется при большом числе опытов среднее арифметическое
этой характеристики (равное, очевидно, относительной частоте
опытов, в которых значение щ{х, t) оказывается удовлетво-
удовлетворяющим неравенству и'^.щ(х, t)^.u"), называется вероят-
вероятностью того, что щ(х,t) примет значение в интервале между и'
и и". Обычно это число р(и', и") может б,ыть представлено в
виде интеграла в пределах от и' до и" от некоторой неотрица-
неотрицательной функции р(и), называемой плотностью распределения
вероятности (или короче — просто плотностью вероятности) ве-
величины щ(х, t). В таком случае совокупность всех и, для кото-
которых р(и) Ф 0, и будет составлять то «множество возможных зна-
значений щ(х, t)*, о котором мы говорили выше; конкретное же
значение Ui(x, t), наблюденное в одном из опытов, мы будем
называть выборочным значением (или реализацией) ^-компо-
^-компоненты скорости. Факт существования плотности р(и) иногда
записывается в виде равенства
Р{и<их(х, t)<u-\ du}=p(u)du,
где знак Р{...} означает вероятность выполнения условия, ука-
указанного в скобках. Теоретико-вероятностное среднее значение
щ(х, t) величины щ(х, t) при этом, очевидно, может быть вы-
выражено через р(и) при помощи равенства
оо
щ {х, t) = j up (и) du. C.8)
— OQ
Одновременно знание плотности вероятности р(и) позволяет
нам определить также и теоретико-вероятностные средние зна-
значения произвольных функций от Ui(x,t): .,
оо
F\Ul(x, t)}= fF(u)p(u)du. C.8')
—оо v
В теории вероятностей величины и, имеющие определенную
плотность вероятности, называются случайными величинами;
совокупность же всевозможных вероятностей р (и', и") =
= Р{и < и < и"), отвечающих величине и, называется ее рас-
распределением вероятности.
Поэтому мы можем заключить, что с точки зрения теории
вероятностей значение скорости в точке турбулентного потока
представляет собой случайную величину, характеризуемую опре-
определённым распределением вероятности.

3.2] § 3. МЕТОДЫ ОСРЕДНЕНИЯ 169
До сих пор мы говорили только о значении Ui{x, t) компо-
компоненты скорости в фиксированной точке X и в фиксированный
момент времени /. Однако аналогичный подход приложим и ко
всему полю значений Ui(X,t), т. е. функции Ui(X,t) =
= щ(Х1, х2, х3, t) от четырех переменных. Повторяя много раз
один и тот же опыт (сводящийся к осуществлению некоторого
турбулентного движения) при одинаковых внешних условиях,
мы будем каждый раз получать новое поле щ(х,t). Таким об-
образом, и здесь можно говорить о «множестве возможных полей
иг(х, t)-», а каждое отдельное поле, наблюдающееся в каком-то
конкретном турбулентном потоке, рассматривать как одного
«представителя», наудачу выбранного из этого множества (ина-
(иначе говоря, как одну реализацию или одно выборочное значение
случайного поля щ{х, t). Нам надо теперь только объяснить,
чем заменяется в этом случае предположение о существовании
плотности вероятности р(и), использовавшееся при рассмотре-
рассмотрении одной величины щ(х, t).
Чтобы о поле Ui(x,t) можно было говорить как о случай-
случайном поле, прежде всего необходимо, чтобы значение Ui(M) =
= т(х, t) этого поля в любой фиксированной точке М = (X,t)
пространства — времени являлось случайной величиной. Поэто-
Поэтому каждой комбинации значений х и t здесь должна отвечать
своя плотность вероятности Рм(и), зависящая от М = (x,t).
Но это еще не все; если выбрать два значения «l(Afi) = tii(xv tr)
и щ (М2) = щ (лг2. h) нашей компоненты скорости, то средние
арифметические любых функций от этих двух величин также
должны быть статистически устойчивыми. Это значит, что для
величин Ui(Mi) и и^Мъ) должна существовать двумерная плот-
плотность вероятности pMlMi(ui,Uz), определяемая соотношением
Р {«1 < щ (Mj) < Й1 + duv и2 < их (М2) < й2+du2] =
Иными словами, при изменении значений щ(Му) и Ui(M2) в
большом числе турбулентных потоков, характеризуемых одина-
одинаковыми внешними условиями, доля случаев, в которых значение
Ui(Mi) оказывается заключающимся между фиксированными
значениями а[ и и*и в то же время значение щЩг) оказывает-
оказывается заключающимся между а'2 и и\, должна колебаться около
некоторого постоянного значения (равного двойному интегралу
в пределах от и[ до и\ и от а'2 до и\ от неотрицательной функ-
функции Pm,m,(uv И2))-Т°чно так же, если Mi'=(xv ti), M2 =
= (-*2' fe). •••. MN = (xN,tN)—произвольные Лоточек про-
пространства— времени, то им должна отвечать функция N

170 ГЛ. И. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [3.2
переменных
Рм1м3...mn(«I, и2, ..., uN), C.9)
определяемая соотношением
Р\их<щ(Mi) <иг-\-duv u2<ul{M2)<u2-\-du2, ...,
uN < и, (Мя) <uN + duN) =
= PMlMi... mn («i, и2. • • •. uN) dux du2... duN
и являющаяся N-мерной плотностью вероятности значений N
случайных величин ut(Mi), Ui(M2), .... Ui(MN). Наличие все-
всевозможных плотностей вероятности C.9) как раз~~й дает осно-
основание считать поле щ(х,Ц ^лучя^ным_ппл?м;_л^ля^его полного
задания (т. е. для задания распределения вероятностйНв функ-~"
циональном пространстве всех его возможных значений) надо
задать все семейство функций C.9), отвечающих всевозможным
целым положительным N и всевозможным наборам N точек
пространства — времени. Два турбулентных потока мы будем
при этом считать одинаковыми, если им отвечают одинаковые
(одномерные и многомерные) плотности вероятности; если "же
некоторый набор плртностей будет близок к тем, которые опи-
описывают заданный турбулентный поток, то этот набор плотно-
плотностей будет определять некоторую приближенную статистиче-
статистическую модель нашего турбулентного потока.
Функции C;9), очевидно, должны быть все неотрицательны-
неотрицательными и такими, что интеграл от каждой из них по всем перемен-
переменным равен единице; кроме того, они должны еще удовлетворять
определенным условиям симметрии и согласованности. А имен-
именно, по самому определению плотности C.9) для любых Mi,
М2, ..., MN должно выполняться соотношение
PMlMi...MN(u1, и2, ..., uN) — рм^м^...MiN(utlt Ut2, ..., uiN),
C.10)
где /i, 4, . • •, In — это те же числа I, 2, ..., N, но расположен-
расположенные в каком-то другом порядке. Далее, если п < N, то для лю-
любых N точек Mi М2, ..., Мп, Mn+i, ..., MN должно выполнять-
выполняться равенство
Рм1...мл(и1 и„) =
оо со
C.11)

3J2J S 3. МЕТОДЫ ОСРЕДНЕНИЙ 171
Любое семейство неотрицательных функций C.9), обладающих
оо
свойствами C.10) —C.11) и таких, что JpM{u)du = \ при всех
—оо
М = (дг, /), определяет некоторое распределение вероятности в
пространстве функций ut(M) = ut(x,t) от четырех переменных
(т. е. задает случайное поле Ui(M) = Ui(x,t)). Вероятностное
среднее значение F произвольной функции F(uu u2, ..., uN) от
значений
{M иг = и1{Мг), ..., uN = Ui(MN)
при этом определяется как интеграл
оо оо оо •
~F= f j ... f F(uv щ uN)X
— OO —00 —OO
XPm1m2...mn{uv Hj, ..., uN)du1du^...duN, C.12)
где^д!,^ ... mn (йц Щ, • • •, uN) — соответствующая плотность ве-
вероятности C.9).
Естественно предположить, что в турбулентном потоке поле
Ui(x, t) и поля остальных компонент скорости, а также поля
давления р(х, t), плотности р(лг, /) (в случае сжимаемой жид-
жидкости), температуры Т(х, t) (в случае температурно-неодно-
родной среды) и других гидродинамических величин яв-
являются случайными полями. В таком случае каждому
из этих полей будет соответствовать своя система многомер-
многомерных плотностей вероятности C.9). Кроме того, различные
гидродинамические поля в турбулентном потоке являются ста-
статистически связанными друг с другом, и следует считать, что
для них существуют также совместные плотности вероятно-
вероятности значений одного из полей в каких-то заданных Л^ точках
пространства — времени, значений второго поля в заданных N2
точках, значений третьего поля в заданных N3 точках и т. д.
Отсюда вытекает, что, имея любую функцию от гидродинами-
гидродинамических характеристик турбулентного потока, мы можем опре-
определить ее среднее значение как интеграл от произведения этой
функции на совместную плотность вероятности всех ее аргу-
аргументов, распространенный по всей области изменения этих ар-
аргументов (ср. C.12)). При этом условия C.3) — C.7) обра-
обращаются в известные свойства теоретико-вероятностных сред-
средних значений, доказательство которых приводится в курсах
теории вероятностей; таким образом, теперь они уже оказы-
оказываются точно выполняющимися и не требуют никакого специ-
специального обоснования.

172 ГЛ. П. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [3.3
3.3 Понятие об эргодичности. Статистическая формулировка
основной задачи теории турбулентности
Намеченный выше подход к полям гидродинамических ха-
характеристик турбулентного потока как к случайным полям,
идущий от работ А. Н. Колмогорова и его учеников (см., напри-
например, Миллионщиков A939)) и работы Кампе де Ферье A939),
является в настоящее время общепринятым во всех исследова-
исследованиях по теории турбулентности (см., например, обзорные, статьи
Кампе де Ферье A953) и Обухова A954)). Приняв предполо-
предположение о существовании распределений вероятности для всех
гидродинамических полей,, мы можем, далее, широко применять
математический аппарат современной теории вероятностей; опе-
операция осреднения при этом определяется вполне однозначно и
обладает всеми свойствами, которых естественно от нее тре-
требовать. Существенно отметить, однако, что при таком подходе
сразу же возникает важный дополнительный вопрос о сопо-
сопоставлении выводов теории с данными непосредственных изме-
измерений.
Дело в том, что согласно нашему новому определению сред-
среднее значение понимается как среднее, взятое по всем возмож-
возможным значениям рассматриваемой величины; поэтому для эмпи-
эмпирического определения средних значений со значительной сте-
степенью точности мы должны были бы иметь результаты большого
числа измерений, производившихся в длинной серии повторяю-
повторяющихся аналогичных опытов. На практике, однако, мы чаще
всего не имеем такого множества опытов и вынуждены опреде-
определять средние значения по данным измерений, проводившихся в
течение одного-единственного опыта1). Во всех таких случаях
обычно используется простейшее осреднение эмпирических дан-
данных по некоторому интервалу временю или пространства. От-
Отсюда видно, что предположение о существовании распределений
вероятности само по себе еще не снимает вопроса о законности
использования в теории турбулентности обычных временных
или пространственных средних, а лишь изменяет постановку
этого вопроса. „А именно, вместо исследования частных свойств
того или иного метода осреднения мы должны теперь выяснить,
насколько близки соответствующие эмпирические средние,к ве-
вероятностным средним значениям, с которыми лишь и имеет
дело теория. Положение дел здесь вполне аналогично тому,
') Исключение в этом отношении представляют лишь опыты по опреде-
определению численных характеристик турбулентной диффузии, в которых чаще
всего одновременно выпускается целое облако одинаковых частиц (например,
клуб дыма), а затем производится «осреднение по облаку>, в известном
смысле эквивалентное осреднению по множеству аналогичных опытов.-

3.3] § 3. МЕТОДЫ ОСРЕДНЕНИЯ 173
которое имеется в обычной статистической механике систем с
конечным числом степеней свободы, где также приходится за-
заменять теоретические «средние по совокупности возможных
состояний системы» (или, как чаще говорят, «средние по ан-
ансамблю») непосредственно наблюдаемыми временными средни-
средними. Известно, что в статистической механике при такой замене
обычно исходят из предположения, что временные средние зна-
значения при неограниченном увеличении интервала осреднения
сходятся к соответствующим теоретическим средним значениям.
Справедливость этого предположения в некоторых специальных
случаях может быть строго доказана (например, с помощью
«эргодической теоремы» Дж. Биркгофа), а в остальных случаях
оно принимается в качестве дополнительной весьма правдопо-
правдоподобной гипотезы («эргодическая гипотеза»). В теории турбу-
турбулентности также иногда вводят предположение о сходимости
временных или пространственных средних при неограниченном
увеличении интервала осреднения к соответствующим вероятно-
вероятностным средним в качестве специальной «эргодической гипотезы».
В применении к временным средним правдоподобность этой
гипотезы в ряде случаев подкрепляется, в частности, общими
представлениями Л. Д. Ландау о характере развитой турбулент-
турбулентности, изложенными на стр. 145. Заметим, однако, что во мно-
многих случаях законность замены теоретико-вероятностных сред-
средних значений гидродинамических полей временными или про-
пространственными средними может быть также строго обоснована
с помощью «эргодических теорем» современной теории случай-
случайных процессов и полей. В связи с большой важностью этого
вопроса мы ниже еще остановимся на нем более подробно (см.
п. 4.7); сейчас же мы постараемся сформулировать общую за-
задачу изучения турбулентности как некоторую задачу о распре-
распределениях вероятности для соответствующих гидродинамических
полей.
Выше мы видели, что в случае ламинарных движений уравне-
уравнения гидродинамики позволяют однозначно определить значения
всех гидродинамических характеристик потока в любой будущий
момент времени по начальным значениям гидродинамических
полей (и соответствующим граничным условиям). При этом в
случае несжимаемой жидкости достаточно знать лишь начальные
значения поля скорости (или поля вихря скорости); в случае же
сжимаемой жидкости требуется задать начальные значения
пяти независимых гидродинамических полей (например, трех
компонент скорости, давления и температуры). В турбулентных
потоках начальные значения соответствующих гидродинами-
гидродинамических полей также будут с помощью уравнений гидродинамики

174 ГЛ. II. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [3.3
определять все их будущие значения1). Однако здесь эти бу-
будущие значения будут существенно зависеть от ничтожных
неконтролируемых возмущений начальных и граничных ус-
условий и, кроме того, будут иметь столь сложный и запутан-
запутанный вид, что точное их определение оказывается бесполезным,
а интегрирование соответствующих дифференциальных уравне-
уравнений практически невыполнимым. Только распределения вероят-
вероятности для соответствующих гидродинамических полей, а вовсе
не сами точные значения этих полей могут в этом случае пред-
представлять интерес. Поэтому и уравнения гидродинамики в случае
турбулентных потоков следует использовать лишь для исследо-
исследования соответствующих распределений вероятности или каких-
либо определяемых этими распределениями величин.
Заметим еще, что для возможности применения уравнений
гидродинамики к случайным полям, задаваемым своими распре-
распределениями вероятности, эти распределения должны обладать
известными свойствами регулярности, гадантирующими, что ре-
реализации соответствующих полей можно считать непрерывными
и достаточно гладкими — имеющими все входящие в уравнения
временные и пространственные производные. Предположим те-
теперь, что распределения вероятности, относящиеся к значениям
полей в фиксированный начальный момент времени / = /0> удо-
удовлетворяют этим условиям^ регулярности. В таком случае каж-
каждая конкретная реализация гидродинамических полей потока
будет закономерно изменяться во времени в соответствии с из-
изменением во времени решения, отвечающего заданным началь-
начальным (и граничным) условиям. Следовательно, вся совокупность
возможных начальных гидродинамических полей перейдет че-
через время т> 0 в строго определенную совокупность функций
от пространственных координат, относящуюся к моменту
t = t0 + x. Отсюда вытекает, что плотность вероятности для ка-
какого-либо гидродинамического поля в момент / можно (во вся-
всяком случае, в принципе) определить, рассчитав с помощью урав-
уравнений гидродинамики, какой совокупности начальных условий
будет соответствовать тот или иной интервал значений нашего
') Заметим, впрочем, что в литературе по теории турбулентности выска-
высказывалось иногда даже мнение о том, что в турбулентном потоке уравнения
гидрТПШнамики вообще неприменимы. Если не принимать во внимание совсем
беспочвенные утверждения, то существенным здесь является лишь вопрос
.о том, не могут ли молекулярные флюктуации вызвать случайные «всплески»,
'способные передавать энергию наиболее мелкомасштабным гидродинамиче-
гидродинамическим возмущениям н тем самым, например, стимулировать переход потока
к турбулентному режиму. В настоящее время, однако, почти все согласны
с тем, что если такие процессы и возможны, то роль их, во всяком случае,
очень невелика, так что в первом приближении их вполне можно не учиты-
учитывать (см. также ниже стр. 21&—217),

3.4] § 3. МЕТОДЫ ОСРЕДНЕНИЯ 175
поля в момент t, и найдя вероятность этой совокупности началь-
начальных условий. Таким образом, в турбулентном потоке уравнения
гидродинамики будут однозначно определять эволюцию во вре-
времени распределения вероятности гидродинамических полей. Это
значит, что более или менее произвольно (с соблюдением лишь
некоторых «условий регулярности») здесь можно выбирать
только распределения вероятности в один фиксированный мо-
момент времени; после этого все остальные распределения вероят-
вероятности, относящиеся к значениям гидродинамических полей во
всевозможных точках пространства — времени, будут уже одно-
однозначно определяться из уравнений движения. Поэтому основную
задачу теории турбулентности (например, для случая несжимае-
несжимаемой жидкости) можно сформулировать следующим образом: по
заданному распределению вероятности значений трех компонент
скорости в различных точках пространства в момент t = t0, со-
сосредоточенному на совокупности дважды дифференцируемых
соленоидальных векторных полей, требуется определить распре-
распределения вероятности значений полей скорости и давления во
все последующие моменты времени (включая и распределения
для значений в несколько различных моментов времени). В слу-
случае сжимаемой жидкости надо только вместо распределений
вероятности трех компонент скорости исходить из распределе-
распределений вероятности значений пяти независимых гидродинамиче-
гидродинамических величин. К сожалению, эта общая задача слишком трудна,
й в настоящее время еще не видно подхода к ее полному реше-
решению. Поэтому дальнейшее обсуждение этой задачи мы отложим
до заключительной главы второй части нашей книги; в осталь-
остальных же главах мы будем заниматься лишь более частными за-
задачами, в которых вместо распределений вероятности фигури-
фигурируют некоторые менее полные статистические характеристики
случайных полей.
3.4. Характеристические функции и характеристический
функционал
Во многих случаях вместо плотностей вероятности C.9) удобно рас-
рассматривать их преобразования Фурье
лг
ft = I * « . . . . .о .оч
— ОО
Такие преобразования Фурье называются характеристическими функциями
соответствующих распределений вероятности; в силу C.12J их, очевидно,

176 ГЛ. II. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [3.4
можно также представить в виде
Ясно, что характеристическая функция однозначно определяет отвечающее
ей распределение вероятности: в самом деле,
Е
C.15)
в силу известной формулы обращения интегралов Фурье. Таким образом,
задание характеристической функции равносильно заданию соответствующей
плотности вероятности.
В силу самого своего определения характеристические функции являются
комплексными непрерывными функциями от аргументов 8i, 82 8W, обла-
обладающими следующими свойствами:
л л
2j ?Л1 M. ...MN\?\ — °1 • °2 °2 °ЛГ °ATjCftW>U t-1')
ft=W=l ' 2
(где звездочкой обозначены комплексно сопряженные величины) при любом
целом п, любых вещественных в\\..., 6'j"'; 6^' 6^"';...; в^' Q$> и
любых комплексных сь ..., с„. В самом деле, левая часть C.17), очевидно,
„ /Е»(,*'в,. 2
равна среднему значению неотрицательной величины ^1 * Л
откуда и вытекает иаписаиное неравенство. Можно также показать, что
любая непрерывная функция от & переменных, обладающая свойствами
C.16) н C.17), является характеристической функцией некоторого ЛГ-мерного
распределения вероятности (которое, правда, может и не иметь плотности
вероятности, а, например, относится к дискретному firny; см. Бохиер A933)).
Это обстоятельство иам еще понадобится во второй части книги.
Нетрудно видеть, что условие симметрии C.10) и условие согласован-
согласованности C.11) в применении к характеристическим функциям переходят
в условия
Vm^ ...mn (\> е2 6лг) - fM^M^ ... MlN (ev е/2 %), C-18)
....jnw(ei.--- 6я- ft--- °)- С3-19)
Таким образом, случайное поле любой гидродинамической величины можно
также задать семейством характеристических функций C.14), удовлетворяю-
удовлетворяющих C.18) и C.19). ч
Из C.19) видно, что характеристическая функция распределения вероят-
вероятности значений поля в заданной системе N точек крайне просто определяет
характеристические функции зиачений поля в любой подсистеме этой системы,
Поэтому естественно попытаться сразу задать все распределения вероятности,

3.4] $ 3. МЕТОДЫ ОСРЕДНЕНИЯ 177
характеризующие поле, при помощи одной-единственной величины — «харак-
«характеристической функции распределения вероятности для значений поля во
всех возможных точках». Оказывается, что такое задание случайного поля
при помощи одной величины — «характеристического функционала:»— дей-
действительно возможно (и в этом состоит одно из важных преимуществ под-
подхода, исходящего из характеристических функций, а не из плотностей веро-
вероятности). Впервые возможность подобного задания случайных функций была
отмечена Колмогоровым A935); в последующие годы ей был посвящен ряд
как чисто математических работ, так и работ прикладного характера (среди
которых особо ¦ следует отметить важную работу Хопфа A952), о которой
мы еще будем подробнее говорить во второй части книги). Здесь мы коротко
изложим лишь самую суть дела, не останавливаясь на математических
тонкостях.
Для простоты сначала рассмотрим вместо случайного поля, зависящего
от четырех переменных, случайную функцию и(х) от одного переменного,
заданную на конечном отрезке а •< х •< Ь оси *. Функция и(х) задается
всевозможными распределениями вероятности для знавеннй u(*i), и(х2), . . .
,. . . , и(хя) этой функции на произвольной системе N .точек Х\, х2, . . . , xN,
таких, что а <!-«?•< 6. Будем теперь безгранично увеличивать число N, выби-
выбирая точки ** так, чтобы все расстояния между двумя соседними из них
стремились к нулю, а в качестве значений параметра 8* выберем умноженные
на Хн+1 — ** значения в точках хк некоторой функции Q(x) на [а, Ь]. Если
функция 6(лс) такова, что интеграл
ь
и [6 (х)] = Г 6 (х) и (х) dx C.20)
а
N
существует для почти всех реализаций функции и(х) '), то 2 "*"* ПРН
N-*-co будет стремиться к интегралу C.20). Переходя к пределу N-*-co
в формуле C.14), мы придем к величине
b
Ф [в (х)] - exp {iu 16 (x)]} = exp III в (х) и (x) dx V. C-21)
Величина Ф [8 (*)], очевидно, является значением характеристической функ-
функции случайной величины u[Q(x)] при аргументе этой функции, равном едини-
единице. Следовательно, при заданной функции 0(*) это есть некоторое комплекс-
комплексное, число. Таким образом, формула C.21) сопоставляет каждой функции
6(*)" некоторое комплексное число, т. е. Ф[6(*)] является функцией от функ-
функции или, как обычно говорят в таких случаях, является функционалом. Мы
будем называть этот функционал характеристическим функционалом случай-
случайной функции и(х).
Покажем, что, зная для некоторой случайной функции и(х) ее характе-
характеристический функционал, можно определить все конечномерные плотности'
вероятности Рх ,х , ...*xN(.ui< > •••> цлг)- Для этого достаточно подставить
в качестве функционального аргумента Q(x) функционала Ф[6(*)] специаль-
специальную функцию
в (х) - 6,8 (х - хх) + 626 (* - х$ + ... + 6„6 (х - xN), C.22)
') То есть для всех реализаций этой функции, за исключением, быть мо-
может, некоторого множества исключительных реализаций, суммарная вероят-
вероятность которых равна нулю.

178 ГЛ. II. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [3.4
где 01, ..., QN — произвольные числа, а 6(х)—функция Дирака, так что
функция C.22) равна нулю всюду, кроме точек Х\, Хг, .. ') П
равенство C.22) в C.21), получим
Ф [в (х)] = ехр | / ^ 6Л J = 9xi хн (в, 6„). C.23)
Следовательно, характеристический функционал в этом случае обращается
в характеристическую функцию многомериого распределения вероятности для
величин u(xi), u(xt),...,u(xN), так что соответствующая плотность распреде-
распределения может быть найдена с помощью формулы обращения интегралов
Фурье.
Характеристический функционал Ф[6(*)], очевидно, обладает следую-
следующими свойствами, аналогичными свойствам C.16) и C.17) характеристи-
характеристических функций:
о-1- C-24)
2 2 Ф [в* (х) - в, (*)] ckc\ > 0 C.25)
k=i i=i
при любых функциях 6i(*),..., вп(*) и комплексных числах с1(....сп (послед-
(последнее свойство называется свойством положительной определенности функцио-
функционала Ф[8.(*)]). Однако обратное утверждение о том, что непрерывный (в
определенном смысле) положительно определенный функционал Ф[8(*)],
обладающий свойствами C.24) и C.25), всегда является характеристическим
функционалом некоторой случайной функции, будет справедливым, лишь если
принять значительно более общее определение случайной функции, чем то,
') При рассмотрении характеристического функционала C.21) обычно
предполагается, что 6(лс)—достаточно гладкая функция (например, непре-
непрерывная или непрерывная и определенное число раз дифференцируемая).
Поэтому, строго говоря, вместо «несобственной функции» C.22) надо рас-
рассмотреть последовательность гладких функций 8(п> (*), л=1,2,..., таких, что
для любого интервала [a, (J], не содержащего ни одной из точек хи i~
Р
Hm (b(n)(x)dx=O
л-»оо J
а
и что для любого достаточно малого в > 0 и i=\,2,...,N
Х1+е
Hm Г
л->об J
Очевидно, что при этом
Hm Ф [6(л) (х)] = Ф [в (х)],
я-»оо
где Q(x) —функция C.22). Отсюда видно, что значение Ф[8(*)] всегда может
быть определено и по одним только значениям характеристического функцио-
функционала для гладких функций е<">(*),

3.4] § з. mei-оды осреднения 179
которым мы здесь пользуемся (см. Гельфанд и Виленкин A961), Прохоров
A961)). .
Совершенно аналогично обстоит дело н тогда, когда вместо случай-
случайной функции и(х) от одного переменного приходится рассматривать случай-
случайное поле U\(x,t), зависящее от четырех переменных. Здесь характеристиче-
характеристическим функционалом называется величина
Ф [8 (*,*)] = ехр
i f f f f 9 (x, t) «, (x, t) dx{ dxt dxs dt I; C.26)
в качестве аргумента она содержит функцию в (х, t) от четырех перемен-
переменных1). Ясно, что и в этом случае характеристический функционал будет
однозначно определять все распределения вероятности для поля и.\(х, t) (и
будет обладать свойствами, аналогичными C.24) и C.25)).
При рассмотрении нескольких статистически связанных между собой
случайных функций или случайных полей приходится рассматривать характе-
характеристический функционал, зависящий от нескольких функциональных аргу-
аргументов. Так, например, поле скорости турбулентного потока а (х, г) =л
«= {«1 (x,t), и2{х, t), u3(x, t)} однозначно определяется характеристическим
функционалом
Ф [в (х, Щ = Ф [в, (х, t), в2 (х, t), 63 (х, t)\ -
Г" - —¦ —
, C.27)
зависящим от трех функций от четырех переменных. В общем случае
^-мерного случайного поля и(х)— [их(х) uN (*)} в пространстве точек
х мы будем иметь
Ф [в (*)] = Ф [в, (х) е„ (*)] = ехр | / J J] \ (х) uk (х) dx . C.27')
Функционал Ф[в (*)], очевидно, также будет обладать свойствами C.24) и
C.25) (с заменой лишь скалярного аргумента в(л-) векторным аргументом
б (х)). Распределение вероятности для поля скорости в фиксированный мо-
момент времени t определяется функционалом
ехр
| ,
V
00
J J J
—00
3
h(x
t) uk
(x,
t)dxdt
eft (x)uk(x, t)dx\, C.28)
I -co t=l j
зависящим от тройки функций в (х) = {в, (х), в2 (х), в3 (х)} от трех перемен-
переменных и от одного скалярного параметра t. Согласно сказанному на стр. 174—
175 об однозначной зависимости распределений вероятности для поля скорости
несжимаемой жидкости во все моменты времени от распределения вероят-
вероятности в начальный момент <=0, характеристический функционал Ф[6 (x),t] в
1} Во избежание затруднений со сходимостью интегралов на бесконеч-
бесконечности можно с самого начала ограничиться лишь такими функциями 8(x,t),
каждая из которых тождественно равна нулю вне некоторой ограниченной
области пространства четырех переменных.

180 ГЛ. II. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4.1
случае несжимаемой жидкости должен однозначно определяться своим на-
начальным значением Ф[6 (х), 0] (и даже более того — функционал Ф [6(Ж, t)]
равенства C.27) также должен однозначно определяться по Ф[в(дс), 0J)
Более сложно обстоит дело для течений сжимаемой жидкости: здесь мы.
должны рассматривать функционал типа
Ф [в (*), в«(*), в6 (*),<] =
'/// 2 е* (*)«*(*. Ф + 0« (*)р (*,"<) +06 (*) Т(х, t)\dx\
C.29)
(р (х, t} — поле плотности, Т(х, t)—поле температуры), зависящий от пяти
функций от трех переменных и одного скалярного аргумента. Только для
этого функционала должна иметь место в случае сжимаемой жидкости одно-
однозначная зависимость значения в любой момент t>0 от соответствующего
начального значения Ф[0(*),64(.х),6в(Х),0].
§ 4. МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ
4.1. Моменты и семиинварианты случайных величин
В предыдущем параграфе мы видели, что для полного ста-
статистического описания полей гидродинамических характеристик
турбулентного потока требуется задать все многомерные рас-
распределения вероятности для значений этих характеристик на
всевозможных множествах точек пространства — времени. Од-
Однако определение таких многомерных распределений является
весьма сложной задачей и редко может быть осуществлено с
достаточной точностью; кроме того, сами эти распределения ча-
часто оказываются мало удобными для приложений в силу своей
громоздкости. Поэтому на практике при решении конкретных
задач теории турбулентности чаще всего ограничиваются рас-
рассмотрением лишь некоторых более простых статистических па-
параметров, описывающих те или иные частные статистические
свойства потока.
Наиболее важными из таких параметров распределений ве-
вероятности являются моменты. Если мы имеем систему N случай-
случайных величин щ, иг, ..., uN с N-мерной плотностью вероят-
вероятности р(щ, u2,..., uN), то моментами этих величин называются
выражения
оо
= //••/ и? 'и*2 • • • unNP {*v иа, .. •, Ид) dux du2... duN, D.1)

4.1] § ¦• МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ 181
где. Ль k2,..., kN—целые неотрицательные числа, сумма кото-
которых называется порядком момента. В частности, моменты пер-
первого порядка — это средние значения величин щ, и2,..., uN.
Наряду с обычными моментами В/,^ ... kN иногда оказы-
оказывается удобным рассматривать некоторые специальные их ком-
комбинации. Например, часто используются так называемые цент-
центральные моменты, т. е. моменты отклонений величин щ, ы2, • • •
..., uN от соответствующих средних значений:
**Л... kN = (и, — я,)*«'(ва —и2р ...(«* — uNfN. D.2)
Раскрыв скобки в правой части D.2), легко выразить централь-
центральный момент Ьк1кг... kN через ?*,*2... *дг и обычные моменты низ-
низших порядков. В частности, при N = 1 мы будем иметь
.. D,3)
(момент &2 = <3и совпадает с теоретико-вероятностной диспер-
дисперсией величины и). Если йг=0, t = 1, ..., N, то центральные
моменты, очевидно, совпадают с обычными, так что момент
bkxk2... *лг является частным случаем момента Bklki...kN- Если
величины щ имеют определенную размерность, то размерными
будут и соответствующие моменты или центральные моменты;
однако, например, отношения
w=s- ж=ь D-4)
всегда безразмерны (отношение s называется асимметрией слу*
чайной величины и, а разность F — 3) — ее эксцессом).
Другими комбинациями моментов Bkik2...kpp представляю-
представляющими специальный интерес, являются так называемые семиин-
семиинварианты (или кумулянты) Skik%... bN. Общее определение этих
величин будет дано несколько позже (см. ниже, стр. 183); сейчас
же мы только отметим, что семиинвариант Sk1ki...kN (так же,
как и центральный момент Ьихк2... kN) получается при помощи
вычитания из момента #*,*а... kN некоторого специального мно-
многочлена относительно моментов низших порядков. В частности,
при N = 1 семиинварианты первых пяти порядков задаются еле*
дующими равенствами:
=*B4 — АВхВг — 3$ + 12B\B2 — 6Я? = Ы — 3*2,
D.5)

182 ТЛ. II. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4.1
В многомерном случае семиинварианты второго и третьего по-
порядков также совпадают с соответствующими центральными
моментами, а общий семиинвариант Sim четвертого порядка
задается формулой
111 — *1111 100^0011 ^1010^0101 *1001*0110- D-6)
Из дальнейшего будет видно, что в некоторых случаях семиин-
семиинварианты оказываются особенно удобными характеристиками
распределений вероятности; пока, однако, мы в их отношении
ограничимся лишь тем, что уже сказано.
Различные моменты величин щ, щ ,..., и^ не могут прини-
принимать произвольные значения, а должны удовлетворять некото-
некоторым условиям, имеющим вид неравенств. Так, например, если
все показатели k\, k2 kN четные, то момент #*,*2... *дг. оче-
очевидно, не может быть отрицательным. Далее, если N = 1, то
2 %Bh+lckCl>Q, D.7)
где Во = 1, а со, с\, ..., сп — произвольные вещественные числа
<ибо левая часть D.7) равна среднему значению неотрицатель-
ной величины 2j cku I • При п = 2 и с0 = 0 отсюда, в част-
частно J /
ности, подучаются неравенства
|?3l<(?AO и |s|<8^ D.8)
(так как Ь& — это частный случай момента Вк). Аналогичные
неравенства могут быть выведены и для моментов высших по-
порядков и моментов многомерных распределений. Тем не менее,
ясно, что даже и при этих ограничениях произвол в выборе
возможных значений различных моментов, остается очень боль-
большим; поэтому задание всех без исключения моментов достав-
доставляет очень много информации о соответствующем распределе-
распределении вероятности. Во многих случаях задание всех моментов
даже просто равносильно заданию самого распределения (см.
ниже мелкий шрифт), так что использование вместо плотности
1вероятности совокупности отвечающих ей моментов не приводит
гк какой-либо потере полноты статистического описания. На
! практике, однако, никогда не бывают известны сразу все мо-
ьменты, а обычно рассматривается лишь несколько моментов
:низших порядков; они уже, разумеется, не определяют одно-
.-значно распределения, а характеризуют лишь некоторые его
•частные свойства. Несмотря на это, подход к изучению случай-
иых величин, опирающийся на рассмотрение лишь нескольких

4.2] § 4. МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ 183
их моментов, часто оказывается весьма целесообразным; в даль-
дальнейшем мы увидим, что в применении к теории турбулентности
он позволяет получить целый ряд конкретных результатов, пред-
представляющих значительный интерес.
Легко видеть, что моменты случайных величин щ, . . . , uN могут быть
просто выражены через соответствующую характеристическую функцию-
<p(9i, . . . , 9N). В самом деле, из сравнения D.1) с C.13) следует,, что
Bft,ft3
'ЛГ
Отсюда, в частности, вытекает, что если характеристическая функция может.'
быть представлена своим рядом Тэйлора, то
ft,, ft2 ftjv W ••• RN
Таким образом, в этом случае, зная все моменты распределения, мы можем
однозначно определить характеристическую функцию, а, следовательно, и
плотность вероятности. Нетрудно показать, что такая однозначность восста-
восстановления плотности по совокупности моментов будет иметь место йР тогда,
когда ряд D.10) является сходящимся лишь в некоторой области значений
9i, 9j, . . . , 9N (для одномерного случая общие условия, при которых эта
однозначность будет иметь место, указаны, например, в книге Ахнезера
A961)).
С помощью характеристической функции легко формулируется также и
общее определение семиинвариантов случайных величин. Для этого надо
рассмотреть логарифм характеристической функции t|>(9i, fk, ...* 6w) =
¦ »1п фFь 9г, ..., 9n); семиинвариант Sft ft ...*«• определяется по
t|>(9i. 9j, ..., 9n) следующим образом:
N
Учитывая, что ф@, О, ..., 0) = 1, отсюда легко получить формулы D.5)—D.6)
и вообще выразить любой конкретный семиинвариант через моменты или
центральные моменты.
4.2. Моменты и семиинварианты случайных полей.
В теории турбулентности приходится иметь дело со случай1*
ными полями — случайными функциями и(М) от точки М четыт
рехмерного пространства — времени. Моментами /С-г.О'порядка-
такого поля называются средние значения произведений К зна-
значений поля:

184 ГЛ. II. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4.2
Эти моменты зависят от координат тех точек, в которых берутся
значения поля, так.что момент К-щ порядка, вообще говоря,
является функцией от 4/С переменных. Следует, однако, иметь
в виду, что некоторые из точек Ми М2, ... , Мк могут и совпа-
совпадать друг с другом; число различных среди них определяет тип
момента. В этой связи мы будем различать моменты одноточеч-
одноточечного типа, двухточечного типа, трехточечного типа и т. д. (ко-
(короче — одноточечные, двухточечные, трехточечные и т. д. мо-
моменты). Если тип момента меньше его порядка, то соответствую-
соответствующий момент [и(Мх)]*' [и(Л*2)]*2 ... \u(MN)]bN будет обозна-
обозначаться символом Ви...и,и...и и...и{Мх, .М^, ...,MN), где
запятыми отделены группы, относящиеся к различным точкам
пространства — времени.
Средние значения произведений значений'нескольких разных
случайных полей, статистически связанных друг с другом, назы-
называются смешанными моментами этих полей. Так, например, поле
вектора скорости и (М) = [щ(М), щ(М), иг(М)} будет иметь Зк
различных (обычных и смешанных) моментов порядка К, обра-
образующих вместе один трехмерный тензор К-го ранга. В частности,
важный для дальнейшего двухточечные моменты второго и
третьего порядков поля скорости являются компонентами сле-
следующих тензоров второго и, соответственно, третьего рангов:
BtJ (Mlt Щ = ui(Ml)uJ(M2),
(где тензор Bijht очевидно, симметричен по индексам t и /).
Аналогичные обозначения будут употребляться и для смешан-
смешанных моментов других гидродинамических полей; например, двух-
двухточечные смешанные моменты поля давления и поля скорости
или поля Давления и поля температуры будут обозначаться
символами Bpi(Mit М2), /=1, 2, 3, или соответственно
ВрТ(Ми М2). В случае моментов, порядок которых превосходит
их тип, группы индексов, относящиеся к различным точкам, бу-
будут отделяться запятыми; например, через Bi}i р>, ты (Ми М2, М3)
будет обозначаться трехточечный смешанный момент .шестого
порядка полей скорости, давления и температуры, содержащий
четыре компоненты скорости и являющийся тензором четвертого
ранга, симметричным по парам индексов t, / и k, l. Центральные
моменты (т. е. моменты пульсаций гидродинамических полей —
их отклонений от своих средних значений) в случае полей с от-
отличными от нуля средними значениями будут обозначаться так
же, как и аналогичные обычные моменты, но с заменой буквы В
на Ь или с добавлением штрихов у соответствующих индексов.

4.2] 5 4. МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ 185
Одноточечные моменты удобнее обозначать просто с помощью
черты сверху (например, uh или uv); впрочем, для Дисперсии
Ьии(М) ==[и(М)—и(М)]2 поля и(М) иногда будет использо-
использоваться также и один из двух следующих специальных символов:
<з2а или U'2 (второе из этих обозначений уже использовалось в
§ 2 —см., например, рис. 7 и 24)-
В тех случаях, когда аргументы Miy М2, ... ,МК являются
произвольными точками четырехмерного пространства — време-
времени, мы будем называть соответствующие моменты пространствен-
пространственно-временными. Чаще всего, однако, в исследованиях по теории
турбулентности ограничиваются рассмотрением лишь моментов,
в которых значения всех полей относятся к одному и тому же
моменту времени t; такие моменты обычно называются про-
пространственными. Иногда приходится иметь дело также со вре-
временными моментами — средними произведениями значений гид-
гидродинамических полей в одной точке (но в разные моменты вре-
времени). В дальнейшем, говоря просто о моментах, мы всегда
будем иметь в виду пространственные моменты; если же речь
будет идти о временных или пространственно-временных мо-
моментах, то это обстоятельство всегда будет специально оговари-
оговариваться..
Особенно часто нам будут встречаться в этой книге так назы-
называемые корреляционные функции — двухточечные моменты вто-
рого порядка. Корреляционная функция Вии (М и М2) =
= и(М1)и(М2) поля и(М), очевидно, симметрично зависит от ар-
аргументов М4 и М2:
Виа (Мх, Щ = Вм (М2, Мх). D.14)
Кроме того, она обладает тем свойством, что
2 2
Вии (Mt, M.) ciCj > 0 D.15)
при любом целом неотрицательном п и любом выборе п точек
Ми ... , Мп и п вещественных чисел cit ... , с„ (ибо правая
часть D.15) совпадает со средним значением неотрицательной
[я П2\
2 и (Mt) с Л ). В частности, при л=2 из D.15) выте*
кает неравенство
\Bau(Mv M2)\^\Bua(Mv M^\Baa(M2, M2)]i D.16)
В дальнейшем мы увидим, что любая функция Вии(Ми М2),
удовлетворяющая D.14) и D.15), может являться корреляцион-
корреляционной функцией некоторого случайного поля (см. сноску на

186 ГЛ. II. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4.2
стр. 192). Смешанный двухточечный момент BUV(MU М2) =
= и (Mi) v (М2) часто называют взаимной корреляционной функ-
функцией полей и и v. Эта функция удовлетворяет аналогичному
{4.16) неравенству
\Bav (М„ М2)\ < [Вии (Ми M,)F \В„ (М2, М2)Р; D.17)
кроме того, очевидно,
BUV(MV М2) = Bvu(M2, М,), D-18)
и если обозначить В^(Ми M2)=ui(Ml)uJ(M2), гДе иу(М), ...
... , uN(M) — произвольные N полей, то
2 2 Bk(kj (Mt, Mj) cfij>0 D.19)
при любом выборе точек Mlt ... , Мп, вещественных чисел
си ... , с„ и целых чисел ku ... , kn (принимающих значения
от 1 до N). Двухточечные моменты выше чем второго порядка,
очевидно, представляют собой корреляционные функции неко-
некоторых новых полей, являющихся произведениями исходных;
поэтому такие двухточечные моменты иногда называют корреля-
корреляционными функциями высших порядков.
Центральные двухточечные моменты второго порядка
Ьии (Mv Щ = [и (М.) - и (М,I [« W2) - и (М2)\ =
= Ваа (М„ М2) - и (М.) и (М2) D.20)
и
Ь„ [Mv М2) = [и (Mt) - и (Mt)] \v (M2) - v (Щ\ =
^Щ D.20')
представляют собой корреляционные функции пульсаций соответ-
соответствующих полей; иногда, когда не будет опасности путаницы,
Мы и их будем называть просто корреляционными функциями 1).
Корреляционные функции пульсаций, разумеется, обладают
всеми свойствами обычных корреляционных функций. Весьма
важно также, что при делении функции ouu(Mi, M2) на
Он(Мi)(Xu(M%), или buv{Mi, Mi) на au(Afi)av(Af2) мы получаем
коэффициент корреляции между и(М^) и и(Мг) или между
') Заметим, что в приложениях часто корреляционными функциями на-
9ЫВаются только корреляционные функцни пульсаций рассматриваемых полей.
Нам, однако, чаще будут встречаться обычные (не центральные) двухточеч-
двухточечные вторые моменты, и поэтому будет удобнее сохранить, термин «корреля-
«корреляционные функции» именно для них,

4.2] § 4- МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ 187
и(Му) и v(M2); поэтому корреляционные функции пульсаций об-
обращаются в нуль каждый раз, как только обращается в нуль
соответствующий коэффициент корреляции. Так как естественно
предполагать, что для любого гидродинамического поля и или
пары таких полей и a v статистическая связь между величинами
u(Mi) и и(М2) или u(Mi) и v(Mz) (характеризуемая величиной
соответствующего коэффициента корреляции) безгранично осла-
ослабевает при неограниченном удалении точек уИ4 и М2 друг от
друга1), то, следовательно, корреляционные функции пульсаций
гидродинамических полей при таком удалении всегда стремятся
к нулю. Это обстоятельство определяет важное свойство корре-
корреляционных функций пульсаций, которым обычные корреляцион-
корреляционные функции, вообще говоря, уже не обладают.
Известно, что для независимых случайных величин среднее
значение произведения равно произведению средних значений
отдельных сомножителей. Так как значения гидродинамических;
полей в очень далеких точках почти независимы, то отсюда
следует, что любые, центральные моменты гидродинамиче-
гидродинамических полей (скажем, взятых в точках Mi MN)t порядок
которых равен их типу, стремятся к нулю при неограниченном
удалении одной из точек Af{ от всех остальных. Однако для цент-
центральных моментов, порядок которых превосходит их тип, послед-
последнее утверждение уже будет неверным. Точно так же, для цент-
центральных моментов порядка К >- 4 стремление к нулю, вообще
говоря, не будет иметь места, если неограниченно удаляться от
остальных будет не одна точка, а некоторая группа точек. В то
же время, в случае, например, общего центрального момента
четвертого порядка нетрудно проверить, что разность
bpuvw(Mv M2> Мг, M4)-bpa(Mv M2)bvw(M3, МА)-
-b^M,, M3)buw(M2, M,)~bpw{Mv M,)buv{Mb Мг) =
= Spuvw{Mv M2, Мг, М4) D.21)
уже будет стремиться к нулю при любом изменении положения
точек Ми М2, M3t Mit таком, что расстояние между хотя бы
двумя из них неограниченно возрастает. Можно показать, что
и в случае любого другого момента (центрального или обыч-
обычного— безразлично) всегда можно подобрать такую комбина-
комбинацию моментов низших порядков, что разность исходного момента
') Две переменные точки М\ =(*i,/i) и М2 = («2.4) пространства — вре-
времени мы называем -неограниченно удаляющимися друг от друга, если в про-
процессе нх'изменения \х2— *1|->соили \t2— fi| —>со (или и то и другое вме-
вместе). В частности, прн U = t2 (случай пространственных корреляционных
функций) точки Х\ н х2 должны неограниченно удаляться друг от друга в
обычном геометрическом смысле.

188 ГЛ. II. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4.2
и этой комбинации стремится к нулю при неограниченном уда-
удалении друг от друга любых двух точек, от которых зависит рас-
рассматриваемый момент (см. мелкий шрифт ниже). Соответствую-
Соответствующие разности момента порядка К и специально подобранных ком-
комбинаций моментов низших порядков как раз и совпадают с теми
семиинвариантами случайных величин, о которых мы говорили
в п. 4.1, и поэтому называются семиинвариантами (кумулян-
(кумулянтами) порядка К рассматриваемых гидродинамических полей.
Воспользовавшись определением семиинварианта, приведенным на стр. 183
(см. равенство D.11)), нетрудно доказать, что семиинварианты гидродина-
гидродинамических полей турбулентного потока действительно обладают указанным
здесь свойством. В самом деле, рассмотрим произвольный семиинвариант
= (-0'
D.22)
= влг=О
где <p(8i, 9j, ..., вя)—характеристическая функция значений «i(Mi),
tbiMi), ..., un(Mk) гидродинамических полей щ, и%, ..., uN (быть может,
частично или полностью совпадающих между собой) в точках Afi, М3 Мк
(которые также могут частично совпадать). Пусть теперь система точек
Ми Мг, ..., MN изменяется таким образом, что расстояние между хотя бы
двумя из них (например, между точками Af< и Afj) неограниченно увеличи-
увеличивается. В таком случае эта система обязательно разобьется иа, по крайней
мере, две такие подсистемы, каждая точка первой из которых неограниченно
удаляется от каждой точки второй (достаточно, например, принять за первую
подсистему совокупность всех точек, неограниченно удаляющихся от
точки Mj). Но так как статистическая связь между значениями любых гидро-
гидродинамических полей неограниченно ослабевает с увеличением расстояния
между точками, в которых берутся эти значения, отсюда вытекает, что
N случайных величин щ(М{), ..., uN(MN) распадаются иа, по крайней мере,
две группы, такие, что величины первой. группы становятся в конце концов
практически независимыми от величии второй группы. Воспользуемся теперь
тем, что характеристическая фуикция совокупиости двух групп статистически
независимых случайных величин равна произведению характеристиче-
характеристических функций каждой из этих групп по отдельности1). Отсюда вытекает,
что при рассматриваемом изменении совокупиости точек Mv M2, ..., MN
фуикция у Fj, в2, ..., вд^стремится распасться в произведение <р(вх ^л)Х
Хт("я+1> ••¦> V)' где "<#• Подставляя это выражение функции
<f (8j, в2, .... в^) в формулу D.22) и учитывая, что k{ > 1 при всех i, убе-
убеждаемся, что семиинвариант Sft ft *v(^r ^2 ^n) пРи таком изме-
изменении системы течек М^ М ,.... Л!„ стремится к нулю.
') В силу C.13) это обстоятельство вытекает из того, что многомерная
плотность вероятности двух групп независимых случайных величин равна
произведению плотностей вероятности для этих двух групп.

4.3] § 4. МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ 189
4.3. Случайные поля с нормальными распределениями
вероятности (гауссовские поля)
Для случайных полей, так же как и для случайных величии,
полное задание распределения вероятности предполагает, вообще
говоря, задание всех моментов всевозможных порядков. Исклю-
Исключение в этом отношении могут представлять лишь случаи, когда
имеются какие-то дополнительные сведения о распределениях
вероятности, позволяющие по некоторым заданным моментам
определить также и все остальные. Сейчас мы рассмотрим один
частный, но очень важный случай такого рода, в котором, как
оказывается, можно ограничиться заданием лишь моментов пер-
первого и второго порядков. А именно, мы рассмотрим случай,- ко-
когда заранее известно, что рассматриваемое поле — гауссовское,
т. е. что все распределения вероятности его значений являются
многомерными нормальными распределениями (распределения-
(распределениями Гаусса).
Напомним, что ^/-мерное распределение вероятности назы-
называется нормальным (или распределением Гаусса), если соответ-
соответствующая плотность вероятности имеет вид
р{их, щ, ..., Идг) =
N |
—j 2 Sik(uj-aj)(uk-ak)\. D.23)
Здесь Oj, j= 1, ..., N — произвольные вещественные постоян-
постоянные; gjk, }, k=l, ... , N — вещественные постоянные такие, что
II gjk II — положительно определенная матрица (т. ¦ е. что
2 gjkcjck > 0 при любых вещественных си -..., cN, не все из
которых равны нулю), а С — постоянная, определяемая из ус-
условия нормировки
? ;i 2 Sjk{ara))(ak-ak)
С j ... fe /.*=1 dul...duN=\ D.24)
ll L
(нетрудно проверить, что С = Q2/BтсJ, где G=\gjk\ =
= det WgjkW '))• Постоянные а, и gjh в формуле D.23) просто
') Вообще говоря, можно рассматривать^ случай, когда ||gj*||—лишь
неотрицательная матрица, т. е. 2 i)kcjck может обращаться в нуль при
каких-то ненулевых значениях с\,..., cN. В этом случае надо лишь считать,
что случайные величины щ,..., Un лннейко зависимы, и распределение веро- '
ятности с плотностью D.23) целиком сосредоточено на некотором линейном
подпространстве ЛГ-мерного пространства, меньшего чем N числа измерений.
Такие распределения вероятности называются вырожденными нормальными
распределениями; иас здесь, однако, они не будут интересовать.

190 ГЛ. П. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4.3
связаны с первыми и вторыми моментами рассматриваемого рас-
распределения. В самом деле, подставив выражение D.23) в общие
формулы D.1) и D.2), легко убедиться, что
D.25)
где, как и выше, O=]\gjk\\, a Ojk = -^~- алгебраическое до-
дополнение элемента gjh в детерминанте G (так что матрицы
II gjk II и || bjk || оказываются взаимно обратными). Из D.25) по-
получается также и выражение для обычных (не центральных)
вторых моментов распределения D.23):
BJk = «^=~ + afik. D.26)
Мы видим, что в случае нормального распределения вероят-
вероятности первые и вторые моменты полностью определяют плот-
плотность вероятности; поэтому они определяют все вообще статисти-
статистические характеристики соответствующих случайных величин и,
в частности, все моменты высших порядков. Так как обычные
(не центральные) моменты любого порядка просто выражаются
через центральные моменты и средние значения, то достаточно
рассмотреть здесь лишь вопрос о вычислении центральных мо-
моментов высших порядков. Нетрудно видеть, что все центральные
моменты нечетных порядков нормального распределения равны
нулю; что же касается центральных моментов четных порядков,
то они могут быть подсчитаны с помощью общего правила, выве-
выведенного Иссерлисом A918)- Согласно этому правилу, если
я>1, W2, • •., и>2к — произвольные 2/С случайных величин (неко-
(некоторые из которых могут и совпадать друг с другом), имеющих
нормальное совместное распределение вероятности и нулевые
средние значения, то - ...
.. w2K = 2 "WixWi2 ¦ wi3wt4 ... Wi2K_xwi2K, D.27)
где сумма справа распространена на всевозможные разбиения
2/С индексов 1, 2, ..., Ж на К пар (t1( t2), (/3, Uh ¦ • •> (*2*-1. hid
(нетрудно подсчитать, что число слагаемых в правой части D.27)
равно |~-=1-3 • 5 ... B/С—1)]- Отсюда следует, что при
= (и, — и,)*i (и2 — Bj)*» ... (uN — uNfN =
ili2K, D.28)

4.3] § 4. М0МЕН1Ы ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ 191
где множители b,-j имеют тот же смысл, что и в D.25), а сумма
справа распространена на все BК)\/2КК\ разбиений 2/С индек-
индексов 1, 1, ..., 1; 2, 2, ..., 2; ; N, N, ..., N (среди кото'
рых 1 повторяется ki раз, ... , N повторяется kN раз) на К пар
(h, h), (»з, h) (izK-i, кк). В частности,
— («1 — Mi) («2 — «а) («з — Из) («4 — «4) =
я; D-29)
что же касается до центральных моментов шестого порядка, то
они уже будут складываться из 15 слагаемых и т. д. О методе
доказательства этого общего правила см. ниже стр. 193.
Из сравнения формул D.6) и D.29) следует, что в случае
нормального распределения 5mi = 0. Можно показать, что этот
результат имеет весьма общий характер: все семиинварианты
порядка К ^> 3 любого многомерного распределения Гаусса
тождественно равны нулю (см. стр. 193).
Отметим, что нормальность распределения вероятности значе-
значений случайного вектора в= (ыь «2 uN) является свойством,
не зависящим от специального выбора системы координат; это
непосредственно вытекает из того, что любые линейные комбина-
комбинации нормально распределенных случайных величин также имеют
нормальное распределение вероятности.
Перейдем теперь к гауссовским случайным полям и(М) или
a(M) = {ul(M), ..., aN(M)}, распределения вероятности любого
конечного числа значений которых являются нормальными рас-
распределениями. Согласно сказанному выше, полное статистиче-
статистическое описание таких полей сводится к заданию их средних зна-
значений и корреляционных функций. Все остальные моменты после
этого можно определить, воспользовавшись формулой D.28) и
тем фактом, что центральные моменты нечетного порядка долж-
должны быть тождественно равны нулю. Существенно отметить, что
для любого (одномерного или многомерного) случайного поля
с конечными моментами первых двух порядков всегда можно
подобрать гауссовское поле, имеющее то же среднее значение
и ту же корреляционную функцию (или корреляционные функ-
функции). В самом деле, например, !для одномерного поля и(М) из
условия D.15), примененного к корреляционной функции пульса-
пульсаций поля buu{Mi, Мг), вытекает, что для любого набора точек
Д^1, Мг, ..., MN можно задать V-мерное нормальное распреде-
распределение с плотностью Pmxm2...mn{u.i, ih, ..., aN), имеющее средние
значения u(Mt), i = \, ..., N, и вторые моменты Buu(Mit M3) =
= buU(Mi, Mj) + u(Mt)a(M'j). Соответствующие распределения
вероятности для всевозможных наборов точек, очевидно, будут

192 ГЛ. !!. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4.3
удовлетворять условиям симметрии C.10) и согласованности
C.11), т. е. будут задавать некоторое случайное поле, имеющее,
те же моменты первых двух порядков, что и исходное случайное
поле и(М). Аналогично будет обстоять дело и в случае много-
многомерного случайного поля и (М) = {ui(M), ..., uN(M)}, с той
разницей, что здесь вместо условия D.15) надо воспользоваться
условием D.19) г). Поэтому при приближенном изучении слу-
случайных полей, использующем лишь данные о моментах первых
двух порядков, всегда можно предполагать, что изучаемые поля
имеют нормальные распределения вероятности. В дальнейшем
мы увидим, что случайные поля гидродинамических характери-
характеристик турбулентного потока часто оказываются и на самом деле
во многих отношениях близкими к гауссовским полям; этим об-
обстоятельством мы еще неоднократно будем пользоваться.
При изучении нормальных распределений вероятности очень удобно ис-
использовать характеристические функции. Нетрудно показать, что в случае
плотности вероятности D.23)
т(в,.в, е„)=
—со
где постоянные п) и Ьц, — те же, что и в равенстве D.25) (при выводе этой
формулы удобно воспользоваться приведением квадратичной формы в пока-
показателе степени формулы D.23) к главным осям). Таким образом, характери-
характеристическая функция нормального распределения вероятности имеет вид экспо-
экспоненциальной функции от многочлена второго порядка относительно пере-
переменных в , в2, ..., в„ с равным нулю свободным членом. Обратное утвержде-
утверждение также верно — такой характеристической функции всегда отвечает плот-
плотность вероятности вида D.23) 2).
') Из того, что при этом рассуждении используются лишь свойства D,15)
и D.19)| корреляционных функций, вытекает, в частности, что любая функ-
функция Buu(Mi, M2) или система функций dj*(Mi, Af2), обладающая такими
свойствами, является корреляционной функцией (или корреляционными функ-
функциями) некоторого (одномерного или многомерного) случайного поля.
2) На самом деле формула D.30) охватывает' н характеристические
функции вырожденных нормальных распределений; в этом случае только
l|oj*ll будет уже не положительно определенной, а лишь неотрицательной
матрицей. Так как нетрудно видеть, что функция вида D.30) может быть
характеристической функцией некоторого распределения вероятности лишь
при условии, что \\Ь)Л является- неотрицательной матрицей, то отсюда выте-
вытекает, что характеристические функции будут иметь вид D.30) только для
(невырожденных или вырожденных} нормальных распределений.

4.3] § *¦ МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ 193
Из формулы D.30) вытекает, что семиинварианты первого и второго по-
порядков распределения Гаусса равны постоянным п), /=1 N и bjh,
j, k — \, ..., N соответственно, а семиинварианты всех порядков выше вто-
второго ¦ тождественно равны нулю. Нетрудно получить из этой формулы также
и общее правило D.28) вычисления произвольных центральных моментов чет-
четного порядка: для этого надо воспользоваться общей формулой D.9), в ко-
которую вместо <р(ва в^.) следует подставить функцию
IJV 1
—
разложив ее предварительно в степенной ряд по переменным 6j, ..., в^.
Метод характеристических функций позволяет просто доказать, что лю-
любые линейные комбинации случайных величии, имеющих нормальное распре-
распределение вероятности, также будут иметь нормальное распределение. В самом
N . ¦
деле, если vj = 2 cjkuk< У = 1 М, то характеристическая функция ве-
величин fj,..., %>м, очевидно, будет равна
(*) (ei ьм)=ехр {l 2
М \ Г / М М
bHsV/--S V
где ?(^i- ••¦• "дг) — характеристическая функция величин «х uN.
Поэтому если tp Fj 6^) задается формулой D.30), то и ?(t,)(ei Лм),
будет экспоненциальной функцией от многочлена второй степенн относительно
переменных в^ ..., в^. Отсюда, в частности, следует, что для задания рас-
распределения вероятности величин Oi, ..., Ом надо только определить их мо-
моменты первых двух порядков, которые без труда находятся по моментам пер-
первых двух порядков величин щ uN.
Последнее замечание позволяет выписать в явном виде характери-
характеристический функционал произвольной гауссовской случайной функции. Рас-
Рассмотрим сначала елучайиую функцию и(х) одного переменного х, опреде-
определенную на интервале <*<*<*. Согласно C.21) характеристический функ-
функционал этой функции совпадает со значением характеристической функции
ь
случайной величины и [в (х)] — I и (х) в (х) dx при аргументе этой функ-
а
ц,ии, равном единице. Но если распределения вероятности всех значений
функции и(х) являются нормальными распределениями, то н все интеграль-
интегральные суммы интеграла и[9(*)], являющиеся линейными комбинациями случай-
случайных величин u(xh), а <Х!<*2< ...<*„<*, имеют нормальное распределе-
распределение вероятности. Поэтому интеграл u[Q(x)] также является случайной
величиной с нормальным законом распределения. Следовательно, для нахо-
нахождения явной формулы для величины Ф[6(х)] надо лишь найтн первые два

194 ГЛ. II. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРВУЛЕИтИОСТИ [4-3
момента случайной величины а[9(*)]. Эти два момента, очевидно, опреде-
определяются формулами
и Iе (¦*)] = / в (х) и (х) dx = Г в (х) и (х) dx. D.32)
ft ft
{«[в (*)] }2 = / / в (*,) в (хг) и (*,) и(хг) dxx dx, =
а а
Ь Ь
= J J 0 (*,) в (хг) В (хи хг) dxx dx2. D.33)
Отсюда вытекает, что
(*„ хг) dxi dx2, D.34)
где b(xuXi)—корреляционная функция пульсаций случайной функции и(х).
Подставляя теперь моменты D.32) и D.34) случайной величины и[9(*)] в
формулу D.30) с N = Л, получаем
Ift ft ft |
'ifo(x)!T(ddx-±f ft (jc.) в (x2) b (xu Xl) dx{ dxA.
a a a J
D.35)
Это и есть общее выражение для характеристического функционала гауссов-
ской случайной функции, указанное еще в первой заметке Колмогорова
A935), посвященной характеристическим функционалам. Аналогично этому
характеристический функционал Ф[9(М)] (или <b[9i(Af) 9*Ш)]) гаус-
совского случайного поли и(М) (или a(M)={ui(M), ..,, uN(M)}) равен
Ф [в (М)] = exp I i J в (М) 1ГрГ) dM —
— jf f* (M^ в (Mi) b (Mi, M2) dMx dM21 D.36)
нли соответственно
f "N
Ф [6j (M) в^ (М)] =* exp j
N
~ i f f
/
"Мг)
естественно, что во всех случаях он однозначно определяется соответствую-
соответствующими средними значениями и корреляционными функциями.

4.4] § *. МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ 195
4.4. Определение моментов и семиинвариантов случайного поля
по его характеристическому функционалу
Так как характеристический функционал содержит в себе полное ста-
статистическое описание случайного поля, то ясно, что он определяет также все
моменты и семиинварианты.этого поля. Сейчас мы выведем явные формулы,
связывающие моменты и семиинварианты с функционалом Ф[6]; при этом
мы придем к естествеийому обобщению формул D.9) и D.11), относящихся
к конечномерному случаю.
Начнем опять с рассмотрения случайной функции и(х), а<х<Ь от од-
одного переменного. Так как моменты и семиинварианты случайного вектора
Я = {«ь ..., uN] выражаются, как мы знаем, через частные производные
соответствующей характеристической фуикции q)(9i, ..., On), to прежде все-
всего нам иадо обобщить поиятие производной на случай фуикции от бесконеч-
бесконечного числа переменных — функционала Ф[9(х)] относительно функции 9(х).
Напомним,, что в конечномерном случае функция <р (8Г ..., 6^) = у (б) назы-
называется дифференцируемой в точке 6° = (b\, ..., в^}, если ее прира-
приращение dtp = <р (в0 -(-de) — <р (в0) при небольшом изменении db = {d6j, ..., de^}
значений аргумента представимо в виде
d?=2M*de*+o(ldf4+ ••• + ld4)
(т. е. с точностью до малых высшего порядка линейно зависит от db). Част-
дЧ (fl) мл. л
ную производную —jag— при этом можно определить как коэффициент Ак
при d9* в линейной части приращения dtp' (так что dtp « V ¦—- d6j \.
Аналогично этому функционал Ф[9(х)] мы будем называть дифференцируе-
дифференцируемым при значении 80(х) его аргумента, если при добавлении к 90(*) не-
небольшой добавки б9(х) главная часть изменения 6Ф[9о(х)] рассматривае-
рассматриваемого функционала линейно зависит от б9(х):
8Ф [в. (х)] = Ф [в. (*)'+ «в (х)] - Ф [в0 (х)} =
г ь -I
J* D.38)
ь г ь -I
J А (х) 86 (х) dx + о J* | 8в (*) | d* D.3
а \_а ]
(иначе говоря, если существует производная 8„Ф [в„ (х)] = -^т- Ф [в0 (х) -\-
+A9i(*)]|ft=0. представимая в виде 80Ф [eo(je)J= Г А (х) в, (х) dx J. Значение
а ' . -
функции А (х) в точке х = х\ в этом случае называется вариацион-
вариационной производной от Ф[90(х)] по 9(х) в точке x=Xi. Учитывая, что А(х) яв-
является коэффициентом при (>Q(x)dx в линейной части приращения 6Ф[9о(х)],
удобно принять для вариационной производной обозначение

196 ГЛ. II. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4.4
Это обозначение подчеркивает также, что фактически вариационная произ-
производная представляет собой двойной предел
»Ф[»о(*I _ „т Мо
bb(x)dx '
где на этот раз под 69(я) понимается функция, отличная от нуля лишь на
малом интервале длины Дх, окружающем точку х. Требование днфференцн-
руемостн функционала Ф[9(*)] накладывает на этот функционал определен-
определенные ограничения, которым, например, не удовлетворяет такой простейший
функционал, как значение 9(х0) функции 9(х) в фиксированной точке х = *о-
Наиболее простым примером дифференцируемого функционала является функ-
ь
цнонал Ф [6 (х)] = J А (х) 6 (х) dx, для которого, очевидно,
а
8 fA(x)Hx)dx\
U b4x)dx =A^- <440>
В примере D.40) вариационная производная sg )J\dx не зависнт от
значения функции 9(я), при котором эта производная берется. Однако в
общем случае это уже, разумеется, будет не так, так что формулы D.38)
н D.39) более правильно было бы писать в виде
ь
8Ф [в. (х)) « f А[% (х); xt] 86 (xt) dx,, l*fflf]t = А [в, (х); х,\.
a
Таким образом, вариационная производная от функционала Ф[9(х)] является
снова функционалом от 9(я), зависящим еще от точки Х\ как от параметра.
Поэтому эта вариационная производная будет уже иметь производные двоя-
двоякого типа: ее можно обычным образом дифференцировать по параметру х,,
а можно также составить ее вариационную производную по 9 (я) в точке
х = Х2, являющуюся второй вариационной производной от исходного функ-
функционала Ф[9(*)]:
8 г 8Ф [6(*I I Ь'ФЩх)] .
86 (хг) dxt I 86 (xt) dx, J ~ 86 (x,) dx, 80 (x2) dx2 ' K >
Вторая вариационная производная будет уже функционалом А[9(*); х,, х2],
зависящим от пары точек х, н хг, причем этот функционал будет не произволь-
произвольным, а удовлетворяющим условию симметрии А[9(*); х,, *г]=^[9(*); хг, x,]t
вытекающему из легко доказываемого тождества
Ь'Ф[Цх)]
86 (х,) dx, 86 (хг) dx% ~ 86 (хг) dx2 86 (х,) dx, '
Простейший пример дважды дифференцируемого функционала доставляет
функционал Ф[в(*)] = Г Г А(х, x')Q(x) b{x')dxdx'\ н этом случае.

4.4] S 4. МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ 197
как нетрудно проверить,
Ib b "I
J J A (x. x') 6 (x) 9 (*') dx dx'
86 (Xi) dxt 86 (x2) dx2 ~ ''
& <4>43)
Аналогично определяются также и вариационные производные высших
порядков: л-я вариационная производная
8"Ф [6 (*)]
(если она существует), очевидно, является фуикциоиалом относительио 9(*),
зависящим еще от п точек х,, ..., хп.
Пусть теперь Ф[6(*)]'— характеристический функциоиал случайиой функ-
функции и(х), задающийся формулой C.21). В таком случае
ь
I f ы (ж)[в (дг)+йв,
b
ь t
= / fu(x)Q(x)dxe
J u(x)b(x)dx
ft=O
a
(так как осреднение переставимо с дифференцированием). Отсюда следует,
что
Рассуждая таким же образом, можно получить и более общее равенство
_
i Г u(x)b(x)dx
показывающее, что
-(-О"
Ь"Ф [6 (л:)]
. D.46)
е (дг)=о
Формула D.46) и является обобщением формулы D.9$ на бесконечномерный
случай.
Совершенно аналогично определяются вариационные производные от
функционалов Ф[в (•*?] и Ф[6 (х)] = фГв, (х), ..., QN(x)\ зависящих от
(скалярной или векторной) функции точки х многомерного пространства.
Так, например, функционал ф[6(х)] называется дифференцируемым по 8j(je)
при заданном значении функции Ь(х) ~= {Qi(x), ..., QK(x)}, если имеет
место равенство
J' Ai[b (*); *,] в? (х,) dxx D.47)

198 ГЛ. II. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4.4
(т. е. если главная часть приращения Ф[6 (х)] при небольшом изменении
86/ (х) функции 8^ (х) линейно зависит от 8fy (x)). В этом случае функ-
функционал
Ш1к\ D48>
зависящий от точки Х\ как от параметра, называется вариационной произ-
производной (нлн, подробнее, частной вариационной пронзнодноЙ) от Ф [6 (х)] по
§i(x) в точке х = х{ (иначе эту производную можно определить как
двойной предел ¦ •
Urn
где hfl (x) — векторная функция, у которой отлична от нуля лишь t-я ком:
понента н притом только в малой окрестности Ьх{ точки х{). Вариацион-
Вариационную производную D.48) можно затем продифференцировать по й](х); при
этом придем ко второй вариационной производной
;xi'x>]- D49)
зависящей уже от пары точек Х\ и х2 н удовлетворяющей условию
»2Ф[0(*)] ЬЩ[Ь(х)]
к '
dxi bbj (x2) dx2 ~ Вву (х2) dx2 Ъв{ (*,) dxx '
Подобным же образом определяются и вариационные производные
8"Ф [8 (х)]
высших порядков. Если под Ф [б (х)] понимать характеристический функцио-
функционал C.27') ЛЛмерного случайного поля и (ж) — ,{ui{x) uN(x)}, то со^
вершенно аналогично выводу формулы D.46) получается равенство
ть (Х)] D 51)
в (х).О
(Заметим, что свойство D.50) вариационных производных обращается при
этом в известное свойство D.18) корреляционных функций).
Семиинварианты случайного поля и(х) = {щ(х) uN(x)} мы теперь
определим при помощи равенства
У Л"
8пФ[8(л:)]
D.52)

4.4}
§ 4. MdMEMtbl гидродинамических Полей
199
Где Ф [б (я)] — характеристический функционал нашего поля. Легко видеть,
что
Slnjexp
в(*)=0
щ (*,) ехр
ехр
в(*)=0
««¦ (л,) ехр
I f Ъиа(х)йа{х) dx
ехр
в (*)= О
и вообще, что St _ i (хг,
(^ ()
величии
ut (x^,
= Щ (*i) uj (x2) — Щ (*i) • uj {x2) = bij (xu x2)
лгя) совпадает с семиинвариантом системы
(лгп), определенным по соответствующей характери-
характеристической функции с помощью формулы D.11). Из формулы D.52) легко
вывести все свойства семиинвариантов (свойство D.50) вариационной про-
производной, например, означает, что корреляционные функции пульсаций дол-
должны обладать тем же свойством D.18), что и обычные корреляционные функ-
функции) .
Для функционала Ф [в (х)], имеющего вариационные производные всеч
порядков, при некоторых условиях можно получить разложение в ряд Тэй-
лора:
1
В применении к характеристическому функционалу случайного поля о.{х)
это разложение обращается в разложение по корреляционным функциям все-
всевозможных порядков:
N
N N
~~ -J
ft=l
N
N
D.54)

200 ГЛ. И. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4.4
Можно показать, что для сходимости ряда в правой части D.54) необходимо
и достаточно, чтобы его п-й член стремился к нулю прн я->со; если же
мы оборвем этот ряд на конечном числе членов, то для остатка можно полу-
получить оценку, близкую к оценке остаточного члена обычного ряда Тэйлора (см.
Новиков A964)). Заметим, однако, что если мы просто оборвем разложение
D.54) функцнонала Ф[9(*)] на каком-либо конечном числе членов, никак
не учитывая остатка, то мы придем к функционалу, обладающему свойством
C.24) характеристического функционала, но наверное не обладающему столь
же обязательным свойством C.25). В самом деле, это следует хотя бы из
того, что функционал, равный сумме конечного числа членов правой части
D.54), не удовлетворяет уже простейшему неравенству |Ф [6 (х)] | <; 1, вы-
вытекающему нз неравенства C.25) с п = 2 (а также и из самого определения
C.27') характеристического функцнонала Ф [в (х)]). Поэтому, предположив,
что все моменты некоторого случайного поля порядка выше данного К то-
тождественно обращаются в нуль, мы можем в конце концов прнйтн к абсурд-
абсурдным выводам, противоречащим, например, условию, что никакая вероятность
не может превосходить единицы.
Несколько более удобным с этой точки зрения представляется применение
разложения Тэйлора к логарнфму характеристического функцнонала Ф [б (х)],
т. е. представление Ф [б (х)] в виде
N
Ф[6(х)] = ехр'
I
N N
- 2 2 / *>*{хь Х
; = 1 t.l
N N
'1 '
Оборвав разложение D.55) на конечном числе членов, мы на этот раз придем
уже к функционалу, удовлетворяющему не только условию C.24), но и необ-
необходимому для характеристического функцнонала условию | Ф [б (х)] | < 1.
Более того, ограничившись лишь линейными и квадратичными по 8^(х) чле-
членами в правой части D.55), мы получим функционал, наверное являющийся
характеристическим функционалом некоторого случайного поля — а именно
гауссовского случайного поля с теми же моментами первых двух порядков,
что и исходное поле И (х) (см. формулу D.37)). Если, однако, мы учтем
в разложении D.55) еще члены третьего порядка по в/(х), т. е. положим
f N
Ф[6(.
N N
- 2 2 / /
N N. N . . |
/=l k.l 1=1 I

4.5]
§ 4. МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ
201
или же оборвем ряд D.55) на любом другом конечном числе членов выше
второго порядка по в/(*>, то мы придем к функционалу, который будет
удовлетворять C.24) и условию | Ф [в (*)] | <; 1, но, вообще говоря, не будет
обладать свойством C.25), необходимым для характеристических функциона-
функционалов. Поэтому, предположив, что все семиинварианты рассматриваемого слу-
случайного поля в (х) порядка выше данного К > 4 обращаются в нуль, мы
также можем в конце концов прийти к противоречию с очевидными свойства-
свойствами распределений вероятности (например, с неотрицательностью вероятности,
из которой следует условие C.25)). В части 2 книги мы еще будем иметь
случай вспомнить об этом неприятном обстоятельстве.
4.5. Стационарные случайные функции
Вернемся теперь к упоминавшемуся выше (см. стр. 173)
важному вопросу о том, при каких условиях временные и про-
пространственные средние значения случайного поля и(х, t) при
неограниченном увеличении интервала осреднения сходятся
к соответствующим теоретико-вероятностным средним значениям.
При этом придем к некоторым специальным классам таких по-
полей, представляющим большой интерес для теории турбулент-
турбулентности.
Будем сначала для определенности говорить лишь о времен-
временном осреднении; тогда зависимость поля и(х, t) от координат х
не будет иметь значения, так что можно рассматривать лишь
функции u(t) от одного переменного t. Нас будет интересовать
вопрос о том, при каких условиях случайная величина
Г/2
D.57)
-Г/2
при Г->оо сходится •) к u(t). Одно весьма важное необходимое
условие этого выводится крайне просто. В самом деле, для лю-
любой ограниченной функции u(t) разность
772
1
-Г/2
/
- f
-Г/2
f u(s)ds— j u(s)ds
т
T+t
т
, D.58)
') Заметим, что речь здесь идет о сходимости случайных величин, тре-
требующей, вообще говоря, специального определения (см. ниже стр. 208).

202 ГЛ. И. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4.5
где t и ti — фиксированные числа (и, например, h> t), при
Г->оо, очевидно, неограниченно убывает. Поэтому пределы при
Г->оо величин цг@ и 2r(?i) (если только они существуют)
должны совпадать друг с Другом, т. е. временное среднее зна-
значение функции u(t) (определяемое как lim uT(t)\ не может за-
V . Г->оо ) ¦
висеть от t. В то же время вероятностное среднее значение u(t)
является, вообще говоря, функцией от t. Следовательно, для ра-
равенства этих двух средних значений необходимо, чтобы выполня-
выполнялось условие
HJF) = U= const. D.59)
Аналогично обстоит дело с применением временного осредне-
осреднения для определения моментов высших порядков и других функ-
функций от значений u(t) в нескольких точках. Так, например, если
использовать осреднение по времени t произведения u(t)u(ti) =
v«= u(t)u(t + s) (где s = U — t считается фиксированным) для
определения корреляционной функции Buu(t, ti), то мы придем
к величине
Btta (t, tx) = lim -i f и (t + x) и (*+ s + x) dx, D.60)
7">0° -TI2
которая может зависеть лишь от s = ti — t, но не от t и ti по-от-
дельности. Поэтому временная корреляционная функция
В( ^2) может быть равна вероятностному среднему значению
u(ti)u(t2) = Buv,{ti, t2), лишь если
Buu(tbt2) = Bm(t2-t,). D.61)
Точно так же для возможности определения момента Л/-го по-
порядка Вии... uitu ?2, ¦•-, tri) при помощи временного осреднения
необходимо, чтобы этот момент зависел лишь от Л? — 1 разно-
разностей h — U,...,tN — U:
Buu...u(tu t%, ..... tN) = Buu...u(t2—th ..-, tN~ ti). D.62)
Наконец, если потребовать, чтобы средние значения всевозмож-
всевозможных функций от величин и(^), u(t2), ... , u(tN) можно было
получить при помощи временного осреднения, то придется огра-
ограничиться лишь такими случайными функциями u(t), для кото-
которых N-мерные плотности вероятности р( t ( (ир и2, ..., uN)
при любых N и tu t2, ... , fjv зависят не от Л^ параметров
h, Н, ••¦ , h, а лишь от N — 1 разностей г? — h, ¦ ¦ ¦ f h — Ц,

4.5] $ *¦ МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ 503
т. е. удовлетворяют условию
= />«,- /, ,„- /, («Г «2 «*)' D-63)
где h — любое вещественное число. Условие D.63) является наи-
наиболее общим — из него вытекают, в частности, и условия D-59),
D.61) и D.62). Заметим еще, что в частном случае гауссовской
случайной функции x(t) из D.59) и D.61) уже вытекают и об-
общие равенства D.62) и D.63).
Итак, мы пришли к специальному классу случайных функций
от времени, для которых все многомерные плотности вероятности
удовлетворяют условиям D.63), т. е. не меняются при сдвиге
соответствующей группы точек ^.нга любой интервал времени h.
Такие случайные функции часто встречаются в самых разнооб-
разнообразных прикладных задачах; они называются стационарными
случайными функциями, или, иначе, стационарными случайными
процессами (поскольку случайные функции от времени в науч-
научной литературе часто называются также случайными процес-
процессами). Математической теории стационарных случайных процес-
процессов посвящен ряд подробных обзоров или глав в специальных
монографиях (см., например, Яглом A952), Дуб A953),
Лоэв A955), Розанов A963)). Однако здесь мы ограничимся
лишь несколькими замечаниями, имеющими непосредственное
отношение к теме настоящей книги (см. также гл. 6 в ч. 2
книги).
Физический смысл условия стационарности совершенно ясен:
оно означает, что физический процесс, численной характеристи-
характеристикой которого является функция u(t), является установившимся,
т. е. что все условия, вызывающие этот процесс, не меняются со
временем. В применении к характеристикам турбулентности
условие стационарности означает, что рассматриваемый турбу-
турбулентный поток должен быть установившимся в обычном гидро-
гидродинамическом смысле: все осредненные характеристики потока
(например, распределение средней скорости, средняя темпера-
температура), так же как и все внешние условия (например, внешние
силы, положение ограничивающих поток поверхностей), должны
оставаться неизменными во времени. Потоки, с достаточной сте-
степенью точности удовлетворяющие этому условию, сравнительно
просто могут быть получены в лаборатории; в случае же при-
природных турбулентных потоков обычно трудно гарантировать не-
неизменность всех осредненных характеристик течения (в особенно
сильной степени это относится к турбулентности в атмосфере,
где средние значения всех гидродинамических элементов обычно

204 ГЛ. И. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4-6
весьма неустойчивы и имеют явно выраженный суточный и го-
годовой ход)- Однако и здесь при рассмотрении мгновенных зна-
значений гидродинамических характеристик в течение сравнительно
небольших промежутков времени (например, порядка нескольких
минут или десятков минут) соответствующие случайные функции
часто вполне можно считать стационарными. Таким образом, и
в этих случаях вероятностные средние значения характеристик
потока часто можно находить при помощи временного осредне-
осреднения; для этого требуется, чтобы временные средние значения при
Т -*¦ оо сходились к вероятностным средним и чтобы средние
за такое время Г, в течение которого рассматриваемый процесс
еще можно считать стационарным, были уже достаточно близ-
близкими к предельным значениям, отвечающим Т -> оо.'
Значения какой:либо гидродинамической характеристики в
нескольких точках установившегося турбулентного потока или
значения нескольких таких характеристик в одной или несколь-
нескольких точках доставляют нам примеры многомерных стационар-
стационарных случайных процессов — векторных функций u(t) ={ui(t),...
..., un(t)}, таких, что плотность вероятности для любого набора
значений Uix(h), m2(ti), ..., uiN(uv) не меняется при одновре-
одновременном сдвиге всех моментов времени U, t2, ... , tN на один и
тот же произвольный интервал времени h. В этом случае, оче-
очевидно, и все смешанные моменты функций Uj(t) будут зависеть
лишь от разностей соответствующих моментов времени (напри-
(например, все взаимные корреляционные функции Sjh(^i, t2) =
= щ (t\) uh (?2) будут зависеть лишь от аргумента т = (*г — *i)-
Ясно, что для того, чтобы статистические характеристики, зави-
зависящие от значений нескольких случайных функций времени,
можно было получить при помощи временного осреднения, сово-
совокупность этих случайных функций должна представлять собой
многомерный стационарный процесс; в противном случае харак-
характеристики, получаемые при временном осреднении, будут даже
зависеть от меньшего числа переменных, чем соответствующие
теоретико-вероятностные средние значения.
4.6. Однородные случайные поля
Прежде чем переходить к выяснению условий, при которых
временные средние значения функций от стационарных случай-
случайных процессов сходятся к соответствующим теоретико-вероят-
теоретико-вероятностным средним, остановимся вкратце на вопросе о тех изме-
изменениях, которые надо внести в наши рассуждения, если исхо-
исходить не из временного, а из пространственного осреднения.
При этом, разумеется, следует рассматривать случайные функ-

4.6] $ *¦ МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ 205
ции и(х) от точки X = (*1, х2, х3), т. е. случайные поля в трех*
мерном пространстве. Пространственные средние значения та-
таких полей определяются равенством
Л/2 В/2 С/2
UA,B,c(X) = ~ffiC f J J «
-Д/2 -В/2 -С/2
Xdlidbdb- D-64)
Требуется определить, при каких условиях величина HAiBiC(x)
при А-*-оо, В-*-оо, С-*-оо (или же при выполнении хотя бы од-
одного из этих предельных переходов) стремится в определенном
смысле к теоретико-вероятностному среднему значению и(х).
Ясно, что для этого прежде всего должно выполняться следую-
следующее условие, аналогичное D.59):
пЩ=и= const, D.65)
т. е. теоретико-вероятностное среднее значение должно быть
одинаковым во всех точках пространства. Точно так же для воз-
возможности определения с помощью пространственного осредне-
осреднения корреляционной функции и(х1)и(х2) = Вши(х1, х2) во вся-
всяком случае необходимо, чтобы эта функция зависела лишь от
векторной разности своих аргументов:
?Ии(*1> Х2> = Виш (х2 — хг). D.66)
Наконец, для того чтобы средние значения всевозможных функ-
функций от значений поля в нескольких точках можно было полу-
получить при помощи пространственного осреднения, требуется,
чтобы N-мерные плотности вероятности величин и(хг), и (х2), ¦ ¦ ¦,
u(xN) при любых N и xv х2, ..., xN зависели лишь от раз-
разностей х2 — xv ..., xN — xv т. е. не менялись при любом
сдвиге (параллельном переносе) системы точек Хх, х2,..., XN
на один и тот же вектор у:
Рху, хг xN(UV «2 UN) = P*1+( )
= Рх%-хх xN-x, («1- «2 %) D-67)
(в случае гауссовского поля и(х) равенство D.67) уже выте-
вытекает из D.65) и D.66)). Поле и(х), удовлетворяющее условию
D.67), называется статистически однородным (или короче —
просто однородным); таким образом, для того чтобы осреднение
по пространству любых функций от значений случайного поля
приводило к тем же результатам, что и осреднение по вероят-
вероятности, рассматриваемое поле должно быть однородным. При
рассмотрении более общих функций от значений нескольких

206 ГЛ. II. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4.6
"случайных полей их(х), и2(*), • • ¦, ип{х) приходится требовать,
чтобы однородным было многомерное (векторное) поле и(х)=
= {Ui(x)t ..., и„(х)\Ут. е. чтобы все плотности вероятности про-
произвольных наборов значений компонент их (х), ..., ип(х) поля
и(х) на некотором множестве точек пространства не менялись
при одновременном сдвиге всех этих точек на один и тот же
вектор у.
В приложении к полям гидродинамических характеристик
турбулентного потока предположение об однородности всегда
является математической идеализацией; точно оно никогда не
выполняется. В самом деле, чтобы можно было говорить об од-
однородности, необходимо, чтобы поток заполнял все неограни-
неограниченное пространство, а уже одно это предположение само по
себе в применении к реальным потокам всегда является идеали-
идеализацией. Далее требуется, чтобы все средние характеристики по-
потока (средняя скорость, давление, температура) были постоян-
постоянными во всем пространстве и чтобы статистический режим
пульсаций не менялся при переходе от одной части простран-
пространства к другой. Разумеется, все эти требования могут выпол-
выполняться с удовлетворительной точностью лишь в пределах не-
некоторых ограниченных областей пространства, малых по срав-
сравнению с масштабами макроскопических неоднородностей и
достаточно удаленных от всех ограничивающих поток твердых
стенок (или свободных поверхностей). Таким образом, на прак-
практике можно говорить лишь об однородности гидродинамических
полей в некоторой определенной области1), но не во всем без-
безграничном пространстве. Тем не менее, при рассмотрении такой
однородной в некоторой области турбулентности часто целесо-
целесообразно считать ее частью однородного турбулентного потока,
заполняющего все пространство: ценность подобного предполо-
предположения связана со значительной математической простотой иде-
идеализированной схемы однородного случайного поля, существен-
существенно упрощающей теоретический анализ. Также 'и эргодическая
теорема (т. е. теорема о сходимости пространственных средних
пА,в,с{х) к теоретико-вероятностным средним значениям и(х))
может быть применена к однородным лишь в некоторой области
случайным полям, если только размеры этой области достаточно
велики (см. по этому поводу замечание на стр. 204, относя-
относящееся к стационарным случайным функциям).
'), Случайное поле и(х) естественно назвать однородным в области G
пространства, если соотношение D.67) оказывается справедливым для лю-
любых Xj, *j, ..., xN и у, таких, что все точки хх, ..., х^ j
*N~\-y располагаются внутри О,

4.6] § 4. МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ 207
О наиболее важном методе экспериментального осуществле-
осуществления турбулентного потока, весьма близкого к однородному, мы
будем говорить в гл. 7 ч. 2 в связи с изучением однородной и
изотропной турбулентности. Здесь мы только отметим, что на-
наряду с полями, однородными во всем трехмерном пространстве,
можно рассматривать также поля и(х) = и(хи х2, х3), однород-
однородные лишь в некоторой плоскости (или вдоль некоторой оси),
т. е. удовлетворяющие условию D.67) для всех векторов у, при-
принадлежащих определенной плоскости (или оси), но, вообще го-
говоря, не удовлетворяющие этому условию для других у. Зна-
Значения такого поля и(х) на любой плоскости или прямой,
параллельной направлению однородности, будут, очевидно,
представлять собой однородное поле на этой плоскости или пря-
прямой; значения же и(х) на нескольких различных таких плоско-
плоскостях или прямых можно рассматривать как многомерное одно-
однородное случайное поле на той же плоскости или прямой.
Естественно ожидать, что осреднение по пространству часто
может быть использовано и тогда, когда гидродинамические
поля не являются однородными во всем пространстве, но одно-
однородными лишь в некоторой плоскости (или вдоль некоторой
прямой); в этих случаях надо только рассматривать осреднение
не по трехмерному объему, а лишь по соответствующей плос-
плоскости или прямой (т. е. трехкратный интеграл в D.64) надо за-
заменить двукратным или однократным).
В некоторых задачах теории турбулентности очень часто
можно считать, что соответствующие гидродинамические поля
являются однородными хотя бы в одном направлении или ста-
стационарными (или даже, что выполняются оба эти условия од-
одновременно). Поэтому если бы удалось доказать, что во всех
случаях при наличии стационарности или однородности теорети-
теоретико-вероятностные средние значения можно заменять средними
по времени или по пространству, то это имело бы очень боль-
большое практическое значение. На самом деле одной лишь стацио-
стационарности или однородности, вообще говоря, еще недостаточно
для сходимости временных или пространственных средних
к средним значениям в смысле теории вероятностей1). Тем не
') Чтобы подтвердить это утверждение, достаточно рассмотреть пример
стационарного процесса u(t), для которого с вероятностью единица u(t) =
= и@) при любом t (так что почти все реализации процесса изображаются
прямыми, параллельными оси t). Здесь, очевидно, «г@ = и@) при любом 7",
и если и@) имеет какое-то распределение вероятности, то для определения'
среднего значения u(t) = и@) необходимо иметь большое число различных
реализаций функции u(t) (каждая из которых сводится к одиому-ёдии-
ственному значению и@)). В прикладных вопросах, однако, этот пример
всегда будет рассматриваться как пример случайной величины « = «@),

208 ГЛ. П. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4.7
менее, как мы сейчас покажем, условия, необходимые для того,
чтобы такая сходимость имела место, носят столь общий харак-
характер, что в прикладных вопросах их почти всегда можно считать
выполняющимися.
4.7. Эргодическая теорема
Будем сначала для определенности говорить только о ста-
стационарных случайных процессах u(t) и о временном осредне-
осреднении; точно те же рассуждения (лишь с заменой времени t про-
пространственной координатой х) будут, разумеется, применимы
и к однородным случайным полям и (я) на прямой. Начнем
с того, что четко определим, что мы будем понимать под сходи-
сходимостью случайной величины UT(t), задаваемой равенством
D.57), при Т-*-оо к константе u(t) = U. Нам будет удобно счи-
считать случайную функцию йт сходящейся при Т -> оо к преде-
пределу U (вообще говоря, являющемуся случайной величиной), если
lim \uT — ?/|2 = 0. D.68)
Г->оо
В силу известного неравенства Чебышева
Р{\йг— E/i>e}< \"т~и\2 D.69)
из D.68) будет также следовать, что
lim Я{|иг — ?/| >t}=0, D.70)
Г->оо
т. е. что вероятность отклонения величины if? от U, превышаю-
превышающего любое заданное е, будет стремиться к^нулю при Г-х»
(и, следовательно, будет сколь угодно малой, если только вы-
выбрать достаточно большое значение Т) *). Равенство D.70) дает
ио не случайной функции; кстати, и многомерные плотности вероятности
Pt t ...t (Mi> M2> •••> un). здесь ие являются обыкновенными функциями, а
выражаются через б-функцию Дирака.
') В теории вероятностей условие D.68) обычно называется условием
сходимости Иг к U при Т -> оо в среднем квадратичном, а условие D.70) —
условием сходимости ит к U по вероятности. Таким образом, мы показали,
что в силу неравенства Чебышева из сходимости случайной функции ит к U
в среднем квадратичном следует тарже ее сходимости к тому же пределу и
По вероятности.

4.7] S 4. МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ 209
достаточные основания для того, чтобы на практике можно
было вместо U использовать значение величины ит, где Т срав-
сравнительно велико; поэтому остается лишь выяснить, при каких
условиях соотношение D.68) будет иметь место.
Легко понять, что правая часть D.68), где ит — временное
среднее D.57) значений стационарного случайного процесса
u(t), a U = u{t)—его теоретико-вероятностное среднее значе-
значение, может быть выражена через корреляционную функцию
пульсаций u(t)
buu (x) = [u(t + x)-U][u{t)-U\ = Вш (т) - U* D.71)
(см. ниже равенство D.83)). Поэтому справедливость равен-
равенства D.68) должна определяться какими-то свойствами функ-
функции Ьии(т). С точки зрения приложений к теории турбулентно-
турбулентности основное значение имеет следующий факт: если Ьии(х) ->0
при т->оо, то сходимость величин Иг@ к вероятностному
среднему значению обязательно имеет место. Этот факт являет-
является следствием следующей общей теоремы, впервые доказанной
Слуцким A938) (см. также Обухов A954)): для того чтобы для
стационарного случайного процесса u(t) выполнялось равенство
D.68), необходимо и достаточно, чтобы корреляционная функ-
функция bUu(i) удовлетворяла условию
т
\im~ [bn(x)d* = 0 D.72)
(доказательство этой теоремы, называемой обычно законом
больших чисел или эргодйческой теоремой') для стационарных
случайных процессов,приведено ниже на стр.212—214).Ясно,что
если bUu(t) -*-0 при т->оо, то и условие D.72) наверное будет
выполняться; отсюда вытекает, что в этом случае равенство
D.68) всегда будет справедливо. Так как корреляционную фун-
функцию buu(i) пульсаций гидродинамического поля u(t) турбу-
турбулентного потока всегда можно считать стремящейся к нулю при
т-»-оо (ср. выше стр. 187), то в теории турбулентности всегда
можно исходить из того, что для установившихся течений тео-
теоретико-вероятностные средние значения любых гидродинамиче-
гидродинамических полей могут быть определены с помощью осреднения по
достаточно большому интервалу времени.
•) Во избежание недоразумений отметим, что в теории вероятностей эр-
эргодйческой теоремой для стационарных случайных процессов иногда назы-
называют н некоторые другие предложения, касающиеся связи вероятностны?!
и временных средних.

210 ГЛ. П. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ {4.7
Если скорость убывания Ьии(х) при возрастании т такова,
что
00
J
<оо, D.73)
о
то существует также простая оценка длины Т тех интервалов,
осреднение по которым достаточно для получения среднего зна-
значения U с заданной точностью. В самом деле, можно показать,
что в этом случае при достаточно большом Т имеет место асим-
асимптотическое равенство
IuT — U\*« 2 -у- bm@), D.74)
где
oo
" «МЛ D.75)
— постоянная размерности времени, которую можно назвать
«временем корреляции» стационарной функции (формула D.74)
была получена еще Тэйлором A921)). Таким образом, для на-
надежного определения величины U надо только воспользоваться
временным осреднением по периоду Т, много большему, чем
соответствующее «время корреляции» 7\. Выбрав желательную
нам степень точности (т. е. наибольшую среднюю квадратичную
ошибку, которую еще можно считать допустимой при замене О
на «г), мы можем определить по формуле D.74) и требуемый
период осреднения Г1).
Скажем теперь еще несколько слов по поводу однородных
случайных полей и{х) и пространственного осреднения. Случай
однородных полей на прямой, как мы уже отмечали, вообще
ничем не отличается от случая стационарных процессов. Что же
касается до однородных случайных полей на плоскости или в
пространстве, то значения такого поля и(х) на любой прямой
будут представлять собой однородное случайное поле на пря-
прямой. Поэтому если только корреляционная функция buu{r) пуль-
пульсаций этого поля такова, что хотя бы для одного направления
(единичного вектора) г0 функция Ьии(мГо) отт удовлетворяет ус-
условию D.72) (например, если 6Uu(r)->0 при \г\ ->оо хотя бы
вдоль одного направления), то средние по пространству (или
') Отметим, что правая часть D.74) вполне аналогична известному вы-
выражению для средней квадратичной ошибки среднего арифметического А'
независимых измерений, если только положить N = Т/2Тг. Таким образом,
осреднение стационарной функции с временем корреляции 7\ по периоду
2NTi эквивалентно осреднению по N независимым измерениям этой функции
(т. е. по N реализациям^;, ' '. ' "

4.7] $ 4. МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ
плоскости) наверное будут сходиться к константе u(x)==L/
(такая сходимость здесь будет иметь место даже при осредне-
осреднении лишь по одной прямой, параллельной г0). Общее условие,
необходимое и достаточное для сходимости Ша,в,с(х) Для всех
JtB среднем квадратичном к U при Л->оо, fl->oo, C->oo для
однородных полей в пространстве имеет вид
ABC
1 Г Г Г
lim л arc III bau(r)drxdr2drz = O D.76)
А-+со, ?->оо, С->оо *-"°° J J J
V —О — С
(изменения для случая двумерных полей являются очевидны-
очевидными); доказательство этого условия почти не отличается от ана-
аналогичного доказательства для одномерного 'случая. Вместо
D.74) мы теперь будем иметь формулу
D.74')
где йу — среднее по объему ABC = V, а Vi — «объем корре-
корреляции»:
00 ОО ОО
f Jbuu{r)drxdr2drz, D.750
^щ f
О —оо —оо
который в формуле D.740, естественно, предполагается ко-
•нечным.
Указанные выше результаты могут быть применены и к вопро-
вопросу о вычислении высших моментов или других теоретико-вероят-
теоретико-вероятностных средних значений каких-либо функций от значений u(t)
или и(х) при помощи временного или пространственного осред-
осреднения; при этом надо только заменить процесс u(t) или по-
поле и(х) новым процессом или полем, являющимся нелиней-
нелинейной функцией исходного. Например, в случае стационарного
процесса u(t) для возможности получения момента Af-го по-
порядка D.62) при помощи осреднения по времени т величины
u(t\ + т) u(ti + м) ... u(tN + т) надо только, чтобы момент
2Л^-го порядка
Ои ...иии ... и(*2 — Ч> • • • i *N — Ч' :' *2 — М I т> • ¦ ч iff — (IT1) ==
D.77)
при фиксированных U, t2, ..., tN являлся функцией от т, удовле-
удовлетворяющей условию D.72). Поскольку обычно из физических

212 ГЛ. II. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ [4.7
соображений можно утверждать, что коэффициент корреляции
между величинами и(^)... u(tN) и u(ti + т) ... u(tN + т) при
т-»-оо стремится к нулю, то нужное нам условие на практике
обычно можно считать выполняющимся, а использование вре-
временного осреднения законным. Для оценки необходимого вре^
мени осреднения надо оценить соответствующее «время кор-
корреляции», т. е. интеграл от указанного коэффициента корреля-
корреляции. В случае гауссовских процессов u(t) момент D.77) можно
выразить через корреляционную функцию и среднее значение
процесса u(t) с помощью общего правила D.28) вычисления
высших моментов. В частности, при определении с помощью вре-
временного осреднения среднего квадрата u2(t) = Вии@) значения
гауссовского стационарного случайного процесса u(t) с нуле-
нулевым средним зйачением роль корреляционной функции buu(t)
будет играть функция
t); D.78)
поэтому здесь формулы D.74) — D.75) принимают вид
fa(x)dx. D.79)
Заметим, что в этом случае из условия
г
hm~ f[buu(x)]*dx = 0, D.80)
г-*°° с.
в которое обращается D.72) при замене функции Ьии(т;) функ-
функцией D.78), будет вытекать также л первоначальное .условие
D.72). Кроме того, для гауссовского стационарного процесса
из D.80) будет следовать, что вероятностное среднее значение
любой функции от значений процесса, имеющей конечное сред-
среднее значение, будет равно пределу при Т-+оо от соответствую-
соответствующего временного среднего за время Т (см., например, Гренан-
дер A950)). Обобщение последнего результата на гауссовские
однородные случайные поля (и на некоторые еще более общие
гауссовские случайные функции) сформулировано в заметке
Темпельмана A962); несколько более слабый результат о та-
таких случайных полях доказан в работе Биркгофа и Кампе де
Ферье A962).
Для доказательства того, что при условии D.72) равенство D.68) обя-
обязательно будет иметь место, выразим средний квадрат разности ит (() — V

4.7] § 4. МОМЕНТЫ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ
через корреляционную функцию Ьии(х):
213
Г/2
Г/2 Г/2
= ^ / f [u(t)-U][u(s)-U]dtds =
-Г/2 -Г/2
Г/2 Г/2 Г т,
2^ / / bm(t-~s)<Uds=ji J J'бвв(х)йхйх, D.81)
-Г/2 -Г/2
О О
(мы использовали подстановку t — s — x, t + s = x\ и учли, что Ьии(—т) =
= Ьии(х)}. Если 6Uu(t) удовлетворяет условию D.72), то для любого
б > 0 будет существовать такое То == ТоF), что
J Ьии (х) dx < ^ xi при х, > Го.
D.82)
С другой стороны, в силу неравенства |6Uu(t)K &uu@) при любом ti
fbaa(z)dz<buu(Q)zl. D.83)
о
Интегрируя неравенство D.83) по ti от нуля до 7, а неравенство D.82) —
от 7"о до некоторого Т > Го, найдем, что при любом Т > То
f f
0 0
f f
0 0
Следовательно,
г т,
If'
О О
5Г2
при
т, е. при
Итак, для любого 5 > 0 при Т > То и Т > 1/
fe"«@)
Т т.
-lLf J Ьш (х) rfx rfx, < 5,
D.85)
о о
т. е. равенство D.68) действительно имеет место.

Й4 ГЛ. И. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПИСАНИЯ ТУРБУЛЕНТНОСТИ D.7
Если предел, фигурирующий в левой части D.72), существует, но равен
отличному от нуля значению с, то условию D.72), очевидно, будет удовлет-
удовлетворять функция 6i(t) = 6Uu(t)—с. Отсюда ясно, что в этом случае
ton Ги_ — ?/]*= ton ~ f fbm
->оо1 ' ' Г->оо * J J
T т, Т х,
^ f flbl(z) + c)dzdzl= Hm ~ f /*61
T J J T_>m T .1 .1
= ton
r->co J T_>m 1
г. е. Иг при Т ->-оо здесь не сходится к U. Но можно показать, что
1 /*
Hm -=- / Ьии (х) </х для корреляционной' функции Ь и „ (т) всегда сущест-
6
вует (см., например, гл. 6 ч. 2 настоящей книги). Отсюда вытекает, что в
случаях, когда условие D.72) нарушается, временные средние ит не будут
при Т ->оо сходиться к соответствующему теоретико-вероятностному сред-
среднему и @ = U.
Если корреляционная функция 6«и(т) удовлетворяет не только D.72), но
и более сильио.му условию D.73), то из D.81) легко следует формула D.74).
Заметим, что из равенства D.68), вообще говоря, еще не следует, что
для любой реализации случайного процесса временные средние ит при
Т ->-оо действительно стремятся к пределу, совпадающему с u(t) = U. Это-
Этому равенству не противоречило бы, если бы даже для любой реализации
иногда встречались такие сколь угодно большие значения Т, при которых
ит было бы далеко от U (так что для отдельных реализаций предел
1 f
Hm -=г / u(t)dt просто не существовал бы). Можно доказать, однако, что
г->°° о
для любого стационарного случайного процесса u(t) с |и(*I < оо для почти
всех реализаций (т. е. для всех реализаций, кроме, быть может, некоторых
«особых> реализаций, суммарная вероятность которых равна нулю) значе-
значения временного среднего ит при 7"^>-оо стремятся к определённому пределу
(так называемая «эргодическая теорема Дж. Биркгофа — Хинчина»; см., на-
например, Дуб A953), гл. XI, § 2, Розанов A963), гл. IV, § 5). Но отсюда
вытекает, что во всех случаях, когда выполняется D.68) (т. е. когда корреля-
корреляционная функция 6uu(t) удовлетворяет условию D.72)), предел временных
средних, составленных по отдельной реализации процесса u(t), с вероятно-
вероятностью единица существует н равняется a(f).

ГЛАВА III
УРАВНЕНИЯ РЕИНОЛЬДСА И ПОЛУЭМПИРИЧЕСКИЕ
ТЕОРИИ ТУРБУЛЕНТНОСТИ
§ 5. ТУРБУЛЕНТНЫЕ ТЕЧЕНИЯ В ТРУБАХ
И В ПОГРАНИЧНОМ СЛОЕ
5.1. Уравнения Рейнольдса
Изучение турбулентных потоков жидкости естественно на-
начать со случая течений в круглых трубах и в пограничном слое
на плоской пластинке, легче всего осуществимых в лаборатории
и имеющих большое значение для многих технических задач.
Богатый экспериментальный материал, накопленный при изуче-
изучении таких течений, позволяет рассматривать их как эталоны
для проверки различных теорий и гипотез о природе турбулент-
турбулентности. Изложение основных сведений о важнейших интеграль-
интегральных характеристиках течений в трубах и в пограничном слое —
профиле продольной скорости, расходе жидкости и законе со-
сопротивления— и займет центральное место в настоящем пара-
параграфе. Далее мы рассмотрим также некоторые гипотезы о тур-
турбулентных течениях, широко используемые при практических
расчетах, и в заключение совсем коротко остановимся на так
называемой свободной турбулентности, на которую не влияют
существенно никакие твердые стенки. Прежде всего, однако, не-
необходимо привести общие соображения Рейнольдса A894), от-
относящиеся к произвольным турбулентным течениям и лежащие
в. основе всей теории турбулентности.
Мы уже. говорили о том, что гидродинамические доля скоро-
скорости, давления, температуры и т. д. в случае турбулентного тече-
течения имеют столь сложную структуру, что их индивидуальное
описание оказывается практически невозможным. Поэтому здесь
приходится рассматривать сразу целую совокупность аналогич-
аналогичных течений и изучать лишь осредненные статистические харак-
характеристики ?тои совокупности, предполагая, что все рассматри-

216 ГЛ. III. УРАВНЕНИЯ РЕИНОЛЬДСА [5.1
ваемые гидродинамические поля являются случайными полями
(© смысле, объясненном в п. 3.2). В дальнейшем мы всегда бу-
будем предполагать, что такой подход является возможным, т. е.
турбулентными мы будем называть лишь такие течения, для
которых существует статистический ансамбль аналогичных тече-
течений, характеризуемый определенными распределениями вероят-
вероятности (с непрерывными плотностями) для значений всевозмож-
всевозможных гидродинамических полей. Отметим в этой связи, что обыч-
обычное определение турбулентных течений просто как течений,
сопровождающихся беспорядочными пульсациями всех гидро-
гидродинамических величин, еще недостаточно для возможности по-
построения математической теории турбулентности. Если же соот-
соответствующий статистический ансамбль существует, то отвечаю-
отвечающее ему статистическое описание гидродинамических полей
турбулентности и с чисто практической точки зрения не будет
«неполным», так как знание всех деталей очень запутанного ин-
индивидуального поля для практики никогда не нужно, а интерес
всегда представляют лишь средние характеристики. Правда, на
практике обычно используются не средние по ансамблю, а вре-
временные или пространственные средние; поэтому с практической
точки зрения следует требовать еще, чтобы случайные поля
гидродинамических величин удовлетворяли какой-то форме
эргодической теоремы. Последнее условие в дальнейшем мы так-
также всегда будем предполагать выполняющимся, не оговаривая
этого.
Важнейшими и одновременно простейшими статистическими
характеристиками случайных гидродинамических полей являют-
являются их средние значения. Разности и' = и — п между индивиду-
индивидуальными значениями поля и и его средним значением п есте-
естественно назвать пульсациями поля и. Разложение гидродинами-
гидродинамических полей на их средние значения и пульсации и играло ос-
основную роль в рассуждениях Рейнольдса (а также и почти во
всех последующих исследованиях турбулентности).
Средние значения гидродинамических полей обычно оказы-
оказываются весьма гладкими и медленно меняющимися; пульсации
же, наоборот, характеризуются боль.шой изменчивостью во вре-
времени и в пространстве. Вообще говоря, допустимо даже пред-
предполагать, что турбулентные неоднородности могут иметь сколь
угодно малые масштабы (вплоть до масштабов, сравнимых со
средней длиной свободного пробега молекул) и сколь угодно
малые периоды (вплоть до периодов, сравнимых со средним
временем между последовательными столкновениями молекул).
Если бы это было так, то использование при бписании турбу-
турбулентности обычных понятий и методов механики сплошных сред
(и, в частности, дифференциальных уравнений гидродинамики),

5.1] § 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 217
разумеется, было бы незаконным. Однако опыт показывает, что
на самом деле турбулентные неоднородности никогда не имеют
столь малых пространственно-временных размеров. Это объяс-
объясняется тем, что неоднородностям очень малых размеров должны
были бы отвечать очень большие градиенты скорости; поэтому
для движений очень малых масштабов затраты энергии на пре-
преодоление сил вязкого трения становятся столь большими, что
делают существование таких движений практически невозмож-
невозможным. В результате минимальные масштабы и периоды тур-
турбулентных неоднородностей оказываются во всех случаях на
несколько порядков превосходящими масштабы и периоды мо-
молекулярных движений. А именно, размеры наименьших неодно-
неоднородностей, наблюдающихся и в воздушных, и в водных турбу-
турбулентных потоках, имеют порядок нескольких миллиметров или,
в крайнем случае, десятых долей миллиметра (ср., например,
ч. 2 настоящей книги, гл. 8), в то время как в нормальных усло-
условиях длина свободного пробега молекул воздуха имеет порядок
10~5 см, а молекул воды — еще много меньший порядок. Так как
к тому же скорости гидродинамических потоков по порядку ве-
величины не превосходят средней скорости теплового движения
молекул (близкой к 5-Ю4 см/сек), то характерные периоды
турбулентных пульсаций также всегда на несколько порядков
превосходят среднее время между двумя молекулярными столкно-
столкновениями. На расстояниях, сравнимых с размерами минимальных
неоднородностей, и в течение промежутков времени, сравни-
сравнимых с минимальными периодами пульсаций, все гидродинамиче-
гидродинамические поля изменяются плавно и могут быть описаны дифферен-
дифференцируемыми функциями. Отсюда вытекает, что описание турбу-
турбулентных течений с помощью обычных дифференциальных урав-
уравнений гидромеханики является вполне оправданным.
Однако непосредственное использование этих уравнений не-
невозможно хотя бы потому, что гидродинамические поля в тур-
турбулентном потоке всегда нестационарны и очень сильно зависят
от мельчайших деталей начальных условий, а эти детали ни-
никогда не бывают известны с достаточной полнотой. Кроме того,
если бы даже начальные значения и были известды точно.товсе
равно решение соответствующей задачи с начальными условия-
условиями из-за ее неустойчивости относительно малых возмущений
начальных данных было бы крайне громоздким и практически
бесполезным. Но отсюда еще не следует, что уравнения гидро-
гидромеханики вообще не могут быть применены при изучении турбу-
турбулентности. Благодаря тому, что индивидуальные реализации
гидродинамических полей турбулентного потока удовлетворяют
определенным дифференциальным уравнениям, статистические
характеристики этих полей оказываются связанными целым

21в M. Hi. УДЛИНЕНИЯ 1>ЕЙН0ЛЬДСА [5.1
рядом важных соотношений, имеющих для теории турбулент-
турбулентности самое первостепенное значение.
Простейшие связи такого рода и были установлены Рей-
нольдсом с помощью непосредственного осреднения уравнений
гидродинамики несжимаемой^ жидкости. Будем исходить из
уравнений баланса импульса, умноженных на р уравнений
Навье — Стокса A.6), в которых нам теперь будет удобно сла-
слагаемые иа -*?г преобразовать с помощью уравнения неразрывно-
д
сти к виду -jj- (UiUa). Применим ко всем членам этих уравнений
операцию осреднения и используем перестановочность этой опе-
операции с дифференцированием по координатам и по времени
(свойство C.6) на стр. 164), а также равенство
~пр = (п1 -(- и';) (и, +. и') = й,й, + и^и'.,
непосредственно вытекающее из C.3) и C.7'). В таком случае
мы получим уравнения
;) = р^—-^+руДЙ„ / = 1,2,3, E.1)
обычно называемые уравнениями Рейнольдса. Эти уравнения
содержат уже только плавно меняющиеся осредненные вели-
величины; поэтому при их использовании не возникает трудностей,
связанных со сложностью и нерегулярностью гидродинамиче-
гидродинамических полей турбулентных потоков. Зато при этом возникает дру-
другая трудность, связанная с наличием в уравнениях Рейнольдса
новых неизвестных величин ¦$} — — щ\и!^ (знак минус здесь по-
поставлен по причине, которая выяснится чуть ниже), характери-
характеризующих пульсационную компоненту поля скорости. Появление
этих новых неизвестных, очевидно, является непосредственным
следствием нелинейности уравнений гидродинамики. При осред-
осреднении же линейных уравнений никаких новых членов, разумеет-
разумеется, не возникает, так что, например, осредненное уравнение не-
неразрывности будет иметь простой вид
Для выяснения физического смысла дополнительных слагае-
слагаемых— риЩ в уравнениях E.1) рассмотрим среднее значение
плотности потока импульса
(да i dtij \
-fa--\"fa~) —вязкий тензор напряжений в не-

5.1] § 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 219
сжимаемой жидкости. Это выражение показывает, что по
отношению к осредненному движению роль вязкого тензора
напряжений играет тензор т^=о^ — pu'tu'j=-olj-\-tf} (для
того чтобы здесь получить сумму, и был добавлен знак ми-
минус в выражении для тЭД. Таким образом, в турбулентном
течении, кроме обмена импульсом между жидкими частицами
благодаря силам молекулярной вязкости (описываемого тензо-
тензором вязких напряжений), имеет место также и передача им-
импульса от одних объемов жидкости к другим, вызываемая пере-
перемешиванием, создаваемым пульсациями скорости. Иначе говоря,
влияние турбулентного перемешивания на осредненное движе-
движение оказывается родственным влиянию вязкости; чтобы под-
подчеркнуть это, уравнения Рейнольдса иногда записываются также
в виде _
др . д I dui ~r~r\ /с чм
i^^Vt-u>^ EЛ)
Мы видим, что величины — pu'fij в уравнениях E.1) для осред-
ненного движения имеют смысл компонент тензора дополни-
дополнительных напряжений, возникающих из-за наличия турбулент-
турбулентных пульсаций подобно тому, как в обычной гидродинамике
микроскопические молекулярные движения приводят к появле-
появлению вязких напряжений. Эти дополнительные напряжения на-
называются в теории турбулентности напряжениями Рейнольдса,
При рассмотрении тензора напряжений Рейнольдса особый
интерес представляет компонента этого тензора, описывающая
передачу импульса жидкости обтекаемому телу. Пусть 2 — не-
небольшая площадка на поверхности обтекаемого тела, которую
приближенно можно считать плоской и совпадающей с частью
плоскости xs = 0. Предположим, далее, что направление осред-
ненного течения в окрестности этой площадки параллельно оси
0*1. В таком случае сила трения, приложенная к площадке 2,
также будет направлена вдоль оси Oxt. Ясно, что величина
силы трения, приходящейся на единицу площади поверхности
тела, будет равна плотности потока ^-компоненты импульса по
направлению Ох3, взятой в точке этой поверхности, т. е. будет
определяться формулой
Величина т0 называется напряжением трения на стенке. Так как
на поверхности обтекаемого тела величины и, и и'{ и их произ-
— / ди, , да* \
водные по xi, очевидно, равняются нулю, а о13 = pv I -^ -f- ^ I,

220 ГЛ. Ш. УРАВНЕНИЯ РЕИНОЛЬДСА [5.1
то величину to можно представить и в более простой форме:
Если, однако, мы выделим площадку, параллельную 2, над по-
поверхностью обтекаемого тела, то для нее напряжение трения
будет уже определяться формулой
* = о13 — ри[и'у E.4)
в важном частном случае, когда осредненная скорость всюду
направлена вдоль оси Охи мы будем иметь
В этом случае, следуя идеям Буссинеска A897), часто фор«
мально полагают
-Р^Х = Р/СЦ, E.5)
где К — новая величина размерности L^T'1, называемая коэф-
коэффициентом турбулентной вязкости; сумму v + К можно назвать
суммарным (или эффективным) коэффициентом вязкости тур-
турбулентного потока. В отличие от обычного коэффициента (моле-
(молекулярной) вязкости v коэффициент турбулентной вязкости К,
очевидно, характеризует не физические свойства жидкости, а
статистические свойства пульсационного движения. Поэтому он
уже не обязан являться постоянной величиной, а может ме-
меняться в пространстве и во времени и даже принимать отри-
отрицательные значения (см. ниже п. 6.3) 1). Существенно под-
подчеркнуть сразу же, что коэффициент турбулентной вязкости К
обычно значительно превосходит коэффициент молекулярной
вязкости v; поэтому вдали от твердых границ напряжение тре-
трения (определяемое потоком лч-компоненты импульса в направ-
направлении оси Ох3) вполне можно noflC4HfbmaTb по формуле
х = та> = -Р^. E.6)
Уравнения Рейнольдса E.3) представляют собой уравнения
баланса импульса осредненного движения; входящие в них на-
напряжения Рейнольдса описывают турбулентный перенос этого
') Помимо того, коэффициент турбулентной вязкости по самому своему
определению зависит также и от принятого способа осреднения, т. е., иначе
говоря, от выбора того статистического ансамбля аналогичных течений, за-
задание которого должно быть включено в определение данного турбулентного
потока. Это замечание оказывается особенно существенным в применении к
«природной» турбулентности в атмосфере или океане, г"де обычно не суще-
существует однозначно определяемого «естественного множества аналогичных те-
течений», и осреднение по различным статистическим совокупностям может при-
привести к значениям К, отличающимся иа несколько порядков.

5.1] § б. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 221
импульса. Аналогичные уравнения баланса могут быть получе-
получены и для произвольной скалярной консервативной субстанции,
переносимой жидкостью (например, для тепла или пассивной
материальной примеои типа водяного пара, дыма или пыли в
атмосфере). Применяя операцию осреднения к уравнению A.72),
описывающему перенос субстанции О в несжимаемой жидко-
жидкости, получим
или, иначе,
(ср. E.1) и E.1')). Если О — это температура, то вектор ppi
описывает адвективный перенос тепла осредненным движением,
%ТзГ 'где х = срРЗУ — перенос тепла за счет молекулярной теп-
теплопроводности, а величина
q^-с^Щ E.8)
будет плотностью турбулентного потока тепла по направлению
отрицательной оси Одс<. Мы видим, что турбулентные пульсации
приводят к появлению дополнительного потока тепла, в ряде от-
отношений родственного потоку тепла, создаваемому молекуляр-
молекулярной теплопроводностью. Аналогично E.5) мы можем формально
положить
E.9)
где величина Кь играет роль нового коэффициента температуро-
температуропроводности, называемого коэффициентом турбулентной темпе-
температуропроводности (вообще говоря, этот коэффициент может
быть различным для разных координатных осей). Если же д в
уравнениях E.7) и E,7') представляет собой концентрацию пас-
пассивной материальной примеси, то величина
Л = -рЩ E.80
будет иметь смысл плотности турбулентного потока примеси по
направлению отрицательной оси Оде*; в таком случае коэффи-
коэффициент Кь в равенстве
-рЩ = рК^ E.9')
называется коэффициентом турбулентной диффузии (этот коэф-
коэффициент был введен Шмидтом A917, 1925)).

222 гл. in. уравнения рейнольдса [5.2
Все сказанное выше по поводу коэффициента турбулентной
вязкости можно, разумеется, повторить и по поводу коэффици-'
ентов турбулентной температуропроводности и диффузии; даль-
дальнейшие сведения о всех этих коэффициентах турбулентного
переноса см. ниже в п. 6.3.
5.2. Общий вид профиля средней скорости течения
около стенки
Перейдем теперь к исследованию общих свойств турбулент-
турбулентных течений около стенки, параллельной направлению средней
скорости течения. Результаты этого исследования будут прило-
жимы и к течениям в круглой трубе или в плоском канале, и к
течениям в пограничном слое на плоской пластинке (в частности,
в приземном или приводном слое атмосферы над ровной подсти-
подстилающей поверхностью при нейтральной, термической стратифи-
стратификации). Мы начнем, однако, с рассмотрения простейшего иде-
идеализированного случая стационарного плоскопараллельного по-
потока жидкости, движущейся по направлению оси Ох в полупро-
полупространстве г > 0 в отсутствие градиента среднего давления.
В случае ламинарного безнапорного плоскопараллельного
течения из первого уравнения гидродинамики, как мы видели на
стр. 41, немедленно вытекает, что профиль скорости u(z) дол-
должен быть линейным. Для аналогичного турбулентного течения
первое уравнение Рейнольдса будет иметь вид
Это уравнение показывает, что поток дс-компоненты импульса
вдоль оси Oz (направленный от жидкости к стенке) здесь будет
одним и тем же на всех расстояниях от стенки:
х (z) = pv ~ — ррда7 = х0 = const, E.11)
где то — напряжение трения на стенке 2 = 0. Однако оно не
позволяет однозначно определить профиль средней скорости
п(г), так как, кроме функции п(г), содержит еще неизвестную
величину u'w'. Тем не менее, некоторые выводы о возможной
форме функции п(г) -в этом случае все же можно получить из
соображений размерности. В самом деле, осредненные характе-
характеристики рассматриваемого течения на расстоянии z от стенки,
очевидно, могут зависеть лишь от напряжения трения to, коор-
координаты г и параметров жидкости v и р. При этом величины to
и р могут входить в кинематические характеристики течения

5,2] § $. ТеЧеНйя В TPVfeAx И в Пог РАЯйчнбМ СЛОЕ 223
лишь в эиде комбинации —, не зависящей от размерности
массы. Вместо отношения — удобно использовать величину
имеющую размерность скорости и являющуюся поэтому есте-
естественным масштабом скоростей для течения около стенки; в
дальнейшем мы ее будем называть динамической скоростью1).
Так как из ut% v и z можно составить единственную безразмер-
безразмерную комбинацию -^*-.то общий вид зависимости профиля сред-
средней скорости п(г) от г, т0. р и v может быть записан в виде
u(z)=uj(^), E.13)
или, что то же самое, в виде
«+=/(*+). где ?+ = ¦?-. г+ = ^- E.13')
Здесь п+ и 2+ — безразмерные скорость и расстояние от стенки,
a f(z+) — некоторая универсальная функция одного переменного.
Важный результат E.13) иногда называется универсальным за-
законом турбулентности вблизи стенки; впервые он был указан
Прандтлем A925) (см. также Прандтль A9326)).
Формулы E.13) и E.13'), разумеется, будут справедливы
лишь в случае, когда стенку можно считать гладкой, т. е. опи-
описываемой простейшим уравнением 2 = 0. Поскольку естествен-
естественным масштабом длин в рассматриваемом течении будет «дина-
«динамическая длина» г, = —-, то мы можем теперь количественно
и*
разъяснить требование гладкости: стенка будет динамически
гладкой, если средняя высота Ао имеющихся на ней бугорков
удовлетворяет условию
(более точные данные см. на стр. 242). Только в этом случае
профиль скорости около стенки будет определяться общей фор-
формулой E.13). В случае же шероховатой стенки, высота неровно-
неровностей которой не удовлетворяет условию E.14), эти неровности
также будут как-то влиять на распределение средней скорости
около стенки. Поэтому формулу E.13) здесь следует заменить
') Иногда эта скорость называется также скоростью трения (в соответ-
соответствии с общепринятым в английской литературе термином friction velocity).

224 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА E.2
более общей формулой
(^ *? ) ' E.15)
где а,.р, ... — безразмерные параметры, характеризующие фор-
форму неровностей и их распределение по поверхности стенки. В
случае сильно шероховатых стенок при использовании форму-
формулы E.15) возникает еще дополнительная трудность, связанная
с тем, что здесь неясно, от какого уровня следует отсчитывать
высоту г; к этому вопросу мы еще вернемся ниже при более
подробном рассмотрении течений около шероховатых стенок.
Прежде чем переходить к обсуждению формы функции f,
остановимся на вопросе о применимости соотношений E.13) и
E.15) к различным реально встречающимся турбулентным те-
течениям. Начнем со случая безнапорного турбулентного течения
жидкости между двумя плоскими стенками, движущимися друг
относительно друга. В этом случае уравнения E.10) и E.11)
будут точными; поэтому, например, при гладких стенках для
применимости формулы E.13) к течению на расстоянии г от од-
одной из стенок надо только, чтобы г было много меньше расстоя-
расстояния Н между стенками1). Однако такое течение само является
идеализированным течением, с трудом моделируемым в лабора-
лаборатории; поэтому для возможности проверки формул E.13) и
E.15) важно знать какие-либо более легко осуществимые тече-
течения, профиль скорости которых описывается этими формулами.
Как уже отмечалось, одним из таких течений может являться
движение воздуха около поверхности земли (или воды) при ней-
нейтральной термической стратификации-. Правда, в земной атмо-
атмосфере горизонтальный градиент давления обычно бывает слегка
отличен от нуля и, кроме того, на скорость ветра влияет еще и
создаваемая вращением Земли сила Кориолиса (см. ниже
п. 6.6). Однако в самом нижнем слое воздуха все эти факторы
играют лишь малую роль и не вызывают заметного измене-
изменения с высотой напряжения трения т: простые оценки (кото-
(которые мы отложим до стр. 349), показывают, что в атмосфере
вплоть до высоты порядка 50 м величина т обычно может счи-
считаться практически постоянной. Следовательно, в пределах
этого слоя в случае нейтральной стратификации можно с доста-
достаточным основанием пользоваться упрощенным уравнением E.11)
') Строго говоря, для турбулентного течения между движущимися стен-
—, . . / гиа г,ил \
камн должна иметь место формула вида и [г) = U.J I —=•, -—-1, где г\ =
= Н—г—расстояние до второй ограничивающей поток стенки. При г\ ~^> г
допустимо считать, что ' * = со, после чего эта формула обращается в фор-
формулу E.13).

5.2] § S. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 225
и формулой E.15) (заметим, что в атмосфере подстилающая по-
поверхность почти всегда оказывается шероховатой, так как ы,
здесь обычно имеет порядок 10 см/сек и, значит, zt не превос-
превосходит нескольких десятых долей миллиметра).
Перейдем теперь к искусственным течениям в трубах, кана-
каналах и пограничном слое на пластинке. В простейшем случае ши-
широкого плоского канала течение можно приближенно рассма-
рассматривать как плоскопараллельное в среднем течение между бес-
бесконечными плоскостями г = 0и2 = // = 2# 4, однородное в пло-
плоскостях г = const. Ясно, что в таком случае первое и третье
уравнения Рейнольдса будут иметь вид
dw'2 dp
<5Л6)
(где, как обычно, >: = P''-^j — pu'w'). Из второго уравнения
E.16) следует, что р + pw'* = Ра зависит только от х (величи-
(величина р0, очевидно, совпадает со средним давлением на стенку).
Но wf не может зависеть от х; поэтому в силу первого урав-
уравнения E.16) _
Обозначим напряжение трения на нижней стенке 2 = 0 через
т0; так как в силу условия симметрии напряжение трения в
центре канала (при 2 = Ht) должно равняться нулю, то послед-
последнюю формулу можно также переписать в виде
E.17)
Отсюда видно, что при 2<C#i можно полагать т(г) = to = const;
поэтому и в этом случае существует слой (примыкающий к
стенке канала), в котором напряжение трения остается практи-
практически постоянным. В пределах этого слоя влиянием градиента
давления можно пренебречь и, следовательно, можно пользо-
пользоваться формулами E.13) и E.15) ').
') Как даииые экспериментов, так и аккуратные расчеты, учитывающие
зависимость напряжения треиия т от z, показывают, что профили средних
гидродинамических полей и основные интегральные характеристики турбу-
турбулентных течений мало чувствительны к даже довольно значительным изме-
изменениям т. Поэтому, например, к слою, в котором т меняется не болыце чем
на 15—20%, почти всегда можно смело прилагать упрощенную теорию, пред-
предполагающую, что т = const. Ниже мы узиднм, что в ряде случаев резуль-
результаты, полученные при таком предположении, дают неплохое приближение
даже и для всего сечеиия канала (или трубы).

226. гл. ш. уравнения рейнольдса [5?
Вполне аналогично обстоит дело и в случае напорного тече-
течения в круглой трубе диаметра D = 2R. В этом случае из уравне-
уравнений Рейнольдса, преобразованных к полярной системе коорди-
координат (х, г, <р), легко выводится, что
2<«, E.17')
где р0— статическое давление на стенку, a z=R — г — расстоя-
расстояние от стенки. Следовательно, при z<C/? напряжение трения
здесь можно снова считать постоянным и задавать профиль
средней скорости той же формулой E.13) (или E.15)), чтоидля
плоскопараллельного безнапорного течения в полуплоскости.
Наконец, в пограничном слое на плоской пластинке уравнения
Рейнольдса получаются при помощи добавления членов, содер-
содержащих напряжения Рейнольдса, к обычным уравнениям погра-
пограничного слоя A.38) — A.39) относительно осреднённых гидроди-
гидродинамических полей. Учитывая, что пульсационные скорости в по-
пограничном слое много меньше средней продольной скорости м,
а производные по х много меньше производных по г, и сохраняя
лишь главные члены, находим, что третье уравнение Рейнольдса
при отсутствии продольного градиента давления в обтекающем
потоке будет иметь вид
— ди , — да д —}—> , д*и /г «О\
Исходя отсюда, можно оценить изменение напряжения трения t
по вертикали и показать, что и в пограничном слое существует
заметный слой, примыкающий к пластинке, внутри которого на-
напряжение трения будет практически постоянным. В пределах
этого слоя течение можно считать плоскопараллельным и опи-
описывать уравнением E.10), а профиль средней скорости — зада-
задавать формулой E.13) или E.15) •).
') Любопытно отметить,'что, как обнаружили Людвиг и Тнльман A949),
формула E.13) с обычной универсальной функцией / оказывается справедли-
справедливой и для пограничных слоев с весьма значительным продольным градиентом
давления, который, казалось бы, должен был вызывать заметное изменение
напряжения трения в пределах рассматриваемого слоя жидкости. Позже
Коулс A955) объяснил это тем, что в пограничных слоях с продольным гра-
градиентом давления изменение величины То вдоль стенки приводит к измене-
изменению величины т по вертикали, в значительной степени компенсирующему из-
меиеиие т по вертикали, вызываемое градиентом среднего давления (ср. Рот-
та A962 а,б)). . .

&3] 5 в. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 227
5.3. Течение около гладкой стенки; вязкий подслой
и логарифмический пограничный слой
Будем пока предполагать, что стенка 2=0 является динами-
динамически гладкой, так что имеет место формула E.13). Тогда вид
входящей в эту формулу функции f (z+) может быть явно опре-
определен для двух предельных случаев — Для больших и для малых
значений аргумента г+.
Непосредственно около стенки основную роль играет то об-
стоятельство, что на самой стенке ри'тю' = 0 и t0 = Pv -g- (см.
формулу E.3)). Поэтому при достаточно малых значениях г
вязкое напряжение трения будет значительно превосходить по-
величиве напряжение Рейнольдса — pu'w'. Слой жидкости, в ко-
котором v
-?-h^> \u'w'\, называется обычно вязким подслоем1).
В пределах этого подслоя, очевидно, можно считать, что
^ = xo = const; E.19)
следовательно, здесь
U\Z) — ~z' J\z+) — z+- (О. Л))
Строго говоря, формула E.20) представляет собой лишь
первый член разложения функции f(z+) в ряд Тэйлора по сте-
степеням 2+ в окрестности точки z+=0. Следующие члены этого
разложения можно получить с помощью дифференцирования
по 2 уравнения E.11) в точке 2=0. При этом существенно,
что и/=у' = ш'=0 при 2=0; следовательно, при 2=0 равны
нулю и все производные, пульсаций скорости по х и у и, кроме
того, (-J—) =0 (в силу уравнения неразрывности).
') Раньше вместо названия вязкий подслой часто употреблялось также
выражение ламинарный подслой, поскольку предполагалось, что движение в
пределах этого подслоя является ламинарным. В дальнейшем, однако, не-
непосредственные ультрамнкроскопическне наблюдения движения частиц, взве-
взвешенных в жидкости около стенкн (Фэндж и Тауненд A932)), подкрепленные
затем и данными тонких термоанемометрическнх измерений (Лауфер A951,
1954), Клебанов A955)), показали, что хотя профиль средней скорости вну-
внутри рассматриваемого подслоя и совпадает с профилем скорости безнапор-
безнапорного плоскопараллельного ламинарного течения (см. A.13)), течение в нем
все же не является ламинарным, а сопровождается заметными турбулентными
пульсациями. Поэтому в настоящее время термин «ламинарный подслой»
представляется мало удачным.

ГЛ. 111. УРАВНЕНИЯ РЕИНОЛЬДСА [5.3
Таким образом,
/ д2и\ 1 / д —г-т\ I i ди' , . , dw'\ n
¦jY = — l-^-u'w) = — -т— w -\-и -д— =0'
д3и
Отсюда вытекает, что разложение Тэйлора профиля средней
скорости по степеням г имеет вид
ф.2(У)
ми-
нус- поставлен в связи с интуитивным представлением о том,
что околб стенки u'w'<0 и поэтому (—Jp~) <0j, a c5 =
— -7—6 (——%- ) • Разложение E.20') было указано (по-види-
мому, впервые) в несколько другой форме Мерфри A932)
(;м. также Таунсенд A956)). Впоследствии некоторыми авто-
авторами (в частности, Дейслером A955), Элродом A957), Леви-
чем A959) и др.; ср. ниже стр. 238) приводились соображения
в пользу того, что с4=0, но они все не являК)тся строгими.
Имеющиеся экспериментальные данные также не позволяют
надежно оценить коэффициент с4 и, следовательно, не дают до-
достаточных оснований определенно утверждать, что d=0. Тем не
менее, равенство нулю второй и третьей производных ?(г+) при
г+ = 0 уже достаточно для того, чтобы изменение скорости в зна-
значительной области -было весьма близко к линейному, т. е. чтобы
понятие о вязком подслое было практически оправданным.
Верхняя граница вязкого подслоя может быть условно опре-
определена, например, как значение г, при котором a'<ze/==O,lv-^-;
можно использовать также и некоторые другие определения,
родственные этому. В любом случае толщина вязкого подслоя б«
может зависеть только от параметров ы* к v; поэтому она дол-
должна задаваться формулой \ —av -ц- = <V^, где аг — универсаль-

5.3] § 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 229.
ная постоянная порядка единицы, точное значение которой, разу-
разумеется, будет зависеть от принятого определения и которую сле-
следует находить по данным экспериментов. То обстоятельство, что
эта постоянная зависит от выбора определения, т. е. не задается
вполне однозначно, является совершенно естественным, так как
вязкий подслой не имеет резкой верхней границы, а плавно пере-
переходит в следующую область течения, в которой вязкое напряже-
напряжение трения и напряжение Рейнольдса имеют одинаковый поря-
порядок величины. Тем не менее, так же как и в случае числового
множителя, определяющего толщину пограничного слоя б, ин-
интервал допустимых значений av здесь оказывается не очень ши-
широким; чаще всего в качестве а„ выбирается число 5, т. е. счи-
считается, что &г>=?=5—- (основой для такого выбора являются экс-
экспериментальные данные, приведенные ниже на рйс. 25).
Перейдем теперь ко второму предельному случаю—к значе-
значениям 2, значительно превосходящим z* — -^- Поскольку в раз-
развитом турбулентном потоке вдали от твердых стенок турбулент-
турбулентные напряжения во много, раз превосходят по величине вязкие
напряжения, то при достаточно большом г (скажем, при г>Ь{)
можно в уравнении E.11) пренебречь членом pv -^- и считать,
что то=—pu'w'. Поэтому закон изменения средней скорости при
2 > 6; также не должен зависеть от вязкости v, а должен как-то
определятьсй лишь значениями плотности р и потока импульса
то, проходящего сквозь жидкость (и равного суммарной силе
взаимодействия жидкости со стенкой, приходящейся на единицу
площади стенки). Существенно подчеркнуть, что мы неслучайно
говорим здесь не о самой скорости, а именно озаконе изме-
изменения Средней скорости. Дело в том, чтр, рассматривая лишь
движение жидкости внутри слоя, в котором можно пренебречь
вязкими напряжениями, мы ничего не можем сказать об абсо-
абсолютных значениях скорости м(г), а можем изучать лишь раз-
разности мB4) —м(г2) значений скорости на двух высотах г4 и г2
в пределах этого слоя (и, в частности, прирост м (г) —м(бг) ско*
рости в слое (г, бг), где z > 6;). Это вытекает из галилеевой ин«
вариантности уравнений механики/согласно которой добавление
ко всем скоростям п{г) при z^-bi постоянного слагаемого не
может изменить передаваемого через жидкость потока им пуль?
са то. Следовательно, абсолютные значения скорости п(г) при
2 > 6; не определяются лишь величинами' то и г, а существенно
зависят от значения м(бг), т. е. от закона изменения скорости В
слое 2<б;, на который уже влияет и.вязкость у. Однако значе-

230 гл. ш. уравнения рейнольдса [5Л
иие -т- градиента средней скорости на высоте г при г > б* не
должно зависеть от v, т. е. должно быть функцией только пара-
параметров те, р и г. Из этих параметров, как легко видеть, можно
т02 а
составить единственную комбинацию —— — —¦ размерности гра-
диента скорости; следовательно, при г > бг должно выполняться
соотношение
Щ?-А^' E-21)
где А ¦— универсальная безразмерная постоянная. Отсюда для
профиля скорости при z > 6j получается логарифмическая фор-
формула
E.22)
где Ai — новая постоянная, которая в силу сказанного выше
может уже зависеть и от коэффициента вязкости v. Слой жидко-
жидкости, в котором выполняется соотношение E.22), называется
логарифмическим пограничным слоем; наличие этого слоя ока-
оказывается весьма существенным для многих задач, в которых
встречаются турбулентные потоки, обтекающие твердые стенки.
Универсальная формула E.22) впервые была выведена Карма-
Карманом A930) и Прандтлем A9326) с помощью совсем других (и
притом различных) соображений. Впоследствии для нее был
найден еще целый ряд других доказательств; некоторые из них
представляют значительный интерес и будут воспроизведены
ниже. Простой вывод этой формулы из соображений размерно-
размерности, приведенный выше, был опубликован в 1944 г. в первом из-
издании книги Ландау и Лифшица A953); см. также Сквайр
A948).
Вместо соображений размерности при выводе формулы E.22)
можно воспользоваться инвариантностью уравнении гидродина-
гидродинамики идеальной жидкости (описывающих рассматриваемое дви-
движение при г > 6*) относительно преобразований подобия x^-kx,
У-ь-ky, z-*-kz и t^>-kt. Поскольку эти преобразования перево-
переводят полупространство г>0 в себя, естественно допустить, что
относительно них будут инвариантны и все статистические ха-
характеристики турбулентности в этом полупространстве (в той
степени, в которой они не зависят от вязкости). Но, как мы уже
видели, пренебрегая вязкостью (т. е. отвлекаясь от граничного
условия и =0 при 2 = 0), мы можем рассматривать лишь отно-
относительные скорости п(гх) — jtB2). Поскольку динамическая

5;3] $ S. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 231
скорость при преобразованиях подобия, очевидно, не изменяет-
изменяется, то согласно принятому допущению об инвариантности без-
и (г2) — ~u{z\)
размерное отношение ц—i-li при не слишком малых «t
и 22 может зависеть лишь от отношения -J-:
E.23)
Из определения E.23) функции g(—-j вытекает, что
g{~-\=g\^-\-\-g\~A\ последнее соотношение в силу равен-
равенства — =-^~-~- можно записать также в виде
g&-ti = g&) + g&)- E.24)
Нетрудно показать, что единственным непрерывным решением
функционального уравнения E.24) является логарифмическая
функция g(l) —A In |; таким образом, мы приходим к соотно-
соотношению
a(zl) = Aatln^-, E.22')
эквивалентному E.22).
Из соображений размерности ясно, что высота 6i нижней гра-
границы логарифмического пограничного слоя должна определять^-
ся формулой 8{ = а, ~, где щ — еще одна универсальная без-
безразмерная постоянная (определяемая примерно с той же сте-
степенью точности, что и постоянная ее). Эмпирические данные
рис. 25 показывают, что допустимо считать аг=30. Из сравне-
сравнения формул E.22) и E.13) вытекает, что постоянная /^должна
быть представима в виде Л, = Аи, 1п — + But, где В — без-
безразмерная универсальная постоянная; при этом E.22) можно
переписать в виде
Aп^+??) при z >«,-?.. E.25)
Отсюда видно, что
/(г+) = Л1пг+ + В при г+>а,. E.250
Заметим еще, что традиционно вместо коэффициента А чаще
используется величина

232 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [5.3
называемая обычно постоянной Кармана. Заменяя Л на — и
обозначая ег*в через р, формулу E.25) можно также переписать
в виде
5(г) = -^1п^./ . E.25")
Численные значения постоянных А (или * = -г) и В (или
р = е-*в), входящих в формулы E.25) — E.25"), могут быть оп-
определены по данным экспериментов. Согласно сказанному в
п, 5,2, соответствующие измерения могут, производиться и в глад-
гладких трубах, и в прямоугольных каналах с гладкими стенками, и
в пограничном слое »а гладких пластинках. Первые пригодные
для этой цели тщательные измерения распределения средней
скорости и напряжения трения то были произведены Никурадзе
A932) в потоках воды в прямых гладких трубах различных ра-
радиусов при Re = —~-~-'г меняющемся в пределах от 4 - 103 до
3,2- 106, Полученные им данные показывают, что действительно
для значительной части течения, начинающейся на расстоянии
порядка 30 —- от стенки и продолжающейся почти до центра
трубы, распределение средней скорости может быть с очень
большой степенью точности описано формулой вида E,25). Для
коэффициентов А и В в этой формуле Никурадзе дал даже два
набора значений: при значениях А = 2,4, В ~ 5,8 (т. е. х=0, 417,
Р « 0,09 « -j-H достигалось наилучшее совпадение формулы
E,25) с опытными данными, относящимися к области 30— <
<г<1000-^-, значительно не доходящей до центра трубы, а
значения Л = 2,5, В=5,5 (т. е. х = 0,40, C «0,11 «-д) оказались
наилучшими при применении формулы E 25) ко всей области от
г = 30:— и до центра трубы, В дальнейшем подобные же изме-
измерения много раз выполнялись и для течений в трубах, и для те-
течений в плоских каналах, и для пограничных слоев на пластин-
пластинках; при этом формула E.25) во всех случаях подтверждалась
достаточно надежно, хотя в получаемых значениях коэффициен-
коэффициентов А и особенно В и имеется небольшой разброс (см., напри-
например, обзорную статью Хинце A962), содержащую сводку боль-

5.3]
§ 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ
233
шого числа данных о величинах А и В) '). Значительное число
данных, относящихся ко всем трем перечисленным типам течений,
30
гь
26
22
го
18
/б
it
12
10
8
6
4
г
¦
а и.
b
¦
)
и*
а
i
=2
Ы
{
*
¦
J
tsuL-
*
Л
f
i
О
/'
A ^
if
A
Л
ж,
¦
t
¦
*
a,
\y
ш
9
\/
Ш
О
У
о
/
о
/
* Шубаузр и Клебаи
* Бребнер и Вягли
л ИикураЙзе
. • Рейхардт и Мощре
* Рейхарвт и Шу
о Лаушер
- г Деистр
о Ван Дриап
о Клебоноо
¦ Фзййж
/
од
льд
W
10*
10*
Рис. 25. Универсальный безразмерный профиль средней скорости
турбулентного течения около гладкой стенки по данным измерений
в трубах, каналах и пограничном слое (по Кестину и Ричардсону A933)).
Разными значками на рисунке отмечены данные разных экспериментаторов.
собрано на сводном рис. 25 (заимствованном из обзора Ке-
стина и Ричардсона A963)). Мы видим, что при г<5-^- все
') Напомним, что согласно приведенному выше теоретическому выводу
значения А и В должны являться универсальными постоянными лишь для
идеализированного плоскопараллельного течения с постоянным напряже-
напряжением трения То- Поэтому для лабораторных наблюдений над реальными

234 гл. ш. уравнения рейнольдса [5.3
наблюденные значения и+=—неплохо укладываются на кри-
кривую и+ = ~- формулы E.20), а при 500-^-< г < 30-^ на-
кривую и+ = 2,5 In -^- + 5,1, соответствующую формуле E.25)
с коэффициентами Л =2,5, В = 5,1 (т. е. х = 0,4, р = 0,13),
рекомендованными Хоулсом A955) и являющимися средними
среди значений этих коэффициентов, получавшихся у различных
исследователей1).
ч
В промежуточной области 5 — < г < 30 — эксперименталь-
ные значения отношения * '. приведенные на рис. 25, явно
уклоняются и от значений, даваемых формулой E:20), и.от тех,
которые должны получаться по формуле E.25). Согласно экс-
экспериментальным данным, значения функции f{z+) в этой об-
области можно изобразить в виде гладкой кривой, плавно перехо-
переходящей в кривую E.20) в точке г+*=5 и в кривую E.25') с
А = 2,5, В — 5,1 в точке z+ = 30 (пунктирная кривая на рис. 25).
Заметим, впрочем, что отклонение пунктирной кривой от лома-
ломаной, изображенной на рис. 25 сплошной линией, не очень велико,
так что в тех случаях, когда не требуется большая точность,
допустимо даже считать, что вплоть до значения 2+= 11,1 (рав-
(равного абсциссе точки пересечения кривых. ы+= z+ и ы+ =
=2,5 In z++5,1) профиль средней скорости задается формулой
E.20), а при 2+> 11,1— формулой E.25). Это предположение,
очевидно, означает, что мы пренебрегаем промежуточной зоной,
du
в которой величины P^-^j и —ри'те/ имеют одинаковый поря-
порядок величины, и считаем, что вслед за вязким подслоем (кото-
(который теперь уже целесообразно считать имеющим толщину
8^=8,= 11,1 -1Л непосредственно следует логарифмический
пограничный слой, в котором вязкие напряжения пренебрежимо
малы по сравнению с напряжениями Рейнольдса.
Заметим еще, что с точки зрения представлений о турбулент-
турбулентной вязкости К (см. формулу E.5)) вязкий подслой, очевидно,
потоками, в которых область применимости формулы E.25) определялась «на
глаз>, небольшой разброс эмпирических значений этих коэффициентов являет-
является вполне объяснимым, даже если не учитывать неизбежных погрешностей
измерений и обработки.
') Близкие значения А = 2,44 и В = 4,9 были предложены Клаузером
A956) на основании обработки данных большого числа опытов, относящихся,
однако, только к пограничному слою на плоской пластинке.

5.3] I s. течения в трубах и в пограничном слое 235
можно определить как подслой, в котором допустимо считать,
что /С=0 (т. е. что эффективная вязкость равна v = const).
Точно так же логарифмический слой можно определить как
слой, в котором молекулярная вязкость пренебрежимо мала по
сравнению с турбулентной вязкостью, задаваемой формулой
К=^- = ш^, х«0,4. E.26)
В таком случае пунктирной кривой на рис. 25, очевидно, будет
отвечать слой, в котором эффективная вязкость как-то плавно
изменяется от значения, близкого к1 v, при 2=5v/«, и до значе-
значения 30xv « 12v при 2 = 30v/«,.
До сих пор мы говорили только о профиле средней скорости
турбулентного потока; однако физические соображения, привед-
приведшие нас к универсальному закону турбулентности вблизи стенки
и к понятию логарифмического пограничного слоя, могут быть с
тем же правом применены и к исследованию любых других од-
одноточечных моментов поля скорости вблизи плоской стенки. Все
эти моменты в пределах слоя постоянного напряжения трения,
очевидно, могут зависеть лишь от параметров 2, т, v и р, т. е.
должны представляться в виде произведения некоторой степени
динамической скорости ы„ на универсальную функцию (свою
для каждого момента) от безразмерного расстояния 2+ = .2«t/v.
При достаточно больших значениях 2+ статистический режим
турбулентных пульсаций не должен уже зависеть и от коэффи-
коэффициента вязкости v; поэтому в случае центральных моментов (не
зависящих от средней скорости п) соответствующие универ-
универсальные функции должны стремиться к постоянным значениям
при 2+ -»- с». Рассмотрим в качестве примера одноточечные вто-
вторые моменты пульсаций ы', v' и w'. Таких моментов всего имеет-
имеется шесть, но два из них (а именно u'v' и v'w') тождественно
обращаются в нуль вследствие симметрии нашей турбулентно-
турбулентности относительно плоскости Одсг, так что остается лишь четыре
ненулевых момента: и/2 = Оц, v'" = al, wn = a\ и u'iso'. Отсюда
ясно, что наряду с формулой E.13) мы будем иметь также че-
четыре формулы вида
E.27)
содержащие четыре новых универсальных функции. Вместо
ФУНКЦИИ М2+) МОЖНО ИСПОЛЬЗОВаТЬ фуНКЦИЮ /5B + )=/4/Л/з>
описывающую изменение с высотой коэффициента корреляции

236.
между и' и w'\
ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА
[5.3
— г —
—"
В пределах логарифмического пограничного слоя функцию
h(•?+). очевидно, можно считать тождественно равной единице,
а функции fi, f2, f3 и f5 — принимающими постоянные значения
fi(oo)=Ai, f2(oo) = А2, fs(oo) - А3 и f5(op) = А& = (AiA3)-K
При приближении к стенке функции fu ¦ ¦., h стремятся к нулю,
причем их разложения в
ряд Тэйлора в точке 2+=О
имеют вид
(так как и' = г/ =•©':=
= ¦^¦=0 при 2 = 0). Ко-
Коэффициенты а4 и 64 . здесь
просто связаны с коэффици-
коэффициентами с4 и с& равенства
E.20'), так как вблизи стен-
стенки Mz+) = 1 — f'B+) (в силу
уравнения E.10)). Точный
вид 'функций fu -.., U не
может быть установлен тео-
теоретически, но приближенно его можно найти, исходя из данных
измерений Лауфера A954) и Клебанова-A955) (см. рис. 26 и
27). Мы видим, что данные измерений в трубе и в пограничном
слое на пластинке в целом неплохо согласуются друг с другом;
в частности, для постоянных А\, Лг и А3 в обоих случаях полу-
получаются примерно одинаковые значения
Рис. 26. Универсальные безразмерные
профили интенсивности флюктуации
трех компонент скорости в течений
около гладкой стенки по данным Кле-
Клебанова (X) н Лауфера (•).
Л, «2,3, Л, да 1,7,
:0,9
(близкие значения постоянных Л4 и А3 были получены также
Гурвичем (I960) и Зубковским A962) при измерениях в атмо-
атмосфере; ср. ниже п. 8.5 и, в частности, рис. 76). Обработав имею-
имеющиеся данные измерений пульсаций скорости в непосредственной
близости от стенки, можно также приближенно оценить (пока
еще лишь с очень невысокой степенью точности) значения ко-

/
i
A
итш
U'li
Уи'г Уш'г
1 1
10 20 30 40 50 ВО 70 80 30 100
5.3] § 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 237
эффициентов fli, ..., ov, при этом оказывается, что
а, ^0,3, а2л;О,О4, а3~0,01, а4=« 0,0006
(см. Лауфер A954), Клебанов A955), Таунсенд A956)).
Что же касается моментов пульсаций скорости выше второго
порядка, то о них пока имеется еще заметно меньше данных,
0,5
0,6
°А
0,2
0
Рис. 27. Универсальные функции /4 (г+)
и /5B+) по даииым измерений Лауфера.
чем о величинах E.27). Укажем, однако, что в работе Конт-
Беллс> A963) можно найти тем не менее предварительные эм-
эмпирические графики универсальных функций /6{г+) = и''/{и'г)*''
и /7(z+) —и'4/(и'2J. определяющих асимметрию и эксцесс ком-
компоненты и'.
В некоторых задачах (в первую очередь при расчете турбулеитиой тепло-
теплопередачи через жидкость; см. ниже п. 5.7) сплошная линия рис. 25 оказывает-
оказывается явно недостаточно точной, а гладкая пунктирная линия — очень неудобной.
В этих задачах желательно иметь аналитическую формулу, описывающую
поведение профиля средней скорости в промежуточной области б„ < t < 8i
и гладко переходящую в предельные выражения E.20) и E.25) при г ¦<
<5,=a,v/u» и соответственно при г>бг=а;у/и,. Целый ряд формул
такого рода для функций /(г+) различной степени сложности и был предло-
предложен в разное время разными авторами. Одной из первых среди них является
формула Кармана A934, 1939), предположившего, что /(г+) =/4ilnz++Bi
при а„ < г+ < а;, причем коэффициенты Ai и В\, отличающиеся от А и В,
таковы, что значение суммы ^4ilnz+ + Si при z+ = а, и при г+ = «; оказы-
оказывается совпадающим со значениями при таком г+ функции E50) и соответ-
соответственно E.25') (т. е., иначе говоря, предложившего соединить прямой линией
точки Do и D.i на рис. 25). В дальнейшем Гофман A940), Рейхардт A940)
н Левич A959), § 4, предложили также иные интерполяционные формулы
для значений f{z+) при aB<z+<a;, несколько лучше соответствующие
данным измерений. Другая идея использовалась в работах Сквайра A948),
Лойцяиского A958) н в очень близких друг к другу работах Ротта A950),
Худнмото A941, 1951) и Майлса A957): здесь область течения делилась
уже лишь иа два слоя z+<aB и z+>av, причем в первой из них принима-
принималась обычная формула E.20), ио зато во второй функции f{z+) задавалась

^38 гл. ш. уравнения рейнольдса [53
более сложным, чем E.25'), аналитическим выражением, асимтотическн
переходившим в E.25') при z+ ->oo и гладко соединяющимся с выражением
E.20) в точке z+ =* а„. В противоположность этому Хама A953), Дейслер
A955, 1959), Рэнни.A956), Левнч A959), § 25, Цай Ко-ен A961) и Тьен и
Васан A963) разбивали поток на слои z+ < «i и z+;>ai и использовали во
втором из них обычную формулу E.25'), а в.первом — более сложное, чем
E.20), выражение для /(z+). В работах Линя, Маултона и Патиема A953)',
Лойцянского A960, 1962а) и Карра A962) рассматривалась сиова трехслойная
модель (т. е. предполагалось, что функция /(z+) задается разными формула-
формулами прн z+ < а„, при «„<*+ <а/ и прн z+>ai), но в отличие от работы
Кармана в первом из этих интервалов для !(г+) принималась более сложная,
чем E.20), формула (разная у разных авторов). Помимо того Лонцянский
A960, 1962а) предложил также и некоторое единое (но весьма сложное) выра-
выражение для функции f(z+), годное при всех значениях z+. Более простые ап-
проксимационные формулы, описывающие поведение функции f(z+) во всей
области постоянства напряжения треиия т и неплохо, согласующиеся со всей
совокупностью эмпирических данных, представленных на рис. 25, были указа-
указаны Рейхардтом A951а), Ван Дристом A956) и Спеллингом A961). Обзор
работ этого направления содержится в книге Хиице A059), § 7.4, и в статьях-
Лойцянского A962а), Ротта A9626) и Кестииа и Ричардсона A963).
Широкую дискуссию вызвал вопрос о детальном поведении функции
/(z+) при z+->-0. В некоторых из перечисленных работ, как уже говорилось
выше, принималось, что f(z+) = z+ при z+-<ae, т. е. считалось, что все про-
производные .функции }(z+) выше первого порядка обращаются в нуль в точке
г+ — 0; это предположение в дальнейшем рядом авторов было подвергнуто
обосноваииой критике. Согласно формулу, предложениой Рэнни, / (г+) = г+ -f-
-+с32^. + ...при z+->0, где с3ф0—этот результат, очевидно, противоречит
-точной формуле E.20'). В то же время формулы Рейхардта, Линя, Маултона
и Патнема, Карра и Тьена н Васана приводят к разложению E.W) с
«47^0, а согласно'Хама, Дейслеру, Левичу, Лойцянскому и Цай Ко-ену в
этом разложении с4 = 0; наконец, Сполдииг приводит сразу два разных вы-
выражения для f(z+) —с с4 9^-0 и с с4 = 0. Большое внимание к вопросу о по-
поведении /(z+) при z+-> 0 объясняется тем, что при достаточно большом чи-
числе Прандтля это поведение существенно влияет на турбулентный теплооб-
теплообмен; об этом еще будет подробнее сказано в п. 5.7.
Заметим еще, что в большинстве перечисленных работ за основу бралась
не сама функция }(г+), а зависимость от г+ эффективного коэффициента тур-
булеитиой вязкости v-{-K = */p -r-; — у [/' (*+)]7 . Предлагаемый вид этой
зависимости иногда просто подбирался иа основе эмпирических данных, но
чаще обосновывался теоретически с помощью рассуждений, близких по духу
к так называемым полуэмпирическим теориям турбулентности (см. ниже
п. 5.8) и использующих те или иные специальные гипотезы, представляющие- '
ся интуитивно довольно правдоподобными. Надо, однако, иметь в виду, что
ни одна из использовавшихся здесь гипотез не была строго доказана; в то
же время разброс кривых u+ — f(z+}, предложенных различными авторами,
имеет тот же порядок величины и тот же характер, что и разброс экспери-
экспериментальных точек на рис. 25. Поэтому в настоящее время иет оснований для
выбора какой-то одной «наилучшей» формулы для /(z+) и при выборе между
различными вариантами таких формул приходится руководствоваться лишь
степенью их удобства для решения той или иной конкретной задачи.
Еще менее удовлетворительно обстоит в настоящее время дело с форму-
формулами для функций fi, ..., /4 и др., описывающих статистический режим пуль-
сашш скорости вблнзн стенкн. Здесь фактически можно указать лишь на

5.4] $ s. течения в трубах и в пограничном слое 239
работы Эйнштейна и Ли A956) и Стернберга A962), предложивших две
различные физические модели процесса возникновения пульсаций скорости
в пределах вязкого подслоя и использовавших эти модели для некоторых
сугубо предварительных расчетов статистических характеристик пульсаций.
Любопытно отметить, однако, что, несмотря на совсем разный характер пред-
предложенных моделей, результаты расчета в обоих случаях оказались во мно-
многом совпадающими с имеющимися эмпирическими данными о пульсациях
скорости (ср. Кистлер A962)).
5.4. Влияние неровностей стенки; параметр шероховатости
и высота вытеснения
Перейдем теперь к рассмотрению турбулентного течения око-
около шероховатой стенки с неровностями высоты й0, не малой по
сравнению с ~. В этом случае профиль средней скорости будет
описываться формулой E.15), содержащей универсальную функ-
функцию /, зависящую от целого ряда параметров. Так как функции
многих переменных обычно бывают мало удобны для практиче-
практических применений, то может показаться, что использование сооб-
соображений размерности в данном случае не очень плодотворно.
На самом деле, однако, дело обстоит вовсе не так плохо.
Будем считать, что Ао^-^-, и рассмотрим опять отдельно
случаи малых и больших значений г. При малых г, сравнимых
с длиной Ао, следует ожидать, что средняя скорость u(z) будет
существенно зависеть от формы и взаимного расположения не-
неровностей стенки и будет различной над вершинами бугров и
над впадинами между ними, так что здесь действительно нельзя
надеяться на нахождение каких-то простых общих закономер-
закономерностей. Во многих случаях, однако, основной интерес представ-
представляет распределение средней скорости не слишком близко к
стенке — на расстояниях z, больших и по сравнению с динами-
динамической длиной г* — ~тг' и по сравнению со средней высотой ho
неровностей стенки. Естественно думать, что на таких расстоя-
расстояниях от стенки ни вязкость, ни локальные свойства поверхности
стенки уже не будут сказываться: существенным здесь будет
лишь наличие постоянного потока импульса вдоль отрицатель-
отрицательного направления оси Ог со «стоком» на плоскости 2 = 0. По-
Поэтому оба вывода формулы E.22), приведенные на стр. 230—231,
в применении к потоку в полупространстве, ограниченном глад-
гладкой стенкой, при z~^> ho> -?- полностью сохраняют силу и в
случае шероховатой стенки. Следовательно,
при z^>h9. E.22а)

240 гл. ш. уравнения рейнольдса [5.4
Так как постоянная Л = —в E.22а) задает значение градиента
средней скорости,. отвечающего заданному потоку импульса
то = ри^, то она и в случае шероховатой стенки должна иметь
то же значение (« 2,5), что и в случае гладкой стенки. Что же
касается коэффициента Ai, то он определяется граничным усло-
условием на нижней границе области применимости формулы EJ22a);
следовательно, он зависит от закона изменения средней скоро-
скорости в непосредственной окрестности стенки, существенно разли-
различающегося для гладких и шероховатых стенок. Заметим, что
начало отсчета расстояний г при z~^>hQ может быть произволь-
произвольно выбрано между основаниями и вершинами бугорков стенки
без заметного изменения результатов; практически оно обычно
выбирается из условия наилучшего совпадения наблюденного
профиля m(z) с логарифмической формулой E.22а) (см. по
этому поводу ниже стр. 248).
Формула E.22а) для. профиля скорости над шероховатой
стенкой может быть несколькими различными способами пере-
переписана в безразмерной форме. Можно, разумеется, воспользо-
воспользоваться записью E.25), применявшейся в случае гладкой стенки,
т. е. положить
я(г) = и,(Л1п-^+д) при гГ>/г0. E.25а)
Однако при этом коэффициент В теперь уже не будет универ-
универсальной постоянной, а будет зависеть от безразмерных параме-
параметров, определяющих размер, форму и расположение неровностей
стенки: В = в(—^± , а, р, ...). Кроме того, запись формулы
E.22а) в виде E.25а) хоть и удобна для сопоставления профи-
профилей средней скорости около гладких и шероховатых стенок, но
Мало естественна (во всяком случае, при Ао^>-^-). В самом
деле, правая часть E.25а) содержит v, в то время как можно
ожидать, что при /to^v/u* профиль средней скорости (а следо-
следовательно, и значение коэффициента /4iB E.22а)) вообще не будет
зависеть от вязкости, а будет определяться лишь размерами
и формой неровностей стенки (полностью определяющими ха-
характер течения в самом нижнем слое). Поэтому при Ао^> —
целесообразнее представить профиль средней скорости в виде
. E.28)
При этом уже можно ожидать, что при достаточно большом
—^-значение коэффициента В' = В-\-А\п-^ не будет менять-

5.4] § 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 241
ся при изменении параметра -^±, содержащего вязкость v
(т. е. будет функцией лишь от параметров а, р, ..., описываю-
описывающих форму и взаимное расположение неровностей). Наконец,
можно еще попытаться выразить постоянную Л4 в формуле
E.22а) непосредственно через характеристики трения жидкости
о стенку, зависящего неизвестным нам образом от геометри-
геометрических свойств стенки. В качестве безразмерной характери-
характеристики трения обычно принимается коэффициент сопротивления
трения
^№)\ E.29)
где U — характерная скорость потока. Однако в рассматривае-
рассматриваемом случае идеализированного течения в безграничном полу-
полупространстве характерная скорость отсутствует, так что здесь
речь может идти лишь о зависящем от высоты (и поэтому мало
удобном) безразмерном коэффициенте c/(z) = 2U=-!- . Но
если мы подставим значение u(z) = —г * в формулу E.22'),
то получим следующий закон изменения Cf(z) с высотой:
Отсюда видно, что в. пределах логарифмического пограничного
слоя
Л1
Таким образом, величина
1
E.30)
имеющая размерность длины, уже не зависит от z. Эта вели-
величина является объективной характеристикой динамического вза-
взаимодействия потока со стенкой (существенно зависящего от
неровностей стенки); ее называют параметром шероховатости,
динамической шероховатостью или даже просто шерохова-
шероховатостью. Подставляя теперь формулу 1/ -9-с/(г)==| ^ 'п ~ 1

242 уравнения рейнольдса E.4
в равенство и (г) = — "* , получим
Zq У. Za
следовательно, го = -^-е~хВ = h<f-xB'. Согласно E.31), пара-
параметр шероховатости можно также определить как ту высоту, на
которой средняя скорость потока обратилась бы в нуль, если бы
логарифмическая формула для п(г) была применима вплоть до
этой высоты (на самом деле, разумеется, логарифмическая фор-
формула перестает действовать уже при значительно больших.зна-
больших.значениях z). . .
Для выяснения зависимости величин В, В' и z0 от высоты
бугорков стенки надо иметь данные опытов, в которых изменял-
изменялся бы только размер, но не форма и не взаимное расположение
этих бугорков. Очень тщательные опыты такого рода были про-
произведены Никурадзе A933) в круглых трубах, стенки которых
были обклеены песчинками заданного размера (меняющегося от
опыта к бпыту), по возможности тесно примыкающими одна к
другой. Полученная в этих опытах зависимость коэффициента
В' в формуле E.28) от -—^ показана на рис. 28 (светлые и
темные точки здесь соответствуют двум разным способам опре-
определения В', первый из которых опирался на непосредственное
сравнение наблюденного распределения скорости с формулой
E.28), а второй будет описан на стр 255). Мы видим, что для
однородной песочной шероховатости при lg—^-<;0,6 (где
lg—десятичный логарифм), т. е. при —2^?-<4, имеет место
формула вида
В' = А\п-^-\-В, где А = 2,5, В — const (« 5,5).
Таким образом, при Ло ^ 4 -^- профиль скорости вовсе не зави-
сит от Ло, т. е. стенка может рассматриваться как динамически
гладкая (заметим, что при таких ft0 бугорки стенки будут пол-
полностью погружены в вязкий подслой; этим, очевидно, и объяс-
объясняется то, что здесь они никак не влияют на течение в области
логарифмического пограничного слоя). При 0,6 ^ lg —^~ <[ 1,7,
т. е. при 4<—^<[60, имеет место промежуточный режим,

5.4)
i. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОВ
243
при котором вершины бугорков выступают из вязкого подслоя и
создают дополнительные возмущения, приводящие к тому, что
оба коэффициента В и В' как-то зависят от —2^-; стенку в этом
случае следует считать динамически слегка шероховатой. Нако-
Наконец, при lg—— >1,7, т. е. при —— >.6О, вязкий род слой
to
В'
9
/
• По
о По
•об
РА*.
сопротивлении
распределению
4v
¦*>J
скоростей
- •«
¦ «с
• t
•
¦ V—
0,2 0,4 0,6 Ofi 1,0 tf 14 IS 18 2,0 21 & 2,6 2,6 3,0 32
Рис. 28. Зависимость коэффициента В' от -5-*- по данным Никурадзе A933).
практически перестает существовать, и течение в непосредствен-
непосредственной близости от стенки целиком состоит из совокупности вих-
вихрей, возникающих при обтекании отдельных бугорков; здесь
распределение средней скорости п(г) оказывается не зависящим
от коэффициента вязкости v, и постоянным оказывается коэффи«
циент В' (а именно, В'~8,5 согласно данным рис. 28). В этом
последнем случае стенку можно назвать динамически вполне
шероховатой. Разумеется, будет ли стенка динамически глад-
гладкой, слегка шероховатой или вполне шероховатой, зависит не
только от характера ее поверхности, но и от величин и, и и
(т. е. в конечном счете от числа Рейнольдса течения). Значения
трех параметров В, В' и z0 для динамически гладкой и дина«
мически вполне шероховатой стенок по данным Никурадзе
(относящимся лишь к однородной песочной шероховатости)

244 ГЛ. Ш. УРАВНЕНИЯ РЕЙНОЛЬДСА [5.4
оказываются равными:
В ж 5,5, В' ж 2,51п ^- +- 5,5, г0 ж \ •?- (гладкая стенка),
Ь-2,5In-^ + 8,5, fi'^8,5, ^o = -^ (вполне шероховатая
стенка).
Имея достаточно полные данные о логарифмическом погра-
пограничном слое около стенки, покрытой песочной шероховатостью,
можно сопоставить шероховатости любого другого типа высо-
высоту hs эквивалентной песочной шероховатости (которой при оди-
одинаковом то отвечает тот же логарифмический профиль средней
скорости). Для ряда искусственных динамически вполне шеро-
шероховатых поверхностей, покрытых геометрически правильными
неоднородностями, эта высота hs была экспериментально опре-
определена Шлихтингом A936) (см. также Шлихтинг A951), гл.XX,
§ 7). В книге Шлихтинга A951) можно найти также дополни-
дополнительные данные и библиографические указания, относящиеся
к вопросу о высоте эквивалентной песочной шероховатости как
для искусственных шероховатых поверхностей, так и для ряда
обычных применяющихся в технике поверхностей (бетонных,
чугунных, стальных и т. д.), оказываюшихся во многих случаях
динамически вполне шероховатыми.
Другой способ описания логарифмических профилей около
стенок с различной шероховатостью состоит в указании соответ-
соответствующего уменьшения средней скорости 6м по сравнению с те-
течением над гладкой стенкой при том же напряжении трения то.
Наличие неровностей всегда приводит к сглаживанию профиля
скорости в непосредственной близости от стенки, т. е. замедляет
нарастание средней скорости при очень малых значениях г. По-
Поэтому в случае шероховатой стенки значение скорости на ниж-
нижней границе логарифмического пограничного слоя (а следова-
следовательно, и во всем этом слое) оказывается меньше, чем в случае
гладкой стенки. Используя формулы E.25) и E.28), мы можем
написать
?± = A\n^ + B-B', E.32)
где Л = const я* 2,5, fi = const»5. Отсюда видно, что — не
зависит от г и что для динамически вполне шероховатой стенки
эта величина при изменении —^ будет линейно зависеть
от In -—¦. При переходе же к слегка шероховатым стенкам

5.4]
зависимость
§ 5. ТЕЧЕНИЯ В ТРУВАХ И В ПОГРАНИЧНОМ СЛОЕ 245
от 1п—— меняет свой вид, и
Ьи
величины —
при значениях Ао, при которых стенка становится динамиче-
динамически гладкой, разность бй становится равной нулю. Значи-
Значили" ,
тельное число эмпирических данных о — (т. е. о значениях ко-
коэффициента В') для различных типов шероховатости, найденных
го
и*
W
>•
S
10
10*
Ш3
Рос. 29. Влияние шероховатости стенки на относительное
уменьшение средней скорости Ьи/и, (по Клаузеру A956)).
Разными значками на рисунке отыечеиы данные, относящиеся к разный
типам шероховатости. Пунктирная линия соответствует данным для
однородной песочной шероховатости.
по результатам измерений в пограничных слоях на пластинках,
было собрано Хама A954) (см. также Клаузер A956)) и Роберт-
соном A957): На рис. 29, заимствованном из статьи Клаузера
A956), представлены полученные значения—. Мы видим, что
при достаточно больших значениях —~ величина — для всех
типов шероховатости действительно оказывается линейно зави-
зависящей от In °v --. что соответствует постоянству коэффициент

246 ГЛ. Ш. УРАВНЕНИЯ РЕЙНОЛЬДСА [5.4
та В' (т. е. случаю вполне шероховатой поверхности). Однако
переход к промежуточному режиму (проявляющийся в откло-
отклонении зависимости ~ от In—~± от простой линейной зависи-
зависимости) для разных типов шероховатости происходит при раз-
различных значениях —^*- (согласно данным рис. 29, обычно
заключающихся между 30 и 100); кроме того, и характер за-
зависимости ~- от —~ для слегка шероховатых поверхностей
разных типов оказывается совершенно различным. Заметим еще,
что рис. 29 позволяет Также для любой представленной на нем
шероховатости легко определить и высоту hs эквивалентной пе-
песочной шероховатости, т. е. такой песочной шероховатости, ко-
которой отвечает то же самое значение —. Для вполне шерохо-
шероховатых стенок (и только для них) высота hs, очевидно, будет
пропорциональна высоте Ао; поэтому и параметр шероховатости
го = -Л здесь будет пропорционален /to-
Выше уже указывалось, что логарифмическая зависимость
средней скорости от высоты должна иметь место также и для.
скорости ветра в нижнем слое атмосферы (толщиной порядка
Ю-т-100 м) при нейтральной (или близкой к нейтральной) тер-
термической стратификации (это обстоятельство, по-видимому,
впервые было отмечено Прандтлем A932а)). То, что дело именно
так обстоит в действительности, было еще в 30-х годах подтвер-
подтверждено на обширном эмпирическом материале Свердрупом
A936), Пешке A936) и другими исследователями. Позже по-
подобные измерения многократно повторялись, причем выводы
всегда оказывались одними и теми же (см., например, обсужде-
обсуждение этого вопроса в книгах Саттона A953) и Пристли A959а)).
В ряде случаев наблюдения над профилем ветра сопровожда-
сопровождались также и измерением напряжения трения то при помо-
помощи предложенного Шеппардом A947) динамометрического
метода, основанного на непосредственном определении силы
трения, действующей на выделенный небольшой участок подсти-
подстилающей поверхности, или же при помощи независимо разрабо-
разработанного в СССР (см. Кречмер A954)) и в Австралии (Суинбенк
A951а, 1955)) пульсационного метода, опирающегося на пред-
представление величины т=то в виде E.6) (подробнее об этом см.
в п. 8.3). Поскольку по наклону логарифмического профиля
можно определить величину и, = 1/ — (считая, что значения.

5.4J I «¦ течения в трубах и в пограничном слое 247
х«0,4, А = -«2,5 известны из лабораторных эксперимен-
экспериментов) ¦, независимое измерение то позволяет значительно более на-
надежно проверить логарифмическую формулу E.31), чем это
можно сделать на основе одних только наблюдений над измене-
изменением скорости ветра с высотой. Следует только иметь в виду, что
из-за сложности непосредственного измерения величины то точ-
точность каждого отдельного измерения такого рода пока еще
остается не очень высокой; поэтому достаточно убедитель-
убедительные результаты здесь удается получить лишь на основе
обработки значительного эмпирического материала. При на-
наличии же такой обработки высокая корреляция значений и,,
определенных по профилю ветра и по данным измерений ве-
величины то, обнаруживается.без труда (см., например, Перепел-
кина A957)).
Все методы определения динамической скорости приводят
к выводу, что в атмосфере она обычно заключается между 10
и 100 см /сек. Так. как для воздуха v ~ 0,15 см2/сек, то отсюда
ясно, что подстилающая поверхность атмосферы почти всегда
является динамически вполне шероховатой. Логарифмический
профиль скорости ветра удобно представлять в виде E.31), ис-
используя понятие о параметре шероховатости z0. При этом су-
существенно, однако, что в условиях атмосферы довольно часто
важную роль играет правильный выбор начала отсчета высот 2.
В самом деле, размеры /t0 неровностей почвы, как известно,
могут принимать сравнительно большие значения (например,
в случае высокой травы или поля, покрытого какой-либо сель-
сельскохозяйственной культурой); в то же время увеличение высо-
высоты измерений z в атмосфере часто оказывается вовсе не без-
безобидным, ибо с ростом z сильно возрастает роль всегда имею-
имеющихся отклонений температурного градиента от равновесного
(см. ниже гл. 4). Поэтому имеет смысл специально остановиться
на вопросе о виде профиля средней скорости u(z) на высотах,
лишь на немного превышающих среднюю высоту Ло неровно-
неровностей почвы (т. е. сравнимых с этой высотой).
При z ~ /to параметр /t0 (размерности длины) также будет
влиять на осредненное течение; что же касается вязкости v, то
в случае вполне шероховатой стенки ею, как мы знаем, можно
пренебречь. Поэтому здесь -^ будет функцией от величин то, р,
z и /to, из которых уже можно составить безразмерную комби-
комбинацию-^-. Отсюда вытекает, что вместо формулы E.21) для
градиента средней скорости при z ~ h0 будет справедлива

248 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [5.4
более общая формула
dll \Z) U, / Ло \ ,т пп\
-1Г-==ъ8[ту E-33)
где х«0,4, a gl —-J—поправочная функция, описывающая
отклонение турбулентного потока от автомодельного режима,
характеризуемого логарифмической формулой {5.31). Это откло-
отклонение непосредственно связано с влиянием неоднородности вы-
высоты /to; при 2^>/to оно должно перестать сказываться, откуда
следует, что g@) = l. Учитывая, что -j < 1, разложим функцию
* )
в Ряд п0 степеням ее аргумента; при этом получим
Введем теперь новое начало отсчета высоты z, полагая
z = z\ + z', где z\ сравнимо по порядку величины с /to. В таком
случае -р- также будет меньше единицы, и мы можем заменить
в правой части E.34) переменную г на z' и вместо разложения
по степеням — воспользоваться разложением по степеням —г.
Легко видеть, что первые члены этого нового разложения будут
иметь вид
Выберем теперь z\ так, чтобы в полученном выражении член
первого порядка малости обратился в нуль (т. е. положим
Zi = ah0 = g' @) /to). Тогда с точностью до членов второго по-
порядка малости получим
откуда
й(г) = ^1п^-. E.37)
Мы видим, что влияние конечной высоты /to в первом прибли-
приближении сводится к тому, что при не слишком малых z профиль
скорости оказывается логарифмическим при отсчете высот от оп-
определенного уровня z=zu а не от уровня 2=^0. Высота Zi может
быть названа высотой вытеснения (по аналогии с понятием тол-
толщины вытеснения, вводимой в теории пограничного слоя).

5.4] § 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 249
Данные о значениях параметра шероховатости z0 и высоты
вытеснения z{ для различных типов естественных поверхностей
могут быть найдены во многих источниках (см., например, Пеш-
Пешке A936), Дикон A949), Колдер A949), Константинов A952),
Саттон A953), Эллисон A956), Пристли A959а)). К сожалению,
эти данные не очень хорошо согласуются между собой (веро-
(вероятно, из-за того, что оба параметра z0 и zx зависят от довольно
тонких деталей подстилающей поверхности). Как и должно
быть для вполне шероховатых поверхностей, параметр шерохо-
шероховатости z0, определяемый по профилю ветра, обычно можно счи-
считать пропорциональным высоте ho неровностей почвы. Однако
и для обычного травяного покрова, и для сельскохозяйственных
культур соответствующий множитель пропорциональности ока-
оказывается заметно большим множителя 1/30 (отвечающего, по
данным Никурадзе, однородной песочной шероховатости) и
обычно бывает близок к 1/10 или даже к 1/5 (Пешке, напри-
например, рекомендует формулуго= ~-\. Высота вытеснения zx при
не слишком высоком травостое вообще может быть принята
равной нулю; однако при высокой растительности ее часто при-
приходится считать заключающейся между h0 и -у.
Заметим еще, что при высокой травяной растительности па-
параметр шероховатости может зависеть от средней скорости
ветра, сгибающего стебли растений и тем самым воздействую-
воздействующего на форму поверхности. Например, Дикон A949) нашел,
что при высокой траве (около 60 см высоты) параметр z0 мо-
может изменяться от 9 см при очень слабом ветре до примерно
4 см при сильном ветре. Аналогично обстоит дело и для водных
поверхностей, для которых и высота, и форма неровностей так-
также, очевидно, зависят от скорости ветра. Если считать, что при
исследовании ветрового волнения можно пренебречь вязкостью
и поверхностным натяжением воды и что шероховатость моря
в данной точке его поверхности определяется лишь атмосфер-
атмосферными условиями вблизи этой точки (т. е. лишь локальным
значением напряжения трения), то из соображений раз-
размерности для параметра шероховатости z0 получается формула
вида
и2
E.38)
Здесь g — ускорение силы тяжести, и* = то/Р (где р — плотность
воздуха), а постоянная Ь может, в частности, зависеть от отно-
отношения плотностей воздуха и воды. Имеющиеся наблюдения

250 ГЛ. Ш. УРАВНЕНИЯ РЕИНОЛЬДСА [5.5
профиля скорости ветра над морем пока очень неполны и неточны;
тем не менее, они не оставляют впечатления, что соотношение
E.38) хорошо оправдывается на опыте (отметим, например, что
Чарнок A9586) и Эллисон A956), использовавшие, это соотно-
соотношение, получили резко различные значения Ь: по Чарноку
Ь «* 1/80, в то время как согласно Эллисону 6» 1/12). В этой
связи многие исследователи склонны считать, что на море z0 за«
висит не только от локальных метеорологических условий (а, на-
например, еще и от разгона ветра, характеризующего путь, про-
проходимый ветром над морем). В то же время все имеющиеся
данные указывают на то, что поверхность моря является аэро-
аэродинамически заметно более гладкой, чем большинство других
встречающихся на Земле естественных поверхностей: даже
при довольно сильном ветре на море zo<O,l см (по данным
ряда авторов морскую поверхность при не очень сильном ветре
часто вообще можно считать аэродинамически гладкой; ср.
Саттон A953), Дикон A962)). Поэтому при изучении ветра
над морем понятие параметра шероховатости используется
сравнительно редко; чаще же вместо значений Zo здесь приво-
приводятся значения коэффициента сопротивления трения cf, отне-
отнесенного к скорости U=u{z) на некоторой фиксированной вы-
высоте г (см., например, Уилсон A960), Дикон A962), Дикон и
Уэбб A962)).
5.5. Турбулентные течения в каналах и круглых трубах;
законы сопротивления
Рассматривавшиеся выше общие закономерности турбу-
турбулентных течений около твердой стенки относились к широкому
классу течений, включающему, в частности, и течения в кана-
каналах и трубах; поэтому многие экспериментальные данные о тур-
турбулентности в каналах и трубах уже использовались в преды-
предыдущем изложении. Однако течения в каналах и трубах обла-
обладают также и важными особенностями, отличающими их от
идеализированных течений в полупространстве г > 0, с кото-
которыми мы до сих пор имели дело. В первую очередь здесь надо
отметить, что в отличие от течения в полупространстве для
течений в каналах и трубах имеется характерная длина tft
(полуширина канала) или R (радиус трубы) и характер-
характерная скорость Uo (максимальная скорость в середине канала или
на оси трубы) или 1/ср (средняя скорость, определяемая как
я, r
jj- J u(z)dz или же ^j I u(r)rdr). Отсюда ясно, что теория
1 о о
течений в слое постоянного трения около стенки не исчерпывает

5.5] I 5. ТЕЧЕНИЯ В ТРУВАХ И В ПОГРАНИЧНОМ СЛОЕ 251
всей теории течений в каналах и трубах, к рассмотрению кото-
которой мы сейчас и перейдем.
Начнем с общих соображений о подобии, причем сначала
для простоты будем считать, что стенки являются аэродинами-
аэродинамически гладкими. Течение мы будем рассматривать лишь на до-.
статочно больших расстояниях от входа в канал или трубу, на
которых условия у входа уже не сказываются, и будем предпо-
предполагать его стационарным и полностью турбулентным. В таком
случае отличной от нуля будет лишь одна компонента п = пх
средней скорости, и все статистические характеристики потока
будут зависеть от единственной координаты z — расстояния от
стенки канала или трубы (для трубы z=R — г, где г — расстоя-
расстояние от оси). При заданных размерах канала или трубы и задан-
заданных плотности и вязкости жидкости мы будем иметь одно-
параметрическую совокупность течений, определяемых значе-
значением «напора» — постоянного продольного градиента давления.
Градиент давления будет уже однозначно определять такие ха-
характеристики течения, как скорости Uo и Ucp и напряжение тре-
трения на стенке то или, иначе, динамическую скорость «,= 1/ —.
Таким образом, значения статистических характеристик тече-
течения на расстоянии z от стенки здесь могут зависеть от следую-
следующих параметров: р, v, z, Hi (для трубы мы теперь через #i
обозначаем радиус, т. е. полагаем Hi=R) и одной из скоростей
Uo, Ucv или и*. Из этих параметров можно составить две без-
безразмерные комбинации: число Рейнольдса S=~*v ' (в качестве
характерной скорости мы выбираем скорость и,) и безразмер-
безразмерное расстояние 71 = 7/~*
Следовательно,
й (г) = иф9 (-^-, -^-) = иФср (S, т,);. E.39)
эта более общая формула заменяет теперь формулу E.13).
Мы видим, что профиль средней скорости течения в канале
или в трубе, вообще говоря, определяется некоторой функцией
от двух переменных (которая, разумеется, может быть различ-
различной для канала и для трубы). Имеются, однако, два важных
предельных случая, в которых функцию <р(|, т\) удается все же
выразить через функции от одного переменного; к ним мы сей-
сейчас и перейдем.
Первый случай (детально рассмотренный в п. 5.2—5.4) —это
случай малых значений z (таких, что ^=-4-<1). В этом

252 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [5.5
случае зависимость скорости п(г) от длины Hi становится не-
несущественной, так что формула E.39) должна обратиться в со-
соотношение
^ =/[—-)=/^--П) при ч<Ч0. E.40)
совпадающее с E.13). Второй же предельный случай, с кото-
которым мы раньше не сталкивались, — случай больших значений
у\ = -jj-. соответствующих «турбулентному ядру» течения, примы-
примыкающему к середине канала или оси трубы. В области больших
значений г\, удаленной от твердых стенок, можно рассчитывать
на применимость тех же рассуждений, которыми мы пользова-
пользовались на стр. 299—230 в связи с выводом логарифмической фор-
формулы для профиля средней скорости. А именно, поскольку вдали
от стенок при развитой турбулентности турбулентное напряжение
трения обычно во много раз превосходит вязкое напряжение,
то есть основания думать, что в «турбулентном ядре» вязкость
не будет оказывать непосредственного влияния на режим дви-
движения (хотя косвенно она все же будет влиять, поскольку от нее
зависят граничные условия на границе «ядра» и значение пара-
параметра и», определяющего в силу E.17) и E.17') величину турбу-
турбулентного напряжения во всех точках потока). При отсутствии
характерного масштаба длины отсюда следовало соотношение
E.21), приводящее к логарифмическому профилю, при наличии
же такого масштаба Ht мы будем иметь более общее равенство
du(z) и, ( г \ ' ' а
—-гг- = -jj- 9i I -jj- I. где ф1 — некоторая функция от одного пере-
переменного. Представив, далее, эту функцию в виде ^ (тч) =—/1'Gl).
где fi(l)=0, и проинтегрировав выражение для —-j—- в пре-
пределах от некоторого значения z до z=Hi, найдем
/Л-п) при ч,<4<1. E.41)
Соотношение E.41), называемое обычно законом дефекта ско-
скорости,.впервые было указано Карманом A930) в применении
к течению в трубе, исходя из экспериментальных данных Фри-
ча A928). В дальнейшем этот закон неоднократно тщательно
проверялся (см. ниже рис. 30 и 31), и теперь уже нет сомнений,
что он представляет собой частный случай весьма общего прин-
принципа подобия по числу Рейнольдса, выполняющегося со зна-
значительной степенью точности для широкого класса турбулент-
турбулентных движений. Согласно этому принципу при достаточно
больших числах Рейнольдса (при v<^K~?/L, где U и L — ха-

5JS] § в. течения в трубах и в пограничном слое 253
рактерные масштабы скорости и длины) для достаточно боль-
большой области турбулентного течения (обычно охватывающей
почти весь поток за исключением сравнительно тонких слоев,
примыкающих к стенкам) осредненное движение не зависит не-
непосредственно от коэффициента вязкости (т. е. от числа Рей-
нольдса), оказывающего влияние на поток только через посред-
посредство граничных условий и величины U (см. Таунсенд A956)).
Заметим еще, что такое «подобие по числу Рейнольдса», вообще
говоря, будет иметь место не только для средней скорости, но
и для всех статистических характеристик течения, не связанных
непосредственно с диссипацией кинетической энергии под дей-
действием вязкости (т. е., например, для и'2 или u'w', но не для
На этом последнем утверждении мы здесь, однако,
уже не будем задерживаться.
Приведем теперь важное рассуждение Изаксона A937) (раз-
(развитое затем в работах Милликена A938) и Мизеса A941)),
позволяющее в некоторых случаях установить точный вид функ-
функций / и f\. А именно, предположим, что ц\ <тH) так что суще-
существует некоторый интервал тI<т1<т1о значений т) = -^-, для
которого общую формулу E.39} можно представить и в виде
E.40), и в виде E.41) (это предположение, разумеется, уже не
может быть обосновано теоретически, а должно проверяться на
конкретных экспериментальных данных). В таком случае, скла-
складывая равенства E.40) и E.41), мы получим
4)=/a(S) при 7h<7,<7tot E.42)
где через f2(?) обозначена величина ~, которая, очевидно,
может зависеть только от числа Рейнольдса % = (но не от
т)= yjH. Но из функционального уравнения E.42) легко сле-
следует, что все три функции /, /i и f2 являются логарифмическими.
В самом деле, продифференцировав равенство E.42) сначала
по |, а затем по т), получим
отсюда.вытекает, что f(|T)) = A lngr] + В, где А и В — постоян-
постоянные интегрирования. Таким образом, мы снова пришли к соот-
соотношению E.25), исходя из немного других соображений. Под-
Подставляя теперь полученное выражение функции Д|т]) в E.42),
убеждаемся, что

254 гл. ш. уравнения реинольдса [5JS
Таким образом, «закон дефекта скорости» в области его пере-
пересечения с законом E.40) должен иметь вид
причём если только формула E.43) может быть применена
вплоть до значения z = Я, (т. е. т) = 1), то, очевидно, В\ = О
(последний вывод, разумеется, не следует автоматически из
приведенных рассуждений, так как они относятся лишь к об-
области тI<т]<т]о). Наконец, логарифмическая формула для
f2(|) дает нам следующую зависимость отношения —- от числа
и»
Реинольдса:
-^- = -1п-^-+Я2. E.44)
Вводя вместо —- коэффициент сопротивления трения cf=
= 2 [-тг-\ > мы можем переписать последнюю формулу
также в виде
1п2
E.45)
До сих пор мы все время предполагали, что стенки рассма-
рассматриваемого канала или трубы являются гладкими. Легко ви-
видеть, однако, что приведенные рассуждения могут быть перене-
перенесены почти без всяких изменений и на случай канала или трубы
с шероховатыми стенками. В этом случае функция <p(g, tj) в
равенстве E.39) и функция f(lr\) в равенстве E.40) могут за-
зависеть также от дополнительных аргументов ——- (или jr)>
а, р, ..., определяющих размеры, форму и взаимное располо-
расположение неровностей стенки. Тем не менее, естественно думать, что
в «ядре» течения наличие шероховатости будет сказываться
только через значения граничных условий и значение турбу-
турбулентного напряжения трения (зависящего от величины трения
о стенку), но не непосредственно; если это так, то соотношение
E.41) должно быть одинаковым и для гладких, и для шерохо-
шероховатых стенок. Но в таком случае, предположив, что области,
в которых выполняются соотношения E.40) и E.41), частично
перекрываются между собой, мы немедленно приходим к функ-
функциональному уравнению E.42) с той только разницей, что те-
теперь функции f и f2 могут зависеть еще от дополнительных па-

5.5J « 5- ТЕЧЕНИЯ В ТРУВАХ И В ПОГРАНИЧНОМ СЛОЕ 255
раметров, характеризующих шероховатость. Отсюда, как и
выше, вытекает, что при t)i <т) < щ все три функции f, ft и $2
должны быть логарифмическими с общим коэффициентомЛ= —
при логарифме; следовательно, этот коэффициент должен яв-
лкться универсальной постоянной (так же как и коэффици-
коэффициент Si). Что же касается коэффициентов В и В2, то они могут
содержать еще некоторое общее слагаемое, зависящее от раз-
размеров и характера шероховатости. Если считать, что формула
E.43) применима вплоть до значения z = Я,, то вообще В, = О
и В2 = В; поэтому при этом предположении данные измерений
коэффициента сопротивления позволяют сразу определить и зна-
значение коэффициента В (или коэффициента В' формулы E.28),
просто связанного с В). Именно таким образом и были полу-
получены значения В' при разных —^.представленные в виде чер-
черных Точек на рис. 28.
В частном случае динамически вполне шероховатой стенки
функция f\b\, ^-5. а, р, ...J не должна зависеть от вязко-
вязкости v, т. е. она будет функцией только от Ь\—Х==Т"' а> Р> • • •
Отсюда вытекает, что функция /2и, —^-. а, р, ...) здесь бу-
V Н
дет зависеть только от I • —г- = ~, а, р, ... Следовательно,
и*па "о
в этом случае соотношения E.44) и E.45) принимают вид
E.45')
где коэффициент В2 может зависеть от формы и взаимного рас-
расположения неоднородностей стенки.
Значительное число экспериментальных данных, подтвер-
подтверждающих справедливость соотношения E.40) (совпадающего
с E.13)) для турбулентных течений r трубах и каналах, было
собрано на рис. 25. Разумеется, для того чтобы указанные здесь
расстояния 2+=-^- можно было перевести в значения пере-
переменной r4==~fj~> надо знать число Е — * ' , которое является
FT ТГ
сложной функцией от числа Рейнольдса Re=—¦5--*-, неявно за-
задаваемой соотношением E.45). Для ориентировки мы лриведем

256
ГЛ. III. УРАВНЕНИЯ РЁЙНОЛЬДСА
[5.5
таблицу, показывающую зависимость нижней границы 8^ = 30-^-
логарифмического пограничного слоя для течений в гладких
трубах от наиболее широко используемого числа Рейнольдса
UcpD
ReD
5- 10s
0,2
Ю4
0,1
1С
0,012
io.
0,0016
(на связи скоростей ?/0 и Ucp мы еще остановимся ниже). С ро-
ростом числа Рейнольдса отношение -А-, естественно, уменьшается,
но это уменьшение не будет безграничным. Для каждой реаль-
реальной трубы при возрастании числа Рейнольдса в конце концов
наступает момент, когда она оказывается уже вполне шерохо-
шероховатой; после этого нижняя граница логарифмического слоя на-
начинает уже зависеть только от Яо и не меняется при дальнейшем
возрастании средней скорости течения.
Что же касается до верхней границы значений z, для кото-
которых оказывается применимой логарифмическая формула E.25),
то выше уже отмечалось, что по данным Никурадзе и в гладких,
и в шероховатых трубах эта граница в широком диапазоне чи-
чисел Рейнольдса оказывается весьма близкой к значению г = R
(так что логарифмический пограничный слой тянется почти до
центра трубы). При этом, однако, для применения логарифми-
логарифмической формулы ко всему течению в трубе Никурадзе пришлось
несколько изменить коэффициенты А и В по сравнению с теми,
которые давали наилучшее совпадение в примыкающей к стен-
стенке части потока. Отсюда ясно, что предложенные Никурадзе
логарифмические формулы для всего течения в целом нельзя
считать совпадающими с теоретическим законом E.25), спра-
справедливым при 6г/#1<т)<тH. В самом деле, коэффициенты А
и В в теоретической формуле E.25), очевидно, должны опреде-
определяться на основании по возможности массового материала, от-
относящегося лишь к пристеночной части турбулентных течений;
только используя такие коэффициенты, можно пытаться выяс-
выяснить, нарушается ли закон изменения скорости, отвечающий
логарифмическому пограничному слою, в центральной части те-
течения. Попытка такого рода впервые была предпринята Мил-
ликеном A938), использовавшим почти все имевшиеся в то вре-
время немногочисленные данные о течениях в трубах и каналах.

5.S]
§ 5. ТЕЧЕНИЯ в ТРУБАХ И в ПОГРАНИЧНОМ СЛОВ
257
Любопытно, что для значений коэффициентов А и В в формуле
E.25) Милликен получил значения А = 2,5, В = 5,0, почти не
отличающиеся от тех, которые считаются наиболее надежными
в настоящее время (см. выше стр. 234). Далее, согласно его
оценкам отклонения профиля средней скорости в круглой трубе
от значений, даваемых формулой E.25), начинаются примерно
при ц = 0,1 (т. е. после изменения значения т на 10%), причем
при всех ц они не превосходят 10% от соответствующего зна-
значения п{г). Несмотря на то, что количество экспериментальных
данных о профиле скорости в круглых трубах к настоящему
времени заметно выросло по сравнению с 1938 г. (см. по' этому
поводу, например, обзорную статью Хинце A962)), эти выводы
Милликена и сейчас полностью остались в силе.
Из результатов Никурадзе ясно также, что если оба коэф-
коэффициента -А = ~ и By в логарифмической форме E.43) закона
дефекта скорости рассматривать как эмпирические постоянные,
то можно считать, что эта формула действует вплоть до z = Hit
т. е. хорошего совпадения с экспериментальными данными мо-
можно достигнуть даже и при Bj = 0. Теоретически, однако, зна-
значение А нельзя считать произвольной постоянной, а надо опре-
определять его из обработки результатов измерений, относящихся
к примыкающей к стенке части течения. В таком случае для
.^5.-2,44 In f +0,8
0,0! 0,02 0,05 0,1 0,2 0,5 1
Рис. 30. Проверка закона дефекта скорости
для турбулентного течения в трубе по данным
Лауфера A954).
получения наилучшего совпадения приходится принять, что
ВфО (см., например, заимствованный из книги Хинце A959)
рис. 30, построенный на материале измерений Лауфера A954);
значение А = 2,44, т. е. х«0,41, здесь выбрано в соответствии
с рекомендацией Клаузера A956)). Аналогичные результаты

$58
ГЛ. Iff.' УРАВНЕНИЯ РЁЯНОЛЬДСА.
получаются и для течений в прямоугольном канале (см. заим-
заимствованный из статьи Шубауэра и Чена A959) рис. 31, где
14
IP
10
в
U0-u(z)
и» 6
А
г
0
1
\
ы
0,01 OfiB WU06 0J0 Щ WU60W
Рис. 31. Проверка закона дефекта скорости для тур-
турбулентного течения_в прямоугольном канале по дан-
данным Лауфера (V) и Дёнха (F. DOnch) (-(-).
положено А = 2,5); отклонения от логарифмической формулы
E.43) в обоих случаях начинаются
примерно при т) = 0,25.
Вопрос о выборе аналитической
формулы для функции /i(t]), дающей
хорошее совпадение с опытными дан-
данными на большем интервале значений
т), обсуждается во многих работах (см.,
* например, Госс A961)).Однако в прак-
практических задачах чаще всего можно
просто считать, что профиль сред-
средней скорости в трубе при турбулент-
турбулентном течении вплоть до самой оси опи-
описывается логарифмической формулой.
Ясно, что такой профиль резко отли-
отличается от параболического профиля
ламинарного течения Пуазейля: вслед-
вследствие гораздо более сильного радиаль-
радиального перемешивания в турбулентном
течении профиль скорости всюду, кроме тонкого пристеноч-
пристеночного слоя, оказывается заметно более сглаженным, чем в лами:
нарном течении "(см. рис. 32). Заметим еще, что при т)>0,25
функция -Inту мало отличается-от функции — 2,03т]3/2; поэтому
Рис. 32. Сравнение профилей
средней скорости при ла-
ламинарном (Л) и турбулент-
турбулентной (Т) течениях в трубе.

5.5J § s. течения в трубах и в пограничном слое 259
неудивительно, что при первых тщательных измерениях про-
профиля скорости около оси трубы, произведенных Дарси A858),
была получена эмпирическая формула, которая в наших обозна-
обозначениях имеет вид
f
=5,08(l — *-f. E.46)
¦ Считая профиль скорости логарифмическим вплоть до оси
трубы и пренебрегая тонким пристеночным слоем толщины
|, = 30-—. к которому уже неприменима логарифмическая фор-
формула, можно установить также простое соотношение между
максимальной скоростью на оси трубы Uo и средней скоростью
(/ср. В самом деле, проинтегрировав равенство E.43) с Si=0,
умноженное на 2я(#1 — г), в пределах от z=0 до 2 = /^ и раз-*
делив результат на ъН\, получим
ио-иср
1
= — 1 Г A — т)) In т) с?т) = const« 3,75.
X J
хо
Следовательно, для гладких труб (ср. E.44))
-^ = i In -^- + B'v B'2 = B2- 3,75. E.47)
Это соотношение также хорошо подтверждается на опыте.
Формула E.47) позволяет установить форму закона сопро-
тивления, т. е. зависимость от числа Реинольдса Кед^=-
безразмерного коэффициента сопротивления Х = ^—5—=
(отличающегося от коэффициента cf в формуле E.45), кроме
несущественного численного множителя, лишь заменой макси-
максимальной скорости Uo более просто измеряемой средней скоро-
скоростью Ucp). В самом деле, представив в E.47) выражение
I UcpD и,
b виде произведения 0/7 , получим
I V -it-/cp
: , , В2~ 3,75 — —In 4КТ
-?=• = —W In (Reг, VT)-\-Bo, Во — ^———.
УТ х>^8 ч D r '^ 3 3 ^8"
E.48)

юоя
ID
9
я
7
6
3
г,5
г
1,5
10
If
X
Ч
S
10* '6
Рис. 33. .
Кривая 1 1
н
\
\
Л
Г
э
^**
"И
1
в Никурадзе
9 Carp и Шодер
в Нцссельт
в #!адяг
в ^w^ J^
ф Стэнтон и Паннел
в Шиллер и Герман
S
*
# В V 2 . * 68w* 2 * 6 8WB * * 68Ю
Зависимость коэффициента сопротивления А. от числа Рейнольдса ReD по данным раз-
различных авторов.
1зображает закон сопротивления X=64/Re для ламинарного течения Харена —Пуазейля; кривая 2—закон
E.48) с х=0,41, Bj=— 0,8; пунктирная кривая 3— приближенный закон Блазиуса E.52).
3
ш
гч
я
I
о
сг
Ja
о
>
СП

5.5] § 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 261
Величина X просто определяется по известному перепаду давле-
давления ,Дг/> = —^- на участке трубы длины I и по расходу Q =
= ^j-Ucp; поэтому количество данных о зависимости X от ReD
очень велико. Как показал Никурадзе A932), все эти данные
очень хорошо согласуются с формулой E.48) при сле-
следующих значениях коэффициентов: -—-^ = 0,87 (чему соответ-
%У 8
ствует и » 0,41), В3=—0,8 (см. рис. 33, где вместе с кривой
64
E.48) нанесена также и прямая ^—1^~> отвечающая в силу
A.26) ламинарному течению в трубах). Согласно формуле
E.48), X неограниченно убывает с ростом ReD; на самом деле
это, разумеется, будет не так, .поскольку при возрастании- ReD
каждая труба в конце концов оказывается вполне шерохова-
шероховатой. Как только это произойдет, коэффициент сопротивления
трубы становится уже независимым от числа Рейнольдса и опре-
определяется по формуле
-4r = —Win — -\-B' E.48')
вытекающей из формулы E.28) с В'=const, прилагаемой ко
всем значениям z из интервала 0<2<Я1. Такое поведение
коэффициента % наглядно иллюстрируется данными рис! 34.
Если не требуется очень большая точность, то можно считать,
что и в случае турбулентного течения в плоском канале ширины
2#i логарифмическая форма закона дефекта скорости E.43)
также выполняется вплоть до значения г=Ни отвечающего
центру канала (при этом, разумеется, Si должно равняться
нулю). Та же формула часто применяется и в случае течения в
открытом плоском канале глубины Ни ограниченном Сверху сво-
свободной поверхностью жидкости (для такого канала максималь-
максимальная скорость и0, очевидно, будет достигаться на верхней гра-
границе течения, так что и здесь Bi=0). Иногда также в случае
открытого канала вместо формулы E.43) используется следую-
следующая формула Кармана A930):
Еще лучшего совпадения с данными опыта можно здесь до-
добиться, приняв несколько более общую формулу
С— 1 А-
, E.49')

262
ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА
[5.5
где С — новый числовой коэффициент, который по данным
Ханта A954) оказывается немного большим единицы. Наконец,
Эллисон A960), исходя из некоторых теоретических соображений,
/ш
о = т/1 (песочная шероховатость)
Гащвич
(технически гладкие трубы)
Рис. 34. Зависимость коэффициеита сопротивлеиия X от числа Рейиольдса ^
для шероховатых труб различной шероховатости.
предложил в случае открытого канала вместо формул E.49) или
E.49') использовать соотношение вида
U0-u(z) _^ 1
и, х
In
г—j-ln-
E.49*)
бравая часть которого при некоторых значениях Ь оказывается
очень близкой и к правой части E.43) (с Bj = O), и к правой
части E.49) или E.49'). Согласно предложенной Эллисоном кос-
косвенной оценке коэффициента Ь (о которой мы еще скажем чуть
подробнее в гл. 5) Ь » 1,4, что не противоречит также и имею-
имеющимся эмпирическим данным о профиле средней скорости в от-

5.6] § 5. ТЕЧЕНИЯ В ТРУВАХ И В ПОГРАНИЧНОМ СЛОЕ 263
Для ограниченного интервала значений числа Рейнольдса общая фор-
формула E.48) может быть приближенно заменена также значительно более
простыми степенными законами сопротивления вида
X = c(ReD)~m. E.50)
Подобные степенные законы получаются, в частности, при аппроксимации
(часто применявшейся в прошлом) профиля скорости и(г) степенными фор-
формулами вида
п(г)
E.51)
при этом, как легко видеть,
^с_Р _ 2 ио _ ,zti(HxUu \STT _ _ 2л
, ^.= cn+l^May+i, m=-^L-. E.51')
Наиболее известным степенным законом сопротивления является эмпири-
эмпирический закон Блазиуса A913)
1
Х = 0,3164 (Reo)"T, E.52)
установленный с помощью обработки данных, относившихся к числам
Рейиольдса Rei>, не превосходящим 5-104 (ср. рис. 33). Согласно E.51'),
закону Блазиуса соответствует «закон 1/7» для профиля скорости, в силу
которого и(г)'^г7; этот «закон 1/7» (хорошо выполняющий при Re^lO5)*'
широко использовался во многих исследованиях, начиная с 20-х годов иа-'
шего столетия. Однако степенные законы ие являются универсальными (т. е.
годными при всех числах Рейиольдса): при больших числах Рейнольдса
приходится использовать меньшие значения л.
Разумеется, помимо степенных формул можно подобрать и другие фор-
формулы для Я,(Re), аппроксимирующие неявное соотношение E.48) на боль-',
шом интервале значений Re. В частности, Никурадзе предложил использо-
использовать приближенную формулу Х= 0,032 -| ' 0237> другими исследователями
было предложено еще несколько формул такого рода (см., например, посвя-
посвященную некоторым таким формулам критическую заметку Колмогорова
A952)).
5.6. Турбулентный пограничный слой на плоской пластинке
Перейдем теперь к рассмотрению турбулентного погранич-
пограничного слоя на длинной плоской пластинке при постоянной ско-
скорости U набегающего потока. Осредненное движение в таком
пограничном слое будет стационарным и почти плоскопараллель-
плоскопараллельным; во многом оно будет близким к течению в трубе, радиус
которой равен толщине 6 пограничного слоя, а скорость на оси—
скорости U вне этого слоя. Имеются, однако, по крайней мере
две причины, нарушающие аналогию между течениями в трубах

264 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [5-6
и в пограничном слое. Во-первых, физические условия на внеш-
внешней границе пограничного слоя весьма отличны от условий в
центре трубы: вне пограничного слоя (т. е. при z > 6) турбу-
турбулентность обычно вовсе отсутствует, в то время как течение в
трубе всюду является полностью турбулентным. Во-вторых, ха-
характеристики пограничного слоя зависят не только от нормаль-
нормальной к пластинке координаты z, но также (хоть и сравнительно
слабо) и от продольной координаты х, отсчитываемой вдоль пла-
пластинки. Указанные причины приводят к тому, что с теоретиче-
теоретической точки зрения течение в пограничном слое оказывается зна-
значительно сложнее течений в канале или трубе.
Разница между течениями в пограничном слое и в трубах и
каналах не затрагивает тонкого слоя жидкости, непосредственно
примыкающего к пластинке, в котором действует универсальный
«закон турбулентности вблизи стенки» E.13). Как хорошо видно
¦из рис. 25, на котором все точки ложатся на одну и ту же кри-
кривую, этот закон одинаков и для труб, и для каналов, и для по-
пограничных слоев. Величина м*, входящая в формулу E.13), в
пограничном слое, разумеется, может изменяться при изменении
х; это изменение, однако, оказывается довольно медленным (см.
ниже стр. 277), так что в каждом сечении х=const поток успе-
успевает приспособиться к местным условиям и зависит уже лишь
от значения м* при данном х. Изменяется с ростом х также и
относительная толщина слоя, к которому приложим закон E.13):
Ux
если при малых Rex= —, не превышающих 106, формулой
E.13) еще можно с известным основанием пользоваться при всех
z вплоть почти до самой границы турбулентного пограничного
слоя, то при Re* порядка 107—108 суммарная толщина вязкого
подслоя и логарифмического пограничного слоя уже не превос-
превосходит 10—20% от толщины б. Это последнее обстоятельство,
очевидно, отличает течение около плоской пластинки от течений
в трубах и каналах, где при всех Re>Recr логарифмическими
формулами можно без большой ошибки пользоваться вплоть до
оси трубы или середины канала.
Профиль средней скорости во внешней части пограничного
слоя естественно характеризовать зависимостью от zx дефекта
скорости U — п(г). Если исходить из хорошо подтверждаю-
подтверждающегося на опыте предположения, что для невозмущенного погра-
пограничного слоя профиль скорости в каждом сечении я—const за^
висит лишь от локальных условий, относящихся к этому же се-
сечению, то разность U — п(г) должна определяться значениями
U и б, параметрами жидкости гири (в случае шероховатой
пластинки) характеристиками шероховатости при данном х. Со~
гласно общему принципу подобия по числу Рейнольдса следует

5.6] § 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 265
ожиДать, что во внешней части течения, достаточно далеко от-
отстоящей от стенки, вязкость v и характеристики шероховатости
будут сказываться только через посредство величины напряже-
напряжения трения на стенке т0 (или динамической скорости at = у —,
или локального коэффициента трения Cf — %\-jj-\ j. Отсюда вы-
вытекает следующая общая форма закона дефекта скорости для
пограничного слоя:
U — п(г) , (г и,
(см. Ротта A962а, б)). Для проверки этого закона целесообраз-
целесообразно построить на графике значения —~~ в виде функции от
^- и попытаться выяснить характер рассеяния .эксперименталь-
.экспериментальных точек в зависимости от значений отношения -А- ¦ При этом,
однако, оказывается, что это рассеяние полностью покрывается
обычным разбросом экспериментальных точек, так что с точ-
U — u(z)
ностью до погрешностей измерении все значения —L-i- пре-
красно ложатся на одну кривую (см., например, рис. 35, заим-
заимствованный из обзорной статьи Клаузера A956)). Таким обра-
U — и (z)
зом, зависимость отношения 1-i- от медленно меняющейся
с изменением Rex величины -у-, если только она имеет место,
является крайне слабой. Это означает, что на практике закон де-
дефекта скорости для пограничного слоя на плоской пластинке
может быть записан в виде
полностью аналогичном тому, который использовался выше при
рассмотрении течений в трубах и каналах.
По сравнению с законом дефекта скорости E.41) для труб
и каналов закон E.54) имеет лишь один недостаток: в то время
как в E.41) фигурирует известная точно длина Ни в формулу
E.54) входит толщина пограничного слоя б, не имеющая точ-
точного определения и лишь весьма приближенно определяемая по
данным эксперимента. В то же время отношение длины б к бо-
более точно определяемым толщинам типа, например, толщины
вытеснения б* в турбулентном пограничном слое (в отличие от

266
ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА
[5.6
ламинарного) оказывается переменным (зависящим от -rf )•
В частности, если выполняется закон E.54), то из самого опре-
определения A.53) толщины вытеснения б* следует, что
1
8* = С-^8, С =
= const
E.55)
(толщиной вязкого подслоя, к которому неприложим закон
E.54), здесь пренебрегается). Учтя это соотношение, Ротта
' 20
U-ti(Z;
18
16
* Ш
12
10
в
'б
4
2
Р
3,
х Данные Фримена
о ,—" — Клебанова и Диля
» —»— Шульц'-ГруноВа
ш —"— Хана
0 " (для шероховатой стенки)
л ' (аля шерохоВотой стенки)
ф —„— Мура Селя .
очень шероховатой стенки)
0,2
Рис. 35. Проверка закона дефекта скорости для турбулентного погра-
пограничного слоя по данным разных авторов.
A951а) предложил использовать в формуле E.54) вместо аргу-
аргумента ц = -| безразмерный аргумент ^i —*7/"' не с°ДеРжа*
щий величины 6; в силу A.53) этот аргумент удобен также и
тем, что для него тождественно выполняется условие нормн-
ровки
Где
оо
/ —7~~ ^i = ^ ¦ Предположим теперь, что —=^-
6 * *
= 0 при т]х = с; тогда, очевидно, 8 = с — 8* и <р, (г^) —

§ S. ТЕЧЕНИЯ В ТРУВАХ И В ПОГРАНИЧНОМ СЛОЕ
267
==/i("j- Следовательно, при обработке наблюдений вполне
можно заменить б на 8* — , и если д окажется однозначной
функцией от ¦>)] = -jji- -jj, то это значит, что выполняется и за-
закон E.54).
Разумеется, равенство E.54) не может выполняться вплоть
до z=0, так как оно не содержит вязкости и не учитывает гра-
граничного условия п@)=0. Непосредственно около етенки дей-
действует универсальный закон E.13) и, как мы уже видели, в об-
области, к которой применимы одновременно оба эти закона,
функции / и f] обязательно будут логарифмическими. Поэтому
неудивительно, что после переноса данных рис. 35 на новый
график, на котором по оси абсцисс нанесена логарифмическая
шкала, функция f$i$ в пределах от т) = 0,01 и до примерно
т) = 0,15 представляется прямой вида —Alrn^+Bi (см. рис. 36,
14
12
10
У-п(г)8
* 6
4
г
х Данные Фритна
} — » — Клебаноба иДиля
—<<— Шульц-Грунова
0,01 0,02 0,04 0,06 0,10 020 0.40 OJBO 1,0
z/b
Рис. 36. Логарифмическая форма закона дефекта ско-
скорости для пограничного слоя.
где учтена лишь часть точек, приведенных на рис. 35). Отметим,
что коэффициент А — — здесь имеет точно то же значение, что и
на рис. 31, относящемся к плоским каналам, как это и должно быть
в силу универсальности логарифмического закона E.25); кбэф^
фициент же В1 для каналов и для пограничных слоев оказы*
вается различным. Кроме того, из сравнения рис. 36 с рис. 31
видно, что при т)>0,15 функция fi(r\) для пограничных слоев
заметно более резко отклоняется от прямой A \nr\+Bi, чем та
же функция для плоских каналов. Согласно данным Хама (J954)

268
ГЛ. Ш. УРАВНЕНИЯ РЕЙНОЛЬДСА
[5.&
значения функции Мл) для пограничных слоев в области
11 > 0,15 хорошо описываются эмпирической формулой fi(t)) =
= 9,6 A—т)J; в случае же течении в плоских каналах функ-
функцию fi(r)) при т] > 0,15 можно неплохо описать формулой
fx (¦>)) = A' In у -f- flj с коэффициентами А' и B'v лишь немного
отличающимися от Л и Si.
Существенная разница между профилем скорости в турбу-
турбулентном пограничном слое около его внешней границы и про-
профилем скорости в трубах и каналах около оси, естественно, объ-
объясняется различием между характером самого турбулентного
течения во внешней части пограничного слоя и в центральной
части трубы или канала. Заметим в этой связи, что в отличие от
ламинарного пограничного слоя, не имеющего сколько-нибудь
резкой границы, турбулентный пограничный слой обычно имеет
отчетливую границу, выше которой турбулентность отсутствует.
Эта граница имеет неправильные очертания, беспорядочно изме-
изменяющиеся во времени, как это хорошо видно на фотографиях
Рис. 37. Теневая фотография турбулентного пограничного елея на
цилиндре (из статей Ротта A962а, б)). Направление течения — слева
направо.
турбулентного пограничного слоя, полученных с помощью ме«
тода теней, позволяющего визуализировать возмущенные области
потока (см., например, рис. 37). Соответствующая такой фото-
фотографии общая схема турбулентного пограничного слоя представ-
представлена на рис. 38. По данным измерений Клебанова A955) верх-
верхняя граница турбулентного пограничного слоя в каждой отдель-

5.6]
§ s. течения в трубах и в пограничном слов
269
ной точке колеблется в пределах примерно от 0,36-^0,46 и до
1,26 (где 6 — расстояние от стенки, на котором средняя скорость
равна 0,99U) почти по нормальному закону со средним значе-
значением 0,786. Доля y(z) времени, в течение которого на расстоя-
расстоянии z от стенки наблюдается турбулентность, убывает с ростом z
к при z=6 равняется всего лишь 0,06 (качественно близкие, хотя
и отличающиеся количественно, результаты указывают также
Корсин и Кистлер A955)). Отсюда ясно, почему логарифмиче-
логарифмический профиль, характерный для развитой турбулентности, может
с неплохой точностью применяться почти до центра канала или
Граница межди пограничным
'слоем и сообооным потоком
Стенка
Рнс. 38. Общая схема турбулентного пограничного слоя на плоской пла-
пластинке.
трубы, но в пограничном слое при большом Re сравнительно
точно выполняется лишь для тонкого слоя жидкости, располо-
расположенного около стенки. Вне этой пристеночной части течения в
каждой точке быстро чередуются периоды наличия и отсутствия
турбулентности, так что среднее значение скорости, получаемое
при осреднении по достаточно большому промежутку времени,
фактически оказывается средним между значениями скорости,
отвечающими турбулентному и ламинарному потокам. Так как
в ламинарном потоке обмен импульсом между соседними слоями
жидкости гораздо меньше, чем в турбулентном потоке, и
поэтому градиенты скорости более резки, то ясно, что во внеш-
внешней части турбулентного пограничного слоя средняя скорость
при удалении от стенки должна возрастать быстрее, чем по ло-
логарифмическому закону, что и подтверждается данными рис. 36.
Естественно также, что в случае пограничного слоя, возникаю'

гл. m: уравнения рейнольдса" J5.6
щего при обтекании плоской пластинки турбулентным потоком,
богатым возмущениями, различие между условиями во внешней
части этого слоя и в центре трубы должно быть менее значи-
значительным. И действительно, опыты Вигхардта A944) и других ис-
исследователей, пропускавших обтекающий поток сначала через
турбулизирующую решетку, показывают, что форма функции
ft(i\) в формуле'E.54) зависит от степени возмущённое™потока
ВдаЛи от пластинки и при увеличении этой степени возмущен-
йости приближается к форме, характерной для течений .в тру-
трубах и каналах. ¦ . .
Интересная попытка объединения универсального пристеноч-
пристеночного закона E.13) с законом дефекта скорости E.54) была
предпринята Коулсом A956). Исходя из E.13), общий вид про;-
филя средней скорости в каждом сечении x=const пограничного
слоя может быть представлен в виде
] E.56)
где f(z+) —функция, изображенная на рис. 25 (и обращающаяся
в Л lnz+ + B при z+ > 30), a h(z) —поправка к универсальному
закону E.13), обращающаяся в нуль непосредственно вблизи
пластинки (скажем, при z<0,!6). Но в таком случае
\h\b) h{) при г>30-^-, и следовательно,
чтобы удовлетворялся также и закон дефекта скорости, функция
h[z) должна зависеть только от у. Исходя отсюда, Коулс пред-
предположил, что
где x = -j='0*4— постоянная Кармана, П—новая постоян-
постоянная, a w(i\)—функция от одного переменного, нормирован-
нормированная условием шA)=2. При этом еще остается некоторая
неопределенность, связанная с тем, что толщина б определяется
не вполне однозначно; воспользовавшись этим, Коулс наложил
на : функцию w(r\) дополнительное условие нормировки
Т w (¦»)) с?7) = 1, которое, как легко видеть, эквивалентно усло-
о
вию 8* — = "^ - S. Тем самы» он задал определенным обра-
образом коэффициент С в E.55), т. е. указал точную связь мас-
масштаба б с легко определяемой по экспериментальным данным

5.6]
§ 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ
271
толщиной вытеснения б*, величиной -jj и параметрами и и П.
Обработав большое число экспериментальных данных, относит"
щихся к профилям скорости в пограничном слое на плоской Ъла:
стинке (как при постоянном давлении, так и при наличии гра-
градиента давления в обтекающем потоке), Коулс обнаружил, что
для ¦ широкого класса двумерных турбулентных пограничных
слоев функция w(i\) оказывается одной и той же. Таким обра-
образом, по данным Коулса внешние условия Обтекания (включая
сюда и распределение давления в свободном потоке) отра-
отражаются лишь на величине множителя П (который в случае слож-
сложного распределения давления приходится считать зависящим от
координаты х); в простейшем случае безнапорного обтекания
пластинки потоком постоянной скорости 11 = 0,55. Универсальная
2.0 г
1,0
0,8
0,6
Ofi
0,2
О
0,1 0,8 0,3 Ofi 0,5 0,6 0,7 OJS 0,9 1,0
Рнс. 39. Универсальная функция следа w On) no
Коулсу A956).
функция w(r\), полученная Коулсом с помощью обработки экс-
экспериментальных данных, изображена графически на рис. -39; она
имеет почти точно антисимметричную S-образную форму и нФ
плохо аппроксимируется отрезком синусоиды w = 1 + sin ^T
при
< 1.

272 гл. ш. уравнения рейнольдса [5.6
Чисто формально в равенстве E.57) можно перейти к пре-
Нелу при м* ->- 0 (т. е. при т0 -*- 0); с помощью E.55) и условия
wA)=2 при этом получается простой результат
Таким образом, функция w{r\) задает форму профиля
средней скорости в точке с То=О, т. е. в точке отрыва по-
пограничного слоя, в которой ^5=0 (ср. схематический рис. 8 на
стр. 85). Исходя отсюда, Коулс назвал функцию w{r\) функ-
функцией следа, а закон E.57), согласно которому отклонения про-
профиля средней скорости в пограничном слое от универсального
пристеночного закона E.13) строго пропорциональны универ-
универсальной функции следа — законом следа. Общая форма профиля
средней скорости п(г), удовлетворяющего этому закону следа,
схематически показана на рис. 40. Здесь пунктиром изображено
распределение средней скорости в верхней половине гипотетиче-
гипотетического турбулентного следа, создаваемое в основном взаимодей-
взаимодействием турбулентного ядра этого следа со внешним ламинарным
потоком и колебаниями границы между турбулентной и нетурбу-
нетурбулентной частями течения в соответствии со схемой рис. 38; раз-
разность средних скоростей в центре и на границе этого следа
2П ,-,
равна —и,. Ьсли мы поместим в центре этого следа твердую
пластинку, то распределение скорости в следе существенно из-
изменится за счет того, что вблизи поверхности пластинки на по-
поток начнет сильно воздействовать вязкость, приводящая к
обязательному выполнению условия прилипания b(z)=0. Это
дополнительное ограничение в чистом виде порождает «универ-
«универсальный пристеночный профиль», изображенный на рио 40 ли-
линией из точек. В результате наложения этого «пристеночного
профиля» на профиль в следе и получается реальный профиль
скорости в турбулентном пограничном слое, изображенный на
рис. 40 сплошной линией.
Как и в случае течений в трубе, из существования части те-
течения, к которой приложим и пристеночный закон E.13), и за-
закон дефекта скорости E.54) (с логарифмическими функциями
f и fi), вытекает, что локальный коэффициент трения
Cf=~i = 2 [jjj должен удовлетворять уравнению вида
= ^ E.58)

5.6]
§ 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ
273
(ср. вывод уравнения E.45) на стр. 254). Аналогично положе-
положению с законом E.54) наличие в формуле E.58) неточно опре-
определяемой толщины б делает эту формулу в таком виде неудоб-
неудобной для приложений; поэтому желательно заменить здесь б
л
/I
У/
7/
7/
УУУУУУУУУУУ/ЛУУУУУУУУУУУУУУУУУУУ/
7/
17
7/
i
i
i
i
Рис. 40. Схематическое изображение профиля скорости, удовле-
удовлетворяющего закону следа Коулса.
каким-либо более легко определяемым масштабом длины.
Проще всего воспользоваться формулой E.55), позволяющей
переписать уравнение E.58) в виде
E-59)

274
ГЛ. III. УРАВНЕНИЯ РЕЙНОЛБДСА
15.6
Сравнение этого соотношения с данными непосредственных йз>
мерений значений локального коэффициента трения в различи
ных тачках пограничного слоя на гладкой, плоской пластинке,
выполненных Шульц-Груновым .(-1940) и Смитом и Уокером
A959), приведено на рис. 41; оно показывает, что эксперимен-
эксперимен-~
E.58) ;(с х = 0,40 и В4=
тальные -значения -~ достаточно точно следуют правой части
22
щ
20
18 -
W
ш ¦
S
S
X
Rea,+2j6'
•
о
¦
X
л
Лонные Шульц-Грунодо
Данные
Смита и Уокеро
при разных i
3ft
3,ff
3,8
4.2
Рис. ^1. Зависимость локального коэффициента сопротивления Cf для по-
пограничного слоя на плоской пластинке от числа Рейнольдса Res« по дан-
данным Шульц-Грунова и Смита и Уокера.
Несколько более сложно обстоит дело,- если желать заменить
б просто длиной х (отсчитываемой от начала пластинки). Для
этого.надо выразить толщину б через х, что можно сделать с по-
помощью следующих приближенных рассуждений. Так как линии
тока вихревого турбулентного движения в пограничном слое не
выходят за границу этого слоя, средняя граница пограничного
слоя должна совпадать с линией тока осредненного движения^
расположенной на расстояний б от пластинки. Отсюда вытекает,
что угол наклона этой границы к оси Ох должен равняться от-
отношению средней вертикальной ' скорости (в направлении оси

S 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 275
Oz) к средне^ горизонтальной скорости в точках границы. Но
средняя горизонтальная скорость на границе пограничного слоя
равна 47; что же касается средней вертикальной скорости, то
она не зависит от U, а определяется лишь относительным пуль-
сационным движением, связанным с переносом импульса в на-
направлении; оси Oz. Следовательно, в силу соображений размер-
размерности эта ^вертикальная скорость должна быть пропорциональ-
пропорциональной динамической скорости «#| составленной по значению т0 при
данном х. [Отсюда вытекает соотношение
§ = Ьг^-. E.60)
где &i — ^исловой коэффициент (порядка единицы). Предпо-
Предположим еще1, что пограничный слой является турбулентным, прак-
практически начиная с самой передней кромки пластинки, так что
равенство! E.60) выполняется, при всех х, начиная 'с х=0 (где
6=0). Величина jjj вообще говоря, является функцией от х, но
посколькуюна изменяется очень медленно, то, интегрируя равен-
равенство E.60|, ее можйо без большой ошибки вынести за знак ин-
интеграла (быть может, немного изменив одновременно значение
коэффициента Ь\). \ Отсюда получается приближенное равен-
равенство1)
E.61)
Подставляя это равенство в уравнение E.58), получим
¦1 "' 1 m
'5- E.62)
Этот результат впервые был' указан Карманом A930, 1934)
(пришедшим к нему из немного других рассуждений); он хо-
хорошо согласуется со старыми экспериментальными данными
Кемпфа A929) (полученными при помощи непосредственного
динамометрического измерения локальных коэффициентов тре-
трения), так же как и с последующими эмпирическими данными
')"Строго говоря, равенство E,61) будет следовать из E.60), лишь
и, л/Г cf '
если ~п = V ~ъ может быть представлено простой степенной
цией от лс^.Как будет. видно из. дальнейшего, такое представление имеет,
довольно высокую степень точности (см., например, формулу E,66), сравне-
сравнение которой с данными измерении приведено, на рнс, 42). , - •

276
ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА
[S.6
Шульц-Грунова A940) и Дхавана A952) (см. рис. 42, где
1 9
коэффициенты —f= = 1,8, т. е. х = 0,39 и Вь=\,1 выбраны
так, чтобы получилось наилучшее совпадение с данными
\
X
\
\
д Дхадам
• Кемтр
о Шульц ~ Грунод
10е
109
%=1Г
Рис. 42. Зависимость коэффициента сопротивлеиия Cf
для пограничного слоя на плоской пластинке от числа
Рейнольдса Re* по данным Кемпфа, Шульц-Груиова
и Дхаваиа.
Кривая /—закон сопротивления Кармана (S.62) с *=0,39 и В6=1,7;
кривая 2 — закон Шульц-Грунова E.64); кривая 3—закон Фок-
нера E.66).
Кемпфа). Заметим еще, что из сравнения численных значений
коэффициентов В4 и В5 в формулах E.59) и E.62), приводящих
к наилучшему сопоставлению с эмпирическими данными, можно
оценить и значение коэффициента Ъ в формуле E.61). В част-
частности, если принять значения этих коэффициентов, использован-
использованные на рис. 41 и 42 (пренебрегая небольшим расхождением

5.6] § S. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 277
в принятых знаниях и), то для толщины 6, определяемой фор*
мулой E.55) с C = -jrj-«*3,9 (т. е. с тем значением С, которое
принимает Коулс A956)), получается 6 — 0,3.
В случае шероховатых пластинок предыдущие формулы
должны быть изменены аналогично тому, как это делалось в
случае шероховатых труб; например, формула E.58) в при-
применении к вполне шероховатой пластинке должна записываться
в виде E.45') (но с 6 вместо Hi). На этом, однако, мы уже не
будем задерживаться (см., например, Шлихтинг A951),
гл. XXI, § 4).
Согласно E.62} С/ является медленно убывающей функцией от х.
Однако явное определение с/ как функции от Rex с помощью уравнения
E.62) является довольно сложным, и на практике обычно используются
более простые интерполяционные или эмпирические формулы. Так, например,
Шлихтииг A936). (исходивший, правда, не из формулы Кармана E.62),
а из более сложных результатов Прандтля, изложенных, например, в книге
Шлихтинга A951)), предложил для с/ расчетную формулу
C/ = BIgRex-O,65)-2'3 E.63)
(где lg — десятичный логарифм), дающую результаты, близкие к вытекаю-
вытекающим из E.62). Позже Шульц-Грунов A940) использовал формулу
c/x=.0C70(lgRer)-2-584, E.64)
результаты сопоставления которой с эмпирическими данными приведены на
рис. 42. Наконец, если принять, что профиль средней скорости в пограничном
слое во всех сечениях дается «законом 1/7> (см. стр. 263), то для С/ может
быть получена совсем простая формула
C/ = c(Rexf5. E.65)
Эта формула при с = 0,0576 также неплохо описывает данные измерений,
относящиеся к интервалу чисел Рейнольдса 5 • 105<Rei<107. При дальней-
дальнейшем увеличении числа Re* формула E.65) начинает давать.заниженные зна-
значения с/, так что для получения лучшего совпадения приходится заменить
показатель степени 1/5 в этой формуле меньшим значением. В частности,
при значениях Rex вплоть до 109 хорошего совпадения с экспериментами
можно добиться, используя формулу Фокнера A943)
cf = 0,0262 (Re,) 7. E.66)
Помимо локального коэффициента сопротивления С/ можно рассматри-
рассматривать также полный коэффициент сопротивления С/ пластинки длины /, опре-
определяемый формулами
С/=-1—- = 1 I cf{x)dx, F=2 fxo(x)dx E.67)
(ср. A.51)—A.52)). Этот полный коэффициент сопротивления значительно
проще поддается измерению, чем локальный коэффициент с/, и относительно

278 гЛ. iit: Ура&нёнйя рёЙнолЬДса [?6
него имеется очень много экспериментальных данных, нанЛШее ранние из Ко-
Которых относятся еще к 1793 г. (см. Шубауэр и Чен A95^гср. также Гольд-
штейн A938) н Шлихтннг 0951)). Исходя нз формулы E.62) для с/,
Шёнгер A932) получил для С/ соотношение
:д Re,=i-^-, E.68)
дающее хорошее совпадение с данными эксперимента; Используя вместо
E.62) более сложные расчеты Прандтля, Шлнхтинг предложил простую
интерполяционную формулу
С/ = 0,455 (lg Re,)'58, E.69)
дающую результаты, почти не отличающиеся от вытекающих из E.68$.
Близкую формулу
С, = 0,427 (lg Re, — 0,407); 2>64 E.70)
использовал Шульц-Грунов A940). Если исходить из «закона 1/7>, то, как
мы уже видели, для С/ получаечся зависимость вида C^~(Re,) ; лучшее
совпадение в широком интервале .чисел Рейнольдса можно, однако, получить,
fecnri, следуя E.66), положить
Cf = 0,0306 Re?. E.71)
Сравнение этого результата с формулой A.52) для коэффициента сопротив-
сопротивления пластннкн при ламинарном обтекании показывает, что при турбу-
турбулентном обтекании сопротивление значительно больше, чем при ламинарном
(например, при Re; = 5-105 больше почти в 2,5 раза) н гораздо медленнее
убывает с ростом числа Рейнольдса.
Все предыдущие рассуждения относились к случаю, когда пограничный
слой можно считать турбулентным, начиная практически от самого переднего
края пластинки. Если же переход к турбулентному режиму происходит лишь
в точке х = Хо, достаточно далекой от переднего края, то в закон сопротивле-
сопротивления необходимо внести поправку на наличие ламинарного участка погранич-
пограничного слоя. Если принять допущение Прандтля A927) о том, что после пере-
перехода к турбулентности пограничный слой ведет себя приблизительно также,
как если бы он был турбулентным, начиная от передней кромки пластннкн,
то эта поправка сводится к следующему: из вычисленной выше силы сопро-
сопротивления F следует вычесть разность снл сопротивления прн турбулентном
н ламинарном режимах для участка пластннкн от передней кромки до точки
перехода х—х0. С учетом этой поправки коэффициент сопротивления будет
равен
С,—
1
где С/ дается, скажем, формулой E.68)' (нлн другой нз приведенных выше
формул), а С\(хо) н Сг(.*о)—коэффициенты сопротивления для пластинки
длины л:0 прн турбулентном н, соответственно, ламинарном обтеканий. Полу-
Полученная поправка позволяет описать переходную область между законом

5.7] § 5. ТЕЧЕНИЯ Б ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 279
сопротивления A.52) для ламинарного режима и рассматривавшимися выше
законами сопротивления для чисто ' турбулентного режима. Коэффициент
A(xq) в формуле E.72) будет, разумеется, зависеть от критического числа
Рейнольдса Re^^Re^,., при котором происходит переход ламинарного тече-
течения в турбулентное; согласно данным Прандтля при ИеЛо= 5-105, например,
Д(*о) = 1700 (значения A(xol при некоторых других значениях Re^ могут
быть найдены в книге ШгГИхтинга A951)).
Приведенные результаты,- касающиеся закона изменения величии с/ и С/
при изменении чисел Рейиольдса Rex и Re;, могут быть использованы также
и для исследования изменения t ростом х профиля средней скорости, зави-
/ :
.. r/f : .
сящего согласно формуле E.57) от и» = U у -^ и 8, Зависимость с/ от х
детально исследовалась выше, измеиениеже 6 с ростом х может быть опре^
делено из формулы E.61), снова содержащей ~ц==\ ~2Ш ^ак как с>
очень медленно убывает с ростом х, толщина б возрастает почти как первая
степень «'(если принять формулу E.66), то пропорционально х Iй).
Существенно, что это возрастание является гораздо более быстрым, чем
возрастание толщины ламинарного пограничного слоя, которая согласно
формуле A.33)' пропорциональна *2 (ср. рис. 4 иа стр. 56, содержащий
данные непосредственных измерений толщины б как в ламинарной, так и
в турбулентной частях пограничного слоя).
5.7. Профиль концентрации пассивной примеси около стенки;
диффузия и теплопередача в турбулентном пограничном слое
Выше мы подробно рассмотрели вопрос о распределении
средней • скорости и о трении в турбулентных потоках около
стенки. Оказывается, что аналогичные соображения могут быть
применены и к исследованию турбулентной диффузии и тепло-
теплопередачи. Ниже будут приведены некоторые основные относя-
относящиеся сюда факты; более подробное изложение (в первую оче-
очередь применительно к теплопередаче, лучше изученной экспери-
экспериментально, чем диффузия) может быть найдено, например, в
рассчитанных на инженеров книгах Гребера и Эрка A955), Мак
Адамса A954) и Эккерта A950), в гл. XIV сводной монографии
под ред. Хоуарта A953), гл. III—IV монографии Левича A959)
и обзорных статьях Дейслера A959) и Кестина и Ричардсона
A963).
Рассмотрим, как и в пп. 5.2—5.3, плоскопараллельное тече-
течение жидкости в полупространстве z > 0 (ограниченном твердой
гладкой стенкой), направленное вдоль оси Ох,в отсутствие про-
продольного градиента давления. Предположим, что на граничной
поверхности z=0 поддерживается постоянное значение Оо кон-
•центрации пассивной примеси. При этом в жидкости будет иметь
место постоянный поток—;/ примеси, направленный от стенки

280 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [5.7
(т. е. вдоль положительного направления оси Oz), и уравнение
E.7') будет иметь вид
J(z) = ?X^-pb'w'=jo = const E.73)
Профиль средней концентрации 0 будет зависеть от стати-
статистических характеристик поля скорости (определяемых парамет-
параметрами v и м*),а также от коэффициента диффузии %, плотности р
и интенсивности переноса примеси, характеризуемой значением
потока /о. Вводя специальную размерность в для величины 0 и
обозначая размерность массы буквой М, будем иметь
Следовательно, в силу соображений размерности
S(z)_S(O) = JjL-T(^, -0 = 6,T(z+, Pr), E.74)
где
9*=ткт E-75)
— величина- размерности в, задающая естественный масштаб
концентраций (безразмерная постоянная Кармана * = -j«*0,4
включена здесь в определение величины 9*, поскольку в даль-
дальнейшем это иногда окажется удобным), а ф(г+, Рг) —новая уни-
универсальная функция от двух переменных, удовлетворяющая
условию ф@, Рг) эО. Если Ф — это температура Т, то формулы
E.73)—E.75), естественно, следует писать в виде
&Т
Я (*) = ср?х gj - cpPT'w' = qQ = const, E.73')
f (г) - f @) = ^ <p (^. j) = T,9 (z+/ Pr), E.74')
где функция ф(г+, Рг) —та же, что и в E.74); Отметим, что для
температуры предположение о пассивности более сомнительно,
чем для материальной примеси, как из-за появления в неодно-
неоднородно нагретой жидкости дополнительных архимедовых сил (об
этом подробнее будет сказано в гл. 4), так и из-за зависимости
от температуры физических констант жидкости типа коэффи-
коэффициентов вязкости и температуропроводности . (по поводу учета
этой зависимости, различной для газов и для жидкостей, см.,
например, статьи Дейслера A959) и Ван Дриста A959)). Тем не
менее, для определенности ниже, как правило, величина 0 будет

5>7j § Б. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 281
называться температурой, и будут использоваться формулы
вида E.73') — E.75'), но с заменой Г на О (в соответствии со
сказанным на стр. 63 употребление буквы О показывает, что
фактически речь все время идет о совершенно произвольной пас-
пассивной примеси).
Формула E.74'), содержащая неизвестную функцию <р, мо-
может быть сильно упрощена в случае достаточно больших
значений z. Под достаточно большими здесь понимаются зна-
значения z, удовлетворяющие прежде всего условию ^
при котором коэффициент вязкости v не оказывает уже влияния
на распределение средней скорости и (по той же причине) не
влияет и на распределение средней температуры. Кроме того, от
рассматриваемых значений z требуется, чтобы турбулентный по-
поток тепла xf^ = — Срр&'да'при таких z был много больше потока
db „
тепла CpPx-j-, связанного с молекулярной теплопроводностью;
при этом условии и коэффициент % также не будет влиять на
изменение величины О с высотой. Заметим теперь, что, поскольку
турбулентный поток тепла порождается тем же вихревым пуль«
сационным движением, что и турбулентный поток импульса
tW=—pu'w', турбулентные коэффициенты вязкости К и темпе-
температуропроводности К» естественно предполагать имеющими
одинаковый порядок величины. Поэтому, если Рг^-1, т. е.
X^v, то при 2>2,= ~- турбулентный коэффициент темпера*
*
туропроводности будет намного больше молекулярного коэф-
коэффициента х, так что в этом случае при z ^> z% Ъущ-* выполнены
оба условия, нужные для того, чтобы значения z можно было
считать достаточно большими. Если же Рг «С 1, то турбулентный
коэффициент температуропроводности (который при z > z* со-
согласно E.26) имеет порядок m*z) будет намного превосходить
молекулярный коэффициент % лишь при z > — = Pr-1 • zt. Та-
Таким образом, вообще говоря, влиянием и v, и % на изменение
средней температуры с высотой можно пренебречь, лишь если
выполняются два условия: z >г* и 2>.Pr~' • z* (второе из них,
очевидно, существенно лишь при Рг <$С 1) •
При выполнении условий z~^> г# и z ^ Рг • z+ градиент
средней температуры должен определяться лишь параметрами
Чо/срр, ы* и z. Отсюда в силу соображений размерности сразу
следует формула

282 ГЛ. 111. УРАВНЕНИЯ РЁЙНОЛЬДСА [5.7
где а — новая безразмерная постоянная (порядка единицы).
Следовательно,
^1 E.77)
(ср. Ландау и Лифшиц A953), ч. 1, § 54), причем постоянная А4
(так же, как и в случае формулы E.22)) здесь должна опреде-
определяться из условия смыкания профиля E.77) с профилем сред-
средней температуры в нижнем слое, к которому формула E.77) уже
неприменима.
Из E.77) видно, что
cp(z+, Pr) = -ilnz++C при z+ ^> max (I, Pr); E.77')
таким образом, при достаточно больших значениях z+ функция
Ф отличается от функции f формулы E.13) лишь значением чис-
числовых коэффициентов (только один из которых — коэффициент
С—может зависеть от числа Прандтля). Заметим еще, что про-
профилю E.77) в силу E.9) отвечает следующее значение коэффи-
коэффициента турбулентной температуропроводности:
K» = **utz. E:78)
Отсюда видно, что постоянная а имеет смысл обратного значе-
значения турбулентного .числа Прандтля для логарифмического по-
пограничного слоя:
* К сожалению, эмпирические данные о профилях концёнтра-
дии пассивной примеси в реальных потоках около плоской стенки
значительно более бедны, чем данные о профилях средней ско-
скорости; поэтому экспериментальная проверка формулы E.77) до
сих пор остается очень неполной. Измерения профилей средней
температуры в приземном слое атмосферы, многократно прово-
проводившиеся метеорологами, мало пригодны для этой цели, так как
в приземном слое при наличии изменения температуры воздуха
с высотой (т. е. при не нейтральной термической стратификации)
значительную роль играет архимедова сила, не позволяющая
рассматривать температуру как пассивную примесь (подробнее
об этом см. в гл. 4). Более подходящими могли бы быть данные
тщательных наблюдений над профилем влажности (т. е. кон*
дентрации водяного пара) в приземном слое атмосферы1); од-
') Разумеется, при наличии значительных температурных градиентов
наличие архимедовых сил будет влиять не только на вертикальное распре-
распределение температуры, но и на вертикальное распределение влажности (см.
главу 4). Однако профиль влажности можно лаблюдать и в «чистых усло-
условиях» при нзотермни, в то время как профиль температуры имеет смысл
изучать лишь при нарушении условия постоянства средней температуры.

8. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОВ
283
5.7]
нако таких данных пока имеется очень немного. Тем не менее,
мы можем сослаться здесь на результаты измерений Паскуилла
A949) и Ра.йдера A954), подтверждающие, что при близкой к
нейтральной температурной стратификации профили влажности
хорошо описываются логарифмическими формулами (см. ниже
П. 8.2). В лабораторных течениях большой скорости, сопрово^
ждающихся вынужденной конвекцией, температуру с большим
1,0
0,9
0,8
0,7
0.В
0,5
ОА
0,3
К х
0,01 6.02 0,05 0,1
02
1"
0,5 1,0
г (или-z/R)
Рис. 43. Распределение средней температуры при
турбулентном течении в трубе и в пограничном
слое по данным Элиаса (О) и Нуннера (X)-
9@)—температура стенки, 9,—температура иа оси трубы или
вые пограничного слоя.
основанием, чем в атмосфере, можно рассматривать как пассив-
пассивную примесь; однако опубликованные измерения профилей тем-
температуры (или, тем более, концентрации материальной примеси)
в лабораторных потоках около стенки весьма немногочисленны
и обычно обладают столь невысокой точностью, что про них
можно сказать только, что они не противоречат закону E.77).
Особо стоит выделить сравнительно старые наблюдения Элиаса
A929), показавшего, что при обтекании нагретой плоской плаг
стинки профиль температуры в пограничном слое для расстоя-
расстояний z, превышающих 0,056, оказывается примерно логарифми-
логарифмическим и подобным профилю средней скорости, и наблюде-
наблюдения Нуннера A956), получившего в неизотермическом течении

284 ГЛ. III. УРАВНЕНИЯ РЕИНОЛЬДСА [5.7
воздуха по трубе с шероховатыми стенками почти точно лога-
логарифмический профиль средней температуры, начиная от z=
=0,027? и вплоть почти до самого центра трубы (см. рис. 43).
Недостаток эмпирических даииых очеиь затрудняет оцеику коэффициента
в (или Рг/ = — J. В большинстве теплотехнических расчетов, относящихся
как к техническим устройствам, так и к атмосфере, до сих пор, следуя
Рейиольдсу A874), обычно предполагают, что а — 1, причем, как правило,
эти расчеты приводят к неплохому согласию с данными измерений. Однако
интегральные характеристики теплопередачи, представляющие основной инте-
интерес для теплотехники, чаще всего малочувствительны к небольшим измене-
изменениям параметра а и поэтому ие позволяют надежно судить о его значении.
Попытки иепосредствеииой оценки величииы а по измеренным профилям
средней скорости и температуры для течений в трубах и каналах чаще
всего приводят к значениям а, немного большим единицы, — порядка
1,1 ч-1,4 (т. е. к выводу, что Рг<<1; см., например, Коркорай и др. A952),
Ка'верс, Хсу я др. A953), Хсу, Сато и Сейдж A956), Людвиг A956), Слейчер
A958), а также обзорные статьи Дейслера A959) и Кестииа и Ричардсона
A963)). Однако иногда (в первую очередь, в ряде экспериментов по тепло-
теплообмену в жидких металлах) получались также и значении а < 1, т. е.
Рг< > 1 (см., например, Субботин, Ибрагимов, Номофилов A963) и Дуайер
A963)). Определение величииы а по профилям ветра и температуры в атмо-
атмосфере может производиться лишь при температурной стратификации, отлич-
отличной от безразличной; при этом, однако, можно попытаться найти- предел,
к которому стремится а при приближении стратификации к состоянию изо-
термии, и приравнять этот предел отношению коэффициентов К» к К для
логарифмического .пограничного слоя. Подобные попытки производились не-
несколько раз, но результаты при этом оказывались различными: Райдер
A954), Пристли A963—1964) и Суинбенк A964) иашли таким образом, что
а>1, а в работах Суинбенка A955) и Гурвича A965) было получено
значение а<1 (см. ниже п. 8.2). Вообще следует иметь в виду, что пока
все имеющиеся данные о турбулентной теплопередаче (и диффузии) через
турбулентный пограничный слой во многом противоречивы, так что к иим
надо относиться с большой осторожностью. Так, например, даже в работах,
дающих примерно одно и ю же среднее значение а, встречаются явно про-
противоречащие друг другу утверждения об изменении коэффициента а при
изменении расстояния до стенки г (согласно Людвигу A956) величина а
слегка возрастает с ростом г, в то время как согласно Коркораиу и др.
A952) и Слейчеру A958), наоборот, а убывает при возрастании г). В^этой
связи целесообразно еще раз подчеркнуть, что, согласно приведенным выше
общим соображениям, в области логарифмического пограничного слоя, в ко-
которой и напряжение трения, и турбулентный поток тепла имеют постоян-
постоянное значение, коэффициент а также должен быть постоянным (т. е.
вовсе ие должен зависеть от г): Существенно также, что, поскольку речь
идет об области течения, в которой молекулярные коэффициенты вязкости
и теплопроводности не играют роли, а ие должно зависеть от этих коэффи-
коэффициентов, а следовательно, и от молекулярного числа Прандтля Рг. Далее,
если верить, что возможны условия вынужденной конвекции, при которой
температура переносится как истинная пассивная примесь, то и значения а
для тепла и для материальной примеси надо считать точно совпадаю-
совпадающими. Если же эти два значения а отличаются, то это может лишь
значить, что существует какой-то (неизвестный • нам) физический механизм,
иначе воздействующий на перенос тепла, чем на перенос материальной
примеси.

5.7] S 5- ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 285
_ ZH,
При очень малых значениях z+ = —*• в случае гладкой стенки, есте-
естественно, должно выполняться равенство
¦» (z) - ? @) - J&L , у (*+1 Рг) = * Рг • г+, E.80)
с?1
аналогичное E.20). Дальнейшие члены разложения функции <p(z+, Рг) в ряд
Тэйлора по степеням z+ в окрестности точки г+ — 0 можно получить, диффе-
дифференцируя по г равенство E.73') в точке г = 0. Так как в случае стенки
постоянной температуры Ь' = 0 при г = 0, то аналогично E.20') с точностью
до членов четвертого порядка по г+ будем иметь
z+, Pr)= * Рг (z+ - сАг\), E.80')
, Cppv3 / дЬ> d*w> v >)
где с4 = 5- I ¦—- —я- I Из обращения в нуль второй и третьей
Ч", \ ^ д* /г=0'
производных функции ф(г+, Рг) по г+ в точке г+ = 0 следует, что изменение
температуры будет близким к линейному в значительной области значений г;
поэтому можно ввести понятие подслоя молекулярной теплопроводности,
в котором значения функции <p(z+, Pr) практически ие отличаются от
%Рг • z . Однако толщина этого подслоя 6$ теперь будет определяться тремя
параметрами v, % и и*, так что, вообще говоря, можно лишь утверждать, что
6& = ф(Рг)—. Непосредственно за подслоем молекулярной теплопровод-
теплопроводности должна следовать какая-то переходная область, промежуточная между
областью применимости соотношения E.80) и логарифмическим слоем. За
этой переходной областью начинается логарифмический температурный по-
пограничный слой, описываемый формулой E.77). К сожалению, в настоящее
время иет никаких непосредственных эмпирических данных о профилях
температуры или концентрации примеси около стеики, позволяющих прове-
проверить все эти общие выводы и построить полный ход функции <p(z+, Pr). По-
Поэтому о значениях этой функции при малых г+ приходится судить лишь иа
основании косвенных данных,, полученных при изучении теплопередачи и
диффузии в турбулентных течениях.
') Заметим, впрочем, что в отличие от точного уравнения E20') уравне-
уравнение E.80') для профиля средней температуры (но ие для профиля концен-
концентрации материальной пассивной примеси) является лишь приближенным.
В самом деле, исходное уравнение E.73'), из которого вытекает E.80'), само
является приближенным, так как при его выводе было отброшено слагаемое,
описывающее прогревание среды в результате диссипации кинетической энер-
энергии, входившее в уравнение A.70) (стр. 61). Если же сохранить это сла-
слагаемое, то в разложении Тэйлора для функции <p(z+) появятся члены порядка
/+иг+ с коэффициентами, выражающимися через статистические характе-
характеристики пульсаций скорости. Оценке величины этих членов посвящена за-
заметка Тьеиа A964), показавшего, что в слое z+<! 10 оии могут играть
какую-то роль, только если ри3/?0 > Ю~3 (где до теперь предполагается
выраженным в единицах размери*ости М7").

28? гл. ш. уравнения реинольдса [5.7-
Эти косвенные данные (которых зато имеется очень много) состоят
в сведениях о значениях безразмерных интегральных характеристик тепло-
теплопередачи — числа Нуссельта Nu = -^—5-г- или коэффициента .теплев
с9Х (9i — "о;
передачи (числа Стэитона) са=^—д- = ¦¦•¦;, Л?—^-г ПРИ различных
Kej ft. CfU (»i — »oJ
значениях Re^ = и Pr = —. Здесь Oo=0(O)—температура стенки
(обычно плоской^ пластинки или трубы), предполагаемая постоянной, <h —
температура потока вне пограничного слоя или на оси трубы, 6 —толщина;
пограничного слоя или радиус трубы, О — скорость невозмущениого.обтекаю-
щего потока или скорость на оси трубы1). Те же безразмерные характери-1
стики определяются обычно и в опытах по диффузии—в этом случае надо
только Цй заменить на. /о, -опустить множитель сР в знаменателях Nu и ел
и понимать под О<> и fh соответствующие концентрации. При теоретическом
изучении теплопередачи в ,трубах (а также и теплопередачи в пограничном
слое при не слишком больших числах РейкольдсаУ изменением величии т
и q вдоль оси Ог в первом приближении можно пренебречь и пользоваться
схемой логарифмического пограничного слоя (обоснование законности такого
упрощения можно иайти, .например, к работдх Дейслера A951, 1954)). Если;
теперь мы перепишем формулу E.77') в виде.
Ъ(г)-К = % (I щ ^s.+ С), E.77")
то для определения разности О] — О0 надо лишь знать параметры и и а
и как-то оценить постоянную С, существенно зависящую от изменения тем-
температуры в тонком пристеночном слое. Для -оценки этой постоянной был.
предложен целый ряд теорий, приводящих к результатам, с разной степенью
точности подтверждающимся на опыте. •
Простейшая гипотеза, позволяющая оценить значение С, была выдви-
выдвинута Рейиольдсом A874). Ои исходил из предположения, что механизмы
переноса тепла и импульса в турбулентном потоке одинаковы; поэтому тур-
турбулентный поток тепла q по теории Рейиольдса должен быть связан с на-
напряжением треиия т соотношением вида
- »i) ~ P {fit -
E.81).
') На практике при изучении теплопередачи в трубах вместо Oi обычно
используется средняя температура
»сР = / »(*) «(') (R- г) <te / J « (г) (R - г) dz
о ' о . Л
массы ц протекающей жидкости,: а вместо V — средняя скорость UCn ='
rR
R
2 Г-
= 'Ш /. и(г)(Л — z)dz.
На этом, однако, можно не останавливаться,
о
так как по данным п. 5.5, зная значения критериев Nu и Сл, состачленных
с помощью <h и U, легко подсчитать также и зиачеиия^этнх критериев,
составленные с помощью ftcp и UCf, и наоборот.

517J $ 5. течения в труйах:И- в- пограничном слое вТ
где Uи Ut и Oi, <Ь — значения средней скорости, и температуры на двух
произвольных уровнях. Согласно этому соотвошению, профили средней ско-
скорости и средней температуры во всем слое постоянства потоков т и q
должны быть точно пропорциональными I с коэффициентом пропорциоиаль-
иости, равным — )• Отсюда вытекает, что <p(z+, Pr)=x/(z+) (так что
функция ф не зависит от Рг) и С= хВ. Сравиивая равеиство E.80) с F.20)
и E.77?). с E.25), легко убедиться, • что такая пропорциональность будет
иметь место, лишь если % = v (т. е. Рг = 1), а = 1 (т. е. Рг, = 1) и, кроме
того, =-==—=- (т. е. Prt"= I) "Также и во всей"промежуточной'области
db ¦ du . .
, "dz - ...':' . .
между вязким подслоем и логарифмическим слоем. Заметим, что условие
Рг=1 лишь весьма приближенно (с точностью, ие превышающей 20—30%)
выполняется для воздуха и большинства других газов и уже. совсем не
выполняется для подавляющего большинства капельных жидкостей; условие
же Рг( = 1 накладывает сильные ограничения на беснорядочные пульсации
полей скорости' и температуры, которые также вряд ли никогда ие нару-
нарушаются. Тем ие менее; предположение Рейнольдса (или, как чаще говорят,
аналогия Рейнольдса, имея в виду аналогию между потЬками тепла и
импульса, виражаемую равенством E.81)), записанное в виде соотношения
. с„ = i cf, E.82)
удивительно хорошо описывает. многие экспериментальные результаты о' тур-
турбулентном теплообмене в газах и поэтому до сих пор довольно часто исполь-
используется иа практика
Существенным недостатком аналогии Рейиольдса является то. что в ией
преиебрегается влиянием иа теплообмен молекулярного числа Праидтля,
в ряде случаев бесспорно играющего определенную роль. Простейшее обоб-
обобщение. формулы E.82), ставящее своей целью хоть как-то учесть влияние.
Параметра Рг, было независимо предложено Прандтлем A910, 1928) и Тэй-
лором A.916). Согласно их .представлениям в области логарифмического
пограничного слоя можно считать, что а = 1, но в вязком подслое (про-
(простирающемся вплоть до z—av— I следует пользоваться строгими форму-
формулами F,20). и E.80), т. е. учитывать точные значения коэффициентов, v и %.
Что же касается промежугочиой области, то в теории Праидтля — Тэйлора
ею преиебрегалос>, т. в. фактически предполагалось, что при. г>а0—
имеют место логарифмические формулы E.25) и E.77). Таким образом,
функция фС2+. Рг) определялась формулой E.80) при z+ <av и формулой
E;77') с а = 1 при г+ > а„; отсюда, в частности, следует, что в этой теории'
&=ая-иРг — 1п а„. Но легко проверить, что этому значению С (и значению
в ш J) отвечает коэффициент теплопередачи
¦'¦• f *>'¦'¦
сА = : ± —^=, E.83)
^— это я, есть оснбвиой результат теории Прандтля — Тэйлора. При Рг ** 1
формула E.83) совпадает с E.82); если же РтфЛ (но не .очень сильно

288 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [6.7
отличается от единицы), то при разумном подборе постоянной а„ (по
Праидтлю, например, а„ = 6,6) оиа дает несколько лучшее совпадение
с опытными данными, чем формула Рейиольдса F.82).
Дальнейшее усовершеиствоваиие схемы Праидтля — Тэйлора было пред-
предпринято Карманом A934, 1939)\ принявшим в расчет «промежуточный слой»
а„<г+<а; (где а„=б, а(=30; см. выше стр. 229 и 231). Как уже отмечалось
иа стр. 237, Карман предположил, что в этой промежуточиой области профиль
скорости также дается логарифмической формулой вида F.26), ио с другими
2
значениями коэффициентов А и В; в частности, ои считал, что А = — « б
и, значит, К=-2и*г = 0t2v*+ при б < г+ < 30. При расчете профиля
средней температуры (т. е. функции <p(z+, Pr)) предполагалось, что в области
г+ < б выполняется соотношение F.80) (т. е. действует только молекулярная
теплопроводность), в области 5<z+<30 действует и молекулярная, и тур-
' „ db " On
булеитная теплопроводность, причем Кь — л, т. е. -з- = -—-,—Гпо—Г•
а_при г+ > 30 коэффициентом % можно пренебречь н считать, что
_ = : 2° (число Рг« в этой теории при г > б v/и* принималось
dz cpf 04иг
всюду равным единице). Исходя отсюда, легко рассчитать весь ход функции
<p(z+, Pr) (определяемой тремя различными аналитическими выражениями)
и, в частности, найти значение постоянной С; для ел при этом получается
формула
сА = 1^- ;=¦ • E.84)
При Рг т 1 эта формула снова обращается в E.82J, ио при значениях Рг
порядка нескольких единиц или одиого-двух десятков (т. е. в случае обыч-
обычных капельных жидкостей) оиа дает заметно лучшее совпадение с опытными
данными, чем формула Праидтля — Тэйлора E.83). Однако при очень боль-
больших или очень малых значениях Рг формула E.84) также приводит к рез-
резким расхождениям с экспериментом.
В дальнейшем разными авторами был предложен ряд новых полуэмпн-
рических (или просто эмпирических) формул для величины сн (или Nn);
см. по этому поводу работы, цитированные иа стр. 237—238, а также статьи
Рибо A941), Капицы A947), Шервуда A950), Левича A951), Рейхардта A9516),
Чепмена и Кестера A953), Дейслера A951, 1954), Ван Дриста A959) и
Сполдинга A963)', в которых можно иайти много дополнительных ссылок.
В значительной части этих работ основиое усовершеиствоваиие теории заклю-
заключалось в выборе, исходя из тех или иных интуитивных или эмпирических
соображений, более сложного выражения для функции <p(z+, Pr), задавае-
задаваемого обычно в виде некоторой формулы для Кь = ^= Х- После
Ctf dbjdz
этого вычисление профиля O(z) (т. е. функции <p(z+, Pr)) и определение
коэффициента съ сводится к некоторому интегрированию (которое в случае
более сложных теорий приходилось выполнять численно). Мы здесь не будем
останавливаться на соответствующих результатах, имеющих в основном чисто
технический характер, а рассмотрим лишь принципиально важный вопрос

5.7] § 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 289
об особенностях теплопередачи при очень больших или очень малых числах
Праидтля.
В обоих этих предельных случаях явно неоправданным является содер-
содержащееся в теории Прандтля — Тэйлора и в теории Кармана предположение,
что толщину слоя молекулярной теплопроводности можно оценить при. по-
помощи формулы \ — %—> где а„ находится по излому профиля средней
*
скорости и, следовательно, не зависит от Рг. Начнем со случая очень малых
чисел Праидтля, характерных, в первую очередь, для жидких металлов.
Поскольку в этом случае % очень велико, слой молекулярной теплопровод-
теплопроводности оказывается много толще вязкого подслоя; поэтому пренебрежение
коэффициентом х во всей области логарифмического профиля средней ско-
скорости здесь безусловно должно привести к серьезным ошибкам. Чтобы их
избежать, многие авторы, специально занимавшиеся теорией турбулентного
теплообмена в жидких металлах (например Мартинелли A947), Лион A951),
Ликудис и Тулукяи A958) и др.), вообще нигде не пренебрегали молекуляр-
молекулярной теплопроводностью. На самом деле это, разумеется, не является необхо-
необходимым (во всяком случае, при рассмотрении идеализированного течения во
всем полупространстве г > 0); но толщину bv слоя, внутри которого коэф-
коэффициент х еще играет роль (т. е. сравним по порядку величины с турбу-
турбулентным коэффициентом /С»), при Рг<^1 следует оценивать при помощи
соотношения \ut ~ х (поскольку К ~ ut z при z ^> —, а коэффициент /(»
по порядку величины должен совпадать с К). Поэтому, например, в простей-
простейшей «двухслойной модели> Прандтля — Тэйлора при Рг <^ 1 следует считать,
что (p(z+, Рг) задается формулой E.80) при г+ < рр-^- = -~ (где 0, уже
ие зависит от Рг и имеет тот же порядок, что и безразмерная толщина
о
вязкого подслоя а,) и задается формулой E.77') при z+>-j=p, так что
6
С = *рр — a In ~. Исходя отсюда, уже легко рассчитать коэффициент
теплопередачи сь. Такой расчет и был выполнен Левичем A959), принявшим,
что Pt> = Н,7. а = 1,2. Несмотря на грубость использованных при этом
расчете предположений, оказалось, что полученная таким путем формула
неплохо соответствует большому числу эмпирических данных о теплопере-
теплопередаче при турбулентном течении жидких металлов в трубах.
Второй предельный случай Prj^g>l, встречающийся при изучении тепло-
теплопередачи в технических маслах или диффузии материальных примесей в
капельных жидкостях, значительно более сложен. Дело в том, что здесь слой
молекулярной теплопроводности гораздо тоньше вязкого подслоя и, следо-
следовательно, уже при г<^ч/и% перенос тепла (или примеси) определяется
в основном турбулентной теплопроводностью (диффузией). В то же время
количественные характеристики турбулентности хуже всего известны как
раз в области z^v/u*, в которой молекулярная вязкость еще играет очень
значительную роль. Так как к задаче независимого определения поведения
сразу двух функций }(г+) и <p(z+) в этой области пока ие видно подходов,
то обычно предполагается, что коэффициенты К и Ks при z-^v/u* или
точно совпадают между собой, или же отличаются лишь постоянным мно-
множителем а (выбираемым более или менее произвольно или же грубо оцени-
оцениваемым по эмпирическим данным). При этом изучение турбулентной тепло-
теплопередачи при Рг_^>1 сводится к исследованию асимптотического поведения
турбулентного напряжения трения — ри' w' (или, что эквивалентно, одной

290 гл. т. уравнения реинольдса [5.?
лишь функции f(z+)) при z<^v/«*(t. e. при г+ <^ 1), которому именно по
этой причине и было посвящено большое число работ (см. выше стр.237—238).
Предположим теперь, что К ~ /С&~zm при z->0 (т. е. что u'w' ~ О'а/ ~ zm
и, значит, [/(¦г+) —¦г+]~[(Р(г+, Рг)—хРг • г+] ~ г^+1). Так как толщина 8„
вязкого подслоя определяется условием K(8V) ~ v, а толщина bv подслоя
молекулярной теплопроводности — условием К$ (b^ ~ х>. то очевидно, что
в рассматриваемом случае
_i_ j_
Профиль Ф(г) в слое bv < г < bv в первом приближении можно опи-
описать уравнением q0 = срр/С» -у— "^ гШ -у— (так что ft (г) ~»const — z~m+l), a
при г > 6„ он обращается в логарифмический профиль E.77). Исходя отсюда,
нетрудно рассчитать и коэффициент теплопередачи (или диффузии} Сд; при
этом получается, что асимптотически при Рг ^> 1
т-\
cA~(Pr)~ m . если Къ~гт E.85)
(ср. Левич A959)). Однако относительно значения показателя т, как уже
отмечалось выше, в настоящее время еще нет окончательного мнения. Мы
видели, что в силу уравнения неразрывности должно быть т ^> 3; если
принять, что т = 3, то согласно E.85)
Ч~(Рг)~3 "Ри Р""^*1- E-85')
Предположение, что т = 3, позволило Мерфри A932) получить формулу
для сн, хорошо описывающую всю совокупность имевшихся тогда данных
о теплопередаче в потоках газов, воды и технических масел (с числами
Прандтля, доходившими до 1000); позже к аналогичным выводам пришел
также Рибо A941). Чисто эмпирически соотношение E.85') ,было найдено
Чилтоном и Кслбэрном A934), изучавшими диффузию в капельных жидко-
жидкостях (без всяких ссылок на работы о теплопередаче); в дальнейшем оно
было подтверждено и рядом других исследователей, из которых следует
отметить Линя, Дентона и др. A951), тщательно измеривших скорость диф-
диффузии ионов в электрохимических реакциях (при числах Прандтля, меняю-
меняющихся от 300 до 3000). В начале 50-х годов предположение о том, что т=3,
снова начало широко использоваться в теоретических работах как по турбу-
турбулентной теплопередаче (Рейхардт A9516)), так и по турбулентной диффузии
(Линь, Маултон, Патнем A953)JL Тем не менее, еще позже Рэнни A956)
допустил, что т—2, и получил, исходя отсюда, формулу Сл'^'(Рг) 2 , не-
неплохо описывающую эмпирические данные по теплопередаче при Рг<П20
(но ие при бблыпих значениях Рг). В то же время многие авторы (например,
Левич A944, 1951, 1959), Дейслер A959), Лойцянский (I960)) склонны
настаивать на том, что т = 4, и, следовательно,
-—
cA~(Pr) 4 при Рг^>1; E.88*)
этот результат также прекрасно описывает всю совокупность эмпирических
данных о турбулентной теплопередаче и диффузии при значениях Рг вплоть

5.8] * 5- ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 291
до 4000. Так как показатели 2/3 и 3/4 отличаются лншь на 1/12, и к тому же
все теории теплопередачи при больших Рг используют некоторые допущения
(например, об отношении а = К»/К) и содержат дополнительные неизвест-
неизвестные параметры, то выяснить по эмпирическим данным, равно ли т трем
или четырем, естественно, очень трудно (тем более, что всегда остается
возможность, что коэффициент с, положителен, но очень мал). Однако
можно утверждать, что пропорциональность коэффициента с& при больших
Рг функции (Рг) (в соответствии с формулами Прандтля — Тэйлора и
Кармана) или функции (Рг) 2 (в соответствии с формулой Рэиии) опре-
определенно опровергается данными опытов, как этого и следовало ожидать,
исходя из теоретических соображений, позволяющих строго доказать, что
т>3.
Разумеется, все предыдущие соображения относились лишь к случаю
теплообмена или диффузии около гладкой стенки. В случае же шероховатой
стенкн проблема еще значительно усложняется (см. Нуннер A956), Оуэи и
Томсон A963)); иа этом, однако, мы не будем останавливаться.
5.8. Полуэмпирические теории турбулентности
Мы уже указывали в п. 5.1, что в случае турбулентных те-
течений законы механики выражаются системой уравнений Рей-
нольдса, число неизвестных в которой превосходит число урав-
уравнений. Поэтому уравнения Рейнольдса позволяют лишь сделать
вывод о наличии определенных связей между различными ста-
статистическими характеристиками турбулентности, но они не мо-
могут быть «решены» в обычном смысле этого слова. Таким об-
образом, при выборе решений уравнений Рейнольдса, имеющих
физический смысл, какие-то функции, описывающие турбулент-
турбулентность, обязательно должны быть заданы независимо от этих
уравнений. В некоторых случаях вид таких функций может быть
найден (с точностью Дй небольшого числа эмпирически опреде-
определяемых констант) исходя из соображений размерности; чаще,
однако, использование соображений размерности все равно
приводит к соотношениям, содержащим неизвестные функции,
которые приходится затем находить по данным экспериментов.
Общее число таких неизвестных функций, необходимых для
описания различных турбулентных течений, встречающихся в
природе или в инженерно-технических устройствах, весьма ве-
велико; поэтому естественно, что многие исследователи стреми-
стремились свести определение этих функций к нахождению неболь-
небольшого числа связей между статистическими характеристиками
турбулентности, применимых сразу ко многим различным те-
течениям. Теории турбулентности, использующие наряду со стро-
строгими уравнениями гидромеханики также некоторые дополни-
дополнительные связи, найденные чисто эмпирически по данным
экспериментов или же выведенные с помощью качественных
рассуждений наглядно-физического характера и затем прове-

292 гл. in. уравнения рейнольдса [5.8
ренные на опыте, называются полуэмпирическими теориями.
Разумеется, все эти теории с точки зрения «чистой» теоретиче-
теоретической физики должны рассматриваться как нестрогие, но для
исследований в области турбулентности они очень характерны;
в развитии наших представлений о турбулентных течениях по-
луэмпрические теории сыграли очень большую роль, и многие
из них до сих пор продолжают широко использоваться в тех-
технике. Поэтому представляется целесообразным дать здесь хотя
бы краткое представление об основных идеях важнейших полу-
полуэмпирических теорий,предложенных Буссинеском A897),Пранд-
тлем A925), Тэйлором A915, 1932) и Карманом A930). Это-
Этому и будет посвящен настоящий пункт; дальнейшее развитие
такого подхода к теории турбулентности и некоторые конкрет-
конкретные примеры применения полуэмпирических теорий будут рас-
рассмотрены в следующем параграфе.
Незамкнутость системы уравнений Рейнольдса относительно
средних значений гидродинамических полей вызывается нали-
наличием в ней дополнительных членов, содержащих турбулентные
напряжения (напряжения Рейнольдса). Отсюда ясно, что про-
простейший путь замыкания этой системы уравнений состоит в ус-
установлении связей между осредненными гидродинамическими
полями, с одной стороны, и напряжениями Рейнольдса, с другой
стороны, позволяющих выразить последние величины через пер-
первые. Ниже мы перечислим несколько связей такого рода, пред-
предложенных различными исследователями в разное время.
Будем рассматривать лишь простейшие плоскопараллель-
плоскопараллельные течения, в которых отлична от нуля только х-компонента
средней скорости йж=й, зависящая лишь от координаты z (или,
что почти то же самое, течения в круглой трубе,, в которых
средняя скорость п всюду направлена вдоль оси Ох и зависит
лишь от расстояния z = R — г до стенки трубы). В таком слу-
случае уравнения Рейнольдса будут иметь вид E.16) (или анало-
аналогичный вид в полярной системе координат); поэтому профиль
средней скорости здесь будет определяться одним уравнением
(первым уравнением E.16) или уравнением E.17')), содер-
содержащим одно-единственное дополнительное неизвестное т*1^
= —pu'w'. Следовательно, для определения функции п(г) надо
только уметь выразить т*1* через п(г).
Простейшее возможное предположение о связи турбулент-
турбулентного напряжения т<1)=—pu'w' с профилем п(г) —это предпо-
предположение Буссинеска A897) о существовании соотношения вида
E,5), содержащего некоторый коэффициент турбулентной вяз-
вязкости К. Собственно говоря, само по себе соотношение E.5)
даже не является предположением и не устанавливает новой

5.8] § 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 293
связи; оно только заменяет неизвестное т*1' новым неизвестным
К=—-=—• Если, однако, предположить, что К зависит от ко-
9(du/dz) . ¦ .
ординат каким-либо определенным образом, то при этом мы
сразу приходим к полуэмпирической теории, основанной на не-
некоторой гипотезе и допускающей проверку на опыте.
.Самое простое допущение о величине К состоит в том, что
ее значение просто считается постоянным. Легко понять, однако,
что в применении к течению в плоском канале или круглой тру-
трубе это допущение приводит к заведомо неверным результатам.
В самом деле, при К = const уравнения для средней скорости
турбулентного течения отличались бы от соответствующих урав-
уравнений для ламинарного течения лишь числовым значением ко-
коэффициента вязкости, и, следовательно, из них следовало бы,
что профиль скорости и в этом случае должен быть параболи-
параболическим. В то же время известно, что такой профиль не соответ-
соответствует данным экспериментов (ср. рис. 32 на стр. 258).
В полученном противоречии, разумеется, нет ничего неожи-
неожиданного— хорошо известно, что при приближении к стенке ко-
коэффициент К должен стремиться к нулю (и притом даже не
медленнее, чем третья степень расстояния от стенки; см. стр. 228);
поэтому предположение о постоянстве К никак не может быть
применено к течению при наличии твердых стенок. Однако в не-
некоторых задачах, касающихся, например, турбулентных струй,
распространяющихся в безграничном пространстве, или турбу-
турбулентности в свободной атмосфере, предположение К = const
оказывается не столь уж плохим. В этих случаях подстановка
соотношения E.5) с постоянным К в уравнение Рейнольдса при-
приводит к полуэмпирическому уравнению, содержащему неизвест-
неизвестный параметр К, который следует определять по данным на-
наблюдений, и которому в разных случаях приходится приписы-
приписывать весьма различные значения.
В случае течений, ограниченных стенками, нельзя считать,
что К = const; но здесь в ряде случаев можно выдвинуть другие
разумные гипотезы о коэффициенте турбулентной вязкости К,
позволяющие доопределить соответствующие уравнения Рей-
Рейнольдса. Так, например, в случае плоскопараллельного течения
около плоской стенки (но не слишком близко от нее — за пре-
пределами вязкого подслоя) к хорошим результатам приводит ги-
гипотеза о пропорциональности коэффициента К расстоянию до
стенки: из нее немедленно вытекает логарифмическая формула
E.22) для профиля скорости, согласующаяся с выводами из
соображений размерности. Для течений в трубах, каналах и
пограничном слое также был предложен ряд гипотез о зависи-
зависимости ^ QT расстояния до стенки z\ в качестве примера можно

294 гл. ш. уравнения рейнольдса [5.8
указать на заметку Госса A961), в которой показано, что для
труб и пограничного слоя к неплохо согласующимся с опытом
результатам приводит предположение о пропорциональности К
1—у| , где 6 — радиус трубы или толщина
пограничного слоя. В непосредственной близости от стенки взаи-
взаимодействие процессов молекулярного и турбулентного трения
приводит к зависимости вида K = xu*Z(p(zudv); некоторые по-
луэмпнрнческне гипотезы о виде функции ф были предложены
Дейслером A955), Рэннн A956), Левичем A959) и другими
авторами (см. выше стр.237—238).В приземном слое атмосферы
при устойчивой термической стратификации, коэффициент К по
всем имеющимся данным с ростом высоты z сначала возрастает
почти линейно, а затем это возрастание становится более мед-
медленным, и при достаточно больших z турбулентную вязкость
можно считать практически постоянной. В соответствии с этим
разными исследователями был предложен ряд формул для К (г),
согласующихся с указанными здесь общими закономерностями
(см., например, Юдин и Швец A940), Дородницын A941), Бер-
лянд A947)). Каждой из этих формул отвечает свой вариант
полуэмпнрнческой теории, позволяющий (после определения по
данным наблюдений всех параметров, входящих в выбранную
формулу для К (г)) с той или иной точностью рассчитать изме-
изменение скорости ветра с высотой и решить некоторые другие ин-
интересные для метеорологии задачи.
При исследовании закономерностей переноса пассивных кон-
консервативных примесей в турбулентном потоке роль турбулент-
турбулентного напряжения т<1)=—pu'w' играет турбулентный поток массы
/(''=—pft'w' или тепла qW =—Cppft'w', а роль коэффициента К —
коэффициент Къ, определяемый соотношением E.9'). По поводу
этого коэффициента можно дословно повторить все то, что выше
говорилось о коэффициенте К (см., в частности, ниже § 10, где
в связи с обсуждением вопроса о диффузии в атмосфере будут
рассмотрены некоторые полуэмпнрнческне теории, использую-
использующие определенную форму зависимости коэффициента /С8 от
координаты г).
Часто, однако, понятие коэффициента турбулентной вязкости
(или теплопроводности, или диффузии) ничем не облегчает за-
задачу исследования турбулентных потоков в связи с тем, что вы-
выбор приемлемого допущения об этой величине наталкивается
на большие трудности, и неясно, чем при таком выборе следует
руководствоваться. Для облегчения этого выбора были разра-
разработаны некоторые другие полуэмпирнческне теории, во многих
из которых основную роль играет понятие пути перемешивания,

5.8] § 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 295
введенное Прандтлем A925) (в слегка отличной форме та же
идея еще раньше высказывалась Тэйлором A915)).
Применение понятия пути перемешивания легче всего про-
проиллюстрировать на примере турбулентного переноса консерва-
консервативной пассивной примеси О. Пусть средняя концентрация О за-
зависит только от координаты z, так что основной интерес пред-
представляет перенос этой примеси по направлению оон Oz. Будем
считать, что перенос осуществляется лишь турбулентными пуль-
пульсациями скорости. Наглядно это можно представить себе так,
что в среде случайным образом возникают отдельные струйки,
переносящие примесь с одного уровня z=const на другой.
Будем считать, что каждая такая струйка проходит по направле-
направлению оси Oz путь V и только после этого перемешивается с окру-
окружающей средой; в таком случае V и будет длиной пути переме-
перемешивания.- Заметим теперь, что согласно принятому предположе-
предположению на уровень z будут попадать только струйки, зародившиеся
на уровне z—Г и двигающиеся вверх, или зародившиеся на
уровне z + l' и двигающиеся вниз. Если еще считать, что пере-
перемешивание струйки происходит не постепенно, а сразу, то струй-
струйка, зародившаяся на уровне z—Г, донесет до уровня z свою
исходную концентрацию примеси, равную в среднем #(z— /'),
а струйка, зародившаяся на уровне z+l', донесет концентрацию,
в среднем равную О (z+/'). Таким образом, попав на уровень z,
рассматриваемые струйки будут содержать примесь в концен-
концентрации, отличающейся от средней концентрации на этом уровне,
т. е. будут приводить к появлению пульсации концентрации, рав-
равной & (z + /') —Ъ(г) « q; /' —j~- Ясно, что струйкам, двигаю-
двигающимся вверх, отвечает положительное значение пульсацнонной
вертикальной скорости w', а двигающимся вниз — отрицатель-
отрицательное значение w'. Поэтому если считать /' также имеющим знак,
положительный для струек, движущихся вверх, и отрицатель-
отрицательный для струек, движущихся вниз, то
/> = —рР5> = рГ^7-Ц. E.86)
Отсюда видно, что коэффициент турбулентной диффузии К"
очень просто выражается через длину пути перемешивания (яв-
(являющуюся, вообще говоря, случайной величиной):
/Г, = Ж E.87)
Формулу E.86) можно попытаться использовать не только
для подсчета потоков пассивных консервативных примесей, но
и для описания турбулентного обмена импульсом. Эта идея

296 гл- т. уравнения рейнольдса [5.8
лежит в основе известной теории переноса импульса Прандтля
A925), предположившего, что для продольной компоненты им-
импульса ри также существует определенный путь перемешивания
V и, следовательно,
тЧ> = — рп^^рГт7^, K=Yw'. E.88)
Длина V здесь, очевидно, в известном смысле аналогична длине
свободного пробега молекул в кинетической теории газов — она
определяет путь, который проходит небольшой элемент жидко-
жидкости («струйка»), прежде чем он перемешается с прочими
жидкими частицами и передаст им свой импульс. В этом смысле
формула E.88) для К аналогична известному из кинетической
теории газов выражению для коэффициента молекулярной вяз-
вязкости: v I- lmum, где lm — длина свободного пробега, и™ — ско-
скорость теплового движения молекул. Разумеется, длина V на
много порядков больше, чем lm; поэтому, несмотря на то, что
ит обычно больше, чем w', формула E.88) приводит к значе-
значениям К, намного превосходящим v.
Заметим теперь, что струйки, попадающие в слой z из слоев
z—/' и z+/', будут в среднем иметь продольную скорость
U(z-l') и соответственно u(z + l'), так что в обоих случаях они
будут создавать пульсацию «'продольной скорости, близкую по
абсолютной величине к W'-j—
Допустив далее, что пульса-
пульсации вертикальной скорости w' по абсолютной величине близки
к пульсациям продольной скорости и', так что
w _и _/ _.,
Прандтль представил турбулентное напряжение тС в виде
du
du
E-89)
где / — новая длина, имеющая тот же порядок, что и среднее
квадратичное значение случайной длины Г1). Знак абсолютной
величины в формуле E.89) поставлен для того, чтобы напряже-
L
') Разумеется, /_ие равно просто U'2J так как w' лишь имеет тот же
,, du
порядок, что и I -jjj, ио ие должно для каждой струйки точно совпадать
с величиной I —г— ¦

5.8] § 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 297
нне iO всегда имело тот же знак, что и -з—, так как импульс
всегда передается от слоев жидкости, двигающихся более
быстро, к слоям, двигающимся более медленно. Длина / в фор-
формуле E.89), которая теперь уже не является случайной величи-
величиной, обычно также называется длиной пути перемешивания.
Формула E.89) позволяет представить коэффициент турбу-
турбулентной вязкости в виде
\^[ E.90)
где / — длина, которая, вообще говоря, зависит от координат и
характеризует масштаб турбулентности (средний размер турбу-
турбулентных возмущений) в данной точке. После этого определение
профиля средней скорости требует лишь задания явного вида
зависимости длины / от координат. Поскольку при течении около
бесконечной плоской стенки, характеризуемом постоянным зна-
значением т, в области за пределами вязкого подслоя не суще-
существует никакого масштаба длины, всякая величина размерности
длины должна быть здесь пропорциональной расстоянию от
стенки. Полагая / = хги xC) = t^p«2^ const, из E.89) получим,
что ~=sz-^-, т. е. й = — lnz + const (см. Прандтль A9326)).
Таким образом, мы снова пришли к логарифмическому закону
для профиля скорости, который, как мы видели, прекрасно под-
подтверждается на опыте. Для течения в плоском канале или в
круглой трубе в качестве первого приближения можно даже
предположить, что соотношение l = xz остается справедливым
вплоть до середины канала или оси трубы. Подставляя это со-
соотношение в E.89) и заменяя здесь левую часть значением
E.17) или E.17') (т. е. снова отождествляя т(') с * = тA) + v-^-),
получим дифференциальное уравнение относительно п(г), кото-
которое при соответственном подборе постоянной к приводит к про-
профилю скорости, неплохо соответствующему данным опыта в зна-
значительной части сечения канала или трубы (см. Гольдштейн
A938)). Однако непосредственно вблизи от центра канала или
трубы это приближение оказывается явно неприемлемым; здесь
значительно лучше считать путь перемешивания приблизительно
постоянным. Полагая, например, для трубы радиуса R, что /=
= Р#, в силу формул E.17') и E.89) будем иметь

298 гл. ш. уравнения реинольдса [5Я
Интегрируя это уравнение при краевом условии u(R) = UQ, по-
получим
*/,-«(*) ... 2 Л __*\Т
Последний результат, как показал еще Дарен A858), при р «
«» 0,13 хорошо соответствует экспериментальным данным в об-
области 0,25 < тг < 1 (см- СТР- 259). Наконец, для того чтобы по-
получить совпадение с опытными данными при всех значениях -&
вне. пределов вязкого подслоя, в случае течения в круглой трубе
следует положить
/ = #[0,14-0,08A _JLJ_o,O6(l -^-L] E.91)
(Ннкурадзе A932)). Последняя формула при -^ <С/1 принимает
г
г2 z
вид / = ОДг — 0,44 -&¦+..* « 0,4г, а при -^ -> 1 она обращается в
соотношение I ~ 0,14/?, т. е. она может рассматриваться как ин-
интерполяционная формула между выражениями для I вблизи
стенки и в центре. Близкое распределение / по сечению трубы
предложил также Обухов A942), высказавший одновременно
некоторую гипотезу о длине /, позволяющую находить ее зави-
зависимость от координат для труб любого сечения. Непосредствен-
Непосредственно около стенки (в пределах вязкого подслоя) /, по-видимому,/
должно убывать при убывании z быстрее, чем по линейному за-
закону; гипотезы о поведении I в этой области течения предлага-
предлагались Ротта A950), Хама A953), Ван Дрнстом A956) и другими
авторами.
В дальнейшем Прандтль указал некоторые обобщения
теории переноса импульса, применимые, например, к трех-
трехмерным течениям "(ср. Гольдштейн A938),_§ 81) или же учи-
учитывающие возможность того, что при -^- = 0 турбулентная
вязкость в противоречии с E.90) будет все же отлична от нуля
(Прандтль A942)). Мы здесь, однако, не будем останавливаться
на этих обобщениях, а перейдем сразу к предложенной Тэйло-
ром теории переноса вихря — второй основной полуэмпнрнческой
теории.
Появление этой теории было связано с попыткой учета влия-
влияния пульсаций давления на перемещающиеся жидкие частицы,
приводящего к изменению их импульса и поэтому не позволяю-
позволяющего считать импульс консервативной примесью, сохраняющейся
при перемещении элементов жидкости. Исходя отсюда, Тэйлор

5.8] i s. течения в трубах и в пограничном слое 299
A915), впервые вводя понятие «пути перемешивания», в отличие
от Прандтля предположил, что «путь перемешивания» должен
существовать для вихря скорости, а не для импульса; впослед-
впоследствии эту идею он развил более подробно (см. Тэйлор A932)).
Идея Тэйлора наиболее обоснована для двумерного потока,
в котором, как известно, в отсутствие вязкости вихрь бкорости
переносится при движении жидких частиц без изменения. По-
Поди dw
этому единственная компонента вихря <оу = -^ -ч— двумер-
двумерного потока С полем скорости и ={и, w} всюду вне вязкого под-
подслоя является консервативной величиной. Турбулентное напря-
напряжение трения т——pu'w' двумерного потока со средней ско-
скоростью и = {и, 0}, всюду параллельной оси Ох, удовлетворяет
соотношению
(здесь использовано уравнение неразрывности для пульсаций
скорости: -^- + ~5F" = 0b В случае потока, однородного вдоль
оси Ох, производные по х от осредненных величин будут равны
нулю; следовательно, в этом случае
|1 = —р^Л7. E.92)
Введем теперь путь перемешивания для вихря 1[, так что
' .' да>у т гг, дау тт
(ву = /, ~-; тогда рда шу = pw ll —^-' Что же касается величины
а/, то ее, как и в теории Прандтля, представим в виде w' = /' -^,
где /' — случайная длина пути перемешивания для скорости. За-
Заметив, что в рассматриваемом случае шу=-^7—dF = F' и>
da>y d2ll
значит, -rg- = -gp- • окончательно получаем
dz л da d2u ,,- по.
где i _/ 1'1'у —характерная длина, играющая в теории
Тэйлора ту же роль, что и длина / в теории Прандтля. Разу-
Разумеется, если учитывать, что на самом деле возмущения поля ско-
скорости плоскопараллельного потока могут быть и трехмерными,

300 гл. ш. уравнения рейнольдса [5.8
то приведенный вывод формулы E.93) теряет свою убедитель-
убедительность— при этом указанную формулу приходится рассматривать
лишь как эмпирическую связь, допускающую проверку на опыте.
Формула E.93) также допускает некоторые дальнейшие обоб-
обобщения (см., например, Тэйлор A935в) или Гольдштейн A938);
§§ 84—85); на этом, однако, мы здесь не будем задержи-
задерживаться.
Если /i = const, то формула E.93) оказывается точно эквива-
эквивалентной формуле Прандтля E.89). В самом деле, при /i = const,
интегрируя E.93) по г, получим t = -j P^i (-^г) • что совпадает
с формулой Прандтля, если положить /, = /\^2. Вообще же
теория Тэйлора приводит к несколько иным результатам, чем
теория Прандтля. В применении к напорным течениям в плос-
плоском канале или круглой трубе теория Тэйлора с /i=XiZ (где
приходится считать, что xi«0,23 в случае канала и Xi«0,19 в
случае трубы) позволяет получить зависимость средней скоро-
скорости от z, которая почти вплоть до самой середины канала или
центра трубы неплохо согласуется с опытными данными (см.
Гольдштейн A938), §§ 156—157).
Аналогично выводу формулы E.89), при помощи подстановки
соотношения wr==l'~jj B равенство E.86) можно вывести ра-
равенство
/I) ft du db „ л du
J =Pl Kb h
где /2 — еще одна длина пути перемешивания, характеризую-
характеризующая теперь уже перенос пассивной консервативной примеси •&.
Соотношение между длинами k и / (или U) определяет значе-
значение турбулентного числа Прандтля Pr, = -vr- (или величины
<х =-пгг-}. Так, например, в области течения, в которой можно
положить /=const, значению k=l отвечает Рг4 = а=1, в то вре-
время как при k=k получается Prt = -y-, a = 2. Теоретически, разу-
разумеется, длина k не обязана совпадать ни с /, ни с U, так что
нельзя считать (как это иногда делается), что из теории пере-
переноса импульса вытекает значение Рг4 = 1, а из теории переноса
вихря — значение Prt^-^; на самом деле соотношение между
длинами /г, / и /i можно пытаться определить лишь на основа-
основании данных экспериментов.
; Как теория переноса импульса Прандтля, так и теория пере-
переноса вихря Тэйлора не решают полностью вопроса о связи ме-

5.3] § S. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 301
жду напряжениями Рейнольдса и полем средней скорости, так
как в этих теориях вводится новая величина — длина пути пере-
перемешивания, определение которой для всех точек течения тре-
требует привлечения дополнительных гипотез. Весьма общей гипо-
гипотезой, позволяющей, в частности, во всех случаях установить
связь между длиной I и осредненным полем скорости, является
предложенная Карманом A930) гипотеза о локальном кинема-
кинематическом подобии поля турбулентных пульсаций скорости. Со-
Согласно этой гипотезе поля турбулентных пульсаций скорости в
окрестности каждой точки развитого турбулентного течения (за
исключением лишь точек гонкого «вязкого подслоя» около сте-
стенок, в котором непосредственно проявляется действие вязкости)
подобны друг другу и отличаются лишь масштабами длины и
времени (или, что то же самое, длины и скорости). Чтобы запи-
записать эту гипотезу математически, введем в окрестности каждой
точки потока х0 подвижную систему отсчета, движущуюся со
скоростью, равной средней скорости и{х0) в данной точке; в та-
таком случае координатами^ в этой системе отсчета будут компо-
компоненты вектора х — xo — u{xo)t. Согласно гипотезе Кармана, в
каждой точке х0 могут быть определены такой масштаб длины
/(•*„) и такой масштаб скорости U(Xq), что в окрестности этой
точки поле турбулентных пульсации скорости будет иметь вид
E-95)
где функция V (|) универсальна, т. е. не зависит от точки х0
(а следовательно, и от поля средней скорости в (•*)). Таким об-
образом, в теории Кармана связь между характеристиками турбу-
турбулентных пульсаций и полем осредненной скорости имеет место
лишь благодаря зависимости масштабов / и U от поля а(х).
Чтобы определить зависимость масштабов / и U от средней
скорости течения в случае плоскопараллельного стационарного
течения со средней скоростью п(г), всюду направленной вдоль
оси Ох и зависящей лишь от г, можно воспользоваться уравне-
уравнением A.7) для вихря скорости, у-компонента которого в прене*
брежении вязкостью будет иметь вид
da>v du>v duv
Подставляя в это уравнение значение полной скорости
и =ы(г0) / +U(zo)v(%), где/—единичный вектор оси Ох, а
~вектор относитель-

302 ГЛ. Ш. УРАВНЕНИЯ РЕЙНОЛЬДСА [5.8
ных безразмерных координат (и предполагается, что Хо—Уо^О),
можно перейти от уравнения E.96) к некоторому уравнению от-
относительно неизвестных va(%), а — 1, 2, 3, с коэффициентами,
содержащими величины U(z0), l(z0), й(г0) и их производные
по г0. Согласно принятой гипотезе об универсальности функций
та(|), коэффициенты последнего уравнения не должны зависеть
от 20. Таким образом, могут быть получены соотношения
*"<«¦>=.const
d\
dz0 , U(z0) dz\
(см., например, Гольдштейн A938), § 158 или Шлихтинг A951),
гл. XIX, § 5, где соответствующий вывод подробно проведен для
частного случая двумерного поля и! (х)). Отсюда вытекает, что
, du I сРи 1Т о, du
где х и В — универсальные постоянные (которым, вообще го-
говоря, можно придать любое значение, так как масштабы / и U
пока определены лишь с точностью до произвольного множи-
теля).
Первое из соотношений E.97), очевидно, может быть выве-
выведено и непосредственно с помощью соображений размерности,
если потребовать, чтобы длина / зависела лишь от ^ и ~^-J);
второе соотношение таким же образом получается из предпо-
du dhi I
ложения, что и и зависит только от ~^j и -^р- 1или от / и
du
Длина / является, очевидно, аналогом длины пути перемеши-
перемешивания / и h в теориях Прандтля и Тэйлора. В самом деле, в си-
силу E.95) и E.97).
г>3@) = const • р/2 (~Х, E.98)
где const=B2yi@)y3@)- Аналогично этому показывается, что
^ ^ p/2f-^ E.99)
') В силу галилеевской инвариантности уравнений движения характер-
характерный масштаб пульсаций_/, очевидно, не может зависеть от абсолютного зна-
значения средней скорости и(г), а зависит только_от изменения м в окрестности
заданной точки, т. е. от производных функции и(г). Предположение о зависи-
зависимости / только от первых двух производных du/dz и d2u/dz2 будет в таком
случае простейшей возможной гипотезой об этой величине.

5.8] 5 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 303
где теперь уже const имеет другое значение. Разумеется, если
заменить const единицей в равенстве E.98) или E.99), т. е.
отождествить длину / с длиной пути перемешивания для им-
импульса или для вихря, то после этого постоянную х в первом ра-
равенстве E.97) уже нельзя выбирать произвольно, а надо опре-
определять, исходя из экспериментальных данных.
Гипотеза Кармана, выраженная соотношением E.95), при ее
буквальном понимании налагает на турбулентные пульсации
скорости непомерно жесткие ограничения, не согласующиеся с
естествен'ным представлением о нерегулярности изменений пуль-
сационной скорости в пространстве и во времени. Как будет
видно из дальнейшего, гипотеза о локальном самоподобии ока-
оказывается приемлемой не для индивидуальных реализаций поля
пульсационной скорости, а лишь для статистических характери-
характеристик такого поля (см. гл. 8 в ч. 2 книги, посвященную гипотезам
подобия, предложенным А. Н. Колмогоровым).. Существенно,
однако, что основные результаты E.97) теории Кармана мо-
могут быть выведены и при гораздо более слабых предположе-
предположениях; как мы уже видели, в некотором смысле они являются
естествевными следствиями соображений размерности. Укажем
еще, что, как показал Лойцянский A935), для вывода формул
E.97) гипотезу о локальном самоподобии достаточно применить
к среднему полю скорости, потребовав, чтобы в каждой точке
хо= {хо, Уа, 2о) был определен такой масштаб l{z0), для которого
при Zo<2<zo-H с точностью до малых третьего порядка отно-
относительно / выполняется условие
E.100)
В самом деле, с указанной степенью точности имеем
!+4
Так как согласно принятой гипотезе последнее выражение не
должно зависеть от z0, то /, очевидно, должно удовлетворять
первому разенству E.97); после этого из условия независимости

304 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [5.9
от 20 отношения
2
Р [и
выводится также и равенство E.98).
Для безнапорного плоскопараллельного течения над безгра-
безграничной плоскостью 2=0 с постоянным напряжением трения
т = ри] соотношение Кармана E.97) для / в соединении с фор-
формулой Прандтля i = pl2(-~l-j (см. E.98)) дает
?" <5Л01>
Отсюда снова получается логарифмический профиль средней
скорости:
Ъ^ E.102)
(исторически именно так он и был выведен впервые). В случае
напорного течения а плоском канале или круглой трубе наряду
, , г? „ / du \3
с формулами / = — %-=- и т = рг(-—-I следует использовать
и \ dz I
еще соотношения E.17) или E.17')..При этом удается получить
формулы для профиля к (г), которые при специальном выборе
постоянной х (различном для канала и для трубы) можно при-
привести в удовлетворительное соответствие с имеющимися опыт-
опытными данными (см. Гольдштейн A938)).
5.9. Свободная турбулентность .
До сих пор в настоящем параграфе мы рассматривали тур-
турбулентные течения в каналах, трубах и пограничных слоях, т.е.
течения около твердых стенок, трение о которые приводит к не-
непрерывному порождению завихренности и оказывает непосред-
непосредственное влияние на весь поток. Но в природе и в технике часто
встречаются также турбулентные течения совершенно другого
рода, в которых непосредственное влияние каких-либо, твердых
стенок отсутствует, и которые называются поэтому свободной
турбулентностью. Важнейшими видами свободных турбулентных
течений являются турбулентные следы за обтекаемыми Жидко-
Жидкостью (или движущимися сквозь жидкость) твердыми телами,
турбулентные струи и зоны турбулентного перемешивания, воз-
возникающие на границе между потоками разной скорости, не раз-
разделенными какими-либо твердыми стенками.

5.9] § 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 305
Свободные турбулентные течения играют большую роль во
многих явлениях природы и в ряде технических устройств. По-
Поэтому неудивительно, что их изучению было посвящено очень
большое число теоретических и экспериментальных исследова-
исследований. Эти исследования привели к ряду результатов, полезных
для практических расчетов, но они пока еще мало что внесли
в наше понимание физической природы турбулентности. Поэто-
Поэтому здесь мы ограничимся лишь кратким рассмотрением неко-
некоторых общих выводов, касающихся перечисленных выше основ-
основных видов свободных турбулентных течений.
Существующие методы описания свободной турбулентности
основаны, во-первых, на некоторых гипотезах об автомодель-
автомодельности соответствующих течений и, во-вторых, на использовании
полуэмпирических теорий турбулентности типа тех, которые бы-
были кратко изложены в предыдущем пункте. Гипотезы об авто-
автомодельности опираются «а некоторые общие свойства течений
жидкости и могут быть обоснованы также с помощью методов
подобия и размерности; их рассмотрение представляет опреде-
определенный физический интерес. Полуэмпирические же теории сво-
свободной турбулентности используют кроме общих законов фи-
физики еще некоторые дополнительные гипотезы более специаль-
специального характера; получаемые при этом выводы важны в первую
очередь для приложений.- В дальнейшем в настоящем пункте
мы ограничимся почти исключительно анализом гипотез об авто-
автомодельности свободных турбулентных течений.
Начнем с того, что постараемся разъяснить общую идею об
автомодельности свободной турбулентности на частном, примере
трехмерной турбулентной струи, бьющей по направлению оси
Ох из конца тонкой трубки диаметра D (но произвольного сече-
сечения) в неограниченное пространство, заполненное той же жид-
жидкостью. Будем сравнивать друг с другом гидродинамические
поля в различных сечениях JC=oonst. Данные наблюдений пока-
показывают, что турбулентная струя обычно оказывается относи-
относительно узкой, так что продольная компонента средней скорости
в струе значительно превосходит поперечную компоненту, а про-
продольные изменения статистических характеристик гидродинами-
гидродинамических полей оказываются много меньшими, чем их поперечные
изменения. Исходя отсюда естественно ожидать, что свойства
гидродинамических полей в данном сечении струи будут в ка-
какой-то мере повторять соответствующие свойства в сечениях
вверх по потоку. Иначе говоря, следует ожидать, что статисти-
статистические характеристики гидродинамических полей струи в раз-
различных ее сечениях (т. е. при различных значениях х) будут по-
подобны между собой. Это означает, что в каждом сечении
jc=const можно ввести такие характерные масштабы длины L(x)

306 гл. ш. уравнения рейнольдса f5.9
я скорости U(x), что безразмерные статистические характери-
характеристики, получаемые при использовании этих масштабов, будут
уже одинаковыми во всех сечениях. Разумеется, такое подобие
не может иметь места начиная сразу же от отверстия, из кото-
которого бьет струя; оно представляется правдоподобным лишь на
достаточно больших (по сравнению с диаметром D) расстояниях
от этого отверстия, на которых его размер и форма перестают
уже сказываться на течении в трубе. Кроме того, для подобия
нужно также, чтобы числа Рейнольдса Re = ———— в рассма-
рассматриваемых сечениях струи были достаточно большими и обеспе-
обеспечивали бы наличие полностью развитой турбулентности (и тем
самым независимость от вязкости статистического режима круп-
крупномасштабных компонент турбулентности, создающих взаимо-
взаимодействие между гидродинамическими полями в близких сече-
сечениях струи, которое и' является физической основой подобия
этих полей).
Высказанное здесь предположение о подобии является еще
одним применением общего принципа подобия по числу Рей-
Рейнольдса, о котором мы говорили на стр. 252; оно может быть
также обосновано с помощью простых рассуждений, родствен-
родственных тем, которые использовались в п. 5.3 при выводе логариф-
логарифмической формулы для профиля средней скорости вблизи стен-
стенки (но за пределами вязкого подслоя). В самом деле, в рассма-
рассматриваемом здесь случае трехмерной затопленной струи течение
зависит от диаметра выходного отверстия D, исходной скорости
истечения струи Uo и параметров жидкости v и р. Поэтому ста-
статистические характеристики течения, например средняя скорость
п или напряжение Рейнольдса,— ры'ш' (где ш' — радиальная
компонента пульсационной скорости в цилиндрической системе
координат (г, ф, х) с осью Ох) в силу соображений размерности
должны задаваться формулами вида
\и и i E.103)
, ~, «р, ReD), где ReD = -^-.
То, что на достаточно большом расстоянии от отверстия трубки
зависимость этих характеристик от x/D практически перестает
сказываться, означает, что при достаточно большом x/D мы мо-
можем положить x/D = oo в E.103) (т. е. является следствием
предположения, что правые части в E.103) стремятся к пре-
пределу при x/D-^oo). Но тогда естественно считать, что «началь-
. ные условия» Uo и D при столь большом x/D уже вообще будут
сказываться лишь через значение «начального импульса» струи,

5.9] * «¦ ТЕЧЕНИЯ 6 ТРУБАХ Й В ПОГРАНИЧНОМ СЛОЕ 307
определяющего медленно изменяющиеся с ростом х интеграль-
интегральные характеристики течения в сечении x=const (типа скорости
Uma.±=U{x) на оси струи и полуширины струи L=L(x), равной
тому значению г, при котором и (г, 0, x) = -^Umax(x)\; весь же
статистический режим^ течения в окрестности плоскости х=const
будет как-то приспосабливаться к значениям масштабов U и L.
Отсюда вытекает, что при больших значениях x/D струю уже
можно считать осесимметрической (так как зависимость от ф
может определяться лишь формой выходного отверстия), и фор«
мулы E.103) здесь будут представимы а виде
u = U{x)fa[J^, Rex].W^ = ~U^(x)g2[T^, Rex]. E.104)
где
Rc Щх)Цх)
Наконец, при достаточно большом Re* мы можем положить
Rea;= с» в формулах E.104), так как при развитом турбулент-
турбулентном режиме турбулентная вязкость всегда намного превосходит
молекулярную и параметр v здесь уже не должен играть роли
(в этом и состоит принцип подобия по числу Рейнольдса). Сле-
Следовательно, при достаточно больших значениях x/D и Re*
EЛ05)
где f(r) и g(r)—некоторые универсальные функции. Эти соот-
соотношения и выражают гипотезу об автомодельности течения в
струе. Заметим еще, что в отличие от случая турбулентных тече-
течений при наличии твердых; стенок автомодельность здесь имеет
место уже для всей области турбулентного течения (но, как и
для течений в трубах, каналах и пограничном слое, она касается
только статистических характеристик крупномасштабных ком-
компонент движения, не связанных с диссипацией энергии под дей-
действием вязкости).
Важные связи между функциями L(x), U(x), f(r) и g(r) мо-
можно получить, подставив формулы E.105) в уравнения Рей*
нольдса. В случае стационарного осесимметричного движения
в пренебрежении слагаемыми, содержащими вязкость, уравне-
уравнения Рейнольдса, как нетрудно показать, могут быть сведены
к одному уравнению
«#+-# — т4?(г*Ъ-?<?-«\_ E.106)
(см., например, Таунсенд A956)). Член -^ (и'2 —да'2) здесь
описывает нормальное турбулентное напряжение и действие

308 гл. ш. уравнения рейнольдса E.9
продольного градиента давления; обычно он оказывается много
меньше других членов (во всяком случае, в центральной части
течения), и чаще всего им просто пренебрегают. В результате
получается уравнение
u + w<ru'w^ <5Л06)
являющееся основой почти всех теоретических исследований,
касающихся турбулентных струй. С помощью уравнения нераз-
неразрывности для осредненного движения
= 0 E.107)
из уравнения E.106') можно исключить поперечную скорость w.
Прежде всего заметим, однако, что, умножая уравнение E.106')
на г и интегрируя по г от 0 до оо, мы в силу E.107) получим
оо оо
Л /* 2 /* 2
-т— / и rdr = 0, т. е. / и rdr = M = const E.108)
дх .1 . J ч '
о о
(это равенство выражает закон сохранения импульса, т. е. ра-
равенство потоков импульса, протекающих через любую достаточ-
достаточно большую сферу с центром вблизи отверстия, из которого бьет
струя). Если теперь мы подставим сюда первую из формул
оо
E.105), то найдем, что U2L? Г/2 (»)) </¦»; = const. Отсюда вытекает,
о
что UL (а следовательно, и число Рейнольдса Rex=f/L/v) не
может зависеть от х. Таким образом, ?/~l/L. Учитывая этот
результат и подставляя формулы E.105) в уравнения E.106')
и E.107), легко найдем, что уравнения эти могут быть удовле-
удовлетворены, лишь если —г— = const (тот же вывод, разумеется, сле-
следует и из более общего уравнения E.106)).
Итак, мы убедились, что автомодельность возможна лишь
при
L(x)~x— xQ, и~(х — хо)~\ E.109)
где х0—постоянная интегрирования. Точка х = х0 при этом
играет роль условного «начала струи». Поскольку нас интере-
интересуют лишь асимптотические закономерности при очень больших
значениях х, то мы можем всюду в. дальнейшем просто считать,
что хо—О. Согласно E.109), на достаточно большом расстоянии
от выходного отверстия трубки ширина струи растет пропорцио-
пропорционально расстоянию (т. е. струя имеет форму прямого круглого

5.9] 5 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 309
конуса), а средняя скорость течения в струе убывает обратно
пропорционально расстоянию. Отметим еще, что количество
жидкости, протекающей через поперечное сечение струи, равно
оо
2тс Г urdr, т. е. возрастает пропорционально х. Это показывает,
о
что в струю все время втягивается жидкость из окружающей ее
неподвижной среды.
При условиях E.109) система уравнений E.106') — E.107)
имеет бесконечное число решений вида E.105). Фактически эта
система позволяет получить лишь одно соотношение, связываю-
связывающее две неизвестные функции f(r\) и g(r\), которое оказывается
имеющим вид
?
g (ч)=-^р- / ъ/Ы d-щ. л =
const
(см., например, Сквайр A948)). Еще хуже будет обстоять дело,
если принять более общее уравнение E.106)" — здесь мы уже
получаем лиш-ь одно соотношение, содержащее четыре неизве-
неизвестных функции (см. Таунсенд A956)). Полное определение всех
неизвестных функций требует привлечения еще каких-либо до-
дополнительных гипотез. Во многих работах с этой целью исполь-
использовались полуэмпирические теории турбулентности; так, напри-
например, Толмин A926) (по-видимому, впервые получивший форму-
формулы вида E.105)) использовал теорию переноса импульса
Л. Прандтля и предположение, что 1=1(х) ~х, а Гертлер A942),
следуя Прандтлю A942), вместо этого принял, что К=К(х)~х
и т. д. (подробнее об этом см., например, книги Бай Ши-и
A954), Хинце A959) и Абрамовича (I960)).
Разумеется, из уравнений Рейнольдса следует лишь, что если
только автомодельность E.105) имеет место, то масштабы U
и L должны удовлетворять соотношениям E.109), но никак не
вытекает, что должна иметь место автомодельность. Наличие
такой автомодельности кажется правдоподобным в силу приве-
приведенных выше общих соображений (которым, как мы покажем
чуть ниже, можно придать также стандартную форму соображе-
соображений размерности); однако окончательно оно может быть установ-
установлено лишь на основе анализа эмпирических данных. В случае
струи, вытекающей в пространство, заполненное неподвижной
жидкостью, формулы E.105) и E.109) проверялись в экспери-
экспериментах большого числа авторов (см., например, Рейхардт A942),
Корсин A943), Хинце и Ван дер Хегге Цийнен A949), Корсин
и Уберои A950), Корсин и Кистлер A954), Форстолл и Гейлорд
A955)). При этом было установлено, что уже на небольших

310
ГЛ. 111. УРАВНЕНИЯ РЕЙНОЛЬДСА
[5.9
расстояниях от отверстия, из которого вытекает струя (при
x>8D), профиль средней продольной скорости п(х, г) хорошо
описывается формулами E.105), E.109). Полная же автомо-
дельность течения, проявляющаяся и в профилях осредненнои
скорости, и во вторых моментах пульсаций скорости, оконча-
окончательно устанавливается лишь в более далеких от отверстия се-
ченийх струи (при x>50D). Наблюдается также некоторая за-
зависимость профилей от числа Рейнольдса Re = —-—, которая
ослабевает с ростом Re и при Re^t 105 уже перестает быть за-
заметной. В качестве примера на рис. 44 приведены (по данным
D.7S
050
t
\
ON
*••
о f-/<?
2Д
3,0
Рис. 44.' Зависимость нормированной средней скорости itjU от ч = r/L
в трех разных сечениях осеснмметричной струи по данным Рейхардта A942).
Рейхардта) профили скорости в трех сечениях струи, нормиро'
ваниые делением на Ume3.—U и отнесенные к расстояниям г,
измеренным масштабом L, таким, что и (L) = -j ?/max. Мы видим,
что подобие профилей выполняется вполне удовлетворительно.
Аналогичные гипотезы об автомодельности могут быть сфор-
сформулированы и для других конкретных типов свободных турбу-
турбулентных течений. Из них мы рассмотрим здесь плоскую турбу-'
лентную струю, бьющую в заполненное той же жидкостью про-

5.9] S »¦ ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 311
странство х>0 по направлению оси Ох из бесконечно длинной
щели, расположенной в плоскости Оуг вдоль оси Оу; трехмер-
трехмерный турбулентный след за расположенным вблизи начала коор-
координат телом конечных размеров, обтекаемым жидкостью по на-
направлению оси Ох; плоский турбулентный след за бесконечно
длинным цилиндром с осью вдоль оси Оу, обтекаемым жидко-
жидкостью по направлению оси Ох; наконец, зону перемешивания ме-
между двумя плоскопараллельными течениями в направлении Ох
в полупространствах г>0 и г<0, имеющими в начальном сече-
сечении Оуг постоянные, но различные скорости (скажем, ?А при
г>0 и Иг при г<0). При этом в случае следов за обтекаемыми
телами естественно перейти к подвижной инерционной системе
координат, перемещающейся вместе с 'невозмущенным обтекаю-
обтекающим потоком (т. е. рассматривать лишь отклонения скорости
течения в следе от невозмущенной скорости, затухающие на
большом расстоянии от тела); в случае же зоны смешения си-
систему координат надо выбрать так, чтобы выполнялось равен-
равенство Иг—— Ui- В таком случае для всех перечисленных течений
следует ожидать, что при достаточно большом числе Реинольдса
профили средней скорости и напряжения трения на достаточно
большом расстоянии х будут представимы в виде E.105), где
г — поперечная координата (расстояние от оси Ох для трехмер-
трехмерных течений и от плоскости 2=0 для плоских течений), w — по-
поперечная скорость. При этом масштабы длины и скорости L(x)
и U(x) всегда оказываются пропорциональными некоторой
степени продольного расстояния от условного начала от-
отсчета х, т. е.
L(x)~xm, U{x)~x-n E.110)
, г. - n U (x)L(x)
(так что число Реинольдса Ke_r = ———-^- пропорционально
хт~п). Показатели тип могут быть определены, как и выше,
из требования, чтобы функции E.105) могли являться точными
решениями соответствующих уравнений Реинольдса (в прене-
пренебрежении молекулярной вязкостью)'. В случае следов за обте-
обтекаемым телом соответствующие уравнения Реинольдса целесо-
целесообразно предварительно упростить, воспользовавшись тем, что
на большом расстоянии от тела средняя продольная скорость п
в пределах следа будет лишь на немного меньше постоянной
скорости Uo обтекающего потока (равной невозмущенной ско-
скорости течения за пределами следа), так что u=U0 — ui где
?/0=const, Mi<Cf/o, а средняя поперечная скорость w будет по
порядку величины не больше, чем ui. Поэтому, например, в
случае трехмерного следа уравнение Реинольдса на большом

312 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [5.9
расстоянии х может быть приближенно записано в виде
-U*%—TW(rib), E.111)
и, следовательно, здесь
со
J пхг dr = N = const. E.112)
о
Дальнейшие рассуждения для всех рассматриваемых типов сво-
свободных турбулентных течений совершенно аналогичны тем, ко-
которые выше использовались в применении к случаю трехмерной
струи. Получаемые при этом результаты сведены в нижеследую-
нижеследующую таблицу:
т
л
т — я
Трехмер-
Трехмерная струя
1
1
0
Плоская
струя
1
1/2
1/2
Трехмер-
Трехмерный след
1/3
2/3
-1/3
Плоский
след
1/2
о
Зэиа
переме-
перемешивания
1
0
1
(см. также Сквайр A948), Шлихтинг A951), Шубауэр и Чен
A959)). Наиболее существенное различие между указанными
здесь типами свободной турбулентности, которое можно усмо-
усмотреть из таблицы, заключается в различной зависимости от рас-
г> - г> U(x)L(x) n
стояния х числа Реинольдса Re^ = — v • ° плоском следе,
как и в трехмерной струе, Re не меняется с расстоянием, тем
не менее, течение в плоском следе оказывается в некотором смы-
смысле более неустойчивым, чем в трехмерной струе; так, согласно
Таунсенду A956), полная автомодельность в плоском следе
устанавливается лишь на расстояниях х> E00 -*- 1000) D, где
D — диаметр обтекаемого цилиндра. В плоской струе и в зоне
перемешивания Re растет с увеличением х. Наконец, в трехмер-
трехмерном следе Re убывает с расстоянием, так что при достаточно
больших х турбулентность должна вырождаться (на таких рас-
расстояниях предположения об автомодельности, конечно, пере-
перестают быть применимыми). Дальнейшие сведения об этих тече-
течениях см., например, в книгах Бай Ши-и A954), Таунсенда
A956), Биркхофа и Царантонелло A957), Хинце A959) и Аб-
Абрамовича (I960).
Упомянем еще одну разновидность свободной турбулентно-
турбулентности— вертикальные турбулентные струи термического происхо-

5.9] § 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 313
ждения, возникающие благодаря действию архимедовых сил
над нагретыми телами. Предположения об а в том одел ьн ости
таких струй впервые были рассмотрены Зельдовичем A937).
Если, как и выше, принять направление течения в струе (т. е.
вертикальное направление) за ось Ох, то эти предположения
заключаются в том, что в каждом сечении струи JC=const мож-
можно ввести такие масштабы длины L(x), скорости U(x) и тем-
температуры Q(x), что безразмерные осредненные характеристики
гидродинамических полей, получаемые при использовании этих
масштабов, будут одинаковыми во всех сечениях. В частности,
будут иметь место формулы E.105) и аналогичные формулы
для распределения в струе средней температуры и радиального
турбулентного потока тепла cppw'T'\
(где w' — радиальная компонента пульсационнои скорости в ци-
цилиндрической системе координат с осью Ох). Подставляя фор-
формулы E.105) и E.113) в. уравнения Рейнольдса, получаемые при
помощи осреднения системы уравнений свободной конвекции
(приведенной в п. 1.5) и пренебрегая в этих уравнениях члена-
членами, содержащими молекулярную вязкость и молекулярную тем-
температуропроводность (но не членом, описывающим архимедову
силу!), получим, аналогично выводу E.109), что
L(x)~x, U(x)~x~\ В(х)~х-ч>. E.114)
Подобное же рассуждение может быть применено и к двумер*
ной конвективной струе,возникающей над нагретым цилиндром,
расположенным в горизонтальной плоскости х=0 вдоль оси Оу.
Здесь мы получим
L(x)~x, */(jc) = const, В(х)~х'1 E.115)
(эти формулы также были получены Зельдовичем).
Заметим еще, что большая часть результатов, собранных в
таблицу на стр. 312, так же как и формулы E.114) и E.115),
легко могут быть получены и из одних только соображений раз-
размерности. В самом деле, в случае, например, трехмерной струн
все осредненные характеристики на большом расстоянии х от
точки истечения струи, очевидно, могут зависеть, кроме расстоя*
ния х — Хо^х, еще только от плотности р и от суммарного им*
пульса 2лрМ массы жидкости, вытекающей из отверстия за
единицу времени. Отсюда следует, что

314 гл. in. уравнения рейнольдса [5.9
(в полном соответствии с формулами E.109)). В случае плоской
струи, вместо величины 2лрМ надо лишь рассмотреть импульс
массы жидкости, вытекающей за единицу времени через еди-
оо
2
и dz. Следовательно, здесь
EЛ17)
(в соответствии со вторым столбцом нашей таблицы). Еще
проще применяются соображения размерности к случаю плос-
плоской зоны смешения: здесь условия в сечении х = const могут
зависеть только от х и от фиксированной разности скоростей
U1 — Ui —:2Ui = Uo, так что, например,
В случае свободных конвективных струй все осредненные
характеристики могут зависеть от полного потока тепла вдоль
оо
струи Q = 2ucpp I u'T'rdr (или потока тепла на единицу длины
о
оо \ .
нагретого цилиндра Qi = cpp lu'T'dziH параметра плавуче-
I
— оо /
сти gP (в случае идеального газа равного g/T0). При этом вели-
величины Q и Qi, естественно, могут входить только в комбинациях
Q/cpp и QJcpp. Отсюда вытекает, что
для трехмерной конвективной струи и
для плоской конвективной струи. Эти результаты, очевидно, со~
ответствуют формулам E.114) и E.115).
Только в случае следов за обтекаемыми телами дело обстоит
немного сложнее, так как здесь, кроме действующей на
оо
тело суммарной силы сопротивления/5^ 2up6yV = 2тср?/0 \ uxr dr
¦ ¦• . ¦ - о
(или приходящейся на единицу длины обтекаемого цилиндра

5.9] I »¦ ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 315
со
силы сопротивления Fi = p^V^i= Р^о Г ui dz) , определяющей
о
«дефект импульса в следе», в условия задачи входит еще одна
размерная величина, а именно — невозмущенная скорость Uo.
Поэтому здесь формулы типа E.116) — E.118) не могут быть уже
выведены на основе одних только соображений размерности.
Однако с помощью немного более специальных рассуждений
и их можно получить, не привлекая точных уравнений гидро-
гидромеханики. В самом деле, воспользуемся тем, что тангенс угла
наклона линии тока осредненного течения в следе к оси Ох ра-
равен -^- = —w - «# —. Отсюда можно заключить, что если
и Uo — щ иа
L(x) —это характерная ширина следа, a U=U(x) —характер-
—характерное значение скоростей hi и w, to
dL U
(
со
Но из постоянства величины N = \ uxrdr в случае трехмерного
о
- со
следа и величины Nx— \ uxdz в случае плоского следа выте-
—со
кает, что UL2 <~ N = const в первом случае и UL~Ni = const
во втором. Эти результаты вместе с соотношением E.121) пока-
/Nx\4* I NU20\4>
зывают, что Z.~ \~тг) ,U—1~т~) -т.е.
в случае трехмерного следа и L—(-77—) '. U—(—!—2-) *, т. е.
в случае плоского следа.
Разумеется, результаты, относящиеся к свободным конвек-
конвективным струям, не надо путать с аналогичными результатами,
относящимися к вынужденной конвекции — переносу пассивной
примеси О (которой может быть также и теплота) свободными
турбулентными потоками динамического происхождения. В этом
случае исходная система уравнений будет состоять нз обычных
уравнений гидромеханики (без члена, описывающего архимедову

316 гл. ш. уравнения рейнольдса [5.9
силу) и уравнения диффузии (или теплопроводности) A.72).
Масштабы длины и скорости здесь, естественно, будут теми
же, что и для соответствующей чисто динамической задачи
(т. е. будут даваться формулами E.110) со значениями показа-
показателей, указанными в таблице), но, кроме того, появится еще
масштаб концентрации (температуры) &(х). Этот новый мас-
масштаб можно определить с помощью дополнительного уравнения
Рейнольдса, получаемого при осреднении уравнения A.72) с
X = 0. Проще, однако, исходить из постоянства массы примеси,
переносимой через любое сечение х = const, сразу показываю-
показывающего, что 6~Ll/s в случае трехмерных течений и Q~L~l в слу-
случае плоских течений. Подробнее о переносе примесей свободны-
свободными турбулентными течениями мы еще будем говорить в гл. 5 в
связи с изучением турбулентной диффузии. Здесь же мы только
отметим, что, зная для свободных турбулентных течений распре-
распределения средней скорости п и средней температуры О и значе-
значения моментов u'wr и Ф'ш', можно определить также значения
соответствующих коэффициентов турбулентного обмена К и Кь и
Л is
найти их отношение а = -р— = -Л-. Измерения, позволяющие
осуществить это, много раз проделывались разными авторами в
течениях разного типа (см., в частности, работы, указанные на
стр. 312); обзор полученных при этом результатов можно найти,
например, в книгах Хинце A959) и Абрамовича A960). В це-
целом все относящиеся сюда результаты сравнительно неплохо
согласуются друг с другом и показывают, что в первом при-
приближении коэффициенты обмена К и-/С» допустимо считать при-
принимающими постоянные значения в каждом поперечном сечении
струи или следа, и что отношение а=К$1К для свободной тур-
турбулентности больше единицы (и именно, а«1,8н-2 для следа
за цилиндром и для плоской струи и а« 1,2-=-1,4 для осесимме-
тричной струи).
Подчеркнем в заключение, что все свободные турбулентные
течения имеют общую очень важную особенность — область
пространства, занятая завихренным турбулентным течением,
здесь в каждый момент времени имеет четкую, но очень непра-
неправильную по форме границу (строго говоря, представляющую со-
собой не поверхность, а очень тонкую зону), вне которой движе-
движение является потенциальным. Как уже объяснялось в п. 2.2,
жидкость может втекать извне в область завихренного движе-
движения, но не может вытекать из него наружу. Проникать же в
область потенциального движения могут только крупномасштаб-
крупномасштабные турбулентные пульсации скорости, затухающие на расстоя-
расстояниях порядка поперечных масштабов L(x) области завихрен-

5.9J 5 5. ТЕЧЕНИЯ В ТРУБАХ И В ПОГРАНИЧНОМ СЛОЕ 317
ного движения. Эти пульсации и создают нерегулярные искрив-
искривления границы.
В качестве иллюстрации к сказанному мы приводим на
рис. 45 великолепную теневую фотографию турбулентного следа
за пролетевшей в воздухе пулей, заимствованную из статьи
Корсина и Кистлёра A954).
Таким образом, всякое свободное турбулентное течение
имеет, по выражению Таунсенда A956), «двойную структуру»:
оно состоит из интенсивной мелкомасштабной турбулентности и
л
Рис. 45. Теневая фотография турбулентного следа за пролетевшей
пулей.
сравнительно мало интерсивных крупномасштабных вихрей,
создающих нерегулярные искривления и движения границы тур-
турбулентной области. Благодаря этим движениям границы в лю-
любой точке свободного турбулентного течения, не слишком дале-
далекой от его оси (или, в случае двумерных течений, от плоскости
симметрии), мелкомасштабная турбулентность будет временами
присутствовать, а временами отсутствовать, т. е. турбулентность
будет перемежающейся. На стр. 268, 269 мы уже указывали па
перемежаемость турбулентности во внешних частях турбулент-
турбулентного пограничного слоя. В свободных турбулентных течениях зона
. перемежающейся турбулентности оказывается, однако, значи-
значительно более широкой, чем в пограничных слоях: если в погра-
пограничных слоях перемежаемость практически наблюдается в пре-
пределах расстояний от стенки от 0,46 до 1,26, то, например, в
плоском турбулентном следе, согласно Корсину и Кистлеру
A954), она имеет место в зоне от 2=0,4L(x) (где г — попереч-
поперечная координата) по меньшей мере' до г = 3,2L(x). Кроме

318 гл. in. уравнения рейнольдса [6.1
свободной турбулентности и внешней части турбулентного погра"-
ничного слоя (во многом схожей со свободными турбулентными
течениями) перемежаемость турбулентности и четкие подвиж-
подвижные границы между турбулентной и нетурбулентной частями
потока наблюдаются, как мы знаем, и в случае течений в тру-
трубах и пограничных слоях при не слишком малых, но и не
слишком больших числах Рейнольдса, способствующих возник-
возникновению турбулентных «пробок» и «пятен» (см. выше. п. 2.1),
а также и в некоторых других случаях (см., например, обзор
Коулса A962)). Можно думать, что подобные явления вообще
счень характерны для широкого круга турбулентных движений
и играют большую роль в возникновении и развитии турбулент-
турбулентности. Однако теоретическое их объяснение пока с наталкивается
на значительные трудности (ср. Коулс A962), Липманн A962)).
§ 6. УРАВНБНИЁ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ
И ЕГО СЛЕДСТВИЯ
6.1. Уравнение для тензора напряжений Рейнольдса
Выше уже отмечалось, что из-за появления в уравнениях
Рейнольдса для среднего движения дополнительных членов, со-
содержащих напряжения Рейнольдса тЭД = — pu'tu'j, система этих
уравнений оказывается незамкнутой. Естественно попытаться
замкнуть ее, дополнив уравнения Рейнольдса новыми уравне-
уравнениями, описывающими изменение во времени самих напряжений
4}]. Эти уравнения для величин zty и будут выведены в на-
настоящем пункте; мы увидим, что и они, в свою очередь, также
содержат ряд дополнительных неизвестных и поэтому снова не
образуют замкнутой системы. Тем не менее, сами уравнения
для величин ъ1}], налагающие на статистические характеристики
турбулентности новые динамические связи, представляют опре-
определенный интерес, так как позволяют сделать ряд качественных
выводов о свойствах турбулентных течений. Особенно полезным
оказывается уравнение баланса турбулентной энергии, описы-
описывающее изменение во времени плотности кинетической энергии
пульсационного движения (или, короче, просто турбулентной
энергии) ?, —-g-РИЖ> подробному рассмотрению этого уравне-
уравнения, все члены которого имеют ясный физический смысл, будет
посвящен ряд последующих пунктов настоящего параграфа.
Для вывода уравнений, описывающих изменение во времени
напряжений Рейнольдса, можно воспользоваться общим мето-
методом составления уравнений для моментов, предложенным Кел-

ftl] § б- УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ- ЭНЕРГИИ 31§
лером и Фридманом A924) (см. также Келлер A925)).
А именно, пусть Ui, и2, ..., uN — какие-то N различных или сов-
совпадающих друг с другом гидродинамических полей турбу-
турбулентного потока сжимаемой жидкости, a xv х2, ...,xN— ка-
какие-то iV различных или совпадающих точек в области про-
пространства, заполненной жидкостью. В таком случае производная
по времени от момента /V-ro порядка
BUlus ... aN(Xv Х2,..., XN, t) = U1(Xvt)u2(X2,t)...UN(XN, t) F.1)
в силу возможности перемены порядка операций осреднения и
дифференцирования может быть представлена в виде
"^" Billet.. uN (Xv Х2,- • • •, XN, t) — ——0j tt2 (X2. t) . . . UN (XN, ty-f-
v t) диЛдх^] ... uN {xN,
_...+«, {xy t) u2 (x2, t)... dUN{*tN't] • F.2)
Теперь достаточно исключить все производные по времени в
правой части последнего равенства с помощью соответствую-
соответствующих гидродинамических уравнений, и мы получим уравнение ба-
баланса для момента Вч.. uN(*i, •••. xN, t), выражающее
-atBUl..,uN (xv ..., xN, t) в виде комбинации моментов самих
гидродинамических полей и их пространственных производных.
Указанный прием, разумеется, может быть применен и к не-
осредненным величинам. Так, например, подставляя уравнения
д dui dui
Навье —Стокса A.6) в равенство -^-ри,и;= ри^-^ + рйу-^-.
получим
доим] л
ди, диЛ I ди, ди,\
Ц +1? - (в|. j± +¦ ом ^). F.3)
дГ
где о,-у = |1 l^"+J~/ — тензор вязких напряжений в несжима-
несжимаемой жидкости. Отсюда, в частности, для плотности кинетиче-
кинетической энергии ?1 = -к-ри?и? получается уравнение

320 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [6.1
где ре = о,,, jp = у 2^ ("ЯГ + 1Г) имеет смысл удельной (на
единицу времени и единицу объема жидкости) диссипации ки-
кинетической энергии. Выражение в скобках в левой части послед-
последнего уравнения представляет собой плотность потока энергии,
обусловленного как непосредственным переносом энергии при
перемещении частиц жидкости, так и работой сил давления и
молекулярных сил внутреннего трения. Правая же часть урав-
уравнения F.4) показывает, что суммарная кинетическая энергия
произвольного объема жидкости изменяется не только вслед-
вследствие механического втекания или вытекания энергии через его
границу и работы приложенных к границе сил давления и моле-
молекулярного трения, но также и вследствие работы объемных сил
и вследствие диссипации, приводящей к переходу части кине-
кинетической энергии в теплоту. '. ¦
Используя теперь вместо уравнений Навье — Стокса урав-
уравнения Рейнольдса E.1)
Т + ТГ 0« А + Р«
и учитывая, что р = const и -^- = 0, аналогично получим сле-
оха
дующее уравнение для тензора
д
[
В частности, для плотности кинетической энергии осредненного
движения Еа = ¦«¦ ?и$и^ получается уравнение
duo
^7' (б-7)
P V^ / « 3 \
где Pes = aa?-^ = -2- 2и\дх7^"дх1 имеет смысл удельной
диссипации энергии осредненного движения под действием

6.1] § 6. УРАВНЕНИЕ БАЛАНСА ТУР8УЛЕНТН0Й ЭНЕРГИИ 321
молекулярной вязкости. Физический смысл всех слагаемых
этого уравнения (за исключением последнего слагаемого, кото-
которое мы подробно рассмотрим ниже) аналогичен смыслу соот-
соответствующих слагаемых уравнения F.4). Заметим лишь, что
плотность потока энергии осредненного движения наряду со
слагаемым и^аа?, описывающим перенос энергии силами моле-
молекулярной вязкости, содержит слагаемое pu'ji'^, описывающее
родственный процесс переноса энергии благодаря действию
«турбулентной вязкости».
Осредняя уравнение F.3) и затем вычитая из него почленно
уравнение F.6), получим искомое уравнение для тензора на*
пряжений Рейнольдса:
Это же уравнение можно получить, составив сначала динамиче-
динамическое уравнение для пульсации скорости и1^=щ—щ (равное
разности 1-х уравнений Навье — Стокса и Рейнольдса)
да, д - _
р+ (p«<+p"
а затем применив формулу F.2) к центральному моменту
и^Иу = 1(/>. Отметим сразу же, что уравнение F.8),
кроме средней скорости щ и напряжений Рейиольдса ри^Иу,
содержит ряд новых неизвестных. Этими новыми неизвест-
неизвестными являются, во-первых, третьи центральные моменты
pu'iU'jit'^, во-вторых, умноженные на v вторые моменты пуль-
пульсаций скорости и ее пространственных производных, входящие
-^ ди'{
в выражения u.aJa и а}а-^~ и непосредственно не выражаю-
выражающиеся через напряжения Рейнольдса; в-третьих, взаимные вто-
-г-, , eu't
рые моменты полей давления и скорости вида р и, и р -~г~
]
(которые с помощью равенства A.9') можно представить в виде
интегралов от двухточечных моментов третьего порядка типа

322 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА - [6.1
u't(x, fyu'jW, f)ti'k(xr, f)). Таким образом, уравнения Рейнольд-
Рейнольдса F.5) и уравнения для напряжений Рейнольдса F.8) снова не
образуют замкнутой системы. Если Теперь мы постараемся до-
дополнить эту систему уравнениями для новых неизвестных, вхо-
входящих в F.8), и начнем с уравнений для третьих моментов
pu'fi'ju'b, то в эти уравнения в свою очередь войдут мно-
многие другие дополнительные неизвестные (например, четвертые
моменты pu^u'jU^ul и третьи моменты типа p'u'ju'k или типа
ди, ди',
-s-^-A-ui; ем. Чжоу Пэй-юань A945а)), и разность между
охт ох„ *
числом неизвестных и числом уравнений станет только еще
больше. Таким образом, составление уравнений для высших мо-
моментов ни на каком этапе не позволяет получить замкнутой
системы уравнений, описывающей турбулентное движение.
Разумеется, систему уравнений F.Б) и F.8) можно попытаться замкнуть,
привлекая для этой пели те или иные дополнительные гипотезы, позволяю-
позволяющие выразить перечисленные выше «новые нензвестные> в уравнениях F.8)
через первые н вторые моменты щ и и{и^. Такие попытки представляют
собой фактически новые варианты «полуэмпирической теории турбулентно-
турбулентности», отличающиеся от теорий, рассмотренных в п. 5.8, лишь тем, что гипоте-
гипотетические связи здесь имеют несколько более сложную структуру, Подобные
усложненные полуэмпнрнческне теории в разное время выдвигались многими
авторами; мы здесь кратко остановимся лишь на некоторых из них. Одной
из первых работ, посвященных попытке замкнуть систему уравнений F.5| и
F.8), была работа Загустнна A938); вслед за ней появилась небольшая
заметка Колмогорова A942), в которой турбулентность характеризовалась
двумя основными параметрами — интенсивностью и масштабом, через которые
выражались затем все члены уравнения баланса турбулентной энергии, выте-
вытекающего из F.8) (близкая идея немного позже была выдвннута также Прандт-
лем A945J). К работе Колмогорова A942) примыкает целая серия работ
Невзглядова A945а, б и др.), предложившего в развитие идеи Колмогорова
несколько различных гипотез для замыкания системы уравнений F.5) н (б.8)\
Аналогичные исследования проводились также в 40-х годах Чжоу Пэй-юанем
A945а, б, 1947). Им, в частности, была впервые предпринята попытка ис-
использовать наряду с уравнениями. F.5) и F.8) также и уравнения для треть-
третьих моментов UiUjU^; появляющиеся при этом четвертые моменты UfUju'^u'i
исключались с помощью гипотезы о равенстве нулю семнинварнантов поля
скорости четвертого порядка или с помощью некоторой родственной гипотезы.
Наконец, уже в 50-х и 60-х годах появились работы Ротта A9516, в) и Да-
Давыдова A958, 1959а, б, 1961), на которых мы остановимся немного более
подробно, чтобы на конкретных примерах, дать представление об общем
характере всего этого круга исследований.
Ротта рассматрииал уравнения F.5) и F.8) для стационарного
плоскопараллельного в среднем турбулентного течения со средней скоростью
Ki(*8) (направленной всюду вдоль оси Ох\) в отсутствие внешних снл. При
этом в целях упрощения предполагалось, Что слагаемыми в квадратных скоб*
ках в левых частях уравнений F.8). описывающими «перенос (диффузию)

6.1] § 6. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ 323
напряжений Рейнольдса», в первом приближении можно пренебречь, рас-
рассматривая лишь те части течения, где турбулентность более или менее близка
к однородной и, следовательно, перенос турбулентных величин из соседних
областей потока играет малую роль. Далее, как и в работах Колмогорова
A942) и Прандтля A945), предполагалось, что турбулентность можно опи-
описать ее интенсивностью * = -j и'^и\ = —- н масштабом / — величиной раз-
размерности длины, определяющей средние размеры «турбулентных возмущений>
и являющейся аналогом «пути перемешиваниям Для вычисления величины
/ Ц да) \
\ dXj + дх, I
Ротта, следуя Чжоу Пэй-юаню A945а, б), воспользовался
тем, что пульсации давления удовлетворяют уравнению Пуассона вида A.9)
и, следовательно, могут быть представлены в виде, родственном (l.EK),
где подынтегральную функцию можно представить в виде двух слагаемых —
одного, зависящего от средней скорости и\(хя), и второго, содержащего толь-
только пульсации скорости. Вклад первой из этих частей в выражение
р' I -з \- -т-^- I может быть представлен в виде ряда последовательных
производных профиля средней скорости и\(х%) с коэффициентами, являющи-
являющимися интегралами от двухточечных вторых моментов поля скорости. Эти
коэффициенты удовлетворяют алгебраическим соотношениям, вытекающим из
уравнения неразрывности, и могут быть приближенно выражены через на-
напряжения РейноЛьдса и масштаб /. Вклад же второй части, зависящий от
двухточечных третьих моментов, Ротта отождествил со значением величины
в однородной турбулентности с постоянной средней ско-
¦*/ '
ростью и предложил вычислять с помощью гипотетического соотношения
(оправдываемого некоторыми качественными соображениями; см. ниже снос-
сноску на стр. 329—330):
т-г 2
где ci — числовой коэффициент, определяемый из эмпирических данных. Ана-
Аналогичную связь вида
, ди, , ди\
la дха >*¦ дха
где С2 и сз —новые числовые постоянные, Ротта предложил использовать для
вычисления «диссипационных слагаемых» в правой части F.8), содержащих
коэффициент вязкости. При использовании этих формул уравнения F.5) и
F.8) позволяют определить зависимость отношений различных напряжений
Рейиольдса от градиента средней скорости и получить некоторые другие ре-
результаты, допускающие проверку иа опыте. При соответствующем подборе
параметров с\, Сг и с3 все эти результаты оказались в неплохом согласии с
данными измерений характеристик турбулентности в канале, выполненных
Рейхардтом A938) и Лауфером A951). Во второй статье Ротта A951в)
в добавление к соотношениям F.10} и F.11) было предложено также диф-
дифференциальное уравнение, описывающее изменение во времени и в простран-
пространстве длины /, и с его помощью было получено более полное объяснение на-
наблюдающихся иа опыте фактов.

324 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [6.1
Более детальная схема получения иа основе уравнений F.5) и F.8)
замкнутой системы полуэмпирическнх уравнений турбулентного движе-
движения была развита Давыдовым. В его работах в отличие от работ Рот--
та в левых частях уравнений F.8) отбрасывались лишь слагаемые
-jr~(p ufija~\~P "/*/«)> описывающие перенос напряжений Рейнольдса, вы-
вызываемый пульсациями давления. Слагаемые уравнений F.8)\ содержащие
множителем коэффициент вязкости ц, могут быть преобразованы к виду
-y—f ди, ди,
(xAu^u, -(- 2ц -з— -^- \ первое слагаемое здесь выражается через иапря-
2
ження Рейнольдса, а второе Давыдов предложил считать равным -g- pEify
(в силу изотропии мелкомасштабных движений, о которой мы еще будем
ди'р ди',
подробно говорить в ч. 2 настоящей книги), где *i = v-g— -g- еще одна
подлежащая определению основная характеристика турбулентности. Для
определения слагаемых в правой части F.8), содержащих давление, Давыдов
использует формулу
2
где С\ — эмпирическая постоянная (родственная постоянной с\ в равенстве
F.10)), a Bij — довольно сложный добавочный тензор, выражающийся через
среднюю скорость, ее пространственные производные н напряжения Рейнольд-
Рейнольдса (этот тензор описывает анизотропию пульсацнонной скорости в погранич-
пограничных слоях около твердых стенок). Далее, для третьих моментов поля ско-
скорости fuiUjUk выводятся уравнения, аналогичные F.8), которые затем под-
подвергаются еще более радикальным упрощениям (в ннх пренебрегается всеми
слагаемыми, содержащими множителем коэффициент вязкости, а также чет-
четвертыми семиинвариантами поля скорости; кроме того, симметричная ком-
комбинация слагаемых вида и',и',-~- заменяется выражением с2 ~ u',u';u't,
1 охъ ¦ о . j
где сг — еще один эмпнрическнй коэффнцнент). Наконец, для определения ei
Давыдов сначала предложил специальное «уравнение переноса», содержащее
кроме Bi только первые, вторые и третьи моменты поля скорости; впослед-
впоследствии, однако, он сам от него отказался (см. Давыдов A961)) и заменил его
уравнением вида:
1 _ д \ dfb е, -7 ди е? d2t.
, ди» ди»
где d — третий эмпирический коэффициент, a 7ft = vUft ~~z~ ~~т~^ > А= 1,2,3 —
еще три дополнительных неизвестных. Теперь уже для замыкания систе-
системы требуется выписать еще и уравнения относительно величии \н, которые
также можно составить, исходя из уравнений F.9) для ut, с помощью об-
общего правила F2}. После значительных упрощений, снова использующих

6.2] § 6. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ 325
некоторые гипотетические связи, эти последние уравнения приводятся к виду
Окончательно, таким образом, получается весьма сложная, но замкнутая си-
система из 23 квазилинейных дифференциальных уравнений относительно 23 не-
неизвестных величин ut, Ujtij, utUjUk, в и ун, содержащая 4 эмпирических
коэффициента, значения которых можно оценить, например, на основании
данных измерений Лауфера A954). Более точная проверка этой системы тре-
требует специальных опытов, в которых тщательно измерялись бы все неизвест-
неизвестные величины, входящие в полученную систему; подобные измерения' до сих
пор, по-видимому, никем не производились.
6.2. Уравнение баланса турбулентной энергии
Аналогично тому, как из уравнения F.3) получается урав-
уравнение F.4) для полной кинетической энергии Е, из уравнения
F.8) после суммирования по I = / получается следующее урав-
уравнение для средней плотности кинетической энергии пульсацион-
ного движения ^
где ре, = авр-^ = -2- 2j [ш+-§?-] имеет смысл средней
. '. /
удельной диссипации энергии пульсационного движения^под
действием вязкости. Выражение в скобках в левой ч'асти
этого уравнения представляет плотность потока турбулентной
энергии, связанного с переносом турбулентной энергии осред-
ненным течением жидкости, пульсациями давления, силами
внутреннего трения (молекулярной вязкостью) и, наконец,
«турбулентной вязкостью», т. е. пульсационной компонентой
1 tv
скорости (слагаемое -^ри'9и'9и'\. Слагаемое
АЩк <6Л6>
входящее в правые части уравнений для Es и Et с разными зна*
ками, очевидно, описывает взаимные превращения энергии
осредненного и пульсационного движений. На вопросе о значе-
значении этого слагаемого мы специально остановимся ниже.

326 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [6.2
Уравнение F.15) и представляет собой общее уравнение ба-
баланса турбулентной энергии. Оно показывает, что плотность тур-
турбулентной энергии в данной точке потока может изменяться
вследствие переноса турбулентной энергии от других частей
жидкости (т. е. диффузии турбулентной энергии), работы пуль-
пульсаций внешних сил, диссипации турбулентной энергии под дей-
действием вязкости и, наконец, вследствие превращения части энер-
энергии осредненного движения в турбулентную энергию или обрат-
обратного превращения части турбулентной энергии в энергию сред-
среднего движения. Энергию турбулентности Et в этом уравнении,
разумеется, можно заменить также интенсивностью турбулент-
турбулентности (т. е. средней кинетической энергией пульсационного
движения единицы массы жидкости) b = — = у и'^. Если при
D д ,Р- д
этом еще обозначить символом -^ =* -=g -f- и„ ^j- индивидуаль-
индивидуальную производную относительно осредненного движения, то в
дп
силу того, что -^-^- = 0, уравнение F.15) можно привести к виду
ОХЛ
Db дпо — д
Уравнение баланса турбулентной энергии F.15) или F.17)
дополняет уравнения Рейнольдса в том отношении, что оно на-
накладывает еще одно важное ограничение на статистические ха-
характеристики турбулентности. Правда, оно содержит новые не-
неизвестные величины ИрИ^, р'и'а и ги не входящие в уравнения
Рейнольдса, т. е. требует более полного описания турбулентного
движения. Однако физический смысл^ слагаемых в уравнении
F.17), содержащих эти новые неизвестные, является достаточно
наглядным, и это очень облегчает попытки их приближенного
выражения через более простые характеристики. Кроме того, в
ряде случаев (например, если турбулентность почти однородна
в пространстве) слагаемыми, описывающими диффузию тур-
турбулентной энергии, вообще можно в первом приближении пре-
пренебречь (в связи с тем, что пространственный перенос энергии
здесь играет малую роль). Использование уравнения баланса
турбулентной энергии в дополнение к уравнениям Рейнольдса
впервые было предложено Колмогоровым A942).
Переходя к более подробному рассмотрению отдельных сла-
слагаемых уравнения баланса турбулентной энергии, начнем со
слагаемых, содержащих пульсации давления. В общем баланс?

6.2) § 6. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ 327
турбулентной энергии Et роль этих слагаемых незначительна;
как показывают уравнения F.15) и F.17), в случае несжимае*
мой жидкости пульсации давления приводят лишь к дополни-
тельному переносу турбулентной энергии от одних частей
жидкости к другим. Поэтому, если рассмотреть объем жидкости,
через границу которого турбулентная энергия не втекает и не вы-
вытекает, то на изменениях полной турбулентной энергии этого
объема наличие пульсаций давления вообще не сказывается.
Кроме того, вклад пульсаций давления в плотность потока тур-
турбулентной энергии, как правило, весьма невелик. Так, например,
в ч. 2 этой книги будет показано, что в случае изотропной тур-
турбулентности р'г имеет тот же порядок, что и ??; следовательно,
\р'а'\^>{р'га'гI ~Et ¦ U', где U'— характерная величина пуль*
сационной скорости. Поэтому относительная роль переноса тур-
турбулентной энергии пульсациями давления по сравнению с пере-
переносом турбулентной энергии осредненным течением жидкости
IpVl U' ,,
здесь определяется значением отношения -^ — — , где и —
| ?<о | и
характерная величина средней скорости. Параметр U'/U («уро-
(«уровень турбулентности») в большинстве реальных турбулентных
течений принимает значения порядка Ш-з-ИО; такой же поря-
порядок будет иметь и относительная величина вклада пульсаций
давления в полный поток энергии в случае изотропной или сла-
слабо анизотропной турбулентности. Поэтому в уравнении балан-
баланса турбулентной энергии пульсациями давления во многих слу-
случаях можно просто пренебречь. Тем не менее, эти пульсации
играют в турбулентном потоке весьма существенную роль. Чтобы
убедиться в этом, рассмотрим величины ?/=урв^ (по i не
суммировать!), имеющие смысл средних плотностей кинетиче«
ской энергии пульсационных движений в направлениях отдель-
отдельных координатных осей. Уравнения F.8) для этих величин в
предположении, что Х\ = 0, могут быть приведены к виду
д
ди, — дщ ¦
ж.-^-^К-ШГ^ F-18)
где р?/ = 1*У] г^Ч > 0; величина реи очевидно, может быть
а
интерпретирована как «диссипация» энергии Е{.
Рассмотрим теперь для наглядности случай, когда осреднен-
ное движение параллельно направлению Oxi (так что йг =»

328 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [6.2
= ы3 = 0) и турбулентность однородна в направлениях осей
Oxt и Ох2 (так что все осредненные характеристики турбулент-
турбулентности могут зависеть лишь от координаты х3). Воспользовав-
ди'
шись уравнением неразрывности -т— = 0, мы можем в этом
случае переписать уравнения F.18) в виде
д /1 -1Г-> дЕх
ди.
Уравнения F.19) показывают, что величины р' -^- и р'-^-
описывают взаимные превращения друг в друга энергии ^про-
^продольных пульсаций и энергий ?2 и Е3 поперечных пульсаций.
Кроме того, из этих уравнений видно, что энергия продольных
пульсаций может еще как-то поддерживаться за счет энергии
среднего _течения (этот процесс описывается слагаемым
— ри^з-з-5- первого уравнения F.19)), но что энергия попереч-
поперечных пульсаций может пополняться только за счет энергии про-
продольных пульсаций. В самом деле, рассматривая стационарный
режим ( т. е. считая, что -~(= СИ и проинтегрировав все урав-
уравнения F.19) по области пространства V, через границу кото-
которой нет потока турбулентной энергии, мы получим соотношения
<6-20>
'S?-dV = 9 f~e3dV>0,
3 v
V V V
Таким образом, энергия осредненного движения, действительно,
передается непосредственно только продольным пульсациям и[.

6.2] § 6. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ . 3.29
а поперечные (Цгльсации и'2 и и'3 получают энергию от продоль-
продольных пульсаций скорости благодаря работе пульсаций давле-
давления. Последни?,. следовательно, осуществляют перераспределе-
перераспределение энергии (Йежду пульсационными движениями различных
направлений, создавая тенденцию к изотропности пульсацион-
ного движений-
Чтобы поручить наглядное представление о механизме
передачи энергии от продольных пульсаций скорости к
поперечным, Заметим, что отрицательный знак величины
, ди, I ¦¦ dtL ди'о \
Р ~fa-^F — \Д -$?¦ -\~Р -л—I означает наличие положительной
корреляции 4ежДУ положительными (отрицательными) пульса-
пульсациями давления и конвергенцией (дивергенцией) продольной
пульсационной скорости. Другими словами, это значит, что кон-
конвергенция и\ приводит преимущественно к положительным, а
дивергенция — к отрицательным пульсациям давления; в то же
время положительные пульсации давления создают преимуще-
преимущественно дивергенцию, а отрицательные — конвергенцию попереч-
поперечных пульсаЦий и\ и и'3. Но так и должно быть: если, например,
два соседних элемента жидкости движутся вдоль осредненного
течения навстречу друг другу, то естественно, что в области
между ними образуется (за счет их энергии) положительная
пульсация.давления и что этот рост давления^приведет к оттоку
жидкости в поперечных направлениях в соответствии с усло-
дц. • s я
вием несжимаемости -^- = 0. Вообще, если «J > и'* и
«j > Ид» так что основную роль играют пульсации скорости
вдоль оси Охи то даже и при отсутствии средней скорости знак
пульсации давления будет <в основном определяться тем, про-
происходит ли сближение или расхождение соседних элементов
_. ди',
жидкости в направлении Одс(; следовательно, величина р' -^~
здесь будет отрицательной и пульсации давления будут стре-
стремиться уравнять энергии различных компонент пульсационной
скорости (ср. работу Бэтчелора A949а), где эта роль пульса-
пульсаций давления была разъяснена на частном примере однородной
турбулентности1)).
') Приведенные соображения оправдывают предположение о том,
ди'х
что величина р' -g^- должна включать слагаемое, пропорциональное
— («1 —иг)~'(и2 ~ из )• содержащееся в формулах F.10) и F.12). Заме-

830 гл- ш уравнения рейнольдса [6.2
Рассмотрим теперь слагаемое А = — ри^ах^» описываю-
описывающее в уравнении баланса турбулентной энергии обмен энергией
между осредненным и пульсационным движением. Если в дан-
данной точке пространства А > 0, то плотность турбулентной энер-
энергии в этой точке возрастает за счет энергии осредненного
движения; наоборот, Л<0 означает, что плотность энергии осред-
осредненного движения в данной точке растет за счет энергии пуль-
пульсаций. Последняя возможность на первый взгляд представ-
представляется парадоксальной; однако этот вопрос требует более
внимательного анализа.
Уравнение F.15) показывает, что при течении несжимаемой
жидкости в поле массовых сил pXi с Jf(=O единственным ис-
источником турбулентной энергии внутри объема, через границы
которого нет притока турбулентной энергии, может быть лишь
трансформация энергии осредненного движения. При этих ус-
условиях возникновение и развитие турбулентности или поддер-
поддержание стационарной турбулентности в указанном объеме воз-
возможны лишь при условии, что интеграл от А по всему объему
положителен (см., например, F.20)). С такими условиями мы
встречаемся, в частности, при течении несжимаемой жидкости
в трубах, каналах и пограничных слоях (при малой «началь-
«начальной турбулентности» набегающего потока), где прямые измере-
—/—; dtls
ния величин риги;. и —- показывают даже, что величина А
здесь всегда оказывается положительной во всех точках тур-
турбулентного потока (в согласии с полуэмпирическими форму-
формулами л. 5.8).
Если же турбулентность имеет какие-либо «внешние» ис-
источники энергии (например еездается искусственным переме-
перемешиванием жидкости или, в случае е-жьщаемой жидкости, обра-
образуется в результате появления пульсаций плотности, возникаю'
щих под действием притока тепла), то не исключена возщ>ж-
/ ди\ да, \
уйм еще, что в сллу тензорного характера величины р 1-т \- ' л от-
(ди, ди, \
л 1" h~ I
дсак это н указано в F.10) н F.12.). Таким образом, естественно думать, что
д
д ТТ
пульсации давления вносят вклад в -^-ри^, Где уф\, пропорциона.льный
—ри^Иу, т. е. приводят к убыванию абсолютной величины все* нэпряисений
Рейнольдса "Щ с / ф J.

6.3] § 6. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИЙ 331
ность превращения энергии турбулентности в энергию осреднен-
ного движения, т. е. выполнения неравенства А < 0. Именно так
обстоит дело в случае атмосферной турбулентности в масштабах
общей циркуляции атмосферы. В этом случае под турбулент-
ностью надо понимать так называемую макротурбулентность —
совокупность нерегулярных крупномасштабных движений типа
циклонов и антициклонов, налагающихся на регулярное тече-
течение общей циркуляции; идея статистического описания такой
макротурбулентности была впервые выдвинута Дефантом
A921). В условиях общей циркуляции отдельные «турбулент-
«турбулентные возмущения» (циклоны и антициклоны) вполне могут воз-
возникать за счет энергии, вносимой локальным притоком тепла,
причем в дальнейшем некоторая часть энергии этих возмуще-
возмущений может передаваться также и осредненному течению общей
циркуляции. Геофизики, изучавшие эмпирические данные о ба-
балансе энергии, импульса и момента количества движения тече-
течений общей циркуляции атмосферы, сравнительно давно уже
пришли к выводу, что данные наблюдений невозможно объяс-
объяснить без допущения о превращениях в некоторых областях ат-
атмосферы энергии нерегулярных возмущений в энергию осред-
ненного течения (см., например, обзорную статью Россби
A948)). Возможность таких превращений энергии была затем
проанализирована и теоретически; см., например, работу Е. Ло-
Лоренца A953), в которой установлены условия, определяющие
знак величины А. Заметим, наконец, что для течений, образую-
образующих общую циркуляцию атмосферы, фактические значения ве-
величины А непосредственно подсчитывались рядом авторов на
основании формулы F.16) по данным метеорологических на-
наблюдений, причем в ряде случаев действительно оказывалось,
что Л<0; по этому поводу см., например, работы Монина
A956в) и Груза A961), содержащие обширную дополнитель-
дополнительную библиографию.
6.3. Общее понятие о коэффициентах турбулентной
вязкости и теплопроводности
Коэффициент турбулентной вязкости был чисто формально
введен в п. 5.1 для случая плоскопараллельного течения жидко-
жидкости; после он несколько раз использовался в § 5 для описания
простейших турбулентных течений в трубах, каналах и погра-
пограничном слое (см. особенно п. 5.8). Сейчас мы покажем, как по-
подобные же коэффициенты могут быть введены и в общем слу-
случае произвольного трехмерного течения.
Будем предполагать, что турбулентность образуется лишь
в результате перехода части энергии осредненного течения в

Зз2 гл. т. уравнения рёйнольдса [6.3
энергию мелкомасштабных возмущений, т. е. за счет того, что
А > 0. Ясно, что в этом случае все статистические характери-
характеристики турбулентности (в частности, напряжения Рёйнольдса)
должны зависеть от поля средней скорости. Учтем теперь то,
что по отношению к среднему движению напряжения Рёйнольд-
Рёйнольдса играют роль, аналогичную роли вязких напряжений в обыч-
обычных движениях жидкости. Поэтому, если -осредненное движе-
движение жидкости имеет характер движения всей жидкости в целом
как твердого тела, т. е. не сопровождается никакими деформа-
деформациями жидких частиц, то естественно предполагать, что рей-
нольдсовы напряжения, действующие на любой выделенный в
жидкости элемент поверхности, будут" направлены по нормали к
этому элементу. Но в таком случае тензор ри^и' будет изотро-
j 2
пен: pu'lu'j = cbiJ, где, очевидно, с =? у ри^и, = -^ pb. Следова-
Следовательно, турбулентная энергия Et = pb в определенном смысле
аналогична давлению. Если же в осредненном движении имеет
место перемещение частиц жидкости друг относительно друга,
то напряжения ^ = щ\и'} должны зависеть от производных
от средней скорости по координатам. Ограничиваясь случаем
небольших градиентов средней скорости, можно в первом при-
ближении учитывать лишь первые производные -^- и зави-
симость "tij от этих производных считать линейной. Это рас-
рассуждение и является основой для попытки описания турбулент-
турбулентности при помощи коэффициентов турбулентной вязкости.
Поскольку напряжения ри^ образуют симметричный тен-
ди.1
зор, их Зависимость от производных -^- должна иметь тензор-
тензорный характер. Величины -^- не образуют симметричного тен-
тензора, но из них_ можно образовать симметричный тензор дефор-
dut да,
мации Фц = <j]jr-+-7jj~' который как раз и характеризует от-
отличие осредненного движения жидкости от движения твердого
тела. Следовательно, тензор pu^u'j естественно считать линей-
dut dui
ной функцией от тензора ®/./=='g3F~+~d* ' обращающейся в
2
jp68,y при Ф^ = 0. Коэффициенты этой линейной функции и
будут иметь смысл коэффициентов «турбулентной вязкости».
Известно, что коэффициенты молекулярной вязкости v и ц
связаны соотношениями v ~ ит1т, ц ~ рит1т со средней скоростью

6.3]' § 6. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ 333
молекул ит и средней длиной свободного пробега молекул 1т.
Можно думать, что для коэффициентов турбулентной вязкости
будут иметь место подобные же соотношения, в которых роль
характеристик молекулярных движений Чщ и 1т будут играть
соответствующие характеристики неупорядоченных турбулент-
турбулентных движений. Аналогичной Um характеристикой, очевидно, яв*
ляется среднее квадратичное значение пульсаций скорости, т. е.
величина У~Ь. Вместо же 1т следует использовать масштаб тур-
турбулентности / — величину размерности длины, описывающую
среднее расстояние, на которое способны перемещаться турбу-
турбулентные образования, сохраняя свою индивидуальность (т. е.
прандтлевский «путь перемешивания», который по порядку ве-
величины совпадает с «длиной корреляции», определяемой по
пространственной корреляционной функции с помощью форму-
формулы вида D.75)). При этом турбулентность может характеризо-
характеризоваться разными масштабами в разных направлениях, так как
турбулентные движения могут быть неизотропными и разные
направления для них вовсе не должны быть равноправными.
Поэтому, строго говоря, в каждой точке потока должен быть
определен эллипсоид масштабов, т. е. задан симметричный тен-
тензор второго ранга 1ц (тензор масштабов), компоненты которого
имеют размерность длины. При надлежащем его определении
величины Mtj — pKtj = pYb 1ц> имеющие размерность коэффи-
коэффициента вязкости, будут иметь смысл коэффициентов турбулент-
турбулентной вязкости. Используя тензор 1ц и учитывая симметрию тен-<
зора pu^u'j, можно положить
ф.,+ /,.*.«)• F.21)
Такая формула была предложена Мониным A9506). Лежащее
в ее основе допущение о линейной зависимости напряжений
Рейнольдса Pu'tu'j от производных -^- можно рассматривать
как еще одну гипотезу того же типа, что и гипотезы, используе*
мые в полуэмпирических теориях турбулентности (см. выше
п. 5.8). Заметим еще, что в наиболее общей форме линейную
зависимость между тензорами риЩ и Фц следовало бы запи-
записать в виде
P"I"y = f ?bbV—РК/М)Ф.|).
где Кца$ — некоторый тензор четвертого ранга, симметрич-
симметричный по t, / и по а, р и удовлетворяющий условию Kjjx? Ф„р=О.

334 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [6.3
Использование формулы F.21) означает, что тензор Кцх? пред-
предполагается вырожденным, а именно — представимым в виде
Впрочем, если не делать никаких дополнительных предполо-
предположений о тензоре 1ц, то формулу F.21) (аналогично формуле
Буссинеска E.5), определяющей скалярный коэффициент турбу-
турбулентной вязкости К) часто можно рассматривать и не как ги-
гипотетическую связь, а просто как определение новых характе-
характеристик турбулентности 1ц, вводимых вместо напряжении Рей-
нольдса %?). В самом деле, равенства F.21) фактически пред-
представляют собой систему шести уравнений относительно шести
неизвестных /n, 1ц, /i3, /22, hs, hs- Перейдя к системе координат,
в которой тензор Фц диагоналей, и учтя, что Фп + Ф22 + Фзз =
= 0, легко убедиться, что детерминант этой системы пропор-
пропорционален (det ||<Dij||J. Поэтому если только det ||Ф^|| Ф 0, т. е.
если тензор Фц не вырождается, то величины li} однозначно
определяются по putuj и наоборот, т. е. формула F.21) всегда
может быть удовлетворена. В этом случае рассуждения, использо-
использовавшиеся при выводе этой" формулы, должны лишь помочь физи-
физической интерпретации величин 1ц и Кц— УЪ1ц, позволяющей,
если надо, сформулировать затем о них определенные гипотезы.
Если же det||Ф»;||= 0, то формула F.21) не только предписы-
предписывает гипотетическую линейную связь между тензорами щ\и'} и
Фг-j, но и налагает определенные ограничения на вид тензора на-
напряжений Рейнольдса, нужные для того, чтобы соответствую-
соответствующая система уравнений относительно 1ц вообще имела решение:
В этом случае рассматриваемая формула иногда может уже ока-
оказаться лишь довольно грубым приближением к действительно-
действительности. Рассмотрим, например, случай, когда оср&дненное движение
является плоскопараллельным, так что ui = ui(xs), Й2=йз=0 и
соответственно этому только компоненты Ф13 и Ф31 тензора
Фц отличны от нуля. Здесь, исходя из геометрических соображе-
соображений, естественно ожидать, что оси Охи Охг, Ох3 будет являться
главными направлениями тензора 1ц. Но тогда формулы F.21)
принимают вид:
Равенство нулю компонент т$ и Т2з согласуется с выводами
из соображений симметрии; однако равенство друг другу сред-

6,3] § 6- УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ 335
них квадратов трех компонент пульсаций скорости является
дополнительным ограничением, вообще говоря, не выполняю-
выполняющимся в реальных плоскопараллельных турбулентных потоках
(ср. выше рис. 26 на стр. 236).
Тем не менее, использование вместо тензора ри'р'. величин
Ь и 1ц часто все же имеет смысл, так как тензор /{,- имеет более
наглядный геометрический смысл и его главные направления
иногда можно задать заранее, исходя из геометрических сооб-
соображений. В ряде случаев можно, даже в качестве первого при-
приближения просто предположить, что 1ц=1'Ьц — изотропный тен-
тензор, т. е. принять за основу гипотезу, выражаемую формулой
F.22)
(заметим, что тензор u'tu'j адесь все равно остается анизотроп-
анизотропным). Гипотеза F.22) близка к той, которая использовалась
еще Буссинеском A897). Фигурирующая здесь величина 1}/Т=К
имеет смысл скалярного коэффициента турбулентной вязкости
(приближенно определяющего сразу все компоненты тензора
напряжений Рейнольдса).
Согласно гипотезе F.22) величина А имеет вид
^ Ф\9, F.23)
', 9
аналогичный выражению для диссипации энергии осредненного
движения pes = -я- V Ф^"; но с заменой коэффициента молеку-
лярной вязкости ц коэффициентом турбулентной вязкости р/С.
Условие Л>0 при этом эквивалентно условию /С>0, так что
формальное использование соотношений F.21), или F.22) в слу-
случаях А<0 означало бы введение в теорию отрицательных коэф-
коэффициентов вязкости. По этой причине понятие о коэффициенте
турбулентной (точнее — макротурбулёнтной) вязкости является
бессмысленным, например, для течений общей циркуляции атмо-
атмосферы (отметим, однако, что «коэффициент макротурбулентной
теплопроводности» для этих течений оказывается, тем не менее,
всегда положительным).
Формулы, аналогичные F.21) или F.22), могут быть напи-
написаны и в применении к турбулентному переносу тепла и мате-
материальных примесей. А именно, если ¦& — концентрация 'примеси,
to плотность турбулентнвго потока примеси по направлению Охи
равную дФ'М/, в общем случае анизотропной турбулентности

336 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА- {6.3
можно предполагать задающейся соотношением
РЩ= — РКШ -^-. F.24)
где компоненты тензора Кы„ имеют смысл коэффициентов тур-
турбулентной диффузии для данной примеси; в случае, когда Ф—
это температура, в обе части F.24) следует еще добавить мно-
житель ср (ср. формулы E.9) и E.9') на стр. 221).
В формуле F.24) учитывается, что турбулентная диффузия,
вообще говоря, анизотропна. При использовании тензора мас-
масштабов турбулентности 1ц можно предполагать, что анизотроп-
анизотропность турбулентной диффузии будет такой же, как и анизотроп-
ность этого тензора, т. е.-что K^}==4?V^hp гДе а» — безраз-
безразмерный параметр. Если предположить, что допустимо пренебречь
анизотропностью тензора масштабов, т. е. принять, что 1ця*1б^,
то F.24) обратится в соотношение
;$-. F.25)
Заметим, что даже в случае плоскопараллельных турбу-
турбулентных течений, для которых F.25) можно рассматривать про-
просто как определение новой величины Кь = <^ьК> это соотношение
становится гипотетическим (и требующим проверни), как только
мы допускаем, что a» = const (т. е. не меняется в пространстве
и времени). Чисто формально здесь можно положить также,что
Ь = V = у и'аи'х, т. е. использовать формулу F.25) для вычис-
вычисления входящих в уравнения F.15) и F.17) третьих моментов
поля скорости:
щ=~ ч?К-щ, F.26)
где а&— численный коэффициент, который может и не совпадать
с а (формула F.26), разумеется, представляет собой еще одну
полуэмпирическую гипотезу). •
Принимая гипотетические соотношения F.22) и F.26), мы
вводим в уравнение баланса турбулентной энергии F.17) зме-
сто характеристик турбулентности ри^Иу и ри^и, характеристики
/и ft (или K=tVb), т: е. существенно уменьшаем число-неиз-
число-неизвестных величин. Дальнейшим шагом в этом направлении будет
установление связи между удельной диссипацией турбулентной
энергии ги также входящей з качестве неизвестной з уравнение
F.17), и величинами / и b (или / и К). Если только допустить,
что такая связь имеет место, то ее зид можно уже однозначно

6.4] 5 6. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ 337
восстановить с помощью соображений размерности:
иЧг 1C
где с4— еще один неотрицательный безразмерный параметр (то,
что мы записываем его как четвертую степень некоторого дру-
другого числа, будет удобно в п. 6.6). Соотношение F.27) опять же
можно рассматривать просто как определение новой величины с,
заменяющей е< (предполагая, что К « / уже заданы, например,
при помощи соотношений zu=pK~{fc~ и К=1УЪ\- Если, од-
однако, мы допустим, что c=const, то тем самым мы сразу пре-
превращаем F.27) в дополнительную гипотезу того же типа, что и
другие гипотезы полуэмпирических теорий турбулентности.
6.4. Баланс турбулентной энергии в сжимаемой жидкости
Учет сжимаемости жидкости и, в частности, пульсаций плот-
плотности р' сразу вносит в изложенные выше расчеты существенное
усложнение. А именно, при этом средняя плотность импульса
оказывается уже равной pu[ = pui-\-pu'r где ри| —p'aj—сред-
—p'aj—средняя плотность импульса пульсационного движения (при отсут-
отсутствии пульсаций плотности обращающаяся в нуль). Аналогично,
средняя плотность кинетической энергии здесь имеет вид
"jnT 1 . " 1 | J
iP«X = Es + Est + Et, F.28)
где Es — плотность энергии среднего движения, Et = -~pu'u' =
1 г-
= -g (р«Х ~Ь Р'ИХ)—плотность энергии пульсационного движе-
движения, a Est = щ'л • их = pV • ив —дополнительная часть пульса-
циоиной энергии, связанная с работой импульса ри[ при пере-
перемещениях жидкости, составляющих осредненное течение.
При составлении уравнений для моментов в случае сжимае-
сжимаемой жидкости в основу должны быть положены общее уравне-
уравнение неразрывности A.1) и уравнения движения A.3), которые
мы здесь перепишем в виде
^Г dJ ~ °'.) = Р*" ' = Ь 2, 3. F.29)
В уравнениях F.29) символом 6и, как обычно, обозначен единич-
единичный тензор, а символом аи—общий тензор вязких напряжений,

338 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [6.4
I dui да, 2 дих \
задающийся формулой at) = ц [щ 4- ^ — -$ -щ; ьи) 4
-j-С-г-^ 8^; остальные обозначения не отличаются от использо-
использовавшихся в уравнениях A.3).Осредняяуравнения A.1) и F.29),
получим соотношения
(»
«? 4- Р~пХ 4- Р~К —
'*;, F.31)
играющие в данном случае ту же роль, которую играют уравне-
уравнения Рейнольдса E.1) в случае турбулентности в несжимаемой
жидкости. С помощью уравнения F.30) и уравнеаия
вытекающего из A.4) (и, следовательно, справедливого лишь в
пренебрежении пульсациями коэффициентов вязкости), можно
найти также выражение для производной ¦¦ L' • При этом мы
получим соотношение
T+di(P"A + P<<4-^-^) = ^4-9; F.32)
где
дри ( др -1 др\ (dix lda,.\
« + te^fed Ft33)
— величина, которая для случая несжимаемой жидкости обра-
обращается в нуль. Сравнение уравнения F.32) (с 6.31) показывает,
что
dt
F.34)
Таким образом, величины ц>{ имеют ясный физический смысл —
они описывают обмен импульсом между осредн&нным и пульса-
ционным движением.
Из уравнений движения F.29) и уравнения неразрывности
A.1) легко получается также уравнение для тензора рщи.], от-
отличающееся от соответствующего уравнения для несжимаемой
жидкости (уравнение F.3) на стр. 319) лишь тем, что под а*,-те-

6.4] § 6. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ 339
перь надо понимать вязкие напряжения в сжимаемой жидкости.
В частности, плотность кинетической энергии Е=-^^иаищ вежи*
маемой жидкости будет удовлетворять уравнению
'&—Р*. "F.86)
отличающемуся внешне от F.4) лишь наличием в правой части
ди.
еще одного слагаемого р -g— , описывающего изменение кинети-
кинетической энергии в результате сжатий и расширений элементов
жидкости (сопровождающихся изменением внутренней энер-
энергии). Взяв среднее значение от всех членов этого уравнения, мы
получим уравнение для средней плотности кинетической энер-
энергии Е. Это уравнение, однако, мы здесь не будем выписывать,
а вместо того выпишем три уравнения для трех составляющих
Es, Est и Et плотности Е:
2_
1 дш 1 Г дпа 1
-35 (*А + ^ « + *&&
где
D д - д - _ дпф Х ..
В этих уравнениях выражение в квадратных скобках описывает
взаимные превращения энергий Es и Est, а выражения в фигур-
фигурных скобках — взаимные превращения Es и Et или Est и Et.
Уравнения F.30) —F.34) и F.36) содержат целый ряд новых
статистических характеристик турбулентности, не содержащих-
содержащихся в соответствующих уравнениях для несжимаемой жидкости.
Наиболее существенными из этих новых характеристик яв-
являются величины ри\—компоненты средней плотности импульса
пульсационного движения, или, что то же самое, компоненты

340 гл. ш. уравнения рейнольдса [64
средней плотности турбулентного потока массы. Если осред-
ненный турбулентный поток массы по направлению среднего
движения отсутствует, то Est = щ'а • иа = 0, и энергия пуль-
сационного движения будет описываться лишь величиной Et.
Самое важное отличие общего уравнения для Et от уравнения
F.15), справедливого для несжимаемой жидкости, заключается
в появлении слагаемого
(%) F.37)
которое мы сейчас рассмотрим несколько более подробно.
В большинстве турбулентных течений, встречающихся на
практике (как в природных условиях, так и в технических уст-
устройствах), основной массовой силой, действующей на жидкость
и производящей работу, является сила тяжести. При этом, на-
направив ось Ох3 вертикально вверх, мы можем положить Х{ =
= Yi—gun, где g— ускорение силы тяжести, a Yt— компоненты
ускорения других массовых сил. Но ускорение силы тяжести
обычно значительно больше, чеминдивидуальное ускорение час-
тиц в осредненном движении -^~ и чем ускорения всех других
массовых сил Yit так что в большинстве задач можно положить
^ F-38)
Смысл этой величины можно уяснить,, заметив, что при наличии
пульсаций плотности о' на турбулентные элементы действует
архимедова сила — p'g, так что В есть средняя работа архиме-
архимедовой силы при турбулентных перемещениях элементов жидко-
жидкости. Таким образом, величина В описывает взаимные превраще-
ния кинетической энергии турбулентности и потенциальной энер-
энергии вертикального столба жидкости непостоянной плотности в
поле тяжести. Особенно существенную роль играют такие вза-
взаимные превращения з случае вертикально стратифицированной
жидкости с переменной по высоте средней плотностью (напри-
(например, в случае атмосферы при отличной от безразличной темпе-
температурной стратификации). Если вертикальная стратификация
жидкости устойчива, то вертикальные перемещения турбулент-
турбулентных элементов сопровождаются затратой энергии на работу
против архимедовых сил, так что В<0 (заметим, что при устой-
устойчивой стратификации плотность убывает с высотой, и пульсации
плотности и вертикальной скорости, очевидно, будут иметь по-
положительную корреляцию). В случае неустойчивой стратифика-
стратификации, наоборот, при вертикальных перемещениях турбулентных
элементов работа архимедовых сил совершается за счет потен-

6.4] § 6. УРАВНЕНИЕ БАЛАНСА ТУРЙУЛЕНТНОЙ ЭНЕРГИИ 341
циальной энергии стратификации и приводит к росту энергии
турбулентности; в этом случае В>0 (корреляция иг3 и р' отри*
цательна).
В случае атмосферной турбулентности и в ряде других важ-
важных случаев для вычисления "величины рп] можно воспользо-
воспользоваться уравнениями теории свободной конвекции и в соответ-
соответствии с A.73) считать, что р'=—Ppf. где р— коэффициент теп*
лового расширения среды. В дальнейшем для определенности
мы будем рассматривать случай газовой среды и в соответствии
с уравнением состояния идеального газа будем считать, что
Р=1/7\ где Т — средняя температура. В таком случае щ\ »
== Т'и'п т. е. турбулентный поток массы оказывается пропор-
пропорциональным турбулентному потоку тепла. Отсюда для величины
В получается выражение
В = ^Щ=^, где q = cjf%. F.39)
/ C
Для приближенного вычисления величины F.39) часто можно
использовать полуэмпирическую формулу q = —
= —срраК-^- (см. F.25)), в силу которой
Иногда, однако, приходится учитывать то, что при вертикальных
перемещениях элементов среды температура Т, вообще говоря,
меняется, т. е. что она не является строго консервативной вели-
величиной. Так как, однако, лучистый и молекулярный теплообмен
между турбулентными элементами и окружающей средой почти
всегда очень мал, то энтропию или функционально с ней связан*
ную потенциальную температуру 6= Т( — Jт (см. выше стр.98)
можно уже считать консервативной величиной. Вследствие ма<
лости пульсаций давления по сравнению с пульсациями темпе-
температуры (на которой основывается все приближение свободной
конвекции) -=-«-=-; поэтому В»~ Ь'и'*. Исходя отсюда, в
То 8
тех случаях, когда соотношение F.40) оказывается неточным
из-за неконсервативности температуры, полуэмпирическое со-
соотношение F.25) обычно можно применить к потенциальной

342 ГЛ. 11Г. УРАВНЕНИЯ РЕЙНОЛЬДСА [6.5
температуре в, положив
В = — а&ЧК-р- F.40')
^ а снова имеет смысл отношения коэффициентов обмена для
теплоты и для импульса).
6.5. Число Ричардсона и коэффициент турбулентной вязкости
в температурно-стратифицированной среде
В предыдущем пункте мы рассмотрели уравнение баланса тур-
турбулентной энергии для произвольной сжимаемой среды. В даль-
дальнейшем, однако, из всех эффектов, связанных со сжимаемостью,
мы будем учитывать только эффект взаимных превращений ки-
кинетической энергии и потенциальной энергии расслоения по плот-
плотности, причем в соответствии со схемой свободной конвекции
плотность будем считать зависящей только от пульсаций темпе-
температуры (но не давления). При этом жидкость можно снова счи-
считать несжимаемой (т. е. использовать уравнение л-^—0);
однако в уравнении для вертикальной компоненты скорости сле-
следует учесть и архимедову силу, в случае газовой среды описы-
описываемую дополнительным слагаемым — ~ V в правой части (ср.
уравнение A.75) на стр 64). Совершенно аналогичные резуль-
результаты получаются также и для несжимаемой жидкости непо-
непостоянной плотности р; в этом случае надо лишь заменить во
всех последующих формулах — •=¦ V на р'.
Итак, будем считать, что сила тяжести — единственная объ-
объемная внешняя сила, производящая работу, и будем исходить
из системы уравнений свободной конвекции, т. е. предположим,
что и3 удовлетворяет уравнению A.75) с р*=1/Г. В таком слу-
случае, повторив снова вывод уравнения баланса турбулентной
энергии, мы придем к уравнению
= -P<^|j+f-7X-PV F-41)
?<*=-2 Р«^- Это уравнение отличается от уравнения F.15),
относящегося к несжимаемой жидкости, только заменой слагае-
слагаемого ри^а z правой части слагаемым В = Щ- Т'и'3, смысл ко-

6.5] § 6. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ ' 343
торого был раскрыт в конце предыдущего пункта. Уравнение
F.41) применимо, в частности, к атмосферной турбулентности,
так как движения воздуха в атмосфере обычно с большой точ-
точностью описываются системой уравнений свободной конвекции.
Заметим теперь, что в условиях развитой турбулентности
вязкие напряжения трения пренебрежимо малы по сравнению
с турбулентными напряжениями Рейнольдса (за исключением
примыкающего к твердым стенкам вязкого подслоя, который мы
здесь не будем рассматривать). Поэтому естественно считать,
что и перенос турбулентной энергии за счет сил вязкости (т. е„
неупорядоченных молекулярных движений) очень мал по срав-
сравнению с переносом энергии турбулентными пульсациями скоро-
скорости, т. е. Что последний член в скобках в левой части F.41)
пренебрежимо мал по сравнению со вторым членом. Рассмот-
Рассмотрим случай, когда осредненное течение однородно в направлении
осей Oxi и Ох2. В таком случае все статистические характери-
характеристики турбулентности будут зависеть только от jc3, причем в силу
уравнения неразрывности здесь -g-- = 0, т. е. мз=0. Будем на-
наряду с обозначениями xt и щ для координат и скоростей исполь-
использовать обозначения х, у, z и и, и, w; тогда, пренебрегая малым
членом g^-"^' мы можем переписать F.41) в виде
<)Ь 1 du'au'aw' I dp'w -1— дп -f— dv g ___ _
— = — — — u'w' v'w' — + г-- Гда'-е..
dt 2 dz p dz dz dz T '*
F.42)
2 2 "¦ 9 P 1 - "
где «X = и' -{-v' -{-w' , a b = ^ = — «X ~ интенсивность
турбулентности (т. е. средняя энергия пульсаций, приходящаяся
на единицу массы жидкости).
Если средняя скорость течения всюду имеет одинаковое на-
направление (скажем, вдоль оси Ох), то уравнение F.42) еще
упрощается; здесь
Последнее уравнение можно также представить в виде
д? .dz \ 2 а а р / dz ^ ' /* \ • /
где
dz dz

344 гл. ш. уравнения рейнольдса [6.5
Безразмерная величина Rf, очевидно, определяет относительную
роль термической конвекции в порождении турбулентной энер^
гии по сравнению с динамическими факторами (передачей энер^
гии от осредненного движения); она называется динамическим
числом Ричардсона. Ясно, что Rf<0 при q>0 (т. е. при неустой-
неустойчивой термической стратификации) и Rf>0 при q<0 (при устой-
устойчивой стратификации); при безразличной же стратификации
Rf=O.
В уравнении F.43) мы уже пренебрегли переносом энергии
силами молекулярной вязкости. Выше также указывалось, что
перенос энергии, обусловленный работой сил давления, обычно
мал по сравнению с ее переносом пульсациями скорости (см.
стр. 327). Поэтому часто в уравнении баланса турбулентной
энергии пренебрегают слагаемым, содержащим пульсации дав-
давления, т. е. полагают
db I du'u'.w' дп —
ж=~ 2 -*?— u'w' -з? о - ВД -«*• • <6-46)
В случае стационарного течения, не сопровождающегося турбу-
турбулентным переносом тепла (т. е. при безразличной термической
стратификации), вблизи стенки образуется логарифмический
пограничный слой, в пределах которого интенсивность турбу-
турбулентности Ь постоянна (равна си\, где с»5 согласно данным
рис. 26 на стр. 236), a u'ji^w' лишь постоянным множителем от-
отличается от «2 • Следовательно, перенос энергии в этом слое
тождественно равен нулю, и в уравнении F.46) здесь отличны
~~i—т ди —
от нуля только слагаемые —и w -^ и —et, которые должны
взаимно компенсироваться. Однако вне логарифмического по-
пограничного слоя и при наличии турбулентного потока тепла
диффузионное слагаемое — ~?~dz u'*u'<iw'> по-видимому, может
иногда оказаться сравнимым по величине с другими слагаемы-
слагаемыми (см. ниже стр. 458—459). Тем не менее, чаще всего им и
здесь пренебрегают, так как обычно это слагаемое все же не
очень велико и, главное, его почти всегда неоткуда определить.
При этом уравнение баланса энергии приобретает относительно
простой вид
^ = _SW^A_Rf)_I,, F.47)
не содержащий уже никаких моментов пульсаций гидродинами-
гидродинамических полей выше второго порядка. Иногда, впрочем, вместо
отбрасывания диффузионного слагаемого предполагают, что в
пограничном' слое это слагаемое пропорционально слагаемому

6.5] § 6. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИЙ 345
— T'w', одновременно с которым оно обращается в нуль
(см., например, Клюг A963), Такеучи и Иокояма A963)). В та-
таком случае вместо уравнения F.47) получается уравнение
*в_ЙЧ?«.A_вК|)_^ F.47')
имеющее столь же простой вид, но содержащее дополнительный
безразмерный параметр а, позволяющий добиться лучшего со-
согласия с эмпирическими данными.
Будем пока исходить из уравнения F.47). Так как всегда
е<>0 и практически всегда — u'w' -^ > 0 (исключительными
случаями, в которых энергия турбулентности передается сред-
среднему течению, мы здесь не будем заниматься), то в силу этого
уравнения стационарная (незатухающая) турбулентность воз-
возможна лишь при
Rf<l. F.48)
Результат F.48) представляет собой фактически критерий воз-
возникновения турбулентности в стратифицированной среде, полу-
полученный с помощью уравнения баланса энергии возмущения (ср.
выше п. 2.9). Как и другие критерии, полученные с помощью
энергетического метода, он, по-видимому, является довольно
грубым, т. е. дает сильно завышенное значение критического
числа Ричардсона. Поэтому исходя отсюда можно лишь утвер-
утверждать, что стационарная турбулентность возможна при Rf<^,
где # = Rfcr наверное меньше единицы (причем, по всей вероят-
вероятности, значительно меньше). Чисто формально значение l/R =
= 1/Rfcr можно отождествить также со значением параметра о
в уравнении F.47') — при таком выборе а энергетический кри-
критерий, получаемый из этого последнего уравнения, оказывается
уже точным.
Воспользовавшись полуэмпирическими соотношениями E.5),
F.26), F.27) и F.40), мы можем преобразовать уравнение
F.46) в следующее полуэмпирическое уравнение баланса тур-
турбулентной энергии:
? g „д? К* , д „db л
Здесь К. — коэффициент турбулентной вязкости (переноса им-
импульса), а аК=Кт и аьК=Кь — коэффициенты турбулентного
переноса тепла и, соответственно, энергии. Пренебрегая диффу-
диффузией энергии (т. е. последним слагаемым в правой части), мы
получим отсюда следующий, эквивалентный F.48) критерий

346 гл. tit. уравнения рейноЛьДсА [6.5
существования незатухающей турбулентности:
Ri<-, * = -?¦- F.50)
Здесь
F.51)
— обычное число Ричардсона (см. формулу B.3') на стр. 98,
д? дЬ дТ „
в которой вместо -^ использовалась величина -§? = -§?—Оа
s соответствии с равенством F.40'), немного более точным, чем
{6.40)). Критерий F.50) , был впервые получен Ричардсоном
A920) (предполагавшим, что а=1); он, очевидно, показывает,
что Ricr < — > но никак не определяет еще тачного значения
RiCr- На стр. 124 мы уже отмечали, что согласно теории гидро-
гидродинамической устойчивости течение расслоенной жидкости ока-
оказывается устойчивым относительно бесконечно малых возмуще-*
ний, если во всех его точках Ri>^; следовательно, RiCr<5
<-^. С другой стороны, однако, есть некоторые основания пред-
предполагать, что, может быть, даже а->-0 при Rf->-Rfcr и турбу-
турбулентность может существовать при сколь угодно больших значе-
значениях Ri (так что Ricr==op; см. ниже стр. 381 и 436).
Так как по определению К-^- = — = и\ то уравнение F.49)
для стационарных условий и в пренебрежении диффузией тур'
булентной энергии может быть представлено в виде
и4 и4 /С3
Отсюда для коэффициента турбулентной вязкости К получается
выражение
К= u,cl (I — Rf)v\ F.52)
Согласно формуле F.52), К как будто бы обращается в нуль
(т. е. прекращается турбулентный обмен) при Rf=l, т. е. Rfcr=l,
Ricr = — в противоречии со сказанным выше. На самом деле,
однако, использование полуэмпирического соотношения F.27)
с с = const при Rf, приближающемся к Rfcr, теряет смысл, так
что и соотношение F.52) здесь не может быть применено.
Заметим теперь, что в отсутствие термической стратификации
в пределах логарифмического пограничного слоя cl—vz (так

6.6] § 6. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ 347
как в силу F.49) здесь cl = К*1' [-?) > а K=*ujs, ~57~
~57
= ^); поэтому при произвольной стратификации удобно поло-
положить
с1 = *г\Щ, К=и,гг\{Щ){\-Щ1и. F.53)
Функция A-i(Rf), очевидно, должна удовлетворять условиям
A,i@) = l и Ki(R)=0, где R = Rfcr. Чтобы подчеркнуть, что
Ki(R)=0, можно ввести в рассмотрение вместо A-i(Rf) функцию
(f такую, что
^^ jL F.54)
с помощью этой новой функции выражение для К записывается
в аналогичном F.53) виде
К= u,%z X (Rf) (l—o Rf)'/4, F.55)
но уже с добавочным множителем а= 1/R при Rf в последних
скобках. Тот же результат F.55), очевидно, можно получить,
если принять, что cl=yzK(Ri), но вместо лренебрежения диффу-
диффузией турбулентной энергии считать эту диффузию пропорцио-
пропорциональной слагаемому 4bT'w' (т. е. использовать вместо F.47)
уравнение F.47') с a=l/R). В соотношении F.55), очевидно,
Я,@) = 1, но теперь уже автоматически K(R)=O, и поэтому мо-
можно допустить, что A-(Rf) нигде не обращается внуль. В п. 7.4
мы увидим, в частности, что разумные в ряде отношений резуль-
результаты получаются, если даже просто положить, что A,(Rf) = l.
Следует, однако, подчеркнуть, что с точки зрения теории такой
выбор функции A-(Rf) ничем не оправдан и он вполне может
быть изменен для получения лучшего согласия с данными экспе-
экспериментов (подробнее об этом мы еще будем говорить в следую-
следующем параграфе).
6.6. Турбулентность в планетарном пограничном слое
атмосферы
В этом и следующем пунктах мы приведем два примера использования
полуэмпирического уравнения баланса турбулентной энергии в конкретных
задачах, иллюстрирующие подход к изучению турбулентных течений, типич-
типичный для полуэмпирических теорий турбулентности.
В качестве первого примера рассмотрим задачу о пограничном слое, 6б-
разующемся в атмосфере около Земли вследствие того, что при движении
воздуха относительно подстилающей поверхности возникают силы трения.
Слой, в котором непосредственно проявляются эти силы, называется Плане-
Планетарным пограничным слоем или, цначе, слщм трения,. Будем рассматривать

318 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [6.6
лишь пограничный слой над плоской однородной подстилающей поверхностью
(которую мы примем за плоскость г •= 0) при стационарных внешних услови-
условиях и в предположении, что термическую стратификацию можно считать без-
безразличной. Кроме того, воспользуемся _тем, что в пределах планетарного
пограничного слоя допустимо полагать p«const; поэтому сжимаемость воз-
воздуха для данной задачи оказывается несущественной. Так как все статисти-
статистические характеристики турбулентности в планетарном пограничном слое
зависят только от г, то здесь можно использовать форму F.42) уравнения
баланса турбулентной энергии. В этом уравнении в рассматриваемом случае
можно пренебречь слагаемым слева (в силу стационарности) и слагаемым
g
~Y T'vd' в правой части (так как стратификацию мы считаем безразличной);
, , 1 djw7
кроме того, мы, как обычно, пренебрежем и членом -=- — , описывающим
р дг
малосущественный эффект переноса турбулентной энергии под действием сил
давления. В результате получается уравнение
ди 6v _
''''
которое после использования полуэмпнрическнх_ гипотез F.22), F.26) н
F.27) (с ab=const) и деления всех членов иа р принимает вид
Это уравнение следует рассматривать совместно с уравнениями Рейиольдса
F.5), которые в данном случае можно записать в виде
dp
(при этом мы пренебрегли вертикальным потоком импульса, связанным с
действием молекулярной вязкости, по сравнению с турбулентным потоком
импульса ри^а» ). Внешние силы Xt, действующие в пограничном слое атмо-
атмосферы, это, во-первых, направленная вертикально вниз сила тяжести и, во-
вторых, перпендикулярная вектору скорости и (т. е. ие производящая рабо-
работы) сила Кориолиса Y =1 [и, «о], где «о—вектор угловой скорости вращения
Земли. Выберем теперь оси Oxi = Ox и Ох2=Оу так, чтобы_ ось Ох была
параллельна приземному ветру. В таком случае величины Х\ и Хг будут
равны соответствующим компонентам ускорения Кориолиса, т. е.
X[ = Yi = 2a>tv, Х4.= У2=—2<BrU, где <вг — вертикальная компонента вектора «о.
Воспользовавшись для вычисления величины рига> полуэмпирической фор-
формулой F.22) и поделив уравнения Рейиольдса на р, мы сможем записать
первые два из этих уравнений (которые нам только и будут нужны) в виде
02 дг р дх дг дг р ду
Горизонтальный градиент давления (-Д, -Д) в рассматриваемой задаче
является заданной величиной, которую мы будем считать не зависящей от

6.6] § 6. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ 349
координат х, у, г (независимость градиента давления от г является обычным
допущением теории пограничного слоя). Вйе слоя трения первыми слагае-
слагаемыми в уравнениях F.59) (которые описывают силу треиия) можно прене-
пренебречь, и движение будет определяться так называемыми формулами геостро-
геострофического ветра:
ii? J^? — Gsina, F.60)
Gcos, FJ
ду 2р<ог дх
1
_ _
где G = ——— | —— -f" [ —*— — скорость геострофического ветра, а a —
2ршг \\дх) \ду I J
f [
рг \\дх) \ду J
I др др\
угол между вектором с компонентами I ^—, -s—I и приземным ветром
(угол полного поворота ветра в слое треиия), подлежащий определению.
Ур_авиеиия F.57) и F.59) позволяют определить распределение ветра
u(z), v(z) и коэффициента турбулентной вязкости К(г) в планетарном по-
пограничном слое атмосферы, если задать каким-либо образом функцию 1(г),
т. е. указать зависимость масштаба турбулентности от высоты. Такая задача
рассматривалась Моиииым A950а) и Блэкедаром A962). Начнем с того, что
оценим изменение с высотой в приземном слое атмосферы х-компоиеиты тур-
турбулентного напряжения трения т^ = ?К-^— = рм*. Интегрируя по высоте
первое уравнение F.59), получим
ul @) - ul (tf0) = f {%>гЪ - i Щ dz < f I-1 Щ dz < %>гНаа.
о7 V P дх] ¦ ^ \ P dxj
Здесь мы воспользовались тем, что отбрасывание члена 2<вги приводит к уси-
усилению неравенства, так как сила Корнолиса частично компенсирует действие
градиента давления. Выберем Но так, чтобы относительное изменение «4 в
слое толщины На не превосходило допуска а, т. е. чтобы выпоиялось не-
U)U0)
равенство s -^в- Для этого, очевидно, достаточно потребовать,
«1@)
чтобы выполнялось следующее неравенство:
Согласно опытным данным, u*/G имеет величину порядка 0,05. Кроме того,
в умеренных широтах 2uh~10~4 сект1, так что при G~10 м/сек получается
«2@)
-j*—^—'250 м. При допуске я=20% получаем оценку толщины приземного
слоя #о~50 м. В пределах этого слоя можно пренебрегать действием силы
Кориолиса (а значит, и обусловленным этой силой вращением ветра с высо-
высотой) и считать и» постоянным, т. е. здесь можно пользоваться обычной тео-
теорией логарифмического пограничного слоя. Следовательно, в этом слое
/^ = хи,г, -г— = —-, -г— = 0, b = c1a* = const, где С\—постоянный коэффи-
OZ f*Z OZ
циент, который можно оценить, например, по данным рис. 26, и, наконец, в

360 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [6.6
силу уравнения F.57)
с1 г 1 F.62)
С
Вернемся теперь к уравнениям F.59). Продифференцировав эти уравне-
уравнения по г, можно записать полученный результат в виде одного равенства
F.63)
, ,,(ди , dv \
где / = л1-з—Г1~§—I— комплексная величина, характеризующая обе
компоненты напряжения треиия (поделенного на плотность р). В призем-
иом слое f, очевидно, принимает значение и». Далее, с помощью величины f
уравнение баланса турбулентной энергии F.57) можно представить в виде
л к
Кроме параметра и*, определяющего режим движения в приземном слое,
уравнения F.63)—F.64) содержат еще параметр Кориолиса 2<вг. Из этих
двух параметров уже можно составить масштаб длины, в качестве которого
мы примем
(постоянная Кармана х здесь добавлена для удобства).
Пользуясь соображениями размерности, теперь можно положить
D-1 F.66)
причем безразмерные функции F(?), Ф(?), ^(S). подлежащие дальнейшему
определению, при ?=0 должны все равняться единице. Для определения
вается, так что Чг(?) 1. При этом допущения уравнения F.63)—F.64)
так что, вообще говоря, необходимо задать еще одно дополнительное урав-
уравнение, определяющее зависимость от высоты масштаба турбулентности /.
В связи с отсутствием надежных данных об этой зависимости в работе Мо-
иииа A950а) для простоты допускалось, что наличие продольного градиента
давления и силы Кориолиса иа масштабе турбулентности вообще не сказы-
сказывается, так что ?EK3 1. При этом допущении уравнения F.63) —F.64)
после подстановки в них формул F.66) принимают вид
СФ ТЕГ = iF< \Р\2-Ф* = -КФ-^ (СФ -|- Ф2), F.67)
где б = а(,х2с2—число порядка единицы. Входящие в эти уравнения функции
F и Ф по своему физическому смыслу должны стремиться к нулю при
. Можно показать, что затухающие решения системы F.67) таковы, что
функция F(t) затухает экспоненциально,' а функция Ф(?)—степенным обра-
образом, а именно—как ^-^1УШ Следовательно, коэффициент турбулентной
вя?кости K{z) здесь асимптотически пропорционален z V® # при 8 > —-

6.6] § 6. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ 351
коэффициент турбулентности неограниченно возрастает с высотой, а при
8 < -я- достигает на некоторой высоте максимума, после чего стремится к
6 •
нулю. Таким образом, учет правой части второго уравнения F.67) (т. е.
учет вертикального переноса турбулентной энергии, создаваемого «турбулент-
«турбулентной вязкостьк») оказывается в рассматриваемой теории существенным для
определения поведения коэффициента турбулентной вязкости К (г) на боль-
больших высотах. .
При 6=0 уравнения F.67) не имеют решений, затухающих при ? ->оо
однако имеется решение, стремящееся к Нулю (по степенному закону) при %,
приближающемся к некоторому конечному значению. Другими словами, тур-
турбулентный пограничный слой имеет в этом случае конечную толщину. Урав-
Уравнения F.67) были проинтегрированы Монииым численно при значениях 0=0
и fl=x2«0,16. В случае fl=0 толщина турбулентного слоя оказалась близкой
к 10Я, т. е. практически весьма большой. Максимум К(г) в этом случае
достигается на высоте г=2,8Я. При г<Ш функции F(t) и Ф(?) для 0=0
и для б=х2 оказались весьма близкими друг к другу.
Когда функция F(?) уже определена, вектор скорости ветра (и, и) иа
различных высотах может быть иайдеи из уравнений F.59), которые удобно
записать для этой цели в виде
и -f iv = G<P -itb-F'{jj\. F.68)
При этом параметры ut и а заранее неизвестны (напомним, что и, входит
также в формулу для масштаба Н), Для их определения воспользуемся тем,
что скорость ветра обращается в нуль на некоторой высоте z0 («высота ше-
роховатости>), которую можно считать заданной. Приравнивая выражение
F.68) при z=zo нулю, получим соотношение
9 (Со) = -^г^ = 1« 2 • F-69)
где Со = Т7« а 1) = -п—— известная величина. Функцию q>(&>) можно
ti ?«0J> N
считать известной, так как функция F(?) уже определена. Следовательно,
F.70)
Кроме того, поскольку г|»=|ф(&>I< T0 ?o»=^(ti), где яр— функция, обратная к
функции |ф|. Последнее соотношение можно переписать в виде
F.71)
чем и завершается определение неизвестных параметров.
Заметим еще, что при аппроксимации распределения ветра во всем слое
трения с помощью формулы F.68) для «шероховатости> z0 следует при-
принимать существенно большие значения, чем при аппроксимации профиля
ветра в приземном слое воздуха. Это естественно, так как при увеличении
вертикальных масштабов рассматриваемого явления необходимо увеличивать
и горизонтальные масштабы и, следовательно, вводить «шероховатость:», ха-
характерную для подстилающей поверхности на больших площадях.
Приведем еще один вывод из рассмотренной теории, полученный в более
поздней работе Казанского и Моиина A961J и касающийся определения

352 гл. in. уравнения рейнольдса F.6
зависимости отношения * — -?¦ от «внешнего параметра> т] = -н ¦¦ Знание
зависимости |(г|) позволяет по измеренной скорости G и известной шерохо-
шероховатости подстилающей поверхности Zo определить также и турбулентное на-
напряжение трения у поверхности Земли, которое является одной из важней-
важнейших характеристик турбулентиостн в прнземиом слое воздухаГ. Как было ука-
указано выше, зависимость 5(г|) можно определить нз соотношения F.69); при
. г0
этом можно воспользоваться малостью аргумента Со=-гг< так что доста-
достаточно определить вид функции F(?) при очень малых С = -тт. Но при ма-
малых г коэффициент турбулентиой вязкости К приблизительио равен ки,г, так
что в первом уравнении F.67) можно заменить множитель Ф единицей.
Тогда решение F этого уравнения, удовлетворяющее очевидному краевому
условию F@) = l, при малых ? будет иметь вид F=l+a?+^ In ?+..., где
а — постоянная интегрирования. Отсюда получаем
где Zi<=?i.H — высота, на которой еще можно полагать /С=хи«г. При этом со-
соотношение ч=«-*—. , вытекающее из F.69), можно переписать в виде
где b=F'(t,\)—Ип (x?i)—комплексная постоянная. Полагая b=A+iB, от-
отсюда получаем
F.72)
Постоянная Ь находится при решении полных уравнений F.67) во всем по-
пограничном слое. При fl=0 для иее получается значение Ь——1,69+2,49 i; при
о=0,16 получается 6=—1,81 + 1,7 i. Сравнение расчетов по формуле F.72) с
экспериментальными данными Леттау A959) показало, что вычисленные при
6=0 значения I оказываются явно завышенными, ио при 6=0,16 они уже
оказываются в качественном согласии с экспериментом (см. рис. 46), причем
можно ожидать, что при некотором увеличении значения в это согласие еще
улучшится.
Близкие результаты были получены также Блэкедаром A962), рассмо-
рассмотревшим ту же задачу, ио пренебрегшим вертикальной диффузией турбу-
турбулентной энергии (т. е. предположившим, что аь=б=0^. Зато в отличие от
Моиниа, этот автор в соответствии с довольно грубыми эмпирическими дан-
данными Леттау A950) принял, что масштаб / возрастает линейно с высотой
лишь в самом нижнем слое атмосферы, а затем скорость его возрастания
убывает, и асимптотически при г->ооои стремится к некоторому постоянно-
постоянному значению к/с. Исходя отсюда, функция cl(z) была выбрана в виде
Что же касается величины к, имеющей размерность длины, то Блэке-
дар предположил, что \ = р -~—, ио одновременно указал, что с тем же

6.6]
§ 6 УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ
353
осиоваиием можно было бы положить \
н-*- = Р1//, т. е. считать, что
jLc) (предположение
я G
р-н—• очевидно, приводит к зна-
значительно более сложному виду функции Ч^)). Числовой параметр 6 был
подобран так, чтобы получаемое значение угла поворота ветра совпало с
данными наблюдений, проводившихся в Брукхевене (недалеко от Нью-
Йорка), Оказалось, что этому условию удовлетворяет значение 0=0,00027,
1/,/в
0,05
0,03
0,02
и
ч.
ч
\
\
V
о Данные Леттау .
в Измерения в брукхевене, июль 1950
д — ч — — .г — 25 ноября 1950
• — п — в Хенсрорде, 1959
Теоретическая кривая Казанского
и Монина (при 0=О,/6)
Теоретическая кривая Блзкедара
о
) О
о
5,0
6J) . 7,0
9,0 10,0
Рис. 46. Зависимость u^/G от 4 =
8,0
по эмпирическим данным
и по теориям Казанского и Моиииа A961) и Блэкедара A962).
Как мы уже видели, задание закона изменения cl с высотой позволяет
получить из уравнений Рейнольдса F.59) и уравнения баланса турбулентной
энергии F.57) замкнутую систему трех уравнений относительно трех неиз-
неизвестных функций (то, что две из этих функций были объединены выше в
оЛну комплексную функцию F, разумеется, не играет никакой роли). Соот-
Соответствующие уравнения были записаны в работе Блэкедара в несколько дру-
другой безразмерной форме, чем в работе Монина, и решались численно. Полу-
чеииые результаты также оказались неплохо соответствующими эмпириче-
? И,
скнм данным о зависимости ветра от высоты и о связи отношения с =-^=г
x.2G
с параметром ¦>) = = (см. рис. 46).

354 гл. ш. уравнения рейноЛьдса . [6.7
6.7. Распределение взвешенных частиц в турбулентном
потоке
Рассмотрим теперь задачу о движении взвешенных частиц в турбулент-
турбулентном потоке несжимаемой жидкости. Теория этого явления была развита в
работах Бареиблатта A953, 1955) (см. также Колмогоров A954)). Основным
предположением указанной теории является допущение о малости размеров
взвешенных частиц (по сравнению с характерным масштабом турбулентно-
турбулентности), позволяющее считать, что они образуют как бы непрерывно распреде-
распределенную в основной жидкости примесь. Полную плотность смеси можно запи-
записать в виде
р = р0 A— s)-f-p,s = po + (pi —PoU F.73)
где ро и pi — плотности среды (т. е. жидкости) и частиц, as — относитель-
относительный объем частиц (в работах по теории движения иаиосов величину s на-
называют «мутностью»). При этом ро и pi являются постоянными, а «мутность»
s в результате турбулентного перемешивания флюктуирует, так что .
Скорость щ движения смеси в данной точке (т. е. скорость движения центра
тяжести бесконечио-малого объема смеси, окружающего данную точку) будет
определяться как среднее взвешенное по массе из скорости движения основ-
основной жидкости Uoi и скорости движения примеси «ц:
^ FJ4)
Уравнения движения для смеси можно записать в виде
-gjT + 3J- tPo A — S) u0iU0a + p,S«1(-«la -f- pblx — aia] = — pg-8,3, F.75)
где p — полное гидродинамическое давление в даииой точке смеси, <^. —
сумма вязкого тензора напряжений в основной жидкости (в присутствии
примеси) и тензора напряжений, возникающих от взаимодействий взвешен-
взвешенных частиц. Из массовых сил мы учитываем" лишь силу тяжести, направлен-
направленную по направлению оси Охг в сторону убывания координаты х3.
Уравнения сохранения массы для основной жидкости и для примеси
имеют вид
<?ро A — 5) , др0 (I — s) Цр, _ n dfls dfjsu^ _-
" di ' дх~а ' dt + дха ~и-
Складывая эти уравнения, получаем уравнение сохранения массы для смеси
<?Р , дрц„
ж + "э^--°- FJ6)
С другой стороны, поделив указанные уравнения соответственно иа ро и pi
и затем складывая, получим уравнение неразрывности для смеси
^ = 0. F.77)
Учитывая малость частиц и приняв дополнительное предположение о ма-
малости индивидуальных ускорений в турбулентном потоке по сравнению с
ускорением силы тяжести g, можно считать, что горизонтальные компоненты
скорости основной жидкости и примеси совпадают, а вертикальные отлн-

6.7] § 6. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ 355
чаются на некоторую величину а — скорость гравитационного оседания ча-
частиц. В дальнейшем мы ограничимся рассмотрением случая малой «мутно-
«мутности», т. е. будем считать, что s<CH- При этом величину а можно считать не
зависящей от s, т. е. постоянной (равной скорости гравитационного оседания
одиночной частицы в неограниченной жидкости). Таким образом, имеем
р0 A — s) uoluOa -f ?isuuuia = р«г«а -+¦ -^- s A — s) а*Ъ13Ъа3.
Уравнения движения F.75) принимают вид
а уравнение неразрывности F.77) запишется в виде
s(l—s)a
-— • F-80)
gj (pi ро) щ;
В дальнейшем нам понадобятся лишь уравнения F.73), F.76), F.79) и
F.80). Рассмотрим с их помощью задачу о распределении взвешенных ча-
частиц в стационарном потоке жидкости, занимающем полупространство, огра-
ограниченное снизу плоскостью *з=0, и однородном в среднем вдоль осей Ох{,
0x2. Прн этом можно считать, что все осредненные характеристики зависят
лишь от координаты г=х3 н что 02=0.
Обозначая ih=w и осредняя уравнение неразрывности F.76), получим
dow r, —
-^— = 0 или pie = const. Поскольку при стационарном режиме вертикаль-
вертикальный перенос массы в среднем , отсутствует, мы должны положить
pw=pw+p'w'=Q. Вспоминая формулу F.73), мы можем переписать послед-
последнее соотношение в виде
w = — <:WI', F.81)
где о = — Из самого существования стационарного распределения
Р
взвешенных частиц следует, что корреляция между w' н s' должна быть
положительной, так как при стационарном режиме регулярное гравитацион-
гравитационное оседание частиц должно быть сбалансировано их турбулентным перено-
переносом вверх, а турбулентный поток массы равен p's>'= (pi — po)w's'. Следова-
Следовательно, w<0, т. е. осредненное движение смеси имеет компоненту, напра-
направленную вниз (напомним, что скорость движения смеси определялась как
среднее взвешенное из скоростей основной жидкости и частиц по массе, а
не по объему).
Осредняя уравнение F.80), получим
д
откуда после интегрирования по г найдем
w = — as (l—s)a -j- const.
Постоянное слагаемое в этой_формуле можно считать равным нулю, так как
при больших г величины s, w's' и, следовательно, w стремятся к нулю.

356 ГЛ. III. УРАВНЕНИЯ РЕЙНОЛЬДСА [6.7
Поэтому, сравнивая последнюю формулу с F.81), имеем
w7? = s(I — s)a « as. F.82)
Если воспользоваться полуэмпирической формулой типа F.25)
^? = -a^|j. F-83)
то последнее соотношение примет вид
°sK^ = -a. F.84)
В качестве осредиеииого уравнения движения смеси используем уравнение
Рейиольдса в проекции иа ось Ох{, которое для не слишком больших г
можно принять имеющим вид' '__
К -^- = и* = const. F.85)
Исключая из F.84)—F.85) величину К, получим
д In s v. ди
- <й
дг ~ и, дг '
где <о = безразмерный параметр. Интегрируя последнее уравнение,
найдем _
_ _ s = ~sae a*, F.86)
где s0— _зиачеии€ s на некоторой условной «высоте шероховатости» го, иа
которой и(г) обращается в нуль.
Приняв для правой части уравнения движения F.79) приближенное зна-
значение— pg6i3, мы убеждаемся, что это. уравнение вместе с уравнением ба-
баланса массы F.76) совпадает с соответствующими уравнениями для сжимае-
сжимаемой жидкости. Поэтому уравнение баланса турбулентной энергии имеет такой
же вид, как в сжимаемой жидкости. Пренебрегая эффектом диффузии энер-
энергии турбулентных пульсаций н другими малыми слагаемыми, запишем ука-
указанное уравнение в виде
(#J-j?-i-V = O, F.87)
причем lV Ь = К, а величина В=—pw'g имеет смысл работы взвешивания
частиц турбулентным потоком в единице объема смеси. Для этой величины
с помощью формул F.73) и F.82) получаем
В = —apgs'w' = — apgs(l — s)a. F.88)
Последнее выражение впервые было получено Великановым A946). Выражая
s'w' с помощью формулы F.83), получим _
С помощью этой формулы уравнение F.87) может быть приведено к виду
* = с4/2AгJA~^К1)' F-89)
где
(ди/дг)г

6.7] S в. УРАВНЕНИЕ БАЛАНСА ТУРБУЛЕНТНОЙ ЭНЕРГИИ 357
— безразмерное число, аналогичное числу Ричардсона. Исключая из F.89)
градиент скорости -g— с помощью уравнения F.85) и соотношения К = i
получим
Ь = С24 1^1 —a Ri, F.90)
При отсутствии взвешенных частиц Ш = 0и6= с2а». Формула F.90) пока-
показывает, что наличие в потоке взвешенных частиц приводит к уменьшению
пульсационной энергии, т. е. влияет на динамику потока. Этот результат
подтверждается прямыми экспериментами. Таким образом, расчет движения
наносов в предположении, что взвешенные частицы не оказывают влияния на
динамику потока (так называемая диффузионная теория), возможен лишь
при достаточно малых Ri. _
Распределение скорости и(г) ¦ в потоке, несущем взвешенные частицы,
может быть найдено с помощью уравнений F.84), F.85) и F.90). Именно,
если ввести безразмерные величины, полагая
«= — FD); К — гм^Ф(Л), с/=%гФ(С), J=S(C), 4=4-, F.91)
и2
где L — —j*—, то указанные уравнения примут вид
№S'= — a>S, l$F' = 1, Ф = W (l 4- -^-V» F-92)
\ F'2 I
Основной интерес представляет функция S(Q, описывающая вертикальное
распределение взвешенных частиц. Исключая из F.92) функции F и Ф, для
величины ДС) = с ... получим уравнение
Баренблатт исследовал решение этого уравнения в общем виде, не зада-
задаваясь конкретной формой функции W, а лишь допуская, что она удовлетво-
удовлетворяет очевидному условию- чР(О) = 1 и является невозрастающей функцией
от числа Ричардсона (поскольку масштаб турбулентности / вследствие нали-
наличия взвеси должен уменьшаться). Результаты анализа показывают, что при
ш<1 и <о>1 характер решения оказывается существенно различным. При
ш>1 (малая скорость потока или крупные частицы) перенос частиц происхо-
происходит в основном вблизи дна потока, причем в придонной области изложенная
теория (основанная на допущении малости s) неприменима и должна быть
заменена более точной теорией. Вне придонной области Ri->0, так что рас-
распределение взвешенных частиц асимптотически приближается к распределе-
распределению, получающемуся согласно диффузионной теории. При ш<1 (большая
скорость потока или же мелкие частицы) перенос частиц происходит в осноз-
ной массе потока. Распределение частиц на больших высотах асимптотически
приближается к некоторому предельному автомодельному распределению
(Ri -> const)-, при котором s обратно пропорционально г, а
и (г) =—In г -f~ const. При этом существует некоторое предельное насыще-
насыщение потока частицами, такое, что при еще большем насыщении изложенная
теория становится неприменимой в придонной области.

ГЛАВА IV
ТУРБУЛЕНТНОСТЬ
В ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННОИ СРЕДЕ
§ 7. ОБОБЩЕНИЕ ТЕОРИИ ЛОГАРИФМИЧЕСКОГО ПОГРАНИЧНОГО
СЛОЯ НА СЛУЧАИ ТЕМПБРАТУРНО-СТРАТИФИЦИРОВАННОЙ СРЕДЫ
7.1. Турбулентный пограничный слой
в температурно-стратифицированной среде как модель
приземного слоя атмосферы
В предыдущей главе были подробно рассмотрены основные
закономерности турбулентных течений жидкости в пограничном
слое над неограниченной плоской пластинкой. Полученные вы-
выводы мы сравнивали с эмпирическими данными, относящимися
как к искусственным течениям, -создаваемым в лаборатории, так
и к наблюдаемым в атмосфере движениям воздуха вблизи по-
поверхности земли. При этом, однако, нам пришлось оговорить, что
из наблюдений в атмосфере для данной цели могут использо-
использоваться только наблюдения, относящиеся к нейтральной (безраз-
(безразличной) стратификации, т. е. к тем случаям, когда в нижних
слоях воздуха температура4 практически не меняется с высо-
высотой '). Но такая нейтральная стратификация довольно редко на-
') Вообще говоря, под нейтральной стратификацией следует понимать
распределение температуры, при котором ее вертикальный градиент dTJdz
точно совпадает с адиабатическим градиентом — Ga, определенным иа
стр. 97. Действительно, только при этом условии вертикальные перемещения
элементов среды не будут сопровождаться ни затратой, ни освобождением
потенциальной энергии. Поскольку, однако, характерные значения вертикаль-
вертикальных градиентов температуры в нижних десяти-пятнадцати метрах земной
зтмосферы почти на два порядка превосходят величину Ga, отличием этой
эеличины от нуля здесь чаще всего можно пренебречь. С этим обстоятель-
обстоятельством связано также и то, что в приземном слое обычно можно не различать
обычную температуру Т и потенциальную температуру 6 формулы B.4).
Поэтому в дальнейшем для простоты мы все время будем говорить
об обычной температуре, хотя, строго говоря, в большинстве случаев
используемые нами соотношения будут точно выполняться лишь для потен-

7.1] S 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 359
блюдается в природе. Действительно, днем обычно температура
заметно понижается с высотой, а ночью она, как правило, повы-
повышается с высотой (как говорят, имеет место инверсия темпера-
температуры), так что нейтральной стратификация оказывается лишь
в течение небольших промежутков времени перед заходом и по-
после восхода Солнца. Следовательно, движения в приземном слое
воздуха в большинстве случаев не могут1 быть уложены в про-
простую схему турбулентного пограничного слоя, рассмотренную
в гл. 3.
Итак, как правило, при изучении турбулентности в призем-
приземном слое атмосферы необходимо учитывать наличие в атмо-
атмосфере температурной стратификации, создающей систематичес-
систематическое изменение плотности среды с высотой. Как известно, в поле
тяжести наличие неоднородностей плотности жидкости р при-
приводит к появлению архимедовых сил, способствующих переме-
перемещению вверх жидких частиц, менее плотных, чем окружающая
среда, и перемещению вниз частиц, более плотных, чем окру-
окружающая среда '). Эти архимедовы силы складываются с силами
чисто гидродинамического происхождения, которые действуют
на жидкие частицы и в отсутствие силы тяжести. В результате
частицы менее (более) плотные, чем окружающая среда, при
движении вверх (вниз) получают дополнительную энергию за
счет работы архимедовых сил, а при движении вниз (вверх),
наоборот, теряют часть своей энергии на преодоление архиме-
архимедовых сил. Тем самым потенциальная энергия расслоенной по
плотности среды в поле тяжести может непосредственно пере-
переходить в энергию турбулентности, а энергия турбулентности мо-
может обратно переходить в потенциальную энергию неоднородной
тяжелой среды. Количественному учету влияния этих переходов
энергии на режим турбулентности и будет посвящена настоя'
щая глава.
В п. 6.4 был подсчитан вклад, вносимый работой -архимедо->
вых сил в баланс турбулентной энергии. Этот вклад (на еди-
единицу объема) дается выражением
? G.1)
циальной температуры. Точно так же и в § 8 мы не будем специально ого-
оговаривать, что в некоторых случаях (относящихся к наблюдениям в относи-
относительно толстом слое воздуха порядка нескольких десятков метров) исполь-
используемые эмпирические данные фактически относились ие к обычной, а к по-
потенциальной температуре.
'), Здесь и ниже под архимедовой силой всегда будет пониматься раз-
разность выталкивающей силы, описываемой законом Архимеда, и объемной
силы тяжести. В однородной (нестратифицироваииой) среде эти две силы
точно уравновешивают друг Друга, и поэтому силу тяжести можно просто-
ие учитывать (ср. сноску на стр. 39).

360 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.1
где w' — пульсация вертикальной скорости (см. формулу F.38)
на стр. 340). Из выражения G.1) видно, что стратификация воз-
воздуха будет влиять на турбулентность, лишь если пульсации
плотности р' будут коррелированы с пульсациями w'. Далее нам
будет удобно перейти от пульсаций плотности, непосредствен-
непосредственное измерение которых в атмосфере очень затруднительно, к
пульсациям температуры, легко доступным, непосредственному
измерению. При этом, как и в п. 6.5, мы будем учитывать только
пульсации плотности, связанные с пульсациями температуры,
а гораздо меньшими пульсациями плотности, вызываемыми от-
относительно очень малыми пульсациями атмосферного давления,
пренебрежем. Так как в случае не слишком больших пульсаций
температуры вполне можно полагать р'~— (plT)T', где Г —аб-
—абсолютная температура, отсчитываемая от абсолютного нуля, то
в этом приближении
-f=-q, G.2)
CJ
где q = cppw'T' — вертикальный турбулентный поток тепла (см.
выше стр. 341). Отсюда видно, что в атмосфере влияние архиме-
архимедовых сил на турбулентность непосредственно связано с турбу-
турбулентной теплопередачей от подстилающей поверхности к атмо-
атмосфере или наоборот. Это обстоятельство снова приводит к вы-
выводу, что указанное влияние должно исчезать при равном нулю
вертикальном градиенте температуры: в самом деле, согласно
основной формуле полуэмпирической теории,
где Кт — коэффициент турбулентной температуропроводности,
и, следовательно,
S = -f 7*7-^. G-4)
так что 5 = 0 при -^- = 0.
Мы видим, что при теоретическом анализе турбулентных
процессов в приземном слое атмосферы надо учитывать нали-
наличие вертикальной температурной стратификации и связанного
с ней вертикального турбулентного потока тепла. С другой сто-
стороны, горизонтальной неоднородностью подстилающей поверх-
поверхности, всегда в какой-то мере имеющейся в реальной атмосфере,
естественно на первых порах пренебречь. В самом деле, можно
надеяться, что по крайней мере в случае сравнительно ровной

7.1] 5 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 361
подстилающей поверхности, характер которой не меняется за-
заметно на протяжении двстатечнв большой еблаети, эта неодно-
неоднородность не будет играть очень большой роли; в то же время
ее учет очень осложняет теоретический анализ. Поэтому в даль-
дальнейшем мы будем рассматривать лишь упрощенную модель тур-
турбулентности в жидкости, заполняющей полупространство над бес-
бесконечной однородной плоской поверхностью z=0 постоянной
шероховатости z0 (высотой вытеснения h0, учет которой сводит-
сводится к простому сдвигу начала отсчета значений г, мы в дальней-
дальнейшем для простоты также будем пренебрегать). В соответствии
с этим в настоящей главе мы всегда будем предполагать, что
все одноточечные осредненные характеристики гидродинамиче-
гидродинамических полей зависят только от вертикальной координаты г.
Допуская, что все одноточечные моменты зависят только от
2, мы тем самым неявно предполагаем, что эти моменты могут
быть определены, т. е. .что значения всех гидродинамических
полей в приземном слое атмосферы обладают определенной ста-
статистической устойчивостью. Вообще говоря, это предположение
также может вызывать сомнения, так как условия в атмосфере
существенно зависят от времени суток и от времени года, при-
причем, кроме регулярных суточных и годовых колебаний, значения
любого гидродинамического элемента в данной точке атмосферы
испытывают еще нерегулярные колебания самых разнообразных
периодов. Эти нерегулярные колебания мОжно рассматривать
как проявления турбулентности различных пространственных
масштабов, от весьма малых (порядка сантиметров, и долей
сантиметра) и до очень больших — порядка размеров циклонов
и антициклонов или даже масштабов неоднородностей общей
циркуляции атмосферы. Поэтому временные средние значения,
например, температуры или скорости ветра в фиксированной
точке атмосферы оказываются, во-первых, существенно завися-
зависящими от величины интервала осреднения и, во-вторых, при дан-
данном масштабе осреднения колеблющимися от выборки к вы-
выборке под действием компонент турбулентности с периодами,
сравнимыми с величиной интервала осреднения или превосходя-
превосходящими эту величину. Указанное явление, называемое «эволюцией
уровня» метеорологических полей, существенно затрудняет по-
попытки определения статистических характеристик таких полей..
Тем не менее, опыт показывает, что если ограничиться лишь на-
наблюдениями, относящимися к определенному сезону года, опре-
определенному времени суток и определенным синоптическим усло-
условиям (т. е. определенной «погоде»), то при осреднении по
временному интервалу т, заметно превосходящему характерный
период «макроструктурных элементов» (турбулентных образова-
образований, содержащих основную долю энергии турбулентности),

362 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.1
средние значения метеорологических полей будут уже относитель-
относительно устойчивыми. Но в таком случае соответствующие наблюдения
можно считать образующими «статистический ансамбль», позво-
позволяющий производить вероятностное осреднение. В приземном
слое воздуха временной, масштаб макроструктурных элементов
можно оценить по порядку величины как отношение L0IU, где
U — характерное значение скорости ветра, a Lo — характерный
горизонтальный масштаб макроструктурных элементов, изме-
измеряющийся десятками или немногими сотнями метров. Поэтому
Lo/U имеет порядок нескольких десятков секунд, и при осред-
осреднении по интервалам времени порядка десяти-двадцати минут
средние значения скорости ветра, температуры и т. д. оказы-
оказываются уже относительно устойчивыми и могут* рассматриваться
как приближенные значения вероятностных средних для соот-
соответствующих случайных полей. Правда, при дальнейшем значи-
значительном увеличении периода осреднения до интервалов порядка
нескольких часов или еще больших средние значения заметно
меняются и могут снова стать малоустойчивыми за счет влияния
длиннопериодных «синоптических колебаний», относящихся уже
к турбулентности средних масштабов, а затем и к макротурбу-
макротурбулентности; однако такой турбулентностью мы здесь не будем
заниматься.
Кроме предположения о горизонтальной однородности, мы
примем еще некоторые упрощающие предположения, касаю-
касающиеся гидродинамических уравнений, описывающих рассматри-
рассматриваемую нами турбулентность. Прежде всего в соответствии со
сказанным выше мы пренебрежем изменениями плотности, вы-
вызываемыми пульсациями давления, и ограничимся уравнениями,
линеаризованными относительно отклонений полей плотности,
температуры и давления от соответствующих «стандартных зна-
значений» ро, То и р0 (зависящих только от z и удовлетворяющих,
уравнению статики dp<Jdz=—pog и уравнению состояния ро=
—RqoTo)- Величины ро=р и То мы будем в дальнейшем даже
считать просто постоянными, так как их изменения с высотой в
приземном слое толщиной в несколько десятков метров прене-
пренебрежимо малы. В таком случае уравнения движения обратятся
в уже известные нам «уравнения теории свободной конвекции»:
да . да . да . да 1 до'
¦dt+u-^+v^+w^=-Ta-o4
dv.dv.dv, dv I dp'
dw , dw . dw . dw 1 dp' . . Z -n

7.1] § 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЙ ЗбЗ
В этих уравнениях член —-М-Т', описывающий «архимедовы
* о
ускорения» жидких частиц, явно учитывает влияние силы тяже-
тяжести. В то же время сила Кориолиса здесь отброшена, так как
согласно оценке, приведенной на стр. 349, эта сила в преде-
пределах нижних 50 м (или околотого) не оказывает заметного влия-
влияния «а осредненное движение, а, значит, и тем более не может
влиять на пульсационное движение, скорость которого в нижней
атмосфере примерло на порядок ниже средней скорости. Разу-
Разумеется, выше немногих десятков метров над поверхностью земли
уравнения G.5) без силы Кориолиса уже становятся неприме-
неприменимыми; это надо иметь в виду при сопоставлении выводов из
указанных уравнений с данными наблюдений.
Уравнение неразрывности в приближении свободной конвек-
конвекции может быть записано так же, как и в случае несжимаемой
жидкости:
ди dv .dw п ._ fi4
В силу горизонтальной однородности отсюда вытекает, что
гу = О, так что осредненное движение здесь является плоскопа-
плоскопараллельным и задаётся вектором средней скорости и(г) =
={U(z), V(z), 0}. Ясно также, что в отсутствие силы Кориолиса
и при постоянном по высоте горизонтальном градиенте давле-
давления направление вектора и {г) не может зависеть от г. Напра-
Направим теперь ось Ох вдоль вектора и (г). В таком случае будет
справедливо равенство v = 0; поэтому распределения вероятно-
вероятностей для гидродинамических полей здесь естественно считать
инвариантными не только по отношению к параллельным пере-
переносам в плоскости Оху, но и по отношению к отражениям отно-
относительно плоскости Oxz. Отсюда, в частности, вытекает, что
тж„ = --ро«'и' = О и т„2=— pot/a/= 0.
Учитывая, что средняя сила ветра в приземном слое меняет-»
ся за сутки на величину порядка 10 м/сек, нетрудно подсчитать,
что в обычных условиях (при которых не проходит какой-либо
особенно быстрой смены погоды) член с производной -?- в ос-
редненном первом уравнении G.5) оказывается даже заметно
меньшим, чем член с градиентом среднего давления -^ или чем
средняя кориолисова сила. Поэтому при осреднении уравнений
G.5) производные по времени также можно откинуть и считать,
что в приземном слое
|i=:i=: const G.7)

364 гл. iv. тёмпературно-стратифицированная среда [7.1
(ср. выше уравнение E.11) на стр. 222). Таким обр азом, среднее
течение в приземном слое можно считать не только плоскопа-
плоскопараллельным, но и стационарным, а напряжение трения t = po«2
(вертикальный поток импульса) —постоянным по высоте.
Кроме уравнений G.5) и G.6), мы должны использовать
еще и уравнение притока тепла, определяющее изменения во
времени температуры Т. Согласно результатам п. 1.5 это урав-
уравнение можно записать в виде
+ u + v + W C^T + Q G<8)
(дТ
где Q — приток тепла за счет излучения и за счет изменений
фазового состояния содержащейся в воздухе влаги (другими
формами притока тепла и, в частности, притоком тепла за
счет диссипации кинетической энергии в приземном слое вполне
можно пренебречь). Если мы пренебрежем и притоком тепла Q,
то получим обычное уравнение теплопроводности
дТ . дТ . дТ . дТ
осреднение которого приводит к выводу, что в стационарных
условиях
q = cp?ow'T' — срРоХ-gj = const, G.9)
т. е. что средний поток тепла по вертикали, создаваемый моле-
молекулярной и турбулентной теплопроводностью, является постоян-
постоянным (ср. уравнение E.73') на стр. 280, отличающееся от G.9)
лишь выбором положительного направления потока q). Если же
учесть и величину Q (основную часть которой обычно состав-
составляет радиационный приток тепла), то вместо G.9) мы получим
более сложное уравнение
<7 + <7, = const, G.9')
где Q = —-gjj-, так что q, обычно можно отождествить со сред-
средним лучистым потокам тепла по вертикали. Согласии предвари-
предварительным данным Робинсона A950) (см. также Халтинер и Мар-
Мартин A957), гл. 15) существенное изменение потока qs с высо-
высотой, по-видимому, обычно имеет место лишь в тонком слое
воздуха около поверхности земли, толщина которого не пре^
восходит (или лишь немного превосходит) 1 м. Если это дей«
ствительно так, то, рассматривая более высокие слои, можно
полагать qs = const, т. е. пренебрегать лучистым притоком
тепла Q. Косвенным подтверждением этого обстоятельства мо-

7.11 S 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 365
жет служить также то, что теория, основанная на уравнении
G.9), как будет видно из дальнейшего, в большинстве случаев
удовлетворительно согласуется с данными наблюдений в при-
приземном слое1). В целом, однако, вопрос о законности при-
приближения G.9) в приземном .слое воздуха пока еще нельзя
считать окончательно выясненным ни теоретически, ни экспери-
экспериментально. Особенно много сомнений с этой точки зрения вызы-
вызывают случаи очень устойчивой стратификации (наблюдаемой,
например, в ночное время), когда турбулентный поток тепла q
очень мал, а изменение с высотой потока qs может быть до-
довольно заметным (см. Функ (I960)). Поэтому попытки более
точного учета влияния радиационного теплообмена на турбу-
турбулентность, начатые работами Таунсенда A958) и Ямамото и
Кондо A959), следует считать вполне актуальными. Поскольку,
однако, в этом направлении пока еще имеются лишь весьма
предварительные оценки, мы ограничимся здесь рассмотрением
только более грубой теории, исходящей из предположения G.9),
построение которой во всяком случае следует считать необходи-
необходимым первым шагом к разъяснению закономерностей турбулент-
турбулентности в приземном слое.
Теперь мы можем окончательно описать ту теоретическую
модель, изучению которой будет посвящена настоящая глава.
Мы будем рассматривать плоскопараллельное стационарное те-
течение жидкости в полупространстве z > 0 над однородной по-
поверхностью 2 = 0 (характеризуемой определенной шерохова-»
тостью 20), описываемое «уравнениями свободной конвекции»
G.5), G.6) и G.8') и удовлетворяющее условиям G.7) и G.9)
с заданными значениями т и q (эти условия играют здесь роль
граничных условий на верхней границе приземного слоя). Со-
Согласно сказанному выше, можно ожидать, что эта модель будет
сравнительно хорошо соответствовать реальным условиям в
нижнем слое атмосферы (порядка нескольких десятков метров)
над относительно ровной и однородной подстилающей поверх-
поверхностью и в условиях устойчивой погоды (за исключением, быть
может, тонкого подслоя, непосредственно примыкающего к
земле, и отдельных случаев, когда турбулентный обмен особен-
особенно мал или изменение по высоте радиационного потока тепла qs
особенно велико). Можно думать также, что та же модель мо-
может быть применена и к некоторым другим течениям — напри-
например, к турбулентности в придонном или приповерхностном слое
') Напомним, впрочем, что логарифмический профиль средней скорости,
вытекающий из теории лишь при т=const, в трубах неплохо выполняется
почти 'вплоть до самого центра трубы, где т=0. Поэтому указанное здесь
косвенное доказательство никак нельзя считать очень убедительным.

366 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.2
моря в условиях изотермии, но заметной вертикальной страти*
фикации по солености (а следовательно, и по плотности р), и к
некоторым искусственным турбулентным потокам, создаваемым
в лаборатории (в случае стратификации по плотности мы долж-
1дТ ' 1 dp
ны только, разумеется, заменить всюду ~jr~g^ на ~~§г' а
Т'/Т— на —р'/р]. В дальнейшем, однако, мы для определенно-
определенности все время будем говорить о турбулентности в приземном
слое атмосферы (так как именно к ней будут относиться почти
все привлекаемые нами эмпирические данные), понижая всюду
под «приземным слоем» указанную идеализированную модель
стратифицированной среды.
7.2. Применение соображении размерности к турбулентности
в стратифицированной среде
Характеристики турбулентности в температурно-стратифици-.
рованной среде, описываемой уравнениями G.5), G.6) и G.8')
и условиями G.7) и G.9), очевидно, могут зависеть только от
небольшого числа физических величин. А именно, они могут
зависеть от параметров у-. р0) у и х. входящих в указанные
уравнения, от значений т (или и*) и q, задающих потоки им-
импульса и тепла, идущие из бесконечности к поверхности 2 = 0
(или наоборот), и характеризующих динамическое и тепловое
взаимодействие приземного слоя воздуха с подстилающей по-
поверхностью, и от параметра шероховатости z0, суммарно опи-
описывающего геометрические свойства подстилающей поверхног
сти. При этом существенно, что не все эти параметры играют
одинаково важную роль. Прежде всего напомним, что в обла-
областях с достаточно развитой турбулентностью (т. е. практически
всюду кроме весьма тонкого подслоя, прилегающего к подсти-
подстилающей поверхности) потоки тепла и импульса, обусловленные
молекулярной теплолроводностью и вязкостью, всегда очень
малы по сравнению с турбулентными потоками тепла и импульса
(см., .например, стр. 220, 229 и 281). Поэтому в этих областях
члены уравнений G.5) и G.8'), содержащие коэффициенты v
и %, обычно можно просто опустить. Но тогда соотношения G.7)
и G.9) можно переписать в более простой форме
— pou'wf = * = const, cpp0T'w' — q = const, G-10)
показывающей, что характеристики турбулентности здесь не
должны зависеть от v и %. Что же касается параметра шерохо-

7.2] § 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 367
ватости z0, то он определяет граничные условия на поверхности
земли и через эти граничные условия влияет также на абсо-
абсолютные значения средней скорости п(г) и на разность средних
температур T(z)—Т@) на значительных расстояниях от под-
подстилающей поверхности.Однако законы изменения средней
скорости и средней температуры на расстояниях z, на которых
непосредственное влияние подстилающей поверхности уже не
ощущается, от z0 не должны зависеть, а должны определяться
лишь значениями т и q потоков импульса и тепла. Иначе го-
говоря, изменение параметра шероховатости z0 может привести
лишь к сдвигу кривых п=п(г) и T=T(z) на некоторое по-
постоянное значение, но не должно влиять на форму профилей
п(г) и T(z). Таким образом, зависимость от высоты градиентов
средней скорости и температуры и других родственных им
осредненных характеристик развитого турбулентного режима
в приземном слое воздуха должна определяться значениями
лишь следующих четырех параметров: плотности ро, «параметра
плавучести» g/T0 (характеризующего влияние архимедовой силы
на турбулентность), турбулентного напряжения трения т (или
и, = l/ — ) и вертикального турбулентного потока тепла q
(или q/cj,p0) '). При этом в случае q = О (т. е. при безразлич-
безразличной стратификации, когда -^ = 6\ влияние архимедовых сил
на турбулентности не должно сказываться, т. е. зависимость
от параметра -М- должна исчезнуть. В этом случае мы возвра-
* о
щаемся к турбулентност-и в однородной среде, для которой
') Заметим, что это основное для последующей теории предположение,
кажущееся совершенно естественным, иногда вызывает некоторые возраже-
возражения. Так, иногда высказывается мнение о том, что профили температуры
и ветра в стратифицированной атмосфере должны зависеть от молекулярных
констант v и х или хотя бы от их отношения — числа Прандтля Pr=»v/x
(см., например, Таунсенд A962а)). В ряде случаев основой для такого мне-
мнения служит вызывающая много разногласий теория турбулентной конвекции
Малкуса A9546) (относительно которой см. также Тауисенд A9626) и Спи-
гел A962)), в которой молекулярные константы играют существенную роль
при всех г. Влиянию числа Рг на турбулеитиую конвекцию посвящена также
работа Крейчнана A962а), результаты которой, относящиеся к умеренным
значениям Рг, не противоречат выводам настоящей главы. С другой стороны,
например, Бюсингер A955) к числу параметров, явно определяющих форму
профилей ветра и температуры, отнес также и параметр шероховатости Z6,
что очень усложнило все его формулы. Еще более далеко идущее предпо-
предположение принял Лайхтмаи A944, 1947а, 1961), у которого вместо обыч-
обычного параметра шероховатости фигурирует явно влияющий на форму
профилей параметр г0 размерности длины, зависящий сложным образом и
от размеров и формы неровностей поверхности, и от термической стра-
стратификации.

368 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.2
справедлива теория логарифмического пограничного слоя, раз-
развитая в п. 5.3.
Таким образом, при z^>z0 характеристики турбулентности на
высоте z будут зависеть лишь от пяти величин: z, p0, -?-• и, и
-У—. Поскольку в данном случае имеется четыре независи-
независимых размерности — длина, время, масса и температура, то из
этих пяти величин можно составить лишь одну (с точностью до
числового множителя) независимую безразмерную комбинацию.
Следуя работам Обухова A946), Монина A950в) и Монина и
Обухова A953, 1954), мы здесь в качестве этой безразмерной
комбинации выберем величину
С — —
L '
G.11)
где
То р
— масштаб длины, составленный из параметров -ё-,и,и -?—
' О *7>Р6
(безразмерная постоянная Кармана х введена в выражение для
L ради удобства некоторых последующих выкладок, а знак
выбран так, чтобы было L>0 при устойчивой термической стра-
стратификации, когда <7<0). Тогда можно утверждать, чтозави-
симость от высоты любой осредненной характеристики / раз-
развитого турбулентного режима в приземном слое воздуха, не
зависящей от свойств подстилающей»- поверхности, может быть
записана в виде _
Z? (i) G.18,
где /о — комбинация размерности J, составленная из парамет-
параметров -?-, р0, и, и ¦——, a F(?) —универсальная функция. В каче-
* о ср9о • .
стве масштаба f0 для осредненной скорости ветра мы примем
¦величину-^-j а для осредненной температуры — величину
Т = LJL
(ср. E.75')), где постоянная х также введена для удобства по-
последующих выкладок, а знак у 7* выбран так, что при устой-
устойчивой термической стратификации Т# > 0. Наконец, укажем,
что для коэффициента турбулентности К естественным масшта-
масштабом будет величина №*\Ц.

7.2] § 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 369
Согласно формуле G.13), вводя с помощью масштабов /0
безразмерные величины, мы можем описать зависимость харак-
характеристик турбулентного режима от высоты универсальными
функциями от ?. Так, например, для вертикальных градиентов
средней скорости ветра и температуры получаются соотношения
где g(t,) и gi(?)—две универсальные функции параметра
?. Формулы G.15) и G.16) были указаны Мониным и Обухо-
Обуховым A953, 1954); их можно рассматривать как непосред-
непосредственное обобщение основных формул E.21) и E.76) теории
логарифмического пограничного слоя на случай температурно-
стратифицированной среды. Подставляя эти формулы в соотно-
соотношения E.5) и E.9), определяющие турбулентные коэффициенты
обмена К и Кт для количества движения и для теплоты, най-
найдем, что
= ^-. G.17)
Отношение коэффициентов обмена Кт и К равно
К и, дТ/dz *,(Q W> K '
вообще говоря, оно является некоторой универсальной функ-
функцией от ?. Число Ричардсона Ri, определенное в пп. 2.4 и 6.5
(см. формулы B.3') и F.51)), в силу G.12) и G.14) — G.1.6)
оказывается равным
№ Л(О 1 GЛ9)
Оно также является универсальной функцией от ?. Аналогично
этому динамическое число Ричардсона Rf формулы F.45), опре-
определяемое по потокам тепла q и количества движения т и про-
профилю скорости м(г), будет равно
S Я
z~dF
Число Rf, очевидно, просто связано с коэффициентом турбулент-
турбулентной вязкости К:
К=ш,Ь-Ш. G.21)

370 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.2
Из анализа общего характера функций g(t,) и gi(Z,), кото-
которому будет посвящен следующий пункт этой главы, можно вы-
вывести, что обе функции Ri(?) и Rf(?) являются монотонными и
поэтому имеют однозначную обратную функцию. Отсюда вы-
вытекает, что величины Ri, Rf и ? могут на равных правах исполь-
использоваться как параметры, характеризующие степень вертикаль-
вертикальной устойчивости воздуха.
Аналогично обстоит дело и с характеристиками поля кон-
концентрации пассивной примеси в стратифицированной среде при
наличии постоянного потока j = pow'®' этой примеси через гра-
границу z = 0 (в случае приземного слоя воздуха в качестве такой
пассивной примеси можно рассматривать, например, водяной
пар; тогда / будет иметь смысл величины испарения с единицы
площади подстилающей поверхности за единицу времени).
Здесь надо только добавить еще величину / к числу параметров,
определяющих осредненные характеристики турбулентного ре-
режима. Однако при этом добавляется также еще одна незави-
независимая размерность величины Ф и, следовательно, мы опять име-
имеем единственную безразмерную характеристику t,=z/L: В ча-
частности, для вертикального градиента дЪ/dz. средней влажно-
влажности Ф (в дальнейшем только эту пассивную примесь мы будем
рассматривать) получается соотношение
G.22)
вполне аналогичное G.15) и G.16); коэффициент обмена для
влаги («коэффициент турбулентной диффузии») при этом равен
G<23)
Сами профили скорости ветра, температуры и влажности в
приземном слое могут быть получены интегрированием ра-
равенств G.15), G.16) и G.22):
G.24)
где
с с ¦ с
/» /» /*
G-25)

7.3] § 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 37Г
7.3. Общий вид универсальных функций, описывающих
турбулентный режим в стратифицированной среде
Согласно сказанному выше, в приземном слое воздуха воз-
возможны два качественно различных универсальных режима, со-
соответствующих случаям устойчивой стратификации (поток теп-
тепла направлен вниз, т. е. <7<0 и, соответственно, L>0 и Г*>0)
и неустойчивой стратификации (q > О, L < О, Г* < 0). Эти два
режима должны сливаться при приближении к безразличной
стратификации (при q->0). Соответственно этому и все уни-
универсальные функции, описывающие универсальный режим, рас-
распадаются на две отдельные ветви: при ^0 и при ?<;0.
В настоящем пункте мы будем рассматривать лишь про-
простейшие характеристики турбулентности, а именно — профили
средней скорости ветра м, средней температуры Т и средней
влажности ¦&. Поэтому нас будут интересовать в первую оче-
очередь функции /(?), fr(?) и f2(?) и их производные ?(?)=/'(?),
g№ =/[<!•) и g2<U=f№.
Начнем с рассмотрения функций /(?) и g(t,). Формулу
G.15) нам будет удобно переписать в виде
If=й- ^ W = ? ? W; 9 W = <* w=Ч' (д. G.15')
Зафиксируем теперь значения г, м* и g/T0 и будем неограничен-
неограниченно уменьшать величину турбулентного потока тепла q, прибли-
приближаясь тем самым к условиям безразличной стратификации.
При этом масштаб L будет неограниченно возрастать по абсо-
абсолютной величине, так что С = -т- стремится к нулю. В пределе
при q -*¦ 0 мы, очевидно, должны получить обычную формулу
теории логарифмического пограничного слоя "л~ —~*"> не со-
содержащую ни q, ни g/T0. Следовательно,
<р@) = НтУ(С)=1. G.26)
С->0
Поскольку функцию ф(?) естественно считать непрерывной,
при фиксированных значениях q и щ, но достаточно малом z
(а именно, при z<&\L\) значение ф(С) будет близко к единице.
Это означает, что при 2^|Z,| условия турбулентного обмена
мало отличаются от условий обмена в температурно-однород-
ной среде, так что турбулентность в слое z<g,\L\ обусловлена в
основном динамическими факторами. Таким образом, масштаб
L определяет толщину слоя, в котором термические факторы не
играют заметной роли; он может быть поэтому назван высотой

372 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.3
подслоя динамической турбулентности1). Из того обстоятель-
обстоятельства, что в самом нижнем слое термическими факторами мож-
можно пренебречь, естественно вытекает, что учет свойств подсти-
подстилающей поверхности в стратифицированной среде должен осу-
осуществляться точно так же, как и в однородной среде. Иначе
говоря, объективной характеристикой свойств подстилающей по-
поверхности в отношении ее динамического воздействия на поток
и в стратифицированной среде является параметр шероховато-
шероховатости 20, определяемый так, как это было указано в п. 5.4. Так
как параметр шероховатости может быть определен по распре-
распределению ветра только в подслое динамической турбулентности,
то ясно, что он не может зависеть от температурной стратифи-
стратификации воздуха. Практически же этот параметр удобнее всего
определять, аппроксимируя логарифмическим законом профили
ветра, относящиеся к нейтральной или почти нейтральной стра-
стратификации, при которой \Ц велико и подслой динамической
турбулентности имеет большую толщину. Учитывая, что на вы-
высоте 20 логарифмический профиль средней скорости обращается
в нуль и что при z<g.\L\ профиль скорости всегда можно счи-
считать логарифмическим, первую формулу G.24) можно перепи-
переписать в виде
*[(*)(*)] G.24')
Отсюда видно, что функция f(z) вместе с параметром шерохо-
шероховатости Zo уже однозначно определяет профиль скорости ветра
во всем приземном слое.
Доминирующая роль динамических факторов при z<g.\L\,
естественно, должна быть связана с малостью числа Ричард-
Ричардсона при таких 2. И действительно, ограничиваясь пока более
удобным для нас числом Rf=aRi, легко вывести из G.20) и
G.26), что
HmRf(z) = 0 и №) =4"? G-27>
z->0 \ ог Лг=0 и.
следовательно, в пределах подслоя динамической турбулент-
турбулентности
IRil^-^^l. G-28)
') Пользуясь этим названием, разумеется, надо не забывать, что толщина
слоя, в котором термические факторы не играют роли, на самом деле равна
длине L, умноженной на постоянный множитель (который,
согласно данным, приведенным в следующем параграфе, по-видимому, имеет
порядок нескольких сотых).

7.3] § 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 373
При небольших значениях ? = 7Г функцию ф(?) = ?f(?)
можно представить в виде степенного ряда:
•• G-29)
Отсюда для функции f(?) в условиях, близких к безразличной
стратификации, получается представление
/(g = const+ln|C| + p,C + -|-C2+...; G.30)
аналогично этому, число Rf здесь оказывается равным сумме
степенного ряда
C3— ... G.31)
Поскольку эмпирические данные не позволяют пока сколько-
нибудь надежно определить несколько коэффициентов рп, прак-
практическое значение может иметь только линейная аппроксима-
аппроксимация функции ф(?):
' G.32)
, G.33)
G.34)
(здесь р — это коэффициент Pi формул G.29) — G.31)).
По поводу формул G.29) — G.34) следует иметь в виду, что
так как случаям ?,%0 и ?<!0 соответствуют два качественно
различных режима турбулентности, то у нас нет Оснований
предполагать, что функция <р(?) является аналитической в точ-
точке ? = 0 (хотя она и непрерывна в этой точке в силу того, что
при ?->-0 оба режима турбулентности сливаются). Поэтому, во-
обще говоря, случаям ? !> О и ? ^ О могут соответствовать раз-
различные значения коэффициентов, разложений G.29) — G.31) и,
в частности, различные значения постоянной р. Кроме того, ко-
коэффициенты рп следует считать универсальными постоянными
(того же типа, что и постоянная Кармана и), только если рас-
рассматривать их как точные значения коэффициентов ряда Тэй-
лора универсальной функции ф(?) (ограничиваясь, например,
лишь неотрицательными значениями ?). Однако в настоящее
время у нас нет возможности определить точный аналитический
вид функции ф(?), не прибегая к каким-либо более или менее
произвольным гипотезам. В то же время эмпирически эта функ-
функция определяется не настолько точно, чтобы. можно было на-
надежно Определить значения ее производных в точке ? = 0. По-
Поэтому на практике коэффициент р обычно находят приближенно.

374 гл. iv. температурно-стратифицированная среда [7.3
аппроксимируя эмпирическую функцию ф(?) на некотором
интервале значений ? формулой G.32) или каким-либо другим
аналитическим выражением. В результате получаемое значение
Р оказывается существенно зависящим от выбора интервала
аппроксимации и от принятой формулы для <р(?), так что не-
неудивительно, что разные авторы приводят сильно различаю-
различающиеся значения этого коэффициента (см. ниже стр. 422—423).
Впрочем, все эти расхождения не касаются вопроса о знаке р,
ответ на который сразу следует из элементарных физических со-
соображений. В самом деле, при устойчивой стратификации (т. е.
при q<0, L>0 и ?>0) турбулентный обмен является затруднен-
затрудненным, и поэтому профиль средней скорости должен быть более
«крутым», чем логарифмический профиль, наблюдающийся при
более интенсивном обмене, отвечающем безразличной страти-
стратификации. Наоборот, при неустойчивой стратификации (q > О,
L < О, ? <0) еще более интенсивное турбулентное перемешива-
перемешивание должно приводить к выравниванию средней скорости, так
что здесь скорость ветра должна возрастать с высотой.медлен-
высотой.медленнее, чем при безразличной стратификации. Поэтому [3—j—-
должно быть положительным при L > О и отрицательным при
L < О, т. е. р > 0 и при I > О, и при ? < 0.
Формулы G.32) — G.34), как мы уже отмечали, могут иметь
смысл лишь при сравнительно небольших по абсолютной вели*
чине значениях ?. Перейдем теперь к вопросу о поведении
функций ф(?) и f(?) при очень больших значениях [С [ == у^—
и начнем со случая сильной .неустойчивости, т. е. больших отри-
отрицательных значений ?. Асимптотическое поведение ф(?) и f(?)
при ?-»—оо можно изучать, рассматривая большие значения
г^>| L | при фиксированных <7>0, ы* и g/T0 (т. е. фиксиро-
фиксированном L<0), или же рассматривая при фиксированных
q > 0, g/T0 и z предельный переход и*->-0( т. е. Z,-vO). Послед-
Последний предельный переход, очевидно, отвечает приближению к
случаю чисто термической турбулентности в условиях так назы-
называемой свободной конвекции (характеризуемой наличием не-
неустойчивой стратификации с q > 0 и отсутствием ветра и свя-
связанного с ним трения воздуха о подстилающую поверхность).
При этом турбулентность имеет весьма своеобразный харак-
характер— она получает энергию не из энергии осредненного дви-
движения, а из энергии температурной неустойчивости, и имеет
характер совокупности тепловых струек, возникающих в отдель-
отдельных точках подстилающей поверхности и сравнительно слабо
перемешивающихся между собой. Если предположить еще, что
имеющееся горизонтальное перемешивание все же достаточно

7.3] § 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 375
для того, чтобы обеспечить инвариантность распределений ве-
вероятностей поля температуры относительно параллельных пе-
переносов и вращений в горизонтальной плоскости, то придется
заключить, что турбулентность в условиях свободной конвекции
представляет собой частный случай рассматриваемой в настоя-
настоящей главе модели турбулентности в стратифицированной среде,
характеризуемый лишь двумя параметрами g/Ta и q/cpp0 (ибо
при «чистой» конвекции и* = 0). Но с точки зрения теории по-
подобия турбулентный режим на высота* z~^>\L\ при фиксирован-
фиксированном и* не должен отличаться от режима при фиксированном z,
но очень малом и*; поэтому при неустойчивой стратификации
турбулентность на больших высотах всегда определяется в основ-
основном термическими факторами, т. е. статистические характери-
характеристики поля температуры здесь зависят только от g/Ta и q/cppa,
но не от и*. С этой точки зрения в предельном случае %-*•—оо
проще сначала рассмотреть поведение функций /i(?) и
gi(?) =/i(?)> характеризующих распределение средней темпе-
температуры, и лишь затем обратиться к фулкциям g(t,) (или
ф(?) = ?g(?))'H /(?) (ибо при изучении поля скорости мы не
можем апеллировать к предельному случаю «чистой» термиче-
термической конвекции, в котором средняя горизонтальная скорость
вообще отсутствует).
Поскольку из величин g/T0 u.q/cpp0 нельзя составить ника-
никакого масштаба длины, то турбулентный режим в условиях сво-
свободной конвекции должен быть автомодельным (ср. выше
исследование конвективных струй на стр. 313—314). В частно-
частности, легко проверить, что соотношение G.16) и второе из соот-
соотношений G.24) не будут содержать величины и*, лишь если
gi(l) ~Zr'h и /i(?) ~?-'/34-const. Таким образом,
1x4-1A G,35)
при СС 1
(множитель х4/з здесь добавлен для удобства). Иначе говоря,
при г^>\Ц, L < 0. Соотлошения G.36) впервые были указаны
Прандтлем A932а), а затем, независимо от него, Обуховым
A946); они, очевидно,-вполне аналогичны выведенным Зельдо-

376 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.3
вичем A937) формулам E.119) —E.120) для распределения
температуры в конвективных восходящих струях и отличаются
от них лишь тем, что здесь речь уже идет не о конвекции над
нагретым шаром или цилиндром, а о конвекции над нагретой
большой плоской пластинкой. В дальнейшем эти соотноше-
соотношения подробно обсуждались в ряде работ (см., например, Мо-
нин и Обухов A953, 1954), Пристли A954, 1955, 1956), Казан-
Казанский и Монин A958)). Из них, в частности, следует, что при
неустойчивой стратификации распределение температуры на
больших высотах приближается к изотермии; это, естественно,
объясняется наличием очень интенсивного перемешивания (уси-
(усиливающегося с высотой за счет появления все более и более
крупных турбулентных возмущений, сравнимых по масштабу с
расстоянием до земли), приводящего к выравниванию темпе-
температуры. Коэффициент обмена для тепла в условиях свободной
конвекции в силу G.36) равен
Кт = L = 3 /j_ JM V»; ' G.37)
с увеличением расстояния до земли он быстро возрастает.
Теперь уже нетрудно понять, какую асимптотическую форму
должны иметь функции g(V), <р(?) = lg(V) и f(?) при ?-»-—оо.
Поскольку предельный переход ?->-¦—оо эквивалентен переходу
и*->-0 (при фиксированных остальных параметрах и фикси-
фиксированном г), то режим турбулентности при ? <S — 1 не может
зависеть от ы*. Но из величин q/cpp0, g/TQ, p0 и z нельзя соста-
составить никакой безразмерной комбинации; поэтому все безраз-
безразмерные характеристики, определяемые указанными парамет-
параметрами, должны иметь постоянное (универсальное) значение.
В частности, естественно считать, что такой безразмерной харак-
характеристикой является отношение коэффициентов обмена для тепла
и для импульса а = Кг/К; следовательно, в условиях свободной
конвекции
? = «— const, Ж=^- = -J-,i~f)''z'' G.38)
(где а_оо= lim а(Q). Но в таком случае, очевидно,
С->-оо
-''' при С<С-Ь G-39)
= Cjr1/s + const при С<С —1» G-39')

7.3] S 7. ОБОБЩЕНИЕ ТЕОРИИ .ПОГРАНИЧНОГО СЛОЯ 377
где С2 = С^'а.оо. Иначе говоря,
IX~4'
дг З*4'»
п(г2) - «(*,) = - С2
при <? > 0, Zi^>\L\, z2^>\L\. Соотношения G.40) также были
впервые получены (в немного другой форме) Прандтлем
A932а) (см. также Обухов A946), Монин и Обухов A954)).
При возрастании г скорость ветра п(г) приближается к по-
постоянному значению по тем же причинам, которые вызывают в
условиях свободной конвекции приближение к изотермии при
z->-oo. Заметим, что в формулы G.40), разумеется, уже входит
величина и*, так какп(г) = 0 при и* = 0, и поэтому функция
п(г) не может не зависеть от и*. Числа Ричардсона Ri и Rf
также будут зависеть от и*; в.условиях свободной конвекции
эти числа в силу G.39), G.19). и G.20) равны
Rl = — -jr-—- ttt • Rf = aRi= —-pr- [jjj) ¦ G.41)
Отсюда видно, что с возрастанием z оба числа Ri и Rf не-
неограниченно возрастают по абсолютной величине (оставаясь
все время отрицательными).
Перейдем теперь ко второму предельному случаю ?-»-+оо.
Исследование асимптотического поведения функций ф(?) и /(?)
при больших положительных ? соответствует рассмотрению про-
профиля средней скорости п.(г) при больших z % случае устойчивой
стратификации (фиксированное L > 0) или же рассмотрению
при фиксированном z случая весьма малых положительных L
(т. е. очень резких инверсий температуры). При этом, однако,
надо иметь в виду, что в предельном случае резкой инверсии
при исчезающе слабом ветре турбулентность вырождается, и
движения среды приобретают совсем иной характер. А именно,
при сильно устойчивой стратификации становится невозмож*
ным существование крупных турбулентных возмущений (так
как эти возмущения должны были бы затрачивать слишком
много энергии на работу против архимедовых сил), и турбу-
турбулентность может существовать лишь в виде мелких вихрей
(иначе это можно объяснить тем, что крупные волны здесь не
теряют устойчивости). При еще большей устойчивости даже
мелкомасштабная турбулентность, по-видимому, будет прак-
практически невозможной, и флуктуирующие движения среды, ве-
вероятно, в основном будут реализовываться в виде случайных
внутренних гравитационных волн. Во всяком случае, ясно, что

378 гл. iv. температурно-стратифйцИрованная среда [7.3
при сильной устойчивости турбулентный обмен между различны-
различными слоями жидкости очень затруднен, и поэтому турбулентность
приобретает локальный характер: характеристики турбулентного
обмена (такие, как коэффициент обмена К, а значит, также
К \
и число Rf = -^-^lпри ?^1 (т. е. при фиксированном L > О,
но большой высоте z~^>L, или же при фиксированной высоте г,
но очень малом Z,>0) не должны явно зависеть от расстояния z
до подстилающей поверхности. Последний вывод можно еще под-
подкрепить следующим рассуждением: согласно известному выводу
Ричардсона (см. выше стр. 345) число Rf ни при каких стацио-
стационарных условиях не может превосходить единицу, т. е. макси-
максимальное возможное значение Rfcr этого числа <1 (по-види-
(по-видимому, Rfor даже заметно меньше единицы, но это для нас
здесь неважно). С другой стороны, естественно предполагать,
что изменение Rf с ростом С==-т- (т. е., при фиксированном г,
с увеличением степени устойчивости стратификации) должно
быть монотонным: невозможно представить себе физические
причины, которые могли бы привести к тому, что с ростом
устойчивости число Rf вдруг начало убывать. Но если Rf(?)
монотонно возрастает с ростом ? и в то же время не может
превзойти некоторого значения Rfcr, то, значит, при ?-*"°° оно
должно приближаться к некоторому предельному значению I?
(которое естественно отождествить с Rfcr).
Итак, в случае устойчивой стратификации должно суще-
существовать такое универсальное значение R, что
Rf^/? = const, K^xutLR при z^>L. G.42)
Но отсюда уже следует, что
S (Ч = Т = const- * W = Тг = CJ-
c G-43)
/(С) = const + -? = const + C3C при С>1,
где C3=l//? = l/RfCr> и, значит,
^ ^^ G.44)
Таким образом, на больших высотах в случае устойчивой стра«
тификации скорость ветра линейно возрастает с высотой, причем
постоянный градиент этой скорости здесь определяется един-
единственным «внешним» параметром, меняющимся от случая к
случаю, а именно — параметром -]р- — — -^-> фактически сов-
совпадающим с отношением турбулентного потока тепла к турбу-

7.3]
§ 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
379
лентному напряжению трения. Этот результат был указан Обу-
Обуховым A946) (см. также Монин и Обухов A954)).
Согласно формулам G.29), G.30), G.39), G.39') и G.43)
универсальные функции ср(С) и /(Q—/(±-1) (слагаемое
—fi — f) здесь Добавлено, чтобы устранить неопределенность
в выборе «начала отсчета» функции f(?)) должны иметь об-
общий вид, близкий к изображенному на рис. 47 и 48. В следую-
следующем параграфе мы увидим, что это заключение' хорошо под-
подтверждается данными непосредственных измерений в приземном
слое атмосферы.
Рис. 48. Схематический вид уни-
универсальной функции
Рис. 47. Схематический вид уни-
универсальной функции <р (С),
Скажем теперь еще несколько слов об общем виде функ-
функций gi(?), /i(?) и g2(?), Ы?)> описывающих вертикальные про-
профили температуры и концентрации пассивной примеси («влаж-
(«влажности») . Согласно п. 5.7
/i К) «^ In |С| +const при |С|<С1; G.45)
здесь а0 = а@)—постоянная, близкая к единице (которую в
п. 5.7 мы обозначали просто а). С другой стороны, как мы ви-
видели, при ?<С—1 (в условиях «свободной конвекции») поведе-
поведение функции /i(?) определяется формулой G.35); от функции
/(?) в этой области /i(?) отличается также лишь постоянным
множителем 1/а_то (точное значение которого, так же как и

380 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.3
точное значение ао, пока остается. неизвестным; см. ниже
стр. 428—429). В дальнейшем мы увидим, что при ?<Ю переход
от режима «вынужденной конвекции», характеризуемого лога-
логарифмическими профилями скорости и температуры, к режиму
«свободной конвекции», определяемому формулами G-35) —
G.41), очень резкий, т. е. происходит на малом интервале
значений ?• Поэтому поведение функции /i (?) на. всей положи-
. тельной полуоси, по-видимому,, достаточно полно описывается
значениями постоянных к, Ct и ао (или к, С2 = Cix4/sa-oo, a0 и
a'-<x>). В частности, вопрос о том, можно или нельзя счи-
считать функцию /i(?) при ?<0 подобной функции /(?), вероят-
вероятно, в первую очередь определяется тем, насколько близки
друг к другу значения постоянных ао и а_оо. Общая же форма
/[(С)—/Л — -s-J при ?<!0 безусловно не должна отличаться от
изображенной на рис. 48 формы функции /(С)—/(— -j).
Несколько более сложным представляется вопрос о поведе-
поведении функции fi(t) при ?> 0. Поскольку
^ +const, G.46)
вопрос о форме функции f^(t,) тесно связан с вопросом о зави-
зависимости величины а(?) от параметра устойчивости ^=7Г" (или
от чисел Rf и Ri). Если считать (как это чаще всего делается
в метеорологической литературе), что-&- = a = const, то функ-
функция /i(S) оказывается совпадающей с функцией /(?) с точ-
точностью до постоянного множителя; если а=1 (как это также
очень часто предполагается), то вообще /!(?)=/(?) (сточностью
до не играющих роли аддитивных постоянных в выражениях
для /i(?) и /'(?)). При малых положительных t, функция /i(g)
задается логарифмической формулой G.45); при немного боль-
больших ? можно использовать «логарифмическую + линейную»
формулу
/1(t) = const + ^-(lnt+pit) G.47)
(с коэффициентом Pi, который, вообще говоря, может отли-
отличаться от соответствующего коэффициента в формуле G.33)).
Если предположить, что а (С) сравнительно мало меняется на
достаточно большом интервале положительных значений ?, за-
захватывающем также и часть области, в которой имеет место

7.3] S 7- ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 381
линейный профиль скорости G.44), то при достаточно боль-
больших значениях ? из этого интервала и профиль температуры бу-
будет неплохо описываться линейной формулой вида
^-, T(z) = -^(^-J^+ const, G.48)
где а — постоянная порядка единицы. Однако наблюдения над
турбулентностью в море при сильно устойчивой стратификации
и примыкающие к ним измерения в водных потоках в лаборато-
лаборатории определенно показывают, что при очень сильной устойчиво-
устойчивости a(i) принимает очень малые значения (см. ниже стр. 435—436
и, в частности, рис. 69). Иначе говоря, при очень большой устой-
устойчивости коэффициент обмена для теплоты Кт оказывается зна-
значительно меньшим, чем коэффициент обмена для импульса К.
Следуя Стюарту A959), нетрудно привести физические сообра-
соображения, объясняющие причину этого. Случай среды с предельно
устойчивой стратификацией можно представить себе в виде слоя
тяжелой жидкости (скажем, воды), над которым помещается
гораздо более легкая среда (например, воздух). При этом тур-
турбулентное движение в нижней жидкости будет приводить к воз-
возмущениям свободной границы и появленэто отдельных «брызг»,
проникающих в верхнюю среду, а затем снова падающих под
действием архимедовых сил. Проникновение «воды» в «воздух»
будет создавать в «воздухе» пульсации давления, осуществляю-
осуществляющие определенный обмен импульсом между двумя средами; в то
же время обмен теплом здесь практически будет отсутствовать
(напомним, что молекулярной теплопроводностью мы услови-
условились пренебрегать). Поэтому можно думать, что при очень
сильной степени устойчивости (возможно, боле'е сильной, чем
та, которая реально наблюдается в атмосферных инверсиях)
коэффициент обмена К будет иметь конечное значение, в то
время как Кт будет близко к нулю. Но если это так, то отсюда
следует, что при очень больших положительных ^ = т профиль
температуры T{z) будет значительно более крутым, чем про-
профиль скорости п(г) (из того, что Кт-+0 при ?->-оо, вытекает,
что крутизна профиля температуры неограниченно возрастает
с ростом z\L). Следовательно, общий вид функций/i (С)—)
и (pj (С) = C/j (С) при очень больших положительных ? будет
отличаться от общего вида функций /(С)—/(V) и ?(*•)' (см-
Rf
рис. 49 и 50). С этим связано также и то, что число Ri = —
при сильной устойчивости, по-видимому, может принимать

382
ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА
[7.3
очень большие значения (так как если а-»-0 ^при Rf-»-Ricr,
то Ri-»-oo); поэтому никакого предельного («критического»)
значения Ri не существует (в отличие от положения с чис-
числом Rf).
Перейдем теперь к функциям /2(С) и g2(C)= /2 (С). До тех
пор, пока всеми принималось, что К = Кт (т. е. что ct=l)^ со-
совершенно естественно было предполагать, что и Кь = К=Кт,
т. е. что функция /?(С) не отличается от /'(С) и /[((.). Однако,
как только мы отказываемся от предположения о равенстве
Рис. 50. Схематический вид уни-
универсальной функции
Рис. 49. Схематический вид уни-
универсальной функции tpi СО-
коэффициентов обмена для импульса и для тепла, перед нами
сразу встает также и вопрос о значении коэффициента турбу-
турбулентной диффузии К», определяющего форму функций /2(Ь и
g2(?). Ниже мы увидим, что эмпирические данные о значениях
Кь и Ы?) еще беднее, чем данные о значениях Кт и /i(?), так
что на их основе пока нельзя сделать никаких заслуживаю-
заслуживающих доверия выводов. Поэтому остается апеллировать лишь
к физической интуиции. Отметим в Этой связи, что в статье
Пристли и Суинбенка A947), одной из первых в метеоро-
метеорологической литературе, в которой серьезно обсуждался во-
вопрос о несовпадении разных коэффициентов обмена, было
в свое время высказано предположение о том, что в силу осо-
особой роли пульсаций температуры в конвективных движе-
движениях под действием архимедовых сил (сказывающейся,
например, в том, что тенденцию двигаться вверх имеют в пер-
первую очередь частицы, более теплые, чем окружающая среда)

7.4] § 1. 060БЩЕНИЁ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 383
коэффициент обмена для тепла Кт может иметь иное значе-
значение, в то время как коэффициенты обмена для импульса К
и для влажности Кь будут совпадать. Однако рассуждения этих
авторов не очень ясны, и их точка зрения разделяется далеко
не всеми (см., например, Робинсон A951)), причем особенно
малоубедительны их аргументы в применении к условиям при-
приземного слоя. Более обоснованным представляется мнение, что
в силу подобия физического механизма обмена теплом и влаж-
влажностью (или другой пассивной субстанцией), осуществляемого
лишь посредством прямого перемешивания воздушных масс, ко-
коэффициенты Кт и Кь будут равны друг другу, в то время как
коэффициент обмена К, на который влияют и пульсации дав-
давления, может быть отличен от Кт — К». Этого последнего мне-
мнения и придерживается в настоящее время большинство специа-
специалистов, (см., например, Эллисон A957), Чарнок A958а)). Мы
здесь также будем считать, что при не слишком большой тем-
температурной неоднородности избирательное влияние архимедо-
архимедовой силы на элементы среды разной температуры не будет
существенно сказываться на турбулентной теплопередаче, так
что до тех пор пока неизвестен никакой другой физический ме-
механизм обмена, по-разному влияющий на обмен теплом и вла-
влагой, нет оснований отказываться от предположения о том, что
Кт = Кь и, следовательно, g2(?) =?i(?), Ы?) = /i(?) + const.
Разумеется, это предположение требует еще тщательной про-
проверки на материале достаточно аккуратных специальных на-
наблюдений в природе и в лаборатории, отсутствующих в настоя-
настоящее время.
7.4, Дальнейшие соображения о виде универсальных функций;
интерполяционные и полуэмпирические формулы
Выше был проанализирован общий ход универсальных функ-
функций /(?),.ср(?) = ?/'(?) и /j(C), cpj (С) = С/| (С) и указаны асимпто-
асимптотические формулы, определяющие поведение этих функций при
близких к нулю больших отрицательных и больших положи-
положительных значениях аргумента. В ряде случаев, однако, удобно
иметь явные формулы, задающие значения перечисленных функ-
функций при всех С = -д-. Проще всего такие явные формулы могут
быть получены с помощью интерполяции, использующей изве-
известные асимптотические закономерности (и учитывающей также
имеющиеся эмпирические данные о поведении функций в про-
промежуточных областях умеренных значений ?). Можно также с
этой целью использовать какой-либо из вариантов полуэмпири-
ческой теории турбулентности, обобщив его на случай стратифи-

384 ГЛ. IV..TEMrtEPATypHO-СТРАТИФИЦЙРОВАННАЯ СРЕДА [7.4
цированной среды, или же просто попытаться подобрать выра-
выражения для статистических характеристик турбулентности в та-
такой среде на основе одних только эмпирических данных без
всяких ссылок на теорию. Трем указанным подходам к задаче
об описании характеристик турбулентности в стратифициро-
стратифицированной среде посвящена обширная литература, насчитывающая
несколько сотен работ. Здесь мы вкратце остановимся, лишь
на некоторых относящихся сюда результатах, основное внима-
внимание уделив работам последних лет.
Начнем с рассмотрения поведения функций /(?) и /i(?). B
области отрицательных значений ?. Как мы уже отмечали, при
малых отрицательных значениях ? обе эти функции должны
аппроксимироваться логарифмической функцией. При- несколь-
несколько больших по абсолютной величине значениях ? можно исполь-?
зовать «логарифмическую + линейную» формулу G.33) или
G.47), а при очень больших отрицательных ? функции f(?) и
fi(?) приближаются к постоянным значениям, причем отклоне-
отклонения их от соответствующих постоянных затухают, как ?~1/з {см.
G.35) и G.39')). Мы уже упоминали выше, что согласно эмпи*
рическим данным переход от режима «вынужденной конвекции»,
описываемого логарифмическими функциями /(?) и Ы?), к Ре*"
жиму «свободной конвекции», которому соответствуют формулы
G.35) и G.391'), происходит весьма быстро, т. е. без заметной
промежуточной области (и притом при очень небольшом зн'аче-
нии \Z\—z/\L\, порядка одной десятой или нескольких сотых;
см. ниже стр. 419 и 428). В соответствии с этим Казанский и
Монин A958) предположили, что значения функции /(?) на всей
отрицательной полуоси будут неплохо описываться простейшей
интерполяционной формулой
> G49)
при С<С1. ( 9)
Аналогично этому для /4(?) можно предложить формулу
при С2<С<0,
G.50)
при С<С2)
где С2/а-оо=С1х1/». Значения безразмерных коэффициентов ао,
а_<х> и ?a/?i, определяющих степень различия функций /(?) и
fi(?), должны быть еще уточнены на основании эмпирических
данных. Пока можно лишь сказать, что все эти коэффициенты,
по-видимому, сравнительно близки к единице (и во многих слу-
случаях всех их вполне можно считать равными единице), Что же

7.4] § 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 385
касается постоянных С2, C2/a_<x, = Six</3 и ?ь входящих в фор-
формулу G.49), то на их значениях мы еще остановимся подроб-
подробнее в следующем параграфе. В применении к функциям
ср (С) = С/' (С) и ?г (С) = а0С/; (С) = аоЬ (С) формулы G.49) -
G.50), очевидно, приводят к соотношениям
1 при С!<
{_ CS.C-* при
и соответственно
при Сг<С<0,
з^С '' при С<С2,
где Сг = ¦ "° С2 = С^1'^. Эти функции, естественно, оказы-
а— оо
ваются разрывными, так как функции G.49) и G.50) непрерыв-
непрерывны, но не дифференцируемы в точках & и соответственно ?г.
Несмотря на наличие разрыва производной, функции G.49)
и G.50) во многих отношениях являются вполне достаточными
для описания профилей ветра и температуры в приземном слое
при произвольной неустойчивой стратификации. В тех же слу-
случаях, когда желательно иметь функцию /(?) с непрерывной про-
производной, можно, например, следуя Пристли A960а), отказать-
отказаться от определения значений ?i и ?г из эмпирических данных, а
/ С \3 / С' \3
положить (.1 = — (~з/ и ^ = —\~з/ (ПРИ этом ФУНКЦИИ
G.51) и G.52), разумеется, уже будут непрерывными). Того же
можно добиться, если, следуя Казанскому и Монину A958),
сохранить также и линейный член в формулах для /(?) и Ы?)
при малых ?, т. е. считать, что, например,/(С) = In |C| +К> СР(^)=
= 1 + рС при 0>С>С и /(С) = 1п|С1| + рС1 + С2(Г1/'-Сг'/8),
<р(С)^ З^С"/snpHC<C!. При этом р можно выбрать так, чтобы
функция 1 + р? хорошо аппроксимировала эмпирические значе-
значения <р(?) при малых С. а & затем определить из условия
l+(^i = ^~^Т''*• обеспечивающего непрерывность ф(?) в точ-
точке С = ?i. С другой стороны, следуя методу Пристли A960а) и
считая обе постоянные р и & неопределенными, можно подо^
брать эти постоянные так, чтобы функция
1-НС при d<C<0,
-^C-v. при

386 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.4
даже имела в точке ?j непрерывную производную (тогда /(С) =
= / ?-t^-(R при всех ? будет иметь уже две непрерывные про-
производные). Вообще, полагая
при Сг < С < О,
| __с при c<Ci, G-54)
мы можем добиться того, чтобы функция G.54) имела п непре-
непрерывных производных (и, следовательно, функция f(?) имела
п+1 непрерывную производную). В самом деле, для этого надо
только приравнять друг другу значения функций 1 +Р^+ • • •
• • • +РЛС и jf"'•"''' и их П^РВЫХ п производных в точке ?=?i,
а затем определить п+l неизвестных U, Рь • • • , Рп из получен-
полученной системы п + \ уравнений. Нетрудно получить явные формулы
для решения этой системы уравнений при любом п; согласно
этим формулам, если п -*~ оо, то ?i -> оо, но значения коэффи-
коэффициентов рй все стремятся к конечным значениям
Т' 3;^ ^2,7 G.55)
(см. Пристли A960а)). Предельным значениям G.55) коэффи-
коэффициентов рА отвечает бесконечно дифференцируемая (даже ана-
аналитическая) предельная интерполяционная функция
= 1&/ et'dL Gl56)
Совершенно аналогичные интерполяционные формулы могут
быть выписаны и для функции Фг(?)> с тои только разницей, что
коэффициент С2 теперь надо заменить на Сг = g°" С2 = Су*lsa0.
Таким образом, придавая п значения 0,1,2, .... и оо, мы получаем
бесконечное число интерполяционных формул вида G.54) для
функций <р(?) и Фг(?). При этом оказывается, что все эти интер-
интерполяционные формулы (включая и предельную формулу G.56))
очень мало отличаются друг от друга и практически одинаково
хорошо описывают имеющиеся эмпирические данные (характе-
(характеризуемые значительным разбросом). Для иллюстрации степени
близости различных интерполяционных формул друг к другу мы
приводим здесь заимствованный из работы Пристли A960а)

7.4J i f- обобщение теории пограничного слоя 387
рис. 51, на котором изображен безразмерный поток тепла
• ч *2(#'
|"ЗГ| г
(обращающийся в постоянную величину в условиях свободной
конвекции), получающийся при использовании для <рт(Е) интер-
интерполяционной формулы вида G.54) с л=0, 2 и 5. При расчетах,
0,001
-Ri
Рис. 51. Зависимость безразмерного потока тепла q от
числа Ричардсона R1.
Ломаная линия соответствует функции чу(С) вша G.52)с (^^-(с^/зK;
пунктирная н сплошная кривые — интерполяционным формулам вида
G.54) для <рг(С) С л = 2 и с /1 = 5.
положенных в основу рис. 5.1, принималось, что ао=1 (и во-
вообще а(?) = 1), х = 0,4 и С2 — С2 —0,95 (последнее значение
соответствует некоторым эмпирическим данным о профилях тем-
температуры в атмосфере); по оси абсцисс здесь отложена величи-
величина Ri = Rf = r-Tjy (при выборе вместо нее аргумента С = -^
расхождение между тремя кривыми было бы еще меньшим).
Вообще при С2=0,95 расхождение между значениями <р(?),
отвечающими «нулевой» интерполяционной формуле G.51)
с Сх==^—г^]и «предельной» формуле G.56), нигде не прево-
превосходит 15%, причем Слизкое к 15% расхождение наблюдается

388 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.4
лишь на коротком интервале значений ? и оно в основном свя-
связано с наличием у кривой G.51) «угловой точки» ?=?i. Первое
же сглаживание с помощью формулы G.53) сразу приводит к
значениям <р(?), нигде не отличающимся от значений G.56) .
больше чем на 5%. Отсюда ясно, что в приложениях к наблюде-
наблюдениям в атмосфере использование более сложных, чем G.53),
интерполяционных формул вида G.54) не имеет большого смыс-
смысла. С этой точки зрения вряд ли достаточно оправданным яв-
является также и предложение Уэбба A960) использовать интер-
интерполяционную функцию вида
1 + рС при d < С < О,
_?С-*+.сс-* при. С < С,, G7>-
где коэффициент С% определяется из эмпирических данных, а р,
С и & подбираются из условия, чтобы функция G.57) имела
две непрерывные производные в точке ? = ?4 (или же ?i нахо-
находится по данным наблюдений, а р, С% и С подбираются из ука-
указанного условия).
Интерполяционную формулу другого типа можно получить,
если, следуя Эллисону A957), принять за основу то, что при
? = -?¦-*¦ 0 (т. е. в условиях безразличной стратификации)
Rf —*- 0 и /(~xu*z, а при ]?]^>1 (т. е. в условиях свободной
конвекции) —-Rf — 1СГ/з и K=xu*L ¦ Rf ~xh1|(z|?|'/» (cm. G.38) и
G.41)), т. е. -^— «(—oRf)V4, где о — некоторая постоянная (рав-
(равная, как легко видеть, C/С2K). Исходя отсюда, можно ожидать,
что на всем интервале изменения Rf от нуля и до —оо (т. е. на
полуоси 0 !> ? >—оо) зависимость К от Rf будет неплохо опи-
описываться формулой вида
K=mtz(\ — oRf)'/4, G.58)
дающей правильные результаты в предельных случаях и малых,
и больших отрицательных значений Rf. Одновременно оказы-
оказывается, что формула G.58) при o=l/Rfcr дает асимптотически
правильные результаты и в предельном случае очень устойчивой
стратификации. В самом деле, из G.58) видно, что в процессе
возрастания числа Rf оно никогда не может превзойти значение
1/с и .что K/Z-+0 при Rf-»-l/a (т. е. при С = -?-»-+оо) в пол-
полном соответствии с формулами G.42). Таким образом, можно на-
надеяться, что, воспользовавшись формулой G.58), содержащей
единственную эмпирическую постоянную а, можно будет при-
приближенно опи'сать профиль средней скорости в турбулентной

7.4] § 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 389
стратифицированной среде при любых условиях стратификации.
Правда, вообще говоря, трудно рассчитывать, что значение
а = 1/Rfcr точно совпадает со значением о = 27Сг, которое
приводит к правильному асимптотическому поведению функции
/C(Rf) в области больших отрицательных значений Rf; однако,
так как в настоящее время значение Rfcr известно лишь крайне
неточно, то у нас пока нет оснований для использования в фор-
формуле G.58) разных значений а при Rf < 0 и при Rf > 0.
Формула G.58) может быть также получена, исходя из про-
простейшей попытки обобщения полуэмпирической теории турбу-
турбулентности на случай стратифицированной среды. В самом деле,
как мы уже видели в п. 6.5 (см. стр. 347), уравнение баланса
турбулентной энергии в стратифицированной среде в рамках по-
полуэмпирической теории может быть преобразовано к виду
К=иМ— о Rf)'/4> G.59)
где li = y,zk(Ri)—соответственным образом определенный «ма-
«масштаб турбулентности». Если теперь предположить, что
A,(Rf)==l, т. е. что масштаб турбулентности U при любой страти-
стратификации задается одним и тем же равенством l\ — %z (верным в
случае равновесной стратификации), то отсюда сразу следует
соотношение G.58). Именно таким образом это соотношение и
было впервые выведено Обуховым A946), использовавшим его
для исследования асимптотического поведения функций /(?) и
<р(?) в области больших положительных и больших отрицатель-
отрицательных значений ?• В последние годы различные методы вывода со-
соотношения G.58) детально обсуждались рядом авторов (см., на-
например, Ямамото A959), Пановский A961а), Пристли A961),
Селлерс A962), Сионо и Хамуро A962), Клюг A963)). По-
Поскольку, однако, все предложенные выводы используют некото-
некоторые произвольные гипотезы, они мало что добавляют к приведен-"
ным выше соображениям Эллисона, рассматривавшего соотно->
шение G.58) просто как интерполяционную формулу для /((Rf),
дающую правильные результаты и для больших отрицательных,
и для близких к нулю, и для больших положительных значений
Поскольку /С=-^р a Rf = —^-, соотношение G.58) мо-
жеть быть переписано в виде следующего простого алгебраиче-
алгебраического уравнения относительно функции <р(?):
ер-* — оСсрЗ —1=0. G.60)
Это уравнение содержит единственную неизвестную постоянную
- Z
о, которую можно исключить, введя вместо !«=:7Г в качестве

390 ГЛ, IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.4
независимой переменной величину т) = оС = ¦?-. где Lt = —;
тогда оно примет вид
i=o. G.61)
Уравнение G.61) было численно решено Ямамото A959), а
затем также и Клюгом A963). В работе Ямамото содержится
таблица значений функции ф(т]) (хорошо согласующаяся со
схематическим рис. 47), приведены несложные аналитические
выражения, аппроксимирующие эту функцию на положительной
и на отрицательной полуосях, и построены графики зависимости
безразмерной скорости ветра хп/ы, от безразмерной высоты z/z0
при различных значениях параметра rj0 = azo/L, определяющего
стратификацию.• Позже Сионо и Хамуро A962) и Ока^ото
A963) выписали решение уравнения четвертой степени G.61) в
радикалах и, исходя из него, более подробно исследовали фор-
форму функции q>0i) и отвечающих ей профилей скорости ветра.
Мы здесь, однако, не будем задерживаться на не представляю-
представляющем большого интереса детальном изучении решения уравнения
G.61), являющегося лишь одной из возможных интерполяцион-
интерполяционных формул для функции ф (и к тому же, по-видимому, не
очень точной).
То, что уравнение G.61) не может быть точным, следует, в частности, из
отмеченного выше факта соответствия этого уравнения физически мало есте-
естественному предположению о независимости масштаба турбулентности h иа
высоте z от температурной стратификации. Если же предположить, что
() G.62)
то для ф получится уравнение
Т4-«СТ'-^ = О, G.63)
содержащее еще одну неизвестную универсальную функцию Х($) (ср. Иокоя-
ма A9626)).
В случае устойчивой стратификации турбулентный обмен затруднен и
большие турбулентные образования не могут существовать; поэтому Есте-
Естественно ожидать, что при положительных ? масштаб t\ будет убывать с
ростом ? (или Rf). В этой связи Казанский и Монин A956) предположили,
что /i = H2A(Rf), где Х@)=1, а прн возрастании Rf от нуля до значения
Rfcr ¦» 1/о" функция X(Rf) монотонно убывает от единицы до нуля. В качестве
__1
конкретного примера они рассмотрели случай, когда A (Rf) = A—aRf) t
где •( > -j- — некоторое число. При таком выборе X(Rf) уразнение G.59) об-
обращается в соотношение
oRf^ G.64)

7.4]
$ 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
391
(такое соотношение с у = 1/2 ранее использовалось Холцменом A943) в ка-
качестве эмпирической формулы для К), Выразив здесь опять К и Rf через
функцию ф(?). найдем, что G.64) эквивалентно уравнению
1 Г, « JT
= [!-
Полагая, что 0? = ц, н вводя в качестве параметра величину ф(п)> нетрудно
получить из G.65) следующее параметрическое представление функции
?
1 = ? — \
G.66)
Поскольку в инверсионных условиях т|=0?>-О, второе из соотношений G.66)
показывает, что в этих условиях ф>1, причем ф@) = 1 и ф(т])->оо при
1]->оо. При малых г\ можно положить ф(п) = 1 + б, где в <^ 1; подставив
эту формулу во второе равенство G.66), найдем, что б = ул. т. е. ф»1 +
+ Y4 = 1 + с\?. Отсюда видно, что произведение ay = p должно совпадать с
коэффициентом {3 в формуле G.32). Далее, прн больших ц в силу того
же второго равенства G.66) будет выполняться асимптотическое соотноше-
соотношение ф ~ ц = 0?, показывающее, „
что а
(ср. G.43)).
Казанский и Моннн рассчитали
значения f(r\) для частного случая
у=0,6 (в этом случае интеграл
в первом равенстве G.66) выра-
выражается через элементарные функ-
функции); полученный исходя из этого
расчета график ¦ зависимости без-
безразмерного коэффициента обмена
K/*u*L от безразмерной .цысоты
ц = аг/Ь приведен на рис. 52
вместе с графиком экспоненциаль-
экспоненциальной функции KI*-u^L = 1 —е~\
использовавшейся в ряде метеоро-
метеорологических работ (Дородницын
A941), Матвеев A960) и др.).
Заметим, что аппроксимация
G.64) целесообразна только при
положительных значениях ? (и R0- Действительно, если попытаться приме-
применить ее одновременно и при отрицательных ? (для неустойчивых стратифика-
стратификации), то обычные закономерности теории свободной конвекции G.35) —G.41)
будут получаться при ?->—с» и Rf~>— с», лишь если у— 1/4. Таким об-
образом, прн ? < 0 надо пользоваться либо уравнением G.60) (т. е. заранее
принять, что Y='/4), либо же применять простые интерполяционные фор-
формулы вида G.51)—G.54). Исходя из этих формул, можно также уточнить
зависимость масштаба турбулентности 1\ от стратификации при неустойчивых
условиях (уравнение G.60), как мы знаем, приводит к неправдоподобно про-
простой формуле: 1\ = кг). В самом деле, если принять, что l\ = xzk(z/L), то в
силу G.63) аг -Ч
MC) = ~[l--?rl '• G-67)
5 z/L
Рис. 52. Зависимость безразмерного
коэффициента обмена Kl^uJL. от безраз-
безразмерной высоты С согласно теории Казан-
Казанского" н Монина (сплошная линия) и со-
согласно эмпирической формуле Дородни-
Дородницына и др. (пунктир).

392 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.4
Поэтому, зная функцию q>(?) (и постоянную а), мы можем найти также и
поправочный множитель м?). В частности, в условиях свободной конвекции
согласно G.67) и G.39)
(97 \/ С, \~Ч* / 27 \'«
**) A + ^г) -»Чсо)=Ы) при ^-
(
(то, что здесь X(oo)=const, т. е. U пропорционально г, естественно вытекает
из отсутствия в условиях свободной конвекции какого-либо фиксированного
масштаба, отличного от г). Так как следует думать, что с ростом неустой-
неустойчивости масштаб турбулентности должен возрастать, то должно быть
А(оо)>1, т. е. С2 <3/Y о. При малых значениях ?, используя формулу
G.32), получим
(J) [(J)f] G.68')
Таким образом, если Р > -т' т0 ПРИ изменении ? от пуля до — оо функция
М?) i/ сначала будет линейно возрастать, затем рост ее замедляется, и
при ?->—с» она будет стремиться к постоянной (в соответствии с фор'му-
лой G.68)). -
Можно также начать с того, что выбрать каким-либо образом функцию
Х(?); тогда из уравнения четвертой степени G.63) легко определить и функ-
функцию ф(?), т. е. найти распределение ветра с высотой, отвечающее заданному
масштабу турбулентности li — Kzk(z/L). В частности, Такеучи и Иокояма
A963), исходя из некоторых довольно грубых эмпирических данных, позво-
позволяющих оценить один из возможных «масштабов,» турбулентности, приняли,
что
* @ = «Iff1+ «-•)*-«.
где а — тот же числовой коэффициент, который входит в G.63).-Исходя от-
отсюда, они рассчитали функцию q>(?), которая, естественно, оказалась не удо-
удовлетворяющей «закону 1/3» G.39) при ? ->—оо (так как выбранная функция
А,(?) не стремится к постоянной при ?->— с»).
Уравнения G.60) (или G.63) при заданном Х(?)) и G.65) представляют
собой частные примеры соотношений, определяющих функцию q>(?) и полу-
получающихся из некоторой полуэмпирической' теории. Как мы уже видели в
предыдущей главе, даже в случае турбулентности в однородной среде суще-
существует целый ряд различных вариантов полуэмпирической теории, приводя-
приводящих к слегка различным результатам. Естественно поэтому, что в значитель-
значительно более сложных условиях стратифицированной среды число возможных по-
полуэмпирических теорий оказывается очень большим, и эти теории приводя^к
весьма разнообразным выражениям для <р(?) и других универсальных функ-
функций. Разумеется, все такие теории содержат те или иные произвольные до-
допущения, требующие дополнительной проверки; получающиеся же выражения
для <р(?) во многих случаях даже не удовлетворяют общим асимптотиче-
асимптотическим соотношениям, выведенным в предыдущем пункте, и, следовательно,
могут применяться лишь на каких-то ограниченных интервалах значений ?.
Так, например, в первой полуэмпирической теории турбулентности в страти-
стратифицированной среде, предложенной Россби и Монтгомери A935), предпола-'
галось, что К =» «»/i, и использовалась специальная гипотеза для определения
зависимости масштаба /[ от высоты и стратификации; в результате указан-
указанные авторы пришли к выводу, что
/С- *"** ,. , G.69)
A -f- a RO'/a '

7-4] § 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 393
где 0= const, т. е. что
9з _ 9 _ аС = 0> G.70)
если а(?)=1 (ср. вывод уравнения G.60) из соотношения G.58)). При
|?| <С! 1 равенства G.69) и G.70), очевидно, приводят к разумной «логариф-
мической+линейной» формуле для профиля ветра (с р = 0/2); однако асим-
асимптотическое поведение q>(?) и при ? -*¦— оо, и при ?-> + оо здесь оказы-
оказывается неправильным (в частности, нз G.69) видно, что в этой теории нет
критического числа Ричардсона), В другой полуэмпирической теории, разви-
развитой Огура A952а), в основу было положено уравнение баланса турбулентной
энергии и гипотезы о том, что К — и isl. При этом для градиента
скорости ветра была получена формула, которая в наших обозначениях мо-
может быть записана в виде
D)'A| G.71)
где 0—эмпирическая постоянная. Ясно, что при |?1<С? 1 и эта формула экви-
эквивалентна «логарифмической+линейной» формуле для профиля ветра (с
Р = 0/2). Поэтому неудивительно, что она оказалась сравнительно хорошо
описывающей профили ветра в условиях, не слишком сильно отклоняющихся
от безразличной стратификации. Однако при ?->—со здесь также не полу-
получается соотношения G.39), отвечающего «закону 1/3» для профиля скорости
ветра (и температуры) в условиях свободной конвекции (в другом предель-
предельном случае ?->+ со асимптотическое соотношение G.43) теперь уже выпол-
выполняется, если принять что и= 1/./?= 1/Rfcr). Основная гипотеза теории Огу-
Огура о коэффициенте обмена К использовалась также Бюсингером A955), но
уже в соединении с гипотезой Россбн н Монтгомери относительно масштаба /i
(вместо использования полуэмпнрнческого уравнения баланса энергии). При
этом им был получен результат, который может быть преобразован к сле-
следующему виду:
<? (О = -j ; G.72)
(как мы уже отмечали в сноске на стр. 367, сам Бюсингер пользовался более
, %г du
сложной записью, так как он считал, что, вообще говоря, —т~ может
зависеть н от Zo/z). Согласно формуле G.72), q>(?) « 1 + 2? при 1?1<^1, но
асимптотическое поведение q>(?) при больших значениях |?| теперь снова
оказывается неверным при любом знаке ? (при сильной устойчивости q>(?)
оказывается даже комплексным).
С помощью специальной гипотезы, представляющейся довольно искус-
искусственной, Суинбенк A960, 1964) получил очень простую формулу
G-73)
так же как и G.72), вовсе ие содержащую эмпирических констант- Эта фор-
формула опять имеет правильную асимптотику (вида G.32) и соответственно
G.43)) при малых и при больших положительных значениях ? (с коэффициен-
коэффициентами р = 0,5, R = С3 = 1), но при ?-> — со и она не переходит в «закон 1/3».
Заметим еще, что соотношение G.73) приводит к простой экспоненциальной
зависимости коэффициента обмена от высоты (изображенной пунктиром
на рис. 52), представляющейся правдоподобной в условиях устойчивой

394 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.4
стратификации. Еще одни вариант полуэмпирической теории был предложен
Као A959), основной результат которого может быть записан в виде
{1 +A+40'/'} при О—^-. G.74)
где а — эмпирическая постоянная. Формула G.74), как и все предыдущие,
приводит к ««логарифмическому+линейному» профилю в близких к равно-
равновесным условиям, но при ?-> + оооиа имеет неправильную асимптотику. Бо-
Более сложное соотношение для q>(Q, которое можно представить в виде
было получено в полуэмпирической теории Бюсингера A959). Последнее со-
соотношение обладает уже тем преимуществом, что соответствующая функция
<р(?) имеет правильное асимптотическое поведение и при ? -»•-{-оо (с Rfcr =
= 1/0, т. е. Сз = а), и при ?-> —оо. Теми же достоинствами обладает н
С
/т (?)
е di, найденная Зилитиикевичем н Лайхтманом
A965), исходя из полуэмпирического уравнения баланса энергии турбулент-
турбулентности, дополненного следующим обобщением гипотезы Кармана E.97) о
«пути перемешивания» /: _
f ^ dz) aT0 dz _
1 9 ^L ^Ё. _ JL d%T
dz dz1 a To dz1
(где v.\ н a — эмпирические константы, a = KT\K).
Примеры применения полуэмпирическнх гипотез для явного определения
функций q>(?) и /(?) можно было бы еще продолжить (см., например, Эллиот
A957, 1960), Кравченко A963), Нанто A964)). Следует, однако, иметь в
виду, что все получаемые таким образом выражения для этих функций
должны рассматриваться лишь как некоторые приближенные формулы, сте-
степень точности которых на заданном интервале значении ? (или чисел Rf, нли
Ri) должна дополнительно устанавливаться на основе сопоставления с дан-
данными наблюдений. В следующем параграфе мы увидим, что разброс имею-
имеющихся данных наблюдений до сих пор остается довольно большим; поэтому
и выбор между различными полуэмпирнческими формулами является за-
затруднительным.
Кроме полуэмпирических формул для профиля ветра, согласующиеся с
общими соображениями размерности (т. е. сводящихся * некоторым предпо-
предположениям относительно функций <р(?) нли /(?)), в метеорологической лите-
литературе можно найти также большое число работ (имеющих, как правило,
более чем десятилетнюю давность), в которых предлагаются полуэмпириче-
ские или же чисто эмпирические формулы для профилей метеорологических
элементов, не опирающиеся на соображения размерности (и содержащие
чаще всего вместо эмпирических постоянных некоторые эмпирические функ-
функции от числа Ричардсона или других характеристик стратификации). Так,
например, в течение ряда лет в научной литературе широко дискутировался
вопрос о возможности использования «логарифмического закона» (с парамет-
параметрами, вообще говоря, зависящими от устойчивости) для описания профиля
ветра в приземном слое воздуха при различных температурных стратифика-
циях. Ряд авторов (например, Россби и Монтгомери A935), Саттон A936,

7.4] § 7- ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 395
1937), Будыко A946, 1948), Бъоргум A953) и др.) отстаивали возможность
применения этого закона при любых условиях. Так, например, Будыко раз-
разработал схему, в которой профиль ветра описывается формулой
п{г)=Ь^\а31, G.76)
где т — параметр, зависящий от температурной стратификации. Для величи-
величины т Будыко предложил формулу, которую, пользуясь введенным выше
, Л i Л* \'1г h и
масштабом L, можно записать в виде /и = 11-f-"тту ] —оГ ' г^е —
«высота приземного слоя воздуха>, близкая к 30 м (наличие в этой формуле
высоты А, очевидно, делает ее несогласующейся с размерностным анали-
дп Q Е *
зом п. 7.2: здесь ¦%— зависит уже, кроме и,, --—, -~г- и z, еще и от Л).
oz Срр0 /0
рр0 0
Позже Бьоргум A953) рассмотрел также более общую формулу вида
w(z) = ——In -, где параметры и, го и Ло зависят от стратификации.
Очевидным иедостатком всех этих формул является то, что оии ие учитывают
реально существующих систематических отклонений профиля ветра при ие-
нейтральной стратификации от логарифмического законз. Кроме того, даже
в самом нижнем слое, в котором температурная стратификация играет очень
малую роль, соответствующие профили ие приближаются к тем, которые на-
наблюдаются в отсутствие градиентов температуры (в частности, экстраполяция
профиля ветра до значения u(zo)=O приводит здесь к значению го, завися-
зависящему от степени устойчивости, т. е. уже ие являющемуся объективной харак-
характеристикой подстилающей поверхности).
Другие авторы, в том числе Шмидт A925), Бест A935), Лайхтман A944,
1947а), Фрост A948), Дикой A949) и Такеда A951), предлагали аппроксими-
аппроксимировать профиль ветра в приземном слое воздуха степенными функциями от г.
При этом Шмидт, Бест и Фрост использовали простейшую формулу вина
и(г)~гг, а Лайхтмаи развил теорию, в которой профиль ветра описывается
формулой
2л~2о
G.77)
\dz 4-4}
так что [ —- = Air , A = —^—- I , где е — параметр, зависящий от
стратификации воздуха (положительный при инверсиях, равный нулю при
безразличной стратификации и отрицательный в случае неустойчивости);
практически ту же формулу позже использовали также Дикон и Такеда.
Формула G.77) позволяет уловить характер отклонений профиля ветра от
логарифмического закона; при е->0 она, очевидно, переходит в обычный
логарифмический профиль (если положить, что А = —— при е=0). Однако,
если, следуя Лайхтману, считать, что параметр го также зависит от страти-
стратификации, то влияние стратификации здесь все равно будет сказываться даже
прн г->0, что противоречит выводам из теории подобия. Вместе с тем число
свободных параметров, подлежащих определению в каждом отдельном слу-
случае по данным наблюдений, в такой теории оказывается слишком большим,
что создает трудности при нахождении этих параметров и снижает точность
расчетов. Если же, следуя "Дикону, принять го постоянным, то приходится
допустить, что е зависит также и от высоты (см., например, Дэвндсои ¦

396 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.4
Баред A956)), что является совсем уж неудовлетворительным. Заметим, что
формула G.77) также не может быть согласована с изложенными в п. 7,2
дп
соображениями размерности; в частности, -g- здесь явно зависит от функции
8 = e(Ri) (где Ri берется на фиксированной высоте) и от параметра шеро-
шероховатости г0 (который в схеме Лайхтмана также зависит от стратифи-
стратификации).
Учет влияния стратификации на профиль ветра путем введеиия линейной
добавки к логарифмическому закону, т. е. использования формулы вида
G.78)
где Ь — параметр, зависящий от степени устойчивости (положительный при
инверсиях и отрицательный при неустойчивой стратификации),, предлагался,
исходя из анализа эмпирических данных, в частности, Хелстедом A943) и Па-,
новским A952). Формула G.78), очевидно, может быть согласована с сооб-
соображениями размерности, для чего надо только положить^ —-j-\ после этого
она переходит в формулу Моиина и Обухова G.33).
Все сказанное выше о профиле ветра может быть перенесено н иа
профили температуры и влажности, если только стратификация является
неустойчивой, безразличной или слегка устойчивой. Однако при очень вы-
высокой степени устойчивости, как мы уже отмечали выше, по-видимому, воз-
возникает особая ситуация: есть основания думать, что при таких условиях
коэффициент ?бмена Кт = Кь гораздо меньше, чем_/С, и поэтому профили
температуры Т и концентрации пассивной примеси О в этом случае отли-
отличаются по форме от профиля средней скорости (ср. рис. 48 и 50).
Теоретический анализ этого явления представляет очень большие труд-
трудности и пока еще не увенчался значительными успехами; однако предприня-
Кг
тдя Эллисоном A957) попытка оценки зависимости величины a — —d- от
1\
числа Ричардсона Rf = ... заслуживает все же упоминания, поскольку она
привела к результатам, которые оказались неожиданно хорошо соответствую-
соответствующими результатам последующих экспериментов Эллисона и Тэрнера A960)
(см. ниже стр. 434). Для расчета величины а Эллисон использовал уравнение
баланса турбулентной энергии Ь —-^(и'г + v'2 + w'2) в стратифицированной
среде и родственные ему уравнения для вторых моментов Т'2, w'2 и w'T'. Как
мы уже видели в п. 6.1, такие уравнения содержат большое число новых
неизвестных членов; поэтому для получения своих выводов Эллисону при-
пришлось принять ряд дополнительных грубых предположений (типа полуэмпи-
полуэмпирических гипотез) о пренебрежимой малости некоторых слагаемых и о свя-
связях, позволяющих выразить не пренебрежимо малые неизвестные члены через
сами рассматриваемые моменты. Использовав эти предположения (неявно
содержащие уже допущение о малости обмена теплом по сравнению с обме-
обменом импульсом при сильной устойчивости), Эллисон пришел к соотношению,
которое можно представить в виде
_,_«т _ «оО -И/Я) "о?(О [Я?(О -С]
«<О—v- (i_RfJ Жт-ГО-Ч1 *
где а0 и R — медленно меняющиеся функции от ?, которые в первом прибли-
приближении можно просто считать эмпирическими постоянными. Ясно, что Оо здесь

7.5] S 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 397
совпадает со значением Кт/К при безразличной стратификации (в условиях
логарифмического пограничного слоя), a R — это критическое значение Rfcr,
которого число Rf никогда не может превзойти, и при котором Кт обра-
обращается в нуль. Весьма грубые оценки, произведенные Эллисопом на основе
некоторых соображений интуитивного характера, привели его к выводу, что
параметр R должен быть значительно меньше единицы (например, близким
к 1/7 или 1/10); это заключение, однако, пока еще нельзя считать окончатель-
окончательным. Если знать характер приближения числа Rf к предельному значе-
значению RfC4 (т. е. порядок члена оA) в асимптотическом разложении
9 (С) =-„-[1 + о A)] функции фE) при больших ?), то, исходя из G.79),
можно определить также и асимптотическое поведение функции ф| (?) (нли
?г (О = — ?i (О I ПРИ Е-*30- В настоящее время, однако, для этого еще иет
1 ао )
необходимых данных.
7.5. Общая формулировка гипотезы подобия для турбулентного
режима в приземном слое атмосферы и ее применение
к исследованию пульсаций метеорологических полей
До сих пор мы рассматривали только профили средних зна-
значений скорости ветра, температуры и влажности в приземном
слое атмосферы и лишь к ним применяли соображения размер-
размерности, изложенные в п. 7.2. На самом деле, однако, эти сообра-
соображения имеют общий характер, и результаты пп. 7.3—7.4 далеко
не исчерпывают всех приложений теории подобия к турбулент-
турбулентности в приземном слое. Сейчас мы рассмотрим некоторые даль-
дальнейшие приложения этой теории, относящиеся к статистическим
характеристикам, отличным от средних значений основных
метеорологических полей.
Начнем с того, что сформулируем в самой общей форме
наши основные предположения о подобии. В п. 7-.1 мы отмечали,
что в случае плоскопараллельного турбулентного течения стра-
стратифицированной жидкости над плоской однородной шероховатой
поверхностью (являющегося естественной моделью «приземного
слоя») все одноточечные моменты гидродинамических полей
будут зависеть только от вертикальной координаты z. Но огра-
ограничение лишь одноточечными моментами было там принято
только потому, что именно они интересовали нас в первую оче-
очередь. Фактически же в такой модели все распределения вероят-
вероятностей для значений гидродинамических полей в каком-то ко-
конечном числе точек будут инвариантными относительно произ-
произвольных параллельных переносов этой совокупности точек в
плоскости Оху и ее отражений в вертикальной плоскости Oxz,
проходящей через направление среднего ветра u(z), а также
стационарными (не зависящими от сдвигов во времени). Иначе
говоря, в этой модели распределение вероятностей для значений

398 гл. tv. телшературно-стратифицированная среда [7.8
произвольных гидродинамических полей в точках (*i, yu zit ti),
..., (*п. Уп, zn, tn) может зависеть лишь от параметров
х2 — *!,..., хп — Xj; у2 — Уь ... , уп — Vi\ Z\, ... , zn;
h — t\, ••• . *n — h и не меняется при изменении направления
оси Оу на противоположное.
Будем рассматривать только поля трех компонент скорости
ветра и, v, w и температуры Т (включение еще и поля влажности
О приведет лишь к появлению очевидных добавочных формул, на
которых не стоит задерживаться). Эти поля можно представить
в виде
u ', v = vf, w = wf, Т=Т{г)-\-Г, G.80)
где u(z) и T(z) —обычные (неслучайные) функции от z, деталь-
детально изученные в предыдущих пунктах настоящего параграфа. Та-
«им образом, достаточно рассмотреть лишь рдспределения ве-
вероятностей, для случайных полей и'(х, у, z, t), v'(x, у, z, t),
w'(x, y, z, t) и Т'{х, у, z, t). При этом общая гипотеза о подобии
турбулентного режима в рассматриваемой нами модели страти-
стратифицированной среды в применении к приземному слою атмосферы
может быть сформулирована следующим образом: совместное
распределение вероятностей для значений безразмерных величин
и'/и*, v'/u*, w'lu* иТ\\Т*\ в точках (хи уи ги t{) (хп, уп,
zn, tn) может зависеть лишь от безразмерных параметров
Щ
если только выполняются следующие два условия: 1) высоты
zlt ..., zn не слишком велики (находятся в пределах слоя, в ко-
котором можно считать, что ы*=const, q—const, и пренебрегать
влиянием силы Кориолиса) и не слишком малы (все много
больше «высоты шероховатости» z0, от которой рассматриваемое
распределение не должно зависеть) и 2) расстояния между лю-
любыми двумя различными точками (xit yit z{) и (*,-, yh Zj) и все
отличные от нуля разности \t{ — tj] не слишком малы (так, что-
<5ы на взаимодействия между пульсациями в рассматриваемых
точках пространства-времени не оказывали влияния молеку-
молекулярные эффекты, определяемые коэффициентами молекулярной
вязкости и теплопроводности воздуха) и не слишком велики
(чтобы не нарушались условия горизонтальной однородности и
стационарности). Через L и 7* здесь обозначены те же вели-
величины G.12) и G.14), что и всюду в этой главе. Обоснование этой
гипотезы фактически уже содержалось в рассуждениях
пп. 7.1—7.2.

7.5J J7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 399
В качестве примера рассмотрим более детально совместное
распределение "вероятностей для пульсаций («', v', w\ T') в фик-
фиксированной . точке (х, у, z, t) пространства-времени. Согласно
сформулированной гипотезе подобия это распределение может
зависеть лишь от вертикальной координаты z и его плотность
вероятности Ф(ы', v', и/, Т') может быть записана в виде
где ~V — универсальная функция от пяти переменных. Разумеет-
Разумеется, функция пяти переменных является очень сложной характе-
характеристикой; поэтому существенно, что в предельных случаях силь-
сильной неустойчивости [-?-*¦—°°)и сильной устойчивости (х"*0I
так же как и в случае безразличной стратификации (-?¦ -> 01,
формула G.81) может быть упрощена. В случае безразличной
стратификации ?->-0 и архимедовы силы не влияют на турбу-
турбулентность, так что параметр g/T0 здесь должен выпасть из соот-
соотношения G.81). Поэтому зависимость от z/L (где L содержит
g/T0) в этом случае отсутствует, т. е. распределение вероятно-
вероятностей не зависит от высоты. Кроме того, при безразличной стра-
стратификации не существует и пульсаций температуры, так что за-
зависимость Ф от Т описывается множителем 6G") (где 6 — это
дельта-функция Дирака). В результате получаем
*L, ^-)b{T') при -|->0, G.82)
где Ч*1 — универсальная функция от трех переменных, описываю-
описывающая распределение вероятности пульсаций скорости в точке ло-
логарифмического пограничного слоя. Предельный случай очень
сильной неустойчивости (свободной конвекции) получается при
q>0, ы*-»-0, так что при этом параметр ы* должен выпасть из
соотношения G.81). Отсюда следует, что
То ср?0 2) Г То срЪ г)
w'
. G.83)

400 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [7.5
где -\р2 — еще одна универсальная функция. Наконец, можно
считать, что при очень сильной устойчивости турбулентные пуль-
пульсации приобретают локальный характер, т. е. что их статистиче-
статистические свойства перестают зависеть от расстояния г до подсти-
подстилающей поверхности. Поэтому следует ожидать, что при
-?-->-|-оо параметр г будет выпадать из соотношения G.81),
т. е., иначе говоря,
Ф(«', v', w', T')->-ir±—wJ—, lL,~L.IL) при f ->oo. G.84)
К сожалению, соотношения G.82) — G.84) все еще трудно
проверяемы, поскольку многомерные распределения вероятно-
вероятностей вообще очень трудно надежно определить по эмпирическим
данным. Поэтому мы далее ограничимся рассмотрением лишь
простейших характеристик распределения G.81), а именно —
младших моментов пульсаций и', v', w', Т' в фиксированной точ-
точке {х, у, z, t). Согласно общей формуле G.13) любой одноточеч-
одноточечный момент этих пульсаций может быть представлен в виде не-
некоторой комбинации из параметров -$-¦> й, и ——¦ , умноженной
1 о -1рРо
на универсальную функцию от С = -?- (тот же результат, разу-
разумеется, следует и из формулы G.81)). По определению пульса-
пульсаций их средние значения равны нулю, поэтому мы сразу перей-
перейдем ко вторым моментам рассматриваемых величин. Таких мо-
моментов всего имеется десять. Однако три из них, а именно u'v',
v'w' и v'T't тождественно равны нулю вследствие симметрии
турбулентности относительно направления среднего ветра (в от-
отношении моментов u'v' и v'w' об этом уже говорилось на
стр. 363). Моменты u'w' — — u\ и w'T'~~- имеют постоян-
постоянные значения; поэтому остается рассмотреть лишь пять момен-
моментов— дисперсии пульсаций и', v', w', T (вместо которых нам
будет удобнее рассматривать стандартные отклонения аи, av,
0«» От) и смешанный второй момент и'Т'. Эти величины в силу
G.13) можно записать в виде
? ? "^=/8 (С).
Таким образом, для описания всех вторых моментов пульсаций
скорости ветра и температуры достаточно определить парамет-

7.5] S 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 401
ры и* и q и знать пять универсальных функций /3» /4, /s, /б и /7-
Через них могут быть выражены, в частности, такие интерес-
интересные характеристики турбулентности, как коэффициенты ани-
анизотропии <х„/<хи и aw/au и коэффициенты корреляции ruw, rwT
и гит:
I* — А 2ж — 1*. г —
__ л <786)
(в последних двух равенствах верхний знак относится к неус-
неустойчивой, а нижний — к устойчивой стратификации).
Функции /3(?), ••• , /б(?), очевидно, являются4 неотрицатель-
неотрицательными при всех значениях Z, по самому их определению. Момент
W77, определяемый функцией hit), описывает турбулентный
перенос тепла по направлению среднего ветра; практически
этот перенос не играет роли, и обычно им вполне можно прене-
пренебречь. При безразличной стратификации и при очень сильной
неустойчивости вообще и'Т' — 0 (см. ниже); однако при дру-
других значениях ? функция hit), возможно, принимает небольшие
положительные значения (за счет того, что при неустойчивой
стратификации неравенство Т > 0, как правило, будет иметь
место тогда, когда w' > 0, и следовательно, при этом пульса-
пульсация и' чаще будет отрицательной, а при устойчивой стратифи-
стратификации дело будет обстоять наоборот).
Асимптотическое поведение функций f3, ... , /7 при ?-»—<х>,
при ?-»-оо и при |?|-»-0 может быть установлено, исходя из
формул G.82) — G.84), .подобно тому как это было сделано
выше в применении к функциям /, /t и h, описывающим осред-
ненные профили. При возрастании неустойчивости (т. е. при
?-*•—сю) величина и* должна выпасть из всех равенств G.85);
следовательно, функции /3, /4 и /5 должны при этом возрастать
асимптотически пропорционально | Z, |'/>, функция /6 — стре-
стремиться к нулю асимптотически пропорционально | Z, \-Ч\ а функ-
функция h — стремиться к некоторой постоянной. Кроме того, надо
еще иметь в виду, что при ы*->-0 и ы(г) ->-0, т. е. турбулент-
турбулентность приближается к режиму, при котором в плоскости Оху
уже нет никакого выделенного направления, и пульсации и' и
v' ничем не различаются между собой (режим «истинной сво-
свободной конвекции» при отсутствии средней горизонтальной ско-
скорости). Поэтому следует ожидать, что при ?-»—сю
/аЮ«/4<9«С4|сГ\ /,Ю-«С,|СГ\

402 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА
или, иначе говоря,
(формула G.87') для ow фактически была известна еще Пранд-
тлюу A932а), но затем была забыта; позже она была незави-
независимо получена Обуховым A960) вместе с формулой для От-
Универсальные постоянные С\ = С&-~ !>, Cb = C's^~'-i> и Сб = С&-!*
в формулах G.87), очевидно, могут быть определены исходя из
эмпирических данных. Из G.87) вытекает также, что в усло-
условиях свободной конвекции-^- да 1, -f- = const, rwT = const, raw —
•—|C|~''-»-0 и гоГда0. В другом предельном случае — при
?-»-оо (т. е. при неограниченном возрастании устойчивости) —
характеристики турбулентности в силу G.84) не должны явно
зависеть от координаты г. Следовательно, при ?->-<эо все функ-
функции G.85) (и их комбинации G.86)) должны приближаться к
некоторым постоянным. Наконец, при |?|->-0 исчезают пульса-
пульсации температуры (см. G.82)), и 7\,-»-0. Поэтому величины f6@)
и /V@) не имеют непосредственного смысла; фактически функ-
функции /$(?) и /7(?) следует рассматривать как состоящие из двух
отдельных ветвей (при % > 0 и при % < 0). Что же касается по-
постоянных fs@)=/43, А@)=/44 и fi@)—A5, то они описывают
интенсивность пульсаций скорости в логарифмическом погра-
пограничном слое однородной жидкости и имеют вполне определен-
определенное значение (см. выше стр. 236, где именно эти постоянные обо-
обозначались как Аи Аг и А3). При малых значениях |?| функции
fs. h и fs Допустимо приближенно описывать двумя членами
ряда Тейлора
/ = 3, 4, 5, G.88)
где коэффициенты р,-, очевидно, все отрицательны (так как
турбулентный обмен ослабевает с возрастанием устойчивости).
Формулы, аналогичные G.85). (и содержащие новые уни-
универсальные функции), могут быть написаны и для моментов
более высокого порядка пульсаций и' v', w' и V. Так, на-
например
G.89)

7.5] «7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 403
Функции fa и fg характеризуют асимметрию распределений ве*
роятностей для w' и для Т :
о.
,3
G.90)
а функции /ю и /и — вертикальную диффузию турбулентной
энергии и интенсивности пульсаций температуры. Исходя из
представления о термической конвекции как о совокупности
восходящих движений нагретого воздуха в форме сравнительно
интенсивных узких струек и нисходящих движений охлажден-
охлажденного воздуха в форме медленного оседания значительных масс,
можно ожидать, что функции f%,..., fu будут положительными,
по крайней мере, при отрицательных ?. Согласно G.82) —G.84)
с ростом неустойчивости (при ?->-—-<х>) функции /8 и /юдолжны
возрастать асимптотически пропорционально |?|, функция /9 —
убывать асимптотически пропорционально |?|-' (так что коэф-
коэффициенты асимметрии /8//f и fg/fl должны стремиться к по-
постоянным), а функция /н(?) — убывать пропорционально
ICI''. С ростом устойчивости (при ?->-оо) все функции jf8, ...
... , fu, так же как и отношения f%jf\ и f^f\, должны стре-
стремиться к постоянным.
Статистические характеристики производных от скорости и
температуры в фиксированной точке (*, у, z, t), вообще говоря,
будут уже зависеть и от коэффициентов молекулярной вязко-
вязкости и температуропроводности v и % (напомним, что в формули-
формулировке гипотезы подобия требовалось, чтобы разности \U — tj\ и
расстояния между различными точками (Xi, yu Z{) и (Xj, yj, Zj)
были не слишком малы). Поэтому применение к таким харак-
характеристикам соображений размерности приводит к более слож-
сложным формулам, содержащим уже универсальные функции от
нескольких переменных. Однако имеются два важных исклю-
исключения из этого правила, относящихся к величинам
G-91)
)V G.92)
В самом деле, эти величины входят в уравнение баланса тур-
турбулентной энергии F.46), где е обозначалось символом et, и в
родственное ему уравнение баланса интенсивности пульсаций
температуры (см, ниже уравнение G.106)) и с их помощью могут

404 ГЛ. IV. ТЕМПеРАТУРНО-СТРАТИФИЦИрОВАННАя СРЕДА [7.5
быть выражены через обычные одноточечные моменты полей ско-
скорости и температуры и их производные. Следовательно, вели-
величины е и N не должны явно зависеть от молекулярных констант
v и х- Это обстоятельство не является случайным — как будет
показано в гл. 8 ч. 2 настоящей книги, величины е и N играют
существенную роль в закономерностях крупномасштабных дви-
движений и могут быть определены по распределениям вероятно-
вероятностей для пульсаций гидродинамических полей в двух достаточно
далеких _точках. Таким образом, для описайия зависимости
величин е и N от высоты z в приземном слое атмосферы можно
воспользоваться обычной формулой теории подобия G.13), не
содержащей v и %¦ А именно, можно положить
- и3 - %и Т2
^ (^ Л/ ^ср(С) G.93)
где ф, и (fN — новые универсальные функции. При |?|->0 функ-
функции ф, и q>N будут стремиться к конечным пределам ф, @) = 1
(так как здесь ъ=и%-^ ; см. выше стр. 344) и ф^@); кроме того,
Ф, (?)~|?1 и Ф*(?) ~|?|~1/з ПРИ ?-*—°°-
Значительно более сложный вид имеют формулы для мо-
моментов пульсаций в нескольких точках, которые,. очевидно, во
-всех случаях будут содержать универсальные функции от не-
нескольких переменных. Так, например, двухточечные моменты
пульсаций гидродинамических полей в точках (*i, y\, Z\) и
(*2, УЬ,, 22) в один и тот же момент времени t будут, вообще го-
говоря, зависеть от четырех переменных-^-. -^. *' L *' и Уг L y' .
Экспериментальное определение функций от четырех перемен-
переменных представляется в настоящее время практически безнадеж-
безнадежным; поэтому большой интерес представляют условия, при
которых число переменных в формулах для двухточечных момен-
моментов может быть уменьшено. Таким условием является, в част-
частности, условие — ? > ?ь где ?i — положительное число, опреде-
определяющее нижнюю границу интервала значений |?|, для которых
турбулентный режим является режимом свободной конвекции
(о порядке величины числа ?i мы будем говорить в следующем
параграфе). При этом условии можно считать, что ы* = 0, так
что из параметров задачи здесь уже нельзя составить никакого
конечного масштаба длины. Кроме того, в этом случае в пло-
плоскости Оху нет выделенного направления, так что все скалярные
(т. е. не зависящие от ориентации координатных осей) двухто-
двухточечные моменты могут зависеть только от го=[(лг2 — *iJ +
+ (У2 — УхJ]'1'* но не от Х2 — *i и Уг — #i п0 отдельности. Из ве-
величин Zi, z2 и го можно составить две безразмерные комбинации,

7.5) * 7- ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 405
в качестве которых_ можно выбрать, например z2/zi и о/у
(или 22/2i и rfVziZ2, где r=[ro+(z2 — ziJ\4'. Поэтому в условиях
свободной конвекции все скалярные двухточечные моменты бу-
будут равны некоторым комбинациям из параметров g/T0, q/cpp0 и
z=Yz\Z2, умноженным на универсальные функции от z2{z\ и
ro/z (или от z2/zx и r/z). В частности,
w'(xv yvzv t)w'(x2, у2, z2, t) =
u'(xv yv zv t)u'(x2, y2, z2, t) = v'(xv yt, zv t)v'\x2, y2, z2, t) =
T'(xu yv zv t)T'(x2, y2, z2,
где Ri, R2. и R3 — универсальные функции от двух переменных
(эти формулы были указаны Обуховым (I960)).
Задача экспериментального определения функций от двух
переменных представляется также достаточно сложной, но уже
не безнадежной. Замечательно, однако, что в некоторых случаях
удается теоретически предсказать форму зависимости соответ-
соответствующих функций двух переменных от одного из них, а для
ряда статистических характеристик вообще свести всю неопре-
неопределенность, имеющуюся в теоретических формулах,, к неопре-
неопределенности в выборе числового коэффициента. Для этого надо
только использовать дополнительные соображения о подобии,
относящиеся к совсем другому классу турбулентных течений,
включающему атмосферную турбулентность в качестве част-
частного случая. Рассмотрению такого подобия будет посвящена
основная часть гл. 8 в ч. 2; поэтому дальнейший анализ фор-
формул типа G.94) мы отложим до ч. 2 настоящей книги.
Как и в случае функций f, fi и fIt ряд дополнительных результатов отно-
относительно функций fa, • • •. fю, Ф, и ф# (не являющихся уже точными)
можно получить с помощью различных вариантов полуэмпирической теории
турбулентности. Так, например, Казанский и Моиии A957) (см. также Мо-
нии A959а)), исходя из уравнения баланса турбулентной энергии F.47),
Дополненного еще некоторыми полуэмпирическими гипотезами, получили для
функция ft(Q приближенное соотношение вида
-71ц]'\ G.95)

406 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЙДА J7.5
где Лб=/б@) —эмпирическая постоянная. Те же соображения, примененные
к уравнению баланса турбулентной энергии в форме F.47'), приводят к со-
соотношению
[-77^)-]1/4. . G-95')
содержащему еще одну эмпирическую постоянную от. Позже Паиовский и
Мак-Кормик A960) выдвинули гипотезу, приведшую их к выводу, что
'/вЮ-ЛвК/'Ю + ДЦ'Ч G.96)
где В — новая эмпирическая постоянная, а Бюсннгер A959) н Манн A961)
с помощью- двух разных предположений о пути перемешивания в стратифи-
стратифицированной среде получили формулы
+ * (/'«)*)']'* I* G 9П
G97)
(or — *гот же коэффициент, что я в G.75)) и соответственно
Л @ — ^|7W" G-98)
Соотношение G.98) с Л6=Г (что противоречит эмпирическим, данным) ис-
использовал также Иокояма A962а). Для функции fe(?) Пристли A9606) и Па-
Паиовский A9616) использовали полуэмпирическое соотношение
/в (С) = 4^/,'(С), 4, = /в@). G.99)
Монин A965) рассмотрел полную снстему динамических уравнений для одно-
одноточечных вторых моментов скорости и температуры и пренебрег в ней слагае-
слагаемыми, описывающими вертикальный перенос рассматриваемых величин (т. е„
в частности, всеми слагаемыми, содержащими третьи моменты), а пульсации
давления исключил с помощью простой полуэмпнрнческой гипотезы типа
F.10) и F.12). При этом он получил приближенное соотношение
связывающее значения функций fg, ft и fs (и при ?=0 хорошо подтверждаю-
подтверждающееся эмпирическими данными, приведенными на стр. 236). Приняв, далее,
еще некоторые полуэмпирические гипотезы (типа гипотезы о постоянстве
коэффициента с в формуле F.27)), он смог выразить коэффициенты анизо-
анизотропности /з(Р//*(?) и ME)/ME) чеРез Ф(?) =?/'(?) и известные из экспери-
экспериментов постоянные Лз=/з@), Л^ЫО) н Ai=fs(O) (причем оказалось, что
при сделанных предположениях дисперсии <хи, ог„ и оги могут быть все поло-
положительными, лишь если Сг— 1/^^5,5). Еще одно полуэмпирическое соот-
соотношение, связывающее функции <р(?), f(Q и Ы?). было предложено Пан-
дольфо A963). Использовав некоторые довольно грубые гипотезы, ПаИчев
A961) получил следующие связи между коэффициентами Cv C'5 и С'6 фор-
формул G.36) и G.87'):'
(из'которых, в частности, следует, что при свободной конвекции г„т = 1, в
прямом противоречии с эмпирическими данными рис. 79 на стр. 457)t

7.5] * 7. ОБОБЩЕНИЕ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ 407
Связь между универсальными функциями <р, (?), f(?) н fio(?) можно
получить из уравнения баланса турбулентной энергии F.46): согласно этому
уравнению
?.<0 = V(C)-C—g-tfotf) G.102)
(см. Моннн A958)). Соотношение G.102) является точным в той степени, в
какой является законным пренебрежение вертикальным переносом энергии
турбулентности, обусловленным работой сил давления и сил вязкого трения.
Если же мы вообще пренебрежем вертикальной диффузией энергии (т. е.
примем уравнение F.47)), то получим
?.<0~V©-t G.103)
а а
а если будем считать эту диффузию пропорциональной величине -=? —
(т. е. примем уравнение F.47')), то будем иметь соотношение
?6(С) = С/'(С)-«С G.103')
Разумеется, оба соотношения G.103) н G.103') являются менее точными,
чем G.102). Вспомнив асимптотические формулы G.33) и G.39) для функции
/(?) и исходя, например, из соотношения G.103'), находим
W "*" ^ОО- G.104)
_а)С при |С|С1
Таким образом, согласно формуле G.103'), при стратификации, близкой к
- и» g
безразличной, е «—; при сильной же неустойчивости е « а-^
, т. е.
перестает зависеть от высоты (те же результаты, но уже с неопределенными
числовыми коэффициентами получаются из одних только соображений раз-
размерности).
Подобные же соотношения можно вывести и для функции ф#(?); при
этом надо только принять за основу уравнение
Т + ^ + ^ + ^-*МГ,^Г,.. G..05,
получающееся из уравнения теплопроводности G.8') после умножения всех
его членов на 27". Подвергнув уравнение G.105) операции осреднения и учи-
учитывая однородность по горизонтали и стационарность турбулентности, мы
получим следующее уравнение баланса интенсивности температурных неод-
нородиостей:
или, иначе,
где, как обычно, N = x(V^'J. Пренебрегая здесь эффектом молекулярной
теплопроводности (первый член в скобках в правой части и последний член
в правой части), получаем соотношение
V1(Q—r-VuQ- G.107)

408 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОБАНЧАЯ СРЕДА [8.1
Если, кроме того, мы пренебрежем и вертикальной диффузией' пульсаций
температуры (второй член в скобках в правой части G.106')'), то получим
9n (С) = С/,(С). G.108)
Функция G.108) обладает свойствами
~Y С, | С | при С -> — со,
* при |С
Следовательно, в этом приближении при стратификации, близкой к безраз-
безразличной, N » , а при сильной неустойчивости Л/ убывает с высотой по
аог
закону
Однако поведение q>w(?) при ?->+со нельзя указать, не зная, как ведет
себя функция a(Q—f{i)/fi (?) при больших положительных значениях ?.
Разумеется, о формулах G.95)—G.101), G.103), G.104) и G.108) —G.110)
можно повторить все то, что выше говорилось по поводу аналогичных полу-
полуэмпирических соотношений, относящихся к функциям /, f\ и f2: все они яв-
являются лишь некоторыми приближениями, степень точности и область
применимости которых должна быть выяснена путем их проверки на
доброкачественном эмпирическом материале. В настоящее время эмпириче-
эмпирические данные о пульсациях еще очень неполны; при этом, однако, полуэмпири-
полуэмпирические формулы все же могут иметь заметную ценность, так как они во мно-
многих случаях помогают оценить с неплохой точностью порядок величины соот-
соответствующих статистических характеристик и дают общую ориентировку при
обработке результатов имеющихся сравнительно грубых наблюдений.
§ 8. СОПОСТАВЛЕНИЕ ВЫВОДОВ ТЕОРИИ С ДАННЫМИ ИЗМЕРЕНИЙ
В ПРИЗЕМНОМ СЛОЕ АТМОСФЕРЫ
8.1. Профили скорости ветра в приземном слое атмосферы
Перейдем теперь к вопросу о сопоставлении данных непо-
непосредственных измерений метеорологических величин в призем-
приземном слое атмосферы с теоретическими выводами § 7. Начнем
с простейших измерений средней скорости ветра на различных
высотах 2, многократно производившихся в разных точках зем-
земной поверхности с помощью тех или иных анемометров (многие
из которых описаны, например, в книгах Мидлтона и Спилхауса
A953), Кедроливанского и Стернзата A953) и Леттау и Дэвид-
Дэвидсона A957)). Как уже указывалось на стр. 246—247, в случае
сравнительно ровной подстилающей поверхности и температур-
температурной стратификации, близкой к безразличной, эмпирические дан-

8.11
§ 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ
409
ные о профиле скорости ветра в нижнем слое атмосферы доста-
достаточно хорошо описываются логарифмической формулой E 31)
Однако при наличии заметных градиентов температуры зависи-
зависимость скорости ветра и (г) от In z (данные о которой можно
"Д например у Торнтвейта и Кейзера A943), Щербаковой
A949), Дикона A949), Паскуила A949), Монина A953) и в
ряде других работ) обнаруживает закономерные отклонения от
простои линейной зависимости. При
этом при неустойчивой стратифика-
стратификации возрастание м(г) с ростом lnz
всегда оказывается более Мед-
Медленным, чем линейное, а при устой-
устойчивой стратификации более быст-
быстрым. В качестве типичных.приме-
типичных.примеров мы приводим на рис. 53' (заим-
(заимствованной из работы Монина
A953)) осредненные профили, по-
полученные в 1951 г. при измерениях
скорости ветра (и температуры)
в условиях открытой степи в Казах-
Казахстане на высотах 0,5, 1, 2, 4, 8 и
15 м. Шесть кривых на. рис. 53
были получены при помощи осред-
осреднения 61 индивидуальных профилей
скорости ветра по шести группам,
однородным в отношении устойчи-
устойчивости, характеризуемой значениями
параметра
0,01
р g Т B) -Т @,5)
1 То ЩГ)
0,51 24 875
Z(метры)
(8 1) *>ис" ^' Эмпирические про-
V • ) фили средней скорости ветра
в приземном слое при различ-
различных термических стратифика-
циях.
где Го — стандартная температура, а
цифры в скобках указывают высоту
(в метрах) точки наблюдения. Число случаев вошедших в
каждую группу, и соответствующее среднее значение параметра
В, приведены в таблице на стр. 410 вместе с качественной ха-
характеристикой отдельных групп. Мы видим, что, действительно
лишь при безразличной стратификации профиль скорости ветра
хорошо описывается логарифмической формулой (т е изобра-
изображается на рис. 53 прямой линией). Во всех же остальных слу-
случаях на достаточно больших высотах наблюдаются отклонения
от логарифмического закона, качественно согласующиеся с тео-
теоретическими предсказаниями предыдущего параграфа В то
же время на' малых высотах профили скорости ветра при всех

410
ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА
Шифр
группы
-3
—2
—1
0
1 ¦
2
Число
случаев
8
19
7
10
11
6
100В,
—0.52
—0.24
—0.11
—0.01
0.17
0.56
Качественная характеристика
Сильная неустойчивость
Умеренная неустойчивость
Слабая неустойчивость
Безразличная стратификация
Слабая устойчивость
Умеренная устойчивость
[8.1
значениях fit могут быть приближенно аппроксимированы форму-
формулой вида u(z) = A\n— с одним и тем же значением «высоты
шероховатости» z0 (наиболее надежно устанавливаемым, разу-
разумеется, по профилям при стратификации, близкой к безразлич-
безразличной); в условиях, к которым относится рис. 53, эта высота ока-
оказалась близкой к 1 см.
Согласно выводам из теории подобия, изложенным в § 7,
изменения скорости ветра с высотой во всех случаях должны
определяться универсальной функцией /(?) от безразмерной вы;
соты С = -?-. где L = — cpp0T0ulJ*gq. Для непосредственной
проверки этого результата и установления точного вида функ-
функции f(t,) надо иметь наряду со значениями п(г) также и значе-
значения величин ut=i — ]' и q, позволяющие подсчитать масштаб
L. Однако непосредственные измерения турбулентных потоков
t и q в приземном слое атмосферы (о которых мы еще спе-
специально будем говорить в п. 8.3) начали производиться лишь
сравнительно недавно и до сих пор являются относительно не-
немногочисленными и довольно неточными. Поэтому первая эм-
эмпирическая проверка общей формулы G.24), содержащей функ-
функцию f(?), позволившая впервые построить примерный график
этой функции, была произведена Мониным и Обуховым A953,
1954) иным путем. В основу этой проверки были положены об-
обширные данные (полученные во время четырех экспедиций, ра-
работавших в 1945, 1947, 1950 и 1951 гг. в различных районах
СССР) об одних только профилях ветра и температуры при
разных метеорологических условиях. Далее, было предполо-
предположено, что «меют место формулы G.24) и, кроме того, были
приняты еще некоторые добавочные предположения о виде
функций /(?) и /i(?). Хорошая согласованность между собой
результатов обработки имеющихся данных, исходящей из этих
предположений, в известной мере подтвердила их справедли-
справедливость и показала, что найденные таким образом эмпирические

8.1] * А- ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ 411
значения функции /(?) являются разумным первым приближе-
приближением.
Добавочные предположения о профилях ветра и темпера-
температуры, принятые в упомянутых работах Монина и Обухова, со-,
стояли в допущении законности «логарифмической + линейной»
аппроксимации G.33) функции /(?) при описании профиля вет-
ветра в нижних четырех метрах и в том, что профиль темпера-
температуры в этом слое предполагается подобным профилю ветра.
Исходя отсюда, все профили ветра, полученные в упомянутых
четырех экспедициях, в пределах нижних четырех метров ап-
аппроксимировались формулой вида
щ (г) = At (lg z+ D) + CiZt (8.2)
где i — номер профиля, а Ai, Cj и D —¦ эмпирические коэффи-
коэффициенты (определявшиеся по методу наименьших квадратов).
Так как все измерения относились к высотам z^>z0, то коэф-
коэффициент D предполагался одинаковым для всех профилей, от-
относящихся к одному и тому же месту наблюдения (т. е. для ка-
каждой из четырех экспедиций), и равным —lgz0,где z0—шерохо-
z0—шероховатость. Значения же коэффициентов Ai и С,- позволяли найти
для каждого профиля величины -?- и ¦-- по формулам
р _ Ct In 10 ,„ .
T— A ' V6'
~~ TiTTo" i
Далее, для каждого профиля вычислялось эмпирическое значе-
значение параметра устойчивости Bi = — 'J~ * ' , которое в
силу G.33) и предположения о подобии профилей п(г) и T(z)
считалось равным следующему выражению:
д ,*т. 44: itfn
"¦
Зная 20=10--°, можно было определить и.число В как коэффи-
коэффициент регрессии совокупности значений Ф(т)(гЛе Т ^ра-
лось из (8.3)) на эмпирические значения Bt. При этом выясни-
выяснилось, что В «* 0,6, причем корреляция между значениями. Ф(--г)
и Bi была достаточно высокой. По значениям — и L = 8'. и
всем данным об й(г) была построена эмпирическая функция
(8.4)

412
ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА
[8.1
где знак плюс соответствует устойчивой, а знак минус — не-
неустойчивой стратификации (значение и(—д—I при этом опреде-
определялось интерполяцией измеренных значений п(г).). Полученные
Рис. 54. Эмпирический график функции / (С) — / ( ± -^) по
Монину и Обухову A953. 1954).
Разными значками на рисунке отмечены данные, полученные в разных
экспедициях.
результаты изображены на рис. 54; они позволяют по-
построить эмпирическую функцию /(?) на интервале — 3 < ? < б.
Мы видим, что несмотря на неточность измерений скорости вет-
ветра и сравнительную грубость использованного приближенного

8.1] $ 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ 413
метода определения величин —- и L, эмпирические точки ло-
ложатся на гладкую кривую (состоящую из двух ветвей) с весьма
небольшим разбросом (кроме, пожалуй, случаев больших поло-
положительных значений ?, для которых разброс оказывается до-
довольно значительным). Тем самым полученный график под-
подтверждает существование универсальной функции f(t), опре-
определяющей зависимость скорости ветра от высоты. Мы видим
также, что эмпирическая функция /(?) в целом согласуется со
схематическим графиком рис. 48, т. е. оказывается обладающей
рядом асимптотических свойств, теоретически предсказанных в
предыдущем параграфе: при условиях, близких к безразличной
стратификации (малые |?|), она близка к функцииЛп |?| + const,
при сильной неустойчивости (?<С—1)—асимптотически при*
ближается к постоянной, а при сильной устойчивости (?^>1) —
возрастает приблизительно как линейная функция (на рис. 54)
эти три асимптоты изображены пунктирными линиями). Заме*
гим тут же, что, как показали последующие исследования, зна-
значения функции /(?), найденные в первых работах Монина и
Обухова, при ? < 0 оказались довольно точными, но при ? > О
они сильно занижены (на самом деле график /(?), по-видимо-
по-видимому, поднимается вверх при возрастании Z, значительно круче,
чем это изображено на рис. 54).
В дальнейшем графики, аналогичные приведенному на рис. 54,
неоднократно строились также и на основе другого эмпириче*
ского материала, причем результаты обычно оказывались близ*
кими к полученным Мониным и Обуховым. Так, Перепелкина
A9596) использовала данные тщательных измерений профилей
ветра и температуры при 2^2я, опубликованные Паскуиллом
A949) и Райдером A954), для детального исследования пове-
поведения' функции /(С)— /(+—) при |С|<-2". Позже она обра-
обработала таким же образом и данные наблюдений над профилями
ветра и температуры до высоты 70 м, проводившиеся летом и
осенью 1960—1961 гг. на специальной 70-метровой вышке в сте*
пи вблизи пос. Цимлянское. Аналогичный рис. 54 график функ-
функции /(С)— /(—y) пРи " < КI < "J и отдельный детальный
график функции /(С) —/( + ^-j при |?| < 0,3, полученные при
помощи обработки, близкой к описанной выше, данных наблю-
наблюдений над профилями ветра и температуры, проводившихся в
1960—1962 гг. на 45-метровой телевизионной вышке около То-
Токио, опубликовал Шиотани A962). После того как появились
данные непосредственных измерений величин и* и q, естествен-
естественно было также попытаться построить график, аналогичный

414 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [8.1
рис. 54, на котором значения L определялись бы по результатам
таких измерений (одновременных с измерениями профилей) без
привлечения каких бы то ни было специальных гипотез. Такое
построение в применении к данным, полученным в 1962 и 1963 гг.'
в районе пос. Цимлянское, было выполнено Гурвичем (см. ниже
рис. 55 и 56).
Графики функции /(С)—/[±-2), приведенные на рис. 54,
очень наглядны и дают хорошее представление об общем ходе
зависимости скорости ветра от высоты при неустойчивой и при
устойчивой стратификации. Однако для количественной оценки
отклонений функции /(?) от логарифмической функции при ма-
малых значениях |?| и ее отклонений от постоянной при больших
отрицательных значениях ? эти графики мало удобны, так как
соответствующие части эмпирической кривой на таких графи-
графиках оказываются сильно сжатыми. Поэтому ряд исследователей
использовал преобразования графика рис. 54 или же преобразо-
преобразования самой эмпирической функции д?), оказывающиеся более
удобными в том или ином отношении. Так, например, Пристли
A959а) преобразовал часть рис. 54, отвечающую отрица-
отрицательным значениям Z, (т. е. неустойчивой стратификации), за-
г.
менив линейную шкалу безразмерных высот С =-г логариф-
логарифмической шкалой. При таком преобразовании отклонения функ-
функции /(?) от логарифмической функции при малых |?| стали зна-
значительно более заметными, и, в частности, стало видно, что даже
при Z, ~ —0,05 эти отклонения оказываются довольно значи-
значительными (хотя на рис. 54 кажется, что сплошная и пунктир-
пунктирная кривые при |?| < 0,5 не различаются друг от друга). Ана-
Аналогичные графики (но с заменой значения и(-^-) значением
во многих случаях проще определяющимся по изме-
измеренным значениям п(г)) были позже опубликованы также
Р. Тэйлором A960а), использовавшим данные измерений Рай-
дера A954) и Суинбенка A955), и Такеучи A961), обработав-
обработавшим собранный в монографиях Леттау и -Дэвидсона A957) и
Бареда A958) обширный материал наблюдений в степи вблизи
О'Нейла (штат Небраска, США), проводившихся в 1953 и
1956 гг. При этом Р. Тэйлор определял значения ~ и L по
данным измерений величин ¦с = р„и^ и q, производившихся Рай-
дером и Суинбенком, в то время как Такеучи использовал для
этой цели аппроксимацию профилей и ветра и температуры
функциями вида (8.2) и формулы G.33) и G.47) (с щ = 1,

8.1]
8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ
413
Pi = P). Одновременно Такеучи на большом материале сравнил,
получающиеся таким образом значения L со значениями, полу-
получающимися при применении близкого по идее (но различаю-
различающегося деталями) метода Монина и Обухова A953, 1954) и
при использовании измеренных значений и* и q. Согласно по-
полученным им результатам все три перечисленных метода опреде-
определения L приводят к сравнительно близким значениям, которые
_ Щг)-п(Ш/2)
г,о
4,0
-2,0
-3,0
-4,0
0,0010,002 0.0050,010,02 0,05 0,1 0,2 0,5 1,0 2,0 5,0
Рис. 55. Эмпирический график функции /(С)—/[—^-
при С < О'по данным Гурвича A965).
в пределах точности существующих метеорологических наблю-
наблюдений во многих случаях можно считать практически эквивалент-
эквивалентными. Наконец, Гурвич A965) построил такие же графики по
данным одновременных измерений профиля ветра, турбулент-
турбулентного потока тепла и напряжения трения, проводившихся
летом 1962 и 1963 гг. вблизи пос. Цимлянское (см. рис. 55 и 56,
точки на которых соответствуют данным, осредненным по ряду
измерений). Значения функции /(?) при ?<0, найденные
Р. Тэйлором, Такеучи и Гурвичем, в общем неплохо согла-
согласуются между собой и со значениями, ранее полученными Мо-
ниным и Обуховым. Если, однако, принять за основу данные
проводившихся в последние годы в Австралии измерений про-
профилей скорости ветра (и темперг»туры) и величин q и т, ука«
занные Суинбенком A964) и Пристли A963—1964), то полу-
получающаяся универсальная функция /(?) оказывается несколько
/
/
?+а
у
s \
? у+соп
rJSty
St

416
ГЛ. IV. ТЕМПЕРАТУРНОСТРАТИФИЦИРОВАННАЯ СРЕДА
[8.1
отличной от той, которая изображена на рис. 55. В частности, со-
согласно Суинбенку функция <р(?) = ?/'(?) при ?<0 неплохо
описывается простой полуэмпирической формулой G.73), а, дан-
данные других авторов этого не подтверждают (см., например, Ба-
ред A963)). По-видимому, это расхождение связано с какими-
то инструментальными ошибками измерений; однако оконча-
окончательное его разъяснение
требует проведения до-
дополнительных исследова-
исследований.
Что же касается дан-
данных, относящихся к поло-
положительным значениям ?
(т. е. к устойчивой стра-
стратификации), то здесь
разброс эмпирических то-
точек оказывается заметно
большим, чем при ?<0,
а : общее число имею-
имеющихся наблюдений, при-
пригодных для определения
/(?), заметно меньшим.
Поэтому приведенный на
рис. 56 график функции
Ш-/@,1) при ?>0
пока должен считаться
лишь ориентировочным.
Заметим, однако, что хотя
его общая форма и со-
согласуется с формой функ-
функции f(t,) при ?>0, найденной Мониным и Обуховым, численные
значения этой функции здесь оказываются заметно отличающи-
отличающимися от найденных ранее; в частности, коэффициент С3 в асимп-
асимптотическом соотношении /(?) «С3? + const теперь уже имеет зна-
значение, близкое к 10 (вместо значения С3~1, следующего из дан-
данных рис. 54).
В ряде случаев при обработке эмпирических данных за ос-
основу принимался не,сам профиль ветра п(г), а значения гра-
— г"~ формуле G.15') для
фаз QW7Q02 0,05/,
'*~lng+CO/7St
~?+const
1
/
/
/
/
,'/
0,70,20,3 OJ
2,03,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
О
-1,0
-2,0
-3,0
-40
Рис. 56. Эмпирический график функции
—/(jo) ПРИ С>° по данным Гур-
вича A965).
диента скорости ветра
Согласно
получения универсальной зависимости надо рассмотреть без-
безразмерную величину
(8.5)

g.l] § 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ 417
или, что то же самое, величину
*?З (8-6)
Поскольку, однако, вычисление значений -?¦ = {- требует зна-
знания турбулентных потоков т = щ\ и q, о последнем из которых
пока имеется сравнительно
мало надежных данных, fay
то значения К чаще опреде- i н№)=о,37/т/}
лялись в зависимости от •' I т
числа Ричардсона Ri = ' ' *-
f п
_ g df II дп \2 _ 1 7,0
— То дг 1\дг ) — а (С)/'-(С)' 0,7
являющегося однозначной '
функцией от ?. Графики ^
функции /((Ri) были у[_
ликованы Райдером A954), 0,0050,0!ЦО2 0,050.1 G20,30,57,02,030&О W'
Диконом A955), Эллисо- „ -_ _ .
НОМ И Тэрнером (I960) и Р«\ 57. .Эмпирический график функ-
Гурвичем A962). На рис. 57 цнн K(Rf) по Гурвнчу A962).
мы приводим один из гра-
графиков Гурвича A962), относящийся к диапазону —0,005 >>
>-Ri >- — 4 и учитывающий также и данные Дикона A955).
Пунктиром на этом графике нанесена зависимость
1 I L ^
^ ^oo = -fy-, (8.7)
отвечающая асимптотическому «закону !/з» G.39) для усло-
условий свободной конвекции, с коэффициентом а — 0,97, найден-
найденным с помощью применения метода наименьших квадратов к
совокупности данных с Ri < —0,05. Сплошной линией отмечено
асимптотическое значение К@) — х ~ 0,4 функции A(Ri) в об'
ласти применимости логарифмического закона, которое весьма
точно определяется по графику функции K(Ri), построенному
с использованием линейной шкалы чисел Ri (именно таким об-
образом и было наиболее убедительно показано, что в атмосфере
также х~0,4). Значения Ri > 0 (устойчивая стратификация)
на рис. 57 отсутствуют, но вообще наблюдения при больших
положительных Ri в метеорологии очень редки. Поэтому наи-»
более обширные данные о значениях /C(Ri) при Ri > 0 были

'418
ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА
[8.1
получены Эллисоном и Тэрнером A960) в лабораторных экспе-
экспериментах, в. которых роль градиента температуры играл гра-
градиент солености воды (ср. ниже стр. 436). Данные Эллисона и
Тэрнера, вообще говоря, характеризуются большим разбросом
точек, но в целом они убедитель-
Р но показывают, что и на_ поло-
*'° жительной полуоси /C(Ri) убы-
убывает с ростом Ri, как этого и сле-
¦30 I довало ожидать.
Зависимость величины <р =
Ш/ ^—-^ от параметра С —jr
Рнс. 58.
Эмпирический гра
универсальной функции <у (С)
данным Гурвнча.
также однозначно связанного с ?,
была изучена на большом эмпи-
эмпирическом материале Пановским,
ff ц/ g? &о< С Блэкедаром и Маквейлом A960).
Согласно их результатам, функ-
дия <р(?') при всех отрицатель-
НЫх • ?' (т, е ПрИ неустойчивой
температурной ,стратификации)
хорошо аппроксимируется реше-
181). Одновременно Уэбб A960)
ф
>афнк
по
нием уравнения G.60) со,
предложил для <р(?') следующую эмпирическую формулу:
.5С'
при О
-0,0317,
0,316 (-C')"Vs-0,00143(-C')"</a при С'<—'0,0317,
(8.8)
приводящую, как оказалось, при всех ?'<0 к значениям <р(?')>
очень близким к тем, которые получаются из уравнения G.60) с
ст=18 (см. Пановский A963)). Несколько более грубый способ
проверки допустимости аппроксимации функции <р(?) решением
уравнения G.60) и подбора наилучшего значения параметра а
использовал Кондо A962а), пришедший к выводу, что <х«13. На
основе эмпирических данных, полученных в различные годы при
измерениях вблизи пос. Цимлянское, график функции <р(?) был
дважды построен Гурвичем A962, 1965); последние его резуль-
результаты приведены на рис. 58. Заметим еще, что, зная функцию
<р(?) (или /(?)), легко найти и зависимость числа Ричардсона
') Поскольку ?' = ?/«(?)> уравнение G.60) относительно ф(?) будет эквива-
эквивалентно такому же уравнению относительно <р(?')> лишь если а(?) = а = const.
При этом, очевидно, коэффициент а в уравнении относительно ф(?') будет
равен старому коэффициенту а, умноженному на а.

8.1] i 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ 419
Rf=?/<p(?) от ?. Точно так же, зная функцию ф(?'), где
?'= г/L'= ?/а(?), легко найти зависимость обыкновенного
числа Ричардсона Ri = Rf/a = ?'Ар(?') от ?'. Последняя зависи-
зависимость, получающаяся по данным Пановского, Блэкедара и Мак-
вейла A960) и Уэбба A960) и по данным Гурвича A962), по-
показана на рис. 59 (для значений ?' < 0, т. е. для неустойчивой
стратификации). Если считать (как это часто делается), что
а(?) = 1, то она будет тожде-
тождественно совпадать и с зависи-
зависимостью Ri от ?. При ?-»-0 и
Ri-^О, разумеется, Rf~? и
Ri — С — ^-(см. G.28)). В об-
области же положительных зна-
значений ? функции ?(Rf) n?'(Ri)
могут быть определены еще ме-
менее точно, чем при ?<0, так как
в этой области рассеяние эмпи- Г, г,
рических точек. больше, чем R, < 0, полученная в результате
при ?<0. Тем не менее, мы все осреднения данных Пановского, Блэ-
же приводим на рис. 60 ориен- кедара и Маквейла A960) и Уэбба
тировочный график зависимо- <196<5> <&mf?Jl ? по даТм Гур"
г г>. . v r ^ г» ¦ вича A962) (кривая Z).
сти Ri от Z, при ?>0, построен- v ' у v '
ный поданным Гурвича A965).
Остановимся вкратце на эмпирической проверке асимптоти-
асимптотических закономерностей, описывающих поведение универсаль-
универсальных функций при больших отрицательных, больших положи-
положительных и малых по абсолютной величине значениях ?. Мы уже
видели, что асимптотический «закон Уз» подтверждается, в
частности, данными Гурвича, представленными на рис. 57, со-
согласно которым он начинает выполняться уже при — ? > 0,05,
причем С2 я* О.ЭЗа!^. Более непосредственная проверка этого
закона была еще раньше осуществлена Р. Тэйлором A960а, б),
который представил значения -^-1«(г) — a (о~) ' найден-
найденные Мониным и Обуховым A954) и подсчитанные по данным
Райдера A954), Суинбенка A955) и Леттау и Дэвидсона A957),
в виде функции от|С|~1/3. При этом он тоже обнаружил, что
уже при — ? я* 0,05—0,08 соотношение G.39), выражающее «за-
«закон Уз», выполняется довольно хорошо. Оказалось также, что
данные Монина и Обухова, Суинбенка, Леттау и Дэвидсона
(при обработке которых использовались три разных способа
оценки длины L) хорошо согласуются друг с другом и приво-
приводят к примерно одинаковым значениям коэффициента C2 =

420
ГЛ, IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА
[8.1
= С1х3а_оо (а именно, к значениям С2 «s 1,3 -f- 1,5, так что Ci «*
«* 4,40-^-*-бог ^; см. рис. 61, где пунктирная прямая отвечает
значению С2 = 1,4), в то время как по данным Райдера
С2 *» 0,8 -т- 0,9 (т. е. С, »2,7а-^-т-За;у. Аналогично этому урав-
уравнение G.60) относительно функции ф(?') с о = 18, эмпирически
полученное Пановским, Блэке-
даром и Маквейлом, и фор-
формула (8.8) Уэбба также приво-
приводят к выводу, что соотношения
/И-
I
• ft
А
Данные
* Монина и Обухова
/? Тэйлора
-д
-2
-1
Рис. 60. Эмпирическая зави-
зависимость Ri от С при устой-
устойчивой стратификации по
данным Гурвича A965).
Рис. 61. Проверка «закона Уа»
для профиля ветра при сильно не-
неустойчивой стратификации (по Тэй-
лору A9606)).
(8.7) и G.39) начинают выполняться уже при сравнительно малых
отрицательных значениях Ri или ?. При этом для коэффициентов
За'Л I
С2 и Сх здесь получаются такие значения: С2
^ » l.laf^,
согласно уравнению Пановского и др. (эквива*
лентному соотношению a(Ri
!) = *(!— 18R1)*) и С,«0;
,95а»
Cj « 3,2а-^ согласно формуле Уэбба. Наконец, данные послед-
последней работы Гурвича A965), представленные на рис. 55, также
хорошо подтверждают «закон 7з» и приводят к выводу, что
Сч ~ 1,4, хорошо согласующемуся с результатами Р.-Тэйлора,
представленными, на рис, 61. Заметим еще, что справедливость

8.1] S «• выводы теории и данные измерений 421
«закона Уз* (теоретически относящегося лишь к случаю очень,
больших отрицательных, ?) уже при очень небольших —?, так
же как и наличие значительных отклонений функции f(?) от ло-
логарифмической функции уже при значениях |?| порядка несколь-
ких сотых, показывают, что толщина подслоя динамической тур-
турбулентности (в котором термические факторы не играют замет-
заметной роли) на самом деле составляет лишь очень небольшую
долю от \L\l).
Менее определенные результаты получаются при проверке
асимптотического закона G.43)—G.44), относящегося к случаю
предельно устойчивой стратификации. Как уже отмечалось
выше, в области больших положительных значений ? эмпириче-
эмпирические данные вообще хуже всего согласуются с предположением
о существовании универсального подобия, определяемого одной
лишь безразмерной высотой -j-. Возможно, что разброс экспе-
экспериментальных точек при таких ? объясняется сильной переме-
перемежаемостью турбулентности при устойчивой температурной стра-
стратификации, приводящей к значительной изменчивости времен-
временных средних значений, ввиду которой для получения надежных
результатов здесь требуется еильно увеличить период осредне-
осреднения. Какую-то роль здесь может играть и то, что мощные ин-
инверсии в приземном слое воздуха обычно сопровождаются силь-
сильным радиационным выхолаживанием, при котором метеорологи-
метеорологические условия оказываются уже нестационарными, a q заметно
меняется с высотой. Отметим, тем не менее, что еще в начале
50-х годов Райдер и Робинсон A951) и Хелстед A952) нашли
из наблюдений, что при очень устойчивой стратификации про-
профиль ветра обычно оказывается примерно линейным. Тот же
вывод можно сделать и из наблюдений Лилиеквиста A954),
проводившихся в Антарктике, где сильные инверсии весьма
обычны. Согласно Маквейлу A964) и Уэббу (см. Ламли и Па-
новский A964), стр. 117) при 0<С'^0,3, где ?' = z/L' (см,
стр. 418), функция <р(?') сравнительно хорошо представляется
формулой <р(С) = 1 + Р?', где Р,' = 7 по данным Маквейла (об*
работавшего результаты наблюдений, проводившихся вблизи
О'Нейла в США и на станции «Южный Полюс» в Антарктике)
и pj я» 4,5 по данным Уэбба. Исходя отсюда, Уэбб выска-
высказал предположение, что функция <р(?) при всех положительных
') С этой точки зрения традиционное включение в знаменатель выраже-
выражения G.12) для масштаба L постоянной Кармана к, приводящее ;к дополнит
тельному увеличению этого масштаба в 2,5 раза, представляется не очень
удачным-.

422 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [8Д
значениях ?, должна неплохо аппроксимироваться выражением
имеющим правильное асимптотическое поведение и при fr-*- + оо,
и при ?->0. Если еще принять, что при степени устойчивости,
характерной для приземных инверсий, а лишь немного отли-
отличается от единицы, то надо будет считать, что коэффициент Pi
по порядку величины близок к С3. Наконец, данные Гурвича
A965), представленные на рис. 56, как будто бы показывают,
что <р(?) ~С3? + const при ? !>0,3, где С3 « 10 (заметим только,
что точность этих данных заметно ниже точности данных той же
работы, относящихся к неустойчивой стратификации). Таким об-
образом, имеющиеся в настоящее время эмпирические данные все
неплохо согласуются с предположением, что при сильной устой-
устойчивости имеют место асимптотические закономерности G.43) —
G.44) с С3 «5-^-10. Отметим в этой связи, что данные лабо-
лабораторных экспериментов Эллисона и Тэрнера (по поводу которых
см. ниже стр. 436) также приводят к выводу, что значение
постоянной R = Rfcr, по-видимому, заключается между 0,10 и
0,15, так что С3 = l/R ~ 7 -f- 10. Однако для более точного оп-
определения значения этой постоянной (и для более полного выяс-
выяснения условий, при которых «линейный закон» G.44) имеет
место) требуется еще организация специальных тщательных
метеорологических наблюдений в условиях сильных инверсий и
проведение дополнительных лабораторных опытов.
Наконец, значение постоянной р в формулах G.32) — G.33),
определяющей поведение функций <р(?) и /(?) при малых |?|,
оказывается весьма неопределенным — оно сильно зависит от
выбора интервала значений ?, по которому это значение нахо-
находится. Мы уже указывали, что в работе Монина и Обухова
A954) было найдено, что р *» 0,6 приводит к неплохой аппро-
аппроксимации профиля ветра в нижнем четырехметровом слое «ло-
«логарифмической + линейной» функцией. Этот результат был позже
подтвержден также Пановским, Блэкедаром и Маквейлом
A960), использовавшими аппроксимацию вида G.32) для-срав-
для-сравнительно широкого диапазона отрицательных значений ?. В то
же время некоторые авторы, определявшие р фактически с по-
помощью формулы P^f-gf (тг-Ег)^ о' получили значительно
большие значения р, порядка нескольких единиц или даже по-
порядка 10 (см., например, эмпирическую формулу (8.8) на стр. 418
и таблицу значений р в работе Кондо A962а)). Отсюда видно,
что определение р из условия наилучшей аппроксимации на ко-
конечном интервале значений ? не совпадает с определением р по

8.2] § ». ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ 423
производным от функции <р(?) в нуле. Положение осложняется
еще тем, что второе определение может дать два разных
значения р в зависимости от того, определяются ли производные
по значениям при устойчивой стратификации (т. е. в точке
? = +0) или по значениям при неустойчивой стратификации
(в точке ? = — 0); первое же определение, вообще говоря, бу-
будет приводить к различным р при любых различных между со-
собой интервалах аппроксимации. Поэтому нет ничего удивитель*
ного в том, что в работах Р. Тэйлора A960а, б), Такеучи A961)'
и Кондо A962а) был получен целый ряд разных значений р.
Исходя отсюда, к использованию «логарифмической + линей-
линейной* аппроксимации вообще надо относиться с известной осто-
осторожностью, и при ? < 0 ее вряд ли целесообразно широко при*
менять (несмотря на то, что согласно результатам Такеучи
A961), оценки турбулентных потоков и длины L, получаемые с
помощью такой аппроксимации, по-видимому, все же можно
считать удовлетворительными). Дело в том, что, в силу данных
рис. 55, при неустойчивой стратификации переход от логарифми-
логарифмического закона к предельному «закону 7з» теории свободной
конвекции происходит в очень тонком слое; поэтому формулы
G.32) и G.33), относящиеся фактически только к этому пере-
переходному слою, здесь не имеют большого смысла.
8.2. Данные о профилях температуры и влажности
Наряду с наблюдениями профиля скорости ветра м B)
к числу весьма обычных метеорологических наблюдений отно-
относятся также и наблюдения профилей средней температуры Т(г)
и (в меньшей мере) средней влажности #(z) в приземном слое
атмосферы. Для измерения температуры используются термо-
термометры разных типов, снабженные специальными приспособле-
приспособлениями, предохраняющими их от непосредственного влияния еол*
ночной радиации. Наиболее удобными для измерения профилей
T(z) являются электрические приборы — термометры сопротив-
сопротивления и термисторы, в которых регистрируются изменения силы
тока, вызванные изменениями сопротивления вынесенного в ат-
атмосферу проводника или специального полупроводника (терми-
стора) при повышении или понижении его температуры, и тер-
термопары, один из спаев которых поддерживается при постоян-
постоянной температуре, а второй выносится в атмосферу (см., напри-
например, Лайхтман и Чудновский A949), Кречмер A957), Леттау
и Дэвидсон A957)). Существенно, что электрические приборы
позволяют непосредственно измерять малые разности "темпера-
"температуры T(z{) —T(z2), что позволяет увеличить точность таких из*
мерений и довести ее до немногих сотых или даже одной сотой

424
ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА
{8.2
градуса. Для измерения влажности d(z) чаще всего исполь-
используется сравнение показаний сухого и смоченного термометров.
В разное время было предложено также много других принци-
принципов, позволяющих производить такие измерения (см., напри-
например, Лайхтман и Чудновский A949), Мидлтон и Спилхаус
A953), Леттау и Дэвидсон A957)); одна-
однако до сих пор ни один из этих принципов не
привел еще к созданию простого и надеж-
надежного прибора, дающего значения д с вы-
высокой относительной точностью. ,Поэтому
получение доброкачественных данных о
профилях Ъ(г) пока остается очень труд-
трудной задачей.
Общая форма профилей температуры
Т(г) как при устойчивой, так и при не-
неустойчивой стратификации в настоящее
время хорошо известна из многих наблю-
наблюдений. В качестве типичного примера, ил-
иллюстрирующего эту форму, мы приводим
на рис. 62 данные Монина A953), получен-
полученные при помощи осреднения 61 индиви-
индивидуальных профилей температуры, наблю-
наблюденных летом 1951 г. в условиях открытой
степи, по шести однородным в отношении
устойчивости группам, охарактеризован-
охарактеризованным в таблице на стр. 410. Из рис. 62 вид-
видно, что при неустойчивой стратификации
убывание T(z) с ростом. In 2 происходит
медленнее, чем по линейному закону, а
при устойчивой стратификации возраста-
возрастание Т(г) с ростом In 2 оказывается бы-
быстрее линейного. Аналогичная закономер-
закономерность выше уже отмечалась и в отношении
зависимости от стратификации закона воз-
возрастания скорости ветра с высотой (см.
рис. 53). Сравнив рис. 53 с рис. 62, можно даже предположить,
что при всех условиях стратификации профили скорости ветра
и температуры подобны друг другу, т. е. что при любой устой-
устойчивости атмосферы отношение
-2
OJ 7 2 4 в 72
z (метры)
Рис. 62. Эмпирические
профили средней тем-
температуры в приземном
слое при различной
стратификации.
(89)
в<*,)-в<*о)
для любых двух высот 2\ и 20 в пределах приземного слоя
принимает одно и то же значение (положительное при инвер-
инверсиях, равное нулю при безразличной стратификации и отрица-

g_2] § 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИИ 425
тельное при неустойчивой стратификации). Для проверки этого
предположения достаточно сравнить функции
j?j[ и /, (810)
где высоты 20 и Zi фиксированы, а г переменно, и выяснить,
совпадают ли они между собой или нет. Такая проверка в раз-
разное время и с разной степенью точности производилась мно-
многими исследователями (в частности, Паскуилом A949), Рай-
дером и Робинсоном A951), Пановским A9616), Пристли
A963—1964),Суинбенком A964), Маквейлом A964) и Гурвичем
A965)). При этом в более старых работах всегда оказыва-
оказывалось, что профили ветра и температуры в приземном слое при
не слишком больших отклонениях от нейтральной стратифика-
стратификации практически подобны друг другу; часто даже утверждалось,
что это подобие имеет место вообще при любой страти-
стратификации (или хотя бы ори любой неустойчивой стратифика-
стратификации). В то же время последние результаты Пристли и Суин-
бенка (в целом ряде отношений расходящиеся с данными всех
других исследователей) указывают на существование очень
значительного различия формы профилей скорости ветра и тем-
температуры при неустойчивой стратификации (случаи устойчи-
устойчивой стратификации эти авторы вообще не рассматривали); не-
некоторое (хотя и заметно меньшее) отклонение от подобия было
обнаружено и Гурвичем. Таким образом, в настоящее время
в вопросе о степени подобия профилей п(г) и Т(г) нет еще
ясности, и окончательное, его решение требует дополнительных
тщательных исследований.
_ Еще хуже обстоит дело с данными о профилях влажности
0B). Имеющиеся пока данные измерений этих профилей (см.,
например, Паскуил A949), Райдер A954)) показывают, что
в пределах нижних нескольких метров функция _ ~ _
Ь (г,) — Ь (г„)
очень близка к функциям (8.10) (см., например, рис, 63, заим-
заимствованный из статьи Райдера A954)). Иначе говоря, имею-
имеющиеся данные о профилях влажности Щг) при различной стра-
стратификации не противоречат и тому, что эти профили подобны
профилям ветра, и тому, что они подобны профилям темпера-
температуры. Это обстоятельство связано со сравнительно низкой точ-
точностью измерения профилей влажности, в силу которой все
имеющиеся данные о профилях влажности должны считаться
пока лишь предварительными и требующими еще тщательной
проверки,

426
ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА
[8.2
В силу общих формул теории подобия G.24) отношение
(8.9) может быть представлено в виде
7-(г,)-7-(г0) = 7> /, (С,)-/, (С)
«!<*,)-о <*,) ut /(С,) -/(Со)
(8.9')
где Ci = -j- > Co = ^r. a /((.) и fx (С) — универсальные функции,
описывающие зависимость профилей ветра и температуры от
безразмерной высоты. Отсюда ясно, что постоянство ^того отно-
отношения при всех zt и z0 означает, что функции /(?) и /t(?)
200
ISO
Z(CM)
JOO
75
SO
37,5
25
15
О
Рис. 63. Эмпирические профили скорости ветра (О).
температуры (X) и влажности (•) в приземном слое при
двух термических стратификациях.
Масштабы (подобранные так, чтобы профили по возможности совпали)
указаны под кривыми. ¦
' Wof/ce/f
/
0,О7г/м3
и
отличаются лишь постоянным множителем. Но
//(С)
f\ С-)
=<х((,) =
= —-; поэтому подобие профилей ветра и температуры равно-
К
сильно независимости от высоты (и от числа Ричардсона) отно-
отношения а "коэффициентов обмена для тепла и для количества
движения. В настоящее время есть известные основания пред-
предполагать, что отношение коэффициентов обмена Кт/К не яв-
является строго постоянным, но нет еще никаких данных для
надежного определения его зависимости от ? = z/L (подробнее
об этом см. ниже). Что же касается коэффициента обмена
Кь для влаги, то пока можно лишь сказать, что эмпирические

8.2]
i 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ
427
данные о профилях влажности не противоречат предположению,
что К»1Кт = const.
Более полное исследование профиля температуры с точки
зрения теории подобия требует построения эмпирической за-
зависимости величины [f B) — Т(а\Ц)уТ, или у--^г от аргу-
аргумента С = 4-1 где а — фиксированный коэффициент (напри-
(например, 1/2 или 1/10) r a L и Т, должны быть определены по зна-
значениям и„ и q (полученным из непосредственных измерений
т*
0
-2,0
-3,0
-4,0
~ln?+cor?st/'
J
»
f
vist
О001ООО2 0.005 ЦЩ02 0.05 0.7 0,2 0.5 1.0 2.0 5,0-^
Рис.64. Эмпирический график функции/, (С) —А I—<А
при С < 0 по данным Гурвича A965).
или оцененным с помощью какого-либо надежного косвен-
косвенного метода) на основе формул G.12) и G.14). Функция
[T(z)—T{a\L\)]IT, была построена, в частности, Р. Тэйлором
A960а) (по данным Райдера A954) и Суинбенка A955)), Та-
кеучи A961) (по данным обширных наблюдений профилей вет-
ветра и температуры, производившихся в 1956 г. вблизи О'Нейла
в США) и Гурвичем A965) (по Данным измерений вблизи
пос. Цимлянское в 1962 и 1963 гг., см. рис. 64 и 65). Поскольку,
однако, Такеучи определял величины L и Tt с помощью кос-
косвенного метода (аналогичного тому, который раньше исполь-
использовался Мониным и Обуховым A953, 1954)) в предположении,

№
ЬЛ. IV.
с!>ЁДА
определения величин L и
ния и» и а, Тэйлор смог
что Кт*=К, то взаимная согласованность полученных им ре-
результатов показывает лишь, что на самом деле а(?), по-види-
по-видимому, не очень сильно уклоняется от единицы. В работе
Р. Тэйлора данные были представлены в виде, ясно показы-
показывающем, что уже при ?«*—0,03 в атмосфере происходит пере-
переход к «режиму свободной конвекции», характеризуемому «за-
«законом Уз» G.35) —G.36). Кроме того, поскольку здесь для
Т, привлекались измеренные значе-
приближенно оценить и величину
а = ПО/Я (?)• Согласно
этим оценкам оказалось,
что при |?|<0,03 (т. е.
в условиях «вынужден-
«вынужденной конвекции») а(?) =
= ао «* 1,2 по данным
Райдера и ао«0,8 по
данным Суинбенка; при
?<—0,03 (при свобод-
свободной конвекции) а (Б) =
= а_<х, ~ 1,7 по данным
Райдера и а-ж =1,3 по
данным . Суинбенка . (см<
также Дикон A959)); на-
наконец, при инверсиях (ког-
(когда ? > 0) а =» 1,8 по дан-
7,0
6,0
5,0
4,0
АО
2.0
го
О
-1,0
-2,0
-3,0
-40
Рис.
:
1
QO0SCL
•'ZlnZ-tconst
~?+const
i
i
/
X.. .,
1-Ц2ЦЗЦ5Ц7
65. Эмпирический график функции
— /i @. 1) при С > 0 по данным Гур-
вича A965).
ным Райдера и а «* 1,0 по
данным Суинбенка. За-
Заметное расхождение ме-
между оценками, вытекаю-
вытекающими из данных Райдера и Суинбенка, является совершенно ес-
естественным, если учесть, что турбулентные потоки измерялись
этими авторами довольно неточно (особенно это относится к зна-
значениям <7, полученным Райдером с помощью замыкания уравне-
уравнения баланса энергии) и что количество использованных наблюде-
наблюдений в обоих случаях было очень небольшим (например, изданных
Райдера удалось использовать лишь 7 профилей). Гурвич, исхо-
исходя из своих данных, построил функцию 91 (?) = у ~дГ(си- Рис- 66)
и также оценил значения а(?) =9(?)Api(?)- Согласно его результа-
результатам, о@) = ссо *** 0,8, а с ростом неустойчивости (т. е. при убыва-
убывании ?) функция а(?) возрастает вплоть до значения а-»~1,3
(с ростом устойчивости, согласно Гурвнчу, значения а(?) также
слегка возрастают, но этот его результат вряд ли можно счи-
считать надежным, учитывая малую точность данных, относя-
относящихся к инверсионным условиям). Таким образом, выводы из

8.2]
8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ
429
работы Гурйича, относящиеся к неустойчивой стратификации,
оказались полностью совпадающими с результатами обработки
наблюдений Суинбенка A955); однако полученное ими значе-
значение сю расходится с данными большинства измерений в лабо-
лабораторных условиях (согласно которым оо слегка больше еди-
единицы, см. стр. 284). Еще более значительно расходятся эти ре-
результаты с последними данными Пристли A963—1964) и
Суинбенка A964), согласно
которым а(?) резко возрастает
при убывании ? от 0 до —оо;
по этим данным ао «* 1, но
а_» ~ 3, т. е. принимает зна-
значение, существенно превосхо-
превосходящее все остальные оценки
этой величины. Таким обра-
образом, имеющиеся сведения о
функции а(?) до сих пор во
многом остаются противоречи-
противоречивыми, и их уточнение требует
еще большой дополнительной
работы.
То, что в земной атмосфе-
¦4,0
¦3,0
-O,6-Q5-U4-Q3-Q2-OJ О QJ 0,2 0,3 0,4
Рис. 66. Эмпирический график уни-
универсальной функции <р, (С) по данным
Гурвича A965).
ре переход от «режима выну-
вынужденной конвекции», харак-
характеризуемого близким к лога-
логарифмическому профилем температуры, к «режиму свободной
конвекции» с его «законом 1/3» происходит при очень неболь-
небольших отрицательных числах Ричардсона (и значениях ?), следует
также и из результатов Уэбба A958), обработавшего данные о
профилях температуры, полученные в ходе многолетних наблю-
наблюдений вблизи Эдитвейла в Австралии. Так, например, Уэбб вы-
вычислил для ряда наблюдений при неустойчивой стратификации
величину
Г(8)-ТB)
(цифры в скобках — высоты в метрах) и графически предста-
представил зависимость этой величины от числа Ri на высоте 1,5 м
(см. рис. 67). Сплошными линиями на рис. 67 нанесены значе-
значения Г = 1 (отвечающее логарифмическому профилю T(z) ~
~const—Inz) и Г=0,73 (отвечающее закону T(z) ~const+z ^).
Мы видим, что . при наименьших наблюдавшихся значе-
значениях—Ri1>5, близких к 0,015 или еще меньших, Г действительно

430
ГЛ. IV. ТЕЛШеРАТУРНО-СТРАТИФИЦИРОВАНнАЯ СРЕДА
[8.2
оказывается близким к 1, но затем оно начинает убывать и
уже при Ri *» —0,03 принимает значение, близкое к 0,73, со-
сохраняющееся затем на значительном интервале чисел Ричард-
Ричардсона. Пунктиром на рис. 67 указан постепенный переход от
Г=1 к Г = 0,73,_который должен.был бы наблюдаться, если бы
соотношение
^отвечающее логарифмическому про-
профилю, точно выполнялось вплоть до высоты 2, на которой
Г=Ц73
0,007
0,01
0.1
Рис. 67. Зависимость величины Г от Ri при неустойчи-
неустойчивой стратификации по эмпирическим данным-
г)Т ——
Ri=—0,03, а выше ее выполнялось бы соотношение -?——z 3 .
Любопытной особенностью рис. 67 является то, что, начиная
примерно с Ri1>5 = — 0,4, значение Г снова начинает умень-
уменьшаться. Если только этот результат верен (что пока не пред-
представляется бесспорным), то отсюда следует, что и при возра-
возрастании неустойчивости (но фиксированной высоте), и при
возрастании высоты (но фиксированной неустойчивой стратифи-
стратификации) наступает момент, когда используемая нами теория по-
подобия (приводящая к «закону 1/3») перестает Действовать.
Последнее обстоятельство в какой-то мере согласуется также
с неподтверждением «закона 1/3» в довольно грубых лабо-
лабораторных экспериментах Томаса и Таунсенда A957) и Таун-
сенда A959), в которых горизонтальная скорость п(г) равня-
равнялась нулю. Может быть, оно объясняется тем, что при нулевой
(или очень малой) горизонтальной скорости очень ослабевает
горизонтальное перемешивание, и в результате турбулентность
на фиксированной высоте г оказывается однородной по гори-
горизонтали лишь при очень большом периоде осреднения по вре-
времени. С другой стороны, есть некоторые основания предпола-
предполагать, что при отсутствии создаваемого горизонтальной ско-

8,2] § 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ 431
ростью горизонтального перемешивания на весь турбулентный
режим будут существенно влиять условия зарождения восхо-
восходящих конвективных струй в пределах подслоя молекулярной
теплопроводности, так что статистические характеристики тур-
турбулентности на всех высотах здесь будут зависеть уже и от
коэффициента % (ср. теорию термической конвекции Малкуса
A9546)). Более детальное обсуждение этого вопроса может
быть найдено в работах Таунсенда A962а), Пристли A962) и
Уэбба A962); однако полученные здесь результаты пока никак
не могут считаться окончательными. Ввиду неясности вопроса
в дальнейшем при рассмотрении неустойчивой стратификации
мы, как правило, будем иметь в виду лишь слой сг< \Ц, в от-
отношении которого нет сомнения, что «закон 1/3» здесь хоро-
хорошо выполняется, начиная с высоты г порядка 0,02|L| -*- 0,05[L|.
Для определения численного значения коэффициента Си
входящего в «закон 1/3» G.36), удобно рассмотреть безраз-
безразмерную величину
Я- f — = —г. (8.11)
являющуюся однозначной функцией от ? и от Ri. В условиях
свободной конвекции эта величина, очевидно, принимает по-
з
• _ / 3 \ 7
стоянное значение Я-т — \Ci) ' гДе С\ — коэффициент в «за-
«законе 1/3» .G.36); ее асимптотическое поведение при малых ? и
• i -i _I
Ri дается формулой ? .f= <*02 х21С | 2=ax2|Rl| 2- Схематиче-
Схематический вид зависимости log ^ (Ri) от log Ri представлен на
рис. 51 на стрг. 387; эмпирически эту зависимость исследовали
Пристли A955, 1956) (на материале Суинбенка A955)),
Р. Тэйлор A956а) и Перепелкина A959а),_ использовавшие
данные одновременных измерений профилей T(z) и u(z) и ве-
величины q. На рис. 68 представлен сводный эмпирический гра-
график <7(Ri), построенный по данным перечисленных выше работ.
На этом графике индивидуальные значения ц{Ш)> полученные
исходя из измерений Р. Тэйлора и Суинбенка, осреднены по
нескольким узким интервалам значений Ri; светлые кружки на
рис. 68 представляют эти осредненные значения, а вертикаль-
вертикальные отрезки характеризуют средние квадратичные отклонения
внутри каждой группы. Эти вертикальные отрезки оказались
довольно большими, что указывает на значительный разброс
индивидуальных значений g(Ri), связанный, по-видимому, со

432
ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА
[8.2
сравнительно невысокой точностью применявшихся методов из-
измерения. Однако средние точки вертикальных отрезков на
рис. 68 хорошо согласуются с предположением о существова-
.— *
нии двух предельных режимов q — |Ri[ 2 и q == q^ = const,
изображенных на рис. 68 сплошными линиями, причем пере-
переходная область между ними по этим данным оказывается очень
узкой. Треугольники на
рис. 68 представляют осред-
ненные данные Перепелки-
ной, хорошо согласующиеся
с данными Пристли и Тэй-
Тэйлора в отношении асимпто-
тического поведения ^(Ri),
но. указывающие на не-
несколько более плавный пе-
переход между предельны-
предельными режимами {как указано
¦в работе Пановского, Блэ-
кедара и Маквейла A960),
более плавный, чем у Прист-
Пристли и Тэйлора, переход ме-
между предельными режимами
получается и при обработ-
обработке американских наблюде-
._,., „ . _ ний> проводившихся вблизи
ОНеила). Эмпирическое значение коэффициента пропорций-
Рис. 68. Зависимость q от Ri по данный
Суинбенка и Тэйлора (О) и Перепелки-
Перепелкиной (Д).
нальности в асимптотическом соотношении <7(Ш)~|Ш|7
близко к 0,17 (Дикон A959)), что хорошо согласуется с обыч-
обычно принимаемыми значениями к =» 0,4, оо ~ 1. Что ка-
касается константы <7_оо, то для нее большинство эмпирических
данных дает почти одинаковые значения: согласно измерениям
Суинбенка и Р. Тэйлора, исправленным посредством введения
инструментальной поправки, ^.„«0,9 (Пристли A959а), Ди-
Дикон A959)), по данным Перепелкиной <7-оо~0,8, по данным
Гурвича A965) (измерившего значение коэффициента Ci =
=3/(<7J/3) получается, что <7«О,73, а по заметно более грубым
данным Крамера и Рекорда н Пановского — что <7-оо~0,95 и
соответственно "?_»«0,75 (см. Дикон A959)). Однако послед-
последние результаты Пристли A963—1964) и в' этом отношении
представляют исключение, так как приводят к значению q~
^ 1,2-н 1,3, заметно превышающему остальные,

8.2] § 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ 433
Зная о-оо, легко вычислить также и коэффициент С, =
3 *
= — Значению <7-оо=0,9 отвечает Ci~3,2, а значениям
<7_оо = 0,73 и <7_со = 1,2 — значения Ci~3,7 и соответственное! = 2,7.
Можно также попытаться непосредственно определить Ct по
эмпирическим данным о значениях q и профилях температуры.
Для этого надо отобрать данные, относящиеся к условиям
«свободной конвекции», и, например, приравнять Ct коэффи-
(г г \
-у) — Т BН)
(где Н — фиксированная высота) на значения Ft(q, Н) =
= (— Y D-) 3\21 — 2"*}Н~* (совпадающие с -^ при вы-
полнении «закона 7з»)- Подобное определение С\ было вы-
выполнено Перепелкиной A962) на материале 52 значений АГ и q
(при условиях с Ri <—0,04), найденных при измерениях в
1958—1959 гг. в открытой степи вблизи пос. Цимлянское. При
этом было получено значение Ct = 3,4, хорошо согласующееся
с большинством имеющихся данных о константе q-<x, (этому
значению отвечает q-^ = 0,83). Позднее Гурвич A965) подоб-
подобным же образом нашел значение Ct «* 3,7, указывавшееся
выше.
Приведенные эмпирические значения коэффициента Ct хо-
хорошо согласуются также с оценками, полученными на стр. 420,
исходя из данных о профиле ветра, если предположить, что
а-оо лишь немного отличается от единицы. Если взять за основу
какую-то одну из приведенных на стр. 420 оценок коэффи-
коэффициента С2 и одно значение Ct (или q-*,), то из их сопоставле-
сопоставления можно даже получить определенную оценку постоянной
ос_оо (именно так в работе Пановского, Блэкедара и Маквейла
A960) была получена оценка а-оо ~ 1,3). Однако имеющаяся
пока неопределенность в эмпирических значениях Ct и С2 не
позволяет придать большой вес получаемым на этом пути зна-
значениям а-оо.
Значение Ri, начиная с которого можно считать справедли-
справедливым «закон 7з»> оценивается достаточно надежно как абс-
цисса точки пересечения двух асимптот функции ^(Ri), т. е.
как корень уравнения <z0x2|Ri| 'г=<7_оо. Отсюда получаем
Ri = — аох4/^1оо' что ПРИ всех разумных значениях ao, x и q~M
приводит к значению Ri, заключающемуся между —0,02 и

434 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [8.2
—0,05, т. е. находящемуся в соответствии с имеющимися эмпи-
эмпирическими данными.
В работах Паскуила A949), Райдера A954) и Перепелки-
ной A959а) была эмпирически построена также функция
^>- (8Л2>
Ясно, что если известна функция f(t), то значения Fi(Ri) по-
позволяют определить также и функцию /ч(?), описывающую
универсальный профиль температуры. Однако недостаточная
точность имеющихся пока данных о значениях ^(Ri) и недо-
недостаточная их согласованность между собой не позволяют ис-
использовать эти данные для дополнительного уточнения поведе-
поведения функции /ч(?) или хотя бы для уточнения значений универ-
универсальных постоянных ао, а_<х> и Ct (например, с помощью соотно-
соотношения Fi@) = оо*2).
Аналогичная функция, относящаяся к профилю влажности,
<8ЛЗ>
была также эмпирически построена Паскуилом A949) и Райде-
ром A954) по данным измерений профилей ветра и влажности
и измерения испарения с помощью почвенных испарителей. По-
Поскольку, очевидно,
(см. формулу (8.6)), сопоставляя значения F2, Fi и К, можно в
принципе сделать определенные выводы и об отношениях /С»/Кт
и Къ/К- Однако очень большая неточность существующих мето-
методов измерения профиля влажности и испарения лишает пока
такие сопоставления какого-либо реального значения.
Разумеется, если интересоваться лишь сравнением различ-
различных коэффициентов обмена, то можно не рассматривать безраз-
безразмерные величины Fi, F2 и К, а сразу определять К=и\-?-,
Кт = — q/ срРо7 и /С» = —у/ р-^- ¦ К сожалению, надежные дан-
данные о j и #(г), позволяющие непосредственно подсчитать зна-
значение коэффициента /С8> пока, по-видимому, отсутствуют; по-
поэтому в настоящее время приходится принять гипотезу о том,
что Я» = Кт (см. стр. 383), без проверки (если не считать

g^j § 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ 435
косвенной проверки Чарнока и Эллисона A959), обнаруживших
сильную корреляцию между пульсациями влажности и темпера-
температуры над морем). Что же касается коэффициентов К и Кт, то
большое число пар значений этих коэффициентов, подсчитанных
по данным одновременных измерений величин т, д, п(г) и Т(г),
выполненных в Австралии, было опубликовано Суинбенком
A955), попытавшимся даже построить графики зависимости
а = Кт/К от Ri и от Rf. Однако очень большой разброс точек
на этих графиках (связанный, очевидно, с неточностью опре-
определения коэффициентов обмена) делает количественную зави-
зависимость а от Ri (или Rf), полученную Суинбенком, крайне не-
ненадежной. Качественно же результаты Суинбенка сводятся
к тому, что а не является постоянной, а возрастает с убыва-
убыванием Ri (или Rf, или ?) и принимает значения меньше единицы
при слабых инверсиях и больше единицы при «свободной кон-
конвекции». В такой форме эти результаты согласуются также с
весьма грубыми оценками Леттау по данным наблюдений
вблизи О'Нейла (см. Леттау и Дэвидсон A957), раздел 7.3).
В той части, которая относится к неустойчивой стратифика-
стратификации, результаты работы Суинбенка A955), как мы уже отме-
отмечали, прекрасно согласуются и с последними результатами
Гурвича (но противоречат последующим данным самого Суин-
Суинбенка и Пристли).
До сих пор рассматривались лишь эмпирические данные, от-
относящиеся лишь к отрицательным или, в крайнем случае,
небольшим положительным значениям Ri и ?. Данных, относя-
относящихся к сильным инверсиям, при измерениях в атмосфере по-
получено пока очень мало, и они обнаруживают сильный разброс
точек, требующий, чтобы-эти ситуации были дополнительно тща-
тщательно изучены. Тем не менее, следует указать, что наблюдения
Лилиеквиста A954) в Антарктике как будто бы подтверждают
в ряде случаев наличие линейного профиля температуры при
сильных инверсиях, предсказываемого теорией подобия при
некоторых дополнительных предположениях (см. стр. 381).
С другой стороны, если принять гипотезу о совпадении коэффи-
коэффициентов обмена для тепла и для пассивной примеси, то при
исследовании вопроса о значениях а = Кт/К = Кь1К в усло-
условиях крайней устойчивости можно воспользоваться данными
океанографических наблюдений и лабораторных экспериментов,
относящимися к течениям жидкости при очень устойчивой плот-
ностной стратификации, создаваемой отрицательным вертикаль-
вертикальным градиентом солености. Первые и наиболее известные дан-
данные такого рода были получены Дж. Тэйлором при океаногра-
океанографических наблюдениях в проливе Каттегат. Они показали, что
заметный турбулентный обмен может существовать даже при

436
ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИцИРб&АНнАЯ СРЕДА
(8.2
Ri порядка 10 и что а = К»/К при этом настолько мало, что
Rf = a Ri остается заметно меньшим единицы (см. книгу Прауд-
Праудмена A953) и дискуссию по докладу Стюарта A959)). Обра-
Обработка этих данных, приведенная а книге Праудмена, показы-
показывает, что а ~ 0,03 -*- 0,05 при 4 < Ri < 10 (см. черные квадрати-
квадратики на рис. 69). Близкие значения a = Кт/К « 0,02 -*- 0,05 были
обнаружены и при непосредственном измерении Кт и К в под-
подледном слое воды оз. Байкал (см. Колесников (I960)). Даль-
Дальнейшие эмпирические данные о зависимости а от Ri при Ri > 0
были получены (в менее чистых условиях) в лабораторных экс-
экспериментах Эллисона и
/.S, 1 ¦ : г-, Тэрнера A960). В этих
экспериментах в трубе
прямоугольного сечения
(со стеклянными боковы-
боковыми стенками) искусствен-
искусственно создавалось турбу-
турбулентное течение соленой
воды с отрицательным
вертикальным градиен-
градиентом солености. После это-
этого в одном сечении трубы
измерялись профили ско-
скорости и плотности, а-так-
а-также (с помощью косвен-
косвенных методов) — коэффи-
коэффициенты обмена К и К»-
Полученные результаты
вместе с океанографиче-
океанографическими данными Тэйло-
Тэйлора—Праудмена предста-
представлены на рис. 69. Мы видим, что разброс экспериментальных
точек здесь оказывается весьма значительным, и, кроме того,
имеется систематическое расхождение данных, относящихся к
2=1 см и 2 = 1,5 см; однако общая тенденция убывания а с
ростом Rf на рис. 69 выявляется достаточно наглядно. Сплош-
Сплошные линии на рис. 69 соответствуют значениям а, получающим-
получающимся исходя из полуэмпирической формулы
Рис. 69. Сравнение эмпирических данных
Дж. Тэйлора и Эллисона и Тэрнера о за-
зависимости а от Ri с формулой Эллисона
(8.14).
• О —данные Эллисона н Тэрнера, относящиеся
к высоте г=*1,5см;
АД—данные, относящиеся к z=l см; И—Данные
Тэйлора. Светлые значки соответствуют менее на-
надежным экспериментальным данным.
= aRi,
(8.14)
предложенной Эллисоном A957). При этом принято, что сю = 1,4
(ср. стр. 284); значения R = RfCr, отвечающие разным кривым,
надписаны над ними. В целом экспериментальные точки на

Щ I 6. ВЫЁОДЫ ТЕОРИЙ Й ДАННЫЕ ИЗМЕНЕНИЙ 43?
рис. 69 более или менее согласуются с выводами, следующими
из формулы (8.14); наилучшая оценка R =* Rfcr. согласно этим
данным, лежит где-то между 0,10 и 0,15.
8.3. Методы измерения турбулентных потоков импульса, тепла
и влаги
Выше уже отмечалось, что полная проверка выводов из тео-
теории подобия, изложенных в § 7, требует знания не только про-
профилей п(г), Т{г) и 0B), но значений турбулентного потока им-
импульса (напряжения трения) v = $u\, потока тепла q и потока
влаги (скорости испарения или конденсации) /. Поскольку к
тому же величины т (или и»), q и / вообще являются очень
важными характеристиками атмосферной турбулентности, наи-
наиболее непосредственно описывающими взаимодействие между
атмосферой и подстилающей поверхностью, естественно, что
задача определения их значений является одной из централь-
центральных в физике приземного слоя воздуха. Поэтому имеет смысл
хотя бы вкратце описать здесь основные методы измерения
турбулентных потоков.
Из прямых методов измерения величин ы*, <7 и/прежде всего
следует назвать пульсационный метод, суть которого состоит
в регистрации временного хода пульсаций и', w', Г и #' в фик-
фиксированной точке атмосферы и последующем вычислении сред-
средних по времени значений произведений u'w', w'T' и w'ib'. По-
Поскольку
7, (8.15)
то эти средние значения уже определяют все интересующие нас
величины. При этом, однако, приборы для пульсационных изме-
измерений должны регистрировать без искажения все детали пуль-
пульсаций метеорологических полей, существенно влияющие на зна-
значения и*, q и /'. Последнее требование накладывает жесткие
ограничения на параметры аппаратуры, причем даже само ак-
аккуратное выяснение характера этих ограничений является не-
нелегким делом; для этого надо заранее знать, какие именно де-
детали пульсаций влияют на турбулентные потоки, а это требует
сведений о спектральном составе турбулентных потоков, остаю-
остающихся до сих пор очень неполными (подробнее об этом будет ска-
сказано в гл. 8 ч. 2 книги). Кроме того, при использовании пульса*
ционного метода для определения турбулентных потоков надо
уметь выбрать интервал временного осреднения так, чтобы по«
лучающиеся средние значения были близки к средним, взя«
тым по некоторой разумно определенной статистической

438 ' ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОбАННАЯ СРЕДА [8.3
совокупности, но чтобы еще не проявлялась постепенная «эво-
«эволюция уровня» метеорологических величин, о которой мы гово-
говорили на стр. 361. Все эти обстоятельства сильно осложняют изме-
измерения и в конечном счете приводят к тому, что результаты не все-
всегда оказываются достаточно точными. Тем не менее, пульсацион-
ный метод до сих пор остается единственным общим методом
непосредственного определения всех трех величин: т, q и /.
Для измерения тонких деталей пульсаций скорости ветра и'
и w' до 1958 г. большинство исследователей применяло принцип
термоанемометра, уже в течение ряда десятилетий с успехом
использующийся для измерений пульсаций скорости потока в
аэродинамических лабораториях. Одной из первых работ, в ко-
которой этот принцип был успешно применен к измерениям в
атмосфере, была работа Гедеке A935). Позже (в 1947—1949 гг.)
удобные приборы такого типа были созданы в СССР Обуховым
и Кречмером (см., например, Кречмер A954)). Более инерцион-
инерционные термоанемометрические приборы примерно в то же время
начали применяться австралийскими и английскими исследова-
исследователями (см., например, Суинбенк A95Ja, 1955), Дикон A955),
Макилрой A955), Джонс и Паскуил A959));. очень тонкая
аппаратура, построенная на принципе термоанемометра, была
разработана Маккриди A953).
Датчиками всех термоанемометрических приборов являются
тонкие металлические нити (чаще всего платиновые), порядка
1 см длиной, которые во время измерений подогреваются током
до температуры порядка нескольких сот градусов. При этом
изменения температуры нити (а следовательно, и ее сопроти-
сопротивления) определяются теплоотдачей в воздух, зависящей от
нормальной к нити компоненты скорости обдувающего нить
потока и практически не зависящей от небольших изменений
температуры воздуха (имеющих обычно порядок долей граду-
градуса). Поэтому, измеряя сопротивление нити, можно определить
нормальную к нити компоненту скорости ветра. Существенным
неудобством является при этом нелинейный характер зависи-
зависимости сопротивления нити от скорости ветра. Измерение пуль-
пульсаций сопротивления нити осуществляется с помощью реги-
регистрации пульсаций силы тока, проходящего через нить. При
вертикальном положении нити термоанемометра эти пульсации
соответствуют пульсациям горизонтальной компоненты скорости
ветра. Если же установить две нити в вертикальной плоскости,
¦проходящей через направление среднего ветра (что достигается
при помощи инерционной флюгарки), и разместить их под
-углами +45° и —45° к вертикали, то разность сопротивлений
этих нитей оказывается пропорциональной вертикальной ком-
компоненте скорости ветра (с коэффициентом пропорциональности,

8.3] § 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ 439
зависящим от скорости среднего ветра). Термоанемометры, ис-
использовавшиеся в СССР, позволяют регистрировать пульсации
скорости ветра с точностью до 1 см/сек и имеют инерцию (по-
(постоянную времени) порядка 0,01 сек; возможны, однако, и еще
более точные и менее инерционные приборы этого типа.
Нелинейность термоанемометра существенно затрудняет вы-
вычисление средних значений произведений пульсаций. При этом
приходится или записывать пульсации силы тока в термоанемо-
термоанемометре на фотобумагу, снимать с этой записи ординаты кривых
и затем уже численно переводить эти ординаты в значения и'
и да' с помощью специальных тарировочных кривых (Кречмер
A954)), или же дополнительно про-
пропускать пульсации тока через нели- г—» ПТ"|
нейный прибор с характеристикой, по- I f I *\
добранной по тарировочным кривым 1j
таким образом, чтобы сигнал на вы- 2Scu \
ходе был уже прямо пропорцио- ' ¦ i
нальным измеряемой пульсации ско- т ¦
рости (Маккриди A953), Р. Тэйлор Y/7,
(.1958)). Чтобы избежать этих ослож- '—
нений и в то же время иметь возмож- Рис 70 Схема расположе-
ность вычисления средних значений ния излучателей и прием-
произведений пульсаций С помощью ников в акустическом ми-
автоматических приборов, в 1958 г. кроанемометре.
Бовшеверовым и Гурвичем был со-
создан линейный прибор для измерений пульсаций скорости — уль-
ультраакустический микроанемометр, основанный на зависимости
времени распространения..звука от излучателя до микрофона от
скорости движения воздуха на его пути (см. Гурвич A959), Бов-
шеверов и Воронов (I960)). Важнейшей частью этого прибора
являются миниатюрные цилиндрические излучатели звука и ми-
микрофоны, имеющие диаметр 2 мм и длину около 5 мм. При-
Прибор содержит два излучателя Hi и Иг и два приемника (ми-
(микрофона) nt и П2, причем пара Hi и П2 помещается на рас-
расстоянии 2,5 см от пары nt и И2 (см. рис. 70). При этом звук
(точнее говоря, ультразвук) распространяется по практически
совпадающим путям от Hi к П[ и от Иг к Пг в противополож-
противоположных направлениях, и при совпадающих фазах колебаний из-
излучателей разность фаз колебаний микрофонов оказывается
пропорциональной компоненте скорости ветра по направлению
базы прибора и фактически не зависящей от температуры воз-
воздуха. Такой прибор также позволяет измерять пульсации скоро-
скорости с точностью до 1 см/сек, а его инерция меньше 0,001 сек.
Помимо термоанемометров и акустических анемометров для-
измерения пульсаций скорости ветра иногда используются

440 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [8.3
также специальные микрофлюгарки, построенные на принципе
обычного флюгера. Особенно удобным оказывается применение
микрофлюгарок для регистрации пульсаций направления ветра,
что вместе с данными о пульсациях полной скорости (опреде-
(определяемыми, например, с помощью термоанемометра) позволяет
определить мгновенные значения всех трех, компонент скорости
uf, v' и w' (см., например, Крамер и Рекорд A953) и Леттау
и Дэвидсон A957), раздел 5.2). Однако инерционность такой
аппаратуры превосходит инерционность аппаратуры, описанной
выше, а возможности автоматизации измерений и их последую-
последующей обработки оказываются здесь меньшими.
Измерение пульсаций температуры Т можно производить
с помощью приборов, основанных на принципе термометра со-
сопротивления (с проводниковыми или полупроводниковыми дат-
датчиками), или с помощью миниатюрных термопар. В качестве
типичного примера прибора.для измерения значений Т можно
упомянуть микротермометр Кречмера A954), представляющий
собой термометр сопротивления с платиновой нитью (тех же
размеров и с той же инерцией, что'и в применявшемся в СССР
термоанемометре) в качестве датчика. При использовании этой
нити для измерения пульсаций температуры через нее пропу-
пропускается очень слабый ток, при котором ее перегрев относитель-
относительно окружающего воздуха не превосходит 0,01°. В таком случае
теплоотдача в воздух практически отсутствует, и температура
нити (а следовательно, и ее сопротивление) зависит поэтому
только от колебаний температуры воздуха л не зависит от
скорости ветра. В результате пульсации силы тока, проходя-
проходящего через нить, оказываются пропорциональными пульсациям
температуры воздуха (с коэффициентом пропорциональности,
определяемым только параметрам^ "прибора).
Для измерения пульсаций влажности О' можно использо-
использовать сухой и смоченный термометры сопротивления (или сухую
и смоченную термопары), дающие мгновенные значения двух
температур V и Т{, по которым значение Ф' определяется с по-
помощью так называемого психрометрического уравнения (см.,
например, Мидлтон и Спил хауз A953) или Кедроливанский и
Стернзат A953)). При этом Ф' можно находить по значениям
V и 7i численно (Макилрой A955)), а можно вместо этого
.подавать пульсации Т и Т{ на вход специального электриче-
электрического аналогового устройства, автоматически выполняющего
операцию, эквивалентную решению психрометрического уравне-
уравнения (Суинбенк A9516), Р. Тэйлор A9566), Тэйлор и Дайер
,A958), Дайер A961)). В обоих случаях задача оценки точности
получаемых значений <У и учета влияния погрешностей и инер-
инерции прибора на значение величины / = рдо'Ф' оказывается за-

8.3]
§ 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ
441
метно более трудной, чем в случае определения величин Т и q
(ср. Р. Тэйлор A963)); поэтому надежное получение значений/
с помощью пульс,ационного метода остается пока еще делом
будущего. Значительные перспективы открывает в этом отно-
отношении использование вместо двух термометров практически
безынерционного оптического метода измерения пульсаций
влажности, основанного на зависимости коэффициента прелом-
преломления воздуха от содержания водяного пара (см. Елагина
A962)). Однако такая аппаратура пока еще не доведена до
состояния, позволяющего
систематически исполь-
использовать ее в полевых ус-
условиях.
Пульсационные изме-
измерения в принципе позво-
позволяют определять для ря-
ряда последовательных мо-
моментов времени одновре-
одновременные значения и' и w'
или w' и Г', или w' и ¦&'.
В качестве примера, ил-
иллюстрирующего полу-
получающиеся при этом ре-
результаты, на рис. 71 (за-
(заимствованном из работы
Монина A953)) приво-
приводится пример корреляци-
корреляционного графика, характе-
характеризующего связь между,
пульсациями w' и Т, по
измерениям на высоте 1,5 м в инверсионных условиях. Этому
графику соответствует коэффициент корреляции rwT между зна-
значениями до' и Т', равный —0,24; турбулентный поток, тепла
здесь равен q = —0,03 кал/см2мин. На рис. 72 (взятом из той
же работы) приводится пример корреляционного графика, ха-
характеризующего связь между пульсациями и' и до', также по
измерениям на высоте 1,5 м. Здесь коэффициент корреляции
ruw равен —0,65, а и* = 0,33 м/сек.
Разумеется, численный подсчет средних значений произведе-
произведений пульсаций и их коэффициентов корреляции по записям типа
изображенных на рис. 1 на стр. 10 весьма трудоемок и утомите-
утомителен. Однако, если используемые приборы линейны (как, напри-
например, микротермометр или ультразвуковой микроанемометр) или
же превращаются в практически линейные с помощью добавления
к ним специальной линеаризирующей приставки, то средние
•
* * *
• •
-fax.
ю,см/сек
• •
• • • "
• •
•" -1-
'-во-
-во-
во
60
, •••
. •
.•
*
•
• * •
..V.
Рис. 71. Пример корреляционного гра-
графика для пульсаций температуры и вер-
вертикальной скорости.

442
ГЛ, IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА
(8.3
значения произведений (или квадратов) пульсаций можно полу-
получать автоматически. Для этого надо только подать сигналы на
выходе пульсационных приборов на вход специального коррело-
коррелометра— интегрирующего устройства, подсчитывающего инте-
интеграл от произведения двух вводимых в него функций. Подобные
автоматические коррелометры были созданы в СССР Бовше-
веровым, Гурвичем, Татарским и Цвангом A959) (см. также
Бовшеверов, Гурвич, Мордухович и Цванг A962)) и были сра-
сразу же использованы ими для определения турбулентного потока
06
0.4
0,2
О
-02
-0,4
-Off
-ов
•
•
.•
щм/ce/f
•
•
1 i* * ...
• • •
•
•
•
•
•
•
•
-1
1'
Рис. 72. Пример корреляционного графика для
пульсаций горизонтальной и вертикальной
компонент скорости ветра.
тепла (Бовшеверов, Гурвич,'Цванг A959)). В Австралии род-
родственная аппаратура была разработана Тэйлором и Уэббом
,A955) и Дайером A958).
Кроме пульсационного метода для измерения турбулент-
турбулентного напряжения трения можно применять также динамометри-
динамометрический метод, впервые предложенный Шеппардом A947), а за-
затем использовавшийся Паскуилом A950), Райдером A954),
некоторыми американскими исследователями (см. Леттау и Дэ-
Дэвидсон A957), раздел 3.2) и Гурвичем A961). Сущность этого
метода заключается в том, что кусок почвы с характерным
для окружающей местности травяным покровом помещается
вровень с поверхностью почвы на подвижную платформу (под-
(подвешенную на нитях в опытах Гурвича и плавающую в жидкости
в опытах других исследователей), удерживаемую на месте спе-
специальной пружиной. Сила трения, действующая на платформу
при наличии ветра, при этом определяется с помощью измере-
измерения либо натяжения пружины (Шеппард, Паскуил и др.), либо

g_3j $ 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЯ 443
смещения платформы (Гурвич). Приборы для измерения вели-
величин t и и* с помощью этого метода весьма капризны и работа
с ними требует большой осторожности, но точность лучших из
них не уступает точности лучших из имеющихся пульсационных
приборов, предназначенных для той же цели.
Турбулентный поток влаги / в метеорологии чаще всего из-
измеряется с помощью почвенных испарителей.' В этих приборах
используется кусок почвы, вырезанный (по возможности без
нарушения его структуры) из своего окружения и помещенный
в специальный открытый сверху сосуд, края которого находят-
находятся на уровне почвы. Вес вырезанного куска измеряется через
определенные промежутки времени, и отсюда находится ско-
скорость потери им влаги. К сожалению, пока трудно сказать, в
какой мере скорость испарения вырезанного образца совпадает
со скоростью испарения неповрежденной почвы. Поэтому в по-
последние годы многие исследователи считают, что данные, полу-
полученные с помощью почвенных испарителей, вообще не имеют
серьезного научного значения. Чтобы опровергнуть это мнение,
необходимо иметь богатый материал одновременных измере-
измерений испарения с помощью испарителей и с помощью пуль-
сационного метода, позволяющего установить, что между пока-
показаниями двух типов приборов действительно имеется значитель-
значительная связь, и выяснить характер этой связи. Пока, однако, такой
материал все еще отсутствует, так как вообще пульсационные
измерения испарения до сих пор очень мало развиты и имеют
небольшую точность.
Для определения турбулентного потока тепла q и испаре-
испарения / можно привлечь также уравнение теплового баланса под-
подстилающей поверхности
(8.16)
где В— радиационный баланс поверхности Земли (т. е. сумма
приходящей длинноволновой и коротковолновой радиации, из
которой вычтена уходящая радиация), Q — поток тепла в почву,
а т — скрытая теплота испарения. В некоторых случаях при
очень сухой почве можно предполагать, что последний член в
правой части мал по сравнению с двумя остальными. Тогда, из*
мерив величины В и Q (определение последней из которых,
впрочем, сопряжено с рядом трудностей и обычно оказывается
не очень надежным), мы можем вычислить и величину q. В дру-
других случаях, когда величина q измеряется с помощью пуль*
сационного .метода, можно воспользоваться уравнением (8.16)
и данными измерений q, В и Q для нахождения испарения /.
Если q неизвестно, но значения /, полученные с помощью испа«
рителей, рассматриваются как достаточно надежные, то по ним

444 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [g,4
с помощью (8.16) можно восстановить и значение ц (ср. Рай-
дер A954)); если же и q, и } измеряются непосредственно, то
уравнение (8.16) можно использовать для дополнительной про-
проверки полученных данных (Дайер A961)). Наконец, если ни q,
ни j не измеряются непосредственно, но имеются данные о про-
профилях температуры и 'влажности, то можно воспользоваться
предположением о равенстве коэффициентов обмена для тепла
и для влаги, из которого следует, что
(8Л7)
где 3"i и Го — значения средней_температуры на двух фиксиро-
фиксированных высотах Zi и Zo, a Oi и О0 — значения влажности на тех
же высотах. Из (8.16) и (8.17) вытекает, что
7(B-Q) ,__ B-Q .Я1_
= -ГП J- ' (8Л8)
где
последние равенства позволяют подсчитать значения q и / по
измеренным значениям В, Q, Tit To, <h и до. Аналогичные фор-
формулы можно получить и исходя из некоторых других предполо-
предположений о связи между разными коэффициентами обмена (см.,
например, Леттау и Дэвидсон A957), раздел 7.3). Заметим,
однако, что, поскольку величины Q и <h — О0 могут быть изме-
измерены лишь с большой ошибкой, точность балансового метода
заметно уступает точности, например, пульсационного определе-
определения q.
8.4. Определение турбулентных потоков по данным о профилях
метеорологических величин
Выше мы перечислили ряд методов измерения величин и*,
д и /. Однако все эти методы довольно сложны и требуют спе-
специального оборудования, имеющегося пока лишь в немногих
научно-исследовательских учреждениях. В то же время для гео-
геофизики большой . интерес представляло бы систематическое
определение турбулентных потоков в большом числе пунктов
земной поверхности. Поэтому большое значение приобретают
методы определения величин и*, q и /по данным более простых

g#4] § 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ 445
измерений и, в первую очередь, обычных измерений профилей
метеорологических полей (т. е., как часто говорят, градиентных
измерений1)).
Мы здесь не будем задерживаться на имеющих значитель-
ную давность многочисленных спекулятивных «полуэмпириче-
«полуэмпирических» формулах, выражающих потоки через профили, так как
почти все они не сравнивались с данными непосредственных
измерений (появившимися лишь в самое последнее время) и
мало надежны. Вместо этого мы воспользуемся развитой в § 7
теорией подобия для турбулентного режима в приземном слое
воздуха. Согласно этой теории, профили скорости ветра и тем-
температуры (влажности пока мы не будем касаться) определяют-
определяются общими формулами G.24), содержащими параметры ut, q,
z0 (от последней величины_зависит полная скорость п(г)),
To = T(Zo) (от Го зависит T(z)), универсальную постоянную
Кармана х и две универсальные функции /(?) и /i(?). Постоян-
Постоянная х близка к 0,4; относительно функций f и Д также имеется
ряд сведений, собранных в § 7 и пп. 8.1—8.2. Будем пока счи-
считать, что эти функции нам точно известны. В таком случае лю-
любые четыре измерения значений скорости и температуры по-
позволяют составить четыре уравнения, в принципе достаточные
для определения четырех параметров ut, q, г0 и Го, причем чис-
число необходимых измерений, вообще говоря, нетрудно даже
уменьшить (например, вовсе не рассматривая значений T(z)
илирассматривая только разности T(z2)—T(z{), не зависящие
от Го). Сложность здесь состоит только в том, что на самом
деле функции f и ft до сих пор известны лишь приближенно
(причем данные о них разных исследователей даже кое в чем
противоречат друг другу) и не задаются никакими простыми
аналитическими формулами, а результаты измерений всегда
содержат некоторые ошибки. Поэтому на практике приходится
пользоваться какими-то приближенными выражениями для f и
fu и разные методы, использующие разные наборы исходных
данных, будут приводить к несколько различным результатам.
Напомним, что описанный на стр. 410—412 метод Монина —
Обухова обработки измерений профилей ветра и температуры уже
содержал в качестве составной части определение значений —
') Это название связано с тем, что измерения профилей отличаются от
стандартных метеорологических измерений на одной фиксированной высоте
(«на уровне метеорологической будки») тем, что здесь дополнительно опре-
определяются еще и значения градиентов метеорологических полей на разных вы-
высотах. Поскольку определение турбулентных потоков во многих случаях явля-
является основной целью измерений профилей, методы определения потоков по про-
профилям часто называются методами интерпретации градиентных измерений.

440 гл. iv. телшературно-стратифицированная среда [8.4
и L (позволяющих найти также и q) по значениям ы(г) и Т(г).
Несмотря на то, что этот метод опирался на использование «ло-
«логарифмической + линейной» формулы для профилей, которая
позже была подвергнута критике, и на предположение, что
as 1, точность его, как показало сопоставление получаемых та-
таким образом значений и* и q с данными непосредственных из-
измерений, оказалась более высокой, чем можно было бы
ожидать. Однако в настоящее время рекомендовать этот метод
в его первоначальном виде для непосредственного практиче-
практического применения, разумеется, нельзя, так как он все же до-
довольно груб и очень громоздок (в частности^ включает опреде-
определение некоторых параметров по материалам ряда измерений с
помощью метода наименьших квадратов).
Близкие методы определения значений ut и q по измере-
измерениям профилей ветра и температуры, также использующие
«логарифмическую+линейную» аппроксимацию универсальных
функций и предположение, что Кт — К, были предложены Таке-
учи A961) и Шиотани A962). В работе Такеучи, в частности,
приведены некоторые практические приемы, позволяющие упро-
упростить вычисления; там же проведено сравнение получающихся
значений и* и q с данными непосредственного измерения потоков
(по некоторым материалам, включающим измерения и пото-
потоков, и профилей). Тем не менее, даже и здесь методы определе-
определения значений и* и q остаются неоправданно сложными; в то же
время они используют лишь небольшую часть имеющихся све-
сведений о функции f(t,).
Методы определения турбулентных потоков по измерениям
профилей рассматривались также в работах Казанского и Мо-
нина A956, 1958, 1962), Пристли A9596), Уэбба A960), Па-
новского, Блэкедара и Маквейла A960), Монина A962а), Кон-
до A9626), Дикона и Уэбба A962) и Пановского A963). Мы
здесь изложим, следуя в основном работам Казанского и Мо-
Монина, общий метод представления данных об универсальных
функциях в виде, удобном для практического нахождения тур-
турбулентных потоков; предварительно, однако, мы сделаем не-
несколько замечаний общего характера.
Начнем с вопроса о выборе величин, наиболее удобных для
определения потоков. Согласно сказанному выше, одних только
значений скорости ветра на трех высотах в принципе уже долж-
должно хватить для нахождения параметров ы*, q и z0; поэтому
может создаться впечатление, что привлечение данных о темпе-
температуре воздуха совершенно излишне. Однако, как показал При*
стли A9596), использование даже значений п(г) для более
чем трех высот г не позволяет надежно определить q, так как

3.41 § 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИИ 447
получаемые при этом значения сильно расходятся с данными
непосредственных измерений и весьма различны при разных
методах обработки. Поэтомупредставляется, что дополнитель-
дополнительное использование значений T(z) имеет большую практическую
ценность. Этот вывод фактически следует и из статьи Панов-
ского, Блэкедара и Маквейла A960), испробовавших метод
определения q по одним лишь значениям п{г) на трех вы-
высотах (и значению z0), но не получивших хороших резуль-
результатов.
Так как нас обычно интересуют в первую очередь значения
и* и q, то можно подумать, что целесообразно с самого начала
исключить величину z0, рассматривая лишь разности m(z2)—
—m(zi),' а не сами значения m(z). Нетрудно понять, однако,
что при этом мы сильно теряем в точности, так как разности
скорости ветра определяются заметно менее точно, чем сам ве-
ветер (особенно, если высоты zt и z2 сравнительно близки друг
к другу). Кроме того, можно показать, что при исключении ве-
величины Zo даже небольшая ошибка в разностях скоростей бу-
будет уже сильно сказываться на величинах и* и q. Поскольку
значение z0 для данного пункта и времени года фактически
надо определить лишь один раз (оно не меняется), и его нахо-
нахождение несложно, более целесообразно заранее найти z0 и за-
затем уже все время пользоваться полученным значением. В то
же время величина f0 = T(z0) непостоянна, и ее исключение не
приводит к вредным последствиям; поэтому данные о профиле
температуры разумно использовать лишь в форме разностей
f(z2) —T(Zi). При этом для определения значений и* и q до-
достаточно иметь данные двух измерений.
Исходя из сказанного выше, можно рекомендовать при оп-
определении значений и* и q по данным о u(z) и T(z) начать
с определения параметра шероховатости Zo, а затем исходить
из скорости ветра U на некоторой фиксированной высоте Я и
из разности 6Г средних температур на двух высотах (напри-
мер, на высотах 2Н и -у). Согласно основной гипотезе подобия
для турбулентного режима в приземном слое атмосферы, вели-
Y) могут быть выражены
через Н, -i-, и,, -г— и z0. Следовательно, ut и -^— (а также
' 0 Ср?0 Ср?0
зависящая от них величина L) в свою очередь могут быть вы-
выражены через Я, ji-, U, ЬТ и z0. Из этих пяти величин можно
составить две независимые безразмерные комбинации, которые

448 гл. lv. темперАтУрно-Стратифицированная среда (8.4
мы запишем в виде
о _ aSH }1_ г — г° (я оп\
где а — произвольный безразмерный коэффициент, об удобном
выборе которого мы еще скажем чуть ниже. Таким образом,
получаем
.7r = Fi(B,^o), ,'I/jt =F2(B, Co), -г = F3(B, Co), (8.21)
где Fi, Fz, F3 — некоторые универсальные функции переменной
В, зависящие также от параметра ?о. Располагая графиками
этих функций, мы имели бы возможность определять с помощью
таких графиков величины и*, q и L по данным градиентных из-
измерений. Графики, же функций Ft, i = 1, 2, 3, можно построить
либо эмпирически, по данным независимых синхронных измере-
измерений величин U, ЬТ, ы* и q, либо теоретически, на основе задания
вида универсальных функций. f(?) и М?). На втором из этих
способов, позволяющем последовательно улучшать точность
определения потоков по мере уточнения наших сведений об уни-
универсальных функциях, мы здесь остановимся немного подробнее.
Примем за основу общие формулы G.24), с помощью кото-
которых были определены универсальные функции /(?) и /i(?).
Тогда первую формулу (8.20) и первые две формулы (8.21)
можно будет переписать в виде
' (а>22)
Первое из этих уравнений задает в неявной форме вид функции
F3(B, ?o). Если функции f(t) и fi(t,) известны, то это уравнение
можно разрешить относительно F3, например, графически, и
тогда два остальных уравнения (8.22) будут параметрически
задавать функции Fi(B, ?o) и F2(B, &>).
В настоящее время различие формы профилей скорости вет-
ветра и температуры не установлено еще вполне убедительно; по-
поэтому пока имеет смысл исходить из предположения о подобии
1 К
этих профилей, т. е. считать, что Л(С)=— /(С), где а==-^- =
= const. В таком случае и коэффициент а в (8.20) и (8.21) так-
также удобно принять равным отношению Кт/К. При этом формулы

8 4] § 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИИ
(8.22) несколько упрощаются и принимают вид
п_ 1 /B//гз)-/A/2/г3)
/7s[/<l//7s)-/(Ce//7s)]t>
449
(8.22')
[/ (l/Z's) - / (Wdl [/ B/^3) -/A/2/%)] '
Поскольку в настоящее время данные о различиях между раз-
разными коэффициентами обмена очень неполны и противоречивы,
пока естественно просто считать, что а = 1. Однако включение
коэффициента а в величину В и функцию /"^позволяет сохранить
и
?o=O,O4
Co = 0,02
to =007
" =0005
О -0,5 -/ -7,5 '2 -2,5- -4 -3 -2,5 -2 -7,5 -1 -0,5 О 0,5
Iff/В/ B
Рис. 73. Номограмма Казанского и Монина для определения без-
безразмерного напряжения трения uJU = Fx по параметру стратифи-"
кации В и параметру шероховатости Со-
ту же схему расчета и после появления более точных данных о
коэффициентах обмена, изменив лишь значение а. Возможно
также, что еще до того, как появятся достаточно надежные
сведения о функции а(?), требующие отказа от формул (8.22')
и возвращения к более общим формулам вида (8.22), станет
целесообразно, тем не менее, считать а различным, например,
при практически нейтральной, неустойчивой и устойчивой
.стратификации.
Казанским и Мониным, исходя из формул (8.22'), были по-
построены номограммы функций Flt F2 и F3 в предположении, что

450
ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА
(8.4
х = 0,43, а функция f(?) при ?<0 задается интерполяционной
формулой G.49) с ?i = 0,03 и С2 = 1, а при ? > 0 — «логариф-
«логарифмической + линейной» формулой G.33) с р = 0,6. Следует
иметь в виду, что использованные при этом построении число-
числовые значения параметров кое в чем отличаются от значений,
которые в настоящее время представляются наилучшими; осо-
особенно это относится к определяющему вид /(?) при устойчи-
;вой стратификации параметру р. Однако изменение значений
Юйраметров в соответствии с последними данными не изменит
кг-
Срросс1/&Т
-3,0 -2,0 -/,0
О
Рис. 74. Номограмма для определения безразмерного потока тепла
qlcpfaaUbT=Ft по В и С„.
общего вида рассматриваемых номограмм и даже, может быть,
не очень сильно изменит числовые значения определяемых по
этим номограммам потоков. В то же время пересчет номограмм
в настоящее время вряд ли был бы оправдан в связи с недавно
обнаружившимся и пока еще не объясненным расхождением в
значениях /(?) и а, полученных австралийскими и всеми осталь-
остальными исследователями. Поэтому мы ограничимся тем, что при-
приведем на рис. 73—75 старые номограммы Казанского и Монина^
дающие достаточное представление о порядке величины турбу-
турбулентных потоков, соответствующих тем или иным значениям
U =п(Н) и 6Т = ТB.Н)—Т(Н/2).
Разумеется, номограмма для F2 может быть использована
не только для определения турбулентного потока тепла q, Щ

8.4]
§ 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИИ
451
также и для определения скорости испарения /, если только,
кроме U и ЬТ, измерена также разность удельных влажностей
на двух высотах Ш =1 BН)—Ъ (~\. Действительно, согласно
Iff/В/ О
1оА
1о=О,О2
Рис. 75. Номограмма для определения L/H=aFt по В и
общим формулам G.24)_и эмпирически обнаруженному по-
подобию профилей Т(г) и #(z),
/VPo
aUbT
(8.23)
где сц = /Cft//C.
С помощью формул' (8.22') нетрудно установить вид функций (8.21) при
стратификации атмосферы, близкой к безразличной, сильно неустойчивой и
очень устойчивой. При близкой к безразличной стратификации ]В| мало, а
|F3| велико, и в (8.22') можно всюду полагать f(?)==ln]?;|. Тогда уравнения
(8.22) сильно упрощаются и могут быть разрешены в явной форме, причем
получается
In(I/Co) '
In 4-In (I/to)'
1п4
¦4". (8-24)
При сильной неустойчивости В будет большим отрицательным, a F3 — малым
отрицательным. Асимптотическое поведение функций (8.21) при этом можно

452 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [8.4
выяснить, положив / (С) » с2—СГ2 i С I Зв формулах (8.22'). Тогда получается
1 _I\7 I I _1
1 •
A -1
U3 —2 3
(8.25)
I -1U
з _, з I
I
,з
- v ч
Наконец, при сильной устойчивости В будет больщим положительиым, a F% —
малым положительиым. Асимптотическое поведение функций (8.21) в этом
случае можно выяснить, положив в (8.22') всюду /(?) => с3 + C3Z,. При этом
оказывается, что В ие может неограниченно возрастать, а приближается к
3
¦ пределу пр /j . .2 ¦ при F3->0. Таким обр-азом, число В при устойчивой
стратификации не может превосходить значения 3/2С3. Для функций Fx и F2
при малых F% получается
/=•, » ? . /'а»—7- ? . (8.26)
С3A-С0) ЗС23A-С0)
Если, например, при сильной устойчивости принять для /(?) асимптотиче-
l-i
)
l
скую формулу / (С) ~ Сз -f- С3 С -\ ^-j (C3C) т . вытекающую из уравнения
G.65) интерполяционной теории Казанского и Монина с а = С3, то для функ-
функции Fs получается следующая асимптотическая формула:
i-l
1-С0 т 2 '-
Особенно простой вид приобретает методика определения турбулентного
потока тепла по данным градиентных измерений в случае сильной неустой-
неустойчивости. А именно, вспоминая формулу G.49), мы видим, что если все вы-
высоты измерения превышают ?iL (для этого достаточно, чтобы выполнялось
Н \
р
Н . \
Н . \
неравенство -g-^di.1, то для интерпретации результатов измерений можно

8.4]
§ 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИИ
453
воспользоваться формулами, справедливыми в предельном случае свободной
конвекции. Критерий -н- > CiZ., обеспечивающий эту возможность, можно
переписать в виде
К^ 21 С Т*
жем привести этот критерий к виду
Пользуясь для Fs формулой (8.25), мы мо-
мо( 1 \ ±
!l2a-lJ|C.|a
0,011
\В\>
где, как и при построении номограмм, принято, что С2 = 1, а |^| = 0,03. Зна-
Значения этого критерия в грубых цифрах изменяются от 0,0005 при ?о=О,ОО5
до 0,004 при ?о=О,О5, так что правую часть неравенства можно для этого
интервала зиачеиий ?о записать приближенио в виде 0,1 ?о. Тогда предложен-
предложенный критерий приводится к виду
где г0 и Я измеряются в метрах, U — в м/сек и 67" — в градусах С.
Если критерий (8.28) выполняется, то это значит, что при
мы находимся в условиях режима свободной коивекции, где
_ з
дг
(8.28)
(Й.29)
(см. G.36) и G.39)). Исходя отсюда, легко показать, что в этом случае
3 11 3
(8.30)
(тот же результат можно получить и из формул (8.21) и (8.25)). Подставляя
это значение q в формулу G.38) для коэффициента турбулентности
К = olZIo Кт иа высоте z= H, получаем
1 1 3 1 -
B3-2~3).
-?-|2 Я2|6Г|2,
(8.31)
1 1
Таким образом, величины q и К(Н) отличаются от //2|5Г|2 и соответ-
ственно Я2|6Г|2 лишь универсальными (но не безразмерными) множи-
множителями Выражая Н в метрах, 67" в градусах, q в ~ и К (Я) в
см мин
мг1сек и полагая * « 0,4, о_00 = С2 « 1 и Го « 300° К, получаем
L 1 11
11
/С(Я)«0,15Я2 |6Г|2.
(8.32)

454
ГЛ. iv: ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА
[8.5
Эти формулы позволяют очень быстро оценивать значения q и К(Н) при
неустойчивой стратификации.
При #=2 м и ?о=0,005 (т. е. Zo=I см, что является типичным значением
«высоты шероховатости» для сухой степи) для параметров L, -А- и _
с помощью номограмм рис. 73—75 получаются следующие характерные знз-
чеиия. При состояниях, близких к безразличной стратификации, с помощью
формул (8.24) получаем
1 =
0,52 1
1
(igCoJ В ~ 10В ' U
«0,08,
aUbT
Эти формулы практически оказываются достаточно точными при
—0,001<В<0,005 (чему соответствуют значения L>20 м. и' L<—100 At).
уменьшаются; с ростом
С ростом устойчивости величины L, -А- и
aUbT
неустойчивости \Ц уменьшается, а -А- и '.._ растут. Характерные значе-
значения этих величии при различных В приведены в следующей таблице:
в .
—0,015
—0,006
—0,001
0,005
0,03
0,1
L м
—2
-10
—100
20
4
1,6
и*
V
0,10
0,09
0,08
0,08
0,07
0,06
ч .
aUbT
—0,13
—0,09
-0,05
—0,05
—0,03
—0,02
Качественная характеристика
Сильная неустойчивость
Умеренная неустойчивость
Слабая неустойчивость
Слабая устойчивость
Умеренная устойчивость
Сильная устойчивость
По данным экспедиции 1951 г. в Заволжье типичные значения,скорости тре-
трения и, в сухой степи в условиях ясной летней погоды (при скоростях ветра
U порядка 2 + 6 At/сек) лежат в интервале 0,2 -^ 0,4 м/сек, а турбулентный
поток тепла q днем принимает значения порядка 0,25 ч- 0,35 кал/см2 мин, а
ночью — порядкаг (—0,04) -=- (—0,06) кал/см2мин (см. Моиии A953)).
8.5. Пульсации скорости ветра и температуры
в приземном слое
Турбулентные потоки импульса и тепла представляют со-
собой лишь частные примеры статистических характеристик
пульсаций скорости ветра и температуры. Многие другие ха-
характеристики этих пульсаций были проанализированы с точки
зрения теории подобия в п. 7.5, и все они могут быть найдены
экспериментально с помощью той же аппаратуры, которая при-
применяется в пульеационном методе определения величин и* и q.
Имея данные одновременных измерений значений и,., q и еще
какой-нибудь статистической характеристики пульсаций (или

8.5]
§ 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ
455
имея данные измерений этой статистической характеристики и
оценив ы* и q с помощью метода, изложенного в п. 8.4), можно
проверить относящиеся к этой характеристике выводы из тео^
рии подобия и эмпирически построить соответствующую уни-
универсальную функцию от ? = т~" Таким образом, данные пуль-
сационных измерений в принципе позволяют определить все
функции /3 /ц, ?, и <pN, введенные в п. 7.5.
К сожалению, имеющиеся в настоящее время эмпирические
данные о характеристиках пульсаций (содержащиеся в ра-
работах Суинбенка A955),
Р. Тэйлора A956а), Пере- ¦ <Ь е*
пелкиной A957, 1962), Гур-
вича A960), Цванга A960),
Пановского и Маккормика
A960), Леттау и Дэвид-
Дэвидсона A957), Бареда A958),
Монина A9626), Зубков-
ского A962), Ламли и Па-
Пановского A964) и в ряде
других работ) еще довольно
неточны, далеко не полны
и позволяют сделать толь-
только некоторые предваритель-
предварительные выводы. Существенно,
однако, что эти выводы во Рис- 76- Эмпирически* график функций
всех случаях в общем не- °A = /i@"'A = /s(^
плохо согласуются с пред-
предсказаниями теории и дают определенное представление о форме
некоторых универсальных функций.
На рис. 76 мы приводим ориентировочные эмпирические
графики функций /3 и /5, на рис. 77 — функцию fe> на рйс. 78 —
график значений коэффициента анизотропии ^f- — -r< на
рис. 79 — графики коэффициентов корреляции ruw = -т—г- и
rwT— ±-J-J-- Согласно этим данным,в частности, при малых |?|
JbJ 6
отношение си/и* = /з близко к 2,3, а/5 = — ~ 0,8'), так что
') Результат /s@) *= 0,8 был впервые получен Перепелкиной A957) и с
точностью до одной десятой подтверждается также и последующими измере-
измерениями Гурвича A960) и лабораторными опытами Шубауэра и Лауфера.
Однако некоторые авторы (Паиовский и Маккормик A960) и Паскуял
A962а)), использовавшие более инерционные приборы, пришли к большему
значению /s@) ~ 1,25 -=- 1,35, заметно отличающемуся от того, которое полу-
получалось при измерениях в лаборатории.
-1 -0,5

456
ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА
[8.5
очень малых
Рис. 77. Эмпирический график функции
/l^lMt)
коэффициент вертикальной анизотропности при безразличной
°т
стратификации имеет порядок 0,3; отношение же \j \ ПРИ
19 принимает значения, близкие к 1. Посколь-
Поскольку значения /з@) = ^з,
fff /4@) =Л4 и fs(O) =А5 оп-
Jfj ределяют интенсивности
пульсаций трех компо-
компонент скорости в логариф-
логарифмическом пограничном
слое однородной жидко-
жидкости, их можно найти так-
также и по данным лабора-
лабораторных пульсационных
измерений в слое по-
постоянного напряжения
трения, проводившихся
Клебановым A955) и
Лауфером A954) (см.
-ту»! —'«v- стр 236 и, в частности,
рис.26). Данные этих ла-
лабораторных измерений, как мы видели, хорошо согласуются ме-
между собой; теперь мы видим, что от них почти не отличаются и зна-
значения Cu/и* и Сш/и*, найденные при измерениях в безразлич-
безразлично стратифицированной ат-
атмосфере. Для величины А^=
= Д@)= -^ лабораторные L/
измерения, представленные
на рис. 26, дают значение, "
близкое к 1,7 (в полном со- ру z^ О 05 1 г-Л.
ответствии с полуэмпириче- ' '
ской формулой G.Ю0)); в
условиях же атмосферы ОТ- Рис 78. Зависимость коэффициента
о анизотропии е^/о^.дат С по эмпирическим
ношение —¦ до сих пор оце- данным.
нивалось лишь очень грубо,
и можно только сказать, что полученные здесь весьма предва-
предварительные данные (собранные, например, в книге Ламли и
Пановского A964)) также не противоречат такому значе-
значению Л4.
С ростом неусточивости функции f3(t,) и /в(?) возрастают,
а функция /б(?). по-видимому, убывает. С ростом устойчи-
устойчивости функции f3 и /5. по-видимому, слегка убывают,
а функция /6 быстро убывает (заметно быстрее, чем с ростом

85]
§ 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ
457
неустойчивости). Коэффициент анизотропности -^- с ростом не-
неустойчивости медленно возрастает. Коэффициент корреляции
fuw, при безразличной стратификации близкий к —0,5, с ростом
неустойчивости слегка уменьшается по абсолютной величине.
Коэффициент корреляции гкт при стратификации, близкой
к безразличной, по-видимому, чуть меньше, чем 0,5, а при воз-
возрастании неустойчивости он слегка возрастает, приближаясь
к 0,5. О коэффициенте горизонтальной анизотропности -^- = ~г
при ненейтральной стратификации прямых эмпирических дан-
данных пока нет; при нейтральной стратификации, согласно при-
приведенным выше лабораторным данным, он близок к 0,7. Можно
ожидать, что при сильной неустойчивости этот коэффициент
'иш
0,5
-0,1
-0,05
О С, -0,1
-0,05
О
Рис. 79. Зависимость коэффициентов корреляции гца) и rwT от С при С < 0
по эмпирическим данным.
должен быть близок к единице и должен убывать при возра-
возрастании ? от больших отрицательных до положительных значе-
значений. О коэффициенте корреляции гаГ = +у-у-, вероятно, очень
небольшом по абсолютной величине, прямых эмпирических дан-
данных также пока нет.
Значения коэффициентов Cs и Се в асимптотических фор-
формулах G.87'), относящихся к условиям свободной конвекции,
были оценены Перепелкиной A962) по данным пульсационных
измерений вблизи пос. Цимлянское (частично опубликованных
в работах Гурвича (I960) и Цванга (I960)) в предположении,
что эти асимптотические формулы справедливы при Ri < —0,04.
При этом оказалось, что Cs« 1,2, С6*» 1,1 (т. е. С5 « 1,6,
С6=;0,3); близкие (но несколько большие) значения этих ко-
коэффициентов получаются и по данным менее точных измерений
Суинбенка A955).
Имеющиеся пока скудные эмпирические данные о коэффи-
w7 ft,
циенте асимметрии —~- =-& недостаточны для построения
графика функции /8(?)> но подтверждают, что при ?<0 эта

458 ГЛ. IV. ТЕМПЕРАТУРНО-СТРАТИФИЦИРОВАННАЯ СРЕДА [8.5
функция положительна (как это и предсказывалось на стр.403).
/3
Так, согласно Дикону A955), значения —д— при неустойчивой
стратификации заключаются между 0,24 и 0,81, причем с ро-
ростом неустойчивости эти значения заметно возрастают. Анало-
Аналоги'3
гично Гурвич A960) получил для -д— ряд положительных
значений порядка 0,4 -5- 0,6. О значениях коэффициента асим-
7^ /
метрии —д- = -4 данных еще меньше, но, исходя из весьма
"г *в
предварительных результатов Перепелкиной A957), можно за-
заключить, что и он положителен.
Из зависимости коэффициентов корреляции гию и rwT и ко*
эффициента асимметрии —j— от ? можно заключить, что плот-
плотов
ность многомерного распределения вероятностей для нормиро-
„ и' v' w' V
ванных пульсации —, —, — и — меняется с изменением
о о о о
и v w Г
е'тратификациИу т. е. что форма этого распределения вероятно-
вероятностей не является универсальной. По-видимому, уже и форма
т' Т'
одномерных распределений величий -j- й -т- не является
й) Г
универсальной, а зависит от ? (см., в частности, работу Пере-
Перепелкиной A957)). Что же касается распределений вероятнбстей
для — и —, то они, вероятно, при любой стратификации
"и av >
близки к распределению Гаусса (это подтверждается, в част-
частности, данными Дикона A955), касающимися третьих и чет-
вертых моментов распределения для — I.
(^кр,тррые оценки величины -г- w' я == "qf/io (*)'
^рпцсыва^рш^й вертикальную диффузию турбулентной энергии,
^со^ерща^ся р .ра^бот^ах IP'. J3ftjipj)a ,A952) и ^анрвского A962)
^рц^р^ врту ффу у
^со^ерж^ея $ .р^бо-^ах IP'. J3ftjipj)a ,A952)
'((см. 'также "«[Га^мли и Ларовс^й fA064Jj);' ^^^
,та^иеГрцёнлкй '^ощр нзвл?Чь",та?же.и;з данных Дикона d
,изменени,и' турбулентной энергии с .высртой. .Согласно д^
[Гэйлора, на ^е^ол^щих .высотах (-большая .часть ,его 'да'нрьцс
.относится к зысо|те 2l= 2 j}i) указанная величина пренебрежимо
.мала по сравнению с рстал1ьн1ым1и членами уравнения 0аланса
турбулентной энергии ,F.46). С этим фактом согласуется и то,
что Дикон обнаружил лишь малую разницу между значениями

8,5] § 8. ВЫВОДЫ ТЕОРИИ И ДАННЫЕ ИЗМЕРЕНИЙ 459
турбулентной энергии на высотах 1,75 и 29 м (кроме случаев
очень сильной неустойчивости). В то же время по предвари*
тельным данным Пановского, относящимся к более высокому
слою в пределах от г = 25 до г = 100 м, на этих высотах
при заметной неустойчивости диффузия энергии играет уже
очень значительную роль в общем балансе турбулентной энер*
гии и по порядку величины совпадает с притоком энергии за
счет термической неустойчивости (т. е. за счет преобразования
потенциальной энергии плотностного расслоения).
Эмпирические данные о функциях <ре (?) и <р^(?) пока так*
же очень бедны. Недавно Такеучи A962) на основе имеющихся
данных о {(?,) построил график функции ср*1*(С) = С/' (С)—С
(совпадающей с <ре(?), если только верна формула G.103));
на этот график он нанес оценки значений —g~ ПРИ различных
?, полученные исходя из некоторых измерений Суинбенка и
Гурвича с помощью метода, о котором мы будем говорить в ч. 2
настоящей книги. При этом, однако, оказалось, что эмпириче-
эмпирические оценки сре (?) обнаруживают очень большой разброс, так
что проверку точности формулы G.103) приходится отложить
до времени, когда появятся более точные и более полные эмпи-
эмпирические данные о значениях е.

ГЛАВА V
ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ
§ 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ
9.1. Уравнения гидродинамики несжимаемой вязкой жидкости
в переменных Лагранжа
В предыдущих главах мы все время пользовались эйлеро-
эйлеровым методом описания движений жидкости. При использова-
использовании этого метода поток_несжимаемой жидкости (которую мы
только и- будем рассматривать в" настоящей главе) в момент /
характеризуется полем скорости и (X,t), т. е. значениями
вектора скорости во всевозможных точках Х= (Xit X2, Х3)
пространства (в настоящей главе по причинам, которые будут
ясны из дальнейшего, нам будет удобно, как правило, обозна*
чать координаты через Х{, а не через Х{, как в предыдущих
главах). Уравнения гидродинамики (из которых давление
можно исключить с помощью A.9)) при этом позволяют (во
всяком случае, в принципе) определить значения переменных
Эйлера и(Х, t) в любой момент времени t>t0 по заданным
начальным значениям и(Х, t0) = uo(X). Однако для изучения
таких явлений, как турбулентная диффузия (т. е. распростра-
распространение примесей в турбулентном потоке) или деформация мате-
материальных (состоящих из фиксированных элементов жидкости)
поверхностей и линий в турбулентном потоке, использование
переменных Эйлера неудобно, а более удобным оказывается
лагранжев метод описания движений жидкости. Этот метод за-
заключается в том, что вместо скоростей жидкости в фиксиро-
фиксированных точках X пространства здесь за основу берется дви-
движение фиксированных «жидких частиц», прослеживаемое на-
начиная от некоторого начального момента времени t = t0. Под
«жидкими частицами» при этом понимаются объемы жидкости,
линейные размеры которых очень велики по сравнению со сред-

9.1] § 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 461
ним расстоянием между молекулами (так что для соответ-
соответствующих объемов имеет смысл говорить об их скорости, оста-
оставаясь в рамках механики сплошной среды), но все же на-
настолько малы, что скорость и давление внутри частицы можно
считать практически постоянными, и что в течение рассматри-
рассматриваемых промежутков времени эти частицы можно считать пере-
перемещающимися «как одно целое» (т. е. без заметной деформа-
деформации). Иначе говоря, «жидкая частица» представляет собой вы-
выделенную «точку» объема жидкости, перемещающуюся внутри
этого объема в соответствии с уравнениями гидромеханики.
Лагранжев метод описания самым непосредственным образом
связан с реальными движениями отдельных элементов жидко-
жидкости, составляющими в совокупности гидродинамический по-
поток, и поэтому он представляется даже более естественным,
чем эйлеров метод описания. В то же время в аналитическом
отношении использование переменных Лагранжа, относящихся
к индивидуальным частицам жидкости, оказывается гораздо
более громоздким, чем использование переменных Эйлера
и(Х, t), вследствие чего уравнения гидродинамики в форме
Лагранжа довольно редко используются при конкретных рас-
расчетах. Если для случая идеальной (невязкой) жидкости такие
уравнения все же приводятся в некоторых учебниках (см., на-
например, Ламб A932)), то для случая вязкой жидкости,соот-
жидкости,соответствующие уравнения до сих пор очень мало изучены; вывод
"этих уравнений, позволяющий записать йх~~в срашштёЯЬНЪ
компактном виде, впервые был опубликован! "по-видимому,
лишь сравнительно недавно Гербером A949) (см. также Мо-
нин A962в)). Хотя использование лагранжевых уравнений гид-
гидродинамики в.язкои, жидкости в задачах теории турбулентности
еще является делом будущего, мы приведем здесь все же вы-
вывод этих уравнений, попутно вводя ряд понятий и обозначений,
которые будут далее постоянно использоваться в настоящей
главе.
Исчерпывающей лагранжевой характеристикой потока не-
несжимаемой жидкости может служить функция Х(х, t), задаю-
задающая для любого момента времени / координаты X всевозмож-
всевозможных «жидких частиц», идентифицируемых по значениям неко-
некоторого параметра х. Уравнения гидродинамики в принципе
должны позволить определить значения Х(х, t) при любых
t > /о по заданным начальным значениям скоростей «жидких
частиц» V(x, t) = -—¦? ' , т. е. по величинам
V(x, to) = \

462 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [9.1
Связь между лагранжевыми и эйлеровыми характеристиками
дается соотношением
±JL tt), t]. (9.1)
Переход от эйлеровых уравнений гидродинамики к лагранже-
вым заключается в замене независимых переменных (X, t) на
(х, t) и переходе от неизвестной функции и(Х, t) к новой не-
неизвестной Х(х, /), связанной с и(Х, t) формулой (9.1),
Далее в настоящем параграфе мы всегда будем использо-
!вать в качестве лагранжевых параметров «жидких частиц» х
начальные значения их пространственных координат X в мо-
.мент / = /0, т. е. положим
х = Х(х, t0). (9.2)
TIfn этом функция двух переменных Х(х, t) описывает семей-
семейств© траекторий «жидких частиц», находившихся в начальный
момент времени t = tQ во всевозможных точках х объема, за-
занятого жидкостью. Ясно, что и в любой момент t > t0 точки
Х=Х (х, t) соответствующие всевозможным допустимым зна-
значениям х, непрерывно заполняют весь объем, занятый
жидкостью. Таким образом, мы видим, что лагранжев метод за-
заключается в задании потока жидкости в виде семейства траек-
траекторий (отличающихся друг от друга значениями х), на каждой
из которых роль параметра играет время t, Отметим, что со-
согласно сказанному выше «жидкие частицы», соответствующие
этим траекториям, фактически представляют собой математи-
математические точки, плывущие вместе с жидкостью.
Перейдем теперь к выводу лагранжевых уравнений дина-
динамики несжимаемой вязкой жидкости. Будем пользоваться де-
декартовыми компонентами векторов X и х, которые обозначим
.(Ai, X2, Аз) и (хи х2, х3) соответственно. Как указывалось
выше, переход от эйлеровых уравнений гидродинамики к-ла-
гранжевым заключается прежде всего в замене независимых
переменных (Xit X2, X3, t) на (хи х% хг, t). Подчеркнем, что
при этой замене переменных мы переходим от декартовых ко-
координат к нестационарным криволинейным и неортогональным
координатам, сопутствующим движению жидкости, Действи-
Действительно, каждая координатная поверхность х% = const во все мо-
моменты времени состоит из одних и тех же «жидких частиц»;
в начальный момент времени такие поверхности суть плоско-
плоскости, но с течением времени они, перемещаясь вместе с
жидкостью, искривляются,

g I! § 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 463'.
Далее мы будем использовать для якобианов по перемен-
переменным (*ь х2, *з) сокращенное обозначение
и будем учитывать, не оговаривая этого, то обстоятельство,
что величина [А, В, С] не меняется при циклической переста-
перестановке переменных А, В, С и меняет знак при их ациклической
перестановке.
При переходе от эйлеровых координат Ха к лагранжевым
х$ большую роль играет матрица •
^М=\М\ = [Хг,Х2,Х3}. (9.4)
Л У
Согласно (9.2) в начальный момент времени -тг- = 81?, т. е.
3 дх
матрица М является единичной, а \М\ = 1. Величины -зу- суть-
элементы обратной матрицы Л!, т. е. алгебраические допол-
нения элементов -^- в матрице М, деленные на \М\. Отсюда'
для вычисления производных по эйлеровым координатам Xt
получаем формулу
;УЗдесь и в дальнейшем под (i, j, k) всегда подразумевается цик-
циклическая перестановка индексов A* 2, 3). В справедливости
формулы (9.5) легко убедиться, записав ее левую часть б виде
y- (где по повторяющемуся индексу а, как обычно, подг
разумевается суммирование); такое же выражение получается!
в правой части при разложении входящего в нее детерминанта!
по элементам столбца /.
Из (9.1) и (9.5) вытекает следующее соотношение для ди-
дивергенции скорости:
дХа dt
— \Ж\ 1 [~дГ ' А2> A3j+ [Л» Sf . ^3J + [Xv Л2, -gj
((где иж — декартовы компоненты поля скорости). В случае не-
несжимаемой жидкости дивергенция скорости тождественно
равна муаю, так что —^—-^0 и, следовательно, |М| не ме-
меняется со времваем. Поскольку в начальный момент времени
\М\ = 1, это рав^дсттво остается справедливым и для любого

464 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ (9.1
момента времени. Вспоминая выражение (9.4) для \М\, имеем
[Xlt Х2,Х3\ = 1. (9.6)
Это равенство и играет роль уравнения неразрывности для не-
несжимаемой жидкости (вязкой или идеальной, безразлично)
в лагранжевых переменных.
Далее мы будем пользоваться формулой (9.5), полагая в ее
правой части \М\ = 1. Дважды используя эту формулу,^ для
оператора Лапласа по эйлеровым координатам Хп получаем
выражение
= [Х2, Х3, \Х2, X3,f] ] + \Х3, Xlt [Х3, Xvf\ ] + [Xlt Х2, [Xlt X2,f\ ].
(9.7)
Теперь мы можем уже без всякого труда перейти к лагранже-
вым переменным в уравнениях Навье — Стокса
Пользуясь формулами (9.1), (9.5) и (9.7), получаем
~ _![*}, Xk, p\ + v{[X2, X*. [X2, X3, *
„ Xv [X3, Xlt *s?]] + [xv X2, [Xv X2, Щ}}. (9.9)
Уравнения (9.6) и (9.9) относительно неизвестных Х{(х, t),
i = 1, 2, 3 и р(х, t) образуют полную систему уравнений ди-
динамики несжимаемой вязкой жидкости в переменных Ла-
гранжа.
Отметим, что нелинейным относительно основных динамиче-
динамических переменных слагаемым в уравнениях движения соответ-
соответствуют силы, описывающие взаимодействие между компонен-
компонентами механической системы. Так, в уравнениях Навье — Стокса
(9.8) нелинейные (а именно, квадратичные) относительно пере-
переменных щ .слагаемые содержатся в выражении для ускорения
—jt-'i им соответствуют силы инерционного взаимодействия ме-
между пространственными неоднородностями поля скорости
U(X, f), через которые (с помощью формулы A.9')) выра-
выражается и градиент давления (подчеркнем, что силы вязкости
описываются в (9.8) линейными выражениями). Однако инер-
инерционные взаимодействия имеют относительный характер — они
устраняются при переходе к сопутствующей системе отсчета.
В лагранжевых уравнениях движения (9.9) нелинейными от-

gji § 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 465
носительно переменных Xt выражениями описываются уже
лишь реальные__сшш взаимодействия между жидкими части-
частицами — силы давления и вязкости (причем силы вязкого взаи-
взаимодействия здесь описываются нелинейными выражениями пя-
пятой степени относительно переменных Л,-). Отношение типичных
для данной задачи значений нелинейных и линейных слагае-
слагаемых в уравнениях движения можно назвать константой взаи-
взаимодействия. Так, в случае уравнений Навье — Стокса (9.8)
константой инерционного взаимодействия является отношение
типичных значений сил инерции и сил вязкости, т. е. число
Рейнольдса Re; при достаточно больших Re (характерных для
развитой турбулентности) инерционные взаимодействия оказы-
оказываются весьма сильными. В лагранжевом описании константой
вязкого взаимодействия является отношение типичных значе-
значений сил вязкости к типичному ускорению, т. е. -^; при боль-
больших Re вязкие взаимодействия оказываются весьма слабыми.
Приведем еще вид лагранжевых уравнений гидродинамики
для двумерного плоскопараллельного течения. Пусть движение
жидкости происходит только в плоскостях х3 = const (так что
Аз = *з), причем Xi и Х2 не зависят от х3. Тогда, используя для
якобианов по (хи x2) обозначения вида
= \А,В], (9.10)
уравнения (9.6) и (9.9) нетрудно привести к виду
]]} (9.11)
[Х2,
В этом случае вязкие силы, очевидно, описываются уже нели-
нелинейными выражениями третьей степени относительно перемен-
переменных Xi.
В заключение настоящего пункта отметим, что, кроме ис-
использования соотношения (9.1), имеется еще один способ
установления связи между лагранжевыми и эйлеровыми ха-
характеристиками потока жидкости, основанный на рассмотрении
произвольных консервативных характеристик «жидких частиц»
(т. е. гидродинамических характеристик, значения которых для
фиксированной «Жидкой частицы» не меняются при ее движе-
движении). При лагранжевом описании каждую такую характери-
характеристику можно записать в виде Ч'(дг), так как при фиксирован-
фиксированном х она не зависит от времени t. При эйлеровом описании,

466 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [9.2'
однако, значения я|э такой характеристики в фиксированной
точке пространства X могут меняться со временем ty т. е.
•ф = ty(X, t). Связь между лагранжевым и эйлеровым описа-
описанием будет, очевидно, даваться соотношением
W(x) = ^\X(x, t\ t\. (9.12)
dW (x)
Так как—gr-*- =0, то и полная производная по времени от
правой части должна быть равна нулю, т. е.
dt~dt~r dXa dt ~ dt ~ru'- dXa ~~u'
где мы воспользовались формулой (9.1). Пользуясь, кроме
того, уравнением неразрывности для несжимаемой жидкости
dua n
-^Y- = 0, получаем
at at
= 0. (9.13)
Это уравнение является дифференциальным аналогом соотно-
соотношения (9.12). Таким образом, эйлерово поле любой консерва-
консервативной характеристики «жидких частиц* удовлетворяет
уравнению переноса (9.13). В частности, консерб^ивной1 характе-
характеристике ^?(х) = 6(х — лг0), отличной от нуля (й равной бес-
бесконечности), лишь для одной «жидкой частицы» (с
координатой Хо) соответствует эйлерово поле
которое является решением уравнения переноса (9.13) при на-
начальном условии
to) = b(X-xo). (9.15)
9.2. Лагранжевы статистические характеристики
турбулентности
При статистическом описании турбулентности необходимо
прежде всего указать, какие именно ее характеристики пред-
предполагаются имеющими распределения вероятностей, т. е. пред-
представляющими собой реализации некоторых случайных полей.
В предыдущих главах при рассмотрении турбулентных потоков
мы всегда предполагали, что случайным полем является эйле-
эйлерово поле скорости tt(X, t). Но в таком случае и лагранжевы
величины
t
, t), t\ и Х(х, t) = x + fV(x, t')dt'

9.2] § 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 467
будут случайными функциями аргументов х и /. Более того,
при этом для любого конечного числа п «жидких частиц» (ха-
(характеризуемых тем, что в момент / = О они находились в точ-
точках Xi, ..., хп) будут существовать многомерные совместные'
плотности вероятности для их координат X и скоростей V
в произвольные моменты времени к, . .., tm, являющиеся функ-
функциями от Зп+т .переменных хп, xi2, х13, ..., xnU xni, xni,
к, ..-, tm (где Хц Xi2, Хц — три компоненты вектора xt). Эти
многомерные плотности вероятности и являются основными
лагранжевыми статистическими характеристиками турбулент-
турбулентности. Заметим еще, что в рассматриваемом случае будут суще-
существовать также и совместные распределения вероятности для
наборов величин, часть из которых является лагранжевыми ве-
величинами (координатами или скоростями фиксированных «жид-
«жидких частиц»), а часть — эйлеровыми величинами (скоростями
потока в фиксированных точках); плотности таких «смешанных
вероятностей» также иногда заслуживают рассмотрения.
Далее мы будем обозначать плотности вероятности симво-
символами вида р(Х, V, ... \xv Хг, ...; к, 4, ...), где в скобках
перед вертикальной чертой указываются возможные значения
рассматриваемых случайных величин (обозначаемые теми же
буквами, что и сами соответствующие величины), а после вер-
вертикальной черты — параметры, от которых эти величины зави-
зависят. В тех случаях, когда параметры, отвечающие нескольким
величинам, совпадают, мы будем их указывать после черты
только один раз (если при этом не возникает опасность пута-
путаницы) .
Между различными, лагранжевыми (и смешанными) стати-
статистическими характеристиками турбулентности существует це-
целый ряд общих соотношений; некоторые из них мы. и укажем
е настоящем пункте. Начнем с соотношений, являющихся след-
следствиями «уравнения переноса» (9.13). Учитывая, что выраже-
выражение (9.14) является решением этого уравнения и что, со-
согласно (9.1),
«.<*, t)b\X-X{x,t)\ =
= «.iXix, f), t\Ь [X-X(x, t)] = Va(x, t)b[X-X(x, /)],
получим
db [X- X{x, t)\ ¦ дУл (x, t) 8 [X- X(x, t)\ n
dt ~*~~* dTa —Ul
Но в силу самого определения теоретико-вероятностного осред-
осреднения (см. C.12))
Ь\Х~Х(х, /)]= р(Х\х, /),
V.4*. i)b[X-X[х, .t)] = j Vj>(X, y\xtt)(iV.

468 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [9.2
. Следовательно, осреднив уравнение для.6 [Л'—X {х, t)],, будем
иметь
d<xJf)f 0- (9л6)
Это уравнение и является статистическим аналогом «уравне-
«уравнения переноса» (9.13)..
Другой тип соотношений между статистическими характери-
характеристиками можно получить, введя в рассмотрение наряду с лаг-
ранжевой скоростью- V(x,t), представляющей собой значение
случайной функции и(Х, t) в случайной точке Х(х, /), также
и случайную величину V(XV x, t), относящуюся к фиксиро-
фиксированной точке Хх=Х(х, t). Значениями этой величины яв-
являются скорости тех жидких частиц, которые в момент / = /0
находились в точке х, а в момент t оказались в фиксирован-
фиксированной точке Xit а её плотность вероятности p(V\Xit x, t) —это
условная плотность вероятности величины V(x, t) при уело*
вии, что Х(х, t)=Xi. Поэтому, строго говоря, величина
V(XV х, t) не является ни чисто лагранжевой, ни чисто эйле-
эйлеровой. Однако можно ожидать, что при возрастании / —10 за-
зависимость распределения вероятности для этой величины от
значения х, как правило, будет становиться все менее и менее
существенной. При достаточно больших по сравнению с лаг-
ранжевым «временем корреляции»
x. t) Vt (x, tp)
c,t)V*(x,to)]4>
значениях t—10 этой зависимостью, по-видимому, в ряде слу-
случаев вообще можно пренебречь, так что случайную величину
V{XV x,t) при таких / — U часто можно считать эквивалент-"
ной эйлеровой случайной величине и(Х^ t). Подчеркнем, впро-
впрочем, что иногда замена V(XV x, t) на и(Хи t) может ока-
оказаться незаконной при любых значениях t—t0; так, например,
в дальнейшем мы увидим, что в турбулентном пограничном
слое над плоскостью х3 = 0 всегда V3(XV x, t) > 0 (в частно-
частности, в области приложимости логарифмического закона для
профиля средней скорости V3(XV x, t) = const « 0,1 и*), в то
время как и3(Хи t) =0.
Нетрудно видеть, что совместную плотность вероятности для
скоростей п «жидких частиц» V(xu ti), ..., V(xn, tn) (взя-
(взятых в разные моменты времени tu ¦ ¦ ¦, tn) можно представить

<J21 § 9. ЛАГРАНЖНВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 469
в виде
p(Vx Vn\xx *„;'/, /„)=»
= f ... fp(Vv ..., Vn\Xv ..., Хп; хх хп; t, ОХ
Xp(Xi, ..., Хп\хг, ..., хп; tx tn)dXx ...dXn, (9.17)
где первый множитель под знаком интеграла есть условная
плотность вероятности для указанных скоростей «жидких ча-
частиц» при условии, что их координаты в соответствующие мо-
моменты времени принимают фиксированные значения Х(хи /4) =
= Xit ..., Х(хп, tn)=Xn. Если все рассматриваемые «жидкие
частицы» различны (т. е. среди начальных точек Х\, ..., хп
никакие две не одинаковы), то этот первый множитель есть
совместная плотность вероятности для случайных величин .
V(Xlt xu U), ..., V(Xn, хп, /„), введенных выше. Второй
множитель под знаком интеграла в (9.17) есть совместная плот-
плотность вероятности для лагранжевых случайных величин
Х{хи ti), ..., Х(хп, tn). Формула (9.17) (принадлежащая,
так же как и рассматриваемые ниже ее следствия, Монину
(I960)) является частным случаем общей «теоремы о полной
вероятности» теории вероятностей. Отметим, что если все рас-
рассматриваемые «жидкие частицы» различны и все разности
h — t0, ..., tn — t0 достаточно велики, то зависимость первого
множителя под знаком интеграла в правой части (9.17) от ар-
аргументов xit ..., хп в ряде случаев можно ¦ считать несуще-
несущественной. При этом указанный множитель можно отожде-
отождествлять с плотностью вероятности для значений поля скорости
Vi = »(Ai, ti), ..., VnF=u(Xn, tn) в фиксированных точках,
так что формула (9.17) здесь становится соотношением между
лагранжевыми и эйлеровыми статистическими характеристи-
характеристиками турбулентности.
Рассмотрим особо частный случай формулы (9.17) прил:^
= Х2= ... = хп( = х), когда эта формула содержит плотности
вероятности для координат и скоростей одной и той же «жид-
«жидкой частицы» в разные моменты времени. При п = 1 получаем
p(V\x, t) = fp(V\X, x, t)p{X\x, t)dX. (9.18)
Как уже отмечалось, при достаточно больших t—10 функцию
p(V\X, x,t) иногда можно отождествить с плотностью вероят-
вероятности для значений V=u(X, t) эйлерова поля скорости в фик-
фиксированной точке пространства-времени (А', /) (в этом смысле
формулу (9.18) можно считать статистическим аналогом основ-
основного соотношения (9.1), связывающего лагранжеву и эйлерову сюь
рости потока). Подставляя теперь формулу (9.18) в выражение

470 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [9.2
для среднего значения V(x, t), вытекающее из общей фор-
формулы C.12), получим
ЩхТТ) = f V(X, х, t)p (X | х, t) dX. (9,19)
В тех случаях, когда зависимость V(X, х, t) от х исчезает при
t—t0 ->¦ оо, последнюю формулу при достаточно больших t—t0
можно переписать в виде
V(x, t) = f a(X, t)p(X | x, t) dX. (9.20)
Для совместного распределения вероятностей значений Vx =
= V{x, t0) и V2=V(x, t) скорости одной и той же «жидкой
частицы» в два последовательных момента времени t0 и t > t0
формула (9.17) приводит к соотношению
p(V» V2\x, /„,/) = f p(VvV2\X;x,to,t)p(X\x,t)dX, (9.21)
где первый множитель под знаком интеграла есть совместная
плотность вероятности для величин V1 = V(x, to)= u(x, t0) и
V2 = V(X, x,- t). Отсюда для лагранжввой корреляционной
функции скорости (т. е. смешанного второго момента VuV2j рас-
распределения (9.21), где индексы i и / нумеруют компоненты век-
векторов Vx и V2) получается соотношение
Vt(x, to)Vj(x, t) = fui(x, to)V,{X, x, t)p(X\x, t)dX. (9.22)
При достаточно больших (по сравнению с лагранжёвым «време-
«временем корреляции») значениях t — t0 корреляционную функцию
скоростей под знаком интеграла можно с известным основанием
отождествить с более простой эйлеровой пространственно-вре-
пространственно-временной корреляционной функцией и( (х, to)Uj(X, t). Однако при
таких t — t0 величины Vt(x, t0) и Vj(x, t) (а также величины
и{(х, to) и щ(Х, t)) уже можно считать практически некоррели-
некоррелированными, так что в данном случае асимптотический вид фор-
формулы не представляет большого интереса. Заметим еще, что ле-
левая часть формулы (9.22) не является самой общей лагранже-
вой корреляционной функцией скорости, так как здесь в один из
рассматриваемых моментов времени (именно, в момент t0) коор-
координата соответствующей «жидкой частицы» имеет фиксирован-
фиксированное значение (равное х). Более общей является лагранжева
корреляционная функция Vt(x, tx) Vj(x, t2), где t2 > U > t0; 2лЯ
нее с помощью формулы (9.17) можно получить выражение

gg, § 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 471
вида
VKx, t,)V,(x, t2)=f f ViiX^x^JVjiXu X2,x, tv t2) X
Xp (*„ X21 x, *„ t2)dX] dX2, (9.23)
..где V{XX, X2, x, t\, t2) означает случайную скорость жидкой
частицы в момент U при условии, что в моменты /0, U и t2 эта
частица находилась в фиксированных точках х, Хх и Х2 соот-
соответственно. При достаточно большом ti— t0 величину V(A',,Jf, ^,)
часто можно с известным основанием считать эквивалентной
U (X\, t\); точно так же при достаточно большом t2—^1 вели-
величину V^i, X2, X, tu t2) часто можно считать эквивалентной
(X t9). ¦
9,3. Характеристики смещения фиксированной жидкой частицы;
случай однородной турбулентности
Движение одной жидкой частицы (скажем, той, которая в
момент t=to находилась в точке х) полностью описывается век-
векторной функцией Х(х, t), задающей положение этой частицы в
произвольный момент времени t. Вместо вектора Х(х, t) можно
использовать также вектор смещения частицы за промежуток
времени т
Y(%) = X{x, to + x)—x= j V(x, t)dt, (9.24)
и
что обычно оказывается более удобным. В настоящем пункте мы
специально рассмотрим вопрос о статистических характеристи-
характеристиках случайного вектора У(х).
Полное описание величины Y (т) требует задания ее трехмер-
трехмерной плотности вероятности p(Y\%; x, t0) (зависящей От t, X и
t0 как от параметров). Нетрудно видеть, что в случае очень ма-
малого (по сравнению с масштабом времени Т, задаваемым типич-
типичным лагранжевым «временем корреляции») значения т эта плот-
плотность вероятности может быть выражена через эйлеровы стати-
статистические характеристики турбулентности. В самом деле, при
-t^ T лагранжева скорость практически не изменится за время
¦?, так что равенство (9.24) здесь можно переписать в виде
}Ki(i)«* V^x, <fo)i = tt(x, t0) т. Поэтому плотность вероятности
•для К,(т) ,в э,то.м с-луч^е .можно преобразовать к виДу
i.x,,t9)&-x-3-p№- х, t0), (9.25)

472 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [9.3
где Р(и\х, t0)—плотность вероятности (эйлеровой) скорости
и(х, t0) в фиксированной точке х в момент t0. Если рассматри-
рассматриваемое турбулентное течение является установившимся, то плот-
плотность Р(и\х, t0) может быть без большого труда определена
с помощью анализа данных наблюдений за скоростью в точке х
в течение длительного промежутка времени. Так, например,
в случае турбулентного потока в аэродинамической трубе, в на-
начальной части которого установлена решетка с квадратными
ячейками (создающая ниже по течению сильную турбулент-
турбулентность), данные измерений Симмонса и Солтера A938) и Таун-
сенда A947) убедительно показывают, что распределениеР (и \х
(а следовательно, и p{Y\i, x) при т<Г) весьма близко к нор-
нормальному распределению.
При не слишком малом т распределение p{Y\x\ x,t0) уже
не может быть выражено через эйлеровы статистические характе-
характеристики. Однако, если т^>7\ то можно использовать то обстоя-
обстоятельство, что правая часть (9.24) в этом случае может быть
представлена в виде суммы ряда интегралов, берущихся по не-
непересекающимся интервалам времени продолжительности > Т,
и являющихся слабо зависимыми случайными величинами. По-
Поэтому можно думать, что к соответствующей сумме должна быть
применима так называемая центральная предельная теорема для
слабо зависимых случайных величин, согласно которой распреде-
распределение вероятностей суммы большого числа таких величин при
некоторых широких условиях оказывается очень близким к нор-
нормальному. В последние годы центральная предельная теорема
была при некоторых условиях доказана и непосредственно для
интегралов вида (9.24) (см., например, Розанов A963), где рас-
рассмотрен случай интеграла от стационарной случайной функции;
близкие теоремы имеются и для интегралов от некоторых неста-
нестационарных случайных функций). К сожалению, прямо восполь-
воспользоваться этими доказательствами все же нельзя, так как фигури-
фигурирующие в них условия, налагаемые на случайные функций, не
могут быть точно проверены в применении к характеристикам
реальных процессов1). Тем не менее, эти условия настолько ес-
естественны, что было бы крайне странно, если бы распределение
вероятностей для смещения У(х) при х^>Т существенно отлича-
отличалось от нормального распределения. В некоторых случаях рас-
') Так, например, ряд доказательств использует так называемое условие
сильного перемешивания, которое в применении к функции V(x, t), грубо го-
говоря, сводится к требованию, чтобы коэффициент корреляции между произ-
произвольным функционалом от значений V(х,г), —co<V <ta, и произвольным
функционалом от значений V(x, t"), ta + т < t" < со, был бы по модулю
меньше такого числа а(т), что а(т) ->0 при т->со,

93] $ 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 473
пределение для У (т) (или хотя бы для отдельных компонент
этого вектора) может быть найдено экспериментально с по-
помощью измерения распределения концентрации в различных се-
сечениях «облака», создаваемого помещенным в поток источником
примеси (например, распределения температуры в различных
сечениях «теплового следа» за нагретым телом). Таким образом
удалось и экспериментально показать, что во многих турбулент-
турбулентных потоках распределение для У (т) при больших т действи-
действительно очень близко к нормальному, причем в частном случае
турбулентности в аэродинамической трубе за решеткой оказа-
оказалось даже, что оно является почти нормальным и при всех
вообще значениях т (см., например, Коллис A948), Таунсенд
A951), Уберои и Корсин A953)). Последнее обстоятельство не
кажется удивительным, так как в этом случае, как мы видели,
распределение Для У (т) должно быть нормальным и при ма-
малых, и при больших значениях т; поэтому его близость к нор-
нормальному при всех т означает только, что при промежуточных
значениях т здесь не происходит очень резкой перестройки фор-
формы соответствующего распределения. В общем же случае нет
никаких оснований ожидать, что- распределение для У (т) будет
близким к нормальному также и* при не слишком больших зна-
значениях т.
Перейдем теперь к рассмотрению важнейших числовых ха-
характеристик случайного вектора У (т) — его первых и вторых
моментов. Среднее значение этого вектора, очевидно, равно
*Ч0= / V(x, t)dt. (9.26)
Исходя отсюда, можно показать, что в ряде важных частных
случаев Y{z)=Ui, где U—соответственно определенная сред-
средняя скорость течения (см. примеры ниже). После этого остается
только еще исследовать характеристики пульсации смещения
Г (,) = Y (,) - Г(Г) = f V (х, t) dt.
¦и
Тензор вторых моментов этого случайного вектора будет зада-
задаваться формулой
Dij(x) = Vt(x)Y'j(x)= f f V'i(x,tl)V'j(x,t2)dtidt2, (9.27)
его естественно назвать тензором Дисперсии смещения «жидкой
частицы». Отметим, что в случаях, когда распределение для

471 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [9.3
Y (т) можно считать нормальным, вектор (9.26) и тензор (9.27)
исчерпывающим образом характеризуют это распределение.
При достаточно малых т, при которых У'(т)« U'(x, to)x, из
(9.27) получаем
DtJ (х)» й; (х, g «;. (*, g • ^ = я .^. (9.28)
Коэффициенты B.J = u'l(x, t^u'j^x, g в случае установившихся
турбулентных течений будут зависеть только от дг, а при допол-
дополнительном предположении об однородности случайного поля
и(х, t) вообще будут постоянными. Конкретные же сведения
о виде функций О^-(т) при не слишком малом т удается полу-
получить только для некоторых частных классов турбулентных по-
потоков.
Рассмотрим, в первую очередь, идеализированный случай
стационарной однородной турбулентности, в которой все гидро-
гидродинамические поля являются однородными случайными полями
в трехмерном пространстве и одновременно стационарными
функциями от времени t. В этом случае средняя скорость и яв-
является постоянной и в пространстве, и во времени и, следова-
следовательно, V(x, t) = a[X(x, t), t] = u, Y(z) — ux. Далее, пульса-
ционная скорость жидкой частицы V (х, t) здесь при всех х бу-
будет иметь одни и те же статистические характеристики и будет
стационарной случайной функцией от t, так что
2 '2\-i
Vl(x, ti)V'j(x, t2) = Bf/(t2-tl) = (u'i u'j J R'tf(h-ti) (9.29)
(буква L здесь указывает, что соответствующие -функции яв-
являются лагранжевыми корреляционными функциями). Перейдя
теперь к переменным s = t2 —1\ и t= ^ *• формулу (9.27)
можно переписать в виде
= //
/ [R'fi (s) -f Rft (s)] dt ds (9.30)
/2 ,2\y
О

931 § 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 475
или, после выполнения интегрирования по t,
= (u'i u'j2)f(z- s)[tftj (s) + /?'/,> (s)] rfs. (9.30')
о
Результат типа (9.30) для дисперсии одной компоненты Y-(z)
впервые был получен в ставшей уже классической работе Тэй-
лора A921); в виде (9.30') он был представлен Кампе де Ферье
A939) в случае i =j и Бэтчелором A9496) в общем случае.
При i = ] формула (9.30') обращается в соотношение
(9-31)
(здесь, так же как и ниже в формулах (9.32)—(9.35), суммиро-
суммирование по i не предполагается!). Примем теперь естественное до-
допущение, что лагранжева корреляционная функция ¦/?«'($) стре-
стремится к нулю при s -*¦ оо и притом настолько быстро, что суще-
существует конечное «время корреляции»
оо
Tt == f MV (s) ds (9.32)
о
(за лагранжев временной масштаб Т, упоминавшийся выше,
при этом можно принять максимальное или среднее значение
трех величин Т{, i = 1, 2, .3). Предполагая еще, что и ^нтеграл
оо
J s/Ui'(«)<& = Si (9.33)
о
является конечным, можно при достаточно большом т (а имен-
именно, при x^>Ji) заменить (9.31) асимптотическим соотношением
оо
Du (х) » 2u? f (x - s) tfti (s)ds = 2uf (Ti x - Si). (9.34)
о
При очень большом t основную роль в правой части (9.34) бу-
будет играть линейный по т член, так что (9.34) можно будет пере-
переписать в виде
0„(т)*2^7> (9.35)

476 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [9.3
(последний результат, как легко видеть, может быть получен
и без предположения о конечности интеграла (9.33)). Анало-
Аналогично этому для Dij(z) при очень большом т получается соотно-
соотношение
(V) f [?/ ?Lh]ds. (9.36)
Равенство (9.35) показывает, что дисперсия смещения час-
частицы за достаточно большое время т оказывается пропорцио-
пропорциональной т. Этот результат вполне аналогичен основному закону
брауновского движения (т. е. молекулярной диффузии), соглас-
согласно которому средний квадрат смещения брауновской частицы
(или любой частицы, участвующей в молекулярной диф|фузии)
пропорционален времени Движения (диффузии). При очень ма-
малых т дисперсия смещения в силу (9.28) квадратично зависит
от т, как это и должно быть при любом движении, происходящем
с конечной скоростью. При промежуточных значениях т зависи-
зависимость /)«(т) от т оказывается более сложной и зависит уже от
формы корреляционной функции R(u(s) (см., например, графики
функций Ьц(т)„ отвечающих нескольким частным формам функ-
функции •/?</'(s). приведенные в работах Френкиля A952, 1953) и в
книге Паскуила A9266)). Заметим еще, что согласно данным
Френкиля и Паскуила большие изменения значений Z),,(t) при
изменении формы функции Ru (s) возникают, лишь если допус-
допустить, что функция Ru (s) может принимать и отрицательные зна-
значения и много раз менять знак при возрастании аргумента s.
В случае же функций R'ti (s), остающихся всюду неотрицатель-
неотрицательными, зависимость D(l(x) от конкретной формы функции RH\s)
оказывается весьма слабой, причем асимптотическая формула
(9.28) здесь достаточно хорошо выполняется при "всех т<Г4,
а асимптотическая формула (9.35) —при всех т>-57\. Таким об-
образом, для неотрицательных функций M/'(s) дисперсия ?>,*(т)
оказывается существенно зависящей от интенсивности турбу-
турбулентности и\ и ее временного масштаба 7\-, но только очень
слабо —от конкретной формы корреляционной функции R{u (s).
Может представиться, что результаты, относящиеся к модели
стационарной однородной турбулентности, не имеют практиче-
практического значения, так как однородная турбулентность в безгранич-
безграничном пространстве вообще является лишь математической идеа-
идеализацией, а предположение о стационарности ещё усугубляет
дело (поскольку из-за наличия- диссипации энергии стационар-
стационарное течение вязкой жидкости должно имет|> какие-то внешние

9.3] § 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 477
источники энергии и поэтому тем более не может быть однород-
однородным). На самом деле, однако, легко видеть, что приведенный
вывод формулы (9.31) требует лишь, чтобы течение было одно-
однородным по направлению оси Ох{. Это позволяет указать вполне
реальные течения, к которым могут быть применены полученные
выше результаты. В частности, в связи с работой Тэйлора A954а)
(о которой мы еще будем подробно говорить в следующем пара-
параграфе) Бэтчелор отметил; что эти результаты могут быть непо-
непосредственно применены к простейшему турбулентному потоку в
достаточно длинной прямой трубе произвольного постоянного
сечения (Бэтчелор и Таунсенд-A956), Бэтчелор A957)). В са-
самом Деле, пусть направление трубы совпадает с осью Oxt;тогда
по этому направлению течение будет однородным, хотя распре-
распределение средней скорости п\(х2, Хз) в плоскости Ох2х3 здесь мо-
может быть весьма сложным. Рассмотрим теперь компоненту Y\(x)
смещения жидкой частицы за время т по направлению Ох\. Со-
Соответствующая лагранжева скорость—-р-^ = Vx (x, to-\-t) будет,
вообще говоря, нестационарной случайной функцией т, зави-
зависящей от выбора начального положения частицы х в плоскости
Ох^Хз- Естественно ожидать, однако, что через некоторое время
после момента выхода t0 рассматриваемой частицы влияние ее
начального положения х практически перестанет сказываться,
так что далее функцию Vi(x, to+i) можно будет уже считать
не зависящей от х и стационарной. В таком случае средняя про-
продольная скорость V\(x, 4 + х)—^i при достаточно большом т
не будет зависеть ни от т, ни от л:, т. е. будет постоянной по вре-
времени и одной и той же для всех «жидких частиц», занимавших
фиксированное положение в момент t0 или раньше. При этом
представляется очевидным (и может быть строго доказано с по-
помощью рассуждений, .о которых мы будем гбворить на
стр. 501—502), что L\ будет совпадать также со средней про-
продольной скоростью совокупности всех жидких, пересекающих
фиксированное сечение трубы в течение заданного промежутка
времени, т. е. со средней скоростью ?/ср, определяемой как от-
отношение объема жидкости, вытекающей из трубы за единицу
времени, к площади ее поперечного сечения. Таким образом,
Y~$) « Ucp ¦ х (9.37)
при достаточно большом т. Далее, в силу формулы (9.35)
[Г,(т)— F7C0P —2Н;2 7,т (9.38)
при достаточно большом т; при чуть меньших значениях т мож-
можно пользоваться более точной формулой (9.34) с (=1. Заметим

478 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [9.4
еще, что характеристики uf и Т\ в (9.38) Должны определяться
параметрами, от которых зависит статистический режим турбу-
турбулентности в трубе. Поскольку в круглой трубе при достаточно
большом числе Рейнольдса вязкий подслой составляет незначи-
незначительную часть сечения (см. выше стр. 256), из результатов п. 5.5
следует, что в этом случае «i и Ту будут зависеть только от
радиуса трубы R и динамической скорости и, = Vzo/?> гДе to —
напряжение трения на стенке. Но в таком случае в силу сооб-
соображений размерности
UxTx = cRut, (9.39)
где с — универсальная постоянная, значение которой можно оце-
оценить по эмпирическим данным (см. ниже п. 10.4). Формула та-
такого же вида будет справедлива также и в случае турбулентного
течения в Прямой трубе или канале некругового сечения при до-
достаточно большом Re; здесь только под R надо понимать типич-
типичный линейный размер сечения трубы или канала, а и* опреде-
определять по среднему значению напряжения трения на стенке.
9.4. Смещение жидких частиц в турбулентности за решеткой
и в турбулентных потоках с градиентом средней скорости
Лагранжевы характеристики автомодельных турбулентных
течений
Вывод формул (9.37)—(9.39) существенно опирается на то,
что в рассматриваемом течении движение жидких частиц в по-
поперечной плоскости О*а*з все время происходит лишь в^преде-
лах фиксированной конечной ее части. Ясно, что это последнее
условие выполняется лишь для некоторых специальных тур-
турбулентных течений. В случае же, например, турбулентного по-
пограничного слоя или турбулентной струи среднее расстояние
частицы от ограничивающей поток стенки или от оси струи бу-
будет неограниченно возрастать с ростом т; поэтому здесь ла-
dYi (т)
гранжеву скорость d^ ни при каком т нельзя считать ста-
стационарной случайной функцией времени. Таким образом, класс
реальных течений, к которым можно непосредственно применить
формулы (9.30) — (9.36), все же довольно узок.
Бэтчелор A957) заметил, однако, что имеется также класс
течений (включающий некоторые практически важные потоки),
к которым, по-видимому, можно применить указанные формулы
после несложного их преобразования. Этот класс состоит из

9.4] § 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 479
установившихся автомодельных течений, в которых средняя
скорость преимущественно направлена вдоль оси Oxt, и стати-
статистический режим турбулентности при разных значениях коор-
координаты Xi является подобным, т. е. отличается лишь значениями
характерного масштаба длины L(Xi) и масштаба скорости
U(Xi). Иначе говоря, в рассматриваемых потоках все эйлеровы
статистические характеристики турбулентности в плоскости
Xi = const, приведенные к безразмерному виду путем деления
на соответствующую комбинацию масштабов L и U, не зависят
от значения Х\. При этом фиксированная жидкая частица все
время будет находиться в практически одинаковых условиях, но
с переменным масштабом скорости ?/(т) = U[Xi(x, to+x)]
и переменным масштабом времени Т(х) = иk,' L' /T^u ¦ По-
этому при изучении движения такой частицы представляется
целесообразным измерять время масштабом Т(х) (т. е. исполь-
использовать вместо времени т переменную т)(т), связанную с т соот-
соотношением di\ = Yj^\]' a скорость — масштабом ?/(т). При этом
естественно предположить, что при достаточно больших значе-
значениях х (таких, что влияние начального положения х уже пере-
перестает сказываться) безразмерная пульсационная лагранжева
скорость V (х, @ + х)/и(т) будет стационарной случайной
функцией Л(т)) переменной тр
Г$?Ц rf,--^. (9.40)
Правда, строгое доказательство этого предположения (и во-
вообще того, что из автомодельности эйлеровых свойств турбу-
турбулентности вытекает автомодельность ее лагранжевых свойств)
пока отсутствует. Однако оно представляет собой очень правдо-
правдоподобную гипотезу, следствия из которой в ряде случаев хо-
хорошо согласуются с имеющимися (к сожалению, еще очень не-
неполными) эмпирическими данными о лагранжевых статистиче-
статистических характеристиках. Заметим еще, что в тех случаях, когда
автомодельность эйлеровых характеристик турбулентности
устанавливается с помощью соображений размерности, этими
же соображениями обычно можно обосновать и автомодель-
автомодельность лагранжевых характеристик;, получаемые таким образом
результаты также совпадают с выводами, следующими из вы-
выделенного курсивом предположения.
Одним из простейших случаев, к которому можно прило-
приложить сформулированную здесь гипотезу, является случай тур-
турбулентности в средней части аэродинамической трубы за ре-
решеткой, специально установленной для турбулизации течения.

480 гл. v движение частиц в турбулентном потоке [9.4
В этом случае средняя скорость u = Uoi1 (где /4 — единичный
вектор оси O*i) является строго постоянной и, следовательно,
К, (х) = Uox, У2 (-с) = Уг (х) = 0. Однако турбулентность здесь все
же не является вполне однородной, так как под действием вяз-
вязкости интенсивность пульсаций скорости слегка убывает с воз-
возрастанием расстояния от решетки. Заметим теперь, что как
показывают результаты измерений характеристик такой турбу-
турбулентности (см. гл. 7 в ч. 2 книги), в течение начального пе-
периода вырождения (т. е. на сравнительно небольших расстоя-
расстояниях от решетки) турбулентность за решеткой обычно пример-
примерно однородна в плоскостях Xi = const и отличается при разных
значениях Х\ лишь масштабом скорости, пропорциональным
(*j—х\у'1г, и масштабом длины, пропорциональным (х2—х0^1'
(где *J — некоторое условное «начало отсчета» на оси Oxi).
Так как в рассматриваемом потоке средняя скорость Uo всегда
много больше пульсаций скорости, то можно считать, что
Jfj(x)—*J = ?/Ox, где т — время движения жидкой частицы, от-
отсчитываемое от условного момента /0 пересечения ею плоско-
плоскости Х1 = х4- За масштаб скорости ?/(т) в плоскости х1 = х^ -\-
-\-UQx можно принять любую постоянную скорость, умножен-
умноженную на t~1/j; удобно, например, при рассмотрении движения
жидкой частицы, находившейся в начальный момент времени
« плоскости Xi — а, положить U(x) = Ua\^A2, где Ua — типич-
а-х\
ное значение пульсации скорости при хг = а, a ia = —n—.
чо
Переменная т) равенства (9.40) в рассматриваемом случае, оче-
очевидно, равна lnt + const; поэтому можно считать, что т) = 1п—.
ха
Отсюда вытекает, что предположение (9.40) здесь сводится к
допущению, что лагранжева корреляционная функция пульса-
пульсаций скорости имеет вид
(9.41)
где Sij — взаимная корреляционная функция стационарных
процессов Ft Ц) = ^щ—'- и Fj(ri)= ' Ц{х)—'-. Подста-
Подставляя (9.41) в общую формулу (9.27) и заменяя в ней интегри-
интегрирование по /4 и /2 интегрированием по «и и тг в пределах от то

04]. § 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 481
до т, аналогично выводу (9.30') получим
ln^
'В. (9.42)
При естественном предположении о достаточно быстром зату-
затухании корреляционной функции (9.41) с ростом Ti— Т2 из (9.42)
следует, что при очень больших значениях t
оо в
DtJ (х) = 2Uha2l/z, Ви = ?/ [Stj F) + SJt (8)] е~* db. (9.43)
о
Тем самым мы показали, что асимптотический закон О^(т)~т,
по-видимому, с известным приближением может быть применен
и к вырождающейся турбулентности за решеткой в аэродинами-
аэродинамической трубе.
Аналогичное рассуждение может быть применено также и к
случаю турбулентного следа за цилиндром произвольного се-
сечения, расположенным вдоль оси Ох2, или за каким-то конеч-
конечным твердым телом с центром в начале координат. Как мы уже
видели в п. 5.9, на достаточно большом расстоянии от обтекае-
обтекаемого тела (там, где турбулентные скорости в следе становятся
малыми по сравнению со средней скоростью Uo обтекаемого по-
потока) турбулентный режим в следе можно считать автомодель-
автомодельным и различающимся при разных значениях продольной ко-
координаты *i лишь масштабом длины L(xi) и масштабом скоро-
сти U(xi). При этом Z.(jci) — Xi, U(xi) — Xi 2 в случае дву-
1 2
If " ~"з"
мерного, следа (за цилиндром) и L(x{) — Jti , U(x\)~X\ в
случае трехмерного следа (за конечным телом). Поскольку в
рассматриваемом случае ^i(t) « Uox при соответственном вы-
выборе начала отсчета времени и достаточно большом t, то, сле-
следовательно, drj=—-, т) = In— как для двумерного, так и для
трехмерного следа. Так как турбулентная жидкость не вытекает из
следа, то фиксированная жидкая частица будет все время блу-
блуждать в пределах объема, занимаемого следом, не выходя за
его границы. Поэтому естественно ожидать, что при достаточно
большом х здесь также будет справедлива гипотеза (9.40)
/ ± 1\
(с С/(х) = иа\^у или соответственно U (х) = Uay-~\ J. Но это

482 гл. v. движение частиц в турбулентном потоке [9.4
означает, что
3I d 9(9-44)
о " a
в случае движения жидкой частицы в двумерном турбулентном
следе и
In-l
Т"г - I il
j3 е~3 — е3 [Stj (8) + Sji (8)] db (9.45)
о
в случае движения в трехмерном следе, причем 5^F) в обоих
случаях имеет тот же смысл, что и в (9.42). Таким образом,
при очень больших значениях т
It для двумерного следа,
2 (9.46)
т3 для трехмерного следа.
Заметим еще, что в случае двумерного следа за длинным ци-
цилиндром, расположенным вдоль оси О*2, очевидно, r2(t)=0.
Что же касается величины Xs(x) в случае плоского следа и
величин X2(t) и Xs(i) в случае трехмерного следа, то. так как
на большом расстоянии от обтекаемого тела плоский след ста-
становится практически симметричным относительно плоскости
O*i*2, а трехмерный след — практически осесимметричны'м,
можно ожидать, что при достаточно большом t они также бу-
будут близки к нулю при любом начальном положении рассма-
рассматриваемой жидкой частицы.
Перейдем теперь к рассмотрению движения жидкой частицы
в плоской или круглой турбулентной струе, распространяющей-
распространяющейся по направлению оси 0*i в заполненном жидкостью про-
пространстве. Здесь также при достаточно большом *4 статистиче-
статистический режим можно считать полностью характеризуемым мас-
масштабом длины L(Xi) и масштабом скорости ?/(*4),как это было
показано в п. 5.9, причем L(xi) — хь U(x\) — xt 2 в случае дву-
двумерной (плоской) струи nL(x{) — jti, U(x\) — х^1 в случае трех-
трехмерной (осесимметричной) струи. Однако, в отличие от случая
турбулентного следа, в турбулентной струе отсутствует основное
движение с постоянной скоростью t/0^>«i'; поэтому здесь уже

9.4] § 9, ЛАГРАНЖЕБО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 483
нельзя считать, что Xi(x) & ?/ot. Поскольку, однако, в струе
осредненное течение также является автомодельным, можно на-
деяться, что в этом случае гипотеза (9.40) с U(t) = U[Xi(x)],
L(x) = L[Xr(x)] при достаточно большом т будет применима
уже не только к пульсациям лагранжевой скорости, но и к са-
самой лагранжевой скорости V(x, to + i). Тогда
rf-де Л —Л (л) = const (ибо ^(л)—стационарный случайный
процесс). Учтя характер зависимости U(xi) от xit получаем от-
отсюда, что при соответственном выборе начала отсчета вре-
времени t
2 _1 2.
X(t) — х3, ?/(х)— т 3, Z.(t)'^-"c3 для двумерной струи,
1 _1 Л
_Х"(х)— х2, ?/(х)—х 2, Z.(x)—^t2 для трехмерной струи.
Следовательно, в обоих случаях dt\ = —, '») = 1п^-. Далее,
аналогично выводу равенств (9.42), (9.44) и (9.45) находим
т
ч" Г _i 2 2 "I
j [{^fe^ " - ^ "J
[StJF)-{-Sji(B)]d9 (9.48)
/ j
для двумерной струи и
= Uli\( \^-e" — eA [Sij F)-j-Sjt F)J rfG (9.49)
для трехмерной струи, где Sij(b) = F'i(ri-{-B)F'j (у). При очень
больших значениях t эти формулы обращаются в асимптотиче-
асимптотические соотношения
х3 для Двумерной струи,
•с для трехмерной струи.
Соображения, примененные при рассмотрении движения
жидких частиц в турбулентных струях, приложимы и к двумер-
двумерным (плоским) и трехмерным конвективным струям над нагре-
нагретыми телами, а также к зоне турбулентного перемешивания
двух плоскопараллельных потоков различной скорости U\ и LJ%.
Как мы знаем из п. 5.9, турбулентное движение и в конвектив-
конвективных струях, и в зоне перемешивания автомодельно при доста-

484 ГЛ. V. ДВИЖЕНИЕ, ЧАСТИЦ В ТУРБУЛЕНТНОМ. ПОТОКЕ [9.4
точно большом Х1.(где ось Oxi считается вертикальной в случае
конвективных струй и параллельной скорости обоих потоков в
случае зоны перемешивания). При этом линейный масштаб
L = L(xi) здесь во всех случаях пропорционален xlt а масштаб
скорости U в случае двумерной конвективной струи над нагре-
нагретым цилиндром и зоны перемешивания оказывается одним и
тем же во всех сечениях xi = const, в то время как в случае
трехмерной конвективной струи U\xi) ~ хг'1г. Отсюда вытекает,
что средняя продольная лагранжева скорость Vl = —j^- в
двумерной конвективной струе и в зоне турбулентного переме-
перемешивания постоянна (в случае зоны перемешивания она, оче-
очевидно, равна (Ui + U2)/2), а в трехмерной конвективной струе —
пропорциональна XT4'. Поэтому гипотеза (9.40) с U(%) =
== U[Xi(x)] и L{x) == L[Xi(t)] в случае двумерной конвективной
струи и зоны перемешивания сводится- к простому утвержде-
утверждению, что V'(x, tt + t) является стационарной случайной, функ-
функцией переменной г\ = In ?¦. В случае же трехмерной конвектив-
\х ¦ _-i ^ 1
ной струи, для которой —jj~-—'-^i » т- е. Xl(t)<^>x*, Z.(x)-~
— X1(t) — х4, f/(x) — х 4, эта гипотеза означает, что стацио-
стационарной случайной функцией от т]==1п— является величина
V' (х, ^oH-t) Uа 1{—У • Отсюда обычным образом получаем, что
\~а/
(9.51)
In —
.о
для двумерной конвективной струи и зоны перемешивания и ;
2 з з
б U4:'B/ J
для трехмерной конвективной струи. В частности, при очень
больших значениях х
для двумерной конвективной струи и
зоны перемешивания,
v (9.53)
для трехмерной конвективной струи

9.4] * 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 48А
(асимптотические формулы (9.43), (9.46), (9.50) и (9.53) были
указаны Бэтчелором и Таунсендом A956), Бэтчелором A957)
и Ягломом A965)).
Покажем теперь, что формулы (9.50) и (9.53) могут быть
выведены и из одних соображений размерности (без использо-
использования гипотезы (9.40)), если только принять, что физические
параметры, от которых зависят эйлеровы статистические харак-
характеристики соответствующих турбулентных течений, определяют
и их лагранжевы характеристики (т. е., иначе говоря, полностью
задают весь «турбулентный режим»). В самом деле, согласно
п. 5.9, для трехмерной струи динамического происхождения оп-
определяющими физическими параметрами являются плотность
жидкости р и суммарный импульс вытекающей за единицу
времени жидкости 2прМ; для двумерной динамической струи —
плотность р и импульс рМи приходящийся на единицу времени
и единицу длины струи; для зоны перемешивания плоскопарал-
плоскопараллельных потоков'-р и скорость Uo = U2 — Ui, для трехмерной
конвективной струи —р, сР, поток тепла вдоль струи Q и пара-
параметр плавучести g/T0; для двумерной конвективной струи — р,
ср, g/To и поток тепла Qi, приходящийся на единицу длины струи.
Но если, например, распределение вероятностей,для смещения
У(т) жидкой частицы за время х при достаточно большом х
может зависеть только от этих параметров и от t, то в силу со-
соображений размерности соответствующая плотность вероят*
ности р(У) = p(Yu Y2, Y3) должна иметь вид
(9.54)
в случае трехмерной струи,
в случае двумерной струи,
в-случае зоны перемешивания,
cP?T0
(9.54'^)

486 гл. v. движение частиц в турбулентном потоке [9.4
в случае трехмерной конвективной струи и
в случае двумерной конвективной струи. Здесь Ж1*, ..., Я<5) —
пять универсальных функций, характеризующих пять указанных
автомодельных турбулентных течений. Из формул (9.54) —
(9.54""), разумеется, сразу вытекают и соотношения (9.50) и
(9.53); вообще, из них легко получаются асимптотические соот-
соотношения для произвольных моментов случайного вектора
Y(x) = (Yit Y2, Ys). Аналогичные (9.54) — (9.54////) формулы мо-
могут быть, очевидно, выписаны для плотности вероятности ла-
гранжеэои скорости V (х) = —^ и других лагранжевых вели-
величин; на этом, однако, мы уже не будем задерживаться.
Дисперсии смещений частиц в потоке с постоянным
градиентом средней скорости
Еще одним примером течения, в котором можно определить
асимптотическое поведение дисперсий Du(i), является идеали-
идеализированное турбулентное течение во всем безграничном простран-
пространстве, такое, что его эйлерово поле лульсаций скорости и! (х, t)
стационарно и статистически однородно, а средняя скорость
и{х) не меняется во времени и линейно зависит от простран-
пространственных координат. Последнее условие, очевидно, необходимо
для того, чтобы поле пульсаций скорости можно было считать
однородным, так как градиент средней скорости существенно
влияет на статистический режим турбулентности, и поэтому' в
однородной турбулентности градиент скорости должен прини-
принимать постоянное значение. Предположим, что средняя скорость
всюду направлена вдоль оси Oxi « изменяется только по на-
направлению Ох3, так что, например, ui = Гдгз, vl% = пз = 0, где
Г = const. He ограничивая общности, достаточно рассмотреть
лишь движение Лидкой частицы, находившейся в момент t = 0
в точке jc = O. Обозначим координаты этой частицы в момент t
через Xt(t), а ее скорость — черезК(/). В таком случае
t\ (9.55)
или, в проекциях на оси координат,
(9.55')

g4] § 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 487
И
Xi(t) = f [rXa(t)+Vi(f)]dt,
t ° t (9-56)
X2 (t) = f V2' (t) dt, X3 (t) = { Vz (t) dt.
о о
Исходя из этих формул, уже нетрудно выразить и величины
Dn(i) через статистические характеристики поля и'(х, t), при-
причем в отличие от рассматривавшихся выше случаев здесь уже
не требуются никакие специальные гипотезы о лагранжевой
автом одедьности.
Так как в' (х, t) = О, то и V (t) s= 0; следовательно, и
X (t) = 0 (в силу (9.56)). Поскольку поле в' (х, t) однородно и
стационарно, лагранжева скорость V (t) также будет стацио-
стационарной случайной функцией; ее корреляционный тензор будет
иметь вид V'i (h) Vj (?2) = B{!f (t\ —1<^. Рассмотрим теперь тен-
тензор дисперсии Dij(x) = Xi(x)Xj(x). Ясно, что наличие осреднен-
ной скорости, направленной вдоль оси Охи никак не сказы-
сказывается на смещениях частицы по направлениям Ох2 и Ох3. По-
Поэтому величины 1J2A), D^ii) и /?2зA) здесь представляются в
обычном для однородной турбулентности виде (9.30'), и их
асимптотическое поведение при малых и больших значениях t
описывается формулами (9.28) и (9.35). Иначе обстоит дел"»
с наиболее интересными компонентами Dn(t) и Di3(i): Для
первой из них из^лервой формулы (9.56) вытекает соотношение
Du(v) = Xi(•*) = } j [VXa(tl)Xa(t^ +
о о
-f- Г [Х3 (ti) V[ (t2) + Хг (t2) V[ (h)) + Mi' (/1 - *2)} dtx
В силу третьего равенства (9.56) первое слагаемое в фигурных
скобках здесь может быть преобразовано к виду
и и
(tt) = ff Vi (в,) Va F2) </в, dh =
о о
0 0
— J ( 1 /l — /2 1

488 гл. v. движение частиц в турбулентном потоке [9.4
Аналогично вычисляется второе слагаемое в фигурных скоб-
скобках:
/ Мз' (h - в) db + / Мз' (/i - 8) db =
о о
J Mi' (8) rf8 + f B'$ (8) rf8 +
Используя полученные выражения, формулу для ?>ц(т) после
многократного интегрирования по частям удается привести к
виду
Dn (х) = у [ B*> — 3x28 + б3) В& (8) dB -f- Г f (х - 8J ВЙ» (8) dS +
о о
х т-
+ Г / (х2 — 82) Мз' (8) rf8 + 2 /* (х - 9) Mi' F) «/6. (9.57)
Совершенно аналогичный расчет приводит к следующей фор-
формуле для Di3:
т т
D13 (х) = Г-:/ (х - 8) В$ (8) db + J (х - 8) [Мз1 (8) + ДЙ} (8)] dB,
о о
(9.570
При больших t из (9.57) и (9.57/) получаются следующие асим-
асимптотические формулы:
Du (x)« 11Х2Г3 • хз, D13 (x)« Г^Г3 • х2. (9.58)
Таким образом, оказывается, что дисперсия смещения жидкой
частицы вдоль оси Oxi (ло направлению осредненного течения)
при больших t асимптотически пропорциональна т3, т. е. растет
со временем значительно быстрее, чем дисперсии поперечных
смещений (асимптотически пропорциональные т). Кроме того,
смещения вдоль осей Oxi и Ох3 оказываются взаимно коррели-
ровашыми. Используя для Da(x) асимптотическую формулу
(9.35), для коэффициента корреляции между величинами Xi(t)
¦н Х&(х) получаем следующее предельное значение:
гх,х, = Di3 (t) [Du (x) D33 (x)j" 2 -> ?± = 0,866 ... (9.59)

g4] 5 9- ЛАГРАНЖЕ?О ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 489
Таким образом, это предельное значение оказывается универ-
универсальным (не зависящим от параметров Г, из2 и Т3). Асимптоти-
Асимптотические формулы (9.58) и (9.59) были опубликованы Корсиным
A9596). Однако эквивалентные выражения еще раньше были
известны из полуэмпирической теории, использующей для опи-
описания движения жидких частиц дифференциальные уравнения
параболического типа; к этому вопросу мы еще вернемся в
следующем параграфе.
Лагранжевы характеристики турбулентности в пограничном слое
Перейдем теперь к вопросу о смещении жидких частиц в
турбулентном пограничном слое. Как и в гл. 3 и 4, будем счи-
считать, что поток заполняет полупространство z > 0, причем
стенку z = 0 для определенности условимся считать динамиче-
динамически вполне шероховатой (с параметром шероховатости z0). Ось
Ох выберем совпадающей с направлением осредненного тече-
течения. Не ограничивая общности, можно считать, что рассматри-
рассматриваемая жидкая частица в момент t = U находилась в точке
с координдтами лг = @, 0, Н). Пусть X (т) = (Х(х), Y(x),
Z\x)) — координаты этой частицы в момент t0 + t, а V (t) =
= (t/(t), V(x), W(x))—ее скорость в этот момент. Случайная
функция V (t), очевидно, не является стационарной — так, на-
например, за достаточно большой промежуток времени х частица
вернее всего поднимется на значительную высоту Z(x), и поэто-
поэтому ее горизонтальная скорость U(x) сильно возрастет. Вообще
говоря, у нас нет.тякже оснований рассчитывать, что функцию
У (t) можно преобразовать в стационармую с помощью про-
простого перехода к новым масштабам длины и времени. Есте-
Естественно предположить, однако, что лагранжевы статистические
характеристики турбулентности в потраничном слое будут зави-
зависеть, кроме параметров т и Я, только от небольшого числа
«внешних» параметров, определяющих «турбулентный режим»,
т. е. входящих в выражения для эйлеровых статистических
характеристик. Это предположение, существенно упрощающее
изучение дагранжевых характеристик, в неявной форме исполь-
использовалось Казанским и Моншым A957) (см. также Монин
A959а)) для расчета формы дымовых струй в приземном слое
атмосферы при разных условиях стратификации. Вслед за тем
оно было подробно исследовано Эллисоном A959) и Бэтчело-
ром A959) в применении к частному случаю логарифмического
пограничного слоя; еще позже Гмффорд A962) (дополнивший
это предположение «екоторыми более специальными гипоте-
гипотезами) и Яглом A965) вывели из него ряд следствий, относя-
относящихся к общему случаю температурно-стратифицированной

490 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [9.4
жидкости, причем выводы Гиффорда были им самим, Малхот-
рой и Сермаком A963) и Сермаком A963) сопоставлены и с
имеющимися эмпирическими данными (см. ниже п. 10.5).
Поскольку высказанное выше предположение включает ут-
утверждение, что турбулентный режим в пограничном слое опи-
описывается небольшим числом параметров, применяя его, целе-
целесообразно ограничиться случаями, когда движение «жидкой
частицы» не выводит ее за пределы слоя постоянства турбу-
турбулентного напряжения трения i = pul и (в случае температурно
стратифицированной жидкости) турбулентного потока тепла q.
Начнем, следуя Эллисону A959) и Бэтчелору A959), со случая
пограничного слоя обычной (нестратифицированной) жидкости,
для которого q'— 0 (для определенности можно считать, на-
например, что речь идет о приземном слое атмосферы в условиях
безразличной стратификации). В этом случае турбулентный ре-
режим определяется параметрами ut « z0. Существенно, однако,
что вне очень тонкого слоя жидкости (толщина которого имеет
тот же порядок величины, что и z0), непосредственно примыкаю-
примыкающего к стенке z = 0, важную роль играет уже только один па-
параметр и,. Изменение же величины z0 (скажем, ее замена на
z'Q) приводит лишь к дополнительному горизонтальному пере-
перемещению всей массы жидкости по направлению оси Оде с по-
постоянной скоростью —*\п~, где х«0,4— постоянная Кармана
(см. выше гл: 3, п. 5.4). Кроме того, представляется очевид-
очевидным, что через достаточно большое время t частица должна
«забыть» про свою начальную высоту Н, т. е. что при больших
т значение Н практически перестает сказываться на статисти-
статистических характеристиках движения жидкой частицы. Отсюда вы-
вытекает, что хотя, вообще говоря, статистические характерисгики
случайного вектора V (t) могут зависеть от четырех парамет-
параметров т, Я, ы, и Zo, влияние второго и четвертого из них является
довольно ограниченным. А именно, влияние величины Н может
сказываться лишь в течение конечного промежутка вреиени
(продолжительность которого в силу соображений размерности
должна иметь тот же порядок величины, что и отношение H/uJy,
а значение параметра ze будет по-настоящему существенным,
только если Н ^ г0, причем и в этом случае лишь в течение про-
промежутка времени порядка го/ы». Если же Н~^> z0 или Н^ ze, но
^. то z0 будет влиять на статистические характеристики
V (т) только через посредство дополнительного постоянного сла-
слаи.
гаемого вида —^lnzo в выражении для t/(t).

9,4] § 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 491
Рассмотрим теперь среднюю скорость V (t) = (?/(t), V{\),
W(x)) жидкой частицы в момент to+x. Из симметрии рассмат-
рассматриваемого течения относительно плоскости Oxz вытекает, что
K(t) =0 при всех t и, следовательно, V(t) = —J^ — 0. Что же
касается компонент U(x) и W(x), то, согласно сказанному выше,
при i^>H/u* (или при т^>2го/ы*, если # = 0 или, вообще,
Н^<- z0) вторая из этих компонент может зависеть только от
ы* и х, а первая должна равняться сумме некоторой функции
от ы* и от х и постоянного слагаемого — ^ In z0. В силу сообра-
соображений размерности отсюда получаются формулы
(9.60)
где b и с =» е^ — безразмерные универсальные постоянные. Ин-
Интегрируя эти формулы по т, найдем, что при достаточно боль-
большом X
Z(x)«K^- " (9-61')
При возрастании начальной высоты Я формулы (9.60')' и (9.610
становятся применимыми позже, но значения параметров b и с
при любом Н остаются одними и теми же. Наличие у частицы
асимптотически постоянной средней вертикальной скорости
W(t) несмотря на то, что средняя вертикальная эйлерова ско-
скорость w{X) во всех точках потока равна нулю (так что, в
частности, и W@) = ш@, 0, Я) =0), очевидно, связано с тем,
что из-за наличия стенки при г = 0'частица не может опустить-
опуститься ниже этого уровня, в то время как ничто не препятствует
ее неограниченному подъему. Поэтому распределение вероятно-
вероятностей для Z(x) с ростом х все более вытягивается вверх по вер-
вертикали, так1 что средняя высота частицы Z(t) возрастает и, зна-
значит, b > 0. Отсюда вытекает, что для любого слоя 0 <; z ^ h
фиксированной толщины h имеет место постоянный оттйк массы
в верхние слои жидкости, который должен компенсироваться
эквивалентным притоком массы из верхних слоев вниз (напом-
ним, что для эйлеровой скорости w{X) неравенство w(X) Ф 0
означало бы, что нарушается закон сохранения массы!). Есте-
Естественно думать, однако, что скорость W(i) должна быть все же

492' ГЛ.ЧГ. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ (9,4
меньше, чем типичное значение пульсаций эйлеровой вертикаль-
«ой скорости (т. е., например, чем величина aw = ('W2)>1')' так
что постоянная b будет заметно меньше единицы (согласно эм-
эмпирическим данным b »0,1; см. ниже стр. 587). Что касается
постоянной с, то ее можно попытаться оценить, исходя из при-
приближенного равенства
(/(*)** и \Z(x)\, (9.62)
где S(Z)—средняя горизонтальная эйлерова скорость на вы-
высоте Z. Подчеркнем только, что в отношении (9.62) нельзя
поставить знак точного равенства, так как в его левой части
среднее значение берется по совокупности жидких частиц, на-
находившихся в момент т = 0 на заданной высоте Я, а в правой
части — по совсем другой совокупности всевозможных жидких
частиц, находящихся (в безразлично какой момент вдемени) на
фиксированной высоте Z(t). Правда, то обстоятельство, что рас-
рассматриваемые жидкие частицы начали свое движение именно на
высоте Я, при t^>— уж'е не будет существенно сказываться на
величине U{i). Тем не менее средняя лагранжева горизонталь-
горизонтальная скорость и при таких t не будет точно равна средней эйле-
эйлеровой горизонтальной скорости на высоте Z(i), так как
W(t) >0, и поэтому в выражении t/(t) = ?/[X(t), K(t), Z(t)]
осреднение преимущественно учитывает частицы, приходящие
на высоту Z(t) снизу. Кроме того, если бы даже и можно было
считать, что U{x) = u.[X{x),Y(x),Z(x)], то все равно равенство
(9.62) не было бы точным, поскольку u(Z) возрастает медлен-
медленнее, чем Z, и, следовательно, u{Z(t)] Ф u[Z{x)]. Заметим еще,
что обе указанные причины должны приводить к тому, что ле-
левая часть (9.62) окажется несколько меньше правой части. Од-
нако можно все же надеяться, что при *^>— различие ме-
между правой и левой частями (9.62) не будет очень значитель-
значительным, так что вытекающее из (9.62), (9.60) и (9.61') соотношу
ние с«*6 будет приемлемым первым приближением (хотя в не-
некоторых случаях, возможно, придется все-таки учесть, что на
самом деле с, по-видимому, немного меньше, чем Ь).
С помощью соображений размерности можно вывести так-
также и выражения для моментов разных порядков векторов'
У'ф_= V(t) - V>) =-(?/'(t), V'(t), W(x)) и Х'(х)=Х(т) -
— X(i) = (X'(i), Y'(ч), Z'{%)). Проще, однако, сразу выписать
общие формулы для плотностей вероятности этих векторов, из
которых уже следуют и выражения для всех их статистических

9 4J * 9." ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 493
характеристик. Как мы уже видели, при х!^^ и ^^jf Рас"
пределение вероятностей для V'(x) может зависеть только от
параметров ы, и х. Следовательно, соответствующая плотность
вероятности должна иметь вид
al
(9.63)
где Pi(u, v, w)—универсальная функция от трех переменных.
Аналогично этому плотность вероятности вектора Х'(х) опре-
определяется формулой вида
1 /У V 7' \
"ТУ Р2[—. —. —)• (9-64)
aV Мат ат ат/
* \ * * * /
а а
* * *
где Рг{х, и, г)—еще одна универсальная функция; отсюда, в
частности, сразу вытекает, что в логарифмическом погранич-
пограничном слое Djj(i)~t2. Согласно равенству (9.61') длину u«t в
(9.64) можно заменить пропорциональной ей длиной Z = Z(t);
поэтому, например, плотность вероятности для вектора Х(т)
можно записать в виде
где функция Р3 получается из Р2 при помощи простого измене-
изменения масштабов на осях координат.
Перейдем теперь к более сложному случаю движения жид-
жидких частиц в пограничном слое температурно-стратифициро-
ванной жидкости (например, в приземном слое воздуха при
стратификации, отличной от безразличной). Здесь уже к числу
«внешних параметров» задачи наряду с и, следует отнести и
параметры д/срр0 и g/T0. Из этих трех величин можно составить
комбинацию размерности длины L — — u3UJh—, игравшую
важную роль в выводах гл. 4. Параметр шероховатости z0 и в
рассматриваемом случае будет существенным, дишь если Н
и одновременно х^^. Если же//^>2о или H<Zz0, но х^^.
то замена z0 на z'o приведет лишь к дополнительному движению
всей массы воздуха по направлению Ох с постоянной скоро-
скоростью •? I / \-?) —/ (х) I > гДе /(?) ~ универсальная функция,
определяющая профиль средней скорости в приземном слое
(см. гл. 4). Следовательно, при х^> — и ^7?>^ должны

494 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [9.4
иметь место соотношения
<9-67>
где \fi и -ф2 — универсальные функции переменной ? = -]г" Ин-
Интегрируя второе из этих соотношений, получим
р (?) ? (?) 0.68)
где ф3 (^) = Г *h fa) rf7!' а ^ — функция, обратная к <|>3- С п0*
о
о
мощью (9.68) равенства (9.66) — (9.67) можно переписать также
в виде
(9.70)
где ф1 и ф — еще две универсальные функции, а постоянная Ь
введена для того, чтобы можно было считать ф@) = 1 (при
этом условии Ь здесь будет иметь то же значение, что и в ра-
равенстве (9.61)). В силу приближенного равенства (9.62) сле-
следует также ожидать, что q>i{t,) ~f(?); поэтому в первом при-
приближении можно -положить
Если, однако, стремиться к большей точности, то следует учесть,
что на самом деле, по-видимому, ццЦ) </(?) при всех ? (но
о величине разности /(?)—q>i(?) пока нет никаких дан-
данных). Соотношения (9.70) и (9.71) использовал Гиффорд A962),
а вслед за ним — Малхотра и Сермак A963) и Сермак A963).
При этом все эти авторы дополнительно предполагали (без до-
достаточных оснований), что функция <р(?) лишь постоянным мно-
множителем отличается от функции /5(?) равенства G.85), опреде-
определяющей среднее квадратичное значение эйлеровой вертикаль-
вертикальной скорости. Исходя отсюда, функция ф(?) в соответствии с
полуэмпирической формулой Казанского иМонина G.95) прини-
принималась равной Jl —т^ТШ ' такои выбор ф(?), впрочем, может
быть в какой-то мере оправдан тем, что при этом выполняются

9.4] $ 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 495
и условие ф@) = 1 и асимптотические закономерности, кото-
которым должна удовлетворять функция <р(?).
Для плотности вероятности р{Х) трехмерного вектора
ЛГ (т) ¦=- (X(x),Y(x),Z(x)) при О^ъ *>^ в силу сообра-
соображений размерности должна иметь место формула вида
^- f ^; !)• <9-72>
ц () nZ=Z(x) определяются из (9.69) (или (9.71))
и (9.70), а Р(х, у, z; ?)—универсальная функция четырех пере-
переменных (последнее из них играет роль параметра, от которого
зависит форма распределения вероятностей). В цитировавшихся
выше работах Гиффорда, Малхотры и Сермака вместо этого
использовалась более простая формула
т. е. неявно предполагалось, что зависимость формы распреде-
распределения вероятностей от параметра стратификации С = -т~ яв"
ляется довольно слабой и в первом приближении ею можно
пренебречь. Это предположение, разумеется, уже не вытекает
из соображений размерности; оно оправдывается лишь некото-
некоторыми имеющимися весьма предварительными эмпирическими
данными (см. Сермак A963)).
При q > 0 (т. е. при неустойчивой стратификации) для ве-
величин WJx) и Z(x) можно получить также ряд заметно более
простых асимптотических результатов, основываясь на предель-
предельных закономерностях свободной конвекции. В самом деле, в
v- |?| / -«^ 0,1 Ш
этом случае при x^>-jj— (и даже уже при х^>?
?
как
А/
это следует из эмпирических данных § 8 гл. 4) и х^>— на вер-
вертикальное движение жидкой частицы не будет оказывать влия-
влияния не только начальная высота Я, но и величина ы*, так как
основное время частица будет проводить в области течения, в
которой господствует режим «чистой» свободной конвекции, не
зависящей от напряжения трения. Поэтому, если q > 0 (т. е.
L<0), то, по-видимому, уже при —1>0,1 функций ip2(g) и
$А\) равенств (9.67) и (9.68) должны принять асимптотиче-
асимптотическую форму iMi) ~ (—I)'1' и Wi) ~ (—ЪУ1'- Точно так же и
функция <р(?) равенства (9.70), вероятно, уже при —?>0,1
мало отличается от своего асимптотического выражение

496 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [9.4
WT
<?{?) ~ (—?)'/з- Но в таком случае при т^>0,1|?|/«. и t^>— бу-
будут выполняться соотношения
(?€'*¦¦ (9-73>
где а — универсальная постоянная, значение которой, в прин-
принципе, можно определить по эмпирическим данным. Формулы
(9.73) и (9.74), разумеется, совершенно аналогичны формулам
для Xi(x) и Vi(x), полученным выше для двумерной и трехмер-
трехмерной конвективных струй. Правая часть (9.74) очень близка
также к правой части формулы G.87') для аи, но это
объясняется лишь тем, что величины аи и W(x) имеют одина-
одинаковую размерность и зависят от почти одних и тех же парамет-
параметров (лишь с заменой координаты z на 2(х))Поэтому из анало-
аналогии формул (9.74) и G.87 ) вовсе не следует еще, что и коэффи-
О
циенты С'ъ и -х с?ь будут иметь близкие значения. Наоборот,
естественно ожидать, что второй из этих коэффициентов замет-
заметно меньше первого, т. е. что а не превышает нескольких де-
десятых. =
Несколько более сложно обстоит дело со средней горизон-
тальной лагранжевой скоростью U{i) = —-^i- в случае режима
свободной конвекции, так как эта скорость уже1 не может быть
независимой от параметра ut (при ut = 0, очевидно, и t/(t) =«¦
= 0). Ясно, однако, что функция ср2 (-jpj = cpj(C) в (9.69) в этом
случае будет стремиться к постоянному значению /(— оо) с ро-
ростом ? (т. е. с ростом т). Это объясняется тем, что с течением
времени частица поднимается в слои жидкости, в которых гори-
горизонтальна^ скорость практически постоянна. Для более точной
оценки U(x) можно использовать приближенную формулу (9.71)
с /(?) = Czt,-'1* + const; возможно также, что в некоторых слу-
случаях целесообразно будет положить cp1(C) = C2C~1/4-const, где
С'ъ принимает немного меньшее значение, чем коэффициент С2
в формуле G.39). Естественно предполагать, однако, что пара-
параметр ы* при Z(x) >0,l|Z.| будет влиять только на среднюю го-
горизонтальную скорость перемещения жидких частиц, но не на
турбулентные пульсации скорости. Поэтому следует ожидать,

9.5] § 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 497
что при достаточно большом т в случае неустойчивой термиче-
термической стратификации будут иметь место соотношения
._ _-.
(9.75')
родственные соотношениям (9.54'f/) и (9.54""), выполняющимся
для турбулентных конвективных струй. Из (9.73) и (9.75'), в ча-
частности, следует, что асимптотически при неустойчивой страти-
стратификации Di^t)"-"!3 (разумеется, все эти выводы предполагают,
что условия-, при которых справедлив «закон 1/3» для эйлеро-
эйлеровой средней скорости и температуры, сохраняются,'по крайней
мере, до высоты Z(x)).
9.5. Лагранжева корреляционная функция скорости и ее связь
с эйлеровыми статистическими характеристиками
Выше мы видели, Что при исследовании движения фиксиро-
фиксированной жидкой частицы очень важную роль играет лагранжёва
корреляционная функция скорости
t* x) = VL(x, h)Vj(x, t2).
Об эмпирических данных, касающихся этой функции, мы скажем
в следующем параграфе. Пока отметим только, что все эти дан-
данные очень малочисленны и неточны, так как в настоящее время
нет никаких надежных методов измерения лагранжевых стати-
статистических характеристик турбулентности. Поэтому имеет смысл
хотя бы вкратце остановиться на вопросе о возможных методах
теоретического определения таких характеристик — непосред-
непосредственно или исходя из их связи с гораздо лучше изученными
эйлеровыми статистическими характеристиками, описывающими
случайное поле и(Х, t).
Легко понять, что задача об определении лагранжевых ста-
статистических характеристик по эйлеровым не может быть простой,

493 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [9.5
В самом деле, в силу основных формул
V(x, t)=u\X(x, t), t], X(x, f) = x+J V(x, t')dt\ (9.76)
являющихся фактически определением величин V(x, t) и
X(x, t), лагранжевы величины в момент t зависят от значений
эйлерова поля и(Х, t) во всех точках случайной траектории
Х(х, t'), to^f.-^t. Траектория же эта определяется как реше-
решение системы интегральных уравнений
с
Х,{х. ?) = xt + f ut\X(x, Г), t"\dt", i = \, 2, S, (9.77)
в свою очередь содержащих поле и {X, t). Поэтому распределе-
распределение вероятностей для каждой лагранжевой величины будет, во-
вообще говоря, зависеть от всего бесконечномерного распределения
вероятностей для значений u(X,t), в функциональном про-
пространстве всевозможных векторных irtwie^ При этом даже и
связь между распределениями в функциональном пространстве
полей и(Х, t) и V(x, t) (или и(Х,t) и X(x,t)) оказываете»
очень сложной, и попытки явно описать ее так и не привели к
результатам, могущим быть примененными к каким-либо кон-
конкретным турбулентным течениям (см. Ламли A9626)).
Рассмотрения распределений вероятностей в функциональном
пространстве можно избежать, допустив^что функции Ui(X, f),
i = 1, 2, 3, — аналитические по всем переменным и поэтому раз-
разлагаются в ряды Тэйлора. Исходя отсюда, можно заключить, что
и все лагранжевы величины в этом случае должны как-то выра-
выражаться через значения эйлеровой скорости и всех ее частных
производных в одной-единственной точке пространства — време-
времени. И действительно, представив значения Х(х, t) и V{x, t) в
виде степенных рядов
Л(Х, t) — 2и^{ W , V — h) —
я=1
(9.78)
я=о '-'•
я=1

95] * 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 499
можно с помощью (9.76) преобразовать коэффициенты этих ря-
рядов к виду
даХ (х, t)
д"У(х, t)
t=ta
_3^V(xJl _ n=li2,...
t=t<,
n = 0, 1, 2, ...,
т. е. выразить их через эйлеровы величины, относящиеся к точке
(х, to). Из формул (9.78) — (9.79) вытекают некоторые важные
общие выводы; например, как было замечено Ламли A962а),
отсюда сразу следует, что если случайное поле и (X,t) является
статистически однородным, то статистически однородными будут
и случайные поля У(х, t) = X(x, t) — х и V(x, t) (этим об-
обстоятельством мы фактически уже пользовались в п. 9.3). Если,
однако, применить эти формулы для определения лагранжевых
статистических характеристик, то результаты окажутся мало-
малоутешительными: для всех моментов полей Y(x, t) и V(x, t)
лри этом получаются очень сложные представления в виде сум-
суммы бесконечного числа одноточечных эйлеровых статистических
характеристик, умноженных на различные степени t ^-.t0. Ясно,
что практически использовать такие представления для кон-
конкретного подсчета лагранжевых характеристик можно лишь
при очень малых значениях t —10, при которых всеми членами
рядов (9.78), кроме небольшого числа первых из них, можно
пренебречь. В частности, в применении к лагранжевой кор.реля-
ционной функции поля скорости таким образом удается оце-
оценить лишь члены порядка не выше (t —10J, причем уже для
членов порядка (t — tQJ получаемая оценка оказывается до-
довольно сложной (см. гл. 7 в ч. 2 настоящей книги).
Лишь в случае членов нулевогр порядка по t —10 (т. е. от-
относящихся к моменту времени ?0) дело обстоит совсем просто,
так как по определению V(x, to) = u(x, t0). Поэтому, например.
о. to, x) =ut(x, to)Uj(x, tQ) = Bu (tQ, tQ; x). Оказывается,
что в случае несжимаемой жидкости и статистически однород-
однородного поля и{Х, t) (а следовательно, и поля V(x, t)) анало-
аналогичный результат имеет место и для всех вообще одноточечных
характеристик поля скорости. Наметим здесь вкратце его до-
доказательство, следуя работе Ламли A962а). Выберем в про-
пространстве точек х объем R и рассмотрим интеграл вида
Jcp(V(x, t))dx, где cp(V) =ф(У4, V2, V3) —некоторая функ-
ция от трех переменных. Перейдем в этом интеграле от пере-

«МО ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКИ (9.5
мёйных Xi, Хг, х3 к новым переменным Xi, X2, Х'з, где Х= Х(х, t).
В случае несжимаемой жидкости (и только в этом случае) та-
такой переход очень упрощается тем, что соответствующий яко-
биан Л ''—-—^-^[Х^ Х2, Х3\ здесь, как мы знаем, тожде-
о (xif Хг, Хз)
ственно равен единице (см. формулу (9.6) на стр. 464). Сле-
Следовательно, в этом случае
f9(V(x,t))dx = /?(в(X, t))dX, (9.80)
R Rt
где Rt — область пространства, которую в момент t заполняет
жидкость, заполнявшая в момент t0 область R. Если, кроме
того, поля V(x, t) и tt(X, ?) являются статистически однород-
однородными, то средние значения функций под знаком интеграла с
обеих сторон (9.80) не зависят от координат. Тем не менее, мы
не можем просто осреднить обе стороны равенства (9.80) и
вынести средние значения функции <р из-под зн^ька интеграла,
поскольку область интегрирования Rt ё правой части является
случайной и зависит от поля и(Х, t). Так как, однако, про-
пространство, заполненное жидкостью, неограниченно (иначе не
могло бы быть однородности),„то мы можем при любом фикси-
фиксированном t выбрать за R, например, шар сколь угодно боль-
большого радиуса. В частности, мы можем выбрать его радиус на-
настолько большим, чтобы область Rt отличалась от R только не-
некоторой частью (неправильной формы), расположенной сравни-
сравнительно близко от границы R и имеющей объем, который с очень
большой вероятностью не будет превосходить достаточно малой
части полного объема шара R. При этом, заменив в правой ча-
части (9.80) интеграл по Rt аналогичным интегралом, распростра-
распространенным по фиксированной области R, мы с очень большой ве-
вероятностью внесем этим лишь очень малую относительную
ошибку. Осреднив теперь обе части полученного приближен-
приближенного равенства и разделив результат на объем R, найдем
)), (9.81)
где мы пишем уже знак точного равенства, так как относитель-
относительная ошибка здесь может быть сделана сколь угодно малой,
если только выбрать достаточно большую область R. В частно-
частности, если ф( V) = ea*v<li то <р( V (х, t)) —это характеристиче-
характеристическая функция лагранжевой скорости V(x, t), а <р(в (X, t))—
характеристическая функция эйлеровой скорости и(Х, t). По-
Поэтому в случае однородной турбулентности в несжимаемой
жидкости распределения вероятностей для эйлеровой и для ла-

9,5] $ 9. ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 501
гранжевой скорости во все моменты времени совпадают ме-
между собой. Таким образом,, в однородной турбулентности невоз-
невозможны парадоксы того типа, с которым мы встретились в слу-
случае пограничного слоя, где и3(х, t) = 0, но V3(х, t) Ф 0.
Разумеется, все наше рассуждение относится только к одно-'
точечным .распределениям вероятностей; для распределений,
относящихся к двум моментам времени, выделенное курсивом
утверждение уже будет, вообще говоря, неверным. Поэтому для
лагранжевой корреляционной функции Bfj{t\, t2; x) отсюда сле-
следует лишь, что в случае однородной турбулентности
B\L} (t, f, x) = Ви (t) = Ui(X, t)uj(X, t),
но ничего не следует о форме зависимости B\}(t\, ^2) от t2 — /1.
Заметим, однако, что если поле скорости и(Х, ^является не
только однородным, но и стационарным, то и функция V(x, t)
будет стационарной по t (этим обстоятельством мы также фак-
фактически уже пользовались выше). В самом деле, представив
Vj(x,t+i)=Uj[X(x, t+x), t+x] в виде ряда Тэйлора (9.78) —
(9.79) (с заменой t0 на t, a t — на /+т), можно записать
корреляционную функцию ft} {t, t + т) = Vt(x, t)Vj(x, * + т)
как сумму одноточечных эйлеровых характеристик (относящих-
(относящихся к точке (Х(х, t), t)), умноженных на степени т. Поэтому,
если соответствующие эйлеровы одноточечные характеристики
не зависят от t (в силу стационарности и однородности поля
и(х, *)), то B?ff(t, ^ + х) = Му'(х).
Равенство (9.81) выше, было доказано для идеализирован-
идеализированного случая однородной турбулентности в безграничном про-
пространстве; однако близкое равенство может быть установлено
и для турбулентного течения в бесконечно длинной прямой трубе.
В этом случае надо только принять за R достаточно длинный
отрезок трубы между сечениями ж4 = а и Xi=b. При любом
фиксированном t=t—t0 мы можем выбрать Ь — а столь боль-
большим, чтобы область Rt отличалась от R лишь небольшими ку-
кусками неправильной формы вблизи краев xi=a и Xi = 6, сум-
суммарный объем которых очень мал по сравнению с полным объ-
объемом R. Но тогда после деления обеих частей равенства (9.80)
на объем R и последующего осреднения мы получим в правой
части величину, почти не отличающуюся от объемного сред-
среднего значения функции (р(и(Х, t)), взятого по цилиндрическому
объему, ограниченному сечениями Jti = a и jc± = 6 и стенками
трубы. В левой же части будет стоять величина tp(V(x, t)),
которую при достаточно большом t — ?0 вообще можно

502 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [9.5
считать не зависящей от х (ср. стр. 477). В частности, при
<р (») == «1 мы таким образом получаем равенство Fi p= Ucp, о
котором шла речь на стр. 477.
Вернемся теперь опять к простейшему случаю однородной и
стационарной турбулентности. В этом случае и = U= const, при-
причем без ограничения общности можно даже считать (как мы и
будем делать в дальнейшем), что U—Q (это эквивалентно про-
простому переходу к новой инерционной системе координат). Если
} (т) = Vi(x, t)Vj(x, t + i) —лагранжев корреляционный
тензор рассматриваемой турбулентности, а 5<,-(gi, ?г, Ез.т) =*
*=щ(хи х2, х3, t)uj(xi +|i, x2 + h, х3 + |з, t + т)' — простран-
пространственно-временной эйлеров корреляционный тензор, то, как мы
знаем, Ett}(Q) = Bij (О, 0, 0, 0). Однако значения #$(т) при
т > 0, вообще говоря, уже не могут быть выражены через зна-
значения Bt;(li. I2, h, t)- В связи с отсутствием надежных дан-
данных о функции B(iL/(i} некоторые авторы- пробовали предполо-
предположить, что Bii))('z) = Bij @, 0, 0, т) (см., например, (работу Бол-
Болдуина и Майкельсена A962), содержащую также сопоставле-
сопоставление следствий из этог^ равенства с эмпирическими данными);
но,такое предположение не имеет никаких теоретических осно-
оснований. Более естественно предположить, что лагранжевы, коэф-
коэффициенты корреляцииR{u {t)=B^ti (i)l Vt (no i не суммируется!),
описывающие связь между i-fi компонентой скорости фиксиро-
фиксированной жидкой частицы в моменты времени t и t+x, будут убы-
убывать с ростом т медленнее, чем эйлеровы коэффициенты корре-.
ляции Ru (т) = ¦ " !—L ' -, описывающие связь между скоро-
*
стями разных элементов жидкости, оказывающихся в момент t
и в момент t + 1 в одной и той же точке пространства. Если это
так, то при 1 > 0 для всех i — 1, 2, 3 должно выполняться нера-
неравенство R'u (т) > Rn (x). Из последнего неравенства, в част-
частности, следует, что лагранжево время корреляции (лагранжев
00
макромасштаб времени) Т'(— \ R^ti'(x)di должно быть больше
о
эйлерова времени корреляции (макромасштаба времени)
00
Т\= ГRlt(i)di, а лагранжев микромасштаб времени 9/==
о ¦ .
_ Г 2/{-т"М/)(т)} I2 точно также должен быть больше

9.5] § 9- ЛАГРАНЖЕВО ОПИСАНИЕ ТУРБУЛЕНТНОСТИ 503
эйлерова микромасштаба 6/ = [—2//?«@)]*. Непосредственная
проверка этих выводов пока, к сожалению, остается невозмож-
невозможной из-за отсутствия данных одновременных измерений эйлеро-
эйлеровых и лагранжевых временных масштабов в условиях, близких,
к тем, которые отвечают однородной и стационарной турбулент-
турбулентности. Однако, как заметил Корсин A963), сопоставление ре-
результатов измерений эйлеровых пространственно-временных
корреляционных функций поля скорости, выполненных Фавром,
Гавильо и Дюма A953) в аэродинамической трубе за турбули-
зирующей решеткой, с данными диффузионных экспериментов
Уберои и Корсина A953), проводившихся в аналогичных усло-
условиях, дает некоторые основания думать, что в таких условиях
¦j-z&OJ. В случае же, когда средняя скорость \и\ — U отлична
от нуля и сравнительно велика, можно ожидать, что коэффи-
коэффициент корреляции Rii(r) = Bn@, 0, 0, т)/и,2 будет убывать с
ростом т еще значительно быстрее, чем при V — 0 (так как те-
теперь* он описывает связь между скоростями элементов жидко-
жидкости, проносящихся в моменты t и t + т с большой скоростью
мимо одной и той же точки пространства, т. е. фактически на-
находящихся на большом расстоянии друг от друга). И'действи-
И'действительно, Хэй и Паскуил A959), предположив, что
Л22(т) = Д$фт) (9.82)
(где направление оси 0x2 совпадает с горизонтальным направ-
направлением, перпендикулярным' среднему ветру), нашли из эмпири-
эмпирических данных о горизонтальной диффузии в атмосфере, что в
первом (весьма грубом) приближении |J«4 (см. ниже стр. 513).
Из равенства (9.82), очевидно, следует, что712 = р712 и в2 ^ рв2;
поэтому значению 0 = 4 отвечает очень значительное превыше-
превышение лагранжевых временных масштабов над эйлеровыми.
Предположение (9.82) о совпадении формы лагранжёвой и
эйлеровой временных корреляционных функций, часто, исполь-
использующееся в исследованиях о турбулентной диффузии, можно
считать допустимым лишь по той причине, что на самом деле точ-
точная форма функций R{u (т), i = 1, 2, 3, во многих случаях ока-
оказывается не очень существенной (см., например, выше стр. 476).
Никаких теоретических оснований это предположение не имеет.
Более того, в гл. 8 ч. 2 настоящей книги будет показано, что
при очень больших значениях числа Рейнольдса PCii (t) **\—С/т
при Щ/Т1<^.ъ^.Т1; в то же время эйлерова временная

504 гл. v. движение частиц в турбулентном потоке [9.5
корреляционная функция Ru(i) при очень большом Re и усло-
условии ы^>(и'2) ' (выполняющемся в опытах Хэя и Паскуила) для
2
/ —
таких т имеет вид^?»(х)«1 — С,т3 (но снова является линей-
линейной по т, если п = 0; ср. Корсин A963), где исходя отсюда при-
приближенно оценивается зависимость отношений различных вре-
менных_масштабов от числа Рейнольдса). Таким образом, при
« ^> (и'2) ' соотношение (9.82) заведомо не может выполняться
при всех 1. О поведении же лагранжевой и эйлеровой корреля-
корреляционных функций при значениях т, сравнимых с соответствую-
соответствующими временами корреляции, в общем случае вообще ничего
нельзя сказать. Поэтому теоретическое определение вида функ-
функций R'ftit) оказывается возможным только на основе каких-
либо специальных чисто эмпирических или же полуэмпириче-
полуэмпирических гипотез.
Сафмен A963) приближенно подсчитал ^наиения функции /?'^'(t) для
одного конкретного вида эйлеровой пространственно-временной корреляцион-
корреляционной функции /?ijEi, Ь. %з, т), предположив, что в соотношении (9.22) ско-
скорость Vj(X,х, t) прн всех t можно заменить эйлеровой скоростью и,( X, t).
Однако мы уже отмечали, что такое предположение необоснованно; поэтому
на нем не стоит задерживаться. Иноуэ A950—1951) н Огура A9526) рассмо-
рассмотрели модель турбулентного движения (задаваемого в виде совокупности
возмущений поля скорости различных масштабов), в которой лагранжевы
корреляционные функции /?н'(т), /=1,2,3, оказались все задающимися следую-
следующей универсальной формулой: R$ (т) = 1 — -н=- прн 0<"c<27*t н Л^(т)=0 прн
х>2Т{. Позже, однако, Иноуэ A952, 1959) пришел к выводу, что более
удобной является другая модель, в которой R$ (т) = е '. Грант A957) ис-
использовал для подсчета функций R $ (т) специальную гипотезу о пути пере-
перемешивания и пришел прн этом к более сложной (но также универсальной)
формуле: /$> (т) = 1 — -^- + -^- In -^- прн 0< т < ATt н &Ц> (т) = 0
прн т>47",-; позже тот же результат получил Мацуока A960) с помощью
небольшого изменения первой модели Иноуэ, о которой говорилось выше.
Еще одну модель турбулентности предложили Вандель н Кофёд-Ханзен
A962); в этой модели для лагранжевой корреляционной функции уже
не получилось универсальной формулы, но зато эта функция оказалась до-
довольно просто выражающейся через эйлерову временную корреляционную
функцию. На самом деле, однако, лагранжева корреляционная функция
не имеет одну н ту же форму во всех однородных н стационарных турбу-
турбулентных течениях н не может быть однрзначно выражена через эйлерову
временную нлн пространственно-временную корреляционную функцию. По-
Поэтому все перечисленные- здесь результаты могут рассматриваться лишь
как некоторые приближения к действительности, степень точности которых
' пока, не" может быть выяснена из-за отсутствия надежных эмпирических
данных, _••--•-

ЮЛ] § 10- ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 505
§ 10. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ
10.1. Постановка задачи об описании турбулентной диффузии
В предыдущем параграфе мы рассматривали движение от-
отдельных «жидких частиц» в турбулентном потоке. При этом под
«жидкой частицей» мы понимали просто объем жидкости, на-
настолько малый, что в рамках теории сплошной среды его мож-
можно отождествить с точкой, перемещающейся вместе с окружаю-
окружающей жидкостью. Ясно, однако, что полученные выводы можно
будет сопоставить с данными наблюдений, лишь если в жидко-
жидкости имеются выделенные «жидкие частицы», за движением
которых можно как-то следить. Поэтому теория, развитая в
предыдущем, параграфе, может иметь значение лишь тогда,
когда в некоторых элементах объема жидкость как-то «отмече-
«отмечена», т. е. обладает какими-то свойствами, отличными от свойств
окружающей среды. Это отличие в свойствах чаще всего бы-
бывает связано с отличием химического состава, т. е. с наличием
в отдельных'элементах объема «посторонних веществ», отлич-
отличных от самой жидкости; однако оно может сводиться, например,
и лишь к разнице температуры. В любом случае при наличии
«отмеченных» частиц мы будем говорить, что в- поток1© имеется
некоторая примесь, понимая под примесью те части жидкости,
которые обладают специальными свойствами, позволяющими
следить за их движением.
Если вводить примесь лишь в определенные места турбу-
турбулентного течения, то в результате ее переноса беспорядочно
перемешивающимися струйками, составляющими в своей сово-
совокупности такое течение, она быстро распространится на весь
занятый жидкостью объем. Это явление, называемое турбулент-
турбулентной диффузией, характерно именно для турбулентных течений;
недаром в классических опытах Рейнольдса возникновение тур-
турбулентности определялось как раз тем, что при добавлении не-
небольшого количества краски вся жидкость быстро становилась
окрашенной. Разумеется, кроме турбулентной диффузии при-
примесь обычно будет участвовать и в молекулярной диффузии, не
связанной с турбулентностью, но этот процесс является несрав-
несравненно более медленным, и поэтому при наличии турбулентности
он играет лишь сравнительно небольшую роль. Именно турбу-
турбулентной диффузией определяются такие всем известные и важ-
важные явления, как распространение в .атмосфере Земли пыльцы
растений, бактерий и вирусов, радиоактивных веществ, вулкани-
вулканической пыли и морской соли, загрязнение воздуха (особенно в
городах) дымами и газами, выделяемыми промышленными

506 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [ЮЛ
предприятиями и транспортом, перенос влаги, испаряемой по-
поверхностью Земли и всевозможными водоемами, рассеяние
предметов, плавающих на поверхности водоемов, и т. д. По-
Поэтому неудивительно, что изучению турбулентной диффузии по-
посвящена обширная литература (см., например, книги Саттона
A953), Френкиля и Шеппарда A959), Паскуила A9626),обзор-
A9626),обзорные статьи Бэтчелора и Таунсенда A956), Эллисона A959),
Монина A959в) и др.).
Для возможности принять частицы жидкости, отмеченные
наличием примеси, за «жидкие частицы» в смысле § 9 прежде
всего необходимо, чтобы примесь была «пассивной» (т. е. не
влияла бы на движение среды) и двигалась бы в потоке со ско-
скоростью, практически совпадающей с мгновенной скоростью те-
течения в соответствующей точке. Отсюда, в частности, вытекает,
что частицы примеси должны быть достаточно мелкими (мень-
(меньшими по линейным размерам, чем те расстояния, на которых
может хоть сколько-нибудь заметно измениться скорость
и (X, t)) и столь близкими по удельному весу к окружающей
среде, чтобы ни гравитационное оседание примеси, ни ее
всплывание вверх под^действием архимедовой силы не играли
бы существенной роли. Разумеется, даже и в этом случае ча-
частицы примеси все равно не будут полностью тождественны
идеальным «жидким частицам». В самом деле, любая примесь
может рассеиваться и в результате молекулярной диффузии
или брауновского движения, связанных с тепловым движением
молекул среды, в то время как на «жидкие частицы» (представ-
(представляющие собой фактически «математические точки» непрерывной
среды, подчиняющейся уравнениям гидромеханики) молекуляр-
молекулярное движение не оказывает никакого влияния. Это обстоятель-
обстоятельство (о котором мы еще будем подробнее говорить в п. 10.2)
имеет, однако, лишь второстепенное значение и в большинстве
случаев им вполне можно пренебречь.
Если частицы примеси могут наблюдаться по отдельности,
то можно, следя за их движением, определить индивидуальную
лагранжеву траекторию X=X(t) и затем попытаться под-
подсчитать лагранжевы статистические характеристики турбулент-
турбулентности с помощью осреднения данных, полученных для ряда
таких траекторий. Этот метод получил довольно широкое рас-
распространение в метеорологии в связи с использованием так на-
называемых уравновешенных шаров-пилотов (вес которых специ-
специально подбирается так, чтобы они плавали в воздухе, не под-
поднимаясь и не опускаясь) и воздушных шаров (см., например,
книгу Паскуила A9626), в которой можно найти и ряд ссылок
на оригинальные работы). Однако полученные таким образом
результаты позволяют получить лишь весьма предварительные

Ю.1] § 10- турбулентная диффузия 507
оценки лагранжевой корреляционной функции скорости и дру-
других лагранжевых характеристик атмосферной турбулентности.
Дело в том, что создание точно уравновешенных шаров весьма
. сложно, а работа с ними очень хлопотлива и трудоемка; кроме
того, такие шары всегда имеют довольно большой объем, и по-
поэтому на них не действуют мелкомасштабные возмущения поля
скорости, сказывающиеся. на движении идеализированных
«жидких частиц».
Как правило, примесь вводится в поток в виде жидкой или
газообразной добавки или в виде большого числа мелких твер-
твердых частиц. При этом ее обычно можно с полным основанием
считать непрерывно распределённой в пространстве и характе-
характеризовать эйлеровым полем объемной концентрации ft(X, t) (в
случае сжимаемой жидкости более удобной характеристикой
была бы массовая удельная концентрадия #/q, но мы здесь бу-
будем для простоты рассматривать лишь диффузию в несжимае-
несжимаемой жидкости). Под описанием турбулентной диффузии мы бу-
будем понимать статистическое описание поля #(Х, t) при задан-
заданных начальных и краевых условиях, включающих и задание всех
источников примеСи. Отметим, что при наличии источников поле
концентрации примеси Ь{Х, t) будет, вообще говоря, неодно-
неоднородным, и его математическое ожидание — средняя концен-
концентрация b{X,t)— будет некоторой функцией от X и t. Опреде-
Определение этой функции является важнейшей (хотя и не единствен-
единственной) задачей теории турбулентной диффузии.
При описании турбулентной диффузии можно исходить из
того, что в каждой индивидуальной реализации турбулентного
потока поле концентрации b(X,t) в областях, не содержащих
источников примеси, удовлетворяет уравнению молекулярной
диффузии
с заданными краевыми условиями на границах рассматривае-
рассматриваемой области пространства. Поскольку примесь пассивна, т. е.
поле и не зависит от распределения концентрации ¦&, уравне-
уравнение A0.1) линейно относительно Ь. Краевые условия, как пра-
правило, также линейны относительно Ь; обычно они имеют вид
где п — нормаль к границе, а р — некоторая постоянная. В слу-
случае твердых стенок, ограничивающих поток, краевые условия
однородны, т. е. /(/) = 0; при этом стенке полностью поглощаю-
поглощающей примесь, соответствует значение Р:=оо, стенке, совершен-
совершенно непроницаемой для примеси, — значение р=0, а значения

508 гл. v. движение частиц в турбулентном потоке [ЮЛ
0 < р < оо соответствуют случаю частичного поглощения и
частичного отражения примеси на границе. В последние годы
в исследованиях В. Феллера, А. Д. Вентцеля и других авторов
по общей теории марковских случайных процессов были изу-
изучены также и более общие (в определенном смысле — наиболее
общие) граничные условия, допускающие возможность времен-
временной остановки примеси в момент достижения границы и ее диф-
диффузии вдоль границы (см., например, Дынкин A963)). По-
Поскольку, однако, эффекты такого рода вряд ли могут иметь
реальное значение при распространении примесей( то на соот-
соответствующих граничных условиях (которые также линейны)
мы не будем задерживаться. В случае неограниченного по ка-
каким-то направлениям потока краевые условия на бесконечности
обычно берутся в виде требования Ф-^-0, т. е. опять же имеют
вид A0.2) (с f(t)=Q и р = оо). Мгновенные источники при-
примеси, очевидно, описываются заданием определенных началь-
начальных условий для поля &{X,t); непрерывно, же действующим
источникам соответствуют неоднородные краевые условия вида
A0.2) с f(t) Н= 0 (подробнее эти условия для различных типов
источников будут рассмотрены ниже).
При однородных краевых условиях эволюция'поля §{Xxt)
в рассматриваемой области будет обусловлена исключительно
переносом примеси полек скорости u(X,t) и молекулярной
диффузией. Поле скорости в принципе однозначно определяется
по начальному полю tt{X,t0) =tto(X) с помощью уравнений
гидродинамики. Следовательно, решение уравнения A0.1) при
заданном начальном поле концентрации Q(X,t0) = Qo(X) мо-
может быть записано в виде
b{X,t) = A [щ {X), t] &o {X), A0.3)
где А — некоторый оператор, зависящий от начального поля
скорости ио{Х), параметра / и вида краевых условий. Подчерк-
Подчеркнем; что вследствие линейности уравнения A0.1) и краевых
условий этот оператор линеен.
При статистическом описании турбулентности начальное
поле скорости ио{Х) рассматривается как случайное, т. е.
предполагается, что ему соответствует некоторое распределение
вероятностей в функциональном пространстве его реализаций
(всевозможных соленоидальных векторных полей). Но в таком
случае и. оператор A[uo(.X),f\, зависящий от случайного поля
U0(X), будет, случайным оператором, характеризуемым .некото-
.некоторым распределением вероятностей в пространстве линейных опе-
операторов, могущих являться реализациями оператора Л. Следо-
Следовательно, при фиксированном О0(А") поле концентрации О(X,-t)

* 10- турбулентная диффузия 509
при t > to будет случайным, (так как оно зависит от А, т. е. от
щ{Х)). При этом среднее значение поля &{Х, t) будет опреде-
определяться равенством
?{Х7Т) = А[и0{X), t\»0{X) = A(t)Ь0{Х). A0.4)
где оператор A(i)=- А\ио(Х), {\ получается из случайного опе-
оператора A[tto{X),f\ с помощью теоретико-вероятностного осред-
осреднения (т. е. интегрирования по вероятностной мере, заданной в
пространстве полей ио(Х)). Поскольку операторы A[uo(X),t]
линейны при любом ио(Х), и осреднение является линейной
операцией, то и результирующий осредненный оператор A(t)
также линеен. Таким образом, при фиксированном начальном
поле концентрации &о{Х) осредненная концентрация #{Х,,t)
удовлетворяет некоторому линейному уравнению. Для корре-
корреляционной функции и для моментов более высокого порядка
случайного поля ft(X,t) с помощью A0.3) также можно полу-
полупить некоторые уравнения; однако эти уравнения будут уже не-
нелинейными и гораздо более сложными, и они рассматриваются
редко. Большинство существующих методов описания турбу-
турбулентной диффузии сводится к конструированию лишь линейного
уравнения для средней концентрации ft(X, t) или, что эквива-
эквивалентно, к нахождению (теоретическому, полуэмпирическому или
чисто эмпирическому) линейного оператора A(t).
В частном случае, когда допускается, что при определении
осредненной концентрации "можно пренебречь молекулярной
диффузией по сравнению с турбулентной (условия, при которых
законно это допущение, будут рассмотрены в следующем
пункте), оператор A(t) может быть представлен в значительно
более конкретном виде, чем. это делалось выше. В самом деле,
рассмотрим прежде всего случай, когда в начальный момент
времени t=to вся примесь (в количестве Q) сосредоточена, в
одной «жидкой частице», находящейся в точке х. В таком слу-
случае,'очевидно, Ъй{Х) = Qb(X— X). Но поскольку молекуляр-
молекулярной диффузией пренебрегаетея, примесь все время будет оста-
оставаться в той же жидкой частице, что и вначале, т. е. в момент
t она будет находиться в точке X(x,t). Следовательно, в рас*
сматриваёмом случае &{Х, ^)= Qfi[X — X(x,t)\. Учитывая,
что '
b[X-X(x,t)\=p(X\x,t); ... . . .
— это плотность вероятности для координат указанной «жи|$0Й
частицы» в момент t, получим A (t) б (X — х) =f р {X | х>, t).
В силу линейности оператора 'Д'(/). при произвольном началь-
начальном поле Ьо(Х) мы можем теперь воспользоваться принципом

510 гл. v. движение частиц в турбулентном потоке [ЮЛ
суперпозиции; отсюда вытекает, что
?Щ7) = Ж[t) К {X) = fp {X\x, t) % {х) dx. A0.5)
Таким образом, нахождение осредненной концентрации ${X,t)
в пренебрежении молекулярной диффузией сводится к опреде-
определению плотности вероятности для координаты X{x,t) одной
«жидкой частицы». Заметим, что саму функцию р(Х\х, t) в
силу A0.5) можно интерпретировать как поле концентрации
примеси ft(X, t) при наличии в начальный момент /= U в
точке X мгновенного точечного источника примеси (единичной
концентрации). Отсюда вытекает возможность эмпирического
определения р(Х\х, f) по данным диффузионных опытов, о ко-
которой мы упоминали на стр. 473.
Зная оператор А (/), т. е. умея вычислить поле средней кон-
концентрации b{X,t), отвечающее заданному начальному полю
Ъ0(Х), легко определить и среднюю1 концентрацию, отвечаю-
отвечающую различным типам источников принеси» встречающимся на
-практике. Рассмотрим, например, снова случай «чисто турбу-
турбулентной» диффузии, определяемой формулой A0.5), причем
поле' скорости u{X,t) для простоты будем предполагать ста-
стационарным (что соответствует установившейся турбулентно-
турбулентности). В таком случае плотность вероятности р(Х\х, t0 + x) для
координат «жидкой частицы» в момент /0 + т при условии, что
в момент /0 она находилась в точке х, удобно обозначить сим-
символом pi(X\x, %); тогда функция р\ в отличие от р уже не бу-
будет зависеть от параметра t0. При этом средняя концентра-
концентрация от мгновенного точечного источника производительности Q
(т. е. создавшего Q единиц массы примеси) будет равна
Qpi(X\x, t — ^о). В случае непрерывно действующего стацио-
стационарного точечного источника в точке х производительности Q
(т. е. создающего Q единиц массы примеси за единицу вре-
времени) средняя концентрация Q(X,t)= Ъ(Х), очевидно, не бу-
будет зависеть от времени и будет даваться формулой
/ 00
= Q fpAX\x, t-to)dto = QfPl(X\x, t)rfx. A0.6)
-аз 0
Ha практике довольно часто приходится также иметь дело с
диффузией в потоке, имеющем постоянную среднюю скорость
й = 0, направленную вдоль оси ОХй в таком случае удобно
сначала перейти к системе координат, движущейся вместе со
средним течением. При этом средняя концентрация от непрерыв-
непрерывно действующего стационарного точечного источника в точке х

|0.1] $ 1°- ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 511
принимает вид
со
ji(X1—Ox, Х2- Х3\х, x)dx, (Ю.б')
где pi(Xi, Х2, Х3\х,х)—плотность вероятности для координат
жидкой частицы при отсутствии средней скорости. В случае
линейного источника, расположенного вдоль оси ОХЬ средняя
концентрация #(Х, t) получается интегрированием по х2 кон-
концентрации от точечного источника в точке @, х2, 0). Отсюда
вытекает, что в случае установившейся турбулентности, одно-
однородной по направлению оси ОХ2, и при наличии средней
скорости потока U по направлению оси OXi средняя концентра-
концентрация от мгновенного линейного источника на оси ОХ2 будет
иметь вид
b(Xv X3,t) = Q Jp^-Uv, X2, Х3\0, t-
— DO
= QA (*i - U-z, X3\0, t - Q. A0.7)
Здесь Q — это количество примеси, внесенное в поток на интер-
интервале оси ОХ2 единичной длины (это количество мы считаем
постоянным, т. е. не зависящим от Х2), a Pi(^i, Х$\0, т) =
0
Г
ь Х3\0, x)dXz — двумерная плотность вероятности
для координат Xi и ^3 «жидкой частицы» в момент to+x (при
условии, что в момент t0 oha находилась в точке X—0) в по-
потоке с нулевой средней скоростью. Точно так же в случае не^
прерывно действующего стационарного линейного источника на
оси ОХ2 производительности Q (т. е. производящего Q единиц
массы примеси за единицу времени на каждую единицу длины)
средняя концентрация #(Xi,X3) равна
l-Ui, X3\0, т)Л. A0.8)
С помощью формул для моментов Х% и Х{Х} координат-
«жидкой частицы», приведенных в предыдущем параграфе, мы
можем теперь выразить через лагранжевы характеристики тур-
турбулентности величины J Xfb(X, t)dX, J XtXjb(X, t)dX и не-
некоторые другие того же типа. С другой стороны, эти величины
Можно определить и по найденной из диффузионных эксперн-

512 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [ЮЛ
ментов средней концентрации Ъ(Х, t), что дает возможность
получить определенные эмпирические сведения о лагранжевых
характеристиках. Рассмотрим в качестве иллюстрации простей-
простейший случай непрерывно действующего линейного источника на
оси ОХ2 в потоке со средней скоростью ?/, намного превосхо-
превосходящей типичные значения пульсаций скорости. В этом случае
основной вклад в интеграл по dx в правой части A0.8) внесут
значения т, близкие к XJU. Поэтому здесь с большой степенью
точности можно положить
»(А„ ^3) = «net. р, (Ai| 0, ¦?-), A0.9)
СО
где Pi(А|0, т)= Гр1(Х1, Х3\0, t)dXl —одномерная плотйость
—со
вероятности для координаты Х3 «жидкой частицы». В силу фор-
формулы Тэйлора (9.31) отсюда, в частности, вытекает, что при
однородной турбулентности с U^\u'l) '
¦О .
с
J
dXz x,/u
7
J Ъ(Хи Х3) dX3
x, A0.10)
где, как и в § 9, изД$(*)= У3@, ^) V^ @, ^ + т). Следователь-
Следовательно, средняя толщина следа за стационарным линейным источ-
источником примеси (которую естественно отождествить с (Х|I/з)
на малых расстояниях от источника возрастает пропорциональ-
но этому расстоянию (так как Х\» ^ при Хх <^ UT3 =*
со
= U ( R$(i)di)>a на больших—пропорционально квадратному
корню из расстояния (так как Xl»—3J при
Это обстоятельство хорошо подтверждается данными диффу-
диффузионных экспериментов Калинске и Пиена A944), Уберои и
Корсина A953), Таунсенда A954) и других исследователей.
Аналогично показывается, что в тех же условиях след за точеч-
точечным стационарным источником должен вначале иметь форму
конуса, а затем — параболоида вращения. Этот факт также уже
давно был известен и из лабораторных экспериментов, и из

ЮЛ]
$ 10. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 513
наблюдений за дымовыми струями, выходящими при сильном
ветре из фабричных труб (ср. Тэйлор A921)).
Согласно формуле A0.10),
так что в принципе по эмпирическим значениям Х\ {Xi) можно
определить и функцию $$(*). На самом деле, однако, точность
такого определения /?зз'(т) оказывается крайне низкой, так как
при этом приходится дважды дифференцировать эксперимен-
экспериментальную кривую, на практике всегда определяемую довольно
ненадежно. Тем не менее, некоторые авторы (в том числе Тэй-
Тэйлор A9356) и Коллис A948)) пробовали получить таким обра-
образом хотя бы ориентировочные значения лагранжевой корреля-
корреляционной функции скорости. Другие исследователи (например,
Калинске и Пиен A944), Уберои и Корсин A953), Майкельсен
A955), Хэй и Паскуил A959)) использовали измерения вели-
величины Х\ (в следе за линейным или точечным стационарным
источником), в первую очередь, для получения более частной
информации о лагранжевых статистических характеристиках и
прежде всего данных о величине лагранжевого масштаба вре-
со
мени Т = Г /Из* (т) dx. В частности, Хэй и Паскуил измеряли
о
(с помощью специальных коллекторов, представляющих собой
небольшие липкие цилиндры) распределение примеси (которой
в их опытах являлись споры ликоподия) вблизи Земли на рас-
расстоянии 100 м от помещенного в атмосферу непрерывного точеч-
точечного источника. Одновременно эти исследователи регистриро-
регистрировали изменения скорости и направления ветра в фиксирован-
фиксированной точке вблизи источника (на высоте 2 м над поверхностью
Земли), что позволило им определить эйлерову временную кор-
корреляционную функцию скорости ветра. Предположив, что эйле-
эйлерова и лагранжева корреляционные функции поперечной компо-
компоненты скорости ветра подобны друг другу (см. формулу (9-82)
на стр. 503), и использовав формулу Тэйлора (9.31), они смогли
оценить по экспериментальным данным величину коэффициента
пропорциональности Р; именно так было получено значение
Р » 4, упоминавшееся на стр. 503. Калинске и Пиен A944) и
Уберои и Корсин Д953) измерили в лабораторных условиях
значения функции Хз {Xi) в следе за линейным стационарным
источником, оценили по ней ^масштаб Т и некоторые другие

514 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ 6 ТУРБУЛЕНТНОМ ПОТОКИ {ЮЛ
параметры функции $&(') и затем использовали эти оценки
для уточнения значений /?зз'(т)> найденных по формуле A0.11);
однако и в этом случае ход функции /?зз (х) определялся нена-
ненадежно. Заметим еще, что в большинстве упоминавшихся опытов
измерения относились к случаю диффузии тепла (работы Тэй-
лора, Коллиса, Уберои и Корсина) или постороннего газа (ра-
(работа Майкельсена) в воздухе, так что пренебрежение молеку-
молекулярной диффузией здесь требовало специального обоснования
(отсутствующего во всех этих работах). В опытах же Калинске
и Пиена, в которых изучалась диффузия в воде мелких капелек
жидкой примеси (того же удельного~веса, что и вода), молеку-
молекулярная диффузия вряд ли могла проявляться, но предположе-
предположение об однородности турбулентности оказывалось, по-видимому,
не очень точным.
Как мы уже указывали в п. 9.3, в случае однородной тур-
турбулентности есть веские основания предполагать, что распреде-
распределение вероятностей для кооодинат «жидкой частицы» при любых
временах диффузии будет довольно близким к гауссовскому
распределению. Иначе говоря, если мы примем за оси коор«
динат главные направления тензора дисперсии координат жид«
кой частицы Dij(x) = [Х{(х) — xf][Xj(%) — г,], то при любом t
допустимо считать, что .
р\ (Х\Х, «) = #—j - X
BЛJ Г?>п(х) Dss(x) Д
2Du(t) 2Dm(x) 2D33(t)
Где величины Оц{%) выражаются с помощью формулы (9.31)
через лагранжевы коэффициенты корреляции /?Ь (х). Подста*
вл'яя эту формулу в общие соотношения A0.5) — A0.9) (в пред*
положении, во многих случаях вполне оправданном, что напра-
направление средней скорости совпадает с одним из главных напра*
влений тензора D(j(t)), можно значительно конкретизировать
эти выражения, исследовать их асимптотическое поведение в раз-
различных предельных случаях, получить для некоторых из них
более простые приближенные формулы и провести детальные
расчеты для отдельных модельных примеров функций /?$'(*)
(Френкиль A952, 1953), Флейшмен и Френкиль A954); ср. так*
же Хинце A959), § 5.5 и начало п. 10.4 настоящей книги),
В ряде случаев примесь можно рассматривать не только как непрерывно
распределенную в пространстве субстанцию, яо и как совокупность дискретных
частиц, причем иногда это последнее рассмотрение даже оказывается в не-
некоторых отношениях более удобным, Несмотря на то, что в дальнейшем мы

ЮЛ] 5 10- ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 515
не будем пользоваться таким рассмотрением, прнзедем здесь все же для
полноты некоторые результаты, касающиеся математического описания поля
дискретной прнмесн. Обозначим общее число частиц примесн через N,
а их суммарную массу примем за единицу. Будем считать все частицы н е
отличающимися друг от. друга и статистически равно-
равноправными в том смысле, что при любом k ¦< N, любых пространственных
областях Vi, ..., Vh н любых различных номерах iit ..., ih, 1<«,<N.
вероятность Р f Xt €V1( ..., Xt € VA, где X?V означает, что точка X
принадлежит области V, ие зависит от номеров f|, '..., h. Отсюда,, в част-
частности, вытекает, что все случайные векторы Aj являются одинаково распре-
распределенными и что Р fXl ? V,, ...,Xl ZV/Л является симметричной функ-
функцией от областей Vlt ..., Vh.
Полной характеристикой распределения дискретной прнмесн в фиксиро-
фиксированный момент времени будет случайная функция области n(V), значение
которой равно массе прнмесн, содержащейся в данный момент в простран-
пространственной области V. Эта случайная функция играет здесь ту же роль, что
и случайное поле О (X) в применении к непрерывно распределенной прнмесн
(точнее говоря, n(V) является аналогом величины j ft(X) dX). Функция
|i,(V), очевидно, является аддитивной функцией области в том смысле, что
\i(Vt + V2) = \i(Vt) + \i(V2). Вместо многомерных распределений вероят-
вероятностей, определяющих случайное поле &(Х), теперь выступают вероятности
= -^f. (ЮДЗ)
заданные для .всевозможных конечных наборов пространственных областей
Vi, ..., Vk- В дальнейшем мы будем для простоты рассматривать Лишь
вероятности A0.13) для непересекающихся между собой областей
Vi, ..., Vh. Отметим, что в частном случае независимых статистически
равноправных частиц прнмесн распределение A0.13) вырождается в так на-
называемое полиномиальное распределение
где
Таким образом, в случае независимых частиц функция u(V) полностью за-
задается значением вероятности Qi(V) для всех областей V. В общем же слу-
случае зависимых статистически равноправных частиц распределение A0.13)
будет представлять собой некоторое обобщение полиномиального распределе-
распределения; для его задания уже надо знать все вероятности
A0.14)

516 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.2
Можно показать, что произвольный момент случайных величин n(Vi), ...,
(V) выражается через вероятности A0.14) с помощью формулы
в.+ ... +nk<m
A0.15)
где m = m1 -)- • • • Ч~ m* — порядок момента, а а™ — так называемые числа
Стирлиига, отличные от иуля лишь при 0<п<тиудовлетворяющие разност-
разностному уравнению^ = a%Zi + па%~'при краевых условияха„ = aj" = 1. От-
Отсюда, в частности, следует, что момент т-го" порядка случайной функции n(V)
полиостью определяется совместным распределением вероятностей для коор-
координат m частиц, т. е., иначе говоря, что вероятности A0.14) с "i+.. .+«* -<m
определяют случайную функцию ц(У) с точностью до моментов т-го по-
порядка.
При т = 1 из A0.15) получается формула
Rv)-Qi.(V),' (юле)
аналогичная формуле A0.5) (точнее говоря, формуле, получающейся нз
A0.5) после интегрирования обеих ее частей по области V переменного ДГ).
При m = 2 из A0.15) и A0.16) получаем ^
= <?г(V) -[Q, {V)] +-!•
[I* ОЛ) - P (V.)] [I* (V.) -[x (Ki)] = Qu (V,. Vi) - Q, (Vj) Q, (Ks) -
¦ " . -^^"(K,, V,). A0.18)
Первая нз этих формул показывает, что при наличии связей между части-
частицами (т. е. при Qz(V) Ф [Qi(V)p) флюктуации количества примеси в фикси-
фиксированном объеме V не убывают неограниченно (по своей средней квадра-
квадратичной величине), даже когда #->оо. Иначе говоря, в случае взаимиозави-
снмых частиц даже при очень большом числе тастнц N значения n(V)
оказываются заметно различными для разных реализаций. Формула A0.18)
показывает, что, кроме того, в таком случае флюктуации количества примесн
в различных (непересекающихся) объемах оказываются взаимно коррелиро-
коррелированными. Заметим, что взаимная зависимость между частицами как раз и
характерна для процесса турбулентной диффузии, где движения частиц, на-
находящихся на не слишком большом расстоянии друг от друга, определяются
в значительной степени одними и теми же возмущениями поля скорости, т. е.
статистически связаны друг с другом. Поэтому при турбулентной диффузии
концентрацнн примесн в каждом объеме заметно флюктуируют и для близких
(но непересекающихся) объемов оказываются зависимыми друг от друга при
любом N и даже прн N =*со — именно этот последний случай и описы-
описывается моделью непрерывно распределенной прнмесн с концентрацией ¦& {X),
непрерывно зависящей от ДГ.
10.2. Взаимодействие между молекулярной
и турбулентной диффузией
Распространение примесей в турбулентной среде в резуль-
результате их переноса движущимися жидкими частицами (т. е. тур-
турбулентная диффузия) обычно происходит много быстрее, чем

§ 10- ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 517
их распространение, создаваемое молекулярным движением
(т. е. молекулярная диффузия). Так, например, в приземном
слое атмосферы условный «коэффициент турбулентной диффу-
диффузии» для пассивных примесей (т. е. отношение турбулентного
потока примеси к градиенту концентрации) обычно имеет зна-
значения порядка 104 н- 105 см2секг1. Иначе говоря, он оказывается
в 105 -г- 106 раз больше коэффициента молекулярной диффузии
1, который для большинства газов имеет порядок 10 см2сек~1.
В результате турбулентной диффузии дым от папиросы в кон-
концентрациях, достаточных для воздействия на человеческое обо-
обоняние, распространяется по комнате за несколько секунд,
в то время как действие одной лишь молекулярной диффузии
привело бы к такому результату лишь через несколько суток.
Однако означает ли все это, что при описании турбулентной
диффузии можно полностью пренебречь молекулярной диффу-
диффузией?
Перенос примеси движущимися жидкими частицами, очевид-
очевидно, приводит к тому, что объем, первоначально занятый при-
примесью, по каким-то направлениям растягивается, а по другим
сжимается, искривляясь при этом самым запутанным образом
(подробнее об этом процессе мы будем говорить в гл. 8 ч. 2 •
книги). Однако суммарный объем примеси при такой деформа-
деформации, разумеется, не меняется. В результате в каждой реализа-
реализации турбулентного течения, удельная концентрация &(X,t) в
каждой точке в любой момент времени будет равной либо
удельному весу примеси р0, либо 0, в зависимости от того, со-
содержала ли соответствующая «жидкая частица» в начальный
момент t = to примесь или не содержала (ср. схематический
рис. 80, заимствованный из обзорной статьи Корсина A959а)).
Таким образом, турбулентная диффузия приводит к образова-
образованию в жидкости очень искривленных и запутанных слоев с рез-
резко различающимися значениями концентрации примеси. Вырав-
Выравнивание концентрации в соседних слоях, сопровождающееся
возрастанием объема, занятого примесью, и сглаживанием поля
концентрации, в результате которого значения функции
ft(X, t) уже, как правило, оказываются промежуточными ме-
между р0 и 0, происходит только вследствие молекулярной диффу-
диффузии и тем медленнее, чем меньше коэффициент %. Отсюда ясно,
что при описании мелкомасштабной статистической структуры',
поля Ь(Х, t) пренебречь молекулярной диффузией невозмож-
невозможно — иначе при большом t мы получим совершенно противоесте-
противоестественное распределение концентрации типа, изображенного в
правой части рис. 80. Однако вопрос о том, нельзя ли прене-
пренебречь молекулярной диффузией по сравнению с турбулентной
при нахождении средней концентрации ${X,t), как

518
ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ Б ТУРБУЛЕНТНОМ ПОТОКЕ
[10.2
это было сделано в предыдущем пункте при выводе формулы
A0.5), более сложен. Этим вопросом мы теперь и займемся.
При выяснении относительной роли молекулярной и турбу-
турбулентной диффузии в формировании поля осредненной концен-
концентрации ft(X,t) мы ограничимся для простоты рассмотрением
задачи о диффузии примеси от мгновенного точечного источника
единичной производительности в поле однородной турбулент-
турбулентности с нулевой средней скоростью. Будем считать, что этот
Рнс. 80. а) Изменение формы объема, занятого
примесью, в результате турбулентной днффузнн.
б) Схематический вид распределения концентра-
концентрации примеси вдоль прямой, пересекающей этот
объем.
источник помещен в момент t=t0 в точкуX =0. Иначе говоря,
мы будем рассматривать поле концентрации О(X, t), соответ-
соответствующее решению уравнения A0.1) при начальном условии
Ь(Х, to) = 6(X). Исследуем диффузию примеси по какому-то од-
одному фиксированному направлению, скажем, по направлению
оси ОХ^ В качестве характеристики роли молекулярной диффу-
диффузии мы используем относительный вклад этой диффузии в дис-
дисперсию распределения средней концентрации О (X, t). При этом
существенно различать, во-первых, дисперсию распределения
средней концентрации относительно местоположения источника
Х=0 ,
A0.19)
и, во-вторых, дисперсию (также относительно местоположения
Источника Х= 0) центра тяжести Xf{t) = J .""

Ю.2] § ю. турбулентная диффузия 519
пределения концентрации #(X,t), т. е. величину
A0.20)
,t)dX].
Помимо того Интерес представляет и дисперсия распределения
концентрации §(X,t) относительно своего центра тяжести
D\ (t) = /[*,- Хс (t)}2 Ъ (X, t) dX. A0.21)
Однако, воспользовавшись условием нормировки j #(X,t)dX=
= 1, выражающим закон сохранения количества примеси (или,
как говорят, ее консервативность), нетрудно проверить,
что
D2c(t) = Dl(t)-X2c(t), A0.22)
так что нам достаточно подсчитать только две величины D\{t)
и ХЩ.
Далее нам будет удобно перейти от неподвижной системы
координат X к подвижной неинерциальной системе координат
У=Х— X @, t), начало отсчета которой в каждый момент
времени совпадает с точкой, в которой в этот момент нахо-
находится жидкая частица, находившаяся в момент t0 в точке
Х= 0. Для поля концентрации в этой новой системе отсчета
мы примем обозначение
ЦУ, i) = b\y+X{0t t),-t]=*b{X, t). A0.23)
В таком случае ясно, что—^v =—^у ¦ • С дру-
J -, dYl dXl \X=Y+X@,t) УУ
гой стороны,
Ж*1Г+^0' 0. <1=-5 + К@, 0^. (Ю.24)
где V@, t) = —JT-*—лагранжева скорость «жидкой части-
частицы», находившейся в момент t0 в точке X = 0. Следовательно,
уравнение A0.1) в рассматриваемой подвижной системе коор-
координат принимает вид
§ + [ui[V+X@,t),t]-Vl@,J)}§; = xM, A0.25)
Где А — оператор Лапласа по переменным (У4, У2, Ys), a
V@, t) — скорость начала отсчета этой подвижной системы
относительно исходной неподвижной системы координат. Поле
б(Y, t) также удовлетворяет условию нормировки J 6 (Y, i)dY=*

520 гл. v. движение частиц в турбулентном потоке [10.2
= 1, которым мы будем пользоваться, не оговаривая этого. Да-
Далее, равенства A0.19) и A0.20) после перехода к новой системе^
координат принимают вид
, t)fb{Y, t)dY=
Л1@, 0 + 2^,@, t)frib{Y,t)dY+frU{Y, t)dY,{\0.26)
и соответственно
, t)]4Y.
= X\{0, 0 + 2^@, t)fr^(Y,t)dY+[f Г,9{Y,t)dYj. A0.27)
Мы ограничимся вычислением величин D\{t) и X*{t) лишь при
малых значениях t — t0. Будем считать, что все моменты
(V*rlYt") = f Y\Y\rl' HY,i)dY A0.28)
(где ku ki, ks*— неотрицательные целые числа) могут быть пред-
представлены в' виде рядов по целым степеням t — t0. В таком слу-
случае и дисперсии D\(t) и X2c{t) будут преДставимы в виде рядов
по степеням t —10, причем для вычисления первых нескольких
членов этих рядов надо знать лишь несколько первых членов
рядов для моментов (Yi) и (Vf), входящих в формулы A0.26)
и A0.27).
Для вычисления моментов A0.28) воспользуемся уравне-
уравнением A0.25). При этом для нас будет существенно, что
«/[Я^О, t), t]= V{@, t), и следовательно, разность скоростей,
стоящая в фигурных скобках в левой части A0.25), может быть
представлена в виде
где все производные от m(Xt t) берутся в точкеХ=Х{0, t),
т. е. являются функциями только от L Подставим теперь разло-
разложение A0.29) в уравнение A0.25), а затем умножим все его
члены на К*'К|'Кз' и проинтегрируем по всем значениям Y. Учи-
тывая, что -gy-^0, мы после интегрирования по частям членов,
содержащих пространственные производные от 6( Y, t), придем

10.2] 5 10- ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 521
к соотношению
¦+
. ,, Ч;
где моменты, содержащие отрицательные степени Yu считаются
тождественно равными нулю.
Из A0.26) видно, что момент нулевого порядка (с ki =» k2 —
= fe3 = 0) тождественно равен единице; поскольку 8(К, ^о) =
= б (У), все остальные моменты стремятся к нулю при t-+t0.
Но в таком случае первый порядок малости по t — f0 будут
иметь только те моменты, для которых правая часть A0.30)
содержит момент нулевого порядка. Нетрудно видеть, что этим
свойством будут обладать лишь моменты (И), причем их глав-
главные члены имеют вид
... A0.31)
Однако, для того чтобы определить также и последующие чле-
члены этого разложения для момента (К?), которые нам понадо-
понадобятся ниже, требуется выписать также и все моменты, имеющие
при t -»- *о порядок (t — to}2.
Ясно, что этим свойством будут обладать те моменты нену-
ненулевого порядка, отличные от (Yt)> для которых среди слагае-
слагаемых в правой части формулы A0.30) встречаются моменты (^).
Нетрудно проверить, что такойыми являются лишь моменты
{Yt), (yf} и (YtYj), (Y2tY)) при i ф j, причем ах главные члены
имеют вид
<10-32)
где все производные от й{Х, t) берутся-в точке X =¦ 0 в мо-
момент t = Ц.

522 гл. v. движение частиц в турбулентном потоке [Ю.2
Поставим задачей вычислить величины Dl(t) и Xl(t) с точ-
точностью до слагаемых порядка (t^-toK включительно. По-
Поскольку
*@ fl @ t)(tt)+ ... A0.33)
для этого надо знать момент (У\) с точностью до слагаемых
порядка (t — toJ, а момент^) — с точностью до слагаемых
порядка (t — toK. Таким образом, равенство A0.32) для (Yi)
достаточно для нашей цели, но разложение A0.31) для (У\)
должно быть уточнено. Чтобы определить недостающие слагае-
слагаемые, выпишем отдельно формулу A0.30) при fei = 2, ^2 = ^3 = 0;
+ J дХадХ?дХ^
Учитывая в правой части этой формулы лишь слаг'аемые порядка
малости не выше (t—toJ, с помощью A0.32) получаем
„ dui dut , d
Так как -W- = -ту- +-Ш
dut
d
ai 0Л1
•» то, следова-
тельно,
A0.34)
где все производные oj tt(X, t) берутся в точке X = 0, t = t0.
Далее нам понадобится только среднее значение момента
{У\). Вспомним теперь, что мы условились считать турбулент-
турбулентность однородной, так что средние значения всех величин, за-
зависящих лишь от одной пространственной трчки Xj сами от X

10.2] « »О. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 523
не зависят. В частности,
Таким образом, в случае однородной турбулентности
Выражение в фигурных скобках легко может быть преобразо-
преобразовано к виду
и мы окончательно получаем
*-g3+ .... (Ю.35)
Отметим еще, что согласно A0.22), A0.26), A0.27) и A0.32)
величина D\(t) с точностью до слагаемых порядка (t — t0K
совпадает с (У1J; поэтому и
В неподвижной жидкости молекулярная диффузия Приводит
к тому, что сосредоточенная в точке единичная масса примеси
за время t — to расплывается в облако, описываемое сфериче-
сферически симметричным распределением концентрации с дисперсией
2%(t — to). Из равенства A0.36) видно, что при t — f0 настоль-
настолько малом, что вторым членом в правой части этого равен-
равенства можно пренебречь по сравнению с первым, среднюю дис-
дисперсию распределения примеси Ъ(Х, ^относительно ее центра
тяжести Xe(t) также можно принять равной 2%{t — to). Иначе
говоря, можно считать (во всяком случае, в той мере, в какой
это касается дисперсий), что на первом этапе турбулентной
диффузии от точечного источника расплывание примеси под
действием молекулярной диффузии накладывается на ее пере-
перенос соответствующей «жидкой частицей*», но не взаимодействует
с этим переносом. Однако при немного больших значениях
t — fo положение изменяется, поскольку начинает сказываться
и второе слагаемое в правой части A0.36). В результате дис-
дисперсия Dc (t) начинает возрастать бцстрее, чем при молеку-
молекулярной диффузии в неподвижной жидкости, причем добавочный

524 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.2
член здесь уже зависит и от коэффициента молекулярной диф-
диффузии жидкости х> и 01> среднего квадрата градиента скорости
в турбулентном движении. Таким образом, возникает взаимо^
действие молекулярной диффузии с турбулентной, приводящее к
«ускорению молекулярной диффузии», т. е. к более быстрому
расширению объема, занятого примесью, и соответственно этому
к более быстрому убыванию максимальной "концентрации. Ис-
Истинной причиной этого явления, очевидно, являются резкие де-
деформации занятого примесью объема в турбулентном потоке
(типа изображенных на рис. 80), существенно увеличивающие
роль молекулярной диффузии. Поэтому неудивительно, что
«ускорение молекулярной диффузии» начинает сказываться не
сразу, а лишь через некоторое время — после того как обычная
молекулярная диффузия превратит точечную массу примеси в
облако, объем которого достаточен для того, чтобы деформи-
деформироваться под влиянием иеоднородностей поля мгновенной ско-
скорости и {X, t).
Эффект «ускорения молекулярной диффузии под действием
турбулентности» был впервые отмечен Таунсендом A951).
В этой работе были даны предварительные оценки указанного
эффекта и приведены результаты специальных экспериментов
(по измерению постепенного падения максимальной темпера-
температуры «тепловых пятен», создаваемых импульсным разрядом
тока в турбулентном потоке), подтвердивших его существование
(и даже показавших, что формулы типа A0.36) неплохо соблю-
соблюдаются Для значительно больших значений t — U, чем можно
было бы заранее предполагать). Дальнейшие более полные
формулы для диффузии от мгновенного линейного источника
(содержащие, впрочем, некоторые ошибки в значениях число-
числовых коэффициентов; см. Сафмен (I960)) были получены Таун-
Таунсендом A954) и Бэтчелором и Таунсендом A956). Заметим, на-
наконец, что второе слагаемое в правой части формулы A0.35)
очень напоминает формулу (9.58) для дисперсии продольной
координаты «жидкой частицы» в однородном турбулентном по-
потоке с постоянным градиентом средней скорости. Это сходство
не случайно: при малых t — /„ вся примесь находится в малой
окрестности источника, в которой поле скорости и(Х, t) допу-
допустимо считать линейно зависящим от координат X (ограничив-
(ограничившись первыми членами соответствующего ряда Тэйлора), и
именно такому представлению поля скорости и соответствует
формула A0.35).
¦ До сих пор мы рассматривали только формулу для диспер-
дисперсии Dl(i) распределения ft(X, t) относительно своего центра
тяжести. Если же мы перейдем к результатам, касающимся дис-

10.2] S №. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 525
Персии Dl(t) облака примеси относительно положения источ-
ника (совпадающего со средним центром тяжести Xc(t)) и
дисперсии X2c(t) самого центра тяжести, то найдем, что здесь
взаимодействие молекулярной и турбулентной диффузии приво-
приводит к противоположному эффекту «замедления диффузии».
В самом деле, для подсчета величин Dl (t) и Х\ (/), согласно
A0.26) и A0.27), надо лишь определить среднее значение
Xi@, t)(Yi). Пользуясь формулами A0.33) и A0.32) для X, @, t)
и (^i), получаем
1
@,
или, поскольку в однородной турбулентности и1ки1= —
1
A0.37)
Отсюда и из A0.26), A0.27), A0.35) и A0.32) следует, что
1
A0.38)
X]{t) = Х\@, t)-х(Va,J(t-tof + ... . A0.39)
Эти формулы впервые были получены Сафменом A960). Вторая
из них показывает, что дисперсия центра тяжести распределе-
распределения примеси О (X, t) при малых t — t0 оказывается меньше дис-
дисперсии Xi@, t) координаты жидкой частицы (определяемой при
малых t — to почти исключительно разбросом начальной скоро-
скорости Vi{Q, to) — Ui@, t0) «жидкой частицы», т. е. близкой к
u\{t — *оJ)- Образно говоря, частица примеси вследствие моле-
молекулярной диффузии в среднем «отстает» от «жидкой частицы»,
с которой она вначале совпадала, т. е. «молекулярная диффу-
диффузия замедляет турбулентную диффузию». Легко понять, в чем
состоит механизм этого «замедления»: величина Х\ @, t) опре-
определяется дисперсией «средней скорости переноса жидкой ча-
частицы» j—r I иЛХ{?), t'\dt', а. молекулярная диффузия при-
водит к тому, что при ? > to полем скорости ui(X, f) перено-
переносится уже не точечная «жидкая частица», а целое облако при-
примеси; поэтому скоростью переноса здесь является скорость
Ui(X, t'), осредненная по некоторому объему, которая, как пра-
правило, меньше мгновенной скорости в точке X @, t'). В резуль-

526 гл. v. движение частиц в турбулентном потоке [10.2
тате того, что Х\{t) оказывается меньше, чем Х\@, t), полная
дисперсия Dl(t) оказывается все же меньше, чем сумма
Xi@, t)-\-2x{t — *о) вкладов от турбулентной и от молекуляр-
молекулярной диффузии по отдельности (без учета их взаимодействия).
«Замедление турбулентной диффузии под действием молеку-
молекулярной диффузии» можно описать также с помощью введен-
введенной Сафменом A962а) «корреляционной функции для примеси»
fi@)((—t0), определяемой как средний коэффициент корреляции
между значениями скорости жидкости в точках, занятых при-
примесью в моменты t > t0 и fa
(t -10) = {ut @, t0) иг [ Y+ X@, t), t\), A0.40)
где угловые скобки, как и выше, являются символом осредне-
осреднения по значениям У с весовой функцией 8 (К, t). Сафмен по-
показал, что дисперсия D\(t) может быть выражена через
B^( — t0) с помощью формулы
Dl (t) = 2X{t-10) + 2f(t-t0- x) B(»> (x) dx, A0.41)
и
которая аналогична формуле Тэйлора (9.31), имеющей вид
t
Х\ @, t) = 2f(t — t0 — x) № (х) dx. A0.42)
Кроме того, подобно тому как B(Li(t — ^0) можно представить
в виде
-t0) = ful@, to)ux(X, t)*/(X, t)dX, A0.43)
где ф(А", t) = b[X — X@, t)\ — решение «уравнения переноса»
Ж ^~ и" Ш~ = ® при начальном условии ty(X, to) = b(X), так
и В<-ь> (t — ^0), очевидно, можно записать в виде
-*o) = f «i @, to) «i (X, t) ^ (X, t) dX, A0.44)
где ^1(X, t)—решение уравнения диффузии ~^--\-иа lS~~
хф при том же начальном условии ф (X, U) = 6(Х). Эф-
Эффект «замедления турбулентной диффузии» в применении к
функции Б(д)(т) выражается в том, что если предполагать
B(L)(z) неотрицательным при всех х, то следует ожидать, что

10,2] S to. турбулентная диффузия 527
() < ^(^(т) при всех t > 0. Образно говоря, можно ска-
сказать, что вследствие молекулярной диффузии частица примеси
скорее «забывает» свою начальную скорость, чем «жидкая ча-
частица» (причиной этого, разумеется, является дополнительное
осреднение по У в A0.40)). Исходя отсюда, Хинце A959) пред-
предложил чисто качественно считать, что В<*>(т) =B(L>(x) -/(т), где
/(т) —монотонно убывающая функция (зависящая от парамет-
параметра х) такая, что /@) = 1. Следуя предложению Бюргерса, он
с/.
специально рассмотрел модель, в которой /(т)=е~а* (rRea—jj,
с — безразмерная постоянная, a L — характерный масштаб тур-
турбулентности). Это предложение, однако, не имеет каких-либо
теоретических оснований (кроме, может быть, частного случая
турбулентности при очень малом числе Пекле Ре = —-—-— ; ср.
Сафмен A962а)). При очень малых т ~ t — t0, при которых ре-
решение уравнения диффузии можно искать в виде ряда по степе-
степеням t и ограничиться лишь слагаемыми порядка не выше t, ис-
ходя из A0.44), можно показать, что функция В*?) (г) предста-
вима в виде
откуда сразу вытекает и равенство A0,38). Естественно ожи-
ожидать, что с возрастанием t — ta (т. е. с возрастанием объема,
занятого примесью) эффект «замедления турбулентной диф«
фузии» усиливается, т. е. что отношение [В1ьЦх) — В<*) (х)]/В<^ (т)
растет с ростом т. Предположив, что при т->оо это отношение
приближается к некоторой постоянной А, Сафмен A960, 1962а)
получил асимптотическую формулу
D$t) = X*@,t) + 2x(t-10)-AX\@, t), A0.45)
верную при больших t —10. Сафмен приводит также некоторые
соображения, согласно которым А ~ (Pr-Re)~! = (Ре), где
Re — число Рейнольдса турбулентности, составленное, напри-
например, из средней квадратичной пульсации скорости \и'$ ' и так
называемого тэйлоровского микромасштаба турбулентности
X = I «J2 / y^-J • Это предсказание оказалось в качествен-
качественном согласии с данными экспериментов Майкельсена A959),
измерившего распределение средней концентрации гелия и угле-
углекислого газа за точечным источником в турбулентном потоке за
решеткой в аэродинамической трубе. Однако ни аккуратного

528 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.2
количественного подтверждения гипотетической асимптотиче-
асимптотической формулы Сафмена A0.45), ни хотя бы качественного под-
подтверждения формулы A0.38), относящейся к малым значениям
t — *о, до сих пор получено не было.
' Чтобы понять причину этого последнего обстоятельства, сле-
следует приближенно оценить относительную роль молекулярной
и турбулентной диффузии и взаимодействия между ними в фор-
формировании поля осредненной концентрации ft(X,t). Для этого
надо сравнить порядок величины трех членов в правых частях
формул A0.38) и A0.45). При очень малых t — t0 следует поль-
пользоваться формулой A0.38), и в ее правой части наибольшим
слагаемым является второе (порядка t —t0), а наименьшим —
третье (порядка (t — *о)8). Однако с ростом t — t0 вклад тур-
турбулентной диффузии растет быстрее, чем вклад молекулярной
диффузии, и при значениях t — t0, превышающих некоторое зна-
значение ti, вклад турбулентной диффузии уже превосходит вели-
величину 2%(t —10)'. Считая, что ti мало по сравнению с лагранже-
вым масштабом времени 7\, определяющим характерное время
изменения скорости «жидкой частицы», можно при оценке tf
воспользоваться формулой A0.33) для А"? (О, t); в таком случае
получаем, что tj = 2yju2. В большинстве реальных турбулентных
потоков это значение xi ничтожно мало; например, в призем-
приземном слое воздуха и\ ~ 102 -*- 103 см2 • сект2, так что ti ~ 10~3 сек
при х ~ 10"' см. 'Сект2. При больших значениях t — f0, когда
величину Х\ @, t) можно оценивать с помощью асимптотической
формулы (9.35), отношение вклада молекулярной диффузии к
вкладу турбулентной диффузии имеет порядок -JL- —
Иначе это отношение еще можно оценить как имеющее поря-
порядок (Pr-Re2) (так как можно показать, что обычно Т{~№/\);
обе эти оценки показывают, что в реальных условиях рассма-
рассматриваемое отношение всегда чрезвычайно мало.
Далее, при достаточно малых t —10, при которых вклад в
дисперсию Do (t) слагаемого, связанного с взаимодействием мо-
молекулярной и турбулентной диффузии, еще можно считать про-
пропорциональным (t — *о)8, этот вклад будет много меньше вкла-
вклада молекулярной диффузии, если (t — t0J >C 6[v "iJ]- Но
в случае стационарной однородной турбулентности (Vu4J =
—- лагранжев микромасштаб времени. Таким образом, при

10.3] S 10. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 529
t — *о <? тх отношение вклада в дисперсию, вызываемого взаи-
взаимодействием молекулярных и турбулентных движений, к вкла-
вкладу молекулярной диффузии является малой величиной (по-
(порядка ¦( ~ ") ) • Наоборот, при t — W^>\ c помощью асимпто-
асимптотической формулы A0.45) можно установить, что указанное
отношение имеет порядок 2Л ~-~-'Ре'т , т. е. может и не
быть малым. При этом, однако, отношение вклада, вносимого
взаимодействием, к вкладу «чистой турбулентной диффузии»
имеет порядок А ~ (Ре), т. е. оно при больших Re (и Рг~1)
очень мало.
Подводя итоги, можно сказать, что молекулярная диффузия
вносит некоторые изменения в зависимость среднего диаметра
облака диффундирующей примеси от времени 't-—_U (и поэтому
еще более затрудняет использование функций X^ — X^t) для
определения лагранжевой корреляционной функции скорости
с помощью формул типа A0.11)). Однако относительное изме-
изменение самой величины D% (t), вызываемое этой диффузией, при
не слишком малом i — /0 и достаточно большом числе Рейнольд -
са обычно пренебрежимо мало. Поэтому можно думать, что в
реальных условиях при вычислении средней концентрации
ft(X, t) допустимо вовсе не принимать во внимание молекуляр-
молекулярную диффузию. Так мы и будем поступать в последующих
пунктах настоящего параграфа.
10.3. Полуэмпирическое уравнение турбулентной диффузии
Вернемся снова к- рассмотрению турбулентной диффузии
непрерывно распределенной примеси в пренебрежении молеку-
молекулярной диффузией. При этом средняя концентрация примеси
Ь(Х, t) в момент t связана с начальной концентрацией &о(Х)
соотношением A0.5). Отсюда видно, что если плотность вероят-
вероятности для координат жидкой частицы p(X\x,t) удовлетворяет
некоторому линейному уравнению по переменным X,t, то та-
кому же уравнению будет удовлетворять и функция Q(X,t).
Постараемся теперь понять, какой вид может иметь это послед-
последнее уравнение.
В пренебрежении молекулярной диффузией поле концентра-
концентрации примеси ib(X, t) удовлетворяет уравнению переноса

530 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.З
получающемуся из уравнения диффузии (ЮЛ) после прирав-
приравнивания нулю его правой части. Осреднив все члены этого ура-
внения, получим
п,» dSa c
где вектор 5= (Sj, S2, S3) имеет смысл плотности турбулент-
турбулентного потока диффундирующей примеси. Простейшая (и наибо-
наиболее ранняя) теория турбулентной диффузии, предложенная
Тэйлором A915) и Шмидтом A917, 1925) (но по существу вос-
восходящая еще к Буссинеску A897)), исходит из предположения,
что поток 5 пропорционален градиенту средней концентрации
примеси, т. е. что .
где К — это коэффициент /С» гл. 3 и 4 (в настоящей главе
мы все время будем иметь дело только с ним, и поэтому ин*
деке Ф нам будет удобно опустить). В более общем анизотроп-
анизотропном случае вместо предположения A0.47) принимается ?уще-
ствование линейной зависимости между векторами S, и -^-:
где тензор коэффициентов турбулентной диффузии /(*,-является,
вообще говоря, функцией от Хи t
Из полуэмпирической гипотезы A0.48) немедленно полу-
получается полуэмпирическое уравнение турбулентной диффузии
* + *»=***. (ю.49)
at дла дла ч> дл$ v '
В силу очень большой важности этого уравнения для дальней-
дальнейшего содержания настоящего параграфа целесообразно прежде
всего рассмотреть некоторые дополнительные соображения, от-
относящиеся к выводу этого уравнения и позволяющие лучше по-
понять область его приложимости. Начнем с простейшего случая
диффузии в поле стационарной Однородной турбулентности, все
статистические характеристики которой не меняются при изме-
изменении начала отсчета времени или сдвига начала системы про-
пространственных координат. В этом случае тензор вторых момен-
моментов смещений жидкой частицы за время % (т. е. величин
Oij (t) = У'1 (t) Y) (t)) определяется обобщенной формулой Тэй-
лора (9.30'),_а среднее значение смещений равно У*(т) = а*т,
где и=(щ, иг, щ)—постоянная (в силу стационарности иод-

10.3] 5 ю- турбулентная диффузия 531
нородности) средняя скорость течения. Кроме того, как мы
знаем из п. 9.3, в этом случае есть веские основания предпола-
предполагать, что совместное распределение вероятностей для величин
(Уь Уг, Уз) и при малых, и при больших (по сравнению с типич-
типичным лагранжевыМ масштабом времени Т) значениях % будет
весьма близким к гауссовскому распределению и, по-видимому,
не будет сильно отличаться от гауссовского при всех вообще
значениях т. Поэтому плотность вероятности р{Х\х, t) здесь
можно приближенно представить в виде трехмерной гауссов-
ской плотности вида D.23) со средними значениями щ =Х) +
+ Uj(t — ^о) и матрицей дисперсий Dn(%) (обратной матрице
коэффициентов g^ в выражений для плотности), определяемой
формулой (9.30') (в частности, при отсутствии средней скорости
и в предположении, что ^(т) = 0 при / Ф i, мы снова прихо-
приходим к формуле A0.12)). Но нетрудно проверить, что такая
функция p(X\x,t) является решением уравнения A0.49) с ко-
коэффициентами Кц вида
/
о
(см. Бэтчелор A9496)). Такому же уравнению будет в этом слу-
случае удовлетворять и средняя концентрация b(X,t); таким об-
образом, предположение о справедливости уравнения вида A0.49)
(но с коэффициентами Кц, определяемыми формулой A0.50),
т. е. зависящими от времени распространения примеси т =
= t — ^о) для диффузии в поле стационарной однородной турбу-
турбулентности точно эквивалентно предположению о том, что рас-
распределение вероятностей для вектора смещения жидкой части-
частицы при любом 1 будет нормальным (гауссовым). Если, однако,
в духе полуэмпирической гипотезы A0.48) желать, чтобы рас-
распределение средней концентрации йри всех t = t0 + % описыва-
описывалось уравнением вида A0.49) с одними и теми же коэффициен-
коэффициентами Kij, то, согласно A0.50), приходится ограничиться лишь
рассмотрением значений т, больших по сравнению с лагранже*
вым масштабом времени Т. При этом, в силу A0.50),
A0.51)
в полном соответствии с полуэмпирическим представлением о
том, что турбулентные коэффициенты обмена должны быть
равны произведению типичной скорости на типичный масштаб
длины (или, что то же самое, квадрата типичной скорости на
типичный масштаб времени).

532 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ • [Ю.З
Мы видим, что для диффузии в поле однородной стационар-
стационарной турбулентности полуэмпирическое уравнение A0.49) (с по-
постоянными коэффициентами диффузии Кг}) выполняется лишь
при t ^t0 + Т, но при таких t зато может быть обосновано
весьма убедительно (оно вытекает из нормальности распреде-
распределения вероятностей для K(t), очень правдоподобного в силу
центральной предельной теоремы; см. выше п. 9.3). Заметим,
однако, что 'В этом случае ценность уравнения A0.49) оказы-
оказывается довольно ограниченной, так как общее выражение для
>Ь (X, t) здесь может быть сразу выписано и независимо от это-
этого уравнения (например, исходя из равенств A0.5) и A0.12)).
Поэтому основная ценность полуэмпирической теории заклю-
заключается в возможности ее применения к более общему случаю
неоднородной (или нестационарной) турбулентности, к кото-
которому мы теперь и перейдем.
Покажем прежде всего, что и в общем случае уравнение
A0.49), строго говоря, может быть применимо, лишь если вре-
время диффузии t = t—t0 значительно превосходит типичный ла-
гранжев масштаб времени. Для этого посмотрим, в чем заклю-
заключается теоретико-вероятностный смысл этого уравнения. Урав-
Уравнение A0.49) является уравнением первого порядка по t;
следовательно, его решение однозначно определяется начальным
значением Ъ{Х ,tQ) — Ь0(Х) (краевые условия мы считаем за-
заранее фиксированными). Обозначим временно плотность веро-
вероятности p{X\x,t) символом р{Х, t\x ,t0) (чтобы подчеркнуть
ее зависимость от начального момента времени ^о); в таком слу-
случае соотношение (Ю.5) можно переписать в виде ®(Х, t)=
=jb(x, to)p(X, t\X, tQ)dx.Полагая здесь Q(X,t0) — 6(X—X),
получим * (Л', ^)=/>(A', /1 jc, /0) при любом t > t0. Используем этот
результат для момента времени U < t и затем решим снова
уравнение A0.49) для интервала времени от момента ti и до t
при начальном условии i>(X, ti) = p(X,tl\x,t0). Тогда получим
p(X,t\ х, t0) = $p{X,t\ Xv tY)p (Xlt ^ | x, t0) dXx, A0.52)
где *о < *i < t. Но такое уравнение для «плотности вероятности
перехода» p(X,4\x,t0) случайной функции X(t) будет спра-
справедливо, лишь если эта функция является марковской, т. е. та-
такой, что условное распределение вероятностей для значения
функции в момент t при условии, что известны ее значения в
произвольные моменты tn < tn-i < ... <to (где /0 < 0. будет
зависеть только от последнего из этих значений X (t0), но не
от значений X (U) с U < /„ (в теории марковских случайных

Ю.З] $ ю. турбулентная диффузия 533
процессов уравнение A0.52) часто называется уравнением
Смолуховскрго). В самом деле, для произвольной (не обяза-
обязательно марковской) случайной функции X(t) при to<h<t
будет иметь место очевидное соотношение
р(Х, t\x, to) = fp(X, t\Xv *,; х, to)p{Xu tx\x, to)dXv
где первый множитель под знаком интеграла есть условная
плотность вероятности для X (t) при условии, что значения
X(t1) = X1 и A(to)—xl фиксированы. Последняя формула
превращается в A0.52), только если указанная плотность ве-
вероятности не зависит от значения X (t0) — х, а это означает,
что случайная функция X (t) является марковской. Подчерк-
Подчеркнем еще раз, что наш вывод не использует явного вида уравне-
уравнения A0.49), а опирается лишь на то, что это уравнение — пер-
первого порядка по t.
Наоборот, есЛи случайная функция X(X,t) является мар-
марковской, то для плотности вероятности р(Х\х, t) — р(Х, t\x, t0)
(а потому, согласно A0.5), и для средней концентрации QiX, t))
при весьма общих условиях может быть получено дифферен-
дифференциальное уравнение вида A0.49)..Этот важный математический
факт был установлен Колмогоровым A931, 1933) (его частные
случаи еще раньше рассматривались физиками Эйнштейном,
Фоккером и Планком). А именно, Колмогоров доказал, что при
некоторых общих условиях «регулярности» (налагаемых на пе-
переходную вероятность p(X\x,t) и гарантирующих, что рассма-
рассматриваемая марковская случайная функция X (t) будет в опре-
определенном смысле непрерывной) существуют производные
A0.53)
г
2Ки(х, *0) = [Ак;(*, t)y'j(x,
(где, как обычно, У(х. t) = X(x, t) — x и Y'=Y— У), и
плотность вероятности p(X\x,t) удовлетворяет уравнению
Ж + Ж ФЖ*)Р\ = т?щ Кр (* ПР\. (Ю.54)
Это уравнение, очевидно, совпадает с A0.49), если положить
V= ui- Смысл последнего равенства заключается в том,
что величина Vit являющаяся, согласно первой формуле A0.53),
средней скоростью движения частицы примеси, в общем случае
равна сумме «скорости переноса» щ и дополнительной скорости

534 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [10.3
¦^Y~, связанной с тем, что в поле неоднородной турбулент-
турбулентности частицы примеси даже и в отсутствие осреднённого тече-
течения могут иметь тенденцию двигаться в определенном напра-
направлении. Подчеркнем, что здесь фигурирует лишь понятие сред-
средней, но не мгновенной скорости движения частицы; мгновенная
скорость в изложенной «марковской модели» не существует.
У(х t) I2
В самом деле, предел lim . __'. , который должен был бы
иметь смысл среднего квадрата мгновенной скорости движения,
частицы в момент А), в силу второго равенства A0.53) не мо-
может быть конечным при Kn(X,t0) Ф0 (так как средний ква-
квадрат длины пути, пройденного частицей за время от момента
U до ti = ^о + т. при т->0, согласно A0.53), имеет порядок т, а
не т2). Заметим, что вторая формула A0.53) дает статистиче-
статистическую интерпретацию «коэффициентов турбулентной диффузии»:
мы видим, что Kij отличается лишь множителем 7г от скорости
изменения тензора дисперсии смещения частицы (изученного
нами в п. 9.3).
Невозможность определения мгновенной скорости движения
-grX(x,t) означает, что случайная функция Х(Х, t) недиффе-
ренцируема. Таким образом, в полуэмпирической теории тур*
булентной диффузии функция Х(Х, t), описывающая движе-
движение фиксированной «жидкой частицы» в турбулентном потоке,
трактуется как нигде не дифференцируемая марковская функ-
функция. На самом деле траектории «жидких частиц» в турбулент-
турбулентном потоке, разумеется, не обладают такими свойствами. Так,
функция Х(х, t) при всех t дифференцируема по t (и, более
того, удовлетворяет лагранжевым уравнениям гидродинамики
(9.6) и (9.9), содержащим первые и вторые производные от
Х(х, t) no Xi и по t). Знание статистических свойств произ-
производной —ft = V(X, t) (т. е. лагранжевой скорости) важ-
важно для многих задач, использующих лагранжево описание тур-
турбулентного движения (см., например, формулу (9.27) для тен-
тензора дисперсии смещения жидкой частицы). С этим связано и
то, что дисперсии смещения «жидкой частицы» за очень малое
время t на самом деле пропорциональны не т, а т2 (см. фор-
формулу (9.28)). Наконец, функция Х(Х, t) не является также и
марковской случайной функцией- например, плотности вероят-
вероятности р(Х, t\x, t0) и p(X,t\x,Vo,to) для величины X (t) при
фиксированном значении^ X (t0) =x и соответственно фиксиро-
фиксированных значениях X (t0) =х и -дт-1 = Vo, которые для мар«

10.3] 5 i°. турбулентная диффузия 535
ковской функции должны совпадать, на самом деле, как легко
понять, будут различными (в частности, при малых .i = t—10
вторая из этих плотностей вероятности будет существенно от-
отлична от нуля лишь при Х^#-\- Vox, а первая не будет обла-
обладать таким свойством).
Если, однако, рассматривать функцию Х{х, t) лишь на
дискретном множестве моментов времени t = tn — t0 + m, где
шаг по времени t велик по сравнению с лагранжевым масшта-
бом времени Т, то практически можно считать, что случайная
последовательность Х(х, tn) является марковской. В самом де-
ле, приращения функции X(x,t) на непересекающихся интер-
валах времени длины х^>Т практически некоррелированы, и
естественно ожидать, что они будут также и почти независимы,
а случайная последовательность с независимыми приращения*
ми заведомо является марковской. Отметим, кроме того, что
дисперсии приращений функции Х(х, t) на интервалах вре-
времени длины i"^>T, согласно (9.35), пропорциональны %, как это
и должно быть при условиях A0.53). Таким образом, если бы
вместо дифференциального уравнения A0.49) мы рассмотрели
аналогичное разностное (по времени) уравнение, соответствую-
соответствующее марковской последовательности Х(х, tn), то оно уже близ-
близко соответствовало бы реальным свойствам движения «жидких
частиц» в турбулентном потоке. Следовательно, можно ожи-
ожидать, что полуэмпирическое уравнение турбулентной диффузии
A0.49) все же имеет определенный смысл, но лишь как диф-
дифференциальный аналог некоторого разностного по времени ура-
уравнения с шагом z"^>T. Но отсюда вытекает, что уравнение
A0.49) можно использовать для описания поля ft(X,t) в фик-
фиксированный момент времени f, где t — to^>T. Иначе говоря,
формулы для распределения примеси #(Х, t) или тех или иных
характеристик этого распределения, получаемые при решении
уравнения A0.49), можно рассматривать как асимптотические
формулы, справедливые при t — to~^>T. В практических зада-
задачах, связанных, например, с диффузией примесей в атмосфере,
как правило, представляет интерес именно описание диффузии
в масштабах, значительно превышающих лагранжев масштаб
времени Т (который в приземном слое воздуха обычно имеет
значения порядка секунд); поэтому в этих задачах обычно мож-
можно пользоваться полуэмпирическим уравнением турбулентной
диффузии. Заметим, впрочем, что даже при больших значениях
t — to полуэмпирическое уравнение может приводить все же к
неверным результатам на очень больших расстояниях от ис-
источников примеси в связи с тем, что эта теория фактически

536 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.З
предполагает, что скорость распространения примеси может
быть бесконечно большой (см. ниже п. 10.6).
В дальнейшем чаще всего нам придется иметь дело со слу-
случаем стационарного и однородного в плоскостях Х3 = Z = const
турбулентного движения со средней скоростью п = U, всюду на-
направленной вдоль оси OXt = ОХ. В этом случае коэффициенты
Kij (как и все другие статистические характеристики турбулент-
турбулентности) могут зависеть только от координаты Z. Кроме того,
здесь естественно считать, что координатные оси ОХХ = ОХ,
0л2 = OY и ОХ3 = OZ совпадают с главными направлениями
тензора Кц (так как именно направления указанных осей здесь
являются выделенными направлениями). Полуэмпирическое
уравнение турбулентной диффузии A0.49) в.этом случае обра-
обращается в уравнение
A0.55)
Заметим, что если необходимо учесть гравитационное оседание
диффундирующих частиц (происходящее с постоянной скоро-
скоростью ш), то к левой части уравнения A0.55) следует добавить
слагаемое —WJZ'' Точно так же возможность распада при-
/ - 1п2\
меси [с периодом полураспада -^-1 приводит к появлению в
левой части добавочного слагаемого а*. Если область течения
по какому-то направлению простирается до бесконечности, то
соответствующим краевым условием обычно будет условие до-
достаточно быстрого убывания p(X,t) при неограниченном уда-
удалении точки X от местоположения всех источников примеси.
Краевые условия на твердых стенках следует подбирать, исходя
из анализа физических процессов, происходящих на этих стен-
стенках, но обязательно так, чтобы получающееся решение соответ-
соответствовало марковской случайной функции X (х, t) (перечисле-
(перечислению всех таких условий как раз и посвящены работы Феллера
и Вентцеля, упоминавшиеся на стр. 508). В соответствии со
сказанным на стр. 507—508 достаточно общим краевым усло-
условием на твердой стенке Z = 0, описывающим практически все
встречающиеся ситуации, является условие вида
K22^- + wb = № при Z = 0, A0.56)
где р — постоянная размерности скорости (для общности мы
даже допускаем здесь наличие гравитационного оседания со
скоростью ш, приводящего к добавлению к вертикальному тур-

10.4] § ю. турбулентная диффузия 537
булентяому потоку примеси — Кгг -^ потока ^— w&. Случай
р = 0 соответствует «отражению» примеси от стенки, случай
р = оо — «поглощению» примеси, а случай 0< р < оо — проме-
промежуточной ситуации частичного отражения и частичного погло-
поглощения (более подробное обсуждение условия A0.56) см. в ра-
работах Монина A956а, 19596) и Колдера A961)).
10.4. Диффузия в поле одиородиой турбулеитиости и в поле
простейших течений с градиентом скорости
Распространение примеси от источников в случае
однородной турбулентности
Вернемся к простейшему случаю диффузии в идеализиро-
идеализированной модели однородной и стационарной турбулентности
с постоянной средней скоростью п = U (которую, как
обычно, мы будем предполагать направленной вдоль оси
OXi = ОХ). Направим оси координат OXt = ОХ, ОХ2 =
= OY и ОХ3 = OZ по главцым осям тензора дисперсии Оц{х) =
= Y\ (x) Y'j (x) (считая ось OXi одной из главных осей) и пре-
пренебрежем молекулярной диффузией по сравнению с турбулент-
турбулентной. Воспользовавшись еще тем, что согласно эмпирическим
данным плотность вероятности р(Х\х, t) в случае однородной
турбулентности при всех % = t—t0 близка к плотности много-
многомерного нормального распределения (причем при больших зна-
значениях х это обстоятельство имеет и определенное теоретическое
оправдание), мы можем для поля осредневной концентрации
b{X,t), отвечающей начальному значению Ь{Х, to) =
написать формулу
При этом для решения любых вопросов, относящихся к осред-
ненной концентрации &(Х, t), надо только знать дисперсии
Ас*(т), Dvv(x) и DzZ(x) компонент смещения жидкой частицы за
время т, которые выражаются по формуле (9.31) через соответ^
ствующие лагранжевы корреляционные функции Вхх(х), В'уу(х)
и fiit'Os). В частности, при t~to = v^> T = max(Tx, Ту, Т2),
(где Тх, Tv и Tz — три лагранжевых масштаба времени) можно

538 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю,4
¦принять, что_О,,(х) =
и йгг (х) = 2w'2Tzi = 1Кгг% при этом правая часть A0.57) будет
совпадать с решением уравнения
~ дЧ
(являющегося частным случаем уравнения A0.55)) при началь-
начальном условии ЩХТТо) =#о{Х). Если\ &0(Х) = Q&(X) =
<= Q6(^N(y)8(Z) (случай мгновенного точечного источника в
точке Х=Ь), то распределение A0.57) будет описыватьэллипсо-
идообразное облако примеси, концентрация которой убывает при
удалении от центра по закону Гаусса. Центр этого облака на-
находится в точке (i/t, 0,0) (т. е. перемещается со средней ско-
скоростью течения), а максимальная концентрация (в центре)
пропорциональна [Dxx{x)Dyy{x)Dzz(x)Yls (т. е., например, при
\
^ Т убывает с ростом t пропорционально х 2). Если o(O
= Q6(XN(Z) (случай мгновенного линейного источника вдоль
15си OY), то облако примеси при любом t будет иметь форму
Цилиндра эллиптического сечения с осью на прямой X *» i/t,
Z = 0. В этом случае максимальная концентрация пропорцио-
пропорциональна {Dxx(x)Dzz(x)Ylls т. е. при больших значениях t убывает
пропорционально т1. В случае непрерывно действующего точеч-
точечного источника в точке X = 0 постоянной производительности Q
следует пользоваться формулами A0.6') и A0.12), причем при
X^>UT мы можем в последней из них без большой ошибки
заменить Z)«(t) на 2Kui. После этого интеграл по t в A0.6')
легко берется в явном виде, и в результате получается формула
{^{Ц^^ ^У}} (,0.59,
Формула A0.59) описывает струю примеси, имеющую форму
эллиптического параболоида, вытянутого вдоль оси ОХ. При
У2 + Z2 эта формула может быть преобразована к виду
Показывающему, что на большом расстоянии от источника при
фиксированных Y и 1 концентрация примеси убывает пример-
примерно пропорционально Х~1, а при фиксированном X и возраста*
нии расстояния от оси струи вблизи оси она убывает экспонен*

10.4] S Ю. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 539
циально. Точно так же в случае стационарного линейного ис-
источника на оси OY производительности Q (на единицу длины)
формулы A0.8) и A0.12) при X^>UT (т. е, тогда, когда мож-
можно принять, что Dxx=*2Kxx*> Dzz=2KZz*) приводят к соотно-
соотношению
где /Со(г) —функция Макдональда (модифицированная функ-
функция Бесселя второго рода). В частном случае, когда UX~^>KXx
и Z •< X, решение A0.61) можно упростить, представив его в
виде
Отсюда видно, что в случае стационарного линейного источника
концентрация примеси в поле однородной турбулентности с по-
постоянной средней скоростью убывает при X-voo (и фиксиро-
фиксированном Z) примерно пропорционально Х-Ч>.
Продольное рассеяние примеси в прямой трубе или канале
Перейдем теперь к значительно более сложной, за даче о тур-
турбулентной диффузии в потоке с градиентом скорости. Интерес-
Интересные результаты здесь удается получить лишь для отдельных
частных классов течений. Начнем с практически важного слу-
случая продольной диффузии примеси в прямой длинной трубе.
(или прямом канале). Важность этого случая диффузии свя-
связана, в первую очередь, с тем, что измерение скорости продоль-
продольного распространения примеси в трубе часто оказывается наи-
наиболее доступным методом измерения средней скорости течения
(и для турбулентных течений, и даже для ламинарных). По
этой причине продольное рассеяние уже сравнительно давно
привлекло внимание экспериментаторов (см., например, иссле-
исследования рассеяния при ламинарном течении в кровеносных со-
сосудах и в стеклянных капиллярах, перечисленные в статье Тэй-
лора A953), и работу Аллена и Е. Тэйлора A923) о рассеянии
при турбулентном течении в трубе). Эксперименты, описанные
в перечисленных работах, состояли в том, что в какой-то мо-
момент времени to в трубу в некоторой точке вводилась опреде-
определенная масса примеси (т. е. имитировался мгновенный точеч-
точечный источник). Затем на некотором расстоянии X от этой точки
вниз по течению измерялось изменение во времени средней (по
сечению трубы) концентрации примеси &m{t). Естественно, что

540 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.4
в течение некоторого времени после введения примеси в трубу
ее концентрация в точке X будет равна нулю. Пусть to = to-\-
+ т0— момент, в который в точке X впервые обнаруживается
примесь; тогда величина итдх = Х/х0, очевидно, будет равна
максимальной скорости течения в трубе (т. е. в случае
осесимметричных труб — скорости течения на оси трубы).
Средняя же скорость течения иср может быть определена по
формуле ыСр = X/xi, где to + xi = U — время, соответствующее
некоторой характерной точке функции Фт@-
Согласно экспериментальным данным (полученным в пря-
прямых круглых трубах) продольное рассеяние примесей в трубах
обладает следующими примечательными особенностями: A) кри-
кривые Qm(t), соответствующие достаточно большим (по сравне-
сравнению с радиусом трубы Я) расстояниям X, оказываются при-
приблизительно симметричными относительно своих максимумов,
хотя распределение скорости течения по сечению трубы мж(г)
(где г — радиальная координата) не симметрично относительно
средней скорости иср; B) если время ti=?to-\ соответствует
"ср
максимуму кривой &m(t), то иср совпадает со средней скоростью
UCp, определяемой как отношение объема жидкости, вытекаю-
вытекающего из трубы за единицу времени, к площади ее поперечного
сечения (иначе говоря, центр тяжести продольного распределе-
распределения концентрации перемещается вниз по течению со скоростью,
равной именно этой средней скорости UCp); C) ширина кривой
Фт@> определяемая как квадратный корень из отношенияод =
т
оо I оо
= f {t — toJbm(i)dtl jbm{t)dt, увеличивается при возрастании
/. It,
расстояния X (или, что эквивалентно, времени xi => X/UCp) про-
пропорционально X1!* (или т'М т. е. дисперсия о8 имеет вид о8 =
^ mm
= 2Kiiu где Ki — некоторая постоянная; D) величина K = KiUlp,
которая, очевидно, играет роль «эффективного коэффициента
продольной диффузии», имеет значение, во много раз превосхо-
превосходящее значение коэффициента радиальной (турбулентной или
молекулярной) диффузии примеси. Особенно любопытна осо-
особенность B), которая показывает, что определение максимума
кривой Qm(t) дает возможность измерить именно ту среднюю
скорость Оср, которая наиболее интересна для большинства ги-
гидротехнических приложений, и особенность C), согласно кото-
которой длина участка трубы (симметричного относительно точки
X— UcpXi), содержащего, скажем, 90% (или 95%, или 99%)
диффундирующей примеси, растет оо временем как i1/», так что

Ю.4] $ Ю. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 541
ее отношение к среднему расстоянию X = f/Cpti этого участка
от источника примеси непрерывно уменьшается. Заметим еще,
что так как участок, заполненный примесью, движется со сред-
средней скоростью UCp, то жидкость вниз по течению от этого участ-
участка, находящаяся у оси трубы (и следовательно, движущаяся со
скоростью, превышающей Ucv), с течением времени догоняет,
а затем и перегоняет этот участок.
Особенности продольного рассеяния примесей в трубах были
теоретически проанализированы (и проверены эксперименталь-
экспериментально) в работах Тэйлора A953, 1954а,б), первая и третья из ко-
которых посвящены ламинарным, а вторая — турбулентным тече-
течениям. Опубликование этих работ обострило интерес к рассма-
рассматриваемому явлению и способствовало выполнению ряда новых
теоретических и экспериментальных исследований (Бэтчелора,
Бинни и Филлипса A955), Ариса A956), Элдера A959), Элли-
сона (I960), Сафмена A9626), Филипа A963) и др.), уточнив-
уточнивших в некоторых деталях результаты Тэйлора и расширивших
область их применимости. При этом, в частности, выяснилось,
что перечисленные выше основные свойства A) — D) продоль-
продольного распространения примеси могут быть просто объяснены,
исходя из общих соображений о движении жидких частиц в пря-
прямых трубах и каналах. А именно, как отмечалось в конце п. 9.3,
продольное перемещение жидкой частицы в прямой трубе (или
прямом канале) при не слишком малом времени движения т =
= t — to подчиняется тем же закономерностям, которые спра-
справедливы в случае однородной турбулентности в потоке жидко-
жидкости с постоянной средней скоростью ы = UCp. Следовательно,
среднее значение продольной координаты X(t0 + т) жидкой ча-
частицы, находившейся в момент t0 в точке X = 0, при большом т
будет весьма точно определяться соотношением X(t0 + т) ^
ж Е/срт, а дисперсия координаты X(t0 + т) будет иметь вид
(X — XJ «* 2/Ст, где_/( = const (в п. 9.3 эту постоянную мы за-
записывали в виде af 7\). Что же касается плотности вероятности
Pi(X\i) для значений X(t0 + т), то центральная предельная тео-
теорема теории вероятностей дает веские основания предполагать,
что при больших т эта плотность вероятности будет близка
к плотности нормального распределения вероятностей. От-
Отсюда вытекает, что продольное распределение облака примеси
от мгновенного точечного источника через большое время т бу-
будет иметь колоколообразную «гауссовскую» форму со средним
значением ?/срт и дисперсией 2/(т. Если фиксировано не ц =
= t —10, a X а х(Х) — время прохождения жидкой частицей
фиксированного участка трубы длины X, то т(Л) = -г? , где

842 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ []0.4
V ,„ — средняя лагранжева скорость частицы за время от to
до to + *W- Поскольку при возрастании X пульсации времени
прохождения i(X) становятся относительно все' менее сущест-
существенными, а т(А') приближается к ЛУ?/Ср,.при достаточно боль-
большом X распределение вероятностей средней за время i(X)
лагранжевой скорости будет с высокой степенью точности со-
совпадать с распределением вероятностей средней за время
лагранжевой скорости Vx/u =XltQ-\-jj—J ¦ —^-- Но
ХМ0-\--ц—) = Х, т.е. xU0-\--^j— \ = X-{- X'; следовательно,
при достаточно большом X
-j^-\ (среднее значение кото-
которого имеет порядок \/Х) и последующими слагаемыми еще бо-
более высокого порядка малости, найдем, что при больших зна-
значениях X
¦К*)«7Г -F-' О0'64)
и ср u ср
где X'—нормально распределенная случайная величина с ну-
нулевым средним. значением и дисперсией 2К-гг—- При этом
^ср
и сама величина i(X) будет иметь нормальное распределение
вероятностей, но со средним значением х = -^— и дисперсией
2K\i, где К\=—— > что вполне соответствует эмпирически уста-
новленным свойствам A) — C) продольного рассеяния примеси.
Указанное выше свойство D) также имеет простое объяснение,
так как в данном случае продольная дисперсия облака примеси
вызывается в первую очередь влиянием поперечного градиента
средней скорости, т. е. порождается разностями скоростей
п(г) — ?/ср, заметно превосходящими как турбулентные пуль-
пульсации продольной скорости и'=и(г) — п(г), приводящие к тур-
турбулентной диффузии, так и тем более молекулярные флюктуа-
флюктуации, вызывающие молекулярную диффузию.
Если, однако, мы захотим оценить численные значения ко-
коэффициентов К и Ki, то приведенные соображения, опираю-
опирающиеся на лагранжево описание течения жидкости, помогут нам
мало. В самом деле, коэффициент К выражается через лагран-

10.4] § lo- турбулентная диффузия 543
жев масштаб времени Ti\ однако этот масштаб определяется
по лагранжевой корреляционной функции скорости, и его очень
трудно связать с непосредственно измеряемыми эйлеровыми
статистическими характеристиками (так что обычно он сам оце-
оценивается только по данным диффузионных экспериментов).
Оказывается, однако, что в рассматриваемом случае продоль-
продольного рассеяния примесей в трубе или канале значение К мож-
можно довольно точно оценить, воспользовавшись полуэмпириче-
ским уравнением турбулентной диффузии для эйлерова поля
концентрации Ф(А\ t)—именно этот путь исследования и был
применен в глубоких работах Тэйлора. Поскольку наша задача
состоит в изучении асимптотических закономерностей при боль-
большом т (или X), следует ожидать, что полуэмпирическое уравне-
уравнение здесь окажется достаточно точным, причем в данном случае
его использование имеет еще и то преимущество, что при этом
одна и та же теория может быть применена к рассеянию и в тур^
булентных, и в ламинарных течениях (в последнем случае при*
ближенное полуэмпирическое уравнение заменяется точным
уравнением молекулярной диффузии A0.1)). Следуя Тэйлору
A953, 1954а), предположим, что средняя концентрация Ф не за-
зависит от угловой переменной ф, и поэтому запишем уравнение
диффузии A0.55) (или в ламинарном случае уравнение A0.1))
для диффузии в прямой круглой трубе в виде
-Ж + МО ох = К** -Ш + 7 IF rKrr (r) sf • A0-65)
Далее нам будет удобно перейти к системе отсчета, движу*
щейся со средней скоростью течения жидкости, т. е. заменить
продольную координату X на координату х = Х — Ucv(t — to);
кроме того, вместо г мы введем безразмерную радиальную пе-
переменную z — ^щ, где # —радиус трубы. Ориентируясь на ука*
занную выше особенность D) продольного рассеяния примесей
в трубах, установленную по экспериментальным данным, мы
сразу же пренебрежем в уравнении A0.65) слагаемым
описываю1Цим продольную диффузию примеси (учет
этого слагаемого почти не изменит рассуждений и приведет
лишь к небольшой поправке в окончательном результате, кото*
рая будет указана ниже). Тогда уравнение A0.65) в перемен*
ных х, 2, t примет вид
§ Лг)-иср]§ = -^±?гКгг(г)?. (Ю.66)

544 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ 6 ТУРБУЛЕНТНОМ ПОТОКЕ [10.4
Мы будем использовать это уравнение для описания распреде-
распределения концентрации О(*,z, t), соответствующего наличию б мо-
момент t = to в точке х = z — 0 мгновенного точечного источника
примеси. Предварительно сравним интервалы времени тй и t<j, в
течение которых концентрация примеси в фиксированной точке
трубы может существенно измениться вследствие одного только
переноса примеси осредненным течением (конвекции) и одной
только поперечной диффузии. Можно положить i.=ab , где
°» @ — стандартное отклонение распределения концентрации
примеси От, осредненной по сечению трубы. С другой стороны,
та есть время, в течение которого поперечная диффузия приво-
приводит к выравниванию неоднородностей распределения концен-
трации по сечению трубы, и можно положить v—т? где /Со —
некоторое типичное значение коэффициента поперечной диф-
диффузий. Ясно, что значениео9 , а потому и т*, растет со време-
временем распространения примеси т (согласно приведенным выше
теоретическим соображениям и экспериментальным данным —
асимптотически пропорционально <c1/j). тогда как ы не меняется
со временем. Поэтому при достаточно большом т (т. е. х) будет
выполняться неравенство Tft^>Td, т. е.
\.»тЕ" <10-67>
Ограничимся рассмотрением лишь таких больших т, при ко-
которых уже выполняется неравенство A0.67), и вычислим значе-
значение Qi полного потока примеси через сечение трубы х — const
(напоминаем, что х = X — ?/срт, так что сечение х — const дви-
движется вдоль трубы со скоростью Ucp). Очевидно,
1
Qi = f f [ux(r)-rUc0dS = 2«R> f [lix(z)-Ucp]bzdz, A0.68)
5 0
где S — сечение трубы; отсюда видно, что Qi может быть от-
отлично от нуля лишь при наличии радиальных неоднородностей
поля концентрации О. При условии A0.67) такие .радиальные
неоднородности весьма быстро выравниваются; поэтому доста-
достаточно длительно могут существовать лишь очень слабые неодно-
неоднородности, постоянно создаваемые неоднородным конвективным
переносом примеси и «приспосабливающиеся» к этому переносу
в том смысле, что для них эффекты конвекции и поперечной
диффузии балансируются, Такие неоднородности удовлетворяют

10.4) § 10. ТУРБУЛЕНТНАЯ ДИФФУЗИЙ 545
уравнению
&%-р± ?**"&)? (Ю.69)
(здесь в левой части мы заменили -g— на -^- вследствие ма-
малости радиальных неоднородностей О — От). Из A0.69) полу-
получаем
г г1
»(*) = » @) + R2^] jrf~yy I ¦ [и, (zT) - Ucp] z" dz";
после этого формула A0.68) легко приводится к виду
где
A0.70)
Подставляя полученное выражение для Qi в уравнение
"K^2~5T~ir~Fx ~®' выРажающее закон сохранения количества
примеси (это уравнение может быть выведено, например, инте-
интегрированием всех членов уравнения диффузии A0.66) по сече-
нию трубы), получим -^р = a -gjp-. Отсюда видно, что про-
продольное рассеяние примеси относительно плоскости, движу-
движущейся вдоль трубы со скоростью UCp, происходит совершенно
аналогично молекулярной диффузии (т. е., в частности, также
приводит к гауссовскому распределению концентрации по на-
направлению О*), но с коэффициентом диффузии К, опреде-
определяемым формулой A0.70). Следовательно, пространственная
дисперсия продольного распределения примеси будет равна
2K(t — t0) и, значит, <&m = 2Kix, где Ki = K/U2cp, % = f — to.
Учитывая, кроме того, что, согласно A0.70), К есть величина
U2 R2
порядка —р—. мы можем привести условие A0.67), при кото-
ром были справедливы наши рассуждения, к виду

546 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.4
Нам остается лишь вычислить значения коэффициента К
для ламинарных и для турбулентных течений. В первом случае
в формуле A0.70) для К в соответствии с формулой A.23) еле-
дует положить пх(г) = 2?/срA —z2) и принять Ктт = Х> гДе X—
коэффициент молекулярной диффузии рассматриваемой при-
примеси. Тогда формула A0.70) для К легко приводится к виду
A0-72)
— ?» 1-у 1 . За исключением чрезвычайно медлен-
так что .. >¦' х
ных течении в особо тонких капиллярах, число у значи-
значительно превосходит единицу, так что /СЭ>х- Нетрудно видеть,
что при учете также и молекулярной диффузии, т. е. при сохра-
нении слагаемого х $хт в уравнении A0.65), мы вместо A0.72)
R2U2
получили бы формулу К== xgCp Ч~Х' обычно почти не отли-
отличающуюся от A0.72).
Ясно, что если бы скорость и (г) была постоянной, то про-
продольная диффузия определялась бы лишь значением коэф-
коэффициента х> таким образом, наличие поперечного градиента
скорости приводит к резкому увеличению продольной дисперсии
примеси. Любопытно отметить, что поперечная диффузия, на-
наоборот, задерживает продольное рассеяние примеси: согласно
A0.72), с увеличением % значение К уменьшается. Если бы по-
поперечной диффузии не было, то, как нетрудно убедиться с по-
помощью уравнения переноса, распределение примеси, вначале
сосредоточенное на участке трубы очець малой длины 6Х (и
равномерное по сечению трубы), за время т превратилось бы в
равномерное распределение, при котором Ьт(Х) = const на уча-
участке длиной 0тахх и $т(Х) = 0 вне этого участка. При наличии
же поперечной диффузии оно, как мы видели, превращается в
гауссовское распределение, в котором почти вся примесь сосре-
сосредоточена на участке трубы длины L ~ ]/7С*> при достаточно
большом т весьма малой по сравнению с t/max т.
Поскольку значение К нетрудно определить эксперименталь-
экспериментально с помощью измерений концентрации Qm(t) или От(Х), то ис-
использование формулы A0.72) открывает возможность получе-
получения по данным таких экспериментов значений коэффициента
молекулярной диффузии %• Этот метод измерения величины %
был проверен Тэйлором A953), экспериментально исследовав-
исследовавшим диффузию марганцевокислого калия в стеклянных капил-

10.4] S Ю- ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 547
лярах и получившим исходя отсюда значение коэффициента мо-
молекулярной диффузии этого вещества, хорошо согласующееся
с данными других измерений. Специально обсуждению такого
метода измерения % посвящена также статья Тэйлора A9546).
В случае турбулентного течения при достаточно большом
числе Рейнольдса (таком, что толщина вязкого подслоя состав-
составляет пренебрежимо малую долю радиуса R) осредненную ско-
скорость пх(г) можно задать с помощью «закона дефекта скоро-
скорости» E.41):
»г@)-»х(г) _ f (, _±_
где и* — «динамическая скорость», определяемая по напряжению
трения на стенке трубы. Учитывая, что турбулентное напряжение
трения в круглой трубе имеет вид т = ри2-р (см. E.17х)), и при-
приняв гипотезу о том, что турбулентный коэффициент диффузии
точно совпадает с турбулентным коэффициентом вязкости (т. е.
воспользовавшись аналогией Рейнольдса, по терминологии'
п. 5.7), можно представить радиальный коэффициент диффузии
в виде
ди.
Используя значения функции fi(r\), полученные с помощью об-
обработки данных измерений Никурадзе и других исследователей,
Тэйлор A954а) получил по формуле A0.70) значение К =
= 10,06 Ru* (так что с« 10 в формуле (9.39) на стр. 478).
К этому значению К нетрудно ввести поправку за счет продоль-
продольной турбулентной диффузии, вычислив соответствующий поток
примеси через сечение трубы
" W-S-dS = ~ %
S 0
Для грубой оценки можно принять простое предположение, что
Kxx(r) = Krr(r); тогда Q[ = — itf^K'-g^f • гДе для К' численное
интегрирование дает значение К' = 0,052 Ru*. Величина К'
очень мала по сравнению с К, но поскольку для KIRu* все рав-
равно удается получить лишь приближенное численное значение,
целесообразно все же добавить К' к полученному выше значе-
значению К, т. е. принять формулу
К= Ю,1Я«, A0.74)

548 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ Б ТУРБУЛЕНТНОМ ПОТОКЕ [10.4
(неточность гипотезы, использованной при вычислении К', здесь
вряд ли может иметь какое-нибудь значение в силу относитель-
относительной малости всего слагаемого К).
Результат A0.74) оказывается хорошо согласующимся с эм-
эмпирическими данными о продольном распространении примеси
в достаточно длинных прямых круглых трубах. Так, например,
опытные данные Аллена и Е. Тэйлора A923), касающиеся диф-
диффузии соли в потоке воды б прямых круглых (но не очень длин-
длинных) трубах, приводят к значению K/Ru* = 10,6 для одной се-
серии экспериментов и K/Ru* =11,7 для другой (см. Тэйлор
A954а)). В аналогичных
опытах самого Тэйлора
(проводившихся при уча-
участии Эллисона), в которых
использовалась значительно
более длинная гладкая тру-
труба, при условиях, наиболее
точно соответствующих опи-
описанной выше теории, было
получено значение KIRu* =
= 10,0; при использовании
же трубы с сильно шеро*
ховатыми стенками оказа-
лось- что KlRu* = 10-5- За-
Зависимость концентрации Фт
Рис. 81. Зависимость концентрации соли от времени t во всех пере-
в фиксированном сечении прямой трубы численных опытах на до-
от времени по данным Тэйлора A9Ма). статочно большом расстоя-
расстоянии от источника примеси
близко соответствовала гауссовской кривой (см., например,
рис. 81, воспроизводящий данные одного из опытов Тэйлора).
В случае же изогнутых труб или, например, промышленных
нефтепроводов, никогда не бывающих идеально прямыми, зна-
значения K/Ru*, естественно, оказываются уже заметно отличаю-
отличающимися от приведенного выше теоретического значения для
прямых труб; в ряде случаев здесь KlRu* принимает значения,
близкие к 20 (Тэйлор A954а)).
Совершенно аналогично может быть рассмотрена и задача
о продольном распространении примеси в широком прямом ка-
канале, ограниченном стенкам-и Z = 0 и Z=H (роль верхней стенки
может играть также свободная поверхность жидкости). Эта за-
задача рассматривалась в работах Элдера A959), Эллисона
A960) и Сафмена A9626). В первых двух указанных работах
был применен изложенный выше метод Тэйлора, а в третьей —
изящный метод Ариса A956), при котором из полуэмпириче-

10.4] § Ю- ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 549
ского уравнения диффузии A0.55) (или уравнения молекуляр-
молекулярной диффузии A0.1)) прежде всего выводятся уравнения для
моментов
со со
bnm(Z, f)= f f Ь(Х, У, Zj)XnYmdXdY. A0.75)
—оо —со
Нетрудно видеть, что, например, в случаях, когда m=0, a n рав-
равно 0, 1 или 2 и используется уравнение A0.55), эти уравне-
уравнения будут иметь вид
1Н' A0-76>
(^#) 2^(Z)e + 2«(Z)V 00.76")
аналогично выглядят и уравнения для моментов 8оь 9ц. See и мо-
моментов высших порядков. Полученные уравнения можно решать
последовательно при начальных и граничных условиях, следую-
щих из начальных и граничных условий для концентрации
О(Л\ t). В таком случае асимптотическое поведение получен-
полученных решений будет описывать среднее распределение примеси
при больших, значениях t в плоскости Z—const (т. е. в тонком
слое, окружающем высоту Z) с точностью до моментов того по-
порядка, на котором была оборвана система уравнений для ве-
величин A0.75). Аналогично этому асимптотическое поведение
н
величин &nm(t) = Г 9„т (Z> t) dZ будет с той же степенью точ-
о
ности описывать среднее распределение примеси во всем трех-
трехмерном объеме, занятом жидкостью. Окончательные результаты,
получаемые на этом пути, разумеется, оказываются такими же,
как и при применении метода Тэйлора. Согласно этим результа-
результатам, если примесь была внесена в поток в момент /=^о в точке
@, 0, Z), где 0<Z<^, и она не поглощается стенками, то
центр тяжести соответствующего облака примеси в момент
/ асимптотически (при больших значениях т) будет иметь
и
^x, 0,-j), где ?/ср = -^ / u(Z)dZ, т. е. будет
о
горизонтально перемещаться вдоль оси ОХ со скоростью Ь'ср
По вертикали примесь будет распределена асимптотически рав-
равномерно (в том смысле, что любой слой жидкости фиксирован-
и
координаты [U 0) ?/

550 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.4
ной толщины AZ при большом т будет содержать одно и то же
количество примеси), причем центр тяжести примеси в каждом
слое также будет перемещаться с асимптотически постоянной
скоростью Ucp (но для разных слоев координаты центра тяже-
тяжести примеси будут при больших т различаться на постоянную
величину, зависящую от соответствующих значений Z и формы
профилей u(Z) и Kzz(Z))- Распределение примеси в плоскостях
X = const в момент t0 + х будет при большом т близко к распре-
распределению Гаусса с нулевым средним значением и дисперсией
я
в» =2#,т+const, Ку = (Куу\ =jj f Kyy(Z)dZ. A0.77)
Распределение же примеси в плоскостях У = const будет близко
к распределению Гаусса со средним значением Х~?/срт и дис-
дисперсией
где
J (Ю.79)
p=^f Kxx(Z)dZ
о
(ср. A0.70)). Дисперсия распределения примеси по направле-
направлению ОХ в тонком слое вблизи фиксированной высоты Z также
будет иметь асимптотическую форму A0.78), но постоянное сла-
слагаемое здесь, вообще говоря, будет зависеть от Z.
Сафмен исследовал продольную диффузию в плоском ка-
канале между двумя твердыми стенками," рассматривая ее как
возможную модель распространения примеси в. атмосфере при
наличии инверсионного слоя, преграждающего дальнейший
подъем примеси на некоторой фиксированной высоте Н. По-
Поскольку такая модель является довольно грубой, профиль ско-
скорости ветра U(Z) он также описывал лишь очень схематически:
кроме простейшего случая ламинарного течения Куэтта, когда
u{Z) = -pl-U<.9, Кгг — x = const и, следовательно, согласно
A0.78) —A0.79),
и2 я2
^ + (Ю.80)

10.4] S 10. турбулентная диффузий 551
~~Н) ^СР'
где a = const, и (в соответствии с аналогией Рейнольдса)
2
и2
и
Кгг(Z)= -* . В этом последнем случае интеграл, входящий
du/dZ
в первую формулу A0.79), также берется в явном виде, и мы
получаем
Элдер рассмотрел диффузию в канале со свободной поверх-
поверхностью на высоте Z=H и сравнил полученные при этом резуль-
результаты с данными специальных экспериментов, в которых иссле-
исследовалось расплывание капель раствора марганцевокислого ка-
калия в слегка наклонном лотке, по которому свободно стекала
вода. Здесь уже требовалось подобрать форму профиля сред-
средней скорости, хорошо соответствующую реальному течению в
лотке, причем результат оказался весьма чувствительным даже
к небольшим изменениям этой формы. В работе Элдера пред-
предполагалось, что профиль скорости в открытом канале дается
логарифмической формой «закона дефекта скорости» E.43) с
постоянной Кармана к=0,41; тогда, если Kzz определять с по-
помощью аналогии Рейнольдса и принять, что Кхх= Кт=Кгг, то
оказывается, что
Кх = E,86+0,068) Ни, = 5,93Hut. ( '
К (К )
Согласно данным измерений Элдера, -^Д- — ^ср «* 0,23, что
примерно втрое превосходит соответствующее значение A0.82);
одним из возможных объяснений получившегося расхождения
может служить несправедливость гипотезы о равенстве трех ко-
коэффициентов Кхх, Куу и Kzz- Если вместо этого принять, что
Kxx=Kyy>_KjZ (напомним, что и ш'2 обычно оказывается мень-
меньшим, чем и'2 и v'2; ср. стр. 236), то коэффициент продольной
диффузии станет равным Кх= E,86+0,23)Яы<: = 6,1Яы*. Это зна-
значение оказывается уже весьма хорошо соответствующим опре-
определенному из экспериментов значению •тг?- = 6,3—даже луч-
лучше, чем можно было ожидать, учитывая, что указанные опыты
производились при сравнительно небольшом значении числа Re,
небольших т и в условиях, не позволяющих рассчитывать на
высокую точность получаемых данных. Впрочем, по мнению
Эллисона (I960), полученное совпадение должно в значительной

552 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.4
мере считаться случайным, так как около свободной поверхно-
поверхности логарифмическая форма профиля скорости не может слу-
служить хорошей аппроксимацией. В этой связи Эллисон повторил
расчеты Элдера, приняв, что профиль скорости задается форму-
формулой E.49"). Согласно его результатам, значение К/Ни* суще-
существенно зависит от значения коэффициента Ь, входящего в
E.49"), причем экспериментальным данным Элдера лучше всего
соответствует значение Ь = 1,4.
Диффузия в свободных турбулентных течениях
Рассмотренный случай продольной диффузии примеси в пря-
прямой трубе или прямом канале весьма специфичен в том отноше-
отношении, что здесь сохраняется ряд свойств, характерных для диф-
диффузии в поле однородной турбулентности. С этой точки зрения
более типичными примерами диффузии в потоке с градиентом
скорости являются, например, случаи диффузии в турбулентных
струях или турбулентных следах за твердыми телами. Однако
теоретическое изучение диффузии в струях или следах с по-
помощью полуэмпирического уравнения турбулентной диффузии
неприятно тем, что при этом обязательно приходится привлекать
еще какие-то дополнительные гипотезы, позволяющие опреде-
определить зависимость коэффициентов турбулентной диффузии (а
также и средней скорости п) от пространственных координат.
В качестве таких дополнительных гипотез обычно используются
те или иные полуэмпирические теории турбулентного обмена,
о которых шла речь в п. 5.8. Получаемые на этом пути резуль-
результаты часто оказываются вполне удовлетворительными с точки
зрения практики (см., например, Хинце A959), Абрамович
(I960)), но теоретически они не очень обоснованы, и мы не бу-
будем на них задерживаться.
В случае, когда исследуется распределение примеси в плос-
плоскости X=const, расположенной вниз по течению за непрерыв-
непрерывным точечным или линейным источником на малом расстоянии
от; него (по сравнению с масштабом L=UT, где U — типичное
значение средней скорости, а Т — типичный лагранжев масштаб
времени), ряд результатов можно получить с помощью перехода
к переменным Лагранжа, если воспользоваться разложением
лагранжевой скорости в ряд Тэйлора (9.78). В частности, как
заметил Хинце A951, 1959), во многих случаях полезным ока-
оказывается уже первое приближение, согласно которому V(x, t) =
= u(x,to)+u'(x,to), так что Х(х, t) = * + (и + и') • V — t0) и
Z(x,t) = w' • (t— tQ), где значения ц, и' и w' относятся к точке
(х, t0) пространства-времени. Отсюда следует, что в устано-
установившемся потоке со средней скоростью, направленной вдоль оси

10.4]
§ 10. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ
553
ОХ, координата Z(t) жидкой частицы, вышедшей в момент t0
из точки х = 0, в момент достижения ею плоскости A=const,
где X<g.L, будет в первом приближении равна
A0.83)
=
u-j-u'
Если |и'|<ы, то согласно этому равенству Z(X) s» (wf/u)X;
поэтому распределение вероятностей для Z(X) здесь только
1.0
as
as
4*
G2
0
я.
* 1
в 1
i '
6 1
*" 1
& 1
к J
4Д 1
& 1
? 1
^ \
+«* 1
>
1*
! \
I л
1 *
1 Л*
i \
! 7*"^
Рис. 82. Распределение температуры в нескольких сече-
сечениях двумерной турбулентной струи, в которую помещена
иагретай проволочка (по Хиице и Ван дер Хегге Цийиеиу).
постоянным множителем отличается от распределения вероятно-
стей для до'@). Если, однако, Значения и' меньше п, но не пре-
пренебрежимо малы, то
Z(X) _ w' u'w' , u'2w'
П Яй — -2 ~Г" —3 • р *
X и и и
A0.84)
Отсюда уже можно без труда выразить моменты распределения
случайной величины Z(X) через моменты эйлеровой пульсацион-
ной скорости и'=(и', w') в точке jc = O, причем обычно при этом
вполне можно ограничиться лишь несколькими первыми члена-
членами ряда A0.84). В тех случаях, когда получающиеся формулы
содержат моменты и' четвертого порядка, по-видимому, до-
допустимо также заменить их комбинациями вторых моментов,

554 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.4
приняв, что соответствующие семиинварианты пренебрежимо
малы (см. Бэтчелор иТаунсенд A956),Хинце A959)). Несмотря
на очевидную грубость подобных приближенных рассмотрений,
они неплохо описывают целый ряд наблюдавшихся Хинце и
Ван дер Хегге Цийненом A951) и Коренном и Уберои A950,
1951) характерных особенностей распределения температуры в
плоскрети X = const в текущей по направлению ОХ турбулент-
турбулентной струе, в которую в фиксированной плоскости Х=0 помеща-
помещалась нагретая проволочка. В качестве примера на рис. 82 при-
приведено такое распределение температуры, полученное в опытах
Хинце и Ван дер Хегге Цийнена, в которых в плоскую струю,
вытекающую из узкого сопла, на расстоянии 100 мм от сопла и
на 6 мм ниже оси струи вводилась тонкая проволочка, нагретая
электрическим током до температуры 400°С. Ось ОХ на рис.82
принималась параллельной направлению средней скорости
у проволочки и проходящей через проволочку (начиная от ко-
которой и измерялось расстояние X); различными значками обо-
обозначены данные измерений при разных значениях X. Мы видим,
что в отличие от аналогичных данных, относящихся к случаю
однородной турбулентности, распределение температуры здесь
оказывается асимметричным — более вытянутым в область поло-
положительных значений Z, которым отвечают большие, чем отрица-
отрицательным Z, значения средней скорости. Полученный результат на-
находится в соответствии с формулой A0.84), поскольку в данном
случае можно считать, что w'=0, а ы'ш'<0. Среднее значение
распределения, приведенного на рис. 82, равно 0,036; в этом опыте
такое же значение имеет и—^=р. Таким образом, в данном слу-
f*(X,Z)
Z dZ
чае при вычислении среднего значения Z(X) = —— уже
Jb(X,Z)dZ
третьим слагаемым в правой части A0.84) можно пренебречь.
Заметим еще, что если бы мы попытались описать распределе-
распределение температуры в струе полуэмпирическим уравнением турбу-
турбулентной диффузии с постоянным коэффициентом /С22,
то в условиях, к которым относится рис. 82, получилось бы
со :
Г Ъ(Х, Z)ZdZ<0, в противоречии с эмпирическими данными.
—во
В другом крайнем случае очень большого X (или, иначе,
очень большого времени диффузии x=t — t0) некоторые резуль-
результаты могут быть получены на основе соображений об автомо-
дельности, рассмотренных в пп. 5.9 и 9.4. Из этих соображений
непосредственно вытекает, что в случае непрерывного источника

10.4] § 10. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 555
примеси (расположенного около обтекаемого тела или сопла, из
которого вытекает струя) распределение средней концентрации
О в любых двух плоскостях X=const с достаточно большими
значениями X (где X отсчитывается от источника по направле-
направлению средней скорости течения) будут подобны друг другу. Точ-
Точно так же в случае мгновенного источника (также расположен-
расположенного около тела или сопла и внесшего в поток примесь в момент
времени t=t0) подобными будут распределения средней концен-
концентрации в трехмерном пространстве в два момента времени t,
достаточно удаленные от момента t0. В силу соображений сим-
симметрии естественно предполагать, что соответствующие распре-
распределения будут симметричными, причем их максимум будет рас-
расположен около оси струи или следа в плоскости A=const (в.
случае непрерывного источника, расположенного достаточно
близко от оси) или же около точки {Х(х), 0, 0), где Х(х) дается
формулами п. 9.4 (в случае мгновенного источника). При этом
результаты пп. 5.9 и 9.4 позволяют просто определить зависи-
зависимость соответствующих максимальных концентраций Ьт(Х) или
От(т) от X или т (хотя они и не дают возможности оценить
форму распределении Ф(У, Z) или $(Х, У, Z)).
Начнем, например, со случая непрерывно действующего ста-
стационарного источника примеси и воспользуемся тем, что в силу
стационарности процесса диффузии поток примеси через любую
плоскость A=const должен быть постоянным. В случае турбу-
турбулентного следа скорость переноса примеси по направлению ОХ
вдали от обтекаемого тела, очевидно, всюду будет практически
равна скорости обтекаемого потока. В то же время размеры
площади в плоскости A=const, на которой имеет место замет-
заметный поток примеси от точечного источника в точке х — 0, в слу-
случае трехмерного следа за конечным телом будут расти пропор-
пропорционально №~Х\ а в случае двумерного следа за цилинд-
ром — пропорционально L (X) \D^ (\)\" — Аг/*Ш221-^г) —X.
В случае следа за цилиндром и линейного источника примеси
(параллельного оси цилиндра) постоянным должен быть поток
примеси на единицу длины оси OY; в плоскости A=const еди-
единичному отрезку оси OY отвечает прямоугольная площадка с
заметно отличной от нуля концентрацией О, имеющая площадь,
пропорциональную L(X) ~ Х1'*. Но поскольку концентрация при-
примеси в плоскости A"=const пропорциональна Ьт(Х), получаем
Х~ '" для точечного источника в трехмерном следе,
Х~г для точечного источника в двумерном следе, A0.85)
Х~Ч* для линейного источника в двумерном следе.

556 гл. v. движение частиц в турбулентном потоке f.io.4
Аналогичное рассуждение применимо и к диффузии примеси
в зоне перемешивания двух плоскопараллельных потоков и в
турбулентных струях (включая сюда и диффузию пассивной ма-
материальной примеси в струях конвективного происхождения).
Однако теперь скорость п переноса примеси через плоскость
X=const уже не будет всюду равна фиксированной скорости Со,
а будет функцией от X, У и Z. Существенно, однако, что при из-
изменении параметра X функция п(Х, У, Z) от У и Z остается
подобной себе, причем ее максимальное значение остается
постоянным в случае плоской зоны перемешивания и двумерной
конвективной струи и убывает пропорционально X'1 в случае
обычной трехмерной струи (бьющей в заполненное той же
жидкостью пространство), пропорционально Х~ч* в случае обыч-
обычной двумерной струи и пропорционально Х~'1а в случае трехмер-
трехмерной конвективной струи. Далее, площадь той части плоскости
X — const, на которой концентрация &(Х, У, Z) заметно отлична
от нуля, в случае точечного источника примеси в трехмерной
струе растет пропорционально L2(X), в случае линейного источ-
источника в двумерной струе или зоне перемешивания — пропорцио-
пропорционально L(X), а в случае точечного источника в двумер-
двумерном течении — пропорционально L(X)[D22(ix)]\ где ^.опреде-
^.определяется по формулам (9.47), или родственным им, из условия, что
Х(хх)<^Х. Поскольку поток примеси пропорционален произве-
произведению концентрации на скорость и на площадь, то рассужде-
ния, приведшие выше к соотношениям A0.85), теперь приводят
к следующим соотношениям:
Х~%1* для линейного источника в двумерной струе'),
Л" для точечного источника в трехмерной струе и
для линейного источника в зоне перемешивания
или двумерной конвективной струе,
Х~'1* для точечного источника в двумерной струе, A0.85')
Х~Ч* для точечного источника в трехмерной конвек-
конвективной струе,
Л" для точечного источника в зоне перемешивания
или двумерной конвективной струе.
В случае мгновенного источника примеси постоянной должна
оставаться общая масса примеси (или, если источник линейный,
масса примеси, приходящаяся на единицу длины оси OY). Но
через время т размер (вдоль оси OXi) облака примеси от мгно-
') Здесь и ниже если не указано, что струя конвективная, то подра-
подразумевается, что речь идет об обычной динамической струе, распространя-
распространяющейся в заполненном той же жидкостью пространстве.

10.4] $ 10. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 557
венного источника характеризуется масштабом [Du(x)]'h (есте-
(естественно, совпадающим с L[X(x)]). В силу результатов п. 9.4, от-
отсюда для максимальной концентрации От(т) облака примеси,
образующегося через время т после момента ее испускания, по-
получаются формулы: -
х для точечного источника в трехмерном следе и ли-
линейного источника в двумерном следе,
х~7» для линейного источника в двумерной струе,
х~ '• для точечного источника в двумерном следе и
в трехмерной струе,
х~2 Для точечного источиика в двумерной струе и для A0.86)
линейного источиика в двумерной конвективной
струе и в зоне перемешивания,
x~s/' для точечного источника в трехмерной конвективной
струе,
х~3 для точечного источиика в двумерной конвективной
струе и зоне перемешивания
(основная часть результатов A0.85) — A0.86) принадлежит Бэт-
челору A957); см. также Яглом A965)).
Диффузия в безграничном турбулентном потоке
с постоянным градиентом средней скорости
В заключение настоящего пункта остановимся на случае
диффузии примеси в безграничном потоке с постоянным попе-
поперечным градиентом скорости ux(Z) и однородным и стационар-
стационарным полем пульсаций и'(А", (). В п. 9.4 мы видели, что в этом
случае взаимодействие градиента скорости с поперечным рас-
рассеянием приводит не к простому увеличению эффективного
коэффициента горизонтальной диффузии, как это было в случае
течения в трубе или в канале, а к качественному изменению
закономерностей продольного рассеяния (выражающемуся в
том, что продольная дисперсия Dxx(x) становится асимптотиче-
асимптотически пропорциональной т3, а не т, как обычно). Поэтому вначале
сферическое облако примеси в таком потоке через некоторое
время принимает форму сильно вытянутого по направлению
оси ОХ эллипсоидообразного веретена, большая ось которого
слегка наклонена по отношению к плоскости Z=0. Поскольку
псле пульсаций и' здесь однородно и стационарно, при исполь-
использовании полуэмпирического уравнения турбулентной диффузии
здесь не возникает трудности с определением зависимости коэф-
коэффициентов турбулентной диффузии от координат: эти коэффи-
коэффициенты естественно считать постоянными в пространстве и во

558 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ 6 ТУРБУЛЕНТНОМ ПОТОКЕ {10.4
времени. Поэтому есть все основания надеяться, что основные
особенности рассматриваемого процесса диффузии можно выяс-
выяснить, рассмотрев решение дифференциального уравнения
при начальном условии $(Х, /о) =6 (X). Нетрудно убедиться,
что искомое решение уравнения A0.87) будет представлять со-
собой трехмерное распределение Гаусса со вторыми моментами
, Dyy = 2Kyy*, Dzz = 2K,s, 1
Dxy = Dyz = 0, Dxz = VKzz*\ j
где т=/ — t0 (этот результат и некоторые его обобщения были
опубликованы Новиковым A958); позже немного более по-
подробно он был изложен такжеЭлриком A962)). Формулы A0.88)
очень наглядно показывают разницу между случаями Г=0 и
Г Ф 0; они полностью согласуются также и с формулами A0.53),
согласно которым удвоенные коэффициенты турбулентной диф-
диффузии Кц равны производным в нуле от компонент тензора
дисперсии бц(х). При сравнении^ же этих формул с формулами
(9.57), (9.57') и (9.58), выведенными на основе лагранжева опи-
описания турбулентности, видно, что наши новые результаты пред-
представляют собой асимптотический вид найденных раньше более
точных выражений для дисперсий Du=Dxx »Da=Dxz при х^>Т3
(причем, как обычно, Kzz=W2T3, Kxx=u'2Ti). Выражения же для
дисперсий при не слишком больших значениях т полуэмпириче-
полуэмпирическая теория турбулентной диффузии не позволяет определить.
Таким образом, мы еще раз убеждаемся в том, что эта теория
описывает только асимптотические закономерности, имеющие
место при больших временах диффузии.
Поскольку максимум многомерной плотности нормального
распределения вероятностей обратно пропорционален корню
квадратному из детерминанта матрицы дисперсий, концентра-
концентрация От(/) в центре облака примеси, созданного в момент t=t0
мгновенным точечным источником, в поле однородной турбу-
турбулентности с градиентом скорости с ростом т = t — t0 будет убы-
убывать асимптотически пропорционально rJ/* (а не пропорцио-
пропорционально тг3'2, как это было при постоянной средней скорости).
Точно так же в случае мгновенного линейного источника на оси
OY максимальная концентрация примеси будет убывать про-
пропорционально т~2 (вместо т). Зная решение, отвечающее мгно-
мгновенному точечному источнику, с помощью формул A0.6) и
A0.8) можно найти также и распределение концентрации, отве-

10.5] 5 ю. турбулентная диффузия 559
чающее стационарному точечному и линейным источникам; на
этом, однако, мы уже не будем задерживаться.
В случае более сложного, чем линейный, профиля средней
скорости u(Z) в безграничном пространстве и зависимости ко-
коэффициентов турбулентной диффузии от координаты Z точное
решение уравнения A0.55), отвечающее мгновенному точечному
источнику, уже не может быть явно выписано. Но если зависи-
зависимость средней скорости и коэффициентов диффузии от Z за-
задается достаточно простыми формулами (например, если функ-
функции m(Z), /Cxx(Z), Kyy(Z) и Kzz(Z) являются степенными), то
основные особенности процесса диффузии, описываемого по-
полуэмпирическим уравнением A0.55), можно исследовать с
помощью уравнений A0.76), A0J6'), A0.76") и т. д. для момен-
моментов 6nm(Z, 0- При этом оказывается, что здесь также взаимо-
взаимодействие вертикального градиента средней скорости п с верти-
вертикальной диффузией, описываемой коэффициентом /С22, приводит
к горизонтальному рассеянию, как правило, при большом вре-
времени диффузии т=/ — t0 много превосходящему обычную гори-
горизонтальную турбулентную диффузию с коэффициентом Кхх- При
этом в отличие от ситуации, с которой мы столкнулись при изу-
изучении горизонтальной диффузии в трубах и каналах, в безгра-
безграничном пространстве это дополнительное горизонтальное рас-
рассеяние обычно не сводится к простому увеличению коэффици-
коэффициента горизонтальной диффузии до некоторого нового значения
К>Кхх, а приводит к тому, что горизонтальная дисперсия а\
оказывается пропорциональной более высокой, чем первая, сте-
степени т. Обо всем этом, однако, мы более подробно будем гово-
говорить в следующем разделе в связи с рассмотрением более важ-
важного практически случая диффузии в полупространстве Z>0,
для которого также сохраняются указанные здесь особенности
процесса горизонтального рассеяния, вызываемого взаимодей-
взаимодействием вертикального градиента средней скорости с вертикаль-
вертикальной диффузией.
10.5. Диффузия в приземном слое воздуха
Среди примеров турбулентной диффузии, упоминавшихся в
начале п. 10.1, наиболее важны, бесспорно, те, в которых идет
речь о диффузии примесей в атмосфере. Поэтому неудивительно,
что в литературе по. проблеме турбулентной диффузии централь-
центральное место занимают работы, посвященные именно диффузии в
атмосфере (к числу таких работ относятся, в частности, и все
книги и обзорные статьи, перечисленные на стр. 506).
При изучении атмосферной диффузии наибольший интерес
представляет диффузия в приземном слое воздуха, наиболее

560 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [10.5
непосредственно связанном с жизнью и деятельностью человека.
Специфика задачи здесь состоит в том, что диффузия происхо-
происходит в турбулентном пограничном слое (вообще говоря, терми-
термически стратифицированном), заполняющем полупространство
над твердой или жидкой подстилающей поверхностью (которую
мы в дальнейшем будем предполагать однородной и примем за
плоскость Z=0). Поэтому результаты предыдущего пункта, в
котором предполагалось, что жидкость либо течет между твер-
твердыми стенками в трубе или канале, либо же заполняет все про-
пространство, непосредственно к атмосферной диффузии неприло-
жимы. Заметим, впрочем, что рассматривавшаяся выше модель
диффузии в плоском канале между стенками Z=0 и Z=H мо-
может быть с известным основанием применена к диффузии в при-
приземном слое воздуха при наличии на высоте Н мощного инвер-
инверсионного слоя (в котором температура растет с высотой), при-
приводящего к резкому уменьшению вертикального обмена на этой
высоте (см., например, Раунде A955), Сафмен A9626), Цейтин
A963)). Ясно, однако, что основной интерес для теории атмо-
атмосферной диффузии представляет все же не эта модель, а слу-
случай диффузии во всем полупространстве Z>0, к рассмотрению
которого мы теперь и перейдем.
Решения полуэмпирического уравнения турбулентной диффузии,
не учитывающие изменения ветра с высотой
Начнем с простейшего подхода, использующего полуэмпири-
полуэмпирическое уравнение турбулентной диффузии. Будем пока, как
обычно, предполагать, что оси системы координат OXYZ, в кото-
которой направление ОХ совпадает с направлением среднего ветра
u=u(Z), являются главными направлениями тензора коэффи-
коэффициентов турбулентной диффузии Ku=Kn(Z). В таком случае
полуэмпирическое уравнение диффузии принимает вид A0.55),
и чтобы все основные задачи теории диффузии свелись к четко
поставленным задачам математической физики, требуется толь-
только еще как-то задать зависимость от высоты скорости ветра п
И КОЭффИЦИеНТОВ ДИффуЗИИ Кхх, Куу И Kzz-
Решение уравнения A0.55) удается получить в аналитиче-
аналитическом виде лишь при некоторых частных предположениях о ха-
характере зависимости коэффициентов этого уравнения от высоты.
Качественные особенности решений, отвечающих различным
типам источников примеси, можно выяснить на простейшем при-
примере уравнения A0.58), т. е. уравнения вида A0.55) с постоян-
постоянными коэффициентами ы, Кхх, Куу и Kzz- Такое простейшее полу-
полуэмпирическое уравнение турбулентной диффузии было исследо-
исследовано Робертсом A923). Воспользовавшись тем, что в этом слу-

10.5] § ю- турбулентная диффузия 561
чае решение, отвечающее наличию в точке Х — х безгранично-
безграничного пространства мгновенного точечного источника производи-
производительности Q, получается из A0.12) с помощью замены Xt на
Xt — пт и Da (т) — на 2/CitT, легко убедиться, что в случае
диффузии в полупространстве Z>0 с краевым условием «отра-
«отражения» \~jyz=® ПРИ Z=Oj решение, отвечающее мгновенному
точечному источнику в точке @, 0, Я) в момент t=to, дается
формулой
Q
Ь(Х, У, Z, ^—--^——рх
Г B-ну (z+ffy-i
у CXD{ ix-ujt-w к» -I /«QRD-Le'^-C-'o)
ХеХР\ 4К„ <*-*„) 4Kyy<t-h)\Le г +е J-
A0.89)
При краевом условии «поглощения» (т. е. при &(Х, У, 0, 0=0)
решение уравнения A0.58) будет отличаться от A0.89) только
тем, что при втором слагаемом в квадратных скобках будет
стоять знак минус, а не знак плюс. Аналогично формулы A0.59)
и A0.61) могут быть использованы для получения решений
уравнения A0.58) в полупространстве Z>0 (с поглощающей
или отражающей примесь границей), отвечающих стационарно-
стационарному точечному или линейному источнику на высоте Z = Н. Эти
решения обычно можно еще упростить, воспользовавшись тем,
что и &^>«'&' и слагаемое и -^ почти всегда значительно пре-
превосходит соответствующий «диффузионный член» —Кхх ду3 =
=дХи'^' (СМ-> напРимеР> оценки Кароля (I960)). Поэтому сла-
слагаемым Кхх-$хг в A0.55) чаще всего можно пренебречь (что
соответствует в формулах A0.59) и A0.61) переходу к пределу
при Кхх-*-0). При этом решение, отвечающее стационарному
точечному источнику производительности Q в точке @, 0, Я) и
условию отражения примеси на границе Z=0, принимает вид
HX,Y,Z)=
В случае поглощения примеси на границе Z=0 мы опять долж-
должны только заменить в последней формуле знак плюс в квадрат-
квадратной скобке знаком минус. Согласно A0.90) распределение при-
примеси поперек направления ветра в горизонтальной плоскости

562 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ш.5
при любых X и Z задается гауссовской функцией со средним
/2КУУХ\Ч,
квадратичным отклонением I —=— I . пропорциональным X» и
обратно пропорциональным п\ При возрастании X (и фиксиро-
фиксированных Y и Z) концентрация Ъ убывает асимптотически пропор-
пропорционально Х~х (как и в случае диффузии в поле однородной
турбулентности в безграничном пространстве). В случае «отра-
«отражения» примеси наибольшая наземная концентрация примеси
?mai= —=—- [——) ' обратно пропорциональна квадрату высоты
источника; она достигается при У=0 на расстоянии от источ-
источника Х=-гр—> прямо пропорциональном Я2. При краевом ус-
ловии поглощения скорость поглощения примеси подстилающей
поверхностью а(Х, Y) — Kzz-$z\ • как легко проверить, убы-
убывает асимптотически пропорционально Х~2. В этом случае наи-
наибольшая скорость оседания а — ,-" (-ТГ-) 'обратно пропор-
пе2ип3 \ КууI _
циональна кубу высоты и достигается при г=0 и ^ =
Решение, отвечающее стационарному линейному источнику,
расположенному на прямой Х=0, Z=H и производящему за
единицу времени массу Q примеси на каждую единицу своей
длины, при краевом условии «отражения» будет иметь вид
(в случае поглощения примеси поверхностью земли мы снова
должны заменить здесь знак плюс на минус). Согласно A0.91)
наземная концентрация от линейного источника на больших
расстояниях от него должна убывать пропорционально Х~Ч*. Ре-
Решения уравнения A0.58), отвечающее более общему гранично-
му условию Кгг -ft?
также могут быть
2=0 „
явно выписаны, но они имеют более сложный вид, и мы на них
не будем останавливаться.
На первый взгляд перечисленные выше результаты, получаю-
получающиеся при использовании уравнения A0.58) для концентра-
концентрации Ф, представляются довольно правдоподобными, но они ни-
рак не согласуются с эмпирическими данными, полученными

10.5] 5 ю. турбулентная диффузия 563
при многочисленных полевых исследованиях диффузии в при-
приземном слое воздуха. Так, например, опыты показывают, что
наземная концентрация примеси, создаваемой стационарным то-
точечным источником, при безразличной температурной стратифи-
стратификации убывает при удалении от источника примерно пропорцио-
пропорционально Х~2 (согласно Саттону A953)—пропорционально A-8),
но никак не пропорционально Л'; наземная же концентрация от
стационарного линейного источника при безразличной стратифи-
стратификации убывает пропорционально А" или Х~°'9 (Саттон A953),
Паскуил A9626)), но не пропорционально А"-1/». Данные, относя-
относящиеся к устойчивой или неустойчивой стратификации, менее оп-
определенны, чем в случае безразличной стратификации, но и они
показывают, что ни при какой стратификации убывание назем-
наземной концентрации не следует простым законам, вытекающим из
формул A0.90) и A0.91) (см., например, Дикон A949)). Та-
Таким образом, приходится заключить, что уравнение A0.58) не-
непригодно для количественного описания процесса турбулентной
диффузии в приземном слое воздуха.
Полученное несоответствие в принципе может объясняться
тем, что полуэмпирическое уравнение турбулентной диффузии
вообще не может быть вполне строго обосновано и не является
точным. Ясно, однако, что только на этом основании еще нельзя
заключить, что полуэмпирическое уравнение диффузии неприме-
неприменимо к рассеянию примесей в атмосфере. В самом деле, все пре-
предыдущие выводы делались на основе очень грубой модели, в ко-
которой полностью пренебрегалось зависимостью скорости ветра
и коэффициентов диффузии от высоты Z. В то же время хорошо
известно, что в действительности в атмосфере и скорость ветра,
и коэффициенты обмена растут с высотой (см. выше гл. 4). По-
Поэтому естественно прежде всего попытаться обобщить исполь-
используемую модель, приняв какие-то разумные предположения
о виде функций m(Z), KXx(Z), Kyy(Z) и Kzz(Z). Такие попытки
предпринимались многими авторами, причем, поскольку реше-
решение уравнения диффузии с переменными коэффициентами на-
наталкивается на значительные аналитические трудности, эти по-
попытки породили обширную литературу, представляющую, глав-
главным образом, прикладной интерес.
Заметим прежде всего, что явное аналитическое решение нестационарных
задач теории диффузии в полупространстве Z > 0 (легко сводящихся к нахо-
нахождению формул для диффузии примеси от мгновенного точечного источника)
в случае меняющейся с высотой скорости ветра u(Z) до сих пор, по-види-
по-видимому, не было получено ни в одном случае. Поэтому при решении задачи
о расплывании облака примеси, созданной мгновенным источником, всегда
используются. те или иные приближенные приемы. Чаще всего при этом
сначала исследуется лишь процесс вертикальной диффузии примеси, т. е.
определяется зависимость от времени суммарной концентрации на высоте Z,

564 гл. v. движение частиц; в турбулентном потоке f 10.5
равной %o(Z,t) = J ?Ъ(&У, Z,t)dXdY(cp. выше формулу A0.75)), и
-СО
только после этого приближенно учитывается-также и горизонтальная диффу-
диффузия. Функция 6оо(?.0> как м" знаем, удовлетворяет уравнений A0.76)
вида
д%о д
соответствующие начальные и краевые условия в случае мгновенного источ-
источника на высоте Z = Я в момент t = U и «отражения> примеси иа грани-
границе Z = О будут иметь внд
, t0) = <?5 (Z — Я), Kz
Z-0
=0, 900 (Z, *) -> 0 при Z -> со. A0.92)
Таким образом, распределение примеси между различными горизонтальными
плоскостями Z = const не зависит от профиля ветра и от коэффициентов
горизонтального обмена и определяется единственной функцией Kzz(Z) (и вы-
высотой источника Н). Решения уравнения A0.76) при условиях A0.92) для
некоторых функций Ku(Z), пригодных для аппроксимации профиля коэффи-
коэффициента вертикального обмена в приземном слое при различных метеорологи-
метеорологических условиях, были найдены, в частности, Лайхтманом в 40-х годах; поз-
позже они исследовались также и другими авторами (см., например, Монин
A956а)). При /(„ = KiZ такое решение имеет вид
где /о — символ функции Бесселя от мнимого аргумента. Поскольку при без-
безразличной температурной стратификации Kzz = a.xut Z, где а = —=- = const
(ср. E.26)), решением A0.93) естественно пользоваться при отсутствии за-
заметного вертикального градиента температуры. В случае наземного источника
(т. е. при Н = 0) формула A0.93). заметно упрощается: здесь
A0>93')
В более общем случае степенной зависимости коэффициента обмена от вы-
высоты, когда К„ = KiZ*, где 0<п<2'), решение задачи A0.92) для урав-
уравнения A0.76) дается формулой
в,» (Z. 0 = : ^ —г/-) 2 е <2-^ к, (/-/.) х
Т 2~"
[) Можно показать, что при п>-2 уравнение A0.76) не имеет решения,
обращающегося в 6(Z — H) при <-*<о. Однако это обстоятельство для нас
не будет играть роли, так как в метеорологических приложениях всегда
можно считать, что п < 2.

10;5] § ю. турбулентная диффузия 565
при #->-0 отсюда следует, что
,1-п
«00 \*-t l} = -
, A0.94')
IKiit-t,)]2-"
Значительно более громоздкие формулы для 9ооB, () получаются при исполь-
использовании функций Kzz(Z), содержащих «изломж, т. е. составленных из двух
аналитических выражении, действующих в различных интервалах высот. Тем
не менее, для случая, когда
К (Z\~iKlZ ПРИ 0<Z<//"
*«(Z)-{*,//,= const при Z>H1,
аналитическое представление функции Qm(Z,t) (в виде некоторого интеграла
от цилиндрических функций) было указано Моиииым A956а), составившим
также таблицу значений этой функции (в безразмерных переменных, позво-
позволяющих исключить неопределенные постоянные Ki и Hi), соответствующей
наземному источнику примеси (т. е. случаю Н = 0).
Следуя развитой в гл. 4 теории подобия для приземного слоя воздуха,
при выборе аналитической формулы для функции /Czz(Z) целесообразно сна-
сначала перейти к безразмерным переменным
где L — естественный масштаб высот в приземном слое, определяемый фор-
формулой G.12). Если, как обычно, считать, что коэффициент обмена для тепла
совпадает с коэффициентом обмена для пассивной примеси, то в силу фор-
формулы G.21) величина К равенства A0.96) будет отличаться от числа Ричард-
Ричардсона Ri (или, в случае неустойчивой стратификации, от его модуля) лишь
множителем а2 = [-р-\ , который, по-видимому, в большинстве случаев не
очень сильно отклоняется от единицы. Функция 3 („, г) = 6(?. t|ti) теперь
будет определяться условиями
¦^- =0, •
in i"» u± ot c_o A0.97)
6->0 при С->со, в(С, 0) = »(C —i)),
которые уже универсальны, т. е. не содержат никаких метеорологических па-
параметров. При этом, теоретически говоря, иам надо рассмотреть лишь случаи
неустойчивой и устойчивой стратификации, которым отвечают две разные
функции /((?), и мы получим формулы, пригодные во всех реальных случаях.
Практически удобно добавить сюда также и третий случай безразличной
стратификации (хотя в принципе его можно получить из любого из двух
предыдущих при помощи предельного перехода |L|->co). В этом третьем
случае, как мы уже говорили, целесообразно полагать /((?) = ? и, следова-
следовательно, применять формулы A0.93) и A0.93'). Что же касается устойчивой
и неустойчивой стратификации, то если бы соответствующие универсальные
функции /((?) были достаточно точно известны, то можно было бы даже не
аппроксимировать эти функции аналитическими формулами, а раз навсегда
решить две задачи A0.97) численно и составить таблицы соответствующих
функций в(?, т|г|) от трех переменных. Поскольку, однако, из § 8 мы знаем,
что функция /((?) и для неустойчивой и, особенно, для устойчивой страти-

566 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.5
фикации известна лишь в общих чертах, и что использование теории подобия
в реальных условиях всегда сопровождается значительным- разбросом эмпи-
эмпирических данных, пока вполие достаточио ограничиться рассмотреиием прибли-
приближенных выражений для /((?). позволяющих получить для в (С, х | т)) явные
формулы. В частности, в случае устойчивой стратификации при слабой устой-
устойчивости (т. е. тогда, когда интерес представляют лишь сравнительно малые
значения ?) можно, следуя Лайхтману A944) и Дикоиу A949), приближенно
заменить K{t) степенной .функцией вида К\?,п с показателем п, немного
меньшим единицы. При сильной устойчивости (т. е. когда речь идет о ши-
широком интервале значений ?) можно воспользоваться тем, что K(t) = oto?
при ?->Юи K(Z)->-W- при ?-*со (см. § 7), и применять функцию К (?) вида
A0.95). Точно так же в случае неустойчивой стратификации при слабой не-
неустойчивости можно приближенно принять, что K(t) = Kit,", где п немного
больше единицы. При более сильной неустойчивости значительно более оправ-
оправданной является «составиаяж формула вида -
К (9 =
A0.98)
—c>C
вытекающая из G.51), а при особо резкой неустойчивости (когда основной
интерес представляют значения I ? I, превосходящие 0,05) можно полагать
К(?) = КЛ>1г и пользоваться формулами A0.94) — A0.94') с п = </з-
Полученные выше результаты позволяют довольно точно описать вер-
вертикальную диффузию в приземном слое воздуха при любой температурной
стратификации. Что же касается учета горизонтальной дцффузии, то простей-
простейший (ио весьма грубый) метод здесь заключается в том, что скорость ветра
u{Z) и коэффициенты Kxx(Z) и Kyy{Z) приближенно заменяются постоян-
постоянными величинами Ucp, (Kxx)cp и (Куу)ср, равными средним значениям со-
соответствующих функций от Z в пределах между верхней и иижней границами
получающегося облака примеси (которые мэжио заранее рассчитать по функ-
функции 0оо (Z,t)). При этом концентрация О(X, Y, Z, t), отвечающая случаю
мгновенного точечного источника производительности Q в точке @, 0, Н),
возникшего в момент времени t = to, будет в первом приближении предста-
представляться в виде
%(ХТ Y, Z, t) и —: ——г. X
4*[<К)<К)]Л<<<)
Y* \
)М (Ю.99)
где 0оо (Z, t) — решение соответствующего уравнения A0.76) при условиях
A0.92). Поскольку коэффициенты Kxx(Z) и Kyy{Z) обычно не очень хорошо
известны, практическое применение формулы A0.99) часто оказывается до-
довольно затруднительным и может привести при разных выборах значений
этих коэффициентов к заметно различающимся результатам. Еще более су-
существенно, однако, то, что независимо от того, как определяются коэффи-
коэффициенты Кхх и КуУ, при использовании формул вида A0.99) с постоянной
средней скоростью ветра мы полностью теряем важный эффект взаимодей-
взаимодействия вертикального перемешивания с вертикальным градиентом скорости,
который, как было показано выше, в турбулентных -потоках в трубе или
в канале и в безграничном пространстве при достаточно большом времени

10.5] S ю. турбулентная диффузия 567
диффузии играет основную роль в горизонтальном рассеянии. Отсюда ясно,
что формула A0.99) и в приземном слое воздуха может быть применима
лишь при сравнительно малых значениях t — to.
Учет горизонтального рассеяния, создаваемого
градиентом скорости ветра
Чтобы приближенно учесть также и влияние градиента сред-
средней скорости на горизонтальное рассеяние, Сафмен A9626) вос-
воспользовался методом Ариса, при котором распределение при-
примеси в плоскости Z=const описывается несколькими первыми
моментами Snm(Z, 0» задаваемыми формулой A0.75). С по-
помощью полуэмпирического уравнения диффузии A0.55) для мо-
моментов боо, бю, бго и т. д. получаются известные нам уравнения
ЛО I
A0.76), в которых, однако, теперь краевое условие -т^ =0
на верхней границе канала Z — H, использовавшееся в п. 10.4,
заменяется условием Qnm (Z, t) ->0 при Z->oo. Так как нас бу-
будет интересовать в первую очередь асимптотическое поведение
облака примеси от мгновенного источника в момент 10 при
t — ^0->оо, то мы можем ограничиться случаем наземного ис-
источника в начале координат — точке @, 0, 0) (поскольку есте-
естественно думать, что при наличии источника на конечной высоте Я
эта высота будет заметно сказываться на процессе рассея-
рассеяния облака примеси лишь в течение ограниченного промежутка
времени). Чтобы уяснить себе основные качественные особенно-
особенности исследуемого эффекта взаимодействия вертикального гра-
градиента скорости с вертикальным перемешиванием, рассмотрим
прежде всего простейший модельный случай, когда m(Z)=TZ
и /Czz(Z)=/C=const (случай m(Z) = U0 + TZ, /(zz = const, могущий
представить интерес при конечной высоте источника Я, лег-
легко получается отсюда при помощи перехода к новой инерци-
инерционной системе координат). В этом случае искомым решением
уравнения A0.76) относительно 8oo(Z, t) будет 8oo(Z, t) =
z1
= 6oo(Z, ^o + t) = ,, e № (символом т здесь и всюду ниже
(тслт) "
будет обозначаться разность t — ^0)- Решение уравнения A0.76')
для функции 6ю (Z, t) при Kzz=K, U(Z)—TZ и таком 8oo(Z, t)
более сложно; ясно, однако, что оно должно быть пропорцио-
пропорционально QT и, следовательно, в силу соображений размерности
должно иметь вид
6l0
(Z, t) = bl0(Z, /0+,) = QI4.9,0(-^r). A0.100)

568 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.5
Здесь <рю(?)—универсальная функция одного переменного та-
такая, что фю(|) ->0 при ?-> оо; с помощью уравнения A0.76') эту
функцию удается явно выразить через ехр (—|2) и так называемые
функции параболического цилиндра математической физики
(см. Сафмен A9626)). Аналогично обстоит дело и с наиболее
интересной для нас функцией 8гоB, /), описывающей дисперсию
распределения примеси в плоскости Z=const по направлению
оси ОХ. Согласно уравнению A0.76"), эта функция зависит уже
и от коэффициента горизонтального обмена КХх', точнее говоря,
она представляет собой сумму двух слагаемых, первое из кото-
которых зависит только от m(Z) и Kzz=K (но не от Кхх), а второе —
от Kxx{Z) и KZt=K (но не от U{Z)). Первое из указанных сла-
слагаемых, очевидно, пропорцибнально QT2 и поэтому в силу сооб-
соображений размерности должно записываться в виде произведе-
произведения СГ2/С(/СтN/гф2оB/G(тI/2); что же касается второго из них,
то его общий вид также легко может быть выписан, если только
Кхх представляет собой степенную функцию от Z. В частности,
если Kxx = Kt*= const или, соответственно, Kxx—K*Z> где К*—
=const, то нужное нам решение уравнения A0.76) будет пред-
ставимо ш виде
=^) при KXX = KV
A0.101)
при Кхх = K\Z.
Здесь <pM(S). TjJ)(^) и Тмф— новые затухающие на" бесконеч-
бесконечности функции, которые, как оказывается, тоже выражаются че-
через функцию ехр(—|2) и функции параболического цилиндра.
Аналогичные (но более сложные) выражения могут быть полу-
получены и для моментов Qnm(Z, 0 высших порядков (с п + т>2).
Согласно формулам A0.100), A0.101) и т. д. моменты рас-
распределения примеси в плоскости Z=const в момент времени
t = to+z представляют собой степенные функции от т, умножен-
умноженные на функции от? = -=^, принимающие, как нетрудно про-
V К%
верить, конечные значения при ?=0. Поэтому в любом слое
0<2<# фиксированной толщины Я моменты распределения
примеси во всех плоскостях Z=const при т-*-оо имеют асимпто-
асимптотически одинаковую форму. Суммарное распределение примеси
между различными плоскостями Z==const, очевидно, описывает-
описывается функцией 6go(^> t) = -iM=^e-Z!iiK\ Эта функция не зави-

tO. 5] § 10. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 569
сит от п (Z)и Kxx(Z) и показывает, что при фиксированном зна-
значении т толщина облака примеси имеет порядок|/7(т; при этом
если //^V^/ft, то примесь почти равномерно распределяется
по вертикали в пределах слоя толщины Я (с постоянной верти-
вертикальной плотностью 600 = —^=^). Выражения для моментов
бюB, to+ч) и 8гоB, *о+т) при Z <^)Л(ч, получающиеся после
подстановки в формулы A0.100) и A0.101) явных выражений
соответствующих специальных функций ?ю($)> Тго^)' Тм^) и
9^E) и перехода к пределу |-*-0, согласно Сафмену оказы-
оказываются равными
„ 7
e
4
2OK, I x V/j
при Kxx=i
A0-102)
при Kxx KZ
Отсюда вытекает, что координата X центра тяжести распределе-
распределения примеси в нижнем слое (толщины //<С V^x) и дисперсия
о» этого распределения по направлению ОХ имеют следующий
вид:
при
К*, г , A0.103)
±У«Кт? при Kxx = KZ
Мы видим, что центр тяжести распределения примеси в нижнем
слое переносится средним течением по направлению оси ОХ со
все возрастающей скоростью g " Г Y К* (пропорциональной
градиенту скорости Г и квадратному корню из коэффициента
вертикального обмена). Что же касается дисперсии этого
распределения, то она, согласно A0.103),складывается из двух
слагаемых. Первое из них пропорционально Г2Кт3 (т. е. только
постоянным множителем отличается от соответствующего сла«
гаемого в выражении A0.88) для горизонтальной дисперсии об-
облака примеси, диффундирующей в безграничном пространстве);
оно, очевидно, создается взаимодействием вертикального тур-
турбулентного переноса с вертикальным градиентом скорости.

570 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.5
Второе же слагаемое в выражении для <з\х описывает обычное
горизонтальное рассеяние, вызываемое турбулентными пульса-
пульсациями горизонтальной скорости (т. е. турбулентной диффузией
с коэффициентом КХх)- Это второе слагаемое при Кхх = Ki имеет
обычный вид 2К\%, а при Kxx = K\Z оно зависит также и от
Кгг=К (т. е. выражает взаимодействие горизонтальной и верти-
вертикальной диффузии) и пропорционально т.3'2. Существенно, од-
однако, что в любом случае при достаточно больших значениях ч
оно оказывается пренебрежимо малым по сравнению с первым
слагаемым (имеющим порядок т.3). Заметим еще, что уравнение
для'бог^, t) будет отличаться от A0.76") отсутствием члена с
%(Z) (в предположении, что средняя скорость при всех Z на-
направлена вдоль оси ОХ). Поэтому дисперсия <з\ будет описы-
ваться лишь вторым слагаемым формулы A0.103) для og (с
очевидной заменой КХх на Куу), т. е. при больших значениях t
будет много меньшей, чем о|^. Максимальная наземная концен-
концентрация От=дт(т) (достигающаяся, очевидно, в точке ((X), 0))
при т -*¦ с» будет убывать асимптотически пропорционально %~*l\
если 7(ra=const, и пропорционально т~"'\ если Kyv~Z. Ясно, что
все эти факты никак не согласуются с упрощенной формулой
A0.99). Кроме того, эта формула оказывается "неверной и в том
отношении, что распределение примеси в плоскости Z=const при
достаточно большом значении x=t — to и по форме не напоми-
напоминает распределения Гаусса. В самом деле, воспользовавшись
аналогичными A0.100) — A0.102) соотношениями для момента
21
6зо> можно показать, что 630 ~2§§ QT^Ki* при достаточно большом
т, откуда вытекает, что асимметрия распределения примеси по
направлению оси ОХ при фиксированном Z и т-*-оо не стремит-
стремится к нулю, а приближается к единице.
Перечисленные результаты относились к модели, в которой u(Z) = TZ,
/(„ = К = const. Естественно ожидать, однако, что и в других случаях при
наличии зависимости скорости ветра от высоты дело будет обстоять ана-
аналогичным образом. Наибольший интерес, разумеется, представляло бы ис-
исследование случая
(т. е. случая диффузии в логарифмическом пограничном слое), а также слу-
случаев, когда u(Z) и /Cn(Z) определяются формулами, выведенными в гл. 4 для
пограничного слоя в температурио-стратифицироваиной жидкости. Однако та-
такое исследование, опирающееся на полуэмпирическое уравнение турбулентной
диффузии, наталкивается на значительные аналитические трудности. Поэтому,
следуя опять Сафмену, мы ограничимся лишь кратким рассмотрением ситуа-
ситуаций, возникающих при использовании аппроксимации всех,вертикальных про-

10.5] § Ю- ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 571
филей степеинымй функциями. Предположим, что
где U\, К, /Ci, Кг — постоянные, и п < 2. В таком случае общий вид решений
уравнений A0.76), A0.76'), A0.76") и т. д. (для случая наземного мгновен-
мгновенного точечного источника производительности Q в начале координат в мо-
момент t = to) снова может быть установлен на основе соображений размер-
размерности. В частности, в уравнение A0.76) для ,0oo(Z, <) теперь входит един-
единственный размерный параметр К; поскольку из К, Z и x = t—t0 можно
составить единственную безразмерную комбииацию ? = Z (К*) 2~". получаем
1_
во» {Z, 0 = 0 (К*) 2-" ?оо (Z (/Сх)-1^-">), A0.105)
где фоо E) — безразмерная универсальная функция (явный вид которой
дается формулой A0.94')). Функция 6тB, t), согласно A0.76') И A0.104),
должна быть пропорциональна Qu,, а в остальном также зависит лишь от К,
Z и т; следовательно,
т-\
9.о {Z, 0 = <?».* (Кт) 2-" ?,о {Z (/Ст)-1/*2-"»), A0.106)
где фю(?)—еще одна универсальная функция. Наконец, 02о в силу A0.76")
и A0.104) представляется в виде суммы слагаемого, пропорционального QUj,
и слагаемого, пропорционального Q К\, а 0м пропорционально Q /Сг", поэтому
2т-\
Ом (Z, 0 = <?«?*2 №) 2-" ?S
),
602 (Z, 0 = Q/C2x (/СтJ-" 9о2 (Z (/Сх)-1^-")).
Поскольку d(Z,0-*0 при Z-K», все функции q>oo(?), ?юB), ?^/{5) и т. д.
должны убывать при ?->оо; в силу A0.105) отсюда вытекает, что толщина
облака примеси в момент to + т должна иметь порядок (/(тJ~л. В слое тол-
толщины Н<^ (KvJ~n распределение примеси будет практически независимым
от высоты и будет иметь плотность
n _
00 ~ (
где 000=900@) (т.е. Оо0 = B —п) 2~" [г (-j^)] в силу A0.94')).
При принятом нами предположении, что скорость u(Z) на всех уровнях па-
параллельна оси ОХ (от которого, впрочем, при необходимости легко освобо-

572 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [10.5
диться, введя в рассмотрение еще и компоненту v(Z) = ViZm'), центр тяже-
тяжести распределения примеси в этом слое будет иметь координаты
(Ю.108)
При том же предположении дисперсии распределения примеси в плоскости
Z •= const, где Z <^ (К1*) 2~ ". будут иметь вид
1т к I
4 = й1Ы2т2 (агх) 2-" + й2/с,т (/ст) 2-в, <4 =63/с2т(л:тJ-\ (шов')
х у
где bi, b2 и Ьг—новые постоянные, а смешанный моменте^ =((Х—(Х)) Y) =
= —1- ^~ будет равен нулю (так как 8О1 = 811 = О). Первое слагаемое
floo floo
первой формулы A0.108') снова описывает горизонтальное рассеяние, вы-
вызываемое взаимодействием вертикального градиента средней скорости с вер-
вертикальным турбулентным переносом, а второе слагаемое 'той же формулы —
обычную горизонтальиую турбулентную диффузию. Ясно, что первый из этих
эффектов при больших т будет преобладающим, если только 2т + 2 — п> к.
В условиях приземного слоя атмосферы последнее условие, по-видимому,
всегда приходится считать выполняющимся (так как при устойчивой или
безразличной стратификации п<! 1 и, вероятно, следует считать, что
п + k <; 2, а при сильной неустойчивости п приближается к */3, но коэффи-
коэффициент Kxx(Z), если только им здесь можно пользоваться, вряд ли будет
заметно возрастать с высотой). Поэтому следует ожидать, что в атмосфере
наличие вертикального градиента скорости ветра всегда играет основную
роль в горизонтальном рассеянии в течение сравнительно больших проме-
промежутков времени. Так как к тому же естественно думать, что Kyy(Z) при-
примерно пропорционально Kxx(Z), то в пренебрежении поворотом ветра с вы-
высотой рассеяние по направлению среднего ветра при больших т будет за-
заметно превосходить рассеяние по перпендикулярному направлению. Кроме
того, дисперсия о| здесь оказывается заметно большей и средней толщины
облака (имеющей порядок (Кх) j^2 ~"'); поэтому облако примеси при боль-
шихт отзывается больше всего вытянутым по направлению среднего ветра.
Формулы Саттона для рассеяния примесей в атмосфере
Приведенные выше оценки горизонтального рассеяния в- приземном слое
воздуха открывают новые возможности для математического анализа про-
процесса распространения примесей от мгновенных источников. Ясно, однако,
что такой анализ неизбежно будет довольно сложным; поэтому в практиче-
практических приложениях широкое применение получили различные довольно гру-
грубые, но зато простые приближенные приемы описания атмосферной диффу-
диффузии. В частности, в Англии и США при расчетах диффузии примесей в ат-
атмосфере часто используются приближениые формулы, предложенные Саттоном
A932, 1949, 1953). Согласно этим формулам, распределение примеси от мгно-
мгновенного точечного источника предполагается имеющим гауссовскую форму
A0.12) (в системе координат, перемещающейся вместе со средним ветром
с постоянной скоростью п), но с дисперсиями Dn(x), растущими быстрее,

J0.5] * W. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 573
чем первая степень т (в соответствии и с формулами A0.108'V н с тем, что
убывание наземной концентрации, отвечающее дисперсиям Ьн(.х), = ЩцХ,
в реальных приложениях оказывается слишком медленным). Чтобы опреде-
определить функциональную форму дисперсий Da(x), Саттои предположил, что при
диффузии в приземном слое атмосферы можно приближенно пользоваться
классической формулой Тэйлора ^9.31) лля &и(х) (строго получающейся
лишь в предположении об однородности турбулентности), приняв прн этому
что лагранжевы корреляционные функции Kff (x) имеют вид
/=1,2,3. A0.109)
Здесь xi — некоторые постоянные масштабы времени, а показатель п, соглас-
согласно Саттону, принимает значения порядка 0,1ч-0,3 (в зависимости от страти-
стратификации). Поскольку предполагается, что п < 1, лагранжев масштаб вре-
времени Тг формулы (9.32) оказывается бесконечно большим; имеиио поэтому
теория Саттона не приводит к асимптотически линейному росту дисперсий
при возрастании времени т (и отсюда же следует, что эта теория, строго
говоря, не является одним из вариантов обычной полуэмпирической теории
турбулентной диффузии, пригодной, как отмечалось выше, лишь при х ~^> Ti).
Однако, как и в обычной полуэмпирической теории, в теории Саттона также
рассматриваются лишь достаточно большие значения х, ио большие не по
сравнению с 7\ (равным здесь бесконечности), а по сравнению с х,. Согласно
A0.109) и (9.31), при x^$>xt дисперсия Du(x) оказывается асимптотически
пропорциональной т*-"; соответствующую асимптотическую формулу Саттон
записывает в виде
С2
^(utf-n. A0.110)
где п — средняя скорость ветра в_рассматриваемом слое воздуха, a Ct — по-
постоянные коэффициенты (при иJ ~ и2 это означает, что т^-^и)).
В случае диффузии примесей от высотных источников Саттои, ориенти-
ориентируясь На экспериментальные данные, рекомендует считать коэффициенты Cf
зависящими от высоты источника Н (н убывающими с ростом Н). Отметим,
что при определении дисперсий Dn(x) "формулой A0.110) функция A0.12)
также оказывается решением уравнения диффузии внда A0.55), но с коэф-
коэффициентами диффузии Кц =—j—С2((иJ~" z1*", зависящими ие от высо-
высоты Z, а от времени диффузии т. Но прн этом уравнение A0.55) уже ие мо-
может быть выведено из статистических предположений полуэмпирнческон тео-
теории днффузин, требующих (см. формулы A0.53)), чтобы коэффициенты
диффузии определялись только полем скорости и (л, t), ио не зависели бы
от того, когда и где в это поле внесены источники примесн (как отметил
Тэйлор A969), то, что коэффициенты турбулентной диффузии в полуэмпнрн-
ческой теории ие могут зависеть от т, вытекает уже нз принципа суперпози-
суперпозиции, соответствующего предположению о линейности уравнения диффузии:
прн зависимости Ки от т значение Ки в фиксированной точке (X, t) прн на-
наличии нескольких мгновенных источников примеси, выделивших примесь не
одновременно, было бы многозначным).
Зная распределение концентрации от мгновенного точечного источника,
можно без труда рассчитать концентрацию н от стационарных точечного н
линейного источников точно так же, как. это было сделано выше- в приме-
применении к формулам Робертса, отвечающим предположению о постоянстве

674 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [10.5
коэффициентов диффузии. Так, например, случаю диффузии от стационарного
точечного источника производительности Q в точке (О, О, Н) при условии
«отражения» примеси поверхностью Земли в теории Саттона отвечает род-
родственная A0.90) формула
к?
Y? Г (Z-H)*
I в случае линейного источника иа прямой X = 0, Z •= Н здесь надо только
1-?
справа опустить множитель, зависящий от У, и заменить Q aaV nQCyX 2
Согласно A0.111), распределение примеси поперек ветра в горизонтальной
С2 1--
плоскости оказывается гауссовским с дисперсией —j- X , а распределе-
распределение наземной концентрации по направлению среднего ветра имеет вид
Я»
— e , A0.112)
т. е. убывает асимптотически пропорционально Хп~2 (в случае линейного
источника — пропорционально X2 /. Максимум наземной концентрации
A0Л12) равен &тах=—— —?- (т. е. обратно пропорционален скорости
пеип2 Су
ветра и квадрату высоты источника) и достигается иа расстоянии от источ-
2
ника ¦^=(~г~1 ~" (которое, в отличие от случая теории Робертса, ие
зависит от скорости ветра и).
Сопоставление формул Саттоиа со сравнительно новыми и полными эм-
эмпирическими данными о диффузии в атмосфере можно найти, например,
в работах Бареда и Хоугеиа A959), Дриммеля и Рейтера A960) и Хоугеиа,
Бареда и Антаиаитиса A961); сопоставлению формулы A0.109) с эмпириче-
эмпирическими данными о лагранжевых корреляционных функциях посвящена работа
Манна A963). Приведенные в указанных статьях материалы показывают,
что формулы Саттоиа весьма неточно описывают реальные лаграижевы кор-
корреляционные функции; тем ие менее, их можно более или менее удовлетвори-
удовлетворительно согласовать с имеющимися эмпирическими данными о диффузии,
если только значительно расширить интервал допустимых значений п и до-
допустить, что ие только параметры С<, но и п могут принимать различные
значения для диффузии по различным направлениям (т. е. заменить в фор-
формуле A0.110) параметр п на п<). Но в таком случае число неопределенных
параметров в формулах теории Саттоиа оказывается настолько большим,
что оно уже само по себе вполне объясняет возможность согласования этих
формул с результатами полевых экспериментов; зависимость же параметров
С, и nt от метеорологических условий все равио оказывается довольио слож-
сложной и плохо изученной. Поэтому представляется естествеииым искать другие
пути приближенного описания данных об атмосферной диффузии, которые
были бы достаточно просты, но более обоснованы теоретически, чем формулы
Саттона,

10.5] S Ю. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 575
Стационарные решения полуэмпирического уравнения
турбулентной диффузии
В частном случае поперечной дисперсии Dyv(x) (по направлению OY,
Перпендикулярному среднему ветру) новые приближенные формулы были
предложены Бютнер и Лайхтманом A963); эти формулы, однако, довольно
сложны и еще требуют эмпирической проверки. Ряд практических формул
для расчета атмосферной диффузии можно найти также в монографии Пас-
Паску ил а A9626). Мы здесь остановимся лишь на некоторых из таких формул,
вытекающих из полуэмпирического уравнения турбулентной диффузии
{10.55). Выше мы рассматривали только решения этого уравнения, отвечаю-
отвечающие случаю мгновенного источника примеси; именно к ним относилось за-
замечание, что никаких точных решений уравнения диффузии, учитывающих
возрастание скорости ветра с высотой, до сих пор не получено. На практике,
однако, часто основной интерес представляет распределение концентрации от
непрерывно действующего стационарного источника примеси, а это распреде-
распределение уже заметно проще поддается_математическому анализу.
Начнем со случая концентрации Ь(Х, Z) от стационарного линей-
линейного источника, перпендикулярного среднему ветру и производящего Q
единиц массы примеси за единицу времени на единицу длины (очевидно,
со
равной также величине ?(Х, Z)= Jb(X. Y. Z)dY. где ЩХ, Y.Z) -концен-
—оо
трация, создаваемая стационарным точечным источником производительно-
производительности Q). В этом случае в уравнении A0.55), очевидно, можно опустить члены,
содержащие -гт* и -gy. Если, кроме того, мы пренебрежем также и слагае-
слагаемым—Кxx-gvT ~~дхи'^'' описывающим продольную диффузию, по срав-
сравнению со слагаемым u(Z)-^r, описывающим перенос примеси средним те-
течением (а в случае стационарных источников это почти всегда не приводит
к заметной ошибке), то уравнение A0.55) еще упростится и превратится
в так называемое двумерное уравнение турбулентной диффузии
В случае отражения примеси поверхностью Земли и источника на высоте Я
искомое решение должно удовлетворять условиям
Ь -> 0 при X -> оо или Z -> оо; К,
дЬ
гг
= 0;
.2=0
A0.114)
jf= 0 при X=*Q, ZфН; I ubdZ = Q при Jf>• О
о
(последние два из этих условий могут быть также записаны в виде
п(#)#@,Z) = Qb(Z— H)). Таким образом, мы приходим к обычной за-
задаче с начальными и краевыми условиями для параболического уравнения
A0.113). в котором роль времени теперь играет переменная X. В частном

576 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.5
случае й (Z) = п =¦ const, /С„ (Z) =/(«=¦ const решение задачи A0.113) —
A0.114), очевидно, будет даваться формулой Робертса A0.91), которая, как
мы знаем, не согласуется с эмпирическими данными. Случай постоянной
скорости ветра й, ио лииейио возрастающего коэффициента обмена
Kn(Z) — K\Z был рассмотрен Бозаике и Пирсоном A936), получившими
(для частного случая наземного источника с Н — 0) очень простую формулу
aZ
b(X,Z) = -jQ—e KlX , A0.115)
уже сравнительно неплохо согласующуюся с данными наблюдений, относя-
относящихся к случаям температурной стратификации, близкой к безразличной.
В дальнейшем ряд авторов изучили также более общий случай произвольной
степенной зависимости-скорости ветра и коэффициентов обмена от высоты
KZZ(Z) = KiZ", u(Z)= u\Zm. A0.116)
В частном случае л=1 — т уравнение A0.113) с такими коэффициен-
коэффициентами, ио при огличиых от A0.114) краевых условиях было сравнительно
давно решено Саттоиом A934) в связи с исследованием процесса испарения
в- приземном слое воздуха; близкую задачу рассмотрел также Лайхтмаи
A9476). Решение уравнения A0.113) при условиях A0.114), отвечающих
наземному источнику, в случае коэффициентов A0.116) было получено, в
частности, Робертсом (см. Колдер A949)), Фростом <1946) (в предположе-
предположении, что п= 1 — т) и Лайхтмаиом A961, 1963); оно имеет следующий вид:
т+1
Г ulzm~n+2
X ехр I — >„,'__„ I 2J к
'(в предположении, что т—п + 2>0). Более общее решение того же урав-
уравнения, отвечающее высотному источнику иа произвольной высоте Н, можно
найти, например, в работах Лайхтмана A961, 1963), Раундса A955), Моиина
A956а) и Смита A957); в этом случае
* )¦ <¦»¦
где /р — функция Бесселя от мнимого аргумента индекса р= 7П~о-
Значительно более громоздкое решение уравнения A0.113) с коэффициентами
A0.116) при краевых условиях, отвечающих общему случаю «частичного или
полного поглощения» примеси, при котором Кгг -Ту-
опубли-
г=о
ковано Лайхтманом A961, 1963); им_же, а также Цейтиным A963), исследо-
исследован случай, когда скорость ветра и и коэффициент обмена Кгг удовлетво-
удовлетворяют степенным формулам A0.116) лишь до некоторой фиксированной высоты
Z = Ни а выше остаются постоянными,

10.5]
§ 10. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ
577
В случае и (Z) = u, In —, /(„(Z) = /f,Z, отвечающем логарифмическо-
логарифмического
му пограничному слою, задачу A0.113) — A0.114) не удается решить анали-
аналитически, но, разумеется, ее можно решить численно. Для нескольких значе-
значений Н такое численное решение было построено Берляндом, Геииховичем
и др. A963, 1964), принявшими, однако, что линейное возрастание коэф-
коэффициента Kzz(Z) сохраняется лишь до некоторой условной «высоты призем-
иого слоя> А, а далее Ku(Z) остается постоянным (или даже изменяется
с высотой причудливым образом, так что график функции Kzz(Z) оказы-
оказывается имеющим несколько изломов). В противоположность этому в работе
Ямамото и Шимануки A960) численное решение уравнения A0.113)
искалось в предположении, что * = Po#» = const и что коэффициент Kzz
7Ов 2* W6
Рис. 83. Зависимость показателя р в законе убывания назем-
наземной концентрации примеси от расстояния от источника и от
параметра устойчивости.
в соответствии с аналогией Рейнольдса всюду совпадает с коэффициентом
турбулентной вязкости, т. е. определяется соотношением Кгг -ку = "^
(приводящим в случае логарифмического профиля ветра к равенству
Azz = KiZ). Однако вместо логарифмической формулы для u(Z) здесь для
профиля ветра использовалась общая формула теории подобия G.24) с уни-
универсальной функцией q>(?) = ?/'(?), удовлетворяющей уравнению четвертого
порядка G.60). Параметр а, входящий в уравнение G.60), в процессе чис-
численного решения удалось исключить с помощью простого перехода к но-
новому масштабу длины L, = L/a. После этого задача о диффузии примеси от
наземного линейного источника (на высоте шероховатости Z — Zo) при усло-
условии «отражения» на поверхности земли свелась к решению одного универ-
универсального уравнения относительно функции от двух переменных, зависящего
' от единственного параметра Со = -=-^- (возникающего в связи с зависимостью
пB) от Zo). Ясно, что положительным значением So отвечает устойчивая
стратификация, а отрицательным значениям — неустойчивая. Полученные
Ямамото и Шимануки численные решения соответствующего уравнения для
ряда значений Со были представлены в виде нескольких графиков. На рис. 83
мы приводим один из них, показывающий зависимость показателя р, харак-

578 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.5
теризующего быстроту убываиия иаземной коицентрации (при Z = Zo) с рас-
расстоянием X от «параметра устойчивости» ?о и безразмериоге расстояния от
источника X/Zo. Параметр р здесь определялся из условия
?(*,, Zp) / А-2 у»
Zo) 1 *, / '
где оба значения Х2 и Х4 брались вблизи определенной координаты X. Мы
видим, что при безразличной стратификации (т. е. при близком к нулю зиа-
чеиии ?о) параметр р вплоть до весьма больших расстояний остается при-
примерно постоянным и близким к 0,9, в полном соответствии с эмпирическими
фактами, о которых говорилось иа стр. 563. Однако при отличной от безраз-
безразличной стратификации ои, как правило, существенно зависит'от расстояния X.
Если при использовании степенных формул A0.116) принять, что Kzz{Z)
может отличаться от коэффициента турбулентной вязкости самое большее
постоянным множителем а, т. е. что KZzjrj = const, то неизбежно, приходится
считать, что л = 1 — т. В частном случае беаразличиой стратификации лога-
логарифмический профиль скорости ветра сравиительио хорошо аппроксимируется
на значительном интервале высот степенной функцией с показателем т = l/j
(ср. выше стр. 263 и 277); поэтому здесь целесообразно принять т — '/г,
n = s/7. И действительно, формулы A0.117) — A0.118) при таких т ил
(и соответствующем подборе коэффициентов 11\ и К\), как оказалось,
очень неплохо соответствуют имеющимся эмпирическим данным о диффу-
диффузии в условиях безразличной стратификации (см., например, Колдер
A949)). Из A0.117) и A0.118), в частности, видно, что при таких т и л
наземная концентрация убывает асимптотически пропорционально Х~*1', что
хорошо согласуется и с опытными данными, и с данными рис. 83 для очень
малых tfi. При стратификации, ие являющейся безразличной, многие авторы
также пробовали применять формулы A0.117) — A0.118), в которых показа-
показатели т и л определялись в зависимости от метеорологических условий (см.,
например, Дикой A949), Воэи A961)), но здесь полученные результаты до-
довольно сильно зависят от метода выбора значений тили поэтому пред-
представляются меиее убедительиыми.
Перейдем теперь к диффузии от стационарного точечного ис-
источника производительности Q в точке @, 0, Н). В этом случае, если мы
снова пренебрежем диффузией по,направлению ОХ по сравнению с перено-
переносом примеси средним течением, то полуэмпирическое уравнение для средней
концентрации будет иметь вид
иЮ \к + (кУ A0Л19)
Интересующее нас решение, уравнения A0.119) должно удовлетворять усло-
условиям
при X2+Y2 + Z2->co, K^~ =0,
dZ
z=o
A0.120)
0, Y, Z)=,
и (Н)
(ср. A0.114)). Увеличение числа независимых переменных от двух до трех
при переходе от уравнения A0.113) к A0.119), естественно, приводит к зна-
значительному усложнению задачи. Дэвис A950) попытался найти точное ре-
решение задачи A0.119) —A0.120) (для случая наземного источника) в предпо-

10.5] S Ю. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 579
ложении, что u(Z)<^Zm, K.zi(Z)~j Zl~m и Куу (Z) ~« Z"; однако он сумел
достигнуть цели лишь в частном случае, когда а = т, т. е. когд^/Суу^) =
«= cu(Z), где с = const. В последнем случае, как легко проверить Q(X, Y,Z)=>
1 / Y2 \ -
= — ехр | • »(*, Z), где b{X,Z)— решение задачи A0.113) —
1\ ъсХ \ icX /
A0.114). Таким образом, при а = m учет диффузии вдоль оси 0У_не пред-
представляет никакой трудности; поэтому предположение, что Куу ~ и, прини-
принималось в целом ряде работ о турбулентной диффузии. К сожалению, получае-
получаемые при таком предположении формулы для концентрации Q(X, Y, Z) во
многих случаях оказались явно противоречащими эмпирическим данным о
распространении примеси от стационарных точечных источников в приземном
слое атмосферы. В связи с этим Смит A957) вернулся к случаю_общего по-
показателя а, но он отказался от точного определения функции Q(X, Y, Z),
а ограничился нахождением лишь двух первых отличных от нуля моментов
распределения концентрации примеси вдоль прямых X = const, Z = const:
СО 00
60(*, Z) = Г Ъ(Х, Y, Z) dY, в2(X, Z) = j Y'~b(X, Y, Z) dY. A0.121)
—00 — OO
Функция Qo(X,Z), очевидно, будет удовлетворять тому же уравнению
A0.113) (с условиями A0.114)), которое описывает распределение концентра-
концентрации в случае линейного стационарного источника, т. е. ее можно определить
из равенства A0.118) с л= 1 — т. Что же касается функции 02(X, Z), то
для нее из A0.119) получается дифференциальное уравнение второго поряд-
порядка, содержащее также и коэффициент KVV(Z). Это уравнение при некоторых
частных значениях т и а может быть решено в общем виде, но при произ-
произвольных т и а его явное решение (выражающееся через сложные специаль-
специальные функции) удалось иайти лишь для случая наземного источника, т. е.
при Н = 0. Естественно думать, однако, что при не слишком большом Н и
большом X решение при Н > 0 будет уже мало отличаться от решения, от-
отвечающего случаю Н = 0. Кроме того, если_ интересоваться лишь наземным
распределением примеси (т. е. значениями Q(X, Y, 0)), то решение для слу--
чая высотного источника может быть выведено из общего решения для слу-
случая наземного источника с помощью доказанной Смитом изящной теоремы
взаимности, выражающей статистическую обратимость процесса диффузии,
описываемого полуэмлирическим уравнением A0.55). Согласно этой теореме,
в случае турбулентной диффузии с условием отражения примеси на поверх-
поверхности 2=0 значение Q(X, Y, 0) функции Q(X, Y, Z), отвечающей высотному
источнику примеси в_ точке X = Y = О, Z = Н, совпадает со значением.
$(Х, Y, Н) функции Ъ(Х, Y, 2), отвечающей такому же наземному источнику
в точке X = Y = 2 = 0 (так что для Q(X, Y, 0) при любом Н можно напи-
написать явную формулу)._Зная 60(Х, 2) и 62(*, 2), можно приближенно
определить и функцию Q(X, Y, 2), допустив (в соответствии с интуитивными
физическими представлениями о поперечной диффузии и с имеющимися
эмпирическими данными), что распределение примеси вдоль прямой X=const,
2 = const при всех X и 2 мало отличается от распределения Гаусса. Следо-
Следовательно, при любых X, Y и 2
- expI-KygKMXZ)]
\2nY*(X Z)]V« '¦ V '

580 гл. v. движение частиц в турбулентном потоке [Ю.б
где
Y2/Y Л— fla(X> Z)
С помощью этой формулы Смит, в частности, нашел скорость убывания на-
наземной концентрации вдоль направления ОХ по оси облака примеси (т. е.
при Y = 0) для т = '/7 и л = а = 6/7- Оказалось, что в этом случае асимпто-
асимптотически Ъ~Х~Ъ1*, что более или менее согласуется с эмпирическими дан-
данными, относящимися к стационарным точечным источникам примеси в атмо-
атмосфере при стратификации, близкой к безразличной.
В общем случае произвольной стратификации Ямамото и Шимануки
A964) попытались оценить коэффициент диффузии в «боковом» направлении
OY с помощью сопоставления эмпирических данных о диффузии от точечных
источников с результатами численного решения задачи A0.119) — A0.120) при
значениях Kyy(Z), содержащих неопределенный параметр. При этом, как и в
предыдущей их работе, предполагалось, что ветер задается формулой G.24),
где ф(^) =?/'(?) удовлетворяет уравнению G.60), и что Kzz = u,xZ/q>(t). Что
же касается до коэффициента Kyy(Z), то в виде первого приближения было
принято,- что ои при любой стратификации линейно зависит от высоты, т. е.
задается формулой вида
где a (Jo) —неизвестная нам функция от So (т. е. от стратификации). Основное
удобство такого выбора Куу состоит в том, что при этом от параметра а
можно легко избавиться с помощью' перехода к безразмерным координатам
Xi *¦ X/Zo, Y{ = K/a'/'Zo, Z, = г/г^зависящим от а. После такого перехода
задача о диффузии от наземного стационарного точечного источника сво-
сводится к решению универсального уравнения относительно функции #№. Уи %\)
от трех переменных, зависящего от единственного параметра to- Это уравне-
уравнение было решено численно для ряда значений So, после чего найденное из
расчета распределение примеси вдоль оси OYi при Xi=32 000 и 2^240 было
сопоставлено с соответствующими данными диффузионных экспериментов
Бареда A958) и других исследователей. Результаты такого сопоставления
позволили приближенно определить неизвестные значения a (So) (значения 20
и L» при этом оценивались по профилям ветра и температуры, измерявшимся
в ходе рассматривавшихся диффузионных экспериментов). Полученные зна-
чеиня a (Jo) легли со сравнительно небольшим разбросом на плавную кривую,
монотонно убывающую при возрастании So; согласно этой кривой, а» 13 при
So = 0 (т. е. при безразличной стратификации), а«100 при ?о=—0.014 и а»3
при So=0,01. Далее, с целью проверки допустимости принятого предположе-
предположения о Kyy(Z) найденные значения a (So) были использованы для теоретиче-
теоретического расчета распределения концентрации вдоль оси ОY при некоторых
других значениях X и 2, результаты которого снова были сопоставлены с дан-
данными наблюдений. Оказалось, что общее согласие теории с опытом удовле-
удовлетворительно, но разброс экспериментальных точек столь велик, что на их
основании нельзя сделать надежного вывода. Для убывания наземной кон-
концентрации вдоль оси облака примеси при безразличной стратификации расчет,
основанный на предположении, что /(„„ = 13 ум Z, привел к соотношению
Ь~Х'х-п, хорошо согласующемуся с имеющимися эмпирическими данными.
Эмпирические данные показывают также, что горизонтальная диффузия
по направлению оси OY становится более быстрой при увеличении горизон-
горизонтального протяжения облака, так что коэффициент Куу как бы возрастает
с ростом времени диффузии x=t—t9 (или координаты X). Это обстоятельство

10.5] t Ю. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 581
объясняется очень важным эффектом ускорения относительной диффузии
облака примеси (т. е. ускорения изменения расстояния между отдельными
составляющими облако частицами) при увеличении размера облака, связан-
связанным с тем, что по мере возрастания размера облака в его рассеянии начи-
начинают принимать активное участие все более и более крупномасштабные воз-
возмущения поля скорости (об .этом мы еще будем говорить в гл. 8 ч. 2
книги). Однако в рамках рассматриваемой здесь полуэмпирической теории
турбулентной диффузии, как уже отмечалось выше, нельзя допустить, чтобы
коэффициенты диффузии зависели от времени т. Тем не менее, Дэвяс A954а)
попробовал учесть и этот эффект, формально допустив, что в уравнении
A0.119) коэффициенты и и Кгг зависят только от 2 (а именно, u~Zm,
Ktt~Zl~m), но Kyy~Z'[Y\? (т. е. Куу фактически зависит от положения
источника примеси, так как только нм выделяется значение Y = 0). В част-
частном случае а=пг, {$=1 — 2/л Дэвису удалось найти точное решение уравне-
уравнения A0.119); однако ясно, что принятое им основное предположение о зави-
зависимости Куу от Y резко противоречит духу полуэмпирической теории. С этой
точки зрения более последовательным представляется предложение Лайхтма-
на A963), согласно которому концентрацию Q(X, Y, 2) в случае точечного
источника следует искать в виде A0.122), где 0о(Х 2) задается как решение
уравнения A0.113), а при определении величины Y2(X, 2) рекомендуется
опираться на представления, связанные с лагранжевым описанием турбулент-
турбулентности (например, на формулу Тэйлора (9.31)), но вовсе ие использовать
полуэмпирическую теорию.
Учет возможного отклонения главных осей тензора
коэффициентов диффузии от осей OX, OY и OZ
Все предыдущие выводы опирались на предположение, что полуэмпири-
полуэмпирическое уравнение атмосферной диффузии имеет вид A0.55). Помимо того,
что и самое общее полуэмпирическое уравиение диффузии может быть полу-
получено лишь при использовании некоторых приближенных гипотез, примени-
применимость которых к диффузии в приземном слое иногда может вызывать сомне-
сомнения, уравнение A0.55) содержит в .себе еще дополнительное допущение, что
оси OZ, ОХ и OY, направленные вертикально вверх, вдоль среднего ветра и
перпендикулярно ветру, являются главными осями тензора коэффициентов
диффузии Kt). Мы ввели это допущение, основываясь на том, что напра-
направления указанных осей выделены самими условиями движения в приземном
слое (ем. выше стр. 536); однако надо иметь в виду, что такая аргументация
не является строгой. Поэтому ие исключено, что впоследствии, когда наше
понимание всех деталей процесса турбулентной диффузии станет более глу-
глубоким, нам придется ввести поправки в полуэмпирическое уравиение A0.55),
учтя в нем еще некоторые дополнительные члены. В самом деле, например,
в п. 7.5 (см. стр. 401) мы уже отмечали, что при теплообмене атмосферы с
однородной подстилающей поверхностью в принципе возможен и небольшой
турбулентный перенос тепла по направлению среднего ветра, описываемый
смешанным моментом u'T'=utTtfJ(Z/L). Представляется довольно правдо-
правдоподобным, что этот момент будет положительным прн положительных гра-
градиентах средней температуры и отрицательным при отрицательных градиен-
градиентах. Но в таком случае в рамках полуэмпнрической теории турбулентности
tff
момент и'Т должен представляться в виде и'Т' —Kxz'Sy'- Наличие отлич-
отличного от нуля коэффициента Кхг, разумеется, означает, что оси координат ие
совпадают с главными направлениями тензора Кц. В полуэмпирической

582 гл. v. движение частиц в турбулентном потоке [10.5
теорнн'турбулентной днффузнн налнчне ненулевого момента и'Т' в условиях,
когда Т зависит только от Z, показывает, что в общем случае турбулентный
поток прнмесн по направлению среднего ветра^должен иметь вид
^ ~. A0.123)
члена
Отсюда вытекает, что в правой части уравнения турбулентной днффузнн
A0.55) в принципе может присутствовать также н слагаемое вида
— ~aV\Kxz "лт- ^а ЭТУ возможность, по-внднмому, впервые обратил вни-
манне Леттау A952) (см. также Пристли A963))'. Позже Дэвнс A9546) по-
попытался оценить возможное влияние этого слагаемого на диффузию от ста-
стационарного точечного источника, _ сравнив решение уравнения
- дЬ д /„ dJ \ , д /„ д»\
и -jt? = — ^т\К„-~г= 1 -f- -jt= \Кгг -А7 )прн некотоРыхспециальных предпо-
предположениях о функциональной форме коэффициентов u(Z), KXz(Z) н Kzz(Z) с
решением обычного двумерного полуэмпнрнческого уравнения A0.113); как
н следовало ожидать, разница, оказалась очень небольшой. Вслед за тем
Мацуока A961) произвел некоторые расчеты для модели^ в которой полу-
д (у. дй\
эмпирическое уравнение содержит, кроме члена -^-у \KXz 'at')' также н член,
характеризуемый коэффициентом Кгх, а Ги н Дэвнс A963) оценили влияние
~дХ\'хг'Ш) на п°Дсчитанные Сафмеиом значения <Х> и п|
(см^ A0.103)) н ^ашлн, что прн некоторых предположениях о Kxz(Z) возни-
возникающие поправки могут иметь порядок 15—20%. Следует, однако, иметь
в виду, что во всех перечисленных работах предполагалось, что коэффициент
КХг (и Kzx) имеет тот же порядок, что и коэффициент Kzz, хотя есте-
естественно предполагать, что на самом деле он будет заметно меньшим.
В целом же по поводу этих поправок к полуэмпнрнческому уравнению4 днф-
днффузнн можно сказать то же самое, что мы в свое время говорили о род-
родственном нм моменте и'Т': пока онн остаются практически совершенно
неизученными, но, по-внднмому, описываемые ими эффекты обычно оказы-
оказываются незначительными. Поэтому в настоящее время нет оснований учи-
учитывать эти поправки прн практических расчетах, хотя теоретически нельзя
исключить возможности, что такие поправки реально существуют и в каких-то
условиях могут даже иметь значение.
Использование гипотезы о подобии лагранжевых статистических
характеристик в теории диффузии в приземном слое
Выше мы все время исходили из полуэмпирического уравне-
уравнения турбулентной диффузии. Представляет интерес, однако, по-
посмотреть, какие выводы о диффузии в приземном слое воздуха
можно сделать, не пользуясь полуэмпирической гипотезой о ли*
нейной зависимости турбулентных потоков примеси от градиен'
та средней концентрации. Оказывается, что значительную по-
помощь здесь может оказать представляющееся вполне естествен-
естественным предположение о подобия лагранжевых характеристик

10.5] § Ю. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 583
турбулентности в приземном слое воздуха, введенное в п. 9.4.
К следствиям из этого предположения мы теперь и перейдем.
Прежде всего напомним, что в пренебрежении действием
молекулярной диффузии средняя концентрация "примеси от мгно-
мгновенного точечного источника единичной производительности в
точке х= (х, у, z) в момент U равна плотности вероятности
лагранжевых координат (X, Y, Z) жидкой частицы, находившей-
находившейся в момент to в точке х (см. выше стр. 509—510). Отсюда, в
частности, следует, что в случае мгновенного наземного источ-
источника производительности Q в начале координат средняя кон-
концентрация в момент t = to+x при безразличной термической
стратификации и достаточно большом т будет определяться
формулой вида
Ь(Х, У, Z, ;0-И) = ^-Я3(Агр* , |, l^ly (ю.124)
где Р$ — некоторая универсальная функция от трех переменных,
Z^bujt, X^^-ln—f-, a b, с и ? = 2,718 ...—универсаль-
ные постоянные (см. (9.65), (9.60') и (9.61'))- В случае источ-
источника на высоте Н можно пользоваться тем же соотношением,
если только т^>— • Впрочем, при не очень больших (но все же
заметно превосходящих — 1 значениях т несколько более точные
результаты ^юлучаются, если допустить, что формулы (9.60') и
(9.61') для Z(x) и Х(х) начинают действовать лишь через время
1,~— после момента t0; за время же от момента t0 до to+x\
центр облака примеси лишь переносится осредненным течением,
т. е. остается на той же высоте Я, но перемещается на расстоя-
расстояние и (Н)хх = -^ In у- вдоль направления ОХ (Бэтчелор
A959)), Такая поправка играет роль лишь в течение сравни-
сравнительно небольшого промежутка времени, но при обработке ре-
реальных экспериментов, в которых часто поневоле приходится
ограничиваться лишь не очень большими значениями т, она
иногда оказывается полезной (см., например, Сермак A963)).
В случае неустойчивой или устойчивой стратификации формула
A0.124) заменяется более общим соотношением
*(*, V, Z, tu + i) = ^p(X=X-, |, ^-; -I), A0.125)
где Р— новая универсальная функция от четырех переменных,
Z = Z(t) и Х^Х(л) определяются равенствами (9,69) и (9.70),

584 гл. v. движение частиц в турбулентном потоке [Ю.5
a L — естественный масштаб длины в стратифицированном по-
пограничном слое, введенный в гл. 4. При не очень большом т
здесь также можно ввести поправку на высоту источника Я, но
на ней мы уже не будем останавливаться.
Из соотношения A0.124), вытекает, в частности, что диспер-
дисперсии облака примеси, созданного мгновенным точечным источни-
источником, определяемые из соотношений
о\ ==Q~1 J f f(X— Xfb(X, V, Z)dXdYdZ,
о\ =Q-X f f fY2b(X,Y, Z)dXdYdZ,
°lz=CTl f f f(Z-ZL(X, Y, Z)dXdYdZ,
при безразличной стратификации должны быть асимптотически
пропорциональны Z2. В силу (9.61') это означает, что диспер-
дисперсии вдоль всех осей облака примеси от мгновенного точечного
источника при безразличной стратификации должны быть асим-
асимптотически пропорциональны т2 (а не т, как в случае однород-
однородной турбулентности, и не т3, как в случае потока с постоянным
градиентом скорости). При наличии же термической стратифи-
стратификации, строго говоря, нельзя уже ручаться, что эти дисперсии
даже при очень большом т будут строго пропорциональны Z2,
так_как здесь форма распределения #(Х, У, Z) может зависеть
от Z/L, т. е. меняться при изменении т. Естественно думать, од-
однако, что зависимость распределения от Z/L не будет прояв-
проявляться очень сильно, так что в первом приближении и здесь
дисперсии можно считать пропорциональными Z2. В случае
сильной неустойчивости последний вывод имеет дополнительные
основания (см. равенство (9.75')); поэтому при этих условиях
для не слишком малых значений т должны иметь место соотно-
соотношения о? —о2, —а\ —Z2 — х3 ( наиболее точным последнее со-
* у * V п .
отношение, вероятно, будет в применении к аь ). Все приведен-
приведенные заключения можно, во всяком случае в принципе, попытать-
попытаться сравнить с эмпирическими данными, относящимися к мгно-
мгновенным точечным источникам примеси. Так как, однако, таких
данных пока имеется очень немного, то более удобными для про-
проверки на опыте являются следствия из предположения об авто-
модельности лагранжевых характеристик, относящихся к рас-
распределению концентрации от стационарных источников примеси,
о которых будет речь ниже.
Согласно формуле A0.125), наземная концентрация примеси
от стационарного точечного источника на достаточно большом

10.5] § Ю. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 585
расстоянии X от этого источника по направлению среднего ветра
будет определяться формулой
Ь(Х, О, 0) = Q /р{^~-, О, -1; j-)-~. A0.126)
В случае линейного источника эту формулу надо заменить соот-
соотношением
со оо
Ь(Х, 0) = Q / /Р(Х~Х , Xr, —1; ~\^^-. A0.127)
О —со
Последние две формулы, очевидно, можно также переписать в1
виде
Х—Х \
Z 1
Z3
-'!¦
I— » v» Ж1
dz dz
и аналогично
- -1- 1)
[ Z dz dz J
Для приближенного вычисления интегралов в правых частях
A0.126') и A0.127') воспользуемся, следуя Бэтчелору A959) и
Эллисону A959), тем, что при большом X облако примеси от
мгновенного точечного источника в начале координат должно
проплыть мимо плоскости X — const за время, много меньшее,
чем время т, требующееся для достижения облаком этой пло-
плоскости. _Иначе это можно еще выразить так: поскольку, оче-
очевидно, Z/X->-0 при т-»-оо, интервал значений X, при которых
У
2'
(( ^)
ся заметно отличным от нуля, при большом X будет составлять
относительно малую долю самого К- Поэтому при достаточно

586 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.5
большом X допустимо считать, что HI—=—, -=-, —1; — —
\ ? ? Li I
———) при любом фиксированном -=¦. Это допущение
вполне аналогично использовавшемуся выше при рассмотрении
полуэмпирической теории пренебрежению продольной диффу-
диффузией (по направлению оси ОХ) по сравнению с переносом при-
примеси средним течением. Из него следует, что равенства A0.126')
и A0.127') могут быть без большой ошибки заменены прибли-
приближенными соотношениями
Ь(Х, 0,0)»—^- f P(l, 0,-U-т)& (Ю.126")
Ъ(Х, 0)»-^- [ [Р(Ъ, ч, -1; x)^^v (Ю.127")
где Z = Z{i) и Х=-Х(х) берутся уже только при таком зна-
значении х, что Х(х)=Х.
Рассмотрим сначала простейший случай диффузии при без-
безразличной стратификации. В этом случае функция Р_не зависит
от Z/L, т. е. при всех Z является одной и той же, а Х(т) и Z(x)
удовлетворяют соотношениям (9.60') — (9.6Г). Поэтому здесь
о (?1п#
Ь(Х, 0, 0) аа си, « ajf A0-128)
'•О) Т^ШТ"*-?*- (Ю.129)
Отсюда видно, что при нейтральной стратификации концентра-
концентрация примеси от линейного стационарного источника должна
убывать примерно пропорционально X'1, а от точечного стацио-
стационарного источника — немного медленнее, чем X'2', как мы знаем,
эмпирические данные достаточно хорошо согласуются с этим
выводом (см.^ыше стр. 563). Более аккуратно показатель р в
соотношении Ь — Х~р можно определить с помощью формулы
= — ¦JlogX' такое его определение было произведено Сер-

10.5] 5 ю. турбулентная диффузия 587
маком A963), принявшим во внимание также и упоминавшуюся
выше поправку к Х{х) и Z(t), связанную с конечной, высотой
источника Н. При этом теоретические значения р = р(Х), вычис-
вычисленные в предположении, что 6 = с=0,1 '), оказались совпадаю-
совпадающими с эмпирическими данными ряда авторов (относящимися
и к лабораторным экспериментам, и к наблюдениям в атмо-
атмосфере при нейтральной стратификации) даже лучше, чем этого
можно было ожидать.
В случае стратификации, отличающейся от безразличной, по-
положение значительно осложняется. Прежде всего здесь уже ин-
интегралы в правых частях равенств A0.126") и A0.127"), вообще
говоря, могут зависеть от Z/L (т. е. от X). Естественно ожидать,
однако, что эта зависимость будет гораздо слабее зависимости
от X множителей перед интегралами, так что и в этом случае
без большой ошибки можно использовать соотношения
Ь (X, 0, 0) -=* , Ь(Х, 0)
щ. dX
¦=dX
Z-
Jw=x
Более существенным является то, что функции' Х(х) и Z(x)
здесь определяются соотношениями (9.69) и (9.70), содержа-
содержащими универсальные функции /(?), cpi(?) и ф(?), только асимп-
асимптотическое поведение которых известно (да и то лишь с точ-
точностью до неопределенных числовых_коэффициентов). Так, при
сильной неустойчивости Z{x) ~ т3/г, Х(х) ~ х и, следовательно,
Ь{Х, 0, 0) ~Х~г, Ь{Х, 0,) ~Х^к Исходя из данных, приведенных
в гл. 4, можно, однако, надеяться, что именно асимптотическое
поведение указанных функций будет играть основную роль при
расчете концентраций, и поэтому в первом приближении мы мо-
можем подставить вместо неизвестных функций почти любые функ-
функции, изменяющиеся так, как надо, при малых и при больших
значениях аргумента. Такая надежда подкрепляется, в частности,
результатами вычислений Гйффорда A962). Этот автор в соответ-
dX — —
ствии с (9.71) предположил, что ф!(^)=/(^) (так что —j- = u(Z),
') Заметим в этой связи, что в силу полуэмпирической формулы A0.93')
при нейтральной стратификации, когда /С22«хи*2,
со
(Z) = j ze00 (z, x) dz = %u,x.
0
Исходя отсюда, Эллисон A959) даже сделал вывод, что, возможно,
6«х«0,4. На самом деле, однако, полуэмпирическая теория не может быть
применена для оценки скорости перемещения частиц примеси (см. ниже
п. 10.7); поэтому такое заключение необоснованно.

588 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.6
а затем выбрал в качестве/(?) функцию вида
1пС + 6С при Х> О,
1п|С| при 0<С<— 0,03, AОЛЗО)
С" з-|_ @,03)" ? + In 0,03 при С<—0^03
и предположил (следуя Казанскому и Монину A957)), что
По найденной исходя из этих' предположений зависимости
безразмерной концентрации -т^- * в случае точечного источ-
источника примеси от безразмерного расстояния *Ь -г Гиффорд
подсчитал показатель р в соотношении Ъ~Х~ъ при различ-
различной термической стратификации и разных расстояниях X.
Полученные им значения р оказались сравнительно неплохо
согласующимися с эмпирическими данными, собранными в
ходе выполнения программы «Прэри Грасс» в О'Нейле (Не-
(Небраска, США) и опубликованными Баредом A958) и др. Позже
Малхотра и Сермак A963) сравнили результаты расчетов Гиф-
форда (опять при 6 = 0,1) с данными некоторых диффузиойных
экспериментов, производившихся в специальной аэродинами-
аэродинамической трубе с подогреваемой нижней стенкой, позволяющей
искусственно создавать неустойчивую температурную стратифи-
стратификацию; полученные результаты также оказались удовлетвори-
удовлетворительными. Дополнительную проверку теории Гиффорда произ-
произвел Сермак A963), который, правда, ограничился лишь случаем
очень слабых отклонений от безразличного равновесия и в этой
связи заменил функцию f(t,) равенства A0.130) более простой
функцией Суинбенка G.73), имеющей неверную асимптотику
при больших отрицательных значениях ?. Но поскольку все ис-
использованные Сермаком экспериментальные данные (получен-
(полученные частично в лаборатории, а частично при полевых наблю-
наблюдениях) относились лишь к очень небольшим значениям |?|,
неудивительно, что совпадение теории с экспериментом и здесь
оказалось довольно хорошим.
10.6. Диффузия с конечной скоростью
Параболический характер полуэмпирического уравнения тур-
турбулентной диффузии A0.55) приводит к тому, что примесь, вне-
внесенная в жидкость в момент времени t0, немедленно распростра-
распространяется по всему пространству и в момент ta+x,- где т сколь

10.6] . S 10. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 589
угодно мало, уже может быть обнаружена, хотя бы и в очень
малом количестве, на сколь угодно большом расстоянии от ис-
источника примеси (см., например, формулу A0.89)). Это обстоя-
обстоятельство явно противоречит фактической ограниченности скоро-
скоростей движения частиц примеси. Оно непосредственно связано с
тем, .что в полуэмпирической теории мгновенная скорость
«жидких частиц», как мы видели на стр. 534, оказывается бес-
бесконечной. На практике, однако, появление в рассматриваемой
теории бесконечной скорости чаще всего не играет большой
роли, так как окружающий источник примеси объем, внутри ко-
которого концентрация не слишком мала, всегда ограничен, и рас-
распределение концентрации внутри этого объема при не слишком
малом времени диффузии, как правило, удовлетворительно опи-
описывается параболическим уравнением диффузии. Тем не менее,
вблизи от реальных границ облака примеси использование пара-
параболического уравнения диффузии может привести к существен-
существенным ошибкам. Например, дым, вышедший из трубы высоты Я,
на самом деле достигает поверхности земли не ближе чем на
расстоянии от трубы, равном -~Н, где и — минимальная ско-
скорость ветра, a v — максимальная скорость вертикальных дви-
движений частиц дыма; в то же время, согласно полуэмпирическому
параболическому уравнению диффузии, дым может быть обна-
обнаружен у поверхности земли сколь угодно близко к трубе. По-
Поэтому в некоторых случаях желательно иметь более общую
полуэмпирическую теорию диффузии, в которой учитывалась бы
ограниченность скорости движения жидких частиц. Подобное
обобщение обычной теории диффузии (не обязательно турбу-
турбулентной) в разное время предлагалось рядом авторов; в настоя-
настоящем пункте мы его изложим, следуя в основном "работам Мо-
нина'A955, 19566);
Будем считать, что случайная функция X (xt t), описывающая
движение «жидкой частицы», почти всюду^дифференцируема по
t, и ее производная — скорость «жидкой частицы» V(x, t) —
ограничена. Функцию Х(х, t) при этом уже нельзя считать
марковской функцией от t. Действительно, выше мы уже видели,
что в случае марковской функции Х(х, t) скорость —dt' ¦
всегда будет бесконечной, если только Кц Ф 0. Если же до-
допустить, что /Cfj=O, то скорость уже не будет бесконечной, но,
как легко видеть, функция Х(х, t) при этом вообще не будет
случайной.
Таким образом, условие ограниченности скорости «жидкой
частицы» несовместимо с предположением, что ее координата
Х(х, t) является марковской случайной функцией от t.

590 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [10.6
Аналогичная ситуация возникает в теории молекулярной
диффузии при попытке учета инерции диффундирующей части-
частицы; благодаря инерции ее траектория X(xJ) оказывается всюду
имеющей конечную производную V(x, t) = —**' ', откуда вы-
вытекает, что функцию Х(х, t) уже нельзя считать марковской.
Известно, что в теории молекулярной диффузии (т. е. браунов-
ского движения) учет инерции частиц осуществляется на осно-
основе предположения, что марковской является не функция Х(х, t),
а шестимерная функция {X(x,t), V(x, t)} (см., например, Улен-
бек и Орнштейн A930) или Чандрасекар A943)). Аналогично
этому будем поступать далее и мы.
Ограничимся для простоты рассмотрением одномерной за-
задачи о диффузии по направлению оси OZ. В соответствии со
сказанным выше попытаемся построить обобщение полуэмпири-
полуэмпирической теории турбулентной диффузии на основе нового полу-
полуэмпирического предположения, более широкого, чем предполо-
предположение о марковском характере функции X{x,t). А именно, до-
допустим, что марковской является двумерная случайная функция
{Z(z, t), W{z, t)}, где Z(z, t)—координата «жидкой частицы»,
a W(Z, t) — —L' —ее. скорость. Поставив при, этом своей
целью только учет ограниченности скорости W, мы мо-
можем ограничиться лишь весьма грубым описанием возможных
значений W. Пусть |№|<С; разобьем всю область возможных
значений скорости — C<W<C на конечное число /V интервалов
А„ и вместо конкретных значений W будем указывать лишь но-
номера п интервалов А„, в которые эти значения попадают. Иначе
говоря, вместо случайной функции W(z, t) мы будем рассматри-
рассматривать случайную функцию n(t), принимающую дискретные зна-
значения 1, 2, ..., /V, и примем предположение, что марковской
является случайная функция {Z(z, t), n(t)}.
Рассмотрим теперь условные вероятности
Z
P{Z(z,t)<Z; n(t) = i\Z(z,to) = z}=fpi(Z\z,t)dZ. A0.131)
— со
Плотность вероятности для координаты «жидкой частицы»
Z(z, t), играющая основную роль в теории турбулентной диффу-
диффузии, выражается через функции Pi(Z\z, t) по формуле
P(Z\z, t) = %pl(Z\z, t). A0.132)
Общие дифференциальные уравнения марковских случайных
процессов, указанные Колмогоровым A931), в данном случае

10.6] § 10. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 591
сводятся к следующей системе уравнений относительно функ-
функций Pi(Z\z, t), заменяющей обычное полуэмпирическое уравне-
уравнение турбулентной диффузии:
Здесь приняты обозначения
Wl = W, (Z, t) = [? r,(x|Z
где Yi(x\Z, t) = Z(z, t + x)—Z(z, t)—это смещение частицы
при условии, что значения ZJz, t)=Z и n(t + x) =
= n(t)=i фиксированы. Очевидно, Wt — это математиче-
математическое ожидание скорости частицы W при условии, что W при-
принадлежит интервалу Д4, так что значение Wi(Z, t) при всех Z
и t лежит где-то внутри интервала At. Смысл величин ац можно
пояснить следующим образом. Поскольку функция n(t) прини-
принимает лишь целочисленные значения, она может изменяться лишь
скачками, переходя от значения n(t — 0)=/ в момент, непосред-
непосредственно предшествующий t, к некоторому другому значению
n(t + 0)=i в момент, сразу следующий за t. Величины а,ц
при 1ф] — это средние частоты переходов от n(t — 0) =/ к
n(t + 0) —i (ибо cijiAt — вероятность скачка от п = j к п = i в
течение промежутка времени (t, t + At) при условии, Что
'2
n(t) = j). Так Kan'2iP[n(t-lrx) = i\Z(z,t) = Z,n(t)=j} = l, то
ясно, что 2а» = 0; следовательно, dj, = —2 а'ц равно взятой
' - «W
со знаком минус средней частоте переходов от п = i к какому-
то Другому значению п.
Уравнения A0.133) образуют полуэмпирическую систему
уравнений диффузии, соответствующую сформулированным
выше предположениям. Эти уравнения надо решать при началь-
начальных условиях
Pi(Z\z, t)-^el(z)b(Z—z) при t-+t0,
to) = z]. A0.134)
Величины et задают распределение вероятностей для n(t0), т. е.
фактически для значений начальной скорости «жидкой частицы».
Рассмотрим более детально простейшую схему, в которой
вся область возможных значений скорости «жидкой частицы»

592 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ Б ТУРБУЛЕНТНОМ ПОТОКЕ [10.6
—C<W<C разбивается лишь на два интервала Д4 и Аг. Выберем
в качестве А4 и Д2 интервалы 0<W<C и —С<№<0; случайная
функция n(t) в этом случае указывает направление движения
«жидкой частицы». Предположим для определенности, что оба
направления равноправны^ так что, в частности, W=0; в этом
случае можно положить W\=—Wz=W (где tF — средняя абсо-
абсолютная скорость частицы) и ац=а.г\=—аи=—агг=а (где а —
частота изменений направления движения). Тогда уравнения
A0.133) принимают вид
;Z . A0.135)
a(A/>)
~дТ az- = a(A-/>2).
Уравнения такого типа (или вытекающее из них телеграф-
телеграфное уравнение, которое мы выведем ниже) впервые были полу-
получены (для описания одномерной диффузии фотонов) Фоком
A926), затем (для описания молекулярной диффузии с учетом
конечности скоростей диффундирующих частиц) — Давыдовым
A935), Каттанео A948—1949), Гольдштейном A951), Р. Дэви-
сом A954) и другими авторами. Для описания турбулентной
диффузии такие уравнения предлагались Ляпиным A948, 1950)
и Мониным A955, 19566).
Предположим, что диффузия происходит в поле стацио-
стационарной турбулентности. В этом случае величины а и W не за-
зависят от t и, следовательно, могут зависеть лишь от 2. Введя
новые неизвестные р=Р\ + Рг (плотность вероятности для коор-
координаты диффундирующей частицы) и q = W(pi-—р2) (плотность
потока диффундирующих частиц), получим
др да
t_\ i_ п.
"' dZ Л A0.136)
да dWp '
I f
Первое из этих уравнений (справедливое и в случае нестацио-
нестационарной турбулентности) выражает закон сохранения количества
диффундирующей примеси. Согласно этому уравнению, можно
положить
Р = Ж' 4 = -Ж' A0Л37)
z
причем W = W(Z\z, t)= Jp{Z'\z, t)dZ' будет иметь смысл ин-

10.6J 5 ГО. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 593
тегральной функции распределения вероятностей для коорди-
координаты Z(z, t) диффундирующей частицы. Подставив формулы
A0.137) во второе уравнение A0.136), мы получим для функ-
функции W так называемое телеграфное уравнение1)
ПО 138)
dt ~W dZ dZ #
Это уравнение — гиперболического типа; ему соответствует
распространение диффундирующей примеси в пространстве с ко-
конечной скоростью, не превосходящей W. Оно также является
лишь приближенным, так как опирается на нестрогую гипотезу
о марковском характере функции {Z(t), n(t)}, но все же оноточ-
нее обычного (одномерного) полуэмпирического уравнения тур-
турбулентной диффузии. В самом деле, нетрудно показать, что наше
новое уравнение диффузии представляет собой обобщение па-
параболического уравнения диффузии: последнее получается из
уравнения A0.138) как некоторый предельный случаи. Этолегче
всего продемонстрировать на примере диффузии в поле стацио-
стационарной однородной турбулентности, в котором коэффициенты
а и W не зависят не только от /, но и от Z, т. е. являются по-
постоянными. В этом случае р (а также р4 и р2) удовлетворяет тако-
такому же уравнению, что и Чг, а именно — телеграфному уравнению
^ + 2af = U^. 00.139)
Если параметры а и W неограниченно возрастают, причем та-
таким образом, что отношение W2/2a стремится к конечному пре-
пределу (который мы обозначим К), то телеграфное уравнение
A0.139) в пределе превращается в параболическое уравнение
диффузии -§?~К-§? (отвечающее рассматриваемому здесь
случаю, когда w(Z)—0).
') Уравнение вида A0.138) называется телеграфным, так как оно опи-
описывает также закон изменения во времени тока в проводнике (например, в
телеграфном кабеле) с сопротивлением R, емкостью С и самоиндукцией L,
если положить а==-п]~ и ^ = (С^) • Используя полученную аналогию,
можно заключить, что электроны как бы совершают в проводнике случайное
блуждание со средней скоростью (С/.)~1'",меняя направление движения в сред-
W 1
нем с частотой R/2L; величина К = -к— — -тто является прн этом анало>
гом коэффициента диффузии.

594
ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ .
[Ю.6
Решение уравнения A0.139) для неограниченного простран-
пространства— oo<Z<oo при начальных условиях A0.134) имеет вид
P{Z\z,
i a
"Г 2W
/0 (ax j/
i+c-o^r
l(^]/l-ri
A0.140)
где т = t'— t0, S = Z — z, /о и /t — символы функций Бесселя
мнимого аргумента, и при |?|>№т функция р принимается рав-
равной нулю. Формула A0.140) показывает, что в рассматриваемой
здесь теории распределение примеси, диффундирующей от мгно-
мгновенного точечного источника, имеет четкую границу — «фронт
волны» ? = ±№т, на котором сосредоточена конечная доля всего
количества диффундирующей примеси (причем эта доля экспо-
экспоненциально убывает со временем). За этим «фронтом» тянется
•непрерывный «след» (образованный частицами примеси, испы-
испытавшими многократное «рассеяние», т. е. изменение направле-
направления движения). В основной части этого «следа», а именно —
при |?|<с№т правая часть A0.140) при т^>— и любых ei и e2,
видеть, почти не отдичается от функции
как
нетрудно
а?
2WH
, являющейся решением параболического урав-
нения
dv д2р W2
~ш
W
=~2^- Таким образом, теория диффузии
с конечной скоростью приводит к заметному расхождению с вы-
выводами из параболического уравнения диффузии только или при
очень малом времени диффузии т^ —, или же вблизи от гра-
границы облака примеси, где концентрация по любой теории очень
мала. В качестве иллюстрации на рис. 84 приведены графики
непрерывной части распределения p{Z\z, t) при et = е2 = 1/2 и
ei = 1, е2 = 0 для двух значений аи вместе с графиками распре-
распределения примеси, отвечающими параболическому уравнению
диффузии.
Математическое ожидание и дисперсия распределения
A0.140) равны
4a*
(ЮЛ41)

10.6] .
при ах [
5 10. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 595
1 они почти не отличаются от значений 2 =
= z -4- тг- (е, — е9) и (Z — ZJ = 2АЧ = . Согласно принятой
здесь модели процесса диффузии, вероятность «рассеяния» на
малом интервале времени т равна ах + о(х), а «рассеяния» на
w ,
~1.ff
Рис. 84. Сопоставление непрерывной части распре-
распределения р (Z\z, t) при ах = 2 и «1 = 5 по теории
диффузии с конечной скоростью с распределением
Гаусса, вытекающим из параболического уравнения
диффузии.
Кривая / отвечает правой части формулы A0.140) (без слагае-
слагаемых, содержащих 5-функции) при 81=?г = '/г; кривая 2 —то же,
при *i = l, «2=0; пунктирная кривая —распределение Гаусса.
непересекающихся интервалах времени суть независимые слу-
случайные события. Поэтому число v(t) «рассеяний» на интервале
времени т — это случайная величина, имеющая распределение
Пуассона с параметром ах:

596 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ . [Ю.6
Если обозначить через рт(?, т) условную плотность вероятности
для Z(z, t)=Z(z, tQ+x) при условиях n(to) = l, v(t)=m, то, оче-
очевидно,
p(Z\z, t) = %^e-"[slPm(Z., xL-ea/»M(—С. х)}. A0.142)
/п=0
Эта формула дает разложение распределения A0.140) по «крат-
«кратности» рассеяний; с помощью A0.140) можно убедиться, что
Ро(?, т)=6(?— Wt), а при т>1 функции рт(?, т) отличны от
нуля лишь при |?| < №т и при этом условии имеют вид
)
<1ан3)
При a->oo, W->oo, -2^--+K распределение A0.140) асимпто-
асимптотически приближается к нормальному распределению с матема-
математическим ожиданием z и дисперсией -~- = 2f(*, являющемуся
решением параболического уравнения диффузии ~&==^~лТг-
Тот же предел, как мы видели, достигается, если а и W (а так-
же -^- = К\ фиксированы и ? фиксировано, но т неограничен-
неограниченно возрастает. Таким образом, при достаточно больших тв точ-
точках ?, далеких от «фронта волны» Z,= ±W%, изложенная схема
описания турбулентной диффузии дает практически такие же
результаты, что и обычная полуэмпирическая теория, основан-
основанная на использовании параболического уравнения. Это обстоя-
обстоятельство еще раз показывает, что изложенная схема действи-
действительно является обобщением полуэмпирической теории в том
смысле, что содержит в себе последнюю в качестве предельного
случая.
В качестве примера применения теории диффузии с конечной скоростью
к случаю неоднородной турбулентности посмотрим, как будет выглядеть эта
теория в применении к вертикальной диффузии в приземном слое воздуха.
В этом случае распределение концентрации b{Z,t) следует определять по
формуле Ъ = -гу, где x?=x?(Z,t) — решение соответствующего телеграфного
уравнения A0.138) прн надлежащих краевых условиях (мы ниже будем
использовать лишь условие «отражения» прнмесн прн 2=0) н начальном
условии, отвечающем наличию в момент t=U мгновенного точечного источ-
источника прнмесн единичной интенсивности в точке @, 0, Я). В силу общих прин-

10.6] t 10. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 597
ципов подобия, развитых в гл. 4, следует ожидать, что коэффициенты W
(размерности скорости) и а (размерности частоты) здесь могут быть пред-
представлены в виде
() () (Ш44)
где (pi к фг — безразмерные универсальные функции, а Я, — введенная для
удобства числовая постоянная, позволяющая наложить на функцию q>i(?)
дополнительное ограничение q>i @) = 1 (при этом Я будет иметь смысл пре-
предельного значения W/и, при -г- -> 0, т. е. отношения W/и, при безразличной
стратификации). Поскольку рассматриваемая теория диффузии все равно не
является точной, имеет смысл привлечь дополнительные приближенные со-
соображения полуэмпнрического характера и для определения функций <Pi(?)
и <Рг(?). Это можно сделать, например, следующим образом. Примем за
основу полуэмпирическое соотношение /(=и»/A — aRf)''4 (см. § 6); если,
кроме того, еще допустить, что /С~ WI, то отсюда вытекает, что
W~u± A — aRfL, т.е.
где /(?) — универсальная функция, определяющая профиль средней скорости
ветра в приземном слое воздуха. Воспользуемся теперь тем, что в стацио-
стационарном случае уравнения A0.136) имеют вид
q = const, 2aq = — W-^r-, A0.146)
где q — вертикальный поток диффундирующей примеси. При безразличной
стратификации, которой мы уделим больше всего внимания в дальнейшем,
w = Яи* = const; поэтому правую часть второго уравнения A0.146) здесь
можно записать в виде — W2 -=-=. В общем случае, строго говоря, это будет
уже не так, но можно надеяться, что и здесь появляющаяся поправка к
Jill
слагаемому —IP'-ту будет относительно невелика и не будет играть боль-
большой роли. Таким образом, в первом приближении можно положить
дЬ lag _ Чд y2 (Q
dZ ~ W2 Х*и,2 [?i (О]2 "
С другой стороны, если пренебречь возможным различием коэффициента тур-
турбулентной диффузии и коэффициента турбулентной вязкости, то, согласно тео-
теории подобия, градиент стационарного распределения концентрации пассивной
прнмеси будет равен
д% _
dZ~~
Сравнивая два приведенных выражения для -^ и используя A0.145), по-
получим
(О = ?С/'(ОГ1 т^жУ- (Ю.147)

598 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [10.6
Формулы A0.144), A0.Н5) н A0.147) прн известной функции /(?) и извест-
известной постоянной а (которую допустимо считать принимающей разные значе-
значения прн устойчивой и прн неустойчивой стратификации) полностью опреде-
определяют внд коэффициентов телеграфного уравнения днффузнн A0.138) ^ля
приземного слоя воздуха. Прн этом предельный переход а -> со, W -> со,
W2
-п > К = const, соответствующий замене телеграфного уравнения обыч-
обычным параболическим уравнением днффузнн, очевидно, будет эквивалентен
переходу к пределу прн X -> со.
Пользуясь полученными формулами и переходя к безразмерным перемен-
переменным ? = -/- н х=—*-Ц- > мы можем привести уравнение A0.138) к
виду
d*V 2n dW
где я = -=—, а переменная ? н функция g(?) определяются формулами
- A0Л49)
Как н функция /(?), переменная ? н функция g(%) в случаях безразличной.,
устойчивой и неустойчивой стратификации определяются по-разному. Так, в
случае безразлнчной стратификации во всех предыдущих форму-
формулах следует перейти к пределу L -*• со нлн ? = -г- -> 0. Но /' (?) и -=-, ? и ?
и g и ? прн малых | С|; поэтому уравнение A0.148) здесь принимает внд
Если теперь мы вернемся от безразмерных переменных (?, т) к размерным
переменным B, i), то масштаб L сократится. Поэтому в случае безразлнчной
стратификации мы можем пользоваться уравнением A0.150), понимая под L
любой конечный масштаб. В случае устойчивой стратификации,
пользуясь для f{t), например, интерполяционной формулой /(?) «In ?+Сг?,
где Сг = 1/Rfcr = о", прн больших ? получаем: ./'@~'о + ^~ > 5~'С* и
g ~< ? "Ч В случае неустойчивой стратификации прн больших ?
имеем /' (?) <~> ? 3, так что ?~? и ^г~'?3. Следовательно, функция g{Q
в уравнении A0.148) прн устойчивой стратификации возрастает с увеличе-
увеличением ^ медленнее, а прн неустойчивой стратификации — быстрее, чем ?; в
этом и заключается основное качественное отлнчне указанных случаев от
случая безразлнчной стратифнкацнн!
Далее мы ограничимся рассмотрением уравнения A0.150), описываю-
описывающего диффузию с конечной скоростью в приземном слое воздуха при без-
безразлнчной температурной стратификации. Прн этом в качестве масштаба L,
используемого для измерения высот 2, удобно выбрать высоту источника Н,
так что безразмерные переменные (?, т) определяются формулами ?=77'
hi, (t - t0) „
< = —^—тз——. Начальные условия для интересующего нас решения

10.6] § 10. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ 599
(S, т) мы сформулируем сначала в терминах условных плотностей вероят-
вероятности р\ и р2, удовлетворяющих уравнениям A0.135):
pi(Z\H, 0->ei4Z — Я), p2(Z\H,t)^-z2b(Z — H) при t-i.t0,
где ei и е2 — вероятности положительного и отрицательного направления на-
начального движения диффундирующей частицы, определяемые из физических
соображений (например, для частиц дыма, выходящих из дымовой трубы,
естественно принять, что ei = l, e2 = 0, а для частиц газа, распространяю-
распространяющихся от точки разрыва снаряда —что ei = е2 = -g")- Но так как
z
Ч? — I (pl-lrpt)dZ и -Z-T- = — W (pi — рг) в силу формул A0.137), то для
о
функции Ч*1 начальные условия записываются в виде
dW (?, х)
1 \ \" /
т=0
где ?(?)—сосредоточенное в точке ? = 0 распределение вероятностей, т. е.
функция, равная нулю при ?<0 и единице при ? > 0.
Интересующее нас решение уравнения A0.150), удовлетворяющее усло-
условию «отражения» ирнмеси на поверхности Земли 2=0, очевидно, будет сов-
совпадать с решением уравнения
во всем пространстве—со<?<со, соответствующим наличию, кроме источ-
источника в точке Н, также и симметрично действующего источника в точке —Н.
Поэтому мы можем положить Ч^!;, t)=4('i(?, т)+Ч'1(^-?,т), где 4fi(?, т) —
решение уравнения A0.152), удовлетворяющее условиям A0.151). В частном
случае наземного источника (при Я=0) в условиях A0.151), очевидно, надо
считать, что ei = 1, е^ = 0, а решение xFi(?, т) здесь обращается в функцию
Ч'о(?> т), которая может зависеть только от отношения своих аргументов
5= —= т—тт—г-г, т. е. имеет вид x?0(t,,x)=F(s). При этом уравнение
х ли, (т — т0)
A0.152) обращается в обыкновенное уравнение второго порядка относительно
F(%), решение которого, отвечающее условиям нашей задачи, как оказы-
оказывается, имеет вид
viro(C> z) = F(i)=\ 1-(-T^f)" прн °<6<1» . A
I 0 прн 5 > 1 или 5 < 0
(Моннн A9566)), Следовательно, концентрация примеси 9 = ._° здесь за-
задается формулой
Отметим, что F(l — 0) = 1 согласно формуле A0.153), т. е. функция F(%)
здесь оказывается непрерывной в точке |=1; иными словами, доля примеси,
находящаяся на «фронте» ее распространения 2=Хмхт, во все моменты вре-
времени равна нулю (это объясняется тем, что в точке 2=0 частота «рассея-

Z/H
1,0
0,8
0,6
ол
0,2
•Л
* **
600 ГЛ. V. ДРИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.6
ний> а = -g—=¦ бесконечно велика, так что частица, вышедшая из источника
в точке 2=0, не может не испытать ни одного рассеяния). Характер поведения
концентрации примеси около «фронта> существенно зависит от значения чис-
числовой постоянной ra = "a7- При га<1 (т. е. А,<2х»0,8) концентрация примеси
неограниченно растет при приближе-
приближении к «фронту>, так что последний
имеет характер сильного разрыва. При
га > 1 (т. е. А, > 2х » 0,8), наоборот, кон-
концентрация примеси при приближении к
фронту стремится к нулю (а при
га = 1 — к некоторому конечному зна-
значению). Экспериментальным данным Ка-
Казанского и Моиина A957) лучше все-
всего соответствует значение га, близкое
к единице. В экспериментах этих авто-
авторов измерялись профили концентрации
примеси в дымовой струе от стационар-
стационарного линейного источника, перпенди-
перпендикулярного направлению ветра, на рас-
_ стоянии от источника в 100 м. Двадцать
Q2 ~д~? ~дд до "Jg измеренных профилей были сведены на
g/'ф ' один_график в форме ¦©¦/¦©¦max = /(•?/#),
т" где Ошах — наибольшее значение кон-
Рис. 85. Вертикальное распреде- центрацни дыма для данного профиля
ление плотности дыма в дымовой (которое из-за того, что дым был теп-
струе. лее воздуха и поэтому стремился под-
подняться вверх, обычно достигалось не
при 2=0, а на небольшой положитель-
положительной высоте), а Н—_высота дымовой струи в точке измерения. Эмпири-
Эмпирические данные о О/От ах следует сравнивать с теоретической кривой
/E) = A—5)n~1(l-f-5)~"~1. Такое сравнение показано на рис. 85, где
пунктирными кривыми проведены теоретические функции с га=1 и n=-j.
График показывает, что концентрация дыма при приближении к «фронту»
остается, по крайней мере, ограниченной (т. е. га!>1) и что теоретическая
кривая с га=1 все же лучше аппроксимирует экспериментальные данные, чем
с га =s-j-. В одном из опытов Казанского и Монина с помощью кинемато-
графиррвания одиночного клуба дыма был также нзучен характер роста его
вертикального диаметра d со временем. При. этом оказалось, что эксперимен-
экспериментальная кривая d(t) хорошо аппроксимируется прямой d = 2W(t—to), причем
W
значение X = — оказалось равным 0,75, чему опять соответствует значение
хи*
га = -я—, близкое к единице.
При сопоставлении теории диффузии с конечной скоростью с обычной
полуэмпирической теорией турбулентной диффузии решение A0.154) целесо-
целесообразно сравнивать с решением A0.93'), отвечающим случаю линейного воз-
возрастания коэффициента обмена /C=xu,2=/Ci2. Такое сопоставление (в пред-
предположении, что га=1,25) представлено на заимствованном из книги Паскуила
A9626) рис, 86. Мы видим, что профиль средней концентрации 0B) при

10.6]
§ m. турбулентная: диффузия
601
каждом фиксированном x=t—to в пределах значений Z, которым еще соот-
соответствуют относительно большие значения концентрации О, принимает очень
близкую форму в теории диффузии с конечной скоростью и в обычной полу-
полуэмпирической теории. Существенное расхождение профилей наблюдается
лишь около «вершины» облака примеси, где согласно теории диффузии с
конечной скоростью концентрация внезапно падает до нулевого значения, в
то время как согласно обычной теории она продолжает плавно убывать,
оставаясь отличной от нуля при сколь угодно больших значениях Z.
dxutl
Q
0.8
0,6
04
0.2
\
i ii i V
0,2
0,6
' 1.0
Рис. 86. Сопоставление вертикального распределе-
распределения концентрации по теории диффузии с конечной
скоростью (пунктирная кривая) с распределением,
получаемым из параболического уравнения диффу-
диффузии с линейным по высоте коэффициентом обмена
(сплошная кривая).
При А.-»оо функция A0.54), естественно, стремится к функции A0.93'),
являющейся решением параболического уравнения диффузии ~~- =а
д дЬ
~ ~dz~xu* ~dz~' B случае наземного точечного источника, производящего
примесь, начиная с момента t = 0, с постоянной (единичной) скоростью, кон-
концентрация Oi (Z, t) находится с помощью интегрирования по времени решения
A0.154); при <->ооотсюда легко получается следующее разложение по сте-
степеням \Ц:
=- /
¦ да
^+...).
<10Л55>

602 ГЛ. V. ДВИЖЕНИЕ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ [Ю.6
Эта формула позволяет оценивать скорость приближения профиля концен-
концентрации к логарифмическому профилю, соответствующему стационарному на-
наземному источнику.
В случае высотного источника (на произвольной высоте Н) решение со-
соответствующей задачи с начальными условиями для уравнения A0.152) мо-
может быть найдено с помощью общего метода Римана решения дифферен-
дифференциальных уравнений второго порядка гиперболического типа. • Это решение,
вообще говоря, имеет значительно более громоздкий вид (оно представляется
в виде интеграла от сложной комбинации гипергеометрических функций; см.
Монин A9566)). Тем не менее, в некоторых случаях оно может быть заметно,
упрощено. Так, например, для наземной концентрации примеси от высотного
мгновенного точечного источника, выпустившего всю примесь вверх (дымовая
труба), получается формула вида
= 21 ('-В", ,>1. A0.156)
Н (t+l)" + 1
Исходя из формул A0.140) и A0.156), для распределения наземной концен-
концентрации по направлению ветра от дымовой трубы высоты Н можно получить
формулу
Щ 1 /(?). (Ю.157)
где
Q — масса дыма, выходящего из трубы за единицу времени, U — скорость
ветра (предполагаемая постоянной), a «i и ах — средняя скорость движения
и частота «рассеяний» частиц, диффундирующих в горизонтальной плоскости
поперек направления ветра. Параметр а следует считать малым, и при оценке
положения и величины максимума функции A0.157) можно приближенно
заменить /(al) единицей.

БИБЛИОГРАФИЯ
Абрамович Г. Н.
1960. Теория турбулентных струй, М., Физматгиз.
АллениТэйлорЕ. (Allen С. М., Taylor E. А.)
1923. The salt velocity method of water measurement, Trans. Amer. Soc
Mech. Engrs, 45, 285—341.
'А и д р о и о в А. А., В и т т А. А. и X а й к и и С. Э.
1959. Теория колебаний, 2 изд. М., Физматгиз.
А р и с (Aris R.)
1956. On the dispersion of a solute in a fluid flowing through a tube,
Prop. Roy. Soc, A235, No: 1200, 67—77.
Ахиезер Н. И.
1961. Классическая проблема моментов, М., Физматгиз.
Бай Ш и - и (Pai Shih-i)
1954. Fluid dynamics of jets, Toronto — N. Y. — London, Van Nostrand
(русск. перевод: Бай Ши-и, Теория струй, М., ИЛ, 1960).
Б а ре д (Barad M. L.)
1958. Project Prairie Grass, a field program in diffusion, vols. 1—2,.Geo-
phys. Res. Pap., No. 59, Cambridge, Mass.
1963. Examination of a wind profile proposed by Swinbank, J. Appl. Me-
Meteor., 2, No. 6, 747—754.
Баред и Хоугеи (Barad M. L., Haugen D. A.)
1Э59. A preliminary evaluation of Sutton's hypothesis for diffusion from
a continuous point source, J. meteorol., 16, No. 1, 12—20.
Бареиблатт Г. И.
1953. О движении взвешенных частиц в турбулентном потоке, Прикл. ма-
тем. мех., 17, № 3, 261—274.
1955. О движении взвешенных частиц в турбулентном потоке, занимаю-
занимающем полупространство или плоский открытый каиал конечной глу-
глубины, Прикл. матем. мех., 19, № 1, 61—88.
Бариес и Кокер (Barnes H. Т., Coker E. G.)
1905. Experiments on streamline motion and the measurements of critical
velocity, Proc. Roy. Soc. London, 74, No. 503, 341—356.
Белякова В. К.
1950. К вопросу об устойчивости движения вязкой жидкости в прямой
круглой трубе. Прикл. матем. мех., 14, № 1, 105—110.
Бенни (Benney D. J.)
1961. A non-lmear theory for oscillations in a parallel flow, J. Fluid Mech.,
JO, No. 2, 209-236,, Г

604 БИБЛИОГРАФИЯ
1964. Finite-amplitude effects in an unstable laminar boundary layer, Phys.
Fluids, 7, № 3, 319—326.
БерляидМ. Е.
1947. Теория изменения ветра с высотой, Труды научно-нссл. учр. Глави.
упр. гидрометслужбы, сер. 1, № 25, 16—67.
БерляндМ. Е., Генихович Е. Л., Ложкина В. П. н Оникул Р.И.
1963. Численное решение уравнений турбулентной диффузии и расчет
загрязнения атмосферы вблизи промышленных предприятий, Труды
Гл. геофиз. обсерв., № 138, 3—17.
1964. Численное исследование атмосферной диффузии при нормальных и
аномальных условиях стратификации, Труды Гл. геофиз. обсерв.,
№ 158, 22—31.
Б ест (Best А. С.)
1935. Transfer of heat and momentum in the lowest layers of the atmo-
atmosphere, Geophys. Mem., 7, No. 65.
Б е т ч о в (Betchov R.)
1960. On the mechanism of turbulent transition, Phys. Fluids, 3, No. 6,
1026—Ш27.
Бетчов и Шевчик (Betchov R., Szewczyk A.)
1963. Stability of shear layer between parallel streams, Phys. Fluids, 6,
No. 10, 1391—1396.
Б и р к г о ф (Birkhoff G.)
1962. Helmholtz and Taylor instability, Proc. Symp. Appl. Math., 13 (Hyd-
rodynamic instability), 55—76_?вусск. перевод в сб. «Гидродинами-
«Гидродинамическая неустойчивость», М., М^Ц5ЩЩ
Биркгоф и Кампе де Ферье (Birkhoff G., Kampe de Feriet J.)
1962. Kinematics of homogeneous turbulence. D. Metric transitivity, J.
Math. Mech., 11, No. 3, 319—340.
Биркгоф и Царантоиелло (Birkhoff G., Zarantonello E. H.)
1957. Jets, wakes and cavities, N. Y. Acad. Press.
Блэкедар (Blackadar A. K-)
1962. The vertical distribution of wind and turbulent exchange in a neu-
neutral atmosphere. J. Geophys. Res., 67, No. 8, 3095—3102.
БовшеверовВ. М. и Воронов В. П.
1960. Акустический флюгер, Изв. АН СССР, сер. геофиз., № 6, 882—
885.'.
Бовшеверов В. М., Гурвич А. С, Мордухович М. И. и
Ц в а н г Л. Р.
1962. Приборы для измерений пульсаций температуры и скорости ветра
и для статистического анализа результатов измерений, сб. «Атмо-
«Атмосферная турбулентность» (Труды Инст. физ. атмосф. АН СССР,
№ 4), 21—29.
Бовшеверов В. М., Гурвич А. С, Татарский В. И. и Цваиг Л. Р.
1959. Приборы для статистического анализа турбулентности, Труды
совещ. по исслед. мерцания звезд, М., Изд. АН СССР,
26—32.
БовшеверовВ. М., Гурвич А. С. иЦваиг Л. Р.
1959. Прямые измерения турбулентного потока тепла в приземном слое
атмосферы, Докл. АН СССР, 125, № 6, 1242—1245.
Бозаике и Пирсон (Bosanquet С. Н., Pearson J. L.)
1936. The spread of smoke and gases from chimneys, Trans. Faraday Soc..
32, No. 8, 1249—126.3..

БИБЛИОГРАФИЯ 605
Болдуин иМайкельсеи (Baldwin L. W., Mickelsen W. R.)
1962. Turbulent diffusion and anemometer measurements, J. Eng. Mech.,
88, No. 1, 37—69; discussion, 151—153.
Б о x н e p (Bochner S.)
1933. Monotone Funktionen, Stieltjessche Integrate und harmonische Ana-
Analyse, Math. Ann., 108, No. 3, 378—410 (русск. перевод в кни-
книге: С. Б о х н е р, Лекции об интегралах Фурье, М., Физматгиз,
1962).
Б у д ы к о М. И.
1946. Распределение метеорологических элементов в приземном слое ат-
атмосферы, Изв. АН СССР, сер. геогр. и геофиз., 10, № 4, 317—
329.
1948. Испарение в естественных условиях, Л., Гидрометеоиздат.
Буссииеск (Boussmesq J.)
1897. Theorie de l'ecoulement tourbillonnant et tumulteux des liquides dans
les lits rectilignes a grande section, I—II, Paris, Gauthier-Villars.
Бьоргум (Bjorgum 0.)
1953. On the velocity, temperature and humidity profiles, Quart. J. Roy.
Meteor. Soc, 79, No. 339, 84—93.
Бэрнс, Чайлдс, Никол и Росс (Burns J. G., Childs W. H. J., Ni-
col A. A., Ross M. A. S.)
1959. Development and use of a vane device for boundary-layer measure-
measurements, J. Fluid Mech., 6, No..l, 97—112.
Бэтчелор (Batchelor G. K.)
1949a. The role of big eddies in homogeneous turbulence, Proc. Roy. Soc,
AI95, No. 1043, 513—532.
19496. Diffusion in a field of homogeneous turbulence, Austr. J. Sci. Res.,
A2, No. 4, 437—450.
1957. Diffusion in free turbulent shear flows, 1 Fluid Mech., 3, No. 1,
67—80.
1969. fliffusion from sources In a turbulent boundary layer (неопублико-
(неопубликованная рукопись).
Бэтчелор, Биннн и Филлнпс (Batchelor G. К., Binnle A. M., Phil-
Phillips О. М.)
1955. The mean velocity of discrete particles In turbulent flow In a pipe,
Proc. Phys. Soc, B68, No. 432, 1095—1104.
Бэтчелор иТаунсенд (Batchelor G. K., Townsend A. A.)
, 1956. Turbulent diffusion, Surveys In Mechanics (ed. by G. K. Batchelor
and R. M. Daivles), Cambridge, Univ. Press, 352—399.
Бюсиигер (Businger J. A.)
1955. On the structure of the atmospheric surface layer, J. Meteor., 12,
No. 6, 553—561.
• 1959. A generalization of the mixing-length concept, J. Meteor., 16, No. 5,
516-523.
Бютиер Э. К. и Лайхтман Д. Л.
1963. О рассеянии пассивных частиц от точечного источника в неодно-
неоднородной среде, Труды Ленингр. гидромет. ин-та, вып. 15,
130-136.
Ванд ель и Кофёд-Ханзен (Wandel С. F., Kofoed-Hansen О.)
1962. On. the Eulerian-Lagrangion transform in the statistical theory of
turbulence, J. Geophys. Res., 67, No. 8, 3089—3093,

606 БИБЛИОГРАФИЯ
Ван Дрист (van Driest E. R.)
1956. On turbulent flow near a wall, J. Aeronaut. Sci., 23, No. 11, 1007—
1011.
1959. Convective heat transfer in gases, Turbulent flows and heat transfer
(ed by С. С. Lin), Princeton, Univ. Press, 339—427 (русск. перевод
в книге «Турбулентные течения и теплопередача», М., ИЛ, 1963,
349—436).
В а зо в (Wasow W.)
1953. On small disturbances of plane Couette flow, J. Res. Nat. Bur. Stan-
darts, 51, 195—202.
Великанов М. A.
1946. Динамика русловых потоков, Л.—М-, Гидрометеоиздат.
В е л ь т е (Velte W.)
- 1962. Ober ein Stabilitatskriterium der Hydrodynamik, Arch. Rat. Mech.
Anal., 9, Nr. 1, 9—20.
Вигхардт (Wieghardt K.)
1940. Uber die Wirkung der Turbulenz auf den Umschalgspunkt, Zs. an-
gew. Math. Mech., 20, Nr. 1, 58—59.
1944. Uber die turbulente Stromung in Rohr und langs der Platte, Zs.
angew. Math. Mech., 24, Nr. 4, 294—296.
Виттинг (Witting H.)
1958. Uber den Einfluss der Stromlinienkrummung auf . die Stabilitat
laminarer Stromungen, Arch. Rat. Mech'. Anal., 2, Nr. 3, 243—283.
В о э н (Vaughan L. M.)
1961. The prediction of atmospheric diffusion by using an eddy diffusivity
based on the vertical transfer of heat, J. Meteor., 18, No. 1,
43—49.
Галлахер иМерсер (Gallagher A. P., Mercer A. McD.)
1962. Qn the b?ha\douT of small disturbances in plane Couette flow. J.
Fluid Mech., 13, No. 1, 91—100.
1964. On the behaviour ol small disturbances in plane Couette flow.
Part 2. The higher eigenvalues, J. Fluid Mech., 18, No. 3, 350—352.
Г а м е л ь (Hamel G.) "=
1911. Zum Turbulenzproblem, Nachr. Ges. Wiss. Gottingen, Math.-Phys. Kl.,
261—270.
Г а с т e p (Gaster M. A.)
1962. A note on the relation between temparally.-increasing and spatially-
increasing disturbances in hydrodynamlc stability, J. Fluid Mecfr.,
14, No. 2, 222—224.
Г е д е к e (Godecke K.)
1935. Messungen der atmospharischen Turbulenz in Bodennahe rait einer
Hitzdrahtmethode, Ann. Hydrogr., Nr. 10, 400—410.
Гейзенберг (Heisenberg W.)
1924. Uber Stabilitat und Turbulenz von Flussigkeitsstromen, Ann. Phys.,
D), 74, 577—627.
Гельмгольц (Helmholtz H.)
1868. Uber discontinuierliche Flussigkeitsbewegungen, Monatsber. Коп.
Akad. Wiss., Berlin, 23, 215—228 (русск. перевод: Г. Гельмгольц,
Два исследования по гидродинамике, СПб, 1902).
Гельфанд И. М. и Виленкин Н. Я.
1961. Некоторые применения гармонического анализа. Оснащенные гиль-
гильбертовы пространства («Обобщенные функции», вып. 5), М., Физ-
матгиз.

БИБЛИОГРАФИЯ 607
Г е р б е р (Gerber R.)
1949. Sur la reduction a un principe variationnel des equations du mouve-
ment d'un fluide visqueux incompressible, Ann. Inst. Fourier, 1,
157—162.
Г е р т л е р (Gortler H.)
1942. Berechnung von Aufgaben der freien Turbulenz auf Grund eines
neuen Naherungsansatzes, Zs. angew. Math. Mech., 22, No. 5, 244—
254.
1959. Ober eine Analogie zwischen der Instabilitaten laminaren Grenz-
schichtstromungen an konkaven Wanflen und an erwarmten Wanden,
Ing. Arch., 28, Nr. 1, 71—78.
Ги иДэвис (Gee J. H., Davies D. R.)
1963. A note on horizontal dispersion from an instantaneous ground sorce,
Quart. J. Roy. Meteor. Soc., 89, No. 382, 542—545.
Гиршфельдер, Кертисс и Берд (Hirschfelder J. О., Curtiss С. F.,
Bird R. B.)
1954. Molecular theory of gases and liquids, N. Y., Viley; London, Chap-
Chapman and Hall (русск. перевод: Дж. Гиршфельдер, Ч. Кертисс,
Р. Берд, Молекулярная теория газов и жидкостей, М., ИЛ, 1961).
Г и ф ф о р д (Gifford F. А.)
1962. Diffusion in the diabatic surface layer, J. Geophys. Res., 67, No. 8,
3207—3212.
Гольдштейн (Goldstein S.)
1931. On the stability of superposed streams of fluids of different densi-
densities, Proc. Roy. Soc, AI32, No. 820, 524—539.
1938. Modern developments in fluid dynamics, vols. 1—2, Oxford Univ.
Press (русск. перевод: Современное состояние гидродинамики
вязкой жидкости, под ред. С. Гольдштейна, т. 1—2, М., ИЛ, 1948).
1951. On diffusion by discontinous movement and on the telegraph equa-
equation, Quart. J. Mech. Appl. Math., 4, No. 1, 129—156.
Горькое Л. П.
1957. Стационарная конвекция в плоском слое жидкости вблизи крити-
критического режима теплопередачи, Ж. эксп теор. физ., 33, № 2(8),
402—411.
Го ее (Gosse J.)
1961. Sur l'ecoulement turbulent des fluids, С. г. Acad. Sci., 253, № 1,
61—63.
Г огф май (Hofmann E.)
1940. Ober die Gesetzmassigkeiten der Warme- und Stoffubertragung auf
Grund des Stromungsverganges im Rohr, Forsch. Gebiete Ingenieur-
wesens, Ail, 159—169.
Грант (Grant A. M.)
1957. Corrected mixing-leght theory of turbulent diffusion, J. Meteor., 14,
No. 4, 297—303.
Гребер и Эрк (Grober H., Erk S.)
1955. Die Grun,dgesetze der Warmeubertragung, Berlin — G6ttingen — Hei-
Heidelberg, Springer (русск. перевод: Г. Гребер, С. Эрк и У. Григулль,
Основы учения о теплообмене, М., ИЛ, 1958).
Гренандер (Grenander U.)
1950. Stochastic processes and statistical inference, Ark. Mat, I, No 3,
195—277 (русск. перевод: У. Гренаидер, Случайные процессы и
статистические выводы, М., ИЛ, 1961),

608 БИБЛИОГРАФИЯ
Грииспан и Бенни (Greenspan H. Р., Веппеу D. J.)
1963. On schear-layer instability, breakdown and transition, J. Fluid Mech..,
15, No. 1, 133—153.
Г р о н e (Grohne D.)
1954. Ober das Spektrum bei Eigenschwingungen ebener Laminarstromun-
gen, Zs. angew. Math. Mech'., 34, Nr. 3, 344—357.
Г р у з а Г. В.
1961. Макротурбулентность в общей циркуляции атмосферы, Л., Гидро-
метеоиздат.
ГурвичА. С. ^
1959. Акустический микроанемометр для исследования микроструктуры
турбулентности, Акустич. журнал, 5, № 3, 368—369.
1960. Экспериментальное исследование частотных спектров и функций
распределения вероятностей вертикальной компоненты скорости вет-
ветра, Изв. АН СССР, сер. геофиз., № 7, 1042—1055.
1961. Измерение напряжения трения в приземном слое атмосферы, Изв.
АН СССР, сер. геофиз., № 3, 458—466.
1962. Турбулентный поток количества движения при неустойчивой стра-
стратификации и в условиях, близких к безразличному равновесию, сб.
«Атмосферная турбулентность» (Труды Инст. физ. атмосф. АН
СССР, №4), 81-100.
1965. Вертикальные профили скорости ветра и температуры в приземном
слое атмосферы, Изв. АН СССР, сер. «Физика атмосферы и океа-
океана», 1, № 1.
Давыдов Б. И.
1935. Уравнение диффузии с учетом молекулярной скорости, Докл. АН
СССР, 2, № 7, 474-478.
1958. Феноменологические уравнения статистической динамики несжимае-
несжимаемой турбулентной жидкости, Ж. эксп. теор. физ.. 35, № 2(8),
527—529. .
1959а. К статистической динамике несжимаемой турбулентной жидкости,
Докл. АН СССР, 127, № 4, 768—771.
19596.'К статистической теории турбулентности, Докл. АН СССР, 127,
№5,980—982.
1961. К статистической динамике несжимаемой турбулентной жидкости,
Докл. АН СССР, 136, № 1, 47—50.
Д а н е-р (Dyer A. J.)
1958. An improved electromagnetic integrator, J. Scient. Instr., 35, No. 7, 240.
1960. Heat transport anemometer of high stability, J. Scient. Instr., 37,
No. 5, 166—169.
1961. Measurements of- evaporation and heat transfer in the lower atmo-
atmosphere by an automatic eddy-correlation technique, Quart. J. Roy.
Meteor. Soc, 87, No. 373, 401—412.
Д а й с о и (Dyson F. J.)
1960. Stability of an idealised atmosphere, II, Zeros of the confluent hy-
pergeometric function, Phys. Fluids, 3, No. 2, 155—158.
Д а р с и (Darcy H.)
1858. Recherches experimentales relatives aux mouvement de l'eau dans les
tuyaux, Mem. Sav. Etrang. Acad. Sci., 15, 265—342
Д е й с л e p (Deissler R. G.)
1951. Investigation of turbulent flow and heat transfer in smooth tubes,
including the effects of variable fluid properties, Trans. Amer. Soc.
Mech. Engrs, 73, No. 1, 101—107.

БИБЛИОГРАФИЯ 609
4. Heat transfer and fluid friction for fully developed turbulent flow of
¦ air and supercritical water with variable fluid properties, Trans.
Amer. Soc. Mech. Engrs, 76, No. 1, 73—86.
1955. Analysis of turbulent heat transfer, mass transfer and friction in
smooth tubes at high Prandtl and Schmidt numbers, Nat. Adv. Com.
Aeronaut. Rep. 1210.
1959. Convective heat transfer and friction in flow of liquids. Turbulent
flow and heat transfer (ed. by С. С. Lin), Princeton, Univ. Press,
288—338 (русск. перевод в книге «Турбулентные течения и тепло-
теплопередача, М., ИЛ, 1963, 297—353).
Д е ф а н т (Defant A.) '
1921. Die Zirkulation der Atmosphere in den gemassigten Breiten der
Erde, Geografiska Annaler, 3, 209—265.
Д ж е ф р и с (Jeffreys H.)
1926. The stability of a layer of fluid heated from below, Phil. Mag.,
G) 2, 833-844.
1928. Some cases of instability in fluid motion, Proc. Roy. Soc, A118,
No. 779, 195—208.
Джонс и Паскуил (Jones J. I. P., Pasquill F.)
1959. An experimental system for directly recording statistics of the in-
intensity of atmospheric turbulence, Quart. J. Roy. Meteor. Soc, 85,
No. 365, 225—236.
Д и к и й Л. А.
-1960а. Об устойчивости плоскопараллёльных потоков неоднородной жид-
жидкости, Прикл. матем. мех., 24, № 2, 249—257.
19606. Устойчивость плоскопараллельиых потоков идеальной жидкости,
Докл. АН СССР, 135, № 5, 1068—1071.
1960в. О корнях функции Уиттекера и функции Макдоиальда ком-
комплексного индекса, Изв. АН СССР, сер. матем„ 24, № 6, 943—
954.
1964. Об устойчивости плоскопараллельного течения Куэтта, Прикл. ма-
матем. мех., 28, Ni 2, 389—392.
Д и к о н (Deacon E. L.)
1949. Vertical diffusion in the lowest layers of the atmosphere, Quart
J. Roy. Meteor. Soc, 75, No. 323, 89—103.
1955. The turbulent transfer of momentum in the lowest layers of the at-
atmosphere, С S. I. R. O., Div. Meteor. Phys., Techn. Pap. No. 4,
Melbourne.
1959. The measurements of turbulent transfer in the lower atmosphere,
Adv. Geophys., 6 (Atmospheric diffusion and air pollution), 211—228
(русск. перевод в сб. «Атмосферная диффузия и загрязнение воз-
воздуха», М., ИЛ, 1962, 236—255).
1962. Aerodynamic roughness of the sea, J. Geophys. Res., 67, No. 8,
3167—3172.
Дикой и Уэбб (Deacon E. L., Webb E. K.)
1962. Interchange of properties between sea and air. Small-scale interac-
interaction, The Sea (ed. by M. N. Hill), vol. 1, N. Y. —London, Inter-
science Publ., 43—87.
Д и Прима (Di Prima R. C.)
,1955. Application of the Galerkin method to the calculation of the stability
of curved flows, Quart. Appl. Math., 13, No. 1, 55—62 (русск. пере-
перевод в сб. «Механика», № 3 C7), 1956),

610 БИБЛИОГРАФИЯ.
1961. Stability of nonrotationally symmetric disturbances for viscous flow
between rotating cylinders, Phys. Fluids, 4, No. 6, 751—755.
Дирдорфф (Deardorff J. W.)
1963. On the stability of viscous plane Couette flow, J. Fluid Mech., 15,
No. 4, 623—631.
Д о н н е л и (Donnelly R. J.)
1962. Experimental determination of stability limits, Proc. Symp. Appl.
Math., 13 (Hydrodynamic instability), 41—53 (русск. перевод в сб.
«Гидродинамическая неустойчивость:», М., Мир, 1964, 54—67).
1963. Experimental confirmation of the Landau law in Couette flow, Phys.
Rev. Letters, 10, No. 7, 282—284.
ДоннелииФультц (Donnely R. J., Fultz D.)
1960. Experiments of the stability of viscous flow between rotating cy-
cylinders, II, Visual observations, Proc. Roy. Soc, A258, No. 1292,
101—123.
Дородницын A. A.
1941. К теории суточного хода температуры в слое перемешивания,
Докл. АН СССР, 30, № 5, 410—413.
Д р а з и н (Drazin P. G.)
1958. The stability of a shear layer in an unbounded heterogeneous fluid,
J. Fluid Mech., 4, No. 2, 214—224.
Дразни иХоуард (Drazin P. G., Howard L. Ш
1962. The instability to long waves of unbounded parallel inviscid flow,
. : J. Fluid Mech., 14, No. 2, 257—283.
Д р а й д е н (Pryden H. L.)
1959. Transition from laminar to turbulent flow, Turbulent flow and heat
transferred, by С. С.-Lin), Princeton, Univ. Press. 3—74 (русск.
перевод в книге «Турбулентные течения и теплопередача», М., ИЛ,
- , . 1963, 9-82).
Драйдеи, Шубауэр, Мок и Скрэмстад (Dryden H. L., Schu-
bauer G. В., Mock W. С, Skramstad H. К.)
1937. Measurements of intensity and scale of wind-tunnel turbulence and
their relation to the critical Reynolds number of spheres, Nat. Adv.
Com. Aeronaut., Rep. No. 581.
Дриммель и Рейтер (Drimmel J., Reuter H.)
1960. Der Exponent n in Sutton's Ansatz fur die Lagrangesche Korrela-
tionsfunktion. Arch. Meteor., Geophys. und Bioklim., AI2, Nr. 1,
24—39.
Д у а й е р (Dwyer О. Е.)
1963. Eddy transport in liquid-metal heat transfer, A. I. Ch. E. Journal,
9, No. 2, 261—268.
Дуб (Doob J. L.)
1953. Stochastic processes, N. -Y., Wiley (русск. перевод: Дж. Л. Дуб,
Вероятностные процессы, М., ИЛ, 1956).
Дхав ан (Dhawan S.)
1952. Direct measurements of skin friction, Nat. Adv. Com. Aeronaut., Tech.
Note, No. 2567.
Дьюти и Рид (Duty R. L., Reid W. H.)
1964. On the stability of viscous flow between rotating cylinders, J. Fluid
Mech., 20, No. 1, 81—94.
Д ы и к и и Е. Б.
1963. Марковские процессы, М.. Физматгиз.

БИБЛИОГРАФИЯ 611
Дэви (Davey A.)
1962. The growth of Taylor vortices in flow between rotating cylinders,
J. Fluid Mech., 14, No. 3, 336—368.
Дэвидсон иБаред (Davidson В., Barad M. L.)
1956. Some comments on the Deacon wind profile, Trans. Am. Geophys.
Union, 37, No. 2, 168—176.
Дэвн с (Davies D. R.)
1950. Three-dimensional turbulence and evaporation in the lower atmos-
atmosphere, I—II, Quart. J. Mech. Appl. Math., 3, No. 1, 51—63,
64—J3.
1954a. On diffusion from a continous point source at ground level into
a turbulent atmosphere, Quart. J. Mech. Appl. Math., 7, No. 2,
168—178.
19546. A note on the two-dimensional equation of diffusion in the atmos-
atmosphere, Quart. J. Roy. Meteor. Soc, 80, No. 345, 429—434.
Дэви с P. (Davies R. W.)
1954. The connection between the Smoluchowski equation and the
Kramers — Chandrasekhar equation, Phys. Rev., 93, No. 6, 1169—
1171.
Дэвис и Уайт (Davies S. J., White С. М.)
1928. An experimental study of the flow of water in pipes of rectangular
section, Proc. Roy. Soc, A119, No. 781, 92—107.
Елагина Л. Г.
1962. Оптический прибор для измерения турбулентных пульсаций влаж-
влажности, Изв. АН СССР, сер. геофиз., № 8, 1100—1107.
Загустин А. И.
1938. Уравнения турбулентного движения жидкостей, Труды Воронеж-
Воронежского уиив., 10, № 2, 7—39.
Зельдович Я. Б.
1937. Предельные законы свободновосходящих турбулентных потоков,
Ж- эксп. теор. физ., 7, № 12, 1463—1465.
Зилитинкевич С. С. и Лайхтман Д. Л.
1965. Турбулентный режим в поиземиом слое атмосферы, Изв. АН СССР,
сер. «Физика атмосферы и океана», 1, № 1.
Зуб ковскийС. Л.
1962. Частотные спектры пульсаций горизонтальной компоненты скорости
ветра в приземном слое воздуха, Изв. АН СССР, сер. геофиз.,
№ 10, 1425—1433.
Изаксои А.
1929. К определению турбулентности, Ж- русск. физ.-хим. общ., 61, № 3,
257—293.
1937. О формуле распределения скоростей вблизи стенки, Ж. экспер.
теор, физ., 7, № 7, 919—924.
И и о у э (Inoue E.)
1950—1951. On the turbulent diffusion in the atmosphere, I—II, J. Meteor.
Soc. Japan, 28, No. 12, 441—456; 29, No. 7, 246—253.
1952. On the Lagrangian correlation coefficient for turbulent diffusion and
its application to atmospheric diffusion phenomena, Geophys. Res.
Pap., No. 19, 397—412.
1959. The effects of thermal stratification on turbulent diffusion in the
atmospheric surface layer, Adv. Geophys:, 6 (Atmospheric diffusion
and air pollution), 319—330 (русск. перевод в сб. «Атмосферная
диффузия и загрязнение воздуха», М., ИЛ, 1962, 354—364).

612 БИБЛИОГРАФИЯ
И о к о я м a (Yokoyama О.)
1962а. On the thickness of smoke plume in diabatic surface layer, J.
Meteor. Soc. Japan, ser. II, 40, No. 2, 83—92.
196?6. On the contradiction and modification of the equation of diabatic
wind profile, J. Meteor, Soc. Japan, ser. II, 40, No. 6, 359—360.
Иссерлис (Isserlis L.)
1918. On a formula for the product-moment coefficient in any number of
variables, Biometrika, 12, No. 1—2, 134—139.
Каверс, Хсу, Шлннгер и Сейдж (Gavers S. D., Hsu N. Y., Schlin-
ger WrG., Sage-B. H.)
1953. Temperature gradients in turbulent gas streams. Behavior near
boundary in two-dimensional flow, Ind. Eng. Chem., 45, No. 9,5139—
2145.
Казанский А. Б. иМонинА. С.
1956. Турбулентность в приземных инверсиях, Изв. АН СССР, сер.
геофиз., № 1, 79—86.
1957. О форме дымовых струй, Изв. АН СССР, сер геофиз., № 8, 1020—
1033.
1958. О турбулентном режиме в приземном слое воздуха при неустойчи-
неустойчивой стратификации, Изв. АН СССР, сер. геофиз., № 6
741-751.
1961. О динамическом взаимодействии между атмосферой и поверх-
поверхностью земли, Изв. АН СССР, сер. геофиз., № 5, 786—788.
1962. Определение турбулентных потоков количества движения, тепла и
влаги по данным градиентных наблюдений, Метеор, и гидрология,
№ 12, 3—8.
Калинске и Пиеи (Kalinske A. A., Pien С. С.)
1944. Eddy diffusion, Ind. Eng. Chem., 36, No. 3, 220—223.
Кампе де Ферье (Kampe de Feriet J.)
1939. Les fonctions aleatoires stationnaires et la theorie statistique de la
turbulence homogene, Ann. Soc. Sci. Bruxelles, 59, 145—194.
1951. Averaging processes and Reynolds. equations in atmospheric turbu-
turbulence, J. Meteor., 8, No. 5, 358—361.
1953. Fonctions aleatoires et theorie statistique de la turbulence (в книге
A. Blanc-Lapierre, R. Fortet, Theorie des fonctions aleatoires, Paris,
Masson, 568—623).
1956. Problemes mathematiques poses par la mecfianique statistique de la
turbulence, Proc. Intern. Congress Math. Amsterdam, 1954, 3, 237—
242, Amsterdam, North-Holland Publ. Co.
К а о (Kao S. K.)
1959. Turbulent transfer in the boundary layer of a stratified fluid, J. Me-
Meteor., 16, No. 5, 497—503.
К а п и ц а П. Л.
1947. Теоретические и эмпирические выражения для теплопередачи в дву-
двумерном турбулентном потоке. Докл. АН СССР, 55, № 7, 595—602.
Карман (Karman Th. von).
1924. Ober die Stabilitat der Laminarstromung und die Theorie der Turbu-
lenz, Proc. 1st Intern. Coiigr. Appl, Mech., Delft, 97—112.
1930. Mechanische Ahnlichkeit und Turbulenz, Nachr. Ges. Wiss. Gottingen,
Math.-Phys. Kl., 58—76 (русск. перевод в сб. «Проблемы турбу-
турбулентности», М.—Л., ОНТИ, 1936, 271—286).
1934. Some aspects of the theory of turbulent motion, Proc. Intern. Congr.
Appl. Mech.. Cambridge (русск. перевод в сб. «Проблемы турбу-
турбулентности», М.-Л., ОНТИ, 1936, 35-74).

БИБЛИОГРАФИЯ 613
1939. The analogy between fluid friction and heat transfer, Trans. Amer.
Soc. Mech. Engrs., 61, 705—710.
К а р о л ь И. Л.
1960. О влиянии турбулентной диффузии в направлении ветра на распре-
распределение концентрации субстанции, диффундирующей в атмосфере,
Докл. АН СССР, 131, № 6, 1283—1286.
К а р р (Carr A. D.) ' •
1962. The transport of heat in a fluid in turbulent pipe flow, Reactor,
1, 6—14.
Карьер и Карлсон (Carrier G. F., Carfson F. D.)
1946. On the propogation of small disturbances in a moving compressible
fluid, Quart. Appl. Math., 4, No. 1, 1—12.
Каттанео (Cattaneo C.)
1948—1949. Sulla conduzione del calore, Atti sem. Mat. Fis. Univ. Modena,
3, 83—101.
Кедроливанский В. Н. и СтернзатМ. С.
1953. Метеорологические приборы, Л., Гндрометеоиздат.
К е л д ы ш М. В.
1951. О собственных значениях и собственных функциях некоторых клас-
классов несамосопряженных уравнений, Докл. АН СССР, 77, № 1,
11—14.
Келдыш М. В. и Лидский В. Б.
1963. Вопросы спектральной теории несамосопряженных операторов, Тру-
Труды 4-го Всесоюэн. матем. съезда, т. 1, Л., Акад. наук СССР, 101—120.
К елле р Л. В.
1925. Ober die Ausstellung eines System von Charakteristiken der atmospha-
rischen Turbulenz, Ж. геофиэ. метеор., 2, № 34, 275^290.
Келлер Л. В. и Фридман А. А.
1924. Differentialgleichung fur die turbulente Bewegung einer kompressib-
len Flussigkeit, Proc. 1st Intern. Congr. Appl. Mech., Delft, 395—405.
К е м п ф (Kempf G.)
1929. Neue Ergebnisse der Wiederstandforschung, Werft, Reederei, Hafen,
10, 234—239, 247—253.
К е р л (Curie N.)
1956. On hydrodynamic stability in unlimited fields of viscous flow, Prec,
Roy. Soc, A238, No. 1216, 489—501.
Кестин и Ричардсон (Kestin J., Richardson P. D.)
1963. Heat transfer across turbulent, incompressible boundary layers, Intern.
J. Heat Mass Transfer, 6, No. 2, 147—189.
К и p x г е с н e p (Kirchgassner K-)
1961. Die Instabilitat der Stromung zwischen zwei rotierenden Zylindern
gegenflber Taylor-Wirbeln fur beliebige Spaltbreiteln, Z. angew. Math.
Phys., 12, Nr. 1, 14-30.
К и с т л е р (Kistler A. L.)
1962. The structure of the laminar sublayer, Mecanique de la turbulence
(Coll. Intern, du CNRS a Marseille), Paris, Ed. CNRS, 287—
297.
К л а у з e p (Clauser F. H.)
1956. The turbulent boundary layer, Adv. Appl. Mech., 4, N. Y., 1—51
(русск. перевод: Ф. Клаузер, Турбулентный пограничный слой, Про-
Проблемы механики, вып. 2, М., 1959, 297—340).

614 БИБЛИОГРАФИЯ
Клебанов (Klebanoff P. S.)
1955. Characteristics of turbulence in a boundary layer with zero pres-
pressure gradient, Nat. Advis. Com. Aeronaut., Rep. No. 1247.
Клебанов и Тидстром (Klebanoff P. S., Tidstrom K- D.)
1959. Evolution of amplified waves leading to transition in a boundary
layer with zero pressure gradient, Nat. Aeronaut. Space Adm., Tech.
note D-195.
Клебанов, Тидстром и Сард жен т (Klebanoff P. S., Tidstrom К. D.,
Sargent L. M.) t
1962. The three-dimensienal nature of boundary-layer instability, J. Fluid
Mech., 12, No. 1, 1—34. .
Кленпюу и Эллиотт (Klenshow С. W., Elliott D.)
1960. A numerical treatment of the Orr — Sommerfeld equation, in the
case of a laminar jet, Qyart. J. Mech. Appl. Math., 13, No. 3, 300—
313.
Клюг (Klug W.)
1963. Zum vertikalen Windprofil, Beitr. Phys. Atmosph., 36, Nr. 3—4,
226—253.
Коважный (Kovasznay L. S. G.)
1953. Turbulence in supersonic flow, J. Aeronaut. Sci., 20, No. 10, 657—674,
682.
Колдер (Calder K. L.)
1949. Eddy diffusion and evaporation in flow over aerodinamically smooth
and rough surfaces: a treatment based on laboratory laws of turbu-
turbulent flow with special reference to conditions in the lower atmosphere,
Quart J. Mech. Appl. Math., 2, No. 2, 153—176.
1961. Atmospheric diffusion of particulate material, considered as a boun-
boundary value problem, J. Meteor., 18, No. 3, 413—416.
Колесников А. Г.
1960. Вертикальный турбулентный обмен в устойчиво-стратифицироваи-
иом море, Изв. АН СССР, сер. геофиз., № 11, 1614—1623.
Ко л лис (Collis D. С.)
1948. The diffusion process in turbulent flow, Austr. Counsil Sci. Ind. Res.,
Div. Aero., Rep. A55.
Колмогоров А. Н.
1931. Ober die analytischen Methoden in der Wahrscheinlichkeitsrechnung,
Math. Ann., 104, 415—458 (русск. перевод в журнале «Усп. матем.
наук», вып. 5, 1938, 5—41).
1933. Zur Theorie der stetigen zufalligen Prozesse, Math. Ann., 108, 149—
160.
1941a. Локальная структура турбулеитиости в несжимаемой жидкости при
очень больших числах Рейиольдса, Докл. АН СССР, 30, № 4,
299—303.
19416. Рассеяние энергии при локально изотропной турбулеитиости, Докл.
АН СССР, 32, № 1, 19—21.
1942. Уравнения турбулентного движения несжимаемой жидкости, Изв.
АН СССР, сер. физ. 6, № 1—2, 56—58.
1952. К вопросу о сопротивлении и профиле скоростей при турбулентном
. течении в трубах, Докл. АН СССР, 84, № 1, 29—30.
1954. О новом варианте гравитационной теории движения взвешенных
наносов, Вестн. МГУ, № 3, 41—45.
1962. A refinement of previous hypotheses concerning the local structure
of turbulence in a viscous incompressible fluid at high Reynolds
number, Fluid Mech., 13, No. 1, 82—85.

БИБЛИОГРАФИЯ 615
К о и д о (Kondo J.)
1962а. Observations on wind and temperature profiles near the ground,
Scu Reports T6hoku Univ., ser. 5, Geophys., 14, No. 2,
41—56.
19626. Evaporation from extensive surfaces of water, Sci. Rep. Tdhoku
Univ., ser. 5, Geophys., 14, No. 3, 107—119.
Константинов A. P.
1952. Расчет испарения с сельскохозяйственных полей с учетом влияния
лесных полос, Труды Гос. гидрологич. ии-та, вып. 34(88), 15—65.
Коит-Белло (Compte-BeHot G.)
1963. Coefficients de dissymetrie et d'aplatissemerit, spectres et correla-
correlations en turbulence- de conduite, J. Mecanique, 2, № 2, 105—
128.
Ко ппе л (Koppel D.)
1964. On the stability of flow of a thermally stratified flow under the
action.of gravity, J. Math. Phys., 5, No. 7, 963—982.
Коркоран, Пейдж, III и иг ер и Сейдж (Corcoran W. H., Page F.,
Schinger W. G., Sage В. Н.)
1952. Gradients in turbulent gas streams, Ind. Eng. Chem., 44, No. 3, 410 —
430.
Коркос и Селларс (Corcos G. M., Sellars J. R.)
1959. On the stability of fully developed flow in a pipe, J. Fluid Mech., 5,
No. 1,97—112.
К о р с и и (Corrsin S.)
1943. Investigation of flow in an axtally symmetric heated jet of air, Nat.
Adv. Com. Aeronaut., Wartime Report W-94.
1959a. Outline of some topics in homogeneous turbulent flow, J. Geophys.
Res., 64, No. 12, 1234—2150.
19596. Progress report on some turbulent diffusion research, Adv. Geophys.,
6 (Atmospheric diffusion and air pollution), 161—164 (русск. 'пере-
'перевод в сб. «Атмосферная диффузия и загрязнение воздуха», М.,
ИЛ, 1962, 187—190).
1963. Estimates of the relations between Eulerian and Lagrangian scales
in large Reynolds number turbulence, J. Atmosph. Sci., 20, No. 2,
115—1-19.
Корсии и Кистлер (Corrsin S., Kistler A. L.)
1955. The free-stream boundaries of turbulent flows, Nat. Adv. Com. Aero-
Aeronaut., Rep. No.-1244.
Корсии и Уберои (Corrsin S.,. Uberoi M. S.)
1950. Further experiments on the flow and heat transfer in a heated turbu-
turbulent air jet, Nat. Adv. Com. Aeronaut., Rep. No. 998.
1951. Spectra and diffusion in a round turbulent jet, Nat. Adv. Com. Aero-
Aeronaut., Rep. No 1040.
Коулс (Coles TJ.) • ,
1955. The law of the wall in turbulent shear flow, 50 Jahre Grenzschicht-
forschung, Vieweg, Braunschweig, 153—163.
1956. The law of the wake in turbulent boundary layer, J. Fluid Mech., 1,
No. 3, 191—226. !
1962..Interface and intermittency in turbulent shear flow, Mecanique de la
turbulence (Coll. Intern, du CNRS a Marseille), Paris, Ed. CNRS,
229—248.
К о ч и и Н. Е., К и б е л ь И. А. и Р о з e H. B.
1963. Теоретическая гидромеханика, т. 1 и 2, 3-е изд., М., Физматгиз.

616 БИБЛИОГРАФИЯ
Кравченко И. М.
1963. О профиле ветра в приземном слое, Изв. АН СССР, сер. геофиз.,
№ 3, 498—499.
Крамер и Рекорд (Cramer H. E., Record F. А.)
1953. The variation with height of the vertical flux of heat and momentum,
J. Meteor., 10, No. 3, 219—226.
Крейчнан (Kraichnan R. H.)
1959. The structure of isotropic turbulence at very high Reynolds numbers,
J. Fluid Mech., 5, No. 4, 497—543,,
1962a. Turbulent thermal convection at arbitrary Prandtl number, Phys.
Fluids, 5, No. 11, 1374—1389.
19626. The closure problem of turbulence theory, Proc. Symp. Appl. Math.,
13 (Hydrodynamic instability), 199—225 (русск. перевод в сб. «Гид-
«Гидродинамическая неустойчивость», М., Мир, 1964, 231—264).
Кречмер С. И.
1954. Методика измерения микропульсаций скорости ветра и температуры
в атмосфере, Труды Геофиз. иист. АН СССР, № 24A51),
43—111.
1957. Полевой градиентометр для измерения градиентов температуры воз-
воздуха, Труды Центр, аэролог, обсерв., № 22, 96—99.
Кристоферсон (Christopherson D. G.)
1940. Note on the vibration of membranes, Quart. J. Math., 11, No. 1,
63—65.
К р о п и к (Kropik K-)
1964. Beitrage zum Stabilitatsproblem der Poiseulleschen Stromung, Acta
Phys. Austr., 17, Nr. 4, 351—377.
К р ы л о в А. Л.
1963. Доказательство неустойчивости одного течения вязкой несжимаемой
жидкости, Докл. АН СССР, 153, № 4, 787—789.
К э й з (Case К. М.)
1960а. Stability of inviscid plane Couette flow, Phys. Fluids, 3, No. 2,
143-149.
19606. Stability of an idealised atmosphere. I Discussion of results, Phys.
Fluids. 3, No. 2, 149—155.
1960b. Taylor instability of an inverted atmosphere, Phys. Fluids, 3, No. 3,
366—368.
1961. Hydrodynamic stability and the invisdd limit, J. Fluid Mech., 10,
No. 3, 420—429.
1962. Hydrodynamic stability and the initial value problem, Proc. Simp.
Appl. Math., 13 (Hydrodynamic instability), 25—33 (русск. пере-
перевод в сб. «Гидродинамическая неустойчивость», М., Мир, 1964,
37—46).
Лайтхилл (Lighthill M. J.)
1952. On sound generated aerodynamically. I. General theory, Proc. Roy.
Soc, A211, No. 1107, 564—587.
1954. On sound generated aerodynamically. II. Turbulence as a source of
sound, Proc. Roy. Soc, A222, No. 1148, 1—32.
ЛайхтмаиД. Л.
1944. Профиль ветра и обмен в приземном слое атмосферы, Изв. АН
СССР, сер. геогр. и геофиз., 8, № 1, 1—5.
1947а. О профиле ветра в приземном слое атмосферы при стационарных
условиях, Труды научио-иссл. учр. гидрометслужбы, сер. 1, № 39,
58—76.

БИБЛИОГРАФИЯ 617
19476. Трансформация воздушной массы под влиянием подстилающей
поверхности, Метеорол. и гидрол., № 1, 17—21.
1961. Физика пограничного слоя атмосферы, Л., Гидрометиздат.
1963. Диффузия примеси от точечных источников в приземном слое атмо-
атмосферы, Труды Леииигр. гидромет. ии-та, вып. 15, 3—9.
Лайхтмаи Д. Л. и Чудиовский А. Ф.
1949. Физика приземного слоя атмосферы, Л.—М., Гостехиздат.
*Л а м б (Lamb H.)
1932. Hydrodynamics, 6th ed., N. Y. Dover, 1932 (русск. перевод: Г. Ламб,
Гидродинамика, М — Л., Гостехиздат, 1947).
Л а м л и (Lumley J. L.) '
1962а. The mathematical nature of the problem of relating Lagrangian
and Eulerian statistical functions in turbulence, Mecanique de la
turbulence (Coll. Intern, du CNRS a Marseille), Paris, Ed.
CNRS.
19626. An approach to the Eulerian—Lagrangian problem, J. Math. Phys,,
3, No. 2, 309—312.
Ламли и Паиоиский (Lumley J. L, Panof sky H. A.)
1964. The structure of atmospheric turbulence, N. Y. — London—Sydney,
Interscience Publ.
Л а н д а у Л. Д.
1944. К проблеме турбулентности, Докл. АН СССР, 44, № 8, 339—
342.
Ландау Л. Д. и Лифшиц Е. М.
1951. Статистическая физика, М., Гостехиздат.
1953. Механика сплошных сред, М„ Гостехиздат.
Л а у ф е р (Laufer J.)
1951. Investigation of turbulent flow in a two-dimensional channel, Nat.
Advis. Com. Aeronaut., Rep. No. 1033.
¦ 1954. The structure of turbulence in fully developed pipe flow, Nat. Advis.
Com. Aeronaut., Rep. No. 1174.
Л е и и ч В. Г.
1944. Теория концентрационной поляризации, Ж- физ. химии, 18, № 9,
335—355.
1951. Теория диффузионных процессов в движущейся жидкости (гидро-
(гидродинамика при больших числах Праидтля), Докл. АН СССР, 78,
№6, 1105—1108.
1959. Физико-химическая гидродинамика, 2 изд., М., Физматгиз.
Л е с с е и (Lessen M.)
1950. On stability of free laminar boundary layer between parallel streams,
Nat. Adv. Com. Aeronaut., Rep. No. 979.
Л етт ay (Lettau H.)
1950. A re-examination of the «Leipzig wind profile> considering some
relations between wind and turbulence in the friction layer, Tellus, 2,
No. 2, 125—129.
1952. On eddy diffusion in shear zones, Geophys. Res. Pap., No. 19,
437—445.
1959. Wind profile, surface stress and geostrophic drag coefficients in the
atmospheric surface layer, Adv. Geophys., 6 (Atmospheric diffusion
and air pollution), 241—257 (русск. перевод в- сб. «Атмосфер-
«Атмосферная диффузия и загрязнение воздуха>, М., ИЛ., 1962, 268—287).

618 БИБЛИОГРАФИЯ
Леттау и Дэвидсон (Lettau H., Davidson В.)
1957. Exploring the atmosphere's first mile, vols. 1—2, London—N. Y.—
Paris, Pergamon Press. ^
Ликудиси Тулукяи (Lykoudis P. S., Touloukian J. S.)
1958. Heat transfer in liquid metals, Trans. Amer. Soc. Mech. Engrs., 80,
No. 3, 653—666.
Лилиеквист (Liljequist G. H.)
1954. Energy exchange of the Antarctic snowfield, Norwegian—British-
Swedish Antarctic expedition 1949—1952, Scientific Results, 2, part
1, Oslo.
Лиидгрен (Lindgren- E. R.)
1957. The transition process and other phenomena in viscous flow, Ark.
Fysik, 12, No. 1^-2, 1—169.
1969. Liquid flow in tabes, 1=—II. Ark. Fysik, 15, No. 2, 97—119; No. 6,
503—5 Г9:
Линь (Lin С, С.)
1945. On the stability of two-dimensional parallel flows. Parts I—III,
Quart. Appl. Math.", 3, No. 2, 117—142, No. 3,218—234, No. 4,277—301.
1955. The theory of hydrodynamic stability, Cambridge, Univ. Ргезв (русск.
перевод: Линь, Теория гидродинамической устойчивости, М., ИЛ,
1958).
1961. Some mathematical problems in the theory of the stability of paral-
parallel flows, J. Fluid Mech., 10, No. 3, 430—438.
Лииь и Бенин (Lin С. С, Веппеу D. J.)
1962. On the instability of shear flows, Proc. Symp. Appl. Math., 13 (Hyd-
(Hydrodynamic instability), 1—24 (русск. перевод в сб. «Гидродинами-
«Гидродинамическая неустойчивость:», М., Мир, 1964, 9—36).
Лииь, Дейтой, Гаскилл и Патнем (Lin С. S., Denfon E. В.,
Gaskill H. S., Putnam G. L.)
1951. Diffusion-controlled electrode reactions, Ind. Eng. Chem., 43, No. 9,
2136—2143.
Лииь, Маултои и Патием (Lin С. S., Moulton R, W., Putnam G. L.)
1953. Mass transfer between solid vails and fluid streams, Ind. Eng.
Chem., 45, No. 3, 636—646.
Лион {Lyon R. N.)
1951. Liquid metal heat-transfer coefficients, Chem. Eng. Progress, 47,
No. 2, 75-79.
Л и n м а н н (Liepmann H. W.)
1962. Free turbulent flows, Mecanique de la turbulence (Coll. Intern, du
CNRS a Marseille), Paris, Ed. CNRS, 211—226.
Лойцяиский Л. Г.
1935. О некоторых приложениях метода подобия в теории турбулентно-
турбулентности, Прикл. матем. мех.% 2, № 2, 180—206.
1941. Аэродинамика пограничного слоя, Л.—М., Гостехиздат.
1958. Гипотеза локальности в турбулентном движении жидкости при на-
наличии вязкости, Прикл. матем. мех., 22, № 5, 600—611.
1960. Перенос тепла в турбулентном движении, Прикл. матем. мех., 24,
№ 4, 637—651. •
1962а. Полуэмпирические теории взаимодействия процессов молекулярно-
молекулярного и молярного обмена в турбулентном движении жидкости, Труды
Всесоюзи. съезда теор. прикл. мех., 1960, М,—Л., Изд. АН СССР,
145—166.
19626. Ламинарный пограничный слой, М., Физматгиз.

619
Л о к к (Lock R. С.)
1955. The stability of the flow of an electrically-conducting fluid between
parallel planes under a transverse magnetic field, Proc. Roy. Sot,
A233,No. 1192, 105—125.
Л о р е и ц (Lorentz H. A.) .
1907. Ober die Entstehung turbulenter Flussigkeitbewegungen und uber
den Einfluss dieses Bewegungen bei der StrSmung durch Rohren,
Abh. theor. Phys., Lpz, 1, 43—71.
Л о р е и ц Е. (Lorenz Е.)
1953. The interaction between a mean flow and random disturbances, Tel-
lus, 5, No. 3, 238—250.
Л о э в (Loeve M.)
1960. Probability theory, 2nd ed., Princeton, van Nostrand (русск. перевод:
M. Лоэв, Теория вероятностей, М., ИЛ, 1962).
Людвиг (Ludwieg H.)
1956. Bestimmung des Verhaltnisses der Austauschkoeffizienten fur Warme
und Impuls bei turbulenten Grenzschichten, Zs. fur Flugwiss., 4,
Nr. 2, 73—81.
ЛюДвиг и Тильмаии (Ludwieg H., Tillmann W.)
1949. Untersuchungen uber die Wandschubspannung in turbulenten Rel-
bungsschichten, Ing. Arch., 17, Nr. 4, 288—299.
Л япии Е. С.
1948. О турбулентном перемешивании воздуха в атмосфере, Метеор, и
гидрол., № 5, 13—23.
1950. О гиперболическом уравнении вертикального турбулентного обмена
в атмосфере, Труды Глави. геофиз. обсерв., № 19(81), 175—184.
Майкельсеи (Mickelsen W. R.)
1955. An experimental comparison of the Lagrangian and Eulerian cor-
correlation coefficients in homogeneous isotropic turbulence, Nat. Adv.
Com. Aeronaut., Techn. note No. 3570.
1959. Measurements of the effect of molecular diffusivity in turbulent
diffusion, J. Fluid Mech., 7, No. 3, 397—400.
Майкл (Michael D. H.) '
1961. Note on the stability of plane parallel flows, J. Fluid Mech., 10,
No. 4, 525—528.
Майлс (Miles J. W.)
1957. On the velocity profile for turbulent flow near a smooth wall,
J. Aeronaut. Sci., 24, No. 9, 704.
1961. On the stability of heterogeneous shear flows, J. Fluid Mech., 10,
No. 4, 496—508.
1963. On the stability of heterogeneous shear flows, Part 2, J. Fluid Mech.,
16, No. 2, 209—227.
Мак Адаме (McAdams W. H.)
1954. Heat transmission, 3rd. ed., N. Y.—Toronto—London, McGraw-Hill
(русск. перевод В. X. Мак-Адаме, Теплопередача, М., Металлург-
издат, 1961).
М а к в е й л (McVehil G. Е.)
1964. Wind and temperature profiles near the ground in stable stratifica-
stratification, Quart. J. Roy. Met. Soc. 90, No. 384. 136—146.
Макилрой (Mcllroy I. C.)
1955. The atmospheric fine structure recorder, C.S.I.R.O., Div, Meteor,
Phys., Techn. Rap. No. 3, Melbourne,

620 БИБЛИОГРАФИЯ
Маккриди (MacCready P. В.)
1953. Atmospheric turbulence measurements and analysis, J. Meteor.,
10, No. 5, 325—337.
M а л к у с (Malkus W. V. R.)
1954a. Discrete transitions in turbulent convection, Proc. Roy. Soc, A225,
No. 1161, 185—195.
19546. The heat transport and spectrum of thermal turbulence, Proc. Roy.
Soc., A225, No. 1161, 196—212.
Малкус и Веронис (Malkus W. V. R., Veronis G.)
1958. Finite amplitude cellular convection, J. Fluid Mech., 4, No. 3,
225—260.
Малхотра и Сермак (Malhotra R. С, Cermak J. _E.)
1963. Wind-tunnel modeling of atmospheric diffusion, J. Geophys. Res.,
68, No. 8, 2181—2184.
Мани (Munn R. E.)
1961. A theoretical expression for the root mean square vertical eddy flu-
fluctuation (ю7*) 2, J. Meteor., 18, No. 1, 38—42.
1963. A reappraisal of Sutton's parameter n, J. Appl. Meteor., 2, No. 4,
440—445.
Мартинелли (Martinelli R. S.)
1947. Heat transfer to molten metals, Trans. Amer. Soc. Mech. Engrs,
69, 947—959.
Матвеев Л. Т.
1960. К установлению зависимости коэффициента турбулентности от вы-
высоты в приземном слое атмосферы, Изв. АН СССР, сер. геофиз.,
с №1, 83—88.
М а ц у о к a (Matsuoka H.)
1960. A corrected turbulon model theory of turbulent diffusion and its
application, J. Meteor. Soc. Japan, 38, No. 3, 148—153.
1961. Note on two dimensional diffusion in the atmospheric surface layer,
J. Meteor. Soc. Japan, 39, No. 6, 324—330.
M e к с и н (Meksyn D.) ^
1946. Stability of viscous flow between rotating cylinders, I—III, Proc.
Roy. Soc, A187, No. 1008, 115—128, No. 1011, 480—491, 492—
504.
1964. Stability of laminar flow between parallel planes for two- and
threedimensional finite disturbances, Zs. Phys., 178, Nr. 2, 159—
172.
Мексин и Стюарт Дж. (Meksyn D., Stuart J. T.)
1951. Stability of viscous motion between parallel planes for finite di-
disturbances, Proc. Roy. Soc, A208, No. 1095, 517—526.
M e p ф р и (Murphree E. V.)
1932. Relation between heat transfer and fluid friction, Ind. Eng. Chem.,
24, No. 7, 726—736.
Мидлтон и Спилхаус (Middleton W. В. К-, Spilhaus A. F.)
1953. Meteorological instruments, Toronto, Univ. Press.
M и з е с (Mises R.)
1941. Some remarks on, the laws of turbulent motion in tubes, Th. v.
Karman anniversary volume, Calif. Inst. Techn. Press,' Pasadena,
317—327.
Миллер и Фейер (Miller J. A., Fejer A. A.) ¦
1964. Transition phenomena in oscillating boundary-layer flows, J. Fluid
Mech., 18, No. 3, 438—448.

БИБЛИОГРАФИЯ 621
Милликен (Millikan С. В.)
1939. A critical discussion of turbulent flows in channels and circular
tubes, Proc. 5th Intern. Congr. Appl. Mech., Cambridge (USA),
386—392.
Миллионщиков М. Д.
1939. Вырождение однородной изотропной турбулентности в вязкой не-
несжимаемой жидкости, Докл. АН СССР, 22, № 5, 236—240.
М и х а л к е (Michalke A.)
1964. On the inviscid instability of the hyperbolictangent velocity profile,
J. Fluid Mech., 19, No. 4, 543—556.
M о н и н А. С
1950a. Динамическая турбулентность в атмосфере, Изв. АН СССР, сер.
геогр., геофиз., 14, № 3, 232—254.
19506. О характеристиках анизотропной турбулентности, Докл. АН
СССР, 75, № 5, 621—624.
1950в. Турбулентный режим в приземном слое воздуха, Информ. сбори.
Гл. упр. гидрометслужбы, N° 1, 13—27.
1953. О механизме нагревания воздуха в открытой степи, сб. «Климати-
«Климатические и микроклиматические исследования в прикаспийской низ-
низменности», М., Изд. АН СССР, 100—123.
1955. О диффузии с конечной скоростью, Изв. АН СССР, сер. геофиз.,
№ 3, 234—248.
1956а. Полуэмпирическая теория турбулентной диффузии, Труды Геоф.
инст. АН СССР, № 33 A60), 3—47.
19566. О турбулентной диффузии в приземном слое воздуха, Изв. АН
СССР, сер. геофиз., № 12, 1461—1473.
1956в. О макротурбулентном обмене в земной атмосфере, Изв. АН СССР,
сер. геофиз., № 4, 452—463.
1958. Структура атмосферной турбулентности, Теор. вероятн. и ее примен.,
3, № 3, 285—317.
1959а. Smoke propagation in the surface layer of the atmosphere, Adv.
Geophys., 6 (Atmospheric diffusion and air pollution), 331—343
(русск. перевод в сб. «Атмосферная диффузия и загрязнение воз-
воздуха», М., ИЛ, 1962, 366—381).
19596. On the boundary condition on the earth surface for diffusing pol-
pollution, Adv. in Geophys., 6 (Atmospheric diffusion and air pollu-
pollution), 435—436 (русск. перевод в сб. «Атмосферная диффузия и
загрязнение воздуха», М., ИЛ, 1962, 477—478).
1959в. Атмосферная диффузия, Усп. физич. наук, 67, № 1, 119—130.
1960. О лагранжевых характеристиках турбулентности, Докл. АН СССР,
134, № 2, 304—307.
1962а. О структуре полей скорости ветра и температуры в приземном
слое воздуха, сб. «Атмосферная турбулентность» (Труды Ин-та
физики атмосф. АН СССР, № 4, 5—20).
19626. Empirical data on turbulence in the surface layer of atmosphere,
J. Geophys. Research, 67, No. 8, 3103—3109.
1962в. О лаграижевых уравнениях гидродинамики несжимаемой вязкой
жидкости, Прикл. матем. мех., 26, № 2, 320—327.
1965. О свойствах симметрии турбулентности в приземном слое воздуха,
Изв. АН СССР, сер. «Физика атмосферы н океана», 1, N° 1.
М он и н А. С. и О б у х о в А. М.
1953. Безразмерные характеристики турбулентности в приземном слое
атмосферы, Докл. АН СССР, 93, № 2, 223—226.

622
1954. Основные закономерности турбулентного перемешивания в призем-
приземном слое атмосферы, Труды Геофиз. инст. АН СССР, № 24A51),
163—187.
МонинА. С. иЯгломА. М.
1962. Гидродинамическая неустойчивость и возникновение турбулентно-
турбулентности, Прикл. мех. тех. физ., № 5, 3—38.
Наито (Naito К.)
1964. Some remarks on the Monin—Obukhov function in the atmosphere
near the ground, J. Met. Soc. Japan, 42, No. 1, 53—63.
Невзглядов В. Г.
1945a. К феноменологической теории турбулентности, Докл. АН СССР,
47, № 3, 169—173.
19456. К статистической теории турбулентности, Докл. АН СССР, 47,
№ 7, 482—485.
Никурадзе (Nikuradse J.)
1932. Gesetzmassigkeiten der turbulenten Stromung in glatten Rohren,
VDI-Forschungsheft Nr. 356 (русск. перевод в сб. «Проблемы тур-
турбулентности», М.—Л., ОНТИ, 1936, 75—150).
1933. Stromungs gesetze in rauhen Rohren, VDI-Forschungsheft Nr. 361.
Новиков Е. A.
1958. О турбулентной диффузии в потоке с поперечным градиентом
скорости, Прикл. матем. мех., 22, № 3, 412—414.
1964. Сходимость функционального ряда Тэйлора для характеристиче-
характеристического функционала случайного поля. Успехи матем. наук, 19,
№ 6A20), 195—197.
Н у н н ер (Nunner W )
1956. Warmeubertragung und Druckabfall in rauhen Rohren, VDI-For-
VDI-Forschungsheft Nr. 455.
Обухов А. М.
1941. О распределении энергии в спектре турбулентного потока, Изв.
АН СССР, сер. геогр. геофиз., 5, № 4—5, 453—466.
1942. О распределении масштаба турбулентности в трубах произвольного
сечения, Прикл. матем. мех., 6, № 2—3, 209—220.
1946. Турбулентность в температурно-неоднородной атмосфере, Труды
Ин-та теорет. геофиз. АН СССР, 1, 95—115.
1954. Статистическое описание непрерывных полей, Труды Геофиз. ин-та
АН СССР, № 24A51), 3—42.
1960. О структуре температурного поля и поля скоростей в условиях
свободной конвекции, Изв. АН СССР, сер. геофиз., № 9, 1392—
1396.
1962. Some specific features of atmospheric turbulence, J. Fluid Mech.,
13, No. 1, 77—81.
Dry pa (Ogura J.)
1952a. Note on the wind velocity profile in the non-adiabatic atmosphere.
J. Meteor. Soc. Japan, ser. II, 30, No. 10, 329—342.
19526. The theory of turbulent diffusion in the atmosphere, I—III, J. Me-
Meteor. Soc. Japan, 30, No. 1, 23—28; No. 2, 53—58; No. 11, 386—397.
Ока mo то (Okamoto M.)
1963. A note on the wind and temperature profiles in the diabatic atmo-
atmosphere near the ground, Geophys. Mag. (Japan), 31, No. 3, 505—514.
О р р (Orr W. McF.)
1906—1907. The stability or instability of the steady motions of a liquid,
Proc. Roy. Irish Acad., A27, 9—27, 69—138.

БИБЛИОГРАФИЯ 623
Оуэн и Томсон (Owen P. R...Thomson W. R.)
1963. Heat transfer across rough surfaces, J. Fluid Mech., 15, No. 3, 321 —
334.
П а л м (Palm E.)
1960 On the tendency towards hexagonal cells in steady convection, J.
Fluid Mech., 8, No. 2, 183—192.
Палм и Эйянн (Palm E., ftann H.)
1964. Contribution to the theory of cellular thermal convection, J. Fluid
Mech., 19, No. 3, 353^365.
Пандольфо (Pandolfo J. P.)
1963. A formula relating various nondimensional parameters of turbulence
fields in atmospheric surface layer under diabatic conditions, J. Geo-
phys. Res., 68, No. 10, 3249—3256. ,
П а новскй й (Panofsky H. A.)
1952. A comparison of different types of stress measurement, Quart. J.
Roy. Meteor. Soc., 78, No. 337, 411—414.
1961a. An alternative derivation of the diabatic wind profile, Quart. J. Roy.
Meteor. Soc, 87, No. 371, 109—110.
19616. Similarity theory and temperature structure in the lower atmo-
atmosphere, Quart. J. Roy. Meteor. Soc, 87, No. 374. 597—601.
1962. The budget of turbulent energy in the lowest 100 meters, J. Geophys.
Research, 67, No. 8, 3161—3165.
1963. Determination of stress from wind and temperature measurements,
Quart. J. Roy. Meteor. Soc, 89, No. 379, 85—93.
Пановский, Блэкедар и Маквейл (Panofsky H,-A., Blackadar А. К.,
McVehil G. Е.)
1960. The diabatic wind profile, Quart. J. Roy. Meteor. Soc, 86, No. 369
390—398.
Пановский и Маккормик (Panofsky H. A., McCormick R. A.)
1960. The spectrum of vertical velocity near the surface, Quart. J. Roy.
Meteor. Soc, 86, No. 370, *95—503.
Па н ч ев Ст.
1961. Некоторые количественные соотношения между статистическими ха-
характеристиками чисто термической турбулентности в атмосфере,
Докл. Болг. Акад. наук, 14, № 8, 791—794.
П а скуй л (Pasquill F.)
1949. Eddy diffusion of water vapour and heat near the ground, Proc
Roy. Soc, AJ98, No. 1052, 116—140.
1950. The aerodynamic drag of the grassland, Proc Roy. Soc, A202,
No. 1068, 143—153.
1962a. Recent broad-band spectral measurements of turbulence in the lower
atmosphere, J. Geophys. Research, 67, No. 8, 3025—3031.
19626. Atmospheric diffusion. A study of the dispersion of windborne ma-
material from industrial and other sources, London—Toronto—N- Y.—
Princeton, Van Nostrand.
ПерепелкинаА. В.
1957. Некоторые результаты исследования турбулентных пульсаций тем-
температуры и вертикальной составляющей скорости ветра, Изв. АН
СССР, сер. геофиз., № 6, 765—778.
1959а. Об определении турбулентного потока тепла, Изв. АН СССР,
сер. геофиз., № 7, 1026—1035.
19596. Статистические характеристики турбулентного обмена в приземном
слое атмосферы, Канд, диссертация, Ин-т физики атмосф, АН
СССР, М.

624 БИБЛИОГРАФИЯ
1962. О характеристиках турбулентности приземного слоя в условиях
свободной конвекции, Изв. АН СССР, сер. геафиз., № 2, 271—
274.
Петров Г. И.
1938. О распространении колебаний в вязкой жидкости и возникновении
турбулентности, Труды ЦАГИ, вып. 345.
Пешке (Paeschke W.)
1936. Experimentelle Untersuchungen zum Rauhigkeits- und Stabilitatspro-
blem in der Bodennahen Luftschicht, Beitr. Phys. fr. Atmosph., 24,
No. 3, 163—189.
Праидтль {Prandtl L.)
1910. Eine Beziehung zwischen Warmeaustausch und Str5mungwiderstand
der Flussigkeiten, Phys. Zs., 11, 1072—1078.
1914. Ober den Luftwiderstand von Kugeln, Nachr. Ges. Wiss. Gottingen,
Math.-Phys. Kl 177—190.
1921. Bemerkungen uber die Entstehung der Turbulenz, Zs. angew. Math.
Mech., I, Nr. 6, 431—436.
1925. Bericht uber Untersuchungen zur ausgebildeten Turbulenz, Zs. angew.
Math. Mech., 5, Nr. 2, 136—139.
1927. Ober der Reibungswiderstand stromender Luft, Ergebn. Aerodyn.
Versuchsanst., Gottingen, 3, 1—5.
1928. Bemerkung uber den Warmeubergang im Rohr, Phys. Zs., 29, Nr. 14,
487—489.
1932a. Meteorologische Anwendungen der Stromungslehre, Beitr. Phys. fr.
Atmosph., 19, Nr. 3, 188—202.
19326. Zur turbulenten Str5mung in Rohren und langs Platten, Ergebn.
Aerodyn. Versuchsanst., Gottingen, 4, 18—29.
1942. Bemerkungen zur Theorie der freien Turbulenz, Zs. angew. Math.
Mech., 22, No. 5, 241—243.
1945. Ober ein neues Formelsystem fur die ausgebildete Turbulenz, Nachr.
Ges. Wiss. Gottingen, Math.-Phys. KL, 6—19.
1949. Fuhrer durch die Stromungslehre, 3ed., Braunschweig, F. Vieweg
{русск. перевод: Л. Прандтль, Гидроаэромеханика, М., ИЛ, 1951).
Праудмен (Proudman J.)
1953. Dynamical oceanography, Loifdon, Methuen (русск. перевод:
Дж. Праудмен, Динамическая океанография, М., ИЛ, 1957).
Преч (Pretsch J.)
1941а. Die Stabilitat einer ebenen Laminarstromung bei Druckgefalle
und Druckansteig, Jahresber. deutsch. Luftfahrtf., I, 158—
175.
19416. Ober die Stabilitat einer Laminarstromung in einem geraden Rohr
mit Kreisformigen Querschnitt, Zs. angew. Math. Mech., 21, Nr. 3,
204—217.
Пристли (Priestley С. Н. B.)
1954. Convection from a large horizontal surface, Austr. J. Phys., 7, No. 2,
176—201.
1955. Free and forced convection in the atmosphere near the ground,
Quart. J. Roy. Meteor. Soc, 81, No. 348, 139—143.
1956. Convection from the Earth's surface, Proc. Roy. Soc, A238, No. 1214,
•287—304.
1959a. Turbulent transfer in the lower atmosphere, Chicago, Univ. Press
(русск. перевод: С. Х. Б. Пристли, Турбулентный перенос в при-
приземном слое атмосферы, Л., Гидрометиздат, 1964).
19596. Estimation of surface stress and heat fiux from orofile data, Quart.
J. Roy. Meteor. Soc, 85, No. 366, 4J5—418.

БИБЛИОГРАФИЯ 625
1960а. A determinant hypothesis for the superadiabatic wind and tempe-
temperature profiles, Quart. J. Roy. Meteor. Soc, 86, No. 368, 232—
236.
19606. Temperature fluctuations in the atmospheric boundary layer, J. Fluid
Mech., 7, No. 3, 375—384.
1961 An alternative derivation of the diabatic wind profile, Quart. J. Roy.
Meteor. Soc, 87, No. 373, 437—438.
1962. Free convection in a wind, Quart. J. Roy. Meteor. Soc, 88, No. 375,
100—101.
1963. Eddy diffusion in shear zones, Quart. J. Roy. Meteor. Soc, 89,
No. 380, 287—288.
1963—1964. Recent flux and profile measurements in Australia, Доклад
иа симпозиуме в Беркли 30 августа 1963 г. и частное сообщение
от 7 апреля 1964 г. <
Пристли и Суиибеик (Priestley С. Н. В., Swinbank W. С.)
1947. Vertical transport of heat by turbulence in the atmosphere, Proc
Roy. Soc, AI89, No. 1019, 543—561.
Прохоров Ю. B.
1961. The method of characteristic functionals, Proc. 4th Berkeley Symp.
Math. Stat. Probab., 2, Berkeley—Los Angeles, Univ. Calif. Press,
403—419.
Пэлью и Саусвелл (Pellew A., Southwell R. V.)
1940. On maintained convective motion in a fluid heated from below, Proc,
Roy. Soc., AI76, No. 966, 312—343.
P а й д е р (Rider N. E.)
1954. Eddy diffusion of. momentum, water vapour and heat near the
ground, Phil. Trans. Roy. Soc., A246, No. 918, 481—501. .
Райдер и Робинсон (Rider N. E., Robinson G. D.)
1951. A study of the transfer of heat and water vapour above a surface of
short grass, Quart. J. Roy. Meteor. Soc, 77, No. 333, 375—401.
Раунде (Rounds W.)
1955. Solutions of the two-dimensional diffusion equations, Trans. Amer.
Geophys. Union, 36, No. 2, 395—405.
Рейнольде (Reynolds O.)
1874. On the extent and action of the heating surface of steam boilers,
Proc. Lit. Phil. Soc. Manchester, 14, 7—12.
1883. An experimental investigation of the circumstances which deter-
determine whether the motion of water shall be direct or sinouos, and the
law of resistance in parallel channels, Phil. Trans. Roy. Soc. London,
174, 935—982.
1894. On the dynamical theory of incompressible viscous fluids and the
determination of the criterion, Phil. Trans. Roy. Soc, London, 186,
123—161 (русск. перевод в сб. «Проблемы турбулентности», М.,
ОНТИ, 1936, 185—227).
Рейхардт (Reichardt H.)
1938. Messungen .turbulenten Schwankungen, Naturwiss., 26, Nr. 24/25,
404-408.
1940. Die Warmeuber.tragung in turbulenten Reibungsschichten, Zs. angew.
Math, Mech., 20, Nr. 6, 297—328.
1942. Gesetzmassigkeiten der freien Turbulenz, VDI-Forschungs, No.
414.
1951a. Vollstandige Darstellung der turbulenten Geschwindigkeitsvertei-
lung in glatten Leitungen, Zs. angew. Math. Mech., 31, Nr. 7,
208—219.

626 БИБЛИОГРАФИЯ
19516. Die Grundlagen des turbulenten Warmeuberganges, Arch. Ges. War-
metech., 2, 129—142.
Рибо (Ribaud G.)
1941. Nouvelle expression du coefficient de convection de la chaleur en
regime d'ecoulement turbulent, J. Phys. Radium (8), 2, Nr. 1,
12-25.
P и и с (Riis E.)
1962. The stability of Couette flow in non-stratified and stratified viscous
fluids, Geofys. Publik. (Oslo), 23, No. 4, 3—37.
Ричардсон (Richardson L. F.)
1920. The supply of energy from and to atmospheric eddies, Proc. Roy.
Soc, A97, No. 686, 3.54—373.
1922. Weather prediction by numerical process, Cambridge, Univ. Press.
1926. Atmospheric diffusion shown on a distance-neighbour graph, Proc.
Roy. Soc, AIIO, No. 756, 709—737.
Роберте (Roberts O. F. T.)
1923. The theoretical scattering of smoke in a turbulent atmosphere, Proc.
Roy. Soc., AI04, No. 728, 640—654.
Робертсон (Robertson J. M.)
1957. The turbulent velocity distribution in rough pipe, Proc 5th Midvestern
Conf. Fluid Mech., Ann. Arbor, Univ. Michigan Press, 67—84.
Робиисои (Robinson G. D.)
1950. Two notes on temperature changes -in 'the troposphere due to radia-
radiation, Centenn. Proc. Roy. Meteor. Soc, 26—33.
1951. The vertical convective heat flux in the atmosphere — a critical
essay, Quart. J. Roy. Meteor. Soc, 77, No. 331, 61—73.
Розанов Ю. A.
1963. Стационарные случайные процессы, М., Физматгиз.
Розенблют и Саймон (Rosenbluth M. N., Simon A.)
1964. Necessary and sufficient condition for the stability of plane parallel
inviscid flow, Phys. Fluids, 7, No. 4, 557—558.
Россби (Rossby C.-G.)
1948. On the nature of the general circulation in the lower atmosphere,
«The atmospheres of the ^arth and planets», ed. by G. P. Kuiper,
Chicago, Univ. Press, ch. 2 (русск. перевод: «Атмосферы Земли и
планет», М„ ИЛ, 1951, 25—57).
Россби и Монтгомери (Rossby C.-G., Montgomery R. В.)
1935. The layer of frictional influence in wind and ocean currents, Pap.
Phys. Oceanogr. Meteor., 3, No. 3.
Рота (Rota G.-C.)
1960. Spectral theory of smoothing operators, Proc Nat. Acad. Sci. USA,
48, No. 6, 863—868.
Pott a (Rotta J. C.)
1950. Das in Wandnahe gultige Geschwindigkeitsgesetz turbulenter Stro-
mungen, Ing.-Arch., 18, Nr. 4, 277—280.
1951a. Beitrag zur Berechnung der turbulenten Grenzschichten, Ing. Arch.,-
19, Nr. 1,31—41.
19516. Statistische Theorie nichthomogener Turbulenz, 1, Zs. Phys., 129,
Nr. 5, 547—572.
1951b. Statistische Theorie nichthomogener Turbulenz, 2, Zs. Phys., 131,
Nr. 1, 51—77.
1956. Experimenteller Beitrag zur Entstehung turbulenter Stromung inj
Rohr, Ing. Arch.; 24, Nr. 4, 258—281,

627
1962а. Incompressible turbulent boundary layers, MecariiqUe de la turbu-
lense (Golloque Intern, du CNRS a Marseille), Paris, Er. CNRS,
255—283.
19626. Turbulent boundary layers in incompressible flow, Progr. Aeronaut.
Sci. 2, Oxford—London—New York—Paris, Pergamon Press, 1—
219.
Рэлей (Rayleigh)
1880, 1887, 1895. On the stability, or instability, of certain fluid motions,
I—III, Sci. Papers, Cambridge, Univ. Press, I, 474—487; 3, 17—23;
4, 203—209.
1894. The theory of sound, London, Macmillan (русск. перевод: Рэлей.
Теория звука, изд. 2-е, т. 1—2, М., Гостехиздат, 1955).
1913. On the stability of the laminar motion of an inviscid fluid, Sci..
Papers, Cambridge, Univ. Press, 6, 1^7—204.
1916a. On the dynamics of revolving fluids, Sci. Papers, Cambridge, Univ.
. Press, 6, 447—453.
19166. On convection currents in a horizontal layer of fluid when the
higher temperature is on the under side, Sci. Papers, Cambridge,
Univ. Press, 6, 432—443.
P э н н и (Rannie W. D.)
1956. Heat transfer in turbulent shear flow, J. Aeronaut. Sci., 23, No. 5,
485—489. .
Саттон (Sutton O. G.)
1932. The theory of eddy diffusion in the atmosphere, Proc. Roy. Soc,
AI35, No. 826, 143—165.
1934. Wind structure and evaporation in a turbulent atmosphere, Proc.
Roy. Soc., AI46, No. 858, 701—722
1936. The logarithmic law of wind structure near the ground, Quart. J.
Roy. Meteor. Soc, 62, No. 271, 124—126.
1937. The logarithmic law of wind structure near the ground, Quart. J.
Roy. Meteor. Soc, 63, No. 275, 105—107.
1949. The application to micrometeorology of the theory of turbulent flow
over rough surfaces, Quart. J. Roy. Meteor. Soc, 75, No. 326, 335—
350.
1950. On the stability of a fluid heated from below, Proc. Roy. Soc, A204,
No. 1078, 297-309.
1953. Micrometeorology, N. Y. — Toronto — London, McGraw-Hill (русск.
перевод: О. Г. Сеттон, Микрометеорология, Л., Гидрометиздат,
1958).
СаусвеллиЧитти (Southwell R. V., Chitty L.)
1930. On the problem of hydrodynamic stability. 1.. Uniform shearing mo-
motion in a viscous fluid, Phil. Trans. Roy. Soc. London, A229, 205—
283.
С а ф м е н (Saffman P. G.)
1960. On the effect of the molecular diffusivity in turbulent diffusion,
J. Fluid Mech., 8, No. 2, 273—283.
1962a. Some aspects of the effects of the molecular diffusivity in turbulent
diffusion, Mecanique de la turbulence (Coll. Intern, du CNRS
a Marseille), Paris, Ed. CNRS, 53—62.
19626. The effect of wind shear on horizontal spread from instantaneous
ground source, Quart. J. Roy. Met. Soc, 88, No. 378, 382—393.
1963. An approximate calculation of the Lagrangian auto-correlation coeffi-
coefficient for stationary homogenous turbulence, Appl. Scient. Res., All,
No. 3, 245—255. ......

628 БИБЛИОГРАФИЯ
Свердруп (Sverdrup H. U.)
1936. The eddy conductivity of the air over a smooth snow field, Geophys.
Pub. II, No. 7.
СекслиШпильберг (Sexl Т., Spielberg J.)
1958. Zum Stabilitatsproblem der Poiseuilleschen Stromung, Acta Phys.
Austr., 12, Nr. 1, 9—28.
С е л л е р с (Sellers W. D.)
1962. A simplified derivation of the diabatic wind profile, J. Atmosph. Sci.,
19, No. 2, 180—181.
С е р м а к (Cermak J. E.)
1963. Lagrangian similarity hypothesis applied to diffusion in turbulent
shear flow, J. Fluid Mech., 15, No. 1, 49—64.
С е р р и н (Serrin J.)
1959. On the stability of viscous fluid motions, Arch. Rat. Mech. Anal., 3,
No. 1, 1—13.
'Сиджел (Segel L. A.)
1962. The non-linear interaction of two disturbances in the thermal con-
convection problem, J. Fluid Mech., 14, No. 1, 97—114.
Сиджел и Стюарт (Segel L. A., Stuart J. Т.)
1962. On the question of the preferred mode in cellular thermal convec-
convection, J. Fluid Mech., 13, No. 2, 289—306.
Симмонс и Солтер (Simmons L. F. G., Salter C.)
1938. An experimental determination of the spectrum of turbulence, Proc.
Roy. Soc, AI65, No. 920. 73—89.
С инг (Synge J. L.)
1933. The stability of heterogeneous liquids, Trans. Roy. Soc. Canada, 27,
No. 1, 1—18.
1938. Hydrodynamic stability, Semi-centennial publications of the Amer.
Math. Soc, 2 (Adresses), 227—269.
Сионо и Хамуро (Syono S., Hamuro M.)
1962. Notes oh the wind-profile in the lower layer of a diabatic atmosphe-
atmosphere, J. Meteor. Soc. Japan, Ser. II, 40, No. 1, 1—12.
Сквайр (Squire H._B.) ¦>
1933. On the stability of the three-dimensional disturbances of viscous
flow between parallel walls, Proc. Roy. Soc, AI42, No. 847, 621—
628.
1948. Reconsideration of the theory of free turbulence, Phil. Mag., 39,
No. 288, 1—14.
С л e и ч e p (S 1 e i с h e г С A., Jr.)
1958. Experimental velocity and temperature profiles for air in turbulent
pipe flow, Trans. Amer. Soc. Mech. Engrs, 80, No. 3, 693—704.
Слуцкий Е. E.
1938. Sur les fonctions aleatoires presque periodiques et sur la decomposi-
decomposition des fonctions aleatoires stationnaires en composantes, Actual.
Scient. Industr., N738, 33—55 (русск. перевод в книге: Е. Е. Слуц-
Слуцкий, Избранные труды, М., Акад. наук. 1960).
Смит (Smith F. В.)
1957. The diffusion of smoke from a continuous elevated point source
into a turbulent atmosphere, J. Fluid Mech., 2, No. 1, 49—76.
Смит и Уокер (Smith D. W., Walker J. H.)
1959. Skin-friction measurements in incompressible flow, Nat. Aeronaut
Space Adm., Rep. R-26.

БИБЛИОГРАФИЯ 629
Сорокин В. С.
1954. О стационарных движениях жидкости, подогреваемой снизу. Прикл.
мат. мех., 18, № 2, 197—204.
С аи г е л (Spiegel E. А.)
1962 On the Malkus theory of turbulence, Mecanique de la turbulence,
(Colloq. Intern, du CNRS a Marseille), Paris, Ed. CNRS 181—201.
Сполдинг (Spalding D. B.)
1961. A single formula for the «law of the wall», J. Appl. Mech., 28E,
No. 3, 455—457.
1963. Исследование теплообмена пластины с турбулентным потоком жид-
жидкости, Инж.-физ. журн., 6, № 3, 21—33.
Спэрроу, Голдстайн и Джоисои (Sparrow E. M., Goldstein R. J.,
Jonsson V. К.)
1964. Thermal instability in a horizontal fluid layer: effect of boundary
condition and non-linear temperature profile, J. Fluid Mech., 18,
No. 4, 513—528.
Спэрроу, Мунро и Джоисон (Sparrow E. M., Munro. W. D., Jons-
Jonsson V. К.)
1964. Instability of the flow between rotating cylinders: the wide-gap pro-
problem, J. Fluid Mech., 20, No. 1, 35—46.
Стейимен (Steinman H.)
1956. The stability of viscous flow between rotating cylinders, Quart. Appl.
Math., 14, No. 1, 27—33.
Стернберг (Sternberg J.)
1962. A theory for the viscous sublayer of a turbulent fluid, J. Fluid
Mech., 13, No. 2, 241—271.
Стюарт (Stewart R. W.)
1956. Irrotational motion associated with free turbulent flows, J. Fluid
Mech., 1, No. 6, 593—606.
1959. The problem of diffusion in a stratified fluid, Adv: Geophys.,6 (Atmosp-
(Atmospheric diffusion and air pollution), 303—311 (русск. перевод веб. «Атмо-
«Атмосферная диффузия и загрязнение воздуха», М., ИЛ, 1962, 337—347).
СтюартДж. (Stuart J. T.)
1958. On the non-linear mechanics of hydrodynamic stability, J. Fluid
Mech., 4, No. 1, 1—21.
1960. On the non-linear mechanics of wave disturbances in stable and
unstable parallel flows. Part I. The basic behaviour in plane
Poiseuille flow, J. Fluid Mech., 9, No. 3, 353—370.
1962. On three-dimensional non-linear effects in the stability of parallel
flow, Advances Aeronaut. Sci., vol. 3, Oxford—London—N. Y.—Paris,
Pergamon Press, 121—142.
1963. Hydrodynamic stability, Laminar boundary layers (ed. by L. Rosen-
head), London, Oxford Univ. Press, 492—579.
1964. On trie cellular patterns in thermal convection, J. Fluid Mech., 18,
No. 4, 481—498.
Субботин В. И., Ибрагимов М. X. и Номофилов Е. В.
1963. Определение отношения между коэффициентами переноса тепла и
количества движения, Атомная энергия, 14, № 4, 414—416.
Суинбенк (Swinbank W. С.)
1951а. The measurement of vertical transfer of heat and water vapour and
momentum in the lower atmosphere with some results, J. Meteor., 8,
No. 2, 135—145.

630 БИБЛИОГРАФИЯ
19516. A sensitive vapour pressure recorder, J. Scienf. Insfr., 28, No. 3,
86-89.
1955. An experimental study of eddy transports in the lower atmosphere,
С S. I. R. O., Div. Meteor. Phys., Techn. Pap. No. 2, Melbourne.
1960. Wind profile in thermally stratified flow. Nature, 186, No. 4723,
463—464.
1964. The exponential wind profile, Quart. J. Roy. Meteor.' Soc, 90,
No. 384, 119—135.
T а к е д a (Takeda K.)
1951. On the atmospheric turbulence. II. On the generalized exponential
formula, J. Meteor. Soc. Japan, 29, No. 7, 243—245.
T а к е у ч и (Takeuchi К.)
1961. On the structure of the turbulent field in the surface boundary
layer, J. Meteor. Soc. Japan, 39, No. 6, 346—367.
1962. On the nondimensional rate of dissipation of turbulent energy in the
surface boundary layer, J. Meteor. Soc. Japan-, 40, No. 3, 127—
135.
Такеучи и Иокояма (Takeuchi K-. Yokoyama О.)
1963. The scale of turbulence and the wind profile in the surface boundary
layer, J. Meteor. Soc. Japan, 41, No. 2, 108—117.
Таунсеид (Tow'nsend A. A.)
1947. The measurement of double and triple correlation derivatives in
isotropic turbulence, Proc. Cambr. Phil. Soc, 43, No. 4, 560—
570.
1951. The diffusion of heat spots in isotropic turbulence, Proc. Roy. Soc,
A209, No. 1098, 418—430.
1954. The diffusion behind a line source in homogeneous turbulence, Proc.
Roy. Soc, A224, No. 1159, 487—512.
1956. The structure of turbulent shear flow, Cambridge, Univ. Press
(русск. перевод: А. А. Тауисенд, Структура турбулентного потока
с поперечным сдвигом, М., ИЛ, 1959).
1958. The effects of radiative transfer on turbulent flow of a stratified
fluid, J. Fluid Mech., 4, No. 4, 361—375.
1959. Temperature fluctuations over a heated horizontal surface, J. Fluid
Mech., 5, No. 2, 209—241.
1962a. Natural convection in the earth's boundary layer, Quart. J. Roy.
Meteor. Soc, 88, No. 375, 51—56.
19626. Remarks on the Malkus theory of turbulent flow, Mecanique de la
turbulence (Coll. Intern, du CNRS a Marseille), Paris, fid. CNRS,
167—180.
T а ц у м и (Tatsumi T.)
1952. Stability of the laminar inlet-flow prior to the formation of Poiseuille
regime, 1—II, J. Phys. Soc. Japan, 7, 489—494, 495—501.
Тацуми и Гото (Tatsumi Т., Gotoh К.)
1960. The stability of free boundary layers between two unifomi streams,
J. Fluid Mech., 7, No. 3, 433—441.
Тацуми и Какутаии (Tatsumi Т., Kakutani Т.)
1958. The stability of a two-dimensional laminar jet, J. Fluid Mech., 4,
No. 3, 261—275.
ТемпельманА. A.
1962. Эргодические свойства однородных случайных полей на группах,
Труды VI Всесоюзи. совещ. теор. верояти, мат. стат., Вильнюс,
Гос, полит, научн. изд., 253—255.

БИБЛИОГРАФИЯ 631
Типпельскирх (Tippelskirch H.)
1956 Ober Konvektionszellen, insbesondere .im flflssigen Schwefel, Beitr.
Phys. Atmosph., 29, Nr. 1, 37—54.
Титьеис (Tietjens O.)
1925. Beitrage zur Entstehung der Turbulenz, Zs. angew. Math. Mech., 5,
Nr. 3, 200—217.
ТолмениФайи (Tolman R. C, Fine P. C.)
1948. On the irreversible production of entropy, Rev. Mod. Phys., 20, No. 1,
51—77.
Толмин (Tollmien W.)
1926. Berechnung turbulenter Ausbreitupgsvorgange, Zs. angew. Math.
Mech., 6, Nr. 6, 468-478.
1929. Ober die Entstehung der Turbulenz, Nachr. Ges. Wiss. Gottingen,
Math.-Phys. Kl., 21—44.
1930. Beitrag zur Theorie der Turbulenz, Proc. 3rd Int. Congr. App.l. Mech.,
Stockholm, 1, 105—108.
1935. Ein allgemeines Kriterium der Instabilitat laminarer Geschwindig-
keitsverteilungen, Nachr. Ges. Wiss. Gottingen, Math.-Phys. Kl.,
79—114.
1947. Asymptotische Integration der Storungsdifferentialglejchung ebener
laminarer Stromungen bei hohen Reynoldsschen Zahlen, Zs. angew.
Math. Mech., 25/27, 33—50, 70—83.
ТолминиПреч (Tollmien W., Pretsch J.)
1946. Instabilitat laminar Grenzechichten, Gottinger Monogr. fiber deut-
schen Luftfahrtforsch., 3, Gottingen.
Томас (Thomas L. H.)
1953. The stability of plane Poiseuille flow, Phys. Rev., 91, No. 5, 780-
783.
Томас и Тауисеид (Thomas D. В., Townsend A. A.)
1957. Turbulent convection over a heated horizontal surface, J. Fluid
Mech, 2, No. 5, 473—492.
Торитвейт и Кейзер (Thornthwaite С. Н., Kaser P.)
1943. Wind-gradient observations, Trans. Amer. Geophys. Union, 24, No. 1,
166—182.
Тьеи (Tien С L.)
1964. A note on distributions of temperature and eddy diffusivity for heat
in turbulent flow near a wall, Zs. angew. Math. Phys., 15, No. 1,
63—66.
Тьеи и Васаи (Tien С. L., Wasan D. T.)
1963. Law of the wall in turbulent channel flow, Phys. Fluids, 6, No. 1,
144—145.
Тэйлор (Taylor G. 1.) [Все статьи Тэйлора за исключением работы
1959 года могут быть также найдены в книге G. 1. Taylor, Scientific pa-
papers, vol. 2, Cambridge, Univ. Press, I960.]
1915. Eddy motion in the atmosphere, Phil. Trans. Roy. Soc, A2I5, 1—26.
1916. Conditions at the surface of a hot body exposed to the wind, Brit.
Adv. Com. Aero. Rep. and Memor., 272.
1921. Diffusion by continuous movements, Proc. London Math. Soc. B),
20, 196-211.
1923. Stability of a viscous liquid contained between two rotating cylin-
cylinders, Phil. Trans. Roy. Soc, London, A223, 289—343.
1931. Effect of variation in density on the stability of superposed streams
of fluid, Proc. Roy. Soc., A132, No. 820, 499—523.

632 БИБЛИОГРАФИЯ
1932. The transport of vorticity and heat through fluids in turbulent mo-
motion, Proc. Roy. Soc, AI85, No. 828, 685—706 (русск. перевод в сб.
«Проблемы турбулентности», М.—Л., ОНТИ, 1936, 228—248).
1935а. Statistical theory of turbulence, 1—III, Proc. Roy. Soc, AI5I,
No. 874, 421—464.
19356. Statistical theory of turbulence. IV. Diffusion in a turbulent air
stream, Proc. Roy. Soc, AI51, No. 874, 465—478.
1935b. Distribution of velocity and temperature between concentric rota-
rotating cylinders, Proc. Roy. Soc, AI5I, No. 874, 494—512.
1936a. Statistical theory of turbulence. V. Effect of turbulence on boundary
layer, Proc Roy. Soc, AI56, No, 888, 307—317.
19366. Fluid friction between rotation cylinders. I. Torque measurements,
Proc. Roy. Soc, AI57, No. 892, 546—564.
1938. Some recent developments in the study of turbulence, Proc. 5th Int.
Congr. Appl. Mech., Cambridge (USA), 294—310.
1953. Dispersion of soluble matter in solvent flowing slowly through a
tube, Proc. Roy. Soc, A2I9, No. 1137, 186—203.
1954a. The dispersion of matter in turbulent flow through a pipe, Proc.
Roy. Soc, A223, No. 1155, 446—468.
19546. Conditions under which dispersion of a solute.in a stream of sol-
solvent can be used to measure molecular diffusion, Proc. Roy. Soc,
A225, No. 1163,473—477.
1959. The present position in the theory of turbulent diffusion, Adv. Geo-
phys., 6 (Atmospheric diffusion and air pollution), 101—112 (русск.
перевод в сб. «Атмосферная диффузия и загрязнение воздуха», М.,
ИЛ, 1962, 124—137).
Т э й л о р P. (Taylor R. J.)
1952. The dissipation of kinetic energy in the lowest layers of the atmo-
atmosphere, Quart. J. Roy. Meteor. Soc, 78, No 336, 179—185.
1956a. Some measurements of heat flux at large negative Richardson num-
number, Quart. J. Roy. Meteor. Soc, 82, No. 351, 89—91.
19566. An electronic analogue of the saturated vapour pressure curve of
water, J. Scient. Instr., 33, No. 11, 436—438.
1958. A linear unidirectional anemometer of rapid response, J. Scient.
Instr., 35, No. 1, 47—52.
1960a. Similarity theory in the relation between fluxes and gradients in the
lower atmosphere, Quart. J. Roy. Meteor. Soc, 86, No. 367, 67—78.
19606. Вид профиля ветра в приземном слое атмосферы. Изв. АН СССР,
сер. геофиз., № 12, 1821-1827.
1963. The effect of instrumental inertia on measurement of the turbulent
flux of water vapour, Austr. J. Appl. Sci., 14, No. 1, 27—37.
Тэйлор и Дайер (Taylor R. J., Dyer A. J.)
1958. An instrument for measuring evaporation from natural surfaces Na-
Nature, 181, No. 4606, 408—409.
Тэйлор и У э б 6 (Taylor R. J., Webb E. K.)
1955. A mechanical computer for micrometeorological research, С S. I. R. O.,
Div. Meteor. Phys., Techn. Pap. No. 6, Melbourne.
Уберои и Корсин (Uberoi M. S., Corrsin S.)
1953. Diffusion of heat from a line source in isotropic turbulence, Nat.
Adv. Com. Aeronaut. Rep., No. 1142.
Унлсон (Wilson B. W.)
1960. Note on surface wind stress over water at low and high wind speed,
J. Geophys. Res., 65, No. 10, 3377—3382.
Уленбек и Орнштейи (Uhlenbeck G. E., Ornstein L. S.)
1930- On the theory of Brownian motion, Phys. Rev., 36, No. 3, 823—84}.

БИБЛИОГРАФИЯ 633
Уотсон (Watson J.)
1960а. On the non-linear mechanics of wave disturbances in stable and
unstable parallel flows. Part 2. The development of solution for
plane Poiseuille and for plane Couette flow, J. Fluid Mech., 9, No. 3,
371—383.
19606. Three-dimensional disturbances in flow between parallel planes, Proc.
Roy. Soc, A254, No. 1279, 562—569.
1962. On spatially-growing finite disturbances in plane Poiseuille flow,
J. Fluid Mech., 14, No. 2, 211-221.
УховскийМ. Р. и ЮдовичВ. И.
1963. Об уравнениях стационарной конвекции, Прикл. матем. мех., 27,
№ 2, 295—300.
У э б б (Webb E. К-)
1958. Vanishing potential temperature gradients in strong convection,
Quart. J. Roy. Meteor. Soc, 84, No. 360, 118—125.
1960. An investigation of the evaporation from Lake Eucumbene,
C.S.I.R.O., Djv. Meteor. Phys., Techn. Pap. No. 10, Melbourne.
1962. Thermal convection with wind shear, Nature, 193, No. 4818, 840—
842.
Фавр, Гавильо и Дючмa (Favre A., Gaviglio J., Dumas R.)
1953. Quelques measures de correlation dans le temps et l'espace en souffle-
rie, La Rech. Aero., N32, 21—28.
Филип (Philip J. R.)
1963. The theory of dispersal during laminar flow in tubes, I—II, Austr.
J. Phys., 16, No. 3, 287—299; 300—310.
Ф и л л и п с (Phillips О. М.)
1955. The irrotational motion outside a free turbulent boundary, Proc.
Cambr. Phil. Soc, 51, No. 1, 220—229.
Флейшмен и Фреикиль (Fleishman В. A., Frenkiel F. N.)
1954. Diffusion of matter emitted from a line source in a non-isotropic
turbulent flow, J. Meteor., 12, No. 2, 141—145.
Ф о к В. A.
1926. Решение одной задачи теории диффузии по методу конечных раз-
разностей и приложение его к диффузии света, Труды Гос. оптич.
• ин-та 4, № 34.
Ф о к н е р (Falkner V. М.)
1943. The resistance of a smooth flat plate with turbulent boundary layer,
Aircr. Eng., 15, 65—69.
Форстолл и Гейлорд (Forstall W., Gaylord E. W.)
1955. Momentum and mass transfer in a submerged water jet, J. Appl:
Mech., 22, No. 2, 161—164.
Фреикиль (Frenkiel F. N.)
1952. Application of the statistical theory of turbulent diffusion to micro-
meteorology, J. Meteor., 9, No. 4, 252—259.
1953. Turbulent diffusion: Mean concentration distribution in a flow field
of homogeneous turbulence, Adv. Appl. Mech., 3, 61—107 (русск.
перевод: Ф. Н. Френкиль, Турбулентная диффузия; распределение
средней концентрации в поле однородного турбулентного потока,
Проблемы механики, М., ИЛ, 1955, стр. 384—421).
ФренкильиШеппард (Frenkiel F. N., Sheppard P. A., ed.)
1959. Atmospheric diffusion and air pollution, Adv. in Geophys., 6, N. Y. —
London, Acad. Press (русск. перевод: Атмосферная диффузия и за-
загрязнение воздуха, М., ИЛ, 1962).

634 БИБЛИОГРАФИЯ
Ф р и ч (Fritsch W.)
1928. Einfluss der Wandrauhigkeit auf die turbulente GeschwindigKeit-
sverteilung in Rinnen, Zs. angew. Math. Mech., 8, Nr. 2, 199—
216.
Ф р о с т (Frost R.)
1946. Turbulence and diffusion in the lower atmosphere, Proc. Roy. Soc,
AI86, No. 1004, 20—35.
1948. Atmospheric turbulence, Quart. J. Roy. Meteor. Soc, 74, No. 321,
316-338.
Функ (Funk J. P.)
1960. Measured radiative flux divergence near the ground at night, Quart.
J. Roy. Meteor. Soc, 86, No. 369, 382—389.
Фэйдж и Тауиеид (Fage A., Townend H. С. Н.)
1932. An examination of turbulent flow with an ultramicroscope, Proc. Roy.
Soc, AI35, No. 828, 656—677 (русск. перевод в сб. «Проблемы тур-
турбулентности», М.—Л, ОНТИ, 1936, 163—184).
X а г е и (Hagen G.)
1839. Ober die Bewegung des Wassers in engen zylindrischen Rohren,
Pogg. Ann., 46, 423—442.
Халтииер и Мартии (Haltiner G. J., Martin F. L.)
1957. Dynamical and physical meteorology, N. Y. — Toronto — London,
McGraw-Hill (русск. перевод: Дж. Халтииер, Ф. Мартии, Динами-
Динамическая и физическая метеорология, М., ИЛ, 1960).
Хама (Наша F. R.)
1953. On'the velocity distribution in the laminar .sublayer and transition
region in turbulent shear flows, J. Aeronaut. Sci., 20, No. 9, 648—
650.
1954. Boundary-layer characteristics for smooth and rough surfaces, Trans.
Soc. Naval Arch. Marine Engrs, 62, 333—358.
Хама, Лонг и Хегарти (Hama F. R., Long J. D.., Hegarty J. C.)
1957. On transition from laminar to- turbulent flow, J. Appl. Phys., 28,
No. 4, 388—394.
X а из е и (Hansen M.)
1928. Die Geschwindigkeitsverteilung in der Grenzschicht an einer eigen-
tauchten Platte, Z. angew. Math. Mech., 8, Nr. 2, 185—199.
X а н т (Hunt J. N.)
1954. The turbulent transport of suspended sediment in open channels,
Proc. Roy. Soc, A224, No. 1158, 322—335.
X e л с т е д (Halstead M.)
1943. A stability term in the wind-gradient equation, Trans. Amer. Geo-
phys. Union, 24, No. 1, 204—208.
1952. The relationship between wind structure and turbulence near the
ground, Geophys. Res. Pap. No. 19, 97—126.
Хннце (Hinze J. O.)
1951. Turbulent diffusion from a source in turbulent shear flow, J. Aero-
Aeronaut. Sci., 18, No. 8, 565—566.
1959. Turbulence. An introduction to its mechanism and theory, N. Y.,
McGrawrHill (русск. перевод: И. О. Хиице, Турбулентность, М.,
Физматгиз, 1963).
1962. Turbulent pipe-flow, Mecanique de la turbulence (Coll. Intern, du
CNRS a Marseille), Paris, Ed. CNRS, 130—165.

БИБЛИОГРАФИЯ 635
Хинце н Ван дер Хегге Цийнеи (Hinze J. О., Van der Hegge
Zijnen B. G.)
1949. Transfer of heat and matter in the turbulent mixing zone of an
axially symmetric jet, Appl. Sci. Res., AI, 435—461.
1951. Local transfer of heat in anisotropic turbulence, Inst. Mech. Eng.,
Proc. Gener. Discus, on Heat Transfer, 188—197.
X о л ц м е н (Holzman B.)
1943. The influence of stability on evaporation, Ann. New York Acad. Sci.,
44, 13—19.
Хопф (Hopf E.)
1952. Statistical hydromechanics and functional calculus, J. Rat. Mech.
Anal., 1, No. 1, 87—123.
X о у а р д (Howard L. N.)
1959. Hydrodynamic stability of a jet, J. Math, and Phys., 89, No. 4,
283—298.
1961. Note on a paper of John W. Miles, J. Fluid Mech., 10, No. 4, 509—512.
1963. Neutral curves and stability boundaries in stratified flow, J. Fluid
Mech.) 16, No. 3, 333—342.
X о у а р т (Howarth L., ed.)
1953. Modern developments in fluid dynamics. High speed flow, Oxford
Univ. Press (русск. перевод: Современное состояние аэродинамики -
больших скоростей, под ред. Л. Хоуарта, М., ИЛ, 1955).
Хоуген, Баред и Антаиаитйс (Haugen D. A., Barad M. L., Anta-
naitis P.)
1961. Values of parameters appearing in Sutton's diffusion models, J. me-
teorol., 18, No. 3, 368—372.
X с у, С а т о и Сейдж (Hsu N. Т., Sato К., Sage В. Н.)
1956. Temperature gradients in turbulent gas streams. Effect of flow con-
condition upon eddy conductivity, Ind. Eng. Chem., 48, No. 12, 2218—
2223.
Худимою (Hudimoto B.)
1941. On the turbulent boundary layer, Trans. Japan Soc. Mech. Eng., 7.
1951. A brief note on the laminar sublayer of the turbulent boundary
layer, Mem. Fac. Eng. Kyoto Univ., 13, 174—179.
Хэйи Паскуил (Hay J. S., Pasquill F.)
1959. Diffusion from a continuous source in relation to the spectrum and
scale of turbulence, Adv. Geophys., 6 (Atmospheric diffusion and air
pollution), 345—365 (русск. перевод в сб. «Атмосферная диффузия
и загрязнение воздуха», М., ИЛ, 1962, 382—404).
Цай Ко-ен
1961. Теплообмен в турбулентном потоке жидкости при больших значе-
значениях чисел Прандтля, Инж.-физ. журн., 4, № 8, 20—29.
Ц в а и г Л. Р.
1960. Измерение частотных спектров температурных пульсаций в призем-
приземном слое атмосферы, Изв. АН СССР, сер. геофиз., № 8, 1252—1262.
Ц е й т и н Г. X.
1963. Распространение примеси от высотного источника, Труды Ленннгр.
гидромет. ин-та. вып. 15, 10—31.
Чандрасекар (Chandrasekhar S.)
1943. Stochastics problems in physics and astronomy, Rev. Mod. Phys., IS,
No. 1, 1—89 (русск. перевод: С. Чандрасекар, Стохастические про-
проблемы в физике и астрономии, М..ИЛ, 1947.)

636 БИБЛИОГРАФИЯ
1953. The stability of viscous flow between rotating cylinders in the pre-
presence of a magnetic field, Proc. Roy. Soc, A2I6, No. 1126, 293—
309.
1954. The stability of viscous flow between rotating cylinders, Mathema-
tika, 1, 5—13.
1958. The stability of viscous flow between rotating cylinders, Proc. Roy.
Soc, A246, No. 1246, 301—311.
1960. The stability of inviscid flow between rotating cylinders, J. Indian
Math. Soc. (N. S.),24, 211—221.
1961. Hydrodynamic and hydromagnetic stability, Oxford, Clarendon Press.
Чандрасекар и Элберт (Chandrasekhar S., Elbert D. D.)
1962. The stability of viscous flow between rotating cylinders. II, Proc.
Roy. Soc, A268, No. 1333, 145—152.
Ч а р н о к (Charnock H.)
1958a. Meteorology, Sci. Progress, 46, No. 183, 470—487.
19586. Physical oceanography, Sci. Progress, 46, No. 183, 487—501.
Чарноки Эллисон (Charnok H., Ellison Т. Н.)
1959. Fluctuations of temperature and humidity at 134m over the sea,
Deutsch. Hydrograph. Zs., 12, Nr. 4, 171—180.
Чепмен и Каулинг (Chapman S., Cowling Т. G.)
1952. The mathematical theory of non-uniform gases. Cambridge, Univ.
Press (русск. перевод: С. Чепмен и Т. Каулинг, Математическая
теория неоднородных газов, М., ИЛ, 1960).
Чепмен и Кестер (Chapman D. R., Kester R. H.)
1953. Measurements of turbulent skin friction on cylinders in axial flow
at subsonic and supersonic velocities, J. Aeronaut Sci., 20, No. 7,
441—448.
Ч ж о у (Chou P. Y.)
1945a. On velocity correlations and the solutions of the equations of tur-
turbulent fluctuation, Quart. Appl. Math., 3, No. 1, 38—54.
19456. Pressure flow of a turbulent fluid between parallel planes, Quart.
Appl. Math., 3, No. 3, 198—209.
1947. Turbulent flow along a semi-infinite plane, Quart. Appl. Math. 5,
No. 3, 346—353.
Чжу и Коважный (Chu В. Т., Kovasznay L. S. G.)
1958. Non-linear interactions in a viscous heat-conducting compressible
gas, J. Fluid Mech., 3, No. 5, 494—514.
Чилтон и Колбэрн (Chilton Т. Н., Colburn A. P.)
1934. Mass transfer (absorption) coefficients, Ind. Eng. Chem., 26, No. 11,
1183—1187.
Шаде (SchadeH.)
1964. Contribution to the nonlinear stability theory of inviscid shear layers,
Phys. Fluids, 7, No. 5, 623—628.
Шёкгер (Schoenherr К. Е.)
1932. Resistance of flat surfaces moving through a fluid, Trans. Soc. Nav.
Arch. Marine Eng., 40, 279—313.
Шеппард (Sheppard P. A.)
1947. The aerodynamic drag of the earth's surface and the value of von
Karman's constant in the lower layer, Proc. Roy. Soc, AI88,
No. 1013, 208—222.
Шервуд (Sherwood Т. К)
1950. Heat transfer, mass transfer and fluid friction relationships in tur-
turbulent flow, Ind. Eng. Chem., 42, No. 10, 2077—2084.

БИБЛИОГРАФИЯ 637
Шиллер (Shiller L.)
1932. Stromung in Rohren, Handbuch der Experimentalphysik, 4, Nr. 4
(русск. перевод: Движение жидкостей в трубах, М., ОНТИ, 1936).
1934. Neue quantitative Versuche zur Turbulenzentstehung, Zs. angew.
Math. Mech., 14, Nr. 1, 36—48.
Ш и о т а и и (Shiotani M.)
1962. The relationship between wind profiles and stabilities of the air
layer in the outskirts of the city, J. Meteor. Soc. Japan, 40, No. 6,
315—329.
Шлихтинг (Schlichting H.) «
1933a. Zur Entstehung der Turbulenz bei der Plattenstromung, Nachr. Ges.
Wiss. Gottingen, Math.-phys. Kl.. 160—19a
19336. Berechnung der Anfachung kleiner Storungen bei der Plattenstrom-
Plattenstromung, Zs. angew. Math. Mech., 13, Nr. 3, 171—174.
1935a. Amplitudenverteilung und Energiebilanz der kleinen Storungen bei
der Plattengrenzschicht, Nachr. Ges. Wiss. Gottingen, Math.-phys.
Kl., I, 47—78.
19356. Turbulenz bei Warmeschichtung, Z. angew. Math. Mech., 15, Nr. 6,
313—338.
1936. Experimentelle Untersuchungen zum Rauhigkeitsproblem, Ing.-Arch.
7, Nr. 1, i—34.
1951. Grenzschicht-Theorie, Verlag G. Braun, Karlsruhe (русск. перевод:
Г. Шлихтииг, Теория пограничного слоя, М., ИЛ, 1956).
1959. Entstehung der Turbulenz, Handbuch der Physik, Berlin (русск. пе-
перевод: Г. Шлихтинг, Возникновение турбулентности, М., ИЛ, 1962).
Шмидт (Schmidt W.)
1917. Der Massenaustausch bei der ungeordneten Stromung In freier Luft
und seine Folgen, Sitzungsber. Akad. Wiss. Wien, Math.-nat. Kl.
Ba), 126, Nr. 6, 757—804.
1925. Der Massenaustausch in freier Luft und verwandte Erscheinungen,
Hamburg, Grand.
Шубауэр и Клебанов (Schubauer G. В., Klebanoff P. S.)
1956. Contributions on the mechanics of boundary-layer transition, Nat.
Adv. Com. Aeronaut. Rep. No. 1289.
Шубауэр и Скрэмстед (Schubauer G. В., Skramstad H. K.)
1947. Laminar boundary-layer oscilations and stability of laminar flow,
J. Aeronaut. Sci., 14, No. 2, 69—78.
Шубауэри Чей (Schubauer G. В., Tcheh С. М.)
1959. Turbulent flow, Turbulent flow and heat transfer (ed. by С. С. Lin),
Princeton, Univ. Press, 75—195 (русск. перевод в книге «Турбулент-
«Турбулентные течения и теплопередача». М., ИЛ, 1963, 83—205).
Шульц-Груиов (SchuUz-Grunow F.)
1940. Neues Reibungswiiiderstandgesetz fur glatte Platten, Luftfahrtforsch.,
17, Nr. 8, 239—246.
Ш э и ь (Shen S. F.)
1954. Calculated amplified oscillations in plane Poiseuille flow and Blasius
flows, J. Aeronaut. Sci., 21, No. 1, 62—64.
Щербакова Л. Ф.
1949. Исследование некоторых способов характеристики турбулентного
обмена на основе данных наблюдений в нижнем слое атмосферы,
Труды Глави. геофиз. обсерв.. № 16G8), 25—51.
ЭйиштейниЛи (Einstein H. A., Li H.)
1956. The viscous sublayer along a smooth boundary, Proc. Amer. Soc.
Civ. Engrs., Pap. 945.

638 БИБЛИОГРАФИЯ
Эйфель (Eiffel G.)
1912. Sur la resistance des spheres dans l'air en mouvement, С. г, Acad.
Sci., 155, 1597—1599.
Э к к е р т (Eckert E. R. G.)
1950. Introduction to the transfer of heat and mass, N. Y., McGraw-Hill
(русск. перевод: Э. Р. Эккерт, Введение в теорию тепло- и массо-
обмена, М. — Л., Госэнергоиздат, 1957).
Э к м а н (Ekman V. W.)
1911. On the change from steady to turbulent motion of liquids, Ark. Mat.
Astron. Fys., 6, No. 12.
Э л д e p (Elder J. W.)
1959. The dispersion of marked fluid in turbulent shear flow, J. Fluid
Mech., 5, No. 4, 544^560.
1960. An experimental investigation of turbulence spots and breakdown
to turbulence, J. Fluid Mech., 9, No. 2, 235—249.
Элиас (Elias F.)
1929. Die Warmeflbertragung einer gehiezten Platte an stromende Luft. I.
Anlage und Ergebnisse der Versuche, Zs. angew. Math. Mech., 9,
Nr. 6, 434—465.
Элиассен, Хойланд и Риис (Eliassen A., Holland Е., Riis E.)
1953. Two-dimensional perturbation of flow with constant shear of a Stra-
Stratified fluid, Publ. Inst. Weath. Clim. Res., Oslo, No. 1.
Эллиот (Elliot W. P.)
1957. A comparision of some approaches to the diabatic. wind profile,
Trans. Amer. Geophys. Union, 38, No. 1, 21—24.
1960. An hypothesis for the diabatic mixing length, J. Meteor., 17, No. 6,
680—681.
Э ллисон (Ellison Т. Н.)
1956. Atmospheric turbulence, Surveys in Mechanics (ed. by G. K. Batche-
lor and R. M. Davies), Cambridge, Univ. Press, 400—430.
1957. Turbulent transfer of heat and momentum from an infinite rough
plane, J. Fluid Mech., 2, No. 5, 456—466.
1959. Turbulent diffusion, Sci. Progress, 47, No. 187, 495—506.
1960. A note on the velocity profile and longitudinal mixing in a broad
open channel, J. Fluid Mech., 8, No. 1, 33—40.
Эллисон и Тэрнер (Ellison Т. H., Turner J. S.)
1960. Mixing of dense fluid in a turbulent pipe flow. Parts 1—2, J Fluid
Mech., 8, No. 4, 514—544.
Э л р и к (Elrick D. E.)
1962. Source functions for diffusion in uniform shear flow, Australian J.
Phys., 15, No. 3, 283—288.
Э л р о д (Elrod H. G.)
1957. Note on the turbulent shear stress near a wall, J. Aeronaut. Sci., 24,
No. 6, 468—469 (см. также Исправление к этой статье^ J. Aeronaut.
Sci., 27, No. 2, 145, 1960).
Э ш (Esch R. E.)
1957. The instability of shear layer between two parallel streams, J. Fluid
Mech., 3, No. 3, 289—303.
Юдин М. И. и ШвецМ. Е.
1940. Стационарная модель распределения ветра с высотой в турбулент-
турбулентной атмосфере, Труды Гл. геофиз. обсерв., № 31, 42—52.

БИБЛИОГРАФИЯ 639
: Я Г Л О М А. М.
1948. Однородная и изотропная турбулентность в вязкой и сжимаемой
жидкости. Изв. АН СССР, сер. географ, и геофиз., 12, № 6, 501—
522.
1952. Введение в теорию стационарных случайных функций, Усп. матем.
наук, 7, №5E1), 3—168.
1965. Лаграижевы характеристики турбулентности в термически страти-
стратифицированном приземном слое и в конвективных струях, Изв. АН
СССР, сер. «Физика атмосферы и океана», 1, № 2.
Ямамото (Yamamoto G.)
1959. Theory of turbulent transfer in non-neutral conditions, Journ. Meteor.
Soc. Japan, 37, No. 2, 60—69.
Ям. амото и Коид о- (Yamamoto G., Kondd J.)
1959. Effect of surface reflectivity for long wave radiation on temperature
profiles near the bare soil surface, Sci. Reports Tohoku Univ., ser. V,
Geophysics, If, No. 1, 1—9.
Ямамото и Шнмануки (Yamamoto G., Shimanuki A.)
1960. Numerical solution of the equation of atmospheric turbulent diffu-
diffusion, Sci. Rep. Tdhoku Univ., ser. V, Geophys., 12, No. 1, 24—35.
1964. The determination of lateral diffusivity in diabatic conditions near
the ground from diffusion experiments, J. Atmosph. Sci., 21, No 2,
Щ-196.

Андрей Сергеевич Монпн.
Акива Моисеевич Яглом
Статистическая гидромеханика
Часть I
М., 1965 г., 640 стр. с илл.
Редактор Л С. Голицын
Техн. редактор И. Ш. Аксельрод
Корректор О. А. Бутусова
Сдано в набор 5/IX 1964 г. Подписано к печати Ю/ХП 1964 г.
Бумага 60X90'/is. Физ. печ. л. 40. Условн. печ. л. 40.
Уч.-изд. л. 37,94. Тираж 7000 экз. Т-17074.
Цена книги 2 р. 05 к. Заказ J6 729
Издательство «Наука»
Главная редакция
физико-математической литературы
Москва, В-71, Ленинский проспект, 15
Ленинградская типография К» 2
имени Евгении Соколовой Главполиграфпрома
Государственного комитета Совета Министров СССР
по печати. Измайловский проспект, 29