Н. С. ПИСКУНОВ
ДИФФЕРЕНЦИАЛЬНОЕ
И ИНТЕГРАЛЬНОЕ
ИСЧИСЛЕНИЯ
для втузов
том первый
ИЗДАНИЕ ТРИНАДЦАТОЕ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия
для высших технических учебных заведений
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1985

22.161Л
П 34
УДК 517
Пискунов Н. С. Дифференциальное и инте-
интегральное исчисления для втузов, т. 1: Учебное пособие
для втузов.—13-е изд.— М.: Наука. Главная редак-
редакция физико-математической литературы, 1985.— 432 с.
Хорошо известное учебное пособие по математике
для втузов с достаточно широкой математической
подготовкой.
Первый том включает разделы: введение в ана-
анализ, дифференциальное исчисление (функций одной
и нескольких переменных), неопределенный и опре-
определенный интегралы.
Настоящее издание не отличается от предыдуще-
предыдущего A978 г.).
Для студентов высших технических учебных за-
заведений*
1702050000-024
053 @2)-85

ОГЛАВЛЕНИЕ
Предисловие к девятому изданию ,., •••••••» 9
Предисловие к пятому изданию ••«•«••*•••»•••»••• И
ГЛАВА I
ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ
§ I. Действительные числа. Изображение действительных чисел точ-
точками числовой оси .«•,,. • . • 13
§ 2. Абсолютная величина действительного числа 15
§ 3. Переменные и постоянные величины • . • • 16
§ 4. Область изменения переменной величины 17
§ 5. Упорядоченная переменная величина. Возрастающая и убываю-
убывающая переменные величины. Ограниченная переменная величина 18
§ 6. Функция ••,»..•••«•»«•......,..»•.• 19
$ 7. Способы задания функции «•••••¦• 20
§ 8. Основные элементарные функции. Элементарные функции . . . • 22
§ 9. Алгебраические функции •••..«*...•••»•••.» 26
§ 10. Полярная система координат ..«,...• 28
Упражнения к главе I ••••••««•••«•,,»••••»•• 29
ГЛАВА II
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
§ 1. Предел переменной величины. Бесконечно большая переменна»
величина • ....«• , • • 31
§ 2. Предел функции ¦......,.,. • 33
§ 3. Функция, стремящаяся к бесконечности. Ограниченные функции 36
§ 4. Бесконечно малые и их основные свойства ••••«••*»•• 39
§ 5. Основные теоремы о пределах • •••••..,....••.. 42
§ 6. Предел функции ?—- при х—^••••••••••••^... 46
§ 7. Число е . 47
§ 8. Натуральные логарифмы . # . . . • 51
§ 9. Непрерывность функций • ¦ ......••••• 53
§ 10. Некоторые свойства непрерывных функций . , 56
§ 11. Сравнение бесконечно малых • • • • • • . ¦ 59
Упражнения к главе II •••••••••••••••«••,•••» 61

4 ОГЛАВЛЕНИЕ
ГЛАВА III
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
§ 1. Скорость движения . • 64
§ 2. Определение производной • 66
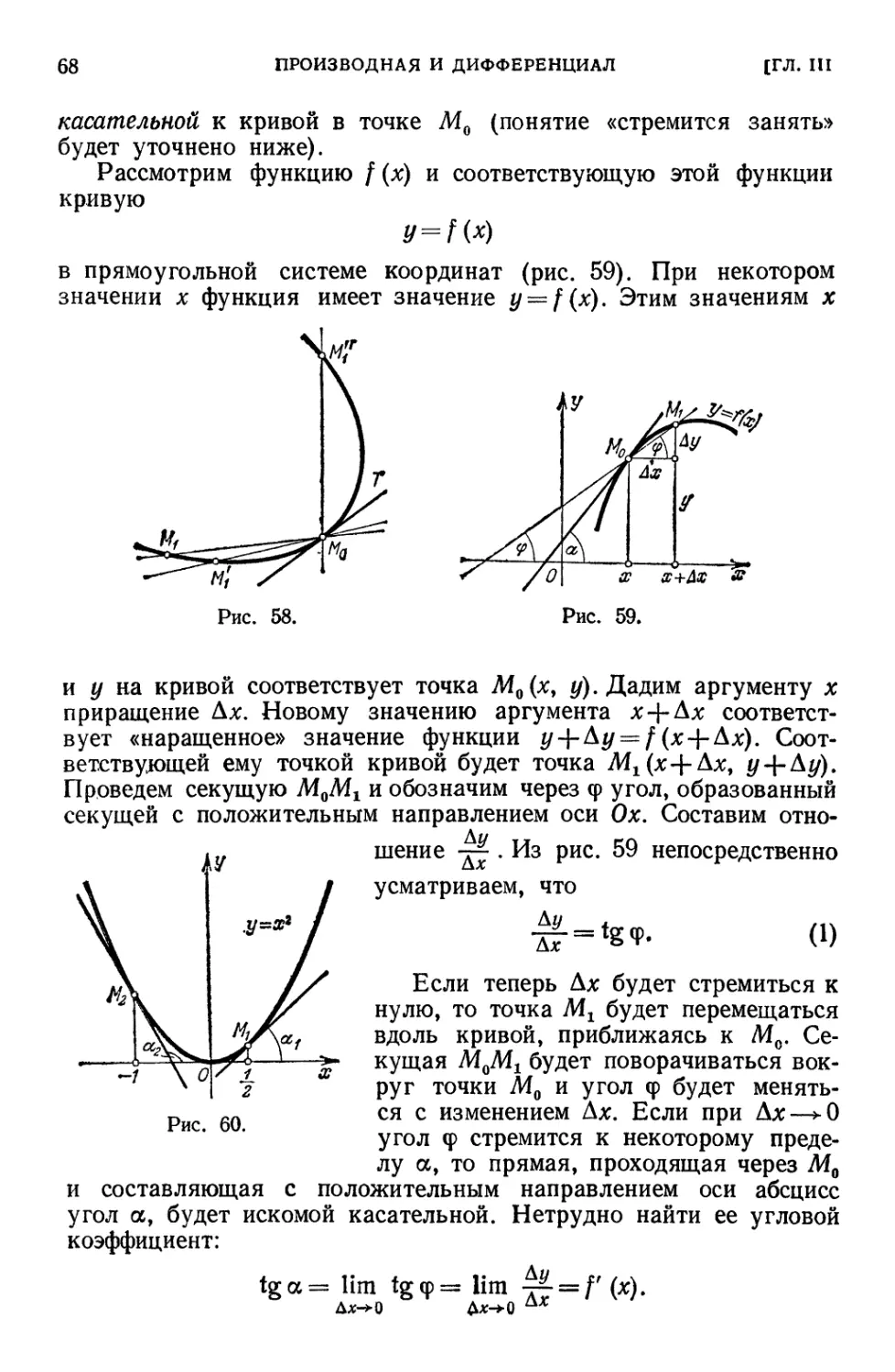
§ 3. Геометрическое значение производной 67
§ 4. Дифференцируемость функций ,.«««•*,. 69
§ 5. Производная от функции у=хп при п целом и положительном 71
§ 6. Производные от функций y = sinxf y = cosx ¦ * 72
§ 7. Производные постоянной, произведения постоянной на функцию,
суммы, произведения, частного 74
§ 8. Производная логарифмической функции 78
§ 9. Производная от сложной функции # 79
§ 10. Производные функций y = tgx, y — ctgx, у— ln| х\ . , 80
§ И. Неявная функция и ее дифференцирование , # # ¦ ¦ 82
§ 12. Производные степенной функции при любом действительном пока-
показателе, показательной функции, сложной показательной функции 83
§ 13. Обратная функция и ее дифференцирование # # , 85
§ 14. Обратные тригонометрические функции и их дифференцирование 88
§ 15. Таблица основных формул дифференцирования 92
§ 16. Параметрическое задание функции 93
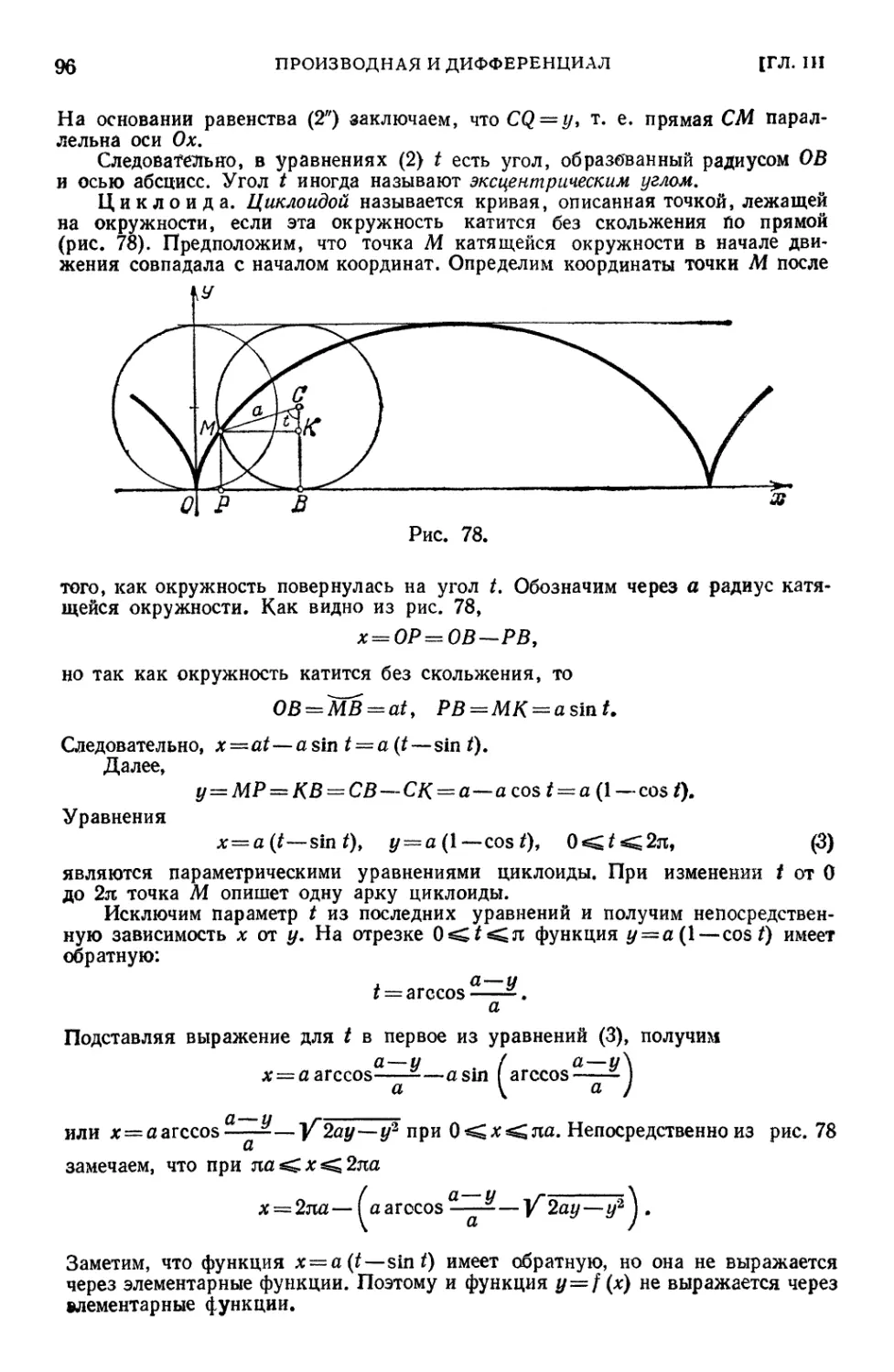
§ 17. Уравнения некоторых кривых в параметрической форме 95
§ 18. Производная функции, заданной параметрически « 97
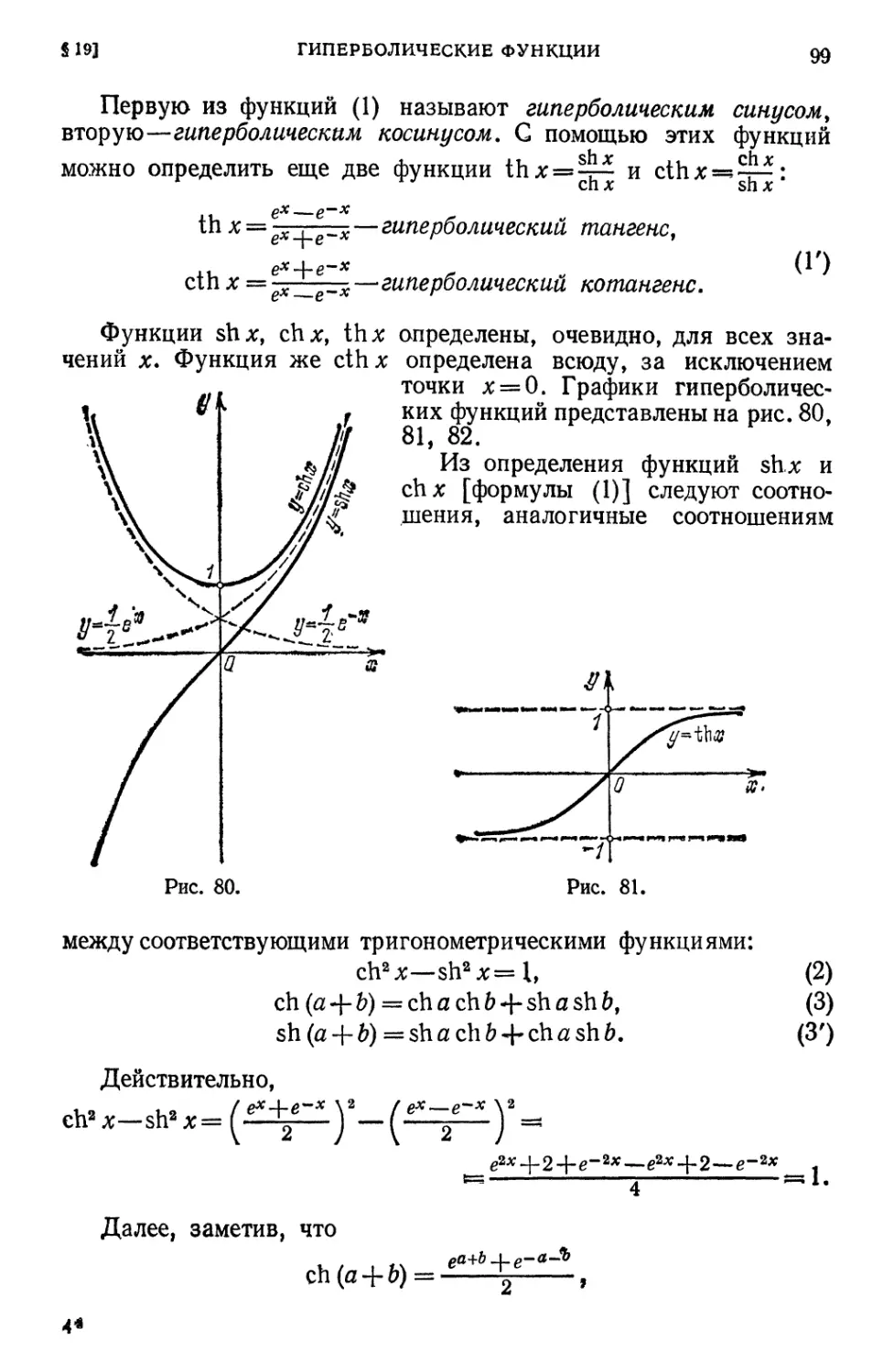
§ 19. Гиперболические функции , ¦ • 98
§ 20. Дифференциал ¦ 101
§ 21. Геометрическое значение дифференциала 105
§ 22. Производные различных порядков 106
§ 23. Дифференциалы различных порядков 108
§ 24. Производные различных порядков от неявных функций и функций,
заданных параметрически 109
§ 25. Механическое значение второй производной 111
§ 26. Уравнения касательной и нормали. Длины подкасательной и под-
поднормали 112
§ 27. Геометрическое значение производной радиус-вектора по поляр-
полярному углу 115
Упражнения к главе III , ,»¦,.,.,« 116
ГЛАВА IV
НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
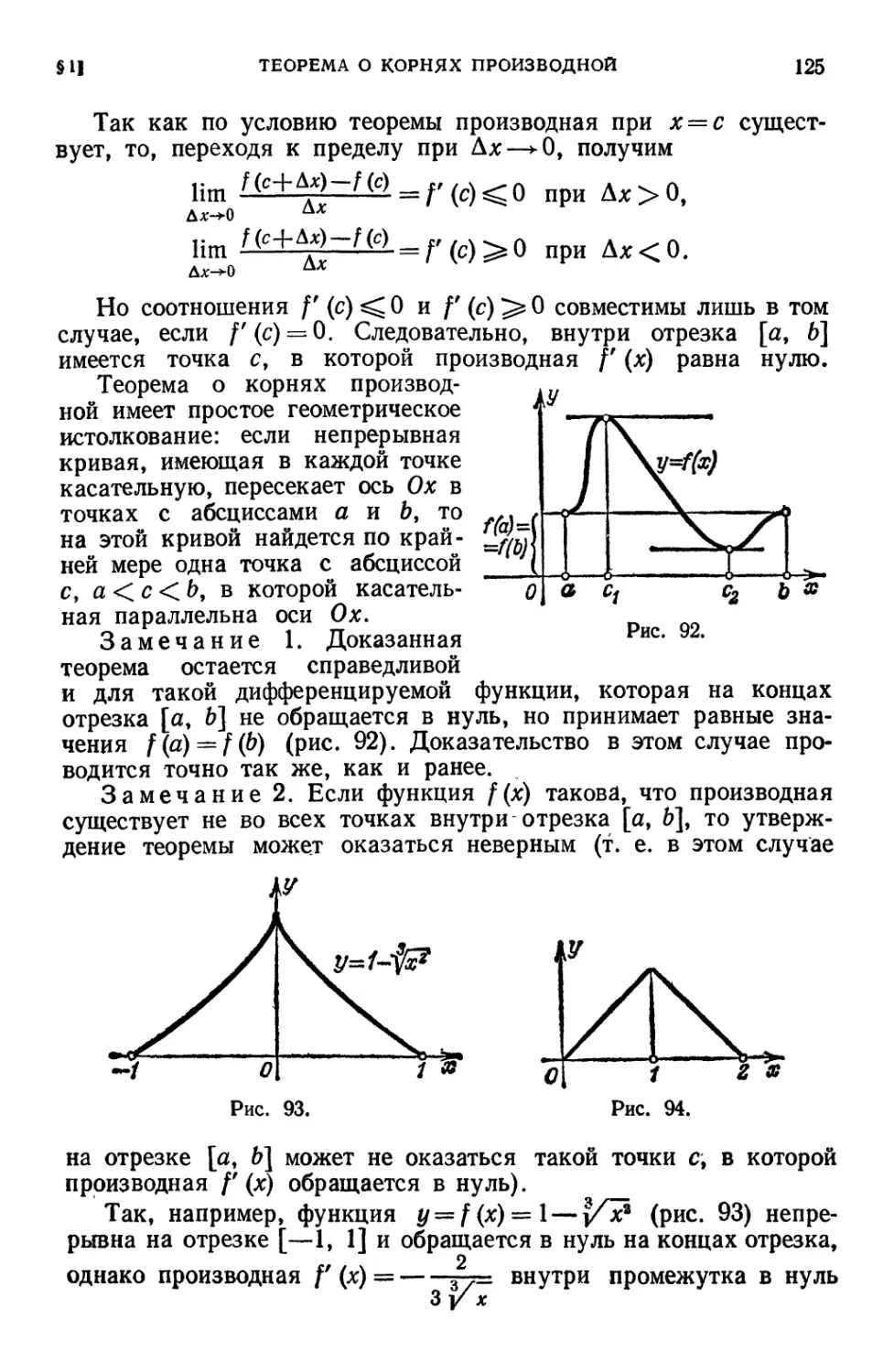
§ 1. Теорема о корнях производной (теорема Ролля) 124
§ 2. Теорема о конечных приращениях (теорема Лагранжа) ...... 126
§ 3. Теорема об отношении приращений двух функций (теорема Коши) 127
§ 4. Предел отношения двух бесконечно малых величин ( «раскрытие
неопределенностей вида -^-» J ¦ • # ••••••••• 128

ОГЛАВЛЕНИЕ 5
§ 5. Предел отношения двух бесконечно больших величин f «раскрытие
со \
неопределенностей вида —» ).#¦«..¦¦.¦• 131
со /
§ 6. Формула Тейлора »«•••»•«*«»««• 135
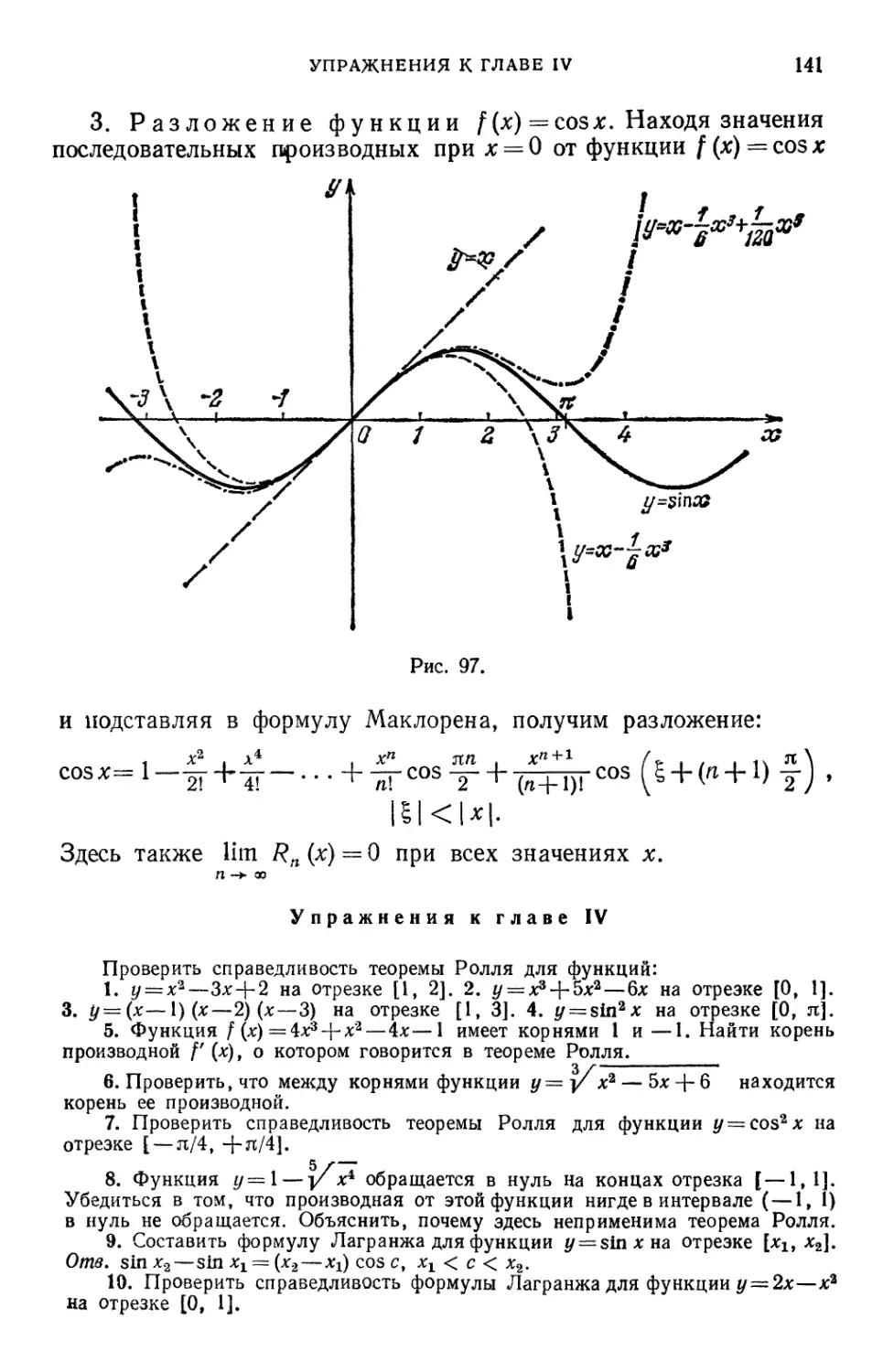
§ 7. Разложение по формуле Тейлора функций ех9 sin лг, cos л: .... 138
Упражнения к главе IV • ¦ • ....¦¦.. 141
глава V
ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
§ 1. Постановка задачи •,•••,«,••«*« « • 144
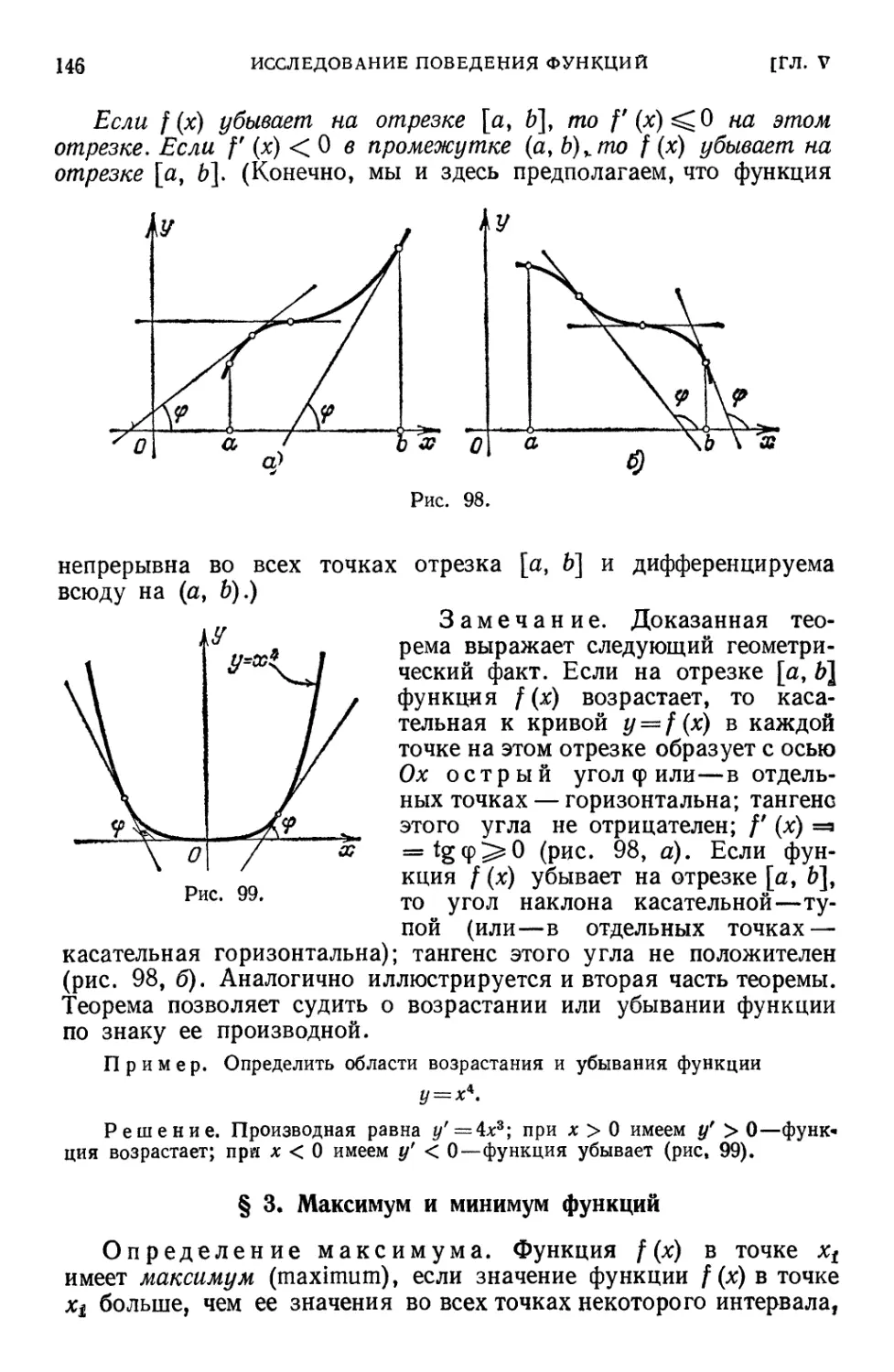
§ 2. Возрастание и убывание функции ¦ • • 145
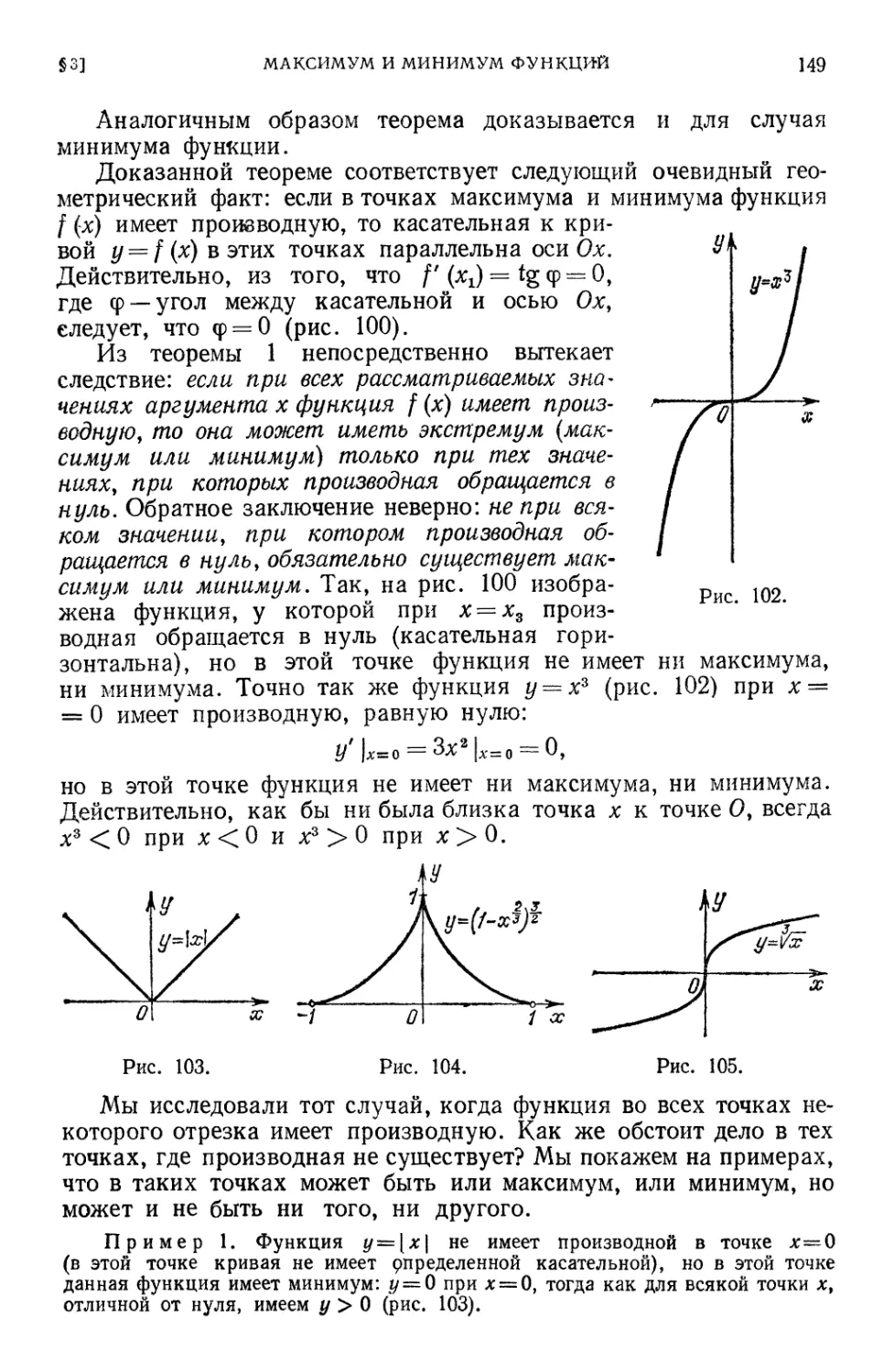
§ 3. Максимум и минимум функций «•# 146
§ 4. Схема исследования дифференцируемой функции на максимум и
минимум с помощью первой производной • • » » • . 152
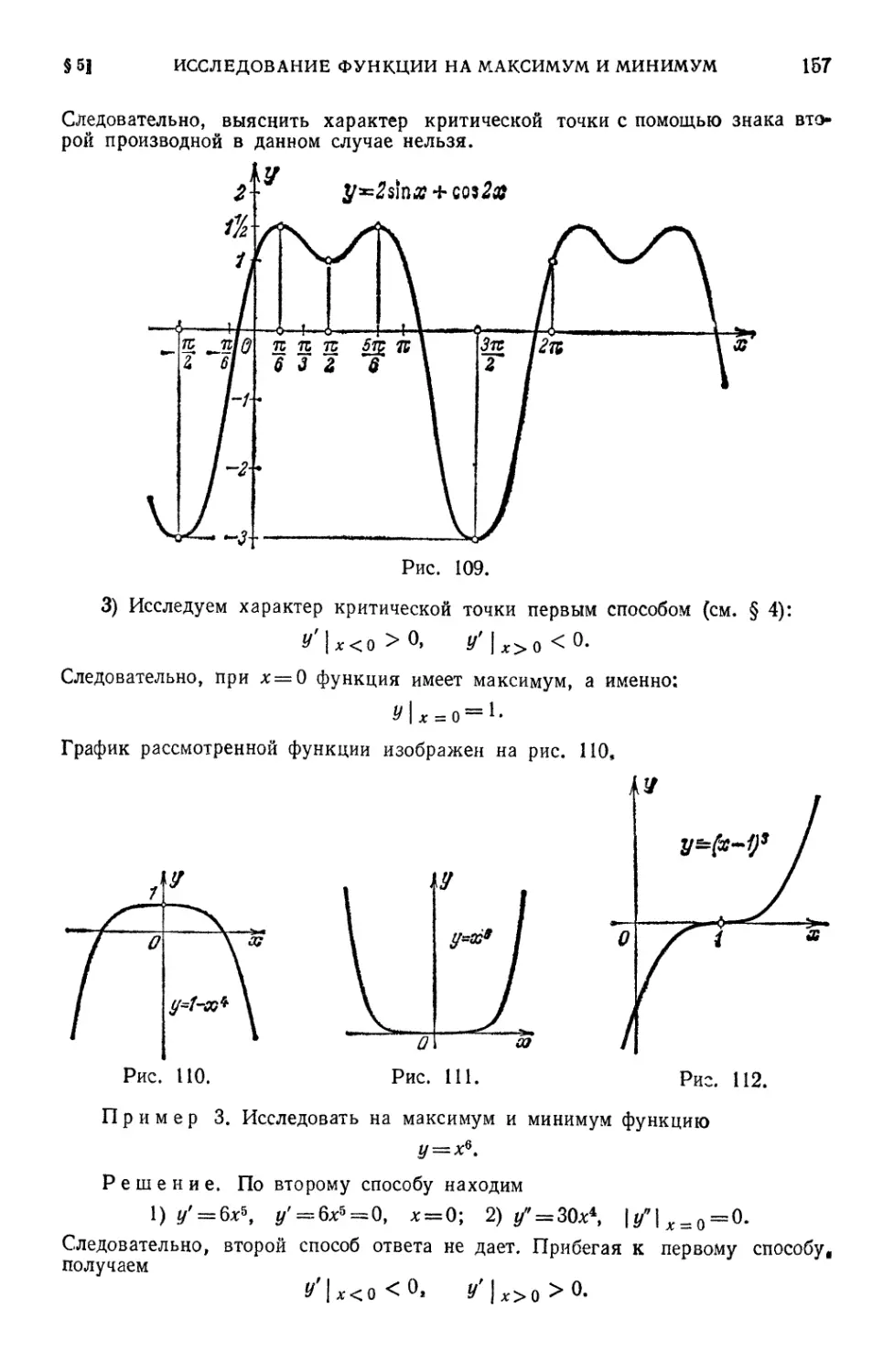
§ 5. Исследование функции на максиму^ и минимум с помощью второй
производной * ¦ ¦ ¦ • ,•,•*.,...,.•*• 155
§ 6. Наибольшее и наименьшее значения функции на отрезке , , . ¦ 158
§ 7. Применение теории максимума и минимума функций к решению
задач * ».«.«•« »•• * 159
§ 8. Исследование функции на максимум и минимум с помощью фор-
формулы Тейлора ••»•.. 160
§ 9. Выпуклость и вогнутость кривой. Точки перегиба • ¦...,<. 162
§ 10. Асимптоты ¦ . ¦ ¦«• 167
§ 11. Общий план исследования функций и построения графиков t . , 171
§ 12. Исследование кривых, заданных параметрически ,,».,,¦. 175
Упражнения к главе V###, ••¦¦•••• ••••••••*»» 179
ГЛАВА VI
КРИВИЗНА КРИВОЙ
§ 1. Длина дуги и ее производная ¦ ¦ • , . . . . 184
§ 2. Кривизна . , , 186
§ 3. Вычисление кривизны ¦•¦¦•,* 187
§ 4. Вычисление кривизны линии, заданной параметрически 190
§ 5. Вычисление кривизны линии, заданной уравнением в полярных
координатах .,.¦¦„.,,,.*,*,¦„......,,, 190
§ 6. Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента 192
§ 7. Свойства эволюты ,¦¦,..,.,, , 196
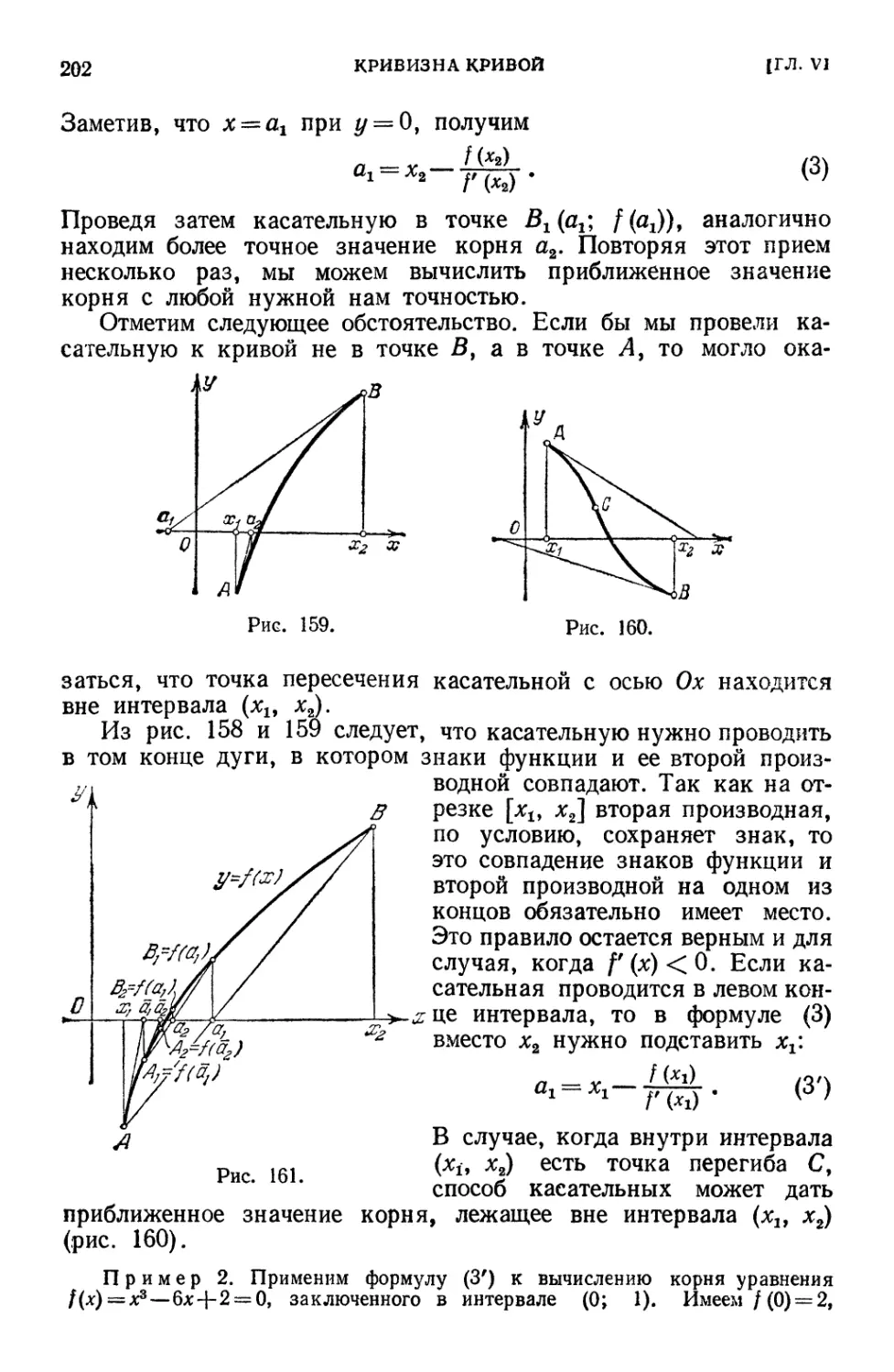
§ 8. Приближенное вычисление действительных корней уравнения . . . 199
Упражнения к главе VI •¦..,, ..•,»••¦• 203
ГЛАВА VII
КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ
§ 1. Комплексные числа. Исходные определения .,.,«*•..•, 206
§ 2. Основные действия над комплексными числами .,,.,,••. 208
§ 3. Возведение комплексного числа в степень и извлечение корня
из комплексного числа .,#..,,..в#, в# 211

В ОГЛАВЛЕНИЕ
§ 4. Показательная функция с комплексным показателем и ее свойства 213
§ 5. Формула Эйлера. Показательная форма комплексного числа • « . 215
§ 6. Разложение многочлена на множители • 217
§ 7. О кратных корнях многочлена , ¦ 220
§ 8. Разложение многочлена на множители в случае комплексных корней 221
§ 9. Интерполирование. Интерполяционная формула Лагранжа , , , 222
§ 10. Интерполяционная формула Ньютона f 224
§11. Численное дифференцирование « • # 226
§ 12. О наилучшем приближении функций многочленами. Теория Че-
бышева • , 227
Упражнения к главе VII . . • « ,,.... 228
ГЛАВА VIII
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 1. Определение функции нескольких переменных ,...••••• 230
§ 2. Геометрическое изображение функции двух переменных ¦ • . . . 233
§ 3. Частное и полное приращение функции , 234
§ 4. Непрерывность функции нескольких переменных 235
§ 5. Частные производные функции нескольких переменных ..... 238
§ 6. Геометрическая интерпретация частных производных функции
двух переменных » 239
§ 7. Полное приращение и полный дифференциал . * 240
§ 8. Применение полного дифференциала в приближенных вычислениях 243
§ 9. Приложение дифференциала к оценке погрешности при вычислениях 244
§ 10. Производная сложной функции. Полная производная. Полный
дифференциал сложной функции ,....«• 247
§ 11. Производная от функции, заданной неявно • 250
§ 12. Частные производные различных порядков , 253
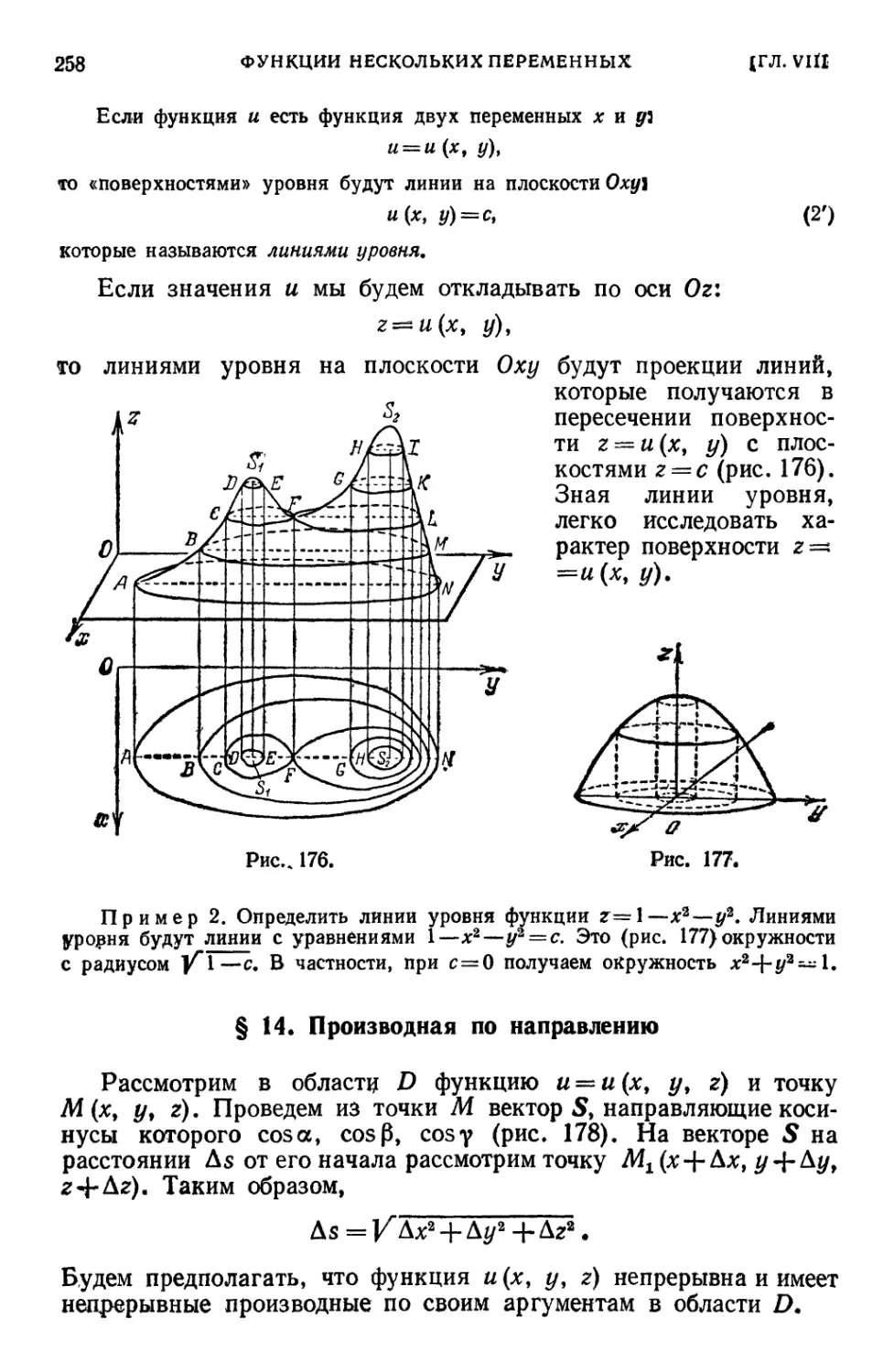
§ 13. Поверхности уровня , 257
§ 14. Производная по направлению 258
§ 15. Градиент » • 260
§ 16. Формула Тейлора для функции двух переменных 263
§ 17. Максимум и минимум функции нескольких переменных • . . ¦ 265
§ 18. Максимум и минимум функции нескольких переменных, связан-
связанных данными уравнениями (условные максимумы и минимумы) 272
§ 19. Получение функции на основании экспериментальных данных по
методу наименьших квадратов 9 276
§ 20. Особые точки кривой « 280
Упражнения к главе VIII , ¦.....•..•• 284
ГЛАВА IX
ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ
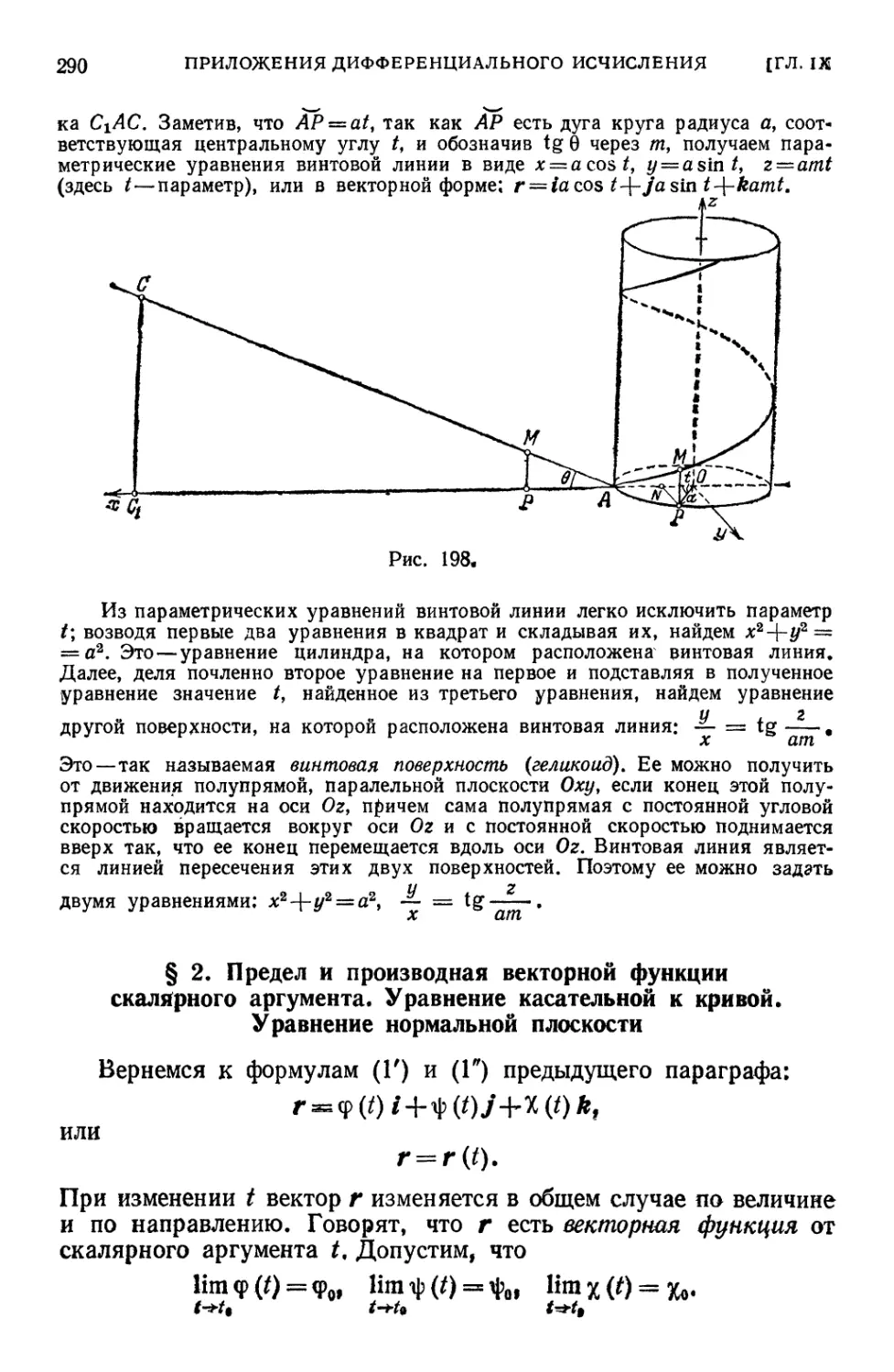
§ I, Уравнения кривой в пространстве ••»•••«••••«.., 288
§ 2. Предел и производная векторной функции скалярного аргумента.
Уравнение касательной к кривой, Уравнение нормальной плоскости 290
§ 3, Правила дифференцирования векторов (векторных функций) . , # 296

ОГЛАВЛЕНИЕ g
§ 4. Первая и вторая производные вектора по длине дуги. Кривизна
кривой. Главная нормаль. Скорость и ускорение точки а криволи-
криволинейном движении 298
§ 5. Соприкасающаяся плоскость. Бинормаль. Кручение 305
§ 6. Касательная плоскость и нормаль к поверхности 309
Упражнения к главе IX м 313
глава х
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Первообразная и неопределенный интеграл « 315
§ 2, Таблица интегралов 317
§ 3. Некоторые свойства неопределенного интеграла 319
§ 4. Интегрирование методом замены переменной или способом под-
подстановки • «•• 321
§ 5. Интегралы от некоторых функций, содержащих квадратный трех-
трехчлен 323
§ 6. Интегрирование по частям 325
§ 7. Рациональные дроби. Простейшие рациональные дроби и их ин-
интегрирование 329
§ 8. Разложение рациональной дроби на простейшие 332
§ 9. Интегрирование рациональных дробей 335
§ 10. Интегралы от иррациональных функций 337
§ 11. Интегралы вида [R (x, Vax*+bx+c)dx 338
§ 12. Интегрирование некоторых классов тригонометрических функций 341
§ 13. Интегрирование некоторых иррациональных функций с помощью
тригонометрических подстановок 345
§ 14. О функциях, интегралы от которых не выражаются через элемен-
элементарные функции 347
Упражнения к главе X . . , • ••••• 348
ГЛАВА XI
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Постановка задачи. Нижняя и верхняя интегральные суммы • ¦ • 356
§ 2, Определенный интеграл. Теорема о существовании определенного
интеграла • ..,•..,..,••*»»,»••»•«*».• 358
§ 3. Основные свойства определенного интеграла ,.*,...,.» 367
§ 4. Вычисление определенного интеграла. Формула Ньютона —
Лейбница » 371
§ 5. Замена переменной в определенном интеграле 374
§ 6. Интегрирование по частям . 376
§ 7. Несобственные интегралы 378
§ 8, Приближенное вычисление определенных интегралов 385
§ 9. Формула Чебышева 389
§ 10. Интегралы, зависящие от параметра. Гамма-функция 393
§ 11. Интегрирование комплексной функции действительной переменной 397
Упражнения к главе XI •*•«•«•••••••••*••,.•. 397

3 ОГЛАВЛЕНИВ
ГЛАВА XII
ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
§ 1. Вычисление площадей в прямоугольных координатах • 401
§ 2. Площадь криволинейного сектора в полярных координатах . ¦ • 404
§ 3. Длина дуги кривой • • • * 405
§ 4. Вычисление объема тела по площадям параллельных сечений • # . 409
§ 5. Объем тела вращения • **, «««««««#• 411
§ 6. Площадь поверхности тела вращения ¦ ¦ • ¦ . 411
§ 7. Вычисление работы с помощью определенного интеграла ¦ ¦ ¦ . ¦ 412
§ 8. Координаты центра масс • «*«*,••««•*«* 414
§ 9. Вычисление момента инерции линии, круга и цилиндра с по-
помощью определенного интеграла • ¦ „ # 417
Упражнения к главе XII 418
Предметный указатель •¦«...«•¦..,...¦¦..,.¦., 424

ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ
Девятое издание данного учебника отличается от его 8-го из-
издания. Это издание полностью соответствует программе по мате-
математике для втузов, рассчитанной на 400—450 часов.
В учебник включены две новые гл. XX и XXI.
Гл. XX «Элементы теории вероятностей и математической
статистики» содержит материал, предусмотренный соответствую-
соответствующим разделом обязательной программы по математике МВССО
СССР.
Гл. XXI «Матрицы. Матричная запись систем и решений
систем линейных дифференциальных уравнений» также содержит
материал, предусмотренный обязательной программой. Но, кроме
того, в этой главе обращено большое внимание на матричную
запись систем линейных дифференциальных уравнений и решений
систем линейных дифференциальных уравнений. Использована
матричная запись последовательных приближенных решений си-
системы линейных дифференциальных уравнений с переменными
коэффициентами. Этот материал необходимо поместить в курсе
дифференциального и интегрального исчисления для втузов по-
потому, что в настоящее время во многих книгах по электротех-
электротехнике, радиотехнике, автоматике исследование решений систем
дифференциальных уравнений производится с использованием
аппарата теории матриц.
Написаны новые §§ 26, 27, 28 гл. XVI. Здесь рассмотрен
метод последовательных приближений решения дифференциаль-
дифференциальных уравнений, доказывается теорема о существовании решения
дифференциального уравнения и теорема единственности. Обращено
внимание на строгость изложения всей главы о дифференциаль-
дифференциальных уравнениях.
Параграф 31 гл. XIII «Понятие о теории устойчивости Ляпу-
Ляпунова» значительно расширен. В этом издании он называется так:
«Понятие о теории устойчивости Ляпунова. Поведение траекто-
траекторий дифференциального уравнения в окрестности особой ^очки».
Здесь параллельно с рассмотрением устойчивости решений систем
дифференциальных уравнений рассмотрено поведение траекторий
вблизи особой точки на фазовой плоскости. Это необходимо было
сделать потому, что при изучении соответствующих вопросов

до ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ
в курсах электротехники, радиотехники, автоматики этими поня-
понятиями необходимо свободно пользоваться. Заново написаны неко-
некоторые параграфы с изложением теории комплексных чисел. Суще-
Существенно расширен § 2 гл. XI, где дано доказательство суще-
существования определенного интеграла от непрерывной функции.
Написан дополнительный § 11 гл. XI «Интегрирование комп-
комплексной функции действительной переменной». Написаны новые
§§ 24 и 25, гл. XVI, посвященные рядам с комплексными членами
и степенным рядам с комплексной переменной. Написан новый
§ 12 гл. XVII, посвященный рядам Фурье в комплексной форме.
Расширено изложение вопроса об интеграле Фурье. Освещены
понятия, используемые в специальной прикладной литературе
(спектр, спектральная функция). Написаны новые § 15 «Ряд Фурье
по ортогональной системе функций» и § 16 «Понятие о линейном
функциональном пространстве. Аналогия между разложением
функций в ряд Фурье и разложением векторов» в гл. XVII. Этот
материал изложен таким образом, чтобы студенты и инженеры
могли понимать материал других дисциплин, опирающийся на
этот математический аппарат.
В гл. XIX написан новый § 20 «Дельта-функция и ее изо-
изображение».
В гл. VIII помещен § 19 «Получение функции на основании
экспериментальных данных по методу наименьших квадратов».
Содержанием этого параграфа ранее являлось Приложение I,
помещавшееся в конце первого тома этого учебника.
В гл. VII даны § 10 «Интерполяционная формула Ньютона»
и § 11 «Численное дифференцирование». Содержанием этих пара-
параграфов ранее явилось Приложение II.
Произведены некоторые дополнения в гл. V, VII, IX, XII, XIII.
Глава XIII «Дифференциальные уравнения» целиком пере-
перенесена во второй том.
Автор
Настоящее издание не отличается от предыдущего {1978 г.).

ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
В пятом издании полностью сохранен без изменений весь
текст четвертого издания, но этот материал разделен на два тома
(для удобства использования настоящего и предыдущих изданий
учебника нумерация глав тоже оставлена без изменения).
Содержание всего учебника определяется программами курса
математики для втузов, рассчитанными на 300—450 часов. Учеб-
Учебник предназначается для изучения курса математики как в ста-
стационарных, так и в заочных втузах. Это учитывалось при изло-
изложении материала; в частности, с этой целью в учебнике разо-
разобрано много примеров, иллюстрирующих изложенный теоретический
материал и дающих образцы решения задач.
Первый том содержит материал, соответствующий программе
1-го курса втуза, за исключением главы XIII «Дифференциаль-
«Дифференциальные уравнения», которая, как правило, проходится на 2-м курсе.
Но так как в некоторых втузах предварительные сведения о диф-
дифференциальных уравнениях, необходимые для последующих дис-
дисциплин, даются на 1-м курсе, то часть этой главы (§§ 1—28) и
помещена в первом томе.
Отметим, что материал, содержащийся в программе втузов,
рассчитанный на число часов порядка 300, почти полностью со-
содержится в первом томе (но в нем содержится и материал, вы-
выходящий за рамки этой программы).
Второй том—конец главы XIII (§§ 29—34), главы XIV —
XIX—содержит материал, соответствующий программе 2-го курса
втуза.
Первые две главы первого тома—«Число. Переменная. Функ-
Функция» и «Предел. Непрерывность функций» написаны в пределах
возможного кратко. Некоторые вопросы, обычно излагаемые
в этих главах, без ущерба для дела перенесены в третью и по-
последующие главы. Это дало возможность раньше перейти к ос-
основному понятию дифференциального исчисления—производной,
его требуют другие дисциплины втузовского курса (целесообраз-
(целесообразность такого расположения материала подтверждается опытом
работы).
В связи с включением во втузовскую программу по высшей
математике вопросов, необходимых для обеспечения курсом мате-

12 ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
матики втузовских дисциплин, связанных с автоматикой и вычис-
вычислительной техникой, в учебнике подробно изложены соответст-
соответствующие разделы: «Численное интегрирование дифференциальных
уравнений и систем дифференциальных уравнений»*),«Интегри-
уравнений»*),«Интегрирование систем линейных дифференциальных уравнений», «Поня-
«Понятие о теории устойчивости Ляпунова», «Оператор Гамильтона»,
«Интеграл Фурье» и т. д.
В гл. XVIII рассмотрены основные уравнения математической
физики. Обращено большое внимание на выяснение характера
физических явлений, приводящих к уравнениям различных типов
и соответствующим краевым задачам. Большое внимание уделено
численным методам решения дифференциальных уравнений в част-
частных производных.
В главе XIX излагаются основные понятия операционного
исчисления и операционный метод решения дифференциальных
уравнений. Это требуется для многих последующих дисциплин,
и особенно электротехнических.
В учебник включено большое количество задач и примеров
для упражнений, многие из которых иллюстрируют связь мате-
математики с другими дисциплинами. Задачи и примеры специально
подобраны по каждому разделу курса, что способствует усвоению
излагаемого материала. Это обстоятельство также делает книгу
удобной для самостоятельного изучения курса математики, в част-
частности для студентов-заочников.
Шестое издание отличается от пятого только тем, что в конце
первого тома дано приложение, где изложен важный для инже-
инженеров вопрос «Получение функции на основании эксперименталь-
экспериментальных данных по методу наименьших квадратов».
Седьмое издание отличается от шестого только тем, что в конце
первого тома дано приложение «Интерполяционная формула Нью-
Ньютона. Численное дифференцирование».
*) Обычно излагаемые численные методы анализа также изложены в дан-
данном учебнике.

ГЛАВА I
ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ
§ 1. Действительные числа.
Изображение действительных чисел точками числовой оси
Одним из основных понятий математики является число. По-
Понятие числа возникло в древности и на протяжении длительного
времени подвергалось расширению и обобщению.
Числа целые и дробные, как положительные, так и отри-
отрицательные, вместе с числом нуль называются рациональными
числами. Каждое рациональное число может быть представлено
в виде отношения — двух целых чисел р и q9 например у,
1,25=4.
В частности, целое число р можно рассматривать как отно-
отношение двух целых чисел -у-, например 6 = у, 0 в= у.
Рациональные числа могут быть представлены в виде конеч-
конечных или бесконечных периодических дробей. Числа, которые
представляются бесконечными, но непериодическими десятичными
дробями, называются иррациональными числами: таковы числа
V29 j/, 5-/2 и т. д.
Совокупность всех рациональных и иррациональных чисел
называется множеством действительных (или вещественных) чисел.
Действительные числа упорядочены по величине, т. е.
для каждой пары действительных чисел х и у имеет место одно
и только одно из соотношений
х<У, х = У, х>У-
Действительные числа можно изображать точками числовой оси.
Числовой осью называется бесконечная прямая, на которой вы-
выбраны: 1) некоторая точка О, называемая началом отсчета,
2) положительное направление, которое указывается стрелкой,
и 3) масштаб для измерения длин. Чаще всего мы будем распо-

14 ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ |ГЛ. 1
лагать числовую ось горизонтально и положительное направле-
направление выбирать слева направо.
Если число Xi положительно, то его изображают точкой Mi9
лежащей справа от точки О на расстоянии ОМХ = хг; если число х2
отрицательно, то его изображают точкой М2, лежащей слева от
точки О на расстоянии ОМ2 = — х2 (рис. 1). Точка О изображает
число нуль. Очевидно, что каждое действительное число изобра-
изображается определенной точкой числовой оси. Два различных дейст-
действительных числа изображаются различными точками числовой
оси.
Справедливо также утверждение: каждая точка числовой оси
является изображением только одного действительного числа
(рационального или иррационального).
Таким образом, между всеми действительными числами и всеми
точками числовой оси существует взаимно однозначное соответ-
ствие: каждому числу соответст-
-ц о 'i 1 о ? t 1 / > ~ вует единственная изображающая
•tf-7 / 2 3 его точка и, наоборот, каждой точ-
Рис | ке соответствует единственное
изображаемое ею число. Это дает
возможность во многих рассуждениях в некотором смысле равно-
равнозначно употреблять понятие «число х» и понятие «точка х». По-
Последним обстоятельством мы будем широко пользоваться в
курсе.
Укажем без доказательства следующее важное свойство сово-
совокупности действительных чисел: между двумя произвольными
действительными числами найдутся как рациональные, так и
иррациональные числа. В терминах геометрических это предло-
предложение формулируется так: между двумя произвольными точками
числовой оси найдутся как рациональные, так и иррациональные
точки.
В заключение отметим следующую теорему, предоставляющую
собой в известном смысле «мостик между теорией и практи-
практикой».
Теорема. Каждое иррациональное число а можно с любой
степенью точности выразить с помощью рациональных чисел.
В самом деле, пусть иррациональное число а > 0 и пусть
требуется вычислить а с точностью до 1/л (например, до 1/10,
до 1/100 и т. д.).
Каково бы ни было а, оно заключается между двумя целыми
числами N и Af-J-l. Разделим отрезок между N и N + 1 на п
частей; тогда а окажется между рациональными числами ЛГ-f—
и N+^—^. Так как разность этих чисел равна 1/п, то, следо-
следовательно, каждое из них выражает а с заданной степенью точ-
точности: первое с недостатком, а второе—с избытком.

I 21 АБСОЛЮТНАЯ ВЕЛИЧИНА ДЕЙСТВИТЕЛЬНОГО ЧИСЛА 15
Пример. Иррациональное число У2 выражается рациональным» чи-
числами:
1,4 и 1,5—с точностью до 1/10,
1,41 и 1,42—с точностью до 1/100,
1,414 и 1,415—с точностью до 1/1000 и т.д.
§ 2. Абсолютная величина действительного Числа
Введем нужное для дальнейшего понятие абсолютной величины
действительного числа.
Определение. Абсолютной величиной (или модулем) дейст-
действительного числа х (обозначается |*|) называется неотрицатель-
неотрицательное действительное число, удовлетворяющее условиям
х9 если ^;
= — xf если #<0.
Примеры: |2| = 2; |—5|=5; |0|=0.
Из определения следует, что для любого х справедливо со-
соотношение л:^|х|.
Рассмотрим некоторые свойства абсолютных величин.
1. Абсолютная величина алгебраической суммы нескольких дей-
действительных чисел не больше суммы абсолютных величин сла-
слагаемых:
Доказательство. Пусть х+у^0, тогда
\х+у\ = х+у^\х\ + \у\ (так как х^\х\ и
Пусть х+ у < 0, тогда
что и требовалось доказать. Проведенное доказательство легко
распространяется на любое число слагаемых.
Примеры:
|-2+3|<|-2| + |3| = 2+3 = 5 или 1< 5;
= 8 или 8=8.
2. Абсолютная величина разности не меньше разности абсо-
абсолютных величин уменьшаемого и вычитаемого:
\х-у\>\х\-\у\, \х\>\у\.
Доказательство. Положим х—г/ = г, тогда #= y + z и по
доказанному
М
откуда
что и требовалось доказать.

16 ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ 1ГЛ. I
3. Абсолютная величина произведения равна произведению аб-
абсолютных величин сомножителей:
\хуг\ = \х\\у\\г\.
4. Абсолютная величина частного равна частному абсолютных
величин делимого и делителя:
Л 1-1*1
У\~~ \У\ #
Последние два свойства непосредственно следуют из опреде-
определения абсолютной величины.
§ 3. Переменные и постоянные величины
В результате измерения таких физических величин, как время,
длина, площадь, объем, масса, скорость, давление, температура
и т. п., определяются числовые значения физических величин.
Математика занимается величинами, отвлекаясь от их конкрет-
конкретного содержания. В дальнейшем, говоря о величинах, мы будем
иметь в виду их числовые значения. В различных явлениях не-
некоторые величины изменяются, т. е. меняются их числовые зна-
значения, другие величины сохраняют свое числовое значение. Так,
при равномерном движении точки время и расстояние меняются;
скорость остается постоянной.
Переменной величиной называется величина, которая прини-
принимает различные числовые значения. Величина, числовые значения
которой не меняются, называется постоянной величиной. В даль-
дальнейшем переменные величины мы будем обозначать буквами х,
у, г, иг ... й т. д., постоянные величины будем обозначать
буквами а, Ьу с, ... и т. д.
Замечание. В математике постоянная величина часто рас-
рассматривается как частный случай переменной, у которой все
числовые значения одинаковы.
Следует отметить, что при рассмотрении конкретных физиче-
физических явлений может иметь место такое положение, что величина
с одним и тем же названием в одном явлении оказывается по-
постоянной, в другом—переменной. Например, скорость равномерного
движения есть величина постоянная, а скорость равномерно
ускоренного движения—величина переменная. Величины, которые
сохраняют свое значение в любом явлении, называются абсолютными
постоянными. Например, отношение длины окружности к диаметру
есть постоянная величина я = 3,14159...
Как мы увидим на протяжении всего курса, понятие пере-
переменной величины является основным понятием дифференциаль-
дифференциального и интегрального исчислений. «Поворотным пунктом в ма-
математике,—писал Ф. Энгельс в «Диалектике природы»,—была
декартова переменная величина. Благодаря этому в математику

§41 ОБЛАСТЬ ИЗМЕНЕНИЯ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ 17
вошли движение и диалектика, и благодаря этому же стало
немедленно необходимым дифференциальное и интегральное ис-
исчисление».
§ 4. Область изменения переменной величины
Переменная величина принимает различные числовые значе-
значения. В зависимости от характера рассматриваемой задачи сово-
совокупность этих значений может быть
различная. Например, температура во-
ды, подогреваемой в обычных условиях,
будет меняться от комнатной темпера-
температуры, равной 15—18° С, до точки кипе-
кипения, 100° С. ^Переменная же величина
л: = cos а может принимать все значе-
значения от —1 до + 1.
Значения переменной величины гео-
метрически изображаются точками чис-
ловой оси. Так, значения переменной
x = cosa при всевозможных значениях а изображаются сово-
совокупностью точек отрезка числовой оси от — 1 до 1, включая
и точки — 1 и 1 (рис. 2).
Определение. Совокупность всех числовых значений пере-
переменной величины называется областью изменения этой перемен-
переменной.
Отметим следующие области изменения переменной величины,
которые часто будут встречаться в дальнейшем.
Промежутком или интервалом называется совокупность всех
чисел х, заключенных между данными числами а и Ь (а < Ь),
при этом сами эти числа не принадлежат рассматриваемой
совокупности чисел; его обозначают так: (а, Ъ) или с помощью
неравенств а<х<&.
Отрезком или сегментом называется совокупность всех чисел
*, заключенных между двумя данными числами а и ft, причем
оба числа а и & принадлежат рассматриваемой совокупно-
совокупности; его обозначают так: [a, ft] или с помощью неравенств
а^.х^.Ь. Иногда отрезок называется замкнутым промежутком
или замкнутым интервалом.
Если одно из чисел а или Ь, например а, присоединяется
к промежутку, а другое—нет, то получается полузамкнутый
промежуток, его можно задать неравенствами a^x<ft и обо-
обозначить [af ft).
Если присоединяется число ft и не присоединяется число а9
то получается полузамкнутый промежуток (а, 6], который можно
задать неравенствами а<х^.Ь.
Если переменная х принимает всевозможные значения, боль-
большие чем а, то такой интервал обозначают (a, +00) и задают

18 ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ {ГЛ, I
условными неравенствами а < х < + а». Так же рассматриваются
бесконечные интервалы и полузамкнутые бесконечные интервалы,
задаваемые условными неравенствами
оо, — оо <x<cf — оо<х*^с9 — оо<х< + оо.
Пример. Область изменения переменной х=cos а при всевозможных
значениях а есть отрезок [—1, 1] и определяется неравенствами — 1^х<\
Данные выше определения можно сформулировать, используя
вместо понятия «число» понятие «точка», например:
Отрезком называется совокупность всех точек х, заключен-
заключенных между данными точками а и Ь (концами отрезка), причем
концы отрезка принадлежат рассматриваемой совокупности.
Окрестностью данной точки х0 называется произвольный
интервал (а, Ь), содержащий эту точку внутри себя, т. е. интер-
0 яь-е^^-яр-^яь+е вал (а» Ь)> К0НВД1 которого удов-
1 L -L -J ^ летворяют условию а < х0 < Ь.
Рис * е Часто рассматривается окрестность
" " (а, Ь) точки #0, для которой х0
является серединой. Тогда х0 называется центром окрестности,
величина (Ь—а)/2 называется радиусом окрестности. На рис. 3
изображена окрестность (х0—е, хо+в) точки х0 с радиусом е.
§ 5. Упорядоченная переменная величина.
Возрастающая и убывающая переменные величины*
Ограниченная переменная величина
Будем говорить, что переменная х есть упорядоченная пере-
переменная величина, если известна область изменения этой перемен-
переменной величины и про каждое из двух любых ее значений можно
сказать, какое значение предыдущее и какое последующее. Здесь
понятия «предыдущее» и «последующее» не связаны со временем,
а являются способом «упорядочения» значений переменной
величины, т. е. установления порядка соответствующих значений
переменной величины.
Частным случаем упорядоченной переменной величины яв-
является переменная величина, значения которой образуют число-
числовую последовательность хь х2, х3, •.., хп, ... Здесь при kr < k
значение х#—«предшествующее», а значение хк—«последующее»
независимо от того, какое из этих значений больше.
Определение 1. Переменная величина называется возра-
возрастающей, если каждое последующее ее значение больше преды-
предыдущего ее значения. Переменная величина называется убывающей,
если каждое ее последующее значение меньше предыдущего.
Возрастающие переменные величины и убывающие переменные
величины называются монотонно изменяющимися переменными
величинами или просто монотонными величинами.

§*] функция 19
Пример. Пря удвоении числа сторон правильного вписанного в круг
многоугольника площадь $ этого многоугольника является возрастающей пере-
переменной величиной. Площадь правильного описанного около круга многоуголь-
многоугольника при удвоении числа сторон является убывающей переменной величиной.
Заметим, что не всякая переменная величина является непременно возрастаю*
щей или убывающей. Так, например, переменная *=sina, если а есть воз-
возрастающая величина на отрезке [0, 2я], не является монотонной величиной.
Она сначала возрастает от 0 до 1, затем убывает от 1 до—-1 и, наконец, возра-
возрастает от —1 до 0.
Определение 2. Переменная величинахназывается ограни-
ограниченной, если существует такое постоянное число М > 0, что все
последующие значения переменной, начиная с некоторого, удов-
удовлетворяют условию —М^.х^М, т. е. |#|<jAf. Иначе говоря,
переменная величина называется ограниченной, если можно ука-
указать такой отрезок [—Af, M], что все последующие значения
переменной, начиная с некоторого, будут принадлежать этому
отрезку. Однако не следует думать, что переменная величина
будет принимать непременно все значения отрезка [—М9 М\.
Например, переменная величина, принимающая всевозможные
рациональные значения на отрезке [—2, 2], ограничена, тем не
менее она не принимает всех значений на [—2, 2], а именно
иррациональных.
§ 6» Функция
При изучении различных явлений природы и решении техни-
технических задач, а следовательно, и в математике приходится рас-
рассматривать изменение одной величины в зависимости от измене-
изменения другой. Так, например, при изучении движения пройденный
путь рассматривается как переменная, изменяющаяся в зависи-
зависимости от изменения времени. Здесь пройденный путь есть функ-
функция времени.
Рассмотрим другой пример. Известно, что площадь круга
выражается через радиус так: Q = я/?2. Если радиус R будет
принимать различные числовые значения, то площадь Q также
будет принимать различные числовые значения. Таким образом, из-
изменение одной переменной влечет изменение другой. Здесь площадь
круга Q есть функция радиуса R. Сформулируем определение
понятия «функция».
Определение 1. Если каждому значению переменной х%
принадлежащему некоторой области, соответствует одно опреде-
определенное значение другой переменной #, то у есть функция от х
или, в символической записи, y = f(x)9 у = у(х) и т. п.
Переменная х называется независимой переменной или аргу-
аргументом. Зависимость переменных х и у называется функциональ-
функциональной зависимостью. Буква / в символической записи функциональ-
функциональной зависимости y = f(x) указывает, что над значением х нужно
произвести какие-то операции, чтобы получить значение у. Вместо

20
ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ
|ГЛ. I
записи y — f(x), я = <р(х) и т. д. иногда пишут# = у (х), и~и(х)
и т. д., т. е. буквы у, и и т. д. обозначают и зависимую перемен-
переменную, и символ совокупности операций над х.
Запись у = С, где С—постоянная, обозначает функцию, зна-
значение которой при любом значении х одно и то же и равно С.
Определение 2. Совокупность значений х, для которых
определяются значения функции у в силу правила / (х), называется
областью определения функции (или областью существования
функции).
Пример 1. Функция у—sin х определена при всех значениях х. Следо-
Следовательно, ее областью определения будет бесконечный интервал — оо < х < +оо.
Замечание 1. Если имеем функциональную зависимость
двух переменных величин х и y = f(x) и если х и y = f(x) рас-
рассматривать как упорядоченные переменные величины, то из двух
значений функции y* = f(x*) и y** = f(x**)9 соответствующих
двум значениям аргумента х* и х**, последующим значением
функции будет то, которое соответствует последующему значению
аргумента. Поэтому естественно, например, следующее определение.
Определение 3. Если функция y = f(x) такова, что боль-
большему значению аргумента х соответствует большее значение функ-
функции, то функция y = f(x) называется возрастающей. Аналогичным
образом определяется убывающая функция.
Пример 2. Функция Q=nR2 при 0 < R < +оо есть функция возра-
возрастающая, так как большему значению R соответствует большее значение Q.
Замечание 2. Иногда в определении понятия функции
допускают, что каждому значению х, принадлежащему некоторой
области, соответствует не одно, а несколько значений у или
даже бесконечное множество значений у. В этом случае функ-
функцию называют многозначной в отличие от определенной выше
функции, которую называют однозначной. В дальнейшем, говоря
о функции, мы будем иметь в виду только однозначные функ-
функции. Если в силу необходимости придется иногда иметь дело
с многозначными функциями, то мы будем делать специальные
оговорки,
§ 7. Способы задания функции
1. Табличный способ задания функции. При этом
Способе выписываются в определенном порядке значения аргу-
аргумента
У» Уъ>
Уп-
хп и соответствующие значения функции
X
У
Ч
У1
*2
У2
ХП
Уп

§71
СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
21
Таковы, например, таблицы тригонометрических функций,
таблицы логарифмов и т. д.
В результате экспериментального изучения явлений также мо-
могут получиться таблицы, выражающие функциональную зависи-
зависимость между измеряемыми величинами. Так, например, в ре-
результате измерения температуры воздуха на метеорологической
площадке в определенный день получается следующая таблица:
Значение температуры Т (в градусах)
(в часах)
t
Т
1
0
2
3
—2
4
—2
в зависимости от времени
5
-0,5
6
1
7
3
8
3,5
t
9
4
Рис. 4.
Эта таблица определяет Т как функцию t.
II. Графический способ задания функции. Если
в прямоугольной системе координат на плоскости имеем некото-
некоторую совокупность точек М(х у), при этом никакие две точки
не лежат на одной прямой, параллельной оси Оу, то эта сово-
совокупность точек определяет некоторую однозначную функцию
y = f(x)\ значениями аргумента являются абсциссы точек, значе-
значениями функции—соответствующие орди-
ординаты (рис. 4).
Совокупность точек плоскости хОу,
абсциссы которых являются значениями V^
независимой переменной, а ординаты —
соответствующими значениями функции,
называется графиком данной функции.
III. Аналитический способ
задания функции. Сначала разъясним понятие «аналити-
«аналитическое выражение». Аналитическим выражением будем называть
символическое обозначение совокупности известных математичес-
математических операций, которые производятся в определенной последо-
последовательности над числами и буквами, обозначающими постоян-
постоянные или переменные величины.
Отметим, что под совокупностью известных математических
операций будем понимать не только математические операции,
известные из курса средней школы (сложение, вычитание, извле-
извлечение корня и т. д.), но и те, которые будут определяться по
мере изучения курса.
Аналитическими выражениями, например, являются хх—2,
(lgx—sinx)/E*2+l), 2*—Vly+Tx и т. д.
Если, функциональная зависимость y = f(x) такова, что /
обозначает аналитическое выражение, то говорят, что функция
у от х задана аналитически.

22 ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ 1ГЛ. I
Примеры функций, заданных аналитически: 1) у = х*—2,
2) y-(x+l)(x— l)-*f 3) у^КГ^Зс, 4) y^sinx, 5) Q=n#*
и т. д.
Здесь функции заданы аналитически с помощью одной формулы
(под формулой понимается равенство двух аналитических выра-
выражений). В таких случаях можно говорить о естественной
области определения функции.
Естественной областью определения функции, заданной ана-
аналитически, является совокупность значений х, при которых
стоящее справа аналитическое выражение имеет вполне опреде-
определенное значение. Так, естественной областью определения функ-
функции # = х4—2 является бесконечный интервал —oo<x< + oo,
так как функция определяется при всех значениях х. Функция
у = (х+1)(х—I)" определена при всех значениях х, кроме зна-
значения jt=l, так как при этом значении знаменатель обращается
в нуль. Для функции г/ = К1—х2 естественной областью опре*
деления будет отрезок — l^x^l и т. д.
Замечание. Иногда бывает нужно рас-
рассматривать не всю естественную область опре-
определения функции, а только некоторую ее часть.
Так, зависимость площади Q круга от радиуса
R определяется функцией Q = я/?2. Областью
определения данной функции при рассмотрении
данного геометрического вопроса является бес-
бесконечный интервал 0</?<+°°- Естествен-
Естественной же областью определения данной функции
г является бесконечный интервал — оо < R <
Рис. 5. Если функция y = f(x) задана аналитичес-
аналитически, то она может быть изображена графичес-
графически на плоскости координат хОу. Так, графиком функции (/ = #a
является парабола, изображенная на рис. 5.
§ 8. Основные элементарные функции. Элементарные функции
Основными элементарными функциями называются следующие
аналитическим способом заданные функции.
I. Степенная функция у=ха, где а—действительное число"*).
II. Показательная функция: у = ах9 где а—положительное
число, не равное единице.
III. Логарифмическая функция: у = loga x, где основание лога-
логарифмов а—положительное число, не равное единице.
*) При а иррациональном эта функция вычисляется путем логарифмиро-
логарифмирования и потенцирования: log у=а log*. При этом предполагается, что х > 0.

ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
IV. Тригонометрические функции:
V. Обратные тригонометрические функции:
у = arcsin x, y = arccos#, t/ = arctgx,
г/ = arcctg x, у = arcsec x, y = arccosec я.
Рассмотрим области определения и графики основных элемен»
тарных функций.
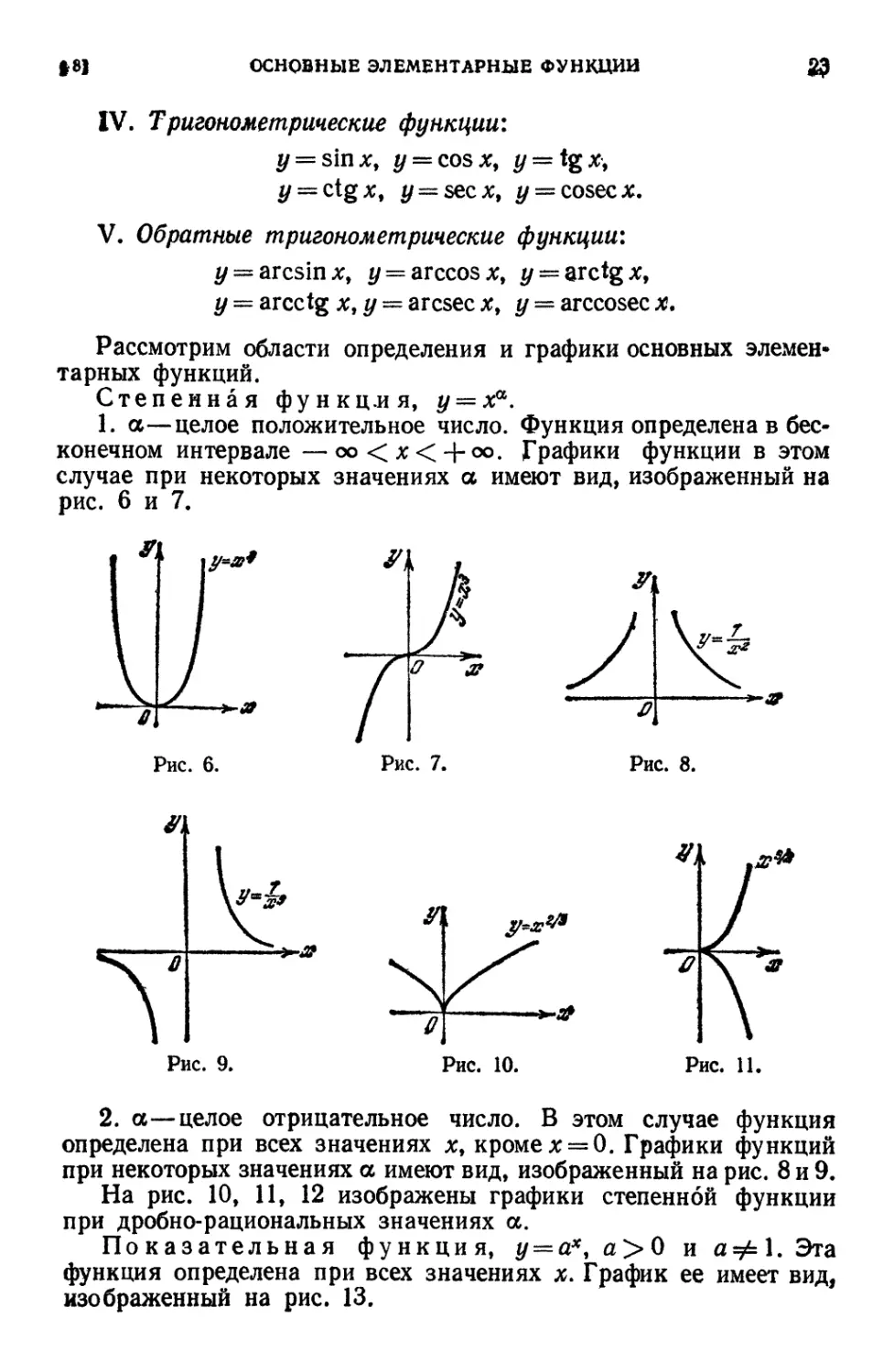
Степенная функц.ия, у = д:а.
1. а—целое положительное число. Функция определена в бес-
бесконечном интервале — оо < х< + оо. Графики функции в этом
случае при некоторых значениях а имеют вид, изображенный на
рис. 6 и 7.
Рис. 6.
Рис. 7.
Рис. 8.
Рис. 9.
Рис. 10.
Рис. 11.
2. а—целое отрицательное число. В этом случае функция
определена при всех значениях х, кроме х = 0. Графики функций
при некоторых значениях а имеют вид, изображенный на рис. 8 и 9.
На рис. 10, 11, 12 изображены графики степенной функции
при дробно-рациональных значениях а.
Показательная функция, у = ах, а>0 и аф\. Эта
функция определена при всех значениях х. График ее имеет вид,
изображенный на рис. 13.

24
ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ
|ГЛ. I
Логарифмическая функция, y^\ogax, a>0 и цф 1.
Эта функция определена при я>0. График ее изображен на
рис. 14.
Тригонометрические функции. Независимая пере-
переменная х в формулах y = sinx и т.д. выражается в радианах.
Все перечисленные тригонометрические функ-
функции—периодические. Сформулируем общее оп-
определение периодической функции.
Определение 1. Функция y~f(x) на-
называется периодической, если существует такое
постоянное число С, от прибавления (или вы-
вычитания) которого к аргументу х значение
функции не изменяется: f(x-\-C) = f(x). Наи-
Наименьшее такое число называется периодом
функции; в дальнейшем будем обозначать его 2/.
Из определения непосредственно следует, что у = sin x есть
периодическая функция с периодом 2я: sin;t = sin(.x;-f2tt). Период
cos я также равен 2я, Период функций у= tg x и y = ctgx равен я.
О.
Рис. 12.
, я?, # , a
У .,
Рис. 14.
Функции у = sin л:, # —cos* определены при всех значениях х\
функции y=tgx и у = sec x определены всюду, кроме точек
(* = 0, ±1, ±2, ...);
и r/ = cosecA: определены при всех значениях ху
; = kn (& = 0, ±1, ±2, ...).
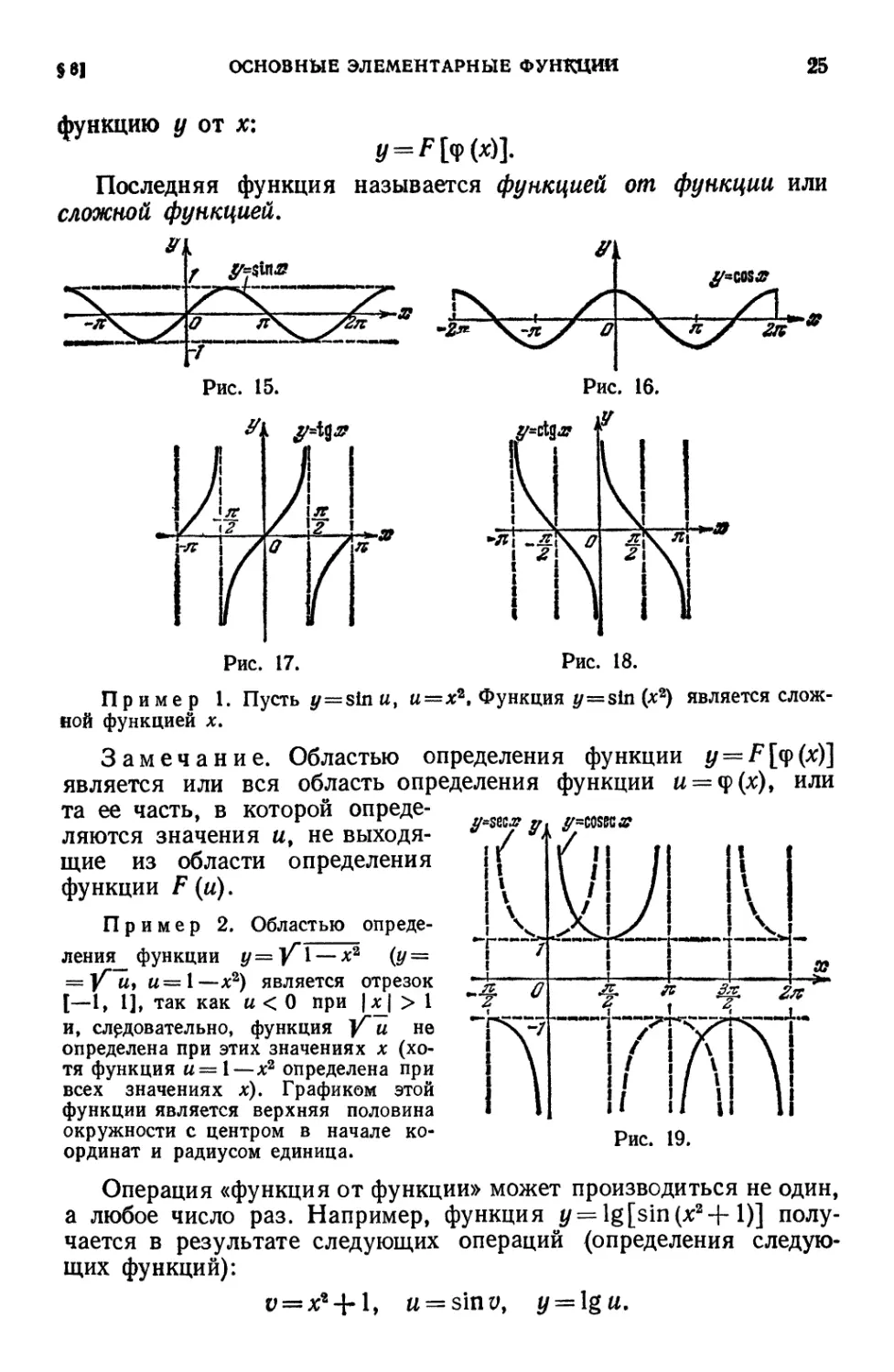
Графики тригонометрических функций изображены на рис. 15—19.
Обратные тригонометрические функции будут нами подробно
рассмотрены позднее.
Введем, далее, понятие функции от функции. Если у является
функцией от м, а и в свою очередь зависит от переменной х, то
у также зависит от х. Пусть y = F(u) и и = ч>(х). Получаем
функции # =
кроме точек

$ 8] ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
функцию у от х:
25
Последняя функция называется функцией от функции или
сложной функцией.
Рис. 15.
Рис. 17. Рис. 18.
Пример 1. Пусть у = sin и, и = х2ш Функция y=sin (л:2) является слож-
сложной функцией х.
Замечание. Областью определения функции y = F[q>(x)]
является или вся область определения функции и = <р(х)> или
та ее часть, в которой опреде-
определяются значения и, не выходя-
выходящие из области определения
функции F(u).
Пример 2. Областью опреде-
определения^ функции у=У"\ — х2 (у =
= У и, и= I —х2) является отрезок
[—1, 1], так как и < 0 при |aJ > 1
и, следовательно, функция У и не
определена при этих значениях х (хо-
(хотя функция и=1—х2 определена при
всех значениях х). Графиком этой
функции является верхняя половина
окружности с центром в начале ко-
координат и радиусом единица.
Рис. 19.
Операция «функция от функции» может производиться не один,
а любое число раз. Например, функция t/ = lg[sin(x2+ 1)] полу-
получается в результате следующих операций (определения следую-
следующих функций):
v — x^ + ly a = sin и, y = lgtt.

2$. ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ 1ГЛ. I
Определим, далее, понятие элементарной функции.
Определение 2. Элементарной функцией называется функ-
функция, которая может быть задана одной формулой вида 1/ = /(х),
где справа стоящее выражение составлено из основных элемен-
элементарных функций и постоянных при помощи конечного числа опе-
операций сложения, вычитания, умножения, деления
и взятия функции от функции.
На основании определения следует, что эле-
элементарные функции являются функциями, задан-
заданными аналитически.
Примеры элементарных функций:
Рис. 20,
10*—
Пример неэлементарной функции:
Функция #=1-2-3« ...-n(y — f (n)) не является элементарной* так как
количество операций, которое нужно произвести для получения #, увеличи-
увеличивается с увеличением я, т. е. не является ограниченным.
Замечание. Функция, изображенная на рис. 20, является
элементарной, хотя она и задается с помощью двух формул:
f(x)~x, если
/(x) = 2x— 1, если
Эту функцию можно задать и одной формулой:
для 0<я<2. (См, также упражнения 130—144 к гл* V.)
§ 9. Алгебраические функции
К числу алгебраических функций относятся элементарные
функции следующего вида:
1. Целая рациональная функция или много-
многочлен
a-%+ ... +ап,
где д0, alf ..., ап—постоянные числа, называемые коэффициен-
коэффициентами', п—целое неотрицательное число, называемое степенью
многочлена. Очевидно, что эта функция определена при всех
значениях х, т.е. определена на бесконечном интервале.
Пример 1, у — ах+Ь—линейная функция. При Ь = 0 линейная функ-
функция у=ах выражает прямую пропорциональную зависимость у от х. При
11=0 функция у=Ь есть постоянная*

АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
27
Пример 2. у=пх2+ЬхЦ-с—-квадратичная функция. График квадра-
квадратичной функции есть парабола (рис. 21).
Эти функции подробно рассматривались в аналитической геометрии,
П. Дробная рациональная функция. Эта функция
определяется как отношение двух многочленов:
Дробной рациональной функцией является, например, функция
у = а/л:, выражающая обратную пропорциональную зависимость.
Ее график изображен на рис. 22,
Очевидно, что дробная рацио-
рациональная функция определена при
всех значениях ху кроме тех, при
которых знаменатель обращается
в нуль.
III. Иррациональная
функция. Если в формуле у=
=f(x) в правой части произво-
производятся операции сложения, вычита-
вычитания, умножения, деления и возведения в степень с рациональ-
рациональными нецелыми показателями, то функция у от х называется
иррациональной. _
2#24-Уг х
Примеры иррациональных функций: « =—-L-1— «='
Рис. 21.
и т.п.
Замечание 1. Перечисленные три вида алгебраических
функций не исчерпывают всех алгебраических функций. Алге-
Алгебраической функцией назы-
называется любая функция у »
= f (x), которая удовлетво-
удовлетворяет уравнению вида
Рис. 22.
л J где Р9(х)9 Pi(x), ...
' ** ... , Рп (х) — некоторые
многочлены от х.
Можно доказать, что
каждая из функций перечисленных трех видов удовлетворяет не-
некоторому уравнению вида A), но не всякая функция, удовлетво-
удовлетворяющая уравнению вида A), является функцией одного из пе-
перечисленных видов.
Замечание 2. Функция, не являющаяся алгебраической,
называется трансцендентной.
Примеры трансцендентных функций: r/ = cosx, у =10* и т.п.

28
ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ
1ГЛ. 1
§ 10. Полярная система координат
Положение точки на плоскости можно определить с помощью
так называемой полярной системы координат.
На плоскости выбираем некоторую точку О, называемую по-
полюсом, и выходящую из этой точки полупрямую, называемую
полярной осью. Положение точки М на плоскости можно опре-
определить двумя числами: числом р, выражающим расстояние точки М
от полюса, и числом <р—величиной угла, образованного отрез-
отрезком ОМ с полярной осью. Положительным направлением отсчета
угла ф считается направление против часовой стрелки. Числа р
и <р называются полярными координатами точки М (рис. 23).
Рис. 23.
Рис. 24.
Радиус-вектор р будем всегда считать неотрицательным. Если
полярный угол ф брать в пределах 0 ^ ф < 2л, то каждой точке
плоскости, кроме полюса, соответствует вполне определенная пара
чисел р и ф. Для полюса р = 0, ф — произвольное.
Установим связь между полярными и прямоугольными декар-
декартовыми координатами. Пусть начало прямоугольной системы ко-
координат совпадает с полюсом, а положительное направление оси
Ох —с полярной осью. Из рис. 24 непосредственно следует:
и, обратно, p = \f y g y
Примечание. При нахождении ф нужно учитывать,в какой
четверти находится точка, и брать соответствующее значение ф.
Уравнение p = F(q>) в полярной системе координат определяет
некоторую линию.
Пример 1. Уравнение р = а, где а = const, определяет в полярных
координатах окружность с центром в полюсе и радиусом а. Уравнение этой
окружности (рис. 25) в прямоугольной системе координат, расположенной так,
как указано на рис. 24, будет
П 2
= а или х2-\-у2 = а2.
С б
ук р , уд У\у \у
Пример 2. р = шр, где a = const. Составим таблицу значений р при
некоторых значениях <р:
ф
р
0
0
я/4
«0,78а
я/2
«1,57а
Зя/4
«2,36а
я
«3,14а
Зя/2
«4,71а
2я
«6,28а
Зя
«9,42а
4я
«12,56а

УПРАЖНЕНИЯ К ГЛАВЕ I
29
Соответствующая кривая изображена на рис. 26, Эта кривая называется спи*
ралью Архимеда.
Пример 3. p = 2acos<p. Это уравнение окружности радиуса а, центр
которой находится в точке ро = а, ф=0 (рис. 27). Напишем уравнение этой
Рис. 25.
Рис. 26.
Рис. 27.
окружности в прямоугольных координатах. Подставляя в данное уравнение
cosq> = :
, будем иметь У"х2-{-у2 =
х2-\-у2 —2ах=0.
Ух2+у2
или
Упражнения к главе I
1. Дана функция f (х)=х2-\-6х—4. Проверить, что /A) = 3, /^3) = 23.
2. /(*) = x2 + l. Вычислить значения: а) / D), Отв. 17. б) /A^2). Отв. 3.
В) /(а-И). Отв. а2 + 2а+2. г) f(a) + \. Отв. а2+2. д) /(а2). Отв. а4+1.
е) U (а)]2. Отв. а4+2а2 + 1. ж) /Bа). Отв. 4а2 + 1.
3. ф(а:) = (а:— 1) (Злт+5)-1. Написать выражения фA/л:) и 1/ф(*). Отв%
4. о|?(л:) = |/'л:2+4. Написать выражения -ф Bд:) и 1р @). Отв.
5. /(e) = tg0. Проверить равенство /B9)==
6. 9(*) = lgjljlf. Проверить равенство ф(а)+Ф (Ь)=Ф (qp)
7. /(x) = lgA:; ф(л:) = ^. Написать выражения: а)/[фB)]. Отв. 3 lg 2.
б) /[ф(а)]. Отв. 31ga. в),ф[/(а)]. Ome. [Iga]3.
8. Найти естественную область определения функции у=2х2+\. Отв.
—оо<х< + оо.
9. Найти естественные области определения функций: а) ]^1—х2. Отв.
. б) Уз+х+уТ^х. Отв. —3<а:<7. в) yjl/^
CL~\- X
Omek—оо <
>. г)
Отв. хфа. д) arcsin2^. Отв. —I
е) y=z\gx. Отв. х>0. ж) у=ах (а > 0). Отв. —оо
Построить графики функций:
10. у = — Зх+5. И. у^^х2 + \. 12. # = 3—2а:2. 13. у = х*+2х--1.
14. у=\/(х— 1). 15. y = sin2x. 16. e/ = cos3*. 17. ^ = д:2—4л:+6. 18. у =

За ЧИСЛО. ПЕРЕМЕННАЯ* ФУНКЦИЯ |ГЛ. I
34. у=\х\. 35. */=1о&1*|. Зв. i/=Iog2(I—^р). 37, 0=
f
Л *= 4 cos (?)
39, Построить график функции /(#), определенной на отрезке [—1; 1)
следующим образом:
/(*) = !-{-* при — 1<*<0з
/(л:)=1— 2х при 0<*<1.
40. Построить график функции [/(*)* определенной на отрезке [0; 2]
следующим образом:
/(*)=*з при 0<л;<1$
f(x)=x при
Построить кривые, данные полярными уравнениями!
41. р=а/<р {гиперболическая спираль). 42. р—аУ (логарифмическая спи-
спираль). 43. p=aVrcos2(p (лемниската), 44. р=сA— cos<p) (кардиоида).
45. p=i39

ГЛАВА II
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
§ 1. Предел переменной величины*
Бесконечно большая переменная величина
В этом параграфе мы будем рассматривать упорядоченные
переменные величины, изменяющиеся специальным образом, кото-
который определяется терминами «переменная величина стремится
к пределу». Во всем дальнейшем курсе понятие предела перемен-
переменной будет играть фундаментальную роль, так как с ним непо-
непосредственно связаны основные понятия математического ана-
анализа—производная, интеграл и др.
Определение 1. Постоянное число а называется пределом
переменной величины х9 если для каждого наперед заданного
произвольно малого положительного —Ъ-
числа е можно указать такое значение "I I jet^****^ *"*
переменной х9 что все последующие зна- С$-а1
чения переменной будут удовлетворять рис 28.
неравенству | х — а | < 8.
Если число а есть предел переменной величины х, то говорят,
что х стремится к пределу а, и пишут х—+а или Шпл; = а*).
В геометрических терминах определение предела может быть
сформулировано следующим образом:
Постоянное число а есть предел переменной, если д,ля любой
наперед заданной как угодно малой окрестности с центром в точке а
и радиусом е найдется такое значение х, что все точки, соответ-
соответствующие последующим значениям переменной, будут находиться
в этой окрестности (рис. 28). Рассмотрим несколько примеров
переменных, стремящихся к пределу.
Пример 1. Переменная величина х последовательно принимает значении
*) tdim* есть сокращение латинского слова limes—предел.

32 ПРЕДЕЛ НЕПРЕРЫВНОСТЬ ФУНКЦИЙ [ГЛ. II
Докажем, что эта переменная величина имеет предел, равный единице. Имеем
Для любого 8 все последующие значения переменной, начиная с номера л,
где 1/л < 8, или п > 1/8, будут удовлетворять неравенству \хп— 1 (< е, что
и требовалось доказать. Заметим, что здесь переменная величина стремится
к пределу, убывая.
Пример 2. Переменная величина х последовательно принимает значения
l 1+ 1 ^1+ *
Эта переменная имеет предел, равный единице. Действительно,
Для любого 8, начиная с номера л, удовлетворяющего соотношению 1/2" < е,
из которого следует
2« > 1/8, п lg 2 > lg A/8), или п >
все последующие значения х будут удовлетворять соотношению | хп— 11 < 8,
Отметим, что здесь значения переменной величины то больше, то меньше
предела. Переменная величина стремится к пределу, «колеблясь вокруг него».
Замечание 1. Как указывалось в § 3, гл. 1, постоянную
величину с часто рассматривают как переменную величину, все
значения которой одинаковы: х = с<
Очевидно, что предел постоянной будет равен самой постоян-
постоянной, так как всегда выполняется неравенство \х — с\~\с — с\ =
5=0 < е при любом е.
Замечание 2. Из определения предела следует, что пере-
переменная величина не может иметь двух пределов. Действительно,
Рис. 29. Рис. 30.
если lira х = а и lim x = b (a < Ь), то * должен удовлетворять
сразу двум неравенствам
|х-а|<в и \х-Ь\<&
при произвольно малом е, а это невозможно, если 8 <(& —а)/2
(рис. 29).
Замечание 3. Не следует думать, что каждая переменная
величина имеет предел. Пусть переменная величина х последова-
последовательно принимает следующие значения:
_j_ ,i 1 _ _i_ К „ L
Х$ л » «^2 * ""

$2J ПРЕДЕЛ ФУНКЦИИ 33
(рис. 30). При достаточно большом k значение х2к и все после-
последующие значения с четными номерами будут как угодно мало
отличаться от единицы, а следующее значение x2k+1 и все после-
последующие значения х с нечетными номерами будут как угодно мало
отличаться от нуля. Следовательно, переменная х не стремится
к пределу.
В определении предела указано, что если переменная вели-
величина стремится к пределу а, то а— постоянное число. Но понятие
«стремится» употребляется и для характеристики другого способа
изменений переменной величины, что видно из следующего опре-
определения.
Определение 2. Переменная х стремится к бесконечности,
если для каждого наперед заданного положительного числа М
можно указать такое значение х, начиная с которого, все после-
последующие значения переменной будут удовлетворять неравенству
\х\>М.
Если переменная х стремится к бесконечности, то ее назы-
называют бесконечно большой переменной величиной и пишут х—^оо.
Пример 3. Переменная величина х принимает значения
*L = —1, Х2 = 2, Х3=— 3, ..., *„=(—1)«Я, ..•
Это —бесконечно большая переменная величина, так как при произвольном
М > 0 все значения переменной, начиная с некоторого, по абсолютной вели-
величине будут больше М.
Переменная величина х «стремится к плюс бесконечности»,
я—^оо, если при произвольном М > 0 все последующие зна-
значения переменной, начиная с некоторого, будут удовлетворять
неравенству М < х.
Примером переменной величины, стремящейся к плюс бесконечности, мо-
может служить переменная величина х, принимающая значения #1=1, х2 — 2} ..,
..., хп = п, ...
Переменная величина х «стремится к минус бесконечности», х—>—оо,
если при произвольном М > 0 все последующие значения переменной, начи-
начиная с некоторого, будут удовлетворять неравенству х < —М.
Например, переменная х> принимающая значения хг = —I, #2 = —2, ...
..., хп — —п, *.., стремится к минус бесконечности.
§ 2. Предел функции
В этом параграфе будем рассматривать некоторые случаи из-
изменения функции при стремлении аргумента х к некоторому пре-
пределу а или к бесконечности.
Определение 1. Пусть функция y = f(x) определена в не-
некоторой окрестности точки а или в некоторых точках этой окрест-
окрестности. Функция y = f{x) стремится к пределу Ъ (у—*Ь) при ху
стремящемся к а (х-^а), если для каждого положительного
числа е, как бы мало оно ни было, можно указать такое поло-
положительное число б, что для всех х, отличных от а и удовлетво-
2 н. С. Пискун<г, т. I

34
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
[ГЛ. II
ряющих неравенству *) | х — а | < б, имеет место неравенство
| /(л:) — Ь\ <е. Если Ъ есть предел функции f(x) при х—>а, то
пишут
lim/(*)=&
х-*-а
или f(x)—+b при х—у а.
Если f(x)—+b при х~^а, то на графике функции y = f(x) это
иллюстрируется следующим образом (рис. 31): так как из нера-
неравенства | х — а | < б следует не-
неравенство | f (х) — b | < е, то это
значит, что для всех точек х,
отстоящих от точки а не далее
чем на б, точки М графика функ-
функции y = f(x) лежат внутри по-
полосы шириной 2е, ограниченной
прямыми у = Ь — е и у = Ь + е.
Замечание 1. Предел функ-
функции f (x) при х—у а можно опре-
определить и следующим образом.
Пусть переменная величина х
принимает значения так (упо-
(упорядочена так), что если J** — a|>|#** — а|, то л;** есть после-
дующее^а х* —^предыдущее значение; если же I** — а| = |л;**—а\
и х*< х**, то л;** есть последующее, a x* — предыдущее значение.
Другими словами, из двух точек числовой прямой последую-
последующей является та точка, которая ближе к точке а; при равных
расстояниях последующая — та, которая правее от точки а.
Пусть упорядоченная таким образом переменная величина х
стремится к пределу а [х—+а или lim jc = aJ.
Рассмотрим, далее, переменную величину y — f(x). При этом
будем считать, как и всюду в дальнейшем, что из двух значений
функции последующим является то значение, которое соответствует
последующему значению аргумента.
Если определенная так переменная величина у при х—+а стре-
стремится к некоторому пределу Ьу то будем писать
lim f(x) = b
Ъ+е
Ъ
h г
0
1
V
а—
Ш
Щ
} а а+д *
Рис. 31.
и говорить, что функция
х—>а.
= f(x) стремится к пределу Ь при
*) Здесь имеются в виду те значения х? удовлетворяющие неравенству
\х—а\ < 6, которые принадлежат области определения функции. Аналогич-
Аналогичные обстоятельства будут встречаться и в дальнейшем. Так, при рассмотре-
рассмотрении поведения функции при х—>-оо может случиться, что функция опреде-
определена только при целых положительных значениях х. Следовательно, в этом
случае х—*-oos принимая только целые положительные значения. Оговорок
об этом мы в дальнейшем делать не будем.

I 21
ПРЕДЕЛ ФУНКЦИИ
35
i
4
4
/
Рис. 32.
Легко доказать, что оба определения предела функции экви-
эквивалентны.
Замечание 2. Если f(x) стремится к пределу Ьг при х,
стремящемся к некоторому числу а так, что х принимает только
значения, меньшие а, то пишут lim / (х) =*
х ->а— О
я= Ь± и называют &i пределом функции f (x)
в точке а слева. Если а; принимает только
значения, большие а, то пишут lim / (х) =з
* ->а + 0
s=a &2 и называют Ь2 пределом функции в
точке а справа (рис. 32). Вместо #-->0+
+ 0 и х—>0—0 обычно пишут л:—> + 0 и
х->-0.
Можно доказать, что если предел спра-
справа и предел слева существуют и равны, т. е.
bf ~Ь2 = Ь, то Ъ и будет пределом в смыс-
смысле данного выше определения предела в точке а. И обратно, если
существует предел функции Ь в точке а, то существуют пределы
функции в точке а справа и слева и они равны.
Пример 1. Док ажем, что lim (Злс+1) = 7. Действительно, пусть задан
#-> 2
произвольное е > 0; для того чтобы выполнялось неравенство | (Зх+1)—71 < 8,
необходимо выполнение следующих неравенств: \Ъх—6|<е, \х—2|<е/3*
— 8/3 < х—2 < 8/3. Таким образом, при любом 8 для всех значений х, удов-
удовлетворяющих неравенству \х—2| < 8/3 = 6, значение функции 3*+1 будет
отличаться от 7 меньше чем на 8. А это и значит, что 7 есть предел функции
при х —* 2.
Замечание 3. Для существования предела функции при
х—>а не требуется, чтобы функция была определена в точке
х = а. При нахождении предела рассматриваются значения функ-
функции в окрестности точки а, отличные от а; это положение наглядно
иллюстрируется следующим примером.
Пример 2. Докажем, что lim {х2—4)/(х—2) =4. Здесь функция
х -*• 2
{х2—4) 1(х—2) не определена при х = 2.
Нужно доказать, что при произвольном 8 найдется такое 6, что будет
выполняться неравенство
если | jc—21 < 6. Но при х Ф 2 неравенство A) эквивалентно неравенству
(х-2)(х+2)
х—2
ИЛИ
Таким образом, при произвольном г неравенство A) будет выполняться,
если будет выполняться неравенство B) (здесь 6 = 8). А это и значит, что
данная функция при х —> 2 имеет пределом число 4.

36
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
1ГЛ. II
Рассмотрим некоторые случаи изменения функции при #—*оо.
Определение 2. Функция f(х) стремится к пределу b
при х —+оо, если для каждого произвольно малого положитель-
положительного числа е можно указать та-
такое положительное число N у что
для всех значений х, удовлетво-
ряющих неравенству \x\>Ny
выполняться неравенство
&1
3. Докажем, что
1 или, в иной записи,
Рис. 33.
lim (l+IW
Нужно доказать, что при произвольном ? будет выполняться неравенство
если только \х\ > N, причем N определяется выбором е. Неравенство C)
эквивалентно следующему неравенству: | \/х\ < 8, которое будет выполняться,
если |л:| > 1/8 = Л^. Это и значит, что lim ( Н )= to iX-=l (рИС, 33).
X -*. оо \ X / х-*- оо X
Зная смысл символов л;—* + оо, х—>—сю, очевидным является
и смысл выражений
«f(x) стремится к Ь при х—> + оо» и
«f(x) стремится к Ъ при х—>¦—оо»,
которые символически записываются так:
lim f(x) = b9 lim
§ 3. Функция, стремящаяся к бесконечности.;
Ограниченные функции
Мы рассмотрели случаи, когда функция / (х) стремится к неко-
некоторому пределу b при х—+а или при х—>оо.
Рассмотрим теперь случай, когда функция y = f(x) стремится
к бесконечности при некотором способе изменения аргумента.
Определение 1. Функция f (х) стремится к бесконечности
при х—*а, т. е. является бесконечно большой величиной при х—+ау
если для каждого положительного числа М, как бы велико оно ни
было, можно найти такое б > 0, что для всех значений х> отлич-
отличных от а, удовлетворяющих условию \х—а|<8, имеет место
неравенство | f (х) \ > М.
Если f (х) стремится к бесконечности при л;—* а, то пишут
lim f (x) = оо
или
оо при х —> а.

ФУНКЦИЯ, СТРЕМЯЩАЯСЯ К БЕСКОНЕЧНОСТИ
37
Если f(x) стремится к бесконечности при х —*а и при этом
принимает только положительные или только отрицательные зна-
значения, соответственно пишут lim / (х) = + оо или 1иц^/ (х)=—оо.
х+а х>а
Пример I. Докажем, что lim A — х)-2 =
х+ 1
оо, Действительно, при лю-
х
бом М > О будем иметь A-х)-2 > М, если только A-хJ < 1/М, 11— х\ <
< 1/"|/и = д. Функция A— *)~2 принимает только положительные значения
(рис. 34).
Рис. 34.
Рис. 35.
Пример 2. Докажем, что lim ( ] =оо. Действительно, при любом
х^о \ х /
М > 0 будем иметь | — 1/х\ > М, если только |л:| = |л:—0| < \/М = д. Здесь
(— 1/х) > 0 при х < 0 и (— 1/лг) < 0 при х > 0 (рис. 35).
Если функция f (х) стремится к бесконечности при х—*оо,
то пишут
lim / (х) = сю,
и, в частности, может быть
lim f(x)=+oo, lim
Например, lim л:2=+оо,
lim f(x) = — со.
lim д:3 = —со и т. п.
я -> -со
Замечание 1. Функция y = f(x) при х—+а или при л;—> со
может не стремиться к конечному пределу или к бесконечности.
Пример 3. Функция y — sinx, определенная на бесконечном интервале
— oo<#<-|-oo, при х—* оо не стремится ни к конечному пределу, ни
к бесконечности (рис. 36).
Пример 4. Функция у = sin —, определенная при всех значениях #f
кроме значения x — Q, не стремится ни к конечному пределу, ни к бесконеч-
бесконечности при х—>-0. График этой функции изображен на рис. 37.

38
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
[ГЛ. til
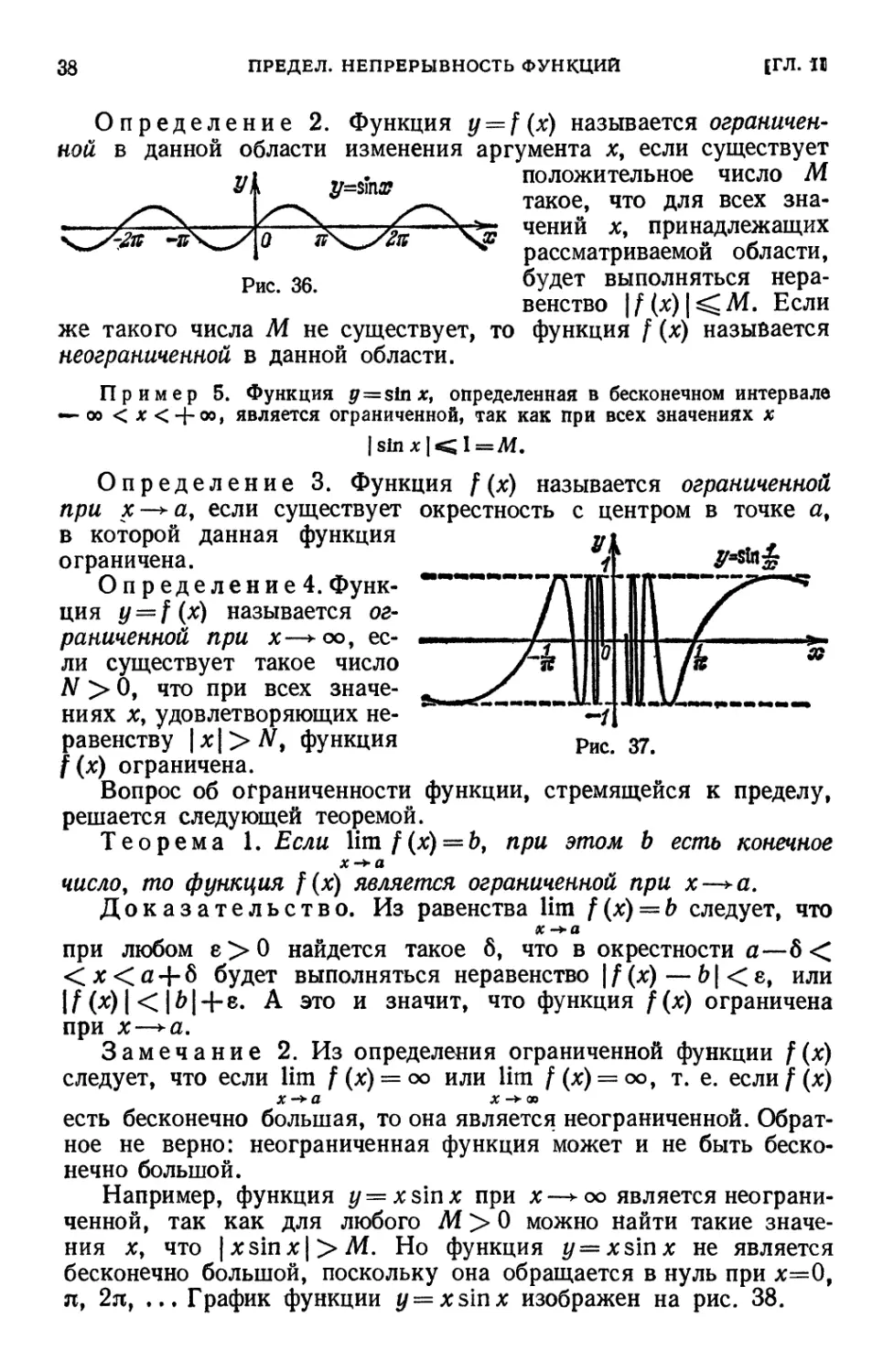
Определение 2. Функция y — f(x) называется ограничен-
ной в данной области изменения аргумента х, если существует
r/=s!na? положительное число М
у ^^ такое,
чений
Рис. 36.
что для всех зна-
х, принадлежащих
рассматриваемой области,
будет выполняться нера-
неравенство | f (я) | <; М. Если
же такого числа М не существует, то функция f (x) называется
неограниченной в данной области.
Пример 5. Функция g=sinx, определенная в бесконечном интервале
— оо < х < + оо, является ограниченной, так как при всех значениях х
Определение 3. Функция f(x) называется ограниченной
при х—+а, если существует окрестность с центром в точке а,
в которой данная функция
ограничена.
Определение 4. Функ-
Функция y = f(x) называется ог-
ограниченной при х—*оо, ес-
если существует такое число
N > 0, что при всех значе-
значениях х, удовлетворяющих не-
неравенству |л;|>#, функция
f(x) ограничена.
Вопрос об ограниченности функции, стремящейся к пределу,
решается следующей теоремой.
Теорема 1. Если lim/(*) = &, при этом Ъ есть конечное
число, то функция f(x) является ограниченной при х—+а.
Доказательство. Из равенства lim f(x) = b следует, что
при любом е>0 найдется такое б, что в окрестности а—б<
<*<а + 6 будет выполняться неравенство |/(д:)—&|<е, или
|/ (х)\ <|fe|+8. А это и значит, что функция f(x) ограничена
при х—+а.
Замечание 2. Из определения ограниченной функции ^(л;)
следует, что если lim /(д:)==оо или lim f (л;) = оо, т. е. если f (х)
х->а х ->¦»
есть бесконечно большая, то она является неограниченной. Обрат-
Обратное не верно: неограниченная функция может и не быть беско-
бесконечно большой.
Например, функция y=xsinx при а:—^оо является неограни-
неограниченной, так как для любого М > 0 можно найти такие значе-
значения х, что |xsinA;| > М. Но функция у = я sin* не является
бесконечно большой, поскольку она обращается в нуль при #=0,
я, 2л, ... График функции y — xsmx изображен на рис. 38.

§4]
БЕСКОНЕЧНО МАЛЫЕ И ИХ ОСНОВНЫЕ СВОЙСТВА
39
Теорема 2. Если lim f (x) = ЬфО, то функция у = 1// (х)
есть ограниченная функция при х—>а.
Доказательство. Из условия теоремы следует, что при
произвольном е > 0 в
некоторой окрестности
точки х=а будем иметь
\f(x)— 6|<8, или
1|/(*)ЦЬ||<в. или
или 161—е<|/(*)|<
Из последних нера-
неравенств следует
1^1^
\Ь\-г > I/WI ^
1
взяв, например, е = у^ | ?
Ю
получаем
1
10
А это и значит, что функция 1// (х) ограничена.
§ 4. Бесконечно малые и их основные свойства
В этом параграфе будем рассматривать функции, стремящиеся
к нулю при некотором характере изменения аргумента.
Определение. Функция а = а(х) называется бесконечно
малой при х—+а или при х—* оо, если lim а (х)=0 или lima (л:)=0.
х -> а х-+(я
Из определения предела следует, что если, например, lim a (x)=0,
то это значит, что для любого наперед заданного произвольно малого
положительного е найдется 6>0 такое, что для всех х, удовлетворяю-
удовлетворяющих условию | х—а | < б, будет удовлетворяться условие) а (х) | < е.
Пример 1. Функция а = (*—-IJ есть бесконечно малая при х—* I,
так как lim a= lira (jc— lJ = 0 (рис. 39).
Пример 2. Функция a=l/# есть бесконечно малая при х—> оо
(рис. 40) (см. пример 3 § 2).
Установим важное для дальнейшего соотношение:
Теорема 1. Если функция y = f(x) представляется в виде
суммы постоянного числа Ь и бесконечно малой а:
A)

40
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
[ГЛ. II
то
limy = & (при х—±а или х—*оо).
Обратно, если limy — b, то можно написать у = Ь+а, где
а—бесконечно малая.
Доказательство. Из равенства A) следует \у—&| = |а|.
Но при произвольном 8 все значения а, начиная с некоторого,
Рис. 40.
удовлетворяют соотношению | а | < е, следовательно, для всех
значений t/, начиная с некоторого, будет выполняться неравен-
неравенство \у—6|<е. А это и значит, что limy = 6.
Обратно: если lim|/ = b, то при произвольном е для всех зна-
значений j/, начиная с некоторого, будет \у—Ь|<е. Но если обо-
обозначим у—fe = a, то, следовательно,
для всех значений а, начиная с не-
некоторого, будет | а | < 8, а это зна-
значит, что a—бесконечно малая.
Пример 3. Пусть дана функция
(рис. 41) у=1-\—, тогда lim у—1, и нао-
борот, так как lim y=l, то переменную
у можно представить в виде суммы предела
1 и бесконечно малой а, равной в данном
случае \/х, т. е. #=1 +
Теорема 2. Если а = а(#)
стремится к нулю при х—+а (или
при х—-юо) и не обращается в нуль, то #=1/а стремится к
бесконечности.
Доказательство. При любом как угодно большомМ > О
будет выполняться неравенство 1/| а | > М, если только будет
выполняться неравенство |а|<1/Л1. Последнее неравенство будет
выполняться для всех значений а, начиная с некоторого, так
как а (л:)—*0.
Теорема 3. Алгебраическая сумма двух, трех и вообще опре-
определенного числа бесконечно малых есть функция бесконечно малая.
Доказательство. Проведем доказательство для двух сла-
слагаемых, так как для любого числа слагаемых оно аналогично.

§ 41 БЕСКОНЕЧНО МАЛЫЕ И ИХ ОСНОВНЫЕ СВОЙСТВА 41
Пусть и(х)=а(х) + $(х), где lima(x) = 0, limP(#) = 0. Дока-
жем, что при произвольном как угодно малом е > 0 найдется
6>0 такое, что при удовлетворении неравенства \х—а|<8
будет выполняться неравенство | и | < е. Так как a (х) есть беско-
бесконечно малая, то найдется такое 6lf что в окрестности с центром
в точке а и радиусом бх будет
|оф)|<е/2.
Так как Р (х) есть бесконечно малая, то найдется такое б2, что
в окрестности с центром в точке а и радиусом ба будет
|Р(*)|<е/2.
Возьмем б равным меньшей из величин бх и б2, тогда в окрест-
окрестности точки а с радиусом б будут выполняться неравенства
|a|<e/2; |р|<е/2. Следовательно, в этой окрестности будет
т. е. |и|<е, что и требовалось доказать.
Аналогично приводится доказательство и для случая, когда
lim a(x) = 0, lim P(x) = 0.
Х-+ со х -*• со
Замечание. В дальнейшем нам придется рассматривать такие
суммы бесконечно малых величин, что с уменьшением каждого сла-
слагаемого число слагаемых увеличивается. В этом случае утвержде-
утверждение теоремы может оказаться и неверным. Рассмотрим, например,
и=—1 \*... Н—, где х принимает только целые положитель-
XX X
х слагаемых
ные значения (х— 1, 2, 3, . ,м /г, ..,). Очевидно, что каждое
слагаемое при х—*оа есть бесконечно малая, но сумма и=1
не есть бесконечно малая.
Теорема 4. Произведение бесконечно малой функции a=a (а:)
на ограниченную функцию z = z(x) при х-^-а (или х —> оо) есть
бесконечно малая величина (функция).
Доказательство Проведем доказательство для случая
х—+а. Для некоторого М>0 найдется такая окрестность точки
# = a, в которой будет удовлетворяться неравенство |г| < М. Для
всякого е > 0 найдется окрестность, в которой будет выполняться
неравенство |а|<е/М. В меньшей из этих двух окрестностей
будет выполняться неравенство
А это и значит, что аг—бесконечно малая. Для случая х—*оо
доказательство проводится аналогично. Из данной теоремы выте-
вытекают:

42 ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ [ГЛ. JI
Следствие 1. Если lim а = О, lim|3 = 0, то 1шоф = О, так
как р (х) есть величина ограниченная. Это справедливо для любого
конечного числа множителей.
Следствие 2. Если lima = 0 и с = const, то Шпдо = 0.
Теорема 5. Частное a (x)/z (x) от деления бесконечно малой
величины а(х) на функцию, предел которой отличен от нуля,
есть величина бесконечно малая.
Доказательство. Пусть lima(x) = 0, Итг(х) = ЬфО. На
основании теоремы 2 § 3 следует, что l/г (а) есть величина ограни-
ограниченная. Поэтому дробь —&> = a (х) —т-у есть произведение вели-
Z \Х) Z \Х)
чины бесконечно малой на величину ограниченную, т. е. величина
бесконечно малая.
§ 5. Основные теоремы о пределах
В этом параграфе, как и в предыдущем, мы будем рассматри-
рассматривать совокупности функций, которые зависят от одного и того
же аргумента х$ при этом Jt—*a или х —>оо.
Мы будем проводить доказательство для одного из этих слу-
случаев, так как для другого доказательство проводится аналогично.
Иногда мы вообще не будем писать ни х—>а, ни х—^оо, под-
подразумевая то или другое.
Теорема 1. Предел алгебраической суммы двух, трех и
вообще определенного числа переменных равен алгебраической сумме
пределов этих переменных:
Мт(и1 + и2+ ... + uk) = \im u1 + \im u2 + ... +\imuk.
Доказательство. Проведем доказательство для двух сла-
слагаемых, так как для любого числа слагаемых оно проводится так
же. Пусть lim «х = а1э \imu2 = az. Тогда на основании теоремы 1 § 4
можем написать
Щ = ai + ai> u2 =
где ax и a2—бесконечно малые. Следовательно,
Щ + и2 = (аг + а2) + (аг+сс2).
Так как (Ях + Яг) есть постоянная величина, а (obi + ^г)—величина
бесконечно малая, то снова по теореме 1 § 4 заключаем, что
lim (ut + и2) = аг + а2 = lim их + lim u2.
Пример 1.
Теорема 2. Предел произведения двух, трех и вообще опре-
определенного числа переменных равен произведению пределов этих

§5J ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ 43
переменных:
lim «-?• «2•... •uk = limuiAimui*... -\imuk.
Доказательство. Для сокращения записи приведем дока-
доказательство для двух множителей. Пусть \imui = a1, lim u2 = a2.
Следовательно,
uxu2 = (at + a*) (a2 + a2) = ага2
Произведение агаъ есть величина постоянная. Величина ага2 +
+ a2a1 + a1a2 на основании теорем § 4 есть величина бесконечно
малая. Следовательно, limw1w2 = a1a2 = limwrlimw2.
Следствие. Постоянный множитель можно выносить за
знак предела.
Действительно, если \\ти± = аи с—постоянная и, следова-
следовательно, lim с = с, то \im(cu1) = limc-limui — C'\imu1, что и требо-
требовалось доказать.
Пример 2. lim 5д^ = 5 lim ^ = 5.8 = 40.
Теорема 3. Предел частного двух переменных равен част-
ному пределов этих переменных, если предел знаменателя отли-
отличен от нуля:
Доказательство. Пусть lima = a, lim^ = 6=^0. Следо-
Следовательно, и = а+а, V — 6 + Р, где а и Р—бесконечно малые.
Напишем тождества
и __ а+а __ а . / а+а а_\ _ а , ab—§а
Т"~~ 6+р "" Ь + \ Ь+$ Ь J-~ b^
или
и а , ab — {За
 5 *""
Дробь — есть постоянное число, а дробь ^.^ по теоремам 4 и 5
§ 4 есть бесконечно малая переменная величина, так как ab—(За
есть бесконечно малая, а знаменатель 6F + Р) имеет пределом
&2#0. Следовательно, lim —==¦?=:-1ш1М
lim у *
Пример 3.
lim C*+5) ЗШиж+5
lim <j-y"^5 *-> 1 *->! ol+o 8^ д
ж™4д:—2"~ lim Dа;—2)"" 4 lim х—2 ~4.1— 2 ~~ 2 ~ ^#
Здесь мы воспользовались доказанной теоремой о пределе дроби, так как
предел знаменателя при х—>• 1 отличен от нуля. Если же предел знаменателя

44 ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ [ГЛ. II
есть нуль, то теорема о пределе дроби не может быть применена. В этом
случае требуется производить специальные рассмотрения.
Пример 4. Найти Нт (х2—4)/(*—2). Здесь знаменатель и числитель
при х—>2 стремятся к нулю и, следовательно, теорема 3 неприменима. Про-
Произведем следующее тождественное преобразование:
х*-4_(х-2)(х+2)
х-2 х~=2
Это преобразование справедливо при всех значениях х, отличных от 2,
Поэтому, имея в виду определение предела, можем написать
.. *2—4 .. (*—2)(*+2) v
hm jr— lim -* 'v^ ; = lim
Пример 5. Найти lim х/(х—1). При х—> 1 знаменатель стремится
х-> 1
к нулю, а числитель к нулю не стремится (числитель стремится к единице).
Следовательно, предел обратной величины есть нуль, т. е.
4 lim (*—1) л
lim = г: = —= 0.
х -* 1 х lim х 1
Отсюда на основании теоремы 2 предыдущего параграфа будем иметь
lim */(*—l)=oo.
X -> 1
Теорема 4. Если между соответствующими значениями
трех функций и = и(х), z = z(x), v = v(x) выполняются неравен-
неравенства u^z^v, при этом и(х) и v (х) при х—> а (или при х—> оо)
стремятся к одному и тому же пределу Ьу то z = z (х) при х—>а
(или при х—> оо) стремится к тому же пределу.
Доказательство. Для определенности будем рассматри-
рассматривать изменение функций при х —> а. Из неравенств и ^ z ^ v
следуют неравенства и—b^iz—b^v—b\ по условию lim u = b,
х -+ а
lim v = b. Следовательно, при любом е>0 найдется некоторая
х-+а
окрестность с центром в точке а, в которой будет выполняться
неравенство \и—6|<е; так же найдется некоторая окрестность
с центром в точке а, в которой будет выполняться неравенство
\v—6|<8. В меньшей из указанных окрестностей будут выпол-
выполняться неравенства — г < и—b < г и —г < v—b < e, а следова-
следовательно, будут выполняться неравенства —е<г—b < е, т. е.
lim z — b.
х-±а
Теорема 5. Если при х—>а (или при х—> оо) функция у
принимает неотрицательные значения у^О и при этом стре-
стремится к пределу Ьу то b есть неотрицательное число: Ь^О.
Доказательство. Предположим, что b < 0, тогда \у—Ь\^>
^|й|, т. е. модуль разности \у—Ь\ больше положительного
числа \Ь\ и, следовательно, не стремится к нулю при х—+а.

§51 ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ 45
Но тогда у при х •—> а не стремится к Ь, что противоречит усло-
условию теоремы. Значит, предположение, что Ь < О, приводит к про-
противоречию. Следовательно, 6^0.
Аналогично доказывается, что если t/^О, то Нту^О.
Теорема 6. Если между соответствующими значениями
двух функций и = и(х) и v = v(x), стремящихся к пределам при
х—+а (или при х—> оо), выполняется неравенство v^u, то имеет
место Шпо^Шпи.
Доказательство. По условию v—w^O, следовательно
(по теореме 5), lim (v—и) > 0, или lim v—lim и ^ 0, т. е. lim v ^
> lim и.
Пример 6. Докажем, что lim sin x = 0,
Из рис. 42 следует: если ОЛ = 1, х > 0, то AC = sinxt AB = x, sinx<x.
Очевидно, что при х < О будет | sin х\ < \ х\. Из этих неравенств на основа-
основании теорем 5 и 6 следует, что lim sin # = 0,
Пример 7. Докажем, что lim sin (xj2) = 0.
Действительно, | sin (jc/2) | < | sin x [. Следовательно, lim sin (x/2) = 0.
Пример 8. Докажем, что limcosx=l; заметим, что cosa;=1—2sin2(*/2),
следовательно, lim cosx= lim A—2 sin2 (x/2)) = 1 — 2 lim sin2 (x/2) = 1—0 = 1.
X-+-Q x-+Q jc->0
В некоторых исследованиях вопроса о пределе переменных при-
приходится решать две самостоятельные задачи:
1) доказывать, что предел переменной
существует, и устанавливать границы, внут-
внутри которых рассматриваемый предел нахо-
находится;
2) вычислять рассматриваемый предел с
нужной степенью точности.
Иногда первый вопрос решается с по-
помощью следующей, важной для дальнейше-
дальнейшего теоремы. v u °
Теорема 7. Если переменная величина Рис- 42»
v возрастающая, т. е. всякое ее последующее
значение больше предыдущего, и если она ограничена, т. е,
v<.M, то эта переменная величина имеет предел lim v = a,
где а^М.
Аналогичное утверждение имеет место и для убывающей огра-
ограниченной переменной величины.
Доказательство этой теоремы мы здесь не приводим, так как
оно основывается на теории действительных чисел, которую мы
здесь не даем*).
*) Доказательство этой теоремы приведено, например, в книге: Фихтен-
гольц Г. М. Основы математического анализа, т. 1.—М.; Наука, 1968.

46
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
[ГЛ. I]
В следующих двух параграфах будут получены пределы двух
функций, имеющие большое применение в математике.
§ 6. Предел функции
при х —> О
Функция не определена при х = 0, так как числитель и
знаменатель дроби обращаются в нуль. Найдем предел этой функ-
функции при х—*0. Рассмотрим окружность
радиуса 1 (рис. 43); обозначим централь-
# ный угол MOB через х, при этом 0 < х < л/2.
Из рис. 43 непосредственно следует
площадь Д МО А < площади сектора МО А <
< площади /\СОА. A)
Площадь
Б А
Рис. 43.
= -<? • 1 • sin х = -? sin x.
Площадь еектора МО А = -^ О А • AM = -^ • 1 • х = -^ х.
Площадь
Неравенства A) после сокращения на */а переписываются так:
sin х < х < tg #.
Разделим все члены на sinx:
sin л:
или
cos*'
cos
Мы вывели это неравенство в предположении, что х > 0; замечая,
sin (— #) sin x
J = —
что
,J_ .
и cos (— х) = cos л:, заключаем, что оно верно
и при х<0. Но lira cos *=1, lira 1 = 1.
0 0
Следовательно, переменная ^—^ заключена между двумя вели-
величинами, имеющими один и тот же предел, равный 1; таким обра-
образом, на основании теоремы 4 предыдущего параграфа
График функции у = ^— изображен на рис. 44.

5 71
ЧИСЛО е
47
Примеры.
COS X v-x) X x-+0 COS X
Рис. 44.
o .. 1 — cos* ..
3. lim = iim -
х-»й x x-+o
2 sin2 -^-
sinT x
^sin4=b0 = 0.
) fx 2
lim
sin a*
l г s*n ax — i: a ш; a ^o ал: ___
# j{!2 sin рлг *mo F * 81прл: ~" Р .. sin рл; ""
I* u ^ r^ r- jim r__
X
^=-2. •-~==^- (a = const, P = const).
§ 7, Число е
Рассмотрим переменную величину
где п—возрастающая переменная величина, принимающая значе-
значения из натурального ряда чисел 1, 2, 3, ...
A Л п
1 + —J при п~>оо
имеет предел, заключенный между 2 и 3.
Доказательство. По формуле бинома Ньютона можем
написать
1.2.....и
0)

48 ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ [ГЛ. II
Произведя очевидные алгебраические преобразования, получим
Из последнего равенства следует, что переменная величина
A \ п
1 + — J —возрастающая переменная величина при возрастаю-
возрастающем п.
Действительно, при переходе от значения п к значению п+1
каждое слагаемое последней суммы возрастает:
и добавляется еще один член. (Все члены разложения—поло-
разложения—положительные.)
/ 1 \ и
Покажем, что переменная величина ( 1 -\— J ограничена.
Замечая, что [\ — ~\ < 1; М—--J М_,_Л < 1 и т. д., из вы-
выражения B) получим неравенство
Замечая, далее, что
Ь2.3^22' Ь2.3-4^23) '"' Ь2-.. .-л
можем написать неравенство
Подчеркнутые члены правой части этого неравенства образуют
геометрическую прогрессию со знаменателем <7=1/2 и первым
членом а=1, поэтому
2
Следовательно, для всех п получаем

$ 71 ЧИСЛО е 49
Из равенства B) следует, что
Таким образом, получаем неравенства
Этим установлено, что переменная величина A + — ) ограничена.
Итак, переменная величина Г1 + — J —возрастающая и огра-
ограниченная, поэтому на основании теоремы 7 § 5 она имеет предел.
Этот предел обозначается буквой е.
Определение. Предел переменной величины (l-\—j при
п —* оо называется *) числом е:
Из неравенства C) на основании теоремы 6 § 5 следует, что
и число е удовлетворяет неравенству 2^в^3. Теорема доказана.
Число е—иррациональное число. Позднее будет указан метод
его вычисления с любой степенью точности. Его значение с де-
десятью верными знаками после запятой:
^ = 2,7182818284...
Теорема 2. Функция A + ~J пРи *> стремящемся к бес-
бесконечности, стремится к пределу е:
lim
Доказательство. Было установлено, что (\-\—j —>е
при п—>оо, если п принимает целые положительные значения.
Пусть теперь х стремится к бесконечности, принимая как дроб-
дробные, так и отрицательные значения.
1) Пусть х—^ + оо. Каждое его значение заключено между
двумя) положительными целыми числами: п ^ х < п+ 1. При этом
/ 1 \п
*) Можно показать, что f 1-|— I —>е при п—)-+оо, если п не является
монотонно возрастающей переменной величиной.

50
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
[ГЛ. И
будут выполняться неравенства
±>±>JL 14-
п ^ х ^ n+V ~
п+1'
Если х —*оо, то, очевидно, и п~>оо. Найдем пределы перемен-
переменных, между которыми заключена переменная (l+ — j :
im^l+JLy^^lhn (l +
s= lim
- Um
следовательно (по теореме 4 § 5),
Um
2) Пусть х—+—oo. Введем новую переменную ^ = —(лг-f-l)
или д: = — (^+0- При t—^ + °° будет дс—¦>—сх>. Можем написать
-7
Рис. 45.
Теорема доказана. График функции y=(l+l\* изображен на
рис. 45.

НАТУРАЛЬНЫЕ ЛОГАРИФМЫ
51
Если в равенстве D) положить 1/х=а, то при х—*оо имеем
а—»0 (но а =7^0) и мы получаем liA4I/a
а-и>
Примеры:
1. lim A+±Г5=1и
1ип
= lim A+—)*• lim f 1+—V = e*l=e.
2. Hm (!+!)"- Ita
[-llm
3. иш
4. lim f —Ц- = lim [ -J— = lim ( 1 ^ г ) s=s
s= bm 1H r sslim 1H— =5
Замечание. Показательная функция с основанием е,
играет исключительно большую роль в дальнейшем курсе матема-
математики. Эта функция играет большую роль при изучении различ-
различных явлений в механике (теория колебаний), в электротехнике и
радиотехнике, в радиохимии и т. д.
Эту функцию часто называют экспо-
нентой (exponential function). Графи-
Графики показательной функции у = ех и
показательной функции у = е~* изоб-
изображены на рис. 46.
§ 8. Натуральные логарифмы
В § 8 главы I была определена
логарифмическая функция у = loga x.
Число а называется основанием лога-
логарифмов. Если a— iO, то у называется
десятичным логарифмом числа х и
обозначается у = lgx. Из школьного курса известны таблицы зна-
значений десятичных логарифмов, которые называются бригговымщ
по имени английского ученого Бригга A556 —1630).

52
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
1ГЛ. II
Логарифмы с основанием е = 2,71828... называются натураль-
натуральными, или неперовыми логарифмами, по имени одного из первых
изобретателей логарифмических таблиц, математика Непера
A550 — 1617). Следовательно, если еУ = х, то у называют натураль-
натуральным логарифмом числа х и пишут # = 1пх вместо у = loge x. Гра-
Графики функций у = 1пх и y = \gx построены на рис. 47.
Рис. 47.
Установим, далее, зависимость между десятичными и натураль-
натуральными логарифмами одного и того же числа х. Пусть у = lg x, или
х=10*. Прологарифмировав левую и правую части последнего
равенства при основании е, получим 1пх = у1пЮ. Определяем
f^
Trflo
"пх* или> п°Дставляя значение^ имеем lgx=
-Inх.
Таким образом, если известен натуральный логарифм числа х,
то десятичный логарифм этого числа находится путем умножения
на множитель Л1= 1п[0 ж 0,434294, не зависящий от*. Число М
называется модулем перехода от натуральных логарифмов к деся-
десятичным:
= Mlnx.
Если положим в этом тождестве х = е, то получим выражение
числа М через десятичные логарифмы:
Натуральные логарифмы через десятичные выражаются так:
1
где
i « 2,302585.
Замечание. Для вычисления натуральных логарифмов чисел
существуют специальные таблицы (например, см. Брон-
Бронштейн И. Н. и СемендяевК. А. Справочник по матема-
математике. -М.: Наука, 1980).

§9]
НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
53
§ 9. Непрерывность функций
Пусть функция y = f(x) определена при некотором значении х0
и в некоторой окрестности с центром в х0. Пусть yo = f(xQ),
Если х получит некоторое поло-
положительное или отрицательное — без-
безразлично — приращение Але и примет
значение x = xQ + Axy то и функция*/
получит некоторое приращение Ау.
Новое, наращенное значение функции
будет yo + Ay = f(xQ + Ax) (рис. 48).
Приращение функции Ау выразится
формулой Ay = f (х0 + Ах) — / (л:0).
Определение 1. Функция у =
= / (л:) называется непрерывной при
значении х = х0 (или в точке х0), Рис.48,
если она определена в некоторой
окрестности точки х0 (очевидно, и в самой точке х0) и если
lim Ау =
Д0
A)
или, что то же самое,
lim
О
B)
Условие непрерывности B) можно записать и так:
lim f(:
ИЛИ
lim f(x)=f(xj9
C)
НО
Xq= lim x.
Следовательно, равенство C) можно записать так:
lim f (x) =
#-* x0
lim x
x0
)
D)
т. е. для того, чтобы найти предел непрерывной функции при
х—>л:0, достаточно в выражение функции подставить вместо
аргумента х его значение х0.
Описательно геометрически непрерывность функции в данной
точке означает, что разность ординат графика функции y = f(x)
в точках хо + Ах и х0 будет по абсолютной величине произвольно
малой, если только |Ах| будет достаточно, мало.

54
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
[ГЛ. II
Пример 1. Докажем, что функция у — х2 непрерывна в произвольной
точке х0. Действительно,
lim \y= lim B*0A*+A*2) = 2*0 lim Ax+ lim Ах* lim Д*=0
Дх->*0 А*-* О А*->0 Д#-> О Ах-> О
при любом способе стремления Ах к нулю (рис. 49, а и б).
у?
Рис. 49.
Пример 2. Докажем, что функция y=sln x непрерывна в произвольной
точке х0. Действительно, #0 = sin*0, yo + Ay = sin (xo + Ax)f
Ах I Ax\
A#=sin (Xq + Ax) —sin Xq = 2 sin -pr— • cos ( Xq -J—^- } ¦
z v * /
Было показано, что lim sin—<?-=0 (пример 7 § 5). Функция cos Гх4~? )
Ax -<> о -6 V «6 /
ограничена. Следовательно, lim Ay = Q.
Аналогичным образом, рассматривая каждую основную элемен-
элементарную функцию, можно доказать, что каждая основная элемен-
элементарная функция непрерывна в каждой точке, в которой она
определена.
Докажем далее следующую теорему.
Теорема 1. Если функции ft{x) и f2(x) непрерывны в точке
х09 то сумма fy(x) = fi(x)+f2(x) также есть непрерывная функ-
функция в точке х0.
Доказательство. Так как fх(л;) и f2(x) непрерывны, то
на основании равенства C) можем написать
lira f± (x) = ft (*0) и Urn f2 (x) = f2 (xQ).
К-+Хо X -*• Xq
На основании теоремы 1 о пределах можем написать
Ига <ф (л:) = lim [ft (x) + f% {x)] = lim ft (x) + lim f2 (x) =
Итак, сумма ty(x) = ft(x)-\-f2(x) есть непрерывная функция.
Теорема доказана.
Как следствие отметим, что теорема справедлива для любого
конечного числа слагаемых.
Опираясь на свойства пределов, так же можно доказать сле-
следующие теоремы:

§92 НЕПРЕРЫВНОСТЬ ФУНКЦИЙ 55
а) Произведение двух непрерывных функций есть функция не-
непрерывная.
б) Частное двух непрерывных функций есть функция непре-
непрерывная^ если знаменатель в рассматриваемой топке не обращается
в нуль,
в) Если и = у(х) непрерывна при х=х0 и f(u) непрерывна
в точке ио = ц>(хо), г*10 сложная функция /[<р(х)] непрерывна
в точке х0.
Используя эти теоремы, можно доказать следующую теорему.
Теорема 2. Всякая элементарная функция непрерывна в каж-
каждой точке, в которой она определена *).
Пример 3. Функция у = х2 непрерывна в любой точке х0 и потому
lim x2 = xl lim *» = За = 9.
х -> Xq х -> 3
Пример 4. Функция y — sinx непрерывна в любой точке и потому
lim sin x = sin (я/4) = У~2/2.
Пример 5. Функция у = ех непрерывна в каждой точке и потому
lim ех = еа.
я-> а
Пример 6. lim lnA+X)= lim — ln(l + *) = lim In 1(\ + хУ/х]. Так
х -* о х х -> о х х •+ о
как lim (\-{-x)l/x = e и функция \пг непрерывна при г > Ои, следовательно,
при г = е, то
lim )n[(l+x)l/x~\ = \n[ lim A + xI
x-*o L J L*-*o
Определение 2. Если функция y = f(x) непрерывна в каж-
каждой точке некоторого интервала (а, Ь), где а < Ь, то говорят,
что функция непрерывна на этом интервале.
Если функция определена и при х = а, и при этом lim / (х)=$
х-*а+ о
= /(а), то говорят, что/(лг)в точке х = а непрерывна справа. Е?ли
lim f(x) = f(b), то говорят, что функция f(x) в точке х = Ь не-
х-+Ь-о
прерывна слева.
Если функция f(x) непрерывна в каждой точке интервала
{а, Ь) и непрерывна на концах интервала соответственно справа
и слева, то говорят, что функция f(x) непрерывна на замкну-
замкнутом интервале или отрезке [а, Ь].
Пример 7. Функция у = х2 непрерывна на любом отрезке [а> Ь], что
следует из примера 1.
Если в какой-то точке х = х0 для функции y = f(x) не выпол-
выполняется по крайней мере одно из условий непрерывности, т. е. если
*) Этот вопрос подробно изложен в книге: ФихтенгольцГ. М.
Основы математического анализа, т. 1.—Мл Наука, 1968»

56
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
[ГЛ. И
при х = х0 функция не определена или не существует предел
lim /(*), или lim f(x)=?f(x0) при произвольном стремлении
X -+ Х0 X -> Х0
х—+х0, хотя выражения, стоящие справа и слева, существуют,
то при х = х0 функция y = f(x) разрывна. Точка х = х0 в этом
случае называется точкой разрыва функции.
Пример 8. Функция у=1/х разрывна при х—0. Действительно, при
х—0 функция не определена: lim 1/*= + оо, lira 1/*=—-оо. Легко по*
казать, что эта функция непрерывна при любом значении х Ф 0.
Пример 9. Функция y—2lfx разрывна при *=0. Действительно,
lim 21/л;=оо, lim 21/*=0. При *=0 функция не определена (рис. 50).
#-*- +о х-*- -о
Пример 10. Рассмотрим функцию / (х) =х/\ х |. При х < 0 будетх/[х{ =
= — 1; при х>0 будет х/\х\ = \. Следовательно,
lim /(*)= lim д:/|д:| = — 1, lim f(x)= lim 1
при х—0 функция не определена. Таким образом, мы установили, что функ-
функция /(*) = */! #1 разрывна при х = 0 (рис. 51).
О
О
Рис. 50.
«2?
Рис. 51.
Пример 11. Функция #=sin (l/x), рассмотренная в примере 4 §3, раз-
разрывна при #=0.
Определение 3. Если функция /(х) такова, что существуют
конечные пределы lim f{x) = f(xo+O) и lim f(x) = f(xo-Q)9
X-*Xq + Q X-*X0-0
но или lim !(х)Ф lim f(x), или значение функции f(x) при
# = л;0 не определено, то х = х0 называется точкой разрыва 1-го
рода. (Например, для функции, рассмотренной в примере 10,
точка х = 0 есть точка разрыва 1-го рода.)
§ 10. Некоторые свойства непрерывных функций
В этом параграфе рассмотрим некоторые свойства функций,
непрерывных на отрезке. Эти свойства будут сформулированы
в виде теорем, которые мы приводим без доказательства *).
*) Доказательства этих теорем можно найти в книге: Ф и х т е н-
гояьц Г. М. Основы математического анализа, т.1.—М.: Наука, 1968.

§10]
НЕКОТОРЫЕ СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ
57
Теорема 1. Если функция y = f(x) непрерывна на некотором
отрезке [a, b] (а^х^Ь), то на отрезке [а, Ь] найдется по
крайней мере одна точка x = xt такая, что значение функции
в этой точке будет удовлетворять соотношению
где х—любая другая точка отрезка, и найдется по крайней мере
одна точка х2 такая, что значение функции в этой точке будет
удовлетворять соотношению
Значение функции / (хг) будем называть наибольшим значением
функции y = f{x) на отрезке [а, Ь], значение функции / (х2) будем
называть наименьшим значением функции на отрезке [а, Ь].
Коротко эту теорему формулируют так:
Непрерывная на отрезке а^.х^.Ь функция достигает на этом
отрезке по меньшей мере один раз наибольшего значения М и
наименьшего значения т.
цат/
Рис. 52.
Рис. 53.
Смысл этой теоремы наглядно иллюстрируется на рис. 52.
Замечание. Утверждение теоремы о существовании наиболь-
наибольшего значения функции может оказаться неверным, если рассмат-
рассматривать значения функции на интервале а < х < 6. Так, например,
если мы будем рассматривать функцию у = х на интервале 0<#<1,
то среди ее значений нет наибольшего и нет наименьшего. Дейст-
Действительно, на интервале нет ни наименьшего, ни наибольшего
значений х. (Нет крайней левой точки, так как, какую бы ни
взяли точку #*, найдется точка левее взятой, например точка^ ;
также нет крайней правой, а следовательно, нет ни наимень-
наименьшего, ни наибольшего значений функции у = х.)
Теорема 2. Пусть функция y = f(x) непрерывна на отрезке
[а, Ь] и на концах этого отрезка принимает значения разных
знаков, тогда между точками а и Ь найдется по крайней мере
одна точка х~с, в которой функция обращается в нуль:

58
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
[ГЛ. II
Эта теорема имеет простой геометрический смысл. График не-
непрерывной функции y = f(x)> соединяющий точки Мг\а, f (а)] и
M2[b, f(b)l где/(а)<0 и /(*)>0 (или /(а)>0 и /(&)<0),
пересекает ось Ох по крайней мере в одной точке (рис. 53).
Пример. Дана функция г/ = *3—2; yU-.i== —I, */|x=2 = 6. На отрезке
[1, 2] она непрерывна. Следовательно, на этом отрезке существует точка, где
# = **—2 обращается в нуль. Действительно, у=0 при х~^/2 (рис. 54).
Теорема 3. Пусть функция y = f(x) определена и непрерывна
на отрезке [а, Ь]. Если на концах этого отрезка функция при-
принимает неравные значения f (а) = А, f (b)— В9
тоу каково бы ни было число |л, заключенное
между числами А и В, найдется такая точка
х = с, заключенная между а и 6, что f (с) = fie
Смысл данной теоремы отчетливо иллюстри-
иллюстрируется на рис. 55. В данном случае всякая
прямая у = [г пересекает график функции у =s
"fix).
Замечание. Отметим, что теорема 2 яв-
является частным случаем этой теоремы, так как
если А и В имеют разные знаки, то в ка-
качестве |Л> можно взять 0 и тогда \i = 0 будет за-
заключено между числами А и В.
Следствие теоремы 3. Если функция
54. y — f^ непрерывна на некотором интервале
и принимает наибольшее и наименьшее значения, то на этом
интервале она принимает по крайней мере один раз любое
Я\
У,
Рис. 56.
значение, заключенное между ее наименьшими и наибольшими
значениями.
Действительно, пусть f(x^ = M, f(x2) = m. Рассмотрим отре-
отрезок [xit х2]. Тогда по теореме 3 на этом отрезке функция y = f(x)
принимает любое значение ц,, заключенное между М и т. Но
отрезок fa, x2] заключен внутри рассматриваемого интервала, на
котором определена функция f(x) (рис. 56).

f 111 СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ 69
§11. Сравнение бесконечно малых
Пусть одновременно несколько бесконечно малых величин
а, Р, y» • • • являются функциями одного и того же аргумента х
и стремятся к нулю при стремлении х к некоторому пределу а
или к бесконечности. Охарактеризуем стремление этих перемен-
переменных к нулю, рассматривая их отношения*).
Будем пользоваться в дальнейшем следующими определениями.
Определение 1. Если отношение Р/а имеет конечный и
отличный от нуля предел, т.е. если lim Р/а = Л ^ О, а следова-
следовательно, lima/P = I/A фО, то бесконечно малые р и а называются
бесконечно малыми одного порядка.
Пример 1. Пусть a = Xj P=sin2*, где х—>-0. Бесконечно малыеаир
одного порядка, так как
lim !=* lira ^?=2.
х-*-о ее х-*о х
Пример 2. При х—>-0 бесконечно малые дг, sin Зх, tg2x* 71п(Г+я)
являются бесконечно малыми одногр и того же порядка. Доказательство прово-
проводится аналогично тому, как это сделано в примере 1.
Определение 2. Если отношение двух бесконечно малых
р/а стремится к нулю, т.е. если lim p/a = О (а Ита/р=*оо), то
бесконечно малая р называется бесконечно малой величиной выс-
высшего порядка, чем бесконечно малая а, а бесконечно малая а
называется бесконечно малой низшего порядка, чем бесконечно
малая р.
Пример 3. Пусть а = х> Р = *п, п > Ь #—>-0. Бесконечно малая Р есть
бесконечно малая высшего порядка, чем бесконечно малая а, так как
Km xn/x= lim xn-1=0.
*-*0 х-+о
При этом бесконечно малая а есть бесконечно малая низшего порядка!
чем бесконечно малая р.
Определение 3. Бесконечно малая р называется бесконечно
малой k-го порядка относительно бесконечно малой а, если р и
а* — бесконечно малые одного порядка, т. е. если limp/a*=Д ^0-
Пример 4. Если а = #, Р = *3, то при х—vO бесконечно малая Р есть
бесконечно малая третьего порядка относительно бесконечно малой а, так как
lim p/a3= lim jr7(xK=l.
х-+0 х ->-0
Определение 4. Если отношение двух бесконечно малых
Р/a стремится к единице, т.е. если НтР/а=1, то бесконечно
малые р и а называют эквивалентными бесконечно малыми **) и
пишут а »р.
*) Будем предполагать, что бесконечно малая, стоящая в знаменателе,
не обращается в нуль в некоторой окрестности точки а.
**) В этом случае аир иногда называют равносильными бесконечно
малыми.

6Q ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ [ГЛ. II
Пример 5. Пусть ос = х и Р = sin х, где х —> 0. Бесконечно малые а и
Р эквивалентны, так как
.. sin х ч
lim =1.
х -» о х
Пример 6. Пусть а = х, P = ln(l+x), где х—> (). Бесконечно малые
аир эквивалентны, так как
lim М±^Ц,
к -*> о х
(см. пример б § 9).
Теорема 1. Если а и р — эквивалентные бесконечно малые,
то их разность а — (J есть бесконечно малая высшего порядка, чем
а и чем р.
Доказательство. Действительно,
lim —? = lim (l-?) = l-lim?=1-1 = 0.
ct \ a / а
Теорема 2. ?сли разность двух бесконечно малых а — р
бесконечно малая высшего порядка, чем а и чем р, то а и р
эквивалентные бесконечно малые.
Доказательство. Пусть limа = 0, тогда lim A — ~ ) ==
а \ а /
= 0, или 1 — lim ~ = 0, или 1 = lim ~, т. е. а ^ р. Если lim ^-g^=
= 0, то lim (|f"~ 0 ==0» lim-^ = 1, т. е. а» р.
Пример 7. Пусть а = лг, $ — х-\-хг, где лс—>-0. Бесконечно малыеаир
эквивалентны, так как их разность Р—а=х3 есть бесконечно малая высшего
порядка, чем а и чем р. Действительно,
Km iz^= iim i!^ цт x* = Of
x -> о ос % .+ q х х -> о
v P—а ,. х3 .. л:2
lim r Q ¦= lim —:—г= lim -j—:
д> 1 j j
Пример 8. При х—>¦ оо бесконечно малые а= 2 и Р= эквива-
эквивах2 х х2
лентные бесконечно малые, так как их разность г
г х2 х х2
есть бесконечно малая высшего порядка, чем а и чем р. Предел отношения а
и Р равен 1:
= Urn i±l= lim
Замечание. Если отношение двух бесконечно малых Р/а
не имеет предела и не стремится к бесконечности, то р и а не
сравнимы между собой в указанном выше смысле.

УПРАЖНЕНИЯ К ГЛАВЕ И 61
Пример 9. Пусть а==лг, P=^sin A/л:), где х—>»0. Бесконечно малые а
и Р не сравнимы, так как их отношение p/a=sin(l/#) при х—>О не стре-
стремится ни к конечному пределу, ни к бесконечности (см. пример 4 § 3).
Упражнения к главе II
Вычислить указанные пределы:
1. lim ^J^!^5 * Отв. 4. 2. lim [2sin*—cos*+ctgA:]. Отв. 2.
3. lim *lJL . Отв. 0. 4. lim B-—+4Л . Отв. 2.
*_2 1^2+л: x->oo\ x^x2 J
5. lim —оЗз—гг-"« Отв- т- 6- lim ——• Отв. 1. 7. lim
1 i2_L924-32-l- 4-п2 1
Отв. 4- »• Иш + + , "+ > Отв. ~.
2 п -+«, /г3 3
Указание. Напишем формулу (k+lK—k3 = 3k2+3k-\-l для ? = 0, 1,
2, ..., п:
18=1;
23—13 = 3-
З3—23 = 3.2
Складывая левые и правые части, получим
откуда
~. Отв. О.
11. lim \ 2То ¦ Отв. i. 12. lim ^—^. Отв. 4. 13. lim -^ f-.
^^.о ох*-\-2.x I х -*¦ 2 -^—<2 х-+1 л:—1
те. -ГГ-. 15. 1
16. Иш у^^.^у . Ота.-±. 17. цМш ^2"р(|^ . Отв. 0.
18. lim v~ ' '"! —. Отв. Зл:2. 19. lim [^ t 3 . 1 . Отв.—\.
20. lim т—. Отв. п (п—целое положительное число).
х -> 1 л:— i
21. lim ' . Отв. —. 22. lim
х -*- 0 ^ 2. х -+¦'&.
23. lim^/l+fl-P. Ome. ±. 24, lim

62 ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ [ГЛ. II
—I при *—->—оо. 29. lim (Vx*+ I —У"*2 — l). Отв. 0.
ЗОф lim *(}Лс2+ 1—*). Отв. -^ при*—>-+оо, — оо при х—> — оо#
Х-+ оо *
л« .. sin л: л t вл .. sin 4л: л А оо .. sin2 (д:/3) л 1
31. lim т . Отв. \. 32. lim . Отв. 4. 33. lim ~-^ . Отв.—.
34, lim л://— cos*. 0тв9 VI. 35. lim *ctg*. Отв. 1.
36. lim l~-2cosi; ^ От у^. 37. lim (l-z)tg ii. Отв. ~.
ло ,. 2arcsinA: л 2 ол .. sin (а+д:) — sin (а—х) л
38. lim 5 • ^тв* "о" • 39« 11т —*—ш— * ¦ • От
X-+Q оХ О X -* О X
40* lim — о . Отв. ~# 41. lim ( Ы— . Отв. е2.
Х-+ О Х * X -+ оо \ X J
42. lim A . Отв. ~. 43. lim ( rf— J . Отв. i-.
A \Л + 5
Н—) *. Отв. е. 45. Иш {п [1п(п+1) —1пл]}. Отв. 1.
46. lim (l + cos*Ksec^ Отв. е*. 47. lim ln(l+ax) л Отв. а.
X -> О
48. lim f|?±r-V+I- Отв. е. 49. lim A+3tg2*)ctg2*. Отв. е\
х-+<х>\ Лх+\ J х-* о
( х \т In A +еа)
50. lim (cos— . Отв. 1. 51. lim —*—! . Отв. I при а—>-+оо,
т-»-оо\ т/ а->°° Сб
Отв 53 lim
х-+ о
при х—>-+оо, 0 при х—>— оо. 54. lim n[a1/f/l—l]. Отв. Ina.
П * 00
О при а—>>—оо. 52. lim —-—я—. Отв. -5-. 53. lim (а>1).Отв.+00
х о sin рл: р ^-^ооЛ:
gax gbx eax е&х
55. lim — — • Отв. а—р. 56. lim —2 1_-. Отв. 1.
*_*о а: к ^ -* о sin ax—sin $x
Определить точки разрыва функций:
х j
57, g= x{x+\){x*—4) ' ОШ' РазРывы ПРИ ^=--2i —Ьч °5 2-
1 2
58. y=tg —. Отв. Разрывы при *=0 и х= ±—;
2 2
± Зя 5 •*#; * 5 ••
59. Найти точки разрыва функции |/=1+21/дс и построить график этой
функции. Отв. Разрыв прих =0 {у —>+ оо при х —>-+0, у —> I при х —*—. 0).

УПРАЖНЕНИЯ К ГЛАВЕ II 63
60. Между следующими бесконечно малыми (при х—>-0) величинами
*а? Vx(l—*)> sin Зя, 2х cos x у tg2 x ? xe2x выбрать бесконечно малые одного
порядка с бесконечно малой х, а также высшего и низшего порядка, чем х.
Отв. Бесконечно малые одного порядка с х: sin3x и хе2х; бесконечно малые
высшего порядка по сравнению с х: х2 и 2#cosa:i/tg2 x> бесконечно малая
низшего порядка по сравнению с х: ]/"# A—х).
61* Среди указанных бесконечно малых (при х—>0) величин найти бес-
бесконечно малые, равносильные бесконечно малой х: 2sin*, -n-tg2x3 к—3jc2|
2
In A+а:), х? + Зх*. Отв. -j
62. Убедиться в том, что при х—^1 бесконечно малые величины I— x и
1 — у х будут одного порядка малости. Будут ли они эквивалентны?
Отв. lim ъ-т=—3, следовательно, данные бесконечно малые одного по-
рядка; но не эквивалентны»

ГЛАВА III
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
§ 1. Скорость движения
Будем рассматривать прямолинейное движение некоторого
твердого тела, например движение камня, брошенного верти-
вертикально вверх, или движение поршня в цилиндре двигателя и т. д.
Отвлекаясь от конкретных размеров и формы тела,
мы будем в дальнейшем представлять его в виде дви-
движущейся точки М. Расстояние s движущейся точки,
отсчитываемое от некоторого начального ее положения
М0У будет зависеть от времени /, т. е. s будет функ-
функцией времени t:
s = f(t). A)
Пусть в некоторый момент времени*) t движущая-
д, ся точка М находилась на расстоянии s от началь-
0 ного положения Мо, а в некоторый следующий мо-
момент t + At точка оказалась в положении Мг—на
Рис. 57. расстоянии s + As от начального положения (рис. 57).
Таким образом, за промежуток времени At расстояние s
изменилось на величину As. В этом случае говорят, что за про-
промежуток времени At величина s получила приращение As.
Рассмотрим отношение ~; оно дает нам среднюю скорость
движения точки за время At:
Средняя скорость не может во всех случаях точно охаракте-
охарактеризовать быстроту перемещения точки М в момент /. Если, на-
например, тело в начале промежутка At перемещалось очень быстро,
а в конце очень медленно, то средняя скорость, очевидно, не, смо-
сможет отразить указанных особенностей движения точки и дать
нам правильное представление об истинной скорости ее движения
*) Здесь, как и в дальнейшем, конкретное значение переменной мы будем
обозначать той же буквой, что и саму переменную,

§ 1] СКОРОСТЬ ДВИЖЕНИЯ 65
в момент t. Для того чтобы точнее выразить эту истинную ско-
скорость с помощью средней скорости, надо взять меньший проме-
промежуток времени At. Наиболее полно характеризует скорость дви-
движения точки в момент t тот предел, к которому стремится средняя
скорость при At—> (). Этот предел и называют скоростью
движения в данный момент:
* = "га ?. C)
Таким образом, скоростью движения в данный момент называется
предел отношения приращения пути As к приращению времени
At, когда приращение времени стремится к нулю.
Напишем равенство C) в развернутом виде. Так как
то
v= Hm 12±Ы?Ж. C')
Это и будет скорость неравномерного движения. Таким обра-
образом, мы видим, что понятие скорости неравномерного движения
органически связано с понятием предела. Только с помощью
понятия предела можно определить скорость неравномерного
движения.
Из формулы C') следует, что v не зависит от приращения
времени At, а зависит от значения t и характера функции f(t).
Пример. Найти скорость равномерно ускоренного движения в произ-
произвольный момент /ив момент / = 2с, если зависимость пути от времени вы-
ражается формулой s=2^-.
gt*
Решение. В момент t имеем s=~-; в момент t-\-M получим
по
Найдем As:>
Составим отношение
As
At"
As.
At1
i
U A
2
At-
2
At gi
As .. /
2
. . 1 \
Таким образом, скорость в любой момент времени t равна v=gt.
При t=2 имеем у 11=2=^2=9,8»2=19,6 м/с.
3 Н. С. Пиокуков, т. I

66 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ 1ГЛ. HI
§ 2. Определение производной
Пусть мы имеем функцию
y = f(x), A)
определенную в некотором промежутке. При каждом значении
аргумента х из этого промежутка функция y — f(x) имеет опре-
определенное значение.
Пусть аргумент х получил некоторое (положительное или
отрицательное—безразлично) приращение Ах. Тогда функция у
получит некоторое приращение Ау. Таким образом:
при значении аргумента х будем иметь y = f{x)9
при значении аргумента х+Ах будем иметь у-\-Ау = / (х + Ах).
Найдем приращение функции Ау:
Ay = f(x+Ax)-f(x). B)
Составим отношение приращения функции к приращению аргу-
аргумента:
Д# f(x+Ах)—f (х) /ov
Д^ At • W
Найдем предел этого отношения при Д#—*0. Если этот предел
существует, то его называют производной данной функции
/ (я) и обозначают /' (х). Таким образом, по определению
/'(*) = Ига -^
ИЛИ
f'(x) — lim ^ *)~-\хУт щ D)
Следовательно, производной данной функции y = f(x) по аргу-
аргументу х называется предел отношения приращения функции Ау
к приращению аргумента Ах, когда последнее произвольным
образом стремится к нулю.
Заметим, что в общем случае для каждого значения х произ-
производная /' (х) имеет определенное значение, т. е, производная
является также функцией от я.
Наряду с обозначением /' (х) для производной употребляются
и другие обозначения, например у% y"Xi -~. Конкретное значе-
значение производной при л; = а обозначается f'(а) или у'!*=<?•
Операция нахождения производной от функции f (х) назы-
называется дифференцированием этой функции.
Пример 1. Дана функция у = х2; найти ее производную у'%
1) в произвольной точке хг
2) при х = 3.
Решение. 1) При значении аргумента, равном #, имеем у — х2. При
значении аргумента, равном jc+Axj имеем у-{-Ау = (х+АхJ. Находим прира-

§ 3] ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ 67
щение функции: А# = (л:+Ал:J—х2 = 2х Ал:+(Ал:J. Составляем отношение
-—-: -Д= г-^——=2л:+Ал:. Переходя к пределу, найдем производную
/лХ /лХ 1л X
от данной функции: yf = lim -Д= lim Bx+Ax) = 2x. Итак, производная
дя _> о Ал: Ах -> о
от функции */ = #2 в произвольной точке равна у'= 2х.
2) При л: = 3 получим */' | х_з = 2»3 = 6.
Пример 2. # = —? найти у'.
Решение. Рассуждая так же, как в предыдущем примере, получаем
X
1 1 х—х—Ал: Ал:
лг+Ал: х л:(#+Ал:)
Ау 1
Ал:™ л:(л:+Ал:)'
у' = lim -Д— lini т——— =й -.
* дл^оД* A^-^oL ^(л:+Ал:)] ^2
Замечание. В предыдущем параграфе было установлено,
что если зависимость расстояния s движущейся точки от вре-
времени i выражается формулой s — /(/), то скорость v в момент t
выражается формулой
у- lim g- Hm
Следовательно, v — st = fr (t), т. е. скорость равна производной*)
от пути по времени t.
§ 3& Геометрическое значение производной
Мы подошли к понятию производной, рассматривая скорость
движущегося тела (точки), т.е. исходя из механических
представлений. Теперь мы дадим не менее важное геометри-
геометрическое истолкование производной. Для этого нам прежде всего
потребуется определение касательной к кривой в данной
точке.
Пусть имеем кривую и на ней фиксированную точку Мо. Возь-
Возьмем на кривой точку Мх и проведем секущую М0Мг (рис. 58).
Если точка Мг неограниченно приближается по кривой к точке М0У
то секущая М0Мг занимает различные положения М0М[, М0М1 и
т. д. Если при неограниченном приближении точки Мг по кривой
к точке Мо с любой стороны секущая стремится занять по-
положение определенной прямой М0Т, то прямая М0Т называется
*) Когда мы говорим «производная по х» или «производная по времени h
и т. д., то под этим мы подразумеваем, что при вычислении производной мы
считаем аргументом переменную х или время t и т. д.
3*

68
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
[ГЛ. Ill
касательной к кривой в точке Мо (понятие «стремится занять»
будет уточнено ниже).
Рассмотрим функцию f (х) и соответствующую этой функции
кривую
в прямоугольной системе координат (рис. 59). При некотором
значении х функция имеет значение y = f(x). Этим значениям х
и у на кривой соответствует точка М0(х, у). Дадим аргументу х
приращение Ал;. Новому значению аргумента х+Ах соответст-
соответствует «наращенное» значение функции y + Ay = f(x + Ax). Соот-
Соответствующей ему точкой кривой будет точка Мх(х-\-Ах, у + Ау).
Проведем секущую М0Мг и обозначим через ф угол, образованный
секущей с положительным направлением оси Ох. Составим отно-
отношение -д^ . Из рис. 59 непосредственно
усматриваем, что
Если теперь Ал: будет стремиться к
нулю, то точка Мг будет перемещаться
вдоль кривой, приближаясь к Мс. Се-
Секущая М0Мг будет поворачиваться вок-
вокруг точки Мо и угол ф будет менять-
меняться с изменением Ах. Если при Ал:—>0
угол ф стремится к некоторому преде-
пределу а, то прямая, проходящая через Мо
и составляющая с положительным направлением оси абсцисс
угол а, будет искомой касательной. Нетрудно найти ее угловой
коэффициент:
tga== lim tg(f=: lim -~ = /'(л;).
Рис. 60.

4] ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ 69
Следовательно,
/'(*) = %«. B)
т. е. значение производной /' (х) при данном значении аргумента х
равняется тангенсу угла, образованного касательной к графику
функции f (x) в соответствующей точке Мо (х, у) с положитель-
положительным направлением оси Ох.
Пример. Найти тангенсы углов наклона касательной к кривой у=х2
в точках AfxO/2, 1/4); М2 (— 1, 1) (рис. 60).
Решение. На основании примера 1 §2 имеем у'—2х; следовательно,
§ 4. Дифференцируемость функций
Определение. Если функция
y = f(x) A)
имеет производную в точке л: = х0, т. е. если существует
иш -г— == ига т , \?)
то мы говорим, что при данном значении х = х0 функция диф-
дифференцируема или (что равносильно этому) имеет производную.
Если функция дифференцируема в каждой точке некото-
некоторого отрезка [а, Ь\ или интервала (а, &), то говорят, что она
дифференцируема на отрезке [а, Ь] или соответственно в интер-
интервале (а, Ь).
Теорема. Если функция y = f(x) дифференцируема в неко-
некоторой точке x = xQy то она в этой точке непрерывна.
Действительно, если
Нто~! = /'(х0),
ТО
где у есть величина, стремящаяся к нулю при Ая->0. Но тогда
отсюда следует, что Ау —> 0 при Ал: —-> 0, а это и значит, что функ-
функция f (х) непрерывна в точке х0 (см. § 9 гл. II).
Таким образом, в точках разрыва функция не мо-
может иметь производной. Обратное заключение неверно,
т.е. из того, что в какой-нибудь точке х = х0 функция y = f(x)
непрерывна, еще не следует, что в этой точке она дифферен-
дифференцируема: функция / (л:) может и не иметь производной в точке х0.

70
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
[ГЛ. III
Для того чтобы убедиться в этом, рассмотрим несколько при-
примеров.
Пример 1. Функция f(x) определена на отрезке [0, 2] следующим
образом (рис. 61):
f(x) = x приО<:л:<:1,
f(x) = 2x— 1 при1<л:<2.
Эта функция при х=\ не имеет производной, хотя и непрерывна в этой точке.
Действительно, при Ал: > 0 имеем
*) — /A)
Ал;
до А*
при Ал: < 0 получаем
Ал:
[1+Ал:] —1 v A* ,
l ^ J == lim -г~ = Ь
Ал: Дд;-*о Ал:
Таким образом, рассматриваемый предел зависит от того, каков знак Ал:, а это
значит, что в точке х=\ функция не имеет производной*). Геометрически
1
Рис. 61.
Рис. 62.
этому соответствует тот факт, что в точке л:=1 данная «кривая» не имеет
определенной касательной.
Непрерывность же функции в точке л:=1 следует из того, что
А# = Ал: при Ал: < 0, А# = 2А* при Ал: > 0,
и, следовательно, в обоих случаях А#—>-0 при Ал:—>-0.
Пример 2. Функция y=ySх, график которой изображен на рис. 62,
определена и непрерывна для всех значенийг независимой переменной. Выяс-
Выясним, имеет ли эта функция производную при х = 0; для этого найдем значе-
значения функции при х = 0 и при л: = 0+Ал:; при л: = 0 имеем у=0, при л: = 0+Ал;
имеем у-\-ку=у/ГКх. Следовательно, А#= ?/"Д#.
Найдем предел отношения приращения функции к приращению аргумента:
lim -Д=; lim
д^-*.о Ал: ддг-*.о
-j
Ал:
л2
*) По определению производной требуется, чтобы отношение —^. стре-
стремилось при Ал:—>-0 к одному и тому же пределу независимо от того, каким
образом стремится к нулю Ал:.

§5] ПРОИЗВОДНАЯ ОТ ФУНКЦИИ у^х" 71
Таким образом, отношение приращения функции к приращению аргумента
в точке х = 0 стремится к бесконечности при Ал:—>0 (и, значит, предела не
имеет). Следовательно, рассматриваемая функция не дифференцируема в точке
х = 0. Касательная к кривой в этой точке образует с осью абсцисс угол я/2,
т. е, совпадает с осью Оу.
§ 5. Производная от функции у = хп
при п целом и положительном
Для нахождения производной от данной функции y = f(x),
исходя из общего определения производной, необходимо произ-
произвести следующие действия:
1) дать аргументу х приращение Дя, вычислить наращенное
значение функции:
2) найти соответствующее приращение функции:
Ay = f(x + Ax)-f(x);
3) составить отношение приращения функции к приращению
аргумента:
Ау __/(*+А*)--/(*).
Ах Ах
4) найти предел данного отношения при Ах—>0:
у-= lim-J* -
Мы применим здесь и в следующих параграфах этот общий
способ для вычисления производных от некоторых элементарных
функций.
Теорема. Производная функций у = хп, где п—целое поло-
жительное число, равна пхп~г, т. е.
если у = хп, то у' = пхп~1. (I)
Доказательство. Имеем функцию
У = хп.
1) Если х получает приращение Ах, то
2) Пользуясь формулой бинома Ньютона, находим
Ау = (х+Axf1 —хп =

72 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ?ГЛ. III
ИЛИ
Ау = пхп-1кх+п(п~21) хп~2 (Аа:J+ ... + (А*)*.
3) Находим отношение
1 = пх + п{п1~1)х"-*Ах+ ...
4) Найдем предел этого отношения
'=lim%L = llm
следовательно, у' = пхп~1, что и требовалось доказать.
Пример 1. ^=а:6, ^' = 5а:6-1 = 5а:4.
Пример 2. #=а:, у' = \х1~1, у' — I. Последний результат имеет простое
геометрическое истолкование: касательная к прямой у = х при любом значе-
значении х совпадает с этой прямой и, следовательно, образует с положительным
направлением оси Ох угол, тангенс которого равен 1.
Отметим, что формула (I) верна и в случае п дробного и от-
отрицательного. (Это будет доказано в § 12.)
Пример 3. у—У
Представим данную функцию в виде степени:
тогда по формуле (I) (учитывая только что сделанное замечание) получаем
или
2У х '
Пример 4. у = —7^=-.
ху х
Представим у в виде степенной функции:
Тогда
о х — 0 л
§ 6. Производные от функций jy = sin дг; ^ =
Теорема 1. Производная от sinx есть cos л:, т.е.
если y~sinx, то t/'==cosjc. (II)

§ 6] ПРОИЗВОДНЫЕ ОТ ФУНКЦИЙ y=sin x; y=cos х 73
Доказательство. Дадим аргументу х приращение Да:;
тогда
л\ а • / i а \ • о • х4-Ах—х х+Ах-{-х
2) /\y = sm(x-\-i\x)—sin x = 2 sin 2 cos п 2 —
. Ах ( . Ал:
sincos^+
1 Ьх
Ал: Ал:
. Ал:
4) yf = lim -?- = lim —^— • lim
AX-+Q Х-+ _
но так как
. А?
lim —г—= 1,
то
'= lim cos [ х + -?-) =cos jc.
Последнее равенство получается на том основании, что cosa:
есть непрерывная функция.
Теорема 2. Производная от cosa: есть —sinx, т.е.
если y = cosx, то у'= —sinx. (Ill)
Доказательство. Дадим аргументу х приращение Да:,
тогда
— cos x= —
. Ах
А Sin—jr—
At/ 2
Ал: Ал:
. Ал: •
lira 4^-= Hm rr-sin ( x + ^) =- lim sin(x+i?

74 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [ГЛ. III
учитывая, что sinx есть непрерывная функция, окончательно
получим
у' = — sinx.
§ 7. Производные постоянной, произведения постоянной
на функцию, суммы, произведения, частного
Теорема 1. Производная постоянной равна нулю, т.е.
если у— С, где С = const, то у' = 0. (IV)
Доказательство. у = С есть такая функция от х, значе-
значения которой при всех х равны С.
Следовательно, при любом значении х y = f(x) = C.
Дадим аргументу х приращение Ал: (АхфО). Так как функ-
функция у сохраняет значение С при всех значениях аргумента, то
y + Ay = f(x + Ax) = C. Значит, приращение функции равно Ау=
= f(x-\-Ax)— f(x) = Oy отношение приращения функции к прира-
приращению аргумента -^ = 0, и, следовательно, у' = lim --^- = 0, т. е.
у' = о.
Последний результат имеет простое геометрическое истолко-
истолкование. Графиком функции у = С служит прямая, параллельная
оси Ох. Касательная к графику в любой ее точке, очевидно,
совпадает с этрй прямой и, следовательно, образует с осью Ох
угол, тангенс которого у' равен нулю.
Теорема 2. Постоянный множитель можно выносить за
знак производной, т. е.
если у=-Си (х), где С = const, то у'= Си' (х). (V)
Доказательство. Рассуждая так же, как и при доказа-
доказательстве предыдущей теоремы, будем иметь:
у = Си(х),
Ау = Си(х + Ах)—Си (х} =
Ау _^и(х + Ах) — и (х)
Ах ~~ U Ал:
у>= lim *L = c lim »
Пример 1. y — 3 .
V x
3
1 I
т. е.

§7] ПРОИЗВОДНЫЕ ПОСТОЯННОЙ, СУММЫ, ПРОИЗВЕДЕНИЯ 75
Теорема 3. Производная суммы конечного числа дифферен-
дифференцируемых функций равна соответствующей сумме производных
этих функций*).
Для случая, например, трех слагаемых имеем
(x). (VI)
Доказательство. Для значений аргумента х
(аргумент х в обозначении функции для краткости письма опу-
опускаем).
Для значения аргумента х + Ах имеем
где Ау, Аи> Av и Aw—приращения функций у, и, v и wt соот-
соответствующие приращению Ал: аргумента х. Следовательно,
или
Пример 2. у — 3jc4— 3 ,
т.е.
A \' 1
Теорема 4. Производная от произведения двух дифферен-
дифференцируемых функций равна произведению производной первой функ-
функции на вторую функцию плюс произведение первой функции на
производную от второй функции, т. е.
если y = uv, то у' = u'v + uv'. (VII)
*) Выражение y = u(x)—v(x) равносильно у = и (х) 4-(—1) v (х) и у'
() + (l)()]' ' () + lv(x)]'=u' (x)-v' (х).

76 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [ГЛ. Ill
Доказательство. Рассуждая, как и при доказательстве
предыдущей теоремы, получим
— (и + Аи) (р + Av)—uv = Аи v + и At>-f Аи Av,
Ax Ax ' Ax l Ax*
,'= Um^-= Hm ^-W+ lim«|+ lim A«?
Д*->-0 A* ДА--+0 Д* Ддг-*О Д* Дл-^-0 Д*
= / lira i^-W«lin» ^+ и д« «ш т2-
(так как « и v не зависят от Ах).
Рассмотрим последний член в правой части
lim Аи lim -r^.
Так как и(х)—дифференцируемая функция, то она непрерывна.
Следовательно, lim Аи = 0. Кроме того,
Ал'->0 ах
Таким образом, рассматриваемый член равен нулю, и мы оконча-
окончательно получаем yf — u'v + uv'. На основании доказанной теоремы
легко получается правило дифференцирования произведения любого
числа функций.
Так, если имеем произведение трех функций y = uvw, то, пред-
представляя правую часть как произведение и й (vw)> получим
у' = и' (vw) + u(vw)' = u'vw + u(v'w + vw')==u'vw + uv'w-\-uvw'.
Таким приемом можем получить аналогичную формулу для произ-
производной произведения любого (конечного) числа функций. Именно,
«ели у — иги2 ... ип, то
у' = и\и% ... ипт.гип + иги'г ... ип_хип + ... + иги2.. • ип„хи'п.
Пример 3. Если y = x2sinx, то
у' = (х*)' sin х+х2 (sin л:)' = 2^ sin лг+л:2 cos x.
Пример 4. Если i/= }f x sin j: cos x, то
у' = (У~х)' sin л; cos л; + >^"^ (sin x)' cos д:+ |/"lc sin x (cos .*)' =
s=s—тг=г sin ^ cos *+1^^ cos Л' cos x + V^ sin л: (— sin x) =
2y x
x
sin x cos АГ+ 1^1 (cos2 л:—sin2 a:) =
—^
л: 4у x
Теорема 5. Производная дроби (m. e. частного от деления
двух функций) равна дроби, у которой знаменатель есть квадрат

§7J ПРОИЗВОДНЫЕ ПОСТОЯННОЙ, СУММЫ, ПРОИЗВЕДЕНИЯ 77
знаменателя данной дроби, а числитель есть разность между
произведением знаменателя на производную числителя и произве-
произведением числителя на производную знаменателя, т. е.
U , llv — UVf /Л7ТТ1Л
= Т, то у' =—^—. (VIII)
Доказательство Если А у, Аи и Av суть приращения
функций у, unv, соответствующие приращению А* аргумента х, то
* «+А« и v Аи—и Av
™ 71—1— Л 71 7)
v-\-Av v v(v-\-Av) '
v Аи—uAv Аи Av
-v—v
Ay Ax Ax Ax
Ax v(v-±-Av) v(v-\-Av) 9
Аи Av .. Аи ,. Av
-r—t;—«-г— v lim --r и lim -r—
lim Ал; — A* ~+ ° Ал: Ax -> о А-У
Ал: ->• 0
Отсюда, заметив, что Av—>0 при Ал;—^0*), получаем
/ «'У — UV*
у =—&—•
Пример 5. Если у— , то
v v cos х
,__(х*У cos x—a;3(cosa:)' ^ 2л;2cos x+a^sin x
У cosT^ "" 'wsTx'
Замечание. Если имеем функцию вида
1/- с ,
где знаменатель С есть постоянная, то, дифференцируя эту функ-
функцию, нет надобности применять формулу (VIII), а целесообраз-
целесообразнее применять формулу (V):
Конечно, этот результат получается и по формуле (VIII).
т-, * т, cos х . (cos xY sin x
Пример 6. Если #=-у-, то y'= v 7 ;^ =s ^—.
*) lim Ау = 0, так как г;(л:)—-дифференцируемая и, следовательно, непре-
рывная функция.

78 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [ГЛ. III
§ 8. Производная логарифмической функции
Теорема. Производная от функции loga х равна — log^ в, т. е.
если y=logax, то y' = — logae. (IX)
Доказательство. Если Ау есть приращение функции
у — loga х, соответствующее приращению Ах аргумента х9 то
Умножим и разделим на х выражение, стоящее в правой части
последнего равенства:
Обозначим величину -?¦ через а. Очевидно, а—>0 при Д#—*0 и
данном я. Следовательно,
Но, как известно (см. § 7 гл. II),
lim
а -> О
Если же выражение, стоящее под знаком логарифма, стремится
к числу е, то логарифм этого выражения стремится к log^e
(в силу непрерывности логарифмической функции). Поэтому окон-
окончательно получаем
у1 = lim -т— = lim —
Ах -> О А* а -> О х
Заметив, что loga е = -^, полученную формулу можно переписать
так: уг = — 1—.
Отметим важный частный случай этой формулы: если а = е,
то \па = 1пе= 1, т. е.
еа/ш у=1п#, то у' = ~. (х)

§91 ПРОИЗВОДНАЯ ОТ СЛОЖНОЙ ФУНКЦИИ 79
§ 9. Производная от сложной функции
Пусть дана сложная функция y = f(x), т. е. такая, что ее
можно представить в следующем виде:
или у = Р[у(х)] (см. гл. I, § 8). В выражении y = F(u) пере-
переменную и называют промежуточным аргументом.
Установим правило дифференцирования сложной функции.
Теорема. Если функция и = <р(х) имеет в некоторой точ-
точке х производную *4 = ср' (х), а функция y = F (и) имеет при соот-
соответствующем значении и производную y'u = F'(и)у то сложная
функция y = F[({){x)] в указанной точке х также имеет произ-
производную, которая равна y'x~F'u (и) ср' (%), где вместо и должно быть
подставлено выражение и = у(х). Коротко,
m. e. производная сложной функции равна произведению производ-
производной данной функции по промежуточному аргументу и на произ-
производную промежуточного аргумента по х.
Доказательство. При определенном значении х будем иметь
При наращенном значении аргумента х + Ах
и -f- Аи = ф (х+А*), y + &y = F (u + Aw).
Таким образом, приращению Дя соответствует приращение Да,
которому соответствует приращение Дх/, причем При Ах —> 0 будет
Аи—>0 и Ау~-+0.
По условию
Hm A? = yl
Из этого соотношения, пользуясь определением предела, получаем
(при АО)
где а—*0 при Аи—*0. Перепишем равенство A) так:
Ау = у'иАи-\-аАи. B)
Равенство B) справедливо и при Аи = 0 при произвольном а, так
как оно превращается в тождество 0 = 0. При Аи = 0 будем пола-
полагать а = 0. Разделим все члены равенства B) на Ал::

80 ПРОИЗВОДНАЯ И Д ИФ^сРБШШАЛ 1ГЛ. III
По условию Hm ^ = «*, lim а = 0. Переходя к пределу при
Ах -* О Лх Ах -> О
Дд:—*0 в равенстве C), получим
Ух=у'ии'х. D)
Пример 1. Пусть дана функция y~sin(x2). Найдем ух. Данную функ-
функцию представим как функцию от функции следующим образом: у—sin и,
и = х2. Находим уи = cos и, и'х = 2х. Следовательно, по формуле D) ух — УФх^1
= cos и -2х. Подставляя вместо и его выражение, окончательно получаем
Пример 2. Дана функция у — (In xK. Найдем у*х.
Данную функцию представим следующим образом: у = и?, м = 1п*. Нахо-
Находим уи = Зи2г их — — . Следовательно, ух = 3w2 — = 3 (In xJ — •
X XX
Если функция у= / (х) такова, что ее можно представить в виде
то нахождение производной у'х производится путем последователь-
последовательного применения предыдущей теоремы.
По доказанному правилу имеем ух=у'иих. Применяя эту же
теорему для нахождения иХУ будем иметь u'x=u'vvx. Подставляя
выражение их в предыдущее равенство, получаем
yx=y'u<vx E)
или
Пример 3. Дана функция у = sin [(In*K]. Найдем ух. Представим дан-
данную функцию следующим образом: # = sin м, w = u3, v~\nx. Находим #tt = cos и,
Uv~3iP> v'x=\/x. Следовательно, по формуле E) получаем y'x~y'uUvv'x~
= 3 (cos и) v2 —, или окончательно ух — cos [(In xK] -3 (In xJ — • Заметим, что
X X
рассмотренная функция определена только при х > 0.
§ 10. Производные функций у = tg х9 у = ctg х, у s In | x \
Теорема 1. Производная от функции tg х равна ^^-, т. е.
если y=tgx, то 1/' = ^- (XI)
Доказательство. Так как
sin х
то по правилу дифференцирования дроби [см. формулу (VIII) § 7]
получаем
, (sin x)' cos л:—sin x (cos x)' cos x cos х — sin х (— sin x)
^ ~~ COS2* COS2 X ~~
_cosa,y+sin2.x_ I
"~ COS2 X "" COS2 X #

$ 10]
ПРОИЗВОДНЫЕ ФУНКЦИЙ y*=ig х, #=ctg х, у=Ых]
81
Теорема2. Производная от функции ctg х равна —^г^ , m, е.
если I/ = ctg л:, то #' = —^rj-
Доказательство. Так как У^~^~> то
sin2 x '
t __ (cos x)' sin л:—cos x (sin *)' __ — sin x sin jc—cos л: cos x
" *~ sin2 л; ~~ sin2 a: ~~
sin2 x
Пример 1. Если y—tg У х, то
Пример 2. Если #=In ctg x, то
ctgx\ sin2A:
—J—- = ^
cos a: sin л: sin 2л:'
Теорема З. Производная от функции \n\x\ (рис. 63) равна
1/х, т. е.
если у = \п\х\, тоу'=1/х.
(XIII)
Доказательство, а) Если х>0, то |#| = х, 1п[#| =
и поэтому у1 = 1/х.
б) Пусть х < 0, тогда \х\ = — х. Но In| х| = In(— х). (Заметим,
что если #<0, то —#>0.) Представим функцию у = In (—х)
Рис. 63.
как сложную функцию, положив у = In и, м=— я. Тогда ^=у^г==
= — (— 1) = — (— 1) = —. Итак, для отрицательных значений х
также имеет место равенство у'х=\/х. Следовательно, форму-
формула (XIII) доказана для любого значения хфО. (При х = 0 функ-
функция 1п\х\ не определена.)

82
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
[ГЛ. Ш
§11. Неявная функция и ее дифференцирование
Пусть значения двух переменных хну связаны между собой
некоторым уравнением, которое мы символически обозначим так:
F(x9 f/) =
A)
Если функция y=f(x), определенная на некотором интервале (а, Ь)у
такова, что уравнение A) при подстановке в него вместо у
#1
Рис. 64.
Рис. 65.
выражения f(x) обращается в тождество относительно л;, то функ-
функция y = f(x) есть неявная функция, определенная уравнением A).
Так, например, уравнение
х2+г/2_а2==о B)
неявно определяет следующие элементарные функции (рис. 64 и 65):
C)
D)
Действительно, после подстановки в уравнение B) этих значений
получаем тождество
х2+(а2—х2)—а2 = 0.
Выражения C) и D) получились путем решения уравнения B)
относительно у. Но не всякую неявно заданную функцию можно
представить явно, т. е. можно представить в виде # = /(#)*),
где f{x) есть элементарная функция.
Так, например, функции, заданные уравнениями t/6—у—#2 = 0
или у—х—-? sin у = 0, не выражаются через элементарные функ-
функции, т. е. эти уравнения нельзя разрешить относительно у.
Замечание 1. Отметим, что термины «явная функция» и
«неявная функция» характеризуют не природу функции, а способ
задания. Каждая явная функция */ = /(#) может быть представ-
представлена и как неявная y—f(x) = O.
*) Если функция задана уравнением вида y=f(x)i то говорят, что функ*
ция задана в явном виде или является явной.

§ 12] ПРОИЗВОДНЫЕ СТЕПЕННОЙ ФУНКЦИИ 83
Укажем, далее, правило нахождения производной неявной
функции, не преобразовывая ее в явную, т. е. не представляя
в виде y = f(x).
Допустим, что функция задана уравнением я2+Уа—а2 = 0.
Если здесь у есть функция от х, определяемая этим равенством,
то это равенство есть тождество.
Дифференцируя обе части этого тождества по ху считая, что у
есть функция от я, получим (пользуясь правилом дифференциро-
дифференцирования сложной функции) 1х + 2уу' = 0, откуда у* — — х/у.
Заметим, что если бы мы стали дифференцировать соответст-
соответствующую явную функцию у = Va*—х2, то получили бы у' =5
t= — - х = — ~, т. е. тот же результат.
Рассмотрим еще один пример неявной функции у от х: t/6 —
— у—#2 = 0. Дифференцируем по х: §уъу'—у1—2л; = 0, откуда
б?/1
Замечание 2. Из приведенных примеров следует, что для
нахождения значения производной неявной функции при данном
значении аргумента х нужно знать и значение функции у при
данном значении х.
§ 12. Производные степенной функции
при любом действительном показателе,
показательной функции, сложной показательной функции
Теорема 1. Производная от функции хп, где п—любое
действительное число, равна nx", т. е.
если у=хп, то yf = nxn. (V)
Доказательство. Пусть х>0. Логарифмируя данную
функцию, будем иметь \пу — п\пх.
Дифференцируем обе части полученного равенства по х, счи-
считая у функцией от х: — =п—, у'= уп— . Подставляя сюда
ух х
значение у=хп, окончательно получаем у'=пхп~1. Легко показать,
что эта формула верна и для х < 0, если только хп имеет смысл *)¦
Теорема 2. Производная от функции а*, где а>0, равна
а* 1п а, т. е.
если у = ах, то у' = ах1па. (XIV)
Доказательство. Логарифмируя равенство у = ах, полу-
получим lny=xlna. Дифференцируем полученное равенство, считая у
функцией от х: —i// = lna, у' = у\па или у' =
*) Эта формула была ранее доказана (§ 5) для случая, когда п является
целым положительным числом. Теперь формула (I) доказана в общем случае
(для любого постоянного числа л).

84 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ?ГЛ. III
Если основание а = е, то1пе—1 и мы получим формулу
у = е\ у' = е*. (XIV)
Пример 1. Дана функция у = ех2. Представим ее как сложную функ-
функцию, введя промежуточный аргумент и: у=еи, и — х2\ тогда у'и = еи, и'х = 2х
и, следовательно, ух = еи -2х — ех% -2х.
Сложной показательной функцией называется функция, у кото-
которой и основание и показатель степени являются функциями от х,
например, (sin#)*2, xtgx, хх, (lnx)*, вообще, всякая функция вида
есть сложная показательная функция*).
Теорема 3.
Если y^uv, то yt = vuv'1uf + uvvf In и. (XV)
Доказательство. Логарифмируем функцию у;
Дифференцируя полученное равенство по х> будем иметь
y' v±
откуда
Подставляя сюда выражение y = uv, получаем
uvvf In и.
Таким образом, производная сложной показательной функции
состоит из двух слагаемых: первое слагаемое получается, если при
дифференцировании предположить, что и есть функция от х, a v
есть постоянная (т. е. если рассматривать uv как степен-
степенную функцию); второе слагаемое получается, если предположить,
что v есть функция от х, а и== const (т. е. если рассматривать
uv как показательную функцию).
Пример 2. Если у = хх, то yf = xxx~ (x')-\-x* (х') \пх или
у'=хх+хх \п х = хх A + In х).
Пример 3. Если # = (sin x)x2t то
yf = x2 (sin х)х*~г (sin *)' + (sin x)x* (x2)' In sin x =
= *2 (sin я)*2-1 cos x + (sin x)xZ -2x In sjn x.
Прием, примененный в этом параграфе для нахождения про-
производных и состоящий в том, что сначала находят производную
*) Часто такую функцию называют показательно-степенной или степенно»
показательной.

§ 13] ОБРАТНАЯ ФУНКЦИЯ И ЕЕ ДИФФЕРЕНЦИРОВАНИЕ 85
логарифма данной функции, широко применяется при
дифференцировании функций. Применение этого приема нередко
значительно упрощает вычисления.
Пример 4. Требуется найти производную от функции
Решение. Логарифмируя, находим
^\п(х— 1)—31п(*+4) —х.
Дифференцируем обе части последнего равенства:
^12| 1 3
_ |
x+l'r2(x—l)
(*+1)]ЛГ=Т
Умножая на у и подставляя -—' ' ' — вместо у, получаем
Г_2_ _J 3 1
{x+l~г2(х— 1) х+4 J"
* ~" (x-\-Afex
и'
Замечание. Выражение ~=Aп*/)', являющееся производ-
производной по х от натурального логарифма данной функции у~у(х),
называется логарифмической производной.
§ 13. Обратная функция и ее дифференцирование
Пусть дана возрастающая (рис. 66) или убывающая функция.
у=/(*). О)
определенная на некотором интервале (а, Ь) (а < Ь) (см. § 6 гл. I).
Пусть / (а) = су f (b) = d. Для определенности будем в дальнейшем
рассматривать возрастающую функ-
функцию.
Рассмотрим два различных значе-
значения xt и х2, принадлежащих интер-
интер( 6) И
&
t 2 р р
валу (а, 6). Из определения возрастаю-
возрастающей функции следует, что если хг <
<х2 и t/1 = /(A:1), #2 = /(*2), то уг< П
< у2. Следовательно, двум различным
значениям Xf и х2 соответствуют два
различных значения функции ух и ис'
у2. Справедливо и обратное, т. е.
если уг<у2, #i = /(#i), a y2 — f{x^, то из определения воз-
возрастающей функции следует, что Xi < x2. Таким образом, между
значениями х и соответствующими им значениями у устанавли-
устанавливается взаимно однозначное соответствие.

86
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
[ГЛ. ГЦ
Рассматривая эти значения у как значения аргумента, а зна-
значения х как значения функции, получаем х как функцию у:
Эта функция называется обратной для функции y = f(x). Оче-
Очевидно, что и функция у = / (х) является обратной для функции
х==Ч(у)- Рассуждая аналогичным образом, можно доказать, что
и убывающая функция имеет обратную.
Замечание 1. Укажем без доказательства, что если воз-
возрастающая (или убывающая) функция y = f(x) непрерывна на
отрезке [а, 6], причем f (a) = c, f (b) = d, то обратная функция
определена и непрерывна на отрезке [с, d].
Пример 1. Пусть дана функция y — xz. Эта функция —возрастающая
на бесконечном интервале —оо<#< + оэ, она имеет обратную х=уу
(рис. 67),
Заметим, что обратная функция х = у(у) находится путем
решения уравнения y = f(x) относительно х.
Рис. 67.
Рис. 68.
Пример 2. Пусть дана функция у — ех. Эта функция—возрастающая
на бесконечном интервале —оо<д:<+оо. Она имеет обратную х = \пу.
Область определения обратной функции 0<#< + оо (рис. 68),
Замечание 2. Если функция y = f(x) не является ни воз-
возрастающей, ни убывающей на некотором интервале, то она может
иметь несколько обратных функций *).
Пример 3, Функция у = х2 определена на бесконечном интервале
— оо < лг< + оо. Она не является ни возрастающей, ни убывающей и не
имеет обратной. Если мы рассмотрим интервал О^х < + оо,_то здесь функ-
функция является возрастающей и обратной для нее будет х=}/~у. На интервале
же — оо < х < 0 функция —убывающая, и обратной для нее будет функция
ж=— Уу (рис, 69).
*) Подчеркнем еще раз, что, говоря о том, что у есть функция от х, мы
понимаем однозначную зависимость у от х»

$13]
ОБРАТНАЯ ФУНКЦИЯ И ЕЕ ДИФФЕРЕНЦИРОВАНИЕ
87
42?=-
Рис. 69.
Замечание 3. Если функции y = f(x) и х = <р(у) являются
взаимно обратными, то графиками их является одна и та же
кривая. Но если аргумент обратной функ-
функции мы обозначим снова через х, а функ-
функцию через у и построим их в одной коор-
координатной системе, то получим уже два
различных графика.
Легко видеть, что графики будут сим-
симметричны относительно биссектрисы пер-
первого координатного угла.
Пример 4. На рис. 68 построены графики
функции у = е* (или х = \пу) и обратной для нее
функции у=\пх, рассмотренных в примере 2.
Докажем, далее, теорему, позволяющую находить производ-
производную у — fix), зная производную обратной функции.
Теорема. Если для функции
У = !(х) О)
существует обратная функция
* = ф(у), B)
которая в рассматриваемой точке у имеет производную <р' (у),
отличную от нуля, то в соответствующей точке х функция
y = f(x) имеет производную /' (х), равную —гг\ > т- е- справедлива
формула
ф' (у)
(XVI)
Таким образом, производная одной из двух взаимно обратных
функций равна единице, деленной на производную второй из этих
функций при соответствующих значениях х и у*).
Доказательство. Возьмем приращение Ау, тогда на
основании B)
. Напишем
C)
Так как ц>(у) есть функций монотонная, то
тождество
А*/^ 1
Ах Ах
*) Когда мы пишем f (x) или у'х, мы считаем, что при вычислении произ-
производной в качестве независимой переменной берется х\ когда же мы пишем
<р' (у) или х'у, то мы считаем, что при вычислении производной роль незави-
независимой переменной играет у. Заметим, что после дифференцирова-
дифференцирования по у, указанного в правой части формулы (XVI), надо
вместо у подставить / (*),

88
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
[ГЛ. III
Так как функция у (у) непрерывна, то Ая-*0 при Д#—*0. Пе-
Переходя к пределу при Д#—>0 в обеих частях равенства C), получим
т. е. получили формулу (XVI).
Замечание. Если пользоваться теоремой о дифференциро-
дифференцировании сложной функции, то формулу (XVI) можно получить так.
Дифференцируем обе части равенства B) по х, считая у функ-
функцией от х. Получим 1 = ср' (у) у'х, откуда #*=-rpj-
Полученный результат наглядно иллюстрируется геометриче-
геометрически. Рассмотрим график функции y = f(x) (рис. 70). Эта же кривая
будет графиком функции х = у(у), где х рас-
рассматривается уже как функция, а у—как не-
независимая переменная. Рассмотрим некото-
некоторую точку М (я, у) этой кривой. Обозначим
углы, образованные данной касательной с по-
положительными направлениями осей Ох и Оу,
соответственно через а и р. На основании
результатов § 3 о геометрическом значении
производной имеем
D)
Рис. 70.
Из рис. 70 следует, что если a<-g-, то
> JT
Если
видеть, р = -?-—с
^ жеа>у, то, как легко g
Следовательно, в любом случае tgP=ctga, откуда tgatgp=:
= tgactga=l или tga=i—^. Подставляя выражения для tga
и tg p из формулы D), получаем
§ 14. Обратные тригонометрические функции
и их дифференцирование
1) Функция t/ = arcsin#.
Рассмотрим функцию
x=smy
A)
и построим ее график, напротив ось Оу вертикально вверх (рис. 71).
Эта функция определена в бесконечном интервале —оо < у < + °°.
На отрезке —п/2 ^ у ^ я/2 функция x = siny—возрастающая, ее
значения заполняют отрезок —1^л:^1. Поэтому функция

§ 141 ПРОИЗВОДНЫЕ ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 89
x—siny имеет обратную, которую обозначают так:
Эта функция определена на отрезке —I^jc^I, ее значения
заполняют отрезок —п/2^.у^.л/2. На рис. 71 график функции
y = arcsinA; изображен жирной линией.
Теорема 1. Производная от функ- \
ции arcsin х равна —===* 9 т. е. г \
если у = arcsin х, то у =-
1
(XVII) _^
Доказательство. На основании
равенства A) находим
По правилу дифференцирования обратной
функции
/ *
\a?=sin^
но
1
Ху
= К1—sin2^
1
cosy1
' = 1/1
)
-х\
поэтому
Рис. 71.
1
I — jr2
перед
корнем берется знак плюс, так как функция у = arcsin x прини-
принимает значения на отрезке —л/2 ^ у ^ я/2 и, следовательно,
cos
Приме р I.
#=arcsine*, у'=
Пример 2.
X
2) Функция t/ = arccosx.
Как и выше, рассмотрим функцию
х = cos у
2 arcsin
B)
*) Отметим, что известное из тригонометрии равенство у = Arcsin x есть
другая запись равенства A). Здесь (при данном я) у обозначает совокупность
значений углов, синус которых равен хь

90 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [ГЛ. III
и построим ее график, направив ось Оу вверх (рис. 72). Эта
функция определена в бесконечном интервале —оо<у< +оо.
функция x = cosy — убывающая и имеет
обратную, которую обозначают так:
у = arccos х.
Эта функция определена на отрезке —1 ^
^#^ 1. Значения функции заполняют отре-
отрезок я^гу^О. На рис. 72 график функции
у = arccos х изображен жирной линией.
Теорема 2. Производная от функции
arccos х равна . , т. е.
если у = arccos х, то у'= г
(XVIII)
Доказательство. На основании равенства B) находим
хгу = — sin у.
Следовательно,
1 1 1
"л ху sin# yi—соз2г/
Но cos у = ху поэтому
В равенстве siny = J/l—cos2 у перед корнем берется знак плюс,
так как значения функции у = arccos x заполняют отрезок 0^
^у^я и, следовательно, siny^O.
Пример 3.
0 = arccos(tg*), у> = -—±== —' l l
3) Функция y = arctg#.
Рассмотрим функцию
x=tgy C)
и построим ее график (рис. 73). Эта функция определена при всех
значениях у, кроме значений y = Bk+l) ~ (& = 0, ±1, ±2, ...).
На интервале —я/2 < у < я/2 функция х= tg у—возрастающая
и имеет обратную, которую обозначают так:
y = arctg#.
Эта функция определена на интервале —оо <#< + <х>. Значения
функции заполняют интервал —я/2 < у < я/2. На рис. 73 график
функции y = arctg# изображен жирной линией.

§ 14] ПРОИЗВОДНЫЕ ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
91
ТеоремаЗ. Производная от функции arctg x равна ртг^2> т- е-
1
если у = arctg х9 то у' =
(XIX)
Доказательство. На основании равенства C) находим
,_ 1
Следовательно,
но
так как
cos2 у =
1
sec2 у 1 + tg2 у '
= x9 то окончательно получаем:
У' =
¦1+*»'
Пример 4. (/ = (arctg д;L,
#' = 4 (arctg xK (tg x)' = 4 (arctg ^K1~Т-^2•
4. Функция y = arcctgA:.
Рассмотрим функцию
x = ctgr/. D)
Эта функция определена при всех, значениях у, кроме значе-
значений y = kn (k = 0, ±1, ±2, .. .)• График этой функции изображен
Рис. 73.
Рис. 74.
на рис. 74. На интервале 0 < у < я функция x = o\g у—убываю-
у—убывающая и имеет обратную, которую обозначают так:

92 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ {ГЛ. III
Эта функция, следовательно, определена на бесконечном интер-
интервале —оо < х < +оо, ее значения заполняют интервал 0 < у < я.
т. е.
Теорема 4. Производная функция arcctgх равна —1 , х%,
если у = arcctg х, то у' = — узг^- (XX)
Доказательство. Из D) получаем
- L.
^ ~~ sin
Следовательно, у; = — sin2 y = —
:=jc. Поэтому
§ 15. Таблица основных формул дифференцирования
Объединим теперь в одну таблицу все основные формулу и пра-
правила дифференцирования, выведенные в предыдущих параграфах.
у = const, у' = 0.
Степенная функция:
у = ха, у'^ах*-1;
в частности,
1 /
У = Т, У
Тригонометрические функции:
t/' = — sinx,
Обратные тригонометрические функции:
//=arcsinx, y'=^=L==
у=arcctg x, t/' =—-q-j.

§ 161 ПАРАМЕТРИЧЕСКОЕ ЗАДАНИЕ ФУНКЦИИ 93
Показательная функция:
у = ах, у'
в частности,
у = е*,
Логарифмическая функция:
в частности,
Общие правила дифференцирования:
у = Си {х), \f = Cu' (х) (С = const),
= U + V—W, у' —
V + mV In «.
Если y = f(x), #=<p(#), где / и <р—взаимно обратные функ-
функции, то
Г{х)=??)> где у=Пх)'
§ 16. Параметрическое задание функции
Даны два уравнения
A)
где ^ принимает значения, содержащиеся на отрезке [7\, Т2].
Каждому значению t соответствуют значения хну (функции <р
и i|> предполагаем однозначными). Если рассматривать значения х
и у как координаты точки на координатной плоскости Оху, то
каждому значению t будет соответствовать определенная точка
плоскости. Когда t изменяется от 7\ до Т2, эта точка на плоско-
плоскости описывает некоторую кривую. Уравнения A) называются пара-
параметрическими уравнениями этой кривой, / называется параметром,
а способ задания кривой уравнениями A) называется параметри-
параметрическим.
Предположим, далее, что функция # = ср(/) имеет обратную
? = <D(#). Тогда, очевидно, у является функцией от х:
У = ¦[<&(*)]¦ B)

94 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [ГЛ. III
Таким образом, уравнения A) определяют у как функцию от х,
и говорят, что функция у от х задается параметрически.
Выражение у = / (х) непосредственной зависимости у от х может
получиться путем исключения параметра t из уравнений A).
Параметрическое задание кривых широко применяется в
механике. Если в плоскости Оху движется некоторая матери-
материальная точка и нам известны законы движения проекций этой
точки на оси координат,
где параметр t есть время, то уравнения
(Г) являются параметрическими уравне-
уравнениями траектории движущейся точки.
Исключая из этих уравнений параметр t,
получим уравнение траектории в форме
y=:f(x) или F (х, #)=0. Рассмотрим, на-
например, такую задачу.
Задача* Определить траекторию и место
падения груза, сброшенного с самолета, движу -
Рис. 75. щегося горизонтально со скоростью vQ на высоте
у0 (сопротивлением воздуха можно пренебречь).
Решение. Возьмем систему координат так, как показано на рис. 75,
предполагая, что самолет сбрасывает груз в тот момент, когда он пересекает
ось Оу. Очевидно, что горизонтальное перемещение груза будет равномерным,
с постоянной скоростью vQ: x = vot. Вертикальное перемещение падающего
gt2
груза под влиянием силы тяжести будет выражаться формулой s = ~-. Сле-
Следовательно ^ расстояние груза от земли в любой момент времени будет выра-
выражаться формулой у — Уъ — Др.
Два уравнения
будут параметрическими уравнениями траектории. Чтобы исключить параметр t,
, х
из первого уравнения находим значение / = — и подставляем это значение
во второе уравнение. Тогда получим уравнение траектории в форме
Это—уравнение параболы с вершиной в точке М (О, #0), причем ось Оу слу-
служит осью симметрии параболы.
Определим величину отрезка ОС. Обозначим абсциссу точки С через X,
заметим, что ордината этой точки у = 0. Подставляя эти значения в преды-
предыдущую формулу, будем иметь
откуда

§17]
УРАВНЕНИЯ КРИВЫХ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ
95
§ 17. Уравнения некоторых кривых в параметрической форме
Окружность, Дана окружность с центром в начале координат и ра-
радиусом г (рис. 76).
Обозначим через / угол, образованный радиусом, проведенным в некото-
некоторую точку М (х, у) окружности, и осью Ох. Тогда координаты любой точки
окружности выразятся через параметр t следующим образом:
#=г cost, y = rsintf 0^t^2n.
Это — параметрические уравнения окружности. Если мы исключим из
П
Рис. 76.
Рио. 77.
этих уравнений параметр /? то получим уравнение окружности * содержащее
только х и у. Возводя в квадрат параметрические уравнения и складывая,
находим
x2-\-y2=,r2 (cos2 *+sin2 t)
или
A)
Эллипс. Дано уравнение эллинса
Положим
л; = a cos/, Bf)
Подставляя это выражение в уравнение A) и производя необходимые преобра-
преобразования, получим
y = bsint. B")
Уравнения
являются параметрическими уравнениями эллипса.
Выясним геометрический смысл параметра t. Проведем две окружности
с центрами в начале координат и радиусами а и b (рис. 77). Пусть точка
М(х, у) лежит на эллипсе, а В—точка большой окружности, имеющая ту же
абсциссу, что и точка М. Обозначим через t угол, образованный радиусом ОВ
с осью Ол\ Непосредственно из рисунка следует
x=OP = acost [это—уравнение B')]i
CQ = bsint.

96
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
[ГЛ. Ill
На основании равенства B;/) заключаем, что CQ = y, т. е. прямая СМ парал-
параллельна оси Ох.
Следовательно, в уравнениях B) t есть угол, образованный радиусом ОБ
и осью абсцисс. Угол t иногда называют эксцентрическим углом.
Циклоида. Циклоидой называется кривая, описанная точкой, лежащей
на окружности, если эта окружность катится без скольжения По прямой
(рис. 78). Предположим, что точка М катящейся окружности в начале дви-
движения совпадала с началом координат. Определим координаты точки М после
Рис. 78.
того, как окружность повернулась на угол t. Обозначим через а радиус катя-
катящейся окружности. Как видно из рис. 78,
х=ОР = ОВ—РВ,
но так как окружность катится без скольжения, то
Следовательно, х=at—a sin t = a (t—sin 0»
Далее,
yz=MP — KB = CB — СК — а—a cos t = a(l—cos 0-
Уравнения
x=a(t—sin t), y — a(l—cosO» 0«^<:2я, C)
являются параметрическими уравнениями циклоиды. При изменении t от О
до 2я точка М опишет одну арку циклоиды.
Исключим параметр t из последних уравнений и получим непосредствен-
непосредственную зависимость х от у. На отрезке 0^*^я функция у = а(\ — cost) имеет
обратную:
,в—У
а
Подставляя выражение для t в первое из уравнений C), получим
¦—-—a sin [arccos
или х—аarccos -—У~2ау—у2 при
замечаем, что при
а )
:. Непосредственно из рис. 78
~2па— ( aarocos ?—?¦—у~2ау—у2 ) .
Заметим, что функция x~a(t—sin t) имеет обратную, но она не выражается
через элементарные функции. Поэтому и функция y=f(x) не выражается через
элементарные функции.

§13]
ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ
Замечание 1. На примере циклоиды легко убедиться, что в некото-
некоторых случаях для исследования функций и кривых параметрические уравнения
удобнее, чем непосредственная зависимость
у от х или х от у.
Астроида. Астроидой называется
кривая, заданная следующими параметричес-
параметрическими уравнениями:
x=aco$3t, y=rasin3tf 0<*<2я. D)
Возводя все члены обоих уравнений в сте-
степень 2/3 и складывая, получим зависимость
между х и у:
или
Рис. 79.
Ниже (см. § 12 гл. V) будет показано, что
эта кривая имеет форму, изображенную на
рис. 79. Эта кривая может быть получена
как траектория некоторой точки окружности радиуса а/4, катящейся без сколь-
скольжения по другой окружности радиуса а причем меньшая окружность все
время остается внутри большей; см. рис. 79).
Замечание 2. Отметим, что уравнения D) и уравнение E) опреде-
определяют не одну функцию y = f(x). Они определяют две непрерывные функции
на отрезке —a«^#^+<z. Одна из них принимает неотрицательные значения,
другая—неположительные.
§ 18. Производная функции, заданной параметрически
Пусть функция у от х задана параметрическими уравнениями
0=*(О. to<t<T. A)
Предположим, что эти функции имеют производные и что функ-
функция jt = <p(Q имеет обратную ? = Ф(л;), которая также имеет про-
производную. Тогда определенную параметрическими уравнениями
функцию y*=f(x) можно рассматривать как сложную функцию
y = ty(t), * = Ф(*), t—промежуточный аргумент.
По правилу дифференцирования сложной функции получим
уГ*=№х = №)<й'я(х). B)
На основании теоремы о дифференцировании обратной функции
следует Ф^ (х) = —,—. Подставляя последнее выражение в равен-
<Pt(t)
ство B), получаем У*==?гУ или
н* - yt
Ух — У *
xt
(XXI)
Выведенная формула дает возможность находить производ-
производную у'х от функции, заданной параметрически, не находя выра-
выражения непосредственной зависимости у от х.
4 н. С. Пискунов, ». I

ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ 1ГЯ. Ш
Пример I. Функция у от х задана параметрическими уравнениями
y = asint,
Найти производную -^-\ 1) при любом значениии t\ 2) при * = -т-'
Решение.
*)' flcos* _
^|/я/4 g(/)
ример 2. Найти угловой коэффициент касательной к циклоиде
x — a(t—sinf),
y=a(\—cosi)
в произвольной точке (^^)
Решение. Угловой коэффициент касательной в каждой точке равен
значению производной у'х в этой точке, т. е. равен
* y't
Ух — т*
Но
дг?=аA— cos Or t
Следовательно,
2 sin тр cos -х-
os -х- , / .
?
Следовательно, угловой коэффициент касательной к циклоиде в каждой ее
точке равен tg f -=—-^-J, где t—значение параметра, соответствующее этой
точке. Но это значит, что угол а наклона касательной к оси х равен ~—~
(для значений t между — п и п) *)»
§19, Гиперболические функции
Во многих приложениях математического анализа встречаются
комбинации показательных функций вида -j (е*—е~х) Иу(^ + е~х).
Эти комбинации рассматривают как новые функции и обозначают
так:
*) Действительно, угловой коэффициент равен тангенсу угла а наклона
касательной к оси Ох. Поэтому
•*(т-4)
н «=|—g ДО тех значений ff для которых у—"j лежит между аил.

$19]
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
99
Первую из функций A) называют гиперболическим синусом,
вторую—гиперболическим косинусом. С помощью этих функций
можно определить еще две функции th# = ^ и ^
ех е-х
™ х = exjL_e-x—гиперболический тангенс,
x =
гиперболический котангенс.
Функции sh#, сЬд:, th;c определены, очевидно, для всех зна-
значений х. Функция же cth* определена всюду, за исключением
точки x = 0. Графики гиперболичес-
гиперболических функций представлены на рис. 80,
81, 82.
Из определения функций shjc и
chx [формулы A)] следуют соотно-
дпения, аналогичные соотношениям
Рис, 80.
Рис. 81.
между соответствующими тригонометрическими функциями:
ch2*—sh2x=l, B)
C)
C')
Действительно,
Далее, заметив, что

100
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
[ГЛ. Ill
получаем:
ch a ch Ь + sh a sh Ь =
еа—е-
о — е-
= ch (a +6).
Аналогично доказывается и справедливость соотношения C').
Название «гиперболические функ-
функции» объясняется тем, что функции
sh/ и ch/ играют ту же роль для
параметрического представления ги-
гиперболы
какую тригонометрические функции
sin/ и cos/—для параметрического
представления окружности
Действительно, исключая пара-
параметр / из уравнений
получим
или
2=
=1 (уравнение окружнос-
окружнос+ у (ур
ти). Аналогично уравнения
Рис.82. X
являются параметрическими уравне-
уравнениями гиперболы.
Действительно, возводя почленно в квадрат эти уравнения и
вычитая из первого второе, получим:
Так как выражение в правой части на основании формулы B)
равно единице, то, следовательно,
а это и есть уравнение гиперболы.
Рассмотрим окружность с уравнением #2-fy2=l (рис. 83).
В уравнениях x = cos/, # = sin/ параметр / численно равен цен-
центральному углу АОМ или удвоенной площади 5 сектора АОМ,
так как / = 25.

§20]
ДИФФЕРЕНЦИАЛ
101
Отметим без доказательства, что в параметрических уравне-
уравнениях гиперболы x = cht, y = sht параметр t также численно равен
удвоенной площади «гиперболического сектора» АОМ (рис. 84).
Рис. 83.
Рис. 84.
Производные гиперболических функций определяются фор-
формулами
(XXII)
которые вытекают из самого определения гиперболических функ-
, , ех—е~х
ции; например, для функции sh;c =—к— имеем
§ 20. Дифференциал
Пусть функция y = f(x) дифференцируема на отрезке [a, ft].
Производная этой функции в некоторой точке х отрезка [а, Ь]
определяется равенством
Отношение ^ при А* —> 0 стремится к определенному числу /' (х)
и, следовательно, отличается от производной. /' (я) на величину
бесконечно малую:
где а—»-0 при Д#—>0.
Умножая все члены последнего равенства на Ах, получим
A)

102 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [ГЛ. III
Так как в общем случае /' (х)фО, то при постоянном х и пере-
переменном Дл: —* 0 произведение /' (а:) Ал: есть бесконечно малая ве-
величина первого порядка относительно А*. Произведение же аДл;
есть всегда величина бесконечно малая высшего порядка относи-
относительно Ал:, так как
"?* a==0.
Таким образом, приращение Ау функции состоит из двух слагае-
слагаемых, из которых первое слагаемое есть [при /' (л:) Ф 0] так назы-
называемая главная часть приращения, линейная относи-
относительно Ал:. Произведение /' (х) Ах называют дифференциалом
функции и обозначают через dy или df(x).
Таким образом, если функция y = f(x) имеет производную /' (л:)
в точке л:, то произведение производной /' (л;) на приращение Ал:
аргумента называется дифференциалом функции и обозначается
символом dy:
йу=Г(х)Ах. B)
Найдем дифференциал функции у=х; в этом случае
я, следовательно, dy—dx=Ax или dx~Ax. Таким образом, диф-
дифференциал ^независимой переменной х совпадает
с ее приращением Алг. Равенство dx=Ax можно было бы
рассматривать также как определение дифференциала независи-
независимой переменной, и тогда рассмотренный пример показывал бы,
что это не противоречит определению дифференциала функции.
В любом случае формулу B) мы можем записать так:
Но из этого соотношения следует, что
Следовательно, производную f (х) иажно рассматри-
рассматривать как отношение дифференциала функции к
дифференциалу независимой переменной.
Вернемся к выражению A), которое с учетом B) перепишем
так:
Ay = dy+tx.Ax. C)
Таким образом, приращение функции отличается от дифферен-
дифференциала функции на величину бесконечно малую высшего порядка
относительно Ал:. Если f {х) ФО, то аДл: является бесконечно
малой высшего порядка и относительно dy и
lim 4f=l+lim тп^Ь=1+ Игл ~-r=l.
Д*-*0 аУ AX-+QI (х)*х АХ-+01 W

$20]
ДИФФЕРЕНЦИАЛ
Поэтому в приближенных вычислениях иногда пользуются при-
приближенным равенством
Ну « dy, D)
или в развернутом виде
f(x + Ax)-f(x)&f'(x)Ax, E)
что сокращает вычисления.
Пример 1. Найти дифференциал dy и приращение Ау функции у = хй:
1) при произвольных значениях х и А*:
2) при х = 20, Д* = 0,1.
Решение. 1) Ау = (х+АхJ —х2 = 2хДх+Д*2,
dy = (x2)' Ах = 2хАх.
2) Если * = 20, Лх = 0,1, то
dy = 2.20-0,1 =4,00.
Погрешность при замене Ау на dy равна 0,01. Во многих случаях
можно считать ее малой по сравнению с Дг/ = 4,01 и пренебречь ею.
Рассмотренная задача наглядно иллюстри-
иллюстрируется рис. 85.
В приближенных вычислениях поль-
пользуются также приближенным равенст-
равенством, которое получается из E),
[х)Ах. F)
Пример 2. Пусть / (х) = sin я, тогда
/' (х) = cos х.
В этом случае приближенное равенство F)
примет вид
sin (х+Ах) « sin лг+cos х Ах. G)
Вычислим приближенное значение sin 46°. Положим *=-т- (что соответствует
углу 45°), Д#=тт^г (соответствует углу 1°), ^+^=="Т+Тол- Подставляя
в G), будем иметь sin 46° = sin ( х~Ьоп ) ^ sin Х~!" Гол cos T" ИЛИ
sin46° « 3-^—ho2 ^=0,7071+ 0,7071-0,0175 =0,7191.
Пример 3. Если в формуле G) положим я=0, Ах = а, то получим
приближенное равенство:
sin a « а.
Пример 4. Если / (х) = tg #, то по формуле F) получаем следующее
приближенное равенство:
при д;=0,
получаем
tg a «a.

204 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ |ГЛ. Ill
Пример 5. Если / (*) = У"х, то формула F) дает
Полагая jc = 1, Д* = а, получаем приближенное равенство
Задача нахождения дифференциала функции равносильна на-
нахождению производной, так как, умножив последнюю на диффе-
дифференциал аргумента, получим дифференциал функции. Следова-
Следовательно, большинство теорем и формул, относящихся к производ-
производным, сохраняют свою силу и для дифференциалов. Так, например:
Дифференциал суммы двух дифференцируемых функций и uv
равен сумме дифференциалов этих функций:
d (u~\*v) = du + dv.
Дифференциал произведения двух дифференцируемых функций
и и v определяется формулой
d (uv) = и do+v du.
Докажем, например, последнюю формулу. Если y = uvt то
dy =zy'dx= (uv' + vur) dx = uv' dx+vu dx, но v' dx = dvt u' dx = duf
поэтому dy = udv+vdu.
Аналогично доказываются и другие формулы, например фор-
формула, определяющая дифференциал частного:
и j v du—и dv
если */ = ~, то dy = ^ .
Решим несколько примеров на вычисление дифференциала
функции.
Пример 6. #=
Пример 7. у =
Найдем выражение для дифференциала сложной функции.
Пусть
у = /(и), и = ф(*), или t/ =
Тогда по правилу дифференцирования сложной функции
следовательно, dy~ f'u (и) q/ (x) dx; но q/ (x) dx = du, поэтому
dy=f'(u)du.
Таким образом, дифференциал сложной функции имеет тот
же вид, какой он имел бы в том случае, если бы промежуточный

§211
ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ ДИФФЕРЕНЦИАЛА
105
аргумент и был независимой переменной. Иначе говоря, форма
дифференциала не зависит от того, является аргумент функции
независимой переменной или функцией другого аргумента. Это
важное свойство дифференциала, называемое инвариантностью
формы дифференциала, будет широко использовано в дальнейшем.
Пример 8. Дана функция y = sin У^х. Найти dy. _
Решение. Представив данную функцию как сложную: у — sin и, и = Y~x >
находим
dy = cos и —-==- dx;
2у х
но —гг=г dx = du, поэтому можно написать
2\Гх
dy — QQSudu или dy = со$ (Ух) d (У х).
§ 21. Геометрическое значение дифференциала
Рассмотрим функцию
y = f(x)
и соответствующую ей кривую (рис. 86).
Возьмем на кривой y = f(x) произвольную точку М(х, у),
проведем касательную к кривой в этой точке и обозначим через
а угол*), который касательная образует с положительным на-
правлением оси Ох. Дадим независимой переменной приращение
Рис. 86. Рис. 87.
; тогда функция получит приращение Ау=Л^М1. Значениям
Л У+&У на кривой y = f(x) будет соответствовать точка
А)
.i + , у+у)
Из треугольника MNT находим NT = MN tg а; так как
g = f'(A:), MN = kx, то NT = f (x)kx\ но согласно определе-
определению дифференциала f (x)Ax = dy. Таким образом, NT = dy. По-
Последнее равенство означает, что дифференциал функции f(x),
соответствующий данным значениям х и Дл:, равен приращению
ординаты касательной к кривой y = f(x) в данной точке х.
*) Предполагая, что функция / (х) имеет конечную производную в точке х,
получаем а ф я/2.

106 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [ГЛ. III
Из рис. 86 непосредственно следует, что МгТ = Ay — dy. По
АЛ Т
доказанному ранее -д^—*0 при Ах—+0.
Не следует думать, что всегда Д у больше dy. Так, на рис. 87
Ду = М1ЛГ, dy^NT, причем Ar/<dr/.
§ 22. Производные различных порядков
Пусть функция y = f(x) дифференцируема на некотором от-
отрезке [а, Ь]. Значения производной /' (х), вообще говоря, зави-
зависят от л:, т.е. производная /' (х) представляет собой
тоже функцию от х. Дифференцируя эту функцию, мы по-
получаем так называемую вторую производную от функции f(x).
Производная от первой производной называется производной
второго порядка или второй производной от первоначальной функ-
функции и обозначается символом у" или f" (х)\ у" = (у'У = f" (х) - Так,
например, если у — хь> то y' = 5#\ у"=Eл;4)' = 20л;3.
Производная от второй производной называется производной
третьего порядка или третьей производной и обозначается
через у или /'" (х).
Вообще, производной п-го порядка от функции f (x) называется
производная (первого порядка) от производной (п — 1)-го порядка
и обозначается символом у{п) или /и) (х):
yin) = (у<п-1)у = fin) (Х)в
(Порядок производной берется в скобки для того, чтобы его
нельзя было принять за показатель степени.)
Производные четвертого, пятого и высших порядков обозна-
обозначаются также с помощью римских цифр: #lV, yv, */vl, ... В таком
случае порядок производной можно писать без скобок. Например,
если у = х\ то у1 = 5х\ у" = 20х3, у"' = 60х\ ylY == уи) = 120х,
VEI20 w »H
Пример 1. Дана функция y = ekx (k = const). Найти выражение ее
производной любого порядка п.
Решение, у'= fie**, у" = ?2е**, ..., (/">
Пример 2. y — sihx. Найти yin).
Решен ие.
'" = --cos * =

S 221 ПРОИЗВОДНЫЕ РАЗЛИЧНЫХ ПОРЯДКОВ \QJ
Аналогично выводятся формулы для производных любого по-
порядка и от некоторых других элементарных функций. Читатель
сам сможет найти формулы для производных n-го порядка от
функций у = хк, y = cosx, y = lnx.
На случай производных любого порядка легко обобщаются
правила, указанные в теоремах 2 и 3 § 7.
В данном случае имеют место очевидные формулы:
Выведем формулу (так называемую формулу Лейбница), даю-
дающую возможность вычислить производную /1-го порядка от про-
произведения двух функций u(x)v(x). Для того чтобы вывести эту
формулу, мы найдем сначала несколько производных, а затем
установим общий закон, пригодный для вычисления производной
любого порядка:
У =ш>,
у1 —u'v +uv\
у№ = u"v -f и'vf -f u'vr + uxf = u'v + 2u'v' + uo\
y"' = u'"v-\-u"v' +2u"v'+2u'xf +u'v"+uvf" =
9
v'" + uvlV.
Закон составления производных сохраняется для производных
любого порядка и заключается, очевидно, в следующем.
Надо выражение (и+v)n разложить по формуле бинома Ньютона
и в полученном разложении заменить показатели степеней для и
и v указателями порядка производных, причем нулевые степени
(tt° = t>°), входящие в крайние члены разложения, надо заменить
самими функциями (т. е. «производными нулевого порядка»):
у™ = (uv)<n} = u™v + nttn~V + n("^l) uin-2>v" + ... + uvm\
Это и есть формула Лейбница.
Строгое доказательство этой формулы можно было бы про-
провести методом полной математической индукции (т. е. доказать,
что из справедливости этой формулы для порядка п следует
справедливость ее для порядка я+1).
Пример 3. у=еахх\ Найти производную #<й>.
Решение.
и =ettx, v =*а,
и' = аеах, v' — 2х,
ип=а4ах, v" = 2,
или

108 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [ГЛ. Ill
§ 23. Дифференциалы различных порядков
Пусть имеем функцию # = /(#), где х — независимая перемен-
переменная. Дифференциал этой функции dy=f'(x)dx есть некоторая
функция от х, но от х может зависеть только первый сомножи-
сомножитель /' (х), второй же сомножитель (dx) является приращением
независимой переменной jc и от значения этой переменной не за-
зависит. Так как dy есть функция от х, то мы имеем право говорить
о дифференциале этой функции.
Дифференциал от дифференциала функции называется вторым
дифференциалом или дифференциалом второго порядка этой
функщщ и обозначается через d2y: d(dy) — d2y. Найдем выраже-
выражение второго дифференциала. В силу общего определения диффе-
дифференциала имеем d2y = [/' (jc) dx]' dx. Так как dx от х не зависит,
то dx при дифференцировании выносится за знак производной,
и мы получаем d2y = f"(x) (dxJ. Принято, записывая степень диф-
дифференциала, опускать скобки; так, например, вместо (dxJ при-
принято писать dx2, подразумевая под этим квадрат выражения dx;
вместо (dxK пишут dxz и т. д.
Третьим дифференциалом или дифференциалом третьего по-
порядка функции называется дифференциал от ее второго диффе-
дифференциала:
d?у = d (d2y) = [/" (х) dx2]f dx = /'" (х) dx\
Вообще, дифференциалом п-го порядка называется первый диф-
дифференциал от дифференциала (п— 1)-го порядка:
dny = d (dn^y) = [/<n-1) (x) dx?1]' dx,
dny=fin)(x)dxn. A)
Пользуясь дифференциалами различных порядков, производную
любого порядка можно представить как отношение дифференциа-
дифференциалов соответствующего порядка:
Замечание. Равенства A) и B) (при п>1) верны только
для того случая, когда х является независимой переменной.
Действительно, пусть имеем сложную функцию
y = F(u), u = <?(x). C)
Мы видели, что дифференциал первого порядка имеет инва-
инвариантную форму, независимо от того, будет ли и независимой
переменной или функцией от х:
dy = F'u(u)du. D)
Второй дифференциал и последующие дифференциалы этим
свойством не обладают.

§24J ПРОИЗВОДНЫЕ ОТ НЕЯВНЫХ ФУНКЦИЙ 109
Действительно, на основании C) и D) получаем d2y=d (F'u(u)du).
Но здесь du = <р' (я) dx зависит от х, и потому мы получаем
= d(F'u(u))du + F'u(u)d(du) или
d2y = F°uu (и) (duJ+F'u (и) d2u% где d2u = q>" (x) (dxJ. E)
Аналогичным образом находятся d3y и т. д.
Пример 1. Найти dy и d2y сложной функции
y = sinut и = У"х.
Решение.
du = cos и • —-==г dx = cos и du.
2V
Далее, по формуле E) получаем
d2y = —- sin и (duJ + cos ud2u = — sin и (duJ + cos и - un (dxJ =
=~sinM (iyrjidxJ+cos" ( ~4"?тг)idx)a
§ 24. Производные различных порядков от неявных функций
и функций, заданных параметрически
1. Покажем на примере способ нахождения производных
различных порядков от неявных функций.
Пусть неявная функция у от х определяется равенством
Дифференцируем по х все члены этого равенства, помня, что у
есть функция от х:
а2 ^ b2
отсюда находим
Последнее равенство снова дифференцируем по х (имея в виду,
что у есть функция от х):
d2y __ _
dx2 ~~
Подставляем сюда вместо производной ~ ее выражение из ра-
равенства B), получаем
ь2 х
dx2 ~" а2 у2 '

110 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ?ГЛ. Ш
или после упрощения
?у__ Ь2(а2у2 + Ь2х2)
dx2 "" а*у*
Из уравнения A) следует, что a2y2 + 62%2 = a2b2, поэтому вто-
вторую производную можно представить в виде
d2y __ ь4
dx2 ~~ tft#
dsi/
Дифференцируя по х последнее равенство, найдем >-~ и т. д.
2. Рассмотрим теперь задачу о нахождении производных выс-
высших порядков от функции, заданной параметрически.
Пусть функция у от х задана параметрическими уравнениями
* = ф@. У = Ф(О, h<t<Tt C)
причем функция x = y(t) на отрезке [/0, Т] имеет обратную функ-
функцию * = Ф()
В § 18 было доказано, что в этом случае производная ~
определяется равенством
dx~~ dx_ • W
dt
Для нахождения второй производной -^§ дифференцируем
по х равенство D), имея в виду, что t есть функция от х:
d?y _d I dt \__ d I dt \ dt
1х*—Щ ЧГ r~"df\ ЧГ )~~
HO
dy \ dx d / dy \ dy d f dx \ dx d2y dy
Ж \_ЖЖ [Ж] Ж Ж [Ж) __ Ж It2 "Ж
[dt J
^
dx\2 fdx\2 »
dt 1
dx dx^
Ж
Подставляя последние выражения в формулу E), получим:
dx d2y dy d2x
d2y __ ЖИР^ЖЖ*
dx2 ~~ ( dxy
\df)

§25] МЕХАНИЧЕСКОЕ ЗНАЧЕНИЕ ВТОРОЙ ПРОИЗВОДНОЙ Щ
Последней формуле можно придать следующий, более компакт-
компактный вид:
dx*- [<р'@13
Аналогичным образом можно найти производные -j| , -р[- и т.д.
Пример. Функция д от х задана параметрически:-
x = acost, y=bsint.
HafiTH производные ~, -рт •
Решение.
dy_ bcost _ b
dx^—asint^ acgtf
(— b sin Q — (b cos t) (— a cos /) __ b 1
dx* (—asin tf "" a2 sin3* *
§ 25< Механическое значение второй производной
Путь s, пройденный поступательно движущимся телом, в за-
зависимости от времени t выражается формулой
*=/('). A)
Как уже известно (см. § 1), скорость v тела в данный момент
равна первой производной от пути по времени:
° B)
Пусть в некоторый момент t скорость тела была равна v.
Если движение не является равномерным, то за промежуток
времени Д?, истекший с момента t$ скорости изменится и полу-
получит приращение Аи.
Средним ускорением за время А* называется отношение при-
приращения скорости Ау к приращению времени:
Ускорением в данный момент называется предел отношения при-
приращения скорости к приращению времени, когда последнее стре-
стремится к нулю:
а= Нш &;

Ц2 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ 1ГЛ. Ш
иначе говоря, ускорение (в данный момент) равно производной
от скорости по времени:
ds
но так как i> = ^, то, следовательно,
л = JL(*L\-?±
dt \dt ) dP >
т. е. ускорение прямолинейного движения равно второй произ-
производной от пути По времени. Исходя из равенства A), получаем
Пример. Найти скорость v и ускорение а свободно падающего тела,
если зависимость расстояния s от времени t дается формулой
*2 + ^ + C)
где ?^=9,8м/с2—ускорение земного тяготения, a so = s|*=o— значение s при
Решение. Дифференцируя, находим
<>=¦?=gt+vQl D)
из этой формулы следует, что уо = Ф=о.
Дифференцируя еще раз, находим:
Заметим, что, обратно, если ускорение некоторого движения постоянно и рав-
равно g, то скорость выражается равенством D), а расстояние—равенством C)
ПрИ УСЛОВИИ, ЧТО Р|*-.О=^о И s|f=0:=SQ.
§ 26. Уравнения касательной и нормали.
Длины подкасательной и поднормали
Рассмотрим кривую, уравнение которой есть
Возьмем на этой кривой точку М (xi9 yj) (рис. 88) и напишем
уравнение касательной к данной кривой в точке Mt предпола-
предполагая, что эта касательная не параллельна оси ординат.
Уравнение прямой с угловым коэффициентом k, проходящей
через точку М, имеет вид у—уг = к(х—х^. Для касательной
(см. § 3) fe = /'(*i)> поэтому уравнение касательной имеет
ВИД у—Уг^ГХх^Х—^).
Наряду с касательной к кривой в данной точке очень часто
приходится рассматривать нормаль.

§261
УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ
ш
Определение. Нормалью к кривой в данной точке назы-
называется прямая, проходящая через данную точку и перпендику-
перпендикулярная к касательной в этой точке.
Рис. 88.
Рис. 89.
Из определения нормали следует, что ее угловой коэффициент
kn связан с угловым коэффициентом kt касательной равенством
и 1 т р а *
Rn-—kt, т.е. яп-
Следовательно, уравнение нормали к кривой y = f(x)
в точке M(xi9 t/j) имеет вид
Пример 1. Написать уравнения касательной и нормали к кривой
у—х3 в точке МA, 1).
Решение. Так как у' = 3х2, то угловой коэффициент касательной ра-
равен ?W=3.
Следовательно, уравнение касательной?
^—1=3(д;—1) или */ = Злг—2.
1 4
Уравнение нормали: г/— 1 =— (дг—1)/3 или у = —о"Л:+— (Рис« Щ*
о о
Длина Т отрезка QM (рис. 88) касательной, заключенного
между точкой касания и осью Ох, называется длиной касатель-
касательной. Проекция этого отрезка на ось Ох, т. е. отрезок QP, на-
называется подкасательной; длина подкасательной обозначается
через Sr. Длина N отрезка MR называется длиной нормали,
а проекция RP отрезка RM на ось Ох называется поднормалью;
длина поднормали обозначается через S#.
Найдем величины Т, Sj* N, S# для кривой y^=f(x) и точки
М (хи уг).
Из рис. 88 видно, что

114
поэтому
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
Ух
[ГЛ. III
Далее, из этого же рисунка ясно, что
поэтому
Эти формулы выведены в предположении, что ^> 1, у[>0.
Однако они сохраняются и в
общем случае.
Пример 2. Найти уравнения ка-
J. сательной и нормали, длины касатель-
Q, ной и ггодкасательнои, длины нормали и
поднормали для эллипса
(I)
Рис. 90. в точке М (х±9 у?% для которой *=j
(рис. 90).
Решение. Из уравнений A) находим:
Av / *у и one/ dv b~*~* dy\ ь
t9 -j|=:6cosr, ^-=—
Находим координаты точки касания М:
Уравнение касательной:
y--^T^-l^--^Ty или bx+ay-ab
Уравнение нормали:
j,_-A-e|V,--^-V или (ах-
Длины подкасательной и поднормали:
Ъ
«ST==
о.
Длины касательной и нормали:
Ъ
ft /¦+(-!)¦

$27]
ПРОИЗВОДНАЯ РАДИУС-ВЕКТОРА
115
§ 27. Геометрическое значение производной радиус-вектора
по полярному углу
Пусть имеем уравнение кривой в полярных координатах:
A)
Напишем формулы перехода от полярных координат к прямо-
прямоугольным декартовым:
Подставляя сюда вместо р его выражение
через 0 из уравнения A), будем иметь:
x=fF)cos9, у = /(9) sinG. B)
Уравнения B) являются параметрически-
параметрическими уравнениями данной кривой, причем
параметром является полярный угол 0 п
(рис. 91).
Если через ср обозначим угол, состав-
составленный касательной к кривой в некото-
некоторой точке М (р, 6) с положительным направлением оси абсцисс,
то будем иметь
л % ^sin8+pcos8
) = Т == dx > ИЛИ
dQ
cos 0—р sinG
Обозначим через \х угол между направлением радиус-вектора и
касательной. Очевидно, что jx = <p—9,
§^~
Подставляя сюда вместо tgcp его выражение C) и производя
преобразование, получим
_ (р' sin 6 + Р cos Q) cos 8 —(р' cos 6—р sin 6) sin 9 _ j)_
g ** — "(P' cos 6 —psin 8) cos 8 + (p' sin 8 + p cos 8) sin 8 ~~ p' *
ИЛИ
pe-pctgfx. D)
Таким образом, производная радиус-вектора по полярному
углу равна длине радиус-вектора, умноженной на котангенс угла
между радиус-вектором и касательной к кривой в данной точке.
Пример. Показать, что касательная к логарифмической спиралиp — eaQ
пересекается с радиус-вектором под постоянным углом.
Решение. Из уравнения спирали находим p' = aeaQ. На основании
формулы D) получаем
ctgjx ;=;?-=а, т, е. ^ = arcctga=
=const г

Цб ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ?ГЛ. III
Упражнения к главе III
Найти производные функций, пользуясь непосредственно определением
производной:
U $г=А Отв. Зх\ 2. //= 1/лг. Отв. —1/х*. 3. у=У~х. Отв. 1/B У"х).
4. у=\/У х. Отв. —\/Bх]/гх), 5. y = sin2x. Отв. 2sinxcosx. 6. #=2*2—*.
Отв. 4л:—1.
Определить тангенсы углов наклона касательных к кривым:
7. у—х*. а) При х=\. Отв. 3. б) При л: ——1. Отв. 3; сделать чертеж.
8. yz=\/x. а) При #=1/2. Отв. —4. б) При х=1. Отв. —1; сделать чертеж.
9. g=V"x при х = 2. Отв. У/4.
Найти производные функций:
10, у=хА+Зх2—6. Отв. у' = 4х?+6х. 11. i/=6a^—*2. Отв. у' = 18л:2—2л:.
*« ^5 л:2 л 5л:4 2л: , ,о д-з_^2 + 1
«—Ь * а+b а—Ь * 5
2*. 14. у = 2««~+с. Отв. у' = 6ах*~.
0 0
15. y = bxV2+4x*/2 + 2x.Ome.y'=2lxb'2 + \0x*'2 + 2. 16. у=
л: . m . л:2 . л2 л . 1 т . 2х 2п2
, Ош. ,'=| ' _ 1 . 20. у=°*
6 V х V х i/x
Отв. у' = ^ах*Ъ~Ьх-™+*-.х-1/ь. 2\. у = (\+4х*)(\+2х*). Отв. у'=*
= 4л:A+Зл:+10л^). 22. ^ = л:Bд;—1) (Зд:+2). Отв. #'=2 (9л:2+л:— 1).
23. #=Bл:—1)(л:2— вх+3). Отв. у'= 6л:2—26х +12. 24. у=^±^.
¦ 37. y = {l+V~*)\ Отв. у '

УПРАЖНЕНИЯ К ГЛАВЕ III Ц7
38. У=*у x+Vx+Vlc* Отв. */' =— = X
2|/ x+Vx+VH
у A-\ г^Х]. 39. у = sin2 л:. Ome. ^' = sin 2x. 40. #=
2Kx+/jc\ 2У*//
= 2sin*+cos3*. Отв. у' = 2 cos x—3 sin За;. 41. y = tg(ax+b).
Отв- У = cos* 42 ^0тл^в
cos* (+) ++
= sin 2л: cos Зх. Отв. ^' = 2cos2jccos3a:—3sin 2л: sin Зл:. 44. y = ctgz5x.
Отв. у' = —10 ctg 5л: cosec2 5л:. 45. y — t sin tf+cos/. Отв. y'~tcost*
46. t/ = sin3/cos/. Отв. t/' = sin2 / Ccos2/—sin2 /)• 47. у = аУ cos 2x.
^2
Отв. у> = ^а^п2х ш 48# r==asin3-|. Отв. rl = a sin2 ^ cos |., 49.
V2 ^ ф « 3
. Ome. * — **???*. 50. ,=flsln*|. Oms. y>
= 2a sin3-j cos у • 51. y=^tg*x. Отв. y'= tgx sec2 x, 52. y=In cos x.
Отв. y' = ~tgx. 53. t/ = lntgA:. Отв. yf = 2/sin2x. 54. ^=
Отв. #r = 2ctg*« 55. #=-^ ¦ Отв. у' = sin л:+cos*. 56.
-Om- у=ш7-57- ^=lntg(t+t)•Отв- у'-
У ()
58. r/ = sin(A:+a)cos(A:+a). Отв. #' = cos2 (л:+а). 59. /(л:) = sin (Inx).
_ г//ч t:os(lnA:) вл г / ч * /i ч л г/, ч sec2 (Inл:)
Отв. /'W^ -• 60- /W = tg(lnx). Отв. f'(x) = Ь 1.
61. /(*) = sin (cosx). Отв. f'(x) = — sin xcos (cosx). 62. r=-^tg*(p—tg<p-}-<p.
Отв. ~=s;tg4(p. 63. /(x) = (A:ctgjtK. Отв. /'(л:) = 2л: ctg x (ctg л:—x cosec2 x).
64. 1/ = 1п(а;с+6). Отв. у' = aj(ax+b). 65. #=logtf (*2+l). Отв. у'
66 yln^
2л:—cos л: co t 1+л:2
*r-t- 1
69. «/= In (**+*). Отв. tfmi-gZ-. 70. i/=ln(*s-
о^2 О
^1 7Ь
72. у =
1п3л:. Отв. ^ = li2lf# 73. i/= In (jc+ у^Г+З^). Отв. у'=
74. г/ = 1пAпх). Отв. ^^^j^. 75. /(х) = In |/l±f. Отв. /' (*) =
^'() 2
Г^-Ъ. 76. /^) = 1п1^1±1—^.# Отв.
— *2 y^ + l+
77. у^уЖТТ^а\па+^Г^7\ Отв. у> = ****. 78. у -
л: л:
. От. у'= J . 79. У=—

118
-jr-. Отв. y'=~: ч
2 sin5» *
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
1
[ГЛ. 1Ц
sin л: л , l+sin2#
Ш~Х- Отв' у =-етпг
--
. Отв. y' = tg*x. 82. у=еах. Отв, у'=
83. у=е*х+ъ. Отв. у' =4е4*+5. 84. у=ах*. Отв, 2*а*81па. 85. */=/
Ome, 0' = 2(*+lO*2+2*ln7. 86. y=ca*~xZ. Отв, у'= — 2хсаг~хг\пс.
87. y=aeV х. Отв, у' = —2_= е *. 88. r=a9. Ome, rf = a9lna.
9. r = a^e. Ome, ^sssflln9lngt 9D# ^=^(l-^)# Ome# ^=
-2х-х*). 91. * =
Отв. y'^
. 92. У^
04, у=esin *. Отв* у'=esin x cos *. 95. ^=ate nx. Отв, у' =
= /ш*? ЛА; sec2 nx In a. 96. у=ez<* x sin j:. Отв. у' = е00** * (cos x—sin2 *).
97. y—eX In sin x. Отв. у'—е" (ctgx+lnsin x). 98. y=xnesinx.
Отв. ^ = xll""^esin^(tt+^cos Jt). 99. y=xx. Отв, ^'=д:^Aпд;+1).
». ^ = jcW. Ome. у'=л:1/д: ^^Ц"^ . 101.
102. y=exX. Отвщ
Отв. у' = п
105. y=(si
Отв. у' =
1
1 + In~у.104.^=
Отв.
103. у={х/п)пх.
+in^cosjkV
106. y = (
108.
=^. Отв. y'=~
cos4
2 V 1—
109. ,= 10***. Отв. ^Ю^^1п1-Г 4OS2^
Найти производные функций* предварительно логарифмируя эти функции:
111. У =
3 2
IJ
ИЗ.
Отв. у'
•. Отв. у'
— 161л:а+480л:—271
60 У(х— If \/(х-
(a—2x) (a
114. -*<'+*>
Ome, y'

УПРАЖНЕНИЯ К ГЛАВЕ Ш Ц9
Найти производные функций:
116. w = arcsin —. Отв, у'= *•• . . 117. */ = (arcsin *J. Отв. у'—
у?2
*•• .
> • И». *,=
. Ome.
/ = arecos(*2). Отв.
. 121. y=a^SSll. отв. y^
х
1 1
^~=. 0тв9 у'= г
у 2 У 1—2х—х2
х* \ \—х2
-
. 123. у=ху а2— л
, у' = 2 У~а2—х2 . 124. у= Y&—*2 +а arcsin ~ . Отв. у'
. Отв. ^=-L_. 126. у—* «rotg
d l + 2 1^3
128.
129.
130.
Отв.
/ (х) = arcsin l/"sin x . Отв.
- Отв- y'="\- Ш. * =
9
Отв. у' =
У 1 —
(
V л;
+1 в 1-й и 4-й четвертях,
-1 во 2-й и 3-й четвертях.
. 134. г/= arcsin (sin Д Отв, у'
136- ^=^т
^'=ет
ш.
x. Отв. if'-
188. У=
Отв. ^'=-
. отв. «/' = •
.Отв. /-
141. ^
Отв, ^

|20 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [ГЛ. Ш
Дифференцирование неявных функций
Найти j-, если:
142. г/2 = 4рх. Отв, gf=—•
**-**. Отв, %=-
. Отв. gf—— у^сш 147#
Найти ~ функций, заданных параметрически:
152. x = acost, y = bsint. Отв. -~= ctg t. 153. x — a(t—sint), у
= a(l—cos/). О/тгв. ^ = ctg-L. 154. A: =
wx ^ ил
Ь . , ,„ 3at 3at* _ dy 2t
~--tgt, 155. х=ТТТ2,у=ТТГг.0тв.Тх=Т-г,.
156. w = 21nctgs, t; = tgs+ctgs. Показать^ что ~=tg2s.
Найти тангенсы углов наклона касательных к кривым:
157. * = cosf, у = sint в точке х = —1/2, у~У^З/2. Сделать чертеж.
Отв. \lYH. 158._a: = 2cos^, y = sin t в точке ^=Ь у = — У/2. Сделать
чертеж. Отв. ^ 3/6. 159. ^ = а(/—sin 0> у = яA—cos 0 при t=л/2. Сделать
чертеж. Отв, 1. 160* x = acos3t, у — a sin31 при t=n/4. Сделать чертеж.
Отв. —1.
161. Тело, брошенное под углом а к горизонту, в безвоздушном прост-
пространстве описало под действием силы тяжести кривую (параболу), уравнения
которой: *=(a0cosa)f, y = (vosln a) t—gt2/2 (g=9,8 м/с2). Зная, что а = 60°,
t/e=50 м/с, определить направление движения при: 1) t = 2 с; 2) f = 7 с.
Сделать чертеж. Отв. 1) tg<pi = 0,948* ф? = 43°30'; 2) teq)s = —1,012,
ф2=+134,3°.
Найти дифференциалы следующих функций:
162. у = (а2—Х2)К Отв. dy =—\0x(a?—x*)*dx. 163!
d ±
Отв. dy= ?dx . 164. y = ±-tg*x+tgx. Отв.
V1 + *2 а
165. y=j—>-+In(l—x). Ome. ^ =
Вычислить приращения и дифференциалы функций:
166. y = 2*2— * при *=Ь Ал: = 0,01. Отв. &у=0,0302, d^=^
167. Дано \у=х9+2х. Найти Ьу и dy при *=—1^ Д*=0,02. Отв.
«0f098808| ф=0,1. 168. Дано y = sinx. Найти dy при *=я/3, A
Ош. ^=л/3б=0,0873.

УПРАЖНЕНИЯ К ГЛАВЕ III 121
169. Зная, что sin 60° =|^3/2 = 0,86602S; cos 60°= 1/2, найти приближен-
ные значения sin60°3' и sin 60° 18'. Результаты сопоставить с данными таб-
таблицы. Отв. sin60°3' «0,866461; sin60°18' «0,868643.
170. Найти приближенное значение tg45°4'30". Отв. 1,00262.
171. Зная, что lg200 = 2,30103, найти приближенное значение lg 200,2.
Отв. 2,30146.
Производные различных порядков
172. #=3л?—2*2 + 5*—1. Найти /. Отв. 18*—4. 173. #=*/?. Найти у"'.
АО /"»
#+ / #* у
АО /"»
Отв. J±x-12/*. 17*. у^х*. Найти t/<6>. Отв. 6!. 175. У = ~. Найти/.
Отв. n(n+1.)C . 176. и= V^^?. Найти у". Отв. —
177. д = 2У"х. Найти #<4>. Отв. ^==. 178. у = ах2+Ьх+с.
Найти у'\ Отв. 0. 179. /(*) = 1п(*+1). Найти /IV (x). Отв. — *
180. ^ = tgjc. Найти у'". Отв. 6sec4x—4sec2a:. 1181. y — \nsinx.
Найти ^. Отв. 2 ctg д: cosec2 х. 182. / (*) = ^sec 2x. Найти //f(je).
Отв. П*)=3[/(*)!¦-/(*). 183. У = ^. Найти /ivW. Отв.
184. p = ft«+rf)arctgi. Найти g. Отв.
Найти ^-|. Отв. -^ . 186. ^ = cos ax. Найти #<»>. Отв. a«cos (ах+пп/2).
187. у = ах. Найти фп\ Отв. (\па)пах. 188. ^ = 1пA+х). Найти фп>. Отв.
^ Найти ^п' 0/ив- 2(-1^
190. у = ехх. Найти ^<п>. Отв. ех(х+п). 191. у = *"-11п*. Найти
Отв. ft1"I ^ 192. i/ = sin2x. Найти у™. Отв. — 2«-icos Bx+nn/2).
193. y = JcsinA:. Найти i/(n). Отв. xsin (x-\-nn/2)—ncos(х+пп/2). 194. Если
у = е* sin л:, то доказать, что у"—2у' + 2у = 0. 195. у2 = 4ах. Найти -j-|-.
Отв. _^. 19в. W+^-Л-. Найти g и g. С -^; -
197. *2+у2 = г2. Найти j?. Отв. —^. 198. у2-2*у=0. Найти -~^.
Отв. 0. 199. p = tg»+p). Найти" ^. Отв. ^-^
200. sec9cosp = C. Найти ~?. Отв. tg'^Ttg>q>. 201.
203# *=в»-««п0. |f = aA-cosO. Найти
Найти .g. Отв. <l^?^^z?L. 202. **+*-3«у=0. Найти
Отв. —i—, A ¦ /n-v. 204. x = acos2f, w=6sln2f. Показать, что -^=0.
4a sin* (t/2) ax?
205. jc=flcosf, y=asin/. Найти -г~ . Отв. а~ТТ7* 2^6# Показать, что

122 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [ГЛ. Ill
Уравнения касательной и нормали.
Длины подкасательной и поднормали
207. Написать уравнение касательной и нормали к кривой у~ х3—Зх2 —
— *+5 в точке М C, 2). Отв. Касательная 8*—у — 22 = 0; нормаль х+8у—
— 19 = 0.
208. Найти уравнение касательной и нормали, длины подкасательной и
поднормали окружности х2+у2 = г2 в точке М (хъ уг). Отв. Касательная ххх+
+ УУ1 = г2\ нормаль x1y—y1x=0; sT = \yl/x1\; sN=\x1\.
209. Показать, что подкасательная параболы у2 = 4рх в любой точке де-
делится вершиной пополам и поднормаль постоянна и равна 2р. Сделать чертеж.
210. Найти уравнение касательной в точке М (хъ ух): а) К эллипсу
2 2 2 2
X
(ъ ух
2 у2
X , У 1 г, ХХ± , уух л *\ тт *> X у , .~, ХХл
^f+fa = 1- От. ^г+т^ = Ь б> К гиперболе ——^=1. Отв. ^-
8а?
211. Найти уравнение касательной и нормали к «локону» у= . 2 2
в точке, где х = 2а. Отв. Касательная х-\-2у — 4а; нормаль у — 2х—За.
212. Показать, что нормаль к кривой Зу=6х—5л:3, проведенная в точке
М A, 1/3), проходит через начало координат.
(х \п / и \п
в точке
\ и у ¦ \ о j
М (а, Ь) есть —1~-|- = 2.
214. Найти уравнение той касательной к параболе у2~20х, которая об-
образует угол 45° с осью Ох. Отв. г/= #+5 [в точке E, 10)].
215. Найти уравнения касательных к окружности х2-\-у2 = 52, параллель-
параллельных прямой 2х+3у = 6. Отв. 2х+3у ± 26 = 0.
216. Найти уравнения касательных к гиперболе 4л;2—9у2=36, перпенди-
перпендикулярных к прямой 2г/+5#=10. Отв. Таких касательных нет.
217. Показать, что заключенный между осями координат отрезок каса-
касательной к гиперболе ху = т делится точкой касания пополам.
218. Доказать, что заключенный между осями Координат отрезок каса-
касательной к астроиде xz^-\-y2^ = a^ имеет постоянную длину.
219. Под каким углом а пересекаются кривые у — ах и ?/ = М? Отв.
In а—1п?
220. Найти длины подкасательной, поднормали, касательной и нормали
циклоиды л: = а@—sin6), у — а(\—cos 0) в точке, для которой 0 = д/2.
Отв. sT = a; sN=a; T = aV^\ N = aV2.
221. Найти величины sr, s^, Т к N для астроиды Ar = 4acos3*, у — Аа sin31.
Отв. sr = |4asin2fcosf |; sN=\4asin* ttg t\; Г = 4a sin2/; # = |42/t/|
Разные задачи
Найти производные функций:
{

УПРАЖНЕНИЯ К ГЛАВЕ III 123
4
228. Из формул для объема и поверхности шара v = -%-nrz и s = 4nr2 сле-
о
дует, что j- = s. Объяснить геометрический смысл этого результата. Найти
аналогичное соотношение между площадью круга и длиной окружности.
229. В треугольнике ABC сторона а выражается через две другие сторо-
стороны Ь, с и угол А между ними формулой a=Y'b2 + c2-~2bc cos А. При по-
постоянных b и с сторона а является функцией угла А. Показать, что-т-г=Ял,
где ha есть высота треугольника, соответствующая основанию а. Пояснить
этот результат геометрическими соображениями.
230. Пользуясь понятием дифференциала, выяснить происхождение при-
приближенных формул У"а? + Ья cl + y » v as+b «a+^, где \Ь\ есть число
малое по сравнению с а.
231. Период колебания маятника равен r = 3xl/"//g. Какое влияние на
погрешность при вычислении периода Т окажет погрешность в 1% при изме-
измерении: 1) длины маятника 1\ 2) ускорения силы тяжести g? Отв. 1) « 1/2%;
2) «1/2%.
232. Трактриса обладает тем свойством, что для любой ее точки отрезок
касательной Т сохраняет постоянную длину. Доказать это, исходя из
1) уравнения трактрисы в форме
— у
2) параметрических уравнений кривой
* = a(lntg(f/2)+cosO. y =
233. Доказать, что функция у~С1е"х-\-С2е"гх удовлетворяет уравнению
%' + 2iy = 0 (здесь Сх и С2 — постоянные).
234. Полагая у=ех sin x, z=ex cos х, доказать равенства #"=2z, г#=—2у.
235. Показать, что функция y=sin (marosin x) удовлетворяет уравнению
236. Доказать, что если (a+bx)ef^x=x, то ж3 -т^= ( * ¦?¦—У) •

ГЛАВА IV
НЕКОТОРЫЕ ТЕОРЕМЫ
О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
§ 1. Теорема о корнях производной (теорема Ролля)
Теорема Ролля. Если функция f (х) непрерывна на отрезке
[а, 6], дифференцируема во всех внутренних точках этого отрезка
и на концах х~а и х = Ь обращается в нуль [/(а) = /F) = 0],
то внутри отрезка [а, Ь] существует по крайней мере одна
точка я = с, а < с < 6, в которой производная /'(х) обращается
в нуль, т. е. /'(г) = 0*).
Доказательство. Так как функция f(x) непрерывна на
отрезке [а, 6], то она имеет на этом отрезке наибольшее значе-
значение М и наименьшее значение т.
Если М = т, то функция f(x) постоянна, т. е. при всех зна-
значениях х имеет постоянное значение /(л;) = 0. Но тогда в любой
точке отрезка будет /'(jt) = O, и теорема доказана.
Предположим, что Мфт. Тогда по крайней мере одно из
этих чисел не равно нулю.
Предположим для определенности, что М > 0 и что функция
принимает свое наибольшее значение при х = с9 т. е. f(c)=M.
При этом заметим, что с не равно ни а, ни &, так как по
условию /(а) = 0, /F) = 0. Так как f(c)—наибольшее значение
функции, то /(с+Л^)—f(c)^O как при Дх>0, так и при
Д0
Отсюда следует, что
/(С) Ах>°> о')
*) Число с называется корнем функции ф(#), если ф(с)=О*

ТЕОРЕМА О КОРНЯХ ПРОИЗВОДНОЙ
125
Так как по условию теоремы производная при х~с сущест-
существует, то, переходя к пределу при Ад:—>0, получим
lim
lim
при Дх>0,
ПрИ
I \^ffr)
Но соотношения /' (с)<0 и /' (с)>0 совместимы лишь в том
случае, если f'(c) = O. Следовательно, внутри отрезка [а, 6]
имеется точка с, в которой производная /' (х) равна нулю.
Теорема о корнях производ-
производной имеет простое геометрическое
истолкование: если непрерывная
кривая, имеющая в каждой точке
касательную, пересекает ось Ох в
точках с абсциссами а и ft, то
на этой кривой найдется по край-
ней мере одна точка с абсциссой
су а < с < &, в которой касатель-
касательная параллельна оси Ох.
Замечание 1. Доказанная
теорема остается справедливой
и для такой дифференцируемой функции, которая на концах
отрезка [а, Ь] не обращается в нуль, но принимает равные зна-
значения f(a) = f(b) (рис. 92). Доказательство в этом случае про-
проводится точно так же, как и ранее.
Замечание 2. Если функция f(x) такова, что производная
существует не во всех точках внутри отрезка [а, 6], то утверж-
утверждение теоремы может оказаться неверным (т. е. в этом случае
I
4
Рис. 92.
i
Рис. 94.
на отрезке [а, Ъ\ может не оказаться такой точки с; в которой
производная /' (х) обращается в нуль).
Так, например, функция y = f(x) = I — j/x5 (рис. 93) непре-
непрерывна на отрезке [—1, 1] и обращается в нуль на концах отрезка,
однако производная f (х) = —
внутри промежутка в нуль

126 НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ [ГЛ. IV
не обращается. Это происходит оттого, что внутри промежутка
существует точка # = 0, в которой производная не существует
(обращается в бесконечность).
График, изображенный на рис. 94, дает нам еще один пример
функции, производная которой не обращается в нуль на отрезке
[0, 2].
Для этой функции также не выполнены условия теоремы
Ролля, так как в точке х=1 функция не имеет производной.
§ 2. Теорема о конечных приращениях (теорема Лагранжа)
Теорема Лагранжа. Если функция f(x) непрерывна на
отрезке [а, Ь] и дифференцируема во всех внутренних точках
этого отрезка, то внутри отрезка [а% Ь] найдется по крайней
мере одна точка с, а < с < ft, что
A)
Доказательство. Обозначим буквой Q число ?¦ ^J ^ ,
т. е. положим
Q-tS^SA, B)
и рассмотрим вспомогательную функцию F(x), определенную
равенством
F(x) = f(x)-f(a)-(x-a)Q. C)
Выясним геометрический смысл функции F(x). Для этого на-
напишем сначала уравнение хорды АВ (рис. 95), учитывая, что ее
угловой коэффициент равен ь~а = ^ и что она ПРОХ°ДИТ
через точку (a; f (a))i
y—f(a) = Q(x-a),
отсюда
y = f(a) + Q(x-a).
Но F (x) = / (х) —[/ (а) + Q (х—а)]. Следовательно, F (х) для каж-
каждого, значения х равняется разности ординат кривой у = /(л;) и
хорды #=f(tfL-Q(*—а) Для точек с одинаковой абсциссой.
Легко видеть, что F (х) непрерывна на отрезке [а, Ь], диффе-
дифференцируема внутри этого отрезка и обращается в нуль на концах
отрезка, т. е. ^(а) = 0, F(b)=0. Следовательно, к функции F (х)
применима теорема Ролля. Согласно этой теореме внутри отрезка
существует точка х = с такая, что F* (с) = 0. Но F' (х) = /' (х)-*» Q.
Значит, Ff(c)^ff(c) — Q=OJ откуда Q = f'(c),
Подставляя значение Q в равенство B), будем иметь:
(Ю

§3]
ТЕОРЕМА ОБ ОТНОШЕНИИ ПРИРАЩЕНИЙ ДВУХ ФУНКЦИЙ
127
откуда непосредственно следует формула A). Таким образом,
теорема доказана.
Чтобы выяснить геометрический смысл теоремы Лагранжа,
обратимся к рис. 95. Из рисунка непосредственно ясно, что вели-
величина ftZfl представляет собой тангенс угла а наклона хорды,
проходящей через точки А и В графи-
графика с абсциссами а и Ь.
С другой стороны, f (с) есть тан-
тангенс угла наклона касательной к кри-
кривой в точке с абсциссой с. Таким об-
образом, геометрический смысл равенства
(Г) или равносильного ему равенства A)
состоит в следующем: если во всех точ-
точках дуги АВ существует касательная,
то на этой дуге найдется точка С меж-
между А и fi, в которой касательная
параллельна хорде, соединяющей
точки А к В.
Заметим, далее, следующее. Так как значение ч удовлетво-
удовлетворяет усдовию а<с<6, то с—а<&—а, или с—а = 9(&—а),
где 9 есть некоторое число, заключенное между 0 и 1, т. е.
0<9< 1. Но тогда с = а + Ь(Ь—а), и формуле A) можно при-
придать следующий вид:
-а)], 0<8<1. (Г)
§ 3.: Теорема об отношении приращений двух функций
(теорема Коши)
Теорема Коши. Если f(x) и у(х)—две функции, непре-
непрерывные на отрезке [а, Ь] и дифференцируемые внутри него,
причем ф' (х) нигде внутри отрезка не обращается в нуль, то
внутри отрезка [а, Ь\ найдется такая точка х = с, а < с < &, что
f(b)-f(a) =Пс) > A)
Доказательство. Определим число Q равенством
q= f(bL(a) 9 B)
Отметим, что Ф F) — ф {а) Ф 0, так как в противном случае ф F)
равнялось бы ф(а), и тогда до теореме Ролля производная у' (х)
обращалась бы в нуль внутри отрезка, что противоречит условию
теоремы.
Составим вспомогательную функцию

128 НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ |ГЛ. JV
Очевидно, что F(a) = 0 и F(b) = 0 (это вытекает из определе-
определения функции F(x) и определения числа Q). Заметив, что функ-
функция F (х) удовлетворяет на отрезке [а, Ь] всем условиям теоремы
Ролля, заключаем, что между а и Ь существует такое значение
х = с (п<с<Ь), 4toF'(c) = Q. Но F* (*) = /' (х)- Qq>'(х), сле-
следовательно,
F'(c) = r(c)-Q9'(c) = 09
откуда
0 _ Г (с)
ф' (с) #
Подставляя значение Q в равенство B), получим равенство A).
Замечание. Теорему Коши нельзя доказать, как это может
показаться с первого взгляда, применением теоремы Лагранжа
к числителю и знаменателю дроби
Действительно, мы получили бы в этом случае (после сокращения
дроби на Ь — а) формулу
f(b)-f(a) ^
)—Ф(а)
в которой a<.Ci<b, а < с2 < Ь. Но так как, вообще говоря,
с* Ф с2, то полученный результат, очевидно, не дает еще теоремы
Коши.
§ 4« Предел отношения двух бесконечно малых величин
[«раскрытие неопределенностей вида -^-»)
Пусть функции f(x) и ф(лг) на некотором отрезке [а, Ь] удов-
удовлетворяют условиям теоремы Коши и обращаются в нуль в точке
х—а этого отрезка, т. е. /(а) = 0 и ф(а) = 0.
f (хЪ
Отношение ~г~ не определено при я = а, но имеет вполне
определенный смысл при значениях хфа. Следовательно, может
быть поставлен вопрос о разыскании предела этого отношения
при х—+а. Вычисление пределов такого типа называется обычно
«раскрытием неопределенностей вида -g-».
С такого рода задачей мы уже имели дело и раньше, например
при рассмотрении предела lim -S^Si f при нахождении производ-
0 х
ных от элементарных функций. Выражение —^ при х = 0 не
имеет смысла, т. е. функция F(x) = ^^ не определена при х=О,

&4J ПРЕДЕЛ ОТНОШЕНИЯ ДВУХ БЕСКОНЕЧНО МАЛЫХ 129
но мы видели, что предел выражения -^-^ при л;—*0 существует
и равняется 1.
Теорема (правило Лопиталя). Пусть функции f(x) и
ц)(х) на некотором отрезке [а,Ь] удовлетворяют условиям тео-
теоремы Коши и обращаются в нуль в точке х = а, т. е. f(a) =
f (х)
=ф(а) = 0; тогда, если существует предел отношения ,* при
а, то существует и lim -^~-, причем
х ->• а Ф \х)
Доказательство. Возьмем на отрезке [а, Ь] какую-нибудь
точку хфа. Применяя формулу Коши, будем иметь
f(x)~f{a) ^/'F)
где I лежит между аи х. Но по условию / (а) = ф (а) = О, значит
/ (х) _ Г (I) т
<р(*) Ф'(9 * к }
Если х—+а, то и Е-^а, так как g заключено между х и а.
При этом, если lim V ' = Л, то lim - ; \У также существует и
я -> я Ф W « -^- а Ф \ъ)
равен Л. Отсюда ясно, что
lim I?U lim 41-= lim 4S-- И™ 4й--Л.
9W Ф© Ф© Ф(*)
и окончательно
limi.= imi^_
Замечание 1. Теорема имеет место и в том случае, если
функции /(я) или ф(х)не определены при х=а, но lim/(x)=0,
hm ф(д:)^0.
Для того чтобы свести этот случай к рассмотренному ранее,
мы доопределяем функции f(х) и у(х) в точке х = а так,
чтобы они стали непрерывными в точке а. Для этого до-
достаточно положить / (а) = lim / (х) = 0, ф (а) = lim ф (х) = 0, так
х -*• а х ->а
как, очевидно, предел отношения -^у при х—>а не зависит
от того, определены ли-функции f(x) и <р(х) в точке л: = а.
Замечание 2. Если /' (а) = ф' (а) = 0 и производные /' (х) и
ф' (х) удовлетворяют тем условиям, которые были наложены
5 Н. С. Пискунов, т. 1

13d НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ [ГЛ. IV
в условиях теоремы на функции f(x) и ф(#), то» применяя
правило Лопиталя к отношению ,' , приходим к формуле
f'() Г()
ит-д-
ЗамечаниеЗ. Если ф' (а) = 0, но /' (л;) Ф О, то теорема при-
ложима к обратному отношению —Щ-, которое стремится к нулю
/ кх)
f (x)
при х—+а. Следовательно, отношение ¦¦ ( стремится к беско-
бесконечности.
_, , ,. sin Ъх .. (sin 5а:)' ,. 5 cos 5а: 5
Пример 1. lim —^—= lim Q ч/ -= lim —5—^z=z~^>
x -> о оХ х -*• 0 ("J^) л; -> о о о
1
г- п ,. 1пA+ДГ) ,. 1 + X 1
Пример 2. lim —-—¦—-= lim —j—=-—t=h
Пример 3.
e-x 2 ex e~x
e_e^2x -.
lim . — ilra __ iim = iim
x-+o x—smx x-+o 1—cosa: x-+o smx x-+q
Здесь три раза пришлось применить правило Лопиталя, так как отноше-
отношения первых, вторых и третьих производных при * = 0 приводят к неопреде-
неопределенности -гг.
Замечание 4. Правило Лопиталя применимо и в том случае,
если
lim f(x) = O и lim <p(*) = 0.
Действительно, полагая х=1/г, видим, что г—^0 при л;--
и, следовательно,
lim / A/г) = 0, lim ф A/г) = 0.
Применяя правило Лопиталя к отношению ¦ Jfi , находим:
что и требовалось доказать.
k k ( 1 \
sin — ^ cos — ( 5-
jc х \ а: у fe
Пример 4. lim —5—= lim \ -^— = lim &cos—=^.
«-#•«» а л -*. оо J_ х -*- 00 л;

§ 5] ПРЕДЕЛ ОТНОШЕНИЯ ДВУХ БЕСКОНЕЧНО БОЛЬШИХ
§ 5. Предел отношения двух бесконечно больших величин
(«раскрытие неопределенностей вида ^»
Рассмотрим, далее, вопрос о пределе отношения двух функций
f(x) и ф(#), стремящихся к бесконечности при х—>а (или при
Теорема. Пусть функции f(x) и <р(х) непрерывны и диффе-
дифференцируемы при всех хфа в окрестности точки а, причем произ-
производная ф'(л;) не обращается в нуль\ пусть, далее%
lim / (х) = оо, lim ф (х) = оо
х-+а х -+а
и пусть существует предел
Иш4й- = Л. A)
/ (х)
Тогда существует предел lim -^Ч- и
Нш IW.-lim 4W =Л., B)
х-+а ФМ к-+а Ф <*)
Доказательство. В рассматриваемой окрестности точки а
возьмем две точки а и jc так, чтобы было а<х<а (или а<
< х < а). По теореме Коши будем иметь
f(x)-f(a) Г (с) 3
Ф(д:)-Ф(а) Ф'(с) » 1 >
где а < с < х. Левую часть равенства C) преобразуем так:
Из соотношений
Отсюда находим
ч
C)
) (х)—ф(сс) ф (х)
и D) получаем
1_
ф'(с) ф(лг) {
1
ф С^О ф' (^)
1 —
ф(а)
Ф(а) •
Ф (^)
Ф (^)
Ф ("^)
Из условия A) следует, что при произвольно малом е>0 можно
а выбрать настолько близким к а, что для всех х = с, где
5*

132 НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ [ГЛ.1У
а < с < а9 будет выполняться неравенство
?§)~А\<&
или
с^ Г (с) <
F)
Далее рассмотрим дробь
1 —
Ф(а)
1 —
/(а) #
Закрепив а так, чтобы обеспечивалось выполнение неравен-
неравенства F), будем х приближать к а. Так как f (х) —> <х> и ср (х) —> оо
при х—^а, то
lim
.= 1
и, следовательно, при ранее выбранном е > 0 для х, достаточно
близких к а, будем иметь
Ф(а)
1 —
-1
или
1—-
G)
Перемножая соответствующие члены неравенств F) и G), получим
1 —
Ф(а)
1 —
JL
или на основании равенства E)
Так как е —произвольно малое число при х, достаточно близком
к ау то из последних неравенств следует, что

§51 ПРЕДЕЛ ОТНОШЕНИЯ ДВУХ БЕСКОНЕЧНО БОЛЬШИХ 133
или на основании A)
что и требовалось доказать.
Замечание 1. Если в условии A) Л = оо, т. е.
limi^Uoo,
то равенство B) остается справедливым и в этом случае. Дейст-
Действительно, из предыдущего выражения следует
Тогда по доказанной теореме
откуда
Замечание 2. Доказанная теорема легко распространяется
на случай, когда х—>оо. Если lim/(*)=oof lim<p(*) = oo и
X -> оо X -> со
lim /, ;ч существует, то
Iimlft=lim4ft. (8)
9W Ф W V
Доказательство проводится путем замены лс=1/г, как это
делалось при аналогичных условиях в случае неопределенности
вида -Q- (см. § 4, замечание 4).
Пример 1. lim —= lim , !, = lim -—=oo.
л -> оо л: jc -> оо (л:) х -*¦ оо 1
Замечание 3. Отметим еще раз, что формулы B) и (8)
справедливы только в том случае, если предел, стоящий справа
(конечный или бесконечный), существует. Может случиться, что
предел, стоящий слева, существует, в то время как предел, стоя-
стоящий справа, не существует. Приведем пример. Пусть требуется
найти
*->оо л
Этот иредел существует и равен 1. Действительно,
lim
#-*• оо
X J

134 НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ [ГЛ. XV
Но отношение производных
\Х) 1
при х—»»оо не стремится ни к какому пределу, а колеблется
между 0 и 2.
Пример 2. iim "*22+; = lim |^=*..
Пример 3.
1
v tgfA; cos2 л: .. 1 cos2 За: v i 2-3 cos За: sin За:
lim .°. as hm —x—= lim -= 5—= lim -% ~ : ==я
*^3л; ^ ^ д/2 3 ^я/гЗ cos2x *-**/* 3 2cosA;sinA;
cos2 3a:
lint ~»i? lim il^= lim
i
^ lint lm = lim 8^з, з.
x->n/2 cos a: x-*n/2 sin л: д:-> я/2 sin a: 1 1 1
Пример 4. lim -r == lim — = 0. Вообще, при любом целом п > 0
# _* оо &* х -> оо 6х
lim
Хп ,. ПА:"* .. П (п—1) •...•! л
— = hm -_=...= lim -^ -? =0.
К предыдущим случаям сводятся случаи других неопределен-
неопределенностей, которые символически записывают так:
а) (Ьоо, б) 0°, в) оо°, г) I00, д) оо —оо,
и смысл которых состоит в следующем.
а) Пусть lim / (х) = 0, lim ф (я) = оо; требуется найти
х-*-а х-*-а
lim [/(#)ф(х)]. Это — неопределенность типаО-оо.
*-> a
Если искомое выражение переписать в виде
Ит[/(*)ф(*)]= lim -Ц^-
х~+ а х-> а
или в виде
lim [Дх)ф(*)]= Ит ^JfL ,
х-+а х-*а
П*)
то при л:~>а мы получим неопределенность вида -тг или вида—
Пример 5. limA:w 1па:= lim —г-= lim = — lim —=0,
X-+Q X -* О J_ Ж-»0 ^ Л-»-О Л
б) Пусть Нт/(д;) = О, Нтф(л:) = О; требуется найти
х-*- а х-*- а
lim [/(я)]ф ш# или, как говорят, раскрыть неопределенность вида О,

§ 6] ФОРМУЛА ТЕЙЛОРА 135
Положив y = [f(x)](p(x\ прологарифмируем обе части получен-
полученного равенства: In у = ср (х) [In / (%)]. При х —>а получим (справа)
неопределенность вида 0- оо. Найдя lim In у, легко получить lim у.
Действительно, в силу непрерывности логарифмической функции,
lim In i/ = In lim z/, и если lnlim y=b, то, очевидно, lim y = eb. Если,
x-+a x->a x-*a x-+a
в частности, b=-f-oo или — oo, то, соответственно, hmy = -\- oo
или 0.
Пример 6. Требуется найти lim хх. Положив у = х*г находим;
х -*• о
In lim y= lim lnz/ = lim \п(хх) = lim (x\nx)i
X-+Q х-+0 х->0 x-+Q
lim (х1пл:)= lim -^-sss lim —^— = — lim x = 0§
следовательноj In lim # = 0, откуда lim z/ = e° = lt т. е.
jt->0 *-> 0
lim x* = l#
x-> о
Аналогичным приемом находятся пределы и в других случаях.
§ 6, Формула Тейлора
Предположим, что функция y = f(x) имеет все производные до
(/г+1)-го порядка включительно в некотором промежутке, содер-
содержащем точку х== а. Найдем многочлен у=Рп (х) степени не выше п,
значение которого в точке х = а равняется значению функции f(x)
в этой точке, а значения его производных до n-го порядка в точке
х = а равняются значениям соответствующих производных от функ-
функции f(x) в этой точке:
Ря ifl) = f (*). К (а) - /' (а), Рп (а) = Г(а)9...9 Р™ (а) = /<»> (а). A)
Естественно ожидать, что такой многочлен в некотором смысле
«близок» к функции f(x).
Будем искать этот многочлен в форме многочлена по степеням
(х — а) с неопределенными коэффициентами:
Р«(*) =
= С0 + Сг(х-а) + С2(х-ау + Сг(х-аУ+...+Сп(х-ау. B)
Неопределенные коэффициенты Си С2, ..., Сп определим так,
чтобы удовлетворялись условия A).

136
НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ [ГЛ. IV
Предварительно найдем производные от Рп(х):
Р'п (х) = С, + 2С2(х - а) + ЗС3 (х - а)* + ... + пСп (х - а)»-*,
Р"п (х) = 2 • 1 • С2+3. 2С3 (х - а) +... +п (п - 1) Сп (х - а)п~\
C)
Подставляя в левые и правые части равенств B) и C) вместо х
значение а и заменяя на основании равенств A) Рп (а) через / (а),
Р'п(а) через /' (а) и т.д., получим
Г (а) = 2.1С,,
/"'W-3.2.1C,,
откуда находим
Подставляя найденные значения Си С2,
получим искомый многочлен
D)
Zn в формулу B),
Обозначим через Rn (х) разность значений данной функции / (х)
и построенного многочлена Рп(х) (рис. 96): Rn(x) = f(x)—Pn(x)f
откуда / (х) = Рп (х) + Rn (x), или в раз-
развернутом виде
F)
Рис. 96.
многочленом у=^Рп(х) с
равной значению остаточного члена Rn(x).
Rn{x) называется остаточным членом.
Для тех значений х, для которых оста-
остаточный член Rn (x) мал, многочлен
Рп (х) дает приближенное представле-
представление функции f(x).
Таким образом, формула F) дает
возможность заменить функциюy=f (x)
соответствующей степенью точности,

§6] ФОРМУЛА ТЕЙЛОРА 137
Дальнейшая наша задача — оценить величину Rn (х) при раз-
различных значениях х.
Запишем остаточный член в форме
i^lQ(x), G)
где Q (х) есть некоторая функция, подлежащая определению, и
в соответствии с этим перепишем формулу F):
При фиксированных х я а функция Q (х) имеет определенное
значение; обозначим его через Q.
Рассмотрим, далее, вспомогательную функцию от t (t заклю-
заключено между а и х):
п\ I W~ (n+l)! W'
где Q имеет значение, определенное соотношением F'); при этом
считаем а и х определенными числами.
Найдем производную F' (t):
или пос^е сокращения
/7'W = _i?^/(»+i)(/)+i?=2lQ. (8)
Итак, функция F (t) имеет производную во всех точках ty лежащих
вблизи точки с абсциссой a {a^t^x при а<хиа>1>х при
а>х).
Далее, замечаем, что (на основании формулы F'))
/?(*) = О, F(a)-0.
Поэтому к функции F(t) применима теорема Ролля, и, следовательно,
существует такое значение f = ?, заключенное между а и х% при
котором F' (|) =0. Отсюда на основании соотношения (8) получаем

138 НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ [ГЛ. IV
откуда
Q = /(n+1)(i)-
Подставляя это выражение в формулу G), получаем
Я (Х) //?)
Это —так называемая форма Лагранжа для остаточного члена.
Так как ? заключено между л: и а, то его можно представить
в форме *)
где 9 —число, заключенное между 0 и 1, т.е. 0<9<1; тогда
формула остаточного члена примет вид
Формула
называется формулой Тейлора для функции /(х).
Если в формуле Тейлора положить а = 0, то она запишется
в виде
/М = /@)+уП0)+?г<^^
A0)
где 6 заключено между числами 0 и 1. Этот частный случай фор-
формулы Тейлора иногда называют формулой Маклорена.
§ 7. Разложение по формуле Тейлора функций ех9 sin*, cos*
1. Разложение функции f(x) — ex> Находя последова-
последовательные производные от f(x), получим
/(*) = **, f@)=l,
/dD^^e*, /Cn)@)=l.
Подставляя полученные выражения в формулу A0) § 6, будем
иметь
уЗ yjz y/j +1
— 4- + — 4*— eQx 0 <Г 9
*) См. конец § 2 настоящей главы.

РАЗЛОЖЕНИЕ ФУНКЦИЙ е*, sin я, cos ж
139
Если \х\ ^ 1, то, взяв п=8, получим оценку остаточного члена:
I
При х=1 получим формулу, позволяющую найти приближенное
значение числа е:
e=l , j I J« —4* 4-J-.
производя вычисления в десятичных дробях с шестью *) десятич-
десятичными знаками, а затем округляя результат до пяти десятичных
знаков, найдем
Здесь погрешность не превосходит числа -^ или 0,00001.
Отметим, что, каково бы ни было х, остаточный член
хп + 1
Кп (л+1)!. **
Действительно, так как Э< 1, то величина eQx при фиксиро-
фиксированном х ограничена (она меньше е* при х > 0 и меньше 1 при
Докажем, что, каково бы ни было фиксированное число х,
Действительно,
___
() при п-+оо.
(п+1)!
XXX
п Я+1Г
Если х — фиксированное число, то найдется такое целое поло-
положительное число N, что
Введем обозначение X^ = q\ тогда, заметив, что
можем написать при п — iV + 1, iV+2, iV + 3 и т.д.
| хп + 1
(л+1)!
потому что
=
X
т
X
X

X
т
X
X
X
п
I
N — 1
XXX
N —
-•q.q.
*Ч= (М-\м У"'
1x1-». I
¦) Иначе суммарная погрешность округления при расчетах может значи-
значительно превысить Rs (например, при количестве слагаемых, равном 10, эта
ошибка может достичь величины 5<10~5).

140 НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ [ГЛ. JV
Но величина (Л/_п| постоянная, т. е. не зависит от п, а д
стремится к нулю при п —>¦ оо. Поэтому
Следовательно, и Rn (х) =^е6х¦ *" { { —>0 при я—^оо.
Из предыдущего следует, что при любом я, взяв достаточное
число членов, мы можем вычислить ех с любой степенью точности.
2. Разложение функции /(A:) = siruc. Находим после-
последовательные производные от f(x) = sinx:
= cos* = sin (*+?), /' @) = 1,
/IV (x) - sinx = sin fx + 4 ?j , /IV @) = 0,
2 '
Подставляя полученные значения в формулу A0) § 6, получим
разложение функции /(jc) = sinA: по формуле Тейлора:
Так как sin (%+(n+l)^-) < I, то lira Rn(x) = 0 при всех
значениях #.
Применим полученную формулу для приближенного вычисле-
вычисления sin20°. Положим /2 = 3, т.е. ограничимся двумя первыми
членами разложения; sin20° = sin-5-^-5-—г(тг) =0,342. Оце-
9 ~ 9 3! V 9
ним сделанную погрешность, которая равна остаточному члену:
Следовательно, погрешность меньше 0,001, т.е. sin20° = 0,342 с
точностью до 0,001.
На рис. 97 даны графики функции f(x) = sinx и первых трех
приближений: S1(x) = x, S2(x) = x—-gy , S3(x)=x—"зТ + -5]-.

УПРАЖНЕНИЯ К ГЛАВЕ IV
141
3. Разложение функции f(x) = cos*. Находя значения
последовательных производных при # = 0 от функции f(x) = cosx
Рис. 97.
и подставляя в формулу Маклорена, получим разложение:
Хп+1
Здесь также lim Rn(x)=0 при всех значениях х.
Упражнения к главе IV
Проверить справедливость теоремы Ролля для функций:
1. у = х*—Зх + 2 на отрезке [1, 2]. 2. у = хг + Ъх2—6х на отрезке [0, 1].
3. у=(х—1) (я—2) (х—3) на отрезке [1, 3]. 4. y = sin2x на отрезке [0, я].
5. Функция f (x)=ixiJrx2—4л:—1 имеет корнями 1 и —1. Найти корень
производной /' {х), о котором говорится в теореме Ролля.
6. Проверить, что между корнями функции у= у х2 — Ъх + 6 находится
корень ее производной.
7. Проверить справедливость теоремы Ролля для функции y = cos2x на
отрезке [ — л/4, +я/4].
8. Функция у—\ — ух* обращается в нуль на концах отрезка [ —1,1].
Убедиться в том, что производная от этой функции нигде в интервале (—1, 1)
в нуль не обращается. Объяснить, почему здесь неприменима теорема Ролля.
9. Составить формулу Лагранжа для функции y = sinxna отрезке [лгх, х2].
Отв. sin х2—sin хг = (х2—хг) cos с, хг < с < х2.
10. Проверить справедливость формулы Лагранжа для функции у = 2х—х%
на отрезке [0, 1].

|42 НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ |ГЛ. IV
11. В какой точке касательная к кривой у = хп параллельна хорде, стя-
а
гивающей точки Мг (О, 0) и М2 (fl, fln)? Ome. В точке с абсциссой с— п_^-*
~V n
12. В какой точке касательная к кривой у — \пх параллельна корде,
стягивающей точки Л^О, 0) и М2 (е, 1)? Отв. В точке с абсциссой с=е—1,
Пользуясь теоремой Лагранжа, доказать неравенства: 13. ех^х1-{-х.
14. ln(l-f*) < х (х > 0). 15. №—ап < пЬп-1(Ь~а)ири b > а. 16. aretg#< x.
17. Написать формулу Коши для функций f(x)—x2, ф (х) = я3 на отрезке
II, 2] и найти с. Отв. с =14/9.
Вычислить следующие пределы:
у 1 1 рХ р — Х to1 V_.Y
18. lim 4т—т. Отв. —, 19. lim ^—A . Отв. 2. 20. lim ё
х-
ьл 4 ^* ' * ¦*»* • • *¦¦ ^ V Mill V ^^ * » i»w • •¦» * ^ ч^ v rf»«.»A<»
. 1 *" — 1 П x-+Q sm x л->0 ^~~
t 2. 21. lim — L Ome. -2. 22. lim sin
cosa: 1
— L Ome. -2. 22. lim
cosa:— 1 ^^o Y\— cosa;
не существует (|Л§ при *—>+(), — У~2 при л;—>—0). 23. lim ^?,
.-* 24. lim 5l=±l. Отв. \п±. 25. Iimf\ Ome,
8 л^»ол; & лг^о sin3 л: 6*
26. lim Sin^Sinfl. Orne, cosa. 27. lim еУ1+УУУ71, Ошв, 2.
28. lim ^+*5~* Ome' 4"* 29# lim ^+В# Ome* Т- 30' lim ^*(гДеЛ > 0)t
1пХ-±1
Отв.. 0. 31. lim —v . л ' . Отв. 1.32. lim ^-7-. Отв. —1. 33. lim -^-.
Отв. 0 при а > 0; оо при а^0. 34. lim ^i?2? Отв. 1. 35. Нт Jfsin3A!
Отв, I. 36. lim 1ПУ1*'. Отв, 1. 37. lim ln (лг"}^^ , Отв. 0.
0 lntg^A: ! j^
ё2л:
38. lim (l_*)tgi* O/iw. 1. 39. lim f-j^ L-l,
X
2€
40. lim
1
42. Ип
Ome, oo. 45. lim*1^. Ome. —, 46. lim \/"l*. Omet 1. 47. Urn f-IVе*.
X-+1 e 1-+00 r й:^0\ X J
Отв. 1. 48. limfl + —V. Ome, e«. 49, Hm (ctgxfi* Ф Отв. —«

УПРАЖНЕНИЯ К ГЛАВЕ IV 143
JL
50« lim (cos хJ . Отв, I. 51, lim ^ <р~/ • От, 6/~~ •
g
52. lim ftg iHL) . От, -L.
53. Разложить по степеням x—2 многочлен я4—5хв + 5х2+х-\-2, Oms.
_7(д:—2) —(д:—2J + 3(д:—2K + (д:—2L.
54. Разложить по степеням *+1 многочлен хъ-\-2х*-—х2+х+1.
От. (л:+1J + 2(л;+1K--3(л;+1L+(л;+1M.
55. Написать формулу Тейлора для функции у = ]/" х при а — 1, п = 3,
+ A)]~7/2, 0<8< 1.
56. Написать формулу Маклорена для функции у=У\-\- х при п—2,
от*. ут+;-1+±*-±*+щ1*^. о <е
57. Пользуясь результатами предыдущего примера, оценить погрешность
а:
приближенного равенства j/T+jc « 1 +-^ а:—- х2 при я=0,2.
Ошв. Меньше
2-103'
Выяснить происхождение приближенных равенств при небольших значе-
значениях х и оценить погрешность этих равенств:
58. In cosx «—1--^L-. 69.tgjc»jc+-j-+^|.. 60. arcsinx « ^+^"-
61. arctgAr^A:-.^.. 62. ' ^ » 1+-^-+^Г> 63-
^ ^ 6 '
Пользуясь формулой Тейлора, вычислить пределы выражений?
64. lim *-sln* , . Oms. I. 65. lim 'nMl+^-stn^ Ошв> Q
66. lim 2(«е*-у*)-*3 0 I „ и Г inf i+I)]. ош. 0.
68. lim C-L—^if). Ome, -L 69. lim f^~ctg'xV Ome, -|.

ГЛАВА V
ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
§ 1. Постановка задачи
Изучение количественной стороны различных явлений при-
природы приводится к установлению и изучению функциональной
зависимости между участвующими в данном явлении переменными
величинами. Если такую функциональную зависимость можно вы-
выразить аналитически, т. е. в виде одной или нескольких формул,
то мы получаем возможность исследовать эту функциональную
зависимость средствами математического анализа. Например, при
исследовании явления полета снаряда в пустоте получается фор-
формула, дающая зависимость дальности полета R от угла возвы-
возвышения а и начальной скорости vQ:
(g—ускорение силы тяжести).
Получив эту формулу, мы имеем возможность выяснить, при
каком а дальность R будет наибольшей, при каком—наименьшей,
каковы должны быть условия, чтобы при увеличении угла а
увеличивалась дальность и т. д.
Рассмотрим другой пример. В результате изучения колебания
груза на рессоре (вагон, автомобиль) получили формулу, показы-
показывающую, как отклонение у груза от положения равновесия зависит
от времени t: y = e~kt(A cos со? + ? sin со/). Величины &, Л, В, ш,
входящие в эту формулу, имеют вполне определенное значение
для данной колебательной системы (они зависят от упругости
рессоры, от величины груза и т. д., но не изменяются с тече-
течением времени t) и поэтому рассматриваются нами как постоянные.
На основании приведенной формулы можно выяснить, при
каких значениях t отклонение у увеличивается с увеличением t,
как меняется величина наибольшего отклонения в зависимости
от времени, при каких значениях t наблюдаются эти наибольшие
отклонения, при каких значениях t получаются наибольшие ско-
скорости движения груза и ряд других вопросов.

S 23 ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ 145
Все перечисленные вопросы входят в понятие «исследовать
поведение функции». Очевидно, выяснить все эти вопросы, вычисляя
значения функции в отдельных точках (подобно тому, как мы это
делали в гл. II), весьма затруднительно. Целью настоящей главы
является установление более общих приемов исследования пове-
поведения функций.
§ 2. Возрастание и убывание функции
В § 6 главы 1 было дано определение возрастающей и убы-
убывающей функций. Теперь мы применим понятие производной для
исследования возрастания и убывания функции.
Теорема. 1) Если функция f(x)y имеющая производную на
отрезке [а, 6], возрастает на этом отрезке, то ее производная
нд отрезке [а, Ь] не отрицательна, т. е. f (х)^0.
2) Если функция f (х) непрерывна на отрезке [а, Ь] и диффе-
дифференцируема в промежутке (а, Ь), причем f (х) > 0 для а < х < 6,
то эта функция возрастает на отрезке [а, Ь].
Доказательство. Докажем сначала первую часть теоремы.
Пусть / (х) возрастает на отрезке [ау Ь]. Придадим аргументу х
приращение Ах и рассмотрим отношение
Ах
Так как f(x) — функция возрастающая, то f(x + Ax) > f (x)
при Ах>0 и f(x + Ax)<f(x) при Ах<0.
В обоих случаях
*)-
Дл:
а следовательно,
lim L
Q
А*-* О АХ '
т. е. у (х) > 0, что и требовалось доказать. (Если бы было /' (х) < О,
то при достаточно малых значениях Ах отношение A) было бы
отрицательным, что противоречит соотношению B).)
Докажем теперь вторую часть теоремы. Пусть /' (х) > 0 при
всех значениях х, принадлежащих промежутку (a, fe).
Рассмотрим два любых значения xt и х2, хг < х2, принадле-
принадлежащих отрезку [а, &].
По теореме Лагранжа о конечных приращениях имеем
/ (Xj — f (Хг) = /' (!) (*,-*,), Xt < I < Х%.
По условию /' (I) > 0, следовательно, / (x2)—f (хг) > 0, а это и
значит, что f(x)—возрастающая функция.
Аналогичная теорема имеет место и для убывающей (дифферен-
(дифференцируемой) функции, а именно:

146
ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
[ГЛ. V
Если f (x) убывает на отрезке [а, 6], то f (х) ^0 на этом
отрезке. Если f (х) < 0 в промежутке (ayb)^mo f (x) убывает на
отрезке [а, 6]. (Конечно, мы и здесь предполагаем, что функция
непрерывна во всех точках отрезка [а, Ь] и дифференцируема
всюду на (а, &).)
Замечание. Доказанная тео-
теорема выражает следующий геометри-
геометрический факт. Если на отрезке [а, Ь\
функция f (х) возрастает, то каса-
касательная к кривой y = f(x) в каждой
точке на этом отрезке образует с осью
Ох острый угол ф или—в отдель-
отдельных точках — горизонтальна; тангенс
этого угла не отрицателен; /' (х) =я
— tgtp^O (рис. 98, а). Если фун-
функция / (х) убывает на отрезке [а, 6],
то угол наклона касательной—ту-
касательной—тупой (или—в отдельных точках —
касательная горизонтальна); тангенс этого угла не положителен
(рис. 98, б). Аналогично иллюстрируется и вторая часть теоремы.
Теорема позволяет судить о возрастании или убывании функции
по знаку ее производной.
Пример. Определить области возрастания и убывания функции
Рис. 99.
Решение. Производная равна у' =4х3; при х > 0 имеем у' > 0—функ>
ция возрастает; при х < 0 имеем у' < 0—функция убывает (рис, 99).
§ 3. Максимум и минимум функций
Определение максимума. Функция f(х) в точке xt
имеет максимум (maximum), если значение функции f(x) в точке
Xfi больше, чем ее значения во всех точках некоторого интервала,

§31
МАКСИМУМ И МИНИМУМ ФУНКЦИЙ
147
содержащего точку хг. Иначе говоря, функция f(x) имеет мак-
максимум при x = xlf если f (x± + Ax) < f (Xj) при любых Ах (поло-
(положительных и отрицательных), достаточно малых по абсолютной
величине*).
Так, например, функция y = f(x), график которой изображен
на рис. 100, имеет максимум при х=^хг.
Определение минимума. Функция / (х) имеет минимум
(minimum) при х = х2У если
f(x2 + Ax)>f(x2)
при любых Ах—как положительных, так и отрицательных,—«до-
отрицательных,—«достаточно малых по абсолютной величине (рис. 100).
Например, функция у = х\ рассмотренная в конце предыду-
предыдущего параграфа (см. рис. 99), при х = 0 имеет минимум, так как
у —0 при х = 0 и у > 0 при других значениях х.
9 j/T
Рис. 100.
Рис. 101.
В связи с определениями максимума и минимума следует
обратить внимание на следующие обстоятельства.
1. Функция, определенная на отрезке, может достигать мак-
максимума и минимума только при значениях ху заключенных
внутри рассматриваемого отрезка.
2. Не следует думать, что максимум и минимум функции яв-
являются соответственно ее наибольшим и наименьшим значениями
на рассматриваемом отрезке: в точке максимума функция имеет
наибольшее значение лишь по сравнению с теми значениями,
которые она имеет во всех точках, достаточно близких
к точке максимума, а в точке минимума—наименьшее значение
лишь по сравнению с теми значениями, которые она имеет во
всех точках, достаточно близких к точке минимума.
*) Иногда это определение формулируют так: функция / (х) имеет макси-
максимум в точке х1у если можно найти такую окрестность (а, р) точки хг (а <
< xi < Р)> что для всех точек этой окрестности, отличных от хи выполняется
неравенство f (х) < f {хг}.

148 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ [ГЛ. V
Так, на рис. 101 изображена функция, определенная на отрезке
[а, 6], которая
при х = хх и х = х3 имеет максимум,
при х = х2 и х = х4 имеет минимум,
но минимум функции при х = х4 больше максимума функции при
х = хг. При х=Ь значение функции больше любого максимума
функции на рассматриваемом отрезке.
Максимумы и минимумы функции называют экстремумами *)
или экстремальными значениями функции.
Экстремальные значения функции и их расположение на отрезке
[а, Ь\ в известной степени характеризуют изменение функции
в зависимости от изменения аргумента.
Ниже будет указан метод нахождения экстремальных значений.
Теорема 1 (необходимое условие существова-
существования экстремума). Если дифференцируемая функция y = f(x)
имеет в точке x = xt максимум или минимум, то ее производная
обращается в нуль в этой точке, т. е. f (х^) = Ъ.
Доказательство. Предположим для определенности, что
в точке x = Xi функция имеет максимум. Тогда при достаточно
малых по абсолютному значению приращениях Ах (Ах Ф 0) имеет
место /ta + AxX/ta), т. е. / (хх + Дх) -/(хх) < 0. Но в таком
случае знак отношения
Ах
определяется знаком Дх, а именно:
>0 при Д
<0 при А
Согласно определению производной имеем
r{Xi) = Hm
Ах -> 0 ах
Если f(x) имеет производную при х = х1у то предел, стоящий
справа, не зависит от того, как Дл: стремится к нулю (оставаясь
положительным или отрицательным).
Но если Ах—*0, оставаясь отрицательным, то /' (xJ^O.
Если же Дх—*0, оставаясь положительным, то /'(х^^О.
Так как f (хг) есть определенное число, не зависящее от спо-
способа стремления Дх к нулю, то два последних неравенства сов-
совместимы только в том случае, если /'(х^^О.
*) Extremum—крайний (лат.).

§3]
МАКСИМУМ И МИНИМУМ ФУНКЦИЙ
149
Аналогичным образом теорема доказывается и для случая
минимума функции.
Доказанной теореме соответствует следующий очевидный гео-
геометрический факт: если в точках максимума и минимума функция
f (х) имеет проиеводную, то касательная к кри-
кривой y — f(x) в этих точках параллельна оси Ох.
Действительно, из того, что f' (хг) = tg ф = О,
где ф —угол между касательной и осью Ох,
следует, что q> = 0 (рис. 100).
Из теоремы 1 непосредственно вытекает
следствие: если при всех рассматриваемых зна-
значениях аргумента х функция f (x) имеет произ-
производную, то она может иметь экстремум (мак-
(максимум или минимум) только при тех значе-
значениях, при которых производная обращается в
нуль. Обратное заключение неверно: не при вся-
всяком значении, при котором производная об-
обращается в нуль, обязательно существует мак-
максимум или минимум. Так, на рис. 100 изобра-
изображена функция, у которой при х = хг произ-
производная обращается в нуль (касательная гори-
горизонтальна), но в этой точке функция не имеет ни максимума,
ни минимума. Точно так же функция у = х3 (рис. 102) при х =
— 0 имеет производную, равную нулю:
Рис. 102.
но в этой точке функция не имеет ни максимума, ни минимума.
Действительно, как бы ни была близка точка х к точке О, всегда
х<0 и х3>0 при х>0.
X
Рис. 103.
Рис. 104.
Рис. 105.
Мы исследовали тот случай, когда функция во всех точках не-
некоторого отрезка имеет производную. Как же обстоит дело в тех
точках, где производная не существует? Мы покажем на примерах,
что в таких точках может быть или максимум, или минимум, но
может и не быть ни того, ни другого.
Пример 1. Функция у—\х\ не имеет производной в точке х=0
(в этой точке кривая не имеет опРеДеленной касательной), но в этой точке
данная функция имеет минимум: у = 0 при * = 0, тогда как для всякой точки х,
отличной от нуля, имеем у > 0 (рис. 103).

150 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ [ГЛ. V
Пример 2. Функция t/ = (l—*2/зK/2 не ИМеет производной при # = 0,
так как у'——A—л:2/3) 1/2дс-i/з обращается в бесконечность при #=0, но
в этой точке функция имеет максимум: f @) = 1, f (х) < 1 при х, отличном от
нуля (рис. 104).
Пример 3. Функция у—ух не имеет производной при х = 0(уг -»- оо
при х —>- 0). В этой точке функция не имеет ни максимума, ни минимума:
/ @) = 0; f(x)<0 для х < 0; / (х) > 0 для х > 0 (рис. 105).
Таким образом, функция может иметь экстремум лишь в двух
случаях: либо в тех точках, где производная существует и равна
нулю, либо в тех точках, где производная не существует.
Заметим, что если производная не существует в какой-либо
точке (но существует в близлежащих точках), то в этой точке
производная терпит разрыв.
Значения аргумента, при которых производная обращается
в нуль или терпит разрыв, называются критическими точками
или критическими значениями.
Из предыдущего следует, что не при всяком критическом зна-
значении функция имеет максимум или минимум. Однако, если в ка-
какой-либо точке функция достигает максимума или минимума, то
эта точка наверняка является критической. Поэтому для разыска-
разыскания экстремумов функции поступают следующим образом: находят
все критические точки, а затем, исследуя отдельно каждую крити-
критическую точку, выясняют, будет ли в этой точке максимум или
минимум функции или же не будет ни максимума, ни минимума.
Исследование функции в критических точках опирается на сле-
следующие теоремы.
Теорема 2 (достаточные условия существования
Экстремума). Пусть функция f (x) непрерывна в некотором ин-
интервале, содержащем критическую точку хь и дифференцируема
во всех точках этого интервала (кроме, быть может, самой
точки xj. Если при переходе слева направо через эту точку про-
производная меняет знак с плюса на минус, то при х~хг функция
имеет максимум. Если же при переходе через точку хг слева на-
направо производная меняет знак с минуса на плюс, то функция
имеет в этой точке минимум.
Таким образом,
если а) /' (х) > 0 при х < хг, f (х) < 0 при х > х19
то в точке Xf функция имеет максимум;
если б) /' (х) < 0 при х < Хц f (х) > 0 при х > хг,
то в точке хг функция имеет минимум. При этом надо иметь
в виду, что условия а) или б) должны выполняться для всех зна-
значений х, достаточно близких к хг, т. е. во всех точках некоторой
достаточно малой окрестности критической точки хг.
Доказательство. Предположим сначала, что производная
меняет знак с плюса на минус, т.е. что для всех ху достаточно

§3]
МАКСИМУМ И МИНИМУМ ФУНКЦИЙ
151
близких к точке х19 имеем
/' (х) > О при х < хи
Г (х) < 0 при л:> хг.
Применяя теорему Лагранжа к разности f (х)—/(#i), получим
где I—точка, лежащая между х и хг.
1) Пусть х < хг; тогда
и, следовательно,
или
f(x)-f(x1)<Ot
A)
2) Пусть х*> хг\ тогда
l>xi9 Г (?)< О, /'©М)<0
и, следовательно,
? /у\ f /Y \ ^ Л
/ \Л/ I \Л1/ "^ vl
ИЛИ
f (у\ ^ f (у \ (О\
I \Х/ ^ч / 1*1/ • \Z/
Соотношения A) и B) показывают, что для всех значений х,
достаточно близких к х1У значения функции меньше, чем значения
функции в точке хг. Следовательно, в точке xt функция f (х) имеет
максимум.
Аналогичным образом доказывается вторая часть теоремы о до-
достаточном условии минимума.
Рис. 106 наглядно иллюстрирует смысл теоремы 2.
Пусть в точке х = хх имеем /' (л^) =*
s=- 0 и для всех х, достаточно близ-
нера-
ких к
венства
/
/
точке
' (*> >
'(*х
Хг,
0
0
выполняются
при
при
х<хи
х~> хг.
я
Рис. J06.
Тогда при х < хг касательная к
кривой образует с осью Ох острый
угол—функция возрастает, а при х >
> хг касательная образует с осью Ох
тупой угол—функция убывает; при х = х± функция переходит от
возрастания к убыванию, т. е. имеет максимум.
Если в точке х2 имеем /' (х2) = 0 и для всех значений х% до-
достаточно близких к точке х2, выполняются неравенства
/'(*)< 0 при х<х2,
f (х) > 0 при х > хг%

152 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ [ГЛ. V
то при х < х2 касательная к кривой образует с осью Ох тупой
угол—функция убывает, а при х > х2 касательная к кривой об-
образует с осью Ох острый угол—функция возрастает. При х = х2
функция переходит от убывания к возрастанию, т. е. имеет ми-
минимум.
Если при х = лг3 имеем /' (х3) = 0и для всех значений к, доста-
достаточно близких к хЗУ выполняются неравенства
/' (а:) > 0 при х < *s,
/' (*) > 0 при х > *3,
то функция возрастает как при jc<jc3, так и при х>хв. Следо-
Следовательно, при х = х3 функция не имеет ни максимума, ни минимума.
Именно такой случай имеет место для функции y = xs при л;=--0.
Действительно, производная у' = Зл:2, следовательно,
t/'U = o = O, y'\x<o>Q, у'\х>о>О,
а это значит, что при х = 0 функция не имеет ни максимума, ни
минимума (см. выше рис. 102).
§ 4. Схема исследования дифференцируемой функции
на максимум и минимум с помощью первой производной
На основании предыдущего параграфа можно сформулировать
следующее правило для исследования дифференцируемой функции
на максимум и минимум:
1. Ищем первую производную функции, т.е. /' (х).
2. Находим критические значения аргумента х\ для этого:
а) приравниваем первую производную нулю и находим действи-
действительные корни полученного уравнения f (х) = 0;
б) находим значения х, при которых производная /' (х) терпит
разрыв.
3. Исследуем знак производной слева и справа от критической
точки. Так как знак производной остается постоянным в интервале
между двумя критическими точками, то для исследования знака
производной слева и справа, например-, от критической точки х2
(рис. 106) достаточно определить знак производной в точках а и E
(xt<a<A:2, #2 < Р <*з> гДе xi и *s — ближайшие критические
точки).
4. Вычисляем значение функции / (х) при каждом критическом
значении аргумента.
Таким образом, имеем следующее схематическое изображение
возможных случаев:

§4]
СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
153
Знаки производной f (x) при переходе через
критическую точку хх
х<хх ,
+
—
+
—
X = Xt
или разрывна
/'(*i)=0
или разрывна
f'(*i)=0
или разрывна
Г№)=0
или разрывна
х> xt
—
+
+
Характер критической точки
Точка максимума
Точка минимума
Нет ни максимума, ни мини-
минимума (функция возрастает)
Нет ни максимума, ни мини-
минимума (функция убывает)
Пример 1. Исследовать на максимум и минимум функцию
Решение. 1) Находим первую производную:
2) Находим действительные корни производной;
Следовательно,
Производная всюду непрерывна. Значит, других критических точек нет.
3) Исследуем критические значения и результаты исследования фиксиру-
фиксируем на рис. 107.
Исследуем первую критическую точку х±=\. Так как у'= (х— 1) (х~3),
то
при х < 1 имеем у' — (—)•( —) > 0;
при х > 1 имеем у' = (-f-)-(—) < 0,
Значит, при переходе (слева направо) через значение х1=\ производная
меняет знак с плюса на минус. Следовательно, при #=1 функция имеет мак-
максимум, а именно:
Исследуем вторую критическую точку х2 — 3:
при х < 3 имеем #' = (+)•(—) < 0;
при х > 3 имеем у' = (-{-).(+) > 0,

154
ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
|ГЛ. V
Значит, при переходе через значение # = 3 производная меняет знак
с минуса на плюс. Следовательно, при х = 3 функция имеет минимум, а именно;
</)* = з = 1.
На основании проведенного исследования строим график функции (рис. 107),
Пример 2, Исследовать на максимум и минимум функцию
*/=Ф-1) У7\
Решение. 1) Находим первую производную:
У - у *2 ^ о з/- — Q з/- •
3 у х 3 у х
2) Находим критические значения аргумента: а) находим точки, в кото-
которых производная обращается в нуль:
, 5х—2 _ 2
3 у х
б) находим точки, в которых производная тер-
терпит разрыв (в данном случае обращается в
Ф
Рис. 107. Рис. 108.
бесконечность), Такой точкой будет, очевидно, точка
(Отметим, что при #2 = 0 рассматриваемая функция определена и непрерывна.)
Других критических точек нет.
3) Исследуем характер полученных критических точек. Исследуем точку
#1 = 2/5. Заметив, что
У'\х<2;ь <°> У'\х>2/в >°»
заключаем, что при х = 2/5 функция имеет минумум. Значение функции в точке
минимума равно
Исследуем вторую критическую точку х — 0. Заметив, что
У'\х<о>°> У'\<Ь
заключаем, что при # = 0 функция имеет максимум^ причем
исследуемой функции изображен на рис. 108,
— в' График

§5J ИССЛЕДОВАНИЕ ФУНКЦИИ НА МАКСИМУМ И МИНИМУМ 155
§ 5.: Исследование функции на максимум и минимум
с помощью второй производной
Пусть при x = xt производная функции y = f(x) обращается
в нуль, т. е. /' (х±) = 0. Пусть, кроме того, вторая производная /" (х)
существует и непрерывна в некоторой окрестности точки xt. Тогда
справедлива следующая теорема.
Теорема. Пусть f (xJ^O; тогда при x = xt функция имеет
максимум, если /" (xj < 0, и минимум, если /" (хг) > 0.
Доказательство. Докажем сначала первую часть теоремы.
Пусть
f(H f()<0
Так как, по условию, /" (л:) непрерывна в некоторой окрестности
точки х = х1У то, очевидно, найдется некоторый малый отрезок, ок-
окружающий точку х = х19 во всех точках которого вторая производ-
производная fr(x) будет отрицательна.
Так как /" (*) есть первая производная от первой производной,
f (х) = (/' (л:))', то из условия (/' (х))' < 0 следует, что /' (*) убы-
убывает на отрезке, содержащем точку х = х± (§2). Но /:'(#i) = 0;
следовательно, на этом отрезке при х < xt имеем /' (х) > 0, а при
х > xt имеем f (х) < 0, т. е. производная /' (х) при переходе
через точку х = хг меняет знак с плюса на минус, а это значит,
что в точке х^ функция f(x) имеет максимум. Первая часть
теоремы доказана.
Аналогичным образом доказывается вторая часть теоремы, а
именно: если f (*i)>°> то /"(*)>° во всех точках некоторого
отрезка, окружающего точку х1У но тогда на этом отрезке /" (х) =s
= (f' (х)У > 0 и, следовательно, /' (х) возрастает. Так как /' (xj)=0,
то, значит, при переходе через точку xt производная /' (х) меняет
знак с минуса на плюс, т.е. функция f(x) имеет минимум при
X = Xi.
Если в критической точке Г(х1) = 0, то в этой точке может
быть или максимум, или минимум или не быть ни максимума, ни
минимума. В этом случае исследование нужно вести первым спосо-
способом (см. § 4).
Схему исследования экстремумов с помощью второй производ-
производной можно изобразить в следующей таблице:
0
0
0
Г to)
t
Характер критической
точки
Точка максимума
Точка минимума
Неизвестен
Пример 1, Исследовать на максимум и минимум функцию
у=2 sin дг-f-cos 2л:#

156 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ [ГЛ. V
Решение. Так как функция является периодической с периодом 2jt,
то достаточно исследовать функцию на отрезке [0, 2я].
1) Находим производную:
у' = 2 cos х—2 sin 2х = 2 (cos х—2 sin x cos х) = 2 cos * A —2 sin *).
2) Находим критические -значения аргумента:
2 cos л: A— 2sinx) = 0,
3) Находим вторую производную:
у" = — 2 sin х—4 cos 2х.
4) Исследуем характер каждой критической точки:
у" | х^т = —2.-1—4-у - — 3 < 0.
Следовательно, в точке *1 = я/6 имеем максимум:
1 _о ! . 1 - 3
^|л:=я/6 — ~2"~^Т~1Г#
Далее,
^"и=Я/2 = --
Следовательно, в точке #2 = я/2 имеем минимум:
В точке д;3 = 5я/6 имеем
44
Следовательно, при д:3 = 5я/6 функция имеет максимум:
i —о l _i_ 1 — 3
^|дг3=5я/6 ~ 7 ' ""*2'
Наконец,
0"изя/2 —2-(-1)-4-(-1)=6>
Следовательно, в точке л4 = Ззх/2 имеем минимум:
График исследуемой функции изображен на рис. 109.
Покажем, далее, на примерах, что если в некоторой точке х = х±
имеем /' (х^^О и f" (x1) = Q, то в этой точке функция f (х) может
иметь либо максимум, либо минимум, либо не иметь ни максимума,
ни минимума.
Пример 2. Исследовать на максимум и минимум функцию
i/= 1 —д:4.
Р еш-е н и е. 1) Находим критические точки:
#' = — 4*3, —4*3 = 0, * = 0.
2) Определяем знак второй производной при * = 0:

ИССЛЕДОВАНИЕ ФУНКЦИИ НА МАКСИМУМ И МИНИМУМ
167
Следовательно, выяснить характер критической точки с помощью знака вто-
второй производной в данном случае нельзя.
Рис. 109.
3) Исследуем характер критической точки первым способом (см. § 4):
У'\х<о >°> У'\х>о<°-
Следовательно, при х — 0 функция имеет максимум, а именно:
График рассмотренной функции изображен на рис. ПО,
№
о
Рис. ПО. Рис. ill. Рис. 112.
Пример 3. Исследовать на максимум и минимум функцию
Решение. По второму способу находим
Следовательно, второй способ ответа не дает. Прибегая к первому способув
получаем

158
ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
{ГЛ. V
Следовательно, при * = 0 функция имеет минимум (рис. Ш).
Пример 4. Исследовать на максимум и минимум функцию
Решение. Второй способ:
^'=3 (л:—IJ, 3(х-1J = 0, х=П
*Г = 6(*-1), y"\Xstl=0\
таким образом, второй способ ответа не дает. По первому способу находим
У'\х<1 >°> У'\х>\ >°-
Следовательно, при #=1 функция не имеет ни максимума, ни минимума
(рис. 112).
§ 6. Наибольшее и наименьшее значения функции на отрезке
Пусть функция y — f(x) непрерывна на отрезке [а, 6]. Тогда на
этом отрезке функция достигает наибольшего значения (см. § 10
гл. II). Будем предполагать, что на данном отрезке функция f(x)
имеет конечное число критических точек. Если наибольшее зна-
значение достигается внутри отрезка [а, 6], то оче-
очевидно, что это значение будет одним из максиму-
максимумов функции (если имеется несколько максиму-
максимумов), а именно, наибольшим максимумом. Но мо-
может случиться, что наибольшее значение будет
достигаться на одном из концов отрезка.
Итак, функция на отрезке [а, Ь] достигает сво-
его наибольшего значения либо на одном из кон-
цов этого отрезка, либо в такой внутренней точ-
точке этого отрезка, которая является точкой ма-
максимума. То же самое можно сказать и о наи-
наименьшем значении функции: оно достигается либо
на одном из концов данного отрезка, либо в такой
внутренней точке, которая является точкой мини-
минимума.
Из предыдущего вытекает следующее правило:
если требуется найти наибольшее значение не-
непрерывной функции на отрезке [а, Ь\ то надо:
1) найти все максимумы функции на отрезке;
2) определить значения функции на концах от-
отрезка, т.е. вычислить f(a) и /(&);
3) из всех полученных выше значений функ-
функции выбрать наибольшее; оно и будет представ-
представлять собой наибольшее значение функции на
отрезке.
Аналогичным образом следует поступать и при определе-
определении наименьшего значения функции на отрезке.

§7!
ПРИМЕНЕНИЕ ТЕОРИИ МАКСИМУМА И МИНИМУМА
159
Пример. Определить на отрезке [—3; 3/2] наибольшее и наименьшее
значения функции у~х?—Зя+З.
Решение. 1) Находим максимумы и минимумы функции на отрезке
[-3; 3/2]: г/' = 3л:2 — 3, Зх2—3 = 0, *i = l, *2 = —1, у" = 6х, тогда у"|ж = 1 =
= б > 0. Следовательно, в точке х=\ имеет место мунимум: g\XSii = l* Да*
лее, #"| ^-._i ==¦— б < 08 Следовательно, в точке #==—1 имеет место макси-
максимум: 0|*в_1=5.
2) Определяем значение функции на. концах отрезка: У\x=3/2 — ^/8j
д\ ^^з2"8—15. Таким образом, наибольшее значение рассматриваемой функ-
функции на отрезке [—3; 3/2] есть ?/ J дг=_ i = 5, а наименьшее значение есть
^1 ___3=—15. График рассматриваемой функции изображен на рис. 113.
§ 7. Применение теории максимума и минимума функций
к решению задач
С помощью теории максимума и минимума решаются многие за-
задачи геометрии, механики и т. д. Рассмотрим некоторые из таких
задач.
Задача 1. Дальность R — OA (рис. 114) полета ядра (в пустоте), выпу-
выпущенного с начальной скоростью v0 из
орудия, наклоненного под углом ф к
горизонту, определяется формулой
v\ sin 2ф
(g—ускорение силы тяжести). Опре-
Определить угол ф, при котором дальность
R будет наибольшей при данной на-
начальной скорости v0. Рис. 114,
Решение. Величина R пред-
представляет собой функцию переменного
угла ф. Исследуем эту функцию на максимум на отрезке
критическое значение ф = -т-;
sin 2ф
g
ф = л/4
—т<0-
Следовательно, при значении ф=п/4 дальность полета R имеет максимум
Значения функции R на концах отрезка [0; л/2] таковы:
Таким образом, найденный максимум и -есть искомое наибольшее зна-
значение Rt

160 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ [ГЛ. V
Задача 2. Какие размеры надо придать цилиндру, чтобы при данном
объеме v его полная поверхность S была наименьшей?
Решение. Обозначая через г радиус основания цилиндра и через h
высоту цилиндра, будем иметь 5 = 2яг2 + 2яг/г.
Так как объем цилиндра задан, по при данном г величина h определяется
формулой v — nr2hf откуда h=—s. Подставляя это выражение h в формулу
для S, получим 5==2дг2 + 2зхг-^2 , или S = 2 (пг2-{-~
Здесь v—заданное число. Таким образом, мы представили S как функцию
одной независимой переменной г.
Найдем наименьшее значение этой функции в промежутке 0 < г < оо:
dr2 r=rx
Следовательно, в точке г — гг функция S имеет минимум. Заметив, что
Jim S=oo и lim /?=оо, т. е. что при стремлении г к нулю или к беско-
Г -> О Г -*- 00
нечности поверхность S неограниченно возрастает, мы приходим к выводу,
что в точке r= ri функция S имеет наименьшее значение.
3 /** 3 /" " '
Но если г=~\/ -^— , то h=—2~^ 1/ -к— =2г. Таким образом, для
того чтобы при данном объеме v полная поверхность S цилиндра была наимень-
наименьшей, высота цилиндра должна равняться его диаметру.
§ 8. Исследование функции на максимум и минимум
с помощью формулы Тейлора
В § 5 было замечено, что если в некоторой точке х = а
имеем /'(а) = 0 и f (а) = 0, то в этой точке может быть либо ма-
максимум, либо минимум, либо нет ни того, ни другого. При этом
указывалось, что для решения вопроса в этом случае нужно ввести
исследование первым способом, т. е. путем исследования знака
первой производной слева и справа от точки х = а.
Теперь мы покажем, что можно в этом случае исследование
вести и с помощью формулы Тейлора, выведенной в § 6 гл. IV.
Для большей общности предположим, что не только /" (х), но
и все производные до n-го порядка включительно от функции / (л)
обращаются в нуль при х = а:
а
Предположим, далее, что f(x) имеет непрерывные производ-
производные до (п + 1)-го порядка включительно в окрестности точки х=а.

$ 8] ИССЛЕДОВАНИЕ ФУНКЦИИ НА МАКСИМУМ И МИНИМУМ 161
Напишем формулу Тейлора для f(x)y принимая во внимание
равенства A):
(УГЬ B)
где ^ —число, заключенное между а п х.
Так как /(w+1) (x) непрерывна в окрестности точки а .и f{n+1)(a)=^0,
то найдется такое малое положительное число /*, что при любом
х9 удовлетворяющем неравенству \х — a|</i, будет f{n+1) (х) фО.
При этом если /(/х+1) (а) > 0, то и во всех точках интервала
(a —ft, a + h) будет /(п+1) (#) > 0; если [{п+г) (а) < 0, то во всех
точках этого интервала будет f{n+1] (х) <0.
Перепишем формулу B) в виде
-/(а) =(^У>+»(|) B')
и рассмотрим различные частные случаи.
Первый случай, п нечетное.
а) Пусть /(и+1)(а)<0. Тогда найдется интервал (я — Л, а )
во всех точках которого (/г+1)-я производная отрицательна. Если
х есть точка этого интервала, то | тоже находится между а — h и
a + ft и, следовательно, fin+1) (g) < 0. Так как п +1 — четное число,
то (х — а)п+г > 0 при хфа, и поэтому правая часть в формуле
B') отрицательна.
Следовательно, при хфа во всех точках интервала (а —Л,
а + Л) имеем f(x) — f (a) <0, а это значит, что при л: = а функ-
функция имеет максимум.
б) Пусть f{n+1) (a) > 0. Тогда при достаточно малом значении h
во всех точках х интервала (а —Л, а + Л) имеет место /(»+1> (?)>0.
Следовательно, правая часть формулы B') будет положительна,
т.е. при хфа во всех точках указанного интервала будет
f(x)-f(a)>0,
а это значит, что при х — а функция имеет минимум.
Второй случай, п четное.
Тогда я+1 нечетное и величина (х — а)п+1 имеет разные знаки
при х<а и #> а.
Если ft достаточно мало по абсолютной величине, то (д+1)-я
производная во всех точках интервала (а — Л, a-\-h) сохраняет тот
же знак, что и в точке а. Следовательно, f(x) — f{a) имеет раз-
разные знаки при х<а и при х>а. Но это значит, что прил; = а
нет ни максимума, ни минимума.
Заметим, что если при п четном /<и+1) (а) > 0, то f(x)<f (a)
для х < а и / (х)> f(a) для х > а.
Если же при л четном f{n+1) (а) < 0, то /(#) > /(а) для л:<а
и / (*)< / (а) Для * > а.
Полученные результаты можно сформулировать следующим
образом.
6 Н. С. Пискунов, т. I

152 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ [ГЛ. V
Если при х = а имеем
/'(а) = Па)=„.=/<»Ча) = 0
и первая не обращающаяся в нуль производная /("+1) (а) есть про-
производная четного порядка, то в точке а
f(x) имеет максимум, если /(л+1)(а)<0;
/ (х) имеет минимум, если fin+ю (а) > 0.
Если же первая не обращающаяся в нуль производная /<«+« (a)
есть производная нечетного порядка, то в точке а функция
не имеет ни максимума, ни минимума. При этом
f(x) возрастает, если /(п+1)(#)>0;
f(x) убывает, если fin+1) (a) < 0.
Пример. Исследовать на максимум и минимум функцию
/ (х) = *4—4*3+6л:2 —4х+ 1.
Решение. Найдем критические значения функции
f (х) = 4х*— 1
Из уравнения 4 (х?—Зл:2 + 3л:—1) = 0 получаем единственную критическую
точку х = 1 (так как данное уравнение имеет лишь один действительный
корень).
Исследуем характер критической точки х=\:
f (х) = \2х2—24*+12=^0 при *=1,
р" (л:) = 24л;—24 =Х) при *=1,
/IV (л:) = 24 > 0 при любом х.
Следовательно, при лг=1 функция f (х) имеет минимум.
§ 9. Выпуклость и вогнутость кривой. Точки перегиба
Рассмотрим на плоскости кривую у = /(*), являющуюся графи-
графиком однозначной дифференцируемой функции f(x).
Определение 1 • Мы говорим, что кривая обращена выпукло-
выпуклостью вверх на интервале (а, Ь)у если все точки кривой лежат ни-
ниже любой ее касательной на этом
интервале.
Мы говорим, что кривая об-
обращена выпуклостью вниз на ин-
интервале (Ь, с), если все точки кри-
кривой лежат выше любой ее каса-
касательной на этом интервале.
Кривую, обращенную выпук-
"$ сТ лостью вверх, будем называть
выпуклой, а обращенную выпук-
Рис> П5# лостью вниз — вогнутой.
На рис. 115 показана кривая, выпуклая на интервале (а, Ь)
и вогнутая на интервале (Ь, с).

$9] ВЫПУКЛОСТЬ И ВОГНУТОСТЬ КРИВОЙ 163
Направление выпуклости кривой является важной характе*
ристикой ее формы. Настоящий параграф посвящен установлению
признаков, по которым можно было бы, исследуя функцию
y=zf(x), судить о направлении выпуклости ее графика на раз-
различных интервалах.
Докажем следующую теорему.
Теорема 1. Если во всех точках интервала (а, Ь) вторая
производная функции f(x) отрицательна, т.е. /"(#)< 0, то
кривая y — f{x) на этом интервале обращена выпуклостью вверх
(кривая выпукла).
Доказательство. Возьмем в интервале (а, Ь) произволь-
произвольную точку х=х0 (рис. 115) и проведем касательную к кривой
в точке с абсциссой х—х0. Теорема будет доказана, если мы
установим, что все точки кривой на интервале (а, Ь) лежат ниже
этой касательной, т.е. что ордината любой точки кривой y = f(x)
меньше ординаты у касательной при одном и том же значении х.
Уравнение кривой имеет вид
y = f(x). A)
Уравнение же касательной к кривой в точке x = xQ имеет ввд
или
» = /(*)+/'(*•)(*-*•). B)
Из уравнений A) и B) следует, что разность ординат кривой
и касательной при одном и том же значении х равна
0-У = /(*)-/(*о)-П*о)(*-*о)-
Применяя теорему Лагранжа к разности /(#) — /(х0), получим
У-У = Г (с) (х-**) -/' (*о) (х- *о)
(где с лежит между х0 и х), или
*/-# = [/'(<0-f (*о)](*-*о).
К выражению, стоящему в квадратных скобках, снова применяем
теорему Лагранжа; тогда
y-y = f"(Ci)(c-Xo)(x-xo) C)
(где Cf лежит между ^0 и с),
Рассмотрим сначала тот случай, когда лс>х0. В этом случае
*o<?i<c<*; так как х — хо>О, с — хо>О и так как, кроме
того^ по условию, /" (сг) < 0, то из равенства C) следует, что
У-У<О.
Рассмотрим теперь случай, когда х < #0. В этом случае #<е<
< Ci < х0 и х — xQ < 0, с — х0 < 0, а так как по условию /" (€г) <0,
то из равенства C) следует, что у — у <0.
6*

164
ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
[ГЛ. V
Таким образом, мы доказали, что любая точка кривой лежит
ниже касательной к кривой, каковы бы ни были значения х и х0
на интервале (а, Ь). А это и значит, что кривая выпукла. Теорема
доказана.
Аналогичным образом доказывается следующая теорема.
Теорема Г. Если во всех точках интервала (Ь> с) вторая
производная функции f(x) положительна, т.е. f (а:) > 0, то
О Ь *
Рис. 117.
с я
кривая y = f(x) на этом интервале обращена выпуклостью вниз
{кривая вогнута).
Замечание. Содержание теорем 1 и Г можно иллюстрировать
геометрически. Рассмотрим кривую y = f(x), обращенную выпук-
выпуклостью вверх на интервале (а, Ь) (рис. 116). Производная /' (х)
равна тангенсу угла а наклона касательной в точке с абсциссой
х, т. е. /' (х) = tg а. Поэтому /" (х) = [tg а];. Если /" (х) < 0 для
всех х на интервале (а, Ь), то это значит, что tg а убывает с возраста-
возрастанием х. Геометрически нагляден тот факт, что если tg а убывает
с возрастанием я, то соответствующая кривая выпукла. Анали-
Аналитическим доказательством этого факта и является теорема 1.
Подобным же образом иллюстрируется геометрически и тео-
теорема Г (рис. 117).
Пример 1. Установить интервалы выпуклости и вогнутости кривой,
заданной уравнением у —2—х2.
Решение. Вторая производная у"——2< 0 для всех значений х. Сле-
Следовательно, кривая всюду обращена выпуклостью вверх (рис. 118).
Пример 2. Кривая задана уравнением у = ех. Так как у" = ех >0 для
всех значений х} то, следовательно, кривая всюду вогнута, т. е. обращена
выпуклостью вниз (рис. 119).
Пример 3. Кривая определяется уравнением y = xz. Так как у" = 6х,
то у" < 0 при х < 0 и у" > 0 при х > 0. Следовательно, при х < 0 кривая
обращена выпуклостью вверх, а при х > 0 — выпуклостью вниз (рис. 120).
Определение 2. Точка, отделяющая выпуклую часть непре-
непрерывной кривой от вогнутой, называется точкой перегиба кривой.
На рис. 120, 121 и 122 точки О, Л и В суть точки перегиба.
Очевидно, дго в точке перегиба касательная, если она суще-
существует, пересекает кривую, так как с одной стороны от этой

§9]
ВЫПУКЛОСТЬ И ВОГНУТОСТЬ КРИВОЙ
165
точки кривая лежит под касательной, а с другой стороны —
над нею.
Установим теперь достаточные условия того, что данная точка
кривой является точкой перегиба.
Теорема 2. Пусть кривая определяется уравнением y — f(x).
Если f" (а) = 0 или /" (а) не существует и при переходе через
Рис. 118.
Рис. 120.
значение х = а производная f"(x) меняет знак, то точка кривой
с абсциссой х = а есть точка перегиба.
Доказательство. 1) Пусть /" (х) <0 при х < а и f" (х)>0
при х> а.
Тогда при х < а кривая обращена выпуклостью вверх и при
х > а — выпуклостью вниз. Следовательно, точка А кривой с абс-
абсциссой х = а есть точка перегиба (рис. 121).
УК
б)
х
Рис. 121.
2) Если Г(х)>0 при х<Ь и f" (х) <0 при х>Ьу то при
х<Ь кривая обращена выпуклостью вниз, а при л:> Ь—-выпук-
Ь—-выпуклостью вверх. Следовательно, точка В кривой с абсциссой х = Ь
есть точка перегиба (см. рис. 122).
Пример 4. Найти точки перегиба и определить интервалы выпуклости
и вогнутой кривой у = е~х2 (кривая Гаусса).

166
ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
[ГЛ. V
Решение. 1) .Находим первую и вторую производные:
у' = — 2хе~*г, уп = 2е-х* Bл:2 —1).
2) Первая и вторая производные существуют всюду. Находим значения дг,
при которых / = 0: 2е-*2Bх*—1) = 0, хг=~1/\Г2, х2=\/У2.
3) Исследуем полученные значения:
при х < —1/У" имеем у" > О,
при х > —1/У~2 имеем #" < 0;
вторая производная меняет знак при переходе через точку х±% следовательно,
при д:г=—lj/ на кривой имеется точка перегиба; ее координаты:
при х < \/У 2 имеем у" < 0,
при х > 1//"~2 имеем у" > 0.
Следовательно, при_дг2 = 1/уг 2 на кривой также имеется точка перегиба: ее
координаты: (Х/У 2, е~1/2). Впрочем, существование второй точки перегиба
вытекает непосредственно из симметрии кривой относительно оси Оу.
п
й)
в
Рис. 122.
4) Из предыдущего следует, что
при —<х> < х < — \/У 2 кривая вогнута,
при —1/У 2 < х < \/У 2 кривая выпукла,
при 1/}^1Г< х < + оо кривая вогнута.
5) Из выражения первой производной у' = — 2xe~*2 следует, что
у' > 0 при х < 0, т. е. функция возрастает,
#' < 0 при х > 0, т. е. функция убывает,
у' = 0 при я = 0.
В этой точке функция имеет максимум, а именно: у—\.
На основании проведенного исследования легко построить график кривой
(рис. 123).
Пример 5. Найти точки перегиба кривой у=х\
Решение. 1) Находим вторую производную: у"=\2х2.
2) Определяем точки, в которых yrf — 0: 12*2=0j л:=0#
3) Исследуем полученное значение х — 0:
у" > 0 при х < 0—кривая вогнута,
у" > 0 при х > 0—кривая вогнута.
Следовательно, кривая не имеет точек перегиба (рис. 124).

10]
АСИМПТОТЫ
Пример 6. Найти точки перегиба кривой у—(х—)
Решение. 1) Находим первую и вторую производные:
«/ — ^v*—ч t У —-—^\х—1)
2) Вторая производная нигде не обращается в нуль^ при
существует (*/"=± оо)«
= 1 она не
Рис. 123.
1У
5
Рис. 124. Рис. 125.
3) Исследуем значение *=ls
#" > 0 при х < 1—кривая вогнута,
у" < 0 при х > 1 — кривая выпукла.
Следовательно, при х=\ имеется точка перегиба; это—точка A;*0),
Заметим, что у' — <х> при *=1, т. е. кривая в этой точке имеет верти-
вертикальную касательную (рис. 125).
§ 10. Асимптоты
Очень часто приходится исследовать форму кривой y = f(x),
а значит, и характер изменения соответствующей функции при
неограниченном возрастании (по абсолютной величине)
абсциссы или ординаты переменной точки кривой или абсциссы
и ординаты одновременно. При этом важным частным случаем
является тот, когда исследуемая кривая при удалении ее пере-
переменной точки в бесконечность *) неограниченно приближается
к некоторой прямой.
*) Мы говорим, что переменная точка М движется по кривой в бесконеч*
ность, если расстояние этой точки от начала координат неограниченно воз-
возрастает.

168
ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
[ГЛ. V
Определение. Прямдя А называется асимптотой кривой,
если расстояние Ь от переменной точки М кривой до этой прямой
при удалении точки М в бесконечность стремится к нулю
(рис. 126 и 127).
Рис. 127.
Мы будем в дальнейшем различать асимптоты вертикальные
(т. е. параллельные оси ординат) и наклонные (т. е. не парал-
параллельные оси ординат).
1. Вертикальные асимптоты. Из определения асимптоты
следует, что если lim f(x) = oo, или lim f(x) = oo, или
lim/(#) = со, то прямая х = а
х-*-а
есть асимптота кривой у = f (x); и
обратно, если прямая х — а есть
асимптота, то выполняется одно из
написанных равенств.
Следовательно, для отыскания
"да" вертикальных асимптот нужно найти
такие значения х = а, при приближе-
приближении к которым функция y = f(x)
стремится к бесконечности. Тогда
прямая х = а будет вертикальной
асимптотой.
2
Рис. 128. Пример 1. Кривая у = = имеет
х—о
вертикальную асимптоту дг==5, так как
у—> оо при х—>-5 (рис. 128).
Пример 2. Кривая y=tgx имеет бесконечно много вертикальных асимп-
асимптот: х= ± я/2, х=± Зя/2, х— ± 5я/2, ... Это следует из того, что tg х —> оо,
когда х стремится к значениям я/2, Зя/2, 5я/2, ... или —я/2,—Зя/2, —5я/2,...
(рис. 129).
как lim
X ->+
р
e1/x
= е1/х
<x> (рис. 130).
Пример 3. Кривая у = е1/х имеет вертикальную асимптоту * = 0, так
1/
II. Наклонные асимптоты. Пусть кривая у = f (x) имеет
наклонную асимптоту, уравнение которой имеет вид
A)

НО]
АСИМПТОТЫ
169
Определим числа k и йм(рис. 131). Пусть М (х, у) —точка, лежащая
на кривой, и N (х, у) — точка, лежащая на асимптоте. Длина
2
5jv
2
Рис. 129.
1
—^^
0
Рис. 130.
Рис. 131.
отрезка МР равна расстоянию от точки М до асимптоты. По усло-
условию
lim MP = 0. B)
Если обозначим через ф угол наклона к оси Ох, то из {\NNIP
найдем
cosq)
Так как <р — постоянный угол (не равный я/2), то в силу преды-
предыдущего равенства
lim ЛГМ = 0, B')
и наоборот, из равенства B') следует равенство B). Но

170 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ ?ГЛ. V
и равенство B') принимает вид
lim [/(*)--Л*-61 = 0. C)
Х-* +00
Итак, если прямая A) есть асимптота, то выполняется равенство
C), наоборот, если при постоянных ft и & выполняется равенство
C), то прямая y = kx + b есть асимптота. Определим теперь ft и
&. Вынося х за скобки в равенстве C), получаем:
Нт
Так как х—* + оо, то должно выполняться равенство
Km
При Ь постоянном lim -- = 0. Следовательно, lim U-^—ft =0,
?-> 00 X JC->+00 L * J
ИЛИ
^. D)
Зная ft, из равенства (З) находим b:
b = lim [/ (x) — kx]. E)
Итак, если прямая y = kx-\-b есть асимптота, то ft и & находятся
по формулам D) и E). Обратно, если существуют пределы D) и E),
то выполняется равенство C) и прямая у = kx+b есть асимптота.
Если хотя бы один из пределов D) или E) не существует, то
кривая асимптоты не имеет.
Заметим, что мы проводили исследование применительно
к рис. 131 при х—»• + °°> но все рассуждения справедливы и для
случая х —>• — оо.
Пример 4. Найти асимптоты кривой
У х
Решение. 1) Ищем вертикальные асимптотыз
у—>+°° ПРИ х—>—0s
у—*—оо при х—> +0.
Следовательно, прямая л- = 0 есть вертикальная асимптота данной кривой.
2) Ищем наклонные асимптоты:
л- У л- х2 + 2х— 1 ,. Г, . 2 11,
= lim ~= 1ш —i—o ^= lim 1-J % =i,

ОБЩИЙ ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИЙ
171
т. е. Л = 1,
Ь= lira [у—*] =
lim
—Х- X =: lim -
X J x -*±oo L
— 1— л:2
1= lim [2-11=2,
J Х-*±оо L Х Л
i. e. 6 = 2.
Следовательно, прямая у = х-\-2 есть наклонная асимптота данной кривой.
Для исследования взаимного расположения кривой и асимптоты рассмот-
рассмотрим разность ординат кривой и асимп-
юты при одном и том же значении х: 1у
При х > 0 эта разность отрицательна, а
при # < 0—положительна; следователь-
следовательно, при х > 0 кривая лежит ниже
асимптоты, при х < 0—выше асимптоты
(рис. 132).
Пример 5. Найти асимптоты кри-
кривой y—e~xsinx+x.
Решение. 1) Вертикальных асимп-
асимптот, очевидно, нет.
2) Ищем наклонные асимптоты:
е~х sinx-^-x
k= lim —= lim
lim
X
г~х sin х
= lim [e-^
+¦]-
= lim e~xsinx =
Рис. 132.
Следовательно, прямая у = х есть наклонная асимптота при х—>+<».
Заданная кривая не имеет асимптоты при х—> — оо. Действительно,
lim ~ не существует, так как i- = -—sinx+1.
^_>-оо Jf л; л;
(Здесь первое слагаемое неограниченно возрастает при х—>—оо и, сле-
следовательно, предела не имеет.)
§11. Общий план исследования функций
и построения графиков
Под «исследованием функции» обычно понимается разыскание:
1) естественной области существования функции;
2) точек разрыва функции;
3) интервалов возрастания и убывания функции;
4) точек максимума и минимума, а также максимальных и
минимальных значений функции;
5) областей выпуклости и вогнутости графика, точек перегиба;
6) асимптот графика функции.

172 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ [ГЛ. V
На основании проведенного исследования строится график
функции (иногда целесообразно намечать элементы графика па-
параллельно с исследованием).
Замечание 1. Если исследуемая функция у — f (x) четная,
т. е. такая, что при изменении знака аргумента значение функции
не изменяется, т. е. если
то достаточно исследовать функцию и построить ее график при
положительных значениях аргумента, принадлежащих области
определения функции. При отрицательных значениях аргумента
график функции строится на том оснований, что график четной
функции симметричен относительно оси ординат.
Пример 1. Функция у = х2 четная, так как (—хJ = х2 (см. рис. 5).
Пример 2. Функция y = cosx четная, так как cos (—х) = cos л (см.
рис. 16).
Замечание 2. Если функция y = f(x) нечетная, т. е. та-
такая, что при изменении аргумента функция меняет знак, т. е.
если
f(-x)=-f(x),
то эту функцию достаточно исследовать при положительных зна-
значениях аргумента. График нечетной функции симметричен отно-
относительно начала координат.
Пример 3. Функция у = х* нечетная, так как (—хK= —х3 (см. рис. 7).
Пример 4. Функция y = sinx нечетная, так как sin (—#)=—sin*
(см. рис. 15).
Замечание 3. Так как знание одних свойств функции
позволяет сделать вывод о других ее свойствах, то иногда поря-
порядок исследования целесообразно выбирать, исходя из конкретных
особенностей данной функции. Так, например, если мы выяснили,
что заданная функция непрерывна и дифференцируема, и нашли
точки максимума и минимума этой функции, то тем самым мы
уже определили и области возрастания и убывания функции.
X
Пример 5. Исследовать функцию у= 1 2 и построить ее график.
Решение. 1) Область существования функции — интервал— со < х <
< + оо. Сразу отметим, что при х < 0 имеем у < 0, а при х > 0 имеем у > 0.
2) Функция всюду непрерывна.
3) Исследуем функцию на максимум и минимум: из равенства
1 v2
У A+*2J
находим критические точки: х± =—1, дг2=1. Исследуем характер критических
точек:
при х < — 1 имеем у' < 0;
при х > — 1 имеем у' > 0.

§ 119 ОБЩИЙ ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИЙ
Следовательно, при х =—1 функция имеет минимум:
Ут\п=У\х=-1~—0,5.
Далее,
при х < 1 имеем у' > 0;
при х > 1 имеем у' < 0.
Следовательно, при х=\ функция имеет максимум;
173
4) Определим области возрастания и убывания функции:
при —оо < х <—1 имеем у' < 0—функция убывает,
при —1 < х < 1 имеем у* > 0—функция возрастает,
при 1 < х < + °° имеем у* < 0—функция убывает.
5) Определим области выпуклости и вогнутости кривой и точки перегиба:
из равенства
У
)
получаем
Х\ = ^ О, Х% "i Хз =
Исследуя у" как функцию от х, находим
при —оо < х < —Уз у" < 0 — кривая выпуклая,
при —УЗ < х < 0 у" > 0—кривая вогнутая,
при 0 < х < У #" < 0—кривая выпуклая,
при УЗ < х < + оо г/'; > 0—кривая вогнутая.
Следовательно, точка с координатами х——У 3, у— — У 3/4 есть точка пе-
перегиба; точно так же точки @, 0) и (]/^3, 1^3/4) суть точки перегиба.
6) Определим асимптоты кривой:
при х—>-{-оо у—^0,
при х—>-—оо у—>().
Следовательно, прямая у —0 есть единственная наклонная асимптота.
Вертикальных асимптот кривая не имеет, так как ни для одного конеч-
конечного значения х функция не стремится к бесконечности.
График исследуемой кривой изображен на рис. 133.
Пример 6. Исследовать функцию у=\/2ах2—х3 (а > 0) и построить
ее график.

174
ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
[ГЛ. V
Р"е ш е н и е. 1) Функция определена при всех значениях х.
2) Функция всюду непрерывна.
3) Исследуем функцию на максимум и минимум:
4ах—3х2
4а—Зх
зУBах*~
Bа —х)*
Производная существует всюду, за исключением точек хг = 0 и х2 — 2а.
Исследуем предельные значения производной при х—*¦—0 и при х+()
4а—Зх
•т =— оо, lim
4а—Зх
'2а—xf
при х < О будет у' < О, при х > О будет #' > О.
Следовательно, при я = О функция имеет минимум. Значение функции в
этой точке равно нулю.
Исследуем теперь функцию в другой критической точке х2 — 2а. При
х—*2а производная также стремится к бесконечности. Однако в данном слу-
случае для всех значений х, близких к 2а (находящихся как справа, так и
слева от точки 2а), производная отрицательна. Следовательно, в этой точке
функция не имеет ни максимума, ни минимума. В точке х2 = 2а, так же как
и вблизи этой точки, функция убывает; касательная к кривой в этой точке
вертикальна.
При * = 4а/3 производная обращается в нуль. Исследуем характер этой
критической точки. Рассматривая выражение первой производной, замечаем,
что при х < 4а/3 будет у' > О, при х > 4а/3 будет у' < 0.
2 з /—
Следовательно, при #=4а/3 функция имеет максимум: #max=-g-а ]/4.
4) На основании проведенного исследования получаем области возрастания
и убывания функции:
при — оо < х < 0 функция убывает^
при 0 < х < 4а/3 функция возрастает,
при 4а/3 < х < + оо функция убывает.
5) Определяем области выпуклос-
выпуклости и вогнутости кривой и точки пере-
перегиба: вторая производная
ни в одной точке не обращается в
нуль. Однако существуют две точки,
в которых вторая производная терпит
разрыв: это точки
Хг = 0 и х2 = 2а>
Рис. 134.
Исследуем знак второй производ-
производной вблизи каждой из этих точек:
при х < 0 имеем у" < 0—кривая обращена выпуклостью вверх;
при х > 0 имеем у? < 0—кривая обращена выпуклостью вверх.
Значит, точка с абсциссой #=0 не является точкой перегиба.
При х <2а имеем у" < 0—кривая обращена выпуклостью вверх; при
X > 2а имеем уп >0—кривая обращена выпуклостью вниз, Значит, точка
Bа; 0) на кривой является точкой перегиба.

§I2J ИССЛЕДОВАНИЕ КРИВЫХ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ 175
6) Определяем асимптоты кривой:
У 1- х/ЪахЪ—х* _.
k— lim — = lim - = lim
#->±:oo X АГ-*;±оо X X
6 = lim [^5*=?+,] = lim
*-±0° х^±
Следовательно, прямая
2a
есть наклонная асимптота кривой у = у 2ахг—х3, График исследуемой функ-
функции изображен на рис. 134,
§ 12. Исследование кривых, заданных параметрически
Пусть кривая задана параметрическими уравнениями
(О
В этом случае исследование и построение кривой проводятся ана-
аналогично тому, как это было сделано для кривой, заданной уравне-
уравнением
y = f(x).
Вычисляем производные
3? = <P'W. ! = *'«. B)
Для тех точек кривой, вблизи которвис кривая является графиком
некоторой функции y = f(x)y вычисляем производную
dx ~~ ср' @ • 1°/
Находим значения параметра t = tti t2, . •., tk> при которых хотя
бы одна из производных <р' (t) или ф' (t) обращается в нуль или
терпит разрыв. (Такие значения t мы будем называть критиче-
критическими значениями.) По формуле C) в каждом из интервалов (tlf t2),
(t2i t3), ..., (tk^b h)> a следовательно, и в каждом из интерва-
интервалов (хь дг2), (л*2, х3), ..., (хк„и xk) (где а:. = ф(^.)) определяем
знак j-, тем самым определяем области возрастания и убывания.
Это дает также возможность определить характер точек, соответ-
соответствующих значениям параметра tb t2> ..., tk. Далее, вычисляем
dx2 [ф'@]3 ' ^ '
На основании этой формулы определяем направление выпуклости
кривой в каждой точке.
Для нахождения асимптот находим такие значения ty при при-
приближений к которым или х, или у стремятся к бесконечности, и

176
ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
[ГЛ. V
такие значения t, при приближении к которыми х, и устре-
устремятся к бесконечности. Затем производим исследование обычным
способом.
Некоторые особенности, появляющиеся при исследовании кри-
кривых, заданных параметрически, выясним на примерах.
Пример 1, Исследовать кривую, заданную уравнениями
x=acosst, y = asindt (a > 0).
0')
Решение. Величины х и у определены для всех значений t. Но так
как функции cos3 t и sin3 t периодические с периодом 2я, достаточно рассмот-
рассмотреть изменение параметра / в пределах от 0 до 2я; при этом областью изме-
изменения х будет отрезок [—а, а] и областью изменения у будет отрезок [—а, а].
Следовательно, рассматриваемая кривая асимптот не имеет. Далее, находим
:?= -Заcos2 *sin/, 7 =
d7 а/
B')
Эти производные обращаются в нуль при / = 0, я/2, я, Зя/2, 2я. Определяем
dy _ За sin2/cos / __ ,
d* —За cos2 tsint
Ha основании формул B'), (Зг) составляем следующую таблицу:
C')
Область изменения
t
0 < / < я/2
я/2 < / < я
п < t < Зя/2
Зя/2 < t < 2я
Соответствующая
область изменения х
а > х > 0
0>*>—а
—а < х < 0
0< х < а
Соответствую-
Соответствующая область из-
изменения у
0 < у < а
а > у > 0
0 > у>—а
—а<у <0
Знак
dy
dx
+
+
Характер
изменения у
как функции
от x(y=f (х))
Убывает
Возрастает
Убывает
Возрастает
Из таблицы следует, что уравнения (Г) определяют две непрерывные
функции вида y = f(x) при (Х;^^я будет у^О (см. две первые строчки
таблицы), при я«^/«?^2я будет у^О (см. две носледние строчки таблицы).
Из формулы C') следует:
dy
-. dy
и lim -f = oo.
В этих точках касательная к кривой вертикальна. Далее, находим:
dy
dt
-0 ^
/=о~ ' dt
=0, 4t
=0.
В этих точках касательная к кривой горизонтальна. Затем находим:
_
dx2 За cos4 t sin t'

§12] ИССЛЕДОВАНИЕ КРИВЫХ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
Отсюда следует:
d2y
-pi > О при О < t < п — кривая вогнута,
d2y
^2 < О ПРИ п < t < 2я—кривая выпукла.
J77
На основании результатов исследования можем построить кривую (рис. 135).
Эта кривая называется астроидой.
Рис. 135.
Пример 2. Построить кривую, заданную уравнениями (декартов
лист)
3at
3at2
О")
Решение. Обе функции определены при всех значениях tt кроме
i = — 1, при этом
lim х = lim
3at
- + ОО,
За/2
lim у= lim t , == —оо;
l + Z3
Заметим, далее, что
lira x— — оо, lim #=+oo#
i o /i o
x = 0, г/ = 0 при * = 0,
^с—->О, г/—>0 при t—>+oo,
х—>, г/—^0 при t—>¦—оо.
Найдем g и §:
/ 1
6a f -.— t
dx__ V 2
dt~~~ A + /3J
d/'
B")

178 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ [ГЛ. V
Для параметра t получаем следующие четыре критических значениям
. « « sv / ^ л & / С\
Далее, находим
dy
dy_dt_
dx" dx'
dt
C")
На основании формул (Iй), B"), C") составляем таблицу!
Область изменения
t
— 00 < t <—1
— 1 < t<0
0 < t < l/j/2
X/l/2 < t< У2
V2<t< + «>
Соответствующая
область изменения
X
0<*<+oo
— oo < x< 0
0 < x < а УА
аУ^>х>аУ2
aj/2 >^>0
Соответствующая
область изменения
У
0 ^ у ^ — оо
+ °° > # > 0
0 < у < a v^2
а V^4 > |/ > 0
Знак
dy
"die
—
+
—
+
Характер
изменения д
как функции
от х
Убывает
Убывает
Возрастает
Убывает
Возрастает
Из формулы C") находим;
dy
dx
= 0, dJ
/=о dx
= oo.
Следовательно, начало координат кривая пересекает дважды: с касательной,
параллельной оси Ох, и с касательной, параллельной оси Оу.
Далее,
|=оо при ^=^ (х-ауТ, ,=
В этой точке касательная к кривой вертикальна.
В этой точке касательная к кривой горизонтальна. Исследуем вопрос о суще*
сгвовании асимптоты:
k= lim — =г lira
b= lim (у—kx)~ lim
3at
Л- пгт+F

УПРАЖНЕНИЯ К ГЛАВЕ V
179
Следовательно, прямая у = —х—а является асимптотой ветви кривой при
х—^ + оо.
Аналогичным образом найдем:
= lim ^-=—1,
#-»- — ОО X
lrm (y—
a.
Таким образом, найденная прямая является асимптотой и для ветви кривой
при х—*—оо#
Рис. 136.
На основании проведенного исследования строим кривую (рис. 136).
Некоторые вопросы, связанные с исследованием кривых, будут дополни-
дополнительно рассмотрены в главе VIII, § 19 «Особые точки кривой».
Упражнения к главе V
Найти экстремумы функций:
1. у==х2—2х+3. Отв.
= 2 при х=1. 2. у=-~~—
о
x=~ при *=
\п=\ при * =
= — 22 при х =
0 5 *
3. у=^х2—
4. у = —
. 0тв9
Отв.
x=W при дс=1, ут\п = — 22 при х = Ь. 4. у = — х4 + 2х2. Отв. #тах=1
при jc=± 1, ут\п = ® при л==0. 5. у = х*—8х2 + 2. Отв. утах = 2 при. Jt=O,
^mifl =—14 при х= ± 2. 6. у = Зхъ—\25х3+2Шх. Отв. Максимум при #=—4
и jc = 3, минимум при х——3 и х~4. 7, у = 2—(х—1J^3. Отв. #шах = 2 при
х~\. 8. у — 3—2(д:+1I^3. Отв. Нет ни максимума, ни минимума. 9. «/ =
= J^^ О/тгв. Минимум при ^="^2, максимум при
а ^
/х 2) C х) 12
10. у=- -$ • Отв< Максимум при х~-^>. II. у =
Минимум при х = jt-. 12. у=-—. Отв. ут\п = е при х-=е. 13, y =
** in х
е~х* Отв.
+ (—ж/2 <; x^ я/2). Ome. #max=}/*2 при jt=ji/4. 14. ^ = si»2x—x
(—л/2^х^п/2). Отв. Максимум при дс=-Я'/6, минимум при х=—я/6.
15. y = x-\-tg х. Отв. Нет ни максимума, ни минимума. 16. y — exsinx. Отв.
максиму ри 2Ы\—?П. 17.
Минимум при x—2kn—j-, максимум при х — 2Ы-\—?П. 17. у = х*—2х2-\-2.
Отв. Максимум при .?=0; два минимума при я=—1 и при #=h 18. г/ =

ISO ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ [ГЛ. V
*=(* — 2KB*+1). Отв. i/mm«-8.24 ПРИ л:=1/8. 19. у=х+—. Отв. Мини-
Минимум при жг= 1; максимум при х = — 1. 20. у=х2 (а—хJ. Отв.
при х = а/2; ут[п = 0 при * = 0 и при х = а. 21. у=Д-+^—^. Отв. Макси-
Максимум при #=-—г ; минимум при л:=—г-^. 22. у = х+У\—х. Отв. утлх^=Ь/4
при * = 3/4; ут-т = 1 при *=1. 23. у=хУ"\—х (*<1). Отв. Утах—-^ j/ -j
2 х
при д;=г^". 24. у—т-;—а- О/Пб- Минимум при х =—1; максимум при *=1.
25. у=д:1пд:. Отв. Минимум при х=\/е. 26. у —л; In2 л;. Отв. утах = 4е~ при
х = в~2, t/min = 0 nPH х=\. 27. */ = 1пл;—arctgA;. Отв. Функция возрастает.
28. y—sin3x—3sin*. Отв. Минимум при х=п/2; максимум при х = Зп/2.
29. у = 2*+arctgA;. Отв. Нет экстремумов. 30._у = sinxcos2x. Отв. Минимум
при х=п/2; два максимума: при ^ = arccosyr2/3 и при * = arccos (—]/*2/3).
31. y = arcsin (sinл:). Отв. Максимум при х=Dт-{-\)я/2; минимум при
D + 3)/2
( + )/
Найти наибольшие и наименьшие значения функции на указанных от-
отрезках:
32. у = —Зл:44-6л:2—1 (—2*^*^2). Отв. Наибольшее значение у=2 при
х=± 1, наименьшее у = — 25 при х=± 2. 33.^=-^—2л:2 + Зд:+1 (—1^д;^5).
о
Отв. Наибольшее значение у = 23/3 при* = 5, наименьшее значение у=—13/3
при х=—1. 34. y=g; 1 @^д:^4). Отв. Наибольшее значение (/ = 3/5 при
х = 4, наименьшее значение у =—1 при *=0. 35. у = sin 2х—х (—л/2<;л:<;л;/2).
Отв. Наибольшее значение у = п/2 при х = — я/2, наименьшее значение
у = —я/2 при х=п/2.
36. Из квадратного жестяного листа со стороной а желают сделать откры-
открытый сверху ящик возможно большего объема, вырезая равные квадраты по
углам, удаляя их и затем загибая жесть, чтобы образовать бока ящика. Какова
должна быть длина стороны вырезаемых квадратов? Отв. а/6.
37. Доказать, что из всех прямоугольников, которые могут быть вписаны
в данный круг, наибольшую площадь имеет квадрат. Показать также, что
у квадрата и периметр будет наибольший.
38. Показать, что из всех равнобедренных треугольников, вписанных
в данный круг, наибольший периметр имеет равносторонний треугольник.
39. Найти прямоугольный треугольник наибольшей площади, имеющий
гипотенузой отрезок h. Отв. Длина каждого катета равна Л/]/" 2.
40. Найти высоту прямого цилиндра с наибольшим объемом, который
может быть вписан в шар радиуса R. Отв. Высота равна 2R/Y^ 3.
41. Найти высоту прямого цилиндра с наибольшей боковой поверхностью,
который может быть вписан в данный шар радиуса R, Отв% Высота равна
42. Найти высоту прямого конуса с наименьшим объемом, описанного
около данного шара радиуса Rt Отв, Высота равна 4R (объем конуса равен
двум объемам шара).
43. Резервуар, который должен иметь квадратное дно и быть открытым
сверху, нужно выложить внутри свинцом. Каковы должны быть размеры ре-
резервуара емкостью 32 л, чтобы выкладка требовала наименьшего количества
свинца? Отв. Высота 0,2 м, сторона основания 0,4 м (т. е. сторона основания
должна быть вдвое больше высоты).
44. Кровельщик желает сделать открытый желоб наибольшей вместимости,
у которого дно и бока были бы шириной 10 см и бока были бы одина-

УПРАЖНЕНИЯ К ГЛАВЕ V 181
ково наклонены ко дну. Какова должна быть ширина желоба наверху?
Отв. 20 см.
45. Доказать, что конический шатер данной вместимости требует наимень-
наименьшего количества материи, когда его высота в У 2 раза больше радиуса ос-
основания.
46. Требуется изготовить цилиндр, открытый сверху, стенки и дно которого
имеют данную толщину. Каковы должны быть размеры цилиндра, чтобы при
данной вместимости на него пошло наименьшее количество материала? Отв.
Если R—внутренний радиус основания, v—внутренний объем цилиндра, то
47. Требуется построить котел, состоящий из цилиндра, завершенного
двумя полусферами, со стенками постоянной толщины так, чтобы при данном
объеме v он имел наименьшую наружную поверхность. Отв. Котел должен
иметь форму шара с внутренним радиусом R = у^Зи/Ап.
48. Построить равнобочную трапецию, которая при данной площади 5
имела бы наименьший периметр; угол при основании трапеции равен а. Отв.
Длина боковой стороны равна ys/sin a.
49. Вписать в данный шар радиуса R правильную^треугольную призму
наибольшего объема. Отв. Высота призмы равна 2R/y 3.
50. Около полушара радиуса R требуется описать конус наименьшего
объема; плоскость основания конуса совпадает с плоскостью основания полу-
полушара; найти высоту конуса. Отв. Высота конуса равна R^~ 3.
51. Описать около данного цилиндра радиуса г прямой конус наимень-
наименьшего объема, полагая, что плоскости и центры круговых оснований цилиндра
и конуса совпадают. Отв. Радиус основания конуса равен Зг/2.
52. Из листа, имеющего форму круга радиуса R, вырезать такой сектор,
чтобы, свернув его, получить воронку наибольшей вместимости. Отв. Цент-
Центральный угол сектора равен 2яуг2/3.
53. Из всех круглых цилиндров, вписанных в данный куб с ребром а
таким образом, что оси их совпадают с диагональю куба, а окружности ос-
оснований касаются его граней, найти наибольшей по объему. Отв. Высота
цилиндра равна аУ 3/3; радиус основания равен а/У 6.
54. В прямоугольной системе координат дана точка (х0, y0), лежащая
в первом квадранте. Провести через эту точку прямую так, чтобы она обра-
образовала с положительными направлениями осей координат треугольник наи-
наименьшей площади. Отв. Прямая отсекает на осях отрезки 2х0 и 2у0, т. е.
имеет уравнение ^L-fJ^ = 1.
55. На оси параболы у2 = 2рх дана точка на расстоянии а от вершины;
найти абсциссу ближайшей к ней точки кривой. Отв. х — а—р.
56. Принимая, что прочность бруска с прямоугольным поперечным сече-
сечением прямо пропорциональна ширине и кубу высоты, найти ширину бруска
наибольшей прочности, который можно вырезать из бревна диаметром 16см.
Отв. Ширина равна 8 см.
57. Миноносец стоит на якоре в 9 км от ближайшей точки берега; с мино-
миноносца надо послать гонца в военный лагерь, расположенный в 15 км, считая
по берегу от ближайшей к миноносцу точки берега. Если гонец может делать
пешком по 5 км в час, а на веслах по 4 км в час, то в каком пункте берега
он должен пристать, чтобы поспеть в лагерь в кратчайшее время. Отв. В Зкм
от лагеря.
58. Точка перемещается прямолинейно по плоскости в среде, расположен-
расположенной вне линии MN со скоростью vlt а по линии MN со скоростью v2. По
какому пути она переместится в наименьший промежуток времени из точки Л
в точку В, расположенную на линии MN? Расстояние точки Л от линии MN
равно h, расстояние проекции а точки А на линию MN от В равно а.

J82 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ [ГЛ. V
Отв. Если ABC—путь точки, то -^z^^L При ^в^~- и аС = аВ при
ЛКл V2 АО U2
аВ vt
AB<F2*
59. Груз с массой w подымают рычагом, причем сила F приложена к од-
одному концу, а точка опоры находится на другом конце рычага. Если груз
привешен к точке, находящейся на расстоянии а см от точки опоры, а масса
стержня рычага равна it на каждый сантиметр длины, то какова должна
быть длина рычага, чтобы сила, потребная для поднятия груза, была наи-
наименьшая? Отв. x=Y^2aw/vcM.
60. При п измерениях неизвестной величины х получены числа:
къ *2> •••> *«• Показать, что сумма Квадратов погрешностей (#—#iJ+
+(*—*2>а+•••+(*—хпJ будет наименьшей, если за х принять число
(xi+x2+...+xn)/n.
61. Чтобы по возможности уменьшить трение жидкости о стенки канала,
площадь, смачиваемая водой, должна быть возможно меньшей. Показать, что
лучшей формой открытого прямоугольного канала с заданной площадью попе-
поперечного сечения является такая, при которой ширина канала вдвое превышает
его высоту.
Определить точки перегиба и интервалы выпуклости и вогнутости кривых:
62. у=хъ. Отв. При х < 0 кривая выпукла; при х > 0 кривая вогнута;
при #=0 точка перегиба. 63. у=\—х2.0тв. Кривая всюду выпукла. 64. у =
= я3—За:2—9*+9. Отв. При х=\ точка перегиба. 65. y = (x—bf. Отв.
При х=Ь точка перегиба. 66. у—_х*. Отв. Кривая всюду вогнута. 67. t/ =
= (^2_|_ 1)—-хж Отв. При х=± 1/У точки перегиба. 68. y=tgx. Отв. При
х=пп точки перегиба. 69. у = хе~х. Отв. При х=2 точка перегиба. 70. # =
=а—yfx—b. Отв. При х ==Ь точка перегиба. 71. у = а— ^/(л:—ЬJ. Отв. Кри-
Кривая не имеет точек перегиба.
Найти асимптоты следующих кривых:
12-y^jni- Отв* *=1; У=о- 73- ^==(^+2)^ • Отв' х==—2> У=°-
а? -
74. у = с+(х __ЬJ- Отв. х=Ь, у = с. 75. у=ех —\.0me. *=0; у=0. 76. у = in x.
Отв. *=0. 77. 1? = &х2+х?. Отв. у=х+2. 78. y* = a?—x*. Отв. у+х=0.
79- У2^2а^хт Ош% х==2а- 80- У2(х—2а) = х?^а3. Отв. х = 2а;
2ах
у=±(х+а).
Исследовать функции и построить их графики:
81. #=**-2*+10. 82. у=-**--вю. у = е~~. 84. У=^~^. 85. у =
«i±i. 86. y^-pl-.gl. y«i±?. 88. У=^гх. 89. у« = *з^. 90. у =
93. у=
95. ^ = Л~^2. 96. ^ = д:—1п(д:+-1). 97. #=1п(*2+1). 98. ^ = sin3A:. 99. у =*
= x-\-sinx. 100* у^дгвшл:. 101. y=e"-xsinx. Ш2. f/ = In sin л:. 103. y=z —.
104. (?. 105. /* = J 106. ^i!"810?; 107.
ly^^ \^ = Л \y = a(l —cos/).

УПРАЖНЕНИЯ К ГЛАВЕ V
Дополнительные задачи
Найти асимптоты линий:
х2 4-1
108. у=г / * 0/п*- *=—1; */ = *—К Ю9. 2/=
+
110. 2у(х+\)* = **. Отв. лг=—1; y=-gx— 1. III. */3 = а3—А Ош, Асимп-
Асимптот нет. 112. ?/ = e-2^sin^. О/ш. # = 0. ИЗ. у=е~х $\п2х+х* Отв. у = х.
114. у = х\п(е-\—) . Отв. х= ; у = х-]—. 115. у = хе:л\ Отв. х = 0;
\ х j e e
= х. 116. x=j°Ш y±X
Исследовать функции и построить их графики:
117. y = \xl 118. у=Ы\х\. 119. у*=х3—х. 120. у=(х+ Ц2 (х—2),
121. У = х+\х\. 122. у=уЛ*—х. 123. y = x2V7+l. 124. yssHjL — lnx.
125. |/=^1пл:. 126. ^-^^-j. 127. ^=^=|^. 528. у = х+™. П9.у=х1пх.
130. у = е*—х. 131. i/ = | sin Злг |. 132. у=;?Н1?. JS3. y^xardg х. 134. // =
= х—2arctgAr. 135. t/ = e-2^sin3A:. 136. ^=|sinx| + Jt. 137. y = sin(x2),
138- |/=cos3^ + sin3A:. 139. ya=-?±!±L. 140. ^f= ^~ ^ ! . 141. |/ =

ГЛАВА VI
КРИВИЗНА КРИВОЙ
§ 1. Длина дуги и ее производная
Пусть дуга кривой М0М (рис. 137) есть график функции y — f(x),
определенной на интервале (а, Ь). Определим длину дуги кривой.
Возьмем на кривой АВ точки Мо, М19 М2, ..., Af/wl, Mh ...
..., Mn-i, M. Соединив взятые точки отрезками, получим ломаную
линию М0М±М^... Mi^M; ... Мп_1М9
вписанную в дугу М0М. Обозначим
длину этой ломаной через Рп.
Длиной дуги М0М называется пре-
предел (обозначим его через s), к которо-
которому стремится длина ломаной при стре-
стремлении к нулю наибольшей из длин
Рис. 137. отрезков ломаной М^М,-, если этот
предел существует и не зависит от вы-
выбора точек ломаной М0МгМ2 .. ,MimmlMt. ¦. МЯ_1Л1.
Отметим, что это определение длины дуги произвольной кри-
кривой аналогично определению длины окружности.
В главе XII будет доказано, что если на отрезке [а, Ь] функ-
функция / (х) и ее производная /' (х) непрерывны, то дуга кривой
y=:f(x)t заключенная между точками [а; /(а)] и [6; /(&)], имеет
вполне определенную длину, причем будет указан способ вычис-
вычисления этой длины. Там же будет установлено (как следствие),
что в указанных условиях отношение длины любой дуги этой
кривой к длине стягивающей ее хорды стремится к 1, когда длина
хорды стремится к 0:
им я я
lim
m JS?L
MQM-+0 MqM
Эта теорема легко может быть доказана для окружности *), однако
в общем случае мы пока примем ее без доказательства.
*) Рассмотрим дугу АВ, центральный угол которой равен 2а (рис. 138).
Длина этой дуги равна 2Ra (R — радиус окружности), а длина стягивающей
ее хорды равна 2R sin а. Поэтому
дл. АВ 2Ra
lim ===== lim „г;—:—= U
а-*0дл. АВ «->O^sma

§11
ДЛИНА ДУГИ И ЕЕ ПРОИЗВОДНАЯ
185
Рассмотрим следующий вопрос. Пусть мы имеем на плоскости
кривую, заданную уравнением y = f(x). Пусть М0(х09 у0) —
некоторая фиксированная точка кривой, а М(ху у) — переменная
точка этой кривой. Обозначим через s длину дуги М0М (рис. 139).
При изменении абсциссы х точки М длина s дуги будет ме-
меняться, т. е. s есть функция х. Найдем производную s по х.
R
Рис. 138.
1
0
4
1
Xq
f
а
М
их
At/
а
а?
' х+Дя
Рис. 139.
Дадим х приращение Ал:. Тогда дуга s получит приращение
А5 = дл. ММг. Пусть ММг — хорда, стягивающая эту дугу. Для
того чтобы найти lim д—, поступим следующим образом: из
Д MMXQ находим ММ±2 = (Ал;J + (АуJ. Умножим и разделим
левую часть на As2:
Разделим все члены равенства на Дх2:
что lim
Ах
Найдем предел левой и правой частей при Ал; -
ММл Л л» Aw dy
—jr-i- = 1 и что lim -f-z=-f получим
As л v . n Ал: ах * J
0. Учитывая,
Для дифференциала дуги получим следующее выражение:
B)
ИЛИ*)
ds=V dx2 + dy2. B')
*) Строго говоря, формула B') верна лишь для того случая, когда dx > 0.
Если же dx < 0, то ds = — Vdx2-j-dy^. Поэтому в общем случае эту формулу
правильнее записать так:

186
КРИВИЗНА КРИВОЙ
liyi. vi
Мы получили выражение дифференциала длины дуги для того
случая, когда кривая задана уравнением y = f(x). Однако фор-
формула B') сохраняется и в том случае, когда кривая задана па-
параметрическими уравнениями. Если кривая задана параметри-
параметрически:
то
= ty' (t)dt,
и выражение B') принимает вид
§ 2. Кривизна
Одним из элементов, характеризующих форму кривой, является
степень ее искривленности.
Пусть мы имеем кривую, которая не пересекает самое себя
и имеет определенную касательную в каждой точке. Проведем
касательные к кривой в каких-нибудь двух ее точках А и В и
обозначим через а угол, образованный этими касательными, или —
точнее—угол поворота касательной при переходе от точки А
к точке В (рис. 140). Этот угол называется углом смежности
дуги АВ. У двух дуг, имеющих одинаковую длину, больше изо-
изогнута та дуга, у которой угол смежности больше (рис. 140 и 141).
Рис. 140.
Рис. 341.
С другой стороны, рассматривая дуги различной длины, мы
не можем оценить степень их искривленности только соответ-
соответствующим углом смежности. Отсюда следует, что полной харак-
характеристикой изогнутости кривой будет отношение угла смежно-
смежности к длине соответствующей дуги.
Определение 1. Средней кривизной /Сср дуги АВ называется
отношение соответствующего угла смежности а к длине дуги:
АВ

§3]
ВЫЧИСЛЕНИЕ КРИВИЗНЫ
187
Для одной и той же кривой средняя кривизна ее различных
частей (дуг) может быть различной; так, например,jym кривой,
показанной на рис. 142, средняя кривизна дуги АВ не равна
средней кривизне дуги АгВ1Ч хотя длины этих дуг равны между
собой. Более того, вблизи различных точек кривая искривлена
по-разному. Для того чтобы охарактеризовать степень искривлен-
искривленности данной линии в непосредственной близости к данной точке Л,
введем понятие кривизны кривой в данной точке.
Рис. 142.
Рис. 143.
Определение 2. Кривизной /Сд линии в данной точке А
называется предел средней кривизны дуги АВ, когда длина этой
дуги стремится к нулю (т. е. когда точка В приближается *)
к точке А)\
В^А Р АВ-+0 АВ
Пример. Для окружности радиуса г: 1) определить среднюю кривизну
дуги АВ, соответствующей центральному углу а (рис. 143); 2) определить
кривизну в точке А. ^
Решение. 1) Очевидно, что угол смежности дуги АВ равен а, длина
дуги равна аг. Следовательно, /ССр=— » или /Сср = —•
2) Кривизна в точке А равна К~ Нт —=—.
а -> о осг г
Таким образом, средняя кривизна дуги окружности радиуса г не зависит
от длины и положения дуги, для всех дуг она равна 1/г. Кривизна окруж-
окружности в любой ее точке также не зависит от выбора этой точки и равна 1/г.
Замечание. Отметим, что для произвольной кривой кривизна
в различных ее точках, вообще говоря, будет различная. Это мы
увидим ниже.
§ 3. Вычисление кривизны
Выведем формулу для вычисления кривизны данной линии
в любой ее точке М(х, у). При этом мы будем предполагать, что
кривая задана в декартовой системе координат уравнением
*) Мы предполагаем, что величина предела не зависит от того, с какой
стороны от точки А мы берем переменную точку В на кривой.

кривизна кривой
[ГЛ. VI
вида
V = f{x) A)
и что функция f(x) имеет непрерывную вторую производную.
Проведем касательные к кривой в точках М и Мх с абсцис-
абсциссами х и х+Ал: и обозначим через ф и ф + Аф углы наклона
этих касательных (рис. 144).
Длину дуги М0М, отсчитываемую отмнекоторой ^постоянной точ-
точки Мо, обозначим через s; тогда As = М0Мг—М0М, a |As|=AiM1.
Как непосредственно видно из
рис. 144, угол смежности, соответст-
соответствующий дуге ММ1У равен абсолют-
абсолютной величине*) разности углов ф и
Ф + Аф, т. е. равен |Аф|.
Согласно определению средней
кривизны кривой на участке MMt
имеем
К
Л^~ |As| ""As •
Чтобы получить кривизну в
точке М, нужно найти предел по-
полученного выражения при условии, что длина дуги ММг стре-
стремится к нулю:
К= lim
As-
Аф
As
Так как величины ф и s обе зависят от х (являются функ-
функциями от х), то, следовательно, ф можно рассматривать как функ-
функцию от s. Мы можем считать, что эта функция задана парамет-
параметрически с помощью параметра х. Тогда
ds
и, следовательно,
Is
B)
Для вычисления ~ используем формулу дифференцирования
ds
функции, заданной параметрически:
d(p
7
ds_
dx
dy
ds
*) Для кривой, изображенной на рис. 144, очевидно, что |Аф| = Аф, так
как Аф > 0.

§31 ВЫЧИСЛЕНИЕ КРИВИЗНЫ 189
Чтобы выразить производную -^ через функцию y=f(x), за-
, du
мечаем, что tg ф = ^ и, следовательно,
Ф-arctgg.
Дифференцируя по х последнее равенство, будем иметь
d2y
dq>dx2
ds
Что же касается производной -т-, то еще в § 1 мы нашли
s
dx
Поэтому
d*y
dx2
d(p
ds
ц
ix
is
ix
Ж
, окончательно
dx2 1
dx2
получаем
C)
Следовательно, в любой точке кривой, где существует и не-
d2u
прерывна вторая производная -^ , можно вычислить кривизну.
Для ее вычисления служит формула C). Заметим, что при вычис-
вычислении кривизны кривой следует брать только арифметическое (т. е.
положительное) значение корня в знаменателе, так как кривизна
линии по определению не может быть отрицательной.
Пример 1. Определить кривизну параболы у2 = 2рх:
а) в ее произвольной точке М (х, у);
б) в точке Mi @, 0);
в) в точке М2 (р/2, р).
Решение. Находим первую и вторую производные функции у—
dy __ р d2y __

190 КРИВИЗНА КРИВОЙ |ГЛ. VI
Подставляя полученные выражения в формулу C), получим
Пример 2. Определить кривизну прямой у—ах-\-Ъ в ее произвольной
точке (х, у).
Решение. i/'=a, у" = 0. Обращаясь к формуле C), получаем К = 0.
Таким образом, прямая представляет собой «линию нулевой кривизны». Этот
же результат легко можно получить непосредственно из определения кривизны.
§ 4. Вычисление кривизны линии, заданной параметрически
Пусть кривая задана параметрически: x = (p(t), y = >ty(t). Тогда
(см. § 24 гл. III)
dx~~ q/ @ ' dx2 ~~ (ф'K
Подставляя полученные выражения в формулу C) предыду-
предыдущего параграфа, получаем
К-
Пример. Определить кривизну циклоиды
x = a(t—-sin /)« 0=-аA— cos 0
в ее произвольной точке (х, у).
Решение.
dx /ч ,ч d2x . , dy
^-=аA— cos 0» -^-=flsm/ ^r
Подставляя полученные выражения в формулу A), находим
_|a(I—cos /) a cos ^—a sin t*asin t \ ___ \o.ost—
~" ?3 A 02+2i203/2 "~23/2<l
1
§ 5* Вычисление кривизны линии, заданной уравнением
в полярных координатах
Пусть кривая задана уравнением вида
Р = /(в). A)
Напишем формулы перехода от полярных координат к декартовым:
B)

§51
ВЫЧИСЛЕНИЕ КРИВИЗНЫ ЛИНИИ
191
Если в эти формулы подставить вместо р его выражение через
9, т. е. /F), то получим:
y=f(Q)sine. C)
Последние уравнения можно рассматривать как параметриче-
параметрические уравнения кривой A), причем параметром является 0,
Тогда
Подставляя последние выражения в формулу A) предыдущего
параграфа, получаем формулу для вычисления кривизны кривой
в полярных координатах:
Пример. Определить кривизну спирали Архимеда р = я0 (а > 0) в про-
произвольной точке (рис. 145).
Рис. 145.
Решение. -т^=®
^=0. Следовательно,
Заметим, что при больших значениях 0 имеют место приближенные равен-
А2_1-2 62-1- 1
ства: ц "^ &\t T яу 1| поэтомуf заменяя в предыдущей формуле
02+2 на б2 и 92+1 на 0% получаем приближенную формулу (для больших
значений 0);
к „ 1
Таким образом-, при: больших значениях 0 спираль Архимеда имеет при-
приблизительно ту же кривизну^ что и окружность радиуса ад.

192
кривизна кривой
[ГЛ. VI
§ 6. Радиус и круг кривизны. Центр кривизны*
Эволюта и эвольвента
Определение. Величина R, обратная кривизне К линии
в данной точке М, называется радиусом кривизны этой линии
в рассматриваемой точке:
R = Щ, A)
или
г> __
ЫШ)
3/2
B)
dx*
Построим в точке М нормаль к кривой (рис. 146), направлен-
направленную в сторону вогнутости кривой, и отложим на этой нормали
отрезок МС, равный радиусу R кривизны кривой в точке М.
д
Рис. 146.
Точка С называется центром кривизны данной кривой в точке М,
круг радиуса R с центром в точке С (проходящий через точку М)
называется кругом кривизны данной кривой в точке М.
Из определения круга кривизны следует, что в данной точке
кривизна кривой и кривизна круга кривизны равны между собой.
Выведем формулы, определяющие координаты центра кривизны.
Пусть кривая задана уравнением
?/ —/W- (о)
Зафиксируем на кривой точку М (х, у) и определим коорди-
координаты аир центра кривизны, соответствующего этой точке (рис. 147).
Для этого напишем уравнение нормали к кривой в точке М:
у fJ L/Y у\ (д\
(Здесь X и Y—текущие координаты точки нормали.)

§ 6] РАДИУС И КРУГ КРИВИЗНЫ, ЭВОЛЮТА И ЭВОЛЬВЕНТА 193
Так как точка С (а, р) лежит на нормали, то ее координаты
должны удовлетворять уравнению D):
Р-у = -у(*-х). E)
Далее, точка С (а, р) находится от точки М(х, у) на расстоя-
расстоянии, равном радиусу кривизны R:
(a—x)* + (P-y)* = R*. F)
Решая совместно уравнения E) и F), определим а и |5:
отсюда
ИЛ_у2\/
а так как R = ' а„.'—, то
Чтобы решить вопрос о том, верхние или нижние знаки сле-
следует брать в последних формулах, нужно рассмотреть случай
/>0и случай у" <0. Если у" > 0, то в этой точке кривая
вогнута и, следовательно, Р > у (рис. 147) и поэтому следует
брать нижние знаки. Учитывая, что в этом случае |#"| = у", фор-
формулы координат центра запишем в следующем виде:
a=x_?i^, P=H-i±A G)
Аналогично можно показать, что формулы G) будут справедливы
и в случае у" <0.
Если кривая задана параметрическими уравнениями
то координаты центра кривизны легко получить из формул G),
подставляя в них вместо у' и у" их выражения через параметр:
xt xt
Тогда
а=х У'(х'2+У'2) р_ | х'(х'* + у'*)
Пример 1. Определить координаты центра кривизны параболы
У2=2рх
а) в произвольной точке М (х, у); б) в точке MQ @,0); в) в точке Afj (р/2, р).
7 Н. С. Пискунов, т. 1

194
КРИВИЗНА КРИВОЙ
[ГЛ. VI
Решение. Подставляя значения ~ и -т-т в формулы G), получим
(рис. 148)
а) а = 3х+р, Р = — /_ ¦; б) при х =
V Р
находим а = р, Р = 0; в) при
х = р/2 имеем а = 5/?/2, 8 = — р.
Если в точке М±{х, у) данной линии кривизна отлична от
нуля, то этой точке соответствует вполне определенный центр
кривизны С1(а1 р). Совокупность всех
центров кривизны данной линии обра-
образует некоторую новую линию, называе-
называемую эволютой по отношению к пер-
первой.
Ш
4 .
Рис. 148. Рис. 149.
Таким образом, геометрическое место центров кривизны дан-
данной линии называется ее эволютой. По отношению к своей эволюте
данная линия называется эвольвентой или инволютой (или раз-
разверткой) .
Если данная кривая определяется уравнением y = f(x), то
уравнения G) можно рассматривать как параметрические урав-
уравнения эволюты с параметром х. Исключая из этих уравнений
параметр х (если это возможно), получим непосредственную за-
зависимость между текущими координатами эволюты а и р. Если
же кривая задана параметрическими уравнениями х=ф (f), y=ty (t),
то уравнения G') дают параметрические уравнения эволюты (так
как величины х> у, х\ у', х\ у" являются функциями от t).
Пример 2. Найти уравнение эволюты параболы у2 = 2рх.
Решение. На основании примера 1 имеем для любой точки (#, у) па-
BхK^2
раболы а = Зх-\-р, C=—¦ ;_ . Исключая из этих уравнений параметр х,
8 ГР
получим р2=г-=-(а — рK. Это—уравнение полукубической параболы (рис. 149).
Пример 3. Найти уравнение эволюты эллипса, заданного параметри-
параметрическими уравнениями * = acos?, y = bsint.
Решение. Вычисляем производные от х и у по t\
' f ' bt
y
х"— — a cos t% y" — —

§61
РАДИУС И .КРУГ КРИВИЗНЫ, ЭВОЛЮТА И ЭВОЛЬВЕНТА
195
Подставляя выражения производных в формулы G'), получим
_ Ь cos t (a2 sin2t + b* cos2 t) _
a — ccos absin2 t+ab cos21 ~~*
Таким образом,
Аналогично получаем:
= a cos f —a cos ^ sin2 ^ cos3^=;[ a—— ] cos3 t.
— cos31.
P= U~ sin3/.
Исключив параметр /, получаем уравнение эволюты эллипса в виде
\ b J \a J \ аЬ 1
Здесь а и Р—текущие кооординаты эволюты (рис. 150).
Пример 4. Найти параметрические уравнения эволюты циклоиды
x — a(t — sin t)t
Решение.
x' = a(\—cos/), у'—asin t,
x" — asintt y" —a cost.
Подставив полученные выражения в
формулу G'), находим
Р = — a(l— cost).
Сделаем преобразование переменных,
положив
а = ?—яа, Р==г]—2д, / = т—я;
тогда уравнения эволюты примут вид
1=:а(т—sinx),
p
они определяют в координатах g, r\
циклоиду с тем же производящим
кругом радиуса а. Таким образом, эволютой циклоиды является такая же
циклоида, но смещенная по оси Ох на величину—па и по оси Оу на
величину—2а (рис. 151).
"К
2а \
\ >
s
yS*— 0
/
(
U па—э-
У
>IPtd крива
г
Рис. 151.

195 кривизна кривой [гл. vi
§ 7. Свойства эволюты
Теорема 1. Нормаль к данной кривой является касатель-
касательной к ее эволюте.
Доказательство. Угловой коэффициент касательной к эво-
эволюте, определяемой параметрическими уравнениями G) предыду-
предыдущего параграфа, равен
d^
сф_ dx
da da
"dx
Заметив, что (в силу тех же уравнений G))
da~ ъ*Гу'*-уГу'"-у'*у'"- 1*ъу'у''г-у'"-у'гу'" /П
7"" 7* у у"* * К}
dx~~ у"* 9 К)
получаем соотношение
d$_ 1_
da ~~ у' '
Но у' есть угловой коэффициент касательной к кривой в соот-
соответствующей точке, поэтому из полученного соотношения следует,
что касательная к кривой и касательная к ее эволюте в соот-
соответствующей точке взаимно перпендикулярны, т. е. нормаль
к кривой является касательной к эволюте.
Теорема 2. Если на некотором участке МгМ2 кривой радиус
кривизны изменяется монотонно (т. е. либо только возрастает,
либо только убывает), то приращение длины дуги эволюты на
этом участке кривой равно (по абсолютной величине) соответ-
соответствующему приращению радиуса кривизны данной кривой.
Доказательство. На основании формулы B') § 1 имеем
где ds — дифференциал длины дуги эволюты; отсюда
( ds у __ (day. /dfi \2
Подставляя сюда выражения A) и B), получим

§ 7J СВОЙСТВА ЭВОЛЮТЫ ]97
Найдем, далее, (-^Л . Так как
А
<
Дифференцируя по х обе части этого равенства, получим после
соответствующих преобразований
OD dR _ 2A + */'2J (W^-tf'-y'V')
2 И _}_ы'2\3/2
Деля обе части равенства на 2R = v ~/ —» получим
(Зу'у-У"'-УгУ)
Возводя в квадрат, получим:
Сравнивая равенства C) и D), находим
откуда
d^ "~ ~*~ dx #
По условию ^ не меняет знак (R только возрастает или только
убывает), следовательно, и ~ не меняет знак. Примем для
определенности 5F<0, ^^° ^что соответствУет Рис- 152)-
Следовательно, ^ = —-^ .
Пусть точка М^ имеет абсциссу хи а М2 —абсциссу д:2. При-
Применим теорему Коши к функциям s(x) nR (x) на отрезке [хи х2]:
dx
1
dx
где I —число, заключенное между хг и x2(Xi<l<x2).
Введем обозначения (рис. 152)
s (х2) = slf s to) = s^ /? (^) = i?2> /? to) = #i-

198
(КРИВИЗНА КРИВОЙ
[ГЛ. VI
Тогда
__д
— 1, или s2 — sx = — (R2 — Rx). Но это значит, что
Совершенно так же доказывается это равенство и при возра-
возрастании радиуса кривизны.
Мы доказали теоремы 1 и 2
для того случая, когда кривая
задана уравнением в явном виде
Если кривая задана парамет-
параметрическими уравнениями, то эти
теоремы остаются в силе, причем
их доказательство проводится со-
совершенно аналогично.
Замечание. Укажем следую-
следующий простой механический способ
для построения кривой (эвольвен-
(эвольвенты) по ее эволюте.
Пусть гибкая линейка согнута
по форме эволюты С0С5 (рис. 153).
Предположим, что нерастяжимая
нить, одним концом укреплен-
укрепленная в точке Со, огибает эту ли-
линейку. Если мы будем эту нить
развертывать, оставляя ее все
время натянутой, то конец нити
опишет кривую М5М0 —эвольвенту. Отсюда происходит и назва-
название «эвольвента» —развертка. Доказательство того, что получен
Рис. 152,
Рис. 153. Рис. 154.
ная кривая действительно является эвольвентой, может быть
проведено с помощью установленных выше свойств эволюты.
Отметим, что одной эволюте соответствует бесчисленное мно-
множество различных эвольвент (рис. 153).

$81 ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ДЕЙСТВ. КОРНЕЙ УРАВНЕНИЯ 199
Пример. Пусгь имеем окружность радиуса а (рис. 154). Возьмем ту из
эвольвент этой окружности, которая проходит через точку Mq (й, 0).
Учитывая, что CM = CM0 — att легко получить уравнения эвольвенты
окружности:
P , PM = y = a(sin / — /cos t).
Отметим, что профиль зуба зубчатого колеса имеет чаще всего форму
эвольвенты окружности.
§ 8. Приближенное вычисление
действительных корней уравнения
Методы исследования поведения функции дают возможность
находить приближенные значения корней уравнения
Если данное уравнение есть алгебраическое уравнение *)
первой, второй, третьей или четвертой степени, то существуют
формулы, позволяющие выра-
выразить корни уравнения через его
коэффициенты с помощью конеч-
конечного числа операций сложения,
Рис. 155.
Рис. 156.
вычитания, умножения, деления и извлечения корней. Для урав-
уравнений выше четвертой степени таких формул, вообще говоря, не
существует. Если коэффициенты любого уравнения, алгебраиче-
алгебраического или неалгебраического (трансцендентного), не буквенные,
а числовые, то корни уравнения могут быть вычислены прибли-
приближенно с любой степенью точности. Отметим, что даже в тех
случаях, когда корни алгебраического уравнения выражаются
через радикалы, на практике иногда целесообразно применять
*) Уравнение f(x) = Q называется алгебраическим, если / (х) есть многочлен
(см. § 6 гл. VII).

200
КРИВИЗНА КРИВОЙ
[ГЛ. VI
приближенный метод решения уравнения. Ниже будут изложены
некоторые методы приближенного вычисления корней уравнения.
1. Способ хорд. Пусть дано уравнение
0, A)
где f(x) — непрерывная дважды дифференцируемая функция на
отрезке [а, 6]. Допустим, что путем исследования функции y = f(x)
внутри отрезка [а, Ь] мы выделим от-
отрезок [хи х2] такой, что внутри этого
отрезка функция монотонная (или воз-
возрастающая, или убывающая), а на его
концах значения функции / (хг) и / (х2) раз-
разных знаков. Примем для определенности,
что/(л:1)<0,/!(х2)>0 (рис. 155). Так как
функция y = f(x) непрерывна на отрезке
[*i» #2]> то ее график пересечет ось Ох в
какой-либо одной точке между х± и х2.
Проведем хорду Л5, соединяющую кон-
концы кривой y = f(x), соответствующие абс-
абсциссам x-i и х2. Абсцисса ах точки пересе-
пересечения этой хорды с осью Ох и будет при-
приближенным значением корня (рис. 156).
Для разыскания этого приближенного зна-
значения напишем уравнение прямой АВУ про-
проходящей через две данные точки А (х19
f (*!» и В (*2, / (*,)): j (^JL/A^ = х7^х\ #
Так как у —0 при х = а19 то, следова-
i7\f (Хпг ^^Т» 0ТКУДа
\Х2) — / \Х1/ *2 *1
B)
тельно,
или после преобразования
B')
Чтобы получить более точное начение корня, определяем [(а,).
Если / (ах) < 0, то повторяем тот же прием, применяя формулу B')
к отрезку [а19 х2]. Если / (ах) > 0, то применяем эту формулу
к отрезку [х19 аг]. Повторяя этот прием несколько раз, мы будем,
очевидно, получать все более точные значения корня а2, az и т.д.
Пример 1. Найти приближенные значения корней уравнения
Решение. Найдем, прежде всего, участки монотонности функции f {х).
Вычислив производную /' (х) = 3х2—6, мы обнаруживаем, что она положи-
положительна при х < — уг21 отрицательна при — Y%< * < Y"% и снова положи-

§8J ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ДЕЙСТВ. КОРНЕЙ УРАВНЕНИЯ 201
тельна при *>>T (рис. 157). Итак, функция имеет три участка монотонности,
на каждом из которых находится по одному корню.
Для удобств дальнейших» вычислений сузим эти участки монотонности
(но так, чтобы на каждом участке лежал соответствующий корень). Для этого,
подставляя в выражение / (х) наугад те или иные значения лс, выделим внутри
каждого участка монотонности такие более короткие отрезки, на концах ко-
которых функция имеет разные знаки:
*i=0, /@)=2,
^3 == — о,
*4 = -2, /(—2) = 6;
*б = 2, /<2)=-2,
*в = 3, /C) = И-
Таким образом, корни находятся в интервалах
(-3; -2), @; 1), B; 3).
Найдем приближенное значение корня в интервале @; 1); по формуле B)
имеем
Так как f @,4) = 0,43—6-0,4 + 2 = — 0,336, /@) = 2, то, следовательно, кЬрень
заключен между 0 и 0,4. Применяя к этому интервалу снова формулу B),
получим следующее приближение:
@,4—0).2
¦_. 0,336—2=
0,8
2,336
=0,342 и т. д.
Аналогичным образом найдем приближенные значения корней в других интер-
интервалах.
2. Способ касательных (способ Ньютона). Пусть
снова f(x1)<0, f(x2)>0, причем на отрезке [хи х2] первая
производная не меняет своего знака. Тогда в интервале
имеется один корень уравнения / (л:) =
= 0. Предположим еще, что и вто-
вторая производная не меняет своего
знака на отрезке [х19 х2]; этого можно
добиться путем уменьшения длины
интервала, содержащего корень.
Сохранение знака второй произ-
производной на отрезке \х1У х2] означает,
что кривая либо только выпукла, ли-
либо только вогнута на участке [х19 х2].
Проведем касательную к кривой
в точке В (рис. 158). Абсцисса аг
точки пересечения касательной с осью Ох будет приближен-
приближенным значением корня. Чтобы найти эту абсциссу, напишем урав-
уравнение касательной в точке В:
У-/(*•) = /'(*i) (*-*¦)•
Рис. 158.

202
КРИВИЗНА КРИВОЙ
[ГЛ. VI
Заметив, что х = аг при # = 0, получим
C)
Проведя затем касательную в точке В1(а1; /(#i)), аналогично
находим более точное значение корня а2. Повторяя этот прием
несколько раз, мы можем вычислить приближенное значение
корня с любой нужной нам точностью.
Отметим следующее обстоятельство. Если бы мы провели ка-
касательную к кривой не в точке Л, а в точке Л, то могло ока-
3
Рис. 159.
Рис. 160.
заться, что точка пересечения касательной с осью Ох находится
вне интервала (х19 х2).
Из рис. 158 и 159 следует, что касательную нужно проводить
в том конце дуги, в котором знаки функции и ее второй произ-
производной совпадают. Так как на от-
отрезке [хи х2] вторая производная,
по условию, сохраняет знак, то
это совпадение знаков функции и
второй производной на одном из
концов обязательно имеет место.
Это правило остается верным и для
случая, когда /'(д:)<0. Если ка-
касательная проводится в левом кон-
:це интервала, то в формуле C)
вместо х2 нужно подставить хг\
п — г
х~ 1
Рис. 161.
В случае, когда внутри интервала
fa, x2) есть точка перегиба С,
способ касательных может дать
приближенное значение корня, лежащее вне интервала (хи х2)
(рис. 160).
Пример 2. Применим формулу C') к вычислению корня уравнения
f(x) = x3—6*+2 = 0, заключенного в интервале @; 1). Имеем f(Q) = 2,

УПРАЖНЕНИЯ К ГЛАВЕ VI 203
С @) = Cjc2—6) |х=о = — 6, f (х) = 6л: ^ 0, поэтому по формуле C') получаем
^=«-^6=1=0,333.
3. Комбинированный способ (рис. 161). Применяя на
отрезке [хь х2] одновременно способ хорд и способ касательных,
мы получаем две точки at и аи лежащие по разные стороны от
искомого корня а (так как /(ах) и [(а^ имеют разные знаки).
Далее, на отрезке [а19 аг] применяем снова метод хорд и метод
касательных. В результате получаем два числа: а2 и й2, еще
более близких к значению корня. Продолжаем таким образом
до тех пор, пока разность между найденными приближенными
значениями не станет меньше, чем требуемая степень точности.
Заметим, что при комбинированном методе мы приближаемся к
искомому корню одновременно с обеих сторон (т. е. мы находим
одновременно как приближенное значение корня с избытком, так
и приближенное значение корня с недостатком).
Так, в рассмотренном нами примере путем подстановки убеждаемся, что
/ @,333) > О, / @,342) < 0. Следовательно, значение корня заключено между
«айденными приближенными значениями: 0,333 < х < 0,342.
Упражнения к главе VI
Найти кривизну кривых в указанных точках:
1. Ь*х2+а?у2 = а2Ь2 в точках @, Ь) и (а, 0). Отв. Ь/а? в точке @, Ь)\ а/Ь*
в точке (а, 0). 2. ху—12 в точке C, 4). Отв. 24/125. 3. у = х3 в точке (хъ ух).
6 i
Отв. 6\ ,9 . 4. 16г/2 = 4д:4—д:6 в точке B,0). Отв. -i . 5.
A+9ед3/ z
(+ед
в произвольной точке. Отв. 1/C ^/| аху |).
Найти радиус кривизны нижеследующих кривых в указанных точках;
вычертить каждую кривую и построить соответствующий круг кривизны:
6. у* = х* в точке D, 8). Отв. #=80Уб/3. 7. *2 = 4ш/ в точке @, 0).
Отв. R=2a. 8. Ь*х*—а*у* = а*Ь* в точке (хь уг). Отв. ^^( ,
9. у = \пх в точке A, 0). Отв. #=2]/Т. 10. */ = sin* в точке (я/2, 1).
Отв. R = \. 11. ^д^з*' } ПРИ ' = 'i- Отв- R=3asinti costf.
Найти радиус кривизны кривых:
12. y^f^fz \ Щ>и ^ = 1. Отв. R=6. 13. Окружность p = asin0. Отв.
Гп4-а)
R=a/2. 14. Спираль Архимеда р = аО. Отв. R—• а_, » % % 15. Кардиоида
р = аA — cos 0). Отв, R = -~-yr2ap. 16. Лемниската p2 = fl2cos20» Отвш
о
^=й2/3р. 17. Парабола p=asec2 (9/2). Отв. R = 2аsec3^ . 18. p = asin3~.
3 8
Отв. R=-j-a sin2-7Г-.
Найти точки кривых, в которых радиус кривизны имеет наименьшее зна-
значение:

204 КРИВИЗНА КРИВОЙ 1ГЛ. VI
19. t/-In*. Отв.(?^, -±1п2). 20. у=*е*. Отв. (-уIn2, -О).
21. Y~x+V!l = V~a- Отв. (-j.-j) • 22. t/ = aln (\ — ^Л . Отв. В точке
@,0) R = t.
Найти координаты центра кривизны (а, р) и уравнения эволюты для каж-
каждой из следующих кривых:
23. -5*—Т5- — 1- Отв. а = -— . ¦—; 0 =— -—"V" 'У- . 24.
а о а о
,-2/3 f\w>n л» ^ I Qvl/^*»2/3 о «._!_ Qv2/3,.l/3 «К «»3 rt2v Л»1Л а*
== п ' . итв. & = х-+-ох у , p = w-j-o^ ' у ' . со. у=п*х. и те. о? =
о
2г r* = ftlnctg(//2)-Acoe<. отв. У=4(е*/*+е-*/«) (трактриса).
I г/ = ^ sin /. z
( х = а(cost+ tsin t)9 . ^ o . лл f^ = acos3^
28. < Ome. a=acos t; P = asin /. 29. <
\ y = a(sin t — tcost). \ y = asUr t.
Ome. a = acos* t+3a cost sin2 t\ $ = asins t + 3асо$2 t sin t.
30. Вычислить с точностью до 0,001 корни уравнения *3—4лс + 2 = 0. Ome*
*!= 1,675, *2 = 0,539, *з = —2,214.
31. Для уравнения t (х)=хь—х—0,2 = 0 определить приближенное зна-
значение корня, заключенное в интервале A; 1,1). Отв. 1,045.
32. Вычислить корни уравнения #4-|-2#2—6#+2 = 0 с точностью до 0,01.
Отв. 0,38 < хг < 0,39; 1,24 < х2 < 1,25.
33. Решить приближенно уравнение х3—5 = 0. Отв. xi»l,71,
*2, 3= *»'1# 2 *
34. Найти приближенное значение корня уравнения х—tg* = O, который
находится между 0 и Зл/2. Отв. 4,4935.
35. Вычислить с точностью до 0,0001 корень уравнения sin х— 1—х*
Указание. Привести уравнение к виду /(#) = 0. Отв. 0,5110 < х < 0,5111.
Разные задачи
36. Показать, что в каждой точке лемнискаты p2 = a2cos2(p кривизна
пропорциональна радиус-вектору этой точки.
37. Найти наибольшее значение радиуса кривизны кривой p=0sin3-^-.
Отв. # = Зд/4.
38. Найти координаты центра кривизны кривой у — х\пх в точке, где
у' = 0. Отв. (е-1, 0).
39. Доказать, что для точек спирали Архимеда р=шр при ц>—*оо вели-
величина разности между радиус-вектором и радиусом кривизны стремится к 0.
40. Найти параболу у = ах2-\-Ьх-\-с, имеющую с синусоидой y — sinx в
точке (я/2, 1) общие касательную и кривизну. Сделать чертеж. Отв. */ =
= ~~Т+Т~'"~~"8"*
41. Функция y = f(x) определена так:
f (х) = х3 в интервале — оо < х <; 1,
f (x) — ax2-\-bx-\-c в интервале 1 < х < + оо.
Каковы должны быть а, Ьу с для того, чтобы линия y = f(x) имела везде
непрерывную кривизну? Сделать чертеж. Отв. а = 3, ? = —3, с—1.

УПРАЖНЕНИЯ К ГЛАВЕ VI 205
42. Показать, что радиус кривизны циклоиды в любой ее точке вдвое
больше длины нормали в той же точке.
43. Написать уравнение окружности кривизны параболы у — х2 в точке
A, 1). Отв. (У
44. Написать уравнение окружности кривизны кривой y = tgx в точке
125
( я
) [х j(J
45. Найти длину всей эволюты эллипса, полуоси которого равны а и Ь.
Отв. 4 (a3—№)lob.
46. Найти приближенное значение корней уравнения хе*=2 с точностью
до 0,01. Отв. Уравнение имеет единственный действительный корень *«0,84.
47. Найти приближенное значение корней уравнения * In* = 0,8 с точ-
точностью до 0,01. Отв. Уравнение имеет единственный действительный корень
164
,64.
48. Найти приближенное значение корней уравнения #2arQtg#=l с точ-
точностью до 0,001. Отв. Уравнение имеет единственный действительный корень
ж» 1,096,

ГЛАВА VII
КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ
§ 1. Комплексные числа. Исходные определения
Комплексным числом z называется выражение
г = а + й>, A)
где а и Ь—действительные числа; i—так называемая мнимая
единица, определяемая равенством
i = V"^A или ia = —1; B)
а ъггыъаекя действительной или вещественной частью, Ь—мнимой
частью числа г. Их обозначают так:
a = Rez, b=lmz.
Если a = 0, то число O + ib = ib называется чисто мнимым;
если & = 0, то получается действительное число: а+ч*0 = а. Два
комплексных числа z = a~\-ib и z = a—ib9 отличающиеся только
знаком мнимой части, называются сопряжен-
ными.
Принимаются два основных определения.
1. Два комплексных числа z1 = a1 + ib1
и z2 — a2-\~ib2 считаются равными: г1 = г2,
если at = a2, bt = b2, т. е. если равны в от-
отдельности их действительные и мнимые части.
рис 162# 2. Комплексное число г равно нулю:
1 " =0, тогда и только тогда, когда
э
1. Геометрическое изображение комплексных
чисел. Всякое комплексное число z = a + ib можно изобразить
на плоскости Оху в виде точки А (а, Ь) с координатами а и Ь.
Обратно, каждой точке плоскости М (х, у) соответствует комплекс-
комплексное число z = x + iy. Плоскость, на которой изображаются комп-
комплексные числа, называется плоскостью комплексной переменной г
(рис. 162) (на плоскости ставить символ z в кружке).

§ ij КОМПЛЕКСНЫЕ ЧИСЛА. ИСХОДНЫЕ ОПРЕДЕЛЕНИЯ 207
Точкам плоскости комплексной переменной г, лежащим на
оси Оху соответствуют действительные числа (Ь = 0). Точки, ле-
лежащие на оси Оу, изображают чисто мнимые числа, так как в
этом случае а = 0. Поэтому при изображении комплексных чисел
на плоскости комплексной переменной г ось О у называют осью
мнимых чисел или мнимой осью, а ось Ох—действительной осью.
Соединив точку А (а, Ь) с началом координат, получим век-
вектор О А. В некоторых случаях удобно считать геометрическим
изображением комплексного числа z = a + ib вектор О А.
2. Тригонометрическая форма записи компле-
комплексного числа. Обозначим через ф и г (г>0) полярные ко-
координаты точки А(а>Ь), считая начало координат полюсом, а
положительное направление оси Ох—полярной осью. Тогда
(рис. 162) имеют место следующие равенства: а = г cos ф, Ь = г sin <p,
а следовательно, комплексное число z можно представить в форме
а + ib = г cos ф + if sin ф
или
z = r (cos ф +1 sin ф). C)
Выражение, стоящее справа, называется тригонометрической
формой записи комплексного числа z = a-\-ib\ r называется мо-
модулем комплексного числа г, ф—аргументом комплексного чис-
числа г; они обозначаются так:
г = \г\, ф = а^г. D)
Величины г и ф выражаются через а и Ь, очевидно, так:
r = VaF+T\ <P = Arctg-j.
Итак,
arg z = arg (a + ib) = Arctg —. W
Аргумент комплексного числа считается положительным, если
он отсчитывается от прложительного направления оси Ох против
часовой стрелки, и отрицательным при противоположном направ-
направлении отсчета. Очевидно, что аргумент ф определяется не одно-
однозначно, а с точностью до слагаемого 2я&, где k—любое целое
число.
_ Замечание. Сопряженные комплексные числа z = a + ib и
z = a—ib имеют равные-модули |г| = |г~|, а их аргументы равны
по абсолютной величине, но отличаются знаком: arg 2 = — argF.
Отметим, что действительное число А также может быть за-
записано в форме C), в именно:
Л = | Л | (cosO + isin0) при Л>0,
A==|4|(cosjt + i'sinn) при А < 0.

КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ
1ГЛ. VII
Модуль комплексного числа 0 равняется нулю 0: |0| = 0, В ка-
качестве же аргумента нуля можно принять любой угол <р. Дейст-
Действительно, для любого угла <р имеет место равенство
O = 0(cosq)-Msin<p).
§ 2. Основные действия над комплексными числами
1. Сложение комплексных чисел. Суммой двух
комплексных чисел zi = a1 + ib1 и z2 = a2 + ib2 называется комп-
комплексное число, определяемое равенством
0)
Из формулы A) следует, что сложение комплексных чисел»
изображенных векторами, производится по правилу сложения
векторов (рис. 163, а).
6)
а
Рис. 163.
2. Вычитание комплексных чисел. Разностью
двух комплексных чисел zi = a1-{'ibi и z2 = a2+ib2 называется
такое комплексное число, которое, будучи сложено с г2, дает в
сумме комплексное число zt:
(h—b,). B)
Отметим, что модуль разности двух комплексных чисел равен
расстоянию ме&сду точками, изображающими эти числа на плос-
плоскости комплексной переценной (рис. 163,6):
3. Умножение комплексных чисел. Произведением
комплексных чисел zt = a1 + ib1 и г2 = а2 + #2 называется такое
комплексное число, которое получается, если мы перемножаем
эти числа как двучлены по правилам алгебры, учитывая только,
что
и вообще при любом целом k
/б=г и т. д.,

§21 ОСНОВНЫЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ 209
На основании этого правила получаем
bt) (о, + ib2) = аха2 + ibxa2 + iaxb2 + i\b2f
или
2i2a= (axa2—bxb2) + i (bxa2+axb2). C)
Пусть комплексные числа даны в тригонометрической форме:
Ч = >Ч (cos <fx -f1 sin ф2), z2 = r2 (cos cp2-+1 sin фа).
Найдем произведение этих чисел:
гхг2 = гх (cos <рх +1 sin фх) ra (cos ф2 + i sin ф2) =
= rxr2 [cos фх cos фа -f t sin фх cos ф2 + i cos ф^ sin ф2 + i* sin (fx sin Фа]^
*= r^jj [(cos <fx cos ф2—sin фх sin ф2) + i (sin фх cos ф2 + cos фх sin Фа)]^
= rxr2 [cos (фх + ф2) + i sin (ф! + ф2)].
Таким образом,
*i*2 = ^ir2 [cos (фх + ф2) +1 sin (фх + ф2)], C')
т. е. произведение двух комплексных чисел есть такое комплекс-
комплексное число, модуль которого равен произведению модулей сомножи-
сомножителей, а аргумент равен сумме аргументов сомножителей.
Замечание 1. Произведение сопряженных комплексных чи-
чисел z = a-\-ib и г = а—ib в силу равенства C) выражается так:
или
Произведение сопряженных комплексных чисел равняется
квадрату модуля каждого из них.
4. Деление комплексных чисел. Деление комплекс-
комплексных чисел определяется как действие, обратное умножению.
Пусть гг = ах + 1Ьх, 22 = а2 + й2, \z2\ = V^+bl?=0. Тогда
— — г есть такое комплексное число, что zt — z2z. Если
ТО
или
«1 + tbt = (а2х - Ьм) + i (a2y+b2x);
хну определяются из системы уравнений

210 КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ [ГЛ. VII
Решая систему, находим
Х = 2 , ,2 > У=='
Окончательно получаем
Ч-*":
Практически деление комплексных чисел выполняется следую-
следующим образом: чтобы разделить z1 = a1-\-ib1 на 22 = a2 + t62, умно-
умножим делимое и делитель на крмплексное число, сопряженное
делителю (т. е. на a2 — ib2).
Тогда делителем будет действительное число; разделив на него
действительную и мнимую части делимого, получим частное:
a—ib2)
«2 + ib2 (at + ib2) (at - ib2) a\ + b\
^l a%+b\
Если комплексные числа даны в тригонометрической форме:
zt = г^ (cos фх +1 sin фх), 2a = ra (соз ф2 + i sinф2),
то
Для проверки этого равенства достаточно умножить делитель на
частное:
r2 (cos ф2 + i sin ф2) 2- [cos (ф^ - ф2) + i sin (ф? - ф2)] =я
е= г2 ^- [cos (ф2 + ф! - ф2) + i sin (ф2 + Фз[ — Ф2)] = rf (cos ф^ Н- i sin ф^.
Таким образом, модуль частного двух комплексных чисел равен
частному модулей делимого и делителя; аргумент частного равен
разности аргументов делимого и делителя.
Замечание 2. Из правил действий над комплексными чис-
числами следует, что в результате операций сложения, вычитания,
умножения и деления комплексных чисел получается снова комп-
комплексное число.
Если правила действий над комплексными числами применить
к действительным числам, рассматривая их как частный случай
комплексных, то эти правила будут совпадать с обычными пра-
правилами действий, известными из арифметики.
Замечание 3. Вернувшись к определениям суммы, разности,
произведения и частного комплексных чисел, легко проверить,
что если в этих выражениях заменить каждое комплексное число
сопряженным, то и результаты указанных действий заменяются

S 3J ВОЗВЕДЕНИЕ КОМПЛЕКСНОГО ЧИСЛА В СТЕПЕНЬ 211
сопряженными числами. Отсюда, в частности, вытекает следую-
следующая теорема.
Теорема. Если в многочлен с действительными коэффици-
коэффициентами Аохп + Агхп~1 + ... + Ап подставить вместо х число
a + ib, а затем сопряженное число а—iby то и результаты этих
подстановок будут взаимно сопряженными.
§ 3. Возведение комплексного числа в степень
и извлечение корня из комплексного числа
1. Возведение в степень. Из формулы C') предыдущего
параграфа следует, что если п— целое положительное число, то
[г (cos ф + i sin cp)]* = rn (cos жр + i sin жр). A)
Эта формула называется формулой Муавра. Она показывает,
что при возведении комплексного числа в целую положительную
степень модуль возводится в эту степень, а аргумент умножа-
умножается на показатель степени.
Рассмотрим теперь еще одно приложение формулы Муавра.
Полагая в этой формуле г = 1, получим
(cos ф + i sin ф)" = cos Пф + i sin mp.
Разлагая левую часть по формуле бинома Ньютона и прирав-
приравнивая действительные и мнимые части, мы сможем выразить
sin/up и cos/ир через степени sincp и созф. Так, например, в
случае /г = 3 получаем
cos3 ф + i • 3 cos2 ф sin ф — 3 cos ф sin2 ф — i sin3 ф = cos Зф + i sin Зф;
используя условие равенства двух комплексных чисел, получим
cos Зф = cos3 ф — 3 cos ф sin2 ф, sin Зф = — sin3 ф + 3 cos2 ф sin ф.
2. Извлечение корня. Корнем n-й степени из комп-
комплексного числа называется такое комплексное число, /г-я степень
которого равняется подкоренному числу, т. е.
\/r (cos ф + i sin ф) = р (cos ф +' $т *Ф)>
если
р* (cos mj> + i sin пф) = r (cos ф + i sin ф).
Так как у равных комплексных чисел модули должны быть
равны, а аргументы могут отличаться на число, кратное 2л, то
р* = г, пф = ф + 2kn. Отсюда находим р == У г, ф = ^"^ , где
k — любое целое число, Y г — арифметическое (т. е. действитель-
действительное положительное) значение корня из положительного числа г.
Следовательно,
(±^ i^). B)

212 КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ [ГЛ. VII
Придавая k значения 0, 1, 2, ,.., п — 1, получим п различ-
различных значений корня. Для других значений k аргументы будут
отличаться от полученных на число, кратное 2я, и, следователь-
следовательно, получатся значения корня, совпадающие
с рассмотренными.
Итак, корень n-й степени из комплекс-
комплексного числа имеет п различных значений.
Корень n-й степени из действительного
числа А у отличного от нуля, также имеет п
значений, так как действительное число яв-
является частным случаем комплексного и мо-
может быть представлено в тригонометричес-
тригонометрической форме:
Рис. 164. если ^ > О» то ^ = | Л | (cos 0 -+-1 sin 0);
если Л<0, то А = |A\(cosn + isinn).
Пример 1. Найти все значения кубического корня из единицы,
Р е щ е н и е. Представим единицу в тригонометрической форме;
I=cos0+*sin0,
По формуле B) получаем
I/ 1 = |/ cos 0 -J- i sin 0 = cos —х— ""Ь * sin —о .
Полагая к равным 0, 1, 2, находим три значения корня:
хг = cos 0+i sin 0 = 1, х2=cos Bя/3) + i sin Bя/3), xz = cos Dя/3) + i sin Dя/3),
Учитывая, что
cos Bя/3) = —1/2, sin Bя/3) = >^3/2, cos Dя/3) =—1/2, sin Dя/3)=—V 3/2,
получаем %=1, *2 =—1/2+^1/2, х3 =—l/2~tl//2.
На рис. 164 точки Л, В, С является геометрическими изображениями
полученных корней,
3. Решениедвучленногоуравнения. Уравнение вида
называется двучленным. Найдем корни этого уравнения. Если А
есть действительное положительное число, то
Выражение в скобках дает все значения корня n-й степени из 1.
Если Л—действительное отрицательное число, то
Выражение в скобках дает все значения корня л-й степени из —1.
Если А — комплексное число, то значения х находятся по
формуле B).

§4] ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ С КОМПЛЕКСНЫМ ПОКАЗАТЕЛЕМ 213
Пример 2. Решить уравнение *4=1.
Решение. *= j/cos2&rc+isin2foi =cos Bfoi/4) + /sin BknJ4). Пола-
гая k равным 0, 1,2, 3, получаем
х2 = cos Bя/4) + i sin Bя/4) = /,
х3 = cos Dя/4) + i sin Dя/4) = — 1 f
х4 = cos Fя/4) + i sin Fя/4) = — i.
§ 4. Показательная функция с комплексным показателем
и ее свойства
Пусть z = x + iy. Если х и у — действительные переменные, то
г называется комплексной переменной. Каждому значению комп-
комплексной переменной г на плоскости Оху (плоскости комп-
комплексной переменной) соответствует определенная точка
(см. рис. 162).
Определение. Если -каждому значению комплексной пере-
переменной г из некоторой области комплексных значений соответ-
соответствует определенное значение другой комплексной величины w, то
w есть функция комплексной переменной z. Функции комплекс-
комплексного аргумента обозначают w = f(z) или w = w(z).
Здесь мы рассмотрим одну функцию комплексной переменной —
показательную функцию
w = ez,
или
Комплексные значения функции w определяются так *):
4*+iy = e*(cosy + isiny), A)
т. е.
w (г) = е* (cos у + i sin у). B)
Примеры:
1. 2=1+—!, е =е ( cos T
2. z = 0+i/, e°+T'=.o^cos|
3. 2=1 + г, e1+^ = e1(cos 1 + tsin 1
4. z — x—действительное число, ex + oi: = ex (cosO+isinO)=e*—обычная
показательная функция.
Свойства показательной функции.
1. Если гх и г2 —два комплексных числа, то
е*1+*. = е*«е**. C)
*) Целесообразность такого определения показательной функции комплекс-
комплексной переменной будет показана и ниже, см. § 21, гл. XIII и § 18 гл. XVI,
(т. II).

214 КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ [ГЛ. VII
Доказательство. Пусть
zl = x1 + iyu z2 =
тогда
= e*e* [cos {yx + y2) + i sin (^ + yt)]. D)
С другой стороны, на основании теоремы о произведении двух
комплексных чисел в тригонометрической форме будем иметь
eziezs = exi + iyxex2+iy2 = exx (cos yi _|_ f sin yj e.v2 (cos y^ ^ f sjn y^ _.
= e*ie*« [cos (yt+yj + i sin (^+y2)]. E)
В равенствах D) и E) правые части равны, следовательно, равны
и левые: ez*+*« = e*e2*.
2. Аналогичным образом доказывается формула
ег'-г< = Й-. (б)
3. Если /п — целое число, то
{^)т = етг% G)
При т > 0 эта формула легко получается на основании формулы
C); если т < 0, то она получается на основании формул C) и F).
4. Справедливо тождество
Действительно, по формулам C) и A) получаем
На основании тождества (8) следует, что показательная функция ег
есть периодическая функция с периодом 2ш.
5. Рассмотрим, далее, комплексную величину
где и (х) и v (х) — действительные функции действительной пере-
переменной х. Это есть комплексная функция действительной пере-
переменной.
а) Пусть существуют пределы
lim и(х) = и (х0), lim v(x) = v (x0),
Х-+ Хо X -> Хо
Тогда a (jc0) + iv (х0) — wQ называют пределом комплексной пере-
переменной w.
б) Если существуют производные и' (х) и v' (x), то выражение
x) (9)
будем называть производной комплексной функции действительной
переменной по действительному аргументу.

§5| ПОКАЗАТЕЛЬНАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА 215
Рассмотрим, далее, следующую показательную функцию:
x
где аир — постоянные действительные числа, а х — действитель-
действительная переменная. Это есть комплексная функция действительной
переменной, которую по формуле A) можно переписать так:
w = еах [cos fix + i sin fix]
или
w = еах cos Рх + *еа* sin fix.
Найдем производную о?. По формуле (9) будем иметь
w'x = (е<** cos р*)' + i (е*х sin Px)' =
= еах (а cos Рд: — Р sin fix) + ieax (а sin fix + p cos pjc) ==
s= a [e°« (cos px + i sin рл:)] + ip [eax (cos px + i sin fix)] =
= (а + /р) [еал; (cos рл: +1 sin fix)] = (a + ifi) e<a+*>*.
Итак, если a; = e(a+W*, то а;' = (а + ф)е(а+'Э>*э или
[е(а+^)*]' = (а + ifi) e(a+Wx. A0)
Таким образом, если k — комплексное число (в частности действи-
действительное) и # —действительное число, то
(e**)' = fe**. (9')
Получили обычную формулу дифференцирования показательной
функции. Далее,
)" = [(е**У]' = k
и при произвольном п
Эти формулы нам потребуются в дальнейшем.
§ 5. Формула Эйлера. Показательная форма
комплексного числа
Если в формуле A) предыдущего параграфа положим # = 0,
то получим:
eiy = cos у + i sin r/. A)
Это есть формула Эйлера, выражающая показательную функцию
с мнимым показателем через тригонометрические функции.
Заменяя в формуле A) у на —у, получим
е-*у = cosy — i sin у. B)
Из равенств A) и B) найдем cos у и sin у:
е*У—е-*9
^ . C)

216 КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ [ГЛ. VII
Последними формулами пользуются, в частности, для выражения
степеней соэф и sin ф и их произведений через синус и косинус
кратных дуг.
Пример 1.
COS2W = I
Пример 2.
cos
2Г-;
Показательная форма комплексного числа.
Представим комплексное число в тригонометрической форме:
где г —модуль комплексного числа, ф —аргумент комплексного
числа. По формуле Эйлера
cos ф + / sin ф = е1**. D)
Следовательно, всякое комплексное число можно представить
в так называемой показательной форме:
z = rei(p.
Пример 3. Представить числа 1, tf —2, —i в показательной форме.
Решение.
1 == cos 2kn + i sin 2kn=
—2=2 (cos я + i sin n) = 2ertl\
На основании свойств (З), F), G) § 4 показательной функции
легко производятся действия над комплексными числами в пока-
показательной форме.
Пусть имеем г1 = г1^, гв = гяе**. Тогда
zi - Z2 = rieiq>i • r2ei(p2 = rir%ei (ф1+ф2); E)
этот результат совпадает с формулой C') § 2.

§61 РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ 217
эта формула совпадает с формулой E) § 2.
гп = (гещ)п — r neinq>. G)
эта формула совпадает с формулой A) § 3.
. ф + 2/гя
Y7di = Y!e~Z~ (? = 0, 1, 2, ..., л-1); (8)
эта формула совпадает с формулой B) § 3.
§ 6. Разложение многочлена на множители
Функция
где п — целое число, как известно, называется многочленом (поли-
(полиномом) или целой рациональной функцией от х\ число п называется
степенью многочлена. Здесь коэффициенты Ло, А19 ..., Л „ — дей-
действительные или комплексные числа; независимая переменная х
также может принимать как действительные, так и комплексные
значения. Корнем многочлена называется такое значение пере-
переменной х, при котором многочлен обращается в нуль.
Теорема 1 (теорема Без у). При делении многочлена f (х)
на разность х — а получается остаток, равный /(а).
Доказательство. При делении f (х) на х — а частным будет
многочлен f±(x)9 степень которого на единицу ниже степени f(x),
остатком будет постоянное число R. Таким образом, можем написать
/(*) = (х-а)/х (*)+*¦ (D
Это равенство справедливо при всех значениях х, отличных от а
(деление на х — а при х = а не имеет смысла).
Заставим теперь х стремиться к а. Тогда предел левой части
равенства A) равен f (a), a предел правой части равен R. Так как
функции f(x) и (x — a)f1(x) + R равны между собой для всех
хфа, то равны и их пределы при х—>а, т.е. f(a) = R.
Следствие. Если а есть корень многрчлена, т. е. f (a) = О,
то f(x) делится без остатка на х — а и, следовательно, пред-
представляется в виде произведения
где fx(x) —многочлен.
Пример 1. Многочлен /(х) = х3—6х2-\-\\x—б при х = 1 обращается
в нуль, т. е. /A) = 0, поэтому данный многочлен делится без остатка на # — 1:
Перейдем теперь к рассмотрению уравнений с одним неизвест-
неизвестным х.
Всякое число (действительное или комплексное), котйрое,
будучи подставлено в уравнение вместо х, обращает уравнение
в тождество, называется корнем уравнения.

218 КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ [ГЛ. VII
Пример 2. Числа *x —л/4, *2 = 5л/4, #3 = 9я/4, ... являются корнями
уравнения cos* = sin*.
Если уравнение имеет вид Р(х) = 0, где Р {х) — многочлен сте-
степени я, то это уравнение называется алгебраическим уравнением
степени п. Из определения следует, что корни алгебраического
уравнения Р(х) = 0 те же, что и корни многочлена Р(х).
Естественно, возникает вопрос: всякое ли уравнение имеет
корни?
В случае неалгебраического уравнения ответ отрицателен:
существуют такие неалгебраические уравнения, которые не имеют
ни одного корня —ни действительного, ни комплексного, напри-
например уравнение е* = 0*).
Однако в случае алгебраического уравнения ответ на постав-
поставленный вопрос положителен. Этот ответ дается основной теоремой
алгебры:
Теорема 2 (основная теорема алгебры). Всякая
целая рациональная функция f (х) имеет по крайней мере один
корень, действительный или комплексный.
Эта теорема доказывается в высшей алгебре. Здесь мы ее
примем без доказательства.
Пользуясь основной теоремой алгебры, легко доказать следую-
следующую теорему.
Теорема 3. Всякий многочлен п-й степени разлагается на п
линейных множителей вида х—а и множитель, равный коэффи-
коэффициенту при хп.
Доказательство. Пусть f(x) есть многочлен степени п:
Этот многочлен в силу основной теоремы имеет по крайней мере
один корень; обозначим его через at. Тогда на основании след-
следствия из теоремы Безу мы можем написать
/(*) = (*-Ox) f Л*).
где ft(x) — многочлен (я — 1)-й степени; fx(x) также имеет корень.
Обозначим его через а2. Тогда
где /2 (х) — многочлен (п — 2)-й степени. Аналогично
*) Действительно, если бы число Xi — a-\-bi было корнем этого уравнения,
то имело бы место тождество ea+bi — § или (на основании формулы Эйлера)
ea(cos6+tsin6)=0. Но еа не может равняться нулю ни при каком действи-
действительном значении а; также не равно нулю cos b-\-i sin b (так как модуль этого
числа равен У^0^*^sin26 = 1 при любых Ь). Следовательно, и произведение
еа (cos b+i sin b) фО> т.е. ee+fc^0, но это значит, что уравнение е* = 0
не имеет корней.

§6] РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ 219
Продолжая этот процесс выделения линейных множителей,
дойдем до соотношения
fn-l(*)=(X-<*n)fn>
где fn — многочлен нулевой степени, т.е. некоторое фиксирован-
фиксированное число. Это число, очевидно, равно коэффициенту при xnt
т.е. fn = A0.
На основании полученных равенств можем написать
Г(х) = Ай(х-а1)(х-аш) ... (x-aj. B)
Из разложения B) следует, что числа aiy a2, ..., ап суть корни
многочлена f (х)> так как при подстановке х = ait х = а2, ..., х=ап
правая часть, а следовательно, и левая обращается в нуль.
Пример 3. Многочлен / (х)=х3 —6#2 + 11*—6 обращается в нуль при
*=1, * = 2, х = 3. Следовательно, я3—б*2+11*—6 = (х— 1) (х—2) (х—3).
Никакое значение х = ау отличное от af, д2, ..., ап% не может
быть корнем многочлена f(x)y так как ни один из множителей
в правой части равенства B) не обращается в нуль при х = а.
Отсюда вытекает следующее предложение.
Многочлен п-й степени не может иметь более п различных
корней.
Но в таком случае имеет место следующая теорема.
Теорема 4. Если значения двух многочленов п-й степени
<Pf (*) и Фг (х) совпадают при п +1 различных значениях а0, ait
аы •••» ап аргумента х, то эти многочлены тождественны.
Доказательство. Обозначим через f(x) разность много-
многочленов
По условию f (x) есть многочлен степени не выше п, обращаю-
обращающийся в нуль в точках а1У ..., ап. Следовательно, его можно
представить в виде
!(х) = А0(х-аг)(х-аш) ... (х-ап).
Но по условию f(x) обращается в нуль также в точке а0.
Тогда f(aQ) = O и при этом ни один из линейных множителей не
равен нулю. Поэтому Л0 = 0, а тогда из равенства B) следует,
что многочлен f(x) тождественно равен нулю. Следовательно,
<Pi (х) - ф2 (х) 5= 0, или фх (х) = ф2 (х).
Теорема 5. Если многочлен
тождественно равен нулю, то все его коэффициенты равны нулю.

220 КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ 1ГЛ. VII
Доказательство. Запишем разложение этого многочлена
на множители по формуле B):
= AQ(x-aJ ...(x-an). (Г)
Если этот многочлен тождественно равен нулю, то он равен нулю
и при некотором значении х, отличном от а19 . ••, ап. Но тогда
ни одна из скобок х — аи ¦ •., х — ап не равна нулю и, следова-
следовательно, Л0 = 0.
Аналогичным образом доказывается, что Лх = 0, Л2 = 0 и т.д.
Теорема 6. Если два многочлена тождественно равны друг
другу, то коэффициенты одного многочлена равны соответствую-
соответствующим коэффициентам другого.
Это следует из того, что разность данных многочленов есть
многочлен, тождественно равный нулю. Следовательно, на осно-
основании предыдущей теоремы все его коэффициенты —нули.
Пример 4. Если многочлен axs + bx2-\-cx+d тождественно равен мно-
многочлену х2—5*, то а=0, 6=1, с——5, й~Ь.
§ 7. О кратных корнях многочлена
Если в разложении многочлена п-и степени на линейные мно-
множители
f(x)^A0(x-a1)(x-a2) ... (х-ап) A)
некоторые линейные множители окажутся одинаковыми, то их
можно объединить, и тогда разложение многочлена на множители
будет иметь вид
!{х) = А.(х-аг)Ъ(х-(ф ... (JC-flJ**- (Г)
При этом
В этом случае корень а% называется корнем кратности kt или
/^-кратным корнем, а2 — корнем кратности k2 и т. д.
Пример. Многочлен f(x)~x*—5*2+8a:—4 разлагается на следующие
линейные множители: f(x) — (x—2)(х—2) (х—1). Это разложение можно на-
написать так: f(x) = (x—2J (х—1). Корень ах = 2—двукратный корень, а2=\ —
простой корень.
Если многочлен имеет корень а кратности ky то мы будем счи-
считать, что многочлен имеет k одинаковых корней. Тогда из теоремы
о разложении многочлена на линейные множители получается
следующая теорема.
Всякий многочлен п-й степени имеет ровно п корней (дейст-
(действительных или комплексных).
Замечание. Все, что говорилось о корнях многочлена
n-*+ ... +Ап,

S8J СЛУЧАЙ КОМПЛЕКСНЫХ КОРНЕЙ 221
можно, очевидно, сформулировать в терминах корней алгебраи-
алгебраического уравнения
Аохп + А1хп~1 + ... + Л„ = 0.
Докажем, далее, следующую теорему.
Теорема. Если аг является для многочлена f (x) корнем крат-
кратности &! > 1, то для производной f (х) это число является кор-
корнем кратности kx — 1.
Доказательство. Если ах есть корень кратности kx> 1,
то из формулы (Г) следует:
где ф {х) = (х — a2)k* •. • (л; — am)k** не обращается в нуль при х = аь
т.е. ^{а^фО. Дифференцируя, получим
/' {х) = k1(x- аг)^ Ф (х) + (* - ах)Ч' (х) =
= (* - а^-1 [*хФ (х) + (х- а,) <р' (х)].
Обозначим
Ф (х) = *хФ W + (* - fli) ф' W-
Тогда
rW-(^-fli)^W,
причем
т.е. х = аг есть корень кратности ^—1 многочлена f (х). Из
проведенного доказательства следует, что если йх=1, то af не
является корнем производной f (х).
Из доказанной теоремы следует, что at является корйем крат-
кратности kx — 2 для производной ftt (х), корнем кратности ?х —3 для
производной f" (х), ..., корнем кратности 1 (простым корнем)
для производной /to-1* (а:) и не является корнем для производ-
производной /to) (*), т. е.
/(*!> = 0, Па^О, ГК) = 0, ..., Р-1)(ах)=0,
но
/ш (ад
§ 8. Разложение многочлена на множители
в случае комплексных корней
В формуле A) § 7 корни а1У а2, ..., ап могут быть как дей-
действительными, так и комплексными. Имеет место следующая
теорема.
Теорема. Если многочлен f (х) с действительными коэффи-
коэффициентами имеет комплексный корень a + ib, то он имеет и со-
сопряженный корень a — ib.
Доказательство. Если мы подставим в многочлен f(x)
вместо х число a + ib, произведем возведение в степень и соберем

.222 КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ \ТЛ. VII
отдельно члены, содержащие i и не содержащие f, то получим
где М и N — выражения, не содержащие /•
Так как a~\*ib — корень многочлена, то
откуда
Подставим теперь в многочлен вместо # выражение a — ib.
Тогда (на основании замечания 3 в конце § 2) мы получим
в результате число, сопряженное с числом M-\-iN', т. е.
Так как М = 0 и iV = 0, то f(a — ib) = 0, т.е. a — tf> есть корень
многочлена.
Итак, в разложении
!(х) = А0(х-аг)(х-а1 ... (х-ап)
комплексные корни входят попарно сопряженными.
Перемножив линейные множители, соответствующие паре ком-
комплексно сопряженных корней, получим трехчлен второй степени
с действительными коэффициентами:
где р = —2а, <7 = ^2+^2 — Действительнце числа.
Если число а+Ы является корнем кратности k, то сопряжен-
сопряженное число а — Ы должно являться корнем той же кратности &,
так что наряду с линейными множителями x — (a + ib) в разло-
разложение многочлена входят столько же линейных множителей вида
x-(a-ib).
Таким образом, многочлен с действительными коэффициентами
разлагается на множители с действительными коэффициентами
первой и второй степени соответствующей кратности, т. е.
/<*) =
= i4e(x-a!)*' (*—aj*«... (x—ar)*' (x'+p.x+q^ ... (x*+psx+qs)**.
этом
§ 9. Интерполирование. Интерполяционная формула Лагранжа
Пусть при изучении некоторого явления установлено, что су-
существует функциональная зависимость между величинами у и х,
описывающая количественную сторону данного явления; при этом

ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА
223
функция у = <р(х) остается нам неизвестной, но на основании
эксперимента установлены значения этой функции у0, у19 у2, ..., уп
при некоторых значениях аргумента х0, xiy х2У . ..,л;„, принад-
принадлежащих отрезку [а, 6].
Задача заключается в том, чтобы найти функцию, по возмож-
возможности более простую с точки зрения вычислительной (например,
многочлен), которая представляла бы неизвестную функцию
у = ф (х) на отрезке [а, Ь] точно или приближенно. В более
отвлеченной форме эту задачу можно сформулировать так: на
отрезке [а, Ь\ заданы значения
неизвестной функции у = <р (х) в
п+ 1 различных точках xQ> х19 ...
• ¦-.у,» = ф (*я);
требуется найти многочленах)
степени ^ д, приближенно выра-
выражающий функцию ф (х).
В качестве такого многочле-
многочлена естественно взять многочлен,
значения которого в точках х0, #f, x2, .
о соответствующими значениями у0У yiy у2У .
Рис. 165.
,, хп совпадают
.,*/„ функции ф(х)
(рис. 165). Тогда поставленная задача, называемая «задачей интер-
интерполирования функции», формулируется так: для данной функции
Ф (л:) найти многочлен Р (х) степени ^ п, который при заданных
значениях х0, х1% ..., хп принимал бы значения
В качестве искомого многочлена возьмем многочлен n-й степени
вида
Р (*)=C0(*-*i) (x-x2)..,(x-xn)+C1 (x—x0) (x—xj...(x-xn) +
+ С2 (X— Хо) (Х—Хг) (Х-Хг) . . . (Х-Хя) +...
...+Cn(X-X0)(X~Xi) ... (Х-Ха-г) A)
и определим коэффициенты Со, Clf ...,С„ так, чтобы выполня-
выполнялись условия
Р (Хо) = yOf P (*i) =Уи • • м Я (^J = У«. B)
Положим в формуле A) # = a;0; тогда, принимая во внимание
равенства B), получим
откуда
0
Уо
)—Х2) • • • (#0—Хп)

224 КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ ЕГЛ. VII
Затем, положив х = хъ получим
Hi = ^ i (xi -^о) (xi хз) • • • \xi хп)»
откуда
Q = !tt
1 (*i — Х0) (Xi—X2) . . . (*1— Хп)
Таким же образом найдем
Q
Подставляя найденные значения коэффициентов в формулу A),
получим
(X—Xp) (Х—Хг) .. . (* — *„-!) Пч
Эта формула называется интерполяционной формулой Лагранжа.
Отметим без доказательства, что если <р (х) имеет производную
(л+1)-го порядка на отрезке [а, 6], то погрешность при замене
функции ф (х) многочленом Р (х), т. е. величина R (х) = () /> ()
удовлетворяет неравенству
\R (x)\< \{x-xQ) (x-xj ... (x-xJI-
Замечание. Из теоремы 4 § 6 следует, что многочлен Р(х)
является единственным, удовлетворяющим поставленным условиям.
Укажем, что существуют и другие интерполяционные фор-
формулы. Одна из них — интерполяционная формула Ньютона — будет
рассмотрена в § 10.
Пример. Из эксперимента получены такие значения функции y = q>(x)t
#0 = 3 при хо=\; 1/1=—5 при хг — 2\ </2 = 4 при х2 = — 4. Требуется предста-
представить приближенно функцию у = у(х) многочленом 2-й степени.
Решение. По формуле C) имеем (при п=>2):
M
()(+) M)() (—1)-(—4—
или
__39 2_Ш 252
§ 10. Интерполяционная формула Ньютона
Пусть известны п+1 значение функции ф(лс), а именно #0,
ffi» •••>&» ПРИ П"М значении аргумента др0, дг1э ..., хп. При
этом разность между соседними значениями аргумента постоянна.

§40]
ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
225
Обозначим ее через h. Таким образом имеем таблицу значений
неизвестной функции у = у>(х) при соответствующих значениях
аргумента.
X
У
Ч
Уо
x1 = x0 + h
У\
x2 = x0 + 2h
У2
...
...
xn = x0 + rih
Уп
Составим многочлен степени не выше п, который принимает
соответствующие значения при соответствующих значениях х.
Этот многочлен будет приближенно представлять функцию ц>(х).
Предварительно введем обозначения
Это так называемые разности 1-го, 2-го, ..., л-го порядка.
Напишем многочлен, принимающий значения у09 yi соответ»
етвенно при х0 и хх. Это будет многочлен 1-й степени
Действительно,
- Уо) =
Напишем многочлен, принимающий значения у0, уи у2 соот-
ветственно при х0, х19 х2. Это будет многочлен 2-й степени
г2\л) ?/о"Г^?/о h -Г 2| h
Действительно,
B)
Многочлен третьего порядка будет иметь вид
+
А3</о х—х0 ( х—х0
3!
Хл ( .
h
C)
Наконец, многочлен n-го порядка, принимающий значения j/0,
Уи Уг> *->Уп соответственно при х0, хг, х2У ..., хп, будет иметь
8 Н. С. Пискунов, т. 1

226 КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ [ГЛ. Vlt
вид
в чем можно убедиться непосредственной подстановкой. Это и
есть интерполяционная формула или интерполяционный многочлен
Ньютона.
По существу, многочлен Лагранжа и многочлен Ньютона для
данной таблицы значений тождественны, но по-разному написаны,
так как многочлен степени не выше п, принимающий заданные
п-\-\ значений при данных п+l значениях ху находится един-
единственным образом.
Во многих случаях интерполяционный многочлен Ньютона
более удобен, чем интерполяционный многочлен Лагранжа. Осо-
Особенность этого многочлена заключается в том, что при переходе
от многочлена &-й степени к многочлену (?+1)-й степени пер-
первые &+1 членов не меняются, а только добавляется новый член,
который равен нулю при всех предыдущих значениях аргумента.
Замечание. По интерполяционным формулам Лагранжа
(см. формулу C) § 9) й Ньютона (формула D)) определяются
значения функции на отрезке хо<х <хп. Если по этим форму-
формулам определяется значение функции при х < х0 (это можно делать
при малом J jc — jc0 |), то говорят, что производится экстраполя-
экстраполяция таблицы назад. Если определяется значение функции при
х > хп, то говорят, что производится экстраполяция таблицы
вперед.
§ 11. Численное дифференцирование
Пусть значения некоторой неизвестной функции ф (х) заданы
таблицей, которая рассматривалась в начале § 10. Требуется
определить приближенно производную этой функции. Эта задача
решается так. Строится интерполяционный многочлен Лагранжа
или Ньютона и от этого многочлена находится производная.
Так как чаще рассматриваются таблицы с равными разностями
между роседними значениями аргумента, то мы будем пользо-
пользоваться интерполяционной формулой Ньютона. Пусть даны три
значения функции у0, уи у2 при значениях аргумента #0, хи х2.
Тогда пишем многочлен B) § 10 и его дифференцируем. Полу-
Получаем приближенное значение производной функции на отрезке
X <^1 X <~^. X *
%Ч*)«ВД = ^+#B^-1). A)
При х=х0 получаем
ф W»/',^)^

§ Щ О НАИЛУЧШЕМ ПРИБЛИЖЕНИИ ФУНКЦИЙ МНОГОЧЛЕНАМИ 227
Если будем рассматривать многочлен 3-го порядка (см. C) § 10),
то после дифференцирования для его производной получим выра-
выражение
В частности, при я = х0 получаем
Если мы будем пользоваться формулой D) § 10, то для при-
приближенного выражения производной при х = х0 получим
Заметим, что для функции, имеющей производные, разность Д*/о
есть бесконечно малая 1-го порядка, Д2#о — бесконечно малая 2-го
порядка, Д3у0"~ бесконечно малая 3-го порядка и т. д. относи-
относительно ft.
§ 12. О наилучшем приближении функций многочленами.
Теория Чебышева
В связи с задачей, рассмотренной в §§ 9 и 10, естественно
поставить такой вопрос: пусть на отрезке [а,6] задана непре-
непрерывная функция <р(х). Можно ли эту функцию с любой
наперед заданной степенью точности приближенно
представить в виде многочлена Р (х)? Иначе говоря, можно ли
подобрать такой многочлен Р(х), чтобы разность между ц>(х)
и Р (х) по абсолютной величине во всех точках отрезка [a, b)
была меньше любого наперед заданного положительного числа е?
Утвердительный ответ *) на этот вопрос содержится в следующей
теореме, которую мы приводим здесь без доказательства:
Теорема Вейерштрасса. Если функция ц>{х) непре-
непрерывна на отрезке [а, 6], то для любого е > 0 существует такой
многочлен Р(х), что во всех точках указанного отрезка выпол-
выполняется неравенство
Выдающийся советский математик академик С. Н. Вернштейн
дал следующий способ непосредственного построения таких много-
*) Заметим, что интерполяционный многочлен Лагранжа [см. C) § 9] не
дает еще ответа на поставленный вопрос. Его значения равны значениям
функции в точках xOi xit x2t ..., хп, но они могут быть очень далеки от
значений функции в других точках отрезка [а, Ь].
8*

228 КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ ?ГЛ. VII
членов, которые приближенно равны непрерывной функции ф (х)
на заданном отрезке.
Пусть, например, функция cp(jt) непрерывна на отрезке [0, 1].
Составим выражение
в„ (*) = Ё ф (f
ш —О
Здесь С{?—~ биномиальные коэффициенты, <р (—) —значение дан-
данной функции ц точке * = ¦—-. Выражение ?„(#) является много-
многочленом п-й степени; его называют многочленом Бернштейна.
Если задано произвольное е > 0, то можно подобрать такой
многочлен Бернштейна (т. е. так выбрать его степень я), чтобы
для всех значений х на отрезке [0, 1] выполнялось неравенство
Отметим, что рассмотрение отрезка [0, 1], а не произвольного
отрезка [а, Ь\ не является существенным ограничением общности,
так как с помощью замены переменной x = a-\-t (b — а) можно
любой Ьтрезок [а, Ь\ преобразовать в отрезок [0, 1]. При этом
многочлен n-й степени преобразуется в многочлен той же степени.
Создателем теории наилучшего приближения функций с по-
помощью многочленов является русский математик П. Л. Чебышев
A821—1894) —один из величайших представителей математиче-
математической мысли. Им получены наиболее глубокие результаты в этой
области, оказавшие исключительное влияние на работу последую-
последующих математиков. Исходной точкой для создания этой теории
была работа П. Л. Чебышева по теории шарнирных механизмов,
широко используемых в машинах. Изучая такие механизмы, он
пришел к задаче разыскания среди всех многочленов данной
степени с коэффициентом при старшем члене, равным единице,
такого многочлена, который меньше всех отклоняется от нуля
на заданном отрезке. Такие многочлены им были найдены и
впоследствии учеными названы многочленами Чебышева. Эти
многочлены обладают многими замечательными свойствами и
в настоящее врегйя являются могучим средством исследования
во многих вопросах математики и техники.
Упражнения к главе VII
1. Найти C + 5()D— 0/ Отв- 17+Ш. 2. Найти F+llt)G+3f>
Отв. 9+95i. 3. Найти -jrrzf- Отв- ??—?Т *' 4' Найти D~(K- О/я*.—524+7*.
5. Найти уТ. Отв. ± Х~^1 . 6. Найти ^—5—12/. Отв. ± B—3i).
7. Привести к тригонометрическому виду выражения: а) 1 + *\
Отв. yjfcos^ + isln^-) .6)\-LOme.Y'2 (cos^+isin—-). 8. Найти

УПРАЖНЕНИЯ К ГЛАВЕ VII 229
Отв. ¦ ?—; —i\ ~-—. 9. Выразить через степени sin* и cos*
следующие выражения: sin 2*, cos 2*, sin 4л:, cos 4*, sin 5*, cos 5л:. 10. Выра-
Выразить cos2л:, cos3*:, cos4*, cos5*, cos6*; sin2*, sin3*, sin4*, sin5* через
синус и косинус кратных дуг. 11. /(*)=*3—4*2 + 8*—1 разделить на *+4.
Отв. /(*) = (*+4)(*2—8* + 40) —161, т. е. частное = *2 —8*+40; остаток
/(—4) =—161. 12. /(*)=*4+12*3 + 54*2+108*+81 разделить на *4-3.
Отв. /(*) = (*+3)(*3+9*2+27*+27). 13. /(*)=*7—1 разделить на *—1.
Отв. /(*) = (*—1)(*6+*5 + *4+*3+*2+*+1).
Разложить на множители с действительными коэффициентами многочлены:
14./(*) = *4-1. Отв. /(*) = (*—1)(*+1)(*2+1). 15./(*) = *2-л:-2.
Отв. /(*) = (*-2)(*+1). 16. /(*) = *3 + 1. Отв. /(*) = (*+1) (*2-*+1).
17. На основании эксперимента получены значения функции у от *:
r/i= 4 при *!==0,
#2= 6 при *2 = 1,
//з=Ю при *з = 2.
Представить приближенно функцию многочленом второй степени.
Отв. *2+*+4.
18. Найти многочлен четвертой степени, принимающий при *=1,2, 3, 4, 5
соответственно значения 2, 1, —1, 5, 0. Отв. —^-*4 +-^-*3 5- *2 А—тг х—35.
о о о о
19. Найти многочлен, по возможности низкой степени, принимающий при
* = 2, 4, 5, 10 соответственно значения 3, 7, 9, 19. Отв. 2*—1.
20. Найти многочлены Бернштейна 1-й, 2-й, 3-й и 4-й степеней для функ-
функции у = sin пх на отрезке [0, 1]. Отв. В1(х) = 0; В2(*) = 2*A—*);

ГЛАВА VIII
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 1. Определение функции нескольких переменных
Рассматривая функции одной переменной, мы указывали, что
при изучении многих явлений приходится встречаться с функ-
функциями двух и более независимых переменных. Приведем несколько
примеров.
Пример 1. Площадь S прямоугольника со сторонами, длины которых
равны хну, выражается формулой S—xy. Каждой паре значений хну
соответствует определенное значение площади S; S есть функция двух пере-
переменных.
Пример 2. Объем V прямоугольного параллелепипеда с ребрами, длины
которых равны х, у, г, выражается формулой V—xyz. Здесь V есть функция
трех переменных х, у, г.
Пример 3. Дальность R полета снаряда, выпущенного с начальной
скоростью v0 из орудия, ствол которого наклонен к горизонту под углом ф,
„ п vl sin 2ф . ^
выражается формулой R= ¦=-- (если пренебречь сопротивлением воз-
воздуха). Здесь g—ускорение силы тяжести. Для каждой пары значений vQ и
Ф эта формула дает определенное значение /?, т. е. R является функцией
двух переменных Vq и ф.
24
Пример 4. « = !— . Здесь и есть функция четырех пере-
переменных х, у, z, t.
Определение 1. Если каждой паре (#, у) значений двух
не зависимых друг от друга переменных величин х и у из неко-
некоторой области их изменения D, соответствует определенное зна-
значение величины г, те мы говорим, что z есть функция двух
независимых переменных х и г/, определенная в области D.
Символически функция двух переменных обозначается так:
* =*/(*» У)> z = F(x, у) и т. д.
Функция двух переменных может быть задана, например,
с помощью таблицы или аналитически — с помощью формулы,
как это сделано в рассмотренных выше четырех примерах. На
основании формулы можно составить таблицу значений функции
для некоторых пар значений независимых переменных. Так, для

§ %1 ОПРЕДЕЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
первого примера можно составить следующую таблицу:
S = xy
231
—^^ х
у ^^"^^
1
2
3
4
0
0
0
i 0
0
1
1
2
3
4
1,5
1,5
3
4,5
6
2
2
4
6
8
3
6
9
12
В этой таблице на пересечении строки и столбца, соответствую-
соответствующих определенным значениям х и у, проставлено соответствую-
соответствующее значение функции S.
Если функциональная зависимость z = f(x, у) получается
в результате измерений величины z при экспериментальном изу-
изучении какого-либо явления, то сразу получается таблица, опре-
определяющая z как функцию двух переменных. В этом случае функ-
функция задается только таблицей.
Как и в случае одной независимой переменной, функция двух
переменных существует, вообще говоря, не при любых значениях
х и у.
Определение 2. Совокупность пар (х, у) значений х и у,
при которых определяется функция г = /(х, у), называется обла-
областью определения или областью существования этой функции.
Область определения функции наглядно иллюстрируется гео-
геометрически. Если каждую пару значений х и у мы будем изоб-
изображать точкой М (ху у) в плоскости Оху, то область определения
функции изобразится в виде некоторой совокупности точек на
плоскости. Эту совокупность точек будем также называть облас-
областью определения функции. В частности, областью определения
может быть и вся плоскость. В дальнейшем мы будем главным
обрааом иметь дело с такими областями, которые представляют
собой части плоскости, ограниченные линиями. Ли-
Линию, ограничивающую данную область, будем называть границей
области. Точки области, не лежащие на границе, будем называть
внутренними точками области. Область, состоящая из одних внут-
внутренних точек, называется открытой или незамкнутой. Если же
к области относятся и точки границы, то область называется замк-
замкнутой. Область называется ограниченной, если существует такая
постоянная С, что расстояние любой точки М области от начала
координат О меньше С, т. е. |СШ|<С.
Пример 5. Определить естественную область определения функции г =
= 2х—у.
Аналитическое выражение 2х—у имеет смысл при любых значениях хну.
Следовательно, естественной областью определения функции является вся
плоскость Оху.

232
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. VIII
Рис. 166.
Примерб. г= у 1 —л:2 — ?/2.
Для того чтобы z имело действительное значение, нужно, чтобы под кор-
корнем стояло неотрицательное число, т. е. х и у должны удовлетворять нера-
неравенству 1—х2—#2^0, или *2 + г/2^1.
Все точки М (дс, у), координаты которых удовлетворяют указанному нера-
неравенству, лежат в круге радиуса 1 с центром в начале координат и на гра-
границе этого круга.
Пример 7. z=\n(x+y).
Так как логарифмы определены только для
положительных чисел, то должно удовлетво-
удовлетворяться неравенство х-\-у > О, или у >—х.
Это значит, что областью определения
функции г является половина плоскости, распо-
расположенная над прямой у — — х, не включая са-
самой прямой (рис. 166).
Пример 8. Площадь треугольника 5
представляет собой функцию основания х и
высоты у: S = xy/2.
Областью определения этой функции яв-
является область х > О, у > О (так как основа-
основание треугольника и его высота не могут быть
ни отрицательными, ни нулем). Заметим, что
область определения рассматриваемой функции
не совпадает с естественной областью определения того аналитического выраже-
выражения, с помощью которого задается функция, так как естественной областью
определения выражения ху/2 является, очевидно, вся плоскость Оху.
Определение функции двух переменных легко обобщить на
случай трех или более переменных.
Определение 3. Если каждой рассматриваемой совокупно-
совокупности значений переменных х, у, г, ..., м, t соответствует опре-
определенное значение переменной w, то будем называть w функцией
независимых переменных х, у, z, ..., и, t и писать w = F (х, у,
г, ..., и, t) или w = f(x9 у, г, ..., и, t) и т. п.
Так же как и для функции двух переменных, можно говорить
об области определения функции трех, четырех и более перемен-
переменных.
Так, например, для функции трех переменных областью опре-
определения является некоторая совокупность троек чисел (х, у, г).
Заметим тут же, что каждая тройка чисел задает некоторую точку
М (х, у\ г) в пространстве Oxyz. Следовательно, областью опре-
определения функции трех переменных является некоторая совокуп-
совокупность точек пространства.
Аналогично этому можно говорить об области определения
функции четырех переменных u = f(x, у, г, /) как о некоторой
совокупности четверок чисел (#, у, г, t). Однако область опреде-
определения функции четырех или большего числа переменных уже не
допускает простого геометрического истолкования.
В примере 2 приведена функция трех переменных, определен-
определенная при всех значениях х, у, г.
В примере 4 приведена функция четырех переменных.

§2] ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ 233
Пример 9. ay = l/"l—jc2—у2—г2 —и2.
Здесь w—функция четырех переменных ху у, z, «, определенная при зна-
значениях переменных, удовлетворяющих соотношению
1—л:3—^г2—г2—
§ 2. Геометрическое изображение функции двух переменных
Рассмотрим функцию
У)>
A)
определенную в области G на плоскости Охд (эта область может
быть, в частности, и всей плоскостью), и систему прямоугольных
декартовых координат Охуг (рис. 167). В каждой точке (л;, у)
восставим перпендикуляр к плоскости Оху и на нем отложим
отрезок, равный /(х, у).
Тогда мы получим в пространстве точку Р с координатами
*, у, * = /(*, у).
Геометрическое место точек Р, координаты которых удовлет-
удовлетворяют уравнению A), называется графиком функции двух пере-
переменных. Из курса аналитической геометрии мы знаем, что урав-
Рис. 167.
Рис. 168.
нение A) в пространстве определяет некоторую поверхность. Таким
образом, графиком функции двух переменных является поверх-
поверхность, проектирующаяся на плоскость Оху в область определения
функции. Каждый перпендикуляр к плоскости Оху пересекает
поверхность z~f(x, у) не более чем водной точке.
Пример. Графиком функции 2 = *2+#2* как известно из аналитической
геометрии, является параболоид вращения (рис. 168).
Замечание. Функцию трех или более переменных изобра-
изобразить с помощью графика в пространстве невозможно.

234
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
f ГЛ. VIИ
§ 3. Частное и полное приращение функции
Рассмотрим линию PS пересечения поверхности
* = /(*. У)
с плоскостью у = const, параллельной плоскости Oxz (рис. 169),
Так как в этой плоскости у
сохраняет постоянное значение,
то z вдоль кривой PS будет ме-
меняться только в зависимости от
изменения х. Дадим независимой
переменной х приращение Ах;
тогда г получит приращение, ко-
которое называют частным прира-
приращением г по х и обозначают че-
через Axz (на рисунке отрезок SS')f
так что
, y)-f(x,y). A)
Аналогично, если х сохраня-
сохраняет постоянное значение, а у полу-
получает приращение Ауу то z получает приращение, называемое част-
частным приращением z no у. Это приращение обозначают символом
Ayz (на рисунке отрезок ТТ')\
B)
Приращение Ayz функция получает «вдоль линии» пересечения
поверхности z = f(x, у) с плоскостью х = const, параллельной
плоскости Oyz.
Наконец, сообщив аргументу х приращение Ах, а аргументу
у—приращение Ау, получим для z новое приращение Дг, кото-
которое называется полным приращением функции z и определяется
формулой
Az = f(x + Ax, y + Ay)-f(x9 у). C)
На рис. 169 Аг изображается отрезком QQ'.
Надо заметить, что, вообще говоря, полное приращение не
равно сумме частных приращений, т. е. AA A
Пример. г = ху.
) у—ху = у Ах,
При *=1, у=2, Д*=0,2, Ау = 0,3 имеем A^2 =
= 0,76.
Аналогичным образом определяются частные и полное прира-
приращения функции любого числа переменных. Так, для функции трех

§41
НЕПРЕРЫВНОСТЬ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
235
переменных u~f(xf у, t) имеем
&xu = f(x + bx9 у, t)—f(x9 у, t)y
Ayu = f(x, у+Ьу, t)-f(xt yy 0.
f( M)f(x, у, t),
, t).
§ 4. Непрерывность функции нескольких переменных
Введем одно важное вспомогательное понятие — понятие окрест-
окрестности данной точки.
Окрестностью радиуса г точки М0(х0> у0) называется сово-
купность всех точек (х, у), удовлетворяющих неравенству
V(x — хоJ+(у — */<>J < г, т. е. совокупность всех точек, лежащих
внутри круга радиуса г с центром в точке М0(х0, у0).
Если мы говорим, что функция /(#, у) обладает каким-либо
свойством «вблизи точки (л:0, у0)» или «в окрестности точки (х0У */0)»,
то под этим подразумеваем, что найдется такой круг с центром
(#<р Уо)» во всех точках которого дан-
данная функция обладает указанным свойст-
свойством.
Прежде чем рассматривать понятие
непрерывности функции нескольких пе-
переменных, рассмотрим понятие преде-
предела функции нескольких переменных*).
Пусть дана функция
определенная в некоторой области G Рис. 170,
плоскости Оху. Рассмотрим некоторую
определенную точку М0(х0, yQ), лежащую в области G или на ее
границе (рис. 170).
Определение 1. Число А называется пределом функции
f(xf у) при стремлении точки М(х, у) к точке М0(х0У yQ), если
для каждого числа г > 0 найдется такое число г > 0, что
для всех точек М(х, у), для которых выполняется неравенство
, < г, имеет место неравенство
Если число А является пределом функции / (х, у) при М (jc, у)
—*Л1в(*д, у0), то пишут
lim f(x, y) = A.
*) Мы будем в основном рассматривать функции двух переменных, так
как рассмотрение трех и более переменных не вносит никаких принципиаль-
принципиальных изменений, но вносит добавочные технические трудности.

236 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. VIII
Определение 2. Пусть точка М0(х0, yQ) принадлежит
области определения функции f (х, у). Функция z = f(x, у) назы-
называется непрерывной в точке Л10(л:0, */0), если имеет место равенство
lim /(*, y) = f(xQy i/0)> 0)
причем точка М (х> у) стремится к точке Мо (#0, у0) произвольным
образом, оставаясь в области определения функции.
Если обозначим х = хо-\-Ах, # = */Q + Aj/, то равенство A)
можно переписать так:
ton / (х0 + Ах, у0 + Ау) = / (х0, у0) (Г)
или
lim [f (X0-f-l\X, Уо-Т^У) — / (Xo, Уо)\ = У. A )
AX-+Q
Обозначим Ap = K(AxJ + (At/)a. При Ах—>0 и Ау—>0 Ар—>0,
и обратно, если Др—»0, то Ад;—>0 и Д#—*0.
Замечая, далее, что выражение, стоящее в квадратных скоб-
скобках в равенстве (Г'), есть полное приращение функции Аг, равен-
равенство (Г) можно переписать в форме
ШпДг = 0. П'")
Др-*0
Функция, непрерывная в каждой точке некоторой области, назы-
называется непрерывной в области.
Если в некоторой точке jV (xq, yQ) не выполняется условие A),
то точка N (х0, у0) называется точкой разрыва функции z=f (xyy).
Условие (Г) может не выполняться, например, в случаях:
1) z = f(x, у) определена во всех точках некоторой окрестно-
окрестности точки N (х0, у0), за исключением самой точки N (х0, у0);
2) функция z = f(x, у) определена во всех точках окрестности
точки #(#0, #0), но не существует предела lim/(л, у);
х
хх0
У-+Уо
3) функция определена во всех точках окрестности N(a:0, yQ)
и существует предел limf(x,y), но
lim
Пример 1. Функция z = x2 + y2 непрерывна при любых значениях х и
</, т. е. в любой точке плоскости Оху.
Действительно, каковы бы ни были числа х и уу Ал: и Аг/, имеем
следовательно, lim Az = 0.
А0

НЕПРЕРЫВНОСТЬ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
237
Приведем пример разрывной функции.
Пример 2. Функция г== 2 *^ а определена всюду, кроме точки *=0,
0=0 (рис. 171, 172). * У
Рассмотрим значения t вдоль прямой y—kx (k~ const). Очевидно, вдоль
этой прямой
<2.Ь,х^ 2h
X ~|~Й X 1 "~р к
т. е. функция 2 вдоль всякой прямой, проходящей через начало координат,
сохраняет постоянное значение, зависящее от углового коэффициента k пря-
прямой» Поэтому, подходя к началу координат по различным путям, мы будем
Рис. 171.
получать различные предельные значения, а это значит, что функция f (*, у)
не имеет предела, когда точка (*, у) на плоскости Оху стремится к началу
координат. Следовательно, функция разрывна в этой точке. Эту функцию нельзя
доопределить в начале координат так, чтобы она стала непрерывной. Легко
видеть, с другой стороны, что в остальных точках эта функция непрерывна.
Укажем без доказательства некоторые важные свойства функ-
функции многих переменных, непрерывной в замкнутой и ограничен-
ограниченной области. Эти свойства аналогичны свойствам непрерывной
на отрезке функции одной переменной (см. § 10 гл. II).
Свойство 1. Если функция f(x, у, ...) определена и не-
непрерывна в замкнутой и ограниченной области D, то в области D
найдется по крайней мере одна точка #(л0, t/0, ...) такая, что
для всех других точек области будет выполняться соотношение
У»
У>
и по крайней мере одна точка N (*0, t/0, •..) такая, что для всех
других точек области будет выполняться соотношение
Значение функции f(xQt yOf ...)=*M будем называть наиболь-
наибольшим значением функции /(*, у% •..) в области D9 а значение
/ (*ot Ум ...) = m — наименьшим значением.

238 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. VIU
Это свойство формулируют и так. Непрерывная функция в замк-
замкнутой ограниченной области D достигает по крайней мере один
раз наибольшего значения М и наименьшего значения т.
Свойство 2. Если функция f(x, у, .,.) непрерывна в замк-
замкнутой и ограниченной области D и если М и т— наибольшее и
наименьшее значения фун-кции f(x9 у, ...) в области, то для
любого числа \i, удовлетворяющего условию т < \i < М, найдется
в области такая точка N*(x*0, yl, ...), что будет выполняться
равенство /(*J, yl, ...) = !*•
Следствие свойства 2. Если функция /(х, у, ...) не-
непрерывна в замкнутой ограниченной области и принимает как
положительные, так и отрицательные значения, то внутри области
найдутся точки, в которых функция f (х,у, ...) обращается в нуль.
§ 5.: Частные производные функции нескольких переменных
Определение. Частной производной по х от функции
z = f{xy у) называется предел отношения частного приращения
Axz по ^ к приращению Ах при стремлении Ах к нулю.
Частная производная по х от функции г — f(x, у) обозначается
одним из символов
* ГЛх. у), 1.1.
Таким образом, по определению,
* lim *?= ton
дх Ax
Аналогично частная производная по у от функции z = f(x, у)
определяется как предел отношения частного приращения функ-
функции Ayz по у к приращению Ау при стремлении Ау к нулю.
Частная производная по у обозначается одним из символов
, г дг_ д[_
Таким образом,
* Нт V = Hm f(x.y+Ay)-nx.y)m
ду д^оАУ А
Заметив, что Axz вычисляется при неизменном у, a A9z при
неизменном дг, мы можем определения частных производных сфор-
сформулировать так: частной производной по хот функции z = f(x, у)
называется производная по ху вычисленная в предположении, что
у — постоянная. Частной производной по у от функции z = f(x,y)
называется производная по у, вычисленная в предположении,
что х — постоянная.
Из этого определения ясно, что правила вычисления частных
производных совпадают с правилами, указанными для функций

§6J ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ 239
одной переменной, и только требуется каждый раз помнить, по
какой переменной ищется проиаводная.
Пример I. Дана функция z = x2siny; требуется найти частные произ-
dz dz
водные дх И Ту'
Решение. ^- = 2xsinyt -^- = х2 cos у.
Пример 2. z=x^.
Здесь % = У>?-\ %=*У^х-
Частные производные функции любого числа переменных опре-
определяются аналогично-. Так, если имеем функцию и четырех пере-
переменных х, у9 zt t:
u = f(x, уу zy t),
то
ди v f(x+&x, уу г, t) — f(x, у, г, /)
ПримерЗ. u =
—-2x4-tz* — -2«/ — Sxtz* du-xz*
§ 6. Геометрическая интерпретация частных производных
функции двух переменных
Пусть уравнение
г = /(^, У)
есть уравнение поверхности, изображенной на рис. 173.
Проведем плоскость # = const. В сечении этой плоскости с по-
поверхностью получится линия РТ. При данном х рассмотрим на
плоскости Оху некоторую точку М(х, у). Точке М соответствует
точка Р(ху у, г), принадлежащая поверхности z = f(x, у). Остав-
Оставляя х неизменным, дадим переменной у приращение Ay = MN =
=*РТ'. Тогда функция z получит приращение Ayz = TT' (точке
N(x* У + ку) соответствует точка Т (х, y + ky, z + kyz) на поверх-
поверхности z^=f(x, у)).
V
Отношение —- равно тангенсу угла, образуемого секущей РТ
с положительным направлением оси Оу:

240
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. VIII
Следовательно, предел
равен тангенсу угла |3, образо-
образованного касательной РВ к кри-
кривой РТ в точке Р с положи-
положительным направлением оси Оу:
dz
Итак, частная производная
-j- численно равна тангенсу уг-
угла наклона касательной к кри-
Рис. 173. вой, получающейся в сечении
поверхности z = f(x, у) плос-
плоскостью х = const.
Аналогично частная производная -—- численно равна тангенсу
угла наклона а касательной к сечению поверхности 2 = f(x, у)
плоскость^ у = const.
§ 7. Полное приращение и полный дифференциал
По определению полного приращения функции г = / (л:, у) имеем
(см. § 3)
Az — f(x + Ax, y + Ay)—f(x, у). A)
Предположим, что / (я, у) в рассматриваемой точке (л:, у) имеет
непрерывные частные производные.
Выразим Дг через частные производные. Для этого в правой
части равенства A) прибавим и вычтем f(x, y-\-Ay):
Выражение
f{x, y + Ay)-f(x, у).
стоящее во второй квадратной скобке, можно рассматривать как
разность двух значений функции одной переменной у (значение х
остается постоянным). Применяя к этой разности теорему Лаг-
ранжа, получим
f(x,
1C)
где у заключено между у и у-\-ку.
Точно так же выражение, стоящее в первой квадратной скобке
равенства B), можно рассматривать как разность двух значений

§ 71 ПОЛНОЕ ПРИРАЩЕНИЕ И ПОЛНЫЙ ДИФФЕРЕНЦИАЛ 241
функции одной переменной х (второй аргумент сохраняет одно
и то же значение у + Ау). Применяя к этой разности теорему
Лагранжа, получим
где х заключено между х и +
Внося выражения C) и D) в равенство B), получим
Аг = Ьх + АуЖ1. E)
Так как, по предположению, частные производные непре-
непрерывны, то
„ dfG, у+Ау) df(x, у)
(так как лиг/ заключены соответственно между х и x-f-^x, »/
и у-\-Ау, то при Ах —*0 иДу—!-0л;и#стремятся соответственно
к х и (/). Равенства F) можно переписать в виде
df(x, y+Ay) _df(x, g) .
. ^ F')
0/(*. у) _^/(^ у), лт 1 ;
ду ду "г^2>
где величины уг и ^2 стремятся к нулю, когда Ах и Ау стремятся
к нулю (т.е. когда Ap = KA*2 + A*/2—* 0)-
В силу равенств F') соотношение E) принимает вид
E')
Сумма двух последних слагаемых правой части является беско-
бесконечно малой высшего порядка относительно Ар= угАх2 + Ау2. Дей-
Действительно, отношение ^-^~>0 при Др—>0, так как уг является
бесконечно малой величиной, а -——ограниченной ( -т^- ^1).
Аналогично проверяется, что Jk-?—>().
Сумма первых двух слагаемых есть выражение, линейное отно-
относительно Ах и Ау. При fx(x9 у)фО и f'y(лс, у) Ф0 это выражение
представляет собой главную часть приращения, отличаясь
от Az на бесконечно малую высшего порядка относительно Ар =

242
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. VIII
Определение. Функция z = f(x> у), полное приращение Дг
которой в данной точке (х, у) может быть представлено в виде
суммы двух слагаемых: выражения, линейного относительно Ах
и Ду, и величины, бесконечно малой высшего порядка относи-
относительно Др, называется дифференцируемой в данной точке, а линей-
линейная часть приращения называется полным дифференциалом и обоз-
обозначается через dz или df.
Из равенства E') следует, что если функция f(x, у) имеет
непрерывные частные производные в дайной точке, то она диффе-
дифференцируема в этой точке и имеет полный дифференциал
Равенство E') можно переписать в виде
и с точностью до бесконечно малых высшего порядка относительно
Ар можно написать следующее приближенное равенство:
Дг &dz.
Приращения независимых переменных Ахи Ау мы будем назы-
называть дифференциалами независимых переменных х и у и обозна-
обозначать соответственно через dx и dy. Тог-
*^„„„„^>„„„~, Да выражение полного дифференциала при-
^ш^ШЩата^ мет в^д ^ * *
Таким образом, если функция z = f(x, у)
имеет непрерывные частные производные,
то она дифференцируема в точке (х, #),
и ее полный дифференциал равен сумме
произведений частных производных на
дифференциалы соответствующих незави-
независимых переменных.
Пример 1. Найти полный дифференциал и полное приращение функции
г=ху в точке B; 3) при Дд; = 0,1, Д#=0,2.
Решение.
Следовательно,
= 3.0,1 +2-0,2+0,1.0,2 = 0,72,
z = 3.0,1+2- 0,2 = 0,7.
На рис. 174 дана иллюстрация к этому примеру.
Предыдущие рассуждения и определения соответственным обра-
образом обобщаются на функции любого числа аргументов.

§¦*} ПРИМЕНЕНИЕ ПОЛНОГО ДИФФЕРЕНЦИАЛА 243
Если имеем функцию любого числа переменных
w=f(x, у, z, и, ..., *),
df df df
причем все частные производные ~, ~, .¦., -~- непрерывны
в точке (х, у, г, иу ..., t), то выражение
является главной частью полного приращения функции и назы-
называется полным дифференциалом. Доказательство того, что разность
Aw—dw является бесконечно малой более высокого порядка, чем
|/г(ДхJ + (А^/J4-. • • + (Д02> проводится совершенно так же, как
и для функции двух переменных.
Пример 2. Найти полный дифференциал функции u=ex2+y2sin2 г трея
переменных дг, у, г.
Решение. Заметив, что частные производные
дх
непрерывны при всех значениях х, у, г, находим
^^-dy+^-dz=ex2+y2 Bxsin2zdx+2ysin2z dy+sin 2z dz).
§ 8. Применение полного дифференциала
в приближенных вычислениях
Пусть функция z = f(x, у) дифференцируема в точке (х, у).
Найдем полное приращение этой функции
Az = f(x + Ax, y+Ay)-f(x9 y)f
откуда
f(x + Ax, y + Ay)^f(x, y) + Az. A)
Мы имели приближенную формулу
Az « dz, B)
где
Подставляя в формулу A) вместо Az развернутое выражение для
dz, получим приближенную формулу
f(x, А+М^Ьс + Ц^Ау, D)

244 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. VIII
верную с точностью до бесконечно малых высшего порядка отно-
относительно Ах и Ау.
Покажем, как используются формулы B) и D) для приближен-
приближенных вычислений.
Задача. Вычислить объем материала, нужного для изготовления цилин-
цилиндрического стакана следующих размеров (рис. 175): радиус внутреннего ци-
. линдра Rt высота внутреннего цилиндра Я, толщина
{ стенок и дна стакана k.
j <т—t—* Решение. Дадим два решения этой задачи: точ-
' | ное и приближенное.
а) Точное решение. Искомый объем v ^авен
' разности объемов внешнего цилиндра и внутреннего ци-
цилиндра. Так как радиус внешнего цилиндра равен R -)-
+kt а высота H + k, то v=n(R+kJ(H+k)—nR2H9
или
E)
I
f б) Приближенное решение. Обозначим че-
* рез/объем внутреннего цилиндра, тогда f=nR2H. Это—
Рис. 175. функция двух переменных R и Я. Если увеличим R и
Я на ky то функция / получит приращение Д/; но это
и будет искомый объем v9 т. е. o^Af.
На основании соотношения A) имеем приближенное равенство v « dft или
J?LbR+-!?LAH. Но так как ^=2nRHt ^L^nR2, Д/? = АЯ=:^, то
получаем
v&7tBRHk + R2k). F)
Сравнивая результаты E) и F), видим, что они отличаются на величину
n(Hk2+2Rk2+ks), состоящую из членов второго и третьего порядка малости
относительно к.
Применим эти формулы к числовым примерам.
Пусть # = 4 см, Я==20 см, ? = 0,1 см.
Применяя E), получим точно
v=k B-4.20.0,1 +42-0,1 +20.0,12+2-4-0,12+0,13)=: 17,881л.
Применяя формулу F), пшучим приближенно
0« л B-4.20.0,1+42.0,1) = 17,6я.
Следовательно, приближенная формула F) дает ответ с погрешностью, мень-
меньшей 0,3л, что составляет 100».^' %, т.е. менее 2% измеренной величины.
§ 9. Приложение дифференциала к оценке погрешности
при вычислениях
Пусть некоторая величина и является функцией величин х, у,
г, ..., *:
ы = /(*. у, г, ..., 0»
причем, определяя каким-то способом значения величин x,ytz9 ...
... f t, мы допускаем погрешности Ах, Ау> ..., Д?. Тогда значение и,
вычисленное по неточным значениям аргументов, получится с

$9] ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛА К ОЦЕНКЕ ПОГРЕШНОСТИ 245
погрешностью
Au = f(x+Ax, у+Ау, ..., z + Az, t + At)-f(x, у, г, ..., t).
Ниже мы займемся оценкой погрешности Аи, если известны пог-
погрешности Ах, At/, ..., At.
При достаточно малых абсолютных значениях величин Ал;,
А у, ..., At можем приближенно заменить полное приращение
полным дифференциалом:
Здесь значения частных производных и значения погрешностей
аргументов могут быть как положительными, так и отрицатель-
отрицательными. Заменяя их абсолютными величинами, получим неравенство
<|. <D
Если через | А*х |, | А*у |, ..., | А*и | обозначим максимальные абсо-
абсолютные погрешности соответствующих величин (границы ддя абсо-
абсолютных величин значений погрешностей), то можно, очевидно,
принять
|?| |f ||Й|А*'|. B)
Примеры.
1. Пусть u=^x+y+z, тогда | А* и |=| А**|+| А* у
2. Пусть и — х—у, тогда | A*w | = | А*л: | +1 А*у |.
3. Пусть и = ху, тогда \ А*и\ = \х\\ А*у\ + \у\\ \*х\.
. _ х
4. Пусть и=—, тогда
\А*х\
а у
У
5. Гипотенуза с и катет а прямоугольного треугольника ЛВС, определен-
определенные с максимальными абсолютными погрешностями |А*с| = 0,2, |Д*а| = 0,1,
соответственно равны с=75, а = 32. Определить угол А по формуле sin A =
= — ; максимальную абсолютную погрешность | АЛ | при вычислении угла А,
Решение. sin^=— ,Л = arcsin — , следовательно,
¦С С
дА 1 дА а
да У~с2—а* ' дс
По формуле B) получим:
1 ОО
I АЛ | = —р= -О,И •====• 0,2 = 0,00273 радианов=9/24//.
1 ' /752322 75]^752322 F
32
Таким образом, >4 = arcsin^ ±9;24/;.

246
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[гл. vat
6. Пусть в прямоугольном треугольнике ABC катет 6—121,56 м, угол
А = 25°2Г40", при этом максимальная абсолютная погрешность при определе-
определении катета Ь равна |Д*6|=0,05м, максимальная абсолютная погрешность
при определении угла А равна |Д*Л| = 12".
Определить максимальную абсолютную погрешность при вычислении ка-
катета а по формуле a = btgA.
Решение, По формуле B) находим
\Ь\
Подставляя соответствующие значения (и помня, что | ДМ | нужно выразить
в радианах), получим
191 ^6 19
| \*а | = tg 25°21Ч0-»0,05+со$225О>21Ч0„ . 2бЙб5=0>°237 + 0,0087 = 0,0324 м,
Отношение погрешности Ах некоторой величины к приближен-
приближенному значению х этой величины называется относительной погреш-
погрешностью величины. Будем его обозначать Ьх:
с Да:
Максимальной относительной погрешностью величины х назы-
называется отношение максимальной абсолютной погрешности к абсо-
абсолютной величине х и обозначается \8*х\:
Для оценки максимальной относительной погрешности функции и
разделим все числа равенства B) на |и\ = \f(jc, у, z, ..., t)j:
df
дх
f
\ Л*
ду
~г
dt
f
но
it iL
дх __ д j |г| ду с
f I .
Поэтому равенство C) можно переписать так:
D)
*•*!..., E)
или коротко
18*гг| = | А*1п|/||. F)
Из формул как C), так и E) следует, что максимальная относи-
относительная погрешность функции равняется максимальной абсолютной
погрешности логарифма этой функции.

$ 101 ПОЛНАЯ ПРОИЗВОДНАЯ 247
Из формулы F) следуют правила, применяемые в приближен-
приближенных вычислениях.
1. Пусть и = ху. Пользуясь результатами примера 3, получим
т. е. максимальная относительная погрешность произведения рав-
равняется сумме максимальных относительных погрешностей сомно-
сомножителей.
2. Если м = ~, то, пользуясь результатами примера 4, находим
\\ \\ + \у\
Замечание. На основании примера 2 следует, что если
и^х—у> то |6»ц|= 'А |]^[л * Если х и У близки, то мо-
может оказаться, что | Ь*и | будет очень велика по сравнению с
определяемой величиной х—у. Это обстоятельство следует учиты-
учитывать при производстве вычислений.
Пример 7. Период колебания маятника равен Т = 2л Y^ljg, где /—длина
маятника, g—ускорение силы тяжести.
Какую относительную погрешность в определении Т мы допустим по этой
формуле, принимая я «3,14 (с точностью до 0,005), /=1 м (с точностью до
0,01 м), g = 9,8 м/с2 (с точностью до 3,02 м/с2).
Решение. По формуле F) максимальная относительная погрешность
равна |6*Г| = |Д*1пГ|. Но \пТ = 1п2 + 1пя+у1п /_ .1 \ng.
Вычислим |А*1пГ|. Учитывая, что л «3,14, Д*л = 0,005, /==1 м, Д*/ =
= 0,01 м, g=9,8 м/с2, A*g=0,02 м/с2, получим:
Итак, максимальная относительная погрешность равна
§ 10. Производная сложной функции. Полная производная.
Полный дифференциал сложной функции
Предположим, что в уравнении
z = F(u,v) A)
и и v являются функциями независимых переменных х и у:
и = (р(х, у), v = ty(x, у). B)
В этом случае z есть сложная функция от аргументов хну.
Конечно, z можно выразить и непосредственно через х, у, а
именно:
* = F[V(x, у), ф(*, у)]. C)
Пример 1. Пусть г = м3у3+и+Ь и = х2+у2, р=е*+0+Ь тогда
B+f)*{*+»+ lK+B+3)+h

248 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. VIII
Предположим, что функции F (и, v)> q>(x> у), -ф(#, у) имеют
непрерывные частные производные по всем своим аргументам и
поставим задачу: вычислить ~- и ¦—-, исходя из уравнений A) и
B) и не пользуясь уравнением C).
Дадим аргументу х приращение Д#, сохраняя значение у неиз-
неизменным. Тогда в силу уравнения B) и и v получат приращения
Ахи и Axv.
Но если и я v получают приращения Ахи и &xv, то и функция
z = F(u, v) получит приращение Дг, определяемое формулой E')
§7:
Разделим все члены этого равенства на Да::
Дг _dF_Axu,dF Axv
Если Дх —^0, то Дхи ->О и Д^ —>0 (в силу непрерывности функ-
функций « и у). Но тогда уг и у2 тоже стремятся к нулю. Переходя
к пределу при Д#—>0, получим
0 ^ дх А0 &х дх
Пт Ух^О, Нт 72 =
Ллг -> 0 Ах -* О
и, следовательно,
Если бы мы дали приращение Ау переменной уу а л: оставили
неизменным, то с помощью аналогичных рассуждений нашли бы
dz __dF ди , dF dw M,v
Пример 2.
г = 1п(«2+у), « = в*+Л г/ =
^2 2ц дг 1
dv M2-|-y'
ду * дх ду
Используя формулы D) и D'), находим
ду
В последние выражения вместо и и v необходимо подставить ех+У* и
х2~\-у соответственно.

§ 10] ПОЛНАЯ ПРОИЗВОДНАЯ 249
Для случая большего числа переменных формулы D) и D')
естественным образом обобщаются.
Например, если w = F(z, и, v, s) есть функция четырех аргу-
аргументов г, иу v, s, а каждый из них зависит от х и у, то фор-
формулы D) и D') принимают вид
dw dw dzj.dwdu.dw dv .dw ds
"д*~ dz dx ' du dx ' dv dx ' ds dx 9 ,p.\
dw dw dz^ .dwdu^dwdv^dwds * '
dy dz dy du dy dv dy ds dy
Если задана функция z = F(x, у, и, v), где у, и, v в свою
очередь зависят от одного аргумента х:
то, по сути дела, г является функцией только одной перемен-
переменной х и можно ставить вопрос о нахождении производной -~ #
Эта производная вычисляется по первой из формул E):
dz dz dx , dz dy , dz du , dz dv
но так как у, и, v — функции только одного я, то частные
производные обращаются в обыкновенные; кроме того, jp=l;
поэтому
dz dz , дг dy , dz <&/ , dz dv
4x~lte^lfyTx*l&lti*lhLx #
Эта формула носит название формулы для вычисления полной
производной -jp (в отличие от частной производной -—И .
Пример 3.
2У' y=sinx,
dz 9
~дх~-гх>
Формула F) дает в этом случае следующий результат:
dz dz . dz dy n , 1 _ . 1
dx dx^ dy dx ^2Vy 2^sinjc
Найдем далее полный дифференциал сложной функции, опре-
определенной равенствами A) и B).
Подставляем выражения — и -~ , определенные равенст-
равенствами D) и D'), в формулу полного дифференциала
b.dy. щ

250 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. VIII
Получаем
dF ди tdF dv
+
dF dU -L- 3F dv \ A
ШТу^до ду)ау-
Произведем следующие преобразования в правой части:
ди
Но
dv . . dv . . W
— dx+^dy^dv.
Равенство G) с учетом равенств (8) можно переписать так:
ИЛИ
Сравнивая F) и (9'), можем сказать, что выражение полного
дифференциала функции нескольких переменных (дифференциала
первого порядка) имеет тот же вид, т. е. форма дифференциала
инвариантна, являются ли и и v независимыми переменными или
функциями независимых переменных.
Пример 4. Найти полный дифференциал сложной функции
z = wV, и = х2 sin у, v = х3еУ.
Решение. По формуле (9') имеем
dz = 2uvz du + 3u2v2 dv=2uv* Bx sinydx+x2 cos у dy) + 3u2v2 (Зх2еУ dx+х*гУ dy).
Последнее выражение можно переписать и так:
dz=Buv*-2xsin y+3u2v2-ЗхЧу) dx+Buv*x2cosy+3u2v2x*ey) dy=-^ dx+-j- dy,
§ 11. Производная от функции, заданной неявно
Начнем рассмотрение этого вопроса с неявной функции одной
переменной *). Пусть некоторая функция у от х определяется
уравнением
F{x, у)=0.
Докажем следующую теорему.
*) В § 11 гл. III мы решали задачу о Дифференцировании неявной функ-
функции одной переменной. Там мы рассматривали отдельные примеры и не нашли
общей формулы, дающей производную от неявной функции, а также не выяс-
выяснили условий существования этой производной»

§ ill ПРОИЗВОДНАЯ ОТ ФУНКЦИИ, ЗАДАННОЙ НЕЯВНО 251
Теорема. Пусть непрерывная функция у от хзадается не-
неявно уравнением
F(x, у)-0, A)
где F(xy у), F'x(x, у), F'x(x, у) — непрерывные функции в некото-
некоторой области D, содержащей точку (х9 у), координаты которой
удовлетворяют у равнению A); кроме того, в этой точке F у (л:, у)фО.
Тогда функция у от х имеет производную
А B)
х> У)
Доказательство. Пусть некоторому значению х соответ-
соответствует значение функции у. При этом
Дадим независимой переменной х приращение Ах. Функция у
получит приращение Д#, т. е. значению аргумента х+Ах соот-
соответствует значение функции у + Ау. В силу уравнения F (х, #) = 0
будем иметь
Следовательно,
F(x+Ax,
Левую часть последнего равенства, являющуюся полным прира-
приращением функции двух переменных, по формуле E') § 7 можно
переписать так:
, y + Ay)-F{x, y)=*jL ^
где Yi и Тг стремятся к нулю при Ах и At/, стремящихся к нулю.
Так как левая часть последнего выражения равна нулю, можно
написать
Разделим последнее равенство на Ал: и вычислим ^:
Ay _ дх
Устремим Але к нулю. Тогда, учитывая, что при этом yt и у*
также стремятся к нулю и что у- Ф 0, в пределе получим
! B')
ду

252 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. VIII
Мы доказали существование производной ух от функции, задан-
заданной неявно, и нашли формулу для ее вычисления.
Пример 1. Уравнение х2-\-у2—1=0 определяет у как неявную функ-
функцию от х. Здесь
Следовательно, по формуле A)
dx 2y у
Заметим, что заданное уравнение определяет две разные функции (так
как каждому значению х в промежутке (—1, 1) соответствуют два значения у);
однако найденное значение у'х справедливо как для одной, так и для другой
функции.
Пример 2. Дано уравнение, связывающее х и у: еУ—ех-\-ху = 0. Здесь
F(x, у) = еУ-е* + ху, J?L=-e*+y, -
Следовательно, по формуле A) получаем:
dx еУ-\-х еУ+х
Рассмотрим теперь уравнение вида
F(x9 у, г) = 0. C)
Если каждой паре чисел х и у из некоторой области соответ-
соответствует одно или несколько значений г, удовлетворяющих уравне-
уравнению C), то это уравнение неявно определяет одну или несколько
однозначных функций z or x и у.
Например, уравнение x2 + y2 + z2 — R2 = 0 неявно определяет
две недрерывные функции z от ху у, которые можно выразить
явно, разрешив уравнение относительно г; в этом случае мы по-
получаем:
г = J//?2 - х2 - у2 и z = — VR2-x2-y2.
Найдем частные производные -—¦ и -j- неявной функции z
от х и у, определяемой уравнением C).
Когда мы ищем -^-, мы считаем у постоянным. Поэтому
здесь применима формула B'), если только независимой перемен-
переменной считать х, а функцией г. Следовательно,
'— дх
г*~~ dF_ *
дг

§ 12] ЧАСТНЫЕ ПРОИЗВОДНЫЕ РАЗЛИЧНЫХ ПОРЯДКОВ 253
Таким же путем находим
г-- ду
Предполагается, что -^
Аналогичным образом определяются неявные функции любого
числа переменных и находятся их частные производные.
Пример 3. x2+y2+z2—#2 = 0,
dz __ 2х^ х dz у
~дх 2г Т* ~ду Т*
Дифференцируя эту функцию как явную (после разрешения уравнения
относительно z), мы получили бы тот же результат.
Пример 4. ег + *2# + 2+5 = 0. Здесь
F(x, у, z)=e
дх У' ду * dz
dz _ 2xy dz _
dx ez -4*-1 * dy
Замечание. Все рассуждения этого параграфа производи-
производились в йредположении, что уравнение F (х, у) = 0 определяет неко-
некоторую функцию одной переменной у = <р (х)\ уравнение F (х, у, г)=0
определяет некоторую функцию двух переменных z = f(x, у).
Укажем без доказательства, какому условию должна удовлетво-
удовлетворять функция F(xy у), чтобы уравнение F(х, #) = 0 определяло
однозначную функцию у~ ц>(х).
Теорема. Пусть функция F(х, у) непрерывна в окрестна-
сти точки (х0, у0) и имеет там непрерывные частные производ-
производные, причем F'y(x, у)фО, и пусть F (х0, уо) = О. Тогда сущест-
существует окрестность, содержатся точку (х0> у0), в которой уравне-
уравнение F (#, у) = 0 определяет однозначную функцию у = у(х).
Аналогичная теорема имеет место и для условий существова-
существования неявной функции, определяемой уравнением F (х, у, г) = 0.
Замечание. При выводе правил дифференцирования неяв-
неявных функций мы пользовались условиями, которые и определяют
существование неявных функций.
§ 12. Частные производные различных порядков
Пусть имеем функцию двух переменных
Частные производные -~- = /^(x, у) и -~- = f'y(x, у), вообще
говоря, являются функциями переменных хну. Поэтому от них

254 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. VJIJ
можно снова находить частные производные. Следовательно, част-
частных производных второго порядна от функции двух переменных
четыре, так как каждую из функций ~- и -—- можно диффе-
дифференцировать как по х, так и по у.
Вторые частные производные обозначают так:
•§j§-= ?*(*» #)» ЗДесь / Дифференцируется последовательно
два раза по х\
fxyi** #)> здесь f сначала дифференцируется по х,
а потом результат дифференцируется по у;
flxi** У) у ЗДесь / дифференцируется сначала по г/,
а потом результат дифференцируется по х\
~дф- = Гуу(х* У)у ЗДесь / дифференцируется последовательно
два раза по у.
Производные второго порядка можно снова дифференцировать
как по х, так и по у. Получим частные производные третьего
порядка. Их будет, очевидно, уже восемь:
dz &z dz &z dz
' дх2ду* дхдудх' дхду2' дудх2' дудхду*
Вообще, частная производная п-го порядка есть первая произ-
производная от производной (п — 1)-го порядка. Например, ^ d"zn,_
есть производная n-го порядка; здесь функция z сначала р раз
дифференцировалась по х, а потом /г — р раз по у.
Для функции любого числа переменных частные производные
высших порядков определяются аналогично.
Пример 1. Вычислить частные производные второго порядка от функ«
ции /(*, у) = х2у+у3.
Решение. Последовательно находим
Пример 2. Вычислить q^-щ и -qT^, если г=у2ех+х2у3+1.
Решение. Последовательно находим
Пример 3. Вычислить 2 ,
если м =

12] ЧАСТНЫЕ ПРОИЗВОДНЫЕ РАЗЛИЧНЫ* ПОРЯДКОВ 265
Решение,
дх дх% дх2ду
Естественно поставить вопрос, зависит ли результат дифферен-
дифференцирования функции нескольких переменных от порядка дифферен-
дифференцирования по разным переменным, т. $. будут ли, например,
тождественно равны производные
дхду " дудх
ИЛИ
dxdydt И
Оказывается, что справедлива следующая теорема.
Теорема. Если функция z = f(x, у) и ее частные производ-
производные f'x, f'y, f"xy и f'yX определены и непрерывны в точке М(х, у) и
в некоторой ее окрестности, то в этой точке
дхду~~ дудх У1ху~1Ух)^
Доказательство, Для доказательства рассмотрим выра-
выражение
-f(x, у)].
Если введем вспомогательную функцию <р(л;), определенную
равенством
ф(*) = /(*> y + by)-f(Xf У)>
то А можно записать в виде
А = <р (л: + Ал:) — ф (х).
Так как, по предположению, f'x определена в окрестности точки
{ху у), то, следовательно, <р(*) дифференцируема на отрезке
[х, x + Ajc\; но тогда, применяя теорему Лагранжа, получим
где х заключено между х и х-\-Ах. Но
Так как fxy определена в окрестности точки (л:, у), то fx диффе-
дифференцируема на отрезке [у, у + Ау], поэтому, применяв к полу-
полученной разности вновь теорему Лагранжа (по переменной у), бу-
будем иметь
где у заключено между у и у-\-Ау.

256 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ |ГЛ. УШ
Следовательно, первоначальное выражение А равно
^y). A)
Переставив средние слагаемые в первоначальном выражении для
Л, получим
Л = [/(* + Д*. y + Ay)-f(x9 y + Ay)]-[f(x+Ax, V)-f(x%y)\
Введем вспомогательную функцию
¦ ДО = /<* + **, У)-Пх, у),
тогда
Применяя снова теорему Лагранжа, получим
где у заключено между у и у + Ау. Но
tfS) = &(*+**. у)-Гу(х, 3-
Применив еще раз теорему Лагранжа, получим
fu(x+Ax9y)-Fy(x, y)=Axf;x(xt y)9
где х заключено между х и х+Ах.
Таким образом, первоначальное выражение А можно записать
Э виде _ _
А = ЬуЬхПх(х, у). B)
Левые части равенств A) и B) равны Л, следовательно,
равны и правые, т. е. _
AxAyf'xy(x, y) = AyAxf'yX(x, у),
откуда
Fxyfc У) = Гух(х, У).
Переходя в этом равенстве к пределу при Ах—>0 и Ау—*0,
получим _ _
lim fxy(x, y)= limFyx&f у).
Лл: -> 0 Ад: -> О
Л|/ -> 0 Ау -> О
Так как производные /^ и /^ непрерывны в точке (х, у), то
lim f"xy(xyly)^f"xy(x, у) и lim f'yx(x, 'y)^fyX(x9 у). Оконча-
А* -> 0 Ал -> О
Ai/ -> о А|/ -> О
тельно получим:
Fxy(X9 y) = Fvx(X, У),
что и требовалось доказать.

§ 13] ПОВЕРХНОСТИ УРОВНЯ 257
Из доказанной теоремы как следствие получается, что если
частные производные ^Цп-ь и dJ-ldxk непрерывны, то
dnf _ dnf
дх* дуп~ * ~~дуп~ * дх* '
Аналогичная теорема имеет место и для функции любого числа
переменных.
Пример 4. Найти а а Л. и а а ^ , если u
у к дхдудг дудгох
Решен ие.
^=уе*У sin 2, JpL=e*y sin г+хуе*У sin г
--^L-=е^ A +^) cos г, ^=±=*ew sin г, Jj?!L=xe*vC0S2,
дхдудг х ^ дхдг
dzu
==g^ cos г+xr/e^ cos 2=e-v^ A + ^) cos 2.
Следовательно,
(см., кроме того, примеры 1—2 этого параграфа).
§ 13. Поверхности уровня
Пусть в пространстве (#, у, г) имеется область D, в которой
задана функция
и = и(х, у, z). A)
8 этом случае говорят, что в области D задано скалярное поле.
Если, например, и (я, #, г) обозначает температуру в точке М (х, у, г),
то говорят, что задано скалярное поле температур; если область D
заполнена жидкостью или газом и и (х, у, г) обозначает давле-
давление, то имеется скалярное поле давлений и т.д.
Рассмотрим точки области D, в которых функция и (я, у, г)
имеет постоянное значение с:
u(xh у, z) = c. B)
Совокупность этих точек образует некоторую поверхность. Если
возьмем другое значение с, то получим другую поверхность. Эти
поверхности называются поверхностями уровня.
Пример 1. Пусть задано скалярное поле
х2 и1 г2
и(х,у, 2)=Т-Н|-+-Ш-.
Здесь поверхностями уровня будут поверхности
4 + 9 + 16 ~С'
т. е. эллипсоиды с полуосями 2 У с, 3 У~с, 4 ]/"~с.
9 Н. С. Пискунов, т. I

258
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
{ГЛ.
Если функция и есть функция двух переменных х и gi
и = и(х, у),
то «поверхностями» уровня будут линии на плоскости Охуч
и(х, t/) = c, B')
которые называются линиями уровня.
Если значения и мы будем откладывать по оси Oz:
z=zu(x, у),
то линиями уровня на плоскости Оху будут проекции линий,
которые получаются в
z Ъ пересечении поверхнос-
поверхности z — u(x, у) с плос-
плоскостями г — с (рис. 176).
Зная линии уровня,
легко исследовать ха-
характер поверхности г=?
=и(х, у).
Рис.. 176.
Пример 2. Определить линии уровня функции г=1— х2—у2. Линиями
уровня будут линии с уравнениями 1— х2—у* = с. Это (рис. 177) окружности
с радиусом уТ^с. В частности, при с=0 получаем окружность х*+у*~1.
§ 14. Производная по направлению
Рассмотрим в областц D функцию и=*и(х, у, г) и точку
М(х9 у, г). Проведем из точки М вектор S, направляющие коси-
косинусы которого cos a, cosp, cosy (рис. 178). На векторе S на
расстоянии As от его начала рассмотрим точку Мг (х-\- Ах> + &
г+Аг). Таким образом,
Будем предполагать, что функция и (ху у, z) непрерывна и имеет
непрерывные производные по своим аргументам в области Z).

ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
259
Аналогично тому, как это делалось в § 7, полное приращение
функции представим так:
*, A)
дх
где бд, е2 и 83 стремятся к нулю при As—>0. Разделим все члены
равенства A) на As:
Am ди Ал: , ди At/ , ди Az , Ах , At/ , Az ,q\
Очевидно, что
Следовательно, равенство B) можно переписать так:
. C)
Аи
Предел отношения ~г- при As~->0 называется производной от
Рис. 178.
Рис. 179.
функции и = и(х, у, г) в точке (х, у, г) по направлению вектора
S и обозначается -^-, т. е.
1. Aw ди
D)
Таким образом, переходя к пределу в равенстве C), получим
ди ди JL^U ft j_ ^u /Ц\
Из формулы E) следует, что, зная частные производные, легко
цайти производную по любому направлению S. Сами частные
производные являются частным случаем производной по направ-

260 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. VIH
лению. Так, например, при а = 0, p = -j, у = у получаем:
ди ди А . ди п . ди л ди
cos0Hcos + cos
Пример. Дана функция
Найти производную -г- в точке М(\, 1, 1): а) в направлении вектора S±
+/+; б) в направлении вектора S2 = +/+
Решение, а) Находим направляющие косинусы вектора Si*.
cos a=2/Y~4+1 +9 = 2/^14, cosp^l/^H, cosv=3/yrl4.
Следовательно,
^ц _ди _2 ди _J , _^w 3
Частные производные
ди л ди л ди
в точке М A, 1, 1) будут
Итак,
?а\ —о *f| —о ^lI —9
аж|м ' ду\м * дг\м
б) Находим направляющие косинусы вектора 52:
cos a
Следовательно,
Заметим для дальнейшего, что 2 }/~3 > 12/^14 (рис. 179).
§ 15* Градиент
В каждой точке области D, в которой задана функция и =*
= w(jc, «/, г), определим вектор, проекциями которого на оси
ди ди ди
координат являются значения частных производных j-, g-, -g-
этой функции в соответствующей точке:
gg4g.*. A)
Этот вектор называется градиентом функции и(ху у, г). Говорят,
что в области D определено векторное поле градиентов. Докажем,

§ 15] ГРАДИЕНТ 261
далее, следующую теорему, устанавливающую связь между гради-
градиентом и производной по направлению.
Теорема. Пусть дано скалярное поле и = и(х, у, z) и опре-
определено в этом скалярном поле поле градиентов
Производная =- по направлению некоторого вектора S равняется
проекции вектора grad и на вектор S.
Доказательство. Рассмотрим единичный вектор S0, соот-
соответствующий вектору S:
Вычислим скалярное произведение векторов gradu и S0*):
(grada,S°) = |cosa+|cosp + gcos?. B)
Выражение, стоящее в правой части этого равенства, есть произ-
-*^$
Рис. 180. Рис. 181,
водная от функции и (х, у, г) по направлению вектора S. Следо-
Следовательно, мы можем написать
(grad и, S»)-^.
Если обозначим угол между векторами gradu и S* через ф
(рис. 180), то можем написать
|grad«|cos<p = |i C)
ИЛИ
пр.sograd */ = -§>. D)
Теорема доказана.
На основании доказанной теоремы наглядно устанавливается
связь между градиентом и производной в данной точке по любому
направлению. В данной точке М(х, у, г) строим вектор grada
(рис. 181). Строим сферу, для которой grad и является диаметром.
*) Скалярное произведение векторов А и В будет обозначаться через
(Л, В) или просто через АВ.—Прим. ред.

262 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ {ГЛ. VIII
Из точки М проводим вектор S. Обозначим точку пересечения век-
вектора S с поверхностью сферы через Р. Тогда очевидно, что МР=*
= | grad и | cos ф, если <р — угол между направлениями градиента и
отрезка МР (при этом <р<~К т. е. МР = -~. Очевидно, что при
изменении направления вектора S на противоположное производ-
производная изменит знак, а ее абсолютная величина останется прежней.
Установим некоторые свойства градиента.
1) Производная в данной точке по направлению вектора S
имеет наибольшее значение, если направление вектора S совпадает
с направлением градиента; это наибольшее значение производной
равно | grad w |.
Справедливость этого утверждения непосредственно следует из
равенства C): наибольшее значение -—- будет при Ф = 0, ив этом
случае
2) Производная по направлению вектора, перпендикулярного
к вектору grad u% равна нулю.
Это утверждение следует из формулы C). Действительно,
в этом случае
Ф = у, совф^О и -тг-в|gradи\cosф = 0.
Пример 1. Дана функция и=х2+у2+г2,
а) Определим градиент в точке М A, 1, 1). Выражение градиента этой
функции в произвольной точке будет
grad и = 2xt+2yf+ 2zk.
Следовательно,
\gradu\\M=2V.
б) Определим производную от функции w в точке М (lt I, 1) в направлен
нии градиента. Направляющие косинусы градиента будут
2 1
cosa= . ¦ = -^=:ж
1^22 + 22+22 1^3
1_ ___ 1
Следовательно,
ди Л 1 ,
Уз"
т. е.

ФОРМУЛА ТЕЙЛОРА ДЛЯ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ 263
Замечание. Если функция и = и(х, у) есть функция двух
переменных, то вектор
лежит в плоскости Оху. Докажем, 4T0grada направлен перпенди-
перпендикулярно к линии уровня и (х, у) == с, лежащей в плоскости Оху и
проходящей через соответствующую точку. Действительно, угловой
коэффициент kx касательной к линии уровня и (#, у) = с будет равен
kf^ ?-. Угловой коэффициент k2 градиента равен &2 = -#-.
Uy Ux
Очевидно, что kxk2 = — 1. Это и доказывает справедливость нашего
Рис. 182.
Рис. 183.
утвержнения (рис. 182). Аналогичное свойство градиента функции
трех переменных будет установлено в § 6 гл. IX.
х2 ф
Пример 2. Определить градиент функции w==-<r""i~"ir (Рис* 183)
в точке М B, 4).
Решение. Здесь
__ I ди_2 I _8
Следовательно,
Уравнение линии уровня (рис. 184), проходящей через данную точку, будет
§ 16. Формула Тейлора для функции двух переменных
Пусть функция двух переменных
* = /(*. У)
непрерывна вместе со всеми своими частными производными до
(п + 1)-го порядка включительно в некоторой окрестности точки

264 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. Vlfl
М(а, 6). Тогда, аналогично тому, как это было в случае функции
одной переменной (см. § 6 гл. IV), функцию двух переменных
представим в виде суммы многочлена /г-го порядка по степеням
х — а и у~Ь и некоторого остаточного члена. Ниже будет
показано, что для случая п=2 эта формула имеет вид
A)
где коэффициенты Ло, D> E, А, В, С не зависят от х и у, а /?2—
остаточный член, структура которого аналогична структуре остаточ-
остаточного члена в формуле Тейлора для функции одной переменной.
Применим формулу Тейлора для функции / (х, у) одной пере-
переменной у, считая х постоянным (ограничимся членами второго по-
порядка):
+ <^Пу(х,Ь)+!^Гт(х,Ъ), B)
где tfa^ft+flifo-ft), 0<61<1. Функции f(x, 6), fy(x9 b)f
t'yy(x, b) разложим по формуле Тейлора по степеням х — а, огра-
ограничиваясь смешанными производными до третьего порядка вклю-
включительно:
?=$тх&, Ь), C)
где g2 = x+6s(x-a), 0 <6, < 1;
Гу,(х, Ь) = Гт,{а, b)+^f'y'y'x(la, *), E)
Подставляя выражения C), D) и E) в формулу B), получим
= /(а, Ь) +*^Гх(а, b) +?zfrxx(fl Ц^

$ 17] МАКСИМУМ И МИНИМУМ 265
Располагая слагаемые так, как указано в формуле A), получим
fix, y) = f{a, Ь) + (х-а)П{а, b) + (y-b)f'y(a, b) +
+ ±{(х -af П» (a, b)+2(x-a) (y-b) f"xy (a,b) + (y-by ГУУ{а,
+ 3(x-a)(y- by Гш (S,, b) + (y- by fy"yy (a, %)]. F)
Это и есть формула Тейлора при п = 2. Выражение
Яш = Ж [(х - с)' Пх* &, Ь) + 3 (х - ау (у - 6) f^y (|2> Ь) +
+ 3 (* - а) (у - by f';y'y (g,, b) + (y- by Гт ifl, тц)]
называется остаточным членом. Обозначим, далее, х — а = Ах,
У . Преобразуем Rz:
^2 = "зГ I До» '*•»* (Si» ^) + 3 ДрЗ / ЛДГ* (?2» ^) Н"
Так как |Дл;|<Др, |Д(/|<Ар и третьи производные, по усло-
условию, ограничены, то коэффициент при Ар3 ограничен в рассмат-
рассматриваемой области; обозначим его через а0.
Тогда можем написать
Формула Тейлора F) в принятых обозначениях для случая я = 2
примет вид
fix, y) = f(a, b) + bxfx(a9 b) + Ayf'y(a, b) +
± ftV. Ff)
При любом п формула Тейлора имеет аналогичный вид.
§17. Максимум и минимум функции нескольких переменных
Определение 1. Мы говорим* что функция г=/(#, у) имеет
максимум в точке M0(x0, у0) (т. е. при д:=х0 и у = у9), если
/(*о> Уо)>!(х, У)
для всех точек (л;, у), достаточно близких к точке (лг0> у0) и от-
отличных от нее.
Определение 2. Совершенно аналогично говорят, что функ-
функция z = f(x7 у) имеет минимум в точке М0(х0, t/0), если
9 у)

266
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. VIII
для всех точек (х, у), достаточно близких к точке (л:0, у0) и от-
отличных от нее.
Максимум и минимум функции называются экстремумами
функции, т. е. говорят, что функция имеет экстремум в данной
точке, если эта функция имеет максимум или минимум в данной
точке.
Пример 1. Функция г = (х—1J + (#—2J—1 достигает минимума при
=1, у = 2, т.е. в точке A, 2). Действительно, /A, 2) = —1, а так как (х—IJ
BJ ф 1 ? 2 AJ + BJ1 1
*=1, у
и (у—2J
/(
, (, ) Д, /(, )
всегда положительны при х ф 1, у •? 2, то (х—1
) /A 2) Г
()
—2J— 1 > — 1,
(у) д р ф , у ? , () + (/)> ,
т.е. /(#, у) > /A, 2). Геометрическая картина, соответствующая данному слу-
случаю, изображена на рис. 185.
Рис. 185.
X
Рис. 186.
Пример 2. Функция *—-^—sin
ПРИ * = 0> */ = 0 (т. е. в начале
координат) достигает максимума (рис. 186).
Действительно, /(О, 0)=1/2. Возьмем внутри окружности х2 + у2 = п/6
точку (х, (/), отличную от точки @, 0); тогда при 0 < *2 + t/2 < я/6 будет
sin (х*+у*) > 0 и поэтому /(*, 0)^i—sin (*2+#2) < у* т. е. /(*, у) < /@, 0).
Данное выше определение максимума и минимума функции
можно перефразировать следующим образом.
Положим х — хо+Ах, у = уо + Ау; тогда
f(*. y)—f{*o, #о) = /(*о + д*> Уо + Ьу)—f{x0, Уо) = А/-
1) Если А/ < 0 при всех достаточно малых приращениях не-
независимых переменных, то функция f(xy у) достигает максимума
в точке М(х0, у0).
2) Если А/ > 0 при всех достаточно малых приращениях не-
независимых переменных, то функция f(x, у) достигает минимума
в точке M(x0J y0).
Эти формулировки переносятся без изменения на функции
любого числа переменных.
Теорема 1 (необходимые условия экстремума).
Если функция z = f(x, у) достигает экстремума при х=х0, у=у0,
то каждая частная производная первого порядка от z или обра-
ищется в нуль при этих значениях аргументов, или не существует.

МАКСИМУМ И МИНИМУМ
267
Действительно, дадим переменной у определенное значение,
именно у = у0. Тогда функция f (х, у0) будет функцией одной
переменной х. Так как при х = х0 она имеет экстремум (макси-
(максимум или минимум), то, следовательно, —•
х=х0
Уо
или равно нулю,
или не существует. Совершенно аналогично можно доказать, что
или равно нулю, или не существует.
Эта теорема не является достаточной для исследования вопроса
об экстремальных значениях функции, но позволяет находить эти
значения в тех случаях, в которых
мы заранее уверены в существова-
существовании максимума или минимума. В про-
противном случае требуется дополнитель-
дополнительное исследование.
Так, например, функция z~ х2—у2 имеет
производные ^-=*2х, ^-=х—2#,которые об-
обращаются в нуль при # = 0 и #=0. Но эта
функция при указанных значениях не име-
имеет ни максимума, ни минимума. Действи- Рис. 187.
тельно, эта функция равна нулю в начале ко-
координат и принимает в как угодно близких
точках от начала координат как положительные, так и отрицательные значе-
значения. Следовательно, значение нуль не является ни максимумом, ни миниму-
минимумом (рис. 187).
Точки, в которых 0j = O (или не существует) и ^ = 0 (или не
существует), называются критическими точками функции z=f(x, у).
Если функция достигает экстремума в какой-либо точке, то (в силу
теоремы 1) это может случиться только в критической точке.
Для исследования функции в критических точках установим
достаточные условия экстремума функции двух переменных.
Теорема 2. Пусть в некоторой области, содержащей точку
Ма(л;0, у о), функция f(x, у) имеет непрерывные частные производ-
производные до третьего порядка включительно; пусть, кроме того, точка
Мо(#о, У о) является критической точкой функции f(x, у), т.е.
д/(*о, Уо) _q df(x0, Уо) ^q
дх ' ду
Тогда при х = х0> у = у0
1) f(x> У) имеет максимум, если
о, Уо) fd2f(x0, уо)\2 п д2/(*о, Уо) ^ п.
, У о)
2) f(x, у) имеет минимум, если
»> Уо)
дхду

268 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. VIII
3) /(*, у) не имеет ни максимума, ни минимума, если
(о, Уо) d*f(xOi у0) (d*f(x0, уо)у Q.
дх* # ду2- \ дхду ) ^ '
4) если d2fixdQxlyo) • т^Уй)- (дН1Хх°еуУо)У = °. то экстремум
может быть и может не быть (в этом случае требуется даль-
дальнейшее исследование).
Доказательство. Напишем формулу Тейлора второго
порядка для функции f(x, у) (формула F) § 16). Полагая a = xQ,
b k &, будем иметь
+ав(Ар)%
где Ap==]/rAx2 + Ay2, a а0 стремится к нулю при Др—>0.
По условию
о, Уо) ^q
^0
дх ' ду
Следовательно,
Обозначим теперь значения вторых частных производных
в точке М0{х0, у0) через Л, В, С:
Обозначив через q> угол между направлением отрезка М0М, где
М есть точка М(хо+Ах, уо + &у), и осью 0х\ тогда Ax = Apcos(p,
Ay = Ар sin <p. Подставляя эти выражения в формулу для А/,
найдем
А/ = i- (АрJ [Л cos2 ф + 25 cos <p sin ф + С sin2 ф + 2<х0 Ар]. B)
Предположим, что ф
Разделив и умножив на А выражение, стоящее в квадратных
скобках, получим
+2а0Ар] . C)
Рассмотрим теперь четыре возможных случая.
1) Пусть ЛС — 52>0, Л<0. Тогда в числителе дроби стоит
сумма двух неотрицательных величин. Они одновременно в нуль

§ 17J МАКСИМУМ И МИНИМУМ 269
не обращаются, так как первый член обращается в нуль при
tg(p = —Л/В, второй при sincp = O.
Если А < О, то дробь есть отрицательная величина, не обра-
обращающаяся в нуль. Обозначим ее через —т2; тогда
где т не зависит от Ар, а0Др-—>0 при Ар-—*0. Следовательно,
при достаточно малых Ар будет А/ < 0, или / (лго + Ал;, уд + Ду) —
— f(*o> #о)<°- Но тогда для всех точек (хо + кх, уо + &У)> до-
достаточно близких к точке (xQf у0), имеет место неравенство
f(xo + kx, y<> + ky)<f{xQy yo)f
а это означает, что в точке (х0, у0) функция f(x, у) достигает
максимума.
2) Пусть АС—В2 > О, А > 0. Тогда, рассуждая аналогично,
получим
или
т. е. f{x, у) имеет минимум в точке (лг0, у0).
3') Пусть ЛС —В2<0, А > 0. В этом случае функция не
имеет ни максимума, ни минимума. Функция возрас-
возрастает, Когда мы движемся из точки (дс0, #0) по одним направле-
направлениям, и убывает, когда мы движемся по другим направлениям.
Действительно, при перемещении вдоль луча <р = 0 имеем
при движении вдоль этого луча функция возрастает. Если же
перемещаться вдоль луча,<р = ср0 такого, что tgq>0 = —А /В, то при
А > 0 будет
при движении вдоль этого луча функция убывает.
3") Пусть АС — В2<0, Л<0. В этом случае функция тоже
не имеет ни максимума, ни минимума. Исследование
проводится так же, как и в случае 3'.
3'") Пусть ЛС-В2<0, Л=0. Тогда ВфО, и равенство B)
можно переписать в виде
При достаточно малых значениях ф выражение, стоящее в круг-
круглых скобках, сохраняет знак, так как оно близко к 25, а множитель

270 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. VIII
sin ф меняет знак в зависимости от того, будет ли <р больше нуля
или меньше нуля (после выбора ф > 0 и ф < 0 мы можем р взять
настолько малым, что 2а0 не будет изменять знак всей квадрат-
квадратной скобки). Следовательно, и в этом случае А/ меняет знак при
различных ф, т. е. при различных А* и Д#, следовательно, и в
этом случае нет ни максимума, ни минимума.
Таким образом, каков бы ни был знак Л, имеем всегда сле-
следующее положение:
Если АС —В2 < 0 в точке (*0, у0), то функция не имеет в этой
точке ни максимума, ни минимума. В этом случае поверхность,
служащая графиком функции, может вблизи этой точки иметь,
например, форму седла (см. выше рис» 187). Говорят, что функ-
функция имеет в этой точке минимакс.
4) Пусть АС — /?2 = 0. В этом случае на основании формул B)
и C) сделать заключение о знаке А/ нельзя. Так, например, при
А Ф 0 будем иметь
+ 2а0 Др];
при cp = arctg(—А/В) знак А/ определяется знаком 2а0, здесь
требуется специальное дальнейшее исследование
(например, с помощью формулы Тейлора более высокого порядка
или каким-либо иным способом). Таким образом, теорема 2 пол-
полностью доказана.
Пример 3. Исследовать на максимум я минимум функцию
Решение. 1) Находим критические точки:
Решая систему уравнений
получаем
* = —4/3, у =1/3.
2) Находим производные второго порядка в критической точке (—4/3; 1/3)
и определяем характер критической точки:
АС—?2 = 2-2—(—1J =
0.
Следовательно, в точке (—4/3; 1/3) данная функция имеет минимум, а именно:
Пример 4. Исследовать ца максимум и минимум функцию

§ 17J МАКСИМУМ И МИНИМУМ 271
Решение, I). Найдем критические точки, пользуясь необходимыми ус«
1иями экстоемума:
)
ловиями экстремума:
Отсюда получаем две критические точки:
*i=l, ух = 1 и *2 = 0, //2=0.
2) Найдем производные второго порядка:
3) Исследуем характер первой критической точки:
a=?l\ =6, в=
АС—В2=36—9=^27>0; А >0.
Следовательно, в точке-A; 1) данная функция имеет минимум, именно:
4) Исследуем характер второй критич;еской точки М2 @, 0):
Л=0, В=г—3, С = 0; ЛС—Я2 = — 9<0.
Следовательно, во второй критической точке функция не имеет ни максимума,
ни минимума (минимакс).
Пример 5. Разложить данное положительное число она три положи-
положительных слагаемых так, чтобы их произведение имело наибольшее значение.
Релгеяие. Обозначим слагаемые: первое через х, второе через у; тогда
третье будет а— лг-~у. Произведение этих слагаемых равно и—ху(а—х—у).
По условии* задали х > О, у > 0* а~-х>—у > 0г т. е\ х+у < а, и > О* Следо-
Следовательно, хну могут принимать значения, принадлежащие области, ограни-
ограниченной прямыми x—Q, y=Ot х-\-у=*а.
Найдем частные производные функции и:
¦?=У(а—2х-~у), Ji=s,x(a—2y—x).
Приравнивая производные нулю, получим систему уравнений
Решая эту систему^ находим критические тачкж
*i = 0, У1 = 0, Л*х@, 0); ^9 = 0, у2 = а, М2@, а);
Первые три точки лежат на границе области, последняя—внутри. На гра-
границе области функция и равна нулю, а внутри области она положительна;
следовательно, в точке (а/3, а/3) функция и имеет максимум (так как это
единственная экстремальная точка внутри треугольника). Максимальное зна-
значение произведения есть
_ а а
••шах "о 5"
t> О

272 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. VIII
Проведем исследование характера критических точек, пользуясь доста-
достаточными условиями. Найдем частные производные второго порядка функции и:
д2и о д2и о о д2и о
дх2 * дхду *' ду*
В точке ЛЫО.О) имеем Л=|?«0, В^^-у=а, С=-|^0, АС-В2^
=—а2 < 0. Следовательно, в точке Мх нет ни максимума, ни минимума.
В точке М2@, а) имеем Л=-^=— 2а, в=^^=—л, С=-^ = 0, ЛС —
— В2 — — а2 < 0. Значит, в точке М2 тоже нет ни максимума, ни минимума.
В точке М3(а, 0) имеем Л = 0, ? = — а, С== —2а, АС—В2 = — а2 > 0.
И в точке Мз нет ни максимума, ни минимума. В точке А/4 (-т, -я- ) имеем
л 2а а 2а „ л 4а2 а2 л
А— , В = , С=—5", АС—В>= 5г- > 0, Л < 0. Следова-
Следовательно, в точке М& имеем максимум.
Замечание. Теория максимумов и минимумов функции не-
нескольких переменных является основой для одного метода полу-
получения формул для изображения функциональных зависимостей на
основании экспериментальных данных. Этот вопрос изложен в § 19.
§ 18. Максимум и минимум функции нескольких переменных,
связанных данными уравнениями
(условные максимумы и минимумы)
Во многих задачах на разыскание наибольших и наименьших
значений функции вопрос сводится к разысканию максимумов и
минимумов функции от нескольких переменных, которые не яв-
являются независимыми, а связаны друг с другом некоторыми доба-
добавочными условиями (например, они должны удовлетворять дан-
данным уравнениям).
Рассмотрим, например, такую задачу. Из данного куска жести
площадью 2а надо сделать закрытую коробку в форме паралле-
параллелепипеда, имеющую наибольший объем.
Обозначим длину, ширину и высоту коробки через х, уу г.
Задача сводится к разысканию максимума функции v = xyz при
условии, что 2xy + 2xz + 2yz = 2a. Здесь мы имеем задачу на
условный экстремум: переменные jc, г/, г связаны условием
2xy-\-2xz + 2yz = 2a. В настоящем параграфе мы рассмотрим ме-
методы решения таких задач.
Рассмотрим сначала вопрос об условном экстремуме функции
двух переменных, если эти переменные связаны одним условием.
Пусть требуется найти максимумы и минимумы функции
u = f(x,y) A)
при условии, что х и у связаны уравнением
<р(х,у)=-0. B)

§ 18] УСЛОВНЫЕ МАКСИМУМЫ И МИНИМУМЫ 273
При наличии условия B) из двух переменных х и у неза-
независимой будет только одна, например х, так как у опреде-
определяется из равенства B) как функция от х. Если бы мы разре-
разрешили уравнение B) относительно у, то, вставляя в равенство A)
вместо у найденное выражение, получили бы функцию одной
переменной х и свели бы задачу к задаче об исследовании на
максимум и минимум функции одной независимой переменной х.
Но можно решить поставленную задачу, не разрешая урав-
уравнения B) относительно х или у. При тех значениях х9 при кото-
которых функция и может иметь максимум или минимум, производная
от и по х должна обращаться в нуль.
Из A) находим -—, помня, что у есть функция от х:
du_dl dj_dy
Следовательно, в точках экстремума
Из равенства B) находим
Это равенство удовлетворяется для всех х и у, удовлетворяющих
уравнению B) (см. § 11).
Умножив члены равенства D) на неопределенный пока коэф-
коэффициент % и сложив их с соответствующими членами равенства C),
получим
df , df dy\>. ( ду , dq> dy
ИЛИ
(^+%^.) + (^+%h.)^L^O. E)
\ дх 1 дх J l \ду 1 ду J dx x '
Последнее равенство выполняется во всех точках экстремума. Под-
Подберем X так, чтобы для значений х и у, соответствующих экстре-
экстремуму функции и> в1горая скобка в равенстве E) обратилась в нуль *):
Но тогда при этих значениях я и у из равенства E) следует равенство
*) Для определенности будем предполагать * что в критических точках
ду * '

274 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. VIH
Таким образом, получается, что в точках экстремума удовлетво-
удовлетворяются три уравнения:
дх ' дх
F)
с тремя неизвестными х, у, X. Из этих уравнений определяем*, у
и X, которое играло только вспомогательную роль и нам в даль-
дальнейшем не требуется.
Из вывода следует, что уравнения F) являются необходимыми
условиями условного экстремума, т. е. в точках экстремума удовле-
удовлетворяются уравнения F). Но не при всяких х и у (и X), удовле-
удовлетворяющих уравнениям F), будет иметь место условный экстремум.
Требуется дополнительное исследование характера критической
точки. При решении конкретных задач иногда удается установить
характер критической точки на основании существа задачи. Заметим,
что левые части уравнений F) суть частные производные функции
Fix, у, Я)=/(*. y)+hf(x9 у) G)
по переменным х, у, X.
Таким образом, для того чтобы найти значения х и у, удовле*
творяющие условию B), при которых функция u=^f(x, у) может
иметь условный максимум или условный минимум, нужно составить
вспомогательную функцию G), приравнять нулю ее производные
по х, у и X и из полученных трех уравнений F) определить иско-
искомые х, у (й вспомогательный множитель X). Рассмотренный метод
распространяется на исследование условного экстремума функции
любого числа переменных.
Пусть требуется найти максимумы и минимумы функции п
переменных u = f(xiy х2, ..., хп) при условии, что переменные
#i» *а> •••! ка связаны т (m<n) уравнениями
n)
. .., хп) = 0,
Для того чтобы найти значения х19 х2У ,.., хпУ при которых
могут быть условные максимумы и минимумы, нужно составить
функцию

§ 18] УСЛОВНЫЕ МАКСИМУМЫ И МИНИМУМЫ 275
приравнять нулю ее частные производные по хи х2, •••, хп\
(9)
^ _l "к d<Pi л. л- 7 ^фст __ о
и из m + n уравнений (8) и (9) определить хг, х2У ...,хп и вспо-
вспомогательные неизвестные к1У ..., кт. Так же как и для функции
двух переменных, вопрос о том, будет ли при найденных значениях
функция иметь максимум или минимум или не будет иметь ни того,
ни другого, мы в общем случае оставляем открытым. Этот вопрос
мы будем решать на основании вспомогательных соображений.
Пример 1. Вернемся к задаче, сформулированной в начале этого пара-
параграфа: найти максимум функции
v = xyz
при условии, что
ху+хг+уг—а = 0 (х > 0, у > 0, г > 0). A0)
Составим вспомогательную функцию
F(x, у, X) = xyz+h(xy+xz+yz—a).
Найдем ее частные производные и приравняем их нулю*
= 0. )
\ A1)
ху+к(х+у) )
Задача сводится к решению системы четырех уравнений A0) и (Л)
с четырьмя неизвестными (х, у, г и К). Для решения этой системы умножим
первое из уравнений A1) на х, второе—на у, третье—на г и сложим их;
принимая во внимание равенство A0), находим Я = ^-. Вставляя в урав-
уравнения (П) найденное значение Я$ получим
] [|] =0.
Так как х, у, г по смыслу задачи отличны от нуля, то из последних уравне-
уравнений имеем
|[(!Н-г)=1, -|(*+*)= 1, |--(х+у) = 1.
Из первых двух уравнений находим х=у, из второго и третьего уравнений
t/=z. На в таком случае из уравнения A0) получаем х~у=*г=;У^а/3. Это —
единственная система значений х, у и 2, при которых может 0ыть макси-
максимум или минимум.
Можно доказать, что полученное решение дает максимум. Впрочем, это
ясно и из геометрических соображений (в условиях задачи объем коробки не
может быть неограниченно большим; следовательно, естественно^ ожидать, что
при какдх-то определенных, значениях, сторон этот объем будет наибольшим).

276 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. VIII
Итак, для того чтобы объем коробки^был наибольшим, эта коробка должна
быть кубом, ребро которого равно "|/"а/3.
Пример 2. Определить наибольшее значение корня /1-й степени из про-
произведения чисел х19 х2, ..., хп при условии, что их сумма равна данному
числу а. Следовательно, задача ставится так: требуется найти максимум функ-
п/ ""
ции и = у хг.. .хп при условии
Xi + x2+...+xn—а = 0 (л:1>6, *2 > 0, ..., хп>0). A2)
Образуем вспомогательную функцию
F(xly ,.., хт k)=i/x1...xn-{-l{x1 + x2+...+xn—a).
Находим ее частные производные:
F' =Д х*х*'-'х» + Я=~ —+ 3t = 0, или «=_/**!,
л* Л "-1 /X Xi
(Xi...Xn) П
f' _ [-Я = 0, или и = —пЫц
Z7' = г-&, = 0, или и = —n^rt.
*п п хп 4 ' л
Из последних равенств находим л^ —#2= f.. =л:л, а на основании уравне-
уравнения (Ц) получаем /
По смыслу задачи эти значения дают максимум функции у хх... хп, рав-
равный ajn.
Таким образом, для любых положительных чисел xlf x2t ..., хПУ связан-
связанных соотношением *1-г*#2+ .. *+хп — а, выполняется неравенство
тУх^..Хп^а/n A3)
l так как, по доказанному, — является наибольшим значением этой функции J.
Подставляя теперь в неравенство A3) вместо а -его значение, полученное из
равенства A2), зайдем
A4)
Это неравенство справедливо для любых положительных чисел #*, х2 ... хп.
Выражение, стоящее в левой части соотношения A4), называется средним
геометрическим этих чисел. Таким образом, среднее геометрическое нескольких
положительных чисел не больше их среднего арифметического.
§ 19. Получение функции на основании
экспериментальных данных по методу наименьших квадратов
Пусть на основании эксперимента требуется установить функ-
функциональную зависимость величины у от величины х:
У = Ф(*). A)
Пусть в результате эксперимента получено п значений функции у
при соответствующих значениях аргумента.

§ 19] МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Результаты записаны в таблицу:
277
X
У
Ух
У*
...
Уп
Вид. функции у = ф (х) устанавливается или из теоретических сооб-
соображений, или на основании характера расположения на коорди-
координатной плоскости точек, соответствующих экспериментальным зна-
значениям. (Эти точки будем называть «экспериментальными точками».)
Пусть, например, экспериментальные точки расположены на коор-
координатной плоскости так, как изображено на рис. 188. Учитывая,
что при проведении эксперимента имеют место погрешности, естест-
естественно предположить, что искомую функцию у = ц>(х) можно искать
в виде линейной функции у =^ax+fa Если экспериментальные точки
расположены так, как указано на рис. 189, то естественно искать
функцию у = ц>(х) в виде у = ахв и т.д.
«27
Рис. 188.
Phcv 18a
При выбранном виде функции у=ф(^ а, &, с, ...) остается
подобрать входящие в нее параметры а, 6, с, ... так, чтобы
в каком-то смысле она наилучшим образом описывдяа рассматри-
рассматриваемый процесс.
Широко распространенным методом решения данной задачи
является метод наименьших квадратов. Этот метод заключается
в следующем. Рассмотрим сумму квадратов разностей значений yh
даваемых экспериментом, и функции <р (х9 а, 6, с, ...) в соответст-
соответствующих точках:
(a, 6, с, ...)=
—<р(*/, а, Ь, с, ...
B)
Подбираем параметры а, й, с, ... так, чтобы эта сумма имела
наименьшее значение:
п
S(a, Ь, с, ...)=.2[У/-Ф(**, а, Ь, с, ...)Р==ш1п. C)

278
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
?ГЛ. УШ
Итак, задача свелась к нахождению значений параметров а, &, с, ...,
при которых функция S(a, 6, с, ¦¦.) имеет минимум.
На основании теоремы 1 (§ 17) следует, что эти значения a}b,c,
удовлетворяют системе уравнений
ds =о — = 0 -^- = 0 ..., D)
' до ос
или в развернутом виде:
(=1
»=1
-q)(*f, а, Ь, с, ...
^-cpfe а, 6, с, ..О
E)
Здесь имеется столько уравнений, сколько и неизвестных. В каж-
каждом конкретном случае исследуется вопрос о существовании реше-
решения системы уравнений E) и о существовании минимума функции
S(a, b, с, .¦.).
Рассмотрим несколько случаев определения функции у =s
5= ф(л;, аь Ь, с, .•.)•
I. Пусть у = ах+Ь. Функция S(a, b) в этом случае имеет вид
(см. выражение B))
$(а, Ь)=
F)
Это функция с двумя переменными а и b (xc и yt — заданные
числа; см. таблицу на с. 277). Следовательно,
да
дЬ
т. е. система уравнений E) в этом случае принимает вид
1=1
1=1
— Ьп = 0.
G)
Получили систему двух линейных уравнений с двумя неизвестными
а и Ь. Очевидно, что система имеет определенное решение и что

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
279
при найденных значениях а и Ь функция S (а, Ь) имеет мини-
минимум*).
II. Пусть за аппроксимирующую функцию взят трехчлен второй
степени
у = ах2-\-Ьх-{-с.
В этом случае выражение B) имеет вид
S(a9 Ь, с)^|[!(г(«? + ^ + * (8)
Это функция трех переменных а, &, с. Система уравнений E) при-
принимает вид
,=о,
)] = О,
2
2
или в развернутом виде:
2 vA-ъ 2 А- ь S А -
11 11 11
t=l
n
1=1J
n
I
i
= 1
n
= 1
2
n
i
i
= 1
n
= 1
1=1
(9)
Получаем систему линейных уравнений для определения неизвест-
неизвестных а, Ьу с. Из характера задачи следует, что система имеет
определенное решение и что при полученных значениях а, Ь, с
функция S(a, by с) имеет минимум.
Пример. Пусть на основании эксперимента получены четыре значения
искомой функции tf~^{x) при четырех значениях аргумента (я = 4), которые
записаны в таблице:
*) Это легко устанавливается и на основании достаточных условий (см.
теорему 2 § 17). Действительно, здесь
dadb
1=1
Следовательно,

280
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
|гл. vm
X 1
1!
у 1 з
2
4
3
2,5
5
0,5
Будем искать функцию <р в виде линейной функции у — ах+Ь. Составляем
выражение 5 (а, Ь):
4
S (а, Ь)= 2] [У1—(#*i+6)l2»
Для составления системы G) для
определения коэффициентов а и Ь
предварительно вычисляем
4 4
Рис. 190.
2^=11, 2^=10.
Система G) принимает вид
21—39а—116=С
10-
—39а—11^=0,1
)_Па—46=0. |
Решая эту систему, находим а и Ь: «=—26/35, 6=159/35. Искомая прямая
(рис. 190) есть
26 . 159
§ 20. Особые точки кривой
Понятие частной производной используется при исследовании
кривкх.
Пусть кривая задана уравнением
Угловой коэффициент касательной к кривой определяется по
формуле
OF
dy дх
~dx"~ W
ду
(см. § И).
Если в данной точке М (х, у) рассматриваемой кривой по край-
Лр лр *
ней мере одна из частных производных -у- и -т- не обращается
в нуль, то в этой точке вполне определяется или -У- или -р . Кри-

§ 20] ОСОБЫЕ ТОЧКИ КРИВОЙ 281
вая F {ху у) = 0 в такой точке имеет вполне определенную касатель-
касательную. В этом случае точка М (я, у) называется обыкновенной точкой.
Если же в некоторой точке М0(х0, у0) имеем
,-,. = 0 и -f _0 = 0,
У=Уо * У=Уо
то угловой коэффициент касательной становится неопределенным.
Определение. Если в точке М0(х0У у0) кривой F(xyy) = 0
* dF dF *
обе частные производные -^ или -g— обращаются в нуль, то такая
точка называется особой точкой кривой. Следовательно, особая
точка кривой определяется системой уравнений
Естественно, что не всякая кривая имеет особые точки. Так,
например, для эллипса
очевидно,
и\- *" -1- У* 1 dF - 2х JL
производные -^ и -j- обращаются в нуль только при л; = 0,
у <= 0, но эти значения х и у не удовлетворяют уравнению эллипса.
Следовательно, эллипс не имеет особых точек.
Не предпринимая подробного исследования поведения кривой
вблизи особой точки, рассмотрим несколько примеров кривых,
имеющих особые точкц.
Пример 1. Исследовать особые точки кривой
у«_*(*_а)*=0 (а>0).
Решение. В данном случае F(х, (/) = ^2—*(*—оJ, поэтому
Решая совместно три уравнения
F(x.v)-0, -g=0, ^=0,
находим единственную удовлетворяющую им систему значений х и у\
хо = а, «/о=О.
Следовательно, точка Мо (а, 0) есть особая точка кривой.
Исследуем поведение кривой вблизи особой точки и построим кривую.
Перепишем данное уравнение в виде у= ± (*—а) Ус. Из этой формулы сле-
следует, что кривая: I) определена лишь при х^0; 2) симметрична относительно

282
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. VIII
оси Ох; 3) пересекает ось Ох в точках @, 0) и (а> 0). Последняя точка, как
было указано, является особой.
Мы рассмотрим сначала ту часть кривой, которая соответствует знаку +:•
у={х—а) Ух. Найдем первую и вторую производные от у по х:
Зх+а
У~
4х}Г
При # = 0 имеем уг=со. Следователь но * кривая касается оси Оу в начале
координат. При х = а/3 имеем #' = 0, у" > 0, т. е. при х — а/3 функ-
функция у имеет минимум: */ = —-^Х/ ~. На отрезке 0 < * < а имеем # < 0;
при х_> а/3 будет у' > 0; при *—> оо будет #—> оо. При х = а имеем у' =
= }/"«, т. е. в особой точке М0(а* 0) ветвь кривой */=(*—а) }/Т имеет
касательную у=Уа (х—а).
Так как вторая ветвь кривой у — —(х—а) У^!с симметрична с первой
относительно оси Ох, то, следовательно, в особой точке кривая имеет и вто-
вторую касательную (ко второй ветви) у = — У а (х—а).
Через особую точку кривая проходит дважды. Такая точка называется
деловой точкой.
Рассмотренная кривая изображена на рис 19К
Пример 2. Исследовать на особые точки кривую (полукубическая па-
парабола) у2—л^=0.
Решение. Координаты особых точек определяются из системы уравне-
уравнений: уг—^ = 0^ 3*2=0, 2# = 0. Следовательно^ MoJO, 0) есть особая точка.
Перепишем данное уравнение в виде у=± Ух3. Для построения кривой
исследуем сначала ветвь, которой в уравнении соответствует знак плюс; ветвь
кривой, соответствующая знаку минус, сим-
симметрична с .первой относительно оси Ох.
Функция у определена только при х^
^0, неотрицательна и возрастает при воз-
возрастании х.
Рис. 191. Рис. 192.
Найдем первую и вторую производные от функции у =

ОСОБЫЕ ТОЧКИ КРИВОЙ
283
При х=0 имеем у = 0, #'=0. Следовательно, рассматриваемая ветвь кривой
имеет в начале координат касательную «/ = 0. Вторая ветвь кривой у=—Ух*
также проходит через начало координат и имеет ту же касательную у — О.
Таким образом, две различные ветви кривой встречаются в начале коор-
координат, имеют одну и ту же касательную и расположены от касательной по
разные стороны. Такая особая точка называется точкой возврата первого рода
(рис. 192).
Замечание. Кривую у2—х* = 0 можно рассматривать как предельный
случай кривой у2 = х(х—аJ (рассмотренной в примере 1), когда а—^0, т. е.
когда петля кривой стягивается в точку.
Пример 3. Исследовать кривую (у—х2J—*5=0.
Решение. Координаты особых точек определяются системой уравнений
—4* (*/—*2) —5*4 = 0, 2 (у—*2)=0,
этого уравнения
которая имеет единственное решение: х = 0, #=0. Следовательно, начало
координат есть особая точка.
Перепишем данное уравнение в виде у = х2 ± Ухъ. Из
следует, что х может принимать значения от 0 до +оо.
Определим производные первого и второго порядка:
15
Исследуем ветви кривой, соответствующие знакам плюс и^инус, в отдель-
отдельности. В обоих случаях при #—0 имеем: у=0, у' = 0, т« е. для обеих вет-
ветвей ось Ох является касательной. Рассмотрим сначала ветвь у=х2-{-Ух?. При
возрастании х от 0 до оо у возрастает от 0 до ооч Вторая ветвь у=х2—У~хЪ
пересекает ось Ох в точках @, 0) и A,_Q).
При x=t 16/25 функция^ у=х2—УхЧ имеет максимум. Если х—^-f-°°> T(>
у—>—оо.
Таким образом, в данном случае в начале координат встречаются две
ветви кривой; обе ветви имеют одну к ту же касательную и расположены по
одну сторону от касательной вблизи
точки касания. Такая особая точка на-
называется точкой возврата второго рода.
График рассматриваемой функции изоб-
изображен на рис. 193.
Пример 4. Исследовать кривую
Решение. Начало координат есть
особая точка. Для исследования кри-
кривой вблизи этой точки перепишем урав-
нение кривой в виде у=±х*У\—х2.
Так как уравнение кривой содер-
содержит только четные степени переменных,
то кривая симметрична относительно
осей координат и, следовательно, доста-
достаточно исследовать часть кривой, соот-
соответствующую положительным значениям
х и у. Из последнего уравнения следует, что х может изменяться на отрезке
от 0 до 1, т. е. 0<х<1.
Вычислим первую производную для той ветви кривой которая является
графиком функции у=х2 j/"l—х2;
Рис. 193.

284
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. VIII
При х=0 имеем у = 0, у' = 0. Следовательно, в начале координат кривая
касается оси Ох.
При #=1 имеем у~0, г/' = оо; следовательно, в точке A, 0) касательная
параллельна оси Оу. При *=уг2/3 функция имеет максимум (рис. 194).
В начале координат (в особой точке) две ветви кривой, соответствующие
знакам плюс л минус перед корнем, взаимно касаются.
Такая особая точка называется точкой соприкоснове-
соприкосновения.
Пример 5. Исследовать кривую у2—х2 (х—1) = 0.
Рис. 194. Рис. 195.
Решение. Напишем систему уравнений, определяющих особые точки:
Эта система имеет решение * = 0, # = 0. Следовательно, точка @, 0) есть
особая точка кривой. Перепишем данное уравнение в виде у— ± х V^x— 1.
Очевидно, что х может изменяться от 1 до +00» а также принимать значе-
значение О (в последнем случае &=0).
Исследуем ветвь кривой, соответствующую знаку плюс перед корнем. При
увеличении х от 1 до оо у увеличивается от 0 до оо. Производная
Злг—2
При лг= 1 имеем у' = so; следовательно, в точке A, 0} касательная парал-
параллельна оси Оу.
Вторая ветвь кривой, соответствующая знаку минус, симметрична с пер-
первой относительно оси Ох.
Точка @, 0) имеет координаты, удовлетворяющие уравнению, и, следова-
следовательно, принадлежит кривой, но вблизи нее нет других точен кривой (рис. 195),
Такая особая точка называется изолированной особой точкой.
Упражнения к главе VIII
Найти частные производные следующих функций:
= x2s'm2y.
Отв. Ч± =
ди
дг_
?
ди
35=
Отв. ~=2xsin2y, -^=Д
дх v ду
2. г =
3. и = е
4.
Отв. ^=
5. z = arotg(xy). Отвч ~ =
дг у
дг
ди
дх'
х
дх \+х2у2* ду~~\+х2у*щ

УПРАЖНЕНИЯ К ГЛАВЕ VIII]
285
6. z = arctgJL. Отв. ?=-
5 л: ал: х
Отв. ^- —
дх
ду у2
dz
9 ду
2x
' ду
7. ,-l
дг
у
8.
9.
xiu . г/и ~ да 1
= ex/y+ez/y. Отв. -~-=:—
^ дх у
Отв. |?
= arctg
^г2. Отв. ^=:
Найти полные дифференциалы от следующих функций:
11. z^xz+xyt + siny. Отв. dz = Bx+y2) dx+Bxy+cos у) dy.
12. z^\n{xy\ Отв. dz = ^+&. 13. z=e*2+*e.
Отв. dz=2ex*+y4xdx+ydy).
Отв. du=^(
—^ t
cos2 Ca:—y)
27^ г
cos*Cx—y
dy+by+z\n6dz.
15. uy =
x ^ ydx—xdy
~~. Отв. dw=——7r==
у \
\y\Yy
16. Вычислить fx B, 3) и f'yB, 3), если f(x, у)-=х*+у*. Отв. fxB, 3) = 4,
f 3) = 27.
17. Вычислить d/ (лг, у) при *=1, ^==Q, йд:=1/2, dy=l/4, если /(дс, у) =з
^"a:2 + i/2. Отв. 1/2.
IS. Составить формулу, дающую при малых абсолютных значениям
величин #, у и г приближенное выражение для
Отв. 1+*2"(лг—у—г).
.. 7\ _^ ^,
19. То же для
20. Найти ~ и
J/ -J±fL.
i (*-?-.г).
«=x24-siny, v = l
«== —cos>;, 0=cosa:.
22. Найти ~ и
, если z = ett~2v, u = sinx, v=x*+y*. Отв. -^ =-
= —4(/е«-2г;, где вместо tt и v над»
— вя-av (cos a:—6a:2), ^ = ea~2& @—
подставить бШдг и а?+(/2.
Найти полные производные данных функций:
dz]
23. 2 = arcsin(« + ^)» «=sinA:cosa, v — cos A* sin a. Ome. ^-вЬ если
2Ля~<^+а<2Лл + у ^ = -1 если2Ля+<х+а<BЛ + 1)л+

286 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ |ГЛ. VIH
24. и—е-—алГТ * y = asinx, z = cosx. Отв. --^-=еахsin x.
25. z;=ln(l— х% х=УШЪ. Отв. -Й-=— 2tg9.
аи
Найти производные неявных функций от х, заданных уравнениями;
*2 У2 dy " Ь2 х __ х* Уг л п dV ъ<1 х
d 2 2 Ъ2 d 2
а2 • &2 d* а2 у a2 Ъ2 dx а2 у
у* = #. Отв. Лу=;ухУ~]]-У\<1пу. 29. sin
йх хух~х —-ху\пх
dy y[cos(xy)—еху—2х] ол х2 . у2 . 22 f „
. -г=^г ^~ =г. 30. —Т+-Т9-Н—- = 1; найти
dx x[x+e*y—cos(xy)] а>^Ь2^с*
д 2 д 2
дг с2х дг с2у
^а; а22 ф 62г
T=VV-z2; показать, что
^|i+i|i=l. 33. -i-Ffi); показать, что ,*+lf^z, ка-
дх* у ду г х \х J ' дх * ду
кова бы ни была дифференцируемая функция F.
Вычислить частные производные второго порядка:
34. z=f-wy+by\ отв. 0-6*-*;
35. г=ех\Пу+*гпу\ПХ. Отв. ft=e
Э2г е*
36. Доказать, что если «= # у то ^-r+^-o+^
У^2-|-1/2-f 22 ^ ^ ^
о- п д:2</2 а2г , а2г о дг
37. Доказать, что если 2=—~~ , то х-%-$-\-у ~, л =2-з~
а:+^ ^ дхду дх
d2z d2z
38. Доказать, что если 2 = In (*2 + #2), то ¦д-т+-^-2' = 0.
522 52г
39. Доказать, что если z = q> (y-\-ax)+ty (у—ах)> то а2-^~2—яРг'^11^ ПРИ
любых дважды дифференцируемых ф и if.
40. Найти производную от функции 2 = 3*4—ху~\-у3 в точке_jW(l, 2)
в направлении, составляющем с осью Ох угол в 60°. Отв. 5+11 У3/2.
41. Найти производную от функции 2 = 5*2—Зх—у—1 в точке М B, 1)
в направлении, идущем от этой точки к точке N E, 5). Отв. 9,4.
42. Найти производную функции / (х, у) в направлении: 1) Биссектрисы
координатного угла Оху. Отв. ( л^"Ь"л^) • ^ Отрицательной полу-
полуоси Ох. Отв. ——-.
дх
43. /(*, у)=х*+3х2 + 4ху+у2. Показать, что в точке М B/3, —4/3)
производная в любом направлении равна нулю («функция стационарна»).
44. Из всех треугольников с одинаковым периметром 2р определить тре-
треугольник с наибольшей площадью. Отв. Равносторонний треугольник.
45. Найти прямоугольный параллелепипед, который имеет наибольший
объем при данной полной поверхности 5. Отв. Куб с ребром ]fS/6.
46. Найти расстояние между двумя прямыми в пространстве, уравнения
У
х—1 ц z х у г ~
которых —J—^у—у» у— i ^Т* Ш*

УПРАЖНЕНИЯ К ГЛАВЕ VIII 287
Исследовать на максимум и минимум функции:
47. г = хгуг(а—х—у). Отв. Максимум г при х = а/2, у = а/3. 48. г = х2-\-
1 • Отв. Минимум г при х = у=\1 у 3. 49. 2 = sin*-f"
+ sin y+sin (х-\-у) @^лс^я/2; 0^у^л/2). Отв. Максимум г при х—у =
= я/3. 50. z = sin* sin у sin (*+#) (О^лг^зх, 0<;(/а^я). Отв. Максимум 2
при х—у — п/З.
Найти особые точки следующих кривых, исследовать их характер и со-
составить уравнения касательных в них:
51. дг3 + г/3—Заху = 0. Отв. МО @, 0)—узел; * = 0, #=0—уравнения
касательных.
52. а4(/2 = а:4 (а2—л:2). Отв. В начале координат точка соприкосновения;
двойная касательная у2 = 0.
53. У2 = ~п • Отв. Мо @, 0)—точка возврата первого рода, t/2~0 —
касательная.
54. е/2 = л:2(9—л:2). Ome. MQ @, 0)—узел; #= ± 3*-— уравнения каса-
касательных.
55. х1—2ах2у—аху2-[-а2х2 — 0. Отв. М0@, 0)—точка возврата второго
рода; #2 = 0—двойная касательная.
66. у*(а24-х2) = х*(а2—х2). Отв. Мо @, 0) — узел; #= ± х—уравнения
касательных.
57. Ь*х?~\-а2у2—х2у2. Отв. М0@, 0)—изолированная точка.
58. Показать, что кривая y—xlnx имеет концевую точку в начале коор-
координат и касательную—ось Оу.
59. Показать, что кривая у= . г имеет узловую точку в начале коор-
координат и что касательные в атой точке: справа tf=O, слева у = #.

ГЛАВА IX
ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ
§ 1. Уравнения кривой в пространстве
Рассмотрим вектор ОЛ = /% начало которого совпадает с нача-
началом координат, а концом является некоторая точка А (ху у, г)
(рис. 196). Такой вектор называют радиус-вектором.
Выразим этот вектор через проекции на оси координат:
r = xi+yj+zk. A)
Пусть проекции вектора г суть функции некоторого параметра t:
* = Ф(О. * = ¦('). * = Х@. B)
Тогда формулу A) можно переписать так:
г = ф@*+*@/+х@*. О')
или коротко
r = r(t). (Г)
При изменении t изменяются х, у, г, и точка А—конец вектора
г—опишет в пространстве некоторую линию, которую называют
годографом вектора r = r(t). Уравнение
(Г) или (Г') называют векторным урав-
уравнением линии в пространстве. Уравнения
B) называются параметрическими урав-
уравнениями линии в пространстве. С помощью
этих уравнений для каждого значения t
определяются координаты х, у, z соответст-
соответствующей точки кривой.
Замечание. Кривая в пространстве
Рис. 196. может быть также определена как геомет-
геометрическое место точек пересечения двух по-
поверхностей; следовательно, такая кривая может быть задана дву-
двумя уравнениями двух поверхностей:
#1 (*> У, г) - О, Ф2 (х, у, г) - 0. C)

§ 1] УРАВНЕНИЯ КРИВОЙ В ПРОСТРАНСТВЕ
Так, например, уравнения
289
являются уравнениями окружности, получающейся в пересечении
сферы и плоскости (рис. 197).
Итак, кривая в пространстве может быть задана или парамет-
параметрическими уравнениями B), или двумя уравнениями поверхнос-
поверхностей C).
Если мы исключим параметр t из уравнений B) и получим
два уравнения, связывающие х9 у," г, то тем самым осуществим
Рис. 197.
переход от параметрического способа задания линии к заданию
ее с помощью поверхностей. Обратно, если положим л: = ф (/)
(ф @ — произвольная функция) и найдем у я z как функции от
t из уравнений
то осуществим переход от задания линии с помощью поверхностей
к параметрическому способу задания.
Пример 1. Уравнения x — At—1, # = 3/, z — t-\-2 являются парамет-
параметрическими уравнениями прямой. Исключая параметр /, получим два уравне-
уравнения, каждое из которых есть уравнение плоскости. Например, если из первого
уравнения почленно вычесть второе и третье, получим х—у— г = — 3. Вычи-
Вычитая же из первого учетверенное третье, получим х—4г = —9. Таким образом,
заданная прямая является линией пересечения плоскостей х—#—2+3 = 0 и
+
Пример 2. Рассмотрим прямой круговой цилиндр радиуса я, ось кото-
которого совпадает с осью Oz (рис. 198). На данный цилиндр будем навивать пря-
прямоугольный треугольник СХАС так, чтобы вершина А треугольника лежала
в точке пересечения образующей цилиндра с осью Ох а катет АСг навивался
на круговое сечение цилиндра, лежащее в плоскости Оху. Тогда гипотенуза
образует на цилиндре линию, которая называется винтовой линией.
Напишем уравнение винтовой линии, обозначая через х, //, г координаты
ее переменной точки М и через t угол АОР (рис. 198). Тогда x = acost,
y==asintt z = PM — АРtg6, где через 0 обозначен острый угол треугольни-
10 Н. С. Пискунов, т. 1!

290
ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ. IX
ка СхАС. Заметив, что ЛР = а/, так как АР есть дуга круга радиуса а, соот-
соответствующая центральному углу t, и обозначив tg 0 через т, получаем пара-
параметрические уравнения винтовой линии в виде x = aco$t, y — as'mt, z — amt
(здесь t—параметр), или в векторной форме; r = iacos t-\-jasint-\-kamt.
Рис. 198.
Из параметрических уравнений винтовой линии легко исключить параметр
t; возводя первые два уравнения в квадрат и складывая их, найдем х2-\-у2 =
— а2. Это—уравнение цилиндра, на котором расположена винтовая линия.
Далее, деля почленно второе уравнение на первое и подставляя в полученное
уравнение значение t, найденное из третьего уравнения, найдем уравнение
другой поверхности, на которой расположена винтовая линия; ~ = tg ,
Это—так называемая винтовая поверхность (геликоид). Ее можно получить
от движения полупрямой, паралельной плоскости Оху, если конец этой полу-
полупрямой находится на оси Ог, причем сама полупрямая с постоянной угловой
скоростью вращается вокруг оси Ог и с постоянной скоростью поднимается
вверх так, что ее конец перемещается вдоль оси Ог. Винтовая линия являет-
является линией пересечения этих двух поверхностей. Поэтому ее можно задать
двумя уравнениями; х2-\-у2 = а2, ~ = tg ,
§ 2. Предел и производная векторной функции
скалярного аргумента. Уравнение касательной к кривой.
Уравнение нормальной плоскости
Вернемся к формулам (Г) и (Г) предыдущего параграфа:
или
При изменении t вектор г изменяется в общем случае па величине
и по направлению. Говорят, что г есть векторная функция от
скалярного аргумента t. Допустим, что

S2J
ПРЕДЕЛ И ПРОИЗВОДНАЯ ВЕКТОРНОЙ ФУНКЦИИ 291
есть предел векто-
Тогда говорят, что вектор ro = %i
ра r = r(t), и пишут (рис. 199)
Из последнего равенства следуют очевидные равенства
Ига | г @ - г,1 = lim V [Ф @ - <Ро]2 + № @ - Ч>.Р + U @ - ЗСо]2 = <>
lim|r@| = |r,|.
Перейдем теперь к вопросу о производной векторной функции
скалярного аргумента
. 0)
предполагая, что начало вектора г @ находится в начале коор-
координат. Мы знаем, что последнее уравнение является уравнением
некоторой пространственной кривой.
Рис. 199.
Возьмем какое-нибудь фиксированное значение t, соответст-
соответствующее определенной точке М на кривой, и дадим / приращение
А*; тогда мы получим вектор
который определяет на кривой некоторую точку Мх (рис. 200).
Найдем приращение вектора
Дг =
На рис. 200, где OM=?_(t),
изображается вектором
Рассмотрим отношение
это приращение
приращения векторной функ-
функции к приращению скалярного аргумента; это, очевидно, есть
ю*

292 ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [ГЛ. IX
вектор, коллинеарный с вектором &r(t), так как получается из
не.го умножением на скалярный множитель 1/ДЛ Мы можем за-
записать этот вектор так:
Ar(Q _ (fl
57
Если функции ф@» "Ф@» х@ имеют производные при выбран-
выбранном значении t, то множители, стоящие при /, /, k> в пределе
при Д?—ьО обратятся в производные ф'@, Ф'(О» %'@- Следо-
Следовательно, в этом случае предел -—- при Ы —> 0 существует и
равен вектору <р'(О|*+'Ф' @/+%'
lim ^- = Ф'(О
Вектор, определяемый последним равенством, называется про-
производной от вектора r(t) по скалярному аргументу ?. Производ-
Производную обозначают символом -? или г'.
Таким образом,
¦^ = г'==ф'@/+*'@У+х'@*. B)
или
Выясним направление вектора -^ .
Так как при Ы —^ 0 точка М? приближается к точке Му то
направление секущей МЛ^- в пределе дает направление касатель-
касательной. Следовательно, вектор производной -~ направлен по каса-
касательной к кривой в точке М. Длина вектора ¦— определяется
формулой*)
На основании полученных результатов легко написать урав-
уравнение касательной к кривой
в точке М(ху у, г), имея в виду, что в уравнении кривой # = ф(/),
7*0.
*) Мы будем предполагать, что в рассматриваемых точках -т~

§2] ПРЕДЕЛ И ПРОИЗВОДНАЯ ВЕКТОРНОЙ ФУНКЦИИ 293
Уравнения прямой, проходящей через точку М(х, у, г), име-
имеют вид
X—х = Y—у = Z — z
т п р '
где X, F, Z—координаты переменной точки прямой, а т, пу р —
величины, пропорциональные направляющим косинусам этой пря-
прямой (т.е. проекциям направляющего вектора прямой).
С другой стороны, мы установили, что вектор
dt - dt l^ dt J~t dt R
направлен по касательной. Поэтому проекции этого вектора яв-
являются числами, пропорциональными направляющим косинусам
касательной, а значит, и числам т, п, р. Следовательно, уравне-
уравнения касательной будут иметь вид
dt
Пример 1. Написать уравнения касательной к винтовой линии х = а cos /,
у = a sin/, z— ami при произвольном значении t и при * = я/4.
Решение.
?L=-asint, ^.= о cos Л ~ = ат.
По формуле D) имеем
X—a cos t _ X—asin t _ Z—amt
—a sin t a cost am
В частности, при t — n/4 получим
аУ2
2
Y а 1П j
2
2
2
— "" 7
am
4
Y~2
Так же как и в случае плоской кривой, прямая, перпенди-
перпендикулярная к касательной и проходящая через точку касания, на-
называется нормалью к пространственной кривой в данной точке.
Нормалей к данной пространственной кривой в данной точке
можно, очевидно, провести бесчисленное множество. Все они ле-
лежат в плоскости, перпендикулярной к касательной прямой. Эта
плоскость называется нормальной плоскостью.

294 ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [ГЛ. IX
Из условия перпендикулярности нормальной плоскости к ка-
касательной D) получаем уравнение нормальной плоскости:
^(X-x) + §.(Y-y) + §(Z-z)=0. E)
Пример 2. Написать уравнение нормальной плоскости к винтовой ли-
линии в точке, для которой / = л;/4.
Решение. На основании примера 1 и формулы E) получаем
ИЛИ
— X+Y+m ^
Выведем теперь уравнения касательной прямой и нормальной
плоскости пространственной кривой в случае, когда эта кривая
дана уравнениями
Фх (х, У, г) = О, Ф2 (*, у, z) = 0. F)
Выразим координаты х, у, z этой кривой как функции неко-
некоторого параметра t:
* = ф@. У = *@. * = Х@. G)
Будем предполагать, что <p(f), ^(t), % (/) — дифференцируемые
функции от t.
Подставляя в уравнения F) вместо х9 у> z выраженные через
t их значения для точек кривой, получим два тождества относи-
относительно t:
0, (8а)
0. (86)
Дифференцируя тождества (8а) и (86) по t, находим
dx , дФг dy , dOj dz _n
d/ "•" dy d^ + аг Л ~" •
Из этих уравнений следует, что
iff dfly дФ2 dOj ^Ф2 ^? d<bj дФ2
iff. ^?
dt ду dz dz ду dt dz дх дх dz
IT ~~ "ЗфГ дФ2 dOi дФ2 1 dz ~"ШГ дФ2 дФ± дФ2
dt дх ду ду дх dt дх ду ду дх
»г дФл дФа
Мы здесь предполагаем, разумеется, что выражение-^--у^-—
—^-^^О» однако можно доказать, что окончательные фор-
формулы A1) и A2) (см. ниже) справедливы и в том случае, когда

ПРЕДЕЛ И ПРОИЗВОДНАЯ ВЕКТОРНОЙ ФУНКЦИИ
295
это выражение равно нулю, если только хоть один из определите-
определителей, фигурирующих в окончательных формулах, отличен от нуля.
Из равенств A0) получаем
dx
dt
dt
dz_
dt
х дФ2 дФл дФ2 дФг дФ2
дФ2
ду dz
dФ2 dФ1 дФ2
dz dy dz dx dx dz dx dy dy dx
Следовательно, на основании формулы D) уравнения касатель-
касательной прямой будут иметь вид
X—х Y—y Z-z
дФ2
dФ1 dФ2
dФ1 дФ2 dФ1 dФ2
dy dz dz dy dz dx dx dz dx dy ду дх
или, пользуясь определителями,
X-
дФ±
ду
дФ2
ду
-X
дФг
dz
дФ2
dz
Y-У
dФ1
dz
дФ2
dz
dФ1
dx
дФ2
dx
Z—z
dФ1
dx
дФ2
dx
dФ1
dy
дФ2
ду
A1)
Нормальная плоскость представляется уравнением
(Х-*)
dy dz
дФ2 дФ2
ду dz
дФг
dz
дФ2
dz
dФ1
dx
дФ2
дх
{Z-z)
дфг
дх
дФ2
ду
дФ2
дх ду
=0.A2)
Эти формулы имеют смысл только тогда, когда хотя бы один
из фигурирующих в них определителей отличен от нуля. Если же
в некоторой точке кривой все три определителя
дФ1 дФг
ЗФ1
ду
дФг
ду
dФ1
dz
dФ2
dz
>
dФ1
dz
дФ2
dz
дФх
дх
дх
дх
дФ9
ду
дФ9
дх ду
обращаются в нуль, то эта точка называется особой точкой про-
пространственной кривой. В этой точке кривая может вообще не
иметь касательной, подобно тому как это имело место в особых
точках у плоских кривых (см. § 20 гл. VIII).
Пример 3. Найти уравнений касательной прямой и нормальной плос-
плоскости к линии пересечения сферы #24-#2+z2 = 4r2 и цилиндра х2-\-у2 = 2гу
в точке М (г, r9 r ]/"~2) (рис. 201).
Решение.
дФ1
дх
=2х, ^=2у,
ду
дФ2
дФ2
dz ~~
дФ2
дг
=0.

296
ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ. IX
Значения производных в данной точ-
точке М будут
дФ9
= 2г =0
Поэтому уравнения касательной прямой
имеют вид
X—г _Y—r _ Z—r У
О "" у ~1
Уравнение нормальной плоскости
или
Рис. 201.
—Z=0.
§ 3. Правила дифференцирования векторов (векторных функций)
Как мы видели, производная от вектора
Г (/) = <р(?)/ + 1ф(/I/-{-5С {t)k A)
по определению равна
Отсюда сразу следует, что основные правила дифференцирова-
дифференцирования функций остаются в силе и для векторов. Мы выведем ниже
некоторые формулы дифференцирования функций от векторов. Эти
формулы нам потребуются в дальнейшем.
I. Производная суммы векторов равна сумме производных от
слагаемых векторов.
В самом деле, пусть, например, даны два вектора:
C)
их сумма равна
По определению производной от переменного вектора имеем
@37+
или

§ 3] ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ ВЕКТОРОВ 297
Следовательно,
dt ~~ dt ~^ dt' \ '
II. Производная от скалярного произведения векторов выра-
выражается формулой
d (/у2) _ drx , dr2 nu
dt —1Гг*~гГ1 df *u'
Действительно, если r1{t), r2(t) определены формулами C),
то, как известно, скалярное произведение этих векторов равно
*х (О Г2 @ =
Поэтому
=ф!ф2+Ф1Ф2
1Ф2+ад;
Теорема доказана.
Из формулы (II) получается важное следствие.
Следствие. Если вектор е единичный, т. е. |е| = 1, то его
производная есть вектор, к нему перпендикулярный.
Доказательство. Если в —единичный вектор, то ее=1.
Возьмем производную по t от обеих частей последнего равен-
равенства: в-^+-^в=0, или 2е-^ = 0, т. е. скалярное произведение
е -^ = 0» а это и означает, что вектор ~ перпендикулярен к век-
вектору е.
III. Если f (t) —скалярная функция и г (t) — векторная функция,
то производная от произведения f (t) r (t) выражается формулой
d(M_d[ fdr (Ш)
dt - dtr^J dV <111'
Доказательство. Если вектор r(t) определен форму-
формулой A), то
По формуле B) получаем

298
ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ. IX
IV. Постоянный числовой множитель можно вынести за знак
производной:
2=e?-or'(Q. (IV)
Это следует из III, если f (t) = a = const. Следовательно,
V. Производная векторного произведения векторов rx (t) и
r2(t) определяется формулой
d (г±Хг2) drx \гку dfj* дг\
Tt "~ dt хг2"гг1х7Г* (V;
Доказывается аналогично формуле (II).
§ 4. Первая и вторая производные вектора по длине дуги.
Кривизна кривой. Главная нормаль.
Скорость и ускорение точки в криволинейном движении
Как и в случае кривых на плоскости, определяется длина
дуги*) пространственной кривой M0A = s (рис. 202). При дви-
движении переменной точки А (х, у, г) по кривой длина дуги s
изменяется; и обратно, при изменении s изменяются координаты
х, j/, z переменной точки Л, лежащей на
кривой. Следовательно, координаты ху
у, z переменной точки кривой А мож-
можно рассматривать как функции длины
дуги s:
В этих параметрических уравнениях
кривой параметром является длина ду-
дуги s.
Вектор ОА = г выразится так:
Рис. 202.
или
A)
т. е. вектор г является функцией длины дуги s.
*) Длина дуги пространственной кривой определяется так же, как и
длина дуги плоской кривой (см. § 1 гл. VI и § 3 гл. XII).

§4] ПЕРВАЯ И ВТОРАЯ ПРОИЗВОДНЫЕ ВЕКТОРА ПО ДЛИНЕ ДУГИ 299
Выясним геометрический смысл производной -~. Как видно из
рис. 202, имеют место следующие равенства:
s, OA = r(s), OB = ri
Мы уже видели в § 2, что вектор ~f-= lim -^ направлен по
as As -+ 0 As
касательной к кривой в точке А в сторону возрастания s. С дру-
г Тв
гои стороны, имеет место равенство lim
длины хорды к длине дуги*)). Следовательно, ^ есть единич-
единичный вектор, направленный по касатель-
касательной; обозначим его через а:
?-•
Если вектор г задан проекциями:
то
причем
(?)•+
= 1 (предел отношения
{^j ^V^^ +\ds) = * Рис.203.
Рассмотрим, далее, вторую производную векторной функции
d2r dr
~, т. е. производную от j-, и выясним ее геометрическое зна-
значение. Из формулы B) следует, что ^==^s [37] =д^. Следова-
тельно, нам нужно найти lim -г—,
As->0As
Из рис. 203 имеем AB = As, AL — e, BK = o + Aa. Проведем
из точки В вектор В^^а. Из треугольника BKLt находим
ВК = BLX + LtK, или
Следовательно, ЬгК=^Аа. Так как по доказанному длина вектора а
не меняется, то |а| = |а + Да|; следовательно, треугольник ВК1ч
равнобедренный.
*) Мы указывали на это соотношение для плоской кривой в § 1 гл. VI.
Оно имеет место и для пространственной кривой г (t) =<p (t) i+тр (t)J+% (() k,
если функции <p(f)t ty@ и %(t) имеют непрерывные производные, не обра*
щающиеся одновременно в нуль.

300
ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ. IX
Угол Дф при вершине этого треугольника есть угол поворота
касательной к кривой при переходе из точки А в точку В, т. е.
соответствует приращению длины дуги As. Из треугольника BKLX
находим
sin
Аф I
sin
Аф|
(так как |a| = 1).
Разделим обе части последнего равенства на As:
Аф
As
Да
As
-2
. Аф
sm 2
As
sinf
Д(р
T
Перейдем к пределу в обеих частях последнего равенства при
As—*0. В-левой части получим
Далее,
litn
As->0
lim
As-* 0
Aa
As
Аф
Аф
do]
ds
i
i f
так как в данном случае мы рассматриваем такие кривые, что
существует предел Ига д2 и, следовательно, Аф-^0 при As—^0.
As -> 0
Таким образом, после перехода к пределу получаем
Аф
l-rh lira
As
As
D)
Отношение угла поворота Аф касательной при переходе от точки А
к точке В к длине As дуги АВ, взятое по абсолютной величине,
называется, так же как и для плоской кривой, средней кривизной
данной линии на участке АВ:
средняя кривизна= д^
Предел средней кривизны при As —> 0 называется кривизной лини»
в точке А и обозначается буквой К:
Аф
As "
Aa
As
К= lim
As->0
Но в этом случае из равенства D) следует, что
= /С, т. е.
длина производной от единичного вектора *) касательной по длине
*) Напоминаем, что производная вектора есть вектор, и поэтому
мы можем говорить о длине производной.

§ 4] ПЕРВАЯ И ВТОРАЯ ПРОИЗВОДНЫЕ ВЕКТОРА ПО ДЛИНЕ ДУГИ 301
дуги равняется кривизне линии в данной точке. Так как вектор а
единичный, то его производная ^ перпендикулярна к нему (см.
§ 3, следствие).
Итак, вектор ~ по длине равен кривизне кривой, а по на-
направлению перпендикулярен к вектору касательной.
Определение. Прямая, имеющая направление вектора -р и
проходящая через соответствующую точку кривой, называется
главной нормалью кривой в данной точке. Единичный вектор этого
направления обозначим через п.
Так как длина вектора ^- равна К—кривизне кривой, то
?-*••
Величина, обратная кривизне, называется радиусом кривизны
линии в данной точке и обозначается через R, т. е. ^- = #- По-
Поэтому можем написать
Из этой формулы следует
sf-S'+S-Z+S*- Следовательно,
i- /(S)'+C)'+(Sy-
Последняя формула дает возможность вычислить кривизну ли-
линии в любой точке, если эта линия задана параметрическими
уравнениями, в которых параметром является длина дуги s (т. е.
если радиус-вектор переменной точки данной линии выражен как
функция от длины дуги).
Рассмотрим случай, когда радиус-вектор г выражен как функ-
функция произвольного параметра t: r = r(t). В этом случае длину
дуги s будем рассматривать как функцию параметра t. Тогда
вычисление кривизны, производится следующим образом:
dr dr ds rj\
!t~~dsTt

302 ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [ГЛ. IX
Так как*) Щ-h то
(dry__(dsy g
[dt) ~[di) • W
Дифференцируя правую и левую части и сокращая на 2, получим
dr^fr_dsd^ Q
dt dt2 ~~ dt dt2' W
Далее, из формулы G) следует
ds ~~ d* ds'
dtf
Дифференцируем по s обе части последнего равенства:
d2s
d2r _ d2r 1 dr dt2 щ
ds2 ~ dt2
dsy dt (dsy>
dt) \dt)
подставляя полученное выражение j? в формулу F), будем иметь
1
Г
d% f fd2r\2/dsy dtrdrdsdh /dryfdhy
dr dt2 I _[dt2 ) \dt) df* dt dtdfi'T~\dt ) \dt2) *
dt2
/dsy dt (ds\a
[dij [Tt) _
?
Выражая ¦? и -^ по формулам (8) и (9) через производные
от г @, получим**)
ю
*) Это равенство следует из того, что
dr
Ar
стягивающая дугу длины As. Поэтому -г- стремится к 1 при As—>-О.
/ds\& ( /ds\2) 3
**) Преобразовываем знаменатель следующим образом: (^l^^fj/) r"==i
ifdr\2\z o fdrY ^ fdrY *• *
t=<(^-J > . Здесь нельзя написать hrl , Под \-гг\ подразумевается
dr {[dr\2\*
скалярный квадрат вектора ^-. Под < ( — J > подразумевается третья
(dr\2 D (dry
пень числа (^т") . Выражение же [-гг\ не, имеет смысла.

§ 4] ПЕРВАЯ И ВТОРАЯ ПРОИЗВОДНЫЕ ВЕКТОРА ПО ДЛИНЕ ДУГИ 303
Формулу A0) можно переписать так*):
\dr . d2rV *
(in
Мы получили формулу, которая дает возможность вычислить
кривизну данной линии в любой ее точке при произвольном
параметрическом задании этой кривой.
Если в частном случае кривая является плоской и лежит в
плоскости Оху, то ее параметрические уравнения имеют вид
Подставляя эти выражения х, у, z в формулу A1), мы получим
выведенную ранее (в гл. VI) формулу, дающую кривизну плоской
кривой, заданной параметрически:
1Ф'@^@-¦»'(*)<!>* @1
А
Пример. Вычислить кривизну винтовой линии r = ia cos /+/д sin t -f*
-\-kamt в произвольной точке.
Решение:
р
Решение:
JL= — ia sin t +ja cos t + k am, gj?= — ^a cos f _ya Sin ^
i j k
—asint a cost am
—a cos I —asint 0
= ia2m sin t—ja2m cos /+/fea2#
Следовательно,
/?2~"[a2 (I+m2)]3
откуда
Таким образом, винтовая линия имеет постоянный радиус кривизны.
Замечание. Если кривая лежит в плоскости, то, не нару-
нарушая общности, можно предположить, что она лежит в плоскости Оху
(этого всегда можно добиться преобразованием координат).
Если же кривая лежит в плоскости Оху, то г = 0; но тогда и
_=0 и, следовательно, вектор п лежит также в плоскости Оху.
*) Мы использовали тождество a2b2—(aftJ = (aXftJ, в справедливости
которого легко убедиться, если переписать тождество в следующем виде;*

304 ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [ГЛ. IX
Отсюда получаем вывод: если кривая лежит в плоскости, то ее
главная нормаль лежит в той же плоскости.
Скорость точки при криволинейном движении.
Пусть движущаяся точка в момент времени / находится в точ-
точке Af, определяемой радиус-вектором OM = r(t) (см. рис. 200),
а в момент t + kt находится в точке Ми определяемой радиус-
вектором 0Mx = r (t+At). Тогда вектор ММг называется вектором
перемещения точки. Отношение вектора перемещения ММХ к
соответствующему приращению времени А* называется средней
скоростью точки за промежуток времени:
=;вд_аг
VW М ~~ At
Вектор средней скорости также направлен по хорде MMi
(см. рис. 200, с. 291) в сторону движения точки (при прямоли-
прямолинейном движении он направлен по самой траектории).
Скорость точки в данный момент определяется так:
<• <• At* dr
д/ дд* at
т. е.
Таким образом можно сказать: Скорость точки в данный мо-
момент равна первой производной от радиус-вектора точки по вре-
времени.
На основании формулы B') § 2 следует, что проекции скоро-
скорости на оси координат будут
dx dy dz
Модуль скорости определяется по формуле C) § 2:
dzy
)
Если ввести длину дуги s, как это делалось в начале этого
параграфа, и рассматривать длину дуги s как функцию времени /,
то формулу A2) можно записать так:
dr dr ds
где t; = ^—абсолютная~величина скорости, а —единичный вектор,
направленный по касательной в сторону движения.
Ускорение точки при криволинейном движении.
Аналогично тому, как это было определено в § 25 гл. III, уско-
ускорением точки w при криволинейном движении называется про-

§ 5] СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ. БИНОРМАЛЬ. КРУЧЕНИЕ 305
изводная от вектора скорости по времени:
Но v = ¦?¦, следовательно,
Если будем исходить из формулы A4), то получим
W- dt ~ dt *
Раскрывая последнюю производную по формуле (III) § 3,
получим
Преобразуем производную ~, пользуясь формулами G) и E):
dt ~~ ds dt ~ R V*
Подставляя в равенство A7), окончательно получаем
Здесь а —единичный вектор, направленный по касательной в
сторону движения, я —единичный вектор, направленный по глав-
главной нормали.
Формула A8) словами формулируется так.
Проекция ускорения точки на касательную равна первой произ-
производной от абсолютной величины скорости, а проекция ускорения
на главную нормаль равна квадрату скорости, деленному на радиус
кривизны траектории в данной точке.
Так как векторы а и п взаимно перпендикулярны, то модуль
ускорения определяется формулой
§ 5. Соприкасающаяся плоскость. Бинормаль. Кручение.
Определение 1. Плоскость, проходящая через касатель-
касательную прямую и главную нормаль к заданной кривой в точке Л,
называется соприкасающейся плоскостью в точке А.
Для плоской кривой соприкасающаяся плоскость совпадает
с плоскостью кривой. Если же кривая не плоская, то, взяв на
ней две точки Р и Р1У мы получим две различные соприкасаю-
соприкасающиеся плоскости, образующие между собой двугранный угол ц.

306 ПРИЛОЖИ НИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ?ГЛ. IX
Чем больше угол fx, тем сильнее кривая по своей форме отли-
отличается от плоской кривой. Для того чтобы это уточнить, введем
еще одно определение.
Определение 2. Нормаль к кривой, перпендикулярная
к соприкасающейся плоскости, называется бинормалью.
Возьмем на бинормали единичный вектор Ь и направим его
так, чтобы вектор а, л, Ь образовывали тройку той же ориен-
ориентации, что и единичные векторы *, jy k, лежащие на осях коор-
координат (рис. 204, 205).
В силу определения векторного и скалярного произведений
векторов имеем
Найдем производную -т-. По формуле (V) § 3
Но-^-=-^- (см. § 4), поэтому ^ хя = -^-яхя = 0, и формула
B) принимает вид
т-*?• <3>
Отсюда следует (на основании определения векторного произве-
произведения), что j- есть вектор, перпендикулярный к вектору каса-
касательной а. С другой стороны, так как 6 —единичый вектор#
то -j- перпендикулярен к b (см. § 3, следствие).
Значит, вектор -j- перпендикулярен и к а и к ft, т. е. кол-
линеарен вектору п.
Обозначим длину вектора -^- через гщч т. е. положим

$ 5] СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ. БИНОРМАЛЬ. КРУЧЕНИЕ 307
Величина у называется кручением данной кривой.
Двугранный угол \i между соприкасающимися плоскостями,
соответствующими двум точкам кривой, равен углу между бинор-
бинормалями. По аналогии с формулой D) § 4 можно написать
db
ds
= lim
Итак, кручение кривой в точке А по абсолютной величине
равно пределу, к которому стремится отношение угла jj> между
соприкасающимися плоскостями в точке А и соседней точке В
к длине | As | дуги АВ, когда As—^0.
Если кривая плоская, то соприкасающаяся плоскость не ме-
меняет своего направления и, следовательно, кручение равно нулю.
Из определения кручения ясно, что оно является мерой от-
отклонения пространственной кривой от плоской кривой. Величина
Т называется радиусом кручения кривой.
Найдем формулу для вычисления кручения. Из формул C) и
D) следует
Умножив скалярно обе части на я, будем иметь
В правой части последнего равенства мы получили так назы-
называемое смешанное (или тройное) произведение трех векторов п,
о и —р . В таком произведении, как известно, можно перестав-
переставлять сомножители в круговом порядке. Учитывая, кроме того,
что пп= 1, мы перепишем последнее равенство в следующем виде:
или
} = -("<!)•
d2r
Но так как п = R -jt > то
ds * ds* "+¦ ds

308 ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО'ИСЧИСЛЕНИЯ [ГЛ. IX
а так как векторное произведение вектора на самого себя равно
нулю, то
~^"Х ds2 ~и-
Таким образом,
ПХ ds —*
Заметив, что о = —г- , и возвращаясь к равенству E), получаем
Если вектор г выражен как функция произвольного пара-
параметра t, то можно показать *) аналогично тому, как это делалось
в предыдущем параграфе, что
_(?_ d?r \ _ dt [ dt2 X dt3
ds V ds* X ds*) jf^
\{dt
*) В самом деле,
dr __ dr ds
dt ~~ds~dt' e
Дифференцируем это равенство еще раз по t:
i!^L—A ( *L\ ds_^idr__^s__^H ( ds \ 2 dr dh
dP ~~ ds\ ds ) dt dt*~ ds dt2 ~~ ds* \dt) +~dT dt1 f
Снова дифференцируем по t:
?jL——(?lL\^±( — \ jl!!lL ods d2s d ( dr\ ds d2s dr d3s _
dt'3'" ds V ^s2 ) dt \dt ) *» ds2 dt dt2 + ds \ ds ) dt dt2~T~4s"dF~~~
_dzr (ds\a d?r_ds_?s_ , dr_ d*s
~~ ds3 [ dt) ^ ds2 dt dt2 ^ ds dt* *
Составим, далее, смешанное (тройное) произведение:
dr ( d2r
( d
dt \ dt* X d
dr ds i\d?r (ds \« , dr (Psl Г d?r ( ds\* d2r ds dh ,dr d*s
Раскрывая это произведение по правилу умножения многочленов и от-
отбрасывая все те члены, которые содержат хотя бы два одинаковых векторных
сомножителя (так как смешанное произведение трех множителей, где хотя бы
два множителя равны, есть нуль), получим
dr ( d2r s/d*r\_dr ( d2r dBr \ ( ds\*
Ж \~dFX dp ) —~ds~ \~dsTX~dF) [it ) *
Наконец, заметив, что
fdsy (dry (ds\s \{dr\*\*
получаем требуемое равенство.

КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ
309
Подставляя это выражение в формулу F) и заменяя R2 его
выражением по формуле A1) § 4, окончательно получаем
dr / d*r d*r \
1 dt \ dt2 X 3 J
Т ~~
J
dr
Эта формула дает возможность вычислить кручение кривой
в любой точке, если кривая задана параметрическими уравнениями
с произвольным параметром t.
В заключение этого параграфа отметим, что формулы, выра-
выражающие производные векторов а, й, я, называются формулами
Серре—Френе:
da п db п dn о Ь
~ds ~~~Т * ~Ш~"Т ' ds ~~ R Т9
Последняя из них получается так:
но
поэтому
пха= —
dn
bxn=
Ь а
a,
Пример. Вычислить кручение винтовой линии
г = ia cos t -\~ja sin t+к ami.
Решение.
dr ( d2r d3r \ __
~dF\~dt2~x~dT '""
—a sin t a cos t am
—a cos t —a sin t 0
a sin t — a cos / 0
2) (см. пример
Следовательно,
§ 6. Касательная плоскость и нормаль к поверхности
Пусть имеем поверхность, заданную уравнением вида
F(x, у¦, г) = 0.
A)
Введем следующее определение.
Определение 1. Прямая линия называется касательной к
поверхности в некоторой точке Р(х, уг г), если она является

310
ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
|ГЛ, IX
касательной к какой-либо кривой, лежащей на поверхности и
проходящей через точку Р.
Так как через точку Р проходит бесконечное число различных
кривых, лежащих на поверхности, то и касательных к поверх-
поверхности, проходящих через эту точку, будет, вообще говоря, беско-
бесконечное множество.
Введем понятие об особых и обыкновенных точках поверх-
поверхности F (х, у, г) = 0.
c)F FiF r)F
Если в точке М (ху у, г) все три производные -^, -^ > ~-^-
равны нулю или хотя бы одна из этих производных не существует,
то точка М называется особой точкой поверхности. Если в точке
«ж/ dF dF dF
М (ху у, г) все три производные -^ , -^ , -^- существуют и не-
непрерывны, причем хотя бы одна из них отлична от нуля, то
точка М называется обыкновенной точкой
поверхности.
Теперь мы можем сформулировать сле-
следующую теорему.
Теорема. Все касательные прямые к
данной поверхности A) в ее обыкновенной
точке Р лежат в одной плоскости.
Доказательство. Рассмотрим на
поверхности некоторую линию L (рис. 206),
проходящую через данную точку Р по-
поверхности. Пусть рассматриваемая кривая
задана параметрическими уравнениями
Рис. 206.
Касательная к кривой будет касательной к поверхности. Урав-
Уравнения этой касательной имеют вид
X х Y у Z z
dx dy_ dz^ •
~df Ж IT
Если выражения B) подставить в уравнение A), то это урав-
уравнение превратится в тождество относительно t, так как кривая B)
лежит на поверхности A). Дифференцируя его по t, получим*)
dx dt + dy dt+ dz dt # W
Рассмотрим, далее, векторы N и — , проходящие через точку Р:
Zk. D)
*) Мы здесь применяем правило дифференцирования сложной функции
трех переменных. Это правило в данном случае применимо, так как все част*
dF dF dF
ные производные
--—
dF dF
, -*— i ~r- по условию непрерывны.

§6]
КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ
311
Проекции этого вектора ~ , 2~ , 4?- зависят от х9 у, г-коор-
г-координат точки Р; заметим, что так как точка Р обыкновенная, то
эти проекции в точке Р одновременно не обращаются в нуль и
потому
Вектор
dt" dt1^ dt J^ dt K
E)
касательный к кривой, проходящей через точку Р и лежащей на
поверхности. Проекции этого вектора вычисляются ца основании
уравнений B) при значении параметра /, соответствующем точке Р.
dr
Вычислим скалярное произведение векторов N и
равно сумме произведений одноименных проекций:
vdr _dF dx . dF dy dF dz
14 ~^ dy dt ^
которое
dt
dx
dz dt
На основании равенства (З) выражение, стоящее в правой
части, равно нулю, следовательно,
*/А
Из последнего равенства следует, что вектор N и касательный
вектор -jg- к кривой B) в точке Р перпендикулярны. Проведен-
Проведенное рассуждение справедливо для любой кривой B), проходящей
через точку Р и лежащей на поверхности. Следовательно, каждая
касательная к поверхности в точке Р перпендикулярна к одному
и тому же вектору N и потому
все эти касательные лежат в одной
плоскости, перпендикулярной к
вектору N. Теорема доказана.
Определение 2. Плоскость,
в которой расположены все ка-
касательные прямые к линиям на по-
поверхности, проходящим через дан-
данную ее точку Р, называется каса-
касательной плоскостью к поверхности
в точке Р (рис. 207).
Заметим, что в особых точках
поверхности может не сущест-
существовать касательной плоскости. В таких точках касательные пря-
прямые к поверхности могут не лежать в одной плоскости. Так, на-
например, вершина конической поверхности является особой точкой.
Рис. 207.

312 ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [ГЛ. IX
Касательные к конической поверхности в этой точке не лежат
в одной плоскости (они сами образуют коническую поверхность).
Напишем уравнение касательной плоскости к поверхности A)
в обыкновенной точке. Так как эта плоскость перпендикулярна
вектору D), то, следовательно, ее уравнение имеет вид
¦?<*-*> + f- (Y-y)+?(Z-z)=0. F)
Если уравнение поверхности задано в форме z = f(x, y)y или
г/ ч л dF df dF df dF ,
*-f(x, y)=0tro _=--^, — =—?.,-—=ifK уравнение
касательной плоскости в этом случае примет вид
?%<y-y). F')
Замечание. Если в формуле F') положим X — х~
Y — у = Д#, то эта формула примет вид
ее правая часть представляет собой полный дифференциал функции
2 = /(jc, у). Следовательно, Z — z = dz. Таким образом, полный
дифференциал функции двух переменных в точке М(х, у), соот-
соответствующий приращениям Дх и Ау независимых переменных х и
у, равен соответствующему приращению аппликаты (г) касатель-
касательной плоскости к поверхности, которая является графиком данной
функции.
Определение 3. Прямая, проведенная через точку Р (х, yt z)
поверхности A) перпендикулярно к касательной плоскости, назы-
называется нормалью к поверхности (рис. 207).
Напишем уравнения нормали. Так как ее направление совпа-
совпадает с направлением вектора N, то ее уравнения будут иметь вид
дх ду дг
Если уравнение поверхности задано в форме z = f(x, у), или:
Z — f{x, y) = 0, то уравнения нормали имеют вид
х—*__ Y—y _ z—z
дх ду
Замечание. Пусть поверхность F (х, у,г) = 0 есть поверх-
поверхность уровня для некоторой функции трех переменных и — и(х, у, z),
т. е.
F(x, У, z)^u{xy yy z)-C = 0.
Очевидно, что вектор N, определенный формулой D), направлен-

УПРАЖНЕНИЯ К ГЛАВЕ IX 313
ный по нормали к поверхности уровня F = и (х, уу z) — С = 0, будет
т. е.
Этим мы доказали, что градиент функции и (х9 у, г) направлен
по нормали к поверхности уровня, проходящей через данную точку.
Пример. Написать уравнение касательной плоскости и уравнения нор*
мали к поверхности шара #2+t/2 + z2 = 14 в точке РA, 2, 3).
Решение. F (х, у, z) = *2+*/2 + г2—14 = 0, -^F^2*' -|? = 2у, IJT^2*'
при дг=1, t/ = 2, z = 3 имеем -^— = 2, -^—=4, -^—==6. Следовательно, урав-
уравнение касательной плоскости будет 2(х—1) + 4(*/ — 2) -J—6 (г—3) = 0, или
+2+Зг—14 = 0.
х— 1 у—2 г — 3 *— 1 у—2 2—3
Уравнения нормали: ^ = . =—^—, или —г—= ^ =—^—
Упражнения к главе IX
Найти производные от векторов:
f. Отв. r'^-^ ^
\ntfc. Отв. r' = —e-n+2j+-j-. 3. г = «—^+-^-.
4. Найти вектор касательной, уравнения касательной и уравнение нор-
нормальной плоскости к кривой r = ti-{-t2j + t3k в точке C, 9, 27). Отв. г' —
х 3 и п у 27
= i + 6j+27k; касательная: -—-—=?-— = ¦; нормальная плоскость:
5. Найти вектор касательной, уравнения касательной и уравнение нор-
мальной плоскости к кривой r = ^cos2y+"o"^sin *+^siny. Oms, г' =
t
=—— * sin t-\—nJ cos ^-h"o* ^ cos "о* t уравнения касательной:
Y—у sin t Z—sin-y
= 7 = -.— ; уравнение нормальной плоскости: X sin t —
cos y
— Fcos f—Zcosy = x-sin t—у cos ^—2 cos у , где х% у, г—координаты
той точки кривой, в которой проводится нормальная плоскость ( т. е.

314 ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИОЛЕНИЯ [ГЛ. IX
6. Найти уравнения касательной к кривой x = t—sin t, y—\—cos tt
г — 4 sin -^ и косинусы углов, составляемых ею с осями координат.
0тв9 • —= з—= —j cos oc = sin2-7j-, cos p = -~-sin /о,
sin ~± cos -± ctg -±
cos y= cos —.
7. Найти уравнение нормальной плоскости к кривой г = х2—у2, у = х
в начале координат. Указание. Написать уравнения кривой в параметри-
параметрической форме. Отв, х-{-у — 0.
8. Найти а, л, Ь в точке t—ir Для кривой г— i (cos /+sin2 /) +
J Ki Ai h
. Отв. а = - ,_
~=r(--i+j + k), п^^~М
9. Найти уравнения главной нормали и бинормали к кривой x =—i
y^s Z=4 в точке (,„, л, го). 0*. ^^|^?
х—дс0 _ у—уо _ г—г0
10. Найти уравнение соприкасающейся плоскости к кривой у2 = х, х2 — г
в точке М A, 1, 1). Отв. 6*—8#—2+3 = 0.
П. Зайти радиус кривизны для кривой, заданной уравнениями *2+г/2 +
+ 22—4 = 0, х+у—2 = 0. Отв. /? = 2.
12. Найти радиус кручения кривой г = i cos t-\-jsin t-\-ksht.
Отв. T = — cht.
13. Найти радиус кривизны и кручения для кривой r = t2i-\-2t3j.
Отв. /? = |-
14. Доказать, что кривая r = (ai^2 + 61^+c1) i+(a2t2 + b2 + 2)j +
+ (a3t2+bst+c3)k плоская. Отв. г'"^=0, поэтому кручение равно нулю.
15. Найти кривизну и кручение кривой x = eti y = e~tt z = iY~2~
V V~2
Отв. Кривизна равна 'r+ ; кручение равно 2 .
16. Найти кривизну и кручение кривой # = e*-*sin /, y = e-icos t\ г = е~*.
т/2 1
Отв. Кривизна равна -Ц—et\ кручение равно —^-е1.
о о
X2 V2
17. Найти уравнение касательной плоскости к гиперболоиду ——-тъ"-•
~?=1 в точке (xlf Л, Zl). Отв. ^L-^-M^i.
18. Найти уравнение нормали к поверхности д:2—4у2+2г2 = 6 в точке
B, 2, 3). Отв. г/+4л:=10, Зл:—2 = 3.
19. Найти уравнение касательной плоскости к поверхности г = 2х2-\-Ауг
в точке МB, 1, 12). Отв. Sx+8y—z=\2.
20. К поверхности х2 + 2у2 + 22 = 1 провести касательную плоскость,
параллельную плоскости х—#+2^ = 0, Отв. х—у-\-2г=± /*

ГЛАВА X
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Первообразная и неопределенный интеграл
В главе III мы рассматривали такую задачу: дана функция F (х);
требуется найти ее производную, т. е. функцию f(x) = F'(x).
В этой главе мы будем рассматривать обратную задачу: дана
функция f (х); требуется найти такую функцию F (х), производная
которой равна f(x)f т. е. F'(x) = f(x).
Определение 1. Функция F(х) называется первообразной
от функции / (х) на отрезке [#, &], если во всех точках этого от-
отрезка выполняется равенство Fr (x)=f(x).
Пример. Найти первообразную от функции / (х) = х2.
Из определения первообразной следует, что функция F(x)—xs/3 является
первообразной, так как (х3/3)'=х2.
Легко видеть, что если для данной функции f(x) существует
первообразная, то эта первообразная не является единственной.
Так, в предыдущем примере можно было взять в качестве перво-
первообразных следующие функции: F (x) = -^ + l, F (х)=~—7 или
вообще F (х) = -j- + С (где С — произвольная постоянная), так как
(Xs \ '
-у +С J = х2. С другой стороны, можно доказать, что функциями
вида 4р+С исчерпываются все первообразные от функции л:2.
Это вытекает из следующей теоремы.
Теорема. Если Ft(x) и F2(x)— две первообразные от функ-
функции f(x) на отрезке [а, 6], то разность между ними равна по-
постоянному числу.
Доказательство. В силу определения первообразной имеем
F'i(x) = f(*)> K(x) = f(x) A)
при любом значении х на отрезке [а, Ь]\
Обозначим

316 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
Тогда на основании равенств A) будет F[ (x) — F2 (х) = f (x)—f (x)=0
или q/ (x) = [Ft (x) — F2 (x)Y = 0 при любом значении х на отрезке
[ау 6]. Но из равенства <р' (х) = 0 следует, что ф (я) есть постоянная.
Действительно, применим теорему Лагранжа (см. § 2 гл. IV)
к функции ф (х), которая, очевидно, непрерывна и дифференцируема
на отрезке [а, 6]. Какова бы ни была точка х на отрезке [а, 6],
мы имеем в силу теоремы Лагранжа ф(х) — <р (а) = (* — а) ф' (?),
где a<g<x.
Так как ф'(|) = 0, то ф(х)— ф(а) = 0, или
Ф(*) = ф(а). C)
Таким образом, функция ф (я) в любой точке х отрезка [а, Ь] со-
сохраняет значение ф (а), а это и значит, что функция ф (я) является
постоянной на отрезке [а, 6]. Обозначая постоянную ф (а) через С,
из равенств B) и C) получаем F1(x)—F2(x) = C.
Из доказанной теоремы следует, что если для данной функции
f(x) найдена какая-нибудь одна первообразная F(x),to лю-
любая другая первообразная для f(x) имеет вид F(x) + С, где
С = const.
Определение 2. Если функция F (х) является первообраз-
первообразной для /(#), то выражение F(x) + C называется неопределенным
интегралом от функции / (х) и обозначается символом \ / (х) dx.
Таким образом, по определению, j / (x) dx = F (х) + С, если
F' (x) = f(x). При этом функцию / (х) называют подынтегральной
функцией, f (x) dx — подынтегральным выражением, знак \ —знаком
интеграла.
Таким образом, неопределенный интеграл представляет собой
семейство функций y = F(x)-\-C.
С геометрической точки зрения неопределенный интеграл пред-
представляет совокупность (семейство) кривых, каждая из которых
получается путем сдвига одной из кривых параллельно самой себе
вверх или вниз, т. е. вдоль оси Оу.
Естественно возникает вопрос: для всякой ли функции /(^су-
/(^существуют первообразные (а значит, и неопределенный интеграл)?
Оказывается, что не для всякой. Заметим, однако, без доказатель-
доказательства, что если функция f (x) непрерывна на отрезке [а, 6], то для
этой функции существует первообразная (а значит, и неопреде-
неопределенный интеграл).
Выяснению методов, с помощью которых находятся пераообраз-
яые (и неопределенные интегралы) от некоторых классов элемен-
элементарных функций, посвящена настоящая глава.
Нахождение первообразной для данной функции / (х) называется
интегрированием функции f(x).
Захметим следующее: если производная от элементарной функции
всегда является элементарной функцией, то первообразная от эле-

§2] ТАБЛИЦА ИНТЕГРАЛОВ 317
ментарной функции может оказаться и не представимой с помощью
конечного числа элементарных функций. К этому вопросу мы вер-
вернемся в конце данной главы.
Из определения 2 следует:
1. Производная от неопределенного интеграла равна подынте-
подынтегральной функции, т. е. если F' (х) = f(x)> то и
/(*). D)
Последнее равенство нужно понимать в том смысле, что производ-
производная от любой первообразной равна подынтегральной функции.
2. Дифференциал от неопределенного интеграла равен подын-
подынтегральному выражению:
) E)
Это получается на основании формулы D).
3. Неопределенный интеграл от дифференциала некоторой функ-
функции равен этой функции плюс произвольная постоянная:
]dF{x)=F{x)+C.
Справедливость последнего равенства легко проверить дифферен-
дифференцированием (дифференциалы от обеих частей равенства равны dF (x)).
§ 2. Таблица интегралов
Прежде чем приступить к изложению методов интегрирования,
приведем таблицу интегралов от. простейших функций.
Непосредственно из определения 2 § 1 и таблицы производ-
производных (§ 15 гл. III) вытекает таблица интегралов. (Сцраведливость
написанных в ней равенств легко проверить дифференцированием,
т. е. установить, что производная от правой части равняется
подынтегральной функции.)
1. \x*dx = -^-r^+C (аф—l). (Здесь и в последующих фор-
формулах под С понимается произвольная постоянная.)
2. ^di = ln|
3. }smxdx=—cosx-f-'C.
4. j
6-
7.
8.

318 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ?ГЛ. X
9.
10
И.
»'•
12.
а2—*2 2а |а—х
13. f /* =
_- = arcsin—|-С.
v2 a •
¦±aa
Замечание. В таблице производных (§ 15 гл. Ill) нет фор-
формул, соответствующих формулам 7, 8, 1Г, 12, 13' и 14. Однако
справедливость последних также легко устанавливается с помощью
дифференцирования.
В случае формулы 7 имеем
g
следовательно, J tg x dx = — In | cos x \ + С.
В случае формулы 8
следовательно, J ctg x dx = In | sin л: | + С.
В случае формулы 12
' а^
следовательно,
Отметим, что последняя формула будет следовать также из
общих результатов § 9.
В случае формулы 14
следовательно,
dx , |
f x2 ± а2-
Эта формула также будет следовать из общих результатов § 10.

§3] НЕКОТОРЫЕ СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА 319
Аналогично проверяются формулы IV и 13'. Заметим, что
эти формулы будут выведены впоследствии из формул 11 и 13
(см. § 4, примеры 3 и 4).
§ 3. Некоторые свойства неопределенного интеграла
Теорема 1. Неопределенный интеграл от алгебраической суммы
двух или нескольких функций равен алгебраической сумме их
интегралов:
% (х) + h (*)] dx = $ h (x) dx + J f2 {x) dx. A)
Для доказательства найдем производные от левой и правой
частей этого равенства. На основании равенства D) § 1 находим
( J [h (х) + h (x)] dx)' = fx (x) + /2 (x),
Таким образом, производные от левой и правой частей равенства A)
равны между собой, т. е. производная от любой первообразной,
стоящая в левой части, равняется производной от любой функции,
стоящей в правой части равенства. Следовательно, по теореме § 1
любая функция, стоящая в левой части равенства A), отличается
от любой функции, стоящей в правой части равенства A), на
постоянное слагаемое. В этом смысле и нужно понимать равен-
равенство A).
Теорема 2. Постоянный множитель можно выносить за знак
интеграла, т. е. если а = const, то
{x)dx. B)
Для доказательства равенства B) найдем производные от левой
и правой его частей: ( J af (x) dx) = af (x)r {a\f (x) dx)' =
= a(lf(x)dx)'=af{x).
Производные от правой и левой частей равны, следовательно,
как и в равенстве A), разность двух любых функций, стоящих
слева и справа, есть постоянная. В этом смысле и следует пони-
понимать равенство B).
При вычислении неопределенных интегралов бывает полезно
иметь в виду следующие правила.
1. Если
C)

320 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
Действительно, дифференцируя левую и правую части равен-
ства C), получим ( J f(ax) dx)'=/(«), {±F (ах)) = 1 (F (ax))'x=
t=-^F'(ax)a = F'(ax) = f(ax). Производные от правой и левой
частей равны, что и требовалось доказать.
II. Если
то
lf(x+b)chc = F(x + b)+C. D)
III. Если
то
§f(ax+b)dx = ±F(ax + b)+C. E)
Равенства D) и E) доказываются дифференцированием правой
и левой частей равенств.
Пример 1.
Г B*3—3sin * +5 V~x) dx= J 2*3 dx— J 3sin хйх+ J 5 V
= 2 jj x*dx— 3 J sin
Пример 2.
КЗ . 1 , V"~\ Л Q Г -1/3 Л X 1 Г
Пример 3.
Пример 4.
\ cos 7xdx — -=- sin 7л: + С.
Пример 5.
V sin Bл;—-6) d* = — -^ cos Bл—6)+ С.

§.4J ИНТЕГРИРОВАНИЕ МЕТОДОМ ЗАМЕНЫ ПЕРЕМЕННОЙ 321
§ 4. Интегрирование методом замены переменной
или способом подстановки
Пусть требуется найти интеграл j / (x) dx, причем непосред-
непосредственно подобрать первообразную для / (х) мы не можем, но нам
известно, что она существует.
Сделаем замену переменной в подынтегральном выражении,
положив
* = ф@. 0)
где ф (/) —- непрерывная функция с непрерывной производной, имею-
имеющая обратную функцию. Тогда dx = y' (t)dt\ докажем, что в этом
случае имеет вдесто следующее равенство:
B)
Здесь подразумевается, что после интегрирования в правой части
равенства вместо t будет подставлено его выражение через х Via
основании равенства (I).
Для того чтобы установить, что выражения, стоящие справа
и слева, одинаковы в указанном выше смысле, нужно доказать,
что их производные по х р-авны между собой. Находим производную
от левой части: (J f(x)dx)x = f(x). Правую часть равенства B)
будем дифференцировать по х как сложную функцию, где / —
промежуточный аргумент. Зависимость t от х выражается равенст-
равенством A), при этом ^- = ф'(<) и по правилу дифференцирования
обратной функции -^ ==:-т-ж • Таким образом, имеем
= /[ф@]ф'@^
Следовательно, производные по х от правой и левой частей равен-
равенства B) равны, что и требовалось доказать.
Функцию х = ф(/) следует выбирать так, чтобы можно было
вычислить неопределенный интеграл, стоящий в правой части
равенства B).
Замечание. При интегрировании иногда целесообразнее под-
подбирать замену переменной не в виде х = <р(/), а в виде t = ty(x).
Проиллюстрируем это на примере. Пусть нужно вычислить интег-
интеграл, имеющий вид
С V (*) dx
С
J
Здесь удобно положить
11 Н. С. Пискунов, т. I

322 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ?ГЛ. X
тогда
Приведем несколько примеров на интегрирование с помощью
замены переменных.
Пример 1, \ j/~sinx cos х dx=? Сделаем подстановку * = sin x; тогда
dt — соьхйх и, следовательно, С J^sta* cos a; dx= С j/T ctf = С *1/2 ctf =
Пример 2. \ « , 2=? Полагаем t~l+x2; тогда dt~2xdx
1
С xdx \ С dt 1
J +1 +J T
Пример 4. i —=— \ . — Полагаем ^ = —; тогда
0)
J ^ J
(предполагается, что a > 0).
В примерах 3 и 4 выведены формулы, приведенные в таблице
интегралов под номерами 11' и 13' (см. выше, § 2).
С dx
Пример 5. \ (In х)* — — ? Полагаем t = In x\ тогда
Гх dx
..r .. -. ^r ^. . T~f—5 = ? Полагаем t=x2; тогда
J 1 + ^
Метод замены переменных является одним из основных методов
вычисления неопределенных интегралов. Даже в тех случаях, когда
мы интегрируем каким-либо другим методом, нам часто приходится
в промежуточных вычислениях прибегать к замене переменных.
Успех интегрирования зависит в значительной степени от того,
сумеем ли мы подобрать такую удачную замену переменных, кото-
которая упростила бы данный интеграл. По существу говоря, изучение
методов интегрирования сводится к выяснению того, какую надо
сделать замену переменной при том или ином виде подынтеграль-
подынтегрального выражения. Этому и посвящена большая часть настоящей
главы.

§5] ИНТЕГРАЛЫ ОТ ФУНКЦИЙ, СОДЕРЖАЩИХ КВАДРАТНЫЙ ТРЕХЧЛЕН 323
§ 5. Интегралы от некоторых функций, содержащих
квадратный трехчлен
1. Рассмотрим интеграл
dx
Преобразуем предварительно трехчлен, стоящий в знаменателе,
представив его в виде суммы или разности квадратов:
где обозначено——-^-т = ± &2. Знак плюс или минус берется в завй-
симости от того, будет ли выражение, стоящее слева, положитель-
положительным или отрицательным, т. е. будут ли корни трехчлена ах*-\-Ьх + с
комплексными или действительными.
Таким образом, интеграл /х принимает вид
dx — 1 Г^
- а)
Сделаем в последнем интеграле замену переменной х + «- = t»dx = <
Тогда получим
dt
• ± k*'
Это — табличные интегралы (см. формулы 11' и 12).
С dx
Пример 1. Вычислить интеграл \ 2 2j.q 4-2Q*
Решение.
J 2x2 + 8jc+20~ J
dx
_J_ С dx _J_ Г dx
~~2 J л:2 + 4л;+4+10-4" J (л: +2J+6*
Делаем замену переменной x+2 = ty dx — dt. Подставляя в интеграл, полу-
получаем табличный интеграл
= 1 Г JL^L _J=- arctg -^=r
2 J p+Q 2 У 6 У 6
Подставляя вместо t его выражение через х, окончательно находим
/ = r arctg *

024 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ?ГЛ. ОС
II. Рассмотрим интеграл более общего вида
I С АХ+В fir
'2 J
Произведем тождественное преобразование подынтегральной функ-
функции:
Г
ЛХ+В
Последний интеграл представим в виде суммы двух интегралов.
Вынося постоянные множители за знак интегралов, получим
. - А С *ах+Ь , . (в АЬ\ С dx
Zl"" 2а J ax*+bx+c ^^[^ 2а J J ax*+bx+c '
Второй интеграл есть интеграл /4, вычислять который мы умеем.
В первом интеграле сделаем замену переменной
а
Следовательно,
Таким образом, окончательно получаем
П р к м е р 2. Вычислить интеграл / = \ -д—Т ¦ ¦, ^л:.
Применим указанный прием:
, f_?±3_, Г | ^-2)+C+1-2)
_1 СBж-2)Дг
-ТJ x*-2*-5+
,n Гб-lx-D
III. Рассмотрим интеграл
dx
С помощью преобразований, рассмотренных в п. I, этот интеграл
сводится, в зависимости от знака а, к табличным интегралам вида
при а>Оили1у1=р- при а<0'
которые уже рассмотрены в таблице интегралов (см. формулы 13'
и 14).

.§ 6). ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ 325
IV, Интеграл вида
С Ах-\-В л
1 —у. (XX
J у ах2+Ьх+с
вычисляется с помощью следующих преобразований, аналогичных
тем, которые были рассмотрены в п. II:
С лх+в C
J Vax*+bx-\-c J
А Г , 2ах+Ь rfr|(P М
2а J }fax2+bx-\-c \ 2а
dx
Применив к первому из подученных интегралов подстановку
ax2-b-bx+c=t$ Bax + b)dx = dt, получим
Второй же интеграл был рассмотрен нами в п. III настоящего
параграфа.
Пример 3.
Г 5*+3 л г
2J |/"jt«+4x + 10 J
= 5 1/*^2+4a: + 10—7 JnJ x+2+ }fx*
§ 6» Интегрирование по частям
Пусть а и ^—две дифференцируемые функции от х. Тогда, как
известно, дифференциал произведения uv вычисляется по следую-
следующей формуле: d(uv) = udv+vdu. Отсюда, интегрируя, получаем
uv= J udv-\- J vdu или
udv=uv— ^ vdu. A)
Последняя формула называется формулой интегрирования по
частям. Эта формула чаще всего применяется к интегрированию
выражений, которые можно так представить в виде произведения
двух сомножителей и и dvf чтобы отыскание функции v по ее диф-
дифференциалу dv и вычисление интеграла }vdu составляли в сово-
совокупности задачу более простую, чем непосредственное вычисление
интеграла S^udv. Умение разбивать разумным образом данное
подынтегральное выражение на множители uudv вырабатывается

32а НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
в процессе решения задач, и мы покажем на ряде примеров, как
это делается.
Пример 1. С хsinxdx=? Положим и=х, dv=shixdx; тогда du=dx,
v=— cos x. Следовательно,
\ л; sin xdx =—#cosa:+\ со5де^л:=—*cos*+sin#+C.
Замечание. При определении функции v по дифференциалу do
мы можем брать любую произвольную постоянную, так как в ко-
конечный результат она не входит (что легко проверить, подставив
в равенство A) вместо v выражение v + Q. Поэтому удобно считать
эту постоянную равной нулю.
Правило интегрирования по частям применяется во многих
случаях. Так, например, интегралы вида
хк sin ах dx, § я* cos ax dxf § хЧах dx% $ xk In x dx,
некоторые интегралы, содержащие обратные тригонометрические
функции, вычисляются с помощью интегрирования по частям.
Пример 2. Требуется вычислить V avdgxdx. Положим w = arctg#,
dv = dx; тогда du=. . 2 , v~x. Следовательно,
тогда
С С xdx 1
\ arcigxdx—xardg х—\ j-ц--%=xarctgx—9"^п| 1+а:2 \+С.
Пример 3. Требуется вычислить \ х2ехdx. Положим и = х2, dv—exdx;
u 2d x
хЧ* dx=x2e*—2 С хе* dx.
Последний интеграл снова интегрируем по частям, полагая %=#, dut~dxt
dvi = ех dxt v1 = ex. Тогда \ хех dx = хех — \ ех dx = хех—ех + С. Окончательно
будем иметь
f x2exdx = x2e*—2 (хех—ех) + С = х2ех—2хех + 2ех + С = ех (л:2—2х+2) + С.
Пример 4. Требуется вычислить \ (л:2 + 7х—Б) cos 2x dx. Положим
и~х2-}-7х—5, dv = cos2xdx; тогда
= Bx+7)dx, v=
_ С
5) ?iL?
Применим интегрирование по частям к последнему интегралу, принимая

ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ 327
их = —i- , dvi^sRnVxdx; тогда
. cos 2x
dx, v1 = - g—
cos2л: \
sin2jc
4+—4—
Поэтому окончательно
Г / 9 i т еч о j / о ¦ я, ех sin 2# , /Л . _ cos 2л: sin 2лг
I (л2+7^—5)со&2л:^ = (^2+7д;-.5)—^—\-Bх+7)— ^
xdx
4
Пример 5. /=\ У л2 — х2 dx = ? Произведем тождественные преобра
зования. Умножим и разделим подынтегральную функцию на У а2—х2:
f V *—x2d — f п2~-х2 dx = c? Г dx С x*dx __
х Г х
~~ Ш~а ] i/~-<
Последний интеграл проинтегрируем по частям, полагая и = х, du = dx,
dv=—F= , у=— Уа2—х2; тогда
У а2—х2
С x2dx Г xdx лГ-х s f _/-5
) "^ д2—-х2 1 1/ Л^—X2 J
Подставляя последний результат в полученное ранее выражение данного ин-
интеграла, будем иметь
Г У^Их1 dx = a2 arcsin -~+д: |/"а2—^2— Г Va2—
Перенося интеграл справа налево и выполнив элементарные преобразования,
окончательно получим
f У"^—2 Лс=^. arcsin ~+4 У^^+а
Пример б. Вычислить интегралы
Применяя метод интегрирования по частям к первому интегралу, получим
u = eaxi du = aea*dx, dv — cosbxdx, a=-r-sin&*;,
С e«^ cos bx dx=~eGX sin ta—у Г eax sin 6л: <fxf

328 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ?ГЛ. X
К последнему интегралу снова применим метод интегрирования по частям:
«=?**, du — aeaxdx, dv = sinbxdxt v = — -j-
i еах slnbxdx — —-г еах cos &#+-т- V еах cos bx dx.
Подставляя полученное выражение в предыдущее равенство, получим
С
1 а а2 Г
еах cos bx dx=-j- eax sin bx-\—r^eax cos bx—-p- \ eax cos bx dx%
Найдем из последнего равенства /t:
{l+w) ^^cosbxdx=e^x(^sinbx+?cosbx)+C (l+^)>
откуда
„*. и s e«x(bsinbx-\-acosbx) , n
Аналогично находим
eax(aslnbx—bcosbx)
§ 7. Рациональные дроби. Простейшие рациональные дроби
и их интегрирование
Как мы увидим ниже, далеко не всякая элементарная функция
имеет интеграл, выражающийся в элементарных функциях. Поэтому
очень важно выделить такие классы функций, интегралы которых
выражаются через элементарные функции. Простейшим из этих
классов является класс рациональных функций.
Всякую рациональную функцию можно представить в виде
рациональной дроби, т. е. в виде отношения двух многочленов:
Q(x)
f(x)
Не ограничивая общности рассуждения, будем предполагать, что
&ти многочлеЕш не имеют общих корней.
Если степень числителя ниже степени знаменателя, то дробь
называется правильной, в противном случае дробь называется
неправильной.
Если дробь неправильная, то, разделив числитель на знамена-
знаменатель (по правилу деления многочленов), можно представить данную
дробь в виде суммы многочлена и некоторой правильной дроби:
Q(x) л, . ч . F (х)
/ (*) w / W '
F (х)
здесь М(х)— многочлен, а у^г—правильная дробь.

§ Ц ПРОСТЕЙШИЕ РАЦИОНАЛЬНЫЕ ДРОБИ И «X ИНТЕГРИРОВАНИЕ 329
Пример t. Пусть дана неправильная рациональная дробь*
л:4—3
Разделив числитель на знаменатель (по правилу делений многочленов),
получим
Так как интегрирование многочленов не представляет затруд-
затруднений, то основная трудность при интегрировании рациональных
дробей заключается в интегрировании правильных раццональных
дробей.
Определение. Правильные рациональные дроби вида
х—а
II. . __ к {fe —целое положительное число )
III. 2 * , (корни знаменателя комплексные, т. е. ~—¦-а <0 { .
JV. ^ 24-Х jg-f- \к №—ВДЛое положительное число ^2; корни
знаменателя комплексные),
называются простейшими дробями I, II, III и IV типов.
Далее будет доказано (сад. § 8), что всякую радцональную
дробь можно представить в виде суммы простейших дробей.
Поэтому мы рассмотрим сначала интегралы от простейших дробей.
Интегрирование простейших дробей типа lf II и III не состав-
составляет большой трудности, поэтому мы проведем их интегрирование
без каких-либо дополнительных пояснений:
Г
J
_ А р 2х+р л„ ,ур Л^з
dx
(см. §5).

330 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
Более сложных вычислений требует интегрирование простейших
дробей IV типа. Пусть нам дан интеграл такого типа:
Лх+В dx
Произведем преобразования:
Zx+P dx\ (в АрU ***
л С Zx+P dx\ (в
~ 2 J (x*+px+q)*ax-r [D
Первый интеграл берется подстановкой **4-/wr-f-<7=f, Bx+p)dx=*
Второй интеграл — обозначим его через Ik — запишем в виде
dx г dt
г dx г
полагая
(по предположению корни знаменателя комплексные, а следова-
тельно, q—^г> 0 1 . Далее поступаем следующим образом:
- Г dt - J f^2+^2)
~~ J (^Н-т2)^^ m2 J (/2 + m
= l Г
/n2 J
Преобразуем интеграл:
-tdt __J_
" 2
С Pdt __ С t-td\
= l [td( X
Интегрируя по частям, будем иметь
\ «»+%»)«¦ = -2 (*!-!) [* (t^l^-1-l-^

§ 7] ПРОСТЕЙШИЕ РАЦИОНАЛЬНЫЕ ДРОБИ И ИХ ИНТЕГРИРОВАНИЕ 331
Прдставляя это выражение в равенство A), получим
7* J (#»+«¦)* =
_ J_ Г dt . 1 1 Г t С dt 1 _
"~ ma J (*2 + m2)ft-li~ m2 2(fe —i) [(^H-m2)*-1 J (P+m*)*-1] ~~~
^ — 3 С
(^— 1) J
t. 2^ — 3 С dt
В правой части содержится интеграл того же типа, что 1к> но
показатель степени знаменателя подынтегральной функции на еди-
единицу ниже (& —1); таким образом, мы выразили 1к через 1кшт1.
Продолжая идти тем же путем, дойдем до известного интеграла:
Подставляя затем всюду вместо t и т их значения, получим вы-
выражение интеграла IV через х и заданные числа А, В, р, q.
Пример 2.
х—1 . f 2 *• ' .
—~ —- ajc= I ^ — . dx=
1 p 2*-f2
.
2
К последнему интегралу применяем подстановку де-{-1 = ^:
J (л:2+2л:+3J Jl(^+lJ+2]2-J (^+2J~2 J
2 J (/2+2)^ at~2 1Л2 B 1Г2 ~ 2
Рассмотрим последний интеграл:
с t*<tt _i г
J (<»+2)«~2 J
/2
(произвольнай постоянной пока не пишем: мы учтем ее только в окончатель-
окончательном результате).
Следовательно,
Г dx |_ tof*+l ±[ х+1 1 . х+\1
Окончательно будем иметь
Л- 2(a:2+2a;+3) 4~arctg V

332 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
§ 8. Разложение рациональной дроби на простейшие
Покажем далее, что всякую правильную рациональную дробь
можно разложить на сумму простейших дробей.
F (х)
Пусть нам дана правильная рациональная дробь -г-?—-.
Будем предполагать, что коэффициенты входящих в нее много-
многочленов—действительные числа и что данная дробь несократима
{последнее означает, что числитель и знаменатель не имеют общих
корней).
Теорема I. Пусть х=а есть корень знаменателя кратности
k, т. е. f(x) = (x-a)kf1(x), где h(a)?=0 (см. § 6 гл. VII); тогда-
данную правильную дробь -г<г можно представить в виде суммы
двух других правильных дробей следующим образом:
F(x)_ Л Ft(x) m
f (v) - {х-а)ь -Г (х~-а)Ь-Чг (х) • W
гд$ А—постоянная, не равная нулю, a Fx(x) —многочлен, степень
которого ниже степени знаменателя (x — a)*~1fx(x).
Доказательство. Напишем тождество
F(x) __ Л Ftf — Ahix) m
(справедливое при любом Л) и определим постоянную А так, чтобы
многочлен F(x) — Af1(x) делился на х — а. Для этого по теореме
Безу необходимо и достаточно, чтобы выполнялось равенство
F{a) — Af1(a) = 0. Так как к(а)ФО, F(a)^O, то А однозначно
определится равенством Л=т~~р При такой А будем иметь
F(x) — А1г(х) = (х — a)F1(x), где Ft(x) есть многочлен, степень
которого ниже степени многочлена (х — a)kf1(x). Сокращая
дробь в формуле B) на х — а, получаем равенство A).
Следствие. К правильной рациональной дроби
входящей в равенство A), можно применять аналогичные рассуж-
рассуждения. Таким образов, если знаменатель имеет корень х = а крат-
кратности k, то можно написать
, Ак_г . Fk(x)
х—а)*-1 "** *Л # "^ х—а "*" /2 (л:) *
где7ТТ—пРавиЛьная несократимая дробь. К ней также можно
применить только что доказанную теорему, если ft (x) имеет другие
действительные корни.

§&J РАЗЛОЖЕНИЕ РАЦИОНАЛЬНОЙ ДРОБИ НА ПРОСТЕЙШИЕ 333
Рассмотрим далее случай комплексных корней знаменателя.
Напомним, что комплексные корни многочлена с действительными
коэффициентами всегда попарно сопряжены (см. § 8 гл. VII).
В разложении многочлена на действительные множители каж-
каждой паре комплексных корней многочлена соответствует выражение
вида x2 + px+q. Если же комплексные корни имеют кратность \if
то им соответствует выражение (x2 + px + q)il.
Теорема 2. Если f (x) = (x2 + px + q)^ifl(x)> где многочлен
ц>г(х) не делится на x2 + px + q* то правильную рациональную
дробь -г~~ можно представать в виде суммы двух других пра-
вильных дробей следующим образом:
F(x) Mx+N Ф^х) п
f(x) -( ^ WJ
где CDj (x) — многочлен, степень которого ниже степени много-
многочлена (х2+рх+q)^1 фх (х).
Доказательство. Напишем тождество
F(x) F(x) Mx+N F(x)^(Mx+N)cpl(x) ,-
f(x) (xz + px+q^qnix) (x* + px+q)n ^ {х* + рх+Я)»ух{х) ' \V
справедливое при любы)с М и N, и определим М и N так, чтобы
многочлен F (х) — (Мх + N) ц>± (х) делился на x2 + px-\-q. Для
этого необходимо и достаточно, чтобы уравнение F (х) —
— (Mx + N)yl(x)=O имело те же корни а±*'Р, что и многочлен
x2+px+q- Следовательно, F (a-f Ф) — [М (a + ify+N]
л>г/ i -оч , at Ffa+ifl) u f(a + ip)
или M (а + Ф) + N = ^^трГ' Но ф1(а+ф) есть
комплексное число, которое можно записать в виде /С+/?, где
и L — некоторые действительные числа. Таким образом, М
#/C/Z,; отсюда Ma + N = Kt M$ = L или
При этих значениях коэффициентов М и N многочлен F (х) —
— (Мх + N) ф! (х) имеет корнем число a + ф, а следовательно, и
сопряженное число a — ifi. Но в таком случае многочлен без
остатка разделится на разности х — (а + ф) и х — (а —10), а сле-
следовательно, и на их произведение, т. е. на x2 + px + q. Обозна-
Обозначая частное от этого деления через Фг(х), получим
f W _ (Mx + N) ф1 (х) = (x2 + px + q) Фх (х).
Сокращая последнюю дробь в равенстве D) на x2 + px + q, получим
равенство C), причем ясно, что степень Фх (х) меньше степени
знаменателя, что и требовалось доказать.
Применяя теперь к правильной дроби j~ результаты теорем
1 и 2, мы можем выделить последовательно все простейшие дроби,

334 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ- X
соответствующие всем корням знаменателя f(x). Таким образом,
из предыдущего вытекает следующий результат.
Если
то дробь jyy может быть представлена в виде
—a)a-i 1" • • • "Г х__а Т"
F(X) __ А , Аг
f(x) ~~ (х—а)<*> "*" (л;
Коэффициенты .4, i4lf ..., 5, Sx, ... можно определить из сле-
следующих соображений. Написанное равенство есть тождество,
поэтому, приведя дроби к общему знаменателю, получим тождест-
тождественные многочлены в числителях справа и слева. Приравнивая
коэффициенты при одинаковых степенях х, получим систему урав-
уравнений для определения неизвестных коэффициентов Л, Аи ...
..., В, В1У . ¦. Этот метод нахождения коэффициентов называется
методом неопределенных коэффициентов.
Наряду с этим для определения коэффициентов можно восполь-
воспользоваться следующим замечанием: так как многочлены, получив-
получившиеся в правой и левой частях равенства, после приведения
к общему знаменателю должны быть тождественно равны, то их
значения равны при любых частных значениях х. Придавая х
частные значения, получим уравнения для определения коэффи-
коэффициентов.
Таким образом, мы видим, что всякая правильная рациональ-
рациональная дробь представляется в виде суммы простейших рациональ-
рациональных дробей.
д>2 j О
Пример. Пусть требуется разложить дробь .i-Us/ §Г на пРосте**-
шие. На основании формулы E) имеем
_ A f At . А» у В
(x—2) — (*+1K ^ (х+\J ^х+1^х—2'
Приводя к общему знаменателю и приравнивая числители, получим
х^+2^А(х^2) + А1(х+\)(х-^2) + А2(х + 1Г(х-2)+В(х+\)\ F)
или
+(—2А—2А±—2А2+В).

?9] ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ 335
Приравнивая коэффициенты при л?, л:2, л:1, х° {свободный член), получим
систему уравнений для определения коэффициентов:
0 = Л—А1 —ЗА2 + ЗВ, 2=—2А—2А1—2А2+В.
Решая эту систему, найдем
Л=—1, А1 = \/Зг Л2 = —2/9, В = 2/9,
Можно было бы также определить некоторые коэффициенты из уравнений,
которые получаются при некоторых частных значениях х из равенства F),
которое является тождеством относительно х.
Так, полагая * =—1, получим 3 = —ЗЛ или А=—I; полагая х = 2,
получим 6 = 27В; В ==2/9. Если к этим двум уравнениям присоединим два
уравнения, получающиеся приравниванием коэффициентов при одинаковых
степенях х, то получим четыре уравнения для определения четырех неизвест-
неизвестных коэффициентов. В результате получаем разложение:
х*+2 __ I . 1 2 2
jc—2) ~~ (x+l)* ^3(*+lJ 9(а:+1)^9(л:—2) #
§ 9. Интегрирование рациональных дробей
Пусть требуется вычислить интеграл от рациональной дроби
Q(x) с QM л
ш, т. е. интеграл )jj^dx.
Если данная дробь неправильная, то мы представляем ее
в виде суммы многочлена М(х) и правильной рациональной
дроби -т4^-(см. § 7). Последнюю же представляем по формуле E)
§ 8 в виде суммы простейших дробей. Таким образом, интег-
интегрирование всякой рациональной дроби сводится к интегрированию
многочлена и нескольких простейших дробей.
Из результатов § 8 следует, что вид простейших дробей опре-
определяется корнями знаменателя f (x). Здесь возможны следующие
случаи.
I случай. Корни знаменателя действительны и различны,
т. е.
F (х\
В этом случае дробь у^ разлагается на простейшие дроби
I типа:
f(x) x—a^x—b^-- * ~^х—d*
и тогда
II случай. Корни знаменателя действительные, причем
некоторые из них кратные:
f(x) = {x-a)a (x-bf ... (x-d)\

336 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ {ТЛ^Х
В этом случае дробь -тгт разлагается на простейшие дроби
i\x)
I и II типов.
Пример 1 (см. пример в § 8).
*2+2 __ Р dx . 1 С dx 2^ С dx ,
IK (x—2)ax- J (х+1K ^ 3 J (jc+1)« ^J x+1 +
2л:—1 2 , 1л:—2
+1п|
III случай. Среди корней знаменателя есть комплексные
неповторяющиеся (т. е. различные):
В этом случае дробь тШ разлагается на простейшие дроби
I, II и III типов.
Пример 2. Требуется вычислить интеграл
xdx
Разложим подынтегральную дробь на простейшие (см. E) § В):
х Ах+В . С
(л;2Н- Г) <л:—1) jca-+-1 ~*~х—1*
Следовательно,
Полагая *=1, получим 1=2С, С=1/2; полагая лс=О, получим 0
# + С Б1/2
+ , /
Приравнивая коэффициенты при ж2, получим 0=Л-}-С, откуда Л=—1/2.
Таким образом,
С xdx 1 С jc—1 А у 1 Г <Гдс_
J <*Ч-1) (*-¦1) "^ 2 J х*+\ аХ^ 2 J ж-1
— * Р *<** . 1 Р djc
IV случай. Среди корней знаменателя есть комплексные
кратные:
F (х)
В этом случае разложение дроби -т~у будет содержать и про-
стейшие дроби IV типа.
Пример 3. Требуется вычислить интеграл
С х*+4х*+Пх*+]2х + 8
J <a+2* + 3J(*+i) *•

ИНТЕГРАЛЫ ОТ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ 337
Решение. Разлагаем дробь на простейшие:
Ах+В Сх+Р ( Е_
3J (х+\)
откуда
Комбинируя указанные выше методы определения коэффициентов, находим
А = \% Я = —1, С=0, D = G, ?• = !.
Таким образом, получаем
С х*+4х* + Пх* + }2х + 8 , р х—
J (*а+2* + 32)(*+1) ^ J (
Первый интеграл, стоящий справа, был рассмотрен в примере 2 § 7. Второй
интеграл берется непосредственно.
Из всего изложенного следует, что интеграл от любой рацио-
рациональной функции может быть выравнен через элементарные функ-
функции в конечном виде, а именно:
1) через логарифмы —в случае простейших дробей I типа;
2) через рациональные функции — в случае простейших дробей
II типа;
3) через логарифмы и арктангенсы —в случае простейших дро-
дробей III типа;
4) через рациональные функции и арктангенсы—в случае
простейших дробей IV типа.
§ 10. Интегралы от иррациональных функций
Не от всякой иррациональной функции интеграл выражается
через элементарные функции. В этом и следующем параграфах мы
рассмотрим те иррациональные функции, интегралы от которых
с помощью подстановок приводятся к интегралам от рациональных
функций и, следовательно, до конца интегрируются.
1. Рассмотрим интеграл § R (*, хт*п, ..., xr<s) dx, где R— ра-
рациональная функция своих аргументов*).
*) Запись, R (*, жш/п, ..., *r/s) указывает, что над величинами, дг, xmfn,,..
..., xrls производятся только рациональные операции-
Точно так же следует понимать в дальнейшем записи йида
«L (~^pjГ'"' '•')•*(*• V*x* + ** + c)> R (sin x, cosx) и г. д. Так, на-
пример, запись R(sinx, cos*) указывает, что над sin* и cos* производятся
рациональные операции.

338
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
?ГЛ.
Пусть к — общий знаменатель дробей m//t, ..., rfs. Сделаем
подстановку x = tk, dx = ktk~x dt.
Тогда каждая дробная степень х выразится через целую
степень t и, следовательно, подынтегральная функция преобра-
преобразуется в рациональную функцию от*.
Пример 1. Требуется вычислить интеграл
xl'*dx
Решение. Общий знаменатель дробей 1/2, 3/4 есть 4; поэтому делаем
подстановку * = ?4, dx~Atzdt\ тогда
II. Рассмотрим теперь интеграл вида
\cx + d) '••" [cx+d)
Этот интеграл сводится к интегралу от рациональной функции
с помощью подстановки
ах+ь __ fk
cx+d ~~l •
где к — общий знаменатель дробей т/п, .«., r/s.
Пример 2. Требуется вычислит* интеграл
-dx.
Решение. Делаем подстановку x+4 — t2, x — t2—4, dx=2tdt; тогда
i = 2 ] р\ dt = 2 I f 1+72ГГ4) dt=2 \ dt+S \ *_ =
r*+T—2
=2^+2 In
t—2
t+2
Vx+4+2
§ 11. Интегралы вида
Рассмотрим интеграл
S R (*, V
где а =7^=0.
)dxt
A)
Такой интеграл приводится к интегралу от рациональной
функции от новой переменной с помощью следующих подстано-
подстановок Эйлера.

§П} ИНТЕГРАЛЫ ВИДА J* Я(хУах*+Ьх+с)<1х 339
1. Первая, подстановка Эйлера, Если а>0, то полагаем
Перед корнем Va возьмем для определенности знак плюс. Тогда
ах2+Ьх+с = ах2+2 j/"a xt -f /2,
откуда д: определяется как рациональная функция от /:
b-2 V a t
(значит, dx тоже будет выражаться рационально через t)9 следо-
следовательно,
Vax2+bx+c=]
+t%
о—2t у а
г. е. ]/rax2-\-bx + c оказывается рациональной функцией от t.
Так как Уах2 + Ьх + с, х и dx выражаются рационально
через ty то, следовательно, данный интеграл A) преобразуется
в интеграл от рациональной функции от t.
Пример 1. Требуется вычислить интеграл
dx
Решение. Так как здесь а — 1 > 0, то полагаем ухл+ с=— #+1\ тогда
откуда
Следовательно,
Возвращаясь к исходному интегралу, получаем
dx
\
2Г
(см. формулу 14 таблицы интегралов).
2. Вторая подстановка Эйлера. Если с>0, то полагаем
V = xt ±
тогда (перед J/Тдля определенности берем знак плюс)

340 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ |ГЛ. X
Отсюда х определяется как рациональная функция от t:
а —Г* *
Так как d# и Vax%-\-bx-\-c тоже выражаются рационально
через tt то, подставляя значениях, V^ax^+bx+c ndx в интеграл
j/? (л:, Ktf*2-b&#+c)d#, мы сведем его к интегралу от рацио-
рациональной функции от t.
Пример 2. Требуется вычислить интеграл
dx.
Решение. Полагаем у i-\-x-\-x2—xt+i; тогда
О/ 1
Подставляя полученные выражения в исходный интеграл, находим
Г (l-Vl+x+x*)* Г (-2/2 + 0г('-^?('-<2)B/г-2<+2)
—у I+j
+с=
3. Третья подстановка Эйлера, Пусть а и Р—действительные
корни трехчлена ах% + Ьх + с. Полагаем
Так как ах2+Ьх+с = а (х-а)(х - Р), то Ка(*-а)(*-р)==(*—а) /,
а(л: —а)(л: —р) = (лг — а)Ч2, а (л; — Р) = (х — а) /2. Отсюда находим
х как рациональную функцию от t:
Так как dx и Vax2 + bx + c тоже рационально зависят от t, то
данный интеграл преобразуется в интеграл от рациональной функ-
функции от t.
Замечание 1. Третья подстановка Эйлера применима не
только при а < 0, но и при а > 0 — лишь бы многочлен а* + Ь +
имел два действительных корня.

12J ИНТЕГРИРОВАНА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 341
Пример 3, Требуется вычислить интеграл
dx
J
Решение. Так как jt2+3*-~4 = (*+4) (x— 1), то полагаем
тогда (*+4) (*-1)=(*+4J /2,*-1 = (*+4) /«, х=~^ , dx= j^~-dt9
У(х+4) (*— 1) = -f I' ~V /a • Возвращаясь к исходному интегралу,
получаем
dx
Г 10/A— /2) ,, f 2 .. , | 1+
ЛГ— 1
+C=ln
У*+4+ УТ-i
+C
Замечание 2. Заметим, что для приведения интеграла A)
к интегралу от рациональной функции достаточно первой и третьей
подстановок Эйлера. Рассмотрим трехчлен ах%-\-Ьх-\-с. Если
fca — 4яс>0, то корни трехчлена действительны и, следовательно,
применима третья подстановка Эйлера. Если б2 — 4яс^:0, то в этом
случае
и, следовательно, трехчлен имеет знак, совпадающий со знакома.
Чтобы Vrax2 + bx + c был действительным, нужно, чтобы трехчлен
был положительным, а следовательно, должно быть а > 0. В этом
случае применима первая подстановка.
§ 12. Интегрирование некоторых классов
тригонометрических функций
До сих пор мы систематически изучали интегралы только от
алгебраических функций (рациональных и иррациональных).
В настоящем параграфе мы рассмотрим интегралы от некоторых
классов неалгебраических, в первую очередь тригонометрических
функций. Рассмотрим интеграл вида
R (sinjc, cosх) dx. (I)
Покажем, что этот интеграл с помощью подстайовки

342 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
всегда сводится к интегралу от рациональной функции. Выразим
sin л: и cos л: через tg~, а следовательно, и через /:
2t
Далее
. х х
i
cos2 Y"~sin2"
1
2 sin y
X
cos y
X X
sin2T+C0S 2
* COS«|~8II1«|.
= 2arctg ty
X
dx Ш
ax l + tt
2tgl
1+tg2
1—tg!
1+tg5
X
T
l±
2
2
Таким образом, sin*, cos л; и их выразились рационально
через t. Так как рациональная функция от рациональных функ-
функций есть функция рациональная, то, подставляя полученные вы-
выражения в интеграл A), получим интеграл от рациональной функции:
Пример 1. Рассмотрим интеграл \ — . На основании написанных
ij- Sill X
выше4>ормул имеем
2dt
Рассмотренная подстановка дает возможность проинтегрировать
всякую функцию вида R(cosx, sin л:). Поэтому ее иногда назы-
называют «универсальной тригонометрической подстановкой». Однако
на практике она часто приводит к слишком сложным рациональ-
рациональным функциям. Поэтому наряду с «универсальной» подстановкой
бывает полезно знать также другие подстановки, которые в неко-
некоторых случаях быстрее приводят к цели.
1) Если интеграл имеет вид \ R (smx)i:osxdx, то подстановка
sin х = t, cosxdx = dt приводит этот интеграл к виду J R (t) dt.
2) Если интеграл имеет вид J R (cos#) slnxdx, то он приво-
приводится к интегралу от рациональной функции заменой cosat = ?,
sinxdx = — dt.
3) Если подынтегральная функция зависит только от tgx, то
замена tg х = /, х = arctg t, dx = t , g приводит этот интеграл

§ 12] ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 343
к интегралу от рациональной функции:
4) Если подынтегральная функция имеет вид /? (sinjc, cosjc),
но sin л: и cos л: входят только в четных степенях, то приме-
применяется та же подстановка
tgx = i$ B')
так как sin2* и cos2* выражаются рационально через tgx:
2 1 1 -2 tg2* t2 й dt
После подстановки мы получим интеграл от рациональной
функции.
С sin3 х
Пример 2. Вычислить интеграл \ j-r- dx.
Решение. Этот интеграл легко, привести к виду \ R (cos x)sin xdx.
Действительно,
Р sin3 л* . _ Г* sin2 х sin x dx С 1 — cos2x
Сделаем замену cosjc = z. Тогда
^2 ГОЧ^ у
=~—2z+3\n(z+2)+C=2 —2-os x+3\n (cos x+2)+C.
С dx
Пример 3. Вычислить \ 2__ . a--. Сделаем вамену tgx — t:
dt
5) Рассмотрим теперь еще один интеграл вида С/? (sin xy cos л:)Л(: —
именно, интеграл, под знаком которого стоит произведение
sin"*л;cos*л:dx (где т и п —целые числа). Здесь рассмотрим три
случая.
а) \ sin7* х cos" x dx, где тип таковы, что по крайней мере
одно из них —нечетное число. Допустим для определенности,
что п нечетное. Положим п = 2р+1 и преобразуем интеграл:
sin"* х qos2p+1 x dx = J sinw x cos2* x cos x dx =
inrt # A — sin2 #)* cos x dx.

344 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
Сделаем замену переменной: sinx = t, cosxdx^dt. Подставляя
новуш переменную в данный интеграл, получим
J sinw х cos" x dx = \tm A - ty dt,
а это есть интеграл от рациональной функции от t.
„ А С cos3 х . С cosaх cos x dx f( 1 —sin2 х) cos x dx ^
Пример 4. l—7-з—dx—\ --r =\i :-? . Обоз-
J sin4* J sin4* J sin4*
i t d dt
J J
начая sinx = tt cos xdx — dt, получим
cos3 x ^ С (I-/2) dt_ С dt С dt _ J_ 1
^^^^J F J /4 J7^ З^^Т"
6) J sinw jc cosn дг^лг, где тип — числа неотрицательные и четные.
Положим m = 2p, /i = 2<7. Напишем формулы, известные из
тригонометрии:
sin2* = Y—-2-cos2#, cos2 x = у + у cos 2л;¦ C)
Подставляя в интеграл, получим
С sin2** ^ cos2^ a: dx = \ (-j—у cos 2^)^(у+у cos 2a:Ja dAT.
Возводя в степень и раскрывая скобки, получим члены, содер-
содержащие cos 2л: в нечетных и четных степенях. Члены с нечетными
степенями интегрируются, как указано в случае а). Четные пока-
показатели степеней снова понижаем по формулам C). Продолжая так,
дойдем до членов вида ^coskxdx, которые легко интегрируются.
Пример 5.
t(
=~{ (I—cos2jcJdjc=jC(i—2cos2jc+cos22jc) dx =
в) Если оба показателя четные, причем хотя бы один из них
отрицателен, то предыдущий прием не приводит к цели. Здесь
следует сделать замену tgx = t (или ctgx = t).
Пример 6.
Положим tgx=t; тогда x=arctgtf dx=. a , и мы получаем
J cos6a: J l + *a J

§ 13f ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ 345
6) Рассмотрим в заключение интегралы вида
J cos mx cos nx dx, j sin mx cos nx dx, j sin mx sin nx dx.
Они берутся при помощи следующих*) формул (тфп):
cos mx cos nx = -g- [cos (m + n) л: + cos (m — n) x]9
sin m# cos nx = -^ [sin (m -f n) л: + sin (m — л) #],
sin mx sin ял; = у [ — cos (m+n) # + cos (m — n
Подставляя и интегрируя, полу'чим
С cos mxcosnxdx = ^ С [cos (m + n) x + cos (m — n)
_ sin (tn + n) x , sin (m—
~^ 2(m+n) "^ 2(m—л
Аналогично вычисляются и два других интеграла.
Пример 7.
§ 13. Интегрирование некоторых иррациональных функций
с помощью тригонометрических подстановок
Вернемся к интегралу, рассмотренному в § И,
J R (*, Vax2+bx+c) dx, A)
где а^Ои с—-^фО (в случае а —0 интеграл имеет вид II § 10,
при с — -т- = 0 выражение ах2 + ак + ? = ш я+о- , и мы имеем
4а
дело с рациональной функцией, если а>0; при а<^0 функция
l^ax^ + bx + c не определена ни при каком значении х). Покажем
здесь метод преобразования этого интеграла к интегралу вида
e, cos г) dz, B)
который, рассмотрен в предыдущем параграфе.
*) Эти формулы легко вывести следующим образом:
cos (m j-я) х — cos mxcos nx—sin m#sin nx,
cos (m—n) x = cos тл: cos па;+sin mx sin я*.
Складывая эти равенства почленно и деля пополам, получим первую из при-
приведенных трех формул. Вычитая почленно и деля пополам, получим третью
формулу. Вторая формула выводится аналогично, если написать аналогичные
равенства для sin (т+п) х и sin (т—п) х и затем почленно их сложить.

346 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
Произведем преобразование трехчлена, стоящего под корнем:
Сделаем замену переменной, положив x+^^t, dx = dt. Тогда
Рассмотрим все возможные случаи.
1. Пусть а > 0, с — j > 0. Введ
s= /г2. В этом случае будем иметь
1. Пусть а > 0, с — j > 0. Введем обозначения а = та, с — -j-
2. Пусть я>0, с—-^<0. Тогда а = т2, с — -^ = — п2. Сле-
Следовательно,
3. Пусть а<0, с —-^-Х). Тогда а = —m2, i?--|i = n2.Сле-
n2.Следовательно,
Vax2+bx+c = {/"n2
4. Пусть д<0, ^ —-4о"<0- В этом случае уах2 + Ьх + с есть
комплексное число при любом значении х.
Таким образом, интеграл A) преобразуется к одному из сле-
следующих типов интегралов:
V C.1)
И. $Я(*, Km2/2-n2)d/. C.2)
III. \R{t, Vn2-m4*)dt. C.3)
Очевидно, что интеграл C.1) приводится к интегралу вида B)
с помощью подстановки t = — tez. Интеграл C.2) приводится
к виду B) с помощью подстановки t = -^secz. Интеграл C.3)
приводится к виду B) с помощью подстановки ? = — sin 2.
Пример. Вычислить интеграл \ =.

ИНТЕГРАЛЫ, НЕ ВЫРАЖАЮЩИЕСЯ В КОНЕЧНОМ ВИДЕ
347
dx = a cos zdz9
x С a cos z dz Г a cos zdz*)__ 1 С dz
-x*)* "" J )Л(а2—a2sin2zK J e3 cos3 z ""a2 J cos2 z
Решение. Это—интеграл типа III. Сделаем замену х—asinz, тогда
d* = acos zdz9
dx _ _ _
i — — i —= г— — - i 7 ^
sin z , ^ 1 д:
-sin2z
§ 14. О функциях, интегралы от которых не выражаются
через элементарные функции
В § 1 гл. X мы уже отмечали (без доказательства), что вся-
всякая функция /(х), непрерывная на интервале (а, &), имеет на
этом интервале первообразную, т. е. существует такая функция
jF(x), что F' (x)=f(x). Однако не всякая первообразная,
даже тогда, когда она существует, выражается в конеч-
конечном виде через элементарные функции.
Таковы первообразные, выраженные интегралами
j!EL?<k,
^. и многие другие.
Во всех подобных случаях первообразная представляет собой,
очевидно, некоторую новую функцию, которая не сводится к ком-
комбинации конечного числа элементарных фуцкций.
Так, например, та из первообразных -у^т- \ е"х dx+C, кото-
V ^ J
рая обращается в нуль при х = 0, называется функцией Лапласа
2 Г 2
и обозначается Ф(х). Таким образом, Ф(х) = -Т=^ \ е"х dx + Clf
если Ф@)-0.
Эта функция хорошо изучена. Составлены подробные таблицы
ее значений при различных значениях х. Как это делается — мы
увидим в § 21 гл. XVI (т. II). На рис. 208 и 209 изображены
график подынтегральной функции у = е~*2 и график функции
Лапласа у = Ф(х).
*) У^\—sin2 2 = | cos z |; мы для определенности останавливаемся лишь
на одном случае: |cosz[ =

348 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 1ГЛ- х
Та из первообразных
(k < 1),
которая обращается в нуль при х = 0, называется эллиптическим
интегралом и обозначается Е (х):
Е(х) = \ V 1—ife2sin2xdx+C2, если ?@)^0.
Для этой функции также составлены таблицы значений при
различных значениях х.
Упражнения к главе X
1. Вычислить интегралы: _
1. [xbdx. Отв. ~+С. 2. [(x+V"lc)dx. Отв. ^-+- о Х+С.
3. ff-JL_*!lf W Ome. б/х—д^Ул+С. 4. Г^^. Отв.
Owe. i- {/? + С- 7. t f ^a+T7=-) ^- Ume' 
о J \ у х /
Интегрирование методом подстановки:
8. ^ebxdx. Отв.-^еЪх + С. 9. \ cos 5л: dx. Отв. Sl" Х-\-С. 10. \ sinaxdx.
Отвт —cosax.^c. И. С— dx. Отв. -j\n*x-\-C. 12. \ . * . Отв.
.. От. —Injl—х|+С. 16. jg^j-. Om -i-ln|5-2* I + C.
17. ftg2;c^ Ome. — Iln|cos2*| + C. I». J ctg Ex-7)dx. Отв.
IlnlsinE^-7)I + C. 19- 5пга* Ome- --з lnIcos3^l+C 20-Jct2-Jd
Ome 31n sin-~ +C. 21. \ tg9sec39d9. Отв. -у tg2q>+C. 22. \(clgex)exdx.
' С f S\ 1
Ome. In I sin e* I + C. 23. \l tg 45—ctg — J d5. Ome. ~j In | cos 4S | —
sin-^-l+C. 24. \ sin2 x cos x dx. Отв. sin *+C. 25. \ cos3 лс sin ^ djc»
4 J . x J
— 4 In
Om. _
ome.

УПРАЖНЕНИЯ К ГЛАВЕ X
349
От. 2
34. V^x+l)dX.
От.
36.
sin2jcd.«r
43.
45.
47-
52.
Отв
65.
Ome
58.
Отв
Отв
64.
Ome
68.
1wF Щт
-i- In B sin *+3)-f C. 49. C-^~ • Ome- ln|ln*|+C. 50. f 2x(x2+\)*dx
Г . , f^ . . Отв. ln|arctg*|+C. 53. С—т
J (t+^2)arctgAr l s i« J cos2
4 fil
i
dx
54.
J COS X
Отв. lniarcsinJcl + C. 56.
dx.
\ cos (a -f 6д?) ^л:.
2+3sin2jt
57. Jcos(lnjc)^t Отв. sin(ln*)+C
Ome. -j sin (a + блг)+С. 59. Г е2х dx
^*dx. Ome. 3ex/* + C. 61. Г esin x cos л: dx
esiax+C. 62. С^2а:^л:. Отв. ^~+С. 63. {ex/a dx. Отв. аех/
i f 3^ 4-C. 66. С е~
J
60.
. 65. f
J
. Ome.
(
Ome. l-
Ome. ±(е*х+^
69.
72.
_^_

35Q
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. X
74. f dx Отв. 4-arcsin^-f С. 75. Г _** ,. Отв
J |/^1б—9л:2 3 4 J 1/^9—л:2
78.
Отв. jz *n
,80. \„ d* „.Ome.l
1 .„3^
dx
8, f
J
dx
Г
J
Отв. L\
\ах- с
2ас
. _ лл Г х2 <iA:
' J 5—д^
—аа| + С.
. 82- С 2 ^ 2-.
Отв-
Отв. -т^г
89.
1/ -^-л:+С. 88.
1 г 3 J
С— dx Отв. arcsin(lnA:) + C.
J ^1— In2 л: V ;
cOs л: d-x: л 1 . / sin х \
. Отв. — arctg (
а ъ\ а )
91.
. 92.
90. Г а^^
Г
[ dx. Отв. -?
J X О
+^ 94. Г
J^ x
Отв. 4КТ+71+С- 95.
xVl + Y^x
Ome. arotg^ + C. 96. f|?
. 97. ( V1+3cos2л:sin 2xdx. Отв. —I
98'
Ome.
f sin 2xdx
99.
-J
sin x
100.
Щ
. [Щ*с1х. Отв. ±VWx+C.
J cos2 x 5 _ •
( /)
Интегралы вида \ —5-j—i—;—dx:
r J ax*+bx+c
- tit arctg w+Cl 104>
105-

УПРАЖНЕНИЯ К ГЛАВЕ X 351
Отв. arctgB*— 1)+С. 107. С Q a d* , о. Ome. --jLrarcfg^=i+C.
J ^* —^дг+z г 5 У 5
Ю8. ГЛ*"!7*?* . Отв. 1п13л;2--7л:+111+С. 109.
От. ! In(**-
|-ln|3*-lH-iln|2*+l|+C. 112. 1ъ^!
arctg+c пз- 3 *¦-«+! fe
Отв.
/7 ^
Интегралы вида \ rf^t
\ . Отв. -Tr-arcsin *-+С. 116, \ —F==
145.
. 117. ^yj?==. Отв. ln\S+a
Г - dx
. 118. Г - dx —. Ome. --Ц-arcsin ^±I
J |Л573^ }^3 V^109
J | }
119. Г f . Om*. -1=- In 16* + 5+ ^12^C^+5I+ C.
J V x (Sx + 5) у 3
120, 1 г Отв. arcsin JL +0. 121. I
Отв. —-^=r ln| IOjc—1+^20E^—л:—1) |+C 122. Г _
}Л 5 J К
Г (+3)fr l
Ome. 2 Y^±bx~+~c +C. 123e Г () ^ Ome^
4 J(
. 125.
126.
II. Интегрирование по частям:
127. Гл:е*^л:. Ome. ел (л:— i) + C 128. Гл:1пл:Же. Отв. ~x2 (\nx — ~ We.
129. ^л:зтл:с(л:. Отв. sin л:—xcosx+C. 130. Пп^^л:. Оатш. л:(Inx— 1) + С.
131. f агсБШл:^. Отв. д:arcsinх+УТ^хР+С. 132. С InA—л:) сГлг.

3$2 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
тА х» In xdx. Отв.
134. \ х arctg х dx. Отв. ~[(*2+1) arctg*—х] + С. 135. \ хarcsin x dx.
Отв. ^[Bx2—l)arcsinx+xVT^x^]+C. 136. ^\n(x2+\)dx. Отв.
x]n(x2+\)—2x+2arcXgx+C. 137. J arctg y^d*. Отв. <jc+ 1) агЫ^У"* —
— /* + С. 138. Г arcsi"У х dx. Отв. 2 V! arcsin V~~x-\-2 |/ТГ? + С#
J У х
139. | arcsin у ~-х dx. Отв. л: arcsin у ^тг| —/"^ + arctg 1^1+С.
| у х у ^
Cjtcos2^^. Отв. ^-+"|"л:81п 2*+~§" cos2jc+C. 141. Г^
Отв. x-YT^arcsinx+C. 142. jp^ii^. Ода. _ф_-f~arctg^-~
_1 arctgх^с^ ш Г ardg y-zziJdx. Отв. ~jc2arctg \Г^И\^
_LYxr^\ + С. 144. [Ш**?Х dx. Отв. JnIil=J^±=l?!J —Larcsinдг+ С.
2 J x2 J x \ x
145
l46-
J
. $ln(*+VT+F)d*. Отв
f дсс?дс л a
Применить тригонометрические подстановки в следующих примерах:
С^2 ^2^\
147.
J х2
Отв.
рномр днов в лдующ
Г*2***. Отв. ->^а2"~^—arcsin—+C. 148. \
2 х Q
1
x. Отв.
151. ¦ . ^ Отв. 4
1ЛB+2K л2
Интегрирование рациональных дробей:
156.
x*dx
п 5х+12 ,
' J(x-}-2)*(X+4)*- иШ- хг+бх+8 +

УПРАЖНЕНИЯ К ГЛАВЕ X
353
г—3*— 3
г—2х+5)
х— 1
166.
1
167.
- , U—II 10 . 2x— 1 2x—1
O/ne. lnr ^=^arctg——= 5—-5
I * I 3^3 УЗ 3(дс2—
Интегрирование иррациональных функций:
170. \ . fj0 dx. Отв. ^
От.
,73. Г Д+К*
dx. От. 4 {^?-|. ^+4 1П_в
5 ^
174.
Ome. In
I—X— у 14-х
i — X*
i™ Г l/x+Vx . .
. 177.
rrrln X — -5-*
12 Н. С. Пискунов, т. 1

354 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Интегралы вида \ R {х, Уах2+Ьх+с) dx:
[ГЛ. X
178.
dx л 1 .
¦ Отв. - . In
хух*—х+3 УЗ
а —лг+3—
179.
180
dx Отв. i=r
х У2+Х—Х* У 2
+С.
J
. он*. l
2
182.
Г
J
у 2х—
184.
. 183.
«те. ^-+J
185»
Отв. In
Г
J
fe
2д:+л:
Отв. In
д:2
-fC.
. 187.
188
. Г
jc+V д:2+4л;
Интегрирование тригонометрических функций:
189. Vsin3^^. Ome. -^-cos3*—cosa:+C, 190. f sin6A:<fA:. Om*. —
1
. Отв. ~~
2. \
COS3 X
. 191. \ cos*
1 f*
Ome. cosec л:—у cosec3 д:+С. 193. \ cos2 x dx.
192.
Отв. JL+±.Sin2x+C. 194. §sin*xdx. Отв. i-x-iE^fL
195, fcose*rf*. Ome. i^5A:+4sm2A:~5i2^+-|
196. Csin4*cos4*dx. Ome.~f3x^sin4x+^~^\^C. 197. Г tg3^^.
i^-+lfljcosA:j+C. 198.
199.
200. §sec*xdx. Отв.
~ ctg4 дг+y ctg2 x +
Отв. — i^?_ln|sin x\+C.
. 201,
Ome, C-cosec*. 204. Г s'_l^l . От. ^cos^x+3 cos'1'3 x+C.
J ?cos*x 5

УПРАЖНЕНИЯ К ГЛАВЕ X
355
206.
I
лл- Г . . о л п sin 4л: , sin 2х , ^
205. \ sin х sin Зх dx. Ome. ^—|—^—|- С.
л sin Их , sin3x , ^ лл„ р о . . , л ^о^л
Отв. -^—|—g—\-С. 207. \ cos 2x sin 4x dx. Отв. ^
208. Csin-i-xcos-|.x^. Отв. — ?^?-j-cos \х+С. 20». С j—
5 sin x *
Отв. -тг In
211.
Г sin
J 1+
J 1+sinx
. Отв.
1+tg-J
+Х+С-
214.
215.

ГЛАВА XI
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Постановка задачи. Нижняя и верхняя
интегральные суммы
Мощным средством исследования в математике, физике, меха-
механике и других дисциплинах является определенный интег-
интеграл—одно из основных понятий математического анализа. Вычис-
Вычисление площадей, ограниченных кривыми, длин дуг, объемов,
работы, скорости, пути, моментов инерции и т. д. сводится
к вычислению определенного интеграла.
/г,
Рис. 210.
0\ Ф<?% «% *&
Рис.
Пусть на отрезке [а, 6] задана непрерывная функция
y=if[x) (рис. 210 и 211). Обозначим через т и М ее наименьшее
й наибольшее значения на этом отрезке. Разобьем отрезок [а, Ь]
на п частей точками деления а = #0, х19 х2, ...9хпят19 #„ = &, при-
причем х0 <х1<.х2<, . •. <хпУ и положим #! — хо = кх19 х2— jcx =====
= Ал:2, ..., хп — хп^1 = Ахп. Обозначим, далее, наименьшее и наи-
наибольшее значения функции f (х) на отрезке [л:0, хг] через тг и Ми
на отрезке [хи х2] через т2 ъ М2, ..., на отрезке [хптт19 хп] через
пгп и Мп. Составим суммы
п
stt = MiAx1+M2Axs.+ ... +МлДх„ =
S
A)
B)

§1]
НИЖНЯЯ И ВЕРХНЯЯ ИНТЕГРАЛЬНЫЕ СУММЫ
357
Сумму sn называют нижней интегральной суммой, а сумму
sn — верхней интегральной суммой.
Если f(x)^Q, то нижняя интеьральная сумма численно рав-
равняется площади «вписанной ступенчатой фигуры» AC0N1C1M2 ...
••• Cn^1ffaBA9 ограниченной «вписанной» ломаной, верхняя ин-
интегральная сумма численно равняется площади «описанной сту-
ступенчатой фигуры»
ft
А
ограниченной «описанной» ломаной.
Отметим некоторые свойства верх-
верхних и нижних интегральных сумм.
а) Так как т(^М( для любого
i (i = 1, 2, ..., я), то на основании
формул A) и B) имеем
?„<5„. C)
(Знак равенства будет тадько в слу-
случае, если / (#) = const.)
б) Так как тх^т, п
значение f(x) на [а, 6], то
Итак,
в) Так как Мг^М, М2^
шее значение / (х) на [а, 6], то
а\ а Т~~^*
Рис. 212.
, где т —наименьшее
.., Мп^.Му где
= т(Ь— а).
D)
—наиболь-
—наиболь... +МпАхп
Итак,
Соединяя вместе полученные неравенства, имеем
тф—а) <; sn
М ф —а).
E)
F)
Если f(x)^O, то последнее неравенство имеет простой гео-
геометрический смысл (рис. 212), так как произведения тф — а) и
М ф — а) соответственно численно равны площадям «вписанного»
прямоугольника ALXL2B и «описанного» прямоугольника ALtL2B.

358
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
§ 2. Определенный интеграл. Теорема о существовании
определенного интеграла
Продолжим рассмотрение вопроса предыдущего параграфа.
В каждом из отрезков [x0J xt"\, [xu х2], .«., [хп„ихп] возьмем по
точке, которые обозначим llf ?я, ..., 1п (рис. 213): *0 < ?х < д^,
Рис. 213.
Xi < ^2 < X2> • • * * ^Я-1 < 5/г < #W
лим значение функции /(Ei), /I
^J7
каждой из этих точек вычис-
вычис»-*м /E„)« Составим сумму
t
Эта сумма называется интегральной суммой для функции f(x) на
отрезке [#, 6]. Так как при произвольном ?,., принадлежащем
отрезку [л:,-^1, ^,-], будет т{</(§/)<Mf и все А^-> 0, то
т,- Ал:; < / (?,) Ал:. < Л!,. Ал;,.,
следовательно,
S
i as 1
2
1=1
или
?Я<5Я<?Я. B)
Геометрический смысл последнего неравенства при f(x)^O состоит
в том, что фигура, площадь которой равна sn, ограничена ломаной,
заключенной между «вписанной» ломаной и «описанной» ломаной.
Сумма sn зависит от способа разделения отрезка [а, Ь] на отрезки
[#!-i> xi\ и от выбора точек g? внутри получающихся отрезков.
Обозначим теперь через max[#f_lt х{] наибольшую из длин от-
отрезков [#0, jc4]t [х19 х2]у ..., [#„_!, хп\. Рассмотрим различные разбие-
разбиения отрезка [а, Ь] на отрезки [ximml9 х(] такие, что тах[^_1э Xi]—+0.
Очевидно, что при этом число отрезков п в разбиении стремится
к бесконечности. Для каждого разбиения, выбрав соответствующие
значения lit можно составить интегральную сумму
2!
C)

§2] ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 359
Рассмотрим некоторую последовательность разбиений, при ко-
которых тахДх;—*0, при этом п—>оо. При каждом разбиении
выбираем значения ?,-. Предположим, что эта последовательность
интегральных сумм*) s* стремится к некоторому пределу
Urn s? = Hm 2/&>**< = «• <4>
max Дд^ -+ 0 max Ьх. -+ 01 - \
Теперь мы можем сформулировать следующее
Определение 1. Если при любых разбиениях отрезка [а> Ь]
таких, что тахДл;;—+0, и при любом выборе точек ^ на отрез-
отрезках [*f_lf x(] интегральная сумма
*п=?г{1()Ь*1 E)
стремится к одному и тому же пределу s, то этот предел назы-
называют определенным интегралом от функции / (х) на отрезке [а, Ь]
и обозначают
ь
lf(x)dx.
а
Таким образом, по определению
ъ
lim fif(li)Axl^lf(x)dx. F)
xA* ^ 0 i^Ti ?
Число а называется нижним пределом интеграла, Ь —верхним пре-
пределом интеграла. Отрезок [а, Ь] называется отрезком интегриро-
интегрирования, х—переменной интегрирования.
Определение 2. Если для функции f(x) предел F) суще-
существует, то функцию называют интегрируемой на отрезке [а, Ь].
Заметим, что нижняя интегральная сумма sn и верхняя интег-
интегральная сумма sn являются частными случаями интегральной сум-
суммы E), поэтому если f(x) интегрируема, то нижняя и верхняя
интегральные суммы стремятся к тому же пределу sf и потому на
основании равенства F) можем написать
lim %mtbxt=\f(x)dxt G)
max 6.х( -* 0 i?x a
*
Jim ^MiAxi=\f(x)dx. (T)
max Д*?. •+ 0; и l a
*) В данном случае сумма является упорядоченной переменной величиной.

360 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
Если построить график подынтегральной функции y = f(x), то
в случае / (х) ^ 0 интеграл
lf(pc)dx
будет численно равен площади так называемой криволинейной
трапеции, ограниченной указанной кривой, прямыми х = а, х = Ь
и осью Ох (рис. 214).
Поэтому если требуется вычислить площадь криволинейной
трапеции, ограниченной кривой y = f(x), прямыми х — а, х = Ь
и осью 0х> то эта площадь Q вычисляется с
помощью интеграла:
ъ
= $/(*)**. (8)
Докажем следующую важную теорему.
М\\\\\\\\\\\\Ч w гт-. * Г* t Г/Ч
а ь х Теорема 1. Если функция f(x) не-
непрерывна на отрезке [а, &], то она интег-
Рис. 214. рируется на этом отрезке.
Доказательство. Снова разобьем от-
отрезок [а, Ь] (а < Ь) на отрезки [*0, л^], [х19 х2], ¦.., [х^г, *,], ...
• • •» [хп-и хпЪ Составим нижнюю и верхнюю интегральные суммы:
п
sn^^miAxi, (9)
п
Для дальнейшего установим некоторые свойства верхних и
нижних интегральных сумм.
Свойство 1. При увеличении числа отрезков, на которые
мы разбиваем отрезок [а, Ь] путем добавления новых точек деле-
деления, нижняя интегральная сумма может только возрастать, а
верхняя интегральная сумма только убывать.
Доказательство. Пусть отрезок [а, Ь] разбит на п' отрез-
отрезков путем добавления новых точек (п' > п). Если какой-то отрезок
[**-!» хк\ будет разбит на несколько отрезков, например, на рк
отрезков, то в новой нижней интегральной сумме sn. отрезку
[*fr_i, xk~\ будет соответствовать рк слагаемых, которые мы обозна-
обозначим через ?Рк. В сумме s_n этому отрезку соответствует одно сла-
слагаемое тк(хк—хк^1). Но для суммы s*Pk и величины щ(хк—хктл1)
справедливо неравенство, аналогичное неравенству D) § 1. Мы
можем написать

§2} ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 361
Написав соответствующие неравенства для каждого отрезка и сум-
суммируя левые и правые части, получим
?„.>?„ (п'>п). (И)
Свойство 1 доказано.
Свойство 2. Нижняя интегрируемая сумма (9) и верхняя
интегральная сумма A0) при неограниченном увеличении Числа
отрезков путем добавления новых точек деления стремятся к не-
некоторым пределам s и s.
Доказательство. На основании неравенства F) § J можем
написать:
т. е. sn ограничена при всех п. На основании свойств 1 ^п моно-
монотонно возрастает при возрастании я. Следовательно, на основании
теоремы 7 о пределах (см. § 5 гл. II) эта переменная величина
имеет предел; обозначим его через s:
«->со- ~ (U)
Аналогично устанавливается, что^ ограничена снизу и моно-
монотонно убывает^ Следовательно, sn имеет предел, который мы обо-
обозначим через s:
lim sn = s.
П -> со
Свойство 3. Если функция f (x) непрерывна на замкнутом
отрезке [а, Ь], то пределы s_u s, определенные в свойстве 2 при
условии, что max Ахг —* 0, равны.
Этот общий предел обозначим через s:
s = I= s. A3)
Доказательство. Рассмотрим разность верхней и нижней
интегральной суммы:
-тп) Ахп - S <Aff—mf) Д*,. A4)
Обозначим через гп наибольшую из разностей Мг—mi при
данном разбиении:
Можно доказать (на чем мы останавливаться не будем), что если
функция f(x) непрерывна на замкнутом отрезке, то при любом

362 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
способе разбиения отрезка [а, Ь] гп —^0, если только шах Ал:,-—*0:
lim вл = 0. A5)
А О
«пах Ах* -> О
Свойство непрерывной функции на замкнутом отрезке, выра-
выражаемое равенством A5), называется равномерной непрерывностью
функции.
Итак, мы будем пользоваться теоремой: Непрерывная функция
на замкнутом отрезке равномерно непрерывна на этом отрезке.
Вернемся к равенству A4). Каждую разность М.—т{ в пра-
правой части заменим не меньшей величиной вп. Получаем неравенство
хп) =вп(Ь—а).
Переходя к пределу при max Л*;—>0 (л —*оо), получаем
lim (sn—sn) <! lim вп (b—а) = (b—a) iim вп = 0,A6)
max A* •-*¦() — тахДл:^-*0 max Дл^->0
т. е.
п п у \ /
или s==s = s, что и требовалось доказать.
Свойство 4. Пусть ^Пх и sUi—нижняя и верхняя интеграль-
интегральные суммы, соответствующие разбиениям отрезка [а, Ь] на пг и
соответственно на п2 отрезков. Тогда имеет место неравенство
М О*, A8)
при любых пг и п2.
Доказательство. Рассмотрим разбиение отрезка [а, Ь] на
п8 = п1 + п2, отрезков, где точками деления будут точки деления
первого и второго разбиений.
На основании неравенства C) § 1 имеем
A9)
На основании свойства I имеем
in,<?^ B0)
s*3<sna. B1)
Пользуясь соотношениями B0) и B1), можно расширить нера-
неравенство A9):

§2] ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 363
или
что и требовалось доказать.
Свойство 5. Если функция f(x) непрерывна на отрезке[ау Ь\
то при любой последовательности разбиений отрезка [а, Ь] на
отрезки [х^и лг,-], не обязательно путем присоединения новых
точек деления, если только max Ах{—*_0, нижняя интегральная
сумма s^ и верхняя интегральная сумма s^ стремятся к пределу s,
определенному в свойстве 3.
Доказательство. Рассмотрим последовательность разбие-
разбиений последовательности верхних интегральных сумм sw, опреде-
определенных в свойстве 2. При любых значениях п и т (на основании
неравенства A8)) можем написать s^^sn.
Переходя к пределу при п—> оо, на основании A5) можем
написать s*^
Аналогичным способом докажем
Итак,
или
s—?>0, "&—s>0. B2)
Рассмотрим предел разности lim (s^—sJJ. Так как функция
max Ах- ->0 "~
f(x) непрерывна на замкнутом отрезке [а, 6], то (так же тц и
при доказательстве свойства 3) докажем (см. равенство A6)), что
lim D-s^) = 0.
max &x- -»• 0 ""*
Перепишем последнее соотношение так:
lim [(S;
igax Ax?-+ 0
На основании B2) каждая из разностей, стоящих в квадратных
скобках, неотрицательна. Следовательно,
lim (s*m—s) = 0, lim (s—s*m) = Qt
max Д#г» -> 0 max A* • -> 0 ~~
и окончательно получаем
lim s*m = s, lim s^ = sf B3)
max A*t- -> Q— max Дд^ -> 0
что и требовалось доказать.
Теперь можно доказать и сформулированную выше теорему.
Пусть f(x) непрерывна на отрезке [а, 6]. Рассмотрим произволь-

364 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
п
ную последовательность интегральных сумм sn = 2 f (S/) А*« та-
такую, что max A*; —»-0, ^- — произвольная точка отрезка [#,-_!, *,-].
Для данной последовательности разбиений рассмотрим соответ-
соответствующие ^последовательности верхних и нижних интегральных
сумм sn и sn. Для каждого разбиения будут справедливы соотно-
соотношения B):
Переходя к пределу при max &х( —> 0 и пользуясь равенствами
B3) и теоремой 4 § 5 гл. II, получаем lim sn=^s, где s —
& О
max &х- -*• О
предел, определенный в свойстве 3.
Этот предел, как уже говорилось выше, и называется опреде-
ь
ленным интегралом }f(x)dx. Ита#, если f (х) непрерывна на от-
а
резке [а, 6], то
ь
2/F/) А*/= $/(*)<**. B4)
тахД^.-т-v а
Отметим, что среди разрывных функций есть как интегрируе-
интегрируемые^ ^гак и' неинтегрируемые.
Замечание 1. Отметим, что определенный интеграл зависит
только от вида функции f(x) и пределов интегрирования, но не
от переменной интегрирования, которую можно обозначить любой
буквой. Шэтому, не изменяя величины определенного интеграла,
можро заменить букву х любой другой буквой:
Замечание 2. При введении понятия определенного инте-
ь
грала J f (x) dx мы предполагали, что а < Ь. В случае 6 < а при-
а
мем по определению
ь а
Sf ( y\ //у — . \ f Iу\ А у /O^V
/ VV ^"^ J / \ / *""•*'• \~^'/
а Ь
О 5
Так, например, \ х% dx = — $ х2dx.
5 О

§2!
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
365
Замечание 3. В случаеа = Ь полагаем по определению,
что для любой функции f(x) имеет место
B6)
Это естественно и с геометрической точки зрения. В самом деле,
основание криволинейной трапеции имеет длину, равную нулю,
следовательно, и площадь этой криволинейной трапеции равна
нулю.
ь
Пример 1» Вычислим интеграл* \ kxdx (b > a).
а
Решение. Геометрически задача эквивалентна вычислению площади Q
трапеции, ограниченной линиями y^=kx, x=*=a, #—0 (рис. 215).
Функция y—kx> стоящая под знаком интеграла, непрерывна. Следова-
Следовательно, для вычисления определенного интеграла мы вправе, как это было
замечено выше, произвести разбиение отрезка [а, Ь] произвольным способом и
произвольно выбрать промежуточные точки ?#. Результат
вычисления определенного интеграла не зависит от спосо-
ба построения интегральной суммы — лишь бы шаг разбие-
разбиения стремился к нулю.
Делим отрезок [а, Ь\ на п равных отрезков.
а х, х2
Рис. 215.
Длина Ах каждого частичного отрезка равна Лд:= ; это число и будет
шагом разбиения. Точки деления имеют координаты xQ = a, хг = а+Ах, *2 =
= а+2Д*, ..., хп — а+пАх. В качестве точек %к возьмем левые концы каж-
каждого отрезка: ?i = a, ?2 = я+Ал:, |3 = «+2Да:, «.., Ъ,п~а+(п — \) Ах.
Составим интегральную сумму A). Так как /(Si) = ^6,-f то
(а+Ах)]
:=-^. Учитывая, что 1+2+i9,
.,. + (п— I) Ах)} Ах =
= k{na+[l+2+...+(n-l)]Ax)Ax9
— l)=n ^Г"" ' (как сумма гео-

366 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
метрической прогрессии), получим
(п—1) 6—а\Ь—а , Г . п—16—
Так как lim ?=lL=1, то lim sn = Q=k\a+^] (b—a) = k
tl -* oo tl Я -> oo L ^ J
Итак, V kxdx=k —о— •
a
a
Площадь >4B6a (рис. 215) легко вычислить методами элементарной гео-
геометрии.
Результат получится тот же.
ь
Пример 2. Вычислить \ х2 dx.
Решение. Данный интеграл равен площади Q криволинейной трапеции,
ограниченной параболой у=х2, ординатой х — Ь и прямой у=0 (рис. 216).
Разобьем отрезок [О, Ь] на п равных частей точкам» *0=0 **~ А*, х2 =
=2Ах1 ..., xn = b = n&xt &x=b/n.
За точки |/ возьмем крайние правые точки каждого ив отрезков* Составим
интегральную сумму:
sn = xl tix+xl Ajc+ .,. +xlAx= [(АхJ Д*+ BА*J Ах+ ...+(« AjcJ Ааг}=
Как известно, р+22+32+,.. + п*=П (п+ 1)^2п+1) 9 поэтому
6
Пример 3. Вычислить \ mdx(m = const).
a
Решение.
b п п
mdx~ lim У1 mAxi— lim m У!
max Дхt- -> 0 j- = | max A^t« -> 0 t- = |
/I
lim ^
Здесь 2 &Xi есть сумма длин отрезков, на которые разбит отрезок [а, Ь].
t = i
При любом способе разбиения эта сумма равна длине отрезка Ь—а.
ь
Пример 4. Вычислить \ ех dx.
а
Решение. Снова разделим отрезок [а, Ь] на п равных частей: лго = а,
¦»,, хп = а-\-п Ах; Дд:=—— t За точки |; возьмем левые крайние

§ 3] ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 367
точки. Составим интегральную сумму:
>л*) Дл:.
Выражение в скобках есть геометрическая прогрессия со знаменателем ед* и
первым членом I, поэтому sn=ea ДЛ.__ « &х = еа (enhx—\) ДЛ._. . Далее,
имеем ntuc — b—а, Кга —^—т" = 1. [ По правилу Лопиталя lim ——г-=
= lim-4"=sl.) Таким образом, lim sn = Q=e<* (г&-*_1). 1 =eb—ea, т.е.
j
а
Замечание 4. Только что рассмотренные примеры показы-
показывают, что непосредственное вычисление определенных интегралов
как пределов интегральных сумм связано с большими трудностями.
Даже в тех случаях, когда подынтегральные функции являются
очень простыми (kxy x2, е*)ч этот способ требует громоздких под-
подсчетов. Нахождение же определенных интегралов от более слож-
сложных функций приводит к еще большим трудностям. Поэтому
естественно возникает задача: найти практически удобный метод
вычисления определенных интегралов. Этот метод, открытый Нью-
Ньютоном и Лейбницем, использует глубокую связь, существующую
между интегрированием и дифференцированием. Изложению и
обоснованию этого метода посвящены следующие параграфы настоя-
настоящей главы.
§ 3, Основные свойства определенного интеграла
Свойство 1. Постоянный множитель можно не выносить за
знак определенного интеграла: если А = const, то
ь ь
\Af{x)dx=A\f{x)dx. A)
а а
Доказательство.
\ Af (х) dx = lira S Л/ (It) Дх,- =
? шах Ах^ -»> 0 i = 1
lim
max Длг
Свойство 2. Определенный интеграл от алгебраической
суммы нескольких функций равен алгебраической сумме интегралов

368 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ {ГЛ. XI
от слагаемых. Так, в случае двух слагаемых
ь ь ъ
\ [П (*) +/, (x)]dx = S U (х) dx+У,(х)dx. B)
а а а
Доказательство.
= lira 2 [fidd+fAh)]^^
max Л^-»- 0 i =1
= Hm f 2 /, &.) Дхг + 2 /2 (I,-) A
max Дл^.-j-O b's=l i* = i
b b
2
max Д^.->0 i=l
Доказательство проводится аналогично для любого числа сла-
слагаемых.
Свойства 1 и 2, хотя и доказаны только для случая а < Ь,
остаются в силе и при а^Ь.
Однако следующее свойство справедливо при а < Ь:
Свойство 3. Если на отрезке [а, 6], где а<6, функции
f(x) и у(х) удовлетворяют условию /(*Х1ф(#), то
ъ ъ
J/(*)dx<J«p(*)<k. C)
а а
Доказательство. Рассмотрим разность
ъ ь ь
Здесь каждая разность <p(?j) — /Ef)^0, Дх/>0. Следовательно,
каждое слагаемое суммы неотрицательно, неотрицательна вся сумма
ь
и неотрицателен ее предел, т, е. )[<р(х) — f(x)]dx^0, или
J Ф -(л;) dx — J / (л:) dx > 0, откуда следует неравенство C).
a a
Если /(#)>0 и ф(х)>0, то указанное свойство наглядно
иллюстрируется геометрически (рис. 217). Так как ф (л) >/(#),

«3]
ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
369
то площадь криволинейной трапеции аАгВгЬ не больше площади
криволинейной трапеции аА2В2Ь.
Свойство 4. Если т и М — наименьшее и наибольшее-зна-
наибольшее-значения функции f (х) на отрезке [а, Ь] и а^Ь, то
ь
т ф—а) < J / (х) dx < М ф—а). D)
а
Доказательство. По условию
На основании свойства C) имеем
ь ь
J mdxt^L J /
а а
Но
ъ ь
M dx.
D0
(см. пример 3 § 2). Подставляя эти выражения в неравенство
получим неравенство D).
о?
т.
О а
Рис. 217.
Рис. 218.
Если f(x)^Oy то это свойство легко иллюстрируется геомет-
геометрически (рис. 218): площадь криволинейной трапеции аАВЬ содер-
содержится между площадями прямоугольников аА}ВгЬ и аА2В2Ь.
Свойство 5 (теорема о среднем). Если функция f(x)
непрерывна на отрезке [а, Ь], то на этом отрезке найдется такая
точка I, что справедливо следующее равенство:
E)
Доказательство. Пусть для определенности а<6. Если
т и М суть соответственно наименьшее и наибольшее значения
13 н. С. Пискунов, *. 1

370
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
f(x) на отрезке [а, Ь]9 то в силу формулы D) m^ g—- \ / (х) dx ^ М.
а
Ь
Отсюда -?zra \ f(x)dx = \if где m
а
Так как / (л:) непрерывна на отрезке [а, Ь\ то она принимает
все промежуточные значения, заключенные между т и М. Сле-
Следовательно, при некотором значении ?(^
g6) будет ji = /(g), т.е.
6
а).
Свойство 6. Для любых трех чи-
чисел а, Ь, с справедливо равенство
ь с ь
f(x)dx, F)
только все эти три интеграла существуют.
Доказательство. Предположим сначала, что а<с<6, и
составим интегральную сумму для функции f (х) на отрезке [а, 6].
Так как предел интегральной суммы не зависит от способа
разбиения отрезка [а, Ь] на части, то мы будем разбивать отрезок
[а, Ь] на малые отрезки так, чтобы точка с была точкой деления.
ъ
Разобьем далее интегральную сумму 2 » соответствующую отрезку
а
с
[а, Ь\ч на две суммы: сумму 2» соответствующую отрезку [а, с],
а
Ь
и сумму 2» соответствующую отрезку [с, 6].
Тогда 2/ F|) Ах, - 2 / di) Ax, + 2/ (&,) А*,.
а а с
Переходя в последнем равенстве к пределу при шах Ах,—*0,
получим соотношение F).
Если а < Ь < с, то на основании доказанного можем написать
с Ь с b о с
lf(x)dx=lf(x)dx+lf(x)dx или J / (*)<&= j/(jc)dx- J /(*)<&;
но на основании формулы D) § 2 имеем ^ f(x)dx = —^ f (x) dx,
b
поэтому j / (х) dx=
/(#) dx.

§4]
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
371
Аналогичным образом доказывается это свойство при любом
другом расположении точек a, b и с.
На рис. 219 дана геометрическая иллюстрация свойства 6 для
того случая, когда f (х) > 0 и а < с < Ь: площадь трапеции аАВЬ
равна сумме площадей трапеций аАСс и сСВЬ.
§ 4. Вычисление определенного интеграла. Формула
Ньютона — Лейбница
ъ
Пусть в определенном интеграле j / (x) dx нижний предел а
а
закреплен, а верхний предел Ь меняется. Тогда будет меняться
и значение интеграла, т. е. интеграл есть функция верх-
верхнего предела.
Для того чтобы иметь привычные обозначения, верхний предел
обозначим через х, а чтобы не смешивать его с переменной интег-
интегрирования, последнюю обозначим через t. (От обозначения пере-
переменной интегрирования значение интеграла не зависит.) Получим
интеграл ^ / (t) dt. При постоянном а этот интеграл будет пред-
а
ставлять собой функцию верхнего предела х. Эту функцию мы
обозначим через Ф (х):
A)
Если /(^—неотрицательная функция, то величина Ф(х) чис-
численно равна площади криволинейной трапеции аАХх (рис. 220).
Очевидно, что эта площадь изменяет-
изменяется в зависимости от изменения х.
Найдем производную от Ф (х) по х,
т. е. найдем производную определенно-
определенного интеграла A) по верхнему пределу.
Теорема 1. Если f (x) — непре-
рыеная функция и Ф(х) = J / (t) dt,
а
то имеет место равенство
Иными словами, производная от определенного интеграла по
верхнему пределу равна подынтегральной функции, в которую
вместо переменной интегрирования подставлено значение верхнего
предела (при условии, что подынтегральная функция непрерывна).
Доказательство. Дадим аргументу х положительное или
отрицательное приращение Ах; тогда (учитывая свойство 6 опреде-
13*

372 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
#4-Ал? х
ленного интеграла) получим Ф(л; + Дл;) = J f (t)dt= J f(t) dt +
x+Lx
f(t)dt. Приращение функции Ф (x) равно ДФ = Ф (х + Ах) —
лг+Дде
@Я + J f{t)dt-\f(t)dt, т. е. АФ= J
а л* а к
К последнему интегралу применим теорему о среднем значении
(свойство 5 определенного интеграла)
где | заключено между д: и х-{-Ах.
Найдем отношение приращения функции к приращению аргу-
ДФ f(l)b
ДФ
мента: _ =
Следовательно, Ф' (х) = lim -г- = lim / (|). Но так как g —> л:
UO Лл: Д0
при Дл;—*0, то lim f(?)= Hm /(?), а вследствие непрерывности
функции f(x) lim~}(I) = f (х)? Таким образом, Ф' (х) = / (х). Тео-
%-+х
рема доказана.
Данная теорема просто иллюстрируется геометрически (рис. 220):
приращение ДФ = /(?)Д* равняется площади криволинейной тра-
трапеции с основанием Да:, а производная Ф' (д:) = f (x) равна длине
отрезка хХ.
Замечание. Из доказанной теоремы, в частности, следует,
что всякая непрерывная функция имеет первообразную. Действи-
Действительно, если функция / (t) непрерывна на отрезке [а, х], то, как
X
указывалось в § 2, в этом случае определенный интеграл
х
существует, т. е. существует функция Ф (я) = J f (t) dt. Но по до-
а
казанному выше она является первообразной от f(x).
Теорема 2. Если F (х) есть какая-либо первообразная от
непрерывной функции /(#), то справедлива формула
а
Эта формула называется формулой Ньютона —Лейбница*),
*) Необходимо отметить, что такое название формулы B) условно, по-
поскольку ни у Ньютона, ни у Лейбница не было такой формулы в точном
смысле этого слова. Но важно то, что именно Лейбниц и Ньютон впервые
установили связь между интегрированием и дифференцированием, позволяю-
позволяющую создать правило для вычисления определенных интегралов.

§4] ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 373
Доказательство. Пусть F (х) есть некоторая первообраз-
X
ная от функции / (х). По теореме 1 функция § / (t) dt есть также
а
первообразная от f(x). Но две любые первообразные от данной
функции отличаются на постоянное слагаемое С*. Следовательно,
можно написать
X
lf(t)dt = F(x) + C*. C)
а
Это равенство при соответствующем выборе С* справедливо при
всех значениях х, т. е. является тождеством. Для определения
постоянного С* положим в этом тождестве х — а\ тогда
а
lf(t)dt = F(a) + C*, или 0 = F(a) + C*, откуда С* = — F(a).
а
Следовательно,
Полагая х = Ь, получим формулу Ньютона —Лейбница:
или, заменив обозначение переменной интегрирования на х:
(x)dx = F(b)-F(a).
Отметим, что разность F (b) — F (а) не зависит от выбора пер-
первообразной Т7, так как все первообразные отличаются на постоян-
постоянную величину, которая при вычитании все равно уничтожается.
Если ввести обозначение *)
F(b)-F{a)=F(x)\>,
io формулу B) можно переписать так:
ь
*) Выражение | а называется знаком двойной подстановки. В литературе
встречаются две формы записи: или
или
F(b)-F(a) = F(x)\ba.
Мы в дальнейшем будем употреблять и тот и другой способы записи.

374 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. ХГ
Формула Ньютона — Лейбница дает практически удобный метод
вычисления определенных интегралов в том случае, когда известна
первообразная подынтегральной функции. Только с открытием
этой формулы определенный интеграл смог получить то значение
в математике, какое он имеет в настоящее время. Хотя с процес-
процессом, аналогичным вычислению определенного интеграла как пре-
предела интегральной суммы, были знакомы еще в древности (Архи-
(Архимед), однако приложения этого метода ограничивались теми
простейшими случаями, когда предел интегральной суммы мог
быть вычислен непосредственно. Формула Ньютона — Лейбница
значительно расширила область применения определенного интег-
интеграла, так как математика получила общий метод для реше-
решения различных задач частного вида и поэтому смогла значительно
расширить круг приложений определенного интеграла к технике,
механике, астрономии и т. д.
ь
Пример 1. \;
а
ь
Пример 2. \j
Пример 3.
Пример 4.
Пример 5. \ sinxdx=—cos* =—(соз2я—cosO) = 0.
о
1
„ rs Г Xdx ,/"i s t 1 чГ<Г
ПриМер6. JF===^1+^ = K2-I.
§ 5. Замена переменной в определенном интеграле
Теорема. Пусть дан интеграл
а
Ь
к1
2
л?
3
b
а
b
а
Ь2—а2
2
б3—а3
" 3 '
а
Ь
где функция f(x) непрерывна на отрезке [а, 6].
Введем новую переменную t no формуле

§5]
ЗАМЕНА ПЕРЕМЕННОЙ В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
375
то
Если
1) <р(а) = а, ф(р) = 6,
2) ф (/) и <р' (t) непрерывны на отрезке [а, $]>
3) /[ф@] определена и непрерывна на отрезке [а,
Доказательство. Если F(х) есть первообразная для функ-
функции /(*), то можем написать следующие равенства:
B)
C)
Справедливость последнего равенства проверяется дифференциро-
дифференцированием обеих частей по t. (Оно также следует из формулы B)
§ 4 гл. X.) Из равенства B) получаем
Из равенства C) получаем
y^/F^
Правые части последних выражений равны, следовательно, равны
и левые.
Замечание. Отметим, что при вычислении определенного
интеграла по формуле A) мы не возвра-
возвращаемся к старой переменной. Если мы вы-
вычислим второй из определенных интегра-
интегралов равенства A), то мы получим неко-
некоторое число; этому же числу равняется
и первый интеграл.
г
Пример. Вычислить интеграл [ V"r2—x2dx.
Рис. 221.
Решение. Сделаем замену переменной: * =
= г sin t, dx=r cos / dt. Определим новые пределы:
лг=О при / = 0, х = г при / = я/2. Следовательно,
Г Я/2 Я/2
/
2—r2sin2trcostdt=r* f /"l— sin2/ cos
о
Л/2
Я/2
Вычисленный интеграл с геометрической точки зрения представляет пло-
площадь V* круга, ограниченного окружностью х2+у*~г* (рис. 221).

376 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
§ 6. Интегрирование по частям
Пусть и и и — дифференцируемые функции от х. Тогда
(uv)' = u'v-{-uv'.
Интегрируя обе части тождества в пределах от а до &, получим
ь ь ь
{uv)f dx=[u'vdx+\uv' dx. A)
а
Ь
С С \ b
Так как ] (uv)' dx = uv + С, то j (uv)' dx = uv | a; поэтому равен-
ство A) может быть записано в виде
ь ь
1ь с с
а= }vdu+] udvt
а а
или окончательно
ь ь
} udv — uv\a— j vdu,
а а
я/2
/
Пример. Вычислить интеграл /ft= \ sinnxdx>
О
Jt/2 я/2 я/2
/я= \ sin"*rf*= V sin*^1 xsin xdx=— \ smn-'1xdcosx=
Я/2
=—sin"~l#cosJt:I" +(n—1) \ sinn-2xcosxcosxdx—
0
Я/2 Я/2
= («—1) f sin«-2A;cos2A:ufA:=(/i~-l) j sin«~2A: A— sin2x)dx=
0 0
Я/2 я/2
= (n—\) [ sinn-zxdx—(n — l) [ sinnxdx.
о о
В выбранных обозначениях последнее равенство можно записать так:
/й = (л-1)/я-«-(я-1)/л,
откуда находим
/»=^/«-t. B)
Тем же приемом найдем
_п-3.
поэтому
n— In—3,

§6] ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ $77
Продолжая таким же образом далее, мы дойдем или до /0 или до 1±
в зависимости от того, будет ли число п четным или нечетным.
Рассмотрим два случая:
1) п—число четное, п = 2т:
2m—l 2т—3 3 I
1 /г
2) п—число нечетное, /i=2m + l:
/ %т 2m—2
2m— i "* 5 3
но так как
Я/2 Я/2 Я/2
С Г я С
то
Я/2
2т—1 2т—3 JL JL _L JL
2т '2т—2 "#1б'4'2*
я/2
Г 2/7г 2т—2 6 4 2
Из этих формул следует формула Валлиса, выражающая число п/2 в виде
бесконечного произведения.
Действительно из последних двух равенств путем почленного деления
находим
rt ( 2>4>6>...>2m у 1 1ШЯ
2 V 3-5.....B/П-1) У 2m+i/2/w+i'
Докажем теперь, что
Для всех д: из интервала I 0, -^- J справедливы неравенства
Интегрируя в пределах от 0 до я/2, получим
откуда
D)
Из равенства B) следует
OT + i 2т
Поэтому
4
щ-*-оо ^2/я + 1 т-*¦

378 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
Из неравенства D) получаем
цт
т -* о
Переходя к пределу в формуле C), получим формулу Валлисся
Л г [7 2-4-6« ... -2т у 1
?[ )
Эту формулу можно записать в следующем виде:
-?L— г (— — -1 -1 А 2т—2 2т 2т \
2 ~п™„ W # 3 # 3 # 5 ' 5 # '" # 2т — 1 # 2т— 1 # 2т+1 У"
§ 7. Несобственные интегралы
1. Интегралы с бесконечными пределами. Пусть
функция f (х) определена и непрерывна при всех значениях х
таких, что а ^ х < + °° • Рассмотрим ин-
интеграл
Этот интеграл имеет смысл при любом
Рис. 222. Ь>а. При изменении Ь интеграл изменя-
изменяется, он является непрерывной функцией Ъ
(см. §4). Рассмотрим вопрос о поведении этого интеграла при
Ъ-+ + оо (рис. 222).
Определение. Если существует конечный предел
ь
Iim ^ / (х) dx,
Ь-> + со а
то этот предел называют несобственным интегралом от функции
f(x) на интервале [а, +<х>) и обозначают так:
S f(x)dx.
а
Следовательно, по определению имеем
+ оо Ь
\ f(x)dx= Iim lf(x)dx.
Говорят, что в этом случае несобственный интеграл $ / (*) dx
а
Ь
существует или сходится. Если )f(x)dx при Ь—>+°° не имеет

НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
379
Ч-да
конечного предела, то говорят, что J f(x)dx не существует или
а
расходится.
Легко выяснить геометрический смысл несобственного интеграла
ь
в случае, когда f(x)^O: если интеграл ^f(x)dx выражает пло-
а
щадь области, ограниченной кривой y = f(x), осью абсцисс и орди-
ординатами х = а, х = Ь} то естественно считать, что несобственный
+ 00
интеграл ^ f(x)dx выражает площадь неограниченной (бесконеч-
а
ной) области, заключенной между линиями y — f{x), x = a и осью
абсцисс.
Рис. 223.
Рис. 224.
Аналогичным образом определяются несобственные интегралы
и для других бесконечных интервалов:
а а
f(x)dx= lim lf(x)dx,
f(x)dx= S f(x)dx+ 5 f(x)dx.
Последнее равенство следует понимать так: если каждый из несоб-
несобственных интегралов, стоящих справа, существует, то существует
(сходится) по определению и интеграл, стоящий слева.
+ 00
Jdx
¦« . 2 (рис. 223 и 224).
о
Решение. По определению несобственного интеграла находим
ь
dx
о
С dx v Г
= lim arotgA: = lim
Рассмотренный интеграл выражает площадь бесконечной криволинейной
трапеции, заштрихованной на рис. 224.

380 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
Пример 2. Установить, при каких значениях а (рис. 225) интеграл
+ 00
С dx
\ —— сходится и при каких расходится.
ь
С dx I \Ъ 1
Решен ие. Так как (приа ф 1) \—= - xlm"a\ =^ (fr1*0*—1),
+ 00
то \ —^-= lim ^ (Ь16 — 1). Следовательно, относительно рассматри-
х) X О -*¦ +|оо ^*
ваемого интеграла можно сделать следующие выводы: если а > 1, то
+Г° dx 1
\ —^- = г, т. е. интеграл сходится; если
{¦ со
+ 00
ся. При а=1 \ —=\пх
+ ОО
, то \ ^-=ioo, т. е. интеграл расходит-
=:оо— интег-
1
а~1 рал расходится.
4 ОН f* rfjf
* П rt м м a r\ Q Т5т_тт*т*о TitrTV 1 -
Рис. 225.
Пример 3. Вычислить \
— 00
+00
^ С dx Г dx , С dx „ „
Решение. ^ f+lc*^ J Г+^+ J T+I1' ВтоРои интеграл равен
— оо —со О
— 00
+ 00 0 +00
-х- (см. пример 1). Вычислим первый интеграл:
о о
= lim (arctg0—arctga)=^-.
dx .. С dx .. .
-i—9= lini \ t , о = lim arctg jc
-оо
Следовательно,
+ 00
Г
J
Во многих случаях бывает достаточно установить, сходится
данный интеграл или расходится, и оценить его значение. Для
этого могут быть полезными следующие теоремы, которые мы при-
приведем без доказательств, а применение их докажем на примерах.
Теорема 1. Если для всех х (х^а) выполняется неравенство
+ 00 +00
и если \ <f(x)dx сходится, то \ f (x) dx также сходится, при

§7] НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 381
этом
+ <» + ю
S /(*)<**< J <?(x)dx.
а а
+ Q0
С dx
Пример 4. Исследовать, сходится ли интеграл \ х2/{\ех\ *
+ 00
1 I Г I
Решение. Заметим, что при 1 < х 2 л , . < -^ . Далее, \ -^ dx =
+ QD
= I. Следовательно, \ ^ tt ,—гт сходится и его значение меньше 1.
1
Теорема 2. ?сла Зля бсг^ х(х^а) выполняется неравенство
<;/(#), причем J ф(л:)^х расходится, то расходится и
а
+ QO
интеграл J / (л:) djc.
а
+ 00
Пример 5. Исследовать, сходится ли интеграл \ Z_ dx,
+ 00
Замечаем,.что —т^=- > —f=== > Но \ . = lim 2у х\ =+°°»
Следовательно, расходится и данный интеграл.
В последних двух теоремах рассматривались несобственные
интегралы от неотрицательных функций. Для случая функции /(#),
меняющей знак в бесконечном интервале, имеет место следующая
теорема.
Теорема 3. Если интеграл J \f(x)\dx сходится, то сходится
и интеграл
+ <ю
J f(x)dx.
а
В этом случае последний интеграл называется абсолютно
сходящимся.
+ <ю
Пример 6. Исследовать сходимость интеграла \ 13 dx.
Решение. Здесь подынтегральная функция знакопеременная. Замечаем,
что
_LI но Г i?- L
= -jr . Следовательно, интег-

&2 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
Ч-со
Г 1 sin х I
рал \ —-§"- dx сходится. Отсюда следует, что сходится и данный ин-
1
1
теграл.
2. Интеграл от разрывной функции. Пусть функция
f(x) определена и непрерывна при а^.х<с, а при х = с функ-
функция либо не определена, либо терпит разрыв. В этом случае
нельзя говорить об интеграле J / (х) dx как о пределе интеграль-
а
ных сумм, так как f(x) не непрерывна на отрезке [а, с], и поэ-
поэтому этот предел может и не существовать.
с
Интеграл j f(x)dx от функции / (я), разрывной в точке с,
а
определяется следующим образом:
с Ь
lf(x)dx= lim \f(x)dx.
{a b ->c -0 а
Если предел, стоящий справа, существует, то интеграл назы-
называют несобственным сходящимся интегралом, в противном случае
интеграл называют расходящимся.
Если функция / (х) имеет разрыв в левом конце отрезка [а, с]
(т. е. при х = а)у то по опр еде лени ю
с с
\f(x)dx= lim \f{x)dx.
a b-*a+Q ?
Если функция f(x) имеет разрыв в некоторой точке х = х0
внутри отрезка [а, с], то полагают
с х0 с
а а Хо
если оба несобственных интеграла, стоящих в правой части равен-
равенства, существуют.
Пример 7. Вычислить \
* х
- lim
= — lim i
J
С dx
Пример 8. Вычислить интеграл \ --у •

§7]
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
383
Решение. Так как внутри отрезка интегрирования существует точка
= 0, где подынтегральная функция разрывна, то интеграл нужно представить
как сумму двух слагаемых:
1 et I
С dx .. С dx , Г dx _,
«с: V —y= lim \ — + lim \ — • Вычис-
-1 е4-*-0 _^ e2->+0 ^
лим каждый предел отдельно: lira \ -^|- = — lim ~| s=
s= — lim ( r )= oo. Следовательно, на участке [ — 1,0] интеграл
6l -> - о V 8i —1/
1
\—4'=— lim [1 ?-)=оо. Значит, на участке
i J Xй e2_^+0v б/
расходится. lim
[О, 1] интеграл также расходится.
Таким образом, данный интеграл расходится на всем отрезке [—1, 1].
Отметим, что если бы мы стали вычислять данный интеграл, не обращая вни-
внимания на разрыв подынтегральной функции в точке * = 0, то получили бы
неверный результат. Действительно, \ —о- = t = ""(l— —г)==~'
J X л 1-1 \ I —1 /
что невозможно (рис. 226).
Замечание. Если функция f(x), определенная на отрезке
[а, Ь], имеет внутри этого отрезка
конечное число точек разрыва аи а2,...
..., ап, то интеграл от функции f(x)
на отрезке [а, Ь\ определяется следую-
следующим образом:
Ь CL* О.*
Ъ
$/(*) dx,
ап
-1 О
1
Рис. 226.
если каждый из несобственных интег-
интегралов в правой части равенства сходит-
сходится. Если же хотя бы один из этих интегралов расходится, то и
ь
^f(x)dx называется расходящимся.
Для определения сходимости несобственных интегралов от раз-
разрывных функций и оценки их значений часто могут быть приме-
применены теоремы, аналогичные теоремам для оценки интегралов
с бесконечными пределами.
Теорема Г. Если на отрезке [а, с] функции f(x) и ц>(х)
разрывны в точке с, причем во всех точках этого отрезка

384 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
выполнены неравенства
с с
и \q>(x)dx сходится, то \jf(x)dx также сходится.
Теорема 1Г. Если на отрезке [а, с] функции f (х) и ц>(х)
разрывны в точке с, причем во всех точках этого отрезка выпол-
выполнены неравенства
с с
и \<p(x)dx расходится, то и \jf(x)dx расходится.
а а
Теорема ИГ. Если f(x) — функция, знакопеременная на от-
отрезке [а, с], разрывная только в точке с, и несобственный интег-
рал \ \f(x)\dx от абсолютной величины этой функции сходится,
а
с
то сходится также интеграл }f(x)dx от самой функции.
а
В качестве функций, с которыми удобно сравнивать функции,
стоящие под знаком несобственного интеграла, часто берут
с
\/(с — х)а. Легко проверить, что \ (c__x)adx сходится при <х< 1,
а
расходится при а ^ 1.
с
Это же относится и к интегралам V . )а^х*
а
1
Пример 9. Сходится ли интеграл \ ~p=r dx?
о " х '
Решение. Подынтегральная функция разрывна в левом конце отрезка
[О, 1]. Сравнивая ее с функцией —=r=i, имеем -= < —^= ¦
ух у х+ 4xz у х
Несобственный интеграл \ -477 существует. Следовательно, несобствен-
1
Г 1
ный интеграл от меньшей функции, т. е. \ —т*= dx, тоже
J У х+ 4х?

§8] ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 385
§ 8. Приближенное вычисление определенных интегралов
В конце главы X указывалось, что не для всякой непрерыв-
непрерывной функции ее первообразная выражается через элементарные
функции. В этих случаях вычисление определенных интегралов по
формуле Ньютона —Лейбница затруднительно, и применяются раз-
различные методы приближенного вычисления определенных
интегралов. Сейчас мы изложим несколько способов приближен-
приближенного интегрирования, исходя из поня-
понятия определенного интеграла как преде-
предела суммы.
I. Формула прямоугольни-
прямоугольников. Пусть на отрезке [а, Ь\ задана не-
непрерывная функция y = f(x). Требуется
вычислить определенный интеграл
ь
\f{x)dx.
а
Разделим отрезок [а, Ь] точками Рис. 227.
a = xQJ x±J х2У ..., xn = b на л равных
частей длины Ах: Ах = -^ .
п
Обозначим далее через y0J уи y2J ..., уп~ъ Уп значения функ-
функции / (х) в точках х07 *!, х2, ..., хп, т. е. #0 = /(*©)» Уг = / (*i). • • •
-.1 Уп = !(Хп)-
Составим суммы у0 Ах + Уг Ах + ... + уп_х Ах, уг Ах + у2 Ах + ...
...+уаАх.
Каждая из этих сумм является интегральной суммой для / (х)
на отрезке [а, Ь] и поэтому приближенно выражает интеграл:
ь
ZZ J, A)
b—a
+ •••+«/„)•
(П
Это и будут формулы прямоугольников. Из рис. 227 ясно, что
если / (х) — положительная и возрастающая функция, то формула
A) выражает площадь ступенчатой фигуры, составленной из
«входящих» прямоугольников, а формула (Г) —площадь ступен-
ступенчатой фигуры, состоящей из «выходящих» прямоугольников.
Ошибка, совершаемая при вычислении интеграла по формуле
прямоугольников, будет тем меньше, чем больше число п (т. е. чем
меньше шаг деления Ах = I .

386
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
П. Формула трапеций. Естественно ожидать, что мы по-
получим более точное значение определенного интеграла, если дан-
данную кривую y = f(x) заменим не ступенчатой линией, как это было
в формуле прямоугольников, а вписанной ломаной (рис. 228),
Тогда площадь криволинейной трапеции аАВЬ заменится суммой
площадей прямолинейных трапеций, ограниченных сверху хордами
AAi9 A±A2y ..., Ап_гВ. Так как площадь первой из этих трапеций
У о +yi
У\ + У 2
—у-
и т. д., то
или
B)
Это и есть формула трапеций. Отметим, что число, стоящее в
правой части формулы B), есть среднее арифметическое чисел,
стоящих в правых частях формул A) и (Г).
Число п выбирается произвольно. Чем больше будет это число
и чем меньше, следовательно, будет шаг Ах = -^у тем с боль-
п
шей точностью сумма, написанная
в правой части приближенного ра-
равенства B), будет давать значение
интеграла.
III. Формула парабол
(формула Симпсона). Разде-
Разделим отрезок [а, Ь] на четное
число равных частей п = 2т. Пло-
Площадь криволинейной трапеции,
соответствующей первым двум
отрезкам [л:0, хг] и [xt, x2] и огра-
ограниченной заданной кривой y=f(x),
заменим площадью криволиней-
криволинейной трапеции, которая ограничена
параболой второй степени, проходящей через три точки
М (х0, у0), М1(х1У #х), М2 (х2, у2) и имеющей ось, параллельную
оси Оу (рис. 229). Такую криволинейную трапецию будем назы-
называть параболической трапецией.
Уравнение параболы с осью, параллельной оси Оу, имеет вид
Рис. 228.
Коэффициенты Л, В и С однозначно определяются из условия,
что парабола проходит через три заданные точки. Аналогичные
параболы строим и для других пар отрезков. Сумма площадей
параболических трапеций и даст приближенное значение интеграла.
Вычислим сначала площадь одной параболической трапеции.

§8] ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 387
Лемма. Если криволинейная трапеция ограничена параболой
осью Ох и двумя ординатами, расстояние между которыми равно
2А, то ее площадь равна
C)
где у0 иу2 — крайние ординаты, ауг — ордината кривой в середине
отрезка.
Доказательство. Расположим вспомогательную систему
координат так, как показано на рис. 230.
Рис. 229.
Коэффициенты в уравнении параболы у = Ах2 + Вх + С опре-
определяются из следующих уравнений:
если хо= — й, то yo = Ah2 — Bh-\-C,
если #i = 0, то #!= С,
если х2 = /г, то y2 = A
D)
Считая коэффициенты А, В, С известными, определим площадь
параболической трапеции с помощью определенного интеграла:
S =
-А
АBЛ/12+6С).
. Сле-
СлеНо из равенств D) следует, что
довательно, S = y (Уо + 4#1+#2)> что и требовалось доказать.
Вернемся снова к основной нашей задаче (см. рис. 229).
Пользуясь формулой C), мы можем написать следующие

388 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
приближенные равенства (h =
. Х?
^Г (yz+
Xt
Ах
а
ИЛИ
ь
Складывая левые и правые части, получим слева искомый
интеграл, справа его приближенное значение:
уш)9
E)
Это и есть формула Симпсона. Здесь число точек деления 2т
произвольно, но чем больше это число, тем точнее сумма в пра-
правой части равенства E) дает значение интеграла *).
2
Пример. Вычислить приближенно In 2 = \ —.
Решение. Разделим отрезок [1, 2] на 10 равных частей (рис.231).
2 1
Полагая Ajc= =0,1, составим таблицу значений подынтегральной функции:
X
*!=!
*з =
*4 =
Х5 =
,0
1,1
1,2
1,3
1,4
1,5
«/0= 1,00000
у* = 0,90909
у2 = 0,83333
Уз = 0,76923
у± = 0,71429
|/5=0,66667
*в=1.6
*7 = 1,7
^=1,8
хв=1,9
лгю=2,0
*/б = 0,62500
у7= 0,58824
ув = 0,55556
у9 = 0,52632
у10 = 0,50000
*) Для того чтобы знать, сколько точек деления надо взять, чтобы под-
подсчитать интеграл с заданной степенью точности, можно воспользоваться фор-
формулами оценки погрешности, получающейся при приближенном вычислении
интеграла. Мы не приводим здесь этих оценок. Читатель может найти их
в более подробных курсах анализа: см., например, Фихтенгольц Г. М.
Курс дифференциального и интегрального исчисления, т. II.—М.: Наука, 1970,
гл. IX, § 5.

ФОРМУЛА ЧЕБЫШЕВА
389
I. По первой формуле прямоугольников A) получим
2
2
С
1
По второй формуле прямоугольников (Г) получим
2
Y ~ °»1 A/1 + 1/2+ •. • +!/ю) = 0,1 -6,68773 = 0,66877.
1
Непосредственно из рис. 231 следует, что в данном случае первая фор-
формула дает значение интеграла с избытком, «у
вторая — с недостатком. *
II. По формуле трапеций B) получим
2
С — я 0,1 ( 1+0°>5 +6,18773 ) =0,69377.
J х \ 2, J
1
III. По формуле Симпсона E) имеем
2
С dx 0 1 - - *
\ — W -~- [Г/0 + ^10 + 2 A/2 + 1/4 + ^6 + 1/8)+ *
Г Рис. 231.
+4(*/1+#з+1/5 + */7+1/9)]=^ 0+0,5 + 2-2,72818 + 4.3,45955) = 0,69315.
2
В действительности In 2= \ —-=0,6931472 (с точностью до седьмого
1
знака).
Таким образом, при разбиении отрезка [0, 1] на 10 частей по формуле
Симпсона мы получили пять верных знаков; по формуле трапеций—лишь три
верных знака; по формуле прямоугольников мы можем ручаться только за
первый знак.
§ 9. Формула Чебышева
В технических вычислениях часто применяется формула Чебы-
Чебышева для приближенного интегрирования.
ь
Пусть снова требуется вычислить \ / (х) dx.
а
Заменим подынтегральную функцию интерполяционным много-
многочленом Лагранжа Р (х) (§9 гл. VII), взяв на отрезке [а, Ь] неко-
некоторые п значений функции / (х^, f (х2), ...,/(*„), где хь х21 ..., хп —
какие угодно точки отрезка [а, Ь]:
n/v\ (х *а) (х #з)...(# хп)
—j^) (JCi—Jca).. .(JCx—j^)
i) (x—x3)... (x—xn) r ,
*).. .(ь-Хп) Г ^
—Xj (X—X2). . .(x — Xn-l

3§0 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
Получим следующую приближенную формулу интегрирования:
ь ь
\f(x)dx*t\P(x)dx\ B)
а а
после некоторых вычислений она примет вид
ь
(xn), C)
где коэффициенты Ci вычисляются по формулам
ь
р Г (* — X1)...(X — XJ-1)(X — Xj + 1)...(x — Xj . ,.ч
1 J (xi-xj).. .(хс-х^г) (*,-*,+1).. .(xt-xj иЛ' V ;
a
Формула (З) громоздка и неудобна для вычислений, так как
коэффициенты С/ выражаются сложными дробями.
Чебышев поставил обратную задачу: задать не абсциссы хи
%г> • • •> хп> а коэффициенты С19 С2, ..., Сп и определить абсциссы
Коэффициенты Ct- задаются так, чтобы формула C) была воз-
возможно проще для вычислений. Очевидно, что это будет тогда,
когда все коэффициенты Ci равны между собой: Сг = С2 = ... = Сп.
Если обозначить общее значение коэффициентов Clf С2, ..., Сп
через Cnf то формула C) примет вид
)l E)
Формула E) представляет вообще приближенное равенство,
но если f(x) есть многочлен степени не выше я — 1, то равенство
будет точным. Это обстоятельство и позволяет определить вели-
величины СпУ х19 х2, ..., хп.
Чтобы получить формулу, удобную для любого промежутка
интегрирования, преобразуем отрезок интегрирования [а, Ь] в отре-
отрезок [—1, 1]. Для этого положим х = ~--\—-^t] тогда при
t = — 1 будет х = а, при /=1 будет х = Ь.
Следовательно,
где через ф (t) обозначена функция от t, стоящая под знаком
интеграла. Таким образом, задача интегрирования данной функции

ФОРМУЛА ЧЕБЫШЕВА
391
f(x) на отрезке [а, Ь] всегда может быть сведена к интегрирова-
интегрированию некоторой другой функции ф(х) на отрезке [—1, 1].
Итак, задача свелась к тому, чтобы в формуле
г
\ F)
-i
подобрать числа СпУ х±, х2У ..., хп так, чтобы эта формула была
точной для всякой функции f(x) вида
/ (х) = а0 + ахх + а2х2 + ... +яй_1д;*~1. G)
Заметим, что
1 г
^^ , если л — число нечетное;
П } (8)
2(ao+~ + ... +-~fp)t если п — число четное.
С другой стороны, сумма, стоящая в правой части равенства
F), на основании G) будет равна
Приравнивая выражения (8) и (9), получим равенство, которое
должно быть справедливо при любых а0, а1У а2, ..., йптя1:
2 (flo + т +х + Т+ • • • )= C«
(х\+х1+ ... +х2п) + ...
Приравняем коэффициенты при я0, а1э а2, а3, ..., а,,.^ в ле-
левой и правой частях равенства:
^Слп, или Ся = -|,
• • • г лп or — Q >
-^l i -^2 -г • • • "Т ^/»==: С~ ~ ~b'
A0)
Из последних п — 1 уравнений находим абсциссы *1Э лс„ ..., хп.
Эти решения найдены Чебышевым для различных значений п.
Ниже приводятся найденные им решения в случаях, когда число п
промежуточных точек равно 3, 4, 5, 6, 7, 9:

39?
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
Число
ординат
п
3
4
5
6
Коэф-
Коэффициент
Сп
2
3
1
2"
2
5
1
3
Значения абсцисо
*1» Хг ХП
^ = — ^3 = 0,707107
*2 = 0
^ = — ^4=^0,794654
*2 = —*3 = 0,187592
^ = — ^ = 0,832498
*2 = —*4 = 0,374541
*з = 0
^=—^ = 0,866247
*2 = --л;5 = 0,422519
*з = —*4 = 0,266635
Число
ординат
п
7
9
Коэф-
Коэффициент
Сп
2
7
2
9
Значения абсцисо
#1, #«> ...» Хп
*! = —х7 = 0,883862
д:2 = —д:б = 0,529657
дг3 = —аг5 = 0,323912
*4 = 0
^ = — ^ = 0,911589
л:2 = — лг8 = 0,601019
лг3=—д:7 = 0,528762
дг4 = —*6 = 0,167906
*5 = 0
Таким образом, приближенное вычисление интеграла на от-
отрезке [ — 1, 1] производится по следующей формуле Чебышева:
§
где п —какое-либо из чисел 3, 4, 5, 6, 7 или 9, a xiy .. .t xn-*~
числа, приведенные в таблице. В качестве п нельзя брать число 8
или числа, превосходящие 9; в этом случае система уравнений
A0) дает мнимые корни. Когда заданный интеграл имеет пределы
интегрирования а и Ь, формула Чебышева принимает вид
[i= 1, 2, ..., л), а X; имеют указанные
в таблице значения.
2
Г dx
Пример. Вычислить \ — ( = 1п2).
Решение. Прежде всего заменой переменной преобразуем этот интеграл
в новый интеграл, у которого границы интегрирования будут—1 и 1;
1+2 . 2 — 1, 3 . t 3+t . dt - Cdx Г dt

§10] ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА. ГАММА-ФУНКЦИЯ 393
числим последний интеграл, приняв п — 3, по формуле Чебышева:
i
J / @ ^ = 4 [/ (°'707107) + / @) + /(—0.707107I.
Так как / @,707107) = 0,269752, f @) = 0,333333, f (—0,707107) =0,436130, то
1
dt 2 2
4 4 0,693.
V
J
J о -pf «3
Сравнивая этот результат с результатами вычисления по формулам пря-
прямоугольников, по формуле трапеций и формуле Симпсона (см. пример в пре-
предыдущем параграфе), мы замечаем, что результат, полученный нами по формуле
Чебышева (с тремя промежуточными точками), лучше согласуется с истинным
значением интеграла, чем результат, полученный по формуле трапеций
(с девятью промежуточными точками).
Отметим, что теория приближенного вычисления интегралов
получила дальнейшее развитие в работах академика А. Н. Кры-
Крылова A863-1945).
§ 10. Интегралы, зависящие от параметра. Гамма-функция
Дифференцирование интегралов, зависящих от
параметра. Пусть дан интеграл
ь
A)
в котором подынтегральная функция зависит от некоторого пара-
параметра а. Если параметр а будет меняться, то будет меняться и
значение определенного интеграла. Таким образом, определенный
интеграл есть функция от а; поэтому мы его можем обозначить
через / (а).
1. Предположим, что f(x, а) и f'a (#> а)—непрерывные функ-
функции при
c<a<d и а<л:<&. B)
Найдем производную интеграла по параметру а:
Iim tz =/а(а)-
Да,-* 0 afX
Для нахождения этой производной заметим, что
Гь ь 1
А^ l^x> v* + k<x)dx—^f(xy a)dx =
Да
a
С f(x, a + Aa) — f(x, a)
'"'J Aa *
a

394 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
Применяя теорему Лагранжа к подынтегральной функции, будем
иметь /fo*+A^)--/(*. а) = /; (^ а + еДа), где 0 < 0 < 1. Так как
/at** a) непрерывна в замкнутой области B),то /« (х, a + QAa) =
= f'a(x, a) + е, где величина е, зависящая от л:, a, Aa, стремится
к нулю при Да—-*0. Таким образом,
Переходя к пределу при Да—*0, получаем*)
Аа-
или
J / (х, a) dx\ = J /а (^, а) Л
a Ja a
Последняя формула называется формулой Лейбница.
2. Предположим теперь, что в интеграле A) пределы ин-
интегрирования a и Ь являются функциями от а:
/(а) = Ф[а, а (а), 6(а)]= j /(^, а) Л. (Г)
а (а)
Ф[а, а (а), Ь(а)] есть сложная функция от а, причем а и Ь
являются промежуточными аргументами» Для того чтобы найти
производную от / (а), применим правило дифференцирования слож-
сложной функции от нескольких переменных (см. § 10 гл. VIII)
На основании теоремы о дифференцировании определенного
интеграла по переменному верхнему пределу (см. § 4) получаем
а
Ъ
*) Подынтегральная функция в интеграле /= \ 8 da стремится к нулю при
а
Да—)-0. Из того, что подынтегральная функция в каждой точке стремится
к нулю, не всегда следует, что интеграл также стремится к нулю. Однако
в данном случае / стремится к нулю при Да—>(). Этот факт мы принимаем
без доказательства.

§1&] ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА. ГАММА-ФУНКЦИЯ 395
Наконец, для вычисления -тг— применяем формулу Лейбница:
а
Подставляя в ф°РмУлУ i?) полученные выражения производных,
будем иметь:
Ь(а)
) Г*(х, *)dx + f[b(a), a]^-f[a(a), a]-g-. D)
а (а)
Ь(а)
()
С помощью формулы Лейбница можно вычислить некоторые опре-
определенные интегралы.
+ «
Пример 1. Вычислить интеграл / (а) = \ е"* —-— dx.
о
Решение. Заметим прежде всего, что непосредственно вычислить этот
л л. у Sin aX
интеграл мы не можем, так как первообразная от функции е~х не вы-
х
ражается через элементарные функции. Для вычисления данного интеграла
будем рассматривать его как функцию от параметра а. Тогда его производная
по а найдется по выведенной выше формуле Лейбница *):
о
Но последний интеграл легко вычисляется с помощью элементарных функ-
функций; он равен 2 . Поэтому /' (ос) = 2 . Интегрируя полученное тож-
тождество, найдем /(а): / (а) = arctg a 4- С. E) Остается определить С. Для этого
замечаем, что
+00
/@)= Г e-*ii?°?d*= Г <и*=
Кроме того, arctg 0 = 0. Подставляя в равенство E) а = 0, найдем 7@) =
= arotgO+C, откуда С = 0. Следовательно, для любого значения а имеет
место равенство / (а) = arctg а, т.е.
+ 00
v sin ax , .
е~х dx = arctg а
*) Формула Лейбница выведена в предположении, что пределы интегриро-
интегрирования а и b конечны. Однако в данном случае формула Лейбница также спра-
справедлива, хотя один из пределов интегрирования равен бесконечности. Об усло-
условиях, при которых допустимо дифференцирование несобственных .интегралов
по параметру, см., например, в книге: Фихтенгольц Г. М. Курс диффе-
дифференциального и интегрального исчисления, т. П.— М.: Наука, 1970, гл. XIV, § 3.

396 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
Пример 2. Гамма-функция.
Рассмотрим интеграл, зависящий от параметра а,
+ 00
x<*-4-xdxm F)
Покажем, что этот несобственный интеграл существует (сходится) при а > 0.
Представим его в виде суммы
+ 00 1 +00
\ ха~1е~х dx~ \ ха~ге~х dx-\- \ хсс~1е~х ^х9
J J J
о о 1
Первый интеграл правой части сходится, так как
1 1
0<
\x^-1e"xdx< f *«-id* = —
Второй интеграл также сходится. Действительно, пусть п—целое число такое,
что п > а—1. Тогда, очевидно,
+ 00 +00
0< С 7P>-4-*dx< \ xne-*dx< + oo.
1 \
Последний интеграл вычисляем путем интегрирования по частям с учетом
того, что
lim ^-=0 G)
при любом целом положительном k. Итак, интеграл F) определяет некото-
некоторую функцию а. Ее обозначают Г (а) и называют гамма-функцией:
+ 00
о
Эта функция часто используется в приложениях математики. Найдем значе-
значения Г (а) при целых а. При а=1 имеем
+ 00
ГA) = J e-*dx=*l. (9)
о
Пусть целое а > 1. Интегрируем по частям:
+ 00 +00 +00
Г(а)= 5 **-\
о
или, учитывая G),
Г(а) = (а~1)Г(а-1). A0)
На основании A0) и (9) находим при а — п
Г(и)»(п-1)!. (И)

УПРАЖНЕНИЯ К ГЛАВЕ XI 397
§11. Интегрирование комплексной функции
действительной переменной
В § 4 гл. VII была определена комплексная функция }(х) =
= и (х) 4- iv (х) действительной переменной л; и ее производная
f
Определение. Функция F (х) = U(x)-f IV(х) называется пер-
первообразной от комплексной функции f(x) действительной пере-
переменной, если
F'{x) = f(x), A)
т. е. если
С/' (х) + iV (x) = u(x) + to (x). B)
Из равенства B) следует, что U' (х) = и(х), V (x) = v(x), т.е.
U(x) есть первообразная для и (х) и V (х) есть первообразная для
Из определения и этого замечания следует: если F (x) — U(x) +
-\-iV(x) есть первообразная для функции /(#), то любая первооб-
первообразная для f(x) имеет вид F(x) + C, где С — комплексная произ-
произвольная постоянная. Выражение F (х) + С будем называть неопре-
неопределенным интегралом от комплексной функции действительной
переменной и писать
l l C)
Определенный интеграл от комплексной функции / (х) — и (х) +
-\- iv (х) действительной переменной определяем так:
ь ь ь
J f{x) dx=lu{x)dx + i \v(x)dx. D)
а а а
Это определение не противоречит, а вполне согласуется с оп-
определением определенного интеграла как предела суммы.
Упражнения кглаве XI
Составляя интегральную сумму sn и переходя к пределу, вычислить
определенные интегралы:
ъ
1. \ x2dx. Указание. Отрезок [а, Ь] разделить на п частей точками
X[=^aql (i = 0, 1, 2, ,.., л), где q = l/ —.
га
2. \ ~ , где 0 < а < Ь. Отв. In— .Указание. Деление отрезка [а, Ь]
%) х а
а
производить так же, как и в предыдущем примере.

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
Ъ
3. \ y"xdx. Ome. -^- (ft*'1—д8/а). Указание. См. предыдущий пример.
а
b
. Ome. cos #—cos b. Указание. Предварительно устано-
установить следующее тождество: sina+sin (a-j-h)-i-sin (a+2A)-(-...-|-sin [a-\-(n—O^J^
cos (a—h) — cos (a-\-nh)
= - j^—-—r—^—! , для этого надо умножить и разделить все члены
? sin ft
левой части на sin h и заменить произведение синусов разностью косинусов.
ь
5. [ cosxdx. Ome, sin b—sin а.
а
Пользуясь формулой Ньютона—Лейбница, вычислить определенные ин-
интегралы:
II я/2 1
6. [x*dx. Отв. — .7.Гe*dx.Ome. г—1.8. f sinxdx. Отвч 1. 9. f гт^ •
oo о о
я/3
/ /
. -^. 10. С dx 2 . От(9. ~. 11. J tg^rfjp. Ome. In2. 12. J~,
. 1. 13. f ~. O/пл ln|jcl. 14. f sln^d*. Oms. 2sin2-~. 15. С х2 cto.
1 * ° V*
2 Л/2
. 16. J
/
^P 0/П<?* ~1п|2г —1[. 17. f
о
18. С
3
б
Я/2
' 4 '
о
Вычислить значения нижеследующих интегралов, применяя указанные
подстановки;
Я/2 Я
dx '.*t.O«m.
19. Г sin х cos2 xdx, cosx=t Отв. ф- 20. Г
о о
COS #
Г 21-1
4/3
От*, х+4-- Cl^^ Г
4/3
*, х+4-- 23. Cl-^^^,^---l=^.Oma.2B-.aretg2).24. Г fz
42 Iх ъ%*** + 1
л/2

УПРАЖНЕНИЯ К ГЛАВЕ Х? 399
Доказать, что
1 1 Ь
26. С*отA—x)ndx~\ *«(i— x)mdx (m>0, n > 0). 27. [ f(x)dx =
0 0 fl
ft а а
f (a+b—x) dx. 28. Г / (*2) dx= у
0 -a
Вычислить следующие несобственные интегралы:
1 +QO + оо
dx л jc
29. С_?^!Ц-. Оя». 1. 30.
о *
1
f е-^^л:, Ол». 1. 3L С fl
о о
оо 1
(a > 0), 32. С rf* . Отв.^ . 33. Г ^. Oms, -i-. 34. С in д; dx. Отв> —I.
о 1 о
+ 00 +00
i. \ xsinxdx. Отв. Интеграл расходится. 36. \ . Отв. Интеграл
+ 00
35,
о
+ 00
dx
расходится. 37.
-оо О V Х О
Отв. Интеграл расходится. 40. \ — х Отв. •-.• 41, \ —j-. Om<9.
Интеграл расходится. 42. \ е"ахsinbxdx (a>Q). Отв. г\иг*
о
+ 00
С а
43. \ е~аХ tosbxdx (а > 0). О/яя. 2 ^.
о
Вычислить приближенные значения интегралов:'
5
44. In 5= \ — по формуле трапеций и по формуле Симпсона (л =12). Отв.
1,6182 (по формуле трапеций); 1,6098 (по формуле Симпсона).
45. \ ? dx по формуле трапеций и по формуле Симпсона (п=10). Ояю.
1
3690, 3660.
1
46. \ y\—xzdx по формуле трапеций (л=6). Отв. 0,8109.
о
з
С dx
47. \ ^ г по формуле Симпсона (я = 4). Отв. 0,8111.
1
ю
48. \ Igxdx по формуле трапеций и по формуле Симпсона (п = 10). Отв0
6,0656; 6,0896.

400 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
1
49. Вычислить значение я из соотношения -j= \ 2, применяя фор-
о
мулу Симпсона (п=Щ. Отв. 3,14159.
50. \ dx по формуле Симпсона (/г=10). Отв. 1,371.
о
+ 00
51. Исходя из равенства \ е-ъ* dx=—, где а > 0, найти при целом
+ со
п >0 величину интеграла \ e~xxndx. Отв. п\.
о
+ 00
52. Исходя из равенства \ * д—5---, найти величину интеграла
*р° dx jt 1>3-5>...*Bя—1)
J (Jt2+1)«+1* 2 2«nJ
о
+ 00
г* \ g~ax
53. Вычислить интеграл \ ^—dx. Отв. 1пA + а) {«>-—1).
о
54. Пользуясь равенством \ хп~* dx~— , вычислить
о
. Отв. (—1^L
интеграл

ГЛАВА XII
ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
§ 1. Вычисление площадей в прямоугольных координатах
Если на отрезке [а, Ь] функция /(#)]> О, то, как известно
(§ 2, гл. XI), площадь криволинейной трапеции, ограниченной
кривой у = / (х), осью Ох и прямыми х = а и х = Ъ (рис. 214), равна
ь
Q=\f(x)dx. A)
а
Ь
Если / (х) ^ 0 на [а, Ь], то определенный интеграл ^ / (х) dx
а
также ^0. По абсолютной величине он равен площади Q соот-
ь
ветствующей криволинейной трапеции: —Q=]f(x)dx.
а
Если f(x) конечное число раз меняет знак на отрезке [а, 6],
то интеграл по всему отрезку [а, Ь] раз-
разбиваем на сумму интегралов по частич-
частичным отрезкам. Интеграл будет положите-
положителен на тех отрезках, где f(x)^O, и от-
отрицателен там, где f(x)^.O. Интеграл по
всему отрезку даст соответствующую ал- ~
гебраическую сумму площадей, лежащих
выше и ниже оси Ох (рис. 232). Для рис 232
того чтобы получить сумму площадей в
обычном смысле, нужно найти сумму абсо-
абсолютных величин интегралов по указанным выше отрезкам или вы-
ь
числить интеграл Q=\\f(x)\dx.
Пример 1. Вычислить площадь Q фигуры, ограниченной синусоидой
y = sinx и осью Ох, при 0«^л:<;2я (рис. 233).
14 Н. С. Пискунов, т. I

402 ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА [ГЛ. XII
Решение. Так как sin х^ 0 при 0 <: х ^ я и sin х ^ 0 при jx < х ^ 2щ
то
2Я
Q=\ sin*^A:+ \ sinxdx =* \ \sinx\dx,
2я
¦s
О
sin xdx = —cos x
о
2я
sin x dx = — cos x
= — (cos я — cosO)=— (— 1 —1)=2,
= — (cos 2л — cos я) = —2.
Следовательно, Q=2 + |—2 | = 4.
Если нужно вычислить площадь области, ограниченной кри-
кривыми y — fi{x), y = f2(x) и ординатами х = а, х = Ь, то при усло-
условии fi(x)^f2(x) будем иметь (рис. 234)
ь ъ ь
а а а
П р_и м е р 2. Вычислить площадь фигуры, ограниченной кривыми (рис. 235)
у = У х и у = х2.
Решение, Находим точки пересечения кривых: У х=х2\ х = х^} откуда
хг = 0, х2 = 1.
Рис. 233.
а
Рис. 234.
Ь я
Рис. 235.
Следовательно,
1 1
x--x*)dx=-jx*'
Рис. 236.
о™ 3
_ _J_
3 3~3 "
Вычислим теперь площадь криволинейной трапеции в случае,
если кривая задана уравнениями в параметрической форме

§ 1J ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ 403
(рис. 236)
* = ф@, #=Ф@. C)
где а^/^C и <р(а)=я, фф) = 6. Пусть уравнения C) опреде-
определяют некоторую функцию y = f(x) на отрезке [а, Ь~\ и, следова-
следовательно, площадь криволинейной трапеции может быть вычислена
по формуле
Сделаем замену переменной в этом интеграле: x = (p(t), dx —
s= q/ (t) dt. На основании уравнений C) получим y = f(x) =ч
s= / [ф (/)] = г|) @. Следовательно,
'@*. D)
Это и есть формула для вычисления площади криволинейной тра-
трапеции в случае кривой, заданной параметрически.
Пример 3. Вычислить площадь области, ограниченной эллипсом
х — а cos /, y = b sin t.
Решение. Вычислим площадь верхней половины эллипса и удвоим.
Здесь х изменяется от —а до +а, следовательно, t изменяется от я до 0,
=2 [ (bsint)(—asintdt) = —2ab [ sm2tdt = 2ab [sin2 tdt=:
0
. о ,Г / sin2n«
я
я
(М— cos 2/
с/
Пример 4. Вычислить площадь области, ограниченной осью Ох и одной
аркой циклоиды x = a(t — sin О» у = а(\—cost).
Решение. Изменению t от 0 до 2л соответствует изменение х от 0 до 2яа,
По формуле D) имеем
2я 2я
Q= С яA—cos 0 а A— cost)dt = a2 J (I—cos*)a<tt =
Q 0
[2я 2я 2я 
Jd/—2 ^ cos/d/+J cos2/^ ,
0 0 0 J
2я 2я
f ^1?==2я, Г cos / ^ = 0, f cos2 / d/= C
во о а
2я 2я
1 + C^s2^ dt=n.
Окончательно получаем Q = a2 Bл+я) = Зла2.
14*

404
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. ХЦ
§ 2. Площадь криволинейного сектора
в полярных координатах
Пусть в полярной системе координат имеем кривую, заданную
уравнением р = /@), где / @) — непрерывная функция при а^
<8р
Д0П
<8<р.
Определим площадь сектора ОАВ, ограниченного кривой
p=^f (В) и радиус-векторами 0 — а и 0 = р.
Разобьем данную область радиус-векторами а = 0о, 0 = 0lt
. >#> вп = $ на п частей. Обозначим через Д0Х, А02, .
углы между проведенными радиус-векторами (рис. 237).
\ i
\
v
V У*
V /
/
\
\
cos 2д
\
Рис. 237.
Рис. 238.
Обозначим через р( длину радиус-вектора, соответствующего
какому-нибудь углу 0,., заключенному между Q[^1 и 6i#
Рассмотрим круговой сектор с радиусом pf и центральным
углом А0Г Его площадь будет равна AQ,- ==yp? A9,.. Сумма
^2/)]2A0t- даст площадь «ступенчатого»
сектора.
Так как эта сумма является интегральной суммой для функции
p2 = [f(Q)]2 на отрезке а^0^р, то ее предел при тахДб,.—>0
1 г
есть определенный интеграл -^{р^сЮ. Он не зависит от того,
какой радиус-вектор р{ мы возьмем внутри угла Д0,-. Этот предел
естественно считать искомой площадью фигуры *). Таким образом,
площадь сектора ОАВ равна
*) Можно было бы показать, что это определение площади не противоре-
противоречит данному ранее; иначе говоря, если вычислять площадь криволинейного
сектора с помощью криволинейных трапеций, то мы получим тот же результат.

$3]
или
ДЛИИА ДУГИ КРИВОЙ
405
Пример. Вычислить площадь фигуры, ограниченной лемнискатой
(рис. 238) р=-а]^соТ20.
Решение. Радиус-вектор опишет область с площадью, равной четверти
искомой площади, если 6 меняется от 0 до л/4:
Я/4 Я/4
Таким образом, площадь фигуры, ограниченной лемнискатой, будет равна
§ 3. Длина дуги кривой
1. Длина дуги кривой в прямоугольных коорди-
координатах. Пусть в прямоугольных координатах на плоскости дана
кривая уравнением y = f(x).
Найдем длину дуги А В этой кривой, заключенной между
вертикальными прямыми х = а и х = Ь
(рис. 239).
В главе VI (§ 1) было дано определение
длины дуги. Напомним это определение.
Возьмем на дуге АВ точки Л, М1ч М2У ...
..., Miy ..., В с абсциссами a = xQy xu х2,
.. ¦, xh ..., хп = Ъ и проведем хорды АМи
МгМ2, ..., Мп_хВ, длины которых обо-
обозначим соответственно через As19 As2, ...
..., Asn. Тогда получим ломаную АМгМ2...
... Мп„гВ, вписанную в дугу А В. Длина
ломаной равна sn=
Длиной s дуги АВ называется тот предел, к которому стре-
стремится длина вписанной ломаной, когда длина ее наибольшего
звена стремится к нулю:
п
s= lira 2 As,-. A)
max Asp*-0 i = 1
Мы докажем сейчас, что если на отрезке a^x^ib функция
/ (х) и ее производная /' (х) непрерывна, то этот предел сущест-
существует. Вместе с тем будет дан и способом вычисления длины дуги.
Введем обозначение Ayt = / (xt) — f (Х;_г). Тогда
2

406 ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА [ГЛ. XII
По теореме Лагранжа имеем д^= ' J* ==/' (?,)» где *,_!<
< \i < х(. Следовательно, As{ = V1 + [/' (S/)]a Да:, .
Таким образом, длина вписанной ломаной равна
По условию, /' (х) непрерывна, следовательно, функция
У\+[Г (х)]* тоже непрерывна. Поэтому существует предел написан-
написанной интегральной суммы, который равен определенному интегралу:
s= lim S У1 + [Г (Б/)Р А^/ = S К1 + [Г (*)]2 Лс. Итак, полу-
max Длг^О t=l #
чили формулу для вычисления длины дуги:
ь ь
Замечание 1. Исходя из последней формулы, можно полу-
получить производную от длины дуги по абсциссе. Если верхний пре-
предел интегрирования будем считать переменным и обозначим через
х (переменную интегрирования менять не будем), то длина дуги s
х
будет функцией от х: s(*) = J у 1 + f^j2^. Дифференцируя
<з>
этот интеграл по верхнему пределу, получим
Эта формула была получена в § 1 гл. VI при иных предположе-
предположениях.
Пример 1. Определить длину окружности х2-\-у2 — г2.
Решение. Вычислим сначала длину четвертой части окружности, ле-
лежащей в первом квадранте. Тогда уравнение дуги АВ будет у=Уг2—х2,
dy х
откуда ^=-^__.
Следовательно,
--s—\ 1/ 1+-= «dx= \ —z
о о г
п
~2%
Длина всей окружности s = 2nr.
Найдем теперь длину дуги кривой в том случае, когда урав-
уравнение кривой задано в параметрической форме:
D)

§ 3] ДЛИНА ДУГИ КРИВОЙ 407
где ф(*) и -ф @ — непрерывные функции с непрерывными произ-
производными, причем ср' (t) на заданном участке не обращается в нуль.
В этом случае уравнения D) определяют некоторую функцию
y = f(x), непрерывную и имеющую непрерывную производную
dyq'jt)
dx ф'(/)"
Пусть а = у(а), Ь = ц>ф). Тогда, сделав в интеграле B) под-
подстановку x = q>(t)y dx = y (t)dty получим
3 у ; g
s= \ у 1-|- ;:J ср' (/) dt, или s =
ос а
Замечание 2. Можно доказать, что формула E) остается
в силе и для таких кривых, которые пересекаются вертикальными
прямыми более чем в одной точке (в частности, для замкнутых
кривых), лишь бы во всех точках кривой были непрерывны обе
производные <р' (t) и -ф' (/).
Пример 2. Вычислить длину астроиды # = acos3/, у —a sin3 /.
Решение. Так как кривая симметрична относительно обеих координат-
координатных осей, то вычислим сначала длину ее четвертой части, расположенной
в первом квадранте. Находим — =*—За cos2 /sin/, ~ = 3asin2 /cos /, Пара-
Параметр / будет изменяться от 0 до л/2. Следовательно,
я/2 я/2
\
о Г • 4 *л о sin2 / |я/2 За
= 6а \ sin t cos t at = 6a —j^— ==;— ; s = 6a,
J * |Q Z
~s = [ /9а2 cos4 t sin2 /+9а2 sin4 / cos2 tdt = 3a Г /cos2 / sin2 / dt
n/2
Замечание З. Если задана пространственная кривая
параметрическими уравнениями
где а^/^р (см. § 1 гл. IX), то длина ее дуги определяется
(так же как и для плоской дуги) как предел, к которому стре-
стремится длина вписанной ломаной, когда длина наибольшего звена
стремится к нулю. Если функции ф(/), «ф@ и %(t) непрерывны
и имеют непрерывные производные на отрезке [а, Р], то кривая
имеет определенную длину (т. е. для нее существует вышеуказан-
вышеуказанный предел), которая вычисляется по формуле
Э
*= S VW (<)Г+№ (*)Р + [Х# (t)fdt. G)
а
Последний результат мы принимаем без доказательства.

408
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. XII
Пример 3. Вычислить длину дуги винтовой линии x = acost, у =
= asin^, z = amt при изменении t от 0 до 2jt.
Решение. Из данных уравнений находим dx = — as'mtdt, dy = aco$tdt,
dz~amdt. Подставляя в формулу G), получим
s=
Длина дуги кривой в полярных координатах.
Пусть в полярных координатах задано урав-
нение кривой
(8)
2.
где р — полярный радиус, 0 —полярный
угол.
Напишем формулы перехода от поляр-
полярных координат к декартовым: x = pcos9,
# = psin9. Если сюда вместо р подставим
его выражение (8) через 6, то получим
уравнения x = f (9) cos 9, y = f(Q) sinO. Эти
уравнения можно рассматривать как парамет-
параметрические уравнения кривой и для вычисления длины дуги при-
применить формулу E). Для этого найдем производные от х и у по
параметру Э:
Рис.240.
fQ = r (в)cos9-/@) sin9, | = /' (9) sin9 + /(9) cos9.
Тогда
Следовательно,
Пример 4. Найти длину кардиоиды р = а A+ cos 0) (рис. 240).
Изменяя полярный угол 9 от 0 до я, получим половину искомой длины.
Здесь р'= — asinO. Следовательно,
s=2
cos 0J
sin
WI)
cos
|
Пример 5. Вычислить длину эллипса
предполагая, что а > b.
Решение. Для вычисления воспользуемся формулой E). Вычислим
сначала 1/4 длины дуги, т. е. длину дуги, соответствующей изменению

§4] ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА 409
параметра от / = 0 до t = n/2:
Jt/2
/
0
У& sin* t+b* cos* tdt =
0
Я/2 Я/2
= С
о
2 — (a2—b
Я/2 я/2
С ^
Я/2
= a С 1/ 1 — 2-=^
я/2
где & = - < 1. Следовательно, s = 4a V у 1—klco§ltdt. Остается
о
только вычислить последний интеграл. Но он, как известно, не выражается
в элементарных функциях (см. § 14 гл. X). Этот интеграл можно вычислить
только приближенными методами (например, по формуле Симпсона).
В частности, если большая полуось эллипса равна 5, а малая равна 4,
Я/2
то & = 3/5, и длина эллипса равна s = 4»5 \ 1/ 1 — ("g") cos2 ?ctf. Вычис-
ВычисЯ/
= 3/5, и длина эллипса равна s = 4»5 \ 1/ 1 — ("g")
отрезок
л/2
Г /^ 3
а: V 1/ 1—=-
ляя последний интеграл по формуле Симпсона (деля отрезок [0, я/2] на че-
чел/2
тыре части), получим приближенное значение интеграла:
1,298, и, следовательно, длина дуги всего эллипса приближенно равна
s х 25,96 единицы длины.
§ 4. Вычисление объема тела
по площадям параллельных сечений
Пусть имеем некоторое тело Т. Предположим, что известна
площадь любого сечения этого тела плоскостью, перпендикулярной
к оси Ох (рис. 241). Эта площадь будет зависеть от положения
секущей плоскости, т. е. будет функцией отх:
Q = Q(x).
Предположим, что Q (х) есть непрерывная функция от ху и опре-
определим объем данного тела. Проведем плоскости х = хо=ау х = хи
Л Хау » » • у Jv П "
Эти плоскости разобьют тело на слои.
В каждом частичном промежутке x^i^.x^.X; выберем про-
произвольную точку ?,. и для каждого значения f=l, 2, ..., п по-
построим цилиндрическое тело, образующая которого параллельна
оси Оху а направляющая представляет собой контур сечения тела Т
плоскостью Аг = |г-. Объем такого элементарного цилиндра с пло-
площадью основания Q Hi) (*/_f ^Si^*i) и высотой kxt равен
п
Q (lt) Ах(. Объем всех цилиндров будет vn= 2 Q (?/) Д*/.

410
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. XII
Предел этой суммы при
зывается объемом данного тела:
v= lim
max Дх,->С
0 (если он существует) на-
наТак как vn представляет собой, очевидно, интегральную сумму
для непрерывной функции Q (х) на отрезке а^х^Ь, то указан-
Рис. 241.
Рис. 242.
ный предел существует и выражается определенным интегралом:
ь
v=\ Q(x)dx.
а
Пример. Вычислить объем трехосного эллипсоида (рис, 242)
(I)
Решение. В сечении эллипсоида плоскостью, параллельной плоскости
Oyz и отстоящей на расстоянии х от нее, получится эллипс
*|2 »2 ^2 »#2 »2
1 ^ , сг — с 1/ 1 2*^°
1 5 J.
Объем эллипсоида будет равен
такого эллипса
В частности, если a~b =
получаем
сг эллипсоид превращается в шар, и в этом случае
4 .

§6]
ПЛОЩАДЬ ПОВЕРХНОСТИ ТЕЛА ВРАЩЕНИЯ
411
§ 5. Объем тела вращения
Рассмотрим тело, образованное вращением вокруг оси Ох кри-
криволинейной трапеции аАВЬ, ограниченной кривой y = f(x), осью
Ох и прямыми х = а, х=^Ь.
В этом случае произвольное сечение тела плоскостью, перпен-
перпендикулярной к оси абсцисс, есть
круг, площадь которого Q = щг =
Применяя общую формулу для
вычисления объема [A) § 4], по-
получим формулу для вычисления
объема тела вращения:
ь ь
Рис. 243.
Пример. Найти объем тела,
образуемого вращением цепной линии
у = -^г{ех1а+е~х1а) вокруг оси Ох на
участке от # = 0 до х = Ь (рис. 243).
Решение.
о
—2e Jo"" 8^ ~~е +Т
§ 6. Площадь поверхности тела вращения
Пусть нам дана поверхность, образованная вращением кривой
y = f(x) вокруг оси Ох. Определим площадь этой поверхности на
участке а ^ х ^ Ь. Функцию / (х) предположим непрерывной
и имеющей непрерывную производную во всех точках отрезка [а, Ь].
Как и в § 3, проведем хорды АМ1У МгМ2У ..., Мп_гВ, длины
которых обозначим через As*, As2, ..., А^„ (рис. 244).
Каждая хорда длины As,- (i=l,2f ..., п) при вращении опишет
усеченный конус, площадь поверхности которого Lpt равна APt. =
= 2пy-±±±^^si. Но As, = KA^+Ayf= у/Т+Щ^Ах^ При-
Применяя теорему Лагранжа, получим -^i = *(**)--/w-0 = р (^л где
Xi-t < h < xt\ следовательно, As,- = V\ +/'2 (gf) A^, APf ~
= 2яУ|" ^ yiV\ + /'2 (li) Ajc,-. Площадь поверхности, описанной
ломаной, будет равна Рп = 2я
+ Г
или

412
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. XU
сумме
1=1
A)
распространенной на все звенья ломаной. Предел этой суммы, когда
наибольшее звено ломаной As,- стремит-
стремится к нулю, называется площадью рас-
рассматриваемой поверхности вращения.
Сумма A) не является интегральной
суммой для функции
W\ B)
Рис. 244.
так как в слагаемом, соответствующем
отрезку [*;_!, *,•], фигурирует нес-
несколько точек этого отрезка Х;_г, х{, ?,..
Но можно доказать, что предел суммы
A) равняется пределу интегральной
суммы для функции B), т.е.
= lim
max &Xj-+ 0 i=l
ИЛИ
C)
Пример. Определить площадь поверхности параболоида, образованного
вращением вокруг оси Ох дуги параболы у2 — 2рх, соответствующей изменению х
от х = 0 до х = а.
Решение.
f2=V 1+^ =
2х+р
2х
По формуле C) получим
а
§ 7. Вычисление работы с помощью определенного интеграла
Пусть под действием некоторой силы F материальная точка М
движется по прямой Os, причем направление силы совпадает с на-
направлением движения. Требуется найти работу, произведенную

§7]
ВЫЧИСЛЕНИЕ РАБОТЫ
413
силой F при перемещении точки М из положения s = a в поло-
положение s — b.
1) Если сила F постоянна, то работа А выражается произве-
произведением силы F на длину пути, т. е.
A = F(b-a).
2) Предположим, что сила F непрерывно меняется в зависимо-
зависимости от положения материальной точки, т. е. представляет собой
функцию F (s), непрерывную на отрезке
РазобьехМ отрезок [а, Ь] на п произ-
произвольных частей с длинами Aslt As2, ...
..., Asny затем в каждом частичном отрезке
1A-i> si\ выберем произвольную точку 1(
и заменим работу силы F (s) на пути As,-
{/=1,2, ..., п) произведением F (%{) As{.
Это значит, что в пределах каждого частич-
частичного отрезка мы принимаем силу F за пос-
постоянную, а именно полагаем F = F (?,-). В та-
таком случае выражение F (gf) As,- при дос-
достаточно малом Asf дает нам приближенное значение работы силы
///////ZyZy//,
Рис. 245.
F на пути As,-, а сумма Ап — 2 f (?,.) As,- будет приближенным
выражением работы силы F на всем отрезке [а, Ь].
Очевидно, Ап представляет собой интегральную сумму, состав-
составленную для функции F = F (s) на отрезке [а, Ь]. Предел этой суммы
при max Asf—^0 существует и выражает работу силы F (s) на
пути от точки s = a до точки s = b:
A)
Пример I. Сжатие S винтовой пружины пропорционально приложенной
силе F. Вычислить работу силы F при сжатии пружины на 5 см, если для
сжатия ее на 1 см нужна сила 10 Н (рис. 245).
Решение. Сила F и перемещение S связаны по условию зависимостью
F = kS, где k—постоянная.
Будем выражать «S в метрах, F—в ньютонах. При S = 0,01 F = 10, т. е.
10 = ^• 0,01, откуда ^ = 1000, F = 1000 S. На основании формулы A) имеем
0,05
С S2 10,05
А= \ 1000 S dS^lOOO-^l =1,25 Дж.
J ^ |о
о
Пример 2, Сила F, о которой электрический заряд ех отталкивает
заряд е2 (того же знака), находящийся от него на расстоянии г, выражается
формулой F =
где k—посгоянная.
Определить работу силы F при перемещении заряда е2 из точки Ai, отстоя-
отстоящей от е± на расстоянии rlf в точку Л2, отстоящую от е± на расстоянии r2f
полагая, что заряд е± помещен в точке Ло, принятой за начало отсчета.

414 ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА [ГЛ. XII
Тг
Решение. По формуле A) имеем А — \ k-^-dr = —kexe2— 2 =
rt
= kexe2 [ ). При г2 = + оо получим А= \ —~^dr = —— . При
\ ri r2 J д r fi
г,
е2—\ \A-k-. Последняя величина называется потенциалом поля, созда-
создаваемого зарядом е±щ
§ 8, Координаты центра масс
Пусть на плоскости Оху дана система материальных точек
Л(*1* */i)> р2 {*** У'2)¦. •••» Рп(хп> Уп) с массами т1У т2У ...,тп.
Произведения x^i и yimi называются статическими моментами
массы т{ относительно осей О у и Ох.
Обозначим через хс и ус координаты центра масс данной
системы. Тогда, как известно из курса механики, координаты
центра масс описанной материальной системы определяются
формулами
а
S ximi
ifnn i= i
_ yitn1\y22+ ... +уптп
Ус~
Мы используем эти формулы при отыскании центров масс раз-
различных фигур и тел.
1. Центр масс плоской линии. Пусть дана кривая АВ
уравнением y = f(x)y a^x^b, и пусть эта кривая представляет
собой материальную линию.
Предположим, что линейная плотность *) такой материальной
кривой равна у. Разобьем линию на п частей длины As^, As2, ..., Asn.
Массы этих частей будут равняться произведению их длин на
(постоянную) плотность: Ami = y^si. На каждой части дуги As{
возьмем произвольную точку с абсциссой lt. Представляя теперь
каждую часть дуги Ast материальной точкой Р( [?,-, / (if)] с мас-
массой yAsf и подставляя в формулы A) и B) вместо xt значение Hf,
вместо у{ значение / (?/), а вместо т( значение yAst (массы частей As {),
получим приближенные формулы для определения центра масс
*) Линейной плотностью называется масса единицы длины данной линии.
Мы предполагаем, что линейная плотность на всех участкам кривой одинакова,

§8] КООРДИНАТЫ ЦЕНТРА МАСС 415
дуги:
Если функция y = f(x) непрерывна и имеет непрерывную произ-
производную, то стоящие в числителе и знаменателе каждой дроби суммы
при max Asj —*0 имеют пределы, равные пределам соответствующих
интегральных сумм. Таким образом, координаты центра масс
дуги выражаются определенными интегралами:
ь ь
\xds С
Ъ
ds j/l+/'»(*)**
а а
Ь Ъ
[f{x)ds
Пример 1. Найти координаты центра масс полуокружности #2-f-#2 = а2
расположенной над осью Ох.
Решение. Определим ординату центра масс:
_/—5 5 du х , -\ /~\ \ (dy\L , . а ,
у=\ а2 —х2, —= . ¦¦•, ds= I/ 1+ — ) dx, ds= Ay
dx у a2-—jc2 ' \dxj ya2—x2
a a
Г y^r^?—rJ- dx a [
a
dx
-a 2a2 2n
Ус ла ла па л1
^ = 0 (так как полуокружность симметрична относительно оси Оу).
2. Центр масс плоской фигуры. Пусть данная фигура,
ограниченная линиями t/ = fl(x)y y = f2{x), x = a, x = b, представ-
представляет собой материальную плоскую фигуру. Поверхностную
плотность, т. е. массу единицы площади поверхности, мы будем
считать постоянной и равной S для всех частей фигуры.
Разобьем данную фигуру прямыми х = а,х = х19 ..., х = хп = Ь
на полоски ширины Ахг1 Ах2У ..., Ахп. Масса каждой полоски будет
равна произведению ее площади на плотность б. Если каждую
полоску заменить прямоугольником (рис. 246) с основанием Ах;
и высотой /2 fa) —/х (?,-), где %. = Х1~г^~Х{, то масса полоски будет
приближенно равна Am( = 8[f2 (?,) — /х A()]Ах( (i=U 2, ..., п).
Приближенно центр масс этой полоски будет находиться в центре
соответствующего прямоугольника: (jc/)c = |/, (y/)g= 2 *

416
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. XII
Заменяя теперь каждую полоску материальной точкой, масса
которой равна массе соответствующей полоски и сосредоточена
п
ч
Рис. 247.
в центре масс этой полоски, найдем приближенное значение коор-
координат центра масс всей фигуры (по формулам A) и B)):
li)]б
Переходя к пределу при Ах? —>0, получим
ь ъ
$ [/«(*)-/j (x)]dx
Эти формулы справедливы для любой однородной (т. е. имеющей
постоянную плотность во всех точках) плоской фигуры. Как мы
видим, координаты центра масс не зависят от плотности б фигуры
(в процессе вычисления б сократилось).
Пример 2. Определить координаты центра масс сегмента параболы
у2 = ах, отсекаемого прямой х — а (рис. 247).
Решение. В данном случае /2 (х) = }fax, fx (x) — — У ах, поэтому
2\х у ах dx
о
-- 2
а1'
с = 0 (так как сегмент симметричен относительно оси Ох).

§9J ВЫЧИСЛЕНИЕ МОМЕНТА ИНЕРЦИИ ЛИНИИ, КРУГА И ЦИЛИНДРА 417
§ 9, Вычисление момента инерции линии, круга и цилиндра
с помощью определенного интеграла
Пусть на плоскости хОу дана система материальных точек
Л.(*1» Уг)у Ръ(хы Уг)> •••» Рп(хт У«)» с массами ти т2, ...,тп.
Тогда, как известно из механики, момент инерции системы мате-
материальных точек относительно точки О определяется так:
п п
'о = ,21 (** + #?) т*> или /о=23г?т„ A)
где rt = ~ "-; _
Как и в § 8, пусть кривая ЛВ дана уравнением y = f(x),
а < х < Ь, где / (х) — непрерывная функция. Пусть эта кривая пред-
представляет собой материальную линию. Пусть
линейная плотность линии равна у. Снова ра- л< Ах I
зобьем линию на п частей длины Asly As2, ...
где Asi = V'Ax*-\-l\y2i, а массы
, ^, д , f+^f,
этих частей Amf == y&s19 Am2 = 7^s2, •.. Рис- 248.
..., Amn = y&sn. На каждой части дуги возь-
возьмем произвольную точку с абсциссой Sf. Ордината этой точки будет
г|,. = / (?,-). Приближенно момент инерции дуги относительно точки О
в соответствии с формулой A) будет
п
/о«2(й+л?)тДв*. B)
i = l
Если функция y = f(x) и ее производная /' (х) непрерывны, то
при As,.—>() сумма B) имеет предел. Этот предел, выражающийся
определенным интегралом, и определяет момент инерции материаль-
материальной линии:
+ f'4x)dx. C)
а
1. Момент инерции тонкого однородного стержня
длины I относительно его конца. Совместим стержень
с отрезком оси Ох: О^.х^.1 (рис. 248). В этом случае Asi = Axh
Ai = yAxi, r\ = x\ и формула C) принимает вид
Если дана масса стержня М, то у = М/1 и формула D) при-
принимает вид
1ос = ±М1*. E)

418
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. XII
2. Момент инерции окружности радиуса т отно-
относительно центра. Так как все точки окружности находятся
на расстоянии г от центра, а его масса
m = 2nr-y, то момент инерции окружности
будет
I0 = mr* = y-2nr-r* = y-2nr*. F)
3. Момент инерции однородно-
однородного кру гарадиусаR относительно
центра. Пусть б —масса единицы пло-
площади круга. Разобьем круг на п колец.
Рассмотрим одно кольцо (рис. 249).
Пусть его внутренний радиус rh внешний
rt + Дг,.. Масса этого кольца Кт{ с точностью
до бесконечно малых высшего порядка относительно Дг,- будет
Ami = b'2nrt Дг{. Момент инерции этой массы относительно центра
в соответствии с формулой F) приближенно будет (AI)
2? к
Рис. 249.
б• 2nrt
у
• кг{.
Момент инерции всего круга как системы колец будет выражаться
приближенной формулой
.53
G)
Переходя к пределу притахАг;—>• 0, получим момент инерции
площади круга относительно центра:
я
о
Если дана масса круга М, то поверхностная плотность б опре-
определяется так: 8 = —-}. Подставляя это значение, окончательно
получаем
I =MRV2.
(9)
4. Очевидно, что если имеем круглый цилиндр, радиус основания
которого R и масса М, то его момент инерции относительно оси
выражается формулой (9).
Упражнения к главе XII
Вычисление площадей
1. Найти площадь фигуры, ограниченной линиями у2 = 9х, у = 3х.
Отв. -j.
2. Найти площадь фигуры, ограниченной равнобочной гиперболой ху = а2,
осью Ох и прямыми х = а, х—2а. Отв. а2\п2.
3. Найти площадь фигуры, заключенной между кривой у = 4—х2 и
осью Ох. Отв. 32/3,

УПРАЖНЕНИЯ К ГЛАВЕ XII 4i9
4. Найти площадь фигуры, ограниченной астроидой х2^+у2^ = а2/3 *
Отв. -5-яа2,
о
5.. Найти площадь фигуры, ограниченной цепной линией y = ach — 9
осью Ох, осью Оу и прямой х = а. Отв. a2 she.
6. Найти площадь фигуры, ограниченной кривой у = х3, прямой у=8
и осью Оу. Отв. 12.
7. Найти площадь области, ограниченной одной полуволной синусоиды
и осью абсцисс. Отв. 2.
8. Найти площадь области, заключенной между параболами у2 = 2рху
Х2 = 2ру. Отв. 4р2/3.
9. Найти всю площадь фигуры, ограниченной линиями у = хъ> y = 2xt
у = х. Отв. 3/2.
10. Найти площадь области, ограниченной одной аркой циклоиды
x = a(t — sin 0, y = a(\ — cost) и осью абсцисс. Отв. Зла2.
11. Найти площадь фигуры, ограниченной астроидой x = acosBt, y = asin3t.
Отв. Зяа2/8.
12. Найти площадь всей области, ограниченной лемнискатой p2-=a2cos2<p.
Отв. а2.
13. Вычислить площадь области, ограниченной одной петлей кривой
р = a sin 2ф. Отв. ко?/8.
14. Вычислить полную площадь области, ограниченной кардиоидой
p = a(l — cos ф). Отв. Зла2/2.
15. Найти площадь области, ограниченной кривой р = асоБф. Отв. ла2/4.
16. Найти площадь области, ограниченной кривой р = асов2ф. Отв. ла?/4.
17. Найти площадь области, ограниченной кривой р = совЗф. Отв. л/4.
18. Найти площадь области, ограниченной кривой р = асов4ф. Отв-. ход2/4,
Вычисление объемов
19. Эллипс-^--]—|з-=1 вращается вокруг оси Ох. Найти объем тела вра-
4
щения. Отв. -~-каЬ2.
d
20. Отрезок прямой, соединяющий начало координат с точкой {а, Ь)> вра-
вращается вокруг оси у. Найти объем полученного конуса. Отв. -z-ncPb.
о
21. Найти объем тора, образованного вращением окружности х2 +
+ (У—ЬJ — а2 вокруг оси Ох (предполагается, что Ь^а). Отв. 2п2а2Ь.
22. Фигура, ограниченная линиями- у2 = 2рх и х=а, вращается вокруг
оси Ох. Найти объем тела вращения. Отв. лра2.
23. Фигура, ограниченная астроидой х2^3 +у2^ —а2^^ вращается вокруг
оси Ох. Найти объем тела вращения. Отв. 32зха3/105.
24. Фигура, ограниченная одной дугой синусоиды у — sinx и осью 0xt
вращается вокруг оси Ох. Найти объем тела вращения. Отв. л2/2.
25. Фигура, ограниченная параболой у2 = 4х и прямой х=4г вращается
вокруг оси Ох. Найти объем тела вращения. Отв. 32л.
26. Фигура, ограниченная кривой у = хех и прямыми у=0$ лс=1, вра-
вращается вокруг оси Ох. Найти объем тела вращения. Отв. ~(еа—1).
27. Фигура, ограниченная одной аркой циклоиды x—a(t—-sin О»
у = а(\ — cost} и осью Ох, вращается вокруг оси Ох. Найти объем тела вра-
вращения. Отв. 5л2а3.
28. Та же фигура, что и в задаче 27, вращается вокруг оси Оу. Найти
объем тела вращения. Отв. 6я&2а3,

420 ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА [ГЛ. XII
29. Та же фигура, что и в задаче 27, вращается вокруг прямой, парал-
параллельной оси Оу и проходящей через вершину циклоиды. Найти объем тела
вращения. Отв. па? (9л2— 16)/б.
30. Та же фигура, что и в задаче 27, вращается вокруг прямой, парал-
параллельной оси Ох и проходящей через вершину циклоиды. Найти объем тела
вращения. Отв. 7я2а3.
31. Цилиндр радиуса R пересечен плоскостью, проходящей через диаметр
основания под углом а к плоскости основания. Найти объем отсеченной части.
Отв. ~R3tga.
о
32. Найти объем, общий двум цилиндрам x2-\-y2 = R2, y<i-\-z2 = R2.
Отв. 16Я3/3.
33. Точка пересечения диагоналей квадрата перемещается вдоль диаметра
круга радиуса а; при этом плоскость, в которой лежит квадрат, все время
остается перпендикулярной к плоскости круга, а две противоположные вер-
вершины квадрата перемещаются по окружности (при движении величина квадрата,
очевидно, меняется). Найти объем тела, образуемого этим движущимся квадра-
квадратом. Отв. 8а3/3.
34. Вычислить объем сегмента, отсекаемого от эллиптического парабо-
ф Z2
лоида ~—|—^—= лс плоскостью # = #. Отв. па2 у pq.
35. Вычислить объем тела, ограниченного плоскостями 2 = 0, # = 0, цилинд-
рическими поверхностями х2=-2ру и z2=^2px и плоскостью х = а. Отв. —
Ту р
(в первом октанте).
36. Прямая движется параллельно плоскости Oyz, пересекая два эллипса
х2 и2 х2 z2
—_—|—^_-==1> —-—|—2~=1, лежаш«их в плоскостях Оху и Oxz. Вычислить
объем полученного тела. Отв. Sabc/3.
Вычисление длин дур
37. Найти всю длину астроиды х2^ +у2^3 —а2^. Отв. 6а.
38. Вычислить длину дуги полукубической параболы ау2 — х* от начала
координат до точки с абсциссой х = Ъа. Отв. ЗЗБа/27,
х
39. Найти длину цепной линии y = ach— от начала координат до
точки (х, у). Отв. ash— =j/\/2—a2.
40. Найти длину одной арки циклоиды x = a(t—sin t) y — a(\—cost).
Отв. Sa.
41. Найти длину дуги кривой у — \пх в пределах от х~У 3 до дг==}^*"8.
1 3
Отв. 1+yltiy.
42. Найти длину дуги кривой t/ = l—In cos а: в пределах от л: = 0 до я = я/4.
Отв. lntgCtt/8).
43. Найти длину спирали Архимеда р = аф от полюса до конца первого
завитка. Отв. па V1 + 4л2-|~тг 1пBя + }Л+4л2).
2
44. Найти длину спирали р = е«Ф от полюса до ' точки (р, ф),
Отв. —: 0&ф = — у \ _|_q^-»#
а. а
45. Найти всю длину кривой p = asin3 (ф/3). Отвч Зла/2.

УПРАЖНЕНИЯ К ГЛАВЕ XII 421
С2 С2
46. Найти длину эволюты эллипса х=— cos3/, У^-тг sin3/.
4 (а3—б3)
Отв. *
—г—*-.
аЬ
47. Найти длину кардиоиды p = aA4-ccs(p). Отв. 8а.
48. Найти длину дуги эвольвенты окружности х = а (cos<p-(-(psin(p),
j/=a(sin(p—срсовф) от ф = 0 до ф=*фх. Отв. aq>\/2.
Вычисление площадей поверхностей тел вращения
49. Найти площадь поверхности, полученной вращением параболы
у2 = 4ах вокруг оси Ох, от начала О до точки с абсциссой х — За. Отв.
56яа2/3.
50. Найти площадь поверхности конуса, образуемого вращением отрезка
прямой у = 2х от х = 0 до х = 2: а) Вокруг оси Ох. Отв. 8пУ~5. б) Вокруг
оси Оу. Отв. 4jt ]/* 5.
51. Найти площадь поверхности тора, полученного вращением круга
х2 + (У—ЪJ = а2 вокруг оси Ох (Ь > а). Отв. 4л2аЬ.
52. Найти площадь поверхности тела, образованного вращением карди-
кардиоиды вокруг оси Ох. Кардиоида задана параметрическими уравнениями
л: = яBсо5ф — соБ2ф), y = aBsin<p — sin 2ф). Отв. 12&юа/5.
53. Найти площадь поверхности тела, полученного вращением одной арки
циклоиды x = a(t — sin t), у = а(\—cos/) около оси Ох. Отв. 64тш2/3.
54. Арка циклоиды (см. задачу 53) вращается около оси Оу. Найти поверх-
поверхность тела вращения. Отв. 16л2а2+—па2.
55. Арка циклоиды (см. задачу 53) вращается около касательной, парал-
параллельной оси Ох и проходящей через вершину. Найти поверхность тела вра-
вращения. Отв. 32зха2/3.
56. Астроида л:=я sin3/, y = acos3i вращается около оси Ох. Найти поверх-
поверхность тела вращения: Отв. \2па2/5.
57. Дуга синусоиды y^sinx от #=0 до х—2п вращается около оси Ох.
Найти поверхность тела вращения. Отв. 4jt[yr 2 + ln (У" 2+0].
2 ф
х2 ф
58. Эллипс —2~-bT2~=l (й>Ь) вращается вокруг оси Ох. Найти поверх-
^ о 1.9 . о ,arcsin е У a2—h2
ность тела вращения. Отв. 2яЬг-\-2паЬ , где с — - .
Различные приложения определенного интеграла
х2 ф
59. Найти центр масс площади четверти эллипса —2"+*р"=^
у^О). Отв. 4а/3л; 4Ь/Зл.
60. Найти центр масс площади фигуры, ограниченной параболой
— 16 = 0 и осью Ох. Отв. @; 8/5).
61. Найти центр масс объема полушара. Отв. На оси симметрии, на
расстоянии 3R/8 от основания.
62. Найти центр масс поверхности полушара. Отв. На оси симметрии,
на расстоянии R/2 от основания.
63. Найти центр масс поверхности кругового прямого конуса, радиУ^
основания которого /?, а высота h. Отв. На оси симметрии, на расстоянии h/3
от основания.
64. Фигура ограничена линиями y = sinx@^x<n)9 y—Q. Найти центр
масс площади этой фигуры. Отв. (я/2, л/8).
65. Найти центр масс площади фигуры, ограниченной параболами
у*=20х, х2 = 20у. Отв. (9; 9).

422 ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА [ГЛ. XII
66. Найти центр масс площади кругового сектора с центральным углом 2<х
и радиусом R. Отв. На оси симметрии, на расстоянии ^ sma от вер-
О (X,
шины сектора.
67. Найти величину давления воды на прямоугольник, вертикально погру-
погруженный в воду, если известно, что основание его равно 8 м, высота 12 м,
верхнее основание параллельно свободной поверхности воды и находится на
глубине 5 м. Отв. 1,056-10* Н.
68. Верхний край шлюза, имеющего форму квадрата со стороной, равной
8 м, лежит на поверхности воды. Определить величину давления на каждую
из частей шлюза, образуемую делением квадрата одной из его диагоналей.
Отв. 853333,3 Н, 1706666,7 Н.
69. Вычислить работу, необходимую для того, чтобы выкачать воду
из полусферического сосуда, диаметр которого равен 20 м. Отв.
2,5-107я Дж.
70. Тело движется прямолинейно по закону x = ct3, где х—длина пути,
проходимого за время t, c = const. Сопротивление среды пропорционально
квадрату скорости, причем коэффициент пропорциональности равен k. Найти
работу, производимую сопротивлением при передвижении тела от точки х — 0
_ 27 , з/—
до точки х — а. Отв. -=¦ k у с*сг.
71. Вычислить работу, которую нужно затратить, чтобы выкачать жидкость
плотностью у из резервуара, имеющего форму обращенного вершиной книзу
конуса, высота которого Я, а радиус основания R. Отв. nyR2H2/l2.
72. Деревянный поплавок цилиндрической формы, площадь основания
которого 5 = 4000 см2, а высота Н = 50 см, плавает на поверхности воды.
Какую работу нужно затратить, чтобы вытащить поплавок на поверхность?
(Плотность дерева 0,8.) Отв. y2H2S/2 = 320 Дж.
73. Вычислить силу, с которой вода давит на плотину, имеющую форму
равнобочной трапеции, верхнее основание которой а = 6,4 м, нижнее 6 = 4,2 м,
а высота Я = 3 м. Отв. 2,22-105 Н.
74. Найти осевую составляющую Р Н полного давления пара на сфери-
сферическое дно котла. Диаметр цилиндрической части котла D мм, давление пара
в котле р Па. Отв. P = npD2/4000000.
75. Конец вертикального вала радиуса г поддерживается плоским подпят-
подпятником. Вес вала Р распределяется равномерно на всю поверхность опоры.
Вычислить полную работу сил трения при одном обороте вала. Коэффициент
трения [X. Отв. 4п\хРг/3.
76. Вертикальный вал оканчивается пятой, имеющей форму усеченного
конуса. Удельное давление пяты на подпятник постоянно и равно Р. Верхний
диаметр пяты D, нижний d, угол при вершине конуса 2а. Коэффициент тре-
трения [I. Найти работу сил трения за один оборот вала. Отв. ^—~-(D3—d3).
77. Призматический стержень длины / растягивается медленно возрастаю-
возрастающей от 0 до Р силой так, что в каждый момент растягивающая сила уравно-
уравновешивается силами упругости стержня. Вычислить работу А, затраченную силой
на растяжение, предполагая, что растяжение происходило в пределах упругости.
Площадь поперечного сечения стержня равна F, модуль упругости материала
равен Е.
Указание. Если х—удлинение стержня, a f—соответствующая сила,
FE PI
то f — —rx. Удлинение под действием силы Р равно А/ = -ртг. Отв. А =
РМ РЧ
~~2 2EF'
78. Призматический брус подвешен вертикально, и к нижнему его концу
приложена растягивающая сила Р. Вычислить удлинение бруса под действием
силы его веса и силы Р, если дано, что длина бруса в нерастянутом состоянии

§8] УПРАЖНЕНИЯ К ГЛАВЕ XII 423
равна I, площадь поперечного сечения F, вес бруса Q и модуль упругости
материала Е. Отв. А1=х ' #
79. Определить время, в течение которого жидкость выльется из призма-
призматического сосуда, наполненного до высоты Я. Площадь поперечного сечения
сосуда F, площадь отверстия /, скорость истечения определяется по формуле
v = \iY'2ghi где |х—коэффициент вязкости, g—ускорение силы тяжести, h —
2FH F /~2Н
расстояние от отверстия до уровня жидкости. Отв. Т= =— 1/ — .
И/ V^gH Vff g
80. Определить расход Q воды (количество воды, вытекающей в единицу
времени) через водослив прямоугольного сечения. Высота водослива Л, ширина Ь.
Отв. Q = ^\ibhV2gh.
о
81. Определить расход воды Q, вытекающей из бокового прямоугольного
отверстия высотой а и шириной Ь, если высота свободной поверхности воды
над нижней стороной отверстия равна Я. Отв. Q = —^~—-[ВЪ12 —(Н—а)
о

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аргумент 19
— комплексного числа 207
— промежуточный 79
Асимптота 168
— вертикальная 168
— наклонная 168
Астроида, 97, 177, 407
Бинормаль 306
Вектор перемещения точки 304
Величина абсолютная 15
— бесконечно большая 33
малая 39, 59
— переменная 16
возрастающая 18
монотонная 18
монотонно изменяющаяся 18
ограниченная 19
убывающая 18
упорядоченная 18
— постоянная 16
абсолютная 16
Величины бесконечно малые одного
порядка 59
¦ эквивалентные 59
Возведение комплексного числа в сте-
степень 211
Выпуклость кривой 162
Выражение аналитическое 21
— подынтегральное 316
Вычисление значений функции при-
приближенное 103
— определенных интегралов прибли-
приближенное 385—393
Вычитание комплексных чисел 208
Гамма-функция 396
Геликоид 290
Годограф вектора 288
Градиент 260
Граница области 231
График гиперболического косинуса 99
График гиперболического котангенса
100
синуса 99
тангенса 99
— функции 21
Деление комплексных чисел 2в9
Дифференциал 102
— второго порядка 108
— дуги 185, 406
— полный 242, 243
— сложной функции 104
полный 250
— п-го порядка 108
Дифференциалы независимых перемен-
переменных 242
Дифференцирование 66
— гиперболических функций 101
— интеграла по параметру 393—395
— логарифмической функции 93
— неявно заданных функций 109
— обратных тригонометрических функ-
функций 92
— показательной функции 93
— степенной функции 92
— тригонометрических функций 92
— функций, заданных параметриче-
параметрически 97, 111
, общие правила 93
Дифференцируемость функций 69
Длина дуги 184, 405
в прямоугольных координатах
406
кривой, заданной в полярных
координатах 408
, — параметрически 407
пространственной кривой 298,
407
— касательной 113
— нормали 113
Дробь рациональная 328
неправильная 328
правильная 328
простейшая 329
Единица мнимая 206

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
425
Зависимость функциональная 19
Задание кривой параметрическое 93
— линии с помощью поверхностей
288
Задача интерполирования функций 223
Замена переменной в неопределенном
интеграле 321
определенном интеграле
374—375
Знак двойной подстановки 373
— интеграла 316
Значение критическое 150, 175
— функции на отрезке наибольшее 158
наименьшее 158
нескольких переменных наиболь-
наибольшее 237
наименьшее 237
одной переменной наибольшее 57
наименьшее 57
— экстремальное 148
Извлечение корня из комплексного
числа 211
Инвариантность формы дифференци-
дифференциала 105
полного дифференциала 250
Инволюта 194
Интеграл, зависящий от параметра
393
— неопределенный 316
от комплексной функции 397
суммы функций 319
— несобственный 378
— определенный 359
от комплексной функции 397
— от разрывной функции 382
— с бесконечными пределами 378
— эллиптический 348
Интегрирование иррациональных
функций 337, 338
— методом замены переменной 321
— неравенства почленное 368
— по частям 325
в случае определенного ин-
интеграла 376
— приближенное 385—393
— простейших рациональных дробей
329—331
— рациональных дробей 335—337
— тригонометрических функций 341—
345
— функций 316
, содержащих квадратный трех-
трехчлен 323—325
Интервал 17
— замкнутый 17
Исследование функций 152, 155, 160,
162, 167, 171, 175
Кардиоида 30, 408
Касательная к кривой 68
— — поверхности 309
Концы отрезка 18
Координаты полярные 28
— центра масс 414
Корень кратности k 220
— многочлена 217
— уравнения 217
— функции 124
Косинус гиперболический 99
Котангенс гиперболический 99
Коэффициент угловой касательной 68
Коэффициенты многочлена 26
Кривая вогнутая 162
— выпуклая 162
— Гаусса 165
Кривизна 187, 189
— кривой, заданной в полярных ко-
координатах 191
, — параметрически 190
— плоской кривой 303
— пространственной кривой 300, 303
средняя 300
— средняя 186
Круг кривизны 192
Кручение кривой 307
Лемниската 30
Линии уровня 258
Линия винтовая 289, 408
Лист декартов 177
Логарифм натуральный 52
Максимум 146
— функции нескольких переменных
Метод замены переменной при нахож-
нахождении неопределенного интеграла
321
— наименьших квадратов 277
— неопределенных коэффициентов 334
Минимакс 270
Минимум 147
— функции нескольких переменных
265
Многочлен 26, 217
— Бернштейна 228
— Ньютона интерполяционный 226
— Чебышева 228
Модуль 15
— комплексного числа 207
— перехода М 52
— скорости 304
Момент инерции 417—418
— статический 414

426
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Независимость значений частной про-
производной от порядка дифференци-
дифференцирования 255
Непрерывность функции нескольких
переменных в области 236
точке 236
одной переменной в точке 53
на интервале 55
отрезке 55
равномерная 362
слева 55
справа 55
Нормаль ИЗ
— главная 301
— к поверхности 312
пространственной кривой 293
Область замкнутая 231
— изменения величины 17
— незамкнутая 231
— ограниченная 231
— определения функции нескольких
переменных 231
одной переменной 20
естественная 22
— открытая 231
— существования функции несколь-
нескольких переменных 231
одной переменной 20
Объем тела 410
вращения 411
— эллипсоида 410
Окрестность 18
— точки 235
Ось действительная 207
— мнимая 207
— полярная 28
— числовая 13
Отрезок 17, 18
— интегрирования 359
Оценка определенного интеграла 369
— погрешности при вычислениях 245—
Параметр 93
Первообразная 315
— комплексной функции 397
Переменная интегрирования 359
— независимая 19
Период показательной функции 214
— функции 19
Плоскость, касательная к поверхности
311
— комплексной переменной 206
—, нормальная к пространственной
кривой 293, 295
— соприкасающаяся 305
Площадь криволинейного сектора 404$
405
Площадь криволинейной трапеции
401
— параболической трапеции 387
— поверхности вращения 412
— эллипса 403
Поверхность винтовая 290
— тела вращения 411
— уровня 257
Погрешность абсолютная 245
максимальная 245
— относительная 246
максимальная 246
Подкасательная ИЗ
Поднормаль 113
Подстановка универсальная тригоно-
тригонометрическая 341, 342
— Эйлера вторая 339
первая 339
третья 340
Подстановки тригонометрические 341—
346
Поле градиентов 260
— скалярное 257
Полином 217
Полюс 28
Последовательность числовая 18
Потенциал поля 414
Правила дифференцирования вектор-
векторных функций 296—298
Правило Л опита л я 129
Предел 31
— векторной функции 291
— интеграла верхний 359
нижний 359
— комплексной переменной 214
— произведения 42, 43
— суммы 42
— функции нескольких переменных
235
одной переменной 33, 34
левосторонний 35
правосторонний 35
sin х
при
46
х
I 1 \х
A +~ 1
при
49
— частного 43
Приращение векторной функции 291
— функции полное 234
частное 234
Произведение комплексных чисел 208
Производная 66
— вектора по длине дуги 299
— векторного произведения векторов
— векторной функции 292
— вторая 106
— высшего порядка 106

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
427
Производная единичного вектора 297
— комплексной функции 214
— логарифмическая 85
— логарифмической функции 78
— обратной функции 87
— от определенного интеграла по пе-
переменному верхнему пределу 371
произведения функций 75
— по направлению 259
— показательной функции 83
— полная 249
— постоянной 74
— произведения скалярной функции
на векторную 297
— скалярного произведения векторов
297
— сложной функции нескольких пере-
переменных 248
одной переменной 79
— степенной функции 71, 83
— суммы векторов 296
функций 76
— функции, заданной неявно 251—253
arcos х 90
arcctg x 92
arcsin x 89
arctg x 91
cos л: 73
ctg x 81
sin л: 72
tg x 80
— частная 238
— частного функций 77
— n-го порядка 106
частная 254
Промежуток 17
— замкнутый 17
— полузамкнутый 17
Радиус-вектор 288
— кривизны 192
пространственной линии 301
— кручения кривой 307
— окрестности 18
Развертка 194
Разложение многочлена на множители
217—222
— рациональной дроби на простейшие
332—335
— функций по формуле Тейлора 138—
141
Разность комплексных чисел 208
Расходимость интеграла 379, 382, 383
Решение двучленного уравнения 212
Свойства интегральных сумм 360—363
— неопределенного интеграла 319—
320
Свойства непрерывных функций 56—
58
— определенного интеграла 367—370
— показательной функции 213
— эволюты 196
Сегмент 17
Синус гиперболический 99
Система координат полярная 28
Скорость движения в данный момент 65
— точки в криволинейном движении
304
средняя 304
Сложение комплексных чисел 208
Спираль Архимеда 29
— гиперболическая 30
— логарифмическая 30
Способ касательных 201
— комбинированный 202
— Ньютона 201
— хорд 200
Сравнение бесконечно малых 59
Степень многочлена 26, 217
Сумма интегральная 358
верхняя 357
нижняя 357
— комплексных чисел 208
Сходимость интеграла 378, 382
абсолютная 381
Таблица интегралов 317, 318
Тангенс гиперболический 99
Теорема алгебры основная 218
— Безу 217
— Вейерштрасса 227
— Коши 127
— Лагранжа 126
— Лопиталя 129
— о конечных приращениях 126
корнях производной 124
среднем для определенного ин-
интеграла 359
— об отношении приращений двух
функций 127
— Ролля 124
— существование неопределенного ин-
интеграла 316
Теоремы о пределах основные 42, 43
Точка возврата второго рода 283
первого рода 283
— кривой обыкновенная 281
особая 281
изолированная 284
узловая 282
— критическая функции двух пере-
переменных 267
одной переменной 150
— области внутренняя 231
— перегиба 164
— поверхности обыкновенная 310

428
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Точка поверхности особая 310
— пространственной кривой особая
295
— разрыва первого рода 56
функции двух переменных 236
одной переменной 56
— соприкосновения 284
Трактриса 123, 204
Трапеция криволинейная 360
— параболическая 386
Угол поворота касательной к кривой
300
— смежности 186
— эксцентрический 96
Умножение комплексных чисел 208
Уравнение алгебраическое 199, 218
— двучленное 212
— касательной к кривой 112
плоскости 312
— линии в пространстве векторное 288
— нормали плоской линии 113
— окружности 100
— трактрисы 123
Уравнения касательной к пространст-
пространственной кривой 293, 295
— нормали к поверхности 312
— параметрические 93
астроиды 97
гиперболы 100
линии в пространстве 288
окружности 95
циклоиды 96
эллипса 95
Ускорение 111
— среднее 111
— точки в криволинейном движении
304
Условие вогнутости кривой 164
— возрастания функции 145
— выпуклости кривой 163
— существования первообразной 372
— убывания функции 146
Условия существования неявной функ-
функции 253
точки перегиба достаточные 165
условного экстремума необхо-
необходимые 274
экстремума функции двух пере-
переменных достаточные 267
необходимые 266
одной переменной доста-
достаточные 150
необходимые 148
Фигура ступенчатая вписанная 357
описанная 357
Форма комплексного числа показа-
показательная 216
тригонометрическая 207
Формула В ал лиса 378
— для вычисления кручения 308
радиуса кривизны 302, 303
— интегрирования по частям 325
— Лагранжа интерполяционная 224
— Лейбница дифференцирования ин-
интеграла по параметру 394
произведения 107
— Маклорена 138
— Муавра 211
— Ньютона интерполяционная 226
— Ньютона — Лейбница 372
— парабол 388
— прямоугольников 385
— Симпсона 388
— Тейлора 138
для функции двух переменных
265
— трапеций 386
— Чебышева 392
— Эйлера 215
Формулы Серре — Френе 309
Функции гиперболические 99
— обратные тригонометрические 23,
88—92
— основные элементарные 22
— тригонометрические 23, 24
Функция 19
— алгебраическая 27
— бесконечно большая 36
малая 40
— возрастающая 20
— двух независимых переменных 230
— дифференцируемая 69
—, — в точке 242
— дробная рациональная 27
—, заданная аналитически 21
—, интегрируемая на отрезке 359
— иррациональная 27
— квадратичная 27
— комплексной переменной 213
— Лапласа 347
— линейная 27
— логарифмическая 22, 24
— многих независимых переменных
232
— многозначная 20
— неограниченная 38
— непрерывная 53, 55; 236
— нечетная 172
— неэлементарная 26
— неявная 82
— обратная 86
— ограниченная 38
— однозначная 20
— от функции 25

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
429
Функция периодическая 24
— подынтегральная 316
— показательная 22, 23
комплексного аргумента 213
— разрывная 56
— рациональная 328
— скалярного аргумента векторная
290
— сложная 25
показательная 84
— степенная 22, 23
— трансцендентная 27
— убывающая 20
— целая рациональная 26, 217
— четная 172
— элементарная 26
— явная 82
— Е (х) 348
Центр кривизны 192
— масс 414
плоской линии 415
фигуры 416
— окрестности 18
Циклоида 96
Часть числа вещественная 206
действительная 206
мнимая 206
Числа сопряженные 206
Число вещественное 13
— действительное 13
— иррациональное 13
— комплексное 206
— рациональное 13
— чисто мнимое 206
— е 49
Эвольвента 194
Эволюта 194
— параболы 194
— циклоиды 194
— эллипса 195
Экспонента 51
Экстраполяция 226
Экстремум 148
— функции нескольких переменных
266
условный 272

Николай Семенович Пискунов
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ
ИСЧИСЛЕНИЯ
для втузов
том 1
Редактор В. В. Донченко
Техн. редактор И. Ш. Ансельрод
Корректор И. Д. Дорохова
ИБ № 12687
Сдано в набор 01.06.84. Подписано к печати 11.12.84.
Формат 60x90Vlfl. Бумага тип. № 3. Литературная
гарнитура. Высокая печать. Усл. печ. л. 2 7. Усл. кр.-
отт. 27,25. Уч.-изд. л. 27,33. Тираж 250 000 экз.
A-й завод 1 — 150 000 экз.). Заказ N° 3167.
Цена 1р. 10 к.
Издательство «Наука»
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
МПО «Первая Образцовая типография» Союзполиграф-
прома при Государственном комитете СССР по де-
делам издательств, полиграфии и книжной торговли.
1130 54 Москва, Валовая, 28